Author: Фоменко А.Т. Фукс Д.Б.
Tags: топология геометрия издательство наука главная редакция физико-математической литературы учебное пособие для вузов теория клеточных комплексов гомотопические группы гомология и когомология метод спектральных последовательностей гомотопические свойства многообразий
ISBN: 5-02-013929-7
Year: 1989
А.Т. Фоменко, Д. Б. Фукс
гомотопической
топологии
ДОПУЩЕНО ГОСУДАРСТВЕННЫМ КОМИТЕТОМ СССР
ПО НАРОДНОМУ ОБРАЗОВАНИЮ
В КАЧЕСТВЕ УЧЕБНОГО ПОСОБИЯ ДЛЯ'СТУДЕНТОВ
ФИЗИКО-МАТЕМАТИЧЕСКИХ СПЕЦИАЛЬНОСТЕЙ УНИВЕРСИТЕТОВ
МОСКВА "НАУКА”
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1989
ББК 22.15
Ф76
УДК 515.143(075.8)
Фоменко А.Т.,Фукс Д.Б. Курс гомотопической топологии: Учеб,
пособие для вузов. — М.: Наука. Гл. ред. физ.-мат. лит., 1989. — 528 с. —
ISBN 5-02-013929-7
Первый в отечественной литературе учебный курс гомотопической топологии и ее мно-
гочисленных приложений. Среди основных тем, затронутых в книге: теория клеточных
комплексов, гомотопические группы, гомологии и когомологии, метод спектральных
последовательностей, гомотопические свойства многообразий. Впервые в доступной
широкому кругу читателей форме рассказывается о месте и роли гомотопической
топологии в современной математике и физике. Читатель, освоивший курс, сможет сво-
бодно ориентироваться в специальной научной литературе.
Для студентов и аспирантов физико-математических специальностей вузов.
Табл. 4. Ил. 255. Библиогр. 140 назв.
Рисунки на вклейках выполнены А. Т. Фоменко
Рецензенты:
кафедра алгебры и геометрии Тбилисского государственного университета
(заведующий кафедрой - академик АН ГССР профессор Г.С. Чогошвили);
доктор физико-математических наук О.Я. Виро
~ 1602060000-035
Ф —----------------54-89
053(02)-89
ISBN 5-02-013929-7
©Издательство ’’Наука”.
Главная редакция
физико-математической литературы,
1989
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ ................................................................. 8
Введение. ВАЖНЕЙШИЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА................................ 11
§ 1. Классические пространства.............................................. IX
1. Евклидовы пространства, сферы и шары (11). 2. Вещественные проективные
пространства (12). 3. Комплексные и кватернионные проективные пространст-
ва (13). 4. Проективная плоскость Кэли (13). 5. Многообразия Грассмана (15).
6. Многообразия флагов (16). 7. Компактные классические группы (16).
8. Многообразия Штифеля (16). 9. Классические действия классических групп
в классических пространствах (16). 10. Классические поверхности (17).
§ 2. Операции над топологическими пространствами........................ 20
1. Произведения (20). 2. Цилиндр, конус и надстройка (21). 3. Приклеивания.
Цилиндр и конус отображения (22). 4. Джойн (22). 5. Пространства отобра-
жений, путей и петель (23). 6. Операции над пространствами с отмеченной
точкой (24).
Глава 1. ГОМОТОПИИ........................................................ 26
§ 3. Гомотопии и гомотопические эквивалентности.......................... 26
1. Определение гомотопии (26). 2. Множества п(Х, У) (26). 3. Гомотопичес-
кая эквивалентность (27). 4. Ретракты (29). 5. Пример гомотопического инва-
рианта: категория Люстерника - Шнирельмана (30). 6. Случай пространств с
отмеченной точкой, пар, троек и Т.Д. (30).
§ 4. Естественные групповые структуры в множествах к(Х, У)................ 31
§ 5. Клеточные пространства........................... ............. 35
1. Основные определения (35). 2. Комментарии к определению клеточного
пространства (36). 3. Отношение к операциям из 3 2 (37). 4. Клеточные
разбиения классических пространств (38). 5. Теорема Борсука о продолжении
гомотопий (43). 6. Следствия из теоремы Борсука (44). 7. Теорема о клеточ-
ной аппроксимации (44). 8. Борьба с химерой: доказательство леммы о сво-
бодной точке (46). 9. Первые применения теоремы о клеточной аппрокси-
мации (48).
§ 6. Фундаментальная группа............................................. 50
1. Определение (50). 2. Зависимость от отмеченной точки (51). 3. Вычисле-
ние фундаментальных групп (51).
§ 7. Накрытия............................................................ 57
1. Определение и примеры (57) . 2. Теорема о накрывающей гомотопии (58).
3. Накрытия и фундаментальная группа (59). 4. Регулярные накрытия (61).
5. Универсальные накрытия (61). 6. Теорема о поднятии отображения (61).
7. Критерий эквивалентности накрытий (62). 8. Существование и классифи-
кация накрытий (62).
§ 8. Гомотопические группы.............................................. 63
1. Определение; коммутативность (63). 2. Зависимость от отмеченной точ-
ки (64). 3. Гомотопические группы и накрытия (64). 4. Относительные го-
мотопические группы (65). 5. "Гомотопические группы” и
я, (X, А; х0) (66). 6. Связи между относительными и абсолютными гомото-
1*
4
ОГЛАВЛЕНИЕ
пическими группами (67). 7. Гомотопическая последовательность пары (67).
8. Следствия точности (68).
§ 9. Расслоения...........................................................
(.Определения (70). 2. Накрывающие гомотопии (71). 3. Доказательство тео-
ремы о накрывающей гомотопии (72). 4. Расслоения в смысле Серра (73).
5. Слои (74). 6. Любое отображение гомотопически эквивалентно расслоению
в смысле Серра (76). 7. Гомотопическая последовательность расслоения (77).
8. Первые применения точности (78) . 9. Заключение: исполнение обещания
из § 8 (79).
§ 10. Теорема о надстройке и гомотопические группы сфер....................
1. Основная теорема (79). 2. Первые применения (82). 3. Степень отображе-
ния Sn-+Sn (83). 4. Стабильные гомотопические группы сфер (84). 5. Ум-
ножение Уайтхеда и ’’трудная часть теоремы Фрейденталя” (84).
§ 11. Гомотопические группы и клеточные пространства.......................
1. Адциционная теорема (86). 2. Применение аддиционной теоремы: гомото-
пические группы букетов (88). 3. Первая нетривиальная гомотопическая
группа клеточного пространства (88). 4. Слабая гомотопическая эквивалент-
ность как отображение (89). 5. Теорема Уайтхеда (91). 6. Клеточная ап-
проксимация топологических пространств (91). 7. Пространства Эйленберга-
Маклейна (K(ir, л)’ы) (92). 8. Единственность К (я, п) ’ов (93). 9. Заклеива-
ние и убивание гомотопических групп (93).
Глава 2. ГОМОЛОГИИ............................................................
§ 12. Сингулярные гомологии................................................
(.Сингулярные симплексы, цепи и гомологии (95). 2. Цепные комплексы,
отображения и гомотопии (96).. 3. Простейшие вычисления (98). 4. Отно-
сительные гомологии (100). 5. Относительные гомологии как абсолют-
ные (101) . 6. Дополнения (105).
§ 13. Вычисление гомологий клеточных пространств...........................
1. Гомологии сфер. Изоморфизм надстройки (106). 2. Гомологии букетов
сфер и вообще букетов (107). 3. Отображения сфер в сферы и букетов сфер в
букеты <^фер (107). 4. Клеточный комплекс (109). 5. Гомологии клеточного
комплекса (111) . 6. Классический комплекс (112). 7. Некоторые вычисле-
ния (113). 8. Цепные отображения клеточных комплексов (116).
§ 14. Гомологии и гомотопии................................................
1. Гомологии и слабые гомотопические эквивалентности (117). 2. Теорема Гу-
ревича (119). 3. Случай п = 1 (120) .4. Относительный вариант теоремы Гуре-
вича (121) . 5. Теорема Уайтхеда (122).
§ 15. Гомологии с коэффициентами и когомологии.............................
1. Определения (123). 2. Перенесение уже известных нам результатов (124).
3. Коэффициентные последовательности (126). 4. Алгебраическая подготовка к
’’формулам универсальных коэффициентов” (127). 5. Формулы универсальных
коэффициентов (128). 6. Формула Кюннета (130).
§ 16. Умножения....................................’.......................
1. Введение (132) . 2. Прямое построение ^-умножения (134). 3. Определение
Х-умножения (135). 4. Применение: инвариант Хопфа (136). 5. Дополнение:
другие умножения (138).
§ 17. Гомологии и многообразия.............................................
1. Гладкие многообразия (140). 2. Фундаментальный класс (143). 3. Изомор-
физм Пуанкаре (144). 4. Индексы пересечения и двойственность Пуанка-
ре (146). 5. Применение: формулы Лефшеца (149). 6. Коэффициенты зацеп-
ления (151). 7. Обратные гомоморфизмы (153). 8. Связь с ^-умножени-
ем(155). 9. Обобщения изоморфизма и двойственности Пуанкаре (156).
§ 18. Теория препятствий...................................................
1. Препятствия к распространению непрерывного отображения (160). 2. Относи-
тельный случай (162). 3. Применение: когомологии и отображения в
К (я, п)'ы (163). 4. Другое применение: теоремы Хопфа (165). 5. Препятствие
к продолжению сечения (165).
§ 19. Векторные расслоения и характеристические классы.....................
1. Векторные расслоения и операции над ними (167). 2. Касательные и нор-
мальные расслоения гладких многообразий (170) . 3. Ассоциированные рас-
70
79
86
95
95
106
117
123
132
139
160
167
ОГЛАВЛЕНИЕ
слоения и характеристические классы (171). 4. Характеристические классы и
классифицирующие пространства (174). 5. Важнейшие свойства классов Шти-
феля - Уитни, Эйлера, Черна и Понтрягина (177). 6. Характеристические клас-
сы в топологии гладких многообразий (181).
Глава 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ............................
§ 20. Спектральная последовательность, ассоциированная с фильтрацией........
1. Общие определения (187). 2. Общие теоремы (189). 3. Присоединенная гра-
дуированная группа (190). 4. Когомологический вариант теории Лере (191).
5. Графическое изображение спектральной последовательности (192). 6. Но-
вое понимание клеточного вычисления гомологий 1.193). 7. Новое понимание
гомологических последовательностей пар и троек (194).8. Обобщение на бес-
конечные фильтрации (194).
§21. Спектральная последовательность расслоения............................... 1
1. Вычисление начальных членов спектральной последовательности в предпо-
ложении гомологической простоты расслоения (195). 2. Случай непростого
расслоения (198). 3. Первые применения (200),
§ 22. Дополнительные свойства спектральных последовательностей расслоений... 21
1. Гомоморфизмы спектральных последовательностей (203). 2. Нулевая строка
и нулевой столбец (205). 3. Трансгрессия (206). 4. Применение: три точных
последовательности (207). 5. Трансгрессия и характеристический класс (210).
§ 23. Мультипликативная структура в когомологической спектральной последова-
тельности ..................................................................... 2
1. Формулировки: свойства мультипликативной структуры (211). 2. Построе-
ние умножения (212). 3. Первое применение: когомологии группы SU(n)(212).
4. Когомологии других классических групп (214). 5. Еще один пример (217).
§ 24. Метод Серра вычисления гомотопических групп............................. 21
1. Когомологии пространств петель (219). 2. Метод убивающих прост-
ранств (220).
§ 25. Ранги гомотопических групп............................................. 22
1. Конечная порожденное!!. и конечность гомотопических групп (222). 2. Вы-
числение колец Н*(К(п, л); Q)(224). 3. Ранги гомотопических групп
сфер (225). 4. Теорема Картана - Серра (227). 5. Комментарии к теореме Кар-
тана - Серра (229).
§ 26. Нечетные компоненты гомотопических групп................................ 23
1. Когомологии H*(X(Z^, л); 7.^) при (р, р*) = 1 (230). 2. Частичное вычисле-
ние кольца H*(K(Zp, л); Z) (230). 3. Частичное вычисление когомологий
X(Z, л) (234). 4. Частичное вычисление p-компонент гомотопических групп
сфер (234).
Глава 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ......................................... 231
§ 27. Общая теория...................................................... 231
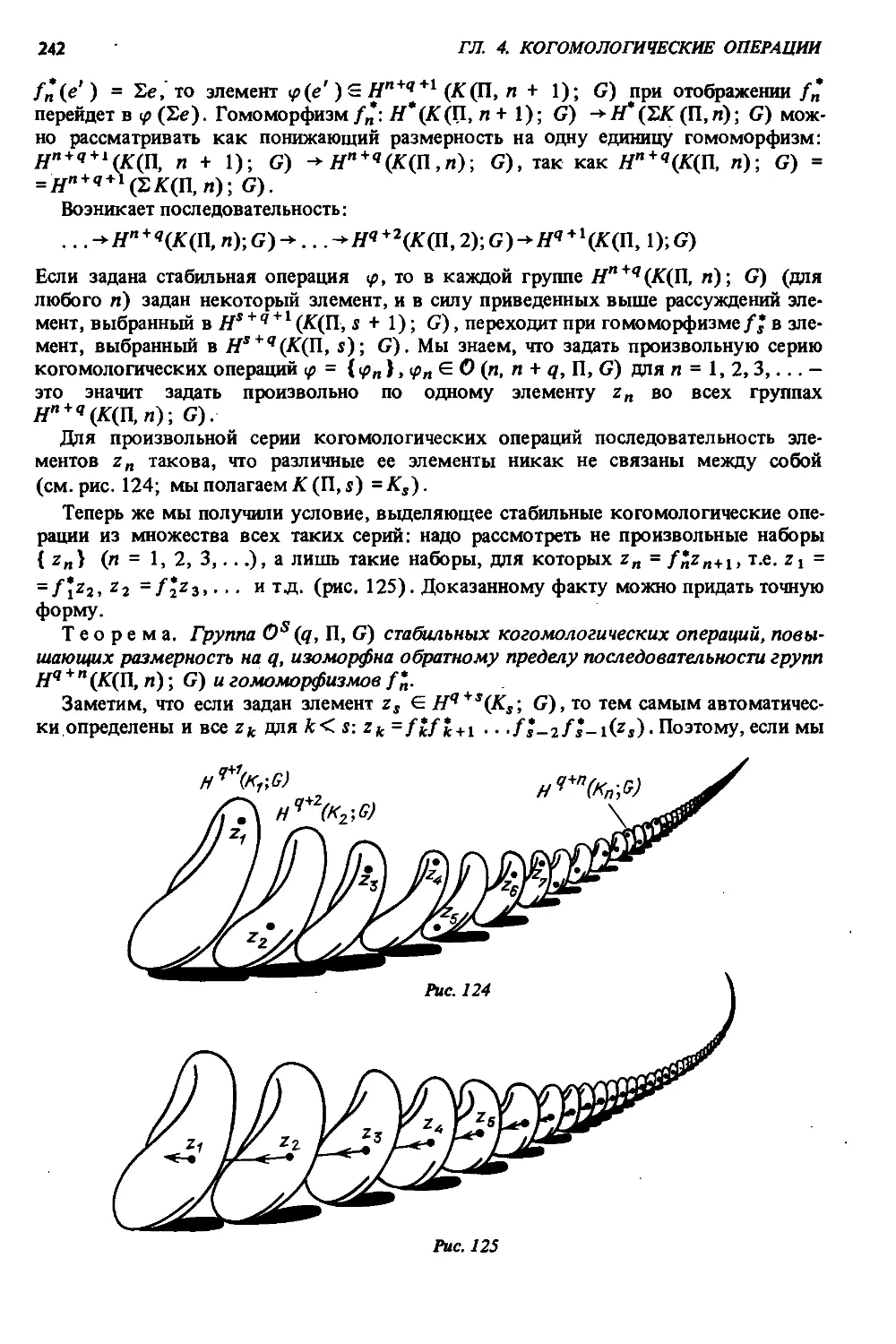
1. Определение (238). 2. Классификация (238). 3. Примеры (239). 4. Стабиль-
ные операции (240). 5. Алгебра стабильных операций (244).
§ 28. Стинродовы квадраты............................................... 244
1. Введение (244). 2. Теорема существования и единственности Sq* (245).
3. Доказательство формулы Картана (247). 4. Другие конструкции стинродо-
вых квадратов (249).
§ 29. Алгебра Стинрода.................................................. 250
1. Строение алгебры Стинрода А,. Формулировки (250). 2. Теорема А.Боре-
ля (251). 3. Теорема Ж.-П. Серра (253). 4. Устройство алгебры А (254). 5. Со-
отношения (254). б. Вычисление (щ, Z, Z,) .(256).7. Алгебра Стинрода
mod р (257). 8. Другие классификационные теоремы (258).
§ 30. Применения стинродовых квадратов.................................. 259
1. Вычисление гомотопических групп (259). 2. Стинродовы квадраты и классы
Шгифеля - Уитни (261). 3. Вторые препятствия (264). 4. Несуществование сфе-
роидов с нечетным инвариантом Хопфа (265). 5. Линзы (265).
6
ОГЛАВЛЕНИЕ
Гл а в а
§ 31.
§ 32.
§ 33.
§ 34.
§ 35.
§ 36.
Глав а
§ 37.
§ 38.
§ 39.
§ 40.
§41.
§ 42.
§ 43.
5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА.............. 268
Общая идея.............................................................. 268
1. Введение (268). 2. Метод Серра и метод Адамса (269). 3. Спектральная по-
следовательность (270).
Необходимый алгебраический материал...................................... 271
1. Модули (271). 2. Проективные модули (272). 3. Проективные резольвен-
ты (273). 4. Тог и Ext (274).
Построение спектральной последовательности............................... 275
1. Топологическая фильтрация Адамса (275). 2. Группы и дифференциалы
спектральной последовательности (278). 3. Теорема Адамса (280). 4. Доказа-
тельство утверждений (1) и (2) (280). 5. Отступление: замечание о резольвен-
тах (283). 6. Продолжение доказательства. Случай конечных стабильных гомо-
топических групп (284). 7. Дополнительные свойства спектральной последова-
тельности Адамса (289). 8. Окончание доказательства теоремы Адамса в общем
случае (291).
Мультипликативные структуры . . ......................................... 293
1. Композиционное умножение в стабильных гомотопических группах сфе-
ры (294). 2. Алгебраическое отступление: алгебры Хопфа (296) . 3. Алгебра
Сгинрода как алгебра Хопфа (297). 4. Умножение в спектральной последова-
тельности Адамса (298).
Применение спектральной последовательности Адамса к вычислению стабиль-
ных гомотопических групп сфер............................................ 301
1. Аддитивная структура члена Et (301). 2. Мультипликативная структура (307).
3. Нечетные компоненты (310). 4. Теоремы Адамса о начальном члене его
спектральной последовательности (311). 5. Заключение (312).
Частичные операции....................................................... 313
1. Построение частичных операций (313). 2. Частичные операции и второй диф-
ференциал в спектральной последовательности Адамса (315). 3. Частичные
операции и гомотопические группы сфер (316). 4. Системы Постникова(316).
6. Х-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ 318
Общая теория.......................................................... 318
1. Введение (318). 2. Определения (319). 3. Периодичность Ботта (324). 4. Ха-
рактер Черна (329). 5. Экстраординарные гомологии и когомологии (331).
Вычисление X-функтора: спектральная последовательность Атиа - Хирцебруха 334
1. Построение спектральной последовательности Атиа - Хирцебруха (334).
2. Примеры вычислений (338). 3. Дифференциалы спектральной последова-
тельности Атиа - Хирцебруха (340).
Операции Адамса....................................................... 341
1. Определение и свойства (341). 2. Простое доказательство несуществования
сфероидов с нечетным инвариантом Хопфа (Адамс - Атиа) (345).
/•функтор............................................................. 346
1. Определение и связь с гомотопическими группами сфер (346). 2. Гипотеза
Адамса (350). 3. Применение к гомотопическим группам сфер (357).
Теорема Римана - Роха................................................. 360
1. Общая теорема Римана - Роха (360). 2. Теорема Римана - Роха в Х-теории
для комплексных расслоений (364). 3. Применение: вычисление е-инвариан-
та (367). 4. Теорема Римана - Роха в Х-теории для спинорных расслое-
ний (369). 5. Первое применение: теоремы целочисленности (376). 6. Второе
применение: теоремы невложимости (377). 7. Заключение: происхождение
названия (379).
Формула Атиа - Зингера (набросок)..................................... 380
1. Эллиптические операторы и их индексы (380) . 2. Примеры (381) . 3. Форму-
ла (383). 4. Снова примеры (383).
Кобордизмы............................................................ 385
1. Определения (385). 2. Вычисления (391). 3. Связь с Х-теорией (395). 4.Ко-
гомологические операции в кобордизмах и спектральная последовательность
Адамса - Новикова (397).
7
ОГЛАВЛЕНИЕ
Дополнение. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ.............................. 401
§ 44. Гомологии и критические точки функций на многообразиях........... 401
§ 45. . Гомологии и точки бифуркации функции. Общие неравенства Морса.. 405
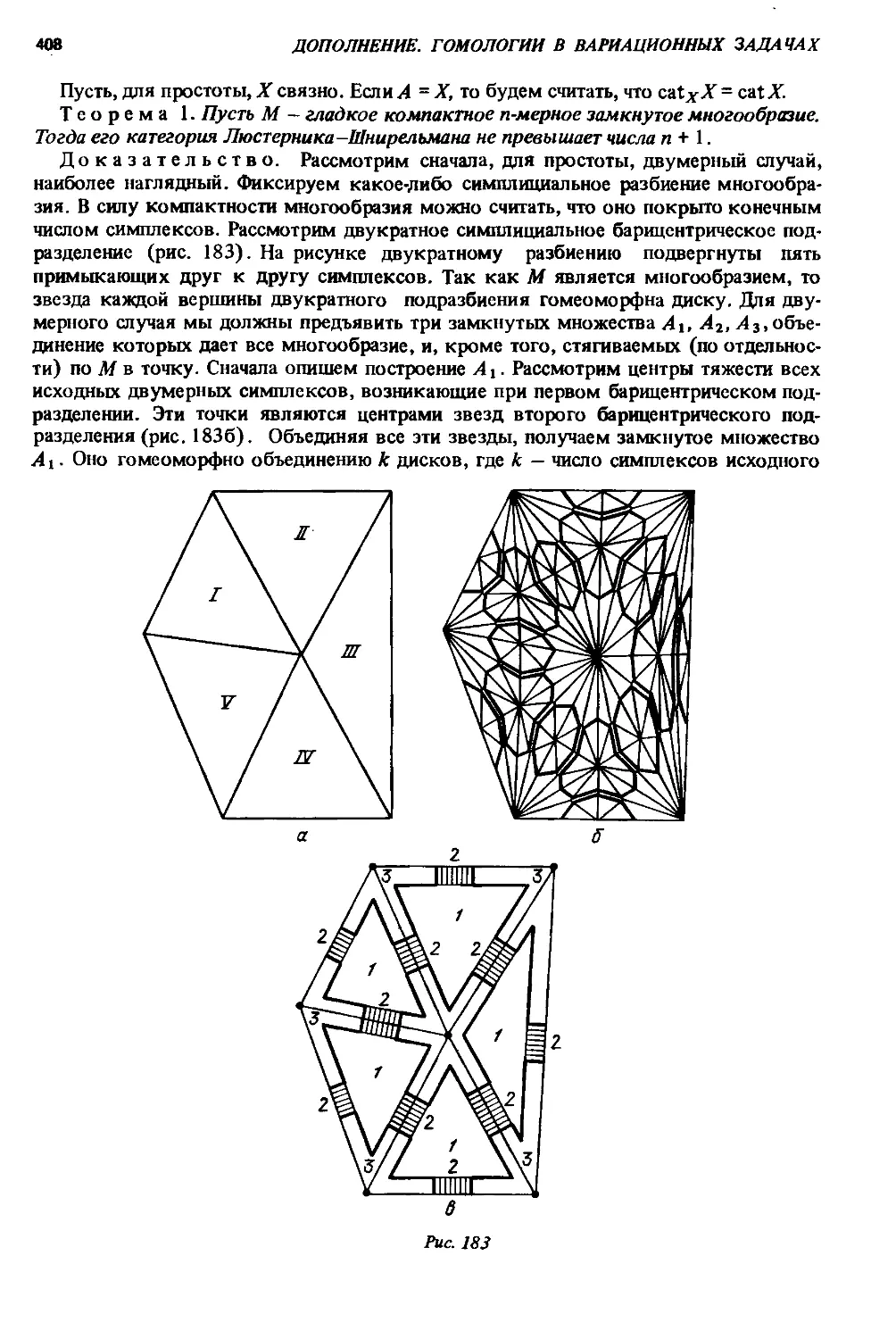
§ 46. Гомологии и категория Люсгерника - Шнирельмана................... 407
§ 47. Гомологии и минимальные поверхности.............................. 414
1. Физические границы раздела двух сред с равными давлениями и их мате-
матическая модель - минималыше поверхности (414). 2. Теорема Дугласа и
Радо (416). 3. Абсолютно минимальные двумерные поверхности (420). 4. Труд-
ности при решении задачи Плато в больших размерностях (421). 5. Гомологии и
многомерные минимальные поверхности (422). 6. Элементы теории препят-
ствий, встречающиеся в вариационных задачах (426). 7. Гомологически три-
виальные минимальные поверхности (429).
§ 48. Бордизмы и минимальные поверхности............................... 432
1. Старшие и младшие страты минимальных поверхностей (432). 2. Бордантные
многообразия и задача минимизации объема (434). 3. Решение задачи Плато в
каждом классе спектральных бордизмов (437). 4. Минимальные поверхности
в гомотопических классах отображений (438).
§ 49. Некоторые топологические свойства минимальных поверхностей....... 439
§ 50. Гомологии и периодические решения интегрируемых гамильтоновых систем. . . 442
§ 51. Теория типа Морса для интегрируемых гамильтоновых систем. Топологи-
ческий инвариант интегрируемых систем............................. 446
§ 52. Когомологии и слоения............................................ 466
1. Слоения (466). 2. Класс Годбийона - Вея (471). 3. Характеристические клас-
сы слоений произвольной коразмерности (477). 4. Отступление: алгебры Ли и
их когомологии (479). 5. Когомологии алгебры Ли и характеристические
классы оснащенных слоений коразмерности q (482).
СПИСОК ЛИТЕРАТУРЫ К ДОПОЛНЕНИЮ............................................ 485
ПРИЛОЖЕНИЕ. О РИСУНКАХ .................................................. 488
СПИСОК КНИГ ПО ТОПОЛОГИИ. . .............................................. 490
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ...................................................... 492
ПРЕДИСЛОВИЕ
Гомотопическая топология, находившаяся в 40—60-е годы в фазе интенсивного
развития, достигла к настоящему времени положения относительного равновесия.
При этом в ней достаточно ясно обозначились границы круга понятий и фактов,
представляющих общематематический интерес. В то же время область применений
топологии, в том числе гомотопической, значительно расширилась, охватив, наряду
с геометрией и анализом, теоретическую физику и ряд прикладных дисциплин.
Поэтому молодому математику, какую бы специальность он себе не избрал, стоит
как можно глубже изучить гомотопическую топологию. В помощь ему мы пред-
лагаем эту книгу.
Книга задумана как универсальное пособие по гомотопической топологии, вклю-
чающее в себя как элементарное введение, так и изложение наиболее совершенных
методов, общематематическое значение которых бесспорно. Первую попытку реа-
лизовать этот замысел мы предприняли 20 лет назад. Ее результатом явились рота-
принтные пособия:
Фукс Д.Б., Фоменко А.Т., Гутенмахер В.Л. Гомотопическая топо-
логия. Часть I. — Изд-во МГУ, 1967.
Фукс Д.Б., Фоменко А.Т. Гомотопическая топология. Часть II. — Изд-во
МГУ, 1968.
В 1969 году зти книги были выпущены издательством МГУ под единой обложкой,
а в 1986 г. венгерское издательство ’’Акаде.миаи” выпустило их английский пере-
вод. Мы использовали в настоящей книге общий план этих изданий (хотя значитель-
но его расширили), а также несколько пунктов из части II (которые, впрочем,
пришлось изрядно переделать).
Главное, что изменилось в книге, — основная цель авторов. Если теперь мы стре-
мимся помочь читателю овладеть разнообразными методами и результатами гомо-
топической топологии, то 20 лет назад мы, в соответствии с идеологией того времени
(лучше сказать, с идеологией конца 50-х годов), считали центральной задачей топо-
логии вычисление гомотопических групп сфер и соответствующим образом ориенти-
ровали читателя. Главное же, что мы старались заимствовать из указанных ротапринт-
ных пособий, - неформальный, лекционный стиль изложения.
ПРЕДИСЛОВИЙ
Достоинства и недостатки лекционного стиля хорошо известны. Достоинства
заключаются в доступности и относительной краткости, недостатки состоят в не-
последовательности изложения и известной вольности в обращении с доказательства-
ми. Мы часто оставляем читателю в качестве упражнения доказательства отдельных
теорем или их части, сохраняя за собой право дальнейшего использования этих
утверждений как доказанных. Особенно легкомысленным (впрочем, по необходи-
мости) является наше отношение к доказательствам в частях книги, соприкасаю-
щихся с топологией многообразий. Непоследовательность изложения проявляется
в двух вещах. Во-первых, мы, как правило, формулируем леммы и теоремы, не
учитывая в деталях потребности дальнейшего, полагая, что небольшие обобщения
или модификации читатель в нужном месте произведет сам. Во-вторых, требования
к читателю у нас не постоянны на протяжении книги: начальные главы ориентиро-
ваны на студента 2—3-го круса, для чтения заключительных глав требуется более
высокий уровень математической культуры.
В свое оправдание мы можем сказать, что изложение грандиозного материала
этой книги более академическим стилем потребовало бы, наверное, многих томов.
(Эти тома частично написаны различными авторами — см. список книг по топологии
на с. 490-491).
Первая часть книги — введение и главы 1 и 2 — содержат более или менее стандарт-
ный курс элементарной гомотопической топологии (гомотопии, расслоения, клеточ-
ные пространства, гомологии). Нестандартными являются § 1 ’’Классические про-
странства”, § 17 ’’Гомологии и многообразия” н § 19 ’’Векторные расслоения и ха-
рактеристические классы”. Глава 3 ’’Спектральная последовательность расслоения”
осуществляет переход от элементарных разделов книги к более сложным вещам.
Изложение в ней сопровождается большим количеством примеров и завершается
применением к вычислению гомотопических групп. На вычисление гомотопических
групп направлены, в основном, две следующие главы, ’’Когомологические опера-
ции” и ’’Спектральная последовательность Адамса”; исключение составляет § 30,
в котором показаны различные применения квадратов Стинрода, такие, как форму-
ла By для классов Штифеля - Уитни, теорема Стинрода о втором препятствии и тео-
ремы о классификации трехмерных линз. Далее идет глава 6, посвященная К-теории
и кобордизмам. Главный упор сделан в ней на применения к различным топологи-
ческим и иным проблемам.
Два заключительных параграфа шестой главы вызовут, по всей вероятности,
особенное неудовольствие у специалистов, которые вообще склонны обращать главное
внимание не на то, что в книге есть, а на то, чего в ней нет. Параграф ’’кобордизмы”
не только не отражает богатства современной теории кобордизмов, но не содержит
даже упоминания о некоторых ее фундаментальных разделах, скажем, о формальных
группах. В свое оправдание мы могли бы сказать, что теории кобордизмов посвяще-
ны отличные книги, а наша цель — только возбудить интерес. Еще более открыт для
критики заключительный параграф ’’формула Атиа — Зингера”, который, впрочем,
мы попытались защитить, вставив в его название слово ’’набросок”.
10 ПРЕДИСЛОВИЕ
Перечисленные главы и составляют курс гомотопической топологии, обещанный
в названии книги. Но мы сочли разумным включить в нее еще Дополнение, содержа-
щее примеры применений гомотопической топологии в геометрии, механике и анализе
и снабженное особым списком литературы. Читатель может воспринимать это как
отражение личных математических вкусов авторов.
За исключением Дополнения, ссылки на журнальную литературу делаются не-
посредственно в тексте. В конце книги мы приводим только более или менее пол-
ный список книг по близким нам разделам топологии, имеющихся на русском
языке. Если в книге сказано ”см. такую-то главу книги такого-то автора”, то имеет-
ся в виду книга из этого списка.
Мы благодарны Сергею Петровичу Новикову за поддержку. Мы благодарны
также В.Л. Гутенмахеру за сотрудничество при составлении ротапринтных пособий,
послуживших прообразом этой книги, и А.В. Зелевинскому, представившему прек-
расный конспект лекций по А-теории.
ВВЕДЕНИЕ
ВАЖНЕЙШИЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Многие лекторы начинают курсы гомотопической (или иной) топологии с ввод-
ной лекции, посвященной ’’теоретико-множественной топологии”, т.е. предмету,
рассматривающему топологические пространства в максимальной общности. Мы
нарушаем эту традицию, предполагая, что читатель либо уже немного знаком с этим
предметом, либо готов терпеть небольшие неудобства, проистекающие из недостаточ-
ного знакомства с ним, либо просмотрит перед чтением нашей книги какое-нибудь
руководство по теоретико-множественной топологии (годится, например, первый
параграф книги Рохлина и Фукса1)). Так или иначе, мы присваиваем себе право
употреблять без пояснений слова ’’хаусдорфово пространство”, ’’компактное прост-
ранство”, ’’пространство со счетной базой” и т.п., а также использовать (явно или
неявно) факты типа ’’непрерывное взаимно однозначное отображение компактного
пространства в хаусдорфово пространство является гомеоморфизмом” или ’’ком-
пактное подмножество хаусдорфова пространства замкнуто”. Вводную же часть
книги мы посвятим рассмотрению не общего понятия топологического пространст-
ва, а конкретного запаса наиболее часто встречающихся топологических пространств,
который будет служить нам источником примеров и мотивировок, а также исполь-
зоваться в разного рода геометрических конструкциях. Сначала мы познакомим-
ся с некоторыми наиболее известными, ’’классическими” пространствами, а затем
опишем важнейшие операции над топологическими пространствами, способствую-
щие размножению нашего запаса пространств и в то же время важные сами по себе.
§ 1. КЛАССИЧЕСКИЕ ПРОСТРАНСТВА
1. Евклидовы пространства, сферы и шары. Обозначения R" и С" имеют у нас
обычный смысл. Пространства С" и R2" отождествляются при помощи соответст-
вия (х, + . . . , хп + 1уп) <-* (Х1, У1,. . . ,хп, уп). Сфера Sn и шар Dn опреде-
ляются соответственно как единичная сфера и единичный шар с центром в начале
координат в пространствах R"+1 и R"; таким образом, S"-1 есть граница шара
1У в R". Символ R“ всегда обозначает объединение (’’индуктивный предел”) цепоч-
ки вложенных пространств R1 С R2 С R3 С. . . ; таким образом R“ есть совокуп-
ность финитных (т.е. нулевых, начиная с некоторого места) бесконечных после-
довательностей (xj, х2, х3, . . . ) вещественных чисел. Топология в R°° вводится
правилом: множество F С R“ замкнуто тогда и только тогда, когда все пересече-
ния F П R" замкнуты в своих пространствах R". Аналогичный смысл придается
COO СО а*ъОО
,S ,D .
1) Список книг по топологии приведен на с. 490-491.
12
ВВЕДЕНИЕ. ВАЖНЕЙШИЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Упражнения. 1. Покажите, что последовательность
(ао,0,0,...), (О, а,, О,...), .... (О,...,0, в„,0,
п
точек пространства R“ имеет предел тогда и только тогда, когда последователь-
ность а0, ej,..., ап,... финитна.
2. Покажите, что ни одно из пространств R“, S”, D°° не метризуемо.
В литературе встречаются другие варианты пространства R“. Например: (1)
’’гильбертово пространство” /2 - совокупность последовательностей (xj, х2, х3,...),
для которых сходится ряд Lx2, топологизированное посредством метрики
p((Xj, х2, ...), (jz,, у2, ... ))2 = ECj/. -x,)2;
(2) ’’тихоновское пространство” Т — совокупность всех последовательностей
(xi, х2> х3,... ) с топологией, определенной правилом
lim (хп, x/2,...) = (xi,x2,...)
«о
тогда и только тогда, когда lim Хц = ху- при каждом/.
i -»<»
Упражнения. 3. Непрерывны ли и являются ли гомеоморфизмами на свои
образы естественные вложения R“ ->Z2,R“ ->7’, l2 -*Т1
4. Метризуемо ли пространство Т?
5. Единичный куб пространства R“, /2 или Т определяется как совокупность
точек (xj, х2, . . . ) этого пространства, таких, что 0 <х< < 1, i =1,2,... Компакт-
ны ли эти кубы?
2. Вещественные проективные пространства. Вещественное п-мерное проективное
пространство RP" определяется как совокупность проходящих через 0 прямых
пространства R"+1, топологизированная угловой метрикой: расстояние между
двумя прямыми равно углу между ними.
Упражнение 6. Докажите, что проективная прямая RP1 гомеоморфна
окружности S1.
Координаты (х0>...»х„) направляющего вектора прямой (определенные, очевид-
но, с точностью до пропорциональности) называются однородными координатами
точки проективного пространства; стандартное обозначение (х0; • • • : х„). Точки,
у которых i-я однородная координата отлична от 0, составляют i-ю основную аф-
финную карту, соответствие (х0 : • • • : хп) •*—> (xq/x,-, . . . , xf _i/xf, xf +i/xf, . . .
. . . , xn/Xi) определяет гомеоморфизм аффинной карты на R" и вносит в нее коор-
динаты.
Сопоставляя с точкой сферы 5” С R"+1 прямую, проходящую через эту точку и 0,
мы получаем непрерывное отображение Sn -> RPn. Это отображение переводит две
различные точки сферы Sn в одну точку пространства RP” тогда и только тогда,
когда эти точки диаметрально противоположны. Таким образом, каждая точка про-,
странства RP” имеет при этом отображении ровно два прообраза (само отображение
является двулистным накрытием - см. § 7). Имея в виду это отображение, говорят,
что пространство RP" получается из сферы 5” посредством отождествления диа-
метрально противоположных точек. (Это выражение имеет точный смысл, который
состоит в следующем. Предположим, что в топологическом пространстве X указано
некоторое множество пар точек, подлежащих отождествлению. После отождествле-
ния получается множество Y и отображение X -* Y. Топология в Y вводится прави-
лом: множество открыто, если его прообраз в X открыт; это — слабейшая из топо-
§ 1. КЛАССИЧЕСКИЕ ПРОСТРАНСТВА
13
логий, в которых отображение X * Y непрерывно1).) Верхняя полусфера сферы Sn
(составленная из точек, у которых неотрицательна (п + 1)-я координата) канони-
чески гомеоморфна шару Л" (гомеоморфизм устанавливается ортогональным проек-
тированием верхней полусферы на экваториальный шар). Сужение предыдущего
отображения Sn -* RP" на верхнюю полусферу есть, таким образом, отображение
Л" -* RP", при котором в одну точку отображаются только диаметрально противопо-
ложные точки граничной сферы Sn~1С1У. Таким образом, пространство RP" может
быть получено также из шара /У отождествлением диаметрально противоположных
точек его границы.
Бесконечномерное проективное пространство RP°° может быть определено при
помощи любой из трех предыдущих конструкций; можно положить также RP“ =
= URPf.
3. Комплексные и кватернионные проективные пространства. Если заменить в
определении пространства RP" пространство R"+1 пространством С"+1 и веществен-
ные прямые комплексными прямыми, то получится определение комплексного
проективного пространства СРп.
Упражнение?. Пространство С-Р1 гомеоморфно S2.
Подобно RP", пространство СР" покрывается п аффинными картами. Сопостав-
ляя с точкой сферы S2n+1 С С"+1 проходящую через эту точку и 0 комплексную
прямую, мы получаем отображение S2n+l -+СРп, переводящее в точку пространства
СР" целую окружность {(zjz, . . . , z„+lz)} , где (zlf . . . , zn+i) - данная точка
сферы S2"+1, a z пробегает окружность | z | = 1. Можно сказать, что СР" получается
из S2"*1 отождествлением точек каждой из этих окружностей. Отображение S2"+1 -*
-►СР" можно сузить на шар D2", вкладывающийся в S2"+1 как совокупность точек,
у которых (п + 1)-я координата вещественна и неотрицательна. Получается отобра-
жение 2>2" -*СР” и с ним — описание СР" как пространства, получающегося из шара
D2n посредством отождествления, аналогичного описанному выше, но производи-
мого только на границе.
Аналогичные конструкции можно произвести, заменив поле комплексных чисел
С телом кватернионов Н. Получается кватернионное проективное пространство HP".
Следует только иметь в виду, что из-за некоммутативиости тела кватернионов
в катернионных пространствах бывают левые и правые прямые; поэтому следует
остановиться на одной из этих возможностей (совершенно равноценных), скажем,
определить кватернионное проективное пространство как пространство левых
прямых.
Очевидным образом определяются также пространства СР°° и НР“.
4. Проективная плоскость Кэли. Читателю может показаться неправомерным,
что кватернионные проективные пространства занимают в списке классических про-
странств столь почетное место - по соседству с шарами и сферами. Можно возра-
зить, что для топологии первостепенную важность имеют не только кватернионные
проективные пространства, но и такое экзотическое образование, как проектив-
ная плоскость Кэли. Определение чисел Кэли (или октав) аналогично определе-
нию комплексных чисел и кватернионов. Мы приведем их общую конструкцию.
*) Термины "слабая топология” и ’’сильная топология” не имеют в математике единого тол-
кования. Мы считаем топологию более слабой, если в ней больше открытых множеств, т.е. мень-
ше предельных точек (у нас слабее всех дискретная топология). Образно выражаясь, слабая
топология - это топология, в которой точки слабее притягиваются друг к другу. Противопо-
ложная терминология исходит из представления, что в топологическом пространстве точки от-
талкиваются друг от друга (по отношению к этой терминологии дискретная топология является
самой сильной).
14 ВВЕДЕНИЕ. ВАЖНЕЙШИЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Предположим, что в пространстве R" с некоторым п определены две операции:
умножение и сопряжение (черта). Мы определяем аналогичные две операции в
R2" формулами
(a, b) (с, d) = (ас - bd , be + ad), (a, b) = (a, -b)
(точки пространства R2" отождествляются с парами точек пространства R"). От-
правляясь от обычного умножения и тождественного сопряжения (а = а) в R1 = R,
мы последовательно получаем умножение и сопряжение в R2, R4, R8, R16, . . .
Умножение в R2 — это обычное умножение комплексных чисел. Умножение в
R4 — это умножение кватернионов. Оно билинейно, ассоциативно и допускает одно-
значное деление (это означает, что уравнение ах = b однозначно разрешимо при
а ¥=0), но не коммутативно. Умножение, возникающее в R8, еще хуже: оно не
только не коммутативно, но и не ассоциативно (хбтя для него справедливы соотно-
шения ассоциативности в которых участвуют только две буквы: (ab)a = а(Ьа),
(ab)b = ab2, (ab)a~l = a(ba~l) и т.д.); правда, оно все еще обладает однозначным
делением. Пространство R8 с этим умножением называется алгеброй Кэли и обозна-
чается через Са; элементы же алгебры Кэли называются числами Кэли или октавами.
(Умножения в R16, R32, . . . не обладают даже этой толикой хороших свойств.)
Забегая значительно вперед, сформулируем гипотезу Фробениуса, доказательство
которой в 1960 г. составило заслугу именно гомотопической топологии: если в
пространстве R" имеется билинейное умножение с однозначным делением, то
п = 1,2,4 или 8.
Неассоциативность умножения в Са препятствует определению в пространствах
Са" с п > 3 каких бы то ни было прямых. (Скажем, если определить прямую, про-
ходящую через 0 и точку х G Са" как совокупность точек вида tx с t G Са, то прямая,
проведенная через 0 и точку tox этой прямой, не будет совпадать с этой прямой —
см. рис. 1.) Поэтому удовлетворительного определения проективных пространств
Кэли не сущестует (мы увидим впоследствии, что пространств, которые обладали бы
ожидаемыми свойствами проективных пространств Кэли, не существует по чисто то-
пологическим причинам); все же удается определить проективную плоскость Кэли.
Для этого мы рассматриваем не целые прямые в Са3, а следы, оставляемые этими
прямыми на объединении Т трех плоскостей x = l,j=l,z = l (х, у, z — кэлиевы
координаты в Са3). Подробнее: точка (а1, b', с') G Са3 — 0 называется коллинеар-
ной точке (a, b, с) G Са3 — 0, если существует такое t 6 Са, что а' = ta, b' = tb, с' =
= tc. Отношение коллинеарности рефлексивно, симметрично, но не транзитивно;
но оно делается транзитивным, если ограничиться точками, лежащими в Т. (На-
пример, если (с, 1, d) = (1, а, b) и (е, f, 1) = t2 (с, 1, d), то 11 = с = а-1 = db’1,
t2 = ее"1 -f^dT2 и (t2ti) (1, a, b) = ((ес-1)с, (№)e, (dT2 (JZ>-1))6) = (e,f, 1).)
Более того, каждая точка каждой из трех плоскостей не коллинеарна никакой
§ 1. КЛАССИЧЕСКИЕ ПРОСТРАНСТВА
15
другой точке этой плоскости и коллинеарна не более, чем одной точке каждой из
двух других плоскостей. Пространство, получающееся из Т при склеивании колли-
неарных точек, и есть проективная плоскость Кэли СаР1 2. Каждая из трех плоскостей
проектируется в СаР2 без складок; образы этих плоскостей составляют в СаР2
аналог покрытия аффинными картами.
Упражнение 8. Что получится, если отождествить все пары коллинеарных
точек в Са3 — О?
5. Многообразия Грассмана. Это — обобщение проективных пространств. Вещест-
венное многообразие Грассмана G(n, к) определяется как пространство £-мер-
ных подпространств пространства R" ’). Очевидно, G(n, к) =G(n,n - к) и G(n, 1)=
= RP"-1. Аналог аффинной карты в G(n, к) определяется так: фиксируется набор
целых чисел 1 <ij < .. . < /^<пи рассматривается часть многообразия Грассмана,
составленная из подпространств, без вырождения проектирующихся на пространство
i j -й, . . . , i к-й координатных осей. Такие подпространства можно рассматривать как
графики линейных отображений пространства указанных координатных осей в до-
полнительное пространство. Таким образом, точки нашей карты характеризуются
к X (п - к)-матрицами, т.е. наборами из к(п - к) вещественных чисел; зто опреде-
ляет гомеоморфизм карты на Rfc и вносит в нее координаты.
Существует-способ ввести координаты сразу во всем пространстве G(n, £). Имен-
но, фиксируем в пространстве a &G(n,k) базис, запишем координаты базисных
векторов (в пространстве R") в виде к X n-матрицы и вычислим у этой матрицы
/ п \
все ( ) миноров порядка к. Получающиеся числа не все равны 0 и при замене
\ к /
базиса в а умножаются на одно и то же число. Они называются плюккеровыми ко-
ординатами подпространства а. Плюккеровы координаты определяют отображение
( " )-i
G(n, к) * RP к . Разумеется, образ этого отображения не покрывает всего
(")-1
RP к , т.е. плюккеровы координаты связаны некоторыми соотношениями.
Пример: 6 плюккеровых координат g]2, £i3> £14. £23. £г4>£з4 (нижние индексы —
номера столбцов, из которых составлен минор) точки пространства G(4, 2) связа-
ны (единственным) соотношением ^]2^34 — 113^24 + £14£гз = 0 (таким образом,
G (4, 2) гомеоморфно гиперповерхности в СР5, задаваемой указанным уравнением
2-й степени).
Все сказанное с очевидными изменениями переносится на комплексный и кватер-
нионный случаи; соответствующие многообразия Грассмана обозначаются через
CG(n, к) и HG(n, к). Еще один важный вариант многообразий Грассмана составляют
пространства G+ (п, к) ориентированных fc-мерных подпространств пространства
R" ; заметим, что G+ (п, к) = G+(n, п - к) uG+(n, 1) = $ п ~ \ Заметим также, что
плюккеровы координаты имеются в CG(n, к) ив G+(n, к). В CG(n, к) они опреде-
лены с точностью до комплексной пропорциональности и определяют отображение
(")-1
CG(n, к) -* СР к , а в 6+ (п, к) они определены с точностью до пропорциональ-
ности с положительном коэффициентом и определяют отображение G+(n, к) -*
с(к)-г
-+S к
Наконец, бесконечномерными вариантами многообразий Грассмана служат про-
странства Грассмана G(°°, к) — объединение цепочки G(k + 1, к} СG(k + 2,fc) С...
1) Существует другая система обозначений, в которой то, что мы обозначаем через G (л, к),
обозначается через G(п — к, Е).
16
ВВЕДЕНИЕ. ВАЖНЕЙШИЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
и G(°°, °°) - объединение цепочки G(°°, 1) CG(«, 2) С. . . , а также пространства
СС(«,Л),...
б. Многообразия флагов. Это — обобщение многообразий Грассмана. Предполо-
жим, что задан набор целых чисел 1 .. .<ks <л - 1. Флагом типа (kt, \., ks)
в R" называется цепочка V\ С... С Vs подпространств пространства R", такая, что
dim V, = kj. Совокупность флагов естественно топологизируется и превращается в
’’многообразие флагов” F (л; klt..., ks). Варианты этого определения CF(n; kt, Л .
. . . , ks), HF(л; kt,'..., ks) и F+ (n; kt, .., ks) очевидны. Пространства F(n; 1,..
. . . , n - 1), CF (n; 1, . . . , n — 1), HF (n; 1,..., n - 1) и F+ (л; 1.n - 1) назы-
ваются (по понятным причинам) многообразиями полных флагов.
7. Компактные классические группы. К их числу относятся: группа О(п) матриц
ортогональных преобразований в R"; группа С7(л) (комплексных) матриц унитар-
ных преобразований в С"; подгруппы SO (л) и5С7(л) групп О (л) и О(л) .составлен-
ные из матриц с определителем 1; группа Sp (л) кватернионных матриц унитарных
преобразований пространства Н".
Заметим, что группа SO (2) поворотов плоскости гомеоморфна окружности.
Группа SO(3) гомеоморфна RP3; гомеоморфизм относит повороту пространства
R3 вокруг ориентированной оси I на угол а < я точку оси I, отстоящую от 0 в поло-
жительном направлении на расстояние a/я. Поскольку поворот на угол я вокруг
ориентированной оси не отличается от поворота на угол я вокруг противоположно
ориентированной оси, образом указанного отображения служит шар D3 с отождест-
вленными диаметрально противоположными точками границы, т.е. RP3. Другую
конструкцию гомеоморфизма SO(3) * RP3 см. в книге Рохлина и Фукса (п. 3.2.3).
Группу SU(2) гомеоморфна S 3: произвольный элемент этой группы записывается
/ а 0 \
в виде ( __ ), где | а| 2 + | 01 ~ 1, т.е. (а, 0) 6 S3 СС2. Наконец, группы С7(1)
V0 а /
и Sp (1),изоморфные, соответственно, группам SO(2) и St7(2), гомеоморфны S1
и53.
8. Многообразия Штифеля. Пространство ортонормированных ^-реперов в R"
называется многообразием Штифеля и обозначается через V(п, к). Это пространство
имеет комплексный и кватернионный аналоги С И (л, к) и НК (л, к). Многообразия
Штифеля обобщают классические группы: К(л, л) = О(п), V(n, п - 1) = SO(ri),
СК(л, л) = С7(л),СК(л, л - 1) = SU(ri), НК (л, л) = Sp(n). Заметим также, что
К(л, 1) =5"-1,СК(л, 1) =52"-1,НК(л, 1) =S4"-1.
9. Классические действия классических групп в классических пространствах.
Действие группы О(п) в R" порождает ее действия в S"-1,1У, G(n, к), У(п, к)\
подгруппа SO (л) группы О (л) действует также в G+ (л, к). В К(л, к) действует еще
группа О (к): матрицы из О (к) применяются к векторам репера. Эти действия имеют
комплексные и кватернионные аналоги.
Действия группы О (л) в S"-1, G(n, к), У(п, к) транзитивны. То же относится к
комплексным и кватернионным аналогам этих действий и к действию группы 50(л) в
G+ (л, к). Таким образом, предыдущие классические многообразия являются одно-
родными пространствами компактных классических групп, т.е. они могут быть пред-
ставлены как факторпространства этих групп по определенным замкнутым подгруп-
пам. Вот эти представления:
S" -1 = <2(л)/О(л - 1) = SO(n)ISO(n - 1);
S2"-1 = щпущп- 1)= SU(n)ISU(n - 1);
S4"-1 =5р(л)/5р(л- 1);
§ 1. КЛАССИЧЕСКИЕ ПРОСТРАНСТВА 17
G(n, к) = 0(п)10{к) ХО(п- к);
CG(n, к) = U(n)/U(k) X U(n - к);
Нб(л, к) = Sp(n)lSp(k) X Sp(n - к)-,
G+ (п, к) = SO(n)/SO(к) X SO (л - к)
(О (к) X 0(п - к) есть подгруппа группы О (л), составленная из блочно диагональ-
ных матриц с блоками к X Ли (л - к) X (и - Л)). Аналогичным образом представ-
ляются многообразия флагов:
/Хл; Л,) = О(л)/О(Л1)Х О(Л2 -Л1)Х... xo^-voxocw-^)
и т.д. В частности, многообразие комплексных полных флагов СЕ(л; 1, . . ., л — 1)
есть факторпространство группы С7(л) по ее максимальному тору 1/(1) X ... Х1/(1).
Действие группы О (к) в К(л, к) и его комплексный и кватернионный аналоги сво-
бодны. При этом
К(л, к)Ю(к) = G(n, к), V(n, k)/SO(k) = G+(n, к),
СК(л, k)IU(k) = СС(и, к), НИ(л, k)ISp(k) = НС(л, к).
10. Классические поверхности. К числу классических поверхностей относятся,
прежде всего, (двумерная) сфера S2, вещественная проективная плоскость RP2
и бутылка Клейна, которая, как это широко известно, реализуется в R3 только как
поверхность с самопересечением (см. рис. 2). Подобная реализация, хотя не столь
широко известная, существует и для проективной плоскости. Она представлена на
рис. 3; чтобы помочь читателю разобраться в устройстве этой поверхности, мы при-
водим на рис. 4 ее сечения семью параллельными плоскостями. Заметим, что: (1)
между сечениями 2 и 3 имеется ’’седло”; сечения горизонтальными плоскостями
Рис. 2 Рис. 3
Рис. 4
18
ВВЕДЕНИЕ. ВАЖНЕЙШИЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Рис. б
вблизи седла ведут себя как горизонтали на географической карте вблизи точки
перевала; (2) в какой-то момент между сечениями 3 и 4 линия проходит через точку
самопересечения, образуя точку тройного самопересечения.
Реализация проективной плоскости в трехмерном пространстве с более сложной
особенностью показана на рис. 5, а (на рис. 5, б более крупно изображена окрест-
ность самой неприятной особой точки).
К числу классических поверхностей относятся также поверхности, получающиеся
из сферы, проективной плоскости и бутылки Клейна присоединением ручек и
высверливанием дыр (рис. 6).
Упражнения. 9. Проективная плоскость с дырой гомеоморфна ленте Мёбиу-
са — рис. 7 (таким образом, лента Мёбиуса относится к числу классических поверх-
ностей) .
10. Поверхность, представляющая собой две бутылки Клейна, соединенные труб-
кой, гомеоморфна бутылке Клейна с ручкой (рис. 8).
11. Поверхность, представляющая собой бутылку Клейна и проективную плос-
кость, соединенные трубкой, гомеоморфна проективной плоскости с ручкой.
12. Поверхность, представляющая собой две проективные плоскости, соединен-
ные трубкой, гомеоморфна бутылке Клейна.
13. Выведите из трех предыдущих упражнений, что поверхность, представляющая
собой две классические поверхности, соединенные трубкой, есть снова классичес-
кая поверхность.
Имеется классический способ склеивания классических поверхностей из много-
угольников. Процедура заключается в следующем. Берется плоский многоугольник
(например правильный). Его стороны (все или некоторые) составляются в пары, и
Рис. 7
Рис. 8
§ I. КЛАССИЧЕСКИЕ ПРОСТРАНСТВА
19
на составленных в пары сторонах ставятся стрелки. После этого в каждой паре произ-
водится склеивание в соответствии со стрелками (иногда это склеивание можно
реально выполнить при помощи клея, но, как правило, оно представляет собой мыс-
ленное отожествление, описанное в п. 2).
Упражнения. 14. На рис. 9 изображены 6 многоугольников. Стороны, обо-
значенные одинаковыми цифрами, составлены в пары и снабжены стрелками. Пока-
жите, что при описанном выше склеивании из этих многоугольников получатся:
(а) кольцо (= сфера с двумя дырами), (б) лента Мёбиуса, (в) тор (= сфера с одной
ручкой), (г) бутылка Клейна, (д) проективная плоскость, (е) поверхность крен-
деля (= сфера с двумя ручками).
15. Покажите, что если в многоугольник вставить 4 стороны, занумерованные и
ориентированные, как показано на рис. 10, то к соответствующей поверхности при-
соединится ручка.
16. Покажите, что если в многоугольник вставить 2 стороны, занумерованные и
ориентированные, как показано на рис. 11, то к поверхности присоединится (труб-
кой) проективная плоскость. (Другое описание последней операции — в поверхности
высверливается дырка и к ее краю приклеивается лента Мёбиуса, край которой,
кстати, гомеоморфен окружности; короче говорят: к поверхности присоединяется
пленка Мёбиуса.)
17. Покажите, что всякая классическая поверхность может быть получена из мно-
гоугольника при помощи нашей процедуры.
18. Всякое ли склеивание многогранника указанного вида приводит к классичес-
кой поверхности?
Тор (сфера с одной ручкой) может быть реализован в R3 как поверхность вра-
Рис. 10
Рис. 11
20
ВВЕДЕНИЕ. ВАЖНЕЙШИЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
мой окружности, называются меридианами тора, а траектории ее точек — паралле-
лями тора. В соответствии с этим на торе вводятся координаты: широта — угол,
отсчитываемый вдоль меридианов от выделенной (скажем, самой длинной) парал-
лели против часовой стрелки, и долгота — угол, отсчитываемый от выделенного ме-
ридиана (скажем, от первоначального положения окружности) вдоль параллелей.
Упражнения. 19. Если иа торе отождествить (при всех у, ф) точку с коорди-
натами (<р, ф) с точкой с координатами (<р + я, ф + я) (т.е. отождествить точки,
симметричные относительно центра симметрии тора), то получится поверхность,
гомеоморфная бутылке Клейна.
20. Если на торе отождествить точки (ip, ф) и (ф, <р), то получится поверхность,
гомеоморфная ленте Мёбиуса.
И в заключение мы займемся вычислением ’’рода комплексных кривых” (тер-
мин ’’род” полезно знать: если поверхность есть сфера с ручками, то число ее ручек
называется ее родом).
Упражнение 21. Подмножество комплексной проективной плоскости
СР2, составленное из точек, однородные координаты (z0: Zj : z2) которых удо-
влетворяют уравнению z" + z" + z"~ 0, гомеоморфно сфере с (п - 1) (л — 2)/2
ручками.
Если вы не справитесь сейчас с этим упражнением, вернитесь к нему после проч-
тения первых трех глав книги.
§ 2. ОПЕРАЦИИ НАД ТОПОЛОГИЧЕСКИМИ ПРОСТРАНСТВАМИ
1. Произведения. Напомним, что произведение X X Y множеств ХиГ -это
множество па)> (х, у), где х G X, у € Y. Если X, Y — топологические пространства,
то произведение X X Yканонически наделяется топологией: базу открытых множеств
в X X Y составляют произведения U X V, где U — открытое множество в X, а V -
открытое множество в Y. (Таким образом, lim (xt, yf) = (х, у) тогда и только тог-
да, когда lim xf = х и lim у,- =у.)
Аналогичным образом определяется произведение трех и более пространств.
Мы уже сталкивались с произведениями в п. 9 § 1: подгруппа группы О(п),
обозначавшаяся у нас через О (к) X О(п - к), действительно не отличается от со-
ответствующего произведения, и то же верно для многочисленных других произве-
дений, упоминавшихся по соседству.
Заметим еще, что тор гомеоморфен произведению S1 X S1 двух окружностей:
это показывают введенные на торе координаты, долгота и широта. Ввиду этого
произведения S1 X ... X S1 (л сомножителей) также называют тором (л-мерным).
Укажем также менее очевидное разложение в произведение: пространство 6+(4, 2)
гомеоморфно S2 X S2. Для доказательства напомним, что плюккеровы координаты
определяют вложение пространства G+ (4, 2) в S5 в качестве поверхности, задавае-
мой уравнением xtx6 - x2xs + Х3Х4 =0 (Xj, . . . , х6 — плюккеровы координаты
Si2,..., £з4 в G+(4, 2)). Введем в R6 новые координаты, положивxt = (yt +уц)12,
х2 = (Уз + 7s)/2, х3 = (у3 + у6)/2,х4 = (уз -Уб)/2, х5 = (у2 -У5) /2, х6 =
= (У1 ~Уа) /2. Тогда предыдущее уравнение примет вид
71 +У2 + Уз -У4-У5-У6 =0,
а уравнение сферы х2 + ... + х% =1 - вид
71 +7г +7з +74 +7s + Уб = 2.
§ 2. ОПЕРАЦИИ НАД ТОПОЛОГИЧЕСКИМИ ПРОСТРАНСТВАМИ 21
Система этих двух уравнений равносильна системе
Уг1 + УI + Уз = 1, Я +у! +Уб = 1,
которая, очевидно, определяет в R6 множество, гомеоморфное S2 X S2: точки этого
множества соответствуют парам (yt, у2, у3), (у4, ys, Ув) точек сферы S2.
Упражнения. 1. Покажите, что комплексная квадратика, т.е. подмножество
комплексного проективного пространства СР3, задаваемое в однородных координа-
тах (г0 : zt : г2 : z3) уравнением zj + z2 + г2 + z3 = 0, гомеоморфно S2 X S2.
2. Покажите, что группа SO(4) гомеоморфна S3 X50(3), т.е. S3 XRP3. (Группа
50(3) могла бы быть гомеоморфна 53 X 5s, поскольку 5О(3)/5О(2) = 5 , т.е.
50(3) отображается в 55 таким образом, что прообраз каждой точки сферы 5 s
гомеоморфен 50(2), т.е. 53, как говорят, расслаивается над 5$ со слоем 53. Тем
не менее, группа 50(3) не гомеоморфна 53 X 5 s , но доказать это вам сейчас вряд
ли удастся — дождитесь главы 4.)
В заключение заметим, что произведение X X Y непрерывно проектируется в X и
в У и что непрерывное отображение третьего пространства, Z, в XX У — это то же,
что пара непрерывных отображений Z ->Х, Z -> У.
2. Цилиндр, конус и надстройка. Символ I обозначает у нас отрезок [0,1]. Произ-
ведение X X I называется цилиндром над X; подмножества X X О, X X 1 цилиндра
называются его {нижним и верхним) основаниями (они не отличаются от X), а под-
множества вида х XI, где х G X, — его образующими (они гомеоморфны/).Если
отождествить между собой все точки основания XXI цилиндра X X Г (как говорят,
профакторизовать X X I по X X 1), то получится конус СХ над X. Запись: СХ =
= XX I/Х X 1. Конус сохраняет одно основание, X X 0. Если профакторизовать конус
Рис. 13
по его основанию, то получится надстройка SX над X; таким образом, LX = СХ/Х X 0.
По-другому можно сказать, что SX получается иэ цилиндра над X отождеств-
лением' в точку каждого иэ оснований (каждого из оснований в свою точку)
(см. рис. 13). Образ ’’срединного сечения” X X —называют иногда основанием
2
надстройки. (Это название мотивируется тем, что надстройку можно представлять
себе как два конуса, приставленные друг к другу основаниями, и эти приставленные
основания и служат основанием надстройки.) Образы отождествленных оснований
называются вершинами: у конуса одна вершина, у надстройки — две. Образы обра-
зующих цилиндра в конусе и надстройке называются образующими конуса и над-
стройки. Точки конуса и надстройки мы будем по-прежнему записывать как пары
(х, I), имея в виду, что в конусе (х', 1) = (х", 1) при любых х', х" е X, а в над-
22
ВВЕДЕНИЕ. ВАЖНЕЙШИЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
стройке еще (х', 0) = (х"> 0). Если нам будет нужно подчеркнуть, что точка (х, t)
лежит в конусе или в надстройке, то мы будем писать (х, t)c или (х, t) £.
Упражнения. 3. Конус и надстройка над Sn гомеоморфны D"+1 и S"+1.
4. Никакая классическая поверхность, кроме S2, не гомеоморфна надстройке
над каким-либо пространством.
3. Приклеивания. Цилиндр и конус отображения. Пусть X, Y — топологические
пространства, А — часть пространства Y, <р: А -*Х — непрерывное отображение. Возь-
мем сумму X U Y (т.е. пространство, составленное из X и Y как из двух несообщаю-
щихся кусков) и произведем в нем отождествление: всякую точку a G А СУ мы
отождествим с точкой <р (а) С X (см. рис. 14). Получающееся пространство обозна-
чается через X У, а описанная процедура его построения называется приклеива-
нием YкХпосредством <р.
Выделим два специальных случая этой конструкции. Пусть /: X ->Y — произволь-
ное непрерывное отображение. Результат приклеивания цилиндра X X I к У посред-
f
ством отображения X X 0 = X У называется цилиндром отображения f и обозна-
чается через Су1(/) (см. рис. 15). Результат приклеивания конуса СХ к У посредст-
вом того же отображения называется конусом отображения f и обозначается через
Con (/). Цилиндр отображения f содержит X и У, конус отображения f содержит X.
Упражнения. 5. Конус двулистного отображения S” -> RP" (см. § 1) гомео-
морфен RP"+1; в частности, конус двукратного накручивания окружности на себя
S1 -> S1, задаваемого формулой (cos <р, sin <р) >-* (cos 2<р, sin 2<р) (или в полярных
координатах (1, у) >-> (1, 2<р), или в комплексных координатах z г1), есть RP2.
6. Сформулируйте и докажите комплексный и кватерионный аналоги первого
из утверждений упражнения 5.
4. Джойн. Джойн X * У пространств X и У удобно представлять себе как объеди-
нение отрезков, соединяющих каждую точку пространства X с каждой точкой прост-
§ 2. ОПЕРАЦИИ НАД ТОПОЛОГИЧЕСКИМИ ПРОСТРАНСТВАМИ
23
ранства Y. Например, джойн двух отрезков, лежащих на скрещивающихся прямых
в R3, — тетраэдр (рис. 16). Формальное определение джойна таково: берем произ-
ведение X X Y X I (отрезок х X у X I соединяет точку х G X с точкой у G У) и в
нем производим отожествление: точку (х,у‘, 0) склеиваем с точкой (х, у", 0) и точку
(х*. у, 1) склеиваем с точкой (х", у , 1) при любых х, х, х" G X, у, у', у" € Y (от-
резки, соединяющие х G X с у' и у" G У, имеют общий левый конец, а отрезки, сое-
диняющие у G Y с х' и х" G X, имеют общий правый конец). Сами X и У вкладывают-
ся в X ♦ У: х -> (х, у, 0) (любое у) и у (х, у, 1) (любое х). Подробнее: подмно-
жество джойна, получающееся при факторизации из X X У X t С.Х X YXI, есть X при
t = 0, У при t = 1 и X X У при 0 < t < 1.
Упражнения. 7. Джойн пространства X и точки (= нульмерного шара/)0)
есть конус СХ над X.
8. Джойн пространства X и двоеточия (= нульмерной сферы 5°) есть надстройка
2ХнадХ.
9. Джойн Sm * Sn гомеоморфен sm+n+1 (ввиду упражнения 8 зто - обобщение
упражнения 3).
Для достаточно хороших пространств операция ’’джойн” ассоциативна: джойны
(X• У)* Z и X* (У * Z) естественно гомеоморфны ’’тройному джойну” X* Y * Z,
который строится как объединение треугольников, вершины которых лежат, соот-
ветственно, в X, У и Z; формально тройной джойн определяется как результат над-
лежащего отождествления в произведении XX У X Z X Д, где Д — треугольник.
Упражнение 10. Опишите это отождествление и постройте естественные
взаймно однозначные соответствия между (X*Y)*Z, X*(Y*Z) и X*Y*Z.
Покажите, что для достаточно хороших пространств X, Y, Z (например, компакт-
ных) эти взаимно однозначные соответствия являются гомеоморфизмами.
(Для плохих топологических пространств эти соответствия гомеоморфизмами не
являются и вообще джойн не ассоциативен. Подробное обследование этого явления
содержится, например, в книге Постникова ’’Основы гомотопической топологии”.)
5. Пространства отображений, путей и петель. Совокупность С(Х, У) всех непре-
рывных отображений пространства X в пространство У наделяется ’‘компактно-
открытой топологией” — топологией равномерной сходимости на компактных мно-
жествах. Базу открытых множеств этой топологии составляют множества вида
U{К, О), где К — компактное подмножество пространства X, О — открытое под-
множество пространства У и //(Х,О) состоит из таких отображений /, что
/(X) С О.
Упражнение 11. Если X — точка, то С (X, У) = У; если X— совокупность л
(изолированных) точек, то С(Х, У) = У X ... X У (и сомножителей). (Последнее
равенство служит основанием для того, чтобы обозначать пространство С(Х, У)
также через Ух.)
Пусть X, У, Z. — топологические пространства. Формула
{/: X -> С(У, Z)) ~ {(х, у) •* [Дх)](у)}
определяет отображение С(Х, C(Y, Z)) * С( X X У, Z).
Упражнение 12. Если пространства X и У хаусдорфовы и локально ком-
пактны, то зто - гомеоморфизм. (В этом случае можно написать (Z Y)x = ZX* Y;
эта формула служит еще одним оправданием обозначения Yx и называется ’’экспо-
ненциальным законом”.)
24
ВВЕДЕНИЕ. ВАЖНЕЙШИЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Путем пространства X называется непрерывное отображение I -+ Х\ точки у (0) и
(1) называются началом и концом пути уг, путь, у которого конец совпадает с нача-
лом, называется петлей. В пространстве C(I, X) путей пространства X рассматри-
вают такие подпространства: пространство Е (Х\ x0,Xj) путей пространства X,
начинающихся в точке х0 и кончающихся в точке Xj; пространство Е(Х, хв) путей
пространства X, начинающихся в точке х0 (и кончающихся где угодно); пространст-
во Sl(X, хе) = Е(Х; х0, хв) петель пространства X с началом х0.
Упражнения. 13. Пространство E(S"-, х0, Xj) не зависит, с точностью до
гомеоморфизма, от х0 и xt (в частности, оно не зависит от тдго, совпадают эти точки
или различны). Какими пространствами можно здесь заменить Sn?
14. Постройте естественный гомеоморфизм между пространством C(X,E(Y;
Уо> У1)) и частью пространства C(SX, Y), составленной из отображений, переводя-
щих вершины надстройки в у0 и yt (в определенном порядке).
Кстати: пространство, любые две точки которого можно соединить путем, назы-
вается линейно связным. Это понятие несколько отличается от понятия связности,
принятого в теоретико-множественной топологии: пространство связно, если в нем
отсутствуют собственные открыто-замкнутые подмножества. Именно, линейно связ-
ное пространство связно, но обратное верно не всегда (докажите первое и приведите
пример, подтверждающий второе). Впрочем, для широких классов пространств
(клеточные пространства, многообразия) понятия связности и линейной связности
равносильны, так что мы будем иногда говорить просто ’’связный”, забывая о ли-
нейности.
6. Операции над пространствами с отмеченной точкой. В топологии часто прихо-
дится рассматривать не просто топологические пространства, а топологические прост-
ранства с отмеченной точкой, т.е. считать, что во всех рассматриваемых пространст-
вах выделены отмеченные точки и все отображения переводят отмеченные точки
в отмеченные; одинаковые пространства с разными отмеченными точками считаются
при этом как бы разными пространствами. Переход к пространствам с отмеченной
точкой в большей или меньшей степени сказывается на всех рассматриваемых опера-
циях. Для некоторых иэ них модификация сводится к тому, что пространство —
результат операции - наделяется отмеченной точкой; например, в произведении
X X У отмечается точка (х0, Уо), где хь, у0 — отмеченные точки сомножителей.
Некоторые операции модифицируются более серьезным образом. Так, в конусе СХ
отождествляются между собой точки образующей, соответствующей отмеченной
точке пространства X, и аналогичным образом модифицируются надстройка, джойн
(в нем отождествляются точки образующей, соединяющие отмеченные точки сомно-
жителей) , цилиндр и конус отображения (которое, конечно, предполагается перево-
дящим отмеченную точку в отмеченную). Образ стянутой образующей во всех
случаях принимается за отмеченную точку.
Упражнение 15. Покажите, что гомеоморфизмы CSn =/)"+1, SS” =Sn+1,
Sm » Sn =sm+n + l сохранятся, если считать сферы и шары пространствами с отмечен-
ной точкой (каковой во всех случаях считается точка (1,0,..., 0)).
Пространство отображений уменьшается до пространства отображений, переводя-
щих отмеченную точку в отмеченную. Отмеченной точкой пространства С(Х, Y)
считается отображение, переводящее все X в отмеченную точку пространства Y.
Если X - пространство с отмеченной точкой, то ЕХ определяется как пространство
путей, начинающихся в отмеченной точке, a SIX — как пространство петель, начинаю-
щихся (и кончающихся) в отмеченной точке.
§ 2. ОПЕРАЦИИ НАД ТОПОЛОГИЧЕСКИМИ ПРОСТРАНСТВАМИ
25
Упражнение 16. Если X, У—пространства с отмеченной точкой, то С(ЪХ, У)=
= С {X, У) (равенство обозначает естественный по X и У1) гомеоморфизм).
В заключение мы опишем две операции, специфические для пространств с отмечен-
ными точками. Букет X v Y пространств с отмеченными точками X, Y получается
из суммы этих пространств посредством отождествления их отмеченных точек.
Например, букет двух окружностей - ’’восьмерка” (рис. 17). Можно определить
Рис. 17
♦
букет X v У как часть произведения X X У, составленную из таких точек (х, у), что
либо х = х0 — отмеченная точка пространства X, либо у = у0 — отмеченная точка
пространства У. Факторпространство X X Y/Хм Y - X# Yназывается ”смеш-произ-
ведением” или тензорным произведением пространств X, У. Отмеченные точки
в пространствах Xv Y и X # У очевидны.
Упражнения. 17. Покажите, что Sm #Sn =Sm+n.
18. Покажите, что для любого пространства X с отмеченной точкой SJV = Х # S1.
1) Слова ’’естественный по X и Y" можно понимать как ’’определяемый единообразно для
всех X и У”, но можно придать этому выражению более формальный смысл. Именно, если
X', Y' - другие пространства с отмеченной точкой, то для любых отображений X' X,
ф: У-+У’ коммутативна диаграмма
C(SX, Y) ------- C(X,[lY)
C(SX’, Y ')
C(X‘, ПУ'),
в которой горизонтальные стрелки обозначают наши гомеоморфизмы, а вертикальные - отобра-
жения, индуцируемые заданными отображениями <р: X' X, ф: У -► У'. (Поясним последнее:
левая вертикальная стрелка относит отображению /: £Х-»У отображение Т.Х* -► У', действую-
щее по формуле (х’, Г) ip(/(,₽ (х'),7)); правая вертикальная стрелка относит отображению
g: X -* ПУ отображение X' -+ ПУ', действующее по формуле х' »-»{г »-» (х'))(Т))} .
Вообще следует иметь в виду, что все наши операции над топологическими пространствами
’’естественны”, т.е. отображению пространства в пространство соответствует направленное в ту
илн иную сторону отображение, связывающее пространства, получающиеся в результате примене-
ния операции.)
ГЛАВА 1
ГОМОТОПИИ
§ 3. Гомотопии и гомотопические эквивалентности
1. Определение гомотопии. Пусть X и Y — топологические пространства. Непре-
рывные отображения /: X -+Y и g: X-+Y называются гомотопными (f ~ g), если
существует семейство отображений X * У, t.&I, такое, что (1) <р0 = f, =g
и (2) отображение Ф: X X I * Y, Ф(х, Г) = </?f(x), непрерывно. (Условие (2) яв-
ляется формализацией требования ’’непрерывной зависимости” <pt от f.) Отображе-
ние Ф (или иногда семейство <pt) называют гомотопией, связывающей f с g.
Очевидная проверка показывает, что отношение гомотопности рефлексивно,
симметрично и транзитивно.
Пример. Все отображения произвольного пространства X в отрезок I гомотоп-
ны между собой. Действительно, отображения х*-*,(1 — t)f (х) + tg(x) составляют
гомотопию, связывающую произвольные отображения f, g: X -* I. (Это же рассуж-
дение применимо к отображениям произвольного топологического пространства X
в произвольное выпуклое подмножество пространства R", в частности, простран-
ства R“.)
Заметим еще, что условие непрерывной зависимости отображения <pt от t можно
выразить по-другому: гомотопия есть путь в пространстве С (X, У), соединяющий
точку / € С {X, У) с точкой g € С (X, У). Впрочем, это определение равносильно
нашему определению гомотопии лишь для достаточно хороших пространств
(см. упражнение 12 в § 2).
2. Множества ir(X, У). Множество классов, на которые отношение гомотопности
разбивает множество С{X, У) (они называются гомотопическими классами),
обозначается через ir(X, У).
Примеры. 1. Множество it ( X, I) состоит (при любом X) из одного элемента.
2. Множество тт(*, У), где ♦ — точка, есть множество компонент линейной связ-
ности пространства У.
Очевидно, что со сделанными выше оговорками множество я (X, У) можно трак-
товать как множество компонент линейной связности пространства С(Х, У).
Пусть X, X', Y. — пространства и Л: Х-+Х' — непрерывное отображение; опреде-
лим отображение Л*: и(Х', У) * tt{X, У) следующим образом: в классе
а € я(У\ У) выберем любой представитель f G С(Х', У) и классу а. поставим
в соответствие класс И*(а), содержащий отображение /° h € С(Х, У), т.е. компо-
л . f
зицию X —► X —► У.
Пусть теперь X, У, У1 — пространства и Л: У * У1 — непрерывное отображение.
Определим отображение Л»: it(X, У) -> п(Х, У*) следующим образом: возьмем
§ 3. ГОМОТОПИИ И ГОМОТОПИЧЕСКИЕ ЭКВИВАЛЕНТНОСТИ
27
а € тг(Х, У), выберем в а любой представитель f G С(Х, У) и классу а поставим
в соответствие класс Л,(а) отображения h о j’ € С(Х, Y*).
Упражнение 1. Проверьте корректность двух последних определений.
3. Гомотопическая эквивалентность. Мы приведем три определения этого понятия.
Определение 1. Пространства Хх, Х2 называются гомотопически эквива-
лентными (Хг ~ Х2), если существуют непрерывные отображения /: Хг -*-Х2,
g: Х2 -+ Xi, такие, что композиции g ° ft Xt -+Xit f.° gt X2-+X2 гомотопны тож-
дественным отображениям Xt -+ Xlf X2 -+ X2 .
Кстати, f и g в этой ситуации называются гомотопически взаимно обратными
гомотопическими эквивалентностями.
Замечание. Если отображения g ° f и f о g не просто гомотопны тождест-
венным отображениям, но и являются таковыми, то f и g — взаимно обратные
гомеоморфизмы. Таким образом, определение гомотопической эквивалентности
аналогично определению гомеоморфизма.
Определение 2. Хг~ Х2, если существует способ определить для любого
пространства Y взаимно однозначное соответствие </>у: it(Xlt Y) ->я(Х2, У.) таким
образом,ато для любого отображения h: У-»-У' диаграмма
я(Хь У) ---------> я(ЛГ2, У)
Л. Л.
я(*2,У')
коммутативна, т.е. ipYt °h, = Л, ° <pY-
Определение 3. Xt ~ Х2, если существует способ определить для любого
пространства У взаимно однозначное соответствие y>Yt я (У, Aj) -►я(У^Х2) таким
образом, что для любого отображения h: Y+Y* диаграмма
л (У, JTi) ----► я(У, Х2)
h* h*
• <oY'
itx'.x^ ——> я(У, X2)
коммутативна, т.е. <pY « h* = h* о tpY .
Теорема. Определения 1, 2 и 3 эквивалентны.
Доказательство. Докажем эквивалентность определений 1 и 2. Пусть
Xt ~ Х2 в смысле определения 2; тогда определено взаимно однозначное соответ-
ствие ч>хл: 77(^1»"* w(Ла, ) • Положим а - <рх* ( [id*. ]) (idz есть тождест-
венное отображение множества Z, квадратные скобки обозначают переход от отобра-
жения к его гомотопическому классу) и выберем f 6 а. В то же время определено
взаимно однозначное соответствие >рх : * и(Х2,Х1). Положим
28
ГЛ. I. ГОМОТОПИИ
0 = <Рх1 ( 1) и выберем g € 0. Покажем, что f ° g ~ idXj. Диаграмма
я(Х,, Х2) -Х*-> п(Х2, Х2)
/. А
?х.
пСХпХ,)----------► п(Х2,Х2)
коммутативна согласно определению. Отсюда <Рхг ° /• = /• ° Фх, • Рассмотрим образ
элемента [id^ ] относительно входящих в диаграмму отображений. Имеем:
/.([idxJ) = [/°idx,] = [/] по определению Л; далее, <рх* ([/]) = [idxJ
в силу выбора f. Следовательно, у>х* °f.([idxj]) = [idxJ]. С другой стороны,
Л° 4>xl ( [idx, ]) = /«([#]) = [/° #]. Из коммутативности диаграммы [/«?] =
= [idx,], т.е. /°g~ idXj.
Аналогичным образом доказывается, что g о / ~ id%x. Таким образом, Хг ~ Х2
в смысле определения 1.
Теперь предположим, что Хх ~ Х2 в смысле определения 1, т.е. что имеются ото-
бражения /: Х2 -^Х2, g.: Х2 -*Л1, такие, что f ° g ~ id, g « id. Возьмем любое
пространство У, положим
<ру =g*: n(Xt, Y) -> тг(Х2, Y)
и покажем, что последнее отображение обратно отображению
f: п(Х2, У) -> n(XltY).
Действительно, пусть й € C(Xit У). Тогда f*o g*( [й]) =f*( [Л о g]) (по. опреде-
лению g*) = [(A«g)o/] (по определению /*) = [A«(go/)] = [Л] (так как
g о f ~ id). Аналогично проверяется, что g* « /* = id. Итак, отображение обла-
дает обратным и потому является взаимно однозначным соответствием. Проверим,
что оно обладает и вторым свойством из определения 2. Пусть У' й к: Y -> У' —
любое пространство и любое непрерывное отображение. Покажем, что диаграмма
= g*
п(Хъ У) ---------> п(Х2, У)
n(Xt,Y') ------>я(У2, У')
коммутативна. Пусть h е С{Х2, У). Тогда, с одной стороны, [Л]) = [itой],
£*([*°Л1) = [(*°Л)°И и, с другой стороны, g*( [й]) = [ftog], fc.([*og]) =
= [b(bg)].
Наше утверждение доказано. Эквивалентность определений 1 и 3 проверяется точ-
но так же.
§ 3. ГОМОТОПИИ И ГОМОТОПИЧЕСКИЕ ЭКВИВАЛЕНТНОСТИ
29
Класс гомотопически эквивалентных пространств называется гомотопическим
типом.
Пример гомотопически эквивалентных не гомеоморфных пространств: Xt — ок-
ружность, Хг — кольцо (см. рис. 18). Здесь можно взять за ft Xt -+Хг естественное
вложение и положить g = f~' ° h: Хг -»-Х1, где Л - сжатие по радиусам.
Пространство X называется стягиваемым, если тождественное отображение Х-+Х
гомотопно отображению X -> X, переводящему все X в точку (’’постоянному” ото-
бражению) .
Упражнения. 2. Докажите, что пространство стягиваемо тогда и только
тогда, когда оно гомотопически эквивалентно точке.
3. Докажите, что конус над любым пространством стягиваем.
4. Докажите, что пространство £ {X, х0) стягиваемо для любого пространства X.
5. Докажите, то цилиндр отображения X-+Y гомотопически эквивалентен прост-
ранству Y.
6. Если Х\ Х%,то SXj ~ ЕЛз.
7. Предыдущее утверждение называют иногда гомотопической инвариантностью
надстройки; сформулируйте и докажите аналогичные утверждения о гомотопической
инвариантности для произведения, джойна, пространств отображений, путей и петель.
4. Ретракты. Подпространство А пространства X называется его ретрактом, если
существует непрерывное отображение г: Х-+ X (’’ретракция”), такое, что г(Х) =А
и г (а ) = а при a G А. Например, любая точка любого пространства является его
ретрактом, а объединение двух концов отрезка его ретрактом не является: мешает
теорема о промежуточном значении непрерывной функции. Не является ретрактом и
граничная окружность в круге и вообще сфера Sn ~1 в шаре 27", но мы пока не рас-
полагаем средствами, чтобы это доказать.
Упражнения. 8. Основания цилиндра являются его ретрактами.
9. Основание конуса СХ является его ретрактом в том и только в том случае,
когда пространство X стягиваемо.
Если ретракцию можно сделать гомотопной тождественному отображению, то А
называется деформационным ретрактом пространства X; если, сверх того, гомото-
пию, соединяющую ретракцию с id, можно выбрать неподвижной на А (т.е. такой,
что (a, t) а при а € A, t.GJ), то А называется строгим деформационным ретрак-
том пространства X.
Очевидно, деформационный ретракт пространства X гомотопически эквивален-
тен А. Более того, А является деформационным ретрактом пространства X в том и.
только в том случае, если включение А -> X является гомотопической эквивалент-
ностью (ср. приведенный выше пример гомотопической эквивалентности:
окружность — кольцо). Таким образом, понятие деформационной ретракции, в сущ-
ности, не ново для нас; о понятии строгой деформационной ретракции этого не
скажешь, но, как мы увидим, его отличие от понятия деформационной ретракции
проявляется лишь в патологических случаях.
30
ГЛ. 1. гомотопии
Упражнения. 10. Точка тогда и только тогда является деформационным
ретрактом пространства X, когда X стягиваемо (это утверждение демонстрирует
различие между ретракцией и деформационной ретракцией).
И. Приведите пример деформационного ретракта, не являющегося строгим де-
формационным ретрактом.
5. Пример гомотопического инварианта: категория Люсгерника — Шнирельмана.
Пространство УС Y называется стягиваемым по У в точку, если вложение X -* У го-
мотопно отображению Х-+ У, переводящему все У в точку.
Пусть X — произвольное топологаческое пространство. Категория Люсгерника -
Шнирельмана cat X пространства Xопределяется как минимальная мощность покры-
тия пространства X стягиваемыми по X замкнутыми множествами. Если удалить
из этого определения слова ”по X ”, то получится определение ’’сильной категории”
s-cat X.
Упражнения. 12. Являются ли cat У и s-cat X гомотопическими инвариан-
тами? (Ответ: cat — да, s-cat — нет.).
13. Найти cat Xи s-cat X в случае, когда X есть сфера с тремя отождествленными
точками (рис. 19).
(Вы можете попытаться продолжить вычисление инвариантов cat и s-cat, но для
этого нет пока эффективных средств.)
6. Случай пространств с отмеченной точкой, пар, троек и т.д. Определения гомо-
топии и гомотопической эквивалентности переносятся на пространства с отмеченны-
ми точками (см. § 2) автоматически. Множество гомотопических классов отображе-
ний пространства с отмеченной точкой X в пространство с отмеченной точкой У мо-
жет обозначаться через я (X, У), но может употребляться и более подробное обозна-
чение яь (У, У) (Ь — от слова ’Sase-point” - отмеченная точка).
Упражнение 14. Доказать гомотопическую инвариантность операций v, #, Я,
а также вариантов с отмеченными точками операций S и *.
Обобщением гомотопической теории пространств с отмеченными точками является
гомотопическая теория пар. Пара — это просто топологическое пространство с выде-
ленным подпространством; запись: (Х,А). (Непрерывное) отображение пары (У, Л)
в пару (У,В) — это такое непрерывное отображение /: У-+У, что /(А) СВ. Оче-
видным образом для пар определяются гомотопии, гомотопические эквивалент-
ности и т.д. Рассматриваются также тройки (Х,А,В), в которых по определению
предполагается, что УЭ А Э В, четверки и вообще n-ки, а также триады (У; А,В),
в которых предполагается лишь, что УЭ А и УЭ В, а также 4-ады и вообще и-ады.
Для троек, триад и т.д. определяются (очевидным образом) отображения, гомотопии
и все прочее.
§ 4. ЕСТЕСТВЕННЫЕ ГРУППОВЫЕ СТРУКТУРЫ В МНОЖЕСТВАХ *(Х, У)
31
§4. ЕСТЕСТВЕННЫЕ ГРУППОВЫЕ СТРУКТУРЫ В МНОЖЕСТВАХ п(Х,У)
Гомотопическая топология изучает дискретные по своей природе инварианты,
соответствующие топологическим пространствам и непрерывным отображениям.
Обычно зти инварианты принимают одинаковые значения на гомотопически экви-
валентных пространствах и гомотопных отображениях. Наиболее распространенная
процедура построения инвариантов состоит в следующем. Фиксируется пространство
У и затем произвольному пространству вставится в соответствие множество ir(X, У)
или множество я(У,Х). (Бывают, конечно, инварианты совершенно другой приро-
ды, как, скажем, категория Люстерника — Шнирельмана — см. п. 5 § 3.)
Изучать эти множества значительно проще, если в них имеется естественная груп-
повая структура. Прежде чем уточнить, о чем идет речь, условимся о форме дальней-
шего изложения. Мы рассматриваем инварианты двух сортов: фиксируется У и каж-
дому X ставится в соответствие я (X, У) или я (У, X). Для каждого сорта доказы-
ваются свои теоремы, причем их теории довольно долго остаются параллельными,
а точнее — двойственными. Двойственность эта занимает важное место в гомотопи-
ческой топологии. Она называется двойственностью Экмана — Хилтона. Мы не будем
явно касаться ее в этой книге, но чтобы дать читателю представление о ней, будем
писать текст в этом параграфе в две колонки, так что двойственные определения,
утверждения и доказательства окажутся написанными рядом.
На протяжении этого параграфа мы считаем все пространства пространствами с
отмеченными точками и соответствующим образом понимаем отображения, гомото-
пии и т.д. Фиксируем пространство У с отмеченной точкой у0.
Предположим, что для любого X
в множестве яь(У, X) введена груп-
повая структура. Такая структура назы-
вается естественной, если для любого
непрерывного отображения >р: X1 ->Х"
отображение </>,: яь(У,Х') ^itb(Y,X"')
является гомоморфизмом?
Определение. Пространство У
называется Н' -пространством, если оп-
ределены отображения
д: У -> У v У
(коумножение) и
w. У-> У
(взятие кообратного), такие, что:
1° (гомотопическая коединица). Отоб-
ражения
Предположим, что для любого X в
множестве тгь (X, У ) введена групповая
структура. Такая структура называется
естественной, если для любого непре-
рывного отображения р: Х'->Х" отоб-
ражение р*: тгь(X", У) ->7ГЬ (X', У)
является гомоморфизмом.
Определение. Пространство У
называется Н-пространством, если опре-
делены отображения
д: УХ У-> У
(умножение) и
V. У-»У
(взятие обратного), такие, что:
1° (гомотопическая единица). Отобра-
жения
У-^-УХ У^У,
ii м
У-^УХ У->У,
где
/1(У) = (У,Уо),
/2(У) = (УО,У),
гомотопны тождественному отображе-
нию id: У-» У.
где Я1 тождественно на первом У и
отображает второе У в у0, а тг2 тож-
дественно на втором У и отображает
первое У в у0, гомотопны тождествен-
ному отображению id: У-> У.
32
ГЛ. 1. ГОМОТОПИИ
2° (гомотопическая ассоциативность).
Отображения
id X д д
УХ (УХ У) -------*УХ У->У,
д X id д
( УХ У)Х У----->УХ У->У
гомотопны.
3° (свойство гомотопического обраще-
ния) . Отображения
2° (гомотопическая
ность). Отображения
д id V д
коассоциатив-
У у(У v У),
д дХ id
У-> У v У----->(У V У) v у
гомотопны.
3° (свойство гомотопического кообра-
шения). Отображения
idX v
У---> УХ
У,
v X id
У—►
д
УХ У- У
гомотопны отображению в точку.
Важный пример //-пространства:
пространство петель S2Z произвольно-
го пространства Z. Отображение
д: 12ZX 12Z->S2Z
определяется формулой
|Г(20, /<1/2,
U(2f -1), t >1/2,
т.е. двум петлям ставится в соответ-
ствие петля, получающаяся при после-
довательном прохожденииобеих петель:
а отображение »; QZ ->12Z определяет-
ся формулой
гомотопны отображению в точку.
Важный пример //'-пространства:
надстройка SZ над произвольным
пространством Z. Отображение
д: SZ->SZv SZ
определяется формулой
I (z, 2/-!)„,/> 1/2
(римские цифры указывают, в каком
из двух SX составляющих букет
ЪХ v SX лежит рассматриваемая точ-
ка) :
а отображение я: SZ-»SZ опреде-
ляется формулой
v(z, t) = (z, 1 — /):
т.е. петля ставится в соответствие эта
"же петля, проходимая в противополож-
ном направлении.
Другой важный пример//-пространст-
ва — топологическая группа.
(Двойственное утверждение форму-
лируется в терминах ’’кокатегории”,
определение которой читатель может
придумать сам.)
(Параллель отсутствует.)
Упражнение. Покажите, что ка-
тегория Люстерника — Шнирельмана
произвольного //'-пространства равна 2.
(Вообще класс Н' -пространств близок
к классу пространств категории 2,
но мы не детализируем это утверж-
дение.)
§ 4. ЕСТЕСТВЕННЫЕ ГРУППОВЫЕ СТРУКТУРЫ В МНОЖЕСТВАХ *(Х, Y)
33
Теорема. Множество яь (X, Y)
тогда и только тогда обладает естест-
венной (поХ) групповой структу-
рой, когда Y есть Н-пространство.
Доказательство необхо-
димости. Пусть в яь (X Y ) введено
естественное по Xумножение. Положим
X- Y X Y и рассмотрим классы [р, ],
[p2]€itb(YXY,Y) проекций произ-
ведения УХ У на сомножители.
Положим [д] = [Pi] [Ра] (умноже-
ние в яь(У X У, У )) и выберем любое
отображение д: УХУ-»У класса [д].
В качестве »: У -» У мы возьмем произ-
вольный представитель класса [»] G
G яь(У> У )> обратного в группе nb(Y,
У) классу [id] тождественного отоб-
ражения id: У-» У.
Свойства 1° — 3° отображений ди v
проверяются автоматически. Проверим,
например, что д ° /1 ~ id у. Отображе-
ние /1: У -» У X У индуцирует отобра-
жение itb(YXY,Y)^>itb(Y, У),ко-
торое переводит [р, ] в [р, о /, ] и
[Рг] в [pi °/2 ]; но pto/t=id и
Р2 ° /1 = *•
(Звездочка всюду обозначает отображение в отмеченную точку или в единицу
группы.)
В силу естественности / , переводит
произведение в произведение; следо-
вательно, /* ([Д ]) =71 ([Pi ] \Рг ]) =
=/T([Pi])/I([P2])= [id] [*] = [id].
Мы показали, что д ° ~ id у.
(Мы воспользовались тем, что класс
постоянного отображения ♦: У-» У
есть единица группы яь(У, У). Для
доказательства достаточно рассмотреть
одноточечное пространство * и (единст-
венное) отображение У-»*. Возникает
гомоморфизмЯь(*, У) -»яь.(У, У),ко"
торый переводит единственный эле-
мент группы яь(*, У), с одной сторо-
ны, в единицу группы яь(У, У) и, с
другой стороны, в класс отображе-
ния *.)
Доказательство достаточ-
ности. Пусть У есть //-пространство
и Xесть любое пространство.
2. А.Т. Фоменко
Теорема. Множество яь (У, X)
тогда и только тогда обладает естест-
венной (по X) групповой структурой,
когда У есть Н' -пространство.
Доказательство необхо-
димости. Пусть в яь (У, У) введено
естественное по X умножение. Поло-
жим X = У v У и рассмотрим классы
[’ll], М2] &nb(Y, У v У) естествен-
ных вложений пространства У в букет
У v У.
Положим д = [т? 1 ] [т?2 ] (умножение
в яь(У, У v У)) и выберем любое
отображение д: У-» У v У класса [д].
В качестве »: У -» У мы возьмем произ-
вольный представитель класса [р] €
£яь(У, У), обратного в группе nb(Y,
У) классу [id] тождественного отоб-
ражения id: У-» У.
Свойства!0 —3° отображений дир
проверяются автоматически. Проверим,
например, что ° р ~ id у. Отображе-
ние я,: У v У-» У индуцирует отобра-
жение Я1,: яь(У, У v У)-»яь(У,У),
которое переводит [77, ] в [я, ° 77, ] и
[т?2] в [я, от?2]; но Я1 о 77,= id и
Я, ° 77з = *.
В силу естественности я,, перево-
дит произведение в произведение; сле-
довательно, я, .([д])=я1.([т?1] [т?2]) =
= ’Г1.([’?1])я,.([7?2]) ₽ [id][*] =
= [id]. Мы показали, что я, ° р ~
~ id у.
(Мы воспользовались тем, что класс
постоянного отображения *: У -» У есть
единица группы яь(У, У). Для доказа-
тельства достаточно рассмотреть одното-
чечное пространство * и (единственное)
отображение * -» У. Возникает гомомор-
физм яь ( У, *) -» яь ( У, У ), который
переводит единственный элемент груп-
пы яь (У, *), с одной стороны, в едини-
цу группы яь (У, У) и, с другой сторо-
ны, в класс отображения *.)
Доказательство достаточ-
ности. Пусть У есть Я' -пространство
и Уесть любое пространство.
34
ГЛ. 1. ГОМОТОПИИ
Рассмотрим множество яь(Х, УХУ).
Отображение д: У X У-> У индуцирует
отображение д ,: яь (X, У X У )
->яь(Х, У), которое, ввиду очевидно-
го равенства яь (X, У X У ) = тгь (X, У) X
X 7ГЬ (X, У ), может рассматриваться
как отображение
яь(Х У)Хтгь(Х, У)-*яь(Х У).
Далее, отображение и: У-> У порож-
дает отображение v ,; ль (X, У ) -*
Умножение д, и операция обраще-
ния и» определяют в irb(X, У) естест-
венную по X структуру группы. Провер-
ка предоставляется читателю.
Упражнение. Группа тгь(X, 1212Z)
абелева.
(Двойственный объект — сфера S ").
(Двойственные факты: формулы
для Н1 (5 ") — см. ниже — и равен-
ство 5 "+1 = 25").
Поскольку Sn = ^Sn~i, яь(У",Х)
является группой. Это группа называет-
ся п-мерной гомотопической группой
пространства X и обозначается через
л„(Х). Предыдущее упражнение пока-
зывает, что группа я„(Х) абелева при
л> 2.
(Двойственный факт: формула для
"/(*„)•)
Вычисление групп itt (5 ") казалось
в свое время очень важной задачей. Эта
задача не решена по сей день (см. под-
робности в гл. 3-6)
Рассмотрим множество яь(У v У,
X). Отображение д: У -» У v У инду-
цирует отображение д *: яъ(У v У,Х)->
->яь (У, X), которое, ввиду очевидного
равенства яь(У v У, X) = itb(Y,X) X
Хяь(У,Х), может рассматриваться
как отображение
тгь (У, х) X тть (У, X ) -> яь(У, X).
Далее, отображение v: У -> У порож-
дает отображение v *: тгь (У, X) ->
->яь(У,Х).
Умножение д * и операция обращения
v* определяют в irb(Y, X) естествен-
ную по X структуру группы. Проверка
предоставляется читателю.
Упражнение. Группа ffb(SSZ,
X) абелева.
Как мы увидим ниже (см. § 11),
при любом л> 1 существует единст-
венное с точностью до гомотопической
эквивалентности пространство Кп, та-
кое, что:
| 0 при i #=л,
(1)яг(К„) =
IZ при i = л;
(2)Х„~ЯХ„+1.
(Определение групп тг{ см. ниже в
левом столбце).
Поскольку Кп~ ПКп+1, тгъ(Х,Кп)
является группой. Эта группа назы-
вается п-мерной (целочисленной) кого-
мологической группой пространства X
и обозначается через Нп(Х; Z) или
Нп(Х). Предыдущее упражнение пока-
зывает, что группа Нп(Х) всегда
абелева.
Как мы увидим,
. ( 0 при /#=л,
H,(Sn) = {
I Z при / = л.
Вычисление групп Н* (Кп) оказа-
лось очень важной задачей. Эта задача
была полностью решена в 50-е годы
усилиями А. Бореля, А. Картана и Ж.-П.
Серра (см. подробности в гл. 3)
§ 5. КЛЕТОЧНЫЕ ПРОСТРАНСТВА
35
§ 5. КЛЕТОЧНЫЕ ПРОСТРАНСТВА
Гомотопическая топология почти никогда не рассматривает совершенно произ-
вольных топологических пространств. Обычно она изучает пространства с той или
иной дополнительной структурой, причем со времен основоположника топологии
Анри Пуанкаре рассматривают структуры двух типов. Первый тип — структуры ана-
литического происхождения: дифференциальная, риманова, симплектическая и
т.д. У нас такие структуры будут встречаться редко, хотя мы и будем иметь с ними
дело (см. §§ 17, 19, 30, 41—52). Отличительной особенностью этих структур яв-
ляется их естественность: обычно рассматриваемое пространство бывает наделено
такой структурой изначально, и мы не должны заботиться об ее построении. Струк-
туры второго, более важного для нас типа — комбинаторные структуры. Они зак-
лючаются в том, что пространство расчленено на более или менее стандартные части,
и изучение пространства сводится к изучению взаимного расположения этих частей.
В этом параграфе мы рассматриваем важнейшую из комбинаторных структур:
клеточную структуру. Хотя мы докажем в заключительной части параграфа неко-
торые теоремы, свидетельствующие о полезности понятия клеточного пространства
для гомотопической топологии, его настоящая роль вскроется позже, в главе ’’Гомо-
логии”, где клеточная структура станет эффективным вычислительным средством.
Все же отложить знакомство с клеточными пространствами до гомологий мы не
можем.
1. Основные определения. Клеточное пространство - это хаусдорфово топологи-
ческое пространство К, представленное в виде объединения U”_o eq попарно
непересекающихся множеств е’ ("клеток”) таким образом, что для каждой клетки
е ’ существует отображение «/-мерного шара Dq в К (характеристическое отображе-
ние, отвечающее клетке eq), сужение которого на внутренность Int D4 шара D4
представляет собой гомеоморфизм Int Л4 eq. При этом предполагаются выпол-
ненными следующие аксиомы.
(С) Граница eq = Fq —eq клетки eq содержится в объединении конечного
числа клеток ej с r<q.
(W) Множество F СК замкнуто тогда и только тогда, когда для любой клетки
eq замкнуто пересечение F П ё"’.
(Иногда характеристические отображения считаются фиксированными, т.е. рас-
сматриваются как элемент структуры. Разумеется, такая модификация определения
будет явно оговариваться.)
Терминологические замечания. 1. Термин ’’клеточное пространст-
во” не является абсолютно общепринятым: говорят также ’’клеточное разбиение”
или ’’клеточный комплекс” или ’’CW-комплекс”. Выражение ’’клеточное разбиение”
мы будем употреблять как синоним выражения ’’разбиение пространства на клет-
ки”; термин же ’’комплекс” будет у нас употребляться исключительно в алгебраичес-
ком значении. 2. Обозначения аксиом (С) и (W) являются стандартными; они проис-
ходят от английских слов ’’closure finite” и ’’weak topology”.
Упражнение 1. Доказать, что топология, описываемая аксиомой (W), яв-
ляется слабейшей из топологий, по отношению к которым все характеристические
отображения непрерывны.
Клеточное подпространство клеточного пространства К — это замкнутое его под-
множество, составленное и целых клеток; клеточные подпространства являются
самостоятельными клеточными пространствами. Важнейшие клеточные подпро-
2*
36
ГЛ. 1. гомотопии
странства клеточного пространства — его остовы: и-й остов есть объединение
всех клеток размерности < п (по определению, размерность клетки ef равна q).
Стандартные обозначения для и-го остова пространства X: Хп или sk„X Кстати,
некоторые говорят ’’«-мерный остов”, но зто неправильно: размерность клеточного
пространства определяется как верхняя грань размерностей его клеток, и, очевидно,
размерность л-го остова меньше или равна л (причем обе возможности реали-
зуются: см. примеры клеточных пространств ниже). Клеточное пространство называ-
ется конечным (счетным), если оно состоит из конечного (счетного) числа клеток.
Заметим, что для конечных клеточных пространств аксиомы (С) и (W) прове-
рять не нужно : они выполняются автоматически.
Упражнение 2. Докажите, что каждая точка клеточного пространства при-
надлежит некоторому его конечному подпространству.
Клеточное пространство называется локально конечным, если каждая его точка
вместе с некоторой окрестностью принадлежит конечному подпространству.
У пражнения. 3. Докажите, что всякое компактное подмножество клеточного
пространства принадлежит некоторому конечному подпространству.
4. Докажите, что клеточное пространство конечно (локально конечно) тогда и
только тогда, когда оно компактно (локально компактно).
5. Докажите, что отображение клеточного пространства в другое топологическое
пространство непрерывно тогда и только тогда, когда оно непрерывно на любом
конечном подпространстве.
6. То же с заменой слов ’’конечном подпространстве” словом ’’остове”.
Непрерывное отображение f клеточного пространства X в клеточное пространст-
во Y называется клеточным, если / (sk„y) Csk„ Y при любом л. Заметим, что это
определение, которое, как читатель убедится, является единственно правильным,
оставляет для отображения довольно большую свободу: клетка не обязана отобра-
жаться при клеточном отображении в клетку, а может размазываться по нескольким
клеткам, задевая при этом клетки меньшей (но не большей!) размерности.
Упражнение 7. Пусть X'я X" обозначают отрезок I, представленный как
клеточное пространство в соответствии с рис. 20. Будут ли клеточными тождест-
венные отображенияX' ->Х" иX" -+Х' 2 (Ответ: первое — да, второе — нет.)
.___________________. X'
Рис. 20
2. Комментарии к определению клеточного пространства. 1°. Замыкание клетки
может не быть клеточным пространством. Пример: разбиение букета S 2 V S 1 на
клетки aG S*,Sl —а и (S2 V S'!) — S 1 делает его клеточным пространством,
но если а не есть отмеченная точка окружности S 1, то замыкание последней клетки
не является подпространством (см. рис. 21).
2°. Из (W) не следует (С). Разбиение диска/)2 на внутренность IntZ)2 и отдель-
ные точки граничной окружности S 1 удовлетворяет аксиоме (W) (потому что
всегда F Г) Int D2 = F ), но не удовлетворяет аксиоме (С).
3°. Из (С) не следует (W). Возьмем бесконечное семейство {Ia I а = 1, 2,...}
копий отрезка I, отождествим нулевые концы и топологизируем получившееся мно-
§ 5. КЛЕТОЧНЫЕ ПРОСТРАНСТВА
37
жество при помощи метрики: расстояние между точками
t' G Ia', t" G 1а» равно | t" — t' | , если а’ = а" , и равно t' +
+ t" , если а’ ¥= а". Рабиение построенного пространства на мно-
жества Int 1а и оставшиеся точки не удовлетворяет, из условий,
входящих в определение клеточного пространства, только ак-
сиоме (W): точки 1/а G 1а составляют последовательность,
сходящуюся к 0, и, значит, незамкнутое множество, но пересече-
ние этой последовательности с замыканием любой клетки
замкнуто.
Кстати' если, как это только что было, разбиение простран-
ства на клетки удовлетворяет всем условиям из опре-
деления клеточного пространства, кроме аксиомы (W), то
можно ослабить в этом пространстве топологию, определив
новую топологию при
емой ’’клеточным ослаблением
зоваться.
а
Рис. 21
помощи аксиомы (W). Этой процедурой, называ-
топологии”, нам придется вскоре восполь-
Упражнение 8. Клеточное пространство метризуемо тогда и только тогда,
когда оно локально конечно.
3. Отношение к операциям из § 2. Все операции над топологическими пространст-
вами, включая специфические операции над пространствами с отмеченными точка-
ми, но исключая операции, вовлекающие пространства отображений (как, скажем,
ПиЕ), действуют в клеточной обстановке. Так, цилиндр, конус и надстрой-
ка над клеточным пространством обладают естественной клеточной структурой
(например, клетки надстройки S X — вершины и надстройки над клетками прост-
ранства X, лишенные вершин). Клеточными пространствами являются цилиндр
и конус клеточного отображения (вот случай убедиться в правильности определе-
ния клеточного отображения!), пространства вида X'J^ Y—при условии, что Хи У
клеточны, а ip есть клеточное отображение клеточного подпространства пространст-
ва Y в X — и, разумеется, факторпространство Х/А клеточного пространства Хпо его
клеточному подпространству А. Правда, некоторая неожиданность подстерегает
нас при попытке внести клеточную структуру в произведение клеточных пространств
и, тем более, в их джойн или тензорное произведение. Клетки, скажем, в XX У оп-
ределяются естественным образом, но с аксиомой (W) — беда: оказывается, что она
не всегда выполнена. Когда топологи обнаружили зто обстоятельство, они принялись
его детально обследовать и накопили большое количество фактов. Мы устраняемся
от обсуждения этого предмета, ограничившись тремя упражнениями (см. ниже)'
и следующим замечанием. Если произведение XX У с естественным разбиением
на клетки не удовлетворяет аксиоме (W), то мы можем проделать клеточное ос-
лабление его топологии (см. предыдущий пункт) и получить клеточное пространст-
во; последнее обычно обозначают через XXW У. К счастью, оказывается, 4ToXXw У
ничем не хуже, чем XX У: замена пространства XX У пространством XXW У настоль-
ко безболезненна, что о возможном различии между пространствами XX У и XXW У
можно просто забыть, что мы и сделаем. Подобное относится к джойнам и тензор-
ным произведениям.
Упражнения. 9. Приведите пример, в котором X Xw У #= XX У.
10. Докажите, что если одно из клеточных пространств X, У локально конечно,
ToXXwy= XX У.
11. Докажите, что если оба пространства X, У локально счетны, ToXXwy=XXy.
38
гл. i. гомотдпии
Что касается пространств отображений, то они слишком велики, чтобы их можно
было разбить на клетки. Все же имеется следующая теорема Милнора:
Теорема (см. Milnor J.W.//Trans.. Amer. Math. Soc. — 1959. — V. 90, № 2. —
P. 272-280). Если X, Y - клеточные пространства, то пространство С(Х, У) гомото-
пически эквивалентно клеточному пространству.
(Как читатель вскоре увидит, быть гомотопически эквивалентным клеточному
пространству — это совсем не плохо; во всяком случае, Милнор предложил назы-
вать пространства, гомотопически эквивалентные клеточным пространствам, го-
мотопически полноценными.)
Завершая разговор о взаимоотношениях клеточных пространств с операциями
из § 2, мы заметим, что всякое клеточное пространство может быть сконструиро-
вано при помощи многократного (иногда бесконечнократного) применения этих
операций к простейшим пространствам: шарам. Действительно, пусть {е”}— все
л-мерные клетки пространства X, f£: Dn-*X — соответствующие характеристичес-
кие отображения. Поскольку f"(S ”-1) Cskn_i X, мы можем сузить f" до отобра-
жения g£: S 1 ->• sk„_ 1 X (отображения g" называются приклеивающими). Рас-
смотрим ’’сумму” 2) = U D" л-мерных шаров, по одному на каждую «-мерную клетку
пространства X, и положим 8 =U<S'”-1 С 3). Далее, рассмотрим отображения gn:
Очевидная лемма:
sk„% = (sk„_1^) и 2), (*)
gn
т.е. sk„Xполучается из sk„_i X приклеиванием п-мерных шаров посредством всех
приклеивающих отображений, отвечающих п-мерным клеткам.
Равенство (*) можно рассматривать как шаг универсальной индуктивной проце-
дуры, позволяющей построить произвольное клеточное пространство из дискрет-
ного пространства (sko^ дискретно) или даже из пустого пространства (sk^JT
пусто) посредством последовательного приклеивания шаров нарастающей размер-
ности. Кстати, если пространство бесконечномерно, то эта индуктивная процедура
включает в себя предельный переход, регулируемый аксиомой (W).
Прямо или косвенно, эта индуктивная процедура лежит в основе доказательства
всякого утверждения, касающегося клеточных пространств: она позволяет свести
доказываемое утверждение к тому или иному утверждению, касающемуся шаров
и сфер.
Упражнения. 12. Докажите, что клеточное пространство линейно связно
тогда и только тогда, когда линейно связен его первый остов.
13. Докажите, что клеточное пространство линейно связно тогда и только тогда,
когда оно связно.
14. Докажите, что всякое конечное клеточное пространство может быть вложено
в евклидово пространство достаточно большой размерности.
4. Клеточные разбиения классических пространств.
А. Сферы и шары. При конечном п имеется два канонических клеточных разбие-
ния сферы 5”. Первое состоит из двух клеток: точки е° (любой, скажем, (1,0,...
. .., 0)) и множества еп = Sn - е° (рис. 22а). Характеристическое отображение
Dn -> Sn, отвечающее второй клетке, — это обычное ’’сворачивание” сферы из шара;
годится, например, отображение, действующее по формуле
(хь . . . , хп) !+ (cos яр, X ! sin пр,... , хп sin пр),
§ 5. КЛЕТОЧНЫЕ ПРОСТРАНСТВА
39
Рис. 22
где р = \/Xi + ... + х% (см. рис. 23). Другое каноническое клеточное разбиение сфе-
ры Sn состоит из 2и + 2 клеток е±,е±,..., е±: клетка еJ состоит из точек (хь ...
... , x„+i) G 5”, у которых xq+2 = .. .=хп + 1 = 0 и ±xq + 1 > 0 (рис. 226). Заботиться
о характеристических отображениях здесь не приходится: замыкание каждой клетки
очевидным образом гомеоморфно шару соответствующей размерности.
Заметим, что оба описанные клеточные разбиения сферы Sn получаются из един-
ственного возможного разбиения сферы S° (двоеточия) посредством применения
канонической конструкции клеточного разбиения надстройки: в первом случае нуж-
но брать надстройку над сферой как над пространством с отмеченной точкой, а во
втором случае — обыкновенную надстройку.
Существует, конечно, масса других клеточных разбиений сферы 5”: ее можно
разбить на 3”+1 — 1 клеток как границу (л + 1)-мерного куба, на 2”+2 - 2 клеток -
как границу (и + 1)-мерного симплекса (см. ниже гл. 2) и тл.
Все описанные клеточные разбиения, кроме самого первого, годятся для сфе-
ры 5“.
Клеточное разбиение шара D” можно получить из любого клеточного разбиения
сферы Sn~1 путем присоединения одной клетки IntD” с характеристическим отоб-
ражением id: Л" ->Л”. Наиболее экономное клеточное разбиение шара Л” состоит,
таким образом, из трех клеток. Правда, ни одно из этих разбиений не годится для
шара D°°.
Упражнение 15. Придумайте клеточное разбиение шара D°°.
В. Проективные пространства. Пр! отождествлении диаметрально противополож-
ных точек сферы Sn клетки е’, е’ (2 л + 2)-клеточного разбиения склеиваются меж-
ду собой и получается (и + 1) -клеточное разбиение пространства RP”, по одной клет-
ке еq в каждой размерности q < п. Это же разбиение можно описать так:
е’= {(x0:xi: ... :x„)GRP"|x, ¥=0, х,+1 = ... = хп = 0}.
Еще одно описание этого разбиения: имеется цепочка включений
ф=ЪР~1 CRP° CRP1 С .. .CRP”,
и мы полагаем eq = RPq - RPq~l. Характеристическим отображением для eq слу-
жит композиция канонической проекции Dq -> RPq (см. § 1) и включения RP4 ->
-+ RPn. При п = °° наша конструкция доставляет клеточное разбиение пространства
RP”, содержащее по одной клетке каждой размерности. Конструкция имеет также
40
ГЛ. 1. ГОМОТОПИИ
комплексный, кватернионный и кэлиев аналоги. Она дает: разбиение пространства
СР” на клетки размерностей 0,2,4,..., 2л; разбиение пространства HP” на клетки
размерностей 0, 4, 8,, 4л; разбиение пространства СаР2 на клетки размерностей
0, 8, 16; клеточные разбиения пространств СР“ и НР“, содержащие по одной клетке
в каждой размерности, делящейся, соответственно, на 2 и 4. Например, пространство
СР" разбивается на клетки
e2q = {(z0:zt : ... : z„)€CP”|z, =#0, zq+1 = . . , = zn = 0}
с характеристическими отображениями
_ каноническая проекция включение
D2q --------------------> СР4----------► СР”.
С. Многообразия Грассмана. Описываемое ниже клеточное разбиение многообра-
зий Грассмана очень важно для геометрии и топологии (особенно для теории харак-
теристических классов). Составляющие его клетки называются клетками Шуберта,
а само оно называется шубертовским.
Пусть mi,. .. , ms — произвольная конечная (возможно, пустая) невозрастаю-
щая последовательность целых положительных чисел, не превосходящих к, причем
s < п — к. Обозначим через e(mi......ms) подмножество пространства G(n, к),
составленное из подпространств я пространства R”, удовлетворяющих следующим
условиям (мы полагаем wj+1 =0):
я Э Rm при m < к - mt;
codim (ffCiR'”) = / при к - nij +j < m< к - my+j + (/ + 1);
IV
я C R”1 при m к + s + 1
(мы считаем,что Re С R* при а < Ь: (хь .... ха) >-> (х1(..., ха, 0,..., 0)). При-
ведем другое, более простое описание множества е (тх.....ms). Напомним, что
диаграмма Юнга набора (mt,..., ms) — это фигура, которая рисуется на клетчатой
бумаге, как показано на рис. 24 (столбцы имеют длины mit..., ms). Число клеток
диаграммы Юнга равно тх + ... + ms. Можно считать, что клетки пространства
G(л, к) отвечают диаграммам Юнга, вмещающимся в прямоугольник к X (л — к)
(рис. 24). Рассмотрим диаграмму Юнга набора (тг,..., ms) и расположим ее,
как показано на рис. 25. Толстая линия на этом рисунке представляет собой график
некоторой неубывающей функции р, и множество e(wt,..., ms) задается усло-
вием dim (я П R”1) = р(т). Ввиду наличия такого простого описания, множество
е (mi,..., ms~) обозначают иногда через е (Д), где Д — обозначение для диаграммы
Юнга набора (тг,... , ms). Еще раз заметим, что размерность клетки е (Д) равна
числу клеток диаграммы Д.
Лемма. Множество e(mt,..., ms) гомеоморфно R 1 ms.
Доказательство. Расчленим диаграмму Юнга набора (тх,. .., ms~), как
показано на рис. 26. Поставим в клетках вдоль косых линий единицы, в заштрихо-
ванные клетки — произвольные числа и в остальные места - нули. Получится к X п-
матрица, строки которой составляют базис некоторого fc-мерного подпространства
пространства R”. Легко понять, что это подпространство принадлежит е (mi,...
. .. , ms) и что всякое подпространство, принадлежащее е(тх,.. ., ms), обладает
, единственным базисом указанного вида. Мы получаем параметризацию клетки
е (тх,..., ms) наборами из mt + ... + ms чисел (числа в заштрихованных клетках).
На самом деле верно больше: множества е(тх,.. ., ms) составляют клеточное
разбиение пространства G (п, к). Для доказательства нужно построить характеристи-
§ 5. КЛЕТОЧНЫЕ ПРОСТРАНСТВА
41
Рис. 24
Рис. 25
ческие отображения, т.е. продолжить построенные гомеоморфизмы mt и
» R 1 5 -> e(mlt..., ms) до непрерывных отображении и
-* G(n, к), отображающих сферу Sm'*"+ms 1 в объединение клеток меньших
размерностей. Мы не будем в это вникать; читатель может найти соответствующие
формулы в книге Рохлина и Фукса или в ’’Лекциях по дифференциальной геометрии
и топологии” Дж. Шварца.
Замечательное свойство шубертовских клеток состоит в том, что при естествен-
ных вложениях G(n, к) в G(n + i, к) ив G(n + 1, к + 1) клетка е (znj,..., zns)
гомеоморфно накладывается на клетку того же наименования. Следовательно,
пространство G(°°, к) разбивается на клетки Шуберта, отвечающие диаграммам
Юнга, содержащимся в горизонтальной полуполосе высоты к, а пространство
G (°°, °°) разбивается на клетки, отвечающие всем без исключения диаграммам Юнга.
Во всех случаях размерности клеток равны числам клеток диаграмм Юнга.
Комплексные и кватернионные аналоги шубертовских клеток очевидны; разу-
меется, размерности комплексных и кватернионных аналогов клеток Шуберта
соответственно в 2 и 4 раза превосходят числа клеток соответствующих диаграмм
Юнга.
Упражнение 16. Построенные выше клеточные разбиения пространств RP" =
= G(n + 1, 1), СР" = CG(n + 1, 1), HP" = HG(n + 1, 1) являются специальными
случаями шубертовского разбиения.
D. Многообразия флагов. Многообразия флагов имеют естественное клеточное
разбиение, обобщающее шубертовское разбиение многообразий Грассмана. Это
разбиение и его клетки также называются шубертовскими. Опишем разбиение в ве-
щественном случае (комплексный и кватернионный случаи отличаются только уд-
воением и учетверением размерностей клеток).
42
ГЛ 1. ГОМОТОПИИ
Шубертовские клетки многообразия флагов характеризуются наборами размер-
ностей d(j пересечений К,- О R7. Числа dy, однако, должны удовлетворять набору
довольно неудобных условий, и мы предпочтем следующее, более рациональное
описание клеток Шуберта.
Клетки пространства F(n\ kit..., ks) отвечают наборам mi,..., тп целых чи-
сел, принимающих значения l,...,s + 1, причем ровно kj — kj_i из этих чисел рав-
ны j (/ = 1....s + 1; мы считаем, что к0 = 0 и ks+i = и). клетка е [mi,... , тп],
отвечающая набору («?],..., тп), состоит из флагов V\ С ... С Vs, у которых
V: HR; (1 при i = т;,
dim------------------------ = Sim. = 1
(K,_i DRO+C^.nR'-1) ’ Ю при i^m,-.
(мы считаем, что Ко = 0 и есть все пространство R”) или, иначе,
dim( И, п R') = card {р < /| кр < / }.
Размерность клетки е [w?i,.. ., тп] равна числу пар (i, j), для которых i < /,
т, > nij.
В частности, многообразие F (и; 1,..., и — 1) полных флагов разбито на п! клеток,
отвечающих обыкновенным перестановкам чисел 1,..., п, причем размерность клет-
ки равна числу инверсий в перестановке.
Если многообразие флагов есть многообразие Грассмана G(n, к), то s = 1 и набор
,..., тп состоит из к единиц и п - к двоек. Построим по этому набору и-звен-
ную ломаную на плоскости, начинающуюся в точке (0, к) и кончающуюся в точке
(п - к, 0). Все звенья ломаной имеют длину 1, причем i-e звено направлено вниз,
если nij = 1, и вправо, если mt = 2. Эта ломаная ограничивает (вместе с координат-
ными осями) некоторую диаграмму Юнга Д, и легко понять, что е [w?j,..., тп] =
= е(Д).
Заметим в заключение, что клетки е [тг,..., т„] (и их комплексные и кватер-
нионные аналоги) могут быть описаны чисто групповым образом: это - орбиты
Рис. 27
группы нижних треугольных п X «-матриц с единицами на диагонали, естественным
образом действующей в многообразии флагов. Именно, клетка e[mlt..., т„]
есть орбита флага, i-e пространство которого порождено координатными вектора-
ми, номера р которых удовлетворяют неравенству тр < i.
Е. Компактные классические группы также обладают хорошими клеточными
разбиениями, но мы их не приводим. Эти клеточные разбиения (неявно) построены
в классической работе Л.С. Понтрягина 30-х годов, перепечатанной в ’’Успехах мате-
матических наук” по случаю 60-летия автора (см. Успехи мат. наук. — 1968. — Т. 23,
№6 (144).-С. 151-185).
§ 5. КЛЕТОЧНЫЕ ПРОСТРАНСТВА
43
F. Классические поверхности. Клеточные разбиения поверхностей S2 и RP2 нами
уже построены. Клеточные разбиения остальных поверхностей без края автомати-
чески получаются при склеивании этих поверхностей из многоугольников (см. § 1):
двумерная клетка получается из внутренности многоугольника, одномерные клет-
ки — из его (открытых) ребер, нульмерные клетки - из его вершин. Каноническое
клеточное разбиение каждой классической поверхности имеет одну двумерную и
одну нульмерную клетку. Кроме того, сфера с g ручками имеет 2g одномерных
клеток (см. рис. 27), проективная плоскость с g ручками имеет 2g + 1 одномер-
ную клетку и бутылка Клейна с g ручками имеет 2g + 2 одномерных клеток.
Упражнение 17. Построить минимальные (по числу клеток) клеточные
разбиения классических поверхностей, имеющих дыры.
Гомотопические свойства клеточных пространств
5. Теорема Борсука о продолжении гомотопий. Определение. Пара (X, А)
называется парой Борсука (или корасслоением), если для любого пространства Y
и любого непрерывного отображения F: X->Y всякая гомотопия ft: А -» У, такая,
что /о ~ ^1 а ’ может быть продолжена до гомотопии Ft: Х-* Y, у которой Fo = F.
Теорема Борсука, Если X - клеточное пространство и А — его клеточное
подпространство, то (X, А) — пара Борсука.
Доказательство. Нам даны отображения Ф: А X I -* Y (гомотопия ft)
и F: X X 0 -> Y, причем F’l^xo = хо- Продолжить гомотопию ft до гомотопии
Ft — это значит продолжить отображение F до отображения F': XX I -* У, такого,
что F'lAX/ = Ф. ^Продолжение мы произведем индуктивно по размерности клеток
пространства X, не входящих в А. Начальным шагом индукции служит продолжение
отображения Ф на (A U Х°) X I:
[ F(x, 0),если х есть нульмерная клетка пространства X, xtfA,
F (х, t) =
( Ф(х, г), если хед.
Допустим теперь, что отображение F1 уже определено на (A U Хп) X I. Возьмем
произвольную (и + 1)-мерную клетку e" + 1 С X - А. По предположению, F' задано
на множестве (F"+1 — e"+I) XI, так как граница ё"+1 =F"+1 — е” + 1 клеткие"+1
содержится в Хп по определению клеточного пространства. Пусть /: Z)"+1 X —
характеристическое отображение, соответствующее клетке еп + 1. Нам надо продол-
жить F' на внутренность ’’цилиндра” f(Dn+i) X I с его ’’стенки” f(Sn) X / и
’’дна” f(Dn+l) X 0. Но из определения клеточного пространства ясно, что это все
равно, что продолжить отображение ф - F’ о f-_ (Sn X Z) U (Z)" + I X 0) -> У до не-
прерывного отображения ф': Dn + 1 XI-*Y.
Пусть ту. Dn + 1 X I -* (Sn X Z) U (Dn + l X 0) — проектирование цилиндра
Z)"*1 X Z из точки, лежащей вне цилиндра вблизи верхнего основания Dn+i X 1
(см. рис. 28); это отображение тождественно на (Sn X Z) U(Z)” + I X 0). Отобра-
жение ф' мы определяем как композицию
Dn + l X I * (5" X Z)U (Dn+l X 0) У.
Эту процедуру можно проделать независимо для всех (и + 1)-мерных клеток
пространства X, и мы получаем продолжение отображения F1 на (A UX"+1) X Z.
Так, остов за остовом, мы строим желаемое продолжение отображения Ф до отоб-
ражения F': X X Z -* У. Подчеркнем, что если пространство X бесконечномерно.
44
ГЛ. 1. гомотопии
то наше индуктивное построение будет состоять из бесконевдого числа шагов;в этом
случае непрерывность окончательного отображения будет следовать из аксиомы (W).
Теорема доказана.
6. Следствия из теоремы Борсука. Следствие 1. Пусть X — клеточное про-
странство и А - его клеточное подпространство. Если А стягиваемо по себе в точку,
то XI А ~ X.
Доказательство. Обозначим через р проектирование X -> Х/А. Так как А
стягиваемо, то существует гомотопия ft: А -*А, такая, что отображение /0: А
Рис. 28
тождественно и /\(Л) есть точка. В силу теоремы Борсука, существует гомотопия
Ft: X, такая, что Fo = id% и FtlA -ft. В частности Fj(4) =* (точка). Это оз-
начает, что Ft можно рассматривать как отображение, заданное на Х/А, точнее, что
Fi = q ° р, где q: Х/А -> X — некоторое непрерывное отображение. По построению,
Fi ~ Fo, т.е. qo р~ id%.
Далее, Ft(A) С А (при любом г), т.е. р ° Ft(A) = *. Следовательно, р ° Ft =
= qt о р, где qt: Х/А -* Х/А — некоторая гомотопия. При этом q0 = idx/A uqi =
= р° q; следовательно, роq ~idx/j4.
Следствие доказано.
Следствие 2. Если X — клеточное пространство и А — его клеточное под-
пространство, то XIА ~ X U СА, где СА - конус над А.
Доказательство. Х/А = (X U СА)/СА ~Х U СА; последнее вытекает
из предыдущего следствия, примененного к клеточному пространству X U СА и его
стягиваемому клеточному подпространству СА.
Замечание. Оба доказанных предложения можно рассматривать не как
следствия из теоремы Борсука, а как самостоятельные теоремы, только предполо-
жения о клеточности X и А нужно тогда заменить в первом случае предположени-
ем, что (X, А) — пара Борсука, а во втором случае — предположением, что (X U СА,
СА) — пара Борсука.
7. Теорема о клеточной аппроксимации.
Теорема. Всякое непрерывное отображение одного клеточного пространства
в другое гомотопно клеточному отображению.
Мы будем доказывать следующее, более сильное утверждение (’’относительный
вариант” нашей теоремы) -
Теорема. Пусть f - непрерывное отображение клеточного пространства X в
клеточное пространство У, причем на клеточном подпространстве А пространства X
отображение f клеточно. Тогда существует такое клеточное отображение g: X-+Y,
что g\A =f\A и, более того, f~g ге1Д.
Поясним запись f ~ g ге1Л (читается: f гомотопно g относительно А), которой
мы будем пользоваться и дальше. Она применяется в ситуации, когда непрерывные
§ 5. КЛЕТОЧНЫЕ ПРОСТРАНСТВА
45
отображения f, g: X ->.У совпадают на подпространстве А пространства X и означа-
ет, что существует гомотопия ht : Х-* Y, соединяющая / с g и неподвижная да А,
т.е. такая, что ht (а) не зависит от t при а €• А. Конечно, иэ g relA следует, что
f ~ g, но не наоборот. Пример: f,g'.I , f - ’’наворачивание” отрезка на окруж-
ность, g — отображение в точку; зти отображения гомотопны, но не гомотопны
rel (О U 1) (строго говоря, это мы докажем только в следующем параграфе).
Доказательство теоремы. Предположим, что отображение f уже сде-
лано клеточным не только на всех клетках из А, но и на всех клетках из X, имеющих
размерность < р. Возьмем р-мерную клетку ер С X - А. Ее образ f(ep) пересека-
ется лишь с конечным числом клеток пространства Y (это следует из компактности
/(ё'р) - см. упражнение 3). Выберем среди этих клеток пространства Y клетку
наибольшей размерности, скажем, eq, dime4 = q. Если q < р, то дам с клеткой ер
делать нечего. В случае же q >рнам потребуется следующая лемма.
Лемма о свободной точке. Пусть U — открытое подмножество про-
странства Rp и U-* \nt Dq - такое непрерывное отображение, что множество V =
= (dq) С U, где dq - некоторый замкнутый шарик в компактно. Если
q> р, то существует непрерывное отображение ф: U-* \nXDq, совпадающее с вне
V и такое, что его образ не покрывает всего шара dq.
Доказательство этой леммы (и обсуждение ее геометрического значения) мы от-
ложим до следующего пункта; ограничимся лишь важным замечанием, что отобра-
жение ф автоматически будет гомотопным относительно U — V: достаточно взять
связывающую с ф ’’прямолинейную” гомотопию, при которой точка (и) равно-
мерно движется к точке ф(и) по прямолинейному отрезку, соединяющему <р(и)
с ф(и).
Завершим доказательство теоремы. Из леммы о свободной точке вытекает, что
сужение /|ли^р-1ив₽ гомотопно ге1(Л UJTp-1) отображению f: A U Хр~1 U
U ер -* Y, такому, что/’(ер) задевает те же клетки, что uf(ep), но заведомо f’ (ер)
не содержит всю клетку eq. В самом деле, пусть h: Dp -> X, k: Dq -> Y - характе-
ристические отображения, соответствующие клеткам ер, еч. Положим U =
= h~^f~\eq) Г> ер) и определим отображение U XnXDq как композицию:
h f к"1
и *+ х у 1—> и = ¥?(ы).
Ф Ф гп гп
и epnf~l(eq) eq IntDff
Обозначим через dq (замкнутый) концентрический подшар шара Dq. Множество
V = ip~\dq) компактно (как замкнутое подмножество шара Dp). Пусть ф: U ->
-> IntZ)’ — отображение, доставляемое леммой о свободной точке. Отображение /’
мы определим как совпадающее с / вне h(U) н как композицию
й"‘ ф к ,
х ।—► и >-* и у = f (х)
ф ф ф ф
h(U) U \nXDq eqCY
на h(U). Ясно, что отображение /' непрерывно (оно совпадает с f на ’’буферном
множестве” Л(1/ - К)) и гомотопно /| ли%р-1и р ге!(Д О Агр-1), и даже
ге!(Л U Хр~1 U (ер - Л(К))) (это вытекает из гомотопности^ ~ ф re\(U- К)).
Ясно также, что f’(ep) не покрывает еq. (См. рис. 29.)
Дальнейшее рассуждение совсем просто. Во-первых, неподвижную на A U Хр~-
гомотопию между /| лихр-1и р и f’ мы можем распространить, по теореме Бор-
46
ГЛ. 1. ГОМОТОПИИ
сука, на все X, и это позволяет считать, что отображение обладающее всеми вы-
шеперечисленными свойствами, определено на всем X. После этого мы берем точку
у0 G еч, не принадлежащую f'(ep), и подвергаем /’| ’’радиальной гомотопии”:
если точка х&ер не принадлежит /'-1(е<!'),то f'(x) стоит на месте, а если f'(x) G
G eq, то f’(x) движется по отрезку, идущему из точки на границу клетки еч
(точнее говоря, по fc-образу прямолинейного отрезка, начинающегося в точке
Л-1(.Уо)> проходящего через точку k.~l(f'(x)) =Л Л.-1(_у0) и кончающегося на гра-
ничной сфере Sq~1 шара Dq), — см. рис. 30. Эту гомотопию мы продолжаем до го-
мотопии отображения /'|лихр-1иер (неподвижной вне ер) и - по теореме Бор-
сука - до гомотопии всего отображения Х~> Y. Получающееся отображение f"
гомотопно f ге1(Л U Хр-1) и обладает тем свойством, что f"(ep) задевает (/-мер-
ных клеток на одну меньше, чем f(ep) (и, как и f(ep}, не задевает клеток размер-
ности >?). Применив эту процедуру нужное число раз, мы прогомотопируем отобра-
жение f к отображению, клеточному на Л UI₽_| и ер, причем гомотопия будет
неподвижной на A U Хр ~1.
Теперь заметим, что ’’исправление” отображения /, которое мы проделали для
клетки ер, можно дословно так же проделать одновременно для всехр-мерных кле-
ток из X - А. Тогда мы придем к отображению, клеточному на A U Хр и гомотоп-
ному f rel(4 U Хр~1).
Неподвижную на А гомотопию, связывающую отображение f с клеточным отоб-
ражением, мы получим, если проделаем последовательно построенные гомотопии
при р = 0, 1, 2,. .. Правда, число этих гомотопий может быть бесконечно, но это не
беда: р-ю гомотопию мы производим на отрезке 1 — 2~р < 1— 2~р~ х. Непрерыв-
ность всей гомотопии обеспечивается аксиомой (W): для каждой клетки е из X го-
мотопия будет неподвижной, начиная с некоторого te < 1.
Теорема доказана.
8. Борьба с химерой: доказательство леммы о свободной точке. Для человека,
не испорченного популярной математической литературой, сама формулировка лем-
мы показалась бы нелепой: как же непрерывный образ пространства меньшей раз-
мерности может покрыть пространство большей размерности? Но кто же не знает,
что это бывает: кривая Пеано, распропагандированная ничуть не меньше, чем, ска-
жем, бутылка Клейна, осуществляет непрерывное (и даже взаимно однозначное)
отображение отрезка на квадрат. Поэтому лемму приходится доказывать, и дело
§ 5. КЛЕТОЧНЫЕ ПРОСТРАНСТВА
47
осложняется тем, что геометрическая интуиция помочь туг не может, она упорно
твердит свое: такое вообще невозможно. С подобными трудностями сталкиваются
всякий раз, когда ’’строгое” определение того или иного понятия (в данном случае
е-6-определение непрерывности) не вполне соответствует исходному интуитивному
представлению: приходится вникать в устройство не реального объекта, а химеры.
Но ничего не поделаешь — доказать лемму надо.
Известны два способа доказать лемму о свободной точке: отображение <р нужно
аппроксимировать либо гладким отображением, либо кусочно линейным отображе-
нием. Первый способ проще, но он предполагает знакомство с теоремой Сарда, не
входящей в стандартный университетский курс анализа (нам эта теорема все равно
понадобится, но лучше мы отложим разговор о ней). В основе второго способа ле-
жит понятие триангуляции. Напомним, что q-мерный евклидов симплекс есть под-
множество пространства R", и > q, являющееся выпуклой оболочкой q + 1 точек,
не лежащих в одной (q — 1)-мерной плоскости. (Евклидовы симплексы размер-
ностей 0, 1, 2, 3: точка, отрезок, треугольник, тетраэдр.) Этид + 1 точек называются
вершинами симплекса. Подсимплексы, т.е. выпуклые оболочки различных подмно-
жеств множества вершин, называются гранями нашего симплекса; это — симплексы
размерности <(/. Нульмерная грань - это вершина. Замечательное свойство симп-
лекса заключается в том, что его линейное отображение в любое пространство Rm
определяется своими значениями на вершинах, причем эти значения могут быть
совершенно произвольны. Конечная триангуляция подмножества евклидова про-
странства - это такое его конечное покрытие евклидовыми симплексами, что любые
два симплекса либо не пересекаются вовсе, либо пересекаются по целой грани. Удоб-
но считать, что грани симплексов триангуляции также принадлежат к числу симплек-
сов триангуляции.
Барицентрическое подразделение (/-мерного симплекса состоит в том, что этот
симплекс разбивается на (q + 1)! более мелких (/-мерных симплексов. Вершины но-
вых симплексов — это центры тяжести граней старого симплекса (в том числе —
его самого). Множество {х0, хх,... , xq} этих центров является множеством вер-
шин некоторого симплекса барицентрического подразделения, если соответствую-
щие грани До, Д!,..., Дд можно составить в цепочку последовательно вложенных
друг в друга, см. рис. 31. (По-другому барицентрическое подразделение (/-мерного
симплекса Д можно описать так: сначала подвергаются барицентрическому подраз-
делению все его (q - 1)-мерные грани, а потом над всеми построенными симплекса-
ми, лежащими на границе симплекса Д, строятся конусы с вершиной в центре этого
симплекса; начать это индуктивное определение можно с q = 0: с нульмерным симп-
лексом при барицентрическом подразделении ничего не происходит. Еще по-другому:
симплекс Д — его совокупность точек вида S t (и{, где и/ — вершины, t( > 0 и S г; =
= 1; симплексы барицентрического подразделения отвечают перестановкам (ia,ix,...
iq) чисел 0, !,...,(/; симплекс, отвечающий этой перестановке, состоит из то-
чек S tjV с tla < tit < . .. < ttq. Барицентрическое подразделение триангуляции -
это триангуляция, составленная из симплексов барицентрических подразделений
симплексов исходной триангуляции (рис. 32). (Проверьте корректность этого опре-
деления!)
Обратимся теперь к нашему отображению <р. Прежде всего мы построим в шарике
d = dq концентрические шарики dx, d2, d3, d4 радиусов p/5, 2p/5, Зр/5,4p/5, где p-
радиус шарика d. Далее, покроем V конечным числом р-мерных симплексов, содер-
жащихся в U, и триангулируем объединение К этих симплексов (объединение конеч-
ного числа как угодно пересекающихся евклидовых симплексов в Rp обладает ко-
нечной триангуляцией — докажите это!). Применив к этой триангуляции достаточное
48
ГЛ. 1. ГОМОТОПИИ
число раз барицентрическое подразделение, мы можем добиться того, чтобы для
любого симплекса Д триангуляции выполнялось неравенство diamy>(A) < р/5.
Пусть — объединение симплексов построенной триангуляции нашего множества К,
«р-образы которых пересекаются с d4. Тогда d4 П >p(U) С <р (А?!) С d. Рассмотрим
отображение <р : -> d, совпадающее с у> на вершинах триангуляции и линейное
на каждом симплексе. Отображения у> | к и у/ гомотопны — они соединяются прямо-
линейной гомотопией y>f: Kt -*d, у>о =lP|x- > <0i = у>’-Теперь’’сошьем” отображе-
ния у> и у/в отображение ф:
<0(“)>
•/(и),
*3-5р(и)(«)>
Ф(и) =
если y>(u) £ d3,
если у>(и) G d2,
если y>(n)Gd3-d2.
Здесь р(и) — расстояние от точки у>(и) до центра шара d. (См. рис. 33.)
Отображение ф непрерывно, совпадает с у> на U— V и его образ пересекается с dx
по конечному числу кусков р-мерных плоскостей, тл. всего шара d2 (а значит, и
всего шара d) не покрывает.
Лемма доказана.
9. Первые применения теоремы о клеточной аппроксимации.
Теорема. Если X - клеточное пространство с единственной вершиной (= нуль-
мерной клеткой), не имеющее других клеток размерности <q, a Y — клеточное
пространство размерности <q, то всякое отображение Y -> X гомотопно отображе-
нию, переводящему все Y в точку. Такое же утверждение справедливо в категории
§ 5. КЛЕТОЧНЫЕ ПРОСТРАНСТВА
49
пространств с отмеченными точками (в клеточной ситуации удобно считать, что отме-
ченными точками являются нульмерные клетки).
Это прямо следует из теоремы о клеточной аппроксимации: если f : Y -> X -
клеточное отображение, то так как q-й. остов пространства У есть все У, а <?-й
остов пространства X есть точка, то /(У) — точка.
В частности, если m < q, то ir(Sm, Sq) = тгь (Sm, Sq) = 0 (т.е. состоит из одного
элемента).
Определение. Пространство X называется п-связным, если при q < и мно-
жество ir(5<?, X) состоит из одного элемента (т.е. если любые два отображения
Sq -*Х с q < и гомотопны). .
Упражнения. 18. Докажите, что каждое из следующих условий эквивалент-
но n-связности: (i) itb(Sq, X) состоит иэ одного элемента при q < и; (ii) любое
непрерывное отображение Sq -* X продолжается до непрерывного отображения
19. Докажите, что 0-связность — это то же самое, что”'линейная связность.
Термин ”1-связность” обьяно заменяют в речй и письме термином ’’односвяз-
ность”.
Те о ре м а. Всякое п-связное клеточное пространство гомотопически эквива-
лентно клеточному пространству с единственной вершиной и без клеток размер-
ностей 1,2,... ,п.
Доказательство. Выберем в нашем пространстве X вершину е0 и соеди-
ним с ней остальные вершины путями. Это можно сделать, так как пространство
и-связно и, в частности, линейно связно. (Пути могут пересекаться.) Используя
теорему о клеточной аппроксимации, мы можем добиться того, чтобы эти пути
лежали в одномерном остове пространства X. Пусть s, — путь, соединяющий вер-
шину е0 с вершиной ef. Приклеим при каждом i к X двумерный диск по отобра-
жению нижней полуокружности в X при помощи пути s; (рис. 34). Получим новое
клеточное пространство X, которое будет содержать X и, кроме того, клетки е}, ef
(верхние полуокружности и внутренности приклеенных дисков). То, что границы
клеток е* лежат в одномерном остове, вытекает из того, что этим свойством обла-
дают пути S/. Л
Ясно, что X есть деформационный ретракт в X: каждый приклеенный диск можно
смять на нижнюю полуокружность.
Обозначим через У объединение замыканий клеток el. Очевидно, У стягиваемо;
следовательно, X/Y ~ Х~ X. Но у Х/Y всего одна вершина.
Дальнейшее рассуждение совершенно аналогично. Предположим, что X ~ X',
причем X' имеет единственную вершину и не имеет клеток размерностей 1, 2,...
Рис. 34
50
ГЛ. I. ГОМОТОПИИ
к — 1, где к < п. В этом случае замыкание каждой ^-мерной клетки представ-
ляет собой ^-мерную сферу. Ввиду «-связности X (и, следовательно, X') включение
этой сферы в X' продолжается до непрерывного отображения (к + 1)-мерного шара,
образ которого, ввиду теоремы о клеточной аппроксимации, можно считать ле-
жащим в (к + 1)-м остове пространства X'. По этому отображению (которое мы
считаем отображением нижней полусферы (к + 1)-мерной сферы) мы приклеиваем
к х'- шар Dk+2, и подобным образом мы поступаем для^каждой /с-мерной клетки
пространства X'. Полученное клеточное пространство л гомотопически эквива-
лентно X и содержит стягиваемое подпространство Y - объединение замыканий
всех вновь приклеенных (к + 1)-мерных клеток (верхних полусфер приклеенных
шаров), содержащее все ^-мерные клетки. Имеем: л/Y ~ X' ~ X1 ~ X, л/Y име-
ет единственную вершину и не имеет клеток размерностей 1,2,.. ., к.
Следствие. Если клеточное прдстранство X п-связно, а клеточное простран-
ство Y п-мерно, то множество ir(Y, X) состоит из одного элемента. Это же верно
для пь (У, X), если Хи Yимеют отмеченные точки, являющиеся вершинами.
Замечание. Использованная в доказательстве последней теоремы процедура
уничтожения ^-мерных клеток предполагает присоединение клеток размерности
к + 2. В случае, если заданное «-связное пространство было (« + 1)-мерно, это могло
привести к увеличению размерности. В действительности можно доказать, что вся-
кое «-связное клеточное пространство размерности п + 1 гомотопически эквивалент-
но букету (н + 1)-мерных сфер. Читатель может с легкостью проделать это после
прочтения гл. 2, а случай л = 0 доступен ему уже теперь. (Добавим, что, как это бу-
дет ясно из гл. 2, л-связное, но не (п + 1)-связное клеточное пространство не может
иметь размерность < п + 1.)
Последняя теорема имеет относительный вариант, для формулировки которого
необходимо понятие п-связной пары. Топологическая пара (X, А) называется «-связ-
ной, если всякое отображение (Dn, 5"-1) -> (X, А) гомотопно (как отображение
пар) отображению, загоняющему все D" в А.
Упражнения. 20. Придумайте эквивалентные определения л-связной пары
в духе упражнения 18 и интерпретации 0-связности и 1-связности пар в духе упраж-
нения 19.
21. Докажите, что всякая л-связная клеточная пара гомотопически эквивалентна
клеточной паре (У, В), у которой В D sk„ У (т.е. разность У - В не содержит кле-
ток размерности <«).
§ 6. ФУНДАМЕНТАЛЬНАЯ ГРУППА
1. Определение. Фундаментальной группой пространства X с отмеченной точкой
х0 называется его одномерная гомотопическая группа irj (X) = irb (S1, X). Посколь-
ку данное в § 4 определение было чересчур общим, мы повторим его в нашем част-
ном случае.
Рассматриваются петли пространства X, т.е. такие отображения </>: I -* X, что
<р(0) = <р(1) = х0. Петли и <р' называются гомотопными, если существует такая
гомотопия tpt: I -+Х, что <р0 = <р, (0) = yt (1) =х0 (0< t < 1). Произ-
ведение <рф петель у и ф - это петля х, у которой х (?) = </> (2г) при t < 1/2 и х (О =
= ф(21 — 1) при t > 1/2. Другими словами, произведение двух петель — это петля,
составленная из этих двух петель, которые проходятся последовательно (ср. § 4).
Как легко проверить, это умножение порождает умножение и в множестве гомо-
топических классов петель (проверять нужно, что если </> ф ~ ф', то <рф ~ у'ф'),
при этом последнее относительно введенной операции является группой (в отличие
§ 6. ФУНДАМЕНТАЛЬНАЯ ГРУППА
51
от самого множества петель, умножение в котором удовлетворяет групповым опе-
рациям лишь ”с точностью до гомотопии”: <р (фх ) ~ (<рф)х и т.д.). Это и есть фун-
даментальная группа Tri (X, х0). Ясно, что обратным к классу петли <р: I + X слу-
жит класс петли <р': I -+Х, определенной формулой tp'(Z) = <р( 1 — Т).
Отображение f: X -*• Y, такое, что /(х0) = у0, очевидным образом индуцирует
групповой гомоморфизм ni(X, х0) -> Я1(У, _у0)- Ясно, что если отображения
f,g'. X -* Y гомотопны (с учетом отмеченных точек), то гомоморфизмы f„g,
совпадают.
2. Зависимость от отмеченной точки.
Теорема 1. Если пространство X линейно связно, то ^(Х, х0) ^я^Х, xj
для любых точек х0, Xj G X.
Доказательство. Поскольку X линейно связно, существует путь а: I -> X,
у которого а(0) = х0, а(1) = xt. Мы построим отображение а#: Я1(Х, х0) -*
-> ni(X, Xi). Пусть Ф G Я1(Х, х0) и G Ф. Положим а#(<р) = (ау)оГ1 (конечно,
можно перемножать не только петли, но и пути, лишь бы только второй путь на-
чинался там, где кончался первый). Получаем петлю с началом (и концом) xt. Оче-
видно, что при замене петли и пути а гомотопными (гомотопность путей пони-
мается в том же смысле, что и гомотопность петель: подразумеваются гомотопии
с закрепленными концами) петля а#(<р) также заменится гомотопной, а потому
а# определяет зависящее только от гомотопического класса пути а отображение
Я1(Х, х0) -* Я1(Х, Xi), также обозначаемое символом а#. Обратное отображение
строится совершенно аналогично: а#1 ([<Д])= [(а'1ф)а].
Легко проверить, что а# есть гомоморфизм и, значит, изоморфизм.
Изоморфизм а# зависит, конечно, от а. При замене пути а на негомотопный
ему путь (3 мы получим, вообще говоря, другой изоморфизм. Точнее: если у = 0а-1,
то для любого Ф G Я1(Х, х0) имеет место равенство 0# (Ф) = [у]а# (Ф) [?]”* (оче-
видно, у есть петля, так что определен элемент [у] группы iri(X, Xj)). В частности,
верно, что если фундаментальная группа коммутативна (и только в этом случае)
изоморфизм а# от а вообще не зависит. В этом случае мы можем говорить о фун-
даментальной группе, не фиксируя отмеченной точки. В общем случае о фундамен-
тальной группе линейно связного пространства без отмеченной точки можно гово-
рить только как об абстрактной группе (т.е. можно сказать, что она, например,
конечна или нильпотентна, но нельзя фиксировать в ней определенный элемент).
Упражнение 1. Докажите, что если f: X -> Y есть гомотопическая эквива-
лентность, тд для любой точки х0 € X гомоморфизм /,: Я1(Х, х0) -* irt(Y, /(х0))
является изоморфизмом.
3. Вычисление фундаментальных групп. Существует два основных метода вычис-
ления фундаментальной группы: ’’метод накрытий” и ’’клеточный метод”. Накры-
тиям будет посвящен следующий параграф, но, не дожидаясь его, мы продемонстри-
руем сущность метода накрытий на примере доказательства теоремы 2 (в котором,
конечно, слово накрытие употребляться не будет). В основе клеточного метода
лежит теорема 4; теорема 3 нужна для ее доказательства.
А. Случай окружности.
Теорема 2. Группа ttj (S1) изоморфна группе Z целых чисел.
Фактически при доказательстве теоремы 2 мы построим ’’универсальное накры-
тие” над окружностью; это понятие будет введено в следующем параграфе, при чте-
нии которого мы советуем читателю держать в уме это доказательство.
Каждой точке окружности S1 мы обычным образом отнесем вещественное число,
определенное с точностью до слагаемого вида 2kir. Отмеченной точкой мы считаемО.
Петля ф: I -* 51 превращается в многозначную функцию на отрезке I, значение кото-
52
ГЛ. 1. ГОМОТОПИИ
рой в каждой точке определено с точностно до слагаемого 2кп и значением которой
в точках 0 и 1 служит само множество чисел вида 2кп. У этой многозначной функ-
ции существует непрерывная однозначная ветвь — непрерывная функция на отрез-
ке I, значение которой в каждой точке принадлежит множеству значений в этой
точке функции <р. Такая однозначная функция # будет определена единственным
образом, если мы наложим на нее дополнительное условие # (0) = 0. (См. рис. 35.)
(Для педантичного читателя приведем детали построения функции <р*. Пусть п
таково, что если |х” — х’| < 1/и, то точки <р(х’), <р(х”) G S1 не диаметрально про-
тивоположны. Мы полагаем <р# (0) = 0. Далее, при 0 < х < 1/и мы берем в качестве
<р# (х) то из значений функции в точке х, которое отличается от 0 меньше, чем
на я. Далее, при 1/л < х < 2/л мы берем в качестве <р# (х) то из значений функции <р,
которое меньше, чем на я, отличается от * (1/л). И т.д.)
Выделим два важных свойства функции <р#: ее значение в точке 1 кратно 2я и
она непрерывно зависит от в том смысле, что если — гомотопия, то и — го-
мотопия. Заметим еще, что всякая непрерывная функция Ф на отрезке /, такая, что
Ф(0) = 0 и Ф(1) кратно 2я, служит функцией <р # для некоторой петли <р.
Теперь для доказательства теоремы 2 осталось сделать четыре простых замечания.
Во-первых, число к = <р# (1)/2я не меняется при гомотопии, поскольку область воз-
можных значений <р#(1) дискретна; таким образом зто число зависит только от
элемента группы я^1). Во-вторых, всякое число к таким образом может полу-
читься: достаточно взять = hk с Л* (х) = 2Лях. В-третьих, если <р* (1) =<р2#(1),
то <pi ~ <р2: функции </># и <р*, очевидно, гомотопны в классе функций с заданными
значениями в 0 и 1 (рис. 36). Наконец, в четвертых, hkhf ~hk+t, потому что
Теорема доказана.
В. Случай букета окружностей.
Теорема 3. Пусть ВА = УаеА8а ~ букет окружностей S& = S1. Тогда
я^) ~ свободная группа, образующие которой соответствуют элементам мно-
жества А.
Доказательство теоремы 3 мы разобьем на две части, вторую из которых отло-
жим до § 7. Стандартное вложение ia: S1 В А мы рассматриваем как петлю;
пусть i]a G Я1 (ВА ) — класс петли ia (отмеченной в букете мы считаем общую точку
окружностей Sa) - Мы покажем, что: 1° всякий элемент группы Ki(BA) представим
в виде конечного произведения элементов вида т]а, ria1', 2° с точностью до сокра-
53
§ 6. ФУНДАМЕНТАЛЬНАЯ ГРУППА
щений идущих подряд множителей т?а, т^1 такое представление единственно. Это
равносильно нашей теореме.
Утверждение 1° доказывается при помощи кусочно линейной аппроксимации
(ср. доказательство леммы о свободной точке в § 5). На каждой из окружностей
8^, входящих в букет, отметим два отрезка, 1а и Ja> не содержащих отмеченной
точки и таких, что JQ С IntJa- Возьмем петлю <р: I ВА и фиксируем такое п,
что если образ некоторого отрезка J С I длины 1/л пересекается с Ja, то он содер-
жится в /а. Обозначим через К объединение отрезков вида [к/п, (к + 1)/и], образы
которых пересекаются с Ua Ja, и заменим отображение отображением<р : / ~^ВА,
совпадающим с вне АГ и во всех точках вида к/п и линейным на каждом из отрез-
ков указанного вида (линейное отображение отрезка в окружность — это отобра-
жение вида х (cos(Xx + д), sin(Xx + д))). Очевидно, у — петля, гомотопная ф.
Выделим теперь в каждом отрезке Ja маленький отрезочек Ка, не содержащий
ни одной точки вида <р'(к/п) ( таких точек конечное число!). Заметим, что прооб-
раз ф' "* (Uа Ка) состоит из конечного числа отрезочков, каждый из которых отобра-
жается на свое Ка линейно. Последний этап: подвергнем гомотопии
ip' hf
Iх* ВА-+вА,
где ht — гомотопия, растягивающая каждый из отрезков Ка равномерно на свою
окружность и сжимающая дополнение 5^ — Ка в отмеченную точку. Мы прихо-
дим к петле / *ВА, устроенной так: на отрезке J расположено некоторое коли-
чество маленьких отрезочков, каждый из которых отображением ф наматывается
на свою окружность Sla (в том или в другом направлении); промежутки между
этими отрезочками загоняются в отмеченную точку. Ясно, что зта петля принадле-
жит классу вида
(₽/ = «)• (*)
Утверждение 1° доказано.
Утверждение 2° заключается в том, что произведение вида (♦), содержащее не
менее одного множителя и не содержащее идущих подряд множителей i?a и i?"1,
не равно единице в Я] (ВА ). Это мы докажем в § 7.
С. Случай произвольного клеточного пространства. Формулировке теоремы 4 мы
предпошлем следующее замечание. Непрерывные отображения окружности в про-
странство X, переводящие отмеченную точку у0 окружности в точку х0, могут
рассматриваться как петли пространства X с началом х0 и определяют элементы
группы Я1(Х х0). Если же отображение <р: S1 -+Х окружности в линейно связное
пространство переводит отмеченную точку у0 неизвестно куда, то оно определяет
элемент группы Я](X, ф(Уо)), связанной с Я1 (X, х0) неканоническим изоморфиз-
мом. Образы класса [<р] в х0) при всевозможных изоморфизмах вида а#
заполняют в Я1(Х х0) целый класс сопряженных элементов (это равносильно ска-
занному после теоремы 1). Это позволяет нам сказать, что отображение окружности,
не обязательно переводящее отмеченную точку в отмеченную, определяет элемент
фундаментальной группы с точностью до сопряженности.
Вернемся к нашей проблеме вычисления фундаментальных групп. Пусть X — кле-
точное пространство с единственной вершиной е°, одномерными клетками е} (i&Г)
и двумерными клетками е? (/€/). Характеристические отображения : D1 X
определяют отображения g^: S1 -> X1 (’’приклеивающие отображения” — см. § 5),
которые, в силу сказанного, определяют некоторые элементы 3/ е Я1(Х*) с точ-
ностью до сопряженности. Добавим, что X1 — это букет окружностей ej и группа
^(Х1, е°) есть, в силу теоремы 3, свободная группа с множеством образующих/.
54
ГЛ 1. ГОМОТОПИИ
Теорема 4. Группа ^(Х, е°) есть группа с системой образующих I и с систе-
мой определяющих соотношений fy= 1, /ел
Доказательство. Если рассматривать окружность как одномерное кле-
точное пространство, у которого отмеченная точка является нульмерной клеткой,
то отображение окружности в X, переводящее отмеченную точку _у0 € S1 в отме-
ченную точку е° е X, есть отображение, клеточное на у0. Поэтому из теоремы о
клеточной аппроксимации вытекает, что всякая петля пространства X с началом е°
гомотопна петле, проходящей по одномерному остову, т.е. что отображение
я1(Х1, е°) -> Я](Х е°), индуцируемое включением X1 X, является эпиморфиз-
мом. Для завершения доказательства нам необходимо установить, что ядро этого
эпиморфизма порождается как нормальная подгруппа группы Я1(Х*, е°) вышеука-
занными элементами 3/ — классами приклеивающих отображений.
”В одну сторону” это утверждение почти очевидно: классы 0у действительно
принадлежат нашему ядру. Действительно, отображение gy: S1 -> X1 продолжается
до отображения fj.D2 + X и потому определяет тривиальный элемент в группе
Я1СХ1, £у(_Уо)); но зтот элемент соответствует элементу 0у при некотором изо-
морфизме Я1(Х*, £у(_Уо)) irifX1, е°). ”В другую сторону” утверждение доказы-
вается опять-таки при помощи кусочно линейной аппроксимации. Чтобы изгнать
из формул многочисленные ff и /у-1, мы будем считать, что клетки е2 отождест-
влены с копиями открытого диска IntZJ2 посредством этих отображений; таким
образом, мы получаем возможность говорить о концентрических дисках, прямоли-
нейных отрезках и т.п. в клетках е2. Построим в каждой клетке е2 концентрические
диски dij,..., d^j радиусов 1/5,..., 4/5 (ср. доказательство леммы о свободной
точке в п. 8 § 5). Пусть-yG Ker [jtiCX1, е°)-*Я1(Х е°)],ипусть<р: S1 —пред-
ставитель класса у. В силу выбора у отображение продолжается до непрерывного
отображения Ф: D2 X, причем теорема о клеточной аппроксимации позволяет
считать, что Ф(£>2) С X2. Триангулируем ZJ4 настолько мелко, что если Д — симп-
лекс триангуляции и Ф(Д) при некотором / пересекается с d4y, то Ф(Д) С е2 и
сНатФ(Д) < 1/5. Пусть К — объединение симплексов нашей триангуляции, Ф-об-
разы которых пересекаются с \Jjd4j. Рассмотрим отображение Ф: К -> X2, совпа-
дающее с Ф на вершинах триангуляции и линейное на каждом симплексе. Отобра-
жения Ф| к и Ф' соединяются прямолинейной (в клетках е2) гомотопией Фг: К ->
-*• Х2, Фо = Ф^, Ф1 = Ф’. Определим отображение Ф": D2 -+X знакомой по § 5
формулой
ф» =
Ф(и), если Ф(М)£и.</3/,
ф'(ц), если
Ф3-5р(И)(МЬ если Ф(И)еиу(с/3у-с/2у),
где р(и) есть расстояние от Ф(м) до центра е2 э Ф(н). Отображение Ф" является
кусочно линейным на прообразе объединения Uydjy. Зафиксируем в каждом d1;-
маленький кружок бу, не пересекающийся с Ф"-образами никаких вершин и ребер
триангуляции К. Тогда Ф''-прообраз каждого из кружков 5у будет состоять из конеч-
ного числа овальных областей (кусков плоскости, ограниченных эллипсами), каж-
дая из которых линейно отображается посредством Ф на Sy. Наконец, рассмотрим
отображение со: -Y2 -* Jf2, тождественное на Xх, линейно растягивающее каждый
кружок 8 у на свою клетку е2 и сминающее е2 — бу на границу клетки е2. Отобра-
жение Ф: D2 X, Ф(и) = со(Ф" (и) ), продолжает, как и Ф, отображение : S1 -> Xх,
§ 6. ФУНДАМЕНТАЛЬНАЯ ГРУППА
55
отображает в Л* дополнение к конечному набору Eit..., Ец неперекрывающихся
овальных областей (см. выше) и отображает каждую из этих овальных областей
линейно на одну из двумерных клеток. Соединим точку у0 G S1 С О2 несамопере-
секающимися и попарно непересекающимися путями st,..., sN с какими-нибудь
точками yi,..., yN границ областей Еи ..., и обозначим через Oj........aN
петли с началами ylt..., yN, обходящие эти границы против часовой стрелки;
при этом можно считать, что пути $1...sN- занумерованы в порядке их выхода,
против часовой стрелки, из точки у0 (см. рис. 37). Очевидно, петля а, обходящая
границу № диска D2 против часовой стрелки из точки у0, гомотопна в D2 — IntP,
петле
(«1 OiSi1) (sjffjSj *) ... (sNaNSj/ )
(см. рис. 38). Следовательно, петля гомотопна (в X1) петле
[♦•(Wf')] [фо (S2O2S21)] . . . [Ф« (tyO^1)].
Но петля [Ф ° (s/O/sr1)] определяет в тг1(ДГ1, е°) элемент, сопряженный С0*1,
где j — номер клетки Ф^,), а знак в показателе зависит от того, в какую сто-
рону петля фо а( обходит ё2. Мы видим, что класс у петли <р действительно
принадлежит нормальной подгруппе группы iri (X1, е°), натянутой на fy.
Теорема доказана.
Следствие. irt (X) = тг i (X2 ) для любого клеточного пространства X.
Доказанная теорема позволяет найти фундаментальные группы классических
пространств, клеточные разбиения которых были построены в § 5. Впрочем, мно-
гие из этих пространств вовсе не имеют одномерных клеток и потому односвяз-
ны, т.е. имеют тривиальные фундаментальные группы (это нам известно уже из
§ 5); таковы, например, сферы S” с п >2, пространства СР", CG(n, к) и неко-
торые другие. Но все же в некоторых случаях вычисление фундаментальных
групп приводит к интересным результатам. Например:
Теорема 5. Фундаментальная группа сферы с g ручками порождена 2g об-
разующими, й1,... ,ag, blt..., bg, связанными одним соотношением
а^а^Ь?... agbga^bg1 = 1.
В частности, фундаментальная группа тора порождена двумя образующими, а и Ь,
связанными соотношением аЬа~хЬ~х = 1, т.е. попросту есть Z ® Z. Этот факт выте-
кает, впрочем, и из очевидной формулы
я, (XX У) = W1(X)Xwj(y)
(докажите ее!).
Рис. 37 Рис. 38
56
ГЛ. 1. ГОМОТОПИИ
Теорема 6. Фундаментальная группа проективной плоскости с g ручками
или бутылки Клейна eg ручками порождена образующими cif..., ch, где в случае
проективной плоскости h = 2g + 1 и в случае бутылки Клейна h=2g + 2, связанными
одним соотношением
В частности, тг i (RP2) = Z2 (циклическая группа порядка 2).
Упражнения. 2. Покажите, что фундаментальные группы, вычисленные в тео-
ремах 5,6, попарно неизоморфны1). Этот результат впервые дает нам возможность
убедиться в том, что сферы с ручками, проективные плоскости с ручками и бутылки
Клейна с ручками попарно не гомеоморфны (даже гомотопически не эквивалентны).
Выведите из этого, что никакие две классические поверхности (см. § 1) не гомео-
морфны.
3. Напомним два алгебраических определения. Пусть Gi, G2 — группы, Ль А2 —
системы их образующих и R i, R2 — соответствующие определяющие системы со-
отношений. Группа с системой образующих At U А2 и определяющей системой
соотношений Rt U R2 называется свободным произведением групп Gt и G2 и обоз-
начается через Gj ♦ G2. Из алгебры известно, что эта группа не зависит от выбора
образующих и соотношений в G, и G2. (По-другому группу Gi ♦ G2 можно описать
как группу ’’слов” g}g2g jg2 .. .gig^megl G Gf.) Докажите, например, что свобод-
ное произведение Z2 * Z2 обладает нормальной подгруппой, изоморфной Z, и
(Z2 ♦ Z2)/Z = Z2.^Обобщение этого определения: пусть Н — еще одна группа и </>i:
Н Gi, v <р2: Н -+G2 — гомоморфизмы. Выберем в Н систему образующих ha и до-
бавим к нашим соотношениям в G] ♦ G2 соотношения (Ла) = <p2(ha) (мы считаем
Gt и G2 подгруппами группы Gt ♦ G2). Получающаяся группа называется амальга-
мированным произведением групп Gx и G2 над Н и обозначается через Gi *н G2.
Попробуйте доказать, например, что группа SZ2(Z) целочисленных 2 X 2-матриц с
определителем 1 изоморфна Z4 *z Z6.
4. Докажите, что (XV У) ^wi(X) ♦ я1(У).
5. Докажите следующую теорему ван Кампена. Пусть X— клеточное пространство,
У и Z — его клеточные подпространства, пересечение V которых связно; пусть е° —
нульмерная клетка, лежащая в V. Тогда Я1(Х, е°) = Я1(У, е°) tt2(Z, е°)
(по отношению к гомоморфизмам 1Г1(К, е°) ->Я1(У, е°), jti(K, е°) -* jti(Z, е°),
индуцированным включениями V У, V -+Z ).
6. Покажите, что всякая группа является фундаментальной группой некоторого
клеточного пространства.
7. Покажите, что всякая группа, задаваемая конечным набором образующих и
соотношений, служит фундаментальной группой некоторого замкнутого многообра-
зия (кто не знает определения, должен дождаться гл. 2). Более того, это многооб-
разие можно выбрать четырехмерным. Однако нельзя понизить его размерность до
трех: группа Z ® Z, например, не является фундаментальной группой никакого
замкнутого трехмерного многообразия (этот факт читатель сможет доказать после
) Не существует универсального алгоритма, позволяющего узнать, изоморфны ли две груп-
пы, заданные образующими и соотношениями, но существуют различные способы решать эту
проблему в частных случаях. Простейший из этих способов, применимый и в рассматриваемой
ситуации, состоит в том, чтобы ’’прокоммутировать” заданные группы, т.е. профакторизовать
их по (нормальной) подгруппе, порожденной ’’коммутаторами”-элементами вида Л , -
и посмотреть, будут ли изоморфны получающиеся коммутативные группы (для конечнопорож-
денных абелевых групп дело обстоит просто: всякая такая группа однозначно представля-
ется в виде Z •... • Z • Zflj е... е Z^, где qt,..., qs - степени простых чисел).
§ 7. НАКРЫТИЯ
57
того, как он прочтет гл. 3; вообще же, вопрос, какие группы могут быть фундамен-
тальными группами замкнутых трехмерных многообразий, не прост).
8. Покажите, что дополнение к стандартно вложенной окружности S1 * в R3 имеет
фундаментальную группу Z. Используя теорему ван Кампена, вычислите фундамен-
тальную группу дополнения к простейшему узлу в R3 — ’’трилистнику” (см. рис. 39).
(Ответ: группа с двумя образующими, а и Ь, и одним соотношением аг = Ь3.) Вы-
ведите из этих результатов, что трилистник нельзя ’’развязать”. Придумайте способ
вычисления фундаментальной группы дополнения к произвольному узлу, задан-
ному картинкой, подобной рис. 40*).
В заключение заметим, что, как показывают проделанные вычисления, фундамен-
тальная группа часто бывает некоммутативной. В этом ее отличие от подавляющего
числа групп, гомотопически инвариантным образом сопоставляемых с топологи-
ческими пространствами. Поэтому изучение фундаментальной группы требует
привлечения специфических и не всегда стандартных алгебраических средств. Чтобы
этого избежать, топологи любят (к месту и не к месту) накладывать на рассматри-
ваемые пространства требование односвязности или хотя бы какие-нибудь требова-
ния, влекущие за собой коммутативность фундаментальной группы. Одна из воз-
можностей зто сделать подсказывается следующим упражнением.
Упражнение 9. Покажите, что если X — топологическая группа (не обяза-
тельно коммутативная) или хотя бы .//-пространство (см. § 4), то фундаментальная
группа Я1 (X) коммутативна.
§ 7. НАКРЫТИЯ
1. Определение и примеры. Линейно связное пространство Т называется накрываю-
щей для линейно связного пространства X, если задано отображение р: Т^-Х, такое,
что у любой точки х € X имеется окрестность U С X, для которой р-1(С7) гомео-
морфно С/Х Г, где Г — дискретное множество, причем диаграмма
p*(U) ~ и* Г
^/проекция
и
коммутативна. Отображение р: Т->Х
называется в этой ситуации накрытием.
1) Как видно из сказанного, фундаментальная группа дополнения к узлу (ее называют иног-
да просто группой узла) доставляет эффективное средство распознавания узлов; бывают все же
узлы, которые не эквивалентны (т.е. один нельзя превратить в другой, не разрывая нити, из ко-
торой он сделан), но Имеют изоморфные группы. Таким образом, теория узлов не сводится к
изучению групп узлов.
58
ГЛ. 1. ГОМОТОПИИ
Примеры. 1. р: R -+S1, S1 — окружность {z € С | | z | = 1}, р: R -►S'1 дей-
ствует по формуле р(х) = е21г1х.
2. р: S1 ->S1, p(z) = z* (к=# 0 — целое число).
3. Т = Sn, X = RP", р: Sn + RP" относит точке сферы S" прямую в R"+1, про-
ходящую через эту точку и точку О G R"+1 (ср. § 1).
Ясно, что если pt: 7\ -+ Х2, р2: Т2 Х2 — накрытия, то и pt X р2: Т2 X Т2 +
-* Х\ X Х2 — накрытие. В частности, квадрат накрытия из примера 1 есть накрытие
R2 ->S* XS1 — плоскость накрывает тор.
Упражнения. 1. Покажите, что при любом g > 2 сфера с g ручками способ-
на накрывать сферу с 2 ручками (’’крендель”). Подумайте, какие из классических
поверхностей способны накрывать друг друга (хотя технические средства, позволяю-
щие ответить на этот вопрос, появятся только в гл. 2).
2. Покажите, что при любом п > 2 букет п окружностей способен накрывать бу-
кет двух окружностей (’’восьмерку”).
2. Теорема о накрывающей гомотопии. Некоторые теоремы этого параграфа тре-
буют наложения на участвующие в них пространства тех или иных условий локаль-
ного характера. Эти условия не особенно ограничительны: всегда достаточно локаль-
ной односвязности (любая окрестность любой точки содержит односвязную окрест-
ность этой точки), а иногда можно обойтись локальной линейной связностью. Эти
условия необходимы для проверки непрерывности различных отображений, и нам
не придется вникать в них, поскольку мы будем систематически такие проверки
пропускать. Поэтому мы будем пользоваться не очень определенным термином
’’достаточно хорошее пространство”, помня при этом, что клеточные пространства
(и многообразия) заведомо достаточно хороши. Читатель, интересующийся подроб-
ностями, с легкостью их восстановит; он может также найти их, скажем, в ’’Основах
гомотопической топологии” Постникова.
Теорема. Пусть р: Т ^Х - накрытие, Z - достаточно хорошее пространство,
F: Z ->Т — непрерывное отображение и fa: Z ->Х — гомотопия, такая, что fa =р° F.
Тогда существует единственная гомотопия Ft: Z ->Т, такая, что Fo = F и fa =р° Ft.
Чтобы доказать эту теорему, мы сначала докажем следующую ’’лемму о накры-
вающем пути”.
Лемма. Для любого пути s: I и любой точких&Т, такой, чтор( х) = s(0),
существует единственный путь st I ->Т, такой, что Г(0) =х и р° s = s.
Доказательство. Окрестности из определения накрытия мы будем назы-
вать элементарными. Для каждого t € I найдем злементарную окрестность <7(Т) С X
точки s (т). В силу компактности отрезка I из этих окрестностей можно выбрать
последовательность U2,..., таким образом, что U/ Э f(tt, t<+1), где 0 = G <
< t2 < .. . < tN+l = 1. Прообраз окрестности Ui гомеоморфен дискретному се-
мейству таких же окрестностей^Пусть Ut — та иэ них, которая содержит точку х.
Возьмем прообраз s: [0, t2] -*U2 куска нашего пути s| j0>rj ] (см. рис. 41). Затем
проделаем то же самое с окрестностью U2, точкой s(t2} и куском пути s|j t t j
и т.д. Так как число окрестностей конечно, то процесс конечен, а так как для каж-
дой окрестности он однозначен, то путь с нужными свойствами существует только
один.
Доказательство теоремы. Пусть z € Z — произвольная точка. Форму-
ла t *+fa (z) определяет путь в X. Этот путь единственным образом можно поднять
в Т так, чтобы поднятый путь начинался в точке F(z). Заставив z пробегать Z,
мы получим отображение Z X I + Т. Это и есть нужная гомотопия. Проверку ее
непрерывности и единственности мы оставляем читателю.
§ 7. НАКРЫТИЯ
59
Замечание. В доказательстве нигде не использовалась связность простран-
ства Т, и действительно она не требуется для этой теоремы. Если из определения
накрытия удалить требование связности Т, то получится определение ’’накрытия
в широком смысле”. Это понятие во многих отношениях не хуже понятия накры-
тия, но в связи с фундаментальной группой удобнее иметь дело именно с накры-
тиями.
Рис. 41
3. Накрытия и фундаменгадеиая группа.
Теорема 2. Если р: Т + X — накрытие, то р,: х0) ->я1(2Г, х0) - моно-
морфизм. Здесь х0 - произвольная точка пространства Т и х0 =р( х0).
Доказательство. Нам надо доказать, что если петля s: I -> Т с началом
х0 проектируется в петлю s : I -> X, гомотопную нулю (т.е. гомотопную постоян-
ной петле), то она и сама гомотопна нулю. Фиксируем гомотопию st: I ->Х, такую,
что s0 = s, st (0) = sr(l) = х0, Si(/) =х0. По теореме о накрывающей гомотопии
существует гомотопия st: / -> Т, такая, что s0 =sap<> st = st. Но так как полный
прообраз точки х0 дискретен в Т, то sr(0) = s(0) = х0, st(l) = s(l) = хо, ?i(/) =
= х0. Таким образом, петля s также гомотопна нулю. Теорема доказана.
Подгруппа х0)) группы irt(X, х0) называется группой накрытия. Ясно,
что если мы изменим точку х0, не меняя точку х0, то подгруппа заменится сопря-
женной (сопряженность определяется классом петли в X, получающейся при проек-
тировании пути, соединяющего две точки х0 в Т — см. рис. 42). При замене же точ-
ки х0 группы накрытия переводятся друг в друга изоморфизмами вида а#.
Теперь мы убедимся в том, что различие между группами Я1(Г) и Я1(Х) изме-
ряется числом прообразов точки пространства X в Т. Именно, мы построим кано-
ническое взаимно однозначное соответствие между элементами фактормножества
П1(Х, х0)/р.(Я1(Т, х0)) и элементами множества р*1 (х0) С Т.
Рассмотрим петлю с началом х0 в X. Поднимем ее в Т как путь с началом в точке
х0. Поставим в соответствие петле конец этого пути. Получим точку изр-1(х0).
Ясно, что эта точка зависит только от гомотопического класса исходной петли:
при гомотопии петли накрывающий путь тоже подвергается гомотопии, но его конец
может варьироваться только в пределах дискретного множества р-1(хо) и потому
стоит на месте. Ясно, далее, что петли Si, s2 тогда и только тогда определяют одну
точку множества р"*(х0), когда петля SjSj1 накрывается в Т петлей (рис. 43), т.е.
определяет элемент группы ni(T, х0). Таким образом, наше соответствие опреде-
ляет отображение Я1(Х х0)/я1(Т, х0) ->Р~1(хо), переводящее разные элементы в
разные. Осталось убедиться в том, что образ этого отображения — все множество
р-1(х0), но это следует из связности Т: любая точка из р-1(х0) соединяется с х0
путем, и проекция этого пути есть петля, поднятие которой есть путь, кончающийся
в выбранной точке.
60
ГЛ. 1. гомотопии
Эта конструкция показывает, что р-прообразы различных точек пространства X
в Т ’’одинаковы” (находятся во взаимно однозначном соответствии). Этот факт
легко вывести и прямо из леммы о накрывающем пути. (Пусть $: I + Т — путь,
соединяющий точки х0, х'^ 6 X. Пути в Т, накрывающие s и начинающиеся в раз-
личных точках множества р-1(х{>), кончаются в р-1(хд) — мы получаем отобра-
жение p-,(xi) -* р-1(хо); обратное отображение строится по пути $-1.) Мощность
Рис. 43
множества р-1(х), где х € X - произвольная точка, называется числом листов
накрытия р: Т -> X. Употребляются также выражения ”и-листное накрытие”, ’’конеч-
нолистное накрытие”, ’’бесконечнолистное накрытие”, ’’счетнолистное накрытие”
итл.
Предыдущая конструкция показывает также, что если х, х' — не совпадающие
точки, такие, что р(х) = р(х'), и s — любой путь, соединяющий х с х , то петля
р о s не гомотопна нулю (в X). Это наблюдение позволяет нам восполнить пробел
в доказательстве теоремы 3 из § 6. Напомним, что там осталось недоказанным, что
е. е.
петля не гомотопна нулю, если среди сомножителей не встречаются иду-
щие подряд элементы i?a ИТ)'1.
Рассмотрим s + 1 экземпляров нашего букета окружностей и расположим их
один над другим, как показано на; рис. 44. Под этими $ + 1 экземплярами располо-
жим еще один экземпляр и будем считать,
что верхние экземпляры вертикально проек-
тируются на нижний экземпляр.
Возьмем теперь первую букву нашего
слова. В первом и втором экземплярах наше-
го букета (снизу) в окружности, соответ-
ствующей нашей букве, вырежем один над
другим по маленькому отрезку и концы об-
разовавшихся дырок соединим крест-нак-
рест, очевидным образом перестроив проек-
цию. Затем аналогичным образом соединяем
второй экземпляр с третьим, используя вто-
рую букву, потом — третий с четвертым и
т.д. Если в нашем слове идут подряд две оди-
наковые буквы, то нам придется выкиды-
вать два отрезка из одной и той же окруж-
ности. Мы сделаем это так, чтобы вторая
дырка предшествовала первой, если соот-
ветствующие буквы стоят в степени +1, и
§ 7. НАКРЫТИЯ
61
следовала за ней, если буквы стоят в степени —1. (Все окружности букета
ориентированы, иначе мы не могли бы говорить о степенях.) Очевидно, что
мы построили (s + 1)-листное накрытие над нашим букетом окружностей и что
наша петля накрывается в нем путем, который начинается в самой нижней точке,
проектирующейся в отмеченную, а кончается в самой верхней (см. опять рис. 44).
Следовательно, наша петля не гомотопна нулю.
4. Регулярные накрытия. Накрытие р: Т-+Х называется регулярным, если группа
накрытия р ,(Я1 (Т, х0 ) ) есть нормальная подгруппа в {X, х0 ).
Упражнения. 3. Докажите, что накрытие р: Т * X регулярно тогда и только
тогда, когда никакая петля в X не служит образом одновременно замкнутого пути
и незамкнутого пути в Т.
4. Докажите, что если р: Т -> X есть регулярное накрытие, то существует свобод-
ное действие группы G = ni(X xq)/ki(T, х0) в Т, такое, что X = Т/G (точнее: такое,
что его орбиты совпадают с множествами р'1 (х)).
5. Докажите, что верно обратное: если группа G действует в пространстве Т сво-
бодно и дискретно (последнее означает, что каждая точка х G Т обладает такой ок-
рестностью U, что множества gU, g G G, попарно не пересекаются), то естественная
проекция Т~* X = Т/G является регулярным накрытием. Более того, в этом случае
я1(Х)/я1(Т) =G.
6. Докажите, что двулистные накрытия всегда регулярны (зто, в действитель-
ности, алгебраический факт: подгруппы индекса 2 всегда нормальны), а трехлистное
накрытие может быть нерегулярным: постройте пример нерегулярного трехлистного
накрытия над кренделем и над восьмеркой.
5. Универсальные накрытия. Накрытие р: Т -+ X называется универсальным,
если Т односвязно. Очевидно, универсальные накрытия всегда регулярны.
Из сказанного выше вытекает, что прообраз произвольной точки пространства X
в его универсальной накрывающей находится во взаимно однозначном соответствии
с группой Я1(У). Более того, упражнение 4 придает этому соответствию смысл груп-
пового изоморфизма. В сущности, именно это обстоятельство лежало в основе дока-
зательства теоремы 1 из § 6. Приведем еще один пример вычисления фундаменталь-
ной группы при помощи ’’метода накрытий”.
Теорема 3. Фундаментальная группа пространства RP п, и > 2, изоморфна Z 2.
Доказательство: естественная проекция 5" -> RP п (см. § 1) есть универ-
сальное накрытие.
(Эту теорему ничего не стоит вывести также из теоремы 4 § 6.)
6. Теорема о поднятии отображения.
Теорема 4. Пусть р: Т -*Х — накрытие и Z — линейно связное топологическое
пространство. Пусть, далее, х0 € Т, х0 =р(х0) G X, z0 G Z - отмеченные точки и f :
Z •+ X - непрерывное отображение, переводящее z0 в х0. Тогда: (i) существует не
более одного непрерывного отображения F: Z -+Т, такого, что F(z0) = х0 и р» F =
= /; (ii) если пространство Z является достаточно хорошим, то для существования
такого отображения необходимо и достаточно, чтобы выполнялось включение
С р,(П!(Т,Х0)).
Доказательство. Пусть F', F" — два таких отображения. Если z G Z —
произвольная точка и s: I ->Z — путь, соединяющий z0 с z, то пути F'°s,F" °s
накрывают путь / » s и имеют общее начало, вследствие чего они совпадают; следо-
вательно, F"(z) = F" о s(l) =F' о s(1) =F'(z). Это же рассуждение подсказывает,
как построить отображение F: для точки z€Z берем путь s: I Z, соединяющий
zo с z, строим поднятие s с началом в точке х0 пути f ° s: I и полагаем F(z) =
- s (1). Для того чтобы эта конструкция была корректной, необходимо (и достаточ-
62
ГЛ. 1. ГОМОТОПИИ
но), чтобы для любого другого пути s': I -> Z, соединяющего z0 с z, соответствую-
щий путь s' кончался в той же точке, что и s, т.е. чтобы петля f ° (ss'-1) накрыва-
лась в Т петлей. Это, очевидно, равносильно вышеуказанному включению.
Следствие. Если Z - односвязное достаточно хорошее пространство и pi
Т -*•X - накрытие, тор,'. Cb (Z, Т) ->Cb (Z, Т) есть гомеоморфизм, ар,'. яь (Z, Г) *
-> яь (Z, Г) — взаимно однозначное соответствие.
7. Критерий эквивалентности накрытий. Накрытия Pi: 7\ -> X, p2i Т2 -> X на-
зываются эквивалентными, если существует такой гомеоморфизм /: 7\ Т2, что
диаграмма
Ъ-----*-—
коммутативна. Отображение / называется при этом эквивалентностью.
Теорема 5. Пусть p2i Т\ -> X, р21 Т2 -+Х - накрытия, х€ X, Xi € Tlt х2 G
G Т2 - такие точки, что pi(xi) = х, р2(х2) = х. Если X - достаточно хорошее
пространство, то накрытия р2, р2 эквивалентны тогда и только тогда, когда группы
РгМ, х2)) сопряжены в Я1(Хх).
В частности, два универсальных накрытия над достаточно хорошим пространством
всегда эквивалентны.
Доказательство. В одну сторону (если эквивалентны, то сопряжены)
зто нам, по существу, уже известно. В другую сторону: изменив, если нужно, точ-
ку х2, мы добиваемся того, что подгруппы Pi»(ffi(7’i, х2)), р2 »(Я1(Г2,х2)) группы
Я1 (X, х) не просто сопряжены, а одинаковы. После этого, применяя теорему о под-
нятии отображения к отображению Pi: 7\ -> X и накрытию р2: Т2 ~*Х, мы полу-
чаем отображение f : Тх -+Т2,а. применив эту теорему к отображению р2: Т2 -+Х
и накрытию Pi: Tt -> X, мы получаем отображение gi Т2 -*• Л. Ясно, что f и g —
взаимно обратные гомеоморфизмы, коммутирующие с проекциями.
Упражнение 7. Постройте изоморфизм между группой автозквивалентностей
накрытия р: Т -> X (с достаточно хорошим X) и группой Normpjri(T)/p,iri(T),
где Norm — нормализатор (нормализатор подгруппы Н группы G - это совокуп-
ность таких g G G, что gHg~l = Я).
8. Существование и классификация накрытий.
Теорема 6. Пусть X - достаточно хорошее линейно связное пространство и
х0 G X - точка. Тогда для любой подгруппы G группы ni(X, х0) существуют накры-
тие pi Т->Хи точка х0 G р-1(хо), такие, что pjinitT, х0)) -G. В частности, над X
существует универсальное накрытие.
Конструкция. В множестве Е(Х, х0) введем отношение эквивалентности:
s ~ s', если s'(l) = s(l) и гомотопический класс петли ss'-1 принадлежит G. Мно-
жество классов эквивалентности принимаем за Т. Отображение pi Т -* X относит
классу путей их общий конец. Определение в Т топологии, выбор точки х0 > провер-
ку того, что р есть накрытие (для достаточно хорошего X) и доказательство ра-
венства р»(яг(Г, х0)) = 6 мы оставляем читателю.
Таким образом, для достаточно хорошего линейно связного пространства X клас-
сы эквивалентных накрытий над X находятся во взаимно однозначном соответствии
с классами сопряженных подгрупп фундаментальной группы пространства X. В част-
ности, над достаточно хорошим односвязным пространством вообще нет нетривиаль-
ных накрытий (тривиальное накрытие — это однолистное накрытие id: X -> X). На-
пример, накрытие (винтовая линия) -> (окружность) не имеет никакого многомер-
ного аналога.
§ 8. ГОМОТОПИЧЕСКИЕ ГРУППЫ
«3
§ 8. ГОМОТОПИЧЕСКИЕ ГРУППЫ
1. Определение; коммутативность. Гомотопические группы я„(Х х0) топологи-
ческого пространства X с отмеченной точкой х0 были определены в § 4 как частный
случай общего ковариантного группового функтора. Напомним, что множество
я„(Х *о) определялось как множество гомотопических классов отображений
Sn * X, переводящих отмеченную точку сферы Sn в точку х0. Сами эти отображе-
ния называются сфероидами. Иначе сфероид можно определить как отображение
л-мерного куба 1п в X, переводящее границу куба Э/л в точку х0.
Сумма двух сфероидов f, g: S” -> X определяется как сфероид f + g: Sn * X,
построенный так: сначала экватор сферы Sn (содержащий отмеченную точку) сжи-
мается в точку, в результате чего сфера превращается в букет двух сфер, затем сфе-
ры, составляющие этот букет, отображаются в X с помощью отображений fug (см.
рис. 45). Иначе зту операцию можно описать на кубическом языке. Если заданы
сфероиды f,g: 1п->Х пространства X с отмеченной точкой х0, то сумма f+g опре-
деляется как отображение 1п + X, совпадающее на левой половине G < 1/2 куба с
композицией f и сжатия куба вдвое, на правой половине — как композиция g и
аналогичного сжатия (рис. 46).
Сложение сфероидов не является групповой операцией. Однако оно гомотопи-
чески инвариантно (т.е. если f ~ /' и g ~ g', то f + g ~ f + g’) и поэтому индуци-
рует операцию в множестве я„(Х х0)> а последняя уже является групповой. Ассо-
циативность и наличие единицы проверяются для этой операции непосредственно
(см. § 4).
При л > 2 эта операция коммутативна — гомотопия, соединяющая сфероиды
f + g и g + f, изображена на рис. 47 (на этом рисунке черные части кубов отобра-
жаются в х0)-
Рис. 46
Рис. 47
64
ГЛ. 1. ГОМОТОПИИ
Если <р: X -> Y — непрерывное отображение, переводящее отмеченную точку
х0 G X в отмеченную точку у0 е то возникает гомоморфизм я„(Х, х0)
->-я„(У, уо), не меняющийся при замене отображения гомотопным. В частности, у
гомотопически эквивалентных пространств с отмеченными точками гомотопические
группы одинаков ы.
Упражнение 1. irn(XX. Y,(x0, у0)) = irn(X, х0)Х. irn(Y, у0).
2. Зависимость от отмеченной точки. Путь а: I-+Х, соединяющий точки х0> *i €
G X, индуцирует изоморфизм а#: ir„(X, х0) ->яи(Х Xj). Построение отображения
а#: на рис. 48 показано отображение со сферы 5" на букет Sn V I этой сферы и от-
резка (это отображение переводит отмеченную точку сферы в удаленный от 5" ко-
нец отрезка I С Sn V I) ; сфероиду /: 5" * X, переводящему отмеченную точку
в х0, ставится в соответствие сфероид
а> fVa
“#(/): S"-*S"VZ-------► X
Легко проверить, что а#(/ + g) ~а#(/) + a#(g) и что (а-1)# = (а#)-1- Ясно
также, что при л = 1 изоморфизм а# совпадает с изоморфизмом а#, построенным
в § 6.
Как мы видели на примере случая л = 1, изоморфизм а# может зависеть от пути.
Если при данном и изоморфизм а# от а не зависит, то пространство X называется
п-простым. Из сказанного в § 6 следует, что 1-простота — зто коммутативность фун-
даментальной группы. Подчеркнем, что при л> 1 л-простота никакого отношения к
коммутативности фундаментальной группы не имеет.
Пространства, л-простые при всех л, называются простыми. Например, односвяз-
ные пространства просты.
Упражнение 2. Докажите, что любое //-пространство просто. (Ср. с упр. 9
к § 6.)
3. Гомотопические группы и иакрьпия.
Теорема 1. Если р: Т -> X - накрытие и л > 2, то р,: тгп(Т, х0) *
-> irn (X, р ( х0 ) ) есть изоморфизм.
Это следует из теоремы 4 § 7 (см. следствие из этой теоремы) и односвязности
сферы 5” с л > 2.
Теорема 1 может быть немедленно использована для вычисления гомотопических
групп у некоторых пространств. Например:
Теорема 2.
Z при п = 1,
О при л > 2.
Первое уже доказано (см. § 6), второе следует из того, что ввиду существования
накрьггия R -> 51 группа я„(№) сл> 2 изоморфна я„(И), а прямая R стягиваема.
^(S1) = (
§ 8. ГОМОТОПИЧЕСКИЕ ГРУППЫ
65
Упражнения. 3. Докажите, что если
В — букет любого числа окружностей, то
1г„ (В) = 0 при и > 2. [Для доказательства
нужно построить универсальную накрываю-
щую над В и убедиться в том, что она стягива-
ема. Универсальная накрывающая над буке-
том двух окружностей изображена на рис. 49.]
4. Докажите, что если X есть связная
классическая поверхность, отличная от S1 2 3 и
RP2, то я„ (X) = 0 при и > 2. [Прежде всего
докажите, что если поверхность имеет непу-
стой край, то она гомотопически эквивалент-
на букету окружностей, так что в этом случае
можно воспользоваться предыдущим упраж- •
нением. Для поверхностей без края можно 49
рассуждать двумя способами. Первый состо-
ит в явном построении над X универсальной
накрывающей, которая оказывается гомеоморфной плоскости. (Подробности см.
в § 20 части II первого тома ’’Современной геометрии” Дубровина, Новикова
и Фоменко.) Другой способ состоит в использовании неуниверсальных накры-
вающих. Именно, пусть X есть поверхность Y с ручкой (из нашего поля зрения
выпадает случай бутылки Клейна, но этот случай тривиален: бутылка Клей-
на двулистно накрывается тором, а универсальной накрывающей над тором,
как нам уже известно, является плоскость). Рассмотрим бесконечнолистное
накрытие Х-> X, изображенное на рис. 50. В силу теоремы 1 пп(Х) « я„(Х). Далее,
ввиду компактности сферы любой сфероид Sn -> X покрывается конечным числом
кусков, на которые поверхность X разбита на рис. 50. Но объединение этих кусков
есть классическая поверхность с непустым краем, и потому наш сфероид стягива-
ется в точку в этом объединении, а значит, и в X.}
4. Относительные гомотопические группы. Пусть (X, А) — пара с отмеченной
точкой х0 G А. Фиксируем и > 2. Относительная гомотопическая группа
пп(Х, А; х0) определяется как множество гомотопических классов п-мерных отно-
сительных сфероидов. Относительные сфероиды (как и абсолютные1)) определя-
ются двумя способами: с помощью шаров и с помощью кубов. Шаровой относитель-
ный сфероид — зто отображение Dn ->Х, загоняющее Sn~ 1 CD"bA и переводящее
Рис. 50
отмеченную точку у0 G Sn 1 С Dn в х0 (рис. 51). Кубический относитель-
ный сфероид — зто отображение In -> X, загоняющее в А границу ЗУ" и переводя-
щее в х0 часть ЗУ” — 1п~1 этой границы.
Относительные сфероиды называются гомотопными, если они гомотопны в классе
относительных сфероидов. Сумма f + g (кубических) относительных сфероидов
1) В отличие от относительных гомотопических групп и относительных сфероидов изучавшие-
ся выше гомотопические группы и сфероиды называют иногда абсолютными.
3 А.Т. Фоменко
66
ГЛ 1. гомотопии
f,g определяется формулой
(/+»)(*..*.......х„) = | Я2"1-*=........еига
I g(2x! - 1,х2(... ,х„), если Х1 >1/2.
Ясно, что если и g ~ g , то f + g ~ f' +g'; следовательно, наша операция ин-
дуцирует некоторую операцию в множестве я„ (X, А; х0 ).
Упражнения. 5. Проверьте для ял(Х, А; х0) выполнение групповых акси-
ом; покажите, в частности, что нулем группы ял(Х, А; х0) служит класс любого
относительного сфероида f : I” -+Х, для которого f(In)CA.
Рис. 51
6. Покажите, что при л > 3 группа ял(Х, А; х0) коммутативна.
7. Найдите относительный аналог упражнения 1.
Если {X, А), (У, В) - пары с отмеченными точками х0 G А, у0€ В, то непрерыв-
ное отображение /: Х-> У, такое, что f(A) С В и /(х0) =у0 (пишут /: {X, А, Хо)-*
-> (У, В, у0)) индуцирует гомоморфизмы ял(Х, Л; х0) ->я„(У, В; у0). Гомо-
топные отображения индуцируют одинаковые гомоморфизмы, в частности, у гомо-
топически эквивалентных пар гомотопические группы одинаковы.
Зависимость групп irn(X, А; х0) от отмеченной точки аналогична зависимости
от отмеченной точки абсолютных гомотопических групп: путь а: 7 А, соединяю-
щий х0 е Л с х, е Л, индуцирует изоморфизм а#: п„(Х, А; х0) ->ял(Х, А; хх).
5. ’’Гомотопические группы” я0 (X, х0) и Я1(Х, Л; х0). Определение множеств
ял(Х, х0) и ял(Х, Л; х0) сохраняет силу, если взять в первом случае л = Оиво вто-
ром случае л = 1. В частности, я0(Х, х0) есть множество компонент линейной связ-
ности пространства X (множество Я1 (X, Л; х0) не имеет столь прозрачного смысла).
Однако в множествах я0(Х х0) и Я1(Х Л; х0) отсутствует естественная групповая
структура (для я0(Х х0) это вытекает из результатов § 4, дляя1(Х Л; х0) читатель
докажет это сам). Впрочем, в этих множествах имеется выделенный элемент — ’’еди-
ница”; это — класс постоянного сфероида 5° ->х0 G X или!)1 ->х0 G X.
Хотя я0(Х х0) и Я1(Х Л; х0) - не группы, не стоит их полностью игнорировать.
Например, утверждение ’’пространство X л-связно тогда и только тогда, когда
я/(Х) = 0 при i < л” при л = 0 ничуть не хуже, чем при л > 0 (равенство я0(Х) = О
означает, что множество я0(Х) состоит из одного элемента, т.е. что X линейно связ-
но) . Более того, мы наберемся смелости сказать, что хотя обозначение я_| (X) не
имеет уж совсем никакого смысла, термин (—1)-связность осмыслен и означает
непустоту (всякое отображение ф -+Х продолжается до отображения ♦ ->-Х). Мож-
но сказать, что я.^Х) — не группа и даже не множество, но может бытья_1(Х) =0
(X непусто) и ff_j(X) ¥= 0 (X пусто). Все это кажется пустословием, но все же
проясняет аналогию, которая подчас имеет место между доказательством существо-
вания, скажем, отображения какого-нибудь типа или решения какого-нибудь урав-
§ 8. ГОМОТОПИЧЕСКИЕ ГРУППЫ
67
нения (вычисление ’’группы я./’) и описанием множества гомотопических классов
этих отображений или решений (вычисление ’’группы я0”).
6. Связи между относительными и абсолютными гомотопическими группами.
Во-первых, абсолютные гомотопические группы - частный случай относительных го-
мотопических групп. Именно, тгп(Х х0) = яп(Х хо; хо) при и > 1.
Во-вторых, относительные гомотопические группы - частный случай абсолютных
гомотопических групп. Именно, по паре (X, А) с отмеченной точкой х0 G А канони-
чески строится некоторое пространство Y с отмеченной точкой у0, такое, что
ir„(X,A; х0) = 1 (Y, Уо) при п > 1. Это равенство объясняет, по чему п„(Х, А; х0)
есть группа только при и > 2и есть коммутативная группа только при и > 3. Опи-
сание пространства Y мы отложим до следующего параграфа.
В-третьих, имеются естественные гомоморфизмы irn(X, х0) А; х0). Эти
гомоморфизмы можно описать при помощи замечания, что всякий абсолютный сфе-
роид (У", ЭУ") -> (X, х0) можно рассматривать как относительный сфероид
(У", ЭУ", Ъ1п — У"-1) -> (X, А, х0); можно сказать также, что эти гомоморфизмы
совпадают с /,, где j есть тождественное отображение Х^ X, рассматриваемое как
отображение (X, х0) -> (X, А).
Упражнение 8. Докажите, что образ гомоморфизма/,: тг2(Х х0)
-> ir2(X, А; х0) лежит в центре группыя2(X, А; х0).
В-четвертых (ив самых важных!) имеются’’связывающие гомоморфизмы”
Э: яп(Х,/1;хо)^я„_1(Л,хо).
Гомоморфизм Э относит классу относительного сфероида f : (1п, д/п, д/п — 1п~1) -►
-> {X, А, х0) класс абсолютного сфероида /| п-1: (У"-1, ЭУ"-1) -> (А, х0); иначе
говоря, $ относит классу сфероида ft (Dn, Sn~l, у0) -> (X, А, х0) класс сфероида
7. Гомотопическая последовательность пары. Так называются последовательность
i • / * э
• • • "*• ^„(Л, х0) -> я„(Х х0) —> Я„(Х, А, х0) *
а /, а /,
-*• wn_i(4,x0) Я!(ХЛ;х0) я0(Л,х0) —> я0(Хх0),
в которой /, и Э — только что описанные отображения,а г,— отображение,индуци-
руемое включением г: А ->X.
Главное свойство этой последовательности заключается в том, что она точна, те.
ядро каждого входящего в нее отображения совпадает с образом предшествующего
отображения (для трех последних стрелок ’’ядро” — это прообраз отмеченной точки).
Доказательство точности. (Мы советуем читателю провести это дока-
зательство самостоятельно.) (1) Кег/,Э Im г,. Действительно, для любого сфероида
ft 1п -> А сфероид i ° f: 1п •+ X определяет нулевой элемент группы я„(Х Л; х0),
поскольку его образ содержится в А — см. упражнение 5. (2) Кет/,С Imz,. Пусть /:
In -> X - сфероид пространства X, представляющий элемент из Кет/,, и пусть Ft
In X.I -+Х - гомотопия, соединяющая f с постоянным отображением в классе отно-
сительных сфероидов пары X, А; очевидно, F есть отображение куба У"+1 в X, совпа-
дающее на грани х„ + 1 = 0 с f, отображающее грань хп = 0 в А и отображающее остав-
шуюся часть границы ЭУ" + 1 в х0; пусть У" СУ"+1 — сечение кубаУ”+1 плоскостью
txn + (1 - 7)x„+i = 0 (см. рис. 52); ясно, что У" « У" и 4toF| 1”=1п-+Х есть
гомотопия, связывающая (в классе абсолютных сфероидов пространства X) сферо-
ид f со сфероидом, образ которого содержится в А. (3) КегЭ Э Im/,. Действитель-
3*
68
ГЛ. 1. ГОМОТОПИИ
но, если f: 1п *X — абсолютный сфероид, то есть постоянное отображение.
(4) КегЭ С Im/,. Пусть /: 1п-+Х— относительный сфероид, и пусть gt: I"-1 -+А —
гомотопия, связывающая абсолютный сфероид /| л-1 пространства Л с постоян-
ным сфероидом; рассмотрим гомотопию ft: Ъ1п -*• X, совпадающую с gt на Z"-1
и переводящую Э/" ~/"-1 в х0, и распространим ее (пользуясь теоремой Борсука)
до гомотопии ht: 1п -+Х сфероида /; очевидно, ht есть гомотопия, соединяющая f
в классе относительных сфероидов с постоянным сфероидом. (5) Кеп, Э 1шЭ.
Если абсолютный сфероид f: 1п 1 -> А является сужением относительного сферои-
да g: In X, то gt =g| и-1 : /”-1 X t -In~l -+Х есть гомотопия, связывающая
в X сфероид f с постоянным сфероидом. (6) Keri, С 1тЭ. Если gt: 1п~1 -> X
есть гомотопия, связывающая (в X) сфероид f = go' Z”-1 ->Л с постоянным сфе-
роидом, то g: 1п X, g(xlt..., хп) = gXfl (*i,хп-1), есть относительный сфе-
роид пары (X, А), сужение которого на Л есть /.
Упражнения. 9. Определите естественное (правое) действие группы Я1 (X, х0)
в множестве iri(X, Л; х0) и заметьте, что орбиты этого действия совпадают с Э-про-
образами элементов множества я0(Л, х0). (Другими словами, точность в члене
Я1(Х, Л; х0), пограничном в гомотопической последовательности между множест-
вами и группами, носит групповой характер.)
. 10. Пусть (X, А, В) — тройка с отмеченной точкой х0 G В. Докажите точность
’’гомотопической последовательности тройки”
пп(А,В,х0) -> 1гп(Х,В,х0) -> я„(ХЛ,х0) * я„_1(Л,В,х0) -* • • •
(в этой последовательности гомоморфизмы, сохраняющие размерности, индуциру-
ются включениями пар (Л, В) -> (X В) -> (X, А), а ’’связывающий гомоморфизм”
я„(Х Л, х0) я„_1(Л, В, х0) определяется как композиция я„(Х, А, х0) ->
э /.
->я„(Л,х0) * я„(Л,5,х0)).
8. Следствия точности. Если противное не оговорено, то рассматриваемые после-
довательности предполагаются последовательностями групп и гомоморфизмов. Три-
виальная группа (состоящая из единичного элемента) обозначается символом 1,
но в ситуации, когда все рассматриваемые группы являются абелевыми, она обозна-
чается символом 0.
§ 8. ГОМОТОПИЧЕСКИЕ ГРУППЫ
69
ч>
Упражнения. 11. Последовательность 1 ->• А * В точна тогда и только тогда,
ч>
когда ч> есть мономорфизм; последовательность А -> В 1 точна тогда и только
тогда, когда «р есть эпиморфизм; таким образом, последовательность 1 -* В -* 1
точна тогда и только тогда, когда есть изоморфизм.
У ф
12. Последовательность 1 -> А -+В -* С->1 (последовательности такого вида на-
зывают ’’короткими”) точна тогда и только тогда, когда «р есть мономорфизм,
С5» В/у (А) и 0 есть естественная проекция.
Следствия. Если А стягиваемо, то я„(Х) «« я„(Х А) (точнее, j, есть изо-
морфизм) при п > 1; если X стягиваемо, то яп (X, А) -1 (^) (точнее, Э есть
изоморфизм) при п > 1; если А есть деформационный ретракт в X, то irn(X, А) = О
при п > 1.
Упражнения. 13. Если А есть ретракт (не обязательно деформационный)
пространства X, то (при всех л)
г,: я„(Л)->я„(Х) есть мономорфизм,
ir„(X) * ir„(X, А) есть эпиморфизм,
Э: тгп(Х, А)->-тг„_1(А) есть нулевой гомоморфизм
и Пп(Х) = п„(Х,А)еяп(А).
14. Если А стягиваемо по X в точку, то
irn(X)-+пп(Х, А) есть мономорфизм,
Э: яп(Х,А)-+ я„_1(Л) есть эпиморфизм,
I,: irn(A)-+irn(X) есть нулевой гомоморфизм
и яп(Х,А) = 1гп(Х)9-пп_1(А).
15. Если существует гомотопия ft: X -> X, загоняющая X в А, т.е. такая, что
/о = id и /1 (X) С А, то
Э: ir„(X,A) -> яи_1(А) есть мономорфизм,
г,: irn(A) -> я„(Х) есть эпиморфизм,
irn(X) -> яп(Х, А) есть нулевой гомоморфизм
и ir„(A) = яп(Х) ® я„ +! (X, А).
16. (”5-лемма”). Если в коммутативной диаграмме
At -+А3 ~^А4 -+As
Iv, lv4 4.ps
Bi ~^В4 ->В5
с точными строками отображения >Pi, >Р2 и <р4, <р5 являются изоморфизмами, то
и <р3 — изоморфизм.
17. Из 8 предположений 5-леммы (‘р1 ,Ч>2,4>4,4>s — мономорфизмы, Ч>1 > Ч>2,
<р5 - эпиморфизмы) для доказательства мономорфности отображения <р3 требуется
только 3, для доказательства его эпиморфности — другие 3 (какие?). Два остав-
шихся предположения являются, таким образом, вообще лишними.
18. Если, сохранив все предположения 5-леммы, исключить из ее диаграммы стрел-
ку <р3, будет ли верно, что А 3 « Дз?
Следствие. Пусть (X, А), (Y, В) - топологические пары с отмеченными точ-
ками xQ G А, у0 € В, и пусть f: X-+Y - такое непрерывное отображение, что f (Л) С
70
ГЛ. 1. ГОМОТОПИИ
С В и f(x0) = у0. Тогда любые два из следующих трех утверждений влекут за собой
третье:
(i) я„(Х х0) * nn(Y, у0) есть изоморфизм при всех п.
(ii) ( f | А ) ,: я„ (А, х0) -> (В, у0 ) есть изоморфизм при всех п.
(iii) Д; яи(Х А;х0) -*• я„(У, В; Уо) есть изоморфизм при всех п.
Упражнение 19. Пусть
1 А1 ->••• -+А„ 1
— точная последовательность. Докажите, что если группы At конечны на; — их по-
рядки, то Е(—1)’а/ = 0, а если At — конечнопорожденные абелевы группы и —
их ранги, то Е(—1)/Г/ = 0.
§ 9. РАССЛОЕНИЯ
В § 7 мы рассматривали накрытия, локально устроенные как произведения на
дискретное пространство D. Накрытия являются частным случаем расслоений, кото-
рым посвящен этот параграф (и многие последующие).
Главное отличие расслоений от накрытий состоит в том, что дискретное простран-
ство!) заменяется произвольным топологическим пространством F.
Можно сказать, что расслоения в той же мере приспособлены к изучению гомото-
пических групп, в какой накрытия приспособлены к изучению фундаментальной
группы, но справедливости ради следует заметить, что понятие расслоения само по
себе по крайней мере не менее важно, чем понятие гомотопической группы.
1. Определения. Расслоением, или локально тривиальным расслоением, называ-
ется четверка (Е, В, F, р), где Е, В, F — пространства, ар — отображение Е~*В, при-
чем любая точка х G В обладает такой окрестностью UC В, что р-1(С7) « и У F-,
более того, существует гомеоморфизм <р: р-1(!/) иУ F, замыкающий коммута-
тивную диаграмму
p~l(U) —^—~U*F
проекция
U
Отображение р называется проекцией, пространства Е, В и F — соответственно
тотальным пространством, базой и слоем расслоения. Иногда расслоением называют
само отображение р: Е -> В. Употребляется также термин ’’расслоенное простран-
ство” — так называют пространство Е. Прообраз р-1(х) точки х€Е В называют слоем
над точкой х; очевидно, этот слой гомеоморфен F, но канонический гомеоморфизм,
вообще говоря, отсутствует.
Расслоение р: Е^В называется тривиальным, еслиЕ« В XF и диаграмма
B*F
проекция
Б
коммутативна.
Примеры расслоений. 0°. Тривиальные расслоения.
1°. Накрытия.
2°. Проекция ленты Мёбиуса на ее среднюю линию (окружность) .Слой этого рас-
слоения — отрезок. (Пожалуй, это — самый популярный пример нетривиального
расслоения.)
§ 9. РАССЛОЕНИЯ
71
3°.E = S3 = {(zljZ2)i ZjZj + z2z2 =1} CC2, B = S2 = CPl, p(.zi,z2) = (zr-Z2),
Р=8*.
Упражнения. 1.Покажите, что (Е, В, F, р) — расслоение. (Это расслоение
называется расслоением Хопфа.) Покажите, что расслоение Хопфа нетривиально.
2. В § 1 вводилось естественное отображение S2n+1 -*СР". Обозначив зто отобра-
жение через р, покажите, что (S2n+1, СР", S1, р) — расслоение. (Это расслоение
обобщает предыдущее расслоение и иногда также называется расслоением Хопфа.)
4°. Пусть G — группа, Ли, Н - ее компактная подгруппа и р: G -* G/H - естествен-
ная проекция.
Упражнение 3. Покажите, что (<7, G/Н, Н, р) — расслоение. Заметьте, что
расслоение (У3, СР1, S1, р) из предыдущего примера является частным случаем
этого расслоения.
5°. Обобщение этого примера: компактная группа Ли G гладко действует (с точ-
ки зрения дальнейшего удобно считать, что справа) в многообразии X.
Упражнение 4. Если действие свободно, то (X, X/G, G, р) ,гдер- естествен-
ная проекция X Х/G, есть расслоение. Заметьте, что расслоение из упражнения 2
является частным случаем этого расслоения.
6° . Пусть X, Y — гладкие компактные многообразия и /: X -* Y - субмерсия, т.е.
отображение, дифференциал которого в каждой точке зпиморфен.
Упражнение 5. (X, Y, /-1(уо), /) есть локально тривиальное расслоение.
[Указание: см. рис. 53.]
2. Накрывающие гомотопии. Расслоения, как и накрытия, обладают свойством
накрывающей гомотопии (сокращенно СНР - от covering homotopy property).
Вот точная формулировка.
Теорема о накрывающей гомотопии. Пусть (Е, В, F, р) - ло-
кально тривиальное расслоение, Z — клеточное пространство, g: Z -+Е - произволь-
ное непрерывное отображение и G: Z X I -* В — гомотопия, такая, что G| ^хо =
= p°g. Тогда существует гомотопия G: Z XI -*Е, такая, что G| zxo =g и р° G = G.
Мы будем доказывать эту теорему в более сильной, относительной, формулиров-
ке. Дополнение заключается в том, что если на клеточном подпространстве Z' С Z
уже задана гомотопия G1: Z1 X/ ->Е, такая, что G’ I ~.vn = и р ° G1 = G| vr,
X U L Ax
то гомотопию на всем Z можно построить так, чтобы на Z1 она совпадала с G1.
Доказательству теоремы мы предпошлем два определения и лемму.
Определение 1. Пусть $ = (Е, В, F, р) - расслоение, и пусть В1 СВ, Е1 =
= р~1(В>). Локально тривиальное расслоение (Е1, в', F, р'), где р': Е' -*В' — су-
Рис. 53
Рис. 54
72
ГЛ. 1. ГОМОТОПИИ
жение отображения р, называется сужением расслоения % на В' и обозначается че-
рез $|в..
Определение 2. Пусть £ = (Е, В, F, р) - расслоение, и пусть /: В ’ ~>В —
непрерывное отображение. Обозначим через Е' подмножество произведения ЕХВ',
составленное из таких точек (е, b'), что р(е) = f(b'}. Определим, далее, отобра-
жение р': Е' -* В1 формулой р(е, b') = о . Локально тривиальное расслоение
(Е1, В', F, р') называется индуцированным расслоением $ посредством f и обозна-
чается через /*$.
Пояснение. Очевидно, р'-1(У) = р-1 (/(&')) — подразумевается канони-
ческий гомеоморфизм, устанавливаемый отображением Е' -* Е, (е, b') »-* е. Это
позволяет сказать, что пространство Е' сделано из слоев расслоения £ над точками
f(b'), где b' пробегает В1. Если несколько точек пространства В1 отображаются в
одну точку пространства В, то слой расслоения % над этой точкой берется соответ-
ствующее количество раз.
Упражнение 6. Докажите, что локально тривиальное расслоение (£', В1,
F, р), для которого существует непрерывное отображение Е' -*Е, гомеоморфно
отображающее слой над точкой b' G В на слой над точкой f (&'), эквивалентно
f*%. (Эквивалентность локально тривиальных расслоений определяется дословно
так .же, как эквивалентность накрытий.)
Лемма (теорема Фельдбау). Всякое локально тривиальное расслоение
(Е, В, F, р) с В = I4 (q-мерный куб) тривиально.
Доказательство теоремы Фельдбау проводится в два шага.
Первый шаг. Положим
/? = {(Хь.-.х,) G I4\ xq< 1/2},
If = {(X1,...,Xg) е i4\Xq > 1/2}.
Покажем, что если сужение нашего расслоения на If и If тривиальны, то и все рас-
слоение тривиально. Пусть рх: Ех ->If, р2. Ег -* If - сужения; можно считать,
что Ег = If X F, Е2 = If Х-. F. Точка из Е\ имеет координаты (х, у), xG If, yGF.
Аналогично, точка из Е2 имеет координаты [х,у]. Если xG Iff1 = If п/’, то точка
(х, у) имеет также координаты [х, у']. Таким образом, для каждого xG
определено отображение fx: F-+F, fx(y) = у'. Определим проекцию п: IfIff1
формулой я(хь ... ,Xq) = (хь ..., Xq_ j, 1/2) и положим ^[х,^] = (х,/я(х) (у))-
Получается гомеоморфизм q>: Е2 X F, который вместе с уже имеющимся (тож-
дественным) гомеоморфизмом Et -* 14 XF составляет гомеоморфизм Е -+I4 X F,
очевидно, удовлетворяющий условию из определения тривиального расслоения.
Первый шаг завершен (см. рис. 54).
Второй шаг. В силу локальной тривиальности расслоения куб I4 можно
разрезать на маленькие кубики, над каждым из которых расслоение тривиально.
Занумеруем эти кубики в последовательность /9(1),..., I4 (N), таким образом,
что при каждом / существует гомеоморфизм U(J) -* I4, где U(j) =
гомеоморфно отображающий U(j — 1) и I4(j) на If и If. После этого, применяя
доказанное на первом шаге утверждение, мы последовательно доказываем триви-
альность нашего расслоения над U(j), j =1.У,в частности U(N) = I4.
3. Доказательство теоремы о накрывающей гомотопии.
Первый случай: данное расслоение тривиально. В этом случае, считая, что
Е = В X F, мы отождествляем отображения в Е с парами отображений в В и в F.
Отображение g и гомотопия G' делаются парами (g = G|zx 0, й: Z -* Е) и
§ 9. РАССЛОЕНИЯ
73
(<7| z<x/, Н’: Z' X /-*F), а то, что мы должны построить, — парой, первый элемент
которой нам уже известен — зто G, а второй есть гомотопия Н: Z X I -* F отобра-
жения h, продолжающая Н'; существование Н прямо следует из теоремы Борсука.
Второй случай: расслоение произвольно, Z = Dk, Z' = Sk~1. Расслоение
G*(E, В, F, р) = (Е1, Dk X I, F, р') тривиально в силу теоремы Фельдбау (Dk XI *
» 1к* *). Напомним, что Е' С (Dk X I) X Е, и обозначим через естественное отоб-
ражение Е' -*Е. Отображение h: Dk -*Е1, й(х) = ((х,0), g(x)) и гомотопии#:
Dk X I -+Dk XI (тождественная) и Й': Sk~l X I ->Е', Н'(х, t) = ((х, t),G'(x, t))
удовлетворяют требованиям теоремы о накрывающей гомотопии, и в силу дока-
занного ранее существует гомотопия Н: Dk X I -* Е' отображения й, накрываю-
щая Н и продолжающая Н'. Ясно, что G = <р ° Н: Dk XI -*Е есть гомотопия отобра-
жения g, накрывающая G и продолжающая G1.
Третий случай: расслоение произвольно, пространство 2конечно. Очевид-
ная индукция позволяет считать, что Z — Z' есть одна клетка е; пусть f: Dk ->Z -
соответствующее характеристическое отображение. Отображение h = g of: Dk -> E
и гомотопии H = G ° (fXI): Dk X I В, Й' =G'o (/| fe_i XI): Sk~l XI-+E
удовлетворяют условиям теоремы о накрывающей гомотопии, и в силу доказанного
ранее существует гомотопия Н: Dk X I -+ Е отображения h, накрывающая Н и про-
должающая Н'. Нужную гомотопию G: Z XI ->Е мы определим на Z1 XI как совпа-
дающую сG' ина е XI формулой
G(f(x),t) = H(x,t) при xGIntDfe.
Корректность определения очевидна.
Четвертый случай: общий. Если Z имеет бесконечное число клеток одной
размерности, не лежащих в Z', то предыдущую конструкцию нужно применить
к ним всем одновременно. Если в Z — Z' содержатся клетки сколь угодно большой
размерности, то предыдущая конструкция применяется бесконечное число раз и не-
прерывность окончательной гомотопии G выводиться из аксиомы (W).
4. Расслоения в смысле Серра.
Определение. Расслоение в смысле Серра — это тройка (Е, В, р), где Е, В -
пространства и р — непрерывное отображение Е -* В, удовлетворяющее условию
СИР для клеточных пространств; другими словами, предполагается, что для лю-
бого клеточного пространства/ и любых отображения Z -* Ей гомотопии G: Z X
XI-+В, таких, что р^° g = G \ z хо> существует гомотопия G; Z X I -* Е’.для кото-
рой G\ z * 0=gvip° G =G.
Подчеркнем, что единственность накрывающей гомотопии не предполагается.
Расслоение в смысле Серра не обязательно является локально тривиальным рас-
слоением. Пример:
Упражнения. 7. Покажите, что расслоение в смысле Серра можно эквива-
лентным образом определить, сузив действие СНР случаем, когда Z есть куб (произ-
вольной размерности).
74
ГЛ. 1. ГОМОТОПИИ
8. Покажите, что расслоение с смысле Серра можно эквивалентным образом
определить, заменив формулировку СНР относительной формулировкой (см. отно-
сительную формулировку теоремы о накрывающей гомотопии).
Еще один вариант определения расслоения в смысле Серра (не эквивалентный
исходному) можно получить, заменив в СНР клеточное пространство Z произволь-
ным пространством Z. Получается определение сильного расслоения в смысле Сер-
ра или расслоения в смысле Гуревича.
П р и м е р ы. 1. Локально тривиальные расслоения.
2 (расслоение путей). Пусть У — произвольное топологическое пространство
с отмеченной точкой у0. Положим Е = E(Y, у0) (пространство путей простран-
ства У, начинающихся в точке у0), В = У и определим отображение р: Е -+ В как
относящее пути s G Е его конец s(l). Получаем (сильное) расслоение в смысле
Серра. В самом деле, пусть g:Z -> Е(У,у0) nG:Z X I -* У — отображение и гомо-
топия, удовлетворяющие посылкам СНР. Накрывающая гомотопия G: Z X /->
-+E(Y,y0) может быть задана формулой (см. рис. 55)
[g(z)](T(l + 0) при 7(1 + 7) <1,
G(z, т(1 +7) - 1) при 7(1+7) >1.
Заметим, что ’’слой” р'1 (у0) расслоения р есть не что иное, как пространство
петель П(У,у0).
[G(z,7)](t) =
3 (обобщение предыдущего примера). Пусть У — произвольное пространство,
(X, А) - пара Борсука (например, клеточная пара). Положим Е = С(Х, У) (про-
странство непрерывных отображений Х-* У), В = С(А, У) и определим отображение
р :Е ~*В формулой р (f) =f | А.
Упражнение 9. Покажите, что (Е, В, р) есть сильное расслоение в смыс-
ле Серра.
5. Слои. Уже из самого первого примера расслоения в смысле Серра (с. 73) видно,
что слои (прообразы точек) не гомеоморфны. Но все же оказывается, что у рас-
слоения в смысле Серра, как и у локально тривиального расслоения, слои в извест-
ном отношении сходны между собой.
Определение. Мы будем говорить, что пространство X слабо гомотопи-
чески эквивалентно пространству У, если для клеточных пространств Z имеет мес-
то равенство n(Z, X) = n(Z, У), естественное по Z. (Подробнее: для каждого кле-
точного пространства Z определено взаимно однозначное соответствие <pz:
w(Z, X) <—> w(Z, У), такое, что для любого клеточного Z и любого непрерывного
§ 9. РАССЛОЕНИЯ
75
отображения/: Z -*Zl коммутативна диаграмма
4>z- a(Z, X) «-> n(Z, У)
tr* t/*
ipz’- ir(Z’, X) it(Z', Y)
— ср. с определением 3 гомотопической эквивалентности из § 3.) '
Замечание. Клеточные пространства X, Y слабо гомотопически эквивалент-
ны тогда и только тогда, когда они гомотопически эквивалентны: берем X и Y в
качестве Z, получаем соответствия
а{Х,Х) = тг(X У), тг(У,Х) = тг(У, У);
классы тождественных отображений id^: Х->Х, idy: У-* У соответствуют некото-
рым элементам множеств тг(Х У), тг(У, X), представители которых — гомотопи-
чески взаимно обратные гомотопические эквивалентности. {Ср. доказательство
эквивалентности определений 1 и 2 гомотопической эквивалентности в § 3.)
Теорема. Если р : Е -* В - расслоение в смысле Серра и х0, Xi - точки из
одной компоненты линейной связности пространства В, то пространства р~' (х0),
р~1 (xj) слабо гомотопически эквивалентны.
Замечание. В случае сильного расслоения в смысле Серра слои гомотопи-
чески эквивалентны в обычном смысле; доказательство то же.
Доказательство. Положим р~1 (х0) = F0,p~1(xi) =F\ и зафиксиру-
ем непрерывное отображение й0: 2 Fo, где Z — клеточное пространство. Зафик-
сируем также путь s: I В, соединяющий х0 с xt. Рассмотрим отображение g =
= /0 ° ft0:Z-*£, где i0 - включение р"1^) в Е, и гомотопию G: Z XI ->В,
G{z, t) = s В силу СНР существует гомотопия G: Z X I -*Е отображения g, та-
кая, что р о G = G, т.е. G(Z X t) Ср" 1 (s(f)). В частности, G(Z X 1) СГ1; ввиду
чего возникает отображение hx: Z ~*РГ. Мы покажем, что гомотопический класс
этого отображения не зависит от выбора накрывающей гомотопии, так что сопо-
ставление h0 ht корректно определяет отображение w(Z, Fo) ->tt(Z, Ft). Более
того, мы покажем, что этот гомотопический класс не меняется при замене пути
гомотопным путем.
Пусть s' - другой путь, соединяющий х0 с х1У и G': Z XI -*В, G’.ZXI ->Е и
h\-.ZFi — гомотопии и отображение, построенные при помощи пути s' так же,
как гомотопии G, G и отображение ht были построены при помощи s. Предполо-
жим, что пути s и s' гомотопны, фиксируем гомотопию S: I X I -+В между ними
и рассмотрим гомотопию Т: I X I -+ В, определяемую формулой T(tt, t2) =
= S(t2, ti). Таким образом, Тесть гомотопия, начальное отображение которой есть
отображение I -> х0 G В, промежуточное отображение есть путь, соединяющий s (?)
с а конечное отображение есть I -* xt & В (см. рис. 56). Рассмотрим, далее,
76
ГЛ. 1. ГОМОТОПИИ
гомотопию G*: (Z X Г) X 1 -*В, определенную формулой G*(z, ty, t2) = T(ty, t2)
и отображение £”*: Z XI -+E, определенное формулой g *(z, tt) = g'(z^. В силу от-
носительного варианта СНР (см. упражнение 8) существует гомотопия G*: (Z XI) X
X I -* Е отображения g'*, накрывающая G* и совпадающая с G на (Z X 0) X I и с
G' на (Z X 1) XI. Конечное отображение этой гомотопии, (z, Z) »->G*(z, t, 1), отобра-
жает Z X I в Fj и представляет собой гомотопию, связывающую отображения Aj и
h\ (см. рис. 57).
Таким образом, путь s.I->B корректно определяет отображение <ps: it(Z,
p~l (s (0))) -* tt(Z, p~ 1 (1))), зависящее только от гомотопического класса пути s.
Добавим, что очевидно, отображение <ps естественно по Z, постоянному пути s:
I -+ (точка) G В отвечает тождественное отображение ips и произведению путей от-
вечает композиция отображений: tpSls2 ~ 4>s2 ° iPsl- Это позволяет завершить до-
казательство: отображения и взаимно обратны и, таким образом, есть
взаимно однозначное соответствие.
6. Любое отображение гомотопически эквивалентно расслоению с смысле Сер-
ра. Пусть даны два непрерывных отображения:/: X Y и g : Ху -* Yy. Мы будем
говорить, что отображения / и g гомотопически эквивалентны, если существуют
гомотопические эквивалентности у: Ху ->Х,^: Yy -* У, такие, что диаграмма
Ху Yy
Ф р . 4 $
X Y
гомотопически коммутативна (/ ° <р ~фо g).
Теорема. Для любого непрерывного отображения f: X * У существует (силь-
ное) расслоение в смысле Серра, р: Ху + Yy, гомотопически эквивалентное этому
отображению.
Дополнение. Как видно из приводимой ниже конструкции, пространство
Yy можно выбрать совпадающим с У и гомотопическую эквивалентность ф: Yy ->
-* У из предыдущего определения можно сделать тождественной. Еще одна особен-
ность конструкции состоит в ее естественности: по отображению /: X -> У канони-
чески строятся расслоение p(f) .Ху -* У и гомотопическая эквивалентность ip(f) :
Ху -+Х с f ° у (f) ~p(f) и по коммутативной диаграмме
a I f" pl
X1 Y1
- коммутативные диаграммы
1р(Л 1р(Г’)
Доказательство теоремы. За Ху мы принимаем пространство пар
(х, s), где X, a s есть путь пространства У, начинающийся в точке f(x). Рас-
слоение p(f) .Ху -* У и гомотопическая эквивалентность ip(/): Ху -*Х определяют-
ся формулами [р(/) ] (х, s) =$(1) и [ip (f) ] (х, s) =х.
Замечание. Доказанная теорема двойственна (в смысле двойственности § 4)
совсем простому утверждению: для любого непрерывного отображения /: X -> У
существует вложение i: Х2 -+ У2, гомотопически эквивалентное этому отображению
§ 9. РАССЛОЕНИЯ
77
(более того, обладающее тем свойством, что (У2> »’(^г)) — паРа Борсука). Доказа-
тельство: в качестве Х2 берем X, а в качестве У2 — цилиндр Су1(/) отображения/,
в качестве i — естественное вложение. Ввиду указанной двойственности пространст-
во Xi, построенное в предыдущем доказательстве, называют иногда коцилиндром
отображения /.
7. Гомотопическая последовательность расслоения.
Лемма. Пусть (Е, В, р) - расслоение в смысле Серра,еСЕ - произвольная
точка. Положим b = р(е), F = p~1(b). Тогда отображение
Р*- Ttn(.E,F,e) -+ п„(В,Ь)
является изоморфизмом при всех п.
Доказательство мономорфности р,. Пусть/ : Dn относи-
тельный сфероид пары (Е, F) wft '. Sn -* В — гомотопия сфероида /: S" -*В, полу-
чающегося из / проектированием, превращающая его в постоянный сфероид Sn -* Ъ.
Гомотопию ft можно рассматривать как гомотопию отображения р ° f: D” -+ В и,
применяя к этой гомотопии и отображению f СНР, мы получим гомотопию, соеди-
няющую / в классе относительных сфероидов со сфероидом, отображающим Dn
в F (строго говоря, мы должны пользоваться относительным вариантом СНР, чтобы
обеспечить неподвижность гомотопии на отмеченной точке). Таким образом, элемент
группы 7Г„ (Е, F, е), переходящий в 0 при отображении р,, сам равен 0.
Доказательство зпиморфностир,. Пусть <pt: Sn~1 -+Sn - гомо-
топия, заметающая сферу S", которая при п = 2 устроена как показано на рис. 58,
и при произвольном п строится аналогичным образом (эта гомотопия нам еще раз
понадобится ниже). Пусть, далее, /: Sn -> В — сфероид. Рассмотрим гомотопию
/ о ipt: Sn~l -*В и поднимем ее, используя СНР, до гомотопии gt: Sn ~1 -+ Е отобра-
жения Sn ~1 -> е G Е, неподвижной на отмеченной точке. Эту гомотопию можно рас-
сматривать как отображение Dn -* Е (шар Dn покрывается (и — 1)-мерными сфера-
ми, как показано на рис. 59, и на этих сферах задаются отображения gt). Последнее
есть относительный сфероид пары (Е, F), проектирующийся в исходный сфероид /.
Заменим теперь в гомотопической последовательности пары (Е, F) группы
пп(Е, F) изоморфными им группами пп(В). Получится точная последовательность
• • •-*• пп(Г,е) -* пп(Е,е) -* itп(В,Ь)->
-* w„_i(F,е) -* ...->• ito(F,e) -+ п0(Е,е) -* п0(В,Ь),
составленная из одних лишь абсолютных гомотопических групп. Эта последова-
тельность называется гомотопической последовательностью расслоения (Е, В, р).
Vi/е
Рис. 58
Рис. 59
78
ГЛ. I. ГОМОТОПИИ
Замечания. 1. В гомотопической последовате-
льности расслоения не только группы, но и гомомор-
физмы могут быть описаны без привлечения относи-
тельных гомотопий. Именно, гомоморфизмы я л (F) -*
-* irn(E) индуцируются (как и в последовательности
пары) включением F -+ Е, гомоморфизмы кп(Е) -*
-* Я„ (В) индуцируются проекцией р: Е -+ В, а го-
моморфизмы п„ (В) -> лп_1 (F) можно опи-
сать при помощи гомотопии <pt: Sn ~ 1 -* Sn, фи-
гурировавшей в доказательстве леммы. Имен-
но, если /: S" -* В — сфероид, то мы накрываем
гомотопию f о ipt-_ sn~1 -> В гомотопией gf:
Sn~ 1 -> Е, такой, что g0 (Sn~ *) = е пере-
водит отмеченную точку в е); тогда g1(S”-1)C
С F, и мы ставим в соответствие классу сфероида f класс получившегося сфероида
пространства F (см. рис. 60).
2. Последний член я0(В) гомотопической последовательности расслоения не полу-
чается из гомотопической последовательности пары, и точность в этом члене нужно
проверять отдельно. Вообще читателю стоит продумать смысл точности гомотопи-
ческих последовательностей в негрупповых членах: зти точности вполне содержа-
тельны и ниже будут использоваться.
8. Первые применения точности.
Упражнения. 10. Выведите из точности гомотопической последовательности
хопфовского расслоения (S3, S2, S1, р) (и информации о гомотопических группах
окружности - см. § § 6, 8), что (а) п2 (S2 ) = irt (S*) и (b) п„ (S3) = п„ (S2 ) при п>3.
Первый изоморфизм показывает, что n2(S2) = Z, откуда мы видим, наконец, что
сфера S2 не стягиваема. Второй изоморфизм выглядит особенно неожиданным
при п = 3 (подумайте, почему).
11. Проанализируйте гомотопическую последовательность накрытия; убеди-
тесь в том, что все следствия этой точности нам уже известны (см. § § 7,8).
12. Используя расслоение S°° + СР°° со слоем S1 и стягиваемость сферы S°°,
покажите, что п„ (СР°°) = 0 при л 2и т2 (СР“) s Z.
13. Используя ’’расслоение путей” из примера 2 в п. 4, покажите, что ял(122Г) а
= ял + ! (X) при любых Уи и > 0.
14. Если база расслоения Серра стягиваема, то включение (любого) слоя в то-
тальное пространство индуцирует изоморфизм гомотопических групп. Если база
расслоения связна и один из его слоев стягиваем, то проекция индуцирует изо-
морфизм гомотопических групп. (Как мы увидим в следующем параграфе, непре-
рывное отображение тогда и только тогда индуцирует изоморфизм гомотопических
групп, когда оно является слабой гомотопической эквивалентностью.)
15. Если все гомотопические группы базы и слоя конечны, то гомотопические
группы тотального пространства тоже конечны и их порядки не больше произведений
порядков соответствующих гомотопических групп базы и слоя. Похожее утвержде-
ние имеет место для конечной порожденное™ и рангов.
16. Покажите, что если расслоение (Е, В, р) обладает сечением (т.е. таким не-
прерывным отображением s: В -* Е, что р ° s = idB) или если слой является рет-
рактом пространства Е, то
^(Е1) s п„(В) ф nn(F).
§10. ТЕОРЕМА О НАДСТРОЙКЕ И ГОМОТОПИЧЕСКИЕ ГРУППЫ СФЕР
79
17. Покажите, что если слой расслоения (Е, В, р) стягивается в точку по Е, то
СВ) яп (Я) ® яя _!<£).
9. Заключение: исполнение обещания иэ § 8. В п. 6 § 8 мы обещали построить
по паре (X, А) пространство Y, для которого пп _ i (5Q = я„ (X, А). Теперь мы можем
это сделать.
Построим по включению А -> X гомотопически эквивалентное ему расслоение
Серра р': А’ -* X (см. выше) и обозначим через Y слой этого расслоения (над произ-
вольной точкой х0 е X) и через / — каноническую гомотопическую эквивалент-
ность А’ -* А. Мы предполагаем, что расслоение р' построено при помощи каноничес-
кой конструкции, так что, в частности, Y есть пространство путей пространства X,
начинающихся в точке х0 и кончающихся в А. Это наблюдение позволяет построить
каноническое отображение irn _ i (У) * пп (X, А): по сфероиду g: S" _ 1 -+ Y сфероид
G-. Dn = CSn~1 -+ X пары (X, А) определяется формулой G(s, t) = [#($)] (г), s 6
GSn ~1, t GI. Легко понять, что эти канонические отображения включаются в комму-
тативную диаграмму
... -* Л„(А') — пл(Х)-* —п^са')-* Л„.1(Х)— ...
II II
... -^ Л„(А)----► Л„(Х)—* Лл(Х,А) — Jt„.t(A)—► ...,
строки которой представляют собой гомотопические последовательности рас-
слоения р' и пары (X, Л). Из 5-леммы вытекает, что отображения ял_1(У)->
itn(X, А) являются изоморфизмами (впрочем, зто очевидно и непосредственно:
наше отображение взаимно однозначно уже на уровне сфероидов).
Таким образом, мы не только нашли обещанную абсолютную интерпретацию
относительных гомотопических групп, но и обнаружили еще одну связь между
гомотопическими последовательностями пары и расслоения.
§ 10. ТЕОРЕМА О НАДСТРОЙКЕ И ГОМОТОПИЧЕСКИЕ ГРУППЫ СФЕР
1. Основная теорема. Рассмотрим «/-мерный сфероид/: Sq -+ X топологического
пространства X (с отмеченной точкой). Отображение S/: SS9 = Sq + l -> SX,
S/(y, = 0s является (q + 1)-мерным сфероидом пространства SX. Ясно,
что если сфероиды /, g’. Sq -* X гомотопны, то гомотопны и сфероиды S/,
Sg: Sq¥1 -+ SX. Легко проверить также, что сфероид S(/+g) гомотопен сфероиду
S/.+ Sg. Таким образом, сопоставление /»->• S/ порождает гомоморфизм nq(X) -+
-* я? + 1(2Х); последний называется гомоморфизмом надстройки и обозначается
через S. В частности, для любых q и п возникает отображение
S: jrq(S")-* 7rq + 1(S" + 1).
Теорема Фрейденталя. Гомоморфизм S: wq(SB)-> лч + 1(5п+1) яв-
ляется изоморфизмом при q<2n — 2 и эпиморфизмом при q = 2n — 1.
Это утверждение называют иногда ’’легкой частью” теоремы Фрейденталя. В чем
заключается ’’трудная часть”, мы расскажем ниже в этом параграфе. Упомянем
еще об одном обобщении теоремы Фрейденталя, которое мы сможем доказать толь-
ко во второй части книги: если X - произвольное клеточное пространство и П/(Х) =
= 0 при i <п,то S: тгч (X) -> (SX) есть изоморфизм при q <2п —2и эпимор-
80
ГЛ. 1. ГОМОТОПИИ'.
физм при q = 2п — 1. (Это - обобщение ’’легкой части”; ’’трудная часть” обобщает-
ся аналогичным образом-)
Доказательство эпиморфности S при q < 2и — 1. Пусть f:
Sq +1 -* S” +1, q < 2и - 1, — сфероид. Мы должны доказать, что существует такой
сфероид Л: Sq -+ S", что сфероид f гомотопен 2Л. Мы смело можем считать, что
п > 0, т.е. что сфера Sn + 1 односвязна, и это позволяет нам при построении гомо-
топий забыть про отмеченные точки.
Пусть а и b - полюса сферы S” +1. Сферу Sq +1 мы будем представлять себе как
R<? + 1 и оо, причем точку =° мы выберем таким образом, что f(°°)^a, f(°°)^b. Вос-
нове доказательства эпиморфности лежат следующие две леммы.
Лемма 1. Существует отображение f\: Sq + 1 -+ Sn+1, гомотопное f (и сколь
угодно близкое к f), такое, что f{*(a) и fil(b) - полиэдры размерности <q -п
в R, + 1 С + (Полиэдр размерности < к - это объединение конечного числа
выпуклых многогранников размерности < к.)
В основе доказательства этой леммы лежит конструкция, уже известная нам по
доказательству ’’леммы о свободной точке” (см. § 5) и теоремы о фундаменталь-
ной группе клеточного пространства (см. теорему 4 из § 6). Оставляя детали чита-
телю, перечислим основные этапы этой конструкции: (1) окружим каждую из точек
а, b пятью маленькими концентрическими шарами: a G др) С ... С В$b G
6 Др) С ... С Д^р (2) берем в R9 + 1 большой (но компактный) многогранник,
содержащий /-1(Др) U Др)); (3) триангулируем его настолько мелко, что если
/-образ симплекса задевает Др), то он содержится в В^\ (i = 1, 2, 3, 4; 7=1,2);
(4) обозначим через К объединение симплексов, /-образы которых пересекаются
с Др) U Др); (5) подправим отображение / на К, заменив его отображением //,
совпадающим с / на вершинах триангуляции и линейным на каждом симплексе
(подразумевается линейность по отношению к линейной структуре bR"+1 = S"+i -
— /(«>)); (6) ’’сошьем” />' с /, т.е. построим отображение /1; совпадающее с/вне
/-1 (Др) U Др)) и с // в/-,(Др) U Др)) и такое, что /х-образ дополнения
к /-1(Др) U Др)) не задевает Др) U дР) (это сшивание описано в § § 5 и 6 - см.
цитированные выше места). Итак, мы аппроксимировали отображение /отображе-
нием Л (которое, очевидно, ему гомотопно) с таким свойством: прообраз окрест-
ности каждой из точек а и b покрывается конечным числом симплексов, на каждом
из которых отображение линейно. Мы можем считать, что ни одна из точек а, b не
принадлежит /х-образу (д + 1)-мерного симплекса, имеющему размерность меньше
п + 1 (при необходимости можно сдвинуть точки а и b с ’’запрещенного множества”
при помощи гомеоморфизма сферы Sh +1, близкого к тождественному). Поскольку
прообраз точки при линейном отображении (q + 1)-мерного симплекса, имеющем
(и + 1)-мерный образ, есть < (q - л)-мерный выпуклый многогранник, отображение
/х удовлетворяет требованиям леммы.
Лемма 2. Пусть K,LC.RP — полиэдры размерностей < к и < I соответственно.
Если k + l + 1 <р,то к и1не зацеплены. Это означает, что существует изотопия (гомо-
топия тождественного отображения, составленная из гомеоморфизмов) Ft: Rp ->
-+ Rp, такая, что Fi(K) и Ft (L) разделяются в Rp гиперплоскостью.
Доказательство. Проведем в Rp гиперплоскость, не задевающую К, и выбе-
рем точку х G R₽, которая отделена от К этой гиперплоскостью и обладает следую-
щим свойством: никакая прямая, проходящая через х, не пересекает одновременно К
и L. Последнее условие можно удовлетворить ввиду неравенства k +1 + 1 <р. Дейст-
вительно, пусть Kt, . . . , Км - плоскости размерности < к, в объединении которых
§ 10. ТЕОРЕМА О НАДСТРОЙКЕ И ГОМОТОПИЧЕСКИЕ ГРУППЫ СФЕР
81
лежит К, и Lt, ... ,LN — плоскости размерности < I, в объединении которых лежит L.
Обозначим через минимальную плоскость, содержащую К, и Z,-; тогда dimPy <
< dim/t/ + dimZy + 1<£ + /+1<р. В качестве х можно взять любую точку из нужно-
го полупространства, не принадлежащую объединению всех плоскостей Ру. Изото-
пию, существование которой утверждается леммой, мы строим так. Каждая точка
пространства R₽ движется прямолинейно по направлению к х, причем скорость
движения пропорциональна расстоянию от х, а коэффициент пропорциональности
свой на каждом луче, исходящем из точки х, равен нулю на лучах, пересекающих К,
и положителен на лучах, пересекающих L (рис. 61).
Замечание. В основе доказательства этой леммы (и всей теоремы Фрейдента-
ля) лежит простое и важное геометрическое соображение, состоящее в том, что,
например, две замкнутых ломаных в трехмерном пространстве могут быть зацепле-
ны (см. рис. 62), а в четырехмерном — не могут.
Окончание доказательства эпиморфности Е при 1.
Пользуясь леммами 1 и 2, мы гомотопируем отображение f к отображению gj:
5<? + i _> 5” + 1 с0 следующим свойством: прообраз северного полюса лежит в север-
ном полушарии, прообраз южного полюса лежит в южном полушарии, образ эква-
тора не задевает полюсов (рис. 63). (Подразумевается следующая нехитрая выклад-
ка: прообразы полюсов имеют размерности q - п, и (q - п) + (q - п) + 1 = 2q -
— (2n — \)<>2q - q<q + V). Более того, существуют окрестности полюсов - поляр-
ные шапки А и В, в которых нет точек образа экватора. Можно произвести гомото-
пию Sn +1 -* Sn+1, которая растягивает А на северное полушарие и В на южное полу-
шарие, а все остальное сжимает на экватор. Компонируя эту гомотопию с отображе-
нием gt, мы получаем уже довольно хорошее отображение g2: Sq+1 -> Sn+1. Оно
переводит экватор в экватор, северное полушарие в северное полушарие и южное
полушарие в южное полушарие. Посмотрим на сферы Sq + 1 и Sn + l сверху — со сто-
роны северного полюса. На рис. 64 изображены образцы (половин) меридианов.
Гомотопию получившегося отображения, окончательно превращающую его в над-
стройку, придумал Александер. Его конструкция ясна из рис. 65.
Доказательство эпиморфности закончено.
Доказательство мономорфности Е при q<,2n — 2 проводится
по той же схеме. Пусть hi'. Sq -*Sn,h2 : Sq -+Sn — сфероиды. Мы должны доказать,
что если сфероиды Lht, Ей2 гомотопны, то и сфероиды hi ,h2 гомотопны. Возьмем
произвольную гомотопию ft, соединяющую ЕЛд с Ей2, и подправим ее так, чтобы
все сфероиды /, тоже были надстройками. Гомотопия ft есть отображение F: Sq + 1 X
82
ГЛ. I. ГОМОТОПИИ
X I * Sn + 1. Рассмотрим снова прообразы полюсов F_,(&) С Sq+1 X I. Эти
прообразы можно сделать полиэдрами, имеющими размерность < (q + 2) — (л + 1) =
= q - п + 1. При 2 (я - п + 1) + 1 < q + 2, т.е. при q < 2л - 2, их можно ’’развести” -
сделать лежащими в произведениях двух полусфер на отрезок. Дальнейшее рассужде-
ние копирует доказательство эпиморфности.
2. Первые применения.
Торема Хопфа. irn(Sn) = Z.
При п = 1, 2 это нам уже известно (см. теорему 2 из § 6 и упражнение 10 к § 9).
При п > 3 мы имеем изоморфизм
S:
Дополнения. 1. Гомоморфизм 2: Яд (S1) * я2 (S2) является, в силу теоре-
мы Фрейденталя, эпиморфизмом. Но так как Яд(5*) = я2(52) = Z, это — изо-
морфизм.
2. Образующей группы я„(5") служит класс тождественного сфероида Sn -+Sn :
при л = 1 это нам известно из § 6, при остальных л вытекает из того, что надстройка
над тождественным сфероидом есть, очевидно, тождественный сфероид.
Следствие из теоремы Хопфа. Сфера Sn не стягиваема ни при
каком п.
§ 10. ТЕОРЕМА О НАДСТРОЙКЕ И ГОМОТОПИЧЕСКИЕ ГРУППЫ СФЕР
83
Это утверждение, доказательство которого оказалось неожиданно длинным,
очень важно: если бы сфера Sn была стягиваема, то группа п„(Х) была бы тривиаль-
на при любом X.
Еще одно с л е д с т в и е. л3(52)й£ Z
В самом деле, из гомотопической последовательности хопфовского расслоения
S3 -> S2 со слоем S1
я3(5’) * я3(Я3) * я3(52) * я2($2)
II II
О О
мы видим, что л3(53) as л3(52). (Ср. упражнение 10 к § 9.)
Из этой же последовательности видно, что образующей группы л3(52) служит
класс проекции S3 -*52 хопфовского расслоения.
3. Степень отображения Sn -* Sn. Отображение f; Sn -> Sn, рассматриваемое
как сфероид «-мерной сферы (с началом в точке /(х0)), определяет элемент груп-
пы я„(5”) = Z, т.е. целде число. Это число называется степенью отображения f и
обозначается через deg/. Перечислим свойства степени, которые нам уже, по сущест-
ву, известны. Отображения Sn •* Sn гомотопны тогда и только тогда, когда они
имеют одинаковые степени. Отображение 5” * S” степени d индуцирует гомомор-
физм тгп(5”) * 7rn(S”), т.е. Z -* Z, который является умножением на d. Гомеомор-
физм всегда имеет степень ± 1. Надстройка над отображением S” * Sn степени d
есть отображение Sn+1 ->5” + 1 той же степени d.
Теперь мы приведем способ вычисления степени. Окрестность U точки х G Sn
мы назовем правильной, если существует гомеоморфизм Sn * Sn, переводящий х
в северный полюс и U в открытую верхнюю полусферу. Точку х eSn мы назовем
правильной для непрерывного отображения /: Sn -+Sn, если/гомеоморфно отобра-
жает некоторую правильную окрестность точки х на правильную окрестность точ-
ки /(х). Если х — правильная точка, то / может сохранять или обращать ориентацию
в точке х (точное определение: совместим /(х) сх вращением сферы Sn, возьмем
на Sn малую (п - 1)-мерную сферу s с центром в точке х и для у е s обозначим
через g(y) точку пересечения короткой дуги большого круга, соединяющей /(у)
с х и сферы s; полученное отображение имеет степень +1 или —1; в соответствии
с этим говорят, что / сохраняет или обращает ориентацию в точке х). Пример: если
отображение / гладко, то правильной является всякая точка, в которой якобиан
отображения / отличен от 0; в окрестности такой точки / сохраняет (обращает)
ориентацию, если соответствующий якобиан положителен (отрицателен). Точка
у е Sn называется регулярным значением отображения /, если прообраз /-,(у)
состоит из конечного числа правильных точек. (Если / гладко, то регулярные зна-
чения в смысле, принятом в анализе, будут регулярными значениями и в нашем
смысле; в силу известных теорем анализа почти все точки сферы Sn будут регу-
лярными значениями отображения/.)
Теорема. Если точка у есть регулярное значение отображения f : Sn -+Sn, то
степень
отображения f
число точек прооб-
раза / ” 1 Су), в ко-
торых / сохраняет
ориентацию
число точек прооб-
раза / “ 1 (у), в ко-
торых f обращает
ориентацию
Замечание. Как правило, отображение / имеет Много регулярных значений у,
и числа точек множества /"* (у) для них неодинаковы; но, как показывает теоре-
ма, разность в правой части равенства зависит только от /.
84
ГЛ. I. ГОМОТОПИИ
Доказательство теоремы. Применим индукцию по числу точек мно-
жества /"* (у). Если f~l (у) состоит из единственной точки х, то отображение /
гомотопируется к надстройке над отображением g: s -> s из определения сохране-
ния и обращения ориентации (гомотопия строится точно так же, как гомотопия
отображения / к надстройке в доказательстве эпиморфности S выше в этом парагра-
фе). Если теорема уже доказана для случая, когда f~l (у) состоит из N — 1 точек
(N > 2), и прообраз f~l (у) состоит иэ N точек, мы располагаем эти N точек так,
чтобы одна из них попала в северное полушарие, остальные - в южное полушарие,
и тогда наш сфероид будет суммой сфероидов, для которых теорема уже доказа-
на. Нам остается воспользоваться тем, что степень суммы сфероидов, по определе-
нию, равна сумме степеней этих сфероидов.
4. Стабильные гомотопические группы сфер. Итак, гомотопические группы сфер
распадаются в стабилизирующиеся ’’серии” групп •nn+k(Sn) с фиксированным к:
Е Е ,, Е
• • • -* *п+к (S”) — я(„+1)+к (Sn+1) -+ ...
Стабилизация в этой последовательности наступает в члене я2ь+2 ($к+2)
. /оЛ+1\___» тг гс»Л+2\_ _ ./с»Л+3\ —
Группы irn+k(Sn) с и > к + 2 называются стабильными (обозначение: я®), группа
Я2Ы-1 (Sk+1) — метастабильной. Информацию о гомотопических группах сфер, ко-
торой мы в настоящее время располагаем, заключена в следующей таблице:
Заметим, что так как тг3 (S2) * тг4 (№) — эпиморфизм, то группа тг4 (S3) = тг? яв-
ляется циклической.
Гомотопические группы сфер полностью по сей день не вычислены. Однако о них
имеется обширная информация как общего, так и табличного характера. На протя-
жении этой книги мы не раз будем обращаться к гомотопическим группам сфер и
узнаем о них довольно много.
5. Умножение Уайтхеда и ’’трудная часть теоремы Фрейденталя”. Произведение
Sm X Sn двух сфер разбивается на 4 клетки размерностей 0, m, п, m + п. Объедине-
ние первых трех — это букет Sm v S". Характеристическое отображение Dm+n -*
-+Sm X Sn, отвечающее четвертой клетке, отображает sm+n~1 в Sm v S"; возника-
ющее отображение Sm+n~l -+Smv Sn называется отображением Уайтхеда.
Точнее говоря, отображением Уайтхеда называется не это отображение, в пост-
роении которого содержится некоторый произвол, а вполне конкретное отображение
w: sm+n~1 -+Sm vSn,
§ 10. ТЕОРЕМА О НАДСТРОЙКЕ И ГОМОТОПИЧЕСКИЕ ГРУППЫ СФЕР 85
определяемое следующим образом. Сфера Sm+n~l разрезается в объединение замк-
нутых областей
U= {(хxm+n)&Sm+n~x |х? + ...+х^<1/2},
V= {(xt,... ,xm+n)eSm+n~x\xl+...+x2m> 1/2}.
Очевидно, U* Dm X Sn~x, V*Sm~x XDn,Uri V^Sm~x XSn~x (случайте = 2,
и = 1 проиллюстрирован на рис. 66; интересным и важным является разбиение сфе-
ры S3 тором S X 51 в объединении двух полноториев). По другому разбиение
Рис. 66
Sm+n-i = и \J у можно построить так: Sm+n~x = dDm+n « Э (Dm X Dn) =
= (Dm X 9Z>”) U (bDm XDn) =U<JV.
Наше отображение sm+n~x * Sm v Sn определяется на U и на V как составная
проекция
U = Dm XSn~x -*Dm -+DmISm~x = Sm CSm vSn,
V = Sm~x XD" -+Dn -+Dn/Sn~x =Sn CSm v Sn
и переводит ’’разрезающую поверхность” Sm ~1 ХУ”-1 в точку.
Пусть теперь /: Sm -+X,g: Sn -+Х — два сфероида в некотором пространстве X
с отмеченной точкой. Вместе они составляют отображение Sm v Sn -+Х,н компози-
ция этого отображения с w: sm+n~x -+Sm v Sn представляет собой некоторый сфе-
роид h: sm+n~x -* X. Гомотопический класс этого сфероида зависит только от
классов сфероидов f,g и называется их произведением Уайтхеда. Произведение Уайт-
хеда обозначается квадратными скобками; таким образом, если a G ят (У), 0 G
е я„ (X), то [а, 0] е ят+„_ 1 (У).
У п р а ж н е н и я. 1) [а, 0 + у] = [а, 0] + [а, у].
2. Если а е ят (У), 0 е я„ (X), то [а, 0] = (— 1)т” [0, а].
3. Если а е ят (X), 0 е я„ (X), у G яр (X), то
(—1)т₽[[а, 0],у] + (- 1)”т[[0,у] ,а] + (-1)₽п[[у,а],0] =0
(’’тождество Якоби”, или, более учено, ’’супертождество Якоби”).
4. Если а G Я1 (X), 0 е я„ (X), и > 1, то [а, 0 ] = Та 0 — 0.
5. Если а G Я1 (X), 0 е (X), то [а, 0] = а0а-10-1.
6. Обозначим через i„ каноническую образующую группы я„ (5”) (класс тождест-
венного сфероида) и через — каноническую образующую группы я3 (S2) (класс
хопфовского отображения). (Оба обозначения являются общепринятыми.) Пока-
жите, что [ij.n] =2т?2-
7. Пусть а € ят (X), 0 е я„ (X). Докажите, что [а, 0] принадлежит ядру гомо-
морфизма S: ят+„_1 (X)->ят+„(ЕХ).
7а. Докажите, что S (Sm X 5”) ~ Sm + X v Sn+X v sm + n+x. (Это утверждение рав-
носильно предыдущему.)
86
ГЛ. 1. ГОМОТОПИИ
8. Пусть X есть Я-пространство. Докажите, что [а, 0] = 0 для любых a G тгт (X),
0 € (X). (Ввиду упражнений 4 и 5 это упражнение обобщает упражнение 9 из § 6
и упражнение 2 из § 8.)
Теорема. (’’Трудная часть теоремы Фрейденталя”). Ядро гомоморфизма S:
я2л+1 (Sk+1) •* Я2*+2 (Sk+2) есть циклическая группа, порожденная квадратом
Уайтхеда [c*+i>tfc+i] класса t*+1.
Эту теорему мы не доказываем, хотя*ее можно доказать чисто геометрически,
воспользовавшись следующим соображением. Прообразы полюсов при отображе-
нии F: S2k+2 X I -* Sk+2 нельзя развести как в доказательстве мономорфности
гомоморфизма 2 (см. выше), но можно их развести так, чтобы они конечное чис-
ло раз трансверсально пересекли друг друга в изолированных точках. Каждое
такое пересечение можно ’’скомпенсировать” прибавлением класса [ifc+i, ijt+i] •
Если читатель не захочет возиться с реализацией этой идеи, он может вернуться
к доказательству теоремы после прочтения главы 2 (а еще лучше — после прочте-
ния § 24) и доказать ее при помощи алгебраических средств, которые он будет
иметь в своем распоряжении.
Заметим, что вместе с упражнением 6 теорема показывает, что тг4 (№) = Z2 (и,
значит, л? = Z2). Альтернатива тг4 (53) = Z2 или О вытекает уже из (довольно прос-
тых) упражнений 6 и 7.
Заметим еще, что при нечетном к циклическая группа, порожденная [i*+1, 1L
есть Z - это мы докажем в § 16. При четном к эта группа есть Z2 или 0 — см. уп-
ражнение 2.
§ 11. ГОМОТОПИЧЕСКИЕ ГРУППЫ И КЛЕТОЧНЫЕ ПРОСТРАНСТВА
Этот параграф, в котором речь идет о различных связях между клеточными про-
странствами и гомотопическими группами, разнороден по содержанию. В нем вы-
числяется первая нетривиальная гомотопическая группа клеточного пространства,
проясняется роль гомотопических групп в гомотопической классификации клеточ-
ных пространств и строятся клеточные пространства с заданными гомотопическими
свойствами.
1. Аддиционная теорема.
Теорема 1. Пусть X - связное топологическое пространство и f: Sn -*Х -
непрерывное отображение. Положим Y = X\j^Dn+i. Гомоморфизм
^(Х,х0)-^щ(У,х0), (*)
где х0 G X С Y - произвольная отмеченная точка, индуцированный включением
X Y, при i < п является изоморфизмом, а при i = п является эпиморфизмом,
ядро которого порождено всевозможными классами вида Ts [/], где з - путь, сое-
диняющий х0 с f-образом /(Уо) отмеченной точки у0 G Sn, a [/J G тти (X, /(у0)) —
гомотопический класс сфероида f
Удобно считать, что f(y0) = х0; тогда ядро отображения (*) с i = п порождается
элементами 7г2 (X, х0)-орбиты класса [/] G яп(Х, х0). Особенно важен случай,ког-
да X односвязно: в этом случае теорема показывает, что при приклеивании (и + 1)-
мерной клетки гомотопические группы размерности < и не меняются, а и-мерная
гомотопическая группа факторизуется по циклической подгруппе, порожденной
классом заклеиваемого сфероида.
Лемма. Пусть Ет есть сфера Sm или шар Dm, где т<п+ Г; при этом мы отож-
дествляем Rm с Sm - у0 или с Dm - dDm (таким образом, у нас всегда Rm С Ет.)
Пусть, далее, Л: Ет -> Y - непрерывное отображение, такое, что h(Em — ROT) С X.
§ 11. ГОМОТОПИЧЕСКИЕ ГРУППЫ И КЛЕТОЧНЫЕ ПРОСТРАНСТВА
87
Тогда существует гомотопное h непрерывное отображение ht: Em -* Y со следую-
щими свойствами'.
(1) Hah~l (У) отображение совпадает ch;
(2) если ш<п, то h (Em) С X;
(3) если m = п + 1,то в Ет лежит конечное семейство попарно непересекающихся
шариков di,..., dN, такое, что (Em - Uf J,) С X и lint dj есть при каждом i
линейный (сохраняющий или обращающий ориентацию) гомеоморфизм открытого
шарика Int dt на Int D”+1 С Y.
Доказательство этой леммы проходит по схеме, уже трижды применявшейся на-
ми (доказательство ’’леммы о свободной точке” в § 5, вычисление фундаменталь-
ной группы клеточного пространства в § 6 и доказательство леммы 1 к теореме
Фрейденталя в § 10) и в первых двух случаях излагавшейся со всеми подробнос-
тями: строим 5 концентрических шаров с центром в центре шара£>" + 1, мелко триан-
гулируем Ет и т.д. Детали читатель восстановит сам, руководствуясь указанными
образцами.
Доказательство теоремы 1. Эпиморфность отображения (*) при
i < л и его мономорфность при i < п вытекает из леммы непосредственно. (При
i < п лемма перерабатывает сфероид h: S'' Y в гомотопный сфероид : S'’ Y,
отображающий S’ в X; при i < п по отображению h: Di+1 -> Y, осуществляющему
гомотопность нулю в Y сфероида h | st: S* -> X С Y, лемма строит отображение
h\: Z),+I -+X С Y, осуществляющее гомотопность нулю этого же сфероида в X.)
Предположим, что гомотопический класс сфероида g'. Sn -> X принадлежит ядру
отображения (*), т.е. g продолжается до некоторого отображения Л: D”+1 -» X.
Заменив отображение А отображением hi со свойствами, указанными в части (3)
леммы, мы получим другое продолжение hi'. Dn+1 -> X этого сфероида. На гра-
нице каждого шарика dt отображение hi совпадает с композицией
(г г
Ы(—>8п-^>Х,
где Ц — линейное отображение.
Дальнейшее рассуждение мало отличается от соответствующей части доказатель-
ства теоремы 4 из § 6. Положим yt = If1 (у0) и соединим при каждом i точку yt
путем af с уо G Sn С Dn+1 таким образом, чтобы эти пути не задевали своими внут-
ренними точками шариков df и попарно не пересекались (см. рис. 37 на с. 55).
В Dn+1 — Uf Inddf существует очевидная гомотопия, соединяющая естественный
сфероид S” -> Dn+1 (включение) с суммой сфероидов ТО{(1{~1) (см. рис. 38 на
с. 55). Переведем эту гомотопию в X посредством отображения hi. Мы получим
гомотопию, соединяющую сфероид g со сфероидом где fi ~ сфероид,
отличающийся от / на линейное преобразование сферы S”. Поскольку [/}] = ±[/]
(знак зависит от того, сохраняет или обращает ориентацию это линейное преобра-
зование), мы видим, что класс [g] действительно является линейной комбинацией
образующих, указанных в теореме. Этим последнее утверждение теоремы доказано
в одну (более трудную) сторону. В другую сторону оно очевидно: класс Ts [/],
разумеется, принадлежит ядру отображения (♦).
Следствие. Если Y - клеточное подпространство пространства X и разность
X - Y не содержит клеток размерности < и, то гомоморфизм щ (У) •* Я/ (Л), инду-
цированный включением, является изоморфизмом при i < п и эпиморфизмом при
i = п. В частности, тгп(Х) = 7r„(sk„+1 X) для любого клеточного пространства X.
88
ГЛ. 1. ГОМОТОПИИ
2. Применение аддиционной теоремы: гомотопические группы букетов.
Теорема 2. Пусть X, Y-клеточные пространства. Если пространство X р-связ-
но, а пространство Y q-связно, то:
(1) nn(Xv Y) = nn(X) nn(Y) припер+ q;
(2) при любом п группа (X v Y) содержит прямое слагаемое, изоморфное
я„(А)®я„(У).
Доказательство. В силу доказанного выше (см. конец § 5) пространст-
ва У и У гомотопически эквивалентны клеточным пространствам с единственной
вершиной и без клеток размерностей 1,..., р и 1,... ,q соответственно; мы будем
считать, что таковы уже X и Y. Букет X v Y является клеточным подпространством
произведения X X Y, и клетки, лежащие в разности (X X У) — (X v Y), имеют раз-
мерности, не меньшие р + q + 2. Ввиду следствия из предыдущей теоремы (а также
того факта, что тгп(Х X У) = пп(Х) ® nn(Y)), отсюда вытекает утверждение (1).
Для доказательства утверждения (2) достаточно заметить, что сквозное отображение
я„(^)®я„(У)—п„(1уУ)-^яи(1Х У)=я„(Х)®я„(У),
где первая стрелка есть сумма гомоморфизмов i,: п„(Х) -^nn(Xv У),/»: я„(У) -*
-> тт„(Х v У), индуцированных включениями i: X~*Xv Y,j: Y-+Xv У, тождест-
венно.
Следствие. я„ (Sn v ... v Sn) = Z ® ... ® Z: систему свободных образующих
я я
составляют классы q естественных вложений Sn -+Sn v ... v Sn.
Упражнение 1. В условиях предыдущей теоремы яр+(?+j (X v У) = пр+ч+1 (X) ®
® 7Тр+<?+1(У) ® [яр+1 (X) ® я9+1 (У)}, где последнее слагаемое вкладывается в
ттр+(?+1 (X v У) посредством формулы а ® 0 [/. В частности, п3 (S2 v S2) =
= Z ® Z ® Z. [Имеется теорема Хилтона — Милнора, согласно которой гомотопичес-
кие группы произвольного букета сфер 5m* v ... v Smr порождаются элементами
гомотопических групп сфер Sm' и их произведениями Уайтхеда; точную формули-
ровку и доказательсто см. в ’’Теории гомотопий клеточных пространств” М.М. Пост-
никова.}
3. Первая нетривиальная гомотопическая группа клеточного пространства. Пусть
X — клеточное пространство с единственной нульмерной клеткой, не имеющее кле-
ток размерностей 1,..., п — 1 (мы предполагаем, что п > 1; случай п = 1 рассмот-
рен в § 6). Отождествим остов sk„Xc букетом vtejSn «-мерных сфер, поставлен-
ным во взаимно однозначное соответствие с «-мерными клетками пространства X.
Пусть ff.. Sn -^sknX=ViSn(j^J) - приклеивающие отображения, отвечающие
(« + 1) -мерным клеткам пространства X, и пусть G ir„(sk.n X)-®i^ zZ — гомотопи-
ческие классы сфероидов fj.
Теорема 3. Группа яп(Х) есть факторгруппа группы ®/e/Z по подгруппе,
порожденной элементами у, (J GJ).
Эта теорема является точным аналогом теоремы 4 из § 6. Ее можно сформули-
ровать менее точным, но более запоминающимся образом: п-я гомотопическая груп-
па пространства X порождается «-мерными клетками, соотношения отвечают (« + !)-
мерным клеткам.
Доказательство теоремы 3 состоит в прямом применении теоремы 1.
Замечание. Поскольку всякое (п — 1)-связное клеточное пространство гомо-
топически эквивалентно пространству рассматриваемого вида, можно сказать, что
теорема 3 описывает первую нетривиальную гомотопическую группу произвольно-
го клеточного пространства. Однако переход от произвольного клеточного прост-
§ 11. ГОМОТОПИЧЕСКИЕ ГРУППЫ И КЛЕТОЧНЫЕ ПРОСТРАНСТВА
89
ранства к пространству нашего вида не вполне эффективен, так что этим дефектом
обладает и наше описание гомотопической группы. Впрочем, главная роль теоре-
мы 3 не в том, что она позволяет вычислить те или иные гомотопические группы,
а в том, что она применяется в доказательстве разного рода общих теорем (с таки-
ми ее применениями мы еще столкнемся).
Упражнения. 2. Докажите следующий относительный вариант теоремы 3
(уточнив надлежащим образом формулировку). Пусть (X, А) — клеточная пара
со связным Л, такая, что в X — А лежат только клетки размерности > и, где л > 3.
Тогда группа яи(Х, А), т.е. первая нетривиальная гомотопическая группа пары
(X, А) порождается как Я1 (А) -модуль и-мерными клетками из X - А; соотно-
шения между этими образующими Я! (А)-модуля кп(Х, А) соответствуют (и + 1)-
мерным клеткам из X — А.
3. Найдите аналог предыдущего утверждения для случая и = 2.
4. Пусть (X, А) — клеточная пара с односвязным А, и пусть клетки, лежащие
в X — А, имеют размерность > и > 2. Покажите, что естественное отображение
пп(Х, А) -+тгп(Х1А) является изоморфизмом. [Эта теорема имеет следующее обоб-
щение. Пусть (X, А) — клеточная пара с А:-связным А, и пусть клетки, лежащие в
X - А, имеют размерность > л > 2. Тогда естественное отображение яч (X, А) -*
* яч(Х/А) является изоморфизмом при q <п + к — 1 и эпиморфизмом при q =
= л + к. Пока мы не имеем средств для доказательства этой теоремы, но читатель
может вернуться к ней после прочтения гл. 2 или, еще лучше, после § 24].
4. Слабая гомотопическая эквивалентность как отображение. В § 9, изучая слои
расслоений в смысле Серра, мы ввели понятие слабо гомотопически эквивалентных
пространств: пространства X и У слабо гомотопически эквивалентны, если можно
определить для любого клеточного пространства Z взаимно однозначное соответ-
ствие <pz: ir(Z, X) -+ir(Z, У), естественное по Z. Как именно строится при этом
не уточняется, но может оказаться, что yz индуцируется некоторым (одним и тем
же при всех Z) непрерывным отображением </>: X * Y.
Определение. Непрерывное отображение X -* Y называется слабой гомо-
топической эквивалентностью, если для любого клеточного пространства Z отоб-
ражение я(7, X) -* ir(Z, У) является взаимно однозначным соответствием.
Очевидно, пространства, которые можно связать слабой гомотопической экви-
валентностью, слабо гомотопически эквивалентны. Обратное неверно, как показы-
вают простейшие примеры. (Множества Q, Z С R слабо гомотопически эквивалент-
ны, но слабой гомотопической эквивалентности Q ->Z не существует: непрерывное
отображение Q -* Z неизбежно будет постоянным на целых интервалах и потому
не будет взаимно однозначным уже индуцируемое им отображение я (точка, <2) ->
* я (точка, Z). Пространства (Q X S1) U Z и (Z X S1) UQ тоже слабо гомотопи-
чески эквивалентны, но слабой гомотопической эквивалентности между ними не
существует ни в одну сторону.) Ниже в этом параграфе мы увидим, что простран-
ства слабо гомотопически эквивалентны тогда и только тогда, когда они могут
быть соединены цепочкой
<-И/2 -* .. . У
слабых гомотопических эквивалентностей (см. упражнение 8).
Наша ближайшая цель — доказать следующую характеризацию слабых гомотопи-
ческих эквивалентностей.
Теорема 4. Для непрерывного отображения f: X -* У следующие свойства
эквивалентны.
(1) f есть слабая гомотопическая эквивалентность.
90
ГЛ 1. ГОМОТОПИИ
(2) Гомоморфизм f*: л„(Х х0) яи(У, /(хо)) является изоморфизмом при
любых пих0.
(3) Если (W, А) - клеточная пара и h: А -* X, g: W -► У - такие непрерывные
отображения, что f о h ~ g\A, то существует непрерывное отображение h: W
такое, что h\A=h и foh ~g.
Доказательство. Импликация (1) =* (2) очевидна. Импликация (3) =* (1)
почти очевидна: взяв в качестве пары (W, А) пару (Z, ф), мы убеждаемся в том, что
отображение /*: n(Z, X) -> it(Z, У) является отображением на, а положив (W, А) =
= (Z X I, (Z X 0) U (Z X 1)), мы видим, что оно переводит разные элементы в разные.
Остается доказать импликацию (2) => (3). Пусть/: X * У - отображение, удов-
летворяющее условию (2), и пусть (W, А) — клеточная пара. Мы предположим
сначала, что W отличается от А единственной клеткой: W = A Ua Dn+1, где
а: S" — непрерывное отображение. Поскольку сквозное отображение а: S п С
С W гомотопно нулю (его продолжением на шар служит естественное отображение
Dn + 1 -* W), гомотопна нулю и композиция (?U) 0 а- Sn -* Y. Значит, гомотопно
нулю отображение f о h° a: Sn-*Y, ас ним - и отображение h о а: 5 ” -+Х: отображе-
ние / переводит в сфероиды, гомотопные нулю, только сфероиды, гомотопные нулю
(/» — мономорфизм). Значит, отображение ho a: Sn -*Х продолжается до непре-
рывного отображения 0: D”+1 -*X, и мы можем составить из отображений й и 0 не-
прерывное отображение h': W -> Х Штрих здесь поставлен потому, что это отображе-
ние еще не годится в качестве й. Нам нужно, чтобы было foh ~g, а есть у нас только
*7 '‘'7
/ ° й |л ~g |л. Фиксируем гомотопию Ф: A XI-+Y, соединяющую g]A cfoh\A=f°h,
ирассмотрим (п + 1)-мерный сфероид у: Sn+1 =d(Dn+1 Х7)-*У, составленный из
отображений:
Dn + 1 X0=Dn + 1 ^W^->Y,
а X I Ф
Sn XI------->A X I--> у
в f
Dn + 1 Xl=Dn + 1--->X-->У.
'’*0
Для того чтобы гомотопия Ф продолжалась до гомотопии, связывающей g с / ° й,
нужно, чтобы сфероид у был гомотопен нулю (см. рис. 67), но на это мы не можем
рассчитывать, потому что не приняли для этого никаких мер. Чтобы исправить дело,
в нашем распоряжении есть выбор отображения 0, продолжающего ho а; если мы
вместо 0 возьмем другое отображение, 0', то к гомотопическому классу сфероида у
§ 11. ГОМОТОПИЧЕСКИЕ ГРУППЫ И КЛЕТОЧНЫЕ ПРОСТРАНСТВА
91
прибавится гомотопический класс сфероида f ° 5, где 6: S" + 1 -> X - сфероид,
составленный из отображений 0': D" + 1 X (согласованных на 3D"+1). Ясно,
что гомотопический класс сфероида 8 может быть сделан произвольным элементом
группы я„+1(Х), но тогда произвольным будет и класс сфероида f° 8 (f,—
эпиморфизм). Этим доказательство завершается в случае, когда W — А есть одна
клетка. В общем случае применяется обычная клеточная индукция: на п-м шаге
предыдущее построение проводится одновременно для всех н-мерных клеток
из разности W — А.
5. Теорема Уайтхеда.
Теорема 5. Пусть X, Y - клеточные пространства. Если непрерывное отобра-
жение f обладает тем свойством, что
f.-. я„(У, х0)-> я„(У,/(х0))
есть изоморфизм при всех пих0, то f есть гомотопическая эквивалентность.
(Если пространства X и Y связны, то условие теоремы достаточно проверять для
некоторой произвольно фиксированной точки х0 G АГ.)
Теорема является прямым следствием теоремы 4 и того факта, что для клеточ-
ных пространств слабая гомотопическая эквивалентность совпадает с обычной (см.
п.4 §9).
Из теоремы Уайтхеда следует, что если все гомотопические группы некоторого
(связного) клеточного пространства тривиальны, то это пространство стягиваемо
(гомотопически эквивалентно точке). Однако в общем случае для гомотопической
эквивалентности клеточных пространств, вообще говоря, недостаточно, чтобы их
гомотопические группы были изоморфны: нужно, чтобы изоморфизм устанавливал-
ся некоторым непрерывным отображением. (См.,впрочем, теорему 8.)
Упражнения. 5. Покажите, что пространства S 2 и S 3 X СР°° имеют одинако-
вые гомотопические группы, но гомотопически не эквивалентны.
6. Покажите, что пространства S m X RP" и RPm X S " (m Ф ri) имеют одинаковые
гомотопические группы, но гомотопически не эквивалентны.
6. Клеточная аппроксимация топологических пространств.
Теорема 6. Для любого топологического пространства X существует клеточное
пространство Y и слабая гомотопическая эквивалентность f: Y -> X.
(Такая пара (У, /) называется клеточной аппроксимацией пространства X.)
Доказательство. Можно ограничиться случаем (линейно) связного прост-
ранства X. Мы построим цепочку пространств Уо С Ух С. .. и систему продолжаю-
щих друг друга отображений fr. Y{ ->АГ, такую, что (/}), : лч(Уг) -+itq(X) будет изо-
морфизмом при q < i. В качестве Yo мы возьмем точку, в качестве f0 : Yo-+X - про-
извольное отображение. Предположим, что уже построены Yo С. .. С Yn_1 nf0,...
• - Положим .Уо = Уо, *о = /о(Уо) Выберем в группе яп(Х, х0) (или даже в
iri(X, х0)-модуле яп(Х, х0)) систему образующих {ч>а}, фиксируем для tpa пред-
ставляющий сфероид ga: Sn -> X, положим У„ = Yn_x V (Va S") и определим
отображение У„ -> X как совпадающее c/n_i на Уп-1 и с ga на а-й компоненте
букета Va S п. В силу теоремы 2 тгч(У^) = itq(.Yn_1') при q < п, поэтому отображение
(/„)» в размерностях < л является изоморфизмом. Отображение же (/„),: я„(У„)^-
->я„(Х) эпиморфно, поскольку все >ра лежат в его образе. Мономорфизмом это
отображение может не быть; возьмем в его ядре К = Кег(/^), систему образующих
{ фр G тг„(У„)} (можно взять систему образующих над я^Уп)). Фиксируем для
фр представляющие сфероиды hp: Sn -+Y„ и приклеим по каждому из них к Y„
(п + 1) -мерную клетку. Полученное пространство примем за У„. Поскольку
92
ГЛ. 1. ГОМОТОПИИ
= композиции fh°h(! гомотопны нулю, и отображение /„ может быть
продолжено на все приклеенные клетки. Результатом такого продолжения и бу-
дет отображение fn: Y„ X. Приклеивание не изменит групп яч с q < п, в силу
же аддиционной теоремы 1 я„(У„) = ^„(Y^/K, вследствие чего (/„),: я„(У„)
-> я„ (У) есть изоморфизм. Теорема доказана.
Упражнение 7. Докажите гомотопическую единственность клеточной ап-
проксимации топологического пространства: если (Y,f), (Z, g) - две клеточных
аппроксимации пространства X, то существует гомотопическая эквивалентность
h: Z -> У, такая, что g=f ° h.
Главный смысл теоремы 6 состоит в том, что она позволяет распространять
гомотопические теоремы, доказываемые для клеточных пространств на произволь-
ные топологические пространства. В качестве упражнения читатель может проде-
лать это с теоремой 2 этого параграфа. Еще одним применением теоремы 6 сле-
дует очередное уточнение понятия слабой гомотопической эквивалентности.
Упражнение 8. Если X, Y - слабо гомотопически эквивалентные простран-
ства, то существует (единственное с точностью до гомотопической эквивалентнос-
ти) клеточное пространство Z, обладающее слабыми гомотопическими эквивалент-
ностями ft Z-+X, gt Z-*Y.
7. Пространства Эйленберга — Маклейна (Д(я, л) ’ы).
Теорема 7. Пусть п - натуральное число и -п - группа, предполагаемая абе-
левой, если п > 1. Тогда существует клеточное пространство X, такое, что
( 0 при i ¥= п,
"/(*)= .
I Я при I = п
(ср. конец § 3).
(Такие пространства называются пространствами Эйленберга - Маклейна или
пространствами типа К(л,п); часто говорят просто ”Х есть К (л, л)”.)
Доказательство. Выберем в я систему образующих {<ра} и систему со-
отношений {Др} (если л>1, то подразумеваются соотношения в я как в абеле-
вой группе). Положим X„ = VaS"; тогда я1(Х„) = 0 при Кп и я„(У„) = ®aZ
(или *aZ при л=1); образующие группы л„(Х„) находятся во взаимно одно-
значном соответствии с ^ра, и мы обозначаем их через уэа. Заменим в левой
части каждого из соотношений Др символы ipa символами <ра ; получатся эле-
менты Гр группы я„(У„). Фиксируем сфероиды, представляющие эти элементы,
и приклеим по этим сфероидам к Хп (л + 1)-мерные клетки. Получится прост-
ранство Хп+1, такое, что я((Х„+1) = 0 при i<n и я„(У„+1) = я. Далее мы берем
произвольную систему образующих в я„ + 1(Х„ + 1), представляем их сфероидами
и приклеиваем по этим сфероидам к Хя+1 (л+ 2)-мерные клетки. Получается
пространство Хп+2, которое имеет нужные гомотопические группы уже до размер-
ности л+ 1. Затем заклеиваем у Х„+2 группу я„+2 ит.д.
Замечание. Эта конструкция совершенно не эффективна: групп
я„+1(Хп + 1), я„+2(У„+2),. .. мы не знаем и не имеем средств вычислить. Мож-
но, конечно, подстраховаться и приклеить к Хп+1 клетки по всем мыслимым
сфероидам Sn+1 ->У„ + 1, затем сделать подобное с пространством Хп+2 и т.д.
Это освободит конструкцию от произвола, но сделает ее уж очень громоздкой.
Ввиду этого представляют интерес, впрочем, немногочисленные, явные конст-
рукции пространств типа К (л, л).
Явные конструкции. (1) Пространство СР°° есть пространство типа
K(Z, 2); это — единственное обозримое пространство, имеющее тип Д(я, л) сл> 1.
§ 11. ГОМОТОПИЧЕСКИЕ ГРУППЫ И КЛЕТОЧНЫЕ ПРОСТРАНСТВА
93
(2) S1 есть K(jL, 1). (3) RP“ есть ,A(Z2, 1). (4) Бесконечномерные линзы L°^ =
= S“/Zm, где образующая Т группы Zm действует в S“ С С” по формуле
Л21> z2> • = (zie2irt/m, z2e2,rt/m,...), есть пространство типа K(Zm, 1). (5) Так
как произведение пространств типаХХти.и) и/^(я2,л) есть,очевидно, пространство
типа Х^(тг1 X я2, и), то конструкции (2) —(4) позволяют построить пространство
типа К(-п, 1) для любой конечнопорожденной абелевой группы я.
Известно такие великое множество пространств типа К (ir, 1) с неабелевыми я.
К их числу относятся, например, все классические поверхности, кроме S2 и RP2
(см.упражнение Зв § 8).
Упражнения. 9. Докажите, что пространство всех неупорядоченных наборов
из п различных точек плоскости есть пространство типа А" (я, 1) для некоторой
группы я; задайте эту группу образующими и соотношениями. (Эта группа назы-
вается группой кос из п нитей', ее придумал Э. Артин.)
10. Сделайте подобное для упорядоченных наборов (соответствующая группа
называется группой крашеных кос).
11. Докажите, что полное риманово многообразие неположительной кривизны
есть пространство типа K(ir, 1) с некоторой группой я. [Указание: любые две точки
такого многообразия соединяются единственной геодезической.]
Пространством типа K(ir, 1) является дополнение к любой замкнутой кривой
("узлу”) в S3, но читатель вряд ли сможет доказать это при помощи имеющихся
в его распоряжении средств.
Упражнения. 12. Построить пространство с заданными гомотопическими
группами.
13. Покажите, что 12А(я, п) = А? (я, п — 1).
8. Единственность К (я, л) *ов.
Теорема 8. Любые два пространства типа К (я, л) слабо гомотопически экви-
валентны. (Следовательно, любые два клеточных пространства типа K(ir, л) гомото-
пически эквивалентны.)
Доказательство. Пусть X — пространство типа K(ir, п), построенное в до-
казательстве теоремы 7, и Y — произвольное пространство типа А? (я, л). Мы по-
строим отображение f: X -> У, индуцирующее изоморфизм гомотопических групп
(т.е. изоморфизм п„(Х) ->я„(У)). Напомним, что л-й остов Х„ пространства X есть
букет Va5 " л-мерных сфер, соответствующих образующим группы я. Поскольку
я„(У) = я, мы можем отождествить эти образующие с элементами группы я„(У).
Отобразим VaS " в У при помощи сфероидов, представляющих эти элементы. Все,
что мы должны еще сделать — как-нибудь продолжить зто отображение до непрерыв-
ного отображения X -> У; любое такое продолжение будет обладать требуемыми
свойствами. Продолжение строится отдельно для каждой клетки пространства X,
и каждый раз оно оказывается возможным, потому что композиция приклеивающе-
го отображения клетки с уже построенным отображением есть сфероид, гомотопный
нулю. Для клеток размерности л + 1 это вытекает из того, что они отвечают соотно-
шениям в группе я, а для клеток больших размерностей - иэ того, что я, (У) = 0
при i > л.
9. Заклеивание и убивание гомотопических групп. В заключение мы обсудим две
гомотопические операции над топологическими пространствами, детерминированным
образом воздействующими на его гомотопические группы. Первой из них мы уже
несколько раз, не называя ее, пользовались: заклеивание гомотопических групп
размерности > л превращает пространство X в пространство X' содержащее X и такое,
что (1)я<,(Х') = 0 при q > п, (2)гомоморфизм irq(X) -> irq(X'), индуцированный
94
ГЛ. 1. ГОМОТОПИИ
включением Х-*Х', является изоморфизмом при q <и. Для построения пространства
X' достаточно сначала приклеить к X (п + 2) -мерные клетки по сфероидам, представ-
ляющим образующие группы itn+1(X), затем приклеить (л + 3)-мерные клетки по
сфероидам, представляющим образующие группы я„+2 полученного пространства и
т.д. Операция заклеивания гомотопически единственна:
Упражнение 14. Пусть X - топологическое пространство, Х[ и Xj — два
пространства, содержащие X и обладающие свойствами (1), (2) из определения
заклеивания. Тогда существует слабая гомотопическая эквивалентность Х{ -+Xj,
гомотопная на X включению X-+Xj .
Заклеивание позволяет определить каноническое отображение произвольного
пространства X в надлежащий К (it, п). Именно, пусть л„(Х) = я — первая нетривиаль-
ная гомотопическая группа пространства X (для простоты предполагаемого связ-
ным) . Заклеим у X гомотопические группы размерностей > п. Получится пространст-
во типа К (it, ri) и отображение (включение) X -+K(it,ri) устанавливает изоморфизм
групп я„. Из упражнения 14 и теоремы 8 легко вывести, что эта конструкция гомото-
пически единственна.
Перейдем теперь к убиванию. Рассмотрим построенное отображение X -+K(it, ri),
где я = itn(X), itq(X) = 0 при q < п. Превратим это отображение в гомотопически
эквивалентное расслоение в смысле Серра (см. § 9) и возьмем слой этого расслое-
ния. Этот слой, определенный канонически с точностью до слабой гомотопической
эквивалентности, называется (первым или (п + 1)-л<) убивающим пространством
для X и обозначается через У| „+1. Имеется (гомотопически единственное) канони-
ческое отображение АП„+1 -* X.
Теорема 9.
О при q^n,
irq(X) при q>n;
более того, каноническое отображение Х|„+1 +X индуцирует изоморфизм гомото-
пических групп в размерностях >п.
Это стандартным образом выводится из точности гомотопической последователь-
ности расслоения, гомотопически эквивалентного отображению X -*K(it,ri).
Конструкцию убивающего пространства можно итерировать. В результате для
произвольного пространства X и произвольного числа m получаются пространство
Х\т и отображение Х\т + X, такие, что индуцированное отображение яд(АГ |т) ->
-* itq(X) является изоморфизмом при q > т, а группы яч(Х|т) с q < т равны 0.
Упражнения. 15. Докажите, что для любого связного пространства X кано-
ническое отображение X |2 -> X слабо гомотопически эквивалентно универсальному
накрытию.
16. Докажите, что52|3 = 53 и |СР" |3 = CP"|2n+1 = 52"+*.
17. Докажите, что в ситуации теоремы 9 слой расслоения, гомотопически экви-
валентного каноническому отображению Х\п + 1-+ X, есть К (it, п — 1).
Итак, для произвольного пространства X имеется два способа сократить гомото-
пические группы. Можно уничтожить гомотопические группы, начиная с некоторой,
и эта операция называется заклеиванием; пространство X отображается в заклеен-
ное пространство. Можно, наоборот, уничтожить гомотопические группы до некото-
рой, и эта операция называется убиванием; убивающее пространство отобра-
жается в X.
ГЛАВА 2
ГОМОЛОГИИ
Наряду с гомотопическими группами ял(Х) топологическому пространству X
ставят в соответствие другие серии групп — гомологические группы Нк(Х)п кого-
мологические группы Нк(Х). По сравнению с гомотопическими группами они обла-
дают важным недостатком — их аккуратное определение связано со значительными
формальными трудностями — и важными достоинствами — они легче вычисляются
(мы более или менее сразу найдем их для большинства известных нам пространств)
и геометрически более наглядны (трудно объяснимых феноменов типа я3(52) = Z
для них не бывает). Информация о топологическом пространстве X, которую несут
его гомологии, в односвязном случае примерно равноценна информации, содер-
жащейся в гомотопических группах.
Геометрическая идея гомологий такова. Сфероиды заменяются циклами; fc-мер-
ный цикл — это замкнутая ^-мерная поверхность (может быть, сфера, а может быть
и нет, скажем, тор). Отношение гомотопности сфероидов заменяется отношением
гомологичности циклов — цикл гомологичен 0, если он ограничивает кусок поверх-
ности на 1 большей размерности.
Как аккуратно определить, что такое циклы (и те ’’куски поверхностей”, кото-
рые они ограничивают, — так называемые цепи) ? Можно было бы попытаться опре-
делить их как отображения стандартных объектов — сфер и чего-нибудь еще, но это
приводит к трудностям, особенно в размерностях > 2. Проще определить циклы (и
цепи) как объединения стандартных элементов (’’кирпичей”). Эту роль принимают
на себя сингулярные симплексы.
Заметим, что для построения гомологических и когомологических групп прост-
ранства X не требуется, чтобы в X была отмечена точка, — в этом одно из их
важных отличий от гомотопических групп.
§ 12. СИНГУЛЯРНЫЕ ГОМОЛОГИИ
1. Сингулярные симплексы, цепи и гомологии. Пусть Ао, А1г..., Aq — точки
пространства R", где n>q, не лежащие в одной (q — 1)-мерной плоскости. Вы-
пуклая оболочка множества этих точек называется евклидовым симплексом с
вершинами Aq, Ai,..., Aq (это определение уже известно нам из § 5); вы-
пуклые оболочки подмножеств этого множества — грани указанного симплекса.
Евклидовы симплексы одной размерности все одинаковы, и это побуждает нас
выбрать стандартный евклидов симплекс. В качестве такового обычно рассматри-
вают евклидов симплекс Тч в R<?+I, вершинами которого являются концы ко-
ординатных ортов:
n = {(To,...,f<?)eR’+‘|To>0,...,T<?>0, 2^=1}.
96
ГЛ 2. ГОМОЛОГИИ
Пусть X — произвольное топологическое пространство. Под q-мерным сингуляр-
ным симплексом пространства X понимается просто непрерывное отображение
стандартного (/-мерного симплекса Tq в X. Под (/-мерной (сингулярной) цепью
пространства X понимается конечная линейная комбинация сингулярных симплек-
сов пространства X с целыми коэффициентами; запись: fa. Tq -*Х. Мно-
жество (/-мерных сингулярных цепей пространства X обозначается через Cq(X).
Сложение цепей как линейных комбинаций делает Cq(X) группой. Говоря иначе,
Cq(X) — свободная абелева группа, порожденная множеством всех (/-мерных сингу-
лярных симплексов пространства X.
Теперь мы определим граничный гомоморфизм Э = dq: Cq(X) -^Cq_i(X). Так как
группа Cq(X) свободна, то достаточно определить Э на сингулярных симплексах.
Для сингулярного симплекса f мы полагаем
а/= SC-iy’nz,
где rtf— сужение отображения/ на i-ю грань
стандартного симплекса Tq. (Грань Т? 1 отождествляется с Г’-1: точке (to,...
..., 0, г/+1,... , rQ)eT^-1 отвечает точка (г0, • •, tt_x, rf+1,... ,tq)G.Tq~l.)
Теорема. Композиция
3Q+i tq
Cq+l(X)------> Cq (X)-> Cq_ t (X)
тривиальна' другими словами, Im 3Q+1 C Ker dq.
Доказательство: прямая проверка, основанная на равенстве
Г/-1Г,/ при />1,
Г/Г<+1/ ПРИ
Основное определение. Факторгруппа
Hq(X)= Ker 3Q/Im 9q+i
называется q-й (q-мерной) гомологической группой (группой гомологий) прост-
ранства X. (Уточнение: это определение имеет силу при q > 1; полагают также
Но(X) = С0(Х)/1т Э j и Hq (X) = 0 при q < 0.)
Употребляют обозначения: КегЭ, = Zq(X), Im3Q + 1 = Bq(X); таким образом,
Hq(X) = Zq(X)/Bq(X)- Цепи из Zq(X), Bq(X) называют, соответственно, циклами
и границами’ циклы, разность которых есть граница, называют гомологичными;
таким образом, элементы группы гомологий — это классы гомологичных циклов,
иногда их называют гомологическими классами.
Если группа Hq(X) конечно порождена, то ее ранг (т.е. число слагаемых Z в кано-
ническом разложении Hq(X) = Z ® . . . ® Z ® Zkj® ... ® Zkg) называется q-м числом
Бетти пространства X.
2. Цепные комплексы, отображения и гомотопии. Цепным комплексом *) (или
просто комплексом) называется последовательность
абелевых групп, в которой Э<г°Э<г+1=О, е » Э1 = 0 и е — эпиморфизм.
*) Не путайте ударение: комплекс неполноценности и комплексная автоматизация, но цеп-
ной комплекс и комплексные числа.
§ 12. СИНГУЛЯРНЫЕ ГОМОЛОГИИ
97
(Это определение вариабельно. Часто в понятие комплекса не включается в качест-
ве обязательного элемента эпиморфизм е; при наличии этого эпиморфизма комплекс
называется пополненным или сегментированным, а само е называется аугментацией.
Иногда комплексами называют бесконечные в обе стороны последовательности
э<?>г -»
но при этом, как правило, ограничиваются рассмотрением "положительных” комп-
лексов, у которых Cq = 0 при q < 0, — т.е., по существу, комплексов в смысле наше-
го определения.)
Группа Нч = Ker + t называется q-H ((/-мерной) гомологической группой
комплекса {q > 1); 0-мерная гомологическая группа определяется как C0/Im 3j.
Группа’Z/o = Ker e/Im Э i называется приведенной О-мерной гомологической группой.
Пополним последовательность
... — Cq(X)---►Св_1(Л)-*-.--*С>о(*)
групп цепей топологического пространства X гомоморфизмом
е: C0(J)^Z, e(S*f/f)=S*,.
Получается ’’сингулярный” цепной комплекс, гомологические группы которого сов-
падают с гомологическими группами пространства X. Приведенные нульмерные го-
мологии пространства X обозначаются символом Я0(Х) 5 пишут также Hq {X) =
= Нч (X) при q ¥= 0. „ „ „
Пусть теперь даны два цепных комплекса С' = {Cq, b'q, е'} и С" = {Cq, b"q, е”).
{Цепное) отображение комплекса С* в комплекс Сп есть, по определению, семейство
гомоморфизмов \pq: Cq -> Cq, таких, что диаграмма
, ач , , а> . е'
► *с/ —
М к-
* а" ♦
__, Ч .
. .rCq ► Cq-i
—>Z
е» j тожд-
Z
Э!
коммутативна. Ясно, что цепное отображение индуцирует отображение гомологий
(Ker b'q ->Ker bq, Im b'q+i -> Im <£+I, Ker Э^/Im 3, + 1 ->Ker bq/Im 3,+1).
Пусть X, Y — два топологических пространства и g: X -* Y— непрерывное отобра-
жение. Естественно возникают гомоморфизмы g# = Z#q'- Cq(X) -+Cq{Y) : сингуляр-
ный симплекс,/: Tq -+Х переходит в сингулярный симплекс# ° f.Tq -> Y. Очевидно,
{g#q} ~ цепное отображение комплекса {Cq{X), bq} в комплекс {Cq{Y), bq}-,
для возникающих отображений в гомологиях употребляется обозначение#, = g,q'-
Hq{X) + Hq{Y).
Очевидная теорема, (а) Если g: X-+Y, h: Y ->Z - непрерывные отобра-
жения, то {hog), = h, ° g9; (Ь) если i: X -> X - тождественное отображение, то
i, - также тождественное отображение: (id^), = id/z^x)-
Пусть снова С' и С" - цепные комплексы, и пусть = {tpq: Cq -* Cq), ф ={фч:
Cq ~*Cq} - два цепных отображения. Цепная гомотопия, связывающая с ф,- это,
по определению, совокупность гомоморфизмов Dq: Cq -* Cj'+i, таких, что при
каждом?
Dq -1 “dg+Sg + i О Dq = фч —<Pq
4. А.Т. Фоменко
98
ГЛ 2. ГОМОЛОГИИ
(считается, что =0). Если такая гомотопия существует, отображения и ф на-
зывают гомотопными (<р ~ф).
Теорема. Гомотопные отображения индуцируют одинаковые отображения в
гомологиях.
Действительно, если a G Cq - цикл (d'qa = 0), то фча - = Dq-^'qOt +
+ Э" + jDqа = dq+lDqa G Im 1 •
Теперь мы установим связь между цепными гомотопиями и обыкновенными го-
мотопиями из главы 1. Если g, h: X -*• Y - гомотопные (в смысле главы 1) отобра-
жения, то цепные отображения, индуцированные отображениями g и h, гомотопны
в смысле последнего определения. В самом деле, пусть Н: X XI -> Y - гомотопия,
связывающая g ch. Тогда для любого сингулярного симплекса/: Тч -*Х определено
отображение Яо (/ X 7) : Т4 X I -> Y. Цилиндр Tq X I канонически разбивается на
симплексы Tf (I = 0,... ,<7); для q = 1, 2 такое разбиение показано на рис. 68,
в общем случае оно определяется формулой
Т- = {(fo, - • •, tq, г) G Tq X 7| t0 +... + ti_! < т< t0 + . .. + t{} .
Поэтому отображение Но (/ X Г) определяет q + 1 сингулярных симплексов раз-
мерности q + 1. Их сумму с надлежащими знаками (выбор котЬрых мы оставляем
читателю) мы принимаем за Dq(f). Проверка показывает, что отображения
Dq'- Cq(X)^Cq^(Y\ Dq& S k^tf) ,
составляют цепную гомотопию, связывающую наши цепные отображения (рис. 69).
Из сказанного вытекает
Теорема. Если g ~h, то g, =ht.
Следствие. У гомотопически эквивалентных пространств гомологии одина-
ковы. Более того, гомотопическая эквивалентность индуцирует гомологический
изоморфизм.
(Естественный вопрос: а слабая гомотопическая эквивалентность? Ответ в § 14.)
3. Простейшие вычисления. Группы сингулярных цепей необъятны и производить
с их помощью вычисления неудобно. Поэтому для вычисления гомологий исполь-
зуются косвенные методы, которые мы начнем излагать в следующем параграфе.
Впрочем, небольшие вычисления, которые мы сейчас все же проведем, даром не
пропадут: они понадобятся, в частности, для обоснования упомянутых косвенных
методов.
Рис. 68
Рис. 69
§ 12. СИНГУЛЯРНЫЕ ГОМОЛОГИИ
99
А. Гомологии точки. Обозначим через pt одноточечное пространство. При любом q
имеется единственный сингулярный симплекс fq: Tq ->pt. Таким образом, CQ(pt) =Z
при всех q > 0. Далее, bfq = S (-l)'Tf/Q = [S (-I)Vq- i> откуда
0 при нечетном q,
= f
fq-1 ПРИ четном q.
Следовательно, наш комплекс имеет вид
id 0 id 0 е = id
—>z—>z—>z—>z-----
Z
и Яо(рО = z, #Q(pt) = 0 при q > 0 (если q нечетно, то Ker bq = Im 3Q+i = Z, а если q
четно, то Ker bq = Im Эч+1 = 0). Добавим, что Но(pt) = 0 (так что Я, (pt) = 0 при
всех <?).
Пространство, имеющее такие же гомологии как точка, называется ацикличным.
Следствие (гомотопической инвариантности гомологий). Всякое стягиваемое
пространство ациклично.
1
(Обратное неверно. Любители функции sin — могут порадоваться контрпримеру
х
на рис. 70; но бывают и более интересные примеры — скажем, проколотая ’’сфера
Пуанкаре”.)
В. Нульмерные гомологии. Если пространство X связно, то Hq(X) = Z. Действи-
тельно, нульмерные сингулярные симплексы — это, в сущности, точки, а одномерные
сингулярные симплексы — это пути, причем граница пути — это конец минус начало.
Отсюда следует, что всякая нульмерная цепь ^kift (которая всегда является цик-
лом) гомологична цепи (S^)/o> где /о — произвольно фиксированный нульмерный
сингулярный симплекс. Из этого видно, что достаточным условием гомологичности
'Zkfft ~ ^kjf'j является равенство Ък{ = ’S.k'f, очевидно, это условие является и не-
обходимым, поскольку у границы сумма коэффициентов равна 0. Наше утверждение
доказано.
Эквивалентные формулировки {X связно!) : Im = Кег е; На(Х) = 0.
В общем случае Hq(X) есть свободная абелева группа, порожденная множеством
компонент (линейной связности) пространства X, т.е. множеством яо(А); кроме
того, всегда Hq(X) as На(Х) ® Z.
Предыдущий переход от связного случая к общему имеет следующее обобщение:
если {Ха} — множество компонент пространства X, то при любом q
Hq(X) = ®Hq(Xa).
а
Упражнение 1. Если f: X -> Y - непрерывное отображение одного связного
пространства в другое, то Н0(Х) ->Я0(У) - изоморфизм.
4*
100
ГЛ. 2. ГОМОЛОГИИ
4. Относительные гомологии. Пусть А — подмножество топологического прост-
ранства X (иначе говоря, (X, А) - топологическая пара). Тогда Cq (А) С Cq (X) и
dq (Cq (4)) С Cq_! (4). Факторгруппа
Cq (X, 4) =Cq(X)ICq(A).
называется группой относительных (сингулярных) цепей пространства X по моду-
лю А; это — свободная абелева группа, множество образующих которой можно отож-
дествить с множеством сингулярных симплексов f : Т4 -> X, таких, что f(T4) <$.А.
Операторы dq: Cq (JV) -> Cq _ j (X) индуцируют операторы
Э,: Cqtf.Ay + Cq-^XA),
и возникает комплекс
Эа . Э. ’
... -> С2 (X, А) —Cl (X, А) -2-* С0(Х, А)
(без аугментации!). Соответствующие гомологические группы обозначаются симво-
лом НЯ(Х, А). Их можно определить более геометрически как факторгруппы групп
относительных циклов по группам относительных границ: относительные циклы —
это цепи пространства X, границы которых лежат в А, относительный цикл является
относительной границей, если он делается настоящей границей после прибавления
некоторой цепи, лежащей в А.
Упражнения. 2. Вычислить Нй(Х, А) в случае, когда X и 4 связны и в об-
щем случае.
3. Для всякого непустого пространства X имеют место естественные изоморфиз-
мы Hq(X) — НЯ(Х, х0), где х0 - произвольная точка в X.
Граница относительного цикла является абсолютным (т.е. обыкновенным) цик-
лом пространства 4; сопоставление а’->Э<га определяет (при каждом q) отобра-
жение
3»: Я<?(Х,4)->Я<?_1(4)
(проверка корректности определения: если а — Р есть относительная граница, то
дча — дчР есть абсолютная граница в А). Отображение Э, включается в точную
гомологическую последовательность пары
. . .^Hq(A)-^Hq(X)-^Hq(X,A)^Hq_i(A)^.. . ,
аналогичную гомотопической последовательности пары (см. § 8). В этой последо-
вательности гомоморфизмы i,: НЧ(А)~*НЯ(Х) индуцируются включением/: 4X
а гомоморфизмы : Hq(X)^Hq(X,A) индуцируются проекциями Cq(X)-+
^Cq(X)ICq(A) = Cq(X,A).
Упражнение 4. Проверить точность гомологической последовательности па-
ры (по образцу проверки точности гомотопической последовательности пары в § 8).
(В известном отношении гомологическая последовательность пары проще гомото-
пической последовательности пары, поскольку она включает в себя только абелевы
группы.)
Заметим, что произвольное отображение /: (X, А) * (У, В) (т.е. непрерывное ото-
бражение /: Х~*У, такое, что f(A)C.B — ср. § 8) индуцирует гомоморфизмы
Д: Hq(X, A)-^Hq(Y, В) и вообще отображение гомологической последовательности
пары (Х,А) в гомологическую последовательность пары (У, В), т.е. ’’коммутатив-
§ 12. СИНГУЛЯРНЫЕ ГОМОЛОГИИ
101
ную лестницу”
... -> Hq (Л) -> Hq (X) -* Hq (X, А) -> Hq_i(А) ->...
/» |г. Л г.
... -> Hq (В) -*Hq (У) -> Hq (Y, В^Н^В)*...,
строки которой — точные последовательности. Добавим, что Hq(X) = Hq(X, ф) (в
этом смысле абсолютные гомологии являются специальным случаем относительных)
и что таинственное отображение /,: Hq (X) -* Hq (X, А) в действительности индуци-
руется отображением / = id: (X, ф) -> (X, А) (ср. § 8).
Упражнение 5. Построить гомологическую последовательность тройки
...-*Hq(A,B)-*Hq (X, В) -► Hq {X, А) -> Hq _ J (А, В) ->...
и доказать ее свойства, аналогичные свойствам гомологической последовательности
пары (включая точность). (Ср. упражнение 10 в § 8.)
Точность гомологической последовательности пары (и тройки) имеет стандартный
набор следствий (ср. § 8), среди которых гомотопическая инвариантность относи-
тельных гомологий: если отображение/: (X, Л) -*( Y, В) обладает тем свойством, что
индуцируемые отображения X -> Y, А -* В являются гомотопическими эквивалент-
ностями, то /,: Hq(X, А) -> Hq(Y, В) есть изоморфизм при любом q.
(Поспешим разочаровать читателя, ожидающего точной ’’гомологической после-
довательноспг расслоения”, - взаимоотношения гомологий с расслоениями доволь-
но сложны и не укладываются в рамки никакой точной последовательности; этим
проблемам посвящена значительная часть всей этой книги.)
5. Относительные гомологии как абсолютные.
Теорема. Пусть (X, А) - топологическая пара.
(i) Если (X, А) — пара Борсука (см. § 5), например, клеточная пара (см. опять
§ 5), то
р. -. Hq(X, A)-*Hq (XIА, а) = Hq (Х/А)
(гдер-. Х-*-Х/А - естественная проекция и а= р(А)) есть изоморфизм при любом q.
Вспомним, что относительные гомотопические группы (X, А) тоже интерпрети-
руются как абсолютные гомотопические группы некоторого пространства, но это
пространство значительно сложнее, чем Х/А (см. § § 8 и 11). Впрочем, эти две интер-
претации (относительных гомотопий и относительных гомологий) двойственны в
смысле двойственности Экмана — Хилтона иэ §4.
(ii) В общем случае включение X -* X UCA, где X UCA получается из X присоеди-
нением конуса СА над А (см. рис. 71), индуцирует изоморфизм
Hq(X, A) sHq(XU СА, СА) = Hq(XU СА, и) = Hq(XO СА).
(Здесь v обозначает вершину конуса СА, предпоследнее равенство является след-
ствием гомотопической инвариатности относительных гомологий и стягиваемости
конуса СА.)
Первая часть теоремы является следствием второй части, ввиду гомотопической
инвариантности гомологий и того факта, что для любой пары Борсука (X, А) проек-
ция X UG4 -*(Х UG4)/CA = Х/А является гомотопической эквивалентностью (см.
§ 5). Доказательство второй части основывается на двух последовательно доказывае-
мых леммах, каждая иэ которых важна сама по себе и каждая из которых обладает
интересными обобщениями, которые мы сформулируем в виде упражнений. Мы нач-
нем с формулировок лемм и упражнений. (Мы рассчитываем, что читатель вникнет
102
ГЛ. 2. ГОМОЛОГИИ
сейчас в формулировки упражнений, но делать их будет после прочтения доказа-
тельств лемм.)
Лемма 1. Пусть % ={Ua} - конечное открытое покрытие пространства X.
Обозначим через Cq(X) подгруппу группы q-мерных сингулярных цепей пространст-
ва X, порожденную такими сингулярными симплексами f : Т4 -*Х, что f(Tq) С Па
при некотором а. Очевидно, ЭЧ(СЧ(ЛЭ) С C^_j(X), так что {Cq(X), Э,} - под-
комплекс комплекса {Cq(X), dq}. Утверждение: гомологии комплекса {Cq(X), bq }
совпадают с гомологиями комплекса {Cq (X), dq}; точнее: включение первого комп-
лекса во второй индуцирует изоморфизм гомологий.
Рис. 71
Упражнения. 6. Пусть 8 — некоторое множество сингулярных симплексов
пространства X (разных размерностей, вообще говоря), включающее вместе с каж-
дым сингулярным симплексом все его грани. Для произвольного сингулярного симп-
лекса f: Т4 -* X его исправлением называется пара, составленная из гомотопии
ft: Т4 -* X и триангуляции (см. § 5) т стандартного симплекса Tq, таких, что f0 =f
и сужение отображения fi на любой симплекс триангуляции т принадлежит 8. Оче-
видно, исправление сингулярного симплекса индуцирует исправление всех его гра-
ней. Множество 8 называется достаточным, если выполняется следующее условие.
Пусть / — сингулярный симплекс, для всех граней которого заданы исправления,
согласованные в их пересечениях (т.е. в гранях граней); тогда существует исправле-
ние сингулярного симплекса /, согласованное с заданными исправлениями граней.
Докажите, что если множество 8 достаточно, то подкомплекс сингулярного цепного
комплекса пространства X, порожденный симплексами из 8, имеет такие же гомоло-
гии, как весь комплекс (точнее, включение подкомплекса в комплекс индуцирует
изоморфизм в гомологиях). Неформально говоря, гомологии пространства X можно
вычислять, пользуясь только сингулярными симплексами из 8.
7. Если — открытое покрытие пространства X, то сингулярные симплексы, за-
ключенные в элементы покрытия, составляют достаточное множество. (Вместе с пре-
дыдущим упражнением это утверждение покрывает лемму 1, освобожденную, к тому
же, от предположения конечности покрытия.)
8. Если X есть область евклидова пространства (или произвольное гладкое много-
образие — см. § 14), то гладкие сингулярные симплексы составляют достаточное
множество. (Таким образом, гомологии гладкого многообразия можно вычислять,
пользуясь только гладкими сингулярными симплексами — этот факт имеет перво-
степенное значение для остающейся за пределами нашего курса теории де Рама — см.
X. Уитни ’’Геометрическая теория интегрирования” или Б.А. Дубровин, С.П. Нови-
ков, А.Т. Фоменко ”Современная геометрия. Часть П”.)
§ 12. СИНГУЛЯРНЫЕ ГОМОЛОГИИ
103
9. Пусть X — область евклидова пространства. Докажите, что достаточное мно-
жество составляют аффинные сингулярные симплексы (аффинные отображения стан-
дартных симплексов в X).
10. Пусть X — триангулированное подмножество евклидова пространства (см.
§ 5, доказательство леммы о свободной точке), или, как говорят,полиэдр. Рассмот-
рим множество 8 сингулярных симплексов, симплициально отображающих стандарт-
ные симплексы на симплексы триангуляции (симплициальное отображение евклидо-
ва симплекса на евклидов симплекс есть, по определению, аффинное отображение,
переводящее вершины в вершины). Докажите, что множество 8 достаточно.
Переходя ко второй лемме, напомним, что в § 5 нами была определена привиле-
гированная барицентрическая триангуляция стандартного симплекса Тч (см. рис. 31
на с. 48). В этой триангуляции ^-мерные симплексы отвечают перестановкам вершин
исходного симплекса. Барицентрическое подразделение 3/ сингулярного симплекса
f: Tq -*Х определяется как сингулярная цепь Ssgn(r)/T, где суммирование рас-
пространяется на все перестановки т множества вершин симплекса Tq, sgn(r) =± 1
в зависимости от четности перестановки т, a fT обозначает сужение отображения/
на ^-мерный симплекс барицентрического подразделения, отвечающий перестанов-
ке т и отождествляемый с Г4 в соответствии с естественным порядком своих вер-
шин. (Последнее означает, что вершина симплекса барицентрического подразделения,
являющаяся центром f-мерной грани симплекса Тч, переходит при отождествлении
в г-ю вершину симплекса Тч\ неформальным оправданием знаков sgn (г) в опреде-
лении 3/ служит тот факт, что гомеоморфизм, при помощи которого производится
указанное отождествление, сохраняет или обращает ориентацию в зависимости от
четности перестановки т.) Положим далее 3 S kt ft = kt 0ft-
Упражнение 11.39 = ЭЗ; таким образом, 3 индуцирует отображения 3. :
Hq(X)^Hq(X).
Лемма 2. Отображение 0, тождественно: 3«(в) = а при любом a^Hq (X). Более
того, существует цепная гомотопия D, связывающая цепное отображение 3 с тождест-
венным отображением и такая, что образы сингулярных симплексов, входящих в
цепь Df, содержатся в образе сингулярного симплекса/.
Упражнения. 12. Предположим, что для любого топологического пространст-
ва X задано цепное отображение ax' {Cq (X), Э } -* {Cq (X), Э } (напомним, что в опре-
деление цепного отображения входит требование согласованности с аугментацией е!),
естественное по отношению к X в том смысле, что для любого непрерывного отобра-
жения /: Х-* Y и для любого q диаграмма
Cq{X)^Cq{X)
а f#
Cq(Y)^Cq(Y)
коммутативна. (Совокупность отображений ах с этим свойством иногда называется
трансформатором.) Тогда отображение at: Hq(X) -*Hq(X), индуцируемое ах, тож-
дественно для любого X. (Более того, существует естественная по X гомотопия,
связывающая ах с id; уточните эту формулировку и докажите уточненное ут-
верждение.)
13. Проверьте, что а%=3 удовлетворяет требованиям определения, содержаще-
гося в предыдущем упражнении. После этого выведите из предыдущего упраж-
нения лемму 2. (’’Более того” в лемме 2 вытекает из ’’более того” в упражне-
нии 12.)
104
ГЛ. 2. ГОМОЛОГИИ
14. Другой пример трансформатора: пусть о>ч: Тч -> Тч - аффинный автомор-
физм, обращающий порядок вершин; для сингулярного симплекса ft Тч -+Х по-
ложим (-l)4^-1^2ax/=/0 w,: Tq -*Х.
Доказательство леммы 2. Построим специальную триангуляцию ци-
линдра Tq X I. При q = 0, 1,2 она показана на рис. 72, в общем случае определя-
ется индуктивно следующим образом. Триангулируем дно Тч X 0 цилиндра Т4 X /
естественным образом (с одним 9-мерным симплексом), а стенки г’ -1 XI - в соот-
ветствии с уже построенной триангуляцией Тч~1 X / (важно, что эта триангуляция
Рис. 72
угодно переставляющие его вершины). После этого триангулируем весь цилиндр,
разбив его на конусы, основаниями которых служат симплексы построенной триан-
гуляции дна и стенок, а вершина находится в центре ’’крышки” — верхнего основа-
ния Тч XI. Теперь для сингулярного симплекса ft Тч + X определим DfG. Сч+1(Х)
как сумму с коэффициентами ± 1 (уточнение знака мы оставляем читателю) сужений
сквозного отображения
pq х I проекция ? ?q f , %
на (q + 1) -мерные симплексы построенной триангуляции цилиндра Тч X /. Возникаю-
щие отображения
D. Cq(X)^Cq+i(X), DZktf^ZkfDfi,
составляют гомотопию, связывающую 3 с тождественным отображением. Эта гомото-
пия удовлетворяет требованиям леммы.
Доказательство леммы 1. Мы должны доказать, что (а) всякий цикл
из Cq (X) гомологичен циклу из Cq(X) и что (Ь) если цикл, лежащий в С“(Х), яв-
ляется границей некоторой цепи из Cq+1(X), то он является границей цепи из Cq+i(X).
Оба факта очевидным образом выводятся из трех утверждений: (а) для любой
9-мерной цепи с цепь finc с достаточно большим и содержится в Cq (X) (очевидно);
(3) циклы с и 3”с гомологичны при любом и (лемма 2); (7) если с — цикл из Cq(X),
то разность с - 0пс является границей цепи из C^+i(X) (вторая часть леммы 2).
Доказательство теоремы. Как было замечено, в доказательстве
нуждается только часть (ii). Рассмотрим покрытие И пространства X и СА, состав-
ленное из открытой части С0А = (X и СА) — X конуса СА и множества X U С А,
где С А - нижняя половина конуса СА (без верхнего основания) (см. рис. 73).
Из относительного варианта леммы 2 (который, с одной стороны, доказывается
§ 12. СИНГУЛЯРНЫЕ ГОМОЛОГИИ
105
точно так же, как абсолютный, и, с другой стороны, является формальным след-
ствием абсолютного варианта и 5-леммы - см. § 8) вытекает, что гомологии пары
(XU СА, СА) можно вычислять при помощи цепей
C*(XUCA,CA) = С®(ХиСА)/С*(СЛ)
(покрытие конуса СА, индуцированное покрытием 41, мы снова обозначаем че-
рез 41). Но, очевидно,
С%(Х\Э СА)!С*(СА) = Cq(X<JCA)!Cq(CA) = Cq{XoCA,CA),
откуда
Hq(XOCA,CA) = Hq(XUCA,CA) = Hq(X,A)
- последнее равенство вытекает иэ гомотопической инвариантности гомологий.
Рис. 73
6. Дополнения. В заключение мы приведем без доказательства (в виде упражне-
ний) еще два важных свойства гомологий.
Упражнения. 15. Пусть (X, А) — топологическая пара, и пусть В С А. Вклю-
чение (X — В,А -В)-* (X,А) индуцирует отображение
Hq(X-B,A— B)-*Hq(X,A),
называемое гомоморфизмом вырезания. Докажите теорему вырезания: ес-
ли В С Int А или если (X, А), (X - В, А - В) - пары Борсука и (X - В)[(А - В) =
= Х/А, то гомоморфизм вырезания является изоморфизмом.
16. Пусть X - топологическое пространство, А С X, В С Х,Я UB = ХиЯ ПВ = С.
Предположим, что гомоморфизмы вырезания
НГ(В,С) -> НГ(Х,А),
НГ(А,С) -* НГ(Х,В)
являются изоморфизмами при всех г (см. предыдущее упражнение) и рассмотрим
последовательность
$Q Уа
... -+Hq(C)—* Hq(A) ® Hq(B) —> Hq(X) —► Hq_1 (С) -> ,..,
в которой aq есть разность гомоморфизмов, определяемых включениями
С -* А и С + В, fiq есть сумма гомоморфизмов, определяемых включениями
Л -> X и В -> X, к yq определяется как одна иэ (совпадающих с точностью до знака -
докажите!) композиций
/. Э.
Я,(Х)--> Hq(X,A) = Hq(B,C)—+ Hq_i(O,
Hq(X) Hq(X,B) = Hq(A,o^ Hq_t(C).
106
ГЛ. 2. ГОМОЛОГИИ
Эта последовательность называется гомологической последовательностью Майера -
Виеториса или гомологической последовательностью триады (Х;А, В). Докажите,
что она точна.
§ 13. ВЫЧИСЛЕНИЕ ГОМОЛОГИЙ КЛЕТОЧНЫХ ПРОСТРАНСТВ
В этом параграфе мы увидим, что гомологии клеточных пространств можно
вычислять при помощи комплекса, неизмеримо более узкого, чем сингулярный
комплекс. Начать мы должны с вычисления гомологий сфер и букетов сфер.
1. Гомологии сфер. Изоморфизм надстройки.
Теорема 1. Если п>0,то
{Z при i = 0, п,
0 при i=£0,n.
Гомологии сферы 5° выглядят немного по-другому: H0(S0) = Z ® Z, Я, (S’0) = 0
при i > 0. Чтобы сделать формулировки более единообразными, лучше говорить
о приведенных гомологиях Я:
Теорема 1. При всех п > 0
~ Г Z при i = n,
Hi(Sn) =
I 0 при i^n.
Доказательство теоремы Г Рассмотрим точную Я-последователь-
ность пары (Dn, Sn ~*) (т.е. гомологическую последовательность тройки
(Dn,Sn -I,pt)):
Ht(Dn) -> Ht(Dn,Sn~l) -> ->
|| (CM. § 12) II (cm. § 12) II
0 Я,(У”) 0
Из точности Hi(Sn) = l), откуда и следует наша теорема (для 0-мерной
сферы ее утверждение нам известно).
Обобщением изоморфизма Hi(Sn) = Hi_1(Sn~1), построенного в доказательст-
ве теоремы 1, служит следующий изоморфизм надстройки.
Теорема 2. Для любого топологического пространства X и любого i
где S - надстройка (см. § 2).
Доказательство: гомологическая последовательность пары (СХ, X),
где СХ — конус над пространством X, отождествляемым с основанием конуса. (За-
метим, что (СХ, X) всегда есть пара Борсука.)
(Это утверждение аналогично гомотопической теореме о надстройке и двойственно
утверждению я/(ПХ) = яДАЭ - см. § 4; впрочем, двойственность § 4 связывает
гомотопические группы, строго говоря, не с гомологиями, а с когомологиями,
с которыми мы познакомимся в § 15).
Упражнения. 1. Теорема 2 уточняется следующим образом. Пусть/: Т'~1 -*
-> X — сингулярный симплекс пространства X. Сквозное отображение
. , . С/ проекция
Ti = СХ—---------► SX
Я,( V S”) =
aG А
§JJ. ВЫЧИСЛЕНИЕ ГОМОЛОГИЙ КЛЕТОЧНЫХ ПРОСТРАНСТВ 107
представляет собой сингулярный симплекс пространства БАГ, обозначаемый через 2/.
Докажите, что отображения
Б: -*• Q(SAT), 2kift н. s ktVfi),
i ’
St
перестановочны с d и определяют изоморфизм H{ _ t (X) -> Ht (БАГ), совпадающий
с изоморфизмом, построенным в доказательстве теоремы 2. Этот изоморфизм
называется изоморфизмом надстройки и обозначается снова через Б.
2. Пользуясь упражнением 1, постройте сингулярные циклы, представляющие
гомологии сфер.
3. Гомеоморфизм Тг -> D' представляет собой относительный сингулярный цикл
пары (Пг, S* ~ 1), представляющий образующую группы Ht (D1, S* ~1) = Z.
4. Постройте относительный вариант изоморфизма Б и докажите естественность
изоморфизма Б по отношению к отображениям Эи/,.
2. Гомологии букетов сфер и вообще букетов.
Теорема 3. Пусть А - произвольное множество, S"(a еЛ) - копии стан-
дартной п-мерной сферы. Тогда
® Za при i = n,
a G А
0 при i^n.
(Здесь V обозначает букет, а ®аеА%а есть свободная абелева группа, порожденная
множеством А, т.е сумма групп Z, которых столько же, сколько сфер в букете.)
Эта теорема вытекает из теоремы 2, поскольку букет УаеА$а гомотопически
эквивалентен надстройке 2(Уаел5"-1) (даже гомеоморфен этой надстройке,
если надстройку понимать в модифицированном смысле, учитывающем отмеченную
точку — см. § 2; для такой надстройки справедлив аналог теоремы 2), а для букета
нульмерных сфер утверждение верно. С другой стороны, она вытекает из следую-
щего общего утверждения о букетах.
Теорема 4. Если (Ха,ха), а е А, - пространства с отмеченными точками,
являющиеся парами Борсука, то при любом i
Ht( V АГа) = ® Ht(Xa).
a G A a G А
Доказательство: букет есть факторпространство суммы по объединению
отмеченных точек.
Упражнение 5. Постройте предыдущий изоморфизм на уровне циклов,
найдите его относительный вариант и проверьте для него всевозможную естест-
венность.
3. Отображения сфер в сферы и букетов сфер в букеты сфер. Напомним, что не-
прерывное отображение S” -* Sn имеет степень — целое число, характеризующее
его гомотопический класс (см. § 8). Непрерывное отображение
g: V S" -> VS»
a G Л 0 G В р
(S", Sp - копии сферы S”) имеет целую матрицу степеней {dap | а &А, 0 &В}\
число есть степень отображения
S’" Va е л V0eBS^ -> Sn,
где ia есть тождественное отображение сферы Sn на S”, а рр есть отображение,
тождественно отображающее сферу S£ на Sn и загоняющее остальные сферы буке-
та в точку.
108
ГЛ. 2. ГОМОЛОГИИ
Упражнение 6. Характеризуют ли степени da$ гомотопический класс отобра-
жения#?
Теорема 5. Матрица отображения
Я„(Уаел52) -> Яп(У0еВ^)
II II
® Za ® Z0
а 0
совпадает с { daj} }. В частности, отображение
f.-. Hn(Sn) - Hn(Sn),
II II
z z
индуцируемое отображением f: Sn -» Sn степени d, есть умножение на d.
Доказательство. Надстройка S/: S” + 1 -> S”+1 над отображением/:
Sn -> Sn степени d тоже имеет степень d. Поэтому, ввиду естественности гомологи-
ческих гомоморфизмов по отношению к 2, доказательство утверждения теоремы 5
при некотором п влечет за собой его доказательство при всех больших п. С другой
стороны, при и = 0 утверждение очевидно; беда, однако, в том, что степень отобра-
жения S’0 -> S° может быть не любым числом (она равна 0 или ±1). Сказанного,
однако, достаточно для доказательства нашего утверждения для некоторых отобра-
жений #, в том числе - для ia и р$ (такие отображения существуют и при и = 0).
Таким образом, ia и р$ индуцируют, соответственно, вложение в проекцию
Z = ZaC®Za, ®Z0 -* Zfl = Z.
а 0
Следовательно, утверждение теоремы достаточно проверить для всех композиций
Рр ° g ° ia> т.е. доказать его для отображений S” -* Sn. Отображение Sn -* Sn степе-
ни d представляется в виде композиции двух отображений (рис. 74). Композиция
отображения /j: Sn -* Sn v . . . v Sn с любым отображением Sn v ... v Sn -*Sn
Puc. 74
гомотопна тождественному отображению и индуцирует в и-мерных гомологиях
отображение id: Z ->Z; поэтому
Л.: Z - Z ® ... ® Z, /1,(1) = (1,..., 1).
Далее, композиция любого отображения ia: Sn -* Sn v ... v Sn с /2: Sn v ...
... v Sn -*Sn тоже гомотопна тождественному отображению, и потому
/2,: Z ® ... ® Z -> Z, /2,(ai,... ,ad) = аг + ... + ad.
Следовательно,
/.(1) = /2. о fi, (1)= /2.(1. ...,1) = d.
Теорема доказана.
§ 13. ВЫЧИСЛЕНИЕ ГОМОЛОГИЙ КЛЕТОЧНЫХ ПРОСТРАНСТВ
109
4. Клеточный комплекс. Пусть X - клеточное пространство, sk„X = Хп(п = 0, 1,
2,...) - его остовы.
Лемма. Ht (Xq, Xq ~1) равна 0 при i^qu является свободной абелевой груп-
пой, порожденной множеством q-мерных клеток пространства X, при i = q.
Доказательство: Ht(Xq ,Xq~l') = Hi(Xq/Xq~1) = Ht(\l Sq).
Г руппа
Kq(X) = Hq(Xq,Xq~l)
называется группой q-мерных клеточных цепей пространства X. Клеточный диф-
ференциал Э = Эч: <Cq (X) -> _ 1 (X) определяется как гомоморфизм
Э.: Я^Х’.Х*-1) Hq_1(Xq~1,Xq~2)
II II
rq(X)
из гомологической последовательности тройки (Xq ,Xq~l, У4 _ 2 ).
Очевидный факт:{ЭоЭ: '6ч(Х)-> '<f4_2(X) }= 0 (следствие равенства
Э о Э = 0 в сингулярном комплексе).
Гомоморфизме: 'Со(Х) = Я0(Х°) "* Z (остовы с отрицательными номерами
мы считаем пустыми) определяется очевидным образом.
Получается комплекс
э ,,, э э , а е
... -> &Ч(Х) <ft(X) -^о(Х) -> z.
Он называется клеточным комплексом. [Терминологическое замеча-
ние. В большинстве книг и статей по топологии, написанных по-русски, термин
’’клеточный комплекс” обозначает то, что у нас называется ’’клеточное пространст-
во”. В последнее время, однако, по крайней мере авторы учебников стремятся
не путать комплексы (алгебраическое понятие) и пространства (топологическое
понятие). Мы тоже следуем этому правилу.]
Относительно клеточного комплекса мы покажем две вещи. Во-первых, мы
увидим, что клеточный комплекс невелик по размерам и без труда вычисляется
для пространств с достаточно явно заданной клеточной, структурой. Во-вторых,
мы покажем, что гомологии клеточного комплекса совпадают с гомологиями сингу-
лярного комплекса, т.е. с гомологиями рассматриваемого клеточного пространства.
После этого мы сможем с легкостью вычислять гомологии не очень сложных клеточ-
ных пространств.
Начнем с реализации первого пункта программы. Как мы уже знаем (см. лемму),
группа $Ч(Х) изоморфна свободной абелевой группе, порожденной ^-мерными
клетками пространства X, т.е. изоморфна группе (конечных) формальных линей-
ных комбинаций где о; — клетка размерности q. Однако изоморфизм между
группой ^>q(X) и этой свободной абелевой группой не вполне каноничен: он зави-
сит от выбора гомеоморфизма Xq/Хч~1 V Sq. Этот гомеоморфизм канонически
строится, если для ^-мерных клеток а( фиксированы характеристические отобра-
жения/}: Dq ->Х: отображение ft определяет гомеоморфизм
fi-. Sq = Dq/Dq~l -* о,/Fra, C X’/X’”1.
Но предполагать, что характеристические отображения фиксированы, неудобно:
обычно мы знаем только, что они существуют. На самом деле фиксировать нужно не
характеристические отображения, а ориентации клеток. Мы скажем, что два характе-
ристические отображения, ft: Efl X и fi': D4 •+ X, определяет одну и ту жеориен-
no
ГЛ. 2. ГОМОЛОГИИ
тацию клетки at , если сквозной гомеоморфизм
fl <fi)'‘ „
Sq —► o,/Fro, -------► S’
имеет степень 1 (гомотопен тождественному); другая возможность состоит в том,
что этот гомеоморфизм имеет степень — 1, и в этом случае говорят, что и // опре-
деляют разные ориентации' В этом смысле каждая клетка имеет две ориентации,
и выбор ориентаций у всех 9-мерных клеток доставляет определенный изоморфизм
между группой %>q(X) и группой линейных комбинаций Ektaf. (Удобно считать,
что в этой записи at — ориентированные клетки и перемена ориентации у клетки at
равносильна перемене знака af -> —of. Заметим еще, что в случае q = 0 характеристи-
ческое отображение единственно, и никакого произвола в выборе изоморфизма
о (X) « {} нет: он каноничен.)
Кстати, употребление выражения ’’ориентированная клетка” вполне оправдано,
ибо это - действительно ориентированная открытая клетка, которая гомеоморфна
евклидову пространству. Например, ориентированная одномерная клетка — это
интервал, на котором задано положительное направление - нарисована стрелка.
Теперь рассмотрим дифференциал Э: 4g q (X) -* 4g q _ t (X). Пусть а и т - соответ-
ственно ^-мерная и (д — 1)-мерная клетки пространства Xnf; Dq -+Х, g : D4~l -*
-*Х — характеристические отображения. Рассмотрим композицию
/'s’-1
S’-1 -----------> X’-1 ->
проекция
---------► Xя 1/(Хя 2 U (все (д — 1)-мерные клетки, кроме т)) =
= r/Frr ~—> S’-1.
Степень этого отображения — целое число - называется коэффициентом инцидент-
ности между а и т и обозначается через [о: т].
Упражнение 7. Хотя по видимости число [а: т] зависит от характеристичес-
ких отображений, на самом деле оно зависит только от ориентаций клеток а и г;
при перемене любой из этих ориентаций число [а :т] меняет знак.
Заметим, что если о и т не пересекаются, то, очевидно, [о:т] =0. Поэтому при
данном а коэффициент [а:т] может быть отличен от нуля лишь для конечного
числа т.
Теорема 6.
Э ( S ki о,) = S kj ( S [of: tJt;,),
i i i
где {ak} и{т,} - все q-мерные и все (q - 1)-мерные клетки пространства X.
Доказательство. Мы должны показать, что т входит в Эт с коэффициен-
том [о:т]. Рассмотрим отображение (О’, S’-1, ф) -* (Xя, Хч~1, Хч~2), опреде-
ляемое характеристическим отображением f : Dq -> X, соответствующим клетке а.
Возникает диаграмма
Z = ЯЧ(О’,5’-1) ——► Яч_1(5’-1) = Z
1 a 4 /?
э*
НЧ(ХЧ1ХЯ-') = Hq(Xq,Xq-1)-------^Яч-ЛйГ’-1,^’-2) = Hq_1(Xq~1/Xq 2)
II II
э
%q(X) ->
§ 13. ВЫЧИСЛЕНИЕ ГОМОЛОГИЙ КЛЕТОЧНЫХ ПРОСТРАНСТВ
111
(аир- гомологические гомоморфизмы, индуцируемые различными производными
отображения f). Ясно, что а(1) = о G 4gq(X), и потому So = 0(Э. (1)) = /3 (1). Но в си-
лу теоремы 5 образ элемента lGHq_1 (Sq ~ *) при сквозном отображении
Hq_1(Xq~l,Xq-2) = Hq_1(Xq~1/Xq~2) =
= ^_1(vs;-1) =
в слагаемом Hq _, (S? “1) = Z, отвечающем клетке т, есть в точности степень соот-
ветствующего отображения Sq ~1 -> Sq ~1, т.е. [а:т]. '
В заключение поговорим еще о геометрическом смысле коэффициентов инци-
дентности. Характеристическое отображение /: Dq -> X, отвечающее клетке о, взаим-
но однозначно на IntD’, а на S’-1 может таковым не быть. Прообраз/*1 (х) точки
х G т лежит в Sq ~1 и может не быть одной точкой. Если / — достаточно хорошее
отображение их— достаточно общая точка, то [а:т] можно определить как ’’ал-
гебраическое число” точек прообраза /**(х). Этот факт, точную формулировку
и доказательство которого мы оставляем читателю, выводится из данного в конце
§ 8 описания степени отображения S" * S" как алгебраического числа прообразов
общей точки. Имея в виду это представление о коэффициентах инцидентности,
можно Придать теореме 6 совершенно тавтологическую форму: ’’граница клетки
есть сумма клеток, входящих в границу клетки, с коэффициентами, равными крат-
ности их вхождения в границу клетки”.
5. Гомологии клеточного комплекса.
Теорема 7. Гомологии клеточного комплекса клеточного пространства X
совпадают с гомологиями пространства X.
(В процессе доказательства будет построен канонический изоморфизм между
теми и другими гомологиями.)
Доказательство осуществляется в 3 шага.
1-й шаг: (?-я группа гомологий клеточного комплекса совпадает с Я^Х4*1, Хч~2)
(здесь, как и выше, остовы с отрицательными номерами считаются пустыми). Рас-
смотрим диаграмму
я„(х*1х9’2) = О
" I
1Р "
нч(хч,х9-') = *,(х) о
я^.дх^х9'2) =r?-t(x),
в которой строка есть отрезок гомологической последовательности тройки
(Xq + 1, Xq, Xq ~2 ), а столбец - отрезок гомологической последовательности трой-
ки (Хч, Xq-1, Xя ~2) (равенства нулю вытекают из леммы в начале предыдущего
пункта). Из точности последовательностей и тривиальности групп Hq(Xq~l ,ХЧ~2),
Hq (Хч +1, Хч) следует, что 0 - мономорфизм, а а — эпиморфизм. Следовательно,
Hq(Xq + 1,Xq~2) = Hq(Xq,Xq~2)/Kera =
= Я,(Х’,Х’~2)/1тЭф = 0ffq(Xq,Xq~2)/0(!mdt) = Im0/Im(0o Э.).
112
ГЛ. 2. ГОМОЛОГИИ
В силу коммутативности диаграммы 0 ° = Эд+1, а в силу точности вертикальной
последовательности 1ш0 = КегЭ,. Таким образом, последняя факторгруппа есть
Kerdg/ImSg + j, что и требуется (небольшую модификацию, необходимую в случае
q = 0, мы оставляем читателю),
2-й шаг: Hq(Xq + x, Xq~2) = Hq(Xq+x). Гомологические последовательности
троек (Хч + х,Х{,Х*-х), i = q — 2, q - 3,..., 1,0,
О = НЯ(Х1,Х1-1) = X Hq(Xq + x,X‘) -*
- = О
дают: Hq(Xq+x Г»"2) = Я,(Х’+1, Xq~3) = ...= Hq(Xq+x, Х°) = Hq(Xq+x).
3-й ша г: Hq(Xq*x) = Hq(X), Гомологические последовательности пар (Х1,Х1~х),
i = q + 2, q + 3,...,
О = ^(Х'.Х'"1) -> Hq(Xl~x) X НЧ(Х‘) - Нч(Х1,Х1~х) =0
дают: Hq(Xq+x) = Hq(Xq+2) = Hq(Xq+3) = . . . Если dimX < <», все доказано.
Если X бесконечномерно, то требуется дополнительное замечание (вытекающее
из аксиомы (W) из определения клеточного пространства и компактности стандарт-
ного симплекса), что всякая сингулярная цепь пространства X фактически является
цепью остова XN с достаточно большим N\ подробности мы оставляем читателю.
Следствие. Если число q-мерных клеток клеточного пространства X равно п,
то группа Hq(X) порождается не более, чем п образующими- в частности, bq (Xq) <
< п, где bq обозначает q-e число Бетти (см. § 12). Например, если у X вовсе нет
q-мерных клеток, то Hq (X) = 0; в частности, если dimХ = т,то Hq(X) = 0 при q>m.
(Не то что гомотопические группы!)
Упражнение 8. Докажите алгебраическую лемму (’’теорема Эйлера — Пуан-
каре”) : пусть
... “* С2 “* Q Cq (-* Z)
- цепной комплекс с конечно порожденной суммой ®/ С(, и пусть q - ранг группы Ct,
Ahj — ранг f-й группы гомологий этого комплекса; тогда
S(-l)% = Z(-l)'Ci.
Выведите из этой леммы следующий факт. Если X - конечное клеточное пространст-
во и с^ — число его i-мерных клеток, то
2(-1)М*) = Z(-I)'c/
(это число называется эйлеровой характеристикой пространства X и обозначается
через х(Х)).
6. Классический комплекс. Пусть X - компактное триангулированное подмно-
жество евклидова пространства (полиэдр). Открытые симплексы триангуляции
составляют клеточное разбиение пространства X. Соответствующий клеточный
комплекс устроен следующим образом. Зафиксируем порядок всех вершин три-
ангуляции; тогда будут упорядочены и вершины каждого симплекса. Клеточная
q-мерная цепь — зто линейная комбинация £ ktot, где о,- — симплексы размерности q;
граничный оператор действует по (хорошо нам знакомой) формуле
я
d^kiOi = 2 Л/ Z Гг ot,
i I г =0
§ 2Л ВЫЧИСЛЕНИЕ ГОМОЛОГИЙ КЛЕТОЧНЫХ ПРОСТРАНСТВ 113
где ГГО| есть г-я грань симплексу о(. Этот комплекс называется классическим',
в силу теоремы 7 его гомологии совпадают с гомологиями пространства X. На протя-
жении длительного времени (с начала века до конца 20-х годов) топологи яе распо-
лагали никаким другим определением гомологий, и они затратили массу усилий
на доказательство независимости гомологий от триангуляции (эта ’’теорема топо-
логической инвариантности гомологий” занимает почетное место и во многих более
поздних учебниках топологии). Классический комплекс замечателен тем, что он
канонически вкладывается в сингулярный комплекс: образ вложения составляют
сингулярные симплексы, аффинно и гомеоморфно отображающие стандартные симп-
лексы на симплексы триангуляции с сохранением порядка вершин.
Упражнение 9. Докажите, что это вложение индуцирует изоморфизм в го-
мологиях, причем тот самый, который построен нами в процессе доказательства
теоремы 7.
Чрезвычайно интересно сопоставить это упражнение с упражнением 10 к § 12.
(Кстати, оба утверждения верны не только для полиэдров, но и для ’’симплициаль-
ных пространств”. Это - абстрактно, наподобие клеточных пространств, опреде-
ляемые пространства, в которых замкнутые клетки — это симплексы, примыкающие
друг к другу строго по граням; подробности см., например, в § 2.2 книги Рохлина
и Фукса).
7. Некоторые вычисления.
А. Сферы. Гомологии сфер нам уже известны, но мы вычислим их еще раз, чтобы
поупражняться в применении теоремы 7. Сфера Sn разбивается на 2 клетки размер-
ностей Ойл (см. § 5). При таком разбиении (мы считаем, что л > 0) $o(S”) ~
= $п (Sn) = Z, остальные $?<j(S") равны 0. Если л > 1, то автоматически все диффе-
ренциалы равны 0, все цепи - циклы, граница — только 0, и группы гомологий
не отличаются от групп клеточных цепей:
Z при 1 = 0, л,
0 при i ¥= 0, л.
Если л = 1, то ответ такой же, но тривиальность дифференциала Э: ^i(S*) *
-> ®0(5*) - уже не тавтология, а следствие важной леммы:
Лемма. Если а - ориентированная одномерная клетка, о0 и — ее "начало"
и "конец", то да = - т0; в частности, если клетка о замкнута (fi =т0), то да = 0.
Упражнение 10. Произведите вычисление гомологий сфер, пользуясь други-
ми клеточными разбиениями — см. § 5:
В. Проективные пространства. Случаи комплексных, кватернионных и калиевых
проективных пространств не сложнее случая сфер: клетки соседних размерностей
отсутствуют (имеется в виду клеточное разбиение, построенное в § 5), клеточный
дифференциал Э всегда тривиален и ЯЧ(С/’") = ^q(CPn) (1 < л < °°), Я, (ИР”) =
= «„(HP") (1<л<оо), Я<?(Са/’2)= (СаР2). Таким образом:
fZ при q = 0,2,4,... [, 2л, если л конечно],
0 при остальных q;
Z при q = 0,4,8,... [,4л,если л конечно],
0 при остальных q;
Hq(CaP2) = ( Z при g = 0,8,16,
I 0 при остальных q.
Hq(HPn) =
114
ГЛ 2. ГОМОЛОГИИ
Вещественный случай сложнее и интереснее. Пространство RP" разбивается на клет-
ки о°, о1, а2,... [, о", если п конечно].
Лемма.
( 2, если i нечетно,
[о/+1 : о*] = ]
( 0, если I четно.
До казательство. Отображение St+1 -» Si+1, степень которого равна, по оп-
ределению, [а,+1 : а/], устроено так: экватор сминается в точку, нижняя из двух
образовавшихся сфер склеивается с верхней по антиподальному отображению
(см. рис. 75). Ясно, что зто отображение имеет степень 2, если антиподальное отобра-
жение сохраняет ориентацию (т.е. если сфера нечетномерна), и степень 0, если анти-
подальное отображение обращает ориентацию.
Лемма доказана. Клеточный комплекс пространства RP" (лишенный аугмента-
ции) имеет, таким образом, вид:
(если п конечно)
4,-1 4,-2 41 ®2 *1 4>
Z —> Z —> Z —> ... —* z —► z —+ z —* z
(л четно) 2 0 2 1
[ ... 020
(л нечетно) 0 2 0 J
О
Ядро и образ гомоморфизма —►: все целые числа и 0; ядро и образ гомомор-
2
фиэма —►: 0 и все четные числа. Производя факторизации, получаем:
(если п конечно)
0 1 2 3 4 ... л-2 л-1 л
Z Z2 0 Z2 0 ... 0 Z2 0, если п четно,
Zj 0 Z, если п нечетно,
т.е.
Z, если <7 = 0 или q = п и п нечетно,
^(RP") = | Z2, если q нечетно и q < п,
0 в остальных случаях.
С. Многообразия Грассмана. Клеточные разбиения описаны в § 5. В комплексном
и кватернионном случаях клетки соседних размерностей отсутствуют и группы гомо-
§ 13. ВЫЧИСЛЕНИЕ ГОМОЛОГИЙ КЛЕТОЧНЫХ ПРОСТРАНСТВ
115
логий совпадают с группами клеточных цепей:
Hq(CG(n,k)) =
' Z®... ® Z, где г есть число диаграмм Юнга из q/2 клеток,
г ' вмещающихся в прямоугольник к X (п - к)
(см. рис. 76)
О в остальных случаях (в частности, если -п нечетно).
Hq(HG(n,k)) - Hq/2(CG(n,k))
(в частности, Hq(HG (п, к)) =0, если q не делится на 4).
Рис. 75
Рис. 76
В вещественном случае ситуация сложнее.
Упражнения. И. Докажите, что [е (Д) : е(Д') ] = 0, если Д' Д; если же
Д' С Д и разность Д — Д' достоит из одной клетки с координатами (s, t), то
[ 0, если s + t нечетно,
[е(Д):е(Д')] =
( ±2, если s + t четно
(знак в последней строке зависит от ориентации клеток; для вычисления гомологий
знать его не обязательно). Вычислите гомологии многообразий G(n, к) с небольши-
ми п и к. Найдите гомологии многообразия G(n, к) размерности dim G(п, к) =
= к(п — к).
12. Найдите числа Бетти многообразий Грассмана.
13. Обследуйте клеточный комплекс многообразия G+(n, к), найдите гомологии
этих многообразий при небольших п и к, а в общем случае найдите гомологии стар-
шей размерности и числа Бетти.
D. Многообразия флагов. В комплексном и кватернионном случаях вычисление
снова не составляет труда.
Упражнение 14. Найдите коэффициенты инцидентности для вещественного
случая.
Е. Классические поверхности. Клеточный комплекс связной замкнутой классиче-
ской поверхности имеет вид
«2 «о
Z Z ® ... ф Z Z,
где число слагаемых Z в равно 2g, 2^ + 1 и 2g + 2 для сферы, проективной
116
ГЛ. 2. ГОМОЛОГИИ
плоскости и бутылки Клейна с g ручками (см. § 5). Дифференциал Э j: -> $0
тривиален в силу последней леммы (см.п. А), а дифференциал Э2 вычисляется на
основании описанной процедуры склеивания классической поверхности из много*
угольника (см. § 1). Именно, границд многоугольника (как двумерной клетки
естественного клеточного разбиения многоугольника) есть сумма всех его сторон,
направленных в одну сторону (против часовой стрелки). При склеивании ориенти-
руемой поверхности стороны попарно склеиваются с обращением ориентации, ввиду
чего все коэффициенты инцидентности между двумерной клеткой ориентируемой
поверхности и ее одномерными клетками равны 0. При склеивании неориентируемой
поверхности стороны склеиваются с сохранением ориентации, и коэффициенты ин-
цидентности равны 2. Таким образом,
(О, ...,0) в ориентируемом случае,
Э2(1) =
(2,..., 2) в неориентируемом случае,
что позволяет вычислить гомологии: для классической поверхности X
Н0(Х) = Z,
Z а ... ® Z, если X есть сфера с g ручками,
2g
Z ® ... ® Z ® Z2, если X есть проективная плоскость с g ручками,
2g
Z ® ... ® Z ® Z2, если X есть бутылка Клейна с g ручками,
2^+1
Z, если X есть сфера с ручками,
О, если X есть проективная плоскость или бутылка Клейна
с ручками.
8. Цепные отображения клеточных комплексов. Заканчивая параграф, мы заме-
тим, что теорию гомологий можно было бы строить, взяв за основу клеточный, а не
сингулярный комплекс (если бы необходимость доказывать топологическую
инвариантность не сводила бы на нет все преимущества этого подхода). В частности,
отображение Л клеточного пространства X в клеточное пространство Y индуцирует
цепное отображение Л#: %>д(Х) -> $Ч(У), если зтоотображение клеточно (см. § 5),
т.е. отображает остовы в соответствующие остовы. Именно, если о и т — клетки
размерности q пространств X и У, то, зафиксировав характеристические отображе-
ния /: Dq -+ X и g: Dq -> У, мы можем определить число dh(a, т) как степень
сквозного отображения
S4 = D^/S4'1 + Xq/Xq~l + Yq/Yq~1 ->
проекция
-------->Yq/(Yq~1 U (все q-мерные клетки, кроме т)) =
_ g
= t/Fit -----> 5^
§ 14. ГОМОЛОГИИ И гомотопии
117
(первые два отображения - это, конечно, не сами f и Л, а отображения, индуцируе-
мые f и h\ второе из них определено ввиду клеточности Л: Л (Xя) С Y4,
Л (Л4-1) С У’-1). Это число, разумеется, зависит только от ориентаций клеток о
и т и меняет знак при изменении любой из этих ориентаций.
При фиксированном о число dh (о, т) может быть отлично от нуля лишь при ко-
нечном числе различных т (докажите!). Поэтому формула
Л#(2 kt о,) = S *f(S dft(o, т)т),
/ i т
где внутреннее суммирование справа распространяется на все ^-мерные клетки
пространства У, корректно определяет гомоморфизм
Л#: Ч8Я(Х) - ®,(У).
Упражнение 15. Покажите, что построенные гомоморфизмы Л# составляют
цепное отображение клеточного комплекса пространства X в клеточный комплекс
пространства У и что индуцированный гомологический гомоморфизм совпа-
дает с Л*.
Если отображение Л не клеточно, то никакого естественного способа построить
цепное отображение Л# не существует; но это не беда, поскольку всякое непрерыв-
ное отображение гомотопно клеточному (теорема о клеточной аппроксимации —
см. § 5). Таким образом, клеточный аппарат приложим, в принципе, и для вычисле-
ния гомологических гомоморфизмов, индуцированных непрерывными отобра-
жениями.
§ 14. Гомологии и гомотопии
Связь между гомологическими и гомотопическими группами топологического
пространства видна уже из предварительного описания гомологий, данного нами
в начале этой главы: сфероиды — это тоже циклы, гомотопные сфероиды —
это гомологичные циклы и, следовательно, гомотопические группы канонически
отображаются в гомологические. Это отображение, называемое ’’гомоморфизмом
Гуревича”, мы изучим в настоящем параграфе. Мы увидим, что связь между гомоло-
гиями и гомотопиями глубже, чем это представляется поначалу, и в то же время
мы приведем примеры, которые должны предупредить читателя, ожидающего от
этой связи слишком многого.
1. Гомологии и слабые гомотопические эквивалентности.
Лемма. Пусть X - топологическое пространство и a G Hq (X). Тогда сущест-
вуют клеточное пространство У, класс гомологий 0G Hq(Y) и непрерывное отобра-
жение f : Y-*-X, такие, что =а.
N
Доказательство. Пусть S ktft, ft: Tq + X,- сингулярный цикл, пред-
i = 1
ставляющий класс а. Рассмотрим сумму N копий стандартного симплекса:
N
Т = U ?/. Произведем в Т следующее отождествление. Пусть Г1 и Г2 — грани
/= 1
одной размерности г < q симплексов и ; вершины граней Г] и Г2 упорядо-
q Q
чены (порядок наследуется от вершин симплексов Тц и 7)2), и это порождает кано-
нический аффинный гомеоморфизм Tj Г2. Мы отождествляем (поточечно)
118
ГЛ. 2. ГОМОЛОГИИ
Я я
rt с Tti с т с Г2 с Т/2 С Т, если fti | - ft* | г*. При отождествлении из Т
получается клеточное пространство, которое мы принимаем за Y. Отображения
ft : ТЧ( + X корректно определяют непрерывное отображение /: У -+Х. Обозначим,
далее, через Ft сквозное отображение
а п вложение проекция
Тч = 7? ----------► Т ---------»• У.
Ясно, что "ZkiFt — сингулярный цикл пространства У и что отображение f перево-
дит F/ в fa и Y,kiFi в Y,ktft, Таким образом,если 0G Hq(У) — гомологический
класс цикла ZfyF/.TO/4(0) =а.
(Замечание. При описанном отождествлении могут отождествляться точки
Q
одного симплекса Т t, но не могут отождествляться точки одной открытой грани;
чтобы лучше понять эту конструкцию, проведите ее явно для сингулярного цикла
Г3-pt.)
Относительный вариант леммы. Пусть {X, А) — топологическая
пара и ft G Hq(X, А). Тогда существуют клеточная пара (У, В), класс гомологий
0 G Hq(Y, В) и отображение- f: (У, В.) + {X, А), такие, что ft ({3) = а.
Доказательство относительного варианта немногим отличается от доказа-
тельства абсолютного варианта. Мы фиксируем (относительный) цикл пред-
ставляющий класс а, и строим клеточное пространство У — факторпространство сум-
q
|иы LI/77 , — сингулярную цепь T.kiFt и отображение /: У -» X, переводящее
T,ktFt в T,ktft. Через В мы обозначаем наибольшее клеточное подпространство
пространства У, отображающееся в А (т.е. объединение замыканий клеток, отобра-
жающихся в А). Тогда f будет отображением (У, В.) -> (X, А), S k(F( - относи-
тельным циклом пары (У, В), и если 0 G Яд(У, Я) — гомологический класс этого
цикла, то f, (3) = <*•
Теорема 1. Если f: Х^ -*Х2 - слабая гомотопическая эквивалентность, то
ft: НЧ(Х2) ->Hq(X2) — изоморфизм при всех q.
Доказательство. Напомним, что отображение /: Х2 -*Х2 называется сла-
бой гомотопической эквивалентностью, если для любого клеточного пространства У
отображение /*: я (У, Хх) -+it(Y,X2') является взаимно однозначным соответст-
вием (см. § § 9 и 11).
Эпиморфность отображения Hq(Xi) — Hq(X2) слерует из леммы: если
а G Hq(X2), то найдется клеточное пространство У, гомологический класс
Д е Hq(Y) и отображение g: Y — Х2, такие, что £*(/?) = ft. Далее, так как f —
слабая гомотопическая эквивалентность, существует отображение Л: У -> Х2, такое,
что foh ~ g. Полагая у = gt(0) G Яд(%1), имеем: /*(у) = (/°й),(?) =
= g.(0) =«•
В доказательстве мономорфности используется относительный вариант леммы.
Ввиду гомотопической инвариантности гомологий можно считать, что / есть вло-
жение, т.е. что (Х2, Xj) — топологическая пара (при необходимости можно заме-
нить Х2 цилиндром отображения f и f — вложением пространства Xt в цилиндр
в качестве верхнего основания; на такую возможность замены произвольного непре-
рывного отображения гомотопически ему эквивалентным вложением мы обращали
внимание в § 9). Если а € HqW И Л (ft) = 0, ю существует /3 € Hq+i(X2, Xi)
§ 14. ГОМОЛОГИИ И ГОМОТОПИИ 119
с &Л0) = а (точность последовательности пары). В силу относительной леммы
существует клеточная пара (У, В), гомологический класс у 6 Я(?+1(У> В.) и отобра-
жение g: (У, В) -* (Xlf X}), такие, что £*(у) = 0. Наконец, так как / есть слабая
гомотопическая эквивалентность, существует отображение Л: У -* Х1} такое, что
h | в = g | в (см. теорему 4 из § 11). Мы имеем: а = Эф(/3) = о #ф(у) =
= (% I в)« ° Э«(1) = Л* °/* ° ЭДу) (где / есть включение В в У) «О (/,<>Э, = 0
в силу точности гомологической последовательности пары (У, В)). Теорема
доказана.
Заметим, что в силу другой части уже цитировавшейся теоремы 4 из § 11 отобра-
жение f является слабой гомотопической эквивалентностью тогда и только тогда,
когда оно индуцирует изоморфизм в гомотопических группах. Таким образом,
доказанное утверждение приобретает следующую запоминающуюся форму.
Теорема 1. Если отображение f: Х2 -*Х2 индуцирует изоморфизм в гомото-
пических группах, то оно индуцирует изоморфизм и в гомологических группах.
(Ср. с теоремой 5 в конце этого параграфа.)
Следующие упражнения показывают, что некоторые утверждения, по звучанию
напоминающие теоремы 1 и 1', неверны.
Упражнения. 1. Покажите, что пространства S2 и СР°° X S3 имеют одинако-
вые гомотопические группы, но разные гомологические группы. То же для прост-
ранств Sm X RP" и Sn X RPm cm/n, ля #= 1, л ¥= 1. (Ср.упражнения 5 и 6к § 11.)
2. Покажите, что пространства S1 v S1 v S2 и S1 X S1 имеют одинаковые гомоло-
гические группы, но разные гомотопические группы.
3. Покажите, что хопфовское отображение S3 -+S2 индуцирует тривиальный гомо-
морфизм в приведенных гомологиях, но индуцирует нетривиальный гомоморфизм
в гомотопических группах.
4. Покажите, что проекция S1 X S1 -> (S1 X S1)/(S1 v S1) =S2 индуцирует три-
виальный гомоморфизм в гомотопических группах, но индуцирует нетривиальный
гомоморфизм в гомологиях (в том числе приведенных).
2. Теорема Гуревича. Пусть X — топологическое пространство с отмеченной точ-
кой Xq. Обозначим через sn каноническую образующую группы Hn(Sn) = Z (и =
= 1,2,...). Для любого G пл (X, хе) положим
Л(<Р) = fM 6 Нп(Х),
где f: Sn -+ X — произвольный сфероид класса <р. Очевидно, что h(<p) не зависит от
выбора /. Ясно также, что сопоставление •-* Л (<р) определяет гомоморфизм
Л: п„(Х,х0) ^Н„(Х);
этот гомоморфизм называется гомоморфизмом Гуревича', он естествен по отноше-
нию к непрерывным отображениям (переводящим отмеченную точку в отмеченную).
Упражнение 5. Докажите, что диаграмма
л„(Х,х0)
Нп(Х)
коммутативна для любого пути s, соединяющего точки хо и хг.
120
ГЛ. 2. ГОМОЛОГИИ
Теорема 2 (Гуревич). Пусть п0(Х, хе) = щ (X, х0) = ... = ял_1(Х, х0) =0
(п > 2). Тогда Hi (X) = ... = Нп_1(Х) = 0 и h: rrn(X, х0) + Нп (X) есть изо-
морфизм.
Доказательство. Согласно теореме 6 из §11 существует клеточное прост-
ранство, слабо гомотопически эквивалентное X; поскольку гомотопии и гомологии
слабо гомотопически инвариантны (по определению и в силу теоремы 1), мы можем
считать, что само X было клеточным. Далее, как было показано в §5, простран-
ство X гомотопически эквивалентно клеточному пространству с единственной
вершиной и без клеток размерностей 1, 2, ..., п — 1. Уже из этого видно, что
Hi (X) = ... = Hn-i(X) = 0 (см. следствие теоремы 7 из § 13), а Я„(X) =
= (Л)/1т Эл+1 не отличается от пл (X) в силу теоремы 3 из § 11.
Следствие (обратная теорема Гуревича). Если пространство X связно и одно-
связно и Н2(Х) =... = Hn^i(X) =0, то тг2 (X) = ...=itn-i(X) = 0 и h: пп(Х) -+Нп(Х)
есть изоморфизм.
Полученные результаты можно выразить одной фразой: у односвязного простран-
ства нетривиальные гомотопические и гомологические группы начинаются с одной
размерности и первые нетривиальные гомотопическая и гомологическая группы
одинаковы.
Следствие (из этого утверждения и теоремы Уайтхеда из § 11). Односвязное
клеточное пространство с тривиальными гомологиями размерностей > 2 стягиваемо.
Упражнение 6. Односвязное клеточное пространство, имеющее такие же
гомологии, как сфера, гомотопически эквивалентно сфере. [Указание: примените
теорему Уайтхеда к сфероиду Sn -> X, представляющему образующую группы
пл (X) = Z ]. То же верно для букетов сфер.
Замечание. Из полученных нами результатов видно, что тривиальность гомо-
логических групп и тривиальность гомотопических групп, каждая по отдельности,
обеспечивают гомотопическую тривиальность (стягиваемость) односвязного клеточ-
ного пространства. В то же время мы видели, что тривиальность индуцированных
гомологических гомоморфизмов и тривиальность индуцированных гомотопических
гомоморфизмов, каждая по отдельности, не обеспечивают гомотопической тривиаль-
ности непрерывного отображения, т.е. что гомотопности постоянному отображению.
Оказывается, что и вместе этих двух тривиальностей недостаточно для гомотопиче-
ской тривиальности отображения.
Упражнения. 7. Композиция
проекция Хопф
S1 x s1 X S1 --------► (S1 X S1 X 8*)/^(8* х S*XS1) = S3 -► S2
индуцирует тривиальное отображение как в гомотопических, так и в гомологических
группах, но не гомотопно постоянному отображению.
8. То же для отображения
S1"-2 XS> (S2»-2 х SSy(J2»-2 , S>) - S2"*' СР".
3. Случай л = 1.
Теорема 3 (Пуанкаре). Для любого связного пространства X гомоморфизм
Гуревича h: Л1(Х) -> Hi(X) является эпиморфизмом, ядром которого служит ком-
мунант [tij (X), rti(X)] группы (X). Таким образом,
Hi(X) m(X)/lm(X), П1(Х)].
§14. ГОМОЛОГИИ И гомотопии
121
(Напомним, что коммутант [G, G] группы G есть ее подгруппа, порожденная
всевозможными коммутаторами [gi, g2] = gig2gixg21, gi ,g2 €G. Группа G/[G,G]
получается из G коммутированием, т.е. наложением дополнительных соотношений:
все образующие коммутируют между собой.)
Доказательство теоремы 3 — копия доказательства теоремы 2: можно считать,
что X — клеточное пространство с единственной вершиной, а для таких пространств
достаточно сопоставить процедуры вычисления фундаментальной группы и одно-
мерной гомологической группы - см. § § 11 и 13.
Упражнения. 9. Покажите, что петля /: 51 X тогда и только тогда опреде-
ляет элемент ядра отображенияh: ir1(X} Н2(Х) (’’гомологична нулю”), когда
она продолжается до непрерывного отображения, ограничиваемого окружностью S1
диска с ручками в X; более того, минимальное число этих ручек равно минимально-
му числу коммутаторов, произведение которых равно представляемому f элементу
ГРУППЫ Л1(Х).
10. Пространство ХвЬ называется абелианизацией (по-другому, квилленизацией)
пространства X, если ХвЬ имеет абелеву фундаментальную группу и существует
отображение X -* ХвЬ, индуцирующее изоморфизм Яд(Х) Hq (ХаЬ) при любом q.
Докажите, что связное пространство X тогда и только тогда обладает абелианиза-
цией, когда
ki(*), *!(*)] = ki(X), kiW, ^(х)]],
т.е. когда всякий элемент группы [tTi (X), it2 (X)] представляется в виде произведе-
ния коммутаторов элементов группы iti (X) с элементами группы [iti (X), Th (X)].
[Наше определение абелианизации представляет собой упрощенный вариант приня-
того определения, в котором ХвЬ предполагается гомотопически простым (см. § 8)
или даже Я-пространством (см. упражнение 2 к § 8) или даже пространством пе-
тель (см. § 4). Настоящее определение абелианизации играет важную техническую
роль в одном из вариантов построения алгебраической К-теории. Проблема существо-
вания абелианизации в этом смысле очень сложна, и никаких общих теорем на сей
счет не известно. Зато известны несколько замечательных примеров абелианизации,
из которых мы упомянем два. Первый открыли Барратт, Кан и Придди в 1971 г.:
X = Х(5(°°), 1), где S’(°°) = U„S(n) — группа финитных перестановок счетного мно-
жества, Хвь = (П~5~)о = ия(Ол5")о (нолик указывает на то, что мы берем только
одну компоненту). Другой пример принадлежит Г. Сигалу (1973 г.): X= К(В(«>), 1),
где В(°°) - бесконечная группа кос, т.е. Xесть пространство таких множеств А С R2,
что при некотором N (своем для каждого А) А содержит точки (N + I1, 0), (N + 2,
0), . . . и еще ровно N точек, ХвЬ = П253. В обоих случаях Xимеет сложную фунда-
ментальную группу и тривиальные старшие гомотопические группы, ХвЬ имеет
простую фундаментальную группу и сложные (по сей день не известные) старшие
гомотопические группы. В обоих случаях совпадение гомологий у Хи ХвЬ совершен-
но не очевидно и кажется чудом. См. обо всем этом Barratt M.G., Kahn D.S., Prid-
dy S.B. // Proc, of AMS Summer Institute of Alg. Topology. — Madison, 1970; Segal G.B. //
Invent, math. - 1973. — V. 21. — P. 213-222; Фукс Д.Б. // Функц. анализ и его прил. —
1974.-8,№2.-С. 36-42.]
11. Доказать, что любой двумерный класс гомологий произвольного топологи-
ческого пространства реализуется сферой с ручками (т.е. для любого а € Я2(Х)
существует сфера с ручками $ и непрерывное отображение f: S -* X, такое, что
отображение Я2(5) -> Я2(Х) переводит каноническую образующую группы
Н2 (S) = Z в а).
4. Относительный вариант теоремы Гуревича. Относительный гомоморфизм
Гуревича h: ля(Х, А) -* Яя(Х, А) определяется аналогично абсолютному: если
122
ГЛ. 2. ГОМОЛОГИИ
f : (D", S"-1)-> (X-4) — относительный сфероид, представляющий класс €
eitn(X,A), то Л(^)€Яя(Х -4) есть образ канонической образующей группы
Hn(Dn, S"-1) = Z при гомоморфизме/,: Hn(fin ,Sn~l)-*Hn(X,A).
Теорема 4. Пусть (X А) - топологическая пара, причем пространства Хи А
связны и односвязны и гг2(Х, А) = 0. (i) Предположим, что я3(Х А) = - =
= я„_1(ХЛ) = 0 (п > 3). Тогда П2(Х,А) = П2(Х,А) = ... = Hn-i(X,A) = 0 и h:
irn(X,A)-*Hn(X,A) есть изоморфизм, (ii) Предположим, что Н3(Х,А~) = ...=
= Нп _ i (X А) = 0. Тогда я3(Х, А) = . . . = irn_ t (Х, А) = 0 и h: rrn(X,A)->Нп (X, А)
есть изоморфизм.
Доказательство теоремы 4 получается из теоремы 2 характерными для перехода
от абсолютного случая к относительному модификациями. Во-первых, нужно по-
строить клеточную аппроксимацию пары (X Л) • Для этого мы строим по отдельнос-
ти клеточные аппроксимации пространств X и А, (Y, f) и (В, g); затем мы находим
отображение h : В -*Y, делающее коммутативной диаграмму
* Г
* включение *
А -----------'+ X
(существование h очевидным образом выводится из свойств клеточной аппроксима-
ции) . После этого h превращается во вложение при помощи перехода к цилиндру
отображения (см. доказательство теоремы 1), и мы получаем клеточную па-
ру (У, В), гомотопические и гомологические группы которой не отличаются от
соответствующих групп для пары (X Л) [это следует из слабой гомотопической ин-
вариантности гомотопий и гомологий и 5-леммы, примененной к гомотопическим
и гомологическим последовательностям пар (X, А) и (Y, В)]. Далее используется
теорема о том, что m -связная клеточная пара гомотопически эквивалентна клеточ-
ной паре (Y', В'), у которой В' Э skm Y' (упражнение 18 к § 5), и клеточное описа-
ние первой нетривиальной гомотопической группы клеточной пары (упражнение 2
к §11).
5. Теорема Уайтхеда (не путать с теоремой того же Уайтхеда из § 11).
Теорема 5. Пусть X и Y - односвязные топологические пространства и f:
X -> Y - непрерывное отображение, индуцирующее эпиморфизм гг2(Х) * ir2(Y).
(i) Если гомоморфизм
f.-. irq(X) -> я,(У)
является изоморфизмом при q < пи эпиморфизмом при q = п, то то же верно для
f,: Hq(X) - Hq(Y).
(ii) To же с заменой -п-^Н.
Доказательство. Можно считать, что/ - вложение, т.е. что (У, X) - пара.
Точность гомотопической последовательности этой пары показывает, что условие
”/,: 71 q W ** *q(Y) есть изоморфизм при q < п и эпиморфизм при q = п ” равно-
сильно условию ”itq(Y, X) = 0 при q < и”; аналогичное верно для гомологий.
Таким образом, теорема Уайтхеда является прямым следствием относительной
теоремы Гуревича.
Следствие. Если отображение f-. X-*Y односвязного топологического прост-
ранства X в односвязное топологическое пространство Y индуцирует эпиморфизм
к2(Х) -> яз(У) и индуцирует изоморфизм Hq(X)~—► Hq(Y) при всех q, то f есть
слабая гомотопическая эквивалентность (даже гомотопическая эквивалентность,
если пространства XuYклеточны).
§ 15. ГОМОЛОГИИ С КОЭФФИЦИЕНТАМИ и когомологии
123
§ 15. ГОМОЛОГИИ С КОЭФФИЦИЕНТАМИ И КОГОМОЛОГИИ
К сингулярному или клеточному комплексу топологического пространства можно
применить алгебраические операции -®G и Hom(—, G). Получатся новые комплек-
сы, которые имею^ свои гомологии; эти гомологии называются, соответственно,
гомологиями и когомологиями пространства с коэффициентами в G. Конечно, пере-
ход к этим гомологиям и когомологиям носит чисто алгебраический характер,
но опыт (например, прекрасных во всех других отношениях ’’Лекций по алгебраичес-
кой топологии” А. Дольда) показывает, что откровенно алгебраическое изложение
этого предмета отпугивает геометрически ориентированного читателя. Щадя чув-
ства такого читателя, мы будем говорить о тензорных произведениях, Нот’ах и дру-
гих подобных вещах только там, где это абсолютно необходимо (таких мест тоже
предостаточно).
1. Определения. Пусть G — абелева группа. Сингулярная «/-мерная цепь пространства
Xс коэффициентами в G есть линейная комбинация вида 'Egifa, raeg{ G-Gii fa-.T4 *
-+Х — сингулярные симплексы. Группа «/-мерных сингулярных цепей пространства У
обозначается через Cq{X\ G); очевидно, Cq(X-, G) = Cq(X) ® G; наша прежняя груп-
па цепей Cq(X) есть в этих обозначениях Cq(X; Z). Сингулярная q -мерная коцепь
пространства X с коэффициентами (со значениями) в G определяется как функция
на множестве «/-мерных сингулярных симплексов пространства X, принимающих
значения в G (никаких условий типа непрерывности на эти функции не накладыва-
ется). Группа этих коцепей обозначается через СЧ(Х', G); очевидно, Cq(X, G) =
= Hom(CQ(AT), G). Значение коцепи с на цепи а обозначается через <с, а). Обобще-
ние: если задано билинейное умножение (спаривание) Gi X G2 ->G3, то для с 6
G С4 (Х-, Gi) и a G Cq (X; G2) можно вычислить <с,a) G G3; например, если G — коль-
цо и с G С4(АГ; G), a G Cq(АГ; G), то (с,a)GG.
Граничный и кограничный операторы
Э = Э,: CQ(Ar;G) -> Cq_1(X-,G),
8 = S’: Cq(X;G) -► Сч + 1(АГ;С)
определяются формулами
ч я
bZgtft~ Zgi S (-l)Tr/,; [8c](/)= S (-1)гс(Гг/).
i i r=Q r=0
Очевидно, для любых сна
<с, да) = <8с,в).
Немедленная проверка показывает, что ЭЭ = 0 и 88 = 0, и мы полагаем
н "ГЛ- Kerldq:Cq(X-,G)^Cq_1(X;G)]
’ Im[3q+1: Cq + 1(X;G)C,(AT;G)]
Ker[8«: Cq(X;G) -> C^ + 1(AT;G)]
Im [8q-1: Cq~l(X-,G) -> Cq(X;G)]
(при q = 0 определения модифицируются очевидным образом). Имеются также ка-
нонические операторы
е: C0(AT;G) -> G (суммакоэффициентов),
е*: G -* С°(АГ, G) (константы),
124
ГЛ 2. ГОМОЛОГИИ
и мы полагаем
H0(X-,G) = Kere/Imdi,
H°(X,G) = Ker 8°/Im е*.
Hq(X', G) = Hq(X\ G), Hq(X; G) = Hq(X; G) при q > 0 (приведенные гомологии и
когомологии). Употребляются также термины цикл, гомологичные циклы (приме-
нительно к цепям с коэффициентами в G), коцикл, когомологичные коциклы.
2. Перенесение уже известных нам результатов. Результаты §§ 12, 13 и отчас-
ти 14 автоматически переносятся на гомологии с коэффициентами и когомологии,
причем в случае гомологий формулировки не меняются, а в случае когомологий
они подвергаются ’’дуализации”, которая заключается, в основном, в обращении
стрелок.
Непрерывное отображение f : X -+ Y индуцирует гомологические и когомологи-
ческие гомоморфизмы, причем первые направлены ”в ту же сторону”, что f, а вто-
рые — ”в противоположную сторону”:
Д: Hq(X,G) Hq(Y,G), f: Hq(Y,G) + Hq(X,G).
Гомологии с коэффициентами и когомологии гомотопически инвариантны: если
f ~ g, то Д = g, и f* = g*; в частности, гомологии с коэффициентами и когомоло-
гии одинаковы у гомотопически эквивалентных пространств.
Для суммы нескольких связных пространств Х=Хх U ... U XN
Hq(Х-, G) = ®Hq(Xi, G), Hq(X\ G) = ®Hq(X-, G).
i i
Если сумма бесконечна, появляется различие между гомологиями и когомологиями:
Hq (A-; G) есть по-прежнему прямая сумма групп Hq(Xi', G), а Нч (X:; G) есть пря-
мое п р о и з в е д е н и е групп Я’(АГ/!; G).
У точки pt
tf0(pt;G) = G = tf°(pt;G),
#Q(pt;G) = 0 = Hq(pt;G) при q>0.
Относительные гомологии с коэффициентами в G определяются дословно так же,
как обычные (целочисленные) относительные гомологии, в определении относитель-
ных когомологий появляется маленькая особенность: группа Cq(X, A; G) есть
не факторгруппа, а подгруппа группы Cq(X; G); она состоит из коцепей, принимаю-
щих нулевое значение на всех цепях из Cq(A) С Cq(X). Последовательность пары
в случае гомологий с коэффициентами строится точно так же, как обычная гомоло-
гическая последовательность пары, когомологическая последовательность пары
(АГ, Л) имеет вид
. 6*
... -> Hq~1(A;G) -> Hq(X,A,G) * Hq(X,G) -> Hq(A\G) -^ ...
Гомоморфизм 8*: Hq~1(A; G) -* Hq(X, A; G) определяется так. Берем в классе
у € ffq~1(A; G) коцикл с: Cq_t(A) -+ G, произвольным образом продолжаем его
до коцепи с: Cq _ i (АГ) -> G и вычисляем кограницу 8 с; очевидно, она принимает
нулевые значения на цепях из Cq(A), т.е. является коциклом из Cq(X, A; G); ее
класс и есть 8 *(7). Все последовательности пары точны. Имеются также точные
гомологические и когомологические последовательности тройки.
Для пары Борсука (АГ, А) имеют место изоморфизмы
Hq(X,A-,G) = Hq(X/A-,G), Hq(X,A;G) = Hq(X/A;G),
§ 15. ГОМОЛОГИИ С КОЭФФИЦИЕНТАМИ и когомологии
125
устанавливаемые проекцией Х-* Х/А. Для произвольной пары (X, Л) имеют место
аналогичные изоморфизмы с заменой пространства Х/А пространством X U СА.
В тех же предположениях, что в § 12, имеют место изоморфизмы вырезания
Hq(X — B,A= Hq(X,A;G), Hq(X-B,A -B,G) = Hq(X,A,G)
и точные последовательности Майера — Виеториса (в когомологической последова-
тельности Майера — Виеториса стрелки повернуты в противоположную, по сравнению
с гомологической последовательностью Майера — Виеториса, сторону).
Для клеточного пространства X гомологии с коэффициентами в произвольной
группе и когомологии можно вычислять при помощи клеточного комплекса. Имен-
но, пусть ^Sq (Х\ G) - группа линейных комбинаций Sgj аь где gt G G и о/ - ориенти-
рованные (/-мерные клетки (замена ориентации клетки et соответствует замене
а, -* -07), и пусть ^(Z; G) - группа функций на множестве ориентированных
q -мерных клеток со значениями в G, таких, что замена ориентации клетки приводит
к изменению знака значения. Граничный и кограничный операторы Э: %q(X; G) ->
-* ®q_i(¥;G), 6: 4Sq(X;G)^- %q + 1(X,G) определяются формулами
3(SftO,)= SftS[a,:T]T,
i i т
[3 c] (o) = Z [а:т]с(т)
t
(в правой части первой формулы внутреннее суммирование распространяется на
(q - 1)-мерные клетки т пространства X, во второй формуле сС ^(A^G),
о есть (q + 1)-мерная клетка пространства X, суммирование в правой части распрост-
раняется на «/-мерные клетки т пространства X).
Приведем некоторые результаты вычисления гомологий и когомологий с различ-
ными коэффициентами для основных клеточных пространств. Для сфер
„ „ ( G прн о = 0, п,
Hq(Sn,G) = H4(S;G) =
I 0 при q^Q,n
(этот факт, конечно, вытекает из сказанного выше о клеточном вычислении гомоло-
гий и когомологий с коэффициентами, но читатель, который пожелает восстановить
доказательства, должен будет доказать его раньше, как зто делалось в §13). Для
комплексных, кватернионных и калиевых проективных пространств, а также для
комплексных и кватернионных многообразий Грассмана и многообразий флагов
гомологии и когомологии не отличаются от соответствующих клеточных цепей и
коцепей, т.е. они устроены точно так же, как целочисленные гомологии (см. § 13),
только все слагаемые Z заменяются слагаемыми G; например,
Hq(CPn,G) = Hq(CPn;G) =
G при q = 0, 2,4,...
... [, 2л, если л конечно],
О при остальных q.
В вещественном случае дело обстоит сложнее (ср. § 13), но при G = Z2 вычисление
резко упрощается, потому что все коэффициенты инцидентности четны и гомологии
и когомологии опять-таки не отличаются от соответствующих групп клеточных
цепей. Например:
fl,(R/»";Z2) = tf’(R/>n;Z2) = I Z* ПРИ 0 < ? < л>
I 0 при q > л.
126
ГЛ. 2. ГОМОЛОГИИ
Добавим,что для классической поверхности X
H2(X;Z2) = №(X;Z2) = Z2,
Я2(Х;г2) = 7/1 (JT; Z2) = Z2 ® ... ® Z2,
r
где
2g,
2g+1,
2g + 2,
если X есть сфера c g ручками,
если Хесть проективная плоскости с g ручками,
еслиХесть бутылка Клейна eg ручками.
Упражнение 1. Найдите гомологии и когомологии вещественных проектив-
ных пространств, вещественных многообразий Грассмана и классических поверх-
ностей с коэффициентами в Zm, где т — нечетное число.
Заканчивая этот пункт, заметим, что если f: X -+ У — слабая гомотопическая эк-
вивалентность, то
tfq(X;G) -> Я,(У;С) и /*: Я’(У;С) -» ЯЧ(Х;С)
- изоморфизмы при любых q и G (ср. § 14).
3. Коэффициентные последовательн : гч. Мы приступаем к выявлению соотноше-
ний между гомологиями и когомологиями с разными коэффициентами. Очевидный
факт заключается в том, что если задан гомоморфизм </>: Gt -* G2 одной абелевой
группы в другую, то для любых X и q возникают гомоморфизмы
Ч>.: Hq (X; G2) -> Hq (X; G2 ), : Я’(Х; G,) -> Я’(Х; G2 )
(в одну сторону!). Однако, как показывают многочисленные примеры (в том числе
и известные нам), мономорфность, зпиморфность и даже нетривиальность гомомор-
физма ip ни в коей мере не влечет за собой аналогичные свойства гомоморфизмов .
Чтобы глубже разобраться в предмете, рассмотрим следующую ситуацию. Пусть G —
абелева группа, Я — ее подгруппа и F — факторгруппа G/Я; обыкновенно все это
записывают в виде короткой точной последовательности
0->Я->С->Я->0.
Наряду с гомоморфизмами Hq(X,H) -+ Hq(X,G) + Hq(X\F) и Hq(X,H) -+
-* Hq(X\ G)-> Hq(X; F) возникают ’’связывающие гомоморфизмы”
Э.: Hq(X\F) -> Я,_1(Х;Я), 8‘; Hq(X,F) -> Яч + 1(Х;Я).
Приведем определение первого. Для a&Hq(X,F) выберем представителя а 6
€ Cq (X; F); так как G -+ F есть эпиморфизм, а обладает прообразом a G Cq (X; G);
граница да G Cq_1(X, G) проектируется в да = О G Gq(X; F) и потому лежит
в Cq_ 1 (X; Я); зто — цикл, его гомологический класс и есть Э, (a) &Hq_2 (X; Я).
Определение гомоморфизма 8* аналогично (у G НЧ(Х, F) * cE.Cq(X,F) ->
-* с е С4 (X; G ) -> 8 с G С 4 +1 (X; Я) -> 8 * (у) G Я q +1 (X; Я) ).
У пражнения. 2. Проверить корректность определений гомоморфизмов
Э.иб*.
3. Доказать точность коэффициентных последовательностей
... - ЯЧ(Х;Я) - Я,(Х;С) -> Hq(X,F) -> Я,_1(Х;Я) ,
... -^ Hq(X,H) Я’(Х;С) -> Hq(X,F) Hq + 1(X;H) -^ ...
1
—-да или
,m J
1 ~
— 5а
[пт
Формула а >-*
§ 15. ГОМОЛОГИИ С КОЭФФИЦИЕНТАМИ И КОГОМОЛОГИИ 127
Историческая и терминологическая справка. Гомоморфиз-
мы Э, и 5, были открыты (в частном случае) М.Ф. Бокштейном задолго до т<
как топологи освоили точные последовательности. Вот построение гомологического
гомоморфизма Бокштейна. Пусть а 6 Hq(X-, Zm); возьмем представляющий а
цикл а; коэффициенты, участвующие в записи а, - вычеты по модулю т, их можно
записать как числа 0,1....т-1,и тогда цикл а станет целочисленной цепью а;
1 ~
граница Э а делится на т (приведенная по модулю т, она равна 0); поделим: — Э а
т
есть целочисленный цикл, он представляет некоторый класс Вт (a) G Hq _ j (Л-; Z);
после приведения по модулю т класс Вт (а) превращается в класс Ът (а) €
G Hq _ 1 (X; Zm ). Мы построили два гомоморфизма Бокштейна
Вт-. Hq(X,Zm) - bm: Hq(X',Zm) - Я,_1(ДГ;гт),
которые на самом деле являются гомоморфизмами Эф, отвечающими коротким
точным последовательностям
0 •* Z > Z Zm 0, 0 •* Zm Zm* •* Zm 0.
Когомологические гомоморфизмы Бокштейна Вт \ НЧ(Х', Zm) -* НЧ + 1(Х', Z) и
bm: НЧ(Х; Zm) -* Нч + 1(Х; Zm) определяются аналогично. Из точности коэффици-
ентных последовательностей следует, что: (i) класс а € Hq(X-, Zm) тогда и только
тогда принадлежит ядру гомоморфизма Вт, когда он является ’’целочисленным”,
т.е. принадлежит образу гомоморфизма приведения Hq(X; Z) -*Hq(X', Zm); (ii) образ
гомоморфизма Вт состоит в точности из элементов группы НЧ(Х', Z), имеющих
порядок т. Аналогичное верно для когомологических гомоморфизмов Бокштейна.
определяет ’’второй” гомоморфизм
Бокштейна, который определен на ядре обычного (’’первого”) гомоморфизма
Бокштейна и принимает значения в факторгруппе по образу первого гомоморфизма
Бокштейна. Свойства второго гомоморфизма Бокштейна, а также третьего, чет-
вертого и т.д. гомоморфизмов Бокштейна мы предлагаем читателю сформулиро-
вать самостоятельно.
4. Алгебраическая подготовка к ’’формулам универсальных коэффициентов”.
Пусть А и В - абелевы группы. Пусть, далее, В = Р2/Р2, где F2 - свободная абеле-
ва группа, F2 - ее подгруппа, которая автоматически тоже будет свободной (такое
представление существует для любой абелевой группы). Каковы взаимоотношения
между тензорными произведениями А ® Fx, А ® F2 иА яВ? Легко понять, что А ® В
есть факторгруппа группы А ® по образу естественного отображения А ® F2 ->
А ® Fi (докажите это!), но последнее не является, вообще говоря, мономор-
физмом. '
Лемма. Ядро Кег[Л ® F2 А ® Fj] не зависит от выбора представления В =
= f2/f2.
Доказательство заключается в построении канонического изоморфизма
Ker [A ®F2 -* А ® F[ ] as Ker [А ® F2 -> А ® F2 ]
для любого другого представления В = F2 /F2. Главным шагом является построение
коммутативной диаграммы
4 4 \в
F2 - F(
128
ГЛ. 2. ГОМОЛОГИИ
и выявление степени неоднозначности этого построения (она измеряется произволь-
ным гомоморфизмом F{ -> F2 ). Детали мы оставляем читателю.
Определение. Ядро Ker [А ® F2 -> А ® Ft ] называется периодическим произ-
ведением групп А и В и обозначается через А * В или (более современное обозначе-
ние) через Тог(4,В).
Упражнения. 4. Покажите, что операция Тог естественна (ковариантна)
по обоим аргументам.
5. Постройте канонический изоморфизм Тог(В, А) = Тог(Л, В).
6. Покажите, что если абелева группа А свободна, то Тог (Л, В) = 0 при любом В.
7. Покажите, что Tor(Zm, Zn) as Zm ® Ln; таким образом, для конечно порожден-
ных абелевых групп А, В
Tor(4,B) as (Круч. А) ® (Круч.В)
(Круч. - кручение, т.е. совокупность элементов конечного порядка.)
8. Для бесконечно порожденных абелевых групп это может быть неверно, приве-
дите пример.
9. Если А = Q, R или С, то Тог (А, В) = 0 для любой абелевой группы В.
’’Двойственная” операция Ext определяется следующим образом. Пусть А нВ —
абелевы группы, и пусть А = Fi/F2 , где Ft и F2 — свободные абелевы группы. Тогда
Нот (А, В) есть ядро отображения Нот^, В) + Hom(F2, В), f н- f | , но это
отображение, вообще говоря, не является эпиморфизмом. Факторгруппа группы
Hom(F2, В) по образу этого отображения (т.е. коядро этого отображения) обозна-
чается через Ext (А, В).
Упражнения. 10. Докажите корректность этого определения (доказательство
должно включать в себя аналог последней леммы).
11. Ext(Z, А) = 0 для любой группы А; Ext(Zm, Zn) a Zm ® Zn; Ext(Zm, Z) as Zm
(в отличие от Tor(Zm, Z) = 0!).
12. Определите операцию Ext по Йонеда: Ext(X,B) есть множество классов изо-
морфных точных последовательностей вида
0->В->С->Л->- 0,
где С - абелева группа. Придумайте независимое описание групповой структуры
в этом множестве и докажите эквивалентность двух определений Ext’а.
13. Если одна из групп А и В есть Q, R или С, то Ext (Л, В) = 0.
S. Формулы универсальных коэффициентов. Мы покажем теперь, что, зная цело-
численные гомологии (или когомологии), можно вычислить гомологии и когомоло-
гии с произвольными коэффициентами.
Теорема. Для любых X, q, G
Hq (X; G) as Hq(X) ® G ® Tor(tfq _ 2 (X), G);
tf4(X;G) as //Q(X;Z) ®G ® Tor(//<? + I(X), G);
Hq(X;G) as Hom(tfq(X),G)®Ext(tfq + i(X),G).
Важное замечание. Эти изоморфизмы не являются естественными. Естест-
венны только отображения, входящие в следующие точные последовательности:
0 -* tfq(X)®G -> Hq(X;G) -> Tor(tfq_i (X), G) -> 0;
0 -* Hq(X;Z) ® G -► Hq(X,G) * Tor(^ + 1(X; Z), G) -► 0;
0 «- Hom(^(X),G) <- Hq(X\G) «- Ext(tfq + i (X), G) *- 0.
Доказательство теоремы. Первые два изоморфизма, или, лучше ска-
зать, первые две из только что выписанных точных последовательностей, без всякого
§ 15. ГОМОЛОГИИ С КОЭФФИЦИЕНТАМИ и когомологии
129
труда получаются из коэффициентных последовательностей. Первая последователь-
ность, например, получается так. Пусть G = Fi/F2, где Ft и F2 — свободные абелевы
группы. Совсем очевидно, что Hq(X\ Ft) = Hq(X) ® Ft-. группа Ft есть сумма некото-
рого множества групп Z, и мы имеем:
Hq(X,Ft) = Hq(X\7.®Z® ...) =
= Hq(X) ® Hq(X)9 ... = Hq(X)®Ft.
Рассмотрим пятичпенный фрагмент коэффициентной последовательности:
Hq(X-,F2) + Д,(Х;Я,) + Hq(X,G) + Hq^!(X,F2) + Hq_1(X,F1')>
т.е.
Hq(X)®F2 Hq(X)»F1 -*Hq(X,G)-*
-* Hq_i(X)®F2 +
*
Произвольная пятичленная точная последовательность А -* В -* С +D -+Е может
быть преобразована в короткую точную последовательность 0 -*Coker (/>-> С-> Кегф ->
-* 0 (Coker — коядро, т.е. Coker = B/Im^). Ясно, что это преобразование превраща-
ет последнюю пятичленную последовательность в первую из наших коротких точ-
ных последовательностей. Вторая получается точно так же из когомологической
коэффициентной последовательности. (Тот факт, что эти короткие точные последо-
вательности расщепляются, т.е. что имеют место изоморфизмы из теоремы, нуждает-
ся в несложной дополнительной аргументации, которую мы оставляем читателю.)
Однако третья из наших последовательностей вряд ли может быть построена таким
образом, поскольку в нее входят и гомологии, и когомологии. Чтобы завершить
дело, мы приведем другое рассуждение, охватывающее первый и третий из наших
изоморфизмов (мы будем сейчас строить изоморфизмы, а не точные последователь-
ности; что в наших построениях будет естественно, а что нет, читатель усмотрит сам).
Поскольку при любом q группа Bq _ i (X) = Im [ dq: Cq (X) -* Cq_1 (X)] свободна
(как абелева группа), существует встречный гомоморфизм (как говорят в анализе,
параметрикс) eq _ 1 : Bq_1 (X) -* Cq (X), dq ° eq _ i = id. Очевидно,
Cq(X) = Ker dq ®Im eq_i =Z?(X)®BQ_1(X).
Дифференциал dq устроен так:
Cq(X) = Zq(X) ® Bq_i(X)
вложение
CQ-1(X) = Zq_i(X)®Bq_2(X).
Это показывает, что весь комплекс {Cq(X), dQ) разлагается в прямую сумму коро-
теньких комплексов
вложение
...0 + 0 + В1?_1(Х) ---------> Zq_i(X) -> о -> о ...
(9) (<? - 1)
У выписанного слагаемого (q - 1)-мерные гомологии совпадают с Я<7_1(Х), осталь-
ные гомологии тривиальны. Тензорное произведение дистрибутивно по отношению
5. А.Т. Фоменко
во
ГЛ. 2. ГОМОЛОГИИ
к прямому сложению. Тензорное умножение слагаемого на G дает:
... О -> 0 -> 5q-i(X) ® G * Zq_i(X) ® G -* 0 * 0 ...
(<?) (я - 1)
Поскольку группы Вq-\{X) свободны и Hq-t (X) = ZQ_i(X)/Bq_i(X),
гомологии этого комплекса, по определению, таковы:
^-мерные Tor(//g_i(X), G),
(#-1)-мерные Hq-itX) ® G.
Поскольку полные гомологии — сумма гомологий этих комплексов, мы получаем
первую из наших формул. Третья формула доказывается точно так же: комплекс
{СЧ(Х; G), 8} есть сумма комплексов
... О 0 * Hom (Bq— J (X), (7) *- Hom (Zq-i(X), G) •*- 0 •*- О ...
и т.д.
Упражнение 14. Покажите, что гомоморфизм Нч (X; G) * Hom (Hq (X), G )
из третьей точной последовательности действует по формуле уь>{а1->(у,а)}.
Следствие. Предположим, что группы Hq(X) конечно порождены. Тогда
^(X.Z) а (Своб.частьHq(X)) ® (Круч.Я^i(X)).
В частности, группа Н1 (Х-, Z) свободна.
Упражнения. 15. Если К = Q, R или С, то
ЯЧ(Х;К) = ЯЧ(Х) ® К, ^(X;K) = Hom (ЯЧ(Х), К).
Таким образом, при переходе от целочисленных коэффициентов к рациональным,
вещественным или комплексным кручение погибает; с другой стороны, числа Бетти
можно вычислять, пользуясь гомологиями с любыми из этих коэффициентов.
16. Если К есть поле (лучше сказать, аддитивная группа поля), в частности, если
K = Zp с простым р, Q, R, С, то
ЯЧ(Х;К) = Ногпк(^(Х;К), К).
(Гомологии и когомологии с коэффициентами в К будут векторными пространства-
ми над полем К. Эту формулу лучше не выводить из формулы универсальных коэф-
фициентов, а доказать непосредственно, пользуясь равенством СЧ(Х-, К) =
= HomK(Cq(X; К), К).)
17. Докажите, что если X есть конечное клеточное пространство и К есть поле, то
выражение
S (-1/ dimKtff(X;K)
не зависит от К и равно эйлеровой характеристике пространства X (см. упражнение 8
к § 13).
18. Обследуйте взаимосвязь формул универсальных коэффициентов с гомомор-
физмами Бокштейна.
6. Формула Кюниета. По своему смыслу зта формула относится, скорее, к следую-
щему параграфу, но она находится в столь тесном родстве с формулами универсалы
§ 15. ГОМОЛОГИИ С КОЭФФИЦИЕНТАМИ и когомологии
131
ных коэффициентов (и действительно, эти формулы являются следствиями одной
общей формулы, т.е. имеют общего предка), что разлучить их не представляется
возможным.
Теорема. Пусть Xt, Х2 - топологические пространства. Для любого q
Hq(Xv X Х2) а ® [Яг№) ® Я,(Х2)] ®
г + J = q
® ® ТогСЯЛХО.Тад))
г + s = q - I
(этот изоморфизм является естественным лишь частично — в точности в том же
смысле, что формулы универсальных коэффициентов).
Доказательство использует понятие тензорного произведения цепных ком-
плексов. Пусть
а, е
... с2 —G ---------> Со Z,
. , э* , е*
... ci —> а —> с; —> z
— цепные комплексы. Их тензорное произведение определяется как комплекс
... (Ci ® Со) ® (Со ® Cj ) ► Cq ® Со ► Z,
дифференциал
bq- ® (Cr ® С/) —> ® (СГ®С/)
г + s = q г + s = q - 1
определяется формулой (в которой с G Сг, с € С/)
Эч(с ® с) = (дгс) ® с' + (—1)гс ® д^с' G
е (Cr_i ® G') ® (Cr ® C/_j) с ® (С„ ® Со').
и + v = q - 1
Формула Кюннета относится, в действительности, к тензорному произведению произ-
вольных свободных комплексов; мы применим ее к клеточным комплексам клеточ-
ных пространств. Основное наблюдение: клеточный комплекс произведения двух
клеточных пространств есть тензорное произведение клеточных комплексов этих
пространств («/-мерные клетки произведения А) X Х2 — это произведения клеток
пространств Х^ и Х2, имеющих сумму размерностей q, поэтому ^(А) X Х2) =
= ®r + s = q ( (Xi) ® (X2) ); однако подумайте, откуда берутся знаки в формуле
для границы). (Подчеркнем, что для сингулярных комплексов подобное неверно!)
Теперь для клеточных пространств формулу Кюннета ничего не стоит доказать:
клеточные комплексы {4Sq(Xi)} и V&q(X2)} разлагаются в суммы коротеньких
комплексов — как сингулярный комплекс в предыдущем доказательстве, —
5*
132
ГЛ. 2. ГОМОЛОГИИ
и их тензорное произведение разлагается в сумму комплексов вида
... О -> 0 ->S9r_1(X1) ® Ss_i(I) ->
(г + 1)
<Г + » - 1)
-S&r(*i) ® ^(^W-0...
(г + S - 2)
( 36 и S3 — границы и циклы клеточного комплекса). Гомологии такого комплекса
находятся без труда:
(г + s)- мерные 0,
(r + s- 1)-мерные Тог HS_1(X2')),
(r + s- 2)-мерные Hr_i(X1)9 HS_1(X2)
(детали оставляются читателю). Формула Кюннета для клеточных пространств тем
самым доказана, а для произвольных пространств она немедленно следует из дока-
занного ввиду слабой гомотопической инвариантности гомологий и существования
клеточной аппроксимации у произвольного топологического пространства (стандарт-
ный прием).
Совместно с формулами универсальных коэффициентов формула Кюннета позво-
ляет найти гомологии и когомологии с произвольными коэффициентами для
произведения любых двух пространств, у которых известны целочисленные гомоло-
гии. Выделим важный случай, когда это вычисление удается провести прямо.
Упражнение 19. Если к - поле, то
Hq(Xt X Х2, к) = ® Нг(Хх; к) ® HS(X2; к),
г + s = q
НЧ(Х1 X Х2; Л) = ® Н\Х1; к) ® НЧХ2; к).
г + s = <?
И в заключение — еще две формулы.
Упражнения. 20. Bq(Xi X Х2) = ^r+s = qBr(Xl')Bs (Х2), где В - числа
Бетти.
21- Х(Х, X Х2) = x(Xi) х№)> где X — эйлерова характеристика. (В обоих уп-
ражнениях предполагается, что правые части равенств определены.)
§ 16. УМНОЖЕНИЯ
1. Введение. Хотя гомологии геометричнее, чем когомологии, они играют в топо-
логии значительно более скромную роль. Тому есть много причин, но главная в том,
что когомологические классы можно перемножать, так что для любого коммутатив-
ного кольца G сумма ®qHq(X‘, G) = Н*(Х\ G) представляет собой ассоциативное
косокоммутативное кольцо; для гомологий ничего подобного нет (см. упражне-
ние 11).
Наиболее прозрачный способ построения когомологического умножения состоит
в следующем. Пусть G — коммутативное кольцо и Х2, Х2 — клеточные пространства.
По клеточным коцепям G ф4» (Xj; G), с2 G ЙЧ'1(Х2; G) мы строим клеточную
§ 16. УМНОЖЕНИЯ
133
коцепь <?! X с2 G +ч* (Xi X Х2; G) : на клетке а X т С Xi X Х2 она принимает
значение, равное (-1)q' Чгс1 (а)с2 (т) [умножение в <7]. Проверка показывает, что
5(cj X с2) = (5ci) X с2 + (-I)’**?! X 5с2, так что если ct и с2 - коциклы, то
Ci X с2 — тоже коцикл. Когомологический класс коцикла Сх Хс2 зависит только от
когомологических классов коциклов ct и с2, так что мы получаем корректно опре-
деленное умножение
[7i etf’-(IbG), 72 бЯ’»(Х2;С7)]к>71 Х72 XX2;G).
Аналогичное умножение есть и в гомологиях: если at = G (Х2; G),
а2 =^jg2iTi G), то Ха2 =2\ ,• gHg2/(а, Хт/) G +<?1(XiXX2; G);
при этом Э (а 1 X в2) = (Э«1) X а2 + (— 1)Q1а 2 X Эа2, ввиду чего получается ум-
ножение
К e^(Xi;G),a2 6^(X2;G)]HttlXa2 X Х2;6).
Два умножения X связаны формулой
<71 х 72,«1 X «2 > = (-1)4'j4'j <71,“1 ><72,«2 >•
Упражнение 1. Другое определение последнего умножения (с G = Z) мож-
но получить из формулы Кюннета: в силу этой формулы мы имеем отображение
НЧ1(Хх) ®ЯЧ1(Х2) ^Hqi+q2(Xx X Х2), и X а2 можно определить как образ
произведения ® а2 при этом отображении. Докажите эквивалентность двух
определений.
Однако дальше сказывается важное различие между гомологиями и когомоло-
гиями, состоящее в том, что первые коварианты, а вторые контраварианты. Для лю-
бого пространства X определено диагональное отображение Д: Х-+ХХХ, Д(х) =
= (х, х). Это отображение индуцирует гомоморфизмы
Д,: Hq(X;G) -► Hq(X X Х\ G),
Д‘: Hq(X X X; G) - ЯЧ(Х; G).
Первый из них нам пока что бесполезен, а второй доставляет умножение в когомоло-
гиях пространства X: мы полагаем для уj G), у2 € Нч* (Х\ G)
71 о 72 = Д’(71 X 72) &Hq^q^X’,G)
(классическое обозначение о (’’чашка”) не особенно удобно, и мы иногда вместо
7t 7г будем писать попросту 71 у2 ).
Этот способ введения умножения был бы хорош, если бы не необходимость дока-
зывать независимость умножения от клеточной структуры. Мы этого делать не
будем. Вместо этого мы приведем другой способ построения -умножения, строго
противоположный предыдущему: мы начнем с независимого определения -умно-
жения, через него определим Х-умножение, а затем выведем для Х-умножения то
описание, с которого мы начали.
(Терминологическое замечание. В этом параграфе мы рассмотрим
три умножения: X, и о (до последнего мы еще не дошли). По-английски они
называются cross-product, cup-product и cap-product. Для о-умножения имеется тер-
мин умножение Колмогорова - Александера — по имени замечательных математи-
134
ГЛ. 2. ГОМОЛОГИИ
ков, открывших это умножение в начале ЗО-х годов. К сожалению, нынешнее поколе-
ние топологов находит это название чрезмерно длинным.)
2. Прямое построение о-умножения. Пусть X — произвольное топологическое
пространство и G - коммутативное кольцо; пусть, далее, Ci G C4i (X; G),
с2 G С41 (Х-, G). Определим коцепь с2 с2 € C4i+q» (X; G) формулой
[Cl4-1 С2 ] ( f) — Cl (/о ...4j ) ^(Д, ... Ч1 +Чз ),
где /: T4l + 4t ->Х, fi9...tr (0<z0 < i'i < — < G <<71 + ?2) обозначает г-мерный
сингулярный симплекс, получающуюся при сужении симплекса f на г-мерную грань
симплекса T4l+c,i, натянутую на вершины с номерами z0...ir. Таким образом,
значение коцепи с2 на сингулярном симплексе f равно произведению значений
коцепей Cj и с2 на двух гранях симплекса /, имеющих одну общую вершину.
Предложение (свойства коцепного -умножения). Пусть cr &С41 (Х\ G),
с2 €СЧ>(Х; G). Тогда:
(0) 5(с2 о с2) = (Sci) о с2 + (-1)’1 с2 о 5с2;
(1) ci (с2 с3) = (с1ч-/ с2) ос3 [с3 £СЧ*(Х-, G)];
(2) обозначим через со = {шу} трансформатор (см. упражнение 12 к § 12), опре-
деленный в упражнении 14 к § 12; для любой (q^ + ц2)-мерной сингулярной цепи а
имеет место равенство
[<?1О с2](а) = (- 1)ч«[с2 cJCwxa);
(3) если g: Y-^-X—непрерывное отображение, то g #(^i с2) = (g#c1)'~/(g Сз);
если h: G ->Н - кольцевой гомоморфизм, то h ° (Cj c2) = (h о Cj) ^(h ° с2).
Доказательство очевидно.
3 амечание. Некоммутативность коцепного -умножения является не случай-
ным дефектом определения, а проявлением глубокой общей закономерности,
имеющей важные последствия.
Из (0) следует, что ^-произведение коциклов есть коцикл, когомологический
класс которого зависит только от когомологических классов сомножителей.
Ввиду этого коцепное -умножение индуцирует когомологическое -умножение
[71 &H^(X,G),y2 еЯ’>(Х;С)] ~ G).
Теорема (свойства когомологического ^-умножения). Пустьу^Н9' (Х-, G),
72 €Ячз(Х; G). Тогда:
(1)71 ^(72'-'7з) = (71'-'7г)^7з (X,G)] \
(2) 71 72 =.(- О*714i 72 71;
(3) для непрерывного отображения g: Y •+ X и кольцевого гомоморфизма h:
G-+H
g*(Ti 7г) = (?*71) (?*7г). Л.(72 ч-/ 72) = (й.71) (Л.7г)-
Это — следствие предложения (доказательство части (2) использует упражне-
ния 12 и 14 к § 12).
Упражнения. 2. Если X связно и 7 G Н° (Х‘, G) = G, то 7 71 = 771 для
любого 71.
§ 16. УМНОЖЕНИЯ
135
3. Постройте относительный вариант о -умножения: если 7i G Н4' (X, А; G),
y2eHq^(X,B; G),Toyi^y2GH^+^(X,AnB; G).
4. Обобщите -умножение на случай, когда 7i G H4t (Х\ G^), у2 G H4t (X; G2)
и имеется спаривание Gj X G2 ->-G3.
3. Определение Х-умножения. Пусть по-прежнему G — кольцо, Xi и Х2 — тополо-
гические пространства. Пусть, далее, 71 ё Hqi (А\; G), у2 Е (Х2; G). Положим
71 Х72=(р?71)^(р2’72)ЕЯ’*+^(У1 XX2;G)
(Pi и р2 — проекции произведения на сомножители).
Упражнения. 5. Постройте относительный вариант Х-умножения.
6. Докажите для Х-умножения всевозможные естественности.
Теорема. Это определение Х-умножения эквивалентно определению, данному
во введении к этому параграфу.
Для доказательства оказывается достаточным явно вычислить Х-умножение в
одном простом частном случае. Так как стандартные симплексы и произведения
стандартных симплексов гомеоморфны шарам, то
Hq (Т4,dTq,Z) = Z,
Hq^q*(Tq' XTq', d(Tq' XT’’);Z) = Z.
Аналогичные формулы имеют место для гомологий, причем относительным циклом
c(q) пары (Тч, дТ4), представляющим каноническую образующую ^-мерных гомо-
логий служит тождественный сингулярный симплекс id: Тч -» Т4, а каноническую
образующую (qi + q2)-мерных гомологий пары (Т4» X Т41, д (Тч> X Т41)) пред-
ставляет относительный цикл c(qi, q2), который есть сумма с надлежащими знака-
ми аффинных сингулярных симплексов
уч» +<?i _> fqt х 7’<?I
с вершинами (м1о, р,о), (Mfj, Vji),..., (и^ +<?
упорядоченные) вершины симплексов Т41,7^г и
iл-1, /j /j+1, ij + /j — s.
v>q +q )> Где M‘> V1 ~ (станДаРтн0
(Мы фактически описали наиболее употребительную триангуляцию произведения
Т41 х Т41, обобщающую триангуляцию цилиндра Tq XI, построенную в § 12 (п. 2).)
Покажем теперь, что X-произведение стандартных образующих
cq ЕЯ’‘(Г’« .ЭГ4* ;Z), а2 eHq>(Tq> ,dTq> ;Z)
есть, с точностью до знака, стандартная образующая
а€Я’«+’>(Т’> ХГ’’,(ЭГ’* ХГ’’)и(Г’* X9r’’);Z) =
= Я<?«+<7>(Г<?‘ XTq*, 9(Т41 X Tq*)-,Z)
(знаки мы нигде не уточняем). Нам достаточно показать, что [cq X a2]c(qlt q2) =
= ± 1. Классы cq и а2 представляются коциклами <q и а2, принимающими значение 1,
соответственно, на c(qi~) и с(q2) и значение 0 на любом сингулярном симплексе,
заключенном в границе симплекса T4i или Т41. По определению,
[«1 Xa2](c(qi,q2y)=Z±ai(uk........и> )a2(v< ,... ,uz ),
v Hi Hi H J • 41
где последовательность вершин в скобках служит обозначением для аффинного
сингулярного симплекса (стандартного симплекса Т4' или Т4*) с указанными вер-
шинами, а суммирование распространяется на все последовательности пар (i'o>7o)> • •
136
ГЛ. 2. ГОМОЛОГИИ
..., {i4i +4j, /41 +4j), обладающие вышеуказанными свойствами. В этой сумме равны
О все слагаемые, кроме одного, отвечающего случаю
l'o =0, h = 1...iql =Q1> jqt =0, /<7,+1 = !,••• ,/<71+<7, = <?2-
Это слагаемое равно ± 1. Наше утверждение доказано.
Дальше мы воспользуемся только естественностью X-умножения.
1-й шаг: X-умножение
Я’*(5’«,р1;г)ХЯ’»(5’»,р1;г)-+ Hq>+q*(Sq* X S’», S’* vS’>; Z)
есть, с точностью до знака, стандартное умножение Z X Z ->Z. Действительно, проек-
ции (7’’*,Э7’’*) ->(S’«,pt), (7’’»,ЭТ’>)->(S’»,pt), (Г’* ХГ’»,Э(Т’« ХТ’»))->
-> (S’* X S’», S’* v S’») индуцируют изоморфизмы в q > -мерных, q2 -мерных и
(?i + <7г) -мерных когомологиях.
2-й шаг: X-умножение
Я’* (S’*; Z) X Я’»(5’»; г)->Я’*+’»(S’* XS’»;Z)
есть, с точностью до знака, стандартное умножение Z X Z -> Z. Действительно, ото-
бражения (S’*, ф) -> (S’*, pt),... индуцируют изоморфизмы в когомологиях нуж-
ных размерностей.
3-й шаг: аналогичное для букетов сфер одной размерности (точную формулиров-
ку мы оставляем читателю).
4-й шаг: вместо Z можно взять произвольное кольцо (7; для доказательства дос-
таточно воспользоваться естественностью по отношению к кольцевым гомоморфиз-
мам коэффициентов Z ->(7.
5-й шаг: пусть Xlt Х2 — клеточные пространства размерностей q2 и q2, когомо-
логические классы 7i £ Я’* (%1; Z) и у2 6 Я’» (Х2; Z) представляются клеточны-
ми коциклами Ci и с2; тогда X у2 е (Д', ХХ2; Z) представляется кле-
точным коциклом
(ci Xc2)(ai X a2) = + ci(a1)c2(a2)-
Для доказательства достаточно рассмотреть проекции Хх ->.¥1/sk4i Х2 = vSqi,
Х2 -+vS41,X1 ХХ2 -> (vS’*) X (vS’»); соответствующие когомологические гомо-
морфизмы зпиморфны.
6-й шаг: общий случай. Для перехода к нему достаточно рассмотреть включения
sk4jXi ->Xi,sk4aX2 ->Х2, sk4jЛГ1 X sk4j Х2 X Х2; соответствующие когомо-
логические гомоморфизмы мономорфны.
Теорема доказана.
4. Применение: инвариант Хопфа. Чтобы сразу продемонстрировать, насколько
мощным инструментом в алгебраической топологии является мультипликативная
структура в когомологиях, мы уже теперь, фактически не умея вычислять умноже-
ние в когомологиях почти ни одного пространства, докажем с помощью этого умно-
жения весьма нетривиальное утверждение о гомотопических группах сфер.
Теорема. Группа ittn-i (<S2n) бесконечна при любом п > 1. Более того, квад-
рат Уайтхеда [i2n, i2n] образующей i2n группы я2„(52") имеет бесконечный поря-
док. (Сопоставьте это утверждение с последней теоремой § 10.)
Доказательство этой теоремы производится при помощи инварианта Хопфа — це-
лого числа, ставящегося в соответствие классу G w4„_i (S2”). Определение этого
инварианта состоит в следующем. Рассмотрим сфероид f: S^n~r -> S2n класса ip
и образуем пространство Х^ = S2" суZ)4" (конус отображения/). Пространство
Ху, с точностью до гомотопической эквивалентности, зависит только от ip (и это
§16. УМНОЖЕНИЯ
137
оправдывает обозначение). Оно обладает естественной клеточной структурой с тре-
мя клетками размерностей 0, 2п и 4л, Таким образом,
[ Z при q = 0, 2п, 4л,
tf’(X„;Z) =
I 0 при q =#0, 2л, 4л.
Когомологии Я2" (Х^,; Z) и//4"^; Z) имеют естественные образующие (опреде-
ляемые каноническими ориентациями сферы S2n и шара Я4”), и мы обозначаем их
через а и Ь. Так как dim а2 = 4 л (в2 = а а), то в2 = fib, где й € Z. Число h =h (/>)
и называется инвариантом Хопфа класса ip. [Инвариант Хопфа имеет многочислен-
ные обобщения, в то числе весьма полезные; с ними можно познакомиться по ’’Лек-
циям по гомотопической топологии” М.М. Постникова.] Доказываемая теорема
покрывается двумя леммами:
Лемма 1. Инвариант Хопфа аддитивен :h(tp + ф~) = h(ip) + h(yj/).
Лемма 2. Инвариант Хопфа нетривиален, в частности, A([i2«, i2«D = 2.
Доказательство леммы 1. Наряду с пространствами Х^, Ху, Xv+y
(построенными по сфероидам f, g, f + g: S4n+1 ->S2n) рассмотрим пространство
Y^y = (S2n UzP4n)UrD4n =S2n (D4n vD*ny
Пространство Y^y разбивается на 4 клетки размерностей 0, 2л, 4л, 4л и имеет сле-
дующие когомологии:
ZeZ при q = 4л,
H4Yv,y,Z) = Z при q = 0, 2л,
1 0 при q #=0,2л, 4л.
Обозначим канонические образующие групп Н2“(Y^y ; Z) к Н4п (Y^y ; Z) через
а’ и Ь\, Ь2. Имеются естественные вложения Х^ -+ Y^y и Ху -> Y^y (в качестве
клеточных подпространств). Имеется также естественное отображение Xv+y ->
-* YVty; оно состоит из тождественного отображения S2n -+S2n и стягивания эква-
ториальной плоскости Я4л ->Я4” v Я4” (эти отображения сшиваются в непрерыв-
ное отображение Xv+y -> Y^ у , поскольку диаграмма
s2"
коммутативна по определению суммы сфероидов). Индуцированные клеточные
цепные отображения для всех трех отображений очевидны; соответствующие кого-
мологические отображения устроены так:
а' н-ц, а' н-дя а' *+а,
Ь\ >+b, Ь{ ^*0, Ь\ i+b,
Ь'г |->0; b'2 »b-, Ь2 *+Ь.
Так как (a')2 G НЛп(Yv Z),to (a')2 =hib'i + h2b2, где hx, h2 е Z. Из естествен-
ности когомологического умножения вытекает, что
а2 = hib в Ху, a2 =h2b в Ху,
a2 =(ht + h2)b в Xv+y.
138
ГЛ. 2. ГОМОЛОГИИ
С другой стороны,
в2 =й(|/>)& в Х^, а2 =Ь(ф)Ь в Хф,
в2 = Л (<^i + </>2 ) /> в Х<р+ф •
Таким образом, Л1 = h (<р), h2 = h (ф) и hi + Л2 = h (<р + ф), откуда h + ф) = h (^) +
+ Л(Ф)- 2я
Доказательство леммы 2. Рассмотрим произведение S X S . Его
когомологии устроены так: H2n(S2n X S2”; Z) = Z ® Z (образующие Ci и с2)>
Я4л(52л X 52л; Z) = Z (образующая d). Умножение: с2 = с2 = 0 (доказательство:
рассмотрим проекции S2n X S2n ->52л), CiC2 = d (см. доказательство предыдущей
теоремы). Следовательно, (с3 + с2) 2 = с2 + 2cj с2 + с2 = 2d. Произведем в S2п X S2n
отождествление: (х, х0) = (х0,х) (здесь х0 — отмеченная точка, она же нульмерная
клетка, сферы S2n, х пробегает всю сферу 52л). Получается пространство X с тремя
клетками размерностей 0, 2п, 4 и. Это пространство есть S2n Uy D ”, где/: S4”-1 ->
->S2” — приклеивающее отображение 4л-мерной клетки (см. § 5). Более того, сли-
чая нашу конструкцию с определением произведения Уайтхеда (см. § 10), мы видим,
что / есть стандартный представитель квадрата Уайтхеда класса с2и е ^2п ($2п) тож-
дественного сфероида id: S2n -+S2n; таким образом, X = ^[i2„,i2„l- Когомологии
пространства X: Н2п (X; Z) = Z,H*n (X; Z) = Z; если а и b - естественные образую-
щие этих групп, то а2 = Л ([i2«» 12л])й- С другой стороны, когомологические гомо-
морфизмы, индуцированные проекцией S2n X S2n -+Х, переводят а в Ci + с2 ubad
Таким образом, (ct + с2)2 = h([i2n, i2nl)d> и. сопоставляя это с предыдущим вы-
числением, МЫ ВИДИМ, ЧТО Л( [t2«, »2л]) = 2.
Доказательство теоремы закончено.
Замечания. 1. Как мы увидим ниже, я4и_ j (52л) = Z ® (конечная группа);
в частности, я3 (№) = Z (это нам уже известно), я7 (S4) = Z ®Z12, яп (S6) = Z,
^15 (S8) = Z ® Z120. Более того, все гомотопические группы сфер, кроме групп
яи (5”) = 7. и я4и_ 1 (52л) конечны.
2. Лемма 2 показывает, что образ гомоморфизма Хопфа h: я4„_] (52л) ->Z —
либо все целые числа, либо все четные числа. Выбор между двумя этими возможнос-
тями сводится к вопросу: существует ли в я4„_! (S2”) элемент с инвариантом Хоп-
фа единица? Эта проблема имеет много замечательных переформулировок; напри-
мер, можно показать, что сфера Sm тогда и только тогда обладает структурой //-про-
странства, когда т нечетно, т.е. имеет вид 2п - 1, и в я4и_! (52л) имеется элемент
с инвариантом Хопфа единица; при этом же условии в Rm+1 имеется билинейное
умножение с однозначным делением. Из упражнения 6 к § 10 и нашей леммы 2 вы-
текает, что инвариант Хопфа хопфовского класса в я3 (52) равен 1 (это соответ-
ствует умножению комплексных чисел). В 1960 г. Адамс доказал, что элементы
с инвариантом Хопфа 1 имеются только в группах я3 (S2), я7 (54) и я15 (58) (этот
результат упоминался в ином контексте в § 1).
5. Дополнение: другие умножения.
А. Гомологическое X -умножение. Оно упоминалось во введении. Его определе-
ние в духе других определений этого параграфа: сингулярные симплексы /3: Т41 ->
~>’Xi,f2: Тч* ->Х2 определяют отображение/t Х/2: T4i X Г’2 ХХ2; триан-
гулируем Тч* X ТЧг как описано выше в этом параграфе и назовем X-произведе-
нием сингулярных симплексов/j и/2 (оно также обозначается через/1 Х/2) цепь
пространства Xi X Х2, являющуюся суммой с коэффициентами ± 1 (это те самые
± 1, которые фигурировали выше в этом параграфе) сужений отображения f2 Xf2
§77. ГОМОЛОГИИ И МНОГООБРАЗИЯ
139
на симплексы триангуляций. По линейности X-умножение распространяется
на сингулярные цепи: S/gii/ц- X ^jgijfn ~ ^tjgugij (fu (gu>g2j - эле-
менты кольца коэффициентов G). Проверка показывает, что Э (ci X с2) = X
X с2 + (— I)’1 Ci X Эс2 (?i = dim ci), ввиду чего возникает X-умножение в гомо-
логиях: если «1 G (Xi; G), а2 G Hqt (X2; G),то X a2 G + (X2 X X2; G).
Доказательство совпадения этого X-умножения с гомологическим X-умножением,
описанным во введении, является копией соответствующего когомологического
доказательства.
Упражнение 7. Обследуйте взаимоотношения гомологического и когомоло-
гического X -умножения с формулой Кюннета.
В. -умножение. Это — смешанная операция, в которой участвуют гомологии
и когомологии. Пусть а = Sg, ft & Cqi(X\ G),c G СЧг (X\ G), qi > q2. Обозначим
через f{ q2 -мерную грань сингулярного симплекса /f, натянутую на q2 + 1 первых
вершин, через //' — его (qi — q2)-мерную грань, натянутую на q^ — q2 + 1 послед-
них вершин, и положим
а - с = с (/?)/," G ъ (X; G).
Упражнение 8. Докажите формулу
Э(а^с) = (Эв)^с + (- l)4’ а -'бс.
Из этой формулы вытекает, что цепно-коцепное ^-умножение индуцирует гомо-
лого-когомологическое ^-умножение.
[a G H4i (Х-, G), у G (X; G)] » а у G H4i _ Чг (У; G).
Упражнения. 9. Докажите для ^-умножения всевозможную естественность.
10. Докажите смешанную ассоциативность: для гомологического класса а и кого-
мологических классов 71 и 72 имеет место равенство
72) = («^71)^72•
С. Умножение Понтрягина-Самельсона.
Упражнение 11. Докажите, что не имеется способа ввести в гомологии
Н, (X; G) = Hq (X, G) всех топологических пространств Xс какими-либо коэф-
фициентами G билинейное естественное умножение таким образом, чтобы произ-
ведение каких-нибудь двух гомологических классов положительной размерности
какого-нибудь пространства было отлично от 0.
Однако умножение в гомологиях пространства X можно определить, если само X
обладает умножением, делающим его топологической группой или хотя бы //-прост-
ранством. Определение очевидно: если д: Х'АХ-^-Х — умножение в X и «i G
{Х\ G), а2 G//gj (X, G), где G - кольцо, то а^а2 =p,(ai Ха2). Это умно-
жение называется умножением Понтрягина — Самельсона. Мы не имеем возможности
уделить этому умножению внимание, которого оно заслуживает, но читателю реко-
мендуется после прочтения главы 3 вернуться к этому умножению и попытаться вы-
числить его в гомологиях известных ему топологических групп и //-пространств.
§ 17. ГОМОЛОГИИ И МНОГООБРАЗИЯ
Среди элементарных вычислительных средств, которыми пользуется теория го-
мологий, наиболее действенными являются средства, доставляемые топологией
многообразий, и мы не можем уклониться от рассмотрения этого предмета. Труд-
ность заключается в том, что основания топологии многообразий, уходяшей корня-
140
ГЛ. 2. ГОМОЛОГИИ
ми в геометрию и анализ, сами по себе способны составить содержание толстого тома.
Первый способ преодолеть эту трудность состоит в том, чтобы написать этот
том; для нас это неприемлемо. Второй способ заключается в замене понятия
гладкого многообразия различными суррогатами (гомологические многообразия,
комплексы Пуанкаре, псевдомногообразия и т.д.), которая позволяет достичь
относительной строгости за счет геометрической наглядности; зто также нам
не годится. Наш подход основан на тезисе, что наиболее эффективный способ
преодоления трудностей состоит в том, чтобы их игнорировать. В этом параграфе
мы будем относиться к доказательствам еше более легкомысленно, чем в других
частях книги, без колебаний принимая на веру наглядно очевидные утверждения,
строгие доказательства которых в ряде случаев довольно мытарны. Мы надеемся,
что читатель этого параграфа сможет свободно пользоваться его результатами при
решении конкретных задач. Если же ему нужно больше, - скажем, сдать экзамен
по гомологической теории многообразий, — он может прочесть, например, "Основы
дифференциальной топологии" Хирша и "Лекции по алгебраической топологии”
Дольда, и при этом знакомство с нашим текстом все равно будет ему полезно.
1. Гладкие многообразия. Хаусдорфово топологическое пространство со счетной
базой (зти топологические требования не в стиле нашего изложения, но мы не ре-
шаемся их отбросить, поскольку без них многое из того, что говорится дальше,
просто неверно) называется п-мерным многообразием, если каждая его точка обла-
дает окрестностью, гомеоморфной пространству R” или полупространству R” =
= {(*!....х„) е R” | х„<0}. Точки «-мерного многообразия X, не имеющие
окрестности, гомеоморфной R", составляют крайЭА'многообразиях Край «-мерного
многообразия есть (п — 1)-мерное многообразие без края (= с пустым краем).
Примеры многообразий: евклидовы пространства, сферы, шары, классические
поверхности, проективные пространства, многообразия Грассмана, многообразия
флагов, группы Ли, многообразия Штифеля, произведения перечисленных прост-
ранств, открытые подмножества перечисленных пространств, лежащие в них замкну-
тые области с гладкой границей и т.д.
Гомеоморфизм между окрестностью точки многообразия и R” или R” опре-
деляет в этой окрестности координаты, называемые локальными координатами на
многообразии. Если области определения локальных координат f: t/-+R”_p#:
r~>R" (как говорят, карты), перекрываются, то возникает "отображение склей-
ки”, т.е. отображение
f(UO V) Ur>V * g(UK К),
п п
R" R”
описываемое обычными числовыми функциями п переменных. Эти функции могут
быть гладкими (у нас слово гладкий означает "принадлежащий классу С “”), анали-
тическими, алгебраическими и т.д. (в смысле определений анализа). Совокупность
карт, покрывающих все многообразие, называется атласом. Атлас называется глад-
ким (аналитическим, алгебраическим и т.д.), если таковы все отображения склейки.
Два гладких (аналитических и т.д.) атласа определяют на многообразии одну и ту
же гладкую (...) структуру, если их объединение — такой же атлас. Многообразие
с гладкой структурой называется гладким многообразием. (Аналогичным образом
определяются аналитические многообразия; алгебраические многообразия обычно
определяются по-другому.)
§ 17. ГОМОЛОГИИ И МНОГООБРАЗИЯ
141
Все перечисленные выше примеры многообразий — это гладкие многообразия
(с естественной гладкой структурой). Добавим еще один пример: гладкие поверх-
ности в евклидовом пространстве, т.е. замкнутые подмножества евклидова прост-
ранства Rm, определяемые в окрестности каждой своей точки системой, состав-
ленной нз уравнений
fi(xi,,хт) — 0, i — 1,...,к,
и, возможно, одного неравенства
/*+101......*п)>о,
где /1....fk ( , /jt+i) - гладкие функции, градиенты которых в области их опреде-
ления линейно независимы.
Фундаментальными в топологии многообразий являются следующие две теоремы
реализации.
Теорема 1. Всякое гладкое многообразие диффеоморфно (т.е. гомеоморфно
с сохранением гладкой структуры) поверхности, лежащей в евклидовом прост-
ранстве.
Теорема 2. Всякое компактное гладкое многообразие гомеоморфно триангу-
лированному подмножеству евклидова пространства, причем гомеоморфизм может
быть сделан гладким на каждом симплексе триангуляции.
Замечания. 1. Если многообразие имеет размерность п, то в обеих теоремах
евклидово пространство может быть взято размерности 2п.
2. Теорема, аналогичная теореме 2, имеет место и для некомпактных многообра-
зий, только, конечно, триангуляция будет бесконечной.
Мы не доказываем этих теорем; во многих конкретных случаях они доказывают-
ся явным построением гомеоморфизма (но не во всех; зто особенно верно по от-
ношению к теореме 2). Теорема 1 доказывается совсем просто, ее доказательство
имеется во многих учебниках топологии. С теоремой 2 дело обстоит хуже. Начиная
с 20-х годов, топологи считают этот факт более или менее очевидным, но попытки
дать ему простое доказательство постоянно терпят неудачу. Первое безупречное до-
казательство было дано Уитни в конце 30-х годов, но это доказательство довольно
сложно. Нам известны два учебных изложения доказательства теоремы 2: в книге
Уитни ’’Геометрическая теория интегрирования” и в ’’Лекциях по дифференциаль-
ной топологии” Манкреса (русский перевод последних составляет приложение
к ’’Лекциям о характеристических классах” Милнора и Сташеффа). Было бы очень
желательно найти простое доказательство теоремы 2, тем более что за последние
полвека топология продвинулась значительно дальше, в частности, многое известно
о триангуляциях негладких многообразий.
Упражнения. 1. Построить реализации в качестве гладких поверхностей
в евклидовых пространствах проективных пространств, многообразий Грассмана,
многообразий флагов и многообразий Штифеля.
2. Докажите, что все классические поверхности гладко реализуются в 4-мерном
пространстве.
3. Постройте триангуляции классических поверхностей; попытайтесь сделать
их минимальными по числу симплексов.
4. Докажите, что число «-мерных симплексов триангуляции «-мерного многообра-
зия, примыкающих к данному (и—1)-мерному симплексу, равно 2, если этот симп-
лекс не лежит на крае, и равно 1, если он лежит на крае.
5. Обобщение этого факта. Рассмотрим совокупность всех симплексов триангули-
рованного n-мерного многообразия, содержащих данный ^-мерный симплекс, и в
каждом из этих симплексов возьмем грань, противоположную этому к-мерному
142
ГЛ. 2. ГОМОЛОГИИ
симплексу (т.е. натянутую на вершины, не входящие в этот к -мерный симплекс).
Объединение этих граней (которое называется линком исходного ^-мерного симп-
лекса) будет гомеоморфно (и — к — 1)-мерной сфере или (и — к — 1)-мерному шару,
в зависимости от того, лежит или не лежит исходный ^-мерный симплекс во внут-
ренности многообразия (т.е. в дополнении к краю). (Если вы не справитесь с этим
упражнением, убедитесь в его справедливости хотя бы для мелкой триангуляции
трехмерного тела.)
Атлас гладкого многообразия называется ориентированным, если у любых его
перекрывающихся карт отображение склейки имеет положительный якобиан. Два
ориентированных атласа определяют одинаковую ориентацию, если их объединение
есть ориентированный атлас. Многообразие называется ориентированным (ориенти-
руемым), если оно наделено (обладает) ориентированным атласом.
Упражнения. 6. Какие из проективных пространств и многообразий Грас-
смана ориентируемы? [Ответ: неориентируемыми могут быть только вещественные
проективные пространства и многообразия Грассмана; именно, RP ” ориентируемо
тогда и только тогда, когда п нечетно, a G(n, к) ориентируемо тогда и только тогда,
когда и четно.]
7. Докажите, что сферы с ручками ориентируемы, а проективные плоскости с
ручками и бутылки Клейна с ручками неориентируемы; высверливание дыр на
ориентируемость не влияет.
8. Связное ориентируемое многообразие положительной размерности имеет ров-
но 2 ориентации.
9. Всякая карта ориентируемого многообразия включается в ориентированный
атлас и, таким образом, определяет ориентацию.
10. Всякое односвязное многообразие ориентируемо.
11. Многообразие ориентируемо тогда и только тогда, когда ориентируема окрест-
ность всякой замкнутой гладкой кривой на этом многообразии.
12. Говорят, что карты ft: Ut ->R"_j, i = 1, ... ,N, составляют цепочку, покры-
i - 1 i
вающую путь : I -+Х, если <р(г) G Uj при —• Петля <р: I -+Х назы-
вается сохраняющей (обращающей) ориентацию, если существует (не существует)
покрывающая цепочка карт ft-. Ut -*R”_pi =1,... ,N, такая, что отображение
склейки между 1-й и 2-й карГой,. .., между (N— 1)-й и Мл картой, между Мл и
1-й картой имеет положительный якобиан. Покажите, что существует гомоморфизм
тт! (X) ->Z2 (X — наше многообразие), такой, что петля сохраняет ориентацию тогда
и только тогда, когда она определяет элемент ядра этого гомоморфизма, а много-
образие X ориентируемо в том и только в том случае, если этот гомоморфизм три-
виален. (Сопоставьте это с упражнением 10.)
13. У связного неориентируемого многообразия имеется ориентируемая двулист-
ная накрывающая. Что это для неориентируемых проективных пространств и мно-
гообразий Грассмана?
14. Край ориентированного многообразия ориентирован.
Ориентации можно определить и пользуясь языком триангуляций. Ориентация
«-мерного симплекса — это заданный с точностью до четной перестановки порядок
его вершин. Ориентация симплекса индуцирует ориентацию его граней коразмер-
ности 1 (сделайте не входящую в грань вершину последней и отбросьте ее). Если
два n-мерных симплекса имеют обшую (и—1)-мерную грань, то их ориентации
называются согласоваными, если они индуцируют на обшей грани разные ориента-
ции (уточнение требуется при п = 1). Чтобы задать ориентацию триангулированного
§17. ГОМОЛОГИИ И МНОГООБРАЗИЯ
143
«-мерного многообразия, нужно задать ориентации всех его «-мерных симплексов
таким образом, чтобы ориентации симплексов, имеющих общую (л —1)-мерную
грань, были согласованы.
Упражнения. 15. Сопоставьте этот подход к ориентациям с предыдущим.
16. Ориентация связного ориентируемого триангулированного многообразия
определяется ориентацией любого его симплекса старшей размерности.
2. Фундаментальный класс. Пусть X — связное гладкое «-мерное многообразие.
Фиксируем его триангуляцию и вычислим его «-мерные гомологии, пользуясь клас-
сическим комплексом. В нижеследующей формулировке используется употреби-
тельный термин: многообразие называется замкнутым, если оно компактно и не
имеет края.
Теорема 3.
{Z, если Xзамкнуто и ориентируемо,
п
О в остальных случаях;
{Z2, если X замкнуто,
О в остальных случаях.
Доказательство. Пусть с = Zk( о/ #= 0 есть «-мерный цикл классического
комплекса с коэффициентами в Z или в Z2. Если симплексы Oi и Oj имеют общую
(п — 1)-мерную грань т, то т входит в д/с с коэффициентом ±(kt — kj), если ориен-
тации симплексов а,- и оу согласованы, и с коэффициентом ±(kt + kj), если они
не согласованы. Так как, очевидно, любые два «-мерных симплекса соединяются
цепочкой «-мерных симплексов, в которой соседние симплексы имеют общую
(« — 1)-мерную грань (это очевидное свойство связных триангулированных много-
образий называется сильной связностью), иэ Эс = 0 следует, что все коэффициенты
kj совпадают с точностью до знака. Если коэффициенты Z2, из этого вытекает, что
наш цикл есть Ео/, где суммирование распространяется на все «-мерные симплексы
многообразия. Такое выражение будет циклом, если выполнены следующие два ус-
ловия: (i) число симплексов конечно, т.е. многообразие компактно; (11) каждый
(и — 1)-мерный симплекс входит ровно в два «-мерных симплекса, т.е. мно-
гообразие не имеет края. Поскольку границ нет (за неимением (п + 1)-мерных
цепей), для коэффициентов Z2 теорема доказана. Если же коэффициенты Z, то
цикл имеет вид S (± k) ot; поменяем ориентацию у некоторых «-мерных симплек-
сов, чтобы наш цикл принял вид kZoj. Тогда ориентации всех симплексов будут
согласованы, и, в дополнение к двум предыдущим условиям, мы получаем усло-
вие (iii): многообразие ориентируемо. Теорема доказана.
Это доказательство содержит, в действительности, явное построение образующей
в группах Нп(Х) и Нп(Х\ Z2), если эти группы нетривиальны. Этой образующей
служит гомологический класс цикла Sa,, где все коэффициенты равны 1 € Z2 или
1 е Z, причем во втором случае все симплексы согласованно ориентированы. Этот
гомологический класс называют фундаментальным классом многообразия. Не
очень точно, но весьма выразительно можно сказать, что фундаментальный класс
есть гомологический класс самого многообразия, рассматриваемого как свой соб-
ственный цикл. Фундаментальный класс многообразия X обычно обозначается сим-
волом [Т] (если хотят подчеркнуть, что речь идет о Z2 -классе, пишут [Т]2).
Если X, Y — связные замкнутые ориентированные многообразия одной размер-
ности п и ft X^Y — непрерывное отображение, то ft [X ] = k [ Y ], где к — некоторое
целое число. Это число называется степенью отображения f и обозначается через
deg f. Мы встречались со степенями в ситуации, когда Х= Y = Sn (см. п. 3 § 10).
144
ГЛ. 2. ГОМОЛОГИИ
Z -* Z®..
• deg/
Как и в этом случае, степень deg/ можно вычислить геометрически: она равна
алгебраическому числу точек прообраза произвольного регулярного значения y€Y
(в частности, это число не зависит от у). Для доказательства возьмем малую шаро-
вую окрестность С7регулярного значения у отображения/; прообраз/~* (t/) СХесть
объединение шаровых множеств С4.......Um. Рассмотрим коммутативную диа-
грамму
Нп(X) = Нп(X-UtZ,, и ЭUi)-Н„_! (U ЭUt)
I i; I г. I г.
я„(У)=яп(?Зц ЭЯ) -* Я^КЭЯ).
Ее левый квадрат имеет вид
m
. ®Z 1 -* (1,1',..., 1)
Г I I
±1±1 ...±1
, deg/»-* deg/.
Утверждение доказано.
Аналогичное справедливо в отсутствие ориентаций по модулю 2.
В заключение — еще один термин. Говорят, что гладкое замкнутое многообразие
У, лежащее-в топологическом пространстве X, реализует класс aG Н^(Х-, Z2) или
Я*(Х) [в последнем случае У предполагается ориентированным], если Г. [У] -а,
где i: Y-+X — включение. Чаще всего о таких реализациях говорят в ситуации, когда
X — тоже гладкое многообразие и У есть его гладкое подмногообразие (смысл этого
слова мы не разъясняем, он понятен).
Упражнение 17. Образующие групп Яд(НРя; Z2), Яд(КР"), Нч(СРп)
реализуются проективными подпространствами пространств RP", СР”. [Ср. также
упражнение 11 к § 14.]
Оказывается, что не всякий (целочисленный) гомологический класс гладкого
многообразия может быть реализован гладким подмногообразием. На этот счет
имеется обширная теория с яркими результатами (см. статью Тома в сборнике
’Тасслоенные пространства”, а также § 43), например, для всякого гомологического
класса найдется кратный ему класс, который реализуется гладким подмногообра-
зием. Впрочем, имеется более простой факт: всякий гомологический класс может
быть реализован гладким подмногообразием с особенностями коразмерности > 2.
(Точное определение: замкнутое подмножество У гладкого многообразия X назы-
вается его (неприводимым) гладким подмногообразием с особенностями коразмер-
ности 2, если у X есть гладкие подмногообразия Zx...Zt, такие, что УП [X-
— (Z j U... UZz) ] есть связное гладкое подмногообразие многообразия X — (Zt U...
... UZt) размерности по крайней мере на 2 больше, чем каждое из многообразии
Zi.....Zj). Для подмногообразий с особенностями коразмерности > 2 можно опре-
делить понятие ориентации; его старшие гомологии (в неприводимом случае) уст-
роены точно так же, как у многообразий без особенностей, т.е. у него есть фундамен-
тальный класс. Как уже было сказано, всякий гомологический класс гладкого мно-
гообразия может быть реализован гладким подмногообразием с особенностями
коразмерности > 2.
3. Изоморфизм Пуанкаре. Главный результат гомологической теории многооб-
разий составляет
§ 17. ГОМОЛОГИИ И МНОГООБРАЗИЯ
145
Теорема 4. Пусть X - замкнутое п-мерное гладкое многообразие. Если X
ориентируемо, то
Hq(X)^Hn-q(X;Z), q любое.
В общем случае
Hq(X;Z2)^Hn-il(X;Z2), q любое.
Мы докажем эту теорему с несколькими важными уточнениями. Первое заклю-
чается в том, что изоморфизмы теоремы задаются явными формулами. Получающие-
ся канонические изоморфизмы называются изоморфизмами Пуанкаре. Формулы
очень просты: изоморфизмы Пуанкаре
D: Hn-4(X;Z)-+Hq(X),
D: Hn~4(X-,Z2)-*’Hq(X;Zi)
(в связном случае) действуют по формуле
£>(а)=[Х]^а,
где [X] — фундаментальный класс (целочисленный или по модулю 2), обозначает
^-умножение (см. § 15).
Доказательство теоремы 4, однако, не включает в себя такое отображение D.
Оно заключается в совершенно ином построении нужных изоморфизмов. Рассмотрим
триангуляцию многообразия X и ее барицентрическое подразделение (см. § 5). Для
симплекса а основной триангуляции обозначим через а* объединение симплексов
барицентрического подразделения, пересекающихся с симплексом а в точности по
его центру. Множество о* называется барицентрической звездой симплекса а. Более
формально о* можно описать так. Вершины барицентрического подразделения сов-
падают с центрами симплексов исходной триангуляции, т.е. находятся с этими симп-
лексами во взаимно однозначном соответствии. Симплексы же барицентрического
подразделения — зто цепочки or D or-i Э .. .D о0 симплексов исходной триангу-
ляции (симплексу т отвечает цепочка, составленная из симплексов, центры которых
служат вершинами т). Барицентрическая звезда а* состоит из симплексов барицент-
рического подразделения, отвечающих цепочкам... Э о, кончающимся симплексом а.
Пример. Рассмотрим триангуляцию куска плоскости (рис. 77). Барицентри-
ческая звезда двумерного симплекса — его центр. Барицентрическая звезда ребра —
двузвенная ломаная, ведущая из центра одного треугольника, примыкающего к
этому ребру, через центр ребра в центр другого примыкающего треугольника. Ба-
рицентрическая звезда вершины — многоугольная область, окружающая вершину.
Следующие свойства барицентрических звезд
очевидны, (i) Барицентрическая звезда q-мер-
ного симплекса гомеоморфна(п - q) -мерному
шару, (ii) Открытые барицентрические звезды
(открытая барицентрическая звезда — это
барицентрическая звезда, из которой удалены
содержащиеся в ней меньшие барицентричес-
кие звезды) составляют клеточное разбиение
рассматриваемого многообразия, (iii) Если
многообразие ориентировано, то ориентации
симплекса его триангуляции естественно соот-
ветствует ориентация его барицентрической звез-
ды. (iv) Соответствие о-«-+а* следующим об-
Рис. 77
146
ГЛ. 2. ГОМОЛОГИИ
разом согласовано с граничным й кограничным операторами. Поставим в соответ-
ствие классической «/-мерной коцепи c={ot ►+ к(}исходной триангуляции кле-
точную (или, как говорят, звездную) (и - q)-мерную цепь De = Xkjrf звездного
разбиения. (Здесь в ориентированном случае kj €Z,ao/ и а? обозначают ориенти-
рованные симплексы и звезды; в неориентированном случае kt G Z2.) Тогда Dbc=
+ Э£>с(знак, как обычно, мы не уточняем).
Последнее равенство показывает, что комплексы, по которым вычисляются
гомологии и когомологии многообразия X, просто не отличаются:
^n_1(Z)-*...-^ ^(ЛГ)-^ «0(ЛГ)
a tn a tn a Id = \ D
6 . 6 8.6
%°(х)^ %*(Х) -> ... «"-‘(хн $"(Т)
(верхняя стрелка обозначает звездный цепной комплекс, нижняя — классический
коцепной; коэффициенты в обоих случаях Z или Z2 — мы их не пишем). Теоре-
ма 4 доказана.
Следствие. Эйлерова характеристика замкнутого нечетномерного многооб-
разия равна 0.
Для доказательства лучше пользоваться изоморфизмом Пуанкаре по модулю 2,
поскольку он имеется и в неориентированном случае:
X(Jr) = S(-l)«dimH,(X-Z2) =
= S (-1)’ dim#"-’(*; Z2) =
= S(-l)« dim^-^ZJ = -х(2Г).
Упражнения. 18. Покажите, что изоморфизм D, построенный в доказатель-
стве теоремы 4, действительно выражается через -умножение, как было сказано
в начале пункта.
19. Просмотрите всю накопленную к настоящему моменту информацию о гомоло-
гиях и когомологиях многообразий (включая теорему 3 этого параграфа) и в каж-
дом случае убедитесь, что эта информация согласуется с изоморфизмами Пуанкаре.
4. Индексы пересечения и двойственность Пуанкаре. Из § 14 мы знаем, как свя-
заны между собой гомологии и когомологии произвольного топологического прост-
ранства. Это позволяет нам переделать канонические изоморфизмы теоремы 4
в неканонические изоморфизмы
НЯ(ХЛ2) - Hn_q(X- Z2)
всегда и
Своб. часть Hq(X) = Своб. часть Hn_q(X),
Круч. Hq(X) * Круч. Hn_q_^X)
в ориентированном случае. Оказывается, что это'— не неестественные изоморфизмы,
а проявления совершенно естественной двойственности, которая называется двойст-
венностью Пуанкаре. Кручением мы займемся немного погодя, а сейчас поговорим
о свободных частях.
В основе двойственности Пуанкаре лежит понятие индекса пересечения. Пусть
а = S ktUj — цепь размерности q классического комплекса некоторой триангуляции
§77. ГОМОЛОГИИ И МНОГООБРАЗИЯ
147
ориентированного гладкого и-мерного многообразия X, с2 = S — цепь размер-
ности и — q звездного комплекса той же триангуляции. Число
с2) = = ±{D~ic2,ci)
называется индексом пересечения цепей Ci и с2. Очевидно, что <Эс\ с” > =
= ±<с*, Ъс” > (это равенство достаточно проверить для случая, когда с1 = о и
с” "= т*} а в этом случае обе части равенства равны ± 1, если т есть грань сим-
плекса а и равны 0 в противном случае). Следовательно, индекс пересечения двух
циклов зависит только от гомологических классов этих циклов. Ввиду этого возни-
кает билинейный индекс пересечения гомологических классов
[a, £Hq(X), а2 eHn_q(X)] ~ ^,а2) 6 Z.
Упражнение 20. Докажите,что <p(ai,<Хг) = (-1)^"” g)<p(a2,ai).
Очевидным образом определен в неориентированной ситуации принимающий
значения в Z2 индекс пересечения Z2-цепей и г2.-классов гомологий. Имеются также
индексы пересечения, отвечающие произвольному спариванию Gi X (72 -+G.
Замечательным свойством индекса пересечения является его геометрическая
наглядность. Очевидно, барицентрическая звезда ’’трансверсально” пересекает свой
симплекс и не пересекается с другими симплексами той же размерности. Поэтому
(ci, с2 ) есть адекватное выражение для ’’алгебраического числа точек пересечения”
цепей С\ и с2. Более того, оказывается, что индекс пересечения может быть опреде-
лен чисто ’’дифференциальным” образом.
Теорема 5. Предположим, что гомологические классы 6 Hq(X) и
02 € реализуются ориентированными гладкими подмногообразиями
Yi С X и У2 С X, находящимися в общем положении (т.е. пресекающимися в ко-
нечном числе точек и при этом трансверсально). Точкам пересечения многообразий
Yi и Y2 естественным образом приписывается знак (ориентации многообразий Yi и
Y2 в точке их пересечения естественно определяют ориентацию объемлющего много-
образия X, которая может совпадать или не совпадать с заданной ориентацией X).
Утверждение: («1, «г) есть алгебраическое число точек пресечения.
Аналогичные утверждения имеют место для гомологических классов по модулю 2
(при этом никаких ориентаций не требуется) и для реализации гомологических
классов многообразиями с особенностями.
Хотя утверждение теоремы 5 выглядит наглядно очевидным, мы не занимаемся
ее доказательством и даже не предлагаем ее читателю в качестве упражнения.
Заметим только, что требование общности положения не является помехой для ис-
пользования теоремы: если подмногообразия Yi и У2 (пурть даже с особенностями)
реализуют нужные гомологические классы, их можно привести в общее положение
малым шевелением любого из них.
Пример. Естественные образующиеуг, уп_г групп Н2г (СРп), Н2п_ 2г(СРл)
имеют индекс пересечения 1: они реализуются проективными подпространствами
пространства СРп (комплексной) размерности г и п - г, которые (в общем поло-
жении) пересекаются в одной точке. Относительно знака мы сделаем важное за-
мечание. Если X есть комплексное многообразие, т.е. его карты.являются ото-
бражениями в С" и отображения склейки являются голоморфными, то X обладает
естественной ’’комплексной” ориентацией. Дело в том, что якобиан голоморфного
отображения С” -> С", рассматриваемого как гладкое отображение R2" -* R2”,
148
ГЛ. 2. ГОМОЛОГИИ
всегда положителен (он равен квадрату модуля комплексного якобиана того же
отображения). Более того, если Yt и У2 — комплексные (локально задаваемые го-
ломорфными уравнениями) подмногообразия многообразия X, имеющие дополни-
тельные размерности и тоже наделенные комплексными ориентациями, то точки их
трансверсального пересечения всегда вносят в индекс пересечения вклад +1 (докажи-
те!). Поэтому <р(уг, Уп-г) = 1, а не —1.
Упражнение 21. Пусть Д — диаграмма Юнга, вписанная в прямоугольник
к X (и — к); обозначим через Д * диаграмму Юнга, полученную путем выбрасывания
Рис. 78
диаграммы Д из указанного прямоугольника и поворота последнего на 180°
(см. рис. 78). Докажите, что индекс пересечения гомологических классов многообра-
зия С(7(п, к), отвечающих диаграммам Юнга Д и Д' (см. § § 5 и 13), равен 1,
если Д' = Д*, и равен 0, если Д' ¥= Д*. То же верно для вещественного грассманиана
и индексов пересечения по модулю 2.
Сам факт, что индекс пересечения пересекаемых циклов зависит только от их го-
мологических классов, часто используется при решении геометрических задач.
Из бесчисленного множества таких задач мы приведем для иллюстрации две.
Упражнения. 22. Докажите, что на гладкой замкнутой двумерной поверх-
ности, лежащей в R4 = С2, найдутся по крайней мере две различные точки, в кото-
рых касательная плоскость является комплексной прямой. (Намек: о том, чтобы их
было две, заботятся ориентации.)
23. Докажите, что если Х2, Х2 — две гладкие замкнутые ориентируемые двумер-
ные поверхности, лежащие в R4, то найдутся по крайней мере 4 пары точек х2& Х2,
х2 G Х2, в которых касательные плоскости к Х\ и Х2 параллельны.
Вернемся теперь к нашему исходному определению индекса пересечения. Из него
очевидным образом выводится следующее принципиальное утверждение.
Теорема 6. Пусть X - гладкое замкнутое ориентированное многообразие.
(i) Для любого гомоморфизма a: Hq(X) -> Z найдется гомологический класс
а* € Яп_д(Л), такой, что <р(аг,0) = а(0) при любом 0 6 Hq(X). (ii) Класс с!
восстанавливается по гомоморфизму а однозначно, с точностью до прибавления эле-
мента конечного порядка.
Аналогичное утверждение верно в неориентированном случае для гомологий и
индексов пересечения по модулю 2, причем в этой ситуации а' восстанавливается
по а уже однозначно.
Таким образом, индексы пересечения определяют невырожденную двойственность
между свободными частями групп Hq(X) и Hn_q (X) (в ориентированном случае),
а также между группами Hq(X-, Z2) и Нп_ q (X; Z2) (всегда). Эта двойственность
и называется двойственностью Пуанкаре. (Удивительно, что в литературе в употреб-
лении терминов ’’изоморфизм Пуанкаре” и ’’двойственность Пуанкаре” царит полная
§77. ГОМОЛОГИИ И МНОГООБРАЗИЯ
149
путаница, — хотя в других случаях математики проявляют повышенную чувствитель-
ность к различиям между пространством и сопряженным пространством и т.п.)
5. Применение: формулы Лефшеца. Пусть X — замкнутое ориентированное глад-
кое многообразие, /: X- гладкое отображение, [/] С X X X — график отобра-
жения f, oti и а2 - гомологические классы многообразия X дополнительной раз-
мерности.
Лемма (очевидная) : <р(Д(оц), а2) = (-l)dimai<p([/ ], «i X Oj).
(В левой части индекс пересечения берется в X, в правой — в X X Х\ [ / ] обозна-
чает гомологический класс, реализуемый в X X X многообразием [/].)
Следствие. Пусть cq,..., — базис в свободной части гомологий многообра-
зия X (сначала берем базис нульмерных гомологий, потом - одномерных и т.д.),
и пусть а*,..., а£[ — двойственный базис (т.е. (а<, оу*) = ). Тогда гомологический
класс диагонали diag = [id] С XXX, с точностью до слагаемых конечного порядка,
равен S (at X а(‘).
Для доказательства существенно, что в XX X (и вообще в Х2 X Х2)
*(<*! X al, а”Х а2 ) = (—l)dim dim “"^(а/, afMaJ, а'2').
Пусть теперь снова ft Х->Х- произвольное гладкое отображение. В каждой раз-
мерности i оно индуцирует эндоморфизм
Д: Своб. часть Hj(X) -> Своб. часть Hi(X),
и этот эндоморфизм имеет след, который мы обозначим через 7/.
Теорема 7 (формулаЛефшеца)
^([/], diag) = S(-l)%
Это — автоматическое следствие двух предыдущих утверждений.
Заметим, что точки пересечения графика отображения [ f ] с диагональю — это в
точности неподвижные точки отображения f. Если неподвижные точки невырожде-
ны, т.е. соответствующие пересечения графика с диагональю трансверсальны (это
просто значит, что дифференциал отображения f в этой точке не имеет собственных
значений, равных 1), то ’’число Лефшеца”
Le(/) = S(-l)f7#
есть алгебраическое число неподвижных точек. (Приписываемый неподвижной точке
знак можно непосредственно описать как четность числа вещественных собственных
значений дифференциала, меньших 1.)
Число Лефшеца определено для непрерывного отображения в себя произвольного
топологического пространства с конечно порожденными гомологиями. Выделим его
важное свойство.
Упражнение 24. Пусть ft Х^Х— клеточное отображение конечного кле-
точного пространства в себя, и пусть 7) — след эндоморфизма /#: (X) -►$/(.¥).
Тогда
Le(/) = S(-l)‘Tf.
(Ср. с упражнением 8 к § 13.)
150
ГЛ. 2. ГОМОЛОГИИ
Следствие!. Если число Лефшеца отлично от 0, то у отображения есть хотя
бы одна неподвижная точка.
Действительно, если неподвижных точек нет, то [ f ] и diag не пересекаются и,
в частности, находятся в общем положении; значит, число Лефшеца равно. 0.
Следствие 2. Если отображение ft Х-+Х обладает только невырожденными
неподвижными точками и гомотопно тождественному, то алгебраическое число его
неподвижных точек равно эйлеровой характеристике х(Х) пространства X.
Действительно, для отображений, гомотопных тождественному, т, = Bt(X) -
число Бетти.
Отображение, гомотопное тождественному, можно построить при помощи вектор-
ного поля, касающегося нашего многообразия (которое мы сейчас представляем
себе как поверхность в евклидовом пространстве): каждая точка немножко сдвигает-
ся в направлении своего вектора. Неподвижные точки такого отображения - это осо-
бенности (нули) векторного поля.
Теорема 8 (следствие следствия 2). Если гладкое замкнутое ориентируемое
многообразие обладает векторным полем без особенностей, то эйлерова характерис-
тика этого многообразия равна 0. (Ниже мы увидим, что, во-первых, для справедли-
вости этого утверждения не требуется ориентируемость и, во-вторых, содержащееся
в нем необходимое условие существования векторного поля без особенностей
является и достаточным.) В общем случае алгебраическое число особенностей век-
торного поля общего положения равно эйлеровой характеристике.
Эта теорема носит имя Хопфа. Мы еще вернемся к ней в следующем параграфе.
Неориентированный Z2-вариант изложенной теории, конечно, имеет место, но он
не нужен, поскольку основные геометрические выводы теории Лефшеца сохраняют
силу в неориентируемом случае (как, впрочем, и в краевом случае) без всякой ре-
дукции по модулю 2. Прежде всего мы заметим, что знак, приписываемый невырож-
денной неподвижной точке гладкого отображения ft X -> X, не изменится, если у
многообразия X поменять ориентацию (при такой замене диагональ и график ото-
бражения оба меняют ориентацию, а X X X ее сохраняет). Отсюда вытекает, что ука-
занные знаки корректно определены и в ситуации, когда многообразие X вообще
неориентируемо.
Теорема 9. Пусть X - не обязательно ориентируемое замкнутое гладкое мно-
гообразие и ft X X - гладкое отображение. Если все неподвижные точки отобра-
жения f невырождены, то их алгебраическое число равно числу Лефшеца.
Доказательство этой теоремы, аналогичное доказательству теоремы 7, использует
неориентируемый целочисленный вариант двойственности Пуанкаре, который корот-
ко излагается в последнем пункте этого параграфа. Впрочем, для довольно широкого
класса отображений f можно воспользоваться более простым соображением:
если f не переводит петли, сохраняющие ориентацию, в петли, обращающие ориента-
цию, то f индуцирует отображение f t Х-*Х ориентирующей двулистной накрываю-
щей (см. упражнение 13). К последнему применима теорема 7, а для него и алгеб-
раическое число неподвижных точек и число Лефшеца вдвое больше, чем для f
(последнее вытекает из упражнения 24).
Теорема 10. Пусть X - компактное многообразие с краем и ft Х-*Х- глад-
кое отображение, не имеющее неподвижных точек на крае. Если все неподвижные
точки отображения f невырождены, то их алгебраическое число равно числу
Лефшеца.
Для доказательства можно воспользоваться ’’удвоением”: к X приклеивается по
краю копия X (рис. 79) и получается замкнутое многообразие. Отображение
§ 17. ГОМОЛОГИИ И МНОГООБРАЗИЯ
151
/: X достраивается до отображения/': Х> -*
X' удвоения: вторая копия отображается так же,
как первая. При этом ни алгебраическое число
неподвижных точек, ни число Лефшеца не меня-
ются. (Это рассуждение требует некоторых до-
делок, которые мы оставляем читателю; в
их числе — сглаживание отображения /': X1 -*•
%'вблизи места склейки.)
Из сказанного вытекает, что теорема 8 сохра-
няет силу для неориентируемых многообразий и
для многообразий с краем; для первых она вер-
на в прежней формулировке, для вторых — в
предположении, что векторное поле на крае не
внутрь многообразия.
имеет особенностей и ’’смотрит”
Упражнение 25. Существует другой подход к доказательству теоремы Леф-
шеца. Прежде всего доказывается, что если X — произвольное (компактное) триангу-
лированное подмножество евклидова пространства и отображение /: Х->Хне имеет
неподвижных точек, то соответствующее число Лефшеца равно 0 (достаточно измель-
чить триашуляцию настолько, чтобы диаметры симплексов были значительно мень-
ше, чем минимальное расстояние между точкой и ее образом; затем к отображению
применяется симплициальная аппроксимация — см. доказательство леммы о свобод-
ной точке в § 5 — и число Лефшеца вычисляется при помощи упражнения 24).
После этого, рассматривая произвольное гладкое отображение /: Х-*-Х с невырож-
денными неподвижными точками, нужно постараться произвести вблизи каждой
неподвижной точки изменение пространства и отображения так, чтобы неподвижных
точек не осталось, а изменение числа Лефшеца было контролируемым. Реализуйте
этот план.
В заключение — одно из бесчисленных применений теории Лефшеца.
Упражнения. 26. Отождествим n-мерный тор Тп с факторпространством
Rn/Z". Очевидно, что отображение R" -> R", определяемое целочисленной матри-
цей А, факторизуется до некоторого отображения Тп -»• Тп-, обозначим последнее
через fA. (Конечно, всякое отображение Тп -* Тп гомотопно единственному отобра-
жению вида fA - докажите!) Вычислите для fA число Лефшеца.
27. Обозначим число Лефшеца, вычислявшееся в предыдущем упражнении,
через La. Докажите, что отображение, гомотопное fA, имеет по крайней мере
ILa | геометрически различных неподвижных точек.
28. Выведите из предыдущего следующее утверждение, называемое ’’гипотезой
/2 1 \
Шуба — Сулливана”: отображение Т2 -* Т2, гомотопное fA, где А = t « «
имеет бесконечно много периодических точек (точка х называется периодической
для отображения g, если g ° ... ° g(x) =х при некотором л). Последние два утверж-
п
дения взяты нами из заметки В.Л. Гинзбурга ”0 числе прообразов точки При непре-
рывном отображении” (Успехи мат. наук. - 1986. - Т. 41, № 2. — С. 187—189).
6. Коэффициенты зацепления. Вернемся к двойственности Пуанкаре. Обещанная
двойственность между
Круч. Hq(X) и Круч. ЯП_„_1(У)
152
ГЛ. 2. ГОМОЛОГИИ
строится при помощи ’’коэффициентов зацепления”. Этот термин употребляется
в топологии в нескольких разных смыслах, в том числе — в двух основных.
Первый — классический — не имеет отношения к двойственности Пуанкаре, а связан
с так называемой ’’двойственностью Александера — Понтрягина”, с которой мы
познакомимся в последнем пункте этого параграфа. Он заключается в следующем.
Предположим, что в ориентированном и-мерном многообразии заданы два (целочис-
ленных) цикла Ci и с2 размерностей q и п — q — 1, гомологичных 0, носители кото-
рых не пересекаются (носитель цепи — объединение образов ее сингулярных сим-
плексов). Возьмем цепь d с границей Cj и вычислим индекс пересечения цепей d и
с2 (можно считать, что все цепи состоят из гладких симплексов, находящихся в об-
щем положении; а можно считать, что Cj и d — классические цепи некоторой триан-
гуляции, а с2 — цепь соответствующего звездного комплекса). Этот индекс назы-
вается коэффициентом зацепления цепей и с2 и обозначается через X (<?i, с2).
Упражнения. 29. Проверьте корректность этого определения: Х(сь с2)
не зависит от d.
30. Докажите формулу
X(ci, с2) = -(-l)dim с> d‘m с’Х(с2, С1).
31. Докажите, что если цикл с2 гомологичен циклу с2 в дополнении к носителю
цикла Ci,то X(ci, с2) = X(ci, с2).
Коэффициент зацепления имеет наглядный геометрический смысл. Например,
он определен для двух ориентированных непересекающихся несамопересекающихся
замкнутых кривых в R3 (или №) и равен алгебраическому числу точек пересечения
пленки, натянутой на одну кривую, с другой. Коэффициент зацепления составляет
первое, самое грубое препятствие к тому, чтобы развести в пространстве две непере-
секающиеся замкнутые кривые, не пронося одну сквозь другую. (Вспомните доказа-
тельство теоремы Фрейденталя в § 10.) Например, коэффициент зацепления двух
соседних звеньев цепи (не сингулярной, а железной) равен (в зависимости оториента-
ций) ± 1. Бывает, конечно, что кривые с нулевым коэффициентом зацепления все же
зацеплены, т.е. не могут быть разведены (см. рис. 80).
Упражнения. 32. Пусть Sj, S2 — две непересекающиеся несамопересекаю-
щиеся ориентированные замкнутые кривые в R3. Рассмотрим отображение
Si X S2 -» S2, ставящее в соответствие паре (s2 6 s.2 € S2) единичный вектор
направления S!S2. Докажите, что степень этого отображения равна коэффициенту
зацепления $! и S2.
33. Многомерное обобщение: Х1г У2 С R” — связные непересекающиеся много-
образия, сумма размерностей которых равна п — 1. Коэффициент зацепления
X (Xi, Х2) равен степени аналогичного отображения Jfj X Х2 -» Sn~l.
34. Коэффициент зацепления двух слоев расслоения Хопфа S3 -* S2 равен 1.
(В действительности справедливо следующее утверждение: коэффициент зацепления
§ п. ГОМОЛОГИИ И МНОГООБРАЗИЯ
153
прообразов двух общих точек сферы S 2n при отображении S4"-1 -> s2n равен
инварианту Хопфа этого отображения (Хопф так и определял свой инвариант!).
Читатель может попытаться доказать эту теорему после прочтения всего параграфа.)
35. [Это упражнение адресовано тем, кто поймет формулировку.] Пусть и —
бездивергентное векторное поле без особенностей на сфере S3, ш — дифференциаль-
ная форма степени 1, получающаяся из и ’’опусканием индексов” по отношению
к стандартной метрике. Возьмем на сфере две случайные точки и будем двигаться
из каждой из них по траектории поля в течение времени Т; после этого две получив-
шиеся незамкнутые кривые мы замкнем дугами больших кругов так, чтобы получи-
лись непересекаюшиеся замкнутые кривые. Коэффициент зацепления этих кривых
мы поделим на Т2 и перейдем к пределу при Т -> «>. Докажите, что получающееся
число (оно называется асимптотическим коэффициентом самозацепления поля и)
не зависит от начальных точек, если только траектории не сталкиваются. Докажите,
что с точностью до не зависящего от поля множителя этот коэффициент равен
f а>л du.
S3
Поскольку коэффициент зацепления определен только для циклов, гомологич-
ных 0, формулировать для него свойство гомологической инвариантности надлежит
аккуратно (см. выше упражнение 31). Например, если А и В - - два непересекающих-
ся подмножества и-мерного ориентированного многообразия X, то коэффициент
зацепления определяет билинейную форму
Kei[Hp(A)^Hp(X)]XKer[Hq(B)^Hq(X)]^Z, p + q = n-l.
В важном случае, когда X есть сфера, мы получаем билинейную форму
НР(А) X Hq(B) -» Z, p + q = n—\, р > О, q>0.
Другая теория коэффициентов зацепления, имеющая прямое отношение к двойст-
венности Пуанкаре, строится в следующей ситуации. Пусть X — гладкое замкнутое
ориентированное «-мерное многообразие, и пусть aG Hq(X), Р G Яя_ч_1(АЭ —
элементы конечного порядка. Пусть, далее, а, Ъ — циклы, представляющие а, Р, и
предположим, что Na = Эс. Определим коэффициент зацепления I (в, 3) как
рациональное
/(а, 0) G Q/Z.
число Ь), приведенное по модулю 1. Таким образом,
Упражнения. 36. Проверьте корректность определения I (а, 0) (что 0 имеет
конечный порядок, существенно именно при проверке корректности).
37. Докажите, что если Na = О, МР = 0 и К = НОД (М, N), то Kl( а, Р) = 0.
38. Докажите, что 1(а, р) = ±1(Р, а); уточните знак.
Основное свойство этих коэффициентов зацепления выражается следующей
теоремой.
Т е о'р е м а 11. Поставим в соответствие классу a G Круч. Hq(X) функцию
0 *-*! (а, 0). Получится изоморфизм
Круч. Я,(У)г Нот (Круч.j (У), Q/Z).
Это и есть ’’вторичная двойственность Пуанкаре”.
Упражнение 39. Докажите теорему 11.
7. Обратные гомоморфизмы. Пусть X и Y — замкнутые ориентированные
связные гладкие многообразия, вообще говоря, разных размерностей m и п, и пусть
154
ГЛ. 2. ГОМОЛОГИИ
f: X -> Y — непрерывное отображение. Наличие изоморфизмов Пуанкаре позволяет
построить по f отображения гомологических и когомологических групп, направлен-
ные ”не в ту сторону”:
. О'1 f* D
f"- Hq(Y)----► Я"-’(У;2)----► Я"-’(ЛГ;2)---► Ят_„+ч(П
D f<. D~l
fl- НУХ-Z)-^ Hm_q(X)-^ Hmq(Y)---------->Hn~m+«(Y-, Z).
Оба гомоморфизма изменяют размерность на т — п: гомоморфизм/1 ”увеличивает”
размерность на т - п (мы берем слово ’’увеличивает” в кавычки, поскольку т — п
может быть отрицательным числом или нулем), а гомоморфизм /( ’’уменьшает”
размерность на т — и. О когомологическом гомоморфизме /j мы скажем немного.
Он представлят собой простейшее проявление необычайно общей и важной конструк-
ции, называемой ’’прямым образом”. Его наглядный аналитический смысл (интуи-
тивные истоки когомологий лежат скорее в анализе, чем в геометрии), во всяком
случае, если / — проекция гладкого расслоения, выражается словами "послойное
интегрирование”, которые будут понятны тем, кто знаком с теорией де Рама. Го-
моморфизм/1: Hq(Y) -» Hm_„+q(X) называется ’’обратным гомоморфизмом Хоп-
фа”. Его геометрический смысл достаточно наглядно иллюстрируется следующей
теоремой.
Теорема 12. Предположим, что гомологический класс a G Hq(Y) реали-
зуется ориентируемым подмногообразием Z СУ и что отображение f трансверсаль-
но регулярно по отношению к Z. Тогда f~l (Z) С X есть ориентированное подмного-
образие, реализующее класс f* («).
Поясним смысл слов, входящих в эту теорему. Отображение /: X -» У назы-
вается трансверсально регулярным по отношению к Z, если для любой точки х €
С /-1 (Z) найдется вложенный в X малый диск размерности dim У — dim Z с цент-
ром х, который отображением / диффеоморфно отображается на диск, лежащий в У
трансверсально к Z. Условие трансверсальной регулярности — зто условие общности
положения; если оно не выполнено, его можно достичь посредством малого шевеле-
ния / (или малого шевеления Z). Легко понять, что если / трансверсально регуляр-
но по отношению к Z, то /"* (Z) есть подмногообразие, имеющее в X такую же ко-
размерность, какую Z имеет в У. Если X, У и Z ориентированы, то и/-1 (Z) приобре-
тает каноническую ориентацию. (Заметим, что если коразмерность Z в У больше раз-
мерности X, то условие трансверсальной регулярности сводится к тому, что f(X)
и Z не пересекаются.)
Мы не доказываем теорему 12; заметим только, что если все ее дифферен-
циальные данные заменить триангуляционными (X и У триангулированы, / симпли-
циально, т.е. аффинно отображает каждый симплекс на симплекс, класс а представ-
лен звездным циклом), то она делается более или менее очевидной (убедитесь в
этом). Заметим еще, что в теореме 12 не сказано, какое из многообразий X, У имеет
большую размерность: она верна в обоих случаях, хотя имеет в них разное геомет-
рическое содержание.
Важно, что аналог теоремы 9 имеет место и для многообразий с особенностя-
ми коразмерности > 2.
Упражнения. 40. Докажите формулу < а,/*0 > =</,«, Р >.
41. Пусть X и У — замкнутые гладкие многообразия одной размерности, и пусть
f : X-+Y — отображение степени d. Тогда композиции
/' /«
Hq(Y)-^Hq(X)-^ Hq(Y),
Hq(Y-,Z~)~-+ rffX.Z)-^-* Hq(Y,Z)
§77. ГОМОЛОГИИ И МНОГООБРАЗИЯ
155
совпадают с умножением на d. Следствие: если f есть отображение степени ±1, то
/, есть эпиморфизм, a f* есть мономорфизм. Обобщение: если f есть отображение
степени d ¥= 0, то всякий гомологический класс многообразия У, умноженный на
d, принадлежит образу отображения/, и всякий когомологический класс многообра-
зия У, принадлежащий ядру отображения /*, аннулируется умножением на d. На-
пример, не существует отображения ненулевой степени S2 -» S1 X S1 (но сущест-
вует отображение S1 X S1 2 степени 1: факторизация S1 X S1 по S1 v S1).
Все, сказанное в этом пункте, имеет очевидный неориентированный Z2-аналог.
8. Связь с ^-умножением.
Теорема 13. Предположим, что Yt и Y2 - гладкие замкнутые ориентирован-
ные подмногообразия гладкого замкнутого ориентированного многообразия X,
находящиеся в общем положении. Последнее означает, что Yt и У2 трансверсально
пересекаются по гладкому подмногообразию Z С X, размерность к которого связана
с размерностями mlt т2 и п многообразий Y}, Y2 и Xсоотношением k = mt +m2 — п.
Пусть, далее, a, G Цп~т> (У; Z), а2 G Нп~т* (Х\ Z), 0 G Я2л“т« "т’ (У; Z) -
когомологические классы, такие, что гомологические классы Dalt Da2, DP реали-
зуются многообразиями У1, Y2,Z. Тогда
aj ot2 = Р.
Аналогичное верно в неориентированном случае с коэффициентами в Z2.
(Заметим, что условие общности положения Yt й У2 равносильно тому, что
включение ij: Y} -> X трансверсально регулярно по отношению к У2 или, что экви-
валентно, включение i2: У2 -> X трансверсально регулярно по отношению к У1.)
Теорема 13 является прямым следствием теоремы 12:
D(tti v/ аг) = [У] (tti <>а2) =
= ([У] tti)>>tt2 = (Й .1^1]) ^«2 =
= й .([у1 ] =
= ^.(^П-ЧйЛУг])) = й.'Сй’&ЛВД =
= йЛй-1^)] = Й[2] = Dfi
(где i — включение Z в X).
Теорема 13 доставляет мощнейшее средство для вычисления мультипликативной
структуры в когомологиях различных многообразий (и, ввиду естественности
умножения, других пространств).
Пример. Если <71 + q2 < п, то произведение канонических образующих
групп Я2(СР”; Z) и Я2<?2(СР”; Z) равно канонической образующей группы
Н2 +ч^ (СР"; Z): действительно, первые две образующие переходят при изомор-
физме Пуанкаре в Гомологические классы, представляемые (п — 44)-мерным и
(п - )-мерным проективными подпространствами, их пересечение в общем поло-
жении есть (п - <71 — <72)-мерное проективное подпространство. Таким образом, i
кольцо Я*(СР”; Z) устроено так: в нем есть 1 G Я0 (СР"; Z) и мультипликативная i
образующая х G Я2 (СР"; Z). Остальные когомологические группы порождаются \
степенями образующей: х2 G Я4 (СР”; Z), х3 6 Я6 (СР"; Z) и т.д. Если п конечно,
то х”+1 = 0. Выражаясь более алгебраически, можно сказать, что Я* (СР” J Z) есть
кольцо многочленов от одной переменной х, профакторизованное по идеалу, по-
рожденному х”+1:
Я‘(СР";г) = Z[x]/(x”+I), dimx = 2.
156
ГЛ. 2. ГОМОЛОГИИ
Аналогично,
H*(RPn; Z2 ) = Z2 [х]/(х"+1), dim х = 1,
Я* (HP"; Z) = Z [x] /(xn+1), dim x = 4,
//•(CaP2;Z) = Z[x]/(x3), dimx =8.
Во всех случаях, кроме RP", можно заменить (в обеих частях равенства) Z любым
коммутативным кольцом с единицей.
Упражнение 42. Покажите, что целочисленное кольцо когомологий сферы
с g ручками X устроено так: в Н1 (X; Z) имеется 2g образующих ах,.'.., ag, bi, .
. . . , bg и a/Of = 0, btbj = 0, atbf = Ьцс, где с — образующая группы Я2 (X; Z). Вычис-
лите когомологические кольца с коэффициентами в Z2 у всех классических по-
верхностей.
Теорема 13 показывает, что умножение в когомологиях многообразия достаточно
богато (много ненулевых произведений). Этот тезис иллюстрируется следующим
предложением.
Следствие из теоремы 13. Если , а2 - когомологические классы
дополнительных размерностей замкнутого ориентированного многообразия X, то
<а2^а2, [ЛГ] > = <р(Яа1,Яа2).
(Справедлив неориентированный 22-аналог.)
Поскольку индекс пересечения представляет собой невырожденную билинейную
форму в гомологиях многообразия (двойственность Пуанкаре), значение произве-
дения на фундаментальном классе представляет собой невырожденную билинейную
форму в когомологиях (когомологическая двойственность Пуанкаре). Особый
интерес представляет зта двойственность в гомологиях и когомологиях средней
размерности.
У пражнение 43. Пусть X — замкнутое ориентированное многообразие четной
размерности 2k. Тогда билинейная форма (ttj, а2) •-* <04 а2, [У] > в свободной
части Hk (Х\ Z) задается (целочисленной) матрицей с определителем ± 1. Эта матри-
ца является симметрической при четном к и кососимметрической при нечетном к.
В частности, если к нечетно, то к-е число Бетти четно. Аналогичный факт для не-
ориентируемых многообразий неверен (бутылка Клейна).
9. Обобщения изоморфизма и двойственности Пуанкаре.
А. Некомпактный случай. Если (связное) многообразие X некомпактно (но по-
прежнему не имеет края), то оно обладает бесконечной триангуляцией. Соответст-
вие между симплексами и барицентрическими звездами сохраняется, но изомор-
физма между цепями и коцепями не возникает, потому что цепи — это конечные
линейные комбинации симплексов, а коцепи — произвольные функции на звездах.
Напрашиваются два выхода из положения, и оба они приемлемы: допустить беско-
нечные цепи или ограничиться финитными коцепями. Эти две модификации приво-
дят к специфическим теориям гомологий и когомологий, которые можно коррект-
но определить для произвольных топологических пространств. Открытые гомологии
Hqpen (Х\ G) топологического пространства X определяются как гомологии комп-
лекса { С£реп (ДГ; G), Э ) , где C£pen (X; G) — группа, вообще говоря, бесконечных
линейных комбинаций S gift ^-мерных сингулярных симплексов, обладающих тем
свойством, что для произвольного компактного подмножества К С X лишь для ко-
нечного числа i пересечение // (Тч) П К непусто; граница определяется обычной
формулой. Компактные когомологии Я?отр (¥; G) пространства X определяются
при помощи комплекса {Clomp(X; G), 6 }, гдеС^отрС'П G) — группа функций
§ 17. ГОМОЛОГИИ И МНОГООБРАЗИЯ
157
на ^-мерных сингулярных симплексах, обладающих тем свойством, что существует
компактное множество К (свое для каждой функции), такое, что значение функции
на сингулярном симплексе /, имеющем пустое пересечение /(Т4) Г> К, равно 0. Де-
фектом и той и другой теории является отсутствие гомотопической инвариантности
и даже индуцированных гомоморфизмов /,,/* (они определены, только если инду-
цирующее отображение f ’’собственно” — прообраз компактного множества ком-
пактен) .
Привлекая вышеописанные гомологии и когомологии, ничего не стоит построить
два разных обобщенных изоморфизма Пуанкаре:
Т е о р е м а 14. Если X - гладкое ориентируемое, вообще говоря, некомпактное
п-мерное многообразие без края, то
f*q(X)* Нпс^(Х-, Z),
Я,ореп(ЛГ)г Я"-’(ЛГ; Z).
Аналогичные изоморфизмы с коэффициентами в Z2 имеют место без предположения
ориентируемости.
Соответствующую этим изоморфизмам Пуанкаре двойственность Пуанкаре
составляют индекс пересечения и коэффициент зацепления между обыкновенными и
открытыми циклами. (Разберите случай, когда X = S1 X R.) Вообще предыдущая
теория переносится на нашу новую ситуацию более или менее вся, но мы не будем
вникать в детали. Зато мы выделим важный случай, когда открытые гомологии и
компактные когомологии сводятся к обыкновенным гомологиям и когомологиям.
Упражнение 44. Если X — компактное топологическое пространство и Л -
его замкнутое подмножество, то имеют место естественные (уточните, в каком
смысле!) изоморфизмы
Я,°Реп(Х - А; G) st Hq(X, А; G),
Я?отр(Х - А; G) a Hq(X, A , G).
В частности, если пространство X локально компактно и X' — его одноточечная
компактификация, то
Hq9*a(X‘,G)Si Hq(X'\G) ; Hqomv(X-, G)* ^(X'; G).
Это утверждение позволяет извлечь из теоремы 14 важное следствие, не вовле-
кающее экзотических гомологий или когомологий.
Следствие (из теоремы 14 и упражнения 44). Пусть X — компактное топо-
логическое пространство, А - его замкнутое подмножество, такое, что X - А есть
гладкое п-мерное ориентируемое многообразие без края. Тогда
Hq(X - Л ) s Hn~q(X, А; Z),
Hq(X, Л) s Нп ” q(X - Л; Z).
Аналогичное верно без предположения ориентируемости с коэффициентами в Z2.
Упражнение 45. Приведите конструкцию этих изоморфизмов при помощи
относительного «^-умножения.
В. Краевой случай. В важном специальном случае, когда X есть связное компакт-
ное ориентируемое многообразие с краем и Л есть его край, предыдущие изоморфиз-
мы принимают форму
Hq(X)^Hn~q(X, дХ- Z),
Hq(X, дХ) a Hn~q(X;Z)
(открытое многообразие X - Э X гомотопически не отличается от X).
158
ГЛ. 2. ГОМОЛОГИИ
Упражнение 46. Эти изоморфизмы, вместе с изоморфизмами Пуанкаре для
ЪХ, составляют изоморфизм между гомологической и когомологической после-
довательностями пары (X, дХ), т.е. коммутативную лестницу
... ----нурх)-----------//V(X)-----*я9(х<?х)—-* ...
II? II? II? II?
... —*~Нп 1 ч(дХ; V(X,dX;Z)^-Hn Ч(Х; Z)—*-tf” ^(дХ; Z)-*-
Предположим, что dim X = 2Л + 1 и рассмотрим фрагмент этой коммутативной
лестницы:
Hk+i(X, ЪХ)~Нк(ЬХ) Нк(Х)^
II? II?
Hk(bX,Z)——* Я*+1(Х ЭХ; Z)-> ...
(где i — включение ЭХ в X). Гомоморфизмы 6* и Э, сопряжены относительно спа-
ривания < , >, и потому ранги групп Coker Э, = Нк (ЭХ)/1т Э, и Кег 6 * совпадают.
Значит, совпадают ранги групп Як(ЭХ)/1т Э, и Кег г, = 1тЭ,. Отсюда получаем
важное следствие:
1
rank Im Э, = — rank Як(ЭХ).
Дальнейшие следствия. 1. Если четномерное ориентируемое много-
образие является краем компактного многообразия, то его срединное число Бетти
четно. (Для неориентируемых многообразий это, конечно, неверно, как показывает
пример все той же бутылки Клейна; верно, однако, что у любого четномерного края
компактного многообразия размерность срединных гомологий с коэффициентами
в Z2 четна. Отсюда следует, например, что ни комплексная проективная плоскость,
ни вещественная проективная плоскость не могут быть краем компактного много-
образия; в списке известных нам многообразий можно найти массу других подобных
примеров.)
2. Эйлерова характеристика края компактного многообразия четна. (Если раз-
мерность края четна, это следует из предыдущего, если она нечетна, то эйлерова ха-
рактеристика края равна 0 в силу следствия из теоремы 4.)
3. Если а, /? € Я^(ЭХ) лежат в образе гомоморфизма Э,, то их индекс пересече-
ния равен 0. (Это имеет наглядное доказательство (см. рис. 81), но легко может
быть доказано и формально: ^(Э.о, Э J?) = /,Э,0) = tp(a, 0) = 0.) Этот факт
особенно важен в случае четного к. Выше уже говорилось, что если срединные гомо-
логии четномерны, то в их свободной части возникает унимодулярная симметричес-
кая билинейная форма. Теперь мы видим, что в случае, когда многообразие есть
край, эта форма имеет нуль-пространство половинной размерности, что возможно
только в случае, когда сигнатура формы равна 0. Выделим подученное утверждение.
Теорема 15. Если ориентируемое многообразие, размерность которого делит-
ся на 4, является краем компактного ориентируемого многообразия, то форма
’’индекс пересечения” в свободной части его срединных гомологий имеет нулевую
сигнатуру.
С. Изоморфизм и двойственность Александера - Понтрягина. Пусть Л — замкну-
тое подмножество сферы Sn. Согласно предыдущему, имеют место изомофизмы
Hq(Sn - Л) а Я"-’(5",Л;г),
Я<г(5я,Л)^Я"-’(5л-Л;г).
§ /7. ГОМОЛОГИИ И МНОГООБРАЗИЯ
159
Но поскольку сфера имеет почти во всех размерностях тривиальные гомологии и
когомологии, из гомологической и когомологической последовательности пары
(5",Д) мы получаем изоморфизмы
Hq(Sn,A) st
H4(Sn,A-,Z)^Hq-l(A;Z)
при 1 < q < п.
Таким образом,
Hp(A)^Hr(Sn -A;Z),
при р + г = п — 1,
ЯР(Л; Z) =*Hr(Sn -А)
р>0, г >0
(условия р > 0, г > 0 можно отбросить, если взять приведенные гомологии и
М
Рис. 81
когомологии). Эти изоморфизмы носят название изоморфизмов Александера -
Понтрягина. Подобно изоморфизмам Пуанкаре, они могут быть представлены в тер-
минах одних гомологий:
Своб.частьЯр(4) = Своб. часть Ял_ 1_р(5л - А),
Круч.ЯР(Л) s Круч.Ял_2_р(5”-Л),
и в этом качестве являются проявлениями двойственности Александера — Понтря-
гина, аналогичной двойственности Пуанкаре. Двойственность между свободными
частями реализуется классическими коэффициентами зацепления (см. выше), двой-
ственность между кручениями — вторичными коэффициентами зацепления, которые
мы не рассматривали, но теорию которых читатель может при желании построить сам.
. D. Целочисленные неориентируемые изоморфизмы Пуанкаре. Эти изоморфизмы
имеют вид
Hq(X-,Z) а ЯЛ-’(У;2Т),
s Hn_q(X,ZT).
Здесь X — гладкое замкнутое, вообще говоря, неориентируемое, n-мериое много-
образие, а гомологии и когомологии с коэффициентами в ZT (индекс Т — от слова
twisted; Zy - ’’подкрученные целые числа”) определяются следующим образом.
Пусть X связно и неориентируемо. Рассмотрим ориентирующее двулистное накрьь
тие X -» X. Тогда в X действует (обращающая ориентацию) инволюция t: X -* X
(точка х Е X переходит в другой прообраз лежащей под ней точки х G X). Возни-
кает преобразование t#: Cq(X) -+Cq(X) с квадратом 1, и получается разложение
C,(f) = Cq(X) ® с-(ху.
Cq(X) - {cGCQ(A') I t#(c) = ±с}. Очевидно, Cq (X) - это то же, что Cq(X).
160
ГЛ. 2. ГОМОЛОГИИ
Другое слагаемое, Cq ( %), мы и примем за Cq (ЛГ; ZT). Очевидно, группы Cq (ЛГ; ZT)
составляют комплекс, его гомологии обозначаются через Hq(X-, Zj), а соответст-
вующие когомологии — через Hq (Х\ Zy). Эти ’’подкрученные” гомологии и кого-
мологии являются предметом теории, параллельной обычной теории гомологий и ко-
гомологий. Мы не будем входить в подробности (нам это еще предстоит, поскольку
с подкрученными гомологиями и когомологиями мы столкнемся в главе 3, причем
в значительно большей общности). Ограничимся голословным утверждением, что
в рассматриваемой теории существуют аналоги коэффициента зацепления и индекса
пересечения и двойственности Пуанкаре (интересующийся читатель, наверное, сможет
восстановить все необходимые определения и формулировки теорем).
§18. ТЕОРИЯ ПРЕПЯТСТВИЙ
1. Препятствия к распространению непрерывного отображения. Очень часто при-
ходится сталкиваться с проблемой продолжения непрерывного отображения А -» Y
на объемлющее А пространство X. Эта задача (и многие ее варианты) рассматривают-
ся в теории препятствий. Мы начнем с рассмотрения технически важного специаль-
ного случая.
Пусть X — клеточное пространство и У — топологическое пространство, предпола-
гаемое гомотопически простым (см. § 8). Рассмотрим проблему продолжения не-
прерывного отображения f:Xn -> Y до непрерывного отображения Хп+1 -» Y (Хп,
У"*1 - остовы).
Пусть е СX— клетка размерности и + 1, Л: D"+1 ->Х соответствующее характерис-
тическое отображение. Поскольку h (S”) С Хп, возникает отображение /е: Sn -> Y,
ft 0) = Z(A(s))- Совершенно очевидно, что отображение g продолжается на Хп Ue
тогда и только тогда, когда отображение/е продолжается до отображения Z>"+1 -»ЛГ,
т.е. когда /е гомотопно 0, т.е. когда /е представляет 0 Е тгл(У) (напомним, что У
гомотопически просто).
Ясно, далее, что возможность продолжить отображение f на ЛГИ+1 равносильно
возможности продолжить его на Хп U е для каждой (и + 1)-мерной клетки е. По-
строив, как выше, по каждой клетке е отображение /е: S" -» X и обозначив через
\ре определяемый им элемент группы irn(Y), мы можем сделать следующее, в сущ-
ности, тавтологическое утверждение: непрерывное отображение f: Хп -* Y тогда и
только тогда может быть продолжено до непрерывного отображения ЛГл+1 -» У,
когда все равны 0.
Сопоставление е >-> может рассматриваться как клеточная коцепь пространст-
ва X с коэффициентами в тгл(У)- Эта коцепь обозначается через су и называется
препятствием к продолжению отображения f на Хп+1. Итак,
суе «"+>(ЛГ; тгл(У)).
Пока все сказанное было тривиальностью; вот первое содержательное утвер-
ждение.
Теорема 1. Препятствие есть коцикл: bcf = 0.
Это утверждение является вариацией на тему ЭЭ = 0 (нужно доказать, что су(Эа) =
= 0 для любой цепи а, но сама коцепь су определяется через посредство границ),
но его аккуратное доказательство сопряжено с некоторыми трудностями. Его мож-
но, например, вывести из относительной теоремы Гуревича (§ 14, теорема 4). Соглас-
но последней, при некоторых ограничениях на X (их мы обсудим ниже), гомомор-
физм Гуревича Л: itq(Xq, Xq~l) -» Hq(Xq, Xq~*) является изоморфизмом. Рас-
§ 18. ТЕОРИЯ ПРЕПЯТСТВИЙ
161
смотрим диаграмму
д
(X) = H„tZ(xa,t, Хп+') л„,2(л ”1хлИ)
(а
Ч.Ж+1)
. I
(X) =Hn^xnt\xn) Д„,дх”+:хя)
Эта диаграмма коммутативна в силу определения коцепи Cf и гомоморфизма
9: Й’„+2(Аг) ->^„ + i(Ar). В то же время, часть правого столбца, отмеченная фигур-
ной скобкой, есть фрагмент гомотопической последовательности пары (Xn+1, Хп),
и потому композиция входящих в нее гомоморфизмов равна 0. Следовательно,
Cf ° 9 = 8cf = 0.
Однако ссылка на относительную теорему Гуревича вынуждает нас уважать пред-
положения, в которых она верна, т.е. вынуждает нас считать, что X односвязно и что
п > 1. Второе ограничение мы проигнорируем (если расшифровать ссылку на теоре-
му Гуревича, то будет видно, что при п = 1 рассуждение совершенно корректно),
а от предположения односвязности X можно избавиться, например, так: рассмотрим
универсальное накрытие X ->Х (клеточное разбиение X индуцирует клеточное разбие-
ние^); очевидно, 7Г#: $*(Х; тг„(У)) ->$*(Х; тг„(У)) есть мономорфизм и в то же
время тг#<у = Cf о п и 8cf о „ = 0 по доказанному.
Когомологический класс коцикла Cf мы обозначаем через Cf. Очень часто имен-
но Cf G Нп+1(Х-, тг„(У)) называется препятствием (a cf называется тогда пре-
пятствующей коцепью).
Теорема 2. Условие Cf = 0 равносильно тому, что отображение f:Xn^>Y
можно продолжить на Хп + 1, предварительно изменив его на Хп, но не меняя
наХ”-1.
(Эту теорему можно применять последовательно к продолжениям отображения с
остова на остов. Именно, если отображение задано на Хп, то возникает препятствие
в (п +1)-мерных когомологиях к продолжению на Хп+1 с возможным исправле-
нием на Хп, не затрагивающим Хп~1. Если такое продолжение существует, то к
продолжению на Хп 2 возникает препятствие в (п + 2)-мерных когомологиях и т.д.
Однако следует помнить, что каждое следующее препятствие зависит от выбора
продолжения отображения на всех предыдущих шагах, и эта неоднозначность нарас-
тает при переходе от остова к остову.)
Прежде чем доказывать теорему 2, мы введем новое понятие, которое будет ис-
пользовано в доказательстве и важно само по себе. Пусть /, g: Хп -> У — два отобра-
жения, совпадающие на X”-1. Рассмотрим произвольную «-мерную клетку е СХ с
характеристическим отображение й: Dn ->Х. Отображения f ° h,g °h : Dn -> У согласо-
ваны на S"-1 (потому что й(5"-1) СХ"-1, а/ ng на X"-1 совпадают) и вместе
определяют отображение ke: S" -> У (область определения f отождествляется с
верхней полусферой, область определения g отождествляется с нижней полусферой).
Определим различающую коцепь
df'gCWCX^tY)),
6. А.Т. Фоменко
162
ГЛ. 2. ГОМОЛОГИИ
приняв за ее значение на е класс сфероида ке. Очевидно, dftg = 0 тогда и только тог-
да, когда f соединяется с g гомотопией, неподвижной на Хп~1. В важном для нас
случае, когда оба отображения /, g с самого начала были определены на всем X
(и совпадали на X”-1), последнее утверждение может быть (ввиду теоремы Бор-
сука) видоизменено следующим образом: существует гомотопия отображения /,
неподвижная на Хп~1 и совмещающая / с g на Хп.
Лемма 1. Для любого отображения f:Xn-*Yu любой коцепи d е 'ё'ЧХ; тг„ (У))
можно найти отображение g: X" -> Y, совпадающее с f на Хп~1 и такое, что df, g = d.
Рис. 82
Доказательство. Рассмотрим произвольную «-мерную клетку е простран-
ства X и выделим около ее центра маленький шарик. Затем изменим отображение
f на этом шарике так, чтобы два отображения шарика — старое и новое — составили
сфероид класса d(e) G (см. рис. 82). Произведя такое изменение на каждой
«-мерной клетке пространства X, мы и получим требуемое отображение g.
Лемма 2. 8df,g -cg - Cf.
Доказательство. Рассмотрим для простоты случай, когда fug различают-
ся на одной «-мерной клетке е (общий случай, по существу, не отличается от этого
специального случая). Пусть а — клетка размерности п + 1, h: Z>"+1 — характе-
ристическое отображение. Мы должны доказать, что
cg(ff) - c/(ff) = [ff: <*лИе)-
Можно считать, что h~l(e) состоит из некоторого количества шариков, каждый из
которых отображается на е гомеоморфно с сохранением или обращением ориентации,
причем разность между числом шариков, отображающихся с сохранением и с обра-
щением ориентации, равна [о: е], В свете сказанного нужное равенство очевидно:
сфероид, представляющий cg(d), получается из сфероида, представляющего <у(о)
прибавлением сфероидов ± dftg(e), алгебраическое число которых есть [о: е].
Доказательство теорем й 2. Если Q = 0, то Cf = 5 d и в силу леммы 1
существует отображение g: Хп -> Y, совпадающее с f на Хп~1 и такое, что df,g =
= — d. Но тогда cg = Cf + 8dftg = 0, т.е. g продолжается на Xn+l. Обратно, если су-
ществует отображение g: Хп -> У, продолжающееся на Ar”+1 и совпадающее с f на
Хп~1, то cg =O,Cf =Cf - cg = — 8df, g и Cf = 0.
Упражнение 1. Докажите, что dftg + dgth = dfь и dgf = - df,g.
2. Относительный случай. Пусть A - клеточное подпространство пространства X,
и пусть отображение f определено на A U Хп. Препятствующая коцепь к продолже-
нию такого отображения на A U/"+1 лежит в %>n+i (X, А; тг„(У)), является коцик-
лом, и соответствующий когомологический класс Cf G Нп+1(Х, А; тг„(У)) называет-
ся препятствием. Теория этих относительных препятствий совершено параллельна
своему абсолютному прототипу, в частности, в ней определяются различающие
и доказываются точные аналоги (как в смысле формулировок, так и в смысле до-
казательств) всех лемм и теорем предыдущего пункта. Мы выделим из относитель-
ной теории следующее важное абсолютное последствие.
Пусть f,gtX^Y — два непрерывных отображения, совпадающих на Хп (условие
совпадения можно заменить условием гомотопности, но с уточнением, что задана
§ 18. ТЕОРИЯ ПРЕПЯТСТВИЙ
163
(х, t) н-
определенная гомотопия между f\xn Hg|%n). Рассматривается проблема построения
гомотопии между fug, неподвижной (или совпадающей с заданной) на Хп. Эта проб-
лема равносильна продолжению на X X I отображения, заданного на (X X 0) U
U (X X 1) U (Хп X /) формулой
f(x) при t = 0 или х G Хп,
g(x) при t = 1 (или х€1").
(В случае гомотопности f\x„ и g\xn формула чуть другая — детали оставляются чи-
тателю.) Препятствие к продолжению этого отображения на (1X0) U (X X 1) U
U(X”+‘ X/) лежит в $л+дА,'Х/, (ЛГХО) UQTX1); тгл+1(У)) = $Л+‘(Х; ял+1(У));
легко понять, что оно равно dfig. Кстати, 8df,g = cg - = 0, так как f ng определе-
ны на всем X. Применяя к этой ситуации относительный вариант теоремы 2, мы полу-
чаем такое утверждение.
Теорема 3. Если f,g:X~>Y - отображения, совпадающие на Хп, то df,g есть
коцикл, когомологический класс Dftg G Hn+1 (X; тгл+1(У)) которого равен О
тогда и только тогда, когда f\x„+i и gl%n+1 можно соединить гомотопией, непод-
вижной на Хп~1'
(Можно сделать замечание, аналогичное замечанию после формулировки теоре-
мы 2.)
3. Применение: когомологии и отображения в Я (я, л) ’ы. Напомним, что построе-
ние пространства /С(я, л) начинается с того, что берется букет «-мерных сфер, постав-
ленных во взаимно однозначное соответствие с элементами некоторой системы
образующих группы я, и этот букет будет л-м остовом строящегося К(тг, л)’а
(см. § И). Поставив в соответствие л-мерной клетке (сфере букета) отвечающую
ей образующую, мы получаем коцепь с € $”(£(я, л); я) (мы допускаем вольность
в обозначениях, обозначая символом К (я, л) определенное пространство типа
К (я, л))-
Лемма. Коцепь с - коцикл.
Доказательство. Клетки размерности л + 1 отвечают соотношениям меж-
ду выбранными образующими в я; если клетка о отвечает соотношению Y.kjgt =
= 0, где gi — образующие, то коэффициент [о: е] равен коэффициенту, с которым
в это соотношение входит образующая, отвечающая е. Обозначая через е/ клетку,
соответствующую образующей g(, получаем:
6с(о) = S[о,е,] с(е() = Sfc/g,- = 0.
Когомологический класс G Нп(К(тт, л); л) коцикла с называется фундамен-
тальным когомологическим классом К(я, л)’а. Другое построение класса F„ произ-
водится при помощи формулы универсальных коэффициентов: так как
Я„_1(/С(я, л)) =0,то
Нп(К(тт, пУ, тг) = Нот(И„(К(тг, л)), тг),
но в силу теоремы Гуревича Нп(К (тг, л)) = тг. Фундаментальный класс F„ отвечает
тождественному гомоморфизму id„ G Нош(Ял(^(тг, л)), тг). Кстати, это построение
применимо к любому (л — 1)-связному пространствуй; в этом случае оно дает фун-
даментальный класс Fx е Нп(Х\ тт^Х) ). К этому классу мы еще вернемся.
Упражнение 2. Докажите эквивалентность двух определений фундаменталь-
ного класса.
6*
164
ГЛ. 2. ГОМОЛОГИИ
Теперь мы переходим к главному предмету этого пункта. Пусть X — произволь-
ное топологическое пространство и /: X -> К (it, п) — непрерывное отображение.
Поставим в соответствие отображению f когомологический класс f^F^ €Е Я”(АГ; л).
Поскольку этот класс зависит только от гомотопического класса отображения f,
мы получаем отображение
тг(Х Х(7Г,«)) ->Я"(Х;я), [/] ^TF*.
Теорема 4. Если пространство X клеточно, то это - взаимно однозначное
соответствие.
(Эта теорема была обещана в § 4.)
Доказательство. Сначала покажем, что для любого а €Е Нп(Х', тг) найдет-
ся такое отображение ft X -+К (it, п), что f*F„ = а. Зададим коцикл a G 'S" (*; я)
класса а. На остове Хп 1 зададим отображение f как отображение в точку. Тогда иа
любой ориентированной и-мериой клетке е отображение f должно быть сфероидом,
и мы потребуем, чтобы этот сфероид принадлежал классу а (е) G тг = тг„(К (тг, п)).
Ясно, что коцепь а будет различающей между f и постоянным отображением
const, все переводящим в точку. Поэтому в силу теоремы 2
О — 8а — 8dconst,f ~ Cf — с const- Cf
(cconst = 0, поскольку const продолжается на все X). Значит, f продолжается на
Хп+1. Продолжение f на Хп+2, Хпг3,... препятствий ие встречает, поскольку
соответствующие препятствия лежат в группах $”+2(А’’; тг„+1(Х’(тг, и)) = 0),
<dn+3(X; itn+2(K(ir, и)) = 0) и тд. Мы приходим к отображению ft X -+K(it, и).
По построению, f*Fv = а.
Теперь покажем, что если f*F„ = g*F^, то/~ g. Будем совмещать/ng, последо-
вательно вычисляя различающие. Эти различающие лежат в нулевых группах до того
момента, пока мы не дошли до различающей в 48n(X; it^(K(ir, и)) = тг). Эта различа-
ющая возникает в тот момент, когда / и g уже совмещены иа Хп~1. В первой части
доказательства мы видели, что f*F.„ и g*F7, — это когомологические классы
^const,/ И Z^const,^ различающих t/const,/ И ^const.g- ПОЭТОМУ Dftg — Dft const "*
+ ^const.g = ^const g - ^const.r (см. упражнение 1) =g_*F„ -f*Fn = 0. Поэтому
/ совмещается на X" c g гомотопией, неподвижной иа У" 2. На последующих шагах
различающие снова тривиальны, и мы последовательно совмещаем / с g на Хп+1'
Хп+2,... Таким образом,/ ~ g. (Если X бесконечномерно, то зти последовательные
гомотопии производятся, когда параметр t изменяется в интервалах 0 < t <1/2,
1/2 < 3/4, 3/4 < t <7/8,...; на каждом остове пространства X гомотопия будет
неподвижной в некоторой окрестности своего конца.)
Упражнение 3. Взаимно однозначное соответствие Нп(Х\ it) « it(X, K(it, и))
является взимно однозначным соответствием между двумя группами: тг(Х К (it, и))
есть группа, поскольку К (it, п) ~ £2(К(тг, и + 1)) есть Я-пространство (см. § 4).
Докажите, что это соответствие является групповым изоморфизмом.
Следствие из теоремы 4 (теорема Брушлинского). Для клеточного
X имеет место изоморфизм Н1(Х; Z) as it (X, S1) (структура абелевой группы в
правой части возникает благодаря наличию естественной структуры топологической
абелевой группы в S1).
Упражнение 4. Еще одно следствие из теоремы 4: всякое отображение
S1 X . . .XS1 -»Sl X .., X S1 гомотопно линейному отображению (т.е. отображению,
п m
получающемуся посредством факторизации из линейного отображения R” ->Rm,
задаваемого целочисленной матрицей).
§ 18. ТЕОРИЯ ПРЕПЯТСТВИЙ
165
4. Другое применение: теоремы Хопфа.
Теорема 5 (Хопф). Для любого п-мерного клеточного пространства X имеет
место взаимно однозначное соответствие
Hn(X;Z)^7t(X,Sn),
где s - каноническая образующая группы Hn(Sn' Z) = Z.
Эта классическая теорема (доказанная, в действительности, раньше, чем появились
не только препятствия, но и когомологии) с современной точки зрения является
следствием предыдущей теоремы. Действительно, если вникнуть в конструкцию
К(тг, л)’а, изложенную в § 11, то можно понять, что K(Z,n) получается из Sn при-
клеиванием клеток размерностей > п + 2 (Z имеет одну образующую и не имеет
соотношений). Поэтому тг (X, К (Z, п) ) = тг (X, S") в силу теоремы о клеточной ап-
проксимации (любое отображение X *+ K(Z, п) гомотопно отображению, образ ко-
торого лежит в п-м остове, а гомотопия между двумя такими отображениями всег-
да может быть сделана протекающей по (п + 1)-му остову).
(Можно доказать теорему 5 и прямо, повторив более или меиее дословно дока-
зательство теоремы 4. Главное различие между двумя доказательствами будет сос-
тоять в том, что старшие препятствия и различающие будут равны 0 ие потому, что
тривиальны старшие гомотопические группы сферы Sn — это неверно! — а потому,
что X не имеет клеток старших размерностей.)
Теорема 6 (Хопф). Пусть п-мерное клеточное пространство X содержит сферу
Sn~l. Для того чтобы эта сфера была ретрактом пространства X, необходимо и
достаточно, чтобы гомоморфизм Hn~l(X,Z)->Hn~1(Sn~1 ;Z), индуцированный
включением, был эпиморфизмом.
Доказательство. Необходимость очевидна: если г: X - ретракция,
то композиция Я"-*(5”“1; Z) r-?Hn~l(X; Z) ->Я”_1(5”-1; Z) (/-включение)
тождественна, и потому /* — эпиморфизм. Обратно, предположим, что /* — эпимор-
физм. Зафиксируем класс a GНп~х(X; Z) .такой, что/*(а) = 1 G Z = Я"-1(5"-1; Z),
и выберем представляющий а коцикл a €Е ^п~1(Х; Z). Построим отображение
q\ X -> 5”-1 следующим образом. Клетки размерности < п — 2 мы отобразим в
точку. На (л — 1)-мерной клетке е отображение q будет сфероидом, и мы потребуем,
чтобы этот сфероид принадлежал классу а(е) G Z = tt„_i(S"-1). Это требование
равносильно тому, что отображение q* переводит 1 G Z =4gn~1(Sn~1; Z) в а. С дру-
гой стороны,' оно показывает, что коцепь а будет различающей между уже постро-
енной частью отображения q и отображением const — в точку. Мы имеем:
О — 8а — 8dq, const — cq ~ cConst = Cq,
ввиду чего отображение q может быть продолжено на Хп = X. Композиция Sn~1
-*•£ индуцирует тождественное отображение в когомологиях: (q о /)*(1) =
=/*(?*G)) = ./*(“) =1,ипотому гомотопна id. Гомотопию, соединяющую это отоб-
ражение с id, мы можем продолжить до гомотопии отображения q, и в результате
получится отображение г: X -+Sn~1, тождественное иа Sn~ г, т.е. ретракция.
5. Препятствие к продолжению сечения. Пусть (£, В, F, р) — локально тривиаль-
ное расслоение. Мы предположим, что слой F гомотопически прост (например, од-
носвязен) и база односвязна. (Предположение об односвязности базы лишне, его
можно заменить предположением о простоте расслоения. Последнее означает, что
расслоение над 5*, индуцированное посредством произвольного непрерывного
отображения S1 -> В, тривиально; с важными примерами такой ситуации мы поз-
накомимся в следующем параграфе.)
166
ГЛ. 2. ГОМОЛОГИИ
Предположим, что пространство В клеточно и что над его и-м остовом задано
сечение s: Вп ->Е. Пусть е — клетка базы размерности п + 1, Л: D"+1 — харак-
теристическое отображение. Расслоение, индуцированное посредством h над D”+1,
тривиально. Сечение s индуцирует сечение индуцированного расслоения над
Sn CDn+l, т.е. отображение Sn X F, т.е. элемент группы tt„(D"+1 X F) =
= Пг№)- (Правильнее было бы сказать, элемент гомотопической группы некоторо-
го слоя над одной из точек клетки е; однако односвязность базы или простота рас-
слоения позволяют отождествить гомотопические группы всех слоев — разберитесь
в этом!) Функция, относящая клетке е построенный элемент группы тг„(Е) , есть ко-
цепь из $"+1(Я; тг„(Е)). Мы обозначим эту коцепь через cs; зто — препятствие (или
препятствующая коцепь) к распространению сечения s на (п + 1)-й остов. Свойства
этого препятствия совершенно аналогичны свойствам препятствия к распростране-
нию отображения, и мы можем ограничиться их перечислением.
(1) Сечение s тогда и только продолжается до сечения над (п + 1)-м остовом базы,
когда с, =0.
(2) 8cs = 0.
(3) Когомологический класс С5 коцикла cs (от также называется препятствием)
равен 0 тогда и только тогда когда сечение можно продолжить на (и + 1)-й остов,
предварительно изменив его иа и-м остове, но не меняя на (п — 1)-м остове.
Вводятся и различающие, также являющиеся аналогами ранее введенных.
Препятствия к распространению отображений являются частным случаем препят-
ствий к распространению сечений: отображение X * У равнозначно своему графику
X -> X X У, который может рассматриваться как сечение тривиального расслоения.
Препятствия к распространению отображения и к распространению графика идентич-
ны. В то же время теория препятствий к распространению сечений не охватывается
теорией препятствий к распространению отображений; в частности, в последней нет
никакого аналога следующей конструкции.
Предположим, что тго(Е) = • = Яп-1(^Э = 0, ^n(f) 0. При к Си препятствие
к распространению сечения на к-к остов базы равно 0 (принимает значение в нулевой
группе). Впервые нетривиальное препятствие возникает в группе Hn*l(B-, ttn{F)).
Оказывается, что это препятствие не зависит от того, как сечение было построено на
и-м остове. Факт этот почти очевиден и доказывается с помощью различающих и
аналога теоремы о том, что 8dftg = cg - Cf. Таким образом, этот класс определяет-
ся самим расслоением. Он называется характеристическим классом расслоения.
Упражнения. 5. (Основное свойство характеристических классов.) Если £ €Е
G Нп+'(В', itn(F)) — характеристический класс расслоения (Е, В, F, р) и /: В'-*В —
непрерывное отображение, то характеристический класс расслоения, индуцированно-
го расслоением (Е, В, F, р) посредством отображения /, равен .
6. Характеристический класс гомотопически инвариантен; в частности, он не за-
висит от клеточного разбиения базы.
С конкретными примерами характеристических классов мы познакомимся в сле-
дующем параграфе. А сейчас — заключительные упражнения.
Упражнения. 7. Постройте теорию препятствий к распространению сечений
в контексте серровских расслоений.
8. Пусть X — клеточное пространство, у которого тг^{Х) = .. . = тг^^У) = 0,
7r„(X) =# 0. Покажите, что характеристический класс серровского расслоения ЕХ ->
-> X со слоем ШГ, лежащий в Нп(Х; тгп_ 1(ШГ)) = Нп(Х\ тгл(^)), есть не что иное,
как фундаментальный класс пространства X. (Отсюда виден инвариантный смысл
фундаментального класса.)
§ 19. ВЕКТОРНЫЕ РАССЛОЕНИЯ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
167
§ 19. ВЕКТОРНЫЕ РАССЛОЕНИЯ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
1. Векторные расслоения и операции над ними.
А. Определения. Мы рассматриваем три типа векторных расслоений: веществен-
ные, ориентированные и комплексные. Вещественное «-мерное векторное расслоение
с базой В - это локально тривиальное расслоение над В со слоем, гомеоморфным
R", наделенное дополнительной структурой: в каждом слое задана структура «-мер-
ного вещественного векторного пространства, причем векторные операции (X, х) *->
»-> \х, (х, у) >->х + у непрерывным образом зависят от слоя в том смысле, что за-
даваемые ими отображения R X Е-> Е, {(х, у) GEXE\p(x) =р(у)} -*Е(греЕ-
пространство расслоения и р — проекция) непрерывны. Комплексные векторные
расслоения определяются точно так же, только поле R заменяется полем С; ориен-
тированные расслоения — это вещественные расслоения, в слоях которых задана
ориентация, непрерывным образом зависящая от слоя.
Последнему можно придать смысл, например, так. В ’’пространстве реперов”
вещественного векторного расслоения % = (Е, R", В, р)
R(£) = {(-Xi, •.. ,хп) &Е X ... X Е |p(Xi)= ... = р(х„); xf линейно независимы }
введем отношение эквивалентности: г = (х{,.. . ,х'„) и г" = (xf,... ,х^) эквива-
лентны, если р (х‘) = р(х") [=6] и реперы {xf,. .., х„} , {xf...х„} опреде-
ляют одинаковую ориентацию в пространстве p-1(Z>). Фактор-пространство про-
странства- R (£) по этому отношению эквивалентности обозначим через До(?)-
Очевидная проекция До(?) В есть накрытие (в широком смысле: без требова-
ния связности), и расслоение £ ориентируемо, если это накрытие тривиально
(ориентировано, если в этом накрытии выбрано сечение).
Для векторных расслоений (всех трех типов) очевидным образом определяются
эквивалентности, сужения, индуцированные расслоения. Тривиальное векторное
расслоение - это проекция R" X В -* В или С" X В -+В с естественной структурой.
Упражнение 1. Векторные расслоения локально тривиальны в векторном
смысле, т.е. сужение векторного расслоения на достаточно малую окрестность произ-
вольной точки базы эквивалентно тривиальному векторному расслоению.
Важный пример. Хопфовское или тавтологическое расслоение над RP" -
это одномерное вещественное векторное расслоение, пространство которого есть со-
вокупность пар (/, х), где I G RP" - прямая в R"+1, х G I - ее точка; проекция
действует по формуле (I, х) »->х. Другими словами, слой хопфовского расслоения
над I G RP" — это сама прямая I. Точно так же определяется (комплексное одно-
мерное) хопфовское или тавтологическое расслоение над СР". Обобщениями служат
тавтологические расслоения над грассманианами G(m, «), G+(m, п) и CG(m, п) —
это «-мерные векторные расслоения, соответственно, вещественное, ориентирован-
ное и комплексное.
В. Овеществление и комплексификация. Комплексное векторное расслоение %
можно овеществить, отбросив часть его структуры, а именно, умножение на мнимые
скаляры. Овеществленное расслоение обозначается через R£. Если расслоение
I «-мерно, то расслоение R£ 2«-мерно. Расслоения вида R£ обладают канонической
ориентацией: достаточно взять в слое этого расслоения комплексный базис
Xi,..., хп и объявить положительно ориентированным вещественный базис Xj,
ixi, •, хп, ixn\ получающаяся ориентация не зависит от базиса х1;..., х„ (ср.
с ’’важным замечанием” в примере к теореме 5 в § 17). Чуть сложнее определяется
комплексификация С£ вещественного векторного расслоения % = (Е, R", Д р).
Нужно в произведении С X £ произвести отождествление (X, rx) = (rX, х) [х G Е,
Х€ С, г 6 R] ; получившееся пространство СЕ — это пространство нашего расслое-
168
ГЛ. 2. ГОМОЛОГИИ
ния, проекция СЕ -> В действует по формуле (X, х ) >->р(х), векторные операции
действуют по формулам д(Х, х) = (д X, х), (Хъ х) + (Х2, х) = (Х2 + Х2, х) [кор-
ректность проверяется молниеносно].
Упражнение 2. Докажите, что Ct — комплексное n-мерное векторное рас-
слоение.
К описанным операциям примыкает операция комплексного сопряжения: если £ —
комплексное векторное расслоение, то сопряженное расслоение £ отличается от £
только тем, что операция умножения на скаляр X € С в f - это то же, что опера-
ция умножения на X в £.
С. Суммы и тензорные произведения. Если £i и £2 — векторные расслоения с об-
щей базой, относящиеся к одному из трех наших типов, то сумма £2 ® £2 и тензор-
ное произведение £х ® £2 — зто векторные расслоения того же типа, что £х и £2,
имеющие ту же базу, что £i и £2, и слои которых над точкой х базы являются, соот-
ветственно, суммами или тензорными произведениями слоев над той же точкой х
расслоений £х и £2. Более формальное определение расслоения £х ® £2 (через К
обозначается R или С): если £t = (Ex, В, К”’, pt) и £2 = (Е2, В, ШПг,р2), то
£i ® £2 - это сужение расслоения £х X £2 = (£I ХЕ2,В ХВ, K"1+”’,Pi Xр2) на
диагональ В С В X В. Другой путь формального определения £ х ® £ 2: пусть р*£2 =
= (Е, Е1,К"» ,р2); по определению, £ 1 ®£2 = (Е, В, K"» + "J ,pt о р2).
Упражнения. 3. Введите структуру векторного расслоения в расслоение
£i ® £2, определенное вторым способом, и докажите эквивалентность двух опре-
делений. (В частности, заметьте, что второе определение по форме не симметрично
относительно £j и £2, но из эквивалентности двух определений вытекает, что эта
несимметричность иллюзорна.)
4. Введите ориентацию в сумму ориентированных расслоений.
5. Придумайте формальное определение для тензорного произведения двух рас-
слоений.
6. Постройте изоморфизм £i ® (£2 ® £з) (£i ®£2) ® ( £i ® £з) (мы не видим
необходимости в разъяснении смысла слова ’’изоморфизм”).
Два векторных расслоения (одного типа, но, возможно, разных размерностей)
называются стабильно эквивалентными, если они делаются эквивалентными после
прибавления к ним тривиальных расслоений. Кстати, стандартное тривиальное п-мер-
ное расслоение (как вещественное, так и комплексное) в теории векторных рас-
слоений обычно обозначается просто символом п. Так что предыдущее определение
можно записать так:
^стаб’? *=* 3m,n: £®m~i?®n.
В заключение укажем на связь операции суммы с операциями предыдущего
пункта.
Упражнения. 7. Постройте канонический изоморфизм RC£ = £ ® £ (£ —
вещественное векторное расслоение). _
8. Постройте канонический изоморфизм CR£ = £ ® £ (£ — комплексное векторное
расслоение).
D. Линейные отображения расслоений, подрасслоения и факторрасслоения. Линей-
ное отображение векторного расслоения £ х в векторное расслоение £ 2 (которые оба
вещественные или оба комплексные) — это пара отображений F: Ех -*-E2,f:Bx -*В2
(Е{ и Bj — пространства и базы расслоений £f), такие, что (i) р2 ° F =f ° Рх (pt —
проекции) и (ii) отображение F линейно отображает каждый слой расслоения £ х в
слой расслоения £2. Подрасслоение векторного расслоения % = (Е, В, К” р) — это
такое векторное расслоение £’ = (Е1, В, Кт, р) с той же базой, что Е1 СЕ и включе-
§ 19. ВЕКТОРНЫЕ РАССЛОЕНИЯ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ 169
ние Е' -+Е составляет с тождественным отображением В -+В линейное отображение
Другими словами, чтобы построить подрасслоение векторного расслоения %,
нужно выделить в каждом слое расслоения £ подпространство, причем эти подпрост-
ранства должны иметь одинаковую размерность и сами составлять векторное рас-
слоение. Если £' — подрасслоение расслоения £, то, производя послойную фактори-
зацию, мы получим факторрасслоение . Другими словами, пространство рас-
слоения %/%' получается из пространства Е расслоения % факторизацией по отноше-
нию эквивалентности:хг ~ х2, еслир(хх) = р(х2) их2 ~х2 (=Е7.
Очевидным образом определяется линейное отображение £ -* {/£’, которое назы-
вается проектированием.
Укажем на два важных примера подрасслоений: Sk$ С $ ®...®£, Ак$ С
к
С £® ... ® £ — симметрическая и внешняя степени расслоения £.
к
Е. Координатное задание векторного расслоения. Обобщение. Пусть £ — вектор-
ное расслоение (одного из наших трех типов). Зафиксируем покрытие {Ut} базы
В, такое, что % |у. тривиально при каждом i, и зафиксируем соответствующие три-
виализации : p-1(G(- ) Ut X К” (р — проекция, К" — слой). Возникает сквоз-
ное отображение (U( П Uj) X К" -> (U( П G,) ХК”, х (х))> которое для
каждой точки у & Uf Cl Uj определяет преобразование К” -> К”, принадлежащее
группе GL(n, R),GZ+(n, R)илиG£(л, С) в зависимости от того, какому типу принад-
лежит расслоение Обозначим эту группу через G; мы получаем набор непрерывных
отображений <р,.: Ц Cl Uj -> G, обладающих следующими свойствами: \ptt (у) = 1,
4>ц (У) = 'Рц(У) -1, ЧНк(у) = 4>ц (У) <P/fc(y) (первое равенство имеет место при у е
G Uj, второе — при у & Ut Cl Uj, третье — при у G G) Cl Uj Cl [/k). Легко понять, что
задание набора отображений <pf/-: Ut Cl Uj ->G, обладающих перечисленными свойст-
вами, равносильно заданию векторного расслоения. Такой способ задания векторно-
го расслоения называется координатным.
Напрашивающееся обобщение таким образом заданных векторных расслоений сос-
тоит в том, чтобы взять произвольную топологическую группу G и произвольное G-
пространство F в качестве слоя. Это обобщение доставляет локально тривиальное
расслоение со слоем F и со специфической дополнительной структурой, учитываю-
щей действие группы G в F. Такие расслоения называются косыми произведениями
или расслоениями Стинрода (более современный термин) со структурной группой
G и стандартным слоем F. Общая тебрия таких расслоений изложена в классической
книге Стинрода ’’Топология косых произведений”, в книге Хьюзмоллера ’’Расслоен-
ные пространства” и в 4-й главе учебника Рохлина — Фукса. Мы ограничимся здесь
рассмотрением примеров.
За примерами далеко ходить не надо: достаточно взять координатным образом
заданное векторное расслоение и предположить, что функции принимают значе-
ния не во всей группе GL(n, R), GL+(n,R) или GL(tf, С), а в какой-нибудь ее под-
группе, скажем, О(п), SO(n) или U(n). Легко понять, что получающееся расслоение
Стинрода может быть адекватным образом описано как векторное расслоение с до-
полнительной структурой в слоях, например, в случае указанных подгрупп — евкли-
довой или эрмитовой метрикой, непрерывно зависящей от слоя. Если в качестве под-
группы группы GL(n, R) взять группу GL (п1, R) X GL(и2, R) блочно диагональных
матриц («1 + п2 = и), то мы придем к «-мерным расслоениям, разложенным в сумму
^-мерного и п2-мерного расслоений. Аналогичным образом можно описать вектор-
ные расслоения с выделенным не обращающимся в нуль сечением, векторные рас-
слоения с выделенным подрасслоением и т.д.
170
ГЛ. 2. ГОМОЛОГИИ
Другие примеры расслоений Стинрода появятся в следующих пунктах.
2. Касательные и нормальные расслоения гладких многообразий. Понятие каса-
тельного вектора к гладкому многообразию очень важно, и потому оно имеет много
эквивалентных определений. Наиболее естественный способ задания касательного
вектора в точке х многообразия X заключается в том, что сначала фиксируется карта
<р: U -> R”, такая, что х G U, и затем задается вектор и пространства R”, приложен-
ный в точке <р (х). Если имеется другая карта, ф: V ->R”, также покрывающая точку
х, то касательный вектор, соответствующий карте <р и вектору и, отождествляется с
касательным вектором, соответствующим карте ф и вектору w = d^t (и), где d^y —
дифференциал отображения tp(UCi К) ->ф(1/ С* V),у ь*Ф(‘Р-1(у)). Другая возмож-
ность, не требующая предварительной фиксации карты, состоит в том, чтобы опре-
делить касательный вектор как класс параметризованных кривых R ->Х, которые
при нулевом значении параметра проходят через х и касаются друг друга (детали
мы оставляем читателю). Еще более благоустроенное определение заключается в том,
чтобы определить касательный вектор к многообразию X в точке х как линейное
отображение а: С" (Х) -> R (первое обозначает пространство С“-функций на АГ),
удовлетворяющее двум аксиомам: (i) если/ = 0 в окрестности точки х, то а(/) =
= 0; (ii) ot(fg) = a(f)g(x) + f(x)a(g) (смысл этого определения заключается в
том, что касательные векторы отождествляются с операциями взятия производной
в направлении этих векторов). Наконец если многобразие X реализовано как глад-
кая поверхность в евклидовом пространстве, то касательный вектор к X— это прос-
то касательный вектор к этой поверхности. Это определение можно увязать с преды-
дущими, сказав, что касательный вектор в некоторой точке к евклидову простран-
ству, рассматриваемому как гладкое многообразие, — зто просто приложенный в
этой точке вектор евклидова пространства, а касательные векторы к подмногообра-
зию всегда являются касательными векторами к объемлющему многообразию.
Совокупность касательных векторов в точке х «-мерного многообразия X — зто
и-мерное пространство; оно обозначается через ТхХ. Объединение всех пространств
ТхХ обладает естественной топологией и даже структурой гладкого многообразия
(размерности 2л); зто многообразие обозначается через ТХ. Естественная проекция
ТХ -> X делает ТХ пространством векторного расслоения с базой X, называемого
касательным расслоением многообразия АГ; обозначение касательного расслоения:
т(Х). Сечение касательного расслоения — это векторное поле на многообразии.
Многообразие, у которого касательное расслоение тривиально, называется парал-
лелизуемым-, таким образом, параллелизуемость — это возможность согласованным
образом выбрать базисы во всех касательных пространствах или, что эквивалентно,
построить и векторных полей, линейно независимых в каждой точке (и — размер-
ность многообразия). Например, окружность параллелизуема, тор параллелизуем, а
двумерная сфера не параллелизуема.Трехмерная сфера параллелизуема: если предста-
вить ее как пространство единичных кватернионов, то базис в касательном прост-
ранстве 7Г/>3 составят (приложенные в точке х) векторы ix,jx, kx, где i ,j, k — ква-
тернионные единицы. Заменяя кватернионы числами Кэли, мы получим параллели-
зацию S1. Замечательный факт заключается в том, что никакие сферы, кроме S1,
S3 и S1 не параллелизуемы; это — одна из редакций доказанной Адамсом гипотезы
Фробениуса (см. § § 1,16).
Упражнение 9. Покажите, что ориентируемость касательного расслоения
многообразия А" равносильна ориентируемости АГ (в смысле § 17).
Если Y есть подмногообразие многообразия X, то на Yвозникают два расслоения:
7 (У) и т (АГ) | у- При этом 7 (У) есть подрасслоение расслоения 7 (АГ) | у (мы замечали
выше, что касательные векторы к подмногообразию являются касательными векто-
§19. ВЕКТОРНЫЕ РАССЛОЕНИЯ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
171
рами к многообразию). Соответствующее факторрасслоение т(У)|у/т(У) называет-
ся нормальным расслоением многообразия У в X и обозначается через vx(Y) или
р(У). Название объясняется тем, что если X расположено в евклидовом прост-
ранстве, то расслоение р^(У) можно представлять себе как составленное из касатель-
ных векторов к X в точках многообразия У, нормальных (перпендикулярных) к У.
Укажем на изоморфизм т (У) + р (У) = т (X) | у. В частности, если X = R", то т(У) +
+ р(У) = п.
Упражнения. 10. Выведите из последнего равенства, что нормальные рас-
слоения многообразия У, получающиеся при разных его вложениях в евклидовы
пространства, стабильно эквивалентны.
11. Покажите, что нормальное расслоение к «-мерной ориентированной поверх-
ности в (п + 1)-мерном пространстве тривиально. Выведите отсюда, что касательное
расслоение к такой поверхности (например, к произвольной сфере с ручками) ста-
бильно тривиально (т.е. стабильно эквивалентно тривиальному). Многообразие,
касательное расслоение к которому стабильно тривиально, называется стабильно
параллелизуемым. Очевидно, многообразие стабильно параллелизуемо тогда и толь-
ко тогда, когда его нормальное расслоение в евклидовом пространстве стабильно
тривиально. Можно доказать, что (это — не упражнение, а просто информация):
многообразие стабильно параллелизуемо тогда и только “тогда, когда оно параллели-
зуемо в дополнении к точке; многообразие стабильно параллелизуемо тогда и толь-
ко тогда, когда оно ориентируемо и погружается в евклидово пространство на еди-
ницу большей размерности; незамкнутое связное многообразие стабильно парал-
лелизуемо тогда и только тогда, когда оно параллелизуемо.
12. Пусть f — хопфовское расслоение над RP". Покажите, что
t(RP")® 1 ® .. ,®f =(п + l)f.
и + 1
Сформулируйте и докажите комплексный аналог этого предложения. (Заметьте,
что касательное расслоение к СР" обладает естественной комплексной структурой.)
3. Ассоциированные расслоения и характеристические классы.
А. Определение характеристических классов. Фиксируем один из трех типов век-
торных расслоений и будем называть расслоения этого типа просто расслоениями.
Мы скажем, что задан «/-мерный характеристический класс а «-мерных расслоений
(нашего типа) с коэффициентами в абелевой группе А, если всякому «-мерному
расслоению % с клеточной базой поставлен в соответствие «/-мерный класс а(£) ко-
гомологий базы с коэффициентами в А, и при этом если ! есть «-мерное расслоение
с базой Ви/: В -+В есть непрерывное отображение клеточного пространства В'в
В, то а(/*£) =/*«(?) (/* в левой части равенства обозначает переход к индуциро-
ванному расслоению, в правой части — индуцированный когомологический гомомор-
физм) .
Само слово ’’характеристический класс” не ново для нас: так мы называли в § 18
первое препятствие к построению сечения, и равенство типа а(/*$) = /*а(£) для
тех характеристических классов было выполнено. Однако непосредственно к вектор-
ным расслоениям такая конструкция характеристических классов неприменима,
потому что у этих расслоений слой стягиваем. (Напомним, что областью коэф-
фициентов для характеристических классов из § 18 служит первая нетривиальная
гомотопическая группа слоя.) Выход из положения состоит в том, чтобы применить
конструкцию § 18 не к векторному расслоению, а к какому-нибудь производному
расслоению, которое естественно строится по векторному. Запас таких производных
расслоений доставляет конструкция ассоциирования.
172
ГЛ. 2. ГОМОЛОГИИ
В. Определение ассоциированного расслоения. Для читателя, который усвоил ска-
занное в п. 1Е, определение ассоциированного расслоения должно показаться
самоочевидным. Берется векторное расслоение, заданное координатным образом —
посредством покрытия {(//} базы и набора отображений Uj A U/-+G, где G =
= GL (и, R), GL+(n, R) или GL (n, С), и произвольное пространство F, в котором
действует групца G. После этого мы строим расслоение с той же базой и слоем F по
схеме п. 1Е: пространство этого расслоения мы склеиваем из произведений Ц-Х F
посредством отождествлений
[(у, f) G Ui X F] ~ [(у, ^О)/) е Uj X л
при любых j, j.y^Ui^UjVif^F. Однако столь общая конструкция нам не пона-
добится, мы приведем два совершенно прозрачных примера и в дальнейшем почти
всегда будем ими ограничиваться.
Пусть % = (Е, В, К" р) — векторное расслоение. 1°. Положим Е' = Е - В, где В
вложено в Е в качестве ’’нулевого сечения” — объединение нулей слоев. Расслоение
£' = (Е”, В, К"- 0, р'), где р’ = р |₽», ассоциировано с £ при F = К" - 0. 2°. Фикси-
руем к, 1 СЕ Си, и обозначим через Ек совокупность Е-реперов в слоях расслоения £.
Более формально:
Ей = {(Xi,.... хк~) G.E X ... X Е | p(xt) = .. . = p(xk), Xi линейно независимы}.
(В случае Е = и это пространство упоминалось в начале параграфа.) Очевидно, %к =
= (Ек, В, Rk, рк), где Rk — пространство Е-реперов в К", и pk(xi,. .. ,хк) = p(xj)
[=...= р(хп) ] есть локально тривиальное расслоение, ассоциированное с £ (F =
= Rk). Заметим, что = %'.
Укажем на маленький дефект вышеприведенных конструкций (скорее, эстети-
ческий, чем технический) : в качестве слоев фигурируют некомпактные пространст-
ва, которые хотелось бы заменить гомотопически эквивалентными им классически-
ми компактными пространствам: сферами и многообразиями Штифеля. Это можно
сделать, воспользовавшись следующей почти очевидной леммой.
Лемма. Если вещественное или комплексное векторное расслоение имеет
клеточную базу, то в его слоях можно ввести непрерывно зависящую от слоя евкли-
дову или эрмитову структуру.
Доказательство. Совокупность всех евклидовых или эрмитовых структур
в слоях векторного расслоения с базой В представляет собой локально тривиальное
расслоение с базой В, слоем которого является совокупность евклидовых или эрми-
товых структур в вещественном или комплексном линейном пространстве. Наше
утверждение состоит в том, что это расслоение обладает сечением. Но совокупность
всех евклидовых структур в вещественном линейном пространстве есть выпуклое
подмножество пространства всех билинейных форм на этом пространстве, и потому
эта совокупность стягиваема. По сходным причинам стягиваема совокупность всех
эрмитовых структур в комплексном линейном пространстве. Таким обра-
зом, мы должны построить расслоение с клеточной базой и стягиваемым слоем,
а это можно сделать, потому что все препятствия к построению такого сечения три-
виальны.
Кстати: тривиальны не только препятствия, но и различающие, и поэтому указан-
ное сечение гомотопически единственно. Это позволяет нам без боязни считать, что
в рассматриваемых векторных расслоениях имеется евклидова или эрмитова струк-
тура, и вместо ненулевых векторов и произвольных реперов говорить об единичных
векторах и ортонормированных реперах. В частности, расслоение превращается
при этом в ’’сферическое” расслоение, слои которого - сферы.
§ 19. ВЕКТОРНЫЕ РАССЛОЕНИЯ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
173
С. Классические характеристические классы векторных расслоений. Пусть I- —
ориентированное n-мерное векторное расслоение с базой В. Рассмотрим сферическое
расслоение % . Легко понять, что ориентируемость расслоения ! влечет за собой
простоту расслоения £' (читатель, который пожелает вникнуть в этот предмет, без
труда убедится в том, что связность структурной группы всегда влечет за собой
простоту косого произведения), а выбор определенной его ориентации доставляет
определенный изоморфизм между (л — 1)-ми гомотопическими группами слоев
расслоения £ и группой Z. Благодаря этому определено первое препятствие к
построению селения в расслоении %и оно является элементом группы Нп(В\ Z).
Этот элемент — характеристический класс расслоения ! — называется классом Эйлера
расслоения % и обозначается через e(g).
Лемма. Пусть 1 < к < п. Тогда:
(i) 1Г/(К(л, Л)) = 0 при Кп - к-,
{Z, если к = 1 или п — к четно,
О в остальных случаях.
Доказательство. Случай п = 2 тривиален (К (2,1) = S *). Предположим,
что для V(n — 1, к) лемма доказана и рассмотрим расслоение
z F(n — l,fc— 1) „
V(n, к) —---------> S " ~1
(проекция ставит в соответствие реперу его первый вектор). Нам нужен фрагмент
его гомотопической последовательности
iti+1(Sn~ *) -> п{(У(п - 1, к - 1)) - я,(К(л, к)) - itt(Sn-*).
Если i < п - 2, то крайние члены - нули, средняя стрелка — изоморфизм, и мы
получаем нужное для V(n, к) при к > 2. Случай К(л, 1) очевиден (V(n, 1) =5"-1),
остается случай К(л, 2). В этом случае наш фрагмент с i = п - к имеет вид:
л„_1(5п-1)^л„_2(5п-2)^1гп-2(И(л,2))^л„_2(5"-1).
Z Z о
Наше утверждение в точности означает, что первая стрелка Z -> Z тривиальна при чет-
ном п и является умножением на 2 при нечетном п. Докажем этот факт. Прежде все-
го, само расслоение есть T^S "-1 где Тцу обозначает пространство единич-
ных касательных векторов. Согласно п. 7 § 9 (см., в особенности, рис. 59), нужно
поднять в пространство расслоения сфероид, в нашем случае тождественный (обра-
зующую группы ir„_i(5 ”-1)), разорвав его в одной точке, и взять получающееся в
этой точке отображение Sn~2 -+ слой = Sn~2. Другими словами, на S”-1 нужно
построить векторное поле с одной особой точкой; векторы этого поля в точках ма-
ленькой сферы, окружающей особую точку, и зададут наше отображение S "~2 ->
-> Sn~2. На Sn~l легко построить векторное поле с двумя особенностями: взять
стрелки, указывающие на север. Если охватить особые точки (полюса) общей сфе-
рой, то на этой сфере поле будет устроено, как показано на рис. 83. Соответствующее
отображение S "~2 -> S п~2 есть сумма двух сфероидов: тождественного и антипо-
дального. Степень такого отображения равна 1 + (—I)"-1, что нам и требуется.
Первое препятствие к построению сечения в расслоении £ к принимает значения в
7/"_fc+1(B; ir„_fc(K(n, Л)) = Z или Z2). Это препятствие обычно приводят по моду-
лю 2 и полученный класс w7-(^) G Н'(В‘, Z2), j = п - к + 1, называют j-м классом
174
ГЛ. 2. ГОМОЛОГИИ
Штиффеля - Уитни расслоения %. Заметим, что ориентируемость расслоения £, нуж-
ная, как и при построении класса Эйлера, для простоты расслоения %к, делается из-
лишней после приведения коэффициентов по модулю 2, так что классы Штифеля —
Уитни определены для произвольных вещественных векторных расслоений (детали
мы оставляем читателю).
Для ориентированных «-мерных векторных расслоений имеет место равенство
wn(£) = Рзе(?), где Pi - приведение по модулю 2.
Рис. 83
я.-(СК(«, &)) “
Пусть теперь £ — комплексное «-мерное векторное расслоение.
Лемма. Пусть 1 <к<п. Тогда
I 0 при i < 2 (и - к) + 1,
I Z при i = 2 (и - к) + 1.
Доказательство этой леммы повторяет первую, тривиальную часть доказательства
предыдущей леммы.
Ввиду этой леммы, первое препятствие к построению сечения в расслоении %к
есть некоторый класс <?,(£) G Н2\В; Z), / = п - к + 1. Этот класс называется j-м
классом Черна (= Чженя) расслоения £.
Наконец, если £ снова есть «-мерное вещественное векторное расслоение, то пола-
гают (-1)'с2/(С£) = ру(£) е я4'(В; Z) и называют классы р,(£) классами Понтря-
гина расслоения £. (Знак (—I)7 имеет чисто историческое происхождение; причина,
по которой мы ограничиваемся четными классами Черна, будет отчасти объяснена
ниже). Классы Понтрягина можно определить и непосредственно: нужно образо-
вать расслоение, ассоциированное с %, слоем которого является пространство
систем из и — 2/ + 2 векторов в слоях, имеющих ранг > и - 2/, и взять первое
препятствие к построению сечения. Это и есть /-й класс Понтрягина (читателю
вряд ли стоит возиться с доказательством этого факта).
Упражнения. 13. Покажите, что vVj(£) = O тогда и только тогда, когда рас-
слоение £ ориентируемо.
14. Покажите, что если £ есть «-мерное комплексное расслоение, то e(R£) =
= с„(£), w2/(R£) = p2cf(%) и w2/+1(R£) = 0.
4. Характеристические классы и классифицирующие пространства.
А. Классифицирующие пространства. В п. 1А мы упоминали тавтологические
расслоения над грассманианами; сейчас зти расслоения выйдут у нас на передо-
вые позиции.
Излагаемая ниже теория имеет три совершенно параллельных варианта для трех
типов векторных расслоений. Мы начнем с вещественного случая, а для двух других
типов ограничимся перечислением формулировок в конце пункта.
Напомним, что пространство тавтологического расслоения (которое мы обозна-
чим через 1? или т;п) над многообразием Грассмана G(N, ri) есть совокупность пар
(я,х), где я G G(N, ri) есть «-мерное подпространство пространства RN их G я CR7^
проекция определяется формулой (я, х) *->• я.
§19. ВЕКТОРНЫЕ РАССЛОЕНИЯ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
175
Теорема. Пусть X — конечное клеточное пространство размерности т, и пусть
7V> т. Тогда-.
(i) для любого п-мерного векторного расслоения £ над X существует непрерывное
отображение f: X -> G(N, п), такое, что £ ~/*1? (~ обозначает эквивалентность
расслоении);
(ii) такое отображение f определено однозначно с точностью до гомотопии, т.е.
ecauf*ri~f2ri, то f\ ~f2 (во втором случае ~ обозначает гомотопность).
Замечания. 1°. Эта теорема показывает, что множество классов эквивалент-
ных «-мерных вещественных векторных расслоений над X находится во взаимно
однозначном соответствии с множеством тг(Х, G(N, «)).
2°. Части (i) и (ii) теоремы покрываются следующим относительным вариантом
часта (i):
(i’) Пусть £ - векторное расслоение над X, Y - клеточное подпространство прост-
ранства X и h: Y -* G(N, п) — такое отображение, что |у. Тогда существует
отображение f: X-*G(N,n), такое, что и f\y = h.
(Чтобы вывести из (if) утверждения (i) и (ii), достаточно применить (i'), соот-
ветственно, к парам (X, ф) и (X X 1, (X X 0) U (X X 1)).)
3°. Условие W > m можно расшифровать в утверждениях (i) и (ii) как N> 2m, а
в утверждении (i’) — как TV> 2m + 1; впрочем, его можно безболезненно заменить
условием N = °°. Дело в том, что Zc-й остов (стандартного клеточного разбиения)
пространства G(N, п) при 7V> п + к не зависит от N, и потому теорема о клеточной
аппроксимации показывает, что -л(Х, G(N, п)) не зависит от N при JV> п + m + 1.
4°. Ссылка на теорему о клеточной аппроксимации в предыдущем замечании —
это единственное место, в котором используется клеточность пары (X, У). Ниже мы
доказываем утверждение (if) в предположении, что X — компактное нормальное
пространство и У — его замкнутое подмножество. Топологические условия на пару
(X, У) нужны для справедливости основной леммы, доказывать которую мы все
равно не будем.
Назовем линейным функционалом на пространстве Е векторного расслоения £
непрерывную функцию Е -> R, которая на каждом слое является линейным функ-
ционалом.
Лемма. Всякий линейный функционал на пространстве расслоения % |у про-
должается до линейного функционала на пространстве расслоения %.
5°. Приведем эквивалентную форму утверждения (i’), в которой его легко
доказать.
(i") Пусть i^i,..., \pN - линейные функционалы на пространстве расслоения
$ |у, такие, что для каждой точки у & У сужения функционалов <pi,, <pN на
слой расслоения % над точкой у линейно порождают пространство линейных функ-
ционалов на этом слое. Тогда функционалы .. ., \pN можно продолжить до
линейных функционалов . .., <pN на пространстве расслоения %, которые облада-
ют тем же свойством в любой точке х G X. (Как и прежде, считается, что N > dim X;
можно считать, что N = °°, но тогда нужно предположить, что все функционалы <pt и
все функционалы <pf, начиная с некоторого, тождественно равны 0.)
Чтобы доказать эквивалентность (/) <==*(1"), достаточно заметить, что функцио-
налы tfi,. .., <pN составляют отображение пространства Е расслоения £ в при
котором каждый слой отображается на некоторое «-мерное подпространство прост-
ранства R7V. Таким образом, каждому слою, т.е. каждой точке базы, отвечает эле-
мент грассманиана G(N, «), и ясно, что получившееся отображение обладает тем
свойством, что
176
ГЛ. 2. ГОМОЛОГИИ
Доказательство утверждения (i”) с N = °°. Начнем, для ясности,
со случая У = ф. Возьмем точку х С Хм выберем на слое надх линейно независимые
функционалы , <рп. В силу леммы, их можно продолжить до линейных функ-
ционалов (^1,.. ., ipn на всем Е, и в некоторой окрестности Ux точки х они будут
линейно независимы. Проделав это во всех точках х G X, мы получим, среди
прочего, открытое покрытие {Ux } пространства X, из которого, ввиду компакт-
ности X, можно выбрать конечное подпокрытие {UXj}. Функционалы <р{-, соответ-
ствующие точкам X,, и составляют нужную систему (мы дополняем ее нулями до бес-
конечной системы). В случае непустого У требуется следующая модификация конст-
рукции. Во-первых, ненулевые функционалы, заданные над У, мы считаем, пользуясь
леммой, заданными над всем X. К полученной системе функционалов мы добавляем
систему функционалов, построенную в первой части доказательства, только каждый
из этих дополнительных функционалов мы умножаем на непрерывную функцию
f: X-* R, равную 0 на У и отличную от нуля вне У. Доказательство закончено.
В вещественном ориентированном и комплексном случаях ситуация в точности
та же, только роль пространства G(N, п) принимают на себя пространства G+(N, п) и
CG(N, ri), а роль расслоения 17 играют аналогичные ориентированное расслоение 17+
над G+(N, п) и комплексное расслоение г?с над CG(N, п).
(В) Характеристические классы и когомологии классифицирующих пространств.
Теорема. Группа q-мерных характеристических классов п-мерных веществен-
ных (п-мерных ориентированных, п-мерных комплексных) векторных расслоений с
коэффициентами в А изоморфна группе Hq(G(N, п);А) [группе Hq(G+(N, п); А),
группеНq(CG(N, п),А)], где N>n.
Доказательство в трех случаях одинаково, мы ограничиваемся вещест-
венным случаем. Заданный характеристический класс может быть вычислен для
расслоения 17; при этом получается элемент группы Hq(G(N, л); А). Нужно дока-
зать, что: (i) значение ненулевого характеристического класса на 17 не может быть
нулевым; (ii) всякий элемент группы Hq(G(N, л); А) является значением на ту не-
которого характеристического класса.
(i) Если характеристический класс принимает нулевое значение на 17, то он прини-
мает нулевое значение на произвольном расслоении с конечной клеточной базой,
поскольку такое расслоение всегда представляется в виде /*17. Если наш характе-
ристический класс принимает ненулевое значение a G Hq (У; А) для некоторого рас-
слоения £ с произвольной клеточной базой X, то мы находим конечное клеточное
пространство У СХ, такое, что при гомоморфизме включения Я4 (У; A) ~>Hq(Y; А)
класс а переходит не в 0. Тогда наш характеристический класс принимает ненулевое
значение на расслоении £ I у, что противоречит доказанному.
(ii) Пусть у С Hq(G(N, л); А). Значение характеристического класса на расслое-
нии /*17 с базой X мы определяем как f*y е ЯЧ(АГ; А), этим класс определен для
всех расслоений с конечными клеточными базами. Если £ — расслоение с бесконечной
клеточной базой X, то для любого конечного подпространства У СХ определено зна-
чение ay С Hq(Y\ А) характеристического класса на расслоении £ |у, и ясно, что
существует единственный класс a G Hq(X\ А), переходящий в oty при .гомомор-
физме, индуцированном каждым включением У -> X', это и есть значение характе-
ристического класса на £.
Теорема доказана.
С. Полнота системы классов Эйлера, Штифеля — Уитни, Черна и Понтрягина.
Т е о р е м a. (i) Всякий характеристический класс с коэффициентами в Z2 ве-
щественных п-мерных векторных расслоений есть полином от классов Штифеля —
§ 19. ВЕКТОРНЫЕ РАССЛОЕНИЯ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
177
Уитни wt,..., w„, причем разным полиномам отвечают разные характеристические
классы.
(ii) Всякий характеристический класс с коэффициентами в Z комплексных п-мер-
ных векторных расслоений есть полином от классов Черна ci,... ,с„, причем раз-
ным полиномам отвечают разные характеристические классы.
(iii) Всякий характеристический класс с коэффициентами в Q или R или С ве-
щественных п-мерных векторных расслоений есть полином от (образов при гомомор-
физме, определяемом включением Z в область коэффициентов) классов Понтря-
гина Pi, Pi,... >Р[п/2]> причем разным полиномам отвечают разные характерис-
тические классы.
(iv) Всякий характеристический класс с коэффициентами в Q или R или С ве-
щественных ориентированных п-мерных векторных расслоений есть полином от
(образов) классов Понтрягина р1г Рг,..., Р[п/2 j и, при четном п, класса Эйлера е,
причем разным полиномам отвечают разные характеристические классы.
Доказательство (каждой части) этой теоремы состоит из двух частей. Во-пер-
вых, необходимо убедиться в том, что соответствующая группаHq(G(N, п), G+(N, п)
или CG(N,n); Z2, Z, Q, R или С) имеет в точности такие размеры, как группа
полиномов указанного вида, имеющих степень q. Этот результат легко извлечь из
вычислений когомологий грассманианов, проделанных в п. 7 § 13. Во-вторых, не-
обходимо установить, что никакой из этих полиномов не является тождествен-
ным нулем как характеристический класс. (В неполевом случае (ii) требуется
чуть больше — уточнение оставляется читателю.) Для этого требуется достаточный
запас явно вычисленных характеристических классов. Такого запаса у нас пока
нет, и мы откладываем вторую часть доказательства до следующего пункта.
D. Обобщения. Аналоги грассманианов и расслоений Г), именуемые классифи-
цирующими пространствами и универсальными расслоениями, имеются для рас-
слоений Стинрода с произвольной структурной группой G. Именно, справедливо
следующее утверждение.
Теорема. Пусть EG - стягиваемое пространство, на котором свободно дей-
ствует группа G, и пусть факторпространство EG/G = BG клеточно. Тогда рас-
слоение EG -* BG универсально в том смысле, что для любого конечного клеточ-
ного пространства X всякое расслоение Стинрода над X со структурной группой
G и произвольным стандартным слоем F индуцируется посредством гомотопи-
чески единственного отображения X -* BG расслоением со слоем F, ассоциирован-
ным с расслоением EG -> BG.
Известны явные конструкции пространств EG и BG (см. Рохлин — Фукс, § 4.4).
При этом пространство BG определяется группой G однозначно с точностью до
гомотопического типа. В полной аналогии с теоремой п. В доказывается
Теорема. Характеристические классы размерности q с коэффициентами в А
расслоений со структурной группой G находятся во взаимно однозначном соот-
ветствии с Hq(BG\ А).
5. Важнейшие свойства классов Штифеля — Уитни, Эйлера, Черна и Понтрягина.
А. Свойства классов Штифеля — Уитни.
Теорема. Классы wt обладают следующими свойствами.
(i) Если f - хопфовское расслоение над В.Рп, то 0 =#Wi(f) G Я1 (RP"; Z2) s Z2
« W;(f) = 0 при i> 1.
(ii) Для любых векторных расслоений с одной (клеточной) базой %, ц
Wi(^S>T))= S wa(^)w/3(7?)
ос + 0= i
(мы считаем, что для любого расслоения w0 = 1).
178
ГЛ. 2. ГОМОЛОГИИ
Доказательство части (i) мы оставляем читателю в виде упражнения. Часть (ii)
удобно доказывать в эквивалентной форме
(ii') wf($Xi?)= S ™«(£)Х w/3(i?),
a + (3 = i
где £, л — расслоения с клеточными (возможно, не одинаковыми базами X, Y, I- Xi) —
прямое произведение этих расслоений (с базой XX У), X в правой части обозначает
когомологическое Х-умножение (см. § 16). Вывод (ii) из (ii') состоит в рассмотре-
нии случая X = Y и применении диагонального отображения. Вывод (ii’) из (ii)
основан на равенстве g X л = (p^g) ® (РуЛ) (гДе Рх> Ру _ проекции произведения
X X Y на сомножители) и аналогичной формуле для когомологий. Доказательство
формулы (ii’) основано на двух леммах (которые являются частными случаями ут-
верждений (ii) и (ii')).
Лемма 1. Классы Штифеля - Уитни стабильно эквивалентных расслоений оди-
наковы.
Действительно, сечение расслоения %к очевидным образом достраивается до сече-
ния расслоения (£ ® л)„ + к .
Лемма 2. Если dim ? = dim X = р и dim i) = dim Y = q, то
Wp + q ($ X л)= wp(?) X wq(if).
Доказательство. Классы Штифеля, участвующие в этом равенстве, — это
препятствия к построению одного ненулевого сечения (приведенные по модулю 2).
Зафиксируем не обращающиеся в 0 сечения <р и ф расслоений £ и л над Агр-1 и У4-1
и продолжим их до сечений и ф над X и У, которым разрешено иметь нули общего
положения. Обозначим через а(е), b(f) н c(g) вычет по модулю 2 числа нулей сече-
ния <р, ф и q> X ф в клетке е, f и g (размерности р, q и р + q) пространства X, У и
X X У. С одной стороны, ясно, что е*-*а(е) ,f*+b(f) vig^c(g) — коциклы, представ-
ляющие когомологическиеклассы wp(g), н’^(л) и wp+Q(g X 17). С другой стороны,
очевидно, с(е X /) = a(e)b(f). Лемма доказана.
Теперь докажем формулу (ii’). Возьмем любые а, |3иа + ^ = 1'и рассмотрим вклю-
чения ja : Ха -> X и кр: Y& -* У и сужения ? |ха, Л |уд. Очевидно, расслоение ? 1ха
стабильно эквивалентно a-мерному расслоению ?0 (°но имеет dim ? — а линейно
независимых сечений), расслоение л1у£ стабильно эквивалентно /3-мерному расслое-
нию т)о и расслоение (£ X л)1(Ха х у^ стабильно эквивалентно i-мерному расслоению
?0 X Ло- Применяя леммы 1 и 2, получаем цепочку равенств:
(Ja X X л) = и'/((?|ха)Х (л1уд)) = и^,(?о X Ло) = и'а(?о)Х w^(7j0) =
= wa (?lxOi) X wp (л IУД) = / * wa(?) X крwp(i)) = (/а X кр)*(wa (?) X wp (7?)) =
= (/«Х^( S M&XwpW))
(последнее равенство вытекает из того, что все слагаемые в последней сумме, кроме
одного, аннулируются гомоморфизмом (/а X кр)*). Таким образом, разность левой
и правой части равенства (ii') принадлежит ядру каждого гомоморфизма (j’a X кр) *.
Остается заметить, что пересечение этих ядер равно 0 (гомоморфизмы (/а X кр)*
составляют вложение Н1 (X X У; Z2) = ®а + д=1-(Я“(Аг; Zj) ® Я^(У; Z2)) С
С ea+p=l(Ha(Xa-,Z2)^ H\yP-Z2))).
Удобно записать формулу (ii) в виде w(? ® л) = н,(?)н’(л), гден1 есть формаль-
ная сумма 1 + и> t + w2 + ...
§ 19. ВЕКТОРНЫЕ РАССЛОЕНИЯ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
179
П ример. Найдем W;(f X . .. X f), где f X ... X f — произведениеп экземпляров
расслоения Хопфа над RPN, А > и. Напомним, что H*(RPN, Z2) = Z2 [x]/xJV+1,
dimx = 1. Согласно (ii') и (i).
X . . .X £)=w(f)X .. .X w(f)=(l + x)X ...X (1 + x)
и, следовательно, wf(f X . .. X f) = et (p* x,... ,p*x), где есть элементарный сим-
метрический полином, р{: RPN X ... X RPN ->RP7V есть i-я проекция.
Следствие. Никакой полином от классов Штифеля — Уитни не есть тождест-
венно нулевой характеристический класс.
В самом деле, этот полином нетривиален уже на произведении f X ... X f с доста-
точно больным числом сомножителей, ибо никакой полином от элементарных
симметрических полиномов не есть 0.
Напомним, что последнее утверждение необходимо для доказательства основной
теоремы п. 4С.
Замечание. Свойства классов Штифеля — Утини, заключенные в предыдущей
теореме, часто кладутся в основу аксиоматического определения классов Штифеля —
Уитни (см. Милнор — Сташефф, ’’Характеристические классы”).
Формулы, выражающие классы Штифеля - Уитни расслоений £ ® ту, Sfcg и Afcg
через классы Штифеля — Уитни расслоений ? и 17 и размерность расслоений £ и V,
существуют, но более сложны. Вот некоторые из этих формул (мы полагаем
dim £ = п, dim т? = т):
wi (£ ® Ч) = mwi (£) + nwx (ту),
w2(t ® ’?) = ^2w2(^) + (тп - Ои^^н’Др) +
, т(т -1) „ п(п - 1)
+ « w2(t?) +---------Wi($)2 +--------Wi(t?)2,
w,(S2e) =(« + l)Wl(0,
(n - 1) (n + 2) ,
w2(S2?) =(h + 2)w2($)+---------------w,(?)2,
Wi(A20 =(«-l)wi($),
, (n — 1) («— 2) _
w2(A2?) = (и-2>2(£) +----------------w,©2,
Общие формулы для w,(g ® 77), wf(Sfcg),. wt(A.k£) можно получить так. Введем
формальные переменные Xj,..., х„, .. ., ут- составим i-й элементарный сим-
метрический полином от тп переменных xs + yt и представим его как полином
от элементарных симметрических полиномов от х и у:
£i(xs +yt) = Р, (eu (x), ev(y)).
Тогда
w,-(? ®t?) =Pj(wu (?), (17)).
Далее, составим f-й элементарный симметрический полином от С^+г переменных
x<t + ... + Xjr , .. . < ir , и выразим его через элементарные симметрические
180
ГЛ. 2. ГОМОЛОГИИ
полиномы от х:
. +xir | й <... < ir}) = Pf(es(x)).
Тогда
^(8ге)=р,(^(0).
Аналогично
^•({xf> +...+x,r|i1 . ,<jr}) = P/(eJ(x))>
^)=«)).
Доказательство всех этих формул лежит за пределами нашего курса. (План доказа-
тельства таков. Для расслоений, расщепляющихся в сумму одномерных расслоений,
все эти формулы без труда выводятся из ’’формул умножения” (часть (ii) основной
теоремы этого пункта), а переход к общему случаю осуществляется на основании
общего принципа расщепления, который, неформально говоря, заключается в том,
что соотношения между характеристическими классами, справедливые для расслое-
ний, расщепляющихся в сумму одномерных расслоений, справедливы для любых рас-
слоений. Формальную основу этого принципа составляет теорема Бореля, утверждаю-
щая, что естественное отображение RP°° X ... X RP°° -> G(°°, и) индуцирует моно-
п
морфизм в когомологиях mod 2.)
В. Свойства классов Эйлера, Черна и Понтрягина. Для класса Эйлера имеет место
формула умножения е(? ® 17) = e(£)e(ri).
На классы Черна дословно переносится все, сказанное для классов Штифеля —
Уитни; в частности, у хопфовского расслоения fc надСР" класс ci есть стандартная
образующая группы Я2 (СР”; Z), а остальные классы Черна равны 0; имеет место
формула умножения
cf($®i?)= S са(Оср(17)
a + fi-i
и формулы для классов Черна тензорных произведений, симметрических и внешних
степеней, дословно повторяющиеся соответствующие формулы для классов Шти-
феля — Уитни. Классы Черна, как и классы Штифеля — Уитни, одинаковы у стабиль-
но эквивалентных расслоений.
Упражнения. 15. Докажите, что с/( £) = (-р^сД?). Выведите из этого, что
для любого вещественного векторного расслоения ? и любого нечетного i имеет
место равенство 2 с,-(С?) = 0. [Ср. комментарий к определению классов Пон-
трягина.]
16. Определим полином Qr от г переменных формулой
Nr = Qr{el,. ...,ег),
где et - элементарные симметрические полиномы, Nr - суммы r-х степеней.
Положим
сМ0= Л Qr(.aG),... ,сг^У)ен2\~ Q).
г!
Характеристический класс (размерно неоднородный) с коэффициентами в Q
ch = ch0 + cht + ch2 + ...
называется характером Черна. (Заметим, что cho(g) G Я°(-; Q) есть просто размер-
ность расслоения £.) Докажите, что
ch(£® 17) = ch? ch 17.
§19. ВЕКТОРНЫЕ РАССЛОЕНИЯ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
181
Для классов Понтрягина формулы умножения и все прочие формулы выводятся
из соответствующих формул для классов Черна и имеют место ”по модулю 2-круче-
ния”. Например, •
2 [р,(? ® 1?) - + г Ра (?)Р(з О?)] = 0.
Упражнение. 17. Докажите, что у стабильно эквивалентных расслоений
классы Понтрягина одинаковы.
С. В заключение мы приведем две формулы при помощи которых классы Штифе-
ля — Уитни и Черна выражаются через класс Эйлера. Пусть £ — вещественное вектор-
ное расслоение размерности п над клеточным пространством X и f — хопфовское
расслоение над RP”. Образуем расслоение £ ® f над X X RP“ (точнее говоря, это —
тензорное произведение расслоений над X X RP°°, индуцируемых расслоениями £ и f
посредством проекций на сомножители). Тогда
p2e(£®f) = S (w,-(£) X х"-') ^//"(Х X RP“; Z2),
i= 0
где x G H1 (RP°°; Z2) - образующая. Аналогично, если £ - комплексное векторное
расслоение размерности п над X и fc — (комплексное) расслоение Хопфа над
СР“,то
е(£®Гс)=еи(£®Гс)= S (с,(£)Хх”-')еЯ2”(ХХСР“; Z),
1 = 0
где х &Н2 (СР°° ;Z) — образующая.
Эти формулы могут рассматриваться как определения классов Штифеля — Уитни
и Черна через класс Эйлера. Кстати, их доказательство заключается в проверке
аксиом (см. замечание в п. А).
6. Характеристические классы в топологии гладких многообразий. Этого необъят-
ного предмета мы можем лишь коснуться.
А. Геометрическая интерпретация первого препятствия. Пусть (£, В, F, р) - гомо-
топически простое локально тривиальное расслоение, в котором Ей В — гладкие мно-
гообразия, причем многообразие В замкнуто, и-мерно и ориентируемо, и р - глад-
кое отображение, имеющее в каждой точке многообразия Е якобневу матрицу
максимального ранга (субмерсия). Предположим, что ir0(F) = . .. = яА._2(/г) = 0 и
7rfe_j(F)=7r. Тогда первое препятствие к построению сечения в нашем расслоении
лежит в Нк(В'. я). Предположим, далее, что нам удалось построить сечение над
В — X, где X — подмногообразие многообразия В (возможно, с особенностями ко-
размерности > 2) размерности п - к (простые соображения типа приведения в
общее положение показывают, что сделать это всегда можно) или объединение
нескольких таких многообразий, пересекающихся трансверсально: Ar=UArl-. Возь-
мем неособую точку одного из этих многообразий X, (мы считаем их связными)
и рассмотрим маленькую (к —1)-мерную сферу, охватывающую многообразие
вблизи этой точки. Поскольку над этой сферой сечение имеется, а расслоение
вблизи рассматриваемой точки считается тривиализованным, мы получаем отобра-
жение Sk~1 -»• (слой), определяющее (ввиду простоты расслоения и слоя) неко-
торый элемент а,- группы ял_1(7*)=я.
Утверждение: класс G/7„_fe(B; я) соответствует при изоморфизме Пуан-
каре первому препятствию к распространению сечения в нашем расслоении. До-
казательство оставляется читателю. (Указание: триангулируйте многообразие В
таким образом, чтобы многообразие X не пересекалось с симплексами размер-
182
ГЛ. 2. ГОМОЛОГИИ
но ста < к, а с каждым симплексом размерности к пересекалось бы трансверсаль-
но, и при этом не более, чем в одной точке.)
В. Дифференциально-топологические интерпретации класса Эйлера.
18. Пусть % = (Е, В, R", р) — гладкое векторное расслоение (т.е. векторное рас-
слоение, у которого Е и В - гладкие многообразия, р — субмерсия и векторные опера-
ции в Е гладки). Предположим, что В есть замкнутое ориентированное многообразие.
Пусть s: В -+Е — сечение расслоения {, находящееся в общем положении с нулевым
сечением. Покажите, что пересечение В С\$(В) (мы считаем В вложенным в £ в качест-
ве образа нулевого сечения) представляет гомологический класс многообразия В,
соответствующий при изоморфизме Пуанкаре классу Эйлера е(£) расслоения £.
19. Пусть Y — замкнутое ориентированное подмногообразие гладкого многообра-
зия X, и пусть Vx(Y) — соответствующее нормальное расслоение. Докажите формулу
D[e(px(YJ)] “/’[Л.
где D - изоморфизм Пуанкаре (в У), i: У-»-X - включение, [У] - гомологический
класс многообразия X, представляемый У. Следствие: если [У] = 0, то e(vx(Y)) = 0;
например, эйлеров класс нормального расслоения многообразия У, вложенного в
евклидово пространство или в сферу, равен 0.
20. Последнее утверждение неверно для погружений. Покажите, в частности, что
если/есть погружение замкнутого ориентированного многообразия Xчетной размер-
ности п в R2” с трансверсальными самопересечениями, то алгебраическое число точек
самопересечения (определение знака, соответствующего точке трансверсального
самопересечения, придумайте сами) равно половине ’’нормального числа Эйлера”,
т.е. значения класса Эйлера нормального расслоения на фундаментальном гомологи-
ческом классе многообразия X.
21. Покажите, что ’’касательное число Эйлера” замкнутого ориентированного мно-
гообразия, т.е. значение класса Эйлера касательного расслоения на фундаментальном
классе, равно эйлеровой характеристике многообразия (для доказательства полезно
вспомнить результаты п. 5 § 17). Выведите отсюда теорему Эйлера: назамкну-
том многообразии тогда и только тогда существует касательное векторное поле,
не обращающееся в нуль, когда его эйлерова характеристика равна нулю. (В одну
сторону эта теорема доказывалась в цитированном п.5 § 17; там же читатель найдет
указания, как получить эту теорему в неориентированном случае.) Докажите вариант
этой теоремы: на замкнутом многообразии тогда и только тогда существует непре-
рывное поле касательных прямых, когда его эйлерова характеристика равна
нулю.
С. Дифференциально-топологические интерпретации классов Штифеля - Уитни.
В этом пункте речь идет только о когомологиях и гомологиях mod 2 и соответствую-
щим образом понимается изоморфизм Пуанкаре D.
Классы Штифеля — Уитни касательного расслоения гладкого многообразия X на-
зываются классами Штифеля — Уитни этого многообразия и обозначаются через
(X) • [В аналогичном смысле говорят о классах Понтрягина р{(Х) гладкого много-
образия X и классах Черна ct(X) комплексного многообразия X.] Поскольку нор-
мальное расслоение гладкого многообразия в евклидовом пространстве не зависит,
с точностью до стабильной эквивалентности, от способа вложения многообразия
(см. упражнение 10), можно говорить о ’’нормальных классах Штифеля — Уитни”
многообразия X — классах Штифеля — Уитни нормального расслоения при каком-
нибудь вложении (или погружении - зто безразлично) многообразия X в евклидо-
во пространство; эти классы обозначаются через wt(X). Из формулы умножения
и того факта, что сумма касательного и нормального расслоения тривиальна,
§ 19. ВЕКТОРНЫЕ РАССЛОЕНИЯ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
183
следует, что
S Wa(X)W^(X) ПРИ г > о,
а + Р = I
и, в частности, нормальные классы Штифеля — Уитни выражаются через касательные
и наоборот.
Упражнения. 22. Рассмотрим гладкое отображение общего положения «-мер-
ного многообразия X в R4, q < л; пусть Y СХ — совокупность точек, в которых это
отображение не является субмерсией (ранг якобиевой матрицы < q). Покажите,
что dim Y = q — 1 и что
Р-*[У] = w„_,+ i(X).
23. Рассмотрим гладкое отображение общего положения замкнутого «-мерного
многообразия X в R4, <? > «; пусть Y С X — совокупность точек, в которых это
отображение не является погружением (ранг якобиевой матрицы < и). Покажите,
что dim Y =2п — - 1 и что
Р-*[У] = w<?+1_„(X).
24. Если «-мерное многообразие X допускает погружение в R" + 4, то w,(X) =0
при i > q. Это утверждение в замкнутом случае следует, конечно, из упражнения 23,
но оно гораздо проще упражнения 23 и более естественно доказывать его прямо.
25. Если «-мерное замкнутое многообразие X допускает вложение в R" + <7, то
w{ (X) = 0 при i > q. В дополнение к предыдущему упражнению нужно воспользо-
ваться упражнением 19.
26. Докажите, что если 2к < п < 2fe + 1, то RP" не погружается в R2fc + 1 - 2 и
не вкладывается в R2 -1. Воспользуйтесь двумя предыдущими упражнениями,
формулами, связывающими касательные и нормальные классы Штифеля, упражне-
нием 12 и частью (i) теоремы п.5А; впрочем, нормальные классы Штифеля —
Уитни вещественных проективных пространств можно найти с помощью упраж-
нения 23.
27. Пусть X — триангулированное замкнутое многообразие. Обозначим через Q
/-мерную классическую цепь барицентрической триангуляции с коэффициентами
в Z2, равную сумме всех /-мерных симплексов барицентрического подразделения.
Покажите, что С/ есть цикл и что
О-1 [С,] = Wi(X).
Значения классов вида wti (X) ... wir(X) с it + ... + ir = и на фундаментальном
классе замкнутого «-мерного многообразия (это — вычеты по модулю 2) называют-
ся числами Штифеля - Уитни многообразия X. Обозначение: [X]. Например,
у двумерных многообразий имеются два числа Штифеля — Уитни: wn [X] и w2 [X].
Упражнение 28. Найти числа Штифеля — Уитни классических поверхностей.
Теорема. Если замкнутое многообразие является краем компактного много-
образия, то все его числа Штифеля - Уитни равны нулю.
Доказательство. Если Х = ЭУ и /: Х-> Y — включение, то тХ= (i*T У) ® 1
(нормальное расслоение к краю всегда тривиально!). Поэтому w;(X) = i*Wj(Y)
ГЛ. 2. ГОМОЛОГИИ
184
при любом /, и
<W/i(X) ... w,r(X), [Х]> =
= < (У)... М7Г(У)), [X] > = < (У) ... W/r(y), i. [X] > = О,
потому что »Ф[Х] = 0 (край компактного многообразия есть граница самого этого
многообразия в гомологическом смысле).
Эта теорема доставляет мощное необходимое условие для того, чтобы данное
замкнутое многообразие ограничивало компактное многообразие.
Упражнение 29. Покажите, что если п + 1 не есть степень двойки, то ни одно
из многообразий RPn, СРп не является краем компактного многообразия.
Самое поразительное заключается, однако, в том, что эта теорема доставляет и
достаточное условие для того, чтобы многообразие ограничивало (Р.Том, Филдсов-
ская медаль 1952 г.). Краткое изложение доказательства этой теоремы содержится
в главах 6 и 7 этой книги. Сейчас мы ограничимся замечанием, что числа Штифеля —
Уитни не являются линейно независимыми. Например, если X — замкнутое одномер-
ное многообразие (т.е. объединение нескольких окружностей), то wx [X] = 0;
читатель, сделавший упражнение 29, знает, что если X — замкнутое двумерное много-
образие, то w, j [X] = w2 [X]. Истина состоит в том, что линейно независимую систе-
му чисел Штифеля — Уитни замкнутых «-мерных многообразий составляют числа
...jr У которых / i + ... + jr = п, < ... <, и ни одно из чисел вида j 3 + 1
не является степенью двойки.
D. Дифференциально топологические интерпретации классов Понтрягина. Аналог
упражнения 22 для классов Понтрягина составляет следующее утверждение. Пусть
X — замкнутое ориентированное «-мерное многообразие и /: X -»• R"-2,+2 —
гладкое отображение общего положения. Обозначим через У совокупность точек
многообразия X, в которых ранг якобиана отображения f не превосходит п — 2q
(т.е. по крайней мере на 2 меньше наибольшего возможного значения). Тогда У есть
ориентированное (и — 4<?)-мерное многообразие (возможно, с особенностями), и
класс [У] G Я„_4<?(Х) соответствует при изоморфизме Пуанкаре классу
рч(Х) G Я4,(Х) Понтрягина (касательного расслоения) многообразия X.
Аналогичное описание существует и для нормальных классов Понтрягина (ср. упраж-
нение 23).
(Ориентированность и даже ориентируемость многообразия X здесь, в действи-
тельности, не нужна; однако, чтобы придать этому высказыванию смысл, необходи-
мо употребить вариант двойственности Пуанкаре, изложенный в п. 9D § 17.)
Если X — замкнутое ориентированное многообразие размерности 4 «г, то значение
класса р^ (X) ... р/г(Х), /1 + ... + jr =m, на фундаментальном гомологическом
классе многообразия X называется числом Понтрягина и обозначается через
Р/ [X]. (Нам удобно считать, что X не обязательно связно; фундаментальный
класс несвязного многообразия есть сумма фундаментальных классов его компо-
нент.) Если X есть край компактного ориентируемого многообразия, то все числа
Понтрягина равны 0 (этот факт доказывается точно так же, как аналогичное утверж-
дение для классов Штифеля — Уитнн). Имеется н теорема Тома, утверждаю-
щая, что если все числа Понтрягина замкнутого ориентированного многообразия
равны 0 (например, если его размерность не делится на 4), то объединение несколь-
ких экземпляров многообразия X (которые все берутся с одинаковой ориентацией)
§19. ВЕКТОРНЫЕ РАССЛОЕНИЯ И ХАРАКТЕРИСТИЧЕСКИЕ КЛАССЫ
185
является краем замкнутого ориентированного многообразия. Более того, всякий
набор целых чисел {р, / | Л + ... + jr = т} делается после умножение на некото-
рое (общее для всех чисел набора} целое положительное число набором чисел
Понтрягина некоторого замкнутого ориентированного многообразия. (В действи-
тельности, зта теорема на порядок проще теоремы Тома для классов Штифеля —
Уитни; читатель сможет в этом убедиться в главе 6.)
Полезным следствием теоремы Тома (и того факта, что если Y = Х2 U Х2 — сум-
ма двух замкнутых ориентированных 4 /п-мерных многообразий, то
для любых /1,..., / г с /1 + ... + jr =ni) является следующее утверждение.
Упражнение 30. Предположим, что всякому замкнутому ориентированному
«-мерному многообразию X поставлено в соответствие целое число а (X), обладаю-
щее следующими свойствами: (i) если X есть край компактного ориентированного
многообразия, то о(Х) = 0; (ii) o(Xi U Х2) = o(Xi) + о(Х2). Тогда
о(Х}= S
/, + ... + ir = "I*
где aj ^jr — некоторые рациональные числа, не зависящие от X. В частности,
о(Х) — 0, если п не делится на 4.
Это утверждение имеет единственное широко известное применение, но зато
какое! Обозначим через о(Х) сигнатуру формы ’’индекс пересечения” в 2 /п-мерных
гомологиях 4/п-мерного многообразия X. Теорема 15 из п. 9 В § 17 показывает, что
о удовлетворяет условию (i) из упражнения 30; условие (ii) для сигнатуры оче-
видно. Следовательно, сигнатура есть линейная комбинация с рациональными коэф-
фициентами чисел Понтрягина. В частности, с(Х) = api [X] при dimX = 4, о(Х) =
= bp2 [X] + epi 1 [X] при dim Х= 8 и т.д. Чтобы найти а, Ь, с,.... необходимо иметь
достаточный запас проделанных вычислений в конкретных примерах. Например,
H2m (CP2m) = Z. Матрица формы пересечений есть (1), значит, а (СР2'”) = 1.
Далее,
тЧСР2'") ® 1 = (2/п + l)fc
(комплексный вариант упражнения 12), значит,
Ст(СР2т) ® 1 = (2/п + 1)(Гс ® Fc)
(единица тоже комплексифицировалась!) и
(Ро -Р1 +Р2 - ... + (-1)"'Р/П)(СР2'") = [(1 + х)(1 -х)]2т + 1 =(1 -х2}2т+1,
где х € Н2 (СР2т) =Z - каноническая образующая (см. п. 5 В, в том числе упражне-
ние 17). Следовательно,
Pi(CP2m) =
C^m + jX2' ПРИ 1 < т>
0
при i > т.
186
ГЛ. 2. ГОМОЛОГИИ
В частности, рх (СР2) = Зх2, ру [СР2] = 3, и так как о(СР2) = 1, то для любого
четырехмерного многообразия X
с(Х) = |Р1[Х]. (*)
(В частности, первое число Понтрягина любого замкнутого ориентированного четы-
рехмерного многообразия делится на 3.) Далее, рц [СР4] = 25, р2 [СР4] = 10,
о(СР4) = 1. Добавим к этому, что
(Ро +Pi +р2)(СР2 ХСР2) = (р0 +Pi)(CP2)X (р0 +Р1)(СР2)
(формула умножения для классов Понтрягина вообще-то справедлива по модулю
2-кручения, но в когомологиях комплексных проективных пространств кручение
отсутствует), и, значит, Pi(CP2 X СР2) = (1 X Зх2) + (Зх2 X 1), р|(СР2 ХСР2) =
= 18(х2 Хх2), р2(СР2 ХСР2) =Pi(CP2) ХР1(СР2) = Зх2 ХЗх2, Р11[СР2 ХСР2] =
= 18, р2[СР2 X СР2] =9; кроме того, о(СР2 X СР2) = 1. (Упражнение 31. Сиг-
натура мультипликативна: а{Х X Y) = о(Х)о(У).) Таким образом, 1 = 10й + 25с,
1 = 9Ь + 18с, откуда b =7/45, с = -1/45. Итак, при dimX=8
7pi[X]-Pii[X]
45 v 7
(Следовательно, 7р2[X] — Pi i [X] делится на 45, и если у восьмимерного многооб-
разия ру = 0, то его сигнатура делится на 7.) Формулы (*), (**) составляют начало
бесконечной цепочки формул. Работа по ее написанию была проделана в 50-е годы
Хирцебрухом. Он вычислил числа Понтрягина многообразий вида CP2m‘ X . ..
... X СР2п,к (это нами, в сущности, проделано) и, воспользовавшись тем, что их
сигнатуры равны 1, нашел коэффициенты, с которыми числа Понтрягина входят
в формулы для сигнатур. Получившиеся формулы приведены в книге Хирцебруха
’’Топологические методы в алгебраической геометрии”.
Е. Проблемы инвариантности характеристических классов многообразий. Как
мы знаем, класс Эйлера многообразия можно вычислить, зная только числа Бетти
этого многообразия. Оказывается, что классы Штифеля—Уитни, хотя они не опре-
деляются группами гомологий этого многообразия, и даже его когомологическим
кольцом, все же являются гомотопическим инвариантом (т.е. отображение одного
замкнутого многообразия в другое, являющееся гомотопической эквивалентностью,
переводит классы Штифеля — Уитни в классы Штифеля — Уитни). Давно известно,
что для классов Понтрягина подобная теорема гомотопической инвариантности
отсутствует: единственной гомотопически инвариантной линейной комбинацией
классов Понтрягина является сигнатура. В 60-е годы С.П. Новиков доказал трудную
теорему топологической инвариантности рациональных классов Понтрягина (го-
меоморфизм между замкнутыми ориентированными гладкими многообразиями
переводит классы Понтрягина в классы, отличающиеся от классов Понтрягина на
элементы конечного порядка; эти элементы конечного порядка могут быть отлич-
ны от нуля - имеются примеры). Ранее В.А. Рохлин, А.С. Шварц и Том доказали
это утверждение для гомеоморфизмов, устанавливающих соответствие между неко-
торыми гладкими триангуляциями двух гладких многообразий. (См. Милнор, Ста-
шефф, ’’Характеристические классы”.) Последний результат естественно приводит
к проблеме ’’комбинаторного вычисления классов Понтрягина”, т.е. их вычисления
через триангуляции (ср. упражнение 27). Внастояшее время эта проблема решена толь-
ко для первого класса Понтрягина (см. А.М. Габриэлов, И.М. Гельфанд, М.В. Лосик,
цикл статей 1975—1976 гг. в журнале ’’Функциональный анализ и его приложения”).
ГЛАВА 3
СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
§ 20. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ,
АССОЦИИРОВАННАЯ С ФИЛЬТРАЦИЕЙ
1. Общие определения. Пусть X - топологическое пространство, в котором задана
последовательность вложенных друг в друга подпространств
ф = Т_1 СХо С Х1 С ..-CXk_i СХк = Х.
Тогда вкладываются друг в друга и группы сингулярных цепей:
0 = Cq(X_1)CCq(Xo)C...CCq (Хк) = С, (X).
Мы скажем, что цепь a G Cq (X) имеет фильтрацию i, если a G Cq (X,) и Cq (Х| + 1).
Таким образом, Cq (Xf) содержит в точности все элементы фильтрации < i.
Имеется общий термин ’’групповая фильтрация”. Его употребляют в ситуации,
когда в (обычно абелевой) группе G задана цепочка подгрупп
...CG.jCGoCGiC... CG,
удовлетворяющая условиям О G{ = 0, U Gt = G. Обычно (но не всегда) мы рассмат-
риваем положительные конечные фильтрации, т.е. предполагаем, что Gt = 0 при
i < 0 и Gj =G при достаточно больших i.
Введем новое обозначение:
= C4(X/,X,_1) = C,(X/)/C,(X,-_1).
Граничный оператор dq: Cq (Х(-, X,_i) (Xt, Xz_ j), введенный в п. 4 § 12, мы
будем теперь обозначать через d^ q_f. Таким образом, dfq_j: Е° f -^E^q_l_t и
d? , .od° . = 0.
i,q -l—i i,q-i
Рассмотрим гомологии полученного комплекса. Это, в действительности, группы
Hq (X,-, Х(-_ i), но мы обозначим их через E/ q_i.
Спектральная последовательность, к построению которой мы теперь приступаем,
состоит из групп Е^,, г = 0,1,2,... В ней каждая следующая группа ’’меньше” пре-
дыдущей, а именно, является для нее группой гомологий по отношению к некоторо-
му дифференциалу. Существует способ (он будет ясен из последующего) определять
группы Ег последовательно при г = 0, 1, 2,.. . Но нам кажется, что читателю проще
будет разобраться в предмете, если мы введем эти группы сразу при всех г.
Определение 1. (Группа ^riq_i CEf {.) Пусть a G E°q_j =
= Cq (Xj)lCq (Xt_ j). Мы будем говорить, что а принадлежит Z[4_f в том и только
в том случае, если в а имеется представитель a G Cq(Xt), граница которого
имеет фильтрацию по крайней мере на г единиц меньше: Эа G Cq_i (X/ _г).
188
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
Таким образом,
Z' — -------------------------
Случай г = 0: Z9(?_f = £’?Q_I. (заведомо d(Cq(Xt'))<ZCq_l(Xi)).
Случай г =1: аб Z- q_j, если существует такое a G а, что да G Cq-i (Х,-_ i),
т.е. а - относительный цикл в Cq (Х;, X, _ i); таким образом, Zgq= Zq (Xit Х(_ i).
Заметим, что если a G Z} t, то включение да G Cq_l(Xi_l) выполнено для
любого aGa.
Упражнение 1. Для элементов групп Z? cr> 1 подобное неверно.
Очевидно, что с ростом г группа Z{ ( уменьшается и при достаточно боль-
шом г она превращается в Zq(Xi)IZq(Xi_1). Таким образом,
E°q_l=Z4q_iDZlq_iD...3Z»q_i =
= ^(x.o/z, (х,-_ о = z"+2,- = •. • = z’q_,.
Определение 2. (Группа Bf t CE?q_..) Пусть а е E°q_.. Мы будем го-
ворить, что а G Bf q_t, если для а найдется представитель a G Cq(Xi), такой, что
а = дЪ, b G Сч+1(Х,+г_ j). Таким образом,
^(хрпэс^!^-,)
‘•ч-‘~
Случай г = 0. Принадлежность а к В^ q_. означает, что у класса a G Efq_i =
= Cq (Xi)/Cq (Xj-i) существует такой представитель a G CQ(X(), что а = дЬ, Ь&
G Сч+1 (Х^ j). Но в этом случае а & Cq (Х(_ ,), т.е. а = 0. Значит, В ° . =0.
Случай г = 1. Если a G В} то у а существует представитель а G СЧ(Х,),
такой, что а = db, b G Сч + 1 (Х(). Таким образом, В° f есть просто подгруппа
относительных границ в Cq(Xt, Х,_!): Вй1д_(-Bq(Xit X^j).
С ростом г группа Brj q_j увеличивается, и для достаточно большого г она
превращается в группу (Bq (X) П Cq (Xi))/(Bq (X) О СЧ(Х,_ i) ).
Заметим еще, что Briq_i С Zst q_t при любых г,s. Итак,
0 = Blq_i CBlq_tC...C B™q_i = в^ =...
II II
Bq (Xi, Xi-1) (Bq (X) n cq (Xi))l(Bq (X) n cq (Xi-1))
-^q_i c ...CZ^q_£ cz“q_f=F«q_r
II II II
Zq(Xi)IZq(Xi- i) Zq(Xi, Xi-!) Cq(Xit X,-_!)
Определение 3. (Группа Ег1ч_(.) Ertq_i = Zriq_ilBriq_i. По-другому,
ЕГ =______________G/x.ona-1^-^-,)_____________________________________
[^(ХОПЭС^^Х,^.!)] +[С,(Х/_1)ПЭ-1С,_,(Х/_Г)]
§ 20. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
189
Очевидно,
= z°(,_f/B»(,_, = од,х/_1)>
= х*ч_,./в?ч_, = г,(х/,х/_1)/од.> х,_1)=я,(х/, xt_^.
Таким образом, определение 3 согласуется с предыдущими определениями.
Из сказанного выше следует, что с ростом г группа Ert q_f уменьшается; уве-
личивается знаменатель и уменьшается числитель. Кроме того, наступает стабили-
зация: при некотором г (которое можно выбрать не зависящим от i и q)
E~q= Zq(Xi)/[Bq(X) О СЧ(ХМ + Z,(X,-_ j).
On ре де ле ние 4. (Дифференциал driq^. E'q_i -> E^_r q+r Пусть
a G. Ei,q-i = Выберем для а представитель a G Z{q_. C
C (X/)/CQ(X/_1) и для а' такой представитель a G. Cq(Xj), что b = да имеет
фильтрацию Ci - г. Тогда смежный класс fl' цепи b в группе
Cq-i (Xi-r)lcq-i (xi-r-i) принадлежит группе Z[_r Q+r_f_j и определяет в
группе Ej_r q+r t некоторый элемент /?. Это и есть dfq_((a).
Упражнение 2. Проверьте корректность этого определения, гомоморфность
di,q-i и равенство dri_rq+r_i_l о dri q_. = 0.
Заметим, что гомоморфизм d^q_f: E°q_. -» Е° l-f совпадает с граничным
оператором Э: Cq(X(, Х,-_]) -> Cq_l(Xi, Х(_1~), а гомоморфизм <7/4_f: Е} f ->
-* E-_l q_j совпадает с гомоморфизмом Э«: Hq(Xit Х,_1) -* Hq_l{Xi_1, Хг_2)
из гомологической последовательности тройки (X,-, Х,_!, Х,_2). (В обоих случаях
определения рассматриваемых гомоморфизмов просто совпадают.)
Последовательность групп Er = ®t E^q_i и дифференциалов dr = ®dr{ q i :
Er ~*Er называется спектральной последовательностью.
(Читатель заметил, конечно, что наличие пространства X, фильтрованного подпро-
странствами X/, не нужно для предыдущих конструкций: достаточно иметь цепной
комплекс
и фильтрации
o = G,_i сс/10с...сс41 = с(,
обладающие тем свойством, что Э,(С|р9) С С,_ i(J.)
2. Общие теоремы.
Теорема. Группа гомологий группы Ег по отношению к дифференциалу dr
ecnEr + i. (Т.е. Er + l = Ker<7r/Im<7r; подробнее-. E'qi_i = K.erdriq_il\mdri+rq_i_r+l}
Доказательство. (Мы пользуемся обозначениями из определения диффе-
ренциала.) Пусть dj q_f(a) = 0. Это означает, что Д’ принадлежит группе
Bri_r q_i+r_1, т.е. существует такой представитель cG 0', что с= де, eG Cq (Х, _,).
Рассмотрим а - е G Cq (Xt). При вычитании е класс в Cq (Х()/Сч (Xf не меняется,
т.е. а - е снова является представителем класса a G Zf f. Так как определение
дифференциала корректно, т.е. не зависит от выбора представителей, то с самого
начала можно было вместо а взять а - е. Но д(а - е) 6 Cq_Y (Х,_г_1). Следова-
190
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
тельно, a’ G Z^q_(. Смежный класс этого а’ в E'^q_( обозначим через а. Относя
элементу а элемент а, мы получим гомоморфизм Kerdf q_( -> E^q_t. Для завер-
шения доказательства осталось:
(i) проверить корректность этого определения, т.е. проверить, что а зависит толь-
ко от а;
(ii) доказать, что отображение зпиморфно;
(Ш) доказать, что ядро этого отображения совпадает с Imc/^+rq_(_r+1.
Это мы оставляем читателю.
Рассмотрим теперь группу E~q= Z~q_t[B~q_(.
Обозначим через (j)Hq (X) образ гомоморфизма Hq (Xt) -*Hq (X), индуцирован-
ного включением Xt -+Х. Возникает групповая фильтрация
0 = (_ 1)Я,(X) С (0)Я, (X) С ... С wHq(X) = Hq(X}.
Т е о ре м a. E~q_{ = {i)Hq (X)/(f_l}Hq(X).
Доказательство. Согласно определениям,
Z-q_i = Zq(Xt)IZq(Xt_i\
= (Bq(X) n Cq(X$l(Bq(X) n C,(X,._!)),
(0Я,(Х) = Zq (Xi)l(Bq (X) n Cq (Xt)),
a-1 )Я,(Х) = zq (xt_! )/(b<?(X) r> cq(xt_!)).
Требуемое равенство Z"q_i/E^q_i = ^Hq(X)l ^._l^Hq(X) следует из следую-
щего очевидного алгебраического утверждения: если А и В — две подгруппы некото-
рой группы, то (А + В)IB =А[А П В (сумма и пересечение подгрупп берутся в обьем-
ляющей группе).
Соберем все, что мы доказали в двух пунктах, в одну формулировку.
Теорема. Если пространство X профильтровано подпространствами Xit ф =
= Х_! С Хо С... CXfc-j С. Хк = X, то существуют группы Epq, определенные
при г >0 и всех puq (причем Epq = 0 при р<. 0 и р> к) ,и гомоморфизмы
dp,я' Ер,я~*Еp-r,q+r-i
(причем drp_r q+r_1 » dp q =0), обладающие следующими свойствами -.
(1) Е'р+' =^drpql\md^rq_r+i.
(2) Eopq=Cp+q(Xp,Xp_i).
(3) dp q совпадает с граничным оператором Э: Cp+q(Xp,Xp_C)-*CpJrq_}(Xp,Xp_l).
(4) Е^ч^Нр^(Хр,Хр_г).
(5) dpq совпадает с гомоморфизмом Э»: Hp+q(Xp, Xp_j) -> Hp+q-i (Xp-lt
Хр-з) из гомологической последовательности тройки (Хр, Xp_lt Хр_2).
_ lm(Hp+q(Xp)^Hp+q(X^ (P)Hp+q(X)
(6) Ер* ~ ^(Нр^Хр.^Нр^хУ) (р-рЯр+^Х) '
Это утверждение носит название теоремы Лере.
3. Присоединенная градуированная группа. Рассмотрим утверждение (6) теоремы
Лере. Оно означает, что при любом m в группе Нт(Х) есть подгруппа (о)Нт(Х) =
= £,Q m; в факторгруппе Ят(Х)/£0>т есть подгруппа и так далее, и,
§ 20. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ 191
наконец, факторгруппа
(... . .)/F;_1>OT_k+1
совпадает с Ект_к. Из этого видно, что прямая сумма ®p+Q=OT E? q тесно связана
с группой ЯОТ(Х); говорят, что эта прямая сумма присоединена к группе Нт{Х)
относительно фильтрации {({)Нт{Х)}. Иногда ее обозначают через GHm{X).
Рассмотрим операцию присоединения в общей алгебраической ситуации. Пусть Л —
абелева группа, 0 = Л С Ло С ... С Ак = А — некоторая ее фильтрация. Положим
А° = Al/Al^1, GA = ®/Л°. Группа GA называется, по отношению к фильтрованной
группе А, присоединенной (градуированной) группой. (Группа называется граду-
ированной, если она представлена в виде прямой суммы некоторой совокупности
своих подгрупп.)
Упражнение 3. Докажите следующие свойства операции присоединения
А н- GA. (i) Если одна из групп A, GA конечно порождена, то и другая группа ко-
нечно порождена, и их ранги совпадают, (ii) Если одна из групп A, GA конечна, то
и другая группа конечна и их порядки совпадают, (iii) Если из групп А° только
одна отлична от нулевой, то А = GA. (iv) Если из групп Л ° только две отличны от
нулевых, а именно, группы Л°>( Л“^, z’j > z2, то Л^ С Л и А/А°? = Afi. (v) Если
все группы Л° (за возможным исключением группы Л§) являются свободными
абелевыми, то Л = GA. (vi) Если Л есть конечномерное векторное пространство
над некоторым полем и At — подпространства, то A=GA.
4. Когомологический вариант теории Лере. Параллельную теорию можно по-
строить, заменив гомологии когомологиями. Вот формулировка окончательного
результата. (Краткости ради мы изгоняем из обозначений коцепей и когомологий
указание на коэффициенты.)
Тео ре ма. Если пространство X профильтровано подпространствами Х{, ф -
- X_t С Хо С ... С Xk_! С Хк = X, то существуют группы Е?’4, определенные при
г > 0 и всех puq {причем Ef’4 - 0 при р< Ои р> к), и гомоморфизмы
dP’4 -. Е™ ^ЕР+гл~г+1
{причем dP+r,q~r+1 о dP’q = 0), обладающие следующими свойствами:
(1) ЕРД =KerdP’’/ImdP-r-<?+'-1.
(2) EP’q=CP+q{Xp,Xp_1).
(3) dg’q совпадает с граничным оператором 6: Ср+ч {Хр, Xp_i) -*
^СР+ч+1(Хр(Хр_1).
(4) ЕРЛ=НР+с>{Хр,Хр_1).
(5) d^,q совпадает с гомоморфизмом 5 *: Нр+ч {Хр, Хр_ х) ->яр+<?+1 {Xp+i, Хр)
из когомологической последовательности тройки {Xp+i, Хр, Xp_i).
Ker{ffp+q{X) -> Hp+q{X„_1)) <^P-^HP+q(X}
(6) Ep,q = ---------------------’>
KeT{Hp+q{X)-> HP+q{Xp)) (p)Hp+q{X)
другими словами, группа ®p+q=m E^q присоединена к Hm{X) относительно ’’убы-
вающей” фильтрации
0 = ^Нт{Х) С 1 }Нт{Х) С ... С (0'>Нт{Х) С <-1 }Нт{Х~) = Нт{Х),
где ^Нт{Х) - ядро отображения Нт{Х} -»If" (JQ), индуцированного включе-
192
ГЛ 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
нием X} -* X. (Термин ’’убывающая фильтрация”, конечно, не является необходи-
мым: стоит нам написать, как зто часто делают, ^_tyHm{X) вместо ^Нт(Х),
и фильтрация станет обычной, возрастающей. Мы предпочитаем, однако, этого не
делать.)
Построение производится так же, как в гомологическом случае. Нужно ввести
в группу Cq (X) убывающую фильтрацию
О = (к>С*?(ЛЭ С ... С <°>СЧ'(Х) С <"1 )С<г(Х) = Cq(X),
где С*7 (X) состоит из коцепей у: Cq (Т) * G, таких, что у (с) =0 при св С, (ХД С
С Cq {X). Далее, нужно положить
Е^-i = а-1 )сч,(Х)/(‘)Сч'(Х)
и в дальнейших построениях всюду заменить граничный оператор Э кограничным
оператором б.
Перенос наших результатов на случай гомологий с произвольными коэффициен-
тами также не составляет труда.
5. Графическое изображение спектральной последовательности. Спектральную
последовательность, как гомологическую, так и когомологическую, принято изобра-
жать на разграфленном листе бумаги. Каждому г отвечает отдельная диаграмма.
Группа E?'q или Epq помещается на пересечении <?-й строки и р-го столбца (рис. 84).
Если группа нулевая, соответствующую клетку можно оставить пустой. Таким об-
разом, заполняются только 0-й, 1-й....к-к столбцы, причем в г-м столбце запол-
няются клетки, начиная с (—г)-й (вверх). Впрочем, в важнейших случаях ненуле-
вые группы стоят только в первой четверти (см. § 21 и дальше). Дифференциал
dp>q (в гомологическом случае) действует из группы, стоящей в некоторой клетке,
в группу, расположенную на р единиц левее (единица = сторона клетки) и р — 1
единиц выше этой клетки. Когомологические дифференциалы действуют в проти-
воположном направлении (рис. 85). Говорят, что ’’дифференциалы действуют хо-
дом коня”, хотя буквально зто верно только для г = 2. При переходе от Е?'4 (ЕргЧ)
к Е^ (Ep*q ) берется ядро стрелки, действующей из (р, <?)-й клетки и фактори-
зуется по образу стрелки, направленной в эту клетку. На практике часто бывает,
что во многих клетках диаграммы стоят нули (ничего не стоит). Но дифференциал
может быть нетривиален, только если ненулевые группы стоят в обеих клетках,
соответствующих концам стрелки. В противном случае дифференциал тривиален.
Это обычно кодируется выражением ”по соображениям размерности”. Например,
если читатель столкнется с фразой ”Е2 =Е3 по соображениям размерности”, он дол-
§ 20. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
193
жен понимать ее так: никакие две нетривиа-
льные группы Е%'4 не стоят в клетках, одна
из которых расположена на одну единицу ни-
же и две единицы правее, чем другая; поэто-
му d?,q = ОиЕ™ =Kerd«‘i'/Imd₽-2’4' + 1 =
= E%q/ {0 } = E^q при любых puq.
В члене Е°° группа, присоединенная к
Нт(Х), есть сумма групп, стоящих на косой
линии р + q = т (рис. 86). Если все эти
группы тривиальны, то Нт(Х) = 0; если все
эти группы, кроме одной, тривиальны, то зта
одна и есть Нт (X); в общем случае самая вер-
хняя нетривиальная группа (на прямой р +
+ q = т) есть подгруппа группы Нт(Х), сле-
дующая есть подгруппа факторгруппы по
этой группе, и т.д., последняя группа совпадает с соответствующей фактор-
группой. В когомологическом случае все так же, только верх и низ меняют-
ся' ролями.
В нижеследующих пп. 6 и 7 мы рассматриваем, краткости ради, только гомоло-
гические спектральные последовательности (с коэффициентами в Z). Перенос на
остальные случаи не составляет никакого труда.
6. Новое понимание клеточного вычисления гомологий. Пусть X - конечное кле-
точное пространство. Профильтруем его остовами, положив X, = X'. В соответствую-
щей спектральной последовательности имеем: Ер q
= Ср+ч(Г’,Г’-1) и
E1Piq^Hp+q(XP,XP-1) =
0 при <7^0,
WplX) при <7 = 0.
Таким образом, в члене Е1 заполненной оказывается только нулевая строка:
(рис. 87). Нетривиальный дифференциал d1 действует только в этой строке и совпа-
дает с клеточным граничным оператором Э. Следовательно, в Е2 тоже нетривиальна
только нулевая строка, и в ней стоят гомологические группы клеточного комплекса
(рис. 88). По соображениям размерности (см. п. 5) .F2 =Е3 = .. .=Е", и, пользуясь
тем, что в Е°° на каждой прямой р + q = т стоит только одна нетривиальная группа,
мы можем написать
Яот(Х) = Кегаот/1тЭот+1.
Мы получили, таким образом, доказательство уже известного нам факта: (сингу-
лярные) гомологии клеточного пространства X совпадают с его клеточными гомоло-
гиями. В действительности, как легко понять, зто ’’новое” доказательство ничем не
отличается от старого доказательства, приведенного в § 13. Таким образом, мы фак-
тически сталкивались со спектральной последовательностью уже в § 13. Впрочем,
мы сталкивались с ней раньше, в § 12, ибо, как мы сейчас увидим, гомологические
7. А.Т. Фоменко
194
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
последовательности пар и троек - это просто способ записи спектральных последо-
вательностей, относящихся к двучленным и трехчленным фильтрациям.
7. Новое понимание гомологических последовательностей пар и троек. Рассмотрим
двучленную фильтрацию ф С Y С X (Хо = Y, = X). Имеем:
^'p.q Cp+q^Xp, Хр_\)
tp.q = ffp+q(Xp,Xp_l) =
I Cq(Y) при p = 0.
I Cq+l(X, Y) при p= 1
f Hq(Y) при p = 0
[ Hq+1(X, Y) при p=l
(рис. 89). В А'1 может быть нетривиальным только дифференциал d\q: Е* Eq q,
который совпадает с соответствующим гомоморфизмом из последовательности
пары. В члене Е2 могут быть отличны от нуля только члены
E20,q = Hq{Y^t{Hq+^X, Y}Y
E\,q = Кег[Э.: Hq+i(X, Y}-Hq{Y)\-
по соображениям размерности E2 = E3 = ... = E“, в E°° на каждой прямой p + q= m
стоят две группы, и мы имеем:
Н,п(Х}
Hm(Y)/lmd.
= КегЭ*.
Полученное равенство можно записать в виде короткой точной последовательности
О -> Н,„ (У)/1ш Э . -> Нт (%) -> Кег Э . -> О
или, что эквивалентно, в виде точной последовательности
э* Э.
+ Y) — Hm(Y)-Hm(X)^Hm(X, У) — Ят_!(Х).
Легко убедиться в том, что это — фрагмент гомологической последовательности
пары (X, У).
Упражнение 4. Рассмотрите спектральную последовательность, отвечающую
трехчленной фильтрации, и убедитесь в том, что наша теорема дает в этом случае
в точности гомологическую последовательность тройки.
8. Обобщение на бесконечные фильтрации. Наши пост-
роения применимы, в принципе, и к случаю бесконечной
фильтрации
.0 = Х-! С Хо С ... С Х„ = X,
хотя в этом случае возникают некоторые новые трудности.
Во-первых, группы E'q (Ер,ч)с ростом г не будут стаби-
лизироваться. В когомологическом случае при г > р группа
EPr'+i изоморфна ядру дифференциала dp’4 (образ дифферен-
циала dpr~r’4+r-1 тривиален по соображениям размерности).
Поэтому
е^эе^з...,
и мы можем положить Ep,q = (\>pEp,(l. В гомологиче-
ском случае при г>р группа Е?** изоморфна факторгруп-
§ 20. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ 195
пе Er„ a[\mdr„.r n_r+y; возникает последовательность эпиморфизмов
pp + l _> с-Р+2 _>
£Р.«? “РЯ ’ ’ ’ ’
и группа Ер ч есть предел этой последовательности, т.е.
ер.,~ Iи Ke'^.V - • - £й">
(Все эти предостережения не особенно существенны для дальнейшего, поскольку
у нас, как правило, будет Ег = 0 при р< 0. Нужно помнить только, что даже в этом
случае в спектральной последовательности, отвечающей бесконечной фильтрации,
стабилизация может наступать в разное время в разных местах.)
Далее, утверждение (6) теоремы Лере сохраняет силу, но фильтрация { ^Нт(Х)}
и ее когомологический аналог делаются бесконечными, и специальной проверки
требуют равенства
и (i)Hm(X) = Hm(X), П &Нт(Х) = 0.
i=o >=о
Упражнение 5. Докажите, что оба равенства справедливы при следующем
дополнительном предположении: для любого компактного множества К С X най-
дется такой номер i, что К С Xj.
Замечание. Для фильтраций, бесконечных в другую сторону, т.е. фильтраций
вида ... С Х_п С ... С X_t С Хо = X с Г) Xt = ф , построение спектральных после-
довательностей проводится без большого труда, хотя гомологический и когомоло-
гический случаи до известной степени меняются ролями. Однако фильтрации, беско-
нечные в обе стороны, к построению спектральных последовательностей непригодны.
Рассмотрим, например, фильтрацию цилиндра X = S1 X R подпространствами X/ =
= S1 X (— °°, /]. У соответствующей спектральной последовательности, если ее опре-
делить дословно как выше, все члены, начиная с первого, будут состоять из одних
нулей, хотя гомологии цилиндра X нетривиальны. Впрочем, вместо цилиндра S1 X R
можно было бы взять прямую R: у нее нетривиальны хоть нульмерные гомологии,
а спектральная последовательность будет чисто нулевой. Разберитесь, в чем тут дело
и к чему сходится такая спектральная последовательность.
§ 21. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
Пусть £ = (Е, В, F, р) — локально тривиальное расслоение с конечной клеточной
базой. Наша цель - вычислить, насколько это возможно, гомологии и когомологии
пространства Е, зная гомологии и когомологии пространств В и F. С этой целью мы
вводим в £ фильтрацию {£(/) =р~1(В1)} прообразами остовов базы,
ф = Е(-1)С£’(0) СЕ(1)С ... СЕ(к) = Е (jt = dim£)
и изучаем соответствующую спектральную последовательность.
Всюду в этом параграфе мы считаем базу В связной (это ограничение совершенно
не существенно).
1. Вычисление начальных членов спектральной последовательности в предполо-
жении гомологической простоты расслоения.
А. Гомологи чески простые расслоения. Пусть х0, Xj - точки базы. 5 - соединяю-
щий их путь. Если слой расслоения клеточен, то очевидное применение теоремы о
накрывающей гомотопии позволяет определить, с точностью до гомотопии, отобра-
жение (гомотопическую эквивалентность) ts: р-1(х0) р~'(хх} слоя над точкой
Г
196
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
Xq в слой над точкой (теорема о накрывающей гомотопии применяется к вклю-
чению Fo -. р-1(х0) и гомотопии ft : р"*(хо) "*«(0 е В)- Замена пути $ гомо-
топным не меняет гомотопического класса [#,]. Поэтому гомотопический класс
путей, соединяющих х0 с xt, определяет при любом q изоморфизм Hq ( р-1 (х0)) -+
Заметим, что такой изоморфизм определен и в случае неклеточного F (по пути $
строится для любого клеточного Z отображение tt(Z, р-1(х0)) -* -n(Z, p_1(xt)), и
этого достаточно).
Определение. Если построенный изоморфизм вовсе не зависит от пути
(а определяется точками х0 и xj, то расслоение % называется гомологически
простым.
В частности, расслоение с односвязной базой гомологически просто. Гомологи-
ческая простота расслоения следует, конечно, и из его простоты в смысле, рассмат-
ривавшемся в п. 5 § 18. С другой стороны, можно ослабить условие гомологической
простоты и говорить, скажем, о G-гомологической простоте расслоения (в опре-
делении которой место целочисленных гомологий занимают гомологии с коэффи-
циентами в G).
Важно, что гомологические и когомологические группы с любыми коэффициен-
тами слоев гомологически простого расслоения могут быть отождествлены: фикси-
рование элемента в гомологической или когомологической группе одного слоя при-
водит к фиксированию элементов в соответствующих группах всех остальных слоев.
Ъ.'Члены Ei иЕ2.
Теорема. Если расслоение £ гомологически просто, то в гомологическом слу-
чае (с коэффициентами в G)
= <8p(B-,Hq(F- G)),
dlp q = Э: <вр(В-, Hq(F- G))-* !(Я; Hq(F\ G)),
Epq=Hp(B;Hq(F-,Gyy,
в когомологическом случае - аналогично.
(Равенства обозначают канонические изоморфизмы, которые будут построены
в процессе доказательства.)
Доказательство мы проводим только в гомологическом случае, полагая
для краткости G = Z. Согласно теореме Лере
^^^(рЪ^р-!));
следовательно,
E1Ptq=Hp+q(P~4Bp\ p-\Bp-1)) = ^Hp+q(p-\ef), р’1^)),
где ер пробегает р-мерные клетки базы В. Пусть ff: Dp *В — характеристическое
отображение для ер. В силу теоремы Фельдбау (п. 2 § 9) расслоение f{*% тривиаль-
но, ввиду чего отображение ft накрывается отображением Dp X F -> р-1(ё;₽), го-
меоморф но отображающим (IntD”) X F на р-1(е/₽) и отображающим S р~1 X F
На р~1(ёр). Очевидно, это отображение индуцирует при любом q изоморфизм
Hp+q(Dp X F, SP-1 X F) Нр^р-^ёР), р-1^))
(для доказательства нужно сначала вывести из теоремы Борсука и теоремы о накры-
вающей гомотопии, что (р~1(ёр), р~1(ёр)) - пара Борсука, и затем применить
§21. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
197
теорему факторизации — см. п. 5 § 12). Очевидно, наконец, что
Яр+ч (DP XF,SP~1XF) = Hq(F)
(это вытекает из относительного варианта формулы Кюннета: Ht(Dp X F,
Sp~l XF) = ®а+(3=/ На(Рр, Sp~l) ® Hp(F)', можно, впрочем, воспользоваться
обычной формулой Кюннета и последовательностью пары). Строго говоря,в послед-
ней формуле F следует понимать как слой над некоторой точкой клетки ер, но го-
мологическая простота расслоения позволяет забыть об этом, ибо у нас гомологи-
ческие группы разных слоев отождествлены между собой. Итак,
^Ч=®ЯЧ(Л= «р(В;Яч(П).
Окончание доказательства мы с легким сердцем оставляем читателю.
Упражнение 1. Перенесите все сказанное в этом параграфе на случай рас-
слоений Серра.
С.Как все это выглядит на картинке. Итак,
^=Яр(В;Яч(П).
Как и было обещано, Epq = 0, если р < О или q < 0. В нулевой строке стоят
группы
£20=Яр(Я;Я0(Я)) = Яр(Я)
(если F связно) — гомологии базы. В нулевом столбце стоят группы
Elq=H0(B-Hq{F))=Hq{F)
— гомологии слоя. Если гомологии базы или гомологии слоя не имеют кручения, то,
в силу формулы универсальных коэффициентов,
E2P,q = Яр(В; Я,(Я)) = Яр(В) * Hq(F) = E*Pi0® E*0<q.
В общем случае это равенство имеет место с точностью до кручения. См. рис. 90.
Следствие. х(Е)= x(B)x(F).
Доказательство. Положим x(Er) = SOT(-l)OTrank ®p+q=m Epq. Из ска-
занного выше следует, что
X(F2) = S (-l)m S гапкЯр(5)гапкЯч(/<Э =
m p+q=m
= S (-1)РгапкЯр(В)(-1)’гапкЯд(Я) = х(В)х(П.
p,q
Из теоремы Эйлера-Пуанкаре (см. упражнение 8 к § 13) следует, что х(£2) =
198
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
= Х(Е3) = ... = х(£”°) и,ввиду равенства rankHm(E) = Zp+q=m rankf”,, х(£“”) =
= X (Е).
Упражнение 2. Покажите, что если расслоение тривиально, то все дифферен-
циалы, начиная со второго, тривиальны (как говорят, спектральная последователь-
ность вырождается во втором члене) и Е°° = Е2. Отсюда следует, что, с точностью
до присоединенности,
Hm(BXF) = ® Яр(В;Яч(П);
p+q=m
впрочем, формулы универсальных коэффициентов и Кюннета показывают, что это
равенство является точным.
3 а м е ч а н и е. Поскольку нетривиальные дифференциалы уменьшают члены
спектральной последовательности, можно сказать, что из всех расслоенных про-
странств с данными базой и слоем наибольшие гомологии имеет прямое произ-
ведение.
2. Случай непростого расслоения.
А. Локальные системы. С гомологиями и когомологиями с коэффициентами в
локальной системе мы уже сталкивались в п. 9D § 17. Теперь мы расскажем о них
более систематически, составив все же детали читателю. Говорят, что над топологи-
ческим пространством X задана локдаьная система групп (= ансамбль групп = ло-
кально постоянный пучок групп), если каждой точке х G X поставлена в соответ-
ствие группа Gx и каждому пути s на X с началом х и концом у поставлен в соот-
ветствие изоморфизм ts: Gx -> Gy, зависящий только от гомотопического класса
пути s. При этом предполагается, что произведению s's" путей s' и s" отвечает изо-
морфизм равный композиции изоморфизмов и т^„. Примеры: (1) Gx =
= тгл(Х х), та = s# (см. п. 2 § 8) ; (2) X — база расслоения р: Y -* X (локально
тривиального или в смысле Серра),GX-Hq(p~l(x)), та — гомоморфизм,построен-
ный выше в п. А (аналогично для когомологий и гомологий с коэффициентами).
Пусть х0 — некоторая отмеченная точка пространства X. Тогда всякая петля с
началом х0 определяет автоморфизм группы GXq и тем самым определяется дей-
ствие группы 7Г1 (X, Хо) в Gx<) посредством групповых автоморфизмов.
Упражнения. 3. Покажите, что если над X заданы две локальные системы,
{Gx, т,} и {Gx, 7>), и при этом существует изоморфизм Gx<i »» Gx<i, согласован-
ный с действиями группы 7Г1(Х х0) (описанными выше), то системы {Gx, т,} и
{G^, та } изоморфны (определение изоморфизма локальных систем самоочевидно).
4. Покажите, что произвольная группа G с произвольным действием группы
Я1(Х х0) посредством автоморфизмов может быть группой GXa локальной системы
групп.
Эти предложения открывают путь к построению большого количества новых ло-
кальных систем. Скажем, пусть X— многообразие, G = Z, элемент а группы 7Г1(Х)
определяет умножение на +1 или —1 в зависимости от того, сохраняет или обращает
ориентацию петля класса а. Получающаяся локальная система обозначается через ZT;
она фигурировала неявно в упоминавшемся п. 9D § 17.
В. Гомологии и когомологии. Пусть $9 = {Gx, та} — локальная система абеле-
вых групп, заданная над пространством X. Обозначим через cq центр стандартного
(/-мерного симплекса Тч, через s f — прямолинейный путь в Тч, соединяющий cq
с центром i-й (q — 1)-мерной грани. Под (/-мерной сингулярной цепью пространства
X с коэффициентами в 'S понимается (конечная) формальная линейная комби-
§ 21. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ 19»
нация где f{: Tq ->X - сингулярные симплексы, gf G Gf^c . Группа таких
цепей обозначается через Cq (Х\ 3), граничный оператор Э: Cq (X; 3) *
-> CQ_! (X; 3 ) определяется формулой
я .
d(gf)= S Д)Г,/.
1=0 Я.1
Возникающие гомологии обозначаются символом/7^ (X; 3). Аналогичным образом
определяются когомологии Hq(X; 3).
Упражнения. 5. Сопоставьте это определение с определениями из п. 9D § 17.
6. Пусть G = GXa \ действие группы Я1(Х, х0) в GXt будем записывать как а,
g ^ag. Покажите, что
№(Х;$) = {gGG\ag=g для любого а&ях{Х, х0)1,
H0(X-,3) = G!G*
где G* — подгруппа, порожденная разностями ag — g (a&iti (X, х0),g G G).
Гомологии и когомологии с коэффициентами в локальной системе в случае кле-
точного X можно вычислять по клеткам. Клеточная цепь размерности q — это фор-
мальная сумма Sg,- of, где о1 - клетка размерности q, g, G GXj, x{ G а, (мы будем
дальше писать вместо GXj прямо Go.). Граница действует по формуле
9(go)= S т?а,ш(х)<о,
dim go =g - I
u> О о ф ф
где оператор i7a u): Ga -* G^ для (ориентированных) инцидентных клеток о, со
определяется следующим образом. Выберем для а характеристические отобра-
жение й: Dq -> X, представляющее выбранную ориентацию клетки q и обладаю-
щую следующим свойством. В со существует маленький шарик U (с центром у),
прообраз Л-1 (t/) С S4-1 которого распадается в объединение U {/,- шариков, каж-
дый из которых отображается на U гомеоморфно с сохранением или обращением
ориентации (мы полагаем е, = ± 1 в зависимости от того, сохраняется или обраща-
ет ориентацию гомеоморфизм t/,- -> U). Пусть с — центр шара Dq, ct = Ut Г» й-1 (у),
Sj — прямолинейный путь в Dq, соединяющий с с Гомоморфизм T?0>tJ: (cj ->
-* Gy определяется теперь формулой g •-> Sef 0 Sj (g)
Упражнение 7. Пусть X = RP", G — абелева группа, Т — ее автоморфизм
с Г2 = id. Пусть, далее, образующая группы тгх (RP") действует в G как Т. Обозна-
чим через 3 соответствующую локальную систему. Покажите, что гомоморфизм
9:«<Z(RP";»)^«(Z_1(RP";»), q<n,
II II
G G
есть id + Г при четном q и id - Гпри нечетному. Вычислите гомологии H„(RPn-,3)
и когомологии Н* (RPn; 3) в общем случае и при G = Z, Т = - id.
С. Основная теорема в случае непростого расслоения.
Теорема.
£2>g= Hp(B-,{Hq(p~\x))}\
где {Hq (р-1 (х)) } — локальная система, описанная в примере (2) из п. А. Аналогич-
ное верно в случае когомологий и гомологий с коэффициентами.
200
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
Доказательство предоставляется читателю.
Упражнение 8. Покажите, что равенство х (Е) = X (5)х (F) (см- п. 1С) сох-
раняет силу и для непростых расслоений.
D. Упражнение 9. Используйте когомологии с локальными коэффициентами
для построения теории препятствий, не связанной условиями простоты (пространств
и расслоений). Определите с помощью этой теории препятствий класса Эйлера не-
ориентированных расслоений.
3. Первые применения. Читателя, который воспринял содержание предыдущего
пункта как нечто вспомогательное и необязательное, мы просим снова напрячь
внимание. Мы увидим сейчас, как даже то немногое, что мы уже знаем о спектраль-
ных последовательностях, может быть использовано для вполне содержательных
вычислений (хотя главные применения спектральных последовательностей впереди).
А. Гомологии специальной унитарной группы SU(n). Как мы знаем, факторпрост-
ранство SU(ri)ISU(ri - 1) есть не что иное, как сфера 52”-1; возникает расслоение
SlZ(n-l) .
SU(n)—------> 52 1 (л >2)
(мы следуем обыкновению писать обозначение слоя над стрелкой, обозначающей
проекцию расслоения).
При п = 2 слоем этого расслоения является одна точка. Следовательно, SU(2) =
= S3. (Это равенство нам известно — см. § 1). Для нас равенство SU (2) = S3 удобно
тем, что гомологии сферы S3 нам уже известны. При п = 3 получаем расслоение
51/(2) с _ 53 ,
SUSs, т.е. 5t/(3)->5s.
Зная гомологии слоя и базы, выписываем диаграмму для члена Ег этого расслое-
ния: Ep<q = Нр (Ss; Нд (53)) (рис. 91). Из диаграммы видно, что d2 = d3 = d4 = ...
... = 0 по соображениям размерности. Значит, Е2 = Е°°. В Е°° на каждой прямой
р + q = const лежит не более одной нетривиальной группы, и мы заключаем, что
SU(3) имеет следующие гомологии: Но = Н3 = Hs = Hs = Z, остальные Hq = 0. Та-
ким образом,
Я.(5{7(3))~Я.(53 X 5s).
Рассмотрим теперь случай п = 4, т.е. расслоение
su(3) „
SU(4)----->57.
Член Е2 показан на рис. 92. По соображениям размерности, Е2 = Е3 = ... = Е°°,
Рис. 92
Рис. 91
§ 21. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
201
и, следовательно, SU(4) имеет такие гомо-
логии: Hq = Н3 = HS = Hq = Hq = Hiq =
= Hi2 = His = Z, остальные Hq = 0. Иными
словами,
H„(SU(4))^H,(S3 X 5s X 57).
Возникает соблазнительная мысль, что
таким образом мы будем двигаться и даль-
ше, усматривая всякий раз тривиальность
дифференциалов спектральной последо-
вательности из соображений размерности.
Оказывается, однако, что случай п = 4 -
последний из случаев, для которых сообра-
жений размерности — пока' что единствен-
ных доступных нам соображений — доста-
точно. Действительно, рассмотрим следу-
SU(4)
ющее расслоение 5 £7(5) ----► S . Член
Е2 показан на рис. 93. По соображениям
размерности Е2 = ... = Е9 и Е10 = ... =
но дифференциалы </9,0: Z * Z и </9,7:
Z -> Z могут оказаться нетривиальными. На самом деле они тривиальны, как три-
виальны и все дифференциалы всех последующих спектральных последователь-
ностей, но с доказательством мы вынуждены повременить до § 23. В § 23 мы дока-
жем, что при любом п
H,(SU(n))^H,(S3 XSs X .. .X s2"-1).
(Заметим, что при л > 3 пространства SU(n) и S3 X S5 X ... X 52"-1 не гомео-
морфны: у них не одинаковы группы 7г4. Читатель может попытаться доказать этот
факт, но лучше отложить это до следующей главы.)
В. Гомологии пространств петель.
Теорема. Пусть X - топологическое пространство (с отмеченной точкой),
и пусть пространство X (п - 1) -связно, т.е.
яо(^) = я1(У)=... = я„_1(Л-
Тогда
Hr(X)^Hr_i^lX)
при г < 2л — 2, и аналогичное равенство имеет место для гомологий с любыми коэф-
фициентами и когомологий.
В доказательстве мы ограничимся случаем клеточного X; переход к общему
случаю (который не кажется нам особенно важным) может быть произведен на ос-
новании результатов п. 6 § 11. д х
Рассмотрим спектральную последовательность расслоения ЕХ —> X из приме-
ра 2 к п. 4 § 9 (это расслоение дальше будет постоянно употребляться) : ЕХ — прост-
ранство путей, начинающихся в отмеченной точке, £2 X — пространство петель. Важ-
но, что ЕХ стягиваемо, поэтому в Е°° все тривиально, кроме Е°^ 0 = Z. В силу теоре-
мы Гуревича Ну (X) = ... = Нп_у(Х) = 0, и потому в Е2 ничего не стоит в полосе,
образуемой 1-м,..., (л — 1)-м столбцами. Следовательно, в заштрихованной на
рис. 94 части нулевого столбца тоже быть ничего не может: по соображениям раз-
мерности эта часть спектральной последовательности не подвержена действию ника-
202
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
ких дифференциалов, и если бы какая-нибудь из этих групп была нетривиальной,
оно осталась бы нетривиальной и в , что невозможно. Итак, (ЯХ) = ... =
= Я„_2(ШГ) = 0, и член Е2 приобретает вид, показанный на рис. 95. В угловой
клетке стоит группа Е„ п_1. Дифференциал из этой клетки попадает в (2л - 2)-ю
клетку нулевого столбца, а в нее попадает дифференциал на 2л-й клетки нулевой
строки. Клетки, стоящие в нулевом столбце и нулевой строке, соответственно,
п-1
Нули
нули
f-2-
п,п-1
Н^Х)
wm. vsssssMVMwa
О п (*1 2п
Рис. 95
Рис. 94
ниже и левее, могут быть связаны дифференциалами только между собой, и так
как в Е°° ничего остаться не должно, мы получаем при г < 2л - 2:
<,0;
II II
II II
НГ(Х) Нг1 (ПХ).
Теорема доказана.
Замечания. 1°. В доказательстве построен канонический изоморфизм
Hr_i (ЯХ) — Hr (X) (г <2п - 2).
2°. В критической размерности дело портит только дифференциал d^ п_ (:
Еп,п-г ^Е9,2п-2- таким образом, дифференциал £22"L'Ij0 ^оХ'-г
изоморфно отображает группу 0 = о = ^2n-i на Ф,актоРгРУП|,У
группы Н2п_2(Х1Х) (по образу дифференциала J" B_j). Этот изоморфизм между
факторгруппой группы Яги-2 (^0 и группой H2n-i (X) равнозначен эпиморфиз-
му Н2п_2 (ЯХ) ^Н2п_1 (X).
3°. В следующем параграфе мы увидим, что этот изоморфизм Hr_l(SlX) =
a Hr (X) (г < 2л - 2) и этот эпиморфизм Н2п_2 (ЯХ) ~>-Н2п_1 (X) индуцируется
на самом деле непрерывным Отображением тх- 22 ЯХ ~>Х, действующим по фор-
муле тгх(з, t) =s(t), st ЯХ, t G [0, 1] (с учетом изоморфизма надстройки 22:
//,_((fiX) -> Hr(X)}. Мы позволим себе воспользоваться сейчас этим фактом,
нс дожидаясь его доказательства.
С. Напомним, что в § 10 нами была доказана теорема Фройденталя:
гомоморфизм надстройки
22: irm (S")-* irm + i (Sn *)
является изоморфизмом при т < 2л - 1 и эпиморфизмом при т = 2л - 1. Сейчас
мы покажем (как это было обещано в § 10), что это утверждение останется верным,
§ 22. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА
203
если в нем заменить сферу Sn произвольным (п — 1)-связным (клеточным) прост-
ранством X, Нам удобно будет считать, что надстройка над пространствами с отме-
ченной точкой (X, пространства петель и т.д.) понимается в смысле определения,
данного в п. 6 § 2 (т.е. образующая над отмеченной точкой стянута).
Наряду с определенным выше отображением тгх: S ПХ -> X мы рассмотрим вло-
жение ix- X -* S2SX, которое ставит в соответствие точке х G X петлю t (х, Г)
(точки (х, 0) и (х, 1) у нас отождествлены!). Очевидно, композиция
X 1у It у» у
XX ►SQSX—► ЪХ
тождественна. В силу сказанного в п. В, отображение тг2Х индуцирует изоморфизм
в гомологиях размерности < 2п (надстройка XX над (л — 1)-связным простран-
ством X л-связна). Значит, и S ix индуцирует изоморфизм в гомологиях размер-
ности < 2л, a ix индуцирует изоморфизм в гомологиях размерности <2л - 1 (го-
мологические гомоморфизмы, индуцируемые отображениями и ix, одинако-
вы с точностью до сдвига размерностей на 1). В силу теоремы Уайтхеда из п. 5 § 14,
ix индуцирует в гомотопических группах изоморфизм в размерностях < 2л — 2
и эпиморфизм в размерности 2л — 1. Для завершения доказательства нам осталось
только доказать следующее утверждение.
Упражнение 10. Гомоморфизм
Ох)»
я, (X)---> nq (ЯХХ) й n4+i (SX)
(где — обозначает изоморфизм из гомотопической последовательности расслоения
й!'
EY —> Y, Y = SX — ср. упражнение 13 к § 9) совпадает с S: тгч (X) ->wQ+i (SX).
§ 22. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА
СПЕКТРАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ РАССЛОЕНИЙ
1. Гомоморфизмы спектральных последовательностей. Пусть
0 = XLt СХо с . . .СХ', ф = Х"_1 cxfc... СХ"
— два фильтрованных пространства. Для соответствующих спектральных последо-
вательностей мы будем употреблять обозначения {'Epq, 'dp q} , {"Epq, "dp q} .
Непрерывное отображение ft X' ->X" называется согласованным с фильтрация-
ми, если /(X/) С X" при всяком i. Поскольку такое отображение / индуцирует
отображения /#: Cq (X*) * Cq (X"), согласованные с дифференциалом и с фильт-
рацией, оно индуцирует при всех р, q и г (включая г = °°) некоторые отображения
/»=(/»)' = 'Ег -+"ЕГ ,
'» v»,p,Q p,q P,q
перестановочные с дифференциалами (рис. 96).
Отображения (ft)rpq наилучшим образом взаимодействуют с утверждениями
(1) —(6) теоремы Лере. В частности,
(А) отображение (/,)р>ч совпадает с индуцируемым / отображением Hp+q (Хр,
(В) отображение (Д)'^1 есть гомологический (по отношению к дифференциа-
лам ,dr,"dr) гомоморфизм, индуцированный отображением (/*)£,</>
204
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
(С) отображение (/,)” индуцируется индуцируемыми1) f отображениями
(оят(у')^(оята").
Доказательство очевидно.
Все эти свойства гомоморфизмов (/,)р>ч принято выражать словами:
{(/,)pjQ} есть гомоморфизм спектральной последовательности { 'EPtq, 'dPtq}
в спектральную последовательность {"Ер>я, "dPtq } ;
Рис. 96
Основной пример. Пусть (Е1, В', F1, р'), (Е", B",F",p") —гомологичес-
ки простые расслоения с клеточными базами и f: Е' -+Е" — послойное отобра-
жение. Последнее означает, что существует непрерывное отображение g: В' -> В",
такое, что диаграмма
коммутативна. Для любой точки х' G В' отображение / индуцирует отображение
Л слоя р'“* (х*) в слой p"-1(g(x’)), которое, ввиду гомологической простоты
расслоений, индуцирует гомоморфизмы Лф: Hq (F') (F").
Ввиду теоремы о клеточной аппроксимации отображение g гомотопно клеточно-
му, а ввиду теоремы о нак рывающей гомотопии гомотопию можно подняГь до гомото-
пии отображения /. Последняя превращает /в отображение, согласованное с фильтра-
циями, которое мы снова обозначим через /. Новое / индуцирует гомоморфизм
спектральной последовательности первого расслоения в спектральную последо-
вательность второго расслоения, который обладает следующими дополнительными
свойствами.
Предложение. (1) Гомоморфизм (ft)p,q совпадает с гомоморфизмом
НР(В'-, Hq(F')) -+Нр(В"-, Hq(F")),индуцируемым g uh,.
(2) Яри г > 2 гомоморфизм (f,)p>q не зависит от произвола конструкции (вы-
бора клеточной аппроксимации и поднятия гомотопии).
Часть (2) этого предложения следует из части (1), доказательство части (1)
мы оставляем читателю (которому придется снова вникнуть в доказательство ра-
венства ЕРгЧ =НР(В\ Hq(F))).
*) Слово ’’индуцированный” топологи употребляют почти так же часто, как слово ’’комп-
лекс”; впрочем, без слова ’’комплекс” мы во многих случаях научились обходиться.
§ 22. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА
205
Все сказанное имеет очевидные аналоги для когомологий и гомологий с коэф-
фициентами.
(Рассмотрение случая гомологически не простых расслоений здесь и далее в этом
параграфе мы оставляем читателю.)
2. Нулевая строка и нулевой столбец. Содержательные следствия из результатов
предыдущего пункта можно получить, применяя их к простейшим отображениям:
(Е, В, F, р) связны. Поскольку все дифференциалы, исходящие из клеток нулевой
строки (гомологической спектральной последовательности с коэффициентами в G),
и все дифференциалы, приходящие в клетки нулевого столбца, тривиальны (см.
рис. 97), группы Егт 0 и Е'о т представляют собой цепочки последовательных, соот-
ветственно, подгрупп и факторгрупп:
Е2т.0^Е^0 о,
„ /Im d „ /1т d
Е2а'~—*Е3'-—> ...^Е~.
и,т и, т и, т
Возникают мономорфизм и эпиморфизм
Ет,о~*ЕтО и Еот ~*Е()<т,
в когомологическом случае
->£2°’т и Е™'° +Е”’°.
В то же время Е°^т и Е°^о ~ это подгруппа и факторгруппа группы Нт (Е; G), а
Е™’0 и Е®'т — подгруппа и факторгруппа группы Нт (Е; G). Рассмотрим цепочки
гомоморфизмов:
Нт (F; G) = Яо (В;Нт (F-, G)) = Е20>т -> Е£т С Нт (Е-, G),
Нт (Е-, G)^E“i0GE2m>0=Hm (В; Но (F; G)) = Нт (В; G),
Нт (B\G) = Нт (В;Н° (F-,G)) = E^'° -+Е™>° С Нт (Е; G),
Нт (Е-. G)+E%mG Е§<т = Н°(В;Нт (F; G)) = Нт (F; G).
206
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
Теорема. Эти гомоморфизмы совпадают с гомоморфизмами, индуцирован-
ными включением F -’’Е и проекцией Е ->В.
Доказательство, как уже было сказано, сводится к применению результатов
предыдущего пункта к отображениям, указанным в начале этого пункта. Детали
мы оставляем читателю.
3. Трансгрессия. Рассмотрим дифференциалы
Л'П pin _*rm jO.m-l. p0,m-l.pm,0
in.О' in,0 in ' m m
гомологической и когомологической спектральной последовательности расслое-
ния (E,B,F,p). Как уже было сказано, Е™п 0 и Е^’"1-1 - подгруппы групп
Я„, (В; G) и Н’”-1 (F; G), a E™m i и Е™’° - факторгруппы групп (F; G)
и Я"' (В; G). Поэтому указанные дифференциалы имеют вид
подгруппа группы Н„, (5; G) факторгруппа группы Hm-AF-, G)
►
подгруппа группы Я'”-1 (Я; G) факторгруппа группы Нт (В; G)
Вообще гомоморфизм подгруппы абелевой группы А в факторгруппу абелевой
группы В называется (по понятным причинам) частичным многозначным гомомор-
физмом группы А в группу В. Мы будем использовать в этом случае запись
А------* В. Важно, что частичные многозначные гомоморфизмы всегда допускают
обращение; в частности, для любого обыкновенного гомоморфизма существует
обратный частичный многозначный гомоморфизм.
Итак, наши дифференциалы — это частичные многозначные гомоморфизмы
H,n(B'G) --------^^„..(F.G),
Hm~\F',G)-------->Hm(B;G).
Эти гомоморфизмы называются, соответственно, гомологической и когомологи-
ческой трансгрессией (рис. 98).
Элементы, входящие в область определения трансгресии, называются трансгрес-
сивными. Насколько нам известно, этот термин употребляют только в когомоло-
гической ситуации.
Теорема. Гомологическая и когомологическая трансгрессии совпадают, соот-
ветственно, со сквозными гомоморфизмами
(ptF1 э*
Яш(В;С) = Ят(В,*;С)---> Hm(E,F'G)->Hm_1(F,G),
Hm-1 (Я; G)Hm (Е, F- G)--- —>Нт (В, *',G) = Hm (В; G).
§ 22. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА
207
Доказательство (в гомологическом случае, G = Z). Можно считать, что
В имеет единственную нульмерную клетку (см. п. 9 § 5). Дифференциал 0 устро-
ен так. Группа Е^ 0 = ZJ" 0 состоит из цепей с G С,„ (р-1 (В'")) С С,„ (В), граница
которых принадлежит Ст_ i (р(В0)) = C,„_i(B) (т.е. из относительных цик-
лов с G Zm (р~1 (В"') , F) , рассматриваемых по модулю цепей из Ст (р~1 (Вт~ *))).
Отождествление с подгруппой группы Н,„ (В) производится при помощи отобра-
жения с [р# с], квадратные скобки обозначают гомологический класс (это оче-
видно непосредственно, а также формально следует из результатов п. 1, примененных
р р и
к отображению (Е -+ В) Дифференциал с?'" 0 переводит класс цепи с в
класс цикла Эс G С,„_ । (F), что равносильно нашему утверждению.
4. Применение: три точных последовательности. В п. 7 § 20 мы столкнулись с
ситуацией, когда информация, заключенная в спектральной последовательности,
может быть записана в виде точной последовательности. Сейчас мы познакомимся
еще с тремя такими ситуациями. Из получающихся трех точных последовательнос-
тей две первых были построены задолго до появления спектральных последователь-
ностей.
А. Последовательность Гизина. Пусть (В, В, Sn, р) — (гомологически простое)
расслоение со сферическим слоем. Устройство члена Е2 соответствующей (гомоло-
гической) спектральной последовательности показано на рис. 99. Априори не три-
виален только (н + 1)-й дифференциал, и он действует, как показано на рис. 99:
Вис. 99
^"10: (В’ (В', G). В члене Е°° остаются группы
В“0 = Кег(/"*‘СЯ,„(В:6’),
Таким образом, в члене Е°° на каждой линии р + q ~ m стоит не более двух нетри-
виальных групп, и мы можем написать
Н,,, (В; G) D EZ _ „, И,„ (В; G’)/B~ _ „ „ = В“ 0,
что записывается, в свою очередь, в виде точной последовательности
0 -> В,7, -> H,„{F.G) -> В,7,. о -> 0.
т.е.
0 Нп1 Im + Ker</Wto“> 0,
208
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
т.е.
п + 1
dm +1, О
-------> tfm_„(B;G) +Hm(E,G) -+
п+1
dm, О
-> Hm{B,G) ------► Ят_„_1(В;С).
Сращивая такие пятичленные фрагменты в одну точную последовательность, мы и
получаем последовательность Гизина
I Pt d
... - Hm_n(B-,G) -> Hm(E,G) -> Hm(B;G) — - ...
Аналогичным образом строится, также точная, когомологическая последователь-
ность Гизина
i Р* d ,
... +-Ят -"(В; G) <-Нт(Е-,G) <— Нт(В‘,G) *-Hm'n \B,G)+- ...
Все гомоморфизмы последовательностей Гизина имеют более или менее прозрач-
ный геометрический смысл.
Упражнения. 1. В последовательности Гизина гомоморфизм р, индуцируется
проекцией, гомоморфизм I (” lifting”) ставит в соответствие гомологическому
классу цикла гомологический класс его полного прообраза (придайте этому выска-
зыванию точный смысл), гомоморфизм d (дифференциал) есть -умножение на
характеристический класс G Нп + 1 (В; Z) расслоения (в смысле §18) (доказатель-
ство этого утверждения лучше отложить до п. 5 и следующего параграфа).
2. В когомологической спектральной последовательности Гизина гомоморфизм р*
индуцируется проекцией, гомоморфизм d есть -умножение на характеристический
класс, а гомоморфизм i есть в гладкой ситуации послойное интегрирование (послед-
нее утверждение должно быть понятно читателю, немного знакомому с теорией
де Рама).
(В гладкой ситуации гомоморфизмы I и i являются специальными случаями об-
ратных гомоморфизмов, рассматривавшихся в п. 7 § 17.)
В. Последовательность Вана. Рассмотрим теперь расслоение (Е, Sn, F, р) со сфе-
рической базой. Спектральная последовательность этого расслоения похожа на преды-
дущую спектральную последовательность, только нетривиальные группы заключены
теперь не в двух строках, а в двух столбцах. Мы снова получаем точную последова-
тельность (в гомологическом и когомологическом случае)
... G) —^Hm(E\ G)-^Hm_n(F- G) _ t(F; G) —...,
... *— Я"1 (F; G) Hm (E; G}<^-Hm~ n(F- G)^ Hm X (F; G) —>...
Эти точные последовательности называются последовательностями Вана.
Упражнения. 3. Восстановите детали построения последовательности Вана и
докажите, что ее гомоморфизмы имеют следующий геометрический смысл (в гомо-
логическом случае). Гомоморфизм it индуцирован включением слоя F в Е, гомо-
морфизм г определяется операцией пересечения циклов с F, гомоморфизм d
§ 22. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА
209
устроен так. Сфера Sn разрезается на два полушария, D" и Dn_, пересекающиеся
по экватору Sn -1. Соответственно, Е = (£)" X F) U (£)" X F) (расслоения над D"
и Dn_ тривиальны по теореме Фельдбау). Мы берем цикл с слоя F, образуем произве-
дение Dn+ X с и пересекаем зто произведение с (£>” X F) Л (£>" X F) = Sn~l X F.
Пересечение мы подвергаем проекции S”-1 X F -> F. В F получается новый цикл,
на и — 1 большей размерности, чем цикл с.
4. Опишите геометрический смысл гомоморфизмов когомологической спектраль-
ной последовательности Вана.
(Ср. снова с п. 7 § 17.)
С. Последовательность Серра. Предположим теперь, что у расслоения (Е, В, F, р)
база л-связна, а слой (л — 1)-связен. Член Е2 этой спектральной последовательности
имеет вид, показанный на рис. 100 (и знакомый нам по п. ЗВ § 21). В этом случае
при m < 2 л + 1
ст - с-2 с"1 - с2
^т, О ^m,0> ^0,m —1 ^0,m —1
и при т < 2 л трансгрессия
г. Hm(B,G) -+Hm_i(F;G)
является не частичным многозначным, а настоящим гомоморфизмом. Далее
при т < 2 л
Ео,™ = Hm(F, G)/1т т С Hm(E;G),
Ет, о = Кегт = Hm(E-,G)IE0,m,
что записывается в виде точной последовательности
«♦ р» т
... -> Hm(F-,G) -> Hm(E,G)-+Hm(B,G) -> Hm_i(F,G) -> ...,
внешне напоминающей гомотопическую последовательность расслоения. Это и есть
Рис. 100
последовательность Серра. Ее отличие от гомотопической последовательности рас-
слоения состоит в том, что последняя бесконечна, а последовательность Серра
конечна:
H2n(F-G) - H2n(E;G) - ... -> Hn(F-G) - Hn(E;G) - 0.
Если в рассматриваемой ситуации пространство Е ациклично (хотя бы в размер-
ностях < 2 л), то мы видим, что трансгрессия т: Нт(В-, G) -^Hm_l{B', G) являет-
ся изоморфизмом при т < 2 п. Читатель помнит, конечно, что мы пользовались этим
210
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
фактом в § 21, когда мы еще не знали слова ’’трансгрессия”. Там мы рассматривали
п х
серровское расслоение ЕХ ---> X. Теперь мы можем доказать неявно использовав-
шееся там
Предложение. Трансгрессия Нщ (X; G) -> Н,п _ i (£2 X; G) является при вся-
ком ш частичным многозначным отображением, обратным гомоморфизму
v <ях>,
Н„, tCSIXiG) H„,(WX\G)------------* Hm(X-,G).
Для доказательства рассмотрим вспомогательное отображение <р: С£1Х -> EX
(С обозначает конус), ставящее в соответствие петле s и числу t & [0,1] ’’укорочен-
ную петлю” — путь т х(гт). [Это отображение иллюстрирует тот факт, что слой
ПХ стягиваем в ЕХ.] Еще мы рассмотрим отображение тгх: СПХ -> X, опреде-
ляемое, как и яЛ, формулой (s, г) •-> s (т), и составим диаграмму
(мы изгоняем из обозначений указание на коэффициенты), которая,очевидно,ком-
мутативна. Из коммугативности видно, что гомоморфизм (ух)* ° S: Hltl_t(£lX) -*
(X) обратен трансгрессии Э, о (р,)-1: Н,„ (X) ->H„,_i (ПХ).
5. Трансгрессия и характеристический класс. Пусть % = (Е, В, F, р) - гомологи-
чески простое расслоение, и пусть тг„ (F) = тг есть первая нетривиальная гомото-
пическая группа слоя F. Рассмотрим когомологическую трансгрессию
т: Hn{F.ir) -* Нп+\В-,я}.
BHn(F; тг) лежит фундаментальный класс с,.- (см. п. 3 § 18), характеризующий-
ся тем своим свойством, что его значение на /г-мерном сфероиде пространства F,
расссматриваемом как «-мерный цикл, равно классу этого сфероида в тг„ (F) = тг.
Упражнения. 5. Образ т (еР) G Я"+1(Д; я) фундаментального класса при
трансгрессии совпадает с характеристическим классом расслоения £ — первым пре-
пятствием к построению сечения. [Указание. Нужно доказать, что фундаментальный
и характеристический классы имеют одинаковые образы при гомоморфизмах
н"(Е;л)
Пп'\е,Е-, л ).
Эти образы равны, в действительности, первому препятствию к распространению тож-
дественного отображения F -*F па Л’.[
6. Найдите аналог упражнения 5 для гомологически непростых расслоений.
§ 23. МУЛЬТИПЛИКАТИВНАЯ СТРУКТУРА
211
§ 23. МУЛЬТИПЛИКАТИВНАЯ СТРУКТУРА
В КОГОМОЛОГИЧЕСКОЙ СПЕКТРАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
До сих пор мы попеременно рассматривали то гомологическую, то когомологи-
ческую спектральную последовательность и не видели между ними особых различий,
разве что стрелки переворачивались. Однако опыт предыдущей главы научил нас, что
когомологии лучше гомологий, поскольку они обладают мультипликативной струк-
турой (и другими отсутствующими в гомологиях структурами, скажем мы, имея
в виду следующую главу). В этом параграфе мы внедрим мультипликативную
структуру в когомологическую спектральную последовательность.
1. Формулировки: свойства мультипликативной структуры. Предположим, что об-
ласть коэффициентов G является коммутативным кольцом, скажем, есть Z или поле.
Мы построим в каждом члене Ег (с г > 2) когомологической спектральной после-
довательности расслоения, (Е, В, F, р) (с клеточной базой) косокоммутативное
(по отношению к полной степени р + q) умножение, обладающее следующими свой-
ствами.
1°. Умножение биоднородно, т.е. если a G ЕР’ 4, /3 G ЕР ' 4 , то аД G ЕРГ+Р ’ 4+4 .
о Р» Q
2 . Дифференциал dr удовлетворяет формуле Лейбница: если a G Е г , 0 G
е ер'' то
, ч + ч _ ^Р, + ^_1у’+ч0(^Р ’ Ч &
3°. Умножение в Ег + 1 индуцируется умножением в Ег : если элементы а, 0ЕЕг + 1
представляются dr-циклами a,b G Ег , то а$ представляется <7г-циклом ab.
4°. Умножение в £2 совпадает с умножением в когомологиях базы В с коэффи-
циентами в кольце H*{F\ G). (Эта формулировка относится к гомологически прос-
тому случаю; в общем случае ее следует модифицировать, введя мультипликативную
структуру в когомологии с локальными коэффициентами, — это мы оставляем
читателю).
5°. Умножение в Е°° присоединено к умножению в Н* (Е; G) в следующем
смысле: если а 6 ^Нт (Я; G), b е <' >ЯЛ(Е; G), то ab е <к + г ^Нт + п(Е- G) и
представляемые а, о. и ab элементы а, р и у групп Еж , Ех и
к+1, т+ п— к— I .
Ех удовлетворяют соотношению у = ар.
В связи с утверждением 5 ° мы введем алгебраическое понятие, которое нам будет
полезно и впредь. Пусть А — кольцо, и пусть
... С А.! С Ао С Xi С ... С А
— фильтрация в кольце А, рассматриваемом как абелева группа. Эта фильтрация назы-
вается мультипликативной, если A^Ai С Ak+i при любых к, I. Группа GA =
= ® (Ap/Ap-i), присоединенная к Л по отношению к мультипликативной фильтра-
ции { Ар}, является градуированным кольцом: если а 6 AkjAk-\, b G Ai/Ai-i и
a Аь , $ Af — представители классов а, Ь, то класс произведения аД 6 Ак+/
в Ak + i /Ак+i -1 зависит только от а и b и принимается за ab.
Заметим, что в известном отношении умножение в присоединенном кольце GA
беднее, чем умножение в исходном кольце А. Например, из того, что в GA произве-
212
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
дение любых двух элементов равно 0, следует лишь, что A^Ai С Ak + i-i
(сдвиньте на 1 фильтрацию в произвольном мультипликативно фильтрованном коль-
це и вы получите кольцо с этим свойством). Напротив, всякое утверждение о нетри-
виальности умножения в GA влечет за собой, как правило, аналогичное утверждение
для А: например, если в GA отсутствуют делители нуля, то они отсутствуют и в Л
(докажите!).
2. Построение умножения. Сначала опишем общую алгебраическую ситуацию,
в которой спектральная последовательность оказывается мультипликативной.
Предположим, что А — фильтрованное дифференциальное градуированное кольцо,
т.е. что в абелевой группе А заданы: умножение, градуировка А = ® Аг, фильтрация
{Лр} и дифференциал d: А -* А, которые согласованы между собой в следующем
смысле: ArAs С Аг + з, АРА<, С Ар+<1, d(Ar) С Ar+1, d(Ap) С Ар, Ар =
= ®г (Ар Г\АГ) и d(ab) = (da)b + (—\)radb при а £ Ar, bGA.B этой ситуации ум-
ножение в спектральной последовательности определяется очевидным образом:
кольцо Ео получается из А посредством присоединения, и прямая проверка показы-
вает, что
" z"'с
что и позволяет определить умножение в Ег , обладающее всеми нужными свойства-
ми, кроме свойства 4°, о котором говорить преждевременно.
Теперь осталось совсем немного: определить в коцепях пространства Е рас-
слоения (Е, В, F., р) с клеточной базой В умножение, которое было бы согласовано
указанным выше образом с уже имеющимися в этих коцепях дифференциалом, гра-
дуировкой и фильтрацией. Такое умножение определяется формулой с1с2 -
= D*(ci X с2)> где D — подходящая аппроксимация диагонального отображения
Е -*Е X Е. Эта аппроксимация строится так. Рассмотрим диаграмму
Е Е X Е
р Р* Р
а "
В —* В X в,
в которой d и d — диагональные отображения. Пусть dt — гомотопия отображения
d = d0, приводящая его к клеточному отображению dr. Построим накрывающую го-
мотопию dt отображения d (строго говоря, это — гомотопия, накрывающая гомото-
пию dto р: Е ->В X В). Отображение dr — это и есть нужное нам отображение D.
Упражнение 1. Докажите, что построенное отображение обладает свойст-
вом 4°.
3. Первое применение: когомологии группы SU(n). Теперь мы имеем возмож-
ность проделать до конца вычисление, начатое в п.ЗА § 21.
Теорема. Я*(5С7(л); Z) a H*(S3 X Ss X ... X S2""1; Z); изоморфизм
мультипликативен.
§ 23. МУЛЬТИПЛИКАТИВНАЯ СТРУКТУРА
213
Замечания. 1 °. Топологи чаще пере-
дают формулировку последней теоремы в ви-
де: H*(SU(n)-, Z) есть внешняя алгебра
(над Z) с образующими размерностей 3, 5,...,
2п - 1; это означает следующее: как коль-
цо с единицей Я*(5Я(л); Z) порождается
образующими Xj, i = 2, 3,..., п, dim xt =
= 2i — 1, связанными соотношениями xtXj =
= -XjXi,x* =0.
2°. Из теоремы следует, что спектральная
последовательность п. ЗА § 21, вырожден-
ность которой мы доказали при п < 4,
вырождена всегда: из наличия у этой спек-
тральной последовательности нетривиальных
что при больших л
дифференциалов следовало бы,
гапкЯ,(5Я(л)) < гапкЯ,(53 X S5 X ... X S2"-1),
что противоречит, ввиду совпадения рангов соответственных гомологических и кого-
мологических групп, нашей теореме.
Доказательство теоремы. Применим индукцию по л (при л = 2 наше
утверждение заведомо верно) и рассмотрим член f2 спектральной последователь-
SU(n-1) 2я_.
ности расслоения SU(n) ------► S (рис. 101). Как мы заметили в §21,
соображения размерности не гарантируют тривиальность дифференциалов этой
спектральной последовательности. Однако дифференциалы, которые могли бы
быть нетривиальны, прилагаются не к мультипликативным образующим кольца
Я*(SU(n — 1); Z), а к разложимым элементам. Образующие же имеют размерности
3, 5, ..., 2л — 3, и от них дифференциалы тривиальны. Значит, все дифференциалы
спектральной последовательности тривиальны — в силу формулы Лейбница.
Доказательство, однако, на этом не кончается. Мы доказали аддитивный изомор-
физм Я* (SU(n); Z) “ Я*(53 X S5 X ... X S2n-1; Z), а должны доказать мульти-
пликативный (это нужно и для индукции). Из доказанного следует, что в
Я*(51/(л); Z), i =3,5,...,2л— 1, имеются элементы х3, х5, .... x2„_j, такие, что
образы элементов х3, х5, ..., х2„_3 в кольце H*(SU(n — 1); Z) являются образую-
щими этого кольца, a x2n-i есть образ стандартной образующей группы
Я2я-1(52”-1; Z) при гомоморфизме, индуцированном проекцией SU(n) -*S2"-1.
Нам достаточно показать, что мономы х* х$’ ... где is = 0 или 1, составляют
аддитивный базис в Я‘(St/(л); Z) (отсутствие в Я*(SU(n) ; Z) кручения гаранти-
рует выполнение равенств х$ = 0). Возьмем любой элемент кольца Я*(SU(л); Z).
Из доказанного следует, что он представляется в виде целочисленной линейной ком-
бинации указанных мономов с точностью до элементов большей фильтрации.
Но элементы большей фильтрации сами представляются в виде комбинаций наших
мономов с точностью до элементов еще большей фильтрации, и так далее.
Теорема доказана.
У п ражнение 2. Я‘(СИ(л,к); Z) =* Я‘(52 (я~ k> + 1 Х52(я-*)+3 X ...
X S2n-‘ Z)
214
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
4. Когомологии других классических групп.
А. Упражнение 3. Покажите, что (мультипликативно) Я‘(£р(л); Z)
5£H*{S3 X S7 X ... X S4"-1; Z).
В. Теорема. Если К = Q, R или С, то
Н* (SO(n)-, К) =
( Я‘(53 X S1 X ... X S4"1-1;»), если п = 2m + 1,
I Я*((53Х57Х ... XS4'”-s)XS2'"-1;K), если п = 2т.
Доказательство. Поскольку SO (2) =S1 и SO (3) = RP3 (см. § 1), при
л = 2 и 3 зто нам известно. Предположим, что утверждение доказано для SO (л’)
сл’< л,и рассмотрим сначала случай нечетного л. Отображение SO (л) -»К(л, 2),
относящее ортогональной матрице совокупность первых двух ее строк, определяет
расслоение
SO(n-2)
SO(n)--------Г (л, 2).
Лемма. Если п нечетно, то H*(V (л, 2); К) = Я*(52"-3; К).
Доказательство. Член Е2 спектральной последовательности расслоения
s"~2
V(n, 2) ---> Sn 1 (с коэффициентами в К) изображен на рис. 102. Априори не из-
вестен дифференциал Z -> Z, но фактически мы его дважды вычисляли:
вп.ЗС § 19 (Я„_2(К(л, 2)) = Z/Imdn-^o = я„_2(К(л, 2)) =Z2 при нечетном л
и Z при четном л; поэтому гомологический дифференциал есть умножение на 2 при
нечетном л и 0 при четном л, и, по соображениям двойственности, то же верно для
когомологического дифференциала) и в п.5 §22 (d*lj 2(1) есть эйлеров класс
нашего расслоения, которое не отличается от сферического расслоения, ассоцииро-
Рис. 102
Рис. 103
§ 23. МУЛЬТИПЛИКАТИВНАЯ СТРУКТУРА
215
О, п—2
ванного с касательным; поэтому a ni (1) = 2 при четном п — 1 и 0 при нечетном
п — 1). Таким образом, H*(V(п, 2); Z) = H*(S"~1 X S"-2; Z) при четном п, а
при нечетном п
Hq(V(n, 2);Z) =
Z при q = 0, 2 п - 3,
Z2 при q = п - 1,
О при остальных q,
откуда и следует наше утверждение.
Вернемся к расслоению SO (л) + V(n, 2). Второй член его когомологической
спектральной последовательности показан на рис. 103. Повторяя слово в слово аргу-
ментацию предыдущего пункта, мы доказываем, что
Я‘(5О(2лг+1);К) = Я‘(53 X S7 X ... X S4m~ К).
Выделим еще одно следствие из тривиальности дифференциалов спектральной по-
следовательности рассматриваемого расслоения: отображение Я*(5О(2лг+1); К) ->
~+H*(SO(2m- 1); К) эпиморфно.
Рассмотрим теперь расслоение
SO(2m) S~m~1X 52m-i
(см. рис. 104). Соображения размерности не обеспечивают тривиальности дифферен-
циалов соответствующей спектральной последовательности, но все же они тривиаль-
ны: сквозное отображение
Я*(5О(2т+1);К) ^-Я*(5О(2ш);К) 4я*(5О(2щ-1);К),
индуцированное сквозным включением SO (2 т - 1) + SO (2 т) ->SO(2 т + 1), яв-
ляется, как мы показали, эпиморфизмом, а значит, эпиморфна и стрелка, помеченная
звездочкой. Последнее равносильно тривиальности дифференциалов рассматривае-
мой спектральной последовательности (образ гомоморфизма * совпадает с ядром
дифференциалов). Доказательство теоремы закончено.
С. Теорема. Имеет место (аддитивный) изоморфизм
H*(SO(n), Z2) ~ Н*(5г X S2 X ... ХУ 'Л).
Более того, существуют элементы x„>t = xt Е Hl(SO(n)-, Z2), i = 1, 2, ..., п — 1,
обладающие следующими свойствами:
(1) мономы xti ... xis, 1 < ii < ... < is < n — 1, составляют в H*(SO(ri)-, Z2)
аддитивный базис-,
(2) x„t t c i < n — 1 переходите x„^itt при гомоморфизме, индуцированном
включением SO(n - 1) -+SO(ri);
(3) x„t n-i есть образ образующей группы H"~l(S"~1-, 7^) при гомоморфизме,
индуцированном проекцией SO(ri) -^S"~1.
Доказательство. Применим индукцию по п. При л = 2 утверждение верно.
SO(n-l)
Рассмотрим спектральную последовательность расслоения SO(n) -------► S
216
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
Рис. 105
Нужно доказать только, что дифференциал (трансгрессия)
d°’-V2: Я"“2(5О(п- 1);^) ->
переводит хп_2 в 0 (все остальное выводится уже привычным для нас образом
из свойств спектральной последовательности). Для доказательства равенства
О, п —2
d п-i (*п - г) = О мы рассмотрим отображение
SO(n) --------► V(n, 2)
SO(n-l) Sn~2
расслоения в расслоение и соответствующий гомоморфизм спектральных последова-
тельностей (рис. 105). Из индуктивного предположения следует, что в членах
О,п-2 п- 2,„п— 2 _ ч
Е2 гомоморфизм переводит образующую группы Н (S ; Z2) в
x„_2 G Hn~2(SO(n — 1); Z2); но в спектральной последовательности расслоения
V(n, 2) Sn~l наш дифференциал, как мы уже знаем, есть 0 (по модулю 2).
Значит, он есть 0 и в нашей спектральной последовательности.
3 амечания. 1. Из теоремы видно, что Я‘(5О (2 w+l); Z2) ^H*(Sp(m+T); Z2),
хотя, как это видно из пп.А, В, H*(SO(2m+l); К) = H*(Sp(m+l); К) прн
K = Q, R, С.
2. Теорема не описывает полностью кольца H*(SO(n); Z2), поскольку остается
неизвестным, чему равно х2. Например, 50(3) = RP3, когомологии RP3 аддитивно
порождаются элементами 1,х, х?, х3, xG№(RP3 ; Z2). Значит, х2 =х2 прип = 3
(а тогда и при п > 3). В действительности верно следующее утверждение. Кольцо
H*(SO(ri); Z2) порождается элементами j>i GЯ2*-1 (SO (n); Z2),/«=1,2. [л/2],
к/
которые связаны (кроме соотношений коммутативности) соотношениями у2 - О,
§ 23. МУЛЬТИПЛИКАТИВНАЯ СТРУКТУРА 217
w • П
где 2 — такая степень двойки, что п < г • 2 < 2 л. Другие сведения о когомоло-
гиях групп Ли и литературные указания читатель может найти в статье Фукса ’’Клас-
сические многообразия” (Итоги науки и техники. Современные проблемы математи-
ки. Фундаментальные направления. Т. 12. — М.: ВИНИТИ, 1986).
5. Еще один пример (иллюстрирующий коварство мультипликативной присоеди-
ненности). Читатель заметил, конечно, что в доказательстве теоремы п. 3 мы осу-
ществляли переход от Е°° к Н*(Е) с большой осторожностью, хотя в конце концов
эти кольца оказались изоморфными. Мы покажем сейчас, что зта осторожность
не была излишней.
Предположим, что нам задано расслоение (Е, S2, S2, р) с базой S2 и слоем S2
(мы не уточняем, какое именно). Член Е2 когомологической спектральной последо-
вательности этого расслоения с коэффициентами в Z показан на рис. 106. По сообра-
_ _ _ _ 0,0
жениям размерности Еж = Е2, т.е. Е^ аддитивно порождается элементами 1 6 Ех ,
0,2 2,0 2,2
хЕЕ„ , у Е Е ж , хуЕЕ„ . Соответственно Н (Е; Z) аддитивно порождается
элементами 1 Е Н° (Е; Z), х, у ЕН2 (Е\ Z), z" Е Н4 (Е\ Z). Здесь у — образ об-
разующей группы Я2(52; Z) — вполне определенный элемент. В противополож-
ность этому, элемент х - представитель класса х Е Е°^ = Я2 (S2; Z)/£’t’° -
определен с точностью до слагаемого вида ку. Наконец, z G Я4 (Я; Z) = Е^ —
снова вполне определенный элемент. Из присоединенности кольца Е°° к Н*(Е-, Z)
мы заключаем, что j' 2 = 0, ху = z, а х2 имеет нулевой образ в факторгруппе я!’°
группы Я (Е; Z), что ни о чем не говорит, ибо Е „ =0. Таким образом, х 2 = Xz,
где X — не известное нам целое число. Мы можем воздействовать на X, прибавив
к х элемент, кратный у: (x + fcy)2=x2 + 2кху + к2 у2 = (X + 2 к) ~z. Поэтому
принципиально возможны два случая: X четно и X нечетно. (Кольца с четным н нечет-
ным X не изоморфны хотя бы потому, что в случае нечетного X элемент z является
квадратом, а в случае четного X не является.) Покажем, что обе эти возможности
реализуются геометрически.
Случай четного X реализуется тривиальным расслоением. Этот случай неинтересен,
поскольку в нем мы опять имеем мультипликативный изоморфизм Е<ю= Н *(£’; Z).
Построим теперь нетривиальное расслоение с базой и слоем S2. Возьмем на ком-
плексной проективной плоскости СР2 точку а и не проходящую через нее прямую
СР1. Построим не пересекающийся с СР1 шар D4 с центром а и положим
X- СР2 — IntD4. Это — четырехмерное многообразие с краем S3. Проведем через
а всевозможные (комплексные) прямые. Они не пересекаются между собой в X,
и каждая из них пересекается с Jfno двумерному диску и с СР1 по точке (’’центру”
218
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
этого диска). В результате X расслаивается над СР1 = S2 со слоем D2 (на bX=S3
это — обычное хопфовское расслоение S3 над S2 со слоем Sl = bD2). Возьмем два
экземпляра такого X и срастим их по ЬХ так, чтобы слои первого расслоения
срастались со слоями второго расслоения. Получится расслоение с базой S2 и слоем
S2 = D2 U D2. Пространство Е этого расслоения — это так называемая связная сум-
ма двух экземпляров многообразия СР2.
(Связная сумма двух связных л-мерных многообразий определяется так:
в каждом из них высверливается шаровое отверстие и края этих отверстий сшивают-
ся или, что эквивалентно, соединяются трубочкой Sn~l X / - см. рис. 107.)
Рис. 107
3 а ьЛ ч а н и е. Если в этой конструкции вместо С взять R, то X станет лентой
Мёбиуса, а Е — бутылкой Клейна, которая является связной суммой двух RP2
(разберитесь в этом).
Когомологии многообразия Е можно найти, например, пользуясь последователь-
ностью Майера — Виеториса (см. п. 6 § 12), применяемой к разложению Е = XU X,
X П X = S3. Кольцо Н*(Е; Z) содержит два подкольца, изоморфных Н*(СР2; Z) и
пересекающихся по Я0 ® Я4; другими словами, кольцо Н*(Е\ Z) аддитивно порож-
дается элементами 1 е Я°, х, у.Е Я2 и z G Я4, причем х2 =у2 = z, ху = 0 (двумер-
ные циклы, лежащие в одном СР2, не пересекаются с двумерными циклами, лежа-
щими в другом СР2). Мы видим, что кольцо Н*(Е‘, Z) не изоморфно (мультипли-
кативно) кольцу Я ‘(S2 X S2; Z) (z есть квадрат), откуда вытекает все, что нам
нужно: расслоение нетривиально и в спектральной последовательности имеется не-
тривиальная мультипликативная присоединенность члена Е°° к Я*(52 X S2; Z).
В заключение — несколько упражнений на применение спектральных последова-
тельностей.
Упражнения. 4. Известны гомологии замкнутого ориентируемого «-мерного
многообразия X. Найдите гомологии многообразия единичных касательных век-
торов к X.
5. Найдите (уже известное вам) кольцо когомологий многообразия СР”, поль-
зуясь спектральной последовательностью расслоения Хопфа S2n + 1 ->• СР”
(со слоем S1).
6. Найдите кольцо когомологий с коэффициентами в Q многообразий
SU(n)ISO(n).
7. Найдите кольцо когомологий с коэффициентами в Q многообразия
SO(2n)ISU(n) с небольшими п (первый интересный случай: л=3).
§ 24. МЕТОД СЕРРА ВЫЧИСЛЕНИЯ ГОМОТОПИЧЕСКИХ ГРУПП
Этот и два следующих параграфа (а также значительная часть последующих глав)
будет посвящена проблеме вычисления гомотопических групп. Мы начнем с того,
что приведем отрывок из интервью, которое дал Жан-Пьер Серр в феврале 1985 г.
в Сингапуре (см. Math. Intelligencer. — 1986. — 8, № 4. — Р. 8—13).
§ 24. МЕТОД СЕРРА ВЫЧИСЛЕНИЯ ГОМОТОПИЧЕСКИХ ГРУПП
219
Вопрос. Были ли в Вашей практике случаи, когда Вы находили проблему
не поддающейся решению и откладывали ее на некоторое время, а затем к Вам
внезапно приходила идея, ведущая к решению?
Ответ. Конечно, это часто случалось. Например, когда я занимался гомотопи-
ческими группами (~195О г.), я пришел к убеждению, что для данного пространст-
ва X должно существовать расслоенное пространство Е с базой X, которое было бы
стягиваемо; такое пространство должно было позволить мне проделать (при помощи
методов Лере) массу вычислений гомотопических групп и когомологий Эйленбер-
га — МакЛейна: Но как найти его? Прошло несколько недель (очень большой срок,
если принять во внимание мой тогдашний возраст1) . . .), прежде чем я понял, что
нужными свойствами обладает пространство ’’путей” на X — если бы я осмелился
назвать его ’’расслоенным пространством”, — что я и сделал. Это было началом
метода пространств петель в алгебраической топологии. Многочисленные результа-
ты были получены в скором времени.
1. Когомологии пространств петель. Первоначальный метод Серра вычисления
гомотопических групп состоял в следующем. Предположим, что мы хотим найти
гомотопические группы пространства X. Рассмотрим последовательность прост-
ранств X, SIX, S1S1X, SISI SIX, . . . Предположим, что мы располагаем способом,
позволяющим находить когомологии пространства 12 Y, если известны когомоло-
гии пространства Y. Тогда мы можем найти первую нетривиальную гомологическую
группу пространства SlkX при любом к, т.е., в силу теоремы Гуревича, первую не-
тривиальную гомотопическую группу этого пространства. Но при г > 1
1,г(ЪкХ) = яг+к(Х),
поэтому всякая гомотопическая группа пространства X станет при некотором к пер-
вой нетривиальной гомотопической группой пространства SlkX. Вычисление же кого-
мологий пространства 12 Y можно попытаться проделать' при помощи спектральной
яг
последовательности расслоения Е Y--► Y.
Мы не будем пользоваться здесь этим методом Серра, а отдадим предпочтение
другому методу Серра - ’’методу убивающих пространств”, который примерно
эквивалентен методу пространств петель по своим возможностям, но алгебраичес-
ки более благоустроен. Однако для иллюстрации петлевого метода мы приведем
здесь поучительное вычисление когомологического кольца пространства петель
сферы.
Теорема.
„ I Z при q = 0, п — 1, 2(л — 1),...,
H4(sisn-,Z) =
I 0, если q не делится на п - 1.
Далее, существуют образующие е Як("-1)(£25"; Z), такие, что xkxt = ак1хк + 1,
где
с1 +1’ С(к + D/2-’ если п нечетно, еслики! четны,
<*к,1 = (-.1/2 ^к + 1-\)/2’ если к нечетно, 1 четно, и п четно.
0, если kul нечетны
Доказательство. Рассмотрим Z-когомологическую спектральную последо-
ях"
вательность расслоения ESn-----* S". Член Е2 состоит из двух совершенно одина-
1) ~ 24 года. - Примеч. авторов.
220
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
ковых (но пока не известных нам) столбцов: 0-го и л-го, в которых стоят когомо-
логии Я*(125"; 2). Дифференциал dn должен уничтожить все, кроме Е§'°, поэтому
Е"’4 ^E§’q + n~1 при 4 +п >0,т.е.Я’(П5";2)^Я’ + "-1(П5";2) (в сущности,
мы пользуемся здесь точной последовательностью Вана). Значит, Hq(£lSn; 2) as
дяz), откуда следует первое утверждение теоремы. Более
того, если® - образующая группы Я "(S"; 2) = £2;’°, то в группах Hk('n~i\£lSn,Z) =
— 2 можно (единственным образом) выбрать образующие хк таким образом, что
d»(xi) ~ STndn(xk) = sxk_ 1, к> 1 (рис. 108). По соображениям размерности должно
бьггьхкх/ = ак txk + l, а1(е2,ив силу мультипликативных свойств дифференциала
<ln(xkxi) = dn(akJxk + l) = +
dn(xkxi) = (d„xk)xi + (-1)*<" ^dxt =
= SXk_lXl + (-l)k("-1)XkSXl_1 = [Ofc-U + (-l)k(""1)ttfc,/_i]sxk + /_1,
откуда
( ak-i,i + ak,i-t при нечетном n,
I ak-i,i + (-l)k“fcj-i при четном л,
откуда и следует нужное нам утверждение.
2. Метод убивающих пространств. Мы знаем из п. 9 § 11 конструкцию убивающего
пространства: пространство Х|„ + 1 строится по пространству X и обладает следую-
щими свойствами:
При этом, если тгп (X) = тг — первая нетривиальная гомотопическая группа пространст-
ва X, то X | „ +! связано с X двумя расслоениями (на выбор) :
(По большей части мы будем пользоваться вторым из этих расслоений.) Таким об-
разом, если мы знаем когомологии пространств К(тг, л), то у нас есть принципиаль-
ная возможность найти когомологии пространства X | „ +1, а с ними первую нетри-
виальную гомологическую группу пространства У|„ + 1, т.е. вторую нетривиальную
гомотопическую группу пространства X. И так далее.
Рис. 108
Рис. 109
§ 24. МЕТОД СЕРРА ВЫЧИСЛЕНИЯ ГОМОТОПИЧЕСКИХ ГРУПП
221
Пока что мы почти ничего не знаем о когомологиях пространств Эйленберга —
Маклейна. Все же нам известно, например, что ET(Z, 2)= S3 |4, и уже зто позволяет
найти H*(S3 |4;Z).
Теорема.
tf’(S3|4;Z) *
Zm при q = 2т + 1, т = 2,3,...
О при ^¥=5,7,9,11,...
Доказательство. Рассмотрим Z-когомологическую спектральную последо-
K(Z,2)
вательность расслоения S3 |4 -----► S . Ее начальный член показан на рис. 109.
Обозначив через х образующую группы №(СР°°; Z) = Ef2(ET(Z, 2); Z) = Е1®’2 и че-
рез s — образующую группы Е3,0 = H3(S 3; Z), мы имеем:
группа Е2’2т = Z порождаетсяхт,
группа Е3’2т = Z порождается sxm,
остальные группы Е%'4 тривиальны.
Очевидно, Е3 = Ег. Далее, так как H3(S3 |4; Z) = 0, то d®’2: Е$’2 -*Е3,0 есть
изоморфизм (должно быть Е3;0 = 0), т.е. d3(x) = ±s; можно считать (хотя зто и не-
существенно) , что d3 (х) = s. Следовательно,
d3(xm) = rnxm~1d3(x) = msxm~l,
т.е. дифференциал d3 устроен, как показано на рис. 110а, и член Е„ устроен, как
показано на рис. 1106.
Теорема доказана.
‘ Из доказанного и формулы универсальных коэффициентов следует, что
f Zm при q = 2т,
Ha(S3\4) =
I 0 при q ¥= 4, 6,8,...
и, значит, tt4(S3 |4) = Z2 и tt4(S3) = Z2.
Последнее равенство уже известно читателю, пробившемуся через все упражне-
ния в конце § 10. Но даже этого читателя легкость, с которой мы доказали зто
равенство теперь, должна убедить, что с появлением спектральных последователь-
ностей наши возможности вычисления гомотопических групп возросли неизме-
римо.
В то же время ясно, что на первый план выходит теперь задача вычисления ’’кого-
мологий Эйленберга — Маклейна” Н*(К{п, п); —). Этим когомологиям посвящена
значительная часть двух оставшихся параграфов этой главы и всей следующей главы.
а
222
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
§ 25. РАНГИ ГОМОТОПИЧЕСКИХ ГРУПП
Вычисление колец Н*(К(я, и); G) оказалось делом не простым; все же задача
была полностью решена в 50-е годы (для абелевых тг) благодаря усилиям, главным
образом, французских топологов А. Бореля, А. Картана и Ж.-П. Серра. Наиболее
простой частью их работы явилось вычисление колец Н*(К(я, и); Q). Этому вы-
числению и его следствиям и посвящен настоящий параграф, который мы начнем
с полезной общей теоремы.
1. Конечная порожденность и конечность гомотопических групп.
А. Теорема. Если группа я конечно порождена (конечна), то для любой
конечно порожденной группы G и любых п > Qu q>0группаНЧ(К(тг,и);G) конеч-
но порождена (конечна).
Доказательство. Формула универсальных коэффициентов позволяет
считать, что G = Z.
При п = 1 утверждение теоремы верно: нам известны соответствующие пространст-
ва К(я, 1) (K(Z, 1) = 51, K(Z2,1)=RP°°, K(Zm, 1) = L% прим > 2 - cm. n. 7 § 11)
и их когомологии:
ч 0 1 2 3 4 5 6 . . .
S' z z 0 0 0 0 0
RP" z 0 z2 0 z2 0 Z2
z 0 Z/n 0 Z/n 0 Zm
Предположим, что утверждение уже доказано для К (я, п — 1), и пусть оно неверно
для К (я, п). Пусть Нт (К (я, п); Z) — бесконечно порожденная (бесконечная) группа
самой маленькой положительной размерности. Рассмотрим спектральную последо-
Х(я,и-1)
вательность расслоения *-----------> К (я, п), где * обозначает стягиваемое прост-
ранство ЕК(я, п). Из определения числа т, индуктивного предположения и формулы
универсальных коэффициентов следует, что группы E?'q с р <т конечно порожде-
ны (конечны), а группа £’2'"’° бесконечно порождена (бесконечна). Группы E?’q
с р < т получаются из соответствующих групп Е$'4 посредством конечного числа
переходов к подгруппам и факторгруппам, поэтому они тоже конечно порождены
(конечны). (См. рнс. 111, на котором светлые квадраты соответствуют конечно
Рис. 111
порожденным (конечным) группам, а темный квадрат соответствует бесконечно
порожденной (бесконечной) группе.) Поскольку факторгруппа бесконечно порож-
денной (бесконечной) группы по конечно порожденной (конечной) подгруппе не
может быть конечно порожденной (конечной), группы
Е?’° = E?'Q/d™ ~2' 1(Е™-2’1),
= Е^’0/бз'~3’2(Е^-3’2),
§ 25. РАНГИ ГОМОТОПИЧЕСКИХ ГРУПП
223
бесконечно порождены (бесконечны), что противоречит равенству £’m+°i = ’° =
= 0. Теорема доказана.
В. Обобщение. Говорят, что задан клас ё абелевых групп, если для всякой абеле-
вой группы указано, принадлежит или не принадлежит она классу ё, причем: (i) изо-
морфные группы принадлежат или не принадлежат классу ё одновременно;
(ii) если группа принадлежит классу ё, то всякая ее подгруппа и всякая ее фактор-
группа принадлежит классу ё; (iii) если подгруппа И группы G и факторгруппа
G/П принадлежит классу ё, то и группа G принадлежит классу ё . Это определение
имеет многочисленные вариации — см. статью Серра ’’Гомотопические группы и клас-
сы абелевых групп” в сборнике ’’Расслоенные пространства”. Примеры: конечно
порожденные группы; конечные группы; периодические группы; конечные
р -группы.
Упражнение 1. Покажите, что если ё есть некоторый класс конечно по-
рожденных абелевых групп, тг G $ и G есть конечно порожденная абелева группа,
то Hq(K(-n, и); G) при любых q > 0, п > 0.
С. Применение. Теорема. Пусть X - односвязное топологическое пространст-
во, такое, что все гомологические группы Hq(X), q > 0 конечно порождены (конеч-
ны). Тогда и все гомотопические группы nq(X) конечно порождены (конечны).
Замечание. Требование односвязности в этой формулировке не является
лишним: например, у букета S1 v S2 гомологические группы конечно порождены,
а группа ^(S1 v S2) таковой не является. Однако требование односвязности можно
все же значительно ослабить: хватило бы, например, условия гомотопической
простоты.
Доказательство теоремы. Лемма. Если у расслоенного пространст-
ва Е база и слой имеют конечно порожденные (конечные) гомологии в положитель-
ных размерностях и база односвязна, то гомологии пространства Е также конечно
порождены (конечны) в положительных размерностях.
Доказательство леммы. В спектральной последовательности нашего
расслоения конечно порождены (конечны) все группы Е?’4 (кроме Е®’°), а значит,
то же верно для групп Е?’4 с любым г, г < °°, и Hm (Е). Лемма доказана.
Для доказательства теоремы мы последовательно применяем лемму к рас-
слоениям
/С(Я2(Х), 1) К(Н3 (Х13),2)
Х|3------------> X, Х\4---------------->Х\3,...
и получаем, что гомологические группы пространств X13, X14,... конечно порожде-
ны (конечны). Следовательно, группа яп(Х) = //„(Х|„) конечно порождена (ко-
нечна) при всяком п.
Следствие. Группы nq(S3) конечны при q > 4.
Действительно, гомологические группы пространства S3 |4 конечны в силу резуль-
татов п. 2 § 24, а 7tq (S3 ) = irq (S3 |4) при q > 4.
Упражнения. 2. Покажите, что если все гомологические группы положитель-
ной размерности односвязного (или гомотопически простого) пространства X при-
надлежит некоторому классу ё конечно порожденных абелевых групп, то и все
его гомотопические группы принадлежат классу ё.
3. Обобщением этого утверждения служит следующая $-теорема Гуревича:
если у односвязного пространства X группы (2Г) с q < п принадлежат $, то и
группы Hq(X) с q < п принадлежат ё, а гомоморфизм Гуревича пп(Х) ->Нп(Х)
является ^-изоморфизмом, т.е. его ядро и коядро принадлежат ё. Верно и обратное
утверждение, в котором Я и тг меняются ролями. Следствием ^-теоремы Гуревича
224
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
является следующий факт, который будет осмыслен и уточнен в следующем парагра-
фе: для любого простого числа р порядок группы ttq(S3) не делится нар при q < 2р.
Для доказательства достаточно применить (обратную) $ -теорему Гуревича к прост-
ранству S3 |4 и классу *8 конечных абелевых групп, порядок которых не делится
на р.
4. Сформулируйте и докажите относительную *8 -теорему Гуревича и $ -теорему
Уайтхеда.
Подробное изложение -теории” читатель найдет в статье Серра, цитирован-
ной в п. А.
2. Вычисление колец Н* (К (я, и); Q). Пусть тг — конечно порожденная абелева
группа. Тогда я = Z ® ® Z ® G, где G — конечная группа. Соответственно if (я, п) =
= K(Z,n) X ... X K(Z,n) X K(G,ri), и в силу формулы Кюннета
Я‘(К(я,л);<3) = H*(K(Z,ny,Q) ® ... ® H*(K(Z, n);Q) ® H*(K(G,ny,Q).
В силу теоремы из п. 1 А
H*(K(G,ny,Q) = tf‘(pt;Q)
(если целочисленные когомологии топологического пространства конечны, то его
рациональные когомологии тривиальны). Значит, последний сомножитель в форму-
ле для Н*(К(я, л); Q) можно отбросить, и вычислить нужно только #*(A?(Z, и); Q).
Теорема.
( Лл(х), dimx = л, при нечетном п,
H-(K(Z,ny,Q)=
( Q[x], dimx = п, при четном п.
Поясним обозначения в зтой формулировке. Если К есть поле, то через Ak(xi , . ..
. . . , xm) обозначается ’’внешняя алгебра”, порожденная Xj.xm, т.е. К-алгебра
с образующими X/ и соотношениями xzxy = — XjXt, х2{ = 0. Размерность этой алгебры
равна 2т, ее К-базис составляют мономы х^ . . . xis, 1 < < ... < is < т. Буква К
иногда обозначает не поле, а достаточно хорошее кольцо, скажем, Z; иногда ее
не пишут вовсе (когда известно, о каком К идет речь). Формула H*(K(Z, л); Q) =
= Aq(x), dimx = п имеет совсем простой смысл: H*(K(Z, п)', Q) = H*(Sn; Q). Че-
рез К [Xi, ... ,хт] обозначается алгебра многочленов otxj, . . . ,хт с коэффици-
ентами в К. Формула H*(K(Z, л); Q) = Q [х], dimx = п, означает, что Hq(K(Z, л); Q) =
= Q при q = 0, л, 2л, ... , Hq(K(Z, л); Q) = 0 при остальных q aHkn(K(Z, n) ;Q)
порождается над К злементомх*, 0 Фх &Hn(K(Z, л); Q).
Доказательство теоремы. При и = 1 (и л = 2) утверждение нам извест-
но (K(Z, 1) = S1 и K(Z, 2) = СР“). Предположим, что теорема доказана для
K(Z, п — 1) и рассмотрим когомологическую спектральную последовательность
расслоения
---------► X(Z,n)
с коэффициентами в Q. Начнем со случая четного л. Тогда, в силу индуктивного пред-
положения, ff*(K(Z, п - 1); Q) s H*(Sn~ ‘; Q) и член Е2 нашей спектральной после-
довательности выглядит, как показано на рис. 112. Так как = 0 (кроме £2’°),
то Hq(K (Z, л); Q) = Hq~"(£(Z, л); Q) при q > 0, т.е.
( Q при q = 0, л, 2л.....
Hq(K(Z,ny,Q) =
I 0 при остальных q. '
225
§ 25. РАНГИ ГОМОТОПИЧЕСКИХ ГРУПП
Более того, существуют 0 4= 6 Hkn(K(Z, и); Q) - Екп,° = Екп,0,к- 1, 2, ... ,и
О ¥= s е Нп-'(К(г, п - 1); Q) = £’f’""1 = Eq,n~l, такие, что dn(s) = х,, d^sx^
=х2,... (рис. 113). Но тогда
1) ~ &п(.3)хк — 1 — х1хк — 1>
откуда хк = хк. Мы установим изоморфизм между H*(K(Z, и); Q) и кольцом мно-
гочленов Q[Xj ].
Рис. 112
Пусть теперь п нечетно. Тогда Е%'к^п ~ = Q с образующей**1, где* - произволь-
ный ненулевой элемент из Е%,п -1 = Hn~1(K(L, и — 1); Q), и E$,q = 0, если q
не делится на и - 1. Так как, далее, HP(K(L, и); Q)= 0 при 0 < р < п и
Hn(K(Z, п)~, Q) = Q (зто хорошо известно нам, но может быть выведено и из рас-
сматриваемой спектральной последовательности), то Ер’4 = 0 при 0<р<п и
£л,к(л-1) _ q с образующей yxfc,rfleyGZT"(llC(Z>n);Q) = £'"’0 - образх при транс-
грессии. Так как, наконец, в строках с номерами, не делящимися на п — 1, ничего
не стоит, то Е2 =Еп. Имеем:
dn(xk) = kxk~ldn&) = кухк~г ¥= О,
т.е. все£,2,<?сР = 0ии (кроме Е%,0) уничтожаются при и-м дифференциале. Предпо-
ложим теперь, что в H*(K(Z, и); Q) есть элементы размерности, большей и, и пусть
O^z € Hm(K(Z, и); Q) имеет среди них самую маленькую размерность. Но в Ер ’4,
р<т, нет элемента, дифференциал которого мог бы попасть в z Gf™’0 (рис. 114).
Это противоречит равенству Е™’° = 0.
Теорема доказана.
Следствие. Пусть rank п = г. Тогда
}Aq (*!,..., хг) при нечетном и.
ЛГ 1
Q [*!,... ,хг] при четном п
(всюду dim*,- = п).
3. Ранги гомотопических групп сфер.
Теорема. 1, если q = n или
rank я, (5”) = если п четно uq = 2n- 1, . 0 в остальных случаях.
Замечание. Мы уже знаем, что пп (S ") = Z (см. п. 2 § 10) и что в я4т _!(52т)
имеется элемент бесконечного порядка - квадрат Уайтхеда образующей группы
я2т(У2т) (см. п. 4§ 16). Теперь мы видим, что
я4т _ г (S2m) = Z ® (конечная группа),
а остальные гомотопические группы (S ") с q #= п конечны.
8. А.Т. Фоменко
226
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
Рис. 115
Доказательство теоремы. Пусть п нечетно. Тогда член Е2 когомоло-
гической спектральной последовательности расслоения
Sn l„ + i
K(Z. п-1)
Sn
с коэффициентами в Q выглядит, как показано на рис. 115. Уже известное нам
рассуждение (dxk = kxk~1dx = ksx11-1) показывает, что = 0, значит,
Hq(Sn („_!*, Q) = 0 при q > 0, и, значит, группы Hq(Sn |„ + 1) конечны при q > О
(они конечно порождены в силу теоремы п. 1С).. Следовательно (опять-таки в си-
лу теоремы п. 1С), все группы я9(5" |„ + 1) конечны, а значит, конечны группы
ttq(5") с q > п. (Несколько иное доказательство более общего факта содержится
в п. 4.)
Пусть теперь п четно. Тогда член Е2 когомологической спектральной последова-
тельности расслоения
K(Z,n-i)
sn\n+1-----------► S"
с коэффициентами в Q выглядит, как показано на рис. 116. Из этой спектральной
последовательности видно, что Я*(5"|„ + 1; Q) = Я*(52"-1; Q). Значит, группы
HQ(Sn In+i) с Я < 2и — 1 конечны, в частности, конечна группа Hn + l(Sn |„ + 1) =
= тг„ +1 (Sn ln + i) = irn + 1(5"). Рассмотрим расслоение
*("n + i(S").n)
$П I п+2 * $П I n + 1-
Так как H*(K(irn + 1(Sn), и); Q) = Я*(pt; Q) (см. п. 1A), спектральная последова-
тельность этого расслоения дает: H*(Sn |„ +2; Q) = H*(Sn |„ + 1; Q) (если , конечно,
п > 2). Отсюда мы последовательно выводим: конечность группы тт„ +2 (5" | п +2) =
= тгп+2(5"); равенство Я*(5" |„+3; Q) = H*(Sn |„+2; Q); конечность группы
тг„+3(S" |„+3) = тгп+3(5"); ...; равенство H*(Sn |2„_i: Q) = H*(Sn l2„_2; Q).
(Читатель, проделавший упражнение 3 в п. 1С, вероятно, знаком с этой процедурой.)
Таким образом,
^V"l2n-i;Q) = tf‘(s"ln+1;Q) = я^2"’1^),
H2n-i(Sn hn-1) = ^2n-i(^" l2n —i) = ^2n-i(Sn) = Z ф (конечнаягруппа),
и спектральная последовательность расслоения
K(”2n-i(Sn);Q)
Sn l2n --------------► Sn I 2„_t
уже известным нам образом приводит к равенству Н*(Sn 12„; Q) = 7Z*(pt; Q). Значит,
§ 25. РАНГИ ГОМОТОПИЧЕСКИХ ГРУПП
227
все группы Hq(Sn 12„) конечны, а с ними конечны и группы тг, (Sn 12„), т.е. группы
nq (S ") с q > 2и. Теорема доказана.
4. Теорема Картана — Серра. Мы скажем, что рациональные когомологии прост-
ранства X с коэффициентами в Q составляют свободную косокоммутативную ал-
гебру с образующими xs G Q), если xs не связаны никакими соотношениями,
кроме соотношений косой коммутативности xsxt = (—Другими словами,
H*(X;Q) = Aq (нечетно мерные х4) ® Q[ четно мерные xj.
Примеры. 1. S" снечетнымп.
2. Sn | 2„ с четными.
3. К(п, п) с конечно порожденной абелевой группой тг.
4.SU(n), SO(n), Sp(n).
5.S2S".
В действительности верно, что рациональные когомологии произвольного //-прост-
ранства, в частности, произвольного пространства петель, представляют собой сво-
бодную косокоммутативную алгебру; читатель может попытаться доказать зто
в качестве упражнения.
Теорема (Картан - Серр). Пусть X - односвязное пространство с конечно
порожденными гомологиями. Предположим, что рациональные когомологии прост-
ранства X представляют собой свободную косокоммутативную алгебру.
H*(X,Q) = AQ(x1,...,xm) ® Q[n,... ,yt],
где xs - некоторые нечетномерные когомологические классы, yt - четномерные
когомологические классы. Тогда ранг группы nq(X) равен числу q-мерных элемен-
тов среди xlt ... ,xm,yi,... ,yt.
Другими словами, у односвязного пространства X со свободными рациональны-
ми когомологиями свободные аддитивные образующие гомотопических групп
находятся в сохраняющем размерность взаимно однозначном соответствии с муль-
типликативными образующими алгебры его рациональных когомологий.
Доказательство. Так как
H*(X-,Q) = H*(X;Z) ® Q
и гомологии пространства X конечно порождены, то найдутся ненулевые целые
числа ai, ... ,am,bi, ... ,bt, такие, что классы aiXi, . . . , amxm, biyi.ЬгУг
принадлежат образу естественного гомоморфизма Н*(Х, Z) -* П*(Х; Q) (индуци-
рованного включением Z->Q). Пусть при этом гомоморфизме xt ^aiXit . . .
. . . , yt •-> biyi- Классам xs,yt целочисленных когомологий пространства Xотвечают
(определенные с точностью до гомотопии) отображения X ->/C(Z, /Д X ->/C(Z, /г),
где is = dimXj, jt = dimyf (см. п. 3 § 18).
Все вместе эти отображения определяют отображение
X Y = ( ПА"(Z, zJ) X ( П K(Z, Л)), ( * )
s t
и ясно, что зто отображение индуцирует изоморфизм в рациональных когомоло-
гиях (из теоремы п. 2 и предположений теоремы вытекает, что рациональные кого-
мологические алгебры пространств X и Y устроены совершенно одинаково, а отобра-
жение (*) индуцирует взаимно однозначное соответствие между образующими
этих алгебр). В силу п. 5 § 9 отображение (*) можно считать расслоением, и кого-
мологическая спектральная последовательность этого расслоения с коэффициента-
8*
228
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
ми в Q показывает, что спой F этого расслоения имеет в положительных размернос-
тях тривиальные рациональные когомологии (ввиду результатов п. 2 § 22 в нулевую
строку этой спектральной последовательности не попадают никакие дифференциалы,
и потому элемент 0 =# z G H4(F; Q) с наименьшим возможным q не уничтожился бы
никаким дифференциалом и остался бы в £«,, в противоречие равенству Н*(Х', Q) =
= Я*(У; Q)). Значит, F имеет конечные гомологические группы (их конечная по-
рожденность вытекает из конечной порожденное™ гомологий пространств Хи Y),
а следовательно, и гомотопические группы пространства F конечны (см. п. 1 С).
Теперь точная гомотопическая последовательность расслоения (*) показывает, что
каждое отображение тг„ (X) -> тг„ (У) имеет конечное ядро и конечное коядро (фак-
тор по образу), а значит, ранги гомотопических групп пространств X и У совпадают,
что нам и требуется.
Из теоремы Картана — Серра вытекают некоторые уже известные нам утверждения
(например, теорема о рангах гомотопических групп нечетномерной сферы), а также
несколько новых утверждений. Например:
Следствие.
{Z ® (конечнаягруппа),еслиq = 3,5,... , 2л + 1,
конечная группа при остальных q;
( Z® (конечнаягруппа),еслиq = 3,7....4m-1,
тг9(5О(2т + 1)) =
I конечная группа при остальных q;
{Z ® (конечная группа), если q = 3,7,..., 4m — 5,2m — 1,
конечная группа при остальных q\
(Z ® (конечнаягруппа),еслиq = 3,7,...,4л - 1,
конечная группа при остальных q.
Замечание. Из точности гомотопических последовательностей расслоений
soW s.->,
вытекает,ввиду равенства nq(Sm) = 0 при q < т, что имеют место изоморфизмы
nq(SO(n - 1)) a irq(SO(n)) при q < п - 2,
nq(SU(n - 1)) a nq(SU(n)) при q <2п-2,
nq(Sp(n - 1)) a nq(Sp(n)) при q < 4л - 2,
индуцируемые соответствующими включениями. (В критических размерностях
q = п — 2, 2п - 2 или 4л - 2 эти включения индуцируют эпиморфизмы левых групп
на правые.) Таким образом, при достаточно большом и группы nq(SO(n)), irq(SU(n)),
nq(Sp(n)) не зависят от п; эта стабильные группы обозначаются через TrQ(SO),
nq(SU), nq(Sp'). Для удобства читателя заметам, что у групп SO(n), SU(n), Sp(n)
стабильными являются гомотопические группы, соответственно, до (л — 2)-й,
(2л - 1)-й и (4л + 1)-й включительно. В отличие от групп nq(SO(n)), nq(SU(n)),
nq(Sp(n)), которые полностью не вычислены, стабильные гомотопические группы
§ 25. РАНГИ ГОМОТОПИЧЕСКИХ ГРУПП
известны:
- [ 0
при нечетном q,
при четном q\
itq{SO) = ff,+4(Sp) =
Z при q = — 1 mod 4,
Z2 при q = 0,1 mod8,
0 при остальных q.
(Ср. с предыдущим следствием.) Этот факт был доказан во второй половине 50-х
годов Боттом, применившим средства вариационного исчисления в целом (весьма
употребительно название ’’периодичность Ботта”). Изложение доказательства Ботта
имеется в заключительной главе книги Милнора ’’Теория Морса”. Другое доказа-
тельство для U будет приведено в гл. 6.
5. Комментарии к теореме Картана - Серра. Как уже говорилось, теорема о ран-
гах гомотопических групп нечетномерной сферы является следствием теоремы
Картана — Серра, но случай четномерной сферы теоремой Картана - Серра не охва-
тывается, потому что в когомологиях четномерной сферы имеется нежелательное
соотношение: квадрат четномерной образующей равен 0. Все же нам удалось вычис-
лить ранги гомотопических групп четномерной сферы, и у читателя может сложиться
впечатление, что, зная рациональное когомологическое кольцо, скажем, односвяз-
ного пространства, всегда можно найти ранги его гомотопических групп. Это впе-
чатление, однако, ошибочно, в чем можно убедиться, рассматривая следующий при-
мер. Возьмем букет S2 v S2 .
Упражнение 5. Пользуясь методами этого параграфа, найдите ранги гомото-
пических групп букета S2 v S2; докажите, в частности, что rankjr4(S2 v S2) = 4.
Возьмем в тг4 (S2 v S2) (или в тг, (S2 v S2) с q > 4) любой элемент бесконечного
порядка, выберем сфероид S4 -* S2 v S2 (Sq + S2 v S2), представляющий этот эле-
мент, и приклеим по этому сфероиду к S2 v S2 пятимерную клетку ((q + 1)-мерную
клетку). Когомологическое кольцо получившегося пространства X не будет отли-
чаться от когомологического кольца букета S2 v S2 v S5 (S2 v S2 v Sq+1) — no
соображениям размерности. Но ранги гомотопических групп у этих пространств
(X и букета) будут, конечно, разными: зто верно уже для группы тг4 (для груп-
пы тг9). Возникает вопрос, нельзя ли все же выразить в чисто когомологических
терминах информацию, позволяющую найти ранги гомотопических групп (односвяз-
ного) пространства. Оказывается, можно. Наряду с обычным когомологическим
умножением в когомологиях топологических пространств имеются ’’высшие умно-
жения” — так называемые умножения Масси.
Вот конструкция первого из них. Пусть а&НР(У; G), Q&H4(Х‘, G), у EHr(X,G)
(G - кольцо) — такие когомологические классы, что а/3 = 0 и 0 у = 0. Выберем ко-
циклы а€а, Ь&$,с&у (неважно какие, сингулярные, или иные, скажем, дифферен-
циальные формы, существенно лишь, чтобы для коцепей рассматриваемого типа
имелось ассоциативное билинейное умножение, удовлетворяющее формуле Лейбни-
ца и индуцирующее обычное когомологическое умножение). Тогда существуют
коцепи е, f, такие, что be = аЪ и 5/= Ьс. Рассмотрим коцепь ее - (— l)paf. Она явля-
ется коциклом:
b(ec - (-l)paf) = (ab)c - (-1)р(-1)ра(Ьс) = 0,
и соответствующий когомологический класс называется произведением Масси клас-
сов а, 0, у; обозначение: {а, у>. Очевидно, произведение <а,0, у> определено с точ-
ностью до прибавления элемента вида аХ + ду, где X G ffq + r~1(X; G), д €
230
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
G Zfp + <7-1(^; G). Таким образом, умножение Масси — частичная многозначная
тернарная операция. (В частности, <а, р, у) есть не один когомологический класс,
а целое множество когомологических классов.)
Упражнение 6. Вычислите умножение Масси в построенном выше прост-
ранстве X = (5 2 v S2) U D5.
Это построение можно продолжить; например, для четверки когомологических
классов a, 0, у, 8, таких, что а0 = 0у = 78 = 0 и <а, р, у> Э 0, {р, у, 8> Э0, можно
построить произведение (а, Р, у, 8 >, определенное с еще большей неточностью, и т.д.
Оказывается, что рациональные когомологии, заданные вместе с обычным умно-
жением и бесконечной последовательностью умножений Масси, определяют ранги
гомотопических групп (а также, с точностью до элементов конечного порядка, умно-
жение Уайтхеда с высшими умножениями Уайтхеда — Масси), разумеется, в одно-
связном случае. Этот вывод можно сделать из так называемой теории минимальных
моделей Сулливана (в построении которой операции Масси явно не участвуют).
Изложение теории Сулливана имеется в известной статье Гриффитса, Делиня, Морга-
на и Сулливана (русский перевод см. Успехи мат. наук. - 1977. - Т. 32, № 3. —
С. 119-152), содержащей также одно из наиболее ярких приложений этой теории
(к топологии кэлеровых многообразий). См. также сборник переводов ’’Гомото-
пическая теория дифференциальных форм”, Мир, 1981 г.
§ 26. НЕЧЕТНЫЕ КОМПОНЕНТЫ ГОМОТОПИЧЕСКИХ ГРУПП
На протяжении этого параграфа р обозначает нечетное простое число (случай
р = 2 мы разберем в следующей главе).
1. Когомологии Я* (К (Z 4,n);Zp') при (р',р)= 1.
Теорема. Если р' не делится на р, то
H\K(ZpS>ny,zP’) — я*(рг,гр-).
Этот факт нам, в сущности, известен (см. упражнение 1 к § 25). Прм и = 1 он
был установлен в главе 2, а в общем случае доказывается индукцией по п при помо-
X(Zp,n-I)
щи расслоений *---------► К (Zp, п).
Следствие. Если G есть конечная абелева группа, порядок которой не делит-
ся на р, то и Hq(K(G, и); Z), q > 0, - конечные абелевы группы, порядок которых
не делится нар.
Это вытекает из предыдущей теоремы ввиду формулы универсальных коэф-
фициентов. (Это вытекает также из упражнения 1 к § 25.)
2. Частичное вычисление кольца H*(K(Zp,n)', Z). Это вычисление будет проделано
до размерности п + 4р — 4 включительно (почему берется именно такая размерность,
будет ясно из вычисления). В следующей главе мы сформулируем полный результат
о когомологиях Н* (К (Zp, и); Zp).
Нам (и читателю) будет удобнее, если, мы начнем вычисление, не формулируя
заранее его окончательного результата.
Когомологии пространства К (Zp, 1) = Lp нам известны:
( Z„ при четном q > 0,
Hq(K(Zp,l)',Z) =\пр
I 0 при нечетном q.
Простые соображения показывают, что в положительных размерностях имеет место
мультипликативный изоморфизм
H*(K(ZP, 1) ;Z) = Zp [х], хе tf2(£(Zp, 1); Z).
§ 26. НЕЧЕТНЫЕ КОМПОНЕНТЫ ГОМОТОПИЧЕСКИХ ГРУПП
231
(Это можно доказать, например, так. Рассмотрим спектральную последовательность
о»
расслоения L“----► СР°° — см. рис. 117. Из формулы Лейбница, или, еще проще,
из информации об аддитивном устройстве когомологий Z) следует, что все
дифференциалы d2: Z -» Z являются умножениями на р. Значит, в Еж остается толь-
ко нулевая строка, и отображение Я* (СР"; Z) ->Я*(£“; Z) эпиморфно, а мульти-
пликативная структура в Н*{СРК; Z) нам известна.)
Рис. 117
Рассмотрим теперь когомологическую спектральную последовательность расслое-
K(Zp,l)
ния ♦-------*K(ZP, 2) с коэффициентами в Z. Эта последовательность (до размер-
ности « 4р) схематически представлена на рис. 118. Из нее видно, что кольцо
H*(K(Zp, 2); Z) до размерности 4р + 1 включительно устроено так: аддитивные
образующие находятся в размерностях 0, 3,2р + 1,2р + 2,2р + 4,2р + 5, мы обозна-
чим их через 1,Уз,У2р+1> • • • ; При ЭТОМ Уз у2 р +1 = У2Р +4>УэУ2Р+2 =У2р + 5-
[Поясним, как это получается. Элемент у3 по определению есть образ х при транс-
грессии. Из d2х = уз вытекает, что
, f =# 0, если т не делится на р,
d3xm = тхт~'у =
I = 0, если т делится нар.
Поскольку d3xp = 0, элементы хр и ухр~г остаются в Е4 и могут уничтожиться
только дифференциалом, отображающим их в нулевую строку. Значит, в нулевой
строке имеются элементы y2p + i и у2р+2, такие, что d2p + i(xp')= y2p+i и
^2р-1(У*р *) = У2р+2 (последнее равенство не противоречит формуле Лейбница,
потому что в Е2р-1 уже нет ни у, ни хр~1, йух Р~1 не разлагается в E2p_2 в про-
изведение). Элементы У2р+\ и у2р+2 присутствуют уже в Е2 (иначе откуда бы они
взялись в Е2р + j и Е2р _ 1 ?). Далее, по формуле Лейбница,
rfsObp+i*) = -У2р+1Уз, d{y2p42x) = у2р42у3,
и если быузу2р+1 илиузУ2р+2 было равно 0, тоу2р + 1х илиу2р+2х осталось бы
в Я»,, чего быть не должно. Положим
УзУ2р+1 ~ У2Р+4, УзУ2р+2 = У2р + 5-
Имеем: d3(P2p + i^k) = ^2р+4^к-1> 4з(У2Р+2*к) = ку2р+5хк~1; эти дифферен-
циалы отличны от 0 при к <р, а произведение у2р-цХр имеет уже самую большую
интересующую нас размерность, и к тому же
^2р+1(х2р') = 2xpd2p + lxp = 2у2р+1хр.
Таким образом, у нас не осталось не уничтожаемых дифференциалами d3, d2p_k
и d2p+1 элементов из Е2 полной степени < 4р + 1.
Ниже мы пропускаем подробные описания рассуждений такого рода, ограничи-
ваясь картинкой.]
Спектральная последовательность расслоения
K(ZP,2)
*---------> K(Zp,3)
232
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
Рис. 119
(см. рис. 119) показывает, что до размерности 4р + 2 включительно кольцо
H*(K(Zp, 3); Z) порождается образующими
24,24,24,2^,24,...,
2
z2p+2> z2p+2 z4> z2p+2 z4 »• • • ,
2
z2p+3»z2p+3 z4>z2p+3 z4 > • • •
(dim zm = m). Заметим, что не все эти элементы имеют разные размерности:
dim 24 2 = dim г2р+2 2*,
и могло бы случиться, что
р+1
_ 2
Pz2p+2 -z4
§ 26. НЕЧЕТНЫЕ КОМПОНЕНТЫ ГОМОТОПИЧЕСКИХ ГРУПП
233
Но этого не происходит, так как тогда бы было
р+1
1 + —
0 = (pz4)z2p+2 =z4 2 *о.
Значит, все указанные элементы имеют (аддитивно) порядок р.
Спектральная последовательность расслоения
* -----Р—^К&Р,4)
устроена совершенно аналогично спектральной последовательности расслоения
K(Zp, 1)
*--------► K{LP, 2) (см. рис. 120) - Образующие размерностей 4,2р + 2 и 2р + 3 соз-
дают в H*(K (Zp, 4); Z) элементы размерностей 5,2р+3 и 2р + 4 и возникают
еше (благодаря равенству ds (zp4 ) = 0) совершенно новые элементы размерностей
4р+1 и 4р+2. Таким образом, H*(K(Zp, 4); Z) в размерностях <4р+2 адди-
тивно порождается элементами
1, H’s , И*2р + з, И’2р + 4, И’гр + ЗИ’з, И’2р + 4 Ws, И’4р+1, W4p+2.
Дальнейшие спектральные последовательности устроены аналогичным образом,
причем р-е степени нетривиальных элементов из Е2 будут иметь уже слишком боль-
шую размерность, и их можно более не принимать во внимание. Вот окончательный
результат.
Теорема. Кольцо Н* (К(Zp, ri); Z) при четном п>2 в положительных раз-
мерностях + 4р — 2 аддитивно порождается элементами порядка р
5л+1> 5n+2p —1,£л+2р> 5л+4р—3> Ёп+4р — 2»
а также £„+1 $и+2р-1 и ?„+i %п+2р, если их размерности входят в наш диапазон.
При нечетном п> 3 это кольцо аддитивно порождается в тех же размерностях эле-
234 ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
ментами порядка р
Пп+i, г}2п+1, Р3п+1, Ч*+1.
Чп+2р-1, Vn + ip-l Пп + 1, Рп + 2р-1 ....
Tln+2pt Чп+грЧп+Ь Чп+2р П„ + 1, . . . ,
Чп+4р — 3, Чп+4р —2-
3. Частичное вычисление когомологий К (Z, л).
Теорема. В положительных размерностях < л + 4р - 3 кольцо Н* (К (Z,ri);
Zp) изоморфно кольцуН* (К(Zр,л —1); Z).
Действительно, во всех положительных размерностях имеет место мультиплика-
тивный изоморфизм Н* (K(Z,2)\ Zp) Э£ Н* (K(ZP, 1); Z). В то же время в про-
деланном в предыдущем пункте вычислении Н * (K(Zp, п); Z) мы не использовали
ничего, кроме мультипликативной структуры Н * (K(Zp, 1) ; Z) и общих свойств
спектральных последовательностей, так что зто вычисление без изменений прило-
жимо кН*(К(1, л); Zp).
Замечание. У читателя не должно возникнуть иллюзии, что одних лишь муль-
типликативных соображений хватило бы для полного вычисления колец
H*(K(Zp, ri)\ Z) и Н * (K(Z,n)', Zp). Довольно скоро возникают ситуации, когда
для дифференциала имеется несколько возможностей, не противоречащих формуле
Лейбница. (Полное вычисление требует привлечения ’’когомологических опера-
ций”, с которыми мы познакомимся в следующей главе.) В частности, при л> 1
кольца Я * (К(Zp, л); Z) и Я * (K(Z, л); Zp) в целом не изоморфны.
Посмотрим теперь, что мы знаем о когомологиях Я * {К(Z, л); Z). В них имеют-
ся, в силу результатов § 25, Z-компоненты в размерности л и, при четном л, в раз-
мерностях 2л, 3л,... При переходе к H*(K(Z,ri)-, Zp) формула универсальных
коэффициентов перерабатывает эти Z в Zp в тех же размерностях, что согласуется
с нашим результатом. Но в Н* (K(Z, ri) -, Zp) нам известны еще некоторые слагае-
мые Zp, в частности, при любом л они имеются в размерностях л + 2р — 2яп + 2р— 1.
Поскольку эти слагаемые не происходят из Z в Я * (К(Z, л); Z ), они (оба) должны
произойти из слагаемого вида ZpS в Hn+2p~1(K(Z,n); Z) (как ZpS<»Zp и
Tor(Zpi,Zp)). Чему равно s, мы не знаем, но в действительности s = 1 и вообще
элементы порядка р2 в Н * (K(Z,ri) ’, Z) появляются впервые в размерности л +
+ 2р2 — 1. Доказательство этого факта мы оставляем читателю (которому мы реко-
мендуем начать с рассмотрения спектральной последовательности расслоения
X(Z,2)
*--------*-K(Z, 3) с коэффициентами в Z).
4. Частичное вычисление p-компонент гомотопических групп сфер.
Теорема. Если л > 3, то яп+2р_з(5") Э Zp, яп+4р_5 (5 я) Э Zp и фактор-
группа
4р —S
I ® я'п+ч(‘У")]/(2р ® Zp)
<7=0
не содержит элементов порядка р.
§ 26. НЕЧЕТНЫЕ КОМПОНЕНТЫ ГОМОТОПИЧЕСКИХ ГРУПП
235
Мы докажем здесь более слабое утверждение. А именно, мы докажем, что p-ком-
понента .группы 7 irn+q (S 'f) сосредоточена в я„+2р_з(5") и равняется Zp.
Для доказательства теоремы в полном объеме нам не хватит вычисления одного
дифференциала. Читатель сможет восполнить этот пробел в доказательстве (и прод-
винуться в вычислении p-компонент групп Trn+q(Sn) дальше, до ?~р2) после
прочтения следующей главы.
Переходим к доказательству. Рассмотрим случай нечетного п > 7. В этом случае
член Ё2 спектральной последовательности расслоения
с коэффициентами в Zp выглядит, как показано на рис. 121. Из спектральной по-
следовательности ясно,что в размерностях Си + 4р-4 когомологии# * (5 "| n+1; Zp)
устроены так:
0 п + 2р - 3 п + 2р — 2 п + 4р — 5 п + 4р - 4
Zp нули ZP ZP нули ZP ZP
Нам известно, что целочисленные когомологии пространства 5"| n + j в положитель-
ных размерностях конечны. Из этого факта и из того, что в когомологиях A(Z,
л+4р-4 3 ЧЙ
п+4р-5 а й
п+2р~2
п+2р~3
Рис. 121
236
ГЛ. 3. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РАССЛОЕНИЯ
п— 1) в рассматриваемом диапазоне размерностей отсутствуют элементы порядка
р2, вытекает, что p-компоненты целочисленных когомологий пространства S"l „+1
имеют устройство
0 п + 2р - 2 п + 4р - 4
Z нули ZP нули ZP
а целочисленные гомологии устроены так же, только размерности Zp-компонент
на 1 меньше.
При переходе к S"ln+2,5"l п+3,..., вплоть до 5"1п+2Р-з. p-компоненты не
меняются, так как слоями расслоений S п I n+Q " I n+q-i с 1 < q <2p- 3 служат
пространства вида K(G, —), у которых G — конечная группа, порядок которой не
делится на р, а (целочисленные) когомологии этого пространства состоят из конеч-
ных групп, порядки которых не делятся на р (см. п. 1). В частности, группа
#2п+р-з($"1 2п+р—з) содержит p-компоненту Zp и не содержит других р-компо-
нент. Мы уже доказали, таким образом, что я„+(7 (5 ") не содержит p-компонент при
1 <<? < 2р — 3 и что p-компонента группы л„+2р_з(5") есть Zp. Далее мы рассмат-
риваем расслоение
Jt(’rn+2p-3(5").»+2p-4) оп1
« 1я + 2р-2 ’л+2р-3-
В силу доказанного,/Г(ffn+2p_3(iS"),я+ 2p-4)=/C(Zp, и+ 2р - 4) X K(G,n + 2р -4),
где G — конечная группа, порядок которой не делится на р. Второй сомножитель
с точки зрения p-компонент не существен, вследствие чего p-компоненты в Z-кого-
мологической спектральной последовательности этого расслоения устроены, как
показано на рис. 122. Из этого рисунка видно, что первая p-компонента в
Н * (5 "| щ-2р-2; Z ) появляется в размерности > п + 4р — 5 (в гомологиях — в раз-
мерности я + 4р — 6). Точнее мы ничего сказать не можем, потому что не знаем,
как действует дифференциал, обозначенный на рис. 122 пунктирной стрелкой. На
самом деле этот дифференциал нетривиален (и этого достаточно для доказательст-
ва утверждения теоремы), но для доказательства необходимо воспользоваться сте-
пенями Стинрода — см. гл. 5. Дальнейшее рассуждение идентично предыдущему:
переходы S"| п+2р-2 n+4P_7 не меняют p-компонент, и мы |уюжем сде-
лать вывод, что группы ffn+q (S ") с 2р — 3 < q < Ар — 6 не включают в себя р-ком-
понент.
В случае нечетного я>7 теорема доказана. Случай я = 3 проще, поскольку мы
знаем целочисленные когомологии пространства .S3| 4 (п. 2 § 24). В случае я = 5
рассуждение совершенно аналогично предыдущему, только следует принять во
внимание, что р(п — 1) = 4р. Наконец, случай четного я, принципиально не отли-
чающийся от рассмотренного случая, но несколько более громоздкий, мы остав-
ляем читателю.
Следствие. Порядок стабильной гомотопической группы (см. я. 4 § 10)
не делится на р при Кк < 2р — 3 и 2р—3<к < 4р — 5 и делится на р, но не делит-
ся на р2 при к = 2р — Зик = 4р — 5.
§ 26. НЕЧЕТНЫЕ КОМПОНЕНТЫ ГОМОТОПИЧЕСКИХ ГРУПП
217
На всякий случай заметим, что для вывода этого следствия достаточно знать
теорему в случае, в котором она была подробно доказана (нечетное п > 7).
Информация. О p-компонентах гомотопических групп сфер в настоящее
время известно довольно много. В частности, при m > 1
Zp, если q = 2i(p - 1) — 1 с i = l,2....р-1,
р-компонента
группы Я2 т +1 +q(S2 т +1)
Zp, если q-2i(p-l)-2 с i=m+l,m+2,...,p-l,
.0 при остальных q < 2р{ р - 1) - 2.
Дальнейшую информацию о нечетных компонентах гомотопических групп сфер
можно почерпнуть в книге X. Тода ’’Композиционные методы в теории гомотопи-
ческих групп сфер” (включая добавление переводчика).
ГЛАВА 4
КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
§ 27. ОБЩАЯ ТЕОРИЯ
1. Определение. Пусть заданы два числа п и q и две абелевы группы П и G. Мы
скажем, что задана когомологическая операция <р типа (л, q, П, G ), если для любого
клеточного пространства X в его когомологиях определено отображение
Нп(Х‘, П) ->Яq (X; G), естественное по Хв том смысле, что диаграмма
*х
Hn(X;\V)-----*Hq(X;G)
f* t f* t
Я”(У;П) Hq(Y;G)
коммутативна для любого непрерывного отображения ft X-*Y.
В случаях, когда зто не может вызвать недоразумений, мы будем писать вместо
рх просто р.
Подчеркнем, что отображение не обязано быть гомоморфизмом группы
Нп(Х; П) в группу Я9 (X; G).
Так как G — абелева группа, то совокупность всех когомологических операций
типа (n,q, П,(7) является абелевой группой, которую мы обозначим через
O(n,q,K,G).
2. Классификация.
Теорема. Имеет место следующее соотношение:
О(п, q, П, G ) “ Я’(А(П, л);G ).
Это красивое и неожиданное предложение почти очевидно, как мы сейчас убедимся.
Доказательство. Мы знаем, что Нп(Х\ П) = тг (X, А(П, л)) (см. п. 3 § 18).
Это равенство устанавливается с помощью некоторого замечательного элемента
е =Fn €Я"(Х(П,л); П); а именно, каждому отображению f: Х-*К(П, п) (точ-
нее, классу отображений, гомотопных /) мы относим элемент f* (е) G Нп(Х; П).
Пусть теперь дана некоторая когомологическая операция ip G О(п, q,H,G).B част-
ности, она определяет отображение >Рк(п,п)- Нп(К(П,п); П) -*Hq (А(П,л),С)
и элемент ^(е)€Я’(Х(П,п); G). Оказывается, что значение </>(е) определяет
операцию р взаимно однозначно, т.е. если <р(е) известно, то однозначно восстанав-
ливается вся операция, и любой элемент х& Hq (7С(П, п); G) представим в виде
<р(е~) для единственной операции р G О(п, q, П, G). Иначе говоря, гомоморфизм
0(л, q, П , G ) -»Я4 (А(П, n); G ), переводящий р в р (е), является изоморфизмом.
Докажем его мономорфность. Пусть X — произвольное клеточное пространство,
р — любая операция, такая, что </>(е) =0, и пусть а€ Нп(Х, П). Тогда существует
§27. ОБЩАЯ ТЕОРИЯ
239
отображение f: Х-*К(Л,ri), такое, что f*(e) = а. В силу естественности операции</>
имеем <₽(а) =</>/*(е) =f =0; мономорфность соответствия </>•-»(/? (е) дока-
зана.
Докажем его эпиморфность. Пусть х - любой элемент из Hq (К (YI ,n); G). По-
ложим <р (е) = х и продолжим это соответствие, заданное пока только на элементе е
до когомологической операции.
Пусть X — любое клеточное пространство, и пусть ?GНп(Х\ П); тогда сущест-
вует fy: X-+К(П, ri), такое, что у = f* (е ). Положим (у) = f* (х). Отображение </>
определено; проверку его естественности (несложную) мы оставляем читателю.
Доказательство теоремы окончено.
Следствие. Нетривиальная когомологическая операция не понижает раз-
мерность (т.е. если 0 ¥= <р G О(п, q, П ; G ), то q > ri).
В самом деле, Нч (Х(П, п); Я) =0 при q < п, так как Х(П ,п), по построению,
не имеет клеток размерности меньшей п.
Замечание. Вот пример когомологической операции, не являющейся гомо-
морфизмом. Пусть П — коммутативное кольцо без элементов второго порядка,
п — четное число. Возведение в квадрат есть отображение q>: Н "(X; П ) -*Я 2 "(X, П ),
которое не есть гомоморфизм. Тем не менее, у, в силу естественности, есть кого-
мологическая операция из О(и,2п,П,П). (Если П =Z2, то >р, конечно, будет го-
моморфизмом) .
3. Примеры. 1°. Нам известны группы Hq (К (П ,и); Q) для всех целых чисел п
и q и конечно порожденных групп П. Дадим интерпретацию наших результатов в тер-
минах когомологических операций. Если группа П конечна, то Н 4 (Х(П, п); Q) =0
для всех q > 0. Это означает, что никаких нетривиальных когомологических опера-
ций из когомологий с конечными коэффициентами в когомологии с рациональными
коэффициентами не существует.
Если П = Z и п нечетно, то Hq (Х(П, п); Q) отлично от нуля только при q =п,
и Я"(Х(П,л); Q) =Q. Образующей группы Я"(Х(П,п);(?) является образ
фундаментального класса е G Нп(К(П, ri); Z ) при гомоморфизме q>: Н"(X(Z, ri);
Z) -+Hn(K(Z,ri); Q), индуцированном включением Z ->Q. Поэтому всякая опера-
ция из нечетномерных целочисленных когомологий в рациональные когомологии
сохраняет размерность и относит каждому элементу аёН п(Х; Z) элемент Xoq G
S//"(l; Q), где X - фиксированное для данной операции рациональное число.
Наконец, если п четно, то Н* (X(Z,n); Q) =Q [cq].. Поэтому всякая операция из
четномерных целочисленных когомологий в рациональные когомологии относит
элементу a G Нп(Х; Z ) элемент X Oq G Н kn(X, Q), где X и к — фиксированные для
данной операции рациональное и целое числа.
Упражнение 1. Докажите, что для любого поля F характеристики нуль лю-
бая когомологическая операция из когомологий с коэффициентами в F в когомо-
логии с коэффициентами в F относит элементу aGHn(X;F) элемент XafcG
€ Я"*(Z; F ), где целое число к и элемент X G ^ фиксированы для данной операции.
2°. Изучим когомологические операции, повышающие размерность на 1.
Пространство X(Z, ri) не имеет (п + 1) -мерных клеток, и потому Я "+1 (К (Z, п);
G J =0 при любой группе G. Следовательно, когомологических операций, действую-
щих из целочисленных когомологий и повышающих размерность на 1, вообше не
существует.
Пусть теперь р — простое число. Пространство X(Zp, ri) имеет при любых р и п
одну (п+1)-мерную клетку. Поэтому Я"+1 (X(Zp, л); Zp) =0 или Zp, и, с точ-
240
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
ностью до множителя, имеется не более одной когомологической операции из
Н п (—; Zp) в Н "+1 ( — ; Zp). Но одна такая операция имеется (при п > 1, конечно):
1
гомоморфизм Бокшгейна Д = — S. Это — нетривиальная операция (она нетривиаль-
Р
на в пространстве S " D"+1, где </> — отображение Sn-*Sn степени р, иначе говоря,
в (n + 1) -м остове К (Zp, п) ’ а). Вывод: 0(п, п + 1, Z р, Zp) = Zp; всякая операция
указанного типа пропорциональна гомоморфизму Бокштейна.
Упражнение 2. Покажите, что всякая когомологическая операция, повышаю-
щая размерность на 1, есть связывающий гомоморфизм в коэффициентной последо-
вательности, ассоциированной с некоторой короткой точной последовательностью
групп коэффициентов.
4. Стабильные операции. '
А. Определение. Стабильной когомологической операцией из когомологий с коэф-
фициентами в П в когомологии с коэффициентами в G, повышающей размерность
на q, называется серия когомологических операций </>nG 0(n,n + q,Xl ,G), опреде-
ленных при п = 1,2, 3,... и таких, что для любого пространства Xи любого числа п
диаграмма
s
Я"(>Г;П) -> Я” + 1(Б%;П).
*п + 1 *
Hn+q(X’,G) +
(где Е — изоморфизм надстройки) коммутативна.
Например, гомоморфизм Бокштейна представляет собой стабильную когомоло-
гическую операцию.
В. Связь с когомологической последовательностью.
Теорема. Стабильная когомологическая операция согласована с когомологи-
ческой последовательностью клеточной пары (X, У), т.е. коммутативна диаграмма:
...->ЯИ(Х;П) Я”(У,П) ——>Яи+1(%/У; П) 4 Я"+1(Т;П)->...
4- ч>п 4- ч>п 4- fn+i 4- >₽п+1
.. .-> Нп+ч (X\G ) + Hn*q(Y,G ) Hn*4(X/Y,G ) + Hn+q+1(X;G )-> ...
Доказательство. В доказательстве нуждается только коммутативность
квадрата, содержащего S. Так как (X, У) — пара Борсука, то X/Y ~ X UCY/CY ~
~ X U СУ. Рассмотрим отображение f : X U CY -> ЕУ; X U CY X U СУ/Х = БУ
(рис. 123) и индуцированный им гомоморфизм f* : Я"+1(ЕУ; П) ->Я"+1(Х/У; П).
Рассмотрим диаграмму:
ЯЛ(У; П)---^->Я”+1(Х У; П)
4- £ 4-»
Я”+1(ЕУ; П)Я”+1(% и СУ; П)
Мы покажем, что эта диаграмма антикоммутативна, т.е. /*Б = — S. Возьмем элемент
f € Я"(У; П) и выберем представляющий его клеточный коцикл z. Рассмотрим ко-
цепь Г G %>" (X; П), принимающую на клетках У те же значения, что и z, а на клетках
§ 27. ОБЩАЯ ТЕОРИЯ 241
X - Y — нулевые значения. Коцепь 6z является относительным коциклом Л'mod У
и определяет в группе Я"+1(Х, У; П) элемент, равный 6f. Коцепь w & <Sn+l(X U
U СУ; П) мы определим как распространение коцепи 6z на X U СУ: на клетках СУ
мы положим ее равной нулю. Эта коцепь является коциклом, представляющим в
Hn+l(X U СУ; П) элемент 6f. Теперь пройдем по двум другим сторонам квадрата.
Напомним, что клетки надстройки ЕУ — это надстройки над клетками У. Коцепь
Ez принимает на клетке Ео то же значение, которое коцепь z принимает на клетке
а. Наконец, коцепь /* Sz е $п+1(Х ОСУ; П), представляющая класс/*Е£, принима-
ет нулевые значения на всех клетках из ХСХ U СУ, а на клетке из СУ, лежащей над
клеткой о С У, принимает значение, равное F(o).
Рис. 123
Теперь сравним коцепи f#Y.z и w. Рассмотрим коцепь и G <ёп(Х иСУ; П), совпа-
дающую на клетках У СХ иСУ с z и .принимающую на клетках из (X иСУ) - У нуле-
вые значения. Очевидно, что би = w + /#Sz, откуда 6J +/*££= 0, что и требовалось.
Осталось вспомнить, что стабильная операция <р перестановочна и с Ей с/*, а по-
тому она перестановочна с гомоморфизмом 6 точной последовательности пары.
Теорема доказана.
С. Связь с трансгрессией. Отметим важное следствие из доказанной теоремы:
трансгрессивность стабильных операций. А именно, пусть — стабильная операция,
(Е, В, F, р) — расслоение с односвязной базой и элемент а С Н' (F; П) = Е%’г транс-
грессивен, т.е. d3a = ... = dra = 0. Тогда элемент (а) G Яг+ч (F; П) = Е%',+ч также
трансгрессивен, т.е. <#3<р(а) =.. . = dr+(?^(a) = 0. Более того, если т(а) = dr+1aG
С £’^+11,0 = Я,+1(В; n)/®j <rImdj содержит элемент 0 С Я, + 1(В; П), то т(<ра)
содержит элемент С Яг+ч + 1(В; П) (менее точно, но более звучно, зто можно
выразить так: трансгрессия т перестановочна с операцией <р).
Все это следует из представления трансгрессии в виде композиции П) ->
-* Hr + 1(E, F; П) -^-4 цг +1 (В; П) и перестановочности сбир*: если ба G Imp *,
а именно ба = р *0, то б (<ра) также принадлежит Imp *, а именно б (<ра) = <рб а = <рр *0=
= р*(ф0).
D. Классификация. Теперь изучим связь между группами стабильных операций и
когомологиями пространств Х(П, л).
Пусть е G Я"(Х(П, л); П) — фундаментальный класс. Тогда Ее еЯ"+1(Х(П, л);
П). Элемент Ее определяет отображение fn: ЕХ(П; л)->Х(П, л + 1) (это отображе-
ние легко строится и непосредственно: вспомним, что Х(П, л) = ЯХ(П, п + 1);
отображение fn: ЕХ(П, п) = ЕЯХ(П, п) -> Х(П, п + 1) определяется формулой
/„(</>, О = ?(/)> где V ~ петля на Х(П, п + 1), т.е. <p(Z) G Х(П, п + 1), t G (0, 1)).
Итак, если е G Я"(Х(П, и); П) и er G Я"+1(Х(П, л + 1); П) - фундаментальные
классы, то /п(е’) = Ее.
Пусть теперь рассматривается стабильная операция <р; тогда ее можно применить
к фундаментальному классу е и получить: <р(е) G Я"+ч(Х(П, л); G). Так как —
стабильная операция, то <p(Se) = Е(<ре) G Нп*ч* *(ЕХ(П, л); G). Так как
242
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
fn(e') = Se, то элемент <р(е') S Я"+<?+1 (Я(П, л + 1); G) при отображении/„*
перейдет в (Ее). Гомоморфизм Н*(К(Ц, п + 1); G) ->Н*(2,К (П, л); G) мож-
но рассматривать как понижающий размерность на одну единицу гомоморфизм:
Яп + ’ + 1(К(П, л + 1); G) Я”+,(Я(П, л); G), так как Яп + ’(Я(П, л); G) =
= Я"+, + 1 (ЕЯ(П, л); G).
Возникает последовательность:
.. .-»Яп+’(К(П, л);С)->.. .^Я’+2(Я(П,2);О)^Я’ + 1(Я(П, 1); G)
Если задана стабильная операция <р, то в каждой группе Я"+ч(Я(П, л); G) (для
любого л) задан некоторый элемент, и в силу приведенных выше рассуждений эле-
мент, выбранный в Hs + ч + 1 (Я(П, s + 1); G), переходит при гомоморфизме f* в эле-
мент, выбранный в Я1+Ч(Я(П, s); G). Мы знаем, что задать произвольную серию
когомологических операций = {ipn }, е О (л, л + q, П, G) для л = 1, 2,3,... -
это значит задать произвольно по одному элементу zn во всех группах
ЯП+’(Я(П, л); G).
Для произвольной серии когомологических операций последовательность эле-
ментов zn такова, что различные ее элементы никак не связаны между собой
(см. рис. 124; мы полагаем К (П,«) = Я,).
Теперь же мы получили условие, выделяющее стабильные когомологические опе-
рации из множества всех таких серий: надо рассмотреть не произвольные наборы
{ zn} (л = 1, 2, 3,...), а лишь такие наборы, для которых zn = fnZn+i> т.е. Zi =
= /Jz2,z2 =/2z3,... и тд. (рис. 125). Доказанному факту можно придать точную
форму.
Теорема. Группа 0s (q, П, G) стабильных когомологических операций, повы-
шающих размерность на q, изоморфна обратному пределу последовательности групп
Нч+п(К(П, л); G) и гомоморфизмов f„.
Заметим, что если задан элемент zs 6 HqJrS(Ks-, G), то тем самым автоматичес-
ки определены и все zk для k< s; zk =fkfk + i .. • Поэтому, если мы
Рис. 125
§ 27. ОБЩАЯ ТЕОРИЯ
243
интересуемся действием стабильной операции только на элементах, размерность ко-
торых не превосходит некоторого фиксированного числа N, то для задания этой опе-
рации достаточно выделить только один элемент zN G HN+q(K(Tl,N) ; G).
С другой стороны, так как пространство К(П, л) является (л - 1)-связным, то
гомоморфизм/п+1: Я"+<7+1(Л(П, л + 1); G) -+Нп+ч(К([[, л); G) для достаточно
больших л, а именно, для л > q, является изоморфизмом (рис. 126). Иначе говоря,
каждая группа HqJrn(K(JX,n)', G) с ростом п, начиная с некоторого N, стабилизи-
руется, т.е. перестает меняться. Отсюда вытекает, что
0 s(q, П, G)= HN+q(K(tt,N); G)
для достаточно большого N (а именно, для N> q).
Полученные результаты поясним при помощи диаграммы, показанной на
рис. 127. В каждой строке (кроме самой верхней) стоят когомологии пространства
К(П, л) с коэффициентами в G (л = 1,2,3.). В левом конце каждой строки стоит
не нулевая, а л-я группа когомологий Я(П, л). Поэтому друг под другом оказывают-
ся группы не одинаковых резмерностей. Зато гомоморфизмы/„ изображаются на этой
диаграмме вертикальными стрелками. В незаштрихованной части диаграммы эти
°°и
/?0
$0
ffiiiiiiiiiiiiiiiiiiiniiiiiiiiiii
nilllllllllllllllllllllllllllllllll
llllllllllllllllllllllllllllllllllll
80
ТППШ1ШШ111Ш1ШШШ1ШШ1
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIH
70
liffliiiiiiiiiiiiiiiiiiiiiiiiniiiiiiiiiiiiiiiiiiM
<?0
50
40
типи
типи ii
niiiiiiiiii
iiiiiiiiiiiii
iiiiiiiiiiiii
iiiiiiiiiiiii
iiiiiiiiiiiii
iiiiiiiiiiiii
iiiiiiiiiiiiii
Ullllllllll
llinillliilllliliii
iiiiiiiiiiiiiiiiiiiii
iiiiiiiiiiiiiiiiiiiii
iiiiiiiiiiiiiiiiiiiii
llllll
IIIIII
llllll
IIIIII_________________________
llllllllllllliilimiilllllllllii
lllillllllllliilimiilllllililii
IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIH
50
Killllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll
miiiiiiiiiiini iiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiuiiiiiiiiiiiiiiiiiiii
iiiiiiiiiiiiiiiiiii
nillllllllllllllllllllll
^iiiiiiiiiiiiiiiiiiiii i
min
min
iiiiii
min
mi
mi
ши
mu
mu
700
1________
7 2 5 4
А
Puc. 127
244
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
Рис. 128
гомоморфизмы являются изоморфизмами, т.е. на каяодой вертикали в этой части
диаграммы стоят одинаковые группы. Из этих групп составляется верхняя строка
диаграммы - ’’группы Н°°+ 4(^(П, °°); G)”. Эти группы уже не являются (в есте-
ственном смысле) группами когомологий никакого пространства, и они изоморфны
группам О s (q, П, G).
Про группу Я"+Ч(£(П, л); G) говорят, что она имеет стабильную размерность
(или просто стабильна), если q < п, и нестабильную размерность (нестабильна), ес-
ли q > л. Таким образом, на нашей диаграмме заштрихованы группы нестабильных
размерностей.
5. Алгебра стабильных операций. Мультипликативная структура в Я*(Л(П, л); G)
не индуцирует мультипликативной структуры в ®q0s(q, П, G), так как гомомор-
физмы
/*: Я*(АГ(П, л);С)->Я*(АГ(П, л — 1); G)
не являются мультипликативными. Это ясно уже потому, что эти гомоморфизмы
не сохраняют размерность и, в частности, для любых а, 0 G Я*(АГ(П, л); G) выполне-
но: dim (/„а • fn&) = dim/,,* (а • 3) - 1. К тому же, как видно из рис. 128,если а,0
имеют стабильные размерности, то а • /? имеет нестабильную размерность.
Однако если П = G, то существует другая возможность введения структуры коль-
ца в ®qOs (q, П, G), а именно, для двух операций ip' G Os(q', П, G) и f>" G
6 б5 (</', n,G) можно рассмотреть их композицию о 0s (q + q", n,G),
которая тоже будет стабильной операцией. Относительно такого’’композиционного”
умножения ®qOs (q, П, G) является ассоциативным (но, вообще говоря, не комму-
тативным) кольцом.
Если G = П = Zp, то это кольцо является Zp-алгеброй. Оно обозначается через Ар
и называется алгеброй Стинрода. В следующих параграфах мы предпримем подроб-
ное ее изучение (в основном при р = 2).
§ 28. СТИНРОДОВЫ КВАДРАТЫ
1. Введение. Мы начнем с построения и изучения некоторых конкретных элементов
алгебры Стинрода Аг, называемых стинродовыми квадратами. Стииродовы квадра-
ты Sq' — это стабильные когомологические операции, являющиеся аддитивными
гомоморфизмами
Sq': Hn(X-,Z2)^Hn + i(X-,Z2).
Они определены для всех I > 0 и обладают следующими свойствами.
§ 28. СТИНРОДОВЫ КВАДРАТЫ
245
(1) Выполнены равенства
0, если
Sq*(a) = а2, если
.а, . если
i > deg а;
i = deg а;
i = 0.
(2) Имеет место формула А. Картана
SqZ(a-0)= S Sq₽a-Sq’0.
р + Ч = /
Замечание. Введем в рассмотрение гомоморфизм Sq = Sq° + Sq1 + ... Тогда
свойство (2) можно записать в виде: Sq (а • /?) = Sqa • Sq0, т.е. гомоморфизм Sq
есть кольцевой гомоморфизм, Sq: Н*(Х\ Z2) Z2).
Свойство (1) может быть записано в виде: если а — однородный элемент степени
к, то Sq(a) = а + Sq'a + ... + Sqfc-1a + а2. Добавим к этому, что в силу сказанного
выше (см. пример 2° в п. 3 § 27) операция Sq1 есть не что иное, как гомоморфизм
Бокштейна /?.
2. Теорема существования и единственности Sq*. Мы докажем существование и
единственность стабильных когомологических операций, обладающих названными
свойствами. При этом, как мы увидим, единственность следует только из стабиль-
ности и свойства (1), а формула Картана является их следствием.
Рассмотрим K(Z2, п) и фундаментальный класс еп 6 Нп (K(Z2, п); Z2).Положим
Sq* (еп) = 0 при i > п. Мы хотим определить Sq1^), Sq2(en),..., Sq"-1(en),
Sq"(en). Положим Sq"(en) = e„.
Почему e„ =# 0? Потому, что существует клеточное пространство X и элемент х =# 0,
х G Нп(Х\ Z2), такой, что х2 =#= 0. (Например, можно положить X = RP”.) Вообще,
все степени при к > 1 отличны от нуля.
Как мы уже отмечали, когомологическая операция вполне определяется своим
значением на фундаментальном классе К(Z2, п) при соответствующем п.
Рис. 129
Таким образом, элемент Sq"e„ задан для всех п (операция Sq", конечно, этим
полностью не определена ни при каком п, так как мы не знаем еще, чему равно
Sq"(e„+k) при fc>0).
Л j t ft — 1 )
Обратимся к расслоению Серра ♦ -------------► K(Z2, п). При этом мы считаем,
что п > 1, иначе K(Z2, п — 1) не существует. Член Е2 имеет вид, показанный на
рис. 129.
Из этой диаграммы видно, что все элементы, стоящие в нулевом столбце ниже
j, трансгрессивны. Трансгрессивность элемента e„_i не следует из соображений
размерности: мог бы быть нетривиальным дифференциал dn: Е°’2п~2 ->Е",п~1.
246
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
HodnCeS-O =2(d„e„_1)en_i =2e„en-i =0в Z2 (к томужЕ*<п 1 =Ерп 1 =
= Z2 и элемент епеп_1 не может быть образом d„, так как dn(enen_1) = е2п =# 0).
Итак, элемент = Sq"-1e„_1 трансгрессивен. При трансгрессии этот элемент
перейдет (обязан перейти, ибо это его последняя возможность исчезнуть) в некото-
рый элемент / G / =£ 0. Очевидно, что ^n-i’0 = ^2”-1’0 =
= Н2п~1{К{г2, л); Z2), т.е. 0 ¥= / е Н2п~1 (AT(Z2, л); Z2). Мы полагаем
Sq”(e„+i)=/ Таким образом, длявсех п> 1 определен элемент Sq"-1 (е„).
Построение дальнейших Sq"-k(e„) очень простое. Предположим, что л > 2.
Тогда элемент Sq”~2(e„_1) уже определен нами и находится в группе Е®*2"-3
рассматриваемой нами спектральной последовательности. Очевидно, что он тран-
сгрессивен, и под действием трансгрессии он переходит в некоторый отличный от
нуля элемент, принадлежащий Е2п~2,й = Я2"-2 (AT(Z2, л); Z2). Этот элемент мы
и объявляем значением операции Sq”-2 на еп. Тем самым мы определили элемент
Sq”-2e„ для всех л > 2. Делаем еще один шаг назад и определяем Sq”-3(en) для
всех л > 3 как образ при трансгрессии элемента Sq"-3(e„_1); и так далее, пока
не доходим до Sq1(e„) (рис. 130).
Таким образом, для всех л > к> 0 мы определили ненулевой элемент Sq"-kenG
G Н2п~к(К(12, л); Z2). Иначе говоря, мы определили элемент Sqke„ при к> 0
и л > 0. Для того чтобы элементы Sqke„ G Нп*к(К(Z2, л); Z2) образовывали
стабильную операцию, нужно, чтобы выполнялось равенство fn*(Sqke„) = Sqken_j
для всех л (см. определение стабильной операции). Докажем его.
(1) Если к > л + 1, то равенство очевидно, так как его левая и правая части равны
нулю.
(2) Пусть к < л — 1. Гомоморфизм
/„‘-г Я‘(^(г2,л);г2)^Я*(/Г(г2, л-1);Z2),
по определению, есть композиция отображения, индуцированного отображением
S^(Z2, л - 1) = 2J1AT(Z2, л) ->^(Z2, л), и изоморфизма надстройки. В п. 3 § 22
было доказано, что этот гомоморфизм обратен трансгрессии расслоения
Рис. 130
§ 28. СТИНРОДОВЫ КВАДРАТЫ
247
K(Zitn-l)
♦ ---------► A^(Z2, л). Так как (по построению) r(Sq e„_i) = Sq кел при к <
< п - 1, то /„*(Sqке„) = Sqke„_ t, что и требуется.
(3) Если к = л, то Sqken_! =0. Мы должны, таким образом, показать, что
/fc(Sqkek) =fke\ ~ 0- Еще раз вспомним, что /к разлагается в композицию
Н*(К(г2, n); Z2) -► tf*(SK(Z2, л - 1); Z2 ) -► Я*(К(г2, л - 1); Z2 ),
причем первый из гомоморфизмов индуцирован непрерывным отображением. При
этом гомоморфизме элемент ек переходит, как мы видели, в следова-
тельно, е2к переходит в (2efc_!)2. Для завершения доказательства нашей форму-
лы нам достаточно усмотреть, что (Se^j)2 =0. Но это вытекает из такого эле-
ментарного утверждения:
Лемма. В любой надстройке когомологическое умножение тривиально, т.е.
если <xG.Hp(Y,X,A'), Hq(SX;A), где р>0, <?>0, А — любое кольцо, то
а • 3=0.
Это сразу следует из того, что диагональное отображение ZX-^'ZX'X.'ZX го-
мотопно композиции ЪХ^-ЪХ v ZXCSXX ZX. Первое из этих ображений бы-
ло определено в § 4, второе отображение — естественное вложение. Построение
гомотопии и вывод утверждения леммы мы оставляем читателю.
Осталось положить Sq°e„ = еп для всех л, и существование стабильных опера-
ций Sq*, удовлетворяющих условию (1), нами доказано. Фактически нами дока-
зана и единственность таких операций, так как наше рассуждение является, по
существу, не построением, а вычислением элементов Sqken на основании равенств
Sq"en = e„ и трансгрессивное™ операций Sqk.
3. Доказательство формулы Картана. Мы должны доказать, что для произвольного
клеточного пространства X, любого номера i и любых элементов х и у, принадле-
жащих Н*(Х, Z2), имеет место следующее соотношение:
Sq*(x.y)= S Sq₽(x).Sq’(y). (*)
Р+Ч=1
Пусть X и У — произвольные клеточные пространства, и пусть хб Н*(Х, Z2),
у G Я*(У; Z2). Если мы вспомним определение когомологического умножения, то
заметим, что вместо формулы (♦) достаточно доказать следующую формулу:
Sq*(x X у) = S Sq’(x) X Sq’( у}.
Р+Ч=1
Если xG Нп(Х-, Z2) и у 6 Я"1 (У; Z2) (очевидно, можно считать, что элементы
х и у однородны), то существуют отображения /: X->^(Z2, л) ng: Y^»K(Z2, m),
такие, что /*(ел) = х и g*(em) = У- Отсюда следует, что достаточно доказать всего
лишь следующее соотношение:
Sq'(emXe„)= S SqP(em)XSq’(e„).
р+ч=/
Предположим сначала, что i > m + л. Тогда и правая и левая части равны нулю.
Пусть теперь i =m + n. Тогда
Sqm+n(em X е„) = (em X e„)2 = е2, X е2 = Sq'"(em) X Sq"(e„).
Справа от всей суммы Sp+</=m+„ остается всего лишь одно слагаемое, и оно
равно Sqm(em) X Sq"(e„). Осталось рассмотреть случай, когда i < m + л. Пред-
положим, что формула верна для i = m + п— (з — 1). Докажем ее для i =m + n-s,
где s — некоторое фиксированное число, большее нуля.
248
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
Подчеркнем, что т и п предполагаются произвольными числами, а индукция
ведется по разности т + п — i.
Итак, рассмотрим Sq'"4”-1 (em X е„). Для краткости будем вместо K(Z2, л)
писать Кп. Рассмотрим тензорное произведение Кт # Кп пространств Кт и Кп.
Напомним, что для любых пространств X и У их тензорное произведение X # Y
определяется как X X Y/X v У. Например, Sp # Х = Y,PX. В частности, S1 # Х= Y,X.
Так как тензорное произведение ассоциативно, то (S1 # X) # Y = Sl # (X# Y},
т.е. (SX) # У = S (X # У). Кроме того, заметим, что Н*(Х# У) = Н*(ХХ Y)/J,
где J есть подгруппа, порожденная элементами вида (х X 1) + (1 X у), где х 6
ея‘(Т),уея‘(У).
Рассмотрим следующие два отображения:
«т * кп сГ
Возникает отображение в когомологиях:
кп‘, zt)
" Яг(2 (кт # кя-1); zt)
или
4 £ * Hr i (Кт.г * Кп; Z2)
нУКт* Kn-'Z2)
Z Нг'4кт* K„-^zz)
Очевидно, что при гомоморфизмах S-1(/OT_i # Цс„)* и #/n-i)*
элемент ет X еп переходит в элементы em_i X еп и ет X e„_j соответственно.
Гомоморфизм
/m-j: Я’(Кт)^Я’(ЕКот_1) = Я’-1(Кт_1)
обратен к трансгрессии в спектральной последовательности серровского расслое-
ния для Кт и является изоморфизмом при 0 < q < 2т (ср. п. 2).
Рассмотрим в
Нг(Кт#Кп-1г)= ® Нр(Кт,Z2) НЧ(Кп,^
p+q=r
пересечение ядер
Т= [KerS-^/m-i [KerS’1^
Пусть
p = ZaiX0t&TCHr(Km #Kn-,z2).
i
' Тогда X Pi = 0 и X (/Л—i в,) = 0, откуда /^-1“/ = 0 и
fn-iPt = О Д’1» всех i. Так как элемент р лежит в когомологиях Кт # Кп, мы
§2S. СТИНРОДОВЫ КВАДРАТЫ
249
можем считать, что среди элементов а; и иет равных 1 и, следовательно, degaf >
> 2т и deg/3; > 2л и degp > 2(wt + л). Итак, доказано, что пересечение ядер не со-
держит элементов степени, меньшей чем 2 (т + л).
Теперь настало время вернуться к формуле Картана. Предположим, что элемент
Р = Sqm+n-4em X е„) - S Sq₽(em) X Sq’(e„)
p+q-m +n-s
отличен от нуля в Я2<т+л)_,(Кт #Kn;Zi}-
Имеем:
#idKn)*p = Sqm+n-\Z-1f*m_1em Хе„)-
- S Sqp(S-1/m-iem) X Sq4en =
p+q=m+n—s
= Sqm+n-,(em_i X en) - S Sq^.j X Sq’en = 0
p+q=tn+n—s
по предположению индукции, и, аналогично, S-1 (idKn #fn-1 )*P = 0-
Так как dimp = 2(m +л) — s< 2(m + n), to p = 0.
Формула Картана доказана.
4. Другие конструкции станродовых квадратов. Доказанная в п. 2 единственность
стинродовых квадратов наводит на мысль, что для них существуют конструкции,
отличающиеся от К(П, л)-ной конструкции п. 2. Такие конструкции действительно
есть. Вот самая известная из них.
Пусть X — клеточное пространство, d-. Х-*XX X — диагональное отображение,Г:
XXХ^XXX— перемена сомножителей местами. Отображение t клеточно,а отобра-
жение d — нет (кроме тривиальных случаев типа Х= pt). Зафиксируем для d клеточ-
ную аппроксимацию d0 и положим
Da = (d0)#: ®‘(XXX;Z2)^ «‘(X;Z2),
T = Г#: «'(XXI;Z2)^ «'(XXI;Z2).
Вообще говоря, D0T ^Do (потому что отображения t ° d0 и d0 не одинаковы),
но D0T ~ Do (потому что t ° d0 ~ d0). Существует понижающее размерность на 1
отображение
Dr. %*(ХХ X;Z2)-> %*(X;Z2),
такое, что Di6 + 8Di = D0T + Do (мы нигде не пишем минуса, потому что коэффи-
циенты G Z2). Далее, DXT Ф Di (гомотопия, связывающая Г ° d0 с d0, не перево-
дится в себя отображением t), но существует понижающее размерность на 2 отоб-
ражение
#2: $*(XXX;Z2)^ ^(Х^),
такое, что D28 + 8D2 =D^T+#i.
Упражнения. 1. Докажите это и докажите, что существует целая последова-
тельность отображений
#,: r(IXI;Z2)^ «‘(X;Z2),
Dq8^bDq=Dq_lT + D(l_i.
2. Докажите, что для коцикла a G $Л(Х; Z2) коцепь#, (а Ха) 6 $2л-<? (X; Z2)
является коциклом, когомологический класс [#, (а Ха)] которой зависит только
отклассаа€Ял(Х; Z2) коциклаа. (Неверно, что еслиа и& — коциклы, то#, (д X Ь)—
коцикл. Выведите формулу для 8#, (а X 8), где а тлЬ — произвольные коцепи.)
250
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
3. Докажите, что в обозначениях предыдущего упражнения [Dq (а Ха)] = Sq"-<,a.
(Доказательство состоит в последовательной проверке, свойств, перечисленных в
начале параграфа.)
Если клеточное пространство X является на самом деле симплициальным, то
предыдущую конструкцию можно сделать совершенно явной.
Упражнение 4. Пусть X — упорядоченное симплициальное пространство,
а 6 $т(Аг; L2), Ъ 6 ^"(У; Z2) и а — симплекс размерности т + п - q нашей
триангуляции. Положим (а X Z>)] (о) = а(Г™а)Ь(Гт+"~ча) (обозначение г[а
(J > 0 употребляется для (/ — i)-мерной грани симплекса а, вершинами которой
служат i-я (i + 1)-я,..., /-я вершины симплекса а). Таким образом, если когомо-
логический класс a 6 Нп(Х; Z2) симппициального пространства представляется
коцепью a G %>п(Х; Z), то Sqfa представляется коцепью b G Й"+/(АГ; Z), опреде-
ляемой формулой b (о) = д(Г" a)a(T”+ia). Такой же формулой определяется сингу-
лярный коцикл Ь, представляющий Sqza, по сингулярному коциклу а, представляю-
щему а.
§ 29. АЛГЕБРА СТИНРОДА
1. Строение алгебры Стинрода А2. Формушровки. Алгебра Стинрода А =А2 есть
алгебра всех стабильных операций над полем Z2, умножение в которой определя-
ется через композиции операций. Оказывается, что А имеет своими мультиплика-
тивными образующими операции
l,Sq‘,SqJ,...,Sq“,...,
т.е. любая стабильная операция в когомологиях mod2 есть линейная комбинация
композиций стинродовыхквадратов.
При этом квадраты Стинрода не образуют свободный мультипликативный базис
в А. Между ними существуют соотношения. В частности, аддитивный базис алгебры А
составляют не все итерации стинродовых квадратов, а только итерации
Sq/ = Sq'»Sq/1 .. . Sq' fc,
у которых набор I = (ij, i2,..., /\) удовлетворяет условиям: Ц > 2i2, i2 >
> 2i3,..., ik-i > 2ik.
Такие последовательности (iit i2,..., ik) мы будем называть допустимыми
последовательностями, а соответствующие им итерации квадратов — допустимыми
итерациями.
Мультипликативная структура в А определяется соотношениями (’’соотноше-
ния Адема”): если а < 2Ь, то
Sq“Sqb = S
С
Заметим, что справа стоит линейная комбинация допустимых итераций. Иными
словами, отсюда следует, что итерацию любых двух стинродовых квадратов можно
разложить по допустимым двухчленным итерациям. Отсюда же следует, что любая
итерация Sq7 сводится к сумме допустимых.
В самом деле, существует лишь конечное число наборов / = (/i,..., ik) с фик-
сированной суммой SQzQ. Упорядочим эти наборы лексикографически, т.е. положим
<i'i,..., ifc)>(i1,..., ik), если ii = ii,..., i'_j =1,-1, i's > is для некоторого s.
Пусть Sq7 = Sq*1 ... Sq'k — любая итерация стинродовых квадратов. Тогда либо
§ 29. АЛГЕБРА СТИНРОДА 251
эта итерация допустима, либо is < 2is+1 для некоторого s. Заменим SqZ®Sq/l+1
по формуле Адема, н мы получим представление Sqz в виде линейной комбинации
итераций Sq7'', причем fr > Ir для каждого г. Затем мы заменяем по формуле
Адема пары соседних Sq и каждый раз индексы I растут в нашем упорядочении.
Следовательно, процесс конечен и мы придем к линейной комбинации допустимых
итераций.
Из формулы Адема вытекает, в частности, что
, . ( Sq*+1, если к четно,
Sq1Sqfc=-
I 0, если к нечетно.
Например, Sq1 Sq1 = 0, что мы знали и раньше, так как Sq1 = 0 и 00 = 0.
Еще пример. Если положить а = Ъ = 2, то получится соотношение Sq2 Sq2 = Sq3 Sq1.
Между прочим, видна некоммутативность алгебры Стинрода: Sq1 Sq2 =А Sq2 Sq1.
Доказательству всех этих утверждений посвящена оставшаяся часть параграфа.
Основным средством будет служить теорема Бореля.
2. Теорема А. Бореля. Предположим, что дана спектральная последовательность
некоторого расслоения, такая, что
(1) =0;
(2) в слое стоит косокоммутативная алгебра с единицей и с системой однородных
образующих Д1, а2,а3,..., где каждая образующая трансгрессивна;
(3) эта сцстема образующих является простой системой, т.е. одночлены д^д^ ...
... aik (где Л < .< iк) являются аддитивным базисом алгебры.
Из (3) следует, что либо д2 = 0, либо элементы д2 разлагаются в сумму одночленов,
в каждом иэ которых д^ встречается только один раз. Например, если Z2) =
= Л2(Д1, д2,..., flfc), то очевидно, что flj, д2,. .. , ак — простая система образующих.
Если H\F-, Z2) = Z2 [д1( д2,..., ак], то дь ..., ак; aj,..., ак‘, а*,..., ак; д.®,...
... , д*; ... — также простая система образующих.
Утверждение теоремы Бореля состоит в том, что при выполнении условий (1), (2),
(3) в базе стоит алгебра полиномов от образующих bt = т(д;).
Доказательство. Мы считаем, что образующие д, расположены в порядке
неубывания размерностей.
Мы построим некоторую абстрактную спектральную последовательность
(E?,q; df) с указанными свойствами. (1), (2), (3), а затем покажем, что она совпа-
дает с нашей.
Алгебру, стоящую в слое нашей спектральной последовательности, обозначим
через А. Рассмотрим тензорное произведение A ®Zj Z2 [&i, b2, b3,... ], где обра-
зующие bi, b2r. .. поставлены во взаимно однозначное соответствие с образующими
Дь д2,... и degb„ = degfl„ + 1 (л= 1,2,3,...). ПоложимЁ2 =А ®Zj Z2 [bltb2,...]
(биградуировка в Е2 определяется естественным образом).
Теперь надо задать дифференциалы dr. На элементах нижней строки естественно
положить их тождественно равными нулю, а на элементах левого столбца определим
их так: dr(at) = 0, пока г < degfl; (что будет означать трансгрессивность всех обра-
зующих Д/ в конструируемой нами спектральной последовательности); <?г(д() = Af,
если г = degfl/ (мы будем в дальнейшем иногда опускать знак тензорного умноже-
ния для сокращения записи). Пусть теперь задан элемент а G Е2. Он представим в
виде линейной комбинации элементов вида (где sm > 0) : а, ... д». ® bs.' ... bSp,
1 К /1 /р
252
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
где Л < ... < ik’, /1 < ... < /р. Мы положим:
1 Л /1 /р
О при г < degaz, если ц
aii...al^bib!.>..bYp
при г = dega(j, если 4 < Ц ;
О при всех г, если >/1.
Легко видеть, что этим определена (аддитивная) спектральная последователь-
ность. Именно, d2d2 = 0. Мы полагаем Е3 = Kerd2/Imd2. Далее, мы считаем, что d3
определено на Е3. Имеем d3d3 = 0. Полагаем Ел = Кег<?3/1т<?з, и так далее. При
этом Е^ = 0. Каждая образующая либо переходит не в ноль при каком-либо диффе-
ренциале, либо сама является образом дифференциала. Осталось проверить муль-
типликативность этой спектральной последовательности. Мы оставляем читателю
эту проверку, разобрав только случай, представляющий главную трудность, а имен-
но, мы докажем, что
dr(AA') = dr(A) -А'+А- dr(A')
при A = a, ... at.9bp ... bSp; A' = a., ... a,, ® bp ... bf , it
1 * A ip A 4’ A ip<
ii < . Имеем: dr(A) -A' = at ... a,® b. bs.1 ... bSp -a,. ... a.,
2 K *1 /1 /p *1
= a. (a, ... at ) (a, ...a, ) ® bt (bP ... bSp) (bP ... b ? ) и, аналогично,
1 к l2 lk> 1 h Ip It lp.
A dr(A') = af] (ait... afjt) (a,.... a.) ® bti (bp ... bSp) (bp ... b£) = dr(A) - A',
= h=r, i2 < jt,
т.е. dr(A) A' + A -dr(A') = G.
Нужно доказать, что d^A - A1) = 0. Ho AA1 = a^ ... ® ... Мы покажем, что a^
представляет собой сумму образующих а^ + ... + а/т. Из условий на саму алгебру Л
это не вытекает: могло бы оказаться, что а* равно произведению а(1 ... а1т (или
сумме таких произведений), и при этом f < it. Но это противоречило бы предпо-
ложениям относительно спектральной последовательности, так как, с одной стороны,
dtl a2ti = 2dti ati = 0, а с другой стороны, dti (a^ ... a,m) =а,г . .. a/m ® Ь,{. Подчерк-
нем, что речь идет о дифференциалах не конструируемой нами, а исходной спектраль-
ной последовательности. Поэтому АА1 начинается с сомножителя а с номером, боль-
шим, чем it, и поэтому dit(A • А') = 0.
Осталось совсем немного. Мы имеем две спектральные последовательности. Обе
они мультипликативны, имеют = 0, и к тому же у них одинаковый левый столбец
в Е2. Нижняя строка во втором члене одной спектральной последовательности есть
Н*(В-, Z2), во втором члене другой последовательности — то, чему должно быть
равно Н*(В\ Z2) по теореме Бореля.
Предположим, что Н *(В; Z2) изоморфно алгебре Z2 [Ь1# Ъ2,... ] (гдеЬ/ = т(а,)€
€ Н*(В\ Z2)) до размерности q, а в размерности q появляется первое различие, те.
в Я *(В; Z2) появляется либо новая образующая с, либо отсутствующее в
§ 29. АЛГЕБРА СТИНРОДА 253
Z2 [&!, b2,... ] соотношение. Но тогда столбцы с номерами 0,1,2,..., q — 1 во вто-
рых членах двух спектральных последовательностей устроены одинаково. Диффе-
ренциалы также действуют одинаково. Поэтому различие приведет к тому, что в
нашей спектральной последовательности Еж Ф 0, а именно, либо новая образующая с
останется в Е^, либо останется в Еж элемент, который в искусственной спектраль-
ной последовательности переходит в элемент, равный нулю в H*(B\ Z2) согласно
соотношению. •
Теорема Бореля доказана.
3. Теорема Ж.-П. Серра. Теорема. Алгебра H*(K(Z2, я); Z2) есть алгебра
полиномов от образующих Sqre„, где enG Hn(K(Z2, и); Z2) - фундаментальный
класс, I - (j'i, i2,..., 4) - допустимая последовательность, т.е. it > 2i2, i2 >
> 2/3, ..., ik_t > 2ik, и, кроме того, def/ < n. Через defI обозначен "дефект
последовательности", определяемый как сумма (i2 — 2i2) + (i2 — 2i3) + ...
• - • + (ik-1 - 24) + 4 = 24 - 0i + 4 +... + 4).
Замечание 1. При W {0 } имеем def I > 1.
Замечание 2. Осмыслим одно из условий теоремы: def/ < п. Откуда могло
возникнуть такое требование? Предположим, что Sq4„ = Sq*1 Sq*2 ... Sq*fe(ея) =A 0.
Тогда 4< и; 4_i < n + ik\ ik_2 < n + ik + ik_! -,... ; ц < n +ik +4_! + ... +i2;
а нз последнего неравенства следует: 2i\ Си + |/| , т.е. def/ Си. Здесь |/| =
= 4 + ... + ik.
Доказательство теоремы Серра. При и = 1 утверждение теоремы
Серра очевидно. Действительно, K(Z2,1) =R/’”, a//*(R/’“; Z2) =Z2 [ej, degei =
= 1, как это мы вычисляли ранее, а допустимых последовательностей дефекта < 1
кроме (0) не существует.
Пусть теорема доказана для всех k С и — 1. Рассмотрим спектральную последова-
ли-!
тельность расслоения •-----► Кп. Заметим, что если / = (4.4....4) >то def/ =
= 24-1/1.
По предположению индукции Z2) есть алгебра полиномов от мульти-
пликативных образующих рг = Sc^(e„_1), где def/ < и - 1 и итерация Sqz до-
пустима.
В рассматриваемом расслоении £«, = 0; еп_1 — трансгрессивный элемент, а по-
тому трансгрессивный все рт = SqIe„_1. Мультипликативная система {рт} не яв-
ляется простой. Как мы уже замечали, простую систему образующих алгебры
2*2 [{Р/}] = Я*(АГ„_1; Z2) составляют элементы р/ , i > 0. Очевидно, что
(Р/)2 = (SqZe„_ 1 )2 = Sq|/|+"-1 о Sq*(en_ j),
(pj2 = Sq2«''+1>o Sq'^""1 - Sq^-J
и так далее, т.е. любая степень вида (pz) допускает подобное представление.
Отсюда следует, что все эти элементы (pz)2 трансгрессивны. Очевидно, что эле-
менты вида (pj)2 не принадлежат исходной системе {рт}, так как
def[... 2(|/| + п - 1); |/| +п - 1; 4, i2,.... 4] = я - 1.
Наоборот, всякий элемент Sqz(en_!), где def/= п — 1, есть элемент вида
(р/()2 , где def/’ < п - 1. В самом деле, пусть / = (4,4..4). Sq/(e„_1) =
= Sq'1...SqZfc(e„_1).
254
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
Имеем: def Z = й — (й + Ь + • • • + *jt) = « — 1, откуда й = (й + ... + iк) + n — 1 =
= deg(SqZ’ ... SqIfce„_i), и Sq/en_1 = (Sq*2 ... SqZke„_!)2 . Далее, либо l' =
= (й > й, • •, й) имеет дефект <и — 1 и Sqze„_ j = (p/.)2, либо def/' = л — 1, /2 =
= deg(SqZ* ... SqZke„_i) и Sqzen_! = (SqZ* ... SqZfce„_1)4. Продолжая это рас-
суждение, приходим к требуемому результату.
Осталось применить к спектральной последовательности нашего расслоения тео-
рему Бореля, воспользовавшись трансгрессивностыо операций Sqz, — и мы получим
утверждение теоремы Серра.
4. Устройство алгебры А. Как мы видели, алгебра Стинрода А получается из
Н*(К (Z2, и); Z2) предельным переходом. Совершив этот предельный переход,
мы получаем следующее утверждение.
Теорема. Аддитивный базис алгебры А составляют операции Sqz, где! пробе-
гает множество всех допустимых последовательностей (без ограничения на дефект).
При этом операция Sqz тривиальна на всех элементах размерности < def/. За-
метим, что это утверждение обобщает равенство Sq"(x) = 0 при dimx < и.
Умножение в алгебре А, как нам известно, не связано с умножением в
Н*(К(Z2, и); Z2), а определяется с помощью композиции операций.
Доказанная теорема означает, что линейные комбинации итераций стинродовых
квадратов исчерпывают все стабильные когомологические операции, определенные
н принимающие значения в когомологиях mod2. Более того, из нее видно, что меж-
ду этими итерациями существует достаточно большое количество соотношений, так
как всякая операция представляется как линейная комбинация допустимых итера-
ций. Мы приступаем к исследованию этих соотношений.
5. Соотношения.
А. Метод отыскания соотношений. Рассмотрим произведение Х= N
экземпляров бесконечномерного вещественного проективного пространства RP”.
Как мы знаем, Н*(Х\ Z2) = Z2 [й,..., xN] - алгебра полиномов от ТУ однородных
образующих. Обозначим через и произведение йй-.. xN& Н*(Х-, Z2).
Алгебра А обладает естественной градуировкой: А = Ао ® Aj ® ..., где Aq =
= 0s (q, Z2, Z2) - совокупность операций, повышающих размерность на q. Зафик-
сируем число q и возьмем N^q.
Построим отображение /: Aq -» Н*(Х', Z2), положив j(p) = <р(йй-.. xN) =
= <р(и) для G Aq. Имеет место замечательный факт: отображение j мрноморфно,
иными словами, если <р(л) = 0 в Н*(Х‘, Z2), то = 0, т.е. для любого Y и любого
элемента а е HP(Y; Z2) любой размерности р имеет место равенство <р(а) = 0.
Докажем это утверждение. Рассмотрим группу Bq =j(Aq) С HN*4 (Х\ Z2). По-
пытаемся описать элементы, принадлежащие Bq. Сейчас мы лишний раз убедимся
в том, что требование естественности — это очень сильное требование, из которого
можно извлекать массу самых интересных следствий. Пусть $ — любая когомологи-
ческая операция (даже не обязательно стабильная). Тогда ф(Х1Х2... xN) есть сим-
метрический полином от х2, х2,..., xN. Для доказательства достаточно рассмотреть
отображение fy: Х-+Х, переставляющее i-Й сомножитель с /-м.
Еще одно следствие иэ естественности: ф(и) делится на и, т.е. ф(и) =.
= и - P(xlt х2,...., xN), где degP = q. Для доказательства рассмотрим вложение
RP” X ... X RP” ->• X, где в произведении слева пропущен i-й сомножитель. Тогда
лг-1
при индуцированном отображении когомолотий ty(u) отобразится в нуль, так как и
отобразится в нуль. Следовательно, делится на й, и это верно для любого i.
§ 29. АЛГЕБРА СТИНРОДА
255
Так как любая стабильная операция есть линейная комбинация итераций Sq1,
то дальнейшие рассуждения достаточно проводить, изучая только итерации стинродо-
вых квадратов. Покажем, что многочлен /(<^) е Zj [х1( х2,..., xw] содержит каж-
дую переменную х,- в степени, являющейся степенью двойки. Рассмотрим RP“.
Из формулы Картана моментально следует, что
« к
Sq‘(x2 ) =
Л Л
х2 при i = О,
2*+1 • ^к
х при1 = 2 ,
О при всех прочих i.
Здесь Sq'(x7) = Cjx?+I. Значит, Sqz(u) есть полином, в котором все степени пере-
менных есть степени двойки. Итак.: / (</>) = и • P(xlt х2, , xN), где degP = q и все
Xj входят в степенях вида 2к — 1 и Р — симметричен.
Оказывается, что н наоборот, любой полином указанного типа есть образ некото-
рого при отображении /. В самом деле, рассмотрим симметрический полином
, fc , k ,fc—1 .к—1
Sym(xi ...<х2+1 ...х22 ...х2л_1 + 1 ...x2fcx„k+1 ...xN),
где Sym означает симметризацию, 1 < «1 < п2 < ... < пк < N — любые числа, та-
кие, что «1(2к - 1) + (и2 - «1) (2fc-1 -!)*<•... + (пк - пк_ i) -q. Ясно, что такие
полиномы составляют аддитивный базис в пространстве всех полиномов. Упорядо-
чим нх лексикографически. Тогда рассматриваемый нами симметрический полином
будет старшим членом в разложении по упорядоченному базису полинома
-к—1 2nt , nt
Sq2 "‘...Sq Sq fy),
откуда и вытекает наше утверждение.
Итак, группа Bq описана полностью. Осталось подсчитать размерности Bq и Aq
(как векторных пространств вида Z2 ). Для того чтобы найти размерность Bq, доста-
точно выяснить, сколькими способами можно представить число q в виде суммы
слагаемых вида 2 к - 1.
Размерность Aq равна числу допустимых последовательностей с модулем, рав-
ным q. Пусть I - любая допустимая последовательность: I = (/’i, i2.......ik),
ii > 2i2, i2 > 2/3,..., ik-i > 2ik, н пусть i2 + i2 + ... + ik = <?.~Положима1 =
-ii — 2i2; a2=i2-2i3; ... ,ak~i=ik-i ~2ik, ak =ik, тогда q = S£=1ap(2₽-1).
Ясно также, что любое такое разложение числа q определяет допустимую последо-
вательность.
Следовательно, число допустимых последовательностей I с модулем, равным q,
равно числу способов представления q в виде суммы 2(2-1). Итак, dimB4 =
= dimт.е. j — мономорфизм, что и требовалось доказать.
Доказанная теорема позволяет без малейшего труда находить в А соотношения:
чтобы доказать, что = Sq1’ ... Sq1" = 0, достаточно проверить, что </>(и) = 0.
Докажем, например, хорошо известное нам соотношение: Sq1 Sq1 = 0. В самом
деле, Sq1Sq1(XiX2... xN) = Sq*(x?X2... xN + X1X2X3.. . xN + . .. + хгх2... x^) =
= ... + хг... xj... xj... x^ + ... + Xj... xj... xj... xN +.. . = 0,ибо каждое сла-
гаемое входит в сумму с коэффициентом 2.
256
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
Упражнение 1.Докажите,что Sq2Sq2 = Sq3Sq1.
В. Соотношения Адема. Как уже говорилось, полную систему соотношений в ал-
гебре А составляют так называемые соотношения Адема:
[а/2]
SqaSqb= S Cr2/iSqe+b“cSqc,
c=max(a —Ь+1,0)
справедливые при д< 2Ь. Для того чтобы доказать такое соотношение, достаточно
проверить, что
Sq‘Sqb(u) = S Са-_2с_ ^-^"‘Sq^),
С
где и = *1*2... xN е HN(X’, Z2). Левая и правая части этого равенства вычисля-
ются по формуле Картана. Левая часть равна:
^b+a-3sSym(*l- • • xixs+l • xa+b-txa+b-s+l • • • XN^ >
s
правая часть равна:
22 СЪ?а-3»‘ Cb~-c-l • • *a+S-s*a+b-s+l • • XN) •
c s
Для доказательства формулы Адема достаточно проверить сравнение:
*
Сь~* 3. = 2 I (mod 2),
Ъ+а— 3s ~ Ь+л—3s о —с—1 х
с
которое после замены переменных d = а - 2s, е = b — s, f = с - s превращается в
следующее:
П/2)
С* = S С' С*-” (mod2).
d+e /=max(O,d —е+1) d+e e~/+1
Это может быть сделано уже элементарными средствами.
Полнота системы соотношений Адема вытекает иэ одного сделанного ранее заме-
чания: с помощью формул Адема можно привести любую итерацию стинродовых
квадратов к линейной комбинации допустимых. Нами доказано, что допустимые
итерации линейно независимы, откуда следует, что любое соотношение между ите-
рациями стинродовых квадратов следует из соотношений Адема.
Упражнения. 2. Доказать, что в качестве мультипликативных образующих
алгебры А можно взять стинродовы квадраты Sq1, Sq2, Sq4, Sq8...причем эту
систему образующих нельзя уменьшить.
3. Найти определяющую систему соотношений между образующими иэ предыду-
щего упражнения. (Это — нерешенная проблема!)
4. Докажите следующую теорему Баллета—Макдональда. Соотношения Адема
можно записать в компактном виде:
P(s2 + st)P(t2) = P(t2 +.sr)P(s2),
гдеР(и) = Su'Sqz.
6. Вычисление 9q 0s (q, Z, Z2). Вычисление когомологий K(Z, ri) mod 2 бы-
ло проведено Серром одновременно с вычислением когомологий К (Z2, ri) mod 2,
§ 29. АЛГЕБРА СТИНРОДА 257
что и не удивительно, так как эти два вычисления совершенно одинаковы (приме-
няются индукция по п и теорема Бореля). Вот окончательный результат.
Теорема. Кольцо Н* (K(Z,ri)-, Z2) при п> 2 есть кольцо полиномов от обра-
зующих SqIe'n,zde Hn(K(Z,n); Z2) - образующая и I = (i'i,i2,... ,ik) -
произвольная допустимая последовательность, такая что def I < п, и ik > 1 (послед-
нее неравенство и составляет все различие между когомологиями K(Z,ri) uK(Z2, ri)).
Переходя к пределу, получаем следующее утверждение.
Теорема. Группа 0s (q, Z, Z2 ) как векторное пространство над Z2 имеет
базис, состоящий из всех операций Sq7, где I = (ii,i2.ik) — допустимая после-
довательность, такая, что ik> 1.
Доказательства обеих теорем оставляются читателю.
Замечание 1. Мы рассматриваем Sqz как элемент из 0s (i, Z, Z2 ), т.е. как
операцию (X; Z) -»Я,+/(ЛГ; Z2). На самом деле Sqz нельзя прямо применять
к целочисленному элементу. Мы имеем в виду, что сначала этот элемент приводится
mod 2, т.е. под Sqz мы фактически понимаем Sqz » Pi, и соответственно под Sq1 по-
нимаем Sq7 о р2, где р2 - приведение целочисленных когомологий mod 2.
Замечание 2. Не нужно думать, что Sq1 действует в Н * (K(Z,ri) \ Z2) три-
виально. Имеет место лишь равенство Sq1 ё„ = 0, хотя в то же время, например,
Sq1 Sq2 ёп = Sq3 ё„ Ф 0 при п > 3.
7. Алгебра Стинрода mod р. При р> 2, как и при р = 2, единственной (с точностью
до множителя) операцией, действующей в когомологиях с коэффициентами в Zp,
является гомоморфизм Бокштейна 0. Однако, если при р = 2 операция 0 - Sq1 ничем
не выделяется среди других стинродовых квадратов, то при р> 2 операция 0 играет
особую роль. Операции, аналогичные другим стинродовым квадратам, также сущест-
вуют. А именно, существует единственная стабильная когомологическая операция
(она называется степенью Стинрода и обозначается через Р z ) из 0s(2i(p — 1);
Zp, Zp), обладающая тем свойством, что Рр(х) =хр при x^H2i(X\ Zp). Как и
в случае р = 2, операция Р° является тождественным отображением и Рр (х) = О
при deg х< 2i. При этом Р2 = Sq2 z.
Оказывается, что алгебра Стинрода Ар мультипликативно порождается операция-
ми рр = 0 и Рр1 . Мы положим
Stit = |PpZ ПРИ k = 2i(p-l),
Рр о Р? при k = 2i(p - 1) + 1.
Таким образом, операции Stfe определены при к = 0,1 mod(2p- 2). Заметим,
что если р = 2, то Stк = Sq к.
Опишем в Zp-алгебре Ар аддитивный базис.
Пусть задана последовательность чисел I = (ii,i 2,...,ik), где im = О,
1 mod(2p —2). Поставим в соответствие этой последовательности операцию St7 =
= StZ1Stz’ ...St‘k.
Последовательность I называется допустимой, если
h ^Pii, ii ^pii, »з • • •
Имеет место теорема: допустимые итерации {St7} образуют аддитивный базис
Zp-модуля Ар.
9. А.Т. Фоменко
258
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
Соотношения между операциями Stz порождаются соотношениями Адема:
[“/pl
pa nb = V / 1\с+а г^а-рс ра+Ъ — с рс .
Р Р с=0 (“0 С(Р-1)(»-с)-1 Р Р’
. [о/р]
Рр‘^р= Л (-1) сгР-с^-еЛраР+ рсР+
[(a-D/pl
+ 2 (_1)*+“+1 С?-Рс~' , pa+b-cp pc а<рЬ.
с=0 v ' (p-V)(b-c}-\ р *р р г
В качестве системы мультипликативных образующих в Ар (как и в случае р = 2)
могут быть взяты операции 1, рр, Рр , рР, РР ,...
Доказательство этой теоремы было впервые получено А. Картаном. Читателю,
желающему познакомиться с ним, мы рекомендуем прочесть статью М.М. Постни-
кова ”К теореме Картана” (Успехи мат. наук. — 1966. — Т. 21, № 4. — С. 35—46) -
8. Другие классификационные теоремы. Введем некоторые обозначения и опре-
деления. Пусть К - поле. Обозначим через Л(т,К) К-алгебру с базисом (1,х), где
dim х = т, х2 =0. Назовем ее внешней алгеброй, ах — образующей внешней алгебры.
Через Р(ш,К) мы обозначим К-алгебру с базисом (1,х<*\х<2\...), где
degx^ =кт, а умножение определено так: х^ x<r> = С^гх^к+г\ Эта алгебра
носит название алгебры модифицированных полиномов, а элементх=х^ называет-
ся ее образующей. Очевидно, элемент х = х действительно является мультипли-
кативной образующей Р(т, К). Под тензорным произведением таких алгебр мы
будем понимать косое тензорное произведение (т.е. (a®b)(c®d) =
= (-l)d,mS d,mc ac®bd), но слово ’’косое” будем опускал., так как обычное
тензорное произведение мы здесь не рассматриваем.
Зафиксируем простое число р и группу n = Z или ZpS и введем определение
набора чисел, удовлетворяющих условию (Ср). Пусть нам дана последовательность
/ = (j’l, i2,... Jk) • Мы скажем, что I удовлетворяет условию (Ср), если:
(l)ii>P4; iz >pi3;... ;ik-2 ^Pik-Г, ik-i^^P-2;
(2)4 =0, если П = Z;
(3) ik - 0 или I, если П = ZpS ( p — простое);
(4) it = 0 или I mod(2p - 2) для I < t < k.
Мы будем использовать стандартное обозначение Н* (П, и; Zp) =Н* (Х(П,и); Zp).
Теорема (А. КартАн). Для п > I и простого р>2 алгебра когомологий
Н* (П, и; Zp) {где П = Z или ZpS) изоморфна тензорному произведению внешних
алгебр Л {m, Zp) с образующими нечетной степени и алгебр обычных полиномов
с образующими четной степени. Для и > 2, р = 2, Н* (П, и; Z2) {где П = Z или Z2s)
изоморфна тензорному произведению алгебр обычных полиномов. В обоих случаях
число образующих, степень которых есть и + q, равно числу последовательностей I,
таких, что q = |/|, удовлетворяющих условию {Ср) и следующему требованию:
р‘1 < {р - 1) (и + q).
Замечание. В этой теореме как частный случай содержатся все предшест-
вующие результаты. Если П = Z, то из условия (Ср) следует, что ik = 0, a ik-i >
> 2р - 2, и если р = 2, то ik-1 > 2, т.е. Sq1 не входит в итерации Sqz.
§ 30. ПРИМЕНЕНИЯ СТИНРОДОВЫХ КВАДРАТОВ
259
При р = 2 условие p‘l < (р - 1) (п + <?) превращается в хорошо знакомое нам
соотношение def I < п.
Оказывается, что и алгебра гомологий пространства Я(П, п) допускает полное
описание. Умножение в гомологиях пространства ЛГ(П, п) индуцируется структу-
рой Я-пространства: К(П, п) - £1К(П, п + 1).
Теорема (А. Картан). При п > 1 и простом р > 2 алгебра гомологий
Н, (И, л; Zp) (где П = Z или ZpS) изоморфна тензорному произведению внешних
алгебр A.(m, Zp) с образующими нечетной степени и алгебр модифицированных по-
линомов с образующими четной степени. Для и > 2, р = 2 алгебра гомологий
Н, (П, п; Z2) (где П = Z или Z2s) изоморфна тензорному произведению алгебр
модифицированных полиномов. В обоих случаях число образующих, стабильная
размерность которых есть q, равно числу последовательностей I, таких, что |Z| = q,
и удовлетворяющих условию (Ср).
Теорема о выборе базиса (А. Картан) .Пусть П =Zue„EH" (Z,n; Zp)~
фундаментальный класс. Тогда в качестве образующих внешних алгебр и алгебр
обычных полиномов, фигурирующих в теореме о Н* (Z, п; Zp), можно выбрать эле-
менты Stp(e„), где I удовлетворяет условию (Ср) ,upi1< (р- 1) (п + |/|).
Доказательство этих утверждений читатель найдет в статьях А. Картана (см: Ма-
тематика: сб. перев. — 1959. - Т. 3, № 5 и № 6). Там же читатель найдет и исчерпы-
вающую информацию о целочисленных когомологиях К(П, п).
§ 30. ПРИМЕНЕНИЯ СТИНРОДОВЫХ КВАДРАТОВ
В этом параграфе мы возвращаемся к случаю р = 2.
Гомотопическая ориентация нашей книги вынуждает нас рассматривать стинро-
довы квадраты, главным образом, как средство вычисления гомотопических групп.
Действительно, в этом отношении они очень полезны; в п. 1 мы покажем, как с их
помощью можно вычислить ття+2 (S”), а в следующей главе вычислим стабильные
группы яи+ч (5”) с q < 13. Не следует, однако, забывать, что гомотопические вычис-
ления — это, так сказать, побочный эффект теории Стинрода. Чтобы убедить в этом
читателя, мы приведем в последующих пунктах подборку применений стинродовых
квадратов, стремясь при этом не столько к полноте, сколько к разнообразию.
1. Вычисление гомотопических групп. Ниже предполагается, что п велико.
Вычислим Н* (Sn | „+!; Z2 ) до размерности п + 4 включительно. Из спектраль-
К(7,,п-1)
ной последовательности расслоения 5 |n+i--------* S (рис. 131) видно, что эти
когомологии устроены так:
я п +1 и + 2 п + 3 П + 4
Нч(5п\п+1-,7.г) Z2 z,
образующие, соотношения и Sq1 и V (Sq2u = 0) Sq‘U = -Sq’Sq'u
Как нам известно, trn+i(Sn) = Z2. Спектральная последовательность расслоения
9*
260
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
л+4
л+3
/г+2
Л+/
п
п-1
Sqffe=Sq*i>=SqzSq,«
Sq4e=y
Sq’e=Sq'i/
Sq*e=tf-
e
Рис. 131
Рис. 132
K(Z2,n)
S |и+2----------*• S |„+i устроена, как показано на рис. 132. Для 5 |„+2 имеем:
<*
ч л + 2 л+ 3
Hq(Sn\n^,Z2} Z, +Z,
образующие W Sqlw X
Мы уже видим, что
tf"+2(S"ln+2) = Z2,
и, значит,
тги+2 (S") = Яи+2 (Sn |„+2) = (Z или Z2s) ® (группа нечетного порядка).
Но группа я„+2 (S”) конечна (п. 3 § 25) и не содержит элементов нечетного поряд-
ка (п. 4 § 26). Значит,
Яи+2 (5") = Zjj.
На самом деле тот факт, что Sq1 w =А 0, т.е. 0(w) =А 0, уже говорит о том, что s = 1.
Однако докажем это с помощью спектральной последовательности. Найденный
нами нулевой элемент w е Я”+2(5”|„+2; Z2) определяет отображение 5”|я+2 -►
K(Z,,n+l)
-► £(Z2, п + 2); рассмотрим расслоение Е---------► 5 |„+2> индуцированное рас-
K(Z,,n+l)
слоением *---------► К (Z2, п + 2) посредством этого отображения. Пространство
Е можно назвать ’’недоубивающим пространством”: из гомотопической последо-
вательности рассматриваемого расслоения видно, что
Ял+2(Я) = Яп+2(^")/Z2 ,
nq (£) = irq (Sn) при q > n + 2.
(На самом деле E — убивающее пространство, мы сейчас в этом убедимся.) Рассмот-
KlZi.n+l)
рим спектральную последовательность расслоения Е---------► 5 |„+2 (рис. 133).
Из нее видно (ввиду Sq1 w =# 0 — от этого не уйти!), что Нп*2 (Е-, Z2) =0, и, зна-
чит, Н„+2(Е‘, Z2) =0, я„+2(£) есть группа нечетного порядка, т.е. 0, поскольку
§ 30. ПРИМЕНЕНИЯ СТИНРОДОВЫХ КВАДРАТОВ
261
я„+2 (5п) есть 2-группа, а яп+2 (£) яп+2 (5,")/Z2. Значит, Е есть убивающее прост-
ранство Sn |„+3 и я„+2 (Sn |„+2) =я„+2($") = Z2.
Кстати, мы видим, что Я„+3 (Е; Z2) = Z2; значит, 2-компонента группы я„+3 (5")
eCTbZ2$.
Упражнение 1. Вычислите я„+3(5"). [Указание. Рассмотрите ’’недоубиваю-
K(Z,,n+2)
щее пространство” Ei с расслоением Ег ----------► S |„+3. Убедитесь в том, что
Hn+3(Ei', Z2) снова есть Z2. То же будет верно для следующего недоубивающего
/7+2 /7+3
Рис. 133
пространства Ег, Е2 -------► Ei, и только третье недоубивающее пространство
Е3 убивает-таки группу я„+3(5"). Значит, 2-компонента группы яп+3(5") есть Z8.
Далее, из п. 4 § 26 мы знаем, что группа я„+3 (5") имеет 3-компоненту Z3 и не
имеет p-компонент с р > 3. Значит, я„+3(5") = Z24. (Сделав это упражнение, вы
передокажете основной результат одной из самых трудных работ дофранцузской
эпохи — работы В.А. Рохлина, в которой группа я„+3 (5") была вычислена геомет-
рическим методом.) ]
2. СТинродовы квадраты и классы Штифеля — Уитни.
А. Формула для Sq*wm. Поставив в соответствие вещественному векторному
расслоению ij когомологический класс Sq* wm его базы, мы получим новый харак-
теристический класс вещественных векторных расслоений. Но ’’новых характерис-
тических классов” не бывает: в п. 4С § 19 мы доказали, что всякий характеристи-
ческий класс вещественных векторных расслоений с коэффициентами в Z2 есть поли-
ном от классов Штифеля — Уитни. Что же это за полином в данном случае? Оказы-
вается, что имеет место равенство
к
Sq* wm = S С'т _к wk4 wm+j.
j=o
Доказательство, детали которого мы оставляем читателю, проводится по следую-
щему плану. Сначала мы проверяем, что левая и правая части равенства принимают
одинаковые значения на расслоении f X ... X J с базой RP7'7 X ... X RP7'7, где J —
хопфовское расслоение над RP7V, a N и число сомножителей достаточно велики.
Затем (или раньше) доказывается, что никакой полином от классов Штифеля не
принимает нулевого значения на расслоении £ X ... X (вычисление для произ-
ведения вещественных проективных пространств — один из ключевых приемов
в теории как классов Штифеля — Уитни, так и квадратов Стинрода).
Пример:
Sq1 wm = wi wm + (m - 1) wm+l.
262
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
В частности, если Wj = 0, т.е. если расслоение ориентируемо, то Sq1 wm - wm + i
при четных т. Но Sq1 — гомоморфизм Бокштейна. Вспомнив определение гомо-
морфизма Бокштейна (п. 3 § 15), мы заключаем, что у ориентируемого расслое-
ния классы Штифеля — Уитни являются целочисленными классами, т.е. образами
целочисленных классов порядка 2 при гомоморфизме приведения р2: Н* (—; Z) ->
-*Я*(-; Z2).
В. Отступление-, пространство Тома и изоморфизм Тома. Пусть f — вещественное
векторное расслоение размерности и. Зафиксируем в слоях евклидову структуру
и обозначим через DQ-) и 5(f) пространства шарового и сферического расслое-
ний (со слоями Dn и 5"-1), ассоциированных с f. Пространство T(f) =
называется пространством Тома расслоения f. Пространство Тома устроено так:
в нем лежит база В расслоения f (бывшее нулевое сечение), и через каждую ее точку
проходит n-мерная сфера. Эти сферы не гомеоморфны Sn канонически, поскольку
слои расслоения £ не гомеоморфны канонически R", но они покрывают все про-
странство T(f) и имеют общую для них всех точку — противоположную точке В,
а в остальном не пересекаются (рис. 134)-
Упражнения 2. Постройте гомеоморфизм между йространством Тома хоп-
фовского расслоения над RP” и пространством RP"+1, Постройте комплексный
аналог этого гомеоморфизма.
3. Что представляет собой пространство Тома тавтологического расслоения над
многообразием Грассмана?
Если база В расслоения f клеточна, то пространство T(f) имеет естественную
клеточную структуру: клетками являются прообразы в D(f) — 5(f) клеток базы В
и точка, получившаяся из 5(f). Таким образом, если В имеет По нульмерных клеток,
И1 одномерных клеток, и2 двумерных клеток.....то T(f) имеет одну нульмерную
клетку, Ио л-мерных клеток, (п + 1)-мерных клеток, л2 (л + 2)-мерных кле-
ток, ... Более того, если расслоение f ориентировано, то ориентированным клет-
кам базы В отвечают ориентированные клетки пространства T(f), и зто соответствие
Рис. 134
согласовано с коэффициентами инцидентности. Поэтому для ориентированного рас-
слоения f имеют место ’’изоморфизмы Тома”
t: Hq (В) a Hq+n (T(f)), t: Нч (В) s Я**”(T(f)).
По модулю 2 аналогичные изоморфизмы строятся независимо от ориентации.
Класс и = t(l) G Hn(T(l-); Z или Z2) называется классом Тома расслоения f.
Упражнение 4. Докажите формулу t(a) = иа. (Умножение в правой части
понимается в следующем смысле. Когомологии базы не отличаются от когомоло-
гий пространства D(f), так что можно считать, что а G Н* (0(1-); —); в то же вре-
MH/T(T(f); -) = Я* (D(f), 5(f) ; -); умножение Я* (0(f)) ®Я* (P(f), 5(f)) -*
§ 30. ПРИМЕНЕНИЯ СТИНРОДОВЫХ КВАДРАТОВ
263
-*Я*(О(£), 5(5)) есть просто частный случай ^-умножения Н* (X) ®Н*(Х, А) -*
-’•Я* (X, А) (см. упражнение 3 к § 16).)
Рассмотрим отдельно случай нормального расслоения. Пусть 5 — нормальное рас-
слоение подмногообразия У многообразия X.
Упражнени я.5. Покажите, что в этом случае Т(5) = Х/Х - U, где U - труб-
чатая окрестность многообразия Y.
6. Сквозное отображение
я*(У)-я*(Т(5))-*я*(Х),
где вторая стрелка обозначает проекцию X ->•Х/(Х - U) = Т(5), совпадает с /, (см.
п. 7 § 17), где i - включение Y ->Х.
С. Sq-определение классов Штифеля - Уитни.
Теорема. Для всякого расслоения 5
wm'(5) = f1 Sqmt(l),
где 1 - нульмерный когомологический класс базы.
Доказательство, детали которого мы оставляем читателю (он может найти их
в книге Милнора и Сташефа "Характеристические классы”), состоит в последова-
тельной проверке аксиом классов Штифеля — Уитни (см. п. 5 § 19) для классов
Г1 Sqm t(l).
Следствие. Если 5 есть нормальное расслоение многообразия Y в X и i: У -+
-»• X есть включение, то
Й (?) - Sqm f, (1) = Sqm (D? [У]).
Упражнение 7. Докажите, что для n-мерного многообразия X имеет место
равенство wm (X) = 0, при m > п - а(п), где а (л) есть число единиц в двоичной за-
писи числа п, a wm обозначает класс Штифеля — Уитни нормального расслоения в
евклидовом пространстве. [Напомним, что в п. 6 § 19 мы доказали, что нетриви-
альность класса wm (X) служит препятствием к существованию погружения много-
образия X в Rn+m-1. Таким образом, нормальные классы Штифеля не препятствуют
существованию погружения произвольного n-мерного многообразия в R2
Недавно Коэн анонсировал доказательство "гипотезы Масси", по которой всякое
n-мерное многообразие погружается в R2. Некоторые подробности см. в
докладе Ланна в семинаре Бурбаки (Lannes J. La conjecture des inunersions//Aste'-
risque. — 1982. — № 92—93. — P. 331—346). (Ранее было известно, что число 2п - а (и)
нельзя уменьшить: в пространство меньшей размерности йе погружается, по причи-
нам нормальных классов Штифеля - Уитни, произведение RP2 1 Х...Х RP2 s,
где 2*> + .., + 2*« — двоичное разложение числа и.) ]
D. Формула By. Положим w= 1 + + w2 + w3 + .. .и Sq = 1 + Sq1 + Sq2 + Sq3 +...
Заметим, что операция Sq: Я‘(-; Z2) -+H*(X\ Z2) обратима: (Sq)-1 = 1 + Sq1 +
+ Sq2 + Sq2 Sq1 +...
Теорема (By, он же У). Пусть X - замкнутое многообразие. Тогда для лю-
бого аЕН*(Х; Z2)
<Sq-1w(X),P(a)> = <Sqa, [X] >.
Эта "формула By” полностью определяет классы Штифеля — Уитни многообразия.
Бе стандартное доказательство можно найти в книге Милнора и Сташефа "Характе-
ристические классы” (§ 11) или в ’’Алгебраической топологии” Спеньера (§ 10
гл. 6); см. также п. 4 § 42. Читатель может попытаться дать другое доказательство,
264
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
следуя такому плану: касательное расслоение многообразия X — это то же, что нор-
мальное расслоение диагонали diag = Х в XX Х\ следовательно,
d\ wm (X) = Sqm (Р^х х [diag]);
так как р о d = id (d — диагональное отображение X -*Х X X, р - проекция на, ска-
жем, второй сомножитель), то
(X) = р\ Sqm [diag]),
apj (а X 0) = < 0, [X] >а; и т,д.
Следствие 1. Классы Штифеля - Уитни замкнутого многообразия являют-
ся его гомотопическими инвариантами (ср. п. 6Е § 19).
Следствие 2 (теорема Штифеля). Всякое ориентируемое замкнутое трех-
мерное многообразие параллелизуема.
Доказательство. Чтобы доказать параллелизуемость ориентируемого трех-
мерного многообразия X, ^достаточно построить на X два линейно независимых
К(3,2)
касательных векторных поля, т.е. построить сечения расслоения Е-----> X, ассо-
циированного с касательным расслоением. Так как К(3, 2) ^RP3,to я> (К(3, 2)) =
= Z2, я2 (V(3, 2)) =0. Первое препятствие к построению сечения лежит в Я2 (X;
Я1(7(3, 2))) = Я2 (X; Z2) и совпадает с классом w2. Нам достаточно доказать,
что w2 = 0, поскольку следующее препятствие будет лежать в нулевой группе
Я3 (X; я2 (V(3, 2))). Чтобы применить формулу By, посмотрим, как в Я* (X; Z2)
действуют квадраты Стинрода, принимающие значения в Я3. Ввиду ориентируемос-
ти многообразия операция Sq1: Я2 (X; Z2) ->Я3(Х; Z2) тривиальна (гомомор-
физм Бокштейна 0: Н2 (X', Z2) -> Я3 (X; Z2) есть по определению композиция
Я2 (X; Z2) -> Я3 (X; Z) ->Я3 (X; Z2), а первая стрелка, будучи отображением ко-
нечной группы в Z, тривиальна). Далее, Sq. Я1 (X; Z2) ->Я3(Х; Z2) есть 0 (по-
тому что Sq/ х = 0 при i > dimx), и тем более Sq3: Я0 (X; Z2) ->Я3 (X; Z2) есть 0.
Следовательно, < Sqa, [X] > = 0 при dima ¥= 3, значит, Sq-1 w(X) может принимать
ненулевые значения только на нульмерных гомологических классах, значит,
Sq-1 w(X) е Я0 (X; Z2), w(X) G Я0 (X; Z2) и w2 (X) = 0.
Упражнения. 8. Пусть X — связное замкнутое ориентируемое четырехмер-
ное многообразие. Докажите, что для любого a G Я2 (X; Z2) имеет место равен-
ство a2 = aw2 (X). [Пояснение. Поскольку область коэффициентов есть Z2, функ-
ционал a •-» < a2, [X] > линеен. Из этого вытекает (ввиду невырожденности умно-
жения) , что существует класс a0 G Я2 (X; Z2), такой, что < аа0, [X] > - < a2, [X] >,
т.е. аа0 = а2. Наше утверждение заключается в том, что a0 = w2 (X).]
9. Найти а0 в неориентируемом случае.
3. Вторые препятствия. Само собой разумеется, квадраты и степени Стинрода
придумал Стинрод. Квадраты Стинрода впервые появились в его работе ’Troducts
of cocycles ond extensions of mappings” (Ann. Math. - 1947. — V. 48, № 2. —
P. 290—320). He все знают, однако, что Стинрод ввел стинродовы квадраты не прос-
то так, а преследуя определенную цель — обобщение классификационной теоремы
Хопфа. Эта теорема Хопфа'доказывалась нами в п. 4 § 18; она заключается в том,
что если X есть и-мерное клеточное пространство, то
я(Х,5") = Я"(Х;г),
причем соответствие относит классу отображения/: X ->-5" когомологический класс
/* («), где s G Я" (S"; Z) - образующая. Стинрод решил следующую по сложности
задачу: найти я(Х, S") в случае, когда dim X = п + 1. Разумеется, и в этом случае
имеется отображение я(Х, 5") -+Я"(Х; Z), [/] »-»/• (s), но оно не обязано быть
§ 30. ПРИМЕНЕНИЯ СТИНРОДОВЫХ КВАДРАТОВ
265
взаимно однозначным. Нужно, во-первых, найти его образ, и, во-вторых, описать
при данном a G Нп (X; Z) множество классов отображений ft X -+Sn, для которых
/* (s) = а. Ответ на этот вопрос (и дальше больше) дает следующая теорема Стин-
рода.
Теорема. Пусть п > 2, и пусть X - клеточное пространство. Тогда: (1) если
dimX < п + 2, то образ отображения ф: ir(X, Sn) -+Нп(Х-, Z), [/] ->•/’ (s), есть
ядро сквозного отображения
Нп (Х\ Z) Д. Нп (Х-, Z2) Нп*2 (Х-, Z2);
(2) если dim А- < п + 1, то множество ф'1 (и) находится во взаимно однозначном
соответствии с коядром сквозного отображения
Нп_ 1 (X; Z) —> Я" _ 1 (Х-,Z2) Hn+i (X; Z2).
Упражнение 10. Докажите теорему Стинрода. [Указание. ДляиЕН"(Х; Z)
рассмотрите соответствующее отображение X ->K(Z, и); у K(L, п) есть одна «-мер-
ная клетка, одна (п + 2)-мерная клетка и еще клетки более высоких размерностей.
Если dim X < п + 2, то можно считать, что X отображается в sk„+2 K(Z, ri); препят-
ствие к тому, чтобы прогомотопировать это отображение в Sn = sk„A?(Z, л), рав-
но Sq2'u; этим доказана первая часть теоремы, доказательство второй части анало-
гично.]
4. Несуществование сфероидов с нечетным инвариантом Хопфа.
Теорема. Если п не есть степень двойки, то в \ (S2”) нет элементов с не-
четным инвариантом Хопфа (см. замечание 2 в конце п. 4 § 16).
Доказательство. Пусть a G я2„_t (5") — элемент с нечетным инвариан-
том Хопфа, и пусть Y = Sn \JfD2n, где f — сфероид класса а. Очевидно,
Яч(У;г2) =
Z2 при q = 0, и, 2п,
0 при остальных q
и, по определению инварианта Хопфа, операция возведения в квадрат Я" (У; Z2) -*
-* H2n(Y; Z2) нетривиальна. Но эта операция есть Sq", а если п не есть степень
двойки, то Sq" представляется как многочлен от Sq' с i < п (например, Sq2n+1 =
= Sq1Sq2", Sq4"+2 = Sq2Sq4” и т д. — см. упражнение 2 к § 29). Так как
Hq (У; Z2) =0 при и < q < 2л, то любая композиция стинродовых квадратов с но-
мерами, меньшими и, тривиальна на Нп (У; Z2) — противоречие.
(Следствие: размерность всякой вещественной алгебры с делением есть сте-
пень двойки.)
Как уже говорилось, элементы с нечетным инвариантом Хопфа в группах
п2я-1(£”) с и > 8 отсутствуют. Одно из возможных доказательств этого факта
(исторически первое) состоит в том, что операции Sq16, Sq32,..., не разложимые
в классе обычных (’’примарных”) когомологических операций, разлагаются в не-
тривиальные композиции так называемых вторичных когомологических операций
(см. § 36). Мы не излагаем этого доказательства, читатель может найти его в книге
Мошера и Тангора. У нас этот факт доказывается средствами К-теории в гл. 6.
S. Линзы. В этом пункте рассматриваются не квадраты Стинрода, а только гомо-
морфизм Бокштейна, причем в случае р > 2.
Пусть р, q - взаимно простые натуральные числа. Рассмотрим преобразование
2Ki 2 nig
Т сферы S3 С С2, действующее по формуле T(zlt z2) = (zte Р , z2e ); оче-
, z2e
266
ГЛ. 4. КОГОМОЛОГИЧЕСКИЕ ОПЕРАЦИИ
видно, Т порождает свободное действие в № группы Zp. Факторпространство сфе-
ры № по этому действию группы Zp обозначается через L(p, q) и называется (трех-
мерной) линзой. (Мы сталкивались раньше с бесконечномерными линзами.) Спра-
шивается, при каких р, q, р', q' линза L (р, q) гомеоморфна или гомотопически эк-
вивалентна линэе L{p', q‘). Так как, очевидно, 74 (L(p, q)) = Zp, мы с самого нача-
ла будем считать, что р' = р (иначе ни гомеоморфными, ни гомотопически эквива-
лентными линзы быть не могут) . '
Теорема. Линзы L(p, q) и L(p, q') гомотопически эквивалентны тогда и
только тогда, когда q' = ±k2 q modp для некоторого целого к.
Мы наметим доказательство части ’’только тогда”; часть ’’тогда” для нас менее
существенна, но читатель может доказать ее в качестве упражнения средствами тео-
рии препятствий (воспользовавшись малостью размерностей линз).
Очевидно, Hr (L (р, q); Zp) = Zp при г = 0, 1, 2, 3. Возьмем на сфере 53 ориенти-
рованную дугу большого круга, идущую из точки (1,0) в точку (e**ilp, 0); зта
дуга определяет некоторый элемент группы я> (Z (р, q)) = Hi (L (р, q)) Zp. Обоз-
начим через а элемент группы И1 (L(p, q)', Zp), принимающий на этом элементе
значение 1 € Zp.
Лемма.
< afi (a), \L (р, q)] > = q (mod р),
где & есть гомоморфизм Бокштейна Н1 (L(p, q); Zp) (L(p, q); Zp).
Набросок доказательства (детали оставляются читателю). Линза
имеет естественное клеточное разбиение, которое получается из Zp-инвариантного
клеточного разбиения сферы S3. Последнее устроено так. Окружность, высекаемая
в S 3 прямой 22=0, делится р точками на р равных дуг — это одномерный остов.
Трехмерные вещественные полупространства, примыкающие в С2 к прямой z2 = 0
и составляющие между собой углы 2я/р, высекают на 53 двумерные полусферы -
это р двумерных клеток. Оставшееся представляет собой р трехмерных клеток,
похожих на дольки мандарина. (См. рис. 135.) Образующая нашей группы Zp пово-
рачивает окружность на угол 2я/р, а двумерные полусферы склеивает через q. Линза,
таким образом, имеет по одной клетке в размерностях 0, 1, 2, 3. Очевидно, а прини-
мает значение 1 на одномерной клетке, a /3(а) принимает значение 1 на двумерной
клетке. Наша задача - найти индекс пересечения замыканий одномерной и двумер-
ной клеток, рассматриваемых как циклы modp. Поднимем зти циклы в S3. Там
получатся выделенная окружность и объединение всех полусфер. Чтобы найти индекс
пересечения, приведем циклы в общее положение, для чего пошевелим одномерный
цикл. Прообраз пошевеленного цикла в S3 будет инвариантной окружностью, кото-
рая, очевидно, q раз охватывает непошевеленную окружность (рис. 136, на котором
§ 30. ПРИМЕНЕНИЯ СГИНРОДОВЫХ КВАДРАТОВ 267
<7 = 2). Поэтому пошевеленная окружность пересекает каждую полусферу в q точках,
а всего точек пересечения будет pq. Значит, соответствующее пересечение в L(p, q)
состоит из q точек. Очевидно, все эти точки совершенно равноправны, в частности,
все имеют одинаковый знак. Значит, индекс пересечения равен ± q (на самом деле q,
но это нйм уже совсем не важно).
Рассмотрим еще линзу L (р, q') и обозначим для нее через а' аналог класса а.
Пусть
<р: L(p,q)^L(p, q')
— гомологическая эквивалентность. Тогда гомоморфизм
: Я3(£(р, <7); Z)-> H3(L(p, q'y Z)
является изоморфизмом; поэтому он переводит [L(p, <7)] в ±[£(р, 47’)]. Пусть,
далее, <р*а' = ка. Тогда
q' = <д'|8(д'), [£(р, <?')]) = ± <л'0(л'), «р. [L(p, <?)]> = + <(<pV) (0(<р*д')), [L(p, <?)]> =
= ± {(ка) (fi(ka)), {L(p, <?)]>=+fc2 <л0(л), [L(p, <?)]>= ± k2q,
что нам и нужно.
Например, £(5, 1) и £(5, 2) гомотопически не эквивалентны (2 ± к2 mod 5).
Кстати, если нас интересуют только гомотопические эквивалентности, сохраняющие
ориентацию или только гомотопические эквивалентности, обращающие ориентацию,
то ± 1 в формулировке теоремы можно заменить, соответственно, плюсом или
минусом. Например, не существует гомотопической эквивалентности, обращающей
ориентацию (т.е. попросту отображения степени — 1) линзы £(3, 1) в себя; этот
факт был доказан Кнезером задолго до построения излагаемой здесь теории.
Добавим, что гомотопически эквивалентные линзы могут быть не гомеоморфны-
ми, как, например, не гомеоморфны линзы L (7, 1) и £ (7, 2), Их различает так на-
зываемое ’’кручение Рейдемейстера - Франца”, которого мы здесь не касаемся.
С ним читатель может познакомиться в книге Дубровина, Новикова и Фоменко ’’Сов-
ременная геометрия. Методы теории гомологий” (гл. I, § 11, задачи 5—8) или, с боль-
шими подробностями, по обзору де Рама, Момэри и Кервера (Leet. Notes in Math. -
1967.-V. 48).
ГЛАВА 5
СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
§ 31. ОБЩАЯ ИДЕЯ
1. Введение. В конце предыдущего параграфа мы видели, как информация о ко-
гомологических операциях может быть использована для нахождения стабильных
гомотопических групп пространств. Зная когомологии пространства X, мы можем
довольно легко найти ’’стабильную часть” когомологий первого убивающего прост-
ранства, затем второго, третьего и т.д. Теорема Гуревича каждый раз дает нам соот-
ветствующую группу гомотопий. Этот метод (метод Серра) не позволяет, однако,
вычислять гомотопические группы без преодоления других трудностей.
Представим себе, например, что мы хотим найти стабильные гомотопические
группы некоторого пространства X, и нам известны когомологии X с любыми коэф-
фициентами и с действием всех когомологических операций. Давайте считать, на-
пример, что первая нетривиальная гомотопическая группа пространства X есть Z2
и расположена она в размерности N. Рассмотрим спектральную последовательность
X(Z,,W- 1)
расслоения Х\ N-----------* X.
Чтобы сделать рисунки более компактными, мы будем рисовать спектральные
последовательности в две строчки. Имеется в виду следующее. Нижняя строчка —
это нижняя строчка прежних рисунков, только начинаем мы ее не с размерности О,
а с размерности, в которой начинаются когомологии. Верхняя строчка — это бывший
нулевой столбец, положенный на нижнюю строчку так, чтобы одинаковые размерно-
сти оказались друг под другом. Стрелка, обозначающая дифференциал, действует
вправо-вниз. Группа, присоединенная к группе когомологий пространства расслое-
ния, стоит в столбце, нижняя группа столбца — подгруппа группы когомологий,
е Sqfe Sq^e ч’®, •.. Sq5?
к к ... ' kSq3°a=ff 0
Рис. 137
верхняя — факторгруппа по ней. Разумеется наша картинка охватывает только ста-
бильные размерности.
Спектральная последовательность нашего расслоения изображена на рис. 137.
В верхней строчке стоят когомологии /T(Z2, N — 1) mod 2, которые в стабильных
размерностях совпадают с алгеброй Стинрода А2. Под действием дифференциала
элемент е переходит в а и, для любой операции <р, элемент ^(е) переходит в tp(a).
В нижней строке останутся все элементы Н*{Х\ Z2), которые не являются образами
операций от а. В верхней строке останутся все операции <р, такие, что tp(a) = 0. Кого-
мологии пространства таким образом, нам полностью известны, но действие
§ 31. ОБЩАЯ ИДЕЯ
269
операций в них известно нам уже не полностью. Представим себе, например, что в
алгебре Стинрода есть соотношение Sq20Sq30 = 0 (такого соотношения, наверное,
нет, но зто неважно), и что Sq30a = 0. Тогда в верхней строке останется элемент
Sq30e, который в когомологиях ЛПдг уже не есть Sq30 ни от какого элемента. Чему
равно Sq2 0 от него? Это не может быть никакой элемент верхней строки (так как
Sq20Sq30 = 0), но вполне может оказаться, что этот элемент не тривиален и лежит
в нижней строке, т.е. может оказаться, что Sq20(/) =у в Я*(Х|^; Z2), где элемент
f происходит из Sq30e G H*(K(Z2, N- 1); Z2) и у происходит из некоторого эле-
мента Н*(Х-, Z2) (рис. 138).
Sq30e
Sq2V
Рис. 138
Таким образом, действие операций в когомологиях X|w нам известно уже не пол-
ностью и когомологии следующего убивающего пространства мы уже не можем
найти.
Способа преодолеть эту трудность современная топология не имеет: гомотопи-
ческие группы сфер, например, по сей день полностью не вычислены. Но есть воз-
можность ’’выделить трудность в чистом виде”, а именно, свести все выкладки, свя-
занные с нахождением гомотопических групп, в одну спектральную последователь-
ность, начальный член которой известен, а в вычислении дифференциалов сосредо-
точивается главная трудность задачи. Это и есть спектральная последовательность
Адамса.
Роль спектральной последовательности Адамса не ограничивается, конечно,
выделением трудностей - она позволяет и преодолевать часть из них. А именно,
эта последовательность наделяется рядом дополнительных структур (например,
мультипликативной), которые на языке обычных убивающих пространств не
просматриваются и которые дают богатую информацию о действии дифференциалов.
2. Метод Серра и метод Адамса. Метод Серра вычисления гомотопических групп
состоит в ’’убивании” когомологий по размерности: убили n-ю группу — переходим
к (и + 1)-й, тд. Метод Адамса — зто тоже ’’убивание” групп когомологий, но в дру-
гом порядке. Берем пространство X. Пусть, например, оно (N — 1)-связно, и мы хо-
тим найти p-компоненты его гомотопий от размерности N до размерности N + п.
На первом шаге мы убиваем все когомологии X mod 2 или modp в этих размер-
ностях. Например, это можно сделать так. Каждая аддитивная образующая группы
HN+q(X', Zp) определяет отображение X-*K(Zp,N+ q). Все они вместе определяют
отображение пространства X в произведение некоторого числа пространств типа
К (ZP,N+ q). Индуцируется расслоение
Х(1)-------£-----X.
Его спектральная последовательность устроена так. В верхней строке стоит
’’свободный Ар-модуль” (т.е. действие когомологических операций в этой строке
свободно: нет никаких соотношений, которые не вытекали бы из соотношений в
самой алгебре Стинрода Ар). См. рис. 139 для случая р = 2.
270
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Дифференциал определяет эпиморфное отображение верхней строки на нижнюю,
и в остается в верхней строчке ядро этого отображения, и в нижней строчке ос-
тается нуль. Эту конструкцию мы можем повторить любое число раз.
Получается последовательность убивающих пространств Адамса: У(1),
Х(2),АГ(3),.. .
Заметим, что убивание всех когомологий X можно было бы осуществить более
экономным образом. А именно, нет необходимости убивать отдельно каждую ад-
дитивную образующую Н*(Х\ Zp). Скажем, если мы убиваем элемент £ и Рр£ =# 0,
то нет необходимости отдельно убивать Р1р%, поскольку он убьется и так. Иначе гово-
ря, достаточно рассмотреть не все аддитивные образующие Н*(Х', Zp), а только об-
разующие Н*(Х\ Zp) как Ар-модуля. Поясним: берем все аддитивные образующие
в HN(X\ Zp), затем в //N+1 (X; Zp) берем уже не все образующие, а только те, кото-
рые не являются образами операций от уже выбранных. И так далее.
Алгебраически то, что мы сделали, можно интерпретировать так. Берем Ар-модуль
//*(%; Zp). На него эпиморфно отображаем свободный Ар-модуль Fr (верхняя стро-
ка спектральной последовательности расслоения Х(1) -> X). На ядро этого отоб-
ражения (т.е. на Я*(Х(1); Zp)),которое тоже является Ар-модулем, снова отобра-
жаем свободный Ар-модуль, и так далее. Получаем точную последовательность
Ар-мо дул ей:
. ..-> F2-> Fj->Я*(Х; Zp)-> 0.
В ней все модули, кроме Н*(Х\ Zp), являются свободными. Такая последователь-
ность называется свободной резольвентой и обладает рядом замечательных свойств,
которые мы перечислим, как только закончим изложение ’’общей идеи”.
3. Спектральная последовательность. Вернемся к геометрии. Наш процесс в неко-
тором смысле является сходящимся, т.е. пространства Х(к) имеют когомологии
все меньше и меньше и, в некотором точном смысле, в пределе не имеют их совсем.
Однако убивание по Серру было прямо связано (через теорему Гуревича) с гомото-
пическими группами пространства. А именно, мы всегда убивали когомологии млад-
шей размерности, и каждое отдельное убивание соответствовало элементу гомотопи-
ческой группы. При убивании по Адамсу это, вообще говоря, не так.
Вернемся к тому примеру, с которого мы начинали: пространство X, Пм(Х) =Z2,
группа HN(X, Z2) имеет образующую a, Sq30a = 0, в когомологиях пространства
Х\м остается элемент f - Sq30e и Sq20/ = у € Н*(Х-, Z2). Если бы производили
убивание по Серру, мы бы не стали отдельно убивать у. он убился бы вместе c/G
G H*(X\N\ Z2). По Адамсу же мы убиваем и а и у на первом же шаге. Таким обра-
§ 32. НЕОБХОДИМЫЙ АЛГЕБРАИЧЕСКИЙ МАТЕРИАЛ
271
зом, метод Адамса содержит большее число убиваний, чем метод Серра. Если мы
подсчитаем, сколько образующих было убито в некоторой размерности N + q при
убивании по-Адамсу на всех шагах, то мы получим верхнюю оценку для р-ком-
поненты группы тгдг+<7 (АГ). Эта верхняя оценка и есть начальный член спектральной
последовательности Адамса. Дифференциалы же в ней уничтожают все лишние эле-
менты. Происходит это примерно так.
Заметим, что не только у оказался напрасно убитым элементом. В когомологиях
пространства АГ(1), как и в когомологиях пространства АГ|N, есть элемент /. Но
Образующие Ар-модуля Н*(Х(.3))
Образующие Ар-модуля H*(x(2)) Sq2®/?
Образующие Ар-модуля
Образующие Ар-модуля Н*(Х) у
Рис. 140
в АП# мы имеем: Sq20/ = у, а в АГ(1) имеем: Sq20/ = 0, что приводит к появлению
лишнего элемента в X(2). А именно, когда мы будем убивать / некоторым элемен-
том g, то Sq20g оста-ется, и этот элемент, который даже и не возникает при уби-
вании по Серру, придется убить на третьем шаге при убивании по Адамсу. Началь-
ный член спектральной последовательности Адамса устроен так, как показано на
рис. 140. Второй дифференциал переведет элемент у в элемент, получившийся из
Sq2 °g, в Н*(Х(2)) и уничтожит оба эти лишние элемента.
Предельный член будет присоединен к p-компонентам стабильных гомотопи-
ческих групп пространства X.
§32. НЕОБХОДИМЫЙ АЛГЕБРАИЧЕСКИЙ МАТЕРИАЛ
1. Модули. Пусть А есть ассоциативная алгебра с единицей над полем К, и пусть
она градуирована целыми степенями:
A = <BqAq = .. .®Л_1 ®Л0 ® ..., ArAsCAr+s.
Левым модулем над А (А-модулем) мы назовем векторное пространство Т над
К, градуированное, т.е. представленное в виде суммы Т„, для которого опреде-
лено отображение Т X А ->Т, такое, что элемент (х, а), х G Т, а&К, переходит в ах G
G Г и при этом:
(1) если a SAq, х G 7), то axG Tq + i,
(2) a(xi + x2) = axi + ax2,
(3) (Д1 + a2)x = a2x + a2x,
(4) b(ax) = (ba)x.
Аналогично определяется правый A-модуль. Левый Л-модуль Т называется сво-
бодным, если он содержит множество элементов Т', такое, что для любого х G Т
существует единственное представление в виде суммы х = (сумма конечная),
где at G A, et &Т'. Множество Т' называется базисом или множеством образующих
свободного А-модуля Т.
Например, сама алгебра А может быть рассмотрена как свободный Л-модуль
(с одной образующей), хотя Л как алгебра может иметь соотношения.
272
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Гомоморфизм Л-модуля Т1 в Л-модуль Т2 — это гомоморфизм/: Т1 ->-7*, такой,
что/(7^) СГ, и/(ox) = af(x) для любых а е А, х G Т1.
Очевидно, что для любого Л-модуля Т существует точная последовательность
0->/r^Fr-=*r->0,
где FT — свободный Л-модуль. В качестве FT можно взять свободный Л-модуль,
базисом которого служит множество всех элементов модуля Г; отображение я пе-
реводит образующие модуля FT в соответствующие элементы модуля Т.
2. Проективные модули. Л-модуль Р называется проективным, если каждую
диаграмму вида
t
Р
с точной строкой можно вложить в коммутативную диаграмму
О
Иначе говоря, модуль Р проективен, если любой гомоморфизм Л-модуля Р в любой
фактормодуль MjR разлагается в сквозной гомоморфизм Р -+М -+MIR, где вторая
стрелка — естественная проекция.
Имеет место следующее утверждение: A-модуль Р тогда и только тогда проекти-
вен, когда он является прямым слагаемым некоторого свободного A-модуля. До-
кажем это. Если Р — свободный Л-модуль, то ои проективен. Действительно, если
Р‘ = { р, } — базис Р и
М——----*
О
- любая диаграмма с точной строкой, п, = f(pi), mt ЕМ - такие элементы, что
л(щ(-) = П{, то отображение : Р -+М можно определить формулой <р (р{) =mt.
Если Р - прямое слагаемое проективного модуля Р', т.е. существуют отобра-
жения а: Р -► Р' и 0: Р' -> Р, такие, что композиция 0 о а: Р -+Р тождественна, то
Р — проективный модуль. Действительно, если
М------—
♦
F|
I, а
Р
Р
О
— любая диаграмма с точной строкой, то /0 — отображение проективного модуля
Р' в N. Поэтому существует отображение </>: Р' -+М, такое, что тпр =/0. Отображение
<ра = ф: Р -+N обладает тем свойством, что тгф - яра = ffia = /. Таким образом, модуль
Рпроективен.
Наконец, всякий проективный модуль является прямым слагаемым свободного
модуля. В самом деле, пусть Р — проективный модуль. Мы видели, что существует
§ 32. НЕОБХОДИМЫЙ АЛГЕБРАИЧЕСКИЙ МАТЕРИАЛ 273
точная последовательность FP Р -> 0, где FP - свободный модуль. Рассмотрим
диаграмму:
Гр —-я - Р-------* О
II
Так как Р — проективный модуль, то эта диаграмма дополняется отображением
Ч>: Р -+FP, и отображение : Р -+Р тождественно. Отсюда FP =Р ® Ker it.
Из доказанного утверждения нам потребуется только то, что свободный модуль
проективен.
3. Проективные резольвенты. Пусть Т — произвольный правый Л-модуль. Тогда
существует точная последовательность:
.. .->Aq .. ->А! ->Л0 -►Г->0,
где Ад (здесь q =0,1,2,...) — правые проективные модули. Эта последователь-
ность называется проективной резольвентой модуля Т. Если все Aq свободны, то
последовательность называется свободной резольвентой. Вот построение свободной
резольвенты. Для каждого модуля Т мы имеем точную последовательность:
0 Fp Г-** 0,
где модуль Fт свободен. Положим Т\ = IT, Т2 = /у > Тз = 1т2, • • • Имеем точные
последовательности:
0-+FT^T^>0,
0^T2^FTi ^7\^0,
0 Гз FP* “*• Т2 0,
Из них можно составить одну точную последовательность:
0 0 0 0
т у
Т
О О
Горизонтальная стрелка и есть нужная резольвента.
Свободная (тем более проективная) резольвента данного модуля не единственна,
и это делает необходимой проверку корректности в конструкциях следующего пунк-
та. Мы оставляем всюду эту проверку читателю, ограничившись замечанием, что она
основана на следующем предложении, которое иногда называют основной леммой
гомологической алгебры.
Упражнение 1. (а) Пусть
<2, d. е
. ..^В2 —^В1 —- В0—>М^0,
. ..^В2—?-> B'l -±-»В'о—> М'^0
274 ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
— проективные резольвенты модулей М и М'. Тогда для любого модульного гомо-
морфизма /: М -> М1 существуют модульные гомоморфизмы ; А/ -> A ,, i =
= 0, 1,.. ., такие, что диаграмма
<2, <2, е
.. ,^В2 ► Во —+М^»0
I <fi I ¥>о 4 4/
, d't , d'i , е'
. ,.^В2 В'1 ——*в0 —> м-»о
коммутативна.
(Ь) Если {} — другое такое семейство гомоморфизмов, то существуют модуль-
ные гомоморфизмыDt: В. -+В'( + i,i =0,1,, такие, что
'Pi 'Pi ~ ^i— l^i "*
(в этой формуле подразумевается, что Do = 0).
4. Тог и Ext. Пусть М и N - два Л-модуля (причем М - правый модуль, a N - ле-
вый) . Зафиксируем проективную резольвенту
... В2 В2 Bq --> М 0
модуля М и применим к ее части . .. -> Во функтор ®л N (со значениями в градуи-
рованных векторных пространствах над К). Мы получим последовательность
• • - ^В2 ®aN^>Bi ®aN->B0 ®aN,
вообще говоря, не точную, но являющуюся комплексом (т.е. композиция двух
соседних гомоморфизмов равна 0). Степень неточности этой последовательности
измеряют гомологии этого комплекса, которые мы обозначим через Тог^(А/, N).
Заметим, что Тог£(Л/, /V) — ковариантный функтор по М и N.
Упражнения. 2.ТоГ(^(Л/,/V) =Л/7V.
3. Если алгебра Л коммутативна, то Tor„ (Af, N) Ss Tor^ (N, М).
4. Если модуль М проективен, то Tor^ (М, N) = 0 при любых Nan>0.
Пространство Тог^(Л/, AQ градуировано:
Tor^ (М, N) = ®g Tor^, (М, N).
Применим теперь к нашей резольвенте функтор Нотл (-, /V). Получаем коцеп-
ной комплекс градуированных пространств над К:
... *-Нотл(В2, /V) *- НотД^, N) «- Нотл(В0, N).
Когомологии этого комплекса обозначаются через Ext" (М, N). Это градуированное
пространство:
Ext^(3f, АГ) = ®g Ext^-q(M, TV).
Итак:
Extq(M N) = КСГ IH0nU^Bn’ N^q H0nU1 ’ 1
где Hom( )q обозначает гомоморфизмы, понижающие степень на q.
Заметим, что Ext^ (М, N) — ковариантный функтор по Л'и контравариантный
функтор по М.
s 33. ПОСТРОЕНИЕ СПЕКТРАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
275
Упражнения. 5. Ext^ (М, N) = Нотл (М, N).
6. Если модуль М проективен, то Ext^ (М, N) = О при любом Я и при п > 0.
7. Абелевы группы А, В могут рассматриваться как Z-модули. Доказать, что
7 ( Тог(Л,В) при л=1,
Тог„г(Л,5)= ’
I 0 при 2,
Ext 2(А, В) =
ЕхЦЛ, В)
О
при п= 1,
при л> 2.
(В правой части Тог и Ext понимаются в смысле п. 4 § 15).
§ 33. ПОСТРОЕНИЕ СПЕКТРАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
1. Топологическая фильтрация Адамса. Пусть X — топологическое пространство.
Мы хотим найти его стабильные гомотопические группы itq(X), т.е. гр/ппы
nN+q(Y,NX), где N > q. Основной случай: X = S° (две точки). Тогда я„(Т) =
= irN+q(SN).
Через А = Ар (р — простое число) мы будем обозначать, как и раньше, ал.ебру
Стинрода. Через Н*(Х' мы будем обозначать Н*(Х; Zp), через Н*(Х) будем обоз-
начать П*(Х; pt), т.е. Я0 (Г) = Н°(Х)/Zp и Н‘ (X) = Я’ (X) при i~> 0.
Так как А действует на Н*(Х), ю естественно рассмотреть Н*(Х) как А-модуль.
Заметим, что как Н*(Х), так и все модули, с которыми мы будем иметь дело
впредь, градуированы только неотрицательными степенями, т.е. слагаемые с отри-
цательными номерами тривиальны.
Построим для A-модуля Н*(Х) свободную резольвенту; напомним, как она
строится.
Выберем в этом A-модуле произвольную систему образующих. Очевидно, эта
операция выбора эквивалентна заданию эпиморфизма некоторого свободного А-мо-
дуля Bi на Н*(Х) :
0<-Я*(А')<-51.
Предположим для простоты, что X — клеточное пространство, имеющее
конечное число клеток в каждой размерности. Тогда все модули, которые будут
возникать на нашем пути, будут иметь конечное число образующих в каждой раз-
мерности.
Рассмотрим ядро построенного гомоморфизма. Это, вообще говоря, не свобод-
ный A-модуль, а поэтому к нему можно вновь применить только что проделанную
процедуру, и так далее. Мы приходим к точной последовательности (свободной ре-
зольвенте)
0<-Я*(%)^В1 ^В2 ^В3^.. .
A-модули В/ не являются модулями когомологий каких-либо пространств. В ко-
гомологиях любого пространства есть, например, соотношения вида Р‘р(х) = 0 при
п > (р - l)dimx Меньше всего соотношений имеет A-модуль H*(K(Zp, л)). Мы
хотим ’’приблизить” Bj модулями такого типа.
Пусть N - большое число. A-модуль H*(X.NX) отличается от A-модуля Я*(Х)
только градуировкой. Пусть а,- G НЯ1 (%) — образы свободных образующих Bt, т.е.
выбранные образующие A-модуля Н*(Х). Рассмотрим отображения Y,NX ->
K(Zp, N + q,), построенные по элементам ^а,- 6 HN+4i (£NX) для всех i, для ко-
торых q, < N. Вместе они определяют отображение "X,NX -* Yt = IIK(ZP,N + qt);
276
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
А-модуль Я*(У1) в размерностях от N до 2Ясовпадает с A-модулем В2 в размернос-
тях от 0 до N, и отображение Y,NX -> индуцирует гомоморфизм Я*(У2 )-►
-> H*(Y,NX), совпадающий в размерностях от N до 2N с гомоморфизмами В2 ->
->Я*(А0 в размерностях от 0 до Я.
Отображение 2NX -> Y2 можно считать расслоением. Обозначим его слой через
Af(l). Кроме того, положим X = Х(0). Описать полностью Я*(АГ(1)) в общем случае
было бы трудно, но, как легко видеть, до размерности 2N — З^А-модуль Я*(У(1))
изоморфен со сдвигом размерности на единицу A-модулю Кег[Я*(У\) ->Я*(2ЛА')],
что очевидно из спектральной последовательности расслоения (рис. 141).
Рис. 141
Сдвиг размерностей происходит потому, что трансгрессия повышает размерность
на 1. Следовательно, Я*(АГ(1)) в размерностях от N — 1 до 2N — 3 изоморфен А-мо-
дулю Кег[Д1 ->Н*(Х)] от размерности 0 до размерности N — 2 со сдвигом размер-
ностей на N — 1.
Замечание. Конечно, X(1) можно было.бы определять не только как слой
v IIK(Zp,W+qf-1) „
отображения 2 X ->У1, но и как пространство расслоения АГ(1)------------->2X,
flK(Zp,N+q{ - 1)
где последнее индуцировано расслоением ♦ ------------------>IIA(Zp, N+ qt) =
с помощью указанного отображения Y,NX -* Yt:
X(l) -> * « pt
nK(Zp,N + qi- 1) I +
N X(I)
ZNX ——> HK(Zp, N + qi) = Yi.
Важно заметить, что мы определили не только пространство АГ(1),но и отображе-
ние АГ(1) -> Y,nX. При этом и пространство АГ(1), и это отображение определены с
точностью до гомотопической эквивалентности.
Далее мы делаем для Af(l) то же, что раньше делали для Y,NX. Берем в А-модуле
Я*(АГ(1)) систему образующих, находящихся (до размерности 2N — 3) во взаимно
однозначном соответствии со свободными образующими A-модуля В2. Напомним,
что мы имеем эпиморфизм В2 -* Ker [Bj -+Н*(Х)]. Выбранные нами образующие
отличаются от предыдущих по размерности на Я — 1. Пусть Д 6 HN~i+ri (А"(1)) —
эти образующие. По ним строим отображение
АГ(1) -+ Y2 = П K(Zp, N - 1 + rf).
А-модули H*(Y2) и B2 совпадают co сдвигом размерности на N — 1 до группы
Я2ЛГ-3(У2). Обозначаем через Х(2) слой расслоения, эквивалентного отображению
Af(l) -> У2. Таким образом, определены пространство Х(2) и отображение X (2) ->
^(1).
Двигаясь дальше таким же путем, получаем последовательность пространств
... -► Х(3) + АГ(2) + Х(1) + Y,nX = *(0).
4 33. ПОСТРОЕНИЕ СПЕКТРАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
277
При этом X(i) — слой расслоения, пространство которого гомотопически экви-
валентно X (i — 1), базой является произведение Y{ пространств типа K(Zр, т).
Зафиксируем п < N; A-модуль Я*(У() до размерности (N - i + 1) + п и А-мо-
дуль Bi до размерности п одинаковы, только градуировки отличаются на N — i + 1.
На самом деле они совпадают и дальше, а именно, H*(Yt ) до размерности ~ 2N и
В, до размерности ~ N, но это для нас не будет существенно, так как в недалеком
будущем мы устремим Na п к бесконечности.
С другой стороны, отображение X(i) -> X (i — 1) само может рассматриваться
как расслоение. Его слоем будет пространство Z/ — произведение такого же числа
К (Zp, т), как и У{, только с номерами соответственно на единицу меньше. Можно
считать, учитывая интересующую нас область размерностей, что Z,- = £2У,- и
SZz=y,-.
_ A-модуль H*(zi) изоморфен В{ со сдвигом градуировок на#-г единиц. Далее,
H*(X(i)) до размерности N - i + п совпадает со сдвигом размерностей на N — i с
ядром гомоморфизма B(i) -► B(i — 1) при i > 2 и гомоморфизма Вх -+Н*(Х) при
i =1. Наконец, композиция отображений Z,- С X(i) -* У, +1 индуцирует гомо-
морфизм Я*(У/ +1) -+H*(Zi), совпадающий (с точностью до различия в градуиров-
ках) с гомоморфизмом Bi -+Bi _ i из резольвенты.
Отметим еще, что все пространства X(q) являются (N— 1)-связными^
Поясним это на примере Х(1). Различие в градуировках Н*(Х(1)) и
Кег[2?1 ->Я*(Х)] составляет N — 1 единицу. Но это ядро в размерности 0 тривиаль-
но: между элементами Н°(Х) не может быть соотношений. Поэтому [Kerffij *
^//•W)Io=Oh/77V-1(X(1)) =0.
Аналогично, используя, что [Кет (В,- -> Bi -i)]/ =0 при / < i, получаем, что
X(i) является (N — 1)-связным для всех i.
Теперь мы хотим заменить цепочку отображений Х(1) фильтрацией. Для этого
надо превратить зти отображения во вложения.
Построим цилиндры всех отображений X(i) ->• X(i — 1) и приставим их один к
другому, как показано на рис. 142. Через X (к) обозначим часть получешюго
х'(ъ)
Рис. 142
пространства, лежащую (на рисунке 142) левее X (к). Очевидно, что цепочка вложений
... С Х'(к) С ... С Х'(2) С Х'(1) С Х'(0)
гомотопически эквивалентна цепочке отображений
...-+Х(к)+... ->Х(2)->-Х(1)->-Х(0) = ZNX.
Мы в дальнейшем не будем использовать обозначение Х'(к), а будем писать прос-
то X (к). Это можно сделать, так как все наши построения производятся с точностью
до гомотопической эквивалентности.
Для дальнейшего нам будет удобно считать, что в фильтрации имеются и члены
вида X (— к) (где к > 0), и ZNX = X (0) = X (—1) = Х(—2) =..., т.е. фильтрация бес-
конечна и вправо и влево. Уместно заметить, что с обозначениями § 20 наша фильт-
рация не согласована: нумерация перевернута.
278
5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
2. Группы и дифференциалы спектральной последовательности. Спектральная
последовательность Адамса строится по полученной фильтрации аналогично тому,
как спектральная последовательность Лере строилась по фильтрации, рассматри-
вавшейся в § 21. Основное отличие состоит в использовании групп гомотопий вместо
групп гомологий. Заметим, что в общем случае группы гомотопий не пригодны к
построению спектральной последовательности из-за отсутствия равенства nq(A, В) =
= •nq(A/B). Но у нас это равенство будет обеспечиваться стабильностью размернос-
тей.
Рассмотрим вложение (X(s), ^(s + г)) (X(s + 1 - r),X(s + 1)), где г > 1 и
введем группы Ef ’f, полагая:
Esr-' = Im[7rv + ,_,(X(s), X(s + r)) -> Ядг+,_,(Х(5 + 1 - r), X(s + 0)1,
где t < n - г. Поясним, зачем нам потребовалось вводить такое ограничение на t.
Конечно, группа Е*’* этим равенством определена для всех г, s и t. Но в ее опре-
делении участвует число N, которое мы выбрали произвольно. Насколько группа
от него зависит? Пространство X(гп) имеет в размерностях от N до N — т + п кого-
мологии, не зависящие от N. Если мы заменим N на большее число М, то пространство
Х(т), которым заменится Х(т), будет гомотопически эквивалентно ’LM~NX(ni)
до размерности М - т + п. Отсюда следует, что Esr’* при указанных ограничениях
на Г от ./Уне зависит.
Устремляя N и п к бесконечности, мы будем в состоянии определить группы
Б*'1 для всехг, s и t инвариантным образом.
Можно дать другое определение, эквивалентное предыдущему. Положим Ers,t =
= Gsr’t!Dsr’t, где
G*’1 = Im X(s + 1))],
Dsr- * - lm[itN+t_s(X(s + 1 - r), A'(.v))^ 7TA+r-i(A'(.v), *(s + 1))].
Это — определение самого Адамса.
Группа G>’f определена с помощью вложения (X(s),X(s +г)) ->(X(s),X(s + 1)).
Группа D?’* определена с помощью граничного оператора гомотопической последо-
вательности тройки (X(s + 1 — г), X(s),X(s + 1)).
Эти два определения эквивалентны. В самом деле, нарисуем соответствующую
картинку для X(s + 1 - г) DI(s) DI(s + 1) D I(s+ г) (рис. 143). Элементами
Df’* являются классы, каждый из которых имеет в качестве представителя абсолют-
ный сфероид размерности N + t — s, лежащий в X(s), но только рассматриваемый
как относительный, по модулю X(s + 1) (сфероидЛ).
При этом во всем X(s + 1 — г) он гомотопен нулю, являясь границей относитель-
ного сфероида. Представителями элементов группы являются относительные
сфероиды в X(s) modX (s + г ), рассматриваемые
как относительные сфероиды в X(s) modX(s + 1)
(где X(s + 1) D X(s+r)). Очевидно, что 2
Э Dr'*. Теперь нам надо профакторизовать Gp* по
Efr’ * Для этого мы должны рассмотреть эти сферои-
ды как сфероиды в X (s + 1 — г ) modX (s + 1).
Осталось только констатировать, что последняя
операция является взятием образа irN+t (X(s),
X(s+r)) в irN+t_s(X(s + 1 - r),X(s + l)) лри
вложении, а эта группа и является Ер'* в нашем
первом определении.
Займемся более подробным рассмотрением
групп Е3Г’*.
§ 33. ПОСТРОЕНИЕ СПЕКТРАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
279
Они определены для любого г > 1 и s > О,
7 > О, кроме того, как очевидно из опреде-
ления, £^,f=0 при t<s. Это утверждение сле-
дует из того, что все A"(s) являются (N— ^-свя-
зными. Положим Er = Член Ег по-
казан на рис. 144. Кстати, на этом рисунке и
всюду в дальнейшем мы отказываемся от
привычного по спектральным последователь-
ностям расслоения порядка осей: группу Esr't мы
располагаем иа пересечении s-й строки и 7-го
столбца. (Это удобно для нас, поскольку, как мы
увидим, в спектральной последовательности
Адамса все главные события будут происходить
в области 0<s <7.)
Проследим за изменением Ег с ростом г. Пока мы не говорим о спектральной
последовательности, так как еще не введены дифференциалы dr. Пусть г увеличи-
вается. Воспользуемся первым определением Е, . Тогда, начиная с г = s + 1 (где s
и 7 фиксированы), группа itN+t_s(X(s + 1 — г), X(s + 1)) стабилизируется и для
всех больших г равна itN+t _S(ZNX, X (s+ 1)). Сказать что-либо подобное о группе
я^+г_^(У(х), У(х + г)) нельзя, ибо заранее ничего не известно о паре (X(s),
X(s + г) ). Поэтому, вообще говоря,. нет оснований ожидать, что группы Ers,t стаби-
лизируются, и вопрос о сходимости спектральной последовательности требует спе-
циального изучения.
Очевидно, что 1т[тгЛГ+г_^(А’(х), Х(з + г)) -> itN+t_s(2NX, X(s + 1))] есть
подгруппа группы 1т[тглг+г_^(А’(х), X(s + г + 1)) ->TrN+t_s(SNX, X(s + 1))],так
как второе отображение есть композиция первого и отображения
nN+t_s(X(s), *(Ж+г+1))^+г_,(*(«), X(s + r)).
Поэтому можно ввести предельную группу £« = где EL,f = С\гЕг’*.
Рис. 145
Можно осуществить предельный переход г и исходя из второго определения,
по которому F/’f = Gr,f ID?’1. А именно, Gi’f = OG/’f,
= 1т[тгЛГ+г_^+1(ЕЛГХ X(s)) + 1))].
Переходим к определению дифференциалов d/’f: Ef,r -> Ef+r,t+r~l. Необходи-
мо запомнить, что в спектральной последовательности Адамса индексы имеют сов-
сем другой смысл, чем в спектральной последовательности Лере. Дифференциалы
dr,f действуют по направлению, близкому к направлению биссектрисы первого
квадранта (рис. 145).
280
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Рассмотрим тройку (X(s), + г), A(s + 2г)) и тройку (Jf(s + 1 — г),
A(s + l),X(s+r + l)) и граничные гомоморфизмы
Э,: irjy+r_,(X(s),X(s +r))-irAr+r_,_1 (X(s +r),X(s +2г))
и
Э2: itN+t_s(X(s + 1 -г),X(s + 1))->-яЛг+г_,_ 1(^(5 + l),I(s + r+l)).
Рассмотрим диаграмму:
di: itN+1-s(X(s), X(s + г))----► itN+(f+r _ j j_+r)(X(s + r), X(s + r + r))
If 4- g
&2- ’’s+t-jW5 + 1 -r),A(s + !))-*• irw+(t+r-i)-o+r)(A(s + 1), X(s :-r + 1)).
Гомоморфизм d3,t по определению есть ограничение нашего гомоморфизма Э2
на £7,f = Im f — подгруппу itN+t _s(X(s + 1 — r), X(s + 1)). Он принимает зна-
чения и действует в Е3 +r>t+r -1 = lmg.
Очевидно,что d3r+r,t+r -1 ° d,’* =0.
И вот наступил подходящий момент для того, чтобы сформулировать основ-
ную теорему, часть которой нами уже осмыслена.
3. Теорема Адамса.
Теорема. Пусть X - клеточное пространство с конечными остовами, р - про-
стое число. Тогда существует спектральная последовательность {Ef,f = E*,f (А)},
где E3,t = 0, если s < 0 или t < s (в частности, E3,t = 0 при Г <0) с дифференциа-
лами d,’1 : Е3г,г -+E3+r,t+r ~1,причем имеют место следующие свойства.
(1) Существует канонический изоморфизм
Е\* ~ Ext д’*(Я*(Л);2р).
Здесь 1р рассматривается как A-модуль с тривиальным действием А, причем един-
ственной образующей этого модуля приписывается размерность 0.
(2) Существует канонический изоморфизм
Е3'+\ = Kerd^^/ImdГr’,_r+,.
(3) При г > s имеем: Im d3 ~г’ * ~г + 1 = о, и поэтому E3,t С E3,t (s <г < к);
положим Е3й* = Hs<r <a,E3r’t. Существуют группы В3’ такие,
что Bs'r СВ’"1''-1 С...С нЕ3’1 =* В3’*/В3+
(4) Df _s = mB3,t = Km — подгруппа тг^(А), состоящая из всех элементов, по-
рядок которых конечен и взаимно прост с р.
Доказательство теоремы Адамса содержится в пп. 4—9.
4. Доказательство утверждений (1) и (2). Группы E3,t и дифференциалы d3,t
у нас уже определены. Выясним структуру Ех и Е2. По определению E3,t =
= ftN+t-j(A(s), A(s + 1)). Из построения просгрансгв{А(£)} следует, что имеет-
X(s + 1)
ся расслоение A(s) --------► ПКт (здесь Кт — обозначение для пространства
К (Zp, т)), откуда itq (X (s ), X(s + 1) ) = itq (П Km) для всех q. Отсюда следует, что
Ег = ®£f’r= « nN + t_s(X(s),X(s + l)) = ® ffAr + f_,(nxm).
3, t S, t 3, t
Здесь следует напомнить, что N выбирается таким образом, что 1 — г = t — 1.
Отсюда видно, что N зависит от t, равно как и X(s) и X(s + 1), которые опреде-
§ 33. ПОСТРОЕНИЕ СПЕКТРАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
281
ляются по N. Но группа X(s + 1)) при достаточно большом N ни
от чего не зависит, так что все слагаемые корректно определены.
Рассмотрим группу Е* = Эта группа равна ®f nN+t _s (ПКт) = ®rZp,
где Zp появляется всякий раз, когда t таково, что N + t — s совпадает с какой-ли-
бо из размерностей т, которые участвуют в образовании этого прямого произве-
дения.
Рис. 146
Следовательно, слагаемые Zp в этой сумме для t <N находятся во взаимно
однозначном соответствии с образующими A-модуля Н*(ПКт) и имеют те же раз-
мерности. То есть они находятся во взаимно однозначном соответствии с образую-
щими A-модуля Bs и имеют размерности на N — s единиц больше.
Это означает, что ядг+1 _s (ПКт) = [HomA (Bs, Zp) ] t.
Гомоморфизм Bs -* Zp может перевести каждую образующую A-модуля Bs в
любой элемент Zp. Элементы же вида <ра, где <р G A.q,q > 0, такой гомоморфизм
обязательно переводит в 0. Поэтому НотА(Б,, Zp) порожден как векторное про-
странство над Zp гомоморфизмами Bs ~*Zp, которые переводят одну из образующих
A-модуля Bs в 1 G Zp, остальные — в ноль. Такой гомоморфизм имеет в гра-
дуированном модуле HomA (Bs, Zp) ту же степень, что и сама образующая.
Итак, £i,f = [HomA(fi,, Zp)]t; = Hom^(Bs, Zp) с учетом градуи-
ровок.
Рассмотрим гомоморфизм di, где di’f: + т.е. [НошА(Д,, Zp)]t ->
[HomA(5i + 1,Zp)]f (рис. 146).
Читатель покажет самостоятельно, что гомоморфизм совпадает с гомоморфиз-
мом, индуцированным отображением Bs + i -* Bs. Тогда, как только мы докажем
'утверждение (2) теоремы Адамса, отсюда будет вытекать, что
Es^= Ext*Xf(^*{X),Zp),
ибо так и были обозначены в начале параграфа гомологии комплекса {HomA(Ss,
Zp)}, где { Bs } - резольвента Н *(Х)
Теперь докажем утверждение (2), т.е. что E^+i = Ker d$~r,f ~r + 1 =
= Im [fljv+f (A"(s), *(s + r +1)) **-s(X(s ~ X(s + 1))]. Нас инте-
ресует Ker dr'f/1т dsr ~r •f ~r + *, где
JJ.f. gS.t £j + r,f + r-l
ds-t,t-r+l. ES-r,t-r + i Es,t
282
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
По определению оператора f имеем:
HN+t-s(X(s),X(s +r))-----------> JTjy+f-j-iWs +t),X(s + 2r))
•I f ds.t Фg
^2- TtN + t-s(X(s + 1 —s),X(s + 1)) ► 1tf/ + t-s-l(X(s + l),X(s + r + 1)),
где = d2 lim/. Рассмотрим цепочку пространств X(s - r) D X(s + 1 — r) D
D X(s) D X(s + 1) Э X(s +r) D X(s +r + 1) Э X(s + 2г).Пустьа e Ef'f =
= Im[7Tjv+f _,(.¥($), X(s + r)) -> nN+t _s (X(s + 1 -г), X (s + 1))]. Согласно
определению, а есть образ при естественном гомоморфизме некоторого элемен-
та 0 G nN+t _s (X(s), X(s + г)). Сфероид, представляющий этот элемент, изобра-
жен на рис. 147. Предположим, что а = 0. Это означает, что gdi (3) = 0, т.е.
граница сфероида /3, как (N + t — s — 1)-мерный сфероид X(s + 1), гомотопна
сфероиду, лежащему в X(s + г + 1). Отсюда вытекает, что сам сфероид 0 гомото-
пен, как сфероид по модулю X(s + 1), сфероиду пространства A'fs) по модулю
пространства X(s + г + 1). Поэтому элемент а лежит не только в
Е°'< = Im[WAr+r_XX(S),X(s + r)) -> Wjv+r_,(X(» + l -г),X(s + 1))],
но и в меньшей группе
1ш[ядг+г_ ,(X(s),X(s + г + 1)) -> itN+t_s(X(s + 1 -f),X(s + 1))]СЕ}'.
Так же доказывается, что и наоборот, из принадлежности элемента а к этой
подгруппе следует, что d^a = 0, т.е.
KerdJ,f = Imlnjv+t-jWs),X(s + r + 1)) -> irN+t_s(X(s + 1 -r),X(s + 1))].
Гомоморфизм nN+t _s (X(s + 1 - r),X(s + 1)) -*itN+t _s (X(s -r),X(s + 1)) ин-
дуцирует гомоморфизм
Ker W = Im[ffjv+t_,(X(S),X(»+r + l)) -> irN+t_s(X(s + 1 -r),X(s + 1))] ->
-* Im[ffAr+f_,(X(s),X(s + l +r)) -> ялг+г_,(Х(в-г),*(« + !))] =
Puc. 147
Puc. 148
§ 33. ПОСТРОЕНИЕ СПЕКТРАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
283
Покажем, что ядро этого гомоморфизма есть Im d3 r,t r +1. По определению
j4-r,f-r+l>HMeeM.
^tt-s+iWs - r), ^(s)) —---------►7TyV+r_J(A'(s)> y(s + r))
V' d lg'
Э4: JTjy+t- j+j (Af(s + 1 — 2r), X(s + 1 —r)) + 1 — r), X(s + 1)),
где d = dsr ~r,t ~r + I = d4 |Imy>. См рис 148.
Если a e Ker d3,t C nN+t _s (X(s + 1 - r), X(s + 1)) переходит в нуль при го-
моморфизме в irN+t_s(X(s — г), X(s + 1)), то это означает, что относительный
сфероид, представленный а (сплошная линия на рис. 148), гомотопен нулю в па-
ре (X(s —r),X(s + 1)). Гомотопия
{DN+t~3, sN^t~s~i) -> (X(s - г), X(s + 1))
представляет собой отображение pJV+f-J X I = £>ЛГ + ,-1 + 1 -+Х(з - г), при ко-
тором нижнее основание DN+t~3 X 0 переходит в сфероид а. Боковая поверх-
ность SN + t ~3 -1 X/ переходит в X(s + 1); верхнее основание — в точку. Таким
образом, имеем (N + t — s + 1)-мерный сфероид X(s - г) mod X(s — г +1), гра-
ница которого получилась из а присоединением некоторой части, содержащейся
в X(s + 1). Наконец, нужно учесть, что а принадлежит образу irN+t (X(s), X(s +
+ г + 1)), т.е. сфероид а можно считать лежащим в (Af(s), X(s + г + 1)), а построен-
ный нами сфероид — относительным сфероидом X(s — г) mod X(s).
Посмотрим на рис. 148. Мы имеем сфероид у € nN+t_j + I (X(s — г), X(s)),
граница которого как относительный сфероид X(s — г + 1) mod X(s +1) совпада-
ет с а, т.е. a=g'b3a&lmdf~r’t~r + l.
Повторяя это рассуждение в обратном порядке, получим, что и наоборот, из при-
надлежности а к образу df ~r,t ~r + 1 вытекает, что а переходит в ноль при гомо-
морфизме Ker d3^3 -*E3r’h.
Утверждение (2), а вместе с ним и утверждение (1), доказано.
5. Отступление: замечание о резольвентах. Для вычисления начального члена
спектральной последовательности Адамса Ext^r (Я*(Х), Zp) нужно выбрать сво-
бодную резольвенту А-модуля Я* (Jf)
... ~*В3 ~*В2 ~*Bi -*Н*(Х)~*0.
Затем нужно применить функтор Нот и потом взять гомологии получившегося
комплекса. При этом от выбора резольвенты конечный результат не зависит, а по-
тому естественно попытаться подобрать наиболее удобную резольвенту.
Рассмотрим Н*(Х) и выберем в этом A-модуле минимальную систему образую-
щих. Построение этой системы будем вести следующим образом. Возьмем систему
аддитивных образующих в первой нетривиальной группе НЧ(Х). Затем во второй
нетривиальной группе мы присоединим к уже выделенным образующим такие ад-
дитивные образующие, которые не получаются из уже выбранных образующих
применением операций. И так далее. Получим некоторую минимальную систему
образующих этого A-модуля at, а2, аэ,..., обладающую тем свойством, что ни
для какой из образующих ag невозможно разложение вида ag = где >р{ G
€ A, deg > 0. На выбранные образующие мы натягиваем свободный А-модуль
284
ГЛ 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Bi. В ядре гомоморфизма -» Н*(Х) мы выберем образующие так же, как
в Н* (X), и так далее.
Очевидно, что для всех к гомоморфизм Ношд(5к, Zp) -*HomA(Bk+1, Zp) три-
виален (при любом гомоморфизме Вк -> Zp все элементы вида Ztipta^ , где а -
образующие Вк, deg <pt > 0, переходят в нуль; при нашем гомоморфизме Вк + 1 -+Вк
все образующие Вк +1 переходят именно в элементы такого вида).
Следовательно, для нашей резольвенты комплекс {HomA(Sfc, Zp)} имеет три-
виальный дифференциал и
Ext*(tf*(*),Zp) = HomA(Bk,Zp).
6. Продолжение доказательства. Случай конечных стабильных гомотопических
групп.
А. Вводные замечания. Переходим к доказательству утверждений (3) и (4) тео-
ремы Адамса. Положим
о
в5’ , = Im{^+f_X^(s))-*[^+r_XS^)] = 7rr_iW} ,
где -V(s) * X — вложение. Получаем цепочку включений (фильтрацию): ..<BS' * С
С в*-1’'’1 С ... С Б°'г-,> где/?0’*""1 =1т[^+г„Д^(0))->^+г_5(%(0))] =
= +1~~ s ( S N^) = я Д s GO • Фильтрация эта в случае любого X существенно бес-
конечна.
Нам надо доказать, что Е^ * = В*’ */Bs+1,t+1 и что Cir_s = mBs' f = Km, где
К” С it™ (X) есть подгруппа всех элементов, порядок которых конечен и взаимно
прост с р.
Замечания. 1. В члене Е2, а значит и в Еж , все элементы имеют порядок р,
как мы это видим вследствие замечания о выборе резольвенты.
2. При t < s наше утверждение очевидно. Действительно, при t < s имеем:
В5- * = Im [jTjv+f-XAXs)) -> 7r.v+r j(^)] =
= 1ш[7Глг + г_,(ВД) ** 0] = О,
и * = 0. Равным образом, если з < 0, то снова Е^*= 0, и Bs’ f = ttn+ t„s(X(0)),
а ^+1>,+ 1 = 1ш[^+,+,(^(5+1))-*я^г_,(^)] = ^+,_,(У(0)),ибо s+1 <0.
Теперь предположим, что все стабильные гомотопические группы пространства X
конечны.
В. Алгебраическая лемма.
Лемма. Пусть М - произвольный А-модуль,
01 01 03
М <----Bl <— в2 <— ...
- его проективная резольвента,
- последовательность проективных A-модулей, в которой композиция двух идущих
подряд отображений тривиальна. Тогда существуют А-гомоморфизмы щ'. Cf+Bj,
§ 33. ПОСТРОЕНИЕ СПЕКТРАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
285
такие, что диаграмма
коммутативна.
Замечания. 1. Ср. с упражнением 1.
2. Эта лемма верна и без-предположения о проективности В/.
Доказательство леммы. Предположим, что имеются гомоморфизмы
<р0: М-> М (тождественный), Рассмотрим диаграмму:
Здесь гомоморфизм С, 5/_2 тривиален, так как =
= <д/_27/_17/. Следовательно, 1т^/_!7/ С Ker 0,_i = Im/?/, т.е. гомоморфизм
<д/_17/: С/ -> можно рассматривать как гомоморфизм С/ -* Im/?/. Так как
Л-модуль Ct проективен, то существует гомоморфизм Q -> В{, композиция кото-
рого с эпиморфизмом В( -* Im (jt совпадает с ^/-17р Его мы и принимаем за <д/.
С. Серровская фильтрация. Наряду с фильтрацией Адамса
... -* %(2) -> У(1) -> T.NX
мы рассмотрим аналогичную фильтрацию, возникающую при убивании гомотопий
по Серру. Пусть m — размерность первой нетривиальной группы когомологий X
(т.е. Н 1 (X; Zp) = 0 при i < m). Отметим, что m > 0, так как если Н ° (X; Zp) ¥= О,
то А- не связно, и я о GO = Z ® ... ® Z, где число слагаемых равно числу связных ком-
понент X, уменьшенному на единицу, а это противоречит предположению о конеч-
ности гомотопий.
Обозначим через К] пространство
K(Hm(X-, Zp),N+m) = K(Zp, N+m) X ... X K(Zp,N+m).
Отображение ZNX -* Ylt индуцирующее изоморфизм групп 7fJV+m(-; Zp)
(оно определено однозначное точностью до гомотопии) превратим в расслоение.
Через Xi обозначим слой этого расслоения.
Отображение nN+m(ZNX) -* я^+т (Yt), очевидно, эпиморфно. Из гомотопи-
ческой последовательности нашего расслоения следует, что TtN+m(X1) есть ядро
этого отображения,откуда порядок я^+т (А)) меньше порядка я^+т (S7VAr).
286
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Дальше мы продолжаем эту же конструкцию и получаем последовательность
убивающих пространств и отображений
... > Х2 -* Xt -> vNx.
Из конечности гомотопий ZNX (до размерности N + п) следует, что для любого
q < п найдется такое з0, что при s >з0 порядок TrN+q(X(s)~) ие делится иа р.
Полученную последовательность мы назовем серровской фильтрацией.
Наша цель — построить такие отображения fs: -Y(s) -> Xs, чтобы диаграмма
Х(2) --------Х(3) *---- ...
X(l)
4
S X
X,’
г
была коммутативна.
D. Отображение адамсовской фильтрации в серровскую. Рассмотрим пространст-
во Yf, возникшее при построении серровской фильтрации. Мы имеем расслоения:
~ Х/+1 ~ ~ zi + i ~ ~ ~
Xi ----► + 1 и Х1 + 1 -----*"Х{, где У/+1 = (в стабильных размерностях).
Второе расслоение индуцирует гомоморфизм Н*(X/ + i) -> H*(Zi + t) (сохраняю-
щий размерность) и H*(Zt + t')-^ H*(Xt') (повышающий размерность на единицу).
Последний гомоморфизм — трансгрессия — определен только в стабильных размер-
ностях. Вместе они определяют повышающий размерность на единицу А-гомомор-
физм Я*(£/ + 1) -+ H*(Xt) + H*(Z t), определенный в стабильных размерностях.
Обозначим через С/ свободный A-модуль такой, что [C/]Q = HN~‘+4(Zt; Zp)
при q < и. Наше отображение 7f*(Z/ + 1) определяет А-гомоморфизм
Q + 1 -> Ct, сохраняющий градуировки. Отображение Ct -> Н*(Х) определяется
с помощью отображения HNX -> Yt = ZZf Получаем последовательность
Ясно, что в этой последовательности композиция двух соседних гомоморфизмов
тривиальна. Уже композиция Я’(%/+1) -> B*(Z<+1) -> H*(Xt) тривиальна.
Согласно нашей лемме, существует диаграмма:
в г---------в2------------в^-------...
Н*\Х)
%!
%
%
Cf* .
Отображение <pi: Ct -> Вi определяет естественное отображение gt'. Yt "* Yt,
такое, что gj = <pt (с точностью до градуировки, в стабильных размерностях).
§ 33. ПОСТРОЕНИЕ СПЕКТРАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
При этом диаграмма
287
гомотопически коммутативна. Это следует из того, что Yt = K(ir, N + т) и из теорем
об отображениях в пространство Эйленберга—Маклейна. Если отображение ENX
в У1 и У1 - расслоения, то слой A'(l) первого содержится в слое Х2 второго из них,
что определяет отображение : У(1) -* Х2. При этом диаграмма
коммутативна. Построим отображение g2: У2 К2, такое, что g2 = <р2 (с точностью
до градуировки в стабильных размерностях) и рассмотрим диаграмму
H*(Y2) ^2- H\Y2)
Н*(Х(1У) H\Xt)
Т* • Т’|
Н*(Л) H^Y.)
В этой диаграмме нижний маленький прямоугольник и большой прямоугольник
коммутативны; т i — мономорфизм (в стабильных размерностях). Отсюда следует
коммутативность верхнего прямоугольника и (из свойств отображений в простран-
ства Эйленберга— Маклейна) гомотопическая коммутативность диаграммы
У2 -------► У2
Х(2)
Х(1) ----> Х2
Последнее обстоятельство позволяет определить отображение слоев f2:
Х(2) ~>Х2, и диаграмма
*(2) ------► Х(1)
1 1
Х2 ---------> X.
гомотопически коммутативна. Дальнейшее построение производится так же.
Е. Фундаментальная лемма.
Лемма. Для любых s и q < п при достаточно большом М гомоморфизм
irN+q(X(s + М)) ->ядг+(г(А'(s)) тривиален на р-компонентах.
Из предыдущего построения ясно, что при достаточно большом М гомомор-
физм nN+q[X{M)) -*itN+q(ENX') тривиален на p-компонентах. Это ясно из
288
ГЛ 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
. диаграммы
^Х(1) <— ... <— Х(М)
X1 * . •. * хм
и из тривиальности p-компоненты nN+q(X(М)) для достаточно большого М.
Для доказательства леммы осталось заметить, что часть адамсовской фильтрации
... -> X(s + 1) -* A'(s) сама является адамсовской фильтрацией для Х(з). Поэтому ут-
верждение леммы следует из доказанного выше факта.
F. Дополнительные замечания. 1°. Группы nm(X(s), X(f)) для всех т, з и t
имеют порядки, равные степеням числа р.
2°. р’-компоненты групп лт (X(s)) для всех т и всех простых рг¥= р ие зависят
от з, и изоморфно отображаются друг иа друга при гомоморфизмах, индуцирован-
ных вложениями Х(з + г) С Х(з).
Оба замечания вытекают из гомотопических последовательностей троек и расслое-
ний Х($) ---*X(s — 1) и из того, что гомотопические группы пространств Ys яв-
ляются р-группами.
G. Вывод из фундаментальной леммы и дополнительных замечаний утверждений
(3) и (4) теоремы Адамса. По определению имеем:
Bs t = Im [яу+,_,(*(«)) -> ^,-,(2^)],
Б,+1.г+1 = 1т[7Гдг+,_,(Х(5+1)) -> =
= Кег [яу+г_,(2№) -> irN+t_s(ZNX, X(s + 1))],
откуда
Bs,t/B3^,t^ = 1т[7^+г_ХВД) -* к„ + '-з(^Х, *(s+l))].
Далее,
ES,t = Im[irN+t_s(X(s),X(3 + M)) -> nN+t.s(^NX, X(s + 1))].
Рассмотрим диаграмму:
5^
Р
n.v+f_s(jr(5-), X(s*M))
^5
1
СХ(5-),2Г($+ 1))
^>10
ny+t. ЛЪ*Х)
2>в
п
* ^^,3
в
(Х(5+М))
О
JX(5 + 1))
§ 33. ПОСТРОЕНИЕ СПЕКТРАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
289
Она коммутативна и три косые строки в ней точны. Пусть а G Е^ , т.е. a G
е irN+t_s(ZNX, X(s + 1)) и а = Ms(fl), где p G nN+t„ s(X(s), X(s + Л/)).
Положим у = $5 (Р)> 8 = 5? (&)• Элемент /3 имеет порядок ph (первое из дополни-
тельных замечаний), потому это же верно и для 6, и поэтому Si 0 (8) =0, а значит,
$8 (?) = о, т.е. Т = h(e), ^N+t- s (Х(з)). Отсюда а = $6$3(е), т.е.
аб В3' */Bs+1’t+1. Так как включение В3’ */Вз+1 ’f+1 С Е^ * при всех М очевидно,
то Bs’ f/Bs+1,t +1 = ОМЕ= Е^ f. Мы доказали утверждение (3).
Утверждение (4) прямо следует из второго из дополнительных замечаний и фунда-
ментальной леммы. См. рис. 149.
7. Дополнительные свойства спектральной последовательности Адамса. Прежде
чем приступать к доказательству утверждений (3) и (4) теоремы Адамса в общем
случае, мы должны рассмотреть вопрос о поведении згой спектральной последова-
тельности при отображениях.
Предположим, что мы построили спектральные последовательности Адамса для
пространств Хи X’, и пусть /: X -* X’ - некоторое отображение. Оно индуцирует
отображение A-модуля Н*(Х’) в A-модуль Н*(Х). Построение, аналогичное
использованному нами при доказательстве последней алгебраической леммы,
дает нам ’’гомоморфизм проективных резольвент”
Н*(Х) *------ Вг <----- В2 <---- ...,
Н*(Х') •<-- В/ <--- В2 <---- ...,
который индуцирует отображение фильтраций:
vNx *— -v(i) <— ад <----------------
T,NX' ♦--- У'(1) *------ Х'(2) «----
Построение аналогично построению отображения адамсовской фильтрации в серров-
10. А.Т. Фоменко
290
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
скую. Это отображение индуцирует, в свою очередь, отображение всех относительных
гомотопических групп, которые участвовали в построении спектральной последова-
тельности Адамса. Совокупность этих отображений индуцирует гомоморфизм
спектральных последовательностей Адамса, обладающий очевидными свойствами.
Этн свойства мы соберем в одной теореме.
Теорема. Отображение f: X * X' индуцирует гомоморфизм спектральной
последовательности Адамса { Е?’ *, d^'*} пространства X в спектральную последова-
тельность Адамса {’Е*г’*, 'd*r'1} пространства X', т.е. набор гомоморфизмов
s. t s, t , s, t
fr:Er -> Er , такой, что'.
(1) Эти гомоморфизмы перестановочны с дифференциалами, т.е. следующая диа-
грамма коммутативна
f3-'
Ер* -----------------
Г + г— 1 ________'Егз + г’ t+r~1
r fS + r,t+r-l
(2) Гомоморфизм fr +i: Er +1 ~+'Er+t есть отображение гомологий комплекса
(Er, dr) в гомологии комплекса ('Er, 'dr), индуцированное отображением fr: Er^'Er.
(3) Гомоморфизм
ft’-. Е^ = Ех13А'(Н\Х), ZpY* ’Е^ = Ы3А*(Н\х'), Zp)
индуцирован гомоморфизмом f*: Н* (X')-* Н* (X).
Сделаем пояснение. Функтор Ext есть контравариантный функтор первого аргу-
мента и ковариантный функтор второго. Отображение Ext д*(^Л > N) “* Ext д (М2, АО,
индуцированное отображением М2 -> Mi строится так. Берется отображение проек-
тивной резольвенты М2 в проективную резольвенту Mi и отображение в противопо-
ложную сторону комплексов, составленных из Ногп’ов. Индуцированное отображе-
ние гомологий этих комплексов — это и есть требуемый гомоморфизм ЕхСов.
(4) Предельное отображение f£’*: Е^ -*’E3-t индуцируется отображением
i^X)-+i^(X').
Мы не доказываем эту теорему, потому что она очевидна. Заметим только, что
ее последнее утверждение, столь же очевидное, как и все остальные, мы не можем
считать доказанным, поскольку не доказано еще то утверждение теоремы Адамса,
на которое оно опирается. Разумеется, при доказательстве этого утверждения теоре-
мы Адамса мы не будем пользоваться приведенной теоремой: нам потребуется
только факт существования отображения адамсовских фильтраций при отображе-
ниях пространств.
Важное следствие. Спектральная последовательность Адамса, начиная со
второго члена, зависит только от стабильного гомотопического типа пространства X.
Иными словами, если пространства X и X' стабильно гомотопически эквивалент-
ны (т.е. их многократные надстройки гомотопически эквивалентны в обычном
смысле), то для всех г > 2, s и t существует изоморфизм Ер f« 'Е3,перестановоч-
ный со всеми дифференциалами; фильтрации в изоморфных группах tt$_s(X) и
7г^_5(Х') одинаковы и присоединенность членов Е„ к стабильным гомотопическим
группам тоже одинакова.
§ 33. ПОСТРОЕНИЕ СПЕКТРАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
291
8. Окончание доказательства теоремы Адамса в общем случае. Фундаментальная
лемма, которой мы пользовались в случае пространства с конечными стабильными
гомотопическими группами, в общем случае бесполезна. Кстати, для общего случая
не проходит и наше доказательство этой леммы. Нам бы хотелось, чтобы
фундаментальная лемма была доказана в такой формулировке: ’’Гомоморфизм
irN + q(X(s +ЛГ))-> irN + q(X(s)) для достаточно большого М тривиален на р-компо-
нентах и на свободных слагаемых”. Но в таком виде она, очевидно, неверна. Если
группа nN + q(X(s)) имеет слагаемое Z, то такое слагаемое имеет и группа
7rw + q(Ar(s + Af)), а ядро гомоморфизма itN + q(X(s + ЛГ)) -> -nN + q(X(s)) конечно,
что следует из того, что различие между гомотопиями A"(s) и X(s + М) измеряется
гомотопиями У5+!, У5+2, ••., которые являются конечными р-группами.
Роль фундаментальной леммы будет играть у нас следующее предложение.
Обобщенная фундаментальная лемма. Любой элемент а 6
яn+q(X(s)), который имеет порядок либо °°, либо рк, не принадлежит образу
гомоморфизма nN+q(X(s + M))-*-rrN+q(X(s)) для достаточно большого М.
Заметим, что отсюда следует тривиальность гомоморфизма 7t^ + q(X(s + М)) +
KN + q(X(s)) ДДя достаточно большого М на р-компонентах:р-компонента группы
тг^+ q(X(s)) состоит из конечного множества элементов.
Доказательство обобщенной фундаментальной леммы. Не ограничивая общности,
можно считать, что s = 0, т.е. X(s) = XNX. Напомним, что последовательность
... Xs + является адамсовской фильтрацией для .¥($)., Из предположе-
ний леммы следует, что элемент а не может бесконечно делиться нар, т.е. найдется
такое число г, что а^р'а ни при каком а1 € Tr^+q(XN X).
Рассмотрим отображение h: XX, определенное следующим образом. Суще-
ствует известное отображение SX+ XX v XX (см. § 4). Применяя его многократно,
мы можем построить отображение SX-*- XX v ... v XX (рг раз). Этот букет можно
отобразить в XX, склеив все его листы (рис. 150). Мы получили отображение ХХ-*
+ XX. По-другому можно описать это отображение так. Как известно, XX = X #SX.
Рассматриваемое нами отображение есть отображение X #S' -+ X #Sr, индуцирован-
ное тождественным отображением X -> X и отображением № степени рг. По
этому отображению мы приклеим к XX конус над XX (рис. 151). Полученное про-
странство мы обозначим через X1. Очевидным образом определяется отображение
XX->Х' (рис. 152). Это отображение индуцирует отображение (N - 1)-кратных
Рис. 152
292
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
надстроек T,N ’(SA') = T,NX-+'SN 1 А'' и адамсовских фильтраций
ZNX<------Х(1)ч—Х(2) «----...
4 4 4
--^(l)*—А"(2)«—
(на основании сделанного выше замечания). Имеем диаграмму:
ZNX <-------Х(1)*—Х(2)*—...
4 4 4
’(A") «— A"(l) <— Х'(2) *—...
Доказываемое утверждение вытекает из нашей старой фундаментальной леммы
и следующих двух предложений:
(1) Стабильные гомотопические группы X' конечны.
(2) Элемент а не принадлежит ядру гомоморфизма
я„+,(2"АЭ^+<г(2"-’Г)-
Доказательство утверждения (1). Напишем гомотопическую после-
довательность пары (ZN~1X', X):
1(-. -)+ ^NX)- я„+г(2"~ lX') - *N+r(-, -)^nN+r_!(SNX).
В стабильных размерностях, которые мы и рассматриваем, имеем:
яЛГ+г+1(2ЛГ-’<2ЛГА') =
= я^+r+1(S^-1A'7S^^)=я^ + r+1(S^+1X) = я^ + r(E^X).
иотображение 3: TtN+r+1(—,—) = TtN+r('SNX)^'nN+r(ZNX) есть умножение нарг.
Ядро и коядро этого гомоморфизма поэтому конечны, и, следовательно, группы
яЛГ+г(2ЛГ-1А’') конечны.
Доказательство утверждения (2). Из этой же точной последователь-
ности имеем, что ядро гомоморфизма irN+q(ZNX)-^irN+q(l,N~1 X') состоит из
элементов, делящихся на рг, т.е. а в него не входит. Осталось заметить, что в силу
старой фундаментальной леммы образ элемента а — ненулевой элемент, порядок
которого есть степень числа р, — не принадлежит образу группы 7tN+q(X' (Л/)) при
достаточно большом М, а отсюда следует, что а не принадлежит образу группы
я^(Х(Л0).
Обобщенная фундаментальная лемма доказана.
Доказательство утверждений (3) и (4) теоремы Адамса.
Для доказательства равенств
Bs’f/Bs+ ’•'*1 = Im[ffjv+r_,(X(s))- X(s + 1)]
и
ESJ =П 1т[ялг+г_5(А'(0,А'(1 + М))-*ялг + г_5(2лгА', A'(s+ 1))]
§ 34. МУЛЬТИПЛИКАТИВНЫЕ СТРУКТУРЫ
293
рассмотрим уже знакомую нам диаграмму:
д
^6
а
%(.$-1))
r.^t_s^x{s+M))
*,о
Р
Она коммутативна и косые строки в ней — точны. Предположим, что элемент
а 6 плг+г_5(2лгX, X(s + 1)) не принадлежит образу гомоморфизма £6$:з:
nAr+f_i(Ar(s))^-nAr+f_J(SArX X(s + 1)). Мы должны показать, что для достаточно
большого М этот элемент не принадлежит образу и гомоморфизма £6 £s.
Положим 0 = £9а 6 TrN + t_s^ 1(X(s + 1)). Элемент 0 имеет конечный порядок,
равный степени числа р. Это следует из того, что этот факт верен для а, как и для
всех элементов группы irN+ t_s(ZN X, X(s + 1)). Поэтому или /3 = 0, или 0не принад-
лежит образу гомоморфизма £10 для достаточно большого М. Если 0 = 0, и
а=1б^(5),тоа = |6(у),где7 = ^(5), 7^ *N+t-sWs), X(s+ 1)).Но£8(7) = £9(а) =
= 0 = 0, отсюда 7 = £3(е), где ебпдг+^/АХх)), иа = £6Ь(«)> что противоречит пред-
положению. Если 0¥=О, то 0$: Im £1о для достаточно большого М. Но если бы а
равнялось £6£s 5, где 5 G ядг+^ДЛХа), Jf(s + М)), то 0 равнялось бы £ю?7 3. Мы снова
пришли к противоречию.
Итак, доказано утверждение (3). Утверждение (4) прямо вытекает из обобщенной
фундаментальной леммы.
Теорема Адамса полностью доказана.
§ 34. МУЛЬТИПЛИКАТИВНЫЕ СТРУКТУРЫ
Мультипликативная структура в спектральной последовательности Лере возникла
из когомологического умножения, и зто было естественно, так как все входившие
в эту спектральную последовательность группы были группами когомологий и их
подгруппами. Группы, составляющие спектральную последовательность Адамса, -
зто гомотопические группы и их подгруппы.
В них никакой мультипликативной структуры нет. Есть, конечно, умножение
Уайтхеда, но оно здесь для нас бесполезно, так как область его применимости —
нестабильные гомотопии. Поэтому в спектральной последовательности Адамса нет
мультипликативной структуры, во всяком случае, настолько же хорошей, как
в спектральной последовательности Лере. Но все же в некоторых предположениях
удается построить аналог мультипликативной структуры, который превращает
спектральную последовательность Адамса в последовательность колец в единствен-
ном случае — когда X есть сфера. Но этот случай весьма интересен.
С него мы и начнем. Представим себе, что обещанная кольцевая структура в чле-
нах спектральной последовательности Адамса уже есть. Тогда кольцом должна быть
s 0
и сумма ®q nq(S ). Каково умножение в этом кольце?
294
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Оказывается, эта естественная кольцевая структура может быть описана геомет-
рически.
1. Композиционное умножение в стабильных гомотопических группах сферы.
Пусть а 6 ядг+*(5ЛГ), /3 6 t^n+i (SN) (где к, I < N). Тогда элемент /3 можно счи-
тать лежащим в группе irN+k + i (SN+k). Сфероиды /3: sN+k + l + SN+k и
a: SN+k + SN, представляющие элементы /3 и а, позволяют определить сквозное
отображение afi: sN+k+I + SN, которое, в свою очередь, определяет элемент иэ
группы Ядг+fc+z (5ЛГ). Мы обозначим этот элемент через а ° (j и назовем компози-
цией элементов а и /3. Дадим другое определение композиционного умножения, вос-
пользовавшись тензорным умножением # (см. п. 6 § 2). Пусть а & nN+k(SN~),
6 nN+1 (SN), ипусть a: SN+k -*SN, SN+l * SN — представляющие отображе-
ния. Можно определить а° (3, положив (-l)7Vfcao р = а # (1: SN+k #SN+I -+SN#
# SN. Другими словами, первый сомножитель отображается с помощью а, второй —
с помощью Этим фактически определено отображение sN+N+k + I -> SN+N или
^N+k+i , так как k + l <N.
Предложение 1. Эти два определения эквивалентны.
Доказательство. Отображение (-l)7Vfc(a #0) = ((-# /3: SN+k #
# SN+1 -+SN # SN можно разложить в композицию двух отображений
S'v+! + $м *
Р id id
5V * 5* * S‘V
id
5Л’ * 5Л
Дополним эту композицию, вставив в середину отображение, меняющее местами
два крайних сомножителя. Это отображение сохраняет ориентацию при четном N и
меняет ее на противоположную при нечетном N. Чтобы оно было гомотопно тождест-
венному, мы третий сомножитель отображаем в первый не тождественно, а с по-
мощью отображения (-1)^id N. Итак, наше отображение гомотопно композиции:
§ 34. МУЛЬТИПЛИКАТИВНЫЕ СТРУКТУРЫ
395
Наконец, добавим к этому отображению отображение, меняющее порядок умно-
жения в последнем произведении (с аналогичной предыдущему поправкой в знаке).
Получаем композицию:
Л-'+' * Л’* #
Итак, имеем отображение sN+k+l # SN ~>SN #SN, которое на втором сомножи-
теле тождественно, а на первом есть композиция
я / , t < \Nk —
$*+*+' _L, sN+k .< 2 -+SN+k « SN,
т.е. a о p. Средняя стрелка обозначает перестановку сомножителей. Наше утвержде-
ние доказано.
Предложение 2. Композиционное умножение антикоммутативно, т. е.
ао 0= (-l)*z0o а.
Доказательство. Очевидно, что элемент а о fi не зависит от числа N, кото-
рое участвует в его определении. Возьмем зто N четным. Тогда а» fi = а # fi и
fi о а = fi # а. Далее, отображение а # fi и fi # а определяют элементы из
n2N+k+i(S2N), отличающиеся на множитель (—l)*z. В самом деле, а # fi есть
композиция SN+k # SN+l -> SN+I # SN+k -+SN # SN ->SN # SN. Здесь две край-
ние стрелки обозначают перестановку сомножителей. Первая перестановка
сомножителей меняет или сохраняет ориентацию в зависимости от четности
числа (—1) (N+k) (N+1\ Вторая перестановка гомотопна тождественному отображению
(N четно) и может не приниматься во внимание. Известно, что замена ориентации
отображаемой сферы приводит к изменению знака у гомотопического класса
сфероида. Это — определение вычитания в гомотопических группах. Поэтому знаки
элементов aofi и (3°а отличаются на (-l)fc/ = (— 1)<ЛГ+Л> (N+I) . Предложение
доказано.
Предложение 3. Композиционное умножение дистрибутивно:
(.fi + 7) 0 а = fi 0 a + У 0 tto(/3 + y) = ao^ + aoy.
До казательство. Так как антикоммутативность нами уже доказана, то
достаточно показать, что верна только какая-нибудь одна из этих формул, например
296
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
формула а ° ((3 + у) = а ° 0 + а ° у. в этой формуле слева стоит класс отображения,
схематически изображенного на рис. 153, а справа — класс отображения, изображен-
ного на рис. 154. Но совершенно очевидно, что это — одно и то же отображение.
Предложение доказано.
Ассоциативность композиционного умножения очевидна.
Итак, нами введена структура градуированного антикоммутативного ассоциатив-
ного кольца в nf (5°) = ®q я, (S°).
Замечание. Композиционное умножение можно, конечно, определить и в не-
стабильной ситуации: композиция элементов аб (S'") и (3 6 um (Sn) есть элемент
Рис. 153
Рис. 154
а о |3 G я, (5"). Однако свойства нестабильного композиционного умножения остав-
ляют желать лучшего. Прежде всего, разрушается коммутативность: композиция
(3°а вышеуказанных элементов вообще не определена (разве что I = т = и).
Неожиданным образом, для нестабильного композиционного умножения не выпол-
няется ’’левый закон дистрибутивности” (0 + у)» а = 0о а + у о а. Простейший при-
мер: пусть аб я3(52) - класс хопфовского отображения h: S3 -*S2 (см.п.2 § 10)
и 21 6 я3 (S3) — класс отображения 53 -> S3 степени 2. Из левого закона дистрибу-
тивности следовало бы, что (21) о а = 2а, но в действительности (2 с) » а = 4а.
Упражнение 1. Докажите это, пользуясь инвариантом Хопфа — см. п.4 §16
и упражнение 34 к п. 6 § 17.
Разнообразную информацию о левом законе дистрибутивности композиционного
умножения и его связях с инвариантом Хопфа и его обобщениями см. в "Теории
гомотопий клеточных пространств" М.М. Постникова.
2. Алгебраическое отступление: алгебры Хопфа. Градуированная алгебра
А = ® Ат с единицей над полем называется алгеброй Хопфа, если:
(1) Ат = 0 для отрицательных т и А0 совпадает с самим полем к.
(2) Определено "диагональное отображение” или "коумножение” Д: А +
которое является гомоморфизмом алгебр. Здесь А А — алгебра:
(а'® /3')-(а" ®/3") = (-l)deg<3'deg“"a*aM®/3'/3".
(3) Для любого элемента а 6 А положительной степени d Д(д) = а ® 1 + ...
... + (-l)dl ® а, где ... обозначает сумму тензорных произведений положительных
степеней.
(4) Операция Д ’’коассоциативна”, что означает коммутативность диаграммы
А 8 А
А 8 А
А8А8А
А ® А 8 А
§ 34. МУЛЬТИПЛИКАТИВНЫЕ СТРУКТУРЫ 297
Замечательным свойством определения алгебры Хопфа является его симметрич-
ность по отношению к умножению д: A®A-+A(a®b^> ab) и коумножеиию Д: А ->
-> А ®Л. Именно, имеет место следующий факт.
Упражнение 2. Если А — алгебра Хопфа, то пространство А * = Ношк (А, К.)
также есть алгебра Хопфа по отношению к умножению Д*: (Л ®А)‘ =А*в>А*^А*
и коумножеиию и*: А* ->А*® А*. (Наличие единицы, ассоциативность,аксиомы (2),
(3), (4) для А * вытекают из аксиомы (3), аксиомы (4), аксиомы (2), наличия еди-
ницы и ассоциативности для А.)
Подробности об алгебрах Хопфа см. в статье Milnor J., Moore J. On the structure
of Hopf algebra //Ann.Math.- 1965. - V. 81, № 2. - P. 211-264.
Пример алгебры Хопфа: когомологии (или гомологии) Я-пространства X с коэф-
фициентами в поле (умножение и коумножение индуцируются диагональным отобра-
жением Х-+ XX X и умножением XX Х-> X).
3. Алгебра Стинрода как алгебра Хопфа. Другой, важный для нас сейчас пример
алгебры Хопфа — алгебра Стинрода: коумножение определяется формулой
д(р)=р®1-1®з, д(рР5 = sj+,=zp;®p/
(если р = 2, то Д Sq" = SJ+r= f Sqs ® Sqf).
Заметим, что если А — алгебра Хопфа, В и С — два Л-модуля, то их тензорное
произведение как векторное пространство над К также является А-модулем. Это
тензорное произведение является, очевидно, А ®к Л-модулем. Наличие же гомомор-
физма А ->Л®к А позволяет превратить его в А-модуль.
Важное замечание. В случае, если Л = А - алгебра Стинрода, то эта кон-
струкция согласована с формулой Кюннета: если X и Y — любые пространства, то
Н*(Х # Y; Zp) =Н*(Х; Zp) 9H*(Y; Zp). Таким образом,Н*(X# Y; Zp) является
A-модулем по двум причинам: во-первых, когомологии любого пространства яв-
ляются A-модулем; во-вторых, структура A-модуля может быть введена с помощью
общей конструкции, так как А — алгебра Хопфа. Формула Картана показывает, что
эти структуры одинаковы.
Упражнение 3. Если В к С- свободные A-модули, то В ®к С - также сво-
бодный А-модуль.
Мы ограничимся для простоты случаем р = 2. Случай р > 2 читатель сможет
разобрать самостоятельно: он отличается от случая р = 2 только наличием в ряде
мест множителя (— 1) .
Для любых A-модулей М*, Мп, N' nN" можно определить умножение
Ext д' ' (M',tf')®Za Ext a ’' (3f",7V")-:>Ext\+S ’'+f"(M'®ZaM";tf'®zaW")
следующим образом. Берем две любые свободные резольвенты:
a.' а' а!
М' <—В{ «------ В2 +— ....
. t; а»» • а” •
М" *-- в" *—- В" .
Рассмотрим следующую свободную резольвенту A-модуля М' ®z М":
а, а. а.
M'®Za М” +----- 5{® В" -г- Вг® Bi+ B’i9 В" +---
Вз ® В" + В'2 9В2 + В\ ®В" ...
298
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
(все тензорные произведения — над Z2), где гомоморфизмы 3; определены ра-
венством:
Эр+<г_1(а'®а") = Эра’®а”+(—1)ра'® Э”а"; а'&Вр, oi'g-b".
Очевидно, определен естественный гомоморфизм
HomA(Bp', N') ® НотА(Я " Я")НотА(Вр ® В”, N' ® N"),
который, после перехода к гомологиям комплексов Нот’ов, даст требуемый гомо-
морфизм Ext’oB.
Упражнение 4. Если М* -М" =N' =N" =М' ®zj М" -N1 ®za NH = Z2 ,
то описанная процедура определяет кольцевую структуру в fExt А? (Z2 , Z2).
Определение. Группы Ext А f(Z2 , Z2) называются группами гомологий ал-
гебры А и обозначаются через Н s> f( А ).
Таким образом, мы определили кольцо гомологий алгебры Стинрода.
Упражнение 5. Это — ассоциативное и коммутативное кольцо.
Если в предыдущем построении М" Ф Z2, то мы получаем гомоморфизм
Ext a ''(Z^Zj)® Ext a* r"(Af",Z2)^ExtA+i"’ ^'"(М"^).
Коротко это можно выразить так: Ext \(М, для любого A-модуля М являет-
ся Н (А)-модулем. Если М -* N — гомоморфизм A-модулей, то индуцированное
отображение
Extl*(JV, Z2) -* ExtACM.Zj)
является Я (А)-гомоморфизмом.
4. Умножение в спектральной последовательности Адамса.
Теорема (Адамс). Если X = S°,to в спектральной последовательности Адамса
„ „s, t „s’ft*- ' „з + з', t+t' '
можно определить умножение Ег ® Ег + Ег , обладающее следующи-
ми свойствами:
(1) умножение коммутативно и ассоциативно-,
(2) умножение ® £2 ’ * е\ s , t + t совпадает с умножением Hs" f(A) ®
,t+t (А) в гомологиях алгебры Стинрода-,
(3) dr(uv) =(dru)v + u(drv):
s, t s, t . s, t
(4) умножение перестановочно с изоморфизмом Er+1 -H(Er ; dr )ucmoho-
s, t s, t , . . , ,
морфизмом E k E r (при s < r < k < «>);
(5) умножение в E^ присоединено к композиционному умножению nSk(S°) ®
® я? (S0) ^я/+/(5°).
До к азательство. Мы хотим получить несколько более общее утверждение,
чем сформулированное, поэтому мы начнем с рассмотрения двух произвольных
§ 34. МУЛЬТИПЛИКАТИВНЫЕ СТРУКТУРЫ
299
пространств X1 й X". Пусть
Я*(Х'; Z2) «--- В! ♦-- В2 4--- ...,
н\х"-,г2) <-----В{’ 4-— в" *— ...
— свободные А-резольвенты A-модулей Я*(Х,;22) иZ2);
ZN'x' *---- Х'(1) *-- Х'(2) «----
SJV"X'' <-- Х"(1) *----- Х"(2) *- ...
соответствующие адамсовские фильтрации. Рассмотрим следующую фильтрацию
в пространстве 2ЛГ X* # ZN X" = SJV + ?v ( X1 # X" ) . Через X(ri) мы обозначим
и/+/=„(Х'(Г) # X"(/)), имея в виду, что Х*(0) = S/vV и X1'(0) = ^"х”.
Положим Yn =Х(п)1Х(п4 1); очевидно,
Yn= v [(Г(П/Г(/+1))#(Г'(/)/^''(/+1))]-
i + / = п
Но пространства Х'(/)/Х'(/ + 1) и X"(j)/X"(j + 1) в стабильных размерностях
гомотопически эквивалентны Y't и Y" — произведениям пространств Эйленберга —
Маклейна, используемым при построении адамсовских фильтраций {X'(i)} и
{У"(/)}. Поэтому H*(Yn) = ®n-j = nH*(Yfr) ® H*(Y’’). Мы видим, что фильтрация
ZN' + N"(x' # др д2)
является адамсовской фильтрацией для резольвенты
Н*(Х’ # X";Z2) * Bi ® В" В2 ® B'i + Bi ® В2 «- ...
Построим спектральные последовательности Адамса для пространств X', X"
и X' #Х" по имеющимся резольвентам и фильтрациям. Умножение
Я/'- f'(X') ® r"(X") -► Ef + '' + г"(ЛГ' # X")
определяется следующим образом. Пусть
a' €= f’(X') =
= 1т17Глг' + г'_Ду,(1')’X'(s' + г» * + 1 -r),X'(s'+ 1))],
a" e r"(X") =
= Im[Jr^ + f«_z(J"(s"),X"(s"+r)) nN„ + t. _z(X"(s" + 1 -r),X"(s" + 1))].
Возьмем в irN< + f, _s, (X'(s), X'(s' + г)) и nN„ + t„ s„(X"(s"), X"(s" + г)) элементы,
образами которых служат а и 0, т.е. отображения кубов IN +f -i и IN +t
в X' и X", при которых сами кубы переходят в и Х’Хх"), а их границы -
bX'(s +г) и X"(s" + r). Эти отображения можно ’’перемножить”, т.е. взять отобра-
жение
jN' + t'-s' x/N" + t"-s" = IN'+N"+t' + t"-y-s" -+х,'АХ" -^Х' #Х".
300
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Последнее отображение переведет куб IN +N + * +* 1 * в JT'(s') # Xя (s") С
CX(s' + s"), а его границу - в R"(s' + r) # X"(s")] U [2"(s') # X"(s" + r)] C
C X(s' + s" + г) (см. рис. 155).
Поэтому оно является относительным сфероидом пары (X(s' + s"), X(s' + s" +r))
и определяет элемент из группы
^'+^ + f' + r''-/-zW + sB)’ W+ *"+')).
Образ этого элемента в + + Ws< + s” + 1 - О, X(s + s" + 1))
и есть элемент Е* +я f +' (X' #ХЯ), который равен, по определению, произведению
выбранных элементов из Ef • * (X') uEf >f (Xя).
Построенное умножение перестановочно с дифференциалами, совпадает на Е2
с рассматривавшимся умножением
Ext”(tf*O");Z2) ® Ext*A*(H*(Xny,Z2) -
Ext~(tf* (X') ® Н*(Х"у,Z2)
и в пределе превращается в умножение
Е£*(Х') ® Е£*(ХЯ) - Е£*(Х' # Xя),
присоединенное к умножению
я£(Г) ® nf(X") - я£+/(Г # Xя).
Проверку этих утверждений мы оставляем читателю.
Если X' = Xя = S°, то доказанное утверждение превращается в сформулированную
выше теорему Адамса.
Если X’ = S0, а Xя = X - произвольно, то наша конструкция снабжает Е**(Х~)
структурой £^*(5°)-модуля, которая при г = 2 совпадает со структурой Я**(А)-
модуля в Ext д’ (Н* (У); Z2), определенной выше; при г = 00 присоединена к струк-
туре n$(S°)-модуля, которой nf(X) обладает для любого X (в том смысле, что
элементы стабильных гомотопических групп сферы в естественном смысле являют-
ся ’’стабильными гомотопическими операциями”, которые действуют в стабильных
гомотопических группах любого X с помощью композиции: операция a G
6 nAr+fc+z(SJV+fc) переводит элемент % 6 nN+k(SNX) в композицию sN+k+l +
SN + k £ ZNX).
§ 35. ВЫЧИСЛЕНИЕ СТАБИЛЬНЫХ ГОМОТОПИЧЕСКИХ ГРУПП СФЕР
301
§ 35. ПРИМЕНЕНИЕ СПЕКТРАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ АДАМСА
К ВЫЧИСЛЕНИЮ
СТАБИЛЬНЫХ ГОМОТОПИЧЕСКИХ ГРУПП СФЕР
Мы рассмотрим задачу о вычислении стабильных гомотопических групп сфер.
Начнем с вычисления члена Е2, т.е. гомологий алгебры Стинрода mod2 с их адди-
тивной и мультипликативной структурами.
1. Аддитивная структура члена Е2. Напишем свободную резольвенту
Z2 *• В\ *• в2 **...
для A-модуля Z2) = Z2. В качестве первого свободного модуля , входяще-
го в эту резольвенту, может быть взята сама алгебра А. Эпиморфизм А -> Z2 пере-
водит образующую этой алгебры в единственный нетривиальный элемент Z2, осталь-
ные элементы — в ноль. Ядром этого эпиморфизма служит А - идеал алгебры А,
составленный из элементов положительных степеней. Следующий шаг состоит в вы-
боре в этом идеале системы A-образующих. Напомним, что мы выбираем минималь-
ную систему образующих, т.е. начинаем с компоненты минимальной размерности
(равной в данном случае единице) и выбираем систему образующих в ней. Вектор-
ное пространство А> одномерно и порождается элементом аг = Sq1. Теперь мы
должны рассмотреть А2. Это тоже одномерное пространство. Так как Sq1^ = 0,
образующая Sq3 этого пространства не выражается через в] и должна быть взята
в качестве следующей образующей. Обозначим ее через а2. Отметим также, что
уже проявилась несвободное» A-модуля А . Для дальнейшего нам полезно выпи-
сывать все соотношения, какие есть в этом А-модуле. В размерности два, очевидно,
есть только одно соотношение: Sq’flj = 0. В размерности 3, как нам известно по
теореме Серра, алгебра Стинрода имеет две аддитивные образующие: Sq3 и Sq2Sq1.
Обе они выражаются через выбранные ранее образующие: Sq3 = Sq’e2, Sq’Sq1 =
- Sq2ai. Соотношений в этой размерности нет. В размерности 4 стоят две аддитив-
ные образующие: Sq4 н Sq3Sq’. При этом Sq3Sq* = Sq3aj, a Sq4, как нам известно,
не выражается через Sq1 и Sq2, и мы должны принять его за новую образующую в3.
Очевидно, в этой размерности должны быть два соотношения (точнее, двумерное
пространство соотношений), потому что применяя элементы алгебры А к образую-
щим fli и а2, мы получаем элементы Sq2e2, Sq3e2 и Sq2Sq*fli. Кроме того, есть но-
вая образующая а3. Поэтому, если бы соотношений не было, то А4 было бы четы-
рехмерно, а оно — двумерно. Поэтому пространство соотношений в этой размер-
ности двумерно. В качестве базиса можно взять соотношения, выражающие Sq2e2
и Sq2Sq1aj через Sq3aj. Такие соотношения мы и определяем, пользуясь формула-
ми Адема: Sq2e2 = Sq3ei, Sq2Sq1e1 = 0.
Дальнейшее вычисление гомологий алгебры Стинрода лучше всего производить
при помощи ЭВМ. Мы не пользовались здесь ЭВМ, но все же произвели выбор обра-
зующих с полным перечислением соотношений до размерности 12. См. таблицу 1.
Впрочем, сам по себе выбор образующих может быть произведен и без вычисле-
ний. Ясно, что таковыми являются Sq2 . Поэтому фактически смысл этой работы
состоит именно в перечислении соотношений. Свободный A-модуль В2 имеет столь-
ко же образующих, сколько А = Ker -> Z2 )], т.е. натянут на образующие
«1. «г, аз> • • размерностей 1, 2, 4, 8,. . . Отображение В2 * Вх = А переводит об-
,fc-l
разующую ак в Sq2 и, где и - образующая В2. Ядро этого эпиморфизма изо-
морфно A-модулю соотношений между образующими aj, а2, а3,. . . A-модуля А .
Аддитивные образующие этого модуля соотношений перечислены в правой колон-
ке таблицы 1.
302
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Таблица 1
Номер клетки Образующие Соотношения
1 а. -
2 “а Sq’a, = 0
3 Sq’a,,Sq’a, -
4 а,, Sq’a, Sq’a, = Sq’a,, Sq’Sq’a, = 0
5 Sq’a,, Sq’a, Sq’Sq’a, =0, Sq’a, =0, Sq’Sq’a, = Sq'a3+Sq4a,
6 Sq’a,, Sq’a, , Sq’a3 Sq’Sq’a, =0, Sq’a, = Sq’Sq’a,
7 Sq’a,, Sq’a, Sq’Sq’a,, Sq’a, Sq’Sq’a, = 0, Sq’a, = Sq’Sq’a, , Sq’Sq’a, = Sq’a,
8 “4> Sq’a,,Sq’a,,Sq’Sq’a, Sq’Sq’a, = 0, Sq4Sq’Sq'a, =0, Sq’Sq’a, = Sq’Sq’a,, Sq’a, = Sq’Sq’a3, Sq’Sq’a, = 0, Sq’a3 = Sq’a, + + Sq8 a,
9 Sq’a,,Sq’a,,Sq7a, , Sq6 Sq1 a,, Sq’Sq’a, Sq7 Sq’a, = 0, Sq’Sq’Sq’a, = 0, Sq’Sq’a, = 0, Sq’a3 = = Sq’a,, Sq’Sq’Sq’a, + Sq’Sq’a, + Sq’Sq’a, =0, Sq’Sq’a, = Sq’a, + Sq*a, + Sq’a,
10 Sq’a,,Sq’a3,Sq7Sq'a2, Sq’Sq’a,,Sq’Sq’a,, Sq’Sq’a, Sq’Sq’a, =0, Sq’Sq’Sq’a, = 0, Sq’Sq’a, = Sq’Sq’a,, Sq’Sq’a, = Sq’a,, Sq’Sq’Sq’a, = Sq’Sq’a, + Sq’a,, Sq‘a, =Sq’Sq’a,, Sq’a, + Sq’Sq’a, + Sq’a, + + Sq’Sq’a, = 0
11 Sq1“a,,Sq’a,,Sq* Sq’a,, Sq’Sq’a,, Sq’a, Sq’Sq’a, =0, Sq’Sq’Sq’a, =0, Sq’Sq’Sq’a, =0, Sq’Sq’a, =0, Sq’Sq’a, = Sq’Sq’a,, Sq’Sq’Sq’a, + + Sq’a, + Sq’Sq’a, + Sq’Sq’a, = 0, Sq’a, + Sq’Sq’a, + + Sq’Sq’a, =0, Sq’Sq’a, = Sq’a, + Sq’a,, Sq’Sq’a, = = Sq’“a,, Sq’Sq’Sq’a, + Sq’“a, + Sq’Sq’a, = 0, Sq’a3 = 0
12 Sq1 ‘a,, Sq"’a, Sq’Sq’a,, Sq’Sq’a,, Sq’ Sq1 a,, Sq*a3, Sq4a4 Sq‘°Sq’a, =0, Sq’Sq’Sq’a, =0, Sq’Sq’Sq’a, =0, Sq’Sq’a, = 0, Sq’Sq’a, = Sq’Sq’a, , Sq’Sq’Sq’a, = = Sq’Sq’a,, Sq’Sq’Sq’a, = Sq’Sq’a, + Sq*Sq’a,, Sq’Sq‘a3 = Sq’Sq’a, , Sq8Sq’a3 = Sq”a, + Sq’Sq’a, + + Sq’°a, + Sq’Sq’a, + Sq’Sq’a,, Sq’Sq’Sq’a, + + Sq* ’ a, + Sq’ Sq’ a, = 0, Sq’ Sq' a, = Sq’1 a,
§ 35. ВЫЧИСЛЕНИЕ СТАБИЛЬНЫХ ГОМОТОПИЧЕСКИХ ГРУПП СФЕР
303
Поэтому наша следующая задача состоит в выборе минимальной системы А-обра-
эующих в этом модуле соотношений.
Первый нетривиальный элемент в этом модуле имеет размерность 2. Это соотно-
шение Sq’fli = 0. Обозначим это соотношение (или этот элемент ядра гомоморфизма
Bi ->H*(S°; Z2)) через bi. В размерности 3 соотношений нет. А чему же равно Sq1 bi 1
Применяя к соотношению Sq'tfj = 0 операцию Sq1, приходим к тождественному
соотношению 0=0 (элемент Sq1 Sq1 равен нулю в А). Соотношение 0 = 0- это
нулевой элемент в модуле соотношений. Поэтому Sq1 £>, = 0. Далее, в размерности 4
стоят два соотношения. Одно из них — это Sq2 bi, другое, очевидно, через bi не вы-
ражается. Это ясно, во-первых, потому, что кроме Sq2 нет операций, повышающих
размерность на 2, а во-вторых потому, что в это соотношение входит д2, и оно ни-
как не может получиться из Ь^, в которое д2 не входит. Итак, в размерности 4 наше-
го A-модуля стоит элемент Sq2 bi и новая образующая Ь2. До размерности 12 этот
A-модуль имеет шесть образующих. Они перечислены в таблице 2.
Таблица 2
Номер клетки Образующие Соотношения
2 0, -
3 - Sq’ft, =0
4 02, Sq’ft, -
5 03, Sq’ft,, Sq1 ft, Sq’Sq1/?, =0
6 Sq4ft,,Sq*ft, Sq’ft, = Sq’ft, + Sq’ft,, Sq’Sq1/?, =0
7 Sq5/?,, Sq’ft,, Sq’ Sq’ft, Sq’Sq’ft, =0, Sq3/?, = Sq5/?,
8 0,, Sq’ft,, Sq’Sq’ft,, Sq4/?,, Sq’Sq*/?,, Sq’ft, Sq’Sq1 ft, =0, Sq’Sq1 ft, = Sq’Sq* ft, + Sq’ft,
9 05, Sq7/?,, Sq’Sq’ft,, Sq5/?,, Sq4ft,,Sq*ft4 Sq’Sq1/?, =0, Sq’Sq’Sq*/?, =0, Sq’ft, =Sq4Sq*ft2, Sq7/?, = Sq’Sq’ft,
10 0,, Sq’ft,, Sq’Sq’ft,, Sq’ft,, Sq’ft, , Sq’/?,, Sq’Sq’ft, Sq’Sq1/?, =0, Sq’Sq’ft, =0, Sq’Sq1/?, =0, Sq*fts = = Sq’ft, + Sq’Sq1/?, + Sq’ft,, Sq’Sq’ft, + Sq4Sq’ft, + + Sq’Sq’ft, =0
11 Sq’ft,, Sq’Sq’ft,, Sq’Sq3/?,, Sq’ft,, Sq’ Sq*ft,, Sq4Sq’Sq*ft Sq’Sq’ft,, Sq’Sq*ft„ ,Sq3 ft„ , Sq106 Sq’Sq’ft, = 0, Sq’Sq’Sq’ft, =0, Sq’Sq’ft, = Sq’ft, + + Sq’Sq’ft,, Sq’ft,+Sq’Sq’Sq’ft,+Sq’ft, +Sq’Sq*ft4 = = 0, Sq’Sq* ft, = Sq’ft,
12 Sq’ft,,Sq’Sq*ft, , Sq3ft,, Sq’Sq’ft,, Sq5Sq’Sq1 /3,, Sq7/33 , Sq5 Sq’ft3 , Sq4ft4 , Sq’“ft,, Sq’Sq’/?,, Sq’Sq3 ft. Sq’Sq’Sq* ft, = Sq4 Sq’ Sq* ft, + Sq*’ft, + Sq’Sq’ft,, Sq’Sq*/?, = Sq’Sq’ft, + Sq’Sq3/?,, Sq’Sq*/?, =0, Sq’Sq1/?, = Sq’ft, + Sq5 Sq2 Sq* ft, , Sq’Sq1 ft, = Sq10ft,, Sq’ Sq’ Sq* ft, = 0, Sq’ Sq3 Sq* ft, = 0, Sq’ ft, + Sq’ Sq’ Sq* ft, + + Sq’ft4 + Sq’ft, + Sq’ft, + Sq’ft, = 0
304
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Далее, свободный А-модуль В3 натянут на образующие 01,02,..., которые соот-
ветствуют выбранным образующим в Кег(Д2 -* Bi). Размерности элементов 01,02,
0з, 04,0$, 06 равны соответственно 2,4,5,8,9,10.
ГомоморфизмВ3 ->В2 действует так:
01 •* Sq*«i,
02 * Sq2a2 + Sq3at,
0э •* Sq2Sq‘a2 + Sqla3 + Sq4oti,
04 •* Sq4a3 + Sq7a! + Sq6a2, ,
0s •* Sq4Sq‘a3 + Sq‘a4 + Sq8ai + Sq7a2,
06 •* Sq2a4 + Sq4Sq2a3 + Sq8a2 + Sq7Sq2a1;
Ядро этого гомоморфизма — зто А-модуль, изоморфный A-модулю соотношений
в A-модуле соотношений в А. Аддитивные образующие этого модуля перечислены
в правой колонке таблицы 3. Выбираем минимальную систему образующих в этом
модуле. До размерности 12 эта система имеет пять образующих (перечислены в таб-
лице 3) в размерностях 3, 6, 10, 11, 12. Образующие свободного A-модуля 54 на-
ходятся с ними во взаимно однозначном соответствии. Обозначим их у], у2, у3, ...
Гомоморфизм В 4 -+Вз действует так:
71 -* Sq‘0i,
7з - Sq202 + Sq,03 + Sq402,
7з * Sq‘05 + Sqs03 + Sq80, + Sq4Sq*03,
74 •* Sqe03 + (Sq4Sq2Sq‘ +Sq7)02 + Sq2Sq104,
7s - Sq206 + Sq305 + Sq404 + Sq703 + (Sq8 + Sq5 Sq2 Sq1 )02,
Таблица 3
Номер клетки Образующие Соотношения
3 7i
4 - Sq17i =0
5 Sq2?, —
6 7г, Sq’?! Sq2Sq*7i =0
7 Sq47i,Sql73 Sq3Sq*7i =0
8 Sqs7i,SqJ72 Sq4Sq*7i =0
9 Sq4 7i, Sq4 Sq’ 7,, Sq3 73, Sq2 Sq173 SqsSq171 = 0
10 73, Sq’7i, Sqs Sq37,, Sq47j , Sq3Sq17, Sq4Sq'7, =0,Sq4Sq2Sq17i =0
11 74, Sq37i, Sq4Sq27>, Sqs72, Sq17S Sq’Sq‘7, = 0, SqsSq2Sq,71 =0, Sq4Sq'75 +Sqs7, + Sq*7, +Sq‘73 =0
12 7s > Sq’ 7i, Sq’Sq371, Sq4Sq37l, Sq4 73, Sq4 Sq2 7,, Sq2 73, Sq17< Sq’Sq‘7, = 0,Sq’Sq‘7, = Sq97,, Sq4 Sq’Sq‘7, =0
§ 35. ВЫЧИСЛЕНИЕ СТАБИЛЬНЫХ ГОМОТОПИЧЕСКИХ ГРУПП СФЕР
305
Таблица 4
Номер Образующие Соотношения
4 -
5 - Sq’6, = 0
6 Sq26, -
7 Sq’6, Sq’Sq’6, =0
8 Sq46, Sq’Sq’a, = 0
9 Sq’8, Sq4Sq’6, =0
10 Sq‘8,, Sq4Sq’6, Sq’Sq’a, =0
11 6,, Sq78,,Sq’Sq’S, Sq‘Sq’6, = 0, Sq4Sq’Sq*8, =0
12 Sq’Sj, Sq’S,, Sq‘Sq’8, Sq’Sq’8, =0, Sq’Sq’Sq’a, =0
Аналогично определяем, что свободный А-модуль55 имеет до размерности 12 две
образующие 81,82 в размерностях 4 и 11, и гомоморфизм 55 +В 4 действует так:
81 •* Sq1?!,
82 (Sq4Sq* + Sqs *)?2 + Sq8?i + Sq1-^,
Свободные А-модули B6, В1г... ,В^з имеют до размерности 12 по одной образую-
щей соответственно в размерностях 5, 6....12 и при гомоморфизмах H5k_t
каждая из этих образующих переходит в Sq1 от предыдущей.
Как мы видели, ExtX’*(Z2, Z2) = Ношд(В,_1, Z2), и, таким образом, аддитив-
ные образующие гомологий Я1’1 (А) алгебры Стинрода при Г < 12 мы можем пол-
ностью перечислить. Иначе говоря, нам известна аддитивная структура второго члена
спектральной последовательности Адамса при t <12 (рис. 156).
Теперь уместно сделать следующее общее наблюдение. Очевидно, минимальная
размерность соотношения в A-модуле Кег(Як -+Bk-i) по крайней мере на единицу
больше минимальной размерности образующей этого модуля. Отсюда следует, что
минимальная размерность образующей модуля Вк больше (по крайней мере на еди-
ницу) минимальной размерности образующей модуля Вк_г. Однако в применении
к нашей спектральной последовательности это наблюдение не дает ровным счетом
ничего. Очевидно и без него, что модуль Вк имеет (к - 1)-мерную образующую и не
имеет образующих меньших размерностей. Поэтому мы не можем гарантировать,
что сколь угодно высоко не появятся ненулевые элементы даже на диагонали t — s =
= 1. Большая информация получается при рассмотрении спектральной последователь-
ности Адамса для первого убивающего пространства 5" |п+1 (в серровском смысле)
n-мерной сферы. A-модуль его когомологий может быть найден иэ расслоения
Sn --------> K(Z, л). Это - часть модуля Z2) размерности >п. Нам
известно, что (со сдвигом размерностей) этот A-модуль равен А, профакторизован-
ному по левому идеалу, порожденному элементом Sq1. Таким образом, нулевая
строка спектральной последовательности Адамса для S" |и+1 такая же, как первая
строка спектральной последовательности для S°, только выкинута образующая at
306
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
и сдвинуты размерности. Легко показать, что и выше спектральные последователь-
ности для 5° и 5" („-и будут отличаться только на сдвиг размерностей (на 1 вверх
и на л — 1 влево) и на элементы, стоящие в спектральной последовательности для S0
на биссектрисе координатного угла. В частности, в исследованных нами размерностях
член Е2 будет выглядеть так, как показано на рис. 157.
Мы оставляем доказательство этой теоремы читателю. Впрочем, ее можно не до-
казывать, а убедиться в ее справедливости прямым вычислением Ext^*(A/ {Sq1} ,
Z2), которое даже проще, чем вычисление Ext^*(Z2, Z2).
Применим к этой спектральной последовательности наше наблюдение относитель-
но минимальной размерности образующей в модуле Вк. Мы получим, что в спект-
ральной последовательности Адамса для «5° размерность второй по порядку обра-
зующей также увеличивается монотонно с ростом к, т.е. число пустых ячеек правее
биссектрисы в s-й строке не убывает с ростом s. Учитывая это обстоятельство, мы по-
лучаем, что при t — s < 7 во втором члене нашей спектральной последовательности
элементов нет. Это дает нам возможность высказать некоторое утверждение о поряд-
ках 2-компонент стабильных гомотопических групп сферы. В самом деле, из сооб-
ражений размерности видно, что в рассматриваемой области может быть два нетри-
виальных дифференциала: во-первых, а2 может уничтожиться любым дифференциа-
лом, во-вторых, 06 может перейти в 62 при дифференциале d2. Первого, во всяком
случае, не происходит, так как если бы а2 уничтожилось, то 2-компонента тг„+1(5")
равнялась бы нулю, в то время, как мы знаем, что лп+1(5п) = Z2. Вопрос о том,
чему равно d2j36, мы отложим до выяснения мультипликативной структуры. Но
§ 35. ВЫЧИСЛЕНИЕ СТАБИЛЬНЫХ ГОМОТОПИЧЕСКИХ ГРУПП СФЕР
307
уже сейчас ясно, что порядки 2-компонент групп nn+k(Sn) при к = 1, 2, 3, 4, 5, 6, 7
равны соответственно 2,2,8, 1,1,2,8 или 16.
2. Мультипликативная структура . Ясно, что из резольвенты Z2 *- Bt *-52 ..
можно получить резольвенту любого модуля Кег(5Л ->5fc_j), оборвав ее в соответ-
ствующем месте. Поэтому и Ext^’f(Ker(Bfc -* Z2) = Ext^+k,f(Z2, Z2) и
действие Hs,t (А) на обоих Ext’ax одинаково.
Предположим, что мы хотим составить ’’таблицу умножения” на некоторьш эле-
мент, например на at G А = Кет(5, ->Z2). Рассмотрим А-гомоморфизм A -»Z2,
переводящий а! в образующую. Этот гомоморфизм понижает степени на 1. Легко
понять, что определенный им гомоморфизм Ext^*(Z2, Z2) в Ext^‘(A, Z2), наобо-
рот, повышает степени на 1. Таким образом, имеем гомоморфизм Ext^ r(Z2,Z2) ->
->Ех1д’,+ 1(А, Z2) = Ext^+1, f+1(Z2, Z2). При этом гомоморфизме элемент 1 перей-
дет в элемент cq и любой элемент £ — в элемент £cq.
Чтобы определить интересующий нас гомоморфизм Ext’oB, мы должны построить
соответствующее отображение резольвент, т.е. коммутативную диаграмму:
д, Э. Э3 д.
Zi—Bt ^-в2 В3^- ...
/,t М М М
в которой верхняя строка представляет собой изученную нами резольвенту модуля
Z2, нижняя — эту же самую резольвенту, оборванную таким образом, чтобы она была
резольвентой модуля А; гомоморфизм — отображение, переводящее at в 1 G Z2.
Остальные гомоморфизмы мы должны определить таким образом, чтобы они пони-
жали размерность на единицу каждый и чтобы вся диаграмма была коммута-
тивна. Поскольку В2,В3, В4 , ... — это свободные A-модули, то для задания
интересующих нас гомоморфизмов достаточно указать, куда переходят их
образующие.
Начнем с В2. Это — свободный А-модуль с образующими cq, cq, а3, . . . Элемент
cq при гомоморфизме Э2 переходит в at. Последний переходит в 1 G Z2 при гомо-
морфизме f!. Поэтому гомоморфизм f2 должен переводить cq в такой элемент В2,
который переходит в 1 6 Z2 при гомоморфизме dj. Но В\ есть просто алгебра Стин-
рода, и в единицу переходит ее образующая и. Поэтому мы должны положить/2(cq ) =
= и. Остальные образующие В2, а именно а2, а3, . . . при сквозном гомоморфизме
д. ~ Л
В2----> А ---> Z2 переходят в 0 G Z2. Поэтому мы можем положить/"2(ак) = 0 при
к > 2. Отметим, что гомоморфизм, который мы строим, определен неоднозначно.
В частности, мы могли бы выбрать в качестве образа ак любой элемент соответ-
ствующей размерности. Мы строим гомоморфизм наиболее простым образом, забо-
тясь о коммутативности диаграммы.
Итак,/"2(cq) = и, f2(ak) = 0 при к > 2. Теперь определим гомоморфизм [з'.В3 -»
d3 fi
-+В2. При сквозном отображении В3---*В2-----*Bi элемент /32 переходит в элемент
Sq'u. Выбираем в В2 любой прообраз этого элемента при гомоморфизме Э2: В2 ->•
-»Bi - Таковым является, например, eq. Полагаем f3(Pt) - cq. Образующая /32 пере-
ходит при сквозном гомоморфизме В3 -*-В2 -*Bi в элемент Sq3n и в этот же элемент
переходит Sq1 cq при гомоморфизме Э2: В2 -*В2. Полагаем/3(Д2) = Sqlcq.
308
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Продолжая это построение, мы приходим к тому, что гомоморфизмы fk: Вк ->
_ 1 в изученной нами области действуют так:
/г: В2 "’’Bi f3: В3 -+В2 fi- B4 -+B3 fs 'Bs ->B4
tti и 01 >-*ai 71 ^01 81 H>7i
a2 н-0 0г '->Sq1a2 T2 н’0з 82 *-*7з
03 Н + SQ*04
04 н- Sq3a3 74 |->Sq204 +Sq*05
05 «4
06 -» Sq7a2 .......................
Осталось рассмотреть индуцированные гомоморфизмы Нот’ов и Ext’oe. Образую-
щие векторного пространства HomA(Bk, Z2) находятся во взаимно однозначном со-
ответствии с образующими A-модуля Вк. Мы их даже обозначали одинаковыми бук-
вами. Ясно, что элемент из HomA(Bfc_i, Z2), соответствующий некоторой образую-
щей A-модуля Вк_ 1, при гомоморфизме
HomA(fifc_ 1, Z2 ) HomA(5k, Z2)
переходит в ноль, если эта образующая не принадлежит образу гомоморфизма Вк -*
-+Вк_г. Если же эта образующая является образом некоторой образующей А-модуля
Вк, то переходит в элемент HomA(Bfc, Z2), соответствующий этой образующей.
Отсюда получаем, что известные нам образующие ExtA*(Z2, Z2) преобразуются на-
шим гомоморфизмом ExtA*(Z2, Z2) -*ExtA*(Z2, Z2) следующим образом:
1 Н-0Ц di >->0i 0i H-7, 7i >->8i
a2 >->0 02 н-0 72 h-0
a3 н>0з 03 h>72 7з h-82
<*4 ^05 04 h-0 74 «-0
05 н>7з 7s h-0
06
откуда aid! = 02, aia2 =0,aia3 =03,aiO4 = 0s,«i0i = 7i,ai02 = O,ai03 = 72>ai04 =
= O,ai0s =73>ai06 = 0,ai7i = 8i,ai72 =0,a1y3 = 82,ai74 =0,ai7s =0.
Аналогично получаем, что a2a2 = ft, a2a4 = 06, otifa = y2, a206 = ys, a3a3 = 04,
a304 = Ts и остальные произведения известных нам элементов равны нулю.
Обычно для элементов групп гомологий алгебры Стинрода используются стан-
дартные обозначения. А именно, элементы at, a2, а3, . . . обозначаются соответ-
ственно через Л©, Ль й2 , ... С этими обозначениями известная (нам) часть второго
члена спектральной последовательности Адамса выглядит так, как показано на
рис. 158. Здесь а — новая мультипликативная образующая. Кстати, теперь ясно, что
^2 06 =^201 й3) = 0, откуда порядок 2-компоненты группы тгл+7(1У") равен 16.
Мы видим, что задача вычисления гомотопических групп сфер разделилась на две
части: вычисление гомологий алгебры Стинрода и вычисление дифференциалов спект-
ральной последовательности Адамса. Первая сводится к чисто механической работе, ко-
торую, очевидно, можно продолжить как угодно далеко. В книге Адамса ’’Стабильная
гомотопическая теория” (Leet. Notes in Math. — 1966. — V.3) результат такого вычис-
ления приводится для t — s <17. Диаграмма для члена £2, заимствованная из этой
§ 35. ВЫЧИСЛЕНИЕ СТАБИЛЬНЫХ ГОМОТОПИЧЕСКИХ ГРУПП СФЕР
309
Рис. 158
dh*~ch*
(*)—дда элемента: и fy в
Нетривиальные дифференциалы: h^~hgh^, hghj—hge, hghtp-*-hge
Рис. 159
книги, показана на рис. 159. Конечно, получение такой диаграммы принципиальных
затруднений не встречает, и мы можем рассматривать ее как доказанную. Для состав-
ления такой диаграммы нужно исследовать алгебру Стинрода не до размерности 12,
как мы это сделали, а до размерности 27. Тогда мы получим, в частности, что Е'г'* =
= 0 при 10 < t < 27 и, следовательно, при 0 < t — s < 17 никаких других элементов,
кроме перечисленных, в Ег нет.
Дифференциалы от мультипликативных образующих й0> Л1, й2, Л3> а, b, с, d, е,
f, i, j равны нулю по соображениям размерности. Поэтому при t - <<13 имеет место
равенство Ег’* = EL’*, и мы можем извлечь следующую информацию о гомотопи-
ческих группах сфер.
310
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Порядки 2-компонент первых тринадцати стабильных групп таковы: 2, 2, 8, 1,
1, 2, 16, 4, 8.2, 8,1,1. Элементы 1, h0, ho, ho,... являются образующими группы
Z2 ® Z2 ® Z2 ® . . . , присоединенной к группе Яо(5°) Z. Ясно, что фильтрация в
группе Z такова: Z D 2Z D 4Z D 8Z D . . . Поэтому элемент является образую-
щей группы 2*Z/2fc+1 Z и представляется элементом 2* G Z с точностью до элементов
высшей фильтрации.
Элемент й2 G Е I’4 является образующей факторгруппы я3 (S0) по некоторой
подгруппе. Выбираем представитель a G Яэ(5°), Так как произведения h0h2 и
hoh2 отличны от нуля, то композиция элемента а с элементами 2 и 4 G я§ (S0) не три-
виальна, т.е. 4а 0(mod2), т.е. а имеет порядок по крайней мере 8. Но 2-компонента
Яз(5°) равна Z8 и 2-компонента it2(S°) равна Z16. В группе, присоединенной к
7^(5°), две образующие (hth3 и а). Произведение hohih3 равняется нулю группы
Е^,’11. Поэтому композиция элемента 2 € я^(5°) и представителя элемента hxh3
имеет фильтрацию > 3. Но таких элементов, как видно из нашей спектральной после-
довательности, в группе я8 (S0) вообще нет. Поэтому 2-компонента этой группы рав-
на Z2 ® Z2. Наконец, я9(|У°) имеет 2-компоненту восьмого порядка. Применяя к
этой группе то же рассуждение, какое мы использовали для я8(5°), мы получаем,
что эта группа не может равняться Z8. Она либо равна Z2 ®Z2 ®Z2, либо равна Z4 ®
® Z2. Во втором случае образующая группы Z4 имеет своим представителем в Е„
элемент h3 = h]h3. Следовательно, сама эта образующая (с точностью до элементов
высшей фильтрации, т.е. порядка 2) является композицией а о а о а, где а — обра-
зующая я3 (S0). Но эта композиция имеет порядок 2, так как уже композиция
а о а имеет порядок 2, будучи элементом группы 2-компонента ко-
торой есть Z 2.
Итак, 2-компоненты групп я„ (5°) при л < 13 нам известны:
Z2, Z2, Z8, о, о, z2, Z j g, Z2 ® Z2, Z2 ® Z2 ® Z2, Z 2, Z8, 0, 0.
Если обозначить образующую я^(5°) через р, то образующей группы я2(№)
является т?2. Элемент т?3 равен 4а, где а - образующая Яз(5°). Группа я‘б(5°)
порождается элементом а2. Элементы из я?(5°) в композицию не разлагаются. Об-
разующую этой группы обозначим через 0. Группа я8(5°) порождена элементами
т?/3 и неразложимой образующей у. Группа я9(5°) порождается элементом а3 =
= т?2 /3 и еще двумя образующими, из которых одна заведомо неразложима,
а другая, возможно, равна riy. Группа я,0(№) порождается произведением
одной из этих образующих на р, группа я$ j (S°) порождается неразложимым:
элементом.
Вся эта информация также содержится в полученном результате о спектральной
последовательности.
3. Нечетные компоненты. В рассматриваемом нами диапазоне размерностей един-
ственная трудность содержится в случае р = 3, в котором требуется рассматривать
спектральную последовательность Адамса. Напомним, что первая нетривиальная
p-компонента находится в группе Я2Р_з(5°), вторая — в группе я4р_5(5°) и обе
они равны Zp. Поэтому кроме компоненты Zs Ся7(5°) и Z7 Ся?1(5°) других р-
компонент дляр > 3 группы я^ (5°) при л <13 не имеют.
3-компоненты этих групп таковы:
0, 0, Z3,0, 0, 0, Z3, 0, 0, Z3, Z9, 0, Z3.
§ J5. ВЫЧИСЛЕНИЕ СТАБИЛЬНЫХ ГОМОТОПИЧЕСКИХ ГРУПП СФЕР
311
Композиционное умножение в этих группах тривиально по соображениям размер-
ности. Итак:
*„(5") = Z, И>1,
Trn+1(S") = Z2, и>3,
7Гп + 2(5") = Z2, и >4,
7Гп + з(5") = Z24, и > 5,
*„+4(5") = 0, И > 6,
7r„+s(S") = 0, и>7,
яп+б(5") = Z2, и >8,
ял+7(5") = Z240, и>9,
я„+8(5") = Z2 ф Z2, и >10,
7Ги+9(‘^И) ~ Z2 ® Z2 ф Z2 , п> 11,
7rH + lo(‘S") = Ze, и >12,
^H + l 1(5") = ZS04, и > 13,
тги+12(5") = 0, и > 14,
’’’h + I з(5") = Z3, и > 15.
Вычисление 14-й и дальнейших групп гомотопий наталкивается на трудность:
соображения размерности не обеспечивают более тривиальность дифференциалов.
И действительно, нетривиальный дифференциал появляется при первой же возмож-
ности. Оказывается, что (Й4) = ЛоЛз.^з(ЛоЙ4) =Ло1>^з(ЛоЙ4) =Ло1 •
4. Теоремы Адамса о начальном члене его спектральной последовательности.
’’Нами показано, что гомологическая алгебра может применяться к стабильной го-
мотопической теории. В этом применении мы имеем дело с A-модулями, где А есть
алгебра Стинрода modp. Чтобы получить этим методом конкретные геометрические
результаты, мы должны проделать работу двух совершенно различных сортов. В
качестве иллюстрации рассмотрим спектральную последовательность
Ext£f(#*(r; Zp), Н*(Х- Zp)), => ртг?( X, У).
Здесь каждая группа Exti,f, входящая в член Е2, может быть эффективно най-
дена; процедура вычисления — чисто алгебраическая. Однако столь же эффективных
методов для вычисления дифференциалов dr спектральной последовательности или
для определения характера присоединенности члена Е«> к pir»(X, У) не существует;
это — топологические проблемы.
Математический логик может быть удовлетворен этой ситуацией: имеется алго-
ритм для вычисления Е2, а нахождение отображений dr требует изобретения новых
методов. Практический математик, однако, вынужден признать, что имеется не
меньше, а больше оснований полагаться на изобретательность математиков, чем на их
готовность произвести большое количество скучной механической работы. (Это
писалось в до-ЭВМ’ную эпоху. — А.Ф и Д.Ф.) Действительно, всякая возможность
установить нетривиальность дифференциала dr воспринимается как интересная за-
дача, которая рано или поздно решается. Однако трудности в вычислении групп
Ext дf (L, М) остаются главным препятствием к применению метода”.
Как видно из этого отрывка, заимствованного иэ предисловия к статье Адамса
”0 периодичности в гомологической алгебре”, ее автор не считает, что наличие алго-
ритма для вычисления гомологий алгебры Стинрода равнозначно их вычислению.
312
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Адамс посвятил.этому вопросу ряд работ. Приводим наиболее важные его резуль-
таты.
Теорема о трех первых строчках. (Adams J.//Ann. Math. — 1960. —
V. 72, № 1. — Р. 20—104; русский перевод: Математика: сб. перев. — Т. 5, № 4. -
С. 3-86.)
(1) Группа Е2 = Ег ’* аддитивно порождается линейно независимыми элемента-
ми ht размерностей 21.
(2) Группа Ег = ®r£’2,f аддитивно порождается линейно независимыми элемента-
ми hj ht при j > i > 0,j =#= i + 1. Произведения hi+l hi равняются нулю при всех i.
п пМ
Рис. 160
(3) В группе Ег - имеют место соотношения-. hi+2 hf = й’+1, й?+2 hf = 0.
Если вычеркнуть из совокупности произведений hk hj hit где k > j > i > 0, произ-
ведения вида hj+l hj hit hkhi+l ht, hi+2 hf, h2+2 ht, то оставшиеся элементы будут
линейно незвависимы в Е2.
Заметим, что эта теорема не дает полной структуры третьей строки Е2 Там могут
быть и элементы, вообще не выражающиеся через hit и мы уже имеем один такой
пример: таковым является элемент a G Е2 ’11.
Теорема о тривиальности. (Adams J. A periodicity theorem in homo-
logical algebra//Proc. Camb. Phil. Soc. - 1966. — V. 61.) Имеют место равенства:
E2'f = 0 при s<t< f(s), где
f(4n) = 12и - 1, и >0,
/(4и + 1)= 12и + 2, и>0,
/(4и + 2) = 12и + 4, и>0,
/(4и + 3)= 12и + 6, и>0.
При этом группаЕг’?^ действительно нетривиальна.
• На рис. 159 мы указали область, в которой по теореме Адамса стоят нули.
Теорема, периодичности. (Там же.) Для каждого к существует окрест-
ность Nk прямой t = 3s, в которой группы E2,f периодичны с периодом 2k+2 по s
и 3 • 2к+2 по t. Объединение этих окрестностей составляет область s< t<g(s),
edeg(s) —некоторая функция, про которую известно, что 4s<g(s) <6s.
5. Заключение. Мы приведем один пример спектральной последовательности
Адамса, в которой будет очевидна нетривиальность некоторого дифференциала.
Обозначим через X пространство X(Z4, и), где и достаточно велико. Стабиль-
ные гомотопические группы этого пространства до размерности 2и таковы:
=Z4,irf (X) = 0 при i =#= п. Алгебра Н* (Х-, Z2) в размерностях до « 2и изо-
морфна Н* (Л7 (Z, и); Z2) ® H*(K(Z, п + 1); Z2), т.е. имеет две образующие: аб
6 Нп (X; Z2), 0 G Hn+l (X; Z2), причем Sq1 а = Sq10=0. Отсюда видно, что в Е2
спектральной последовательности Адамса для этого пространства есть две полностью
занятые нетривиальными группами диагонали (рис. 160). Ясно, что d20 = айо, так
как иначе порядок группы тг„ (X) не мог бы равняться четырем.
§ 36. ЧАСТИЧНЫЕ ОПЕРАЦИИ
313
§ 36. ЧАСТИЧНЫЕ ОПЕРАЦИИ
Излагая спектральную последовательность Адамса, мы обошлись без понятия
частичной операции. Даже само название не было нами упомянуто, хотя, возможно,
его стоило упомянуть в параграфе ’’Общая идея”. Все же есть все основания счи-
тать, что понятие частичной операции составляет основу адамсовского метода.
1. Построение частных операций. Пусть
Z 3/0, = О (*)
i= 1
— соотношение в алгебре Стинрода Ар, где а,-, 0,- — стабильные операции степеней,
соответственно, qt, и - q,. При любом N каждая операция а,- определяет, с точностью
до гомотопии, отображение
at: K(Zp,N)-*K(Zp,N + qt),
а все эти операции вместе — отображение
a,: K(Zp,N)^nK(Zp,N + qt).
I
Рассмотрим индуцированное расслоение
Е---------►*
nA(Zp^+qz-l) । । nX(Zp^+41.-l)
X(Zp,7V)“ nK(Zp,N + qi).
Спектральная последовательность этого расслоения изображена на рис. 161. Мы ви-
дим, что элемент S/0/ц,- остается в Ет и определяет, ввиду этого, в группе
ffN+n-i 2р) смежный класс относительно подгруппы Im [HN+n~1 (K(Zp, TV);
Zp)-*^"-1^; Zp)].
Выберем в этом классе любой элемент и обозначим его через и. Из определения
видно, что образ элемента v при гомоморфизме
HN+n~l (E,Zp)^HN*n~l (UK(Zp,N+qt- l);Zp)
есть S/ Uj. Элемент и G HN (К (Zp, N); Zp) также остается в Ет и однозначно оп-
ределяет элемент в группе HN (Е\ Zp). Последний мы снова обозначим через и.
314
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Для любого пространства X мы определим (естественный по X) гомоморфизм
П Ker[az: HN (X-,ZP)-+HN+qi(X-,ZP)] -*
i= 1
HN+n-l(X;Zp)
----------------------—---------------- .
f
+ Im [ft: HN*qi-1 (X\Zp) ->HN+n~l (X;Zp)]
это и есть вторичная операция.
Пусть £ G HN (Х\ Zp), и пусть at (%) =0 при i = 1, 2,..., m. Рассмотрим отобра-
жение £ : X -> X(Zp, Л) соответствующее элементу £. Его композиция с отображе-
нием а гомотопически тривиальна, и потому расслоение, индуцированное над X
расслоением Е -*• К(Zp, N), тривиально (оно совпадает с расслоением, индуцирован-
ным расслоением » -*• IIK(Zp, N + qt) при отображении а ° £ ) Следовательно, оно
допускает сечение:
Е~Х*ПК (Zp ,N+4t -1)
Композиция этого сечения с верхним горизонтальным отображением представляет
собой отображение т?: X -> Е, которое вместе с другими отображениями диаграммы
составляет коммутативный треугольник
Очевидно, ri*u = %. Примем за<р(^) (X; Zp) элемент ц*о. Этот элемент
определен неоднозначно, поскольку неоднозначно определено сечение, с помощью
которого строилось отображение т?.
С точностью до чего определено сечение? Его существование выводилось нами из
равенства Е1 = XX TlK(Zp, N + qt — 1). Само сечение задавалось формулой х *+
>-> (х, »). Любое другое сечение задается формулой х •-> (х, f (х)), где f: X *
->nK(Zp,7V + qt — 1) — произвольное непрерывное отображение.
Упражнение 1. При такой замене сечения элемент </>(£) заменяется элемен-
том </>($) + S ™ , ft f * (и,), где и, е HN*qi~1 {K{Zp,N + qt - 1); Zp) - фундамен-
тальные классы.
Из этого утверждения следует, что как элемент указанной факторгруппы элемент
((•) определен однозначно.
Итак, мы построили стабильную вторичную операцию >р. Она представляет собой
совокупность заданных для всех X и N частичных многозначных гомоморфизмов
HN (X; Zp)-----> jjN+n-1 . (Частичных потому, что они определены на пе-
ресечении ядер операций а,-; многозначных потому, что они определены с точностью
до образов операций ft.)
Заметим, что операция <р определяется соотношением (») с точностью до при-
бавления обычных (примарных) операций (эта неопределенность является прояв-
лением неоднозначной определенности класса v G (Е; Zp) — см. выше).
§ 36. ЧАСТИЧНЫЕ ОПЕРАЦИИ
315
Упражнение 2. Сформулируйте и докажите свойства вторичных операций,
в том числе их стабильность и естественность.
Пример вторичной операции мы уже знаем: ’’второй гомоморфизм Бокштейна”
(см. п. 4 § 15). Он строится по соотношению 00 = 0, и, в согласии с общей конструк-
цией, определен на тех элементах g G HN (X', Zp),для которых 0(g) = 0, и принимает
значения в факторгруппе по образу 0. Напомним его прямое построение. Пусть х —
коцикл, представляющий элемент g, х — целочисленная коцепь, проектирующаяся
в х Равенство 0(g) = 0 означает, что существует такая целочисленная коцепь у, что
1 ~ ~ _ 2 1
— 5х = 8у modp, т.е. 8(х - ру) = 0 modp . Коцикл — 8 (х - ру), приведен-
Р
ный по модулю р, и определяет элемент 02 (g) G HN+1 (2f; Zp).
Упражнение 3. Что представляют собой пространство Е и когомологический
класс и, соответствующие, в силу конструкции этого пункта, соотношению 00 = О?
Аналогично второму гомоморфизму Бокштейна строится ’’третий гомоморфизм
Бокштейна” (— 8(х - ру — р2у') j и так далее. Это — примеры третичных и т.д.
операций. Третичная операция определяется по соотношению 2 0; = 0, где —
вторичные, а 0,- — примарные операции. Читатель, которого все это интересует, может
построить теорию и-ичных операций для любого п.
Бели при этом не ограничиваться стабильными операциями и брать в качестве
области коэффициентов не Zp, а произвольную группу, то частичных операций будет
настолько много, что они полностью определяют гомотопический тип пространства.
Этой формулировке можно, по размышлении, придать точный смысл, но тогда она
сделается тавтологической. Более интересное утверждение в этом роде составляет
содержание п. 4 этого параграфа.
2. Частичные операции и второй дифференциал в спектральной последователь-
ности Адамса. Связь между дифференциалами спектральной последовательности
Адамса и частичными операциями мы не будем обсуждать в полном объеме. Огра-
ничимся простым замечанием. Преположим, что в спектральной последовательнос-
ти Адамса для некоторого пространства X имеются элементы уi 6 E2,f ,у2 G Е2,г
и г € £2+2,f+1 (рис. 162). Элементы yt и у2 — это образующие А-модуля
Рис. 162
Н* (X (s); Zp). Предположим, что у2 = 'Z’O'i), где у> — вторичная операция, построен-
ная по соотношению 2 0,- а, = 0 в алгебре Стинрода.
В силу определения вторичных операций, =0 при всех i. Это - соотношение
в A-модуле H*(X(s); Zp). Если применить к соотношению a, yi =0 операцию 0,
и все полученные соотношения сложить, то получится соотношение 0 = 0. Таким обра-
зом, имеется соотношение в модуле соотношений. Предположим, что это соотно-
шение является одной из образующих A-модуля соотношений в модуле//* (X(s); Zp)
и что эта образующая как раз есть z (по размерности это возможно).
316
ГЛ. 5. СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АДАМСА
Упражнение 4. Докажите, что в спектральной последовательности Адамса
d2y2 =z.
3. Частичные операции и гомотопические группы сфер. Гомологии алгебры Стин-
рода связаны с частичными операциями очевидным образом: первая строка — это
примарные операции, вторая — соотношения в алгебре Стинрода, т.е. вторичные опе-
рации, третья — соотношения между ними, т.е. третичные операции, и т.д. Каждый
элемент p-компоненты стабильной гомотопической группы сферы происходит из не-
которого элемента члена Е2 спектральной последовательности Адамса. Какова связь
между операциями и элементами гомотопических групп сфер?
Элемент а группы яЛГ+Л(5ЛГ) определяет отображение SN+k -+SN. Приклеим по
этому отображению к шар DN+k+1. Получается некоторое пространство Ха,
гомотопический тип которого зависит только от а и когомологии которого нетри-
виальны в размерностях N и N + к + 1.
Упражнение 5. Частичная операция, соответствующая элементу члена Е2
спектральной последовательности Адамса, который дает в Е^ элемент а, нетриви-
альна в Ха. [Указание: рассмотрите спектральные последовательности Адамса для
Ха и Sn и их отображение, соответствующее естественному вложению S" -*• Ха.]
Рассмотрим, например, элементы, стоящие в нижней строке: Sq2, Sq4, Sq8,... G
6 A2. Те из них, которые доживают до Ет, определяют элементы из тги+1(5"),
я„+з (S"), тги+7 (S, такие, что в соответствующих пространствах Sn U Dn+2,
Sn U Dn+4,Sn U Dn+8,.. . нетривиальны операции Sq2, Sq4, Sq8,...
Адамсом было показано, что ни один из элементов Л4> hs, h6,... не доживает
до Ет, т.е. от них имеются нетривиальные дифференциалы. Например, d2h4 =hoh2 =#=
=#= 0. Из этого следует, что пространство S" U Dn+q, в котором нетривиальным обра-
зом действует Sq4, существует только при q = 1, 2,4, 8. Как объяснялось в п. 4 § 30,
из этого вытекает, что группа я2п_1(<У") содержит элемент с нечетным инвариан-
том Хопфа только при и = 2, 4, 8. Как уже было обещано, мы докажем этот факт
в главе 6 средствами Х-теории.
4. Системы Постникова. Как нам известно, гомотопические группы пространства
не определяют полностью его гомотопический тип. Исключение составляют два слу-
чая: когда все гомотопические группы пространства тривиальны и когда нетриви-
альна только одна гомотопическая группа. В этом случае пространство восстанав-
ливается по своим гомотопическим группам с точностью до слабой гомотопической
эквивалентности.
Уже в сдучае пространства с двумя нетривиальными гомотопическими группами
это, вообще говоря, не так. В самом деле, пусть Wj и ir2 — две абелевы группы, И1
и и2 — два натуральных числа, причем 1 < Hj < и2. Предположим, что пространство
X имеет тривиальные гомотопические группы во всех размерностях, кроме nt и и2,
и что тгИ1 (X) = 7Г1, тг„а (X) = тг2. Существует отображение пространства X в X(tti , п2),
индуцирующее изоморфизм nj-x гомотопических групп. Если превратить это отоб-
ражение в расслоение, то слоем этого расслоения будет пространство К(тг2, и2).
В когомологической спектральной последовательности этого расслоения с коэффи-
циентами в группе я2 элемент е G Нп* (K(ir2, и2); тг2) переходит при трансгрессии
в некоторый элемент группы Hn>+1 (X(tti, гц); я2). Последний, с одной стороны,
может быть любым элементом указанной группы и, с другой стороны, полностью
определяет гомотопический тип пространства X. Таким образом, гомотопический
тип пространства с двумя нетривиальными гомотопическими группами вполне опре-
деляется этими группами и некоторым элементом из (X(tti, И1); тг2). Пос-
ледний естественно рассматривать как когомологическую операцию, которая назы-
вается (первым) постниковским фактором пространства X.
§ 36. ЧАСТИЧНЫЕ ОПЕРАЦИИ
317
Если пространство X имеет три нетривиальные гомотопические группы Я1, тг2, тг3
в размерностях Л1 < л2 < п3, Hi >1, то, заклеивая старшую гомотопическую груп-
пу, мы получаем отображение пространства X в пространство У с двумя нетри-
виальными гомотопическими группами: яЛ1 (У) = и яи> (У) = тг2. Это отображение
можно рассматривать как расслоение со слоем K(tr3> л2). Образ фундаментального
класса этого слоя при трансгрессии представляет собой элемент группы Я"»+ 1 (У; я3).
Этот элемент может принимать любое значение и вполне определяет гомотопический
тип пространства X.
Как мы знаем, этот элемент можно рассматривать как вторичную когомологи-
ческую операцию, определенную на ядре примарной когомологической операции —
первого постниковского фактора пространства У. Эта вторичная операция называ-
ется вторым постниковским фактором пространства X. Таким образом, гомото-
пический тип пространства X полностью определяется его гомотопическими груп-
пами и двумя когомологическими операциями: примарной, определенной на Л1-
мерных когомологиях с коэффициентами в я2 и принимающей значения в (л2 + 1) -
мерных когомологиях с коэффициентами в тг2, и вторичной, определенной на ядре
этой примарной операции в принимающей значения в (л3 + 1)-мерных когомоло-
гиях с коэффициентами в тг3. Продолжая эту конструкцию и совершая предель-
ный переход (мы не касаемся возникающих при этом трудностей), мы приходим
к такому результату.
Гомотопический тип односвязного клеточного пространства определяется его го-
мотопическими группами и последовательностью когомологических операций: при-
марной, вторичной, третичной и т.д., каждая из которых определена на ядре пре-
дыдущей.
Эти операции называются постниковскими факторами пространства, а вся сис-
тема инвариантов — постниковской системой (башней) пространства.
ГЛАВА 6
А-ТЕОРИЯ
И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
§ 37. ОБЩАЯ ТЕОРИЯ
1. Введение. Х-теория возникла как самостоятельный раздел топологии в конце
50-х годов, когда обозначились пределы возможностей методов, основанных на
спектральных последовательностях и когомологических операциях (и изучавшихся
нами выше, в главах 3 — 5). В это время прогресс гомотопической топологии заметно
замедлился, ведущие топологи погрязли в громоздких вычислениях, результаты
получались все менее впечатляющие, и для их получения требовалось соединение
большой изобретательности с огромной усидчивостью. Для оживления этой деятель-
ности требовалось радикальное средство, и такое средство нашлось. Оно состояло
в том, чтобы — ни много ни мало! — отказаться от когомологий как от основного го-
мотопического инварианта и заменить его совершенно другим объектом — так назы-
ваемым Л?-функтором.
История A-теории поучительна. Период ее активного развития был краток: первые
работы по /^-теории появились в 1959 г., и уже к 1963 г. было получено большинство
ее результатов (в том числе все результаты, о которых пойдет речь ниже, кроме дока-
зательства гипотезы Адамса). При этом все без исключения работы по /Г-теории, от-
носящиеся к этому периоду, принадлежат четырем авторам: Адамсу, Атиах), Ботту
и Хирцебруху. В этом списке отсутствует Гротендик, который не имеет работ по то-
пологии; однако, по общему признанию, именно Гротендику принадлежат ключевые
идеи /Г-теории, которые применяются совсем не только в топологии.
Приложения Х-теории, полученные в ее ’’героический период”, были очень ярки-
ми. Упомянем простое доказательство теоремы о несуществовании сфероидов с не-
четным инвариантом Хопфа, точное вычисление максимального количества линейно
независимых векторных полей на сфере произвольной размерности, вычисление
£
порядка образа ’’/-гомоморфизма” ir„(SO) -> тги, теоремы о невложимости и
непогружаемости различных многообразий в евклидовы пространства, различные
теоремы целочисленности для рациональных линейных комбинаций характеристиче-
ских классов. Без /Г-теории было бы немыслимо решение проблемы индекса эллип-
тического оператора, найденное в 1963 г. Атиа и Зингером.
Большинство топологов спохватилось, когда построение Х-теории было в основ-
ном завершено и ее яркие приложения были в основном получены. Дело для них,
однако, нашлось. Они включили /^-теорию в рамки общей теории ’’экстраординар-
ных когомологий”. При этом оказалось, что Х-теория занимает среди других экстра-
ординарных теорий довольно скромное положение. Дело вот в чем. Как читатель
помнит, для обычных когомологий (с коэффициентами, например, в Z) справедлива
1) Это имя по-русски часто передается как Атья. Следует учесть, однако, что ударение в нем
приходится как раз на ”и” - это подтверждает и сам Атиа.
§ 37. ОБЩАЯ ТЕОРИЯ
319
теорема Уайтхеда: если X и Y — односвязные клеточные пространства и непрерывное
отображение /: X -» Y индуцирует изоморфизм /*: H*(Y; Z) -*Н*(Х; Z),to /
есть гомотопическая эквивалентность (см. п. 5 § 14). A-теория тоже ставит в соот-
ветствие (конечному) клеточному пространству функториальным образом завися-
щую от него градуированную группу, ио аналог теоремы Уайтхеда отсутствует:
прекрасно может быть, что /*: K*(Y) -+К\Х) — изоморфизм, a f — не гомотопи-
ческая эквивалентность. Были придуманы (лучше сказать, припомнены) экстраорди-
нарные теории, обладающие всеми достоинствами Х-теории, но свободные от этого
недостатка.
Наиболее совершенной иэ этих теорий является теория кобордизмов, которая
(как, впрочем, и /Г-теория) существует в большом числе вариантов. Для теории ко-
бордизмов существует аналог теоремы Уайтхеда, так что с гомотопической точки
зрения кобордизмы не хуже когомологий. Для них удалось построить даже аналог
спектральной последовательности Адамса — так называемую ’’спектральную последо-
вательность Адамса —Новикова”, — неоднократно с успехом применявшийся
к гомотопическим вычислениям. Чрезвычайно полезной оказалась теория характе-
ристических классов векторных расслоений со значениями в кобордизмах базы.
Наконец, утверждение, что кобордизмы лучше Л?-теории, имеет точную формулиров-
ку: A-теория вкладывается в кобордизмы в качестве прямого слагаемого. Мы воз-
даем теории кобордизмов должное, посвятив ей отдельный параграф ( § 43).
Все же необходимо признать, что по качеству своих применений A-теория значи-
тельно опережает другие экстраординарные теории когомологий; и именно ей мы
уделим главное внимание в этой главе. По необходимости мы ограничиваемся,
главным образом, комплексным случаем.
2. Определения. Группы К(Х). Пусть X — конечное клеточное пространство.
Обозначим через F (Т) совокупность классов эквивалентности комплексных вектор-
ных расслоений с базой X. Если X связно, то F(X) = U„ > 0Fn (X), где F„ (Т) —
совокупность классов «-мерных расслоений. Если X не связно, то мы не предпола-
гаем, что размерности слоев над разными компонентами базы одинаковы; размер-
ность расслоения определяется в этом случае как размерность слоя над отмеченной
точкой.
В множестве F(X) есть две операции: сложение и умножение (тензорное).
Относительно сложения F (X) представляет собой коммутативную полугруппу
с нулем; умножение дистрибутивно по отношению к сложению, коммутативно,
ассоциативно и обладает единицей.
В алгебре имеется общая операция, превращающая полугруппу с нулем в группу
(так называемую ’’группу Гротендика”). Именно, пусть F — коммутативная полу-
группа с нулем. Рассмотрим совокупность формальных разностей а — b, а G F,
b 6 F, и введем в этой совокупности отношение эквивалентности: а — b ~ с — d,
если существует такое е 6 F, что а + d + е = b + с + е. Очевидно, это отношение
рефлексивно и симметрично.
Упражнение 1. Проверьте, что оно транзитивно.
Обозначим через G(F) совокупность классов эквивалентности и введем в G(F)
операцию сложения формулой {а - } + { с — d} = {(а + с) — (b +d)}.
Упражнение 2. Проверьте, что G (F) с введенной операцией — группа.
Это и есть группа Гротендика полугруппы F. Формула а ь> {а — 0} определяет
отображение F -*G (F).
Упражнения. 3. Проверьте, что зто отображение является гомоморфизмом
(по отношению к сложению в F uaG(F)).
320
ГЛ. 6. К ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
4. Это отображение не обязательно является вложением — приведите пример.
5. Пусть G — абелева группа. Докажите, что всякий гомоморфизм F -»G единст-
венным образом разлагается в композицию канонического отображения F -*G(F)
(см. выше) и некоторого группового гомоморфизма G (F) -+G.
6. Покажите, что последнее свойство группы G(F) и гомоморфизма F -^G(F)
определяет и то и другое (по F) единственным образом.
Вернемся к расслоениям.
Определение. К (X) -G(F (У) ). Элементы группы К (Л) иногда называют
виртуальными расслоениями.
Всякое непрерывное отображение /: X -*• У очевидным образом определяет ’’ин-
дуцированный гомоморфизм” /*: K(Y) -+К(X). Гомотопные отображения опреде-
ляют одинаковые отображения, так что К (X) есть гомотопический инвариант прост-
ранства X.
Пример. F(pt) = Z + , X(pt) = Z; то же верно, если вместо pt взять любое
стягиваемое пространство.
Гомоморфизм dim: F (X) -+ Z определяет гомоморфизм dim: К(Х) ->Z; это
видно из упражнения 5, но ясно и непосредственно: dim {а — b) = dima — dimh
(проверьте корректность последнего определения). Заметим, что размерность вир-
туального расслоения может быть отрицательной.
Предложение, (i) Для всякого виртуального расслоения а& К (У) найдет-
ся обыкновенное расслоение а и число N, такие, что а = {а — N } .(Напомним,
что в теории векторных расслоений N обозначает векторное расслоение размер-
ности N.)
(ii) Виртуальные расслоения а = {а — N)u (3 = { b — М} в том и только в том
случае одинаковы, если dim а = dim 0 и расслоения а и b стабильно эквивалентны.
(См. п. 1 § 19.)
Доказательство основано на следующей лемме.
Лемма. Для всякого векторного расслоения а с (конечной клеточ-
ной) базой X найдется расслоение а с базой X, такое, что сумма а & а три-
виальна.
Доказательство леммы. Согласно п. 4 § 19, а = f *f, где f — тавтоло-
гическое расслоение над надлежащим комплексным грассманианом, a f — непрерыв-
ное отображение пространства X в этот грассманиан. Отсюда видно, что утверждение
леммы достаточно доказать для случая, когда само а есть тавтологическое рас-
слоение над грассманианом CG(N, и). Обозначим через f1 ’’дуальное тавтологиче-
ское расслоение”, слой которого над х G С G (N, и) есть ортогональное дополнение
х1 к х в CN. Слоем расслоения f ® f1 над х будет х фх1 = CN. Значит, расслоение
f ф f1 тривиально, что и требовалось.
Вывод предложения из леммы, (i) Пусть а = {с — d}, и пусть
d — такое расслоение, что d ® d = N. Тогда виртуальное расслоение с — d эквива-
лентно (с ф d) — (d ф d) = а — N, где а = с ®d. (ii ) Равенство {а — N} = { Ь — М}
означает, что а ф М ф с = beN ® с для некоторого с. Подберем такое с\ что с ® F= К;
тогда а ® М ® К - a ®M®c&c=b®N®c®c = b®N®K. Обратно, если расслоения
а и b стабильно эквивалентны, то a <s К = b ® L при некоторых К тлЬ. Следователь-
но, a®X®M®JV=d®L ф MsN. Так как dim (a -N) =dim(Z> — М) и dim (а 9 К) =
= dim(Z> ф L), то К + N = L +М,и, значит, a eM9c = beN9c, где с = К + N = L +М
и а — N эквивалентно b — М.
§ 37. ОБЩАЯ ТЕОРИЯ
321
В. Группы К (X).
Определение. К(Х) = Ker [dim; К (X) + Z ].
Так как A'(pt) = Z и dim: /T(pt) + Z есть изоморфизм, то наше определение
эквивалентно следующему определению:
К(Х) = КегЩХ) - К(х0)],
где х0 - отмеченная точка пространства X.
Очевидно, всегда К (J) = К (J) е Z.
Теорема. К (Т) есть множество классов стабильно эквивалентных расслоений
над X.
Доказательство. Из предложения следует, что всякий элемент a G К (X)
представляется разностью а - dime, где а — расслоение, причем а по а восстанав-
ливается однозначно с точностью до стабильной эквивалентности. В то же время для
всякого расслоения а разность а - dim а определяет некоторый элемент из К (Т).
Положим
BU = CG(oo, оо), U = U U(n)
п = 1
(см. п. 5 § 1). Доказанная теорема имеет важное
Следствие. К(X) =п(Х, В17).
Доказательство. Мы должны показать, что классы стабильно эквивалент-
ных векторных расслоений над (конечным клеточным) пространством X находятся
во взаимно однозначном соответствии с гомотопическими классами отображений
X + BU. Согласно п.4 § 19 всякое расслоение (размерности п) над X определяет
отображение X + CG(<x>, п) и, так как CG(°o, и) С СС7(<», оо), - отображение
X + CG(oo, оо). Но очевидно, что отображения X + CG(°o, пг), X->CG(<x>, «2),
отвечающие двум расслоениям с базой X, гомотопны в СС7(«>, оо) тогда и только
тогда, когда эти расслоения стабильно эквивалентны.
Гомотопическая лемма. При всяком г имеет место изоморфизм
nr(U) = irr + i(BU). Это остается верным, если вместо BU и U взять BU(n) =
= СС7(оо, п) (обозначение из п. 4 § 19) и U(п).
Докажем утверждение, относящееся к BU(ri) и U(n) (часть, касающаяся BU и
U, получается очевидным предельным переходом по п). У нас есть расслоение
t/(") £/(«)
СК(оо, и)---► CG(oo, и), т.е. ЕЩп)----> ВЩп)
со стягиваемым пространством EU(n). (Стягиваемость пространства СК(оо,и)
читатель может доказать в качестве упражнения; впрочем, для наших целей доста-
точно знать, что лг(СГ(», п)) = 0 при всяком г, а это вытекает из равенства
тгг (СК (N, и)) = 0 при г < 2 (N - п) - см. п. 3 § 19.) Нужный нам изоморфизм
получается из точности гомотопической последовательности этого расслоения.
Упражнения. 7. Докажите усиление гомотопической леммы: пространства
Г25 U и U гомотопически эквивалентны, и пространства £1В U (п) н U (п) гомотопи-
чески эквивалентны.
8. Дальнейшее усиление: указанные пространства гомотопически эквивалентны
как //-пространства.
11. А.Т. Фоменко
322
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Применение. K(Sr) =nr(BU) = яг _! (U). В частности, К (52) = 714 (U) = Z.
Заметим, что образующей группы K(S2) = Z является класс хопфовского рас-
слоения f над S2 - СР1. Действительно, расслоение f не является стабильно три-
виальным, поскольку первый класс Черна Су (f) отличен от 0 (см. п. 5 § 19); зна-
чит, f определяет в K(S2) ненулевой элемент. Но этот элемент не может быть дели-
мым, так как всегда су (£> ф £2) = ct (£j) + Cj (£2) и, значит, (n£) = псу (£),
a Cj (f) есть образующая группы Н2 (52; Z) — неделимый элемент.
Далее, K(S2) = K(S2) ®Z = Z®Z. Эта группа порождается f и 1. Умножение
в K(S2) определяется формулой f2 = 2 f + 1: расслоения f2 ® 1 и 2 f имеют оди-
наковый класс Су и потому стабильно эквивалентны (в действительности они просто
эквивалентны).
С. Группы Kq (X, А), q < 0. Пусть (Л, Л) — пара, составленная из конечного кле-
точного пространства и его клеточного подпространства. Положим при q < 0:
Kq(X,A) = K(h~q(XlA)),
Kq(X) = Kq(X, ф),
Kq(X) = Kq(X,x0),
где x0 — отмеченная точка. Очевидно,
К°(Х) = К(Х/ф)= К(Х U pt) = £(X)®Z = К(Х),
К°(Х) = К(Х/х0) = К(Х).
(Заметим, сколь это ни тривиально, что факторпространство Х/ф состоит из X и еще
одной изолированной точки: по определению, элементами множества Х]ф служат
точки разности X— ф = X и еще одна точка { ф}.)
Пример. К’(pt) =X;(S"‘7(pt/0)) =£(S-’(pt U pt)) =£(S-’(50)) =
= K(S~q) =n_q(BU).
В Л>теории рассматриваются, конечно, и группы К4 (X, А) с q > 0, но чтобы их
определить, требуется так называемая периодичность Ботта, и разговор о них мы
отложим до п. 3.
D. Последовательность пары.
Лемма. Для любой (конечной клеточной) пары (X, А) последовательность
К(Х/А) К(Х) -> К(А)
гомоморфизмов, индуцированных включением А и проекцией X-+Х/А, точна.
Доказательство леммы мы оставляем читателю.
Построим теперь по паре (X, А) следующую диаграмму:
А ----„ х ----> х/А
2Л
11 I
хисл —>стисл--------> SX.
Вертикальные стрелки этой диаграммы обозначают гомотопические эквивалент-
§ 37. ОБЩАЯ ТЕОРИЯ
3»
ности: факторизацию по С А и факторизацию по СХ. Все строки имеют вид
В -> Y -> Y/В. Поэтому можно отождествить К -функторы пространств, стоящих в од-
ном вертикальном ряду, и получить последовательность
К(Л) «— К(Х) <— К{Х/А) К(2Л) К(ЪХ),
точную в силу леммы, причем первая, вторая и четвертая стрелки в ней индуцируют-
ся, соответственна, включением А -* X, проекцией X -> Х/А и включением
2 Л -> 2 X. Точно так же, отправляясь от пары (2 X, 2 Л), мы строим точную после-
довательность
К(2Л) £(2Х) £(2Х/2Л) £(22Л) К(ЪгХ)
и, далее,
К(ЪЧА) ^K(XqX) ^K(ZqX/ZqA) «- K(Sq + 1A) «- +
при любом q. Все эти последовательности можно срастить в единую точную последо-
вательность
£(2Л) «- £(2 X) «- ^(2Х/2Л) .
... *- £(2’X/2^) *- £(2’+1Л) *- tf(2’+1X) «- ...
Заменяя в этой последовательности пространства X и Л сначала пространствами
X LI pt и Л Upt, а затем пространствами Х/В и А/В, где В — клеточное подпрост-
ранство пространства Л, мы получаем (пользуясь определениями из п.С) точные
последовательности
К°(А) *- №(Х) «- К°(Х, Л) «- К'1 (А)
... +- K~q(X) «- Г’(1,Л) *-K~q~l(A)
К°(А,В) *- К°(Х,В) «- К.й(Х,А) «- К-\А,В)
.. . «- К~Ч(Х,В) *- K~q(X,A) «- K~q-\A,B) *- К-Ч-'(Х,В) -^ ...
— последовательности пары и тройки в /Г-теории.
Разумеется, непрерывное отображение пары в пару индуцирует (направленные
в противоположную сторону) гомотопически инвариантные отображения всех
групп Kq, и эти отображения согласованы с последовательностями пар и троек.
Замечание. Геометрическое построение, с которого мы начали, можно про-
должить. В результате получится последовательность
Л -* X -* Х/А ---► 2Л -> 2Х -> 2(Х/Л) ---► 22Л -> . . . ,
в которой пунктирные стрелки определены с точностью до гомотопии. Эта последова-
тельность называется последовательностью Пуппе. Последовательность Пуппе точна
в том смысле, что любой трехчленный фрагмент этой последовательности гомотопи-
чески эквивалентен фрагменту вида В -+Y -*У/В.
Е. Попытки обобщения на случай бесконечных клеточных пространств. Удовлет-
ворительного обобщения изложенной теории на случай бесконечных клеточных
11*
324 ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
пространств не существует. Мы рассмотрим несколько возможных вариантов опреде-
ления Л'-функтора в этом случае.
Вариант 1. А (X) — группа Гротендика полугруппы классов эквивалентных
векторных расслоений.
Вариант 2. К(Х) = я(Х, BU), А'(Х) = А(Х) eZ.
Вариант 3. Л' (A) = lim К (У), где предел берется по всем конечным подпрост-
ранствам пространства X.
Вариант 1 выглядит особенно естественно, но про такой ”Л'-функтор” ничего не
известно; вряд ли он обладает какими-нибудь хорошими свойствами. Не видно, как
вычислять его даже, скажем, в случае X = СР°°. Варианты 2 и 3 более осмысленны;
определяемые таким образом Л'-функторы обозначаются, соответственно, символа-
ми к и X.
Достоинством теории X является ее легкая вычислимость: методы вычисления
Л'-функтора, которые будут изложены в следующем параграфе, будучи применены
к бесконечному клеточному пространству, дают именно X. Однако в этой теории
отсутствуют точные последовательности пар: может случиться, скажем, что
X{XjY^ = 0 и J5T(K) = 0, но Х(Х) =# 0 (читатель сможет построить такой пример
после прочтения § 38). Напротив, fc-функтор точен, но его значения трудно вычис-
лять. Действительно, вникнем в разницу между к и X. Существует очевидное отобра-
жение к -> X (отображение X -*BU определяет отображение Y -*BUи тем самым —
элемент из А (Y) для любого конечного подпространства Y пространства Х\
эти элементы составляют элемент из lim K(Y) =X(X)j.
Упражнение. 9. Докажите, что это отображение эпиморфно.
Что же является его ядром? Классы отображений X^-BU. гомотопных нулю на
любом конечном подпространстве Y С X, но, возможно, не гомотопных нулю в це-
лом. Возможно ли такое? Оказывается, да!
Определение. Отображение клеточного пространства X в пространство V
называется призрачным (phantom mapping), если оно не гомотопно нулю, но сужение
его на любое конечное подпространство пространства X гомотопно нулю.
Первый пример призрака — довольно сложный — был построен Адамсом и
Уокером (перевод их работы см. Математика: сб. перев. — 1965. — Т. 9, № 1).
Впоследствии были найдены более простые примеры, и в настоящее время известен
пример призрачного отображения СР°° + S3 (читатель может попытаться такое
отображение построить).
Взаимоотношения к- и Л*-теорий обследовались сначала Атиа и Хирцебрухом, а
затем Бухштабером и Мищенко; см. работы последних в Докладах АН СССР
(1968. - Т. 178, № 6) ив Известиях АН СССР (1968. - Т. 32, № 3; исправление -
Т. 33, № 1). Сформулируем два результата Бухштабера и Мищенко. (1) Если все не-
четные числа Бетти пространства X равны 0, то к (X) =Х(Х). (2) Пусть Х=К (Z, 3).
Тогда Х(Х) = 0, а к(Х) = Z/Z, где Z - пополнение группы Z по всем подгруппам
конечного индекса. (Другими словами, Z есть совокупность последовательностей
{а2, а3, а4 ,. . . } неотрицательных целых чисел, удовлетворяющих условиям
a(J <q, aq = а^ mod (<?, q' ). Z вкладывается в Z формулой //^-{resj/t, res3«,...),
т.е. Z есть подгруппа группы Z, составленная из стабилизирующихся последователь-
ностей; ясно, что Z значительно больше Z.)
3. Периодичность Ботта. А. Формулировка теоремы Ботта. Как уже говорилось,
A'(S2) = Z е Z, причем образующими этих групп служат классы Inf тривиального
§ 37. ОБЩАЯ ТЕОРИЯ
325
и хопфовского расслоения. Пусть X — клеточное пространство, и пусть ax,a2SK(X}.
Тогда можно образовать элемент
(а, 1) + (а2 ® Г) G К(Х X S2).
Теорема (Ботт). Для любого X отображение
К(Х)®К(Х) -* К(ХХ S2), (а1(а2) н- (а, ® 1) + (а2 ® f)
является изоморфизмом.
К доказательству этой теоремы мы обратимся в п. С, а сейчас мы приведем ее
формулировку к более удобному для нас (и более привычному) виду.
Рассмотрим ^-последовательность пары {X X S2, X v S2 ):
... ->К-х(ХА S2)->K~s(X v S2)-> К(Х X S2, X v S2) К(Х X S2) K(Xv S2).
Очевидно, К(Х v S2) = К(Х) + K(S2); в то же время произвольный элемент а & К(Х)
есть образ при гомоморфизме * элемента р*а G К(Х X №), а произвольный элемент
b SK(S2) есть образ элемента р2Ь SK(X X S2), где Pi и р2 — проекции произведе-
ния XX S2 на сомножители. Значит, * есть эпиморфизм, и по аналогичным причинам
эпиморфно отображение К'1 (XX S2) (X v S2). Значит, К(Х X S2, X v S2) есть
просто ядро гомоморфизма *. Посмотрим, какие элементы принадлежат этому ядру.
Согласно теореме Ботта, всякий элемент из К(Х X S2) представляется в виде
(«1 э 1) + (а2 <& f). Перепишем последнюю сумму как (а ® (f - 1)) + (0 ® 1).
Сужение этого виртуального расслоения на ХС XX S2 равно a-dim(f —1)+0 - dim 1=0.
Сужение этого виртуального расслоения на S2 С X X S2 равно dima(f — 1) +
+ di m 0 • 1. Таким образом, наше виртуальное расслоение принадлежит ядру гомомор-
физма * в том и только в том случае, если 0 = 0 и dima = 0, т.е. если оно имеет вид
a ® (f — 1) с aS К (X). Мы видим, что отображение
а ь» a ® (.f - 1)
устанавливает изоморфизм
К(Х)^К(ХХ S2,Xv S2) = K(XXS2/XvS2) = X(S2X).
Нами доказано
Следствие. Имеет место естественный по X изоморфизм
К(Х) — К(Ъ2Х)
Применяя это следствие к случаю X = Sq, мы получаем (ввиду равенства
K(S‘) =T4(BU))
Следствие из еле дстви я. При любом q
irq(BU) = 1Гд_2(В1Г),
и, значит,
= ^_2(f/).
326
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Собственно, это и есть ’’периодичность Ботта”. Так как tti (U) = Z и я2 (U) =
= я2 (S U) =0, то
я,(^) =
Z при нечетном I,
0 при четном i.
и
K(S‘) = я,(В17) =
Z при четном i,
0 при нечетном i.
В. Окончание построения К-теории. Отложив на время доказательство теоремы
Ботта, мы покажем, как с ее помощью завершить построение К-теории. Следствие
из теоремы Ботта, выделенное в п. А, показывает, что для любой пары (X, А) и лю-
бого q < 0 имеет место естественный по (X, А) (и по отношению к связывающим
гомоморфизмам Kq(X, А) ^Kq~I (А, В)) изоморфизм
Kq(X,A)~Kq~2(X,A).
Мы используем это равенство для определения К4 (X, А) при всех q: по определению,
Kq(X,A) = Kq~2N(X,A), N > | max(0,<7).
Получается 2-периодическая обобщенная теория когомологий (разъяснение этого
термина — ниже, в п. 5), т.е. правило, относящее конечной клеточной паре (Х,А)
последовательность групп КЧ(Х,А), q G Z, и последовательность гомоморфизмов
Kq(A) =КЧ(А, ф) + Kq+l (X, А) и непрерывному отображению (Х,А) -* (Y,B) —
последовательность гомоморфизмов К4 (Y, В) ->-Kq(X, Л), причем все эти группы и
гомоморфизмы гомотопически инвариантны и удовлетворяют надлежащим условиям
коммутативности диаграмм и точности последовательностей (подробности в п. 5).
К тому же имеются согласованные со всеми этими стр' ктурами изоморфизмы
Kq(X, А) = Kq~2 (X, Л). (Последнее составляет' важюе отличие К от Н,
поскольку Hq = 0 при q < 0.)
Теперь мы можем применять к К-теории все стандартные следствия точности по-
следовательностей пары и тройки. Например, имеют место изоморфизмы надстройки
S: К’(Х) Kq+1(ZX)
(из точности последовательности пары (СХ, X)
Kq(CX) —> Kq(X) —► К’+1(СХ,Х) —> Kq + l(CX)
II
0
II
о
следует, что Кq(X) - Kq+1 (СХ, X) = Kq+1 (SX)).
§ 37. ОБЩАЯ ТЕОРИЯ
327
Упражнение 10. Придумайте в A-теории естественное умножение
КЧ(Х,А) ® КГ(Х,А) —► К’+Г(Х,Л).
С. Доказательство теоремы Ботта мы проведем в одну сторону, а именно, дока-
жем, что отображение К(Х) е К(Х) -+К(ХХ S2), (ai} а2) ь* (at ® 1) + (а2 ® f)
эпиморфно. Доказательство мономорфности основано на близких соображениях и
может быть проведено читателем самостоятельно. (Оно изложено в лекциях Атиа
по A-теории, а также в книгах Каруби, А.С.Мищенко, Дж.Шварца и Хьюзмоллера.)
Рассмотрим расслоение I над X X S2. База X X S2 разлагается в объединение
(XX D2) U (X XD2). Над каждым куском расслоение представляет собой прямое
произведение некоторого расслоения над X (мы обозначим его через а) на D2.
Склейка двух кусков происходит над XX S* (S1 — экватор сферы S2); при каждом
z 6 S1 она задается отображением u(z): а -> а, накрывающим тождественное
отображение базы X. Для каждого х 6 X мы имеем зависящий от z автоморфизм
и (х, z) : ах -> ах слоя ах расслоения а над х. Итак, наше расслоение I определяет-
ся парой а, и; мы используем обозначение: < = [а, и ].
Разложим функцию и (x,z) в ряд Фурье по z (мы считаем, что zSS’^dz^lJCC2):
u(x,z) = S uk(x)zk.
k e Z
Подчеркнем, что uk(x) — это, вообще говоря, вырожденные эндоморфизмы прост-
ранства ах.
Ясно, что если заменить и достаточно близким отображением и, то расслоение $
не изменится: [а, и.] = [а, м]. Поэтому можно считать, что и — тригонометрический
полином:
N
и(х, z) = S uk(x)zk.
k = -N
Умножение функции и на z соответствует тензорному умножению расслоения £ ня
f = f-1 (действительно, [ai.Ui] ® [а2, и2 ] = [оц ®а2, «i ®wj] и, как легко понять.
f_> = (1, z]). Заменим расслоение $ расслоением Имеем: £'
= [а, и'. ], где
и(х, z) - S uk(x}zk (m = 2 7V).
к = о
Положим £м = ® (ma ® 1) = [а", пм ], где а" = (т + 1)а, и" =и' ®1 ф ... «> 1
Таким образом, матрица имеет вид
328
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Умножим эту матрицу слева и справа на
m
U*k = Ъ ur(x)zr~k.
г — к
где
Это умножение не изменяет расслоения (обе матрицы гомотопны, как отображения
X X S1 -> {матрицы} , постоянной единичной матрице) и приводит матрицу u "(х, z)
к виду а(х) + b(x)z.
Лемма из линейной алгебры. Пусть а и b - два эндоморфизма про-
странства V, пересечение ядер которых есть нуль. Положим ckill = \a + pb (X, д G
G С, (X, д) #= (0, 0)), и пусть ( X/: д/) G СР1, i = 1, -все попарно различ-
ные корни уравнения det м = 0. Тогда существуют прямые разложения
V = Ai ф Аг © ... © Am , V = Вг ® В2 ® ... ® Вт ,
и
такие, что ck ,ц(А^ С В{ при всех Х,р, причем А{----->5/ есть изоморфизм при
X: Д #=Х^: др
Доказательство мы оставляем читателю.
Положим , д(х) = Ха (х) + д&(х): ах ->ах. Так как эндоморфизм а (х) + zb(x)
с \z | = 1 невырожден, то уравнение detcx, м = 0 не имеет решений (X, д) с
I X | /1 д | = 1. Из леммы следует, что существуют разложения ах = 0Х + ух и
«х = 0х + 7х, такие, что ех,д(х)(0х) С 0Х, cKtlt(x)(yx) С ух и м(х)(0х) = 0Х
при | X | /1 д | > 1 и сх, м(х)(7х) = 7х ПРИ I X | /1 д | < 1. В частности,
я(х) - Ь(х) _
Их ---* 0Х И ух ----------> Ух
- изоморфизмы. Обозначим через м (х) и ек> д(х) отображения
сх,д(*) — о(х)"‘ сХ,д(*) — b(x)-'
0х-------&х ------* Рх И ух ------------► ух ----* 7х-
Ввиду сказанного выше, dK> д(х) невырождено при | X | / | д | > 1 и eki д(х) невы-
рождено при | X | /1 д | < 1.
Предположим, что X связно (это предположение безвредно). Тогда 0Х > Тх > 0х > 7х
составляют подрасслоения 0,у,0,У расслоения а”, и мы имеем:
Г' = [ft di,z ] Ф [г е1>2].
§ 37. ОБЩАЯ ТЕОРИЯ
УВ
Но d1>z гомотопно d1>0 nel<z гомотопно во,z в классе невырожденных преобразо-
ваний (гомотопии d1>fz и ef> z ). Значит,
= [ft di,o ] ® 1% eo,z] =
= [0, 1] ф [% z] = (0 ® 1) ® (у ® Г1).
Окончательно имеем:
(£ ® ® (wa ® 1) = (0 ® 1)ф (у ® f-1),
т.е.
$ ={[(0-/па)® 1] + (у ®f-1)} ® $N.
Доказательство эпиморфности закончено.
Упражнение И. Выведите мономорфность отображения К (X) ф *(*) ->
-> А^(ХХ S2) из его эпиморфности, пользуясь следующей схемой. Из эпиморфности
следует, что отображение тг{ (BU) ->я/+2 (BU) эпиморфно при любом /. Но (BU) -
- О, я2 (BU) = Z и rank2r(Bt/) = 1 при любом г (см. п. 4 § 25). Из этого следует,
что я,- (BU) -* я;+2(ВС/) есть при любом i изоморфизм, а из этого легко вывести и
что К (X) ф К (X) -+К (XX S2) - изоморфизм.
4. Характер Черна.
А. В п. 5 § 19 мы определили ’’характер Черна” - характеристический класс ком-
плексных векторных расслоений, принимающий значения в Яе',еп (X; Q) =
= Н° (X; Q) ф Н2 (X; Q) ® ..., где X - база расслоения; обозначение: £ н- ch£.
Этот характеристический класс аддитивен и мультипликативен:
ch (£1 ® £2) = ch £i + ch £2, ch (£t ® £2) = ch £2 ch £2.
Первое свойство позволяет перенести ch в А'-теорию:
ch: К(Х) Heven(X; Q);
второе свойство делает этот А-теорный характер мультипликативным. Кроме того,
это определение очевидным образом превращается в определение характера
ch: Kq(X, А) —>
//even^ 4- q) ПрИ четном д
Я°а<1(Х, A; Q) при нечетному
(Нodd = Я1 ® Я3 ® ...). Удобно ввести такое обозначение:
№(Х,Л) =
^even^y д. Q) При четном q
НоЛЛ{Х, A; Q) при нечетном q.
Тогда JC станет похоже на А: останутся индуцированные гомоморфизмы и точные
последовательности пар и троек, но появится 2-периодичность: = JC,+ 2. Отображе-
330
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
ние ch станет тогда набором гомоморфизмов
ch: Kq(X, А) —* Xq(X, А),
перестановочным с индуцированными гомоморфизмами, последовательностями пар
и троек и периодичностью
Упражнение 12. Покажите, что это отображение ch мультипликативно
(см. упражнение 10).
В. Положим
chQ = ch® Q: Kq(X, Л)®0 —► JCQ(X>1)®Q = Xq(X, A).
Теорема. Отображение chQ является изоморфизмом при любом q и для лю-
бой (конечной клеточной) пары (X, А). В частности,
К(Х) ® Q = Неуеа(Х; Q),
и ранг группы К (Я) равен сумме четных чисел Бетти пространства X. (Например,
rank К (S2) = 2 - в согласии с утверждением теоремы.)
Доказательство. Достаточно рассмотреть случай А = ф (поскольку
Kq(X, A) = Kq (Х/А) и №(Х, А) = ЗС’(Х/Л)).
Утверждение теоремы очевидно, если dim Л' = 0, т.е. X есть конечное множество.
Так как для К ® Q и JC есть изоморфизмы надстройки и отображение chQ с ними
перестановочно, то chQ является изоморфизмом и для надстроек над конечными
множествами, т.е. для букетов сфер одинаковой размерности. Дальше —индукция по
dimX.
Предположим, что dimX = «>lH что для пространств размерности < п теорема
уже доказана. Рассмотрим JC- и (К ® Q)-последовательности пары (X, Хп~1) и отоб-
ражение chQ одной в другую:
/C’-i(Xn-i) ® Q —> Kq(X, Xn~l) ® Q —►
chQ
I
chQ
—* Xq(X, Xn~l )
—> Kq(X) ® Q —► Kq(Xni) ® Q —> Kq+i(X,Xn~l'>) ® Q
chQ chQ ChQ
—*Xq(X) —’Xq(Xn-1) —> Kq + 1(X,Xn-1 ).
Все вертикальные гомоморфизмы, кроме среднего являются изоморфизмами в силу
уже доказанного: два — потому что dim.Y"-1 < и и два других — потому что
Х/Хп -1 есть букет «-мерных сфер. Остается применить 5-лемму.
§ 37. ОБЩАЯ ТЕОРИЯ
331
5. Экстраординарные гомологии и когомологии.
А. Аксиомы Эйленберга - Стинрода. Вернемся к главе 2. В этой главе мы поста-
вили в соответствие конечной клеточной (на самом деле — произвольной топологи-
ческой, но забудем сейчас об этом) паре (X, А) последовательность групп ffq{X,A),
q G Z (мы подразумеваем, что Hq{X,A} = 0 при q < 0), и гомоморфизмов
Э,: Hq{X, А) -+ЯЧ_1(Л) (мы полагаем Н г (У) =Hr(Y, ф)) и каждому непрерыв-
ному отображению f: {X, А) -* (У, В} - последовательность гомоморфизмов
Hq (X, Л ) (У, В), согласованных с отображением Э При этом справедливы
следующие утверждения:
Аксиома гомотопии: если f ~ g, то /, = gt.
Аксиома точности: последовательности пар точны. (Следствие:
последовательности троек точны.)
Аксиома факторизации: проекция {X, Л) -* {Х]А, pt) индуцирует
при всех q изоморфизм Hq {X, Л) = Hq{X/A, pt) =Hq(X/A).
Аксиома размерности: Яд(р1) = 0 при q #=0.
Эти утверждения называются аксиомами Эйленберга - Стинрода. Если мы при-
соединим к аксиомам Эйленберга — Стинрода утверждение, что Но (pt) = Z, то будет
справедлива ’’теорема единственности”: теория {Hq, f.,}, удовлетворяющая
всем перечисленным условиям, единственна и совпадает с теорией обычных {сингу-
лярных} гомологий. Эта теорема, по существу, доказывалась нами в § 13, где мы
вычисляли гомологии клеточных пространств (и клеточных пар), пользуясь как
исходным материалом только перечисленными здесь свойствами гомологий.
Отбросим требование Яо(рО = Z и назовем группу G = H0{pt) группой коэф-
фициентов. Аналог теоремы единственности утверждает в этом случае, что теория,
удовлетворяющая всем аксиомам Эйленберга - Стинрода, совпадает с теорией обыч-
ных гомологий с коэффициентами в G.
Аналогичным образом составляется система когомологических аксиом Эйленбер-
га - Стинрода с такими же теоремами единственности.
В. Экстраординарные теории. Предположим, что каждой конечной клеточной паре
{X, А) поставлена в соответствие последовательность групп hq{X, А) и гомомор-
физмов Э,: hq(X, A) -*hq^1{A) (мы полагаем hr (У) =ЛГ(У, ф)) и каждому не-
прерывному отображению f: {X, А} -* (У, В) поставлена в соответствие последова-
тельность гомоморфизмов hq(X,A) -+hq{Y, В), согласованных с Э,. Предполо-
жим теперь, что выполняются аксиомы гомотопии, точности и факторизации, а аксио-
ма размерности, вообще говоря, не выполнена. Тогда говорят, что {hq, Э,, ft} —
экстраординарная {обобщенная) теория гомологий. Аналогично определяются
экстраординарные {обобщенные} теории когомологий.
Примером экстраординарной теории когомологий служит A-теория. Другие при-
меры рассматриваются в п. D и в § 43.
Упражнение 13. Докажите, что hq{Xx U Х2) = hq{Xi) ф hq{X2} для любой
экстраординарной теории гомологий h (и аналогичное для когомологий).
С. Обобщенная теорема единственности. Пусть h и q - две экстраординарные тео-
рии когомологий (или гомологий; в гомологическом случае все, что говорится ни-
же, верно с надлежащими модификациями: опускаются некоторые индексы, обра-
щаются некоторые стрелки и т.д.). Говорят, что задано отображение <р: h -+Л,если
для всякой конечной клеточной пары {X, А) определены гомоморфизмы
= *Р(х, а)- &{Х,А) k*{X,A},
332
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
такие, что для любых (X, А) и f: (X, А) -> (У, В) коммутативны диаграммы
й
fiq(X,A) <----hqX(A)
ip ip и
6*
kq(X,A) <----kq '(А)
fiq(X,A) hq(Y, В)
ч>
kq(X,A) kq(Y,B).
Т е о р е м а. Пусть h ->к - отображение теории h в теорию к, такое, что при
любом и
Apt, фу л</(р‘) —*
есть изоморфизм. Тогда
Ах, и): hq(X,A) kq(X,A)
есть изоморфизм при любых ц и (X, А ); в частности, в этом случае h = к.
Доказательство повторяет доказательство теоремы п. 4В (в котором роль
играет ch), только нужно доказать, что <(>(х а) есть изоморфизм при dimX = О,
А = ф. Это можно вывести из упражнения 13, но можно доказать и прямо, восполь-
зовавшись индукцией по числу точек в X. Пусть X состоит из и > 2 точек. Тогда
X = У/ ф, где У состоит из и - 1 точек. Из Л- и ^-последовательностей пары (У, pt)
составляется коммутативная лестница
hq 1 (pt) hq(X,pt) hq(X) //"(pt) —> Л"+1(Х, pt)
kq !(pt) —> kq(X, pt) —► kq(X) —> A"(pt) —> kq + 1(X, pt),
в которой все - изоморфизмы, кроме среднего (ибо hr (X, pt) = Иг(У1ф, pt) =
-Лг(У, ф) = hr(Y~)). Значит,и среднее — изоморфизм.
Замечание. Если Л" (pt) = kq (pt), но изоморфизм не индуцирован отобра-
жением h -+к,то изоморфизма h к может не быть. Например,
/("(pt) ~ -Kz(pt),
где ^Kz(X, А) = Heven(°dd)(X,A-, Z), но, как мы увидим в §38,
K(RPn) $ H*ven(RPn;Z).
D. Примеры экстраординарных теорий. Наряду с комплексной /(-теорией сущест-
вует вещественная /(-теория. Мы не касаемся ее здесь, хотя в некоторых случаях зто
будет стоить нам небольшого ослабления результата (см., например, замечания
в п. 3 § 40 и п. 5 § 41). Роль BU в вещественной /(-теории играет BSO = G+ («>,«>)
(в другом варианте ВО = (И°°, «>)), роль 2-периодичности Ботта — вещественная
8-псриодичность Ботта = nf + 8(5O). Подробности см. в лекциях Атиа
(включая добавленную в переводе статью Атиа ’’/(-теория и вещественность”)
или в книге Кару би.
§ 37. ОБЩАЯ ТЕОРИЯ
333
Существует общая конструкция, обобщающая как комплексную и вещественную
/С-теорию, так и обыкновенные когомологии (и гомологии).
Определение. Спектром, или ^l-спектром, называется последовательность
клеточных пространств и непрерывных отображений: И7/ ->£2H/z+i (/> 1).
Заметим, что для любых пространств с отмеченными точками А, В. задание непре-
рывного отображения А -* SIB равнозначно заданию непрерывного отображения
S А -*• В (надстройка понимается в смысле конструкции, учитывающей отмеченную
точку, см. п. 6 §2): отображению /: А -* ПВ соответствует отображение
/: 2А->В, f(a, t) = 17(a)] (/). В частности, тг(А, ПВ) = -и (X А, В).
Определение. Пусть (X, А) - конечная клеточная пара и V7= { Wf, } -
произвольный £2-спектр. Гомологические и когомологические группы пары (X, Л)
с коэффициентами в 117определяются формулами (в которых q G Z):
If’tX.A .V) = lim тг(2л,(Х/Л). И'дг+ч);
N
hq(X,A:H7) = йттгдг+.ДИ^ # (Х/А)).
N
Пояснение. Отображение
А^\Х/А). WN+q) -> it(SN+l(X/A),WN+i+q) =
= n(SN(X/^), £2 И^+1+(/).
при помощи которого образуется первый предел, индуцируется отображением
fN + ч- И7дг+ч S2 И7jv + 4+i . Отображение
irN + q(^N # (Х/А)) Ядг+1+ч(В//у+1 # (Л'/Д)),
при помощи которого образуется второй предел, определяется при помощи соответ-
ствующего fN отображения S И7 Л'-» IV д,+ 1 как сквозное отображение
яд+ч(^ # (Х/А)) 7Глг+1+ч(Е(И/дг # (Х/А))) =
= TtK+t+qCSWn # (Х/А)) > irN+i+q(WN+i # (Х/А)).
Упражнение 14. Определите для групп hQ(X, А ,177) и ltq (X, Л; ЭДР ) инду-
цированные и связывающие гомоморфизмы таким образом, чтобы получилась
теория экстраординарных гомологий и теория экстраординарных когомологий.
П р и м с р ы. Обычные гомологии и когомологии (с коэффициентами в (?)
отвечают спектру Эйленберга - Маклейна, в котором И7/ есть K(G, i). f{ есть стан-
дартная гомотопическая эквивалентность K(G,i) -+&K(G, i.+ 1). (Для когомоло-
гий это нам известно, для гомологий - упражнение.) Комплексная Л'-теорйя соответ-
ствует периодическому £2-сиектру U, BU, U, BU, ... с гомотопическими эквивалент-
ностями U-+ £1ВU и BU -*Пи (наличие первой эквивалентности составляет содержа-
ние упражнения 7, наличие второй - одну из формулировок периодичности Ботта).
334
ГЛ. 6. КТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Большой интерес представляют гомологии с коэффициентами в этом спектре —
так называемые А-гомологии, но мы их не рассматриваем. Вещественная А-теория
определяется при помощи 8-периодического спектра, в котором
И'8г = BSO, = SO,...
Еще один пример: сферический Q-спектр S, в котором W{ = S1 и отображение
S‘ -* nSt + ] соответствует стандартному гомеоморфизму ->5f + 1, Соответст-
вующие гомологические и когомологические группы — зто стабильные гомотопиче-
ские группы -п q (X, А) и так называемые стабильные кого метопические группы
•п$(Х,А) = lim 7r(SJV+4(JVM), SN).
N
В заключение заметим, что произвольная теория экстраординарных гомологий или
когомологий получается при помощи указанной выше процедуры из некоторого
£2-спектра. Это нетрудно вывести из так называемой теоремы Брауна о представи-
мости, которую читатель найдет, например, в книге Спеньера.
§ 38. ВЫЧИСЛЕНИЕ К-ФУНКТОРА:
СПЕКТРАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ АТИА - ХИРЦЕБРУХА
1. Построение спектральной последовательности Атиа - Хирцебруха.
А. Формулировка. Мы изложим сейчас конструкцию, относящую конечному кле-
р р
точному пространству X набор абелевых групп Er = Еr (X) и гомоморфизмов
р р р + г
dr : Е r -+ЕГ , г = 2,3,.... р = 0,1,.... обладающих следующими свойствами.
(1) ЕР2=НР(Х- Z);
р р р— г р — г
(2) Er+i =Ker dr/\mdr (подразумевается, что Im dr = 0 при г >р);
р р р
(3) dr = 0 и Ег + 1 =ЕГ при любом четном г и любом р.
Ввиду конечности пространства X из (1) и (2) следует, что d, = 0 и Е’г₽+1 = Ер
р
также при любом достаточно большом г. Эти не зависящие от г группы Ег мы обо-
гр
значим через .
р = Кег[*Р(*) Кр(Хр2)]
" Кег[/Г₽(АГ) -+ КР(ХР)]
Поясним это свойство. Положим
<-г'>Кр(Х) = Кег[А₽(Х) -> КР(ХГ)].
Эти группы составляют фильтрации (ввиду периодичности Ботта мы можем считать,
что р = 0,1)
К°(Х) = (-^^(Х) D (°>К0(Х) Э ... Э (">А°(Х) = О,
К1(Х) = ^-^К^Х) Э <°>№(X) Э ... Э = О,
где n = dim X. Заметим, что если X связно, то К0 (X) = К(X).
§ 38. ВЫЧИСЛЕНИЕ К-ФУНКТОРА
335
Лемма. При четном г
(г)К°(Х) = <г+1>Х°(Х), <’-1>Х1(Х) = ^'(Х).
Доказательство. Рассмотрим фрагмент последовательности тройки
(X, Xr+1, Хг):
K°(X.Xr+1) К°(Х,ХГ) -+ К°(Хг+1,Хг)
II
О = К~г1(у 5°) = X°(v5r+1)
ввиду периодичности Ботта
Из точности видно, что естественное отображение
К°(Х, Xr + 1) -+ К°(Х, Хг)
эпиморфно. Теперь рассмотрим кусок коммутативной лестницы, составленной из
последовательностей пар (X, Хг ) и (X, Xr + 1):
а 0
Х°(Х,ХГ) -> К°(Х) -> К°(ХГ)
le II
К0(X, Хг+1) К°(X) К°(Хг+1).
Из эпиморфности е следует, что Im а = Im у, но Im а = Кег 0, Im у = Кет 8. Значит,
Кег/3 = Кет 6, что и требовалось.
Часть, относящаяся к К1, доказывается точно так же.
Ввиду леммы вышеуказанные фильтрации в К° (X) и X1 (X) принимают вид
К° (X) = (-2)Х0 (X) Э (0)Х°(Х) Э (2)Х° (X) D ...,
Х*(Х)= (~1)Х1(Х)Э(1)Х1(Х)Э(3)Х1(Х)Э ...,
и утверждение (4) показывает, что к этим двум фильтрациям присоединены группы
®£^®£1®Л’1®...,
/.'L ® ХД ® А’Х Ф /;’L ® • • .
,(5) Непрерывное отображение /: X -► У индуцирует (зависящие только от гомо-
топического класса отображения /) отображения/*: EP(Y) -+£’£(Х), обладающие
следующими свойствами: (а) диаграммы
dP
Ер Ep+r(Y)
f* dp Ы
Ер (Х)——~> Ер+г(Х)
коммутативны; (Ь) /*: Ер+1 (У) -> (X) совпадает с гомологическим гомо-
морфизмом, индуцированным отображением/*: EP(Y) -+Ер(Ху, (с) /*: Е£(У) -»
-» Е^(Х) совпадает с /*: Нр (У; Z) -»Нр (X; Z); (d) отображение/*: Epa>(Y)
^Е^ (X) индуцировано гомоморфизмом/*: К* (У) -+Х* (X).
Заметим, что в (5) содержится топологическая, и даже гомотопическая, инва-
риантность спектральной последовательности, в частности, ее члена Е2-
336
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
(6) Спектральная последовательность мультипликативна: все Е* = ®рЕр — гра-
дуированные кольца, дифференциалы удовлетворяют формуле Лейбница, умноже-
ние в Ег совпадает с умножением в Н* (АГ; Z), умножение в Е\ присоединено к ум-
ножению в К* (X) (см. упражнение (10) к § 37).
(7) Все дифференциалы dp имеют конечный порядок.
Это свойство мы можем доказать уже теперь, не дожидаясь построения спектраль-
ной последовательности. Если бы какой-нибудь дифференциал имел бесконечный
порядок, то было бы
rank (К°(Х) ® № (АГ)) = rank Е*„ < rank Е*„ = rank Н*(Х\ Z),
что противоречит сказанному в п. 4 § 37.
Умножим тензорно нашу спектральную последовательность на Q. Ввиду свой-
ства (7) все дифференциалы станут нулевыми и будет Ег = ЕЖ. Мы приходим к изо-
морфизмам К°'Х) « Q s tfeven (Х-, Q), К* (Л) 0 Q = Нойй (X; Q).
(8) Эти изоморфизмы совпадают с cHq (см. п. 4 § 37).
(Последнее утверждение нуждается в уточнении, поскольку изоморфизмы, дос-
тавляемые спектральной последовательностью, не являются каноническими, тогда
как изоморфизм cItq каноничен; уточнение мы оставляем читателю.)
В. Построение спектральной последовательности. Положим
p-r)^Kp*g(Xp,Xp~r)]
Кы{Кр*д(Хр*г-\Хр
Кы[Кр+д (Хр*г~1 ,Х‘
-^Kp+q(Xp-\Xp~r)]
и определим дифференциал dp,g: Ep,g -+Ep+r,g r+1 следующим образом. Рас-
смотрим коммутативную диаграмму
Кр+д (Хр+г~\Хр-г) -----?—>
6* I
j^p+<y+1 ^yp+2r—I jyo+r—I) А
Kp+g(Xp,Xp~r)
16*
F^lfjpUr-ljp)
Композиция 6* О a = /3 об*: Kp+g (Xp*r~1-,Xp-r) ->Л’₽+<?+1 (Xp+2r~1,Xp) может
рассматриваться как отображение
Kp*g (Хр+г~ 1, хр~Г)/Кет а Im /3.
Но по определению Ер,д есть подгруппа группы Kp*g (A'₽+,_I, Хр~г)/Кета, а
^fp+r,<7-r+i есть (факторгруппа группы Im/3 = Кет[Кр+д** (Хр+2г~1, X1*) -*
кр+д+1 (Хр+г, Хр) ] .Поэтому последнее отображение индуцирует некоторый го-
моморфизм
£Р,Ч -+ gp+r,q-r+l
Это и есть dp,g.
Легкая проверка показывает, что dp+',g~r+1 о dPi g - 0 и что
Ep:g = Kerdp-gl\mdp~r-g”-1.
г+1 г 1
Мы уже построили некоторую спектральную последовательность, но не ту, кото-
рую должны построить, поскольку построенная последовательность состоит из групп
с двумя верхними индексами, а нам нужны группы с одним верхним индексом.
§ 38. ВЫЧИСЛЕНИЕ К-ФУНКТОРА
337
Вычислим Ei’4 и Ер’ q. Имеем:
~pq_ K.et[Kp^q(Xp,Xp~1)^Kp+q(Xp-l,Xp-1)] _
E1 ~K.et[Kp+q(Xp,Xp~1)-+Kp+q(Xp,Xp~1)]
= KpJrq (Xp ,xp~l) = Kp+q ( V 5₽) =
р-мерные
клетки
= ® Kp+q(Sp)= ® X4(pt) ='£p (X,Kq (ptj).
р-мерные р-мерные
клетки клетки
Легко показать (детали мы оставляем читателю), что
df •4 = 6: rg р (X- Kq (pt)) -+ Цр+1 (X; Kq (pt))
и, следовательно,
E$-q =Hp(X,Kq(&y).
Другими словами, второй член нашей спектральной последовательности устроен
так: нечетные строки состоят из одних нулей, а в четных строках стоят целочислен-
ные когомологии пространства X (см. рис. 163),
Теперь заметим, что мы могли сразу доказать 2-периодичность нашей спектраль-
ной последовательности по q: из определений (и периодичности Ботта) следует, что
Ep,q = Ep,q+2 и dp,q = dp,q+2 при всех р, q, г. Поэтому мы можем отождествить
группы Ep,2s в одну группу Ер и дифференциалы dp,2s-. Ep,2s -+Ep+r,2s~r+l с не-
четным г в один дифференциал dp: Ер -* Ер+Г (остальные Ep,q и dp,q равны 0).
Мы приходим к нужной спектральной последовательности. Кстати, делается очевид-
ным неожиданное свойство (3).
Проверку остальных свойств мы оставляем читателю.
Построенная спектральная последовательность называется спектральной последо-
вательностью Атиа — Хирцебруха.
Спектральная последовательность Атиа — Хирцебруха имеет (очевидные) относи-
тельный вариант Я* (X, A; Z) =>Х* (X, А) и приведенный вариант Н* (X; Z) ^>К* (X).
[Запись G =* F применительно к спектральной последовательности означает, что на-
чальный (обыкновенно второй) член спектральной последовательности есть G, а
ее предельный член присоединен к F.]
Упражнение 1. Докажите, что порядок кручения в группах К° (X), К1 (X)
делит порядок кручения в группах Heven (X; Z), Я<м,<| (X; Z).
С. Обобщения. Спектральная последовательность Атиа —
Хирцебруха (точнее, ее вариант {kp,q, d%,q}), существует
для любой экстраординарной теории гомологий или ко-
гомологий; оиа имеет вид
Я,(Х;Л,(Р0)=>Л.(Х) или tf*(X;A*(pt))=>h*(X).
Обобщением этой спектральной последовательности явля-
ется ’’спектральная последовательность расслоения
{E,B,F,p) ”
Hjp-,h,(F))=*h,(E} или (F))=>ft*(F).
(Построение обеих последовательностей абсолютно
аналогично предыдущему.)
H*(X-Z)
Нули
H*(X,Z)
Нули
Н*(Х;2)
Нули
H*(X;Z)
нули
Н*(Х;2)
338
ГЛ. 6. К-ТЕОРИЯ и ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Разумеется, вторая спектральная последовательность может быть нетривиаль-
ной даже для тривиального расслоения. Все же с ее помощью можно получить /^-ана-
лог формулы Кюннета (см. статью Атиа в Topology. — 1962. — V. 1, July—Sept.).
2. Примеры вычислений.
А. К*(СРп). Второй член спектральной последовательности Атиа — Хирцебруха
имеет вид
Z О Z ... О Z
О I 2 ... In-1 2п
Все дифференциалы тривиальны по соображениям размерности. Вспомнив свойства
операции перехода к присоединенной группе, мы заключаем, что
К° (СР") = Z ® ... ® Z (п + 1 слагаемых),
Х1(СР") = О.
Мы докажем следующее уточнение этого утверждения.
Теорема. А0 (СР") = Z(7]/(7"+1), где 7 = f — 1 (f - расслоение Хопфа).
Лемма. Образ гомоморфизма
ch: £(52")->-tf*(52";Q) = #2"(52";Q)
II II
Z Q
совпадает с Н2п (52"; Z) = Z С Q = Н2п (52"; Q).
Доказательство леммы. При п = 1 зто нам известно, а общий случай
получается из этого индукцией по п ввиду коммутативности диаграммы
К° (АГ) —>//even(A';Q)
Is’ Is2
К2(Ъ2Х) Нечеп (У; Q)
II II
A°(V2A') -^//even (X; Q).
Доказательство теоремы. Пусть х G Н2 (СР"; Z) — образующая. Вы-
числим характеры Черна:
ъ
chy* =xk + — xfc+I + .. .;
ch7n=x", ch7"+1=O.
Это вычисление показывает, что у"*1 = 0и 1,7, ...,7" линейно независимые
А(СР"), и значит (поскольку А (СР") = Z"+1), они порождают А (СР") над Q. По-
кажем, что они порождают fr(tPn) над Z. Для СР1 это нам известно, пусть это уже
доказано для СР"-1. Пусть г0 + 7 + .. . + rn уп G К (СР"). Тогда r0 + rt 7 + ... +
§ 38. ВЫЧИСЛЕНИЕ К-ФУНКТОРА 339
+ /„-! у"-1 € К(СРп~х), и потому r0, rlt..., r„~i G Z. Значит, r0 + ^7 +.. .+
+ r„_17n"1 €K(CPn)~ иг„7"е/С(СР").Таккакг„7" ^0еЛ'(СГ,'1).тог„7''e
G K(CP", CP"-1) = К (Sln) (это получается из ^-последовательности пары (СР",
СР"-1) ввидуК~1 (СР"-1) =0).Hochr„7" = г„х", значит,
r„G Im [ch: X(S2")->#2"(52";Q) = Q],
и, ввиду леммы, rn G Z. Теорема доказана.
В. X*(RP"). Начальный член приведенной спектральной последовательности
Атиа - Хирцебруха имеет вид
при п = 2m 0 0 z2 0 0 z2 2m + I
0 1 2 3 2m-l 2m
при п = 2m + 1 0 0 z2 0 0 z2 z
Все дифференциалы тривиальны по соображениям размерности, и мы имеем:
[ 0 при и = 2m,
№(RP") =
I Z при и = 2m + 1,
порядок группы К° (RPn) равен 2^"^21.
Теорема. X°(RP") есть циклическая группа порядка 21 "/2 L
Доказательство. Поскольку включение RP2"1 -+ Rp2m+1 индуцирует,
как это видно из спектральной последовательности Атиа — Хирцебруха, изоморфизм
группы К0, достаточно доказать теорему для п = 2m. Естественное вложение
RPlm -+CP2m гомотопно, в силу теоремы о клеточной аппроксимации, некоторому
отображению/: RP2"1 ->CPm. Легко понять, что индуцированный когомологический
гомоморфизм
/*: tf*(CP",;Z)->tf*(RP2"’;Z)
является эпиморфизмом. Применяя к отображению / свойство (5) спектральной по-
следовательности Атиа — Хирцебруха, мы находим, что и отображение
/*: K0(CPm)^k°(RPlm)
эпиморфно, ввиду чего (и предыдущей теоремы) k° (RP2m) порождается /3, /З2,...
..., /Г”, где 0 = f*y. Но 7 = f — 1. Легко понять, что/*f = Cfr — комплексификация
вещественного расслоения Хопфа над RP2"1. Легко понять также, что (fR)2 = 1 (се-
чение расслоения (fR)2 = 52fR есть евклидова структура в расслоении fr). Значит,
(CfR)2 = 1, 02 = (CfR - I)2 = —2CfR + 2 =—20,03 = (—20)0 = 40,... ,0m =
= (— 2)m~10. Из этого видно, что произвольный элемент из К° (RP2"1) кратен 0,
т.е. Х° (RP2m) — циклическая группа.
Следствие из доказательства. Всякое комплексное векторное рас-
слоение над RPlm или RP2m+I стабильно эквивалентно расслоению fcCfR, причем
расслоения &CfR и ZCfR стабильно эквивалентны между собой в том и только в
том случае, если k = I mod 2m.
С. Другие вычисления К-функтора, в частности, для грассмановых многообразий
и многообразий флагов читатель найдет в книге Каруби (гл. IV). При этом Каруби
340 ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
не пользуется спектральной последовательностью Атиа — Хирцебруха, и читатель
может попытаться местами усовершенствовать его вычисления. О вычислении К-
функтора классических групп см. статью Атиа ”0 Х-теории компактных групп Ли”,
включенную в качестве приложения в русский перевод его ’’Лекций по Х-теории”.
3. Дифференциалы спектральной последовательности Атиа — Хирцебруха. Первый
нетривиальный дифференциал есть
d3 = d?: Я" (X; Z) Н"+3 (X; Z).
Упражнение 2. Покажите, что d3 есть стабильная когомологическая
операция.
Хотя мы не проводили вычисления Н* (К(Z, п); Z), читатель без труда может
вывести из результатов § 26, что
tf"+3(X(Z,«);Z)=Z2 (п>3).
Таким образом, имеется единственная нетривиальная стабильная когомологическая
операция, действующая из целочисленных когомологий в целочисленные и повы-
шающая размерность на 3. Эта операция действует так:
Я" (X; Z) Н" (X; Z2) Я"+ 2 (X; Z2 ) Я"+ 3 (X; Z).
После приведения mod 2 эта операция превращается в Sq1 Sq2 = Sq3, и се есте-
ственно обозначить через Sq3.
Теорема. d3 = Sq3.
Доказательство. Поскольку единственной альтернативой этому равенству
является равенство d3 = 0, нам достаточно указать пример, в котором действие
дифференциала d3 нетривиально.
Возьмем гомотопически нетривиальное отображение a: S5 -+S4 и составим прост-
ранство 54 О6. Так как я5(У4) = Z2, отображение (1: Ss —>Ss —*54 с degX = 2
гомотопно 0 и существует отображение у: D6 с 7I55 = /3. Это отображение сос-
тавляет с отображением
О6 = CSs CS5 = Г? ->54 иа Db
отображение 5: (Я6 U О6) = Sb -+S4 Ua D6, и мы полагаем X = (5 4 UaD6) ий О7.
Относительно X нам необходимо помнить, что X D S4 и что когомологии X устроены
так:
q <4 4 5 6 7 >7
//"(X;Z) 0 Z 0 0 Z2 0
яч(Х;г2) о z2 о Z2 Zj 0
причем операция Sq3 : Я4(Х; z2) -> H1 (X; Z2) нетривиальна. (Последнее доказы-
вастся так: операция Sq2: Я4 -* Я6 нетривиальна в X и„ О6, как нам известно из
§ 30, а в Х/S4 нетривиален гомоморфизм БокштейнаЯ6(Х/54; Z2) -*Я7(Х/54;г2).)
Если бы дифференциал </4: Я4(Х) -* Л’з(Х) спектральной последовательности
Атиа — Хирцебруха был тривиален, то отображение Х(Х) ->K(S4) было бы изомор-
физмом. В частности, отображение : S4 -+BU, соответствующее образующей группы
X(S4) = Z, продолжалось бы до некоторого непрерывного отображения ф: X -+BU.
Но отображение <р*:Я4(/Ш; Z2) ->Я4(54; Z2) нетривиально. [Действительно, у
образующей £ группы K(S4) характер Черна есть образующая группы Я4(S'4; Z);
8 39. ОПЕРАЦИИ АДАМСА
341
в то же время ch2 (О = — с2(£) -с2($) = -с2(^); следовательно, у>*(Н4 (В U; Z)) Э
Э-с2($) = 1 6Я4(Х4; Z), и, значит,^*(Я4(В(/; Z2)) Э 1 GH4(S4- Z2).] Значит,
и отображение ф*: H\BU\ Z2) -*Я4(Х; Z2) должно быть нетривиальным, что про-
тиворечит коммутативности диаграммы
Я4 (В U-, Z2)--> Я4 (X; Z2)
&1Ч I Sq 3
0 = //’(Bi/;Z2)-^—► H\X;Z2).
Следствие из доказательства. Существуют конечные клеточные
пространства X, Y и непрерывное отображение f : X -* Y, не являющееся гомотопи-
ческой эквивалентностью, но индуцирующее изоморфизм f*: K*(Y) —К*(Х).
(Этот факт был обещан и прокомментирован в п. 1 § 37.)
До казательство. Достаточно взять X из предыдущего доказательства и
положить Y = S4. Легко показать, что отображение S4 -+ S4 степени 2 продолжается
до отображения X ->S4; это и есть/. Что/*: К*(У) ->К*(Х) есть изоморфизм, пря-
мо следует из предыдущего вычисления, что / не есть гомотопическая эквивалент-
ность, видно из того, что уже/*: Я*(У; Z2) ->Я*(Х; Z2) не есть изоморфизм.
Добавим, что о дальнейших дифференциалах имеется лишь частичная информа-
ция; известно, например, что при г < 2р - 1 дифференциал dr имеет порядок, не
делящийся на р, а дифференциал d2p_i имеет порядок, не делящийся нар2. Подроб-
ности см. в статье Бухштабера в Математическом сборнике (1969. — Т. 78, № 2. —
С. 307-320).
§ 39. ОПЕРАЦИИ АДАМСА
1. Определение и свойства.
А. Введение. Когомологическая операция в Я-теории (да и в любой экстраорди-
нарной теории когомологий) определяется совершенно так же, как когомологичес-
кая операция в когомологиях. Она представляет собой класс гомоморфизмов
ах'. К(Х)^К(Х)
(или К‘1(Х) -> КЧ(Х), но мы предпочтем пройти мимо этой возможности), под-
чиненных условию коммутативности диаграмм
К(Х)——-+ К(Х)
f*l I f*
K(Y)~ K(Y)
(f: Y ->X - непрерывное отображение). Подход к классификации таких операций
диктуется общей идеей и. 2 § 27, которая сводит классификационную проблему к
проблеме вычисления К-функтора для пространства BU (с попутным преодолением
трудностей, связанных с бесконечностью BU, — см. н. 2Е § 37). Все эти проблемы
давно решены; результаты, относящиеся к комплексному случаю, содержатся в § 7
главы 4 книги Каруби, вещественный случай изучен в работе Андерсона (см.
Proc. Nat. Acad. Sci. USA. - 1964. - V. 51. - P. 634-636).
Мы систематически игнорируем вещественный случай. Что же касается комплекс-
ного случая, мы ограничимся рассмотрением наиболее важных конкретных когомо-
342 ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
логических операций в К-теории — так называемых операций Адамса. Читатель книги
Каруби знает, что, по существу, эти операции исчерпывают все многообразие когомо-
логических операций в комплексной Х-теории — в той же мере, в какой квадраты
и степени Стинрода исчерпывают все многообразие когомологических операций в
обычных когомологиях.
В. Определение операций Адамса. Операция в К-теории должна естественным
образом ставить в соответствие виртуальному векторному расслоению с базой X
другое виртуальное векторное расслоение с той же базой X. Если отбросить здесь
виртуальность, то понятие операции станет в высшей степени прозрачным. Действи-
тельно, мы знаем массу способов естественного построения векторного расслоения
по векторному расслоению: расслоению £ можно поставить в соответствие расслое-
ние $ ® | или Л2|, или 52| или вообще взять любое представление (размерности
N) группы U(n) и ассоциировать с era помощью с и-мерным расслоением | некото-
рое TV-мерное расслоение. Общая беда всех этих конструкций состоит в их неад-
дитивности: (|| ® |2) ® ($1 ® (Si ®$i) ® (?2® 1г) ит.д.; поэтому отсутству-
ет возможность прямого перенесения их в /С-теорию. Конструкция Адамса достав-
ляет способ (в известном смысле, единственный — см. цитированный параграф
из книги Каруби) составить из этих операций аддитивную комбинацию.
Пусть ej, е2, . . . — элементарные симметрические многочлены, Nlt N2, . . . —
ньютоновские симметрические многочлены (суммы степеней). Пусть
Wj =Л(е,),
N2 =Л(е1, е2>
Мз =Рз(е1, е2, е3),
Для расслоения (настоящего) | положим
= Л2|,.. ., Л*|).
Например,
Ф1(8 = 1
*2(1) = 1*|-2Л2$,
ф3(£) = |®$®$ -з$ ®л2$ + зл3$,
В силу этого определения ф*(£) — виртуальные расслоения.
Лемма, ф *(£ ® п) = Ф *(£) ® Ф *(т?).
Доказательство. Разобьем совокупность переменных Xj,.. ., xN на две
группы:уj,. . . ,ум и Zj,.. ., Z/, (L, MnN= L + Мочень велики). Очевидно,
M-(x) = ATr(y)+ATr(z),
е,(х) = S_ es(y)et(z).
Следовательно,
Рк (ei ( У), е2 (У), •..) + Рк («1 (z), е2 (z),...) =
= Л:( 2 es(y)et(z), S es(y)et(z),. ..),
s+t=l s+t=2
т.е.
Pk(°4,ot2, ) + Pk(Pi,Pz, -) = pk( 2 «jft, S <*,&,.••)•
s+t=l s+t=2
§ 39. ОПЕРАЦИИ АДАМСА
343
Подставляя в последнюю формулу As£ и Afr? вместо as и и пользуясь равенством
® As£ ® Лгт? = Лг(£ ® 17),
s+t=r
мы приходим к равенству
P*(t, Л2£,... ) +Рк(п, Л2п, ...) = Pk(^V, Л2(| ® п), • • •),
т.е. ф*(|) + ф*(т?) = ф*(| ® т?).
Доказанная лемма позволяет распространить определение операции фк на вирту-
альные расслоения. Получается когомологическая операция
фк: K(X)^K(Y)
(перестановочность фк с гомоморфизмами f* очевидна), которая по построению
аддитивна, т.е.
Ф*(1+П) = Ф*(1) + Ф*(1).
С. Свойства операций фк.
Теорема. (1) dim фк(£) = dim £.
(2) фк(^) = (фк^)(фкч).
(3) фк °Ф1(П = фк1(!-).
(4) ch4 фк (!) = к4 ch4 $.
(5) Если £ есть геометрическое (т.е. не виртуальное) одномерное расслоение,
тофк(^)=е.
(6) Если р - простое число, что ф ₽(£) =^р mod р. _
(7) Положим ф°(£) = dim£,^“'(£) = £, ф~к($) = фк (?). Для таким образом оп-
ределенных фк,к€2, выполнены свойства (1) - (5).
Доказательство. (1) Ввиду аддитивности операций фк и dim достаточно
рассмотреть случай, когда £ есть геометрическое расслоение. В этом случае мы имеем
(п = dim|) =
dim фк(£) =Pk(dim £, dim Л2£,..., dim Лк£) =
= Рк(п,С2,...,Ск) =
= PfcCeJl,... ,]),е2(1,...,1). . . . ,efc(l,...,l))=Afc(l,...,l)= lk + ... + lk=n.
п п п п П
(5) Если £ — геометрическое одномерное расслоение, то Л'£ = 0 при г > 1 и
Фк«)=^а,о,о,...,о) = ек.
(6) Утверждение следует из сравнения Np = (ei )р modp.
Наиболее естественное доказательство утверждений (2) — (4) основано на приме-
нении ’’принципа расщепления”, упоминавшегося в п. 5 § 19; этот принцип заклю-
чается в том, что различные формулы, включающие векторные расслоения, можно
доказывать в предположении, что эти расслоения разлагаются в сумму одномерных
расслоений. Обоснованием этого принципа служит тот факт, что естественное вложе-
ние (СР”)" п) индуцирует мономорфизм как в когомологиях (это нам,
по существу, известно), так и в A-теории (это легко доказать при помощи спектраль-
ной последовательности Атиа — Хирцебруха). Мы, однако, приведем более короткое
доказательство, использующее принцип расщепления в завуалированном виде.
(4) Формула £ (ch’i/^t — A/’ch’t) определяет характеристический класс век-
торных расслоений со значениями в 2<?-мерных рациональных когомологиях. Сог-
ласно результатам § 19 этот класс представляется как (рациональный) полином от
344
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
классов Черта. Там же было доказано, что ненулевой полином от классов Черна обя-
зательно принимает ненулевое значение на расслоении f X . . . X f (п сомножителей)
с базой (СР°°)", где п — достаточно большое число. Имеем:
ch^ex...x0«ch^(p;f®...®p‘n=
= ch !/,*(/>;;£)] =
= ch[(p;f*)®...®(P*f*)] ^(cho* +...+p;(chn* =
n CO faQ n
= piekx + ...+p*ekx= 2 ekxi= 2 — 2 x?.
i = l <f=0 q\ i= 1
(Обозначения: pt — проекция на i-й сомножитель, x € H2 (CP°°; Z) и xj,..., xn G
G//2((CP°°)"; Z) — когомологические образующие.) Значит,
kq n
ch^k(fX...Xf) = —- 2 x?,
1 = 1
в частности,
ch’(f X ... X f) = —- S
q\ i=i
откуда
ch<tyk(f X ... X f) = ch’(f X ... X f),
что и требовалось.
(3) Формулу достаточно доказать в случае, когда £ — тавтологическое расслоение
над грассманианом. Так как когомологии грассманиана не имеют кручения, то и его
.^-функтор не имеет кручения (зто видно из спектральной последовательности Атиа—
Хирцебруха — ср. упражнение 1 к § 38). Значит, характер Черна мономорфен (его
ядро должно быть конечно), и нам достаточно доказать, что
сЬ(фкоф'(|))=ф*'(П
Имеем:
сЬч(фкф‘(^ = А5сЬ<?(ф/(|)) = Arch’S =
= (JW)’ch’$ = chq (фк1$)).
(2) Доказательство аналогично предыдущему: достаточно рассмотреть случай,
когда % и Т) — расслоения над произведением двух грассманианов, служащие подня-
тием тавтологических расслоений над сомножителями. Когомологии произведения
грассманианов опять-таки не имеют кручения, и мы можем безболезненно приме-
нить к двум частям доказываемого равенства характер Черна. Имеем:
ch<7^*(|n) = *<?ch<’(^) = )t4' 2 ch^ch'n =
j+ t = Q
= 2 (fcschs£) (fcfchf7j) = 2 (chsi//k{) (ch'^ij) =
j + t = q s+t = q
= сЬ’[(фк|)(фкЧ)].
Наконец, утверждение (7) является очевидным следствием доказанного.
Следствие и з~ (1). фк(К (X) ) СК (X); таким образом, фк молено рассмат-
ривать как операцию К (X) -* К(Х).
§59. ОПЕРАЦИИ АДАМСА
345
Следствие из (3). фк о ф1 = ф1 о фк.
2. Простое доказательство несуществования сфероидов с нечетным инвариантом
Хопфа (Адамс — Атиа). Пусть X £ я4п_1(52"). Приклеим к сфере S2n шар Л4"
посредством сфероида 54"-’ -> S2n класса X. У полученного пространства X такие
когомологии:
„ I Z при а = 0, 2п, 4п,
H4(X-,Z) = н
I 0 при остальных
Пусть a G Н2п(Х-, Z) и b G Н4п(Х\ Z) — естественные образующие. Тогда а2 = hb,
где h G Z. Число h называется инвариантом Хопфа класса X. Следующая теорема уже
неоднократно формулировалась и комментировалась на протяжении книги (см.,
в особенности, п. 4 § 16 и п. 4 § 30).
Теорема. Если п Ф 1,2, 4, то в л4п-1($2п) отсутствуют элементы с нечетным
инвариантом Хопфа.
Доказательство. Ввиду наличия элементов с инвариантом Хопфа 2 и ад-
дитивности инварианта Хопфа (см. п. 4 § 16), нам достаточно доказать, что при л ¥=
¥= 1, 2, 4 отсутствуют элементы с инвариантом Хопфа 1. Пусть все же h = 1, т.е.
а2 = Ь.
Вычислим К (%). Из /^-последовательности
0^K(S4n)^K(X) -^А(52п)-*0
пары (X, S2n) мы имеем: К(Х) Z ©Z. В группах k(S2n) и К (S4n) имеются кано-
нические образующие а и /3. В группе К (X) имеются образующие а и /3, одна из кото-
рых, /3, определяется как образ (3, а другая, а, есть произвольный прообраз а и опре-
делена с точностью до прибавления кратного /3. Характеры Черна виртуальных рас-
слоений а и /3 — образующие групп Я2"(52"; Z) и H4n(S4n-, Z). Отсюда мы заклю-
чаем, что ch/3 = b, a ch а = а + eb, где е — не известное нам рациональное число. (Это
число не будет иметь никакого значения в настоящем доказательстве, но оно сыг-
рает важную роль в следующем параграфе.) Так как
cha 2 = (ch а )2 = (а + eb)2 - а2 = b = ch (3,
то а2 = /3. Далее, в силу свойства (4) операций фк
фка = кпа, фк0 = к2п0.
Следовательно,
фка = кпа + ркр (рк £ Z), фк0 = к2п0.
Из сравнения ф2 а = a2 mod 2 следует, что р2 нечетно (это — центральный момент
доказательства!). В то же время,
ф2ф3 а = |//2(3" а + д3/3) = 6" а + 3”д2/3 + 22"д3/3,
ф3ф2 а = ф3(2па + р2(3) = 6" а + 2"д3/3 + 32пд2/3,
откуда, ввиду ф2 ф3 = ф3 ф2,
Зпц2 + 22”д3 = 2"д3 + 32"д2 ,
д23"(3"-1) =Дз2л(2"-1).
346
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Так как р2 нечетно, то 3" - 1 делится на 2”, что возможно только прн п = 1, 2, 4.
[Действительно, очевидно, 32s = 1 mod 8 и 32l+1 = 3mod8. Поэтому, если
п = 2Z • т, где т нечетно, то (при I > 1)
3” - 1 = (З2''1т + 1)(32,~2т + 1) ... (Зт + 1)(Зт - 1) =
~ 2-2 • • ' 2 ' 4 • 2 = 2'+2 mod 2/+3,
I - 1
т.е. при четном п число двоек в разложении 3" - 1 на простые множители равно
I + 2; а при нечетном п оно и того меньше: равно 1. Значит, из делимости 3" — 1
на 2" вытекает, что п = 2l т > I +2; при т = 1 это неравенство выполнено для
I < 2, при т > 3 - не выполнено ни для каких /.]
Напомним, что существование в Я4П_1(52") элемента с нечетным инвариантом
Хопфа равносильно параллелизуемости сферы 52"-1. Поэтому рассмотренная
проблема имеет естественное уточнение; каково максимальное число линейно неза-
висимых векторных полей на сфере Sm ? Если сфера Sm параллелизуема, то это чис-
ло равно т, если же она не параллелизуема, то можно сказать только, что это число
меньше т. Чему же оно равно? Ответ на этот вопрос дает следующая
Теорема. Представим число п в виде (2а + 1)24ь + с, где а,Ь, с — неотрица-
тельные целые числа и с <3. Положим, далее, р(п) = 2е + 8 Ь. Тогда на сфере Sn~1
существует р(п) — 1 линейно независимых векторных полей и не существует боль-
шего их количества.
Первая часть этой теоремы является классической — она доказана Радоном и Гур-
вицем — и не затрагивает гомотопической топологии. Вторая же часть теоремы
(что не существует большего количества векторных полей) была доказана Адамсом,
который свел ее к вычислению операций ф* в А-функторе ’’усеченных проективных
пространств” RP1 /RPT. Подробности читатель может найти в оригинальной работе
Адамса (русский перевод — Математика: сб. перев. — 1963. — Т. 7, № 6; эта работа
замечательна тем, что в ней впервые появились операции ф*); более удобным для чи-
тателя образом (без внешних ссылок) этот предмет изложен в ’’Дифференциальной
геометрии и топологии” Дж. Шварца.
§ 40. / ФУНКТОР
1. Определение и связь с гомотопическими группами сфер.
А. Определение. Пусть £ и т? — векторные расслоения одной размерности с общей
базой, 5(|) и 5 (т?) — соответствующие сферические расслоения. Расслоения £ и г/
называются послойно гомотопически эквивалентными или J-эквивалентными, если
существует отображение 5(£) -> 5 (т?), тождественное на базе и имеющее степень 1
на каждом слое.
Пусть X — конечное клеточное пространство. Элемент a G К (%) называется J-три-
виалъным, если а = {£ — т?} и расслоения £ и т? /-эквивалентны. Очевидно, /-три-
виальные виртуальные расслоения составляют подгруппу группы К(Х) С К(Х)',
мы обозначим ее через Т (X) и положим
/(X) = К(Х)/Т(Х), 7(Х) = К(Х)/Т(Х).
Таким образом, /(A)=Ker[dim: /(%)-> Z], J(X) = Z® 7(X).
§ 40. J-ФУНКТОР
347
У'п ражнение 1. Покажите, что Т (X) С К (X) состоит из классов стабильно
эквивалентных расслоений над X, таких, что произвольное расслоение достаточно
большой размерности из этого класса /-эквивалентно тривиальному расслоению.
Непрерывному отображению f: X-*Y отвечают отображения /*: J (У) -> J (X) и
/*: J(Y)-> J(X). Мы увидим,однако,что функтор J не является полу точным, т.е. по-
следовательность
/'(Х/А) —> J(X) —► 7(Л),
индуцированная включением А -> X и проекцией X -> Х/А, не обязана быть точной
даже для конечных клеточных пар.
В. J-гомоморфизм и J-функтор сферы. Действие группы U(n) в S2"-1 опреде-
ляет отображение (/(л) -> C(S2"-1, 52"-1). Если мы возьмем композицию этого
отображения с надстройкой S: C(S2"-1, S2"-1) ->• C(S2n, S2n), то получим
отображение группы U(п) в пространство отображений S2n -* S2n, оставляющих
на месте некоторую точку (любой полюс), т.е. отображение
U(n) —► n2nS2n.
Соответствующий гомоморфизм гомотопических групп
^•((/(л)) - я,(П2"52п) - я2п+,-($2")
называется /-гомоморфизмом. Особенно интересен стабильный J-гомоморфизм
(n&i) в случае нечетного i:
^2к-1(и(пУ) = Z П2п+2к-1($2п) = irS2k-i.
Образ этого гомоморфизма представляет собой циклическую подгруппу группы
я2*-1, которая, как мы увидим, может иметь весьма большой порядок; вычисле-
нием этого порядка мы будем заниматься как в этом, так и в следующем параграфе.
(В действительности, интерес представляет образ ’’вещественного /-гомоморфизма”
/: Я4*_!(50(л)) -* Я4*_1, который может оказаться немного (вдвое) больше об-
раза комплексного /-гомоморфизма. Различие между этими образами мы проком-
ментируем в следующем параграфе.)
Посмотрим теперь, что представляет из себя / (Sm).
Теорема. / (Sm) = Im [/: ят_!(1/) ->Ят_1 ].
Этот факт, в сущности, очевиден. Векторное расслоение размерности п над Sm
определяется ’’отображением склейки” Sm~l -> U(ri), посредством которого
склеиваются два тривиальных расслоения над полусферами D™ С £т; /-тривиаль-
ность расслоения в точности означает, что отображение склейки гомотопно постоян-
ному отображению в C(S2"-1, S2"-1) D 1/(л).
С. J-функтор как образ К-функтора в полуточном функторе. Рассмотрим для ко-
нечного клеточного пространства X совокупность всевозможных ориентированных
сферических расслоений над X, т.е. локально тривиальных расслоений над X со слоем
348
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
сфера, слои которого могут быть согласованным образом ориентированы. Два таких
расслоения, Pi: Et -> X и р2: Е2 X, считаются эквивалентными, если существует
непрерывное отображение Ех -+ Е2, при каждом х G X отображающее р\1 (х) на
р 2* (х) со степенью +1.
Упражнение 2. Проверьте, что зто — отношение эквивалентности.
Совокупность классов эквивалентных расслоений мы обозначим через 5 (X).
Размерность сферического расслоения определяется как размерность слоя +1;
у эквивалентных расслоений размерности одинаковы.
Сферические расслоения можно складывать: сумма двух расслоений определяется
при помощи послойного джойна
Л1 * f Е2 -
{01.Уз, t) G Ej X Е2 X /(PiCy,) = Р2(у2)}
(УьМ
{если yi =У1, t = t'=O,
или у2 =у2, t-t = 1
(рис. 164). Эта операция превращает S (X) в коммутативную полугруппу. Соответ-
ствующая группа Гротендика обозначается через П(Х). Очевидным образом опреде-
ляется гомоморфизм dim: П(Х) ->Z. Ясно, что
П(Х) = Z ф П(Х),
где П(Х) = Ker dim.
Упражнение 3. Покажите, что П (X) - группа классов стабильно эквива-
лентных ориентированных сферических расслоений. (Сферические расслоения ста-
бильно эквивалентны, если эквивалентны их некоторые кратные надстройки.
Надстройка над сферическим расслоением определяется как послойная надстройка;
другими словами, кратная надстройка — это сумма с тривиальным сферическим
расслоением.)
Для непрерывного отображения /: X -> Y очевидным образом определяются
гомоморфизмы /*: П(У) ->П(Х), /*: П(У) ->П(Х).
Рис. 164
§ 40. J-ФУНКТОР
349
Упражнение 4. Покажите, что П - полуточный фактор, т.е. последова-
тельность
ff(х/а) п(А) -> П(Л)
точна для любой конечной клеточной пары {X, А).
Имеется естественный по X гомоморфизм К(Х) -> П(А) (векторному рас-
слоению ставится в соответствие соответствующее сферическое расслоение). Очевид-
но, J (А) есть образ К (X) в П (А).
Теорема.
П(5”) =
s
я»—1
при
при
п = 1,
п > 1.
О
Доказательство. Ориентированное сферическое расслоение размерности N
над5" определяется отображением склейки 5"-1 ->С1(5ЛГ-1 ,SN~I) , где Ct обо-
значает совокупность отображений степени 1. Но С) (SN ~1,SN ~1) расслаивается над
Slv~1 со слоем 1, £lN1)o (индекс 0 обозначает связную компоненту). Поэто-
му при п > 1 гомотопические классы отображений склейки составляют группу
Таким образом, группа П(5") конечна при любом п.
Теорема. Группа П (А) конечна для любого клеточного пространства X.
Доказательство. Очевидно, П (pt) = 0. Если утверждение уже доказано для
пространств, в которых клеток меньше, чем в А, то мы обозначаем через Y простран-
ство, полученное из А выбрасыванием одной клетки максимальной размерности
(скажем, п ) и выводим нужное из точной последовательности
П(5”) -> П(А) -> П(Г).
Следствие. Группа J (А) конечна для любого конечного клеточного прост-
ранства А.
Действительно, J (А) С П(А). ~
D. Некоторые свойства функтора П. Полуточ-
ный функтор П можно использовать для построе-
ния ’’половины теории когомологий”:
ПЧ'(А, А) = П(2’(А/Л)),
q < 0.
Однако отсутствие периодичности Ботта препят-
ствует определению групп ПЧ(А, А) с q > 0.
Впрочем, для П (как и для любого полуточного
функтора) есть аналог спектральной последова-
тельности Атиа — Хирцебруха: группы Ef,q
определены при р > 0 и q < 0, причем E%,q =
350
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
= НР{Х;, П(№<7)); группы E&q с р + q =г < 0 составляют группу, присоединенную
к П~Г(Х) (см. рис. 165).
Заметим еще, что если X = S У, то
ПШ = я(У, nNSN),
т.е. П(Х) = Р°(У) = Р1(Х), где Р — экстраординарная ’’когомотопическая теория
когомологий”, — см. п. 5D § 38. Следовательно, для любой конечной клеточной
пары
П’(ХЛ) = Pq*\X,A) при <?<-!.
Это позволяет сказать, что функтор П близок к когомотопической теории, в кото-
рой размерности сдвинуты на 1. К сожалению, не удается установить равенства
П°(Х, А) = Р1(Х, А) для произвольной клеточной пары (X, А).
2. Гипотеза Адамса.
А. Введение. Гипотезой Адамса по инерции продолжают называть давно доказан-
ное утверждение, что для любых a G К(Х) h£GZ+ найдется такое 7У,что
к*(фк(а) - а) G Т(Х).
Адамс сформулировал свою гипотезу в статье ”0 группах J (X). I ” (Topology. -
1963. — V. 2. — Р. 181 -195; русский перевод — Математика: сб. перев. — 1966. -
Т. 10, № 5). Сам он доказал ее для одномерных геометрических расслоений. В после-
дующие годы гипотеза Адамса постоянно находилась в центре внимания ведущих
топологов, но доказана она было только в 1970 г. В этом году сначала Квиллен
анонсировал доказательство гипотезы Адамса (подробное изложение работы Квил-
лена появилось позже), а затем Сулливан, используя некоторые идеи Квиллена,
получил полное доказательство. Доказательство Сулливана, вместе с подготовкой и
большим количеством побочных результатов, составило целую книгу, переведенную
на русский язык под названием ’’Геометрическая топология” (Мир, 1975).
Однако в 1975 г. Беккеру и Готтлибу удалось найти относительно простое доказа-
тельство гипотезы Адамса, основанное на понятии трансфера (Topology. — 1975. —
V. 14, № 1); это доказательство мы изложим ниже в этом пункте (воспользовавшись
одним простым фактом из теории представлений, доказательство которого выходит
за рамки нашего курса).
В. Случай одномерного расслоения. Если а - геометрическое одномерное рас-
слоение, то утверждение гипотезы Адамса является следствием следующей теоремы
Адамса — Дольда.
Теорема. Пусть 11- два комплексных векторных расслоения одной раз-
мерности с конечной клеточной базой X. Предположим, что существует послойное
отображение S (£ i) -* S (|2 ), накрывающее тождественное отображение id X и имею-
щее на каждом слое степень k>0 (S, как обычно, обозначает переход к сферическо-
му расслоению). Тогда для некоторых N и М расслоения kN^t ф Ми kNl2 ® М
J-эквивалентны.
Выведем из этой теоремы утверждение гипотезы Адамса для геометрических одно-
мерных расслоений. Пусть а — такое расслоение. Согласно свойству (5) операций
Адамса, ф*а = ак. Очевидно, далее, что существует отображение S(a) -> S(ak),
имеющее на каждом слое степень к: оно задается в слоях формулой z н z*.
§ 40. J-ФУНКТОР
351
Таким образом, расслоение kNtyk(a) ® М /-эквивалентно kNа ® М, откуда
kN(фк(а) — а) е Т(Х).
Доказательство теоремы Адамса — Дольд а. Сначала сведем
общий случай этой теоремы к случаю, когда расслоение |2 тривиально. Предполо-
жим, что в этом случае теорема уже доказана, и подберем расслоение q, такое, что
сумма q ® |2 тривиальна. Послойное отображение 5(11) ->5(|2) степени к превра-
щается, после прибавления q, в послойное отображение S(q ® $1) ® |2) сте-
пени к. По предположению, при некоторых N и М расслоение kN (q ® Ii) ® М
/-эквивалентно расслоению kN (q ® |2) ® М. Но тогда /-эквивалентны расслоения
kN (ji ® Ii) ® М ® kN%2 и kN (v ® 1г) ® М ® kN , т.е. kN® М' й kN 1-2 & М1,
где М* =Ms kN (|2 ® г?). Таким образом, теорема верна и в общем случае.
Переходим теперь к рассмотрению случая тривиального |2. Пусть £ — векторное
расслоение размерности п с базой X, Е — пространство соответствующего сфе-
рического расслоения. Предположим, что существует послойное отображение
f: Е -» АХ 52л-1, имеющее на каждом слое степень к. Обозначим через IЕ простран-
ство сферического расслоения, соответствующего расслоению таким образом,
IE есть пространство расслоения над X со слоем 52/я-1, причем слой этого рас-
слоения над точкой х 6 X есть джойн I экземпляров слоя расслоения Е -> X над точ-
кой х. Обозначим, далее, через I f отображение IЕ-+ХУ. S2nl~x, которое представ-
ляет собой Z-кратный послойный джойн отображения f. Мы докажем следующее
утверждение.
Существуют натуральное число N и послойное отображение g: kNE -* X X
.N
X S2n * 1, имеющее степень 1 на каждом слое, такие, что диаграмма
кГЕ ---—------*~Х* S2nl,>l~'
X. idx«*
x^s2"*"',
в которой h - отображение степени kN, послойно гомотопически коммутативна.
Разумеется, нам этого достаточно: достаточно уже существования отображения g.
Это утверждение мы докажем индукцией по числу клеток в X. Именно, мы пред-
положим, что X получается прибавлением одной тп-мерной клетки из некоторого
пространства Y, для которого утверждение уже доказано (с N1 вместо N). Зафикси-
руем для дополнительной клетки характеристическое отображение (/У", 5т-1) ->
-> (X, К) и возьмем над Dm индуцированное расслоение, которое, разумеется, будет
тривиально. Наша задача сводится к следующей. Имеется диаграмма
f 1И-1 JU-1
s х <$• ----$ X 1
в которой все отображения послойны (над S'"-1), отображение /' имеет на слоях
I
степень к , отображение g имеет на слоях степень 1 и вся диаграмма послойно
гомотопически коммутативна. Известно, что отображение /’ продолжается до по-
352
ГЛ 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
слойного отображения F: ГТ1 X 5м-1 -> SM~l. Наша цель - продолжить при неко-
тором N" отображение kN g': S'”-1 X SM~* X SM-1, где M = kN"M,
до отображения G': LfnXSM~1 таким образом,что диаграмма
» Д ** X
в которой h имеет степень kN, N = N1 + N", будет послойно гомотопически ком-
мутативна. Другими словами, задача такова. Обозначим через G(М, г) пространство
отображений SM~1 -> SM~l степени г. Отображение g' определяет по формуле
g'(x, у) = (х, ['>'(-*)]€>’)) некоторое отображение у: Sm~l -+G(M, 1),обладаю-
щее тем свойством, что композиция
S'"-1 —G(M, 1) G(M,kN), (♦)
в которой вторая стрелка есть взятие композиции с фиксированным отображением
й': Sm~l -* S'"-1 степени kN , гомотопна постоянному отображению. Но у есть
сфероид, представляющий некоторый элемент с группы
Ят — I (G(М, 1)) = Ят _ 1 ,
и гомотопность нулю композиции ( ♦) означает в точности, что kN с = 0.
Гомотопическая лемма. Если сфероид a: S1 -*G(M, 1), М > 1,пред-
s i
ставляет элемент а& п1 ,то сфероид а * ... ♦ а: S -> G(qM, 1),
я
а ♦ ... * а(х) =
= [а(х)* ... *а(х): ♦ ... ♦ S""1 * SMi ♦ ... ♦ SM~1 ],
s
представляет элемент qa 6 я,.
Доказательство леммы. Можно считать, что а переводит отмеченную
точку сферы S1 в тождественное отображение. Заменим отображение а* ... * а
гомотопным ему отображением «1 ♦... *aq, где at = ao(}{t s' -> Sl -
отображение, загоняющее в отмеченную точку дополнение к шарику dt С S1 и
растягивающее этот шарик на всю сферу S1; шарики dt предполагаются попарно
непересекающимися. Очевидно, ♦ ... ♦ ая есть сумма q сфероидов, каждый из ко-
s
торых представляет в я, тот же элемент, что и а.
Теперь мы завершим доказательство, положив N" = N1. Из леммы следует, "что
отображение 7 ♦... *7 (kN сомножителей) гомотопно 0, а это отображение индуци-
§ 40. J-ФУНКТОР
353
руется отображением kN gc, так что kN gr продолжается до отображения G;
в качестве h мы берем h * ... * h (к N сомножителей).
-Теорема Адамса — До льда доказана.
С. Теорема Беккера - Готтлиба о существовании трансфера. Сведение общего
случая гипотезы Адамса к ее одномерному случаю осуществляется при помощи
чисто геометрической теоремы Беккера — Готтлиба.
Пусть G — компактная группа Ли (компактная подгруппа группы GL(N, R)),
М — замкнутое многообразие с гладким действием группы G. Пусть, далее,
р: Е-+Х— гладкое расслоение со слоем М и структурной группой G.
Обозначим для пространства Y через Y+ сумму Y LI pt. Для нас важно, что
ZN Y+ = УХ Sn/YX pt,
т.е. TV-кратная надстройка над У+ состоит из TV-мерных сфер, проходящих через точ-
ки пространства У и скрепленных в одной точке (рис. 166).
Заметим еще, что ZN У+ есть пространство Тома TV-мерного тривиального вещест-
венного векторного расслоения над У (см. п. 2 § 30).
Теорема (Беккер — Готтлиб). При некотором достаточно большом N сущест-
вует отображение t: "LNX* -> 2ЛГЕ+, такое, что при композиции
t 2"
ZN X* —► £nE* ZNX+
каждая из N-мерных сфер, из которых сделана надстройка ZNX*, отображается в
себя со степенью х (М) (эйлерова характеристика многообразия М).
Отображение t называется трансфером.
Пример. Пусть р: Е -+Х — конечнолистное накрытие. Можно считать, что Е С
С X X RAr и р — сужение проекции X X Rw -+Х. Нормальное расслоение к Е в X X RAr
Рис. 166
тривиально (нормальные пространства к Е без вырождения проектируются в сом-
ножитель R7*). Обозначим через D открытый шар в R7*, такой,чтоТ?СXXD, и через
U — узкую трубчатую окрестность Е в X X RAr. Имеем отображение
ArXRJV/[ATX(RAr-Z))] X RA'/[(^X RA')-17]
II II
y,nx+ zne\
Это отображение мы и принимаем за t; проверьте, что требования теоремы для не-
го выполнены.
12. А.Т. Фоменко
354 ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Доказательство теоремы Беккера — Готтлиба. Конструкция
отображения t в общем случае обобщает конструкцию предыдущего примера.
Лемма. Пусть М - компактное гладкое многообразие, в котором действует
компактная группа Ли G. Тогда существует линейное представление группы G в не-
котором пространстве RN и эквивариантное (т.е. перестановочное с операторами
из G) С°° -вложение M-*RN.
Доказательство. Пусть L — пространство С°° -функций на М. Формула
gf(x) = f(gx) ,g€G,f€L,x€M, определяет представление группы G в L. Как из-
вестно из теории представлений (см. Кириллов А.А. Элементы теории представле-
ний. - М.: Наука, 1972, п. 9.2), конечномерные подпредставления представления
L порождают в L плотное подпространство; другими словами, для всякой_функции
f G L найдется сколь угодно близкая к ней (в С°* -топологии) функция Д содержа-
щаяся в конечномерном инвариантном подпространстве L С L. Возьмем теперь про-
извольное С°° -вложение М -> Rk; пусть/!,..., Д: М -»R — его координатные функ-
ции. Выберем функции Д,., fk'. М -» R, которые содержатся в конечномерных
подпредставлениях L , Lk С L и которые настолько близки к Д,..., fk, что
отображение М -> R* с координатными функциями Д...Д снова является вло-
жением. Пусть gn,..., gjn. — базис пространства L, (п{ = dim Lf). Это - функции,
составляющие отображение М -> R”'^которое является, в действительности, экви-
вариантным отображением g,: М -» Lt- (штрих обозначает переход к пространству
функционалов). Вместе отображения gi,..., gk составляют эквивариантное отоб-
ражение М -+ Lf X ... У L'k, которое является вложением,-Поскольку среди линей-
ных комбинаций его координатных функций содержатся Д,..., Д. Лемма дока-
зана.
Зафиксируем теперь эквивариантное вложение многообразия М в пространство
Rn представления группы G. Поскольку группа G компактна, ее действие в прост-
ранство R7^ можно считать ортогональным. (Образ группы G в GL(N, R) компак-
тен, а всякая компактная подгруппа группы GL(N, R) сопряжена с подгруппой
группы О (А) ) Возьмем открытую е-окрестность Т многообразия М в RN с до-
статочно малым е; ввиду ортогональности действия окрестность Т G-инвариантна.
Вложим теперь R77 в SN = RN U °° и продолжим действие группы G в RN на SN
условием g (°°) = °® при любом g 6 G. Факторпространство SN/(SN - Т) есть прост-
ранство Тома нормального расслоение v к многообразию М в R7V; итак, мы постро-
или эквивариантное отображение SN -» Т(у). Далее, расслоение v вкладывается в
сумму v ® т, где т — касательное расслоение многообразия М, и это определяет отоб-
ражение Т(у) -> Т(у ®т), разумеется, также эквивариантное. Так как v ®т = N, то
Т(у ® т) = ^,NМ+ . Итак, мы построили эквивариантное отображение SN
§ 40. J-ФУНКТОР
355
(действие группы G в М+ = (М XSN)I(M X pt) индуцируется действиями G в
MnSN).
Покажем, что степень сквозного отображения
5ЛГ->2ЛГМ+-»5ЛГ
равна х (Af). Отображение устроено так: точки из SN - Тпереходят в 00 G SN, а точ-
ка х G Т переходит в вектор v 6 R7V С SN, параллельный перпендикуляру, опущен-
ному из точки х на М, направленный противоположно этому перпендикуляру и име-
ющий длину ф (/), где I — длина перпендикуляра, а - монотонная функция [0, е) -»
-> [0, оо), такая, что ф (0) = 0, ф' (0) = 1, ф (г) при t (рис. 167). Найдем степень
этого отображения. Возьмем вектор и0 6 RN — 0 С SN и посмотрим, каков его
прообраз. Этот прообраз состоит из точек х 6 SN, находящихся от М на расстоянии
Z = (|и0 I) и таких, что направление перпендикуляра, опущенного иэ точки х на
М, совпадает с направлением вектора - и0 • Рассмотрим на М поле векторов длины I,
параллельных —v0, и спроектируем все векторы этого поля на М (рис. 168). Полу-
чается векторное поле на М, особенности которого в точности соответствуют точкам
нашего прообраза. Читатель без труда убедится в том, что знаки, с которыми точ-
ки прообраза учитываются при вычислении степени отображения, совпадают со зна-
ками, с которыми особенности векторного поля учитываются при вычислении эй-
леровой характеристики. Это показывает, что степень рассматриваемого отображе-
ния SN -*SN действительно равна х (И) •
Для каждого слоя нашего расслоения р: Е -* X его диффеоморфизм с М задан
с точностью до преобразования из G. Так как наша конструкция эквивариантна,
ее можно применять к слоям расслоения р: Е +Х. В результате для каждой точки
х 6 X получится отображение SN = S* -> (р~1 (х)) + , переводящее точку в от-
меченную точку надстройки ZN (р-1 (х)) + . Вместе эти отображения составят отоб-
ражение пространства, составленного из сфер S* , склеенных по точке °°, в простран-
ство, составленное из надстроек 2ЛГ (р-1 (х)) + , склеенных по их отмеченной точ-
ке. Очевидно, оба эти пространства являются пространствами Тома: первое — прост-
ранство Тома расслоения | над X со слоем R77, ассоциированного с расслоением
р: Е -» X посредством нашего представления G в R77; второе - пространство Тома
расслоения р*% над Е (тоже со слоем R77). Композиция этого отображения Т($) -*
-» Т(р*|) с естественной проекцией Г(р*^) * T(g) имеет степень на каждой
из Димерных сфер, из которых сделано пространство Тома Т(£). Если расслоение £
тривиально, то этим все доказано. Если оно нетривиально, то мы найдем векторное
расслоение т? над X (уже не имеющее отношения к G), такое, что сумма £ ® т? три-
виальна; после этого мы достраиваем очевидным образом наше отображение
12*
356
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
до отображения
та © то->/(?* а ®т?))-
(При переходе от Г(5) к Т(£ ©т?) каждая из сфер Sx, из которых сделано прост-
ранство Т(£), тенэорно умножается на пополненный слой 17JJ = r)x U <» расслоения
17 над х; равным образом, при переходе от Т(р*|) к Т(р*(1- ®i?)) часть простран-
ства Т(р*%), лежащая над слоем р-1 (х) расслоения р: Е -+Х, тензорно умножается
на 17JJ. ’’Достройка”, упомянутая выше, заключается в том, что отображение Sx
-» 2ЛГ (р-1 (х)) + , построенное на предыдущем этапе, тензорно умножается на 17*.)
Последнее отображение и есть t. Теорема Беккера — Готтлиба доказана.
Следствие. Пусть р: Е -> X и М обозначают то же, что в теореме Беккера —
Готтлиба, и пусть х(М) = 1. Тогда р*‘. Р(Х) -*Р(Е) есть мономорфизм для любо-
го полуточного функтора Р.
Доказательство. Трансфер t индуцирует гомоморфизм
Г: H*(E,G)-* H*(X,G)
и композиция
р* t*
Н*(Х-, G)—*H*(E', G) —> Н'(Х- G)
есть умножение на х (И). Если х (Л/) = 1, то р‘ о = id, ввиду чего р* — мономор-
физм, более того, мономорфизм на прямое слагаемое. (Группа коэффициентов про-
извольна.) Теперь спектральная последовательность Атиа — Хирцебруха показы-
вает, что в точности то же верно для любого полуточного функтора.
D. Прямой образ (случай накрытий). Как мы хорошо знаем, непрерывное отоб-
ражение X -» Y индуцирует отображение К (У) -+К(Х). Однако уже в теории обыч-
ных когомологий и гомологий мы сталкивались с ситуацией, когда непрерывное
отображение индуцирует когомологические и гомологические гомоморфизмы,
’’направленные не в ту сторону” (см. п. 7 § 17). Соответствующее явление в К-тео-
рии мы обсудим в следующем параграфе, а сейчас мы познакомимся с ним в прос-
тейшей ситуации.
Пусть тг: Y -+Х — конечнолистное накрытие, и пусть £ - (комплексное) вектор-
ное расслоение размерности п над Y. Тогда над X возникает расслоение я, £ размер-
ности hn, где h — число листов накрытия: слой расслоения я;£ над точкой х 6 X
есть сумма слоев расслоения % над точками прообраза я-1 (х). Операция Я; адди-
тивна, поэтому она превращается в гомоморфизм я>: K(Y) -+К(Х). Равенство
дш1(я!|) = /г dim % показывает, что Я!(К(У)) с Б(Х). Ясно также, что гомомор-
физм я, перестановочен с ф* с переходит J-тривиальные виртуальные расслоения в
/-тривиальные виртуальные расслоения.
Е. Доказательство гипотезы Адамса в общем случае. Мы должны доказать, что
^ (>//*(£) - $) G Т(Х) для любых £ G К(Х) и к и для достаточно большого N.
Можно считать, что £ — настоящее расслоение; пусть dim £ = п. Рассмотрим главное
расслоение р: Е ->X со слоем U(ri), ассоциированное с £. В группе 1/(л) выделим
следующие подгруппы:
Т — диагональные матрицы;
N — нормализатор группы Т (т.е. группа унитарных матриц, сохраняющих объе-
динение координатных осей как множество);
Т — подгруппа группы N, состоящая из матриц, сохраняющих л-ю координат-
ную ось.
§ 40. J-ФУНКТОР
357
Очевидно, Т С Т С N, причем | N/ Т | = и! и | Г/Г| = (л-1)!. Рассмотрим последова-
тельность расслоений
Т (л-1)! ~ Л U(n)IN
/;’---> Е/Т-----> Е/Т-----► E/N------> X.
Pi Рг Рз Pt
Лемма. x((/(«)//V) = 1.
Это, в действительности, совершенно общий факт: эйлерова характеристика
факторпространства простой компактной группы Ли G по ее максимальному тору
Т равна порядку | W | группы Вейля, нормализатор N тора Г накрывает тор | W |-лист-
но, поэтому x(G/N) = 1. В нашем случае G/Т = U(n)IT есть многообразие полных
флагов с С”, а это многообразие обладает клеточным разбиением на л! клеток, ко-
торые все четномерны, поэтому x(U(n)IT) = л!. Другой способ доказательства пос-
леднего равенства состоит в рассмотрении цепочки расслоений
и(п)!тп---------► сг"-1,...
С/(2)/Т2
.. ., 1/(3)/Г3 ---> СР2, 17(2)/Г2 = СР1
(где Тк обозначает подгруппу диагональных матриц в U(Л)): нужное равенство
вытекает из равенства х (СРк ) = к + 1 и теоремы об эйлеровой характеристике рас-
слоенного пространства в п. 1 § 21 Наконец, х (^(л) 1Ю ~ 1 ввиду существования
л!-листного накрытия U (л)/Г-+U(n)/N.
В силу результатов п. С (см. следствие) проекция р4: Е/N -+Х индуцирует моно-
морфизм П (X) -» П (Е/N). Поэтому нам достаточно доказать /-тривиальность для
kN (фк - 1)т?, где т? = р4*£. Пространство Е/N устроено так: его точка - это пара
(х, а), где х G X, а а - неупорядоченная система_из л попарно ортогональных прямых
в слое расслоения £. Точка пространства Е/Т есть тройка (х, а, I), в которой х
и а — то же, что прежде, а I — одна из прямых, составляющих а. Рассмотрим над
£/Г одномерное расслоение со, слоем которого над точкой (х, а, I) является пря-
мая I. Очевидно, (рз);со = т?. Значит, (рз) i[kN ~ 1)ш] = kN (фк - 1)т?. Но
виртуальное расслоение kN($к — Г) cj /-эквивалентно 0 по доказанному (п.В),а
значит, и kN($k —1)1? /-эквивалентно 0. Доказательство гипотезы Адамса закончено.
3. Применение к гомотопическим группам сфер. В этом пункте мы займемся
вычислением порядка циклической группы
7(52")=Im(/: я2„_!((/)->^„.i).
А. Верхняя оценка. Нам известно, что К (S2n) = Z и фк: К (52") -*К (S2n) есть
умножение на кп. Таким образом, из гипотезы Адамса следует, что при любом к и
достаточно большом N (зависящем от А: и л)
kN(kn - 1)ZC Г(52").
Обозначим через d„ наибольшее целое число, обладающее следующим свойством: для
любого к найдется N, такое, что kN (кп — 1) делится на dn.
Теорема. |7(52")|</„.
Это — прямое следствие доказанной в п. 2 гипотезы Адамса.
Что такое dn?
Найдем d2. Наибольший общий делитель чисел 2ЛГ(22— 1) = 2N • 3 и 3ЛГ(32 — 1) =
= 3N • 8 равен 24. С другой стороны, kN (к2 — 1) всегда делится на 24 (это доста-
точно проверить для |Л| <6, поскольку прибавление к к числа, делящегося на 12,
не изменяет делимости числа kN (к2 — 1) на 24). Значит, d2 =24.
358
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Найдем d3. Набольший общий делитель чисел 2N (23 - 1) = 2N • 7 и 3N (З3 - 1) =
= 3N • 26 равен 2. Число kN (к3 - 1) всегда четно. Значит, d3 = 2.
Найдем d4. Наибольший общий делитель чисел 2N (24 — 1) = 2N • 15 и 3ЛГ(34 — 1) =
= 3N 80 равен 240. Проверка показывает, что kN (к4 — 1) всегда делится на 240.
Значит, d4 = 240.
Легко показать, что d* = 2 при любом нечетном к. При четных к числа d* выра-
жаются через так называемые числа Бернулли. Напомним, что числа Бернулли В„
s > 1, определяются при помощи степенного ряда
х
\-е~х
ОО у
i=o s!
формулой Bs = (- I)1 1 ^23. (Заметим, что fas+i = О ПРИ s > 0-) В следующей таб-
лице проведены несколько первых чисел Бернулли.
5 1 2 3 4 5 6 7 8
£ 6 1 30 1 42 1 30 5 66 691 2730 7_ 6 3617 510
знаменатель Bsl4s 24 240 504 480 264 65520 24 16230
Числам Бернулли уделяется большое внимание в учебниках по теории чисел (см.,
например, Боревич З.И., Шафаревич ИТ. Теория чисел. — М.: Наука, 1972, § 8 гл. V).
В то же время, как читатель увидит в этом и в следующем параграфе, числа Бернул-
ли чрезвычайно важны для топологии и топологи потратили значительные усилия
на их изучение. Информация о числах Бернулли, полезная для топологии, собрана
в § 2 статьи Адамса ”0 группах J(Х), П” (Математика: сб. перев. — 1967. — Т. 11,
№ 4). В частности, там доказана
Теорема. Число d2, равно знаменателю несократимой дроби, равной B,jAs.
(См. третью строку предыдущей таблицы.)
Таким образом, числа, стоящие в третьей строке таблицы, служат верхними оцен-
ками для порядка образа /-гомоморфизма в t!S4s_ j .
В. Нижняя оценка. Пусть X G ^2W+2n-i (<52ЛГ)- Приклеим к S2N клетку /)2ЛГ+2п
по сфероиду 52ЛГ+2"-1 ->£2ЛГ класса X. Получится пространство Х\, для которого
[ Z при <? = О, 2N, 2N+2n,
I 0 при остальных q.
Обозначим череза и Ъ естественные образующие групп H2N (A\; Z) и я2ЛГ+2п ; Z).
Так как X\IS2N = 52ЛГ+2",имеет место точная последовательность
О ->K(S2N+2n) -> К(Хк) -> K(S2N) -> О,
II II
0GZ a£Z
из которой К(Х\) as Z ©Z. Одна из образующих этой группы, мы обозначим ее че-
рез /3, определена канонически — это образ образующей /3 группы K(S2N+2n)-, дру-
§ 40. J-ФУНКТОР
359
гая, а, определенная с точностью до прибавления кратного /3: это - прообраз обра-
зующей а группы К(S2N). Имеем:
cha=a + eh, е 6Q,
ch/3 =д
(ср. п. 2 § 39). Поскольку а определено с точностью до прибавления кратного /3,
число е определено лишь mod 1. Пусть е = е(Х) G Q/Z - соответствующий вычет.
Этот вычет называется е-инвариантом Адамса класса X.
Упражнения. 5. Докажите, что е: яцч+гп-1 (S2JV) -* Q/Z — гомоморфизм.
6. Докажите, что е (S X) = е (X).
Пример. Пусть у G тг7 (54) — класс хопфовского отображения 57 -> 54. Вы-
числим е (у).
Очевидно, Ху = HP2; рассмотрим в К (HP2) класс тавтологического расслоения
?н> рассматриваемого как комплексное векторное расслоение. Классы Черна рас-
слоения fn нам известны: Ci (£н) = 0 (потому что Я2 (HP2; Z) = 0), сг (£н) - я
(это — класс Эйлера расслоения — первое препятствие к построению сечения в
соответствующем сферическом расслоении), с,- (f н) = 0 при i > 2 (потому что
dimcfH = 2). Компоненты характера Черна выражаются через классы Черна. В
частности,
1 ,
ch2 = - (с2 - 2с2),
ch4 = — (с4 - 4с2 с2 + 2с2 + 4ciC3 + 4с4).
24
Ъ
Поэтому ch2 (fH) = -а, ch4(fH) =
12
= —, т.е
1
ch f н = 2 — а + — Ъ.
12
II
dimc fH
Таким образом, за а мы можем взять 2 — и е(у) = — 1/12.
Это означает, что подгруппа, порождаемая классом ZNy в hn+t(Sn+4), имеет
порядок по крайней мере 12. (На самом деле она имеет порядок 24 - см. гл. 5).
Этот пример подсказывает способ получения нижних оценок для порядка об-
раза /-гомоморфизма: вычислить е-инвариант для /-образа группы (^0 и взять
знаменатель.
Упражнение 7. Пусть £ — векторное расслоение (настоящее), представля-
ющее элемент а группы К (S2n), и пусть dime | = N. Тогда пространство Тома Г(|)
имеет гомотопический тип Х\, где X = / (a) G я2ЛГ+2 п _ ] (52ЛГ).
Это утверждение показывает, что для нахождения нижних оценок порядка об-
раза /-гомоморфизма нужно уметь вычислять характер Черна элементов XS-функ-
тора от пространства Тома. Это и есть предмет следующего параграфа.
360 гл. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
§ 41. ТЕОРЕМА РИМАНА-РОХА
1. Общая теорема Римана — Роха.
А. Ориентируемость векторного расслоения по отношению к теории когомо-
логий. Пусть h - экстраординарная (возможно, обычная) теория когомологий
(см. п. 5 § 37), £ = (Е, X, V, р) — некоторое (вещественное или комплексное)
векторное расслоение. Рассмотрим пространство Тома Т(|). Как известно (см.
п. 2В § 30), имеет место изоморфизм
я*(*; с) = я‘(Т(|); G),
сдвигающий размерности на л = dimR где G есть в общем случае группа Z2, а
при условии ориентируемости расслоения | - произвольная абелева группа. Спра-
шивается: имеет ли место подобный изоморфизм для теории й? Ответ подсказы-
вают предыдущие формулировки: изоморфизм имеет место при некотором усло-
вии ’’ориентируемости”, зависящем от h.
Далее мы ограничиваемся случаем мультипликативных теорий, т.е. предполага-
ем, что h(X) есть для любого X градуированное кольцо с единицей 1 G й°(Х);
более того, предполагается наличие умножения
hp(X,A) ® hq(X, В) -> hp+q(X,A UB).
Все умножения должны быть естественны по отношению к индуцированным го-
моморфизмам. (Точно сформулировать аксиомы мы оставляем читателю.) В част-
ности, все h*(X, А) оказываются модулями над кольцом ft*(pt) [ft*(pt) естествен-
но отображается в h*(X) : гомоморфизм индуцируется отображением pt].
Изоморфизм надстройки Л4 (pt) -»й<?+"(5") позволяет определить (как образ
единицы 1 6 h° (pt)) каноническую образующую s” G й"(5я).
Упражнение 1. Для любого X изоморфизм надстройки S”: hq (X) ->
-*hq + n(SnX) выражается через s”:
hv(X) =A?(X,pt)
а ।---------
h9(X^S”s")
^(^Х)
uj
UJ uj
лл(кп) =А"«рО h\x*s”x)
Опре деление. (Вещественное или комплексное) векторное расслоение £
называется ориентируемым по отношению к теории h, короче, h-ориентируемым,
если существует элемент и 6 Л”(Т(£))> п = dimR £, такой, что гомоморфизм
й"(Т(£)) -> Л” (5”), индуцированный вложением в Т(£) пополненного слоя ££ =
= %хи о°« S”, переводит и в элемент вида es”, где е - обратимый элемент коль-
ца й° (pt). Всякий элемент и с этим свойством называется h-ориентацией расслое-
ния £.
§ 41. ТЕОРЕМА РИМАНА-РОХА
361
Очевидно, всякое векторное расслоение является Н*(—; Z2)-ориентируемым,
а Я*(—; Z)-ориентируемость — это ориентируемость в обычном смысле. Ниже в
этом параграфе мы обследуем ориентируемость расслоений по отношению к Х-тео-
рии; в п. 2 мы покажем, что всякое комплексное векторное расслоение Х-ориен-
тируемо, а в п. 4 мы увидим, что необходимым и достаточным условием X-ориен-
тируемости ориентируемого вещественного расслоения является равенство нулю
целочисленного аналога класса w3.
В. Изоморфизм Тома. Предположим, что векторное расслоение % = (Е, X, V, р)
является й-ориентируемым и зафиксируем ^ориентацию и G Л"(7’(^)), п = dimR
Обозначим через Е' дополнение к нулевому сечению в Е; очевидно, hr =
= hr (Е, Е'). Отображение
t: Л’(Х) = hq(E) -е/1 й<7+”(Е, Е') = Л1?+"(7’|)
называется гомоморфизмом Тома. Иногда вместо t мы будем использовать раз-
вернутые обозначения t А или t*.
Замечание. Очевидно, t (а0) = at (0) = t (a) 0 [ = a0u].
Теорема. Гомоморфизм Тома является изоморфизмом.
Доказательство. Для А С X очевидным образом определен относительный
гомоморфизм Тома
t: hq(X,A) -> Л’+и(Г«),Г«1л)),
причем диаграмма
hq~\A) * hq(X,A) -> hq(X)
ф t ф t ф t
hq+n -1 (ra U)) - hq+n (ПО. Г(5 1л)) -> hq+n(T(g)~) ->
•* hq(A) •* hq + i(X,A}
41 It (*)
- hq+n(TQ \A^^hq + h + l(T(K), T(l- U))
коммутативна. Если X — А есть одна клетка размерности, скажем тп, то независи-
мо от расслоения £ относительный гомоморфизм t превратится в гомоморфизм
hq(Sm) -> hq™(Sm+n),
и упражнение 1 показывает, что это — S”, в частности, изоморфизм. Предпола-
гая по индукции, что для £ 1л изоморфность t уже установлена, мы получаем ее для
£, применяя 5-лемму к коммутативной лестнице (*).
Впредь вместо названия ’’гомоморфизм Тома” мы будем употреблять назва-
ние "изоморфизм Тома”.
С. Теорема Римана - Роха. Пусть h и к — две мультипликативные теории кого-
мологий и т: h +к - мультипликативное отображение, переводящее 1 G A°(pt) в
1 G к° (pt). Пусть £ — векторное расслоение, ориентированное по отношению к
обеим теориям, X — его база. Рассмотрим диаграмму
Л’(Т(£)) к*(Т(1М
ttf ttf
h к
h*(X) —-—► к*(Х).
362
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Спрашивается, коммутативна ли она. Известные нам примеры показывают, что
нет. Действительно, пусть h = к = Н*(—; Z2)HT = Sq=l + Sq1 + Sq2 + ... (муль-
типликативность этого отображения утверждается формулой Картана, см. § 28).
Как мы знаем,
Г1 Sqt(l) G //*(X;Z2)
есть не 1, a w(£) =1 + W; (£) + w2 (£) + ... - полный класс Штифеля-Уитни рас-
слоения £ (см. п. 2 § 30).
Определение. Элемент
5г(1)= (t*rlo7ot«(l)
называется классом Тодда расслоения £.
Это - характеристический класс расслоений, одновременно /{-ориентированных и
к -ориентированных. Предыдущий пример показывает, что <S*s q =w-
Теорема. Для любого a G h*(X)
(ф'1 ото^(а) = т(а)<^.(£).
Доказательство: r(t/,(a)) = т(а-t^(l)) = т(а)т^(1) = т(а)- S”T(£) =
= ^(т(«)- JT(£)).
Это очевидное предложение и есть общая теорема Римана — Роха.Оно перестает
быть тривиальным в конкретных примерах, поскольку в них оно включает в себя
явное описание класса ориентируемых расслоений и явное вычисление Sr. Мы
убедимся в этом в последующих пунктах этого параграфа, где в качестве т высту-
пает характер Черна ch. А в заключение этого пункта мы приведем одно следствие
из общей теоремы Римана — Роха.
D. Прямой образ в экстраординарных когомологиях. (Сопоставление этого пунк-
та с п. 2D § 40 мы оставляем читателю.) Компактное многообразие называется А-
ориептируемым, если /{ориентируемо его нормальное расслоение в сфере большой
размерности. Пусть X и Y - два /{ориентированных многообразия и /: X -* Y — не-
прерывное отображение. Возьмем большое, сравнительно с dim X и dim У, число
N, зафиксируем гладкое вложение <р: Y ->SN и аппроксимируем отображение ° ft
X SN гладким вложением ф . X SN. Многообразие ф(Х) будет лежать в узкой
трубчатой окрестности V многообразия </>( У); обозначим через U столь узкую труб-
чатую окрестность многообразия ф(Х), что она содержится в V. Мы получаем
отображение
SNI(SN - U) SN/(SN - V),
II II
Т(у(Х)) T(y(Y))
где v (X) н v (У) — нормальные расслоения многообразий У и X в SN. Воспользовав-
шись A-ориентированностью расслоений v (X) н v (У), составим отображение
t * Г'
h'(X) nW)) Л’(Г(КП)) Л’(У).
Упражнения. 2. Это отображение определяется отображением/.
3. Если h — обычные когомологии (с произвольными коэффициентами, если
многообразия X и У ориентированы, и с коэффициентами в Z2 в общем случае),
то это отображение совпадает с гомоморфизмом/; из п. 7 § 17.
И в общем случае этот гомоморфизм обозначается через/;. Элемент/;aG А*(У)
называется прямым образом элемента a G h*(X).
§ 41. ТЕОРЕМА РИМАНА-РОХА
363
Упражнение 4. Докажите, что для любых х G h*(X), у G й*(У)
Л(ГО')х) =УЛ(х).
Пусть h и к -мультипликативные теории когомологий, т : h -+к - мультиплика-
тивное отображение, и пусть X — многообразие, одновременно являющееся й-ориен-
тируемым и к -ориентируемым. Класс Тодда расслоения v(X) по отношению к т,
т.е. элемент
(t”(X))-1 orot^W(l) е к*(Х)
называется классом Тодда многообразия X и обозначается через У(Х) или ^Т(Х).
Теорема Римана — Роха имеет такое следствие (которое тоже иногда называют
теоремой Римана - Роха).
Теорема. Пусть X и Y — замкнутые многообразия, одновременно h-ориенти-
рованные и k-ориентированные, и пусть f: X -> У - непрерывное отображение.
Классы Тодда S'(X) и ^(У) измеряют степень некоммутативности диаграммы
h^X) к*(Х)
1 /| I fi
h'(Y) — Й’(У);
Точнее-, для любого х G й*(X)
^(т^.^СХ)) = т(/,(х))-^(У).
„ v(Y)
Доказательство. Применим к левой и правой части tk
U(n[/!(7(x)<S’(X))] =
= tk [(t* ) g tk (т(х)-(1к ) Tth (1))] =
. v(.X) v(X) -1 v(X) . v(X)
= 4r(x).(V ) 7t/ 41)) = r(7(x) Tt/ 41)) =
= Tg (x- th (1)) = Tg th (x);
^(Г)[7(/,(Х))-^(У)] =
v(Y) v(Y) -1 . v(X) v(Y) -1 v(Y)
= tk [r((t/ 4 s’t/ 4x))4(t/ 4 r(t? 41))] =
р(У) -1 , v(X) v(Y) . v(X)
= 7[((t/ g*th( 4x)) t/ (l)] = 7g’t/ 4x).
(Мы постоянно пользуемся мультипликативным свойством изоморфизма Тома:
а • t(/3) = t(a) -0 = t(a- 0).)
Пример. Пусть h = к = Н*(- ; Z2), т = Sq, X — произвольное многообразие,
У - точка. Из описания когомологического прямого образа, данного в п. 7 § 17,
видно, что гомоморфизм /, : Н*(Х; Z2) ->-H*(Y; Z2) =Z2 действует по формуле
х»-> <х, [ X] >. Далее, (X) = t-1 Sq t (1) = 1 + Wj (X) + w2 (X) + ... - полный нор-
364
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
мапьный класс Штифеля — Уитни многообразия X (см. п. 2С § 30), т.е. «^(Х) =
= н'(Л’)1,где w(X) — полный (касательный) класс Штифеля — Уитни многообра-
зия X. (И, конечно, «^(У) = 1 и Sq в H*(Y; Z2) - Z2 есть тождественное отображе-
ние.) Применим теорему Римана - Роха:
< Sqx^ w(A')-1, f X] > = <х, ]Х] >.
Положим Sqx w(X)~1 = Sq а. Тогда Sqx = Sq a о w(X'), х = а <-> Sq-1 w(X), и
мы имеем:
< Sqa, [У] > = < Sq-‘w(X), fX] > = < Sq'1 w(X), D(a) >,
где D — изоморфизм Пуанкаре. Это — формула By (см. п. 2D § 30).
2. Теорема Римана — Роха в Х-теории для комплексных расслоений. Цель этого
пункта — доказать, что комплексные векторные расслоения ориентируемы и обла-
дают канонической ориентацией по отношению к Х-теории, и вычислить соответствую-
щий класс Тодда.
Пусть % = (Е, X, Сп, р) — комплексное векторное расслоение с (конечной клеточ-
ной) базой X. Положим
х0(£) = 1 ч> л2£фл4£ф...,
xj£) - £ф Л3£ф Л5£ ф ....
Х(Н = МО - Xi(OGA^X).
Лемма. Если расслоение % обладает не обращающимся в 0 сечением, то
X ( ( £) ~ Хо(£) • Более того, имеется естественная конструкция, ставящая в соответ-
ствие сечению расслоения £, не обращающемуся в 0, эквивалентность Хо (£) X j (£).
Конструкция. Сечение расслоения £, не обращающееся в 0, — это то же, что
расщепление £ = 1 ф tj. Но Лг (1 ®tj) = ®J+r (As 1 ® A'tj) = Ari? <i> Ar~ *tj. Поэтому
X0(l ®tj)
= 1 ® tj ф A2t? ф A3tj Ф A4tj ф А5 я ф ...
Xi(l фт?)
Рассмотрим расслоение /?*£ над E. Это расслоение обладает каноническим сече-
нием: слой расслоения /т*£ над точкой .у G Е естественно отождествляется со слоем
6 у расслоения £ над точкой р(у), и мы ставим в соответствие точке у G Е
точку .у G £;,(у). Это сечение обращается в 0 в точности над нулевым сечением
X С Е, а в точках пространства Е: = Е — X оно в 0 не обращается. Поэтому предыду-
щая лемма доставляет каноническую эквивалентность между Х0(р*£) и Xj(p*£)
над Е( С Е, а с ней эквивалентность между Хо (Р*£ ) и X] (/?*£ ). Это позволяет
рассматривать
Х(р*£) = Хо(рЧ) - Х,(р’£)
как элемент из К (Е, Е') = К (Т (£ )). Обозначим этот элемент через и (£ ).
§41. ТЕОРЕМА РИМАНА-РОХА
365
(Здесь используется следующее соображение. Если Si, £2 — расслоения над X,
между сужениями которых на А С X задана эквивалентность, то разность Si — 1г
может рассматриваться как элемент нз К(Х, Л). Подробнее: пусть 17 — расслоение
над X, такое, что сумма ® ri тривиальна; зафиксируем эквивалентность S2
Тогда $1 - $2 = (Si ® т?) - (?2 ® *?) = (£i ® *?) --W и для расслоения Si Ф77 над Л
задана тривиализация. Это позволяет склеить слои этого расслоения над Л и получить
расслоение над Х/А.) ~
Теорема, (i) Класс u (S ) ё К(Т (S ) ) представляет собой К-ориентацию рас-
слоения £; эта ориентация естественна в том смысле, что если S* — другое ком-
плексное векторное расслоение той же размерности и S1 -> S — отображение, изо-
морфно отображающее каждый слой расслоения S’ на некоторый слой расслоения S,
то соответствующее отображение Т (J-1 ) -> Т (S) индуцирует отображение
К(Т (S)) -+К(Т (S',)),переводящее u(i-) в и(%')'.
Чтобы сформулировать следующее утверждение, рассмотрим симметрический
степенной ряд
" l-е
...хп) = П
1 = 1 % i
и определим степенной ряд G ( ,..., уп) формулой
F(*i....х„) = (/’(Мх,...х„)...e„(xt....х„)),
где -•» *н) - элементарные симметрические функции. Вычисление показы-
вает, что
G’C.i’i.,V„) = 1 - .1’1 + (2.1’1 -с2) -
- 0’1 - Vi.r2)+y^ (6.1’1 —9.i’iI’2 +2.1’1 —,|’1.|’з +.1’4)+-
(i i ) Соответствующий ориентации u(S) класс Тодда
^(S) = (tn)'* ch«(S) е н\х-, Q)
равен G(<i(S)..<’„(S)).
Доказательство. Покажем прежде всего, что из (ii ) следует (i ). Мы
должны показать, «по сужение класса //(S) на пополненный слой расслоения S.
S2" С Т (S), есть образующая группы А' (52") = Z. Это сужение есть w (So), где
So (тривиальное) л-мерное комплексное векторное расслоение над точкой.
Но у So все классы Черна тривиальны, следовательно,
(tj/ )-,cli//(So) = G(ci(So).<•„(&>)) = I
и ch //(So) = t/,° (1) есть образующая группы H2" (S2"; Z). А это и означает, что
//(So) G A'(S2") есть образующая.
366
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Часть утверждения (i ), касающаяся естественности, очевидна.
Докажем теперь утверждение (i i ). Априори очевидно, что !) есть характерис-
тический класс расслоения £, т.е. однородные составляющие класса &(!) являются
полиномами от классов Черна с рациональными коэффициентами. Поэтому достаточ-
но убедиться в справедливости нашей формулы для &(!) в случае, когда % есть
произведение f X ... X f некоторого количества хопфовских расслоений над CPN.
Рис. 169
Далее, очевидно, что ® £2) = ^(Г1)^(|2) (зто — следствие очевидного равен-
ства X(£t ® £2) = X(£j)X(£2)). Ввиду этого можно ограничиться случаем, когда £
есть просто хопфовское расслоение f над CPN. В этом случае наша формула приоб-
' 1 е~х , н
ретает вид «/(£) = -------, где х^ Н (СР ; Q) - образующая. Теперь заметим,
что Т (f) = СР14 +1. Действительно, фиксируем точку a G CP7V+1 - CPN и проведем
через а всевозможные (комплексные проективные) прямые (рис. 169). Каждая из
этих прямых пересекает CPN в своей точке, т.е. CP7V+I сделано из двумерных сфер
S2 , х G CPN, скрепленных в одной точке. Значит, CP/V+1 есть пространство Тома
некоторого расслоения над CPN, а именно расслоения, пространство которого есть
CPN + i ^а. Это - нормальное расслоение CPN в СРЛ7+1, т.е. f.
Теперь покажем, что w(f) 6 К (CPN + I) есть виртуальное расслоение 1 — J над
CPN + 1. Действительно, точка из CPN - это прямая в C7V+I ; точка из CPN + 1 —
прямая в С77+ 2, и в качестве а естественно взять прямую, перпендикулярную C7V + I.
Проекция р: CPN+i ~ а -> CPN индуцируется ортогональным проектированием
Cw + 2 -> C7V + I. Слой расслоения f над / G CPN - это сама прямая / С C7V + 1,
слой расслоения над I G CPW + 1 - а - это проекция прямой I в C/v+1;
эта проекция естественно отождествляется с /. Таким образом, поднятое расслоение
есть f | Cp,v+i (мы используем обозначение f для хопфовского расслоения как
над СР77, так и над СР77 + *). Вне CPN это расслоение тривиализуется: слои без вы-
рождения проектируются на прямую а С С774"2. Поэтому при проектировании
CP7V + 1 — л -> Т (f) = Cp77 + I (которое гомотопически не отличается от включения
СР7741 — а -> CPW + 1) расслоение превращается в хопфовское расслоение f над
§ 41. ТЕОРЕМА РИМАНА-РОХА
367
CPN + 1. Из этого видно, что //(f) = Х (p*f )= 1 -p*f как виртуальное расслоение над
7’f = CP/v+I действительно есть 1-f. Значит, ch//(f) = ch( 1-f )= 1 -е~х.
Наконец, когомологический изоморфизм Тома t/y: H*(CPN; Z) H*(CPN +1: Z)
действует, очевидно, по формуле хк ►+ хЛ + 1. Поэтому
, 1 -е~х
&(П = tf/o -е-Л) = —-—.
Теорема доказана.
Таким образом, в рассматриваемом случае теорема Римана — Роха принимает та-
кую форму.
Теорема. Для n-мерного комплексного векторного расслоения £ . существует
естественный (по %) изоморфизм Тома Л'(Х)-> А'(Т(^)), где X - база расслое-
ния при этом
ch(tj-a) = t//(cha ^(S)),
где a 6 Л(Х), tf, - когомологический изоморфизм Тома и ^’(?) = G(c,i(?), • • •
... , /„(£)), где G - степенной ряд. определяемый формулой
1 — е~х‘
G(ei(xt,. .. ). e2(.rj.. .) = П ----------
-V/
3. Применение: вычисление е-инварианта. Напомним определение е-инварианта
класса X G ttjn + z/i-i (52Л ): по X строится пространство Х\ =S2N U f D2N + 2",
где f: s2N + 2"~' ->S2N есть сфероид класса X; в Л'(Л\) = Z ®Z берется произ-
вольный элемент а, сужение которого на S2N С X есть стандартная образующая
группы Л' (S2 Л ) = Z; далее,
ch а = а + е Ь,
где д G H2N (Х\-, Q), b G Н2 N+2n (Х\-, Q) — стандартные образующие и е G Q;
вычет е(Х) G Q/Z числа е по модулю 1 определяется классом X; это и есть его
е -инвариант.
Наша цель — вычислить е(Х) для случая, когда X есть J-образ образующей груп-
пы К (S2") = Z. В § 40 мы заметили, что Х^ в этом случае есть пространство Тома
?’(?), где £ есть расслоение над S2", представляющее образующую группы Л'(52")
(см. упражнение 7 к § 40). Добавим теперь, что в качестве а можно взять
//(?) G Л (Г(?)); сужение //(£) на S2N как раз есть образующая группы К(S2N)
по определению ориентации. Согласно теореме Римана — Роха,
ch//((•) = tH^(?) = tHG(Ci(^, е2(^}.
368
ГЛ. б. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Но классы ct (£) с i < п равны 0 (ибо тривиальны соответствующие когомологии
сферы), а сп (£ ) легко вычислить:
ch| = dim$ + s2„ G H*(Sln;Q),
где s2n - образующая группы №”(S2"; Z). Найдем коэффициент, с которым сп
входит в chn. Имеем:
еЬИ = РП (с 1г — > Сп ) >
п I
п
S х" = Рп(е1(х),...,еп(хУ).
1= 1
Подставим в последнее равенство xt = е„, где еп — первообразный корень степени п
из 1. Тогда будет Ci (х) = ... = еп _j (х) = 0, е„ (х) = ± 1, S х” = п. Отсюда следует,
что сп входит в Рп с коэффициентом ± п, и, значит,
sn = ch«(£) = ~7(±«)cn(S),
C„(S) = ±(n- l)!s„.
Итак,
ch a = ch w(S) = tn(l ± (n - 1) ! д s„) = a ± (n - 1) ! д b,
где p. — коэффициент, с которым cn (I) входит в G(ci ($), c2 (£),...); таким обра-
зом,
e = ±(n - 1) ! д.
Легко показать, что если п нечетно и больше 1, то д = 0. Если же п = 2т четно,
то оказывается, что д = ±----- (при т = 1, 2 это видно из формулы для начальной
2 т!
части ряда ••)> приведенной в п.2). Это доказывается так. Рассмотрим
класс ^-1(S)= ^(c^S), МО, • ••), где
^l(ei(x), е2(х),...) = П-------.
~xi
1-е ’
Очевидно, для нашего £ этот класс равен
а + (п - 1)дЬ.
Далее, элементарными средствами доказывается, что в ряде ’Н при любом к совпа-
дают коэффициенты при Ci(x)fc и ек(х) [доказательство см. в книге Хирцебруха
’’Топологические методы в алгебраической геометрии”, замечание 2) в п. 7 § 1 гл. 1].
Коэффициент же при е1(х)2пг легко находится: положим Xi = z, х2 = ... = х„ = 0;
§ 41. ТЕОРЕМА РИМАНА-РОХА
369
тогда el(x) = z, е2(х)=... = 0,
„ xi z
П----— =--------= 1 +
1—е~г
+ 2 (-I/"1
S = 1
Bs
(2 s)!
1
2 2
^(^i(x),e2(x),...) = ^(z.O, ...),
т.е. коэффициент при е t (х)2т
Итак, при и = 2 т
Вт
е(Х) = ±(2т-1)1——^—
(2т)1
действительно равен ± Вт / (2 т)!.
” В™
i
2 т '
Нами доказана
Теорема. \ J (54ш)| не меньше знаменателя несократимой дроби, равной
Вт 12 nt.
Сопоставим этот результат с теоремой иэ п. 3 § 40. Мы видим, что верхняя оценка
для | J (54ш)| в два раза больше нижней (числитель дроби Вт всегда нечетен),
причем, поскольку в обоих случаях знак > следует читать ’’делится на”, т.е. мы до-
казали, что этот порядок равен либо знаменателю дроби Bmj2 т, либо знаменателю
дроби Вт!4 т.
В действительности дело обстоит так (см. книгу Каруби). Если т четно, то поря-
док группы | J (54ш)| равен знаменателю дроби Вт12т. Но в этом случае гомо-
морфизм
= ^4т-1(^) * ^4т-1(О) = Z
есть умножение на 2, ввиду чего J-образ группы ir^m-i(P) в n4m_i имеет поря-
док, равный знаменателю Вт14 т. Если же т нечетно, то указанный гомоморфизм
Z -> Z является тождественным, но зато порядок группы | J (5 4 т) | совпадает со
своей верхней оценкой: знаменателем дроби Вт/4 т. Таким образом, группа я4т-1
при любом т содержит циклическую подгруппу, порядок которой равен знаменате-
лю дроби ВтЦт - образ при J-гомоморфизме группы it4m-i(O). Про зту под-
s
группу известно также, что она выделяется в п4ш_1 прямым слагаемым.
4. Теорема Римана — Роха в Х-теории для спинорных расслоений. Ориентируемы-
ми по отношению к ЛГ-теории являются не только комплексные расслоения. В дейст-
вительности справедлива следующая
Теорема. Ориентируемое вещественное векторное расслоение £ в том и толь-
Z Z
ко в том случае является К-ориентируемым, когда w3 (£) = 0, где w3 - ха-
рактеристический класс, соответствующий нетривиальному элементу группы
Н3 (G* (оо, л.); Z2); равносильное условие: класс w2 (£) G Н2 (X; Z2) (где X -
база) является целочисленным, т.е. принадлежит образу гомоморфизма приведения
р2: Н2 (Х\ Z) -> Н2 (X; Z2). Выбор К-ориентации равнозначен выбору прообраза
w2(£) G Н2 (X; Z) класса w2(|). (К-ориентация комплексного векторного рас-
слоения соответствует классу w2(|) = <?!($)•)
370 ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Мы ограничимся здесь построением А-ориентации для расслоения с выбранным
классом w2. Полное доказательство сформулированной теоремы читатель найдет
в книге Каруби.
А. Группа Spinc. В основе построения К -ориентации комплексного векторного
расслоения лежит следующее наблюдение: естественное представление группы
U(n) в Л*С" разлагается в сумму AevenC" ® AoddС", причем слагаемые эквива-
лентны как представления группы U(n — 1) С Мы увидим сейчас, что анало-
гичными свойствами обладают некоторые группы, действующие в Л* С” и значи-
тельно более обширные, чем унитарные группы.
В пространстве Л* С" есть каноническая эрмитова метрика, благодаря чему
в End Л* С" имеется сопряжение * с *2 = 1. Для и & С” определим Fv G End Л*С"
как оператор внешнего умножения на и и положим уи = Fu + F*. Очевидно,
= <PV , = II v || 2 (действительно, FVF* +F*FV = || и || 2, F* = О, F*2 = 0) и
и ►+ </>у есть линейное вложение С" -> End Л* С“.
Обозначим через Pinc (2 и) часть пространства End Л*С", составленную из эндо-
морфизмов х: Л* С” -> Л* С", удовлетворяющих трем условиям:
(i ) х* ° х = 1 (в частности,эндоморфизмх обратим);
(ii) эндоморфизм х однороден по отношению к Z2-градуировке Л*С" =
= AevenC" ® Aodd С";
(iii ) для любого и G С'' существует wG С” с xy>vx* = <pw.
Очевидно, Pinc(2 н) — группа Ли.
Обозначим через Spinc (2 н) часть группы Pinc (2 и), составленную из отображе-
ний, имеющих по отношению к указанной градуировке степень 0: x(AevenC”) С
С AevenC", x(AoddC") С AoddC''. Очевидно, Spinc(2 л) есть подгруппа ин-
декса 2 в группе Р inc (2 н).
Каждому х G Pinc (2 и) поставим в соответствие вещественное линейное преобра-
зование пространства С", определенное формулой и >-» w (см. условие (iii)) при
х G Spinc (2 п) и формулой и ►+ — w при х £ Spinc (2 н). Очевидно, это преобразо-
вание ортогонально (норма оператора tpv равна длине вектора и, норма операто-
ра х, ввиду х *х = 1, равна 1.) Получается гомоморфизм
Piii2z, -► 0(2 н). (*)
Предложение 1. Это - эпиморфизм, ядром которого служит группа
Sl С SpinC(2/z), составленная из операторов умножения на комплексные числа,
по модулю равные единице. Группа Spinc(2//) является прообразом группы
SO(2 и) при эпиморфизме (*).
С
Доказательство. Очевидно, G Р in 2,, для всякого единичного вектора
и G С". Далее, соответствующее ipv преобразование пространства С" есть отражение
в вещественной гиперплоскости, ортогональной и. (В самом деле, —</>y</>y<pJ =
= -'flu = -<Ри =<Р-У; -'Pv'Piv'Pv = ~(Гу + Fv)(Fiv + Fiv)(Fv + Fv) = (Fv +
+ FJ)(FV - Fl)(Fv + = -/(^FyFy* - FVF*FV) = -z(F; - F„)
§ 41. ТЕОРЕМА РИМАНА-РОХА
371
* 2 ч
если v и w комплексно ортогональны, то -'pvfpwfpv = -fpv<pw*pu =yu*pw = v>w.)
Следовательно, образ гомоморфизма (*) содержит все отражения в гиперплос-
костях, и, значит, он содержит всю группу 0(2 п).
Докажем теперь, что ядро гомоморфизма (*) составляют операторы умножения
на комплексные числа, по модулю равные 1. Пусть х €Е Pinc(2n) — элемент ядра.
Предположим, что х е Spinc(2n); тогда принадлежность ядру означает, что
„ «—i
= <Р»х при любом и GC. Обозначим через Си ортогональное дополнение
к у в С". Очевидно, всякий элемент из Л*С" единственным образом представ-
ляется в виде
* л- 1
(1 + у) л а + (1 — у) л Ь, где a, b G Л Си ,
и оператор х должен переводить этот элемент в элемент вида
(1 + у) л у(а) + (1 -у) л z(b),
где у, z. G Spinc(2n — 2) — элементы ядра гомоморфизма, аналогичного (*).
По индукции мы можем считать, что у и z - операторы умножения на числа 0и и
, по модулю равные 1. Но для любых линейно независимых у, w должно быть
х((1 +и)л(1 +w)) = (l + у) Л j3u(l + w) = 0w(l +у)л(1 + w).
Отсюда 0и = 0W, т.е. 0 не зависит от у. Аналогично, у не зависит от у. Наконец, 0 =
= 0и = 0 = уu = у, т.е. х есть действительно умножение на константу, по модулю
равную 1.
Еще более простая индукция показывает, что элемент ядра оператора (*), лежа-
щий вне Spinc(2w), равен 0.
Из доказанного видно, что Pin с (2л) порождается умножениями на константы и
операторами <ри. Для всех образующих, а значит, и для всех элементов группы
Pin с (2л) верно, что их образ при гомоморфизме ( * ) тогда и только тогда принад-
лежит SO(2n), когда сами они принадлежат SpinC (2л). Из этого вытекает последнее
утверждение нашего предложения.
Замечания. 1. Аналогичная вещественная конструкция дает группы PinR(к)
и SpinR(fc); группа SpinR(fc) двулистно накрывает группу SO(k), группа PinR(fc)
состоит из двух компонент, одна из которых есть SpinR(fc). Группа SpinR(2n) со-
держится в Spinc (2л), причем проекции этих двух групп в SO(2л) согласованы.
2. Очевидно, С/(л) включается в Spinc(2n) в качестве подгруппы, составленной
из преобразований, сохраняющих не только разложение Л*С" = AevenC" ® AoddC",
но и более тонкое разложение Л*С” = ® Р$Сп. Сужение на SU(n) проекции
Spinc(2n) ->5О(2л) есть естественное вложение SU(n) ~>SO(2n).
Итак, нами построены группа Spinc(2n) и ее (унитарное) представление в Л*С",
причем это представление разложено в сумму двух подпредставлений: Л*С" =
= AevenC" ®AoddC".
Предложение 2. AevenC" u AoddC” изоморфны как представления группы
Spinc (2л — 2) С Spinc (2л).
Доказательство. Вложение Spinc(2n - 2) -> Spinc(2n) индуцируется
вложением С"-1 -> С"; пусть и — единичный ортогональный вектор к С"-1 в С".
Тогда оператор tpv : AevenC” -> AoddC" является Spinc(2n — 2)-изоморфизмом.
372 ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
В заключение рассмотрим когомологии группы Spinc (2л).
Предложение 3.Я1 (Spinc(2n)) = Z, Н2(Spinc(2n)) = 0.
Лемма. Расслоение Spinc (2л) ->5О(2л) (со слоем S’) нетривиально.
Доказательство леммы. В Spine(2л) содержится двулистная накры-
вающая SpinR (2л) группы 5О(2л). Если бы рассматриваемое расслоение было
тривиально, то сквозное отображение
Spin *(2л) -> Spinc(2n) -про-ек-^ s 1
переводило бы точки слоя двулистного накрытия в диаметрально противоположные
точки окружности, и мы получили бы коммутативную диаграмму
SpinR(2n)-> 5*
4, ;
5О(2л) -> S1,
вертикальные стрелки которой являются двулистными накрытиями. Но отображение
5O(2n)->S* должно быть гомотопно нулю, потому что № (5О(2л); Z) = 0, а это про-
тиворечит петривиальностирасслоения Spin R (2л) ->5О(2л).
Доказательство предложения 3. Расслоение Spinc(2n) -> £О(2л)
просто, потому что его слои, будучи смежными классами группы S1, обладают ка-
нонической ориентацией. В спектральной последовательности этого расслоения
(рис. 170) дифференциал J?1 нетривиален, поскольку его образ содержит первое
(и единственное) препятствие к построению сечения (см. н. 5 § 18). Таким образом,
из спектральной последовательности вытекает нужное нам утверждение.
В. Спинорные расслоения и их характеристические классы. Спинорной структурой,
или, подробнее', комплексно спинорной структурой или §р\пс-структурой в 2л-мер-
ном вещественном ориентированном векторном расслоении называется редукция его
структурной группы к SpinC (2л). Поясним это. Как было сказано в н. 1Е § 19,2л-
мерное вещественное ориентированное векторное расслоение над X может быть
задано посредством покрытия {С7,-} пространства X и набора отображений
Uj И Uj -> SO(2ri), удовлетворяющего определенным условиям [именно,
(x)<p/-*(x)<pfc,-(х) = 1 прих€Ц Cl Uj Cl U fc]. Редукция заключается в том, что для
отображения фиксируется поднятие : U{ И Uj ->Spinc(2n), такое, что выстав-
ленное условие продолжает выполняться. Эквивалентность редукций читатель опре-
делит самостоятельно.
Векторные расслоения, структурная группа которых редуцирована к Spinc(2n),
мы будем называть (комплексно) спинорными расслоениями.
Чтобы двигаться дальше, нам нужно немного расширить наши познания относи-
тельно классифицирующих пространств. Для всякой топологической группы G су-
§ 41. ТЕОРЕМА РИМАНА-РОХА
373
ществует клеточное пространство BG, такое, что расслоения с конечной клеточной
базой X и структурной группой G находятся во взаимно однозначном соответ-
ствии с гомотопическими классами отображений X ->BG. Пространство с этим свой-
ством единственно с точностью до гомотопической эквивалентности. Другие свойства
классифицирующих пространств: существует стягиваемое пространство EG со сво-
бодным действием группы G, такое, что BG = EG/G, в частности, имеется расслоение
EG -> BG со слоем G; гомоморфизму G -> Н отвечает отображение BG -+ВН', более
того, если G -+Н — эпиморфизм с ядром F, то имеется расслоение BG -+ВН со слоем
BF. Все зто нетрудно доказать, самое сложное — построить пространство BG; эта
трудность преодолевается при помощи универсальной конструкции Милнора, в кото-
рой EG есть бесконечный джойн группы G :
EG= ... ((G * G) * G) * G...
Классифицирующие пространства некоторых групп нам известны; BU(n) = CG(°°, и),
ВО{п) = G(°°, л), BSO(n) = G+(°°, п), и если я — дискретная группа, то Вп=К{п, 1).
Дальнейшие подробности см., например, в § 4.4 книги Рохлина и Фукса.
Таким образом, существует классифицирующее пространство BSpinC(2n), обла-
дающее тем свойством, что (комплексно) спинорные расслоения с конечной кле-
точной базой X находятся во взаимно однозначном соответствии с гомотопическими
классами отображений X ->BSpinc (2л), и при этом характеристические классы спи-
норных расслоений соответствуют когомологиям этого пространства. Групповое
r s1 r bs'
расслоение Spin (2л)----->5О(2л) превращается в расслоение BSpin (2л) ------>
bs'
----->BSO(n), в котором BSO(n) = G+(°°, л), BS1 = BG(1) = CG(°°, 1) = СР” =
= K(Z, 2). Можно сказать больше: внедрение спинорной структуры в вещественное
ориентированное векторное расслоение соответствует поднятию отображения X ->
-+BSO(n) до отображениях->Z?Spinc(2n).
Из предложения 3 и спектральных последовательностей расслоений
f. Spin^(2n) г- SO(2n)
/TSpinc(2n)----------->В8рщс(2л), ESO(2n)----------> BSO(2n) обычным обра-
зом выводится, что Н‘ (BSO(2n); Z) = 0 при i = 1, 2, Я3(Д$О(2л); Z) = Z2 и
//Э(В SpinC (2л); Z) = 0. Из этого следует, что в спектральной последовательности
r K(Z,2)
расслоения BSpin (2л) -------> BSO(2n) (рис. 171) дифференциал нетривиа-
лен; его образ содержит единственный нетривиальный элемент группы Я3 (Д$О(2л);
Z), который мы обозначим через w%. Теперь мы можем классифицировать спинор-
ные структуры в ориентированных вещественных векторных расслоениях. Ориенти-
рованное вещественное 2л-мерпое векторное расслоение % над X — это отображение
Д: X -> BSO(2n); спинорная структура - это поднятие этого отображения в
BSpinc(2n) (см. выше), т.е. сечение расслоения У->Х, индуцированного расслое-
нием В Spinc (2л) ->BSO(2n) посредством отображения Д :
В Spinc(2 п)
K(Z,2)
K(Z,2)
G
BSO(2n).
Единственным препятствием к построению этого сечения служит класст.е.
соответствующий wf характеристический класс расслоения £. Принимая во внима-
374
ГЛ 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
ние, что W3 = (iw2, где w2 G H2(BSO(2n); Z2) — универсальный класс Штифеля -
Уитни, а Р — гомоморфизм Бокштейна, мы приходим к следующему результату.
Предложение 4. Ориентированное вещественное векторное расслоение I
с конечной клеточной базой X тогда и только тогда обладает комплексно спинорной
структурой, когда wf (£) = 0, или', что эквивалентно, класс w2(|) является целочис-
ленным, т.е. принадлежит образу гомоморфизма приведения р2: Н2(Х; Z) ->
-> Н2(Х', Z2). Более того, классы эквивалентных спинорных структур в £ находят-
ся во взаимно однозначном соответствии с элементами множества р21(у>г($У) С
СЯ2(Х; Z).
Упражнения. 5. Докажите последнее утверждение предложения 4 (указание:
различающие).
6. Комплексное векторное расслоение обладает канонической спинорной структу-
рой ввиду включения U(n) С SpinC (2и). Докажите, что эта структура отвечает клас-
су ci«) Cp7'(w2(O)-
Предложение 5. //*(BSpinc (2n); Q) есть кольцо многочленов от следую-
щих переменных: с (dime = 2), р1(.. ., рп (dimp/ = 4i), X (dimx =2и). Таким об-
разом, рациональные характеристические классы спинорного расслоения — это поли-
номы от классов Понтрягина и Эйлера этого расслоения, рассматриваемого как
ориентированное вещественное векторное расслоение без спинорной структуры, и
характеристического класса с, который является образом в рациональных когомоло-
гиях целочисленного класса из р£* (w2(|)) .задающего спинорную структуру.
Первое утверждение вытекает из спектральной последовательности расслоения
' K(Z,2)
В Spin (2 л)-------* BSO(2n) и вычисления рациональных когомологий простран-
ства BSO(2n)„ проделанного в § 19. Остальное оставляется читателю в качестве
упражнения.
Как уже не раз говорилось, комплексные векторные расслоения являются спи-
норными расслоениями. Поэтому характеристические классы спинорных расслоений
являются и характеристическими классами комплексных векторных расслоений
и должны выражаться через классы Черна. Это выражение легко найти, вычислив
классы с, pt, х Для расслоения f X . .. X f над СР™ X ... X CPN (п сомножителей).
Вычисление приводит к следующим результатам.
с(ГХ...ХГ) = х1 +...+х„,
Р,(ГХ...ХГ) = е,(х?,...,х2),
Х(ГХ...ХГ) = х1 ...х„,
где ei — элементарные симметрические многочлены. Это позволяет прямо выразить
с, Pi>X через с{:
С = Cl, Pi = С2 + Cj-iCi+i + ...+ c2i, Х~ сп.
Впрочем, это прямое выражение не столь полезно, как предыдущее косвенное.
С. К-ориентация спинорных расслоений, класс Тодда и теорема Римана - Роха.
^-ориентация спинорного расслоения £ = (Е, X, V, р) строится по образцу /С-ориента-
ции комплексного векторного расслоения. Унитарные представления группы
SpinC(2n) в AevenC" и AoddC" позволяют построить по £ ассоциированные расслое-
ния с базой X и слоями AevenC" и AoddC”; эти расслоения мы обозначим через
Хо(£) и Х1(|). Поднятые расслоения р’Хо(£) и p’Xj(£) канонически изоморфны
над Е' = Е - X в силу предложения 2; поэтому разность р*Хо(£) — p*Xj(£) может
§ 41. ТЕОРЕМА РИМАНА-РОХА
375
рассматриваться как элемент группы К (Е, Е‘) = АС(Т(£)); этот элемент мы обозна-
чим через и (£).
Теорема, (i) Элемент ц(£) представляет собой К-ориентацию расслоения %.
(ii) Класс Тодда
^«)=t^ chaG)etfe’e"(X;Q)
равен
ес/2Л(Р1(0, Р2(0, - •
где степенной ряд А определяется формулой
A(et(x2i, xl,. .. е2(х2, х22,...),.. )= П—.
Xitl
Замечания. 1. Характеристический класс A (Pi(Jj), рг(£),. • •) называется
(приведенным) классом Атиа - Хирцебруха вещественного расслоения £.
2. Заметим, что определенная в п. 2 АГ-ориентация комплексного векторного рас-
слоения £ совпадает с АС-ориентацией в спинорном смысле расслоения £.
Доказательство теоремы, по существу, нам уже известно. Как и для аналогичной
теоремы из п. 2, утверждение (i) следует из утверждения (ii). Вычисление же класса
<£F(j) производится из следующих соображений. Во-первых, если расслоение % комп-
лексно, то наш класс &(%) совпадает с классом У(£) из п. 2. Во-вторых, класс
&(%) является стабильным, т.е. ^(£ ® 2) = У(£). Поэтому 3(1-) не может зависеть
от х- Эти свойства &(!) полностью его определяют (поскольку симметрический мно-
гочлен от Xi,... не может выражаться через ei(xit . . .) и е,- (х2, . ..) разными спо-
собами) . Остается воспользоваться тождеством
1-е-* sh(x/2)
__ = £ — -
х_______________________х/2
Приведем результаты вычисления начальных отрезков рядов А (р) и А (р)~1:
-4(Р)= * +~Pi + c_,n (3Pi +4Р2) + - • >
24 5760
. 1 1
А(р) = 1-------рх +---------------(7pi - 4р2 ) + . . .
24 5760
Сопоставляя общие теоремы из п. 1 с результатами проделанных выше вычисле-
ний, Мы приходим к главным результатам этого пункта — теоремам Римана — Роха
для изоморфизма Тома и прямого образа.
Теорема. Пусть % — комплексно спинорное векторное расслоение с конечной
клеточной базой X. Тогда для любого a G К (X)
ch(t|a)=t^(cha- ec(i)l2A(pl(^\ р2(%),... ).
Теорема. ПустьХ, Y - многообразия, нормальные расслоения , р(у) ко-
торых в сфере большой размерности наделены комплексной спинорной структурой,
и пусть f: X -+Y - непрерывное отображение. Тогда для любого а&К (X)
f,(cha-e~c^x'>'>A(pi(X))= ch(f,a) • е-с<*'<г>)Л(р/(Г))
(Pi(X) = pi(v(X)), Pi(Y) = Pi(v(Y)) — нормальные классы Понтрягина многообразий
X, Y).
Большое количество других формулировок в этом роде читатель найдет в § 4
гл. V книги Каруби.
376
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
5. Первое применение: теоремы целочисленности. Последняя теорема весьма
содержательна уже в случае, когда Y есть точка.
Теорема. Пусть X - замкнутое гладкое ориентированное многообразие, такое,
что класс w2(X) является целочисленным, и пусть с G Н2(Х\ Z) — какой-нибудь
класс, переходящий при приведении mod2 в класс w2(X). Тогда для любого a G
€ К (X) класс
е-с'2сЬаА-1(р^Ху, р2(Х),...)
принимает целое значение на фундаментальном гомологическом классе [X] много-
образия X.
Доказательство. Применим последнюю теорему предыдущего пункта
к отображению/: X-*pt. Имеем:
Z 3dim/|0! = ch/;a = (ch f,a) -Si(pt) =
=/l(cha- есЫх»!2А(р2(Х). p,(.¥),... ) =
=Л(<Г c'2 • ch a • A -1 ( p, (X), p2 (X),... ) =
= <е-с/2 сЬа Л-1(р1(ДЭ, p2(X),...), [X]>
(мы воспользовались равенством A(p) = A“’(p-), являющимся следствием очевид-
ной мультипликативности класса А: А (£ ® т?) = А (£)А (ц) ).
Положим в последней формулировке а = 1 (случай а ¥= 1 тоже весьма содержа-
телен, как мы увидим в следующем пункте). Получаем утверждение о делимости
характеристических чисел многообразий с целочисленным классом w2.
Примеры. Пусть X — замкнутое ориентированное многообразие, с G Я2(Х; Z) -
произвольный класс, переходящий в w2 при приведении mod2. Если dim X = 4, то pt —
— Зе2 делится на 24. Если dimX = 6, то с3 - срг делится на 48. Если dimX = 8, то
15с4 + 30piC2 + 7р2 - 4р2 делится на 5760. (Всюду подразумевается делимость в
группеHdimX(X-, Z).)
Использование вещественного /С-функтора позволяет иногда несколько усилить
эти результаты. Именно, ориентируемость по отношению к вещественной Х-теории
ориентируемого вещественного векторного.расслоения равносильна редуцируемое™
его структурной группы не к группе Spinc, а к меньшей группе SpinR. Последнее
означает, что класс w2 уже не просто является целочисленным, а равен 0. Зато веще-
ственный класс Тодда отличается от комплексного класса Тодда множителем 1/2,
и зто позволяет в случае w2 = 0 улучшить теоремы делимости на множитель 2.
Прим еры. Пусть X - замкнутое ориентированное многообразие с w2 =0.
Если dimX = 4, то Pl делится на 48. Если dimX = 8, то 7р2 - 4р2 делится на 11520.
На первый взгляд это дополнение кажется мало существенным. Для иллюстра-
ции противоположного рассмотрим случай, когда X — замкнутое односвязное глад-
кое четырехмерное многообразие с w2(X) - 0. Из формул By для классов Штифеля -
Уитни (см. п. 2 § 30) с легкостью выводится, что последнее утверждение равносиль-
но тривиальности гомоморфизма Sq2: Я2(Х; Z2) ->Я4(Х; Z2), который является
не чем иным, как возведением в квадрат. На языке целочисленных гомологий
зто означает, что квадрат любого двумерного когомологического класса четен, т.е
что у матрицы формы пересечений Н2(Х\ Z) X Я2(Х; Z) -> Z на диагонали стоят
четные числа. В алгебре есть термин, описывающий зту ситуацию: четная форма;
имеется теорема Серра, утверждающая, что сигнатура четной унимодулярной цело-
численной формы делится на 8. Но, как известно (см. п. 5 § 19), сигнатура этой фор-
мы равна <р! (X), [X] >/3. Значит, наша комплексная теорема целочисленности только
повторяет алгебраический результат, а более тонкая вещественная теорема превра-
щается в следующий весьма содержательный факт.
§41. ТЕОРЕМА РИМАНА-РОХА
377
Теорема. Сигнатура формы пересечений замкнутого односвязного гладкого
четырехмерного многообразия Xс - 0 делится на 16.
Это - знаменитая теорема Рохлина, доказанная в 1952 г. Она показывает, что не
всякая целочисленная унимодулярная квадратичная форма может быть формой пе-
ресечений замкнутого гладкого односвязного четырехмерного многообразия; этот
факт имеет в топологии бесчисленные применения. Заметим, что до 1982 г, кроме
форм, запрещаемых теоремой Рохлина, не было известно никаких квадратичных
форм, не способных быть формами пересечений односвязных замкнутых гладких
четырехмерных многообразий. Такие формы стали в большом количестве известны
после работы Доналдсона, доказавшего,что если форма пересечений гладкого замкну-
того односвязного четырехмерного многообразия положительно определена, то она
приводится над Z к сумме квадратов.
6. Второе применение: теоремы невложнмости. Теорема Римана — Роха и теоремы
целочисленности допускают следующее усиление. Пусть т: й -> к — мультипликатив-
ное отображение одной мультипликативной теории когомологий в другую, и пусть
% — векторное расслоение, ориентируемое по отношению к теории к, но, вообще го-
воря, не ориентируемое по отношению к теории й. Пусть ик €к(Т(£У) есть й-ориен-
тация и € й(Т(£)) есть произвольный элемент. По ик и uh строятся, соответ-
ственно, изоморфизм Тома tk и гомоморфизм Тома th, причем последний, как и
первый, обладает мультипликативным свойством.
Теорема. Для любого aGh (X) (X - база расслоения £)
где <5'«) = tfc1Tth(l)e*(X).
Доказательство прежнее (см. п. 1).
Формулировки теоремы Римана — Роха для прямого образа и теоремы целочис-
ленности (для случая т = ch) остаются прежними, и мы их не повторяем.
Рассмотрим следующий пример. Группа SO(2k) обладает унитарным представле-
нием в Л*С2к. Определен оператор
*: Л'С2*-> Л2*-'С2*,
в частности,
*: AkC2k->AkC2k.
Пространство ЛкС2к разлагается в ортогональную сумму пространств Л$С2к и
ЛкС2к, соответствующих собственным значениям 1 и —1 этого оператора. Положим
С - Л’С2к +Л2С2к - ... +(-1)к-1Лк"1С2к + (—1)*ЛкС2к = То - Т1;
где То и Г] - унитарные представления группы SO(2k). Очевидно, эти представления
эквивалентны как представления группы SO(2k — 1). Поэтому для любого 2й-мер-
ного ориентированного вещественного векторного расслоения £ = (Е, X, V, р) мы, в
полной аналогии с предыдущим, получаем элемент
п® = T0P*t- Т1Р*^К(Е, Е- Х) = К(Т&.
Обозначим через В (%) аналог класса Тодда для и (О- Вычисление (совершенно
аналогичное предыдущему) показывает, что
1 Г * ех‘ - е~х> к (е*« - 1)(е-*'— 1)
В(£) = - П ------------+ П ------------------- ,
2 . i= 1 Xj i= 1 Xi
Pi(£) = Mx2.....x2k), x® = *i •• • xk.
378
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Упражнение 7. На основании этого вычисления покажите, что п(£), вообще
говоря, не есть К-ориентация.
Соединяя все результаты этого пункта, мы приходим к следующему результату.
Теорема. Число
<eha- B(i>(X)),[X[>
является целым для любого а&К(X).
Введем теперь несколько обозначений. Для z G №ven (Х\ Q),z =z0 + zt +z2 + ...,
Zj e H2' (X; Q), положим z напомним, что если z = cha и t G Z, to
z (f) = chi//a (cm. n. 1 § 39). Положим для замкнутого 2л-мерного многообразия
X, класса с G Н2 (X; Q) и виртуального расслоения a G К (АЭ
H(t) = <е"2 • (cha)<'> • Л'1 (р,(Х), р2(Х),...), [Х]>.
Это — многочлен от t степени п с рациональными коэффициентами; коэффициент
при t" в нем равен <ch„a, [Х]>. Доказанная в п. 5 теорема (вместе с замечанием,
что (cha/f) =сЬ^га) показывает, что если w£(X) = 0 и р2с = w2(X"), то многочлен
H(t) принимает в целых точках целые значения. Применение последней теоремы
целочисленности позволяет доказать, в дополнение к этому, следующее утвержде-
ние.
Теорема. Если многообразие X допускает гладкое вложение в S2n+2k, то
число
2n + k~lH(l/2)
является целым.
Доказательство. Как было доказано в п. 6 § 19, класс Эйлера нормаль-
ного расслоения вложенного многообразия в сфере всегда равен 0. Поэтому в выра-
жении для В(v (X)) второй член, а именно,
п (е*'- 1)(е-*'- 1)
xi
равен 0: он делится на Xj ... xfc. Значит, в выражении для В(у(Х)) мы можем
оставить только первый член, откуда видно, что
cha - В(р(Х)) = (-1)к2п + к~1 Н(1/2).
[Действительно,
cha exi-e~Xi ... ,sh(x,-/2)
----П ---------- и г"**-1 (cha)1'2 П -
2 х,- х,/2
имеют одинаковые 2и-мерные составляющие (формальные переменные х/ имеют
размерность 2). ]
Теперь мы можем доказать сильную теорему невложимости.
Теорема. Пусть X — гладкое замкнутое многообразие размерности 2п>2 с
wf (J) = 0, и пусть существует такое a G К (J), что (заведомо целое) число
<n!ch„a, [Х]> нечетно. Тогда X не вкладывается в S4n~2a^, где а(п) - число еди-
ниц в двоичной записи числа п.
Доказательство. Рассмотрим многочлен Н (Т), построенный по произволь-
ному с G pj1 (w2(X)) и по а из формулировки теоремы. Согласно сказанному выше,
§ 41. ТЕОРЕМА РИМАНА-РОХА
379
этот многочлен принимает в целых точках целые значения. Значит,
t(t- 1)... (/-п + 1) t(t- 1) .. .(t-n +2)
Я(7) = ап-------------------+ Д„_!----------------------и
л!
Г(Г-1)
... + а2-------+ а,Г + а0,
2
с целыми а, . Так как ап = < и! ch„a, [X] > (см. выше), то а„ нечетно. В силу преды-
дущей теоремы, 2n+k~t Я(1/2) — целое число. В то же время предыдущее выраже-
ние для Н показывает, что
2я + к -1 /2) = 2к -1 (ап b + пс)/п<,
где b — нечетно число, а с — четное число. Наконец, хорошо известно, что в разложе-
ние числа и! на простые множители входит ровно п — а (и) двоек. Значит, к — 1 >
> п - а (и). Теорема доказана.
Условие теоремы, касающееся существования а, выполнено, если в Н2(Х; Z)
имеется такой элемент d, что число < d", [X ] > нечетно: в этом случае в качестве а
мы берем класс одномерного расслоения £ с сД?) = d, и будет ch£ = ес,(^) = ed,
ch„ I = dn/n!.B частности, теорема приложима к комплексным проективным прост-
ранствам:
Следстви е. СР" не вкладывается в s4"~2a^"^.
Чтобы оценить силу этого результата, сравните его с теоремами невложимости из
п. 6 § 19. Например, СР1000 в силу результатов § 19 не может быть вложено в
R2046, а в силу наших теперешних результатов - в R3988. (Добавим, что в силу
общих теорем дифференциальной топологии СР1000 вкладывается в R3999.)
Все результаты этого пункта принадлежат Атиа и Хирцебруху и изложены в их
статье ”0 невложимости дифференцируемых многообразий” (Математика: сб. перев.
1961. — Т. 5, № 3). В этой статье читатель найдет и другие интересные результаты.
Предостережение: переводчик этой статьи то, что мы называем вложениями, называл
погружениями.
7. Заключение: происхождение названия. Название ’’теорема Римана - Роха”
известно в алгебраической геометрии. Там так называется формула
r(-D)-i(D) = d(P)-g+l,
где D — дивизор на римановой поверхности Xрода#, d(D) — его степень, r(-D) -
размерность пространства мероморфных функций на X, дивизор которых больше
или равен —D, и /(D) — размерность пространства мероморфных форм степени 1
на X, дивизор которых больше или равен D. Эта теорема может рассматриваться
как вычисление эйлеровой характеристики пучка ростков голоморфных сечений
голоморфного расслоения над X, определяемого дивизором D. Первоначальная
редакция теоремы целочисленности (см. п. 5) выглядела как обобщение теоремы
Римана — Роха; см. статью Атиа и Хирцебруха ’’Riemann - Roch theorems for differenti-
able manifolds” (Bull. Amer. Math. Soc. — 1959. — V. 65. — P. 276 — 281):
T e о p e м а. Пусть X - неособое комплексное проективное алгебраическое
многообразие, с - его первый класс Черна, S- — голоморфное расслоение над X.
Тогда значение на [X] когомологического класса
ес'2 cht-A-l(Pi(X), р2(Х),...)
равно эйлеровой характеристике пучка ростков голоморфных сечений расслоения %.
При перенесении этой теоремы из голоморфной ситуации в дифференциальную
эйлерова характеристика исчезла, осталось утверждение о целочисленности. Но тео-
380
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
рема по-прежнему называлась теоремой Римана — Роха. Затем это название стало
прилагаться к более общим теоремам — вплоть до теорем п. 1.
Вообще стоит сказать, что среди создателей /С-теории только Адамс был
’’чистым топологом”; Ботт был известен своими работами по геометрии и вариа-
ционному исчислению в целом, Атиа, Хирцебрух и особенно Гротендик — работами
по алгебраической геометрии. Последнее обстоятельство сказалось на принятой
в X-теории терминологии. Кроме названия ’’теорема Римана — Роха” алгебро-гео-
метрическое происхождение имеет сам термин "К-функтор”. Добавим, что рассмат-
ривавшийся в п. 6 многочлен Н (г) бьш назван Атиа и Хирцебрухом многочленом
Гильберта многообразия X — на том основании, что он является таковым в случае,
когда X — проективное алгебраическое многообразие, с — его первый класс Черна и
а. — сужение на X хопфовского расслоения над объемлющим проективным прост-
ранством.
§ 42. ФОРМУЛА АТИА - ЗИНГЕРА (НАБРОСОК)
Формула Атиа — Зингера для индекса эллиптического оператора является
одним из наиболее значительных достижений математики последних десятилетий.
Ее значение не исчерпывается; ее бесчисленными приложениями: она напомнила ана-
литикам о необходимости изучать топологию и топологам о необходимости изучать
анализ, способствовав тем самым возрождению математики как единой науки.
Теореме Атиа — Зингера посвящены целые книги (наиболее известен ’’Се-
минар по теореме Атиа — Зингера об индексе” Р. Пале, переведенный на русский
язык). На этом фоне настоящий параграф преследует скромные цели: возбуждение
у читателя интереса и общее знакомство с предметом.
1. Эллиптические операторы и их индексы. Пусть U — область в R", С ”((/)-
пространство комплекснозначных функций класса С на Uh
D:
— дифференциальный оператор порядка к. (Последнее проще всего выразить на
языке координат, но можно описать и инвариантным образом: если функции f,g^
6 С” ((/) имеют в точке х G Uодинаковые £-струи, то Df(x) = Dg (х).)
(Напомним определение струи. Если X, Y - многообразия и хб/, у G Y — точки,
то т-струя с источником х и устьем (значением) у определяется как класс отображе-
ний /: (X,х) -> (К,у) относительно следующей эквивалентности: g, если
II/(z) — g(z) II = О( II z — х II m), нормы берутся по отношению к произвольным
локальным системам координат.)
Предположим, что D есть оператор порядка к (и не есть оператор порядка к — 1).
Символ (или главный символ) oD оператора D есть функция на пространстве T*U
кокасательного расслоения т * (U) области U. В координатах символ определяется
так: если
Э*
D = S <рк к (х) —£-----------------------к— + члены меньших порядков,
к1+... + кп=к ‘ “ " ЭХ] 1 ... Эхп"
ТО
ао(х1;... ,х„;£1,... ,?«)= S tpk к (х)£ *1... £ " ,
к,+... + кп=к 1 " "
rp,eli = dXi — координаты в кокасательном пространстве. Существенно, что символ
может быть описан бескоординатным образом. Именно, отождествим пространство
§ 42. ФОРМУЛА АТИА—ЗИНГЕРА (НАБРОСОК)
381
Т * Uс пространством J1 (U, R) 0 1 -струй функций со значением 0. Тогда
Od№ = Dfk(x),
где (U, R) о, / — произвольный представитель 1 -струи .
Это инвариантное определение символа позволяет обобщить его на случай, когда
D есть дифференциальный оператор С°° (X) ->С°° (X), где X - произвольное глад-
кое многообразие; в этом случае oD есть функция на пространстве Т *Х ко касатель-
ного расслоения т * (X) многообразия X. Дальнейшее обобщение: пусть £, т? — ком-
плексные векторные расслоения с базой X. Очевидный смысл имеет высказывание,
что
D: С “(?)-> С “(т?)
(где С°° (£), С °° (т?) — пространства гладких сечений) есть дифференциальный
оператор порядка к. Пусть р — проекция расслоения т * (X). Тогда символ операто-
ра D определяется как отображение
oD:
действующее по формуле
crD( v, z)=( У.
где y&J(X, R)o — кокасательный вектор к X в точке х& X, z G gx — точка слоя
расслоения g над х и g - такое сечение расслоения g, что g(x) = z. Таким образом,
символ oD линейно отображает слой расслоения p*g над кокасательным вектором
к многообразию X в слой расслоения р*г] над тем же кокасательным вектором.
Очевидно, над нулевым сечением ХС Т*Х символ а о представляет собой нулевое
отображение.
Оператор D называется эллиптическим, если для любого ненулевого кокасатель-
ного вектора и оператор Од определяет изоморфизм (p*g)„ "*(p*’?)v-
В анализе доказывается
Теорема. Эллиптический оператор на компактном многообразии X имеет ко-
нечномерное ядро и конечномерное коядро.
Доказательство см. в книге Пале.
Оператор с конечномерным ядром н конечномерным коядром называется фред-
гольмовым. Индекс ind Ь фредгольмова, в частности эллиптического, оператора D
определяется формулой
ind D = dim Ker D - dim Coker D.
Мотивировкой этого определения служит тот факт, что при деформации оператора в
классе фредгольмовых операторов размерности ядра и коядра могут измениться,
но индекс не меняется. Этот же факт послужил мотивировкой обшей проблемы,
поставленной в 50-е годы И.М. Гельфандом: выразить индекс эллиптического опе-
ратора в топологических терминах.
Формула Атиа — Зингера и является решением этой обшей проблемы Гельфанда.
Прежде чем перейти к рассмотрению формулы, мы рассмотрим несколько при-
меров.
2. Примеры. (Все примеры, рассматриваемые здесь и в п. 4, предполагают зна-
комство с теорией де Рама, не вошедшей в нашу книгу. Читатель, не знакомый с
этой теорией, должен либо пропустить этот пункт и п. 4, или, что лучше, выучить тео-
382 ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
рию де Рама. Она изложена во многих книгах, например, в книге Дубровина, Но-
викова и Фоменко’’Современная геометрия. Методы теории гомологий” и в книге де
Рама ’’Дифференцируемые многообразия”.)
А. Пусть X — замкнутое гладкое ориентированное 2и-мерное многообразие с
фиксированной римановой метрикой (т.е. с фиксированными евклидовыми струк-
турами в слоях косательного расслоения, гладко зависящими от точки базы). Обоз-
начим через £lk X пространство внешних дифференциальных С “-форм степени к
на X. Имеются операторы:
d: ПкХ->^к+1Х,
»: акх-*а2п-кх,
5:
где d — внешний дифференциал, * - послойный оператор, определяемый формулой
[*<р] (Wi,...,W2n-fc) =
Vol(i>1,...,ihw-fc,>v1,...,wifc)
^(Wi,..., wk)
в которой v!,. .., v2n-k — касательные векторы в некоторой точке многообразия
X,wt,... ,wk — произвольные линейно независимые векторы, ортогональные векто-
рам Wi,..., v2n_k (проверьте корректность этого определения), и 5 =» d «.Очевид-
но, d и 5 — сопряженные операторы. Рассмотрим оператор
d + 5: П*Х^П*Х.
Упражнение 1. Докажите, что d + 5 — эллиптический оператор.
Вычислять индекс' этого оператора бессмысленно: он самосопряжен, его ядро и
коядро сопряжены друг другу и имеют одинаковые размерности, и, значит, индекс
равен 0. Чтобы поправить дело, рассмотрим оператор
(d+5)| : I2evenX -> I2oddX.
1 |nevenx
Очевидно, форма ipGfi211! принадлежит ядру оператора <7 + 6 тогда и только
тогда, когда d<p = 0 и = 0. Формы с этим свойством называются гармоническими.
Известна теорема Ходжа: каждый класс дерамовских когомологий содержит одну
и только одну гармоническую форму (т.е. если форма ф замкнута, dtp = 0, то сущест-
вует единственная гармоническая форма такая, что ф — G Im<7). Это позволяет
(ввиду теоремы де Рама) произвести отождествление
Ker(d + 5)|nevenx=^eVeV.R).
Коядро Coker(d + 5) | еуеп есть ядро сопряженного оператора, который есть не что
иное, как (d + 5) I . . : J2oddX-+ J2evenX. Значит,
4 ’ In odd..
Coker(dtS)|ne,e^-№"(XR)
И
+ 5) | n even
= dim 7/even(X; R) - dim tfodd(X; R) = X(X ).
§ 42. ФОРМУЛА АТИА—ЗИНГЕРА (НАБРОСОК) 383
В. Очевидно, ( ♦ | к )2 = (-1)к. Определим оператор
а: акХ-*а2п~к X
как * •Ясно, что а2 = 1, Положим
S2* X =( Я* I а(^>) = ± ф}
Упражнения. 2. (d + 5) (Я* X ) С Я* X.
3. Покажите, что если л нечетно, то индекс оператора (с?+ 5) |п, х равен 0, а
если п четно, то он равен сигнатуре формы пересечений многообразия X.
3. Формула. Пусть
D: С“(0^С“(т?)
- эллиптический оператор,
oD- Р*^Р*Р
— его символ (более подробные обозначения см. в п. 1). Поскольку оо есть изомор-
физм над дополнением к нулевому сечению, оно позволяет рассматривать разность
p*V - р*% как элемент из К(Т(т\Х)')~) (ср. пп. 2, 4, 6 § 41). Обозначим этот элемент
через SD и положим
(№ven(%;Q), если X четномерно,
ch D - ch Sn G J н
d (X;Q), если X нечетномерно.
Теорема.
ind D = ((ch О • ^-’(Ст(О> [X] >,
где S' (Ст(Х)) обозначает класс Тодда (в смысле п. 2 § 41) комплексификации
касательного расслоения. Другими словами,
S'~1(Ct(X))= U(pt(X), р2(Х ),...),
где степенной ряд U определяется формулой
х2
U(ex(x}), е2(х^), ...)=- II -------— .
(1-е х')(1 - ех‘)
Эта теорема по форме напоминает теорему Римана — Роха. Во всяком случае,
целочисленность правой части может быть установлена средствами § 41 (см. п. 6).
Но, конечно, главным в этой теореме является тот факт, что эта правая часть равна
индексу оператора. Мы не излагаем здесь доказательства этой теоремы, укажем
только его общий план. Нетрудно показать, что если расслоения £ и tj продолжаются
до расслоений £ н т? над компактным многообразием W с краем X и эллиптический
оператор D продолжается до эллиптического оператора D: С“(1-) -> то
индекс оператора D равен 0. К тому же индекс эллиптического оператора аддитивен
(если X = Xi U Х2 и D = Dx U D2, то ind D = ind D\ + ind D2) и мультипликативен
(если X = X\ X X2 н D = Dx ® D2,to ind D =ind Dx ind D2). Все это позволяет свести
общую задачу вычисления индекса к задаче вычисления индекса нескольких конкрет-
ных операторов, которая решается без труда.
4. Снова примеры. А. Символ оператора d + 5 (рассматриваемого во всем прост-
ранстве £1*Х) устроен так. Над кокасательным вектором v G Тх*Х к многообразию
X в точке х G X это — оператор : (Л*Тх*Х) ® С -> (А*ГЛ*%) ® С (см. п. 2 § 41).
384 ГЛ 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Положим D = (d + 5) lnevenx- Сравнивая конструкцию SD с построением из п. 2
§ 41, мы находим, что есть в точности каноническая Х-ориентация и (Ст* (Л)) G
G Х(Т(Ст*(Х)))комплексного расслоения Ст*(Х), суженная с Т(Ст*(Х)) на Т(т*(Х)).
Упражнение 4. Пусть £ - произвольное ориентированное (в обычном смысле)
вещественное векторное расслоение, С£ — его комплексификация, i?:T(£) -*7’(С£) —
вложение, индуцируемое естественным вложением £ -» Q-. Тогда для любого a G
G Я*(Г(С£); G) имеет место равенство
(4)-,п’а=(Гн?Г1(а)-х(Л.
Теперь применим формулу Атиа — Зингера:
indZ) = <(chZ)- ^_1(Ст*(Х))), [X] > =
= < ((tTH(X))” ch SD • ST (Ст*(АГ))), [X] > =
= <((tTH(X)T1ch7?.«(CT*(X))- ^-’(Ст*(АГ))), [Х]> =
= <((^*^))-17?.сЬМ(Ст*(АГ)) -5-,(Ст*(АГ))), [X] > =
= <(x(r*W) (tST’(X)r,ch и(Ст*(Х))- Г-ЧСт*(Х))), [X] > =
= < х(т*(X)) • У(Ст*(X)) • (Ст* (X)), [X] > = < Х(т*(X)), [X] > = Х(Х).
— эйлерова характеристика X. Таким образом, вычисление при помощи формулы
Атиа — Зингера привело нас к тому же результату, что прямое вычисление в п. 2 А.
В. Вычисляя при помощи формулы Атиа - Зингера индекс эллиптического
оператора, рассматривавшегося в п. 2В, мы приходим к выражению индекса этого
оператора, т.е. сигнатуры многообразия, через классы Понтрягина. Читатель может
самостоятельно убедиться в том, что получаются в точности формулы, известные нам
ло п. 6 § 19.
С. Пусть X — комплексное многообразие, т? — голоморфное расслоение над
ним. Рассмотрим пространство £2Р,<?(Х; т?) дифференциальных форм типар, q на X
с коэффициентами в сечениях расслоения р и дифференциал d" : S2p,,(X; р) -*
-» 12 р>\X,ri). В силу известной теоремы Дольбо (см. например, книгу Черна
’’Комплексные многообразия”) когомологии пучка '6‘w(t?) ростков голоморфных
сечений расслоения т? могут быть вычислены при помощи комплекса
...->I2°’4(X;n)^ Q0’4+i(X;t?)->...
Из этого с легкостью выводится, что индекс оператора (d" +5”) lno,even(x- n)
есть не что иное, как эйлерова характеристика S(—l)r dim Hr (X; J?) пучка $и>(т?)-
Вычисляя этот же индекс при помощи формулы Атиа — Зингера, мы получаем выра-
жение этой эйлеровой характеристики через топологические инварианты — разумеет-
ся то самое, которое содержится в теореме Атиа — Хирцебруха, приведенной в
п. 7 § 41.
D. Добавим, что все теоремы целочисленности иэ § 41, не исключая теоремы из
п. 6 этого параграфа, могут быть выведены из формулы Атиа — Зингера при надле-
жащем подборе операторов.
§ 43. КОБОРДИЗМЫ
385
§ 43. КОБОРДИЗМЫ
Как и теорема Атиа — Зингера, теория кобордизмов является предметом целых
книг (см., например, ’’Заметки по теории кобордизмов” Стонга). В этом параграфе
мы ограничиваемся определением кобордизмов, перечислением их основных свойств
и сопоставлением их с /^-теорией.
1. Определения.
А. Бордизмы. Пусть X — топологическое пространство. (Замкнутым) п-мерным
сингулярным многообразием пространства X называется пара (М, f), гдеЛУ —замк-
нутое гладкое «-мерное многообразие и/ — его непрерывное отображение в X. Сингу-
лярные многообразия (M2,fi) называются бордантными, если существует
компактное многообразие W с краем 9 W = Мi U М2 и непрерывное отображение
F: W-* X, такое, что F\M=fi, F |ЛГа = /2. Множество классов бордантных «-мерных
сингулярных многообразий пространства X обозначается через Операция
дизъюнктного суммирования U многообразий делает это множество абелевой груп-
пой (в которой, кстати, любой элемент имеет порядок 2: бордизм 2(М, f) ~ (ф, -) =
= 0 осуществляют многообразие W = М X / и композиция проекции МУ. I -+М cf).
Отображение X -* У очевидным образом индуцирует гомоморфизм £1%(Х) -+ £l°(Y),
и, полагая
П„о(Х)=0 при и<0,
Я^(АГ) = Кег(Я „(АГ)-* Я „(pt)),
П^(Х,А) = ^(Х/А),
мы составляем из групп теорию экстраординарных гомологий, называемую
теорией (неориентированных) бордизмов.
Внедряя в это определение ориентации, мы приходим к определению ориентиро-
ванных бордизмов £1п°- Подчеркнем, что при этом ориентированными считаются
как многообразия М в определении сингулярных многообразий, так и многообразия
W в определении бордантности, причем в дополнение к равенству dW = Mt U М2
предполагается, что ориентация многообразия Мi согласована, а ориентация много-
образия Мг противоположна ориентации, согласованной с ориентацией многообра-
зия W. Операция обращения в группе П^°(Х) соответствует операции обращения
ориентации у отображаемого многообразия. Ниоткуда не следует и, как мы увидим,
неверно, что все элементы группы (X) обязаны иметь порядок 2.
Еще один вариант определения бордизмов получится, если предположить, что
многообразия М и И7.согласованным образом наделены стабильно почти комплекс-
ной структурой, т.е. что расслоения т(М) ® N и т(И') ® N (с некоторым N) сделаны
комплексными векторными расслоениями. Соответствующее обозначение:
Стоит сказать, что в современной топологии рассматривается огромное количество
других вариантов теории бордизмов (и кобордизмов). Некоторые из них мы упомя-
нем очень коротко ниже — в п. 2D. Дальнейшие сведения о них см. в цитировавшейся
книге Стонга.
В. Спектры Тома. Теории бордизмов укладываются в общую схему построения
экстраординарных гомологий при помощи спектров (см. п. 5 § 37).
Обозначим через МО(п) пространство Тома тавтологического векторного расслое-
ния над ВО(п) = G(°°, п) и через MSO(n) и MU(n) - пространства Тома тавтоло-
гических расслоений и над BSO(n) =G+(°°,n) и BU(n) = CG(°°, п). Построим
отображения W(«) -*МО(п + 1), YMSO(n) -*MSO(n + 1), Z2MU(n) ->MU(n + 1).
Сужение расслоения |„+ j на G (°°, п) есть, очевидно, & 1; включение £„ ® 1 -*£„+1
13. А.Т. Фоменко
386
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
определяет отображение Т(£п ® 1) -* Т(£„+ i). Но ясно, что Т(т? ® 1) = ST(t?) для
любого векторного расслоения т?; таким образом, мы получаем отображение
ХМО(п) -*МО(п + 1). Остальные два отображения строятся аналогично.
Пространства МО(п), MSO(n), MU(ri) вместе с построенными отображениями
составляют спектры
...,МО(п), МО(п+\),...
...,MSO(n), MSO(n +1),...
.... MU(ri), ЪМЩп), MU(n + 1), £MU(n + 1),...
(отображения, составляющие последний спектр, — это id 2Aft/(«) и наше отображе-
ние S(SA/t/(n)) = T?MU(n) -* MU(n +1)). Эти спектры называются спектрами Тома
и обозначаются через МО, MSO, MU.
Теорема. Теории бордизмов совпадают с теориями экстраординарных гомоло-
гий с коэффициентами в спектрах Тома. Другими словами,
П°(Х) = lim лп +N(X #MO(N)),
ns„°(X) = lim irn+N(X #MSO(N)\
Й^(Т)=Иттгп + 2Л,(% #MU(N)). .
(♦)
Прежде чем доказывать эту теорему, уместно сделать следующее замечание. На
протяжении книги мы несколько раз сталкивались с пространствами Тома по самым
разным поводам: в связи с характеристическими классами (§ 30), в связи с ориента-
циями расслоений по отношению к теориям когомологий (§ 41) и тд. Но все это —
побочные продукты теории Тома, главный результат которой составляют именно
равенства (*) в случае X = S°. В этом случае равенства (*) принимают следующий
вид:
Й^(5°) = Я<£(pt) = lim тг„ +лг(5° #MO(NJ) = lim тг„ +n(M0(N)),
Я5ЛрО = Um лп+„(Л«О(Л0),
я£(рО = Итя„ + 2лг(М/(ЛГ)).
Заметим еще, что при больших N группы тг„ +n(M0(N)), irn + N(MSO(N)'),
я п + 2 N (MU (N)) от N не зависят (докажите это!), так что во всех этих равенствах
можно отбросить знак lim.
Теперь посмотрим, что такое Яп (pt) (Г - О, SO, U). Сингулярное многообра-
зие точки — это пара, составленная иэ многообразия М (с той или иной структурой) и
отображения М -* pt. Но отображение в pt есть всего одно, поэтому его можно
не указывать.
г г о
Принято обозначение Q„(pt) = Ял. Элементами группы Ял служат классы
замкнутых гладких «-мерных многообразий, рассматриваемых абстрактно
(т.е. никуда не вложенных и не отображенных), по отношению к следующей эквива-
лентности, называемой кобордантностью: Mi ~ М2, если существует компактное
многообразие W с Э W = Мj И М2. Сумма, она же разность (все элементы имеют
порядок 2), определяется как U . Операция прямого произведения превращает
„О
= ®п“и в градуированное кольцо.
В п. 6 § 19 были сформулированы результаты Тома, доставляющие классифика-
цию гладких замкнутых многообразий с точностью до кобордантности. Там же
были приведены частичные результаты аналогичного вычисления для кольца
§ 43. КОБОРДИЗМЫ
387
„SО „SО
S2, - ® \1 п классов ориентированно кобордантных ориентированных замкнутых
гладких многообразий (ориентированные многообразия Мх и М2 ориентированно
кобордантны, если существует компактное ориентированное многообразие W с
dW = Мх U (-Л/2), где -М2 обозначает многообразие М2 с противоположной
ориентацией). Теперь мы можем добавить к этим кольцам кольцо J2^ = ® £2^ клас-
сов замкнутых стабильно почти комплексных многообразий по отношению к соот-
ветствующей кобордантности.
Докажем, что £2°п = irn + N(МО(N)). Построим отображение £2^ -»тг„ + N(МО(N)).
Пусть X — замкнутое и-мерное многообразие; вложим его B .Sn+N, где N достаточ-
но велико. Согласно результатам л. 1 § 19, нормальное расслоение v мнообразия X
в Sn + N отображается в тавтологическое расслоение над BO(N) = G(«>, N),
причем отображение гомотопически единственно. Возникает отображение простран-
ства Тома Т(п) в T(U) =MO(N). Но Т (п) = 5n + JV/(5" + JV - U(X)), где U(X) -
трубчатая окрестность многообразия X в Sn + N. Композиция
Sn+N Sn + N/(Sn + N - U(X)) = Т(у) MO(N)
определяет элемент группы тг„ + n(MO(N)) , который, как читатель проверит само-
стоятельно, зависит только от класса многообразия X в £2^; возникает отображение
£2„ ** ^n+N(MO(N)). Построим теперь отображение nn + N(MO(N)) -» J2„.
Элемент группы тгп +(MO(N')') представляется сфероидом у: Sn + N -» МО(N).
Можно считать, что образ этого отображения содержится в пространстве Тома тавто-
логического расслоения над многообразием Грассмана G(M,N.) с достаточно боль-
шим Л/; чтобы избежать громоздких обозначений, мы это конечномерное простран-
ство Тома по-прежнему обозначаем через MO(N). Далее, отображение Sn + N -*
-» MO(N) можно считать гладким вне прообраза отмеченной точки «> пространства
МО (N) [МО (7V) — °° есть гладкое многообразие ]. Наконец, малое шевеление этого
отображения приводит его в общее положение по' отношению к многообразию
G(M, TV) С MO(N) в следующем смысле: если <р-(х) G G(M,N), то,образ при ото-
бражении (лучше сказать, при дифференциале отображения^) касательного прост-
ранства TxSn + N к сфере Sn + N составляет в сумме с (X)G(M,N.) все простран-
ство T^^yMO^N). Это свойство отображения называется трансверсальной регу-
лярностью по отношению к G(M,N) (см. рис. 172). Из трансверсальной регуляр-
ности следует, что прообраз (G (М, N}) = ХС Sn + N есть гладкое подмногообра-
зие сферы Sn + N, коразмерность которого в сфере равна коразмерности много-
образия G(M, N) в MO(N}, т.е. равна TV; другими словами, dim % = п. (Подроб-
ности, относящиеся к трансверсальной регулярности, см. в § 3.4 книги Рохлина и
Фукса или в гл.З книги Хирша.) Можно показать (подробности мы снова оставляем
читателю), что класс многообразия X в £2„ зависит только от исходного элемента
группы яп+ N (МО(N\), так что получается отображение itn + N(MO(N)) -> £2„.
Мы оставляем читателю также доказательство того факта, что построенные отображе-
ния £2° * >^п + N (МО(N)) взаимно обратны.
Доказательство равенств nSn° = irn + N(MSO(N)) и £2^ = ^n+2N(MU (N))
совершенно аналогичны (нужно только заметить, что задание ориентации или ста-
13*
388
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
бильной комплексной структуры в касательном расслоении к многообразию равно-
сильно заданию ориентации илн стабильной комплексной структуры в нормальном
расслоении в сфере большой размерности).
Этим доказательство теоремы завершено в случае X = S0. Переход к общему слу-
чаю не вызывает серьезных затруднений, и мы ограничимся общими указаниями.
Пусть (М, f) - замкнутое п-мерное сингулярное многообразие пространства X.
Вложим М в Sn+N. Как выше, определяется отображение Sn+N -* MO(N),
Рис. 172
переводящее в отмеченную точку дополнение к трубчатой окрестности U многообра-
зия М в S"+N. Отображение f: М -* X естественно продолжается до отображения
/: U-*X. и отображения у? и f составляют отображение Sn + N -* (А’Х MO(NJ)IX:
отмеченная точка, если s ф U,
[ (/($), $($)), если s G U.
Композиция этого отображения с проекцией (%Х MO(N))[X-*X #MO(N) опреде-
ляет элемент группы я„+N(X # МО (7V)), и нетрудно показать, что этим корректно
определено отображение Л^(А') -* tt„ + n(X # MO(N)), в частности, 12^ (А-) -*
Пп + n(X # MO(N)). Что это изоморфизм, можно доказать прямо, а можно вы-
вести из общей теории п. 5 § 37; рассмотрим £2^ и гомологии с коэффициентами
в спектре Тома МО как две разные экстраординарные теории гомологий; можно
проверить, что описанная конструкция определяет гомоморфизм одной теории в дру-
гую и затем воспользоваться теоремой единственности из п. 5 С § 37.
Ориентированный и комплексный случаи совершенно аналогичны.
С. Кобордизмы. В п.5 § 37 по спектру построена не только теория экстраорди-
нарных гомологий, но и теория экстраординарных когомологий. Экстраординарные
когомологии, соответствующие спектрам Тома, называются кобордизмами. Их обо-
значения: J2p = ® O.Q. £lso = ® S2^o, Г2у = ® S2y. Таким образом,
= яСг^Х/Л), MO(N+n)),
ti's^X.A) = я(£л(*/А). MSO(N +п)),
п":(Х/А) = я(22Л’ + '!(-¥/Л), MU(N + n)y.
в частности,
Яо(Р») = я(5л’, MO(N + л)) = nN(MO(N + п)) = nf„(pt).
§ 43. КОБОРДИЗМЫ
389
и,аналогично,
I2^(pt) = ^(pt) = «"„(pt).
Заметим, что «г (pt) = 0 при п >О (Г = О, SO, U).
Упражнения. 1. Кобордизмы обладают естественной мультипликативной
структурой; восстановите детали.
2. Пусть X - замкнутое многообразие размерности т. Тогда (X) есть группа
классов эквивалентности пар (Л/, /), где М — замкнутое многообразие размер-
ности т - п п f: М-*Х - непрерывное отображение. Группы П^О(Х) и
описываются точно так же, но с дополнительным условием, что виртуальное рас-
слоение f т (А-) — т (М) (над М) обладает соответственно ориентацией или стабиль-
ной комплексной структурой. В частности,
Пп(Х) = П(Х) всегда,
12п°(Л’) = n”so\X'), если X ориентировано,
Пп(Х) = п”и \Х), если в расслоении т(X) задана стабильная комплексная
структура
(’’изоморфизмы Пуанкаре”).
D. Связь с обыкновенными гомологиями и когомологиями. Бордизмы разного
вида связаны между собой и с гомологиями естественными отображениями, состав-
ляющими диаграмму:
и so о
tln(X)------ Я„ (X) ----> Я„(Х)
Н„(Х) = Нп(Х) —> Нп(Х, Z2).
Верхние горизонтальные стрелки определяются посредством отбрасывания у сингу-
лярного многообразия структуры (или ее части), нижняя горизонтальная стрелка
есть приведение mod 2, вертикальные стрелки действуют по формуле (ЛГ,/)>-*
[ЛГ]. Эти вертикальные гомоморфизмы имеют прозрачный геометрический
so
смысл. Именно, класс a G Нп(Х) принадлежит образу гомоморфизма £ln (X) -*
-» Нп (X) тогда и только тогда, когда он представляется циклом, реализуемым как
ориентированное сингулярное многообразие. Если при этом X есть многообразие
размерности > 2 п, то это сингулярное многообразие можно малым шевелением
превратить во вложенное многообразие. Таким образом, наш гомоморфизм имеет
прямое отношение к проблеме реализации гомологических классов (неособыми)
подмногообразиями, которую мы обсуждали в п. 2 § 17. Аналогичный смысл (но без
о
ориентации и с коэффициентами в Z2) имеет гомоморфизм «„(А’) ~*Нп (Х\ Z2).
Заметим, что рассматриваемые гомоморфизмы тесно связаны также со спектральной
последовательностью Атиа — Хирцебруха, точнее, с ее дифференциалами. Именно', хотя
390 ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
мы еще ничего не знаем о бордизмах точки (им посвящен следующий пункт),
априори ясно, что £ln (pt) = Пп (pt) = 0 при п < 0 и J20 (pt) = Z2, I20 (pt) =Z.
о
Поэтому спектральная последовательность Атиа - Хирцебруха для J2, (ЛГ) и
SO
J2, (У) имеет вид, показанный на рис. 173. Ядра дифференциалов, действующих
из Н.(Х; Z2) и Ht(X), представляют собой факторгруппы групп ЯДХ) и
Jlf°(X); этим и определяются наши гомоморфизмы Slf(A’) -* Я, (X; Z2) и
J2, (X) -* Н9 (X). Таким образом, реализуемости гомологического класса сингу-
лярным многообразием, в частности, подмногообразием препятствует нетривиаль-
ность дифференциалов в спектральной последовательности Атиа — Хирцебруха.
Подробности см. в двух статьях Бухштабера в Математическом сборнике (1969. —
Т. 78. — № 2; 1970. — Т. 83, № 1). Мы ограничимся замечанием, что все дифферен-
циалы спектральных последовательностей Атиа — Хирцебруха имеют конечный поря-
док, и потому гомоморфизмы (X) -* Я, (X) и 12^ (X) -* Я, (У) имеют
(для произвольного конечного клеточного пространства X) конечное коядро.
Е. Гомотопическая достаточность. Как мы замечали выше (см. п. 1 § 37 и
п. 1 § 38), У-теория не является гомотопически достаточной, в том смысле, что
отображение односвязного конечного клеточного пространства X в односвязное ко-
нечное клеточное пространство Y, индуцирующее изоморфизм К* (У) К*(Х),
не обязано быть гомотопической эквивалентностью. В противоположность этому
so и » »
теории J2, и J2, (равно как Qso и fi^) являются гомотопически достаточными.
Теорема. Если непрерывное отображение f.X-^Y одного односвязного ко-
нечного клеточного пространства в другое обладает тем свойством, что один из гомо-
морфизмов
f, -. (X)-+as°(Y),
f,-. ^(У) + 12^ (У),
Г-
f*-.
является изоморфизмом, то f — гомотопическая эквивалентность.
Достаточно доказать, что f индуцирует изоморфизм в целочисленных гомологиях
или когомологиях. Далее, превращая отображение f в гомотопически эквивалентное
§ 43. КОБОРДИЗМЫ
391
ему вложение и пользуясь точностью последовательностей пары, мы приходим к сле-
дующей эквивалентной формулировке: если конечное клеточное пространство Z
обладает тем свойством, что Я^° (Z) =0 или ПУ(2) =0 (т.е. Stf°(Z) = fi?°(pt)
или fi^(Z) =S2i(pt)), то H*(Z)=0, а если £2*o(Z)=0 или £2^(Z)=0, то
Н* (Z; Z) =0. Предположим, например, что Slf°(Z) = Я^ ° (pt), но H,(Z) =А0.
Пусть q — самое маленькое положительное число, при котором Hq (Z ) =А0. По тео-
реме Гуревича irq(Z) -+Hq(Z) есть изоморфизм, т.е. существует нетривиальный эле-
мент аЕ Hq(Z), представляемый сфероидом Sq-*Z. Но Sq — ориентированное
многообразие, так что сфероид может рассматриваться и как ориентированное син-
гулярное многообразие. В этом качестве он определяет элемент из S2^(Z), нену-
левой, поскольку он имеет ненулевой образ в Hq (Z ). Однако образ этого элемента
в (pt) равен 0 (сфера есть край шара). Противоречие. Разбор остальных слу-
чаев мы оставляем читателю.
2. Вычисления.
А. Я®. Теорема 1. Я^ есть кольцо многочленов (над Z2) от переменных
xt,dimxt =i, где i пробегает все натуральные числа, не имеющие вида 2s —1,
s > 1. В качестве х,- можно взять класс произвольного гладкого замкнутого {-мерно-
го многообразия X, у которого
<^(wi,w2,...,W/), [X] > = 0,
где Р( — (приведенный по модулю 2) многочлен, выражающий симметрическую
функцию Ъх* через элементарные симметрические функции (см. § 39), [X] обоз-
начает фундаментальный гомологический класс mod 2.
Эта теорема принадлежит Тому (см. статью в сборнике ’’Расслоенные пространст-
ва”). Ее доказательство заключается в следующем. Мы должны найти гомотопи-
ческие группы irn+N(MO(Ny), N. Априори ясно, что все элементы этих групп
имеют порядок 2. Когомологии mod 2 пространства M0(N) нам известны: изомор-
физм Тома связывает их с когомологиями пространства BO(N) = G (°°,7V), вычис-
лявшимися в § 19. Их легко описать, пользуясь умножением
Н* (M0(N ); Z2) X H*(BO(N); Z2) -*H*(M0(N ); Z2 ):
когомологии H (M0(N); Z2) аддитивно порождаются элементами вида uwj
.. .w/r, ICi-! <. ..<1г,гдеп€ Hn(M0(N\, Z2) — класс Тома, w{ & Hl (BO(N); Z2) -
классы Штифеля — Уитни. Пользуясь формулами Sqfcwm = С1 k wk_j wm+j и
= (см. п. 2 § 30), можно вычислить действие стинродовых квадратов в
Н*(М0(Ы);7ъ). Вычисление приводит к следующему результату: до размерности
~ 2N когомологии Н* (M0(N)‘, Z2) представляют собой свободный модуль над
алгеброй Стинрода А2, причем образующие этого модуля явно указываются (мы
рекомендуем читателю проделать зто вычисление). (Заметим, что свободность А2-
модуля Н (M0(N); Z2) имеет совсем простое доказательство, практически не
содержащее вычислений, — см. книгу Стонга.)
Воспользуемся спектральной последовательностью Адамса (гл. 5). Мы видим,
что в начальном члене этой спектральной последовательности отлична от нуля только
первая строка, причем стоящие в ней элементы соответствуют свободным образую-
щим А2 -модуля Н* (МО(N); Z2). (В последующих строках стоят соотношения, со-
отношения между соотношениями и т.д., но всего этого нет, потому что модуль сво-
392
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
боден.) Значит, в спектральной последовательности Адамса тривиальны дифферен-
циалы и тривиальна присоединенность, и это позволяет немедленно найти гомотопи-
ческие группы. (В действительности можно показать, что до размерности ~ 27Vпрост-
ранство MO(N) гомотопически эквивалентно произведению пространств типа
K(Z2,N+k).)
Следствием этого вычисления является уже известное нам по § 19 утверждение,
что класс многообразия в £2,° определяется его числами Штифеля - Уитни (вывод
этого утверждения из предыдущего вычисления мы оставляем читателю). В § 19
говорилось, что числа Штифеля — Уитни не являются независимыми, и приводились
примеры соотношений между ними. Теперь мы можем дать полное перечисление этих
соотношений.
Теорема 2. Пусть Hn(BO(N); Z2) -*Z2 - гомоморфизм. Для того чтобы
существовало замкнутое гладкое п-мерное многообразие М, такое, что для любого
a&Hn(BO(N)-, Z2)
, [М] > =
где ам- характеристический класс (касательного расслоения) многообразия М,
отвечающий а, необходимо и достаточно, чтобы для любого IlCH' (BO(N); Z2)
выполнялось равенство
^(Sq (3 + /3 Sq-1 w) = О
(где Sq = l+ Sq1 + ... и w = 1 + Wj +...).
(Читатель может найти доказательство самостоятельно или в книге Стонга.)
Посмотрим, что эта формулировка дает для малых размерностей. Простое вычис-
ление показывает, что
Sq-1 W = 1 + + (W2 + W2) + И>1 W2 + (w2 + WjWs + w4) + ...
Обозначая через F4 (/3) часть когомологического класса Sq(3 + (3 Sq-1 w, имеющую
размерность < 4, имеем:
Г4(1) = И>1 + (w2 + W2) + Wj W2 + (w2 + Wj w3 + w4),
F4(W1) = (wf + WjW2) + w2 w2,
F4(W2) = + w\ W2,
F4(w2) = w3 + w\ w2,
F4(wl)=F4(w3) = 0,
F4(W1 W2) = W!W3 + W 1W2 .
В силу теоремы 2 каждая однородная составляющая любого из этих классов прини-
мает нулевое значение на фундаментальном классе любого замкнутого многообра-
зия своей размерности, и этим исчерпываются все соотношения между числами
Штифеля — Уитни замкнутых многообразий. В частности, все характеристические
числа одномерных и трехмерных многообразий равны 0 (для одномерных много-
образий это очевидно, для трехмерных было доказано Рохлиным за несколько лет
до появления работы Тома); если dimХ=2, то w2 [У] =w2[Ar] (это мы уже
знаем); если dimХ= 4, то wjw2 [А-] = wtw3 [X] = 0и w2 [JV] = w4 [У].
В заключение приведем одно из возможных описаний мультипликативных обра-
зующих xt кольца (см. теорему 1). Если i четно, то xt = RPi; если i =
= 2p(2q + 1) — 1, 1, 1, то Xj есть подмногообразие произведения RPm X
XRP”, m =2p+1 q,n = 2p, задаваемое в однородных координатах (ц,:... : ит),
§ 43. КОБОРДИЗМЫ
393
(и0:...:и„) уравнением F(z/,u)=O, где F - произвольная билинейная форма
ранга л. (Эта система образующих была указана в 1965 г. Милнором. Другая систе-
ма образующих была указана в 1956 г. Дольдом.)
В. . Теорема 3. ® Q есть кольцо многочленов (над Q) от перемен-
ных размерности 4i (i = 1.2. 3,...). Точнее: гомоморфизм -*Z t2, ].
deg tj = 4i, определяемый формулой
имеет в каждой размерности конечное ядро и конечное коядро.
Этот факт, который уже упоминался в п. 6 D § 19, может быть сформулирован
так: (1) если размерность ориентированного многообразия Мне делится на 4, то при
некотором к многообразие кМ ориентированно кобордантно нулю: (ii) если ориен-
тированные многообразия и М2 имеют одинаковые размерности, делящиеся
на 4, и имеют одинаковые числа Понтрягина, то при некотором к многообразия
кМ\ и кМ2 ориентированно кобордантны; (iii) любой Ha6op{pZi .. .Iz'i + i2 +...
. ..+ i'i =г) целых чисел пропорционален набору чисел Понтрягина некоторого
ориентированного 4г-мерного многообразия. Из формулируемых ниже теорем 4 и 6
следует, что в утверждениях (i) и (ii) можно взять к = 2.
Доказательство теоремы 3 относительно несложно: оно основано на применении
теоремы Картана - Серра. Прежде всего вспомним, что при JV> s
гапкЯДД5О(У)) =
О, если $ не делится на 4,
числу представлений числа t в виде суммы
натуральных слагаемых, если s =4t.
Ввиду изоморфизма Тома, таков же ранг группы Hn+s(MSO(N)). Если мы огра-
ничимся размерностями < 2N, мы можем считать, что кольцо рациональных кого-
мологий пространства MSO(N) свободно (соотношения могут появиться в раз-
мерностях > 2К). Значит, при $ < /Vранг группы £1$° =яn+s(MSO(N)) совпадает
с рангом группы Hs(BSO(N)). Легко видеть, что вычисленный нами ранг группы
таков, как это утверждается теоремой 3. Остается заметить, что числа Понтря-
гина Pi ... ,-г линейно независимы (см. и. 6 D § 19), и потому они определяют моно-
морфизм пространства £1®® ® Q в Q [rt, t2,... ], deg tt = 4i. Ввиду совпадения раз-
мерностей однородных составляющих, этот мономорфизм должен быть изомор-
физмом.
Произведем обзор дальнейших результатов; большая часть утверждений доказана
в книге Стонга, там же имеются литературные указания.
Теорема 4 (Милнор, Авербух). Кольцо нс имеет элементов нечетного
порядка.
Наиболее рациональное доказательство этой теоремы использует спектральную
последовательность Адамса по модулю нечетного простого числа.
Теорема 5 (Милнор, Новиков). Кольцо £2f°/Tors изоморфно кольцу цело-
численных многочленов от переменных размерностей 4i, i = 1. 2, 3,...
(Эта теорема служит уточнением теоремы 3.)
Теорема 6 (Рохлин, Уолл). В £1$ ° отсутствуют элементы четвертого порядка.
Теорема 7. Факторкольцо /2£1$° можно описать следующим образом.
Пусть W - подкольцо кольца полиномов над Z2 с образующими x(.i =1,2.....
394
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
порожденное элементами x2k,x2k-i (&¥=27) и (х^у)2, и пусть 9: W->W — диф-
ференциал, действующий по формулам Эх2Л_1=О, Эх2Л =x2fc_i, 9 (х .) 2 = 0.
27
Тогда !2£1$° изоморфно КегЭь причем образ Tors Я^ ° в КегЭ совпадает
с Im 9.
Ввиду отсутствия в Я$ ° 4-кручения (теорема 6), для доказательства этой теоре-
мы достаточно знать А2-модуль Н * (MSO(N); Z2). Вычисление этого модуля про-
делал С.П. Новиков. Он показал, что как А2-модуль H*(MSO(N)-, Z2) совпадает
(до размерности ~ 2Л7) с Z2-когомологиями произведения некоторого количества
пространств типа K(Z,N+k) и K(Z2,N+k). Заметим, что даже в стабильных раз-
мерностях пространство MSO(N) не имеет гомотопического типа произведения
пространств Эйленберга - Маклейна: постниковские факторы (см. п. 4 § 36) нетри-
виальны, но имеют нечетный порядок.
Теорема 8. При гомоморфизме забывания ориентации кольцо
Я У*/2 Я® изоморфно отображается на подкольцо Кег 9 СЯ° = Z2 [х2, х4, х5,... ],
где х, — (специально выбранные) образующие кольца Я?.
Как уже говорилось, теорема 3 показывает, что любой набор целых чисел
{pt,... t | i j + . .. + is = t} после умножения на некоторое целое число делается
набором чисел Понтрягина некоторого замкнутого гладкого ориентированного
4f-мерно го многообразия. Остается вопрос, каково это целое число. Ответ дает
Теорема 9 (Стонг). Набор {pit ... является набором чисел Понтрягина
некоторого замкнутого гладкого ориентированного 4t-мерного многообразия тогда
и только тогда, когда это не противоречит теоремам целочисленности из § 41.
Полезно запомнить вытекающую из вышеназванных результатов конкретную
формулировку, относящуюся к малым размерностям.
Следствие. При п<3 всякое замкнутое ориентированное гладкое п-мерное
многообразие является краем гладкого компактного ориентированного (л+1)-
мерного многообразия. Всякое гладкое замкнутое ориентированное 4-мерное мно-
гообразие ориентированно кобордантно связной сумме некоторого количества
многообразий СР2 или —СР2. (Знак определяется знаком сигнатуры данного
многообразия, а число слагаемых равно модулю сигнатуры).
(Эти результаты принадлежат В.А. Рохлину, они были получены до доказатель-
ства общих теорем об устройстве Я?° )
С. ЯУ Теорема 10 (Милнор, Новиков). Кольцо ЯУ изоморфно кольцу це-
лочисленных полиномов от образующих размерности 2i(i = i, 2,... ). В качестве
представителей образующих можно взять классы кобордизма некоторых комплекс-
ных проективных алгебраических многообразий.
Заметим, что после тензорного умножения на Q эта теорема делается следствием
теоремы Картана - Серра (ср. теорему 3). При этом оказывается, что полным набо-
ром инвариантов класса кобордизмов в ЯУ является набор чисел Черна.
Теорема 11 (Стонг, Хаттори). Набор целых чисел (с, ... ir | i i + ... + ir = t}
тогда и только тогда является набором чисел Черна замкнутого стабильно почти
комплексного 2 t-мерного многообразия, когда это не противоречит теоремам цело-
численности § 41.
Теорема 12 (Милнор, Новиков). При гомоморфизме забывания структуры
£1^кольцо £1^ эпиморфно отображается на Я^ °/Tors. При гомоморфизме
Я^->Я® кольцо Я^ эпиморфно отображается на подкольцо, составленное из квад-
ратов элементов кольца Я®.
§ 43. КОБОРДИЗМЫ
395
D Другие типы кобордизмов. Пионером вычисления групп кобордизмов явился
Л.С. Понтрягин, доказавший в ЗО-е годы, что кольцо £1** классов кобордизмов мно-
гообразий с тривиализованным нормальным расслоением совпадает с (компози-
ционным) кольцом стабильных гомотопических групп сфер. (Работа Понтрягина
содержит и соответствующую нестабильную формулировку. Подробности см. в книге
Понтрягина ’’Гладкие многообразия и их применения в теории гомотопий”.)
В настоящее время известно вычисление колец кобордизмов точки для большого
количества разновидностей кобордизмов (см. обзор результатов в гл. 4 книги
Стонга). Выделим вычисление ^^-кобордизмов, проделанное Коннером, Флойдом и
Уоллом, и вычисление спинорных кобордизмов, произведенное Андерсоном, Брау-
ном и Петерсоном (в обоих случаях важные предварительные результаты принад-
лежат Новикову).
3. Связь с К-теорией. В соответствии с общими установками этой главы мы огра-
ничимся комплексным случаем; более подробное и полное изложение предмета
см. в статье Коннера и Флойда ”0 соотношении теории бордизмов и Х-теории”,
русский перевод которой включен в качестве дополнения в перевод книги тех же
авторов ’’Гладкие периодические отображения”.
А. Гомоморфизм р. Сейчас мы определим мультипликативное отображение
Д:
теории унитарных бордизмов в (комплексную) X-теорию. Пусть a6fl"(I), и
пустьМ>| л| + dim X. Элемента представляется отображением
/; Е2ЛГ-"Х -»Г({),
где ? - (комплексное) тавтологическое расслоение над CG{M,N). Согласно п. 2
§ 41, расслоение % обладает канонической Х-ориентацией и (£) G К (Т ()•)); положим
д(а) = (//(£)) е К (S 2N~ п X) = Кп - 2N{X) = К” {X ).
Очевидно, это определение корректно.
Упражнения. 3. Проверьте, что р — мультипликативное отображение теории
£2^ в Х-теорию.
4. Покажите, что гомоморфизм
р: Q'2" (pt)->X“2n (pt) = Z
относит классу 2л-мерного стабильного почти комплексного многообразия М его
’’род Тодда”
&(М) = (Я(т(М)), [М]>,
где 5"(т(М )) = G(c,(М ), с2(М ),.. . ),
\-e~xt
• • • ), e2(xit)=П ------------- .
5. Опишите сквозной гомоморфизм
, ц ch ,
Я^Х + Я*(- ;Q).
В. Классы Черна со значениями в кобордизмах.
Теорема. Существует единственная функция, относящая комплекс-
ному векторному расслоению £ с конечной клеточной базой X ’’классы
Черна <Т|(?) G£2^(X), i = 1, 2,..., dun обладающая следующими
свойствами {через а(^) мы обозначаем формальную сумму l+oi ({)+.,. .
396
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
• - • + ^dinif (£)) ;
(1)
(2) o(£®i?) = a(^)a(ri);
(3) если '$ - (одномерное) хопфовское расслоение над СРп, то o(f) = 1 +7,
где £12у(СРп) - класс кобордизмов, представляемый СРп~1 ССРп (см. уп-
ражнение 2).
Доказательство мы изложим конспективно, отсылая читателя за подробностями
к цитированной статье Коннера и Флойда.
Конструкция, доказывающая и существование, и единственность классов ajt
заключается в следующем. Если расслоение % одномерно, то оно индуцируется хон-
фовским расслоением над СР Nc достаточно большим /V (В U(i) =CP°°), и класс
o(£) = l+oj(£) определяется условием (3). Предположим, что кобордические
классы Черна, обладающие нужными свойствами, уже построены для расслоений
размерности < п, и пycurdim £ = п. Рассмотрим расслоение р: Х^-Хсо слоем СР п~1,
ассоциированное с £ (точками пространства X служат прямые, проходящие через О,
в слоях расслоения £). Расслоение р*£ распадается в сумму одномерного расслое-
ния и некоторого (л — 1)-мерного расслоения: слой (р*£)|, где / G X — прямая
в слое £х, х~p(l) С X, совпадает с £х и канонически расщепляется: £х=/ + Z1.
Поэтому, ввиду предположения индукции и условия (2), определены классы Черна
расслоения/?*£. В силу условия (1) должно быть
Р*(а(%)) = a(P*(i)),
и наша цель будет достигнута, если мы покажем, что
р-: ^(Х^П^Х)
есть мономорфизм. А это утверждение является следствием общего факта, дока-
занного Дольдом:
Лемма. Пусть h - мультипликативная экстраординарная теория когомологий и
я: Е->Х - локально тривиальное расслоение со слоем F, причем X и F - конечные
клеточные пространства и X связно. Пусть.далее, i- F -+Е - включение. Предполо-
жим, что eh* (Е) имеются элементы ct,... ,с„, такие, что h* (F) есть свободный
h* (pt) -модуль с образующими i*cx,... ,i*cn. Тогда h* (Е) есть свободный h*(X)-
модуль с образующими Ci,...,c„; другими словами, для всякого элемента а&
G Л* (Е) существует единственное представление
a = 7t,(ai)ci + . . . + я*(ап)с„ ,
где а,,. .. ,a„G h* (X). В частности, я*: h* (X) -+h* (Е) - мономорфизм.
Доказательство леммы мы оставляем читателю. Ее нетрудно доказать при по-
мощи спектральной последовательности. Другой план, реализованный в статье Кон-
нера и Флойда, заключается в том, что сначала теорема доказывается для тривиаль-
ных расслоений, а затем многократно применяется аддиционная последовательность
типа последовательности Мейера — Вьсториса (ср. п. 6 § 12).
Лемма Дольда применима к нашему расслоению р: Х~>-Х. Действительно, при
помощи спектральной последовательности Атиа - Хирцебруха легко показать,
что £1*и(СРп~1) есть свободный Q^(pt)-модуль с образующими 1,7,72,.. . ,7"“',
где 76 Ll^(CPn~l) - элемент, упоминавшийся в условии (3) пашей теоремы.
В частности, 7 = <4 (Г), где t — хопфовское расслоение над СР " 1. 11о расслоение t
§ 43. КОБОРДИЗМЫ
397
является сужением некоторого одномерного расслоения над СР"-1, именно,
одномерного слагаемого из вышеописанного расщепления расслоения в сумму.
Значит, класс у является образом при гомоморфизме включения СР"-1 -*Хнеко-
торого класса у G П2и{Х) (первого класса Черна указанного одномерного расслое-
ния) . а классы у2,..., у 1 являются образами классов у2,..., у 1.
Доказательство теоремы закончено.
С. Взаимодействие а и р . Так как
СТ1(?<®7?) = СТ1(0 + СТ1(Р).
то возникает гомоморфизм
а,: А(%. A)->Q ^.(А, А).
Обозначим через а? композицию
А (%, А ) = К{Х/А) = К~2(А/А) =
= A(S 2 {Х/А ))-!-> Q2V (S 2 {Х/А)) = S2 °, {Х/А) = П {Х.А ).
Упражнение 6. Покажите, что композиция
К{Х. А) —^{Х. А ) -* К{Х. А )
совпадает с — id. (Указание: достаточно проверить это для X = pt, А = ф.)
Следствия (из упражнения 6). (i) Существует естественное аддитивное вло-
жение
К{Х, A )-Я° {X. А )
в качестве прямого слагаемого.
(ii) Имеет место мультипликативный 7.2-градуированный изоморфизм
К*{Х. А ) = П*{Х. А )« Z,
n^(pt)
где действие Q^(pt) в Z определяется родом Тодда £2(,(pt) -*Z {см. упражнение 4).
4. Когомологические операции в кобордизмах и спектральная последовательность
Адамса—Новикова. Как уже говорилось (см. первую фразу § 39),когомологические
операции могут быть определены в любой экстраординарной теории когомологий.
Здесь мы рассмотрим когомологические операции в теории Пи.
А. Примеры операций. При построении когомологической операции а мы будем
ограничиваться описанием отображения
av: J2*,(A)-S2^(A)
в случае, когда X— замкнутое стабильно почти комплексное многообразие. Этого дос-
таточно, поскольку произвольное конечное клеточное пространство Y может быть
представлено как ретракт такого многообразия X (например, декартова квадрата
удвоения замыкания своей окрестности в евклидовом пространстве), и тогда £2*;(У)
будет прямым слагаемым в S2 (А). В рассматриваемом случае мы будем пользо-
ваться интерпретацией кобордизмов, содержащейся в упражнении 2.
Мы рассмотрим два способа построения операций. Первый применим, в действи-
тельности, к любой мультипликативной теории когомологий. Он состоит в том. что
элемент а кольца Q*z(pt) определяет операцию умножения на а:
я;,(*) - яц(Х).
398 ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
Приведем геометрическую расшифровку этой конструкции. Если элемент
G (pt) представлен 2г-мерным многообразием А, а рассматриваемый элемент
кольца SlyfX) представлен отображением /: Z-+X (с надлежащей структурой,
мы ее не напоминаем,онаописанав упражнении 2), то образ этого элемента при нашей
когомологической операции представляется сквозным отображением
проекция f
ZXA—---------> Z^X.
Эта операция понижает размерность на 2г.
Другой способ построения операции предполагает фиксированной финитную
последовательность со = (со15 со2,... ) неотрицательных целых чисел. Пусть снова
рассматривается элемент кольца П^Х), представленный отображением/: Z-+Х
и комплексным векторным расслоением % над Z, стабильно эквивалентным вир-
туальному расслоению f*r(X) — r(Z). Согласно п. 3, определен характеристический
класс
(О = а. ог ($)"’ • • • S '(Z),
где |а>| = а>! + 2со? +... Этот класс представляется некоторым отображением
g: W -* Z (снова с надлежащей структурой). Образ рассматриваемого элемента
кольца £2у(АЭ при когомологической операции представляется сквозным отоб-
ражением
Операция обозначается через . Она повышает размерность на 21 а> |.
Все рассмотренные когомологические операции являются, очевидно, стабиль-
ными (т.е. перестановочны с изоморфизмами надстройки).
В. Алгебра Ландвебера — Новикова. Обозначим через Аи алгебру стабильных
когомологических операций в теории Qy. Следующая теорема (которую мы сооб-
щаем без доказательства) независимо доказана в 1967 г. Ландвебером и Новико-
вым.
Теорема, (i) Подгруппа S алгебры А и, порожденная операциями sw, замкну-
та относительно композиции, т.е. является подалгеброй.
(ii) Отображение Пц ® 5 -+ A Ut определенное формулой а ® $ »->а ° s, мономорф-
но и имеет плотный образ.
Алгебра S С А и называется алгеброй Ландвебера — Новикова.
Следующая интерпретация алгебры Ландвебера - Новикова была найдена Бух-
штабером и Шокуровым (Функц. анал. и его прил. - 1978. — Т. 12, № 3. - С. 1-11).
Обозначим через Diffх (Z) группу формальных диффеоморфизмов прямой, име-
ющих вид
t ь+t +xit2 + х2Г3 + ..., x1,x1,...GZ.
Заметим, что группа Difft (Z) действует в кольце Р = Z [xj, х2,... ] функций на
себе самой посредством левых сдвигов. Обозначим через S алгебру всех Diffj (Z)-
инвариантных формальных дифференциальных операторов в Р, т.е. формальных
Э Э
степенных рядов от — , — .... с коэффициентами в Q [xj, х2,. ..], переводя-
9xj Эх2
щих элементы из Р в элементы из Р и перестановочных с преобразованиями, произ-
водимыми элементами группы Diff2 (Z). Для произвольной финитной последова-
тельности со = (о>!, а>2,...) неотрицательных целых чисел определим оператор
§ 43. КОБОРДИЗМЫ
399
G £ формулой
P(x°y)=S DwP(x)y^,
в которой х = (xi, х2 ,...), У ~ (УI > Ут > • • •) > операция ° отвечает умножению в
Diff\ (Z) и уш обозначает у . Например,
Ъ
Э
Р(03.о....)=
“ Э
+ S кхк_г —,
k = T 0Xk
“ э
+ S (*-l)xfc_2—.
k=3 OXk
Главный результат Бухштабера и Шокурова составляет следующая
Теорема. Сопоставление «* определяет изоморфизм между кольцами
SuS.
Изоморфизм 8 = S превращает Р в 5-модуль, и этот модуль также имеет интерпре-
тацию в кобордизмах. Именно, обозначим через Q^(Z) часть тензорного произ-
ведения £2 у (pt) ® Q, выделяемую условием целости всех чисел Черна. Таким обра-
зом, S2^(pt) С Qy(Z) С S2^(pt) ® Q; из результатов п. 2С следует, что фактор-
группа ClyiTyiCLy конечна. Действие операций из S распространяется с £2^ на
ПЪ (2) •
Теорема. Изоморфизм между S и 8 продолжается до изоморфизма между
S-модулем и * -модулем Р.
С. Спектральная последовательность Адамса — Новикова. Гомотопическая дос-
таточность теории унитарных кобордизмов (см. п. 1Е) создает принципиальную
возможность вычисления стабильных гомотопических групп пространства, у ко-
торого известны группы кобордизмов. Реализацией этой возможности является
кобордический аналог спектральной последовательности Адамса — так называе-
мая спектральная последовательность Адамса — Новикова. Она определяется для
произвольного конечного клеточного пространства X, имеет начальный член
Ext аг/ (£2 с/ (X), Пц (pt) ) и сходится к стабильным гомотопическим группам прост-
ранства X U pt. В случае одноточечного X мы получаем спектральную последо-
вательность
Ext Ау (S2fr (pt), £2<> (pt)) => я®,
сходящуюся к стабильным гомотопическим группам сфер. Применение этой спект-
ральной последовательности осложняется тем, что мало что известно об ее началь-
ном члене. Упомянем некоторые результаты, относящиеся к вычислению этого на-
чального члена.
Из части (ii) теоремы Ландвебера — Новикова следует, что
Ext а у («сл (Pt), &u (Pt)) = Ext s (Z, (pt)),
и теорема Бухштабера — Шокурова позволяет заменить в этом равенстве кольцо S
кольцом $ . Нетрудно показать, что
Ext #(Z,P) = 0.
Бухштабер предложил использовать для вычисления Extj(Z, (pt))фильтрацию
0CNoCNlC...CN„=au(Z),
где No = £2у (pt), N[ = { a G (Z) | зш о G , при | со | > 0 }. Факторгруппы
400
ГЛ. 6. К-ТЕОРИЯ И ДРУГИЕ ЭКСТРАОРДИНАРНЫЕ ТЕОРИИ КОГОМОЛОГИЙ
NfrINj_l конечны и тривиальны как 5-модули. (В настоящее время вычислены
Ni/N0 и Ni/Ni — см. Шокуров А.В.//Мат. заметки. — 1979. — Т. 26, № 1.) С фильтра-
цией Бухштабера ассоциируется триградуированная спектральная последователь-
ность
$>0, ?>0, s + t<0, dp*’4: Ер*'4 -+E*-'.t+r-i,q j
у которой fO’*’* = Ext "(Z.Sljy (pt) ),£«, = e2,’°’° = 2ипри5>0
F*-' ♦ = Ext-<^'>’4Z,A^_ j).
Так как Ns/Ns_ г есть тривиальный 5-модуль, то (в силу формулы Кюннета)
Ext-<i+'^(Z,^/2Vs_1) =
= ® {[Ext;<,+,>’’> (z, z) ® (n;4* In;^ )] ®
® Tor(Ext-(s+,)+,’«' (Z, Z), (N~^ IN^l))}.
Таким образом, для вычисления начального члена спектральной последователь-
ности Бухштабера необходимо знать группы Exts(Z, Z), а эта задача, благодаря
равенству 5 = S, переносится в рамки когомологической теории бесконечномер-
ных групп и алгебр Ли. В рамках этой теории удается доказать (см. книгу Фукса
’’Когомологии бесконечномерных алгебр Ли”), что
„ ( 1, если v = Зи2 ± и,
rank Ext • (Z,Z) = <
d ( 0 в остальных случаях.
ДОПОЛНЕНИЕ
ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
§ 44. ГОМОЛОГИИ И КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИЙ
НА МНОГООБРАЗИЯХ
При изучении многих задач механики, математической физики возникает необ-
ходимость изучения свойств гладких функций (например, потенциалов и т.п.) на
многообразиях, например, на конфигурационных или фазовых пространствах ме-
ханических систем.
Пусть f — гладкая вещественная функция на гладком n-мерном многообразии
М, пусть х — точка на М и Xi,..., хп — локальные регулярные координаты в ок-
рестности точки. Точка называется критической для функции/, если все частные про-
Э
изводные — равны нулю в этой точке. В критической точке корректно опреде-
дх/
лена симметричная матрица вторых частных производных функции /, называемая
, / Э2/ \
иногда гессианом функции, а именно d f = (-----1. Критическая точка невы-
\дХ{ дх,/
рождена, если гессиан — невырожденная матрица (в этой точке). Так как гессиан —
симметричная матрица, то определен ее индекс, т.е. число отрицательных квадра-
тов, возникающих на диагонали матрицы после ее приведения к диагональному
Рис. 174
виду. Это число не зависит от выбора координат в окрестности течки. Этот индекс
и называется индексом невырожденной критической точки. Он может принимать
любые значения от нуля до п (где п - размерность многообразия). Гладкая функция
называется функцией Морса, если все ее критические точки невырождены.
Каждая функция f на многообразии задает его отображение в прямую (рис. 174).
Если а — точка на прямой, то ее полный прообраз мы обозначим fa, т.е. fa =
= { х G Af|/(x) = а}. Число а называется критическим значением функции f, если
в fa содержится хотя бы одна критическая точка функции. В этом случае fa назо-
вем критическим уровнем функции.
Важную роль в теории гладких многообразий играет теорема, восходящая к
М. Морсу и в окончательном виде доказанная С. Смейлом.
402
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
Теорема 1. На любом гладком компактном многообразии существуют функ-
ции Морса. Они всюду плотны в пространстве всех гладких функций на много-
образии. Каждая функция Морса имеет на замкнутом многообразии лишь конеч-
ное число критических точек. В множестве всех функций Морса существует всюду
плотное подмножество (всюду плотное, следовательно, и в пространстве всех глад-
ких функций), состоящее из функций, у которых каждый критический уровень
содержит ровно одну критическую точку. На каждом п-мерном, связном глад-
ком замкнутом многообразии существует функция Морса, принимающая значения
от нуля до п, имеющая ровно один минимум, ровно один максимум и каждая крити-
ческая точка индекса X расположена на критическом уровне j\.
См. рис. 175. На рис. 175а видно, что на каждом критическом уровне расположе-
на ровно одна критическая точка. Любая функция Морса может быть превращена
в такую функцию сколь угодно ’’малым шевелением”. Функция на рис. 1756 носит
более специальный характер. Такие функции уже не являются всюду плотными в
пространстве гладких функций. Здесь все критические точки одного индекса X рас-
положены на одном критическом уровне, отвечающем критическому значению X.
Такие функции иногда называются правильными функциями Морса. Здесь крити-
ческие точки расположены в порядке возрастания их индекса: чем больше индекс
X, тем ’’выше” (при выбранном нами на рис. 1756 направлении оси R) расположе-
на критическая точка. Минимум имеет индекс ноль, а максимум — индекс п. Пра-
вильная функция Морса не имеет локальных минимумов и максимумов, отлич-
ных от абсолютных.
Почему функции Морса приобрели большое значение в топологии? Оказывает-
ся, задание такой функции позволяет довольно много сказать о топологии мно-
гообразия.
Предложение 1 (известная ’’лемма Морса”). Пусть Хо — невырожденная
критическая точка индекса X гладкой функции. Тогда в некоторой открытой ок-
рестности этой точки на многообразии Мп всегда существуют такие регулярные
локальные координаты xt,..., хп, в которых функция запишется так:
f(x) = f(x0)-x2i - ...-х2х+х2х+1 + ...+х2п.
Смысл леммы Морса (см. [1]; в настоящей главе ссылки в квадратных скоб-
ках указывают на список литературы к Дополнению с. 485 — 487) в том, что в раз-
ложении функции f в ряд Тейлора по степеням переменных Xj,..., хп можно, ока-
зывается, всегда убрать все члены, начиная с порядка три и выше, выбрав для этого
подходящие координаты. Применим лемму Морса для разложения многообразия
в сумму клеток по заданной на нем функции Морса. Пусть Ма = {х G М|/(х) <а},
Рис. 175
§ 44. ГОМОЛОГИИ И КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИЙ
403
тогда дМа = fa, т.е. fa — край Ма (рис. 176). Если а — регулярное (т.е. не крити-
ческое) значение, то в силу известной теоремы о неявных функциях подмножест-
во Ма является гладким n-мерным многообразием с границей fa, которая, в свою
очередь, является гладким (п — 1)-мерным многообразием.
Лемма 1. Пусть f - функция Морса и отрезок [а, Ь] (где а < Ь) не содержит
критических значений функции f Тогда многообразия fa и fb диффеоморфны. Мно-
гообразия Ма и Мь также диффеоморфны.
Рис. 177
Доказательство достаточно наглядно и понятно из рис. 177. Достаточно рассмот-
реть интегральные траектории векторного поля v = — grad f и построить гладкую
деформацию поверхности fb вдоль этих траекторий вниз до встречи с поверх-
ностью fa.
Изучим структуру поверхностей уровня около критических точек функции. В силу
леммы Морса в достаточно малой окрестности невырожденной критической точки
х0 можно ввести криволинейные координаты, такие, что f(x) = f(x0) — х2 — ...
••• ~хх + jd+i + ••• + х„. Пусть центр О окрестности U совмещен с xb uf(O) = 0.
Рассмотрим гиперповерхности: где е > 0 — малое число. Поверхности за-
даются квадратичными уравнениями:
~ х2 ~ ~х{ + х1+1 + .. . + хп = {-е,0, е},
где X — индекс критической точки. Поверхность/0 — конус, а поверхности f±e —
гиперболоиды. На рис. 178 см. случай л = 2, X = 1, на рис. 179 - случай л = 3, X = 1.
Лемма 2. Пусть в слое f~l [— е, е] = Ме — М_е имеется только одна критичес-
кая точка индекса X. Тогда многообразие Ме гомотопически эквивалентно конечно-
му клеточному пространству, получающемуся из М_е приклеиванием одной клет-
ки ок размерности X (к границе дМ_е = /_е) •
Итак,Л/е имеет гомотопический типЛ/_е U а\
Доказательство можно легко извлечь из рис. 180 и рис. 181. Построим поле и =
= — grad/и заставим точки слоя Afe — Л/_е вне окрестности U скользить вдоль траек-
торий поля и (рис. 180). В окрестности U деформация показана на рис. 180. Отрезок
404
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
АВ изображает диск Dx (xi,... ,хк), граница которого вложена в край области Af_e.
Результат деформации см. на рис. 181.
Теорема 2. Пусть f - функция Морса на гладком компактном связном замк-
нутом многообразии М. Тогда М гомотопически эквивалентно конечному клеточ-
ному пространству, причем каждой критической точке индекса X отвечает ровно
одна клетка размерности X.
Так как на любом компактном гладком многообразии есть функции Морса, то
каждое такое многообразие допускает описанное клеточное разбиение. Доказатель-
ство теоремы 2 следует из лемм 1, 2. Так как М компактно, то число критических
точек функции f конечно. Если на каждом критическом уровне функции имеется
только одна критическая точка, то утверждение теоремы сразу следует из леммы 2.
Если же на одном критическом уровне находится несколько критических точек, то
вследствие их изолированности можно считать, что к многообразию М_е одновремен-
но приклеивается несколько клеток.
Теорема 2 позволяет восстанавливать гомотопический тип многообразия по функ-
ции Морса далеко не однозначно. Мы можем вычислить только число клеток и их
размерности, но в общем случае ничего не можем сказать о способе приклейки кле-
ток друг к другу.
Рассмотрим фиксированное многообразие и всевозможные функции Морса на
нем. Какое количество критических точек обязана иметь функция f на Ml Из преды-
дущего ясно, что чем сложнее многообразие, тем сложнее функция Морса на нем.
Можно ли придать этой связи количественный характер? Для приложений, например,
в механике, полезно знать — сколько положений равновесия (т.е. критических
точек потенциала) имеет данная механическая система, если известна структура
конфигурационного пространства. Оказывается, зная гомологии многообразия, мож-
но оценить снизу число критических точек функции Морса.
Теорема 3. Пусть fik (М, G) — ранг группы гомологий Hk (М, G) с коэффи-
циентами в поле G (т.е. 0к - число Бетти для гомологий с коэффициентами в G).
Тогда для любой функции Морса на М всегда выполняются неравенства Морса:
где рк - число критических точек индекса к функции f Здесь к = 0,.. . ,п.
Доказательство фактически следует из предыдущих лемм. По функции Морса
строим представление М в виде клеточного пространства. При этом количество
A-мерных клеток в точности равно числу рк критических точек индекса к. Следо-
вательно, А-мсрная группа клеточных цепей многообразия имеет рк образующих.
Так как число 0к образующих группы А-мерных гомологий не превосходит числа об-
разующих в группе А-мерных цепей, то теорема доказана.
§ 45. ОБЩИЕ НЕРАВЕНСТВА МОРСА
405
§ 45. ГОМОЛОГИИ И ТОЧКИ БИФУРКАЦИИ ФУНКЦИИ.
ОБЩИЕ НЕРАВЕНСТВА МОРСА
Существует более тесная связь между критическими точками функции Морса
и гомологиями многообразия чем та, которая указана в § 44. Эта связь имеется не
только для функций Морса, но и для непрерывных функций с ’’правильными” крити-
ческими точками, определение которых см. ниже. Общие неравенства Морса мож-
но выписать не только для многообразий, но и для клеточных пространств (и даже
для компактных метрических пространств, не являющихся клеточными), снабжен-
ных непрерывными функциями с ’’правильными” критическими точками. Чтобы
не углубляться в технические детали, ограничимся здесь случаем непрерывных функ-
ций на многообразиях, предоставляя читателю перенесение всех нижеследующих
конструкций на случай клеточных пространств.
Определение 1. Пусть X — топологическое пространство и / — непрерыв-
ная функция на нем. Точка х G X называется правильной для функции /, если су-
ществует открытая окрестность U этой точки такая, что U гомеоморфна прямому
произведению fa XI, где а = /(х), I — единичный отрезок, fa — полный прообраз зна-
чения а. При этом требуется, чтобы гомеоморфизм U был послойным
в том смысле, что fa
См. рис. 182, где видно, в каком смысле расслоение U в прямое произведение сог-
ласовано со слоями/).
Определение 2. Точка х 6 X называется точкой бифуркции функции f,
если х не является правильной точкой.
Если f — функция Морса на гладком многообразии, то ясно, что все ее критичес-
кие точки являются точками бифуркации в смысле определения 1.
Однако если f нс является функцией Морса, то ее критические точки могут не
быть точками бифуркации. Пример: /(х) = х3 на вещественной прямой. Точка О
очевидно является вырожденной критической точкой, но в то же время это — пра-
вильная точка (докажите!).
Поскольку дальнейшие приложения связаны с функциями на многообразиях,
то для простоты ограничимся рассмотрением гладких функций на многообразиях
(но не обязательно функций Морса). Пусть / имеет на М лишь конечное число точек
бифуркации. Рассмотрим группы гомологий Я, (М, G), где G — поле (например, R
или Zp). Обозначение G будем опускать и писать просто Н* (М). Пусть (Зк — размер-
ность группы Нк (М) (Л-мерное число Бетти).
Определение 3. Полиномом Пуанкаре пространства М называется полином
Р(М, t) = Zk = 0(iktk, где п = dim М.
Определение 4. Значение с для функции f называется бифуркационным,
если поверхность уровня/-1 (с) содержит хотя бы одну точку бифуркации.
406
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
Пусть cN — бифуркационные значения функции. Пусть Аа — множест-
во бифуркационных точек на поверхности уровня /<.&. Рассмотрим Ма =
= { х G М|/(х) < са } и группы гомологий Нк (Ма, Ма - Аа). Здесь мы имеем в ви-
ду группу Нк(Ма, Ма — Ua), где Ua — достаточно малая открытая окрестность то-
чек Аа. Рассмотрим целые числа fa>a = dim Нк (Ма, Ма - Аа).
Определение 5. Полиномом Пуанкаре функции f на М назовем полином
e(/,0=E^=1E{x)aE2 = o^,eZfc.
Теорема 1 (Морс, Смейл). Пусть Q(f, f) и Р(М, t) - полиномы Пуанкаре
функции и многообразия. Тогда разность Q - Р делится на 1 + Г и отношение поли-
номов (Q - Р)/(1 + 0 является полиномом с неотрицательными целыми коэф-
фициентами.
Доказательство. Предположим, что [д, Ь] — такой отрезок, что он не со-
держит бифуркационных значений функции f. Тогда Мь стягивается на Ма и
Н,(МЬ, Ма) =0. Доказательство этого факта во многом аналогично доказатель-
ству утверждения из § 44 для функций Морса, и мы предоставляем его читателю.
Вместо интегральных траекторий градиентного поля здесь нужно взять траектории —
прообразы отрезка при гомеоморфизме <р Для каждой отдельной открытой окрестнос-
ти, окружающей правильную точку функции. Рассмотрим теперь следующие полино-
мы Пуанкаре.
l)P(Ma)=Zkfa(Ma)tk-,
2)P(Mb, Ma)=Zkfa(Mb,Ma)tk, где а<Ь‘,
3)P(Im Э)= Sfc(dim Im 3fc+i)r*, где Hk+i(Mb, — граничный
оператор гомологической последовательности пары (Мь, Ма ).
Оказывается, выполнено равенство:
Р(МЬ, Ма) - Р(МЬ) + Р(Ма) = (1 + 0 P(Im Э)
В самом деле, рассмотрим точную последовательность пары, а именно:
Hk+1(Mb, Ma)-^Hk(Ma )-^Hk(Mb)-^Hk(Mb, Ма)^Нк-1(Ма}.
Отсюда имеем:
fa (Mb, Ма) = dim Im /, + dim Im дк;
dim Im/, = fa(Mb) - dim Im i, = fa(Mb) - fa(Ma) +
+ dim Im 3^+1 = fa(Mb) - fa(Ma) + dim Im dk+i;
fa(Mb, Ma) - dim Im/, =
= &k (Mb, Ma) - fa (Mb) + fa (Ma) - dim Im Э*+1 =
= Rk — dim Im Э^+1 = dim Im bk',
Rk = fa(Mb, Ma) - fa(Mb) +
Итак, tkRk = f*dimlm3fc+1 + z(z*_1dim Imd*), т.е. T,ktkRk = (1 + ?)P(Imd),
что и требовалось.
Теперь рассмотрим все бифуркационные значения ,..., cN. Пусть числа а0,
......aN , ац+\ таковы, что
ab <ci,..., а, <с, <л,+1 . •. cN <aN+i.
Тогда для каждого i имеем:
Р(М»1, Mi)-Р(М1+1)+Р(М.) = (1 +z)P(Imd)z,
§ 46. ГОМОЛОГИИ И КАТЕГОРИЯ ЛЮСТЕРНИКА - ШНИРЕЛЬМАНА
407
где полином P(Imd)z имеет неотрицательные целые коэффициенты. Суммируя
эти равенства (по всем i ), мы и получаем утверждение теоремы.
Извлечем следствия. Возьмем в качестве коэффициентов поле R, пусть f — функ-
ция Морса. Тогда Р(М, t) = 2,(iktk. Полином Q(f, t) запишем в ’’приведенном виде”,
собрав вместе члены, содержащие одну и ту же степень t. Имеем Q = Ърктк. Здесь
д* — числа Морса функции /. Легко видеть, что д* равно числу критических точек
индекса к. Доказательство следует из леммы Морса и определения полинома Пуан-
каре.
Извлечем классические неравенства Морса из теоремы 1. Имеем: С(/) — Р(М) =
= ^к(рк ~ Pit)?* = (1 + где полином, стоящий в правой части равенства,
имеет неотрицательные коэффициенты. Следовательно, числа Бетти (!к многообразия
М оценивают снизу числа Морса рк.
Рассмотрим еще одно утверждение, вытекающее из теоремы 1, а именно: 'S,p.ktk =
= E0ktk + (1 + t)K(t). При t = — 1 получаем: Б(-1)*д* = E(-l)*0fc, где справа
стоит величина, называемая эйлеровой характеристикой многообразия (альтер-
нированная сумма чисел Бетти).
Наконец, разложим выражение (1 + Г)-1 в ряд по степеням переменной t. Полу-
чим 2"=о(-1)^' • Отсюда получаем, что ряд (2(д* - 0&)ffc) £" = o(~l)^z имеет
(после приведения подобных членов) неотрицательные коэффициенты. Фиксировав
какое-либо к, получаем систему неравенств:
(До - М (-1 )* + (Mi - 01) (-1)*-1 + • • • + (Д* - flt) > о,
отсюда:
Д*~Д*г-1 +Д*:-2 ----±^0 >0Jt -0Jt-l +0Jt-2-...±0O-
§ 46. ГОМОЛОГИИ И КАТЕГОРИЯ ЛЮСТЕРНИКА-ШНИРЕЛЬМАНА
Как было доказано выше, если f - функция Морса на многообразии М, то число
ее критических точек индекса X не менее числа Бетти 0х- Однако когда мы рассмат-
риваем не морсовские функции, в частности, допускаем слияние невырожденных
особенностей в вырожденные, ситуация усложняется. Как мы знаем, для точек би-
фуркации неравенства типа (± дх) > (± 0л.) по-прежнему выполнены, но теперь
числа Д\ не имеют того простого смысла, как для функций Морса. В общем случае
числа дх описывают ’’степень сложности” точек бифуркации, которая довольно слож-
но вычисляется через гомологии поверхностей уровня, близких к бифуркационной
поверхности уровня. Число д\ уже не дает прямой информации о том, сколько име-
ется точек бифуркации. Но в приложениях часто важно знать: сколько точек бифур-
кации имеется у данной функции; каково наименьшее возможное число таких точек
на данном многообразии? Оказывается, этот вопрос решается в терминах уже из-
вестного нам по предыдущим главам топологического инварианта — категории Люс-
терника— Шнирельмана.
Определение 1. Пусть X — хаусдорфово топологическое пространство
и А — замкнутое подмножество в X. Категорией Люстерника-Шнирелъмана cat^-Л
замкнутого подмножества А относительно пространства X называется минимальное
число к, для которого существуют замкнутые подмножества A i,..., Ак в X, такие,
что А является их объединением и каждое из этих подмножеств стягивается в точку
по пространству X (ср. п. 5 § 3). Связность подмножеств Aj при этом не предпо-
лагается.
408
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
Пусть, для простоты, X связно. Если А = X, то будем считать, что cat^X = catX
Теорема 1. Пусть М - гладкое компактное п-мерное замкнутое многообразие.
Тогда его категория Люстерника-Шнирелъмана не превышает числа п + 1.
Доказательство. Рассмотрим сначала, для простоты, двумерный случай,
наиболее наглядный. Фиксируем какое-либо симплициальное разбиение многообра-
зия. В силу компактности многообразия можно считать, что оно покрыто конечным
числом симплексов. Рассмотрим двукратное симплициальное барицентрическое под-
разделение (рис. 183). На рисунке двукратному разбиению подвергнуты пять
примыкающих друг к другу симплексов. Так как М является многообразием, то
звезда каждой вершины двукратного подразбиения гомеоморфна диску. Для дву-
мерного случая мы должны предъявить три замкнутых множества Ai, А2, Аз, объе-
динение которых дает все многообразие, и, кроме того, стягиваемых (по отдельнос-
ти) по М в точку. Сначала опишем построение A i. Рассмотрим центры тяжести всех
исходных двумерных симплексов, возникающие при первом барицентрическом под-
разделении. Эти точки являются центрами звезд второго барицентрического под-
разделения (рис. 1836). Объединяя все эти звезды, получаем замкнутое множество
Ai. Оно гомеоморфно объединению к дисков, где к — число симплексов исходного
Рис. 183
§ 46. ГОМОЛОГИИ И КАТЕГОРИЯ ЛЮСГЕРНИКА - ШНИРЕЛЬМАНА
409
симплициального разбиения многообразия. Ясно, что А\ стягивается в точку по
многообразию. Затем рассматриваем центры одномерных ребер (для двумерного
случая) исходного симплициального разбиения, являющиеся центрами звезд второго
барицентрического подразделения. Объединяя эти звезды, получаем замкнутое мно-
жество Аг, стягиваемое по многообразию в точку. Ясно, что оставшаяся часть второ-
го барицентрического подразделения распадается в объединение звезд вершин исход-
ного разбиения. Это множество Аз также стягиваемо. На рис. 183в этот же процесс
показан более наглядно. Сначала выбрасываем достаточно малые шары,окружающие
центры тяжести исходных л-мерных симплексов. Затем выбрасываем шары, окру-
жающие центры (л + 1)-мерных граней исходных симплексов. Эти шары зануме-
рованы цифрами 2 на рис. 183в, Остаются шары (занумерованные цифрами 3), ок-
ружающие вершины исходных симплексов. Ясно, что этот процесс точно так же
(как и в двумерном случае) приводит к доказательству теоремы. Теорема доказана.
Таким образом, верхняя оценка на категорию многообразия получается очень
просто. Значительно сложнее получить нижнюю оценку на категорию. К этому воп-
росу мы сейчас и перейдем. Предварительно опишем простейшие топологические
ствойства категории. Доказательства перечисляемых ниже предложений 1 — 6 мы
предоставляем читателю в качестве упражнения.
Предложение 1. Если А С В - замкнутые подмножества в X, то cat^ Л <
Ccat^R
Предложение 2. Пусть А и В — два произвольных замкнутых подмножества
в X. Тогда cat^A UВ < cat^А + cat^R
Предложение 3. Пусть А С В — замкнутые подмножества в X. Тогда
catxR - А > catxB - catxA, г&е через В - А обозначено замыкание множества
В-АвХ.
Предложение 4. Пусть А С.В — замкнутые подмножества, и пусть множество
В непрерывно деформируется по пространству X в подмножество А, т.е. существует
гомотопия <pt вложения i : В ->Х в такое отображение : В ->Х, при котором у^В С
QA. Тогда са^Л > cat^R
Множество y>iB может быть не гомеоморфно множеству В.
Предложение 5. Пусть А - замкнутое подмножество в многообразии X
(здесь, в отличие от предыдущих предложений, мы предполагаем, что X -
многообразие). Тогда существует число е > 0 (зависящее, вообще говоря, от А)
такое, что catxUeA = catxA, где через UeA обозначена замкнутая е-окрестность
подмножества Ав X.
Если X — не многообразие, то это утверждение, вообще говоря, неверно
(рис. 184),
Предложение 6. Пусть А, Вп (где л = 1, 2, ... ) - замкнутые подмножества
в многообразии X, снабженном метрикой р. Пусть А - lim Вп,т.е. р(А, Вп) -*Г)при
п~^ж. Если catxBn > к при всех п, то тогда и catxA = cat (limR„) > к.
410
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
Теорема 2. Пусть М — гладкое компактное связное замкнутое многообразие
и f - гладкая функция на М. Тогда всегда выполнено неравенство k > cat М, где к -
число различных точек бифуркации функции f. Аналогично, р > сгЛМ, где р - число
различных критических точек (быть может, вырожденных) функции f.
Для простоты мы докажем эту теорему лишь для случая критических точек (в
обычном смысле), так как для точек бифуркации рассуждения повторяются практи-
чески дословно, но с заменой интегральных траекторий векторного поля grad/ на
слоение окрестностей U траекториями-прообразами сомножителя I при гомеомор-
физме U&fa X/.
Пусть М{ — класс всех замкнутых подмножеств X С М таких, что catM X > i.
Ясно, что Mi D М{ +1. Пусть в — пространство всех замкнутых подмножеств в М.
Тогда в снабжается естественной структурой метрического пространства введением
метрики р(Х, Y), обычным образом задающей расстояние между замкнутыми мно-
жествами
р(Х, Y) = sup inf р(х,у) + sup inf p(x,y).
xGX yS У y<=YxGX
Будем говорить, что Y = lim Xq, если p(Xq, У) -> 0 при q -> <».
q —> o©
Предложение 7. Каждый класс Mt является подмножеством в в, замкну-
тым относительно двух операций: а) предельного перехода, т.е. Y € М{, если
Y = lim Xq, Xq G Mt; б) непрерывной деформации подмножеств по многообра-
q —► ос
зию JM, т.е. YGMt, если Y = у^Х, где <pt: Х~*М — гомотопия.
Доказательство вытекает из предложений 4 и 6.
Фиксируем класс Afz, и пусть XG Mt. Построим число Xz = inf max/(x).
х е м{ хе х
Пусть N — категория М. В условиях теоремы 2 имеем N < <». Получаем це-
почку вложений: в = Мо = Mt Э М2 Э ... Э Mjy. Можно считать, что 0 = Мо =
= {X G в, catMX > 0}. Ясно, что catMX > 0 для любого X G в. Совпадение классов
Мо и М1 очевидно. Отсюда имеем, что Хо = Xz.
Функция / индуцирует функции /0, ..., /у, определенные, соответственно, на
классах Мо, .... MN. А именно, fi(X) = max f(x), где X G Mt. Тогда X/ =
x e x
= inf fi (X). Так как Afz D Mt+i, то с ростом i числа Xt не убывают. Так как
X G Mt
классы Mf замкнуты в в относительно предельного перехода (предложение 7), то
в каждом классе Mt существует элемент Х°{ (замкнутое подмножество в много-
образии) , такое, что /z (AfJ) = Xf.
Предложение 8. На поверхности уровня имеется по крайней мере
одна критическая (бифуркационная) точка функции f.
Доказательство. Допустим противное, что на нет критических точек.
Рассмотрим Mf, и пусть Х°{ G М{ — замкнутое подмножество, для которого
max f(x) = Тогда существует точка G X°t, такая, что /(х°) = Xz. Так как
X е х®
мы предположили, что grad / Ф 0 на /Л/, то существует малая деформация поверх-
§ 46. ГОМОЛОГИИ И КАТЕГОРИЯ ЛЮСГЕРНИКА - ШНИРЕЛЬМАНА
411
ности f\{ вдоль интегральных траекторий поля —grad/ в область меньших, чем
X/, значений (рис. 185). Строим далее гладкую гомотопию, тождественную вне слоя
Хг - h < / < X/ + <7 (где Хг - h < X/ - е, X* < X/ + q) и переводящую поверх-
ность /х, в Пусть Х° — зто образ Х° при этой деформации. Из леммы 4
имеем, что catMX° > catMX^- *• Итак, Х° G М{. Отсюда
inf sup f(x) < sup /(x) < Xf - e < X/,
X x g x x ex*
что невозможно в силу определения X/. Лемма доказана.
Предложение 9. Предположим, что в последовательности Хо <... < Xjv
есть совпадающие числа. Пусть, например, X/ = X/ + Q, где q> 0. Пусть К - множе-
ство всех критических точек функции f на поверхности Тогда catM К > q+1.
Доказательство. В силу леммы 5 существует е > 0, такое, что catM/^ =
= catMt/eX:. Допустим противное: catM/^ < q. Рассмотрим классы М{ р ...
... р Mf+g. Пусть Xi+q таково, sup f(x) = Xi+q = Х(. Рассмотрим замкнутое
* xi+q
О о
множество Y = Xt+q — (Xl+q О К) (рис. 186). Тогда из предыдущих предложений
следует, что сагмУ > /, т.е. Y G М/. . Далее: X,- = Xl+(? = sup f (х) >
х е xt+q
> sup f(x) > X/ = Xf+<? = sup / (x). Отсюда следует, что sup /(x) = X/.
x 6 Y vex’ x 6 У
x e Xl+q
В то же время Y Г) К = ф, что противоречит предложению 8. Лемма доказана.
Перейдем к доказательству теоремы. Рассмотрим классы Мо = М1 р Мг р ...
... р MN. Пусть сначала Хо = X! < Х2 < ... < Xjy. Тогда из предложения 8 следует,
что на каждой поверхности /х, есть хотя бы одна критическая точка, поэтому их
общее число не меньше N = catЛ/. Пусть теперь, например, X, = Xt+q. Из предложе-
ния 9 следует, что cat^/X^ > i, где К — множество критических точек на поверхности
/Х/. Следовательно, на К можно выбрать по крайней мере <7 + 1 различных точек.
Итак, ’’однократное” значение X/ дает вклад в виде по крайней мере одной крити-
ческой точки, а каждое ”(<7 + 1)-кратное” значение X, дает вклад по крайней мере
Рис. 185
l/tS
Рис. 186
412
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
в виде <7 + 1 различных критических точек. Отсюда очевидно следует утверждение
теоремы.
Вопрос: является ли полученная выше оценка наилучшей, т.е. существуют ли та-
кие примеры, в которых оценка достигается?
Теорема 3. Категория Люстерника-Шнирельмана для сферы Sn равна двум.
Наименьшее число критических (бифуркационных) точек для гладкой функции
на сфере равно двум (т.е. категории сферы). Категория двумерного замкнутого
гладкого многообразия, не гомеоморфного сфере, равна трем. Наименьшее число
критических (бифуркационных) точек для гладкой функции на таком много-
образии равно трем (т.е. категории).
Доказательство. Для сферы утверждение очевидно. Достаточно предста-
вить ее как объединение двух полусфер, а в качестве функции взять функцию высо-
ты при стандартном вложении сферы S" в R" +1. Здесь мы используем тот факт, что
категория сферы больше единицы, т.е. что она нестягиваема. Теперь рассмотрим дву-
мерную поверхность, не гомеоморфную сфере. Ее категория строго больше 2.
В самом деле, в противном случае, как легко доказать, оно было бы гомеоморфно
сфере. А в силу теоремы 1 категория двумерного многообразия не превышает трех.
Следовательно, она равна 3. Чтобы построить функцию с тремя критическими точ-
ками, нужно рассмотреть фундаментальный многоугольник поверхности, задающий
ееввиде<71 ... ак а;1... а^ (рис. 187). Стрелки и буквы на сторонах много-
угольника указывают правило склейки сторон. Разобьем многоугольник диагональю
(рис. 187). Слева от диагонали зададим точку минимума, справа — точку максиму-
ма, а в вершинах многоугольника (изображающих в действительности одну точку
на поверхности) зададим седловую (вырожденную, вообще говоря) критическую
точку. Линии уровня такой функции см. на рис. 187. Теорема доказана.
Категория - зто трудновычислимый инвариант многообразий. Ограничимся описа-
нием одного способа ее оценки снизу, основанного на понятии когомологической
длины многообразия.
Пусть Н*(М-, А) — кольцо когомологий многообразия М, где А - Z или R,
если М ориентируемо, и А - Z2, если М неориентируемо. Рассмотрим все такие
целые числа <7, что в кольце Н*(М-, А) существуют элементы «j, ...,ая, dima1>0,
1 < i < <7, произведение которых (в смысле умножения в кольце когомологий)
Н*(М\ А) отлично от нуля. Когомологической длиной многообразия называется
максимальное из таких чисел.
Теорема 4. Если к - когомологическая длина многообразия М, то
cat Af > k + 1.
§ 46. ГОМОЛОГИИ И КАТЕГОРИЯ ЛЮСТЕРНИКА - ШНИРЕЛЬМАНА 413
Доказательство. Напомним свойства изоморфизма Пуанкаре (см. § 17).
Пусть, для простоты, Мп замкнуто и ориентируемо. Тогда изоморфизм двойствен-
ности D связывает группу Hk (М; Z) и группу Нп-кZ),T.e. D: Нк(М-, Z) *
-> ЯП_Л(Л/; Z), причем Dla^ ...ар) = D(ai) Г)... П D(ap), где at & Н\М) —
коциклы, через а -Ь обозначено произведение коциклов. Далее, D(a) — зто цикл,
двойственный (по Пуанкаре) коциклу а. Через а Л Р обозначен цикл, являющийся
пересечением двух циклов а и Р в М. Для этого нужно реализовать оба цикла в виде
симплициальных подкомплексов, привести их затем в общее положение и взять пере-
сечение.
Рассмотрим коциклы ау, ..., , такие, что ai ... а* =# 0, и пусть ух,..., ук — цик-
лы, соответствующие этим коциклам при двойственности. Тогда D(ai ... ак) =
= 7! Л ... лук = у, где через 7j Л ... Л ук обозначено пересечение всех циклов 7/.
Ясно, что 7 не гомологичен нулю. Предположим, что cat М = s < к. Тогда в М суще-
ствуют замкнутые подмножества A i, ..., As , стягиваемые в точку и объединение ко-
к
торых дает М. Можно считать, что s =к и М = U А/. Сопоставим циклу у/ множе-
i = 1
ство А/. Так как каждое А/ стягивается в точку, то из точной гомологической после-
довательности пары
... --> Hs(Aj) -> HS(M}-----> HS(M, At) -> ...
получаем, что /, = 0, т.е. - мономорфизм. Итак, каждый цикл 7/ гомологичен
циклу 7/ из H,(M,At), т.е. можно считать, что носитель цикла yt ~ у{ лежит
в М - А/. Другими словами, можно ’’снять” каждый цикл 7/ с подмножества А{
(рис. 188). Итак, цикл у гомологичен циклу 7 = 7i п п Тк- В ю же время
у С.\М - Ai) Л... Л (М — Ак) = ф, так как М =Ai U ... U Ак. Это означает,
что 7 гомологичен нулю, что противоречит условию. Если многообразие неориенти-
руемо, то нужно повторить все рассуждения для группы коэффициентов Z2 .'Теорема
доказана.
Следствие 1. Категория вещественного проективного пространства RPn
равна п + 1. Категория n-мерного тора Тп равна л + 1.
Доказательство. Так как оба многообразия имеют размерность л, то из
теоремы 1 следует, что их категория не превышает л + 1. Найдем когомологическую
длину этих многообразий. Это легко сделать, так как когомологиц этих пространств
были подсчитаны нами выше. Имеем: Я*(ЯР"; Z2) =Z2 [е]/ (en + I), где dege = l.
Очевидно, что произведение еп = ее ... е (л раз) отлично от нуля, что и требовалось
доказать. В случае тора имеем Я*(Т"; Z) = А(е1, ...,еп) - внешняя алгебра с обра-
зующими «!, ..., еп. Ясно, что e,e2 ... еп =# 0, что и дает искомое утверждение.
Теорема доказана.
При вычислении категории Люстерника — Шнирельмана полезно также следующее
утверждение, доказательство которого мы оставляем читателю.
F
Теорема 5. Пусть р: Е ’-------► В - локально тривиальное расслоение. Тогда
cat В < catEF- cat В, где F С Е - слой расслоения.
414
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
Существуют расслоения, для которых это неравенство превращается в равенство.
Рассмотрим, например, расслоение Хопфа р: № ------. Имеем: cat 53 = cat № =2,
cat^j S1 = 1, так как слой S1 стягивается по сфере в точку. Итак, 2 = 1-2.
§ 47. ГОМОЛОГИИ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
1. Физические границы раздела двух сред с равными давлениями и их математи-
ческая модель — минимальные поверхности. Все мы знакомы со следующей двумер-
ной вариационной задачей. В R3 задан фиксированный замкнутый проволочный
контур, гомеоморфный окружности или системе непересекающихся окружностей.
Нужно найти поверхность наименьшей площади, затягивающей контур, т.е. имеющей
его в качестве границы. Физической моделью таких поверхностей являются мыльные
пленки, повисающие на проволочных контурах после того, как их извлекают из
мыльного раствора (достаточно концентрированного). С математической точки зре-
ния такие пленки описываются как решения дифференциального уравнения второго
порядка в частных производных. Поведение мыльных пленок достаточно сложно и
до конца еще не изучено.’
Мыльные пленки — частный случай более широкого класса поверхностей — так на-
зываемых границ раздела двух сред.
Напомним сначала определение средней кривизны Н гладкой двумерной поверх-
ности М2 в R3. Пусть Р — точка на поверхности (рис. 189) и da - бесконечно малая
окрестность этой точки (площадка) на поверхности. Ее площадь мы также обозна-
чим через da. Отложим на нормалях к поверхности М в одном направлении отрезки
постоянной длины а. Концы отложенных отрезков описывают некоторую поверх-
ность М*, которую можно назвать ’’параллельной” поверхности М. Тогда площадке
da будет ’’параллельна” некоторая площадка da* на поверхности М*. Обозначим ее
da — da*
площадь также через da*. Построим следующее выражение ------------. Переходя
2 ada
к пределу при а * 0, получаем число, зависящее, вообще говоря, от выбора точки
на поверхности. Это число и называется средней кривизной Н поверхности М в точ-
da— da*
ке Р. Итак, Н(Р) = lim ----------. Средняя кривизна — важный локальный инва-
а-о 2ada
риант поверхности. Эта функция естественно возникает в теории мембран и тонких
оболочек (в химии, физике, биологии и т.п.). Например, почти у всех млекопитаю-
§ 47. ГОМОЛОГИИ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
415
щих эритроциты (в крови) похожи на двояковогнутый диск. Исключения из этого
правила крайне редки. В состоянии покоя красная клетка является фигурой враще-
ния, образованной незамкнутой восьмеркой. В 1970 г. П.Кенхзм (Канада) предпо-
ложил, что форме клетки нужно искать чисто энергетическое объяснение. Когда
эритроцит переходит из одной формы в другую, его мембрана (граница раздела двух
сред) изменяется, поэтому изменяется и ее энергия. Энергия мембраны вычисляется
так: J J D-H2da, и минимум этой энергии соответствует оптимальной форме зритро-
м
цита. Оказалось, что среди нескольких семейств поверхностей вращения, исследован-
ных Кенхзмом, эритроцит (толстый диск, сплющенный в середине) действительно
имеет наименьшую энергию. В данном примере средняя кривизна была переменной
функцией. Оказывается, в механике и физике встречаются ситуации, когда средняя
кривизна постоянна. Еще в 1828 г. Пуассон доказал важное утверждение, связываю-
щее условия равновесия физических сред со свойствами их границ раздела. Пусть
в R3 находятся две среды I и II, разделенные границей раздела, которую будем
считать гладкой поверхностью. Пусть Pi и р2 — давления в средах I и II соответ-
ственно.
Теорема 1 (Пуассон). Предположим, что среды I u II находятся в равнове-
сии. Тогда в каждой регулярной точке поверхности М,являющейся границей раздела
сред, выполняется равенство Н = X(pi — Рг),где X — некоторая постоянная, не зави-
сящая от выбора точки на М. В частности, средняя кривизна поверхности раздела
(в указанных предположениях) постоянна.
Число X имеет простой физический смысл. Величина 1/X является коэффициентом
поверхностного натяжения на границе раздела сред. Рассмотрим два простейших при-
мера. Выдуем из трубки мыльный пузырь. Он оторвется от трубки и начнет планиро-
вать, приобретая форму сферы. Это не случайно. Здесь мыльная пленка (сферический
пузырь) является границей раздела двух сред: шаровой объем газа (воздуха) с дав-
лением Pi и внешняя среда с давлением р2. Из условия опыта ясно, что Pi > р2,
поэтому Н = const > 0. Можно доказать (хотя зто и нетривиально), что любая
замкнутая гладкая двумерная связная поверхность (без самопересечений) постоян-
ной положительной средней кривизны в R3 является стандартной сферой.
Второй пример, представляющий здесь для нас больший интерес, реализуется так.
Рассмотрим мыльную пленку, ограничивающую какой-либо замкнутый проволочный
контур (и не содержащую в себе замкнутых пузырей). Здесь пленка является грани-
цей раздела двух сред: воздух ’’над” пленкой и воздух ’’под” пленкой, причем давле-
ния Pi и р2 с обеих сторон, очевидно, равны. Следовательно, по теореме Пуассона
Рис. 190
мы имеем Н = const = 0. Итак, мыльная пленка, ограничивающая контур, имеет ну-
левую среднюю кривизну. Это ее свойство допускает характеризацию в терминах
площади пленки.
Рассмотрим в R3 гладкую поверхность, возьмем на ней точку и окружим ее ма-
лым замкнутым контуром, нарисованным на поверхности и гомеоморфным окруж-
ности (рис. 190). Рассмотрим малое возмущение поверхности внутри контура,
416
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
затухающее к границе области, ограниченной контуром, и не смещающее поверх-
ности вне контура. Такие возмущения назовем возмущениями малой амплитуды
с малым носителем.
Опр еделение 1. Поверхность М2 в R3 называется локально минимальной,
если любое малое ее возмущение малой амплитуды с малым носителем не уменьшает
ее площадь.
Точно так же можно определить локальную минимальность и в многомерном слу-
чае: Мк С Rn.
Теорема 2. Двумерная поверхность в R3 является локально минимальной
тогда и только тогда, когда ее средняя кривизна тождественно равна нулю.
Доказательство этого классического утверждения мы опускаем. Теорема 2 пока-
зывает, что физической моделью локально минимальных поверхностей являются,
например, мыльные пленки 2-го типа, т.е. ограниченные замкнутым контуром.
Простые примеры показывают, что на один и тот же контур можно натянуть,
вообще говоря, несколько разных локально минимальных поверхностей. Все эти
пленки имеют, вообще говоря, разные площади. Более того, можно предъявить прос-
той контур, состоящий из четырех непересекающихся гладких окружностей, на кото-
рый можно натянуть континуум ( !) различных (не совпадающих) минимальных по-
верхностей. Этот замечательный пример построил Ф. Морган [64]. Возникает
вопрос: существует ли пленка, затягивающая данный контур и имеющая наимень-
шую возможную площадь среди всех пленок с той же границей? Сегодня эта задача
называется проблемой Плато по имени известного бельгийского профессора физики
и анатомии Жозефа Плато (1801-1883), который провел серию фундаментальных
опытов по изучению конфигурации мыльных пленок и экспериментально обнаружил
несколько важных принципов, управляющих их геометрией и топологией.
2. Теорема Дугласа и Радо. В 30-е и 40-е годы нашего столетия был достигнут
большой прогресс в изучении свойств двумерных минимальных поверхностей.
Замечательные результаты были получены Дуг-
ласом и Радо [4], [6], [7], Курантом и др.
Вкратце остановимся на теореме Дугласа и
Радо, решающей задачу Плато для двумерных
поверхностей. Будем называть минимальную
пленку, реализующую абсолютный минимум
площади в классе всех поверхностей с данной
границей, абсолютно минимальной поверхно-
стью, чтобы отличать ее от локально минималь-
ных поверхностей. Абсолютно минимальных
поверхностей с одной и той же границей так-
же может быть несколько (как и локально ми-
нимальных). Все они имеют в таком случае
одинаковую площадь (абсолютный минимум).
Сферы с ручками
Сферы с пленками Мёбиуса
Наиболее важным результатом Дугласа яв-
ляется теорема существования абсолютно ми-
нимальной поверхности в классе поверхностей
фиксированного топологического типа. Снача-
ла напомним (см. п. 10 § 1), что каждое
гладкое замкнутое связное двумерное много-
образие И^диффеоморфнолибо сфере с некото-
рым количеством ручек, либо сфере, заклеен-
ной несколькими пленками Мебиуса (рис. 191).
Рис. 191
§ 41. ГОМОЛОГИИ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
417
Ручка - это обыкновенный цилиндр, приклеиваемый своими двумя краями к краям
двух дырок в сфере. Пленка Мёбиуса — это лента Мёбиуса, приклеенная по своей
границе к границе дырки в сфере.
Предположим, что для многообразия W данного топологического типа (т.е. с за-
данным числом ручек и пленок Мёбиуса) существует гладкое отображение
f: W -*• R3 с конечной площадью, причем край поверхности отображается на задан-
ный набор замкнутых жордановых кривых в R3. Требование ’’конечной площади”
надо понимать так. При отображении /: W -*• R3 возникает образ X = f(W) поверх-
ности W. Нужно подсчитать площадь этого образа, причем ”с кратностью”, т.е. часть
образа, покрытая несколькими листами поверхности W, засчитывается столько раз,
сколько листов ее покрывает. Можно рассматривать также задачу Плато, подсчиты-
вая просто площадь образа X = /(И'), т.е. без учета кратностей. В этом случае мы
интересуемся площадью той геометрической поверхности (без параметризации),
на которую отобразилась поверхность W.
Определим теперь операцию (введенную Дугласом) перетягивания трубок и
выбрасывания из поверхности ручки или пленки Мёбиуса. На рис. 192 показана
поверхность, например, с двумя ручками. Перетягиваем одну из них, как показано
на рис. 192, т.е. сдавливаем трубку. Перетяжка превращается в точку, затем ручка
распадается, причем новых дырок при этом не возникает, так как в момент перетяж-
ки они ’’запаиваются”. В результате число ручек уменьшилось на единицу. Другой
способ удаления ручки показан на рис. 193. Ручка ’’отрывается” от поверхности,
а место отрыва ’’запаивается”, так что край поверхности не меняется. Ясно, что точно
так же определяется операция выбрасывания пленки Мёбиуса (рис. 194). Здесь от
поверхности ’’отрывается” проективное пространство, а место разрыва запаивается
(т.е. дырка заклеивается диском).
Теорема 3 (Дуглас). Предположим, что минимум (точнее, точная нижняя
грань) площадей погружений поверхности W фиксированного топологического типа
в R3 с фиксированным краем строго меньше, чем минимум площадей всех погруже-
ний в R3 (с тем же краем) всех поверхностей, получающихся из исходной поверхно-
Рис. 192
14 А.Т. Фоменко
Рис. 193
418
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
сти выбрасыванием одной ручки или выбрасыванием одной пленки Мёбиуса.
Тогда существует непрерывное и абсолютно минимальное отображение f0: W -> R3,
т.е. оно реализует минимум площади в классе всех погружений поверхности в R3
с заданной границей. Эта поверхность fo(W) имеет нулевую среднюю кривизну
во всех своих неособых точках и почти всюду регулярна.
Прокомментируем условие существования хотя бы одного погружения W в R3
с конечной площадью. Дело в том, что существуют кривые, на которые нельзя натя-
нуть ни одной поверхности с конечной площадью (рис. 195). Изображены две орто-
гональные проекции пространственной кривой на две плоскости. Уравнение кривой
в стандартных сферических координатах г, 0, записывается так: г = cos в,
= tg5 в. Здесь г — длина радиус-вектора, — полярный угол на плоскости х, у,
— угол, образуемый радиус-вектором с вертикальной осью 2. Когда в
стремится к ± тг/2, то I I г. -> 0, что и дает картину проекций. Прямое вычис-
ление показывает, что эта кривая не является границей никакой погруженной в R3
поверхности с конечной площадью. Более того, существуют примеры таких экзоти-
ческих кривых, каждая точка которых имеет похожую сложную структуру, и,
следовательно, заклейка любого сколь угодно малого участка границы требует
построения поверхности бесконечной площади.
Поскольку рассматриваются гладкие отображения поверхности в R3, то мини-
мальные пленки могут иметь самопересечения и точки ветвления. Ясно, что сущест-
вуют простые контуры, для которых минимальной пленки в классе вложений не су-
ществует. Простейший такой контур (заузленный трилистник) см. на рис. 196. Он не
затягивается в R3 никаким вложенным диском. В то же время существует гладкое
отображение диска D2 в R3 (с самопересечениями), реализующее абсолютный мини-
мум площади в классе всех отображений диска с данной границей. Это верно,
кстати, для любого жорданова замкнутого контура, гомеоморфного окружности.
На рис. 196 показан также известный пример локально минимальной (но не абсолют-
но минимальной) пленки, затягивающей вложенную в R3 окружность, заузленную
Рис. 196
Рис. 197
$47. ГОМОЛОГИИ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
419
в виде трилистника. Эта поверхность имеет не только самопересечения (три отрезка,
сходящиеся в одной точке), но и точку ветвления в центре.
Прокомментируем теперь условие теоремы Дугласа, связанное с выбрасыванием
ручек или пленок Мёбиуса. Рассмотрим простой пример граничного контура 7 —
две соосные окружности одинакового радиуса, расположенные в двух параллельных
плоскостях. Центры окружностей расположены на одной прямой, ортогональной
плоскостям. Будем менять расстояние h между плоскостями (рис. 197). Рассмот-
рим пленку фиксированного топологического типа — цилиндр с краями, прикреп-
ленными к двум указанным окружностям у. Пусть сначала расстояние h мало.
Рис. 199
Тогда иэ физических соображений ясно, что абсолютный минимум площади в классе
цилиндров с фиксированным краем достигается на так называемом катеноиде
(слегка прогнутом цилиндре, образованном вращением цепной линии). Катеноид
реализуется реальной мыльной пленкой (рис. 198). Напомним, что цепная линия -
это форма провисания тяжелой цепи с закрепленными концами (гиперболический
косинус). Обозначим площадь этой пленки через a(W, у), указывая явно как кон-
тур 7, так и топологический тип W исследуемой пленки. Применим теперь описанную
выше операцию Дугласа перетяжки трубок. У нас есть одна трубка - цилиндр.
Перетягивая его, мы перестраиваем цилиндр в пару дисков .затягивающих по-прежне-
му тот же контур (рис. 199). Полученную поверхность обозначим через W*.
Если обозначим через а (W', 7) абсолютный минимум площади в классе всех поверх-
ностей этого топологического типа (пара дисков), то ясно, что этот минимум дости-
гается на паре плоских дисков, затягивающих окружности в плоскостях (рис. 199) .
Если h мало, то очевидно, что a(W, 7.) < a(Wr, 7). Следовательно, условия теоре-
мы Дугласа выполнены и, в самом деле, при малом h абсолютный минимум площади
в классе цилиндров действительно достигается на катеноиде.
Покажем теперь, что при увеличении h условие теоремы Дугласа перестает выпол-
няться и в результате в классе цилиндров может вскоре не оказаться абсолютно ми-
нимальной поверхности с данной границей. Эта ситуация показана на рис. 200.
Когда h достаточно велико, то цилиндр W начинает обтягивать вертикальный отре-
зок, соединяющий центры окружностей, и ясно, что минимум площади в классе по-
верхностей, получающихся ’’сдавливанием” цилиндра, достигается на паре плоских
дисков, соединенных вертикальным отрезком. Так как двумерная площадь отрезка
14*
420
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
равна нулю, то этот минимум равен числу a(W*, 7) , введенному выше. Итак, в слу-
чае большого h мы имеем: a(W, 7) = a (Wr, 7). В общем случае следует отметить,
что всегда a(W, 7) < a(Wr, 7).
Итак, условие теоремы Дугласа здесь не выполнено. И в самом деле, в классе
цилиндров не существует абсолютно минимальной поверхности с данной границей.
Следовательно, условие Дугласа действительно существенно и отказ от него сразу
приводит к простым контрпримерам.
3. Абсолютно минимальные двумерные поверхности. Сколько минимальных дис-
ков могут иметь одну и ту же границу? Леви и Курант построили интересный пример
спрямляемой жордановой кривой, гладкой всюду за исключением одной точки и
ограничивающей несчетное число минимальных дисков. Если же кривая является
вещественно-аналитической, то, как показал Томи, она может ограничивать лишь
конечное число локально минимальных дисков.
Минимальные поверхности могут иметь самопересечения и точки ветвления.
Оссерман сформулировал теорему о том, что абсолютно минимальная двумерная
поверхность, решающая задачу Плато в классе дисков в R3 (с фиксированной гра-
ницей) , регулярна в каждой своей внутренней точке, т.е. не имеет точек ветвления
(хотя самопересечения допускаются). Первоначальное доказательство Оссермана
было уточнено Альтом и Гулливером. В случае когда жорданова кривая является
вещественно-аналитической, Гулливер и Лесли доказали, что решение задачи Плато
(т.е. абсолютно минимальная поверхность) не имеет ветвлений не только внут-
ри, но и на границе. Следовательно, в этом случае решение задачи Плато задается
погруженной поверхностью. Если же граничная кривая является всего лишь
гладкой, то существование точек ветвления на границе остается пока открытой
проблемой.
Все сказанное выше относится, конечно, не только к минимальным дискам, но и
к минимальным поверхностям любого топологического типа, участвующим в теоре-
мах Дугласа и Радо (так называемым обобщенным минимальным поверхностям).
Особый интерес представляет следующий вопрос: каковы условия на граничную
кривую 7 в римановом многообразии М п (например, в R" ), при которых абсолютно
минимальная поверхность W2 в многообразии Мп, ограниченная кривой 7 (и ре-
шающая, следовательно, задачу Плато для данного контура), является вложенной
поверхностью, т.е. не имеет не только ветвлений, но даже и самопересечений?
Оссерман высказал гипотезу, что это справедливо в том случае, когда кривая 7
лежит на границе выпуклой области в R3, например, на стандартной двумерной сфе-
ре. Существенные продвижения в решении этой проблемы были получены Гулливе-
ром, Шпраком, Симоном, Альмгреном. Однако в полном объеме гипотеза Оссермана
была доказана Яо и Миксом III, причем не только для выпуклых областей в R3, но и
для выпуклых трехмерных многообразий, т.е. для многообразий с выпуклой дву-
мерной границей. Дело в том, что понятие выпуклости, очевидно, можно определить
не только для двумерных поверхностей в R3, но и для двумерной границы трехмер-
ного риманова многообразия. Однако для наглядности читатель может представлять
себе просто выпуклую область в R3 .
Теорема 4 (Яо.Микс III). Пусть М3 - трехмерное выпуклое многообразие.
Если 7 - жорданова кривая (например, гладкая окружность), лежащая на грани-
це дМ и многообразия М3 и стягиваемая в точку по многообразию М3, то имеют
место следующие утверждения :
(1) Для контура у всегда существует решение задачи Плато (т.е. абсолютно мини-
мальная двумерная поверхность) с конечной площадью.
§ 47. ГОМОЛОГИИ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
421
(2) Любое такое решение задачи Плато яв-
ляется вложенной поверхностью (без ветвлений
и самопересечений в М3).
(3) Любые две абсолютно минимальные по-
верхности с одной и той же границей у либо сов-
падают (как подмножества в М3, т.е. соответ-
ствующие поверхности могут отличаться друг
от друга лишь параметризацией), либо образы
поверхностей пересекаются в М3 только вдоль
кривой у.
Эта теорема называется иногда обобщенной
леммой Дена. В теореме 4 речь шла о двумерных
поверхностях абсолютно минимальной плошали. В
отображений диска D2 с границей у (в условиях
вует вложенный диск абсолютно минимальной
Рис. 200
действительности в классе
теоремы 4) всегда сущест-
(в классе погружений диска)
площади. (
4. Трудности при решении задачи Плато в больших размерностях. У читателя, ве-
роятно, возник вопрос: причем здесь гомологии? Пока мы говорили о двумерной
задаче минимизации площади, необходимость в гомологиях не возникла.
Однако ситуация меняется при переходе в большие размерности. Рассмотрим в рима-
новом многообразии Мп фиксированный ’’контур” — замкнутое компактное
(к — 1)-мерное подмногообразие А. Всегда ли существует локально минимальная
или абсолютно минимальная ^-мерная поверхность Wk в Мп такая, что граница Э W
совпадает с А ? При этом мы стремимся минимизировать Л-мерный объем поверх-
ности Wk. Методы, позволившие решить задачу Плато в размерности 2, оказывается,
не действуют в больших размерностях. Укажем причины этого явления.
Вернемся на время к двумерному случаю. Возьмем контур у на рис. 200, т.е. две
соосные окружности, значительно удаленные друг от друга.
Попробуем натянуть на них минимальную поверхность, имеющую топологический
тип цилиндра. В классе погруженных цилиндров задача решения не имеет. Абсолют-
ный минимум площади достигается на паре дисков, соединенных отрезком, на кото-
рый ’’схлопывается” значительная часть первоначально вложенного цилиндра. Мини-
мизирующее отображение вырождено на значительной части цилиндра, переводя ее
в отрезок. Образ цилиндра состоит из нескольких кусков разной размерности: два
двумерных диска и один одномерный отрезок. Эти куски сцеплены друг с другом,
поскольку их объединение является образом одного двумерного многообразия.
Итак, все-таки существует кусочно гладкое отображение /0 цилиндра IV2 в R3,
образ которого X = /0(IV2) имеет абсолютно минимальную площадь. Но зто ’’реше-
ние” является составным (состоит из кусков разных размерностей), и минимизирую-
щее отображение /0 не является погружением (так как имеет большие ’’зоны вырож-
дения”) (рис. 201). В двумерном случае обнаруженную трудность легко обойти,
выбросив одномерный отрезок и перейдя от рассмотрения цилиндра к рассмотрению
пары дисков, т.е. изменив топологический тип минимизируемой пленки. Именно это
и делает теорема Дугласа. В новом классе пленок (пара дисков) мы уже найдем
абсолютно минимальную пленку. Однако внешняя легкость этой процедуры Дугласа
превращается в серьезную задачу в многомерном случае. Дело в том, что естественно-
го многомерного аналога операции Дугласа нет. При минимизации объема образа
Л-мерного многообразия К* (при отображениях /: Й* -> Мп) мы не можем так же
легко отбрасывать ’’мешающие” нам куски малых размерностей, поскольку можем
422
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
потерять основное свойство пленки — быть непрерывным образом гладкого много-
образия с данным краем.
Пытаясь решить задачу Плато в классе пленок, являющихся образами многообра-
зия с фиксированным краем, мы сталкиваемся с еще одной трудностью, которую
мы сейчас проиллюстрируем на двумерных поверхностях, когда условие теоремы
Дугласа не выполнено. Растягивая граничные окружности у катеноида мы, оказыва-
ется, не можем даже приблизиться к искомой минимальной поверхности на рис. 201
(т.е. к паре дисков, соединенных отрезком) в классе вложенных минимальных
Рис. 201
поверхностей. Дело в том, что при малых Л существуют два различных катеноида
с одной и той же границей: внутренний и внешний (рис. 202). При увеличении h
эти катеноиды движутся навстречу друг другу. Внешний становится тоньше, внутрен-
ний становится толще. Они встречаются и сливаются, образовав на мгновение некото-
рый общий катеноид, который затем сразу лопается. Все это происходит ’’вдали”
от стратифицированной поверхности: пары дисков с отрезком между ними. Итак,
искомая стратифицированная поверхность не аппроксимируется вложенными (или
погруженными) катеноидами. В многомерном случае ситуация, естественно, усугуб-
ляется.
Итак, перед нами два пути. Первый: пытаться решать задачу Плато в терминах,
максимально близких к терминам двумерной теоремы Дугласа и Радо, т.е. рассмат-
ривать стратифицированные образы X = /(И**) многообразий Wk с фиксированным
краем и минимизировать их fc-мерный объем в классе ’’составных” (стратифици-
рованных) поверхностей. Второй путь: отказаться от жесткого представления о
поверхности (образ многообразия), ослабить его и рассмотреть более широкий
класс поверхностей, уже не являющихся, вообще говоря, образами многообразий.
Расширив класс поверхностей, мы получим большую свободу в обращении с ними.
Гомологии естественно появляются в задаче Плато на втором пути. Они позволяют
сформировать новое понятие ’’поверхности” и ее ’’границы”.
5. Гомологии и многомерные минимальные поверхности. Бурное развитие много-
мерных вариационных задач, связанных с проблемой Плато, началось примерно в
60-е годы и связано с именами Федерера, Флеминга, Альмгрена, Миранды, Райфенбер-
га, Морри, Джусти, де Джорджи, Оссермана, Ниче, Лоусона, Саймонса, Хсианга,
Алларда, Бомбьерн, Гильдебрандта, Бёма, Моргана, Микса, Уленбек, Харви, Яо,
Постона, Сью, Томи, Тромба, Шоена и многих других (этот список, конечно, не пре-
тендует на полноту). Мы отсылаем читателя за более детальным обзором,например,
к [3], [2], [11], [12], [15]. Здесь же мы в качестве иллюстрации вкратце изложим
геометрический подход Райфенберга и Адамса (развитый затем Морри). Более
функциональный подход на языке потоков, разработанный Федерером, Флемингом
и др., хотя и отличается от подхода Райфенберга и Адамса, но гомологии также
играют в этих исследованиях важную роль [2], [3], [5], [8].
При расширении понятия поверхности следует расширить и понятие ее площади,
объема. В качестве ’’объема” замкнутых к -мерных компактных подмножеств в R"
§47. ГОМОЛОГИИ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
423
берется &-мерная сферическая мера Хаусдорфа, которую мы обозначим через volfc.
Мы не будем здесь давать ее определение, ограничившись указанием, что если под-
множество Хк является гладким подмногообразием, то vol* X совпадает с обычным
А-мерным римановым объемом.
В качестве поверхностей рассматриваются измеримые (т.е. имеющие конечную
меру Хаусдорфа) компактные подмножества в R" (или в римановом многообразии).
Осталось сформулировать понятие границы.
Фиксируем теорию гомологий с коэффициентами в абелевой группе G. Если
поверхность X является конечным клеточным комплексом (полиэдром) или глад-
ким многообразием, то можно брать обычные группы гомологий Hq(X; G), напри-
мер, клеточные, симплициальные или сингулярные. Для указанных объектов все
эти типы групп совпадают. Если же X является всего лишь измеримым компактным
множеством, то в качестве Hq(X-, G) следует брать так называемые спектральные
гомологии (гомологии Чеха). Они строятся так. Известно, что каждый компакт
можно представить в виде обратного предела нервов всевозможных его конечных
открытых покрытий, т.е. X = lim N(Ua), где N(Ua) — полиэдр, являющийся нервом
а
покрытия Ua. Нерв покрытия Ua определяется как полиэдр, вершины которого
соответствуют множествам Vt >а, составляющим данное покрытие t/a; одномерные
симплексы нерва N(Ua) соответствуют парам множеств Е)>а и Vj>a, имеющим
непустое пересечение; двумерные симплексы нерва N(Ua) соответствуют тройкам
множеств И/>а, Рц,а> имеющим непустое совместное пересечение. И так далее.
Получается полиэдр, состоящий из тем большего числа симплексов, чем более мелко
рассматриваемое покрьпие. Определяя понятие вписанных друг в друга покрытий,
мы определяем отображения соответствующих нервов. Переходя к обратному преде-
лу, мы и получаем исходный компакт. Другими словами, нервы покрытий являются
аппроксимациями данного множества, причем аппроксимация ’’тем лучше”, чем
мельче покрытие. Рассмотрим теперь группу симплициальных гомологий
Hq(N(Ua)'. G) нерва N(Ua). Тогда можно рассмотреть обратный предел этих групп
lim Hq(N(Ua)). Получающаяся абелева группа и называется ^-мерной спектральной
группой гомологий компакта АГ. Можно записать
Hq (X) = Я,(НтЛГ(Г/а)) = Пт Hq(N(Ua)).
а а
В случае конечных клеточных пространств, полиэдров, гладких многообразий эти
спектральные группы совпадают с обычными группами симплициальных (клеточ-
ных) гомологий этих объектов. В этом смысле спектральные гомологии являются
естественным расширением обычных гомологий с класса ’’хороших пространств”
(многообразий, полиэдров и т.п.) на более широкий класс измеримых компактных
множеств. Можно показать, что спектральные гомологии обладают всеми свойствами
обычных гомологий. В дальнейшем, используя гомологии в вариационных задачах,
мы будем иметь в виду спектральные гомологии, не оговаривая этого каждый раз
специально.
Группы гомологий хорошо приспособлены для того, чтобы сформулировать
естественное понятие границы для широкого класса пространств. Будем говорить,
следуя Дж.Ф. Адамсу и Райфенбергу, что замкнутое Л-мерное множество X С R"
является (7-поверхностью, затягивающей (заклеивающей) замкнутое (к — 1)-мерное
множество А для данной абелевой группы коэффициентов G, если: (1) А содержится
в X, (2) гомоморфизм г,: Нк(А; G) ~>Нк_1(Х', (7), индуцированный вложением
424
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
i: А X, тождественно равен нулю, т.е. вся группаНк_ г(А; G) отображается в ноль.
Тогда множество А называется гомологической границей поверхности X.
Соответствующее определение когомологической границы компакта было сфор-
мулировано в [16], [17].
Данное выше определение границы хорошо согласуется с интуитивным представ-
лением о геометрической границе множеств. Рассмотрим некоторые простейшие
примеры.
1. Пусть Мк — гладкое компактное ориентируемое многообразие с краем Л*-1.
Тогда гомоморфизм (4; G) -* G) тривиален, т.е. А является гомоло-
гической границей М.
2. Пусть А —конечное клеточное пространство и X — конус над А. Тогда гомомор-
физм Нк_1(А\ G) -*Нк-!(Х; G) тривиален для всех Л (рис. 203а).
Понятие G-поверхности зависит от выбора группы G. Множество А может быть
гомологической границей X для одной группы коэффициентов и не бьггь его грани-
цей для другой группы.
3. Если А — окружность, а X — лента Мёбиуса, то гомоморфизм i,: И, (A; Z) *
-* Ну(Х; Z) является мономорфизмом, так как i, умножает каждый 1-цикл на
число 2. Дело в том, что вложение i: А -> X эквивалентно (с гомотопической точки
зрения) отображению окружности на себя со степенью два (рис. 2036). Итак, лента
Мёбиуса не является Z -поверхностью с границей окружность (хотя является гладким
многообразием с краем окружность). В то же время лента Мёбиуса является Z2-по-
верхностью с границей окружность. Для группы G = Z2 имеем, что гомоморфизм :
Нг (А; Z2 ) -> Ну (Х-, Z2 ) тривиален.
4. Пусть А — окружность, X — тройная лента Мёбиуса, получающаяся так. Рассмот-
рим обычную окружность в R3 и трилистник — три отрезка одинаковой длины,
сходящиеся в некоторой точке окружности ортогонально ей и образующие друг с
другом углы 2тг/3. Будем перемещать трилистник вдоль окружности, оставляя его
все время ортогональным к окружности и так, чтобы после полного оборота отрезки
подверглись перестановке 1 -> 2 -* 3 -> 1 (рис. 203в). Границей получившейся поверх^
ности является окружность. Если трилистник достаточно мал, то эта поверх-
ность очевидно реализуется как устойчивая мыльная пленка с границей А. Однако X
не является ни Z-поверхностью, ни Z2-поверхностью с границей А (докажите!).
Рис. 203
§ 47. ГОМОЛОГИИ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
425
В то же время тройная лента Мёбиуса является Z3-поверхностью с границей окруж-
ность.
Итак, варьируя группы коэффициентов, можно представлять различные пары
пространств (X А) в виде G-поверхностей с границей А. Интересно, что в примере 4
граничная окружность, три раза обходящая вокруг вертикальной оси, является в то
же время границей и обычной ленты Мёбиуса (рис. 203).
Одним из основных фундаментальных результатов, доказанных в рамках много-
мерной задачи Плато, является известная теорема Райфенберга для случая компакт-
ных поверхностей в R", расширенная затем Морри на случай произвольных римано-
вых многообразий.
Теорема 5 (Райфенберг, Морри). Пусть М — гладкое полное риманово много-
образие и А СМ — компактное измеримое (к — 1) -мерное подмножество. Пусть G —
компактная абелева группа, и пусть fik_l(A-, G) =# 0. Пусть существует хотя бы
одно измеримое k-мерное подмножество X, вложенное в М и являющееся G-noeepx-
ностью с границей А. Рассмотрим класс {X} всех таких поверхностей и положим
d = inf volfc(X — А), X С{Х}, т.е. число d является точной нижней гранью объемов
всех G-поверхностей с данной границей А. Тогда утверждается, что d>Qu что суще-
ствует минимальная поверхность Хо из класса{X}, такая, что d = volfc(X0 - А).
За исключением множества S точек k-мерной меры нуль, эта поверхность Хо - А
является открытым гладким минимальным подмногообразием в смысле обычной
дифференциальной геометрии, т.е. его средняя кривизна равна нулю. Если объем-
ляющее многообразие было аналитическим, то и подмногообразие Хо - (A U S)
также аналитическое.
Такие поверхности, реализующие абсолютный минимум объема, будем по-преж-
нему называть абсолютно минимальными. Когомологический вариант этой теоремы
доказан затем в [16], [17].
Рассмотрим группу относительных гомологий //fc(R", А). Так как Hk_ j(A) =#=0,
то группа Hk(Rn, А) отлична от нуля и изоморфна группе Hk_ i(<4) (см. точную
последовательность пары). Согласно теореме Райфенберга, существует минимальный
относительный цикл в группе Hk(Rn, А), т.е. ^мерная поверхность X, реализующая
ненулевой цикл в группе Hk(Rn,A). Интересно выяснить - какие метрические
свойства характеризуют этот абсолютно минимальный относительный цикл (по моду-
лю подпространства А). Оказывается, минимальная относительная пленка всегда
содержится в выпуклой оболочке своей границы. Эта теорема обобщает многочислен-
ные варианты классических теорем о свойствах обычных двумерных и многомерных
минимальных поверхностей. Более того, оказывается, можно оценить сверху Л-мер-
ный объем относительного минимального цикла X через {к — 1) -мерный объем его
границы (которая совпадает с Л и предполагается фиксированной). Имеет место
замечательное изопериметрическое неравенство: volfc X < с (volfc_, A)k^k~1^,
где с — некоторая постоянная, не зависящая от выбора границы А в R" и выражаю-
щаяся только через размерности кип. Это неравенство играет большую роль в
теории минимальных поверхностей.
Укажем некоторые общие топологические свойства минимальных А-мерных
поверхностей X, заклеивающих в гомологическом смысле (к — 1)-мерные ’’контуры”
А в римановом многообразии. В общем случае такие минимальные поверхности
могут содержать в себе А-мерные ’’пузыри”, т.е. ненулевые к -мерные циклы. Это не
противоречит тому, что средняя кривизна поверхности равна нулю. Таких ’’пузырей”
не может быть для двумерной пленки в R3, но для минимальных пленок в римано-
вом многообразии ’’пузыри” могут появиться.
Особый интерес представляют А:-мерные минимальные поверхности, не содержа-
щие ни одного А-мерно го пузыря. Оказывается, существуют чисто топологические
426
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
критерии, гарантирующие такое свойство минимальных пленок. Так как -мерные
пузыри” имеются в пленке X тогда и только тогда, когда ^-мерная группа гомологий
поверхности X отлична от нуля, то отсутствие пузырей эквивалентно условию
Нк(Х\ G) = 0 (для данной группы коэффициентов).
Теорема 6 (см. [16], [17]). Пусть М - полное гладкое риманово многообра-
зие и А СМ- компактное измеримое (к - 1)-мерное подмножество, например,
подмногообразие. Пусть G - абелева группа, являющаяся одномерным векторным
пространством над некоторым полем F. Например, G - группа R вещественных чисел
или G = Zp, гдер - простое число. Пусть существует хотя бы одна G-поверхность в М
с границей А. Тогда абсолютно минимальная поверхность X с границей А обладает
тем свойством, что Hk(X- G) = 0, т.е. поверхность не содержит ни одного нетривиаль-
ного "пузыря ”, k-мерного цикла.
Если объемлющее многообразие М не является евклидовым пространством, то
группа Hk(M‘, G) может быть отлична от нуля. Поэтому наряду с задачей заклейки
границы А при помощи минимальной пленки возникает не менее естественная гео-
метрическая задача реализации при помощи минимальных замкнутых поверхностей
нетривиальных циклов в многообразии М.
Пусть Р — нетривиальная подгруппа в группе Нк(М\ G). Будем говорить, что
подмножество X СМ реализует подгруппу Р, т.е. реализует циклы этой подгруппы,
если при гомоморфизме /,: Нк(Х; G) -> Нк(М\ G), индуцированном вложением
/ : X ->М, подгруппа Р содержится в образе группы Нк(Х; G).
Рассмотрим класс (Р) всех компактных подмножеств X, где А СX СМ и где X
реализует подгруппу Р. Оказывается, в этом классе также всегда существует абсо-
лютно минимальная поверхность, т.е. такая поверхность Хо, что ее объем равен
inf vol Y, где YC{P].
Естественно ожидать, что минимальная поверхность Хо, реализующая Р, не содер-
жит в себе никаких ’’лишних” ^-мерных циклов, т.е. содержит только те циклы,
которые переходят в ненулевые циклы в многообразии М. При этом поверхность Хо
может реализовывать и какие-то дополнительные циклы,не лежащие в первоначально
выбранной подгруппе Р. Другими словами, наша гипотеза состоит в том, что гомо-
морфизм Hk(H0; G) -*Нк(М-, G) должен быть мономорфизмом. Никакой нену-
левой цикл из пленки Хо не должен ’’растворяться” в многообразии М, если пленка
минимальна. Интуитивно ясно, что если какой-то цикл из пленки Хо стал нулевым
после вложения пленки в многообразие, то часть пленки - носитель этого цикла -
можно ’’выбросить”, не влияя на реализуемость пленкой циклов из подгруппы Р,
но уменьшая объем пленки. Для минимальной пленки такая процедура невозможна.
Теорема? (см. [16], [17]). Пусть М - компактное замкнутое риманово
многообразие и G - одномерное векторное пространство над полем, например, G -
группа R или Z р для простого р. Тогда для любой нетривиальной подгруппы Р С
CHk(M\ G) всегда существует абсолютно минимальная поверхность Хо в М, реали-
зующая эту подгруппу, причем для любой такой поверхности гомоморфизм jr
Hk(Xr G) ->Hk(M; G), индуцированный вложением j: Xo -*•M, является мономор-
физмом, т.е. на поверхности Хо нет ’’лишних циклов”.
Утверждения теорем 6 и 7 точны в том смысле, что отказ от условий, наложенных
на группу коэффициентов G, приводит к появлению контрпримеров (см. подробно-
сти в [16], [17], [15]).
6. Элементы теории препятствий, встречающиеся в вариационных задачах. В этом
пункте мы сделаем небольшой экскурс в теорию препятствий и докажем теорему
Хопфа о ретракции (см.п.4 § 18). Пусть t/=R1(mod 1) - абелева группа (по сложе-
нию) , т.е. окружность.
§ 47. ГОМОЛОГИИ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
427
Т с о р с м а 8 (Хопф). Пусть задано вложение i сферы S"~-1 в конечное п-мерное
клеточное пространство К. Пусть гомоморфизм iHn_t(Sn~l; U) -*Hn_i(X\ U),
индуцированный этим вожением, является мономорфизмом. Тогда сфера Sq~ 1 =
= i S"~l является ретрактом К, т.е. существует непрерывное отображение ft К ->
->S'o~', тождественное на сфере S'o~1 (ретракция).
Доказательство. Воспользуемся свойствами пространств Эйленберга—Мак-
лейна. Фиксируем натуральное число л > 1 и группу я (абелеву нрил> 1). Условие
теоремы Хопфа, переформулированное в терминах когомологий, означает, что гомо-
морфизм /*: Н"~ 1 (Л';Z)-> Нп~ 1(S"~ 1; Z), индуцированный вложением, является
эпиморфизмом. Следовательно, существует элемент € Н" ’(А; Z), та кой, что I* (} = а =
= 1 G H"~l(S "~l; Z). Тогда существует непрерывное отображение f.K -+K(Z,n - 1),
такое, что f*a = /?. Так как (fi) *а = а, то ограничение отображения /па сферу iS"~ ’,
вложенную в К, гомотопно тождественному отображению сферы па себя. Докажем,
что f можно про деформировать в отображение, тождественное на сфере 5"-1 и
отображающее на нее все пространство К. Так как пространство К л-мерно, а про-
странство A(Z, п - 1) нс содержит клеток размерности п. то из теоремы о клеточной
аппроксимации следует, что можно считать, что / переводит К в (п - 1)-мерный
остов пространства K(L,n - 1), т.е. в сферу S"~1. Теорема доказана.
Приведенное доказательство носит алгебраический характер. Для некоторых
приложений удобно иметь другое, геометрическое доказательство, которое мы сей-
час приведем, следуя работе [28].
Выберем для сферы клеточное разбиение в сумму двух клеток: нульмерной
* = о°н (п — 1)-мерной а"-1. Мы сконструируем искомое отображение так. чтобы
оно переводило весь остов А"-2 пространства А' в точку на сфере. Достаточно пост-
роить отображение факторпространства А/А"~2 в сферу S"-’. Здесь А = А". Для
применимости теории препятствий нужно рассматривать (п - 1)-простое прост-
ранство. Для сферы 5"-1 это выполнено. Так как остов А'"-* стянут в точку, то
можно считать, что остов А"-1 есть букет сфер So-1 v S"~l v . . . Ясно.
что сферу iS"~ 1 можно считать одной из них. Пусть это будет сфера Sq~ 1. Каждую
из сфер представим в виде простейшего клеточного разбиения и обозначим со-
ответствующие (п - 1)-мерные клетки через о"~1. Пусть о".а” все л-мерные
клетки пространства А'. Можно считать, что А = a0 Uo'0'~1 и... Оо*-1 ио'/ и... иа"
(рис. 204). Сначала мы построим такое отображение#j: А"~* которое.во-
обще говоря, нс продолжится до отображения всего
А' в5"-1, однако может быть использовано для по-
строения окончательного отображения у2, продолжа-
ющегося до отображения /’: А ->5" “ 1. Так как остов
А" - 1 - букет сфер, то достаточно задать на каж-
дой из них. На сфере 5'0' ~ мы зададим тождествен-
ное отображение S" ’ 1 S"~ *. а все остальные
сферы отобразим в точку *6 S"~l. Подсчитаем
препятствие с" для отображения #i.
Рассмотрим* клетку о". Нужно рассмотреть сквоз-
ное отображение границы клетки в сферу S" ~ 1 и най-
ти его степень. Мы знаем, что я„_ ] (S" ')= Z и го-
мотопические классы отображений сферы в сферу
классифицируются степенью отображения. Сквозное
отображение есть композиция характеристическо-
го отображения и g, : А"- 1 *. Часть сферы
428 ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
до", отобразившаяся в букет S"~ 1 v ... vSnk~ 1 (т.е. не инцидентная с Sq~ *),
отобразится в точку *. Итак, эти участки сферы до" не принимают участия в
формировании искомой степени (вклад—нулевой). Остальная часть до" ото-
бражается на S"_ 1 и ’’намотается” на нее столько раз, каков коэффициент
инцидентности [о" : До-1], после чего с помощью тождественного отображе-
ния отобразится на Sn~1. Итак, мы нашли, что Cg ((о”) = [о" : о"~1 ] - Утверждается,
что эта коцепь представима как кограница некоторой (и — 1)-мерной коцепи d.
Лемма. В предположениях теоремы Хопфа коцепь является кограницей,
т.е. c^t = 8d, гдеd & Рп~} (K,Trn_1(Sn~i)),d(Xoo~l) = 0,0<Х<1; Р"-1 -клеточ-
ные цепи.
Доказательство. Пусть, для простоты, среди п-мерных клеток прост-
ранства К есть лишь одна клетка о", имеющая ненулевой коэффициент инцидент-
ности с клеткой о”-1. Мы хотим построить (л — 1)-мерную коцепь d на букете сфер,
равную нулю на клетке о”-1 (на цепи X • Оо-1) и, быть может, нетривиальную на
остальных сферах букета. Другими словами, мы хотим ’’снять” коцепь со сферы
5”'1. Напомним, что цикл 5"-1 не гомологичен нулю в К. Имеем: до" =
= [а" : о"“1 ] Оо~1 + . . . + [о" : о*-1] о*-1. Обозначая [о" :о"-1] через а,-, запи-
шем до" = Доо"-1 + . . . + akok~'. Итак, цепь -д0о"-1, гомологична цепи
ajo"-1 + . . . + akuk~l. Определяемые ими циклы совпадают как элементы группы
гомологий (над Z). Из условия вытекает, что цикл Хо"-1, где 0 < X < 1, отличен
от нуля в Я„_ । (У; U). Рассмотрим следующие случаи.
(а) Все целые числа a j,... ,ak взаимно просты.
(б) Числа Д],. . . , ак имеют наибольший общий делитель р, отличный от единицы,
причем число а0/р не целое.
(в) Числа д,, . . . , ак имеют наибольший общий делительр, отличный от единицы,
и р делит д0 •
В случае (а) существуют целые числа Xj, . . . , хк, такие, что до = Xjfli + • • •
. . . + Xjtfljt- Определим (л—1)-мерную коцепь d на остове Кп~х так: с/(Хо"-1) =
= Хх,° xt S Z = nn-i(Sn l)’ 1 rf(Xo"-1) = 0- Здесь хь . . . , хк реализу-
ются как степени отображений сфер S"-1 на 5"-1. Ясно, что 8d = сg , так как
(8d) о” = d(don) = = S*= iXffl,- = a0 = Cgt(on'). В случае (а) лемма
доказана.
В случае (б) имеем: д (Хо") - Хд0о"_1 = Xp(iio”-1 + .. . + bkок~*), где д,- =
= pbj, 1 < i < к. Здесь , . . . , bk — взаимно простые. Так как д0/р не целое, то су-
ществует ненулевой цикл —• оо-1 (при X = 1/р) в гомологиях Hn_l(Sn~l; U),
Р
который становится гомологичным нулю в Нп-.Х(К-, U), так как — • Oq-1 =
Р
= д ( — о" ) (mod 1). Это противоречит мономорфности гомоморфизма Нп_ i(Sn~1;
ХР /
U) । (К; U). Итак, случай (б) не реализуется.
В случае (в) число р — наибольший общий делитель чисел дп..., ак, т.е. д,- =
= рЬ,, 1 < i ^к, а0 = тр, пг G Z и числа ij,. .., взаимно просты. Существуют це-
лые числа xt,. .., хк, такие, что т = хгЬх + ... + хкЬк. Реализуем числа х(- как сте-
пени отображений сфер S"~l в S"-1 и определим коцепь d так: d(o"-1) = х,- G
G тг„_I(-$"”1), d(uo~l) = 0. Утверждается, что 8d = Cgt. В самом деле, (8d)un =
= б/(д0о"-1 + • + akok~l) = аох, + ... + акхк = тр = д0 = с£ (о"). Лемма дока-
зана.
§ 47. ГОМОЛОГИИ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
429
Возвращаемся к доказательству теоремы Хопфа. В силу теории препятствий для
отображения gy: К”-1 -> S"-1 и коцепи d, построенной выше, можно подобрать
отображение g2: Кп~х -> 5"-1, такое, что d = d^1 . Имеем: &dg~g3 = 8d = сg3 -
- Cg2, т.е. Cg3 - 0. Итак, мы нашли отображение g2 (n-l)-ro остова К в Sn~l,
продолжающееся до отображения /: Кп -> 5"-1. Убедимся, что f тождественно на
Sn~1. В самом деле,^2 отличается от#] лишь на тех (п — 1)-мерных клетках, где ко-
цепь d отлична от нуля. Но коцепь d была построена так, что она равна нулю на це-
пях вида Хо"-1, следовательно, g2, как и g2, тождественно отображает на
5"-1. Если имеется несколько n-мерных клеток, инцидентных с а"-1, то доказа-
тельство проводится по такой же схеме. Теорема Хопфа доказана.
7. Гомологически тривиальные минимальные поверхности. Основным ограниче-
нием, несколько сужающим область применимости замечательной теоремы Райфен-
берга, является то, что существуют естественные мыльные пленки, заклеивающие
’’хорошую границу” А, однако не являющиеся G-поверхностями с границей А ни для
какой абелевой группы коэффициентов G. Это обстоятельство мы проиллюстрируем
на примере, построенном Адамсом.
Казалось бы, подходящим образом подбирая группу G, всегда можно представить
любую ’’разумную пленку” как некоторую G-поверхность. Однако это не так. Рас-
смотрим контур А, показанный на рис. 205а и являющийся границей устойчивой
мыльной пленки X, показанной на рис. 2056 и получающейся, если мы склеим
двойную и тройную ленты Мёбиуса, соединив их тонкой полоской-мостиком (т.е.
взяв их связную сумму). Эта пленка реализуется физической мыльной пленкой и
устойчива. Ее граница — окружность.
Однако ни для какой абелевой группы G эта пленка не является G-поверхностью
с границей окружность. Дело в том, что эти пленка ретрагируется на свою границу.
Доказательство этого факта мы дадим ниже, а сейчас извлечем из него необходимые
для нас следствия.
Пусть i: А -> X - вложение и/: X *А - ретракция. Тогда сквозной гомомор-
i» /.
физм Я1(Л; G)—-+Hi(X-, G)------>НХ(А\ G) является тождественным и г, - моно-
морфизм. Это и означает, что для любой группы G пленка X не заклеивает ни одно-
го цикла в группе Н2(A; G).
А теперь докажем ретрагируемость пленки на границу. Так как X гомотопически
эквивалентно букету двух окружностей, то Нг(Х; U) = U ® U и i »(Х) = (2Х, ЗХ),
где 0 <Х < 1. Отсюда видно, что /» — мономорфизм, что и требовалось доказать
в силу теоремы Хопфа.
Рис. 205
Рис. 206
430
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
Отметим, что хотя А является здесь ретрактом X, но А не является деформа-
ционным ретрактом X. Это следует из того, что А и X гомотопически не экви-
валентны.
Мы извлекли выше существование ретракции из алгебраических теорем. Однако
полезно наглядно представить себе — как именно происходит зта ретракция. Эта наг-
лядная картина описана в [28] и опирается на геометрическое доказательство теоре-
мы Хопфа (вкратце изложенное в п. 6).
В нашем случае X двумерно и его одномерный остов — это букет двух окружнос-
тей (ось обычной и ось тройной ленты Мёбиуса) .Можно считать, что X = о0 U a] Uoj U
U о2, где о2 — двумерная клетка. Разрежем пленку вдоль осей биди вдоль отрезка
с — оси мостика, соединяющего две ленты Мёбиуса (рис. 206). Представим Xтак:
X = о0 UaUiUcUl2, где Л2 - кольцо. Разрезая пленку по одномерному остову,
получаем кольцо к2. Его граница — две окружности: внешняя А и внутренняя, сос-
тавленная из семи дуг (рис. 207). Выполним деформационную ретракцию, чтобы
внутренняя граница в одной точке соприкоснулась с внешней границей.
Для установления соответствия с обозначениями теоремы Хопфа обозначим А
через So, окружность а через 5] и окружность b через S%. Тогда коэффициенты ин-
цидентности клетки о2 с этими окружностями таковы: [о2 : А] = 1, [о2 : д] =
= 3, [а2 : А] =2. Следуя схеме п. 6, построим отображение g одномерного остова
пленки X на А. Отобразим А на себя тождественно. Определим теперь g на а и Ь.
Нужно подобрать такие целые числа т и п, чтобы т[о2 : а] - и [о2 : 6] = 1, т.е.
Зт — 2п = 1. Затем построим отображение g, отображающее а со степенью т на А,
а b — со степенью п на А. Достаточно положить т = п = 1, т.е. можно считать, что
а и b отображаются на А гомеоморфно. Согласно теореме Хопфа, отображение g
продолжается до отображения f всей пленки на А, что и требуется. Изобразим это
отображение наглядно. Подробности см. в [28].
Фиксируем А и растянем сторону с так, чтобы она намоталась на А со степенью 1
(рис. 208). Но мы не будем отождествлять А и с и прервем операцию, сохранив уз-
кую полоску, ограниченную на рисунке окружностями А и с . Оставшаяся часть
двумерной клетки образует диск, приклеенный к точке о° и получившейся полоске
между А и с. Берем ребро д и наматываем его вдоль А, как показано на рис. 208
Рис 207 Рис. 208
§ 47. ГОМОЛОГИИ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
431
Рис. 209
и рис. 209 (7), (2). В результате получается мешок, дырка в котором имеет гра-
ницу bbc~xaa. Это слово выписано при движении против часовой стрелки на границе
дырки. Степень + 1 или —1 указывает ориентацию соответствующих ребер. Про-
должаем намотку двумерной клетки, как показано на рис. 209 (5) - (74). Этим и
завершается построение искомой ретракции.
Тот же механизм действует и в случае связной суммы p-к ратной и «/-кратной лент
Мёбиуса, если р и q взаимно просты. Наглядное изображение ретракции сохраняет-
ся, но добавляется намотка окружностей а и b со степенями т и п на окружность
А, где тип таковы, что тр - nq = 1.
Приведем также второй пример Адамса — минимальную пленку X, затягивающую
контур А на рис. 210. Контур гомеоморфен окружности, вложенной в R3. Пленка
на рисунке является ’’хорошей пленкой”, правда неустойчивой и имеющей особен-
Рис. 210
432
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
Рис. 211
Рис. 212
ности. Эта пленка также не является G-поверхностью с границей А ни для какой
группы G. Дело в том; что она не только ретрагируется на свою границу, но даже
деформационно ретрагируется на границу. Это стягивание показано на рис. 211,
212. Две ручки справа и слева образованы парами соосных окружностей. Окружнос-
ти близки друг к другу и ограничивают часть мыльной пленки, похожую на катено-
ид. Горловина каждого из них затянута плоским диском. В двух особых точках плен-
ки Q и Q1 сходятся по 4 сингулярных ребра пленки под углами примерно в 109°.
§48. БОРДИЗМЫ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
1. Старшие и младшие страты минимальных поверхностей. В предыдущем параг-
рафе мы говорили о двух путях исследования проблемы Плато и о ее решении на вто-
ром пути, т.е. в классе гомологических G-поверхностей. Вернемся теперь к подхо-
дам к задаче Плато, основанным на идеях Дугласа и Радо.
Сначала еще раз обратимся к примеру на рис. 200 в § 47. Увеличивая высоту ка-
теноида, мы заставляем его перестраиваться в пару дисков, соединенных отрезком.
Процесс перестройки заслуживает того, чтобы остановиться на нем подробнее. Когда
высота h достигает критического значения йтах, внешний и внутренний катеноды
встречаются, сливаются и превращаются в один катеноид. Дальнейшее увеличение h
разрушает его. Оставаясь в рамках прежних методов, мы не можем сохранить преж-
нюю минимальную поверхность, оставаясь в топологическом классе цилиндров или
в классе конформных отображений цилиндра в R3. Но с другой стороны, интуитив-
§ 48. БОРДИЗМЫ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
433
но ясно, что возникшее препятствие можно преодолеть (оставаясь в ’’прежнем топо-
логическом классе поверхностей”), если допустить у поверхности склейки. Изгото-
вив цилиндр из тонкой резины и увеличивая h за критическое значение, мы можем
добиться того, что цилиндр (уже не являясь локально минимальной поверхностью)
превращается в пару дисков, соединенных тонкой трубкой (рис. 200 в § 47), после
чего естественно считать, что трубка стягивается в отрезок, соединяющий пару плос-
ких дисков. Эти события происходят вне класса минимальных поверхностей. Но
в результате мы снова получаем минимальную (правда, стратифицированную, состоя-
щую из нескольких стратов разных размерностей) поверхность: пару дисков с от-
резком. Однако естественно ожидать, что многомерная задача Плато имеет решение,
непрерывно зависящее (в некотором точном смысле) от начальных данных. В нашем
примере мы можем убедиться в этом. К значению Лтах мы можем приблизиться
в классе минимальных поверхностей: двух катеноидов. При h = Лтах мы получаем
один катеноид критической высоты, затем ”в принудительном порядке” мы сжимаем
его, превращая в пару плоских дисков, соединенных прямолинейным отрезком, т.е.
превращая в минимальную поверхность. Дальнейшее увеличение h приводит лишь к
растяжению отрезка. При этом он остается одномерной минимальной поверхностью,
линией кратчайшей длины, соединяющей пару дисков (их центры).
Будем теперь произвольно перемещать в пространстве плоские граничные окруж-
ности, не соблюдая их параллельность. Два минимальных диска, оставаясь плоскими,
будут менять взаимное положение, а соединяющий их отрезок (который удобно
представлять резиновой нитью) будет скользить своими двумя концами по этим дис-
кам, стремясь занять положение, отвечающее наименьшей длине (рис. 213). Мы при-
ходим к естественной идее рассматривать каждый страт размерностно-неоднородной
поверхности как минимальную поверхность в своей размерности. Видно, что страты
меньших (младших) размерностей занимают минимальное положение в пространст-
ве, реагируя на взаимное расположение минимальных стратов большей размерности.
Минимальные диски, располагаясь разными способами в R3, индуцируют перемеще-
ния одномерного минимального страта относительно двумерных стратов. Если в
некоторый момент два диска снова сблизятся на расстояние h <Лтах> то ПРИ пра-
вильной постановке вариационной задачи отрезок снова превратится в тонкий ци-
линдр, а вся пленка — в катеноид. Максималь-
ную размерность стратов назовем старшей
размерностью. Итак, страты младших раз-
мерностей ’’помнят” о первоначальной топо-
логической структуре всей пленки (в це-
лом) и в подходящие моменты позволяют
осуществлять перестройку образа пленки,
чтобы она могла занять положение с мини-
мальной площадью (объемом).
Итак, хотя проблема Плато в классе под-
многообразий не имеет буквального реше-
ния, однако если допустить к рассмотре-
нию естественно возникающие страты млад-
ших размерностей, мы сохраняем главное
условие задачи Плато — поиск минимума в
классе образов гладких многообразий с
фиксированным краем.
Поясним геометрический смысл предыду-
щих переформулировок задачи Плато на язы-
ке гомологий. Дело в том, что для обычных
Рис. 213
434
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
гомологий (и когомологий) выполнено следующее свойство. Если приклеить к
^-мерному комплексу X (к-1)-мерный комплекс Y (рис. 214), то Нк(Х U У) =
= Нк(Х), так как Я* (У) = 0. Это свойство обычных гомологий следует из так
называемой ’’аксиомы точки”, согласно которой Як(*) = 0, при к =# 0. Поэтому
при формулировке задачи Плато в терминах гомологий мы игнорировали воз-
никающие в минимальных пленках страты младших размерностей. С одной сто-
роны, это облегчало задачу минимизации объема, но с другой стороны, мы, вообще
говоря, теряли свойство пленки быть непрерывным образом многообразия с краем.
к-1
Рис. 214
Рис. 215
2. Бордантные многообразия и задача минимизации объема. Рассмотрим пары
(IV, /), где W — гладкое компактное многообразие размерности к с краем Э W,
гомеоморфным A, a/: W ->М - непрерывное (липшицево, кусочно гладкое) отоб-
ражение, тождественное на крае ЭИ\ т.е. совпадающее с фиксированным вложением
i: А -+М. Далее обозначение i будем опускать.
Задача А. Можно ли среди всех пар (W, /), где W — всевозможные многооб-
разия с краем А, найти пару (IVq, /о) такую, чтобы отображение f0 или пленка
Хо = /о ОМ (образ многообразия JV0) обладали бы разумными свойствами мини-
мальности, в частности, чтобы volk Хо < volk X, тле X=f (W) - любая пленка из ука-
занного класса.
Задача Б. Пусть (К, g) — пара, где V — замкнутое /с-мерное многообразие,
g: V -+ М - непрерывное (липшицево, кусочно гладкое) отображение в Мп, X =
= g(V) — образ V в М. Мы скажем, что пара (Y',gr) является бордизм-вариацией
пары (К,g), если существует компактное многообразие Z с краем 9Z = KU (± К')
и непрерывное отображение F: Z -+М, такое, что F 1к = g, F\v> = g' (рис. 215).
Можно ли среди всех пар (К, g) найти пару (Ко, £о)> такую, чтобы образ Хо =
= go(Vo) обладал бы разумными свойствами минимальности, в частности, чтобы
volk Хо <volk X, где X = g (К) - любая поверхность из указанного класса?
Математическая природа задачи минимизации вынуждает нас ввести: а) стратифи-
цированные поверхности X = Хк UX*-1 U. . . , где каждое подмножество (страт)
Xя является «/-мерной поверхностью в М, имеющей в каждой своей точке размер-
ность q и Xя содержится в X - = q+JXl , причем Xя П (U*_ q+lX') = ф; б) стра-
тифицированный объем SV(X) = (volkX*, vol*А*-1, . . . ), изображаемый век-
тором, каждая компонента которого равна объему соответствующего страта (в каж-
дой размерности).
Итак, стратифицированная поверхность состоит из кусков разных размерностей,
наподобие пары дисков с отрезков, подробно описанных в предыдущем пункте. На-
хождение минимальной поверхности означает доказательство существования поверх-
ности, стратифицированный объем которой является наименьшим в смысле лекси-
кографического упорядочивания. Другими словами, под минимизацией вектора
§ 48. БОРДИЗМЫ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
435
стратифицированного объема нужно понимать следующее. Сначала минимизируем
его первую координату, т.е. старший fc-мерный объем. Фиксировав это минимальное
значение старшего объема, минимизируем вторую координату. т.е. (к — 1)-мерный
объем стратов. Фиксировав минимальные значения первых двух координат вектора
объема, минимизируем третью и т.д. Различные способы появления младших стратов
см. на рис. 216,217.
Сопоставляя каждой стратифицированной поверхности X = U, X' вектор ее стра-
тифицированного объема SV(Xj = (уо\кХк, . . .), мы можем изобразить 5К(ЙГ)'сак
вектор в R*. Меняя поверхности, получаем множество векторов (Лк, Хк_], . . .),
заметающих в R* некоторое подмножество (рис. 218). Лексикографическое упоря-
дочение позволяет определить наименьший вектор. Задача заключается в поиске
поверхности, стратифицированный объем которой в точности равен минимальному
вектору.
Для реализации этой программы нужен подходящий язык. Оказывается, он су-
ществует и используется в топологии. Это язык бордизмов, с которым мы знакомы
по предыдущим главам. Отношение бордантности является отношением эквивалент-
ности на классе замкнутых ориентированных {к — 1)-мерных многообразий.
Множество 12*-!-классов эквивалентности является абелевой группой, в
которой сложение индуцировано несвязным объединением многообразий (рис. 219).
Ориентированным сингулярным многообразием пары (У, Z) называется пара
(Кк-1,/), где Кк-1 — компактное ориентированное многообразие с краем Э V, а/—
непрерывное отображение (К, ЭР) -* (У, Z), т.е./(К) С У,/(ЭК) CZ. Если Z = ф,
то полагаем, что и ЭК = ф. Ориентированное сингулярное многообразие (К*-1,/)
пары (У, Z) называется бордантным нулю, если существуют компактное ориенти-
рованное многообразие WK и непрерывное отображение F: Wk -+ У такие, что:
436
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
Рис. 220
бордизм (A, i)
а) многообразие V есть регулярное подмногообразие
края W (т.е. V CbW),K ориентация V совпадает с ори-
ентацией, индуцированной на нем ориентацией W; б)
F ly = f, F(3B' - К) С Z (рис. 220).
Класс бордизмов сингулярного ориентированного
многообразия (V, f) называется синулярным бордиз-
мом. Множество таких классов обозначается через
S2a_1(}^Z)h называется (к-1)-мерной группой ориен-
тированных сингулярных бордизмов пары (Y, Z). Ана-
логично определяются неориентированные сингуляр-
ные бордизмы Nt _ 1 (У, Z ) (здесь ориентация много-
образий игнорируется).
Вернемся к задаче Плато. Пусть Ак ~ 1 — компак-
тное замкнутое ориентированное подмногообразие
в М, г: А -+ X — вложение, где X подмножество в М.
Задача А. Можно ли среди всех компактов X,
содержащих А и обладающих тем свойством, что син-
зквивалентен нулю в X, найти такой компакт Хо, кото-
рый обладал бы свойством минимальности?
Поскольку тождественное отображение е: А -+ А определяет элемент о G
G S2fc_ j (А) (и элемент о (А) в случае неориентированных бордизмов),
то введенный выше класс пленок-компактов X характеризуется тем, что f, (о) =
= 0, где it : Пк_1 (А) -> I2k_1 (X) —гомоморфизм групп бордизмов, индуцирован-
ный вложением i : А ->Х.
Ясно, как переформулировать на языке групп сингулярных бордизмов и вто-
рую задачу Б (см. выше, т.е. задачу реализации).
’Задача Б. Можно ли среди всех сингулярных многообразий (К, g) g: V -+М,
бордантных данному сингулярному ьиогообразию (V', g')> найти такое многооб-
разие (V0,g0), чтобы пленка Хо = go(Vo) была минимальной?
Мы видели, что минимальные поверхности чаще всего являются не многообрази-
ями, а поверхностями с особенностями. Сегодня хорошо известно, что эти особен-
ности могут быть очень сложными. Поэтому нужно уметь вычислять группы бордиз-
мов для широкого класса пространств (а не только для конечных клеточных). Ока-
зывается, достаточно рассмотреть класс компактов в римановом многообразии.
Для того чтобы распространить определение групп бордизмов с категории конечных
клеточных пространств (полиэдров, многообразий) на категорию компактов, нужно
воспользоваться уже знакомым нам спектральным процессом — процессом Чеха.
Напомним, что каждый компакт X можно представить в виде обратного предела
полиэдров N(Ua), являющихся нервами его открытых покрытий. Обратный пре-
дел берется по множеству измельчающихся покрытий компакта. Можно записать,
что X = limA(t/tt). Положим, по определению, £lk(X) ~ lim Elk (N(Ua)). Группу
а а
Пк (X) будем называть А:-мерной группой спектральных бордизмов компакта X
(или просто спектральными бордизмами).
Теорема 1. Если компакт является конечным клеточным пространством
(полиэдром, многообразием), то его группы спектральных бордизмов совпадают
с группами обычных бордизмов.
Элементом группы спектральных бордизмов является бесконечная последова-
тельность (спектр) многообразий и отображений. В случае конечных полиэдров
эта последовательность стабшшзируется (начиная с некоторого момента), т.е. все
§ 48. БОРДИЗМЫ И МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ
437
многообразия спектра совпадают с каким-то одним фиксированным многообра-
зием.
3. Решение задачи Плато в каждом классе спектральных бордизмов. Рассмотрим,
для простоты, в евклидовом пространстве R" ’’контур” Ак~1, например, замкнутое
гладкое подмногообразие. Пусть А (о) — класс всех измеримых компактных под-
множеств X в R", содержащих А и аннулирующих бордизм о = (А, е), где е: А -+А -
тождественное отображение. Другими словами, сингулярное многообразие (A, i),
где i : А X — вложение, бордантно нулю (в смысле спектральных бордизмов) в
пленке X. Это означает, что i„ (о) = 0, где - гомоморфизм, отображающий
(к — 1)-мерные бордизмы границы А в (к — 1)-мерные спектральные бордизмы
пленки X. Через vol* обозначим либо риманов объем пленки X, либо ее Л-мерную
хаусдорфову меру, когда пленка содержит сложные особенности.
Теорема 2 (Фоменко [16], [17]). Пусть Ак~* — произвольное гладкое замк-
нутое подмногообразие в R". Тогда в классе поверхностей А (о), граница которых
совпадает с А (см. выше), всегда существует абсолютно минимальная поверхность
X = Xk U Xk~l U ..., старший к-мерный объем которой является наименьшим. Эта
поверхность стратифицирована стратами X', каждый из которых имеет размерность
i (некоторые страты могут быть пустыми), причем Х‘ С X- (A UI;+i U...Xk).
Кроме того, эта поверхность такова, что ее стратифицированный объем SV(X) =
= (vol* Xk, vol*-! Xk~l,... ) является наименьшим в лексикографическом упо-
рядочении среди всех стратифицированных объемов других поверхностей из клас-
са А (о). Это означает, что поверхность X является абсолютно минимальной не толь-
ко в старшей, но и во всех младших размерностях. Кроме того, каждый из стратов
Х‘ поверхности X является, за исключением, быть может, множества i-мерной ме-
ры нуль, аналитическим минимальным подмногообразием в R" (рис. 221).
Следствие. Если минимальная поверхность из предыдущей теоремы явля-
ется конечным клеточным комплексом (полиэдром, многообразием), то ее спект-
ральные бордизмы совпадают с обычными и, следовательно, эта поверхность является
непрерывным образом какого-то одного многообразия ivj с краем Ak~l. В этом
случае поверхность Хо является решением классической задачи Плато.
(1-1)-мерный страт
'11-мерный страт
-^.Объединение стратов „
больших размерностей
Рис. 221
Следует отметить, что все известные сегодня конкретные примеры минималь-
ных поверхностей, граница которых — гладкое компактное многообразие, действи-
тельно являются конечными клеточными пространствами. В действительности тео-
рема 2 доказана в существенно более общей ситуации. Оказывается, минимальная
поверхность существует для произвольного ’’контура” Ак~1, являющегося компакт-
ным подмножеством в римановом многообразии Мп. При этом, конечно, должна
существовать хотя бы одна поверхность Хк, заклеивающая А в. смысле спектраль-
ных бордизмов. В общем случае минимальная поверхность является пределом по-
438
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
верхностей, допускающих непрерывную параметризацию гладкими многообра-
зиями.
Проследим процесс минимизации вниз по размерностям в условиях теоремы 2.
1. Оказывается, существуют поверхности Хк, аннулирующие спектральный бор-
дизм (А, е) и имеющие наименьший старший объем vol*. Каждая из них содержит
однозначно определенный ^-мерный старший страт, являющийся почти всюду глад-
ким /с-мерным минимальным подмногообразием в Мп.
2. Среди этих поверхностей существуют поверхности, у которых абсолютно ми-
нимальным является не только старший страт, но и следующий за ним вниз по раз-
мерности младший {к - 1)-мерный страт (если он непуст). Этот (к - 1)-мерный
страт однозначно определен в дополнении X — (старший страт) и является, за иск-
лючением, быть может, множества меры нуль особых точек, гладким минимальным
(к - 1)-мерным подмногообразием в М.
И так далее, спускаясь вниз по размерностям, мы обнаруживаем в итоге, что
существуют поверхности, все страты которых (как старшие, так и младшие) аб-
солютно минимальны. Эти поверхности и являются решениями задачи Плато.
Далее, проблема Плато имеет решение и в классе поверхностей, реализующих лю-
бой ненулевой класс обычных борднзмов произвольного компактного риманова
многообразия М. См. [16], [17]. Это означает, что среди компактных поверхнос-
тей X, таких, что при их вложении i: X ->М данный элемент о G 12* (Л/) (из группы
обычных бордизмов многообразия М) принадлежит образу гомоморфизма
12* (X) -> 12* (Л/) (где 12* (X) - группа спектральных бордизмов поверхности X),
всегда существует абсолютно минимальная (во всех размерностях) поверхность
Хо. Еще раз отметим, что минимальную реализацию здесь всегда допускает элемент
обычной группы бордизмов многообразия.
Абсолютно минимальная поверхность всегда существует и в классе компактов,
реализующих ненулевые элементы стабильных гомотопических групп гладких пол-
ных римановых многообразий. Это означает, что среди компактных поверхностей X
таких, что при их вложении i: X -> М данный элемент a G я* (Л/) принадлежит обра-
зу гомоморфизма я* (X) ->я®(Л1), всегда существует абсолютно минимальная
(во всех размерностях) поверхность Хо. Как и в случае бордизмов, стабильные
гомотопические группы компактов определяются при помощи спектрального про-
цесса.
Абсолютно минимальная поверхность всегда существует и в классе носителей
стабильно нетривиального векторного расслоения на многообразии М. Компакт
X С М называется носителем такого расслоения £, если ограничение £ | х по-преж-
нему стабильно нетривиально. Таким образом, можно рассмотреть вариационную
задачу в классе таких носителей. Оказывается (см. [16|, [17|), среди этих носи-
телей всегда имеется абсолютно минимальная поверхность.
Другие примеры решения проблемы Плато в различных топологических клас-
сах поверхностей см. в [16], [17]. Во всех этих случаях абсолютный минимум дос-
тигается на стратифицированной поверхности. Все се страты, в том числе и стар-
ший, абсолютно минимальны и являются почти всюду гладкими подмногообразия-
ми (аналитическими, если объемлющее многообразие аналитическое). Замыкание
каждого отдельного непустого страта не содержится в замыкании объединения всех
стратов больших размерностей (см. рис. 221). Поэтому удалить какой-либо из не-
пустых стратов нельзя: это сразу разрушит топологические свойства минимальной
поверхности.
4. Минимальные поверхности в гомотопических классах отображений. Введен-
ные в [16], [17| понятия стратифицированной поверхности и стратифицировапно-
§ 49. НЕКОТОРЫЕ ТОПОЛОГИИ МИНИМАЛЬНЫХ ПОВЕРХНОСТЕЙ
439
го объема допускают, как выяснилось, естественное развитие на функциональном
языке, что и было сделано в работах Дао Чонг Тхи [21] — [23].
Теорема 3 (Дао Чонг Тхи). Пусть М - полное связное риманово многооб-
разие, W - некоторое фиксированное k-мерное компактное многообразие с краем.
Рассмотрим все локально липшицевы отображения f : W -+М, такие, что огртиче-
ние f на край Э W совпадает с некоторым заданным отображением g: dW ->М.
Тогда каждому отображению f: W -+М отвечает "параметризованный мультивари-
фолд" [ W, f ] — функциональный аналог стратифицированной поверхности
X = f (ИО (см. [21] - [23] ). Каждый параметризованный мультиварифолд обладает
"массой" - аналогом риманова объема Утверждается, что в каждом гомотопическом
классе параметризованных мультиварифолдов существует параметризованный муль-
тиварифолд [И7, /о] минимальной массы (решающий, следовательно, проблему
Плато в данном гомотопическом классе).
Если многообразие М компактно, то теорема 3 остается справедливой и при
dW = ф, т.е. когда W — компактное замкнутое многообразие. Далее, аналогичная
теорема существования справедлива и для вариационных задач с подвижной грани-
цей, т.е. когда граница пленки может скользить по некоторому фиксированному
подмногообразию. В теореме 3 минимизируется старший объем стратифицирован-
ной поверхности (на функциональном языке — мультиварифолда, [21]-[23]).
Младшие страты здесь не минимизируются.
§ 49. НЕКОТОРЫЕ ТОПОЛОГИЧЕСКИЕ СВОЙСТВА
МИНИМАЛЬНЫХ ПОВЕРХНОСТЕЙ
Существует интересная связь между разрешимостью задачи Дирихле для ми-
нимальных поверхностей и их гомотопическими свойствами. Рассмотрим разло-
жение Rn+* в прямую сумму R* © R" и пусть Вп — открытое подмножество в R"
с гладкой или кусочно гладкой границей.
Предположим, что задано гладкое отображение f: Вп -> Rk. Рассмотрим график
Г этого отображения, т.е. множество точек вида (x,f(x)) в Rn+k, где х G Вп
(рис. 222). График Г является и-мерным подмногообразием в R"+k. Сформули-
руем задачу Дирихле. Пусть задано гладкое отображение границы ЪВ области В
в R*. Требуется найти отображение /: В ->Rk, такое, чтобы f было непрерывно на
замыкании области В, локально липшицевым (или гладким) в области В и, кроме
того, чтобы график Г отображения f был минимальным подмногообразием в Rn+*.
Мы считаем, что объем графика конечен, следовательно, имеет смысл рассматривать
ограниченные области В в R". Выражаясь языком теории дифференциальных урав-
440
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
нений, мы ставим задачу Дирихле для уравнения минимальной поверхности кораз-
мерности к на области Вп с граничными условиями у>.
Хорошо известно, что в случае, когда график Г является гиперповерхностью
(т.е. при к = 1), задача Дирихле для выпуклых областей В всегда имеет единствен-
ное решение для любых заранее заданных непрерывных граничных условий. При этом
решение f: Вп ->R* единственно, является вещественно-аналитическим и график Г
является не только локально минимальной, но даже абсолютно минимальной поверх-
ностью в R"+1. Более точно, гиперповерхность Г в R"+1 имеет наименьший возмож-
ный объем в классе всех поверхностей с той же границей {(х, (х))} , где х G ЪВ.
Для случая больших коразмерностей следует выделить двумерные графики, за-
дающие отображения двумерных выпуклых областей В2 и Rk. Оказывается (см.,
например, обзор в работах Оссермана и Лоусона [9], [12]), что при и = 2 и при
любом к > 1 для любой выпуклой области В2 всегда существует решение задачи
Дирихле для любых непрерывных граничных данных. Правда, в этом случае мини-
мальная поверхность может быть не единственной, решение задачи Дирихле может
быть неустойчиво. Другими словами, график искомого отображения f: В2 -> Rk
может быть локально минимальной, но не абсолютно минимальной поверхностью
BRfc+2.
Теперь рассмотрим минимальные поверхности коразмерностей, больших чем
единица, т.е. к > 2. В качестве выпуклой области В" возьмем стандартный откры-
тый диск D" единичного радиуса. Оказывается, при п > 4 задача Дирихле может
вообще не иметь решения и препятствие к существованию решения носит чисто
гомотопический характер, см. [9].
Теорема 1 (Лоусон, Оссерман). Пусть п > к > 2, Sa~1 = dDn, Sk~1 С R*,
где Sn~1 и Sk~1 - стандартные сферы единичного радиуса. Пусть у. Sn~1 ->Sk~1 -
любое отображение класса С2, определяющее нетривиальный (отличный от нуля)
элемент гомотопической группы itn~i(Sk~l). Тогда существует число R^>, такое,
что для каждого R > не существует решения задачи Дирихле в шаре Dn для
уравнения минимальной поверхности коразмерности к с граничной функцией =
= R • (рис. 223).
Лоусон и Оссерман рассматривают, следовательно, график отображения, реали-
зующего ненулевой элемент гомотопической группы, затем растягивают область
значений с коэффициентом подобия R. Попросту говоря, увеличивается радиус сфе-
ры в области значений. Начиная с некоторого момента, решение задачи Дирихле
исчезает. При этом следует сказать, что задача Дирихле всегда разрешима для
выпуклой области (и для любой коразмерности) для достаточно малых граничных
§ 49. НЕКОТОРЫЕ ТОПОЛОГИ МИНИМАЛЬНЫХ ПОВЕРХНОСТЕЙ
441
данных. Другими словами, если функция мала на ЭД, то всегда существует ми-
нимальная поверхность, близкая к В и совпадающая на ЭВ с графиком \р.
В качестве примера рассмотрим отображение (расслоение) Хопфа. Его можно
задать отображением р: S3 -* S2, записывающимся в координатах z, w так: p(z, w) =
= (| z |2 — | w |2, 2z w). Здесь z, w — эрмитовы координаты в С2. Сфера S3 задается
так: |z |2 + | w|2 = 1, асфера S2 реализована как единичная сфера в R3 =RXC. Легко
убедиться (проверьте!), что вектор p(z, w) пробегает двумерную сферу в R3. Как
мы знаем, отображение р негомотопно нулю, определяет ненулевой элемент груп-
пы тг3 (№) = Z. Следовательно, в силу теоремы Лоусона и Оссермана, при достаточ-
но больших R задача Дирихле на четырехмерном шаре с граничными условиями
R<p не имеет решения в виде минимального графика некоторого отображения F:
Da -> R3. Оказывается, в качестве граничного значения R^ можно взять число 4,2
при единичных радиусах сфер.
Отсутствие решения задачи Дирихле (в классе графиков) не препятствует нали-
чию 4-мерной минимальной поверхности, имеющей в качестве граничного ’’конту-
ра” трехмерную сферу, вложенную в R7 как график отображения <р: S3 -*S2 С R3.
Как мы видели, иэ общих теорем существования абсолютно минимальных поверх-
ностей следует, что для любого непрерывного <р всегда существует абсолютно ми-
нимальная поверхность, решающая задачу Плато. Однако она не представима как
график (при указанных условиях).
Минимальные поверхности обладают и другими интересными топологическими
свойствами. Харви и Лоусон в известной работе [31] доказали, что любое локально
минимальное лагранжево подмногообразие в С" * R2" (со стандартной кэлеровой
метрикой) является специально лагранжевым, а потому абсолютно минимальным.
Любое специально лагранжево подмногообразие — абсолютно минимально, см. [31].
Возникает вопрос об описании топологических классов минимальных лагранжевых
подмногообразий в произвольном кэлеровом многообразии. При этом считается,
что риманова метрика и симплектическая структура задаются кэлеровой структу-
рой. Хорошо известно, что лагранжево подмногообразие в симплектическом прост-
ранстве R2" (а также в некоторых других кэлеровых многообразиях М2п) облада-
ет естественным топологическим инвариантом — индексом Маслова, и, более общо,
— характеристическими классами Маслова — Арнольда. А.Т. Фоменко сформули-
ровал гипотезу, согласно которой минимальность лагранжева подмногообразия
влечет аннулирование многих характеристических классов at Маслова — Арноль-
да. Для случая М2п = R2" зта гипотеза оказалась справедливой, см. [30].
Теорема 2 (Ле Хонг Ван, А.Т. Фоменко). Для минимальных лагранжевых
многообразий в R2" характеристические классы Маслова - Арнольда а,-(mod 2)
и классы а, (для группы коэффициентов Z) равны нулю.
При доказательстве использованы, в частности, результаты Д.Б. Фукса [27].
Современная теория минимальных поверхностей тесно связана с теорией гар-
монических отображений. Хотя эта теория выходит за рамки настоящей главы, мы
приведем здесь один из ее результатов, связанный с гомотопическими свойства-
ми римановых многообразий.
Напомним, что функционалом Дирихле (или функционалом энергии) называет-
ся отображение, ставящее в соответствие каждому достаточно гладкому отобра-
жению /: М -+N компактного ориентируемого риманова многообразия М в римано-
во многообразие N число
..Э/“ Э/^
D(f) = f T-7gapdo,
М t,j дх дх'
iA2
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
где ht/- и gap — римановы метрики на многообразиях М и N соответственно, h*1 —
коэффициенты обратной матрицы к матрице (Л//), х1,..., хт — локальные коор-
динаты на М, а функции /“ = fa (х1,..., хт ) задают отображение /: М -+N.
Отображение f: М -+Nназывается гармоническим, если оно является экстремалью
функционала Дирихле. Обозначим через D(M) следующее число: D(M) - \niD(g),
g
где g: М -* М — отображения, гомотопные тождественному отображению многооб-
разия М на себя.
Теорема 3 (А.И. Плужников [32]). Пусть М — замкнутое гладкое риманово
многообразие. Тогда D(M) = 0 тогда и только тогда, когда каждая компонента связ-
ности многообразия М является двусвязной, т.е. ее первая и вторая гомотопические
группы' тривиал ьны.
Так как отображения, гомотопные тождественному, топологически нетривиаль-
ны (не гомотопны отображению в точку), то равенство D(M) = 0 означает, что функ-
ционал Дирихле (в условиях теоремы Плужникова) не достигает минимума на го-
мотопическом классе тождественного отображения многообразия на себя.
§ SO. ГОМОЛОГИИ И ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ
ИНТЕГРИРУЕМЫХ ГАМИЛЬТОНОВЫХ СИСТЕМ
Группы гомологий естественно возникают и в других вариационных задачах,
среди которых особое место занимает задача интегрирования так называемых га-
мильтоновых систем, возникающих во многих вопросах механики, теоретической и
математической физики.
Рассмотрим чсгырехмерное гладкое многообразие МА без края (компактное или
некомпактное, все равно). Пусть на нем задана дополнительная структура, называе-
мая симплектической. Это означает, что на касательных векторах к многообразию М
в каждой его точке задано кососимметрическое невырожденное скалярное произ-
ведение, определяемое невырожденной кососимметрической матрицей Я = (<<ty(x)),
где х G М, соц - — сор. Кроме того, требуется, чтобы в окрестности каждой точки х
существовали такие локальные регулярные криволинейные координаты (называе-
мые каноническими или симплектическими) q(, q2, Pi > Рг > что в каждой точке этой
окрестности кососкалярное произведение одновременно задавалось бы в этих коор-
/ О Е\ /1 0\
динатах следующей простейшей матрицей Я = I & \, где Е = ) — единич-
ная матрица. Другими словами, требуется, чтобы сразу в целой окрестности косо-
симметрическое скалярное произведение приводилось бы (путем выбора координат)
к указанному каноническому виду.
Если а и b - касательные векторы к Л/4, задаваемые координатами (а,-), (Л,-),
то их кососимметрическое скалярное произведение задается так: {a, b) - T,b>ijaibj.
Многообразие М с такой структурой называется симплектическим.
Если Н - гладкая функция на многообразии, то задание невырожденного скаляр-
ного произведения позволяет определить так называемый косой градиент sgradЯ
функции Н посредством формулы < sgrad Н, и> = и (Я), где и — произвольное глад-
кое векторное поле на М, а через и (Я) обозначена производная функции Н вдоль
векторного поля у. Из условия невырожденности матрицы Я следует, что поле
sgrad// корректно и однозначно определено. Векторные поля вида sgradЯ называют-
ся гамильтоновыми, а функция Я называется гамильтонианом такого поля.
Важность гамильтоновых полей объясняется тем, что огромное число конкрет-
ных механических и физических систем описывается гамильтоновыми полями на
соответствующих симплектических многообразиях. В качестве примера достаточно
§ 50. ПЕРИОДИЧЕСКИЕ РЕШЕНИИ
443
указать известные уравнения движения трехмерного твердого тела с закрепленной
точкой в поле силы тяжести.
Так как любое векторное поле можно интерпретировать как систему обыкновен-
ных дифференциальных уравнений на многообразии, то эквивалентным образом
можно говорить о гамильтоновых системах дифференциальных уравнений. Напри-
мер, в канонических координатах (см. выше) такие системы записываются так:
ЭЯ
Qi =-—
Эр,-
ЭЯ
Pi =-—'
Э?,-
Такой вид следует из данных выше определений.
Интерпретируя гамильтонову систему как векторное поле (динамическую систе-
му) на симплектическом многообразии М, мы можем интерпретировать ее решения
как интегральные траектории векторного поля. Одной из центральных задач га-
мильтоновой механики является изучение свойств этих траекторий, в частности,
поиск устойчивых периодических решений гамильтоновой системы. Такие решения
соответствуют устойчивым периодическим движениям механической (физической)
системы, изображаемой данным гамильтоновым полем. Оказывается, в некоторых
случаях информацию о существовании и о количестве таких решений можно извле-
кать из данных о гомологиях поверхностей уровня гамильтониана Я.
Во многих физически важных случаях гамильтонова система и = sgrad# имеет на
Л/4 , так называемый дополнительный независимый интеграл, находящийся в инво-
люции с гамильтонианом Я. Функция f на М называется интегралом поля
sgгadЯ, коммутирующим, или находящимся в инволюции с Я, если (sgrad Я,
sgrad/) s 0 в каждой точке многообразия. Особый интерес представляют случаи,
когда функции f и Я функционально независимы почти всюду на М. Такие системы
называются вполне интегрируемыми по Лиувиллю. Если данная система допускает
второй независимый инволютивный интеграл /, то это дает много информации о
поведении интегральных траекторий системы, однако, к сожалению, не всегда поз-
воляет проинтегрировать систему до конца в явном виде. Поэтому вопрос о сущест-
вовании о и количестве устойчивых периодических движений системы остается не-
решенным даже в этом случае.
Рассмотрим неособую фиксированную трехмерную поверхность (3-миогообразие)
Q постоянной энергии, т.е. задаваемую уравнением Я = const, причем grad Я 0 всю-
ду на поверхности Q. Такие поверхности иногда называются изоэнергетическими.
Пусть гамильтонова система sgrad// интегрируема на этой поверхности Q при помо-
щи второго дополнительного гладкого интеграла /, коммутирующего с Я. Вне по-
верхности Q интеграл f вообще может быть не определен.
Определение 1. Интеграл f назовем боттовским (или морсовским) на изо-
энергетической поверхности Q, если его критические точки (как гладкой функции
на б), образуют на Q невырожденные критические подмногообразия, т.е. гессиан
d2f функции f невырожден на подпространствах, нормальных к этим подмного-
образиям.
Накопленный опыт исследования конкретных механических систем показывает,
что в большинстве известных случаев обнаруженные интегралы являются боттовски-
ми на почти всех изоэнергетических поверхностях. Легко убедиться в том, что век-
торное поле sgrad Я всегда касается поверхностей уровня Q гамильтониана Я Это
означает, что эти 3-поверхности целиком состоят из интегральных траекторий систе-
444
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
мы. Поэтому систему sgrad// всегда можно ограничить на любую поверхность пос-
тоянной энергии.
Определение 2. Пусть у — замкнутая интегральная траектория гамильто-
новой системы sgrad// на изоэнергетической поверхности Q, т.е. — периодическое
решение системы. Мы скажем, что траектория у устойчива, если некоторая ее труб-
чатая трехмерная окрестность в Q целиком расслоена на двумерные торы, инва-
риантные относительно системы sgrad/Z
Это определение означает, что все интегральные траектории системы, близкие к
устойчивой траектории, не уходят далеко и все время движутся около нее, наматы-
ваясь на двумерные концентрические торы (общей осью которых и является перио-
дическое решение).
Гамильтонова система может быть интегрируемой по Лиувиллю, но не иметь при
этом ни одной устойчивой периодической траектории.
Оказывается, существует тесная связь между следующими тремя важными объек-
тами: (1) боттовский интеграл f на поверхности постоянной энергии б, (2) устойчи-
вые периодические решения (траектории) системы sgradT/наб, (3) группы целочис-
ленных гомологий Нх (б, Z) или фундаментальная группа ти (б) •
Определение 3. Будем говорить, что боттовский интеграл f на изоэнергетичес-
кой поверхности Q является ориентируемым, если все его критические подмного-
образия ориентируемы. Если хотя бы одно критическое многообразие неориенти-
руемо, то скажем, что интеграл f неориентируем.
Теорема 1. (А.Т. Фоменко). Связные критические многообразия боттовско-
го интеграла f на изоэнергетической поверхности Q могут быть лишь следующих
четырех типов: (а) минимаксная окружность, (б) минимаксный двумерный тор,
(в) минимаксная бутылка Клейна, (г) седловая критическая окружность. Пусть
U(Q) - малая трубчатая окрестность поверхности Q в М4. Тогда существует двулист-
ное накрытие я: (U(б), Н, f) -> (U(Q), Н, f) (со слоем Т.2), где U(Q) - симплею
тическое многообразие с гамильтоновой системой v = sgrad/7 (где гамильтониан Н
имеет вид Н = я*Н), интегрируемое на поверхности Q = я’ 1 (б) при помощи
боттовского ориентируемого интеграла f - ir*f. При этом все минимаксные
бутылки Клейна интеграла f "разворачиваются" в минимаксные торы интеграла
f на Q.
Следовательно, без существенного ограничения общности можно изучать лишь
ориентируемые интегралы. Из теоремы 1 следует, что если f - неориентируемый
интеграл на Q, то автоматически я^б) =/= О и в группе Я1(б) содержится подгруппа
индекса 2. Например, если Q гомеоморфно сфере S3 (частый случай в механике),
то любой боттовский интеграл f на 53 всегда ориентируем.
Обозначим через m = пг (б) число устойчивых периодических решений системы
и на б Пусть г =r(Q) — число минимаксных бутылок Клейна для интеграла f наб-
Если интеграл ориентируем, то г =0. Пусть р — число критических минимаксных
торов, q — число седловых критических окружностей с ориентируемой сепаратрис-
ной диаграммой.
В предыдущих параграфах мы познакомились со способами оценки снизу числа
точек бифуркации (критических точек) гладкой функции на многообразии. Анало-
гичная задача возникает и в гамильтоновой геометрии: как оценить снизу число, на-
пример, устойчивых периодических решений интегрируемой системы? По своему
характеру эта задача близка к изученным выше, но для ее решения необходимо
привлечь новые методы. Дело в том, что в этом случае роль изолированных крити-
ческих точек исполняют критические подмногообразия (в частности, окружности)
§ 50. ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ
445
' и, как легко убедиться, неравенства ’’типа Морса” не дают здесь необходимой
оценки.
Теорема 2. (А.Т. Фоменко). Пусть f - боттовский интеграл. Тогда число m
устойчивых периодических решений системы v на Q следующим образом оценивает-
ся снизу через топологические инварианты изоэнергетической поверхности.
1. В случае, когда интеграл f ориентируем:
(a) m > 2, если группа гомологий Hi (б; Z) конечна-,
(б) m > 2, если фундаментальная группа тп (б) равна Z.
2. В случае, когда интеграл f неориентируем:
(a) m + г >2, если группа Hi (Q, Z) конечна-,
(б) m > 2, если Hi(Q,Z) =0 (при этом группа ai(Q) может быть бесконечной);
(в) т> 1,если Hi(Q, Z) — конечная циклическая группа-,
(г) m > 1, если (Q) = Z или если тг j (б) - конечная группа.
В обоих случаях 1 и 2 теоремы 2 интеграл f достигает локального минимума или
максимума на каждом из этих устойчивых периодических решений системы (или на
бутылках Клейна). Если группа гомологий HX(Q, Z) бесконечна, т.е. ранг Hi > 1,
то система и может вообще не иметь на изоэнергетической поверхности Q устой-
чивых периодических решений (такие примеры легко строятся).
Подробности этой теоремы см. в работах [34], [35].
У многих интегрируемых механических систем иэоэнергетические поверхности
диффеоморфны либо сфере S3, либо проективному пространству RP3, либо прямо-
му произведению 5* X S2. Например, для уравнений движения тяжелого твердого
тела с закрепленной точкой в интегрируемом случае Ковалевской некоторые изоэнер-
гетические поверхности (после факторизации) гомеоморфны Sl X S2. Если гамильто-
ниан Н имеет изолированный минимум или максимум (т.е. изолированное положение
равновесия системы) на Q, то все достаточно близкие поверхности уровня Q (Н =
= const) являются сферами S3.
Оказывается, число критических многообразий интеграла f на Q (а иногда число
устойчивых периодических решений) можно оценить снизу некоторой универсаль-
ной постоянной, зависящей только от первой группы гомологий Hi(Q, Z). Пусть
3 = ранг Hi(Q, Z) (т.е. одномерное число Бетти), е — число элементарных множи-
телей в конечной части Tors Hi группы Hi(Q, Z). Если группа Tors/Л разложена в
упорядоченную сумму подгрупп, где порядок каждой подгруппы делит порядок
предыдущей подгруппы, то е — это число слагаемых.
Теорема 3 (А.Т. Фоменко, X. Цишанг). Пусть Q - компактная неособая изо-
энергетическая поверхность интегрируемой системы (с боттовским интегралом).
Пусть m - число устойчивых периодических решений системы, s - число неустойчи-
вых периодических решений системы с неориентируемой сепаратрисной диаграммой
(т.е. число критических седловых окружностей с неориентируемой сепаратрисной
диаграммой), г — число критических бутылок Клейна. Тогда выполняются условия:
если q + s > 0, р + пг >0,то т' >е - 20+ l,q' >т' - 2,а также q> т+г -2
(где числа т', q' имеют вид: т' = т + s +2r,q' = q + s +г).Прир = 1 (гдер — число
минимаксных торов) и т = г = 0 имеем : 0 > е -2/3. Если интеграл f ориенти-
руем и все сепаратрисные диаграммы его критических подмногообразий также
ориентируемы, то имеем s = г = 0, т.е. в этом случае мы получаем оценку снизу
на число m устойчивых периодических решений системы: т> е — 2/3+1, а так-
же q > т- 2.
Эта теорема дополняет теорему 2 в некоторых случаях. Области применения тео-
рем 2 и 3 не совпадают. Подробности см. в [36], [47].
446
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
§ 51. ТЕОРИЯ ТИПА МОРСА
ДЛЯ ИНТЕГРИРУЕМЫХ ГАМИЛЬТОНОВЫХ СИСТЕМ.
ТОПОЛОГИЧЕСКИЙ ИНВАРИАНТ ИНТЕГРИРУЕМЫХ СИСТЕМ
В предыдущих параграфах мы познакомились с классической теорией Морса глад-
ких функций на многообразиях. Затем мы вкратце осветили ее развитие в рамках
теории Люстерника—Шнирельмана. Было показано, что эта теория тесно связана с
исследованием групп гомологий многообразий (именно поэтому мы и поместили ее
в главу ’’Гомологии в вариационных задачах”). В настоящем параграфе мы изложим
новую теорию ’’типа Морса”, построенную А.Т. Фоменко для гладких интегралов
гамильтоновых систем, причем интеграл рассматривается как гладкая функция на
изоэнергетической поверхности данной системы. Подробности см. в [34], [35].
В целях упрощения изложения мы остановимся лишь на случае четырехмерных
симплёктических многообразий (здесь поверхности постоянной энергии, т.е. изо-
энергетические поверхности являются трехмерными).
Одно из центральных мест классической теории Морса заключается в описании
перестроек поверхностей уровня функции в окрестности ее критического значения.
В общем случае их классификация невозможна, так как поверхности уровня могут
иметь очень сложную топологическую структуру. Оказывается, если функция явля-
ется интегралом гамильтоновой системы, то можно дать полную классификацию
таких перестроек, что позволяет полностью описать топологию самих поверхностей
постоянной энергии. Это позволяет построить теорию ’’типа Морса” для функций,
являющихся интегралами гамильтоновых систем.
Через (М) мы обозначим класс всех замкнутых компактных ориентируемых
трехмерных многообразий. Пусть (Н) — класс всех компактных замкнутых неосо-
бых изоэнергетических поверхностей гамильтоновых систем, интегрируемых при
помощи боттовских интегралов. Оказывается, класс (Н) ’’меньше” класса (М) и,
более того, в некотором точном смысле класс (Н) является ’’тощим” подмножест-
вом в классе (М); см. [35]. Оказывается, далее, что класс (Н) допускает другое
важное представление, а именно, многообразия из этого класса являются склейками
’’элементарных кирпичей” двух типов. Это утверждение следует из теории, элементы
которой мы сейчас кратко изложим.
Рассмотрим 5 простейших трехмерных многообразий с краем. Пусть О" обозначает
n-мерный диск.
Т и п 1. Прямое произведение S1 X D3 назовем полноторием. Его край - один
двумерный тор Т3 (рис. 224).
Т и п 2. Прямое произведение Т2 X D1 назовем цилиндром. Его край — два тора
(рис. 225).
Тип 3. Прямое произведение N3 X S1 назовем ориентированным седлом (или
’’штанами ”, или просто седлом), где № - двумерный диск с двумя дырками. Много-
образие N3 X S * гомотопически эквивалентно прямому произведению окружности
на восьмерку. Краем многообразия N3 X S1 являются три тора. Его можно реализо-
вать в R3. Для этого достаточно высверлить из стандартного полнотория два тонких
параллельных полнотория, обходящие ровно один раз вдоль оси основного ’’боль-
шого полнотория” (рис. 226).
Т и п 4. Снова рассмотрим в R3 стандартно вложенное полноторие и высверлим
из него теперь одно тонкое полноторие, два раза обходящее вдоль оси первого
полнотория (рис. 227). Назовем получившееся трехмерное многообразие неориен-
тированным или скрученным седлом (или неориентированными, скрученными
штанами).
§ 51. ТЕОРИЯ ТИПА МОРСА ДЛЯ ГАМИЛЬТОНОВЫХ СИСТЕМ
447
Рис. 225
Рис. 226
Прокомментируем многообразия типов 3 и 4. В типе 3 мы имеем (с гомотопи-
ческой точки зрения) прямое произведение окружности на восьмерку. В типе 4
восьмерка движется по окружности так (оставаясь ей ортогональной), что после
полного оборота две ее петли меняются местами. Ясно, что скрученное седло можно
рассматривать как косое произведение N2 X S1 диска с двумя дырками на окруж-
ность. Край скрученного седла состоит иэ двух торов. ~
Т и п 5. Пусть К2 — обычная двумерная бутылка Клейна. Через К2 X Z)1 обозна-
чим косое произведение бутылки Клейна на отрезок. Его можно представить себе
так. Рассмотрим стандартное погружение бутылки Клейна в R3, рассмотрим ее
малую трубчатую окрестность. Легко видеть, что граница трубчатой окрестности
является тором, погруженным в R3. Он стягивается внутри трубчатой окрестности
на бутылку Клейна, двулистно накрывая ее. Следовательно, границей многообразия
К2 X D1 является один тор. Назовем многообразие К2 XD1 неориентированным или
скрученным цилиндром (рис. 228).
448
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
Заметим, что все перечисленные выше пять многообразий являются ориентируе-
мыми. Термин ’’неориентируемый”, использованный выше, имеет смысл, который
ниже будет специально прояснен.
Для краткости обозначим многообразия, перечисленные выше, через I, II, III,
IV, V. Оказывается (см. [35]), с топологической точки зрения многообразия П, IV,
V новыми не являются, а именно, они получаются склейками многообразий I и III.
Можно доказать, что II = I + III, IV = I + Ш, V = 2 • I + III. Здесь знак ’’плюс” условно
Рис. 228
обозначает склейку указанных элементарных кирпичей I и III по некоторым диффео-
морфизмам их граничных торов. Конкретный вид этих склеивающих диффеомор-
физмов нам здесь не понадобится, поэтому мы опускаем доказательство сформули-
рованного выше утверждения.
Рассмотрим новый класс (Q) замкнутых компактных ориентируемых трехмер-
ных многообразий, получающихся склейкой произвольного числа полноторий и
штанов по произвольным диффеоморфизмам их граничных торов. Замечательным
фактом оказывается совпадение классов (Н) и (Q), см. [62].
Предложение 1 (см. [35]). Пусть f - боттовский интеграл на какой-то
трехмерной компактной неособой изоэнергетической поверхности Q (интегрируемой
гамильтоновой системы). Тогда его критические подмногообразия в Q могут быть
только следующих типов: (а) минимаксные окружности (т.е. критические окруж-
ности, на которых интеграл достигает своего локального минимума или макси-
мума), (б) минимаксные двумерные бутылки Клейна, (г) седловые критические
окружности.
Напомним понятие сепаратрисной диаграммы критического многообразия Т для
функции Ботта. Пусть х G Т — произвольная точка и NXT — нормальный диск малого
радиуса в точке х к подмногообразию Т. В силу боттовости интеграла /, его ограни-
чение на нормальный диск NXT является обычной функцией Морса с критической
точкой х некоторого индекса X. Сепаратрисой критической точки х называется
интегральная траектория поля grad f, входящая (асимптотически) в точку х или
исходящая из точки х. Рассмотрим множество сепаратрис, входящих в критическую
точку х и исходящих иэ нее (в нормальном диске). Объединение всех входящих
сепаратрис дает диск размерности X и называется входящей сепаратрисной диаграм-
мой (входящим сепаратрисным диском). Объединение всех исходящих сепаратрис
дает диск дополнительной размерности и называется исходящей сепаратрисной
диаграммой (исходящим сепаратрисным диском). Меняя точку х <= Т и строя для
каждой точки х ее входящие и исходящие сепаратрисные диски, мы и получаем
§ 51. ТЕОРИЯ ТИПА МОРСА ДЛЯ ГАМИЛЬТОНОВЫХ СИСТЕМ
449
входящую и исходящую сепаратрисные диаграммы всего критического многообра-
зия Т (рис. 229).
Назовем интеграл 5-ориентируемым, если все сепаратрисные диаграммы его
критических многообразий — ориентируемы. В противном случае назовем интег-
рал 5-неориентируемым (если у него есть хотя бы одна неориентируемая сепарат-
рисная диаграмма).
Пусть f — боттовский интеграл на компактной неособой изоэнергетической трех-
мерной поверхности Q. Через m мы обозначим число минимаксных критических
окружностей интеграла. Через р мы обозначим число минимаксных критических
двумерных торов для интеграла. Через q мы обозначим число седловых критических
окружностей интеграла с ориентируемой сепаратрисной диаграммой. Пусть далее s -
число седловых критических окружностей интеграла с неориентируемой сепаратрис-
ной диаграммой. Наконец, пусть г — число критических минимаксных бутылок
Клейна.
Теорема! (о топологической классификации трехмерных поверхностей посто-
янной энергии интегрируемых систем; А.Т. Фоменко). Пусть М4 — гладкое симплек-
тическое многообразие (компактное или некомпактное), и = sgrad Н - гамильто-
нова система, интегрируемая по Лиувиллю на какой-то одной неособой компактной
трехмерной изоэнергетической поверхности Q при помощи боттовского интеграла f.
Тогда многообразие Q представляется в виде склейки (по некоторым диффеомор-
физмам граничных торов) следующих элементарных кирпичей:
Q = m(Si XD2) + p(7’2X51) + <?(№ X5*) + s(№ XS*) + r(^2 XZ>’)_
Это разложение многообразия Q можно назвать гамильтоновым. Оно ’’помнит”,
сколько критических многообразий каждого типа имел интеграл f на Q. Другими
словами, эта структурная теорема является ’’разложением типа Морса” для изо-
энергетической поверхности, порожденным данным интегралом. Другой интеграл
даст, вообще говоря, другое разложение. Таким образом, сузив класс рассматривае-
мых многообразий до класса изоэнергетических поверхностей, удается существенно
Рис. 229
усилить классическую теорию Морса, а именно — в явном виде указать ’ элементарные
кирпичи” (их лишь 5 типов), в сумму которых разлагается многообразие, см. [35].
Следствие 1. Пусть Q — компактная неособая изоэнергетическая поверхность
системы, интегрируемой при помощи боттовского интеграла. Тогда Q допускает
следующее топологическое разложение fn I + q III, где числа fn и q следующим обра-
зом связаны с числами из теоремы 1: fn = пг + р + s + 2r ,q = q +р + s + г.
Отсюда вытекает, что (Н) С (Q). Верно и обратное включение: (Н) Э (Q)
(А.Б. Браилов, А.Т. Фоменко), т.е. классы (Н) и (Q) совпадают.
15. А.Т. Фоменко
450
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
Теперь можно дать классификацию всех возможных перестроек торов Лиувилля,
возникающих при изменении значения интеграла f. Напомним, что компактные
неособые совместные поверхности уровня обоих интегралов Н и f на Q являются
двумерными торами, которые и называются торами Лиувилля.
Рассмотрим следующие пять перестроек торов, отвечающие указанным элемен-
тарным многообразиям I, II, III, IV, V. Реализуем тор как одну из компонент края
соответствующего элементарного многообразия. Тогда тор, увлекаемый изменением
значения интеграла, преобразуется в объединение других торов, являющихся осталь-
ными компонентами края того же элементарного многообразия.
1. Тор стягивается на осевую окружность полнотория и ’’исчезает” затем с поверх-
ности уровня интеграла. Обозначим эту перестройку так: Т2 -+ S1 -*0. Она происхо-
дит в окрестности минимаксной окружности интеграла. Условно изобразим эту
перестройку черным кружком (изображающим минимаксную окружность) с входя-
щим в него (или исходящим) ребром. Каждая точка ребра условно изображает тор
Лиувилля (рис. 230).
2. Два тора движутся навстречу друг другу по цилиндру Г2 X D1, сливаются в
один тор и затем ’’исчезают”. Это происходит в окрестности минимаксного тора
для интеграла. Обозначим эту перестройку так: 2 Г2 ->7'2 ->0. Условно изобразим ее
белым кружком (минимаксный тор) с двумя исходящими (входящими) ребрами.
Движение точек вдоль ребер наглядно показывает движение соответствующих торов
Лиувилля (рис. 230).
3. Тор распадается на два тора, проходя через центр седлаА2Х 51 (т.е. штанов).
Эти торы затем ’’остаются” на поверхности уровня интеграла. Обозначение: Т2 -+2Т2.
Это событие происходит в окрестности критической седловой окружности с ориенти-
рованной сепаратрисной диаграммой. Изобразим графически эту перестройку в виде
трилистника (треножника). При этом одно ребро графа распадается на два ребра.
Все три ребра встречаются в одной вершине графа (рис. 230).
4. Тор два раза наматывается на другой тор, следуя при этом топологии скручен-
ного седла N2 XS1 и остается затем (после своего преобразования) на поверхности
уровня интеграла. Обозначение: Т2 ->Т'2.Это событие происходит внутри многооб-
разия N2 X S1. Изобразим эту перестройку в виде ребра, в середине которого постав-
лена звездочка. Точка, изображающая тор, входит в эту звездочку, а затем выходит
из нее, прочерчивая следующее ребро графа (рис. 230).
12 3 4 5
Рис. 230
5. Тор превращается в бутылку Клейна, два раза накрывая ее. Затем тор исчезает
с поверхности уровня интеграла. Обозначение: Т2 ->К2 ->-0. Это событие происходит
в многообразии К2 X D1, т.е. внутри скрученного цилиндра. Графически изобразим
эту перестройку в виде белого кружка с точкой внутри, причем в кружок входит
(или выходит) одно ребро графа (рис. 230).
При желании можно снабдить построенные выше ребра графа стрелками, указы-
вающими движение торов Лиувилля. Перестройки, получающиеся из перечисленных
выше перестроек заменой стрелок на обратные, мы не будем считать новыми.
Следствие 2 (теорема классификации перестроек, бифуркаций двумерных
торов Лиувилля в интегрируемых системах; А.Т. Фоменко). Пусть f — боттовский
§ 51. ТЕОРИЯ ТИПА МОРСА ДЛЯ ГАМИЛЬТОНОВЫХ СИСТЕМ
451
интеграл на неособой поверхности постоянной энергии Q. Тогда любая перестройка
тора Лиувилля, возникающая при его проходе через критическую поверхностность
уровня интеграла, является композицией некоторого числа указанных выше элемен-
тарных перестроек типов 1, 2, 3, 4, 5. Из этих пяти перестроек независимы (с топо-
логической точки зрения) лишь первые три. Перестройки 4 и 5 распадаются в компо-
зиции перестроек видов 1 и 3.
Аналогичная теорема верна и для перестроек многомерных торов Лиувилля.
Подробности см. в [34], [35]. Более подробно перестройки двумерных торов Лиу-
вилля изображены на рис. XXX, XXXI, XXXII. На рис. XXX изображено седло
(штаны), на рис. XXXI - скрученное седло, на рис. XXXII - трубчатая окрестность
бутылки Клейна, стандартно погруженной в R3.
Что здесь имеется в виду под ’’композицией перестроек”? Дело в том, что боттов-
ский интеграл, рассматриваемый как гладкая функция на трехмерной изоэнергети-
ческой поверхности, может иметь на одном критическом уровне несколько крити-
ческих многообразий. Например, на одном критическом уровне может лежать не-
сколько критических седловых окружностей. В обычной теории Морса хорошо
известна теорема о том, что сколь угодно малым шевелением (возмущением) функ-
ции Морса можно добиться, чтобы на каждом критическом уровне была лишь одна
критическая точка. В некотором смысле аналог этого утверждения имеется и в
рассматриваемой здесь теории ’’типа Морса” для боттовских интегралов (здесь это
утверждение существенно менее тривиально). Оказывается (см. [34], [35]), каждый
боттовский интеграл f можно путем сколь угодно малого возмущения превратить
в гладкую боттовскую функцию /' (близкую к /) со следующими свойствами:
(a) f является боттовским интегралом системы и'= sgrad Н' с гамильтониа-
ном Н , (б) на каждом критическом уровне интеграла /' расположено ровно одно
связное критическое многообразие, (в) всюду, кроме, быть может, открытого мно-
жества малой меры (эта мера может считаться меньше заранее заданного числа е),
функции// и f' совпадают, соответственно, с функциями Я и f на £2.
При этом происходит, вообще говоря, преобразование прежних критических
уровней интеграла f, если на них было расположено несколько критических много-
образий интеграла Все перестройки торов Лиувилля у системы (Н*, /') имеют
вид элементарных перестроек, перечисленных выше. В этом смысле мы и говорим
о том, что любая перестройка торов Лиувилля у исходной системы (Н, f) распадается
в композицию элементарных перестроек типов 1,2, 3,4,5. Конечно, это разложение
неоднозначно, так как пару (Я, /) можно разными способами превратить в новую
пару (Я , /'). Поэтому представляет интерес изучить перестройки торов Лиувилля,
возникающие у исходного интеграла f в том случае, когда на одном критическом
уровне расположено несколько критических многообразий. Эта задача будет ниже
полностью решена.
Итак, сформулированная выше теорема 1 (и следствие 1) является аналогом
теоремы Морса о клеточном разложении многообразия по заданной на нем функции
Морса. Однако здесь вместо клеток выступают более сложные объекты: многообра-
зия типов I, II, III, IV, V. С другой стороны, они склеиваются более просто, чем
клетки в классической теории Морса.
Перейдем теперь к построению топологического инварианта интегрируемых
гамильтоновых систем. Этот инвариант позволяет классифицировать интегрируемые
случаи по их топологическому типу.
Назовем гамильтониан Я нерезонансным на данной изоэнергетической поверх-
ности Q, если в Q всюду плотны торы Лиувилля, на которых траектории системы
и = sgrad Я образуют всюду плотную иррациональную обмотку.
15*
452
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
Прокомментируем это определение. Из классической теоремы Лиувилля известно,
что совместные поверхности уровня интегралов Ни f являются двумерными торами.
Кроме того, в окрестности каждого тора всегда можно ввести такие регулярные
координаты, относительно которых интегральные траектории системы и на торе
будут определять прямолинейную обмотку, т.е. соответствующее векторное поле
будет иметь постоянные компоненты. Интегральные траектории (в этих координатах,
называемых иногда ’’действие-угол”) будут изображаться прямыми (если рассмот-
реть универсальное накрытие над тором Лиувилля). На торе интегральные траекто-
рии могут быть одновременно все замкнуты (рациональная обмотка тора), либо
одновременно все незамкнуты (иррациональная обмотка тора).
Опыт изучения конкретных механических и физических систем показывает, что
на четырехмерных симплектических многообразиях в большинстве случаев гамиль-
тониан Н является нерезонансным (на почти всех изознергетических поверхностях).
В многомерном случае (когда изо энергетическая поверхность имеет размерность,
большую чем 3) известны примеры, когда гамильтониан Н является резонансным.
В [37] проанализированы все основные известные на сегодя случаи так называемой
некоммутативной интегрируемости. В этих случаях система интегрируется при помо-
щи интегралов, образующих некоммутативную алгебру Ли относительно скобки
Пуассона. Здесь гамильтониан будет, вообще говоря, резонансным. Однако посколь-
ку в настоящем параграфе мы изучаем, в основном, случай четырехмерных симплек-
тических многообразий, то здесь нерезонансность гамильтониана является ’’типичным
случаем”.
Т ео р е м а 2 (А.Т. Фоменко). Пусть v — гамильтонова система с нерезонансным
гамильтонианом Н, интегрируемая при помощи некоторого боттовского интеграла f
на компактной неособой изоэнергетической поверхности Q. Тогда можно однозначно
построить некоторый граф Г(Q, f) со следующим свойством: по графу Г(Q, f)
однозначно (с точностью до гомеоморфизма) восстанавливается вся топологическая
картина эволюции и перестроек (бифуркаций) торов Лиувилля внутри поверхности
Q при изменении значения интеграла f.
Пусть f: Q -+ R — боттовский интеграл, a G Rh fa - f~* (а) — связная компонента
поверхности уровня интеграла (особая или неособая). Если а = а — регулярное
(некритическое) значение для f, то f0 — объединение конечного числа торов Лиу-
вилля. Критические значения для интеграла f обозначим через с, связную компо-
ненту критической (особой) поверхности уровня интеграла — через fc, а множество
критических точек интеграла f на fc — через Nc.
Оказывается (см. [34], [35]), связные компоненты множеств Nc могут быть
только следующих типов.
Тип I — минимаксная окружность S1 (локальный минимум или максимум для
интеграла/), тогда Nc = fc = S1. Тип II — минимаксный тор Г2, тогда Nc = fc = Т2.
Тип III — седловая критическая окружность S1 с ориентируемой сепаратрисной
диаграммой, тогда Nc = S1 ¥= fc. Тип IV — седловая критическая окружность №
с неориентируемой сепаратрисной диаграммой, тогда Nc - S1 Ф fc. Тип V — мини-
максная бутылка Клейна К2 ; тогда Nc =fc = К2.
Через U(fc) (где с - критическое значение интеграла) обозначим регулярную,
связную замкнутую трубчатую окрестность компоненты fc в многообразии Q3
Можно считать, что U(fc) — связное трехмерное многообразие, край которого
состоит из несвязного объединения торов Лиувилля. В качестве U(fc) можно взять
связную компоненту многообразия /-1[с — е, с + е]. Можно также считать, что
Q - T,cU(fc), т.е. Q получается из всех'многообразий U(fc) склейкой их границ
(торов) по некоторым диффеоморфизмам граничных торов Лиувилля.
§ 51. ТЕОРИЯ ТИПА МОРСА ДЛЯ ГАМИЛЬТОНОВЫХ СИСТЕМ
453
Теорема 3 (А.Т. Фоменко). Пусть Q - компактная неособая изознергети-
ческая поверхность системы v с гамильтонианом Н (не обязательно нерезонансным),
интегрируемой при помощи некоторого боттовского интеграла f Тогда многообра-
зия U(fc), входящие в разложение Q = T,cU(fc), допускают следующее представле-
ние, в зависимости от типа множества Nc.
Тип I: С/(/с) = Л?Х 51, где Р2 = D2 (диск);
Тип II: U(fc) = Р2СХ S', где Р2 = S'X D' (цилиндр);
Тип III: lKfc) = Р2 X S', где Р2 — некоторая двумерная поверхность с краем;
Тип IV: U(fc) = Р% X где Р% - некоторая двумерная поверхность с краем,
а Р% X 51 - пространство расслоения Зейферта с базой и слоем 51 (точное описа-
ние см. ниже);
Тип N: U(fc) = Р% X 51, где Р2 = р (лента Мёбиуса), а рХ. S' обозначает косое
произведение (с краем - тор Т2).
Следствие 3. С каждой изоэнергетической поверхностью Q (в условиях
теоремы 3) можно однозначно (с точностью до гомеоморфизма) связать некоторую
замкнутую двумерную поверхность Р2 (Q, f) = Т,СР2, получающуюся склейкой
поверхностей Р%, индуцируемой склейкой Q~T,cU(fc).
Теорема4 (основная; А.Т. Фоменко). Пусть и - гамильтонова система, инте-
грируемая на Q при помощи некоторого боттовского интеграла f. Тогда существует
однозначное (с точностью до гомеоморфизма) каноническое вложение h(Q, f)
графа T(Q, f) в поверхность Pi(Q, f). Если гамильтониан Н - нерезонансный на Q,
то тройка (Г, Р, Л) не зависит от выбора интеграла f. А именно, если f и f‘ — лю-
бые боттовские интегралы системы и, то соответствующие графы T(Q, f) и
Г (Q, /'), поверхности P(Q, f) и P(Q,f') - гомеоморфны, а следующая диаграмма
коммутативна:
h: Г -+Р
гг «
h'-. Г’^Р'.
Следствие 4. В нерезонансном случае тройка (Г, Р, h) является топологи-
ческим инвариантом самого интегрируемого случая (гамильтониана ) и позволяет
классифицировать интегрируемые гамильтонианы (системы) по их топологическому
типу и сложности.
Тройку Г (Q), P(Q), h(Q) естественно назвать топологическим портретом инте-
грируемого гамильтониана. Вложение графа в поверхность P(Q) определяет ее раз-
биение на области. Следовательно, зто разбиение также является топологическим
инвариантом интегрируемого гамильтониана и описывает его топологическую слож-
ность. Поверхность P(Q) не обязана вкладывать в многообразие Q.
Определим теперь Р2 X 51. Расслоенным полноторием типа (а, Ь) называется
полноторие, полученное склейкой двух оснований полного (заполненного) цилиндра
D2 X D1 при помощи отображения (z, 0) -> (exp(2nib/a), 1), где z G. С, | z | < 1;
a, b G Z, а и b взаимно простые. Слоем является {(z, t), (exp(2iri b/a) z, t),
(ехр(4яй>/д) z,t),..., (ехр(2тп (a — l)b/a) z, t), 0 < t < 1} . Тогда на полнотории
Й X 51 определяется расслоение со слоем 51 над D2, локально тривиальное для всех
ненулевых точек диска D2. Слой — окружность { (0, t), 0 < t <1 } является особым,
если а > 1. Теперь рассмотрим многообразие Р% с отмеченными на нем точками
. . . , х,п и окружим их малыми дисками ,Ь^,. Затем возьмем прямое
произведение Р% X 51 и выбросим из него набор из тполноториев Z^X 51, 1 < i < m.
Вклеим вместо них расслоенные полнотория типа (2, 1). Полученное многообразие
454 ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
обозначим через ^5*. Оно является расслоением Зейферта, а Р% — база рас-
слоения.
Таким образом, теперь можно наглядно продемонстрировать — чем, например,
знаменитый случай Ковалевской топологически отличается от случая Горячева — Чап-
лыгина (в теории движения твердого тела).
Построим теперь явным образом граф Пусть f: — гладкое отобра-
жение, определяемое данным боттовским интегралом f. Через fa обозначим поверх-
ность уровня интеграла f на Q, т.е. fa . Если а - некритическое (регулярное)
значение для /, то fa является объединениём конечного числа торов Лиувилля. Изо-
бразим их условно точками в R3, лежащими на высоте а (в плоскости). Меняя зна-
чение а (так, чтобы оно оставалось регулярным), мы заставляем эти точки переме-
щаться по вертикали в R3. В результате они заметают некоторые отрезки — часть
ребер будущего графа Г. Будем считать, что ось R направлена вертикально вверх.
Если значение а становится критическим (такие значения мы обозначим через с), то
критический (особый) уровень интеграла f, вообще говоря, усложняется и превра-
щается в некоторый клеточный комплекс. Пусть /с — какая-либо связная компонен-
та этого критического уровня интеграла. Пусть Nc — множество критических точек
интеграла f на fc. Множество Nc может быть несвязно.
Выделим два случая: (a) Nc = fc, т.е. вся компонента связности критического
уровня состоит из критических точек интеграла; (б) NcCfc, т.е. критические точки
не заполняют весь критический уровень. В работах [34], [35] (см. также настоящий
параграф) дано полное описание всех возможных случаев и указано — какие именно
критические множества Nc возникают и какова топология критических уровней fc.
Рассмотрим случай (а). Возможны лишь следующие три типа критических мно-
жеств.
Тип ’’минимаксная окружность”. Здесь Nc = fc, и это множество гомеоморфно
окружности, на которой интеграл достигает локального минимума или максимума.
Трубчатая окрестность S1 X D2 этой окружности в б3 гомеоморфна полноторию, т.е.
многообразию типа I в классификации теоремы 1. Когда а -*с, то неособые торы
стягиваются на ось полнотория и при а = с вырождаются в критическую окружность.
Выше мы условно изобразили эту минимаксную окружность черной жирной точкой
(вершиной графа), в которую входит (или из которой выходит) одно ребро буду-
щего графа Г.
Тип ”тор”. Здесь Nc = fc, и это множество гомеоморфно тору, на котором интег-
рал достигает локального минимума или максимума. Трубчатая окрестность
Т2 X D1 этого тора является цилиндром, т.е. многообразием типа II в классифика-
ции теоремы 1. Мы изобразили выше минимаксный тор белым кружком (вершина
графа), в которую входят (или выходят) два ребра графа.
Тип ’’бутылка Клейна”. Здесь Nc = fc,n это множество гомеоморфно бутылке
Клейна, на которой интеграл достигает локального минимума или максимума.
Трубчатая окрестность К2 X D1 этой бутылки Клейна является скрученным ци-
линдром, т.е. многообразием типа V в классификации теоремы 1. Выше мы условно
изобразили эту минимаксную бутылку Клейна белым кружком с черной точкой
внутри (вершина графа), в которую входит (выходит) одно ребро графа.
Теперь рассмотрим случай (б). Здесь Nc<2 fc и Nc^ fc, так как Nc одномерно,
a fс — двумерно. Оказывается (см. [35] ), что Nc состоит из несвязного объедине-
ния непересекающихся критических седловых окружностей, лежащих на fc. Соответ-
ствующую компоненту связности [с также назовем седловой. Условно можно изо-
бразить каждую седловую компоненту fc в виде плоского квадрата в R3, располо-
§ 51. ТЕОРИЯ ТИПА МОРСА ДЛЯ ГАМИЛЬТОНОВЫХ СИСТЕМ
455
женного горизонтально на уровне с (рис. 231). Снизу в него втыкаются некоторые
ребра графа (подходящие к нему, когда а ->• с и а < с). Вверх от квадрата уходят
другие ребра графа, когда а > с. Сейчас мы опишем способ соединения этих входя-
щих и исходящих ребер, чем и завершим процесс построения графа Г. Пока что мы
определили некоторый граф А, состоящий из одномерных регулярных ребер,
некоторые из которых заканчиваются вершинами. Вершины могут быть трех типов:
черная вершина, белая вершина и белая вершина с черной точкой внутри. Другими
словами, все вершины графа А являются минимаксными для интеграла.
Фиксируем теперь связную компоненту fc ц построим соответствующий ей
граф Тс, показывающий, как именно соединяются входящие и исходящие ребра
графа, взаимодействующие с данной компонентой fc. Рассмотрим на многообра-
зии Q векторное поле w = grad/. Его интегральные траектории, исходящие из кри-
тических точек (лежащих на критических многообразиях) или входящие в них,
называются сепаратрисами. Их объединение - это сепаратрисные диаграммы крити-
ческих многообразий. Из каждой седловой критической окружности S1 на критиче-
ском уровне fc выпустим ее сепаратрисную диаграмму. Она является двумерным
клеточным комплексом. Ориентируемая сепаратрисная диаграмма получается
склейкой двух плоских колец (цилиндров) по их осевой окружности. Неориенти-
руемая сепаратрисная диаграмма получается склейкой двух листов Мёбиуса по их
осевой окружности. Рассмотрим два некритических значения с — е и с + е, близких
к с. Они определяют неособые торы Лиувилля, расположенные ниже [с и выше /с
(рис. 232). Сепаратрисные диаграммы критических окружностей, лежащих на /с,
встречаются с этими торами и пересекают их по некоторым гладким окружностям.
Эти линии пересечения разбивают каждый тор в объединение двумерных областей,
которые мы назовем регулярными. Каждая точка регулярной области лежит на ин-
тегральной траектории поля н>, не являющейся сепаратрисой. Выберем в каждой
регулярной области на уровне [с—^ по одной точке и выпустим из нее вверх интег-
ральные траектории поля w. Поднимаясь вверх, эти траектории пройдут мимо крити-
ческих седловых окружностей и обязательно встретят некоторые торы, расположен-
ные на ’’верхнем” уровне fc+e. Траектории попадут в некоторые точки регулярных
областей ’’верхних” торов. Мы получили гомеоморфизм между регулярными облас-
тями на уровне fc^.e и на уровне fc + e- Он устанавливается вдоль интегральных
траекторий поля w.
Теперь мы можем построить подграф Тс. Рассмотрим сначала случай, когда все
сепаратрисные диаграммы критических окружностей на fc — ориентируемы
(т.е. нет листов Мёбиуса). Так как каждый неособый тор Лиувилля изображается
точкой на графе А, мы можем соединить соответствующие точки (на уровне fc_e
и на уровне /с + е) отрезками (дугами), которые можно считать изображением
456
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
Рис. 232
пучка интегральных траекторий поля w. В результате мы получили некоторый
граф, который мы и обозначим через Тс. Его ребра показывают нам движение от-
дельных регулярных областей торов Лиувилля. Эти торы разваливаются на отдель-
ные куски, которые затем как-то перегруппировываются и склеиваются в новые
торы Лиувилля, расположенные уже по другую сторону от критического уровня
интеграла. Каждый верхний тор составлен из кусков нижних торов (и наоборот).
Геометрическая картина этих перестроек может быть очень сложной. Она и характе-
ризует сложность изучаемой гамильтоновой системы.
Теперь рассмотрим неориентируемый случай, т.е. когда на компоненте [с есть хо-
тя бы одна критическая окружность с неориентируемой сепаратрисной диаграммой
(гомеоморфной, следовательно, склейке двух листов Мёбиуса). На каждом торе
Лиувилля, взаимодействующей с fc, отметим окружности, по которым тор пересе-
кается с этими листами Мёбиуса. Далее, пометим звездочками регулярные области,
инцидентные с листами Мёбиуса (т.е. области, на границе которых есть отрезки
окружностей пересечения листов Мёбиуса с торами Лиувилля). Следовательно, те-
перь мы можем пометить звездочками соответствующие ребра конструируемого
нами подграфа. В качестве примера см. рис. 233. Получающийся граф обозначим
через Тс. Граф Тс удобно назвать седловым. Концы его ребер — это нёособые торы
Лиувилля. Граф Тс наглядно демонстрирует нам процесс распада и перестройки ниж-
них торов Лиувилля в верхние торы в момент их взаимодействия со связной ком-
понентой fc.
Окончательно мы определим граф Г (Q, f ) как объединение графа А со всеми
графами вида Тс, т.е. положим Г = А + S с Тс, где { с } — критические значения.
Прокомментируем ту часть теоремы 2, где говорится о гомеоморфизме графов
Г (С, /) и Г (С,/*) для любых двух боттовскихинтегралов данной гамильтоновой
системы. Оказывается, что при гомеоморфизме h (Q, f, f* ) : Г (Q, f ) ->• Г (Q, f’)
(см. теорему 2) седловые подграфы Tc для интеграла f гомеоморфно переходят
в седловые подграфы Г/ для интеграла f*. При этом звездочки графа Г (на его
ребрах) переходят в звездочки графа Г*. Вершины типов ’’минимаксная окруж-
ность” и ’’бутылка Клейна” графа Г переходят в вершины того же типа (соответ-
ственно) на графе Г*. Вершины типа ”тор” графа Г могут изменить свой тип и
отобразиться в обычную внутреннюю точку какого-то ребра графа Г*. И, наконец,
§ 51. ТЕОРИЯ ТИПА МОРСА ДЛЯ ГАМИЛЬТОНОВЫХ СИСТЕМ
457
обычные внутренние точки ребер графа Г могут отобразиться при гомеоморфизме Л
в вершины типа ”тор” на графе Г*. С аналитической точки зрения это событие
(изменение типа вершины) локально соответствует операции возведения в квадрат
интеграла /, т.е. f -> f2, либо, напротив, извлечению из него квадратного корня,
т.е. f -► хЛЛ
Если нерезонансный гамильтониан Н фиксирован, то можно рассмотреть все его
неособые компактные изоэнергетические поверхности Q. Следовательно, полным
топологическим инвариантом (назовем его полным топологическим портретом)
интегрируемого гамильтониана является весь набор троек {(Г (Q), P(Q), }
(т.е. по всем {(?}). В конкретных случаях практически всегда набор различных
(т.е. недиффеоморфных) изоэнергетических поверхностей конечен.
Из теоремы 4 сразу получаем следствие: если две интегрируемые системы обла-
дают негомеоморфными топологическими портретами, то не существует замены
переменных (на данном многообразии Q), которая устанавливала бы эквивалент-
ность этих систем (например, траекторный изоморфизм). Следовательно,системы
с негомеоморфными топологическими портретами не эквивалентны. Однако сущест-
вуют заведомо не эквивалентные интегрируемые системы с одинаковыми топологи-
ческими портретами.
Переходим теперь к построению двумерной поверхности Р2 (Q, f) для интегри-
руемого гамильтониана Н на Q. Мы получим поверхность Р2 как объединение
(склейку) вида Р(А) + Т,СР(ТС), где Р (Л) нР(Тс) - двумерные поверхности
с краем. Край каждой из них состоит, вообще говоря, из нескольких непересекаю-
щихся окружностей. Построим сначала поверхность Р (А). Определим ее так:
Р (Л) = (51 X 1п1Л)’ + SZ)2 + SjLt2 + S (S1 X Л1). Здесь через Int/l обозначено
объединение всех открытых ребер графа А, т.е. Int А состоит только из ребер, заме-
таемых регулярными торами Лиувилля при изменении регулярного значения а
(см. выше). Следовательно, № X Int Л состоит из несвязного объединения двумер-
ных цилиндров, соответствующих ребрам графа Int Л. Многообразие S1 X Int Л
открыто. Присоединим к нему граничные окружности. В результате получится ком-
пактное многообразие с краем, которое мы и обозначаем через (S1 X Int Л) ".
Пусть некоторое ребро графа Л заканчивается черной вершиной (минимаксная ок-
ружность). Тогда соответствующий ему цилиндр из поверхности (S1 X Int Л) за-
канчивается окружностью. Заклеим ее двумерным диском D2. Тем самым мы сопо-
ставим каждой черной вершине графа Л двумерный диск. Приклеивая их к поверх-
ности (S1 X Int Л)", мы частично заклеиваем некоторые компоненты ее края.
Приклейку указанных дисков мы и обозначили выше через Z D2.
Пусть некоторое ребро графа Int Л заканчивается белой вершиной. Тогда в нее
входит еще одно ребро. Соответственно, на поверхности (S1 X Int Л)" выделяются
два цилиндра с краем — две окружности. Заклеим их двумерным цилиндром
№ X D1. В результате уменьшим число компонент края поверхности (S1 X Int Л)’
на два. Объединение этих цилиндров мы и обозначили выше через S (S1 X D1).
Наконец, пусть некоторое ребро графа Int Л заканчивается белой вершиной с точ-
кой внутри. На соответствующей поверхности (S1 X Int Л) "этому ребру отвечает дву-
мерный цилиндр с краем окружность. Заклеим ее листом Мёбиуса д2. Объединение
этих листов Мёбиуса мы обозначили выше через Ед2. Таким образом, поверхность
Р(Л) полностью и однозначно определяется графом Л. При этом объединение SD2
соответствует вершинам типа "минимаксная окружность”, объединение S (№ X Л1)
458
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
соответствует вершинам типа ”тор”,объединение S д2 соответствует вершинам типа
’’бутылка Клейна”.
Теперь нужно сконструировать поверхности Р(ТС). Рассмотрим сначала для
простоты ориентируемый случай, т.е. когда на связной компоненте fc все крити-
ческие окружности имеют ориентированные сепаратрисные диаграммы. Сначала
опишем топологию клеточного комплекса fc.
Предложение 2 (см. [34], [35]). Если все критические седловые окруж-
ности, лежащие на fc, имеют ориентируемые сепаратрисные диаграммы, то fc го-
меоморфно прямому произведению Кс X S1, где Кс - некоторый граф, получаю-
щийся из нескольких окружностей путем отождествления на них некоторых пар
точек. В частности, локально, из каждой вершины графа Кс выходит ровно че-
тыре ребра.
В действительности верно более сильное утверждение.
Предложение 3 (см. [34], [35]). Двумерное клеточное пространство fc
(здесь никакого ограничения на ориентируемость сепаратрисных диаграмм не на-
кладывается) всегда получается склейкой нескольких экземпляров двумерных
торов. Склейки производятся по окружностям, реализующим нетривиальные (не-
нулевые) циклы на торах. Если на одном торе лежит несколько таких окружностей,
то они не пересекаются (а потому гомологичны и изотопны). Окружности, по кото-
рым касаются торы, являются критическими седловыми окружностями для ин-
теграла f.
Критические окружности, лежащие на fc, разрезают этот комплекс на несколько
плоских колец. Следовательно, на fc однозначно определена окружность-цикл у,
негомологичная нулю. Ей параллельны все остальные критические окружности,
лежащие иа fc. Выберем на каждом торе, входящем в состав fc, некоторую обра-
зующую-цикл а, дополнительную к циклу у, т.е. пересекающуюся с у ровно в одной
Рис. 234
точке. Назовем этот дополнительный цикл овалом. Он, конечно, определен неод-
нозначно. Легко видеть, что можно считать эти овалы соприкасающимися в точках
касания торов, т.е. в точках, лежащих на критических окружностях интеграла
(рис. 234). Если мы рассматриваем, например, ориентируемый случай (все сепа-
ратрисные диаграммы ориентируемы), то объединение всех овалов а и дает нам
граф Кс. Из рис. 234 видно, что fc=Kc'X.y (см. [34], [35]). При этом отметим,
что граф Кс не обязан быть плоским. Можно всегда считать, впрочем, что он вложен
в R3, хотя это для нас здесь неважно.
§ 51. ТЕОРИЯ ТИПА МОРСА ДЛЯ ГАМИЛЬТОНОВЫХ СИСТЕМ
459
Снова рассмотрим, для простоты, ориентируемый случай. Пусть два овала кос-
нулись друг друга в некоторой точке. Она является критической для интеграла,
т.е. лежит на критической окружности. Из условия боттовости легко следует, что
в малой окрестности этой точки можно рассмотреть отрезки интегральных траек-
торий векторного поля w. Рассматривая часть линии уровня интеграла f (рис. 235),
можно считать, что около каждой критической точки однозначно определен ’’коор-
динатный крест”, на каждом конце которого поставлена стрелка, показывающая
направление поля w. Построим такие координатные кресты в каждой точке каса-
ния овалов, т.е. в каждой вершине графа Кс. Следовательно, мы снабдили каждую
вершину графа Кс двумерным диском (в виде креста), причем на четырех кон-
цах креста указаны ориентации вдоль градиента функции /. Соединим теперь кон-
цы крестов лентами (узкими полосками), идущими вдоль дуг овалов. Каждую
из этих лент можно получить, рассмотрев семейство отрезков малой длины, рас-
положенных вдоль интегральных траекторий поля w (рис. 236). В результате мы
получаем двумерную поверхность с краем. Она показана на рис. 236. Ее край
состоит из двух семейств окружностей. Общее их число равно числу торов, кос-
нувшихся друг друга и образовавших в результате комплекс fc. Пометим знаком
’’минус” те окружности, которые отвечают торам, подошедшим снизу к уровню
fc. Знаком ’’плюс” пометим те торы, которые подошли к fc сверху. На рис. 236 в
качестве примера показано шесть ’’отрицательных торов” и три ’’положительных
тора”. Число отрицательных торов в точности равно числу ребер графа Г, снизу
подходящих к уровню fc, а число положительных торов — числу ребер графа Г,
уходящих вверх от уровня fc.
Получившуюся поверхность с краем мы и обозначим через Р (Тс). Каждая ок-
ружность, являющаяся компонентой края поверхности Р(ТС), принадлежит либо
нижнему (отрицательному) семейству, либо верхнему (положительному) се-
мейству.
Ясно, что граф К с однозначно (с точностью до гомеоморфизма поверхности)
вложен в поверхность Р(ГС).
Построим поверхность Р(ТС) в неориентируемом случае. Схема рассужде-
ний в основном сохраняется. Поэтому обратим внимание читателя лишь на отли-
чия, обусловленные неориентируемостью некоторых сепаратрисных диаграмм кри-
тических окружностей. Пусть, для простоты, на fc лежит ровно одна критическая
окружность с неориентируемой диаграммой. Тогда критическая поверхность уров-
Рис. 235
Рис. 236
440
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
ня fc имеет вид, показанный на рис. 237. Следовательно, каждый овал а, лежащий
на торе, на котором есть окружность-цикл у’, являющийся основанием листа Мё-
биуса, должен быть удвоен. Следовательно, любая другая критическая окружность
с ориентируемой сепаратрисной диаграммой, лежащая на fc, встречает два цикла а
в двух точках. Это заставляет нас удваивать циклы а и на тех торах, которые ка-
саются друг друга вдоль окружностей с ориентируемыми диаграммами, но входят
в состав fc, содержащего окружность с неориентируемой диаграммой. Можно по-
казать (подробный анализ мы здесь опускаем ввиду недостатка места), что коли-
чество окружностей с неориентируемыми диаграммами не влияет на процесс удвое-
ния. Другими словами, удвоение не зависит от числа критических окружностей
с неориентируемыми диаграммами (лишь бы это число было отлично от нуля).
В результате мы получаем граф Кс (каждая вершина которого по-прежнему
имеет кратность 4, т.е. в нее входит ровно 4 отрезка ребер), вложенный в fc. Окру-
жая каждую его вершину (т.е. критическую точку) координатным крестом и до-
полняя их связующими лентами, мы получаем поверхность Р(ТС). Ее граничные
окружности по-прежнему разбиваются на два семейства: нижние и верхние. Но в
отличие от ориентируемого случая теперь каждая граничная окружность встреча-
ется в двух экземплярах. Это означает, что каждое ребро графа Г, подходящее
снизу к fc, определяет на Р (Тс) ровно две нижние граничные окружности. То же
самое верно и для ребер графа Г, подходящих сверху к fc. Из построения повер-
хности Р(ТС) видно, что на ней корректно определено гладкое действие груп-
пы Z2 (инволюция а). При этом а(х) = х в том и только в том случае, когда точ-
ка х принадлежит критической окружности с неориентируемой сепаратрисной
диаграммой. Обозначим такие точки через Xi......xm, а соответствующие им
окружности через ..., Sm. Рассмотрим факторпространство Р(ТС) = Р (Тс)/Z2.
Ясно, что Рс = Р(ТС) является двумерным многообразием с краем. Теперь каж-
дая его граничная окружность отвечает ровно одному тору Лиувилля (верхнему
или нижнему). Легко видеть, что точки Xj,..., xm являются внутренними точка-
ми на поверхности Р(ГС). Отметим их звездочками. В частном случае, когда [с
имеет вид, показанный на рис. 237 (т.е. m = 1), поверхность Р(ТС) является дву-
мерным цилиндром с одной звездочкой (рис. 238).
Теперь мы можем построить всю поверхность P(Q, f). Возьмем поверхность
Р (А), уже построенную ранее, и возьмем все поверхности вида Р (Тс). Из нашей
конструкции ясно, что существует взаимно однозначное соответствие между гра-
ничными окружностями поверхности Р(А) и граничными окружностями объедине-
ния (несвязного) поверхностей Р(ТС). Отождествим эти соответствующие окруж-
Рис. 237
Рис. 238
§ 51. ТЕОРИЯ ТИПА МОРСА ДЛЯ ГАМИЛЬТОНОВЫХ СИСТЕМ
461
ности при помощи некоторых гомеоморфиз-
мов. Их выбор произволен, так как замена
склеивающих гомеоморфизмов другими инду-
цирует лишь гомеоморфизм поверхности на се-
бя. В результате получим некоторую замкну-
тую двумерную поверхность (ориентируемую
или неориентируемую), которую и обозначим
через Р (б). Отметим, что на ней однозначно
(с точностью до гомеоморфизма поверхности)
расположен некоторый граф, который мы обо-
значим через K(Q). Определим его так. Рас-
смотрим окружности, рассекающие пополам
цилиндры, входящие в состав поверхности
S1 X Int А. Можно считать, что каждая из этих
окружностей имеет вид S1 Хр, где р — середи-
на соответствующего ребра графа А. Теперь
определим граф К как несвязное объединение
всех графов Кс и окружностей вида S1 X р. Этот граф имеет лишь вершины крат-
ности 4 (локально), отвечающие касаниям окружностей-овалов.
Построение поверхности P(Q, f) полностью завершено (рис. 239). Кроме того,
мы построили некоторый граф K(Q, f) однозначно вложенный в поверхность
P(Q, /). Теорема 4 (см. выше) утверждает, что поверхность Р и граф К не зави-
сят от конкретного выбора второго интеграла f. Оказывается, имеется простая
и замечательная связь между графом Г (Q) и графом К (Q).
Теорема 5 (А.Т. Фоменко). Граф Г совпадает с графом К*, где К* -
граф, сопряженный графу К в поверхности Р.
Напомним определение сопряженного графа. Граф К разбивает поверхность Р
на области. В каждой из них поставим точку, которую возьмем за вершину сопря-
женного графа. Затем соединим эти вершины ребрами, проходящими через се-
редины ребер графа К. Полученный граф и называется графом, сопряженным к К.
Так как граф К* очевидно однозначно (с точностью до гомеоморфизма по-
верхности) вкладывается в поверхность Р, то мы и получаем искомое вложе-
ние* (Q) :Г(б) ^Р(б).
Тем самым построение тройки Г (Q), Р (Q), h (Q) полностью завершено. От-
метим, что граф К разбивает поверхность Р на области, каждая из которых гомео-
морфна либо диску, либо плоскому кольцу, либо ленте Мёбиуса; при этом Г = К*.
Поскольку с каждой замкнутой двумерной поверхностью можно связать
ее род (целое число, которое можно определить как в ориентируемом, так и в
неориентируемом случаях), то, как следует из теоремы 4, с каждой интегрируемой
гамильтоновой системой связан некоторый целочисленный инвариант — род по-
верхности Р. Чем больше этот род, тем ’’сложнее” интегрируемая система. Из тео-
ремы 4 следует также, что граф Г (Q), поверхность Р (Q) и вложение Л (Q) можно
определить, не привлекая интеграл f (хотя нужно знать о факте его существования).
Мы не будем здесь этого делать, поскольку читатель сможет при желании восста-
новить необходимые рассуждения, руководствуясь, в частности [34] и [35].
Прокомментируем утверждение о возможном изменении типа вершин ”тор”
при гомеоморфизме графов Г и Г . Рассматривая окрестность какого-либо неособо-
го тора Лиувилля и локально возводя интеграл f в квадрат, мы, очевидно, сохра-
няем его боттовость в окрестности данного тора. Но зато появляется новый кри-
тический тор. Ясно, что определена и обратная операция — извлечения корня. Все
другие возможные функциональные операции, сохраняющие (локально) ботто-
462
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
вость интеграла, сводятся к этим, поскольку морсовская функция на одномер-
ном многообразии может иметь лишь квадратичные особенности. С геометриче-
ской точки зрения операция возведения в квадрат сводится к перегибанию ребра
графа и локального подъема точки перегиба вверх (или опускания вниз). Это
приводит к появлению новой белой вершины с двумя исходящими (входящими)
ребрами. Извлечение корня геометрически изображается как распрямление реб-
ра (если это в принципе можно сделать) и исчезновение белой вершины.
Приведем теперь два примера. Классические уравнения движения твердого
тяжелого тела имеют вид:
Ай + ы X Аш =vX grad П, v=vXw,
где а X b — векторное произведение, П — потенциал. Интегралы имеют здесь сле-
дующий вид:
F= v2 + l>2 + V3 =1,
G =Ai<jJiVi + Л2а»2р2 + А3ы3и3 = g,
H = — (Ai а»? + Л2о>2 + A3a>2 ) + П (p) = h.
(а) Случай Ковалевской характеризуется тем, что Лj = Аг = 2Л3, П = — . Тогда
возникает еще один дополнительный независимый интеграл f = (со2 — о>2 + »i)2 +
+ (2a»ia»2 + р2)2 Рассмотрим четырехмерное симплектическое многообразие
М* = { F(a>, р) = 1; (7 (со, р) = g} Оно диффеоморфно касательному расслоению
к сфере, т.е. TS2. На этом многообразии задан гамильтониан Н (см. выше) и до-
полнительный интеграл f. Следовательно, можно применить изложенную выше
теорию и вычислить топологический портрет интегрируемого случая Ковалевской.
Это исследование было проведено А.А. Ошемковым и А.Т. Фоменко. В данном
случае Ковалевской трехмерные связные компоненты неособых изознергетиче-
ских поверхностей задаются уравнениями Q3 = {F=\,G=g,H = h}. Оказалось,
что полный список всех графов Г (Q), встречающихся в случае Ковалевской, со-
стоит из шести графов. Этот набор графов см. на рис. 240.
1 2 3 4 5 6 1
Рис. 240
(б) Случай Горячева—Чаплыгина. Он характеризуется тем, что At = А2 = 4Л3,
П = —?1. Известно, что при G = 0 существует дополнительный интеграл / =
= 2со3 (со2 + со2) + 2a»1i>3. Вычисления показывают, что здесь полный список гра-
фов Г (Q) содержит два графа (рис. 241).
(в) Можно обобщить решение Горячева—Чаплыгина на случай гиростата. В урав-
нениях движения и в интегралах G нН нужно заменить Аа> на Аа> + X. Тогда допол-
нительный интеграл будет иметь вид/ = 2(со3 — X) (со2 + со2) + 2a>ii>3. При X = 0
мы получаем обычный случай Горячева—Чаплыгина. При X =# 0 полный список гра-
фов Г (2), встречающихся в этом интегрируемом случае, представлен на рис. 242.
Здесь мы снова имеем шесть типов графов.
§ 51. ТЕОРИЯ ТИПА МОРСА ДЛЯ ГАМИЛЬТОНОВЫХ СИСТЕМ
463
Вывод: полные топологические портреты трех перечисленных выше интегриру-
емых случаев не гомеоморфны. В частности, в случае Ковалевской графы, зану-
мерованные цифрами 5 и 6, не гомеоморфны никакому графу из случая Горячева-
Чаплыгина (гиростат). И наоборот, графы 5 и 6 случая гиростата не гомеоморфны
никакому графу случая Ковалевской. Таким образом, топологические портреты
действительно наглядно различают между собой три классических случая интег-
рируемости уравнений движения тяжелого твердого тела.
Осталось построить вложения графов Г (Q) в соответствующие замкнутые по-
верхности Р(6). Эта задача также решена А.А. Ошемковым и А.Т. Фоменко. В
! YYY Y
7 2 5 4 5 6
Рис, 242
качестве иллюстрации приведем результат для случая Ковалевской. Он показан
на рис. 243. Видно, что здесь во всех шести случаях поверхность Р (2) гомеоморф-
на двумерной сфере. На сфере сплошными дугами показаны графы Г (2), а пунк-
тирными дугами - графы К (2). Отчетливо видно, что графы Г сопряжены гра-
фам К. На рис. 244 графы Г и К изображены на двумерной плоскости, получаю-
щейся выкалыванием точки из сферы S2. Возникают системы овалов, дальнейшее
изучение которых можно и нужно проводить методами теории классификации ал-
гебраических кривых. Хорошо известно, что в алгебраическом случае реализуется
далеко не любая комбинация овалов.
Отметим, что построенные выше поверхности P(Q) можно рассматривать (в
целом) как базы расслоений Зейферта (детали мы здесь опускаем). Отметим
также, что на рис. 243 графы Г изображены сплошными черными дугами, а гра-
фы К изображены пунктирными дугами. Наглядно иллюстрируется сформулиро-
ванная выше теорема о том, что граф Г сопряжен графу К в поверхности Р2.
Теория, построенная в [34], [35], была затем развита в серии работ [36], [38],
[39], [40]. Вкратце изложим те из этих результатов, которые наиболее тесно свя-
заны с топологией многообразий и теорией гомотопий. Оказалось, что введенный
А.Т. Фоменко класс многообразий (Н) = (Q) допускает еще два важных пред-
ставления. Ранее, исходя из внутренних задач трехмерной топологии, Вальдхай-
зен в [41] ввел класс (W) трехмерных многоообразий, таких, что в многообразии
И/е (W) существует набор непересекающихся двумерных торов, выбросив кото-
рые, мы получим многообразие, каждая связная компонента которого расслаи-
вается со слоем окружность над некоторым двумерным многообразием (возможно,
с краем). Как доказали А.Т. Фоменко и X. Цишанг, классы (W) и (Q) совпадают,
см. [47]. Недавно С.В. Матвеев и А.Б. Бурмистрова рассмотрели класс (S) трех-
мерных многообразий, на которых существует гладкая функция g, все критиче-
ские точки которой организованы в невырожденные критические окружности (бот-
товская функция), а все неособые поверхности уровня функции g являются объеди-
нениями двумерных торов. При этом функция g не обязана быть интегралом ка-
кой-либо гамильтоновой системы. Как доказал С.В. Матвеев (см. [39]), классы
(S) и (Q) совпадают. Совпадение классов (Н) и (Q) было ранее доказано А.В. Бра-
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
Рис. 244
§ 51. ТЕОРИЯ ТИПА МОРСА ДЛЯ ГАМИЛЬТОНОВЫХ СИСТЕМ
465
иловым и Т.А. Фоменко. Собирая вместе все эти результаты, получаем следующую
важную (и нетривиальную) теорему.
Теорема 3. Все четыре класса трехмерных многообразий, описанных выше,
совпадают, т.е. (Н) = (Q) = (W) = (S).
Далеко не всякое трехмерное компактное замкнутое ориентируемое многообра-
зие может выступать в роли поверхности постоянной энергии некоторой гамильто-
новой системы, интегрируемой при помощи боттовского интеграла (см. [35]).
Класс (Н) = (Q) = (W) = (S) является в некотором смысле ’’тощим” подмножест-
вом в классе (М) всех трехмерных многообразий.
Итак, препятствием к интегрируемости гамильтоновой системы (в классе бот-
товских интегралов) может служить топология рассматриваемой изоэнергетической
поверхности. Подробности см. в [35].
В то же время, как доказал Г. Мамедов, из штанов и полноторий можно склеить
трехмерное многообразие с любыми возможными (для трехмерных замкнутых
ориентированных многообразий) группами целочисленных гомологий. Другими
словами, опираясь на группы гомологий, можно (как показано в [35]) эффектив-
но вычислять препятствия к интегрируемости, но нельзя (как показал Г. Мамедов)
эффективно выделить класс изоэнергетических поверхностей среди всех трехмер-
ных многообразий.
Утверждение о том, что класс (Н) является ’’тощим” подмножеством в (М),
следует из теоремы Бальцхаузена [41] и из теоремы А.Т. Фоменко [35].
Возникает важный вопрос: насколько существенно в описанной выше теории,
что интеграл / является боттовским? Хотя этот случай является типичным, однако
встречаются ситуации, когда интеграл f боттовским не является. Изучение реаль-
ных механических систем показало, что встречающиеся не боттовские (но глад-
кие) интегралы относятся к классу функций, которые естественно назвать ’’руч-
ными”. Термин заимствован из топологии, где им обозначают объекты, локально
устроенные ’’достаточно хорошо”, в отличие от патологических, ’’диких” прост-
ранств. Оказалось, что многие из перечисленных результатов остаются справед-
ливыми и в том случае, когда гладкий интеграл является всего лишь ручным (но
не обязан быть боттовским).
Определение. Гладкий интеграл f назовем ручным, если для любого кри-
тического значения с G R множество (с) является ручным, т.е. существует
гомеоморфизм всего многообразия Q на себя, сдвигающий зто множество в полиэдр.
Обозначим через (Н*) класс трехмерных компактных замкнутых многообра-
зий, являющихся изоэнергетическими поверхностями гамильтоновых систем,
интегрируемых при помощи некоторого ручного интеграла. Так как каждый глад-
кий боттовский интеграл очевидно является ручным, то имеет место тривиальное
включение (Н*) Э (Н).
Предложение 5 (С.В. Матвеев, А.Т. Фоменко). Классы (Н*) и (Н) сов-
падают.
Укажем теперь на еще один класс (R) трехмерных многообразий, активно
изучающийся сегодня. Круглой функцией Морса называется боттовская функция
на многообразии, все критические подмногообразия которой являются окруж-
ностями. Мы скажем, что многообразие принадлежит классу (R), если оно допу-
скает круглую функцию Морса. Подчеркнем, что здесь, в отличие от многооб-
разий класса (5), не требуется, чтобы неособые поверхности уровня функции
были торами. Круглые функции Морса тесно связаны с разложением многообра-
зия в сумму так называемых круглых ручек (см. [42]-[46]). Мийоши (см.
[43]) доказал, что многообразие Мп (произвольной размерности п) разлагается
в сумму круглых ручек тогда и только тогда, когда М” допускает круглую функ-
16. А.Т. Фоменко
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
466
цию Морса. Азимов в [45] доказал, что многообразие Мп размерности п > 4 раз-
лагается в сумму круглых ручек в том и только в том случае, когда эйлерова ха-
рактеристика х(Л/) многообразия равна нулю. Однако для трехмерных многооб-
разий (т.е. для случая, который здесь нам особенно интересен) картина оказалась
существенно сложнее.
Ясно что (R) Э (Н), т.е. любая изоэнергетическая поверхность интегрируемой
гамильтоновой системы допускает круглую функцию. Это сразу следует из теоре-
мы 3, поскольку (Н) = (S), а класс (S) как раз и состоит из многообразий с
круглыми функциями (у которых, кроме того, все неособые поверхности уров-
ня являются торами). Оказывается,класс (R) строго больше класса (Н). Это
означает, что существуют многообразия, допускающие круглые функции Морса,
но при этом не реализующиеся как изоэнергетические поверхности интегрируемых
систем. Различие между классами (R) и (Н) обусловлено их различным поведе-
нием по отношению к операции взятия связной суммы # двух многообразий.
Согласно работе Моргана [44], если М — произвольное трехмерное многообразие
(мы не будем оговаривать каждый раз, что рассматриваются компактные замк-
нутые ориентируемые многообразия), то рассматривая его связную сумму с до-
статочно большим числом экземпляров многообразия S1 X S2, мы в конце концов
обязательно попадем в класс (R). Другими словами при достаточно большом т мы
будем иметь: М # (#7=1 5* Х S2) G (R).
С другой стороны, изучая свойства класса (Н) = (S), С.В. Матвеев доказал сле-
дующее важное свойство класса (И). А именно, если М G (Н) и М - Мt # М2, то
многообразия и М2 также обязательно принадлежат классу (Н). Усиление
этого результата (распространение его на многообразия, снабженные боттовским
интегралом, т.е. на пары вида (М, /)) было получено А.Т, Фоменко и Х.Цишангом
в [47]. Отсюда сразу следует, что класс (R) строго больше класса (Н). В самом
деле, достаточно взять многообразие Мо, не принадлежащее классу (Н) (такие,
как мы знаем, существуют). Беря его связную сумму с достаточно большим чис-
лом экземпляров многообразия S1 X S2, мы в конце концов попадаем в класс
(R). Однако полученное при этом многообразие не лежит в классе (Н), так как
в противном случае исходное многообразие Мо также должно было бы лежать в
(Н),что противоречит выборуМо.
Рассмотрим теперь класс неприводимых многообразий, т.е. не представимых в
виде связной суммы Mi # М2, где Мг и М2 отличны от сферы S3. Рассмотрим пе-
ресечение (R)o этого класса с классом (R). Другими словами, многообразие
М принадлежит классу (R)o в том и только в том случае, когда оно неприводимо
и допускает круглую функцию Морса. Рассмотрим также класс (Н)о, состоящий
из неприводимых многообразий класса (Н).
Предложениеб (А.Т. Фоменко, X. Цишанг). Классы (Н) 0 и (R)o совпадают.
Следовательно, имеется тождество: (Н)о = (Q)o = (W)o = (S)o = (R)o-
§ 52. КОГОМОЛОГИИ И СЛОЕНИЯ
В большей части этого параграфа мы предполагаем, что читатель знаком с кого-
мологической теорией дифференциальных форм, включая теорему де Рама (см. ли-
тературные указания в п. 2 § 42).
1. Слоения.
к. Определение слоения. Пусть АГ—гладкое п-мерное многообразие без края, и
пусть 0 < р < и. Говорят, что на X задано (гладкое) слоение размерности р, ес-
ли Xнаделено разбиениемна (линейно) связные подмножества /^.обладающие следую-
щим свойством: в окрестности произвольной точки многообразия X найдется
§ 52. КОГОМОЛОГИИ И СЛОЕНИЯ
467
система локальных координат х1г___,хп, принадлежащая выбранной гладкой
структуре многообразия X и такая, что связные компоненты пересечений множеств
Fa с областью определения этой системы координат задаются уравнениями вида
хр+1 = const,, х„ = const. Множества Fa называются слоями слоения, само
X называется его тотальным многообразием. Числа р и п —р называются размер-
ностью и коразмерностью слоения; размерность и коразмерность слоения ^обоз-
начаются через dim^H codim £
Слоения на многообразиях с краем будут иногда у нас встречаться, но будут иг-
рать чисто техническую роль. При этом каждая компонента края либо будет слоем
(это возможно при codim S' - 1), либо будет трансверсальна слоям.
Слои слоения целесообразно наделять не индуцированной топологией, а тополо-
гией, базу которой составляют компоненты пересечения слоя с открытыми подмно-
жествами тотального многообразия. По отношению к этой топологии слой являет-
ся р-мерным многообразием. Он обладает и естественной гладкостью, делающей
его включение в тотальное многообразие (взаимно однозначным) погружением.
Например, слои обмотки тора с иррациональным наклоном (см. ниже) диффеоморф-
ны прямым.
В. Примеры слоений. Тривиальные примеры слоений доставляют гладкие рас-
слоения: если X — тотальное многообразие гладкого расслоения с (и — р) -мерной
базой (и = dim АГ), то разбиение многообразия X на слои расслоения естьр-мерное
слоение. Следующий по сложности пример — обмотка тора, т.е. разбиение тора R2/Z2
на образы прямых у = Хх + с с фиксированным X. Если X рационально, то это
слоение относится к предыдущему классу, в случае же иррационального X каждый
слой плотен в торе. Последний пример иллюстрирует различие между слоениями и
расслоениями, слоения не имеют базы. (Конечно, всегда можно образовать фактор-
пространство тотального многообразия по разбиению на слои, но, как показывает
последний пример, результат может оказаться неудовлетворительным.)
Следующий важный для дальнейшего пример обобщает обмотку тора. Пусть G —
группа Ли, Н - ее связная подгруппа, Г - ее дискретная подгруппа. Правые смеж-
ные классы группы Н составляют в G слоение, инвариантное относительно левых
сдвигов, производимых элементами группы G, в частности, элементами группы Г.
Благодаря последнему, в G/Г возникает слоение, коразмерность которого равна
коразмерности группы Н в G; мы обозначаем его через £(G, Н, Г). Это слоение
превращается в обмотку тора, если G = R2, Н= R, Г =Z2. В общем случае это слое-
ние является вещественно-аналитическим; его слоидиффеоморфныфакторпростран-
ствамЯ/(ЯП^_ 1 Tg) cgGG.
Пожалуй, этот пример не очень типичен для классической теории слоений. За-
пас примеров, которым располагает эта теория, состоит, в основном, из слоений
коразмерности 1, построенных в разное время с целью доказать существование
слоения коразмерности 1 на том или ином многообразии. Сама проблема суще-
ствования слоений коразмерности 1 в настоящее время полностью решена: на |связ-
ном) открытом многообразии такое слоение всегда существует, а в случае замкну-
того многообразия равенство нулю эйлеровой характер!стики этого многообразия,
очевидно, необходимое для существования слоения коразмерности 1, является
для него и достаточным. Последний факт доказан Тэрстоном [46]. Однако доказа-
тельство Тэрстона трудно назвать геометрически наглядным, так что классические
конструкции слоений не утратили своего значения. Наиболее известной среди них
является конструкция слоения коразмерности 1 на S3, принадлежащая Ребу [48].
Слоение Реба строится следующим образом. Рассмотрим сначала слоение в цилинд-
ре {(х, у, z) € R3 |х2 + у2 <1 }, слоями которого служат край цилиндра
16*
468
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
х2 + j2 = 1 и поверхности z = ехр(1 - х2 - у2) "1 + с. Обычная проекция цилиндра на
полноторий S1 X D2 наделяет последний слоением коразмерности 1. Это слоение в
S1 X D2 называется ребовской компонентой-, его осевое сечение изображено на
рис. 245. Слоение в сфере S3 получается при обычном склеивании этой сферы из
двух полното риев.
Заметим, что у слоения Реба в S3 все слои, кроме одного, диффеоморфны плос-
кости, а один диффеоморфен тору. В связи с этим уместно упомянуть теорему
Новикова [49] (ее доказательство изложено также в книге [50]), согласно которой
всякое двумерное слоение на трехмерном многообразии с нестягиваемой универ-
сальной накрывающей имеет замкнутый слой, причем если слоение не является
ни в каком открытом подмножестве тотального многообразия гладким расслое-
нием с компактным слоем, то один из замкнутых слоев обязательно является то-
ром, ограничивающим ребовскую компоненту.
Упражнение 1. Построить слоение на замкнутом ориентируемом трехмер-
ном многообразии, имеющее конечное число замкнутых слоев и такое, что один из
этих слоев есть наперед заданная (ориентируемая или неориентируемая) замкну-
тая двумерная поверхность.
Заметим еще, что слоение Реба является гладким, но не аналитическим. Этот де-
фект представляется непоправимым из-за односторонней голономии. Под этим
понимается следующее. Если у тора, являющегося слоем нашего слоения, взять
меридиан и составить из коротеньких нормалей к слою в точках этого меридиана
кольцо S1 X R, то слоение будет высекать на этом кольце с одной стороны от то-
ра семейство концентрических окружностей, а с другой — семейство спиралей (см.
рис. 246), что в аналитической ситуации, конечно, невозможно. Вообще имеется
теорема Хефлигера, согласно которой на замкнутых односвязных многообразиях
не бывает аналитических слоений коразмерности 1 (см. [51], а также [49]).
Наряду с конструкцией Реба имеются явные конструкции слоений коразмерно-
сти 1 на целом ряде других многообразий, в том числе на всех нечетномерных сфе-
рах. Отсылая читателя за подробностями к обзорной статье Лоусона [52], мы при-
ведем поучительную конструкцию слоения коразмерности 1 на 5s, принадлежащую
тому же Лоусону [53].
Конструкция основывается на таком наблюдении: если компактное многообра-
зие X, вообще говоря, имеющее край, гладко расслаивается над окружностью, то X
обладает слоением коразмерности 1, у которого край является слоем. Для дока-
Рис. 245
Рис. 246
§ 52. КОГОМОЛОГИИ И СЛОЕНИЯ
469
Рис. 247
эательства достаточно построить гладкую
функцию X -> R+> равную 0 на дХ, поло-
жительную в Int X и не имеющую крити-
ческих значений, меньших 1. Эта функция
составляет с проекцией X^S1 гладкое отоб-
ражение X -> S1 X R+, трансверсальное слое-
нию, изображенному на рис. 247 [в S1 X
X (1, °°) слои этого слоения совпадают с пря-
мыми t X (1, оо) ]. Индуцированное в X слое-
ние и будет требуемым. (Слои построенного
слоения в X будут в достаточном отдалении
от края совпадать со слоями расслоения
X -> $*, а при приближении к краю будет
накручиваться на край; такую структуру
имеет и ребовская компонента.)
Очевидно, эта конструкция позволяет
построить слоение коразмерности 1 иа прои-
звольном замкнутом многообразии, которое разрезается подмногообразием ко-
размерности 1 на два куска, каждый из которых расслаивается над окружностью.
А сфера S5 так разрезается: разрез производится поверхностью | z3 + z3 + zj | = е,
где е достаточно мало (мы считаем, что Ss С С3). Часть |zj + z% + z3 | > е рас-
слаивается над 51 посредством проекции (zt, z2, z3) ^arg(z3 + z% + z3) (это —
так называемое расслоение Милнора), часть |z3 + z| + z3 | <е расслаивается над
неособой кубической кривой в С/*2, которая диффеоморфна тору S1 XS1.
Упражнение 2. Сформулируйте условия для того, чтобы замкнутое глад-
кое многообразие разрезалось подмногообразием коразмерности 1 на два куска,
гладко расслаивающиеся над окружностью. В частности, разрезается ли таким об-
разом S’? (Это - нерешеннаяпроблема!).
С. Касательное и нормальное расслоения. Касательное расслоение тотального мно-
гообразия слоения обладает подрасслоением,которое естественно считать касатель-
ным расслоением слоения: его составляют векторы, касающиеся слоев. Соответ-
ствующее факторрасслоение называется нормальным расслоением слоения; его раз-
мерность равна коразмерности слоения. Обозначения для касательного и нормального
расслоения слоения S--. т (F) и v (£).
Слоение называется ориентированным, если ориентировано его нормальное рас-
слоение. Подчеркнем, что ни слои, ни тотальное многообразие ориентированного
слоения не обязаны даже быть ориентируемыми. Слоение называется оснащенным,
если его нормальное расслоение тривиально и наделено определенной тривиализа-
цией (т.е. если на тотальном многообразии задано codim ^-реперное поле, транс-
версальное к слоению).
Упражнение 3. Все слоения, рассматривавшиеся в п. В, являются ориенти-
руемыми (за исключением некоторых из слоений, которые читатель должен был
построить, решая упражнение 1).
Слоение 3\G, Н, Г) обладает естественным оснащением: слои нормального
расслоения этого слоения канонически изоморфны пространству g/h, где g, h —
алгебры Ли, соответствующие группам G, Н, и слоение делается оснащенным, если
в g/h фиксировать базис.
Гладкое отображение f гладкого многообразия Y без края в тотальное много-
образие X слоения $ называется трансверсальным к &, если f трансверсально ре-
гулярно по отношению к каждому слою слоения £”(см. п. 1 § 43). Конечно, это
♦70
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
возможно, только если dim Y > codim £ Если f трансверсально то компонен-
ты прообразов слоев слоения 3 составляют слоение многообразия Y. Последнее
называется индуцированным S' посредством f и обозначается через /*£ Ясно,
что codim /*^= codim *£) = f*v(3).
Важный пример: замкнутые трансверсали к слоям коразмерности 1. Речь идет
о гладких замкнутых кривых в тотальном многообразии, включение которых в
тотальное многообразие трансверсально слоению.
Упражнение 4. Покажите, что если L — некомпактный слой слоения кораз-
мерности 1 на замкнутом многообразии и х € L — произвольная точка, то существу-
ет замкнутая трансверсаль, пересекающая L в точке х и только в этой точке.
D. Отношения эквивалентности. Мы рассматриваем четыре отношения эквивалент-
ности между слоениями: диффеоморфность, гомотопность, конкордантность и кобор-
дантность.
Диффеоморфностъ слоений определяется очевидным образом.
Упражнение 5. Какие обмотки тора (см. п. В) диффеоморфны?
Гомотопия слоения 3 - зто семейство {3t | 0 <7 < 1 } слоений одной размер-
ности на одном многообразии X, такое, что Зо = ^ичго для любой точки х£Х про-
странство, касательное к слою слоения 3t в точке х, непрерывно зависит от t. Если
{ — гомотопия, то слоения и называются гомотопными. Например, все
обмотки тора гомотопны. (Это показывает,, ввиду упражнения 5, что гомотопные
слоения могут быть недиффеоморфны.)
Слоения За и одной размерности на многообразии X называются конкор-
датными, если существует слоение ^(той же коразмерности) в X X R, такое, что
вложения т0> й ’ X -> XX R, :\(х) = (х, X), трансверсальны £и i* 3= 30, i* 3=
Упражнения 6. Покажите, что разные обмотки тора конкордантны. (За-
мечание: хотя разные обмотки тора, таким образом, и гомотопны, и конкордантны,
читатель, проделав это утверждение, увидит различие между гомотопностью и кон-
корданностью; примеры гомотопных, но не конкордатных слоений появятся в
п. 2.)
7. Покажите, что слоение тора, изображенное на рис. 248, конкордантно, но не
гомотопно обмотке (скажем, составленной из параллелей).
Слоения 30 и одной размерности на замкнутых многообразиях Хо и Хх одной
размерности называются кобордантными, если существует компактное многообра-
зие X со слоением 3 такое, что (i) ЪХ = Хй U Хг; (ii) слоение 3 трансверсально
к краю ЪХ и индуцирует на Хо и Хх слоения 30 и Разумеется, конкордатные
слоения на замкнутом многообразии кобордантны. Обратное неверно, но мы не
сможем привести пример. Понятия диффеоморфности,
конкордантности и кобордантности слоений имеют
очевидные ориентированные и оснащенные варианты.
Е. Определяющая система форм. Пусть 3 - слое-
ние коразмерности q на многообразии X. Определяю-
щая система форм слоения 3 в открытом множестве
U С X — зто набор ........гладких 1-форм, за-
данных в U и обладающих следующими свойствами:
(i) формы о>1.....<oq линейно независимы в каж-
дой точке множества (ii) сужение каждой из
этих форм на любую компоненту пересечения любого
слоя с U тривиально. Очевидно, для задания слоения
достаточно задать определяющие системы форм в от-
§ 52. КОГОМОЛОГИИ И СЛОЕНИЯ
471
крытых множествах, составляющих покрытие тотального многообразия. Ясно, так-
же, что если { Wi,..Wg} , { ш'1,— определяющие системы форм в U,
U', то (в U П U') о, = где ч>ц — такие гладкие функции, что det || <pf/- ||
не обращается в U d U' в нуль.
Если U = X.„ro мы имеем дело с глобальной определяющей системой форм. Оче-
видно, для существования глобальной определяющей системы форм необходимо и
достаточно, чтобы было тривиально нормальное расслоение к слоению, и задание
глобальной определяющей системы форм приводит к выбору определенного го-
мотопического класса оснащения этого слоения.
Подчеркнем, что система ,..., гладких 1-форм, заданных в открытом мно-
жестве U С X, может не быть определяющей системой форм ни для какого слое-
ния коразмерности q, даже если она удовлетворяет условию (i): требуется еще,
чтобы был выполнен ’’критерий интегрируемости”. Последний формулируется
* так: при каждом i дифференциал dwt должен представляться в виде S/ty л оу,
где q, — некоторые гладкие 1-формы; равносильная (если выполняется (i)) фор-
мулировка: со, а ... a (jjq a da>t = 0 при / = 1,..., q. Что этот критерий выпол-
няется для любой определяющей системы форм, совсем очевидно: можно считать,
что система задана в пределах зоны действия локальной системы координат, описан-
ной в определении слоения, а в таких локальных координатах всякая определяю-
щая система форм имеет вид 'LjfijdXp+jti = 1,..., q) с det \\ftj || # 0. Обратное ут-
верждение, доказательство которого чуть более длинно, представляет собой хоро-
шо известную теорему анализа.
Упражнение 8. Докажите эту теорему анализа. Для удобства читателя при-
ведем ее формулировку в традиционных аналитических терминах. Пусть со,,...
....Wq-система гладких 1-форм, определенных в окрестности точки 0 € R" и ли-
нейно независимых в этой точке. Если cjj а .., а a dсо, = 0 при i - 1,..., q,
то существуют гладкие функции /,у, gt (i,j = 1,..., q), такие, что det || /,/ II #
=#= 0 и со, = 'Lfijdgj. (Доказательство имеется в некоторых учебниках анализа, на-
пример, в [54].)
2. Класс Годбийона—Вея.
А. Определение. Нижеследующая конструкция относит произвольному ориенти-
руемому слоению & коразмерности 1 трехмерный вещественный когомологический
класс его тотального многообразия, называемый, по имени своих авторов, клас-
сом Годбийона—Вея слоения ^(см. [55]). Поскольку слоение & ориентируемо,
оно может бьпь глобально задано 1-формой со, не обращающейся в 0, и эта фор-
ма определяется слоением с точностью до умножения на необращающуюся в 0
функцию. Форма со удовлетворяет условию интегрируемости, которое равносиль-
но существованию 1-формыт? ст?асо =<7со.
Упражнения. 9. Форма qKdq замкнута.
10. Когомологический класс этой формы не зависит от произвола в выборе форм
со и q, а определяется слоением £
Когомологический класс формы q a dq называется классом Годбийона—Вея слое-
ния ^и обозначается через gv(SF).
Упражнение 11. Распространите конструкцию класса Годбийона—Вея на
случай неориентируемых слоений.
Замечания. 1°. Если /: Y -> X — гладкое отображение, трансверсальное слое-
нию 9(коразмерности 1) на X, то gv (/ *У) = f *gv (£). Из этого очевидного наблю-
дения вытекает, что у конкордатных слоений классы Годбийона—Вея одинаковы.
Гомотопическим инвариантом класс Годбийона—Вея, как мы увидим ниже, не
является.
472
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
2°. Наряду с классом Годбийона-Вея можно определить число Годбийона-Вея.
Последнее возникает, если слоение коразмерности 1 задано на трехмерном замкну-
том ориентированном многообразии, и равно значению класса Годбийона-Вея на
фундаментальном гомологическом классе. Очевидно, числа Годбийона-Вея у ориен-
тированно кобордантных слоений одинаковы.
В. Нетривиальность. Пусть М - некоторое «-мерное риманово многообразие
отрицательной кривизны, х2, х2 € М — точки, vlt и2 — единичные касательные век-
торы в точках Xi, х2 и у,: R+ ->ЛГ, 7 2: R+ ~*М - геодезические, определяемые век-
торами i?i, и2 и отнесенные к натуральному параметру. Векторы иi и v2 называют-
ся параллельными, если существует предел lim p(7i(0, 7г (О) > и называются
Г -» оо
строго параллельными, если этот предел равен 0. Легко понять, что векторы иi ии2
параллельны тогда и только тогда, когда векторы скорости в некоторых точках
геодезических и 72 строго параллельны (см. рис. 249, на котором векторы Uj и
i>2 параллельны, а векторы Wj и w2 строго параллельны).
Обозначим через N многообразие единичных касательных векторов многообра-
зия М (таким образом, dim N = 2п — 1). Назовем орициклами (чистыми орицикла-
ми) многообразия М подмногообразия многообразия N, составленные из всех век-
торов, параллельных (строго параллельных) одному вектору v G N. Очевидно,
орициклы имеют размерность п, а чистые орициклы — размерность и — 1.
Упражнение 12. Если кривизна многообразия М постоянна, то орициклы и
чистые орициклы составляют слоения многообразия N. (Условие постоянства кри-
визны, кажущееся на первый взгляд излишним, необходимо для того, чтобы слое-
ния были гладкими.)
Напомним, что замкнутая ориентированная поверхность М произвольного ро-
да g > 2 обладает метрикой постоянной отрицательной кривизны, поскольку она
получается из плоскости Лобачевского факторизацией по дискретной группе изо-
метрий Да Я) (М), действующей без неподвижных точек (подробности см. в ’’Со-
временной геометрии” Дубровина, Новикова и Фоменко, ч. И, гл. 4, § 20).
Соответствующее орициклическое слоение представляет собой двумерное слоение на
замкнутом трехмерном многообразии N — многообразии единичных касательных
векторов поверхности М.
Теорема. У этого слоения класс Годбийона-Вея нетривиален.
Доказательство. Положим G = SL(2, R). Обозначим через Н подгруппу
группы G, составленную из матриц вида
а Ъ
0 а'1
с а > 0 и через Г - прообраз
группы A s /Г1 (М) (см. выше) в группе SL(2,R) при проекции
SL(2,R) -> SL(2,R)/{+ 1} =
группа движений
плоскости
Лобачевского
§ 52. КОГОМОЛОГИИ И СЛОЕНИЯ
473
Тогда наше слоение есть &(G, Н, Г) (в частности, N есть G/Г). (Доказательство
этого факта мы оставляем читателю в качестве упражнения; те, кто с этим упраж-
нением не справятся, не должны особенно сокрушаться: наша цель заключается в
том, чтобы построить слоение с нетривиальным классом Годбийона—Вея, и не так
уж важно, будет ли зто орициклическое слоение или слоение F(G, Я, Г).)
Касательное пространство si (2, R) к группе SL(2, R) в точке Е (единичная матри-
ца) отождествляется с пространством матриц, имеющих нулевой след: элемент
группы SL(2, R), отстоящий от Е на расстояние ~е, имеет вид
/ а Ь\
Е + е I ) + о (е).
\С-П/
Рассмотрим линейные функционалы s/(2, R) -*R, действующие по формулам
с -а
»-> с>
а b
с -а
а,
а b
с -а
Ъ,
а Ъ
и превратим их в 1-формы на SL(2, R), перенося точку Е в другие точки
группы SL(2, R) посредством правых сдвигов. Обозначим эти 1-формы через
СО _ । , COq , CJj •
Упражнения. 13. Покажите, что то _ , л то0 л то, - форма объема в SL(2, R).
14. Докажите, что = 2то_ , л то0, dcoQ = со- , л то,, doji = 2тоол то, [ Указа-
ние. Докажите следующее правило для вычисления дифференциалов правоинвариант-
ных 1-форм: если то — такая форма и и,, и2 ~ касательные векторы в точке Е, то
dco(Ui,u2) = то( [и,, г2 ]), где квадратные скобки обозначают коммутатор: [А, В] =
=АВ-ВА.]
Формы со-i, то0, то, получаются поднятием из некоторых форм то_,, Too, то',,
определенных на G/Г, и ясно, что форма то'_, интегрируема (перечисленные выше
соотношения между формами то и их дифференциалами сохраняются при перехо-
де к формам то') и определяет в G/Г как раз слоение $(G, Н, Г). Поскольку Jto'_, =
= — 2тооЛсо11, класс Годбийона—Вея представляется формой — 2toqaJ(—2toq) =
= — 4то'_ , л тоо л то], которая не является точной, потому что то'_ , л Тод л то', — форма
объема.
С. Геометрический смысл класса Годбийона—Вея по сей день остается загадоч-
ным. Имеется целый ряд теорем, показывающих, что слоение с нетривиальным клас-
сом Годбийона—Вея является достаточно запутанным.
Упражнение 15. Покажите, что у слоения Реба на 53 (см. п. В) класс Год-
бийона—Вея равен 0. [Указание. Подберите для слоения Реба определяющую фор-
му то, такую, что (/то = т? лее и форма т? в каждом из двух полноториев, составляю-
щих 53, зависит от двух переменных, т.е. индуцируется некоторой 1-формой на дву-
мерном многообразии при проекции на него полнотория. В этой ситуации, очевид-
но, т? л dq = 0.]
Как показали Мицутани, Морита и Цубой [56], тривиальность класса Годбийо-
на—Вея у слоения Реба предопределяется характером его голономии. Упоминание
о голоиомии проскользнуло выше в этом параграфе, теперь мы дадим ей точное
определение. Пусть s - гладкий путь на слое L слоения^ коразмерности q. По-
строим вдоль этого пути семейство трансверсальных шариков; они составят ци-
линдр DA XI. Слои слоения будут высекать на этом цилиндре линии, и эти линии опре-
делят диффеоморфизм окрестности центра одного основания в окрестность цент-
ра другого основания. Этот диффеоморфизм не меняется при гомотопии пути (с
закрепленными концами). Рассматривая же замкнутые пути, мы получим представ-
474
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
пение фундаментальной группы слоя L в группе локальных диффеоморфизмов
(Л4,0) •-> (DP, 0). Это и есть голономия. (См. рис. 250.)
Если всякому элементу фундаментальной группы слоя отвечает тождественный
диффеоморфизм, то говорят, что этот слой не имеет голономии. Если ни один слой
слоения у не имеет голономии, то говорят, что слоение & не имеет голономии.
Если голономию могут иметь только компактные слои слоения то говорят,
что & почти не имеет голономии. Например, слоение Реба почти не имеет го-
лономии.
Теорема (Мицутани, Морита, Цубой). Если слоение коразмерности 1 почти
не имеет голономии, то его класс Годбийона—Вея равен 0.
Дальнейшее обобщение этой теоремы принадлежит Думини. Назовем слой слое-
ния коразмерности 1 пружинным, если он бесконечно наматывается сам на себя
(рис. 251).
Теорема (Думини — для замкнутых многообразий, Кантвелл и Конлон - в
общем случае). Если слоение коразмерности 1 не имеет пружинных слоев, то его
класс Годбийона-Вея равен 0.
Одним из следствий теоремы Думини является следующий факт, связывающий
класс Годбийона—Вея с характером роста слоев. Пусть слоение на замкнутом
многообразии X. Введем в X произвольную риманову метрику, выберем слой L и
точку х G L и для г > Ообозначим через и(г) объем шара радиуса г с центром х
на L (в индуцированной метрике). Говорят, что £ имеет экспоненциальный, суб-
экспоненциальный, полиномиальный и т.д. рост, если такой рост имеет функция и (г).
Упражнение 16. Покажите, что это определение корректно, т.е. что харак-
тер роста слоя ие зависит от выбора римановой метрики и точки х.
Теорема (Думини). Если класс Годбийона-Вея слоения коразмерности 1 на
замкнутом многообразии отличен от 0, то это слоение обладает слоем экспонен-
циального роста.
Упражнение 17. Выше мы показали, что класс Годбийона—Вея орицикли-
ческого слоения замкнутой поверхности постоянной отрицательной кривизны имеет
ненулевой класс Годбийона—Вея. Значит, в силу результатов Думини, это слоение
должно иметь пружинные слои и слои экспоненциального роста. Найдите такие слои.
D. Варьируемость. Ниже излагается конструкция Тэрстона [57] гладкого семей-
ства слоений на S3, число Годбийона—Вея которых изменяется с изменением пара-
Рис. 250
Рис. 251
§ 52. КОГОМОЛОГИИ И СЛОЕНИЯ
475
метра. Это показывает, что слоения этого семейства попарно не диффеоморфны
и даже попарно не конкордантны, и даже попарно не кобордантны.
Пусть т > 3. Возьмем на плоскости Лобачевского L произвольный w-угольник
Q и симметричный ему относительно какой-нибудь прямой w-угольник Q*. Выбро-
сим из Q и Q* вершины и обозначим через R, R* прообразы остающихся частей при
проекции N -+L, где N — многообразие единичных касательных векторов к L. Выше
Рис. 252
(в п. В) мы построили в N орициклическое слоение. Это слоение высекает неко-
торые слоения коразмерности 1 в R и R*. Теперь заметим, что орициклическое слое-
ние инвариантно относительно движений плоскости Лобачевского. Склеим Л с R*,
отождествив компоненту края многообразия R, отвечающую стороне АВ много-
угольника Q, с компонентой края многообразия R*, отвечающую симметричной
стороне А*В* многоугольника Q* (А* симметрично А и В* симметрично В),
по диффеоморфизму, определяемому движением плоскости Лобачевского,
совмещающим А с А* и В с В*. Многообразие R U Л*естественно сглаживается, и
слоения в Л и R* составляют слоение коразмерности 1 на склееном многообразии.
Последнее представляет собой произведение сферы с т проколами на окружность.
Отождествим это многообразие с внутренней частью произведения сферы с т ды-
рами на окружность. Последнее есть компактное многообразие с краем, который
представляет собой объединение т торов. При естественном продолжении слоения
на край мы получим на каждом их этих торов обмотку.
Упражнение 18. Убедитесь в справедливости последнего высказывания
и найдите углы наклона этих обмоток (выразите их через углы многоуголь-
ника Q).
Имеется стандартная процедура, позволяющая продолжить обмотку тора до слое-
ния в полнотории, трансверсального краю. Это слоение в полноюрии состоит из
двух частей. Для построения первой мы возьмем слоение в плоском слое R2 X
X I, слои которого трансверсально подходят к плоскости R2 X 0, высекая на ней
семейство параллельных прямых, и асимптотически приближаются к плоскости
R2 X 1 (рис. 252). Профакторизуем R2 X I по группе Z ® Z параллельных пере-
носов, действующих в направлении R2. Получится торический слой (тор) X /, со
слоением, у которого одна из компонент края является слоем, а на другой компо-
ненте края высекается обмотка с наперед заданным углом наклона. К этому то-
рическому слою мы присоединяем полноторий с ребовской компонентой (разу-
меется, со стороны компоненты края, являющейся слоем). Все вместе дает слое-
ние в полнотории, продолжающее обмотку тора.
Теперь заклеим торы, составляющие край построенного выше многообразия
со слоением, полноториями таким образом, чтобы получилась сфера 53, и продол-
476
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
жим слоение на эти полнотории указанным образом. Получится слоение в 53, ко-
торое мы обозначим через &q.
TeopeMa:<gv( 9q) , [S3 ] > = 4яагеа Q.
Доказательство. Выше (в п. В) мы уже строили для орициклического
слоения в /V формы со, т?(со определяет слоение и с!аз = 1)лаз). При этом оказалось,
что форма Годбийона—Вея tjac/t? есть стандартная форма объема в N. Значит,
J -q^dri = vol(/?U/?*) = R U R * длина единичной окружности площадь 2UQ*
= 2тг • 2area Q = 4warea Q.
Далее, легко убедиться в том (детали мы оставляем читателю), что формы аз, г] с
указанными свойствами можно продолжить на вклеенные полнотории таким обра-
зом, что форма тг будет зависеть в действительности от двух переменных (ср. ука-
зание к упражнению 16), вследствие чего в полноториях будет rj л dri = 0. Значит, и
J 1? л dij = 4irarea Q.
s3
Из доказанной теоремы видно, что, варьируя многоугольник Q, мы получаем се-
мейство слоений коразмерности 1 (гладко зависящее от параметра) с непостоян-
ным классом Годбийона — Вся.
Е. Комментарии к конструкции Тэрстона. 1 °. Существуют многочисленные моди-
фикации конструкции Тэрстона: в частности, можно построить на некотором замк-
нутом (разумеется, неодносвязном) трехмерном многообразии аналитическое се-
мейство аналитических слоений коразмерности 1 с переменным классом Годбийо-
на — Вся.
2°. Как известно, площадь m-угольника на плоскости Лобачевского изменяется в
пределах от 0 до ir(m — 2). Поэтому число Годбийона — Вея слоений указанного
семейства может изменяться от 0 до 4тг2 (тп — 2) (легко понять, что включительно).
В связи с этим возникает вопрос о характере возможного изменения числа Годбийо-
на — Вея в семействе слоений на замкнутом ориентируемом трехмерном многооб-
разии. Например, может ли это число изменяться неограниченно в одну и или обе
стороны; если да, то может ли это изменение быть монотонным, и т.д.
.3°. Единственное известное (авторам) ограничение на вариации класса Годбийо-
на — Вея составляет теорема, доказанная Гельфандом,Фейгиными Фуксом [58].
Эта теорема относится в действительности к произвольным характеристическим клас-
сам слоений (см. пп. 3 и 5); для класса Годбийона — Вея ее утверждение можно до-
казать элементарными средствами.
Упражнение 19. Пусть — гладкое семейство слоений коразмернос-
ти 1. Тогда при любом t имеет место равенство
d
gv(^i) — gv(5j = 0
dt
(имеется в виду когомологическое умножение).
4°. Для иллюстрации последнего утверждения рассмотрим следующий любопыт-
ный пример. Пусть {^} — гладкое однопараметрическое семейство слоений на мно-
гообразии S3 X S3, и пусть gv(#J = («(/), 0(t)) е R2 = Н3 (S3 Х53; R) - класс
§ 52. КОГОМОЛОГИИ И СЛОЕНИЯ
477
Годбийона — Вея слоения &t. В силу последнего
утверждения,
d , ,
О = gv (•—gv (£)=(«(0,0(0) • («'(0.0 (0) =
dt
= a(t)0'(t)-a'(t)0(t)eR = #6(S3 X 53;R),
т.е. а: 0 = а : 0'. Из этого видно, что класс
Годбийона - Вея слоения на S3 X S3 может
изменяться только по лучам, исходящим нз
точки О G R2 =Я3 (S3 XS3; R) (см. рис. 253).
Это наблюдение интересно сопоставить с
другими фактами, касающимися слоений на
S3 X S3. Слоение коразмерности 1 на S3 X S3
можно построить, взяв произвольное слоение
коразмерности 1 на S3 и умножив каждый его
слой на S3. Класс Годбийона — Вея такого слое-
ния будет иметь вид («, 0). Подвергая слоение
действию автоморфизмов многообразия S3 X S3, мы можем получить слоение с
классом Годбийона — Вея (а, 0) с произвольными рационально соизмеримыми
а, 0. Проблема: существует ли на S3 X S3 слоение коразмерности 1, класс Год-
бийона - Вея которого имеет рационально несоизмеримые координаты?
Если нет, то это прекрасно объясняет предыдущее наблюдение, но порождает
вопрос, какие вообще значения может принимать класс Годбийона — Вея. Если да,
то в чем состоит геометрическая природа запрета на ’’поперечные” деформации клас-
са Годбийона — Вея?
Аналогичные проблемы существуют для других характеристических классов
слоений. Читатель может их сформулировать, прочитав остающуюся часть параграфа.
3. Характеристические классы слоений произвольной коразмерности.
А. Случай оснащенного слоения. Прямое обобщение конструкции Годбийона —
Вея проходит в предположении, что предложенное слоение & коразмерности q явля-
ется оснащенным или, что эквивалентно, наделено глобальной системой ..... со(/
определяющих форм. Интегрируемость системы cjj,. .., означает существова-
ние 1-форм Tjy (i, j = 1,. . ., q), для которых 2; (рц л coj) = du, (i = 1,.... q).
Дифференцируя последнее равенство, получаем:
S {dritj - S (nik a rikj)) л o>} = 0.
i k
Обозначим 2-форму dpn — S* л рк, через f,y. Равенство Sy r]y л wy =0 ноказы-
вуют.что все формы £,у принадлежат идеалу (в кольце дифференциальных форм
на тотальном многообразии X), порожденному формами gjj,..., a>q. Поэтому
у л ... л ff- у = 0 при г > q
и любых i’i ,..., ir, ji.jr.
Обозначим через W(q) факторкольцо кольца А (уу | 1 1 </ <q) ®
® R [dytj | 1 < / <<?, 1 </ <<?] (уц, dyy — формальные переменные) по идеалу, по-
рожденному всевозможными произведениями zfj ... zf- j с г > q, где z,y = dyy -
- 2*(у/Л л ук)). Градуируем это факторкольцо, положив degуц = l.degdyy = 2.
Сопоставленияуу^ dyy, dyy »-* 0 определяют мультипликативный дифференциал
1Р(</) W(q). за которым сохраняется обозначение d. Таким образом, IPO?) — гра-
478
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
дуированный мультипликативный комплекс. (По причинам, изложение которых
мы пропускаем, этот комплекс называется усеченной алгеброй Вейля алгебры Ли
?/(<? R))
Найденные выше соотношения между формами 17,7 показывают, что если набор
форм rjjj, ассоциированный со слоением фиксирован, то сопоставление^^- *-*77^
определяет морфизм W (</) -> J2(X) в категории градуированных мультипликатив-
ных комлексов, где X — тотальное многообразие слоения S\ a J2 обозначает комп-
лекс дифференциальных форм (комплекс де Рама). Можно показать, что замена
форм qy другими формами, удовлетворяющими соотношениям S (??,/ л со;) = dcj;-
(с теми же со,), приводит к замене этого гомоморфизма гомотопным. Таким об-
разом, чтобы определить характеристические классы оснащенных слоений кораз-
мерности q, достаточно найти когомологии комплекса W(q) (что не очень трудно,
мы рассмотрим эту проблему в п. 4), выбрать коциклы, представляющие найден-
ные когомологические классы, — эти коциклы будут многочленами от уц и dy^ —
и составить такие же многочлены от i?y- и dTty; получатся замкнутые дифферен-
циальные формы на X, и их когомологические классы, которые будут зависеть толь-
ко от слоения и оснащения, и являются характеристическими классами оснащенно-
го слоения 3. Оказывается, что при q = 1 такая форма (с точностью до множите-
ля) всего одна: t?i i л dqx 1, т.е. форма Годбийона — Вея. При q = 2 пространство
таких форм пятимерно и порождается формами:
d(yii 1 + т]2з)2 л Oil 1 + Ч22);
(Jfh 1 л df?22 - d’h 2 л <й?21) л 1 + 7Ъг);
(dTh 1 л dq22 ~ diji 2 Kdq21 )л Oh 1 ~ ^22) л ’h 2 л tj2 1;
(drill bdri22 - dqi2 Л<Й?2 1)Л1711 лт?22 ЛТ?12 AT?2i;
dOh 1 +Ч12)2 A 7?! 1 Л Г)2 2 л Th 2 A q2 1 J
таким образом, оснащенные слоения коразмерности 2 имеют 5 характеристичес-
ких классов размерностей 5, 5,7, 8, 8. Этим способом можно построить и характе-
ристические классы оснащенных слоений произвольной коразмерности q. Получаю-
щиеся таким образом классы имеют размерности от 2q + 1 до q(q + 2), и среди
них при любом q присутствуют классы форм
(SdT?,-,)’ л2т7/7,
i i
(S dq,,)4 Л ( Л q,j)
‘ ‘J
степеней 2q + 1 и q (q + 2). Каждый из этих классов обобщает класс Годбийона — Вея.
В. Общий случай. Чтобы совершить переход к неоснащенным слоениям, подни-
мем наше слоение ^(неоснащенное) на тотальное многообразие X главного O(q)-
расслоения, ассоциированного с v (3) [<? = codim 3\. Поднятое слоение мы обозна-
чаем через 3. Очевидно, оно обладает каноническим оснащением. Значит,_оно кано-
нически определяет гомотопический_класс гомоморфизмов W (q) -» Q (X). Комп-
лекс J2(Y) естественно вложен в J2(X). Оказывается, что комплекс И'(д) содержит
такую часть, которая указанным гомоморфизмом W (q) -> J2 (¥) заведомо перево-
дится в J2(X). Эта часть обозначается через WO(q) и определяется следующим об-
разом. Обозначим для q X ^-матрицы А = || || через ТА отображение W(q) -> W (q),
определяемое соотношениями: ТА (уц) = ац (последнее есть скаляр — элемент нуле-
вой степени); ТА (z,;) = 0; ТА (^q) = ТА (?)т? + (- l)deg{ £ ТА (q) для любых одно-
родных %, q G W(q). Очевидно, Гд имеет степень -1. Ясно также, что действие ал-
§ 52. КОГОМОЛОГИИ И СЛОЕНИЯ
47?
гебры Лиgl(п, R) в W(д'), определяемое формулой (А, 5) ^dTA £ - TAd%, явля-
ется дифференциалом естественного действия группы GL(n, R) в W (?) [для пос-
леднего употребляется запись (В, О *-*В£]. По определению, £ G W (q) принадлежит
WO(q), если ТА £ = 0 для всякой кососимметрической матрицы А и В^ = 0 для вся-
кой ортогональной матрицы В. Когомологии комплекса WO(q) также могут быть
легко вычислены, и им соответствуют характеристические классы (неоснащенных)
слоений коразмерности q. Например, при q = 2 таких классов 3; они представляют-
ся формами (вХ):
j Л dT]2 2 - 2 л 1
(dihi hdq22 ~dqi2 * dq21) л i +тъг);
d(ihi +J122)2 a(t?ii +T?22>-
С. Теорема Ботта. Как оказывается, к числу форм, определяющих характеристи-
ческие классы неоснащенных слоений коразмерности q, при любом q принадлежат
формы
<7
Пк = S Г/ i * Ji i * • • • A , i
К. , _ , *2 J'2 '» Э‘2*‘1
'1...’2k~ 1
с k = 1,2,..., [q/2] (если q = 2, то iti пропорционально dqn a dq22 ~ ^12 ^dq2i)-
Определяемые этими формами характеристические классы слоения $ являются в
действительности полиномами от классов Понтрягина расслоения v($-), и классы
Понтрягина являются полиномами от этих классов. (Это сразу видно из черн-вейлев-
ской конструкции классов Понтрягина — см. книгу Дж. Шварца.)Сопоставляя это с
тем фактом, что мономы f, л ... л /rc r>q равны 0, мы приходим к следующей
теореме Ботта [59]:
Теорема. Полиномы от вещественных классов Понтрягина нормального рас-
слоения слоения коразмерности q, имеющие степень > 2q, тривиальны.
(Для целочисленных классов Понтрягина подобное утверждение неверно: см.
[60].)
Теорема Ботта доставляет содержательное топологическое препятствие к интег-
рируемости: она дает необходимое условие для того, чтобы подрасслоение (более,
чем половинной размерности) касательного расслоения многообразия было гомо-
топно (в классе подрасслоений) касательному расслоению некоторого слоения. Эта
теорема может быть слегка усилена: если pi,.. ., рг — полиномы от вещественных
классов Понтрягина расслоения, нормального слоению коразмерности ?, и dim р, +
+ dim pi > 2q при 1 = 2,...,?, то произведение Масси {pi,..., рг) (см. п. 5 § 25)
определено и тривиально: действительно, произведения j cr>q не прос-
то гомологичны нулю (чего было бы уже достаточно для теоремы Ботта), а в точ-
ности равняются нулю.
4. Отступление: алгебры Ли и их когомологии. Алгебра Ли — это векторное прост-
ранство над каким-нибудь полем — у нас это всегда будет поле R вещественных чи-
сел, — наделенное билинейной операцией a, *+ [«, 0] с двумя следующими свой-
ствами:
[«, 0] = - [0,«] (антикоммутативность)
[[«,/?],?] + [[(3, ?],«] + [[?, «],/?] =0 (тождество Якоби).
Простейший пример: пространство всех вещественных nXn-матриц с операцией
[А, В] = АВ - ВА (коммутатор). Основной (в действительности универсальный)
источник примеров конечномерных алгебр Ли — конструкция Ли, относящая груп-
480
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
пе Ли (гладкому многообразию, наделенному групповой структурой с гладкими
групповыми операциями) G алгебру Ли g: касательное пространство Те G в едини-
це е G G со следующей операцией. Если R -> G, ф: R -> (7 — гладкие кривые с
<р (0) = ф (0) = е и <р (0), ф (0) 6 Те G =g — векторы скорости, то
1Ф(о),ф(о)] ={ ^ш^Мх/О^ФеЛ)’1) ;=0.
Если, скажем, G = GL(n, R), то g есть описанная выше алгебра Ли п Хп-матриц.
Среди бесконечномерных алгебр Ли для нас интерес представляют алгебры Ли век-
торных полей, особенно — алгебра Ли W„ формальных векторных полей в R". Ее
элементы имеют вид
« Э
S fi(xlt. .. ,х„)—,
/= I дх,
где ft(xi..х„) — формальные степенные ряды, коммутатор определяется фор-
мулой
По определению, q-мерные коцепи алгебры Ли g — зто кососимметрические ве-
щественные «/-линейные формы на g:
A’g^R;
если dimg = °°, то обычно предполагается, что в g имеется топология и коцепи не-
прерывны; в частности, в W„ имеется топология: степенные ряды fm сходятся к
степенному ряду /, если сходимость имеет место для всех коэффициентов. Прост-
ранство «/-мерных коцепей алгебры Ли g обозначается через С4 (g). Формула
• • • ,gq + l) =
= S (- l)s+,_1 a([gs,gf] ,gj.........gS- - gt - gq+l)
(aec’(g); gi,.. .,gq+i eg)
определяет дифференциал d: Cq (g) -» Cq+l (g).
У п p а ж н e н и e. 20. Проверьте, что d2 = 0.
Возникают когомологии //4(g), называемые когомологиями алгебры Ли g.
Упражнения. 21. Найдите когомологии n-мерной абелевой алгебры Ли,
т.е. алгебры Hng с dimg = п и [«,= О.
22. Докажите, что матрицы со следом 0 составляют подалгебру алгебры Ли
gl (п, R) всех п X л-матриц. (Эта алгебра отвечает группе Ли SL(n, R) и в соответст-
вии с этим обозначается через s/(n, R). Найдите когомологии алгебры Лих/(2, R).
(Ответ: Hq (sl(2, R)) s R при </ = 0, 3 и H4 (sl(2, R)) =0при остальных q.) Заме-
чание. Это вычисление фактически проделывалось нами выше, в п. 2В — см. упраж-
неие 14. Дело в том, что комплекс коцепей алгебры Ли g, отвечающей группе Ли G,
не отличается от комплекса правоинвариантных дифференциальных форм группы G;
это — одна из исходных мотивировок определения когомологий алгебр Ли.
23. Вычислите Н* (IVj). Указани е.Обозначим символом у"' ... у™ч «/-линей-
ный функционал на W„, действующий по формуле
/ d d\
IS almxm —,.. .,T,aqmxm mJ ..aqm.
\m dx m dxj q
§ 52. КОГОМОЛОГИИ И СЛОЕНИЯ
481
Это обозначение позволяет отождествить Сч (Wx) с пространством кососимметри-
ческих многочленов от q переменных. Дифференциал <Г. Сч(И^) Сч+1 (И^) за-
писывается при таком отождествлении формулой
dP(yl,...,yq+i) =
= S Ot-ys)P(ys+^t>yi,... j-, ...yt- ,yq+i>-
1
Из этой формулы видно, что дифференциал переводит однородные многочлены в
однородные, увеличивая их степени на 1; поэтому однородные составляющие ко-
цикла снова являются коциклами. Пусть Р — однородный коцикл степени т. По-
ложим
Л01. ,УЧ-1) = Р'Ч(У1, • .Jq-i.O)
(P's есть производная многочлена Р по s-му переменному). Дифференцируя равен-
ство 0 = dP 01...yq+i) по jg+i и полагая затем yq+i = 0, мы приходим (ввиду
формулы Эйлера %sysP's =тР) к равенству
0 = dR-(-l)q(q-m)P,
которое показывает, что если q # т, то коцикл Р когомологичен 0. Остается рас-
смотреть кососимметрические однородные многочлены, у которых степень равна
числу переменных, но таких многочленов почти нет. Замечание. Изоморфизм
H*(sl(2, R)) = H*(WX) не вполне случаен: он устанавливается вложением
d d d
si (2, R) -*Wt, образ которого натянут на векторные поля-, х— , х —.
dx dx dx
Когомологии алгебры Ли векторных полей (не только формальных и не только
с коэффициентами в R) вычислялись в конце 60-х и начале 70-хгодов И.М. Гель-
фандом и Д.Б. Фуксом и в последующие годы - многими авторами (см. список
литературы в книге Фукса ’’Когомологии бесконечномерных алгебр Ли”). Мы при-
ведем здесь один из ключевых результатов Гельфанда и Фукса [61].
Обозначим через Хп прообраз 2л-мерного остова (стандартного клеточного раз-
биения) комплексного грассманиана CG (7V, л), N > п в расслоении С V(N, п) -*
-*CG (N, л) (со слоем U(л) — см. п. 9 § 1). Например, Хх =S3.
Теорема. H*(Wn) = H*(Xn\R).
Когомологии пространства Хп вычисляются стандартными методами алгебра-
ической топологии (см. гл. 3). Приведем некоторые результаты этого вычисления.
Следствие. (1) dini^*(lV„)<°°;
(2) Нч (Wn) = 0 при 0 < q < 2п + 1 и при q>n(n + 2);
R при q = 0, 3,
О при остальных q~,
(3) Hq(Wx) =
R ф R при q = 5,8,
(4)Z^(JV2) = R при q = 0,7,
0 при остальных q-,
(5) dim//2n+,(JV„) = р(л + 1)- 1, dim^n<,, + 2)(M/„) = р(л)
(р обозначает число разбиений в сумму натуральных слагаемых).
482
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
5. Когомологии алгебры Ли Wq и характеристические классы оснащенных
слоений коразмерности q.
А. g-структуры и их характеристические классы. Пусть g — алгебра Ли и X —
гладкое многообразие. Дифференциальная (/-форма на I со значениями в g — это
гладкое семейство линейных отображений {АчТхХ -> g | х 6 X}; пространство та-
ких отображений обозначается через Slq(X‘ g). Обычным образом определяется
внешний дифференциал d: Slq(X; g) ->S2q + 1(X; g). (Ни одно из этих определений
не использует структуры алгебры Ли в g.) Говорят, что дифференциальная 1-форма
со на X со значениями в g удовлетворяет условию Маурера — Картана, если для лю-
бых касательных векторов v, w ё ТхХ
dco(v, w) = — [со(п), co(vv)];
сокращенно это условие записывается так: dto +у [со, со] =0. Дифференциальные
1-формы со значениями в g, удовлетворяющие условию Маурера — Картана, назы-
вают также g-структурами.
Упражнения. 24. Пусть g — алгебра Ли, отвечающая группе Ли G, и пусть
/: X * G — гладкое отображение. Определим 1-форму на X со значениями в g как
семейство отображений
ТхХ Tf(x}G ----------> TeG = g,
где вторая стрелка обозначает правый сдвиг. Докажите, что зта форма удовлетворяет
условию Маурера - Картана.
25. Пусть g обозначает то же, что в упражнении 24. Если X односвязно, то всякая
g-структура на X получается конструкцией этого упражнения. Как обстоит дело
в неодносвязном случае?
Для g-структуры со на X определим отображение
Cq(g) ----► П’(Х)
формулой
[с<о(«)](«1, •••.^) = ...
Упражнение 26. Докажите, что сш перестановочно с дифференциалом (име-
ется в виду внешний дифференциал в дифференциальных формах и определенный
выше дифференциал в коцепях алгебры Ли). (Желательно доказать это утвержде-
ние в такой форме: условие Маурера — Картана — зто в точности то, что нужно для
перестановочности отображения с дифференциалом.)
Отображение сш индуцирует отображение в когомологиях:
Hq(g) ----► Hq{X- R).
Если задан класс 0 ё Hq(g), то всякой g-структуре со на У будет соответство-
вать класс c^jP ё Н q(X-, R). Соответствие со <-> с ш ((3) называется ((/-мерным веще-
ственным) характеристическим классом g-структур. Это название оправдывается
следующим свойством нашего соответствия: если /: Y ->Х — гладкое отображение и
/*со — индуцированная g-структура на Y (читатель должен сам понять, что это
§ 52. КОГОМОЛОГИИ И СЛОЕНИЯ
483
значит), то (очевидно)
Г«(Ю) = yj/3).
Упражнение 27. Пусть X — одномерная коммутативная алгебра Ли. Дока-
жите, что Л-структура на X - это просто замкнутая дифференциальная 1-форма
на X, и соответствие, относящее такой форме ее когомологический класс, представ-
ляет собой (по существу, единственный) характеристический класс g-структур.
В. Оснащенные слоения коразмерности q и W ч-структуры. Пусть S' — слоение
коразмерности q на многообразии X, р: N -* X — его нормальное расслоение.
Обычным образом определяется экспоненциальное отображение е: N * X, которое
отображает р~1 (х) на трансверсальную площадку к слоению S^ в точке х (рис. 254).
Конечно, такое отображение определяется не единственным образом, но любые два
экспоненциальных отображения гомотопны в классе экспоненциальных отображений,
во всяком случае, в окрестности нулевого сечения в N. Если слоение 3? оснащено, то
N = X X R4, и сужение экспоненциального отображения на X X Р’ есть отображение
X X D4 *X с двумя свойствами: (i) точка (х, 0), где 0 — центр шара, переходит
в точку х; (ii) сужение отображения нах XD4 трансверсально слоению. Для доста-
точно близких точек Xi, х2 G X слоение определяет частичное отображение, даже час-
тичный диффеоморфизм,Xi X Р’ ->х2 X D4, т.е. Р’ -+Dq (рис. 255). Если v G ТхХ—
касательный вектор и у: R *X — гладкая кривая с 7 (0) = х, у (0) = 0, то мы полу-
чаем гладкое семейство частичных диффеоморфизмов <pt: Р’ -’•Р'7, <р0 = id, которое
определяет гладкое векторное поле {(<pty)j = 0 | у 6 Р’ } в D4. Относя вектору и
оо-струю этого векторного поля, мы получаем на X дифференциальную 1-форму со
значениями в Wq.
Упражнения. 28. Проверьте корректность этого определения.
29. Докажите, что построенная 1-я форма удовлетворяет условию Маурера — Кар-
тана, т.е. является ^-структурой.
Можно показать, что возникающий гомоморфизм
---> Я‘(У; R)
не зависит от произвола конструкции и, таким образом, доставляет характеристи-
Рис. 254
Рис. 255
484
ДОПОЛНЕНИЕ. ГОМОЛОГИИ В ВАРИАЦИОННЫХ ЗАДАЧАХ
ческие классы оснащенных слоений. Более того, оказывается, что эта конструкция
дает в точности те же классы, что конструкция, изложенная в п. 3. (В действитель-
ности приведенная выше теорема Гельфанда — Фукса иногда формулируется так:
когомологии алгебры Ли Wn совпадают с когомологиями усеченной алгебры Вейля
алгебры Ли gl (п, R) — см. п. 3.)
Чтобы прояснить связь между Wq-структурами и оснащенными слоениями кораз-
мерности q, приведем обратную конструкцию.
Упражнение 30. Пусть w есть ^-структура на гладком многообразии X.
Пусть для н G ТхХ
д Э
w(h) = 2 <о,(н)— + 2 + ...
i ij Ьх/
Покажите, что если дифференциальные формы ыь ..., w, 6 Я* (У) линейно незави-
симы в каждой точке, то они удовлетворяют условию интегрируемости, и опреде-
ляемое ими оснащенное слоение доставляет, прн применении к нему предыдущей
конструкции, исходную И^-структуру.
Характеристические классы неоснащенных слоений могут быть описаны аналогич-
ным образом, но требуют привлечения так называемых относительных когомологий
алгебр Ли.
Упомянем еще, что для многих алгебр Ли g существует геометрическая интерпре-
тация g -структур как тех или иных разновидностей слоений, и это позволяет рас-
сматривать их когомологии как характеристические классы. Подробности см.
в § ЗЛ книги Д.Б.Фукса ’’Когомологии бесконечномерных алгебр Ли”.
СПИСОК ЛИТЕРАТУРЫ К ДОПОЛНЕНИЮ
1. Милнор Дж. Теория Морса. - М.: Мир, 1965.
2. Федерер Г. Геометрическая теория меры. - М.: Наука, 1987.
3. Morrey Ch. В. Multiple integrals in the calculus of variations. — Berlin: Springer-Verlag, 1966.
4. Redo T. On the problem of Plateau. - Berlin: Springer Verlag, 1933. - (Ergebnisse der Mathematik
und ihrer Grenzgebiete).
5. Reifenberg E.R. Solution of Plateau problem for m-dimensional surfaces of varying topological type//
Acta Math. - 1960. - V. 104, № 1. - P. 1 -92.
6. Douglas J. Minimal surfaces of general topological structure // J. Math. Phys. — 1936. - V. 15. -
P. 105-123.
7. Douglas J. The most general form of the problem of Plateau // Proc. Nat. Acad. Sci. USA. - 1938. -
V. 24.-P. 360-364.
8. Almgren F. J. Existence and regularity almost everywhere of solutions to elliptic variational problem
among surfaces of varying topological type and singularity structure // Ann. Math. Ser. 2. - 1968. —
V. 87,№2. -P. 321-391.
9. Lawson H.B., Osserman R. Non-existence, non-uniqueness and irregularity of solutions to the minimal
surface system // Acta Math. - 1977. - V. 139,№ 1.
10. Lawson H.B. The equivariant Plateau problem and interior regularity // Trans. Amer. Math. Soc. -
1972. - V. 173. - P. 231 -249.
11. Nitsche J.C. Vorlesungen uber Minimalflachen. - Berlin: Springcr-Vcrlag, 1975. - (Die Grundlehren
der Mathematischen Wissenschaften in Einzeldarstellungen. Bd 199).
12. Osserman R. Global properties of minimal surfaces in E3 and En // Ann. Math. - 1964. - V. 80,
№2. — P. 340-364.
13. Hildebrandt S. Boundary behavior of minimal surfaces// Arch. Rational Meeh, and Anal. - 1969. -
V. 35,№1.-P. 47-82.
14. Hildebrandt S., Kaul H. Two-dimensional variational problems with obstructions, and Plateau’s
problem for Я-surfaces in a Riemannian manifold // Comm. Pure AppL Math. - 1972. - V. 25,
№2.-P. 187-223.
15. Фоменко A. T. Вариационные методы в топологии. - М.: Наука, 1982.
16. Фоменко А.Т. Минимальные компакты в римановых многообразиях и гипотеза Райфенбер-
га // Изв. АН СССР. Математика. - 1972. - Т. 36, № 5. - С. 1049-1080.
17. Фоменко А.Т. Многомерная задача Плато в римановых многообразиях // Мат. сб. - 1972. -
Т. 89, №3. - С. 475-520.
18. Фоменко А.Т. Топологические вариационные задачи. - М.: Изд-во МГУ, 1984.
19. Фоменко А.Т. О минимальных объемах топологических глобально минимальных поверхно-
стей в кобордизмах // Изв. АН СССР. Математика. - 1981. —Т. 45,№ 1. - С. 187-212.
20. Фоменко А.Т. Многомерные вариационные задачи в топологии экстремалей // УМН. - 1981.-
Т. 36, №6. - С. 105-135.
21. Дао Чонг Тхи. Мультиварифолды и классические многомерные задачи Плато // Изв.
АН СССР. Математика. - 1980. - Т. 44, № 5. - С. 1031 - 1065.
22. Дао Чонг Тхи. Мультиварифолды и задачи минимизации функционалов типа многомерного
объема // ДАН СССР. - 1984. - Т. 276, № 5. - С. 1042- 1045.
23. Дао Чонг Тхи. Изоперимстричсскис неравенства для мультиварифолдов // Изв. АН СССР.
Математика. - 1984. - Т. 48, № 6.
24. Fomenko А.Т Symmetries of soap films // Comp. & Math, with AppL — 1986. - V. 12B,№3/4. —
P. 825-834.
486
СПИСОК ЛИТЕРАТУРЫ К ДОПОЛНЕНИЮ
25. Fomenko А.Т. On certain properties of extremals in variational problems. - Berlin: Springer-Verlag,
1984. - P. 209-217. - (Leet. Notes in Math. V. 1108).
26. Ле Хонг Ван. Рост двумерной минимальной поверхности // УМН. - 1985. - Т. 40, № 3. -
С. 209-210.
21. Фукс Д.Б. О характеристических классах Маслова-Арнольда // ДАН СССР.- 1968. -
Т. 178, №2. - С. 303-306.
28. Фоменко Т.Н. Об эффективном построении ретракции некоторых пространств на сферу //
Новое в глобальном анализе: Анализ на многообразиях и дифференциальные уравнения. -
Воронеж: Изд-во Воронеж, ун-та, 1986. - С. 164—173.
29. Ле Хонг Ван. Абсолютно минимальные поверхности и калибровки на орбитах присоединенно-
го представления классических групп Ли // ДАН СССР. - 1987.
30. Ле Хонг Ван, Фоменко А.Т. Лагранжевы многообразия и индекс Маслова в теории минималь-
ных поверхностей//ДАН СССР. — 1987.
31. Harvey R., Lawson Н.В. Calibrated foliations (foliations and mass-minimizing currents) // Amer. J.
Math. - 1982. — V. 104, № 3. — P. 607—633.
32. Плужников А. И. Задача минимизации функционала энергии / ИПУ АН СССР. - Деп. в
ВИНИТИ. - 1984, № 5584-84. - 40 с.
33. Плужников А.И. О минимумах функционала Дирихле // ДАН СССР. - 1986. - Т. 290, № 2. -
С. 289-293.
34. Фоменко А.Т. Теория Морса интегрируемых гамильтоновых систем // ДАН СССР. - 1986. -
Т. 287, №5.-С. 1071-1075.
35. Фоменко А.Т. Топология поверхностей постоянной энергии интегрируемых гамильтоновых
систем и препятствия к интегрируемости // Изв. АН СССР. Математика. - 1986. - Т. 50,
№6.-С. 1276-1230.
36. Фоменко А.Т., Цишанг X. О топологии трехмерных многообразий, возникающих в гамильто-
новой механике // ДАН СССР. - 1987. - Т. 294, № 2. - С. 283 - 287.
37. Трофимов В.В., Фоменко А.Т. Интегрируемость по Лиувиллю гамильтоновых систем на ал-
гебрах Ли // УМН. - 1984. - Т. 39, № 2. - С. 3 - 56.
38. Ошемков А.А. Боттовские интегралы некоторых интегрируемых гамильтоновых систем //
Геометрия, дифференциальные уравнения и механика. - М.: Изд-во МГУ, 1986. -
С. 115-117.
39. Матвеев С.В., Бурмистрова А.Б. Структура S-функций на ориентируемых 3-многообразиях //
Тезисы XI Всесоюзной школы по теории операторов в функциональных пространствах. -
Челябинск, 1986. - Т. 1. - С. 70.
40. Матвеев С.В., Фоменко А.Т., Шарко В.В. Круглые функции Морса и изоэнергетические поверх-
ности интегрируемых гамильтоновых систем // Мат. сб. - 1988. - Т. 52, № 2. - С. 378-
407.
41. Waldhausen F. Eine Klasse von 3-dimensional Mannigfaltigkeiten, I // Invent. Math. - 1967. -V. 3,
№4.-P. 308-333.
42. Orlik P., Vogt E., Zieschang H. Zur Topologie gefaserter dreidimensional Mannigfaltigkeiten // Topo-
logy. - 1967. - V. 6, № 1. - P. 49-65.
43. Miyoshi S. Foliated round surgery of codimension-one foliated manifolds // Topology. - 1982. -
V. 21,№3. -P. 245-262.
44. Morgan J. Non-singular Morse—Smale flows on 3-dimensional manifolds // Topology. — 1979. -
V. 18,№1. -P.41-54.
45. Asimov D. Round handles and non-singular Morse-Smale flows // Ann. Math. - 1975. - V. 102,
№1. -P. 41-54.
46. Thurston W. Existence of codimension-one foliations // Ann. Math. - 1976. - V. 104, № 2. -
P. 249-268.
47. Фоменко A.T., Цишанг X. О типичных топологических свойствах интегрируемых гамильтоно-
вых систем // Изв. АН СССР. Математика. - 1988. - Т. 52, № 2. - С. 300-320.
48. Reeb G. Sur certaines proprietes topologiques des variete's feuilletees. - Paris: Hermann, 1952. -
(Actualites Sci. Indust. № 1183).
49. Новиков С.П. Топология слоений // Тр. Моск. мат. о-ва. - 1965. - Т. 14. - С. 249-278.
50. Тамура И. Топология слоений. - М.: Мир, 1979.
51. Haefliger A. Sur les feuilletages analytiques // C.r. Acad. sci. - 1956. - V. 242, № 5. - P. 2908-
2910.
52. Lawson H.B. Foliations // BuU Amer. Math. Soc. - 1974. - V. 80, № 3. - P. 369-418.
53. Lawson H.B. Codimension one foliations on spheres // Ann. Math. — 1971. — V. 94, №3. - P.494-
503.
54. КартанА. Дифференциальное исчисление. Дифференциальные формы. — М.: Мир, 1971.
СПИСОК ЛИТЕРАТУРЫ К ДОПОЛНЕНИЮ
487
55. Godbillon С., Vey J. Un invariant des feuilletages de codimension un // C.r.Acad. sci. - 1971. -
V. 273, №2. -P. 92-95.
56. Mizutani T., Morita S., Tsuboi T The Godbillon — Vey classes of codimension one foliations which
are almost without holonomy // Ann. Math. - 1981. -V. 113. — P. 515—527.
57. Thurston W. Non-cobordant foliations of SP // Bull. Amer. Math. Soc. - 1972. - V. 78, №4.-
P. 511-514.
58. Гельфанд ИМ., Фейгин Б.Л., ФуксД.Б. Когомологии алгебры Ли формальных векторных по-
лей с коэффициентами в сопряженном с ней пространстве и вариации характеристических
классов слоений // Функц. анал. н его прил. - 1974. - Т. 8, № 2. - С. 13- 29.
59. Bott R. On topological obstruction to integrability // Actes Congr. Int. Mat. 1970. - Paris, 1971. -
V. l.-P. 27-36.
60. Bott R., Heitsh J. A remark on the integral cohomology of Brq // Topology. - 1972. - V. 11,
№2. — P. 141-146.
61. Гельфанд ИМ., Фукс Д.Б. Когомологии алгебры Ли формальных векторных полей // Изв.
АН СССР. Математика. - 1970. - Т. 34, № 2. - С. 322-337.
62. Браилов А.В., Фоменко А.Т. Топология интегральных многообразий вполне интегрируемых
гамильтоновых систем // Мат. сб. - 1987. - Т. 133, № 3. - С. 375-385.
63. Матвеев С.В., Фоменко А.Т. Изоэнергетические поверхности гамильтоновых систем, пере-
числение трехмерных многообразий в порядке возрастания их сложности и вычисление объе-
мов замкнутых гиперболических многообразий // УМН. - 1988. - Т. 43, № 1. - С 5-22.
64. Morgan F. A smooth curve in R* bounding a continuum of minimal surfaces // Arch. Rational Meeh.
AnaL — 1981.— V. 71, №2. — P. 193-197.
65.1>o Camo M., Peng C.K. The stable minimal surfaces in R* are plane // Bull. Amer. Math. Soc.
1979. - V. 1, №6. - P. 903-906.
66. Beeson M.J., Tromba A.J. The cusp catastrophe of Tome in the bifurcation of minimal surfaces
// Manusc. Math. - 1984. - V. 46. - P. 273-308.
ПРИЛОЖЕНИЕ. О РИСУНКАХ
Рисунки, помещенные в книге, разбиваются на две группы. Первая состоит из
чертежей, иллюстрирующих конкретные конструкции, описываемые в тексте. Вто-
рая группа, состоящая из 32 рисунков (занумерованных римскими цифрами),
иллюстрирует более сложные понятия, иногда лишь кратко отраженные в тек-
сте книги.
На рис. I представлена стандартная двумерная сфера — многообразие, играющее
важную роль во многих разделах книги. На рис. II показана так называемая ’’рога-
тая сфера” Александера— вложение сферы S2 в R3, не являющееся локально плоским
и разбивающее R3 на неодносвязные области. В этом — существенное отличие ’’рога-
той сферы” от обьиной, разбивающей R3 на односвязные области. На рис. III пред-
ставлены двумерные поверхности: сфера с двумя ручками (т.н. крендель), листы
Мёбиуса и проективные плоскости. Листы Мёбиуса представлены в виде ’’скрещен-
ных колпаков”. Они же показаны на рис. IV, где можно увидеть также сферу с тремя
отождествленными точками. На рис. V условно изображено вложение клеточного
пространства в евклидово пространство. На рис. VI изображен полиэдр, на
рис. VII — линзовое пространство (линза). Известно, что двумерную сферу мож-
но ’’вывернуть” в R3, т.е. построить непрерывную последовательность ее гладких
погружений (самопересечения разрешаются), начинающуюся на стандартном вложе-
нии сферы, а кончающуюся на вложении, при котором прежняя внутренность сферы
оказывается снаружи. На рис. VIII показан момент деформации сферы, отвечаю-
щий значению параметра t = 1/2. Более подробно этот процесс показан на рис. XXVI,
где изображено девять последовательных положений сферы. Девятое положение наибо-
лее симметрично, и в этот момент сфера оказывается в окрестности погружения проек-
тивной плоскости в R3 (т.е. около так называемой поверхности Боя). В этом поло-
жении сфера выворачивается, после чего процесс повторяется в обратной после-
довательности — от девятого положения до первого. На рис. IX условно изображено
разбиение сферы S3 на два оолнотория. Эта картина полезна при изображении струк-
туры расслоения Хопфа. Полнотории склеиваются так, что их граничные торы ото-
ждествляются с переменой местами параллели и меридиана. На рис. X показано дей-
ствие фундаментальной группы на высших гомотопических группах: к каждому
многомерному сфероиду приклеивается тонкая трубка, идущая вдоль одномерной
петли (элемент фундаментальной группы). В более условной форме это действие
см. на рис. XI. На рис. XII изображен фрагмент унитарной периодичности Ботта.
Середины геодезических, соединяющих две точки на унитарной группе, образуют
многообразие Грассмана. На рис. XIII условно изображены вращения стандартной
сферы. Стандартная метрика на сфере выделяется из множества всех других метрик
тем, что обладает максимально возможной группой изометрий. Рис. XIV изображает
расслоение. Вертикальные фигуры — слои, горизонтальная полоса — база расслоения.
ПРИЛОЖЕНИЕ. О РИСУНКАХ
489
На рис. XV представлено локально компактное хаусдорфово пространство, не являю-
щееся локально гомологически связны / (в смысле Чеха) в размерности 1. Это оз-
начает, что любая открытая окрестность концевой точки (на переднем плане рисун-
ка) имеет нетривиальную группу одномерных гомологий. Разложение этого прост-
ранства на составные элементы (’’ракушки”) показано на рис. XVII. На рис. XVI
условно изображена одна из главных идей доказательства теоремы о клеточной ап-
проксимации: образ симплекса при непрерывном отображении ’’выдавливается” в
остов той же размерности путем проектирования из некоторой внутренней точки,
которая не принадлежала образу симплекса. На рис. XVII кроме ’’ракушек” — обра-
зующих пространства с рис. XV, присутствуют: соленоид (первый шаг в построении),
ожерелье Антуана (также первый шаг в построении), пример Адамса. Ожерелье
Антуана получается путем пересечения показанной на рисунке последовательности
полноторий. Оно является вполне несвязным компактным совершенным метричес-
ким пространством, а потому гомеоморфно канторову множеству. Его дополнение
в R3 неодносвязно. Соленоид показан более подробно на рис. XXVIII. Для его по-
строения берется полноторие, внутрь которого вкладывается второе полноторие,
два раза намотанное вдоль оси первого. Внутрь второго полнотория точно таким же
способом вкладывается третье полноторие. Процесс повторяется до бесконечности.
Получающееся пространство называется 2-адическим соленоидом. Топологический
пример Адамса получается взятием связной суммы обычного листа Мёбиуса с трой-
ным листом Мёбиуса, который можно задать в трехмерном пространстве в цилиндри-
ческих координатах формулами: г = 1 + et cos и; в = Зи; z = et sin и; е = const, 0 <
< t < 1. Получающийся клеточный комплекс не является многообразием, так как
при t = 0 получаем сингулярную окружность пересечения трех листов под углами
2тг/3. Несмотря на то, что границей комплекса Адамса является окружность, комп-
лекс ретрагируется на эту окружность. Пример имеет большое иллюстративное
значение, например, в теории минимальных поверхностей. Комплекс Адамса изо-
бражает минимальную поверхность, которая не является гомологической G-по-
верхностью с границей окружность ни для какой группы коэффициентов G.
Рисунки XVIII, XIX, XX, XXI, XXII, XXIII, XXIV, XXV допускают истолкование
в терминах спектральных последовательностей. Они изображают различные кон-
струкции, присутствующие в тексте книги. На рис. XXVII показано разбиение дву-
мерной поверхности в сумму треугольников и квадратов. Ясно, что чем больше кри-
визна поверхности (около некоторой точки), тем более мелким должно быть соот-
ветствующее разбиение. Напротив, области малой кривизны допускают покрытие
большими симплексами. На рис. XXIX изображена деформация алгебраической
(римановой) поверхности в комплексном пространстве C2(z, w). Поверхность
гомеоморфна (после проективизации) обычному тору. На рисунке видны две точки,
играющие роль кратных точек. При слиянии корней полинома соответствующие
трубки поверхности ’’перетягиваются” и два листа поверхности начинают касаться
друг друга. Тор представлен в виде двух сфер, соединенных двумя трубками. При
раздувании верхней сферы, нижняя, наоборот, сжимается.
На рисунках XXX, XXXI, XXXII, XXXIII изображены перестройки торов
Лиувилля (см. Дополнение). На рис. XXX изображено многообразие с краем —
три тора (в книге обозначено как N2 X S1). Один тор (внешний) перестра-
ивается в сумму двух торов. На рис. XXXI изображено скрученное седло N2 X
X S1. Здесь тор перестраивается в jrop путем двукратной намотки. На рис. XXXII
показан скрученный цилиндр К2 О1. Здесь тор перестраивается в двумерную
бутылку Клейна. При этом тор реализован как граница трубчатой окрестности
бутылки Клейна, стандартно погруженной в терхмерное пространство. Стрелка-
ми показано стягивание тора на бутылку Клейна.
список книг по топологии
1. Адамс Дж. Лекции по группам Ли. - М.: Наука, 1979.
2. Адамс Дж. Бесконечнократные пространства петель. - М.: Мир, 1982.
3. Александров П.С. Комбинаторная топология. - М.; Л.: ОГИЗ, 1947.
4. Александров П.С. Введение в общую теорию множеств и функций. - М.: Л.: ОГИЗ, 1948.
5. Арнольд В.И. Математические методы классической механики. - М.: Наука, 1974.
б. Атья М. Лекции по А>геории. - М.: Мир, 1967.
7. Бишоп Р., Криттенден Р. Геометрия многообразий. — М.: Мир, 1967.
8. Бордман Дж., Фогт Р. Гомотопически инвариантные алгебраические структуры на тополо-
гических пространствах. - М.: Мир, 1977.
9. Браудер В. Перестройки односвязных многообразий. - М.: Наука, 1984.
10. Бреддн Г. Введение в теорию компактных групп преобразований. - М.: Наука, 1980.
11. Вейль А. Введение в теорию кэлеровых многообразий. - М.: ИЛ, 1961.
12. Годбийон К. Дифференциальная геометрия и аналитическая механика. - М.: Мир, 1973.
13. Гуревич В., Волмэн Г. Теория размерности. — М.: ИЛ, 1948.
14. ДольдА. Лекции по алгебраической топологии. - М.: Мир, 1976.
15. Дубровин БА., Новиков С.П., Фоменко А.Т. Современная геометрия. Методы и приложе-
ния. - М.: Наука, 1986.
16. Дубровин БА., Новиков С.П., Фоменко А.Т. Современная геометрия. Методы теории гомо-
логий. - М.: Наука, 1984.
17. ЗейфертГ., Трельфалль В. Топология. - М.; Л.: ГОНТИ, 1938.
18. Зейферт Г., Трельфалль В. Вариационное исчисление в целом. — М.: ИЛ, 1947.
19. Каруби М. A-теория. Введение. — М.: Мир, 1981.
20. Коннер П., Флойд Э. Гладкие периодические отображения. - М.: Мир, 1969.
21. Кроуэлл Р., ФоксР. Введение в теорию узлов. - М.: Мир, 1967.
22. Ленг С. Введение в теорию дифференцируемых многообразий. — М.: Мир, 1968.
23. Мадсен И., Милграм Р. Классифицирующие пространства для перестроек и кобордизмов мно-
гообразий. - М.: Мир, 1984.
24. Мандельбаум Р. Четырехмерная топология. - М.: Мир, 1981.
25. Масси У., Столлингс Д. Алгебраическая топология. Введение. - М.: Мир, 1977.
26. Масси У. Теория гомологий и когомологий. — М.: Мир, 1981.
27. Милнор Дж. Теория Морса. - М.: Мир, 1965.
28. Милнор Дж. Теорема об А-кобордизме. - М.: Мир, 1969.
29. Милнор Дж. Особые точки комплексных гиперповерхностей. - М.: Мир, 1971.
30. Милнор Дж., Уоллес А. Дифференциальная топология. Начальный курс. - М.: Мир, 1972.
31. Милнор Дж., Сташеф Дж. Характеристические классы. — М.: Мир, 1979.
32. Мищенко А.С., Фоменко А.Т. Курс дифференциальной геометрии и топологии. — М.: Изд-во
МГУ, 1980.
33. Мищенко А.С. Векторные расслоения и их применения. - М.: Наука, 1984.
34. Мошер Р., Тангора М. Когомологические операции и их приложения в теории гомотопии. -
М.: Мир, 1970.
35. Новиков С.П., Мищенко А.С., Соловьев Ю.П., Фоменко А.Т. Задачи по геометрии. — М.: Изд-
во МГУ, 1978.
36. Номидзу К. Группы Ли и дифференциальная геометрия. - М.: ИЛ, 1960.
37. ПалеР. Семинар по теореме Атьи - Зингера об индексе. - М.: Мир, 1970.
38. Понтрягин Л.С. Непрерывные группы. - М. : Наука, 1984.
39. Понтрягин Л.С. Основы комбинаторной топологии. - М.: Наука, 1986.
491
СЛИСОК КНИГ ПО ТОПОЛОГИИ
40. Понтрягин Л.С. Гладкие многообразия и их применения в теории гомотопий. - М.: Наука,
1985.
41. Постников ММ. Вариационная теория геодезических. — М.: Наука, 1965.
42. Постников ММ. Введение в теорию Морса. - М.: Наука, 1971.
43. Постников ММ. Группы и алгебры Ли. - М.: Наука, 1982.
44. Постников ММ. Лекции по алгебраической топологии. Основы теории гомотопий. - М.:
Наука, 1984.
45. Постников ММ. Лекции по алгебраической топологии. Теория гомотопий клеточных прост-
ранств. - М.: Наука, 1985.
46. де Рам Ж. Дифференцируемые многообразия. - М.: ИЛ, 1956.
47. Рохлин 2L4., Фукс Д.Б. Начальный курс топологии. Геометрические главы. - М.: Наука,
1977.
48. Рурк К, Сандерсон Б. Введение в кусочно линейную топологию. — М.: Мир, 1974.
49. СнэйтВ. Алгебраический кобордизм и A-теория. - М.: Мир, 1983.
50. Спеньер Э. Алгебраическая топология. - М.: Мир, 1971.
51. СпивакМ. Математический анализ на многообразиях. - М.: Мир, 1968.
52. Спрингер Дж. Введение в теорию римановых поверхностей. - М.: ИЛ, 1960.
53. Стинрод Н. Топология косых произведений. — М.: ИЛ, 1953.
54. Стинрод И., Эйленберг С. Основания алгебраической топологии. - М.: Физматтиз, 1958.
55. Стинрод И., Эпстейн Д. Когомологические операции. - М.: Наука, 1983.
56. Стонг Р. Заметки по теории кобордизмов. - М.: Мир, 1973.
57. СулливанД. Геометрическая топология. - М.: Мир, 1975.
58. Сян У.И. Когомологическая теория топологических групп преобразований. - М.: Мир, 1979.
59. Тамура И. Топология слоений. - М.: Мир, 1979.
60. Телеман К. Элементы топологии и дифференцируемые многообразия. - М.: Мир, 1967.
61. Toda X. Композиционные методы в теории гомотопических групп сфер. - М.: Наука, 1982.
62. Уайтхед Дж. Новейшие достижения в теории гомотопий. — М.: Мир, 1974.
63. Уитни X. Геометрическая теория интегрирования. — М.: ИЛ, 1960.
64. Фоменко А.Т. Вариационные методы в топологии. — М.: Наука, 1982.
65. Фоменко А.Т. Дифференциальная геометрия и топология. Дополнительные главы. - М.:
Изд-во МГУ, 1983.
66. Фоменко А.Т. Топологические вариационные задачи. — М.: Изд-во МГУ, 1984.
67. Фоменко А.Т. Симплектическая геометрия. Методы и приложения. - М.: Изд-во МГУ, 1988.
68. Фукс Д.Б., Фоменко А.Т., Гутенмахер В.Л. Гомотопическая топология. - М.: Изд-во МГУ,
1969.
69. ФуксД.Б. Когомологии бесконечномерных алгебр Ли. - М.: Наука, 1984.
70. Фултон У., Мак-Фёрсон Р. Категорный подход к изучению пространств с особенностями. -
М.: Мир, 1983.
71. Хирцебрух Ф. Топологические методы в алгебраической геометрии. — М.: Мир, 1973.
72. Хирш М. Дифференциальная топология. - М.: Мир, 1979.
73. Хилтон П, Уайли С. Теория гомологий. - М.: Мир, 1966.
74. Ху С.Ц. Теория гомотопий. - М.: Мир, 1964.
И.Цишанг X., Фогт Э., Колдевай Х.-Д. Поверхности и разрывные группы. - М.: Наука, 1988.
76. Чепмен Т., Лекции о ^-многообразиях. — М.: Мир, 1981.
77. Чжень Ш. Комплексные многообразия. - М., ИЛ, 1961.
78. Шафаревич И.Р. Основы алгебраической геометрии. - М.: Наука, 1972.
79. Шварц Дж. Дифференциальная геометрия и топология. - М.: Мир,-1970.
80. Расслоенные пространства и их приложения. Сб. перев. - М.: ИЛ, 1958.
81. Теория алгебр Ли. Топология группы Ли. Сб. перев. — М.: ИЛ, 1962.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аксиомы Стинрода-Эйленберга 331
Алгебра Ландвебера-Новикова 398
- Стинрода 244
- Хопфа 296
Аугментация 97
Ацикличность 99
База 70
Барицентрическая звезда 145
Барицентрическое подразделение 47
Башня Постникова 317
Бордизмы 385
Букет 25
Векторное расслоение 167
Вырезание 105
Гипотеза Адамса 350
Голономия 4 74
Гомологические последовательности 100, 101
Гомоморфизм Бокштейна 127
- Гуревича 119
- надстройки 79, 106
Гомотопическая группа 34, 63
--стабильная 84
— эквивалентность 27,76
--слабая 74, 89
Гомотопические последовательности 67, 77
Гомотопический тип 29
Гомотопия 26
— цепная 97
Группа гомологий 96
- когомологий 34,123
- узла 57
Двойственность Александера—Понтрягина 158
- Пуанкаре 146
Джойн 36
Диаграмма Юнга 40
Задача Плато 416
Изоморфизм Пуанкаре 145
— Тома 262, 361
Инвариант Адамса 359, 367
- Хопфа 137
Индекс пересечения 146
- эллиптического оператора 381
Интеграл боттовский 443
Интегрируемость по Лиувиллю 443
Категория Люстерника-Шнирельмана 30,407
Классифицирующее пространство 174
Классические поверхности 17
Клетка 35
- Шуберта 40,41
Клеточное пространство 35
--конечное 36
--локально конечное 36
--счетное 36
Кобордизмы 388
Когомологическая длина 412
— операция 238
--стабильная 240
Комплекс цепной 96
- классический 112
- клеточный 109
Конус 21
- отображения 22
Коцепь 123
Коцикл 124
Коэффициент зацепления 152
- инцидентности ПО
Коэффициентная последовательность 126
Лемма Морса 403
— о свободной точке 45
Линейная связность 24
Линза 265
Локальная система 198
Минимальная поверхность 416
Многообразие 140
— Грассмана 15
- замкнутое 143
- параллелизуемое 171
— флагов 16
полных 16
- Штифеля 16
Надстройка 21
Накрытие 57
— регулярное 61
- универсальное 61
Обратные гомоморфизмы 154
Односвязность 49
ПРЕДМЕТНЫЙ У КА ЗА ТЕЛЬ
493
Операция Адамса 342
Ориентация 109, 142, 360, 444, 469
Орицикл 472
Остов 36
Пара Борсука 43
Периодичность Ботта 229, 324
Петля 24
Плюккеровы координаты 15
Полипом Пуанкаре 405
Полиэдр 80, 103
Последовательность Вана 208
- Гизина 208
- Майсра-Виеториса 125
- Пуппе 323
- Серра 208
Препятствие 160, 161, 166
Приклеивающее отображение 38
Присоединенная группа 191
Произведение пространств 20, 37
Проективная плоскость Кэли 12
Проективное пространство вещественное 11
--кватернионное 12
--комплексное 12
Пространство гомотопически полноценное 38
- Тома 262
- убивающее 94
- Эйлснберга-Маклейна ПО
Прямой образ 154, 362
Путь 24
Различающая 161
Расслоение ассоциированное 172
- в смысле Серра 73
------- сильное 74
- виртуальное 320
- индуцированное 72
- касательное 170
- локально тривиальное 70
- нормальное 170
- простое 165,196
- спинорное 372
- Стинрода 169
- тавтологическое 167
- Хопфа 71, 167
Ретракт 29
- деформационный 29
строгий 29
Сигнатура многообразия 185
Сильная связность 143
Символ эллиптического оператора 131
Симплекс евклидов 95
- сингулярный 96
Слоение 466
-Реба 467
Слой 70
Соотношения Адема 250
Спектр 333
- Тома 385
Спектральная последовательность 189
--Адамса 278
--Адамса-Новикова 399
Спектральная последовательность Атиа-Хир
цебруха 334
---расслоения 195
Стабильная эквивалентность 168
Степень отображения 83, 143
- Стинрода 257
Сгинродов квадрат 244
Сфера 11
Сфероид 63
Тензорное произведение пространств 25
Теорема Адамса 280, 312
- Адамса-Дольда 350
- Баллета-Макдональда 256
- Беккера-Готтлиба 353
- Бореля 251
- Борсука 43
- Ботта 479
- ван Кампена 56
- Гуревича 119
- Дугласа-Радо 416
- Картана 258
- Картана-Серра 227
- Лера 190, 191
- о клеточной аппроксимации 44
- о накрывающей гомотопии 58, 71
- о поднятии отображения 61
- Пуанкаре 120
- Римана-Роха 361
— Рохлина 377
- Серра 253
- Стинрода 265
- Тома 184
- Уайтхеда 91, 122
- Фельдбау 72
- Фрейденталя 79, 86
- Хопфа 150, 165,427
- Штифеля 264
- Эйлера-Пуанкаре 112
Теоремы целочисленности 376
Тождество Якоби 85,479
Точная последовательность 68
Трансгрессия 206
Триангуляция 47
Умножение Масси 229
— Понтрягина -Самельс она 139
- Уайтхеда 84
Фильтрация 187
- Адамса 245
- мультипликативная 211
Формула Атиа-Зингера 380
- By 263
- Картана 245
- Кюннета 131
- Лефшеца 149
- универсальных коэффициентов 128
- Хирцебруха 186
Фундаментальная группа 50
Фундаментальный класс 143, 163
494 ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Функция Морса 401 Числа Бернулли 358 - Бетти 96
Характер Черна 180 Характеристический класс 166, 171 Атиа-Хирцебруха 375 Годбийона-Вея 471 Понтрягина 174 Тодда 362 Черна 174 Штифеля-Уитни 174 Эйлера 173 ^-структуры 482 Характеристическое отображение 36 Шар И Эйлерова характеристика 112 Экстраординарные теории 331 Эллиптический оператор 380 -теория 223 Ext 128, 274 //-пространство 31 Н' -пространство 31 /•функтор 346 Х-функтор 319
Цепь 96 Цикл 96 Цилиндр 21 - отображения 22 Частичная операция 313 л-простота 64 л-связность 49 Тог 128, 274 5-лемма 69 ^умножение 133 '''-умножение 139
Учебное издание
Ф о м е и к о Анатолий Тимофеевич
Фукс Дмитрий Борисович
КУРС ГОМОТОПИЧЕСКОЙ ТОПОЛОГИИ.
Заведующий редакцией НЛ. Угарова
Редактор Ф.И. Кизнер
Художественный редактор Т.Н. Кольченко
Технические редакторы С.В. Геворкян,С.Н. Баронина
Корректоры Н.П. Круглова, Т.В. Обод, Т.А. Печко
Набор осуществлен в издательстве
на наборно-печатающих автоматах
ИБ № 32388
Сдано в набор 22.08.88. Подписано к печати 14.11.88
Формат 70 X 100/16. Бумага офсетная № 1
Гарнитура Пресс-Роман. Печать офсетная
Усл.печ.л. 42,57. Усл.кр.-отт. 42,57. Уч.-изд.л. 43,08
Тираж 9250 экз. Тип.заК. .338. Цена 1 р. 70 к.
Ордена Трудового Красного Знамени
издательство ’’Наука”
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
Типография им. Котлякова
издательства ’’Финансы и статистика”
Государственного комитета СССР
по делам издательств, полиграфии и книжной торговли
195273 Ленинград, ул. Руставели 13
Anatole Fomenko,Dmitry Fuchs
A COURSE IN HOMOTOPY TOPOLOGY
Moscow, Nauka, Main Editorial Board for
Physical and Mathematical Literature, 1989
Readership: The book is addressed to University students and researchers in various domains of Ma-
thematics and Physics.
From the book’s review: ”... The book presents an unique course in homotopy topology. It contains
everything that may be needed for reconstructing the proofs and in the same time includes nothing
unnecessary. In uses methodical achievements of the almost twenty years’ teaching experience.”
Professor O.Ya. VIRO (Leningrad)
Summary: The book contains an account on all methods and results of homotopy topology whose
value for the whole mathematics is indisputable. It includes both elementary and sophisticated
chapters of the subject.
Contents: The most important topological spaces. Homotopy. Homology. The spectral sequence of a
fibration. Cohomology operations. The Adams spectral sequence. А-theory and other extraor-
dinary cohomology theories. Homology in variational problems.
Authors: Anatole Timofeevich Fomenko is Professor of Mathematics at the Moscow State University,
D. Sci. in Mathematics, the author of numerous papers in geometry, topology, classical mecha-
nics and computer science.
Dmitry Borisovich Fuchs is Leading Scientific Associate at the Moscow State University, D.
Sci in Mathematics, the author of numerous papers in topology, homological algebra, and rep-
resentations theory.
II
!^ТГГПТГГПТПТПТГПТТПТШ
VI
VIII
IX
XII
XIII
XV
XVIII
XX
XXI
XXII
Tl li I I I IIJJX
i / / 4 4-
тш
плтп
fining
шнпм
WUHJfT)
тшшт
mini
«пмо
WWWff
wwwr
wwww
SSWWWWW
58й8^^1ЖЕ5Е!.Ш//27///ЯИЙ
^88888®^КЯЯЕЕЙЙМ
jW.LaZC p L- - "и;г ^rssssxs^br.^-.
i^-. aiLL^SC'’ Г 1 '- Г7^7ХХХХ^ЖХЖ^^
XXVII
XXVIII
шш»;
IIXXX
1