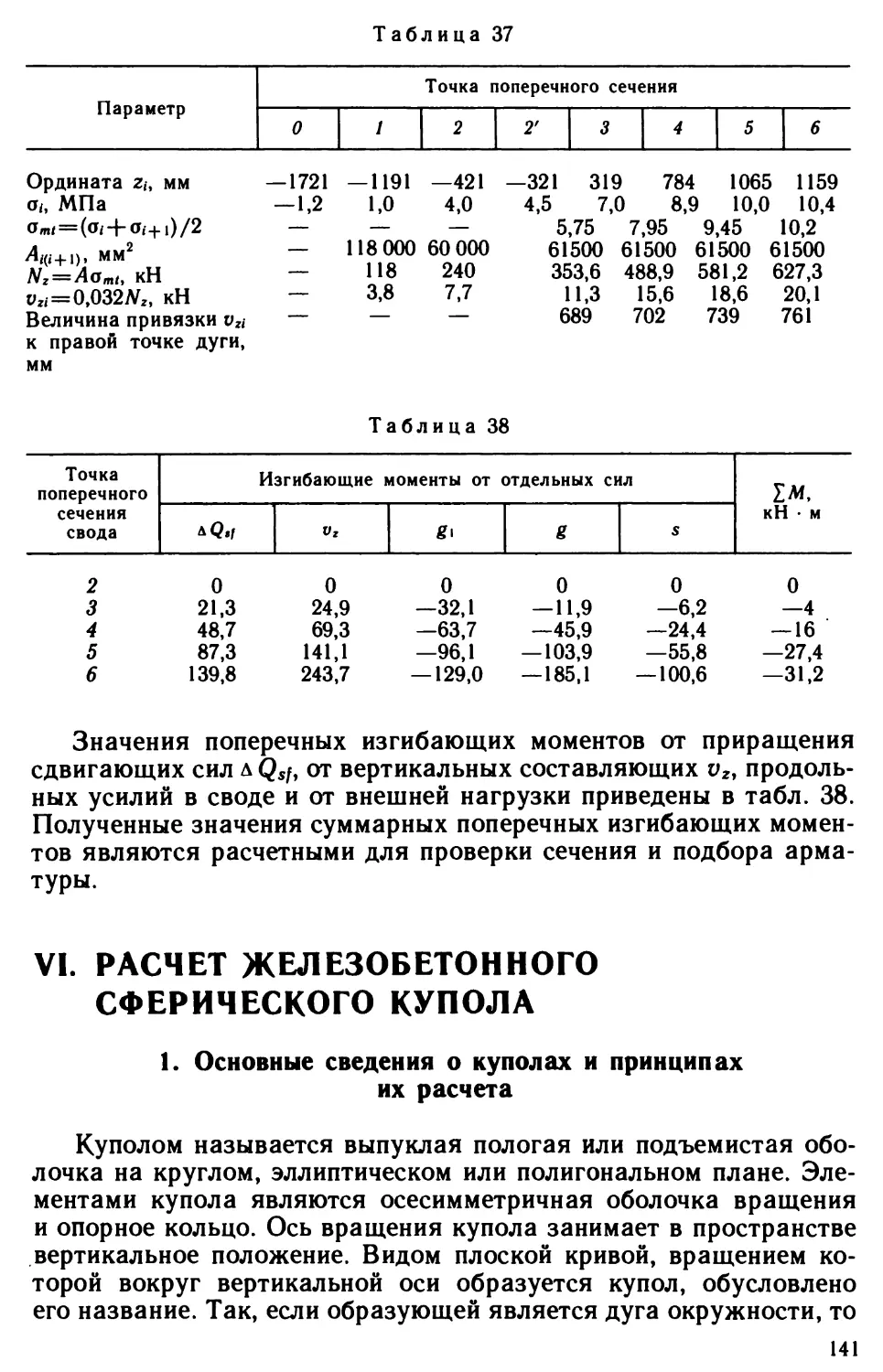
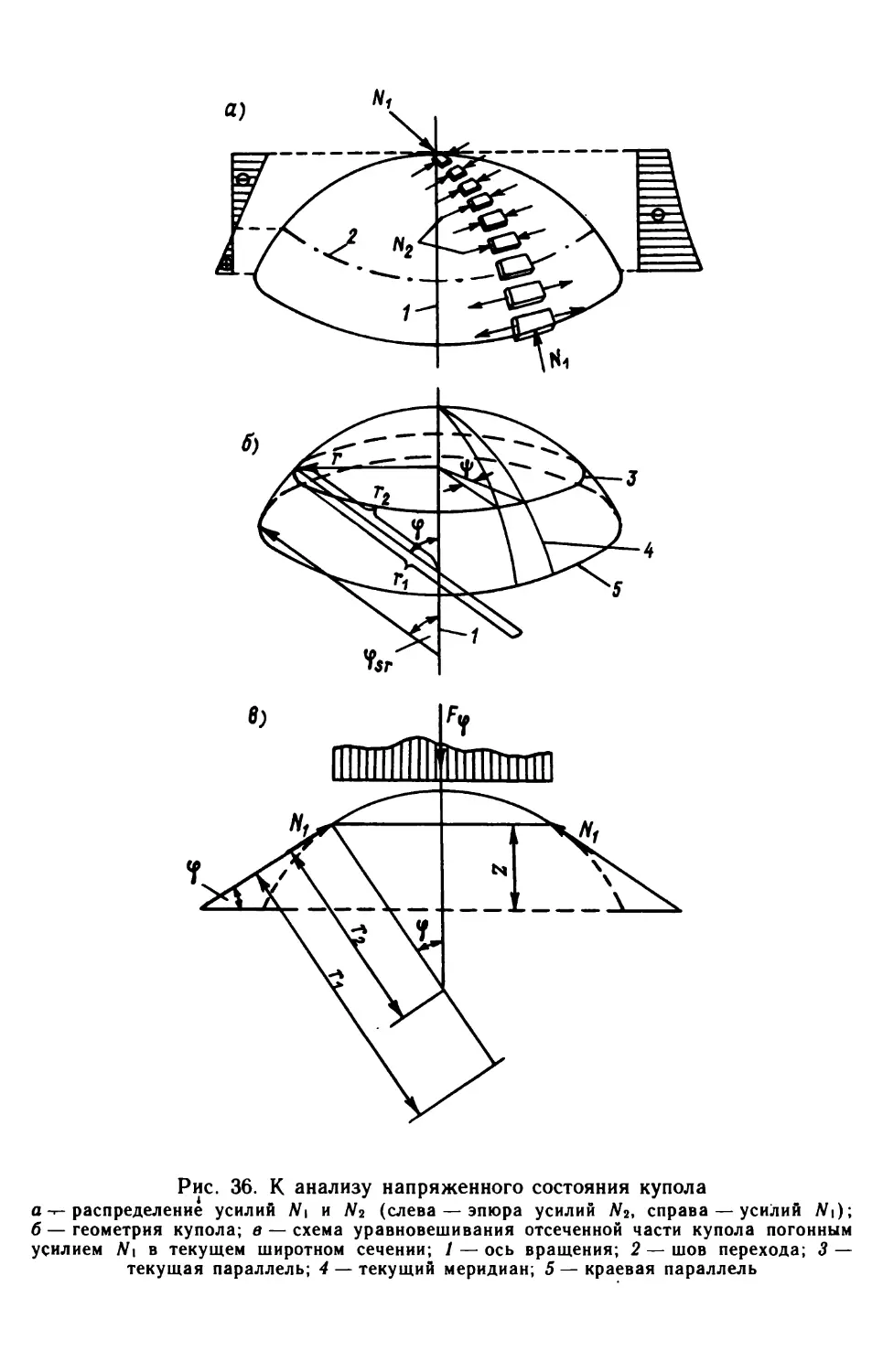
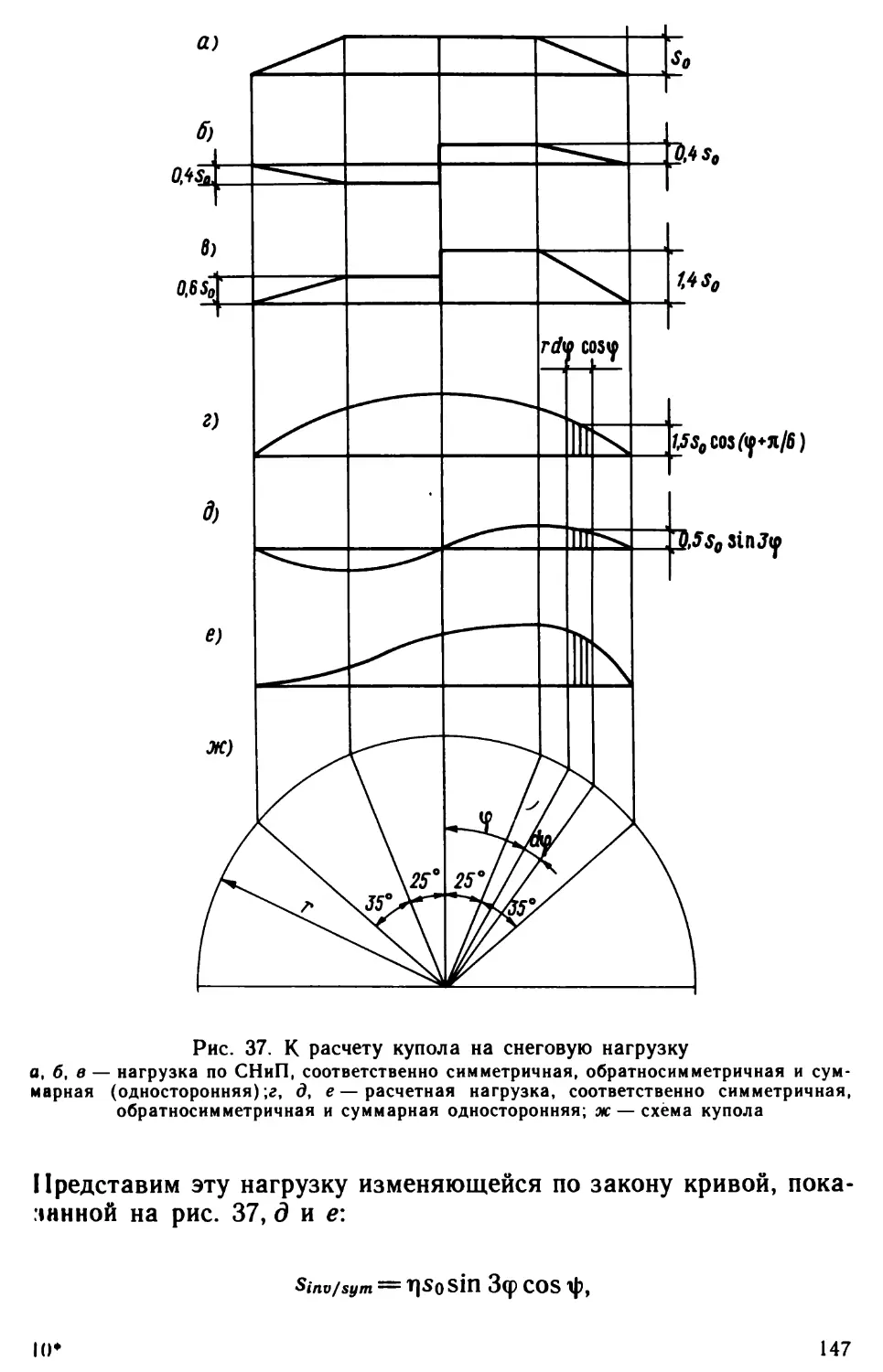
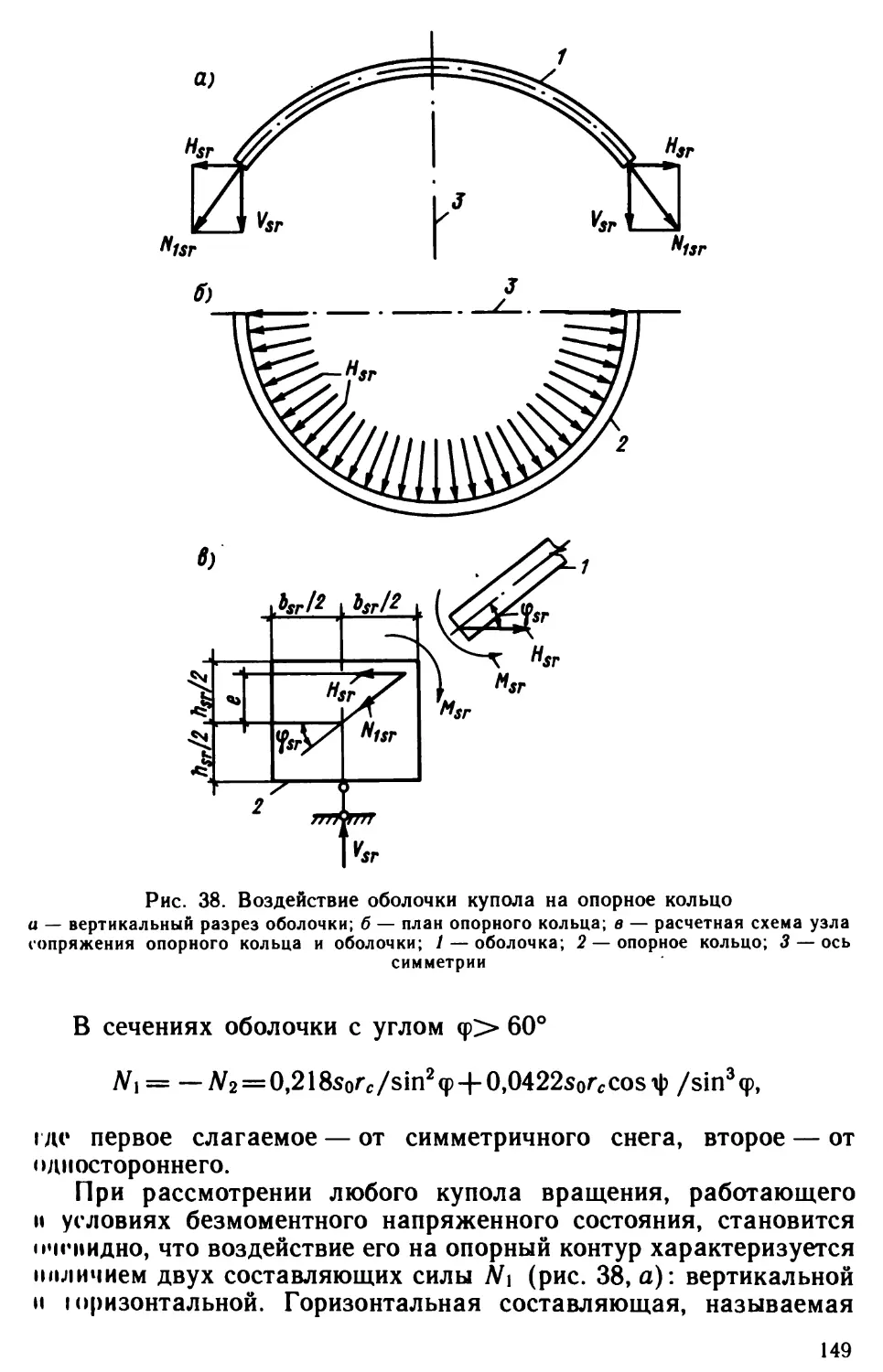
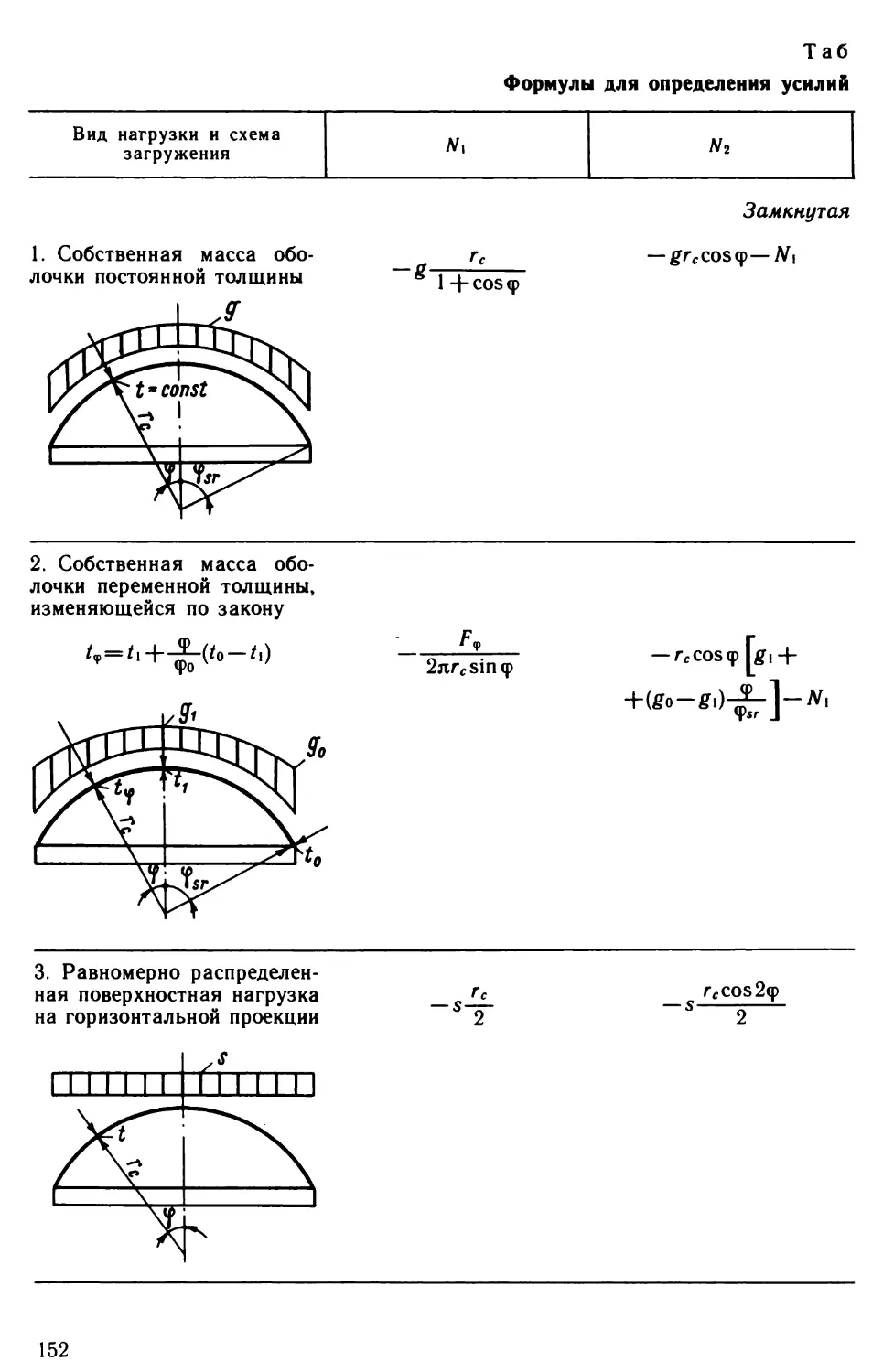
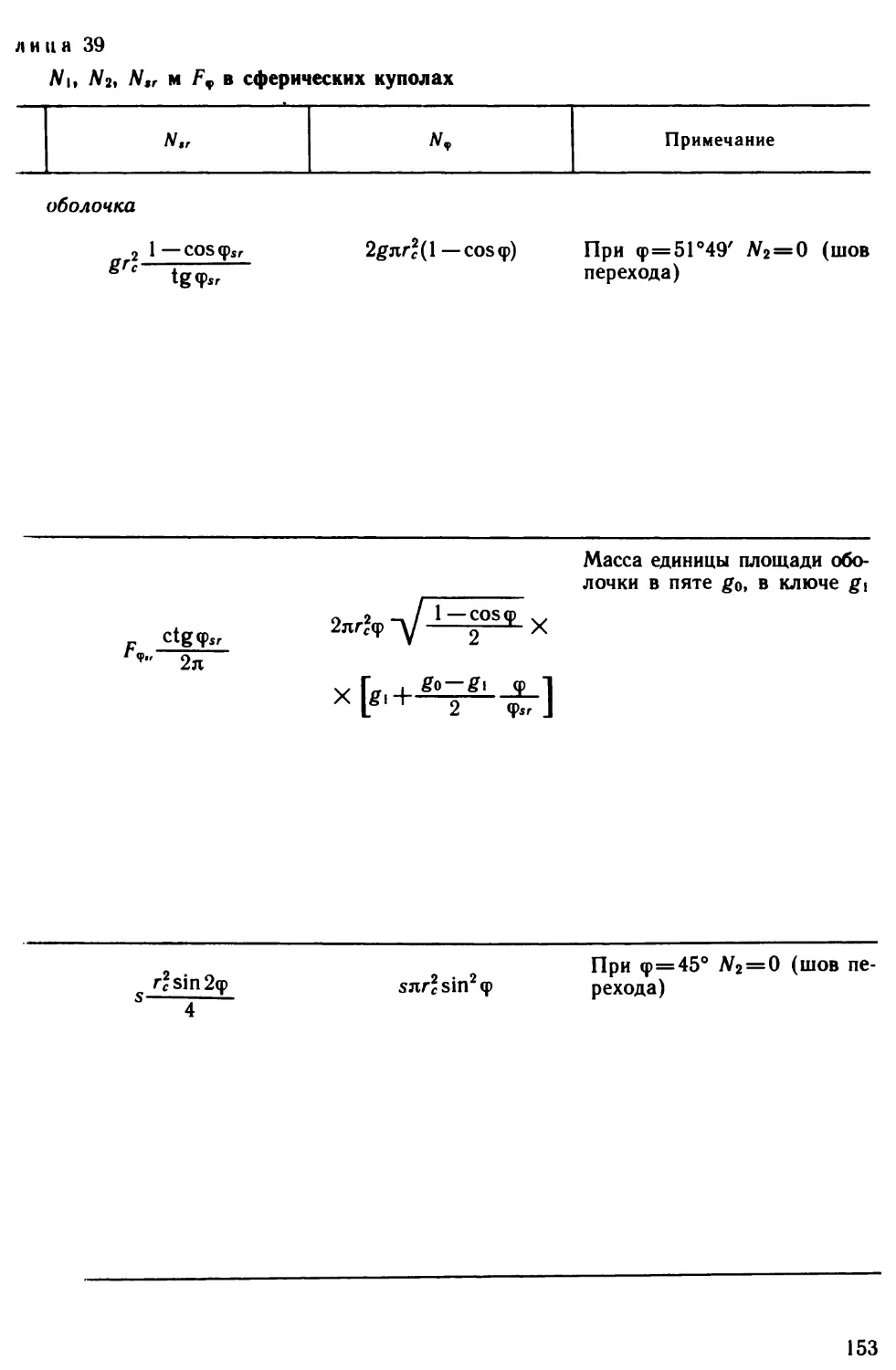
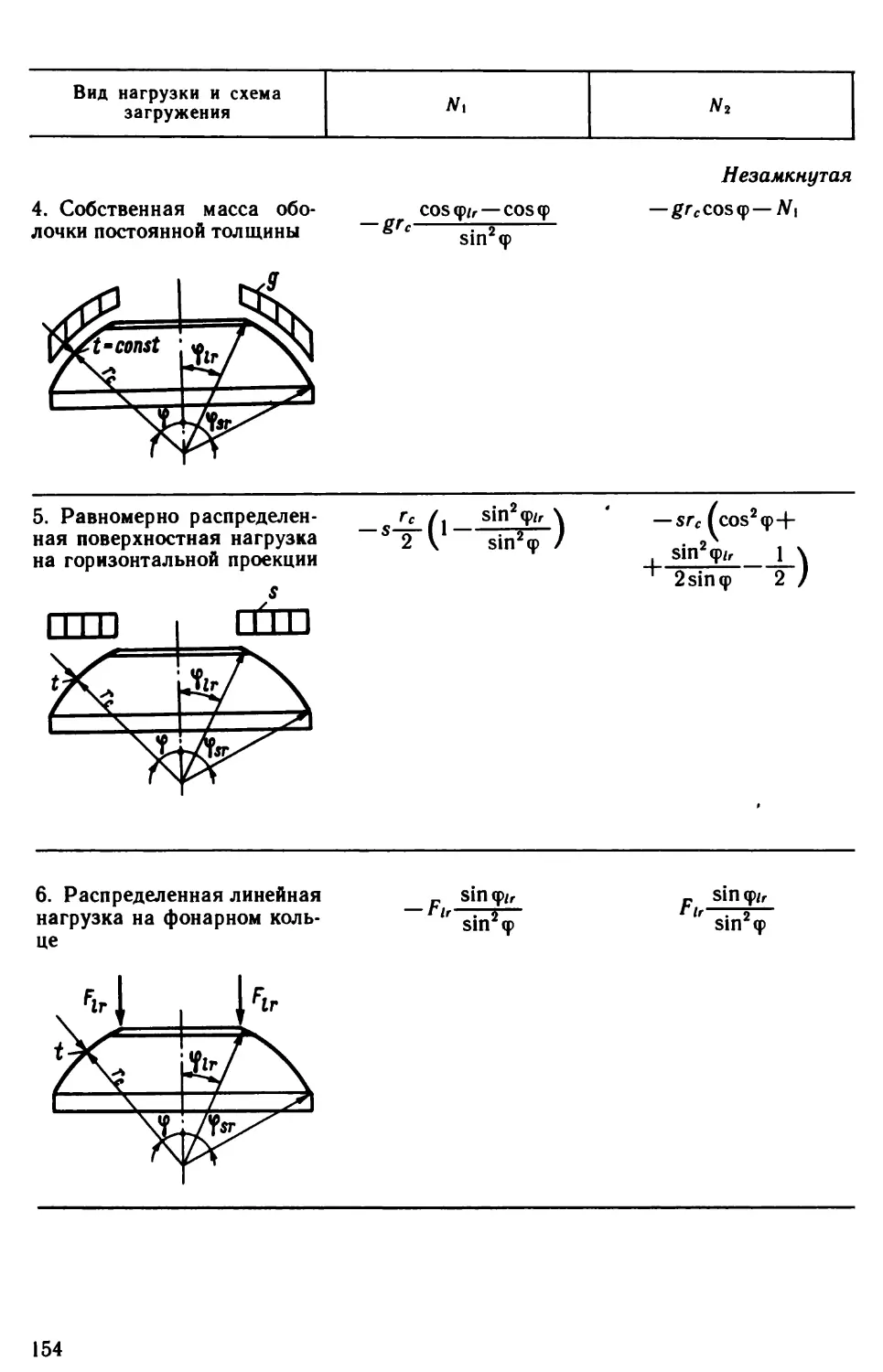
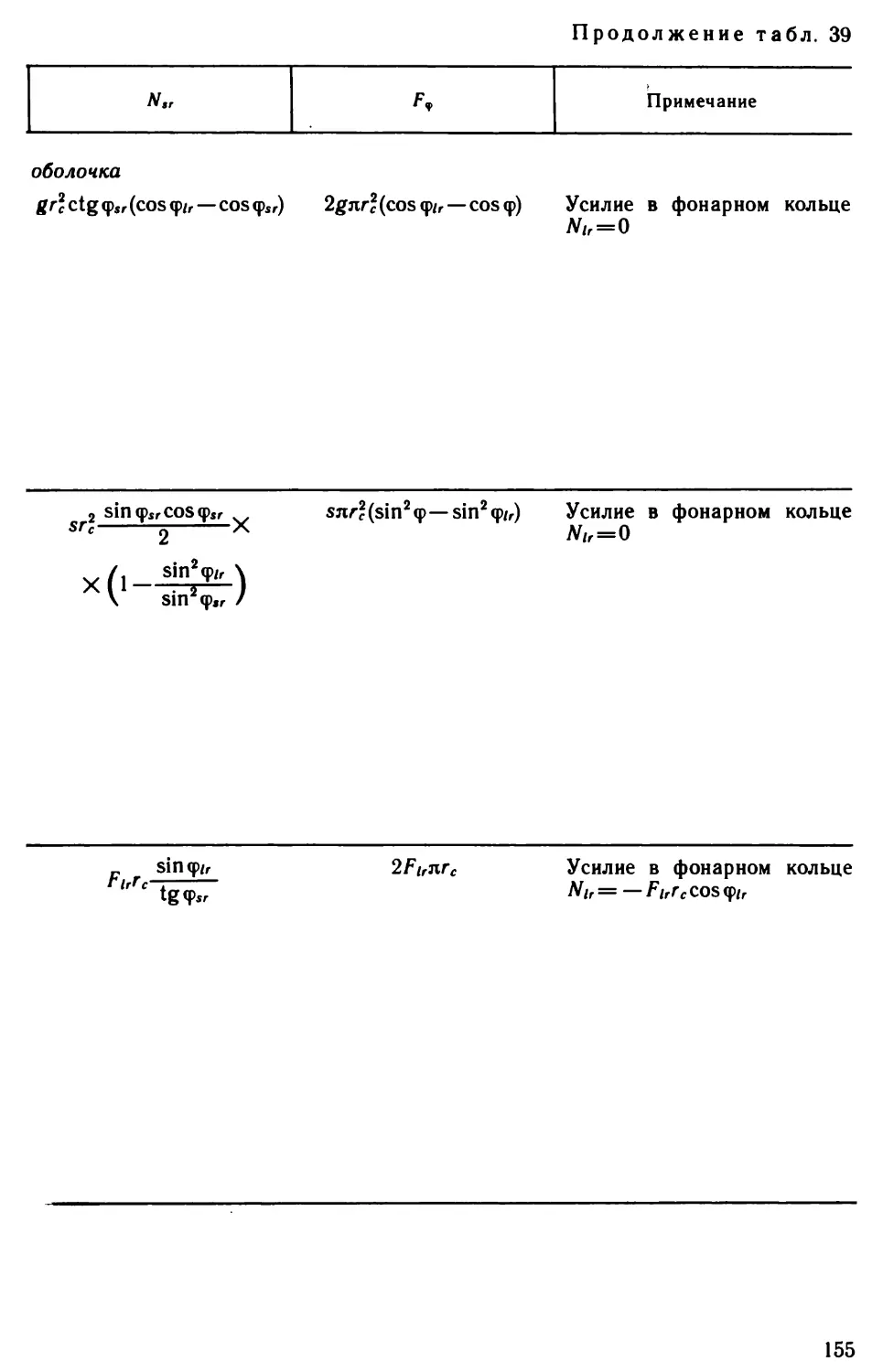
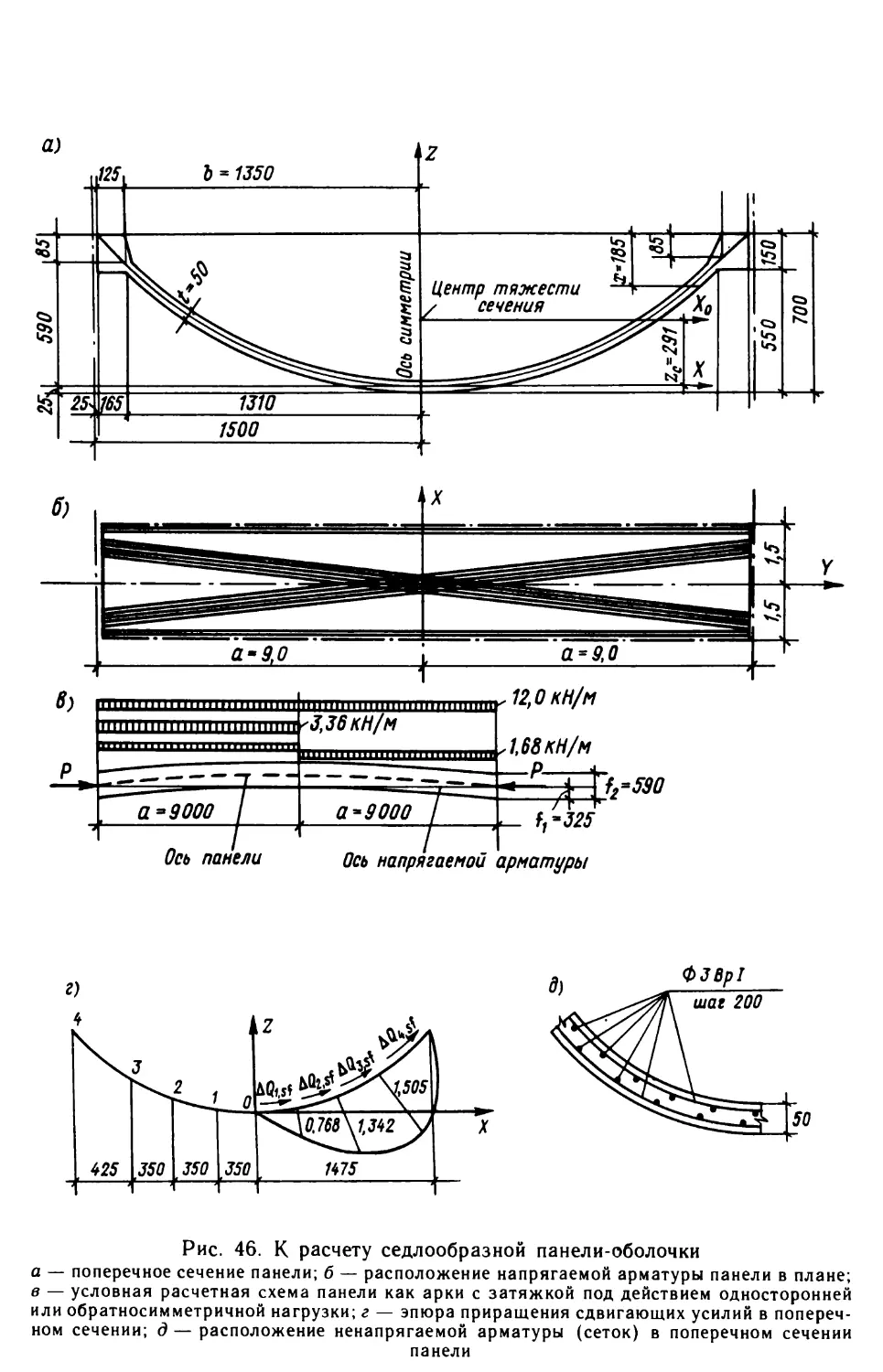
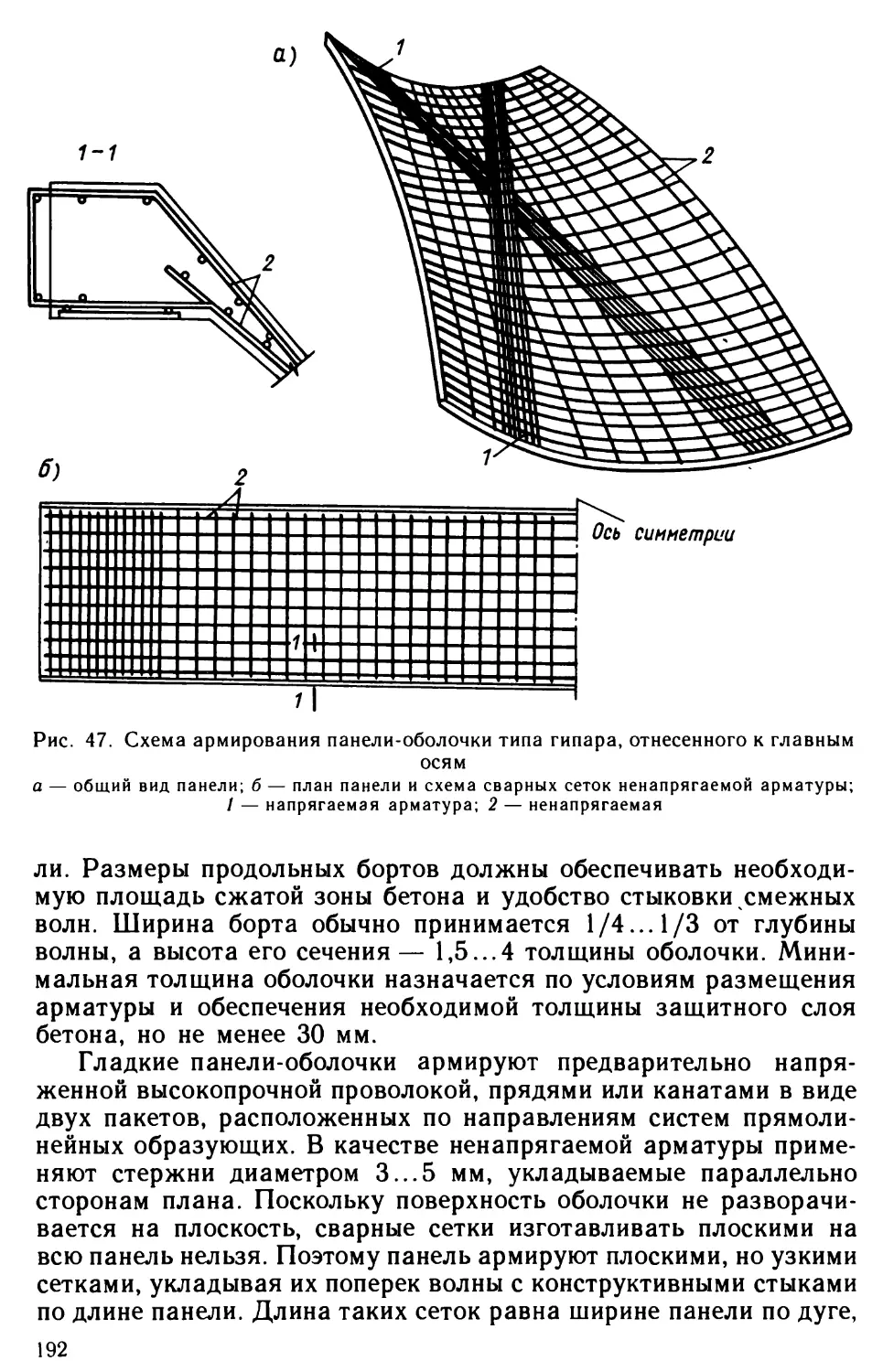
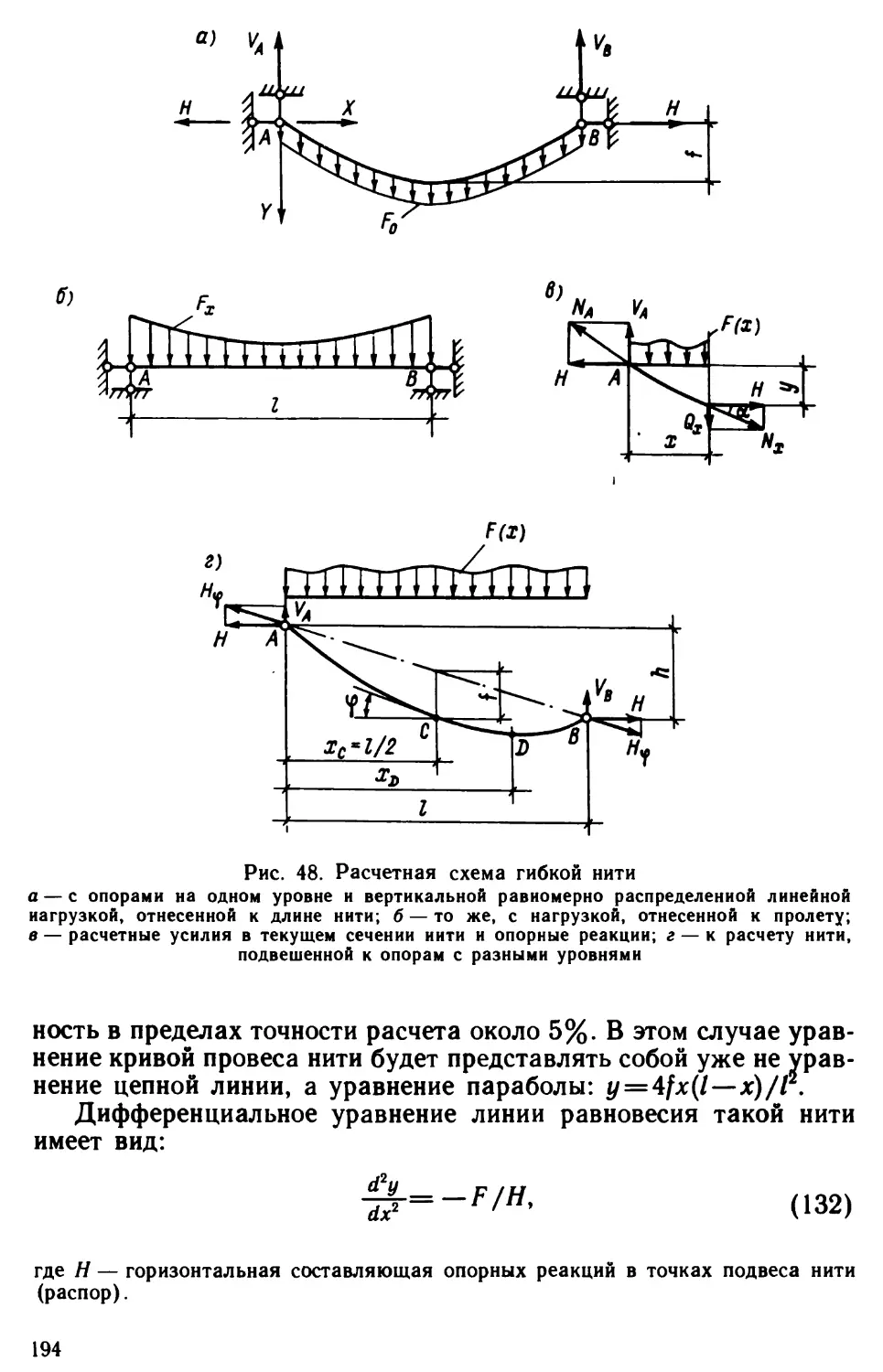
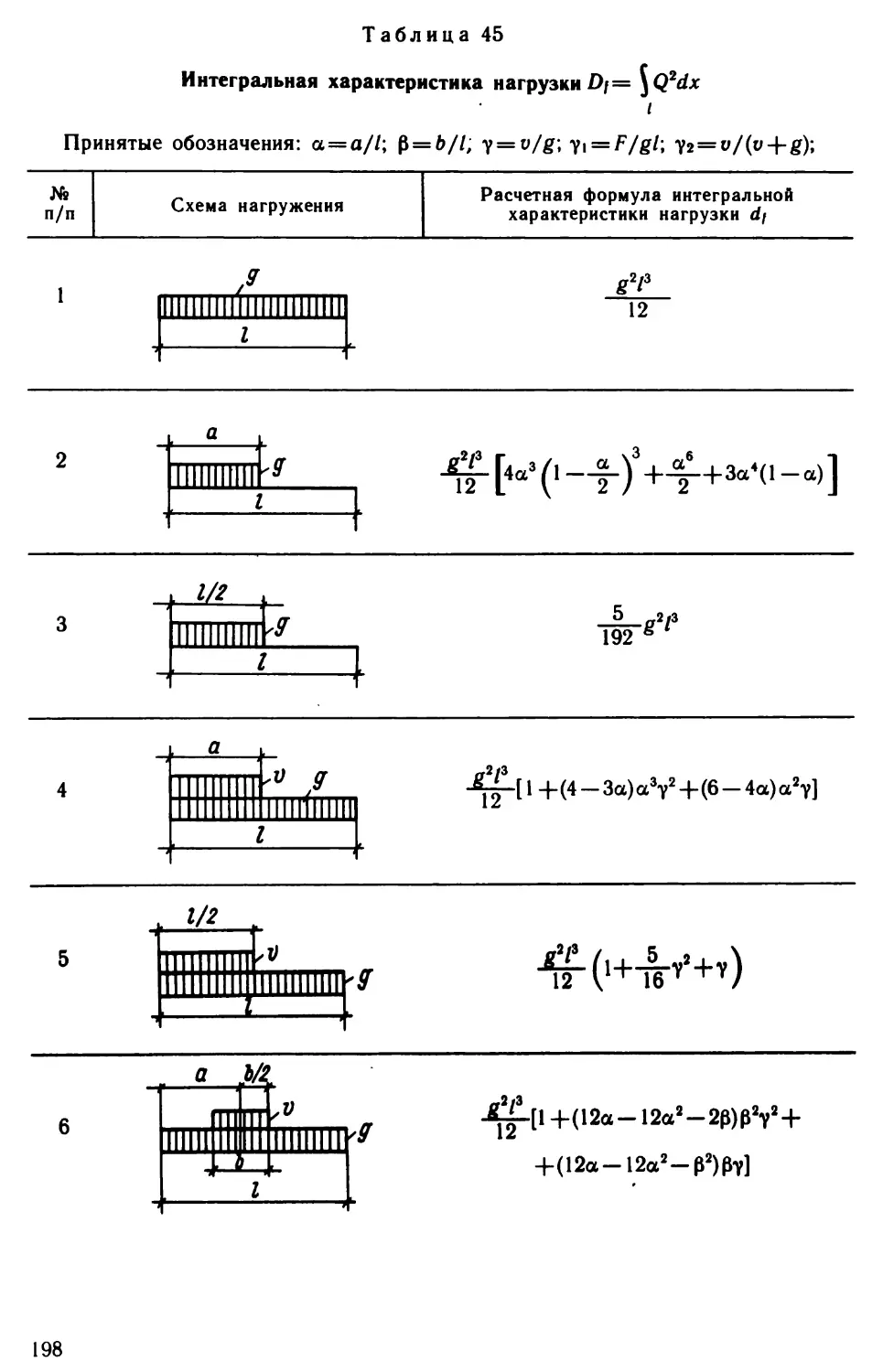
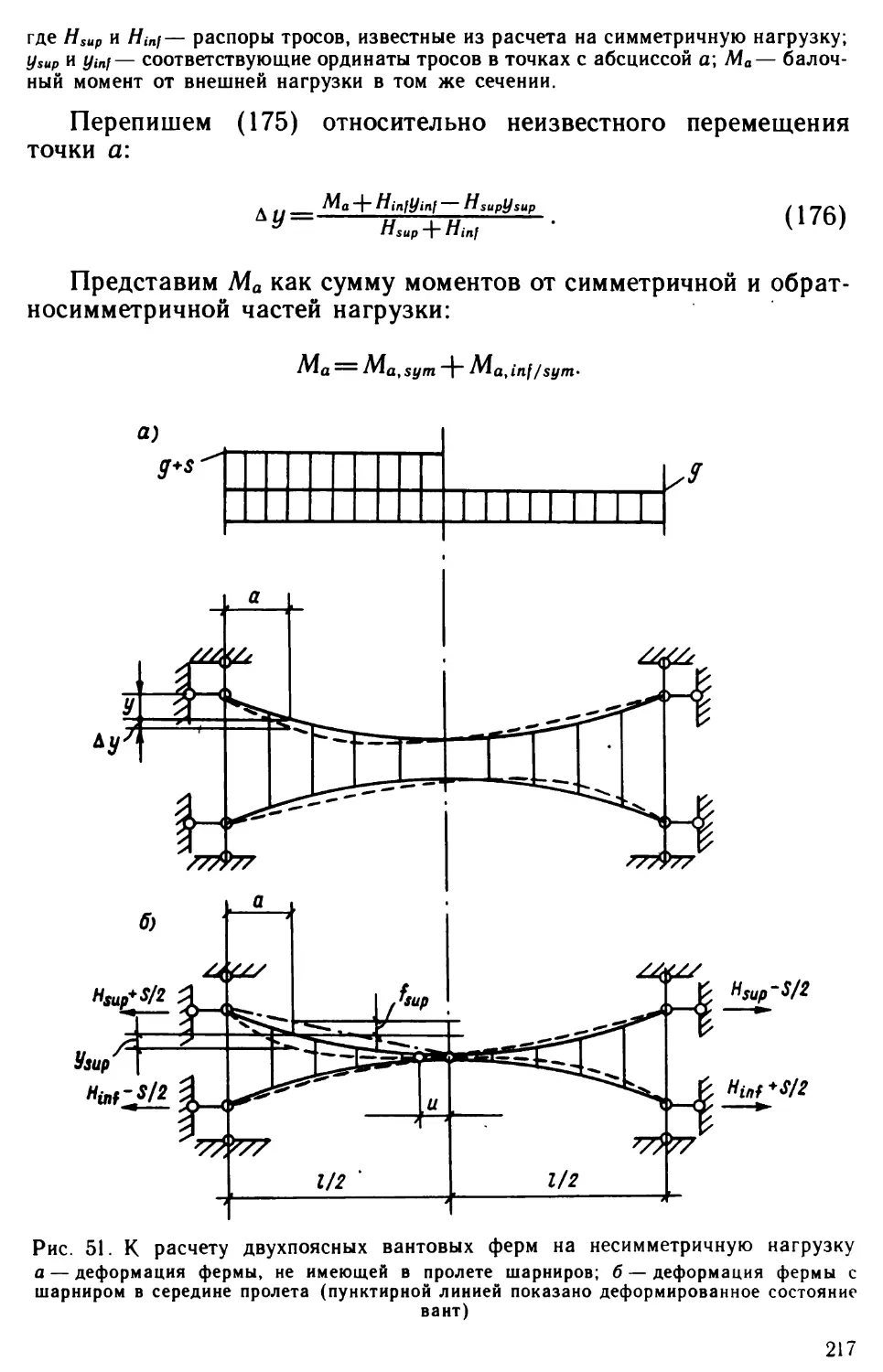
Author: Виноградов Г.Г.
Tags: конструктивные элементы несущие конструкции строительство строительные конструкции
ISBN: 5-274-01015-6
Year: 1990
Text
Расчет строительных пространственных конструкцийГ. Г. ВиноградовРасчетстроительныхпространственныхконструкций
ББК 38.5
В 49
УДК 624.074DWG.ru, июнь 2012Сканы - Verloc;
Обработка - Armin.Рецензент — канд. техн. наук Б. А МиронковВиноградов Г. Г.Расчет строительных пространственных конструкций. J1.:
Стройиздат, Ленингр. отд-ние, 1990.— 264 с.: ил.ISBN 5-274-01015-6.Точные методы расчета оболочек с помощью ЭВМ по специально разрабо¬
танным программам обеспечивают высокую точность результатов, которая, однако,
не всегда требуется проектировщику. В то же время отладка программ для
расчета на существующих типах машин для многообразных видов оболочек тре¬
бует больших затрат труда высококвалифицированных специалистов. Предлага¬
емые автором примеры позволяют выполнять расчеты оболочек на прочность, тре-
щиностойкость и устойчивость с достаточной для практических целей точностью
доступными каждому проектировщику методами и без больших трудовых затрат.Для инженерно-технических работников проектных организаций.Производственное изданиеВиноградов Григорий ГригорьевичРАСЧЕТ СТРОИТЕЛЬНЫХ
ПРОСТРАНСТВЕННЫХ КОНСТРУКЦИЙЗав. редакцией Н. Н. Днепрова
Редактор И. И. Кудревич
Художественный редактор О. В. Сперанская
Художник-оформитель М. А. Федорова
Технический редактор Е. В. Полиектова
Корректоры Т. Б. Верникова и Н. С. ЛукьянчукСдано в набор 26.12.89. Подписано в печать 25.07.90. М-19614. Формат 60X90'/i6- Бумага
офсетная. Гарнитура «Литературная». Печать офсетная. Фотонабор. Уел. печ. л. 16,5.
Уч.-изд. л. 16,91. Уел. кр.-отт. 16,75. Изд. № 2598Л. Тираж 9900 экз. Заказ № 61.Цена 90 коп.Стройиздат, Ленинградское отделение. 191011, Ленинград, пл. Островского, 6ББК 38.5ИБ № 4369ПО-3 Ленуприздата. 191104, Ленинград, Литейный пр., 55ISBN 5-274-01015-6© Г. Г. Виноградов, 1990„ 3302000000—159 пл
047(01)—90В 49
ПРЕДИСЛОВИЕСовременные направления экономического и социального раз¬
вития СССР в большой степени зависят от правильной политики
в капитальном строительстве. Отсюда вывод — нужно изыскать
пути сокращения инвестиционного цикла, ускорения внедрения
достижений науки и техники, улучшения структуры применяемых
строительных конструкций и материалов, обеспечения наиболее
эффективного использования материальных и финансовых ресур¬
сов, выделяемых на капитальное строительство.Стоимость покрытий составляет примерно 2...5% от стоимости
зданий, и снижение их материалоемкости и стоимости является
существенным вкладом в решение поставленных задач.Среди всевозможных конструктивных решений покрытий зда¬
ний особое место занимают оболочки — тонкостенные простран¬
ственные системы, имеющие криволинейную поверхность. Приме¬
нение оболочек в качестве одной из эффективных конструкций
покрытий зданий может с успехом способствовать достижению
намечаемых в сфере строительства целей.Железобетонные оболочки являются наиболее экономичными
конструкциями покрытий зданий, они зачастую совмещают в себе
как несущие, так и ограждающие (разделяющие) функции и при
этом обладают высокими прочностными и жесткостными каче¬
ствами.Оболочки наиболее полно отвечают требованиям по улуч¬
шению структуры и рациональному применению строительных
конструкций, повышению качества архитектурных, градострои¬
тельных и объемно-планировочных решений зданий и сооружений,
уменьшению их материалоемкости и стоимости.Сегодня невозможно представить архитектуру и строитель¬
ство без оболочек. Роль этих конструкций возрастает из года
в год. Вместе с тем современное состояние строительной индустрии
позволяет более широко внедрять пространственные конструкции
в практику строительства. Для этого необходимо квалифициро¬
ванно проектировать и уметь быстро рассчитывать эти конструк¬
ции силами массовых проектировщиков на качественном уровне.Между тем в настоящее время механика оболочек достигла
такого уровня математизации, что расчет пространственных кон¬
струкций стал привилегией отдельных высококвалифицированных3
специалистов. Отдавая должное точным методам расчета оболочек
с помощью ЭВМ по специально разработанным программам
(с использованием в исходных уравнениях всех функций, харак¬
теризующих напряженно-деформированное состояние оболочки,
в том числе и таких, которые не могут заметно повлиять на окон¬
чательные результаты) следует отметить весьма высокую трудо¬
емкость составления и отладки программы для каждого типа
машины и различных видов оболочек, что не под силу большин¬
ству проектных организаций и тем более отдельным инженерам.При этом получаемая на ЭВМ высокая точность результа¬
тов расчета не всегда требуется разработчику конструкции. Вслед¬
ствие этого важное значение приобретают практические способы
расчета пространственных систем. Наряду с точными методами
в практике проектирования оболочек существуют так называ¬
емые инженерные методы расчета, которые дают возможность
достаточно быстро определить величины усилий для назначения
сечений конструктивных элементов, арматуры и т. д.Практические, приближенные методы расчета оболочек разра¬
батывались многими учеными. Так, методы расчета цилиндриче¬
ских оболочек и складок имеются в работах С. А. Амбарцумяна,
Л. С. Гильмана, X. X. Лаула, И. Е. Милейковского, П. Л. Пастер¬
нака; расчет куполов — в работах Н. В. Ахвледиани и М. А. Да-
ниелашвили, П. Л. Пастернака; оболочек двоякой кривизны —
в работах В. С. Бартенева, В. В. Горенштейна, В. М. Никиреева
и В. Л. Шадурского и др.Большой вклад в развитие практических методов расчета
висячих нитей и конструкций внесли В. К. Качурин, Р. Н. Маце-
линский и др.Методы, по которым выполнены примеры расчетов в настоящей
книге, в основном освещены в трудах Б. В. Горенштейна «Желе¬
зобетонные пространственные конструкции»; М. Е. Липницкого,
Б. В. Горенштейна, Г. Г. Виноградова «Железобетонные про¬
странственные покрытия зданий»; рекомендации по армированию
железобетонных оболочек — в работе автора «Конструирование
железобетонных элементов промышленных зданий».Эти методы использовались при расчете конструкций, осуще¬
ствленных в разные годы на различных объектах строительства.
При этом многие оболочки были подвержены испытаниям на мо¬
делях и на натуре с доведением конструкции до разрушения.
Результаты испытания полностью подтвердили верность методов
и надежность спроектированных по ним пространственных кон¬
струкций, что нашло отражение в работах Ю. В. Чиненкова,Н. Н. Коровина, Г. К. Хайдукова, В. В. Шугаева, В. П. Абовского,
А. А. Цейтлина, А. Д. Либермана, Д. А. Коршунова, А. П. Пав¬
лова и других специалистов.Предлагаемые читателю примеры расчета инженерными при¬
ближенными методами позволяют рассчитывать строительные про¬4
странственные конструкции по прочности, по образованию и рас¬
крытию трещин, деформации и устойчивости известными из
институтского курса средствами и приемами с достаточной для
практических целей точностью при относительной простоте. При этом
немаловажно, что методы доступны инженеру-практику, так как
обладают несомненными преимуществами физической наглядно¬
сти и позволяют достаточно надежно принимать необходимые
проектные решения на разных стадиях разработки конструкции.В примерах, с целью сокращения объема книги, приводятся
расчеты исключительно пространственных элементов. Расчеты
плоскостных элементов оболочек (ребра, затяжки и др.), а также
расчеты по подбору сечений бетона и арматуры здесь опущены,
так как выполняются известными способами в соответствии с
действующими нормами и имеющимися пособиями.В расчетных формулах использованы буквенные обозначения
и индексы, установленные для основных величин, применяемых
в строительстве, стандартом СЭВ 1565—79 «Буквенные обозна¬
чения». Отсутствующие в стандарте индексы приняты в примерах
(как это и рекомендуется стандартом) из строчных букв латин¬
ского алфавита и характеризуют данное понятие на английском
языке.Автор полагает, что данная книга будет способствовать раз¬
витию творческой инициативы и повышению уровня професси¬
ональных знаний работников проектных организаций, а также
поможет студентам строительных специальностей вузов в овла¬
дении навыками расчета пространственных конструкций.В настоящее время применение оболочек характеризует уро¬
вень инженерного мастерства и прогресс в строительной технике,
чему, как надеется автор, будет способствовать предлагаемая
работа.ОСНОВНЫЕ БУКВЕННЫЕ ОБОЗНАЧЕНИЯ И ИНДЕКСЫ
Буквенные обозначенияГеометрические величины:L— длина геометрической оси арки, дуги, ванта;1— пролет;S— длина кривой;а— расстояние, размер, половина длины оболочки;b— ширина, половина ширины оболочки;bf— ширина полки таврового сечения;h— высота;h0— рабочая высота сечения;t— толщина;s— шаг;r— радиус;d— диаметр;A— площадь сечения;f— стрела подъема, прогиба или провеса;5
во — эксцентриситет продольной оси относительно центра тяжести сечения;е — расстояние от точки приложения продольной силы до равнодейству¬ющей усилий в арматуре;
е0р — эксцентриситет силы предварительного напряжения относительно цен¬тра тяжести сечения;/ — момент инерции сечения;W — момент сопротивления сечения;г — ядровое расстояние;х — высота сжатой зоны сечения;S — статический момент сечения.Усилия воздействия и характеристики материалов:М — изгибающий момент;N — продольная сила;Q — поперечная сила, сила сдвига;Р — сила предварительного напряжения;S — усилие;V — вертикальная составляющая опорной реакции;Н — горизонтальная составляющая опорной реакции (распор);F — нагрузка;g — нагрузка постоянная распределенная;s — нагрузка снеговая распределенная;п — продольная сила на единицу длины;q — поперечная сила, сдвигающее усилие на единицу длины;v — вертикальная составляющая продольного усилия;h — горизонтальная составляющая продольного усилия;R — сопротивление материала;Rby Rb.ser — расчетные сопротивления бетона осевому сжатию для предельных
состояний соответственно первой и второй групп;Rbt, Rbt.ser—то же, осевому растяжению;RbP — передаточная прочность бетона;Rs, Rs,ser — расчетные сопротивления арматуры растяжению для предельных со¬
стояний соответственно первой и второй групп;
а — нормальные напряжения;т — касательные напряжения;Е — модуль упругости;В — жесткость сечения;Df — интегральная характеристика нагрузки.Индексы и поясняющие словаа — арка (arch);а — нагрузка особая;Ъ — бетон, бетон сжатый (beton);с — купол (cupola)\саг — несущий (carrying)-,сг — критический (critical);сгс — трещина (crack);cur, pi — криволинейная плита (curved plate);cut —отсеченный (cut off);d — расчетный (design);ed — бортовой элемент (edge)\est — оцененный (estimate);ext — наружный (external);f — нагрузка (force);fact — фактический (factual);g — нагрузка постоянная (gravity);gr — решетка (grating);6 I
inf — нижний (iinferior);int — внутренний (internal);inv/sym — обратносимметричный (inversely symmetrical),,I — левый (left)\I — фонарный (lantern);lr — фонарное кольцо (lantern ring);Is — потери напряжений в арматуре (loss);т — монолитный (monolith);mt — средний (middle);п — нормативный (normative);on — односторонний (onesided);р _ предварительное напряжение (prestressing);pi — пластичный (plastic);pr — главный (principal);г — балка, ребро (rafter, rib);г — правый (right);red — приведенный (reduction);s — арматура, вант (steel);ser — эксплуатационный (service);sf — перерезывающее (сдвигающее) усилие (sher forse);sh — оболочка (shell);sp — арматура напрягаемая;sr — опорное кольцо (supporting ring);st — стабилизирующий (stabilizing);sup — верхний (super);sup — опорный (support);sur — поверхность (surface);sym — симметричный (symmetrical);t — поперечный (transverse);t — растяжение (tention);td — затяжка (tightening device);tot — суммарный, общий (total);и — предельный, крайний (ultimate);у — предел текучести (yield point).
I. РАСЧЕТ ДЛИННОЙ ЦИЛИНДРИЧЕСКОЙ
ОБОЛОЧКИ1. Некоторые сведения о длинных
цилиндрических оболочках,
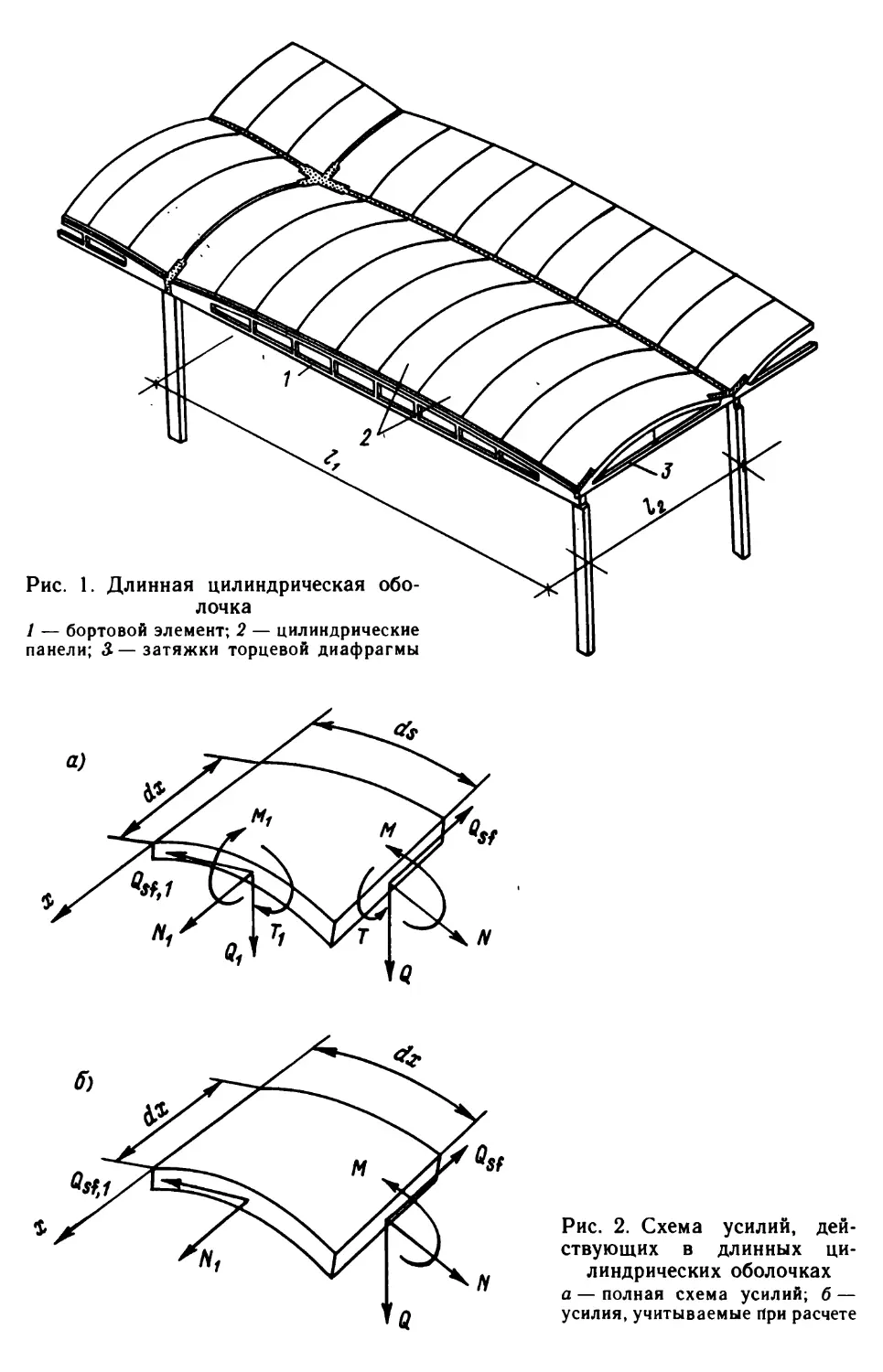
основные положения их расчетаДлинными цилиндрическими оболочками (рис. 1) называются
строительные пространственные конструкции, имеющие:тонкую криволинейную плиту (собственно оболочку), средин¬
ная поверхность которой очерчена по цилиндрической (как пра¬
вило, круговой, и следовательно, наиболее простой и удобной)
поверхности;бортовые элементы, окаймляющие оболочку вдоль крайних
образующих;поперечные диафрагмы по криволинейным краям (творцам)
оболочки.Расстояние между осями опорных (торцевых) диафрагм Л
называется пролетом оболочки, расстояние между бортовыми эле¬
ментами /2— длиной волны или шириной оболочки. Высота обо¬
лочки, включая бортовые элементы, обозначается Л5л. Стрела
подъема оболочки, т. е. криволинейной плиты без бортовых эле¬
ментов, обозначается fCur,p/. Направление по образующей вдоль
пролета U называется продольным, а вдоль пролета /2— попереч¬
ным. Если /i//2^1, то оболочки считаются длинными.Оболочки могут быть однопролетными, многопролетными и
консольными, а также одноволновыми и многоволновыми. Смеж¬
ные волны многоволновых оболочек, как правило, имеют общие
бортовые элементы и монолитно связаны между собой. Различают
крайние и средние (промежуточные) болтовые элементы. Пролет
бортового элемента соответствует пролету оболочки, а пролет
диафрагмы не обязательно равен длине волны оболочки. Бортовые
элементы длинных цилиндрических оболочек выполняют обычно
в виде вертикальных балок, расположенных ниже края криво¬
линейной плиты, а торцевые диафрагмы — в виде арок, ферм
или балок.Высоту оболочки hshy включая сечение бортовой балки, назна¬
чают в пределах */ю !/i5 пролета Л, а стрелу подъема криволи¬
нейной плиты fcur,Pi принимают равной /в длины волны U.Криволинейные плиты сборных и сборно-монолитных оболо¬
чек, как правило, ребристые, а монолитных — гладкие.Для расчета длинных цилиндрических оболочек используется
полумоментная теория. При этом исследования показали, что
изгибающие моменты Afi, действующие на площадках поперечного
сечения криволинейной плиты, соответствующие им поперечные8
Рис. 2. Схема усилий, дей¬
ствующих в длинных ци¬
линдрических оболочках
а — полная схема усилий; б —
усилия, учитываемые При расчетеРис. 1. Длинная цилиндрическая обо¬
лочка1 — бортовой элемент; 2 — цилиндрические
панели; 5—затяжки торцевой диафрагмы
силы Qi, а также крутящие моменты Т и Т\ незначительны по
величине, их можно принять равными нулю. Таким образом,
при расчете длинных цилиндрических оболочек на подбор сечений
в первую очередь влияют (рис. 2) нормальные силы Ni, сдвига¬
ющие силы Qs/ti и изгибающие моменты М. Силы N, действующие
нормально к площадкам продольного сечения плиты, и возника¬
ющие на этих же площадках поперечные силы Q учитываются
в расчете, но непосредственного влияния на расчет сечений не ока¬
зывают.Как показали многочисленные натурные и лабораторные экс¬
периментальные исследования длинных цилиндрических оболочек,
обычно применяемых в практике строительства покрытий произ¬
водственных зданий (для которых характерны опирание конструк¬
ций по углам, равномерно распределенные нагрузки, достаточно
большая жесткость поперечных ребер и контура оболочки, отно¬
шение /1//2 1), взаимное влияние поперечных изгибающих и
продольных нормальных сил отсутствует или это влияние столь
незначительно, что для упрощения расчета им можно пренебречь.
Рассчитывать такие оболочки можно раздельно в продольном,
а затем в поперечном направлении, причем в продольном направ¬
лении оболочки рассчитываются как балки корытообразного се¬
чения, а в поперечном — как арки (в виде элементарной поло¬
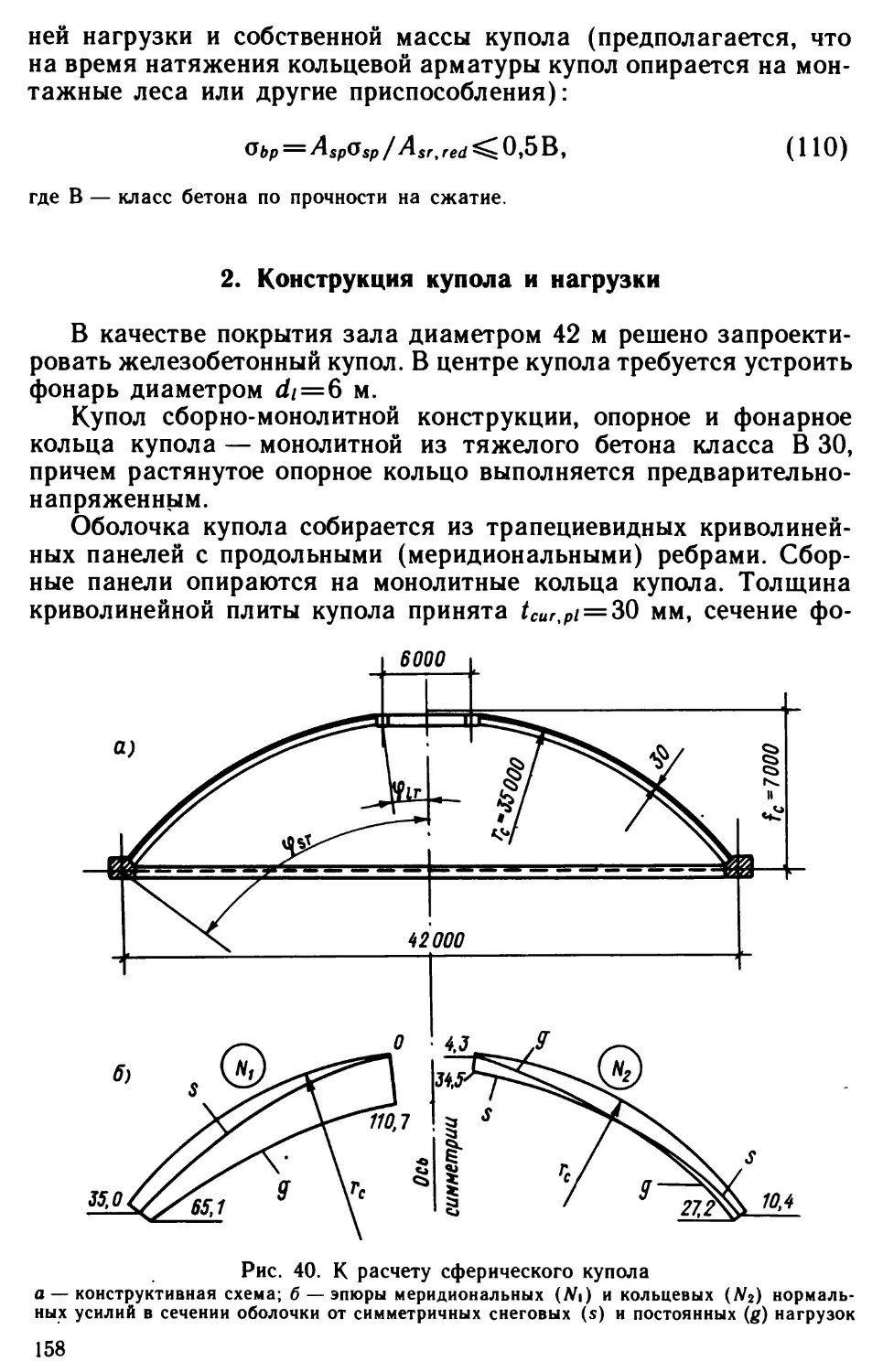
ски, вырезанной в пределах длины оболочки).2. Конструкция оболочки и нагрузки,
принятые в примереТребуется запроектировать цилиндрическую оболочку в ка¬
честве конструкции покрытия промышленного здания с сеткой
колонн 30X12 м.Прежде всего с учетом рекомендаций по расчету оболочек
складчатого типа зададимся конструкцией оболочки и всеми ее
геометрическими характеристиками, которые затем проверяем в
процессе расчета. При этом следует иметь в виду, что полученная
в результате расчета жесткость элементов оболочки не должна
отличаться от предварительно принятой более чем на 30%. В про¬
тивном случае расчет придется повторить с уточненными раз¬
мерами.Оболочку принимаем сборно-монолитной конструкции с вер¬
тикальными бортовыми элементами, располагаемыми под кри¬
волинейной частью. Бортовые элементы изготавливаются отдельно
длиной на пролет, т. е. 30 м в виде сборных балок. Криволинейная
часть состоит из сборных панелей цилиндрической формы раз¬
мером 3X12 м. Панели смежных волн опираются на общий для
них бортовой элемент, где замоноличиваются, образуя жесткий
узел. Шаг бортовых элементов принят равным шагу колонн,10
Таблица 1Вид нагрузкиНормативноезначениенагрузки,кПаКоэффициент
надежности
по нагрузке,
V/Расчетноезначениенагрузки,кПаСобственная масса оболочки,
приведенная к горизонтальной
проекции *2,51,12,75Теплоизоляция, пароизоляция,
гидроизоляционный ковер1,31,31,69Снег (III район)1,01,41,4Итого4,81,22**5,84Итого с учетом коэффициента
надежности по назначению уп=
=0,955,55* С учетом массы бортового элемента после замоноличивания стыковой
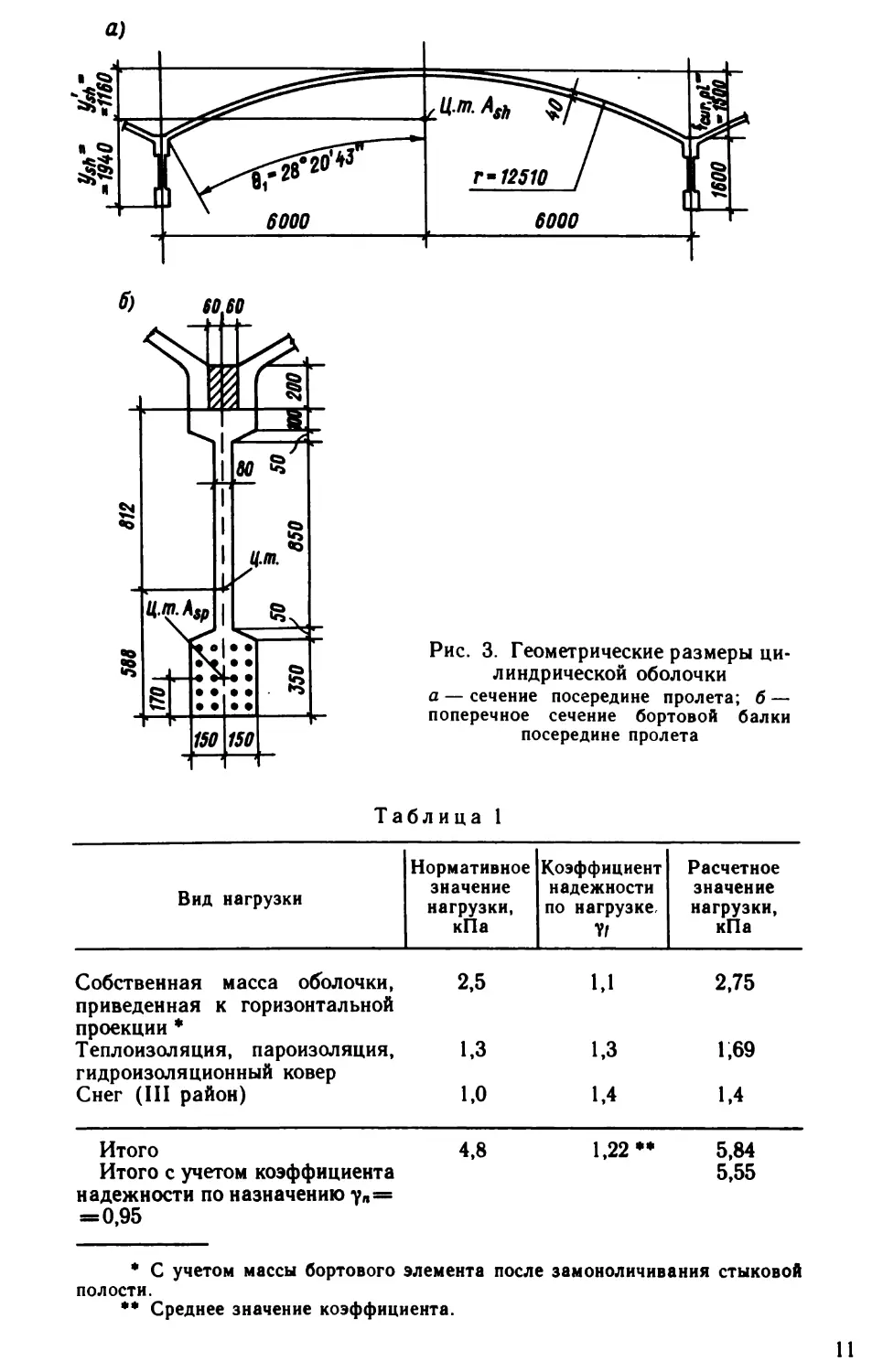
полости.** Среднее значение коэффициента.11Рис. 3. Геометрические размеры ци¬
линдрической оболочки
а — сечение посередине пролета; б —
поперечное сечение бортовой балки
посередине пролета
т. е. 12 м. Таким образом, оболочка представляет собой однопро¬
летную многоволновую конструкцию. Поперечное сечение балки
принято переменной высоты — на опорах 800 мм, а в середине
пролета 1400 мм. При этом верхнему поясу придано сегментное
очертание, в результате чего оболочка имеет небольшую вторую
кривизну в продольном направлении. Выбор такой поверхности
обусловлен ее преимуществами — обеспечивается надежный отвод
атмосферной воды с кровли без устройства специальных набето-
нок. Кроме того, такая форма оболочки способствует более эффек¬
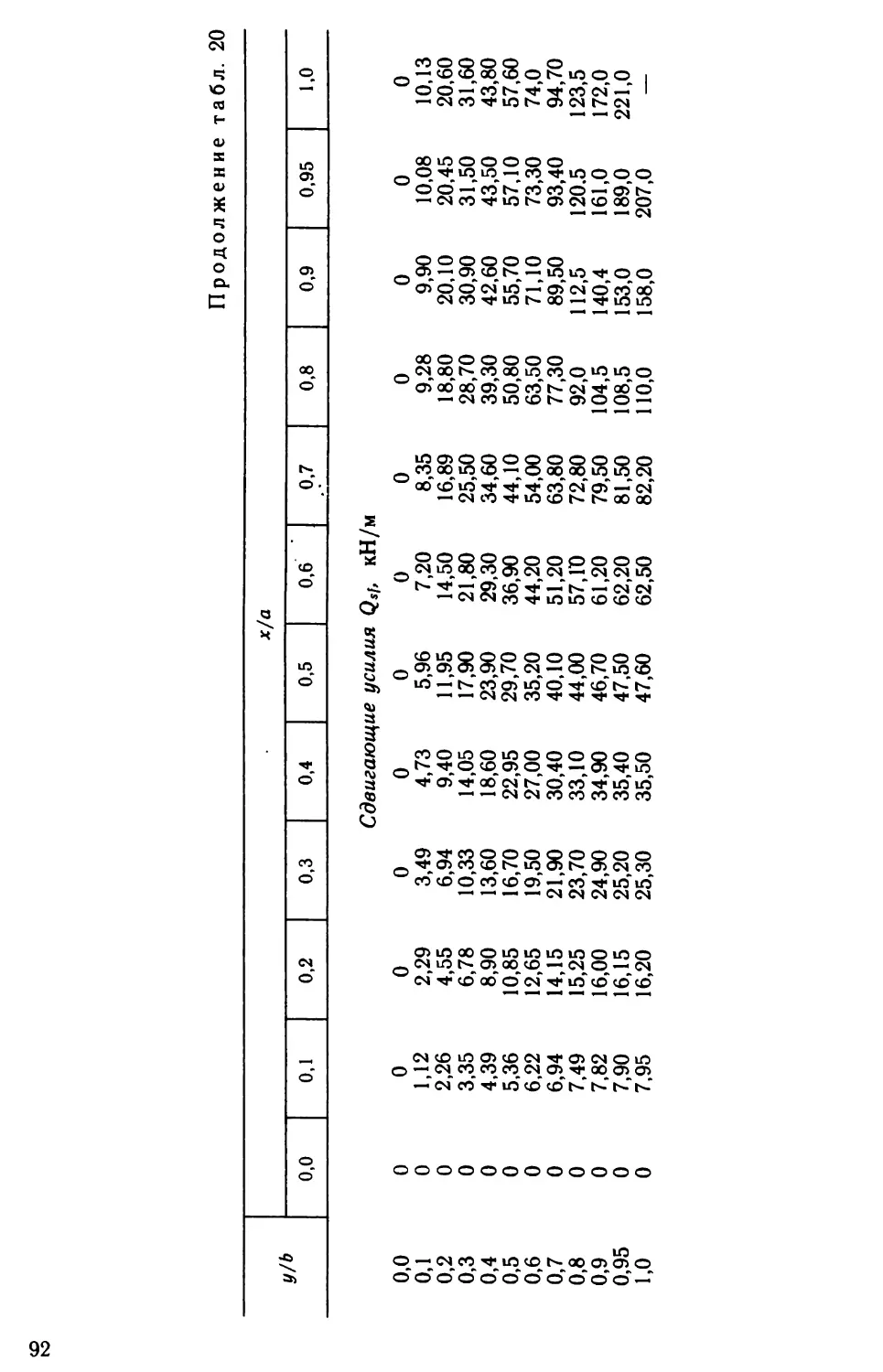
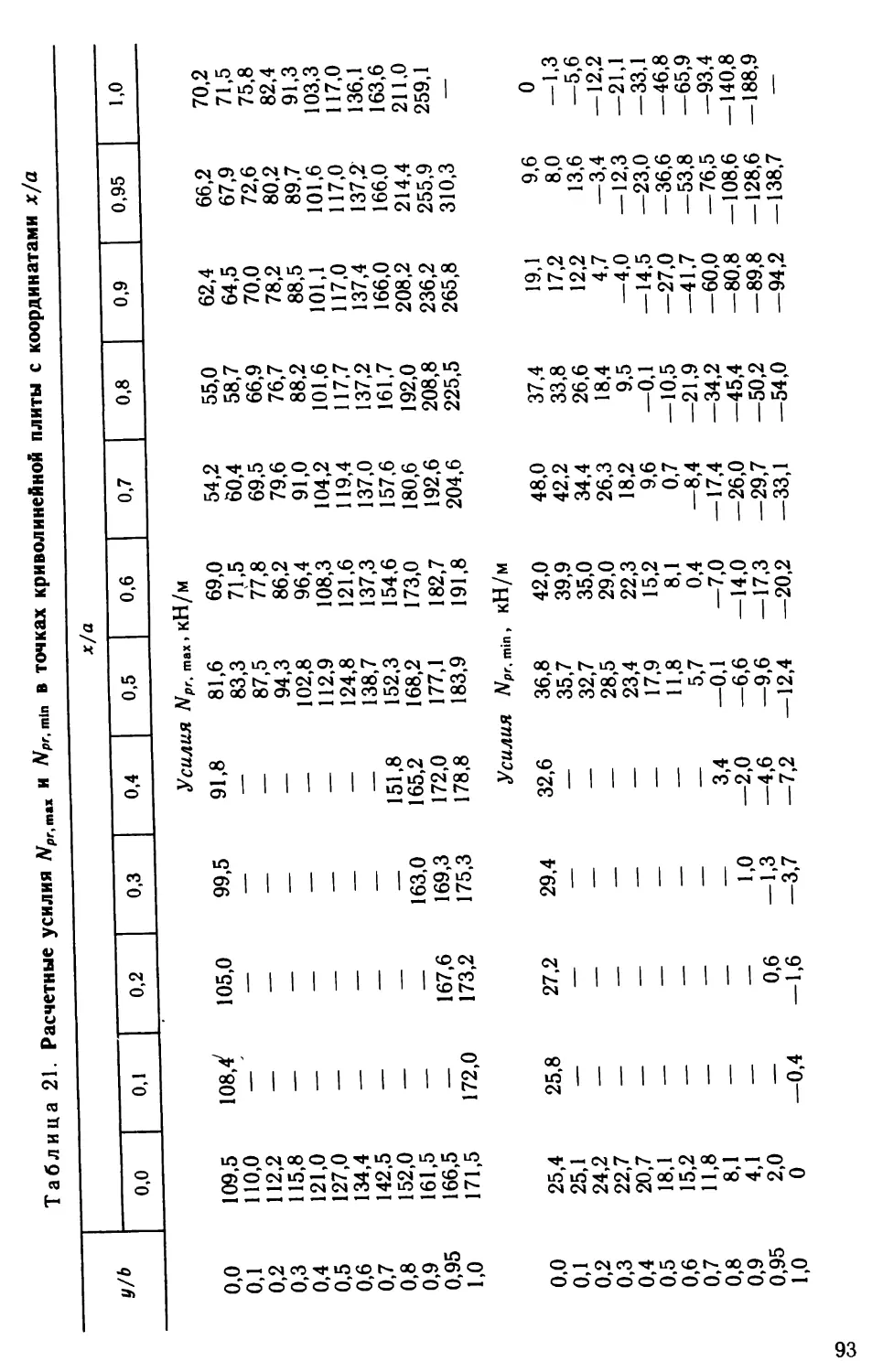
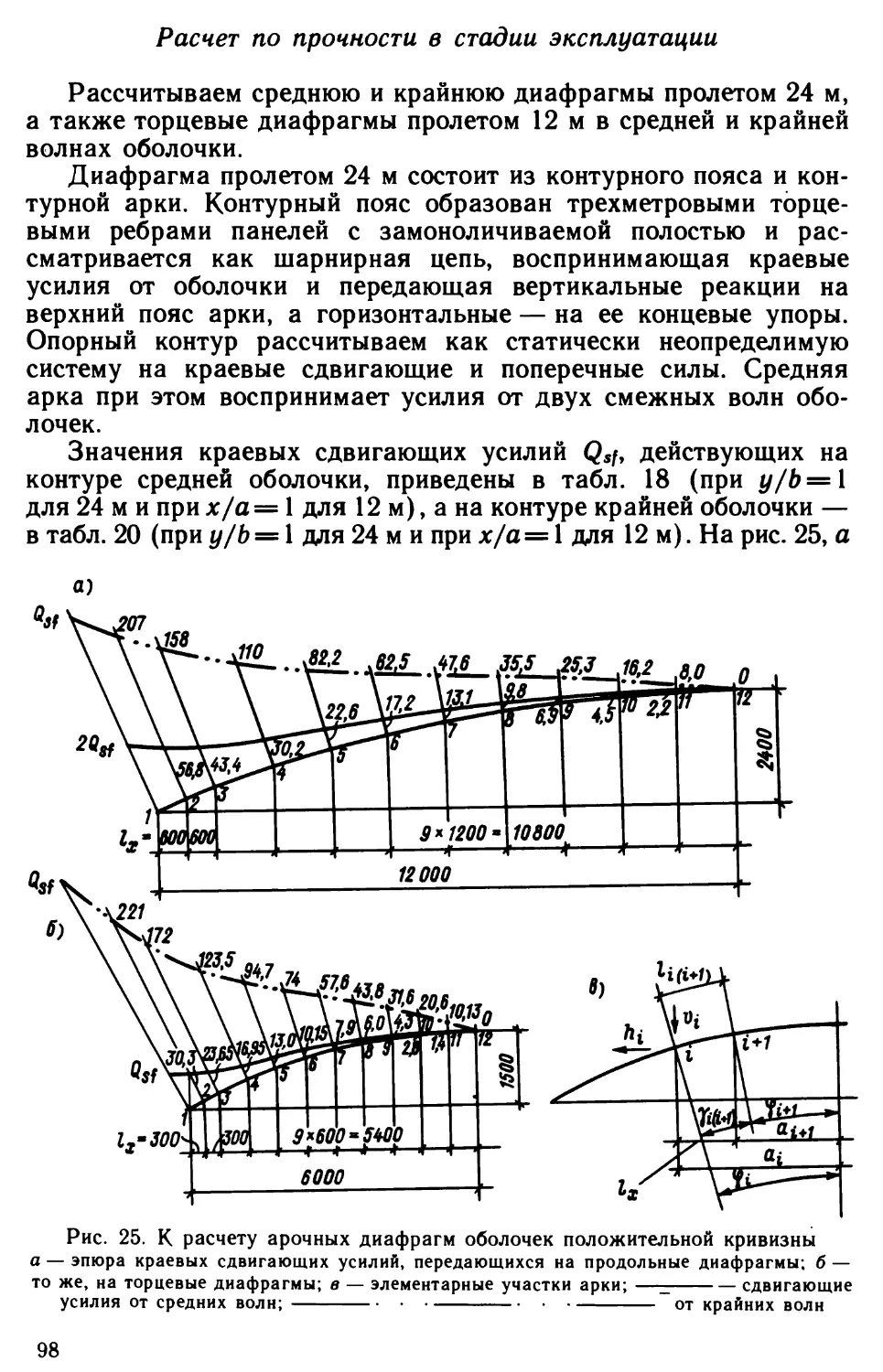
тивному распределению усилий по пролету.Торцевая диафрагма оболочки имеет пролет 12 м и принята
в виде арки, верхний пояс которой является ребром торцевой
панели. Затяжка этой арки изготовляется отдельно в виде железо¬
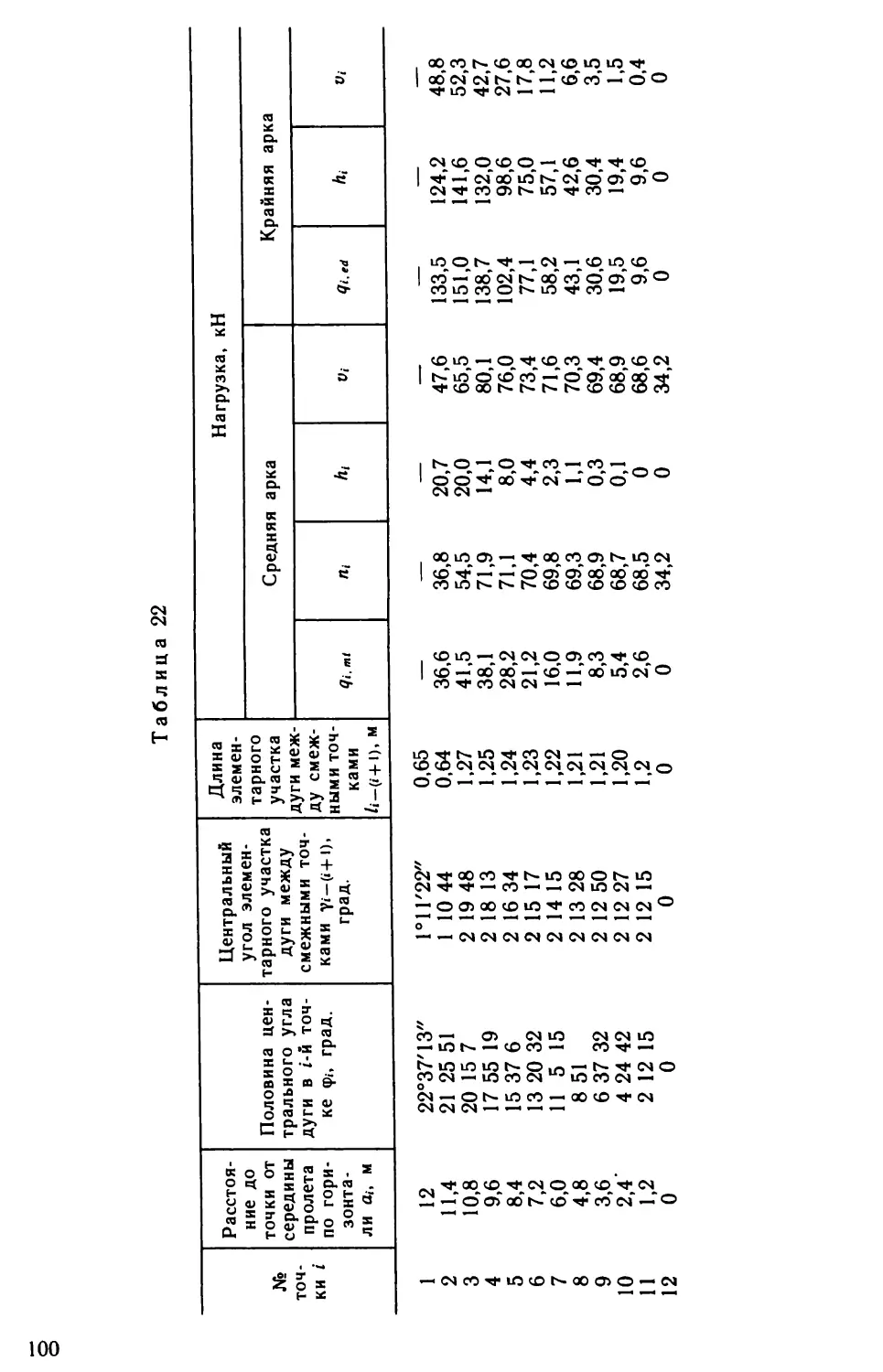
бетонного предварительно напряженного бруса.Конструкция оболочки показана на рис. 1 и 3.Элементы оболочки выполняются из тяжелого бетона клас¬
са В 35.Нагрузки на оболочку, принятые в расчете, приведены в табл. 1.3. Геометрические характеристики оболочкиНазначаем высоту поперечного сечения оболочки Л*л, посере¬
дине пролета, включая сечение бортовой балки, равной 3100 мм,
что соответствует примерно Л/10, а стрелу подъема fCur,Pi криволи¬
нейной части оболочки — равной 1500 мм, т. е. около 1/8 ширины
оболочки (пролета /2).Криволинейную часть внешней поверхности оболочки прини¬
маем очерченной по дуге круга радиусом:г = (/2 + 4fcur, pi) / (8/cur, pi) —=[(12-2 • 0,Об)2 + 4 • 1,52]/(8 • 1,5)= 12,51 м.Радиус срединной поверхности будет 12,51—0,02=12,49 м.
Значение h принимается в соответствии с конструкцией узла
соединения плиты оболочки с бортовым элементом (рис. 3, б).Исходя из радиуса г находим центральный угол 6| для поло¬
вины дуги криволинейной части оболочки:sin0, = /2/(2r)=(12—2 • 0,06)/(2 • 12,51)=0,475;cos 0|=О,88, чему соответствует угол 0| =28°20/43"=0,495 рад.Площадь поперечного сечения криволинейной плиты (размеры
на рис. 3, а) :Лсиг, pi=2rQltcurt pi=2 • 12,49 • 0,495 • 0,04 = 0,495 м2.12
Площадь бортовой балки в сечении посередине пролета (до за-
моноличивания стыковой полости оболочки):Л^ = 0,08* 1,4 + 0,22(0,1+0,05 + 0,35) = 0,222 м2.Общая площадь поперечного сечения оболочки посередине
пролета с учетом площади сечения замоноличенной стыковой
полости 0,3 • 0,2 = 0,06 м2.ASh = 0,495 + 0,222 + 0,060 = 0,777 м2.Определяем момент инерции поперечного сечения оболочки.
Для этого сначала находим положение центра тяжести сечения:
криволинейной плитыу'сиг,Р1&г( 1 —sin 6i/0i)или приблизительно при sin 0i = 0iy'curtPl=f/3= 1,48/3 = 0,493 м;бортовой балки в сечении посередине пролета (до замоноли-
чивания стыковой полости оболочки)y'ed = [0,08 1,4 0,7 + 0,22(0,1 • 0,05 + 0,05 • 0,575 ++ 0,35 • 1,225)]/0,222 = 0,812 м;1/^ =1,4 — 0,812 = 0,588 м;всего поперечного сечения оболочки посередине пролета с
учетом замоноличенной стыковой полостиy'sh = [0,495 • 0,493 + 0,222(0,812 + 0,2 + 1,5) ++ 0,2 • 0,3(0,1 + 1,5)/0,777= 1,16 м;= 3,1 — 1,16=1,94 м.Теперь определим момент инерции сечения криволинейной
плитыIcur,Pi=r*tCUr,pi(Q\ + sin Gicos 0i — 2sin20i/0i) == 12,493 • 0,04(0,495 + 0,475 • 0,88-2 • 0,4752/0,495)= (1)
= 0,0965 m413
и момент инерции бортовой балки в сечении посередине пролета
до замоноличивания стыковой полости приводим без вычислений;
/^ = 0,0493 м4. В результате момент инерции всего поперечного
сечения оболочки посередине пролета с учетом замоноличенной
стыковой полости составитIsh = 0,0965 + 0,0493 + 0,3 • 0,23/12 + 0,495 • 0,6572 ++ 0,222 • 1,3422+0,3 • 0,2 • 0,432 = 0,77 м4.4. Расчет оболочки в продольном направлении4.1. Расчет по прочности на действие
изгибающих моментов и подбор продольной
арматуры бортовых балокОболочка выполняется из тяжелого бетона класса В 35, Еь =
= 31000МПа. Величина расчетных сопротивлений бетона по проч¬
ности на сжатие Rb и на осевое растяжение Rbt для предельных
состояний первой группы соответственно равна 19,5 и 1,30 МПа.В целях экономии арматуры, а также повышения трещино-
стойкости и жесткости конструкции арматуру бортовых элементов
оболочки выполняем предварительно напряженной. В качестве
напрягаемой арматуры для армирования бортовой балки прини¬
маем арматурные канаты диаметром 15 мм класса К-7 с расчет¬
ным сопротивлением растяжению Rs = 1080 МПа. Максимальный
изгибающий момент в середине пролета от расчетной нагрузки
на оболочку шириной 12 м /\/ = 5,55 • 12 = 66,6 кН/м составляет:
М„=0,125 • 66,6 • 29,62=7294 кН • м.Оболочку на прочность в продольном направлении рассчиты¬
ваем по предельным состояниям как простую балку. Целью рас¬
чета является определение необходимого сечения растянутой
арматуры и проверка прочности сжатой зоны бетона. При этом
продольную рабочую арматуру располагаем в нижней части
бортовых элементов для получения наибольшего значения плеча
сил внутренней пары, т. е. расстояния между центрами тяжести
растянутой арматуры и сжатого бетона. Зная величину максималь¬
ного изгибающего момента в пролете и плечо сил внутренней
пары, можно легко определить необходимое количество растяну¬
той арматуры.Итак, необходимо найти плечо сил внутренней пары. Для этого
нужно задаться количеством рабочей арматуры, найти границу
сжатой зоны бетона и определить ее центр тяжести. Принимая
очертание криволинейной части сечения оболочки по дуге окруж¬
ности,расчет оболочки в продольном направлении можно упростить
воспользовавшись формулами, предложенными П. Л. Пастерна-14
Рис. 4. Схема усилий и эпюра напряжений в сечении, нормальном к продольной
оси изгибаемой цилиндрической оболочки, при расчете по прочностиком. Запишем суммарный момент сжимающих усилий относитель¬
но центра дуги поперечного сечения оболочки:%RbtCur,pir2\ cos ada = RbtCurtpir2s\n 0£.оЕсли а (рис. 4) — расстояние от центра дуги поперечного се¬
чения оболочки до центра рабочей продольной арматуры, то
h0 sh = r — a — расстояние от центра рабочей продольной арматуры
до осевой линии дуги поперечного сечения оболочки; 0£— поло¬
вина центрального угла, охватывающего дугу сжатой зоны сечения
оболочки; а — текущая угловая координата.Сравнивая внешний изгибающий момент с выражением мо¬
мента внутренних сил относительно центра дуги поперечного
сечения оболочки, получим:Md = 2(Rbtcur,pir2sin в'ь — ciRsAs). (2)Запишем также условие равновесия продольных сил в сеченииRbQbrtcur,pi=RsAs (3)
и решим совместно уравнения (2) и (3):sin 0J-4-0» =0.2Rbtcur,pirИмея в виду, что угол 0£ относительно мал, и приняв приближенно15
sin0£«0£, найдем выражение для половины центрального угла,
охватывающего участок сжатой зоны дуги поперечного сечения
оболочки:6*= 2Rbtcur.plrh0 ' WПодставляя численные значения в (4), получим 0£ = О,129.Полная площадь сечения растянутой арматуры, размещаемой
в одной промежуточной бортовой балке, вычисляется по форму¬
ле (3). Учитывая, что в этой формуле As— половина необходимой
площади, вводим коэффициент 2, тогдал __0 %rtCUT,piRb __ 2 • 0,129 • 12490 • 40 • 19,5 ООГГ7 ____2
5 Rs 1080 —2627 мм .Принимаем 20 арматурных канатов класса К-7 диаметром 15 мм.
Таким образом, площадь напрягаемой арматуры составит Asp =
= 2830 мм2. Другие расчеты и конструирование балки выполня¬
ются по аналогии с плоскими балками и здесь не приводятся.4.2. Расчет по прочности на действие
поперечных сил и подбор арматуры
криволинейной плитыНа поперечные силы оболочку рассчитываем как обычную
упругую систему, в данном случае представляющую собой простую
балку. Такой расчет для крайних четвертей оболочки вполне при¬
емлем. В средней зоне оболочки, где поперечные силы имеют
минимальные значения, а изгибающие моменты — максимальные,
криволинейная часть оболочки работает на сжатие в продольном
направлении, и лимитирующим здесь является устойчивость пли¬
ты. Однако учитывая, что сборные оболочки снабжены продоль¬
ными и поперечными ребрами, устойчивость криволинейной пли¬
ты, как правило, обеспечивается.Итак, рассчитываем криволинейную плиту крайних четвертей
оболочки.Для определения нормальных напряжений в плите от расчет¬
ной нагрузки допускается использовать формулу Навье, а для
определения сдвигающих усилий — формулу Журавского: Мх% /л QxSyЗакон изменения этих усилий по длине оболочки принимается
такой же, как и для простой балки.16
Главные растягивающие напряжения определяются исходя
из плоского напряженного состояния. При этом можно учитывать
нормальные напряжения, действующие в обоих направлениях,
по формуле:0^4^=р7(^у+^. (5)Имея в виду, что нормальные напряжения в поперечном направ¬
лении относительно малы, их можно не учитывать, приняв 0^ = 0.Каждая панель, имеющая ширину 3 м, рассчитывается на
среднее значение ординаты балочной эпюры поперечной силы, т. е.
в сечениях на расстояниях от опоры х\ = 1,3 м, *2 = 4,3 м, *3 = 7,3 м.Рассчитаем две панели: первую от опоры (торцевую) и вторую
(рядовую).Расчет криволинейной плиты торцевой панели. Геометрические
характеристики поперечного сечения оболочки в сечении на рас¬
стоянии *1 = 1,3 м от опоры:1) бортовая балка: Ле{*=1,1 м, Aed = 0,242 м2, z'ed = 0,56 м,
/^ = 0,032 м4;2) полное сечение оболочки: Л5Л = 0,737 м2, 2^ = 0,996 м, Ish =
= 0,5235 м4;3) изгибающий момент в сечении: Mx = Q$Fdx(l\ — х) =
= 0,5 • 66,6 • 1,3(29,6-1,3) =1225 кН • м;4) поперечная сила в сечении: Qx = Fd(0y5li — jc) = 66,6X
X (0,5 • 29,6-1,3) =899 кН.На участках, где opr> Rbu сечение арматуры определяется
исходя из растягивающих напряжений, действующих под углом 45°
к образующей.Главные растягивающие напряжения, действующие в плите
оболочки, определяем по формуле (5), принимая ау = 0:ОрГ = ах/2 + V (ох/2)2+т* ,
где ax = Mxy,/lsh\ тx = Q,Si/(Ishb)\yi— ордината точки рассматриваемого сечения дуги (криволинейной плиты обо¬
лочки); Si— статический момент дуги площадью Л = 2га|*Сиг,р/, находящейся выше
рассматриваемого сечения и имеющей стрелу fi = r(\ — cos a,); Si = Ai(z'sh — z't)\
b — ширина элемента: b = 2tCUr,pi\ 2, = /,/3 — расстояние до центра тяжести
i-й дуги.Вычисление главных растягивающих напряжений сводим в
табл. 2. Из результатов расчета видно, что во всех точках сечения
криволинейной плиты торцевой панели оболочки главные растяги¬
вающие напряжения превышают Rbt= 1,30 МПа и, следовательно
для подбора арматуры необходимо вычислить W45.Усилие N45, действующее в точках сечения криволинейной
плиты под углом 45° к образующей, определяем по формуле2 Заказ 6117
ПараметрТочки поперечного сечения (рис.4)/2345а/, град, (рад.)28°20'43"21°15'14°10'7°5'0(0,4947)(0,371)(0,2474)(0,1237)(0)sin a,0,4750,3620,2450,12350cos a,0,880,9310,970,9931Ai, m20,4950,370,250,1240fi. M1,480,860,370,0870Zi, M0,490,290,120,030Si, m30,250,260,220,120Тх, МПа5,365,584,722,580yi. м0,4840,1560,6360,9260,996ox/2, МПа0,57—0,19—0,74— 1,08— 1,17apr, МПа5,965,44,051.71018N<b=^-+QSf,a , (6)™ т-^'»-''г-тт1к0'м'-,бда*здесь z — расстояние от точек дуги до центра тяжести сечения оболочки; Qsf,a —
сдвигающее усилие, действующее в точке сечения криволинейной плиты одно¬
волновой оболочки с угловой координатой а:Qst.a 2(sina —л«), (7)Qx— поперечная сила в рассматриваемом сечении оболочки от нагрузки,
приходящейся на половину единичной плоскости оболочки.Подставив все значения величин в (7), получим:= 899 2°о45235’492 2(sin а-Ла)= 10691(sin а-0,92а),где л=(г - z'sh)/г=(12,49—0,996) /12,49=0,92.Расчет криволинейной плиты второй от торца панели. Расчет
второй от торца панели (сечение на расстоянии дс2=4,3 м от опо¬
ры) выполняется аналогично. В этом случаеhe,t= 1,3 м; Aed = 0,258 м2; z'tt=0,663 м;led=0,0508 м4; ASh=0,753 м2; 2^=1,053 м;/*а=0,618 м4; М*=3622 кН • м; Qx=698 кН;Л =0,916; ^/2 = 117,2; Qs/.a =7046(sin a-0,916a).Вычисление усилий N45 по формуле (6) сведено в табл. 3 (зна¬
чения функций углов см. табл. 2).Таблица 2
Таблица 3ПанельНомер точкиZ, мQsf, а , КН/М0,5Nx, кН/мЛГ45. кН/мТорцевая (пер¬1—0,484212,4622,67235,1вая от опоры)20,156221,1—7,31213,830,636185,9—29,79156,140,926103,7—43,3760,350,9960—46,65—46,7Рядовая (вто¬1—0,427153,950,04203,9рая от опоры)20,213156,2—24,96131,230,693129,55—81,2248,340,98371,82— 115,2—43,451,0530— 123,4— 123,4Исходя из опыта применения длинных цилиндрических обо¬
лочек и результатов исследований, на арматуру можно передать
не полное усилие N45, а лишь 70% от вычисленного выше. Остальная
часть усилий воспринимается бетоном. Таким образом, в точках /,
2, 3 дуги оболочки второй от опоры панели усилие Ns, восприни¬
маемое арматурой, соответственно составляет 142,7; 91,8; 33,8 кН/м.
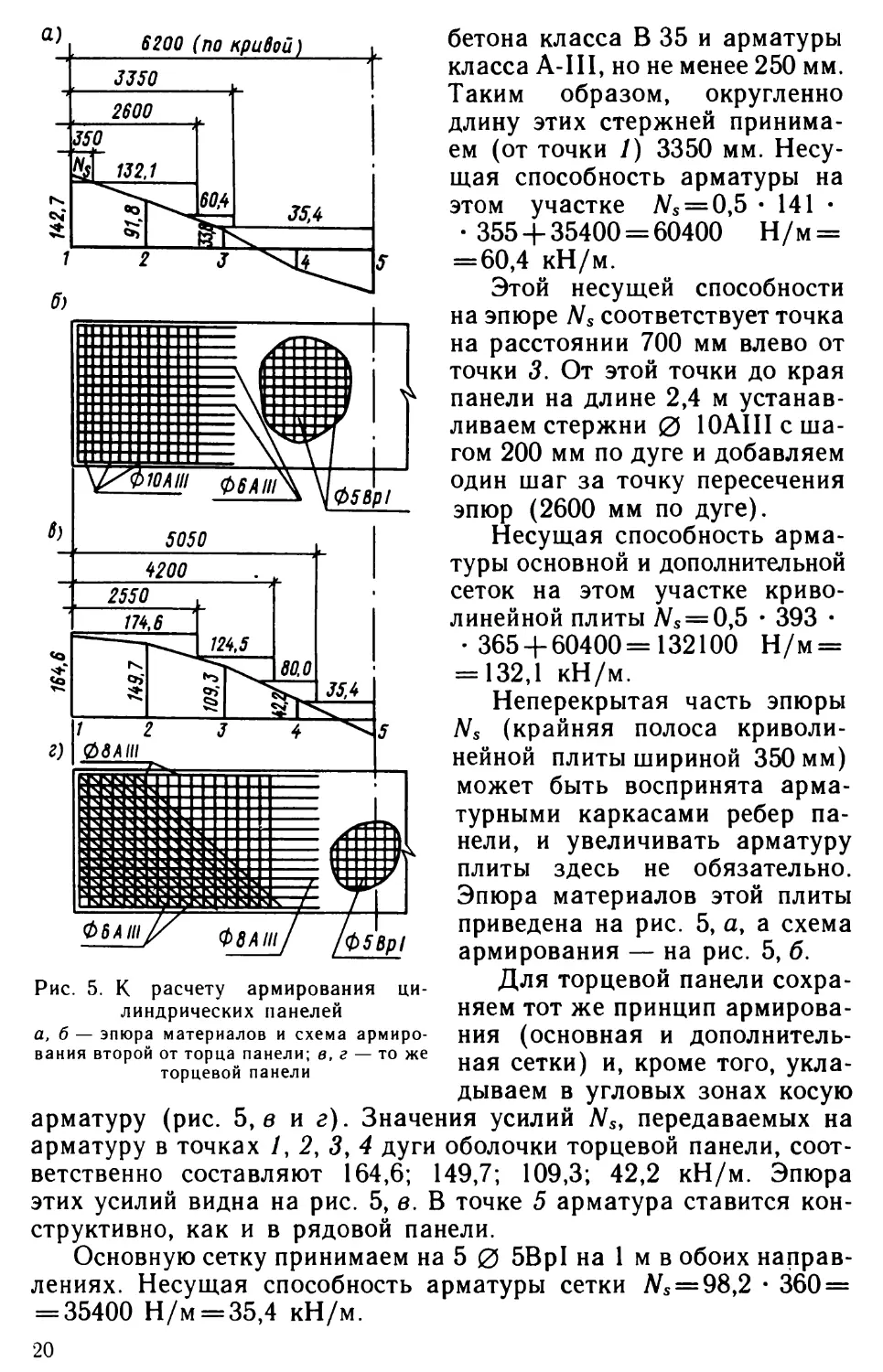
Эпюра этих усилий дана на рис. 5, а.Вторую от торца панель армируем основной сеткой, уклады¬
ваемой по всей площади криволинейной плиты, и дополнительными
сетками на крайних участках в зонах, прилегающих к бортовым
балкам.Продольную арматуру в сжатой зоне оболочки (в точках 4
и 5 сечения криволинейной плиты) устанавливаем конструктивно,
причем площадь сечения этой арматуры должна быть не менее
0,2% сечения бетона. Следовательно, As=0,002 • 1000 • 40 =
= 80 мм2/м. Принимаем здесь 505Вр1 на 1 м, Л* = 98,2 мм2.
Такую же арматуру устанавливаем в качестве поперечной (Л5а; =
= 98,2 мм2).Таким образом, основная сетка, укладываемая по всей пло¬
щади второй панели, конструируется из стержней 0 5Вр1 с ша¬
гом 200 мм в обоих направлениях. Несущая способность этой
сетки на единицу длины составляетNs = 0,5(i4s + Asw)Rs = 0,5(98,2 + 98,2) 360 == 35352 Н/м«35,4 кН/м.На крайних участках плиты (точки /, 2, 3) устанавливаем
дополнительные сетки из стержней 0 6AIII (поперечная арматура
оболочки) и 0 10AIII (продольная арматура оболочки) с шагом
200 мм в каждом направлении (рис. 5,6). Длину стержней0 6AIII в сетке назначаем такой, чтобы они перешли за точку, где
они не требуются по расчету (точка на расстоянии 40 мм от точки 3
по дуге влево), на длину анкеровки, равную 24 диаметрам для2*19
6200 (по кривой)бетона класса В 35 и арматуры
класса A-III, но не менее 250 мм.
Таким образом, округленно
длину этих стержней принима¬
ем (от точки 1) 3350 мм. Несу¬
щая способность арматуры на
этом участке Ns = 0,5 - 141 -
• 355 + 35400 = 60400 Н/м =
= 60,4 кН/м.Этой несущей способности
на эпюре Ns соответствует точка
на расстоянии 700 мм влево от
точки 3. От этой точки до края
панели на длине 2,4 м устанав¬
ливаем стержни 0 10AIII с ша¬
гом 200 мм по дуге и добавляем
один шаг за точку пересечения
эпюр (2600 мм по дуге).Несущая способность арма¬
туры основной и дополнительной
сеток на этом участке криво¬
линейной плиты Ns = 0,5 • 393 •
•365 + 60400=132100 Н/м =
= 132,1 кН/м.Неперекрытая часть эпюры
Ns (крайняя полоса криволи¬
нейной плиты шириной 350 мм)
может быть воспринята арма¬
турными каркасами ребер па¬
нели, и увеличивать арматуру
плиты здесь не обязательно.
Эпюра материалов этой плиты
приведена на рис. 5, а, а схема
армирования — на рис. 5, б.Для торцевой панели сохра¬
няем тот же принцип армирова¬
ния (основная и дополнитель¬
ная сетки) и, кроме того, укла¬
дываем в угловых зонах косую
арматуру (рис. 5, в и г). Значения усилий Ns, передаваемых на
арматуру в точках /, 2, 3, 4 дуги оболочки торцевой панели, соот¬
ветственно составляют 164,6; 149,7; 109,3; 42,2 кН/м. Эпюра
этих усилий видна на рис. 5, в. В точке 5 арматура ставится кон¬
структивно, как и в рядовой панели.Основную сетку принимаем на 5 0 5Вр1 на 1 м в обоих направ¬
лениях. Несущая способность арматуры сетки Ns = 98,2 • 360 =
= 35400 Н/м = 35,4 кН/м.20Рис. 5. К расчету армирования ци¬
линдрических панелей
а, б — эпюра материалов и схема армиро¬
вания второй от торца панели; в, г — то же
торцевой панели
От точки пересечения вычисленного значения эпюры мате¬
риалов Ns с эпюрой усилий N45 (140 мм вправо от точки 4) уклады¬
ваем дополнительную поперечную арматуру оболочки — 5 0 8AIII
на 1 м и заводим стержни этой арматуры за указанную точку
на длину анкеровки /ап=250 мм. Полная длина этих стержней
по дуге составит 1,55 -3 + 0,14 + 0,25 = 5,05 м. Тогда несущая
способность арматуры: Ns = 35400 + 0,5 • 251 • 355 = 80000 Н/м =
= 80 кН • м.В точке пересечения этого значения Ns с эпюрой усилий (0,85 м
влево от точки 4) добавляем продольную арматуру оболочки —
5 0 8AIII с прибавлением одного шага для перекрытия эпюры.
В результате общая несущая способность основной и дополни¬
тельной сеток N* = 35,4 + 251 • 355=124,5 кН/м.Оставшуюся часть эпюры Ns перекрываем добавлением косой
арматуры. Принимаем эту арматуру из 0 6AIII с шагом 200 мм
и устанавливаем ее в угловой зоне начиная с точки пересечения
эпюры усилий с полученным значением Ns (0,5 м влево от точки 3).
Несущая способность всей арматуры, установленной в угловой
зоне криволинейной плиты, N*=124,5+141 355=174,6 кН/м,
что больше максимального усилия Ns> действующего в торцевой
панели оболочки, и, следовательно, прочность плиты оболочки
обеспечена.4.3. Расчет по трещиностойкости
(по образованию трещин, нормальных к продольной оси оболочки)Для расчета трещиностойкости оболочки в стадии эксплуата¬
ции необходимо учесть напряжения, возникающие в бортовой
балке на всех этапах ее работы, в том числе на всех этапах мон¬
тажа.Для этого рассмотрим порядок монтажа оболочки:1) на несущие колонны цеха устанавливаются бортовые эле¬
менты оболочки, работающие как балки пролетом 30 м;2) под каждую балку в точках на расстоянии 11,8 м от обеих
колонн для уменьшения монтажных усилий подводятся две времен¬
ные промежуточные опоры в виде стоек (без вывески собственной
массы балки);3) по балкам укладываются криволинейные 12-метровые па¬
нели, после чего производится замоноличивание швов оболочки;
на этом этапе балка еще работает по трехпролетной схеме, причем
криволинейные панели в работе не участвуют, а представляют
собой нагрузку на балку;4) после набора необходимой прочности бетоном замоноли-
чивания швов временные промежуточные опоры убираются, и
оболочка включается в работу полным сечением.Расчет оболочки по образованию трещин производим для21
упругой стадии работы конструкции от действия постоянных и
временных (длительных и кратковременных) нормативных нагрузок
(yf= 1), с учетом коэффициента точности натяжения напрягаемой
арматуры. Оболочка относится к третьей категории требований
к трещиностойкости.Расчетные сопротивления бетона по прочности на осевое сжатие
и на осевое растяжение для предельных состояний второй группы
соответственно составляют RbtSer = 25,5 МПа и RbttSer = 1,95 МПа.
Предельную величину предварительного напряжения назначаем
osp = Rs,ser — p, где Rs,ser= 1295 МПа и p = 0,05asp, откуда о8рж
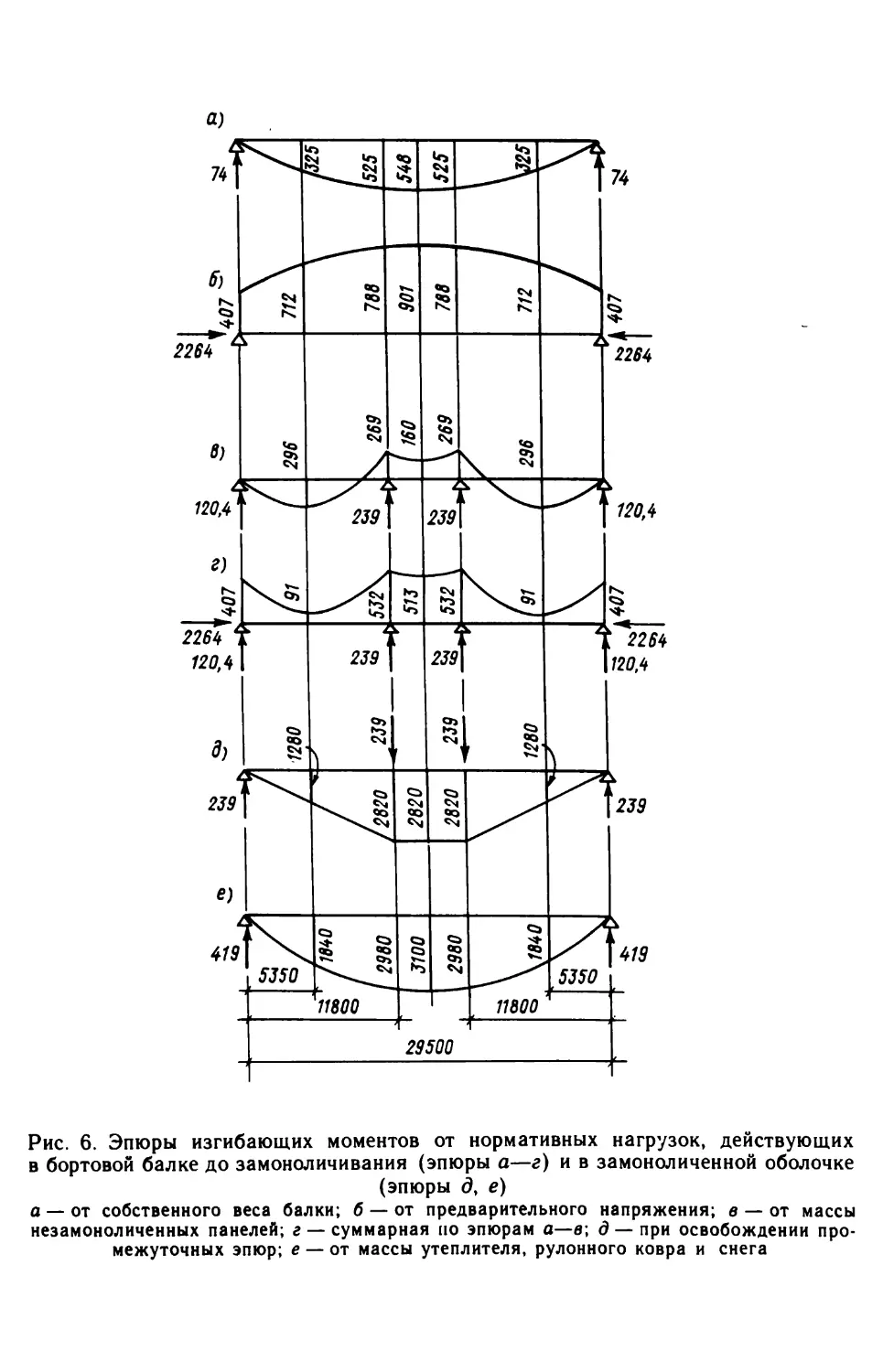
«1230 МПа.Без приведения подсчетов на рис. 6 показаны эпюры изгиба¬
ющих моментов на различных этапах загружения балки и обо¬
лочки, построенные по приведенным ниже значениям воздействий:а) от собственной массы балки (&я = 5 кН/м)Мп = 0,125 • 5 • 29,62 = 548 кН • м (рис. 6, а) ;б) от предварительного натяжения арматуры (расчет величин
потерь предварительного напряжения опущен) силой Р:P = (osp-ois)Asysp = ( 1230-430)2830 • 1 =2264000 Н = 2264 кН;на опореMSup = PeSup = 2264 • 0,18 = 407 кН • м;в пролетеМша* = /><?тах = 2264 . 0,398 = 901 кН • м (рис. 6,6) ;в) от массы криволинейных панелейgn = 24,3 кН/м (рис. 6, в);г) суммарная эпюра от собственной массы балки, от предва¬
рительного натяжения арматуры и от массы криволинейных па¬
нелей — при работе балки по трехпролетной схеме (рис. 6, г);д) от реакций временных опор величиной 239 кН, передава¬
емых на оболочку в момент снятия временных промежуточных
стоек (рис. 6, д);е) от массы теплоизоляции, кровли и снегаgn-\-sn=57,6 — 24,3 = 28,3 кН/м (рис. 6, е).Для определения трещиностойкости оболочки вычислим зна¬
чения напряжений в предварительно напряженном бортовом эле-22 '
d)Рис. 6. Эпюры изгибающих моментов от нормативных нагрузок, действующих
в бортовой балке до замоноличивания (эпюры а—г) и в замоноличенной оболочке(эпюры д, е)а — от собственного веса балки; б — от предварительного напряжения; в — от массы
незамоноличенных панелей; г — суммарная по эпюрам а—в; д — при освобождении про¬
межуточных эпюр; е — от массы утеплителя, рулонного ковра и снега
менте, возникающих в нем до замоноличивания, от действия
изгибающего момента Мп = 548— 901 —160= —513 кН • м и про¬
дольной силы Nn = 2264 кН (рис. 6, а, б и в).Для этого нам нужны параметры приведенного сечения посе¬
редине пролета. Приводим их без вычислений: Аел,гел = 233700 мм2;
Ied,red = 49,3 • ю9 ММ4; y'edtred = 832 MM', yed,red = 568 ММ.Напряжения в бетоне балки до замоноличивания вычислим
по формуле N . Myed, red .А =*= led,red ‘
в крайнем верхнем волокне, 2264000 . 513 • 106 - 832 i п мгт~ 233700 + 49,3 • 10м = _1’° МПа;в крайнем нижнем волокне2264000 513 • 106 568 , с с Х)1Г1
°ed= 233700 ШЛУ = _15’6 МПа(минус обозначает сжатие).Определяем также значения напряжений в элементах оболочки
после замоноличивания и снятия временных опор на действие
изгибающего момента Мп = 2820 + 3100 = 5920 кН • м (рис. 6, д
и е). Параметры приведенного сечения оболочки посередине про¬
лета даем без вычислений: ASh,re<i = 788700 мм2; /«*,red = 816,5X
XlO9 ММ4; y'sh,red ^ 1 160 ММ; ysh,red = 1940 мм.Напряжения:в крайнем сжатом волокне бетона обол9чки
. ■ 5920 • 1160 ■ 106 0 . МГ1sA 816,5 • ю9 — ’ МПа,на уровне верхнего волокна бетона балки, 5920 • 537 • 106 0 п ХДГ1
Р*'= 816,5 • 109 =3’9 МПа;в крайнем растянутом волокне бетона оболочки5920- 1945 • 10е ...
g*=" -816,5-10^ =14’1 МПа’Эпюры напряжений в сечении оболочки по этапам загружения,
в т. ч. результирующая, приведены на рис. 7. Как видно из резуль¬
тирующей эпюры (рис. 7, в), трещиностойкость оболочки обеспе-24
Рис. 7. Эпюры нормальных напряжений в сечении оболочки посередине пролета
а — до замоноличивания; б — после замоноличивания; в — суммарнаячена, так как нижнее краевое напряжение в зоне размещения
напрягаемой арматуры — сжимающее, равное 1,5 МПа.Расчеты для других сечений оболочки аналогичны и здесь
не приводятся, так же как и расчеты балки в стадии изготовления
и монтажа.4.4. Расчет по деформациямЭтот расчет выполнен в соответствии с указаниями
СНиП 2.03.01—84, ф-ла (155).При расчете оболочки по деформациям учитываем действие
постоянны*, длительных и кратковременных нагрузок, а также
обратный выгиб бортового элемента от действия предварительного
обжатия и вследствие усадки и ползучести бетона. При этом
принимаем во внимание установленный выше (см. с. 21) порядок
монтажа оболочки. Расчет производим на нормативные нагрузкиДля определения кривизны оси оболочки от действия кратко¬
временной нагрузки (в нашем случае от снега) вычисляем изги¬
бающий момент от этой нагрузки: М* = 0,125 • 1 • 12 • 29,62 =
= 1310 кН • м.От этой нагрузки кривизна будет составлять/ 1 \ Ms<pt2 1310 • ю6 • 1 1П_6 , ,YT)i = ФНЕЛ* = 0,85 • 31000 • 816,5 • 10* =°’0Ь ‘ 10 1/ММ*Изгибающий момент от длительных нагрузок, прикладываемых
к оболочке после замоноличивания и снятия временных опор,М/=(2820 + 3100)/1,22-1310 = 3542 кН • м.25
Величина кривизны оси оболочки от действия этого момента(-!-) = 3542 106 • 2 =0,33 • 10“6 1/мм.' г /2 0,85 • 31000 • 816,5 • 109Для определения обратной кривизны, обусловленной выгибом
бортового элемента под действием предварительного обжатия,
возникающего до замоноличивания оболочки, рассматриваем на¬
грузки, изображенные на схемах рис. 6, а и б. Схему, приведенную
на рис. 6, а, не учитываем ввиду незначительности ее влияния
на прогиб. Усилие предварительного напряжения принято здесь
с коэффициентом точности натяжения ysp = 0t9.Кривизна оси балки от выгиба/ 1 \ Pyfe0P (901 • 0,9 — 548) 106 . in—6 i/ммV Г /з 4b\Eblred ~ 0,85 • 31000 • 49,3 • 10* ’ 'Для определения кривизны, обусловленной выгибом балки
вследствие усадки и ползучести бетона от усилия предваритель¬
ного обжатия, вычисляем соответствующие относительные дефор¬
мации бетона на уровне центра тяжести растянутой продольной
арматуры и крайнего сжатого волокна.Напряжения в бетоне на уровне центра тяжести напрягаемой
арматуры2264000 ■ 353 • 106 /глп 17m 10с пл
Р»'’==-233700~+ 49,3 • 10^ ( 170)= 12,5 МПа.Величины напряжений для определения относительных дефор¬
маций бетона принимаем численно равными сумме потерь предва¬
рительного напряжения арматуры от усадки и ползучести бетона
по поз. 8 и 9 табл. 5 СНиП 2.03.01—84. При передаточной прочно¬
сти бетона /?*р=0,5 • 35= 17,5 МПа для Obp/Rbp= 12,5/17,5 =
=0,71 потери от усадки бетона составляют ав=35,0 МПа, а от
ползучести — ст9= 150 • 0,85 • 0,71 =90,5 МПа.Таким образом, относительная деформация бетона на уровне
центра тяжести растянутой продольной арматуры£*=(ов + а9)/Е,=(35+90,5)/18 . 1 о4=0,697 • 10"3.То же, на уровне крайнего сжатого волокна/ 2264000 353 * 106 qq ^ q 7^ лдпл.а»=~тт— 49,3- ю* 83'2=3-73 МПа;
oi/Rbp=3,73/17,5=0,21; ст$ = 35,0 МПа;
ад = 150 • 0,85 • 0,21=26,77 МПа.26
Следовательно, относительная деформация бетона на уровне
крайнего сжатого волокна££ = (<*в + о'д)/Es=(35,0 + 26,77)/18 • 104 =0,343 • 10~3.Кривизну балки вследствие усадки и ползучести от предва¬
рительного обжатия находим, учитывая, что усадка и ползучесть
бетона на момент монтажа проявятся еще не полностью. Условно
принимаем их в размере 50%. Тогда(~г)4 =^ТГ~= °'69^23о’343 10~3 • 0,5=0,14 • 10"6 1/мм.Полная величина кривизныl/r = (l/r),+(l/r)2-(l/r)3-(l/r)4 ==(0,06 + 0,33 -0,2 - 0,14)10"6 = 0,05 • 10“6 1/мм.Стрелку прогиба однопролетной оболочки от равномерно рас¬
пределенной нагрузки определяем по известной формуле:f = 5/?/48r = 5 • 296002 • 0,05 • 10"6/48 = 4,56 мм.Таким образом, величина наибольшего прогиба составляет
1/6490 пролета, что свидетельствует о достаточной жесткости
конструкции.5. Расчет оболочки в поперечном направленииДля расчета в поперечном направлении оболочки, загружен¬
ной распределенной поверхностной нагрузкой постоянной интен¬
сивности, необходимо рассмотреть условия равновесия полоски
единичной ширины, вырезанной в любом сечении х по длине обо¬
лочки. Такая полоска представляет собой криволинейную плиту.
Эту плиту можно рассчитать как круговую бесшарнирную арку
пролетом, равным ширине оболочки. На рис. 8, а и б показаны
действующие на вырезанную из оболочки элементарную полоску
внешние нагрузки и внутренние усилия. Из рисунка видно, что
внешняя нагрузка F, приходящаяся на вырезанную полоску, урав¬
новешивается приращением поперечной силы или, что то же, при¬
ращением сдвигающих усилий bqSf. Зная закон изменения сдви¬
гающих усилий по сечению оболочки, можно записать условия
их равновесия, из которых и определить интересующие нас уси¬
лия — поперечные изгибающие моменты и соответствующие им
поперечные и нормальные усилия, действующие в сечении выре¬
занной полоски.27
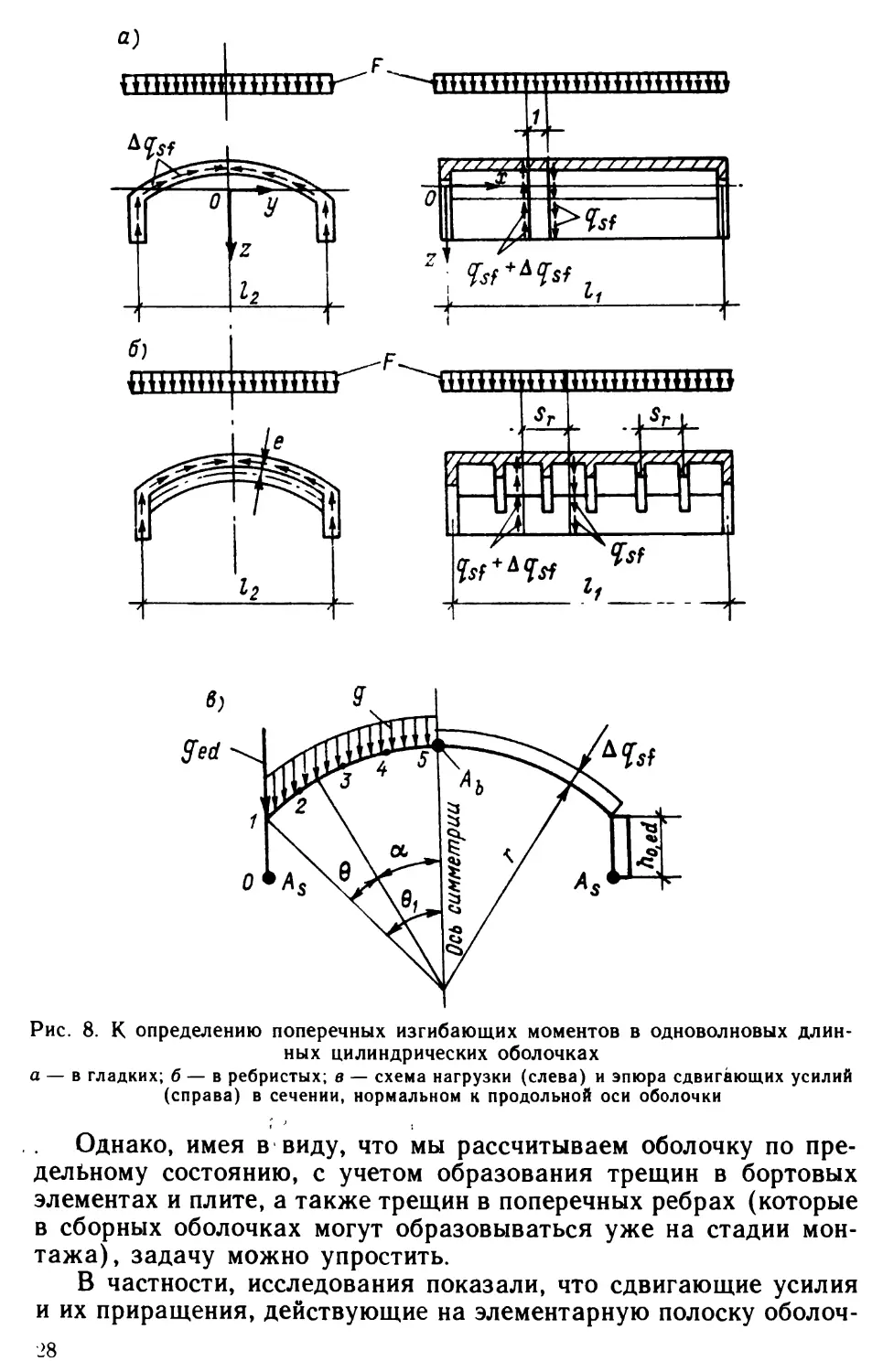
Рис. 8. К определению поперечных изгибающих моментов в одноволновых длин¬
ных цилиндрических оболочках
а — в гладких; б — в ребристых; в — схема нагрузки (слева) и эпюра сдвигающих усилий
(справа) в сечении, нормальном к продольной оси оболочкиОднако, имея в виду, что мы рассчитываем оболочку по пре¬
дельному состоянию, с учетом образования трещин в бортовых
элементах и плите, а также трещин в поперечных ребрах (которые
в сборных оболочках могут образовываться уже на стадии мон¬
тажа), задачу можно упростить.В частности, исследования показали, что сдвигающие усилия
и их приращения, действующие на элементарную полоску оболоч¬28
ки, можно представить в виде эпюры постоянной напряженности
по всему сечению оболочки (рис. 8, в). Такое допущение базиру¬
ется на условии, что сжатая зона оболочки относительно мала,
а именно 0£<CO,50i (см. рис. 4). Такая предпосылка позволяет
условно представить сечение оболочки в виде двух стержней —
продольного жесткого сжатого стрингера и продольного растяну¬
того одиночного стержня. В стрингере условно концентрируют
всю площадь сжатой зоны бетона. Его располагают в центре
тяжести этой зоны (или условно в шелыге). В растянутом стержне
условно сосредоточивают сечение всей рабочей арматуры, име¬
ющейся в нижней зоне бортового элемента. Размещают этот стер¬
жень в центре тяжести площади сечения рабочей арматуры в
каждом бортовом элементе (рис. 8, в). При этом допущении ве¬
личину интенсивности сдвигающих усилий qsf можно определить
как частное от деления поперечной силы Qx в данном сечении
на расстояние между центрами тяжести арматуры и сжатого
бетона. Таким же образом получим и интенсивность приращения
сдвигающих усилий &qsf— путем деления приращения поперечной
силы на плечо пары внутренних сил в сечении:Д0 _ AQjt £0|Г + 5Г sin 01 +ged /044st z /io.** + (l-cos0,)r ' К }Поперечные изгибающие моменты определяются из суммы
моментов всех сил, взятых с одной стороны, относительно сечения
с угловой координатой а по следующим формулам:для отдельно стоящей одноволновой оболочким =-^г[А я „ +*,) - (-^+до о+s*c)]± Ne, (9)для средней волны многоволновой оболочкиMmt = M + Xx • 0,01п|)А + Х2±М>; (10)в формуле (9) первый член в квадратных скобках, умноженный на (0,1 г)", пред¬
ставляет собой изгибающий момент от приращения сдвигающих сил A</Sf* а вто¬
рой — от внешней нагрузки; N — продольное усилие на единицу длины оболочки;
е — расстояние между серединой сечения плиты оболочки и центром тяжести
таврового сечения ребристой оболочки.Эксцентриситет е приложения продольной силы в гладких
оболочках равен нулю. Если же имеются ребра, расположенные
под плитой оболочки, то перед последним членом уравнений ста¬
вится знак «минус». Положительному значению моментов соответ¬
ствует растяжение в волокнах нижней поверхности плиты оболоч¬
ки, а положительному значению продольных усилий — растяже¬
ние. В формуле (10) значение М принимается по (9), но без
последнего члена.29
Коэффициенты i|) в формулах (9) и (10) определяются по сле¬
дующим выражениям:■ф0=(sin 01 —sin а) 100; "Чi|)i,=(cos а — cos 0i) 100;•фс= (sin 0i —sin а)2 50; ► (11)i|)i=(0 — sin 0)100;i|?o=(cos a—Osin a—cos 0i)lOO.^/Величины коэффициентов -ф для ряда значений углов 0| и а
(в пяти точках поперечного сечения) даны в табл. 4.Продольная сила в плите у пересечения с бортовым элементом
(точка 1 на рис. 8, в) вычисляется по формулеN\=(ged—A<7s/Ao.*<)sin0i+.*iCos0i. (12)Продольная сила в других точках плиты далее по дуге имеет сле¬
дующее выражение:Nt=(ged + grQ i + 0,01 sn|>a) sin a—a qSf (ho, ed sin a ++ rsin0)+Jti cos a. (13)Бортовые элементы (балки) средних волн оболочки будем
условно считать не смещающимися в горизонтальном направлении
и не поворачивающимися вокруг горизонтальной оси. Тогда рас¬
четная схема арки, представляющей собой полоску единичной
ширины, будет иметь вид, приведенный на рис. 9, а, а задача
определения усилий сведется к расчету дважды статически неопре¬
делимой схемы. Разрешается такая задача системой канонических
уравнений метода сил:•^1611+^2612=—61/; \■^1621 + -^гб22=—621> )гдеу 6226 |f — 61262^ .1 611622 — 621612 *
v 61162; — 62161; ^ ^2 6ц 622 62|6|2 * J30
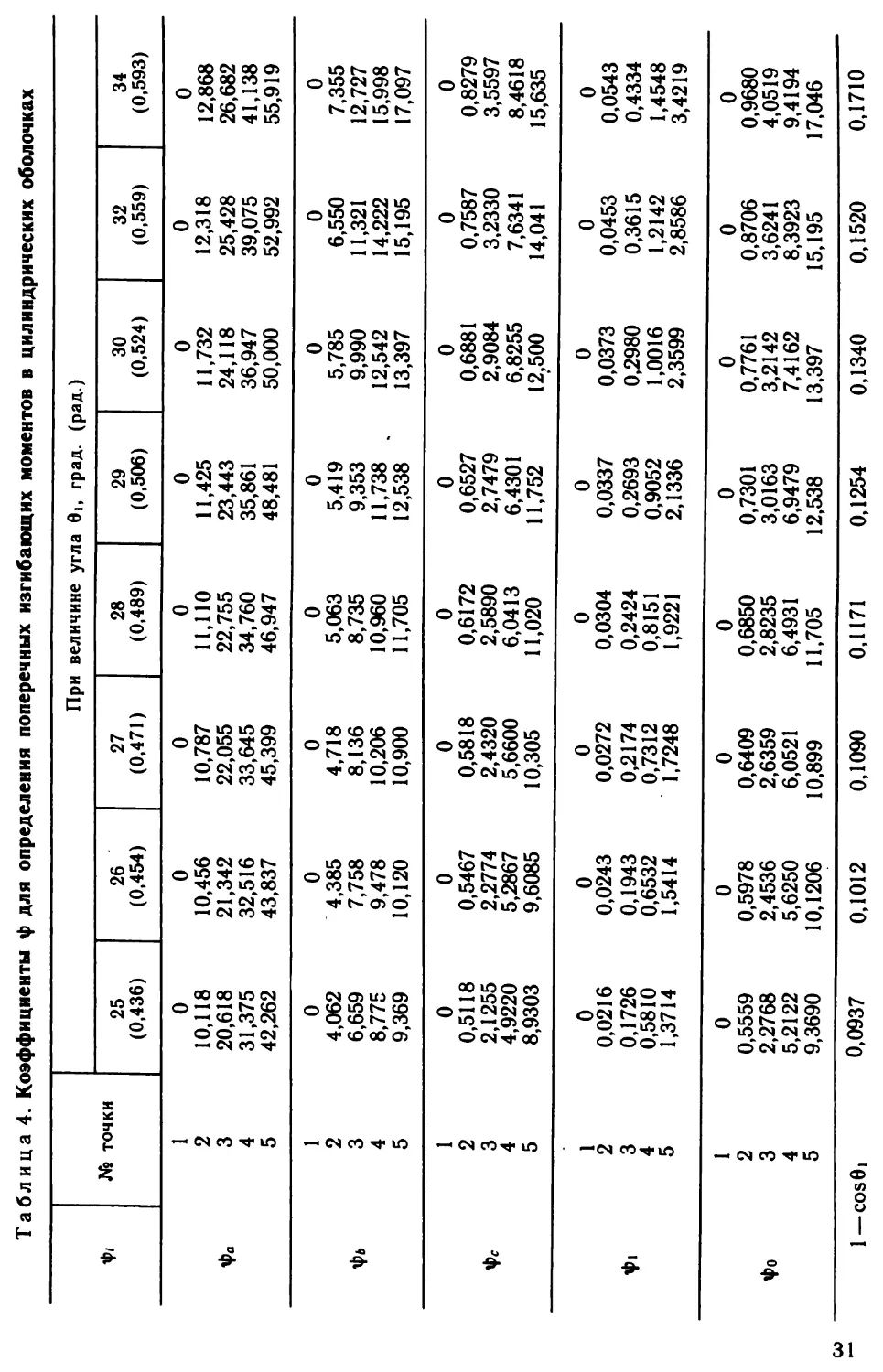
Таблица 4. Коэффициенты ф для определения поперечных изгибающих моментов в цилиндрических оболочках34(0,593)012,86826,68241,13855,91907,35512,72715,99817,09700,82793,55978,461815,63500,05430,43341,45483,421900,96804,05199,419417,0460,1710(0,559)012,31825,42839,07552,99206,55011,32114,22215,19500,75873,23307,634114,04100,04530,36151,21422,858600,87063,62418,392315,1950,1520При величине угла 6|, град, (рад.)30(0,524)011,73224,11836,94750,00005,7859,99012,54213,39700,68812,90846,825512,50000,03730,29801,00162,359900,77613,21427,416213,3970,134029(0,506)011,42523,44335,86148,48105,419
9,353
11,738 .
12,53800,65272,74796,430111,75200,03370,26930,90522,133600,73013,01636,947912,5380,1254оо(0,489)011,11022,75534,76046,94705,0638,73510,96011,70500,61722,58906,041311,02000,03040,24240,81511,922100,68502,82356,493111,7050,117127(0,471)010,78722,05533,64545,39904,7188,13610,20610,90000,58182,43205,660010,30500,02720,21740,73121,724800,64092,63596,052110,8990,109026(0,454)010,45621,34232,51643,83704,3857,7589,47810,12000,54672,27745,28679,608500,02430,19430,65321,541400,59782,45365,625010,12060,101225(0,436)010,11820,61831,37542,26204,0626,6598,7759,36900,51182,12554,92208,930300,02160,17260,58101,371400,55592,27685,21229,36900,0937№ точки12345123451234512345123451 —COS0IФа4>ь4>сфо31
Коэффициенты при неизвестных и свободные члены уравнений (14)
определяются по формулам, предложенным X. X. Лаулем:6n=-^jrCi; 612=621=^-^5; 622 = 1;
61/=-^г[д^(-^С2+Сз)-(-^-С2+гС7+5С8)]; • (15)62/=-|q3-[Ms/( lt°r“l С4 + Сб)— (-^C4+gC9 + sC,o)}Значения коэффициентов С, в уравнениях (15) вычисляются по
следующим формулам:С, =[0,50,(24- cos 20,) - 0,75 sin 20, ]104;С2 = (0,5 sin2 01 — 0,501 sin 201 + 2 cos 01 sin2 01 /2) 104;Сз =(sin2 0i —O,502cos 01 — 0,501 sin 0i)lO4;C4 =(0isin0i+cos0i —1)102;C5=(sin 0i — 0iCOS0i)lO2;C6=(0,50! -(-cos 0i — 1) 102;г (16)C7=[0,50, - 0,125 sin 20, - 0,25 cos 20, - 0,5 sin2 0, +-(-cos 01(01 0, cos 0i —2 sin 0i)]lO4;C8=[0,1667 sin3 01 — cos 01(0,501 sin2 01 — sin 0, ++ 0,75 sin 0i cos 0i 4- O,250i)] 104;C9=[2sin 0i -0,(1 +cos ©OJIO2;Сю=[0,250, + sin 0,(0,501 sin 0, + 0,75cos 0, -1)]102. -Коэффициенты Ci получены путем перемножения эпюр единичных
моментов по методу Верещагина (рис. 9, б и в), а свободные
члены — перемножением этих эпюр на эпюры от внешней нагруз¬
ки, вычисленные по формуле (9).Величины коэффициентов С; для ряда значений 0, криволи¬
нейных плит в поперечных сечениях волны оболочки приведены
в табл. 5 (0i — половина центрального угла). Изложенные рас¬
суждения и формулы позволяют приступить непосредственно к
расчету.32
Рис. 9. К определению поперечных
изгибающих моментов в средней
волне длинной цилиндрической обо¬
лочкиа — расчетная схема; б — эпюра мо¬
ментов от Х\ = \\ в — эпюра моментов
от Х2 = 1Итак, нам необходимо рассчитать арочную полоску шириной1 м, расположенную между ребрами панели средней волны обо¬
лочки.Расчетная схема элементарной арки показана на рис. 9.
На элементарную арочную полоску действуют следующие расчет¬
ные нагрузки (см. табл. 1): постоянная, равномерно распреде¬
ленная по криволинейной поверхности g = 3,5 кН/м; временная
(снег), равномерно распределенная по горизонтальной проекции
s= 1,4 кН/м; постоянная от массы бортовых элементов ged = 4,0 кН.
Схема приложения нагрузок дана на рис. 10, а.Приращения сдвигающих усилий для полоски посередине про¬
лета оболочки, где высота сечения бортового элемента (с учетом
замоноличенной стыковой полости) hed= 1,6 м, находим из (8):А„ 3,5 • 0,495 12,51 + 1,4 • 12,51 • 0,475 + 4,0 1 1 7 и /
M«f=- ! 1 43_j_ I 4g :—^^=11,7 кН/м.Неизвестные Х\ и Лг (рис. 10, а) получаем из решения системы
канонических уравнений метода сил (14).Коэффициенты при неизвестных определяем по формулам (15)
и табл. 5:6,,=-^Uo, 1=7,8; 6i2=-4^-4,014=6,26;622= 12,49 • 0,495 = 6,18;3 Заказ 6133
ТабКоэффициентыС,При величине2526272829С\20,33524,66729,69835,50642,175с270,92182,54095,476109,810125,620С31,3111,6552,0722,5723,167с49,0719,77210,49411,23712,000Съ2,7173,0513,4113,7984,212Се0,1500,1750,2040,2360,271с711,35113,76116,55619,78023,480С610,73012,94615,50018,42621,756С91,3451,5101,6861,8762,079Сю1,2701,5181,6761,8452,023—Ц^-[‘1 •7(-га^-119-‘+3-026)-(-гелэ-119-‘ ++ 3,5 • 22,26+1,4 • 20,62)]= 121,7;62/=-LT^-[I 1 >7(lW11 >55 + 0,2573 ) - (-jgg-11,55 ++ 3,5 • 1,98+1,4 • 1,83)]= 103,1.Найденные значения коэффициентов подставляем в канониче¬
ские уравнения (14): 7,8*i + 6,26X2= —121,7; 6,26Х| + 6,18Х2 =
= — 103,1.В результате решения этих уравнений по (14а) получаем Х\ =
= -11,2 кН; Х2= -5.4 кН • м.Для вычисления значений продольных сил и изгибающих мо¬
ментов в точках дуги поперечного сечения оболочки определяем
некоторые необходимые для подстановки в формулы (10), (12)
и (13) геометрические характеристики сечения посередине проле¬
та. Значение характеристик для точек / ...5 поперечного сечения
записываем в табл. 6.Величину продольной силы для точки 1 находим по (12): Ni =
= (4,0-11,7 • 1,43)0,475-11,2 -0,88=—15,9 кН, а для осталь¬
ных точек дуги — по (13): М = (9,0 +0,2i|)a)sina — 146,4 sin 0 +
-|- 11,2 cos ct.Изгибающий момент для точки 1 вычисляем по (10), при этом
первое и второе слагаемые формулы в точке 1 обращаются в ноль:
Mmi,i =Х2 — N\e= —5,4+ 15,9 *0,032=—4,9 кН • м.Для вычисления изгибающих моментов Mmt,i в остальных
точках дуги необходимо сначала определить значения моментов
в этих точках по (9) как для одноволновой оболочки, но без по¬
следнего члена формулы: Af*= l,6i|)a+ 18,3i|)i — 5,5я|)о — 2,2я|эс.Опуская арифметические выкладки, приводим на рис. 10,6
эпюры N (кН/м) и М (кН • м/м), вычисленные по формуле (10).34
лица 5Эксцентриситет продольной силы при вычислении Mmt, 1 принят
в = 32 мм.В случае применения гладких оболочек по полученным мамен-
там рассчитывают поперечную арматуру оболочки, расположен¬
ную в криволинейной плите (как растянутую арматуру для плоскихРис. 10. К расчету средней волны оболочки на поперечные изгибающие моменты
а — расчетная схема; б — эпюры нормальных сил (кН) и изгибающих моментов (кН м)на 1 м длины оболочки3*35угла 0|, град.30323436384049,79468,26291,720121,070157,280201,400143,000182,790229,820284,710348,070420,4503,8745,6808,13111,39915,67821,20312,78214,40116,08717,83319,63321,4794,7555,6286,7237,9469,30310,7990,3100,4010,5110,6410,7940,97427,70137,91450,85967,01186,890111,04025,52734,54145,76759,51676,10295,8322,3952,7693,3013,8934,5475,2642,1062,6173,0633,5484,0704,527
Таблица 6ПараметрТочкипоперечного сечения123450, град, (рад.)07°5'14°10'21 ° 15'28°20'43"(0)(0,1237)(0,2475)(0,371)(0,4947)sin000,12350,2450,3620,475COS010,9930,970,9310,88а, град, (рад.)28°20'21°15'14°10'7°5'0(0,4947)(0,371)(0,2474)(0,1237)(0)sin а0,4750,3620,2450,12350cos а0,880,9310,970,9931фа011,32335,1547,5Уь05,1911.312Фс00,642,656,1811,28ф|00,030,250,92фо00,692,946,7212Zcur,ply М00,641.121.411.48плит), и устанавливают ее соответственно эпюре моментов —
ближе к растянутой зоне. Продольной силой при этом пренебре¬
гают из-за малости значений.В нашем примере оболочка ребристая — поперечные ребра
с шагом 3 м, поэтому значения вычисленных величин поперечных
изгибающих моментов и продольных сил умножают на 3 м и по¬
лученное усилие передают на основную арматуру ребер, рассчи¬
тывая тавровое сечение ребристой плиты. Ребра армируем обыч¬
ной двойной арматурой, связанной поперечными стержнями.6. Расчет торцевой диафрагмыДиафрагмы длинных цилиндрических оболочек рассчитыва¬
ются как плоские стержневые или балочные конструкции — на
собственную массу и внешнюю нагрузку, действующую на обо¬
лочку, которая передается в виде сдвигающих сил (рис. 11). Эти
силы, касательные к срединной поверхности криволинейной пли¬
ты, обратны по направлению и равны по величине сдвигающим
усилиям в криволинейной плите на контуре — по линии ее сопря¬
жения с диафрагмой. Величина сдвигающих сил определяется
из расчета криволинейной плиты (оболочки) как упругой системы.
Вместе с тем опыт показал, что вблизи опорных диафрагм часто
возникают косые трещины, что свидетельствует о более сложном
законе распределения усилий в приопорных зонах.Сумма проекций сдвигающих сил на вертикальную ось должна
уравновешиваться балочной опорной реакцией оболочки. На ха¬
рактер же распределения сдвигающих сил влияет степень попе¬36
Рис. 11. Схема усилий, передаваемых с обо
лочки на торцевую диафрагмуречной деформации контура (диафрагмы). Чем жестче контур,
тем ближе характер распределения сдвигающих сил к закону
Журавского. Но поскольку характер распределения сдвигающих
сил на контуре оболочки незначительно отражается на величине
расчетных усилий в ней, то с поперечной жесткостью практически
можно не считаться.Для вычисления сдвигающих сил по формуле Журавского
необходимо знать величину статического момента отсеченной
части сечения криволинейной плиты с центральным углом 2а
(рис. 10, а), которая может быть определена по следующей фор¬
муле (приводим без вывода) :аsa = \ rtcur,pi[rcosy — (r — z)\dy = 2r2tcur,pi(sina — r)a). (17)оВеличину сдвигающих сил qSf в любой точке срединной поверх¬
ности криволинейной плиты, очерченной по дуге окружности,
имеющей ось симметрии и вертикальные бортовые элементы, рас¬
положенные ниже края криволинейной плиты, можно вычислять
по формуле (7), принимая для Q значение величины нагрузки,
приходящейся на половину длины оболочки и диафрагмы, т. е.
опорную реакцию торцевой диафрагмы.Если просуммировать проекции сдвигающих сил на вертикаль¬
ную ось по всей криволинейной части сечения оболочки, то по¬
лучим:аQsf,z= ®‘си'1Р‘г 2^ (sin а — г]а) sin Qda=0= Wcy,r [(8i — sin 0i cos 0i)—2t|(sin 0i — 0i cos 0i)]
или после упрощения записи:(18)здесь т] — коэффициент, определяющий положение центра тяжести сечения плиты
оболочки: т]=(г — z)/r\ z — расстояние от точки на срединной поверхности в ше-
лыге криволинейной плиты до центра тяжести ее сечения.37
Поперечный изгибающий момент, нормальная и поперечная
силы в сечении оболочки с угловой координатой а могут быть
определены по аналогии с выражениями (9) и (13) последующим
формулам:м* -гН'-тёЙО'-чадМН —(^4 — Л^Ь) }—iqq" —|- ДОо + ±Ne. (19)=(ged + gr0,+sr-i^-)sina-Q{[i_i£^lx 'X(*i - T|*2)]sin a +-^^(^6 - Л^7>};I (20>Q/a = (ged + grQ 1 + Sr-^-)cOS tt — Q {[l — - XX(0.-^2)]cosa+-^l^8-^9)}. JПервое слагаемое в (19) представляет собой изгибающий мо¬
мент от сдвигающих усилий, а второе — от внешней нагрузки.
Обозначения приняты по (9), коэффициенты г|> — по табл. 4. Влия¬
ние нормальной силы учитывается третьим слагаемым, как в
формуле (9).В формуле (20) Q — нагрузка, приходящаяся на половину
торцевой диафрагмы.Коэффициенты определяются по следующим формулам:Ф, = 100(0,- sin 0, cos 0,);= 200(sin 0,-0, cos 0,);#з= 100(sin 0, — sin a);#4= 100[2cosa — 2cos0, — sin 0isin (0i — a)—(0, — a)sin a];
#5=lOO[0i —a2 —20isin(0i —a)—2cos(0i —a) + 2]; > (21)fte= 100[sin 0] sin (0i — a)+(0i — a)sin a];Ф7 = 2OO[0, sin (0, - a) + cos (01 - a) -1 ];#8 = 100[sin a+(01 — a)cos a — sin 01 cos (01 — a)];Ф9 = 200[sin (0, - a)+a - 0, cos (0, - a)]. J38
Для облегчения вычислений по формулам (21) в табл. 7 при¬
ведены значения коэффициентов подсчитанные для углов 0
в пяти точках дуги (см. рис. 10, а).Поскольку в нашем примере оболочка примыкает к торцевой
арке поверху (рис. 12, б), сдвигающие силы передаются от плиты
оболочки на ось арки с эксцентриситетом е=180 мм. Кроме того,
опорный узел арки выполнен так, что затяжка присоединяется
к арке с эксцентриситетом 250 мм (рис. 12, а). Эти эксцентриситеты
учитываются расчетом. Примыкающее к торцевой диафрагме опор¬
ное сечение оболочки имеет следующие параметры: площадь се¬
чения бортовой балки Aed = 0y3 • 1,0 = 0,3 м2; площадь сечения
криволинейной плиты ACUr,pi = 0,495 м2; общая площадь опорного
сечения оболочки ASh = 0,795 м2; момент инерции сечения оболочки
Ish sup = 0,541 м4; расстояние от центра тяжести сечения оболочки
до оси сечения криволинейной плиты в шелыге z=l,07 м; г\ =
= ( 12,49 - 1,07) /12,49 = 0,915.Внешнюю нагрузку на торцевую арочную диафрагму в виде
сдвигающих сил, действующих в торцевом опорном сечении обо¬
лочки, будем определять в тех же пяти точках (точки 1...5 на
рис. 12, а), в которых вычислены коэффициенты О, в табл. 7. Уси¬
лия Af/a , Nfa и Qfa от сдвигающих сил, действующих на арку,
определим для сечений в пяти точках с угловой координатой а
(точки /'...5'), показанных на рис. 12, в. Для вычисления усилий
воспользуемся следующими формулами:= Q{[(#i — Л<Ь)0,0103 — $4 + У — (Ф& — Ц#7)е}\Nfa = Q[fl6 —тift7 —(fli —Ti<h)sina]; (22)Qfa = Q[(ft I — ^)cos a — + rj#9}где Q = QtCur,pir3/( 100/); Q — опорная реакция торцевой диафрагмы (половина
опорной реакции оболочки).Найдем значения этих усилий:Q=5,55 • 12,0 • 0,5 • 29,6 • 0,5=492,8 кН,
Q=492>8WTW=710,0 кН.Подставив в выражения (22) известные величины, получим:М,а = 710,0{ [(О, - 0,915<Ь) 0,01 д3 - Ъ + 0,915d6] X
X 12,49 - (д6—0,915<b)0,18};Nfa =710,0[Ф6—0,915Ф7 - (Oi - 0,915<h) sin а].39
При величине угла 0|, град.3412.98212.98212.98212.98212.98213.44613.44613.44613.44613.446012,86826,68241,13855,91900,0570,4291,3432,92300,060,451,4023,043210.91110.91110.91110.91110.91111.25611.25611.25611.25611.256012,31825,42839,07552,99200,0450,3391,0612,30900,0470,3531,1012,391309.0599.0599.0599.0599.0599.319.319.319.319.31011,73224,11836,94750,000,0350,2630,8241,79500,0370,2730,8521,851298,2128,2128,2128,2128,2128.4258.4258.4258.4258.425011,42523,44335,86148,48100,0310,230,7211,57200,0320,2380,7441,618287.4177.4177.4177.4177.4177.5967.5967.5967.5967.596011,1122,75534,7646,94700,0270,2010,6291,37000,0280,2070,6471,407276.6736.6736.6736.6736.6736.8236.8236.8236.8236.823010,78722,05533,64545,39900,0230,1740,5451,18800,0240,1790,561,218265.9785.9785.9785.9785.9786,1026,1026,1026,1026,102010,45621,34232,51743,83700,0200,1500,4701,02400,0210,1540,4811,048255.3315.3315.3315.3315.3315.4335.4335.4335.4335.433010,11820,61831,37542,26200,0170,1290,4020,87800,0180,1320,4120,897№ точки1234512345123451234512345Коэффи¬циентыО,О.02Оз040540
014.652
25,02430.652
31,270015,34625,96031,61132,17401,1364,1358,32512,98101,1954,3198,65213,446013,05422,30427,38328,081013,59923,04128,14228,80200,9533,4686,98610,91000,9963,6047,22911,256011,53619,71724,26025,000011,958
20,289
24,850
25,56500,7902,8735,7929,05800,8212,9725,9689,310010,80718,47522,75623,504011,17618,97523,27324,00000,7152,6025,2478,21100,7422,6865,3968,425010,10017,26921,29122,040010,42117,70421,74222,47500,6452,3484,7367,41700,6882,4184,8627,59609,414
16,099
19,868
20,61109,69116,47620,25920,98900,5802,1114,2586,67200,5992,1694,3636,82308,74914,96518,48619,21708,98815,29018,92419,54400,5191,8893,8125,97800,5341,9383,8996,10208,10713,86917,14717,86108,31214,14717,43718,14200,4631,6833,3985,33100,4751,7233,4695,43312345123451, 2345123450*#841
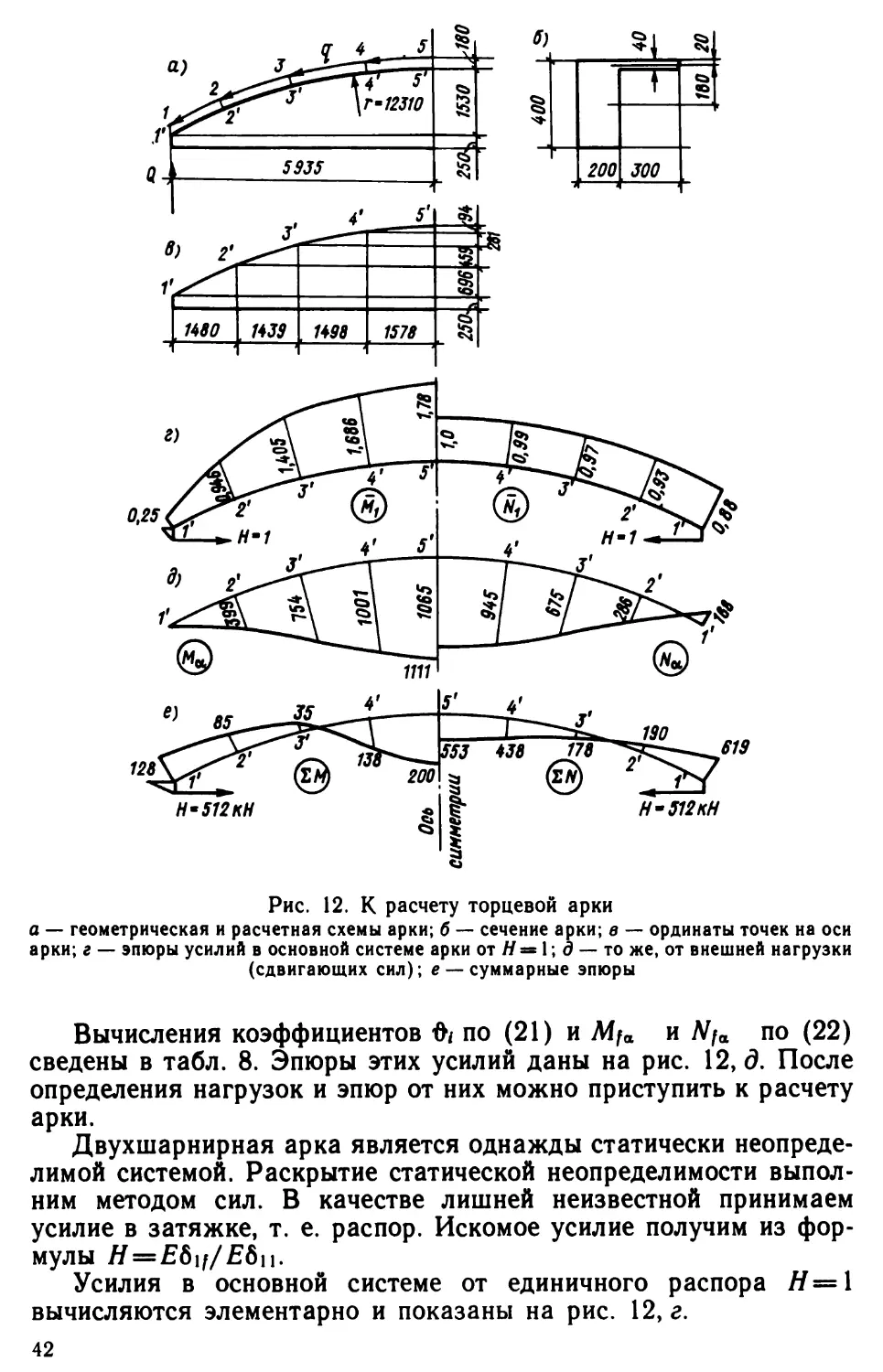
Рис. 12. К расчету торцевой арки
а — геометрическая и расчетная схемы арки; б — сечение арки; в — ординаты точек на оси
арки; г — эпюры усилий в основной системе арки от Н = 1; д — то же, от внешней нагрузки
(сдвигающих сил); в —суммарные эпюрыВычисления коэффициентов по (21) и Mfa и N/a по (22)
сведены в табл. 8. Эпюры этих усилий даны на рис. 12, д. После
определения нагрузок и эпюр от них можно приступить к расчету
арки.Двухшарнирная арка является однажды статически неопреде¬
лимой системой. Раскрытие статической неопределимости выпол¬
ним методом сил. В качестве лишней неизвестной принимаем
усилие в затяжке, т. е. распор. Искомое усилие получим из фор¬
мулы Н=ЕЬц/ ЕЬ\\.Усилия в основной системе от единичного распора Я= 1
вычисляются элементарно и показаны на рис. 12, г.42
Таблица 8№
точки
в се¬
ченииQtcur, р1?аОз04#50607М. ,
кН»мN* ,
кН100/$h, supкНГ7107,77,88000000— 1682'7107,77,8811,30,02820,028610,3410,673992863'7107,77,8823,00,2210,22817,6818,157546754'7107,77,8835,10,6600,67921,7922,3010019455'7107,77,8847,51,4401,4822,5423,011111065Опуская перемножение эпюр по методу Верещагина, приводим
окончательный результат вычисления перемещений. При этом
сечение арки принято по рис. 12, б. Площадь поперечного сечения
и момент инерции арки соответственно Аа=0,095 м , /а = 0,00145 м1
Сечение затяжки Лм =0,2 • 0,2=0,04 м2.a.-H^+JV^-TnlSr+w-M •11,04 | 5,7 | 6 _0 „ .„3
~ 0,00145 "г* 0,095 "r 0,04 — ' 1U •откуда tf = 4,3 • 106/8,4 • 103 = 512 кН.Суммарные эпюры изгибающих моментов (кН • м) и продоль¬
ных сил (кН) показаны на рис. 12, е.7. Некоторые положения по конструированию
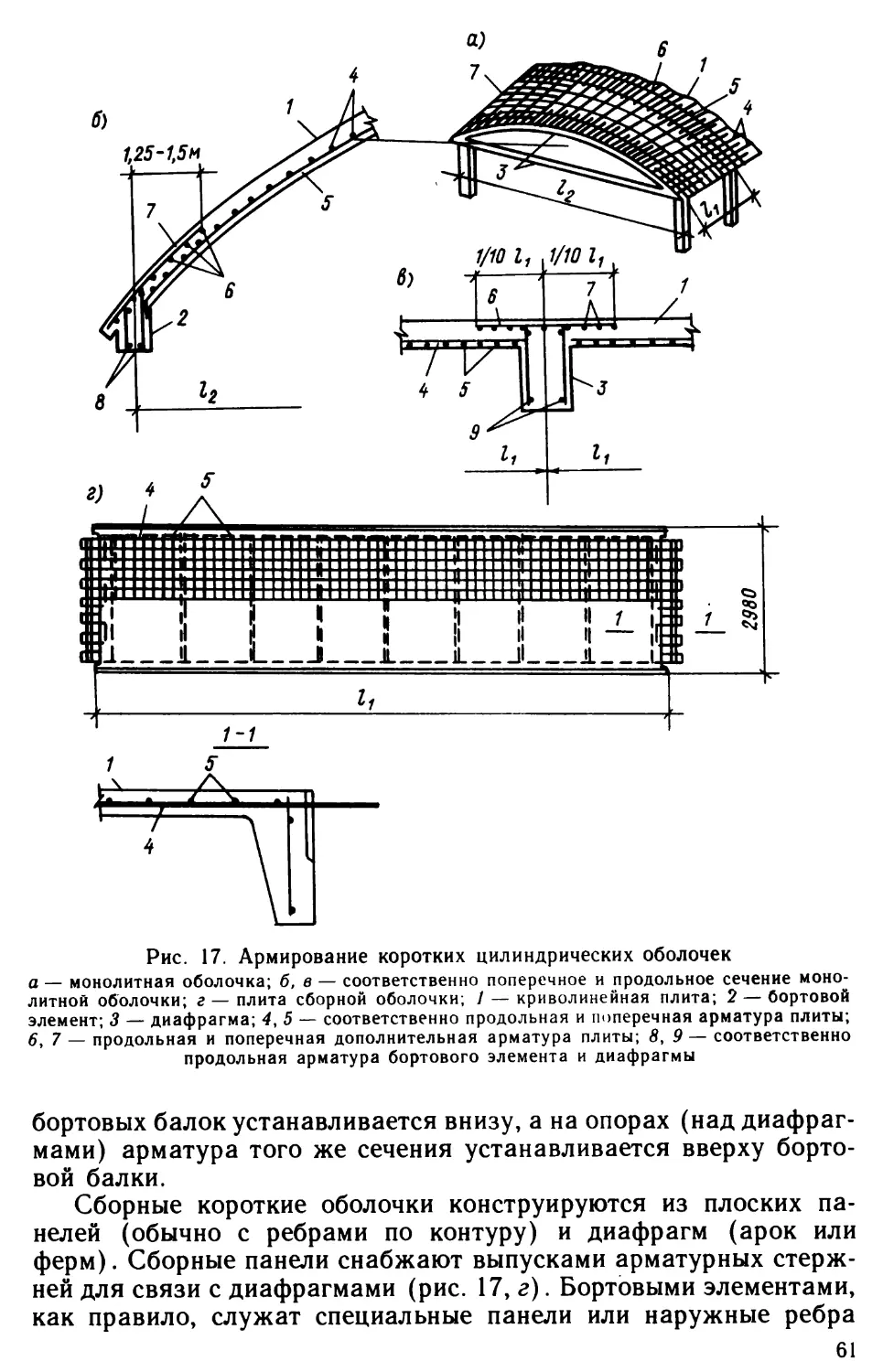
длинных цилиндрических оболочек (рис. 13)В монолитных оболочках криволинейную плиту, если ее тол¬
щина находится в пределах до 80 мм, армируют одиночной сеткой
(основной), располагаемой у растянутой грани. При сжатых
плитах больших толщин арматура должна быть двойной, причем
сетки располагают симметрично относительно срединной поверх¬
ности. На полосе плиты, определяемой по расчету, но шириной
не менее 1/10 h по обе стороны вдоль бортовых элементов при
армировании криволинейной плиты одиночной арматурой необ¬
ходимо сверху укладывать дополнительную арматурную сетку.
В этом случае плита на данном участке утолщается. Стержни
основной сетки должны быть доведены до соответствующих сторон
криволинейной плиты и заведены в контурные элементы по пра¬
вилам анкеровки арматуры на крайних опорах плоских плит.43
Поперечные (по отношению к оболочке) арматурные стержни
дополнительных сеток (или сплошных верхних сеток при двойной
арматуре) должны быть заведены в бортовую балку не менее
чем на величину анкеровки, принятую для растянутых стержней
в соответствии с требованиями СНиП 2.03.01—84.В углах оболочки криволинейную плиту рекомендуется арми¬
ровать косыми стержнями переменной длины, направленными
к осям оболочки под углом 45°. Количество стержней определя¬
ется расчетом. Стержни заводятся в продольную балку с одной
стороны и торцевую диафрагму с другой не менее, чем на длину
анкеровки, принятую для растянутых стержней.Шаг стержней арматуры криволинейной плиты необходимо
назначать не более 4—5 толщин плиты и не более 200 мм. Диаметр
стержней определяется расчетом и должен быть не менее 6 мм
для монолитных оболочек и не менее 4 мм для сборных. Для кон¬
структивной, не требующейся по расчету арматуры плит допуска¬
ется применять сварные сетки из стержней d = 3 мм. Продольную
арматуру криволинейных плит сборной оболочки допускается
не стыковать и специальных выпусков из панелей не делать.Бортовые балки монолитных длинных цилиндрических оболо¬
чек армируют продольными, поперечными и при вязаной арма¬
туре — отогнутыми стержнями. Принципы конструирования этих
балок аналогичны общим принципам конструирования железо¬
бетонных балок.Балки и затяжки диафрагм рекомендуется конструировать
предварительно напряженными. С большим эффектом и степенью
индустриальности это может быть осуществлено при конструиро¬
вании сборных и сборно-монолитных оболочек, когда элементы
выполняются в заводских условиях.Конструкция панелей сборной оболочки зависит от принятой
системы разрезки ее на отдельные сборочные единицы. Практика
показала, что наиболее рациональным является членение ци¬
линдрических оболочек, когда бортовые элементы (балки, фермы)
и торцевые диафрагмы (затяжки) отделяются от криволинейной
плиты. Плита, в свою очередь, поперечными сечениями (например,
с шагом 3 м) разрезается на сборные панели, которые обычно
окаймляются ребрами. При необходимости, например по условиям
изготовления, транспортировки и монтажа, эти панели можно
разрезать еще и продольными (по отношению к оболочке) швами,
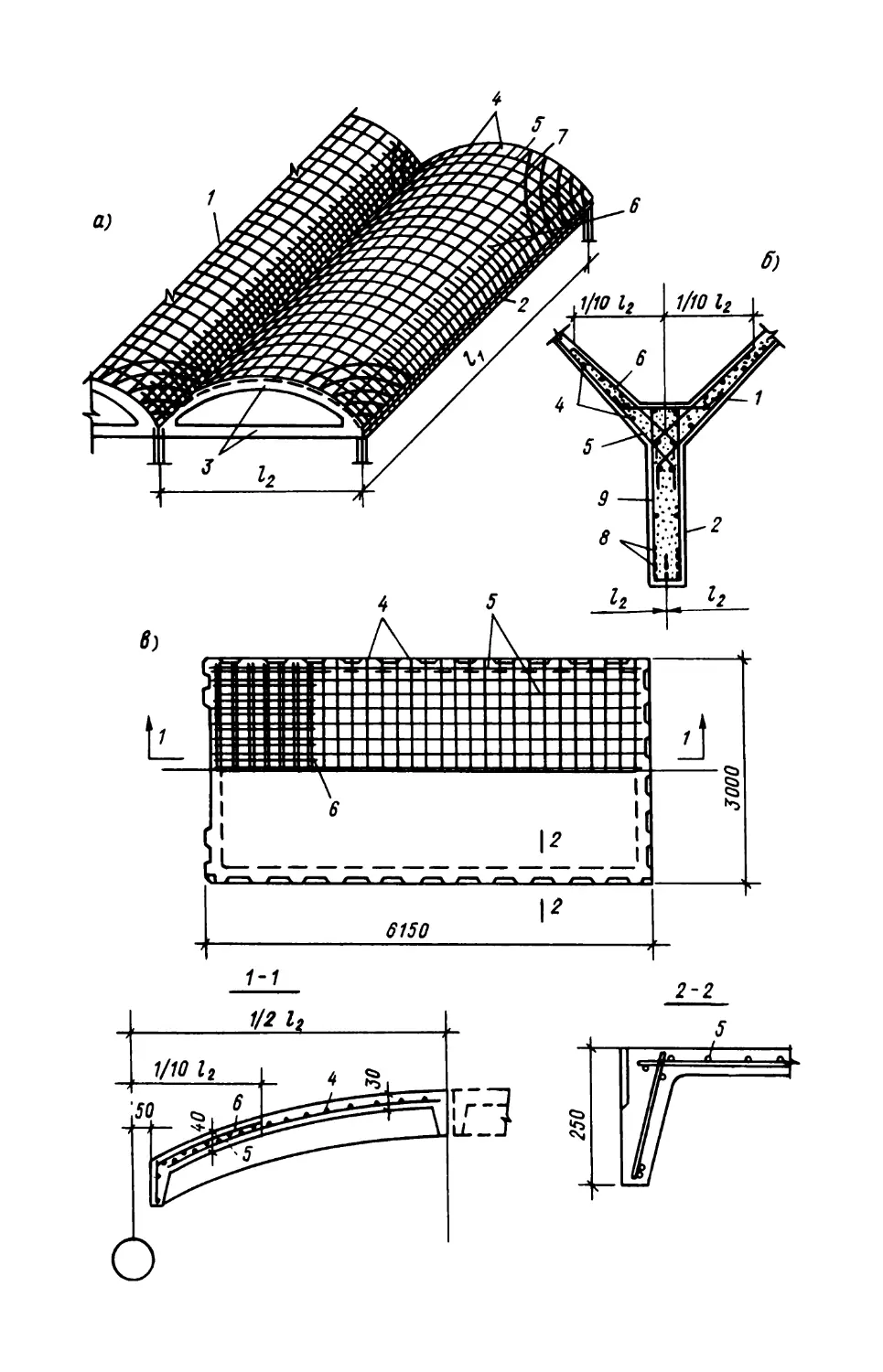
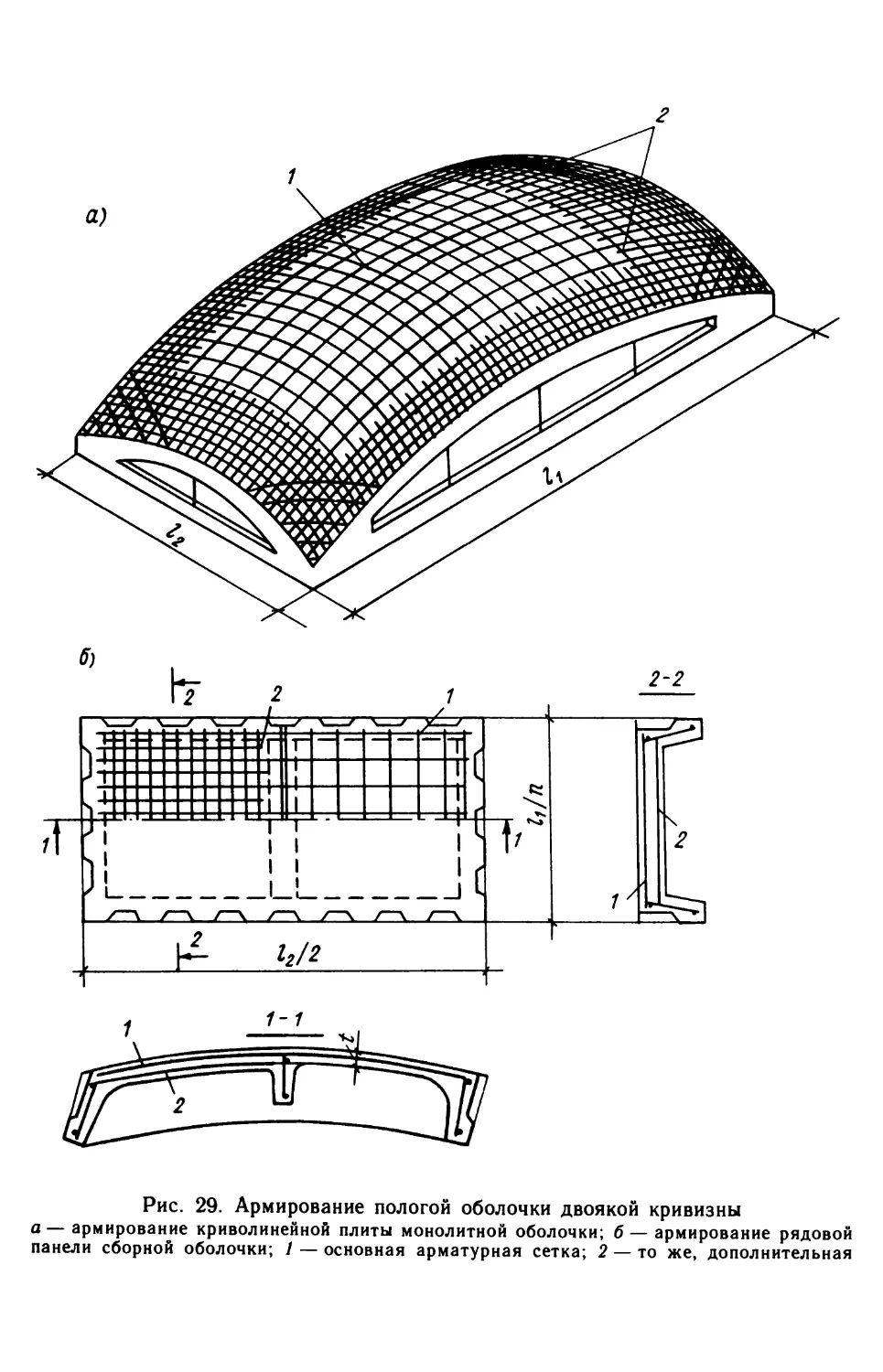
расчленяя панели на два или три элемента. Сборные панелиРис. 13. Армирование длинных цилиндрических оболочек
а — монолитная оболочка; б — поперечное сечение бортового элемента монолитной обо¬
лочки; в — панель сборной оболочки; / — криволинейная плита; 2 — бортовой элемент;
3 — торцевая диафрагма; 4, 5 — соответственно продольная и поперечная арматура
плиты; 6 — дополнительная поперечная арматура плиты; 7 — косая арматура плиты;8, 9 — соответственно продольная и поперечная арматура бортового элемента45
длинных цилиндрических оболочек бывают двух типов: рядовые
и торцевые.Криволинейная плита сборных рядовых панелей должна иметь
толщину не менее 30 мм, но по условиям размещения арматуры
толщина может быть и больше (в частности, при укладке в плите
второй арматурной сетки вдоль бортовых элементов). Торцевые
панели всегда делают толще рядовых. Участки, где главные рас¬
тягивающие напряжения орг> Rbu должны армироваться исходя
из условий полного восприятия арматурой растягивающих уси¬
лий. Не рекомендуется допускать арг> 3/?*/, во избежание этого в
соответствующих участках криволинейной плиты размеры по тол¬
щине следует увеличивать. В торцевых панелях дополнительные
сетки снабжаются косыми рабочими стержнями.Ребра панелей армируются плоскими сварными каркасами.
Для связи ребер смежных панелей между собой они должны
иметь закладные детали, надежно приваренные к их продольной
арматуре и соединяемые после монтажа накладками.В верхней поверхности железобетонных бортовых балок сле¬
дует предусматривать выпуск стержней поперечной арматуры
каркаса балки для связи с криволинейными панелями — с вы¬
пусками арматурных стержней сеток (стык внахлестку) или с за¬
кладными пластинами по прямому ребру панели (сварной стык).
Рекомендуется первый стык как менее трудоемкий. Связь эта
нужна для восприятия контурного изгибающего момента оболочки.Все наружные поверхности контурных ребер панелей, а также
верхняя поверхность бортовой балки должны иметь шпонки, чтобы
после замоноличивания обеспечить восприятие сдвигающих уси¬
лий в швах. На наиболее напряженных участках (стык панелей
с балкой на крайних четвертях пролета) поверхность сопрягаемых
элементов рекомендуется выполнять пилообразной, а при необхо¬
димости — устраивать специальные упоры.Арматурные сетки криволинейных плит цилиндрических оболо¬
чек конструируют и изготавливают плоскими. Необходимую кри¬
визну они приобретают под действием собственной массы во время
укладки в опалубку.8. Расчет оболочки комбинированной конструкции
(металложелезобетонной)8.1. Основные расчетные положенияПри пролетах цилиндрической оболочки длиной более 24...30 м
вместо железобетонных балочных бортовых элементов целесооб¬
разно применять стальные решетчатые фермы с параллельными
поясами (или с малоуклонным верхним поясом). Такие бортовые
элементы рассчитываются как стержневые конструкции. Усилия46
в элементах фермы определяются по двум стадиям — монтажной
и эксплуатационной. В первом случае нагрузкой на ферму явля¬
ется собственная масса всех элементов оболочки. Конструкция
работает как плоская статически определимая, расчет которой
особого труда не представляет и поэтому здесь не рассматривается.После замоноличивания ферма работает в составе оболочки
как ее бортовой элемент. В этом случае верхний пояс может
рассматриваться как арматура зоны замоноличивания, где он
работает совместно с прямолинейными ребрами железобетонных
панелей и участками криволинейных плит, примыкающими к этим
ребрам. Опыт показывает, что сечение верхнего пояса, подобран¬
ное из расчета фермы в монтажной стадии, как правило, доста¬
точно и для стадии эксплуатации, а потому не требует усиления.
Сечение нижнего пояса может быть подобрано из расчета ци¬
линдрической оболочки в продольном направлении как простой
балки. При этом нижний пояс фермы можно рассматривать как
рабочую растянутую арматуру оболочки, а криволинейную пли¬
ту — как сжатую зону.Сечения стержней решетки фермы подбираются по усилиям,
действующим в эксплуатационной стадии. На величину усилия
в любом раскосе влияют величина поперечной силы, действующей
в сечении, проходящем через данный раскос, угол наклона раскоса
к горизонтали, а также закон распределения величины поперечной
силы между сечениями железобетонной оболочки и раскоса.
При этом остается в силе гипотеза о распределении сдвигающих
сил по сечению оболочки в соответствии с законом Журавского:Qsf=QScut/Ish,red. (23)Из рис. 14, в видно, что доля поперечной силы, которая при¬
ходится на решетку фермы, определяется заштрихованной пло¬
щадью эпюры сдвигающих сил в сечении оболочки:Рис. 14. Схема металложелезобетонной длинной цилиндрической оболочки
а — продольный разрез; б — поперечный разрез; в — эпюра сдвигающих усилий47
Qsi,er=QKvAin,yhK/I, (24)где \ = ES/Eb—отношение модулей упругости стали бортовой фермы и бетона
оболочки; Ainf— площадь поперечного сечения нижнего пояса фермы; у — рас¬
стояние от оси нижнего пояса фермы до центра тяжести приведенного сечения
комбинированной конструкции.Тогда искомое усилие в /с-м раскосе (действительное для
бортовых элементов — ферм с параллельными поясами)NK = QKvAinfyhK/(I cos а). (25)Для фермы с наклонным верхним поясом необходимо учиты¬
вать вертикальную составляющую продольного усилия, действу¬
ющего в наклонном верхнем поясе, что приводит к соответству¬
ющему уменьшению величины поперечной силы QK. Однако при
достаточно малых уклонах пояса в фермах цилиндрических оболо¬
чек рассматриваемого вида этой составляющей можно пренебречь,
она войдет в запас прочности.Усилия в стойках решетки можно определить приближенно,
имея в виду, что стойка воспринимает нагрузку Fd, приходящуюся
на панель верхнего пояса фермы длиной 1т и пропорциональную
воспринимаемой фермой доле поперечной силы:Nc = FdlmvAinfyht/I. (26)8.2. Конструкция оболочки и нагрузкиДля конструкции покрытия промышленного здания с сеткой
колонн 36X 12 м применена цилиндрическая оболочка. Принципи¬
альную конструкцию оболочки принимаем по аналогии с рас¬
смотренной в расчете железобетонной оболочки. Отличием в дан¬
ном случае является конструкция бортового элемента, который
принят в виде стальной решетчатой фермы с параллельными
поясами пролетом 36 м. Для отвода воды с кровли предусматри¬
вается набетонка вдоль ендовы, масса которой учитывается в
расчете.Здесь приводятся только расчеты по прочности в продоль¬
ном направлении на действие изгибающего момента с определе¬
нием сечений элементов бортовой фермы и расчет по деформациям
(расчет оболочки на поперечные изгибающие моменты и на по¬
перечные силы, а также расчет торцевой диафрагмы изложены
выше).Нагрузки на оболочку приведены в табл. 9.Нагрузка на 1 м оболочки составляет: нормативная Fn =
= 3,88 • 12= 46,56 кН/м; расчетная /^ = 4,5 • 12 = 54,0 кН/м.48
Таблица 9Вид нагрузкиНормативноезначениенагрузки,кПаКоэффициент
надежности
по нагрузке
V/Расчетноезначениенагрузки,кПаСобственная масса оболочки,2,01,12,2приведенная к горизонтальной
проекции *Теплоизоляция, пароизоляция,0,881,31,14гидроизоляционный ковер
Снег (III район)1,01,41,4Итого3,884,74Итого с учетом коэффициента
надежности по назначению уп =
= 0,954,5* С учетом собственной массы бортового элемента (стальной фермы),
бетона замоноличивания стыковой полости и набетонки вдоль ендовы 0,5 кПа.8.3. Геометрические характеристики оболочки (рис. 15)Высоту поперечного сечения оболочки, включая сечение борто¬
вого элемента, назначаем равной 4,2 м, что примерно соответствует
1/8,5 пролета 1\. Конструкция и параметры криволинейной части
оболочки идентичны принятым в предыдущем примере.Площадь поперечного сечения криволинейной плиты оболочкиACur,pi = 2rQ\tCur,pi = 2(l2t5l —-0,035/2)0,495 • 0,035 = 0,433 м2.Площадь поперечного сечения зоны замоноличивания Ат =
= 0,25 • 0,2 = 0,05 м2.Отношение модулей упругости стали бортовой фермы и бетона
класса В 35:v = Es/Eb = 2,06 • 105/(31,0 • 103) = 6,65.Предварительно, с последующей проверкой, назначаем следу¬
ющие сечения поясов фермы: верхнего — из двух уголков
140* 90*8 мм, i4sup = 3600 мм2; нижнего — из двух уголков
160 • 10 мм, A„f = 6280 мм2.Приведенная площадь сечения поясов фермы Лг^ = (3600 +
+ 6280)6,65 = 65700 мм2. Общая площадь поперечного сечения
оболочки A5h, red=(0,433 + 0,05 + 0,0657) • 106 = 0,5487 • 106 мм2.4 Заказ 6149
Рис. 15. Геометрические размеры комбинированной оболочки
а — поперечное сечение; б — схема стальной бортовой фермыПоложение центра тяжести поперечного сечения оболочкиУл.red=[0,433(2 • 1,4825/3+2,72)+0,05 х
Х2,62 + 36,0 • 6,65 • 10"4 • 2,5]/0,5487 = 3,28 м.Момент инерции поперечного сечения оболочки находим с
учетом податливости решетки бортовой фермы путем введения
коэффициента 0,9:Isk.red = \r3tcur,pl (01 + sin 01 COS 01 —2 ) ++ Асиг,р1Усиг, pi+ Amy2m + AsupVylup + AinfVyfnf] 0,9 == [l2,4925s • 0,035(0,495 + 0,475 • 0,88-2-^^-)++ 0,433 • 0,4462 + 0,05 • 0,662+36 • 6,65 • 10"4 • 0,782+
+62,8 • 6,65 • 10“4 • 3,282]0,9 = 0,6 m4.8.4. Расчет оболочки в продольном направленииРасчет по прочности на действие изгибающего момента
и проверка сечений бортовой фермыКриволинейная часть оболочки (панели) выполняется из бе¬
тона класса В 35, бортовая ферма из стали по ТУ 14-1-3023—8050
марки 09Г2С-6-2 (нижний пояс) и марки ВСтЗпсб-2 (верхний
пояс).Максимальный изгибающий момент в середине пролета от рас¬
четной нагрузки составляет Мл,шах = 0,125 • 54 • 35,6 =8550 кН • м.Полагая, что угол 0£ относительно мал и, следовательно,
0i«sin06, имеем согласно (5):а/ max 8550 • 106 П 1 1 QЬ~ 2Rbtcr,„irho ~ 2 • 19,5 • 35 • 12492,5 • 4220 ’ ,Сечение нижнего пояса фермы составит по формуле (3) с уче¬
том положений СНиП по проектированию стальных конструкций:Л outer,?,Rb 2 - 0,119 • 12492,5 -35 • 19,5 „СЛОо ....2inf Ryfc 360 • 0,95 'Принятое выше сечение нижнего пояса фермы .4^=6280 мм2
больше требуемого расчетом, следовательно несущая способность
по прочности обеспечена.Сечение верхнего пояса фермы рассчитываем с учетом работы
оболочки в стадии монтажа. На выбор ширины пояса влияют
конструкция узла соединения криволинейных панелей с фермой,
условия опирания панелей и размеры стыковой полости. В данном
случае ширина верхнего пояса должна быть не менее 250 мм.С целью экономии металла целесообразно на период монтажа
оболочки подпереть ферму временной стойкой посередине пролета.В период монтажа на ферму действуют расчетные нагрузки
от собственной массы фермы, сборных железобетонных панелей
и бетона замоноличивания, составляющие 1,8 • 1,1 = 2 кПа, а так¬
же монтажная нагрузка 0,5 • 1,2=0,6 кПа, что составляет в сумме
2,6 кПа. Таким образом, линейная нагрузка на ферму Fa—
=2,6 • 12 = 31,5 кН/м.Из расчета фермы как двухпролетной балки на симметричную
нагрузку изгибающий момент на средней опоре будет М =
= —1233 кН • м, в пролетах М = 693 кН • м, а опорные реакции
на крайней и средней опорах соответственно равны 208 и 693 кН.Проверяем сечение нижнего пояса фермы на сжатие, возни¬
кающее в нем в период монтажа. Усилие сжатия составит:N= —(31,2 • 14,82 • 0,5-208 • 14,8)/2,5=-136 кН.Устанавливаем посередине пролета фермы вертикальную связь,
и тогда расчетная длина сжатого нижнего пояса будет lef = 6 м.
Коэффициент ф продольного изгиба (при гибкости \ = lef/i =
■=6000/49,6=121) равен 0,283. Несущая способность сжатого
нижнего пояса составит N = ARyyc<р = 6280 • 360 • 0,283 =
— 608000 Н, что больше действующего в нем усилия сжатия.451
Проверяем сечение верхнего пояса. Усилие растяжения, дей¬
ствующее в нем, составляет N = 1233/2,5=493,2 кН, а усилие
сжатия — N = {208 • 5,8-31,2 • 5,82 • 0,5)/2,5 = 273 кН.Несущая способность сжатого верхнего пояса при гибкости
А,=3000/25,8= 117 и коэффициенте <р=0,393 составит: N =
= 3600 • 270 • 0,95 • 0,393 = 363000 Н, а растянутого — N=
= 3600 • 270 • 0,95=92^400 Н. Таким образом, несущая способ¬
ность верхнего пояса больше действующих в нем усилий. Следо¬
вательно, сечение его достаточно.Для определения усилий в стержнях решетки бортовой фермы
в k-м сечении воспользуемся формулой (25):Л 6,65 • 6280 • 3280 • 2500
Nk = Qk 0,768 • 0,6 ■ 10» =°-74<?*-Теперь получим усилия в раскосах фермы: раскос 1 — N\ =
= —0,74 • 54(17,8— 1,4)= —655 кН; раскос 2 — N2 = 0,74 • 54 X
Х(17,8-4,3) = 539 кН.Усилие в стойке 3 определим из формулы (26):ЛГ3=— 54 • 3-6,65 • 6,28 *3,28 • 2,5 • 1012/0,6 • 10,2 = 92461 Н.Усилия в остальных элементах решетки вычисляются анало¬
гично.Для обеспечения совместной работы железобетонной оболочки
со стальным бортовым элементом необходимо сборные панели
приварить в углах к верхнему поясу фермы и снабдить его уст¬
ройствами, надежно воспринимающими сдвигающие усилия, воз¬
никающие в зоне контакта. Усилия сдвига найдем по форму¬
ле (23):Qs, = (0,433+00б05)(10^-°’61) Q* = 0,27Qk,где в числителе — статический момент площади сечения сбор¬
ной панели и зоны монолита относительно центра тяжести сечения
оболочки.Величина усилий сдвига определяется площадью эпюры по¬
перечных сил на длине соответствующей панели (в данном случае
на 2,8 м для торцевой панели и на трехметровом участке пролета
для второй панели). Так, усилие сдвига для первой (торцевой)
панели QSfi =0,27 • 54(17,8—1,4) • 2,8 = 669 кН, для второй па¬
нели — Qsf2 = 0,27 • 54(17,8-4,3) • 3 = 590 кН.Усилия сдвига воспринимаются с помощью стальных упоров,
размещаемых в стыковой полости и привариваемых к верхнему
поясу фермы. Размеры упоров и их количество на длине стыка52
каждой панели должны удовлетворять расчету на смятие бетона
замоноличивания и на срез, причем на срез проверяются как бетон
замоноличивания между упорами, так и сварное соединение упо¬
ров к стальной ферме. Эти расчеты выполняются известными
методами и здесь не приводятся.Расчет по деформациямМеталложелезобетонная оболочка рассчитывается по дефор¬
мациям так же, как железобетонная простая балка приведенного
сечения.Расчет производим на нормативные нагрузки (yf=l) в соот¬
ветствии с положениями СНиП.Изгибающий момент от кратковременной (снеговой) нагрузки
5=1,0. 12 = 12 кН/м составит Ms = 0,125 • 12 -35,62=1900 кН • м.Кривизна оси оболочки от действия кратковременной на¬
грузки( 1 \ Msq>b2 1900 • 106 - 1 10 1Л_7 i / ( г )i — <fnEbl,ed ~ 0,85 • 31,0 • 103 • 0,6 • Ю12 ’ ’ 1/мм.Изгибающий момент от действия постоянных и длительных
нагрузок gn = 2,88 • 12 = 34,56 кН/м; Afn = 0,125 • 34,56 * 35,62 =
= 5475 кН • м.Кривизна оси оболочки от действия длительной нагрузки со¬
ставит:/ 1 \ _ 5475 • 106 • 2 Л ,л-7 1 /____\ г )2 0,85 - 31,0 * 103 • 0,6 • 1012 ’ 1/ММ.Полную величину кривизны оси оболочки рассчитываем по
формуле(1/г) = (1/г),+(1/г)2 = (1,2 + 6,9)10-7 = 8,1 • 10"7 1/мм.Прогиб оболочки от кратковременной, постоянной и длитель¬
ной нагрузок составит:/ = 5/2/48г = 5 • 356002 • 8,1 • 10”7/48= 107 мм == //333 <//250.Для уменьшения стрелы прогиба стальной фермы рекоменду¬
ется придать ей при изготовлении строительный подъем.53
II. РАСЧЕТ КОРОТКОЙ ЦИЛИНДРИЧЕСКОЙ
ОБОЛОЧКИ (ПРИЗМАТИЧЕСКОЙ СКЛАДКИ)1. Общие положенияОболочки, имеющие отношение сторон (/i//2)<0,5, относятся
к классу очень коротких оболочек. Такие оболочки, широко встре¬
чающиеся в практике, как правило, имеют пролет /1^12 м, а
/2 <^30 м и распределенную поверхностную нагрузку. Конструиро¬
вать их можно по результатам приближенного расчета. Этот же
расчет используется и для предварительного назначения конструк¬
тивных размеров и арматуры коротких оболочек, которые требуют
применения точных методов расчета.При упрощенном методе расчета короткой оболочки на равно¬
мерно распределенную поверхностную нагрузку усилия в плите
оболочки можно не определять. Сечение бетона и армирование
плиты назначают из конструктивных соображений.Для плит сборных оболочек в этом случае расчетными явля¬
ются усилия при изготовлении, транспортировке и монтаже кон¬
струкций.2. Конструкция оболочки и нагрузкиТребуется запроектировать короткую цилиндрическую оболоч¬
ку в качестве конструкции бесфонарного покрытия производ¬
ственного здания с сеткой колонн 6X18 м.Оболочку принимаем сборно-монолитной конструкции из плос¬
ких ребристых панелей размером 3X6 м, диафрагм в виде арок,Таблица 10Вид нагрузкиНормативноезначениенагрузки,кПаКоэффициент
надежности
по нагрузке
V/Расчетноезначениенагрузки,кПаСобственная масса оболочки,2,01,12,2приведенная к горизонтальной
проекции *Теплоизоляция, пароизоляция,0,751,30,75гидроизоляционный ковер
Снег (III район)1,01,41,4ИтогоИтого с учетом коэффициента
надежности по назначению уп=
=0,953,754,5754,4* С учетом массы арочной диафрагмы после замоноличивания стыковой
полости, составляющей 0,6 кПа.54
Рис. 16. К расчету короткой цилиндрической оболочки
а — общий вид оболочки; б — геометрия арочной диафрагмы; в — суммарные эпюрыусилий в аркепо которым укладываются эти панели, и бортовых элементов
в виде балок прямоугольного сечения, отдельных для каждой
волны. В продольном направлении оболочку принимаем нераз¬
резной с арочными диафрагмами, общими для смежных проле¬
тов. Для обеспечения совместной работы элементов сборно-моно¬
литной оболочки устраиваем по верхней поверхности арки-диаф-
рагмы бетонные шипы, по наружным боковым граням контурных
ребер плит и бортовых элементов — пазы, а в швах замоноличи¬
вания устанавливаем арматурные каркасы.Конструкция оболочки и необходимые размеры приведены
на рис. 16. Нагрузки на оболочку, принятые в расчете, даны
в табл. 10.55
Расчет выполняем на симметричную нагрузку для среднего
пролета многопролетной оболочки.3. Расчет оболочки в продольном направленииВ продольном направлении основным является расчет борто¬
вых элементов. В бортовом элементе однопролетной одноволновой
оболочки рассматриваемого класса усилие растяжения определя¬
ется из условия, что плечо пары внутренних продольных усилий
составляет 0,5...0,6(fCur,Pi + hed)- Растягивающее усилие Ned в одном
бортовом элементе отдельно стоящей оболочки можно найти по
средней величине пары внутренних сил:ДТ Md Md z ~ cur,pished) —_ Fdhtt _ FM /o748 • 2 • 0,55(Scur,pl + hed) 9(fcur,pl + hed) ’ K ’где Fd— приведенная расчетная нагрузка на 1 м2 горизонтальной проекции
(с учетом собственной массы бортовых элементов, но без учета массы диафрагм).В средних пролетах монолитной короткой неразрезной мно¬
гопролетной одноволновой оболочки растягивающее усилие в
пролете бортового элемента следует уменьшать вдвое, а в крайних
пролетах — на 30%. Конструктивную неразрезность оболочек не¬
обходимо обеспечивать, предусматривая, например, верхнюю
арматуру. В противном случае оболочку следует рассматривать
как однопролетную.В многоволновых оболочках везде усилие в среднем бортовом
элементе должно быть увеличено пропорционально грузовой пло¬
щади, приходящейся на этот элемент от обеих примыкающих
к нему волн. При равных пролетах величина Ned удваивается.В данном примере пролет оболочки Л = 6 м < 12 м, соотноше¬
ние сторон /1 //2 = 6/18 < 0,5, а нагрузка равномерно распреде¬
ленная. Это позволяет выполнять расчет упрощенным методом.Растягивающее усилие Ned в одном бортовом элементе в сред¬
нем пролете (нижняя зона) многопролетной оболочки определяем
по формуле (27):АГ (4,4-0,6 • 1,1 • 0,95)18 • 62 с
N'd=1 9(2+0,4)2 = 56>6 кНТо же, на опоре бортового элемента (верхняя зона):(4,4-0,6. 1,1 -0,95)18 - 62 _212 6 н
Med— l6 . 09 . 035 . 2 — ко.Здесь 0,35 — рабочая высота сечения бортового элемента (Ло).56
Площадь арматуры бортового элемента (класса А-III, Rs == 365 МПа) составит:пролетной As = Ned/Rs = 56600/365= 155 мм2;
опорной As = Ned/Rs = 242600/365 = 665 мм2.Таким образом, бортовой элемент в пролете армируем одним
плоским арматурным каркасом с рабочей растянутой арматурой
внизу из стержня 0 14AIII (As— 153,9 мм2), а на средних опорах
в шов замоноличивания между бортовым элементом и крайней
панелью устанавливаем один плоский арматурный каркас с ра¬
бочей растянутой арматурой вверху из стержня 0 32AIII (As =
= 804,3 мм2). Заводим этот каркас на (Л/З) =2 м в каждую сто¬
рону от диафрагмы.Усилия в плите оболочки не определяем, поскольку расчет
оболочки выполняется упрощенным методом. Из конструктивных
соображений принимаем толщину плиты панелей равной 30 мм,
ее армирование — в виде сетки из стержней 0 4Вр1 с шагом
200 мм в обоих направлениях (As = 62,8 мм2/м).Сечения и армирование ребер панелей назначаются из условий
работы их в стадии изготовления и монтажа.4. Расчет оболочки в поперечном направлении
(расчет арочной диафрагмы)Продольное усилие N в сечении посередине пролета /2 допуска¬
ется определять по безмоментной теории. Если нагрузка равно¬
мерно распределена по поверхности оболочки, то:N = Frl\. (28)Полученная таким образом величина продольной силы исполь¬
зуется при расчете промежуточных средних диафрагм. Крайние
диафрагмы многопролетных оболочек или диафрагмы отдельно
стоящих оболочек рассчитываются на воздействие половины этого
усилия.Продольные усилия приближенно можно считать изменяющи¬
мися вдоль волны оболочки /2 по параболической кривой. При рас¬
чете средних арочных диафрагм их сечение принимается тавро¬
вым. Ширина полки берется равной расстоянию между диафраг¬
мами /i=6 м (см. рис. 16,6, сеч. /—/).В многоволновой оболочке диафрагма с прилегающими к ней
частями смежных оболочек делится на не связанные между собой
отдельные волны.Для расчета собственно арочных диафрагм надо определить
усилия, приходящиеся на оболочку, при этом изгибающими мо¬
ментами и поперечными силами, действующими непосредственно
в плите коротких оболочек, можно пренебречь. Полное продольное57
сжимающее усилие Nx в сечении х по длине средней диафрагмы
находят по формулеNx=^r-x(l2—x). (29)Для крайней диафрагмы, когда примыкает лишь один полупролет
оболочкиЫХ=Щ-'-x(h-x\ (30)где г — радиус кривизны срединной поверхности плиты оболочки в середине
пролета; х — расстояние по горизонтали до сечения оболочки от опоры (рис. 16, б).Найдем полное продольное сжимающее усилие в сечении обо¬
лочки для средней диафрагмы (29):Г} 4 • 4,4 • 21,46 • 6 /10 ч 7/ю \Nx= 18s jc(18 — х) = 7х(18 — х).Диафрагма представляет собой двухшарнирную арку с затяж¬
кой и является статически неопределимой конструкцией. Расчет
такой арки выполняется методом сил. Для раскрытия статической
неопределимости принимаем за основную систему арку с разрезан¬
ной затяжкой, а за основную неизвестную — усилие в затяжке
(распор).Усилия в основной системе находим из условий равновесия
рассматриваемого сечения арки по формулам:Mx = M°x-Nxex^NX = N°X + NX- ^ (31)Qx=Qx, Jгде М°х, Nx и QS— соответственно изгибающий момент, продольная и поперечная
силы, определяемые в основной системе от полной вертикальной нагрузки на
оболочку и отнесенные к оси арки в любом сечении на расстоянии х от опоры; ех —
расстояние от оси арки до срединной поверхности плиты оболочки, измеряемое
по нормали к оси арки вдоль сечения по направлению радиуса (рис. 16, б). Вели¬
чина ех считается положительной, если оболочка (криволинейная плита) находится
выше оси арки, отрицательной — если ниже оси; Nx вводится в формулы (31)
со знаком «плюс».Усилия в основной системе арочной диафрагмы найдем из
условия (31). Для этого рассчитываем М°х и Nx.М°=^х(/2-х)=4^-1*(18-*)=13,2х(18-х);№X = QXsina=-4,4 • 6(9-*)-§^=—1,242(9-x)2.58
Таблица 11Точка
дуги арких, мУ, мМх,кН‘мNx, кНМ|, мNt0000— 100,60—0,90611,50,61290,3103,4—0,64—0,936231,11527,8270,3— 1,15—0,%34,51,5712,6400,1— 1,532—0,978461,78844,6492,8— 1,788—0,9957,51,95923,7548,5— 1,957—0,998692950,1567,0—2— 1После подстановки в формулу (31) получимМх=х{ 13,2-7,0 • 0,21)(18—х)= 11,73х(18 —х);Nx= — 1,242(9 — х)2 + 7,0jc(1 8—х).Значения изгибающего момента и продольной силы в основной
системе от единичного распора Н = хi = l составят Mi=y\ Ni =
= cos ах. Вычисленные значения изгибающих моментов и продоль¬
ных сил в основной системе сведены в табл. 11.Для определения перемещений 6ц и 61/ вычисляем интегралы
Мора по правилу Верещагина (табл. 12).Геометрические характеристики арочной диафрагмы:
площадь поперечного сечения арки Аа = 0,2 • 0,45 = 0,09 м2;
момент инерции поперечного сечения арки 1а=0,2 • 0,453/12 =
= 0,00152 м4;площадь поперечного сечения затяжки Atd = 0,2 • 0,25 = 0,05 м2
Таким образом, получим значения перемещений для подста¬
новки в каноническое уравнение метода сил:Е{1 = ( 0,00152 )2 = 26488;- (-SS-+^wlL)2=|2242128-Таблица 12УчастокДлинаПеремещениядуги аркиучастка дуги,
м\NfN\ds\NUs0—11,651— 102,22,90,2251,41—21,582—595,1—280,71,3011,422—31,545-1294—502,12,801,453—41,526— 1976,6—670,54,211,484—51,509—2499,9—781,05,291,495—61,502—2784,3—836,95,881,5Сумма9,315—9252,1—3074,119,718,7459
Основную неизвестную (распор) найдем из решения канони¬
ческого уравнения: х = Н= 12242128/26488 = 462,2 кН.После того как распор найден, можно определить усилия в
любом сечении арки. Опуская арифметические вычисления, при¬
водим суммарные эпюры изгибающих моментов (кН • м) и про¬
дольных сил (кН) на рис. 16, в.Расчет сечений бетона и арматуры плоской арки выполняется
обычными методами и здесь не приводится.5. Основные положения по конструированию
коротких цилиндрических оболочек (рис. 17)В коротких монолитных оболочках с нагрузкой только от
собственной массы, массы утеплителя и снега, при пролетах
Zi^6 м и /2<30 м и стреле подъема не менее (1/8) /2, толщина
плиты может быть назначена 50 мм. Если же 6</i ^ 12 м, то на¬
значение толщины плиты зависит от класса бетона: при бетонах
класса В 30, В 35 толщина плиты принимается 70...80 мм, а при
классе В 25 — 80...90 мм.При упрощенном расчете короткой оболочки плита армируется
конструктивно прямоугольной сеткой из стержней диаметром
4...6 мм и шагом 100 или 150 мм. Стержни сетки заделываются
в контурные элементы так же, как на крайних опорах плоских
плит (рис. 17, бив).В многопролетных монолитных оболочках для восприятия дей¬
ствующих над опорами растягивающих усилий в приконтурных
зонах сверху укладываются дополнительные сетки (рис. 17, в) —
над диафрагмой на расстоянии 0,11\ в обе стороны от оси (рабочие
стержни прямолинейные, а монтажные — криволинейные) и вдоль
бортовых балок на расстоянии 1,25... 1,50 м от оси бортового эле¬
мента (рабочие стержни криволинейные, а монтажные — прямо¬
линейные) .Рабочие стержни дополнительных сеток следует укладывать
ближе к наружной поверхности бетона с минимальным защитным
слоем. На крайних контурных элементах эти стержни должны
быть заведены в бетон контурных элементов на длину анкеровки
растянутых стержней. Для размещения всей арматуры в прикон¬
турных зонах толщину плиты допускается увеличивать.Высота сечения бортовых элементов, выполненных без пред¬
варительного напряжения, принимается не менее (l/15)/i, а ши¬
рина— 1/5... 1/2 высоты сечения. При этих размерах горизон¬
тальная жесткость бортового элемента оказывается достаточной.Бортовые балки, а также торцевые диафрагмы, которые вы¬
полнены в виде арок с затяжками или ферм, армируются в соот¬
ветствии с расчетом по общим правилам конструирования подоб¬
ных плоскостных конструкций. В пролете большая часть арматурыво
Рис. 17. Армирование коротких цилиндрических оболочек
а— монолитная оболочка; б, в — соответственно поперечное и продольное сечение моно¬
литной оболочки; г — плита сборной оболочки; 1 — криволинейная плита; 2 — бортовой
элемент; 3 — диафрагма; 4,5 — соответственно продольная и поперечная арматура плиты;
6,7 — продольная и поперечная дополнительная арматура плиты; 8, 9 — соответственно
продольная арматура бортового элемента и диафрагмыбортовых балок устанавливается внизу, а на опорах (над диафраг¬
мами) арматура того же сечения устанавливается вверху борто¬
вой балки.Сборные короткие оболочки конструируются из плоских па¬
нелей (обычно с ребрами по контуру) и диафрагм (арок или
ферм). Сборные панели снабжают выпусками арматурных стерж¬
ней для связи с диафрагмами (рис. 17, г). Бортовыми элементами,
как правило, служат специальные панели или наружные ребра61
крайних панелей, в которых в этих случаях предусматривается
дополнительная арматура.Толщина плиты сборных панелей назначается из условия раз¬
мещения арматуры и защитных слоев. Жесткость обеспечивается
небольшими промежуточными ребрами. Конструирование сборных
элементов коротких оболочек принципиально не отличается от
конструирования подобных плоскостных элементов покрытий
зданий.Складчатые железобетонные пространственные конструкции
треугольного или трапециевидного сечения (рис. 18) состоят
из плоских элементов — граней, соединенных между собой под
углом так, что в месте их сопряжения образуется прямолинейное
а)III. РАСЧЕТ ДЛИННОЙ ТРЕУГОЛЬНОЙ
СКЛАДКИ1. Особенности расчета62Рис. 18. Схемы призматических
складок и примеры приведения
их поперечных сечений к форме,
удобной для расчета
а — треугольные складки, образу¬
емые из плоских граней; б — то же,
из Г-образных элементов; в —трапе¬
циевидные складки, образуемые из
z-образных элементов; г — складка,
приведенная к прямоугольному сече¬
нию; д — то же, к тавровому сече¬
нию; е — то же, к двутавровому
ребро. Складки с достаточно жестким поперечным сечением, ко¬
торое под нагрузкой не испытывает кручения и, следовательно,
не приводит к его депланации (к таким складкам относятся сред¬
ние волны многоволновой складки или отдельные складки, под¬
крепленные поперечными ребрами и диафрагмами), практически
рассчитываются так же, как и длинные цилиндрические (призма¬
тические) оболочки балочного типа.На симметричную нагрузку тонкостенный элемент такой склад¬
чатой конструкции может быть рассчитан по схеме простой балки
в предположении линейного распределения продольных дефор¬
маций по высоте сечения. В этих случаях дополнительные каса¬
тельные и нормальные усилия в поперечных сечениях волн складки
несущественны и в расчете не учитываются.2. Конструкция складки и нагрузкиЗапроектируем складчатое покрытие промышленного здания
с сеткой несущих колонн 6X24 м.Складку принимаем однопролетной, многоволновой, сборно¬
монолитной конструкции с вертикальными бортовыми элементами
(рис. 19, а). Последние изготовляются отдельно в виде предвари¬
тельно напряженных балок длиной на пролет, т. е. 24 м. Попереч¬
ное сечение балок имеет уширения внизу для размещения напря¬
гаемой арматуры.Складка состоит из двух граней (плоских панелей размером
3,1 X 12 м), соединенных между собой под углом по верхней кром¬
ке. В месте их сопряжения образовано прямолинейное ребро,
состоящее из двух продольных ребер сборных панелей и замоно¬
личенной полости между ними. В панелях для повышения ихТаблица 13Вид нагрузкиНормативноезначениенагрузки,кПаКоэффициент
надежности
по нагрузке
VIРасчетноезначениенагрузки,кПаСобственная масса складки1,31,11,43Собственная масса бортового
элемента0,71,10,77Теплоизоляция, пароизоля-
ция, гидроизоляционный ко¬
вер0,751,30,975Снег (III район)1,01,41,4Итого3,751,24,5Итого с учетом коэффициен¬
та надежности по назначе¬
нию y„ = 0,954,363
Рис. 19. К расчету складки
а — конструкция складки; б — приведенное сечение; в — эпюра сдвигающих сил (главных
растягивающих сил) по нейтральной оси грани; г — армирование плиты наклонной грани;
д— геометрическая схема и нумерация точек складки; е —схема торцевой диафрагмыжесткости из плоскости устроены поперечные ребра с шагом 2 м.
В торцах складки предусмотрены жесткие диафрагмы в виде
треугольных рам. Связь граней между собой по верхней кромке,
а также с бортовым элементом по нижней кромке и с диафрагмами
по торцам осуществляется при помощи выпусков арматуры, свар¬
ки закладных деталей и замоноличивания.Толщина плиты граней (панелей) принята 30 мм, высота сече¬
ния ребер панелей — 200 мм, или примерно 1/15 их длины, что
несколько больше рекомендуемого соотношения 1/20. Высота,,
сечения балки (бортового элемента) принята 800 мм и постоянна
по длине пролета.64
Все элементы складки выполняются из бетона класса В 25
(Rb = 14,5 МПа, Rbt = 1,05 МПа, £* = 27000 МПа).Нагрузки для расчета даны в табл. 13.3. Расчет складки в продольном направленииРасчет по прочности на действие
изгибающих моментов и подбор
арматуры бортовых элементовДля подбора продольной растянутой рабочей арматуры и
вычисления прогибов балочных симметричных складок трапе¬
циевидного или треугольного сечения, работающих на симметрич¬
ную нагрузку, допускается сечение складок приводить к тавровому
или двутавровому виду. Такое приведенное сечение легко может
быть рассчитано по предельным состояниям с помощью «Пособия
по проектированию бетонных и железобетонных конструкций из
тяжелых и легких бетонов без предварительного напряжения
арматуры» (М., 1986). При этом размеры тавровых и двутавровых
сечений подбираются так, чтобы элементы их были равновелики
по площади фактическим сечениям складок. Так, если обозначить
угол наклона плоских боковых граней складки а, то толщина
бетона приведенной вертикальной стенки bred для складок на
рис. 18, г, д и е составит:bred = 2tpi/sin а. (32)Учитывая, что складка в нашем примере находится под воздей¬
ствием симметричной равномерно распределенной нагрузки и
не испытывает кручения или поперечных симметричных или асим¬
метричных деформаций, рассчитываем и конструируем ее по схеме
простой балки в предположении линейного распределения про¬
дольных деформаций на высоте сечения.Складку в продольном направлении рассчитываем на нагрузку
Fd = 4,3 • 6 = 25,8 кН/м. Соответственно максимальный изгиба¬
ющий момент в пролете от действия этой нагрузки Md = 0,125Х
Х25,8 • 23,72= 1811 кН • м.Преобразовываем треугольное поперечное сечение складки в
двутавровое (рис. 19,6). Для этого определим угол а наклона
грани складки:tg а = 800/3000 = 0,267; а= 14°57'; sin а = 0,258.Приведенная ширина сечения бетонной стенки по формуле (32):
bred = 2 • 30/0,258 = 230 мм. Ширина полки верхнего участка при¬
веденного сечения с учетом ребра у верхней кромки граней складки
составляет Ь\ = 580 мм, высота Щ = 200 мм.5 Заказ 61 65
В качестве продольной напрягаемой арматуры бортового эле¬
мента принимаем термически упрочненную арматурную сталь
класса AtIVC с расчетным сопротивлением растяжению Rs =
= 510 МПа. Рабочая высота сечения складки йо=1700 мм.Используя указанные параметры, рассчитаем площадь сечения
продольной растянутой арматуры.Приведенное сечение складки рассчитываем как тавровое.
ПосколькуМь = уьАьЬШЬ* - °>5М) == 0,9 • 14,5 • 580 • 200(1700 — 0,5 • 200) = 2413 • 106 кН • ми, следовательно, Мь> Md, то граница сжатой зоны сечения про¬
ходит в полке, и расчет производится как для прямоугольного
сечения шириной bj = 580 мм. При этом сжатой арматуры в сече¬
нии не требуется, так как соблюдается условие [ф-ла (22) По¬
собия] :Md 1811 • 106 л ~°"п ~ yaRbbhl 0.9 14,5 580 • 1700й ’ < ®R~ °-422'При отсутствии сжатой арматуры площадь сечения растянутой
арматуры определяем следующим образом [ф-ла (23) Пособия]:А - Md - 1811 • 106 91 НО мм2ад/io — 510 • 0,955 • 1700 — ’где £ = 0,955 при ат = 0,0856 (табл. 20 Пособия).Принимаем 4 0 28AtIVC, As = 2463 мм2.Расчет предварительно напряженной бортовой балки на рас¬
крытие трещин и по деформациям производится в соответствии
с «Пособием по проектированию предварительно напряженных
железобетонных конструкций из тяжелых и легких бетонов» и
здесь не приводится.Расчет по прочности на действие поперечных сил
и подбор арматуры плитПри расчете прочности складки на поперечную силу по наклон¬
ному сечению следует учитывать фактическую толщину наклонных
стенок с поправкой на угол наклона. Величина поперечной силы
на опоре составляет: Qsur = 0,5 • 4,3 • 6 • 23,7 = 306 кН.Для определения касательных напряжений приводим без вы¬
числений необходимые значения геометрических характеристик
поперечного сечения складки (размеры см. на рис. 19): площадь
А =0,4 м2; положение центра тяжести сечения z' = 0,67 м; момент66
инерции /х =0,1165 м4; статический момент площади относительно
нейтральной оси S* = 0,0917 м3.Касательные напряжения на нейтральной оси в опорном сече¬
нии складки при толщине плиты 30 мм:т = 306 • 0,0917 • 1012/(2 - 0,1165 • 30 • 1012)=4,0 МПа.Касательные напряжения на нейтральной оси численно равны
главным растягивающим. Учитывая, что допускать opr> 3Rbt =
= 3,15 МПа не рекомендуется, увеличиваем без пересчета толщину
плиты приопорного участка панели и принимаем ее равной 45 мм.
Тогда т = 4,0в 30/45 = 2,7 МПа<3/?*,*.Величина сдвигающих усилий в опорном сечении складки 306 • 0,0917 • 10‘2qsf 2 • 0,1165 • 10‘2 —120»4кН/ *Плиту граней складки армируем из предположения, что 30%
главных растягивающих напряжений (или касательных на ней¬
тральной оси) воспринимается бетоном. С учетом сказанного
на арматуру в опорном сечении передаются ^ = 0,7 • 120,4 =
= 84,3 кН/м.Далее по пролету в сечениях через каждые 2 м от опоры зна¬
чения сдвигающих усилий следующие (вычисления опускаем):
70,8, 56,4, 42,1, 27,7, 14,3 кН/м, посередине пролета ^/ = 0
(рис. 19, в).Плиту армируем основной арматурной сеткой, укладываемой
по всей площади грани. Участки плиты, где несущей способности
этой сетки недостаточно, армируем дополнительно косой армату¬
рой (рис. 19, г). Несущая способность основной сетки, которая
принята из стержней 0 6AIII с шагом 200 мм в обоих направле¬
ниях, равна 0,5(28 • 5 + 28 • 5)355 = 49700 Н/м.Первые от опоры три панели грани, где qSf> 49700 Н/м, снаб¬
жаем косой арматурой — стержнями 0 6AIII с шагом 200 мм.Полная несущая способность приопорной зоны составляет:
49700 + 28 • 5 • 355=99400 Н/м, что больше величины сдвига¬
ющего усилия в опорном сечении, передаваемого на арматуру.
Принятую в приопорной зоне толщину плиты 45 мм распростра¬
няем на панели плиты, где укладывается косая арматура, что
позволит разместить обе сетки и обеспечить необходимую толщину
защитного слоя бетона.4. Расчет складки в поперечном направленииРасчет складок открытого профиля рекомендуется произво¬дить с учетом моментов, вызывающих поперечный изгиб граней.67
Поперечные изгибающие моменты в гранях складки, рассматри¬
ваемой как балка с недеформируемым поперечным сечением,
допускается определять как в неразрезной многопролетной плите
на неподвижных шарнирных опорах. За неподвижные опоры
принимаются ребра складки (линии сопряжения граней), а за
пролет — ширина грани. Расчет выполняется для полосы единич¬
ной ширины. Число пролетов, вводимых в расчет, должно быть
не менее двух и не более пяти. Крайняя опора многопролетной
плиты, в зависимости от конструктивного решения, рассматрива¬
ется как шарнирная упругозащемленная или жесткозащемленная.Нормальные усилия для расчета сечений граней можно вы¬
числять без учета неразрезности плиты, как статически опреде¬
лимые величины.Предварительный расчет поперечных моментов в отдельных
складках трапециевидного и прямоугольного сечения произво¬
дится как для консольных плит с защемлением по вертикальной
плоскости симметрии. Учитывая, что в нашем примере грани
складки имеют подкрепляющие поперечные ребра с шагом 2 м,
поперечные изгибающие моменты будем определять как для плиты
размером 2X3 м, опертой по контуру. Условия закрепления на
опорах для расчета этих плит принимаются соответственно кон¬
структивному решению грани; контурные ребра грани будем счи¬
тать упругозащемленными опорами плит, а промежуточные реб¬
ра — жесткозащемленными.Поперечные ребра грани рассчитываются как однопролетные
простые балки на нагрузку, передаваемую плитой.Подбор арматуры в плите складок производится так же, как
и в длинных цилиндрических оболочках, на усилия W45. При этом
поперечная арматура складок проверяется еще на действие по¬
перечных изгибающих моментов (из расчета многопролетной пли¬
ты). Кроме того, армирование плит и подкрепляющих ребер
граней, а также их сопряжений следует выполнять с учетом из¬
гибающих моментов от возможной местной нагрузки. Расчет плит
и балок выполняется элементарно и здесь не приводится, так же
как и подбор арматуры, выполняемый по указанному выше По¬
собию.5. Проверка устойчивости складкиПри проверке устойчивости граней складки критическое на¬
пряжение продольно-сжатой прямоугольной пластинки может
быть найдено из решения дифференциального уравнения ее рав¬
новесия в зависимости от отношения приведенной толщины пла¬
стинки tred к ее ширине fcs/, условий закрепления ее продольных
граней и от характера распределения напряжений по ширине68
пластинки. Решение дифференциального уравнения приводит к
выражениюСЛ Еь / tred \°сг = 12(1-v2) \~/ ‘Если вместо модуля упругости бетона Еь подставить модуль де¬
формации бетона Еь\=0у25Еь (что учитывает фактор ползучести
бетона и его неоднородность), а также ввести коэффициент запаса
на устойчивость, равный 2,4, то получим:,33)где v = 0,2 — коэффициент Пуассона; vi— коэффициент, зависящий от распреде¬
ления напряжения по ширине грани и условий закрепления ее продольных
краев: vi =сл2/[115(1 — v2)]=0,089 с\ при продольных краях грани, опертых шар¬
нирно, коэффициент vi =0,35; при жестко защемленных краях vi = 0,63; при
упругой заделке в смежных гранях допускается принимать vi=0,45.Поскольку в нашем примере подкрепляющие поперечные ребра
грани достаточно жесткие и препятствуют повороту продольных
ребер грани, полагаем плиту жесткозащемленной по продольным
краям.Вычислим продольные напряжения в середине плиты грани
(среднее напряжение):Omt = My/I= 1811 • 106 • 270/(0,1165 • 1012) = 4,2 МПа,где у — ордината середины сечения плиты; г/ = 670 — 800/2 = 270 мм.Приведенная толщина плиты с учетом ребер tred = 54 мм. Для обес¬
печения устойчивости грани необходимо соблюдение условия (33):<тсг = 0,63 • 27 • 103(54/2800)2 = 6,3 МПа.Так как ат/<асг, то условие устойчивости грани складки удов¬
летворено.Диафрагмы складок рассчитываются так же, как диафрагмы
длинных цилиндрических оболочек. Диафрагмы, выполненные ввиде треугольной или трапециевидной рамы с затяжкой (см.рис. 19, е) и работающие на симметричную нагрузку, можно рас¬
считывать без учета эксцентриситета приложения сдвигающих
сил к стержням диафрагмы относительно их оси. Если пренебречьпродольными деформациями стержней диафрагмы, то изгибающиемоменты в стержнях рамной диафрагмы обратятся в нуль, и каж¬дый стержень будет подвержен растяжению или сжатию от сдви-6. Расчет диафрагмы
Таблица 14ТочкасеченияСтатический
момент отсе¬
ченной части
сечения Scui,
м3Сдвигающее
усилие qsf =
= QsupScut/2I,
кН/мУчастоксеченияРасчетная
сдвигающая
сила, кН00010,068690,00—274,520,0897117,82—3121,430,0895117,53—4110,840,073396,34—562,1500гающих усилий, которые передаются непосредственно на него.В нашем примере диафрагма треугольная, поэтому рассчиты¬
ваем ее как треугольную раму. Нагрузкой на раму являются
сдвигающие силы, которые действуют в опорном сечении складки
и передаются от плиты по линии сопряжения. Значения сдвига¬
ющих сил в точках диафрагмы (см. рис. 19, д) приведены
в табл. 14.Продольное усилие в наклонном элементе рамы представляет
собой сумму расчетных сдвигающих сил в опорном сечении на¬
клонной грани: N= 121,4 + 110,8 + 62,1 =294,3 кН. Зная усилие
в наклонном элементе, найдем растяжение в затяжке (распор):
Я = 294,3 • 3,0/3,1=284,8 кН.Подбор сечений элементов диафрагмы по полученным усилиям
опущен. При подборе сечений наклонного элемента рамы необ¬
ходимо учесть изгибающий момент от местной нагрузки, если
таковая есть на примыкающем участке плиты.7. Основные принципы конструирования складокСкладчатые конструкции можно проектировать сборными,
сборно-монолитными или из монолитного железобетона. Целесо¬
образно конструировать складки из сборных гладких или ребри¬
стых пластин (граней) с монолитными пересечениями — прямо¬
линейными ребрами. В стыке граней обычно предусматривают
утолщение типа вутов, что предопределяет более качественную
работу сопряжений граней на изгиб, позволяет рациональней
разместить арматуру, упростить конструкцию опалубки. Рабочую
растянутую арматуру располагают в продольных ребрах сборных
граней или в замоноличиваемой полости ребра, а в трапециевид¬
ных складках также и в нижних горизонтальных гранях.Толщину стенок складок, конструкцию ребер и диафрагм
принимают по тем же требованиям, что и для приведенных выше
цилиндрических оболочек.70
Призматические складки треугольного и трапециевидного се¬
чения применяют для покрытий однопролетных зданий с проле¬
тами до 30 м. Грани таких складок лучше делать целиком на
пролет, а торцы складок конструировать такой ширины, чтобы
они опирались непосредственно на колонны здания. При складках
шириной менее 3 м их опирают на подстропильные балки, фермы
или на стены.Основную рабочую растянутую арматуру балочных складок
конструируют прямолинейной. При относительно больших проле¬
тах складки выполняют предварительно напряженными. В каче¬
стве напрягаемой применяются арматурные стержни классов
A-IV, А-V или арматурные канаты. При этом диаметр напрягаемой
арматуры назначается по возможности наибольший, а распола¬
гается она в утолщенных частях складок и граней.Если грани балочных складок не подвержены местному изгибу
и исключена возможность потери их устойчивости, то они арми¬
руются одинарными сварными сетками в срединной плоскости
граней. В других случаях, а также при толщине грани 80 мм и
больше они армируются двойными сетками, расположенными в
соответствии с эпюрой поперечных изгибающих моментов.Следует обращать особое внимание на узлы сопряжения граней
складок между собой. Необходимо конструировать их жесткими
и армировать как входящие углы железобетонных рамных кон¬
струкций с использованием пересекающихся стержней или сеток,
чтобы обеспечить совместную их работу. При этом как растянутые,
так и сжатые стержни должны быть заделаны на требуемую
нормами длину анкеровки.Сборные складки треугольной и трапециевидной формы се¬
чения, работающие как простые балки, обычно конструируют
из ребристых панелей длиной на пролет или, при больших проле¬
тах, из отдельных элементов, соединяемых по длине на месте
строительства. Стыки таких элементов следует располагать в ме¬
нее напряженных поперечных сечениях складки. Ширина стыка
не должна превышать 250 мм, чтобы обеспечить возможность
надежной стыковки арматурных стержней и соединения конструк¬
ции в целом.Если грани и диафрагмы изготовляются отдельно, то их соеди¬
нения конструируют с выпусками арматурных стержней, чтобы
после замоноличивания надежно обеспечить их совместную работу.71
IV. РАСЧЕТ ПОЛОГОЙ ОБОЛОЧКИ
ПОЛОЖИТЕЛЬНОЙ ГАУССОВОЙ КРИВИЗНЫ
НА ПРЯМОУГОЛЬНОМ ПЛАНЕ1. Некоторые сведения об оболочках
и принятые положения
их расчетаК рассматриваемому виду оболочек относятся строительные
пространственные конструкции, имеющие выпуклую поверхность
на прямоугольном плане (рис. 20, а).Эти поверхности, или собственно оболочки, делятся на два
класса — пологие и подъемистые. По ряду известных причин и
преимуществ именно пологие оболочки получили наиболее широ¬
кое распространение в практике строительства. Немаловажное
значение имеет и тот факт, что при расчете пологих оболочек
может быть принят ряд гипотез, которые справедливы для тех¬
нической теории расчета оболочек, существенно упрощают урав¬
нения равновесия и вместе с тем обеспечивают достаточную для
практики точность.Пологими считаются оболочки, имеющие подъем над опорным
планом в пределах /i^a/5; f2^b/5, где 2а и 2Ь — размеры сто¬
роны оболочки в плане; f\ и f2— стрелы подъема оболочки на
контуре.Кроме того, для пологих оболочек гауссова кривизна Х/Г\Г2
в любой точке срединной поверхности мала по сравнению с I//2,
где / — ширина прямоугольника, перекрываемого оболочкой. В си¬
лу этих предпосылок внутренняя геометрия срединной поверхности
пологой оболочки может быть отождествлена с внутренней гео¬
метрией плоскости.Форму оболочки характеризует тип ее срединной поверхности.Следует заметить, что сведения из теории поверхностей необ¬
ходимы при исследовании теории так называемых точных расчетов
тонких оболочек, так как деформация всей оболочки может быть
описана, если известна деформация ее срединной поверхности,
которая, в свою очередь, определяется геометрией этой поверх¬
ности до и после деформации.Форма поверхности пологих оболочек, как правило, выбирается
из соображений удобства изготовления конструкции, простоты
опалубки, легкости монтажа и заделки стыков и условий унифи¬
кации (при сборных конструкциях). Краткие сведения из теории
поверхностей необходимы также проектировщику-конструктору
для правильного построения поверхности, разбивки ее на сборные
элементы и определения их размеров, проектирования опалуб¬
ки и пр.72
*Рис. 20. Схема оболочек положительной гауссовой кривизны
а — оболочка с поверхностью гиперболического параболоида; б — оболочка с тороидаль¬
ной поверхностью и схема членения исходной поверхности на сборные элементы радиаль¬
ными секущими плоскостямиОболочки по контуру опираются на диафрагмы, которые могут
выполняться из различных конструкций — арок, ферм, балок,
криволинейных брусьев. Контурные элементы опираются на ко¬
лонны каркаса здания.В зависимости от структуры здания оболочки могут быть
одноволновыми (отдельно стоящими) и многоволновыми в одном
и двух направлениях.Поскольку в этом примере рассматривается сборно-монолитная
оболочка, то нами выбрана поверхность тора, а именно наружная
его часть, имеющая положительную кривизну. Такая поверхность
имеет ряд известных преимуществ.73
Тор является поверхностью четвертого порядка (см. рис. 20, б),
уравнение которой имеет видг*={го+лГ7^)2-х2:Если начало координат перенести в вершину поверхности (в точ¬
ку Oi), то уравнение в новой системе запишется так:z2 = (го 4“ V r<1—У* )2 — (го~\~г)2 — 2(го + г) z—х2.Параметры сплошной поверхности тороидальной оболочки,
имеющей положительную кривизну, теоретически связаны между
собой зависимостями, которые выражаются следующими фор¬
мулами:радиусы кривизны контураг\ = г0+л/ г2— Ь2 ; Г2=У г2 — (г0 — а)2 ; (34)главные радиусы кривизныгрг,1 = г0 + г; v,2 = r; (34а)стрелы подъема поверхности на контуре
fi = rt( 1 —cosai);f2 = rpr, i cos a — ri cos a 1, (346)угол a отыскивается из значения sin a = a/rpr,i, а a\—из
sinai=a/ri;полная стрела подъема поверхности в вершине поверхности
оболочки/ == грГ, 1 — г 1 cos ос 1. (34в)Известны и другие формы поверхности положительной гауссо¬
вой кривизны, но мы на них не останавливаемся, так как при
расчетах пологих оболочек с принятыми упрощениями геометрия
других применяемых иногда видов поверхностей практически
не оказывает влияния на результаты расчета. В частности, в на¬
стоящем примере приводится расчет оболочки с поверхностью
эллиптического параболоида, позволяющей существенно упро¬
стить расчетные формулы, но таким же методом могут быть рас¬
считаны пологие оболочки и с другими поверхностями.Уравнение поверхности эллиптического параболоида в системе
координат по рис. 20, а, заданное в явной форме, имеет вид:74
Рис. 21. Схема усилий, действу¬
ющих в пологих оболочках2=/i-fr+/2-p- • (35)Радиус кривизны главной параболыV2Z = hjrяожет быть вычислен в любой точке по формулеr _(i+z;)3/2Отсюда радиус кривизны в вершине параболы при х = 0roi=ir=w- <36>и2Аналогично для главной параболы z=f2-^г имеемro2=lf=W- <37>В пологой оболочке возникает система усилий N\, N2, QSf> Q, а так¬
же изгибающих моментов Мь М2 и крутящих моментов Т12 и Г21
(рис. 21).В зависимости от конструктивных особенностей, условий опи-
рания на контуре и вида нагрузки оболочки могут рассчитываться
разными методами. В нашем примере для тонкой оболочки с отно¬
сительно большим подъемом в центре (///>20) и равномерно
распределенной нагрузкой может быть использован метод расчета
по безмоментной линейной теории с последующим учетом изгиба¬
ющих моментов, возникающих в приконтурных зонах (так называ¬
емый краевой эффект). При этом допускается считать шарнирным
опирание оболочки на достаточно жесткие в своей плоскости и
гибкие из плоскости диафрагмы.75
Пренебрегая при расчете оболочек изгибающими моментами,
мы тем самым пренебрегаем тангенциальными деформациями
срединной поверхности, учитывая только ее вертикальные переме¬
щения.Дифференциальные уравнения равновесия элемента оболочки
под действием вертикальной распределенной поверхностной на¬
грузки F с учетом принятых гипотез имеют вид:£*=0; -^-+-^-=0; Ли дх дуЬ=0; ^+^=0; . (38)2> = 0; ^-/V,+ ^-№ + 2^-Q„ = F. ^Первые два уравнения — это известные уравнения равновесия
плоской задачи, третье уравнение получено непосредственно из
приращений горизонтальных проекций усилий N\ и N2. Если про¬
извести необходимые подстановки, раскрыть производные и учесть,
что кручение поверхности переноса (эллиптического параболоида)отсутствует, т. е. -qxq =0, а вторые производные по х и у являют¬
ся кривизнами главных парабол в вершине оболочки, то получим
третье уравнение равновесия, которое примет вид:N\/r\ + N2/r2 = F. (39)Выражение (39) является не чем иным, как уравнением равно¬
весия между внутренними силами и внешней нагрузкой, спроек¬
тированными на вертикальную ось. Строго говоря, кривизны по¬
верхности гиперболического параболоида не одинаковы в различ¬
ных точках поверхности, но приближенно будем полагать эти
кривизны идентичными во всех точках поверхности и равными
главным кривизнам, что позволит применить уравнение (39) для
любой точки поверхности оболочки.Три полученных уравнения равновесия для определения нор¬
мальных (продольных) сил N\y N2 и сил сдвига QSf можно при¬
вести к одному дифференциальному уравнению Пуассона путем
некоторых преобразований.Исходя из уравнения (39), можно с помощью гиперболотри¬
гонометрических рядов дать решение в замкнутой форме, если
выразить три неизвестные функции JVi, JV2 и QSf через функцию
напряжений Ф следующим образом:д2Ф it д2Ф кт д2Ф ~ //|т■W=N'- 1хг= ’ —5rfF=e"- <40176
Эти выражения удовлетворяют первому и второму уравнениям
равновесия. Из третьего уравнения (39) с учетом выражения (40)
получим дифференциальное уравнение:1 д2Ф . 1 д2Ф Р—-ду*-+—-ьГ=Р- (41)При этом по краям оболочки Ф = 0, так как из условий N\ =
д2Ф д2Ф— и N2= &хъ вытекает, что вдоль краев оболочки, парал¬
лельных осям хну, ^_^-=0 и -^£-=0. В углах оболочки всег¬
да можно Ф приравнять нулю, так как усилия выражаются через
вторые производные. Следовательно,Ф принимает нулевое значе¬
ние по всему контуру оболочки.После замены переменных преобразованием у = ц/^[77 \ х =
= 1/^/~г2~ получим следующее выражение:д2Ф , д2Ф сдV + ЙТ)2 ’ (42)которое и называется гармоническим уравнением Пуассона.
При его решении необходимо учитывать граничные условия обо¬
лочки, т. е. характер ее закрепления к контурным элементам.Для отдельно стоящей оболочки с шарнирным опиранием на
контуре и равномерно распределенной нагрузкой F нормальные
и сдвигающие силы можно определить из решения гиперболотри¬
гонометрических рядов:О 2 ” Л=1. . сЛ-££-*о«/Ni=^ri~F Т (-о 2 4- пп хЯ fl п=Г3.5 " Ch.f-*0Xcos-^-x; (43). «-I , ch -rrr-koy/1 = 1,2,3 2xcosir*]; (44)” «=L . sh-!£-koy
Qsf=- — -^—F У (-1) 2 4 75 x* Ш -Г2.ЗXsin-^-x; (45)здесь h0 = ^ f2/fi .77
Хорошая сходимость рядов в выражениях (43), (44), (45)
ограничена средней зоной оболочки. Для получения быстрой
сходимости по всей поверхности оболочки, включая приконтурные
зоны, выражения эти преобразованы, и необходимая для практики
точность достигается удержанием только первого члена ряда.Окончательно выражения искомых сил в замкнутой форме
приобретают следующий вид: -T-f <«>о,— — F Пп(*6+*7)(/г8~*7)-1+ ^K-Fe-nkok9k7. (47)v*f—— „ г\}п (kb-k7)(kt+k7) яНормальную силу N2 можно определить из (39), имея в виду,
что силы N\ и N2 сжимающие и имеют знак «минус»:N2=-(F+Nt/n)r2. (48)В формулах (46) и (47) приняты следующие значения коэф¬
фициентов ki'.fci=cos-^-; *2 = sh-^-(l —
кз=sh-^-(l —I—ki = ch-^-ko\
ft5=ch-^-&o', fte = ch-^-(l —
fe7=sin-^- ; ft8=ch-^-(l-|—|-);
sh~^~feo
9_ Ch^-feor\ и г2— главные радиусы кривизны срединной поверхности
в вершине оболочки. Это справедливо, даже если фактическая
поверхность оболочки отличается от поверхности гиперболического
параболоида, которая была принята при выведении формул (46),
(47) и (48).Следует отметить, что сдвигающие силы по всей поверхно¬
сти оболочки, кроме угловых зон, имеют конечные значения.
В угловых зонах безмоментная теория не дает возможности опре¬
делить сдвигающие силы, так как при приближении к углам они
резко возрастают и при х = 0 стремятся к бесконечности. Объяс¬
няется это исходным допущением, что диафрагмы приняты абсо¬
лютно гибкими в горизонтальном направлении на всем своем78
протяжении. В действительности же диафрагмы в углах жестко
соединены и оказывают сопротивление горизонтальному смещению
краев оболочки. Это свидетельствует о том, что в углах оболочки
равновесие может быть обеспечено только с учетом действительно
возникающих в этих сечениях усилий (изгибающих моментов,
нормальных и сдвигающих сил). Эти усилия существенно умень¬
шают сдвигающие силы в угловой зоне. Поэтому для практики
при расчете оболочки достаточно величины сдвигающих сил при¬
нимать по значениям, вычисленным в точке, на расстоянии
0,04...0,05 а (или Ь) от теоретического (расчетного) угла оболоч¬
ки, что приблизительно соответствует внутренней грани диафрагм
на опоре оболочки.Для облегчения и ускорения процесса расчета в табл. 15 при¬
ведены вычисленные по формулам (46) и (47) коэффициенты
(условные силы Ni и QSf) для некоторых значений /2//1.При помощи указанных таблиц искомые силы вычисляются
по следующим формулам:Nl = NlrlF; Qsf = QsnTwF-, (49)с учетом выражения (48)N2=(\—Ni)r2F. (50)Напомним, что формулы (49) и (50) в представленном виде
годны для расчета отдельно стоящих оболочек со свободным
опиранием на контуры диафрагмы. Чтобы воспользоваться этими
формулами для расчета оболочек с другими вариантами закреп¬
ления на контуре (например, многоволновых однопролетных обо¬
лочек, которые, как правило, и встречаются в практике строитель¬
ства), необходимо усилия, вычисленные по формулам (49) и (50),
умножить на поправочный коэффициент х, который вычисляется по
формулех= ——; (51)(a>+l)2+(<o-i)2-ijr^здесь (o = r2/riv a ko—то же, что и в (43)...(45).Запишем выражения безмоментных составных частей искомых
усилий для случая, когда две продольные стороны оболочки, па¬
раллельные оси лг, жестко защемлены, а другие две стороны,
параллельные оси у, шарнирно оперты на соответствующие контур¬
ные диафрагмы (см. рис. 22, расчетная схема /):Nx =xtf,r,F; N2= -(1 — xtf i)r2f;_ (52)Qsf= xQsfV Г1Г2 F.79
Таблица 15. Коэффициенты N, и Qsf для вычисления продольных и сдвигающих усилий в пологих оболочкахположительной кривизны .в точках с координатами х/а80х/а1,00Ni при f2/f\ = 1/2000000000000Qsf при f2/fi = \/200,09580,19420,29830,41180,54020,69160,88201,14501,58892,03140,950,06730,06820,07100,07620,08440,09710,11720,15160,21900,39310,60901,0000,09520,19290,29600,40820,53460,68260,86541,10751,46031,68181,81090,900,13360,13540,14100,15080,16660,19470,22790,28880,39720,61080,78511,0000,09320,18870,28920,39780,51840,65660,82031,03051,24131,33371,37140,800,26040,26360,27330,29080,31760,35700,41410,49730,61860,78880,89121,0000,08600,17370,26450,36030,46250,57200,68810,80300,89720,92550,93550,700,37470,37870,39100,41240,44440,48930,55030,63100,73430,85990,92901,0000,07570,15220,23000,30960,39090,47250,55090,61960,66820,68160,68620,600,47330,47760,49080,51320,54590,59010,64090,71760,80170,89750,94831,0000,06380,12760,19160,25530,31780,37740,43120,47500,50420,51190,51440,500,55490,55910,57200,59370,62460,66520,71560,77580,84470,92050,96001,0000,05160,10290,15350,20290,25000,29320,33080,36030,37920,38400,38570,400,61950,62360,63360,65570,68400,72040,76450,81590,87340,93550,96761,0000,03980,07930,11770,15470,18930,22040,24660,26680,27950,28280,28380,300,66810,67180,68300,70150,72710,75970,79870,84350,89280,94550,97271,0000,02890,05740,08510,11130,13560,15700,17490,18840,19690,19900,19970,200,70180,70530,71560,73270,75640,78610.82140,86140,90540,95200,97591,000. 0,0181
0,0372
0,0550
0,0718
0,0872
0,1008
0,1119
0,1203
0,1255
0,1268
0,12730,100,72160,72490,73480,75100,77330,80130,83430,87170,91240,95560,97781,0000,00920,01820,02700,03520,04260,04920,05460,05860,06110,06170,06190,000,72810,73140,74100,75690,77880,80620,83860,87500,91480,95680,97841,00000000000000У/Ь0,000,100,200,300,400,500,600,700,800,900,951,000,000,100,200,300,400,500,600,700,800,900,951,00
6Заказ 6181Ni при f2/f i=2/3000000000000QSf при f2/f 1=2/300,09210,18700,28760,39800,52350,67270,86101,12251,56562,00780,05600,05680,05940,06400,07130,08260,10040,13080,19080,35060,56471.000,0916
0,1859
0,2859
0,3952
0,5192
0,6657
0,8483
1,0943
1,4646
1,7163
1,87890,11150,11310,11810,12600,14120,16280,19650,25190,35300,56560,75421.000,0901
0,1827
0,2806
0,3871
0,5067
0,6456
0,8132
1,0222
1,2746
1,3892
1,43840,21820,22110,23030,24660,27180,30900,36390,44580,57030,75620,87341.000,0843
0,1707
0,2609
0,3571
0,4620
0,5770
0,7032
0,8351
0,9503
0,9868
1,00000,31620,32010,33210,35320,38490,43000,49260,57780,69130,83500,91601.000,07580,15280,23210,31470,40100,49040,57990,66200,72310,74030,74620,40260,40710,42060,44400,47840,52550,58750,66850,76350,87670,93781.000,06550,13150,19830,26630,33480,40220,46530,51870,55550,56530,56870,47590,48050,49460,51850,55290,59870,65670,72720,80980,90210,95071.000,05420,10850,16280,21690,26970,31970,36450,40060,42440,43070,43270,53530,53990,55380,57730,61040,65360,70670,76950,84080,91860,95911.000,04290,08550,12770,16900,20840,24490,27650,30120,31720,32140,32280,58090,58540,59890,62140,65290,69320,74200,79860,86160,92950,96461.000,03170,06300,09390,12360,15170,17710,19870,21540,22590,22870,22960,61310,61740,63040,65200,68200,72000,76560,81770,87520,93670,96821,000,02080,04140,06160,08080,09880,11490,12840,13880,14520,14690,14140,63210,63700,64910,67000,69960,73560,77910,82850,88280,94050,97021,000,01020,02050,03040,03990,04870,05650,06300,06800,07110,07180,07220,63840,64270,65520,67600,70460,74170,78350,83200,88530,94180,97081,00000000000000,000,100,200,300,400,500,600,700,800,900,951,000,000,100,200,300,400,500,600,700,800,900,951,00
Продолжение табл. 1582х/а1,00Ni при /2//1 =4/5000000000000Qsf при f2/f i=4/500,08890,18060,27820,38590,50890,65600,84261,10291,53551,98730,950,04940,05010,05250,05680,06370,07420,09070,11880,17440,32490,53591,000,08440,17970,27670,38350,50530,65020,83201,07921,45911,72951,91690,900,09820,09970,10450,11290,12620,14650,17810,23020,32030,53630,73291,000,08720,17700,27230,37660,49460,63310,80201,01701,28781,41731,47530,800,19270,19560,20440,22000,24410,28000,33310,41350,53890,73390,86091,000,08220,16650,25520,35070,44570,57320,70490,84720,97721,01991,03550,700,28030,28410,29590,31660,34800,39290,45580,54310,66230,81760,90691,000,0746
0,1507
0,2296
0,3129
0,4011
0,4946
0,5908
0,6820
0,7522
0,7724
0,77940,600,35830,36280,37650,40020,43540,48390,54850,63220,73720,86220,93031,000,06520,13120,19870,26830,33970,41160,48070,54330,58320,59480,59870,500,42530.43010,44480,46980,50610,55480,61710,69410,78550,88920,94421,000,05460,10970,16530,22140,27720,33130,38080,42180,44930,45650,45890,400,48020,48520,50010,52540,56130,60850,66720,73740,81790,90670,95311,000,04360,08740,13110,17440,21660,25630,29160,31970,33800,34280,34440,300,52290,52780,54270,56760,60260,64770,70290,76730,83970,91830,95891,000,03260,06510,09730,12880,15900,18700,21110,23000,24210,24520,24630,200,55320,55800,57270,59700,63100,67440,72670,78690,85390,92570,96271,000,02160,04310,06420,08480,10420,12190,13710,14880,15620,15820,15880,100,57120,57610,59050,61450,64770,68990,74040,79810,86180,92980,96481,000,01080,02140,03190,04200,05150,06020,06750,07310,07660,07750,07850,000,57720,58210,59640,62020,65330,69500,74480,80180,86440,93110,96541,0000000000000у/ь0,000,100,200,300,400,500,600,700,800,900,951,000,000,100,200,300,400,500,600,700,800,900,951,00
В табл. 16 приведены значения коэффициентов х, применяемых
для расчета оболочек, закрепленных по двум сторонам, причем
для таких геометрических параметров /2//1 и а/Ь, при которых
погрешность, вызванная допущениями при выводе х, не превы¬
шает 5%.После вычисления нормальных и сдвигающих усилий по фор¬
мулам (52) можем перейти к определению главных растягивающих
и главных сжимающих усилий по формулеN,,™ =Щ^-± У(^Т^)2 + <Й • (52а)Формулы (52) и (52а) позволяют вычислять необходимые
усилия, возникающие в любой точке криволинейной плиты от
воздействия на оболочку внешней нагрузки F.2. Конструкция оболочки и нагрузкиДля промышленного здания с сеткой колонн 12X24 м необ¬
ходимо запроектировать покрытие в виде пологой оболочки поло¬
жительной кривизны. Покрытие принимаем сборно-монолитной
конструкции из многоволновых однопролетных оболочек по ароч¬
ным контурным элементам с предварительно-напряженными за¬
тяжками.Оболочка собирается из панелей размером ЗХ 12 м с цилиндри¬
ческой поверхностью и ребрами по периметру. Панели смежных
волн трехметровыми сторонами опираются на сборную арочную
диафрагму пролетом 24 м и замоноличиваются. Арка торцевой
диафрагмы оболочки является одновременно ребром торцевой
панели. Затяжка арки изготовляется отдельно в виде железобе¬
тонного предварительно-напряженного бруса.В качестве исходной срединной поверхности оболочки служит
наружная часть тора, имеющая положительную кривизну (см.
рис. 20, б). Подъем срединной поверхности над опорным контуром
принимаем по длинной стороне f\ =2,4 м, что составляет 1 /5 от по¬
ловины большего пролета оболочки, а по короткой стороне /2 =
= 1,5 м, или 1/4 от половины меньшего пролета оболочки.Членение оболочки на плиты производится системой радиаль¬
ных секущих плоскостей, проходящих через ось вращения тора,
при этом панели приняты прямоугольного плана, а швы между
ними — клиновидными. Такая система членения на сборные па¬
нели позволяет сократить количество их типоразмеров, так как
все промежуточные панели одинаковые.Главными радиусами кривизны поверхности являются г\ =
= 31,2 м и г2= 12,75 м.Толщину криволинейной плиты средней полосы сборных рядо¬
вых панелей оболочки принимаем tcurtPi=35 мм, что определяется6*83
Таби/иКоэффици2/34/516/55/41/22/34/51,06171,01011,01210,92140,84460,84150,70840,61470,66720,52060,43110,62560,47980,3934Вид нагрузкиНормативноезначениенагрузки,кПаКоэффициент
надежности
по нагрузке
Y/Расчетноезначениенагрузки,кПаСобственная масса оболочки2,181,12,4Теплоизоляция, пароизоляция,
гидроизоляционный ковер1,01,31,3Снег (IV район)1,51,42,1ИтогоИтого с учетом коэффициента
надежности по назначению уп =
= 0,954,685,85,5технологическими возможностями изготовления и необходимой
величиной защитного слоя бетона для поперечных и продольных
стержней арматурной сетки. Плиту крайних полос этих панелей
принимаем на 10 мм толще, учитывая необходимость установки
в краевых зонах дополнительных сеток арматуры.Нагрузки на оболочку, заданные для расчета, приведены
в табл. 17.3. Расчет оболочки по безмоментной теорииПо безмоментной линейной теории определяем продольные
и сдвигающие усилия, действующие на оболочку. При этом счи¬
таем опирание оболочки на диафрагмы шарнирным, так как
диафрагмы по принятой гипотезе являются жесткими в своей
плоскости и гибкими из плоскости.Расчетная схема многоволновой однорядной оболочки приве¬
дена на рис. 22. Средние волны и половины крайних волн, примы¬
кающие к средним продольным диафрагмам (расчетная схема 1)>
рассчитываем по формулам для средних оболочек. Крайние волны
(расчетная схема 2) условно дополняем до целой волны и рассчи¬
тываем по формулам для отдельно стоящих оболочек.84Таблица 17
лица 16Расчет средней волныРасчетные усилия в точках криволинейной плиты оболочки
определяются по формулам (52) с помощью табл. 15 и 16. Посколь¬
ку f2/f 1 = 1,5/2,4 ж 2/3 и а/Ь = 12/6 = 2, поправка составит х =
= 0,1372.Подставляя исходные значения в (52), получаем усилия:продольныеNx = FdrxxNx=5,5 31,2 • 0,1372ДГ, =23,5Wi;W2 = /V2(l-xW,)=5,5 • 12,75(1 —0,1372Л/1) = 70,2 — 9,63Ni;сдвигающиеQsf = Fd^/ Г1Г2 xQs/ = 5,5y 31,2 • 12,75 • 0,1372Qs/= 15,1QS/.Учитывая симметричность оболочки и внешней нагрузки, зна¬
чения усилий Nx, N2 и Qsf достаточно вычислить для точек одной
четверти криволинейной плиты оболочки. Результаты расчетов
по приведенным выражениям для средней волны даны в табл. 18.Результаты вычислений главных усилий в точках криволиней¬
ной плиты средней волны оболочки по формуле (52а) приведены
в табл. 19.Рис. 22. Расчетная схема многоволновой оболочки1 — средние волны; 2 — крайние волны85енты х при а/Ь4/33/25/325/20,55950,44190,34580,21040,10370,41760,31480,23730,13720,06500,33730,24820,18350,10360,0483
Таблица 18. Расчетные усилия Ni, N2 и QSf в точках криволинейной плиты с координатами х/а86х/а1.0Продольные усилия N\, кН/м000000000000Продольные усилия N2, кН/м70.270.270.270.270.270.270.270.270.270.270.20,951.31.31.41.5
1,7
1,92.43.14.58.2
13,3
23,569.769.769.669.669.569.4
69,2
68,968.466.8
64,860.60,92,62.72.8
3,03.33.8
4,65.98.3
13,3
17,7
23,569.169.169.069.0
68,8
68,6
68,367.866.864.862.9
60,60,85.15.25.4
5,86.47.3
8,6
10,513.4
17,820.523.568,168,168,067.867.6
67,266.765.964.762.961.8
60,60,77.47.5
7,8
8,39.110.1
11,613.6
16,319.621.523.567,267,167.0
66,866.566.165.564.663.5
62,2
61,460.60,69.59.6
9,910.4
11,2
12,313.815.617.920.6
22,123.566.366.3
66,2
65,9
65,665.164.563.862.9
61,861.260.60,511,211.3
11,6
*2,213.014.115.417.1
19,021.222.423.565.665.6
65,565.264.964.463.963.262.461.5
61,060.60,412,612,713.013.614.315.416.618.1
19,7
21,6
22,623.565,165.064.964.664.363.963.4
62,862.161.4
61,060.60,313.613.8
14,114.615.316.317.418.8
20,3
22,022.723.564,664,564.464.163.963.563.162.561.9
61,360.960.60,214.414.514.8
15,3
16,016.9
18,0
19,220.6
22,0
22,7
23,564,364.264.163.963.663.3
62,862.3
61,861.260.960.60,114,915.015.315.716.417.318.319.520.722.122.823.564,264.063.963.763.563.162.762.261.7
61,160.960.60,015.015.115.4
15,916.517.418.419.5
20,822.2
22,823.564.164.063.963.7
63,463.062.762.261.761.160.9
60,6у/ь0,00,10,20,30,40,50,60,70,80,90,951,00,00,10,20,30,40,50,60,70,80,90,951,0
87Сдвигающие усилия Qsf, кН/м0.0 0000000000000,1 0 0,15 0,31 0,48 0,65 0,82 0,99 1,14 1 27 1 36 1 38 10.2 0 0,31 0,63 0,95 1,29 1,63 1,98 2,30 2^58 2J6 2^81 2^820.3 0 0,46 0,93 1,42 1,93 2,46 3,00 3,50 3,94 4.24 4 32 4 340.4 0 0,60 1,22 1,86 2,55 3,28 4,02 4,75 5,40 5,85 5,96 б!о10.5 0 0,74 1,49 2,29 3,15 4,06 5,06 6,05 6,97 7 65 7 84 7 910.6 0 0,85 1,74 2,67 3,70 4,83 6,07 7,40 8,70 9,75 10,05 10*150.7 0 0,95 1,94 3,00 4,17 5,50 7,02 8,75 10,50 12,25 12,80 13,000.8 0 1,03 2,09 3,25 4,55 6,04 7,83 10,0 12,60 15,40 16,50 16,950.9 0 1,07 2,19 3,41 4,78 6,40 8,38 10,90 14,35 19,25 22,10 23,650,95 0 1,08 2,22 3,46 4,85 6,50 8,53 11,18 14,90 21,00 25,90 30,30'•О 0 1.09 2,23 3,47 4,88 6,53 8,58 11,28 15,10 21,70 28,40 —
Таблица 19. Расчетные значения усилий Ырг,тлх и Npr>mXn в точках криволинейной плитыс координатами х/а88х/а1,0Усилия Npr, max, кН/м70.270.370.370.5
70,7
71,171.6
72,5
74,077.474.5Усилия Npr, rnin, кН /м0—0,1
—0,1
—0,3
—0,5
—0,9
— 1,4
—2,3
—3,8
—7,2
—4,30,9569.769.869.869.970.070.370.671.372.4
74,375.676.01.31.31.3
1,2
1,2
1,0
1,0
0,7
0,7
0,7
2,5
8,10,969.169.269.269.369.469.5
69,870.270.671.2
71,170.62,62,62.72.72.72.9
3,13.54.56.99.513.50,868,168,268,168,168,168,068,067,967.6
67,166.6
66,05.15.25.35.5
5,96.57.38.5
10,413.615.7
18,20,767.267.2
67,167.066.9
66,8
66,566.1
65,164.964.3
63,87.47.47.78,18.79.4
10,6
12,1
14,1
16,9
18,6
20,40,666.366.366.3
66,1
65,9
65,665.2
64,864.263.4
63,062.59.59.6
9,810,210,911,813,114.616.6
19,0
20,3
21,60,565.665.6
65,565.465.164.7
64,3
63,963.262.5
62,161.711,211.3
11,6
12,0
12,8
13,8
15,016.4
18,2
20,221.322.40,465,161,312,622,90,364,661,013,623,20,264,360,814,423,30,164,260,714,923,40,064.164.063.963.7
63,463.062.762.261.761.160.9
60,615.015.115.4
15,916.517.418.419.5
20,822.2
22,823.5У/Ь0,00,10,20,30,40,50,60,70,80,90,951,00,00,10,20,30,40,50,60,70,80,90,951,0
а) 6)Рис. 23. Изостаты главных усилий в криволинейной плите оболочкиа — в средней волне; б — в крайней волне; главные сжимающие усилия; • • главные растягивающие усилияНа рис. 23 изображены изостаты вычисленных по приведенным
выше формулам главных сжимающих и главных растягивающих
усилий (кН/м) на 1/4 поля криволинейной плиты средней волны
оболочки. Изостаты построены по 144 точкам.Расчет крайней волныРасчетные усилия определяем по формулам (49) и (50), при¬
нимая поправку х=1.Продольные усилияNx = FdrxNi = 5,5 -31,2^1 = 171,5^,;W2 = /V2(1-Wi) = 5,5 • 12,75(1 —Wi) = 70,2(l —N\).89
Сдвигающие усилияQSf = F<r\j Г\Г2 Qs/ = 5,5V 31,2 • 12,75 Qs/=110Qs/.Результаты вычислений этих усилий по формулам для крайней
волны приведены в табл. 20.Главные растягивающие и главные сжимающие усилия в кри¬
волинейной плите крайней волны оболочки вычисляем по форму¬
ле (52а). Значения вычисленных усилий представлены в табл. 21.Подбор арматуры в криволинейной плите оболочки положи¬
тельной гауссовой кривизны производится на действие главных
растягивающих усилий. Расчет необходимого количества арма¬
туры здесь такой же, как для плиты цилиндрической оболочки
(см. пример расчета I).4. Расчет оболочки на действие изгибающих моментов
(учет краевого эффекта)Как уже отмечалось, практически приемлемым является метод
расчета пологих оболочек в два этапа: на первом этапе выполня¬
ется расчет безмоментного (мембранного) состояния оболочки,
на втором этапе вычисляются изгибающие моменты, возникающие
в приконтурной зоне. Действительное напряженное состояние
определяется путем наложения усилий, полученных в результате
расчета этапов.Известно, что изгибное состояние оболочки имеет характер
краевого эффекта, который практически быстро затухает по мере
удаления от контура. Для определения краевого изгибающего
момента воспользуемся параметром s, предложенным П. J1. Пас¬
тернаком. Этот параметр зависит от главного радиуса кривизны
оболочки и от ее толщины:S, = 0,76VW7 > \ (53)5</==:0,76л/ tcur,plf2 •Зона действия изгибающих моментов в зависимости от способа
закрепления оболочки на контуре изменяется в пределах (3...4)s,
а величина s колеблется в пределах (0,01 ...0,05) а (или Ь). Для уп¬
рощения задачи рассмотрим только два способа закрепления обо¬
лочки к контуру — по наружному краю и по внутреннему, смеж¬
ному с соседней оболочкой (волной). При первом способе пере¬
мещения краев оболочек перпендикулярно к своим плоскостям
могут реализоваться свободно (в соответствии с принятой гипо¬
тезой о податливости контура в горизонтальном направлении,
перпендикулярном плоскости диафрагмы). Такое закрепление бу-90
Таблица 20. Расчетные значения усилий Ni, N2 и QSf в точках криволинейной плиты с координатами х/а91х/а1,0Продольные усилия N\, кН/м000000000000Продольные усилия N2, кН/м70.270.270.270.270.270.270.270.270.270.270.20,959,69,810,211,012,214.217.2
22,432.760.296.8
171,566,266,166,065.7
65,264.4
63,2
61,056.846.530.5
00,919.119.4
20,3
21,624.2
27,9
33,743.260.5
97,0129,0171,562,462.3
61,961.360.3
58,755.452.545.430.4
17,300,837.4
37,939.542.346.6
53,062.576.597.3129.5
149,7171.555.054.654.0
52,851.1
48,544.738.830.2
17,18,900,7,54,254,957.060.566.0
73,884.5
99,0118.5143.0157.0171.548.0
47,7
46,9
45,4
43,240.035.629.621.7
11,65,900,669.0
69,872.276.282.090.2
100,7114.3131.0150.4161.0171.542.041.640.639.036.733.329.023.4
16,68,64,40.. 0,581,682,584.8
89,094.8102.5112.5124.8138.8
154,7
164,0171.536.8
36,535.433.831.4
28,224.119.213.3
6,9
3,5
010,491,892,595.099.0104.5
112,0
121,0132.0144.0157.5164.5171.532.632.331.329.727.4
24,3
20,6
16,2
11,25,72,900,399,5100.0102.5106.5
112,0119.0127.0137.0147.5159.0165.5171.529.429.128.2
26,624.421.5
18,1
14,19,75,02,500,2105.0106.0
108,0
112,0117.0123.5131.0140.0150.0160.5166.0171.527.2
26,9
26,024.422.3
19,616.5
12,88,84,42,200,1108.4109.2111.2115.0120.0
126,0133.5142.0151.5161.0
166,2171.525,825.524.6
23,2
21,118.515.5
12,08,24,22,100,0109,5110,0112,2115,8121,0127.0134.4142.5152.0161.5166.5171.525,425.124.222.720.7
18,115.211.8
8,1
4,1
2,0
0У/Ь0,00,10,20,30,40,50,60,70,80,90,951,00,00,10,20,30,40,50,60,70,80,90,951,0
Продолжение табл. 2092х/а1,0010,1320,6031.60
43,8057.60
74,0
94,70123,5172.0221.00,95010,0820,4531.5043.50
57,10
73,30
93,40120,5161,0189.0207.00,909,9020,1030,9042,6055,7071,1089,50112,5140,4153.0158.00,809,2818,8028,7039.30
50,80
63,5077.30
92,0104.5108.5
110,00,7Сдвигающие усилия QSf, кН/м08,3516,8925.50
34,60
44,10
54,0063.8072.8079.5081.50
82,200,607,2014.50
21,80
29,30
36,9044.2051.20
57,11)61.20
62,2062.500,505,9611,9517.9023.9029.70
35,20
40,10
44,0046.70
47,50
47,600,404,739,4014,0518,6022,9527,0030.40
33,10
34,9035.40
35,500,303,496,9410,3313,6016.70
19,5021.9023.7024.90
25,20
25,300,202,294,556,788,9010,8512,6514.15
15,25
16,0016.15
16,200,101,122,263.35
4,395.36
6,226.94
7,49
7,82
7,907.950,0000000000000у/ь0,00,10,20,30,40,50,60,70,80,90,951,0
Таблица 21. Расчетные усилия ЛГ„.-« и » точках криволинейной плиты с координатами х/а931,070.2
71,5
75,8
82,491.3
103,3117.0136.1
163,6
211,0259.1Усилия Npr, min , кН/М0— 1.3
—5,6
— 12,2
—21,1
—33,1
—46,8
—65,9
—93,4— 140,8— 188,9"Г0,9566,267.972.6
80,289.7
101,6117.0137.2166.0
214,4255.9310.39.6
8,013.6
—3,4— 12,3
—23,0
—36,6
—53,8
—76,5
— 108,6
— 128,6
— 138,7 г0,962.464.570.0
78,288.5
101,1117.0
137,4166.0
208,2
236,2
265,819.117.212.2
4,7—4,0
— 14,5
—27,0
—41,7
—60,0
—80,8
—89,8
—94,2г 0,855.058.7
66,976.7
88,2101,6117.7
137,2161.7192.0208.8
225,537.4
33,8
26,618.4
9,5—0,1
— 10,5
—21,9
—34,2
—45,4
—50,2
—54,00,754.260.469.579.691.0104.2
119,4137.0157.6180.6192.6204.648,042.2
34,426.3
18,29,6
0,7
—8,4
— 17,4
—26,0
—29,7
—33,1'а0,6кН/м69.0
71,5
77,8
86,2
96,4108.3
121,6137.3154.6173.0182.7191.842.0
39,935.029.0
22,3
15,28,10,4—7,0— 14,0— 17,3
—20,2х/0,5■Я NрГ, max *81,683.3
87,594.3
102,8
112,9124.8
138,7152.3
168,2
177,1183.936.835.732.7
28,5
23,417.911.8
5,7—0,1
—6,6
-9,6
— 12,40,4Усили91.8151.8
165,2
172,0178.832,63,4—2,0—4,6—7,2 0,399,5163,0169.3175.329,41,0
— 1,3
—3,7 0,2I— 1105,0167,6173,227,20,6
— 1,60,11 —I108,4^
172,025,8—0,410,01 1109,5110,0112,2115,8121,0127.0134.4142.5152.0161.5166.5171.525,425.124.222.720.7
18,115.211.8
8,1
4,1
2,0
0у/ь-10,00,10,20,30,40,50,60,70,80,90,951,00,00,10,20,30,40,50,60,70,80,90,951,0
дем считать шарнирным. Во втором случае принято жесткое
присоединение оболочки к диафрагме и предполагается, что в го¬
ризонтальном направлении перемещения краев оболочки отсут¬
ствуют.В соответствии с принятыми двумя способами крепления обо¬
лочки на контуре и тремя вытекающими из этой предпосылки
возможными вариантами закрепления оболочки в углах (шарнир¬
ное с обеих сторон, шарнирное с одной стороны и жесткое с дру¬
гой, жесткое с обеих сторон угла) существуют два вида основных
функций, характеризующих изгибное состояние оболочки на кон¬
туре, и три триады выражений для изгибающих и крутящих мо¬
ментов (Мх, Му и Тху). На основе этих выражений выведены
формулы для вычисления значений максимальных изгибающих
и крутящих моментов:со стороны защемленного края—MXltnax=—Fsl/2 при х = 0; (54)MXimax=Fs2x/2 при x = nsx/2; (55)со стороны шарнирного краяMXlmax=Fsx/6 При X = 7lSx/4. (56)В формулах (54), (55), (56) начало координат совпадает
с углом оболочки.Аналогичный вид имеют выражения для Му , max с соответству¬
ющей заменой индекса, обозначающего координатную ось.Максимальные значения крутящих моментов могут быть вы¬
числены по выражениям, зависящим от варианта закрепления
оболочки в углу.Так, для случая шарнирного крепления с обеих сторон углаГшах= F*f- при Х = у = 0- (57)шарнирного с одной стороны угла и жесткого с другойTmax—F^f- при х=0, y = nsy/4; (58)жесткого с обеих сторон углаTmax = F^~ при x=nsx/4, y = nsy/4. (59)Все приведенные выражения относятся к гладким оболочкам,
которые обычно выполняются из монолитного железобетона.94
Поскольку в нашем примере рассматриваются сборные обо¬
лочки, монтируемые из ребристых панелей, которые в основном
и применяются в современном строительстве, заслуживает внима¬
ния способ учета ребер. Для оболочек с постоянным шагом ре¬
бер sr и равномерно распределенной поверхностной нагрузкой
можно, с достаточной для практических целей точностью, учиты¬
вать наличие ребер приближенно, путем замены ребристой кри¬
волинейной плиты на гладкую, но приведенной толщины. При этом
в зависимости от решаемой задачи основанием для определения
приведенной (фиктивной) толщины плиты может быть принята
площадь сечения или его изгибная жесткость. Так, при расчете
на мембранные усилия важной является площадь сечения, поэтому
приведенная толщина вычисляется от эквивалентного по площади
таврового сечения:tred==z tcur,pl~\~(hr tcur,pl)~tr~ • (60)При расчете краевой зоны на действие изгибающих моментов
существенным является изгибная жесткость сечения, поэтому
приведенная толщина вычисляется от эквивалентного по жестко¬
сти таврового сечения:3 / tred==~\J 121/Sr • (61)В формулах (60) и (61) принято: tred—приведенная толщина
криволинейной плиты; Ъг и hr— соответственно ширина и высота
ребра таврового сечения; / — момент инерции таврового сечения;
sr— шаг ребер.При расчете ребристых оболочек полученное по формуле (61)
значение приведенной толщины подставляют в выражение (53)
для вычисления ширины зоны действия моментов, а затем самих
моментов. По величине отрицательного момента подбирают арма¬
туру плиты, а нижнюю арматуру ребер рассчитывают по положи¬
тельному моменту.Учитывая, что в данном примере оболочка имеет поперечные
ребра с шагом 3 м, в расчет вводим тавровое сечение с полкой
шириной 3 м (рис. 24). Площадь этого сечения составляет А =
= 1415 см2, а момент инерции / = 51310 см4.Рис. 24. Расчетное сечение ребри¬
стой плиты оболочкиШШ95
Приведенная толщина сечения:tred=^l 12 • 51310/300 = 12,7 см.Зная толщину оболочки, вычислим по формуле (53) параметр
П. Л. Пастернака:sy = 0,76-yJ12,7 • 1275 =97 см.По формуле (54) определим максимальный изгибающий мо¬
мент со стороны защемленного края оболочки, т. е. у средней
арки:— Му,max = -5,5 • 3 • 0,972 /2= -7,75 кН • м.То же, со стороны свободного края, т. е. у крайней арки, по
формуле (56):Му,тах =5,5 • 3 • 0,972/6 = 2,6 кН . м.Аналогично в перпендикулярном направлении оболочки, где
опирание с обеих сторон свободное, имеем:s* = 0,76y 12,7-3120 =151 см;Мтах=5,5 • 3 • 1,512/6 = 6,3 кН • м.Арматура ребер определяется по усилиям, действующим на
трехметровой полосе (т. е. ЪМу,тгх). Кроме того, эта арматура
должна удовлетворять прочности по усилиям, действующим в
стадиях изготовления и монтажа. Расчет арматуры выполняется
по нормам.5. Расчет железобетонных арок-диафрагмНекоторые особенности расчетаВ качестве контурных элементов (диафрагм) пологих оболо¬
чек положительной кривизны в практике находят применение
балки, фермы с различной решеткой, арки с затяжкой, криволи¬
нейные балки по стенам и пр. В нашем примере рассматриваем
в качестве диафрагмы арку с затяжкой, которая имеет ряд преиму¬
ществ в изготовлении и эксплуатации по сравнению с другими
конструкциями диафрагм, хотя и более податлива в своей плоско¬
сти, чем ферма. Нагрузкой на диафрагму является передаваемое
контуром оболочки опорное давление в виде сдвигающих QSf и96
продольных сил. Силы Qsf касательны к срединной поверхности
оболочки, обратны по направлению и равны по величине сдвига¬
ющим усилиям, действующим в криволинейной плите оболочки.
Влияние продольных сил, как показали исследования, тем больше,
чем меньше стрела подъема. При переносе сил, нагружающих
диафрагму со срединной поверхности плиты оболочки на ось
арки-диафрагмы, следует учитывать возникающие при этом до¬
полнительные моменты.При проектировании многоволновых оболочек расчету подле¬
жат средние и крайние диафрагмы, так как они работают на раз¬
ные нагрузки. Так, по принятым допущениям, связанным с усло¬
виями закрепления, на крайние диафрагмы передаются только
сдвигающие силы, поскольку продольные силы на контуре равны
нулю (согласно принятой гипотезе о податливости диафрагмы
из плоскости). Что же касается средних диафрагм, то здесь кон¬
турные продольные силы не обращаются в нуль, а, действуя под
углом ф к диафрагме, раскладываются на горизонтальные и,нор¬
мальные к оси диафрагмы составляющие. Горизонтальные состав¬
ляющие взаимно уравновешиваются, а нормальные складываются
и нагружают диафрагму.Таким образом, крайние диафрагмы рассчитывают только на
сдвигающие силы, а средние — на сдвигающие и нормальные
составляющие контурных продольных сил оболочки.Нагрузка на диафрагму от нормальных составляющих вычис¬
ляется по формулам:/ii = 2Nisin<pi; n2 = SA^2sin фг. (62)Поскольку в нашем примере рассчитывается оболочка круго¬
вого переноса, для которой sin ф1 == а/г,; зтф2 = 6/г2, тоn\ = 2N\a/r\\ п2 = 2 N2b /г2. (63)При расчете арочной диафрагмы площадь сечения верхнего
пояса может быть принята несколько увеличенной за счет примы¬
кающих участков плиты оболочки. Этот прием допустим, если
учесть, что оболочка не только нагружает арку, но, будучи моно¬
литно связанной с верхним поясом, подвергается тем же деформа¬
циям, что и этот пояс. Учитывая жесткость криволинейной плиты
и наличие ребер, в расчетное сечение верхнего пояса можно вклю¬
чить 6...8 толщин плиты. Возможность этого подтверждена экспе¬
риментальными проверками запроектированных с указанными
допущениями оболочек.7 Заказ 6197
Расчет по прочности в стадии эксплуатацииРассчитываем среднюю и крайнюю диафрагмы пролетом 24 м,
а также торцевые диафрагмы пролетом 12 м в средней и крайней
волнах оболочки.Диафрагма пролетом 24 м состоит из контурного пояса и кон¬
турной арки. Контурный пояс образован трехметровыми торце¬
выми ребрами панелей с замоноличиваемой полостью и рас¬
сматривается как шарнирная цепь, воспринимающая краевые
усилия от оболочки и передающая вертикальные реакции на
верхний пояс арки, а горизонтальные — на ее концевые упоры.
Опорный контур рассчитываем как статически неопределимую
систему на краевые сдвигающие и поперечные силы. Средняя
арка при этом воспринимает усилия от двух смежных волн обо¬
лочек.Значения краевых сдвигающих усилий QSf, действующих на
контуре средней оболочки, приведены в табл. 18 (при y/b= 1
для 24 м и при х/а= 1 для 12 м), а на контуре крайней оболочки —
в табл. 20 (при у/Ь = 1 для 24 м и при х/а= 1 для 12 м). На рис. 25, аРис. 25. К расчету арочных диафрагм оболочек положительной кривизны
а — эпюра краевых сдвигающих усилий, передающихся на продольные диафрагмы; б —то же, на торцевые диафрагмы; в — элементарные участки арки; —= сдвигающиеусилия от средних волн; от крайних волн98
показаны эпюры усилий 2QSf, действующих на среднюю 24-метро¬
вую арку, и усилий QSf— на крайнюю, а на рис. 25, б — эпюры
усилий Qsf, действующих на торцевые 12-метровые арки средней
и крайней волн оболочки.Нормальные составляющие продольных краевых усилий в
оболочке, передающиеся на верхний пояс средней 24-метровой
арки, определим по формуле (62):п2 = 2 • 60,6 • 0,471 =57 кН/м,где #2 = 60,6 кН/м (см. табл. 18), a sin<р = 6/г2=6/12,75 = 0,471.Для удобства расчета арки нагрузки, действующие на нее,
представляем в виде вертикальных (а) и горизонтальных (Л)
составляющих контурных (сдвигающих и нормальных) усилий
в оболочке. При этом верхний пояс арки расчленяем на элемен¬
тарные участки длиной /* (рис. 25, в). В пролете размер горизон¬
тальной проекции участка /,= 1,2 м, у опоры /, = 0,6 м.На каждом элементарном участке средней 24-метровой арки
действуют сдвигающие силы величиной qi,mt = 2QSf,ili и нормальные
силы Л/ = /гг/«, а на участках крайней 24-метровой и торцевых
12-метровых арок — только сдвигающие силы qi,ed = Qsf,ili, где
Qsfj принимается по табл. 15 и 18.Вертикальные (а,) и горизонтальные (А*) проекции сдвига¬
ющих сил, действующие на участках дуги средней 24-метровой
арки, будем вычислять по следующим формулам:Vi = qi,mt sin <p/ + /i/cos фi\hi = qit mt cos ф, + rii sin ф/.Аналогично для остальных (крайних) диафрагм, на которые
не передаются нормальные усилия от оболочек, имеемVi — qi,ed sin ф/ И А/ — qit gd COS ф/.Результаты вычислений вертикальных и горизонтальных со¬
ставляющих нагрузки на арки пролетом 24 м приведены в табл. 22,
а на арки пролетом 12 м — в табл. 23. При этом некоторые про¬
межуточные элементарные вычисления опущены, а результаты
представлены для половин арок (до оси симметрии).Расчет арок на нагрузки из табл. 22 и 23 производим методом
сил. Арки рассматриваются как двухшарнирные однократно ста¬
тически неопределимые системы. За основную систему принимаем
трехшарнирную арку. В качестве лишней неизвестной введем
изгибающий момент в ключе арки.Ниже приводятся сокращенные расчеты арок средней продоль¬
ной диафрагмы пролетом 24 м и торцевой диафрагмы крайней7*99
Таблица 22100Крайняя аркаVi48,852,342.7
27,617.8
11,26,63.51.5
0,4
0hi124,2141,6132,098.675.057.142.630.419.4
9,6
0Нагрузка, кНQi. ed133,5151,0138,7102,477.158.2
43,1
30,6
19,5
9,6
0Средняя аркаVi47,665.5
80,1
76,0
73,471.670.369.4
68,968.6
34,2hi20,720,014,18,04,42,31,10,30,100tii36.8
54,571.971.170.469.8
69,368.9
68,768.534.2Qi. mt36,641,538.128.2
21,2
16,0
11,98.35.4
2,6
0Длина
элемен¬
тарного
участка
дуги меж¬
ду смеж¬
ными точ¬
ками0,650,641,271,251,241,231,221,211,211,201,20Центральный
угол элемен¬
тарного участка
дуги между
смежными точ¬
ками Yi_(,+ i),
град.1 °11 '22"1 10 442 19 48
2 18 13
2 16 34
2 15 17
2 14 15
2 13 28
2 12 50
2 12 27
2 12 150Половина цен¬
трального угла
дуги в /-й точ¬
ке ф„ град.22°37'13"
21 25 51
20 15 7
17 55 19
15 37 6
13 20 32
11 5 15
8 51
6 37 32
4 24 42
2 12 15
0Расстоя¬
ние до
точки от
середины
пролета
по гори¬
зонта¬
ли а„ м1211.4
10,89.68.47.2
6,0
4,83.6
2,4'1.2
0№
точ¬
ки i 112345678
9101112
Таблица 23101Крайняя волнаVi33,136.030.1
19,813.1
8,4
5,0
2,7
1,2
0,30hi66.377.074.2
56,944.4
34,626.319.012.4
6,1
0Нагрузка, кНqi.ed74.185.080.060.246.3
35,6
26,8
19,212.4
6,1
0Средняя волнаVi4,55,04.22.71.81.2
0,7
0,4
0,2
0
0hi9.1
10,6
10,27,86.1
4,73.62.6
1,7
0,80<7i. mi10,211,711,08.36.4
4,93.7
2,61.7
0,80Длина элемен¬
тарного участка
дуги между
смежными точ¬
ками //-(l-f 1).
м0,340,330,650,640,630,620,610,610,60,60,60Центральный
угол элементар¬
ного участка
дуги между
смежными точ¬
ками у»—(*+ О*
град.1°31'2"1 29 502 56 33
2 52 57
2 49 56
2 47 30
2 45 32
2 44 2
2 42 56
2 42 12
2 41 500Половина цен¬
трального угла
дуги в /-й точ¬
ке <р<, град.28° 4' 20"
26 33 18
25 3 28
22 6 55
19 13 58
16 24 2
13 36 32
10 51
8 6 58
5 24 2
2 41 50
0Расстояние
до точки
от середины
пролета
по горизон¬
тали CLi, м6,05.75.44.84.2
3,6
3,02.41.81.2
0,60№
точ¬
ки I12345678
9101112
Рис. 26. Сечения арочных диафрагм
а — средняя диафрагма пролетом 24 м; б — торцевая диафрагма пролетом 12 м; в —
стальная диафрагма пролетом 24 м; 1 — сборные плиты; 2 — зона замоноличивания;3 — верхний пояс сборной арки; 4 — верхний пояс стальной аркиволны пролетом 12 м для эксплуатационной стадии работы обо¬
лочки.Арка продольной диафрагмы. В расчете учитывается совмест¬
ная работа поперечного сечения дуги арки с примыкающими
к ней с обеих сторон участками криволинейных плит оболочки.
В расчетное сечение вводим по шесть толщин криволинейной
плиты с каждой стороны, а также замоноличенную стыковую
полость с опорными трехметровыми ребрами сборных панелей
(рис. 26, а). В результате центр тяжести площади поперечного
сечения арки несколько поднимается и соответственно возрастает
стрела подъема арки. Опуская элементарные вычисления, запишем
геометрические характеристики арки: площадь поперечного сече¬
ния дуги Аа= 1650 см2, момент инерции дуги /„ = 723000 см4, пло¬
щадь поперечного сечения затяжки Л^ = 875 см2, стрела подъема
/ = 263 см, начальный модуль упругости бетона класса В 30 Еь =
= 29 • 103 МПа.Под действием симметричной внешней нагрузки (см. табл. 22)
в основной системе получаем следующие опорные реакцииVf=lvi = 725,6 кН;Hj= Vfa + Ihiyj-ZviCH = 725,6 • 12+130,5-4450,5 _ jggg rH
На рис. 27, а и б приведены без вычислений эпюры изгибающих
моментов от внешней нагрузки и от единичного момента, прило¬
женного в ключевом шарнире.Искомые перемещения находим путем перемножения соответ¬
ствующих эпюр усилий по методу Верещагина только для поло¬
вины арки, имея в виду ее симметрию:Г 6и_ iMUla , iNUla . H\Ud _СЬ 2 1а “Г Аа “Г 2Aid ~~_ 6,55 , 1,69 , 1,74 _п07
— 0,00723 “Г 0,165 ' 0,0875 — '_ -98,5 7720 7610 _ t АМпп
— 0,00723 0,165 0,0875 “ 1«X3UU,откуда получим искомый момент в ключе аркиjc=—6i//6ii = 146300/937= 156 кН - м.Суммарные эпюры изгибающих моментов и продольных сил
показаны на рис. 27, виг.Расчетная комбинация усилий в арке: Af = 156 кН • м,N = Ni2=—Nfi2 + Ni2x= —(К4 —Z^i_i2)sin ф!2 —— (// —Z/ll-12) COS Ф12+ С°-у^12 * == -(1668-71) • 1+0,38 • 156=-1538 кН.Усилие в затяжке (распор) #=1609 кН.Проверка железобетонного сечения арки и подбор рабочей
арматуры выполняются известными методами и здесь не приво¬
дятся.Арка торцевой диафрагмы крайней волны оболочки. Расчет
12-метровой арки выполняется аналогично предыдущему. В рас¬
четное сечение арки также вводится участок плиты оболочки
(см. рис. 26, б). В связи с этим несколько поднимется центр тя¬
жести арки и стрела подъема составит 1,8 м. Геометрические
характеристики арки приводим без вычислений: Ла = 800 см2,
/а =135000 см4, Лм = 300 см2, /=1800 мм, Еь = 29 • 103.В основной системе от действия внешней нагрузки получим
опорные реакции, записанные в табл. 23: 149,7 кН; Я == 293 кН.103
Рис. 27. Эпюры усилий в арочных диафрагмах
а — эпюры изгибающих моментов от внешней нагрузки в основной системе для средней
диафрагмы пролетом 24 м; б — то же, от М = 1, приложенного в ключе арки; в, г — суммар¬
ные эпюры изгибающих моментов и продольных сил; д — суммарная эпюра изгибающих
моментов в стальной диафрагме; е, ж — эпюры изгибающих моментов и продольных
сил от внешней нагрузки в основной^системе для торцевой диафрагмы- пролетом 12 м;
и — эпюра изгибающих моментов от М = 1, приложенного в ключе арки; к, л — суммарные
эпюры моментов и продольных силЭпюры изгибающих моментов и продольных сил в арке от
внешней нагрузки и от единичного момента, приложенного в клю¬
че, для пяти промежуточных точек показаны на рис. 27, е, жу и,
а суммарные эпюры изгибающих моментов и продольных сил —
на рис. 27, к ил. Значения последних вычислены после отыскания
неизвестного изгибающего момента в ключе:М= —х = — б,//6,, = 69570/2567 = 27,1 кН • м.104
Рис. 28. К расчету арочной диафрагмы на
монтажные нагрузки
а — схема монтажных нагрузок на арку; б —
эпюра изгибающих моментова)Запишем расчетные комбинации усилий в сечениях арки для
подбора арматуры:1) Afmax = 27,l кН • м; N = 68 кН;2) Afmin= —15,1 кН • м; N= — ПОкН;3) М = 0; Мпах= —314 кН.Распор в затяжке #=278 кН.Проверку железобетонного сечения арки и затяжки и подбор
рабочей арматуры опускаем.Расчет по прочности в стадии монтажаВсе элементы сборной оболочки должны быть проверены на
усилия, возникающие в процессе монтажа. Выполним поверочный
расчет сборной железобетонной предварительно напряженной
арки пролетом 24 м. Наиболее невыгодное сочетание нагрузок
на эту арку во время монтажа оболочки возникает в момент, когда
с одной стороны арки уложены все панели волны оболочки, а с дру¬
гой — только на половине пролета (рис. 28, а). Снеговая нагрузка
при таком сочетании может не учитываться.Вычислим величину указанной нагрузки на 1 м арки. Собствен¬
ная масса арки составляет 110 кН, или 110/24 = 4,6 кН/м. Соб¬
ственная масса средних панелей составляет 47 кН, или 47/(3 • 2) =
= 7,8 кН/м.Нагрузка от бетона замоноличивания 0,18 • 0,2 • 25 = 0,9 кН/м.
Монтажная нагрузка составляет 0,3 кПа, или 0,3 • 6=1,8 кН/м.Таким образом, нагрузка, приложенная ко всему пролету, со¬
ставит g = 4,6 • 1,1+7,8 * 1,1+ 1,8 • 1,2 + 0,9 • 1,1 = 16,8 кН/м;
односторонняя нагрузка (приложенная на половине пролета)
gon = 7,8 • 1,1 + 1,8 * 1,2=11 кН/м.Расчет двухшарнирной арки ведется по известным формулам.
Поперечные сечения арки и затяжки имеют следующие стати¬
ческие характеристики: осевой момент инерции площади сечения
арки в ключе /а= 126500 см4; площадь поперечного сечения арки
в ключе Ла = 825 см2; площадь поперечного сечения затяжки Ам =
= 875 см2.Начальные модули упругости бетона арки и затяжки Еа =
= £,* = 29 • 103 МПа.Коэффициент, учитывающий влияние обжатия арки продоль¬
ной силой, что приводит к уменьшению распора и увеличению
изгибающих моментов, вычисляем по формулам (72) и (73):k = 1/(1 + v)= 1/(1 +0,009) = 0,99,где 15/а ( Ей . г\ \ v~~5P~\euau —15 • 1265 • 106 / 1 | 0.948 \ n nnq.8 • 24502 V 87500 ~ 82500 / —Л =0,948 при f /1=2450/23600 = 1 /9,63.Нагрузку, действующую на арку, разделяем на симметричную
(gsym) И обратносимметричную (ginj/sym):gsym= g + 0,5gOn =16,8 + 0,5 • 11,0 = 22,3 кН/м;gini/sym=0,5gon = 0,5 • 11,0 = 5,5 кН/м.Усилия от симметричной нагрузки:
распор с учетом обжатия аркиH=l^Lk= 2У, 22Г 0,99 = 627 кН;изгибающий момент в ключеMma* = 0,125gS!,m/2(l-fe)=0,125 • 22,3 • 23,62Х
Х(1-0,99)= 15,5 кН • м;
изгибающий момент в четверти пролетаМ, = 0,125gsyml2 (1 - 0,25)(1 - к) ==0,125 • 22,3 • 23,62(1-0,25)(1 -0,99)= 11,6 кН • м.106
От обратносимметричной нагрузки изгибающий момент в чет¬
верти пролета составит:M2=±gini/Syml2/4 • 8= ±5,5 • 23,62/32= ±95,7 кН • м.Суммарная эпюра изгибающих моментов в арке показана
на рис. 28, б.Напишем расчетные комбинации усилий в сечениях арки для
подбора арматуры: 1) Af = 107,3 кН • м; N=634 кН; 2) Af =
= —84 кН • м; N=634 кН.Проверка сечений опускается.Нагрузки на оболочку, а также ее конструкция (кроме про¬
дольной диафрагмы) аналогичны принятым выше.Сечение арки-диафрагмы и элементов оболочки, примыкающих
к ее верхнему поясу, приведено на рис. 26, в. Стрела подъема
арки / = 265 см.Запишем геометрические характеристики арки по сечению,
приведенному к бетону класса В 30: v = Es/Еь = 2,06 • 105/29Х
X 103 = 7,1; расчетная площадь приведенного поперечного сечения
арки Ared = 20 • 30 + 4,5 • 2 • 35 + 65,6 • 7,1 = 1380 см2; осевой мо¬
мент инерции этого сечения Ired = 638000 см4, площадь сечения
стальной затяжки из двух равнобоких уголков размерами
160 • 10 мм — Atd = 62,8 см .Внешнюю нагрузку, как и в примере расчета полностью же¬
лезобетонной оболочки, принимаем по табл. 17. Эпюры усилий
в основной системе от внешней нагрузки и единичного момента,
приложенного в ключе, принимаем, как и в предыдущем расчете,
по рис. 27, а и б.Для вычисления перемещений используем значения статиче¬
ских характеристик сечений арки, полученные для металложеле¬
зобетонной оболочки:6,, 6,55 . 1,69 . 1,74 1ПЯП-2 ” 0,00638 ' 0,1380 ' 7,1 • 0,00628 ”6ij _ 98,5 7720 7610 _ ттсол
2 0,00638 0,1380 0,0431“Отсюда jc = 217684/1080 = 202 кН • м.Суммарная эпюра изгибающих моментов в арке показана на
рис. 27, д. В результате получаем следующие расчетные комби¬6. Расчет стальной арки-диафрагмы
при варианте комбинированной конструкции
оболочки (металложелезобетонной)107
нации усилий в сечениях арки: N=—1508 кН, Af = 202 кН • м.
Усилие в затяжке #=1585 кН.Проверку принятых в расчете сечений арки и затяжки не при¬
водим.7. Некоторые положения по конструированию
оболочек положительной гауссовой кривизныПоверхность выпуклых оболочек, в отличие от поверхности
цилиндрических оболочек, нельзя развернуть на плоскости. Это
качество, являясь достоинством для обеспечения прочности, жест¬
кости и общей устойчивости конструкции, налагает определенные
геометрические требования при назначении размеров сварных
арматурных сеток для монолитных оболочек.Армировать криволинейную плиту (скорлупу) монолитной обо¬
лочки рекомендуется стержнями, расположенными параллельно
диафрагмам (рис. 29, а).В средней безмоментной зоне гладкой оболочки, где действуют
только сжимающие усилия, толщину бетона и армирование назна¬
чают конструктивно, согласно требованиям норм.При толщине плиты до 80 мм она армируется одиночной сет¬
кой. Конструктивная арматура принимается диаметром 3...4 мм
с шагом не более 150 или 200 мм. Располагается она у нижней
грани сечения. При толщине плиты более 80 мм, во избежание
появления усадочных и температурных трещин, укладывается
двойная арматурная сетка.В приконтурных зонах и углах, где действуют растягивающие
усилия, плиту необходимо принимать большей толщины, чем
в средней зоне. Армируют здесь стержнями больших диаметров
или предусматривают дополнительные сетки. Ширина и толщина
плиты и количество дополнительной арматуры приконтурных зон
принимаются в соответствии с расчетом.В угловых зонах укладывают косую арматуру под углом 45°
к контуру перпендикулярно диагонали плана. Толщина плиты
в угловых зонах оболочки обычно в два-три раза превосходит
толщину плиты в середине оболочки.Толщина плиты оболочки должна обеспечивать размещение
необходимого количества арматуры и требуемую толщину двух
защитных слоев. Переход от одной толщины плиты к другой
должен быть плавным.Все стержни арматуры криволинейной плиты заводятся в со¬
ответствующий контурный элемент оболочки не менее, чем на дли¬
ну анкеровки для растянутой арматуры. При армировании свар¬
ными сетками заделка может осуществляться дополнительными
гнутыми стержнями, заводимыми в плиту на нормативную вели¬
чину нахлестки.108
Рис. 29. Армирование пологой оболочки двоякой кривизны
а — армирование криволинейной плиты монолитной оболочки; б — армирование рядовой
панели сборной оболочки; / — основная арматурная сетка; 2 — то же, дополнительная
Для восприятия растягивающих усилий, действующих парал¬
лельно контуру, у нижней грани криволинейной плиты на при-
опорных участках укладывается расчетная или конструктивная
арматура.Конструкция панелей сборных оболочек зависит от схемы
разрезки криволинейной плиты на отдельные элементы. Рекомен¬
дуется конструировать панели с цилиндрической формой поверх¬
ности. Такая конструкция позволяет упростить арматурные изде¬
лия и работы по их заготовке, а также по изготовлению панелей.
Кроме того, такие панели экономичны по расходу материалов,
технологичны по изготовлению и монтажу, позволяют обеспечить
широкую унификацию. Применяют также и плоские панели.
При плоских панелях фактическая поверхность оболочки пред¬
ставляет собой многогранник. Чем меньше размеры плоских па¬
нелей, тем ближе поверхность многогранника к исходной, но
такая разрезка сильно увеличивает число панелей и количество
стыков.Крупные же плоские панели создают ощутимые изломы поверх¬
ности, что сказывается на работе оболочки, создает дополни¬
тельные изгибающие моменты.В любом случае габариты панелей и схема разрезки сборной
оболочки определяются технико-экономическими расчетами.
В отечественной практике нашли применение цилиндрические
панели размером 3X12 и 3X6 м, а также плоские размером
3X3 м.Панели рекомендуется проектировать с контурными и проме¬
жуточными ребрами. Система ребер должна обеспечивать проч¬
ность и жесткость панелей в стадии транспортирования и мон¬
тажа, прочность и устойчивость оболочки в стадии эксплуатации,
возможность выполнения проемов для светоаэрационных устройств
и подвесок для сосредоточенных грузов. Поперечные ребра па¬
нелей в местах стыков рекомендуется соединять сваркой заклад¬
ных деталей, в том числе и ребер, находящихся на диафрагме.Для восприятия сдвигающих сил в швах между панелями
наружные поверхности контурных ребер должны иметь череду¬
ющиеся выступы и впадины, создающие после замоноличивания
бетонные шпонки.Плиты панелей армируют сварными сетками, а ребра — кар¬
касами. Арматура плиты панели надежно заделывается по кон-
туру приваркой поперечных стержней в пределах ребер. Конструк¬
ция и армирование цилиндрических панелей пологой оболочки,
рассмотренной в настоящем примере, идентичны панелям длинной
цилиндрической оболочки (см. рис. 13).Диафрагмы пологих оболочек двоякой положительной кри¬
визны конструируются так же, как аналогичные плоскостные
конструкции (арки, фермы и пр.). Особенностью является необ¬
ходимость мероприятий, обеспечивающих возможность восприя¬110
тия сил сдвига оболочки по контурному элементу, а также сил
отрыва контура оболочки от диафрагмы. Для этого на верхней
поверхности пояса арки (фермы) устраивают выпуски арматуры
и бетонные шпонки. Выпуски арматурных стержней устраивают
также из панелей, при этом они должны отвечать выпускам из
диафрагмы. В углах панелей предусматриваются закладные де¬
тали для приварки к закладным деталям на поверхности диаф¬
рагмы.Торцы взаимно перпендикулярных контурных элементов обо¬
лочки соединяют между собой сварными накладками сверху, а сни¬
зу приваривают их к закладной детали на колонне, что должно
обеспечить восприятие главных растягивающих усилий, которые
в углу имеют максимальное значение.V. РАСЧЕТ ВОЛНИСТОГО СВОДА-ОБОЛОЧКИ
А. РАСЧЕТ ЖЕЛЕЗОБЕТОННОГО СВОДА-ОБОЛОЧКИВолнистыми сводами-оболочками называют распорные строи¬
тельные пространственные конструкции, у которых поперечное
сечение (вдоль образующей) имеет цилиндрическую, складчатую
или волнистую форму (рис. 30), а пролет в четыре и более раз пре¬
вышает длину волны. Волнистые своды-оболочки проектируют
в качестве покрытий зданий больших пролетов — до 100 м и бо¬
лее. Такая возможность связана с тем, что волнистая форма по¬
перечного сечения значительно повышает несущую способность
и жесткость сводчатой конструкции. Волны применяют как само¬
несущие конструкции или, при больших пролетах, в сочетании
с арками, поддерживающими их. Такие арки ужесточают конструк¬
цию свода, что очень существенно при необходимости устройства1. Основные сведения о волнистых
сводах-оболочках и принципах их расчетаРис. 30. Типы поперечных сечений волнистых
сводов-оболочек
а, б — складчатые; в — переменной гауссовой кри¬
визны; г,д — отрицательной гауссовой кривизны;
е — положительной гауссовой кривизны111
подвесного транспорта, а также упрощают монтаж. Арки могут
быть железобетонными или стальными.Волнистые своды-оболочки проектируют, как правило, сбор¬
ными. Очертание свода можно принимать по дуге окружности,
параболе, цепной линии или другим близким к ним кривым. Наи¬
более целесообразным очертанием является дуга окружности,
позволяющая унифицировать сборные элементы и, следовательно,
сокращать число их типоразмеров. По продольным краям своды
можно опирать на колонны, подстропильные конструкции, стены
или непосредственно на фундаменты. Конструкция сводов рас¬
порная. Для восприятия распора применяют затяжки, рамы, контр¬
форсы, используют жесткие диафрагмы в виде перекрытий, а
при опирании сводов на уровне земли устраивают фундаменты
соответствующей конструкции.При проектировании сводов следует учитывать податливость
элементов или конструкций, воспринимающих распор. В случае
применения железобетонных затяжек целесообразно проектиро¬
вать их предварительно напряженными, что позволяет несколько
уменьшить деформацию свода. Желательно, чтобы шаг затяжек
совпадал с шагом волны свода. В противном случае при шаге
затяжек, превышающем шаг волны, для восприятия распора
от волн между затяжками необходимо предусматривать специ¬
альную продольную конструкцию, пролет которой равен шагу
затяжек.Стрелу подъема свода (в ключе) в зависимости от конструк¬
тивных особенностей и функциональных условий назначают в
пределах /i/10.../i/2, а высоту волны в продольном сечении сво¬
да— из соображений устойчивости в пределах Zi /60.../1 /30,
а также в пределах /2/12.../2/7, где U — пролет свода; /2— длина
волны.Высоту (поперечное сечение) волны рекомендуется принимать
одинаковой по всей ее длине (пролету /1), включая торец. Однако,
в ряде случаев высоту сечения профиля уменьшают к опорам
свода, трансформируя ее на самой опоре в прямую линию, тогда
конструкция приопорной зоны переходит в коноид, балку-стенку
и т. п.Применение волнистых сводов сопряжено с усложнением уст¬
ройства кровли и укладки утеплителя, и с увеличением их площади.
Для устранения этого недостатка по гребням волн иногда укла¬
дывают плоские плиты, образующие цилиндрическую поверхность,
что упрощает кровельные и теплоизоляционные работы и сокра¬
щает их объем.Плоские плиты могут изготовляться из теплоизоляционного
(легкого) бетона со слоями паро- и гидроизоляции.Деформативность волнистых сводов в продольном направлении
позволяет проектировать их без температурно-усадочных швов112
(с соответствующим расчетом каркаса здания на температурные
воздействия).Волнистые своды хорошо работают на равномерно распреде¬
ленную вертикальную симметричную нагрузку, но неудовлетво¬
рительно — на одностороннюю, вызывающую кручение профиля
волны при одноволновом решении. В последнем случае для вос¬
приятия несимметричной нагрузки требуются специальные кон¬
структивные мероприятия (усиление, применение жестких подве¬
сок и др.). Следует отметить, что многоволновые своды более
приспособлены для работы на одностороннюю, особенно местную,
нагрузку.Для обеспечения устойчивости сечения волны при воздействии
односторонних и сосредоточенных нагрузок, а также для восприя¬
тия нагрузок, возникающих при транспортировке и монтаже,
пространственные элементы сборных волнистых сводов рекомен¬
дуется выполнять ребристыми.В продольном направлении волнистые своды рассчитывают
как двухшарнирные или трехшарнирные тонкостенные арки.
В расчетное сечение верхнего пояса тонкостенной арки вводится
полное сечение волны. Если шаг волн не соответствует шагу
затяжек, то в расчетное сечение верхнего пояса вводится сечение,
равное размеру шага затяжек. При этом поперечное сечение
считается недеформируемым.Допущение о недеформируемости поперечного сечения волны
неоднократно обосновано экспериментально для средних волн
сводов. Что же касается крайних волн и одноволновых сводов,
которые не имеют ограничений для поперечных деформаций, то
их следует рассчитывать с учетом деформативности поперечного
сечения. В этом случае в дополнение к вычислению продольных
усилий в плоской арке необходимо определять поперечные изги¬
бающие моменты.В расчете на сосредоточенные и полосовые нагрузки учиты¬
вается работа только той волны, к которой непосредственно при¬
ложена данная нагрузка. Взаимодействие со смежными волнами
свода не учитывается.При расчете волнистых сводов с постоянной высотой профиля
поперечного сечения и со стрелой подъема fi^li/S нагрузка
от собственной массы g должна вводиться в расчет с учетом фак¬
тического увеличения ее интенсивности к пятам. Распределение
этой нагрузки принимается по закону кривой (рис. 31, а):g*=g(l/cosq>,— 1), (64)где gx—дополнительная интенсивность нагрузки, вызываемая уклоном свода,
изменяется от нуля (в ключе) до gi (в сечении у пяты); g — интенсивность нагрузки
в ключе свода; <рх— угол наклона касательной к оси свода в рассматриваемом
сечении на расстоянии х от опоры.8 Заказ 61113
Рис. 31. Расчетная схема (а), схемы нагрузок и опорных реакций свода-обо¬
лочки (б)
Таблица 24Коэффи¬циентыПри/./*»1/31/41/51/61/71/81/91/10h0,0990,1270,1420,1500,155h0,0310,0610,0930,1160,150———л0,6960,7850,8430,8810,9110,9310,9420,952л .=/-//.1,2961,1671,1071,0741,0541,0421,0331,027При очертании оси свода по дуге окружности его геометриче¬
ские параметры определяются по формулам:г=(/?+4/?)/8/,; (65)sin q>*=(0,5/i —x)/r ; (66)cos ф*=У 1 —sin2<p* ; (67)y=fi — r(l— совф,). (68)Опорные реакции в двухшарнирной арке вычисляются с учетом
влияния смещения опор и упругого обжатия оси арки (рис. 31, б)
по формулам:
от нагрузки gVA = VB—0,bgl\\ //=0,125-^-*; (69)от нагрузки g 1VA = VB=l\g\h; H=Ugihk; (70)от нагрузки 5Ki=0,375s/i, Vb=0,125s/,, Я=0,0625 Щ-k. (71)В формулах (69)...(71) введены обозначения: g, gi и s — рас¬
пределенная линейная нагрузка, кН/м, отнесенная к ширине се¬
чения волны или к шагу затяжек; коэффициенты h и £2 принима¬
ются по табл. 24; ft — коэффициент, учитывающий влияние про¬
дольных деформаций вследствие упругого удлинения затяжек
и обжатия свода:ft=l/(l+v). (72)8*115 *
При определении распора от собственной массы панелей сбор¬
ного волнистого свода допускается принимать к=\. Для сводов
со стрелой подъема fi^h/З коэффициент к при любых нагрузках
можно не учитывать.Величина v зависит от соотношения жесткостей затяжки и
свода в ключе:<73>где /„, Аа и Еа— соответственно момент инерции, площадь сечения арки и модуль
упругости ее материала; Etd и Atd— модуль упругости материала затяжки и пло¬
щадь ее сечения; т| — коэффициент, зависящий от отношения стрелы подъема
свода к его пролету, принимается по табл. 24.При расчете волнистых сводов с предварительно напряжен¬
ными железобетонными затяжками, категория требований к тре¬
щиностойкости которых допускает раскрытие трещин, следует
иметь в виду, что входящая в выражение (73) жесткость затяжки
под нагрузкой значительно уменьшается по причине выключения
из работы растянутого бетона с трещинами. Жесткость железо¬
бетонной затяжки с трещинами в работе на этой стадии может
быть заменена (с определенной долей приближения) на жесткость
ее рабочей арматуры, т. е. Es,tdAs,td- При этом должна учитываться
вся арматура затяжки — как напрягаемая, так и обычная, с со¬
ответствующим модулем упругости.Таким образом, при расчете волнистых сводов на расчетные
нагрузки в случаях, когда в затяжках допускается раскрытие
трещин и они рассчитываются на нормативные нагрузки (yf=l),
следует учитывать повышенную деформативность затяжки при
работе ее с трещинами и влияние этого эффекта на увеличение
изгибающих моментов в своде.Чтобы примерно оценить удлинение затяжки от появления
трещин, можно разложить полную расчетную нагрузку, действу¬
ющую на волнистый свод, на две части: на нагрузку Fcrc, при ко¬
торой трещиностойкость затяжки обеспечивается, и на некую
дополнительную нагрузку д F, при которой трещины уже раскрыты:Fd = F tot=F crc+д F. (74)При вычислении Fcrc принимаем коэффициент точности натя¬
жения арматуры ysp=l.Исходя из этого формулу (73) можно преобразовать в выра¬
жениеVerc=J^^('^‘+£7^7)+X‘]’ (75)которое и используется для определения окончательных усилив
в своде.116
Рис. 32. К определению эксцентриси¬
тета приложения продольной силы в
волнистых сводах-оболочках полиго¬
нального очертанияИзгибающие моменты Мх и продольные силы Nx в поперечных
сечениях волнистых сводов средней зоны волны определяются
по формулам для трех-, двух- и бесшарнирных арок с затяжками
или без них:Afx=Af0— Ну, (76)Nx — Q0 sin q> + Ясов ф, (77)где Мо и Qo— изгибающий момент и поперечная сила в соответствующем сечении
простой однопролетной балки пролетом h \ Н — распор волны свода; у — ордината
оси свода в рассматриваемом сечении.При расчете сборных сводов, имеющих полигональное очерта¬
ние (из прямолинейных элементов), следует учитывать дополни¬
тельный положительный изгибающий момент М\, возникающий
вследствие прямолинейности элементов свода (рис. 32):M\ = Ne\. (78)Величина эксцентриситета е\ определяется по формулее\ =го ( 1 — cos-y-) или е, = го—V Н>—а2 , (79)где г0— радиус оси свода; <ро— центральный угол, ограничивающий края элемента
длиной 2а полигонального свода.Метод расчета приопорных зон сводов определяется их кон¬
структивным решением. Они могут рассчитываться как оболочка,
как балка-стенка и т. д.Волнистые своды-оболочки с затяжками, особенно имеющие
большие пролеты, как правило, снабжаются подвесками. Подвески
обычно имеют определенную жесткость и несомненно помогают
работе на продольный изгиб двухшарнирного свода при потере
устойчивости. Даже если считать подвески прикрепленными к
арке и затяжке шарнирно, т. е. не учитывать наклон подвесок,
возникающий в процессе потери аркой устойчивости, критическая
нагрузка для такой арки, как показывают исследования, значи¬
тельно выше, чем для арки без учета подвесок. В процессе потери117
Таблица 25ЧислоподвесокЗначение коэффициента р при т — ,• 1/31/41/51/61/71/81/91/1030,3750,3400,3120,2970,2820,2750,2690,26440,3790,3350,2950,2750,2620,2500,2400,23750,3830,3280,2820,2560,2370,2250,2160,21260,3620,3180,2700,2380,2180,2060,1970,19370,3560,3080,2660,2300,2060,1870,1810,175>70,3420,2920,2350,1940,1690,1500,1370,125устойчивости подвески, способные воспринимать сжимающие уси¬
лия, передают перемещения затяжке по вертикали. Растянутая
затяжка, являясь как бы упругим основанием, оказывает отпор
подвескам, передавая им давление, направленное в противополож¬
ную перемещениям сторону, подкрепляющее арку. Особенно это
относится к предварительно напряженным затяжкам, представля¬
ющим собой как бы натянутую упругую струну. Таким образом,
величина критической нагрузки и, соответственно, критического
продольного усилия центрально-сжатых и сжато-изогнутых арок
при потере ими устойчивости в плоскости кривизны значительно
возрастает. Это обстоятельство можно учитывать при вычислении
расчетной (приведенной) длины дуги арки Lo путем умножения
геометрической длины дуги арки Lo на коэффициент \i. Для опре¬
деления этого коэффициента произведем следующие выкладки.Известную формулу распора арки H=Fl2 /8/ перепишем отно¬
сительно нагрузки, заменив ее и распор критическими значениями:
Fcr=S fHcr/l\Имея в виду, что в шелыге арочного свода распор численно
равен продольной силе H=Ny напишем полученное выражение
в следующем виде: Fcr=SfNcr/l2.Для параболической арки А. Н. Динник * получил зависимость
FCr=KEIa/l3, где К — коэффициент устойчивости. Приравняв это
выражение к выражению для Fcr, полученному выше, и опуская
простейшие преобразования, имеем K=SflNcr/Е1а.Подставим в эту формулу величину критической силы по Эйле¬
ру, которая равна NCr = n2EIa/Lo.Тогда окончательно /(=8n2/f/Lo.Обозначим f//=m, а длину пологой параболической арки
вдоль ее геометрической оси приближенно примем равной L =
= /[1 +(8/3)m2] и учтем, что Lo = \iLa. В результате получим вы¬
ражение коэффициента для приведения геометрической длины
дуги арки к расчетной:М’= l+(8/3)miI V8m//C .* Динник А. Н. Устойчивость арок. М. Гостехиздат, 1946.118
Этой формулой можно пользоваться для определения расчетной
длины пологих параболических арок постоянного сечения с жест¬
кими подвесками при расчете на продольный изгиб. Коэффи¬
циент К зависит от отношения / к /, способа закрепления опор
и от количества жестких подвесок. В табл. 25 приводятся коэффи¬
циенты ji для ряда значений т при разном количестве подвесок.
Коэффициенты К подсчитаны по методике А. Ф. Смирнова.2. Конструкция свода-оболочки и нагрузкиВ качестве конструкции покрытия для здания с сеткой колонн
12X72 м принят многоволновый свод-оболочка, собираемый из
сборных железобетонных элементов. Свод опирается на колонны.
В поперечном сечении свода (вдоль образующей) для повышения
несущей способности и жесткости принимаем волнистое очертание
по рис. 30, е.Поперечная конструкция свода-оболочки состоит из железо¬
бетонных ребристых панелей с цилиндрической поверхностью, а
продольная — из сборной железобетонной арки с предварительно
напряженной затяжкой. Затяжка собирается из сборных предва¬
рительно напряженных элементов длиной по 18 м, которые изго¬
тавливаются на стендах с натяжением стержневой арматуры на
упоры механическим способом. На монтаже затяжка объединяется
сваркой арматуры. С целью уменьшения деформативности затяж¬
ки и повышения ее трещиностойкости стыки сборных элементов
замоноличены бетоном на расширяющемся цементе. Напрягаемая
арматура изготовлена из стержневой термомеханически и терми¬
чески упрочненной свариваемой арматурной стали периодического
профиля класса Ат-IVC с расчетным сопротивлением растяжению
для предельных состояний первой группы Rs=510 МПа и началь¬
ным модулем упругости £s=190 • 103 МПа.Торцевую конструкцию принимаем в виде арочной железобе¬
тонной диафрагмы, аналогичной принятой в цилиндрической обо¬
лочке (см. пример I).Материал свода-оболочки — тяжелый бетон класса В 30
(/?б =17 МПа, /?ы=1,2 МПа), предварительно напряженная за¬
тяжка — из бетона класса В 40. Элементы свода соединяются
сваркой закладных деталей с последующим замоноличиванием
стыков. Швы между сборными элементами замоноличены мелко¬
зернистым бетоном класса В 15.Свод рассчитывается на нагрузки, приведенные в табл. 26.Собственная масса продольной арки— 13,8 кН/м.Полная нагрузка на погонный метр волны свода шириной 12 м
составит: нормативная Fn=3,85 • 12+13,8=60 кН/м; расчетная
/\*=4,6 • 12+13,8 • 1,1=70,4 кН/м, в том числе постоянная на¬
грузка gn = 48 кН/м; gd = 54,4 кН/м, а нагрузка от собственной119
Таблица 26Вид нагрузкиНормативноезначениенагрузки,кПаКоэффициент
надежности
по нагрузке
Y1Расчетноезначениенагрузки,кПаСобственная масса оболочки,
приведенная к горизонтальной
проекции1,61,11,76Теплоизоляция, пароизоляция,
гидроизоляционный ковер1,251,31,63Снег (III район)1,01,41,4Итого3,854,79Итого с учетом коэффициента
надежности по назначению уп=
= 0,954,6массы элементов свода (сборных панелей) g„p = 18 кН/м; gdP —
= 20 кН/м.3. Геометрические характеристики волнистого
свода-оболочкиКонструкция и размеры свода-оболочки показаны на рис. 33.
С целью сокращения числа типоразмеров элементов очертание
свода принято по дуге окружности:Расчетный пролет свода Л =72—0,5=71,5 м. Стрелу подъема
продольной арки свода принимаем равной f i„=7,20 м, т. е. около
1/10 пролета.Радиус кривизны оси арки Г\ =92,35 м. Сечение арки прини¬
маем двутавровое с размерами, указанными на рис. 33, б. Высота
волны поперечного сечения свода равна /2=1,5 м, а ширина
сборного элемента в поперечном сечении свода составит 12 — 2Х
Х0,06= 11,88 м. Радиус кривизны поверхности волны (вдоль
образующей) Гг= 12,51 м; радиус кривизны поверхности свода
в шелыге (рис. 33, а) Л=92,35 +0,6 + 0,2 + 1,5=94,65 м.Полная стрела подъема свода-оболочки в ключе будет (от оси
затяжки): ft0t=7,20+0,6+0,2+1,5=9,5 м.Площадь поперечного сечения свода-оболочки включает пло¬
щади сечений криволинейной плиты, зоны замоноличивания сты¬
ковой полости и двутаврового сечения арки Л=0,492+0,06 +
+0,23=0,782 м2. Центр тяжести этого сечения расположен на
расстоянии 1,12 м от шелыги.Осевой момент инерции волны относительно центра тяжести
сечения /=0,7065 м4.Половина центрального угла волны в поперечном сечении
свода 0, =28°20'43"=0,494718; sin0, = 0,47482; cos0, = 0,8801.120
Рис. 33. Схема многоволнового свода пролетом 72 м
а, б — конструкция свода; в — расчетная схема свода в поперечном направлении; г —
суммарная эпюра изгибающих моментов в поперечном сечении свода; д — сечение свода
со стальной арочной диафрагмой
Стрела подъема свода в ключе по осям поперечных сечений
затяжки и волны ft =9,5—1,12=8,38 м; f\/l\ «1/8,5.Радиус оси свода г=Г\ —1,12 м=94,65—1,12 = 93,53 м. Сече¬
ние затяжки принято 500 X 800 мм, Atd—0,4 м2.4. Расчет свода-оболочки в продольном
направлении4.1. Расчет на равномерно распределенную
симметричную нагрузкуОпределим вертикальные опорные реакции и ориентировочно
оценим величину распора при k = 1 по формулам (69) от полной
расчетной нагрузки Fa=70,4 кН/м:Va = Vb=0,5Fdh = 0,5 • 71,5 • 70,4 = 2516,8 кН; 5368,5 КН.Площадь сечения напрягаемой арматуры из расчета затяжки
по прочности: Asp=Hest/Rs=5368500/510= 10526,5 мм2.Принимаем армирование из 36 0 22Ат1УС площадью сечения
А,р= 13683,6 мм .Для расчета трещиностойкости предварительно напряженной
затяжки необходимо найти величину распора свода с учетом влия¬
ния упругого обжатия арки от массы кровли и снеговой нагрузки.
Коэффициент, учитывающий податливость свода при трещино¬
стойкой затяжке, определяем по (72): k= 1/(1 +0,065)=0,939,
где согласно формуле (73)15 0,7065 / 0,892 . 0,9365 \ лпа-Коэффициент ц =0,9365 при f\ /1\ = 1 /8,5 принимается по
табл. 24. Отношение начальных модулей упругости бетона арки
и затяжки Ea/Eid=29 • 103/32,5 • 103=0,892.Распор от собственной массы элементов сборного свода вы¬
числяем при коэффициенте k=\.Распор волны свода от полной расчетной нагрузки по форму¬
ле (69) составит:Hd=0,125 • 71,52(20 + 50,4 . 0,939)/8,38 = 5134 кН.То же от полной нормативной нагрузки:Я„=0,125 • 71,52 (18+42 • 0,939)/8,38 = 4380 кН.122122
Определим трещиностойкость предварительно напряженной
затяжки. В соответствии со СНиП 2.03.01—84 к трещиностойко¬
сти затяжки предъявляются требования третьей категории, по¬
этому проверяем трещиностойкость от действия нормативных
усилий (-у/=1).Предельную величину предварительного напряжения прини¬
маем osp = 500 МПа, что удовлетворяет условию oSp^.Rs ser—р,
где Rs,ser=590 МПа, p=0,05osp=25 МПа.Чтобы определить контролируемое напряжение в напрягаемой
арматуре по окончании натяжения на упоры вычислим первые
и вторые потери напряжений по табл. 5 СНиП.Первые потери:от релаксации напряжений арматуры 0,1сг*р—20=0,IX
X500 — 20 = 30 МПа;от температурного перепада: 1,25д/= 1,25 • 65=81,0 МПа;
от быстронатекающей ползучести: 0,85 • 40 • 0,665=22,6 МПа
(при а»„/Л»р=(500—30—81) 13683,6/0,4 • 106 • 0,5 • 40 = 0,665<
<а, где а=0,25+0,025/?»р=0,75).Вторые потери:от усадки бетона: 35,0 МПа;от ползучести бетона 150а • а»р//?»р= 150 • 0,85 • 0,627 =
=80 МПа (при оьР/Rbp=(500 — 30 — 81 — 22,6)13683,6/0,4 • 106Х
Х0,5 • 40=0,627 <0,75).Полные потери напряжения в арматуре составят: <х4/=30+
+81+22,6 + 35 + 80 = 248,6 МПа.Усилие, воспринимаемое сечением предварительно напряжен¬
ной затяжки при образовании трещин (Ncre), т. е. предел ее тре¬
щиностойкости, определяем по ф-ле (123) СНиП 2.03.01—84.Ncrc = Rb,,ser(Au+2vAs)+P= 2,Ю(о,4 • 106 + 2 3'|5 XX13683,б) + (500-248,6)13683,6=4616042 Н> Я, =4380000 Н,т. е. количество принятой выше напрягаемой арматуры доста¬
точно, так как трещиностойкость затяжки обеспечена.Далее находим величину раскрытия трещин от постоянных и
длительных нормативных нагрузок. Для этого сначала вычисляем
коэффициент армирования сечения: ц=Л(р/Лм= 13683,6/400000=
=0,034> 0,02. Так как этот коэффициент не должен быть бо¬
лее 0,02, принимаем {1=0,02. ^Вычислим также напряжения в арматуреN-P 4380 • 103-(500- 248,6)13683,6 М7ип* Щб— 68*7 МПа-123
Величина раскрытия трещин по ф-ле (144) СНиП:
аСгс=бф/Т] -g.20 (3,5 — 100\i)\[~d == 1,2 • 1,3 • 11|^5-20(3,5-100 • 0,02)^[22 = 0,047 мм,где 6=1,2; <р,= 1,6—15*1= 1,6—15 • 0,02=1,3; ц=\.Величина раскрытия трещин меньше допустимой СНиПом
для конструкций третьей категории трещиностойкости, равной0,3 мм.Нагрузка, соответствующая трещиностойкой затяжке:Р Ncr&fi 4616 • 8 • 8,38 г** с и /Рсгс~~^Г~~ 71,5й • 0,939” Ь4,5 кН/м.Как уже отмечалось,деформативность затяжки влияет на ве¬
личину изгибающих моментов в своде, а с появлением в затяжке
трещин ее деформативность увеличивается. Учтем повышение
деформативности затяжки при расчетных нагрузках за пределами
ее трещиностойкости. Превышение расчетной нагрузки над на¬
грузкой, при которой трещиностойкость затяжки обеспечена, со¬
ставит aF = 70,4—64,5 = 5,9 кН/м.Коэффициент, учитывающий продольные деформации свода
и затяжки за пределами ее трещиностойкости, находим по фор¬
муле (75):_ 15 • 0,7065 Г 29000 / 64500 . 5900 \ ,Vcrc — 8.838й [70400 V 32500 • 0,4 ' 1,9 • 10ь * 0,13636 / ■+ 0^]=0,0788.Коэффициент, учитывающий влияние продольных деформаций
вследствие удлинения затяжки с трещинами, по формуле (72)
равен: kcrc= 1/(1 +0,0788) = 0,927.Величину распора с учетом деформативности затяжки опре¬
деляем по (69):Ясгс=0,125^-(20+50,4 • 0,927)=5088 кН.Зная величины вертикальной опорной реакции и распора, мож¬
но перейти к определению усилий в сечениях свода. При расчете
внецентренно сжатых сечений свода необходимо учесть влияние
прогиба.По табл. 24 найдем длину дуги свода L = l,035/i = 1,035 • 71,5=
=74 м.
Таблица 27ПараметрПри х/110,20,250,30,350,40,450,5У, м5,886,677,387,818,098,308,38sin ф0,26520,2210,17680,13260,08840,04420СОвф0,96420,97530,98420,99120,99610,9991Мо, кН • м28795337333779140940431884453844978Qo, кН1506126110077534992540М, кН • м— 1122—2042421203202623082341N, кН5305524151865143511250945088Mi, кН • м64636262616161По табл. 25 при семи подвесках и fi/h = 1/8,5 коэффициент
приведения длины арки к расчетной \х = 0,184, расчетная (приве¬
денная) длина оси свода Lo = 0,184* 74=13,6 м.Радиус инерции поперечного сечения свода /=У0,7065/0,782 =
=0,95 м. Гибкость свода Х= 13,6/0,95» 14,0. Влияние прогиба
на несущую способность можно не учитывать; т| = 1.Изгибающие моменты М и продольные силы N в поперечных
сечениях свода от действия расчетной нагрузки Fd = 70,4 кПа
вычисляем по формулам (76) и (77). Величину распора в этих
формулах следует принимать вычисленную с учетом деформатив-
ности затяжки.Поскольку свод имеет полигональное очертание, при расчете
следует учесть дополнительный положительный изгибающий мо¬
мент по формуле (78), возникающий вследствие прямолинейности
элементов свода. Величина эксцентриситета продольной силы
(см. рис. 32) по формуле (79)е| = 93,53—V 93,532 — 1,52 =0,012 м.Расчет усилий выполняем для точек свода с абсциссами х =
=(0,2...0,5)/i, взятых с интервалом через 0,05/i. Данные расчета
представлены в табл. 27. Ряд элементарных вычислений опущен.Зоны свода вблизи опор рассчитываются как оболочка двой¬
ной кривизны (см. пример IV). Проверка прочности сечений свода
производится по усилиям Af + Afi и N, приведенным в табл. 27.4.2. Расчет на несимметричную (одностороннюю снеговую) нагрузкуДля удобства расчета разбиваем снеговую нагрузку на сим¬
метричную и обратносимметричную части. Снеговую нагрузку
на одной половине свода считаем с коэффициентом 1,4, а на дру¬
гой — с коэффициентом 0,6. Полная расчетная симметричная125
Таблица 28Вид нагрузкиУси¬лиеПри х/1\0,20,250,30,350,40,450,5СимметричнаяМ— 1122—2042421203202623082341N5305524151865143511250945088Обратносиммет¬М1030110010309106903900ричнаяN200—20—50—70— 100— 120Суммарная слеваМ—9289612722113271626482341N5325524151665093504249944968Суммарная спра¬М—2152— 1304—788293133619182341ваN5285524152065193518251945208нагрузка составляет Fd = 70,4 кН/м, обратносимметричная на¬
грузка от одностороннего снега:Sinv/sym == (1 »4 0,6) • 1,4 • 12/2 = 6,7 кН/м.Усилия от симметричной части нагрузки определены выше
и приведены в табл. 27. Усилия от обратносимметричной нагрузки
вычисляются как для простой балки, так как распор от такой
нагрузки Н= 0. Величины этих усилий, а также суммарные усилия
от симметричной и односторонней нагрузок приведены в табл. 28.Прочность свода при внецентренном сжатии проверяют на
расчетные комбинации усилий Мшах и Mmin с соответствующими
значениями продольных сил. Проверка сечений свода и затяжки
на полученные значения усилий, а также расчет арочной диафраг¬
мы на монтажные нагрузки не приводятся.5. Расчет свода-оболочки в поперечном
направленииВ поперечном направлении расчету подлежат средние и край¬
ние волны сводов. При этом крайние волны, у которых с одной
стороны отсутствуют ограничения деформаций поперечного сече¬
ния, рассчитывают как одноволновый отдельно стоящий свод.
Расчет средних волн выполняется в предположении, что горизон¬
тальному перемещению и повороту сечения препятствуют допол¬
нительные закрепления в виде смежных волн.Для расчета крайней волны рассмотрим равновесие элемента
оболочки волнистого свода (рис. 34), поверхность которого имеет
положительную кривизну и очерчена в продольном и поперечном
направлениях по окружности (бочарный свод). На рис. 34 пока¬
зана внешняя нагрузка F, действующая на элемент, а также126
N, + ANfРис. 34. Схема усилий и условия равновесия элементов волны волнистого свода
а — общий вид элемента; 6 — вид элемента сбоку {Мг = М\ + дМt); в — схема к опре¬
делению вертикальных составляющих усилийусилия и их приращения, уравновешивающие внешнюю нагруз¬
ку. Если не пренебрегать продольными деформациями волнистого
свода, то в условии равновесия элемента следует учесть не только
продольные силы N\, но и поперечные силы Q и силы сдвига QSf.
Как указывалось выше, продольные деформации волны свода
учитываются введением коэффициента Л, который всегда меньше
единицы. Отсюда можно сделать вывод, что продольные силы Ni
в арочной волне свода уравновешивают не всю вертикальную
нагрузку F (здесь F — распределенная линейная нагрузка, отне-127
сенная к сечению арки — ширине одной волны), а только ту ее
часть, которая равна Fk. Часть нагрузки, равная F( 1—Л), урав¬
новешивается силами сдвига Qs/, действующими в срединной
поверхности оболочки. Из рис. 34, б следует, что проекция про¬
дольных сил N1 на вертикальную ось выражается формулой (при¬
ращения, представляющие собой малые второго порядка малости,
несущественны)Vz=2Nlsin±f=Nl±- (80)или с учетом того, что N\—интегральное усилие в поперечном
сечении волны, имеем:1,‘-(-Т-±-Т-гУ-7Г- (*■)где N\ w М\ — соответственно продольная сила и изгибающий момент, полученные
из расчета волны свода в продольном направлении как арки; t — толщина плиты
оболочки.В общем случае при симметричной вертикальной нагрузке
волна свода сжата по всей длине, и силы Vz, как видно из рис. 34, а,
направлены вверх и уравновешивают внешнюю нагрузку. Однако
при односторонней (снеговой) нагрузке продольные изгибающие
моменты могут достигать значительных величин и тогда, как сле¬
дует из формулы (81), эпюра напряжений в поперечном сечении
волны может поменять знак, т. е. иметь зону растяжения (рис. 34, б).
Это означает, что силы Vz на этом участке направлены вниз, т. е.
суммируются с внешней нагрузкой. Но в случае больших изгиба¬
ющих моментов в поперечном сечении возникают также попереч¬
ные силы и силы сдвига. Для их определения можно сделать
допущение, что поперечные сечения волны при изгибе и вне-
центренном сжатии остаются плоскими (гипотеза плоских сече¬
ний), и воспользоваться гипотезой Журавского, согласно которой
касательные напряжения распределены по ширине сечения волны
равномерно.При односторонней нагрузке (рис. 35, а), состоящей из сим¬
метричной и обратносимметричной частей, приращение попереч¬
ной силы на метр длины арки имеет вид: aQ = F(1 — k) + s/2,
где 5 — односторонняя снеговая распределенная линейная на¬
грузка, отнесенная, как и F, к ширине сечения арки. При наличии
в элементах арки поперечных ребер это усилие умножается на
размер шага ребер для определения величины нагрузки на ребро.Приращение поперечной силы можно также получить непо¬
средственно как разность между полной внешней нагрузкой, при¬
ходящейся на выделенный элемент свода, и суммой нормальных
составляющих продольных сил вч данном сечении свода, т. е.&Q = Ftot-lV'.,. (82)128
Рис. 35. К расчету волнистых сво¬
дов-оболочек на несимметричную
нагрузкуа — схема несимметричной нагрузки;
б — схема симметричной и обратносим¬
метричной частей нагрузок, заменя¬
ющих несимметричную нагрузку; в —
эпюры изгибающих моментов и пере¬
резывающих сил от действия на свод
обратносимметричной части нагрузкиДля определения приращений сил сдвига воспользуемся фор¬
мулой Журавского (как аналогом) и вспомним выражение (17)
статического момента сечения кругового (или близкого к нему)
очертания. Приращение сил сдвига имеет вид:a QSf= *®j2t 2(sin а — т]а), (83)где Т1=(г2—2о)/гг; 2о— расстояние от центра тяжести сечения до шелыги волны.Изгибающий момент в сечениях с цилиндрической поверхностью
волны от сил сдвига вычисляется по формуле, выведенной для
цилиндрических оболочек:-JIr±rh+JIr^+^5)} (84)Поперечные изгибающие моменты М2 в сечениях крайних
волн определяются из условия равновесия элемента волны как
сумма моментов всех сил с одной стороны рассматриваемой точки
поперечного сечения (см. рис. 34, в), а именно от внешней нагруз¬
ки, от сил Vz и от приращений сил сдвига.Для средних волн необходимо, кроме того, определить влияние
соседних волн свода. В тех случаях, когда волны имеют симметрич¬
ное сечение, можно ввести предположение об отсутствии горизон¬
тальных перемещений и равенстве нулю угла поворота крайней
точки сечения волны. Такое допущение позволяет свести задачу
к расчету бесшарнирной арки (для волн кругового очертания,9 Заказ 61129
Таблица 29ПараметрТочка поперечного сечения0122'3456Ордината z„ мм— 1980— 1182—482—38225872310041120a*, МПа— 1,161,94,65,07,49,210,310,7ат<=(а* + а|Ч_ i)/2———6,2 8,3 9,75 10,5At(i+1), мм2—23000060 00061500 61500 61500 61500NZy кН—437276381,3 510,5 600,0 645,8Vz.i, kH—14,08,812,2 16,3 19,2 20,7которые здесь рассматриваются) как дважды статически неопре¬
делимой и легко разрешается системой двух канонических урав¬
нений метода сил. При этом можно воспользоваться формулами
и таблицами, приведенными в расчете цилиндрической оболочки
(см. пример I).Рассмотрим условия равновесия элемента средней волны свода
шириной 6 = 3 м от действия комбинаций усилий из расчета свода
на несимметричную нагрузку (см. табл. 28; нагрузка суммарная
слева, х = 0,4): Mitmax=2716 кН • м; Wi = 5042 кН.Внешняя расчетная нагрузка, действующая на поверхность
трехметрового элемента свода; постоянная g=(l,76+ 1,63)Х
X0,95 = 9,7 кН/м; временная s=l,4 -3-1,4 0,95 = 5,6 кН/м;
от арочной диафрагмы g, = 13,8 • 1,1 • 1,5 0,95 = 21,63 кН/м.Вычисленные напряжения и усилия в точках поперечного се¬
чения свода записываем в табл. 29. Значения напряжений в точках
поперечного сечения волны будем определять из расчета свода
в продольном направлении: 2716 106 ^ | 5042 • 103 л ллооу!„ i о аан /лап \1 0,7065 • ю12 782000 *00384zi+6,447 (МПа).Знак «плюс» в формуле соответствует сжатию.Усилие Nz между двумя соседними точками поперечного сече¬
ния вычисляем, умножая площадь участка сечения на значение
средней величины напряжения на этом участке amt.Нормальную составляющую vz продольных усилий в сечениях
свода определяем по формуле (80) :Vz = Nzb /г, = Лгг3/93,53 = 0,032Nz.Точка приложения усилия vz находится в центре тяжести
участка эпюры а между смежными точками дуги поперечного
сечения волны. Привязку усилий vz к правым точкам дуги (для слу¬
чая возрастания значений от края к середине поперечного сечения
волны) можно определить по формулеAi-iy(2a(,-i) + a/)(cos o^,_i) + cos /qk\a‘ = 6(<X(J_|) + C() •130
Таблица 30Точкапоперечногосечениясвода' Изгибающие моменты, кН • м, от отдельных сйлX M,
кН • мbQsfVzgtgs20/00000314,841,9—32,3— 11,9—6,26,3433,2104,8—64,0—45,9—24,43,7558,3196,5—96,6— 103,9—55,8— 1,5691,5320,2—129,8— 185,1— 100,6—3,8Например, привязка 1>гз к точке 3 будет_ 1540(2 • Б,0 + 7.4)(0,88 + 0,932)3— 6(5,0+7,4) —ЬМ ММ.Привязка усилий иг к точкам поперечного сечения волны по¬
казана на рис. 33, в.Полная величина нормальной составляющей продольной силы
в сечении свода Уг=ХУг/ = 91,2 кН (табл. 29).По формуле (82) определяем долю нагрузки, воспринимаемую
сдвигающими силами: aQ = 5,6 • 6+9,7 -6,15 + 21,63 — 91,2 =
=23,7 кН.Сдвигающие силы, распределение которых принимаем по за¬
кону Журавского, находим по формуле (83):д Qsl = 23,7 ‘ 0^5' 0,04 2(sin а—0,9104а)=420(sin а - 0,9104а),где Т1=(г2 — 2о)/г2=(1251 — 112)/1251 =0,9104; го— расстояние от центра тяжести
сечения криволинейной плиты до шелыги.Поперечные изгибающие моменты Ма от действия сдвига¬
ющих сил вычисляем в точках поперечного сечения оболочки с
угловой координатой а (см. рис. 33, в и 34, в). Воспользуемся
для этого формулой (84), заменив М2 на Ма . Коэффициенты О
определяются по формулам (21). Их величины даны в табл. 8.Значения изгибающих моментов в основной системе относи¬
тельно точек поперечного сечения свода, вычисленные от действия
сдвигающих сил, вертикальной составляющей продольной силы
и внешней нагрузки, приведены в табл. 30.Для нахождения неизвестных в основной системе (см. рис. 9)
составляем канонические уравнения метода сил по формулам (14):^1611 -I- A2fii2 + Si/ = 0;^1^21 + А2622 + ^2/= 0.9*131
Вычисление коэффициентов при неизвестных и свободных чле¬
нах канонических уравнений выполняется путем перемножения
эпюр по формулам (15) и (16) и по табл. 5:6ц = 12,513[0,5 • 0,4947(2+0,5492)—0,75 • 0,8357]=7,38;6,2 = 621 = 12,512(0,4749-0,4947 • 0,8801)=6,18;622=12,51-0,4947=6,19; 6„=4,6; 62/=10,2.В результате канонические уравнения примут вид:7,38^1+6,18^2= —4^0.6,18^,+6,19^2=-10,2.Отсюда по формулам (14а)v 6,18-10,2-6,19-4,6 л uЛ,= 7,38 • 6,19-6,18й =4’615 кН;Y 6,18 • 4,6-7,38 . 10,2 а u2 7,38* 6,19 — 6,18* “ 6,255 кН • м.Суммарная эпюра изгибающих моментов дана на рис. 33, г.
Проверка сечений и подбор арматуры в примере не приводятся.6. Некоторые указания по конструированию
волнистых сводов-оболочекКонструирование элементов волнистых сводов и сводов в целом
зависит от профиля поперечного сечения (вдоль образующей)
сводчатого покрытия — треугольного, трапециевидного или вол¬
нистого, от материала элементов свода (железобетон, армоцемент),
а также от принятых условий изготовления или монтажа конструк¬
ций и способов их стыковки.Своды рекомендуется проектировать из тяжелого или легкого
бетона и из армоцемента. Волнистые своды могут быть монолит¬
ными или сборными. Монолитные своды проектируются преиму¬
щественно цилиндрическими. Сборные волнистые своды пролетом
более 24 м рекомендуется проектировать с применением диафрагм
в виде железобетонных или стальных арок или ферм, устанавли¬
ваемых в направлении перекрываемого сводом пролета. При про¬
летах более 24 м затяжки арок предусматриваются предваритель¬
но напряженными, они должны поддерживаться не менее чем дву¬
мя подвесками, закрепленными в швах между панелями свода.Крайние волны сводов, в частности, примыкающие к дефор¬
мационным швам или торцам здания; конструируют жесткими
в поперечном направлении, чтобы исключить возможность дефор¬
мации контура поперечного сечения. Для этого следует предусма¬132
тривать жесткие ребра-диафрагмы, затяжки-распорки и т. д.
Конструкция сопряжения крайних волн с торцевыми стенами
зданий не должна препятствовать вертикальным перемещениям
свода.Сборные своды лучше проектировать из прямолинейных (в на¬
правлении перекрываемого сводом пролета) панелей, в результате
чего свод приобретает полигональное очертание.Панели проектируют тонкостенными с ребрами по контуру,
а панели складчатых сводов — плоскими из толстых трапециевид¬
ных панелей. Ребра панелей армируют плоскими сварными арма¬
турными каркасами. Криволинейная или складчатая плита пане¬
лей (обычно толщиной 30 мм) армируется сварной сеткой из
обыкновенной арматурной проволоки диаметром 3...4 мм с разме¬
ром ячейки 200X200 мм.При трапециевидном сечении волны толщину горизонтальных
полок панелей, в которых устанавливается рабочая арматура
свода (при отсутствии диафрагм вдоль перекрываемого пролета),
надо принимать не менее 60 мм.Соединение панелей свода между собой выполняется сваркой
закладных деталей, которые привариваются к концам арматурных
стержней с последующим замонолячиванием стыков. Все панели
свода, за исключением опорных, должны иметь одинаковые опа¬
лубочные размеры.В опорных панелях волнистых сводов, где возникают значи¬
тельные по величине главные растягивающие напряжения, прихо¬
дится утолщать криволинейную плиту и укладывать косую арма¬
туру.Конструкция опорных элементов свода зависит от профиля
сечения волны свода (вдоль образующей) и способа опирания.
При опирании на колонны опорными элементами могут служить
треугольные фермы (при складчатых сводах) или арки (при вол¬
нистых сводах) со стальным нижним поясом (затяжкой) из
прокатных профилей или из предварительно напряженного же¬
лезобетона.Б. РАСЧЕТ ВОЛНИСТОГО СВОДА-ОБОЛОЧКИ
КОМБИНИРОВАННОЙ КОНСТРУКЦИИ
(МЕТАЛЛОЖЕЛЕЗОБЕТОННОГО)Б.1. РАСЧЕТ СРЕДНЕЙ ВОЛНЫ СВОДА-ОБОЛОЧКИ1. Конструкция свода-оболочки и нагрузкиНеобходимо запроектировать покрытие, конструкция которого
описана в предыдущем примере (см. пример V.A), за исключением
продольной диафрагмы. Конструкцию этой диафрагмы принимаем133
из металлопроката. Поперечное сечение железобетонного свода
со стальной продольной конструкцией показано на рис. 33, д.Нагрузки для расчета свода принимаем по табл. 26. Собствен¬
ная масса стальной арки-диафрагмы 5 кН/м.Полная нагрузка на метр волны свода шириной 12 м: норма¬
тивная F„ = 3,85 12+ 5 = 51,2 кН/м; расчетная Fd = 4,6 • 12 +
+ 5 . 1,1=60,7 кН/м, в том числе постоянная нагрузка gn =
= 39,2 кН/м; gd = 43,9 кН/м.2. Геометрические характеристики свода-оболочкиКонструкция железобетонных элементов свода и их размеры
приняты по примеру V.A. Необходимые для расчета размеры сталь-
. ной продольной конструкции приведены на рис. 33, д.Геометрические параметры свода следующие: площадь по¬
перечного сечения свода А =0,492 + 0,06 + 0,134 = 0,686 м2, где0,492 м2— площадь поперечного сечения оболочки; 0,06 м2—
площадь зоны замоноличивания; 0,134 м2— приведенная площадь
верхнего пояса арки.Коэффициент приведения v=2,06 • 105 /29 • 103 = 7,1, площадь
поперечного сечения стальной затяжки Atd = 200 см2.Момент инерции поперечного сечения свода / = 0,483 м2.
Стрела подъема свода в ключе / = 7,2 + 0,67 + 0,2+0,568 =
= 8,64 м.3. Расчет свода-оболочки в продольном
направлении3.1. Расчет на равномерно распределенную
симметричную нагрузкуДля расчета свода в продольном направлении прежде всего
определим коэффициент к> учитывающий влияние смещения пят
вследствие упругого удлинения затяжек и обжатия свода на
величину распора. Для вычисления распора от собственной массы
элементов свода принимается k = l.По формуле (73)15 0,483 / 29 • 103 , 0,9342 \_Л1то
v—2,06 • 10* • 0,02 + 0,686 ) и>1ЩУ’где по табл. 24 т)=0,9342 при f\/l\ = 1/8,3.По формуле (72) к = 1/1,1019=0,907. Распор свода от полной
расчетной равномерно распределенной нагрузки составит:Я„=0,125^-(20+40,7 • 0,907) = 4209 кН.134
Таблица 31Изгибающий
момент, кН • мПри x/h0,20,250,30,350,40,450,5М о = 0,5FdX X24702289483242235124372383840138789ХЦ-х)У, М6,066,877,618,058,348,558,64Ну=4203у25506289163203033842351033598636366М = Мо — Ну—804323921242213524152423Расчетная (приведенная) длина волны свода по устойчивости
(см. пример V.A) L0=13,6 м.Расчет изгибающих моментов по формуле (76) в поперечных
сечениях волны свода от действия симметричной нагрузки приве¬
ден в табл. 23.3.2. Расчет на несимметричную нагрузкуРасчет на одностороннюю снеговую нагрузку выполнен по
аналогии с проделанным в примере V.A. Величину снеговой нагруз¬
ки берем из табл. 26, а величины изгибающих моментов от односто¬
ронней нагрузки — из табл. 32.Для расчета армирования и проверки сечений свода выбира¬
ем из табл. 39 и 40 две расчетные комбинации усилий в сечении
свода: с максимальным моментом и соответствующей продольной
силой и с минимальным моментом и соответствующей продольной
силой:1) Мтах = 2825 кН • м; N = Я/cos 06 = 4209/0,999 = 4213 кН;2) Мтщ = -1834 кН . м; N=*H/cos 0i =4209/0,9642 = 4365 кН;где cos 0/=V 1 — (l/r)2(\ —xi/l)2 .Таблица 32Изгибающий момент,
кН • мПри jc//i0,20,250,30,350,40,450,5От симметричной на- —804 32 392 1242 2135 2415 2423
грузкиОт кососимметричной 1030 1100 1030 910 690 390 0
нагрузкиУ Ml 226 1132 1422 2152 2825 2805 2423
IMr —1834 —1068 —638 332 1445 2025 2423135
Поскольку рассчитываемый нами свод имеет полигональное
очертание, в приведенных выше комбинациях усилий необходимо
учесть положительный изгибающий момент, определяемый по
формуле (78).Проверка сечений железобетонного свода и стальной затяжки
на приведенные комбинации, а также расчет стальной диафрагмы
на монтажную нагрузку выполняются известными методами.4. Расчет свода-оболочки в поперечном направленииКак и в предыдущем примере расчет волны выполняем на
поперечные изгибающие моменты из условия равновесия элемента
свода от действия комбинации усилий из расчета свода в продоль¬
ном направлении на одностороннюю нагрузку.Расчетная комбинация усилий: М* = 2825 кН • м; М*=4213 кН.Внешняя расчетная нагрузка, действующая на трехметровый
элемент свода: постоянная g=9,7 кН/м; временная 5 = 5,6 кН/м;
от арочной диафрагмы ^=5,5 • 3/2 = 8,25 кН/м.Напряжения в точках поперечного сечения волны свода4213000 . 2825- 106 ctoo , Л ллсос
688000 483 109 6,123 + 0,005852/.Вычисление сил и2 = 0,032Nz сведено в табл. 33.Доля нагрузки, воспринимаемая сдвигающими силами по фор¬
муле (82): лQ = 8,25+9,7 • 6,15 + 5,6 • 6,0-64,4 = 37,1 кН.Определяем сдвигающие силы, принимая распределение их
по закону Журавского [формула (83) ]:Д Qsf= 37-' • ‘02458з • °’°?-2(sin а—0,925а)=961,7(sin а—0,925а),где т\ = (г2 — zq)/г2 = (1251 —93,2)/1251 =0,925; z0— расстояние от центра тяжести
сечения оболочки до ее шелыги.Изгибающие моменты в поперечном сечении волны определяем
по той же методике, что и в предыдущем примере. Вычисление
суммарных значений изгибающих моментов в точках поперечного
сечения в основной системе сведено в табл. 34.Составляем канонические уравнения метода сил:*,6,, +^26i2 + 6i/ = 0;-^1621 + Л2622 + &2f 0.Определяем коэффициенты при неизвестных:6И=7,38; 612 = 621 =6,18; 622 = 6,19 (см. пример V.A);136
Таблица 33Таблица 34ТочкапоперечногосечениясводаИзгибающие моменты от отдельных сил, кН • мХМ,
кН • мA QsfVz818s2000000319,12,22— 12,3— 11,9—6,2—9,08444,124,83—24,4—45,9—24,4—25,77580,971,58—36,9— 103,9—55,8—44,126132,9153,22—49,5— 185,1— 100,6—49,586,/= - Ь-54 ’ 9ff ‘ 0,660 —~^~(4 • 25,77 • 1,124 ++ 2 • 9,08 • 0,66+9,08 • 1,124+25,77 - 0,66 ++ 4 - 44,12 • 1,406+25,77 • 1,406+44,12 • 1,124 ++ 2 • 49,58 • 1,5+44,12 • 1,5+49,58 • 1,406)=-201,3;62, = -1,54 • 9,08 -0,5-1,537 ( 9,08+49’58 ++25,77+44,12)=-159,4.Перепишем полученные значения коэффициентов в канониче¬
ские уравнения:7,38Х, + 6,18*2=201,3;6,18X1 + 6,19*2 = 159,4.137Параметр•Точки поперечного сечения0122'3456Ордината Z/, мм— 1968— 1438—668—56872537818932а/, МПа—5,4—2,32,22,86,59,310,911,54-tf/+i)/2———4,65 7,9 10,1 11,2
61500 61500 61500 61500Ащ+1), мм2—59 00030 000285,9 485,9 621,2 688,8Nz, кН—— 135,766,09,1 15,6 19,9 22,0Vz,i, кНПривязка tмм,
к правой точке
дуги по форму¬
ле (85)——4,32,1604 688 730 758
Отсюда по формуле (14а)Y _ 201,3 • 6,19-159,4 • 6,18 _~л р н.1 7,38*6,19 — 6,18-6,18 ’v _ 7,38 • 159,4-6,18 • 201,3 _ 0 п н
2 7,38 • 6,19 — 6,18 • 6,18 “ ’ ‘ М*Значения изгибающих моментов в точках поперечного сечения
волны свода в результирующей эпюре: Мг= — 9,0 кН . м; М3 =
= 4,36 кН • м; М4 = 3,45 кН . м; М5=-5,32 кН . м; М6 =
= —7,58 кН • м.Проверка сечений и подбор арматуры в примере не приводятся.Б.2. РАСЧЕТ КРАЙНЕЙ ВОЛНЫ СВОДА-ОБОЛОЧКИ1. Конструкция свода-оболочки и нагрузкиЖелезобетонная конструкция свода принимается из примера V.
Стальная продольная диафрагма принимается из примера VI.
Поперечное сечение свода показано на рис. 33, д. Равномерно
распределенные нагрузки принимаем по табл. 26. Масса продоль¬
ной диафрагмы и зона замоноличивания берутся удвоенными
против принятого в примере VI, поскольку крайняя волна рассчи¬
тывается как отдельно стоящий свод с двумя полными диафраг¬
мами по краям.Полная нагрузка на 1 м волны свода составит: нормативная —
Fn = 3,85 • 12 + 5 • 2 + 0,06 • 25 = 57,7 кН/м; расчетная — Fa =
= 4,6 • 12+(10+1,5)1,1=67,9 кН/м.2. Геометрические характеристики
металложелезобетонного свода-оболочкиСоответствующие параметры свода и размеры его элементов
принимаются такие же, как в примерах V.A и V.B.I.Площадь поперечного сечения оболочки ASh = 0,492 м2; зоны
замоноличивания Ат = 0,12 м2. Приведенная площадь поперечного
сечения стальной арки Аа = 0,268 м2. Полная площадь поперечного
сечения свода А =0,492+0,12+0,268=0,88 м2.Момент инерции поперечного сечения свода /=0,692 м4. Рас¬
стояние от центра тяжести поперечного сечения свода до верха
замоноличиваемой полости z=0,32 м. Стрела подъема свода в
ключе jF=7,2+ 0,67+0,2+ 0,32=8,39 м.Площадь поперечного сечения стальной затяжки в обеих
диафрагмах принята, как и в предыдущем примере, Atd = 200 см2.138
3. Расчет свода-оболочки в продольном
направлении3.1. Расчет на равномерно распределенную
симметричную нагрузкуДля учета податливости свода и деформативности затяжки
вычислим по формуле (72) коэффициент к. При f\/l\ = 1/8,5 по
табл. 24 г\ = 0,9365.Коэффициент v находим по формуле (73):15 • 0,692 / 29 103 . 0,9365 \ п nftr8 • 8,392 V 2,06 • 105 • 0,04 0,88 )Следовательно, Л = 1/(1 +0,085) = 0,92.Распор от полной расчетной равномерно распределенной на¬
грузки с учетом податливости свода по формуле (69) составитЯ„ = 0,125-^-(20+47,9 • 0,92)=4880 кН.Таблица 35Изгибающий момент,
кН • мПри х/1\0,20,250,30,350,40,450,5Mo = 0,bFd(l-x)27770325433644839485416654295643390У, м5,896,677,397,828,18,38,39Ну=4880у28743325503606338062395284050440943М = Мо — Ну—973—73851323212724522447Изгибающие моменты, вычисленные в точках поперечного се¬
чения свода, приведены в табл. 35 (расположение расчетных
точек сечений и их характеристики см. пример V.A).3.2. Расчет на несимметричную нагрузкуРасчет на одностороннюю снеговую нагрузку производим по
аналогии с выполненным в примере V.A. Величину снеговой нагруз¬
ки берем из табл. 34. Величины изгибающих моментов от односто¬
ронней нагрузки определены в табл. 36, откуда выбираем расчет¬
ные комбинации усилий для расчета сечений свода по прочности
на внецентренное сжатие:1) Мшах = 2842 кН • м; Д^=^|®^-=5044 кН.2) Mmin = —2003 кН • м; Л^=-д^-=5248 кН.139
Таблица 36Изгибающий момент,
кН • мПри х/1\0,20,250,30,350,40,450,5От симметричной на¬—973—73851323212724522447грузкиОт кососимметричной1030110010309106903900нагрузкиТМ,571093141522332817284224471МГ—2003— 1107—645413143720622447На приведенные комбинации усилий производится известными
методами проверка сечений свода.4. Расчет свода-оболочки в поперечном
направленииВ поперечном направлении крайняя волна свода рассчитыва¬
ется на поперечные изгибающие моменты исходя из тех же усло¬
вий, что и аналогичный расчет в примере V.Расчетные усилия в сечении x = 0,45/i (см. табл. 36): М<* =
=2842 кН . м; Nd=—5044 кН.Внешняя расчетная нагрузка, действующая на элемент свода:
постоянная g=9,7 кН/м; gi =(5,5 + 0,06 • 25 • 1,1)3 = 21,5 кН/м;
временная 5 = 5,6 кН/м.Напряжения в точках поперечного сечения свода от усилий
из расчета свода в продольном направлении: 5044000 , 2842 • 106 с 700 , Л880000 692 • 1О9 5,732 + 0,0042/.Из примера V.B.1 известно, что вертикальна^ составляющая
продольных усилий в сечениях свода vz = 0,032N. Привязка усилий
vz в поперечном сечении свода видна из рис. 33. Вычисление на¬
пряжений и усилий в точках поперечного сечения свода приведено
в табл. 37. Полная величина вертикальной составляющей про¬
дольной силы в сечении свода Vz = Y,Vzi = 77,1 кН.Долю нагрузки, воспринимаемую сдвигающими силами, найдем
по формуле (82):a Q=Z(g+g.+s)-Vz=9,7 - 6-15+21,5 + 5,6 • 6-77,1=37,7 кН.Для определения приращений сил сдвига воспользуемся фор¬
мулой (83):дQsf= 37,7 ' ^ ' °'04 2(sin а —0,907а) = 977,2(sin а —0,907а),
где i\=(1251 —115,9)/1251 =0,907.140
Таблица 37ПараметрТочка поперечного сечения0122'3456Ордината z,, мм— 1721— 1191—421—32131978410651159Oi, МПа— 1,21,04,04,57,08,910,010,4ат, = (а/ + а/+ \)/2———5,75 7,95 9,45 10,2A(i+1)> мм2
Nz = Aomt, кН—118 000 60 00061500 61500 61500 61500—118240353,6 488,9 581,2 627,3vzi = 0t032Nz, кН—3,87,711,3 15,6 18,620,1Величина привязки t/zl
к правой точке дуги,
мм689 702 739761Таблица 38ТочкапоперечногосечениясводаИзгибающие моменты от отдельных силXM,
кН • м*QsfVzg\gs2000000321,324,9—32,1— 11,9—6,2—4448,769,3—63,7—45,9—24,4— 16587,3141,1—96,1— 103,9—55,8—27,46139,8243,7— 129,0— 185,1— 100,6—31,2Значения поперечных изгибающих моментов от приращения
сдвигающих сил л Qs/, от вертикальных составляющих vZy продоль¬
ных усилий в своде и от внешней нагрузки приведены в табл. 38.
Полученные значения суммарных поперечных изгибающих момен¬
тов являются расчетными для проверки сечения и подбора арма¬
туры.VI. РАСЧЕТ ЖЕЛЕЗОБЕТОННОГО
СФЕРИЧЕСКОГО КУПОЛА1. Основные сведения о куполах и принципах
их расчетаКуполом называется выпуклая пологая или подъемистая обо¬
лочка на круглом, эллиптическом или полигональном плане. Эле¬
ментами купола являются осесимметричная оболочка вращения
и опорное кольцо. Ось вращения купола занимает в пространстве
вертикальное положение. Видом плоской кривой, вращением ко¬
торой вокруг вертикальной оси образуется купол, обусловлено
его название. Так, если образующей является дуга окружности, то141
купол сферический; если отрезок дуги эллипса — эллиптический;
если отрезок одной ветви двухполосной гиперболы — гиперболи¬
ческий, если прямая пересекает ось вращения — конический и т. д.
Могут также быть и сочетания кривых.Образующая купола называется меридианом. Оболочка купола
может быть также образована волнистыми и складчатыми эле¬
ментами. В практике строительства покрытий равным образом
находят применение железобетонные многогранные купола. Если
оболочка купола в вершине имеет фонарный проем, то она счита¬
ется незамкнутой.Опорное кольцо купола является его контурным элементом.
Оно может покоиться на сплошном основании в виде стены или
на отдельных колоннах. При наличии фонарного проема устраива¬
ется также фонарное кольцо.Стрелу подъема купола не рекомендуется принимать меньше
1/10 диаметра опорного контура. Верхний предел стрелы подъема
купола, а также диаметр опорного кольца теоретически не огра¬
ничивается и зависит от технико-экономической целесообразно¬
сти, функциональных особенностей здания или сооружения и прак¬
тических возможностей строительной техники.По конструктивным особенностям различают купола гладкие
(купола-оболочки), ребристые или ребристо-кольцевые.Ребристые купола могут быть с ребрами меридионального
направления, ромбического (по направлениям встречных спира¬
лей) и др. Ребристо-кольцевые купола имеют ребра кольцевого
и меридионального направления или кольцевого и по направле¬
ниям встречных спиралей (с треугольными ячейками). В послед¬
нем случае могут быть еще и меридиональные ребра (также с ячей¬
ками треугольного очертания). В зависимости от архитектурного
решения интерьера или других требований встречаются и иные
рисунки ребер куполов. Железобетонные купола можно проектиро¬
вать в виде монолитных, сборно-монолитных или сборных кон¬
струкций. Монолитные купола выполняют гладкими, а сборные —
ребристыми.Разрезку сборного купола на отдельные панели выполняют
по-разному, это зависит от принятого рисунка ребер и способа
монтажа. Обычно членение купола производят по меридиональ¬
ному и кольцевому направлениям.При небольших диаметрах опорного кольца панели можно
образовывать разрезкой купола только по меридиональным на¬
правлениям, в этом случае длина панелей зависит от возможностей
перевозки. Панели могут быть криволинейными или (при больших
размерах купола) плоскими, и тогда поверхность становится
многогранником.Оболочка купола под действием распределенной поверхностной
нагрузки в условиях безмоментного напряженного состояния ра¬
ботает главным образом на сжатие. Зона действия изгибающих142
моментов ограничивается областью вблизи опорного кольца. Опор¬
ное кольцо при вертикальной нагрузке работает на растяжение, а
фонарное кольцо — на сжатие. Для создания условий безмомент¬
ной работы купола опорное кольцо должно иметь возможность
свободно перемещаться в радиальных и угловых направлениях
при температурных воздействиях, колебаниях величины нагруз¬
ки и пр. При этом меридиональные усилия должны быть направ¬
лены по касательной к меридиану. При условии, что толщина
стенок купола и радиуса кривизны его меридиана изменяется
плавно (не скачкообразно), усилия в куполе можно определять
по безмоментной теории с наложением вычисленных отдельно
усилий краевого эффекта.Напомним основные положения расчета куполов по безмомент¬
ной теории.При действии на купол осесимметричной вертикальной нагруз¬
ки в оболочке исключается кручение, вследствие чего обращается
в ноль сдвигающая сила. В связи с этим в стенке купола действуют
только продольные силы — меридиональные N\=o\t и кольцевые
N2 = G2t (рис. 36, а). Усилие Ni на единицу длины меридиана опре¬
деляется из условия равновесия сегмента, отсеченного от купола
конической поверхностью с углом раствора ф (рис. 36, в).Для точки с ординатой z введем следующие обозначения:
г\— радиус кривизны срединной поверхности оболочки в направ¬
лении меридиана; г2— то же, в направлении, нормальном к мери¬
диану. Радиус г2 перпендикулярен к касательной в данной точке
меридиана.Радиусы г\ и г2, являющиеся функцией лишь угла ф, полностью
определяют поверхность вращения и связаны следующей диффе¬
ренциальной зависимостью:dr 2 sin®—^-2-= Г, COS ф.Уравнения равновесия элементарного участка срединной по¬
верхности оболочки купола имеют вид:2 jiN 1 г 2 sin2 ф — /4=0; >} (86)
Nl/rx + N2/r2-Fn=0. >Первое уравнение (86) представляет собой равенство нулю
проекций всех сил на вертикаль. Из него получим меридиональное
усилие:Ы'=2пгХ\ • (87)143
Рис. 36. К анализу напряженного состояния купола
а -н- распределение усилий Ni и N2 (слева — эпюра усилий N2, справа — усилий N\)\
б — геометрия купола; в — схема уравновешивания отсеченной части купола погонным
усилием N\ в текущем широтном сечении; / — ось вращения; 2 — шов перехода; 3 —
текущая параллель; 4 — текущий меридиан; 5 — краевая параллель
Второе уравнение (86) взято из системы дифференциальных
уравнений равновесия элемента оболочки, полученных с извест¬
ными допущениями в безмоментной теории оболочек вращения.
Из этого уравнения найдем величину кольцевого усилия:N2 = r2{Fn-Nx/rx). (88)В формулах (86)...(88) вертикальная равнодействующая внешней нагрузки,
действующая на часть оболочки, расположенную выше рассматриваемого гори¬
зонтального сечения с углом раствора 2<р (рис. 36, в) ; Fn— нормальная к поверх¬
ности купола в рассматриваемом сечении составляющая внешней нагрузки на
единицу площади поверхности.Для сферического купола, воспринимающего только собствен¬
ную массу g (масса элемента оболочки с площадью срединной
поверхности, равной единице), можно определить зависимости для
усилий N\ и N2 следующим образом.Так как купол сферический, то г\ = r2 = rc, a r2sin (p = rcsin ф = г.
Касательная составляющая собственной массы купола в точке
меридиана с углом раствора ф будет g\=gsinq), а нормальная
к поверхности купола gn= —g cos (р. Далее для нахождения уси¬
лий N\ и N2 воспользуемся формуламил/, = ——;1 + COS ф * Vt } (89)N*=-ere( cos<p—пр^г).В полюсе купола при <р=0 усилия N\ = N2— —grc/2. Эпюры
усилий Ni и N2 показаны на рис. 36, а. Меридиональные усилия Ni
независимо от угла <р всегда сжимающие.Кольцевая продольная сила N2 из сжимающей в районе полюса
переходит через нулевое значение и становится растягивающей.
Кольцевое сечение с нулевыми значениями усилия N2 называют
швом перехода. Этот шов соответствует углу <ро, определяемому
из условия N2=0:cos <ре —1/(1 +совфо)=0 или cos^o+cos фо—1 =0,откуда фо=51°49'.Таким образом, если центральный угол раствора пологого
купола меньше 2фо=103°38', то в нем не возникает растяжения в
кольцевом направлении; при угле 2фо больше указанного — в
кольцевых сечениях, ниже шва перехода, возникают растягива¬
ющие кольцевые усилия.При нагрузке, равномерно распределенной по горизонтальной
проекции купола #2=0 при ф0=45°, следовательно полностью
сжатый купол может существовать только при условии, что10 Заказ 61145
2фо<90°. Это обстоятельство рекомендуется учитывать при проек¬
тировании куполов.Снеговая симметричная нагрузка на купол при ф^25° при¬
нимается, согласно СНиП 2.01.07—85 «Нагрузки и воздействия»,
в виде равномерно распределенной поверхностной нагрузки по¬
стоянной интенсивности (рис. 37). Для удобства расчетов куполов
с любым ф симметричную снеговую нагрузку можно представить
изменяющейся по закону s = l,5socos^ + tt/6), где so— нагрузка
равномерной интенсивности по СНиП в пределах широты с углом
раствора 2ф^50°. При 2ф^120° нагрузка обращается в ноль.
Суммарная снеговая нагрузка выше широты с углом ф^60°
составит<р ф5ф= \ds= 1,55о2яг? J cos (ф +я/6) sin фсов фйф =о о= 3soJirc [0,29 (1 — cos3 ф) — 0,167 sin3 ф].Коэффициент 1,5 принят здесь из условия равенства объемов эпюр
снеговой нагрузки, принятой по СНиПу и в данном расчете.Отсюда, имея в виду (87), получим выражение для мери¬
дионального усилия от снеговой нагрузкиNt = 6 s\ | = 1,5s0rc Г 0,29(1~/О83ф) -0,167sin ф! (87а)2nrcsirr<p * L sirrtp Т J v 7Нормальная к поверхности оболочки составляющая снеговой
нагрузки Sn = 1,5so cos (ф-f- я/6) соэ2ф, что позволяет получить
из (88) выражение для кольцевого усилия от симметричной сне¬
говой нагрузки:N2= l,5Sorc [cos (ф + я/6) С052ф— Q,29^~2^OS’” ++ 0,167sin ф^ (88а)Максимальные сжимающие усилия от снеговой симметричной
нагрузки, возникающие в полюсе купола, равны: N{ = N2 =
= — 0,65sorc. Для расчета купола на несимметричную снеговую
нагрузку будем полагать, что эта схема реализуется за счет
переноса 40% снега с одной стороны купольного покрытия на
другую (см. рис. 37, бив).Несимметричную снеговую нагрузку представим в виде сим¬
метричной и обратносимметричной составляющих. Объем поло¬
вины обратносимметричной снеговой нагрузкиSinv/sym =l,36sor? • 0,4 • 0,5=0,272r?So.146
Рис. 37. К расчету купола на снеговую нагрузку
а, б, в — нагрузка по СНиП, соответственно симметричная, обратносимметричная и сум¬
марная (односторонняя)^, д, е—расчетная нагрузка, соответственно симметричная,
обратносимметричная и суммарная односторонняя; ж — схема куполаПредставим эту нагрузку изменяющейся по закону кривой, пока¬
янной на рис. 37, д и е:Sinv/sym === T|s0Sin Зф COS tjj,К)1147
где гр — центральный угол в горизонтальной плоскости, отсчиты¬
вающий долготу меридиана от оси симметрии снеговой нагрузки
(рис. 36, б). Половина объема этой нагрузки составляетур = л/2 ф = л/3Sinv/sym = 5 5 sin Зф COS ф Sin ф COS tydydty = 0,52т)5оГ?.i>= — n/2 <p=0После этого определяется величина коэффициента:т| = 0,272г?5о / (0,52r?So)« 0,5.Таким образом, полная несимметричная снеговая нагрузка со¬
ставит:Son = 1,5so cos (ф + я/6) + 0,5so sin Зф cos г|).В правой части этого выражения первое слагаемое — симметрич¬
ная составляющая снеговой нагрузки; второе — обратносим¬
метричная. Обратносимметричная нагрузка и соответственно уси¬
лия N\ и N2 от нее распределяются в горизонтальном сечении
купола пропорционально cos\|).Чтобы определить усилия Nь отсечем от купола верхнюю часть
широтным сечением с углом раствора 2ф и рассмотрим условия
равновесия элементарного сферического сегмента с центральным
углом d\р. Для удобства предположим, что элементарный сегмент
расположен на оси симметрии нагрузки. Тогда cos -ф = 1. Момент
от внешней нагрузки относительно полюса куполафdM = 0,5sor?dt|) \ sin Зф sin2 ф cos фйф =о= 0,5sor? [(3/4) sin4 ф — (4/5)sin6 ф]йф.По условиям равновесияdM = N\r2csin3ф^ф, откуда N\ = 0,5sorc(0,75sinф — 0,8sin3ф)X
Xcos ф. (876)Далее вычисляем нормальную к поверхности оболочки состав¬
ляющую снеговой нагрузки: sn=0,5sosin Зфа^фсоэг!), которая
дает возможность определить кольцевое усилие N2:N2== snr с — N \ = 0,5so/* c(sin ЗфСоз2ф — 0,75 sin ф ++ 0,8sin^)cos -ф. (886)Множитель cos ф отражает закон циклических систем. Полное
усилие N\ от действия снеговой нагрузки получим, суммируя (87а)
и (876), а усилие N2—суммируя (88а) и (886).148
Рис. 38. Воздействие оболочки купола на опорное кольцо
а — вертикальный разрез оболочки; б — план опорного кольца; в — расчетная схема узла
сопряжения опорного кольца и оболочки; 1 — оболочка; 2— опорное кольцо; 3 — осьсимметрииВ сечениях оболочки с углом ф> 60°N\ = — N2 = 0,218s0rc/sin29 + 0,0422s<)rccos,i|) /sin3(p,где* первое слагаемое — от симметричного снега, второе — от
одностороннего.При рассмотрении любого купола вращения, работающего
и условиях безмоментного напряженного состояния, становится
мчгиидно, что воздействие его на опорный контур характеризуется
нпличием двух составляющих силы N\ (рис. 38, а) : вертикальной
и юризонтальной. Горизонтальная составляющая, называемая149
распором, воспринимается полностью опорным кольцом, которое
монолитно связано с оболочкой. В пологом куполе опорное кольцо
обычно попадает выше шва перехода. Поэтому кольцевые усилия
в сечении оболочки, непосредственно примыкающем к кольцу, сжи¬
мающие, в то время как само опорное кольцо растянуто. В связи
с этим, если не принять никаких мер, в сопряжении появляются
меридиональные изгибающие моменты, правда, быстро затуха¬
ющие с удалением от опорного кольца вдоль меридиана (краевой
эффект). Схема действующих в узле сопряжения оболочки с коль¬
цом усилий видна на рис. 38, в. Таким образом, купола, у которых
нет шва перехода, не могут работать как безмоментные. Избежать
влияния краевого эффекта в этом случае можно, если создать
в опорном кольце предварительное обжатие напрягаемой армату¬
рой. В принципе можно выбрать такую величину обжатия, при
которой обеспечиваются равенство кольцевых усилий опорного
кольца и кольцевого волокна оболочки купола. Следует при этом
заметить, что устранение краевого эффекта возможно только для
какой-либо одной определенной нагрузки, например для полной
или только для постоянной. При изменении величины нагрузки
краевой эффект все же проявляется, но в значительно меньших
размерах.Погонный распор купола Hsr определяют как горизонтальную
проекцию N\ :HSr = M,<p,rcos <psr или, с учетом (87),//.r = /4.,/(2jir2sin q>srtg фД (90)где F{v„— полная вертикальная нагрузка на купол; <psr— половина центрального
угла дуги оболочки купола в меридиональном направлении.Распор купола Hsr вызывает в поперечных сечениях опорного
кольца продольные усилия Nsr:N Sr= Hsr? 2 sin (fsr= Fф„ / (2ntg Ф$г)* (91)Продольные усилия Ni, в фонарном кольце незамкнутого купо¬
ла (которое при вертикальной нагрузке всегда сжато), опреде¬
ляются по формулег гNtr= —fg—j^j-rzsin <р,, = -/V2cos <р 1г, (92)где Fu— распределенная линейная нагрузка на 1 м фонарного кольца; г*г— радиус
кольца; <р/г— половина центрального угла раствора дуги оболочки в меридиональ¬
ном направлении на уровне фонарного кольца.В табл. 39 приведены формулы для определения значенийусилий N\t N2, Nsr и /\р при некоторых видах осесимметричной
нагрузки на сферические купола. Как уже отмечалось, для сфери¬
ческого купола п=Г2 = гс. В таблице приняты следующие обозна¬150
чения (кроме упомянутых выше): t — толщина оболочки; г —
радиус параллели (r = r2Sin (p = rcsin ф); ф — переменный угол
в меридиональном сечении оболочки, отсчитываемый от оси вра¬
щения оболочки; Fv— вертикальная равнодействующая внешней
нагрузки на часть оболочки, расположенную выше рассматри¬
ваемого сечения с углом раствора 2ф.Далее разберемся, как определить краевой эффект и как
уменьшить его влияние на условия работы оболочки.Как отмечалось выше, из-за разности знаков усилий в опорном
кольце и в крайнем волокне пологой оболочки купола, примыка¬
ющем к кольцу, в пограничном сечении возникают местные на¬
пряжения, так называемый краевой эффект. Величина усилия
краевого эффекта зависит от жесткости опорного кольца, харак¬
тера взаимного соединения оболочки с кольцом и коэффициента
затухания £, характеризующего ширину кольца оболочки, на ко¬
торую распространяется влияние краевого эффекта. Коэффи¬
циент к для гладкой сферической оболочки можно вычислить
по формуле:&=У rc/t V 3(1 —v2) . (93)Ниже приведены формулы для определения усилий краевого
эффекта на границе заделки сферического купола в опорном коль¬
це при разных опорных условиях.При защемляющей опоре (жесткая заделка оболочки в кольце)
в месте заделки усилия достигают максимальных значений(94)N2=-N'sr; (95)Mi.»ln = -iVJr-£-; (96)Af 2 = vAf,; (97)Q=~iT~ ■ (98)В сечении на расстоянии nrc/2k от края по меридиану нахо¬
дится максимальное значение положительных моментов Mi
(рис. 39, а):Afi.max =0,208Mi,min , (99)151
ТабФормулы для определения усилий152Вид нагрузки и схема
загруженияNiN2Замкнутая1. Собственная масса обо- гс ~~grccostp— Ni
лочкн постоянной толщины 8 i_|_C0S(p2. Собственная масса обо¬
лочки переменной толщины,
изменяющейся по закону2nrcsin(j>" r£cos<p[g,+3. Равномерно распределен¬
ная поверхностная нагрузка _ гс „ г с cos2<p
на горизонтальной проекции 2 2ПТГ1 1 Г (\ ГМ 1 1
л и ц a 39N i, N2, Nsr м Fw в сферических куполах153N„N,Примечаниеоболочкап 1 — COS ф$г
gr‘ tg<ps,2gnrf(l — cosq>)При ф = 51°49' N2 = 0 (шов
перехода)Масса единицы площади обо¬
лочки в пяте go, в ключе g 1г. Ctg(p„2л2яг?<р “^/ g—^ xXr? sin 2m
S 4sjir2 sin2 фПри ф=45° N2 = 0 (шов пе¬
рехода)
Вид нагрузки и схема
загруженияNiN24. Собственная масса обо¬
лочки постоянной толщиныCOS ф if COS ф— grc Z—2 —sin фНезамкнутая
— grccosy — Nid0 1 ^1%%-const5. Равномерно распределен¬
ная поверхностная нагрузка
на горизонтальной проекцииrc /t sin2 ф/г \
s 2 I1 sif.4 )— src ^С082ф +. sin2 ф/г 1 \
2зтф 2 /SПТП | гТтрX* hV'N( X ["/.—31'6. Распределенная линейная
нагрузка на фонарном коль¬
цеc sin ф/г• Ir . A ""sin фr sin ф/г• lr . 2 'Sin Ф\F,ri 1 !*Я к/\( \ г/
Продолжение табл. 39155NsrПримечаниеоболочкаgr2c ctg ф5Г (cos ф 1, — COS ф5г)2 gJir2 (cos ф/r — COS ф)Усилие в фонарном кольце
Ntr=02 8Шф5гС08ф*г ^src 2 Xsnr2 (sin2 ф—sin2 ф i,)Усилие в фонарном кольце
Nu=0x(i 4^)V Sin ф,г /г. - Sin ф/rlr С irrrr,б ф®^2 FirJircУсилие в фонарном кольце
Ntr=— Fur с cos ф/г
Рис. 39. Эпюры меридиональных изгибающих моментов в оболочке купола (крае¬
вой эффект) при разных условиях сопряжения оболочки с опорным кольцом
а — при жесткой заделке; б — при шарнирном соединенииПри шарнирном опирании оболочки на жесткое неподвижное
опорное кольцо:N^N'sr-g=-; (100)Af,=0; N2=-N'sr; (101)м'=т!т^ге; <l02>Q=-N'sr/(2ky, (103)Q = N'srk/(Et). (104)где 0 — угол поворота касательной к меридиану.Наибольшее значение Mi находится в сечении на расстоя¬
нии nrc/(4k) от края по меридиану (рис. 39,6):Mi.„ax=0,161^^r. (105)При проектировании ребристой оболочки можно пользоваться
формулами (94)...(105) только если в формулу (93) вместо зна¬
чения толщины оболочки t подставить значение приведенной
толщины tredy которая учитывает наличие ребер:trea = lj 12It/Sr , (106)где It— момент инерции таврового сечения с шириной полки, равной шагу мери¬
диональных ребер; sr— шаг меридиональных ребер у опорного кольца.В зоне действия краевого эффекта усилия от него должны
суммироваться с усилиями, полученными из расчета безмомент-
ного напряженного состояния.156
Следует отметить, что в практике проектирования куполов
невозможно в месте сопряжения обеспечить ни абсолютно жесткую
заделку оболочки в опорное кольцо, ни чистый шарнир. Обычно
это соединение бывает конечной жесткости, т. е. упругим, поэтому
в зоне действия краевого эффекта рекомендуется подбирать такое
сечение арматуры, чтобы оно удовлетворяло как формулам
(94)...(99), так и (100)... (105).Выше уже говорилось, что путем предварительного обжатия
кольца можно уменьшить влияние краевого эффекта при одно¬
временном удовлетворении условию прочности.Если обжатие опорного кольца выполнить усилием, получен¬
ным от полной расчетной нагрузки на купол, то, например, при
отсутствии снега краевой эффект проявится, но величина его
усилий будет меньше, а знак их поменяется, и дополнительные
кольцевые усилия будут не растягивающие, а сжимающие, что
для железобетона благоприятно. Чтобы уменьшить влияние крае¬
вого эффекта, силу обжатия (площадь напрягаемой арматуры)
опорного кольца следует назначать такой величины, чтобы она,
с учетом потерь, уравновешивала растягивающее усилие в опорном
кольце от полной вертикальной нагрузки и в примыкающем во¬
локне оболочки, т. е.ASp(oSp Asr, redfosr O2)ИЛИASp>Asr,red^ZZ =A°r.red\l. (107)Как видно из выражения (107), отношение разностей напря¬
жений представляет собой не что иное, как коэффициент армиро¬
вания напрягаемой арматурой опорного кольца:-%=£■-* <108)I At* osr = Nsr /Asr,red, 02 = N2/(tb)\ osp — предварительное напряжение в напряга¬
емой арматуре до проявления потерь; asi — суммарные потери в напрягаемой
арматуре, определяемые по СНиП 2.03.01—84.Предварительное сечение напрягаемой арматуры подбирается
•и расчета центрально-растянутого сечения опорного кольца на
прочность по формулеК >Nsr/Rsp, (109)*• штем проверяется по формуле (107).Очение опорного кольца должно быть также проверено на
прочность в момент обжатия до передачи на него усилия от внеш¬157
ней нагрузки и собственной массы купола (предполагается, что
на время натяжения кольцевой арматуры купол опирается на мон¬
тажные леса или другие приспособления):Obp ^AspOsp/^sr, red 0,5 В, (110)где В — класс бетона по прочности на сжатие.2. Конструкция купола и нагрузкиВ качестве покрытия зала диаметром 42 м решено запроекти¬
ровать железобетонный купол. В центре купола требуется устроить
фонарь диаметром d/ = 6 м.Купол сборно-монолитной конструкции, опорное и фонарное
кольца купола — монолитной из тяжелого бетона класса В 30,
причем растянутое опорное кольцо выполняется предварительно¬
напряженным.Оболочка купола собирается из трапециевидных криволиней¬
ных панелей с продольными (меридиональными) ребрами. Сбор¬
ные панели опираются на монолитные кольца купола. Толщина
криволинейной плиты купола принята tCur,Pi = 30 мм, сечение фо-Рис. 40. К расчету сферического купола
а — конструктивная схема; б — эпюры меридиональных (Ni) и кольцевых (Nг) нормаль¬
ных усилий в сечении оболочки от симметричных снеговых (5) и постоянных (g) нагрузок158
Таблица 40Вид нагрузкиНормативноезначениенагрузки,кПаКоэффициент
надежности
по нагрузке
VIРасчетное
значение
нагрузки,
к Г] аСобственная масса купола1,981,12,18Теплоизоляция, пароизоляция,
гидроизоляционный ковер1,01,31,3Итого постоянная3,48Снег1,51,42,1Всего4,481,255,58Всего с учетом коэффициента надежности по назначениюY„=0,955,3В том числе постоянная: 0,95 • 3,483,3нарного сжатого кольца — 200X250 мм, а площадь сечения
опорного растянутого кольца Л5Г=1600 см2.При монтаже купола сборные элементы опираются на под¬
мости, убираемые после натяжения всей напрягаемой арматуры
нижнего кольца. Конструктивная схема купола показана на рис. 40.Бетон для сборных элементов купола принимаем тяжелый,
класса В 25.Нагрузки на купол, принятые в расчете, приведены в табл. 40.
Нагрузка, приходящаяся на 1 м верхнего кольца от собственной
массы фонаря, принята 9 кН/м (нормативная) и 10 кН/м (рас¬
четная). С учетом коэффициента надежности по назначению
нагрузка составляет: нормативная g/n = 0,95 • 9 = 8,6 кН/м; рас¬
четная g/d = 0,95 • 10 = 9,5 кН/м. Нагрузка от симметричного
снега: нормативная sin=yndis/4=0,95 • 6 • 1,5/4=2,1 кН/м, рас¬
четная sid = 2,1 • 1,4 = 3,0 кН/м.3. Геометрические характеристики куполаКупол диаметром dsr = 42 м принимаем в виде тонкостенной
сферической пологой оболочки со стрелой подъема fc = 7 м. Радиус
кривизны оболочки купола при этом составитг с=(г*г + f ?) / (2/с)=(212 + 72) / (2 • 7)=35 м.Значения половины центрального угла дуги оболочки в мери¬
диональном направлении на уровне опорного и фонарного колец
Оулут:sin q>sr = rsr/rc=21/35=0,6; ф*г=36052'12"; cos<psr = 0,8;
*lii ф/г = г/г /гс=3/35=0,0858; ф/г = 4°55'20"; cos ф/л = 0,996.159
4. Определение усилий в куполе
по безмоментной теорииУсилия от симметричной нагрузки в оболочке купола мери¬
диональные N1 и кольцевые N2 вычисляем по формулам табл. 39.
Усилия от постоянной нагрузки у нижнего опорного кольца:^■=_i%ri(0’996 ~0’8)~9’5'2wL= ~65)1 кН/м;N2= -35 • 3,3 (0,8- 0>990У'8 ) + 9,5-^|р-= -27,2 кН/м.То же, у фонарного кольца:^l = _9’5oir=_ 110)7 кН/м;N2= -35 • 3,3 • 0,996 + 9,5-^55-= -4,3 кН/м.Усилия от симметричной снеговой нагрузки у опорного кольца
составят (см. табл. 39, п. 5 и 6):N, (1 _ з,0 = -35,0 кН/м;N,= -2,0 • 35(0,8’—i-+f^)+ 3,0-М|£-= -10,4 кН/м.
То же, у фонарного кольца:N1= 0; N2= -2,0 • 35 • 0,9962 + 3,0-^5g-= -34,5 кН/м.Усилия от односторонней снеговой нагрузки в вершине купола,
условно принимаемого сплошным, будут М = N2= —0,65 • 2,0X
Х35= —45,5 кН/м.Меридиональные усилия у опорного кольца вычисляем по
формулам (87а) и (876):N,= -1,5 • 2,0 • 35(0,29 '"У' -0,167 • 0,6)--0,5 • 2,0 • 35(-|-0,6—g-0,63) • 1 = —40,5 кН/м.То же, кольцевые усилия — по формулам (88а) и (886):N2= —1,5 • 2,0 • 35 • 0,39 • 0,82 —0,5 • 2,0 • 35 • 0,937 • 0,82 +
+40,5= —6,7 кН/м.160
Усилия от односторонней снеговой нагрузки у фонарного
кольца:JV, = -1,5 • 2,0 • 35(0,29 '"ggf -0,167 • 0,0858)-
-0,5 • 2,0 • 35 (-|-0,0858 —1-0,08583)= -50,2 кН/м,
N2= -1,5 • 2,0 • 35 • 0,82 • 0,9962 - 0,5 • 2,0 • 35 • 0,255X
X 0.9962 + 50,2 = —44,1 кН/м.
Усилие в фонарном кольце от полной нагрузки на купол со¬
ставит (см. табл. 39, п. 6): Nu=—(9,5+3,0) • 35 • 0,996 =
= -435,8 кН.
Усилие в опорном кольце от постоянной нагрузки (см. табл. 39,
п. 4):
Nsr= 3,3075—(0,996-0,8)+ 9057535 0,0858=1094,5 кН.То же, от симметричного снега (см. табл. 39, п. 5):Nsr= 2,0 4 352 0,96 (1 - -]fff--)+ 3 о 7535 0,0858 = 588 кН.Сумма усилий в опорном кольце от полной нагрузки: Nsr,tot =
= 1682 кН.5. Подбор арматуры элементов куполовАрматуру криволинейной плиты купола принимаем из расчета
на максимальное усилие. Из статического расчета видно, что
максимальное усилие возникает в меридиональном направлении
оболочки у фонарного кольца от действия постоянной нагрузки
и одностороннего снега: yvl max= 110,7 + 50,5= 161,2 кН/м.Поскольку Gmax = N\,max/{bt) = 161200/(1000 * 30) = 5,4 МПа
меньше Rb= 14,5 МПа, армирование оболочки купола принимаем
конструктивное.Проверка сечения верхнего кольца купола и подбор арматуры
выполняются на сжимающее усилие Nu = 435,8 кН и здесь не при¬
водятся.В предварительно напряженном нижнем опорном кольце дей¬
ствует растягивающее усилие 7VSr= 1682 кН. Выполним расчет
этого кольца. В качестве напрягаемой арматуры принимаем стерж¬
невую арматуру класса A-IV с расчетным сопротивлением растя¬
жению RS = 510 МПа и нормативным Rsser = 590 МПа.I I Заказ 61161
Натяжение стержней осуществляется на бетон электротерми¬
ческим способом. Необходимая площадь поперечного сечения
этой арматуры из расчета по прочности по формуле (109): Asp =
= 1682000/510 = 3298 мм2. Принимаем арматуру из 8 0 25AIV,
площадь ее составляет Asp = 3927 мм2.Вычислим площадь приведенного сечения опорного кольца:Asr.red= 160000 + 3927(190/32,5- 1)= 179000 мм2.Предварительное напряжение asp в напрягаемой арматуре
назначаем с учетом допустимых отклонений р от значения пред¬
варительного напряжения, чтобы выполнялись условия
0,3R$, ser Р ^ ^sp ^ Rs, ser Р*Для стержневой арматуры при электротермическом способе
натяжения на бетон р = 30+ 360//= 30+ 360/(3,14 • 42) = ЗЗМПа.
Принимаем р = 40 МПа, a osP=550 МПа. Далее вычисляем потери
напряжений в напрягаемой арматуре.Первые потери составляют: от релаксации напряжений арма¬
туры 0,lasp —20 = 35 МПа; от усадки бетона — 30 МПа. Итого
первые потери 35 + 30 = 65 МПа.В качестве вторых потерь учитывается только ползучесть
бетона: а*р = (550-65) • 3927/179000= 10,6 МПа; Rbp = 0,5 • 30 =
= 15 МПа. При obp/Rbp= 10,6/15 = 0,707<0,75 эти потери вычис¬
ляются по формуле 150а(аЬр/Rbp)= 150 • 0,707= 106 МПа, где
a — коэффициент, принимаемый для бетона естественного тверде¬
ния равным 1. Таким образом, суммарные потери напряжений
as/=65+ 106= 171 МПа.Вычисляем кольцевые напряжения в оболочке на уровне опор¬
ного кольца:от постоянной нагрузки a2= —N2/tb= —27200/(30 • 1000) =
= -0,9 МПа;от снега а2= — 10400/(30 • 1000)=—0,35 МПа;от полной нагрузки а2=—(0,9 + 0,35)=—1,25 МПа.Теперь определим напряжения в опорном кольце от полной
расчетной нагрузки на купол: Qsp = Nsr/Asr red= 1682000/179000 =
= 9,4 МПа.Необходимую площадь напрягаемой арматуры, обеспечива¬
ющую безмоментное состояние оболочки купола, найдем из услот
вия равенства напряжений, действующих в кольце и в оболочке.Сначала вычислим минимальный коэффициент армирования
по формуле (108): |ш = (9,4 — 1,25)/(550— 171) = 0,0215, после чего
по формуле (107) определим необходимую площадь арматуры:
j4Sp=0,0215 • 179000 = 3849 мм2. Принято Asp = 3927 мм >
>3849 мм2.Следует также проверить прочность сечения опорного кольца
на действие силы обжатия напрягаемой арматурой в момент от¬162
пуска натяжения до передачи на него растяжения от нагрузок
на купол (сборные панели еще поддерживаются подмостями)
и с учетом первых потерь напряжения.Величина напряжений в бетоне в этом случае будет:аЬр= А--а~Т'] = 329?7ОТ00 65) =8’9 МПа< 15 МПа-
Следовательно, сечение опорного кольца достаточное.6. Определение усилий краевого эффектаДаем без вычислений приведенную к прямоугольной толщину
оболочки купола с меридиональными ребрами по формуле (106):
tred = 0,0675 м. По формуле (93) определим коэффициент затуха¬
ния &, характеризующий величину зоны купола, в которой дей¬
ствуют краевые изгибающие моменты:k—^j 35/0,0675 V3"=30.Шаг меридиональных ребер купола у опорного кольца 3 м, а коэф¬
фициент Пуассона принят равным нулю.Определим напряжения, действующие в опорном кольце после
его обжатия и приложения постоянных нагрузок:_ _ Nsr-Asp(asp-osl) _ 1094500-3927(550-171) _ ООМПл°8Г “ Asr,red ~ 179000 — М11а-То же, после приложения всей нагрузки на купол:1682000-3927(550-171) , . мп
Gsr 179000 ’ Mlia.Теперь вычислим кольцевое усилие в оболочке на границе с
опорным кольцом (в месте заделки) от полной нагрузки на купол:Nsr=-{a2-Osr)tb= -(-1,25 +1,1)30 • 1000 = 4,5 кН/м.Усилия в результате краевого эффекта в этом же сечении
для случая полного защемления оболочки в опорном кольце вы¬
числим по формулам (94)...(96):N, = -5,7 -0,8/(30- 0,6)= -0,25 кН/м; N2=-5J кН/м;Afi min = —5,7 • 35/(2 • 302)= —0,11 кН • м/м.и*163
Для этого же сечения, но в случае шарнирного опирания обо¬
лочки на жесткое опорное кольцо, усилия находим по форму¬
лам (100) ... (104):yV, =5,7 • 0,8/(2 • 30 • 0,6) = 0,13 кН/м; Л^2= —5,7 кН/м.Сечение, где действует максимальный изгибающий момент
в меридиональном направлении, находится на расстоянии
3,14 • 35/(4 • 30) = 0,9 м от линии примыкания оболочки к кольцу,
а величина этого момента вычисляется по формуле (105):Ml,шах =0,161 • 5,7 • 35/302 = 0,4 кН • м/м.По этим же формулам вычисляем усилия от действия краевого
эффекта при работе купола только на постоянные нагрузки, т. е.
при отсутствии снега.Усилия для варианта полного защемления оболочки в кольце:N'sr = — (—0,9 — 2,2) • 30 • 1000 • 10~3 = 93 кН/м;Ni = -93 • 0,8/(30 • 0,6)= -4,1 кН/м; N2= -93 кН/м;
vVfi = —93 • 35/(2 • 302)= —1,8 кН • м/м.164
То же, для варианта шарнирного опирания:Ni = -93 • 0,8/(2 • 30- 0,6)= -2,1 кН/м; N2= -93 кН/м;
М^ах =0,161 • 93 • 35/302 = 0,6 кН • м/м.На полученные усилия от действия краевого эффекта рассчи¬
тываются ребра купола. Проверка сечений ребер купола здесь
не приводится.7. Некоторые положения по конструированию
куполовМонолитные купола проектируются, как правило, гладкими.
Толщину их стенок обычно принимают в пределах 1/800... 1/600
радиуса кривизны оболочки в вершине, но не менее 50 мм. В зоне
Примыкания к опорному кольцу, где действует краевой эффект,
толщину стенки следует плавно увеличивать. Армирование глад¬
ких стенок толщиной до 70 мм, как правило, выполняют конструк¬
тивно в виде одиночной сетки из.стержней диаметром 4...5 мм,
но при большей толщине во избежание усадочных трещин стенкиРис. 41. Конструирование элементов куполов
а — сопряжение в монолитном куполе оболочки
с опорным и фонарным кольцами и армирование
монолитного купола; б — жесткое сопряжение
сборной ребристой оболочки купола с опорным
и фонарным кольцами; в — то же, шарнирное со¬
пряжение; г — ребристая панель сборного купола
(слева — армирование, справа — опалубочный
вид); /—оболочка купола; 2—опорное кольцо;3 — фонарное кольцо; 4 — предварительно на¬
пряженная арматура; 5 — бетон омоноличивания;6 — стальные закладные детали; 7 — соединитель¬
ные детали, привариваемые на монтаже к заклад¬
ным; 8 — ось симметрии165
купола армируют двумя сетками. В приконтурной утолщенной
зоне всегда предусматривают двойную арматуру (рис. 41, а). Кри¬
волинейную плиту монолитных куполов обычно армируют отдель¬
ными стержнями, которые укладывают в меридиональном и коль¬
цевом направлениях. Шаг кольцевой арматуры принимают
150...200 мм. Расстояние между меридиональными стержнями
внизу, у опорного кольца, обычно 200 мм. По мере приближения
к вершине это расстояние уменьшается, и когда оно становится
равным 100 мм, один из двух стержней обрывается, стержней
остается вдвое меньше, но с шагом 200 мм и т. д. При этом надо
обеспечивать нормативную величину нахлестки стержней в стыках.
Вблизи опорного кольца, в утолщенной зоне, арматура ставится
в меридиональном направлении по расчету на восприятие опорного
изгибающего момента. Диаметр ее 6...8 мм. Арматурные стержни
меридионального направления заделываются в опорное и фонар¬
ное кольца на длину анкеровки по нормам.Сборные купола конструируют из ребристых панелей (рис. 41, б)
сборного, сборно-монолитного или монолитного опорного кольца.Конструкция панелей зависит от схемы разрезки оболочки
и от диаметра купола. Толщина плиты определяется условиями
размещения арматуры и нормативной толщиной защитных слоев.
Обычно толщину плиты сборных панелей не назначают менее
30 мм. Размеры сечений ребер панелей диктуются условиями устой¬
чивости купола в стадии эксплуатации, а также требованиями
по изготовлению, транспортировке и монтажу. Поверхность пане¬
лей рекомендуется делать криволинейной только в одном направ¬
лении — меридиональном. При разрезке оболочки на мелкие пане¬
ли их целесообразно делать плоскими. Плита панелей армируется
сварной сеткой из стержней диаметром 3...4 мм с ячейкой
200X200 мм. Ребра армируются сварными каркасами. Панели
следует соединять между собой, а также с опорным и фонарным
кольцами сваркой закладных деталей (рис. 41,6). При монолит¬
ных кольцах арматура меридиональных ребер заводится в них
на длину анкеровки. В приконтурной зоне арматура меридиональ¬
ных ребер проверяется из условия восприятия краевых изгиба¬
ющих моментов при расчетной нагрузке.При сборном опорном кольце продольная арматура его эле¬
ментов должна иметь выпуски для соединения их сваркой, если
кольцо из обычного железобетона, или внахлестку без сварки, если
после замоноличивания предусмотрено предварительное напря¬
жение. Предварительное напряжение опорного кольца можно
выполнять электротермическим или электротермомеханическим
способом при стержневой арматуре или путем обмотки его с по¬
мощью карусельной машины при арматуре из высокопрочной тон¬
кой проволоки. Могут быть и другие способы натяжения кольце¬
вой арматуры, но они менее индустриальны.166
VII. РАСЧЕТ ПОЛОГИХ ОБОЛОЧЕК
ОТРИЦАТЕЛЬНОЙ ГАУССОВОЙ КРИВИЗНЫОболочки, срединная поверхность которых имеет отрицатель¬
ную гауссову кривизну, называются гиперболическими парабо¬
лоидами (гипар). У таких оболочек центры кривизны всех нор¬
мальных сечений, проведенных через рассматриваемую точку
поверхности, лежат на нормали с разных сторон поверхности.Гипары обладают многими положительными свойствами: с кон¬
структивной стороны они привлекательны линейчатостью поверх¬
ности, с архитектурной стороны — возможностью создания огром¬
ного числа оригинальных форм и их сочетаний. Наконец, одно
из главных свойств таких поверхностей — отсутствие крученияd'*z(в каждой точке поверхности смешанная производная ^--=0)
существенно облегчает их расчет.В практике строительства широкое распространение получили
в основном два типа гипаров.Гипар первого типа имеет поверхность, отнесенную к его
главным осям. Эта поверхность описывается уравнением относи¬
тельно осей координат, параллельных осям гиперболы, и имеет
начало координат в вершине (рис. 42, а):(»•>Если оболочка очерчена по поверхности гиперболического
параболоида над прямоугольным планом со сторонами 2а и 2b
и задается параболой, выпуклой кверху со стрелой f 1 над сторо¬
ной 2а, и параболой, выпуклой книзу со стрелой провеса /г под
стороной 26, уравнение (111) принимает вид (рис. 42, б)2=^1(‘5“) ^2(тг) • (112)Главные параболы этого гипара лежат в плоскостях XZ и YZ,
называемых плоскостями ортогональной симметрии параболоида,
и описываются уравнениями2=/i(x) > 2=—/2(х) ' <113)Второй тип оболочек — это гипары, поверхность которых отне¬
сена к асимптотам горизонтальных гипербол. Для этого принятую
систему прямоугольных координат (рис. 42, в) трансформируют167
Рис. 42. Геометрия гиперболических параболоидов
а — поверхность гиперболического параболоида; / — главные параболы; 2— асимптоты;
б — поверхность гиперболического параболоида, отнесенного к главным осям; в — пре¬
образование прямоугольной системы координат в косоугольную и гипербола, отнесенная
к косоугольным координатам асимптот (XOY и X»OY•—соответственно старая и новая
системы координат); г — поверхность четырехлепесткового гиперболического параболоида,
отнесенного к асимптотам; д— геометрия лепестка гипарав косоугольную координатную систему, у которой вертикальную
ось OZ сохраняют, а новые оси Я* и У* направляют по асимптотам
горизонтальных гипербол так, чтоx = cosa(xm+yJ; y = sin а({/*—хф).Поверхность этого гипара описывается уравнением относитель¬
но осей координат, направленных по асимптотам с началом коор¬
динат в вершине, и имеет видz=-^rX.y.. (114)Если учесть, что асимптоты равностороннего гиперболического
параболоида расположены взаимно перпендикулярно, то уравне¬
ние поверхности четырехлепестковой оболочки (рис. 42, г) с двумя
взаимно перпендикулярными коньками можно записать так:г=^ьх°У°' (115)168
где ось OZ направлена вниз и проходит через точку пересечения
коньков, а коньки являются осями ОХ о и OYo.При проектировании, как правило, возникает необходимость
в определении площади поверхности гипара. Для гипара, урав¬
нение которого отнесено к главным осям, площадь поверхности,
с достаточной для практики степенью точности, может быть вы¬
числена по формулеAsh.sur^4ab[\+-L(^+-^)\ (116)Если же уравнение гипара отнесено к асимптотам, то площадь
его поверхности составитAsh,sur=ab[ 1 (117)А. РАСЧЕТ ГИПЕРБОЛИЧЕСКОГО ПАРАБОЛОИДА,
ОТНЕСЕННОГО К АСИМПТОТАМ1. Основные сведения о конструкциях
и принципах расчетаЭти оболочки представляют собой квадратные или прямо¬
угольные панели («скрученные» прямоугольники), как правило,
с ребрами по контуру, которые всегда прямолинейны. В покрытиях
зданий применяются как однолепестковые, так и многолепестковые
гипары. Такими конструкциями можно перекрывать пролеты до
70 м и более.Конструкция покрытия может иметь по контуру или по диаго¬
налям затяжки для обеспечения общей неизменяемости системы.
При небольших пролетах покрытия ребра панелей служат одно¬
временно контурными элементами. При значительных пролетах
панели укладывают обычно на треугольные фермы и предусматри¬
вают меры, обеспечивающие их совместную работу.Оболочки могут опираться по контуру также на ряд стоек.
В зависимости от взаимного расположения оболочек при действии
равномерно распределенной нагрузки в контурных элементах и
коньковых балках возникают сжимающие либо растягивающие
усилия.Расчет гипаров приближенно может производиться по безмо¬
ментной теории. Для этого в дифференциальных уравнениях (40),
выражающих равновесие элемента пологой оболочки под дей¬
ствием вертикальной распределенной нагрузки, нужно неизвест¬
ную функцию Ф найти из уравненияд2Ф d2z ^ д2Ф d2z | д2Ф d2z \ р ^ /1 iq\-dF-d?-2dxdy dxdy+-a^W+Fz=0- (1 8)169
Для равностороннего гипара, отнесенного к асимптотам,—=—=0- д*г (119)дх2 ду2 ' дхду ^ ab • г11*'Тогда уравнение (118) принимает видд2Ф 2Л _ р
дхду ab ~~ *ИЛИQ„ = /vg-. (120)Таким образом, сила сдвига постоянна по всей срединной по¬
верхности оболочки.Опуская выкладки, отметим, что усилия N\ и N2 являются
в этой оболочке функциями, зависящими только от одной орди¬
наты. Так, усилия N\ действуют параллельно оси X, зависят только
от у и для какой-то определенной ординаты у имеют постоянное
значение по всей длине оболочки.Эпюра для N2 аналогична. Если допустить, что контур гипара
абсолютно податлив из плоскости, то нормальные усилия здесь
обращаются в нуль, а следовательно, они равны нулю и по всей
срединной поверхности оболочки. Таким образом, под действием
вертикальной равномерно распределенной поверхностной нагруз¬
ки напряженное состояние гипара характеризуется только сдви¬
гающими усилиями постоянной интенсивности. Из этого следует,
что главные напряжения равны по интенсивности сдвигающим,
но направлены под углом 45° к ним, т. е. совпадают с направле¬
ниями главных парабол. По направлению выпуклой параболы
действуют сжимающие усилия, а по направлению вогнутой —
растягивающие.Нагрузкой на контурные элементы является собственная масса
(если они выполняются в виде самостоятельных ферм) и опорное
давление оболочки, передаваемое в виде сдвигающих сил. Эти
силы равны по величине и обратны по направлению силам сдвига,
действующим в оболочке на контуре. В результате контурные
элементы гипара испытывают сжатие или (в некоторых системах)
растяжение. Система, принятая для расчета в этом примере, со¬
стоит из четырех конгруэнтных гипаров. Контурные элементы
(ребра панелей) сжаты; при этом наклонные сжаты в направлении
к опорам (причем величина силы сжатия изменяется от нуля
в коньке, на оси симметрии системы, до максимального значения
у опоры), а коньковые (горизонтальные) —в направлении к оси
симметрии (причем сжимающие силы достигают максимума в
центре системы).170
Максимальная величина силы сжатия в контурных ребрах
гипаровNmax = Qsfl, (121)где / — длина соответствующего ребра гипара.Усилия в контурных затяжках (распоры) найдем из условия
равновесия соответствующего опорного узла как горизонтальную
составляющую силы сжатия в наклонном ребреН = N max С OS ОС, (122)где а — угол наклона соответствующего ребра; Nmax—продольная сила в этом
ребре.Главные растягивающие усилия Npr,t в плите оболочки пол¬
ностью воспринимаются арматурой.Стержни арматуры укладываются не по направлениям пара¬
бол, а по прямым линиям — направляющим и образующим гипара.
Поэтому в каждом направлении арматура воспринимает не все
усилия Npr,ty а только его проекцию на данное направление, т. е.As = Ns/Rs = Npr,tcos450/Rs = Qsf cos 45°/Rs. (123)Прочность сечений четырехлепесткового гипара на действие
вертикальной симметричной нагрузки можно также проверить,
рассчитав конструкцию как трехшарнирную арку с затяжкой
известными методами строительной механики. Расчет этот приво¬
дится в примере.При несимметричных нагрузках систему следует рассчитывать
по более точной моментной теории.2. Конструкция оболочки четырехлепесткового
гипара и нагрузкиДля покрытия цеха с сеткой колонн 6X18 м применены четы¬
рехлепестковые гиперболические параболоиды, представляющие
собой пологую оболочку отрицательной гауссовой кривизны, от¬
несенную к асимптотам (рис. 43, а). Стрела подъема оболочки
/*л = 2 м. Оболочка выполняется сборной из^четьфех плит. Каждая
плита является скрученным прямоугольником с номинальным раз¬
мером 3X9 м. Плиты по краям окаймляются ребрами. Учитывая
небольшой пролет оболочки, гипары выполняются в виде распор¬
ной конструкции без отдельных контурных элементов. Возника¬
ющий распор воспринимается предварительно-напряженными же¬
лезобетонными затяжками. Для обеспечения надежного восприя¬
тия сдвигающих и продольных усилий стыки плит выполнены
со шпонками, расположенными на наружной поверхности контур¬
ных ребер. Толщина криволинейной плиты принимается 30 мм.171
Рис. 43. Схема четырехлепесткового гиперболического параболоида
а — схема оболочки; б — схема оболочки как трехшарнирной системы; в — сечение всреднем шарниреГеометрические размеры и армирование контурных ребер назнача¬
ются из условий монтажа. Оболочка выполняется из тяжелого
бетона класса В 25.Рассчитываем гипар на действие равномерно распределенной
симметричной нагрузки. Величины нагрузок приведены в табл. 41.3. Расчет по безмоментной теорииОпределяем погонное сдвигающее усилие по формуле (120):
Qsf = 3,7 • 3 • 9/(2 • 2) = 25,0 кН/м.Вычисляем главные напряжения. Они по интенсивности равны
сдвигающим и направлены под углом 45° к ним, т. е. параллельны
направлениям главных парабол. Напомним, что по направлению
выпуклой параболы действуют сжимающие напряжения, и по на¬
правлению вогнутой — растягивающие:т = орг,t = Qsf/tb = 25000/(30 • 1000) = 0,83 МПа</?*,= 1,0 МПа.Армирование гипаров выполняется сварной сеткой из холодно¬
тянутой проволоки 04Вр1 с расчетным сопротивлением растяже-172
Таблица 41Вид нагрузкиНормативноезначениенагрузки,кПаКоэффициент
надежности
по нагрузке
Y/Расчетноезначениенагрузки,кПаСобственная масса оболочки1,331,11,46Теплоизоляция, пароизоляция,0,81,31,04гидроизоляционный коверИтого постоянная2,132,5Снег1,01,41,4Всего:3,133,9Всего с учетом коэффициента
надежности по назначению у„ =
= 0,953,7нию Rs = 365 МПа. Стержни сетки располагаем по прямолинейным
образующим и направляющим поверхности. Стержни каждого
направления должны быть рассчитаны на восприятие полных
растягивающих усилий.Получим необходимую площадь сечения этой арматуры на1 м плиты каждого направления:Asl=As2 = QSfcos45°/Rs = 25000 • 0,707/365 = 48,4 мм2.Сетка из стержней 0 4 мм с шагом 200 мм в каждом направ¬
лении имеет j4s = 62,8 мм2, т. е. установлена с запасом. Армиро¬
вание нижних (опорных) углов гипаров косыми стержнями в
данном случае не требуется.Наклонные контурные ребра панелей гипара рассматриваемой
оболочки в результате передачи на них сдвигающих усилий с кон¬
тура криволинейных плит оболочки испытывают продольное сжа¬
тие, равное нулю в коньковом сечении и максимальное у опорного
сечения оболочки. Горизонтальные ребра имеют максимальное
сжатие в центре оболочки. Вычислим усилия в наклонных ребрах
по формуле (121) :Nh.n,ax = 25,0V92 + 22 =230,5 кН; ЛГи.т« = 25,0V32+22 =90,1 кН.То же, в горизонтальных (коньковых) ребрах оболочки:
Ыы,та* =25 • 9 = 225 Кн; Nb2,max=25-3 = 75 кН. В контурных
затяжках растягивающие усилия определяем из условия равно¬
весия опорного узла по формуле (122): Н\ =230,5 • 0,976 =
=225 кН; #2 = 90,1 • 0,832 = 75 кН.Расчеты сечений ребер и затяжек выполняются по соответ¬
ствующим пособиям и здесь не приводятся.173
4. Расчет четырехлепесткового гипара
как трехшарнирной системы с затяжкойРассмотрим четырехлепестковую оболочку как трехшарнир¬
ную плоскостную систему, в которой от вертикальной равномерно
распределенной симметричной нагрузки возникают сжимающие
усилия в контурных ребрах и растяжение в затяжке. Кроме того,
нагрузка вызывает поперечные изгибающие моменты (рис. 43, б).Если за нулевую точку принять сечение в шарнире арки, то
уравнение изгибающих моментов будет иметь следующий вид:
Мх = 0,Об/7 • х(а—х\ где нагрузка F = 3J • 6 = 22,2 кН/м.Момент сопротивления складки (рис. 43, б, сеч. 1—/) также
изменяется от нуля (условного) до максимального значения на
опоре по следующему закону (контурные ребра условно не учиты¬
ваются, что идет в запас прочности):Wx = tlxfshx/За.Если подставить в эту формулу известные величины, то по¬
лучимГ,=0,001*745+* м3; Мх= 11,1*(9,0-*) кН • м.Имея изгибающий момент и момент сопротивления, получим
выражение для нормальных напряжений в крайних волокнах
складчатого профиляах =-w-= И-|дс(9’°~^ = 11100-(-:-—L .0,001*745 + * У45+7Отсюда следует, что максимальные нормальные напряжения
в складчатом профиле арки от равномерно распределенной сим¬
метричной нагрузки возникают в сечении, где х = 0, т. е. в сечении,
где расположен средний шарнир. Это сечение мы и проверим
на возникающие в нем усилия, причем в данном случае ребра
в расчете будем учитывать (рис. 43, в). Так как в сечении, где х =
=0, есть шарнир и, следовательно, изгибающий момент здесь равен
нулю, то расчет выполним на действие условного момента, вычис¬
ленного в сечении на расстоянии х = 0,5 м от шарнирного сечения.Усилие в наклонных продольных ребрах складки: Nb =
= 2ЛГм,тах = 2 • 230,5 = 461 кН.Условный изгибающий момент при х = 0,5 м: М = 11,1Х
X0,5(9,0 — 0,5) = 47,2 кН • м.Эксцентриситет продольной силы при этих условиях составит
(см. рис. 43, в) : е0 = 47200/461 = 102 мм, е = 338 — 40 = 298 мм.Принимая во внимание большую жесткость панелей оболочки,174
расчет ведем по недеформированной схеме, а значение коэффи¬
циента г), учитывающего влияние прогиба на величину эксцентри¬
ситета продольного усилия еоу принимаем равным 1.В ребрах установлена арматура 4 0 16AIII общей площадью
Л* = 804 мм2, Rb = 14,5 МПа.Определяем высоту сжатой зоны сечения показанного на
рис. 43, в, при этом сечением сжатой арматуры пренебрегаем:N + RgAs _ 461 • 103 + З65 • 804 _0 п
Х~ Rb Ь ~~ 14,5 -6000 —о,/ ММ.Так как х = 8,7 мм <£/?Ло = 0,604 • 260=157 мм, то прочность
сечения определяем из условияRbbx(ho — 0,5x)=l4,5 • 6000 • 8,7(260-4,4) == 193 • 106 Н • мм = 193,0 кН • м;Ne = 461 • 103 • 298=137,378 • 106 Н • мм= 137,4 кН • м.Поскольку несущая способность поперечного сечения складки
больше действующего в сечении усилия, то прочность сечения
обеспечена.5. Принципы армирования гипаров,
отнесенных к асимптотамЭти гипары представляют собой пропеллерообразные конструк¬
ции в виде скрученного квадрата, прямоугольника или параллело¬
грамма. Они применяются обычно как сборные панели целых
систем. Разрезка на панели осуществляется по направлению пря¬
молинейных образующих и направляющих. Гипары могут выпол¬
няться и монолитными, особенно для уникальных сооружений.
Толщина монолитных плит должна быть не менее 50 мм. В сборном
варианте панели окаймляются по периметру ребрами. Геометри¬
ческие размеры и армирование ребер назначают, как правило, из
условий перевозки и монтажа. В смонтированной многолепестко¬
вой оболочке совпадение фактически собранной поверхности с ис¬
ходной достигается за счет устройства швов замоноличивания
переменной толщины. На наружных поверхностях ребер, окаймля¬
ющих панель, предусматриваются чередующиеся выступы и впа¬
дины, чтобы бетон замоноличивания образовывал шпонки. Шпон¬
ки должны быть рассчитаны на срез и на смятие от силы сдвига,
действующей в стыке между панелями. По линии примыкания
плиты к ребрам следует предусматривать плавный вут. Толщина
плиты сборных панелей назначается по условиям размещения
арматуры с необходимыми по толщине защитными слоями бето-175
б)Рис. 44. Схема армирования сборного гипара, отнесенного к асимтотам
а — сборное покрытие в виде четырехлепесткового гипара; б — панель в виде скрученного
пропеллерообразного прямоугольникана. В зависимости от класса бетона плиты обычно принимаются
толщиной 25...30 мм. Арматурные стержни располагают в плите,
используя линейчатость поверхности, по прямолинейным образу¬
ющим и направляющим (рис. 44). Для армирования плит приме¬
няют плоские сварные одиночные сетки из холоднотянутой прово¬
локи диаметром 3...5 мм с ячейкой 150X150 или 200X200 мм.
Если требуется по расчету, нижние углы (у опор) однолепестковых
и многолепестковых гипаров армируются косыми стержнями для
восприятия главных растягивающих усилий. Эти стержни имеют
криволинейное очертание и укладываются под основную сетку.
Угловая зона плиты в этом случае утолщается. Стержни сетки,
армирующей плиту, в том числе и косые, следует заводить в
окаймляющие ребра или предусматривать для этой цели специаль¬176
ные гнутые углом стержни. Ребра панелей армируются плоскими
прямолинейными сварными каркасами. В пересечении ребер сле¬
дует устанавливать не менее двух уголковых стержней диаметром
не менее половины диаметра рабочего стержня каркаса и не ме¬
нее 8 мм. Для соединения со смежными панелями в углах предусма¬
тривают закладные детали.Затяжки распорных гипаров небольших пролетов можно вы¬
полнять стальными, в частности из стержневой арматуры. При боль¬
ших пролетах затяжки выполняют железобетонными предвари¬
тельно напряженными. Чтобы обеспечить безмоментное состояние
плиты, затяжки в опорных узлах следует тщательно центрировать.Б. РАСЧЕТ ГИПЕРБОЛИЧЕСКОГО ПАРАБОЛОИДА,
ОТНЕСЕННОГО К ГЛАВНЫМ ОСЯМ1. Некоторые сведения о седлообразных
панелях-оболочках и их расчетеСведения о геометрии поверхности этой оболочки изложены
в предыдущем примере.Гипары, отнесенные к главным осям, так называемые седло¬
образные конструкции, представляют собой панель-оболочку и,
как правило, применяются в многоволновых покрытиях зданий.
Широкое распространение в строительной практике получили
гипары с отношением сторон а/6 ^4 для пролетов 2а равных
от 9 до 24 м. Панель-оболочку гипар обрамляют продольными
бортами и иногда торцевыми диафрагмами (вертикальными или
наклонными), имеющими горизонтальные грани понизу для опира-
ния на нижележащие конструкции (стены, подстропильные бал¬
ки и пр.). Панели применяют как для однопролетных, так и для
многопролетных зданий. При больших пролетах, чтобы исключить
распор панели-оболочки проектируют с затяжками или с ребром
по продольной оси (так называемые килевые панели-оболочки).Гипары целесообразно делать предварительно напряженными
с расположением напрягаемой арматуры вдоль прямолинейных
образующих. При этом классически используется удобное для
этой цели свойство поверхности гипара, обладающего двумя
пересекающимися семействами прямолинейных образующих.Обычно поверхность гипара принимают с таким расчетом,
чтобы в середине пролета центр тяжести напрягаемой арматуры
совпадал с центром срединной поверхности оболочки (началом
координат), а у опор — пересекал центр тяжести поперечного
сечения (рис. 45, а). В таком случае положение центров тяжести
напрягаемой арматуры относительно криволинейной оси панели-
оболочки изменяется по закону параболы, по которому изменяется12 Заказ 61177
лг=/Рис. 45. К расчету панелей-оболо-
чек гипар, отнесенных к главным
осяма — вид панели-оболочки (к расчету в
продольном направлении) — уподобле¬
ние пологой арке с затяжкой; б —
то же, прямолинейной балке с криволи¬
нейной напрягаемой арматурой; в —
элемент оболочки единичной длины
(к расчету на усилия поперечного на¬
правления); / — геометрическая ось
панели; 2 — ось равнодействующей на¬
прягаемой арматурыи эпюра балочных моментов от симметричной распределенной
нагрузки, что дает определенные преимущества.В продольном направлении панель-оболочка рассчитывается
как пологая арка с затяжкой (рис. 45, а) или как простая балка
с криволинейной напрягаемой арматурой (рис. 45, б) и криволи¬
нейным поперечным сечением. При этом, как будет показано
ниже, в расчете учитываются особенности формы поверхности
гипара. Расчет гиперболических панелей-оболочек в продольном
направлении на действие вертикальных нагрузок производится
из предположения о недеформируемости контура поперечного
сечения оболочки.Площадь сечения напрягаемой арматуры предварительно опре¬
деляют из расчета по прочности и увеличивают ее на 20...25%,
что, как показывает опыт, необходимо для обеспечения трещино¬
стойкости.Сечение рабочей продольной арматуры определяется из фор¬
мулыMdjot>AsRskho. (124)Коэффициент k ориентировочно принимают равным 0,85.При проверке принятых размеров поперечного сечения и арми¬
рования панели-оболочки высоту сжатой зоны бетона х опреде¬
ляют методом подбора путем решения уравнения длины дуги
в растянутой зоне сечениях1ы= 5-у1 + (£)* dx. (125)178 0
Расчет по прочности сечений, наклонных к продольной оси,
выполняют для упругой стадии работы конструкции. Сечения
поперечной арматуры определяют из расчета на растягивающие
напряжения, действующие под углом 45° к образующей:а4 5= — (Ji/2 + т, (126)где а|— нормальные напряжения в бетоне от предварительного обжатия сечения
напрягаемой арматурой с учетом потерь; т — касательные напряжения, вычисля¬
емые по формулеx = QS/2It. (127)Расчеты по образованию и раскрытию трещин и по деформа¬
циям проводятся согласно действующему СНиП.В зоне действия максимальных изгибающих моментов при
неравномерной нагрузке оболочка должна быть проверена на дей¬
ствие усилий поперечного направления. В поперечном направ¬
лении рассчитывается отдельно стоящая панель-оболочка, не име¬
ющая креплений с соседними волнами. При этом панель-оболочка
рассматривается как пологая арка с абсолютно жесткой затяжкой
(предварительное напряжение позволяет принять эту гипотезу).Известно, что в сечениях пологих арок, очерченных по квад¬
ратной параболе или по кривой, близкой к ней по очертанию и
с постоянным или мало изменяющимся по пролету поперечным
сечением, сплошная равномерная симметричная нагрузка вызыва¬
ет только продольные силы, которые и уравновешивают полностью
внешнюю нагрузку. Изгибающие моменты и поперечные силы
в таких арках несущественны и их можно принять равными нулю.
Можно утверждать, что поперечные изгибающие моменты воз¬
никают в результате действия в сечениях сил сдвига, которые
сами являются следствием существования поперечных сил. По¬
этому надо обеспечить прочность гипара в поперечном направле¬
нии от нагрузки, которая вызывает поперечные силы. Такой на¬
грузкой является несимметричная односторонняя вертикальная
нагрузка, в частности снег. Для удобства расчета имеет смысл
одностороннюю нагрузку рассматривать как сумму симметричной
и обратносимметричной нагрузок. Именно при обратносимметрич¬
ной нагрузке отсутствует распор, и в арке, как в балке, возникают
только изгибающие моменты и поперечные силы. Таким образом,
внешнюю нагрузку в данном случае уравновешивают именно
сдвигающие усилия, а конкретно — их приращения.Из условия равновесия элемента гипара длиной, равной еди¬
нице (рис. 45, в) видно, что сдвигающие силы по обеим сторонам
полоски одинаковы по величине и обратны по направлению. Ве¬
личина их меняется пропорционально поперечной силе, т. е. зави¬
сит от места сечения в пролете, где вырезана элементарная по¬
лоска. Что же касается приращения сдвигающих сил, то при12'179
Рис. 46. К расчету седлообразной панели-оболочки
а — поперечное сечение панели; б — расположение напрягаемой арматуры панели в плане;
в — условная расчетная схема панели как арки с затяжкой под действием односторонней
или обратносимметричной нагрузки; г — эпюра приращения сдвигающих усилий в попереч¬
ном сечении; д — расположение ненапрягаемой арматуры (сеток) в поперечном сечениипанелиЦентр тяжести
/ сечения
нагрузке постоянной интенсивности (а именно такую мы рассмат¬
риваем) величина приращения также постоянна, т. е. не зависит
от места расположения сечения в пролете. Распределение сдви¬
гающих сил Qsf и, следовательно, их приращений &QSf по попереч¬
ному сечению оболочки принимается по закону Журавского(128)Поперечный изгибающий момент Mt в сечении панели-оболоч¬
ки определится из условия равновесия моментов от внешней
нагрузки Mf и от приращений сил сдвига MSf относительно точки
условного закрепления в середине поперечного сечения волны
с координатами х = 0 и z = 0 (рис. 46, а):Mt = Mf-Msf. (129)В формуле (129) знаки принимаются положительными, если рас¬
тянутое волокно расположено сверху условной консоли.Момент от приращений сдвигающих сил вычисляется для каж¬
дой элементарной площадки поперечного сечения и затем сумми¬
руется:Msf,i= &Qsf,i&i\ (130)i = nMs,= I MsM, (131)i = 1где aQs/,/—обобщенное приращение сдвигающего усилия, действующего на эле¬
ментарной площадке половины поперечного сечения, ограниченной точками i
и /+1, и приложенное в центре тяжести площадки; а,— расстояние силы aQs/,/
до точки условного закрепления.2. Конструкция и геометрические параметры
панели-оболочки. НагрузкиПроектируется многоволновое покрытие производственного
здания. Пролет 18 м. В качестве элемента покрытия принята
седлообразная панель-оболочка размером 18X3 м (рис. 46) ба¬
лочного типа, т. е. без затяжки. Поверхность оболочки представ¬
ляет собой поверхность отрицательной гауссовой кривизны в виде
гиперболического параболоида, отнесенного к главным осям, и
является поверхностью параллельного переноса, что имеет извест¬
ные преимущества при изготовлении панели.181
Таблица 42Вид нагрузкиНормативноезначениенагрузки,кПаКоэффициент
надежности
по нагрузке
V/Расчетноезначениенагрузки,кПаСобственная масса1,41,11,54Теплоизоляция, пароизоляция,
гидроизоляционный ковер0,981,31,27Снег1,01,41,40Итого3,384,20Итого с учетом коэффициента
надежности по назначению уп=
= 0,953,24,0Уравнение срединной поверхности оболочки с осью Y направ¬
ленной параллельно стороне 2а, имеет вид [см. формулу (112)]:z = l±- у2 Ь ,.2_ 0,59 л 0,325 2 Ъ2 Х а2 У 1,352 “9^ У= 0,324х2 — 0,004t/2;откуда -g^-=0,648x; ^-=0,008i/.Длина половины дуги поперечного сечения составляет по (125)1,35L= S V 1+0,648V djt= 1,51 м.0.Геометрия поперечного сечения панели видна на рис. 46, а.
Панель-оболочка снабжена напрягаемой арматурой, расположен¬
ной вдоль прямолинейных образующих срединной поверхности
(рис. 46, б). В качестве напрягаемой арматуры применены семи¬
проволочные пряди диаметром 9 мм класса К-7 (Rs=\\45 МПа,
Rs ser=\370 МПа, £s=18 • 104 МПа). Пряди натягиваются меха¬
ническим способом на упоры. Ненапрягаемая арматура — стерж¬
невая класса A-III и обыкновенная проволочная арматура клас¬
са Вр-1. Бетон принимаем класса В 35 (/?»= 19,5 МПа, Еь =
= 31000 МПа).Панель-оболочку необходимо рассчитать на внешнюю нагруз¬
ку, значения которой приведены в табл. 42.Кроме равномерно распределенной поверхностной нагрузки,
на панель-оболочку действует приложенная в середине пролета
сосредоточенная сила F\ = 9,5 кН. С учетом коэффициентов надеж¬
ности по нагрузке Yf = 1.3 и по назначению y„=0,95, имеем Fi„ =
= 9,0 кН, Fid = 11,7 кН.182
Распределенная линейная нагрузка на панель шириной 3 м
составляет: нормативная Fn=3,2 • 3=9,6 кН/м, расчетная Fa=
=4,0 • 3=12,0 кН/м.3. Расчет панели-оболочки в продольном
направлении3.1. Расчет по прочности сечений, нормальных
к продольной оси элементаМаксимальный изгибающий момент от линейной нагрузки
находится в середине пролета и равен:Мп =0,125 • 9,6 • 17,92=385 кН • м, Afd=0,125 • 12,ОХ
X 17,92=481 кН • м.То же, от сосредоточенной силы:Мя=0,25 • 9,0 • 17,9=40 кН • м; Md=0,25 • 11,7 • 17,9== 52,3 кН • м.Определяем предварительно количество напрягаемой армату¬
ры из формулы (124):Л*=533,3 • 106/(1145 • 0,85 • 6,75)=812 мм2.Принимаем 20 семипроволочных прядей 0 9К.-7 As= 1020 мм2,
что примерно на 25% больше требуемого из расчета по прочности.Приведенная площадь поперечного сечения панели с учетом
только напрягаемой арматуры:Ared= [1510 • 50 + 145 • 150+1020 ^ — l)]=Q,2 • 106 мм2.Статический момент дуги поперечного сечения панели относи¬
тельно оси X (см. рис. 46, а).Ь 1,35Sx=2\ tzdL =2 • 0,05 • 0,324 \ х2У 1 + 0,648V dx =о о=0,032 м3 = 32 • 10® мм3.Находим положение центра тяжести приведенного поперечного
сечения панели:z0=(32 • 106+2 • 145 • 150 • 600)/0,2 • 106=291 мм.183
9 мм4.Момент инерции криволинейной части поперечного сечения
панели относительно оси X:Ь 1,35Ix=2\tz2ds = 2 • 0,05 • 0.3242 J *47 1 +0,648V dx=ll,7 • 109 мм4о оПолный момент инерции приведенного сечения относительно
центра тяжести (относительно оси Хо) составит:I0 red= 11,7 • Ю9 + 2 • 145 • 150 • 6002 —— 0,2 • 106 • 2912 + 290 • 1503/12 +1020 • 2912 == 10,6 • 109 мм4.Вычислим необходимую площадь сжатой зоны бетона в попе¬
речном сечении панели:Ab=AsRs/Rb= 1020 • 1145/19,5=6 • 104 мм2.Определим длину дуги сжатой зоны сечения панели (для по¬
ловины дуги), имея в виду, что Ab — 2Af — 2Lbt:L6 = 60000—145 • 150 • 2/(2 • 50)= 165 мм.Оставшаяся часть дуги находится в растянутой зоне. Устано¬
вим ее длину до оси Z: /(,/=1510—165=1345 мм.Высоту сжатой зоны бетона х найдем из решения уравне¬
ния (125), имея в виду, что Lbt = 1345 мм:X XЦ, = 1,345 = J У1 + (-g-Уdx = \ л/ 1+0.6482*2 dx =0 0=0,324*7 2,381+*2 + 0,771 In(х + 7 2,381 +х2 ) - 0,335.Это уравнение удовлетворяется при х= 1,23 м, откуда по (113):
z = 0,324jc2 = 0,324 • 1,232 = 0,490 м. После этого расчета опреде¬
лится высота сжатой зоны бетона х = 0,675 — 0,490 = 0,185 м,
а относительная высота сжатой зоны бетона \ = x/hc= 185/675 =
= 0,274.Определим также граничное значение относительной высоты
сжатой зоны бетона, как того требует СНиП 2.03.01—84, ф-ла (25):бЛ (д \ = , . 295^?94 0,694 \ = 0>570> 1=0,274,М" Osc.uV 1,1/ 500 V 1,1 /где to — характеристика сжатой зоны бетона: а) = а— 0,008#ь = 0,85 — 0,008X
X 19,5 = 0,694;184
osr = Rs-\-400 — Osp= 1145 + 400— 1250 = 295 МПа;
asc>w = 500 МПа (при y62=1,0).Поскольку то сжатой арматуры по расчету не требуется.Эта арматура устанавливается из конструктивных соображений.Статический момент сжатой зоны сечения относительно центра
тяжести напрягаемой арматурыS(,=43500 • 600+165 • 2 • 50 • 520 = 34,7 • 106 мм3.Расстояние центра тяжести сжатой зоны бетона от центра
тяжести сечения напрягаемой арматуры (плечо пары внутренних
сил)z = Sb/Ab=MJ • 106/60000 = 578 мм.Необходимая площадь сечения рабочей растянутой арматуры
по формуле (124), где khQ = z:Л*=(481+52,3) . 106/(1 145 • 578) = 806 мм2.Ранее ориентировочно было принято Л*=1020 мм2, следова¬
тельно прочность растянутой зоны и всего сечения панели в целом
обеспечена.3.2. Расчет по прочности сечений, наклонных
к продольной оси элементаРасчет панели-оболочки по наклонным сечениям выполняем
на поперечные силы для упругой стадии работы конструкции:
Q =0,5/\*/ = 0,5 • 12,0 • 17,9=107,4 кН.Сечение поперечной арматуры устанавливается из расчета
на главные растягивающие напряжения. Они действуют под
углом 45° к образующей и определяются по формуле (126).Для вычисления нормальных напряжений в бетоне от предва¬
рительного обжатия сечения напрягаемой арматурой a1 необхо¬
димо определить потери напряжений в напрягаемой арматуре.
Но сначала надо знать величину предварительного напряже¬
ния Ospy которую назначаем с учетом допустимого отклонения
р значения напряжения при натяжении арматуры. Принимаем
р = 120 МПа, asp=1250 МПа. Величина р должна удовлетворять
условию СНиП 2.03.01—84, ф-ла (1):Osp ~\~ Р Rs,ser\ Osp P^^0,3Rs,ser’Проверяем это условие: 1250+120=1370; 1250—120>18."
>0,3 • 1370. Следовательно, величины предварительного напря¬
жения и допустимое отклонение от него установлены правильно.Теперь определим потери предварительного напряжения так¬
же по СНиП.Первые потери, происходящие до окончания обжатия бетона:
от деформации анкеров, расположенных у натяжных устройств,('.25+0,15 9)|'« |0-_г6 „Па;
от релаксации напряжений в арматуре
(0,22asp/Rs,ser — 0,1)asp=(0,22 • 1250/1370-0,1)1250=126 МПа;от температурного перепада л/ = 65°: 1,25л/= 1,25 • 65 =
= 81 МПа.Для определения потерь от быстронатекающей ползучести
бетона сначала находим сжимающие напряжения в бетоне в ста¬
дии предварительного обжатия (при этом учтем, что потери, вы¬
численные выше, составляют 26+126 + 81=233 МПа):■’•'•='>(х7+тЙ-)='02°(|250 - 233)(ж2Ьг+. 291 • 316 \ , , 0+ m-W)=H'2 МПа’где во = zc показано на рис. 46, a; t/ = eo + 25.Отношение сжимающих напряжений в бетоне к его передаточ¬
ной прочности:оьр/Rbp= 14,2/(0,5 • 35)=0,81; a = 0,25+ 0,025/?*,=0,687;0,81> 0,687, следовательно потери от быстронатекающей ползу¬
чести бетона составляют0,85[40a + 85$(obp/Rbp— а)]= 0,85[40 • 0,687 ++ 85 • 2,01(0,81-0,687)]=41,0 МПа,где 0 = 5,25 — 0,1 S5Rbp = 2,01; коэффициент 0,85 принят в связи с тем, что бетон
панели подвергается при изготовлении тепловой обработке.Итого первые потери: 233 + 41=274 МПа.Вторые потери, происходящие после окончания обжатия бе¬
тона, складываются из потерь от усадки бетона, составляющих
35 МПа, и потерь от ползучести бетона, которые приоьР= 1020(1250 — 274)[1 /0,2 • 106 + 291 • 316/10,6Х
ХЮ91=13,6 МПа,186
obp/Rbp= 13,6/17,5 = 0,777> 0,75 и a = 0,85равны 300а(оьР/Rbp — 0,375)= 102,5 МПа.Итого вторые потери: 35+103=138 МПа.Суммируя первые и вторые потери, получаем общие потери
предварительного напряжения в арматуре: as/ = 274+138 =
= 412 МПа.Теперь, зная потери напряжений в арматуре, можно найти
нормальные напряжения в бетоне о\ от предварительного обжатия
напрягаемой арматурой:a, = g»~g,< Aspk= 'о”~у2 • Ю20 • 0,5 = 2,1 МПа.В последней формуле введен коэффициент ft = 0,5, учитыва¬
ющий, что рассматриваемое сечение находится в зоне передачи
напряжений напрягаемой арматурой на бетон, где эта арматура
еще не полностью включена в работу. Длина этой зоны составляет
в данном случае 1250 мм, расчет ее не приводится.При вычислении а = 45° принято, что центр тяжести напряга¬
емой арматуры совпадает с центром тяжести сечения панели.Определяем касательные напряжения в бетоне:Q S 107400 • 0,0178 ■ Ю9 i о п
T=1W= 2 ■ 10,6 • 109 • 50 =1’8 МПа'Подставляя полученные значения в формулу (126), получим
а45о= -2,1/2 + 1,8 = 0,75 МПа.Сечение арматуры на 1 м рассчитывается по формулама45° • / • 1000 = 0,75 • 50 • 1000 = 37500// == 0,5(>4S + Asw)Rswjоткуда As + Asw = 37500/(0,5 • 270) = 278 мм2.Устанавливаем в сечении две сетки из стержней диаметром
3 мм класса Вр.-I. Принимаем шаг стержней в приопорных зонах
длиной по 1500 мм равным 100 мм в каждом направлении, в про¬
лете — 200 мм (рис. 46, д). Площадь сечения установленной
арматуры составляет As+Asw = 2(7l +71) = 284 мм2>278 мм2.3.3. Расчет по образованию трещин,
нормальных к продольной оси элементаОбразование трещин проверяем в зоне сечения, растянутой
от действия внешних нагрузок, но сжатой от действия усилия
предварительного обжатия. Расчет выполняем по СНиП из усло¬187
вия: Mr^Mere, где Mr— момент внешних сил, расположенных по
одну сторону от рассматриваемого сечения, относительно оси, па¬
раллельной нулевой линии и проходящей через ядровую точку,
наиболее удаленную от растянутой зоны, трещинообразование
которой проверяется; Мсгс— момент, воспринимаемый сечением,
нормальным к продольной оси элемента при образовании трещин
и определяемый по формуле МСГс = Rbt,serWpi±Mrp, где Мгр— мо¬
мент усилия Р относительно той же оси, что и для определения
Мг. Для изгибаемых элементов МГ = М.Рассчитываемая панель относится к конструкциям третьей
категории требований к трещиностойкости. Расчет начинаем с
определения ядрового расстояния. Для этого сначала вычислим
момент сопротивления приведенного сечения панели для крайнего
растянутого волокна, имея в виду работу панели как упругого
тела:Wred = Ired/y=\Ofi * 109/(291+25) = 33,5 • 106 мм3;МГр=Р(вор “1” г).Расстояние г от центра тяжести приведенного сечения до ядро¬
вой точки, наиболее удаленной от растянутой зоны, трещийо-
образование которой проверяется, найдем по формулеr = yWred/Ared=\ ■ 33,5- 106/0,2 • 106= 162 мм,где ф= 1,6 — оь/Rb,ser= 1,6 — 6,4/25,5= 1,35; принимаем <р=1; оь—максимальное
напряжение в сжатом бетоне от внешней нагрузки и усилия предварительного
напряжения, вычисляемое как для упругого тела по приведенному сечению:(,»• 1°*—- 1020(1250-412)2,91]=6,4 МПа.Момент сопротивления приведенного сечения для крайнего
растянутого волокна с учетом неупругих деформаций растянутого
бетона вычисляется по формулеWpt = 2(1 ьо + vi so)/(h — x) + Sbto.Положение нулевой линии сечения определяется из условия
S'bo — vSso=(h — x)Abt/2.Находим значения величин, входящих в эти формулы.188
Статический момент сжатой зоны бетона относительно нуле
вой линии:S'bo = 43500(х —-75) + 50 • 0,5 1,67 2(*-85)2 == 83,5*2 + 29300* — 2659000,где коэффициент 1,67, на который умножается толщина панели,
представляет собой усредненное значение величины 1 /cos а (а —
угол наклона осевой линии плиты сжатой зоны оболочки).Статический момент растянутой арматуры относительно нуле¬
вой линии с учетом коэффициента v:v = Es/Eb= 18 • 104/3,1 • 104 = 5,8;vSs0 = 5,8 • 1020(700 -25 — *) = 3993300-5916*.Площадь сечения растянутой зоны бетона:Abt = 50- 1510 • 2-50 • 1,67 • 2(jc — 85)= 165195— 167*.После подстановки полученных выражений в условие для опре¬
деления положения нулевой линии получим уравнение (здесь
не приводится), решая которое относительно х} найдем, что х =
= 392 мм. Обращается внимание на то, что высота сжатой зоны
бетона, полученная из расчета по трещиностойкости, отличается
от полученной ранее из расчета по прочности.Зная положение нулевой линии можем перейти к определению
величин, входящих в выражение момента сопротивления приве¬
денного сечения.Момент инерции площади сечения сжатой зоны бетона отно¬
сительно нулевой линии:/60=2[145|215°3 +145 • 150(392—75)2 +. 50 • 1,67(392-85)3 л с пс tn9 4
+- —1=6,06 • 10 мм4.Момент инерции напрягаемой арматуры относительно нулевой
линии:v/s0 = 5,8 • 1020 • 2832 = 0,47 • 109 мм4.Статический момент растянутой зоны бетона относительно
нулевой линии:Sbto =2/3(165195— 167 • 392)(675-392)= 18,8 • 106 мм3.189
Подставляя полученные величины в формулу момента сопро¬
тивления приведенного сечения для крайнего растянутого волок¬
на, с учетом неупругих деформаций растянутого бетона получим:yw-igg^+b47-|0,)+l8,8 • 106 = 61,2 • 106 мм3.После того как необходимые величины вычислены, подставим их
в выражение для определения Мсгс и получим искомый момент
воспринимаемый сечением:Mcrc = Rbt.serWpl + Mrp= 1,95 • 61,2 • 106 ++ 1020(1250 —412)(291 +162)= 511-106 Н • мм.Сопоставим этот момент с действующим в сечении моментом
от нормативных нагрузок Мп,ш = 385 + 40 = 425 кН • м..Сравнение
показывает, что Мп,ш<Мсгс. Следовательно, в растянутой зоне
панели-оболочки имеет место сжатие при нормативных нагрузках,
и проверку по образованию и ширине раскрытия трещин произ¬
водить не требуется.4. Расчет панели-оболочки в поперечном
направленииРасчет панели-оболочки выполняем на поперечные изгибающие
моменты от действия односторонней снеговой нагрузки на отдель¬
но стоящую волну, так как именно такой случай будет неблаго¬
приятным для конструкции (рис. 46, б).Панель рассчитывается как условная арка с затяжкой, в ко¬
торой при действии обратносимметричной нагрузки не возникает
распор, который мог бы уравновесить внешнюю нагрузку сжима¬
ющими усилиями. В этом случае внешняя нагрузка уравновеши¬
вается поперечными (сдвигающими) силами.Интенсивность распределенной поверхностной односторонней
снеговой нагрузки на 1 м панели-оболочки шириной 3 м состав¬
ляет: Son=(1,4 — 0,6) 1,4 • 3 = 3,36 кН. Обратносимметричная со¬
ставляющая этой нагрузки sirtt,/S!/m = 0,5 • 3,36=1,68 кН. Эта же
нагрузка, распределенная по вырезанной в панели полоске шири¬
ной 1 м, на 1 м длины полоски составит SinV/sym= 1,68/3 = 0,56 кН.Приращение поперечных (сдвигающих) усилий для полоски
единичной ширины вычисляется по формуле (128):А Qsf= 2 ''l0,6 ‘°109 S™< = 79’2 ' 10'9 ’ S“‘*
где Scut— статический момент отсеченной части сечения панели.190
Таблица 43Точки поперечного сеченияПараметр точки0/23■> 4ху мм035070010501475Z, ММ040159357675Scut • 10-6, мм309,716,95190bQsfj, Н/мм00,7681,3421,5050Параметр точкиУчасток поперечного сечения0—11—2 '2—33—4bQsfj-j, Н162390574534di, мм1083214397Mgfj, Н • м1,6232,37122,84212,0Расчет приращений сдвигающих усилий производится в точках
поперечного сечения, указанных на рис. 46, г, и дан в табл. 43.Поперечные изгибающие моменты в точках поперечного сече¬
ния панели, определенные по формуле (130), вычислены также
в табличной форме (табл. 44).Суммарный поперечный изгибающий момент в сечении от при¬
ращения сдвигающих сил находим по (131): Msf= 1,62 + 32,37 +
+ 122,84 + 212 = 368,8 Н • м«0,37 кН • м. Поперечный изгиба¬
ющий момент в сечении определим по формуле (129): М2 =
= 0,56 • 1,52/2-0,37=0,26 кН • м/м.Сечение поперечной арматуры панели определяется из расчета
панели как плоской плиты на момент Л12 = 0,26 кН • м/м и здесь
не приводится. Деталь армирования криволинейной плиты пока¬
зана на рис. 46, д.5. Основные положения по конструированию
гипаров, отнесенных к главным осямГиперболическая гладкая оболочка выполняется в виде отдель¬
ных панелей обычно для пролетов до 18 м. При больших пролетах
применяют килевидные панели-оболочки или гладкие панели в
виде арки с затяжкой. Сечение гладкой панели-оболочки в сере¬
дине пролета рекомендуется делать высотой 1/25... 1/15 пролета.
Стрелу подъема таких оболочек в продольном направлении назна¬
чают в пределах 1/60... 1/40 пролета, а глубину волн (стрелу
в поперечном направлении — в пределах 1/8... 1/4 ширины пане-191Таблица 44
Рис. 47. Схема армирования панели-оболочки типа гипара, отнесенного к главнымосяма — общий вид панели; б — план панели и схема сварных сеток ненапрягаемой арматуры;
/ — напрягаемая арматура; 2 — ненапрягаемаяли. Размеры продольных бортов должны обеспечивать необходи¬
мую площадь сжатой зоны бетона и удобство стыковки смежных
волн. Ширина борта обычно принимается 1/4... 1/3 от глубины
волны, а высота его сечения— 1,5...4 толщины оболочки. Мини¬
мальная толщина оболочки назначается по условиям размещения
арматуры и обеспечения необходимой толщины защитного слоя
бетона, но не менее 30 мм.Гладкие панели-оболочки армируют предварительно напря¬
женной высокопрочной проволокой, прядями или канатами в виде
двух пакетов, расположенных по направлениям систем прямоли¬
нейных образующих. В качестве ненапрягаемой арматуры приме¬
няют стержни диаметром 3...5 мм, укладываемые параллельно
сторонам плана. Поскольку поверхность оболочки не разворачи¬
вается на плоскость, сварные сетки изготавливать плоскими на
всю панель нельзя. Поэтому панель армируют плоскими, но узкими
сетками, укладывая их поперек волны с конструктивными стыками
по длине панели. Длина таких сеток равна ширине панели по дуге,192Ось симметрии
а ширина 1 ...2 м. В приопорных зонах шаг поперечных стержней
сеток уменьшают.Продольные борта армируются гнутыми сварными каркасами
и отдельными стержнями. Армирование гипара показано на рис. 47.Для связи панелей между собой предусматривают выпуски
арматуры из продольных бортов панелей-оболочек. Кроме того,
соседние волны соединяют сваркой закладных деталей и стык
замоноличивают.Килевые и арочные панели-оболочки конструируются аналогич¬
но. Отличие заключается только в расположении напрягаемой
арматуры, которую укладывают в киле, а в арочных оболочках —
в наличии затяжки.А. РАСЧЕТ НЕСУЩИХ ВАНТ
1.Основные расчетные положенияВантами называют гибкие провисающие нити, которые при над¬
лежащем закреплении концов на опорах способны нести верти¬
кальные и ветровые нагрузки. Гибкая нить является геометриче¬
ски изменяемой системой с бесконечно большим числом степеней
свободы. Расчет гибких нитей производят при проектировании
вантовых покрытий, когда нити служат основной несущей кон¬
струкцией и рассчитываются на эксплуатационные нагрузки, или
висячих железобетонных оболочек, в которых нити выполняют
роль рабочей арматуры и рассчитываются на монтажные на¬
грузки. При любых нагрузках в вантах возникают только растяги¬
вающие усилия.Величина линейной распределенной по длине нити нагрузки,
отнесенной к пролету, меняется в зависимости от угла наклона
нити в данной точке к горизонту по закону Fx = Fo/cos а, где Fo—
величина нагрузки в середине пролета нити; а — угол наклона
касательной к нити по отношению к горизонту (см. рис. 48, а ив).Абсолютно гибкая нить под действием линейной распределен¬
ной нагрузки провисает по закону цепной линии в соответствии
с уравнениемУ = у^(сЪ-д-Х—\') .В строительной практике обычно применяют пологие гибкие
нити с относительно небольшим провесом, в пределах 1/10 проле¬
та. Для таких отношений угол а мал, и cos а можно принять
равным 1 по всей длине нити. Тогда FX = F0 = F, что дает погреш-VIII. РАСЧЕТ ВАНТОВЫХ СИСТЕМ13 Заказ 61193
Рис. 48. Расчетная схема гибкой нити
а — с опорами на одном уровне и вертикальной равномерно распределенной линейной
нагрузкой, отнесенной к длине нити; б — то же, с нагрузкой, отнесенной к пролету;
в — расчетные усилия в текущем сечении нити и опорные реакции; г — к расчету нити,
подвешенной к опорам с разными уровняминость в пределах точности расчета около 5%. В этом случае урав¬
нение кривой провеса нити будет представлять собой уже не урав¬
нение цепной линии, а уравнение параболы: y=4fx(l—x)/t.Дифференциальное уравнение линии равновесия такой нити
имеет вид:d2y г /и1?-=-F/H' (132)где Н — горизонтальная составляющая опорных реакций в точках подвеса нити
(распор).194
Уравнение (132) аналогично дифференциальному уравнению
эпюры изгибающих моментов простой балки, несущей вертикаль¬
ную нагрузку:d2M _ F
dx2Таким образом, линия равновесия гибкой нити под действием
вертикальной нагрузки F совпадает с эпюрой изгибающих мо¬
ментов балки пролетом /, находящейся под действием такой же
нагрузки F. Если проинтегрировать уравнение (132), то получим
выражение для ординаты у линии равновесия гибкой нити:у = М/Н, или Н = М/у, (133)где М — изгибающий момент в шарнирно-опертой однопролетной балке проле¬
том / под действием нагрузки F Фбалочный момент).Из формулы (133) следует, что ординаты линии провисания
гибкой нити под любой нагрузкой равны ординатам эпюры мо¬
ментов простой балки при той же нагрузке, деленным на горизон¬
тальную составляющую усилия в нити (распор) Я, которая при
вертикальной нагрузке по всей длине нити (включая опоры) по¬
стоянна. Эту формулу можно получить также из условия равенства
нулю суммы моментов всех сил, расположенных с одной стороны
промежуточной точки на нити, относительно этой точки.Как видно из формулы (133), для расчета гибкой нити необхо¬
димо знать величину распора Н или ординату у хотя бы одной про¬
межуточной точки нити. Одна такая точка нам известна. Это
наибольшая ордината линии провисания нити в середине пролета
при * = 0,5/. Таким образом, если на нить действует равномерно
распределенная линейная нагрузка F = const и известна стрела f
провеса нити в середине пролета, то Н можно определить по фор¬
мулеH=Fl2/{8f). (134)Определим теперь закон изменения продольной силы в сечениях
нити по ее длине. Из рис. 48, в видно,что по условию равновесия
усилие Nx в отрезке нити длиной х на горизонтальной проекции,
направлено под углом а к горизонту по касательной к оси нити.
Из равенства нулю суммы проекций сил на горизонтальную ось
получим NX = H/cos а, следовательно, с увеличением абсолютного
значения угла а усилие увеличивается. В середине пролета а = 0
и Nmin = H. Наибольшая величина усилия будет у опоры. Ее можно
определить по формулеyVmax=VW2 + Q8 t*H + Ff, (135)13*195
где Qo— значение балочной поперечной силы на опоре (вертикаль¬
ная составляющая опорной реакции). Следует отметить, что в по¬
логих нитях наибольшее усилие мало отличается от наименьшего,
т. е. от распора. Так,при ///=1/20 Мпах» 1,020//; *\ (135а)при ///=1/10 Млах» 1,078//. IДлина пологой нити при действии равномерно распределенной
линейной нагрузки вычисляется как длина пологой параболы по
приближенной формулеL = /[l+-|-(i-)2]=/£. (136)Для нити с опорами на разных уровнях (рис. 48, г) формула
(136) приобретает видl=-dT+TTC0S’f- <>зба)Все приведенные выше формулы относятся к нерастяжимой
гибкой нити. В большинстве случаев точно рассчитать нить непо¬
средственно по приведенным выше формулам не удается. Более
точный расчет возможен, если связать уравнение нерастяжимой
нити с ее длиной и нагрузкой. Для этого проделаем следующие
выкладки.Длину пологой нити определим с помощью линейного интегралаLL=\dL=\V(dx)2 + (dy)2 = \V 1 + (dy/dx)2 dx.
о / /Имея в виду, что (dy | dx)2^ 1 и что в соответствии с правилами
приближенных вычисленийдлину нити можно представить следующим образом:
L=)[l+~r(ir) ]dx=\dx += 1+Ър-№(х)<1х = 1+^г, <137)где (■af") ='нг; D,= №wdx — интегральная характеристика нагрузки.196
Выражение (137) связывает длину нити с произвольной нагруз¬
кой. Следует заметить, что вычисление \Q2(x)dx довольно тру¬
доемко. Однако в простейших случаях, когда одна из эпюр прямо¬
линейна, задача может быть решена с помощью метода Вереща¬
гина. Для некоторых распространенных нагрузок значение D/
приводится в табл. 45.Сравнивая формулы (136) и (137), получим выражение для
определения распора при заданном провесе нити:н=±Щ_ (138)Если известна длина нити, а не провес, то распор можно по¬
лучить непосредственно из (137):и-ЧжЬг- О39*Ниже без вывода даются формулы для расчета нерастяжимых
гибких пологих нитей подвешенных к опорам, находящимся на
разных уровнях (рис. 48, г).Из формулы (133) получим выражение для ординаты у (см.
рис. 48, в).y = M/H + xtgy = M/H+x-h/l\ (140)из (134) для равномерно распределенной линейной нагрузки
величина распора составит:H=M/{f + h/2); (141)из (135) получим усилиеWmaW H2+[Qo + H{h/l)f ; (142)длина пологой нити из (137):‘■-ТЯ7+&ая?* <143>Если на нить действует не равномерно распределенная нагруз¬
ка, а произвольная, то распор определяется по формуле//=УD/cos3(p/[2(L — //cosq))] . (144)Если известен провес нити с опорами на разных уровнях, то
распор определяется по (138), т. е. так же, как и для нитей с опо¬
рами на одном уровне.197
Таблица 45
Интегральная характеристика нагрузки Df= \ Q2dxПринятые обозначения: a = a/l; $ = b/l, y = v/g, yx = F/gl\ y2 = v/(v + g)\Схема нагружения198№п/п123456Расчетная формула интегральной
характеристики нагрузки dfgY
12
5 gy192 ы.^.[i +(4-3a)aV+(6-4a)aJT]^-[1+(12«-12aJ-2p)pV+
+(12a— 12a2—P2)Py]
Продолжение табл. 45Схема нагружения199нп/п789101112Расчетная формула интегральной
характеристики нагрузки dj-£j-[l+(3-2p)pV+(3-p*)f>Y][l-i-(^2a-l2a2-2P)PavS--(12a-12a2-P2)PY2]-i^-(4g?+4g!+7g1<?2)g2/3452^-(3g?+8g5+9g,gs)g2/380
Продолжение табл. 45Схема нагружения200№п/п131415161718
19Расчетная формула интегральной
характеристики нагрузки dj-2^-(13g?+10g,g2+13gl)13g¥2880F2la(l-a)F2l4-j[F,(l-a)+F2bf +
+±lFta+F4l-b)f+2F2a
1,25 FH
Продолжение табл. 45Схема нагруженияРасчетная формула интегральной
характеристики нагрузки df2 F2l-^-[l + 12aY.(l-a)(l+Yl)]-^-[l+3Yi(H-Y.)]-^f-+2F2a+2Fga(l-a)FHa{ 1 -a)+-A-(4g?+4gI + 7glg2) +
a(l-a)(2-a)++-^-g2a(l — a)(l + a)F4a(\ - а)+-&г-+Цё-а(1 - a2)201№n/n202122232425
Кривая провисания нити с опорами на разных уровнях (см.
рис. 48, г) имеет две особые, заслуживающие внимания, точки,
Первая точка С — находится в середине пролета. Касательная
в этой точке параллельна наклонной линии, соединяющей точки
опоры. Вторая — это точка D, низшая точка на кривой. Касатель¬
ная в этой точке горизонтальна, а усилйе в ванте принимает наи¬
меньшее значение, равное распору Я, и, следовательно, здесь
Q = 0. При проектировании обычно стремятся кровлю устроить
так, чтобы был наружный водоотвод. В этом случае необходимо,
чтобы хd^U т. е. выносят низшую точку за пределы пролета по¬
крытия, а кривую провисания принимают такой, чтобы угол на¬
клона касательной к горизонту в точке подвески при максимальной
нагрузке был равен нулю. Расстояние от левой опоры до точки D
и ее ордината определяются по формуламxd — Va/F-, » (145)
yD=FxD/(2H), >гдеVa=FI/2 + H tgq>; VB=Fl/2-Htgy. (146)Вместе с тем, если провес задать малым и хd оставить далеко
за пределами покрытия, то усилия в вантах возрастут и на низшей
опоре появится вертикальная составляющая опорной реакции,
направленная вверх, что создает угрозу отрыва опоры от поддер¬
живающих конструкций.Пологую нерастяжимую нить легко рассчитать, если известны
пролет нити, нагрузка, действующая на нее, и ордината хотя бы
одной промежуточной точки нити. Однако в большинстве прак¬
тических случаев ни одна из промежуточных ординат линии рав¬
новесия нити не бывает заранее известна. Это объясняется тем,
что гибкие нити в конструкциях, нагруженные некоторой началь¬
ной нагрузкой, подвергаются также воздействиям различных вре¬
менных нагрузок. Последние вызывают изменение формы равно¬
весия нити за счет ее удлинения, что существенно влияет на
величины провеса и распора. Поэтому расчет нитей без учета
их упругого удлинения вести нельзя. Для того чтобы учесть
упругое удлинение нити под нагрузкой, необходимо использовать
закон Гука, связав его с длиной нити при начальной нагрузке
и с длиной нити после добавления нагрузки.Удлинение нити постоянного по длине сечения\L = bL=-j-L=-^-L. (147)202
Если иметь в виду, что мы рассматриваем пологие нити, для
которых приемлемо условие (135а), т. е. Nmax = ( 1,020... 1,078)Я,
или в среднем Mnax=l,05tf, то удлинение нитиЛ / _ 1,05HL _ 1,05HL _ 1,05ЦН /1у1очEsAs ~ Bs ~ В5 'где BS = ESAs— жесткость сечения нити; L = £/.Между величинами Lo, L и aL существует следующая зависи¬
мость:Lo = L+^L. (148а)Подставляя в эту формулу выражения, полученные выше,
можно переписать ее в следующем виде:_ 8 ,/ / \2 , 1,05нц2#2 3 \ / / ' В5 *После некоторых преобразований получим решение в виде
кубического уравненияЯ3+2,54-||-Я2-0,476-^-=0. (149)Похожее решение предложено Р. Н. Мацелинским и вошло
в нормативную литературу:h3+t-^h2-W-=0' (150)В уравнениях (148)... (150) принято\=l/f- l = L/l. (151)Пользуясь аналогичными рассуждениями, можно вывести
уравнения распора и от других различных воздействий. Эти урав¬
нения приводятся ниже без вывода.Для нити с опорами в разных уровнях уравнение (150) при¬
нимает видЯ3_|_ (£i-1)B,cos<p Я2_0 5 P,B,cos6<y =Q ^152JПри смещении одной из опор нити, подвешенной к опорам,
расположенным на одном уровнеуЗ | ( DfBs и BS&1 \ и2 DfBs /1 го\2 \ 2Я?/£2 1 /£2 / 2 211? '203
То же, если опоры расположены на разных уровняхиЗ I / DfBscos5q> „ Bscos2фда ч 2 D,BS cos5 <р Л /1С,Ч—я' 1$—)и2 2?s? °- (154>Знак минус перед третьим членом выражения в скобках в фор¬
мулах (153) и (154) обозначает увеличение пролета при смещении
опоры. Если пролет уменьшается в результате смещения опоры,
то следует принимать плюс. В этих формулах распор и длина нити
до. смещения опоры обозначены Н\ и L\ (и соответственно £i),
а после смещения — Н2, L2 и £2.При изменении температуры нити на a t уравнение распора
нити с опорами в одном уровне имеет вид:я*+(1щг_я,+"^)я|_'§г=0- (155)То же для нити с опорами в разных уровняхl/3 I / Df Bscos4(p и , Bsabtcosq> \ и2 DfBscos\ Л мн2+\~2im— я 1 +—ci—)н2 —а#—"= °- (156)Перед третьим членом выражения в скобках принимается знак
минус, если температура уменьшается. В формулах (155) и (156)
а — коэффициент линейного расширения материала нити.Если упругая нить загружена нагрузкой с интегральной грузо¬
вой характеристикой D/,и распор Hi определен из формулы (150),
а затем нить догружается дополнительно, причем D/2— суммарная
характеристика, то суммарный распор Н2 находят из следующего
уравнения: у _ D _ D<‘57>а когда опоры находятся на разных уровнях, тоЯ|+ ( -И,)Н\- =0. (158)Для горизонтальной предварительно напряженной струны, на¬
тянутой силой Р, начальная длина которой равна /:Н3-РН2-^-.=0. (159)То же, для наклонной струны, начальная длина которой равна
расстоянию между точками подвеса:Н3 — Р cos фЯ2- =0. (160)204
илиР=— -S&-cos4- (161)cos(p 2/Я YРаспор предварительно напряженной струны для случая сме¬
щения опоры определяется из уравнений (153) или (154), а если
изменяется температура — из(155) или (156). Если предваритель¬
но напряженную струну после первого загружения нагружают
дополнительной нагрузкой, то новый распор вычисляется по (157)
или (158).Допускаемая расчетная нагрузка на нить при ее работе за
пределом упругости (в упругопластической стадии) определяется
по формулеFadm + ( j g2)а при опорах на разном уровнер 3,8AsOy~)J 4~£i 1 . мсо\Fadm= Шi * (163>здесь <зу— предел текучести, принимаемый условно равным 80% предела прочности
материала нити; — предельно допустимое относительное удлинение.Расчет упругих нитей по прочности выполняется на расчетные
нагрузки, а по деформациям — на нормативные, причем на каж¬
дую из этих нагрузок, учитывая нелинейность системы, нить не¬
обходимо рассчитывать отдельно.2. Расчет гибкой нити с опорами
на одном уровнеНеобходимо рассчитать гибкую нить пролетом /=40 м, подве¬
шенную в точках А и В, расположенных на одном уровне (см.
рис. 48, а). На нить действует равномерно распределенная расчет¬
ная нагрузка gd=2,4 кН/м. Начальный провес нити в середине
пролета /=2,5 м.В качестве гибкой нити принят высокопрочный трос с попереч¬
ным сечением j4s=200 мм2. Расчетное сопротивление троса растя¬
жению Rs — 930 МПа, модуль упругости Es^ 18 • 104 МПа. Коэф¬
фициент надежности работы троса у»=1,1. Отношение пролета
к провесу нити 1=40/2,5=16.Вначале определяем величину горизонтальной составляющей
опорной реакции (распора) Но без учета продольных деформаций
(как нерастяжимой нити) по формуле (134): Яо=2,4 • 402/(8Х
X 2,5) =192 кН.205
Максимальное усилие в пологой нити по формуле (135) Nmax =
= 192 + 2,4 • 2,5=198 кН.Фактическая несущая способность принятого троса составляетN,act=RAs/ys=930 • 200/1,1 = 169100 Н = 169,1 кН.Сечение троса недостаточно, так как Nfaci<.Nmax, поэтому
выполняем расчет с учетом упругих деформаций.Для этого по формуле (136) определяем длину нити:L = /[l+8/(3 • 162)]=£/= 1,0104/.Вычислим жесткость сечения нити на растяжение:В, = £И.= 1,8 • 105 • 200 = 36 • 106 Н.Величину распора с учетом упругих деформаций нити найдем
из формулы (150).Вычислим сначала интегральную характеристику по табл. 45
для равномерно распределенной нагрузки:Df = g2/7l 2 = 2,42 . 400003/12 = 30,72 • 1012Н2 • мм.Далее вычислим постоянные величины в выражении (150):B&S 8 ' 36 * 106 ft ЛД 1 I q5.З|2£3 — 3 • 162 • 1.01043 — ’D,BS _ 30,72 • 36 • 10" _ . ^ 1П162/£3 2 • 4 • 104 • 1.01043 ’ ' ’После подстановки этих величин в выражение (150) получим
следующее кубическое уравнение: Я3+ 3,64 • 105Н2—1,34 • 10|6 =
= 0, решая которое, найдем Я=160 кН.Вертикальные составляющие опорных реакций висячей нити:Va = Vb = Qo=2,4 ■ 20=48 кН.Максимальное продольное усилие в гибкой висячей нити нахо¬
дится в точках подвеса (на опорах) и равно по формуле (135)Nmах =У 1602 + 482 =167 кН.Сечение троса достаточно, так как Nfact= 169,1 кН> Nmax =
= 167 кН.Вычислим упругий провес нити при нормативной нагрузке
gn = 2,0 кН/м. Для этого вначале найдем величину распора при
этой нагрузке.206
Определяем интегральную характеристику нагрузки по табл. 45
D,=g2„l3/12 = 2,02 • 40000712 = 21,3 • 1012
и значение свободного члена в кубическом уравненииD,BS 21,3 36 10|а по? 1П,6
21? 2 • 4 • 104 • 1,0104® ’ 'В результате запишем следующее кубическое уравнение:Я3+3,64 • 105 • Я2 —0,93 • 1016=0,откуда распор Я= 137,1 кН.Таким образом, искомый упругий провис из формулы (134):/=2,0 • 402/(8 • 137,1)=2,92 м.Теперь рассчитаем эту же нить на работу в упругопластической
стадии. Принимаем предел текучести троса as=0,8 • 1470 =
= 1175 МПа. Предельно допустимое относительное удлинение
троса еи = 0,01. Вычислим по (162) допускаемую расчетную на¬
грузку:gd,odm= 3,8 '4^01175 V 1,0104 • 0,01 + 1,0104-1 =3,2 кН/м.Из этого расчета следует, что при работе в упруго-пластической
стадии допустимая на висячую нить нагрузка на 33% превышает
нагрузку, на которую рассчитан трос по упругой стадии. Проверим
при этих условиях усилия в тросе для случая, когда его темпера¬
тура изменяется на л/==ьЗО°С. Сначала определим по (155)
горизонтальную составляющую опорной реакции (распор), кото¬
рая будет иметь место после изменения длины нити при .коэффи¬
циенте линейного расширения стальной нити а = 0,12 • 10”4.Вычислим выражение в круглых скобках в уравнении (155):DfBs j, . Bsa&t
2 HW 1=±= С ~_ 30,72 • 1012 • 36 • 106 lfif) lft32 • 1602 • 106 • 40 • 103 • 1,01042 * ±± 36 • 106 ■ 0,.2^.0-V- З0_=(0)369.|-0>013) . 106 H;При Д t= +30 °C это выражение равно 0,382 • 10®, а при л t=
= —30 °С оно равно 0,356 • 106 Н.Теперь вычислим свободный член в уравнении (155):D,Bs _ 30,72 • 36 • 1018 _ , OR . 1П162 /£2 2 40 1 03 1.01042 ’ ’ '207
Запишем кубическое уравнение с полученными коэффициен¬
тами:при л/=+30° #2 + 0,382 • 106#2 —1,35 • 1016 = 0; (а)
при л/ = —30° Н\ + 0,356 • 106#2 — 1,35 • 1016 = 0. (б)Решая эти кубические уравнения, найдем горизонтальные со¬
ставляющие опорной реакции (распор): Я^а) = 158 кН; Н^б) =
= 162 кН.3. Расчет предварительно напряженной струныНеобходимо рассчитать предварительно напряженную горизон¬
тальную струну пролетом / = 20 м, подвешенную в точках А и В,
натянутую усилием Р = 50 кН, и определить ее провис. Струна
нагружена равномерно распределенной линейной расчетной на¬
грузкой gd = 2,3 кН/м. Кроме того, на струну действуют две сосре¬
доточенные вертикальные расчетные силы по Fvd=\0 кН, прило¬
женные на расстоянии а = 5 м от каждой опоры. Материал стру¬
ны — трос, площадь его поперечного сечения Л* = 350 мм2. Расчет¬
ное сопротивление троса растяжению Rs = 825 МПа, модуль упру¬
гости £s=l,8 • 105 МПа. Коэффициент надежности работы троса
Ys= 1,1. Следует проверить сечение троса и определить его провисИнтегральная характеристика нагрузки по табл. 45:Df=gll3 /12 + 2 Flda + 2 Fvdgd(l -a)a == 2,32 • 200003 /12 + 2 • 100002 • 5000 ++ 2 • 10000 • 2,3(20000 - 5000) • 5000 = 7,98 • 1012.Распор горизонтальной предварительно напряженной струны
определим из уравнения (159):H*-PH2-DfBs/2l = 0Вычислим значение свободного члена уравненияDfBs _ 7,98 • 10‘2 • 1,8 ■ 105 • 350 _ 10 ^ 1л16
21 2 • 20000 ' ' ’ 1U •Подставив результаты подсчетов в формулу (159), получим
следующее кубическое уравнение:Я3—50 • 103Я2-12,57 • 1016 = 0,
решая которое, найдем искомый распор Я = 250,5 кН.208
Вертикальная опорная реакция Ул=33 кН.Максимальное усилие в предварительно напряженной струне
составит по формуле (135) :Wma* H2+V2A =V 250.52 —ЗЗ2 =252,7 кН.Определим несущую способность струны:Nfad = RsAs/ys = 825 • 350/1,1 • 103 = 262,5 кН.Поскольку Nfaci> Мчах, принятое сечение струны достаточно.
Провис струны найдем из расчета на действие нормативных
нагрузок gn = 2 кН/м и Fvn = 8 кН. Для этого сначала посчитаем
максимальный балочный изгибающий моментМп,max = gnl2/8 + Fona = 2 • 202/8 + 8 • 5= 140 кН • ми по табл. 45 интегральную характеристику нагрузкиD, = 22(2 • 104)3/12 Н- 2(8 • 103)2 • 5 • 103 ++ 4 • 8 • 103(20—5) • 5 • 106 = 4,37 • 10'2.Вычисленное позволяет определить свободный член в уравне¬
нии (159):-^-=12,57 • 1016 • if-=6,9 • 1016.Перепишем уравнение (159), подставив известные величины, и
решив его, найдем распор от действия указанных выше нагрузок:Нп + 5000#2 — 6,9 • 1016 = 0, откуда #„ = 226 кН.Зная распор, найдем по формуле (133) искомый провис струны:Утах = /=140 • 103 /226 = 620 мм.4. Расчет гибкой нити с опорами
на разных уровняхТребуется определить усилия от полной нагрузки и вычислить
приращение провиса от временной нагрузки в нити, подвешенной
к расположенным на разных уровнях точкам: А (верхняя) и В (ниж¬
няя). Пролет нити (расстояние между точками подвеса по гори¬
зонтали) / = 42 м, перепад опор (расстояние между точками подве¬14 Заказ 61209
са по вертикали) составляет h = 7 м. Расстояние между точками
подвеса по наклонной линии а=У 422 + 72 =42,58 м. В качестве
нити принят арматурный стержень 0 40АШв (с контролем удли¬
нения) . Характеристики арматурного стержня R,=450 МПа, Е,=
= 1,8 • 105 МПа, As= 1256,6 мм2, fls = 2,26 • 10® Н. Коэффициент
условий работы по арматуре принят y*=1-Начальная длина нити (до загрузки) Lo=42680 мм. На нить
действует распределенная линейная нагрузка, компоненты которой
имеют следующие значения: расчетная постоянная gd = 3 кН/м;
расчетная временная ^=1,2 кН/м; нормативная постоянная
gn=2,7 кН/м; нормативная временная у„=1 кН/м.Приводим без вычислений интегральные характеристики по¬
стоянной и полной нагрузок (см. табл. 45):расчетные dfd=5,56 • 1013 Н2 • мм; Di,lot= 10,89 • 1013Н2 • мм;нормативные Dfd = 4,5 • 1013 Н2 • мм; Df,lot=8,45 • 1013 Н2 • мм.Определим отношение £i начальной длины нити Lo к расстоя¬
нию между точками подвеса a: £i — Lo/а = 42680/42580= 1,0024.Распор найдем из решения кубического уравнения упругой
наклонной нити (152):(£, - l)B,cos<p (1,0024- 1) • 2,26 • 10е • 0,986 _ „по?/! s! = Гош3 5dU9/4-Вычислим коэффициенты при неизвестном этого уравнения
(в свободном члене сосчитаем только постоянную величину):Bscos5<p _ 2,26 • 10* • 0.9865
2/£? _ 2 • 42000 • 1.00243 —здесь cos ф=//а=42/42,58=0,986.Перепишем кубическое уравнение, подставив полученные коэф¬
фициенты: Я3 + 530974Я2 —2490D/=0. Решая это уравнение с уче¬
том вычисленных выше значений характеристик нагрузок (£>f),
получим величину распора:при полной расчетной нагрузке (Df,td= 10,89 • 1013) Нш=
=525000 Н. Зная распор, вычислим по (146) вертикальные со¬
ставляющие опорных реакцийVA=(gd + vd)l/2 + H • Л//=(3 +1,2)42/2 ++ 525 • 7/42=175,7 кН;VB=(3 + 1,2)42/2 -525 • 7/42=0,7 кН.210
при постоянной нормативной нагрузке (Dfg = 4,5* 1013):
rf" =354 кН; Va = 115,7 кН; VB = -2,3 кН;при полной нормативной нагрузке (Df,t0t = 8,45 • 1013):Я(2) = 460 кН; Va = 154,4 кН; VB = 1 кН.Определим усилие в нити от полной расчетной нагрузки по (135):
Afma* =л/5252+175,72 = 553,6 кН.Несущая способность нити составляет: Nfact= 1256,6 • 450 =
= 565470 Н> 553600 Н. Следовательно, прочность нити обеспечена.Теперь вычислим приращение провиса от временной нагрузки,
переписав формулу (134) относительно стрелы провиса и разло-'
жив нагрузку на составляющие:Л f / go+Ул gn \ч- 8 \~н® ж)=42! • 10* / 2,7+1 2.7 \ п| 0
—1354-iF)=91’8Б. РАСЧЕТ ВАНТОВЫХ ФЕРМ
1. Основные положенияОдним из видов висячих конструкций, получивших широкое
распространение в строительной практике, являются плоские ван¬
товые фермы (рис. 49). Подобные системы имеют ряд преимуществ
перед системами из параллельных вант, в частности, в отношении
восприятия несимметричных и ветровых нагрузок, в том числе
отрицательных (отсосов). В вантовых фермах тросы расположены
в два яруса, причем один трос является несущим, а другой — ста¬
билизирующим (напрягающим). Между этими тросами имеются
стойки, которые могут быть распорками (рис. 49, а) или подвес¬
ками (рис. 49, б), а сами тросы соединяются между собой в одной
или двух промежуточных точках-шарнирах (рис. 49, г) или не со¬
единяются вовсе. Вместо стоек тросы могут объединяться гибкой
раскосной решеткой (рис. 49,(9). Тросы подтягивают так, чтобы
от действия внешней нагрузки в элементах фермы не могли по¬
явиться сжимающие усилия (если применены подвески) или рас¬
тягивающие усилия (если применены распорки). Отсюда следует,
что эта система является предварительно напряженной и имеет
повышенную жесткость. Такие системы могут применяться как14*211
Рис. 49. Примеры двухпоясных вантовых
ферма — со сжатыми стойками (распорками); б —
с растянутыми стойками (подвесками); в —
с центральным шарниром; г — с распорками
и подвесками и с двумя шарнирами в пролете;
д — с треугольной решеткой; 1 — несущий
трос; 2 — стабилизирующий (напрягающий)
трос; 3 — стойки-распорки; 4 — стойки-подвес¬
ки; 5 — раскосы треугольной решетки; 6 — со¬
единительный шарнирна прямоугольном, так и на круглом или многоугольном плане.
Различие типов вантовых ферм предопределяет и различные
способы их расчета. При рассмотрении напряженно-деформиро¬
ванного состояния вантовых ферм принимаются некоторые допу¬
щения: нити-пояса фермы считаются пологими относительно гори¬
зонтальной оси, а распорки (подвески) —абсолютно жесткими,
исключающими взаимное смещение соответствующих точек нитей-
поясов в вертикальной плоскости. В деформированном состоянии
распорки (подвески) остаются вертикальными. Так же, как и рас¬
чет гибких нитей, расчет вантовых ферм выполняется по нелиней¬
ной теории и основан на приближенных решениях. Для правомоч¬
ности использования дифференциальной формы записи уравнений
будем считать, что связи между поясами расположены так часто,
что позволяют считать их непрерывными (сплошными). Это дает
возможность предположить, что нагрузка, приложенная к верх¬
нему поясу, распределяется на нижнем поясе по тому же закону.Рассмотрим, например, ферму, показанную на рис. 49, б.Расчетной комбинацией нагрузки на несущий трос является
полная нагрузка на ферму и усилие в стабилизирующем тросе,
которое передается через систему связей (стоек). Расчетной
комбинацией нагрузок для стабилизирующего троса является212
предварительное напряжение (поэтому он еще называется напря¬
гающим). Причем, если напряжение создается до приложения
внешней нагрузки, то усилие в тросе оказывается значительным,
и поэтому выгодней осуществлять натяжение после приложения
постоянной нагрузки (собственной массы конструкций покрытия).
Тогда нагрузкой на ферму для расчета стабилизирующего троса
будет масса конструкций покрытия в сочетании с ветровым отсо¬
сом. Предварительное напряжение можно производить в два
этапа: до приложения нагрузок от конструкций покрытия и после
окончания их монтажа.Стрелу провиса несущего троса принимают в пределах
1/20... 1/10 пролета, а стабилизирующего — несколько меньше.
Сечение несущего троса определяют исходя из расчета фермы
на полную расчетную нагрузку по формулам (133) и (134), пред¬
варительно назначив стрелки провиса обоих тросов. Влияние
стабилизирующего троса на работу несущего троса учитывают
увеличением нагрузки на 10... 15%. Сечение стабилизирующего
троса задается предварительно в пределах 0,2...0,4 от сечения
несущего троса. Если окажется, что сечения тросов приняты не¬
верно, то расчет следует повторить с новыми сечениями. Зная
сечения и провисы тросов фермы, а также действующие на нее
нагрузки, можно определить по формуле (137) их длину, а по фор¬
мулам (148) и (148а) —длину их заготовок.Представим нагрузку на несущий трос в виде суммы нагрузок:FSUp = F + Fa; (164)здесь Fa— неизвестная особая нагрузка, воспринимаемая стабилизирующим тро¬
сом и передаваемая на несущий.Балочные моменты от этих нагрузок соответственно будут:Msup = M + Ma, (165)или согласно (133)Hsupf sup = M + Hafa. (166)Перепишем выражение (166) следующим образом:(Н sup bHSUp)(fsup — у) = М +(Яа+Л Ha)(fa-\-y), (167)обозначим через у искомое приращение провисов тросов. Согласно
принятым допущениям вертикальные перемещения обоих тросов
равны между собой. В выражении (167) величины Hsup, fSuP, На
и fa— это известные распоры и провисы обоих поясов в исходном
состоянии при полной нагрузке.При увеличении провиса троса приращение его длины равно213
разности между длинами нити в обоих состоянйях. Согласно (136)
и (148а) имеем (простейшие преобразования опускаем):д/,=-|-(2 f+y). (168)При уменьшении провиса—1-(2 f-y). (169)На основании формулы (148):AL= . (170)Приравнивая между собой правые части формул (168) и (170),
получим выражение для приращения распора:Mi=2,54jt(2f+y)y, (171)а при уменьшении провисаД# = — 2,54-j£-(2f—y)y. (172)Подставим формулы (171) и (172) в (167), предварительно
обозначив2t54Bs, sup r , 2tb4Be,inf ,IUP -Саи»' ~щ;, Cinh(Csup “Ь Clnf)y3 3(Csupf аир С inf fInf) У^ “Ь
“Ь (Н sup 2С aupfaup “Ь 2Cinff?nf)y —— (Hsupfaup — Hinfflnl — Л4) = 0. (173)Выражение H,Upfaup—Hintfini представляет собой балочный мо¬
мент от полной расчетной внешней нагрузки Мш, а свободный
член уравнения является разностью балочных моментов, отража¬
ющих два состояния системы — исходное и то, которое мы ищем
и которое заключает в себе момент от «снимаемой» нагрузки. Если
рассматривать ферму без этой нагрузки, то свободный член обра¬
щается В Mtol-После определения приращения провиса можно вычислить
значения провисов обоих тросов в новом состоянии: по форму¬
ле (168) или (169)—приращение их длины, а по (171) или214
Рис. 50. Эпюры несимметричной нагрузки, действующей на вантовые фермы
а — равномерно распределенная несимметричная нагрузка и разложение ее на симметрич¬
ную и обратносимметричную части; б — то же, нагрузка, изменяющаяся по законутреугольника(172) — приращение распоров. Вычисление ординат, а следова¬
тельно, и перемещений любой точки тросов при известном распоре
выполняется по формуле (133).Рассмотрим теперь расчет вантовой фермы на одностороннюю
нагрузку. Представим эту нагрузку в виде равномерной (рис. 50, а)
и по закону треугольника (рис. 50, б) в виде симметричной и обрат¬
носимметричной частей. Примем допущение, что распор нити вы¬
зывается только симметричной нагрузкой, имея в виду, что от
обратносимметричной нагрузки посередине пролета балочный мо¬
мент равен нулю и, следовательно, на величину распора не влияет.
Для расчета упругой нити это предположение не справедливо,
поскольку средняя точка при несимметричной нагрузке смещается
и по вертикали и по горизонтали. Вертикальное перемещение
практически несущественно и им можно пренебречь. Это дает
возможность применить принцип независимости действия сил для
решения поставленной задачи. Границы применимости такого
подхода определяются величиной погрешности в результате при¬
нятого допущения.В качестве примера можно воспользоваться значениями инте¬
гральных характеристик симметричной D/, и несимметричной D/
нагрузок:П._Л*(i+o,313y4y) . n _ fVo-HW-H)и< п ’ п ГЗ ’где y = s/g (отношение временной нагрузки от снега к постоянной).215
Приведенные выражения отличаются коэффициентами при у2,
что и определяет величину погрешности в интегральной характе¬
ристике при использовании выражения D/, вместо Df. При вычисле¬
нии распора погрешность всегда меньше величины квадратного
корня из отношения обеих интегральных характеристик нагрузки,
так как Df входит в свободный член кубического уравнения рас¬
пора (150).При равномерно распределенной линейной нагрузке (рис. 50, а)Е tr-t/V 1+0,25y2 + Y ’при треугольной нагрузке (рис. 50, б)/ 1+0,361y2 + yl\= V 1+0,25y2 + y ’Ниже приводятся значения £ и 1\ в зависимости от величины у:У00,5123411,0051,0131,0321,0451,055h11,0091,0251,0551,0801,095При равномерной нагрузке погрешность в определении распора
не превышает 5% (при v^4).В большинстве случаев это отношение меньше единицы и обес¬
печивает удовлетворительную точность такого способа расчета.
Если указанная величина погрешности превышена, то следует
пользоваться методом последовательных приближений.Из сказанного следует, что распор и провис тросов в середине
пролета с достаточной точностью определяются из решения для
симметричной нагрузки. Остается определить деформированную
кривую тросов в результате действия обратносимметричной части
нагрузки и нагрузку, действующую на правые и левые ветви
тросов.Условие равновесия фермы в сечении на расстоянии а от левой
опоры (рис. 51, а) можем записать по аналогии с выражением(165):Ma,sup = Ma + Ma,inf (174)ИЛИН sup(y supЬ у) = Ма-\- Hinf(yinf (175)216
где HSUp и Hinf— распоры тросов, известные из расчета на симметричную нагрузку;
У sup и у inf— соответствующие ординаты тросов в точках с абсциссой а; Ма— балоч¬
ный момент от внешней нагрузки в том же сечении.Перепишем (175) относительно неизвестного перемещения
точки а:д ц Mg -{- Hinfyinf Hsupysup (176)Hsup "H HinfПредставим Ma как сумму моментов от симметричной и обрат¬
носимметричной частей нагрузки:Ма = М a, st/m "Ь* Ma,inf/sym•Рис. 51. К расчету двухпоясных вантовых ферм на несимметричную нагрузку
а — деформация фермы, не имеющей в пролете шарниров; б — деформация фермы с
шарниром в середине пролета (пунктирной линией показано деформированное состояниевант)217
Момент от симметричной нагрузки уравновешивается произве¬
дениями распоров на соответствующие провисы тросов, т. е.Ма.аут ~ Н зирУ sup “I” ^ inf У inf== 0.Таким образом,^ Ma,inf/sym / (Н Hinf)- (177)В правой половине фермы перемещение симметричной точки
равно —д у. Зная ду, можно определить интенсивность нагрузок,
действующих на тросы фермы, и проверить правильность расчетов
из решения уравненияFa,sup ~ Fa~\~ $а “I” F a.inf-Имея величину нагрузки на каждый трос, можно записать
уравнение изогнутой оси по (133).Для определения горизонтального смещения средних точек
тросов воспользуемся выражением (143). Представим это пере¬
мещение как разность длин двух кривых (рис. 51, а) — пунктирной
(за пролет которой примем полупролет фермы, а за разницу
отметок опор — величину провиса всей нити) и сплошной (за дли¬
ну которой примем половину длины троса):=-2^W,>, (178)где DI, — характеристика нагрузки на несущий трос, вычисленная для полупролета
фермы от всей нагрузки; Df,— то же, но только от симметричной части нагрузки.Из выражения (178) видно, что взаимное смещение средних
точек обоих тросов равно сумме смещений каждого.Рассмотрим теперь ферму, показанную на рис. 51, б, в которой
средние точки тросов соединены между собой, образуя шарнир.
При симметричной нагрузке на ферму горизонтальное усилие S
взаимодействия тросов в шарнире равно нулю. Поэтому расчет
фермы с шарниром в центре на симметричную нагрузку не отлича¬
ется от расчета на ту же нагрузку фермы без соединения в середине
пролета. При несимметричной нагрузке в шарнире появляется
горизонтальное усилие S, отражающее взаимодействие тросов.Представим всю нагрузку на ферму в виде суммы симметрич¬
ной и обратносимметричной частей. При обратносимметричной
нагрузке величина провиса посередине пролета не меняется, сред¬
няя точка перемещается только по горизонтали, причем перемеще¬
ние направлено в сторону пригружаемой полуфермы. Усилие S,218
возникающее при этом в шарнире, передается на опоры тросов,
изменяя величины распоров каждого троса, перераспределяя их
так, как показано на рис. 51, б и в соответствии с данной эпюрой
нагрузки. Естественно, что 0.5S должно быть меньше Я, т. е. уси¬
лия в обоих тросах должны сохранять свой знак.Рассмотрим сечение на расстоянии а от левой опоры. В данном
случае обратносимметричная часть нагрузки пригружает этот
полупролет фермы. Запишем условие равновесия по выражению(166) для точки, где балочный момент и провис f,Up имеют макси¬
мальные значения (хотя оно справедливо для любой точки):(Н,ир + 0,5 S)(fsup+ </)=M +(Ям/ - 0,5 S)(f,nl -у). (179)Здесь стрелки провиса отсчитываются от наклонной хорды,
соединяющей точки подвеса нити с центральным шарниром фер¬
мы. Момент для балки пролетом 1/2 представим в виде суммы
моментов от симметричной и обратносимметричной частей на¬
грузки:М == Msym Mlnv/sym-Имея в виду, что M,ym — H,Upfsup-\-Hinifint=0, получим урав¬
нение, связывающее приращение провиса и усилие взаимодействия
тросов в шарнире:S(fsup~\~ftni)^2Mino/jyin 2у (Hsup Я inf)', (180)другие величины, не входящие в (180), определяются из расчета
фермы на симметричную нагрузку.Второе уравнение, связывающее приращение провиса и усилие
взаимодействия тросов в шарнире, получим из геометрических
выкладок (136а).Приращение длины левой половины несущего троса:А W" 2cosф,Г У"*+у)2 cos3 “ 2conw —~з7~f*uPcos3<ftup — 16с%3^ (2fSUpy+y2). (181)Полученное приращение является результатом удлинения тро¬
са от увеличения распора на 0,55 и перемещения срединного
шарнира фермы вдоль оси X на и (рис. 51,6):. (182)Приравняв (181) и (182), будем иметьи=^.^Ч21,„у+у’)-0.264 ■ <183)2 19
Аналогично--£^№»-!l‘)+0,264 . (184)Сопоставив (183) и (184), найдем искомое выражение, связы¬
вающее приращение провиса и усилие взаимодействия тросов в
шарнире.■^f[(2fsupy + y2)C0S3 (f>sup + (2/Vnfy — y2)cOS3 ф(п/]== 0,264/S ( я U И я Ь:' V (185)\ Вs, sup COS (psup D s. inf COS (pinf /Решая совместно уравнения (180) и (185), вычислим величину
дополнительного провиса тросов и усилие их взаимодействия
в ключе фермы.Перемещение срединного шарнира фермы определяется по
(183). Правильность результатов расчета проверяется по условию
равновесия (164).2. Расчет бесшарнирной фермыНадо перекрыть зал вантовыми фермами пролетом 60 м. Ферму
принимаем по рис. 51, б с верхним несущим и нижним стабилизи¬
рующим тросами и с растянутыми стойками. Стрелу провиса не¬
сущего троса назначаем f\ = //15 = 60/15 = 4,0 м, а стабилизиру¬
ющего— /2 = //24 = 60/24 = 2,5 м.Схема фермы и эпюры нагрузок видны из рис. 52.Ферму необходимо рассчитать на следующие распределенные
линейные нагрузки:постоянная симметричная gd = 7,0 кН/м; gn = 6,0 кН/м;
временная симметричная (снег) — s<* = 5,0 кН/м; sn = 3,5 кН/м;
полная симметричная нагрузка (рис. 52, a) Fd,tot= 12,0 кН/м;
/Ч/о/ = 9,5 кН/м.Требуется определить максимальные расчетные усилия в эле¬
ментах фермы, длины тросов в рабочем состоянии и при их заго¬
товке, а также прогиб. Сечение несущего троса принято 4 0 15К=7
Вычислим жесткость сечения верхнего троса на растяжение:BS,SUP = ES,SUPAS,SUP= 1,8 • 105 • 4 • 143,0=103 • 106 Н,
а также интегральную характеристику нагрузки, пользуясь табл. 53:13' Г00’ =45.63 ■ 10'-220
Рис. 52. К расчету вантовой фермы
а схема фермы и симметричные нагрузки; б — несимметричные нагрузки на фермуДлина верхнего троса по формуле (137)Lsup = l(l+-fi^r) = 6 • 104 • 1,016=60960 мм,гдеDf — 45,63 - 1013 _q Qjg
2lH28Up 2 • 6 • 104 • 487,52 • 106 U’U1D*Определим теперь упругое удлинение верхнего троса по (148):
- 487500 • 60960 • 1,05 огм По* =304 мм'Зная длину троса и его упругое удлинение под нагрузкой, вы¬
числим необходимую длину заготовки этого троса по (148а):
LotSup = 60960 — 304 = 60656 мм.Жесткость сечения нижнего (стабилизирующего) троса на рас¬
тяжение (сечение этого троса принято 1 0 15К = 7):Bs,ini=EsMAs,in,= 1,8 • 10е • 143,0=25,74 • 106 Н.221
Горизонтальная составляющая опорной реакции (распор) в
точке подвеса нижнего троса на опоре А при полной нагрузке на
ферму составит:гг Fd.infP 1,0 • 60s • 1012 СЛППП 14И‘п'=-Щ-= 24 • 2500 = 60000 н-Приводим без вычисления значения величин, необходимых
для расчета длины нижнего (стабилизирующего) троса по (137):D,,in, —2,7 • 1012 Н2 • мм; 0,,,„//2Ш,2„,=0,00625.Длина нижнего (стабилизирующего) тросаLi„f=60000(1 +0,00625)=60000 • 1,00625 = 60375 мм.Длина заготовки этого троса:Lo,tnf=60375- 60' 6°’375,Аб106 1,056 = 60375-148=60227 мм.25,74 • 10Очертание обоих тросов фермы определяется из уравнения
нити (133):„ М(х) F, /1х , х1 , х3 \У~~ Н — Н \ 4 2 31 )■Предварительное напряжение фермы производим без нагрузки.
При этом собственной массой фермы пренебрегаем, т. е. балочный
момент от собственной массы М=0.Приращение провисов обоих тросов (д/) найдем из кубического
уравнения (173). Для решения кубического уравнения вычислим
коэффициенты при неизвестном и свободный член этого уравнения: 2,54 В$ sup 2,54 * 103 * 10^ л г\*ч\ с и / 2С’“Р=-Г-ПГ= 6 •'6,096 10» =0’0715 н/мм ;2,54 В,Лп, 2,54 • 25,74 • 106 ЛЛ1ои/ 2
1п1=~1 Тщ~= б • 6,0375 • 10* =°’018 Н/ММ ;Csup+Ctn,=0,895 Н/мм2;3(Wi-C/n/f2)=3(0,0715 • 4,0-0,018 • 2,5)103 = 723 Н/мм;Я«|р + ///я/ + 2с»цр/2 +2C(n/fl == 106(0,4875+0,06+2 • 0,0715 • 42 + 2 ■ 0,018 • 2,52) =
=3,06 • 10* Н;222
_'г 'У |0У — ,.8 - IQ, И-т..После того как полученные значения коэффициентов подставим
в кубическое уравнение (173), имеем:0,0895у3—723у2+3,06 • 106у-1,8 • 109=0,откуда */=дf=695 мм. В результате провис несущего троса
составит fsuP=4000—695=3305 мм, его длина по формуле (136):Цир = 6 • 104(l + V.36o°o'2H • Ю4 • 1,0081=60485 мм,а горизонтальная составляющая опорной реакции (распор)
равна:Нsup = Hsup—лЯ5ир=(487,5 — 363,0) • 103= 124,5 * 103 Н= 124,5кН,
где приращение распора вычислено по формуле (172):А и _ 2,54 • 103 • 10ls(2 • 4 - 0,695) • 0,695 осо Л ,л3 и_осо „илЯ5И,= (60.0 • 60,96)10» =363,0- 10 Н=363 кН.Вычислим расчетную нагрузку, на которую работает несущий
трос:Fd,suP= 24У“* = 24 • 3-э°5 • 124-5 ■ 108 =2,75 Н/мм = 2,75 кН/м.I 60 • 10Теперь определим провис стабилизирующего троса: fin\ —
= 2500 + 695 = 3195 мм.Рассчитаем также длину стабилизирующего троса:Lin,=6 • 104(l+ 8 31952 )=6 . ю4 • 1,0076 = 60454 мм' V з • во2 • ю6 /и горизонтальную составляющую опорной реакции (распор)
Я,'П/=Я,П/+ДЯ„, = 60 + 71,5= 131,5 кН,
где приращение распора по (172), и 2,54 • 25,74 * 1012(2 • 2,50,695)0,695 "tiaok. u>w71 к
ДЯМ 60 • 60.375 • 105 71435 Н*71>5 КН-223
Наконец определим расчетную нагрузку, на которую работает
стабилизирующий трос:rv 24 • 3,195 • 131,5 • Ю6 отпи/ о 7п и/Fd,inf= 1q6 =2,79 Н/мм = 2,79 кН/м.Одинаковое значение полученных величин нагрузок, на кото¬
рые работают несущий и стабилизирующий тросы, служит дока¬
зательством правильности расчетов.Определим теперь прогиб фермы. Он вычисляется от действия
временной нормативной нагрузки как разность положений средней
точки фермы при полной нагрузке и при действии постоянной
нагрузки в сочетании с ветровым отсосом.Для определения прогиба воспользуемся приведенным выше
кубическим уравнением, вычисленные коэффициенты которого
можно использовать и для расчета прогиба, а свободный член
для случая полной нормативной нагрузки/4/0/=9,5 кН/м найдем:М„,ш — Мп.ш= 1,8 • 109 — 9,5(6 • 104)2/24 = 0,375 • 109 Н • мм.Перепишем кубическое уравнение с новым свободным членом:0,0895у3 — 723у2 + 3,06 • 10*у — 0,375 • 109 = 0;решение этого уравнения дает у =127 мм.При действии на ферму постоянной нормативной нагрузки
gnz= 6,0 кН/м в сочетании с ветровым отсосом wn=1,5 кН/м, т. е.
при нагрузке Fnw = 4,5 кН/м, значение свободного члена уравнения
будетMr,tot-Mr,nw =1,8 • 109 —4,5(6 • 104)2/24= 1,125 • 109 H • мм.Подставим это значение в уравнение и решим его:0,0895у3 — 723у2 + 3,06 • 106у- 1,125 • 109 = 0; у = 406 мм.Полный прогиб фермы при нормативных нагрузках составит
406— 127 = 279 мм, или 1/215 пролета, что удовлетворяет эксплуа¬
тационным требованиям.Рассчитаем ферму на действие односторонней снеговой нагруз¬
ки. Для этого одностороннюю нагрузку представим в виде суммы
симметричной и обратносимметричной частей. Несимметричная
нагрузка (рис. 52,6) в левой части схемы имеет значение F/ =
= 7,0+1,4 -5,0=14,0 кН/м, а в правой Fr = 7,0 + 0,6 • 5,0 =
= 10,0 кН/м.Установим значения симметричной и обратносимметричной
частей нагрузок:224
Fsym=(Fl+Fr)/2=(l4,0 +10,0)/2= 12,0 кН/м;Finv/sym ^ it 2,0 kH/M.Распор и провис тросов от симметричной нагрузки Fsym =
= 12,0 кН/м уже известны из предыдущего расчета. Будем пола¬
гать, что при приложении обратносимметричной части нагрузки
провис средней точки фермы и распор неизменны.Запишем выражение для балочного изгибающего момента в
левой половине фермы от обратносимметричной нагрузки:Мх = F inv/sym[l /6-Х/2+ Х'7(3/)] X.Точка фермы, где изгибающий момент имеет максимальное
значение, находится на расстоянии от левой опоры:*=а=(3—Уз”)//6=0,211/=0,211 • 60 • 103 = 12660 мм.Подставив значение х в выражение для МХу определим
Мтах= 115,4 * 106 Н ‘ ММ.Кинематическое перемещение этой точки фермы найдем из
формулы (177):. Мтах 115,4 ‘ 10б 91 1 П \лалУа~ Нпр+Ны, ~ 487,5 • 103 + 60 ■ 10» 211,0 ММДалее необходимо распределить обратносимметричную нагруз¬
ку между верхним (несущим) и нижним (стабилизирующим)
тросами фермы, учитывая при этом, что на условном пролете, рав¬
ном половине пролета фермы, т. е. /с = 30,0 м, нагрузка распреде¬
лена по закону треугольника.Часть этой нагрузки, приходящуюся на верхний трос, найдем
из выражения для максимального значения балочного моментаMsup, max == 0,064 15F d, suplc == Н sup^ У а z== 487,5 • 103 • 211,0=102,9 • 106 Н • мм,
откуда искомая нагрузкаFd,sup= '°,2:9ОЛ10' =1,78 Н/мм = 1,78 кН/м.' р 0,06415(30 • 103)2 'Аналогично вычисляется часть нагрузки, приходящаяся на
нижний трос:Hinfb у а = —60 • 103 • 211,0=-12,66 • 106 Н • мм,2 15 Заказ 61 225
откуда доля расчетной нагрузки, приходящаяся на нижний трос,
составитFd inf= 12-66 • 106 -г= -0,22 Н/мм = -0,22 кН/м.• ' 0,06415(30 • 103)2. Полная обратносимметричная нагрузка на половине пролета
фермыFd,sup — Fdjnf = 1,78+0,22 = 2,0 кН/м.Следовательно, условие равновесия удовлетворено.Проверка сечений на усилия, полученные из расчета, в данном
примере опущена.Рассчитаем ферму, приведенную на рис. 51, б на действие одно¬
сторонней нагрузки //=14,0 кН/м. Эта нагрузка, как и в предыду¬
щем примере, состоит из двух частей: FitSup и Fвоспринимаемых
соответственно верхним и нижним тросом.Максимальный балочный изгибающий момент М шах в левой
половине фермы от обратносимметричной нагрузки 2,0 кН/м нахо¬
дится на расстоянии х= 12660 мм от левой опоры и равен
115,4 • 106 Н • мм.Значения начальных провисов тросов, считая от линий, соеди¬
няющих точки подвеса соответствующих тросов с шарниром, при¬
водим без вычислений: fsup= 1540,0 мм и /ш/ =965,0 мм.Подставим в уравнение (180) значения известных величин:5(1540,0 + 965,0) = 2 • 115,4 • 106-2у(487,5 • 103 + 60 • 103),откуда после выполнения необходимых преобразований S =
= 92136 — 437у. Для расчета нам будет необходимо уравне¬
ние (185).Вычислим значения величин, входящих в это уравнение, имея
в виду треугольную эпюру нагрузки:16 • cos3([w = 16 0,9911 =8,65 • 10"5 1/мм;Ji-^=fr^=8’8 •10-5 */-;0,264/U, = 0.264^ 6(Ь103о1 016 6 . ш-з мм/н;Bs,supc0sysup 103 • 10б • 0,9913. Расчет фермы с центральным шарниром226
0,264/U =0,264 - 60 JO3 ^1 00625 =Q 62 . 1Q-3 MM^H-
B,,,„/cos<p,„/ 25,8 • 10* • 0,9967 'здесь ф5ир и фinf— угол между линией, соединяющей точку подвеса соответ¬
ствующего троса с шарниром и горизонталью.После подстановки вычисленных величин в уравнение (185)
получим выражение для усилия в шарнире S = 0,224y2 +559,97у.
Приравняв оба уравнения и решив полученное квадратное урав¬
нение, будем иметь у=91 мм, откуда S = 52,8 кН.Действующую на каждый трос нагрузку найдем из выраженияс _ М _ 0,06415F//?И' H±S/2 'которое получено из формулы (133). Преобразуя это выражение
относительно нагрузки Fi и используя соответствующий знак
перед у, можем вычислить величину нагрузки, приходящуюся на
каждый трос.Так, нагрузка на верхний трос составляет:р _ (1«*+й(w-o+4) (1540+91) (48,75+2,64)■ 104 _ со Н 'мм
0,06415/? “ 0,6415 • З2 • 10» 14,52 М/ММ-То же, на нижний трос:(finf—y) (Нщ 2~) (965 —91 )(б—2,64) • 104 nc:tu/0,06415/? 0,06415 З2 108 ’ Н/мм-Проверим условие равновесияFl = Fl,sup-Fltinf= 14,52-0,51 = 14,0 Н/мм=14,0 кН/м.Следовательно, расчеты проделаны правильно, так как в резуль¬
тате получена суммарная исходная нагрузка.IX. РАСЧЕТ ВИСЯЧЕГО ШАТРОВОГО ПОКРЫТИЯ
НА КРУГЛОМ ПЛАНЕ1. Общие вопросыКруглые в плане висячие покрытия имеют, как правило, за¬
мкнутый опорный контур и радиальную систему вант, сходящихся
в общем центральном узле. Кольцевой опорный контур восприни¬
мает распор вант и передает на поддерживающие конструкции227
Рис. 53. Примеры круглых висячих
покрытий с радиальной системой
ванта — план покрытия; б — разрез покры¬
тия с однопоясной шатровой системой;
а — то же, без центральной опоры;
г, д — то же, с двухпоясной системой;
1 — опорный контур; 2 — ванты; 3 —
центральное кольцо; 4 — центральная
опоратолько вертикальные нагрузки. Контур в основном работает на
сжатие. В центральном узле, как правило, устраивают внутреннее
кольцо, к которому крепят ванты. Это кольцо работает главным
образом на растяжение. Известны также висячие системы, в ко¬
торых оба кольца работают на сжатие *. Работа таких покрытий
под нагрузкой, их статическая схема показывают, что эти системы
довольно эффективны и могут применяться для перекрытия очень
больших пролетов. Круглый контур является оптимальным для
таких систем, так как он получается безмоментным.Круглые висячие покрытия проектируют в виде однопоясных
или двухпоясных систем, с центральной стойкой или без нее. Каж¬
дая из систем обладает своими особенностями, преимуществами
и недостатками. Выбор той или иной конструктивной схемы за¬
висит от архитектурных, функциональных, технико-экономических
и других требований. Некоторые примеры круглых висячих систем
показаны на рис. 53.Однопоясные системы могут предусматриваться предваритель¬
но напряженными, но их проектируют и без предварительного
напряжения. Двухпоясные системы рекомендуется выполнять
только предварительно напряженными.В покрытиях с центральной опорой последняя воспринимает
значительную вертикальную нагрузку, величина которой зависит* А. с. 1030510 (СССР). Висячее покрытие; Авт. изобрет. Г. Г. Виноградов.—
Заявл. 10.02.81 № 3244855/29—33.— Опубл. в Б. И., 1983, № 27; МКИ Е 04В7/14.228
от принятой стрелы провисания вант. Если опору сделать жесткой,
сопротивляющейся горизонтальным смещениям, то расчет ра¬
диальной системы вант сводится к расчету отдельных нитей. По¬
лучающаяся в этом случае неуравновешенность всего покрытия
в горизонтальной плоскости при односторонней нагрузке может
компенсироваться изгибной жесткостью опорного контура и цен¬
тральной стойки. В случае, если центральный узел висячей системы
опирается на подвижную стойку и имеет возможность смещаться
в горизонтальной плоскости, характер напряженно-деформирован-
ного состояния покрытия будет иной. При односторонней нагрузке
величйны натяжений во всех вантах покрытия связаны с величиной
этого смещения.В настоящем примере рассмотрим однопоясные висячие си¬
стемы без центральной опоры и с центральной качающейся (под¬
вижной) опорой.При расчете круглых висячих покрытий вводятся некоторые
допущения: центральный узел рассматривается как единая точка,
отдельные нити в кольцевом направлении не связаны между
собой, наружный опорный контур является жестким и недефор-
мируемым, продольные деформации центральной стойки пренебре¬
жимо малы.Как уже было сказано выше, при осесимметричной нагрузке
ванты рассчитываются как отдельные нити. Для расчета на несим¬
метричную нагрузку, под которой понимается неравномерное от¬
ложение снега на покрытии, необходимо знать характер этого
отложения. Для покрытий шатрового типа ЦНИИСК рекомендует
снеговую нагрузку принимать по законуs = s0(l+0,5cosp)-^77^7, (186)а для провисающих покрытийs = s0(l +0,5cos Р), (187)где р — угловая координата в горизонтальной плоскости, отсчитываемая от самого
нагруженного «нулевого» ванта; г — радиус-вектор, полярная координата; г5Г —
радиус опорного кольца (покрытия).Максимальная интенсивность снеговой нагрузки при р = 0
и r = rST составляет s=l,5so, а минимальная (на диаметрально
противоположной стороне покрытия при 0=180°) 5 = 0,5io.
На перпендикулярном к «нулевому» диаметре при 0 = 90° и 270°
и r = rsr интенсивность s = so.В формулах (186) и (187) первый член представляет собой
симметричную часть нагрузки, которая может быть просуммиро¬
вана с постоянной нагрузкой, что даст возможность получить
распор, усилия в вантах, уравнение кривой и максимальный провис
от симметричной части нагрузки. Второй член в указанных форму¬229
лах представляет собой полярно обратносимметричную часть
нагрузки, подчиняющуюся тригонометрическому закону. Усилия
от обратносимметричной нагрузки можно суммировать с усилиями
от симметричной нагрузки. При этом величина распора опреде¬
ляется только симметричной нагрузкой, а прогрешность расчета
измеряется величиной £ (см. табл. на стр. 216). В данном случае
отношение односторонней снеговой нагрузки к симметричной
Y=0,5, и с учетом даже минимальной постоянной нагрузки (легкие
покрытия) величина погрешности не превышает 1%.При обратносимметричной нагрузке горизонтальное перемеще¬
ние самого нагруженного «нулевого» ванта в центральном узле
определяется по формуле (178). Расчет любого другого троса,
находящегося под углом р к «нулевому», можно выполнять неза¬
висимо от системы как для отдельного троса, а перемещение вдоль
его оси будет aP=acosP, причем обратносимметричная нагрузка
на этот трос определяется величиной s0cos р. Таким образом, рас¬
чет радиальной вантовой системы без центральной стойки на обрат¬
носимметричную нагрузку сводится к расчету нулевого ванта, а
усилия и перемещения других определяются умножением соответ¬
ствующих значений на cos р.При проектировании шатровых висячих систем, имеющих цен¬
тральную стойку, целесообразно перепад отметок подвески вант
назначать таким, чтобы угол наклона касательной в точке креп¬
ления вант к наружному опорному контуру был равен нулю. Тогда
вся вертикальная нагрузка передается на центральную стойку,
а опорное кольцо нагружено исключительно распором от вант
и работает только на сжатие. Имеет также смысл делать верхнюю
точку центральной опоры подвижной, а саму опору качающейся
или с минимальной изгибной жесткостью. Это позволяет исклю¬
чить передачу на нее и на опорный контур больших горизонтальных
сил, возникающих в радиальной системе, особенно от действия
односторонней нагрузки.Расчет вант шатровой системы на симметричную нагрузку
выполняется по формулам расчета отдельных гибких нитей (см.
пример VIII.А).При расчете вант на одностороннюю снеговую нагрузку интен¬
сивность ее вычисляют по формуле (186). При этом распор опре¬
деляется из расчета только на симметричную нагрузку и прини¬
мается одинаковым для всех вант. Обратносимметричная нагрузка
вызывает только горизонтальное перемещение центрального узла
радиальной системы. Приближенное решение задачи можно полу¬
чить из раздельных расчетов системы на симметричную и обратно¬
симметричную нагрузки.Дополнительный провис нити от действия обратносимметрич¬
ной нагрузкиА^ = Мтах/Н, (188)230
где Mmax— момент от обратносимметричной нагрузки; Н — распор от осесим¬
метричной нагрузки.Если иметь в виду, что в результате действия обратносим¬
метричной нагрузки длина ванта и распор остаются прежними,
а горизонтальное перемещение центрального узла вызывает изме¬
нение только длины хорды, связывающей точки крепления ванты,
то на основании формулы (143) можем записать:г . D/Ocos3<p г ж . Df.cos3®cos ф “I 2Я5 — cos ф C0S 2fp ’откуда■ , (189)где л — горизонтальное перемещение центрального узла в результате действия
обратносимметричной нагрузки; D/0 и D/,— интегральные характеристики нагру¬
зок, отнесенные к пролету, равному радиусу шатрового покрытия, соответственно
от симметричной и суммарной нагрузок; угол ф принят одинаковым до и после
перемещения из-за малости последнего.Для расчета опорного контура радиальной вантовой системы
на обратносимметричную нагрузку необходимо знать горизонталь¬
ную и вертикальную составляющие опорной реакции вант. Что
касается горизонтальной составляющей, то, как отмечалось выше,
под действием обратносимметричной нагрузки величина распора
не меняется. Следовательно, расчетным состоянием является сим¬
метричная нагрузка, и опорное кольцо работает на равномерное
сжатие. Вертикальная составляющая под действием рассматри¬
ваемой нагрузки перераспределяется: она становится больше в
зоне пригружаемых вант (с максимумом на опоре «нулевого»
ванта) и меньше в зоне разгружаемых. На вертикальную нагрузку
опорное кольцо рассчитывается в случае, если оно опирается
на отдельно стоящие по периметру покрытия колонны.Сжатые опорные кольца круглых висячих покрытий должны
быть проверены на устойчивость. Критическую продольную си¬
лу Ncr в плоскости кривизны кругового опорного контура рекомен¬
дуется определять по формулеNcr>2^J Eblredk , (190)где Ebhed— изгибная жесткость контура; k — коэффициент, равный для провиса¬
ющих радиальных вантовых систем с горизонтальной касательной в центральном
узлеЛ = 5F/(24ц3), (191)231
а для шатровых висячих оболочек*,=5F/(3ti?) (192)т\=f/rsr; r\\=f\/rSr4,f — стрелка провиса центрального кольца висячей оболочки; f\ — величина подъ¬
ема центрального кольца над уровнем контурного кольца шатрового покрытия;
rsr— радиус центра тяжести сечения контурного кольца.Как уже отмечалось выше, в случаях, когда в шатровых систе¬
мах угол наклона касательной у опорного контура ср^О, вся на¬
грузка от покрытия передается на центральную опору и осадка
ее основания может оказаться существенно большей, чем осадка
опор контура. Если не будут приняты необходимые меры по
предотвращению осадки основания центральной опоры, разность
осадок следует учесть при определении коэффициента rji. В этом
случае y\i=(fi+e)/rsn где е — взаимная осадка центральной и
периферийной опор.2. Конструкция покрытия и нагрузкиНужно запроектировать покрытие над круглым залом со стой¬
кой в центре. Диаметр зала 80 м. Покрытие принято висячее,
шатрового вида с 72 радиальными вантами (рис. 54). Ванты
закреплены вверху к внутреннему кольцу, наружный диаметр
которого составляет 12 м, и внизу — к наружному кольцу, внутрен¬
ний диаметр которого 80 м. Шаг вант по внутреннему кольцу:
sm/ = n • 12 • 103 /72 = 524 мм; шаг по наружному кольцу: =
= п • 80 • 103/72 = 3490 мм.В качестве ванты приняты два стержня диаметром по 40 мм
из арматуры класса А-Шв: Rs = 450 МПа, Es= 18* 104 МПа.Наружное кольцо принимаем из монолитного железобетона се¬
чением 1200X500 мм, бетон класса В 25, /?&=14,5 МПа, Еь =
= 3 • 104 МПа. Арматура кольца принята (5 + 5) 0 40, клас¬
са A-III, /?5 = 365 МПа, Es— 2 • 105 МПа, As= 12566 мм2.Перепад уровней подвески вант 5,3 м. Центральную стойку
принимаем качающейся. Значения нагрузок, действующих на по¬
крытие, даны в табл. 46. Таким образом, для расчета принимаем
нагрузку Fdtt3,5 КПа.Вычислим полную распределенную линейную расчетную на¬
грузку, действующую на вант: Fd,ш=0,524 • 3,5= 1,83 кН/м;
Fdtext = 3,490 • 3,5= 12,2 кН/м, и нормативную: ^=0,524 • 2,9=
= 1,5 кН/м; Fn,ext = 3,490 • 2,9=10,1 кН/м.Выделим из полной нагрузки только постоянную составля¬
ющую:Fngtint = 0,524 • 1,9= 1,0 кН/м; Fng,ext = 3,49 • 1,9 = 6,63 кН/м.232
Рис. 54. К расчету кругового шатрового покрытия
а — схема покрытия и симметричные нагрузки; б — расчетная схема вантТаблица 46Вид нагрузкиНормативноезначениенагрузки,кПаКоэффициент
надежности
по нагрузке
V/Расчетноезначениенагрузки,кПаСобственная масса оболочки1,151,11,27Теплоизоляция и пароизоляция
кровли, гидроизоляционный ко¬
вер0,751,30,98Итого постоянная1,92,25Снег1,01,41,4ВсегоВсего с учетом коэффициента
надежности по назначению уп =
= 0,952,93,653,47233
3. Расчет вант по симметричной схемеПримем за исходное такое состояние вант, когда на покрытие
действует полная нагрузка и при этом касательная в точке сопря¬
жения ванты с наружным кольцом горизонтальна. В этом случае
на наружное кольцо передается только горизонтальная нагрузка,
а самой низкой точкой висячего троса является точка его крепле¬
ния к опорному кольцу. Такой трос может быть рассчитан как
симметричный с опорами на одном уровне, если принять условную
схему, показанную на рис. 54, б в качестве расчетной.Определим интегральную характеристику нагрузки по табл. 53,
для троса по схеме 54, а:Dfd(a) ==-Г80”(4 Fdtext + 4 Fd,int + 7 Fd,extFd,int) =• 12>22 + 4 • 1,832 + 7 • 12,2 • 1,83)== 1,67 • 105 кН2 • м = 1,67 • 1014 Н2 • мм.Интегральные характеристики нагрузки по схеме рис. 54, б:
Dfd{6) =_2^о”(3 Fdtint + 8Fd,ext + 9Fd,intFd,ext) ==-^f(3 • 1,832 + 8 • 12,22+9 • 1,83 • 12,2)== 18,41 • 105 кН2 • м= 18,41 • 1014 Н2 • мм.Найдем балочный момент в тросе по схеме рис. 54, б:Мы = ода.,* + /ч«<)(0,5/)2 - 0,5/ч,„/(0,5/)2 -
-(Fd,e*t-Fd,intm5l)2/6 == ‘-83+12’2 342—1,83-^—(12,2 —1,83)-^-=5055 кН • м,после чего вычислим значение распора по формуле (133): #<* =
= 5055/5,3 = 953,8 кН.Для определения максимального усилия в растянутом тросе
по формуле (135) необходимо сначала рассчитать вертикальную
реакцию в точке подвеса, которая составляет VOi =0,5(1,83 +
+ 12,2)34 =239 кН, тогдаNd=^Hl + Vl =V 953,82 + 2392 = 985 кН.234
Несущая способность принятого выше ванта 204ОАШв
(i4s = 2513 мм2) составляетNfact=ASRS = 2513 • 450/103= 1130,85 кН,т. е. установленные ванты удовлетворяют условиям прочности,
так как Nfact> Nd.Рассчитаем теперь длину заготовки ванта.Жесткость сечения ванта на растяжение:Bs=AsEs = 2513 • 18 • 104/103 = 452,3 • 103 кН.Длина ванта при полной нагрузке по формуле (137):'■=('+И)т= О*'101+т^)т=34511 ““Расстояние между точками крепления наклонного ванта (см.
рис. 54, а): а=У342 + 5,32 =34,41 м. Косинус угла наклона ли¬
нии, соединяющей точки подвеса, cos ср = 34/34,41 =0,9881.Находим отношение длины троса (при полной нагрузке) к рас¬
стоянию между точками подвеса ванта по формуле (151):£ = L/a = 34,511 /34,41 = 1,00294.Вычисляем удлинение наклонного ванта по (148):1,05Hat _ 1.05 ■ 953800 ■ 34410 • 1,00294 _7Q
£scosq> 452,3 • 106 • 0,9881 MM*Зная длину ванта под нагрузкой и его упругое удлинение, вы¬
числим длину заготовки ванта по (148а): L0 = L —aL = 3451 1 —— 78 = 34433 мм, что и требовалось.4. Определение провиса наклонного вантаВертикальная составляющая реакции опоры А наклонного ван-
П1 в точке крепления к верхнему кольцу (балочная реакция)
будетКл=0,5 • 1,83 • 34 + (12,2—1,83) • 34/6 = 90 кН.Сечение, где балочный изгибающий момент имеет максималь¬
ное значение, найдем из уравнения балочной поперечной силы,
приравняв ее нулю:Q = Fd.intx+(Fd.exl-Fd,inl)x2/(2l')-К4 =— I,83л:—(12,2— 1,83)л:2/(2 • 34)-90 = 0, откуда *=19 м.235
Вычислим максимальный изгибающий момент в указанной
точке:Md,ma*=90 • 19-1,83 • 192/2—(12,2— 1,83)Х
X193/(34 • 6)= 1030 кН • м.Величина провиса ванта от воздействия этого момента полу¬
чится по (133):/шах = Md,max/Hd = 1030 - 106/953800= 1080 мм.5. Определение прогиба покрытияЧтобы определить прогиб от воздействия на покрытие полной
нормативной нагрузки (рис. 54, а), вычислим для нее интеграль¬
ную характеристику по табл. 45:D'«=w(4 • Ю.12+4 • 1.547 • 10,1 • 1,5)== 11,42 • 104 кН2 • м = 11,42 • 1013 Н2 • мм.Значение распора найдем из решения кубического уравне¬
ния (158). Подставим в уравнение известные величины:„3 , / 1,67 • 1014 • 452,3 • 106 • 0,98814 ПСООЛл\ и2
Ип+К 2 -953800»- 34410 -1.00294» 9*3800) Я„-11,42 ■ 1013 • 452,3 ■ 106 • 0,98814 _q.2 • 34410 • 1,002942после выполнения необходимых вычислений и упрощений пере¬
пишем уравнение в следующем виде:Н\ + 2 • 105 Я2—0,71 • 1018=0,откуда распор Я„ = 826 кН.Для определения максимального изгибающего момента от нор¬
мативной нагрузки воспользуемся вычисленным ранее его значе¬
нием для расчетной нагрузки: Мп,тах= 1030- 2,9/3,5 = 853 кН • м.
После этого найдем искомый провис от полной нормативной на¬
грузки по (133):/„ = 853 • 106/0,826 • 106 = 1033 мм.236
Найдем теперь провис от воздействия на покрытие только
постоянной части нормативной нагрузки. Значение интегральной
характеристики нагрузки при этом составит:' 6,632 + 4 • 1,02 + 7 • 1,0 • 6,63) ==4,94 • 104 кН2 • м = 4,94 • 1013 Н2 • мм.Подставив вычисленные коэффициенты при неизвестном рас¬
поре в кубическое уравнение, получимH3ng + 2 • 105Я^-0,31 • 1018 = 0,откуда распор Hng=602,3 кн.Изгибающий момент от постоянной части нормативной нагруз¬
ки М„*=1030 • 1,9/3,5 = 559 кН • м.По формуле (133) находим провис ванта от указанной на¬
грузки:/„* = 559 • 106/0,6023 • 106 = 928 мм.В результате прогиб покрытия Af = fn — fng= 1033 — 928 =
= 105 мм составляет 1/325 пролета покрытия.6. Расчет покрытия на одностороннюю
снеговую нагрузкуУчитывая, что конструкция центральной стойки принята ка¬
чающейся, будем считать распор неизменным и равным распору
от воздействия полной нагрузки.Горизонтальное смещение верхней точки центральной опоры
от воздействия нормативной нагрузки определим по (189):b=(Df,on — Dfn) cos2 <р/ (2#2),где Dfn— интегральная характеристика нагрузки при полной нормативной на¬
грузке на покрытие: D/„= 11,42 • 1013 Н2 • мм; Dft0n— то же, при нормативных
постоянной и односторонней снеговой нагрузках.Считая, что перегрузка снегом на одной стороне шатрового
покрытия составляет 40%, получим искомые значения нагрузок
(гм. табл. 46):Fanoint = 0,524(1,9 + 1,4)= 1,73 кН/м;Fon,g,ext = 3,49(1,9 + 1,4) = 11,5 кН/м.2 37
Зная величины нагрузок, найдем D,l0n по табл. 45:
D,.on=ig-(4 • 11,52 + 4 • 1,732 + 7 • 11,5 • 1,73)== 14,854 • 104 кН2 • м = 14,854 • 1013 Н2 • мми после подстановки в формулу (189) получим искомое горизон¬
тальное смещение:д =(14,854—11,42) • 10'3 • 0,98812/(2 • 8260002)=24,6 мм.7. Расчет нижнего опорного кольцаПроверяем сначала прочность сечения. Для этого вычислим
сжимающее усилие в кольце от воздействия полной расчетной
нагрузки:Nrd = 72Hd/(2я) = 72 • 953,8/(2 • 3,14)= 10935 кН.Определим фактическую несущую способность кольца по проч¬
ности:Nlacl = hbRb+AsRs=(500 • 1200 • 14,5+12566 • З65)/103 == 13287 кН, т. е. Niact> Nrd-Следовательно, прочность кольца обеспечена.Расчет на устойчивость конструкции кольца производим по
формуле (190). Для этого сначала вычислим:радиус центра тяжести кольца rsr=40+1,2/2=40,6 м;
приведенный момент инерции кольца/rod = 500 • 12003/12+12566 • 5402 • 2 • 105/3,0 • 104 ==96,4 • 109 мм4.Вычислим коэффициенты i]i и ^ по формуле (192):ц,—f,/r„ = 5,3/40,6 = 0,13; k, = 5 • 2,9 • 10_3/3 • 0,133=2,2.Полученные значения подставляем в формулу (190) для NCr
и находим величину продольной сжимающей критической силы
в железобетонном кольце:Ncr=2V30 • 96,4 • 2,2 • 10'4 =159,5 • 106 Н = 159,5 • 103 кН.238
Свободная длина кольца вычисляется по известной формуле:
, I nEbI,ed / 3,14 • 30 • 103 • 96,4 • 109/o=V^- = V 15^5—Ш5 =754? ММ'Гибкость кольца при данной свободной длине /0/Л = 7547/1200=
= 6,3. Поскольку /0/Л< 14, сечение следует рассчитывать, как вне-
центренно сжатое, с учетом случайного эксцентриситета, согласно
рекомендациям СНиП по проектированию железобетонных кон¬
струкций: еа = h/30= 1200/30 = 40 мм.Расчет внецентренно сжатого железобетонного сечения по
полученным усилиям не приводится.X. РАСЧЕТ ВИСЯЧЕГО ПОКРЫТИЯ
С ПЕРЕКРЕСТНОЙ СИСТЕМОЙ ВАНТ
И КРИВОЛИНЕЙНЫМ КОНТУРОМ1. Основные положенияВисячая система, образуемая сеткой растянутых вант, самая
распространенная в строительной практике. Одним из достоинств
ее является возможность регулирования усилий в вантах. Находят
применение сетки с вантами, пересекающимися под разными
углами и образующими соответственно разнообразные ячейки,
при этом сетки могут натягиваться на жесткий или гибкий опор¬
ный контур.В нашем примере рассматриваются сетки с ортогональной
системой вант, натягиваемых на жесткий замкнутый криволиней¬
ный контур и образующих висячую оболочку. Такие конструкции
целесообразно проектировать в виде поверхностей эллиптического
параболоида, гиперболического параболоида или параболоида
вращения, уравнения которых соответственно имеют вид:2 = f(-^r+|r); (193>*«/«7—(194)
z=fS+!L. (195)где f — стрела провисания в центре эллиптического параболоида или парабо¬
лоида вращения; fx и fy—стрелы провисания вантов, соответственно параллель¬
ных оси х и у гиперболического параболоида; а и Ь — полуоси контурного эллипса;
г — радиус контурной окружности.239
Уравнения дают описание поверхности при полном загружении
вант. Поверхность образуется двумя взаимно перпендикулярными
семействами вант, причем ванты каждого семейства конгруэнтны,
параллельны друг другу в плане и имеют одинаковый шаг.
При этом ванты одного семейства являются несущими и имеют
выпуклость вниз, а ванты другого семейства — стабилизирующи¬
ми (напрягающими) и имеют выпуклость вверх. Предварительное
напряжение системы создается натяжением стабилизирующих
вант. Расчетом предполагается, что ванты упругие, а контур
абсолютно жесткий. В примере рассматривается эллипсовидный
контур (рис. 55), уравнение которого имеет вид:('96)tear 1stНа несущие ванты, кроме расчетной нагрузки от покрытия,
действует дополнительная нагрузка от натяжения стабилизиру¬
ющих вант. Величина дополнительной нагрузки принимается10... 15% от расчетной.Если провисы главных вант считать заданными fcar и f st для
исходного состояния системы, то, имея в виду зависимость в фор¬
муле (134), можем записать:Я/7 carScarlcar . гг FusJi,car Qf , *1 st — qcOf car Of siПоскольку ванты (параболы) каждого семейства конгруэнтны,
то их распоры от одной и той же нагрузки одинаковы. Следова¬
тельно, составляющие опорных реакций и усилия в главных и
остальных вантах могут быть определены по формулам для расчета
гибких нитей (см. пример VIII.А). Это позволяет подобрать сече¬
ние несущих вант. Сечением стабилизирующих вант необходимо
задаться заранее в пределахBs,st=(0,2... 0,4)BS, car-^- (197)Л carи затем в процессе расчета проверить его. За исходное состояние
системы принимается вантовая сетка без нагрузки (собственной
массой пренебрегают) или сетка, загруженная незамоноличен-
ными плитами покрытия в сочетании с ветровым отсосом.Условие равновесия вантовой сетки можно записать в следу¬
ющем виде:Fcar = F\-\-Fst> (198)где F\—внешняя нагрузка в новом состоянии системы; Fcar и Fst—нагрузки,
воспринимаемые вантами соответствующих направлений.240
Рис. 55. Схема висячего покрытия с перекрестной системой вант и криволинейнымконтуромНагрузки отнесены к единице горизонтальной проекции пло¬
щади. Значение нагрузки на ванту получим из формулы (134),
учитывая при этом, что при снятии части нагрузки распор и провес
ванты уменьшатся:г» 8Мсаг 8{Hear &Hcar){fcar %) . / 1 ОП\Г саг “ /2 — —л > У1™)bcartcar bcartcarFst= 8(tf.«+Ay.«±gL • (200)Ssdstздесь z={±fcar=bfst—неизвестное приращение провиса.Приращение распоров определим по формулам (171) и (172):A Hcar=2MBs.car(2fcar-z)z . (2()1)IcarLcarд// 2,54Д„,(2/„+г)г (202)IstLstПодставим (201) и (202) в (199) и (200), а затем в (198). В ре¬241
зультате получим кубическое уравнение относительно неизвестного
приращения провиса z:(Ссаг “1“ Cst) Z3 3(Ccarf car Cstfst) Z? -(-(fTlcar fTlst~\~2Ccarfcar~\~2Cstfst)Z (F Fl) = 0, (203)где F — полная нагрузка на покрытие в исходном состоянии (кПа).Здесь введены обозначения для сокращения записи:_ 20,3Вs, саг . 20,3BStSt 'СйГ"" Scarltar&r ’ ’ 8//саг . ^ 8 Hst•fl car — "lst — 72 •Scarlcar SstlstЭллиптический опорный контур висячего покрытия с ортого¬
нальной вантовой сеткой в виде поверхности гиперболического
параболоида с двумя осями симметрии представляет собой эллипс
с поверхностью второго порядка [см. уравнение (196)]. Опорный
контур работает главным образом на сжатие с изгибом в горизон¬
тальной и вертикальной плоскостях. Чтобы контур не испытывал
кручения, ванты следует центрировать на ось его поперечного
сечения.Линейная нагрузка на контур от каждого семейства вант
(см. рис. 55) равна:Fcar = Нсаг /5сап |(204)F st — Hst/Sst• J
Условие безмоментности контура имеет вид: С fcarсаг — г т——I— ,fcar — fst(205)FSI=F-г-Ц-.fcar — fstЕстественно, что от всех нагрузок, действующих на покрытие,
невозможно обеспечить безмоментность контура. Поэтому имеел
смысл обеспечивать безмоментность или только от постоянной
нагрузки, или от постоянной и половины временной. Другие на¬
грузки при этом будут создавать моменты, но величина этих мо¬
ментов будет не столь велика, как от полной нагрузки.Расчет контура на действие нагрузок по формулам (204) це¬
лесообразно выполнять методом сил. Замкнутый контур представ¬
ляет собой трижды статически неопределимую систему. Введя242
шарниры в двух диаметрально противоположных сечениях на оси
симметрии, контур превращают в статически определимую систе¬
му. По условиям симметрии третье неизвестное — поперечные
силы в шарнирах — обращается в нуль, а продольные силы в шар¬
нирах — в Fstlcar/2. Неизвестные изгибающие моменты в шарнирах
равны между собой. Таким образом, расчет системы на сим¬
метричную нагрузку сводится к решению одного уравнения метода
сил с одним неизвестным, в качестве которого принимаются изги¬
бающие моменты в шарнирах.Максимальные по абсолютной величине изгибающие моменты
в эллипсовидном опорном контуре возникают в сечениях, распо¬
ложенных на пересечении с главными осями эллипса. Опорный
контур следует также проверить на устойчивость. При этом учи¬
тывается влияние вантовой сетки, которая рассматривается как
упругое основание, поддерживающее кольцо. Значение продоль¬
ной сжимающей критической силы можно рассчитать по форму¬
ле (206) *:+ (206)Коэффициент упругого основания k определяется по формуле(207)где ф — угол наклона линии, соединяющей опорные точки ванта.Проверкой опорного контура на устойчивость расчет заканчи¬
вается.2. Конструкция покрытия и нагрузкиПроектируется покрытие здания, имеющего в плане криволи¬
нейный контур. Очертание контура выбираем так, чтобы в плане
не возникали изгибающие моменты, т. е. чтобы контур был безмо-
ментным. Таким является контур, имеющий очертание эллипса.
Принимаем покрытие в форме гиперболического параболоида,
уравнение поверхности которого имеет вид (194):^—/.£+/.£—/~-£-+Иг (|94а)* Кузнецов Э. Н. Радиальные вантовые системы, теория и расчет. М.: Строй¬
издат, 1963.2 43
Таблица 47Вид нагрузкиНормативноезначениенагрузки,кПаКоэффициент
надежности
по нагрузке
VfРасчетноезначениенагрузки,кПаСобственная масса покрытия1,11,11,21Теплоизоляция, пароизоляция
кровли, гидроизоляционный ко¬
вер0,41,30,52Итого постоянная1,51,73Снег1,01,41,4Всего2,53,13Конструкция покрытия принимается в виде висячей оболочки
с ортогональной системой перекрестных вант, несущих и стабили¬
зирующих, опирающихся на жесткий замкнутый криволинейный
контур (см. рис. 55). Уравнение контура имеет вид х* /а2-\-у2/Ь2 =
= 1. Полуоси контурного эллипса: а = 30 м, Ь = 20 м.Несущие (провисающие) ванты расположены параллельно
оси X с шагом в плане sCflr=1250 мм, а стабилизирующие (на¬
прягающие) — параллельно оси Y с шагом в плане ss*=1500 мм.
Материал вант — стержневая арматурная сталь класса A-V
(#s = 680 МПа; Es= 190 • 103 МПа); опорный контур — моно¬
литный железобетонный сечением 400X4000 мм из бетона клас¬
са В 30 (Rb= 17,0 МПа, £* = 32,5 • 103 МПа).Стрелы провисания вантов составляют: несущего fcar = 4,5 м,
стабилизирующего fst= 1,2 м. Значения нагрузок, действующих
на покрытие, приведены в табл. 47. Коэффициент надежности
по назначению Yn=l-3. Расчет перекрестных вантПри расчете системы вант за исходное принимаем состояние,
когда на покрытие действует полная расчетная нагрузка. При этом
несущие ванты работают на полную расчетную и дополнительную
нагрузку от натяжения стабилизирующих вант, составляющую10... 15% от полной расчетной нагрузки. В данном случае прини¬
маем дополнительную нагрузку равной 0,4 кПа. Таким образом,
каждый несущий вант рассчитываем на линейную нагрузку
(3,13 + 0,4) • 1,25 = 4,4 кН/м.Распор от действия этой нагрузки по формуле (134) ://саг = 4,4 • 602/(8 • 4,5) = 440 кН.244
Вертикальная реакция на опоре A: Va = 4,4 • 60/2=132 кН.
Отсюда усилие в несущем ванте, рассчитанное по (135), составитNcar=^J 4402+ 1322 =459 кН.Несущая способность стержня 032AV, принятого для этого
ванта, составляетNfaci = AsRs = 804,3 • 680/103 = 547 кН> 459 кН,т. е. прочность несущих вант обеспечена.Вычислим теперь длину заготовки главного несущего ванта.
Длина этого ванта по (136):Lcar = Ucar = U(\+^-) == 60 • 103(1 + 83 4/, ) = 60 • 103 • 1,015 = 60,9 • 103 мм.Длина его заготовки по (148а):j j \%0ЬHear linear L>0, car — Lear ~А~Ё —СП n m3 1.05 • 440 • 60 ■ 1,015 • I06’ ' 10 0.8043 ■ 0.19 . 10- =6°715Распор, возникающий на опорах стабилизирующего ванта от
действия дополнительной линейной нагрузки 0,4 • 1,5 = 0,6 кН/м,
рассчитываем по (134): Hst = 0,6 • 402/(8 • 1,2)= 100 кН.Длина стабилизирующего ванта по (136):Ь (.+f)=40.10»(l +4^-).= 40 • 103 • 1,0024 = 40096 мм.Сечение стабилизирующих вант принимаем 02OAV (AStSt =
= 314,2 мм2), что удовлетворяет условию (197), так какAs,stEs,stScar / (As,carEs,carSst) ^0,32.Сечение стабилизирующего ванта проверяется из условия
равновесия вантовой сети. За расчетное состояние принимаем
систему без внешней нагрузки (собственной массой вант пре¬
небрегаем), нагруженную только напрягающими вантами.
При этом для равновесия сети должно быть соблюдено условие245
равенства приращения провисов в точках пересечения вант. Ре¬
шение получим из кубического уравнения относительно прираще¬
ния провиса (203), но сначала вычислим значения коэффициентов
в уравнении:Ссаг = 20,3 • 0,19 0,8043 • 109/604 • 1,25 • 1,0152 • 10,5 =
=0,186 • 10-'2;
tncar = 8 • 0,44 • 106/602 • 1,25 • 109 = 0,782 • 10~6;
cs/ = 20,3 • 0,19 • 0,3142 • 109/404 • 1,5 • 1,00242 • 10,5 == 0,314 • 10-'2;nts, = 8 • 0,1 • 106/402 • 1,5 • 10_9=0,33 • 10"®,'F — Fi =3,53 —0,4 = 3,13 кПа = 0,00313 МПа.Полученные величины ccar, c$t, тсаг и msi используем для вы-
числения коэффициентов при неизвестной z (вычисления опуска¬
ем) и перепишем кубическое уравнение:0,5 • 10-V-1,381 • 10-V + 9,552z —3130 = 0.Это уравнение имеет одно действительное решение при z = 340 мм.
Следовательно, и приращение провиса вант д^аг=д/^ = 340 мм.
В результате провис главного несущего ванта при отсутствии
внешней нагрузки составит fo,car = 4500—340 = 4160 мм, а распор
этого ванта Но.саг = Нсаг—ьНсаг = 440 — 312,8 = 127,2 кН, где при¬
ращение распора по формуле (201):л//сал = 2,54 • 0,19 • 0,8043(2 • 4,5—0,34)0,34 • 10,5/602Х
X 1,015 • 109 = 312,8 кН.Проделаем такие же расчеты для главного стабилизирующего
ванта: провис fo,st= 1200 + 340= 1540 мм; распори и I » и inn i 2.54 • 0,19 • 0,3142(2 • 1,2 + 0,34)0,34 • 1015
Ho,st = Hsl + bHsl=m+ 40* ■ 1,0024 -10» = 188,0 кН.Проверим расчеты по условию равновесия вант сети, найдя
значения нагрузок, приходящихся на несущий и стабилизирующий
ванты, по формулам (199) и (200):246
_ 8 • 127,2(4,5-0,34) 109 „ „test,car- j 25 . 602 . 10® KUa^p 8- 188,0(1,2 + 0,34) 109 % „— J 5 . 402. 109 —и,УЬ Kiia,т. e. равновесие обеспечено. Следовательно, расчеты верны.Проверим принятое сечение стабилизирующих вант. Для этого
сначала найдем значение вертикальной опорной реакции этого
ванта и величину продольной силы, действующей в нем от вычис¬
ленной выше равновесной нагрузки:VA=Fes,ss,±-= 1,0 • lf5-£~j5r=30,0 кН;Nst=V (Hsl + A Hslf + Vl =V 188,02 + 30,02 =190,0 кН.Несущая способность принятого сечения стабилизирующего
ванта Nfact = 314,2 • 680/103 = 213,7 кН; Nfact> Nst. Фактическая
несущая способность ванта больше действующей продольной
силы и, следовательно, прочность этого ванта обеспечена.Теперь необходимо вычислить длину заготовки стабилизиру¬
ющего ванта. Для этого воспользуемся формулами (148) и (148а),
объединив их:, 1,05//,,/^ _■“О, st — L,st л F —As,st£s,stллллй >.05 0.1 4 1.0024 10'“= 40096 0.3142 ■ 0.19 10* 40026Для обеспечения безмоментности контура при действии на
покрытие постоянной части расчетной нагрузки Fgd= 1,73 кПа
(без снега) нужно сначала определить от нее усилия в вантах.
С этой целью решим приведенное выше кубическое уравнение
относительно приращения провиса вант. Поскольку изменилась
величина нагрузки, заменим в нем свободный член, который в дан¬
ном случае будет равен (3,13— 1,73) 10“3= 1,4 • 10-3. Уравнение
примет следующий вид:0,5 • 10-12 • z3—1410 • 10-12 • z2 ++ 9,63 • 10_6 • z—1,4 • 10“3 = 0,откуда ,Z=A/car = д/*/= 148 мм.247
Зная приращения провиса вант, можем определить прираще¬
ние распора по (201) и полный распор от постоянной нагрузки:Hear — A НСаг = 440 • 103-8 • 0,19 • 0,8043(2 • 4,5 — 0,148)0,148 • 1015 _ОП/| „ц.3 • 602 • 1,015 • 10е _ ’Hst + bHst=l00 • 103 +, 8 • 0,19 • 0,3142(2 • 1,2 + 0,148)0,148 • 1015 _ 1003 • 402 • 1,0024 • 10е К4. Определение прогиба покрытияПрогиб покрытия определяется от действия нормативной на¬
грузки. Полная нормативная нагрузка составляет 2,5 кПа, а по¬
стоянная ее часть— 1,5 кПа. Прогиб покрытия определится как
разность положений центральной точки покрытия в результате
расчета йокрытия при воздействии снеговой нагрузки и при ее
отсутствии. В этом случае коэффициенты приведенного выше
кубического уравнения не меняются, за исключением свободного
члена, который в первом случае равен (3,13—1,5) 10“3= 1,63 • 10-3,
а во втором — (3 • 13 — 2,50) 10-3 = 0,63 • 10_3.Итак, запишем кубические уравнения для обоих вариантов
нагрузки:1) снеговая нагрузка на покрытии имеется:0,5 • 10"12 • zf—1410 • 10"12 • z2 + 9,63 • 10"6 • zi-
-1,63 • 10"3 = 0,откуда Zi = 174 мм;2) снеговая нагрузка на покрытии отсутствует:0,5 • 10"12 • zl—1410 • 10"12 • zi + 9,63 • 10"6 • z2-
-0,63 • 10"3 = 0,откуда z2 = 66 мм. В итоге разность положений центральной точки
или прогиб покрытия составит az= 174 — 66= 108 мм.5. Расчет опорного контураЖелезобетонный опорный контур рассчитывают по прочностии по устойчивости.248
Таблица 48КомбинациянагрузкиНагрузка, кН/мF сагFst135266,72108125,93243,290,7Расчет опорного контура по прочности. Расчет эллиптического
контура по прочности выполняется на возможную комбинацию
из трех нагрузок: 1) на покрытие действует полная расчетная
нагрузка; 2) на покрытии отсутствуют какие-либо нагрузки (ста¬
дия напряжения вантовой сети); 3) на покрытие действует только
постоянная часть расчетной нагрузки.Нагрузки, передающиеся на контур, вычислены и приведены
в табл. 48 для всех трех случаев по формулам (204):Fcar ^ Нcar /Scar И Fst^Hst/Sst'Контурную кривую произвольно разбиваем на близкие по длине
участки. В нашем примере четверть дуги эллипса длиной 39580 мм
содержит 8 участков.Замкнутый контур является трижды статически неопределимой
системой, однако благодаря симметрии системы и нагрузок доста¬
точно ввести два шарнира и система превращается в статически
определимую. Шарниры располагаем на большой оси эллипса
(рис. 56, а). В силу симметрии системы оба неизвестных изгиба¬
ющих момента равны между собой, поперечные силы в шарнирах
обращаются в ноль, и задача может быть решена методом сил
с помощью одного канонического уравнения: х=— 6i//6n.Разбивка дуги контура на участки, а также эпюры изгибающих
моментов в основной системе от действия единичных сил Fcar =
= 1,0 кН/м и Fst= 1,0 кН/м приведены на рис. 56,6. Эпюра из¬
гибающих моментов от приложения в шарнирах единичного из¬
гибающего момента х=1 показана на рис. 56, в.Производя вычисления перемещений на одной четверти дуги
контура, имеем £/бц =39,580. Площади-эпюр моментов несущего
и стабилизирующего ванта (вычисления сшускаем): Mf Саг =
= 4353,0 кН • м2; М/*/ = 9796,0 кН • 0,25 м2; отсюда El8\f =
= 9796,OF,/ —4353,0/wПодставляя полученные EIбц и Elbif в каноническое уравне¬
ние, запишем выражение для определения искомого изгибающего
момента:* = (4353,0/w -9796,0/7*,)/39,58= 110,0FCfl,-247,5Fs/.16 Заказ 61 ^49
Рис. 56. К расчету контура ортогональной вантовой сети
а — эллиптический контур — основная система; б — расчетные участки эллиптического
контура и эпюры изгибающих моментов в основной системе: Mf>car от действия Fcar =
= 1 кН/м и Mf,st от действия Fst= 1 кН/м; в — эпюра изгибающих моментов от Х=\
Таблица 49КомбинациянагрузкиРасчетные усилияMi, кН • мN\, кНМ2, кН ■ мN2, кН1222122000-1817370402— 19280Ъ111157752160342682720—35574864Последовательно подставляя величины нагрузок из табл. 48
в последнее выражение, получим значения ху которые соответ¬
ствуют значениям изгибающих моментов М\ на большой оси
контура для трех указанных выше комбинаций нагрузок. Значения
изгибающих моментов на малой оси Мг находим из следующего
выражения (см. рис. 56,6): Af2 = 450/7S/ — 200/7сал + х, а продоль¬
ные усилия в тех же точках определим из условий: N\ = 30Fst
и N2 = 20FCar.Расчетные усилия для трех комбинаций нагрузок приведены
в табл. 49.Вычисление усилий в промежуточных точках контура выполня¬
ется по формуле Mi = MstFst — McarFcar+x, где Mst и Мсаг—соот¬
ветствующие значения единичных изгибающих моментов в инте¬
ресующей нас точке. Получив значения усилий, проверяем условие
безмоментности контура.Как известно, условие безмоментности может быть удовлетво¬
рено при действии на покрытие только одной из нагрузок, и оно
нарушается при изменении величины этой нагрузки. В данном
расчете, как видно из табл. 49, наименьшие по абсолютной вели¬
чине изгибающие моменты имеют место при действии на покрытие
постоянной части расчетных нагрузок (комбинация 3).Условие безмоментности проверяем по формуле (205):17 |7 fear А/саг Гсаг—Tgd (fcar-bfcar)-Qsl + bfsl) —-1 7о 4500-148 _g , „’ (4500—148)—(1200+148) П11а'Значения нагрузок, приходящихся на несущий и стабилизи¬
рующий ванты для указанной комбинации нагрузок, найдем по
формуле (199):г* 8{Hear Л Н car){f саг Л1 саг)°аГ~ Sccrtl ~8 • 293,89 • 4,352 о о п осп
П25-605 =2'3 кПа»2-5 кПа.251251
Примерное равенство полученных значений нагрузок свиде¬
тельствует о том, что геометрия покрытия отвечает условию без-
моментности контура. При других комбинациях нагрузок значения
положительных и отрицательных изгибающих моментов близки
по абсолютной величине.Расчет опорного контура по устойчивости. Оценку устойчи¬
вости сжато-изогнутого железобетонного опорного контура произ¬
ведем приближенно для второй комбинации нагрузок — когда
поддерживающая контур оболочка еще не работает. Значение
сжимающей критической продольной силы в опорном контуре Ncr
с учетом влияния вантовой системы, играющей роль упругого
основания, поддерживающего кольцо, определяем по формуле (206):лг„=(1 + 77+та£).^.Значение приведенной расчетной длины найдем, приравняв это
выражение известному выражению Эйлера для критической силы:N сг Eblred,i/lred-В результате сравнения правых частей формул и после преоб¬
разований получаем формулу для определения приведенной рас¬
четной длины опорного контура:, 2,22 гbed — j ~,V 1+V \ -\~kr2 / (Еь1 red,i)
где к — коэффициент упругого основания:*= * .Н О.саг/(Е$А$,саг) (£ саг l)/cos2<pРадиус кривизны эллипса в вершинах, пересекаемых большой
его осью, равен: rmin =202/30= 13,33 м, а в вершинах, пересека¬
емых малой осью, гтах =302/20 = 45 м.Жесткость опорного контураEbIred.i = 32500 400 \40003 =6,93 • 1016 Н • мм2.Провис главного несущего ванта при отсутствии нагрузки
вычислен выше и составляет f0tCar = 4160 мм. Продольная сила
для второй комбинации нагрузок по табл. 57 Ni = 3777 кН. Угол
наклона линии, соединяющей опорные точки ванта, ср = 0.Коэффициент, характеризующий отношение длины нити к ее
пролету, найдем из формулы (136)V 1 I 8fo,car 1 . 8 4,1602 J ni QUr- 1 +-^2— 1 + 3.60)02 -252
Таким образом,U = 3,777 • 106 , 4 . 108 н1 0,1272 • 106/(0,19 • 0,8043 • 109)+ 1,0132- 1Подставив в выражение приведенной расчетной длины опор¬
ного контура полученные значения по несущему ванту, найдем ее
величину:, 2,2 • 13,33 • 103 10~ 1Гк3lred=—— — =19,6 • 10' мм.У 1+У 1 + 1,4 • 108 • 1,3332 • 108/(6,93 • 1016)В результате аналогичных вычислений для стабилизирующего
ванта получим второе значение приведенной длины опорного
контура:/о,*,= 1540 мм; W2 = 2,16 • 106 Н;£s/=l+8 • 1,542/(3 • 402)= 1,0039.и 2,16 • 106 • 1 Q . iq8 тт.2 0,188 • 106 / (0,19 • 0,3142 • 109) + 1,00392 — 1, 2,22 • 45 • 103 гоп m3lred=— =52,9 * 10 ММ.V 1 +V 1 + 1,9 • 108 • 4,52 • 108/6,93 • 10'6Подбор арматуры и проверка железобетонного сечения опор¬
ного контура выполняются известными методами и здесь не при¬
водятся.XI. РАСЧЕТ ВИСЯЧЕГО ПОКРЫТИЯ
С ПЕРЕКРЕСТНОЙ СИСТЕМОЙ ВАНТ
И ОПОРНЫМ КОНТУРОМ ИЗ ДВУХ АРОК,
ЛЕЖАЩИХ В НАКЛОННЫХ ПЛОСКОСТЯХ1. Основные принципы расчета
на равномерно распределенную симметричную нагрузкуПерекрестная система вант образует висячее покрытие с по¬
верхностью гиперболического параболоида (рис. 57). Расчет ван¬
товой сети, поверхность которой описывается уравнением (194),
выполняется по формулам предыдущего примера. Поэтому здесь
рассмотрим принцип расчета главным образом опорного контура.253
Рис. 57. Схема висячего покрытия с перекрестной системой вант и опорным
контуром в виде двух арок, лежащих в наклонных плоскостяхУравнение плоскости, в которой лежит арка, имеет вид:2 = 2 (fcar + fst) / (Icar fst)»Уравнение оси арки получим, решая это выражение совместно
с (194а):_2U/_4^coso sjn ч - =4f^_ ogUar \ tear / lstгде а — угол наклона плоскости, в которой лежит арка.Уравнение (208) составлено относительно системы координат,
имеющей начало в ключе арки, причем ось х направлена по оси
ее симметрии. Уравнение оси арки в обобщенных координатах г\и\
примет следующий вид:W+(l-b)t) = £2. (209)где_2_£cosa_ £ = 2i-; Х = -Ь- ,1 lea, hi 1st254
причем £ имеет действительные значения при 1 +Х(т| —1)^0.
Так как 0<т| < 1, то при т^О условие действительности обраща¬
ется В ИЛИ fcar^fst-В общем случае уравнение оси арки представляет собой пара¬
болу второго порядка, которая при Х,= 1 обращается в прямую.
Значения X рекомендуется принимать в пределах 1/3... 1/2.Арки опорного контура рассчитываются на действие нагрузок
от натяжения вант, поддерживающих кровлю. Нагрузки, пере¬
дающиеся вантами на арку, могут быть разложены на две состав¬
ляющие: одну, действующую в плоскости арки, и другую —
нормально к ней (последние вызывают кручение арки). Таким
образом, условие безмоментности контура здесь не обеспечивается.Усилия в арках опорного контура можно определить методом
сил. В качестве основной системы принимаются трехшарнирные
арки, для чего вводятся шарниры на главных осях контура. Расчет
сводится к решению системы из двух канонических уравнений
с двумя неизвестными, поскольку при равномерной симметричной
нагрузке усилия в противоположных шарнирах попарно равны.Из условия равновесия полуарки, продольное усилие в ключе¬
вом шарниреж г F carlcar ___ i F sticar /01 а\~4/Ii ”^"4cosa ' <2l0>Нагрузки, действующие в плоскости арки:/2Fa,car==Fcar~Qf COS Ot;Of carI2Fa,st = Fst^r cos a.01stИзгибающий момент в арке для точки с координатами х, у:Мх = NqX Fa>car\ Fatst~2~ *Подставим в эту формулу значения N о из (210), произведем
необходимые упрощения и перейдем к обобщенным координа¬
там г\ и £. Тогда:м-—H^-(f»'cos“+lSk-)(1-4),l (211)или^=}(fa,a2A+Fa,s^)(l-4)T|. (211а)255
От единичного момента в опорном шарнире арки Mi = т|, от мо¬
мента в ключевом шарнире М2= 1—л*После определения усилий, действующих в сечениях арки,
принятые в расчете сечения бетона и арматуры проверяются по
соответствующим нормам и пособиям.При проектировании ортогональных вантовых сеток, подвешен¬
ных к наклоненным аркам, целесообразно угол наклона арок и
величины провиса вант подбирать так, чтобы нормальная состав¬
ляющая усилия в точках подвеса вант уравновешивалась соб¬
ственной массой арки. В этом случае при определенном значении
нагрузки на покрытие арка будет работать только в своей плоско¬
сти. Вертикальные оттяжки (стойки), поддерживающие арку,
включатся в работу только при изменении величины этой нагрузки.2. Конструкция покрытия и нагрузкиТребуется рассчитать покрытие здания приблизительно оваль¬
ной формы в плане, размеры которого 36X50 м. Покрытие под¬
держивается ортогональной системой перекрестных вант, натя¬
нутых на опорный контур, который представляет собой две бес-
шарнирные железобетонные параболические арки, лежащие в на¬
клонных плоскостях на нескольких опорных стойках (см. рис. 57).
Уравнение оси арки в обобщенных координатах ц и £ имеет вид
(209): 0,5385л2+ 0,4615л —S2 = 0, где k=fCar/fst = 3,5/6,5 = 0,5385Находим косинус угла наклона плоскости, в которой лежит
арка:cos а = 2,5/У 252 + 102 = 0,93.Седловидное покрытие имеет форму гиперболического парабо¬
лоида. Уравнение поверхности покрытия в исходном состоянии
имеет вид [см. формулу (194)]:~ 4/car JL | 4fst ti2 ^ /2 Л I /2 У 1у_4-3,6-10» о ■ 4-6.Б- 10» о gg . ш-в„2 ,52 10е + 3,62 • 108 У ’ ++ 0,2006 • 10“У.Несущие ванты (параллельные оси X) приняты из арматурного
стержня 04ОАШв (As,car = 1256,6 мм2; /?s,car = 450 МПа; Es,Car =
=0,18 • 106 МПа). Стабилизирующие ванты (параллельные
оси К) приняты из арматурного стержня 0 14AV (/1S,S(= 153,9 мм2;
Rs.st = 680 МПа; £s,s( = 0,19 • 10* МПа).256
Таблица 50Вид нагрузкиНормативноезначениенагрузки,кПаКоэффициент
надежности
по нагрузке
Y fРасчетноезначениенагрузки,кПаСобственная масса оболочки1,01,11,1Теплоизоляция, пароизоляция
кровли, гидроизоляционный ко¬
вер0,421,30,55Итого постоянная1,41,65Снег1,01,41,4Всего2,43,05Всего с учетом коэффициента надежности по назначению
Y„ = 0,952,9Необходимо проверить принятое сечение вант и определить
усилия в арке опорного контура на действие нагрузок, приведенных
в табл. 50.3. Расчет вантВ качестве исходного состояния для расчета принимается
покрытие, на которое действует полная расчетная нагрузка F =
= 2,9 кПа. Дополнительная нагрузка от натяжения стабилизи¬
рующих вант принимается в данном случае 0,6 кПа. Таким обра¬
зом, несущие ванты рассчитываем на нагрузку 1 величиной
2,9 + 0,6 = 3,5 кПа, или линейная нагрузка на вант Fcar=3,5 • 1,6=
= 5,6 кН/м.Определяем от этой нагрузки вертикальную и горизонтальную
(распор) реакции в точках подвески несущего ванта по (134):Va,car = 5,6 • 50 • 0,5=140 кН; Нсаг = 5,6 • 502/(8 • 3,5) =500 кН.Усилие в несущем ванте находим по (135): Near, тах =
=V 1402 + 5002 = 520 кН, а нормальные напряжения в сечении
ванта всаг = 520000/1256,6 = 419 МПа</?5,саг = 450 МПа. Таким
образом, прочность несущего ванта обеспечена.Теперь необходимо определить длину главного несущего ванта
и длину его заготовки.Жесткость несущего ванта: Bscar = 0,18 • 106 • 1256,6 = 2,26X
X Ю8 Н.Длина несущего ванта по (136):Lear = Ucar = 50000(1 +8 • 3,52 • 106/(3 • 502 • 106) == 50 • 103 • 1,013 = 50650 мм.257
Длина заготовки несущего ванта по (148) и (148а):Lo, саг = 50,65 • 103 —1,05 • 1,0132 • 50 • 0,5 • 109 /2,26 • 108 == 50532 мм.Проделаем те же расчеты для стабилизирующего ванта.Жесткость стабилизирующего ванта: Bs st = 0,19 • 106 • 153,9 =
=0,292 • 108 H.Распор стабилизирующего ванта от его натяжения по (134):
Hst = 0fi • 1,8 • 362/(8 • 6,5) = 26,9 кН.Длина стабилизирующего ванта по (136):Lst = ly£>st = 36 • 103(1+8 • 6,52 • 108/(3 • 362 • 108) == 36 • 103 • 1,087 = 39132 мм.Сечение стабилизирующего ванта проверим из условия равно¬
весия вантовой сети. За расчетное состояние в данном случае
принимаем систему, напряжение которой производится под дей¬
ствием собственной массы оболочки покрытия до замоноличивания
швов сборных плит. Эта нагрузка составит F0 = 0,9 кПа. Равно¬
весие системы обеспечивается равенством приращения провисов
в точках пересечения вант. Для определения приращения прови¬
сов необходимо решить кубическое уравнение (203). Но прежде
всего найдем значение коэффициентов этого уравнения. Для этого
вычислим величины, введенные в формулу (203) для сокращения
записи:Ссаг= 21,3 ' 2’26- '-2—— =4,7 • 10"18 Н/мм5;50 • 1,6 • 1.0132 ■ 1015 'сsl = ,21 '3 ' °'29---2= 1,74 • 10“13’ Н/мм5;364 • 1,8 • 1,087 • 10158 ■ 0,5 • 10е , п 1Л_6 и / зтСаг= 5Q2, 1 6 , 109 = 1.0 • 10 Н/мм ;8 • 0,026 • 10е п поп 1Л_6 u / 3т"= 36- 1.8 - 10' =0’089 • 10 Н/"“ ;F—F\ =2,9—0,9 = 2,0 кПа = 0,002 МПа.Подставив коэффициенты в кубическое уравнение, получим
(вычисление коэффициентов опущено):0,644 • 10-V-1,542 • 10-V + 27,307z-2000 = 0,2581
откудаZ = &fcar = bfst = 74 ММ.Провис главного несущего ванта при действии нагрузки от
собственной массы оболочки покрытия до замоноличивания швов
f\car = 3500 — 74=3426 мм.Распор по (201):и и . и АС m3 2,54 • 2,26 • 108(2 • 3500-74)74
HiCar = Hcar-bHcar = 0,5 • 10 isoio: 50,65 • ю9 == 383,8 кН.То же для главного стабилизирующего ванта по (202):/is/ = 6500 + 74=6574 мм;Hlsl = Hs,+bHsl = 26,9+ 2=54 :P|g-J°8J.o.^±74H.4, = 77,8 кН.Проверяем условие равновесия по нагрузкам из расчета урав¬
нений (199) и (200):Fest,car = 8 • 383,8 • 3,426/(1,6 • 502) = 2,63 кПа;Fest,st = 8 • 77,8 • 6,574/(1,8 • 362)= 1,75 кПа;Fest,car= Fq-|- Fest,st= 0,9 -|- 1,75 = 2,65 кПа^/2,63 кПа,т. е. условие равновесия по нагрузкам выдержано.Проверим принятое сечение стабилизирующих вант.
Вертикальная опорная реакция от нагрузки, полученной из
условия равновесия:Vst = Fesl,slSsl±= 1,75 • 1,8-|—56,7 кН.Продольная сила при этой нагрузке:JV,/=Vtff.<+ V\t =V77,82 + 56,7i =96,3 кН.Несущая способность стабилизирующих вантNsi,tact=As,siRs,si= 153,9 • 680 • 10~3 == 104,65 кН> Ns,=96,3 кН.259
Следовательно, сечение и несущая способность стабилизирую¬
щих вант достаточны.Длина заготовки стабилизирующего ванта по (148) и (148а):/ опюо 2»69 • 3,6 • 1,05 • 1,087 • 108 оппЛ/(^o,s/= 39132 ■ Г()-5 =39094 мм.Прогиб покрытия определяется по аналогии с предыдущим
примером и здесь не приводится.4. Расчет арки опорного контураДля расчета арки принимаем следующие комбинации нагрузок:
1) полная расчетная нагрузка; 2) напряжение вантовой сети;
3) постоянная часть расчетной нагрузки. В настоящем примере
дается расчет только на две первые комбинации нагрузок.
Для 1-й комбинации нагрузки составляют: F = 2,9, Fst = 0,6,
Fcar = 3,5 кПа, а для 2-й — соответственно 0,9, 1,53 и 2,63 кПа.Определение усилий в арках
контура производим методом сил.
В качестве основной системы рас¬
сматриваем трехшарнирную арку
с шарнирами, введенными в точ¬
ках пересечения дуг с главными
осями контура в плане. Учитывая,
что усилия в противоположных
шарнирах при равномерной на¬
грузке попарно равны, задача ре¬
шается системой из двух канони¬
ческих уравнений (14) с двумя
неизвестными.Изгибающие моменты в полу¬
арке от действия полной расчетной
нагрузки (комбинация 1) найдем
по формуле (211):М б2 • 3.6* • 101 (0,0035 • 0,93 +, 64 • 6,5 ■ 103 VРис. 58. Эпюры изгибающих моментов в
половине арки
а — от внешней нагрузки и единичных усилий
в основной системе; б — суммарная эпюра260
+-2oii§_)(I—11>Т1=:30375 •106' ^о-ч)-Вычислим значения изгибающих моментов в точках с коорди¬
натами т| = 0,25, т] = 0,75 и т| = 0,5.Значение момента при т| = 0,25 и т] = 0,75:м,=0.25; 0.75 =30375 • 1О6 • 0,25 • 0,75 == 5695 • 10® Н • мм = 5695 кН • м;Af,_о,5 = 30375 • 106 • 0,5 • 0,5 = 7594 • 10® Н • мм = 7594 кН • м.Изгибающие моменты в арке от действия нагрузки при напря¬
жении сети (комбинация 2) найдем по той же формуле:52 • 3,62 • Ю,6/гк пг\с\пъ лло, 0,00153 \ ,,М*= 64 6573 (°’°0263 • °>93 + -Щ- )(1-т1)т1 ==31510 • ю6 • л(1 —л);м„ =0,25:0.75 = 31510 • 106 • 0,25 • 0,75 == 5908 • 10® Н • мм = 5908 кН • м;Af„=0.5 = 31510 • 106 • 0,52 = 7878 • 10® Н • мм = 7878кН • м.Из приведенного расчета видно, что значения изгибающих
моментов, вычисленные для стадии напряжения вантовой сети,
превышают значения моментов, полученные для стадии действия
полной расчетной нагрузки. Поэтому дальше расчет производим
только для второй комбинации нагрузок.Эпюры изгибающих моментов от действия внешней нагрузки
и от единичных усилий показаны на рис. 58. Для удобства пере¬
множения эпюр длину полуарки разбиваем на четыре участка
с абсциссами г] = 0; 0,25; 0,5; 0,75; 1,0.При этом длины дуг отдельных участков имеют следующие
значения: S0i =9350 мм, Si2 = 7380 мм, S23 = 7220 мм, S34=7160 ммВвиду различной длины участков использование для интегри¬
рования формулы Симпсона невозможно, поэтому интегрирование
выполняем по участкам приближенно, как для треугольных или
трапециевидных площадей. Путем перемножения соответству¬
ющих эпюр получим искомые перемещения:8п=^-(1,02 + 0,752 + 0,75 . i>0)+i|?-(0,752 ++ 0,52+0,75 • 0,5)+^-(0,52 + 0,252 + 0,5 • 0,25) ++i|L . о,252 = 9,65;261
622=i|l(l,02+0,752 + 0,75 • l,0)+^-(0,752 ++ 0,52 + 0,75 • 0,5)+^-(0,52 + 0,252 + 0,5 • 0,25)++-^- • 0,252= 11,33;621 = 6,2=-^-(0,25 • 1,0 + 2 • 0,25 • 0,75)++-^-(2 • 0,75 • 0,25 + 2 • 0,52 + 0,75 • 0,5 + 0,25 • 0,5) +
+I|L(2 . 0,52 + 2 • 0,75 • 0,25 + 0,5 • 0,75 + 0,25 • 0,5)+-|_Л|1(2 • 0,25 • 0,75 + 0,25 • 1,0)=5,07;6lf=^-(5908 • 1,0 + 2 • 5908 • 0,75)+-|_I|L(2 • 5908 • 0,75 + 5908 • 0,5 + 7878 • 0,75 ++ 2 • 7878 • 0,5)+^-(2 • 7878 • 0,5 + 2 • 5908 • 0,25 ++ 7878 • 0,25 + 5908 • 0,5)+-^ • 5908 • 0,25 = 72416;62,=^- • 5908 • 0,25+^-(2 • 7878 • 0,5 ++ 2 • 5908 • 0,25 + 7878 • 0,25 + 5908 • 0,5) ++-^-(2 • 5908 • 0,75 + 5908 • 0,5 + 7878 • 0,75 ++ 2 • 7878 • 0,5)+-^(5908 • 1,0 + 2 • 5908 • 0,75)=76922.Перепишем канонические уравнения (14) с полученными коэф¬
фициентами:9,65Xi + 5,07*2 + 72416 = 0;5,07*i + 11,33*2 + 76922 = 0.Решение уравнения выполним по формулам (14а), откуда
*i = —5159 кН-м; Х2 = —4481 кН • м.Суммарная эпюра моментов показана на рис. 58.На полученные усилия производится проверка принятых в
расчете сечений железобетонных арок. Здесь этот расчет не при¬
водится.262
ОГЛАВЛЕНИЕПредисловие 3I. Расчет длинной цилиндрической оболочки 81. Некоторые сведения о длинных цилиндрических оболочках, основ¬
ные положения их расчета 82. Конструкция оболочки и нагрузки, принятые в примере .... 103. Геометрические характеристики оболочки 124. Расчет оболочки в продольном направлении 144.1. Расчет по прочности на действие изгибающих моментов и подбор
продольной арматуры бортовых балок 144.2. Расчет по прочности на действие поперечных сил и подбор
арматуры криволинейной плиты 164.3. Расчет по трещиностойкости (по образованию трещин, нормаль¬
ных к продольной оси оболочки) ... 214.4. Расчет по деформациям 255. Расчет оболочки в поперечном направлении 276. Расчет торцевой диафрагмы 367. Некоторые положения по конструированию длинных цилиндрических
оболочек (рис. 13) 438. Расчет оболочки комбинированной конструкции (металложелезо¬
бетонной) 468.1. Основные расчетные положения 468.2. Конструкция оболочки и нагрузки 488.3. Геометрические характеристики оболочки (рис. 15) ... • 498.4. Расчет оболочки в продольном направлении 50II. Расчет короткой цилиндрической оболочки (призматической складки) 541. Общие положения ... 542. Конструкция складки и нагрузки 543. Расчет оболочки в продольном направлении 564. Расчет оболочки в поперечном направлении (расчет арочной
диафрагмы) 575. Основные положения по конструированию коротких цилиндрических
оболочек (рис. 17) 60III. Расчет длинной треугольной складки 621. Особенности расчета ... • • 622. Конструкция складки и нагрузки ... *633. Расчет складки в продольном направлении 654. Расчет складки в поперечном направлении 675. Проверка устойчивости складки .686. Расчет диафрагмы .697. Основные принципы конструирования складок 70IV. Расчет пологой оболочки положительной гауссовой кривизны на прямо¬
угольном плане 721. Некоторые сведения об оболочках и принятые положения их расчета 722. Конструкция оболочки и нагрузки 833. Расчет оболочки по безмоментной теории 844. Расчет оболочки на действие изгибающих моментов (учет краевого
эффекта) 90263
5. Расчет железобетонных арок-диафрагм 966. Расчет стальной арки-диафрагмы при варианте комбинированной
конструкции оболочки (металложелезобетонной) 1077. Некоторые положения по конструированию оболочек положительной
гауссовой кривизны 108V. Расчет волнистого свода-оболочки 111
А. Расчет железобетонного свода-оболочки 1111. Основные сведения о волнистых сводах-оболочках и принципахих расчета 1112. Конструкция свода-оболочки и нагрузки 1193. Геометрические характеристики волнистого свода-оболочки 1204. Расчет свода-оболочки в продольном направлении 1224.1. Расчет на равномерно распределенную симметричную нагрузку 1224.2. Расчет на несимметричную (одностороннюю снеговую) нагрузку 1255. Расчет свода-оболочки в поперечном направлении 1266. Некоторые указания по конструированию волнистых сводов-оболочек 132
Б. Расчет волнистого свода-оболочки комбинированной конструкции (ме¬
талложелезобетонного) 133Б.1. Расчет средней волны свода-оболочки ... 1331. Конструкция свода-оболочки и нагрузки 1332. Геометрические характеристики свода-оболочки 1343. Расчет свода-оболочки в продольном направлении 1343.1. Расчет на равномерно распределенную симметричную нагрузку 1343.2. Расчет на несимметричную нагрузку ... 1354. Расчет свода-оболочки в поперечном направлении 136
Б.2. Расчет крайней волны свода-оболочки 1381. Конструкция свода-оболочки и нагрузки 1382. Геометрические характеристики металложелезобетонного свода-
оболочки 1383. Расчет свода-оболочки в продольном направлении 1393.1. Расчет на равномерно распределенную симметричную нагрузку 1393.2. Расчет на несимметричную нагрузку ... 1394. Расчет с вода-оболочки в поперечном направлении 140VI. Расчет железобетонного сферического купола .... 1411. Основные сведения о куполах и принципах их расчета 1412. Конструкция купола и нагрузки ... 1583. Геометрические характеристики купола 1594. Определение усилий в куполе по безмоментной теории 1605. Подбор арматуры элементов куполов 1616. Определение усилий краевого эффекта 1637. Некоторые положения по конструированию куполов 165VII. Расчет пологих оболочек отрицательной гауссовой кривизны 167
А. Расчет гиперболического параболоида, отнесенного к асимптотам . 1691. Основные сведения о конструкциях и принципах расчета .... 1692. Конструкция оболочки четырехлепесткового гипара и нагрузки 1713. Расчет по безмоментной теории 1724. Расчет четырехлепесткового гипара как трехшарнирной системыс затяжкой 1745. Принципы армирования гипаров, отнесенных к асимптотам . . . 175
Б. Расчет гиперболического параболоида, отнесенного к главным осям 1771. Некоторые сведения о седлообразных панелях-оболочках и их расчете 1772. Конструкция и геометрические параметры панели-оболочки. Нагрузки 1813. Расчет панели-оболочки в продольном направлении 1833.1. Расчет по прочности сечений, нормальных к продольной оси
элемента 1833.2. Расчет по прочности сечений, наклонных к продольной оси
элемента 1853.3. Расчет по образованию трещин, нормальных к продольной оси
элемента .... .... 187264
4. Расчет панели-оболочки в поперечном направлении 1905. Основные положения по конструированию гипаров, отнесенных к
главным осям .... ... .191VIII. Расчет вантовых систем 193
А. Расчет несущих вант 1931. Основные расчетные положения 1932. Расчет гибкрй нити с опорами на одном уровне 2053. Расчет предварительно напряженной струны . . 2084. Расчет гибкой нити с опорами на разных уровнях 209
Б. Расчет вантовых ферм 2111. Оснорные положения .... ... 2112. Расчет бесшарнирной фермы ... 2203. Расчет фермы с центральным шарниром 226IX. Расчет висячего шатрового покрытия на круглом плане 2271. Общие вопросы 2272. Конструкция покрытия и нагрузки 2323. Расчет вант по симметричной схеме 2344. Определение провиса наклонного ванта ... 2355. Определение прогиба покрытия 2366. Расчет покрытия на одностороннюю снеговую нагрузку 2377. Расчет нижнего опорного кольца 238X. Расчет висячего покрытия с перекрестной системой вант и криволиней¬
ным контуром .... 2391. Основные положения .... ... 2392. Конструкция покрытия и нагрузки 2433. Расчет перекрестных вант ... 2444. Определение прогиба покрытия ... 2485. Расчет опорного контура 248XI. Расчет висячего покрытия с перекрестной системой вант и опорным
контуром из двух арок, лежащих в наклонных плоскостях 2531. Основные принципы расчета на равномерно распределенную сим¬
метричную нагрузку 2532. Конструкция покрытия и нагрузки 2563. Расчет вант 2574. Расчет арки опорного контура . . 260