Saunders Mac Lane
CATEGORIES
FOR
THE WORKING
MATHEMATICIAN
Second Edition
SPRINGER
1998

С. МАКЛЕИН
КАТЕГОРИИ
ДЛЯ
РАБОТАЮЩЕГО
МАТЕМАТИКА
Перевод под редакцией
В А. Артамонова
МОСКВА
ФИЗМАТЛИТ
2004

УДК 512.58
Г Г Издание осуществлено при поддержке
ББК 22.144 :рс±Ь>:и Российского фонда фундаментальных
у[ 25 * * исследований по проекту 02-01-Ц035д
Маклейн С. Категории для работающего математика /
Перевод с англ. под ред. В.А. Артамонова. — М.: ФИЗМАТЛИТ, 2004. — 352 с. —
ISBN 5-9221-0400-4.
Книга написана выдающимся американским математиком С. Маклей-
ном, одним из создателей теории категорий, рассматривающей свойства
отображений (морфизмов) между объектами с определённой структурой.
Овладение категорным языком и умение его использовать позволяет
современному математику видеть и осознавать единство науки. Особое внимание
в книге уделено понятиям сопряжённого функтора и моноидальной
категории, которые находят разнообразные применения.
Для широкого круга специалистов, интересующихся современными
проблемами математики, включая студентов и аспирантов. Перевод
осуществлён со второго издания книги.
ISBN 5-9221-0400-4 (русск.) © Springer, 1998
ISBN 0-387-98403-8 (англ.) © ФИЗМАТЛИТ, 2004

ОГЛАВЛЕНИЕ
Предисловие редактора перевода 8
Предисловие ко второму изданию 9
Предисловие к первому изданию 9
Введение 12
Глава 1. Категории, функторы и естественные
преобразования 17
1.1. Аксиомы категорий 17
1.2. Категории 20
1.3. Функторы 23
1.4. Естественные преобразования 27
1.5. Мономорфизмы, эпиморфизмы и нулевые морфизмы 30
1.6. Основания теории 33
1.7. Большие категории 36
1.8. Множества hom 39
Глава 2. Конструкции в категориях 43
2.1. Двойственность 43
2.2. Контравариантность и двойственные категории 45
2.3. Произведения категорий 48
2.4. Категории функторов 53
2.5. Категория всех категорий 55
2.6. Категории запятой 58
2.7. Графы и свободные категории 61
2.8. Фактор-категории 65
Глава 3. Универсальные конструкции и пределы 68
3.1. Универсальные стрелки 68
3.2. Лемма Ионеды 73
3.3. Копроизведения и копределы 76
3.4. Произведения и пределы 83
3.5. Категории с конечными произведениями 88
3.6. Группы в категориях 90
3.7. Копределы представимых функторов 92
Глава 4. Сопряженные функторы 95
4.1. Сопряжение 95
4.2. Примеры сопряженных функторов 103
4.3. Рефлективные подкатегории 107
4.4. Эквивалентность категорий 110
4.5. Сопряженные функторы в случае предпорядков 113
4.6. Декартово замкнутые категории 115
4.7. Преобразования сопряженных функторов 117

6 Оглавление
4.8. Композиция сопряженных функторов 122
4.9. Подмножества и характеристические функции 124
4.10. Категории, похожие на Sets 126
Глава 5. Пределы 129
5.1. Создание пределов 129
5.2. Связь пределов с произведениями и уравнителями 133
5.3. Пределы с параметрами 136
5.4. Сохранение пределов 137
5.5. Действие сопряженных функторов на пределы 140
5.6. Теорема Фрейда о сопряженном функторе 142
5.7. Подобъекты и порождающие семейства 148
5.8. Специальная теорема о сопряженном функторе 152
5.9. Сопряженные функторы в топологии 156
Глава 6. Монады и алгебры 162
6.1. Монады в категории 162
6.2. Алгебры над монадой 164
6.3. Сравнение с алгебрами 168
6.4. Слова и свободные полугруппы 169
6.5. Свободные монадические алгебры 172
6.6. Расщепление коуравнителей 174
6.7. Теорема Бека 177
6.8. Алгебры являются Т-алгебрами 183
6.9. Компактные хаусдорфовы пространства 184
Глава 7. Моноиды 188
7.1. Моноидальные категории 188
7.2. Когерентность 192
7.3. Моноиды 198
7.4. Действия моноидов 202
7.5. Симплициальная категория 204
7.6. Монады и гомология 210
7.7. Замкнутые категории 213
7.8. Компактно порожденные пространства 215
7.9. Петли и надстройки 219
Глава 8. Абелевы категории 222
8.1. Ядра и коядра 222
8.2. Аддитивные категории 225
8.3. Абелевы категории 230
8.4. Леммы о диаграммах 234
Глава 9. Специальные пределы 244
9.1. Фильтрованные пределы 244

Оглавление 7
9.2. Перестановка пределов 248
9.3. Финальные функторы 251
9.4. Диагональная естественность 252
9.5. Концы 257
9.6. Ко-концы 261
9.7. Концы с параметрами 263
9.8. Повторные концы и пределы 266
Глава 10. Расширения Кана 269
10.1. Сопряженные функторы и пределы 269
10.2. Слабая универсальность 272
10.3. Расширение Кана 273
10.4. Расширения Кана как ко-концы 278
10.5. Поточечные расширения Кана 281
10.6. Плотность 283
10.7. Все категорные понятия являются расширениями Кана 286
Глава 11. Симметрия и заузливание в моноидальных
категориях 290
11.1. Симметричные моноидальные категории 290
11.2. Моноидальные функторы 294
11.3. Строго моноидальные категории 297
11.4. Группы кос Вп и категория кос 299
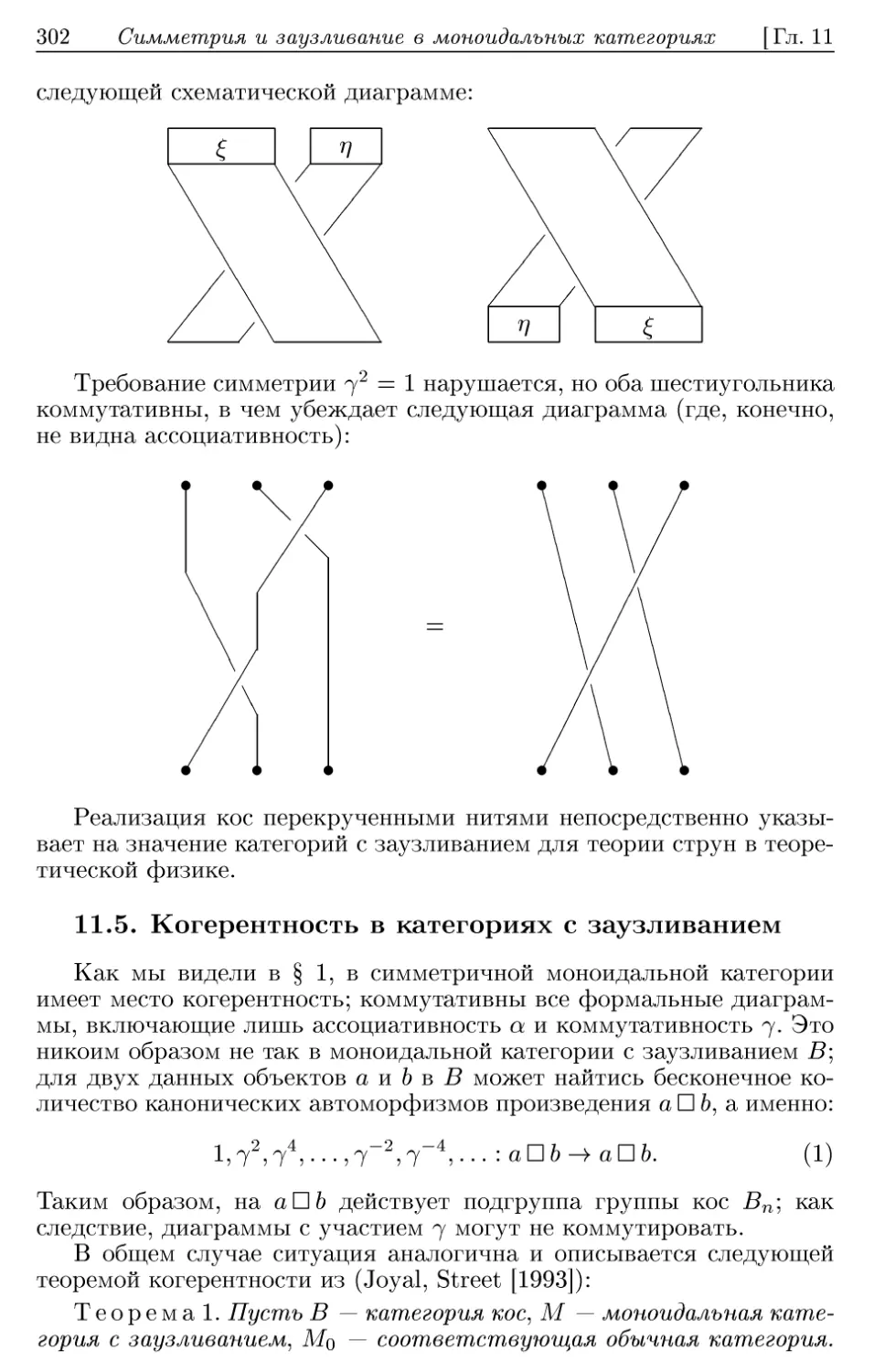
11.5. Когерентность в категориях с заузливанием 302
11.6. Перспективы 305
Глава 12. Структуры в категориях 307
12.1. Внутренние категории 307
12.2. Нерв категории 310
12.3. 2-категории 312
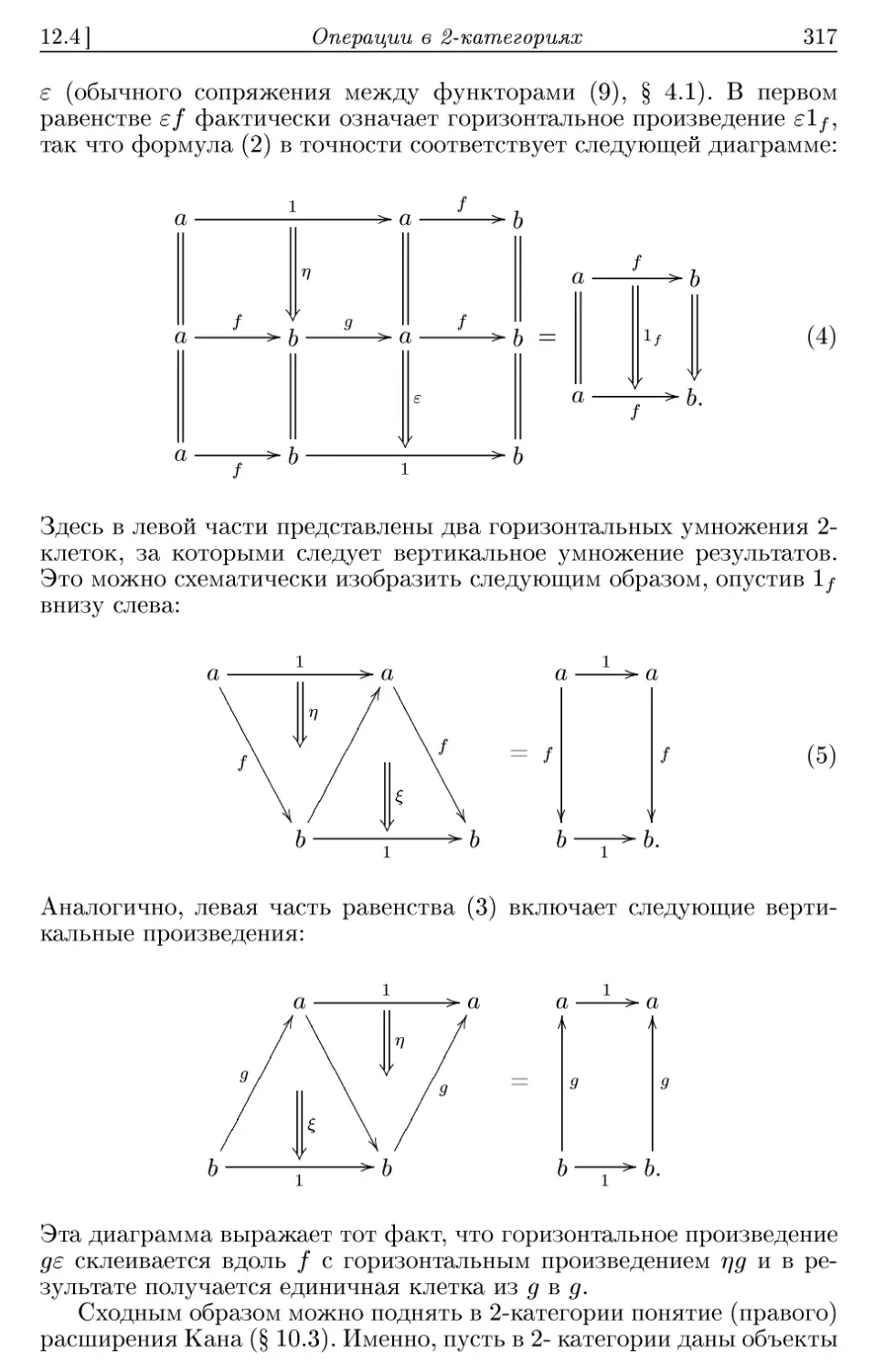
12.4. Операции в 2-категориях 316
12.5. Категория как одно множество 320
12.6. Бикатегории 322
12.7. Примеры бикатегории 324
12.8. Скрещенные модули и категории в Grp 326
Дополнение. Основания теории категорий 329
Указатель обозначений 333
Терминология 336
Список литературы 338
Список дополнительной литературы 344
Предметный указатель 348

8
Предисловие редактора перевода
Предисловие редактора перевода
Предлагаемая читателю книга написана выдающимся
американским математиком С. Маклейном, одним из создателей теории
категорий и гомологической алгебры. Эта книга предназначена для
широкого круга математиков. Она знакомит читателя с основами
теории и указывает ее многочисленные применения в различных
разделах математики. Эти применения основаны на том, что в
математике изучаются не только свойства элементов объектов, наделенных
определенной структурой, но и отображения между этими
объектами, согласованные с рассматриваемыми структурами. Теория
категорий концентрируется на изучении свойств отображений (морфизмов)
между объектами. В математике принято отображения на картинках
изображать стрелками. Поэтому автор в книге использует термин
«стрелка» для обозначения морфизмов в категориях.
В книге наглядно демонстрируется, что язык категорий —
функторы, морфизмы, (ко)пределы, (ко)произведения, резольвенты,
сопряженные функторы и т. д. — широко используется в различных
разделах математики. Поэтому овладение этим языком и умение его
использовать позволяет современному образованному математику
видеть и осознавать единство науки. Таким образом, знакомство с этой
книгой является важной частью образования современного
математика. Автор не ставил своей целью отразить достаточно подробно все
направления развития теории категорий. Например, в книге почти не
отражены такие разделы теории категорий, как абелевы категории,
производные категории и производные функторы, категории
многообразий алгебраических систем, упорядоченные категории, теория
алгебр, коалгебр, биалгебр и алгебр Хопфа в моноидальных
категориях и связь с теорией квантовых групп и т. д. Читатель,
заинтересовавшийся этими разделами, может найти соответствующие ссылки,
используя дополнительный список, приведенный в конце книги.
Книга небольшая по объему. Она написана достаточно просто
и рассчитана на студентов-математиков. Книга выдержала два
издания на английском языке. Настоящий перевод осуществлен со второго
издания.
Библиография, приведенная автором, разумеется, не является
полной. В ней мало отражена, например, литература на русском языке.
При переводе библиография пополнена рядом основных монографий
и статей, вышедших в последние годы. В тексте ссылка на
дополнительную литературу отмечена знаком *. Выражаю глубокую
благодарность Е. С. Голоду, Е. Б. Кацову и Е. Г. Шульгейферу за помощь
при обсуждении терминологии и списка литературы.
Надеюсь, что публикация этой книги на русском языке будет
способствовать знакомству нового поколения математиков с теорией
категорий и ее применениями в математике.
Перевод книги выполнен Б. Р. Френкиным.
В. А. Артамонов

Предисловие к первому изданию
9
Предисловие ко второму изданию
Во втором издании книги «Категории работают» г) добавлены две
главы, предмет которых вызывает сейчас активный интерес. Одна
из этих глав посвящена симметрическим моноидальным категориям,
категориям кос и теоремам когерентности для них. Эти темы
представляют интерес как сами по себе, так и в связи с применением
в квантовой теории поля, именно, в теории струн. Во второй из новых
глав рассмотрены 2-категории и категории высших размерностей,
которые в последнее время привлекают большое внимание. Кроме того,
пополнена библиография, чтобы в какой-то мере отразить прогресс
в изучении категорий за прошедший период.
Остальные десять глав подверглись небольшим изменениям, что
позволило в ряде мест достичь большей ясности; во многих случаях
этому помогли полезные предложения Георгия Джанелидзе. В гл. 3
я добавил описание копределов представимых функторов, а гл. 4
теперь включает краткое описание характеристических функций
подмножеств и элементарных топосов.
Дюн Эйкрз, 27 марта 1997 г. Сондерс Маклейн
Предисловие к первому изданию
Теория категорий развивалась быстро. Цель этой книги —
представить те ее идеи и методы, которые ныне могут эффективно
применяться математиками, работающими во многих других областях.
Такое применение осуществляется на нескольких уровнях. Во-первых,
категории дают удобный язык мышления, основанный на понятиях
категории, функтора, естественного преобразования, контравариант-
ности и категории функторов. Эти понятия рассмотрены (с
подходящими примерами) в главах 1 и 2. Затем появляется фундаментальная
идея пары сопряженных функторов. Это происходит во многих, по
существу эквивалентных, формах, таких как универсальная
конструкция, прямой и обратный пределы, пара функторов с естественным
изоморфизмом между соответствующими множествами стрелок. Все
эти формы и их взаимосвязи изучаются в главах с 3 по 5 под девизом
«Сопряженные функторы вездесущи».
Другим основным понятием теории категорий является моноид —
множество с бинарной операцией умножения, ассоциативной и
имеющей единицу; категория сама может рассматриваться как своего рода
обобщенный моноид. Это понятие и его обобщения изучаются в
главах 6 и 7. Его тесная связь с понятием сопряженного функтора
позволяет прояснить идеи универсальной алгебры и в итоге приводит к
теореме Бека, характеризующей категории алгебр. С другой стороны,
1) Формулировка автора. — Прим. пер.

10
Предисловие к первому изданию
рассмотрение категорий с моноидальной структурой (порождаемой
тензорным произведением) позволяет, например, ввести некоторые
категории топологических пространств, обладающие хорошими
свойствами.
Поскольку категория состоит из стрелок, то теория категорий —
это и наука о том, как прожить без элементов, заменив их стрелками.
Это направление мысли, присутствуя с самого начала, становится
центральным в гл. 8, которая содержит элементарную теорию абе-
левых категорий и учит, как доказать любую лемму о диаграммах, не
«прогоняя» по диаграмме ни одного элемента *).
В итоге все основные понятия теории категорий соединяются
в двух последних главах 2), где рассмотрены: более сильные
свойства пределов, в особенности фильтрованных пределов; исчисление
концевых морфизмов; понятие расширения Кана. Это более глубокая
форма базовой конструкции сопряженных функторов. В заключение
мы показываем, что все объекты теории категорий являются
частными случаями расширений Кана (§ 10.7).
У меня было много возможностей излагать материал этих глав
на лекциях: в Чикаго; в Боулдере, в цикле лекций на коллоквиуме
Американского математического общества; в Сент-Эндрюс, благодаря
Эдинбургскому математическому обществу; в Цюрихе это сделали
возможным Бено Экман и Институт математических исследований;
в Лондоне — А. Фрелих, Кинге- и Куинс-колледжи; в Гейдельберге —
X. Зейферт и Альбрехт Дольд; в Канберре — Нейманы и Фулбрай-
товский грант; в Баудойне — Дэн Кристи и Национальный научный
фонд; в Тьюлене — Поль Мостерт и Фонд Форда; наконец, за
повторные лекции в Чикаго я благодарен Роберту Мейнарду Хатчинсу
и Маршаллу Харви Стоуну.
Моим исследованиям помогли многие коллеги. Очень полезным
было общение с математиками, посещавшими Чикаго (благодаря
эффективной поддержке со стороны Управления научных исследований
Военно-воздушных сил, Управления морских исследований и
Национального научного фонда): это М. Андре, Ж. Бенабу, Э. Дюбюк,
Ф. У. Ловер, Ф.Э.Дж. Линтон. Полезные соображения высказали
Майкл Барр, Джон Грэй, Майлз Тьерни и Фриц Ульмер. Разумные
советы дали мне Брайан Абрахамсон, Роналд Браун, У. X. Кокрофт
и Поль Халмош. Даниэл Фейгин и Джеффри Филипс сумели привести
ряд моих лекций в удобочитаемый вид. Мой старый друг А. X.
Клиффорд и другие коллеги в Тьюлене также оказали большую помощь.
По нескольким главам существенные советы дали Джон Макдоналд
и Росс Стрит; другие материалы критически прочли Спенсер
Диксон, С. А. Хак и Мигель Л а Плаза. Острые суждения Питера Мэя
помогли существенно улучшить отбор и подачу материала, а Макс
) Здесь и в других местах, подразумевая использование элементов при
работе с диаграммами, автор употребляет слово chase, которое можно
перевести как «прогон». — Прим. пер.
2) Главы 9 и 10. — Прим. пер.

Предисловие к первому изданию
11
Келли своим зорким глазом усмотрел многие сырые места в готовой
рукописи. Дороти Маклейн и Тир Шуман заслуживают
признательности за печатание, Дороти Маклейн также за составление указателя,
а М. К. Квонг за тщательное чтение гранок. При всем этом оставшиеся
ошибки, равно как отбор и подача материала, принадлежат мне.
Дюн Эйкрз, 27 марта 1971 г.
Сондерс Маклейн

ВВЕДЕНИЕ
Теория категорий начинается с наблюдения, что многие свойства
математических систем можно представить просто и единообразно
посредством диаграмм, состоящих из стрелок. Каждая стрелка / : X —>
—> Y обозначает функцию, т. е. множество X, множество Y и правило
ж I—)- /ж, которое сопоставляет каждому элементу х Е X некоторый
элемент fx Е Y. Всюду, где это возможно, мы будем писать /ж, а не
/(ж), опуская ненужные скобки. Типичная диаграмма из множеств
и функций имеет вид
Л
она коммутативна, если h = д о /, где д о /, как обычно, обозначает
сложную функцию д о / : X —У Z, определяемую как ж н-» g(fx).
Такие же диаграммы можно применять и в иных математических
контекстах; так, в категории всех топологических пространств буквы
X, Y и Z обозначают топологические пространства, а /, д, h —
непрерывные отображения. Точно так же в категории всех групп X,
Y и Z обозначают группы, а /, д, h — гомоморфизмы.
Многие свойства математических конструкций можно выразить
в терминах свойств универсальности диаграмм. Рассмотрим
декартово произведение X х Y двух множеств, состоящее, как обычно, из всех
упорядоченных пар (ж, у) элементов ж G X и у G Y. Проекции
произведения (ж, у) I-)- х,(х,у) I-)- у на его оси X и Y представляют собой
функции р : X xY ^ X, q : X xY ^Y. Любая функция h :W ^ X х
х У из третьего множества W однозначно определяется композициями
ро h и q о h. Обратно, если дано множество W и функции fug, такие,
как на последующей диаграмме, то существует единственная функция
/i, которая делает диаграмму коммутативной; а именно, hw = (fw, gw)
для каждого w G W:
x+—XxY^+Y.
Таким образом, для данных X и Y функция (р, q) универсальна среди
всех пар функций, отображающих некоторое множество в X и в У,
поскольку любая другая такая пара (/, д) однозначно пропускается
(посредством К) через пару (р, q). Это свойство определяет декартово

Введение
13
произведение единственным образом (с точностью до биекции); та
же диаграмма в категории топологических пространств или групп
определяет топологическое произведение или прямое произведение
групп.
Другим примером таких свойств универсальности является
сопряженность. Если hom (РУ, X) обозначает множество всех функций
/ : W —У X, a hom (([/, У), (X, У)) — множество всех пар функций
/ : U —У X, g : V —У У, то соответствие h \-У (ph,qh) = (/,#),
показанное на предыдущей диаграмме, является биекцией:
hom (W, X х Y) = hom ((VF, VF), (X, У)).
Эта биекция естественна в том смысле (уточняемом ниже), что она
определяется единообразно для всех множеств W и всех пар
множеств (X, Y) (и точно так же естественна в случае топологических
пространств или групп). Эта естественная биекция включает две
теоретико-множественные конструкции: конструкцию W —У (W,W),
отображающую каждое множество в диагональную пару АРУ =
= (ТУ, РУ), и конструкцию (X, У) \-у X х У, сопоставляющую
каждой паре множеств их декартово произведение. Если дана описанная
биекция, то мы говорим, что конструкция X х У сопрлэюена справа
конструкции А, а А сопряжена слева произведению. Как мы увидим,
сопряженность встречается повсюду в математике.
Конструкция декартова произведения называется функтором,
поскольку она применяется к множествам и к функциям между ними;
декартовым произведением двух функций к : X —у X' и / : У —у Y'
является функция к х I:
kxl:X х У -+Х1 х У, (х,у)^У (кх, 1у).
Отметим также, что одноточечное множество 1 = {0} служит
единицей для операции «декартово произведение» ввиду биекций
lxxAx^Xxl, (1)
имеющих вид Л(0,ж) = ж, д(х,0) = х.
Важнейшую роль в теории категорий играет понятие моноида
(полугруппы с единицей). Моноид М можно описать как множество
М с двумя функциями
fi : М х М -* М, г) : 1 -* М (2)
такими, что следующие диаграммы коммутативны:
М х М х М^М х М 1 х М^М х М^-М х 1
11
Y
Л
11
Y
М х М ^ М, М = М = М\

14
Введение
здесь 1 в выражении 1 х /i — тождественная функция М х М, а 1
в выражении 1 х М — одноточечное множество 1 = {0}, тогда как
Л и q — биекции из (1). Коммутативность диаграмм означает, что
следующие произведения совпадают:
\i о (1 х /i) = \i о (jjl х 1), \i о (ту х 1) = Л, \i о (1 х г]) = д.
Эти диаграммы можно переписать с использованием элементов,
записывая, скажем, функцию \i как произведение /л(ж, у) = ху при
ж, у Е Ми заменяя функцию г) на одноточечном множестве 1 =
= {0} ее (единственным) значением — элементом 77(0) = и Е М. Тогда
предыдущие диаграммы принимают вид
(x,y,z)\-
(x,yz)
(ху, z) I ^ [xy)z = x(yz),
(0, ж) l—^ (и,х) (х,и) -<—|(ж,0)
их,
хи
X.
Получаем, что эти диаграммы не что иное, как известные аксиомы
моноида: умножение в них ассоциативно, а элемент и служит левой
и правой единицей. Справедливо и обратное утверждение, поскольку
те же соображения показывают, как можно выразить алгебраические
тождества в виде коммутативных диаграмм. Эту процедуру можно
применить и к другим тождествам: например, можно описать группу
как моноид М, снабженный функцией ( : М —>■ М (конечно, это
функция х ь->- ж-1), для которой коммутативна следующая диаграмма:
М —6—^ М х М 1Х > М х М х I ^ (ж, ж) l ^ (ж, ж-1)
-^М
0Ь
-^ и
(4)
Здесь S : М —>• М хМ — диагональная функция ж \-^ (ж, ж) при ж G М,
а безымянная вертикальная стрелка М 4 1 = {0} - это очевидная
(и единственная) функция из М в одноточечное множество. Как
показано на правой диаграмме, ( сопоставляет каждому элементу ж G
G М элемент ж-1, который является для него правым обратным.
Определение группы посредством стрелок /i, 77 и £ в подобных
коммутативных диаграммах не использует явно элементов группы
и потому применимо в различных ситуациях. Если буква М
обозначает топологическое пространство (а не просто множество), причем
стрелки — это непрерывные отображения (а не просто функции), то
условия (3) и (4) определяют топологическую группу: они
утверждают, что М является топологическим пространством с бинарной
операцией умножения /i, которая непрерывна (по совокупности
аргументов) и имеет непрерывную правую обратную операцию, причем

Введение
15
выполнены обычные аксиомы группы. Точно так же, если буква М
обозначает дифференцируемое многообразие (класса С00), причем
1 — одноточечное многообразие, а стрелки /i, г\ и ( — гладкие
отображения многообразий, то диаграммы (3) и (4) становятся определением
группы Ли. Таким образом, группы, топологические группы и группы
Ли можно описать с помощью диаграмм, соответственно, в категориях
множеств, топологических пространств и дифференцируемых
многообразий.
Такое определение группы в категории зависит (для обратного
элемента в диаграмме (4)) от диагонального отображения в декартово
произведение S : М —у М х М. Определение моноида носит более
общий характер, поскольку декартово умножение х в произведении М х
х М можно заменить любой другой операцией □ от двух переменных,
если только она ассоциативна и имеет единицу 1, обеспечивающую
изоморфизмы (1). Поэтому можно говорить о моноиде в системе
(С, □ , 1), где С — категория, □ — такая операция, а 1 — ее единица.
Например, рассмотрим моноид М в системе (АЬ, ®, Z), где АЬ —
категория абелевых групп, х заменено на тензорное произведение
абелевых групп, а единица заменена на Z — аддитивную группу целых
чисел; тогда (1) превращается в известный изоморфизм
Z® X = X = X ®Z, X — абелева группа.
Мы утверждаем, что моноид М в системе (АЬ, (g), Z) — это просто
кольцо. В самом деле, соответствующий морфизм \i : М ® М —у М
в силу определения операции ® является билинейной функцией М х
х М —У М, т. е. дистрибутивен слева и справа относительно сложения.
Назовем его умножением. Морфизм абелевых групп г) : Z —у М
полностью определяется выбором одного элемента в группе М, а именно
образа и образующего 1 группы Z. Коммутативность диаграммы (3)
означает, что умножение \i в абелевой группе М ассоциативно, причем
и является левой и правой единицей, — другими словами, М является
кольцом (с единицей).
(Гомо)морфизмы алгебраической системы также можно описать
с помощью диаграмм. Если (M,/i,t]} и (М',//,//) — два моноида,
описанных вышеприведенными диаграммами, то морфизм из первого
моноида во второй можно определить как такую функцию / : М —>
—у М'', что коммутативны следующие диаграммы:
М МхМ—^М 1—^М
/ /х/ / / (5)
М', М' хМ'-^М', 1^-^М'.
В терминах элементов это означает, что f(xy) = (fx)(fy) и fu =
= и', где и и и' — единицы. Таким образом, гомоморфизм — это,
как обычно, функция, сохраняющая произведение и единицу. Если

16
Введение
М и М' — моноиды в системе (Ab,(g),Z), т. е. М, М' — кольца, то
определенный здесь гомоморфизм / — это в точности морфизм колец
(сохраняющий единицу).
Наконец, действие моноида (М, /i, 77) на множестве S определяется
как такая функция v : М х S —> 5, что коммутативны две следующие
диаграммы:
М х М х S-^^M х S lxS^>MxS
/1X1 V
Y Y
M x S >■ 5,
Если результат действия элемента моноида х на элемент s G S
обозначается через i/(x,s) = ж • s, то указанные диаграммы означают, что
х • (у • s) = (xy) • s, и • s = s
при всех ж, у G Ми всех s E S. Это обычные формулы для
действия моноида на множестве, особенно широко известные для случая
группы, действующей на множестве как группа преобразований. Если
из категории множеств мы перейдем в категорию топологических
пространств, то получим непрерывное действие топологического
моноида М на топологическом пространстве S. Если же (М, /i, 77) —
моноид в системе (Ab,0,Z), то действие моноида М на объекте S
из категории АЬ — это в точности левый модуль S над кольцом М.

Глава 1
КАТЕГОРИИ, ФУНКТОРЫ И ЕСТЕСТВЕННЫЕ
ПРЕОБРАЗОВАНИЯ
1.1. Аксиомы категорий
Вначале мы опишем категории непосредственно с помощью
аксиом, не опираясь на аксиоматику теории множеств, и назовем их
метакатегориями. Однако начнем мы с более простого понятия
(мета) графа.
Метаграф включает в себя объекты а, Ъ, с,..., стрелки f,g,h,...
и следующие две операции:
область, которая сопоставляет каждой стрелке / объект а =
= dom/;
кообласть, которая сопоставляет каждой стрелке / объект Ь =
= cod/.
Удобнее всего представить эти операции, изобразив / стрелкой,
которая начинается в области (источнике, области определения) и
кончается в кообласти (цели, области значений):
f : а —>• Ъ или а —>• Ъ.
Тогда легко изобразить и конечный граф, например: •—>-•—>-• или
• =4 ••
Метакатегория — это метаграф, в котором имеются две
дополнительные операции:
единица, сопоставляющая каждому объекту а стрелку ida =
= 1а : а -»> а;
композиция (умножение стрелок), когда каждым двум
стрелкам (/,#), для которых domg = cod/, сопоставляется стрелка
g о / : dom/ —>• codg, называемая их произведением (композицией).
Такая операция изображается диаграммой
А
а ^ с,
9°f
в которой представлены все упомянутые области определения и
значений. Эти операции в метакатегории подчинены следующим двум
аксиомам.

18 Категории, функторы и естественные преобразования [Гл. 1
Ассоциативность. Для конфигурации объектов и стрелок
Л и ^^ К л
а —У о —У с —У а
всегда выполнено равенство
ko(gof) = (kog)of. (1)
Эта аксиома утверждает, что ассоциативный закон выполнен для
операции композиции всегда, когда она имеет смысл (т. е. всегда, когда
определены произведения в каждой части равенства (1)). В наглядной
форме это выражается в коммутативности следующей диаграммы:
Аксиома единицы. Для всех стрелок f:a^bng:b^c
умножение на единичную стрелку 1^ обладает свойствами:
h°f = f и golb = g. (2)
Эта аксиома утверждает, что единичная стрелка 1& любого объекта
Ъ действует как единица относительно операции умножения, если
произведение имеет смысл. В наглядной форме уравнения (2)
выражаются в коммутативности следующей диаграммы:
Нам встретится много таких диаграмм, состоящих из вершин
(метками при которых служат объекты категории) и ребер (где метками
служат стрелки той же категории). Такая диаграмма коммутативна,
если любые два ориентированных пути между произвольной парой
вершин с и с' дают при композиции их меток одну и ту же стрелку
из с в с'. Эффективность теоретико-категорных методов в
значительной мере основана на наглядности таких диаграмм, представляющих
действие стрелок в конкретных случаях.
Если Ъ — объект в метакатегории С, то соответствующая
единичная стрелка 1& определяется свойствами (2) однозначно. По этой
причине иногда бывает удобно отождествить стрелку 1^ с объектом Ъ
и записать Ъ : Ъ —у Ъ. Таким образом, в случае необходимости можно
писать 1ь = Ъ = id&.

Ml
Аксиомы категорий
19
Метакатегорией является любая модель для перечисленных
аксиом. Примером может служить категория множеств, объектами
которой являются все множества, а стрелками — все функции с
тождественными отображениями в качестве единиц и с обычной
композицией функций. Здесь «функция» означает функцию с заданной
областью и кообластью. Таким образом, функция / : X —у Y состоит из
множества X (области), множества Y (кообласти) и правила х4/ж
(т. е. соответствующего множества упорядоченных пар (ж,/ж)),
которое сопоставляет каждому элементу х Е X некоторый элемент fx Е
Е Y. В зависимости от удобства эти значения будут записываться как
fx,fx или f(x). Например, для любого множества S запись s \-> s
для всех s Е S описывает тождественное отображение Is : S —> S.
Если S — подмножество в У, то соответствие s —> s описывает также
отображение включения или вложения S —>• У'. Эти отображения
различны, за исключением случая S = Y. Для данных функций
f: X^Yng-.Y^Z сложная функция g о / : X —>• Z определяется
как g о f(x) = g(fx) при всех х Е X. Отметим, что запись g о f
означает применение сначала /, потом g — в соответствии с тем, что
функция / записывается слева от аргумента. Многие авторы, однако,
придерживаются противоположного соглашения.
Таким образом, объектами метакатегории всех множеств служат
все множества, а стрелками — все функции с обычным правилом
композиции. Аналогично определяется метакатегория всех групп:
объектами являются все группы G,H,K...; стрелками — все те функции
f из множества G в множество Н, для которых G —^ Н является
гомоморфизмом групп. Существует и много других метакатегории:
все топологические пространства с непрерывными функциями в
качестве стрелок; все компактные хаусдорфовы пространства с теми же
стрелками; все окольцованные пространства с их морфизмами и т.д.
Стрелки метакатегории часто называют ее морфизмами.
Поскольку объекты метакатегории в точности соответствуют ее
единичным стрелкам, то технически возможно обойтись вообще без
объектов и работать только со стрелками. Метакатегория стрелок С
состоит из стрелок, некоторых перемножаемых упорядоченных пар
(д, /) и операции, которая сопоставляет каждой такой паре (д, /)
стрелку д о /, называемую ее произведением или композицией. Если
(#? /) — перемножаемая пара, то мы говорим также, что (д, /)
определено.
Определим единицу в С как такую стрелку и, что / о и = /, если
только определено /ои, и иод = д, если только определено иод.
Далее, потребуем выполнения следующих аксиом:
1) Произведение (к о д) о f определено, если и только если
определено произведение к о [д о f). Если они определены, то они равны
между собой (и это тройное произведение записывается как kgf).
2) Тройное произведение kgf определено всегда, когда определены
произведения kg и gf.
3) Для каждой стрелки g в С существуют такие единичные стрелки
и и и' в С, что определены и' о g и g о и.

20 Категории, функторы и естественные преобразования [Гл. 1
С учетом явного определения единичных стрелок, данного
выше, последняя аксиома оказывается достаточно мощной; стрелки и
и и' в аксиоме (3) единственны, а каждой стрелке д сопоставляется
кообласть и' и область и. Эти аксиомы равносильны предыдущим.
Именно, если дана метакатегория с объектами и стрелками, то ее
стрелки с обычной композицией удовлетворяют аксиомам только для
стрелок. Обратно, метакатегория только из стрелок удовлетворяет
аксиомам метакатегории с объектами и стрелками, если объектами
считаются определенные выше единичные стрелки. (Доказательство
предоставляется читателю в качестве упражнения.)
1.2. Категории
Категория (в отличие от метакатегории) будет означать любую
теоретико-множественную модель для аксиом категории. Поясним это
подробнее. Направленный граф (его называют также диаграммной
схемой) — это множество объектов О, множество стрелок А и две
функции
dom
А ГО. (1)
cod
Умножение в этом графе определено для пар стрелок из множества
Ax0A = {(g,f)\g, feA и domg = cod/},
называемого произведением над О.
Категория — это граф с двумя дополнительными функциями
О—^А, Ах0А >А, ^
ci ^idc, (gj)\ ^g°f,
которые называются единицей и композицией или умножением
(последнее записывают также gf). При этом для всех объектов a Е О
и всех перемножаемых пар стрелок (д, /) Е А х о А справедливы
равенства
dom (id a) — a — cod (id a), dom {go f) = dom /, cod (go f) = cod g (3)
и выполняются аксиомы ассоциативности и единицы (1.1) и (1.2). При
рассмотрении категории С мы часто будем опускать буквы А и О,
записывая
CGC, JbC (4)
в смысле «с — объект в С» и «/ — стрелка в С» соответственно.
Множество стрелок из Ъ в с будет обозначаться
horn (b, с) = {/|/ в С, dom / = b, cod / = с}. (5)

Ml
Категории
21
Категории можно определить и непосредственно в терминах
композиции в этих hom-множествах (см. ниже § 1.8). Мы этого не делаем,
так как нас больше интересуют не множества (категория достаточно
частного вида), а аксиомы, стрелки и диаграммы. Позже мы увидим,
что наше определение категории равносильно утверждению, что
категория — это моноид относительно произведения Xq (определение
дано во введении). Рассмотрим ряд примеров:
0 — пустая категория (нет ни объектов, ни стрелок);
1 — категория с одним объектом и одной (единичной) стрелкой;
2 — категория с двумя объектами а, Ъ и одной неединичной
стрелкой а —у Ь]
3 — категория с тремя объектами, причем неединичные стрелки
образуют треугольник / \ ;
Ц — категория с двумя объектами а, Ъ и двумя неединичными
стрелками а —> Ь. Такие стрелки мы называем параллельными.
Во всех перечисленных случаях композиция определяется
единственным образом.
Дискретные категории. Категория дискретна, если все стрелки —
единичные. Каждое множество X является множеством объектов
дискретной категории. Действительно, можно ввести по одной единичной
стрелке х —> х для каждого х Е X. Каждая дискретная категория
однозначно определяется множеством своих объектов. Таким образом,
дискретные категории — это, по существу, множества.
Моноиды. Моноид — это категория с одним объектом. Как
следствие, моноид определяется множеством своих стрелок, единичной
стрелкой и правилом композиции стрелок. Поскольку произведение
определено для любой пары стрелок, то моноид можно описать как
множество М с бинарной операцией М х М —У М, ассоциативной
и имеющей единицу. Таким образом, моноид — то же самое, что
полугруппа с единицей. Для любой категории С и любого объекта
a Е С множество hom (а, а) всех стрелок а —у а является моноидом.
Группы. Группа — это категория с одним объектом, в которой
любая стрелка имеет (двустороннюю) обратную относительно
композиции.
Матрицы. Для любого коммутативного кольца К г) множество
Matr^ всех прямоугольных матриц с коэффициентами из К является
категорией; ее объектами являются все натуральные числа ?тг,п,...,
а каждая т х п-матрица А рассматривается как стрелка А : п —> т,
с обычным умножением матриц в качестве композиции.
Множества. Если V — некоторое семейство множеств, то Ensy
будет означать категорию, объекты которой — все множества X G
) В книге все кольца предполагаются ассоциативными и содержащими
единичный элемент. В этом примере требование коммутативности кольца
К можно опустить. Прим. ред. пер.

22 Категории, функторы и естественные преобразования [Гл. 1
Е V, а стрелки — все функции / : X —У Y с обычным правилом
композиции. Под Ens будем понимать любую из таких категорий.
Предпорядки. Под предпорядком мы понимаем категорию Р, в
которой для любых данных объектов р,р' существует не более одной
стрелки р —у р'. В любом предпорядке Р можно определить бинарное
отношение ^ на его объектах таким образом, что р ^ р1', если и только
если в Р существует стрелка р —у р'. Это бинарное отношение
рефлексивно (поскольку для каждого р имеется единичная стрелка р —у
—у р) и транзитивно (поскольку стрелки можно перемножать). Таким
образом, предпорядок — это множество объектов, наделенное
рефлексивным и транзитивным бинарным отношением. Обратно, любое
множество Р с таким отношением определяет предпорядок, в котором
стрелки р —у р' — это в точности те упорядоченные пары {р,р'),
для которых р ^ р1'. Поскольку отношение транзитивно, то имеется
единственный способ перемножения этих стрелок; рефлексивность
обеспечивает наличие единичных стрелок.
В число предпорядков входят частичные порядки, т. е.
предпорядки с дополнительным требованием, что из р ^ р' и р' ^ р вытекает
р = р'', и линейные порядки, т. е. предпорядки, в которых для любых
р и р' либо р ^ р', либо р' ^ р.
Порядковые числа. Будем рассматривать каждый ординал
(порядковое число) п как линейно упорядоченное множество всех
предшествующих ординалов: п = {0,1,...,п — 1};в частности, 0
обозначает пустое множество, а первый бесконечный ординал равен и =
= {0,1,2,...}. Каждый ординал п линейно упорядочен и потому
является категорией (предпорядком). Например, категории 1, 2 и 3,
перечисленные выше, являются предпорядками, которые
соответствуют (линейно упорядоченным) ординалам 1, 2 и 3. Другим примером
служит линейный порядок и. Как категория он состоит из стрелок
0-^1-^2-^3-^...,
их всевозможных произведений и единичных стрелок для каждого
объекта.
В категории А объектами являются все конечные ординалы,
а стрелками / : т —У п — все функции, сохраняющие порядок (из
г ^ j в т вытекает fi ^ fj в п). Эта категория А, которую иногда
называют симплициальной, играет важнейшую роль (см. гл. 7).
В категории Finord = Set^ объектами являются все конечные
ординалы п, а стрелками / : т —у п — все функции из т в п. По
существу это категория всех конечных множеств, в которой взято по
одному конечному множеству для каждой конечной мощности п.
Большие категории. В дополнение к метакатегории всех
множеств — которая не является множеством — мы хотим ввести и
категорию Set всех малых множеств 1). Пусть имеется достаточно большое
множество U («универсум»). Будем считать множество х малым,
:) Часто используется также обозначение Sets. Прим. ред. пер.

L3]
Функторы
23
если оно является элементом универсума. Пусть Set — категория,
множеством объектов которой служит эта совокупность U всех малых
множеств, а стрелками — все функции из одного малого множества
в другое. По этой схеме (подробности см. ниже в § 1.7) строятся
и другие известные большие категории, а именно:
Set: Объекты — все малые множества; стрелки — все функции
между ними.
Set*: Множества с отмеченной точкой. Объекты — малые
множества, в каждом из которых отмечена точка; стрелки — функции,
сохраняющие отмеченную точку.
Ens: Категория всех множеств и функций внутри (переменного)
семейства V.
Cat: Объекты — все малые категории; стрелки — все функторы
(см. § 1.3).
Моп: Объекты — все малые моноиды; стрелки — все морфизмы
моноидов.
Grp: Объекты — все малые группы; стрелки — все морфизмы
групп.
АЬ: Объекты — все малые (аддитивные) абелевы группы, с их
морфизмами.
Rng: Все малые кольца, с морфизмами колец (сохраняющими
единицу) между ними г) .
С Rng: Все малые коммутативные кольца и их морфизмы 2).
R-Mod: Все малые левые модули над кольцом R и их линейные
отображения 3).
Mod-i?: Малые правые Л-модули 4).
К-Mod: Малые модули над коммутативным кольцом К.
Тор: Малые топологические пространства и непрерывные
отображения.
Toph: Топологические пространства с классами гомотопных
отображений в качестве стрелок.
Тор^: Топологические пространства с отмеченной точкой и
непрерывные отображения, сохраняющие отмеченную точку.
Название той или иной категории всегда будет (как выше)
выделяться жирным шрифтом. Многие авторы обозначают категории
заглавными рукописными буквами.
1.3. Функторы
Функтором называется морфизм категорий. Более подробно, если
имеются категории С и В, то функтор Т : С —> В с областью С
и кообластью В состоит из двух взаимосвязанных функций: функции
объектов Т, которая каждому объекту с из С сопоставляет объект Тс
; Часто используется также обозначение Ass. Прим. ред. пер.
2) Часто используется также обозначение Comm. — Прим. ред. пер.
3) Часто используется также обозначение rM, rM. Прим. ред. пер.
4) Часто используются также обозначения Mr, Mr. Прим. ред. пер.

24 Категории, функторы и естественные преобразования [Гл. 1
из Б, и функции стрелок (также обозначаемой Т), которая каждой
стрелке / : с —У с' из С сопоставляет стрелку Тf : Тс —у Тс' из В,
причем
Т(1с) = 1Тс, T{gof)=TgoTf (1)
(последнее равенство должно выполняться всякий раз, когда
композиция до f определена в С). Можно описать функтор, как и категорию,
пользуясь одними стрелками: это функция Т, которая стрелкам /
из С сопоставляет стрелки Тf из В, переводит каждую единицу из
С в единицу из В, а каждую перемножаемую пару (д, /) из С —
в перемножаемую пару (Тд, Т'/) из 5, причем Тд о Тf = T(g о /).
Простым примером служит функтор степени множеств Р : Set —>■
—у Set. Его функция объектов сопоставляет каждому множеству А
множество-степень VX, элементами которого являются все
подмножества S С X; его функция стрелок сопоставляет функции / : X —У Y
отображение Vf : VX —у VY, которое переводит каждое
подмножество S С X в его образ fS С Y. Так как V(lx) = 1-рх и V(g ° f) =
= Vg о Vf, то, очевидно, мы определили функтор V : Set —у Set.
Функторы впервые появились в явном виде в алгебраической
топологии, где они естественно возникают при описании
геометрических свойств посредством алгебраических инвариантов. Например,
сингулярная гомология в данной размерности п (где п —
натуральное число) сопоставляет каждому топологическому пространству X
абелеву группу Нп(Х), т.е. п-ю группу гомологии пространства X,
а каждому непрерывному отображению топологических пространств
/ : X —У Y — соответствующий гомоморфизм групп Hn(f) : Нп(Х) —у
—У Hn(Y), причем Нп оказывается функтором Тор —у АЬ. Например,
если X = Y = S1 — окружность, то Hi(S1) = Z, и гомоморфизм групп
Hi(f) : Z —у Z определяется целым числом d (образом единицы); это
число — обычная степень непрерывного отображения / : X —У Y.
В данном случае (как и в общем) гомотопные отображения f,g:X^
—У Y дают один и тот же гомоморфизм Нп(Х) —у Hn(Y), так что
Нп в действительности можно рассматривать как функтор Toph —>■
—У Grp, определенный на категории гомотопий. Аксиомы гомологии
Эйленберга-Стинрода начинаются с утверждения, что Нп при
каждом натуральном п является функтором на Toph, и содержат
некоторые дополнительные свойства таких функторов. Созданные позднее
теории исключительных гомологии и когомологий тоже имеют дело
с функторами на Toph. Группы гомотопий 7ГП(А) пространства X
также можно рассматривать как функторы. Так как они зависят от
выбора начальной точки в А, то группы гомотопий являются
функторами Toph^ —у Grp. Основная идея при использовании функторов
в топологии состоит в том, что Нп или 7гп дает алгебраическую
картину или образ не только топологических пространств, но и всех
непрерывных отображений между ними.
Функторы естественным образом возникают и в алгебре. Для
любого коммутативного кольца К множество всех невырожденных пхп-
матриц с коэффициентами из К составляет полную линейную группу
GLn(K); далее, каждый гомоморфизм колец / : К —У К' очевидным

L3]
Функторы
25
образом порождает гомоморфизм групп GLn(K) —у GLn(K'). Тем
самым для всякого натурального п определен функтор GLn : CRng —у
—у Grp. Для каждой группы G множество всех произведений
коммутаторов хух~1у~1(х,у Е G) является нормальной подгруппой [G, G]
в G и называется коммутантом или коммутаторной подгруппой.
Поскольку любой гомоморфизм групп G —У Н переводит
коммутаторы в коммутаторы, то сопоставление G \-У [G, G] определяет
очевидный функтор Grp —у АЬ, а именно факторизацию по коммутанту.
Заметим, однако, что центр Z(G) группы G (все a Е G такие, что
ах = ха при всех х) не определяет подобным образом функтор Grp —у
—у Grp, поскольку гомоморфизм G —У Н может перевести элемент из
центра группы G в элемент, не принадлежащий центру группы Н.
Функтор, который просто «забывает» частично или полностью
структуру алгебраического объекта, обычно называется забывающим
(или стирающим) функтором. Так, забывающий функтор U : Grp —у
—У Set сопоставляет каждой группе G множество ее элементов UG
(забывая умножение и тем самым — групповую структуру), а
каждому морфизму групп / : G —У G' сопоставляет то же отображение,
рассматриваемое как отображение множеств. Забывающий функтор
U : Rng —у АЬ сопоставляет каждому кольцу его аддитивную абелеву
группу, а каждому морфизму колец / : R —У R' — то же самое
отображение, рассматриваемое как морфизм аддитивных групп.
Функторы можно перемножать. А именно, если даны функторы
С ^уВ^уА
между категориями А, В и (7, то сложные функции
c^S(Tc) и f^S(Tf)
от объектов с и стрелок / категории С определяют функтор
S о Т : С —У А, который называется композицией или произведением
S и Т (в таком порядке). Такая композиция ассоциативна. Для
каждой категории В существует тождественный функтор 1в • В —>-
—У В, который действует как единица относительно этой композиции.
Таким образом, мы можем говорить о метакатегории всех категорий:
ее объектами являются все категории, а стрелки — все функторы
с описанной композицией. Аналогично, мы можем образовать
категорию Cat всех малых категорий — но не категорию всех
категорий.
Изоморфизм категорий Т : С —» В — это функтор Т из С в В,
который является биекцией как на объектах, так и на стрелках. Иными
словами, функтор Т : С —» В является изоморфизмом, если и только
если существует функтор S : В —у С, для которого оба произведения
S о Т и Т о S являются тождественными функторами; в этом случае
S — двусторонний обратный функтор S = Т-1.
Окажутся полезными и некоторые свойства, гораздо более слабые,
чем изоморфизм.

26 Категории, функторы и естественные преобразования [Гл. 1
Функтор Т : С —У В называется полным (full), если для каждой
пары с, с' объектов из С и каждой стрелки д : Тс —у 7V из 5 найдется
стрелка / : с —у с' в С, для которой g = Т/. Ясно, что композиция
двух полных функторов является полным функтором.
Функтор называется унивалентпным или вложением, если для
любой пары с, с' объектов из С и любой параллельной пары Д, /2 : с ^ с'
стрелок в С из равенства ТД = ТД : Тс —у 7V следует Д = Д. При
этом композиция унивалентных функторов унивалентна. Например,
забывающий функтор Grp —у Set унивалентен, но не полон и не
является биекцией на объектах.
Эти два свойства можно сделать наглядными с помощью hom-
множеств (см. (2.5)). Для данной пары объектов с,с' Е С функция
стрелок функтора Т : С —У В сопоставляет каждой стрелке f : с —У с'
стрелку Тf : Тс —у Тс' и тем самым определяет функцию
Гс,с/ : hom (с, с') -+ hom (Тс, Тс'), f н> Г/.
Функтор Т полон, когда каждая такая функция сюръективна, и
унивалентен, когда каждая такая функция взаимно однозначна. Если
функтор и полон, и унивалентен (т. е. вполне унивалентен — fully
faithful), то эти функции являются биекциями, но сам функтор может
и не быть изоморфизмом категорий, поскольку в категории В могут
найтись объекты, не принадлежащие образу функтора Т.
Подкатегория S категории С — это совокупность некоторых
объектов и стрелок из С, которая вместе с каждой стрелкой / включает
объекты dom / и cod Д вместе с каждым объектом s — его единичную
стрелку ls, а вместе с каждой парой перемножаемых стрелок s —>■
—у s' —У s" — их композицию. При этих условиях совокупность
объектов и стрелок составляет некоторую категорию S. Далее,
отображение вложения (включения) S —У С, сопоставляющее каждый
объект и каждую стрелку из S самим себе (в С), является функтором,
а именно функтором вложения. Этот функтор вложения
автоматически оказывается унивалентным. Если он полон, то мы говорим, что
S — полная подкатегория в С. Если дана категория С, то полная
подкатегория определяется указанием множества ее объектов, поскольку
стрелки между двумя из этих объектов s,s' — это всевозможные
морфизмы s —У s' в С. Например, категория Setf всех конечных
множеств является полной подкатегорией в Set.
Упражнения
1. Покажите, что каждая из следующих конструкций может
рассматриваться как функтор: поле частных целостного кольца; алгебра Ли группы
Ли.
2. Покажите, что функторы 1—^С,2—^СиЗ—^С соответствуют
объектам, стрелкам и перемножаемым парам стрелок в С.
3. Интерпретируйте понятие функтора в следующих частных случаях
категорий: а) функтор между двумя предпорядками — это монотонная
функция Т (т. е. из р ^ р' следует Тр ^ Тр'); б) функтор между двумя
группами (как категориями с одним объектом) — это морфизм групп; с) если

L4]
Естественные преобразования
27
G — группа, то функтор G —У Set — это ее представление перестановками,
тогда как функтор G —У Mat г к — представление группы G матрицами.
4. Докажите, что не существует функтора Grp —у Ab, который бы
отображал каждую группу в ее центр (рассмотрите симметрические группы:
S2 -+ S3 -+ S2).
5. Найдите два различных функтора Т : Grp —у Grp с тождественной
функцией объектов: T(G) = G для каждой группы G.
1.4. Естественные преобразования
Пусть даны два функтора S,T : С —У В. Естественное
преобразование т : S -^ Т — это функция, которая каждому объекту с из С
сопоставляет стрелку тс = тс : Sc —у Тс из 5 таким образом, что для
каждой стрелки / : с —у с' из С следующая диаграмма коммутативна:
5с^^^Гс
5/
Sc'
Tf
(1)
Т^Тс'.
В этом случае мы говорим также, что стрелка тс : Sc —у Тс
естественна по с. Если считать, что функтор 5 создает в 5 изображение (всех
объектов и всех стрелок) категории С, то естественное преобразование
г — это совокупность стрелок, отображающих (или переводящих)
картинку S в картинку Т, причем коммутативны всевозможные
квадраты (и параллелограммы!) вроде изображенного выше. Мы называем
та, тЪ, тс,... компонентами естественного преобразования т.
Ь Sh
Естественное преобразование часто называют морфизмом
торов', если каждая компонента тс естественного преобразования т
обратима в категории В, то т называется естественной
эквивалентностью или, лучше, естественным изоморфизмом] в символической
записи т : S = Т. В этом случае обратные стрелки (тс)-1 в В являются
компонентами естественного изоморфизма г-1 : Т^> S.
Примером естественного преобразования служит определитель.
А именно, пусть det^ М — определитель п х n-матрицы М с
коэффициентами в коммутативном кольце К, а К* обозначает группу единиц
(обратимых элементов) в К. Тогда матрица М невырождена, если
clet^ M обратим, и det^ является морфизмом групп GLnK —у К*
(стрелкой в Grp). Поскольку определитель выражается одинаковой

28 Категории, функторы и естественные преобразования [Гл. 1
формулой во всех кольцах К, то каждый морфизм коммутативных
колец f : К —> К' порождает коммутативную диаграмму
GLnK >■ if*
GLnf
GLnK'—^K'*.
(2)
Это означает, что det : GLn —>•()*— естественное преобразование
между двумя функторами CRng —> Grp.
Для любой группы G проекция ро : G —>• G/[G,G] на
факторгруппу по коммутанту определяет преобразование р тождественного
функтора на Grp в фактор-функтор Grp —> АЬ —> Grp. При этом
р естественно, так как каждый гомоморфизм групп / : G —>- Н
определяет очевидный гомоморфизм /', для которого коммутативна
следующая диаграмма:
G
PG
■G/[G,G\
Г
Н^^Н/[Н,Н].
(3)
В категории АЬ всех абелевых групп наглядным примером служ:ит
вторая группа характеров. Пусть D(G) обозначает группу характеров
группы G, т. е. DG = hom (G, R/Z) — множество всех гомоморфизмов
t : G —> R/Z с естественной групповой структурой (здесь R/Z —
аддитивная группа вещественных чисел по модулю 1). Каждая стрелка
/ : G' —>■ G определяет в категории АЬ стрелку Df : DG —У DG'
(противоположного направления!), причем (Df)t = tf : G' —>- R/Z
при каждом t. Отметим, что для перемножаемых стрелок D(g о f) =
= Df о Dg. Из-за обращения стрелок отображение D не является
функтором. Это контравариантный функтор из АЬ в АЬ, см. § 2.2.
Однако вторая группа характеров G н->- D(DG) и тождественное
отображение 1(G) = G задают функторы АЬ —>• АЬ. Для каждой
группы G имеет место гомоморфизм
rG :G^D(DG),
конструкция которого хорошо известна: каждому д G G сопоставим
функцию год : DG —> R/Z, которая имеет вид t \-> tg для
любого характера t G DG; тогда {rog)t — t(g). Без труда
проверяется, что т является естественным преобразованием т : I —> DD. Это
утверждение выражает в точной форме тот элементарный факт, что
определение преобразования т не зависит от специального выбора
базисов, образующих элементов и т. п. Если группа G конечна, то т
является изоморфизмом. Поэтому если мы ограничим все функторы

L4]
Естественные преобразования
29
на категорию АЬ/ конечных абелевых групп, то т будет естественным
изоморфизмом.
С другой стороны, для каждой конечной абелевой группы G
имеется изоморфизм а : G = DG на ее группу характеров, но этот
изоморфизм зависит от представления G в виде прямого произведения
циклических групп и потому не может считаться естественным. Более
точно: мы можем превратить D в ковариантный функтор D'Ahf^ —>
—> Abf^ на категории Ab/?i, объектами которой являются все
конечные абелевы группы, а стрелки — все изоморфизмы / между ними.
Для этого положим D'G = DG и D'f = Df~l. Тогда oG : G -> D'G
задает отображение а : I —> D' функторов Aby^ —> Ab/?i, но оно не
является естественным в смысле нашего определения.
Аналогичный пример — хорошо известный естественный
изоморфизм конечномерного векторного пространства и его второго
сопряженного.
Другой пример естественного изоморфизма возникает, если
сопоставить категорию Finord всех конечных порядковых чисел п и
категорию Setf всех конечных множеств (в некотором универсуме U).
Каждое порядковое число п = {0,1,...,п — 1} — это конечное
множество. Поэтому имеется функтор вложения S : Finord —> Set/. С
другой стороны, каждое конечное множество X определяет порядковое
число п = #Х, а именно число элементов в X. Для каждого
множества X можно выбрать биекцию вх • X —> фХ. Теперь для каждого
отображения / : X —у Y между конечными множествами определим
соответствующее отображение #/ : фХ —> #У между ординалами,
положив #/ = @Y fOx . Получается коммутативная диаграмма
/ #/
показывающая, что # является функтором # : Set/ —> Finord. Если
X само является ординалом, то в качестве вх можно взять
тождественное отображение. В этом случае композиция функторов # о S
будет тождественным функтором Г в категории Finord. С другой
стороны, композиция S о ф не является тождественным функтором
/ : Set/ —> Set/, поскольку она отображает каждое множество X
в конечное множество специального типа — ординал п с тем же числом
элементов, что и X. Тем не менее, приведенный выше коммутативный
квадрат показывает, что 6 : I —> 5# является естественным
изоморфизмом. В итоге имеем / = So#, /' = # о S.
В общем случае эквивалентность между категориями С и D
определяется как пара функторов S : С —>■ D, Т : D —» С вместе с
естественными изоморфизмами 1с — Т о S, Id — S о Т. Приведенный
пример показывает, что это понятие, изучаемое в § 4.4, позволяет
сравнивать категории похожие, но очень разного размера.

30 Категории, функторы и естественные преобразования [Гл. 1
Мы будем использовать и многие другие примеры естественных
преобразований. Как впервые отметили Эйленберг и Маклейн,
категория была определена, чтобы можно было определить функтор,
а функтор — чтобы можно было определить естественное
преобразование.
Упражнения
1. Пусть S — фиксированное множество, X — множество всех функций
h : S —> X. Покажите, что отображение X н->- X является функцией
объектов для некоторого функтора Set —»■ Set, а сопоставление ех '• X х
х S —> X, определенное как e(h,s) = h(s), т. е. как значение функции h при
s G S, является естественным преобразованием.
2. Пусть Н — фиксированная группа. Покажите, что соответствие G н-»-
н->" Н х G определяет функтор Н х — : Grp —»> Grp, а каждый морфизм
групп / : Н —>- К определяет естественное преобразование Н х —'■* К х —.
3. Пусть В и С — группы (рассматриваемые как категории с одним
объектом), a S,T : В —>- С — функторы (гомоморфизмы групп). Покажите, что
естественное преобразование S -^Т существует тогда и только тогда, когда
S и Т сопряжены, т. е. когда для некоторого элемента h E С выполнено
равенство Тд = h (Sg) h~x при всех д Е В.
4. Пусть С — категория, Р — предпорядок, S,T : С —»■ Р — функторы.
Покажите, что естественное преобразование S —>Т существует (и
единственно) в том и только том случае, когда Sc ^ Тс для любого объекта с £ С.
5. Покажите, что каждое естественное преобразование т : S -^Т
определяет функцию, также обозначаемую г, которая каждой стрелке / : с —»■ с
в С сопоставляет стрелку rf : Sc —»■ Тс7 в 5, причем Тд Т/ = r(gf) =
= тд 5/ для любой перемножаемой пары (д, /). Докажите обратный факт,
что каждая такая функция т возникает из единственного естественного
преобразования, для которого тс = т(1с). (Это позволяет описать естественное
преобразование с помощью одних лишь стрелок.)
6. Пусть F — поле. Покажите, что категория всех конечномерных
векторных пространств над F, где морфизмами являются все линейные
отображения, эквивалентна категории Matr^, описанной в § 1.2.
1.5. Мономорфизмы, эпиморфизмы и нулевые
морфизмы
Многие факты, которые обычно описываются в терминах
элементов, например, элементов множества или группы, на теоретико-
категорном языке формулируются в терминах стрелок. Например,
вместо того чтобы говорить, что множество X имеет ровно один
элемент, можно сказать, что для любого другого множества Y существует
ровно одна функция Y —> X. Приведем еще несколько примеров такой
«работы без элементов».
Стрелка е : а —> Ь обратима в С, если существует такая стрелка
е' : Ъ —> а в С, для которой е'е = 1а и ее' = 1&. Если стрелка е'
существует, то она единственна и обозначается е' = е-1. Обычным
образом доказывается, что (е^)-1 = е^"1е^1, если произведение е\е2

1.5] Мономорфизмы, эпиморфизмы и нулевые морфизмы 31
определено, а е\ и е<± обратимы. Два объекта а и Ь изоморфны в
категории С, если существует обратимая стрелка (изоморфизм) е : а —>
—у Ь; тогда мы пишем а = Ъ. Ясно, что отношение изоморфизма
рефлексивно, симметрично и транзитивно.
Стрелка т : а —>■ Ъ является мономорфизмом в С, если для любых
двух параллельных стрелок Д, Д : d —> а из равенства т о Д =
= шо/2 вытекает Д = Д. Другими словами, стрелка m
является мономорфизмом, если на нее всегда можно сократить слева (т
сократима слева). Мономорфизмы в Set и в Grp — то же самое,
что вложения или мономорфизмы в обычном смысле, т. е. взаимно
однозначные функции.
Стрелка h : а —>■ Ь является эпиморфизмом, если для любых двух
стрелок gi,#2 • cl —> Ь из равенства д\ о h = д2 ° h вытекает д\ —
— #2- Другими словами, стрелка h является эпиморфизмом, если она
сократима справа. Эпиморфизмы в категории Set — то же самое, что
сюръекции или эпиморфизмы в обычном смысле, т. е. отображения
на.
Правой обратной для стрелки h : а —>• Ъ является стрелка г : Ъ —>•
—> а со свойством hr = 1&. Правая обратная стрелка (обычно не
единственная) называется также сечением для /i. Если /i имеет правую
обратную, то h заведомо является эпиморфизмом. Обратное верно
в Set, но не в Grp. Аналогично, левая обратная стрелка для h
называется ее ретракцией, и любая стрелка с левой обратной обязательно
является мономорфизмом. Если gh = 1а, то д является расщепляющим
эпиморфизмом, h — расщепляющим мономорфизмом, а композиция
/ — hg определена и идемпотентна. В общем случае стрелка / : Ъ —>■ Ъ
называется идемпотентом, когда /2 = /. Идемпотент расщепляется,
если существуют стрелки g и /i, такие что / — hg и gh = 1.
Объект называется терминальным в С, если для каждого объекта
а в С имеется ровно одна стрелка а —> t. Если объект t терминален,
то единственной стрелкой t —> t будет единичная. Любые два
терминальных объекта в С изоморфны. Объект s называется начальным
или инициальным в категории С', если для каждого объекта а имеется
ровно одна стрелка s —> а. Например, в категории Set пустое
множество является начальным, а любое одноэлементное множество —
терминальным объектом. В категории Grp одноэлементная группа
является и начальным, и терминальным объектом.
Нулевой объект z в С — это объект, который одновременно
является начальным и терминальным. Если нулевой объект в С существует,
то он единственен с точностью до изоморфизма, и для любых двух
объектов а и Ъ в С существует единственная стрелка а —> z —> Ъ,
которая называется нулевой стрелкой из а в Ь. Любая композиция
с нулевой стрелкой также является нулевой стрелкой. Например,
в категориях АЬ и Л-Mod существует нулевой объект (а именно О!),
так же как и в Set* (а именно одноточечное множество).
Группоид — это категория, в которой любая стрелка обратима.
Типичным примером служит фундаментальный группоид 7г(Х)
топологического пространства X. Объект в 7г(Х) — это точка в X, а стрелка

32 Категории, функторы и естественные преобразования [Гл. 1
х —У х' в 7г(Х) — это класс гомотопных путей из ж в ж'. (Напомним,
что путь / — это непрерывная функция / —у X, где / — отрезок / =
= [0,1], причем /(0) = ж, /(1) = х'. Два пути /,д с общими концами
ж, х' гомотопны, если существует непрерывная функция F : / —У / х X
такая, что F(t,0) = /(£), F(t, 1) = #(£) и F(0, s) = ж, F(l,s) = ж' при
всех s и £ в /.) Композиция (произведение) путей g : х' —у ж" и / : ж —>•
—>- ж' — это путь /i, в котором за / следует д, а именно
h(t) = f(2t), O^t^ 1/2,
= 0(2i-l), 1/2 ^ t ^ 1.
Композиция может применяться и к классам гомотопий, превращая
7г(Х) в категорию и группоид, где путь, обратный к данному, — это
тот же путь, но пройденный в противоположном направлении.
Поскольку в группоиде G любая стрелка обратима, то каждый
объект ж в G определяет группу hom^ (ж, ж), состоящую из всех стрелок
g : ж —у ж. Если существует стрелка / : ж —у ж', то между группами
пот<з(ж,ж) и Ьот^(ж/,ж/) имеется изоморфизм, а именно
сопряжение g \-у jgj~x'. Группоид называется связным, если любые два его
объекта соединены стрелкой. Легко показать, что связный группоид
с точностью до изоморфизма определяется группой, именно любой
из групп hom<3 (ж, ж)), и множеством всех объектов. Таким образом,
фундаментальный группоид 7г(Х) линейно связного пространства X
определяется множеством точек пространства и группой hom^ (ж, ж),
т. е. фундаментальной группой пространства X.
Упражнения
1. Найдите категорию, в которой некоторая стрелка является
эпиморфизмом и мономорфизмом, но не обратима. (Указание: рассмотрите
плотное подмножество топологического пространства.)
2. Докажите, что произведение мономорфизмов является
мономорфизмом, и аналогично для эпиморфизмов.
3. Если композиция g о f является мономорфизмом, то это верно и для
/. Верно ли это для д?
4. Покажите, что в категории Rng вложение Z —у Q является
эпиморфизмом.
5. Докажите, что в Grp любой эпиморфизм сюръективен. (Указание.
Пусть образ М морфизма ср : G —У Н не совпадает с Н. Если М имеет
индекс 2, то рассмотрите факторгруппу Н/М. В противном случае пусть
Perm H — группа всех перестановок множества Н, причем существуют три
различных смежных класса М, Ми, Mv по подгруппе М. Определим а Е
Е Permit, положив а(хи) = xv, a(xv) = хи при х Е М. В остальных случаях
а действует тождественно. Пусть ф : Н —У Permit отображает каждый
элемент h Е Н в умножение фн слева на h, a ф'н = сг~1ф}1сг. Тогда ф(р = ф'ср,
но ^ ф ф''.)
6. Покажите, что в категории Set все идемпотенты расщепляются.
7. Стрелка / : а —у Ъ в категории С называется регулярной, если
существует стрелка д : Ъ —У а такая, что fgf = /. Покажите, что / регулярна,
если она имеет левую либо правую обратную, и докажите, что в категории
Set регулярна любая стрелка, для которой а ф 0.

L6]
Основания теории
33
8. Рассмотрим категорию с объектами (X,e,t), где X — некоторое
множество, е G X, t : X —»> X, и со стрелками / : (X, е,£) —»■ {Х',е',^), где
/ : X —»■ X7, /е = е', ft = t'. Докажите, что в этой категории существует
начальный объект, для которого X — множество натуральных чисел, е = О,
at — функция следования, т. е. t : п \-> п + 1.
9. Докажите, что если функтор Т : С ^ В унивалентен, а Тf —
мономорфизм, той/ — мономорфизм.
1.6. Основания теории
Одна из главных задач теории категорий состоит в изучении
свойств совокупностей математических объектов, таких как
множество всех групп или множество всех гомоморфизмов между
двумя группами. Сейчас обычно рассматривают группу как множество
с некоторой дополнительной структурой, и мы здесь намереваемся
рассматривать множества всех множеств с некоторой заданной
структурой. Это соответствует признанию принципа выделения: если дано
свойство (р(х) множеств ж, то можно образовать множество {х \ ц>(х)}
всех множеств х с этим свойством. Однако этот принцип не может
быть принят в полной общности, так как он приводит к известным
парадоксальным множествам, таким как множество всех множеств,
не являющихся элементами самих себя.
По этой причине в наивной теории множеств с обычным
отношением принадлежности Е применение принципа выделения обычно
ограничивается. Разрешается построить по данным множествам и, v
множество {u,v}, элементами которого являются и, v и только они,
упорядоченную пару (u,v), бесконечное множество (множество со =
= {0,1,2,...} всех конечных ординалов), а также
декартово произведение и х v = {(ж, у)\ х Е и и у Е v},
множество-степень Ти — {v | v С и},
объединение Ux = {у | у G z для некоторого z G х}.
(семейства х множеств)
Наконец, пусть дано множество и и свойство (р(х), в
формулировке которого участвуют ж, отношение принадлежности и обычные
логические связки, включая выражения «для всех множеств £» и
«существует множество £». Тогда допускается
выделение элементов из и: {х | х G и и (р(х)}.
Это свойство можно выразить следующими словами: существует
множество всех тех х с данным свойством (р, которые являются
элементами заранее данного множества и.
Добавим к этому стандартному набору еще одно допущение:
существование универсума. Универсум определяется как множество U со
следующими (отчасти избыточными) свойствами:
1) из х е и е U следует х G U;
2)h3uGUhvGU следует {и, v}, (и, v), и х v G U;

34 Категории, функторы и естественные преобразования [Гл. 1
3) из х е U следует Тх Е U и Ux Е U;
4) и Е U (здесь и = {0,1,2,...} — множество всех конечных
ординалов);
5) если / : а —у Ъ — сюръективная функция, причем a Е U и Ъ С U,
то Ь Е U.
Эти условия замкнутости для U гарантируют, что применение
стандартных теоретико-множественных операций к элементам из U
всегда дает элементы из [/; в частности, благодаря условию и Е U
универсум содержит все обычно рассматриваемые множества
вещественных чисел и связанные с ними бесконечные множества. Поэтому
можно считать, что обычная математика работает исключительно
внутри U, т. е. с элементами из U, тогда как само U и множества, с ним
связанные, применяются для построения искомых больших категорий.
Зафиксируем универсум U, а множества и Е U будем называть
малыми множествами. Таким образом, универсум U — это
множество всех малых множеств. Аналогично, назовем функцию / : и —>- v
малой, если и и v — малые множества. Тогда можно рассматривать
и / как малое множество — например, как упорядоченную тройку
(u,Gf,v), где Gf С и х v — множество всех (х,у), для которых
х G и, у = fx. Как следствие, принцип ограниченного выделения
позволяет построить множество А всех тех множеств, которые
являются малыми функциями, поскольку эти функции — элементы из
U. Теперь мы можем определить категорию Set всех малых
множеств как такую категорию, в которой U, т. е. множество всех малых
множеств, является множеством объектов, а А, т. е. множество всех
малых функций, — множеством стрелок. В дальнейшем Set всегда
обозначает эту категорию.
Аналогично, малая группа — это малое множество с групповой
структурой, т. е. упорядоченная пара (и, т), где и — малое множество,
am: и х и ^ и — функция, т. е. бинарная операция на и, которая
удовлетворяет обычным аксиомам группы. Поскольку любая малая
группа является элементом в U, мы можем образовать множество
всех малых групп и множество всех гомоморфизмов между малыми
группами. Они составляют категорию Grp всех малых групп.
Тот же процесс приводит к категориям всех малых
математических объектов других типов. Например, категория является малой,
если множества ее объектов и стрелок — малые. Далее мы построим
категорию Cat всех малых категорий. Заметим, однако, что Set не
является малой категорией, поскольку множество ее объектов U не
является малым. В противном случае U G U, что противоречит аксиоме
регулярности, которая утверждает, что не существует бесконечных
цепочек ...хп G xn-\ G жп-2 £ ••• £ #о- Аналогично, не является
малой и категория Grp.
Такому описанию оснований математики можно придать
аксиоматическую форму. Примем стандартные аксиомы теории множеств
Цермело-Френкеля плюс существование множества U, играющего
роль универсума. В систему Цермело-Френкеля для отношения
принадлежности G входят следующие аксиомы: экстенсиональность (мно-

L6]
Основания теории
35
жества, имеющие одни и те же элементы, равны); существование
пустого множества; существование множеств {u,v}, (u,v),Vu и Ux
для всех множеств и, v, ж; аксиома бесконечности; аксиома выбора;
аксиома регулярности и аксиома замещения.
Замещение. Пусть а — некоторое множество, а свойство (р(х, у)
определяет функцию на элементах ж из а в следующем смысле: из
(р(х,у) = ср(х,у') при х Е а вытекает у = у', причем для любого х Е а
найдется такое у, что (р(х,у). Тогда существует множество, состоящее
из всех таких у, что ср(х,у) выполнено при каком-либо х Е а.
Кратко говоря, аксиома замещения утверждает, что образ
множества а при действии функции ip является множеством. Можно
показать, что из аксиомы замещения следует аксиома выделения,
сформулированная выше. Далее, из наших условий, определяющих
универсум U, вытекает, что все множества в U (все малые множества)
удовлетворяют аксиомам Цермело-Френкеля. Например, условие (5)
в определении универсума соответствует замещению. Мы увидим, что
наше допущение о существовании единственного универсума вполне
достаточно для целей теории категорий.
Некоторые авторы предполагают существование как множеств, так
и классов, используя аксиомы Геделя-Бернайса. Чтобы пояснить этот
подход, определим класс С как произвольное подмножество
универсума С С U. Поскольку из х Е и Е U вытекает х Е U, то каждый элемент
из U является его подмножеством, так что любое малое множество
является также и классом. Однако некоторые классы, такие как само
U, не являются малыми множествами. Они называются
собственными классами. Малые множества и классы вместе удовлетворяют
стандартным аксиомам Геделя-Бернайса (см. Godel [1940]).
Большая категория — это такая категория, в которой
множества объектов и стрелок являются классами, собственными или нет.
Используя только малые множества и произвольные классы, можно
описать многие необходимые категории. В частности, наши категории
Set, Grp и т. д. являются собственными классами и, значит, большими
категориями в данном смысле. Вначале теория категорий
ограничивалась изучением малых и больших категорий и основывалась на
аксиомах Геделя-Бернайса. Однако во многих случаях нам придется
образовывать категории, не являющиеся классами. Одной из них является
категория всех классов Cls: ее объекты — все классы, а стрелки — все
функции f : С —> С между классами. Таким образом, множество
объектов категории Cls — это множество V всех подмножеств в U.
Это не класс, так как его мощность больше, чем мощность универсума
U. Другим полезным примером служит Cat7, категория всех больших
категорий. Она не является классом.
В дальнейшем мы опускаем обозначение выбранного универсума
U и говорим просто о малых множествах, классах и множествах, имея
в виду, что множества включают малые множества и классы, так же
и многое другое, — например, V(U), W(U), {U} и т.п. Отметим,
в частности, что {U} — это множество, имеющее единственный
элемент (а именно универсум U). Поэтому на интуитивном уровне оно

36 Категории, функторы и естественные преобразования [Гл. 1
очень мало, но в нашем смысле малым множеством не является; из
{U} Е U следовало бы U Е U, в противоречии с аксиомой
регулярности. Таким образом, малое множество означает для нас элемент
универсума, а не множество малой мощности.
Такое построение оснований математики с помощью единственного
универсума обеспечивает (в рамках теории множеств) корректный
способ рассмотрения категорий всех малых множеств и всех малых
групп. Но здесь отсутствуют множества для реализации некоторых
метакатегории, таких как метакатегория всех множеств или всех
групп. Гротендик использует иной подход. Он принимает, что для
каждого множества X имеется универсум U такой, что X Е U.
Ясно, что это, более сильное, допущение обеспечивает для
каждого универсума U существование категории всех тех групп, которые
являются элементами из U. Однако отсюда не возникает категория
всех групп. По этой причине серьезно обсуждалась возможность
построения теории категорий (и всей математики) вне рамок теории
множеств. Вот почему мы вначале дали определение категории С
без использования понятия множества, рассматривая аксиомы просто
как аксиомы первого порядка с неопределяемыми терминами «объект
категории С», «стрелка в категории С», «композиция», «единица»,
«область» и «кообласть». На этом языке можно сформулировать
аксиомы элементарной теории, т. е. теории первого порядка, категории
всех множеств — в противовес обычным аксиомам для отношения
принадлежности, — получив понятие элементарного топоса (см. Мае
Lane, Moerdijk [1992]) х).
Упражнения
1. Пусть дан универсум U, а также функция f : I —> b с областью
определения I £ U, причем все ее значения fi (г Е U) принадлежат U.
Докажите, что декартово произведение П^ fi является элементом из U.
2. а) Для данного универсума U и функции f : I —> b с областью
определения I € U покажите, что объединение Uifi является множеством
из U.
б) Покажите, что в определении универсума U можно заменить условие
(5) на свойство из п. (а) этого упражнения, а из условия х Е U вытекает,
что Ux E U.
1.7. Большие категории
Во многих существенных случаях категория состоит из всех
(малых) математических объектов с данной структурой, причем ее
стрелками служат все функции, сохраняющие эту структуру. Перечислим
некоторые полезные примеры, указав соответствующие
мономорфизмы.
:) Логические вопросы, связанные с построением теории категорий,
обсуждаются в работе (Захаров, Михалев [2002]). — Прим ред. пер.

ш
Большие категории
37
В категории АЬ всех малых абелевых групп объектами являются
все малые (аддитивные) абелевы группы А, £?,..., а стрелками — все
гомоморфизмы / : А —У В с обычным умножением. В этой категории
стрелка является мономорфизмом, если и только если она задает
инъективное отображение (вложение). Точно так же сюръективный
гомоморфизм заведомо является эпиморфизмом. Обратно,
гомоморфизм f : А —У В, который является эпиморфизмом как стрелка
в категории АЬ, должен быть отображением на. В противном случае
факторгруппа В/f А состоит не только из нуля, и существуют два
различных морфизма В —У В/f А (проекция р и нулевой морфизм
0), для которых pf = 0 = 0/, что противоречит определению
эпиморфизма. Нулевая группа в категории АЬ является и начальным,
и терминальным объектом.
Малое кольцо R — это малое множество с бинарными
операциями сложения и умножения, удовлетворяющими обычным аксиомам
кольца — включая существование двусторонней единицы 1 по
умножению. Категория всех малых колец будет обозначаться Rng; ее
объекты — малые кольца Л, стрелки / : R —у S — (гомо)морфизмы колец,
причем предполагается, что единица кольца R переходит в единицу
кольца S. В этой категории нулевое кольцо является терминальным
объектом, а кольцо целых чисел Z — начальным, поскольку
существует ровно одна стрелка Z —у R, которая переводит 1 Е Z в единицу
кольца R. Мономорфизмы в этой категории — это обычные
мономорфизмы (вложения) колец. Каждый эпиморфизм колец является
эпиморфизмом и как стрелка в категории. Однако вложение Z —у
—У Q кольца Z в поле рациональных чисел Q является эпиморфизмом
в категорном смысле, но не сюръекцией.
В случае малого кольца R объектами категории Л-Mod являются
все малые левые Л-модули А, В,..., а стрелками / : А —у В — все
морфизмы Л-модулей (R-линейные отображения). В этой категории
понятия мономорфизма и эпиморфизма имеют обычный смысл, а
нулевой модуль является начальным и терминальным объектом. В
случае поля F категория F-Mod, иначе обозначаемая Vct^, состоит из
всех векторных (линейных) пространств над F. Категория всех малых
правых Л-модулей будет обозначаться Mod-i?. Если R и S — два
кольца, то i^-Mod-S обозначает категорию всех малых Л-5-бимодулей
(левых R- и правых 5-модулей, в которых г (as) = г (as) для всех г Е
Е R, a Е A, s G S). Аналогично можно построить категории малых
алгебраических объектов любого заданного типа.
Объектами категории топологических пространств Тор служат
все малые топологические пространства X, У,..., а морфизмами —
все непрерывные отображения / : X —У Y. Снова мономорфизмами
являются вложения, а эпиморфизмами — сюръекции. Одноточечное
пространство служит терминальным, а пустое множество —
начальным объектом. Аналогично можно образовать категорию всех малых
хаусдорфовых пространств или всех малых компактных хаусдорфо-
вых пространств.

38 Категории, функторы и естественные преобразования [Гл. 1
В категории Toph объектами являются все малые топологические
пространства X, У,..., а морфизм а : X —У У — это класс гомо-
топии непрерывных отображений / : X —У У; таким образом, два
гомотопных отображения / = д : X —у У определяют один и тот же
морфизм из X в Y. Умножение морфизмов — это обычное умножение
классов гомотопных отображений. В этой категории класс гомотопии
вложения не обязательно является мономорфизмом, как можно
видеть на примере вложения окружности в круг в качестве его границы.
Категория Toph естественно возникает в теории гомотопии, и на ее
примере мы видим, что стрелка в категории — не то же самое, что
функция. В теории гомотопии используются и многие другие
категории: например, категории CW-комплексов, симлициальных множеств,
компактно порожденных пространств (см. § 7.8) и комплексов Кана.
Категория множеств с отмеченной точкой (иногда называемых
базированными множествами) будет обозначаться Set*. Мноэюество
с отмеченной точкой Р непусто и имеет отмеченный элемент,
который обозначается * или *р. Отображение множеств с отмеченной
точкой / : Р —у Q — это функция из множества Р в множество Q,
которая переводит отмеченную точку в отмеченную, т. е.
удовлетворяет условию /(*р) = *q. Множества с отмеченной точкой и с такими
отображениями в качестве морфизмов составляют категорию Set*.
В этой категории множество {*} из одной (отмеченной) точки
является и начальным, и терминальным объектом. Морфизм / является
мономорфизмом в категории Set*, если и только если он обратим
слева, и эпимофризмом — если и только если он обратим справа. Он
обратим, если и только если является моно- и эпиморфизмом.
Аналогично, Тор^ обозначает категорию малых топологических
пространств с отмеченной точкой: ее объекты — пространства X с
отмеченной точкой *; морфизмы — непрерывные отображения / : X —У
—У У, которые переводят отмеченную точку в отмеченную. Точно
так же, Toph* — это категория, объектами которой являются
пространства с отмеченной точкой, а морфизмами — классы гомотопии
непрерывных отображений, сохраняющих отмеченную точку (причем
гомотопии также должны ее сохранять). Обе категории возникают
в теории гомотопии, где всегда бывает необходимо выбрать
отмеченную точку при определении фундаментальной группы или высших
групп гомотопии, см. § 1.5.
Бинарные отношения можно рассматривать как стрелки в
категории Rel. Ее объекты — все малые множества X, У,..., а стрелками
R : X —У У являются все бинарные отношения между X и У, т. е. все
подмножества R С X xY. Если S : У —У Z — другое такое отношение,
то произведение отношений S о R : X —У Z определяется обычным
образом:
S о R = {(ж, z)\ для некоторого у G У верно,
что (х,у) е Rn (y,z) е S}.
Единичной стрелкой X —У X служит тождественное отношение на
X, состоящее из всех пар вида (ж, ж) для всех х G X. Аксиомы

Ml
Множества horn
39
категории очевидным образом выполняются. Категория Rel содержит
Set в качестве подкатегории с теми же объектами, поскольку
каждую функцию / : X —У Y можно интерпретировать как отношение,
состоящее из всех пар вида (x,fx) для всех х Е X. Но в Rel есть
и дополнительная структура: для каждого R : X —У Y существует
обратное отношение R# : Y —У X, состоящее из всех пар вида (у,х),
где (х,у) е R.
Конкретная категория — это пара (С, С/), где С — некоторая
категория, U — унивалентный функтор U : С —У Set. Поскольку
U унивалентен, то можно отождествить каждую стрелку / из С
с функцией Uf. В этом смысле можно описать конкретную категорию
как такую категорию С, где каждый объект наделен множеством-
носителем Uc, каждая стрелка / : Ъ —У с в действительности
является функцией Ub —У Uc, а композиция стрелок — это композиция
функций. Многие из больших категорий, описанных выше, являются
конкретными категориями в таком смысле, каждая по отношению
к своему очевидному забывающему функтору. Но это неверно в
случаях Toph и Rel. Что касается приложений, то понятие категории
проще (и более абстрактно), чем понятие конкретной категории.
1.8. Множества hom
Для объектов а и Ъ в категории С hom-множество
home (a, b) = {f \ f — это стрелка / : а —У Ъ в С}
состоит из всех стрелок с областью а и кообластью Ъ. Его обозначение
часто и разнообразно сокращается:
home (а, Ъ) = С(а, Ъ) = hom (а, Ъ) = (а, Ъ) = (а, Ь)с-
В терминах hom-множеств понятие категории можно
сформулировать следующим образом. Малая категория задана, если имеется
следующая совокупность данных:
1) множество объектов а, Ь, с,...;
2) функция, которая каждой упорядоченной паре объектов (а, Ь)
сопоставляет множество hom (a, b);
3) для каждой упорядоченной тройки объектов (а, Ь, с) — функция
hom (6, с) х hom (а, Ь) —у hom (а, с),
называемая композицией (умножением); при д G hom (6, с), / G
G hom (а, Ь) она записывается как (д, /) \-у д о /;
4) для каждого объекта Ъ — элемент tb G hom (b,b), который
называется единицей объекта Ъ.
При этом требуется выполнение обычных аксиом ассоциативности
(1.1) и единицы (1.2) плюс дополнительная аксиома разделения:
5) если (а, Ъ) ф (а;, Ь'), то hom (а, 6)nhom (а;, Ъ') = 0, где 0 — пустое
множество.

40 Категории, функторы и естественные преобразования [Гл. 1
В частности, аксиому ассоциативности можно сформулировать как
утверждение о коммутативности следующей диаграммы (где каждая
стрелка получается очевидным образом из умножения морфизмов):
hom (с, d) х hom (b, с) х hom (a, b) >■ hom (b, d) x hom (a, b)
hom (c, d) x hom (a, c) >■ hom (a, d).
Это определение категории равносильно первоначальному
определению из § 1.2. Аксиома (5) требует, чтобы различные hom-множества
не пересекались; она включена для того, чтобы каждая стрелка
имела единственную область и кообласть. Если в конкретном примере
эта аксиома не выполнена, то это легко устранить, подправив hom-
множества так, чтобы они не пересекались. Например, можно
заменить каждое из исходных множеств hom (a, b) на множество {а} х
х hom (a, b) x {b}. Это означает, что каждый морфизм / Е hom (a, b)
помечается своей областью а и кообластью Ь. Некоторые авторы
опускают аксиому (5).
Функтор Т : С —>- В описывается на языке hom-множеств как
(обычная) функция объектов Т вместе с семейством функций
Тс,х:С(с,с')^В(Тс,Тс')
(а именно функций / н-» Т f для / Е С (с, с')) таких, что всегда Тс?с1с =
= 1тс и коммутативна любая диаграмма
C(d, с") х С (с, с') >• С (с, с")
Т, пхТ
тп
В(Тс',Тс") х В(Тс,Тс') ^В(Тс,Тс"),
где горизонтальные стрелки соответствуют композиции в В и в С.
Предоставляем читателю описать естественное преобразование
t:S4Tb терминах функций С (с, с') —>• B(Sc, Тс').
Во многих существенных примерах категорий сами hom-
множества имеют определенную структуру; так, в категории
векторных пространств У, W,... над фиксированным полем каждое
множество hom (У, W) само является векторным пространством (всех
линейных отображений V —> W). В простейшем из таких случаев hom-
множества являются абелевыми группами. Определим формально
А Ъ- категорию (называемую также пред аддитивной категорией) как
такую категорию А, в которой каждое hom-множество является
абелевой группой по сложению, причем композиция билинейна: для
любых стрелок f,f':a—>bHg,g':b—>c справедливо равенство
(9 + g,)°(f + f,)=9°f + 9°f' + g'<>f + g,°f'-

Ml
Множества horn
41
Таким образом, Ab, i?-Mod, Mod-i? и т. п. являются АЬ-категориями.
Поскольку композиция (д, /) ^ д о f билинейна,
А(Ь, с) х А(а, Ь) -)► А(а, с),
то ее можно записать и как линейное отображение, используя
тензорное произведение ® = ®z:
А(Ъ, с) ® A(a, 6) -)► А(а, с),
и полностью описать АЬ-категорию А в этих терминах, не предполагая
заранее, что это категория. Таким образом, для задания АЬ-категории
нужна следующая совокупность данных:
1) множество объектов а, 6, с,...;
2) функция, сопоставляющая каждой упорядоченной паре
объектов (Ъ, с) абелеву группу А(Ь,с);
3) для каждой упорядоченной тройки объектов (а, Ь, с) — морфизм
абелевых групп
А(Ь, с) ® А(а, Ь) -)► А(а, с),
который называется композицией и записывается как д (8) / *-> д о /;
4) для каждого объекта а — морфизм Z —» А(а,а). (Здесь Z —
абелева группа целых чисел по сложению; этот морфизм полностью
определяется образом числа 1 G Z, который можно обозначить через
При этом должны выполняться аксиомы ассоциативности и
единицы (1.1) и (1.2), см. также диаграммы. Определение Аб-категории
вполне аналогично определению категории через hom-множества: Set
заменяется на АЬ, декартово произведение множеств х — на
тензорное произведение в АЬ, а одноточечное множество * на Z. Это
определение очевидным образом обобщается на категории А, в которых
hom-объекты А(Ъ, с) принадлежат категории типа АЬ, т. е. наделенной
умножением типа (8) и единицей типа Z относительно такого
умножения. Такие категории называются обогащенными (enriched, Kelly,
[1982]).
Функтор Т : А —>■ В между Аб-категориями А и В называется
аддитивным, если каждая функция Т : А(а,а') —> В (Та, Та') является
гомоморфизмом абелевых групп, т. е. T(f + /') = Тf + Tf для всех
параллельных пар / и /'. Ясно, что композиция аддитивных
функторов аддитивна. Ab-cat будет обозначать категорию всех малых АЪ-
категорий с аддитивными функторами в качестве стрелок.
Замечания
Эти неформальные замечания, как и в конце последующих глав,
касаются предпосылок и перспектив исследований по затронутым темам, а также
содержат библиографические ссылки (например, Petard [1980b] означает
вторую из цитированных статей этого автора, вышедших в 1980 г.).
Основополагающая идея представления функции стрелкой впервые
появилась в топологии около 1940 г., вероятно в статьях или лекциях В. Гу-
ревича о группах относительных гомотопий (см. Hurewicz [1941]).

42 Категории, функторы и естественные преобразования [Гл. 1
Его нововведение немедленно привлекло внимание Р. X. Фокса (см.
Fox [1943]) и Н. Э. Стинрода, который использовал стрелки и (неявно)
функторы; см. также (Hurewicz, Steenrod [1941]). Стрелка / : X —»■ Y
быстро вытеснила менее удачное обозначение функции f(X) С Y. Она
хорошо выразила предмет главного интереса в топологии. Таким образом,
обозначение стрелка породило понятие категории.
Коммутативные диаграммы впервые были применены, вероятно, также
Гуревичем.
Сами категории, функторы и естественные преобразования были
открыты Эйленбергом и Маклейном (Eilenberg, Mac Lane [1942a]) при
изучении пределов (при естественных преобразованиях) в связи с теоремами об
универсальных коэффициентах когомологий Чеха. В этой статье были
напечатаны коммутативные диаграммы (вероятно, впервые). Таким образом,
одним из первых рассмотренных функторов оказался Ext. Категории как
самостоятельный предмет впервые изучались в работе (Eilenberg, Mac Lane
[1945]). Столь широкие обобщения в основном бывают проявлением
дерзости и стремления к спекулятивному абстрагированию, которое в данном
случае подкреплялось удовольствием от похищения терминов у философов:
«категория» заимствована у Аристотеля и Канта, «функтор» — у Карна-
па (Logische Syntax der Sprache), а «естественное преобразование» — из
тогдашней повседневной речи. Вначале категории применялись в основном
как язык; в том числе существенно и эффективно — в аксиомах Эйленберга-
Стинрода в теории гомологии и когомологий. В дальнейшем применение
категорий расширялось, и вопрос надежного обоснования вышел на первый
план. Согласия среди специалистов здесь до сих пор нет; принятое нами
допущение «единственного универсума» является подходящей временной
мерой, но не предсказанием будущего.
Теория категорий спрашивает о каждом типе математического объекта:
«Что здесь служит в качестве морфизмов?»; она требует, чтобы эти мор-
физмы были описаны одновременно с объектами. Однако «категорщики»
обычно называют свои большие категории общим именем их объектов,
как например Set, Cat. Только Эресман (Ehresmann [1965]) и его школа
отважились называть каждую категорию общим именем ее стрелок: наша
категория Cat — это их категория функторов. Такое внимание к
(гомоморфизмам в большой мере восходит к Эмми Нетер, которая широко
их использовала в теории групп и колец.

Глава 2
КОНСТРУКЦИИ В КАТЕГОРИЯХ
2.1. Двойственность
Категорная двойственность состоит в обращении всех стрелок.
В этом параграфе мы дадим точное описание такой процедуры на
основе аксиом, а в следующем — на теоретико-множественной основе.
Таким образом, в этом параграфе категория описывается аксиомами,
как в § 1.1, а не в терминах множеств (объектов и стрелок) и функций
(область, кообласть, композиция).
Элементарная теория абстрактной категории (ЕТАС) — это
некоторая совокупность утверждений Е, где используются буквы
а, Ь, с,... для объектов и /, д, /г,... для стрелок. Эти утверждения
строятся из атомарных утверждений, включающих
неопределимые исходные понятия теории категорий; таким образом, атомарные
утверждения имеют вид «а является областью определения функции
/», «Ь является кообластью функции /», «г — тождественная стрелка
объекта а», «д можно умножить на /, получив /г», «а = Ь» и «f = g».
Эти атомарные утверждения можно также записать как знакомые
уравнения: а = dom/, h = go f. В общем случае утверждение Е — это
любая фраза (правильно построенная формула), полученная из
атомарных утверждений перечисленных типов с помощью стандартных
пропозициональных связок (и, или, не, влечет, если и только если)
и стандартных кванторов («для всех а», «для всех /», «существует
а...», «существует /...»). Таким образом, запись «f : а —> Ь»
употребляется нами как сокращение утверждения «а является областью
для функции /, а Ъ — ее кообластью».
Предложение — это утверждение, в котором на все переменные
навешены кванторы (т.е. все переменные связаны, а не свободны).
Пример предложения: «для каждой функции / существуют такие
а и Ь, что / : а —>■ Ь» (это даже аксиома, выполненная в любой
категории). Другой пример — аксиомы ЕТАС (приведенные в § 1.1).
Утверждение, двойственное к данному утверждению Е из ЕТАС,
образуется следующим способом: всюду в Е область заменяется на
кообласть, кообласть на область, соотношение «h является
произведением g на /» заменяется на «h является произведением / на д»;
стрелки и композиции поворачиваются в обратную сторону.
Логические операции (и, или, ...) не затрагиваются. Получаем следующую
таблицу (дополнение к ней см. в упр. 1 § 4.3).

44
Конструкции в категориях
[Гл. 2
Утверждение Е Двойственное утверждение Е*
/ : а -» Ъ f :b -» а
а = dom / а = cod /
г = 1а г = 1а
h = go f ft = f од
f — мономорфизм / — эпиморфизм
стрелка и — правая обратная стрелка и — левая обратная
для ft для ft
стрелка / обратима стрелка / обратима
объект t — терминальный объект t — начальный.
Отметим, что двойственное к двойственному утверждению совпадает
с исходным (Е** = Е). Если утверждение включает диаграмму, то
в двойственном утверждении все стрелки в диаграмме нужно
перевернуть.
Утверждения, двойственные к аксиомам категорий, также
являются аксиомами. Таким образом, если при выводе теоретико-категорной
теоремы из аксиом каждое утверждение заменить на двойственное,
то мы получим правильное доказательство (двойственной теоремы).
В этом состоит принцип двойственности: если утверждение Е
элементарной теории абстрактной категории можно вывести из аксиом,
то это верно и для двойственного утверждения Е*. Например, мы
упоминали (элементарную) теорему, что если в категории существует
терминальный объект, то он единствен с точностью до изоморфизма.
Принцип двойственности и в более сложных случаях дает удобный
способ получить (причем сразу) двойственную теорему. Ее не
требуется доказывать. Даже ее формулировку мы обычно будем
предоставлять читателю.
Принцип двойственности можно применять и к утверждениям,
включающим несколько категорий и функторов между ними.
Простейший (и характерный) случай — элементарная теория одного
функтора, т. е. двух категорий С и В и функтора Т : С —>■ В.
Атомарными утверждениями в этой теории служат, во-первых, атомарные
утверждения для категории С, перечисленные выше; во-вторых,
соответствующий список для категории В; в-третьих, утверждения вида
«Тс = Ь» и «Tf = ft», которые определяют значения функции
объектов и функции стрелок функтора Т на объектах с и стрелках /
категории С. Аксиомами теории служат аксиомы категорий С и В, а также
утверждения вида T(gf) = (Tg)(Tf) и Т(1а) = 1Та, означающие,
что Т является функтором. Дуализация (переход к двойственному
утверждению) состоит в замене его атомарных составляющих,
относящихся к С и к В, на двойственные (т. е. в обращении стрелок в обеих
категориях). Принцип двойственности справедлив и здесь, поскольку
утверждение о том, что Т является функтором, самодвойственно.

2.2] Контравариантностъ и двойственные категории 45
Подчеркнем, что при дуализации утверждения, включающего
несколько категорий и функторов между ними, поворачиваются стрелки
в каждой категории, но функторы не поворачиваются.
2.2. Контравариантностъ и двойственные категории
Каждой категории С мы сопоставим двойственную категорию Сор.
Ее объекты — те же, что и в категории С, а стрелки fop находятся во
взаимно однозначном соответствии / \—у fop со стрелками категории
С. Для каждой стрелки / : а —> Ъ из С имеем fop : Ъ —> а
(направление противоположно). Произведение fopgop = (gf)op определено
в Сор тогда же, когда произведение gf определено в С. Ясно, что
тогда Сор является категорией. При этом область для fop совпадает
с кообластью для /, стрелка fop является мономорфизмом тогда же,
когда / является эпиморфизмом, и т. д. Действительно, при такой
процедуре любое утверждение Е о категории С переходит в
двойственное утверждение Е* о категории Сор. Более подробно: пусть
утверждение Е в элементарной теории абстрактной категории содержит
свободные переменные /,#,... Очевидная индукция, отвечающая его
построению из атомарных утверждений, показывает, что Е выполнено
для стрелок /, д,... в категории С, если и только если двойственное
утверждение Е* выполнено для стрелок /ор,дор,... в двойственной
категории Сор. Как следствие, предложение Е верно в категории Сор,
если и только если двойственное предложение Е* верно в категории
С. Это наблюдение позволяет рассматривать свойство, двойственное
к свойству Е, как исходное свойство, но в двойственной категории.
(Некоторые авторы обозначают двойственную категорию через С*.)
Пусть Т : С —» В — некоторый функтор. Его функция объектов
с^Тси функция стрелок / \-^ Т/, преобразованная в /ор \-^ (Т/)ор,
вместе определяют функтор из Сор в 5ор, который мы обозначим
через Гор : Сор -^ Бор. Соответствия СиСориТи Гор определяют
(ковариантный!) функтор Cat —у Cat.
Рассмотрим некоторый функтор S : Сор —> В. В силу определения
функтора, он каждому объекту с G Сор сопоставляет объект Sc G
G В, а каждой стрелке /ор : Ъ —>• а из Сор — стрелку 5/ор : Sb —>•
—>• Sa из Б, причем S(fopgop) = (5/op)(5^op), если только определено
fopgop. Такой функтор S можно описать непосредственно в терминах
исходной категории С, обозначив 5/ор через Sf; тогда S становится
контравариантным функтором из С в В. Он сопоставляет
произвольному объекту с G С объект Sc G В, а каждой стрелке / : а —>■ Ъ —
стрелку Sf : Sb —>■ Sa (противоположного направления), причем
5(1с) = 15с, 5(/5) = (Sg)(Sf) (1)
(последнее выполнено, если только произведение fg определено в С).
Отметим, что функция стрелок S контравариантного функтора
меняет порядок умножения. Конкретные контравариантные функторы
бывает удобно представлять в таком виде, т. е. как функции 5, меняющие

46
Конструкции в категориях
[Гл. 2
порядок умножения. Примером служит контравариантный функтор
булевой степени Р из Set в Set. Множество РХ = {S | S С X} —
это множество всех подмножеств данного множества X; если / : X —У
—у Y — некоторая стрелка, то Pf : PY —у РХ отображает каждое
подмножество Т С Y в его полный прообраз /_1Т С X. Другой
пример хорошо известен: это процедура, сопоставляющая каждому
векторному пространству V его двойственное (сопряженное)
векторное пространство У*, а каждому линейному отображению / : V —У
—У W — сопряженное отображение /* : VF* —У У*. Эти соответствия
определяют контравариантный функтор из категории всех векторных
пространств (над фиксированным полем) в нее же.
Напротив, функтор Т : С —У В, определенный ранее (в § 1.3),
называется ковариантным функтором из С в В. При общих
рассмотрениях бывает гораздо удобнее представлять контравариантный
функтор S из С в В как ковариантный функтор S : Сор —У В,
а иногда как ковариантный функтор S : С —У Вор. В этой книге
стрелка между категориями (т. е. между их обозначениями) всегда
будет означать ковариантный функтор Т : С —» В или S : Сор —У В
между указанными категорями.
Важный пример ко- и контравариантных функторов дают hom-
множества. Пусть С — категория с малыми hom-множествами, так
что каждое множество hom (а, Ь) = {/ | / : а —У Ъ в С} является
малым и потому входит как объект в категорию Set всех малых
множеств. Тогда для каждого объекта a G С имеется ковариантный
hom-функтор
С (а, -) = hom (а, -) : С -* Set; (2)
его функция объектов отображает каждый объект Ъ в множество
hom (a, b), a функция стрелок отображает каждую стрелку к : Ь —У
—у Ъ' в функцию
hom (а, к): hom (а, Ь) —у hom (а, &'), (3)
которая строится по правилу / \-у к о f для каждой стрелки / : а —У
—У Ь. Ради простоты обозначений эта функция hom (а, к) иногда
обозначается fc* и называется умножением на к слева или отображением,
которое индуцировано стрелкой к.
Контравариантный hom-функтор для произвольного объекта Ъ G
G С можно записать в ковариантном виде как
С(-, Ъ) = hom (-, Ъ) : Сор -+ Set; (4)
он отображает каждый объект а в множество hom (а, 6), а каждую
стрелку д : а —у а' категории С в функцию
hom (g, b) : hom (af, 6) —у hom (a, 6), (5)
которая строится по правилу / \-у f о д. Опуская объект 6, эту
функцию hom (g, b) иногда записывают просто как д* и называют
умножением на д справа. Таким образом, для каждой стрелки / : а' —у b

2.2] Контравариантностъ и двойственные категории 47
имеем
&*/ = &<>/, g*f = f°g-
Для двух таких стрелок g : а ^ а' и k : b ^ b' следующая
диаграмма в категории Set коммутативна:
hom
к*
'
у, ъ)-
'
>■ hom
1
(М)
к*
'
(6)
hom (а', Ь') >- hom (а, Ь'),
поскольку оба пути переводят / Е hom (а', Ъ) в fc/#.
Мы определили hom-функторы лишь для категории С с малыми
hom-множествами. Таковы известные большие категории Grp, Set,
Тор и т. п. Чтобы охватить категории без этого свойства, можно
поступить следующим образом. Пусть дана категория С. Возьмем
достаточно большое множество V, содержащее все подмножества в
множестве стрелок категории С (например, множество всех подмножеств
этого множества). Пусть в категории Ens = Set у объектами являются
все множества X Е V, стрелками — все функции / : X —> Y между
такими множествами, а произведение определено как обычная
композиция функций. Тогда каждое hom-множество С(а, b) = hom (а, Ь)
является объектом категории Ens, так что описанная выше процедура
определяет два hom-функтора
С(а, -) : С -> Ens, С(-, Ъ) : Сор -> Ens. (7)
В частности, если в качестве V взять универсум, состоящий из всех
малых множеств, то Ens = Set; в общем случае Ens — это
(переменная) категория множеств, которая служит областью значений hom-
функторов в интересующей нас категории или категориях.
Существует и много других примеров контравариантных
функторов. Пусть X — топологическое пространство. Упорядочив
(частично) по включению множество Ореп(Х), получим категорию; стрелка
V —У U существует в ней в точности тогда, когда V С U. Пусть
С(U) обозначает множество всех непрерывных вещественнозначных
функций h : U —> R; при каждом V С U соответствие h н->- h\V,
ограничивающее каждую функцию h на подмножество V,
определяет функцию С(U) —> С{V). Возникает контравариантный
функтор С из Open (X) в Set. Этот функтор называют пучком ростков
непрерывных функций на X. Аналогично строится пучок ростков
С°°-дифференцируемых функций на гладком многообразии (см. Мае
Lane, Moerdijk [1992]).
Примером контравариантного функтора из колец в категории
служит Mod-i?. Более конкретно, пусть g : R —>■ S — морфизм (малых)
колец. Тогда каждый правый 5-модуль В превращается в правый
Л-модуль Bg = (Mod g)B при обратном ходе вдоль д: каждый
элемент г G R действует на Ъ G В по формуле Ъ • г = Ъ • (дг). Ясно,

48
Конструкции в категориях
[Гл. 2
что Mod д — это функтор Mod-5 —У Mod-i?, причем Mod (^1^2) =
= (Mod Q2)(Mod £1), так что Mod, в свою очередь, можно
рассматривать как контравариантный функтор из Rng в Cat7, категорию всех
больших категорий.
Можно построить и категорию Mod всех (правых) модулей над
всеми кольцами. Ее объекты — это пары (R, А), где R — малое кольцо,
А — малый правый Л-модуль. Морфизм (Л, А) —у (5, В) — это пара
(g,f), где д : R —у S — морфизм колец, f : А —> (Mod д)В —
морфизм правых Л-модулей. Определив умножение очевидным образом,
получаем категорию Mod. Функтор проецирования Mod —у Rng
определяется соответствием (Л, А) \-у R. Дальнейшее исследование
связи этого функтора с вышеописанным функтором Rng —у Cat
приводит к теории расслоенных категорий. (Категория Mod расслоена
над Rng, и слоем над каждым R служит категория Mod-i?.)
2.3. Произведения категорий
Из двух данных категорий В ж С можно следующим образом
построить новую категорию В х С, которая называется их
произведением. Ее объекты — это пары (6, с) объектов Ъ из В и с из С; ее
стрелки (Ь, с) —у (£/, с'} — это пары (/, д) стрелок / : Ъ —у Ь' и д : с —у с',
а композиция двух таких стрелок
(Ь, с) JIU- (V, с') ^U (Ъ", с")
определяется в терминах композиции в категориях В и С по формуле
{f',9')o{f,g) = {f'of,g'og). (1)
Функторы
В ^ВхС %С
определены на (объектах и) стрелках формулой
P(f,g) = f, Q(f,g)=g
и называются проекциями произведения. Они обладают следующим
свойством: для каждой категории D и функторов
В £ D^yC
существует единственный функтор F : D —у В х С такой, что PF =
= R, QF = Т. Ясно, что в силу этих условий для каждой стрелки
h из D имеем Fh = (Rh,Th); обратно, определив Fh таким образом,
получаем функтор F с нужными свойствами. Можно наглядно
представить построение функтора F (обозначенного штриховой стрелкой)

2.3]
Произведения категорий
49
с помощью следующей коммутативной диаграммы:
В^
(2)
ВхС-
*с.
Это свойство произведения категорий означает, что проекции Р и Q
универсальны среди пар функторов, направленных в В и С. Оно
совпадает со свойством проекций (декартова) произведения двух
множеств, групп или топологических пространств. Общие свойства таких
произведений в произвольной категории рассмотрены в гл. 3.
Для двух функторов U : В —у В' и V : С —У С существует
произведение U х V : В х С —У В' х С, которое можно определить на
объектах и стрелках явным образом:
(U xV) (Ь, с) = (Ub, Vc), (U xV) (/, g) = (Uf, Vg).
Этот функтор U х V можно описать и иначе: как единственный
функтор (как на диаграмме (2)), который делает коммутативной
следующую диаграмму:
В^
В'*
р'
ВхС
UxV
В' х С
^С
(3)
-^с.
Таким образом, произведение х — это пара функций: каждой паре
категорий (В, С) ставится в соответствие новая категория ВхС,
а каждой паре функторов (U, V) — новый функтор UxV. Если при
этом определены произведения U' о U и V' о V, то заведомо (U' х
х V') о (U х V) = U'U х V'V. Поэтому операция х сама является
функтором; более точно (если ограничиться малыми категориями),
это функтор
х : Cat х Cat -» Cat.
Аналогично строятся функторы Grp x Grp —у Grp, Top x Тор —у
—У Тор и т. д.
В определении произведения категорий с помощью диаграммы (2)
присутствовал функтор F : D —У В х С. С другой стороны, функторы
S : В х С —> D из произведения категорий называются бифункторами
(на категориях В ж С) или функторами от двух объектных
переменных (в В и в С). Такие бифункторы встречаются часто; например,
декартово произведение X х Y двух множеств X и Y — это бифунктор
Set х Set —у Set (точнее, его функция объектов). Таким образом, наше
определение произведения категорий автоматически приводит к
определению функтора двух переменных — точно так же, как определение

50
Конструкции в категориях
[Гл. 2
произведения X х Y двух топологических пространств автоматически
приводит к определению непрерывной функции двух переменных.
Фиксировав один аргумент в бифункторе S, получаем
одноместный функтор от оставшегося аргумента. Бифунктор S в целом
определяется этими двумя наборами одноместных функторов по следующей
элементарной схеме.
Предложение 1. Пусть даны категории В,С и D. Для всех
объектов Ъ Е В и с Е С рассмотрим такие функторы
LC:B -+ D, Mb:C -+ D,
что Мь (с) = Lc(b) при любых hue. Тогда бифунктор S : В х С —>-
—>• D, для которого S(—, с) = Ьс при всех с и 5(6,—) = Мь при всех
Ь, существует в том и только том случае, если для каэюдой пары
стрелок f : Ъ —>■ Ь' и g : с —>■ с' выполнено равенство
MblgoLcf = LclfoMbg. (4)
В этом случае каэюдая из частей равенства является значением
S(f,g) функции стрелок функтора S на паре f,g.
Доказательство. Используем обозначения Ъ и с для
соответствующих единичных стрелок. Из определения (1) умножения в
категории В х С видно, что
(Ь',9) ° </,с> = (b'f,gc) = (f,g) = {fb,c'g) = </,</> о (b,g).
Применяя функтор S к этому равенству, получаем
S(b',g)S(f,c) = S(f,c')S(b,g);
соответствующая коммутативная диаграмма имеет вид
S(b, с) -iM- S(b, с')
S(f,c)
S(J,c')
S(b',c')^£s(b',c').
Но это — условие (4), которое, таким образом, необходимо. Обратно,
если даны все Lc и Мь, то это условие определяет S(f,g) для каждой
пары /, д; можно проверить, что мы получаем бифунктор S с
нужными свойствами. □
Можно строить произведения трех и более категорий, а также
комбинировать построение произведений и переход к двойственным
категориям. Имеется очевидный изоморфизм (В х С)ор = Вор х
х Сор. Часто говорят, что функтор Вор х С —>■ D — это бифунктор,
контравариантный в В и ковариантный в С со значениями в D.

2.3]
Произведения категорий
51
Например, пусть С — категория с малыми hom-множествами. Тогда
hom-множества определяют следующий бифунктор:
hom :СорхСч Set.
Действительно, коммутативная диаграмма (6) из § 2.2 в точности
означает, что ко- и контравариантные hom-функторы
hom (-, с) : (7ор -> Set, hom (6, -) : С -> Set
удовлетворяют условию (4) теоремы, которое необходимо для
получения бифунктора.
Теперь рассмотрим естественные преобразования между
бифункторами 5, S' : В х С —>■ D. Пусть функция а каждой паре объектов
Ъ Е В, с Е С сопоставляет стрелку в категории D:
а(Ъ,с) :S(b,c) -> S'(b,c). (5)
Назовем преобразование естественным по Ь, если для каждого с Е
Е С компоненты а(6, с) со всевозможными Ъ определяют естественное
преобразование функторов В —>• D:
a(-,c):S(-,c)^S'(-,c).
Читатель легко докажет следующий полезный факт:
Предложение2. Пусть 5, S' — бифункторы, а функция а
определена формулой (5). Эта функция является естественным
преобразованием бифункторов а : S —>S' тогда и только тогда, когда
преобразование а(Ь, с) естественно по Ъ при любом с G С и естественно
по с при любом Ъ G В.
Такие естественные преобразования участвуют в важнейшем
определении сопряженных функторов (гл. 4). Функтор F : X —> С
сопряжен слева к функтору G : С —> X (противоположного направления),
если существует биекция
home (Fx, с) = homx (ж, Gc),
естественная по х G X и по с G С. Здесь hom (F—, —) — бифунктор,
равный произведению
XoPxC™_VPxC^Set;
аналогично определяется hom (—, G—) (по крайней мере если X и С
имеют малые hom-множества).
Произведение категорий можно наглядно представить в случае С х
х 2, где 2 — категория с одной неединичной стрелкой 0 —> 1; а именно,
(7x2 состоит из двух экземпляров С х 0 и С х 1 категории С и стрелок,
соединяющих первый экземпляр со вторым. Для (7 = 3 это показано

52
Конструкции в категориях
[Гл. 2
на следующем рисунке, где опущены диагональные стрелки (С
это треугольная категория из § 1.2):
С х 1
СхО
Здесь функторы Xb,Ti : С —> С х 2 («верх» и «низ»
соответственно) определяются для каждой стрелки / из С по формулам То/ =
= (/,0) и Ti/ = (/,1)- Пусть I обозначает единственную
неединичную стрелку 0 —> 1 категории 2. Определим преобразование между
Г0, Тх : С -»> С х 2 по формуле
/х:То^>Ть /ic=(c,|),
для каждого объекта с. Оно отображает «низ» в «верх» и
заведомо является естественным. Назовем \i универсальным естественным
преобразованием из С по следующей причине. Для каждого
естественного преобразования г : S -^ Т между функторами 5, Т : С ^ В
существует единственный функтор F : С х 2 —>■ В такой, что F/ic =
= тс для любого объекта с. А именно, если / : с —>- с;, то пусть
F(f,0) = Sf, F(f,l)=Tf, F(f,i)=TfoTC = Tc'oSf. (6)
Непосредственно проверяется, что мы получаем бифунктор F х 2 —>
—>■ 5, причем F/i = г.
Упражнения
1. Покажите, что следующие известные понятия являются частными
случаями произведения категорий: произведение моноидов (категорий с
одним объектом), групп, множеств (дискретных категорий).
2. Покажите, что произведение двух предпорядков является предпоряд-
ком.
3. Пусть {d | г G /} — семейство категорий, / — соответствующее
множество индексов. Опишите произведение С = Y\i Ci, его проекции
Pi : С —> Ci и найдите универсальное свойство этих проекций.
4. Опишите категорию, двойственную к категории Matrx из § 1.2.
5. Покажите, что кольцо непрерывных вещественнозначных функций
на топологическом пространстве является функцией объектов контравари-
антного функтора из Тор в Rng.

2.4]
Категории функторов
53
2.4. Категории функторов
Пусть даны категории Си В. Рассмотрим все функторы
R, S, Т : С —>■ В. Если сг : R^ S и г : S ^ Т — два естественных
преобразования, то их компоненты для каждого с Е С определяют
произведения стрелок (т • а) с = тс о ас, которые являются
компонентами преобразования т • а : R^r T. Покажем, что т • а —
естественное преобразование. Для этого возьмем произвольную
стрелку / : с —> с' в С и рассмотрим диаграмму
(т-*)с\ Sc
Так как преобразования сг и г естественны, то оба маленьких
прямоугольника коммутативны. Поэтому коммутативен квадрат, и
произведение т • а является естественным.
Умножение преобразований ассоциативно; при этом с каждым
функтором Т связывается единичное естественное преобразование
1т : Т —> Т с компонентами 1тс = ±хс- Таким образом, для данных
категорий В и С можно формально построить категорию функторов
Вс = Funct {С, В), объектами которой являются функторы Т : С —>
—> В, а морфизмами — естественные преобразования между такими
функторами. Часто бывает естественно обозначить hom-множество
в такой категории через
Nat (5, Г) = Вс (5, Г) = {т | преобразование т : S -^Т естественно}.
(1)
Это множество не обязательно мало.
Мы будем широко использовать категории функторов. Например,
если В и С — множества (категории, где все стрелки единичные),
то Вс также является множеством, а именно известным множеством
функций, которое состоит из всех функций С —> В. В частности, если
множество В = {0,1} состоит из двух элементов, то {0,1}^ —
множество (с точностью до изоморфизма) всех подмножеств в С (булева
степень VC). Если В — любая категория, то В и В1 изоморфны, а В2
называется категорией стрелок для В] ее объекты — стрелки / : а —>•
—> Ъ из В, а ее стрелки / —>- /' — это пары (/i, k) стрелок из В, для

54
Конструкции в категориях
[Гл. 2
которых коммутативен квадрат
(2)
Если М — моноид (категория с одним объектом), то объектами
категории Set являются его реализации преобразованиями некоторого
множества, а стрелками — морфизмы между такими реализациями.
В категории функторов Grp объектами являются группы с
полугруппой операторов М.
Если К — коммутативное кольцо, a G — группа, то категория
функторов (K-~M.od)G — это категория (К-линейных) представлений
группы G. Каждый функтор Т : G —>■ if-Mod определяется К-
модулем V (образом единственного объекта категории G) и морфиз-
мом групп Т : G —>- Aut (V) (представлением группы G линейными
представлениями V —> V). Если Т' — другое такое представление, то
естественное представление а : Т -^ Т' определяется своей
компонентой на единственном объекте в G — единственной стрелкой а : V —>-
—> V, для которой диаграмма
У-^У
(3)
Тд
Т'д
коммутативна при любом д G G. В теории представлений а
называется сплетающим оператором. Таким образом, объектами категории
(K-~M.od)G являются представления группы G, а морфизмами —
сплетающие операторы.
Если С — большая категория, то категория функторов Вс не
обязательно является подмножеством универсума. Например, если
В = {0,1} — множество из двух элементов, а С совпадает с U, то
функтор U —^ В — это функция из U в двухэлементное множество.
Такие функции соответствуют (в качестве характеристических
функций) подмножествам в U. Поэтому множество объектов категории
{0,1}и равномощно множеству V(U) всех подмножеств в(7, а
последнее имеет большую мощность, чем U.
Упражнения
1. Пусть R — некоторое кольцо. Опишите .R-Mod как полную
подкатегорию в категории функторов АЬЛ.
2. Пусть X — конечное множество (конечная дискретная категория).
Опишите категорию Вх.

2.5]
Категория всех категорий
55
3. Пусть N — дискретная категория натуральных чисел. Опишите
категорию функторов AbN (известную как категория градуированных абеле-
вых групп).
4. Пусть Р и Q — предпорядки. Опишите категорию функторов Qp
и покажите, что она является предпорядком.
5. Пусть Fin — категория всех конечных множеств, G — конечная
группа. Опишите Fin (категорию всех представлений группы G
перестановками) .
6. Пусть М — бесконечный циклический моноид (с элементами
1, т, т2,.. .). Покажите, что в категориях функторов (Matrx)2 и
(MatrK)M объектами являются матрицы, причем объекты изоморфны
в точности тогда, когда матрицы, соответственно, эквивалентны или
подобны в смысле линейной алгебры ). О категории Matr см. § 1.2.
7. Пусть даны категории В, С л категория функторов В . Покажите,
что каждый функтор Н : С —У В2 определяет два функтора S, Т : С —»■
—У В и естественное преобразование т : S -^ Т, причем это соответствие
Н н->" (S, Т, т) биективно.
8. Найдите связь функтора Н из упр. 7 с функтором F из (3.6).
2.5. Категория всех категорий
Мы определили вертикальное умножение т • а естественных
преобразований:
Они допускают и другое, горизонтальное умножение. Если даны
функторы и естественные преобразования
S S'
->■ >■
С 1т ^ В ir'^ А, (1)
т ' г'
можно сначала образовать произведения функторов S'S и Т'Т : С —>■
—у А, а затем построить квадрат
5;5с -^^ T'Sc
S'tc
Т'тс
S'Tc^^T'Tc,
который коммутативен, поскольку т естественно на стрелках г с из С.
Определим теперь (т' о г) с как диагональ этого квадрата:
(г' о т) с = Т'тс о t'Sc = т'Тс о S'tc. (2)
:) См. Ф.Р. Гантпмахер. Теория матриц. — М.: Наука, 1988, с. 70, 75. —
Прим. пер.

56
Конструкции в категориях
[Гл. 2
Чтобы показать, что преобразование r'or: S'S-^ Т'Т естественно,
составим для каждой стрелки / из С диаграмму
S'Sc -^^ S'Tc r'Tc> Т'Тс
S'Sfl
S'Sb-
S'Tf
S'rb
S'Tb -
т'ТЪ
T'Tf
Т'ТЪ,
Ъ.
Произведения по горизонтали равны по определению (т' о г) с
и (т' от) Ъ. Левый квадрат коммутативен, поскольку т — естественное
преобразование, a S' — функтор. Правый квадрат коммутативен,
так как т' естественно, а Тf : Тс —у ТЪ — стрелка в категории В.
Коммутативность внешнего квадрата означает, что преобразование
т'от естественно.
Непосредственно проверяется, что введенное умножение (т'^т) —>
Чт'от ассоциативно. Оно обладает единицами. Если 1в • В —^ В —
тождественный функтор в категории В, а 1# : 1в —> 1в —
тождественное преобразование в себя, то 1в °т = тт' о1в = т'. Таким образом, 1#
является единицей как относительно умножения о, так и относительно
умножения •. Обозначение функтора S удобно использовать и для
тождественного преобразования S -^S. В этих обозначениях получаем
в рассматриваемой ситуации естественные преобразования
^or^'oS^S'oT, т' о Т : S" о Г^> Г о Т.
Определение (2), используя и вертикальное умножение, можно тогда
переписать в виде
г'ог = (Т'от)- (т' о S) = (т' о Г) • (S" о г).
(3)
Имеется более общее правило. Пусть даны три категории и четыре
преобразования:
С -^ В ^- А,
|т.
1т'
(4)
Тогда вертикальное умножение • и горизонтальное умножение о
связаны тождеством (законом чередования)
(V • а') о (г • а) = (V о т) • (а' о а).
(5)
В качестве упражнения читатель может выписать очевидные
диаграммы, нужные для доказательства этого факта.
Эти результаты можно просуммировать следующим образом
(ограничиваясь случаем малых категорий):
Теорема 1. Совокупность всех естественных преобразований —
это множество стрелок двух различных категорий, на котором

2.5]
Категория всех категорий
57
определены две различных операции умножения • и о, которые
удовлетворяют закону чередования (5). Если при этом стрелка
является единицей относительно умножения о, то она является единицей
и относительно умножения •.
Отметим, что для горизонтального умножения о объектами
являются категории, а для вертикального умножения • — функторы.
При использовании этих операций часто опускают обозначение о
для горизонтального умножения (как делается обычно при
композиции стрелок в категории), тогда как жирная точка, обозначающая
вертикальное умножение, всегда сохраняется. Заметим, что объекты
и стрелки из С можно записать как функторы с : 1 —у С или f : 2 —>■
—> С. Тогда такие обозначения, как а о с = ас, в ситуациях типа
имеют свой обычный смысл.
Двойной категорией (double category, Ehresmann) называется
множество, которое (подобно множеству всех естественных
преобразований) состоит из стрелок с двумя различными умножениями, в
совокупности удовлетворяющими условию (5). Если при этом каждая
единичная стрелка по первому умножению является единичной и по
второму, то двойная категория называется 2-категорией (сокращение
для двумерной категории). Например, категория всех коммутативных
квадратов категории Set является двойной категорией (с очевидным
горизонтальным и вертикальным умножением), но не 2-категорией.
Существуют n-категории и для больших п, см. гл. 12.
Мы говорим, что две (частично упорядоченные) бинарные
операции • и о удовлетворяют закону чередования, если (5) выполнено
во всех случаях, когда определены произведения в обеих частях.
Приведем еще некоторые примеры. Пусть С — категория, • : С х С —>
—> С — функтор (например, тензорное произведение), а, а', т, г' —
стрелки из С, для которых определены произведения а' о а и т' о т.
Тогда закон чередования (5) выполняется; действительно, он сводится
к требованию, чтобы функтор • сохранял произведение о . Условие (5)
выполняется и в том случае, когда а, а', г, т' — квадратные матрицы,
для которых определены обычные матричные произведения а' о а
иг'ог, а т • а обозначает матрицу
с блоками т и а на диагонали и нулями на остальных местах.
Категория функторов Вс сама является функтором между
категориями В и С, ковариантным в В и контравариантным в С. Более
конкретно, если ограничиться категорией Cat всех малых категорий,
то это функтор Catop x Cat —у Cat; функция объектов отображает
пару категорий (С, В) в категорию функторов Вс', а функция стрелок

58
Конструкции в категориях
[Гл. 2
отображает пару функторов F : В —> В' и G : С —> С в функтор
FG :ВС -+ В'с\
определенный на объектах S Е Вс по правилу FGS = F о 5 о G, а на
стрелках г : 54Г из Вс по правилу FGr = F о т о G. Отметим,
например, что Fc — не что иное, как умножение на F слева, тогда
как BG — умножение на G справа. Этот функтор является точным
аналогом hom-функтора Setop x Set —у Set.
Упражнения
1. Для малых категорий А, В и С установите существование биекции
Cat (A х Б, С) ^ Cat (А, Св)
и покажите, что она естественна по А, В и С. Покажите, что функтор
— х В : Cat —у Cat имеет правый сопряженный (см. гл. 9).
2. Для категорий А,ВиС докажите существование естественных
изоморфизмов
(А х В)с й/х Вс, СЛхВ S* {СВ)А.
Сопоставьте второй изоморфизм с биекцией из упр. 1.
3. С помощью теоремы 1 покажите, что горизонтальное умножение
является функтором
о:АвхВс^ Ас.
4. Пусть G — топологическая группа с единицей е, а а, а', т, т' —
непрерывные пути с началом и концом в е (т. е. непрерывные отображения
единичного отрезка I в G, переводящие концы отрезка в е). Как ив (1.5.1),
определим т о а как путь, в котором за а следует т. Определим т • а как
поточечное произведение путей т и сг, так что (г • a)t = (rt) (at) при 0 ^
^ t ^ 1. Докажите, что выполнен закон чередования (5).
5. (Hilton-Eckmann). Пусть S — множество с двумя (всюду
определенными) бинарными операциями • : S x S ^ S, о : S x S ^ S, которые имеют
общую (двустороннюю) единицу е и удовлетворяют закону чередования (5).
Докажите, что операции • и о совпадают и коммутативны.
6. Соединив упр. 4 и 5, докажите, что фундаментальная группа
топологической группы абелева.
7. Пусть Т : А —>- D — некоторый функтор. Покажите, что функции
стрелок Та,ъ : А (а, Ъ) —»■ D (Та,ТЪ) определяют естественное
преобразование между функторами Аор xi4 Set.
8. Если 1с — тождественный функтор некоторой категории, то
естественные преобразования а : 1с —> 1с образуют коммутативный моноид.
Найдите этот моноид для случаев С = Grp, Ab и Set.
2.6. Категории запятой
Существует и другая общая конструкция категории, объектами
которой являются стрелки. Опишем сначала несколько частных случаев.
Пусть Ъ — объект категории С. Построим категорию объектов под
Ь, которая обозначается (b l С). Ее объектами являются все пары

2.6]
Категории запятой
59
(/, с), где с — объект из С, а / : Ъ —>• с — стрелка из С. Ее стрелки
ft : (/, с) —>■ (/', с') — это те стрелки ft, : с —>■ с', для которых ft о / = /'.
Таким образом, объект в категории (Ь ^ С) — это стрелка в категории
C, исходящая из 6, а стрелка в категории (Ъ \,С) — это коммутативный
треугольник с верхней вершиной Ъ. В наглядной форме:
Ъ Ъ
объекты (/, с) : I/; стрелки (/, с) Л (/', с') : / \ . (1)
* с —^ с'
С /г С
Умножение стрелок в категории (b l С) определяется умножением
оснований ft таких треугольников в категории С.
Пусть, например, * обозначает множество из одной точки, а X —
произвольное множество. Тогда каждая функция * —> X — не что
иное, как выбор точки в множестве X; таким образом, (* ^ Set) —
это категория множеств с отмеченной точкой (§ 1.7). Аналогично,
(Z I Ab) — категория абелевых групп, в каждой из которых отмечен
элемент.
Пусть теперь а — некоторый объект в категории С. Категория
(С I а) объектов над а имеет вид
С h ,
объекты : |/ ; стрелки : \ / , (2)
а а
где треугольник коммутативен. Например, множество * терминально
в категории Set, и потому всегда существует единственная стрелка
X —У *; следовательно, категория (Set ^ *) изоморфна Set. Еще
пример: в случае кольца Z объекты категории (Rng ^ Z) — это кольца,
снабженные морфизмом г : R —> Z (кольцо R с пополнением г),
а морфизмы — это морфизмы колец, сохраняющие пополнение.
Пусть Ъ — объект в категории С, a S : D —у С — некоторый
функтор. Тогда в категории (b I S) объектов под Ъ относительно
S объектами являются все такие пары (/, d), что d G ObjD, / : Ь —>
—>• Sd, а стрелками ft : (/, d) —>• (f'jd') — все те стрелки ft : d —>• d! из
D, для которых /; = 5ft о /. В наглядном виде
Ъ Ь
объекты : |/ ; стрелки ft : У V , (3)
Sd Sd ~sT Sd'
причем треугольник коммутативен. Умножение здесь определяется
умножением стрелок ft в D. Отдельно отметим, что равенство стрелок
в категории {Ъ \, S) означает их равенство в категории D.
Пусть, например, U : Grp —>• Set — забывающий функтор. Тогда
для каждого множества х объектами категории (х I U) являются

60
Конструкции в категориях
[Гл. 2
функции х —у Ug из ж в носитель некоторой группы д; такова,
например, функция, отображающая х в носитель свободной группы,
порожденной элементами множества х. Эта категория (х \,U) — и
другие ей подобные — будут широко использоваться при рассмотрении
сопряженных функторов.
Аналогично, если а Е С и Т : Е ^ С — некоторый функтор, то
можно построить категорию (Т ^ а) объектов над а относительно Т.
Приведем общую конструкцию. Пусть даны категории и функторы
Е^С ^- D.
Объектами категории запятой (Т I 5), которая обозначается также
(Т, 5), являются все тройки (е, d, /), где d Е Obj D, e G Obj E, f :Te —>•
—>■ Sd. Стрелками (e,d,/) —>■ (e',d',f) в этой категории являются все
пары (fc, /i) стрелок fc : e —>• е'', h : <i —>• d'', для которых f oTk = Shof.
В наглядном виде
Те
объекты (е, d, /) :
Sd
Те ^^ Те'
f ; стрелки (к, h) :
Г
Sd^Sd',
(4)
причем квадрат коммутативен. Произведение (k',h') о (k,h) равно
(к' о к, Ы о h), если оно определено.
Под это общее определение категории запятой (Т I S) подпадают
все перечисленные случаи. Действительно, объект Ъ из С можно
рассматривать как функтор Ъ : 1 —> С. Если при этом взять Т = 6, то
категория запятой (Т I S) превращается в категорию (b I S) объектов
под Ъ относительно S. В частности, если S = С — тождественный
функтор категории С, то мы получаем категорию (b ^ С) объектов
из С под Ъ. Аналогично, можно взять в качестве S функтор 1 —> С,
т. е. объект а из С Пусть теперь S = Т — тождественный функтор
в С. Тогда (С I С) — в точности категория С2 всех стрелок из С.
В качестве S и Т можно взять также объекты а и Ъ категории С;
тогда в категории (Т \. S) = (b l а) объектами являются все стрелки
/ : Ъ —у а, а морфизмами — лишь единичные стрелки всех объектов;
иначе говоря, (b l а) совпадает с множеством (дискретной категорией)
home (b, а). Именно этот пример и породил название категория
запятой и обозначение (Т, S) — которого мы будем избегать, поскольку
запятая и так несет большую нагрузку.
Построение категории запятой (Т I S) можно наглядно
представить на следующей коммутативной диаграмме из категорий и
функторов:
(TIS)
\ О
(5)

2.7] Графы и свободные категории 61
Здесь do j d\ — функторы 1—^2, категория функторов С2 — не что
иное, как категория стрелок / из С, и потому функторы Cd°, Cdl,
определенные как в конце предыдущего параграфа, сопоставляют
каждой такой стрелке, соответственно, ее область и кообласть.
Функторы Р и Q (проекции категории запятой) и функтор R определяются
(на объектах) в соответствии с диаграммой
(e,d,/: Те^ Sd)
e^Te^Cf: Те ^ Sd) ^^ Sd^ d.
Упражнения
1. Пусть if — коммутативное кольцо. Покажите, что категория запятой
(К \, CRng) совпадает с категорией всех малых коммутативных if-алгебр.
2. Пусть t — терминальный объект в С. Докажите, что категория (С J, t)
изоморфна С.
3. Дополните диаграмму (6), доопределив Р, Q и R на стрелках.
4. (S.A. Huq). Пусть даны функторы T,S : D —»> С. Покажите, что
естественное преобразование т : Т -^ S совпадает с функтором т : D —»■
—»■ (Т 4- £), таким что Рт = Qr = id^», где Р, Q — проекции на диаграмме
(5).
5. Пусть дана коммутативная диаграмма категорий функторов вида
(нижняя строка как на диаграмме (5)). Докажите, что существует
единственный функтор L : X —> (Т \. S), для которого Р' = PL, Q' = QL
ий' = RL. (Это характеризует (Т I S) как обратный предел, см. § 3.4.)
6. (а) Пусть фиксированы малые категории C,D и Е. Покажите, что
(Т, S) ^ (Т 4- S) - функция объектов функтора (СЕ)ор х (CD) -> Cat.
(b) Опишите аналогичный функтор для переменных С, D и Е.
2.7. Графы и свободные категории
Напомним сначала построение свободного моноида FX,
порожденного множеством X. Он состоит из всех конечных
последовательностей х\Х2 • • -хп элементов xi множества X; умножение таких
последовательностей состоит в приписывании одной последовательности
к другой, так что пустая строка служит единицей в FX.
Характеристическое свойство этого свободного моноида можно
сформулировать следующим образом. Пусть UM обозначает множество элементов
произвольного моноида М. Тогда любая функция / : X —у UM
продолжается до единственного морфизма моноидов:
g:FX -+ М.

62
Конструкции в категориях
[Гл. 2
Чтобы получить соответствующее определение свободной категории,
нужно заменить исходное множество X ориентированным графом G.
Напомним, что (ориентированный) граф G (§ 1.2) — это множество
объектов (вершин) О, множество стрелок (ребер) А и две функции
А^О:
до
A s О, до = dom /, д\ = cod / .
Морфизм графов D : G ^ G' — это пара таких функций Do : О ^ О'
и DA : А^ А', что
D0dof = d0DAf и D0d1f = d1DAf
для любой стрелки / Е А. Такие морфизмы, с очевидным
умножением, являются стрелками категории всех малых графов Grph (граф
является малым, если О и А — малые множества). Любой граф можно
изобразить на диаграмме, состоящей из вершин (объектов) и стрелок.
Отличие от категорной диаграммы здесь заключается в том, что не
предусмотрено ни умножение стрелок, ни единичные стрелки.
Поэтому граф часто называют диаграммной схемой или предкатегорией.
Каждая категория С превращается в граф UC с теми же
объектами и стрелками, если забыть об умножении стрелок и о единицах.
Каждый функтор F : С —>• С' является и морфизмом UF : UC —>• UC'
между соответствующими графами. В результате определяется
забывающий функтор U : Cat —> Grph из категории малых категорий
в категорию графов.
Фиксируем множество О. Граф с множеством вершин О назовем
О-графом; в морфизме О-графов D отображение Do : О —>■ О
обязательно тождественное. Простейший О-граф О имеет вид 0^0,
где обе функции «область» и «кообласть» — тождественные. Если
А и В — два О-графа (т.е. два множества стрелок в О), то их
произведение над О равно
Ax0B = {(g,f)\do9 = d1f, geA, f e В}; (1)
/ 9
это множество состоит из перемножаемых пар стрелок •—>-•—>-•.
Положив
d0(g,f)=d0f, d1(g,f) = d1g, (2)
мы превращаем это множество в О-граф. Такое умножение О-графов
ассоциативно, поскольку для любых трех О-графов А,ВиС
существует очевидный изоморфизм А х о(В х qC) = (Ах о В) х оС. Для
простейшего О-графа О существует также изоморфизм А = А х qO,
который имеет вид / н->- (/, dof). Аналогично, А = О х о А.

2.7]
Графы и свободные категории
63
Категорию с множеством объектов О можно описать как О-граф
А, снабженный двумя морфизмами О-графов с : Ах о А —» Ажг : О —>
—у А (умножение и единица), для которых коммутативны диаграммы
(А х 0А) х 0А = А х о (А х 0А) >■ А х 0А
cxl
т
А х 0А - *- Л
0xoi гх > Ах о А < Ах О0
А
(3)
Здесь 1 х с служит сокращением для 1 х qc и т. п. Действительно, для
перемножаемых стрелок (д, /) морфизм с определяет их произведение
c(g,f); каждый объект b E О имеет единичную стрелку вида i(b) Е
Е А. При этом первая диаграмма утверждает, что умножение
ассоциативно, а вторая — что каждое г (А) действует как левая и правая
единица относительно умножения. В этом смысле категория подобна
моноиду, как и отмечено во введении: Set нужно заменить на О —
— Grph, а произведение множеств на Xq.
С помощью любого О-графа G можно породить категорию С на
том же множестве объектов О; стрелками этой категории будут строки
перемножаемых стрелок из G, так что стрелку из Ъ в а в категории С
можно изобразить как путь из Ъ в а, состоящий из последовательных
ребер графа G. Эта категория будет обозначаться С = C{G) и
называться свободной категорией, порожденной графом G. Ее основные
свойства можно сформулировать следующим образом.
Теорема 1. Пусть дан малый граф G = {А =4 О}. Тогда
существует малая категория С = Со с множеством объектов О
и морфизм графов Р : G —>• UC из G в граф-носитель UC категории
С, причем выполнено следующее утверждение. Для любой категории
В и любого морфизма графов D : G —> UB существует единственный
функтор D' : С —>• В такой, что (UD')oP = D, см. коммутативную
диаграмму
С G^^UC
D'
У
в,
(4)
В частности, если О — множество объектов категории В, a D —
морфизм О-графов, то функтор D' тождествен на объектах.
Свойство морфизма Р, выраженное в диаграмме (4), равносильно
утверждению, что стрелка Р : G —> UC является начальным объектом

64
Конструкции в категориях
[Гл. 2
в категории запятой (G \, U). Поэтому Р единствен с точностью до
изоморфизма (категории С). Подобное свойство встречается часто;
будем говорить, что Р универсален среди морфизмов из G в
забывающий функтор U.
Доказательство. Пусть объекты в С те же, что и в G, а
стрелками являются конечные строки (или пути) вида
Л h ^ ^т1
а\ -4 а2 -4 а3 ->• • • • -4 ап,
которые состоят из п объектов графа G, соединенных п — 1 его
стрелками fi : ai -4 c^+i. Рассмотрим каждую такую строку как стрелку
(^lj/ij • • • ?/п-1?^п) : ai —>• ап категории С и определим умножение
строк как сцепление (последовательное приписывание) с
отождествлением общего конца. Такое умножение заведомо ассоциативно, и его
единицами служат строки (ai) длины п = 1. Каждая строка длины
п > 1 является произведением строк длины 2:
(ai,/i,a2,...,an_i,/n_i,an) = (an_b /n_b an) о ... о (ab/i,a2). (5)
Искомый морфизм графов Р : G —>■ С/С отображает каждую стрелку
/ : а\ —у CL2 данного графа G в граф-носитель некоторой категории В.
Если существует функтор D' : С —^ В такой, что UD' о Р = D, как на
коммутативной диаграмме (4), то D; должен иметь вид D' (а) = Da на
объектах и D'(ai,f, a2) = Z)/i на стрелках. Поскольку любая строка
длины п > 1 является произведением вида (5) в (7, то D' должен
иметь вид
JD/(ai,/i,a2,...,an_i,/n_i,an) = £>/n-i ° ••• °£>Л-
И обратно, эта формула определяет функтор D'В —у С, для которого
указанная диаграмма коммутативна. □
Вот некоторые простые примеры. Если граф состоит из
единственной стрелки /, для которой dof = <9i/, то свободная категория состоит
из всех стрелок вида 1, /, /2, ... Если граф состоит из единственной
стрелки с несовпадающими концами, то свободная категория состоит
из этой стрелки плюс две единичные стрелки (на каждом конце).
Для графа •—>-•—>-• с тремя различными вершинами свободная
категория представляет собой коммутативный трегольник (добавим
одно произведение стрелок и три единичные стрелки).
Если О состоит из одной точки, то граф G сводится к множеству
X (множеству стрелок X = А), и теорема приводит к общеизвестному
построению свободного моноида М, порожденного множеством X,
а именно:
Следствие 2. Для каждого множества X существует моноид
М и функция р : X —> UM, где UM — носитель моноида М со
следующим универсальным свойством: для каждого моноида L и любой
функции h : X -4 UL существует единственный такой морфизм
моноидов Ы : М —>■ L, что h = Uh' op.

2.8]
Фактор-категории
65
Элементами моноида М служат единица и строки вида (х\,...
... ,xn_i), где xi e X.
Графы можно использовать для описания диаграмм. Если G —
некоторый граф, то можно определить диаграмму вида G в категории
В как морфизм графов D : G —> UB. Согласно доказанной теореме,
такие морфизмы D в точности соответствуют функторам D' : Со ~~**
—у В при биекции D' \-t D = UD' о Р. Эта биекция
Cat (CG, В) ** Grph (G, UB) (6)
естественна по G и по В. Таким образом, она означает, что функтор
С : Grph —> Cat является левым сопряженным (см. гл. 4) к
забывающему функтору U : Cat —> Grph.
Упражнения
1. Дайте определения противоположного графа и произведения графов,
согласованные с соответствующими определениями для категорий (т. е. так,
чтобы функтор U сохранял произведения и переход к противоположному
графу).
2. Покажите, что каждый конечный ординал является свободной
категорией.
3. Покажите, что каждый граф G порождает свободный группоид F
(т. е. удовлетворяющий теореме 1, в которой категория С заменена на
группоид F, а категория В — на группоид Е). Выведите как следствие,
что каждое множество X порождает свободную группу.
2.8. Фактор-категории
Некоторые категории можно описать с помощью образующих и
соотношений следующим образом:
Предложение 1. Пусть С — некоторая категория, а функция
R сопоставляет каждой паре объектов а,Ь из С бинарное
отношение Raj ua hom-множестве С(а,Ь). Тогда существуют категория
C/R и функтор Q = Qr : С —>• C/R такие, что: 1) если fRa,bf
принадлежит С, то Qf = Qf; 2) если Н : С —» D — функтор из
С, для которого из fRa,bf следует Hf = Hf при всех f и f, то
существует единственный функтор Н' : С/R —>• D, для которого
Н' о QR = Н. При этом функтор Qr является биекцией на
объектах.
Говоря кратко: Q является универсальным функтором в категории
С, для которого из fRf следует Qf = Qf.
Например, пусть С = Top, a fRf означает, что / и /' гомотопны.
Тогда соответствующая фактор-категория С/R — не что иное, как
категория Toph из § 1.7, в которой объектами служат
топологические пространства, а стрелками — классы гомотопии непрерывных
отображений. Такое непосредственное построение категории Toph
возможно, поскольку отношение гомотопии отображений является

66
Конструкции в категориях
[Гл. 2
эквивалентностью и сохраняется при их композиции. В общем
случае требуются предварительные манипуляции с отношением R для
получения таких свойств.
Набросок доказательства. Отношение R на С называется
конгруэнтностью, если: 1) Ra^ является рефлексивным, симметричным
и транзитивным отношением на С (а, Ь) для любой пары объектов а, Ь;
2) если для /,/' : а —>• Ь верно, что fRa,bf'j то при всех д : а' —>•
—>■ а и ft, : 6 —» Ь' имеем (hfg)Ra>j'(hf'g). Для каждого Л существует
наименьшая конгруэнтность Л' на С такая, что R С R' (докажите
в качестве упражнения). Возьмем в качестве объектов категории С/R
объекты из С, а в качестве любого hom-множества (C/R)(a, b) возьмем
фактормножество C(a,b)/R'a ъ множества С(а,Ь) по
соответствующему отношению эквивалентности R'. Поскольку это отношение
согласовано с умножением, то произведение в С соответствует произведению
в С /R при очевидной проекции Q : С —>■ С JR. При этом ясно, что для
любого функтора Н : С —>■ D множества Sa^ = {/, /; • а —> Ъ \ Н f =
= Hf'} определяют конгруэнтность на С. Значит, из С D R вытекает
S D R', и Н можно представить как Н = Н' о QR. □
Если здесь С — свободная категория, порожденная графом G, то
мы называем С/R категорией с образующими G и соотношениями
R. Например, 3 можно описать как категорию, порожденную тремя
объектами 0, 1, 2, тремя стрелками / : 0 —>■ 1, д : 1 —> 2, ft:0—> 2
и одним соотношением ft = g о f. В качестве частного случая (с
одним объектом) сюда входит случай моноида, заданного образующими
и соотношениями.
Упражнения
1. Покажите, что категория, порожденная графом
9
Л /'
9
с одним соотношением д f = / д, имеет четыре единичные стрелки и ровно
пять неединичных стрелок /, д, /', д' и д' f = f g.
2. Пусть С — группа (рассматриваемая как категория с одним
объектом). Покажите, что для каждой конгруэнтности Я на С существует
нормальная подгруппа N в G такая, что fRg, если и только если д~х f E N.
Замечания
Главная идея этой главы — научиться применять простое понятие
функтора в сложных случаях путем построения соответствующих сложных
категорий: двойственной категории в случае контравариантных функторов,
произведения категорий в случае бифункторов, категории функторов
фактически как сопряженной произведению и категории запятой для редукции

2.8]
Фактор-категории
67
универсальных морфизмов к инициальным объектам. Важность
использования категорий функторов (которые иногда называются категориями
диаграмм) была осознана Гротендиком (Grothendieck [1957]) и Фрейдом
(Freyd [1964]). Понятие категории запятой, часто применявшееся в частных
случаях, было в полной общности введено в (неопубликованных) тезисах
Ловера (Lawvere [1963]), с тем чтобы дать определение сопряженного
функтора без использования множеств элементов. На некоторое время оно стало
своего рода тайным орудием в арсенале посвященных.
Двойственность имеет долгую историю. Наличие двойственности между
точкой и прямой в геометрии, особенно проективной, привело к строгому
аксиоматическому определению двойственности в монументальном
трактате Веблена-Юнга по проективной геометрии. Явное описание
двойственности с помощью двойственных категорий часто оказывается
предпочтительным, например в случае двойственности Понтрягина, которая
формулируется (§ 4.4) как эквивалентность между категориями или как
эквивалентность между категорией и двойственной категорией (см. Negrepontis [1971]).

Глава 3
УНИВЕРСАЛЬНЫЕ КОНСТРУКЦИИ И ПРЕДЕЛЫ
Универсальные конструкции в разном обличье появляются во
многих разделах математики — как универсальные морфизмы в данный
функтор, как универсальные морфизмы из данного функтора, как
универсальные элементы функтора в категорию множеств. Каждая
универсальная конструкция определяет представление
соответствующего функтора (со значениями в категории множеств) в виде hom-
функтора. В свою очередь, для анализа таких представлений служит
лемма Ионеды. Важным примером универсальных конструкций
являются пределы — как обратные (= проективные пределы = пределы
= левые корни), так и двойственные к ним прямые (= индуктивные
пределы = копределы = правые корни). В этой главе мы дадим
определения универсальных объектов и пределов и рассмотрим несколько
основных случаев (произведения, коуниверсальные квадраты,
уравнители ...). Более глубокие их свойства появятся в гл. 9, посвященной
специальным типам пределов. Связь с сопряженными функторами
будет рассмотрена в гл. 5.
3.1. Универсальные стрелки
В § 2.7, исходя из забывающего функтора U : Cat —> Grph
и графа G, мы построили свободную категорию С над G и морфизм
графов Р : G —> UC, который вкладывает G в С. Мы показали, что
эта стрелка Р универсальна среди стрелок из G в U. Аналогичное
свойство универсальности присуще морфизмам, которые вкладывают
порождающие элементы в свободные алгебраические системы других
типов — например, группы или кольца. Введем общее определение.
Определение. Пусть S : D —» С — некоторый функтор, с —
объект из С. Универсальная стрелка из с в S — это пара (г, и), состоящая
из объекта г в D и стрелки и : с —> Sr в С такая, что для каждой пары
(d,/), где d — объект в D, а / : с —> Sd — стрелка в С, существует
единственная стрелка f : г —> d в D, для которой Sf о и = /. Иначе
говоря, каждая стрелка / из S пропускается единственным образом
через универсальную стрелку и, как на коммутативной диаграмме
и „
с ^ Sr r
II \sf \f (1)
с —^ Sd, d.

ЗЛ]
Универсальные стрелки
69
Другими словами, и : с —у Sr является универсальной стрелкой
из ев 5, если пара (г,и) является начальным объектом в категории
запятой (с I 5), объектами которой служат стрелки с —у Sd. Как
и сам начальный объект, пара (г, и) единственна с точностью до
изоморфизма в (с I S); в частности, объект г в D единствен с точностью
до изоморфизма в категории D. Это типичный случай применения
категорий запятой.
Существует огромное число примеров универсальных стрелок;
перечислим лишь некоторые из них.
Базисы векторных пространств. Пусть Vct^ обозначает
категорию всех векторных пространств над фиксированным полем К,
в которой стрелками являются линейные преобразования. Через
U : Vct^ —у Set обозначим забывающий функтор, который каждому
векторному пространству V сопоставляет множество его элементов.
Для каждого множества X, как известно, существует векторное
пространство Vx с базисом X; оно состоит из всех формальных К-
линейных комбинаций элементов из X. Функция, сопоставляющая
каждому элементу х Е X тот же элемент, рассматриваемый как
вектор в Ух, является стрелкой j : X —> U(Vx)- Как известно,
для любого другого векторного пространства W каждую функцию
/ : X —у U(W) можно продолжить до единственного линейного
преобразования /' : Vx —> W такого, что Uf о j = /. Этот стандартный
факт равносилен тому, что j — универсальная стрелка из X в U.
Свободные категории над графами. Теорема I, § 2.7 о свободной
категории С над графом G в точности означает, что функтор Р : G —>
—У UС универсален. Это замечание относится и к свободному
моноиду с фиксированным множеством образующих, свободной группе
с фиксированным множеством образующих, свободному Л-модулю
(над фиксированным кольцом R) с фиксированным множеством
образующих, алгебре многочленов над данным коммутативным кольцом с
фиксированным множеством образующих, и аналогично для
всевозможных типов свободных алгебраических систем г).
Поля частных. Для каждого целостного кольца D существует
известный способ построить его поле частных Q(D) вместе с
мономорфизмом j : D —> Q(D) (часто при этом D объявляется подкольцом
в Q(D)). Это поле частных обычно описывается как наименьшее
поле, содержащее D, в том смысле что для каждого поля К D D
имеется мономорфизм полей / : Q(D) —> К, тождественный на общем
подкольце D. Однако вложение D С К без труда можно заменить
на любой мономорфизм целостных колец D —» К. Таким образом,
наше утверждение означает, что пара (Q(D),j) универсальна
относительно забывающего функтора Fid —у Domm из категории полей
в категорию целостных колец — если стрелками в Domm считать
мономорфизмы целостных колец (заметим, что гомоморфизм полей
обязательно является мономорфизмом). Однако в большей категории
1) Определение свободных алгебраических систем см. в книге (*Мальцев
[1970]), с. 315-316. — Прим. ред. пер.

70 Универсальные конструкции и пределы [Гл. 3
Dom, где стрелками служат все гомоморфизмы целостных колец, не
существует универсальной стрелки из каждого кольца в поле.
Например, в кольце целых Z для каждого простого числа р существует
гомоморфизм Z —у Zp; читатель может убедиться, что это делает
невозможным наличие универсальной стрелки из Z в функтор Fid —>
-» Dom.
Полные метрические пространства. Пусть Met — категория всех
метрических пространств X, У,..., в которой стрелками X —> Y
служат функции, сохраняющие метрику — и потому взаимно
однозначные. Полные метрические пространства составляют, как объекты,
полную подкатегорию. Общеизвестное пополнение X метрического
пространства X порождает стрелку X —У X, универсальную
относительно очевидного забывающего функтора (из категории полных
метрических пространств в категорию всех метрических пространств).
Функция, вкладывающая математический объект в его
подходящее пополнение, может рассматриваться как универсальная стрелка
и во многих других случаях. Общее утверждение о единственности
универсальной стрелки влечет единственность пополнения, с
точностью до единственного изоморфизма (что еще можно желать?)
Идею универсальности иногда выражают в терминах
«универсальных элементов». Пусть D — некоторая категория, Н : D —>■ Set —
некоторый функтор. Универсальный элемент функтора Н — это пара
(г, е), состоящая из объекта г Е D и элемента е Е Нг такая, что для
каждой пары (d, х), х Е Hd существует единственная стрелка / : г —>
—> d в D, для которой (Hf) е — х.
Естественными примерами универсальных элементов служат
многие известные конструкции. Например, рассмотрим отношение
эквивалентности Е на множестве S (соответствующее фактормножество
S/E состоит из классов эквивалентности элементов из S относительно
Е) и проекцию р : S —>■ S/E, которая отображает каждый элемент s G
G S в его класс .Е-эквивалентности. Множество S/E обладает тем
известным свойством, что каждая функция / на S, сохраняющая
отношение эквивалентности, может рассматриваться как функция на
S/E. Более формально, это означает, что если функция / : S —>■ X
такова, что sEs' влечет fs = fs', то / можно записать как композицию
/ = f'p для единственной функции /; : S/E —У X:
ii !/'
Это в точности означает, что (S/E,p) — универсальный элемент для
функтора Н : Set —У Set, сопоставляющего каждому множеству X
множество НХ тех функций / : 5 —> X, для которых sEs' влечет
fs = fs'.
Пусть теперь N — нормальная подгруппа в группе G, а функтор
Н : Grp —> Set сопоставляет каждой группе G' множество HG' всех

ЗЛ]
Универсальные стрелки
71
тех гомоморфизмов / : G —> G', которые аннулируют N (т. е. fN =
= 1). Тогда стандартная проекция р : G —> G/N, сопоставляющая
каждому элементу д Е G его смежный класс рд = gN в
факторгруппе G/N, является универсальным элементом для Н. В самом
деле, каждый из указанных гомоморфизмов можно представить как
/ = f'p для единственного /' : G/N —>• G'. Далее, факторгруппу
обычно описывают как группу, элементами которой служат смежные
классы. Однако, доказав с помощью смежных классов одно указанное
универсальное свойство гомоморфизма р : G —> G/N, можно затем
доказать все остальные свойства факторгрупп — например, теоремы
об изоморфизме, — уже без упоминания о смежных классах (см. Мае
Lane, Birkhoff [1967]). Требуется лишь существование универсального
элемента р для функтора Н. Более того, его существование можно
доказать без использования смежных классов (см. теорему о
сопряженном функторе, сформулированную в § 5.6).
Тензорные произведения дают другой пример универсальных
элементов. Пусть даны векторные пространства У и У над полем К
и функция Н, которая сопоставляет каждому векторному
пространству W множество HW = Bilin (V, V; W) всех билинейных
функций V х V' —> W. Она служит функцией объектов для функтора
Н : Vct^ —у Set. В обычной конструкции тензорного произведения
участвуют векторное пространство V (8) V и билинейная функция
(8) : V х V —>• V (8) V, записываемая как (v,v') \-^ v ® v'. При этом
пара (V (8) V,(8)) является универсальным элементом для функтора
Н = Bilin (У, V'; —). Все это распространяется на случай, когда поле
К заменено на коммутативное кольцо (а векторные пространства —
на if-модули).
Понятие универсального элемента — это частный случай понятия
универсальной стрелки. В самом деле, пусть * — множество из одной
точки. Тогда любой элемент е G Нг можно рассматривать как стрелку
е : * —> Нг в категории Ens. Как следствие, универсальный элемент
(г, е) для Н — это в точности универсальная стрелка из * в Н.
Обратно, если С имеет малые hom-множества, то понятие «универсальная
стрелка» является частным случаем понятия «универсальный
элемент». В самом деле, пусть S : D —>■ С — некоторый функтор, а с G
G С — некоторый объект. Тогда (г, и) : с —>■ Sr является универсальной
стрелкой из с в 5, если и только если пара (г, и) G C(c, Sr) является
универсальным элементом для функтора Н = С (с, S-). Этот функтор
действует на объект d и стрелку h из D по формулам
d^C(c,Sd), h^C(c,Sh).
До сих пор мы рассматривали универсальные стрелки из объекта
с G С в функтор S : D —>■ С. Двойственное понятие также полезно.
Универсальная стрелка из S в с — это пара (r,v), состоящая из
объекта г G D и стрелки v : Sr —> с с такой кообластью с, что для
любой пары (d,/), где / : Sd —> с, существует единственная стрелка

72
Универсальные конструкции и пределы
[Гл. 3
/' : d —у г, такая что / = v о Sf, см. коммутативную диаграмму
d Sd^-^c
f \ sf \ ||
г, SV —^ с.
Проекции р : а х Ъ —>■ а, q : a x b ^ b произведения в категории
С (где С = Grp, Set, Cat,...) являются примером такой
универсальности. Действительно, для любой другой пары стрелок / : с —у
—> а,д : с —> b с кообластями а и b существует единственная такая
стрелка h : с —>• а х 6, что ph = f,qh = д. Таким образом, (р, д) —
универсальная пара. Чтобы сделать ее универсальной стрелкой, введем
диагональный функтор Л : С —> С х С такой, что Лс = (с, с). Тогда
пара /, д превращается в стрелку (/, д) : Лс —>• (а, Ь) в категории С х
х С, и (р, #) становится универсальной стрелкой из Л в объект (а, 6).
Аналогично, ядро любого гомоморфизма (в категориях Ab, Grp,
Rng, i?-Mod, ...) универсально — точнее, универсально для
подходящего контравариантного функтора.
Отметим, что мы говорим «универсальная стрелка в 5» и
«универсальная стрелка из 5», а не «универсальная» и «коуниверсальная»
стрелка.
Упражнения
1. Покажите, как интерпретируются в виде универсальных стрелок
следующие известные конструкции:
а) целочисленное групповое кольцо группы (и вообще моноида);
б) тензорная алгебра векторного пространства;
в) внешняя алгебра векторного пространства.
2. Найдите универсальный элемент для контравариантного функтора
множества-степени V : Setop —»■ Set.
3. Найдите универсальные стрелки (из данного произвольного объекта)
в следующие забывающие функторы: АЬ —»■ Grp, Rng —»■ Ab (забывается
умножение), Тор —»■ Set, Set* —»■ Set.
4. Используя лишь универсальность (проекций), докажите следующие
теоретико-групповые изоморфизмы:
а) если М, N — нормальные подгруппы в группе G, причем М С N, то
(G/M)/(N/M) ~ G/M-
б) если S,N — подгруппы в группе G, вместе порождающие подгруппу
SN, причем N нормальна, то SN/N = S/S П N.
5. Покажите, что Х-фактормодуль A/ S (где S — подмодуль в А) может
быть описан в терминах универсальности. Выведите теоремы об
изоморфизмах.
6. Опишите факторкольца по двусторонним идеалам колец в терминах
универсальности.
7. Покажите, что построение кольца К[х] многочленов над
коммутативным кольцом К от переменного х является универсальной конструкцией.

3.2]
Лемма Йонеды
73
3.2. Лемма Йонеды
Теперь рассмотрим некоторые основные свойства, вытекающие из
универсальности. Во-первых, это понятие может быть
сформулировано в терминах hom-множеств, а именно:
Предложение 1. Для данного функтора S : D —>• С пара
(г, и : с —> Sr) универсальна из с в 5, если и только если функция,,
отображающая каждую стрелку f : г —> d в Sf о и : с —>• Sd,
является биекцией hom-множеств
D(r,d) = C(c,Sd). (1)
Эта биекция естественна по d. Обратно, для данных г и с любой
естественный изоморфизм (1) соответствует в указанном смысле
единственной стрелке и : с —>• Sr, для которой пара (г, и)
универсальна из с в S.
Доказательство. Утверждение об универсальности пары (г,и)
в точности означает, что соответствие /' н-» Sf о и = f биективно.
Эта биекция естественна по d, так как для g' : d —>- d' верно, что
S(g'f)ou = Sg'o(Sfou).
Обратно, естественный изоморфизм (1) сопоставляет каждому
объекту d e D биекцию ера : D{r,d) —>• C(s,d). В частности, пусть
d — г\ тогда единичная стрелка lr Е D(r,r) переходит под действием
ipr в стрелку и : с —> Sr из С Для любой стрелки f : г —> d диаграмма
Z>(r,r)-^C(c,Sr)
D(rJ')
c(c,sf) (2)
L>(r,d)^^C(c,Sd)
коммутативна, поскольку ip естественно. Но на этой диаграмме lr Е
Е D(r, r) переходит по верхней и правой стрелке в Sf о и, а по левой
и нижней — в (pd(f')- Так как ср^ биективно, то это в точности значит,
что каждая стрелка / : с —>■ Sd имеет вид / = Sf'ou для единственной
стрелки /'. Но это как раз и означает, что пара (г, и) универсальна. □
Если категории С и D имеют малые hom-множества, то (1)
означает, что функтор С(с, S-) в категорию Set естественно изоморфен
ковариантному hom-функтору D(r, —). Такие изоморфизмы
называются представлениями (representations):
Определение. Пусть D — категория с малымиhom-множест-
вами. Представлением функтора К : D —>• Set называется пара
(г,ф), где г — объект из D, а
ф : D(r, -)*<K (3)
— естественный изоморфизм. Объект г называется
представляющим объектом. Если такое представление существует, то функтор
К называется представимым.

74
Универсальные конструкции и пределы
[Гл. 3
Таким образом, представимый функтор с точностью до
изоморфизма совпадает с ковариантным функтором D(r,—). Введенное
понятие можно распространить на универсальные стрелки следующим
образом.
Предложение2. Пусть * обозначает одноточечное
множество, D — категория с малыми hom-множествами, (г,и : * —>•
—> Кг) — универсальная стрелка из * в К : D —» Set, а функция
ф отображает стрелку f'-.r—tde K(f')(u*) G Kd для каждого
объекта d из D. Тогда ф является представлением функтора К,
и каждое его представление получается таким способом из ровно
одной универсальной стрелки такого вида.
Доказательство. Функция /:*—>■ X из одноточечного
множества * в произвольное множество X определяется элементом /(*) G X.
Это соответствие / н-» /(*) является биекцией Set (*,X) —> X и
естественно по X Е Set. Композиция с К дает естественный изоморфизм
Set (*, К—) —> К. С учетом представления ф из (3) получаем
Set (*,#-) ^K^D(r,-).
Таким образом, представление функтора К соответствует
естественному изоморфизму Set(*,K—) = D(r,—). Теперь наше утверждение
вытекает из предыдущего предложения.
Столь же легко доказать его и непосредственно: если и —
универсальная стрелка, то /' н-» K(f')(u(*)) — представление; если ф таково,
как в формуле (3), то фг отображает 1 : г -У г в элемент из Кг,
который универсален, а потому является универсальной стрелкой * —>
-+ Кг. □
Отметим, что каждое из понятий «универсальная стрелка»,
«универсальный элемент» и «представимый функтор» фактически
охватывает два остальных. Так, универсальная стрелка из с
в S : D —>- С соответствует (см. предложение 1) естественному
изоморфизму D(r,d) = C(c,Sd), а значит и представлению функтора
С(с, S-) : D —> Set или, равносильно, универсальному элементу для
этого функтора.
Доказательство предложения 1 основано на наблюдении, что
каждое естественное преобразование ip : D(r,—)—>K полностью
определяется образом единичной стрелки 1 : г —> г при отображении срг.
Этот факт можно сформулировать следующим образом:
Лемма (Yoneda). Пусть К : D —>• Set — некоторый функтор,
а г — объект из категории D (причем D — категория с малыми
hom-множествами). Тогда имеется биекция
y:N<it(D(r,-),K)^Kr, (4)
которая переводит каждое естественное преобразование
а : D(r,—) -^ К в аг1г, т. е. в образ единичной стрелки г —>■ г.

3.2]
Лемма Йонеды
75
Доказательство выражается следующей коммутативной
диаграммой:
D(r,r) r-^K(r) r
f*=D(rJ)
K(f)
(5)
D(r,d)-^K(d), d.
Следствие. Для любых объектов r,s G D любое естественное
преобразование D(r, —) -1» D(s, —) имеет вид D(h, —) для
единственной стрелки h : s —>• г.
Отображение Йонеды у из формулы (4) естественно по К и по
г. Чтобы точно сформулировать этот факт, нужно рассмотреть К
как объект в категории функторов Set , а область и кообласть
отображения у считать значениями функторов на паре (К, г) и затем
рассмотреть эту пару как объект в категории Set x D. Тогда
кообласть для у — это функтор оценки (evaluation functor) E, который
отображает каждую пару (К, г) в значение Кг функтора К на объекте
г; область для у — это функтор N, который отображает объект (К, г)
в множество Nat (D(r, —), К) всех естественных преобразований, а
пару стрелок F : К —>• К', f : г —>• г' в Nat (D(f, —), F). После этих
замечаний можно без труда получить добавление к лемме Йонеды:
Лемма. Биекция из формулы (4) является естественным
изоморфизмом у : N -^ Е между функторами Е, N : Set x D —У Set.
Функция объектов г \-> D(r, —) и функция стрелок
(/ : a -► г) .-> Л(/, -) : £>(r, -) ^ D(s, -),
где / — стрелка в категории D, вместе определяют полный и унива-
лентный функтор
У : Dop -> SetD, (6)
который называется функтором Йонеды. Двойственный к нему
функтор
Y' : D -+ Set^°P (7)
(также унивалентный) отображает /:Мгв естественное
преобразование
£>(-,/): !>(-, в) -4 £>(-, г) : Dop -»• Set.
Чтобы эти функторы были определены, категория D должна иметь
малые horn-множества (поскольку Set — это категория всех малых
множеств). Для более обширных категорий D лемма Йонеды и
добавление к ней остаются верными, если заменить Set на любую
категорию Ens, объектами которой являются множества X, У,..., причем
Ens (X, Y) состоит из всех функций из X в У\ разумеется, horn-
множества категории D должны быть объектами из Ens. (Дальнейшее

76
Универсальные конструкции и пределы
[Гл. 3
расширение категории Ens не влияет на понятие естественности; см.
упр. 4.)
Упражнения
1. Пусть функторы К, К' : D —»■ Set имеют представления (г, ^) и (г7, ?//)
соответственно. Докажите, что для каждого естественного преобразования
т : К —ь К' существует единственный морфизм h : г —»■ г7 из D такой, что
тоф = ф' о D(h, -) : £>(r, -) -^ if'.
2. Сформулируйте утверждение, двойственное к лемме Ионеды (с
заменой D на Dop).
3. (Кап; «лемма ко-Ионеды».) Пусть К : D —»■ Set — функтор; (* 4- if) —
категория элементов ж Е ifd; Q : (* I К) ^> D — проекция х Е if с/ н-»- с?;
а : (* 4- ^) -^ ^) при любом а £ D — диагональный функтор, образом
которого является константа а. Установите естественный изоморфизм
Nat (if, D(a, -)) ** Nat (a, Q).
4. (Естественность не затрагивается при расширении категории-
кообласти.) Пусть Е — полная подкатегория в Е', a J : Е —>- .Б7 —
соответствующее вложение. Докажите для функторов if, L : D —»■ £7, что
Nat (if, L) ^Nat(Jif, JL).
3.3. Копроизведения и копределы
Понятие копредела мы продемонстрируем на множестве частных
случаев, где фигурируют универсальные объекты.
Копроизведения. Пусть С — произвольная категория.
Диагональный функтор Л : С —> С х С на объектах имеет вид Л (с) = (с, с),
а на стрелках A(f) = (/,/). Универсальная стрелка из объекта (а,Ь)
категории СхС в функтор Л называется диаграммой копроизведения.
Она состоит из объекта с Е С и стрелки (а, 6) —> (с, с) из С х С,
т. е. пары стрелок г : а —>■ с, j : b —> d с областями а и 6 и общей
кообластью с. Эта пара имеет известное свойство универсальности:
для любой пары стрелок / : а —>■ d, g : b ^ d существует единственная
такая стрелка h : с —>■ d, что / = bi, g = ho j. Если такая диаграмма
копроизведения существует, то объект с обязательно единствен (с
точностью до изоморфизма в категории С); он обозначается с = а П b
или с = а + b и называется объектом копроизведения. Диаграмма
копроизведения тогда имеет вид
а 1-*~ aUb •< b;
стрелки i и j называются инъекциями копроизведения а П b (хотя
они не обязаны быть инъективными как функции). Универсальность
этой диаграммы означает, что любая диаграмма следующего вида

3.3]
Копроизведения и копределы
77
однозначно дополняется до коммутативной (посредством стрелки ft):
а ^ aUb^ b
d.
Тогда соответствие (/, g) н-» ft является биекцией
С(а, d) х С(Ъ, d) ^ С {а II Ь, d), (2)
естественной по d, и соответствие ft н->- (fti,ftj) к нему обратно. Если
каждая пара объектов a, b в категории С имеет копроизведение, то,
составив для каждой пары диаграмму копроизведения, мы получаем
бифунктор II : С х С —> С; при этом ft II к определяется для стрелок
ft : а —>■ а', к : b ^ b' как единственная стрелка /illfc : aII6->■ а' II Ь',
для которой (ft, II к) г = z'ft, (ft II к) j = j'fc (нарисуйте диаграмму!).
Диаграмма (1) чаще встречается в ином виде. Например, возьмем
в категории Set в качестве аII b дизъюнктное объединение множеств а
и b (т. е. объединение их непересекающихся экземпляров), а в качестве
г и j — отображения вложения а С a YL b, b С a YL Ь. Функция ft
на дизъюнктном объединении однозначно определяется независимым
заданием ее значений на а и на 6, т. е. заданием композиций hi и hj.
Это как раз и означает, что в диаграмме (1) стрелка ft определяется
однозначно. Говоря строго, дизъюнктное объединение не единственно,
но оно единственно с точностью до биекции, что и требуется от
универсального объекта.
Копроизведение двух объектов существует во многих известных
категориях и имеет в них разнообразные названия, приведенные в
следующем списке:
дизъюнктное объединение множеств,
дизъюнктное объединение топологических
пространств,
объединение топологических пространств с
отождествленной точкой,
прямая сумма А 0 В,
свободное произведение,
тензорное произведение R® S.
В предпорядке Р наименьшая верхняя грань a U b двух элементов
а и b (если она существует) — это элемент a U b со следующими
свойствами: 1) а ^ aUfr, b ^ aUb; 2) если а ^ с, b ^ с, то aUb ^ с. Эти
свойства в точности означают, что a U b является копроизведением
элементов а и 6, если рассматривать Р как категорию.
Бесконечные копроизведения. В определении копроизведения
заменим С х С = С2 на (7х, где X — некоторое множество. Здесь
Set
Тор
Тор,
АЬ, Л-Mod
Grp
CRng

78
Универсальные конструкции и пределы
[Гл. 3
это множество рассматривается как дискретная категория, и поэтому
объектами категории функторов Сх являются семейства а = {ах \ х Е
Е X} объектов из С, проиндексированных элементами из X.
Соответствующий диагональный функтор Л : С —> Сх отображает
каждый объект с в семейство, где все сх совпадают с с. Универсальная
стрелка из а в Л — это диаграмма копроизведения по множеству
индексов X; она состоит из объекта YLxax Е Си стрелок (инъекций
копроизведения) гх : ах —> YLxax из С с соответствующим свойством
универсальности. Оно состоит в том, что отображение / \-> {fix \ х Е
Е X} является биекцией
c(Uax,c) 9* П С(ах,с), (3)
\ж / хех
которая естественна по с. В категории Set копроизведение множеств,
индексированных множеством X, — это их дизъюнктное объединение.
Костепени. Если все множители копроизведения совпадают (ах =
= Ъ при всех ж), то копроизведение Jlxb называется костепенъю
и обозначается X • Ь; в этих обозначениях
С(Х-Ъ,с)^С(Ъ,с)х,
и это соответствие естественно по с. Например, если в категории Set
все сомножители равны некоторому множеству Ъ = X, то костепень
X • Y = X х Y совпадает с декартовым произведением множеств X
и У.
Коядра. Предположим, что С имеет нулевой объект z, так что для
любых двух объектов 6, с G С существует нулевая стрелка 0 : Ъ —у z —>
—> с. Тогда коядро стрелки / : а —>■ Ъ — это такая стрелка и : Ъ —>■ е,
что: 1) ix/ = 0 : а —> е; 2) если для h : 6 —>■ с верно, что ft/ = 0, то
ft = ft'ix для единственной стрелки ft7 : е —>■ с. В наглядной форме:
а ^ Ь —^—^ е uf = О,
В категории АЬ коядром стрелки f : А ^ В является проекция В —>■
—>■ 5/А на факторгруппу группы 5, и во многих подобных категориях
коядро — это по существу некоторый факторобъект. Однако в
категориях без нулевого объекта понятие коядра неприменимо. Поэтому
рассмотрим более общее понятие коуравнителя.
Коуравнители. Пусть в категории С дана пара стрелок /, g : а —>
—>• Ъ с общей областью а и общей кообластью Ъ. Коуравнитель пары
(f,g) — это такая стрелка и : Ъ —>• е (или пара (е,га)), что 1) га/ = ад;
2) если для ft : Ъ —> с верно, что ft/ = hg, то ft = h'u для единственной

3.3]
Копроизведения и копределы
79
стрелки Ы : е —У с. В наглядной форме:
uf = ug,
hf = hg.
(6)
Можно следующим образом описать коуравнитель как
универсальную стрелку. Пусть Ц обозначает категорию, которая содержит
ровно два объекта и две неединичные стрелки из первого объекта во
второй; таким образом, категория имеет вид • =£ •. Образуем категорию
функторов С^. Объектом в ней служит функтор из • 4 • в С, т. е.
параллельная пара (/, д) : а —> Ъ стрелок а =4 Ь в категории С. Стрелка
в категории С^ из одной такой пары (f,g) в другую (/',#') — это
естественное преобразование между соответствующими функторами;
иначе говоря, это пара (h, к) стрелок h : а —>• а' и к : Ъ —>• Ъ' в категории
С:
/
a s 6 kg = #'/i,
*/ = /'Л,
которая делает коммутативными /-квадрат и ^-квадрат. На объектах
с и стрелках г из С определен также диагональный функтор Л,
а именно: Ас — (1С, 1С) и ^г = (г,г). Если теперь имеется пара
(f,g) : а —)► 6, то стрелка h : 6 —>• с, для которой /i/ = /ig, — это
то же самое, что стрелка (hf = hg,h) : (f,g) —>■ (1С,1С) в категории
функторов С^:
л/
/г hf = hg.
Иначе говоря, стрелки /i, которые уравнивают fug — это стрелки
из {ft я) в ^- Поэтому уравнитель (е,и) пары (f,g) — это в точности
универсальная стрелка из (f,g) в функтор Л.
Коуравнители любого множества отображений из а в Ъ
определяются аналогично.
В категории АЬ коуравнитель двух гомоморфизмов f^g'.A^B —
это проекция В —> B/(f — g) А на факторгруппу группы В по образу
гомоморфизма / — д. В категории Set коуравнитель двух функций
/, д : X —У Y — это проекция р : Y —у Y/E на фактормножество
по наименьшему отношению эквивалентности Е С Y х У, которое

80
Универсальные конструкции и пределы
[Гл. 3
содержит все пары (fx,gx), где х Е X. Коуравнители в категории
Тор определяются аналогично с помощью фактортопологии.
Универсальные квадраты. Пусть в категории С дана пара стрелок
/ : а —>• 6, g : а ^ с с общей областью а. Универсальный квадрат для
(f,g) — это коммутативный квадрат (см. ниже слева)
такой, что для каждого коммутативного квадрата (см. выше справа),
построенного на стрелках /, д, найдется единственная стрелка t : г —>
—У s, для которой tu = h и tv = к г). Иначе говоря, универсальный
квадрат — это универсальное средство дополнить стрелки /, д до
коммутативного квадрата. Его можно интерпретировать как
универсальную стрелку. Пусть •<—•—>• обозначает категорию, которая
имеет этот вид. Тогда объект в категории функторов С'А у' — это
пара стрелок (f,g) из С с общей областью, причем Л (с) = (1с, 1С) —
это функция объектов очевидного диагонального функтора Л : С —>
—> С'А *"'. Коммутативный квадрат hf = kg, изображенный наверху
справа, может тогда рассматриваться как стрелка
(f,9) Ь^ а—^с
h
Y
'
hf=kg
As s •< s >- s
в категории С'А >ч из (f,g) в Лв. Универсальный квадрат — это
универсальная стрелка такого вида. Ее конец г, однозначно определенный
с точностью до (единственного) изоморфизма, часто записывается как
копроизведение над а:
г = bYLc = Ъ П с
(М
и носит название расслоенной суммы или (вершины) кодекартова
квадрата. В категории Set универсальный квадрат существует для
любой пары (f,g)', это дизъюнктное объединение 6Пс, в котором для
каждого х G а отождествлены элементы fxngx. Аналогично строятся
универсальные квадраты в категории Тор — к ним принадлежит
такая полезная конструкция, как присоединенное пространство.
Существуют универсальные квадраты и в категории Grp; в частности, если
:) Обращаем внимание читателя, что, согласно устоявшейся
терминологии, универсальный квадрат (pushout) является копределом, а коунивер-
сальный квадрат (pullback, см. § 4) — пределом! При этом оба они
образованы универсальными стрелками. — Прим. пер.

3.3]
Копроизведения и копределы
81
стрелки /, g (в прежних обозначениях) являются мономорфизмами, то
это верно и для стрелок универсального квадрата и, v. В этом случае
вершина г называется амальгамой для Ь и с.
Коядерная пара. Пусть / : а —>• Ъ — стрелка в категории в С.
Универсальный квадрат для пары (/, /) называется коядерной
парой для /. Таким образом, коядерная пара для / состоит из объекта
г и параллельной пары стрелок и, v : Ь —> г с областью Ь, для которой
выполнено равенство uf = bf и для любой пары ft, к : Ъ —> s из
равенства ft/ = fc/ вытекает существование единственной стрелки
t : г —>• s со свойствами tu = h и tv = к:
uf = v/,
ft/ = fe/.
Копределы. Все предыдущие примеры относятся к различным
категориям функторов и строятся по следующей схеме. Пусть С и J —
две категории (J — категория индексов, обычно малая и часто
конечная). Диагональный функтор
Л : С -+ CJ
отображает каждый объект в постоянный функтор Лс, который на
любом объекте г G J принимает значение с, а на любой стрелке из
J — значение 1С. Если / : с —> с' — некоторая стрелка из С, то
Aj — естественное преобразование Aj : Ac^r Ac', которое на любом
объекте г G J принимает значение /. Каждый функтор F : J —>■
—у С является объектом в С3. Универсальная стрелка (г, и) из F
в А называется копределом (прямым пределом или индуктивным
пределом) диаграммы функтора F. Она состоит из объекта г G С,
обычно обозначаемого г = LimF или г = ColimF, и
естественного преобразования и : F -^ Аг, универсального среди естественных
преобразований т : F -^ Ас. Поскольку Ас — постоянный функтор,
то естественное преобразование т состоит из стрелок ri : F{ —> с
в С, по одной для каждого объекта г G J, причем Tj о Fu = Ti для
каждой стрелки и : i —> j в J. В наглядном виде это означает, что
коммутативны все квадраты в следующей схематической диаграмме
(с определенной категорией J):
F! +
:iV
с.
На такой диаграмме бывает удобно отождествить все нижние
объекты. По этой причине естественное преобразование т : F -^ Ас (часто

82
Универсальные конструкции и пределы
[Гл. 3
обозначаемое просто г : F -^ с), называется конусом с основанием F
и вершиной с, см. следующий рисунок:
(все треугольники коммутативны). В этих терминах копредел для
F : J —у С состоит из объекта Lim FgCh конуса \i : F -^ ^(Lim F) с
основанием F и вершиной LimF, причем этот конус универсален: для
каждого конуса т : F -^ Ас с основанием F существует единственная
стрелка t' : Lim F —> с такая, что Ti = t'jii для каждого индекса г Е J.
Будем называть \i предельным конусом или универсальным конусом
(с основанием F).
Например, пусть J = cj = {0—)>1—)>2—)-3—)>•••}. Рассмотрим
функтор F : и —> Set, который отображает каждую стрелку из и
в некоторое вложение (подмножества в множество). Такой функтор
F — это просто возрастающая цепь множеств Fq С F\ С F^ С •.
Тогда Lim F — это объединение U всех таких множеств Fn вместе
с конусом вложений Fn —>■ U. Точно так же можно интерпретировать
объединения как частный случай копределов в Grp, Ab и других
известных категориях. Возможно, теперь читатель захочет проверить
факт, который мы вскоре докажем (упр. 5.1.8): если J — малая
категория, то любой функтор F : J —> Set имеет копредел.
Упражнения
1. Покажите, что если в категории коммутативных колец диаграмма
R^-R^S-^Sc отображениями г \-> г <8> 1,1 <g> s <—< s определяет
копроизведение.
2. Покажите, что если в категории всегда существуют (бинарные) ко-
произведения и коуравнители, то в ней всегда существуют и универсальные
квадраты. Примените этот результат в случаях Set, Grp и Тор.
3. В категории Mat г к из § 1.2 опишите коуравнитель двух m x гг-матриц
А, В (т. е. двух стрелок п —»■ m в этой категории).
4. Опишите копроизведения (и покажите, что они существуют) в
категориях Cat, Mon и Grph.
5. Пусть Е — отношение эквивалентности на множестве X. Покажите,
что множество классов эквивалентности X/Е можно описать через понятие
коуравнителя в категории Set.
6. Покажите, что для объектов а и Ъ категории С существует
копроизведение, если и только если функтор С(а, —) х С(Ъ, —) : С —»■ Set представим.
Используйте соответствие с \-ь С {а, с) х С(Ь,с).
7. (Каждая абелева группа является копределом своих конечно
порожденных подгрупп.) Пусть А — абелева группа, J a — предпорядок,
состоящий из всех конечно порожденных подгрупп S С А, упорядоченных по

3.4]
Произведения и пределы
83
включению. Покажите, что А является копределом очевидного функтора
J а —>- АЬ. Обобщите этот факт.
3.4. Произведения и пределы
Понятие предела двойственно к понятию копредела. Пусть
имеются категории С, J и диагональный функтор Л : С —>• CJ. Предел
функтора F : J —> С — это универсальная стрелка (г, и) из Л в F.
При этом объект г Е С обычно обозначается г = LimF или LimF.
Его иногда называют обратным пределом или проективным пределом
функтора F. Естественное преобразование v : Лг -^ F универсально
среди естественных преобразований т : Лс^- F, где с — объект из
С. Поскольку значения функтора Лс : J —>■ С сводятся к с, то такое
естественное преобразование т для каждого объекта г G J состоит из
одной стрелки т« : с —> Fi такой, что для любой стрелки и : г —>■ j
в категории J выполнено равенство Tj = Fu о tj. Назовем т : с—> F
конусом с основанием F и вершиной с. (Мы предпочитаем говорить
«конус с основанием F», а не «коконус».) Универсальное свойство
преобразования v состоит в следующем: это конус с основанием F
и вершиной Lim F\ для любого конуса т с основанием F и вершиной
с существует единственная такая стрелка t : с —> LimF, что Т{ = V{t
при всех г. Наглядно это изображается так:
п l ^ Lim F — Lim Fj
с ' <-j
v — предельный конус.
Fu
Здесь каждый конус представлен одним коммутативным
треугольником (из многих), вершина конуса находится наверху; существует
единственная стрелка £, которая делает коммутативными все
дополнительные треугольники (с одной вершиной внизу). Объект Lim F и его
предельный конус v : Lim F —>• F, как и любой универсальный объект,
однозначно определяются функтором F с точностью до изоморфизма
в категории С.
Свойства понятий Lim и Lim собраны в диаграмме
Lim F = Lim F
LimF = ColimF
(1)

84
Универсальные конструкции и пределы
[Гл. 3
где горизонтальные стрелки соответствуют конусам, а
вертикальные — стрелкам в С. Если пределы существуют, то имеются
естественные изоморфизмы
С (с, Lim F) = Nat (Лс, F) = Cone (с, F), (2)
Cone (F, с) = Nat (F, Л с) ^ C(Lim F, с). (3)
В различных частных случаях пределы имеют хорошо известные
названия, двойственные к названиям соответствующих копределов:
Произведения. Пусть J — дискретная категория {1,2}, а функтор
F : {1,2} —у С — это пара объектов (а, 6) из С. Его предел называется
произведением объектов а и 6 и обозначается а х 6 или а П Ь; диаграмма
предела состоит из объекта а х Ь и двух стрелок р, д, которые иногда
обозначаются рт\, pr<i и называются проекциями произведения:
а £- а х b -U Ь.
Они образуют конус с вершиной а х Ъ, и в силу данного выше
определения предела существует биекция множеств
С(с,ахЪ) **С(с,а) хС(с,Ъ), (4)
естественная по с; она отображает каждую стрелку h : с —>■ ахЬв пару
произведений (p/i, g/i). Обратно, если даны стрелки /:с-Уаи^:с-У
—>- 6, то существует единственная стрелка h : с —>■ а х Ъ такая, что
ph — j^qh — g. Будем писать
h=(f,g):c->axb
и называть h стрелкой с компонентами fug. Мы уже отметили
(в § 2.3), что произведение любых двух объектов существует в таких
категориях, как Cat, Grp, Top, Mon; в этих (и многих других)
случаях оно называется прямым произведением. Произведение в предпо-
рядке — это наибольшая нижняя грань.
Бесконечные произведения. Пусть J — некоторое множество
(= дискретная категория = категория, в которой все стрелки
единичные). Тогда функтор F : J —^ С — это просто множество
объектов aj G С, проиндексированное множеством J. Конус
с вершиной с и основанием aj — это семейство стрелок /j : с —>■ aj,
проиндексированное множеством J. Следовательно, универсальный
конус pj : Uj aj —> aj состоит из объекта П^- aj, который называется
произведением множителей aj, и стрелок pj — проекций произведения,
со следующим свойством универсальности. Для каждого семейства
(= конуса) fj : с —> aj, индексированного множеством J, существует
единственная стрелка
/ : с —у Пaj, для которой pjf = fj, j G J.

3.4]
Произведения и пределы
85
Стрелка /, однозначно определяемая этими свойствами, называется
отображением (в произведение) с компонентами fj,j Е J. При этом
{fj \i ^ J] *-> f — биекция
IIС (с, a j) S*nC(c,aj), (5)
j j
естественная по с. Здесь произведение в правой части взято в
категории С, а в левой — в категории Set (предполагается, что С —
категория с малыми hom-множествами). Отметим, что hom-функтор С (с, —)
переводит произведения в смысле С в произведения в смысле Set (см.
§ 5.4). В категориях Set, Top, Grp существуют произведения любого
семейства объектов, индексированного любым малым множеством J;
во всех случаях это обычное декартово произведение.
Степени. Если все сомножители произведения совпадают (ctj =
= bj G С при всех j), то произведение Hj ctj = Hj b называется
степенью и обозначается nj b = bJ. Имеется биекция
C(c,b)J=C(c,bJ), (6)
естественная по с. Степень в левой части взята в смысле категории
Set, где существует любая малая степень XJ (и совпадает с
множеством всех функций J —> X).
Уравнители. Пусть J = Ц. Функтор F : Ц —> С — это
параллельная пара стрелок /, g : b —> а в категории С. Предельный объект d для
F, если он существует, называется уравнителем (или ядром разности)
для fag. Диаграмма предела имеет вид
/
d -4- Ъ ^ a, fe = ge (7)
9
(стрелка е соответствует конусу а «— d —> b с вершиной d). Стрелку
предела часто также называют уравнителем для / и д; ее свойство
универсальности состоит в следующем: для каждой стрелки h : с —> Ь,
такой что fh = gh, существует единственная стрелка Ы : с —>■ d, для
которой eh' = h.
В категории Set уравнитель всегда существует; множество d имеет
вид {х G b | fx = дх}, а е : d —> b — это его вложение в качестве
подмножества в Ь. Так же описывается уравнитель в категории Тор
(причем d имеет топологию подпространства). В категории АЬ
уравнитель d стрелок fug — ядро разности гомоморфизмов / — д : b —>■ а.
Аналогично определяются уравнители любого множества стрелок
из b в а. Любой уравнитель е обязан быть мономорфизмом.
Коунив ер сальные квадраты. Пусть J = (—> • <—). Функтор F :
(—>• • ^—) —>• С — это пара стрелок 5 ^ а ^- d из С с общей кообластью
а. Конус над таким функтором — это пара стрелок из вершины с, для

Универсальные конструкции и пределы
[Гл. 3
которой коммутативен (левый) квадрат
&—«,
Ь х ad ^ d
(8)
->■ а.
Тогда универсальный конус — это коммутативный квадрат подобного
вида с новой вершиной Ь х ad и стрелками р, q (как показано справа),
такой что для любого квадрата с вершиной с существует единственная
стрелка г : с —>• 6 х ad, для которой k = pr,h = qr. Квадрат,
образованный этим универсальным конусом, называется коунив ер сальным
или декартовым квадратом г), а его вершина Ъ х ad называется
расслоенным произведением или произведением над (объектом) а. Эта
конструкция, возможная во многих категориях, вначале приобрела
значение в категории Тор. Если g : d —>■ a — отображение расслоения
(некоторого типа) с базой а, а / — непрерывное отображение в
базу, то проекция коуниверсального квадрата р — это индуцированное
отображение расслоения (того же типа).
Если существует коуниверсальный квадрат для пары
совпадающих стрелок f : Ь —> а ^г- Ь : /, то он называется ядерной парой для
/. Он состоит из объекта d и пары стрелок p,q : d —>■ b такой, что
fp — fq. '• d ~^ aJ причем любая пара ft, k : с —>• a со свойством /ft, = /fc
имеет вид ft = pr, k — qr для единственной стрелки г : с —>■ d.
Пусть J = 0 — пустая категория. Тогда существует единственный
функтор 0 —у С, а именно пустой функтор; конус над ним — просто
объект с G С (т. е. состоит лишь из вершины). Значит, универсальный
конус над 0 — это объект t из С, такой что для каждого объекта с G С
существует единственная стрелка с —у t. Иначе говоря, предел пустого
функтора в категорию С — это терминальный объект в С.
Иногда пределы определяются не для функторов, а для диаграмм.
Подробнее: пусть С — категория, UC — соответствующий граф, G —
произвольный граф. Тогда диаграмма в С вида G — это морфизм
графов D : G —> UC. Определим теперь конус \i как функцию, которая
каждому объекту г G G сопоставляет такую стрелку /^ : с —> Di из С,
что Dho^ = jjij для каждой стрелки ft : г —> j графа G. Это совпадает
с прежним определением конуса как естественного преобразования
\i : Лс^-D, если добавить замечание, что в этом определении
используется умножение стрелок в категории С, но не в области G морфизма
D. Пределом для диаграммы D теперь является универсальный конус
X:c^D.
Эта модификация определения предела ничего по существу не
меняет. Действительно, пусть свободная категория FG, порождена
графом G, а Р : G —>• U(FG) — соответствующая универсальная
:) См. сноску на с. 80. — Прим. пер.

3.4]
Произведения и пределы
87
диаграмма. Тогда каждая диаграмма D : G —> UC однозначно
записывается в виде D = UD' о Р для некоторого (единственного) функтора
D' : FG —> С. Без труда проверяется, что пределы (и предельные
конусы) для D' в точности соответствуют таковым для D.
Упражнения
1. Покажите, что в категории Set универсальный объект для f : X —>
—»■ Z и g : Y —»■ Z имеет вид {{х,у) \ х Е X, у € Y, fx = g?/}. Опишите
универсальные объекты в категории Тор.
2. Покажите, что декартово произведение над множеством индексов J
с обычными проекциями является произведением (в категорном смысле)
в Set и в Тор.
3. Пусть категория J имеет начальный объект s. Докажите, что любой
функтор F : J —>- С в любую категорию (7 имеет предел, а именно F(s).
Сформулируйте двойственный факт.
4. Докажите, что в любой категории стрелка / : а —»■ 6 является
эпиморфизмом, если и только если универсален квадрат
/ ,
а ^ Ъ
Л 1
т т
Ъ—j-э-Ь.
5. Покажите, что если в коуниверсальном квадрате (8) / является
мономорфизмом, то и q является мономорфизмом.
6. Покажите, что в категории Set ядерная пара для / : X —>- Y
определяется отношением эквивалентности Е = {(ж, х') \ х,х Е X, fx =
= fx'} вместе с подходящими отображениями Е =£ X.
7. (Ядерные пары в терминах произведений и уравнителей.) Пусть С —
категория с конечными произведениями и уравнителями. Покажите, что
каждую ядерную пару для / : а —»■ Ъ можно выразить через проекции
pi,P2 : а х а -> о в виде pie, рге, где е — уравнитель для fpi,fp2 '• а х
х а —>- 6 (см. упр. 6). Сформулируйте двойственный факт.
8. Рассмотрим следующую коммутативную диаграмму:
т
а) Пусть оба квадрата коммутативны. Докажите, что внешний
прямоугольник (с очевидными композициями вверху и внизу) универсален.
б) Если внешний прямоугольник и правый квадрат коммутативны, то
это верно и для левого квадрата.
9. (Уравнители в терминах произведений и коуниверсальных
квадратов.) Покажите, что уравнитель для f,g\h^-a можно определить с
помощью коуниверсального квадрата для
(1ь,/) :b^bxa^b: (lb,g).

88 Универсальные конструкции и пределы [Гл. 3
10. Пусть С — категория с коуниверсальными квадратами и
терминальным объектом. Докажите, что в С всегда существуют конечные
произведения и уравнители.
3.5. Категории с конечными произведениями
Мы говорим, что С — категория с конечными произведениями,
если для каждого конечного множества объектов с\,..., сп Е С
имеется диаграмма произведения, состоящая из объекта с\ х ... х сп и п
проекций pi : с\ х ... х сп —> ci (ъ = 1,... , п) с обычным свойством
универсальности. В частности, тогда в С существует произведение
пустого множества объектов: это просто терминальный объект.
Существует и произведение любых двух объектов. Диагональное
отображение 8с : с —>■ с х с определяется для любого с условиями р\8с =
— 1с = Р2$с] оно является естественным преобразованием.
Предложение 1. Пусть в категории С существует
терминальный объект, t и произведение а «— axb —>■ Ъ любых двух объектов.
Тогда в С существуют любые конечные произведения. Объекты
произведений определяют (через соответствие (а, Ъ) н-» axb) бифунктор
С х С —>• С. Для любых трех объектов а, 6, с имеется изоморфизм
ol — оса,ъ,с '• & х (Ь х с) = (а х b) x с, (1)
естественный по а,Ь и с. Для каждого объекта а имеются
изоморфизмы
А = Аа : t х а = а, g = ga : a x t = а, (2)
которые естественны по а; здесь t — терминальный объект в С.
Доказательство. Произведение одного объекта с — это просто
диаграмма с ^ с, состоящая из единичной стрелки для с; она
присутствует в любой категории. Пусть теперь для любых двух объектов
ai, a2 в С существует произведение. Если для каждой пары объектов
выбрано по одной диаграмме произведения а\ «— а\ х а<± —> ^2, то
мы получим функтор х, определив Д х /2 для стрелок Д условиями
Pi(fi х /2) = fiPi- Итерируя, можно образовать произведение трех
объектов а, 6, с, состоящее из объекта ах (bxс) и проекций, показанных
на диаграмме:
а ^ а х (Ь х с) ^ Ьх с
Проекция на а и две показанные здесь композиции определяют три
стрелки из а х {Ъ х с) — соответственно в а, Ъ и с. Из универсальности
проекций произведения двух сомножителей вытекает, что эти три
стрелки образуют диаграмму произведения для a, b, с. Диаграммы
произведения для большего числа сомножителей можно сходным
образом построить по индукции. Для трех сомножителей можно также

3.5] Категории с конечными произведениями 89
построить диаграмму произведения посредством итерации (а х b) x
х с; из единственности объекта произведения вытекает
существование единственного изоморфизма а х (Ь х с) = (а х 6) х с, который
коммутирует с данными проекциями на а, 6 и с. Это изоморфизм
а из предложения, и он естествен. Наконец, поскольку из каждого
объекта ведет единственная стрелка в терминальный объект £, то
диаграмма t «— а —у а определяет произведение объектов t и а. Ввиду
единственности объекта произведения t x а существует изоморфизм
Ла : t х а —У а, и аналогично существует изоморфизм £>а : а х £ —>> а,
причем оба они естественны. Построенные здесь изоморфизмы а, А
и q называются каноническими. □
Для конечных копроизведений верен двойственный факт; в
частности, копроизведение пустого множества сомножителей — это
начальный объект. Для т объектов clj диаграмма копроизведения
состоит из т инъекций ij : clj —У а± П ... II ат, и любое отображение
/ : а\ II ... II аш —у с однозначно определяется своими т кокомпо-
нентами fij = fj : ctj —у с (j = l,...,m). В частности, если С —
категория с конечными произведениями и конечными копроизведени-
ями, то стрелки
а\ II... II аш —у Ъ\ х ... х Ъп
из копроизведения в произведение однозначно определяются т х п-
матрицей стрелок fjk = Pkfij '• &j —* bk, где j = 1,..., m, к = 1,..., п.
В категориях конечномерных векторных пространств, где конечное
копроизведение совпадает с конечным произведением, эта матрица
выражает линейное преобразование, связывающее заданные базисы
в его области и кообласти.
В общем случае пусть С — любая категория с нулевым объектом
z (т. е. объект z одновременно и начальный, и терминальный). Тогда
любая стрелка а —У z —У Ь, проходящая через z, — это нулевая стрелка
а —У Ъ. Если в С существуют также конечные произведения и конечные
копроизведения, то имеется каноническая стрелка
а\ II... II ап —у а\ х ... х ап
из копроизведения в произведение — а именно, стрелка с единичной
п х n-матрицей (единицы на диагонали и нули в остальных местах).
Эта каноническая стрелка может быть изоморфизмом (в категориях
АЬ и Л-Mod), собственным мономорфизмом (в Тор^ и Set*),
собственным эпиморфизмом (в Grp).
Упражнения
1. Докажите, что диагональное отображение 5С : с х с —у с естественно
по с.
2. Докажите, что в любой категории с конечными произведениями
всегда коммутативны следующие диаграммы, включающие канонические

90
Универсальные конструкции и пределы
[Гл. 3
отображения а, £>, Л из формул (1) и (2):
а х (Ь х (с х с/)) —^->- (а х Ь) х (с х d) —^—>
1Ха
т
а х ((6 х с) х d) >■
t x (b x с) —^->- (t x b) х с а х (t x с)
Лх1
b х с
Ъ х с,
1хЛ
((а х 6) х с) х d
«Xl
(а х (b x с)) х d,
—^—>- (а х t) х с
QXl
3. а) Докажите, что в категории Cat существуют коуниверсальные
квадраты (см. упр. 2.6.5).
б) Покажите, что категории запятой (Ь \. С) и (С 4- °) являются
коуниверсальными квадратами в категории Cat.
4. Докажите, что в категории Cat всегда существуют малые копроизве-
дения х).
5. Пусть В — категория с (конечными) произведениями. Покажите, что
в любой категории функторов В также всегда существуют (конечные)
произведения, вычисляемые поточечно.
3.6. Группы в категориях
Вернемся к идее о представлении алгебраических тождеств
диаграммами, высказанной во введении. Пусть С — категория с
конечными произведениями и терминальным объектом t. Моноид в категории
С — это тройка (с, \i : с х с —у с, r\ : t —> с), для которой коммутативны
следующие диаграммы:
/ ч а / ч д х 1
с х (с х с) >■ {с х с) х с >■ с х с
lX/i М
с х с >■ с,
(1)
77X1 1X77
£ х с >■ с х с^ с х t
с.
(2)
(Это в точности совпадает с определением из введения, исключая
явное использование в первой диаграмме изоморфизма
ассоциативности а из (5.1).) Определим теперь группу в С как моноид (с, /i, 77) со
*) Т.е. произведения малых семейств, состоящих из малых множеств.
Прим. ред. пер.

3.6]
Группы в категориях
91
стрелкой ( : с —у с, для которой коммутативна следующая диаграмма,
где 8с — диагональное отображение:
С >■ С X С >■ С X С
I L (з)
(это означает, что ( отображает каждый элемент х Е с в правый
обратный к нему).
Посредством аналогичных диаграмм можно определить кольца
в категории С, решетки и т. п.; такая процедура применима к
любому классу алгебраических систем, который определяется операциями
и связывающими их тождествами.
Хорошо известно, что для любой группы G (в обычном смысле)
множество функций Gx также является группой при любом X;
действительно, произведение двух функций /, /' в Gx можно определить
поточечно: (/ • f')(x) = fx • f'x. В данном контексте эта конструкция
принимает следующий вид.
Предложение 1. Пусть С — категория с конечными
произведениями. Тогда объект, с является группой (соответственно
моноидом) в категории С, если и только если hom-функтор С(—,с)
является группой (соответственно моноидом) в категории функторов
Setc°P.
Доказательство. Каждая операция умножения \± на
объекте с определяет соответствующее умножение ~р на hom-множестве
С(—, с) : Сор —У Set как композицию
С(-,с) х С(-,с) Л С(-,с х с) А С(-,с),
где v — /i* = C(—,/i), а первый естественный изоморфизм существует
(см. (4.4)) в силу определения объекта произведения с х с. Обратно,
пусть дано естественное преобразование v указанного вида. Тогда по
лемме Ионеды существует единственная стрелка \i : с х с —у с, для
которой г/ = /л*. Прогон по диаграмме показывает, что /а
ассоциативно тогда и только тогда, когда ассоциативно ~р; при этом нужно
использовать определение изоморфизма ассоциативности а в
терминах коммутирования с проекциями произведения трех сомножителей.
Конец доказательства предоставляется в качестве упражнения. □
В категории функторов Set всегда существуют конечные
произведения (упр. 5.5). Поэтому даже при отсутствии конечных
произведений в категории С можно рассматривать объекты с G С, для
которых С(—,с) является группой в категории функторов. Однако я
не вижу реальной пользы в таком увеличении общности.

92
Универсальные конструкции и пределы
[Гл. 3
Упражнения
(Здесь С — категория с конечными произведениями и терминальным
объектом t.)
1. Опишите категорию моноидов в С и покажите, что в ней всегда
существуют конечные произведения.
2. Покажите, что категория групп в С — категория с конечными
произведениями.
3. Покажите, что функтор Т : В —»■ Set является группой в категории
Set , если и только если каждое множество ТЬ, где Ъ — объект из В,
является группой в обычном смысле, а каждая стрелка Т/, где / — стрелка
из В, является морфизмом групп.
4. а) Пусть А — абелева группа в категории Set. Покажите, что
соответствующее умножение А х А —»■ А, единица 1 —»■ А и взятие обратного
А ^ А являются морфизмами групп, если под А х А понимается прямое
произведение групп. Получите отсюда, что А с такими структурными
отображениями является группой в категории Grp.
б) Докажите, что каждая группа в категории Grp имеет указанный вид.
3.7. Копределы представимых функторов
Полезность представимых функторов horn (d, —) хорошо видна из
следующего основного результата о функторах со значениями в
категории множеств.
Теорема 1. Любой функтор К : D —» Set из малой категории
D в категорию множеств можно представить {каноническим
образом) как копредел диаграммы представимых функторов horn (d, —)
для объектов d из D.
Доказательство. Вначале построим для данного К искомую
категорию диаграмм (для копредела) J в виде так называемой
категории элементов из К. А именно, это категория запятой (1 \. К)
(см. диаграмму (3) в § 2.6), в которой объектами служат пары (d,ж),
где d G D,x G K(d), а стрелками / : (d,x) —> (d',x') — те стрелки
/ : d —> d' из D, для которых K(f)x = x' (более кратко, / * x = x').
Мы утверждаем теперь, что данный функтор К является копределом
диаграммы в категории (1 \. К), которая соответствует функтору
М :JD -+ SetD.
Каждый объект (d,x) переходит в horn-функтор D(d, —), а
каждая стрелка / — в индуцированное естественное преобразование
/* : D(d', —) —>• D(d, —). В силу изоморфизма Йонеды
у-1 : K(d) -+ Nat (D(d, -),K)
существует конус в категории Set с основанием М и вершиной
К, который на нижеприведенной диаграмме изображен стрелками,

3.7]
Копределы представимых функторов
93
идущими в К (внизу слева):
J: (d,x)* (d',x')
f*x = x',
f:d^d'
Мы утверждаем, что этот конус определяет копредел для D(d,—).
Во-первых, рассмотрим любой другой конус над D(d,—), вершиной
которого служит некоторый функтор L : D —> Set. Стрелки этого
конуса (стрелки в категории Set ) — это естественные преобразования
D(d, —) —у L, и в силу леммы Ионеды они имеют вид y~xz : D(d, —) —>
—> L для некоторого z G L(d), а также y~xz' : D{d!, —) —> L, где z' = fz
(поскольку это конус).
Покажем, что этот конус с вершиной К универсален. Нужно найти
единственное естественное преобразование в : К —>■ L, переводящее
первый конус во второй. Для этого возьмем произвольный объект
х е K{d) и рассмотрим объект (d,x) G Jop (как в верхней части
диаграммы (1)). Положим
6dx = z
для объекта z G L(d), фигурирующего в естественном преобразовании
y~xz из конуса для L. Чтобы показать, что в естественно, рассмотрим
любую стрелку / : d —>• d!, для которой fx = x'. Тогда и fz = z', а так
как преобразование у~х естественно, то f(y~1z) = y~1(fz) = y~1z'.
Следовательно, в естественно. Его единственность очевидна. □
Двойственное рассуждение показывает, что любой контравариант-
ный функтор Dop —> Set можно представить как копредел диаграммы
представимых контравариантных функторов hom (—, d).
Если С — малая категория, то контравариантный функтор
F : Сор —> Set часто называют предпучком. Чтобы мотивировать
это название, рассмотрим ситуацию, когда С — категория открытых
множеств U некоторого топологического пространства, F(U) —
множество гладких (в некотором смысле) функций на U, а включению
V С U соответствует отображение F(U) —У F(V), которое заменяет
функцию, определенную на U, ее ограничением на V. Категория
Set всех таких функторов (предпучков) часто обозначается
С. Некоторые из таких функторов (со свойством «взаимности»)
называются пучками (см. Mac Lane, Moerdijk [1992]).

94
Универсальные конструкции и пределы
[Гл. 3
Замечания
Японский математик Н. Ионеда впервый сформулировал лемму,
носящую его имя, в 1954 г. (частное сообщение Маклейну). С течением времени
ее значение возросло.
Представимые функторы, вероятно, впервые появились в топологии
в виде универсальных примеров, таких как универсальные примеры
когомологических операций (например, при вычислении Ж. П. Серром в 1953 г.
когомологий по модулю 2 пространств Эйленберга-Маклейна).
Универсальные стрелки единственны лишь с точностью до
изоморфизма; возможно, именно из-за отсутствия абсолютной единственности
это понятие формировалось медленно. Примеры существовали в течение
долгого времени; решительный шаг был сделан в работе (Samuel [1948]),
где действительно сформулировано общее понятие универсальной
стрелки; затем Бурбаки придали этому общему понятию широкую известность.
Примерно тогда же была высказана идея, что обычное декартово
произведение можно описать на основе свойства универсальности его проекций
(Mac Lane [1948, 1950]). С другой стороны, понятия предела и копредела
имеют долгую историю в виде разнообразных конкретных примеров. Так,
копределы применялись при доказательстве теорем о представлении
бесконечных абелевых групп в виде объединения их конечно порожденных
подгрупп. Пределы (по упорядоченным множествам) появляются в теории
р-адических чисел Гензеля и при построении гомологии и когомологий
Чеха посредством предельных процессов, формализованных Понтрягиным.
Стремление разобраться в естественных изоморфизмах, связанных с
такими пределами, лежало в основе первой статьи Эйленберга-Маклейна по
теории категорий (Eilenberg, Mac Lane [1945]). Э. X. Мур при общем построении
анализа (около 1913 г.) использовал пределы по некоторым направленным
множествам. Во всех этих классических примерах возникали пределы лишь
для функторов F : J —»■ С, где J — линейно или частично упорядоченное
множество. В работе (Кап [1958]) был сделан шаг к рассмотрению пределов
для произвольных функторов; в книге Freyd [1964] для общего случая
используется термин корень, а не предел. Его последователи предпочли
распространить и на общий случай первоначальный термин предел. Свойства,
специфичные для пределов по направленным множествам, будут изучены
в гл. 9.

Глава 4
СОПРЯЖЕННЫЕ ФУНКТОРЫ
4.1. Сопряжение
Мы определим теперь важнейшее понятие, введенное Каном,
которое позволяет по-новому сформулировать свойства свободных
объектов и других универсальных конструкций. Чтобы понять
необходимость этого, вспомним построение векторного пространства Vx с
базисом X (§ 3.1). Фиксировав поле К, рассмотрим следующие
функторы:
v
и
Здесь U — забывающий функтор, т. е. U(W) для произвольного
векторного пространства W обозначает множество всех его векторов;
если X — произвольное множество, то через V(X) обозначается
векторное пространство с базисом X. Таким образом, векторы из V(X) —
это формальные линейные комбинации Ег^, где Т{ Е К — скалярные
коэффициенты, Х{ Е X, а операции над векторами определены
очевидным образом. Каждая функция д : X —У U(W) продолжается до
единственного линейного преобразования / : V(X) —> W, имеющего
вид fiYiViXi) = T<ri(gxi) (т.е. формальные линейные комбинации
из V(X) отображаются в реальные линейные комбинации из W).
Для этого соответствия ф : д ь->- / существует обратное, а именно
(р : f \-> X — ограничение функции / на1; таким образом, имеется
биекция
ip : VctK(V(X),W) ^ Set (X, U(W)).
Биекция (р = (fx,w определяется одинаковым образом для всех
множеств X и всех векторных пространств W. Это означает, что
отображения (fx,w являются компонентами естественного
преобразования (р, если рассматривать обе части указанной эквивалентности как
функторы между X и W. Достаточно проверить отдельно
естественность по X и по W. Естественность по X означает, что для каждой
стрелки h : X' —> X коммутативна диаграмма
VctK(V(X),W) —^ Set (X, U(W))
(Vh)*
h*
VctK(V(X'),W) —^ Set (X', U(W)),

96
Сопряженные функторы
[Гл.4
где h*g = д о h. Но это выводится из определения биекции ср
посредством стандартных выкладок. То же относится и к естественности по
W.
Рассмотрим еще несколько подобных примеров.
Свободная категория С = FG над данным (малым) графом G —
это функтор Grph —> Cat, который связан с забывающим
функтором Cat —> Grph таким образом, что каждый морфизм графов
D : G —> UB продолжается до единственного отображения категорий
D' : FG —> В, причем соответствие D ь->- D' является естественным
изоморфизмом
Cat (FG, В) ** Grph (G, UB).
В категории малых множеств каждую функцию двух переменных
д : S х Т —» R можно рассматривать как функцию ipg : S —> hom (T, R)
одного переменного (принимающего значения в 5), причем значения
этой функции зависят от второго переменного (принимающего
значения в Т); а именно, [((pg)s] t = g(s,t), где s G 5, t G Т. Следовательно,
(p является биекцией:
if : hom (S xT,R)^ hom (5, hom (Г, R)).
Она естественна по 5, T и R. Если фиксировать множество Т и
определить функторы F, G : Set —> Set по формулам F(S) = 5 х Т, G(i?) =
= hom (T, i?), то биекция принимает вид
hom (F(S),R) S* hom (5, G(R)).
Теперь она естественна по S и по Л, и видно сходство с предыдущими
примерами.
Аналогично, если А, В и С — модули над коммутативным кольцом
К, то имеется изоморфизм
hom (А ек В, С) ^ hom (A, homK(B, С)),
естественный по всем трем переменным.
Определение. Пусть АиХ — некоторые категории.
Сопряжение между X и А — это тройка (F, G, if) : X —^ А, где F и G —
функторы
а функция (^ каждой паре объектов х Е X, а Е А сопоставляет
биекцию множеств
<р = <рх,а : A(Frr, a) ^ X(x, Go), (1)
естественную по ж и по а.
Здесь левая часть A(Fx, a) — это бифунктор
-тгглъ л Fop xld hom <->, .
Хор х А >■ Аор х А >■ Set,

41]
Сопряжение
97
который каждую пару объектов (ж, а) отображает в hom-множество
A(Fx, а). Правая часть — это аналогичный бифунктор Хор х А —> Set.
Поэтому естественность биекции ср означает, что для всех к : а —> а'
и h : х —у х' коммутативны диаграммы
A(Fx,a) -
к*
т
A(Fx,a')
-X(x,Ga)
(Gk),
•X(x,Ga')
A{Fx,a)
(Fh)*
A(Fx',a)
■X(x,Ga)
\h* (2)
■X(x',Ga),
где к* — сокращение для A(Fx, к) — операции умножения на к, и h* =
= X(h,Ga).
Подразумевается, что все hom-множества в категориях X и А
малы. В противном случае нужно просто расширить Set до подходящей
категории множеств Ens.
Сопряжение можно описать и без помощи hom-множеств —
непосредственно в терминах стрелок. Это биекция, которая каждой
стрелке / : Fx —> а сопоставляет стрелку iff = rad / : х —> Ga,
сопряженную к f справа, причем условия естественности (2), имеющие вид
if (к о /) = Gk о <р/, ip{f о Fh) = iff oh,
(3)
выполнены для всех / и для всех стрелок h : х' —>- х и к : а —>- а'. Это
равносильно естественности преобразования у?-1; иначе говоря, при
всех h,k и д : х —>■ Ga должны выполняться равенства
<Р
-\дК) = уГ1^ о F/l, if-^Gk og)=ko ^(g).
(4)
В описанной ситуации функтор F называется левым
сопряженным для G, а G — правым сопряженным для F. (Некоторые авторы
пишут F —У G; другие говорят, что F сопряжен к G, а G косопряжен
kF, но некоторые говорят и наоборот; поэтому мы будем
придерживаться терминов левый и правый сопряженный.)
Каждое сопряжение определяет универсальную стрелку. Именно,
в формуле (1) положим а = Fx. Тогда в hom-множестве из левой части
содержится единичная стрелка 1 : Fx —> Fx; ее (р-образ обозначим т\х.
Ввиду предл. 1 Ионеды из § 3.2 г)х является универсальной стрелкой
г]х : х -> GFx, j]x = if{lFx)
из х Е X в G. При сопряжении такая универсальная стрелка
сопоставляется каждому объекту х. При этом функция х \-> г)х является
естественным преобразованием 1х —> GF', поскольку коммутативна
любая диаграмма
х' —^ GFx'
h GFh
GFx.

98
Сопряженные функторы
[Гл.4
Это доказывается следующей выкладкой:
GFh о <p(lFx,) = <p(Fh о lFx,) = <p(lFx о Fh) = ip(lFx) o ft,
которая основана на уравнениях (3), означающих, что ср естественно.
В наглядном виде это выражается коммутативной диаграммой
A(Fx', Fx') -^—^ A(Fx', Fx) i—^- A(Fx, Fx)
X(x',GFx')
>■ X(V, GFx) * X(x, GFx),
(GFh), V ' J h* V ' У'
где ft* = X(h, 1) и ft* = X(l, ft).
Биекция (p может быть выражена в терминах стрелок г\х, а именно
ip(f) = G(f)r]x для всех / : Fx -> a; (5)
действительно, ввиду условий естественности (3) имеем
<£(/) = <Р(/ ° 1Fx) = Gf о y?lFa. = G/ о туж.
Мы наглядно изобразим эту выкладку, подставив единичную стрелку
1 в коммутативный квадрат
A(Fx,Fx)
A(Fx,a)-
■X{x,GFx)
(Gf),
V
■X(x,Ga)
lb
^Vx
f oil ^<p/ = Gf oj]x.
В силу двойственности, сопряжение определяет универсальную
стрелку из F. В самом деле, в формуле (1) положим х = Ga. Тогда
в правом hom-множестве содержится единичная стрелка 1 : Ga —> Ga;
ее образ при отображении (р-1 обозначается еа:
ea\FGa^ а, га = ^_1(1<-а), а G А,
и является универсальной стрелкой из F в а. Как и выше, г — это
естественное преобразование г : FG -^ 1а •> причем
ср~1(д) = еа о Fg для всех д : ж —>■ Ga.
Наконец, возьмем ж = Ga. Тогда из еа = ср~1(1оа) ввиду формулы (5)
вытекает, что
iGa = <p(ea) = G(ea) о ^Ga-

41]
Сопряжение.
99
Это значит, что естественное преобразование
G -L-^ GFG -^ G
является тождественным.
В итоге доказана следующая теорема.
Теорема 1. Сопряжение (F,G,if) : X —^ А определяет:
1) естественное преобразование r\ : Ix -^GF такое, что для
каждого объекта х стрелка г\х является универсальной стрелкой из х в G
и для каснсдой стрелки f : Fx —> а правая сопряэюенная к ней имеет
вид
iff = Gf oj]x :x -> Ga; (6)
2) естественное преобразование г : FG —> 1а такое, что каэюдая
стрелка га является универсальной стрелкой из а в F, а каэюдая
стрелка g : х —>■ G имеет левую сопряженную
^~Х9 = eaoFg:Fx^a. (7)
При этом следующие композиции являются тождественными
преобразованиями (функторов G и F соответственно):
G^^GFG^^G, FJ^FGF^L^R (8)
Назовем г\ единицей (unit), а г — коединицей (counit) сопряжения.
(В прошлом мы употребляли термины сопряжение вперед (front
adjunction) и сопряжение назад (back adjunction).)
Заданное сопряжение на самом деле можно полностью определить
той или иной частью перечисленных данных. Именно, справедлива
следующая теорема.
Теорема2. Любой из следующих наборов данных полностью
определяет сопряжение (F,G,if) : X —^ А.
1) Функторы F,G и естественное преобразование г\ : 1х —> GF
такое, что каэюдая стрелка г\х : х —> GFx универсальна как стрелка
из G в х. В этом случае if имеет вид (6).
2) Функтор G : А —» X и для каждого х Е X — объект Fqx E А
и универсальная стрелка г\х : х —> GFqx из х в G. Тогда функтор F
имеет функцию объектов F0 и определяется для стрелки h : х —>• х'
по формуле GFh о г\х — т]х' о h.
3) Функторы F,G и естественное преобразование г : FG -^ 1а
такое, что каэюдая стрелка га : FGa —>• а универсальна как стрелка
из F в а. В этом случае if-1 определяется по формуле (7).
4) Функтор F : X —» А и для каждого a Е А — объект G$a Е X
и стрелка во : FG^a —>• а, универсальная как стрелка из F в а.
5) Функторы F,G и естественные преобразования г\ : 1х —> GF
и г : FG -^ 1а такие, что обе композиции из (8) являются
тождественными преобразованиями. В этом случае if определяется
формулой (6), a if-1 — формулой (7).

100
Сопряженные функторы
[Гл.4
Ввиду п. 5) мы часто будем обозначать сопряжение (F, G, ср) как
(F,G,r,,e):X^A.
Доказательство. Универсальность стрелки г)х означает, что
для каждой стрелки / : х —> Ga существует ровно одна стрелка д,
для которой коммутативна диаграмма
Fx х —^->. GFx
; 9
У
а,
Это в точности означает, что 0(d) = Gg о г\х определяет биекцию
в: A(Fx,a) -+X{x,Ga).
Эта биекция в естественна по ж, поскольку естественно ту, и
естественна по а, поскольку G — функтор. Следовательно, определено
сопряжение (F, G,#). Если т\ — единица сопряжения (F, G,(p), то в =
Набор (2) можно расширить до (1), и потому он определяет
сопряжение. В самом деле, в случае (2) для каждого объекта х G X
дана универсальная стрелка (Fqx, t]x); покажем, что существует ровно
один способ превратить Fq в функцию объектов такого функтора
F, что преобразование т\ : 1х —> GF будет естественным. Именно,
из универсальности т\х вытекает, что для каждой стрелки h : х —>
—у х' существует единственная (прерывистая) стрелка, которая делает
коммутативной следующую диаграмму:
F0x х ^ GF0x
\h
У Y У
F0x' x'^^GFox'.
Эту стрелку возьмем в качестве морфизма Fh : Fqx —> Fqx';
коммутативность означает, что преобразование г) естественно. Легко
проверить, что F при таком определении является функтором.
В силу двойственности доказываются пп. 3) и 4).
Чтобы доказать (5), определим с помощью г) и г функции
A(Fx,a) ^=^ X(x,Ga),
в
положив iff = Gf о т]х при всех / : Fx —> а и вд = га о Fg при
всех д : х —> Ga. Поскольку G — функтор, а т\ — естественное
преобразование, то
срвд = Gsa о GFg о цх = Cr)a ° ЦОа ° 9-

41]
Сопряжение
101
Но мы приняли допущение (8), т.е. Gea о j]Ga = 1. Поэтому срв =
= id. Двойственно, в(р = id. Значит, отображение ip является биекцией
(и в обратно ему). Очевидно, что эта биекция естественна и потому
является сопряжением (и если мы начали с сопряжения, то ср с ним
совпадает). □
Эта теорема очень полезна. Например, пп. 2) и 4) позволяют
построить сопряжение, если дана универсальная стрелка из любого
объекта (или в любой объект) данной категории. В частности, категория
С имеет конечные произведения, если для любой пары (a, b) Е С х
х С существует универсальная стрелка из А : С —>• С х С в (а, Ь). Из
доказанной теоремы мы получаем, что функтор (а, Ь) —> а х Ь, который
определяет объект произведения, в действительности является
функтором С х С —>■ С, причем сопряжен справа диагональному функтору
А:
ip: (СхС)(Ас,(а,Ъ)) ^С(с,ахЪ).
Вспомнив определение стрелок в категории С х С, получаем:
if : С(с, а) х С(а, Ь) ^ С (с, а х Ь).
Коединица этого сопряжения (положим с = а х Ъ справа) является
стрелкой (ахЪ,ахЪ) —>• (а, Ь); иначе говоря, это пара стрелок а ^— ах
х Ъ —> Ь, а именно проекции произведения р : а х b ^ а и q : ахЪ ^ Ъ.
Сопряжение (р~г отображает каждую стрелку / : с —>■ а х Ъ в пару
(pf,qf), тем самым ip определяется по коединице е.
Аналогично, если категория С имеет копроизведения (а, Ь) н-» аН6,
то они определяют функтор копроизведения С хС —> С, сопряженный
слева к А:
С(аиЪ,с)**(СхС)((а,Ъ),Ас).
Точно так же, все другие примеры пределов (если эти пределы
существуют в данной категории) можно интерпретировать как примеры
сопряженных функторов. Во многих дальнейших приложениях
окажется, что доказать универсальность — это легкий способ доказать
существование сопряженного функтора.
С другой стороны, в п. 5) сопряжение описано посредством двух
простых условий относительно его единицы и коединицы:
Fr] r]G
F >■ FGF GFG ■< G
sF
(9)
Эти треугольные тождества не содержат явно объектов категорий
А и X и потому удобны в обращении. Как мы вскоре увидим, это
полезно при рассмотрении свойств сопряжения. (Некоторые авторы
в ситуации (9) называют преобразование г\ квазиобратным для е.)
Следствие 1. Если два функтора F, F' сопряжены слева к
функтору G : А —» X, то они естественно изоморфны.

102
Сопряженные функторы
[Гл.4
Доказательство сводится к использованию того факта, что
универсальная стрелка (подобно начальному объекту) единственна с
точностью до изоморфизма. Именно, сопряжения (F,G,ip) и {F',G,if')
сопоставляют каждому х две универсальные стрелки х —> GFx их-}
—> GF'x. Поэтому существует единственный изоморфизм вх : Fx —>■
—>• F'x, для которого G0X о г\х = г]'х; легко проверить, что
преобразование 0 : F —> F' естественно.
Следствие 2. Функтор G : А —» X имеет левый
сопряженный, если и только если для каждого объекта х Е X функтор
X(x,Ga) представим как функтор, действующий на a Е А. Если
if : A(Fqx,cl) = X(x,Ga) — представление этого функтора, то Fq
является функцией объектов функтора, сопряженного слева к G,
причем биекция if естественна по а и реализует сопряжение.
На самом деле это переформулировка п. 2) теоремы 2.
Равносильно, функтор G имеет левый сопряженный, если и только если
из любого х Е X существует универсальная стрелка в G.
Предоставляем читателю сформулировать двойственные
утверждения.
Функторы, сопряженные аддитивным, аддитивны.
Теорема 3. Пусть аддитивный функтор G : А —» М между АЪ-
категориями А и М имеет левый сопряэюенный F : М —» А. Тогда
F аддитивен, а биекции сопряжения
if : A(Fm,a) ^ M(m,Ga)
являются изоморфизмами абелевых групп {при всех т Е M, a Е А).
Доказательство. Пусть г) : I —> GF — единица сопряжения.
Тогда if имеет вид iff = Gf о т\ш для произвольной стрелки / : Fm —>■
—у а. Если имеется также стрелка /' : Fm —> а, то ввиду аддитивности
функтора G получаем
4>U + Л = GU + Л Vrn = (Gf + Gf) Vrn =
= Gf о цш + Gf о цш = iff + ^f.
Таким образом, if является морфизмом абелевых групп. Возьмем
теперь g,g' : m —>• п в категории М. Поскольку преобразование г\
естественно, то
GF(g + g') о r]m = цп(д + д') = г]пд + г)пд'.
С другой стороны, ввиду аддитивности функтора G
G(Fg + Fg') о Vm = (GFg + GFg') Vm =
= GFg or]m-\- GFg' о цш = ^ + 77^.
Совпадение этих двух результатов показывает с учетом
универсальности стрелки г\ш, что F(g + д') = Fg + Fg'. Значит, функтор F
аддитивен. □

4.2]
Примеры сопряженных функторов
103
В силу двойственности, если функтор сопряжен справа
аддитивному функтору, то он аддитивен.
Упражнения
1. Покажите, что к теореме 2 можно добавить еще один пункт (и
двойственный ему):
6) Функтор G : А —»■ X и для каждого х Е X — представление срх
функтора Х(х, G-) : А —»> Set.
2. (Lawvere.) Пусть даны функторы G : А—Ь X тя. F : X —Ь А. Покажите,
что любое сопряжение (F, G, ср) можно описать как изоморфизм в между
категориями запятой, для которого следующая диаграмма коммутативна:
в : {F 4 1А) * (1х 4- G)
X х А = X х А.
Здесь компонентами вертикальных стрелок являются функторы
проектирования Р и Q из (5), § 2.6.
3. Для сопряжения (^, х,(р) (произведение сопряжено справа
диагональному функтору) покажите, что если с Е С, то единица дс : с —»■ с х с —
это единственная стрелка, для которой коммутативна диаграмма
(Эту стрелку дс часто называют диагональной стрелкой объекта с.) В
случае С = Set покажите, что дсх = (х,х) при любом х Е с.
4. (Pare.) Пусть даны функторы G : А —^ X, К : I 4 i и
естественные преобразования е : KG —> icU, £ : idx —> GX, причем Ge •
• £>£? = \g '• G—> GKG —t G. Докажите, что eK • i^£> : К ^ К является
идемпотентом в А и что G имеет левый сопряженный, если и только
если этот идемпотент расщепляется. А именно, если еК • Kg = а • /3, где
(За = 1,/3 : К ^ F, то функтор F сопряжен слева к G с единицей G/3 • g
и коединицей е • olG.
4.2. Примеры сопряженных функторов
В этом параграфе содержатся различные примеры сопряженных;
вначале приведем таблицу левых сопряженных для наиболее
известных забывающих функторов (табл. 1).
Аналогично описываются коединицы. Пусть, например,
свободный Л-модуль FX порожден элементами jx = (ж), где х Е X. Его
элементы записываются как конечные суммы Ег^ж^), где Т{ Е R.
Тогда для любого Л-модуля А коединица г а • FUA —у А имеет вид
Y,ri(a,i) н-» &i<2i (линейные комбинации в А). Иначе говоря, г а — это

104
Сопряженные функторы
[Гл.4
Таблица 1.
Забывающий функтор
U : R-Mod -^ Set
U : Cat -^ Grph
U : Grp -> Set
С/ : Ab -> Set
С/ : Ab -^ Grp
С/ : Я-Mod -^ Ab
С/ : Rng -^ Моп
см. упр. 1, § 3.1
U : К - Alg -^ К - Mod
С/ : Fid -^ Domm
(см. § 3.1)
С/ : Compmet -> Met
Левый сопряженный F
X \-> FX. Свободный R-
модуль с базисом X
G \-ь CG. Свободная
категория над графом G
X \-ь FX. Свободная
группа над X
X \-ь FaX. Свободная
абелева группа над X
G ь+ G/[G, G]. Фактор по
коммутанту
А \ч> Я0 А
М \-> Z(M)
(целочисленное) моноидальное
кольцо
V \-> TV. Тензорная
алгебра над V
D \-> QD. Поле частных
Пополнение метрических
пространств
Единица сопряжения
j : X -+ UFX
(см. § 3.1). Вложение
образующих
G -> UCG. Вложение
образующих
X -> UFX. Вложение
образующих
Вложение
образующих
G -> G/[G, G].
Проекция на фактор по
коммутанту
А^ U(R®A)
М -+ UZ(M)
т \-> т
V С TV. Вложение
образующих
D С UQD. Вложение
а \-> а/1
(§ зл)
стандартный эпиморфизм на произвольный Л-модуль из свободного
модуля, натянутого на его элементы как на образующие.
Теперь перечислим левые и правые сопряженные (которые не
обязательно существуют в каждой категории С) для диагональных
функторов; в случае С = Set укажем также единицу (табл. 2).
В случае предела вид единицы зависит от числа связных
компонент в категории J. Категория называется связной, если в ней для
любых двух объектов j,k Е J существует конечная
последовательность стрелок, соединяющая их:
j = jo -)► ji <- j2 -> > hn-i <~ hn = к (возможны оба направл.);
см. упр. 7 и 8.
Двойственные функторы дают новые примеры. Пусть У, W —
векторные пространства над полем К. Дуализация D — это контрава-
риантный функтор из Vet в Vet, который на объектах равен DV =
= Vet (У, К) с обычной структурой векторного пространства, а на
стрелке h : У —>• W имеет вид Dh : W —>• У, где (Dh)f = fh для
любого линейного отображения / : W —>■ К. Функция
<р = <pvw : Vet (У, Vet (W, К)) -> Vet (W, Vet (У, К))
(1)

4.2]
Примеры сопряженных функторов
105
Таблица 2.
Диаг. функтор Сопряженные
А : С —> С х С Левый: копроизведе-
ние П : С х С -> С
(а, 6) i->- a II 6
Правый: произведение
П : С х С^ С
(й,&)ИйХ&
С —»■ 1 Левый: начальный
объект s
Правый:
терминальный объект t
A'.C^r С^ Левый: коуравнитель
(3.3.6)
(3.4.7)
А : С -> С*
A:C^CJ
(/? 9) ^ объект ко-
уравнителя е
Правый: уравнитель d
(/? 9) ^ объект
уравнителя
Левый: Вершина унив.
квадрата (7), § 3.3
Правый: Вершина коу-
нив. квадрата (8), § 3.4
Левый: объект
копредела
Правый: объект
предела
Единица
вложения
г:й->йП&
j : b -> а П b
Диаг. отобр.
8 с '• с —» с х с
х ь-» (ж, ж)
t
Коединица
свертывающее
отобр. сПсчс
гх \-t x,jx \-> х
проекции
р : а х b \-> a
q : а X b \-> b
Коуравн. Единичная
стрелка стрелка
(uf,u)
if, 9) —> (е,е>1:с->с
Единичная Уравн. стрелка
стрелка {d, d) —» (/, g)
Универс.
конус
Универс. конус
определяется для h : V —> DW по формуле [(cph)w] v = (hv)w при всех
г> G V, w G W. Поскольку отображение ipv,w<Pw,v ~ тождественное,
то каждое ip является биекцией. Ее можно превратить в сопряжение
следующим образом. Контравариантный функтор D порождает два
различных (ковариантных!) функтора с одинаковой функцией
объектов:
D : Vctop -+ Vet, Dop : Vet -+ Vctop,
которые определяются (как обычно) для стрелок /iop : W —> V
и h : V —>• W по формулам
Dhop = Dh : DW -+ DV; Doph = (Dh)op : DV -+ DW.
Биекцию if из формулы (1) теперь можно записать как соответствие
Vctop(DopW, V) ** Vet (W, DV), (2)
естественное по V и W. Следовательно, функтор D сопряжен слева
к D. (Предупреждение: он не сопряжен D справа, см. § 5.5, упр.
2.) Пусть к,\у • W —>■ DDW — каноническое отображение во второе

106
Сопряженные функторы
[Гл.4
сопряженное пространство. Тогда единица сопряжения (положим V =
= DopW в формуле (2)) совпадает с этим отображением: r\w —
= к\у • W —>• DDopW, а коединица — это стрелка гу : DopDV —>• У из
Vctop, которая на самом деле равна еу — (к,у)ор с тем же к,.
Этот пример показывает, каким образом сопряжения могут
заменять изоморфизмы категорий. Для конечномерных векторных
пространств D и Dop являются изоморфизмами; в общем случае это
неверно, но D остается правым сопряженным для Dop.
Этот пример имеет отношение и к сопряженным для других кон-
травариантных функторов. Два контравариантных функтора S : А —У
—> X и Т : X —> А сопряжены справа (Freyd), если имеется биекция
А(а,Тх) = X(x,Sa), естественная по а и по х. Мы не нуждаемся
в этом термине, поскольку S и Т можно заменить ковариантными
функторами S : Аор ч!иГ: Хор —> А и построить двойственный
функтор 5ор : А —> Хор, также ковариантный. Тогда предыдущая
естественная биекция принимает вид Хор(5ора,ж) = А(а,Тх) и,
таким образом, функтор 5ор сопряжен слева (в нашем смысле) Т. Это
равносильно тому, что Тор сопряжен слева к S. Но это не всегда
эквивалентно тому, что Т и S сопряжены справа.
Три следующих параграфа посвящены трем другим типам
сопряженных. Левый сопряженный функтору вложения (полной
подкатегории) называется рефлектором; другие частные виды сопряженных —
это эквивалентности категорий. Ниже в упражнениях приведены
еще некоторые любопытные примеры сопряженных функторов; в
ряде случаев требуется знание соответствующей тематики. В работе
(Goguen [1971]) показано, что для автомата с конечным числом
состояний функтор минимальная реализация сопряжен слева к функтору
поведение. Приглашаем читателя поискать и свои собственные
примеры.
Упражнения
1. Пусть V — векторное пространство над полем К. Тогда можно
построить внешнюю алгебру E(V), которая является градуированной
антикоммутативной алгеброй. Покажите, что функтор Е сопряжен слева
соответствующему забывающему функтору (который не является унивалентным).
2. Покажите, что функтор U : R-NLod —»■ Ab имеет не только левый
сопряженный А \-> R © А, но и правый сопряженный А \-> homz (R, А).
3. Пусть IjIgk — категория всех (малых) алгебр Ли L над полем К,
в которой стрелками являются морфизмы if-модулей, сохраняющие лиево
умножение (а, Ь) \-> [а,Ь]. Пусть функтор V : AlgK —»■ Liex каждой
ассоциативной алгебре А сопоставляет алгебру Ли VА на том же векторном
пространстве с умножением [a, b] = ah — Ъа при а, Ъ Е А. С помощью
теоремы Пуанкаре-Биркгофа-Витта покажите, что функтор Е, где EL —
обертывающая ассоциативная алгебра для L, сопряжен слева к V.
4. Пусть Rng7 обозначает категорию колец R, не обязательно имеющих
единицу по умножению. Покажите, что стандартная процедура
присоединения к R единицы порождает левый сопряженный для забывающего
функтора Rng —»■ Rng7 (забывающего наличие единицы).

4.3]
Рефлективные подкатегории
107
5. Рассмотрим моноид М как дискретную категорию, объектами
которой являются элементы х Е М. Тогда умножение в М становится
бифунктором р : М х М —> М. Покажите, что если М является группой, то
переход к обратному элементу определяет правые сопряженные к функторам
р(х,—) и р(—,у) :М —»■ М. Обратный вопрос: означает ли наличие таких
сопряженных, что моноид является группой?
6. Опишите единицы и коединицы для универсального и коуниверсаль-
ного квадрата.
7. Пусть категория J является дизъюнктным объединением (копроизве-
дением) 11J к категорий Jk, где индекс к пробегает некоторое множество К.
Инъекции копроизведения обозначим Ik '• J к —>- J. Тогда каждый функтор
F : J —»> С определяет функторы Fk = Flk : Jk —> С.
а) Докажите, что LimF — П& LimF/., если существуют пределы в
правой части.
б) Покажите, что любая категория J является дизъюнктным
объединением связных категорий (которые называются ее связными
компонентами).
в) Отсюда выведите, что все пределы можно получить из произведений
и пределов в связных категориях.
8. Пусть категория J связна, а Л.с : J —>- С — постоянный функтор.
а) Докажите, что Lim Лс = с и Colim Лс = с.
б) Опишите единицу для правого сопряженного С Л. : С —>- С .
9. (Smythe.) Пусть функтор О : Cat —»■ Set сопоставляет каждой
категории С множество ее объектов. Покажите, что он имеет левый сопряженный
D, который сопоставляет каждому множеству X дискретную категорию на
X, a D в свою очередь имеет левый сопряженный, который сопоставляет
каждой категории множество ее связных компонент. Покажите также, что
О имеет правый сопряженный, который сопоставляет каждому множеству
X категорию с множеством объектов X и с единственной стрелкой в каждом
hom-множестве.
10. Пусть категория С имеет коядерные пары и уравнители, а функтор
К : С2 —>- С^ сопоставляет каждой стрелке из С ее коядерную пару.
Покажите, что он имеет правый сопряженный, который каждой параллельной
паре стрелок сопоставляет ее уравнитель.
11. Пусть С имеет конечные копроизведения и а Е С. Покажите, что
проекция Q : (а 4- С) —»■ С категории запятой (Q(a —> с) = с) имеет левый
сопряженный вида с4 (a4allc).
12. Пусть X — некоторое множество, С — категория со степенями
и костепенями. Докажите, что костепень с \-> X • с сопряжена слева со
степенью с4 сх.
4.3. Рефлективные подкатегории
Для многих забывающих функторов из списка в § 4.2 коедини-
ца сопряжения г : FU -^ 1а сопоставляет каждому объекту а Е А
стандартный эпиморфизм га : F(Ua) —> а, отображающий свободный
объект на а. Это общий факт. Именно, если правый сопряженный G
унивалентен, то каждая коединица сопряжения га является
эпиморфизмом.
Теорема 1. Пусть (F,G;rj,e) : X —>• А — некоторое
сопряжение. Тогда: 1) функтор G унивалентен, если и только если каждая

108
Сопряженные функторы
[Гл.4
компонента га коединицы г является эпиморфизмом; 2) функтор
G полон, если и только если каждая компонента га является
мономорфизмом и расщепляется. Как следствие, G полон и унивалентен,
если и только если каждая компонента еа является изоморфизмом
FGa ^ а.
В доказательстве используется следующая
Лемма. Пусть /* : А(а, —) -^ А(Ь, —) — естественное
преобразование, индуцированное стрелкой f : Ъ —>■ а категории А. Тогда /*
мономорфно, если и только если f эпиморфна. С другой стороны,, /*
эпиморфно, если и только если f мономорфна и расщепляется (т. е.
имеет левую обратную стрелку).
Отметим, что соответствие /* н-» / — это биекция
Nat (А(а, —),А{Ъ, —)) = А{Ъ, а) из леммы Йонеды.
Заметим также, что для любых функторов S,T : С —>- В = Set
естественное преобразование т : S -^ Т эпиморфно (соответственно,
мономорфно) в категории Вс, если и только если каждая компонента
тс : Sc —> Тс эпиморфна (соответственно мономорфна) в категории В;
это можно получить из упр. 4, § 3.4, вычислив универсальный квадрат
поточечно, как в упр. 5, § 3.5.
Доказательство. Если h G А(а,с), то f*h = hf. Поэтому
первое утверждение как раз означает, что стрелка / эпиморфна. Если
отображение /* эпиморфно, то существует стрелка ho : а —> Ь, для
которой f*ho = hof = 1 : b —> b, т. е. / имеет левую обратную стрелку.
Обратное утверждение очевидно.
Теперь докажем теорему. Применим лемму Йонеды к
естественному преобразованию (функция стрелок функтора G, затем
сопряжение)
А(а, с) ^> X(Ga, Gc) ^ A(FGa, с).
Это преобразование определяется (положим с = а) образом стрелки
1 : а —> а, и это в точности — определение коединицы sa : FGa —>■
—> а. Но Lp~x является изоморфизмом, поэтому данное естественное
преобразование эпиморфно или мономорфно, если каждое Ga?c
соответственно инъективно или сюръективно — иначе говоря, когда
функтор G соответственно унивалентен или полон. Теперь остается
применить лемму. □
Подкатегория А называется рефлективной в категории В, если
функтор вложения К : А —> В имеет левый сопряженный F : В —»
—> А. Этот функтор F можно назвать рефлектором, а сопряжение
(F,K,if) = (F,if) : В —^ А — репликой (reflection) категории В
в ее подкатегорию А. Поскольку функтор вложения К всегда
унивалентен, то коединица отражения г всегда является эпиморфизмом.
Можно описать отражение в терминах композиции функторов R =
= KF : В —» В; действительно, подкатегория А С В рефлективна
в В, если и только если существует функтор R : В —> В со значениями
в А и биекция множеств
A(Rb,a) 9*B(b,a),

4.3]
Рефлективные подкатегории
109
естественная по & G 5 и по a G А. Можно также описать отражение
в терминах универсальных стрелок: подкатегория А С В рефлектив-
на, если и только если для каждого Ъ Е В существуют объект Kb в А
и стрелка щ '• Ъ —>■ Rb, такие что каждая стрелка g : b —>■ a Е А
имеет вид g = / о щ для единственной стрелки / : Rb —>■ а из А. Как
обычно, тогда R оказывается функцией объектов функтора В —>■ В
(со значениями в А).
Если полная подкатегория А С В рефлективна в В, то по теореме
1 каждый объект a Е А изоморфен FKa, и потому Ra = а при всех а.
Двойственно, подкатегория А С В корефлективна в Б, если
функтор вложения А —» В имеет правый сопряженный. (Предупреждение:
в книге (Mitchell [1965]) термины рефлективный и корефлективный
поменялись местами.)
Вот некоторые примеры. Подкатегория АЬ рефлективна в
категории Grp. В самом деле, пусть G/[G,G] — факторгруппа по
коммутанту группы G. Тогда hom (G/[G, G],A) = hom (G, А), если группа А
абелева, и при этом АЬ полна в Grp. Теперь рассмотрим категорию
всех метрических пространств X, взяв в качестве стрелок равномерно
непрерывные функции. Полная (full) подкатегория полных (complete)
метрических пространств рефлективна; рефлектор отображает
каждое метрическое пространство в его пополнение. Далее,
рассмотрим категорию всех вполне регулярных хаусдорфовых пространств
(стрелки — все непрерывные функции). Тогда (полная) подкатегория
всех компактных хаусдорфовых пространств рефлективна; рефлектор
отображает каждое вполне регулярное пространство в его компакти-
фикацию Стоуна-Чеха *).
В категории АЬ корефлективна полная подкатегория всех абеле-
вых групп кручения (в группе кручения все элементы имеют
конечный порядок); корефлектор отображает каждую абелеву группу А
в подгруппу ТА, состоящую из всех ее элементов конечного порядка.
Упражнения
1. Покажите, что таблицу двойственных утверждений (§ 2.1) можно
продолжить следующим образом:
) Рассмотрим более общую категорию К всех универсальных алгебр
сигнатуры Q (см. *Мальцев [1970], с. 46-47). Полная подкатегория Р в К
называется предмногообразием, если выполнены следующие условия:
1) если алгебра А лежит в Р и изоморфна алгебре В, то В £ Р\
2) одноэлементная алгебра принадлежит Р\
3) категория Р замкнута относительно подалгебр и прямых произведений.
Можно показать, что Р является рефлективной подкатегорией в К.
Верно и обратное: если полная рефлективная подкатегория М в К
удовлетворяет условию 1), то она является предмногообразием (*Мальцев [1970],
с. 292-293). — Прим. ред. пер.

по
Сопряженные функторы
[Гл.4
Утверждение Двойственное утверждение
S,T : С -> В — функторы S,T : С -> В — функторы
Т полон Т полон
Т унивалентен Т унивалентен
г] : S -^Т — естественное преобразо- ц : Т -^ S — естественное преобразова-
вание ние
(F, G,(p) : X —^ А — сопряжение (G, F, (р-1) : А —^ X — сопряжение
г] — единица для {F, G,(p) r\ — коединица для (G, F, (f_1).
2. Покажите, что абелевы группы, свободные от кручения, составляют
полную рефлективную подкатегорию в АЬ.
3. Пусть (F, G,<p) : X —^ А — сопряжение, причем функтор G полон,
а каждая единица цх мономорфна. Тогда все цх также и эпиморфны.
4. Покажите, что следующие подкатегории рефлективны:
а) полная подкатегория всех частичных порядков в категории Preord
всех предпорядков, где стрелками являются все монотонные функции.
б) полная подкатегория То-пространств в категории Тор.
5. Пусть дано сопряжение (F, G,tp) : X —^ А. Докажите, что G
унивалентен, если и только если <^-1 переводит эпиморфизмы в эпиморфизмы.
6. Пусть дано сопряжение (F, G; г], е), где один из функторов F, G полон.
Докажите, что преобразование Ge : GFG —»■ G обратимо, причем обратным
является r]G : G —»■ GFG.
7. Пусть А — полная рефлективная подкатегория в В. Докажите, что
если функтор S : J —»■ А имеет предел в В, то он имеет предел в А.
4.4. Эквивалентность категорий
Функтор S : А —> С является изоморфизмом категорий, если
существует (противоположно направленный) функтор Т : С —> А такой,
что ST = / : С —>■ С и TS = I : А —> А. В этом случае имеется
сопряжение (Т, S]rj,e) : С —^ А, где т] : I —>ST и г : TS —>1 — тождественные
естественные преобразования. Иначе говоря, двусторонний обратный
Т к функтору S сопряжен к нему слева, — а в действительности также
и справа.
Имеется более общее (и более полезное) понятие: функтор S : А —>
—>• С является эквивалентностью категорий (и тогда категории АиС
эквивалентны), если существуют (противоположно направленный)
функтор Т : С —> А и естественные изоморфизмы ST = / : С —>
-^ С и TS = I : А ^ А. В этом случае Г : С -> А также
является эквивалентностью категорий. Вскоре мы увидим, что тогда
Т сопряжен к S и слева, и справа.
Приведем пример. Скелетом категории С называется любая ее
полная подкатегория А, такая что любой объект из С изоморфен (в С)
ровно одному объекту из А. Тогда А ж С эквивалентны, и вложение
К : А —у С является эквивалентностью категорий. Действительно,
для каждого с G С выберем некоторый изоморфизм вс : с = Тс
с объектом Тс из А. Тогда существует ровно один способ превратить Т
в функтор Т : С —У А, так чтобы получить естественный изоморфизм
6:1 = КТ. При этом ТК = /, поэтому К действительно является

4.4]
Эквивалентность категорий
111
эквивалентностью. Таким образом, любая категория эквивалентна
(любому) своему скелету. Например, скелетом категории всех
конечных множеств является полная подкатегория, объекты которой —
все конечные ординалы 0,1,2,...,п,... (Здесь 0 обозначает пустое
множество, а каждое п — множество {0,1,...,п — 1}.)
Категория называется скелетной, если любые два изоморфных
объекта совпадают, т. е. когда категория является своим скелетом.
Сопряжение-эквивалентность (adjoint equivalence) между
категориями — это сопряжение (Т, 5;?7,s) : С —^ А, в котором единица
г) : I —> ST и коединица г : TS -^ I являются естественными
изоморфизмами: / = ST, TS = /. Тогда ту-1 и г-1 также являются
естественными изоморфизмами, и треугольные тождества еТ • Тг) —
= 1, Se • r]S = 1 можно записать в виде Т/у-1 • е~хТ = 1, r\~1S x
х 5г-1 = 1 соответственно. Теперь эти тождества означают, что
(5, Т;г_1,ту-1) : А —^ С — сопряжение, для которого е~х : I—> TS
является единицей, а ту-1 : ST -^ I — коединицей. Как следствие,
в сопряжении-эквивалентности (Т, 5;—,—) функтор Т : С —> А
сопряжен слева функтору S : А —У С с единицей 77, и одновременно Т
сопряжен справа S с единицей г-1.
Теперь мы готовы сформулировать основные утверждения об
эквивалентности.
Теорема 1. Следующие свойства функтора S : А —>• С логически
равносильны:
1) функтор S является эквивалентностью категорий;
2) S входит в состав сопряжения-эквивалентность
(T,S;V,e):C^A;
3) функтор S полон и унивалентен, причем каждый объект с G С
изоморфен Sa для некоторого объекта a G А.
Доказательство. Ясно, что из (2) вытекает (1). Покажем, что
из (1) следует (3). Для этого заметим, что поскольку ST = /, то
каждый объект с G С имеет вид с = S(Tc) для некоторого а = Тс G
G А. Для каждой стрелки f : а —> а' ввиду естественного изоморфизма
в : TS = / существует коммутативный квадрат
TSa ^a
f
TSf
TSa' -—>■ а
Поэтому / = ва' о TSf о в~х] следовательно, функтор S унивалентен.
Симметричным образом из естественного изоморфизма ST = /
следует, что Т унивалентен. Покажем, что S полон. Для этого возьмем
любую стрелку h : Sa —> Sa' и положим / = 6а> о Th о в~х. Тогда
вышеприведенный квадрат останется коммутативным после замены
Sf на h; значит, TSf = Th. Поскольку функтор Т унивалентен, то
Sf = /1, и это означает, что S полон.

112
Сопряженные функторы
[Гл.4
Докажем, что из (3) вытекает (2). Нужно построить для S (левый)
сопряженный Т. Для каждого с Е С мы можем выбрать объект а$ =
= Tq с Е А и изоморфизм /7С, для которых коммутативна диаграмма
Vc'.c - S(T0c)
\sg. g : Г0с -»> а.
5а
Для каждой стрелки / : с —у Sa композиция / о /у-1 имеет вид Sg
для некоторой стрелки д, поскольку S полон; д единственна, так
как S унивалентен. Иначе говоря, / = Sg о г\с для единственной
стрелки д, т. е. г\с — универсальная стрелка из ев S. Следовательно,
существует ровно один способ превратить Т в функтор Т : С —> А
так, чтобы преобразование rj : I —У ST было естественным, и тогда Т
сопряжен слева к S, причем изоморфизм г) является единицей. Как
и для любого сопряжения, Sea • T]sa — 1 (положим на предыдущей
диаграмме с = Sa,f = 1). Таким образом, стрелка Sea = (ту^а)-1
обратима. Поскольку S полон и унивалентен, коединица га также
обратима. Следовательно, (T,S]rj,e) : С —^ А является сопряжением-
эквивалентностью, и доказательство завершено. □
Примем в этом доказательстве, что А — полная подкатегория в С
и S = К : А —>- С является вложением. Тогда для объектов a G А С С
мы можем положить а$ = а = Ха и считать ?7ка единичной стрелкой.
Теперь Кеа = 1, поэтому еа = 1 при всех а. Доказано
Предложение 2. Пусть А — полная подкатегория в С, и
каждый объект с G С изоморфен (в С) некоторому объекту из А.
Тогда вложение К : А —>• С является эквивалентностью и входит
в состав сопряжения-эквивалентности (Т, К;т],1) : С —> А, где
коединицей является единичная стрелка. Как следствие, А рефлек-
тивна в категории С.
В частности, сюда включается уже упомянутый случай, когда А
является скелетом для С.
Функтор F : X —>• А называется сопряженным и обратным слева
(left-adjoint-left-inverse) для G : А —> X, если имеется сопряжение
(F, G; 77,1) : X —^ А, где коединицей служит единичная стрелка. Это
означает (упр. 4), что G является изоморфизмом между А и
рефлективной подкатегорией в X. В ситуации из предложения 2 мы
показали, что вложение А —>■ С имеет сопряженный и обратный слева
функторы.
Теоремы двойственности в функциональном анализе часто дают
примеры категорной эквивалентности. Например, пусть САЬ —
категория компактных топологических абелевых групп, а отображение
Р сопоставляет каждой такой группе G ее группу характеров PG,
состоящую из всех непрерывных гомоморфизмов G —> R/Z. Согласно
теореме двойственности Понтрягина, Р : САЬ —у АЬор является
эквивалентностью категорий. Аналогично, теорема Гельфанда-Наймарка

4.5] Сопряженные функторы в случае предпорядков 113
утверждает, что эквивалентностью категорий является функтор С,
сопставляющий каждому компактному хаусдорфову пространству X
абелеву С*-алгебру непрерывных комплекснозначных функций на X
(см. Negrepontis [1971]).
Упражнения
1. Докажите следующее:
а) Любые два скелета данной категории С изоморфны.
б) Пусть Aq — скелет для А, а Со — скелет для С. Тогда А и С
эквивалентны, если и только если Aq и Со изоморфны.
2. а) Докажите, что композиция двух эквивалентностей D —»■ С, С —»■ А
является эквивалентностью.
б) Сформулируйте и докажите соответствующий факт для сопряжений-
эквивалентностей.
3. Пусть функтор S : А —»■ С унивалентен, полон и сюръективен на
объектах (каждый объект с Е С равен Sa для некоторого а Е А). Докажите,
что имеется сопряжение-эквивалентность (Т, S;l,e) : С —^ А, где единицей
служит единичная стрелка (и, как следствие, Т является сопряженным
слева и обратным справа к S).
4. Пусть дан функтор G : А —>- X. Докажите равносильность следующих
трех условий:
а) G имеет сопряженный и обратный слева функтор;
б) G имеет левый сопряженный, полон, унивалентен и взаимно
однозначен на объектах;
в) имеются полная рефлективная подкатегория Y в X и изоморфизм
Н : А = У такие, что G = КН, где К : Y —»■ X — вложение.
5. Пусть J — связная категория, Л : С —»■ CJ имеет левый сопряженный
(копредел). Покажите, что можно выбрать левый сопряженный так, что он
будет и левым обратным.
4.5. Сопряженные функторы в случае предпорядков
Напомним, что предпорядок Р — это множество Р = {р,//,•••},
наделенное рефлексивным и транзитивным бинарным отношением
р ^ р'. Предпорядки можно рассматривать как категории, причем
функции, сохраняющие порядок (бинарное отношение), становятся
функторами. Тогда функция L : Р —У Q, обращающая порядок,
становится функтором L : Р —> Qop.
Теорема 1. Пусть P,Q — два предпорядка,, а функции L : Р —>•
—> Qop,R : Qop —> Р сохраняют порядок. Тогда L как функтор
сопряжен слева к R, если и только если при всех р G Р и q G Q
выполнено следующее:
Lp ^ q в Q, если и только если р ^ Rq в Р. (1)
В этом случае существует ровно одно сопряжение ср, при котором
L сопряжен слева к R. При всех р и q верно, что р ^ RLp и LRq ^ q;
как следствие,
Lp ^ LRLp ^ Lp, Rq ^ RLRq ^ Rq. (2)

114
Сопряженные функторы
[Гл.4
Доказательство. Напомним, что Р можно рассматривать как
категорию, в которой существует (ровно) одна стрелка р —>■ р' в
случае р ^ р'. Поэтому условие (1) означает, что имеется биекция
honiQoP(Lp, q) = homp(p, Rq); эта биекция естественна, поскольку
каждое hom-множество содержит не более одного элемента. Единица
сопряжения соответствует неравенству р ^ RLp для всех р, а коедини-
ца — неравенству LRq ^ q для всех q. Два условия (2) — это
треугольные тождества, связывающие единицу и коединицу. Случай, когда Р
и Q частично упорядочены (т. е. оба отношения ^ антисимметричны),
выглядит наиболее просто: предыдущие условия принимают вид L =
= LRL и R = RLR (три отображения сводятся к одному!) □
Пара функций Ьий, сохраняющих порядок и удовлетворяющих
условию (1), называется соответствием Галуа между Р и Q.
Приведем основной пример. Пусть группа G действует на множестве U по
формуле (а, х) и-» а-х, где a Е G, x Е U. В качестве Р возьмем V{U) —
множество всех подмножеств X С U, упорядоченное по включению,
а в качестве Q — множество всех подмножеств S С G, также
упорядоченное их по включению (S ^ S", если и только если S С S"). Пусть
LX = {сг|жЕХ=>сг-ж = ж}, Д5 = {ж|сгЕ5=>сг-ж = ж};
иначе говоря, LX — это подгруппа в G, оставляющая на месте все
точки х Е X, a i?5 — множество неподвижных точек автоморфизмов
из S. Ясно, что LX ^ S в Q, если и только если сг • х = ж при всех
a Е 5 и всех ж Е X, что в свою очередь равносильно неравенству
X ^ i?5 в Р. Следовательно, L и R составляют пару сопряженных
функторов (соответствие Галуа). В исходном варианте G является
группой автоморфизмов поля U, как в классической теории Галуа.
Пусть U и V — два множества. Тогда множество V(U) всех
подмножеств из U является предпорядком по включению. Для каждой
функции / : U —> V ее образ /*, определяемый условием /*(Х) =
= {f(x) | х Е X}, является функцией на множествах, сохраняющей
порядок. Таким образом, получаем функтор /* : V(U) —> V(V).
Прообраз f*(Y) = {х | fx = у для некоторого у Е F} определяет
функтор V{V) —>• V(U), направленный в обратную сторону.
Поскольку /*Х С F <£> X С f*Y, то функтор образа /* сопряжен слева
к функтору прообраза /*.
Некоторые сопряженные функторы в теории булевых алгебр тесно
связаны с логическими связками. Снова будем рассматривать V(U)
как предпорядок и, следовательно, как категорию. Как мы уже
отметили, диагональный функтор Л : V(U) —> V(U) x V(U) имеет правый
сопряженный П, который отображает подмножества X, Y в их
пересечение 1ПУ,и левый сопряженный U, т. е. объединение (X, Y) н-» X U
U У. Если фиксировано подмножество X в [/, то пересечение с ним
становится функтором X П — : Р(?7) —>• V(U). Если X' обозначает
дополнение к!в[/, то 1 П У ^ Z тогда и только тогда, когда Y ^
^ X' П Z. Поэтому правым сопряженным для X П — является X' U —.
Таким образом, при построении сопряженных функторов
используются булевы операции D,U и ', которые соответствуют связкам и, или,
не.

4.6]
Декартово замкнутые категории
115
Теперь рассмотрим первую проекцию Р : U xV —>■ U произведения
множеств U и V. Каждое подмножество S С U х V определяет два
подмножества в U по формулам
Р*5 = {ж | 3 у, у е V, причем (ж, у) е S} ,
Р*5 = {ж | У у, у е V всегда (х,у) е S} .
Они получаются при применении к (х,у) квантора существования
Зу (существует у) и квантора общности \/у (для всех у). При этом
P*S является образом множества S при проекции Р. Для любого
подмножества X С U справедливы соотношения
S <: Р*х & Р*5 ^ X; Р*х <с S & х <с Р*5.
Это означает, что для Р*, т. е. для взятия прообраза, существует как
левый сопряженный Р*, так и правый сопряженный Р*. В этом смысле
кванторы 3 и V можно интерпретировать как сопряженные функторы.
Здесь возможна и геометрическая интерпретация: Р*Х — это
цилиндр XxU С U xV с основанием X С U; P*S — проекция множества
S С U х V на основание [/, a P*S — такое наибольшее подмножество
X С U, что построенный над ним цилиндр целиком содержится в S.
Таким образом, мы убедились, что важнейшие логические связки (и,
или, не, \/у, Зу) можно истолковать как сопряженные функторы. Это
иллюстрирует наш девиз «сопряженные функторы вездесущи».
Упражнения
1. Пусть Н — пространство со скалярным произведением (например,
гильбертово пространство). Далее, пусть Р = Q — множество всех
подмножеств S С Н, упорядоченное по включению. Покажите, что ортогональное
дополнение к S (равное RS и LS) определяет соответствие Галуа.
2. Рассмотрим соответствие Галуа между частично упорядоченными
множествами. Покажите, что подмножество {р \ р = RLp} совпадает с
подмножеством {р | р = Rq для некоторого q]. Найдите биекцию между этим
множеством и подмножеством в Q вида {q \ q = LRq]. Каковы эти
множества в случае группы автоморфизмов поля? Распространяется ли этот
результат на произвольные сопряжения?
3. Если С — категория с коуниверсальными квадратами, то каждая
стрелка / : а —»■ а определяет функтор (С \. /) = /* : (С \. а) —»■ (С \. а'),
который переводит каждый объект х —»■ а категории (С \. а) в композицию
х —>- а —>- а . Покажите, что /* имеет правый сопряженный /*, для которого
f*(x' —> af) = у —> а, где у — вершина коуниверсального квадрата а —»■
->• а' «— х'.
4.6. Декартово замкнутые категории
Как мы увидим, эффективность теории категорий в значительной
мере основывается на применении категорий с дополнительной
аддитивной структурой. Одним из основных примеров служат замкнутые

116
Сопряженные функторы
[Гл.4
категории (см. § 7.7); сейчас мы уже можем ввести их частный
случай — декартово замкнутые категории.
Когда мы говорим, что категория С имеет конечные произведения
и копроизведения, то это означает, что всегда существуют конечные
произведения и копроизведения, а также терминальные и начальные
объекты. В этом случае функторы Сч1иЛ:СчСхС имеют
левый и правый сопряженный. В самом деле, их левые сопряженные
соответствуют начальному объекту и копроизведению, а правые
сопряженные — терминальному объекту и произведению.
Используя лишь понятие сопряженного функтора, мы определим
теперь декартово замкнутые категории. Категория С, в которой
однозначно г) заданы все конечные произведения, называется декартово
замкнутой, если каждый из следующих функторов:
снО, с\->(с,с), а и-» а х Ъ
имеет заданный правый сопряженный (с заданным сопряжением). Эти
сопряженные имеют следующий вид:
Поэтому однозначно задать первый из них — значит однозначно
задать терминальный объект в категории С, а однозначно задать
второй означает для каждой пары объектов а, Ь Е С однозначно
задать объект произведения а х Ъ и его проекции а «— а х Ъ —>■ Ъ. Эти
проекции определяют сопряжение (и образуют его коединицу); как
уже отмечалось, в этом случае х становится бифунктором. Третье
искомое сопряжение однозначно определяет для каждого функтора
— х Ъ : С —>- С правый сопряженный, а также соответствующую
биекцию
hom (а х 5, с) = hom (а, с6),
естественную по а и по с. По теореме о параметрах (которая будет
доказана в следующем параграфе) отображение (6, с) н-» съ является
функцией объектов бифунктора (7ор х С —> С. Однозначно задать
сопряжение — значит задать для каждых с и Ъ стрелку
е : сь х Ь ->• с,
естественную по с и универсальную среди стрелок из — х Ъ в с.
Назовем такую стрелку е = е^с отображением оценки (evaluation map).
В следующих двух случаях такое отображение сводится к (/, х) н-» /ж,
т. е. обычному взятию значения функции / при значении аргумента х.
Категория Set декартово замкнута, причем съ = hom (Ь, с).
х) А не только с точностью до изоморфизма. — Прим. пер.

4.7]
Преобразования сопряженных функторов
117
Категория Cat декартово замкнута, причем Св —
функторов.
Примером аналогичного явления служит функтор
это категория
- ®к В : K-Mod -+ K-Mod,
которому сопряжен справа функтор hom^ (£?, —);
сопряжение определяется коединицей, а именно отображением оценки
horrid (В, А) ®к В -> А.
Упражнения
1. а) Пусть U — произвольное множество. Покажите, что предпорядок
V(U), состоящий из всех его подмножеств, является декартово замкнутой
категорией.
б) Покажите, что любая булева алгебра, рассматриваемая как
предпорядок, декартово замкнута.
2. Пусть Т — элементарная теория. Рассмотрим множество ее
предложений S = {р, д,...} как предпорядок, в котором р ^ q означает «р влечет q»
(т. е. q следует из р с учетом аксиом теории Т). Докажите, что категория S
декартово замкнута, причем произведением служит конъюнкция, a qp имеет
вид «из р следует q».
3. Докажите, что в любой декартово замкнутой категории с* = с
и СЬХ6' s (с6)Ь'
4. В произвольной декартово замкнутой категории найдите естественное
преобразование съ х Ъа —»■ са, в случае категории Set согласованное с
композицией функций. Докажите, что оно (как и композиция) ассоциативно.
5. Покажите, что из декартовой замкнутости категории А не вытекает,
что категория А3 также декартово замкнута.
4.7. Преобразования сопряженных функторов
Теперь изучим преобразования, которые связывают различные
сопряжения. Пусть даны два сопряжения:
{F, G, ^, V,е) : X - A, {F', G',<p', v',e') : X' - А'.
(1)
Отображение сопряжений (первого во второе) — это пара функторов
К : А —> А' и L : X —> X', для которой коммутативны оба квадрата
на следующей диаграмме:
(2)

118
Сопряженные функторы
[Гл.4
и для всех объектов х Е X и a Е А коммутативна диаграмма
A(F
=KFx,a
ж, а)
A'(KFx,Ka)
II
A'(F'Lx,Ka) —
у
ч>'
—-х(ж
Ga)
L=LX,G
Х'(£ж,.гХ?а)
II
-^X'(Lx,
G'Ka)
(3)
Здесь Крх,а означает отображение / н-» X/, состоящее в применении
функтора К к каждой стрелке / : Fx —> а.
Предложение 1. Пусть даны сопряжения (1) и функторы
К и L, для которых выполнено (2). Тогда условие (3) для /шга-
множеств эквивалентно равенству Lrj = т/L, а таксисе г'К = If е.
Доказательство. Пусть диаграмма (3) коммутативна.
Положим а = Fx и добавим к (3) единичную стрелку 1 : Fx —> Fx.
Получим единицы е,е' и равенство
(Lri:L-> LGF) = (т/L : L -> G'F'L),
где LGF = G'F'L в силу (2). Обратно, если дано равенство Lr\ = rj'L,
то (3) вытекает из определения сопряжений ip и у/ в терминах их
единиц. Случай коединиц двойствен к этому. □
Пусть теперь даны два сопряжения
{F,G,V,ri,e), <F',GV,r/,£'>:X-A (4)
между одними и теми же категориями. Естественные преобразования
a:F^F', т : G' ^ G
называются сопряженными (посредством данных сопряжений), если
для любой пары объектов х Е X, a Е А коммутативна диаграмма
A(F'x,a)^X(x,G'a)
(ах)*=А((тх,а)
Х(х,Та) = (та)*
(5)
A(Fx,a) <*X{x,Ga).

4.7]
Преобразования сопряженных функторов
119
Теорема2. Пусть дана пара сопряжений (4). Тогда
естественные преобразования а и т сопряжены, если и только если
коммутативна одна из следующих четырех диаграмм:
G' —
\r,G'
GFG' -
GaG'
^G
Ge'
GF'G'
Fr,'
FG'F'
FtF'
A
\eF'
-^ FGF'
(6)
FG' -^ FG
\aG'
T
F'G' -
Ia,
G'F'
tF'
-^GF
Gct
i
*~GF'.
(7)
При этом для данной пары сопряжений (4) и естественного
преобразования а : F -^ F' существует единственное такое г : G -^ G,
что пара (сг,т) сопряжена. Двойственно, если даны (4) и т, то
существует единственное такое а, что пара (а, т) сопряжена.
Доказательство. Прежде всего, из (5) вытекает (6) и (7).
В самом деле, положим на диаграмме (5) х = G'а, в верхнем правом
углу возьмем единичную стрелку 1 : G'а —> G'a и проведем ее по
диаграмме, используя определение отображений ip и ip' в терминах
единицы и коединицы:
"11 = iG'a
е'а ° o-G'a ^ Ge'a о GaG>a о r)G,a = та.
Справа внизу получаем первое равенство из (6). Несколько другой
обход дает следующий результат:
£п ■<-
41
Y
S'a ° aG'a =£a° Fra -<Ч Та.
Получаем коммутативность первой диаграммы из (7). По
двойственности коммутативны и вторые диаграммы.
Пусть теперь фиксировано а, но не т. Применим лемму Ионеды
к преобразованию ср о {ах)* о (р1-1 (три стороны диаграммы (5)). Мы
видим, что имеется единственное семейство стрелок т'а, делающее
диаграмму коммутативной, и это семейство определяет естественное

120
Сопряженные функторы
[Гл.4
преобразование. Поскольку каждая стрелка sa : FGa —у а
универсальна среди стрелок из F в а, то существует и единственное семейство
стрелок г" : G'a —у Ga, делающее коммутативной первую диаграмму
из (7). Так как из (5) вытекает (7), то т'а = т". Иначе говоря, если т =
= т" делает коммутативным первый квадрат из (7), то это верно и для
(5). Поэтому из коммутативности первого квадрата в (7) вытекает (5).
Если дано сг, то, очевидно, первый квадрат из (6) коммутативен ровно
для одного естественного преобразования т : G' -4 G. Так как из (5)
следует (6), то т'а = та и потому отображения т'а из (5) определяют
естественное преобразование; при этом из (6) следует (5).
Построив соответствующие диаграммы из естественных
преобразований, читатель может также убедиться, что из (6) вытекают (5)
и (7). □
Теперь рассмотрим сопряженную пару (а, т) естественных
преобразований как преобразование (или морфизм) первого сопряжения во
второе. Вертикальная композиция двух таких морфизмов:
(F, G, г,, e) %} (F1, G', г,',е') ^4 } (F", G", г,",е") (8)
заведомо является (например, в силу условия (5)) преобразованием
(о~',т') о (а,т) = (сг'-,т • т') первого сопряжения в третье. Таким
образом, по двум данным категориям X и А строится новая
категория A(ad^x — категория сопряжений между X и А. Ее объектами
являются сопряжения (F,G;t],s), а стрелками — преобразования
(сопряженные пары) (а, т) с определенным выше умножением. Два
очевидных забывающих функтора связывают эту категорию с обычными
категориями функторов, а именно:
■ ^(adj)J
[^(adj)
х ар
X1
F^
ч < F,G,/y,s >^
<(Т,Т>
V
4<F',G",t/,s' >ь
G
—^G'.
В случае категории Set характерным примером служит биекция
hom (S х Г, R) ^ hom (5, hom (Г, R)), (9)
которая обсуждалась в § 1 как пример сопряжения (для каждого
данного множества Т). Пусть t : Т —у Т' — функция между двумя
такими множествами; тогда — х t — естественное преобразование
функторов = хТ^> — хХ". Ему сопряжено естественное
преобразование hom (£, —) : hom (Т', —) -4 hom (T, —), направленное в обратную
сторону, в соответствии с тем, что функтор SxT ковариантен, а
функтор hom (T, R) контравариантен по аргументу Т. Можно назвать (9)
сопряжением с параметром Т Е Set. В случае коммутативного кольца

4.7]
Преобразования сопряженных функторов
121
К сопряжение Mod^ (А ®к В, С) = Mod^ (A,RomK (В, С)) имеет
параметр В Е Mod^. В общем случае справедлива
ТеоремаЗ(о сопряжениях с параметром). Пусть дан бифунктор
F : X х Р —>> А, причем для каэюдого объекта р Е Р функтор
F(—,p) : X —> А имеет правый сопряэюенный G(p,—) : А —» X с
сопряжением
hom (F(x,p),a) = hom (ж, G(p, a)), (10)
естественным по х и по а. Тогда существует единственный способ
сопоставить каждой стрелке h : р —>• р' из Р и каждому
объекту a Е А стрелку G(h,a) : G(p',a) —> G(p,a) из X так, чтобы
получить бифунктор G : Рор х А —> X, для которого биекция из
сопряжения (10) естественна по х,р и а. Это соответствие между
G(h, а) и (h, а) можно таксисе описать как единственный способ
превратить G(h, —) в естественное преобразование, сопряженное
KF(-,h).
Доказательство. Естественность сопряжения (10) в р Е Р
соответствует коммутативности квадрата
hom (F(x,p),a) = hom (ж, G(p, a))
F(x,h)*
G(h,a)*
hom(F(x,p'),a) ~ hom (ж, G(p', a)).
Но его коммутативность для всех а означает, что в качестве
G(h, —) : G(p', —) —>G(p, —) можно взять преобразование, сопряженное
к F(—,h) : F(—,р)—> F(—,p'). Ввиду предыдущей теоремы такой
выбор единствен — и условие сопряженности можно выразить любым
из пяти указанных там способов. Для любой другой стрелки Ы : р' —>-
—>• р" эта единственность означает, что G{h'h, —) = G(h, —) о G(h', —).
Следовательно, G(—, а) является функтором, а G — бифунктором. □
Двойственно, если дан бифунктор G : Рор х i 4 I, причем
каждый функтор G(p,—) имеет правый сопряженный F(—,p), то
существует единственный способ превратить F в бифунктор X х Р —у А.
Упражнения
1. Покажите, что костепени X • а в категории С, определенные условием
С(Х • а,с) = Set (X, С (с, а)), можно интерпретировать как сопряжение
с параметром а.
2. Пусть г]х : ж —»■ G(p,F(x,p)) — единица сопряжения с параметром.
Оно естественно по х\ какое свойство преобразования ц соответствует
естественности сопряжения (10) по р?
3. Пусть Ах — категория функторов, S — полная подкатегория в ней,
состоящая из тех функторов F : X —у А, которые имеют правый
сопряженный RF : А —> X. Превратите R в функтор Sop —»■ X , выбрав по одному
RF для каждого F, причем Ra должно быть сопряжено с а.

122
Сопряженные функторы
[Гл.4
4. (Kelly.) Квадрат сопряжений (adjoint square) — это совокупность
категорий, функторов, сопряжений и естественных преобразований
<F,G,<p>
X' <F'*GW>-A',
a: F'H^KF,
r.HG^G'K,
для которой всегда коммутативна следующая диаграмма hom-множеств:
A(Fx,a)
^Af(KFx,Ka)
(ах)*
^Af(FfHx,Ka)
Х(х, Go) ^—>- Х'(Нх, HGa) (rQ)% X'(Hx, G'Ka).
Выразите последнее условие различными способами в терминах единиц
и коединиц сопряжений; покажите, что каждое из преобразований а, г
определяет другое. (Выше в тексте рассмотрен случай Н = К = тождественный
функтор.)
5. (Palmquist.) Пусть даны Н,К и два сопряжения из упр. 4.
Найдите биекцию между естественными преобразованиями а : F'HG^ К
и /3: H^G'KF.
4.8. Композиция сопряженных функторов
Произведение двух последовательных сопряжений является
сопряжением в следующем смысле:
Теорема 1. Пусть даны два сопряжения:
(F,G,V,s) : X - A, (F,G,rj,s):A^D.
Тогда произведения функторов определяют сопряжение
(FF,GG,GrjF -п,ё- FsG) : X -- D.
Доказательство. Применительно к hom-множествам два
данные сопряжения определяют следующий изоморфизм, естественный
по х Е X и по d Е D:
D{FFx,d) £* A(Fx,Gd) £* X(x,GGd).
Он означает, что произведение функторов FF сопряжено слева с GG.
Положим d = FFx и применим эти два изоморфизма к единичной
стрелке 1 : FFx —> FFx. Тогда единица произведения сопряжений
равна х —^ GFx > GGFFx, т. е. GrjF • 77, как и утверждалось.

4.8]
Композиция сопряженных функторов
123
Двойственное рассуждение показывает, что коединица равна г • FsG.
Можно непосредственно проверить, что последние формулы
определяют естественные преобразования / -^ GGFF и FFGG -^ /, которые
удовлетворяют треугольным тождествам. □
Используя такое умножение, можно образовать категорию Adj,
объектами которой служат все (малые) категории X, A, D,..., а
стрелками — сопряжения (F,G,rj,e) : X —^ А с введенным умножением;
единичной стрелкой для каждой категории А служит тождественное
сопряжение А —^ А.
Эта категория обладает и аддитивной структурой. Каждое hom-
множество Adj (X, А) можно рассматривать как категорию — а
именно, как категорию A^ad^x сопряжений между X и А, описанную
в предыдущем параграфе. Ее объекты — указанные сопряжения, а ее
стрелки — сопряженные пары (а, т) с вертикальным умножением,
введенным в формуле (7.8).
Теорема2. Пусть даны две сопряженные пары
(а, т) : (F, G, г,, е) -4 {F', G', rf, е1) : X - А,
(а,т) : (F,G,r],e) -4 (F,&,т?,?) :A^D.
Тогда (горизонтальные) произведения естественных преобразований
~до и тт определяют сопряженную пару естественных
преобразований ~до : FF -^ F F'', тт: G'G -^ GG , которая соответствует
произведениям сопряжений.
Доказательство можно выразить диаграммой hom-множеств
D(F'F'x,d) = A(F'x,G'd) =X(x,G'G'd)
(crcrx)*
(ax)* (rd)*
(TTd)
D(FFx,d) = A(Fx,Gd) = X(x,GGd).
Операция горизонтального умножения в действительности
является бифунктором
Adj (A, D) х Adj (X, А) -»• Adj (X, D). (1)
Это значит, что Adj является двумерной категорией, подобной Cat
(см. § 2.5).
Дополнительное обсуждение см. в гл. 12.
Упражнения
1. Докажите, что горизонтальное умножение является бифунктором
вида (1) и что отсюда вытекает закон чередования между горизонтальным
и вертикальным умножением сопряженных пар.

124
Сопряженные функторы
[Гл.4
2. Покажите, что сопряжение забывающего функтора Rng —>- Set с его
правым сопряженным можно получить как умножение сопряжений двумя
способами: Rng —»■ Ab —»■ Set и Rng —»> Mon —»> Set.
3. Пусть R,S,T — некоторые кольца.
а) Пусть rEs — некоторый бимодуль. Покажите, что — 0д Е : Мос1д —>-
—> Mods имеет правый сопряженный homs (E, —).
б) Покажите, что получено сопряжение с параметром Е £ .R-Mod-S'.
в) Опишите композицию этого сопряжения с аналогичным сопряжением
Mods -^ ModT.
4.9. Подмножества и характеристические функции
это функ-
Характеристическая функция подмножества S С X
ция грз • X —> {0,1}, принимающая два значения:
ф3х = 0 при х е S; ijisx = 1 при х G X, х ^ 5.
(1)
При этом {0} С {0,1} является простейшим случаем
нетривиального подмножества. Произвольное множество S С X можно
отобразить в это подмножество, используя определение характеристической
функции. Это отображение порождает коуниверсальный квадрат
S-
X
'Фб
{0}
{0,1}.
(2)
Характеристические функции часто применяются в теории
вероятностей; в логике множество {0,1} состоит из значений истинности.
Мономорфизм (простейшее вложение подмножества) t : {0} —> {0,1}
называется классификатором подобъсктов в категории множеств.
Оказывается, подобные классификаторы подобъектов существуют
и в других категориях. В общем случае классификатор подобъсктов
в категории С с терминальным объектом 1 — это такой мономорфизм
t : 1 ь-> П, что каждый мономорфизм т из С единственным способом
включается в коуниверсальный квадрат для t. Иначе говоря, для
каждого т существует единственный коуниверсальный квадрат
(3)
Верхняя горизонтальная стрелка этого квадрата — единственное
отображение в терминальный объект 1, нижняя горизонтальная стрелка
соответствует характеристической функции данного подобъекта 5,
а универсальный мономорфизм t : 1 —> П играет роль истины.

4.9] Подмножества и характеристические функции 125
Например, возьмем в качестве С категорию функций / : X —У Y.
В этом случае мономорфизм g >—> f — это функция g : S —У Т между
подмножествами S С X и Т С К, такая что g(s) = /(s) при всех s Е 5.
Это означает, что коммутативна диаграмма
5-
X
Y.
При этом все элементы множества X делятся на три класса: элементы
из S; элементы х не из 5, но такие, что gx G Т; наконец, элементы ж
не из 5, для которых дх (£ Т. Поэтому можно определить
характеристическую функцию, принимающую три значения, положив:
ф3х = 0 при х е 5,
i/jsx = 1 при х £ S , но fx e T,
т/^ = 2, когда ж ^ Т (и потому х £ S).
Аналогично предыдущему, получаем коуниверсальный квадрат в
категории функций:
{0,2}
Здесь объектами являются стрелки X —у Y и j : {0,1,2} —у {0,2}, где
функция j имеет вид j0 = 0, jl = 0, j2 = 2. Таким образом, вложение
j, показанное справа, является классификатором подобъектов в
категории функций.
Классификаторы подобъектов существуют и во многих других
случаях. Вспомним, что категория-стрелка 2 содержит два объекта
0 и 1 и единственную неединичную стрелку а : 0 —У 1. Поэтому
произвольная функция / — то же самое, что функтор 2 —у Sets.
Следовательно, выше мы построили классификатор подобъектов для
категории функторов Sets . Если С — произвольная категория, то
в категории функторов Sets
(найдите его!).
существует классификатор подобъектов

126
Сопряженные функторы
[Гл.4
4.10. Категории, похожие на Sets
(Элементарный) топос — это, по определению, категория Е со
следующими свойствами:
1) всегда существуют конечные пределы;
2) имеется классификатор подобъектов;
3) категория Е декартово замкнута.
Напомним, что декартова замкнутость означает, что при всех Ъ Е Е
функтор «умножение на Ь» (т. е. а \-> axb) имеет правый сопряженный
с I—у с&, для которого, таким образом, выполнено условие
hom (а х 5, с) = hom (а, сь).
Иначе говоря, в Е существуют экспоненты.
Категория Sets всех (малых) множеств является топосом, так же
как и категория Sets всех контравариантных функторов из малой
категории С в Sets. Такой функтор F : Сор н->- Sets называется
также предпучком. Это название возникло в топологии. Пусть С —
множество всех открытых множеств U в топологическом пространстве
X. В этом случае предпучок F сопоставляет каждому открытому
множеству U множество F(U) и обладает свойствами функтора по
отношению к непрерывным отображениям U —> V. Например, в качестве
F(U) можно взять множество всех непрерывных вещественнозначных
функций на U. В этом случае F называется пучком (вспомним пучок
коэффициентов в теории когомологий!). Эта и другие категории
пучков играют центральную роль в алгебраической геометрии и
алгебраической топологии; понятно, что слово «топос» произведено от слова
«топология». Основание состоит в том, что топологическая структура
по существу описывается своим топосом пучков.
Изучение категорий пучков на топологических пространствах и их
обобщений привело и к изучению топосов (см. Mac Lane, Moerdijk
[1992]). В частности, многие их логические характеристики
отражаются в классификаторе подобъектов П. Во многих случаях топосы
позволяют по-новому взглянуть на основания математики; например,
применение форсинга в доказательстве независимости континуум-
гипотезы хорошо описывается посредством конструкций в топосах
(см. Mac Lane, Moerdijk [1992], Ch. VI). Кроме того, соответствующие
топосы могут заменить категорию множеств как основу математики.
Из аксиом топоса вытекает много полезных следствий. Например,
в топосе всегда существуют все конечные копределы.
Замечания
Многочисленные примеры сопряженных функторов, приведенные здесь
и в других источниках, показывают, что сопряженность постоянно
встречается во многих областях математики. Идея этой книги состоит в том, что

4.10]
Категории, похожие, на Sets
127
систематическое применение сопряженности позволяет прояснить многие
вопросы. Несмотря на это, понятие пары сопряженных функторов
сформировалось очень поздно. По-видимому, термин «сопряженный» вначале
(и уже очень давно) применялся в теории линейных дифференциальных
операторов. Около 1930 г. это понятие было перенесено в гильбертово
пространство Н, где данному линейному преобразованию Т соответствует
сопряженное преобразование, которое определяется через равенство
скалярных произведений:
(Т*х,у) = (х,Ту)
для всех векторов ж, у Е Н. Ясно, что здесь имеется формальная аналогия
с определением сопряженного функтора.
Дэниел Кан (Кап [1958]) первым ввел и начал изучать сопряженные
функторы. Они потребовались ему при рассмотрении симплициальных
объектов, и Кан ввел основные понятия: единицы и коединицы,
пределы как сопряженные функторы, сопряжения с параметром,
сопряженные преобразования. Он также доказал важную теорему
существования (для расширения Кана — см. гл. 10). Заметим,
что его открытие произошло лишь через десять лет после точного
определения универсальных конструкций. Вначале идеи, связанные
с сопряженностью, развивались медленно, и не была ясна связь
с понятием универсальности. Важнейшая роль сопряженности была
раскрыта в 1960 в принстонских тезисах Фрейда
(неопубликованных, но широко циркулировавших), а также в его книге (Freyd
[1964]) и в работах (Lawvere [1963, 1964]). Здесь уместно задаться
вопросом, не предстоит ли открытие еще каких-то основных общих
понятий.
Можно также задуматься, почему введение сопряженных функторов
так задержалось. К нему могло бы привести изучение гильбертовых
пространств или универсальных конструкций в общей топологии, но
этого не произошло; возможно, этому помешала война 1939-1945 гг.
В следующем десятилетии, 1945-1955 гг., категории изучались мало,
теория категорий была лишь языком, а потенциальных исследователей
расхолаживало распространенное прагматичное недоверие к всеобщей
абстрактной чепухе (т.е. теории категорий). Бурбаки, однако, избежал
этого (Bourbaki [1948], Appendix III). Его определение универсальной
конструкции было громоздким, так как не применялся категорный
язык, но оно означало рассмотрение бифунктора W : Хор х А —»■
—>- Set и отыскание универсального элемента в W(x,—) для каждого
х. Это, в свою очередь, означает отыскание объектов вида Fx E А
и естественного изоморфизма W(x,a) = A(Fx,a)', сюда включается
задача отыскания левого сопряженного F функтору G : А —»■
—»■ X: тогда W(x,a) = homx (x,Ga). Сюда включается также задача
отыскания тензорного произведения двух модулей А и В, когда
в качестве W((A,B),C) берется множество билинейных функций А х
х В —> С. Отметим, что при таком подходе тензорное произведение
А 0 В не является примером левого сопряженного функтора (хотя это
пример универсальных стрелок). Иначе говоря, идея универсальной
конструкции была сформулирована Бурбаки таким образом, чтобы
охватить как можно больше — в частности, чтобы включить идеи
полилинейной алгебры, столь важные для традиций французской
математики. Задним числом эта дополнительная общность выглядит
излишней; в формулировке Бурбаки выдвигались на первый план

128
Сопряженные функторы
[Гл.4
представимые функторы и ставилась задача найти Fx, для которого
W(x,a) = A(Fx,a). При этом пропадает симметрия, присущая задаче
построения сопряженного: найти Fx, для которого X(x,Ga) = A(Fx,a).
В результате главное открытие не состоялось: оно было предоставлено
более молодому человеку, быть может менее скованному традицией
или модой. По этому поводу можно сказать, что хорошая общая
теория стремится не к максимальной общности, а к разумной
общности.

Глава 5
ПРЕДЕЛЫ
В этой главе исследуются свойства и строение пределов, а также
их связь с сопряженными функторами. Затем эта связь используется
в важнейших теоремах, обеспечивающих существование сопряженных
функторов и универсальных объектов в широком классе ситуаций.
В заключение мы покажем, как используются сопряженные функторы
в топологии.
5.1. Создание пределов
Категория С называется полной в малом (small-complete), а чаще
просто полной (complete), если в С существуют пределы для всех
малых диаграмм, т. е. существует предел любого функтора F : J —>
—> С из малой категории J в С. Покажем, что Set, Grp, Ab и многие
другие категории алгебр полны в малом.
Чтобы показать, как строятся пределы в категории Set,
рассмотрим предел функтора F : иор —> Set; здесь и — линейно
упорядоченное множество всех конечных ординалов, и мы интерпретируем его
как свободную категорию, порожденную графом
{0^1^2^3^---}.
Функтор F : соор —> Set — это перечень множеств Fn и функций /п,
см. первую строку следующей диаграммы:
Fn •< Fn+i -*-•••
к sf
I / (1)
LimF
,Х\, . . . | Хп е Fn} -<ч {ж0,ж1,... | fnXn+i = хп е Fn}.
Если функтор F задан, то сначала мы образуем произведение Hi Ff,
оно состоит из всех строк вида х = {жо,жъЖ2,...}, гл>е всегДа хп £
G Fn, и семейства проекций рп : Hi Fi —у Fn. Но эти проекции не
обязательно порождают коммутативные треугольники, т. е.,
возможно, fnPn+i Ф Рп- Предел должен быть, во всяком случае, вершиной
множества коммутативных треугольников (конуса). Поэтому возьмем
подмножество L, состоящее из тех строк ж, которые согласованы с /

130
Пределы
[Гл.5
(т. е. fnXn+i = хп при всех п). Затем определим функции \in : L —У Fn,
положив \inx — хп; так как строка х согласована с /, то /n/in+i = \лп
при всех п. Следовательно, \± : L -^ F — это конус с вершиной L Е Set
и основанием F. Пусть т : М -^ F — другой конус, вершиной которого
является множество М. Тогда любой элемент m Е М определяет
строку {тптп}, согласованную с /. Тем самым определена функция
g : М —» L, для которой gm = {тптп} и потому jig = т. Поскольку
такая функция g единственна, то \i является универсальным конусом
с основанием F, т. е. L — предельное множество для F.
Строка х, согласованная с /, — то же самое, что конус х : * —у F
с основанием F и вершиной в одноточечном множестве *. Поэтому
построенный предел L можно описать как множество L = Cone (*, F),
состоящее из всех таких конусов. Та же конструкция применима и
после замены иоор на любую категорию.
Теорема 1 (полнота категории Set). Пусть J — малая
категория. Тогда каэюдый функтор F : J —>• Set имеет предел, которым
является множество Cone (*, F) всех конусов а : * -^F с основанием
F и вершиной в одноточечном множестве *. Предельный конус v
состоит из стрелок
Vj : Cone (*, F) -> Fj, a \-^ Gj, (2)
каждая из которых — это функция, отображающая конус а в
элемент o~j G Fj.
Если, например, категория J дискретна, то множество J-конусов
Cone (*, F) — это просто декартово произведение П^- Fj.
Доказательство. Поскольку J — малая категория, то
Cone(*,F) — малое множество и, значит, объект в категории Set.
Пусть и : j —>■ к — произвольная стрелка из J. Поскольку а —
конус, то Fuo~j = o~k] следовательно, формула (2) определяет конус
v с основанием F. Чтобы доказать его универсальность, рассмотрим
любой другой конус т : J4Fc основанием F и вершиной в некотором
множестве X. Если х G X, то тх — конус над F с вершиной
в одноточечном множестве. Поэтому существует единственная
функция h : X —У Cone(*,F), которая отображает каждый элемент х
в тх. □
Ключевую роль в доказательстве сыграла (естественная) биекция
Cone (X, F) = Set (X, Cone (*, F)), (3)
которая имеет вид т н-» h. Поскольку конус — не что иное, как
естественное преобразование, то получаем сопряжение
Nat (AX, F) ^ Set (X, Cone (*, F)).
Тогда в силу определения предела LimF = Cone (*, F).
Пределы в Grp и других категориях строятся во многом
аналогично с помощью множества всех конусов. Например, пусть дан

5Л]
Создание пределов
131
функтор F : cj°p —>• Grp (см. диаграмму (1)). Тогда каждый объект
Fn является группой. Множество L, состоящее из всех конусов (всех
строк ж, согласованных с /), также является группой относительно
поточечного умножения ((ху)п = хпуп), и проекция \in : L —У Fn
вида х н-» хп оказывается гомоморфизмом групп. Следовательно,
\i : L -^ F — предельный конус в категории Grp.
Теперь продемонстрируем эту конструкцию для случая целых р-
адических чисел Zp (где р — простое число). Пусть дан функтор
F : иоор —у Rng, причем Fn = Z/pnZ — кольцо целых по модулю
рп, a Fn+i —>• Fn — каноническая проекция Z/pn+1Z —>• Z/pnZ. Тогда
существует Zp = Lim F. Элемент Л Е Zp — это конус над F с вершиной
*. Иначе говоря, Л можно представить как последовательность целых
чисел Л = {Ло, Ai,...}, где An+i = An (modpn) при всех п, причем А =
= А', если Ап = А^ (modpn) при всех п. Два р-адических числа Аи/i
мож:но слож:ить и перемножить почленно, по формулам
(А + /i)n = Ап + /in, (A/i)n = Xnfin.
Тогда Zp = LimF превращается в кольцо (р-адических чисел), и оно
полностью определяется таким описанием. Это описание короче, чем
традиционное, когда вначале вводится р-адическая норма (а тем
самым и топология) в кольце Z, а затем р-адическое число определяется
фундаментальной последовательностью в этой топологии.
С помощью понятия предела можно построить и кольцо
формальных степенных рядов (упр. 7).
Перейдя в категорию Тор, возьмем в качестве объекта Fn
окружность 51, а в качестве стрелки fn : S1 —> S1 — непрерывное
отображение, п раз равномерно наматывающее окружность S1 на себя.
Пределом в смысле категории Set здесь служит некоторое множество
L; превратим его в топологическое пространство, объявив открытыми
лишь такие его подмножества, чтобы все отображения \in : L —> S1
стали непрерывными. Полученное пространство является пределом
уже в категории Тор; оно известно как р-адический соленоид.
Опишем общую конструкцию предела для случая групп.
Теорема2. Пусть Н : J —» Grp — некоторый функтор,
U : Grp —> Set — забывающий функтор, причем UH имеет в
категории Set предел L и предельный конус v : L—> UH. Тогда существует
единственная структура группы на множестве L такая, что все
стрелки i/j : L —>■ UHj конуса v становятся морфизмами групп; эта
группа L является пределом для Н в категории Grp с предельным
конусом v.
Доказательство. Ввиду теоремы 1 возьмем L = Cone(*,i?);
произведение двух конусов a,r G Cone (*,UH) зададим формулой
(o~r)j = cfjTj, а обратный элемент — формулой (o~~1)j = aj1 (здесь
произведение и обратный элемент взяты в группе Н). Эти
определения превращают L в группу, а каждую компоненту конуса v —
в морфизм групп. Обратно, если v имеет вид т \-л Tj и при каждом j

132
Пределы
[Гл.5
определяет морфизм групп, то произведение конусов а, г Е L должно
иметь указанный вид.
Пусть теперь G — произвольная группа, Л : G -^ Н — некоторый
конус в категории Grp (состоящий из морфизмов групп Xj : G —>
—>• Hj, j G J). Тогда UX : UG-^ UH — конус в категории Set,
и по универсальности получаем, что (UX = (Uv)h для единственной
функции h : UG —> L. Для любых двух элементов gi,g2 £ G имеем
(h(gig2))j = \j(gi92) = (Xjg1)(Xjg2) = (hg1)j(hg2)j = ((hg1)(hg2))j;
поскольку Л — морфизм групп, то это верно и для h. Это означает,
что L действительно является пределом в Grp. □
Приведенное рассуждение на самом деле формализует обычное
покомпонентное определение умножения в декартовых произведениях
групп, в кольце р-адических чисел и т. д. При этом пределы в
категории Grp однозначно строятся с помощью функтора U, исходя
из пределов в категории Set. Аналогичное рассуждение позволяет
построить с помощью забывающих функторов пределы любых
малых семейств в категориях Rng, Ab, i?-Mod и тому подобных
алгебраических категориях. Иначе говоря, забывающий функтор создает
пределы в смысле следующего определения:
Определение. Функтор V : X —>• А создает пределы для
функтора F : J —>• А, если выполнены следующие два условия:
1) для каждого предельного конуса т : х -^ VF в категории X
существует единственная пара (а, а), состоящая из объекта a G А
и конуса а : а ^> F такая, что Va = х и Va = г;
2) этот конус а : а^> F является предельным в категории А.
Аналогично можно определить смысл выражений «V создает
произведения» (считая в предыдущем определении категорию J
дискретной), «V создает конечные пределы» (считая J конечной) или
«V создает копределы» (обратив стрелки во всех конусах). Отдельно
отметим, что выражение «V создает пределы» означает лишь, что V
определяет пределы для функторов F в тех случаях, когда
произведения VF уже имеют пределы.
В этих терминах теорема 2 принимает следующий вид:
Теорема 3. Забывающий функтор U : Grp —> Set создает
пределы.
Упражнения
1. Докажите, что проекция категории запятой (ж J^ С) —> С создает
пределы.
2. Пусть Comp Haus С Тор — полная подкатегория всех
компактных хаусдорфовых пространств. Покажите, что забывающий функтор
Comp Haus —»> Set создает пределы.
3. Пусть X — произвольная категория. Покажите, что проекция X2 —»■
-4- X х X, отображающая каждую стрелку / : х —»■ у из X в пару (х,у),
создает пределы.
4. Докажите, что категория всех малых конечных множеств конечно
полна (т. е. в ней всегда существуют конечные пределы).

5.2] Связь пределов с произведениями и уравнителями 133
5. Докажите, что категория Cat полна в малом.
6. Покажите, что каждое р-адическое число Л определяется строкой
целых чисел а; Е {0,1,... ,р — I}, причем Лп = а<э + а±р + ... + an-ipn~1 x
х (modpn). Покажите, что сложение и умножение р-адических чисел
соответствует операциям сложения и умножения бесконечных десятичных
дробей ... ап ... ао, не ограниченных влево и взятых по модулю р.
7. Пусть К[х] — кольцо многочленов от ж с коэффициентами в
коммутативном кольце К, а функтор F : иор —»■ Rng задан формулой Fn =
= К[х]/(хп), где проекции очевидны, а (хп) — главный идеал. Докажите,
что Lim F — это кольцо формальных степенных рядов от ж с
коэффициентами из К.
8. Покажите, что категория множеств кополна.
5.2. Связь пределов с произведениями
и уравнителями
Предел для функтора F : J —> Set как семейство всех конусов
Cone (*, F) С UFj
з
можно построить в два этапа. Каждый конус а — это элемент х
произведения П j Fj с проекциями pj; такой элемент является конусом
в том случае, когда (Fu)xj = Xk для каждой стрелки и : Xj —>
—> Xk из J; это равносильно требованию, чтобы х лежал в уравнителе
стрелок (Fu)pj и pk : П; Fj —>• F&. Сформулируем эту процедуру для
произвольной категории.
Теорема 1. Пусть в категории С существуют уравнители всех
пар морфизмов, а также произведения всех семейств объектов,
индексированных объектами и стрелками категории J. Тогда в С
существует предел любого функтора F : J —» С.
Для доказательства нужно поэтапно построить следующую
диаграмму (1). Здесь г обозначает объект, а и : j —>■ к — стрелку
категории индексов J. По предположению существуют произведения
П^ F{ и Uu Fk и их проекции; второе произведение взято по всем
стрелкам и из J, причем множитель с индексом и — это значение
Fk = Fcodw функтора F на кообласти стрелки и. Для произведения
nw Fk существует единственная пара стрелок / и д, делающих
коммутативными при всех и соответственно верхний и нижний квадрат. Для
этой пары по предположению существует уравнитель е. Умножая его
на проекции произведения pi, получаем стрелки \i{ — pie : d —>■ F{ для
всех г. Поскольку е уравнивает / и д, а два квадрата на диаграмме
коммутируют, то Fu/ij = /ik для всех и : j —>■ к. Следовательно,
\i : Ad^t F — конус над F с вершиной d. Пусть т — другой такой
конус, но с вершиной с. Его отображения Т{ однозначно определяют
отображение h : с —> Hi Ff, так как т является конусом, то fh =
= gh. Таким образом, h однозначно пропускается через е, и потому
конус т однозначно пропускается через конус \i. Это означает, что d
с конусом \i образует предел функтора F. Зафиксируем результат,

134
Пределы
[Гл.5
который близок к случаю категории Set:
*-*-u:j^k ^ к
Теорема2 (связь пределов с произведениями и уравнителями,
продолжение). Пределом функтора F : J —» С является уравнитель
Е пары f,g : П; F; -)► UuFcodu (и G arr J, г G J), где pu/ = pcodu,
pug = Fwopdomw. Предельный конус /л состоит из отображений /ij =
— Pje? Э ^ J {обозначения соответствуют диаграмме (1)).
Эта теорема имеет несколько полезных следствий и частных
случаев.
Следствие 1. Пусть в категории С существуют уравнители
всех пар стрелок, произведения всех объектов и терминальный
объект. Тогда в С существуют все конечные пределы.
Здесь конечный предел означает предел функтора J —> С, где
категория J конечна.
Следствие2. Пусть в категории С существуют уравнители
всех пар стрелок и все малые произведения. Тогда С полна в малом.
Отсюда, в частности, вытекает другое доказательство полноты
в малом для категории Set.
Понятие полноты наиболее полезно в случае больших категорий
или предпорядков. В предпорядке Р произведение объектов aj, j Е
Е J, — это такой объект d, что d ^ aj при всех j, причем из условия
с ^ aj при всех j вытекает, что с ^ d; иначе говоря, произведение
совпадает с наибольшей нижней гранью или пересечением
множителей aj (двойственно, копроизведение — это наименьшая верхняя грань
или объединение).
Предложение 3 (Freyd). Если малая категория С полна в
малом, то она является предпорядком, причем каждое малое
множество его элементов имеет наибольшую нижнюю грань.
Доказательство. Предположим, что С не является предпоряд-
ком. Тогда найдутся объекты а, Ъ Е С со стрелками / ф g : а —>■ Ъ. Для
каждого малого множества J образуем произведение nj b, в котором
все множители bj равны Ъ. Любая стрелка h : а —> Uj Ъ определяется
своими компонентами, каждая из которых может равняться / или
д. Таким образом, существует не менее 2J стрелок aj —у Uj Ъ. Если
в малом множестве J больше элементов, чем стрелок в категории С,
то получаем противоречие. □
Г codu
А
\Ри
^codu
/
Fi
А
Пп Fcodu < П^ Fi <■■
(i)
- cod и
■Fa от и

5.2] Связь пределов с произведениями и уравнителями 135
Упражнения
1. (Manes.) Параллельная пара стрелок /, g : а —>- 6 в категории С имеет
обилую левую обратную стрелку h : Ъ —»■ а, если hf = 1 = hg.
а) Пусть в категории С всегда существуют малые произведения и
уравнители параллельных пар стрелок, имеющих общую левую обратную.
Докажите, что С полна в малом. (Указание: параллельная пара из
доказательства теоремы 1 в действительности имеет общую левую обратную.)
б) Покажите, что в категории Set параллельная пара стрелок /, g : X —>-
—> Y имеет общую правую обратную, если и только если образ
соответствующей функции (f,g):X—>YxY содержит диагональ {(у, у) | у Е У}.
2. Покажите, что если категории Ci,C2 полны (или кополны), то это
верно и для их произведения С\ х С2.
3. (Lim и Lim как функторы.) Пусть функторы F, F' : J —»■ С имеют
предельные конусы //,// (или копредельные конусы v,v'). Покажите, что
каждое естественное преобразование (3 : F —»■ F' однозначно определяет
стрелку lim (3 (соответственно lim (3), для которой коммутативна следующая
диаграмма, где Л : С —»■ С — диагональный функтор:
Л Lim F ^_
^ F
Д(Ит(3)
Л LimF' »' у р, »' ^ A(LimF
^(LimF)
A(lim(3)
Получите как следствие, что если С полна, то Lim (соответственно Lim)
является функтором С3 -Л С.
4. (Пределы композиций.) Пусть дана композиция функторов
а также предельные конусы v для F, v' для HFW. Проверьте, что
Л.ji (Не) = Н о Л.jс о W : J —> С , и покажите, что существует
единственная каноническая стрелка t : Н о LimF —»■ Lim HFW, для которой
коммутативна следующая диаграмма:
Aj, (Я о Lim F) Huw^ Hpw /? Aj, (Lim HFW)
*j,(t)
Л,,(е)
A j, (Lim HFW) "', HFW H»w. A j, (H о Lim F).
Двойственно, постройте стрелку s : Lim HFW —»■ H о Lim F в соответствии
с правой частью диаграммы.
5. (Предел как функтор из категории запятой, состоящей из всех
диаграмм категории С.)

136
Пределы
[Гл.5
а) Рассмотрев функтор W из упр. 4 как стрелку в категории (Cat l С),
покажите, что если категория С полна, то Lim является функтором
(Cat 4. С)ор -► С.
б) Пусть (Cat-J/C) — категория сверх-запятой, объектами которой
являются функторы F : J —У С, а стрелками (/3,W) : F' —у F — пары,
состоящие из функтора W : J —У J и естественного преобразования
/9 : PVF —У F . Объединив упр. 3 и 4, покажите, что если категория С полна,
то Lim является функтором (Cat\|/C)op —У С. Сформулируйте и докажите
двойственный факт.
5.3. Пределы с параметрами
Пусть Т : J х Р —у X — некоторый бифунктор, причем при каждом
значении р G Р параметра р функтор Т(—,р) : J —>• X имеет предел.
Тогда эти пределы для всех р G Р определяют функцию объектов
р ь->- Linij T(j,p) некоторого функтора Р —> X.
Мы не будем доказывать этот факт непосредственно, а заменим
функторы Р —у X объектами категории функторов Хр. Тогда
функтор Т : J х Р —» X будет заменен на сопряженный ему S : J —> Хр;
здесь сопряжение имеет вид Cat (J х Р, X) = Cat (J, Xp). Напомним,
что каждому объекту р G Р соответствует функтор Ер : Хр —у
—У X, значение при р, который действует на стрелку (естественное
преобразование) а : Н -^ Н' из Хр по формулам
ЕРН = Нр, ЕрО = Ор : Нр —у Нр. (1)
Теорема 1. Пусть S : J —У Хр — некоторый функтор, причем
для каждого объекта р G Р композиция EPS : J —У X имеет предел
Ьр с предельным конусом тр : Lp^ EPS. Тогда существует
единственный функтор L : Р —у X с функцией объектов р \-у Lp такой,
что отображение р \-у тр определяет естественное преобразование
г : ЛЬ = AjJ^ S. При этом г является предельным конусом
с основанием S : J —У Хр и вершиной L G Хр.
Доказательство. Пусть h : р —у q — произвольная стрелка из
Р. Тогда конусы тр и rq для произвольной стрелки и : j —у к из J
имеют следующий вид, где Sp обозначает EPS:

5.4]
Сохранение пределов
137
Треугольники коммутативны, поскольку тр и rq являются конусами,
а параллелограмм коммутативен, так как S является функтором.
Поскольку внутренний конус универсален, то существует единственная
стрелка Lh : Lp —У Lq такая, что rqj о L^ = Shj ° rpj при всех j Е J.
Соответствие h \-у L^ определяет функтор L (чтобы доказать это,
нарисуем снаружи еще один конус) и естественное преобразование
т : AL^r S (конус из объекта L Е Хр в функтор S : J —У Хр).
Этот конус — предельный. В самом деле, пусть а : М -^ S — еще один
конус. Тогда существуют единственные стрелки Мр —У Lp 1),
поскольку L является пределом; они определяют единственное естественное
преобразование М -^ L. □
Результат можно записать в виде
Ep(LimS) = Lim (EPS) :
в категории функторов пределы можно вычислять поточечно (если
существуют поточечные пределы).
Следствие. Если категория X полна в малом,, то это верно
и для любой категории функторов Хр.
Этот факт превращаетя в частный случай создания пределов, если
рассмотреть дискретную категорию |Р|, состоящую из всех объектов
и единичных стрелок категории Р.
Теорема 2. Пусть X и Р — произвольные категории. Тогда
функтор вложения i : |Р| —у Р индуцирует функтор г* = Хг : Хр —у
—У Xlpl, создающий пределы.
5.4. Сохранение пределов
Говорят, что функтор Н : С —» D сохраняет пределы функтора
F : J —У С, если каждый предельный конус г/ : b—У F для функтора
F в категории С переходит под действием функтора Н предельный
конус Ни : НЪ^- HF в категории D. Это означает, что Н не только
переводит каждый предельный объект категории С в предельный
объект категории D, но и переводит предельные конусы в
предельные. Функтор называется непрерывным, если он сохраняет все малые
пределы.
Теорема1. Пусть С — категория с малыми hom-
множествами. Тогда каждый hom-функтор С{с, —) : С —У Set
сохраняет все пределы — в частности, все малые пределы.
Доказательство приведет и к более общему результату. Именно,
пусть hom-множества категории С принадлежат некоторой категории
множеств Ens, причем Ens (X, Y) всегда состоит из всех функций
X —У Y. Тогда каждый hom-функтор С(с,—):С—У Ens сохраняет все
пределы, которые существуют в категории С.
) Которые сохраняли бы коммутативность диаграммы. — Прим. пер.

138
Пределы
[Гл.5
Доказательство. Пусть J — произвольная категория, F : J —>
—> С — функтор с предельным конусом v : Lim F -^ F в категории С.
Применив hom-функтор С (с, —), получим конус v* — С (с, г/),
показанный на следующей диаграмме для категории Set:
С(с,Ыш^^С(с,^), ie J
А
I* II
X T-i-+C(c,Fi).
Пусть т — другой конус с тем же основанием и с вершиной в
множестве X. Каждому элементу х Е X соответствует конус Т{Х : с —>
—> F{ в категории С, и ввиду универсальности конуса v существует
единственная стрелка hx : с —у LimF такая, что щкх = Т{Х. Положив
п>Х == fix
при всех ж, мы построим функцию, а тем самым и стрелку
к в категории Ens (см. диаграмму) такую, что v^k = Т{ при всех г.
Очевидно, что стрелка к с таким свойством единственна, и потому
конус i/* является предельным в категории Set. □
При ином изложении можно было бы начать доказательство с
того, что виду определения функтора С (с, F-) : J —> Set конус
Л : с^> F в категории С отвечает конусу Л : * -^ C(c,F—) в
категории Set с вершиной в точке *. Поскольку в соответствии с (1.3)
Cone (X, -) ^ Set (X, Cone (*, -)), то
Cone (X, С (с, F-)) = Set (X, Cone (*, С(с, F-))) =
= Set (X, Cone (с, F)) ^ Set (X, С (с, Lim F)),
где Cone означает J-конус. На последнем шаге используется
определение LimF. Но LimS для каждого S : J —> Set определяется
сопряжением Cone (X, 5) = Set (X, Lim 5). Поэтому из предыдущих
уравнений следует, что в данном случае Lim S (с соответствующим
предельным конусом) имеет вид
Lim C(c,F-) ^ C(c, LimF). (1)
Некоторые авторы с помощью этого равенства определяют
пределы в категории С в терминах пределов в Set; например, произведение
объектов di из С определяется как
ПС{с,щ)^С(с,Па1). (2)
г г
Контравариантный hom-функтор можно записать как
С(-,с) = Сор(с,-) :Cop^Set;
поэтому из теоремы 1 следует, что этот функтор переводит малые
копределы (и их копредельные конусы) в категории С в
соответствующие пределы и предельные конусы в Set. Например, из определения

5.4]
Сохранение пределов
139
малого копроизведения вытекает изоморфизм (между копроизведени-
ем и произведением):
C(Uaj,c) =ПС(алс).
3 3
Вообще, копредел функтора F : J —у С можно определить по формуле
С (Сбит F, с) ** LimC(F-,c). (3)
Создание и сохранение пределов связаны между собой.
Теорема 2. Пусть функтор V : X —> А создает пределы для
F : J —>• А, причем композиция VF : J —>• X имеет предел. Тогда V
сохраняет пределы для F.
Как следствие, если V сохраняет малые пределы, а категория X
полна в малом, то это верно и для А, причем функтор V непрерывен.
Доказательство. Пусть г : а^> F и а : х -^ VF — предельные
конусы в А и в X соответственно. Поскольку V создает пределы, то
существует единственный конус g : b^-F в А такой, что Vg : Vb-^VF
совпадает с а : х -^ VF; при этом конус g является предельным. Но
пределы единственны с точностью до изоморфизма, поэтому
существует такой изоморфизм О : b = а, что тв = д. Следовательно,
V6 : Vb = х = Va, причем Уг о У# = Vд = ст. Поэтому Уа является
пределом и У сохраняет пределы. □
Объект р некоторой категории называется проективным, если для
каждой стрелки вида h : р —> с и любого эпиморфизма д : 6 —>■ с
существует такая стрелка /г/, что /i = g/z/:
^' .-■■■"'
А''
Это равносильно следующему требованию: если д — эпиморфизм, то
отображение hom (р, д) : hom (p, 6) —>■ hom (p, с) является
эпиморфизмом в категории Set. Иначе говоря, объект р проективен, если и
только если функтор hom (p, —) сохраняет эпиморфизмы. Двойственно,
объект q называется инъективным, если hom (—,q) переводит
мономорфизмы в эпиморфизмы. Эти понятия особенно полезны в случае
i?-Mod и других АЪ-категорий; в категории i?-Mod проективными
объектами являются прямые слагаемые свободных модулей.
Упражнения
1. Докажите, что композиция непрерывных функторов непрерывна.
2. Пусть категория С полна, а функтор Н : С —> D сохраняет малые
произведения и уравнители (параллельных пар). Докажите, что Н
непрерывен.

140
Пределы
[Гл.5
3. Покажите, что функтор F : Set —у Ab, который отображает каждое
множество X в порожденную им свободную абелеву группу, не является
непрерывным.
4. Пусть X — малое множество. Покажите, что функтор (прямого
умножения на X) X х — : Set —у Set сохраняет пределы.
5. (Сохранение пределов.) Пусть даны функторы Н : С —У С' и F : J —»■
—>- С, причем F и i^F имеют пределы. Докажите, что if сохраняет предел
функтора F, если и только если каноническая стрелка Н о Lim F —»■ Lim if F
из упр. 2.4 является изоморфизмом. (Это естественная характеризация
сохранения пределов, если в категориях С и С' пределы заданы однозначно.)
5.5. Действие сопряженных функторов на пределы
Одно из наиболее полезных свойств сопряженных функторов
состоит в следующем: функтор, сопряженный справа, сохраняет все
пределы, существующие в его области.
Теорема1. Пусть функтор G : А —у X имеет левый
сопряженный, а функтор Т : J —у А имеет предельный конус г : а ^> Т
в категории А. Тогда GT имеет предельный конус Gr : Ga^- GT
в категории X.
Доказательство. Очевидно, что Gr действительно является
конусом над X с вершиной Ga. Пусть функтор F сопряжен с G
слева. Применив изоморфизм сопряжения к каждой стрелке конуса
а : ж^> GT, получаем стрелки (о$ : Fx —>• Тг, г G J, которые
составляют конус а : Fx -4Тв категории А. Но конус г : а^-Т универсален
среди конусов из Т в А, поэтому существует единственная стрелка
h : Fx —у а, для которой г ft- = <т°. Снова применив сопряжение,
получаем единственную стрелку ft^ : х —у Ga со свойством Gr • h$ =
= (rft)tf = (<7 )Й = ст. Единственность стрелки ft^ в точности означает,
что конус Gr : Ga -^ T универсален. □
Проиллюстрируем доказательство следующими диаграммами (где
и : г —у j — произвольная стрелка в категории J)
Менее элементарный вариант доказательства использует тот факт,
что функтор Lim сопряжен справа диагональному функтору Л. В
самом деле, пусть дано сопряжение
{F,G,r,,s) : X ^ А

5.5] Действие сопряженных функторов на пределы 141
и некоторая категория индексов J. Рассмотрим категории функторов
из J в X и в А; получаем диаграмму
(FJ,GJ,r)J,sJ) :XJ ^ AJ,
где FJ(S) = FS для каждого функтора S : J —> X, а также ?7J5 =
= r]S : 5 ^> GFS и т. д. Из треугольных тождеств для 77 и г вытекают
такие же тождества для г)J и sJ, поэтому диаграмма действительно
определяет сопряжение (короче говоря, сопряжения переносятся в
категорию функторов). В итоге получена диаграмма сопряженных пар
Непосредственно из определения диагональных функторов А
вытекает, что F3 А = AF, поэтому диаграмма левых сопряженных в этом
квадрате коммутативна. Поскольку при композиции сопряженных
функторов сопряженность сохраняется, то оба функтора Lim oGJ
и G о Lim сопряжены справа функтору FJ о А = А о F. Но
правый сопряженный для данного функтора единствен с точностью до
естественного изоморфизма, и потому Lim о GJ = Go Lim. Таким
образом, для любого функтора Т : J —> А с пределом а (и предельным
конусом т:й4Тв категории А) вновь доказано, что Ga = G Lim T =
= Lim GJ (T) = Lim GT. Рекомендуем читателю показать с помощью
аналогичного рассуждения, что G сохраняет предельные конусы
(подставить в предыдущую диаграмму единицы и коединицы и вспомнить,
что предельный конус т : а -^Т — не что иное, как значение коединицы
сопряжения (A, Lim ...) : А —^ AJ на функторе Т).
Столь же полезно и двойственное утверждение: если функтор Р
имеет правый сопряженный (т. е. является левым сопряженным),
то он должен сохранять копределы (копроизведения, коуравнители
и т. д.). Это объясняет, почему копроизведение (свободное
произведение) двух свободных групп снова является свободной группой (над
дизъюнктным объединением множеств образующих).
Аналогично (ввиду исходного варианта теоремы) типичные
забывающие функторы в алгебре сохраняют произведения, ядра,
уравнители и прочие виды пределов. Как правило, носителем произведения
двух алгебраических систем (групп, колец и т. д.) служит декартово
произведение носителей множителей. Этот и другие подобные факты
непосредственно вытекают из (нетрудной) теоремы 1. С ее помощью
можно также доказать отсутствие сопряженных у некоторых
функторов.

142
Пределы
[Гл.5
Упражнения
1. Пусть X — фиксированное множество. Покажите, что функтор
X х — : Set —>- Set не может иметь левого сопряженного, если X содержит
более одного элемента.
2. Покажите, что функтор D : Vctop —»■ Vet из (2), § 4.2 не имеет
правого сопряженного (и потому, в частности, не сопряжен слева функтору
Dop).
3. Пусть С — полная и рефлективная подкатегория в категории D,
кополной в малом. Докажите, что С кополна в малом.
4. Докажите, что категория Setop не является декартово замкнутой.
5.6. Теорема Фрейда о сопряженном функторе
Сформулируем теперь основную теорему существования левого
сопряженного для данного функтора. Сначала рассмотрим вопрос
о существовании начального объекта в данной категории, а затем
используем тот факт, что каждая универсальная стрелка,
определяемая единицей левого сопряженного, является начальным объектом
в подходящей категории запятой.
Теорема 1 (существование начального объекта). Пусть D —
категория, полная в малом и имеющая малые hom-множества. Тогда
существование начального объекта в D равносильно следующему
условию существования разрешающего множества: имеется малое
множество I и проиндексированное им семейство {ki} объектов из
D такое, что для каждого d Е D при некотором г Е / существует
стрелка ki —>■ d в D.
Доказательство. Существование разрешающего множества
необходимо. В самом деле, пусть D имеет начальный объект к.
Проиндексировав его одноэлементным множеством, мы получим
разрешающее множество, поскольку из к в любой объект имеется
единственная стрелка.
Обратно, пусть разрешающее множество существует. Поскольку
категория D полна в малом, то для этого множества существует
объект произведения w = П/^. Для каждого d Е D найдется некоторая
стрелка w —>■ d — например, композиция w = Uki —> ki —> d, где
первая стрелка — это проекция произведения. По предположению,
множество эндоморфизмов D(w,w) объекта w мало, а категория D
полна. Поэтому можно построить уравнитель е : v —> w этого
множества эндоморфизмов. Для каждого d G D найдется хотя бы одна
стрелка v —> d, например v —>■ w —>■ d. Пусть имеется две таких стрелки
f,g:v—>d. Возьмем их уравнитель е± (см. диаграмму).
ei $ ^ .
и *~v z^id
А I 9 \
: S е
т
eeis
w ^ w = П кг ^ ki.

5.6] Теорема Фрейда о сопряженном функторе 143
По определению объекта w имеется стрелка s : w —> и, поэтому
композиция ee\s, как и lw, является эндоморфизмом объекта w. Но
е по определению служит уравнителем всех таких эндоморфизмов,
и потому
ee\se = lwe = elv.
Поскольку е является уравнителем, то это мономорфизм; сократив на
него слева, получаем: e\se — lv. Это означает, что уравнитель в\
стрелок / и g имеет правую обратную стрелку. Как и любой уравнитель, е±
является мономорфизмом — а значит и изоморфизмом. Поэтому / =
= д; это значит, что v является начальным объектом в категории D. □
Иную формулировку этого доказательства см. в § 10.2.
Теорема2 (теорема Фрейда о сопряженном функторе). Пусть
дана категория А с малыми hom-множествами, полная в малом.
Тогда функтор G : А —>• X имеет левый сопряженный, если и только
если он сохраняет все малые пределы и выполнено следующее
условие существования разрешающего множества: для каждого объекта
х е X существует малое множество I и проиндексированное им
семейство стрелок /^ : ж —>■ Gai такое, что каждая стрелка h : х —>
—>• Ga может быть представлена как композиция h = Gt о fi для
некоторого индекса г и некоторого t : а\ —>• а.
Доказательство. Если G имеет левый сопряженный F, то
G сохраняет все пределы, в том числе малые, которые существуют
в его области А. При этом универсальная стрелка г\х : х —у GFx,
которая является единицей сопряжения, служит для х разрешающим
множеством с одноэлементным /.
Обратно, пусть условия теоремы выполнены. Достаточно
построить универсальную стрелку х —у Ga из каждого х G X в функтор G;
тогда левый сопряженный для G строится поточечно. Такая
универсальная стрелка является начальным объектом в категории запятой
(х I G) = D, так что нужно лишь проверить условия предыдущей
теоремы для этой категории. Ясно, что из существования
разрешающего множества для G вытекает существование такого множества
для (х I G) = D. Поскольку А имеет малые hom-множества, то это
верно и для D. Чтобы показать, что D полна в малом, нужно лишь
доказать существование любых малых произведений и уравнителей
параллельных пар. Их можно построить следующим образом:
Лемма. Пусть функтор G : А —у X сохраняет все малые
произведения (соответственно, все уравнители). Тогда при любом
х G X проекция категории запятой
Q : (х I G) -у А, (х Л Ga) \-> a
создает все малые произведения (соответственно, все уравнители).
Доказательство. Пусть J — некоторое множество (дискретная
категория), a fj : х —> Gaj — проиндексированное им семейство
объектов из (х ^ G), причем в категории А имеется диаграмма произведения
Pj : HcLj —> aj. Поскольку G сохраняет произведения, то в категории

144
Пределы
[Гл.5
X имеется диаграмма произведения Gpj
в X существует единственная стрелка / :
(Gpj)f = fj при всех j:
: GHcij —>• Gctj. Поэтому
х —> GUctj, для которой
Па.
Pj
CLj,
fj
GUaj
GPj
Gdi
Это означает, что семейство pj : / —у fj является конусом в категории
(х I G) — и на самом деле единственным конусом, который под
действием Q проецируется в данный конус pj : Hctj —> ctj. Можно
проверить, что этот конусу служит диаграммой произведения в
категории (х I G); эти два факта показывают, что Q создает произведения.
Аналогично мы создадим уравнитель двух стрелок s,t : / —>■ g
в категории (х I G) (см. диаграмму ниже). Пусть дан уравнитель е
стрелок Qs, Qt — т. е. дан уравнитель для s и t как стрелок из А.
Поскольку G сохраняет уравнители, то Ge является уравнителем для
Gs и Gt. Но Gs о f = g = Gt о f, поэтому существует единственная
стрелка h : х —> Ga, для которой Ge о f (см. диаграмму). Иначе говоря,
стрелка е : h —> f в категории (х I G) — единственная, которая под
действием Q переходит в е : а —> Ъ.
Остается показать, что стрелка е является уравнителем в
категории (х I G). Возьмем в этой категории другой объект к : х —> Gd
и стрелку г : к —> /, для которой sr = tr. Тогда равенство sr = tr
верно и в А, и потому существует единственная стрелка г'вД для
которой г = ег'. Осталось лишь показать, что г' является стрелкой
к —>• h в категории (ж | G); но Ge{Gr' о к) = G{er') о к = Gr о к =
= /, и ввиду единственности стрелки /i получаем, что Gr; ok = h. Это
означает, что г; является стрелкой категории (х I G). □
Такая схема рассуждений применима не только к произведениям
или уравнителям, но и к созданию любого предела (упр. 1).
ТеоремаЗ (теорема о представимости). Пусть D —
категория с малыми hom-множествами, полная в малом. Тогда функтор
К : D —>• Set представим, если и только если он сохраняет все малые
пределы и выполнено следующее условие.

5.6] Теорема Фрейда о сопряженном функторе 145
Существование разрешающего множества. Существует малое
множество S объектов из D такое, что для любого объекта d Е
Е D и любого элемента х Е Kd существуют sGS, элемент у Е Ks
и стрелка f : s —У <i, для которых (Kf)y = х.
Доказательство. Фактически мы по-новому
сформулировали теорему 1 о существовании начальных объектов. Действительно,
представление для К — это универсальная стрелка из
одноэлементного множества * в К (предложение 2, § 3.2), т.е. начальный объект
в категории запятой (* \. К), которая полна в малом, поскольку
функтор К предполагается непрерывным. Обратно, если функтор К
представим, то он заведомо непрерывен. □
Существование разрешающих множеств (или что-то подобное)
необходимо во всех трех теоремах. Пусть, например, Ord —
упорядоченное множество всех малых порядковых чисел а,/?,...; это
категория с hom-множеством Ord (а,/?), которое пусто или одноэлементно
в зависимости от того, а > /3 или а ^ /3. Категория Ordop полна
в малом, поскольку произведение любого малого множества
ординалов равно их наименьшей верхней грани. Функтор К : Ordop —у Set,
отображающий любое а в одноэлементное множество *, заведомо
непрерывен. Однако он не представим: если К а = Ordop(^,a) при
некотором Д то а ^ /3 для всех а, т. е. /3 — наибольший малый
ординал, а такого, как известно, не существует.
Случай полных булевых алгебр также показывает, что необходимо
какое-то условие типа существования разрешающих множеств.
Заданное счетное множество D порождает сколь угодно большие полные
булевы алгебры (Solovay [1966]); как следствие, не существует
свободной полной булевой алгебры, порожденной множеством D, и потому
забывающий функтор Comp Bool —у Set не имеет сопряженного
слева — хотя он непрерывен, а категория Comp Bool полна в малом.
Теорема о сопряженном функторе имеет много приложений.
Например, она обеспечивает существование левого сопряженного
для забывающего функтора Grp —у Set. Действительно, мы уже
знаем, что U создает все пределы (теорема 3, § 5.1), поэтому категория
Grp полна в малом, а функтор U непрерывен. Остается найти
разрешающее множество для каждого X G Set. Рассмотрим некоторую
функцию / : X —> UG, где G — группа, и возьмем подгруппу S С G,
порожденную всеми элементами вида /ж, х G X. Каждый элемент
из S равен произведению этих образующих и обратных к ним
элементов — например, (fxi)±1(fx2)±1 • • • (/жп)^1; поэтому для данного
X мощность множества S ограничена. Взяв по одному экземпляру
из каждого класса изоморфных групп 5, получаем малое множество
групп, и разрешающим множеством будет совокупность всех функций
X^US.
Построенный левый сопряженный F : Set —у Grp сопоставляет
каждому множеству X порожденную им свободную группу FX.
Таким образом, наша теорема позволяет построить эту группу, избежав
обычного (довольно кропотливого) явного построения ее элементов
как классов эквивалентности слов над алфавитом X. Ради точности

146
Пределы
[Гл.5
отметим, что обычное построение заодно показывает, что
универсальная стрелка X —> UFX инъективна (различные элементы из
X различны и как элементы свободной группы). Однако при нашем
подходе также можно установить этот факт, вспомнив, что существует
группа Н с двумя различными элементами h ф к. В самом деле, пусть
х е у в X. Возьмем такую функцию f : X —> UH, что fx = hnfy = k.
Она должна пропускаться через универсальную стрелку X —у UFX,
которая поэтому обязана быть вложением.
Эта конструкция применима не только к Grp, но и к категории
всех малых алгебраических систем г) данного типа т. Тип г
алгебраической системы определяется множеством операторов П и
множеством тождеств Е. Множество операторов П градуировано, т. е.
каждому его элементу со Е П сопоставлено натуральное число п,
которое называется его арностью. Таким образом, оператор арности
2 — это бинарный оператор, арности 3 — тернарный и т. д. Действие
операторов из П на некотором множестве S — это функция А, которая
сопоставляет каждому оператору и арности п некоторую п-арную
операцию и а • Sn —> S (здесь Sn = Sx... х 5, число множителей равно
п). По данному множеству операторов П строится множество Л всех
производных операторов; если дан оператор и арности п, а также п
производных операторов Ai,..., Лп арностей mi,..., mn, то очевидная
композиция cj(Ai, ..., Ап) является производным оператором арности
TTii + • •. + mn. Если же дан оператор А арности п и функция / : п —>- т
из {1,...,п} в {1,...,т}, то ее подстановка в А дает производный
оператор в арности т, который записывается через переменные Х{
в виде 6(xi,... ,хт) = А(ж/1,... ,ж/п). (Такое описание в терминах
переменных зависит от действия операторов из П на данном
множестве; абстрактный подход к композиции операторов см. в стандартных
курсах универсальной алгебры, например (Cohn [1965]) или (Gratzer
[1968]).) Во всяком случае, каждое действие А операторов из П на
множестве S однозначно продолжается до действия множества
производных операторов Л.
Множество тождеств Е в алгебраических системах типа т — это
множество упорядоченных пар (A, pi) производных операторов,
причем Аи/i имеют одинаковую арность п. Действие А операторов из П
на множестве S удовлетворяет тождеству (A, /i), если А^ = pi а • Sn —>
—> S. Алгебра А типа г — или (П, Е)-алгебра — это множество 5,
на котором задано действие А операторов из П, удовлетворяющее
всем тождествам из Е; мы будем называть S носителем алгебры
и часто писать \А\ = S. Морфизм (П, .Е)-алгебр g : А —>• А' — это
отображение носителей g : S —>■ S', сохраняющее все операторы из П
(и, следовательно, из Л) в том смысле, что
gu)A(ai,...,an) = UA'(gai,...,gan) (l)
1) В русском языке принят (в данном значении) термин универсальная
алгебра. — Прим. ред. пер.

5.6] Теорема Фрейда о сопряженном функторе 147
для всех cti Е А. Совокупность всех малых (П, .Е)-алгебр с
указанными морфизмами в качестве стрелок образует категорию (Q,E) —
— Alg, которую называют многообразием алгебр. Сюда относятся
такие известные примеры, как Grp, Rng, Ab, а также многие менее
известные (например, группы класса нильпотентности не выше
данного). Опишем в этих терминах, например, Grp. Пусть П содержит
три оператора: умножение, взятие обратного и выбор единицы е,
с арностями соответственно 2, 1 и 0. Тогда Е включает аксиомы для
единицы (еж — х — же), аксиомы для обратного элемента [хх~х — е —
— х~хх) и закон ассоциативности.
Для каждого многообразия алгебр теорема о сопряженном
функторе гарантирует существование левого сопряженного к забывающему
функтору (0,,Е) — Alg —>• Set; разрешающее множество строится
так же, как в случае групп (см. также § 5.7 ниже). Таким образом,
эта теорема для каждого множества X гарантирует существование
порожденного им свободного кольца, свободной абелевой группы,
свободного Л-модуля и т. п. Свободные поля при этом не появляются:
обратная операция к умножению в поле не всюду определена, так что
поля не являются алгебраическими системами в описанном смысле
(и в действительности свободных полей не существует) г).
Другая иллюстрация теоремы о сопряженном функторе —
построение левого сопряженного для забывающего функтора
V : Comp Haus -> Set, (2)
который отображает каждый хаусдорфов компакт в множество его
точек. Если даны хаусдорфовы компакты Х^ то декартово
произведение их носителей Y = П^ VXi с топологией произведения также
является хаусдорфовым компактным пространством (последнее в
силу теоремы Тихонова); следовательно, в Comp Haus существуют все
малые произведения и V сохраняет их. В действительности V создает
произведения. Топология произведения включает наименьший набор
открытых множеств, при котором все проекции^ : Y —> Х{
непрерывны; поэтому в любой другой компактной топологии Y' на том же
множестве У, обеспечивающей непрерывность проекций pi, присутствует
больше открытых множеств; значит, отображение id : Y' —> Y
является непрерывным вложением компакта в хаусдорфово пространство
и потому — изоморфизмом. Аналогичное рассуждение показывает,
что V создает все уравнители, а следовательно и все малые пределы.
Остается найти для каждого множества S разрешающее множество
стрелок / : S —> VX, где каждое X — хаусдорфов компакт. Поскольку
можно заменить X на замыкание fS С X, то можно считать fS
плотным в X. Для каждой точки х G X рассмотрим множество Lx =
= {D\DcSnxe fD}; таким образом, Lx — непустое семейство
) Конструкция свободной алгебры применима также к предмногообрази-
ям (реплично полным классам) универсальных алгебр (см. *Мальцев [1970],
с. 303-305); (*В. А. Артамонов [1991]). — Прим. ред. пер.

148
Пределы
[Гл.5
подмножеств в S. Если х ф х' разделены в X непересекающимися
открытыми множествами U и U', то f~xU G Lx, но f~xU £ Lx',
поэтому Lx т^ Lx;. Таким образом, L является вложением множества
X в повторную булеву степень VVS множества S. Если взять все
подмножества X в TVS, все топологии на каждом множестве X и все
функции / : S —У VX, то мы получим малое разрешающее множество
для S. Теорема о сопряженном функторе гарантирует теперь наличие
левого сопряженного для V; он сопоставляет каждому множеству S
компактификацию Стоуна-Чеха дискретной топологии на S.
Упражнения
1. Пусть функтор G : А —у X непрерывен. Покажите, что проекция
(х J, G) —>- А создает все малые пределы.
2. С помощью теоремы о сопряженном функторе найдите левый
сопряженный для каждого из забывающих функторов Rng —»■ Set, Rng —»■
—»■ Ab, Cat —у Ab, Cat —»■ Grph. Сопоставьте это с обычным построением
сопряженных в явном виде.
3. Пусть дан коуниверсальный квадрат в категории Cat:
причем Н создает пределы, аСих сохраняет. Докажите, что Н' создает
пределы.
4. С помощью упр. 3 и того факта, что (х \, X) —> X создает пределы,
дайте новое решение упр. 1.
5.7. Подобъекты и порождающие семейства
Такие понятия, как подкольцо, подгруппа или подполе, мы
рассмотрим теперь с категорной точки зрения, используя стрелки вместо
элементов. Например, подгруппа S группы G будет пониматься не как
множество элементов из G, а как мономорфизм S —> G,
реализованный как вложение множеств.
Пусть А — произвольная категория, u:s—>a,Hv:t—>a —
два мономорфизма с общей кообластью а. Будем писать и ^ v, если
и пропускается через v, т. е. если и = vu' для некоторой стрелки
и' (которая обязательно мономорфна). Если одновременно и ^ v
и v ^ и, то будем писать и = v; тем самым определено отношение
эквивалентности = на множестве мономорфизмов с кообластью а.
Классы этой эквивалентности называются под объектами объекта а.
Часто бывает удобно сказать, что мономорфизм и : s —> а является
подобъектом в а — т. е. отождествить и с классом эквивалентности,
состоящим из всех v = ив, где в : s —>■ s' — обратимая стрелка. Такие
подобъекты соответствуют подобъектам в обычном смысле
(определяемым в терминах элементов) в таких известных больших категориях,
как Rng, Grp, Ab и R-M.od, но не в Тор.

57]
Подобъекты и порождающие, семейства
149
Лемма 1. В любом коуниверсальном квадрате:
h
'- - tP
k I
S
если стрелка f мономорфна, то и f мономорфна (и если g
мономорфна, то и д' мономорфна).
Кратко говоря, коуниверсальные квадраты для мономорфизмов
состоят из мономорфизмов.
Доказательство. Рассмотрим, как показано на диаграмме,
параллельную пару /i, k, для которой f'h = f'k. Тогда gf'h = gf'k
и потому fg'h = fg'k. Поскольку / — мономорфизм, то g'h = g'k.
Но одновременно f'h = f'k] поскольку квадрат универсален, то из
этих двух равенств вытекает, что h = к. Следовательно, /' является
мономорфизмом. □
Для каждого a Е А множество всех подобъектов частично
упорядочено посредством отношения и ^ v. Пусть и : s —> а и v : t —>
—у а — два подобъекта, причем в категории А всегда существуют
коуниверсальные квадраты. В силу предыдущей леммы коунивер-
сальный квадрат для стрелок unv определяет еще один мономорфизм
w : р —>• а с кообластью а, причем w ^ u,w ^ v; это пересечение (или
наибольшая ниж^няя грань) подобъектов unv в частично
упорядоченном множестве всех подобъектов для a G А. Аналогично, пусть J —
произвольное множество, которое индексирует семейство подобъектов
щ : Si —>■ а (г G J) объекта a G А; тогда предел всех этих стрелок,
если он существует, определяет пересечение подобъектов щ. При
дополнительных предположениях можно построить и объединение (или
наименьшую верхнюю грань) семейства подобъектов.
Двойственно, два эпиморфизма г, s с областью а эквивалентны,
если г = 6s для обратимой стрелки в. Классы эквивалентности
таких эпиморфизмов называются фактор объектами объекта а; они
частично упорядочены отношением г ^ s, которое означает, что г
пропускается через s, т. е. г = r's. Такое определение факторобъектов
по двойственности проще, чем обычное определение факторалгебр
в терминах классов эквивалентности, и оно согласуется с обычным
определением в тех категориях, где эпиморфизмы — это сюръектив-
ные отображения. Например, так обстоит дело в Grp. Как следствие,
каждый факторобъект группы G в этой категории определяется
проекцией р : G —>• G/N группы G на ее факторгруппу G/N по некоторой
нормальной подгруппе N; при этом отношение G/M ^ G/N имеет
место, если и только если М D N (в общем случае отношение г ^
^ s для факторобъектов означает, что при переходе к фактору по г
больший объект s нужно отбросить!).
Г
>t
-^ а,

150
Пределы
[Гл.5
Мы говорим, что множество S объектов категории С порождает
эту категорию, если для каждой параллельной пары несовпадающих
стрелок ft, ft' : с —>■ d из С существуют объект s Е S и стрелка
/ : s —> с, для которой ft/ 7^ ft'/ (термин «порождает» устоялся, но
выбран неудачно; лучше подошло бы «разделяет»). Сюда включается
и случай, когда категорию порождает один объект s. Например, любое
одноэлементное множество порождает Set; Z порождает АЬ и Grp;
R порождает Л-Mod. Множество конечных циклических групп
порождает категорию всех конечных абелевых групп (а также — всех
абелевых групп кручения).
Двойственно, множество объектов Q является копорождающим
множеством для категории С, если для каждой параллельной пары
стрелок ft ф Ы : а —>- Ъ в этой категории существуют объект q
и стрелка g : Ъ —>■ д, для которой gft 7^ #/&'• Объект q называется
копорождающим, если множество {q} является копорождающим.
Например, любое двухэлементное множество является копорождающим
в категории Set.
Пользуясь понятием подобъекта, можно глубже исследовать
строение разрешающих множеств. Пусть дан функтор G : А —> X; мы
говорим, что стрелка / : х —> Ga охватывает (spans) объект а, если
в категории А не существует собственного 1) мономорфизма s —У а
такого, что / пропускается через Gs —> Ga.
Лемма 2. Пусть в категории А любое множество подовьектов
объекта а имеет предел. Тогда если функтор G : А —>• X сохраняет
все эти пределы, то каждая стрелка ft : х —>• Ga пропускается через
стрелку / : х —> Gb, которая охватывает Ъ.
Доказательство. Рассмотрим множество всех таких подобъек-
тов Uj : Sj —> а, что ft = Guj о hj для некоторой стрелки hj. Возьмем
предел v : Ъ —>■ а всех Uj. Тогда (см. диаграммы)
Ъ х- f->Gb
из Guj
стрелка Gv : Gb —у Ga также является пределом (для Guj), и ft
пропускается через Gv с помощью некоторой стрелки /, как показано
на диаграмме. По построению / охватывает Ь. □
Эта лемма означает, что разрешающим множеством для х может
служить множество всех исходящих из него стрелок, которые
охватывают какой-либо объект.
В качестве приложения рассмотрим категорию алгебр данного
типа т. Пусть в ней задана стрелка / : S —> GA. В алгебре А имеется
:) Т. е. не являющегося изоморфизмом. — Прим. пер.
Gv

5,7]
Подобъекты и порождающие, семейства
151
подалгебра, получаемая многократным применением операторов со Е
Е П к элементам множества f(S). Мощность этой подалгебры Af
ограничена мощностями множеств S и П. Поскольку / пропускается через
S —У GAf, то такие стрелки из множества S г) образуют малое
множество, которое является разрешающим для функтора G : Algr —>
—у Set. Эти стрелки являются охватывающими в смысле предыдущей
леммы, если вместо подобъекта а рассмотреть такой морфизм и : s —>
—> а, что стрелка Gu инъективна в категории Set.
Другим примером совместного применения этой леммы и
теоремы о сопряженном функторе служит доказательство существования
тензорного произведения модулей. Пусть даны модули А ж В над
коммутативным кольцом К. Их тензорное произведение — это
универсальный элемент множества Bilin (А, В; С) билинейных функций
/3 : А х В ^ С в некоторый третий if-модуль С. Это множество
служит функцией объектов некоторого функтора из категории С. Чтобы
построить разрешающее множество для данных А и В, достаточно
рассмотреть лишь те билинейные функции /?, которые охватывают
С (не пропускаются через его собственный подмодуль). Модуль С
состоит из всех конечных сумм ^ /3(ai,bi), т. е. указанное множество
действительно является разрешающим. Категория К — Mod полна
в малом, а функтор Bilin : К — Mod —у Set непрерывен; поэтому
тензорное произведение (g) : А х В ^ А ® В существует. Обычное
построение (в явном виде) становится совершенно излишним, так как
все свойства тензорного произведения непосредственно вытекают из
универсальности.
Упражнения
1. С помощью теоремы о сопряженном функторе постройте копроизве-
дение G II Н в категории Grp (оно обычно называется свободным
произведением). Используя произведение G х Н, покажите также, что инъекции
копроизведения G —»■ G II Н и Н —у G II Н мономорфны, а их образы
пересекаются по единичной подгруппе.
2. Аналогично постройте копроизведение колец.
3. Пусть R — некоторое кольцо, А — правый Я-модуль, В — левый R-
модуль. С помощью теоремы о сопряженном функторе постройте А 0д В.
(Такое тензорное произведение — это абелева группа, наделенная функцией
(а, Ь) I—>-а®&£ A<g>R В; эта функция биаддитивна, удовлетворяет условию
аг 0 6 = а 0 гЪ при всех а £ А,г £ R,b £ В и универсальна среди функций
с такими свойствами.) Докажите, что А ®д В порождается (как абелева
группа) элементами а 0 Ь. Исследуйте связь между A(&s В и A(&r В для
данного морфизма колец S —У R.
4. С помощью теоремы о сопряженном функторе постройте коуравни-
тели в категории Algr.
х) Для всевозможных /. — Прим. пер.

152
Пределы
[Гл.5
5.8. Специальная теорема о сопряженном функторе
Теперь рассмотрим другую теорему о существовании
сопряженных, в которой вместо разрешающего множества требуется малое
копорождающее множество объектов.
Теорема 1 (специальная теорема о начальном объекте). Пусть
категория D полна в малом, имеет малые hom-множества и малое
копорождающее множество Q, причем для каждого множества
подобъектов любого объекта d Е D существует пересечение. Тогда
D имеет начальный объект.
Доказательство. Образуем произведение qo = ^lqeQ Q всех
элементов малого копорождающего множества Q и возьмем пересечение
г всех подобъектов в qo. Для каждого объекта d Е D существует
не более одной стрелки г —> d; в самом деле, уравнитель двух
различных стрелок такого вида был бы собственным мономорфизмом
с кообластью г, т. е. подобъектом в qo, меньшим чем пересечение всех
подобъектов.
Чтобы показать теперь, что г является начальным объектом
категории D, нужно лишь построить стрелку г —>■ d для каждого d.
Рассмотрим множество Н всех стрелок h : d —>■ q G Q и (малое)
произведение Пнен Q- Возьмем стрелку j : d —>■ UheH Q с компонентами
h (т. е. ph о j = h для всех проекций р^). Поскольку множество Q —
копорождающее, стрелка j мономорфна. Образуем коуниверсальный
квадрат
с J-^UqeQq = q0
k
У j I
d ^ЩеЯ<7,
где стрелка к имеет компоненты Ph ° k = pq для всех h : d —>■ q.
Тогда и стрелка j' мономорфна, как предел для мономорфизма j.
Значит, с является подобъектом в qo. Но г — это пересечение всех
таких подобъектов, поэтому имеется стрелка г —>■ с. Композиция г —>
—> с —> d служит искомой стрелкой. □
Теорема2 (специальная теорема о сопряженном функторе).
Пусть категория А полна в малом, имеет малые hom-множества
и малое копорождающее множество Q, причем для каждого
множества подобъектов любого объекта a G А существует предел
(а значит, и пересечение). Пусть категория X таксисе имеет малые
hom-множества. Тогда для функтора G : А —>• X существует левый
сопряженный, если и только если G сохраняет все малые пределы
и все пределы семейств мономорфизмов.
Доказательство. Условия теоремы необходимы, поскольку
правый сопряженный функтор должен в действительности сохранять
все пределы. Чтобы доказать обратное, достаточно построить для

5.8] Специальная теорема о сопряженном функторе 153
каждого ж Е X начальный объект в категории запятой D = (х \, G).
Покажем, что эта категория удовлетворяет условиям предыдущей
теоремы (о существовании начального объекта). Вначале убедимся,
что подобъекты в категории (ж ^ G) имеют нужный вид.
Лемма. Стрелка h : (f : х —> Ga,a) —»(/': ж —>• Ga',a')
в категории (х I G) мономорфна, если и только если стрелка h : а —>
—>• а' мономорфна в категории А.
Доказательство. Ясно, что если h : а —>■ а' мономорфна, то
и h : f —> f мономорфна. Для доказательства обратного заметим,
что мономорфность стрелки h в точности означает, что ее ядерная
пара (коуниверсальный квадрат для пары /i, К) имеет вид 1а, 1а : а —у
—у а. С другой стороны, в силу леммы из § 5.6 проекция категории
запятой
(х I G) -» А, (/ : х -» Ga, a) \-> a
создает все пределы и, в частности, ядерные пары. При этом в А
всегда существуют ядерные пары. Поэтому (теорема 4.2) проекция
категории запятой сохраняет все ядерные пары и в том числе пару
1а, 1а; как следствие, она переводит мономорфизмы категории (ж I G)
в мономорфизмы категории А. □
Вернемся к доказательству теоремы. Дано малое копорождающее
множество в категории А. Поскольку X имеет малые hom-множества,
то множество Q' всех объектов к : х —> Gq (q G Q) является малым —
и при этом копорождающим в категории (х \, G). Если в этой
категории даны стрелки s ф t : (/ : х —>• Ga,a) —»(/': ж —>• Ga',a'), то
найдутся qo Е Q и стрелка h : а' —> qo, для которой hs ф Ы. При этом
h можно рассматривать как стрелку
h : (/' : х -+ Go!, a') -+ (f0 : x -+ Gq0, qo),
где /о = Gh о /', причем hs ф Ы в категории (ж \. G). Таким образом,
Q копорождает (х I G).
Поскольку категория А полна в малом, а функтор G
непрерывен, то категория (ж ^ G) полна в малом. Остается лишь построить
в этой категории пересечение произвольного множества подобъектов
hi : (fi : х —>• Gai,ai) —>•(/: ж —>• Ga,a), где i e J. Согласно лемме,
соответствующие стрелки hi : ai —У а мономорфны в категории А. По
предположению они тогда имеют предел h : Ъ —> а в А:
х = х = х
i /о л /
\i U Y V
h Ч Y <^Si ^/ <3fci
6 ■■■ > a, G6 >■ Са; >■ Ga.
Поскольку функтор G сохраняет пределы, то Gh : Gb —>• Ga, где G/i =
= G/if o Gsi, является пределом для Ghi в X. Так как одновременно
G/ii ° fi — f ПРИ всех г Е J, то существует единственная стрелка
си

154
Пределы
[Гл.5
/о • х —> Gb, для которой fi = Gsi о /0; в итоге получаем
стрелку h : (fo,b) —> (f, а), которая является пределом семейства {/if}
в категории (ж ^ G) (мы снова воспользовались тем, что проекция
категории запятой создает пределы). Этот предел является искомым
пересечением всех hi. □
Доказанной теореме можно придать и другую форму. Будем
говорить, что категория мала в смысле подобъектов (well-powered) l),
если подобъекты любого объекта a Е А можно проиндексировать
малым множеством; иначе говоря, для каждого а существует малое
множество Ja, обладающее биекцией на множество всех
подобъектов в а. Многие известные большие категории — Top, Grp, i?-Mod
и т. д. — малы в смысле подобъектов; двойственное понятие —
категория, малая в смысле фактор объектов 2). Если категория А мала
в смысле подобъектов и полна в малом, то любое множество
подобъектов объекта a Е А имеет пересечение, которым служит их обычный
предел. Как следствие, специальная теорема о сопряженном функторе
принимает следующий вид:
Следствие. Пусть категория А полна в малом, мала в смысле
подобъектов, имеет малые hom-множества и малое копорождающее
множество, а категория X имеет малые hom-множества. Тогда
функтор G : А —>• X имеет левый сопряженный, если и только если
он непрерывен. Как следствие, любой непрерывный функтор К : А —>•
—> Set представим.
Этот классический вариант специальной теоремы о
сопряженном функторе (иногда обозначаемой SAFT — Special Adjoint Functor
Theorem) часто встречается без явного упоминания о малости horn-
множеств — если в данной работе рассматриваются лишь категории
с малыми horn-множествами. Некоторые авторы используют для
категорий, малых в смысле подобъектов, термин «локально малые
категории», но другие называют так категории с малыми horn-множествами,
так что мы вообще отказались от этого термина!
Классический вариант теоремы SAFT можно непосредственно
вывести из общей теоремы о сопряженном функторе путем построения
разрешающего множества (см. Freyd [1964], р. 89 или Schubert [1970a],
р. 88).
В качестве типичного примера рассмотрим функтор вложения
G : Comp Haus С Тор (1)
полной подкатегории хаусдорфовых компактов в категорию Тор. Как
уже отмечено, категория Comp Haus полна в малом; она имеет
и малые hom-множества. Согласно лемме Урысона, для любых двух
точек ж/|/в компактном хаусдорфовом пространстве X существует
) В русской терминологии — категория локально мала слева. — Прим.
ред. пер.
2) В русской терминологии — категория, локально малая справа. — Прим.
ред. пер.

5.8] Специальная теорема о сопряженном функторе 155
непрерывное отображение / : X —у I на единичный отрезок /, такое
что fx = 0, fy = 1. Как следствие, / копорождает Comp Haus. По
специальной теореме о сопряженном функторе указанное вложение G
имеет левый сопряженный. Этот функтор (или, иногда, его
ограничение на полную подкатегорию вполне регулярных пространств)
называется компактификацией Стоуна- Чеха. Сюда включается и случай
дискретного пространства, см. § 5.6.
Другим примером служит теорема из работы (Watts [I960]). Любое
кольцо R порождает категорию R-Mod и потому копорождает
категорию i?-Modop. Как следствие, любой контравариантный аддитивный
функтор Т : i?-Mod —> Ab, переводящий малые копределы в
пределы, реализуется посредством изоморфизма групп Т = hom# (—,С)
для некоторого Л-модуля С. Действительно, по специальной теореме
о сопряженном функторе Т : (i?-Mod)op —> Ab имеет левый
сопряженный F. Поскольку функтор Т аддитивен, то сопряжение
Ab (G, ТА) ^ потя (A, FG), G Е Ab, Ae Я-Mod
является изоморфизмом абелевых групп; положив G = Z, получаем
ТА ^ Ab (Z, ТА) ^ потя(А, FZ).
Упражнения
1. Пусть дан функтор К : А —>- Set. Докажите, что если для К
существует левый сопряженный, то он представим. Обратно, пусть А — категория
с малыми костепенями, а функтор К представим в виде К = А(а,—) для
некоторого а Е А. Докажите, что К имеет левый сопряженный (который
сопоставляет каждому множеству X малую костепень X • а).
2. Пусть А — левый Я-модуль, В — правый Я-модуль, G — абелева
группа.
а) Докажите наличие следующих сопряжений:
homR(A,homz(B,G)) ^ homz (В ®д A, G) ^ hom# (В, homz (A, G)), где
homz (5, G) имеет естественную структуру (левого или правого) Я-модуля,
Ьотд обозначает hom-множество в категории Я-Mod, a homz — в Ab.
б) Известно, что аддитивная группа Q/Z рациональных чисел по
модулю 1 является инъективным кообразующим в категории Ab. Используя
п. а), докажите, что homz (Я,Q/Z) является инъективным кообразующим
в категории .R-Mod (определение инъективного объекта см. в § 5.4).
3. С помощью упр. 2 б) и специальной теоремы о сопряженном функторе
докажите, что любой непрерывный аддитивный функтор Т : Я-Mod —»■ Ab
представим. (Теорема Уотта.)
4. (Компактификация Стоуна-Чеха.) Пусть X — вполне регулярное
топологическое пространство. Покажите, что универсальная стрелка X —>-
—>- GFX для левого сопряженного к функтору (1) является инъекцией.
(Примените лемму Урысона: если х ф у во вполне регулярном пространстве
X, то существует непрерывное отображение f : X —> I (I — единичный
отрезок), такое что fx ф fy.) В классических источниках эта компактификация
описывается лишь для вполне регулярного X. Это ограничение излишне;
оно связано с тем, что рассматривались лишь универсальные инъекции,
а не универсальные морфизмы вообще.

156
Пределы
[Гл.5
5.9. Сопряженные функторы в топологии
В категории Тор объектами являются все (малые) топологические
пространства X, У, ..., а стрелками — все непрерывные отображения
/ : X —У Y. Забывающий функтор (обычно безымянный)
G : Тор -у Set
отображает X в множество его точек GX; он унивалентен и имеет
левый сопряженный D, который сопоставляет каждому множеству S
дискретную топологию на нем (когда все подмножества в S открыты).
Как следствие, G сохраняет все пределы, какие могут существовать
в категории Тор (поэтому носителем произведения пространств
является декартово произведение их носителей). Забывающий функтор G
имеет также правый сопряженный D', который сопоставляет каждому
множеству S тривиальную топологию на нем (когда открыты только
S и 0). Как следствие, G сохраняет все копределы, какие могут
существовать в категории Тор — и вот почему копроизведением двух
пространств служит их дизъюнктное объединение с сохранением их
топологии.
Теперь рассмотрим топологию подпространства на множестве
S CGX.
Если пространство X фиксировано, то G индуцирует функтор
G I X : (Тор | X) -+ (Set | GX)
f Gf
Y —-> X GY -^ GX
h
\-У
/'
Gh ||
Gf
(1)
Y' >■ X GY' >■ GX
Здесь / и /; — объекты, a h — стрелка в категории запятой (Top ^ X).
Функтор G I X имеет правый сопряженный L. Действительно, объект
t : S —У GX категории (Set ^ GX) — это множество S и функция
t : S —У GX. Введем топологию на 5, объявив открытыми все
множества вида £-1£/, где U открыто в X. Назовем полученное пространство
LS; тогда t становится непрерывным отображением Lt : LS —У X.
(Например, если S — подмножество в GX, то LS — это S с
топологией подпространства.) Как известно, такая топология на S имеет
свойство универсальности: если непрерывное отображение / : Y —У X
пропускается через t в категории Set по формуле Gf = t о s:
Gf
GY ^GX
II Gf = tos,
S^^GX,

5.9]
Сопряженные функторы в топологии
157
то отображение s : Y —у LS непрерывно. На самом деле это
свойство выражает искомую сопряженность: hom (G/, t) = hom (/, Lt).
Заметим, что (G \, X) о L = Id; функтор L является сопряженным
и обратным справа для (G I X).
Отдельно отметим, что свойство универсальности индуцированной
топологии на подмножестве S С GX касается не только других
подпространств в X, но и других пространств Y и любого непрерывного
отображения / : Y —> X, которое пропускается через вложение t : S —>
—у GX (т. е. его образ содержится в подмножестве S).
С помощью описанного сопряженного функтора можно построить
в категории Тор (стандартные) уравнители посредством следующей
общей процедуры:
Предложение!. Пусть функтор G : С —У D унивалентен,
в категории D всегда существуют уравнители и при любом х Е
Е С функтор (G I х) : {С \. х) —>• {D \. Gx) имеет сопряженный
и обратный справа функтор L. Тогда в категории С всегда
существуют уравнители.
Доказательство. Чтобы построить уравнитель параллельной
пары /, /; : х —у у, применим G, возьмем в D уравнитель t : s —>
—> Gx пары G/, Gf и применим L; ввиду универсальности
сопряжения стрелка Lt : Ls —>■ х является уравнителем в С. □
Это рассуждение — не что иное, как обычное определение
уравнителя, освобожденное от упоминаний об элементах: если даны два
непрерывных отображения /, /; : X —у У, то берем множество S
точек х G X, где fx = f'x, и вводим топологию подпространства.
Наличие сопряженности объясняет, почему нужна именно топология
подпространства.
Хорошо известно, что категория Тор полна (complete). Чтобы
доказать это, требуется построить лишь уравнители (параллельных пар)
и произведения. Чтобы построить произведение любого семейства
пространств Xi,i G J, нужно взять произведение их носителей UGXi
и ввести на нем (универсальную) топологию, в которой непрерывны
все проекции pi : UGXi —у GXi, г G J. В терминах категорий
можно выразить тот факт, что для любых пространств Х^ множества
S и функций ti : S —> GXi существует универсальная топология,
содержащая лишь те подмножества в 5, которые необходимы для
непрерывности отображений ti (см. упр. 3).
Двойственное рассуждение применимо к копределам. Пусть X —
произвольное топологическое пространство. Функтор
(X I G) : (X I Тор) -у (GX | Set)
имеет левый сопряженный М. Действительно, объект из (GX I Set) —
это некоторая функция t : GF —у S. Введем на ее кообласти S
топологию, состоящую из всех тех подмножеств V С 5, прообразы
которых t~xV открыты в X, и назовем полученное пространство
MS. (Если отображение t : GX —у S сюръективно, то мы получаем
хорошо известную фактортопологию или топологию отождествления

158
Пределы
[Гл.5
на S.) Теперь функция t превращается в непрерывное отображение
Mt : X —>• MS. При этом, если отображение / : X —>• Y непрерывно
и Gf = к о t для некоторой функции к:
X GX
ТоР : Mt/ \ / Set : */ \ g/
MS - >У, 5 ■■ >ОУ,
А; к
то отображение fc : MS —>■ У непрерывно. Таким образом,
соответствие к \-^ к — это сопряжение
(X ; Top)(Mi, /) S (GX ; Set)(i, G/),
единицей которого служит тождественное отображение. Как
следствие, функтор М сопряжен слева и обратен справа к {X \. G).
Предложение 1 опирается лишь на аксиомы категорий, поэтому
верно и двойственное утверждение. С учетом указанной
сопряженности оно означает, что в категории Тор всегда существуют коуравни-
тели.
Аналогично в категории Тор строятся копроизведения
(дизъюнктные объединения) и копределы общего вида. Такие копределы
встречаются часто, обычно под другими названиями, например в
стандартной процедуре склеивания пространства из кусков. Пусть,
скажем, {Ui | i Е J} — открытое покрытие пространства X. Каждое
непрерывное отображение / : X —> Y определяет семейство своих
ограничений f\Ui : Ui —> Y (i G J). Обратно, хорошо известен тот
факт, что семейство непрерывных отображений fa : Ui —>■ Y (i G J)
определяет непрерывное отображение / всего пространства X, если
и только если fi\(UiC\Uj) = fj\(Ui П Uj) при всех г и j. Этот факт
означает, что следующая диаграмма определяет уравнитель:
Top(X,F) ->IlTop(Ui,Y) =* IlTop (Ui П Uj,Y),
где стрелки соответствуют ограничениям отображений.
Эквивалентно, результат можно сформулировать следующим образом.
Пространство X является копределом в категории Тор для функтора U : J' —>
—у Тор, причем копредельный конус состоит из вложений Ui —>
—> X; при этом объектами категории J' являются пары индексов (г, j)
и отдельные индексы (г), а неединичные стрелки имеют вид (г, j) —>■
—у (г), (i,j) —> (j); функтор U действует на объекты по формулам
U(i,j) = Ui П Uj, U(г) = Ui, а неединичные стрелки переводит во
вложения.
Другим примером коуравнителя служит пространство Х/А,
которое получается из пространства X сжатием подмножества А

5.9]
Сопряженные функторы в топологии
159
в точку. Это коуравнитель
а
* • X -+ Х/А
^^
множества всех стрелок, отображающих одноточечное пространство
* в какую-либо из точек a Е А. Такой коуравнитель используется
в теории гомотопии. Рассмотрим категорию Тор^ \ объектами
которой являются пары (X, А) (пространство X с подмножеством А),
а стрелками — (X, А) —> (Х',А') — непрерывные отображения X —>
—у X', отображающие А в А'. Если У — топологическое пространство
с отмеченной точкой, то определению пространства Х/А можно
придать следующий вид:
ТорДХ/А,У) = Тор^((Х,А),(У,*)).
Как следствие, функтор (X, А) и-» Х/А сопряжен слева к функтору
У н-» (У,*), отображающему каждое пространство с отмеченной
точкой в пару (У, *).
Многие подкатегории в Тор широко известны.
Предложение 2. Полная подкатегория Haus категории Тор,
состоящая из всех хаусдорфовых пространств, полна и кополна.
Функтор вложения Haus —> Тор, так же как и забывающий
функтор Haus —>• Set, имеет левый сопряженный Н.
Доказательство. Покажем, что существование левого
сопряженного Н вытекает из теоремы о сопряженном функторе. Прежде
всего, произведения и подпространства хаусдорфовых пространств
также хаусдорфовы, поэтому категория Haus полна (complete), а ее
вложение в Тор является непрерывным функтором (т. е.
сохраняет малые пределы). Остается лишь проверить существование
разрешающего множества для каждого топологического пространства X.
Но любое непрерывное отображение пространства X в хаусдорфово
пространство Y пропускается через свой образ, который является
подпространством в У и потому хаусдорфов. Этот образ является
фактормножеством для X с некоторой топологией, поэтому
существует не более чем малое множество (неизоморфных) сюръекций X —>
—> У на хаусдорфово пространство У. Это значит, что разрешающее
множество существует. Полученный левый сопряженный функтор Н
сопоставляет каждому пространству X хаусдорфово пространство
ИХ и непрерывное отображение г\ : X —> НХ, универсальное среди
непрерывных отображений из X в хаусдорфовы пространства. Из
универсальности отображения г] вытекает его сюръективность, поэтому
ИХ можно описать как наибольшее хаусдорфово факторпространство
для X. Если само X хаусдорфово, то можно положить ИХ — X
иг] = 1, и тогда Н является сопряженным и обратным слева для
вложения.

160
Пределы
[Гл.5
Поскольку функтор Н является левым сопряженным, то он
сохраняет копределы. Как следствие, категория Haus кополна, т. е.
в ней существуют все малые копределы. В частности, копроизведе-
ние в Haus совпадает с копроизведением в Тор (поскольку копро-
изведение хаусдорфовых пространств хаусдорфово), а коуравнитель
в Haus — это наибольшее хаусдорфово фактор-отображение для ко-
уравнителя в Тор.
Полная подкатегория компактно порожденных хаусдорфовых
пространств особенно полезна, поскольку она декартово замкнута (§ 7.8).
Упражнения
1. Пусть L conn — полная подкатегория локально связных пространств
в категории Тор. Докажите, что функтор D : Set —»■ L conn имеет левый
сопряженный С, который сопоставляет каждому пространству X
множество его связных компонент. Покажите, что функтор С уже не имеет левого
сопряженного (из-за неправильного действия на уравнители).
2. Покажите, что правый сопряженный D' : Set —»■ Тор к забывающему
функтору не имеет правого сопряженного (из-за неправильного действия
на копроизведения).
3. Категорное построение обычных произведений топологических
пространств.
а) Пусть Л : С -► С\ А : D -► DJ — диагональные функторы.
Для любого Т G CJ каждый функтор G : С —»■ D определяет функтор
G* : (Л I Т) -+ {Л' 4- GT) по формуле (г : с^ Т) ^ (Gr : Gc^r GT).
Пусть G* имеет левый сопряженный, a GT имеет предел в категории D.
Докажите, что Т имеет предел в категории С.
б) Пусть G — забывающий функтор Тор —»> Set, a J — дискретная
категория. Постройте левый сопряженный для G>, показав, что он вводит
на произвольном множестве S слабейшую топологию, в которой является
непрерывным заданное семейство функций fj-.S—t GXj,
проиндексированное множеством J.
в) Выведите из предыдущего, что в категории Тор существуют все
произведения (в обычном смысле).
4. Постройте левый сопряженный для каждого из функторов вложения
Торп+1 —»> Торп, п = 0,1,2,3, где Торп обозначает полную подкатегорию
всех Тп-пространств в категории Тор. Условие Т\ означает нормальность
пространства, Тз — его регулярность, Т2 — хаусдорфовость и т. д. х)
5. Покажите, что вложение Haus —»■ Тор не имеет правого
сопряженного. Для этого покажите, что коуравнитель отображений хаусдорфовых
пространств в категории Тор не обязательно хаусдорфов. Отсюда получите,
что забывающий функтор Haus —»■ Set не имеет правого сопряженного.
Замечания
Известны многочисленные примеры и частные случаи теоремы о
сопряженном функторе; произошло множество частичных открытий и
переоткрытий. Упомянем условие Бурбаки (Bourbaki [1957]) для существования
х) См. Математический энциклопедический словарь. — М.: Советская
энциклопедия. 1988, с. 443-444. — Прим. пер.

5.9] Сопряженные функторы в топологии 161
универсальных стрелок; в этом варианте теоремы явно сформулирована
роль разрешающих множеств, но он оказался громоздким, поскольку
понятие структуры у Бурбаки не использует категорных идей. Современный
вариант теоремы о сопряженном функторе был сформулирован и
приобрел известность благодаря Фрейду (Freyd [1964]), который сформулировал
и специальную теорему о сопряженном функторе (SAFT). Наш вариант
специальной теоремы о начальном объекте принадлежит Келли (G. M. Kelly,
частное сообщение).

Глава 6
МОНАДЫ И АЛГЕБРЫ
Теперь мы более подробно изучим роль сопряженных функторов
в универсальной алгебре. Для каждого типа алгебр т (§ 5.6)
имеется категория Algr всех алгебр данного типа, забывающий функтор
G : Algr —у Set и его левый сопряженный F, который сопоставляет
каждому множеству S свободную алгебру FS типа т, порожденную
элементами из S. Эта сопряженность отражается в категории Set;
действительно, композиция Т = GF — это функтор Set —у Set,
который сопоставляет каждому множеству S множество всех
элементов соответствующей свободной алгебры. С функтором Т связаны
и определенные естественные преобразования, которые придают ему
структуру монады, напоминающую моноид. Замечательно то, что всю
категорию Algr можно восстановить по ее монаде в категории Set.
Другой важнейший результат принадлежит Беку (Beck) и
характеризует те категории А с сопряжениями (F, G,(p) : X —^ А, которые
можно восстановить таким образом по монаде Т в данной категории
X. В итоге оказывается, что алгебра в смысле Бека — настолько общее
понятие, что включает компактные хаусдорфовы пространства (§ 6.9).
6.1. Монады в категории
Каждый эндофунктор *) Т : X —у X определяет композиции Т2 =
= ТоТ: Х^ХиТ3 = Т2оТ: Х^Х. Пусть и : Т2 ^ Т -
естественное преобразование с компонентами /лх : Т х —У Тх для
каждого х е X. Тогда Т/л : Т3 -^Т2 обозначает естественное
преобразование с компонентами (T/i)x = Т(цх) : Т3х —у Т2ж, а преобразование
/iT : Т3 -^Т2 имеет компоненты (цТ)х = /1тх- В действительности Т/г
и /±Т — это «горизонтальные» произведения в смысле § 2.5.
Определение. Монада Т = (Т,т/,/л) в категории X состоит из
функтора Г:1-^1и двух естественных преобразований
r/iIx^T, /i:T2^T,
делающих коммутативными следующие диаграммы:
тз Тм> у2
г)Т п Тг)
IT >■ Г2 ^ TI
II
г
II
г.
(1)
(2)
1) Т. е. функтор, у которого область и кообласть совпадают. — Прим. пер.

6Л]
Монады в категории
163
Определение монады формально похоже на определение моноида
М в категории множеств, данное во введении. Множество
элементов моноида М заменено на эндофунктор Т : X —У X, декартово
произведение двух множеств х — на композицию двух функторов,
бинарная операция умножения /i : М х М ^ М — на преобразование
[1 : Т2 -1» Т, а единица г\ : 1 —>• М — на преобразование г\ : 1х -> Т.
Поэтому мы назовем г\ единицей, a \i — умножением в монаде Т; тогда
первая коммутативная диаграмма из (1) выражает ассоциативность
умножения, а вторая и третья характеризуют соответственно левую
и правую единицу. Ввиду сказанного, монада в категории X — это
моноид в категории ее эндофункторов, где умножение х заменено на
композицию эндофункторов, а единица — на тождественный
эндофунктор.
Терминология. Объекты (X, Т, 77, /i) имеют много названий:
двойственная стандартная конструкция, тройка, моноид и триада. Частое
и неудачное употребеление в этом смысле слова тройка (triple)
породило массу недоразумений, например из-за путаницы с
упорядоченными тройками и использования родственных терминов типа
троичные производные функторы (triple derived functors), притом что эти
функторы не произведены три раза от чего бы то ни было. Поэтому
целесообразен термин монада.
Каждое сопряжение (F, G, ту, е) : X —^ А порождает монаду в
категории X. Именно, композицией двух функторов F : X —> А и G : А —>
—> X является эндофунктор Т = GF, единица сопряжения г] является
естественным преобразованием т] : I ^>Т, а коединица г : FG —>1а пРи
горизонтальном умножении порождает естественное преобразование
\i — GeF : GFGF -^ GF = Т. Ассоциативный закон (2) для такого
умножения \i соответствует коммутативности первой из следующих
диаграмм:
GFGeF
GFGFGF >■ GFGF
GsFGF
GFGF
GeF
GeF
Y
■GF,
FG f
FGFG >■ FG
\eFG
Y
FG —
Ia-
Поменяв местами G и F, получаем коммутативность второй
диаграммы, которая вытекает уже из определения (§ 2.4) горизонтального
произведения ее = e-(FGe) = e-{eFG) (т. е. из закона чередования для
функторов и естественных преобразований). Аналогично, аксиомы
левой и правой единицы из (2) соответствуют диаграммам
IxGF^GFGF°E?LGFIx

164
Монады и алгебры
[Гл.6
которые по существу сводятся к треугольным тождествам для
сопряжения:
1 = Ge • r]G : G ^ G, 1 = sF • Frj : F ^ F.
Следовательно, (GF, 77, GsF) действительно является монадой в
категории X. Будем говорить, что эта монада определена сопряэюением
(F,G,r,,e).
Например, монада свободной группы в категории Set — это монада,
определенная сопряжением (F,G,cp) : Set —^ Grp, где G : Grp —>•
—> Set — забывающий функтор.
Двойственно, комонада в категории состоит из функтора L и
преобразований
L : А -> А, е : L-+I,
для которых коммутативны диаграммы
S:L^L2
(1°Р)
L
II
sL
L
L2
Ls
L
II
Каждое сопряжение (F,G,rj,e) : X —^ А определяет комонаду
(FG,s,Ft]G) в категории А.
Что такое монада в предпорядке Р1 Функтор Т : Р —у Р — не
что иное, как монотонная функция Т: Р^-Р(х^увР влечет
Тх ^ Ту). Естественные преобразования т\ и \i из (1) существуют
в точности тогда, когда
х ^ Тх, Т(Тх) ^ Тх
(3)
при всех х Е Р; в этом случае диаграммы (2) коммутативны,
поскольку в предпорядке существует не более одной стрелки с заданными
концами. Из первого уравнения в (3) вытекает, что Тх ^ Т(Тх). Пред-
пол ожим теперь, что предпорядок Р является частичным порядком
(ж ^ у ^ х влечет х ^ у). Тогда из (3) следует, что Т{Тх) = Тх.
Следовательно, монада Т в частичном порядке Р — не что иное, как
операция замыкания t в Р, т. е. монотонная функция t : Р —У Р, для
которой х ^ tx и t(tx) = tx при всех х Е Р.
Предоставляем читателю определить морфизм монад (Т, /i, ту) —>
—>• (Т',//,//) (соответствующее естественное преобразование Т—> Т')
и категорию всех монад в данной категории X.
6.2. Алгебры над монадой
Естественный вопрос: «Всякая ли монада определяется парой
сопряженных функторов?» имеет положительный ответ, а на самом деле

6.2]
Алгебры над монадой
165
два положительных ответа, отвечающие двум парам сопряженных
функторов. При первом ответе (Eilenberg, Moore [1965]) по монаде
(Т, ту, /i) в категории X строится категория Т-алгебр Хт и сопряжение
X —^ Хт, которое и определяет монаду (Т, 77,/i) в X. Формально
Т-алгебра — это множество, на котором действует моноид Т (см.
Введение).
Определение. Пусть Т = (Т,77,/i) — монада в категории X.
Тогда алгебра над монадой Т (Т-алгебра) (ж, h) — это пара, включающая
объект ж Е X (носитель алгебры) и стрелку /i : Тх —> х в категории
X (называемую структурным отображением алгебры), для которой
коммутативны диаграммы
Т2х -^ Тх
Тх
-^ ж,
(1)
(Первая диаграмма означает ассоциативность, вторая — наличие
единицы.) Морфизм Т-алгебр / : (ж, h) —> (х', h') — это стрелка / : х —> х'
в категории X, для которой коммутативна диаграмма
х -*-
ж'^
/г'
Тж
у
Тх'.
(2)
Теорема 1. {Каждая монада определяется своими Т-
алгебрами.) Если (T,tj,/jl) — монада в категории X, то множество
всех Т-алгебр и их морфизмов образует категорию ХТ. Имеется
сопряжение
{FT,GT;r1T,eT):X^XT,
в котором функторы FT и GT определяются соответствиями
GT
(ж,/г) \—
/
(ж',/г')ь
->- ж
f FT :
ЖЬ
f
x'\-
- (Tx,fix)
i
(Tx',fixi),
(3)
и при этом г] =77 и a (x,h) = h для каждой Т-алгебры (ж, К).
Монада, соответствующая в категории X этому сопряжению, совпадает
с исходной монадой (T,tj,/jl).
Доказательство этих утверждений состоит в их прямой проверке.
Если / : (ж,/г) —>• (ж',/г/) и g : (x',h')(x",h") — морфизмы Т-алгебр,

166
Монады и алгебры
[Гл.6
то это верно и для их композиции gf; при таком умножении Т-
алгебры очевидно образуют категорию, как и утверждалось. Функтор
просто забывает структурное отображение Т-алгебры.
С другой стороны, для каждого х Е X пара (Тх,/ах : Т(Тж) —>■
—> Тх) является Т-алгеброй (свободной Т-алгеброй над X) в силу
закона ассоциативности и наличия левой и правой единицы в монаде
Т. Следовательно, соответствие х н-» (Тх,/ах) действительно
определяет функтор FT : X —у Хт, как и утверждалось. Тогда GTFTx =
= GT(Tx, цх) = Тж, поэтому единица ту данной монады является
естественным преобразованием j] = j]T : Ix ^ GTFT. С другой стороны,
FTGT(x,h) = (Тх,/лх). При этом первый квадрат в определении (1)
Т-алгебры (ж, /i) означает, что структурное отображение h : Тж —>• ж
является морфизмом Т-алгебр (Tx,/ix) —>■ (ж,/г). В итоге получаем
естественное преобразование
4г,л>=Л:^ГСт<а;,Л>-^<а;,Л>)
которое соответствует определению морфизма Т-алгебр. Треугольные
тождества для сопряжения имеют вид
Тг)х
Тх >■ ТТж
^
1
Их
х -
*». т
> 1
^
ж
h
Тх, ж.
Первое выполнено в силу аксиомы (правой) единицы для Т, а второе —
в силу аксиомы единицы для Т-алгебры (см. (1)). Следовательно, т]Т
и гт определяют сопряжение, как и утверждалось.
Это сопряжение, в свою очередь, определяет монаду в категории
X. Эндофунктор G FT совпадает с исходным Т, единица г]т — с
исходной единицей, для умножения fiT = GTsTFT выполнены равенства
/jTx = GTet(Tx,iix) = GT\ix — \ix, т.е. оно совпадает с исходным
умножением в Т. Доказательство завершено. □
Теперь покажем на нескольких примерах, что Т-алгебры для
некоторых известных монад — это также известные алгебры.
Замыкание. Операция замыкания Т на предпорядке Р — это
монада в категории Р (см. § 1); соответствующая Т-алгебра — это
элемент ж Е р, для которого Тж ^ ж (стрелка служит структурным
отображением). Поскольку ж ^ Тж при всех ж, то Т-алгебра — это
такой элемент ж Е Р, для которого ж ^ Тж ^ ж. Если Р — частичный
порядок, то в такой ситуации ж = Тж, и тогда Т-алгебра — это элемент
ж, замкнутый в обычном смысле.
Действие группы. Пусть G — (малая) группа, X — (малое)
множество, причем выполнены условия
ТХ = G х X, X -^ G х X, Gx(GxX) ^GxX,
^ (и,х), (pi, (#2,я» Н> (9192,х),

6.2]
Алгебры над монадой
167
где х Е X, gi,#2 £ G, а -и — единица группы G. Тогда в категории
Set определена монада (Т, ту, /i). В этой ситуации Т-алгеброй является
множество X с функцией (структурным отображением) h : G х X —>■
—>■ X, таким что
h(g1g2jx) = h(gljh(g2jx)) , h(u,x) = х.
Если положить # • ж = h(g,x), то получаем стандартное определение
действия (д,х) ^Л д-х группы G на множестве X. Неудивительно, что
Т-алгебры для монады Т — это действия группы: наше определение
Т-алгебр построено по образцу определения действия группы.
Модули. Пусть R — (малое) кольцо, А — (малая) абелева группа.
Тогда условия
TA = R®A, A^R®A, R®(R®A)^R®A,
ан1®а, ri ® (r2 0 а) И- т\т2 ® а,
где oG А,Г1,Г2 G Д, определяют монаду в категории АЬ. Рассуждая
как в предыдущем случае, получаем, что Т-алгебры — это левые R-
модули.
Упражнения
1. Полные полурешетки (Е. Manes, диссертация.) Напомним, что полная
полу решетка — это частичный порядок Q, в котором каждое подмножество
S С Q имеет супремум (наименьшую верхнюю грань). Пусть V — кова-
риантный функтор булевой степени в категории Set. Это означает, что
VX — множество всех подмножеств S С X, a (Vf)S, где / : X —»■ У, —
это образ множества S при отображении /. Пусть X — произвольное
множество, rjx '• X —>- VX отображает каждый элемент х Е X в одноточечное
множество {ж}, a fix '• VVX —»■ VX отображает каждое семейство множеств
в их объединение.
а) Докажите, что (V,r],fi) — некоторая монада V в категории Set.
б) Докажите, что каждая Р-алгебра (X, h) становится полной
полурешеткой, если определить отношение х ^ у условием h{x,y} = у и положить
sup S = hS для всех S С X.
в) Докажите обратное: каждая (малая) полная полу решетка
превращается таким способом в V- алгебру.
г) Из в) получите, что категория Р-алгебр — это категория всех (малых)
полных полу решеток, где морфизмами являются функции, сохраняющие
порядок и супремум.
2. Покажите, что функтор GT : ХТ —»■ X сохраняет пределы.
3. а) Пусть (T,rj,fj) и (Т',т/,//) — монады на множестве X.
Определите морфизм монад в как соответствующее естественное преобразование
в : Т —> Т' и постройте категорию всех монад на X.
б) Исходя из 9, постройте функтор #* : Хт —»■ Хт, такой что GT о #* =
= GT , а также естественное преобразование FT -^ в* о FT .

168
Монады и алгебры
[Гл.6
6.3. Сравнение с алгебрами
Исходя из сопряжения X —^ А, можно построить монаду Т в
категории X, а затем категорию Т-алгебр. Спрашивается, как она связана
с исходной категорией А? Полный ответ зависит не только от самих
категорий, но и от сопряжения. Он содержится в следующей теореме.
Теорема 1 (сравнение сопряжений с алгебрами). Пусть
(F,G,r1,e):X^A
— некоторое сопряжение, Т = (GF,r],GeF) — определяемая им
монада в категории X. Тогда существует единственный функтор
К :А^ ХТ такой, что GT К = G и KF = FT.
Доказательство. Утверждение теоремы означает, что
следующую диаграмму мы можем дополнить стрелкой К, которая сделает
коммутативными и F-, и G-квадрат:
А
X
к
■■^х1
X.
(1)
Коедница е заданного сопряжения определяет для каждого a Е А
стрелку Gea : GFGa —> Ga. Эту стрелку можно рассматривать как
структурное отображение h в Т-алгебре на объекте Ga = ж;
действительно, диаграммы (2.1) здесь принимают вид
GFGsa
GFGFGa >■ GFGa
/iGa=GsFGa
GFGa-
Gsa
\Gea
Y
Ga,
Они коммутативны (первая является определением Gee, а вторая —
одним из треугольных тождеств данного сопряжения). Поэтому для
любой стрелки / : а —у а' из А мы определим К по формулам
Ка = (Ga,Gea), Kf = Gf: (Ga,Gea) ->■ (Ga1,Gea,);
(2)
поскольку преобразование е естественно, то такая стрелка Kf
коммутирует с Ge и потому является морфизмом Т-алгебр. Стандартная
проверка показывает, что К является функтором, причем
KF = FT,
G1 =G.
(3)

6.4]
Слова и свободные полугруппы
169
Остается показать, что функтор К единствен. Прежде всего,
каждый объект Ка должен быть Т-алгеброй, а условие коммутативности
GTК = G означает, что соответствующим Х-объектом является Ga.
Таким образом, Ка имеет вид Ка = (Ga, h) для некоторого
структурного отображения h; при этом равенство GTК = G означает,
что значение функтора К на стрелке / из А равно Kf = G/,
что соответствует равенству (2). Остается лишь найти структурное
отображение h. Диаграмма (1) коммутативна, сопряжения (F, G,...)
и (FT, GT,...) имеют общую единицу ту, и поэтому функторы К : А —У
—у Хт и / : X —У X (тождественный) определяют отображение
первого сопряжения во второе в смысле § 4.7. Применив к этому
отображению предложение 1 из § 4.7, получаем, что Кг = етК. Но К
при действии на стрелки совпадает с G, поэтому Кга = Gea для всех
a Е А, а из определения коединицы алгебры ат вытекает, что е1К а =
= sT(Ga,h) = h. Таким образом, из Кг = етК следует, что Gea = h.
Тем самым структурное отображение h определено, и единственность
функтора К доказана. □
Во многих известных сопряжениях (F, G,...) сравнивающий
функтор К является изоморфизмом; в этом случае мы называем функтор
G монадическим (monadic, tripleable). У других авторов (Barr, Wells
[1985]) tripleable означает лишь, что К является эквивалентностью
категорий. Однако имеется простой пример, когда К не является ни
изоморфизмом, ни даже эквивалентностью. Забывающий функтор
G : Тор —у Set имеет левый сопряженный D, который
сопоставляет каждому множеству X дискретное топологическое пространство
(все подмножества в X открыты); действительно, единичная стрелка
т]х • X —У GDX заведомо универсальна среди стрелок из объекта
X в функтор G. Сопряжение (D,G,?7,...) : Set —^ Тор определяет
в категории Set тождественную монаду / = (/,1,1) (с
тождественным функтором и тождественными естественными
преобразованиями). При этом /-алгебры в категории Set — это просто множества,
поэтому сравнивающий функтор Тор —у Тор = Set в данном случае
совпадает с забывающим функтором G.
6.4. Слова и свободные полугруппы
В случае свободных полугрупп сравнивающий функтор можно
построить в явном виде. Полугруппа — это множество 5, наделенное
ассоциативной бинарной операцией v : S x S —У S. Свободная
полугруппа WX над множеством X похожа на соответствующий свободный
моноид (§ 2.7). Она состоит из всех слов (xi)... (хп) положительной
длины п, записанных посредством символов ^ G X; мы пишем (ж),
чтобы отличить слово (х) из WX от элемента х G X. Умножение слов
состоит в их приписывании друг к другу:
((Ж1> . . . (ЖП))(Ы • • • (Уп)) = (Xl) • • • (Хп)(У1) • • • (Уп);
такое умножение ассоциативно и превращает FX = (WX, v) в
полугруппу. Здесь WX — дизъюнктное объединение ПХП, п = 1,2,...

170
Монады и алгебры
[Гл.6
Пусть G : Smgrp —у Set — забывающий функтор из категории всех
малых полугрупп (забывающий умножение). Тогда стрелка т\х • X —>
—У GFX, определяемая соответствием х \-> (ж), универсальна среди
стрелок из X в G. Поэтому F является функтором, сопряженным
слева с G, а ту определяет сопряжение
(F,G,ri,e} : Set -^ Smgrp.
Пусть S — произвольная полугруппа (множество S с ассоциативной
бинарной операцией S x S —> 5, записываемой мультипликативно);
тогда коединицей ss данного сопряжения по определению является
тот морфизм полугрупп ss : FGS —> S, для которого тождественна
композиция Gss о T]Gs '• GS —> GFGS —> GS. Иначе говоря, ss —
единственный морфизм полугрупп, который отображает каждый
образующий (s) в s. Это означает, что
es((si)... (sn>) = si ... sn (произведение в S) (1)
при всех s G S. Таким образом, коединица снимает угловые скобки ( ).
Предложение 1. Монада в категории Set, определяемая
сопряжением Set —^ Smgrp, имеет вид
W = (W : Set -► Set, rj : / ^ W, p : W2 ^ W),
оо
где WX = П Хп, г)хх = (ж) ^л«я каэюдого х G X, a /ix имеет вид
п=1
»x(((xii) • • • (Ж1П1>)... ((хк1)... (хкПк)}) =
= (жи)... (xlni)... (хк1)... (хкПк)
для всех положительных к, всех наборов ni,..., пк из к натуральных
чисел и всех хц G X.
Доказательство. По определению г\х = (ж), а /л =
= GsF : W2 -^ W определяется вышеприведенной формулой для ss,
где каждый элемент из W2X записан как слово (длины к) от к слов
длины ni,... ,Пк соответственно. Короче говоря, \±х при применении
к слову из слов удаляет внешние угловые скобки. □
Отметим, что это определение позволяет непосредственно
проверить аксиомы единицы и ассоциативности в монаде W, не обращаясь
явно к понятию полугруппы. Например, ассоциативность умножения
\i означает, что в случае трех пар угловых скобок результат будет
одинаков, если удалить средние, а затем внешние скобки, или если
удалить сначала внешние скобки, а затем средние.
Предложение2. В случае описанной монады слов W в
категории Set, W-алгебры имеют вид (5, i/i, &% • • •)• Более конкретно, на
мноснсестве S для каэюдого натурального п задана п-арная операция

6.4]
Слова и свободные полугруппы
171
vn : Sn —>• 5, причем v\ — \ и для каждого натурального к и каждого
набора к натуральных чисел п\,..., п/. выполнено тождество
vk(vni x...xunh)= zv+...+п, : Sni+-+n" -»• 5. (2)
Морфизм W-алгебр f : (5, z/i,...) —>■ (S",z/{,...) — это функция
f : S —> S', коммутирующая со всеми vn, т. е. jvn = i/'nfn : S' ^ S.
Доказательство. Рассмотрим И^-алгебру (S,h : WS —>• S).
Поскольку WS = П5П, то структурное отображение h — это
совокупность n-арных операций i/n : Sn —> 5, по одной для каждого п.
В силу аксиомы единицы для И^-алгебр hr\x — 1, поэтому
отображение v\ — тождественное. С другой стороны, произведение множеств
дистрибутивно относительно копроизведения, и потому
W(WX) = П(П1П)^ = ПП(ХП1 х ... х ХПк) =■ UUXni+"+nfc,
fen fen fen
где n в средней и правой части пробегает все наборы вида (ni,..., Пк).
В этих обозначениях аксиома ассоциативности для структурного
отображения h принимает вид (2). □
Рассмотрим простейший случай тождества (2): 3 = 2 + 1 = 1 + 2,
отображение г/\ — тождественное. Тогда
v<i{y\ х 1) = i/3 — г/2(I х г/2) : S x S x S ^ S.
Если записать бинарную операцию г/2 как умножение, то мы
получаем, что тернарная операция г/% при всех x,y,z Е S удовлетворяет
тождеству
[xy)z = i/3(x,y,z) =x(yz).
Аналогично, г/п совпадает с произведением п элементов. По индукции
без труда доказывается
Следствие. Система (5, v\, 1/2, • • •) является W-алгеброй
описанного вида, если и только если v\ = 1, V2 : S x S —>• 5 —
ассоциативная бинарная операция на S и при всех п ^ 2 верно, что
vn+i = ^2 х 1) : 5n+1 -> 5.
Таким образом, если мы рассматриваем полугруппы как
множества с одной бинарной ассоциативной операцией, определяем
соответствующую монаду W в категории Set и строим категорию VF-алгебр,
то получаем те же полугруппы, но уже как алгебраические системы
вида (5, i/i, г/2, • • •), где v\ — 1,1/2 — v, а все vn+i являются итерациями
операции г/2- Сравнивающий функтор К : Smgrp —> Set — это
очевидное отображение (5, v) \-л (5,1, г/2, • • •, ^п5 • • •)? где z/n —
итерация бинарной операции v. Иначе говоря, К — это изоморфизм, но
он заменяет алгебраическую систему (5, г/) с одной ассоциативной
бинарной операцией тем же множеством со всеми производными от
нее операциями.
Аналогично описываются алгебры над другими известными
монадами (упр. 1, 2).

172
Монады и алгебры
[Гл.6
Упражнения
1. Пусть Wo — монада в категории Set, определяемая забывающим
функтором Моп —>- Set. Покажите, что Wo — это множество М со строкой
г/0,1/1,..., состоящей из гг-арных операций г/п, где г/о : * —»■ N — единица
моноида М, а г/п — произведение п множителей.
2. Пусть R — кольцо с единицей. Забывающий функтор G : Я-Mod —>>
—> Set из категории левых ^-модулей имеет левый сопряженный и потому
определяет монаду {Tr,t],ii) в категории Set.
а) Докажите, что эту монаду можно описать следующим образом. Если
X — произвольное множество, то TrX состоит из вех функций f : X —> R,
имеющих лишь конечное число ненулевых значений; если t : X —>- Y —
некоторая функция, у Е Y, то [(TRt)f]y = ^ fx, где сумма берется по всем
х Е X, для которых tx = у; если ж Е X, то цх '• X —»■ Я определяется по
формулам (7/ж)ж = 1, (r]x)xf = 0 г); если к Е Tr(TrX), то //ж& : X —»> Я
определяется для х Е X по формуле (/1хк)х = ^2f kffx, где сумма берется
по всем / Е ТдХ.
б) Проверьте непосредственно, что {Tr,t],ii) из п. а) является монадой.
в) Покажите, что (Tr, ц, //)-алгебры совпадают с Я-модулями, если в
последних рассматривать в качестве операций не только сложение и
умножение на скаляры, но и любые линейные комбинации. (Структурное
отображение h сопоставляет каждому / линейную комбинацию с коэффициентами
fx для каждого х Е X.)
3. Дайте аналогичное полное описание сопряжения, определяемого
забывающим функтором CRng —>- Set. Используйте тот факт, что здесь
ТХ — это кольцо всех многочленов с целыми коэффициентами от символов
(переменных) х Е X.
4. Сопряжение (F, G, (р) : АЬ —^ Rng, где функтор G забывает
умножение в кольце, определяет монаду Т в категории АЬ.
а) Дайте прямое описание этой монады, как сделано в тексте для W,
но заменив Хп на тензорное произведение п множителей, а копроизведение
П — на (бесконечную) прямую сумму абелевых групп.
б) Дайте соответствующее описание Т-алгебр и покажите, что
сравнивающий функтор из колец в Т-алгебры является изоморфизмом.
6.5. Свободные монадические алгебры
Пусть дано сопряжение
(F,G,<p) : X ^ А.
Любая полная подкатегория В С А, содержащая объекты Вх для всех
х G X, порождает другое сопряжение:
(Fb,Gb,<Pb):X^B,
где Fb — это функтор F, кообласть которого ограничена с А на В,
функтор Gb — это G, область которого ограничена на В, и при х G X
и Ъ G В исходное сопряжение определяет биекцию (рв'-
hom# (Fbx, b) = hom^ (Fx, b) = homx (x, Gb) = homx (x, Gsty,
1) При x Ф x. — Прим. пер.

6.5]
Свободные монадические алгебры
173
заведомо естественную по ж и по Ъ. При этом второе сопряжение срв
определяет в категории X ту же монаду, что и первое. Это наблюдение
показывает, что и та же монада в X может определяться многими
сопряжениями. Для наименьшего такого сопряжения В = FX; это
полная подкатегория в А, состоящая из всех свободных объектов Fx Е
Е А. Известные свойства морфизмов Fx —> Fy между свободными
объектами подсказывают способ построения подкатегории FX и
сопряжения (рв непосредственно по монаде. Приведем это построение,
при котором категория FX описывается внутренним образом, а не
как подкатегория (см. упр. 3).
Теорема 1 (Монадическая категория, Kleisli [1965]). Пусть дана
монада (Т, r\, fi) в категории X. Каждому объекту х Е X сопоставим
новый объект хт-> а каждой стрелке f : х —> Ту из X — новую
стрелку /ь : хт —У Ут- Эти новые объекты и стрелки образуют
категорию, если определить композицию стрелок /ь и д9 : ут —У zt
по правилу
9bofb = (nzoTgof)K (1)
При этом функторы Ft : X —> Хт и Gt • Хт —> X соответственно
определяются по формулам
FT : k:x^y^(j]yok)b:xT^ Ут, (2)
GT- /b :xT^yT^VyoTf:Tx^ T2y -> Ту, (3)
и потому для объектов выполнено равенство Gt%t — Тх. Биекция
fb \-> f определяет сопряжение (Ft,Gt,^Pt) • X —^ Хт, которому
соответствует в категории X исходная монада.
Набросок доказательства. В силу определения стрелок /ь
имеется биекция hom-множеств Хт{хт-> Ут) — Х(х, Ту), а определение
композиции в категории Хт соответствует композиции
х—UTy^Ttz-^Tz
в категории X. С помощью подходящей диаграммы можно показать
ассоциативность введенной композиции. Другие диаграммы
показывают, что левой и правой единицей служит (tjx) '- хт —У %т- Из
дальнейших выкладок следует, что Ft и Gt действительно являются
функторами. По построению, /ь —у f — это биекция
XT(FTx, ут) = Хт(хт, Ут) = Х(х, Ту) = Х(х, GTyT);
она естественна по х и по ут и потому определяет искомое сопряжение
(рт- Его единицей служит т\, а коединица определяется по формуле
(вт)ут — (Хту) '- (Ту)т ~~** Ут- Умножение в категории X имеет вид
Gt^tFt-, что совпадает с исходным умножением \± в силу определения
Gt- В итоге сопряжение определяет исходную монаду Т. □

174
Монады и алгебры
[Гл.6
Теорема2 (теорема сравнения для конструкции Клейсли).
Пусть дано сопряжение (F,G,f],s) : X —^ А, которое определяет
в категории X монаду Т = (GF,rj,GeF). Тогда существует
единственный функтор L : Хт —>• А такой, что GL = GtLFt = F.
Предоставляем доказательство читателю. Отметим лишь, что для
установления единственности функтора L требуется снова (и
несколько по-иному) применить предложение 1 из § 4.7 об отображениях
сопряжений.
Две теоремы сравнения можно объединить следующим образом:
Теорема 3. Пусть дана монада (Т, 77,/i) в категории X.
Рассмотрим категорию, объектами которой являются все те
сопряжения (F, G, г\, г) : X —^ А, которые порождают эту монаду, а
стрелками — те отображения сопряжений (§ 4.7), которые тождественны
на X. В этой категории имеется начальный объект — конструкция
Клейсли — и терминальный объект (FT,GT,rj,eT) : X —^ ХТ со
сравнивающим функтором
ХТ L >А К>ХТ.
Упражнения
1. Постройте сравнивающий функтор Клейсли L, докажите его
единственность и покажите, что образ категории Хт при его действии является
полной подкатегорией FX С А, объекты которой имеют вид Fx для
всевозможных iGl.
2. Покажите, что ограничение функтора L определяет эквивалентность
категорий Хт —>■ FX.
3. Постройте пример сопряжения, в котором F не является биекцией на
объектах. Отсюда получите, что эквивалентность Хт —> FX из упр. 2 не
обязательно является изоморфизмом. (Указание: отображение S *->■ T(S)
с одноэлементным образом определяет монаду в категории Set.)
4. Рассмотрим заключительное сравнение из теоремы 3. Существует ли
на самом деле категория всех сопряжений?
5. Пусть (F,G,rj,£) : X —^ В определяет монаду (Т, т/,//) в категории
X, а другое сопряжение (L,R,rjr, е') : В —^ А определяет тождественную
монаду в категории В (т.е. RL = 1в, п = 1 и Re L = 1). Докажите,
что композиция сопряжений X —^ А определяет в категории X исходную
монаду (Г,7/,//>.
6.6. Расщепление коуравнителей
Нам потребуются некоторые специальные типы коуравнителей.
Под вилкой в категории С будем понимать диаграмму

6.6]
Расщепление коуравнителей
175
где едо = ед±. Таким образом, вилка — это просто конус с основанием
а =4 Ь и вершиной с. Напомним, что стрелка е называется
коуравнителем параллельной пары стрелок до и <9i, если она порождает
вилку, причем любая стрелка / : Ь —>■ d, для которой /до = /с?ь
имеет вид / = f'e для единственной стрелки f : с —> d. Стрелка
е называется абсолютным коуравнителем для <9о и д\ в категории
С, если для любого функтора Т : С —> X (в любую категорию X)
в полученной вилке
Тд0 т
Та =£ ТЪ >■ Тс
Тдг
коуравнителем для Тдо и Тд\ является Те. Как следствие,
абсолютный коуравнитель является коуравнителем. Аналогично можно
определить абсолютные копределы (и абсолютные пределы) любого
типа (Pare [1971]).
Расщепленная вилка в категории С — это вилка (1) с двумя
дополнительными стрелками
а -*-
■Ь^-с, (2)
для которой выполнены условия
e<90 = e<9i, es = 1, dot = 1, d\t — se. (3)
Будем говорить, что s и £ расщепляют, вилку (1). Из этих условий
вытекает, что е — расщепленный эпиморфизм с правым обратным s.
Расщепленную вилку можно также представить как пару
коммутативных квадратов
где произведения по горизонтали — единичные стрелки. Иначе говоря,
если стрелки д\ и е рассматривать как объекты в категории
функторов С2, то (<9о, е) : д\ —> е — стрелка между ними, для которой стрелка
(t,s) служит правой обратной: (do,e)(t,s) = (1,1).
Лемма. В любой расщепленной вилке е является коуравнителем
для до и д\.
Доказательство. Пусть для стрелки / : Ь —>■ d верно, что /до =
= jd\. Положим f = fs : с —> d. Из уравнений расщепленной вилки
(3) получаем
f'e = fse = fd!t = fdot = /,
т. е. / пропускается через е. С другой стороны, если j — he для
некоторой стрелки к : с —>• d, то fs = kes = к, поэтому к = f =
= /s, и стрелка /; единственна. □

176
Монады и алгебры
[Гл.6
Под расщепленным коуравнителем для до и д\ будем понимать
стрелку е из такой расщепленной вилки. Существует характеризация
тех параллельных пар <9o,<9i, для которых некоторый (а тогда и
любой) коуравнитель расщеплен (упр. 2).
Поскольку расщепленная вилка определяется уравнениями,
включающими только композиции и единичные стрелки, то она остается
расщепленной вилкой при действии любого функтора. Отсюда
вытекает
Следствие. В любой расщепленной вилке е является
абсолютным коуравнителем для до и д\.
Приведем пример вилки в категории Cat {С — любая категория):
дг
Здесь С2 — категория, объектами которой служат стрелки из С; через
до и д\ обозначены функторы, сопоставляющие каждой стрелке ее
область и кообласть соответственно; е — это функтор, который
отображает каждый объект категории С в единственный объект категории
1. Если С имеет терминальный объект ао, то эту вилку расщепляют
функторы s и t: первый отображает единственный объект категории 1
в ао, а второй отображает любой объект с Е С в единственную стрелку
с —>• ао-
Теперь приведем пример вилки в категории Grp. Пусть N <G —
нормальная подгруппа группы G; образуем полу прямое произведение
G х 0iV, состоящее из пар (ж,п), где х Е G,n Е N, с (заведомо
ассоциативным) умножением (х,п)(у,т) = (ху, (у~1пу)т). Тогда имеется
вилка
G х oN ~^Г G ^-^ G/N.
Здесь р — проекция на факторгруппу G/N, до(х,п) = ж, di(x,n) =
= хп. Очевидно, что в этой вилке р является коуравнителем для до
и д\. В общем случае эта вилка не расщеплена, но после применения
забывающего функтора U : Grp —у Set получится расщепленная
вилка в категории Set. В качестве s возьмем функцию, выбирающую по
представителю из каждого смежного класса (элемента факторгруппы
G/N), и положим tx = (ж, x~1(spx)). Этот пример, кстати, показывает,
что факторгруппу можно рассматривать как коуравнитель в
категории групп.
Упражнения
1. Покажите с помощью аналогичной конструкции, что в категории
Rng факторкольцо R/A кольца R по идеалу А можно рассматривать как
коуравнитель, причем полученная вилка расщепляется под действием
забывающего функтора в категорию множеств.

G_7\
Теорема Бека
177
2. Параллельная пара до,д\ : а =4 Ъ называется (Веек) сжимаемой
(contractible), если существует стрелка t : Ъ —»■ а, такая что % = 1и сМ<9о =
а) Докажите, что в любой расщепленной вилке (1) пара до, д\ сжимаема.
б) Докажите, что если сжимаемая пара имеет коуравнитель, то он
расщеплен.
6.7. Теорема Бека
В наиболее известных категориях алгебр важнейшую роль играет
построение коуравнителей — факторгрупп в категории Grp, фактор-
модулей в Л-Mod и т. п. Теорема Бека характеризует категорию Т-
алгебр для произвольной монады Т как категорию с сопряжением,
забывающий функтор которого создает определенные коуравнители.
Напомним (§ 5.1), что функтор G : А —> X создает коуравнители
для параллельной пары /, g : а =^ 6 в категории А, если для каждого
коуравнителя и : Gb —> z стрелок G/, Gg из категории X существуют
единственный объект с и единственная стрелка е : b —> с, для которых
Gc = z и Ge = и, причем е служит коуравнителем для fag.
Теорема1 (теорема Бека о характеризации алгебр). Пусть
(F,G,ri,e) : X ^ А (1)
— некоторое сопряжение; (Т, tj^/jl) — определяемая им монада в
категории X; ХТ — категория Т-алгебр;
(FT,GT,r1T,eT):X^XT (2)
— соответствующее сопряжение. Тогда следующие условия
равносильны:
1) {единственный) сравнивающий функтор К : А —» ХТ является
изоморфизмом;
2) функтор G : А —» X создает коуравнители для тех
параллельных пар f,g из А, для которых пара Gf, Gg имеет абсолютный
коуравнитель в категории X;
3) функтор G : А —» X создает коуравнители для тех
параллельных пар f,g из А, для которых пара Gf, Gg имеет расщепленный
коуравнитель в категории X.
Доказательство. Вначале покажем, что из (1) вытекает (2).
Рассмотрим два отображения Т-алгебр
do
(x,h) =Л (y,k),
d\
которым соответствуют стрелки из X, имеющие абсолютный
коуравнитель
do p
х tV >z.
di

178
Монады и алгебры
[Гл.6
Чтобы создать коуравнитель для этой параллельной пары, нужно
вначале найти единственную структуру Т-алгебры т : Tz —> z на объекте
z, при которой е станет морфизмом Т-алгебр, а затем доказать, что
в действительности е является коуравнителем для do,d\ в категории
Т-алгебр ХТ. Но в левой части диаграммы
Td0
коммутативен и верхний квадрат (включающий do), и нижний
(включающий di), поскольку do и d\ являются морфизмами Т-алгебр. Как
следствие, ек при умножении на Tdo и на Td\ дает одну и ту же
стрелку. Но е — абсолютный коуравнитель, и потому Те является
коуравнителем. Значит, существует единственная вертикальная стрелка
m (показанная штрихами), которая делает правый квадрат
коммутативным.
Теперь мы хотим показать, что тп служит структурным
отображением для z. На диаграмме (3) показана связь аксиомы
ассоциативности для m (внешний квадрат) с аксиомой ассоциативности для
структурного отображения к (внутренний квадрат).
Тгп
(3)
Левая трапеция коммутативна, поскольку преобразование \±
естественно, а остальные три трапеции коммутативны в силу определения
m посредством кие. Следовательно,
m о Тгп о Т2е = m о цг о Т2е.
Но е является абсолютным коуравнителем, поэтому Т2е —
коуравнитель и, следовательно, эпиморфизм; сократив на Т2е, получаем закон
ассоциативности для тп. Рассуждение того же рода показывает, что
выполнена аксиома единицы m о rjz = 1 : z —У z.
Мы нашли, как и намеревались, единственную структуру Т-
алгебры тп на объекте z, причем е является морфизмом Т-алгебр

67]
Теорема Бека
179
в силу построения т. Чтобы показать, что е является коуравнителем
в Хт, рассмотрим любое другое отображение Т-алгебр / : (у, к) —>■
—у (w,n), для которого /do = /di. Тогда стрелка / : у —>■ w в категории
X удовлетворяет условию /do = /di, причем е является (абсолютным)
коуравнителем для do,di : х =4 у. Поэтому существует отображение
f : z —> w, для которого / = /'е. Рассуждая как в случае диаграммы
(3), получаем, что /' является морфизмом Т-алгебр. Поскольку это
единственная стрелка с условием / = f е, то е - коуравнитель в
категории Хт, и из 1) следует 2).
Далее, каждый расщепленный коуравнитель является
абсолютным, поэтому условие 2) позволяет функтору G создать больше, чем
3). Таким образом, из 2) следует 3).
Остается доказать, что из 3) следует 1). Рассмотрим для этого Т-
алгебру (x,h). Отображение h : Тх —у х является структурным в том
и только том случае, когда диаграмма
Т2х =^S Тх —^ х (4)
Th
является вилкой в категории X, причем ее расщепляют стрелки
Т2х <—— Тх <-^- х. Действительно, условие наличия вилки в (4):
h о цх = h о Th — это в точности закон ассоциативности для h;
композиция h о г\х равна 1 в силу аксиомы единицы для (ж, h); уравнения
Vx ° VTx = 1, Th о г)Тх =r]xoh
выполнены в силу аксиомы единицы для монады Т, а также
естественности преобразования г\.
Для каждого объекта a G А сопряжение (F,G,e,rj) : X —^ А
порождает вилку
FGFGa £FGal FGa £a > а, (5)
FGsa V J
которую мы назовем каноническим представлением объекта а. В
случае А = Grp оно совпадает со стандартным представлением; здесь
га — это проекция на группу а свободной группы, порожденной
множеством ее элементов. Применив функтор G к вилке (5), мы
получаем расщепленную вилку в категории X — именно, частный
случай расщепленной вилки (4), когда (ж, h) — это Т-алгебра (Ga, Gsa)
из теоремы сравнения.
Рассмотрим теперь другое сопряжение (F', G',rj',e'} : X —^ А',
которое определяет ту же монаду в категории X. Под сравнением
(между F' и F) мы понимаем такой функтор М : А' —у А, что
MF' = F и GM = Gf; как уже отмечено, такое сравнение является
морфизмом сопряжений и потому удовлетворяет условию Me' = eM.

180
Монады и алгебры
[Гл.6
Лемма. Если G удовлетворяет предположению 2) теоремы
о создании коуравнителей, то существует единственное сравнение
М :А' -+ А.
Как мы теперь знаем, GT удовлетворяет этому предположению;
поэтому лемма попутно даст новое доказательство теоремы сравнения
(§ б.з).
Доказательство. Если М существует, то FGM = MF'G
и Me' = еМ, поэтому М переводит каноническое представление для а'
в каноническое представление для Ма'. Значит, объект Ма' включен
в некоторую вилку
FGFG'a' = FG'F'G'a' FG'°'l FG'a' - >■ Ма'
FG'e'a,
в категории А, причем стрелка к должна совпадать с Ме'а = ема1-
Отобразим эту вилку в категорию X посредством функтора G.
Получим вилку
GFGFG'a' ^'"'g GFG'a' е-^-+ G'a'
TG'e',
a'
в категории X, причем расщепленную. Так как Т = GF, то мы
получили частный случай вилки (4), где х = G'a'. Но в силу предположения
3) в этом случае G создает коуравнители. Поэтому к и Ма' можно
выбрать ровно одним способом (причем если объект Ма' выбран, то
ема1 имеет свойство, определяющее к, и потому совпадает с к). Мы
показали, что сравнение М единственно, если оно существует.
Теперь выберем к и Ма' указанным образом и покажем, что М
является функтором. Рассмотрим произвольную стрелку / : а' —>■ Ъ'
в категории А. На диаграмме
FG'F'G'a' ^=S FG'a' —^ Ма'
FG'F'G'f
FG'f
Mf
FG'F'G'b' =^ FG'b' -^^ Mb'
оба левых квадрата коммутативны, поэтому koFG' f пропускается
через первый коуравнитель к посредством единственной стрелки Ма' —>■
—у Mb', как показано на диаграмме. Взяв эту стрелку в качестве Mf,
мы, очевидно, превратим М в функтор А' —> А, что и требуется. □
С помощью этой леммы можно построить и исходный
сравнивающий функтор К : А —> Хт, и сравнивающий функтор М : Хт —у
—> А. Их композиция МК : А —> А тогда является сравнением
(сопряжения F... с самим собой) и, снова в силу леммы, должна
быть тождественным функтором. Аналогично, функтор КМ : Хт —У
—у Хт является сравнением между FT и FT и потому должен быть

G_7\
Теорема Бека
181
тождественным. Поскольку КМ = 1 и МК = 1, то К является
изоморфизмом, что и требуется для пункта 1). □
Можно и дальше анализировать конструкцию функтора М в этой
теореме, используя (для случая параллельных пар) следующее
понятие отражения:
Определение. Функтор G : А —» X отражает копределы
функтора Т : J —>• А, есл-u каждый конус \ : Т ^± а из Т в а е А,
для которого GX : GT ^ Ga является копредельным конусом в X,
уже является копредельным конусом в А.
В частности, G отражает коуравнители, если каждая вилка в А,
которая становится коуравнителем в X, уже является коуравнителем
в А. Аналогично, G отражает изоморфизмы, если из того, что Gt —
изоморфизм для некоторой стрелки t из А, вытекает, что и t —
изоморфизм.
Теорема Бека сокращенно обозначается РТТ (precise tripleability
theorem). У нее имеется много вариантов: слабый вариант, с более
легким доказательством, когда делается больше предположений о ко-
уравнителях пар (упр. 2, 3); вариант для эквивалентностей, который
дает условия, при которых сравнивающий функтор К : А —> Хт
является не изоморфизмом, а эквивалентностью категорий (упр. 2,
6); конструктивный вариант, когда анализируются предположения
(некоторые из них обеспечивают существование левого сопряженного
для К; другие превращают это сопряжение в эквивалентность: упр.
2, 5); грубый вариант (СТТ или VTT) с сильными предположениями,
подходящими в случае произведения нескольких забывающих
функторов (упр. 9-11). Однако отметим, что в работе (Barr, Wells [1985])
имеются и более категоричные формулировки вариантов СТТ и VTT.
Упражнения
(Коуравнитель здесь означает коуравнитель параллельной пары.)
1. Докажите, что если функтор G создает коуравнители, то он их
и отражает.
2. Слабая теорема о троичности (из диссертации Бека). Пусть дано
сопряжение (1) и соответствующий сравнивающий функтор К. Дайте прямое
доказательство следующих фактов:
а) Если в категории А всегда существуют коуравнители, то К имеет
левый сопряженный L.
б) Если при этом G сохраняет коуравнители, то единица этого
сопряжения является изоморфизмом / = KL.
в) Если при этом G отражает коуравнители, то коединица этого
сопряжения является изоморфизмом LK = I.
3. (Альтернативное условие для упр. 2.) Пусть в категории А всегда
существуют коуравнители, G сохраняет коуравнители и отражает
изоморфизмы. Докажите, что G отражает коуравнители.
4. а) Покажите, что Т-алгебра (x,/i) имеет каноническое представление
{Т2хфТх) ^3: (Тх,цх) -^-^ (x,h).
Th

182
Монады и алгебры
[Гл.6
б) Покажите, что сравнивающий функтор М : Хт —»> А в теореме Бека
определяется диаграммой коуравнителей
FGFx ==t Fx ■>■ М(ж, К).
Fh
5. Пусть даны сопряжения (1), (2) и сравнивающий функтор К. Далее,
пусть Р — множество всех параллельных пар /, g : а =£ 6 в категории А
таких, что Gf, Gg имеют расщепленный коуравнитель. С помощью упр. 4 б)
докажите следующее.
а) Если в А существуют коуравнители всех пар из Р, то К имеет левый
сопряженный М.
б) Если при этом G сохраняет коуравнители всех пар из Р, то единица
этого сопряжения rj : I —> КМ является изоморфизмом.
в) Если, в дополнение к a), G отражает коуравнители всех пар из Р, то
коединица этого сопряжения МК —ь I является изоморфизмом.
6. С помощью результатов упр. 5 и теоремы 1 из § 4.4 докажите
следующий вариант теоремы Бека, характеризующий категорию Т-алгебр с
точностью до эквивалентности. Если даны сопряжения (1) и (2), то следующие
утверждения равносильны:
1) Сравнивающий функтор К : А —»■ Хт является эквивалентностью
категорий.
2) Пусть f,g — параллельная пара в категории А, причем пара Gf, Gg
имеет абсолютный коуравнитель. Тогда в А существует коуравнитель для
/, д, причем G сохраняет и отражает коуравнитель такой пары.
3) То же с заменой абсолютного уравнителя на расщепленный.
В дальнейших упражнениях используются определения свойств СТТ',
VTT, РТТ для функтора G : А —»> X. Пусть Cg (соответственно Sg) —
множество всех параллельных пар (/, д) в категории А таких, что пара
(Gf, Gg) имеет коуравнитель в X (соответственно, расщепленный
коуравнитель). Тогда G обладает свойством СТТ', если G имеет левый
сопряженный, сохраняет и отражает все существующие коуравнители, причем в А
существуют коуравнители всех пар из Cg- Далее, G имеет свойство VTT,
если G имеет левый сопряженный, отражает коуравнители всех пар из Sg,
а в категории А существуют расщепленные коуравнители всех пар из Sg-
Наконец, G имеет свойство РТТ, если G имеет левый сопряженный,
сохраняет и отражает коуравнители всех пар из Sg и в категории А существуют
коуравнители всех пар из Sg- Ясно, что из СТТ и VTT следует РТТ.
7. СТТ (Crude Tripleability Theorem — грубая теорема о троичности;
Barr-Beck). Пусть G имеет свойство СТТ. Докажите, что сравнивающий
функтор К является эквивалентностью категорий.
8. VTT (Vulgar Tripleability Theorem — простая теорема о троичности).
Пусть G имеет свойство VTT. Докажите, что сравнивающий функтор К
является эквивалентностью категорий.
9. Пусть даны функторы G\ : А ->• X, G2 - X ->• У, <23 : У ->• Z,
соответственно обладающие свойствами СТТ, РТТ и VTT. Докажите, что
функтор G3G2G1 обладает свойством РТТ.
10. Докажите, что композиция двух функторов со свойством VTT также
обладает этим свойством.
11. Докажите, что композиция двух функторов со свойством СТТ также
обладает этим свойством.

6.8]
Алгебры являются Т-алгебрами
183
6.8. Алгебры являются Т-алгебрами
Мы уже знаем, что в случае полугрупп, моноидов и колец
сравнивающий функтор является изоморфизмом (§ 6.4). Этот результат
верен и для любого многообразия (в смысле определения из § 5.6):
Теорема 1. Пусть П — некоторое множество операторов, Е —
некоторое множество тождеств (в терминах операторов,
производных от П), G — забывающий функтор из категории (0,,Е) — Alg
всех малых (П, Е) -алгебр в категорию Set, aT — соответствующая
монада в категории Set. Тогда сравнивающий функтор К : (0,,Е) —
— Alg —У Set является изоморфизмом.
Доказательство использует теорему Бека. Рассмотрим
параллельную пару морфизмов (П, .Е)-алгебр f,g : A =4 В, которым
соответствуют функции, имеющие абсолютный коуравнитель е:
Gf
GA Г GB
Gg
+ х.
(1)
Чтобы создать коуравнители, мы должны показать, что отображение
множеств е поднимается до единственного морфизма алгебр В —>-?,
который является коуравнителем морфизмов алгебр /, д. Для этого
рассмотрим произвольный n-арный оператор со Е П и его действия uj a
и и в в алгебрах А ж В (как обычно, мы не будем различать алгебру
А и ее носитель \А\). На следующей диаграмме (не обращаем пока
внимания на правый квадрат):
Г
Ап jr Bn
В
-*• Хп ■-"■■"■>■ Сп
^х
ы
(2)
■>с
два левых квадрата (включающих соответственно fug)
коммутативны, поскольку fag являются морфизмами П-алгебр. Функция е
является абсолютным коуравнителем в категории Set, поэтому ее п-я
степень еп остается коуравнителем (для fug). Но
eujBfn = efujA = egujA = еивдп,
поэтому еив пропускается через этот коуравнитель единственным
образом по формуле ей в — оохе71. Тем самым на X определена операция
ujx, делающая средний квадрат на диаграмме (2) коммутативным;
это означает, что е является морфизмом П-алгебр. Для производных
операторов Л строится аналогичная диаграмма, однозначно
определяющая Хх] как следствие, из справедливости тождества Хв = \1в

184
Монады и алгебры
[Гл.6
в алгебре В следует его справедливость в X, и потому X является
(П, .Е)-алгеброй.
Остается показать, что е является коуравнителем для алгебр.
Рассмотрим произвольный морфизм алгебр h : В —у С, для которого hf =
= hg. Тогда hf = hgB категории Set (применим забывающий функтор
G), поэтому h имеет вид Ые для единственной функции Ы. Нужно
показать, что правый квадрат на диаграмме (2) коммутативен для
каждого из операторов и. Но h является морфизмом алгебр, поэтому
h'ujxen = h'eujB = hcoB = oochn = ujch,nen.
Так как еп — коуравнитель, то это эпиморфизм, поэтому h'ux =
= исЫп, что и требуется.
Упражнения
1. Докажите теорему 1, используя вместо абсолютных коуравнителей
расщепленные и заметив, что каждая операция их определяется в терминах
расщепления (s,t) вилки (1) по формуле
ux(xi,... ,хп) = eojB(sxi,... ,sxn), xi G X.
(Отметим, что при п = 2 это напоминает обычное определение умножения
смежных классов по нормальной подгруппе.)
2. Пусть К — коммутативное кольцо. Покажите, что теорема Бека
справедлива для забывающего функтора К — Alg —»■ К — Mod.
6.9. Компактные хаусдорфовы пространства
Теорема 1. Забывающий функтор
G : Cmpt Haus -» Set,
сопоставляющий каждому {малому) компактному хаусдорфову
пространству его носитель, является монадическим.
Доказательство. Мы уже знаем, что G имеет левый
сопряженный F; действительно, в качестве FX можно взять компактификацию
Стоуна-Чеха (2) из § 5.6 множества X с дискретной топологией.
В оставшейся части доказательства (мы следуем Pare [1971])
будет удобно рассматривать топологическое пространство как пару
(X, (—)x)i состоящую из множества X и операции замыкания S \-> 5,
которая определена для всех подмножеств 5, Т С X и имеет обычные
свойства:
0 = 0, 5с5, 5 = 5, 5UT = 5UT,
где 0 — пустое множество. Тогда непрерывное отображение
f : (Х,(~)х) -> (Y, (~)у) — это такая функция f : X -> Y,
что fS D fS для всех 5 С X. Нам будет полезна хорошо известная

6.9]
Компактные хаусдорфовы пространства
185
Лемма. Пусть X — компакт, Y — хаусдорфово пространство.
Тогда каждое непрерывное отображение f : (X, ( )х) —> (У, ( )у)
замкнуто.
Нужно проверить, что забывающий функтор
G:(X,(-)X)^X
создает коуравнители для соответствующих пар. Пусть /, g :
(X, ( )х) =4 (У, ( )у) — пара непрерывных отображений, для
которой существует множество W и абсолютный коуравнитель е:
X
/
У
W,
в категории Set. Пусть Р обозначает ковариантный функтор булевой
степени Set —>• Set; таким образом, если S С У, то (Ре)5 — это
образ множества 5 при отображении е. Поскольку это абсолютный
коуравнитель, то Ре является коуравнителем в следующей диаграмме
(в категории множеств):
РХ
~р7
PY
Ре
Pf
РХ ГРУ
Рд
(")у
Ре
^PW
^PW
(1)
Так как отображения fag непрерывны, то коммутативны оба
квадрата слева (включающие / и д соответственно). Как следствие,
Ре о (-)Y о Pf = Ре о (-)Y о Рд.
Но Ре является коуравнителем, поэтому через него пропускается
Ре о ( )у. Тем самым определяется единственное отображение
( )w, обозначенное прерывистой стрелкой на диаграмме (1), которое
делает коммутативным правый квадрат. Это отображение можно
описать следующим образом. Пусть дано подмножество Г С W; возьмем
любое подмножество S С Y, для которого (Ре)S = Г; тогда Г = (Ре)S
независимо от выбора S. Как следствие, если е-1 Г С Y — полный
прообраз множества Г, то Г = Ре(е_1Т). Без труда проверяется,
что это операция замыкания на множестве W, которое превращается
в топологическое пространство.
Поскольку диаграмма коммутативна, то отображение е
непрерывно и замкнуто. Так как пространство Y компактно, а отображение
е : Y —у W сюръективно, то W также компактно. Поскольку Y
хаусдорфово, то каждая его точка замкнута; так как отображение е
замкнуто и сюръективно, то точки пространства W также замкнуты.

186
Монады и алгебры
[Гл.6
Чтобы показать, что W хаусдорфово, рассмотрим две точки w\ ф w^ G
Е W. Они замкнуты, поэтому e~lrw\ и e~lrW2 — непересекающиеся
замкнутые множества в Y. По известному свойству хаудорфовых
компактов, такие множества можно разделить непересекающимися
открытыми множествами (любой хаудорфов компакт нормален).
Поэтому существуют открытые множества U\,U2 С Y такие, что U\ П
П U2 = 0, e~xWi e Щ. Их дополнения U[ и Щ в пространстве Y
замкнуты, причем ЩиЩ — Y. Поскольку отображение е замкнуто,
то множества e(U[) и efJJ^) замкнуты в W, причем
(Pe)U[ U (Ре)Щ = W, иог£ (Pe)U[.
Снова возьмем дополнения, на этот раз в W: тогда [(Pe)U[]
и [(-Ре)[/2] — эт0 непересекающиеся открытые окрестности в W
точек w\ и W2 соответственно. Значит, пространство W хаусдорфово.
Исходя из абсолютного коуравнителя е в категории Set, мы
построили в его кообласти W единственную топологию, в которой он
непрерывен, причем эта топология компактна и хаусдорфова.
Остается показать, что непрерывное отображение е : У, ( )у) —> (W, ( )w)
является коуравнителем в категории Comp Haus. Рассмотрим хаус-
дорфов компакт (Z, ( — )z) и непрерывное отображение h : Y —> Z,
для которого равны обе композиции на диаграмме
f h
X Г Y -^ Z.
9
Поскольку е — коуравнитель в категории Set, то существует
единственная функция h : W —>■ Z, для которой h = h'e : Y —>■ Z; осталось
показать, что она непрерывна. Возьмем Т С W и S С Y такие, что
(Pe)S = Г. Тогда Г = (Ре)5 и потому
(РЛ')Т = (P/i,)(Pe)5 = Р(Л)5 = Р(Щ = (Phf)(Pe)S = (РЛ')Т.
Значит, отображение Ы непрерывно (и замкнуто). Доказательство
завершено. П
Упралснение
1. Покаж:ите, что топология на W, введенная в предыдущем
доказательстве, — это фактортопология, определяемая отображением е : Y -Л
—>- W (в этой топологии множество открыто, если и только если его полный
прообраз открыт в У).
Замечания
Эффективность и простота использования монад и комонад
осознавалась крайне медленно. Вначале они применялись в гомологической алгебре
(см. § 7.6). В работе (Mac Lane [1956]) мимоходом отмечено (§ 3), что
все стандартные резольвенты можно получить из универсальных стрелок
(т.е. из сопряжений). Затем в книге (Godement [1958]) эти резольвенты

6.9]
Компактные хаусдорфовы пространства
187
были систематизированы с помощью стандартных конструкций (комонад).
В статье (Huber [1961]) на основе теории гомотопии в смысле Экмана-
Хилтона изучались примеры производных функторов, которые могут быть
определены в терминах комонад, а в статье (Huber [1962]) — возникающие
при этом функторные симплициальные резольвенты в абелевых категориях
более общего вида. Затем Хилтон (как и другие) поставил вопрос, всякая
ли монада возникает из сопряжения. Независимо появились два ответа:
конструкции свободных алгебр (Kleisli [1965]) и важнейшая конструкция
категории монадических алгебр (Eilenberg, Moore [1965]). Исходя из такого
описания алгебр, в работе (Barr, Beck [1966]) было показано, что
резольвенты, полученные с помощью монад и комонад, можно использовать даже
в неабелевых категориях. При этом был получен неожиданный результат:
рассмотрение монады свободной группы в категории Set приводит к
стандартной когомологии групп. Дальнейшее продвижение в этом направлении
отражено в работе (Barr, Beck [1969]).
В результате около 1965 г. стал актуален вопрос об описании категории
алгебр над монадой. В работе (Linton [1966]) рассмотрен случай монад
в категории Set, а затем Бек доказал свою теорему (тогда
неопубликованную, но доложенную на конференции в 1966 г.). В статье (Pare [1971])
эта теорема сформулирована в терминах абсолютных коуравнителей, что
позволило Паре (§9) дать изящное доказательство того факта, что
компактные хаусдорфовы пространства являются монадическими. Многие другие
результаты в этом направлении содержатся в диссертации Манеса (Manes
[1969]).
Описание алгебр в терминах монад тесно связано с другим их
описанием, в терминах алгебраических теорий (Lawvere [1963], изложено в книге
Pareigis [1970]).

Глава 7
МОНОИДЫ
Теперь мы исследуем общее понятие моноида в категории. Как мы
уже видели во введении, обычный моноид в категории Set
определяется стандартными диаграммами для декартова произведения х,
а в категории АЬ кольцо является моноидом относительно операции
тензорного произведения. Поэтому мы начнем с категорий В,
наделенных подходящим бифунктором х или О, который чаще обозначается
□ . Сами эти категории будут называться моноидальными, поскольку
бифунктор □ : ВхВ —>■ В предполагается ассоциативным. Обычно он
бывает ассоциативен лишь «с точностью до изоморфизма»; например,
для тензорного произведения векторных пространств имеется
изоморфизм U®(V®W) = (U®V)®W. Чаще всего мы просто отождествляем
эти тройные произведения посредством такого изоморфизма.
Дальнейший анализ показывает, что при таком отождествлении требуется
аккуратность — нужно правильно выбрать изоморфизм и убедиться,
что полученное отождествление повторных произведений будет
когерентным г).
Решив вопросы когерентности в моноидальных категориях, мы
сможем определить в них моноиды, действие моноидов на объекты
категории, а также построить свободные моноиды. Затем мы
определим симплициальную категорию Л, которая окажется основной
моноидальной категорией, поскольку она содержит универсальный
моноид и играет важную роль в симплициальных разбиениях и сим-
плициальной топологии. В заключение мы рассмотрим замкнутые
моноидальные категории на примере компактно порожденных
пространств.
7.1. Моноидальные категории
Категория называется моноидальной, если она наделена
произведением типа прямого произведения х, прямой суммы 0 или
тензорного произведения ®. Во всех случаях мы будем одинаково
обозначать это произведение через □ (многие авторы пишут ®). Сначала
мы рассмотрим категории с умножением □ , строго ассоциативным
и имеющим строгую двустороннюю единицу е. Более подробно, строго
моноидальпал категория (В, □ , е) — это категория В, наделенная
бифунктором □ : В х В —» В, который ассоциативен:
□ (□ х 1) = □ (1 х □) : В х В х В -+ В, (1)
х) См. § 7.2. — Прим. ред. пер..

Lil
Моноидалъные категории
189
а также объектом е, который является левой и правой единицей для
□ :
D(exl) = id# = П(1 х е). (2)
При записи закона ассоциативности (1) мы отождествили (В х В) х
х В и В х (В х В); в записи аксиомы единицы (2) е х 1 обозначает
функтор си (е,с) : В —» В х В. Бифунктор □ сопоставляет каждой
паре объектов а,Ь е В объект а □ Ъ Е В, а каждой паре стрелок / : а —>•
—>• а', g :Ъ ^ Ъ' — стрелку /D^:aD^a'D5'. Утверждение, что □
является бифунктором, означает, что выполнен закон чередования:
10П16 = 1вПЬ, (/'П </)(/□<?) = (/'/) □(</<?), (3)
если определены композиции /'/и g'g. Аксиома ассоциативности (1)
означает, что бинарная операция □ ассоциативна и на объектах, и на
стрелках. Аналогично, аксиома единицы (2) означает, что е П с = с =
= с□ е для объекта с гл что 1е □/ = / = /□ 1е для стрелки /.
Любой моноид М (в обычном смысле, т. е. в категории Set),
рассматриваемый как дискретная категория, является строго моноидаль-
ным, причем в качестве □ нужно взять умножение его элементов.
Если X — любая категория, то категория End(X), объектами которой
служат все эндофункторы S : X —у X, а стрелками — все
естественные преобразования О : S4T, является строго моноидальной, если
в качестве □ взять умножение функторов.
(Нестрого) моноидальная категория — это категория В с
умножением, т. е. бифунктором □ , который ассоциативен с точностью до
естественного изоморфизма а и имеет объект е, являющийся левой
и правой единицей для □ с точностью до естественных изоморфизмов
Л и g соответственно. При этом должны быть коммутативны все
диаграммы, включающие а,Х и д.
Говоря формально, моноидальная категория В = (Б, □ , е, а, Л, д) -
это категория В, бифунктор □ : В х В —» В, объект е Е
Е В и три естественных преобразования а, А, д. Более конкретно,
преобразование
а = ааЛс : а □ (Ъ □ с) ^ (а □ 6) □ с (4)
естественно по а, 6, с Е 5, и пятиугольная диаграмма
a □ (6 □ (с □ d)) —^ (а □ 6) □ (с □ d) —^ ((a □ Ь) □ с) □ d
Ша
аП1 (5)
а □ ((6 □ с) □ d) >■ (а □ (6 □ с)) □ d
коммутативна при всех a,b,c,d Е 5. Точно так же, преобразования Л
и £> естественны по всем объектам a Е В:
Ха : е □ а = а, £>а : а □ е = а, (6)

190
Моноиды
[Гл.7
треугольная диаграмма
а □ (е □ с)
IDA
(аПе)Пс
£□1
(7)
аПс = аПс
коммутативна при всех а, с Е 5, и при этом
Ле = де : еПе —>• е.
(8)
Вскоре мы увидим, что из коммутативности этих трех диаграмм
вытекает, что коммутативны и все подобные диаграммы. Отметим
лишь (см. упр. 1), что из нее вытекает коммутативность диаграмм
е □ (Ъ □ с) —^+ (е □ Ъ) □ с а □ (6 □ е) -^ (аПЪ)Пе
ЬП(
ЛП1
т
6Пс,
1ЕЫ
т
аП6
(9)
аП6.
Любая категория с конечными произведениями становится монои-
дальной, если в качестве а □ Ъ взять (однозначно выбранное)
произведение объектов а, Ь; в качестве е — терминальный объект; в качестве
а, А и д — единственные изоморфизмы (предл. 1, § 3.5), которые
коммутируют с соответствующими проекциями. Тогда пятиугольник
(5) коммутативен (обе вертикальные стрелки коммутируют с
проекциями четырехкратного произведения), так же как и треугольник
(7). Аналогично, любую категорию с конечными копроизведениями
можно сделать моноидальной, взяв в качестве □ копроизведение,
а в качестве е — начальный объект.
Обычные тензорные произведения также приводят к моноидаль-
ным категориям. Например, тензорное произведение двух абелевых
групп А и В определено, если задана функция А х В —у А 0 В,
о,Ь н> а 0 Ь, универсальная среди билинейных функций из А х В
в абелевы группы. Ее итерация дает универсальную трилинейную
функцию А х (В х С) —>■ А0 (В® С); поскольку она единственна с
точностью до изоморфизма, то существует единственный изоморфизм
а : А®(В®С) —> (i05)0C, и притом естественный (вследствие его
единственности). Соответствующий пятиугольник (5) коммутативен,
поскольку обе вертикальные стрелки — это единственные сравнения
универсальных 4-линейных функций. Изоморфизмы Л : Z (8) А = А,
д : А (8) Z = А хорошо известны (и позволяют отождествить Z 0 А с А).
В целом сказанное означает, что (АЬ, 0, Z, а, Л, д) — моноидальная
категория.
Коммутативность пятиугольника (5) для (8) в категории АЬ можно
непосредственно проверить на элементах a G A,b G В, с G С, заметив,

Lil
Моноидалъные категории
191
что а [а (g) (Ь (g) с)] = (a 0 b) 0 с. Отсюда видна еще одна роль этого
условия: оно предотвращает использование ложной ассоциативности —
например, для изоморфизма а' : А (g) (В (g)C) —>• (А® В)® С, заданного
на этих абелевых группах по формуле а'[а (g) (Ь (g) с)] = — (a (g) Ь) (g) с.
В данном случае диаграмма (5) некоммутативна из-за неправильного
знака.
Существует и много других примеров. Рассуждая как в случае АЬ,
можно показать, что для любого коммутативного кольца К категория
(if-Mod, (g)^, if) моноидальна. То же верно для градуированных К-
модулей и дифференциальных градуированных if-модулей (т. е.
цепных комплексов if-модулей) при традиционном определении
тензорного произведения этих объектов (Mac Lane [1963a]). Аналогично,
категория всех if-алгебр (или всех дифференциальных градуированных
if-алгебр) также моноидальна относительно их обычного тензорного
произведения. Для каждого кольца R категория всех R — Л-бимодулей
моноидальна относительно (g)#.
(Строгий) морфизм моноидальных категорий
Г : (Б, □ , е, а, А, в) -»• (В', □', е', а', Л', в')
— это такой функтор Т : В —>■ В'', что при всех а, 6, с, / и g выполнены
равенства
Т(аПЪ) = Ta\J'Tb, T{fUg) = TfU'Tg, Te = e', (10)
Taa,b,c = a'TaTbTc, TXa = X'Ta, Tga = g'Ta. (11)
Взяв такие морфизмы в качестве стрелок, можно образовать Моп-
cat — категорию всех малых моноидальных категорий. В ней
(очевидно) всегда существуют конечные произведения; в частности, объект 1
с очевидной (строго) моноидальной структурой является
терминальным объектом в Moncat. В ней имеется полная подкатегория,
состоящая из всех строго моноидальных категорий; в них, естественно, при
определении морфизмов Т можно опустить условия (11) для а, А и £>.
Однако многие полезные морфизмы между моноидальными
категориями не являются строгими в смысле условий (10) и (11).
Например, забывающий функтор U : (if-Mod, (g)#, —) —>• (Ab, (g),...) не
является строгим. В самом деле, если А и В — два if-модуля, то
может не иметь места ни равенство U(A ®к В) = UA (g) UB, ни даже
изоморфизм, а лишь естественный морфизм UA (g) UB —у U(A ®к В),
который выражает тот факт, что i%5 является фактормодулем
для A (g)z В. Аналогичное положение возникает для забывающего
функтора (Ab, (g),...) —>• (Set, x,...). Мы не будем формулировать
здесь свойства этих нестрогих морфизмов между моноидальными
категориями (см. § 12.5).
Возникает искушение избавиться от всех этих хлопот са,Аи^,
просто отождествив все изоморфные объекты из В. Но это
невозможно, как показывает следующее рассуждение, принадлежащее Избеллу.
Пусть Seto — скелет категории множеств; в нем существует
произведение X х Y с обычными проекциями р\ и р2- Если D — счетное

192
Моноиды
[Гл.7
множество, то D = D x D, и обе проекции этого произведения —
эпиморфизмы pi,p2 : D —> D. Предположим, что стандартный
изоморфизм а : X х (Y x Z) = (X х У) х Z), коммутирующий со всеми
тремя проекциями, всегда тождествен; тогда он тождествен и при X =
— У — Z — D. Поскольку он естествен, то / х (д х К) = (/ х д) х h
для любых f,g,h : .D —>■ Z). Но операция х на функциях определяется
в терминах проекций р\ и р<±, и потому
М =Pi(/ х (# х ft)) = Pi((/ x 9) х ^) = (/ х 0)Pi '.D^D.
Так как pi является эпиморфизмом, то это верно и для / = / х д.
Такое же рассуждение относительно pi показывает, что / х д = д,
и потому j — д для любых /, д : D —> D, что абсурдно. Аналогичное
рассуж:дение применимо к скелету категории (АЬ, О,...).
Упралснения
1. Докажите, что из (5) и (7) вытекает (9). Подсказка: в пятиугольнике
(5) положим а = Ъ = е и добавим диагонали, два раза подставив £>, два
раза — основное тождество (7), а также подходящие естественные
преобразования. Получим (Л □ 1)аЛ = ЛЛ : е □ (е □ (с □ с/)) -^cDd, и поскольку Л —
изоморфизм, то (ЛП 1)а = Л.
2. Постройте в категории Moncat произведение двух моноидальных
категорий.
3. Покажите, что если категория В моноидальна, то и Вор имеет
(очевидную) моноидальную структуру.
4. Пусть В — моноидальная, а С — произвольная категория.
Покажите, что категория функторов В моноидальна, причем умножение S\3T
определяется по формуле (БПТ)с = ScHTc. В качестве е : С —»■ В нужно
взять постоянный (константный) функтор е. Покажите, что сопряжение
В х = (В ) является изоморфизмом моноидальных категорий.
5. Докажите, что строго моноидальная категория с одним объектом —
это множество (стрелок) с двумя бинарными операциями о, □, которые
удовлетворяют закону чередования и имеют общую (левую и правую)
единицу ide. Примените упр. 5 из § 2.5.
6. Покажите на примерах, что аксиомы (5) и (7) независимы.
7.2. Когерентность
Теорема когерентности утверждает: любая диаграмма
коммутативна; в более умеренном варианте — любая диаграмма определенного
класса коммутативна. Предмет нашего внимания сейчас — диаграммы
в моноидальной категории, которые, подобно пятиугольнику (5) из
§7.1, строятся с помощью умножения □ из реализаций изоморфизмов
а,Хи д. Однако две формально различных вершины такой диаграммы
могут совпасть в отдельной моноидальной категории, причем таким
образом, что коммутативность не сохранится. Поэтому мы докажем
лишь, что коммутирует каждая формальная диаграмма, в которой
вершинами служат итерированные формальные □ -произведения
переменных. Такие формальные произведения мы назовем бинарными

7.2]
Когерентность
193
словами; они соответствуют правильно построенным формулам и
термам в логическом синтаксисе теории доказательств.
Дадим точное рекурсивное определение. Бинарное слово длины
О — это символ во (пустое слово); бинарное слово длины 1 — это
символ (—) (переменное или заменяющий его знак). Если v и w —
бинарные слова длины тип соответственно, то выражение v □ w =
= (v) □ (w) является бинарным словом длины т + п. Например,
выражение ((— □— )Пео)П — является бинарным словом длины 3;
оно обозначает □ -произведение четырех сомножителей с заданной
расстановкой скобок и заданной совокупностью множителей,
состоящей из во- Для любых двух бинарных слов v и w одинаковой длины
введем единственную стрелку v —> w. Такие слова и стрелки образуют
категорию W (предпорядок, в котором каждая стрелка обратима).
Эта категория является моноидальной с умножением v,w н-» v\I\w
и единицей во, где в качестве а,\и g нужно взять соответствующие
стрелки (заведомо единственные).
По самому своему построению (стрелка v —> w единственна) любая
диаграмма в категории W коммутативна. Поэтому морфизмы из W
в В дают искомые диаграммы, коммутативные в других моноидаль-
ных категориях. Существование этих морфизмов вытекает из
следующей теоремы, которая в действительности означает, что W является
свободной моноидальной категорией с одним образующим (—):
Теорема 1. Для любой моноидальной категории В и любого
объекта Ъ Е В существует единственный морфизм моноидальных
категорий W —>• В такой, что (—) \-^ Ъ.
Доказательство. Запишем искомый морфизм как w \-> Wb,
поскольку на самом деле он означает: Подставим Ъ во все свободные
позиции слова w. На объектах w следует положить
(е0)ь = е, (-)Ь = Ъ, (v\Jw)b = vb\Jwb; (1)
по индукции эти формулы однозначно определяют все wb.
Для слов фиксированной длины п построим теперь базисный граф
Gn = Gn,6- Его вершины — все слова w длины п, не включающие
во, а его ребра v —> w совпадают с некоторыми стрелками vb —> wb
в категории В. Назовем их базисными стрелками. При этом каждая
реализация ассоциативности
а : щ □ (уь □ Wb) —> (щ □ Уъ) □ Wb
или изоморфизма а-1 является базисной стрелкой, так же как все
стрелки вида /3 □ 1 и 1 □ /?, где 1 : уь —> Уь — единичная стрелка,
причем стрелка /3 уже отнесена к базисным. Неформально говоря,
базисная стрелка — это стрелка типа (1Па)П(1П1) — реализация
изоморфизма а, умноженная на единичные стрелки. Заметим, что
каждая базисная стрелка направлена либо прямо (если включает а),
либо обратно (если включает а-1). Таким образом, пути в графе
Gn из v в w — это перемножаемые последовательности базисных

194
Моноиды
[Гл.7
стрелок из щ в Wb; в качестве произведения получаем стрелку щ —у
—> гпь в категории В. Ключевой пункт нашего доказательства будет
состоять в том, что два пути из и в w дают в произведении одну
и ту же стрелку щ —> uw в категории В — т. е. граф Gn определяет
коммутативную диаграмму в В.
Сначала возьмем в качестве w^ единственное слово длины п,
в котором все пары скобок вынесены влево. В графе Gn из любого
слова w длины п существует ориентированный путь в слово w^;
в самом деле, такой путь можно выбрать каноническим образом,
последовательно передвигая влево скобки — от наружных к
внутренним — в реализациях изоморфизма а. Если v и w — два слова длины
п, то можно объединить два канонических пути, получив путь v —>■
—> w(n) —).щ фактически мы доказали обобщенную ассоциативность
итерированного произведения в случае ассоциативности для трех
множителей.
Рекурсивно определим ранг g слова w, положив део = 0, д(-) = О
и
g(v □ w) = g(v) + g(w) + длина слова w — 1;
тогда равенство gw = 0 означает, что все пары скобок в слове w
вынесены влево.
Покажем теперь, что диаграмма Gn коммутативна. Все вершины
пути из v в w соединим с отмеченной вершиной w^ каноническим
направленным путем. Из полученной диаграммы
-^ V\
^v2
w
(n)
w
(n)
w
(n)
^v3^
w
(n)
w
(n)
ясно, что достаточно доказать равенство произведений по любым
направленным путям (только а, ни одного а~х) из vi в w^n\ Проведем
индукцию по рангу слова vi = v. Пусть утверждение верно для всех
слов v меньших рангов. Рассмотрим два различных направленных
пути, которые начинаются (направленными) базисными стрелками /3
и 7, исходящими из v, см. диаграмму:
w
(п)
■■■\ Л"
Z
У
W
(п)

7.2] Когерентность 195
Обе стрелки /3 и 7 понижают ранг. Поэтому достаточно показать,
что можно соединить их кообласти v' и v" направленными путями
с некоторой общей вершиной z, создав коммутативный ромб между v
и z. Рассмотрим возможные случаи. Если /3 = 7? т0 возьмем z = v' =
= v". Если /3 ф 7? т0 запишем v в виде v = uUw и заметим, что /3
имеет одну из трех возможных форм:
/3 = /3' □ lw; /? действует внутри первого множителя и,
/3 = 1и\3 /3"', (3 действует внутри второго множителя,
Р = &u,s,tj где v = uDw = uD(sDt).
Для 7 возможны аналогичные три случая.
Теперь сравним различные случаи для /3 и для j. Если оба
действуют внутри одного и того же множителя и, то можно применить
индукцию по длине п. Если /3 действует внутри и, а 7 — внутри ги, то
коммутативен ромб
u'Uw u\I\w'
поскольку □ является бифунктором. Остается случай, когда одна
из стрелок /3 и 7, например /?, имеет вид /3 = а = aUjSjt (третий
случай в приведенном перечне). Поскольку 7 7^ /?? то 7 действует
внутри и или внутри w. Если 7 действует внутри и, то нам
подходит ромб между un(snt) и (и' □ s) Dt, коммутативный в силу
естественности изоморфизма а. Если 7 действует внутри w = sDt
и при этом внутри s или внутри £, то аналогичный ромб существует
в силу естественности изоморфизма а. Остается лишь случай, когда
7 действует внутри w = s □ t, но не внутри s или £. Тогда 7 является
реализацией изоморфизма a, t равняется произведению pOq, и наш
ромб должен начинаться со стрелок
(uDs)D(pDq) uD ((sDp) D ^).
Тогда в качестве ромба можно взять пятиугольник (5) из § 7.1. Это
показывает, что граф Gn определяет коммутативную диаграмму в
категории В; доказательство когерентности завершено — в том, что
касается ассоциативности.

196
Моноиды
[Гл.7
Случаи применения изоморфизмов Аи^ тривиально
укладываются в это доказательство. Говоря формально, рассмотрим следующий
граф G'n. Его вершинами являются все слова длины п, в том числе
и слова, содержащие во- Ребрами этого графа служат все базисные
стрелки, построенные, как и выше, по реализациям изоморфизмов
а, А и g (и их обратных) посредством П-умножения на единичные
стрелки. Граф G'n бесконечен, но содержит прежний (конечный) граф
Gn, построенный лишь с помощью а. Нужно показать, что диаграмма
G'n коммутативна в категории В. Для каждого слова w по-прежнему
найдется хотя бы один путь w —у w^n\ Но композиция стрелок,
полученная из любого такого пути, равна композиции для другого
пути, где вначале устраняются все вхождения е, а затем применяется
а. Действительно, если е устраняется под действием изоморфизма
Л : е □ Ъ = Ъ после некоторого применения а, то это вхождение е
можно устранить и раньше — в силу естественности а, диаграммы (7)
или диаграммы (9). В случае произведения е □ е ввиду равенства (8)
безразлично, устраняется е под действием Л или д. В итоге получаем
ту же композицию стрелок, что и для канонического пути, в котором
все вхождения е устраняются в некотором определенном порядке
(например, слева направо). Эта процедура сводит G'n к Gn, и коль
скоро диаграмма Gn коммутативна, то это верно и для G'n.
Теперь мы можем построить морфизм W —> В, о котором
говорится в теореме. По построению категории W, слова v и w одинаковой
длины п соединены в ней ровно одной стрелкой v —> w. Искомый
морфизм отображает эту стрелку в композицию стрелок вдоль любого
пути уъ —> Wb в G'n: мы теперь знаем, что эта композиция единственна
(не зависит от выбора пути). Благодаря той же единственности такая
конструкция определяет функтор W —^ В. Этот функтор является
морфизмом моноидальных категорий, поскольку
/П5 = /о1П1о5 = (/П1)о(1П5)
для любых стрелок / и д. □
Утверждение о когерентности можно сформулировать в терминах
графов, ребрами которых служат естественные преобразования а, X
и д. Вначале заметим, что каждое слово w длины п (от одного
переменного) определяет для каждой моноидальной категории В функтор
wb '• Вп = Вх...хВ^Вотп переменных: для этого нужно каждый
пробел (-) в слове w заменить на тождественный функтор категории
В. Возможно и явное рекурсивное определение этого функтора
(аналогичное формуле (1)): (во)б : 1 —> В — это константный функтор
е G В; (-)в — тождественный функтор В —» В. Если wb и w'b уже
определены в терминах слов w и w' длин соответственно п и п', то
(w\I\w')b — это композиция функторов
(wUw')b : Вп+п' =Впх Вп' WBXW'B) BxB^B. (2)
В таких терминах утверждение о когерентности формулируется
следующим образом:

7.2]
Когерентность
197
Следствие. Пусть В — моноидальная категория. Существует
функция, сопоставляющая каждой паре слов v,w одинаковой длины
п (единственный) естественный изоморфизм
сап#(v,w) : vB -^ wB '• Вп -» В, (3)
который называется каноническим отображением из vb в wb,
причем канонической является единичная стрелка е —>• е (между
функторами от 0 переменных), а также тождественное преобразование
id.B : 1в —> 1в-> естественные изоморфизмы а, а-1, Л, Л-1, £>, £>-1,
композиция и □ -произведение двух канонических стрелок.
Такая формулировка, как выяснится из доказательства,
применима и к случаю, рассмотренному в самой теореме: для каждого Ь Е
Е В существует функция, сопоставляющая каждой паре слов v,w
одинаковой длины каноническую стрелку с&щ(у,и)) : уь —> и)ь и по
своим свойствам напоминающая сап#.
Доказательство. По данной моноидальной категории В мы
построим категорию It(B), объектами которой служат все пары (n, Т),
где Т — любой функтор Т : Вп —>• В, а стрелками / : (п,Т) —>• (п,Т')
являются все естественные преобразования / : Т —> Т'. В этой
категории мы определим умножение по формуле (m, S) □ (п, Т) = (т +
+ n, S □ Т), где 5 □ Т — композиция
S U Т : Бт+П ^Вш хВп ^^> В х В ^ В.
В качестве единицы е возьмем функтор 1 -f Бс единственным
значением е и определим Л : еПГ4Г для каждого Т и для каждого a Е £?п
как стрелку Хта '• е □ Та —>■ Та в категории 5. Такое преобразование Л
естественно по Т. Аналогично определим поточечно g и а; без труда
проверяется, что It (В) — (нестрого) моноидальная категория. □
Тождественный функтор / : В —» В является объектом в It(B).
Согласно доказанной теореме, W является свободной моноидальной
категорией над (-); положив Ъ = /, получаем единственный морфизм
моноидальных категорий W —> It (В) такой, что (—) 4/.В частности,
этот морфизм отображает каждое слово w в функтор wb,
описанный в формуле (2), а единственная стрелка v —> w между
словами одинаковой длины отображается в естественное преобразование
vb —> wb, которое мы обозначим c&ub(v,w), как ив (3). Поскольку
этот функтор является морфизмом моноидальных категорий, то он
должен сохранять а, А и д. Таким образом, в наших обозначениях для
слов получаем следующее:
сапв(е0,е0) = 1е : е^>е, сапБ((-), (-)) = id^ : B^ В,
сапБ(- □ (- □ -), (- □ -) □ -) = а : В □ (В □ В) ^ (В □ В) □ Б,
сапБ(е0 □-,(-)) = Л, сапБ(-Пе0,(-)) = д,
сап#(г> Пг/ ,w \Z\wf) = с&пв(у,и)) □ сапв(у' ,w').

198
Моноиды
[Гл.7
Это следствие означает, что коммутативны все диаграммы
следующего вида.
Вершины. Слова w длины п, которые представляют функторы
wB :Вп -+ В.
Ребра. Естественные преобразования le,id#, а, A, g и их П-
произведения. При этом рассматриваются функторы вида е, /, — □ —
и их композиции, а каждое ребро является естественным
преобразованием между функторами, отвечающими его концам.
Упражнения
1. Начертите диаграмму, включающую все канонические отображения
между бинарными словами длины 5. (Ее можно рассматривать как
полиэдральное разбиение поверхности сферы на 19 областей — 16 пятиугольников
(реализаций изоморфизма а) и 3 квадрата (коммутативных в силу
естественности).)
2. (Stasheff [1963].) Покажите, что диаграмма, включающая все
канонические отображения между словами длины п + 3, может рассматриваться
как полиэдральное разбиение поверхности n-мерной сферы.
3. Постройте свободную моноидальную категорию над произвольным
множеством X и докажите для нее соответствующее свойство
универсальности. (Подсказка: ее объектами служат слова, причем словом длины 1
является любой элемент х Е X, и существует сюръекция Wx —> Мх из
множества слов Wx на свободный моноид над X. Существует
(единственная) стрелка v —»■ w, если и только если слова v и w имеют одинаковый
образ в моноиде Мх-)
7.3. Моноиды
Следуя идеям введения, определим теперь понятие моноида в
произвольной моноидальной категории (В, □ , е).
Моноид с в категории В — это объект с Е В с двумя стрелками
/i : с П с —>- с, г] : е —>- с, которые делают коммутативными диаграммы
с П (с П с) ■
т
сПс —
(сПс)Пс ^сПс
-^с,
(1)
ryDl lDry
е □ с ^ сП с^ сП е
(2)
Морфизм моноидов / : (с,/1,т]} —>■ (с',//,ту)' — это стрелка f : с —> с'
такая, что
/M = M'(/D/):cDc^C', fr, = rj[:e^d.

7.3]
Моноиды
199
Моноиды в категории В с такими стрелками образуют категорию
Моп#, причем соответствие (с, /1,т]} н-» с определяет забывающий
функтор U : Моп# _> В.
Это определение охватывает множество случаев; некоторые из них
Моноиды в категории
(обычные) моноиды
топологические моноиды
монады (см. гл. б!)
кольца
if-алгебры
Градуированные алгебры
Дифференциальные
градуированные if-алгебры
комоноиды в категории В
if-коалгебры
строго моноидальные
категории
категории (см. (2.7.3)).
Выполняется обобщенный закон ассоциативности, который
утверждает, что в моноиде (с, /i, 77) равны любые n-кратные произведения.
Более подробно, пусть w — произвольное бинарное слово, wc Е В —
соответствующий объект из В (в обозначениях из доказательства
теоремы 2.1). Тогда ги-кратное произведение \iw — это стрелка /jlw : wc —>
—> с, определяемая рекурсивно. Если w = во, то /ieo : е —> с равна
ту; если w = (—), то /i(_) : с —>■ с — единичная стрелка; если w =
= (—)□(—), то \iw — /i, и вообще, если w = иПу, то /iu\jv равна
очевидной композиции
(гл □ v)c = uc\Jvc !—> с П с —>> с. (3)
Предложение 1 (обобщенный закон ассоциативности). Пусть
(c,/jL,rj) — моноид в категории В. Тогда кратные произведения fiv
и \iw для любых двух слов v и w одинаковой длины п удовлетворяют
равенству
fiw о canc (v, w) = /jlv : v —>• с, (4)
где сапс (v,w) : г;с —>• wc — каноническая стрелка из теоремы 1 § 7.2.
Доказательство. Аксиомы моноида (1) и (2) — это как раз
те случаи равенства (4), когда каноническая стрелка равна а, А или
q. Остальные случаи можно проверить по индукции, поскольку все
канонические стрелки являются композициями стрелок вида а,Х и д.
уже упоминались во введении:
Моноидальная категория
(Set,x,l)
(Тор, х,*)
<Cc,o,Id>
(Ab,(g),Z)
(Градуированные модули, ...)
(DG-K-Mod,®K,K)
(Бор, Пор,е)
(K-Mod°»,®°»K,)
(Cat,x,l)
(O-Grph, xo,0^0)

200
Моноиды
[Гл.7
Например, можно определить п-ю □ -степень элемента Ъ Е В,
положив
Ъп = (ЪПЪ)П ••• ПЬ, (5)
где все скобки вынесены влево; таким образом, Ь° = е, б1 = 6, 6n+1 =
= 6П □ Ь. Тогда в моноиде (с, /i, 77) рекурсивно определяется п-кратное
произведение //п) : сп —>• с:
Д(0)=»?, /х
«=icL
м
(2)
/х, i^n+1'=/i(/i(")Dg). (6)
Как следствие, из (4) вытекает более известное равенство —
обобщенный закон ассоциативности, верный при всех натуральных п и к±,...
... ,кп\
/iW^'D ... П//*»>) = /x(*i+-+*»). (7)
Теорема2 (построение свободных моноидов). Пусть в монои-
дальной категории В существуют счетные конроизведения, причем
для каждого a Е В функторы а П — и —Па : В —» В сохраняют эти
конроизведения. Тогда забывающий функтор U : Моп# —> В имеет
левый сопряженный.
Замечание: во многих случаях (В = Set, В = АЬ,...) сами
функторы а □ — и —Па имеют правый сопряженный и потому
автоматически сохраняют копроизведения.
Доказательство. Для каждого счетного
копроизведения ИпЬп объектов Ъп Е В выполнен дистрибутивный закон
в : Пп(аП6п) = аП Пп Ьп, так как аП— сохраняет копроизведения.
Действительно, в силу определения инъекций копроизведения
in '• Ьп —>■ ИпЬп и jn существует единственная стрелка в, делающая
коммутативной диаграмму
a\Jbn
1Шта
аПЬп
Jn
a\J Unbn-< Пп(аП6п),
и сохранение копределов в точности означает, что в является
изоморфизмом. Обратная стрелка строится аналогично.
Для данного а пусть Ъп = а71 обозначает n-ю степень, заданную по
формуле (5). Определим умножение копроизведений IInan формулой
ат П an = am+n. Формально \i — это единственная стрелка, делающая
коммутативной диаграмму
(Umam) □ (Ппо")
■П„
гат П an -i-
Пап
Ukak
1n-\-n
-.m+n

7.3]
Моноиды
201
Здесь вертикальная стрелка сап — это каноническое отображение
(итерированной ассоциативности), существующее в категории В по
теореме когерентности; ср — единственное отображение копроизведе-
ния Пп?т, которое делает квадрат с инъекциями копроизведения jm,n
и in+m коммутативным при всех натуральных тип; отображение
в о в — композиция двух упомянутых канонических изоморфизмов
в (поскольку операция □ дистрибутивна относительно Пт и Пп);
умножение \i имеет вид \i — (р(6 о в). Большая, но стандартная
диаграмма (упражнение!) показывает, что \± ассоциативно в смысле
(1). Соответствующая единица г\а : е —> IInan по определению есть
инъекция копроизведения io : е = а0 —> Ппап. Сказанное означает,
что (IInan, /i, f]a) является моноидом в категории В. Инъекция
копроизведения Qa = i\ : a = а1 —>■ IInan — это стрелка
Qa : a -> t/(IIan,/i,7ya
\ п
в забывающий функтор U : Моп# —> В.
Эта стрелка универсальна среди стрелок из а в U. Действительно,
пусть (с,/ic,?7c) — любой моноид, а / : a —>- с = t/(c,/ic,?7c) — стрелка
в категории В. Определим стрелку /; : IInan —> с как композицию
в нижней строке коммутативной диаграммы
с
и\ II
Unan >Uncn ->с,
построенной следующим образом. В качестве w возьмем слово длины
п, в котором все скобки вынесены влево, так что ъиь = Ъп согласно
нашему определению Ъп. Далее, пусть \iw : сп —>■ с обозначает п-кратное
произведение, определенное в обобщенном законе ассоциативности
(6). Пусть гп и jn — инъекции копроизведения, а прерывистые стрелки
в нижней строке делают квадраты на диаграмме коммутативными
при всех п (эти стрелки существуют по свойству универсальности
копроизведений). С помощью большой, но стандартной диаграммы
можно показать, что /; является морфизмом моноидов. По
построению /; о да = /, и поэтому стрелка да действительно универсальна —
а значит, Ппап — свободный моноид над а, как и утверждается в
теореме. □
В этом совершенно формальном доказательстве важно, что оно
охватывает многие частные случаи одной и той же конструкции.
В случае £? = (Set,x,l,...) это стандартная конструкция свободного
моноида над множеством а (следствие 2, § 2.7); в этом случае ап
состоит из слов длины п, записанных через символы из а, а свободный
моноид является дизъюнктным объединением Лпап с композицией
в качестве умножения. В случае В = (К — Mod, ®к, К,...) получаем
стандартную конструкцию (см., например, Мае Lane [1963a], р. 179)

202
Моноиды
[Гл.7
тензорной алгебры ®пАп над if-модулем А. Та же конструкция дает
дифференциальные градуированные тензорные алгебры, свободные
топологические моноиды и т. д.
Упражнения
1. Докажите, что если в категории В существуют конечные
произведения, то это верно и для Мопв.
2. (Когерентность для моноидов.) Интерпретируйте предложение 1 о
канонических отображениях fiw как следующую теорему когерентности для
моноида (с,//,т/). Рассмотрим граф, вершинами которого служат бинарные
слова w, а стрелками v —> w — следующие стрелки vc —»■ wc- l, //, v,
реализации a(ufc,vfc,wfc) изоморфизма а, реализации изоморфизмов Аи^,
а также все □ -произведения таких стрелок. Докажите, что любые два пути
w —>- (—) в этом графе дают равные композиции стрелок, но это будет
неверно, если концом пути служит не (-), а слово (—)□(—) длины 2.
3. а) (Подстановка слов в слово.) Каждое слово и длины п определяет
функтор uw • Wn —>- W. Пусть даны слова vi,..., vn\ покажите, что длина
слова uw(vi,..., vn) равна сумме длин слов vi и что оно (неформально)
соответствует последовательной подстановке слов v\,..., vn в слово и вместо
пробелов (-).
б) Пусть w = uw(vi,..., vn). Покажите, что для канонических
отображений /iw из предложения 1 композиция
V>w(lJ>v1---lJ>vri) ци
Wc = Uw{Vlc, • • • , VnC) >■ Uc >• С
равна /iw : wc —>- с. Покажите, что отсюда вытекает предложение 1.
7.4. Действия моноидов
Пусть снова фиксирована моноидальная категория В. Левое
действие моноида (с, /i, 77) на объекте a Е В — это стрелка v : с □ а —> а
в категории В, для которой коммутативна диаграмма
cD(cDa)^^(cDc)Da—-^cDa^ eUa
f Y Y
cDa ^a = a.
(i)
Например, с действует на себя посредством левого регулярного
представления \i : с □ с —> с. Морфизм f : г/ —> и' левых действий моноида
с — это стрелка / : а —>• а' в категории Б такая, что г/(1П/) =
= jv : сП а —> а'. Взяв левые действия моноида с в качестве объектов
и такие морфизмы в качестве стрелок, получаем категорию cLact.
Ясно, что эти определения включают некоторые известные случаи:
действие обычного моноида на множестве; левый Л-модуль,
рассматриваемый как действие кольца R на абелевой группе; то же с заменой
колец на if-алгебры или DG-алгебры (DG означает
дифференциальные градуированные).

7.4]
Действия моноидов
203
Забывающий функтор cLact —у В определяется по формуле
(и : с П а —> а) н-» а; он имеет левый сопряженный, который отоб-
ражает каждый объект Ъ Е В в с □ 6, причем действие моноида с на
с □ 6 определяется композицией
сП(сПб) —► (сПс)Пб —► сП6.
Аналогично определяются правые действия сг : 6 П с —>- 6 моноида
с. По аналогии с бимодулями (левыми и правыми Л-модулями) можно
определить левое и правое действия с на а, коммутирующие между
собой 1).
Упражнения
1. (Dubuc [1970], предл. 1, § 2.1.) Пусть (Т, 77, /i) — монада в категории X.
Покажите, что можно определить ее действие на эндофункторе S : X —»■ X,
если и только если можно поднять S* в категорию Т-алгебр X по формуле
5 = G1S'', причем эти действия взаимно однозначно соответствуют
подъемам S^ :X->XT.
2. Пусть малая строго моноидальная категория В действует на
категории С (как моноид в категории (Cat, x,...)). Определите действие моноида
в категории В на объекте из С и с помощью этого действия распространите
результат упр. 1 на случай функторов S : X —»■ А из произвольной
категории А.
3. Опишите действия if-коалгебры.
4. Пусть в категории В существуют копроизведения и их сохраняют
все функторы вида аП—. Покажите, что в категории cLact существуют
копроизведения и их сохраняет забывающий функтор в категорию В.
5. Если в исходной категории В существуют конечные произведения,
то это верно и для cLact, причем проекции а х а —»■ а, а' произведения
в категории В становятся морфизмами действий в категории cLact.
6. (Обобщение тензорного произведения правого модуля на левый.)
Пусть в категории В существуют коуравнители, с — некоторый моноид,
а : Ъ□ с —>- Ъ — его правое, а г/ : cDa ч a — левое действие. Постройте
тензорное произведение b\3ca E В как коуравнитель двух отображений
Ъ □ (с □ а) —>- Ъ □ а, определяемых действиями, и докажите, что □ с является
функтором Пс : Ractc x cLact —»■ 5.
7. (Теорема когерентности для действия.) Пусть дано левое действие
v : с П а —>- а моноида с. Опишите свойства канонических отображений
^™ • и)с,а —>- а, где ги — произвольное слово длины не меньше чем 1
с последним символом (-) (определите, что это значит), a wc,a получается
из ги, если подставить а вместо последнего символа, ас — вместо остальных.
:) Обзор результатов по свойствам категории cLact можно найти в работе
(*М. Kilp e.a. [2000]). Прим. ред. пер..

204
Моноиды
[Гл.7
7.5. Симплициальная категория
Опишем теперь одну строго моноидальную категорию А, которая
играет важнейшую роль в топологии и при этом порождает
универсальный моноид.
Объектами этой категории Л служат все конечные порядковые
числа п = {0,1,... ,п — 1}, а стрелками / : п —у п' — все (нестрого)
монотонные функции, т. е. такие функции /, что из 0 ^ г ^ j <
< п следует fi ^ fj. В этой категории порядковое число 0 является
начальным объектом, а 1 — терминальным. Порядковое сложение
(ordinal addition) — это бифунктор + : Л х Л —У Л, определенный
на ординалах п, т как обычная сумма п + т, а на стрелках / : п —У
—У п', g : т —У т' — по формуле
(f + g)(i) = fh i = 0, ...,n-l,
= п' + g(i — п), г = n,... , n + m — 1.
(Таким образом, функция f + g — это просто fug, поставленные
рядом.) Тогда (^,+,0) становится строго моноидальной категорией.
Поскольку объект 1 в ней терминален, то существуют единственные
стрелки /i : 2 —>■ 1, 77 : 0 —>■ 1; по той же причине эти стрелки образуют
моноид (1,/i, 77) в категории Л. Он универсален в следующем смысле.
Предложение 1. Пусть дан моноид (с,//,т/) в строго
моноидальной категории (В, □,/*). Тогда существует единственный мор-
физм F : (Л, + , 0) —У (В, □ , г) такой, что F1 = с, F/i = // и Frj = ту7:
0 —^ 1 -< 2 = 1 + 1 < А +, 0>
е ^с^ сПс, (В, П,е).
Доказательство основано на том, что стрелки из ^ — не что иное,
как итерации бинарного произведения \i. Более подробно, пусть /л^
обозначает единственную стрелку /л^ : к —У 1. Таким образом, //°) =
= 77, /Z1) — единичная стрелка, //2) = \i : 2 —У 1,
^(3) =^ + 1) = /х(1 + д) :3-И
и т. д. Поскольку объект 1 терминален в Л, то
^(n)^(*i) + ш ш ш + ^(М) = ^(fci+...+Лп) (2)
(обобщенный закон ассоциативности). С другой стороны, если / : т —У
—У п — любая стрелка из Л, то пусть mi — (порядковое) число

7_5]
Симплициалъная категория
205
элементов в подмножестве / 1i С т; тогда
г=0
(отметим, что некоторые из rrii могут равняться нулю).
Следовательно, каждая стрелка / — это сумма повторных произведений,
построенных из \i и г].
Рассмотрим теперь функтор F из формулировки предложения 1.
Поскольку F(l) = с и F должен быть морфизмом моноидальных
категорий, то Fn = c^n); тем самым определена функция объектов
для F. Далее, из равенств F/jl = ц' и Fr\ — rj' вытекает, что F/jl^ =
= /i'(n); с учетом представления (3) для стрелок из Л определена
функция стрелок Ff для /. Следовательно, функтор F единствен.
Осталось лишь показать, что указанные функции объектов и
стрелок действительно определяют функтор. Но композиции в категории
Л определяются формулой (2). Они согласованы с композициями
в категории В, поскольку в ней также справедлив закон обобщенной
ассоциативности. Доказательство завершено. □
Полученное свойство универсальности полностью характеризует
категорию Л. Ее объекты образуют свободный моноид, порожденный
объектом 1 (относительно сложения); ее стрелки строятся из \i : 2 —> 1
и Т] : 0 —> 1 посредством сложения и композиции с учетом аксиомы
ассоциативности для \± и аксиом левой и правой единицы для г) и \±.
Возможно и другое описание стрелок из Л, основанное на том, что
монотонная функция f : п —> п' представляется в виде / = д о h, где
функция h : п —>■ п" монотонна и сюръективна, а д : п" —>■ п'
монотонна и инъективна. При этом инъективная функция д определяется
указанием ее образа, т. е. некоторого подмножества из п" ординалов
в множестве п'. Как следствие, существует ровно п + 1 инъективных
монотонных функций п —> п +1, а именно функции 8f (i = 0,1,..., n),
образ каждой из которых не содержит соответствующее г:
6?:п^п + 1, 5?{0,...,п- 1} = {0,..., ?,..., п}, (4)
где г означает, что г пропускается. Можно изобразить совокупность
этих стрелок (опустив индекс п) в виде
0 -^^ 1 ==£ 2 ^=г 3,..., 50,...,5п :п-^п + 1. (5)
Si
С другой стороны, сюръективная монотонная функция h : п —>- п"
определяется подмножеством {j \ hj = h(j + 1), 0 ^ j ^ п —
— 2}, состоящим из тех значений j, при которых h не возрастает. Как
следствие, имеется п таких стрелок п + 1 —у щ они определяются по
формуле
<т?:п + 1->п, а?(г) = <т?(г + 1) (г = 0,1,... ,п - 1). (6)

206
Моноиды
[Гл.7
Изобразим их совокупность (опустив индексы) в виде
0 ■< 1 ^— 2 $== 3 |= 4 ..., сг0,..., crn_i : n + 1 -^ п. (7)
Эти стрелки можно также выразить через \± и г). Действительно,
So : 0 —> 1 совпадает с ту, сто : 2 —> 1 совпадает с /i, и из определений
следует, что
5™ = U + ту + ln-i : n ^ n + 1, г = 0,..., п, (8)
сггп = 1; + /i + ln-i-i : n + 1 -)► п, г = 0,..., п - 1. (9)
Лемма. В категории Л каждая стрелка f : п —> п' имеет
единственное представление в виде
f = 5ilo...o5ih oah o-..о^, (10)
где порядковые числа h и к удовлетворяют условию п — h + к = п',
а строки индексов г и j — условиям
п' > н > • • • > ik ^ 0, 0 ^ ji < • • • < jh < n - 1.
Доказательство. Индукция по п показывает, что любая
монотонная функция / определяется своим образом — подмножеством
вп'-и совокупностью тех j Е n, при которых / не возрастает [f(j) =
= f(j + 1)]. Элементы из п', не принадлежащие образу функции /,
занумеруем индексами ii,...,i/. (в обратном порядке). Элементы j
из п, на которых / не возрастает, занумеруем индексами ji,...,jh
(в прямом порядке). Мы видим, что функции в обеих частях равенства
(10) совпадают. □
Как следствие, композиция любых двух S или а приводится к
каноническому виду (10). Отсюда вытекает, что эти бинарные композиции
удовлетворяют тождествам трех видов:
SiSj = Sj+tSi, i ^ j, (11)
(jj(Ji = (Ji(jj+i, i^j, (12)
( 5^-!, i < j,
o-j8i = < 1, i = j,i = j + 1, (13)
[ £i-icrj, i > j + 1.
Можно проверить эти тождества непосредственно. Например, (11)
означает, что 6™+16™ = б^+^б™ : п —>• п + 2 для любого j ^ п; можно
проверить, что обе части этого равенства — монотонные инъекции,
имеющие одинаковый образ.

7_5]
Симплициалъная категория
207
Предложение 2. Категория А, объекты которой — все
конечные ординалы, порождается стрелками 6™ : п —>n + luo~f: п + 1—>
—>• п, подчиненными соотношениям (11), (12) и (13).
Доказательство. С помощью этих соотношений любая
композиция стрелок 6 и а приводится, и притом единственным образом,
к виду (10) из формулировки леммы. □
Категория А имеет непосредственную геометрическую
интерпретацию в терминах аффинных симплексов, которой соответствует
функтор
А : А -+ Тор, (14)
представляющий А как подкатегорию в Тор. На объектах п из А
он действует следующим образом. В качестве Aq возьмем пустое
топологическое пространство, а в качестве An+i — стандартный п-
мерный аффинный сиплекс, т. е. подпространство в Rn+1, состоящее
из следующих точек:
Ап+1 = {р= (to,.-.,tn) | t0 ^ 0, ...,tn ^ 0, У$2и = 1};
неотрицательные вещественные числа to,..., tn — это
барицентрические координаты точки р Е An+i. Если / : п + 1 —> т — стрелка из А,
то определим А/ : An+i —> Am+i как (аффинное) отображение вида
A/(t0,...,tn) = (s0,...,Sm), Sj = Yl ti'
fi=3
Обратим внимание, что (в таких обозначениях) An+i имеет п + 1
вершин и размерность п, а А/ — это (единственное) аффинное
отображение, которое переводит вершину i симплекса An+i в вершину fi
симплекса Am+i; например, А^. : An+i —> An+2 — это аффинное
отображение, переводящее n-мерный симплекс An+i в n-мерную грань
симплекса Ап+25 противолеж:ащую вершине г. Поверхность тетраэдра
А4 геометрически состоит из четырех треугольных граней, которые
являются образами симплекса Аз при отображениях 60,61,62 и 6%.
Используя стандартные факты из аффинной геометрии (Mac Lane,
Birkhoff [1967], ch. 12) можно проверить (упражнение), что А при
таком определении действительно является функтором Л —> Тор.
Отметим, что функтор А отображает порядковое число п + 1 в п-
мерный симплекс: геометрическая размерность на единицу меньше,
чем арифметическая, используемая в Л.
Пусть Л+ обозначает полную подкатегорию в Л, объектами
которой являются все положительные ординалы {1,2,3,...} (удален
только 0). Топологи обозначают эту категорию А, а ее объекты —
{0,1,2,...} (в соответствии с геометрической размерностью). Здесь
мы добавили к Л настоящий 0 — объект, необходимый для того,
чтобы, аналогично формуле (3), выразить все операции перехода
к грани и вырождения в терминах бинарного умножения \± и
единицы Г].

208
Моноиды
[Гл.7
Контравариантные функторы из Л+ в Set традиционно
называются симплициальными множествами.
С учетом сказанного, симплициалъный объект S в некоторой
категории X — это, по определению, функтор S : (^+)ор —>• X, а морфизм
симплициальных объектов S —>■ S" — естественное преобразование
# : S —> S'. Запишем функтор S в виде
п + 1 ь->- 5n, #i ь->- di, (Tj \-> Sj,
так что 5П имеет геометрическую размерность п. Тогда симплици-
альный объект X можно описать традиционным (и более сложным)
образом как перечень So, Si,..., Sn,... объектов из X (где Sn
соответствует n-мерному симплексу). При этом стрелками служат операторы
грани di : Sn —>■ Sn_i (г = 0,... ,n;n > 0) и операторы вырождения
Si : Sn —>■ 5n+i (г = 0, ...,п;п > 0), удовлетворяющие тождествам,
двойственным к (11), (12) и (13):
didj+г = djdi, г ^ j, (11дв)
Sj+iSi = SiSj, ^j, (12дв)
diSj
1, i = i,i + l, (13дв)
Sjdi-i г > j + 1.
Пусть, например, Y — это аффинный симплекс, вершины которого
линейно упорядочены. Тогда d{Y — это его г-я грань, полученная
удалением вершины г, a SiY — вырожденный симплекс с удвоенной
вершиной г. Перечисленные выше правила при этом выполняются.
Пополненный симплициалъный объект в категории X — это
функтор S' : Аор —> X. Симплициальный объект S можно пополнить
(т. е. продолжить до функтора S'), найдя в категории X объект S_i
и стрелку г : So —> S_i, для которых г do = sdi : Si —>■ S_i; тогда
S'(So) = е. Такая стрелка г (традиционно) называется пополнением
объекта S.
Симплициальный объект S в абелевой категории А (например,
в АЬ) определяет гомологию с помощью подходящего оператора
границы. Именно, построим, исходя из S, стрелки
S0 Д 5! Д S2 Д ..., (15)
где гомоморфизм границы д : Sn+i —> Sn определен как
альтернирующая сумма д = do — di + ... + (—l)n+1dn+i. Из соотношений (11дв) для
граней di вытекает, что дд = 0. (Это означает, что диаграмма (15)
определяет цепной комплекс в категории А.) Поскольку дд = 0, то
Im {3 : Sn+1 ->■ Sn} «С Ker {д : 5„ -»■ S„_i},

7_5]
Симплициалъная категория
209
и можно взять факторобъект (см. гл. 8) в качестве n-й гомологии
объекта S:
H0(S)=So/Im{d:S1^S0},
Hn(S) = Кет{д : Sn -> 5n_i}/Im{a : Sn+1 -> Sn}, n > 0.
Каждое пополнение функтора S определяет пополнение этого цепного
комплекса, т. е. объект S-i Е А и стрелку г : So —> S_i, для которой
eS = 0; тем самым определена и стрелка Hq(S) —> S_i.
Классическим примером служит сингулярная гомология
топологического пространства. Рассмотрим композицию функторов
ЛоР х Тор hom(A-,...)) get Д Abj
где А : Л —>• Тор — функтор из формулы (14), a Z сопоставляет
каждому множеству свободную абелеву группу, порожденную его
элементами. Описанная композиция определяет для каждого
топологического пространства X пополненный симплициальный объект
S = S(X) в категории АЬ. Каждая стрелка h G hom(An+i,X) —
это сингулярный n-симплекс в пространстве X, поэтому 5n+i — это
свободная абелева группа, порожденная всеми такими симплексами
(она состоит из всех конечных целочисленных линейных
комбинаций всех сингулярных n-симплексов). Соответствующий цепной
комплекс называется сингулярным цепным комплексом пространства X,
а его гомология — сингулярной гомологией (см., например, Mac Lane
[1963а], ch. 3).
Многообразные свойства категории Л можно подытожить
следующим образом:
а) категория Л состоит из конечных порядковых чисел и,
соответственно, является полной подкатегорией в категории Ord всех
(линейно) упорядоченных множеств;
б) Л является полной подкатегорией в Cat, если интерпретировать
каждый ординал п как категорию (конечный предпорядок); тогда
объектами в Л являются категории 0,1,2,3,...;
в) категория Л является строго моноидальной и содержит
универсальный моноид; ее стрелки — это всевозможные итерированные
произведения //т°) + ... + //Шп_1);
г) Л как подкатегория в Тор состоит из стандартных
упорядоченных симплексов (по одному в каждой размерности) и аффинных
отображений между ними, сохраняющих порядок.
Симплициальные объекты, определяемые с помощью категории
Л, служат орудием исследования многих вопросов алгебраической
топологии, в особенности связанных с гомологией, CW-комплексами,
пространствами Эйленберга-Маклейна и когомологическими
операциями. Эта линия развития представлена работами (May [1967]),
(Lamotke [1968]) и (Gabriel, Zisman [1967]), причем в последней работе
категорные приемы используются в полную силу.

210
Моноиды
[Гл.7
Упражнения
1. Покажите, что в категории Л. стрелка / : п —>- п является
мономорфизмом (соответственно эпиморфизмом), если и только если функция
/ инъективна (соответственно сюръективна).
2. а) Покажите, что подкатегория Лт0п С Л. всех мономорфизмов из Л.
порождается стрелками Si, подчиненными соотношениям (11).
б) Покажите, что каждая стрелка из Zlmon однозначно представляется
как итерированная сумма стрелок 77 : 0 —>■ 1 и id. : 1 —>> 1.
3. а) Покажите, что подкатегория ^epi С Л. всех эпиморфизмов из Л.
порождается стрелками ai, подчиненными соотношениям (12). Покажите
также, что категория Лер[ является строго моноидальной.
б) Полугруппа (с, ц) в строго моноидальной категории (С, □ , е) — это
объект с и стрелка /и, : с □ с —»■ с, ассоциативная в том смысле, что /i(/i □ 1с) =
= /i(lcD/i). Покажите, что стрелка 2 —»■ 1 определяет универсальную
полугруппу в категории Лер[.
4. Покажите, что категория симплициальных объектов в категории Set
полна в малом.
7.6. Монады и гомология
Монады и двойственные им комонады играют в гомологической
алгебре центральную роль благодаря категории Л, что мы теперь
вкратце и поясним. Пусть L = (L,e,S) — комонада в категории А;
иначе говоря, дан эндофунктор L : А —» А и естественные
преобразования г : L -^ Id а •> S : L —>■ L2, удовлетворяющие соотношениям
SL-S = LS'S :L^L3, sL - S = 1L = Ls - S : L^ L. (1)
Это определение двойственно к формуле (2) из определения монады
в § 6.1. Оно равносильно тому, что (L,e,S) — комоноид в строго
моноидальной категории АА эндофункторов категории А, где функтор
умножения □ — это композиция функторов.
Поскольку Л содержит универсальный моноид (1,0—>-1,1 + 1—>-
—> 1), то Лор содержит универсальный комоноид (1,1 —> 0,1 —> 1 +
+ 1). Перейдя от предложения 1 § 7.5 к двойственному, получаем,
что для любого комоноида в строго моноидальной категории (В, □ , е)
существует единственный морфизм моноидальных категорий Лор —>
—у В, при котором универсальный комоноид переходит в данный.
Этот морфизм — не что иное, как пополненный симплициальный
объект в категории В (а (^+)ор —> В — симплициальный объект).
В частности, любая комонада (Z/,£, S) в категории А,
рассматриваемая как комоноид в категории функторов АА, определяет
пополненный симплициальный объект (функтор) Лор —> А с диаграммой
(1, 0^ 1 ^1 + 1)
(L, Id^^L—^LoL).

7_6]
Монады и гомология
211
Здесь п отображается в Ln = L о • • • о L; г является пополнением,
a S = so : L —» L2 — отображением вырождения. Переход к грани
и вырождение в высших размерностях определяются уравнениями,
двойственными к (8) и (9) из § 7.5 (где 5 и сг выражены через /i и ту):
d? = L^L"-* : Ln+1 ^> Ln, г = 0,..., п, (2)
s? = VSL71-1-1 : Ln ^> Ln+1, г = 0,..., п - 1. (3)
В целом симплициальный объект имеет вид
Smp L=\b j-^- L2 j== L3 ..., L ^ L2 Г L3 ...).
Пусть теперь А является Ab-категорией (например, абелевой
категорией, или же к Smp L применен функтор в некоторую АЪ-
категорию). Из симплициальных тождеств для операций перехода
к граням di тогда вытекает, что альтернирующие суммы
д = d0 - di + d2 - ... + (-l)ndn : Ln+1a -+ Lna
удовлетворяют условию дд = 0 и поэтому являются морфизмами
границы для некоторого цепного комплекса, обозначаемого L*a:
L*a :La£ L2a£- L3a£ ...
с пополнением га : La —> а. Этот комплекс является стандартной
резольвентой для a G А в смысле гомологической алгебры, поэтому
с его помощью можно строить производные функторы — в частности,
различные гомологические функторы.
Примером может служить когомология групп.
Забывающий функтор U : Rng —> Моп (забывающий умножение)
имеет (по теореме о сопряженном функторе) левый сопряженный Z,
который отображает каждый моноид М в моноидальное кольцо ЪМ.
В частности, если М — П — (мультипликативная) группа, то Z П —
групповое кольцо: его аддитивная группа — это свободная абелева
группа, порожденная элементами х G П, а умножение в нем — это
единственное билинейное отображение, при котором (ж, у)
отображается в ху (произведение в П) при любых ж, у G П. Пусть П-Mod
обозначает категорию левых П-модулей А.
Забывающий функтор U : П-Mod —> АЬ имеет левый
сопряженный Z(n)(g), который сопоставляет каждой (аддитивной) абелевой
группе В левый Z(П)-мoдyль Z(n) ®B. Единицей и коединицей этого
сопряжения служат отображения
т] : В -> Z(n) <8)Я, Ьн>1®Ь, be В,
г : Z(n) ®UA-> A, x®a^xa, a G А.

212
Моноиды
[Гл.7
Композиция П-Mod —У АЬ —У П-Mod определяет комонаду
(L,s,S) в категории П-Mod, где L : П-Mod —>• П-Mod — функтор
L = Z(n) (8) — (точнее говоря, Z(n) (8) ?7—), преобразование г : L -^ Id
определено как выше. Преобразование S : L ^ L2 имеет вид S =
= Z(n) (8) ??£/, или в явном виде для произвольного модуля А:
SA'-LA = Z(n) <8> А -► Z(n) <8> А -► Z(n) (8) Z(n) ®i = L2A,
где 1 — единица группы П. Рассмотрим абелеву группу Z как
тривиальный П-модуль А (х • т = т при всех ж Е П и всех целых т). Тогда
Z(n) (8) Z = Z(n), и симплициальный объект (SmpL)Z принимает вид
z(n) 3= z(n)(2) J • • • z(n)(n) 2: z(n)(n+1)
где Z(II)(m) обозначает п-кратное тензорное произведение Ап =
= Z(n) (8)---(8)Z(n) !). При этом An+i — свободная абелева группа,
порожденная всеми элементами
х (8) х\ ... (8) жп = х (8) [xi | ... |жп]
(традиционным является правое обозначение), где х,Х{ пробегают П.
Структура П-модуля определяется соответствием (где у Е П)
(У,Х[Х!\ ...| ...|ЖП]) Н> yx[xi| ...|ЖП].
Операторы грани d{ : Z(n)(n+1) —>• Z(II)(n), которые в формуле (2)
выражены через г, имеют вид
di{x[x1\...\xn]) = xxi[x2| ...|жп], г = О,
= x[xi\ ... \xiXi+i\ ... |жп], 0 < г < п,
= x[xi| ...|xn_i], г = п.
Операторы вырождения s« : Z(Pi)(n) —» Z(Pi)(n+1), выраженные
в формуле (3) через S, — это отображения П-модулей
Si(x[xi| ... |xn_i]) = х[хг\ ... |xi_i|l|xi| ... |xn_i], 0 ^ г ^ п - 1.
Поскольку сама категория П —Mod абелева, то этот (пополненный)
симплициальный объект определяет в ней пополненный цепной
комплекс вида
z <- z(n) <- z(n)(2) <- ... <- z(n)(n) <-...
:) Принято также обозначение Z(II)®m. — Прим. ред. пер.

7.7]
Замкнутые категории
213
Получена свободная резольвента тривиального П-модуля Z; на самом
деле это стандартная резольвента, с помощью которой
определяется гомология и когомология группы П (Mac Lane [1963a], Theorem
IV.5.1).
Когомология группы П получается из этой резольвенты
следующим образом. Возьмем П-модуль А и соответствующий функтор
homn (—,^4) : (П-Мос1)ор —>• АЬ, где homn (—, —) обозначает абелеву
группу морфизмов П-модулей. Применив этот функтор к
упомянутому цепному комплексу (исключая пополнение Z(n) —> Z), получаем
коцепной комплекс
homn(Z(n),A) 4homn(Z(II)(2\A) 4...
с кограницей 5 = homn (<Э, А). Группы когомологий этого комплекса —
это в точности группы когомологий Нп(И, А) группы П с
коэффициентами в А. Формулы для di, приведенные выше, дают явное
выражение для S. Так, например, H°(U, A) = {a | a Е А и ха = а для всех ж};
^(П, А) — это группа скрещенных гомоморфизмов П —> А по
модулю главных скрещенных гомоморфизмов, а Н2(И,А) — группа всех
расширений аддитивной группы А посредством мультипликативной
группы П, с операцией сопряжения, которая определяется структурой
П-модуля A (Mac Lane [1963a], IV.2, IV.3) х).
Группы высших когомологий групп встречаются в теории
препятствий (Mac Lane [1963a], IV.8), в теории К(И, 1)-пространств в
топологии (Mac Lane [1963a], IV. 11), в теории полей классов (Cassels,
Frohlich [1967]) 2).
Гомология группы П с коэффициентами в правом П-модуле С
строится аналогично. К стандартным резольвентам нужно теперь
применять не функтор homn (—,A), а (ковариантный, аддитивный)
функтор С ®п — : П-Mod —> АЬ. Гомология полученного цепного
комплекса в категории АЬ — это гомология Нп(И, С) группы П с
коэффициентами в С. Например (Mac Lane [1963a], Prop. X.5.2),
tf0(n,Z) = Z, tf!(n,Z)=n/[n,n];
последняя группа получена факторизацией группы П по коммутанту.
7.7. Замкнутые категории
Идеи, о которых идет речь в этой главе, получили в дальнейшем
мощное развитие, которого мы коснемся вкратце. Моноидальная
категория В называется симметричной, если она наделена
изоморфизмами
7а,б '.аПЬ^ЬПа, (1)
х) См. также (*Brown [1994]). — Прим. ред. пер.
2) См. также (*Serre [1968]). — Прим. ред. пер.

214
Моноиды
[Гл.7
естественными по а, Ъ Е В, причем коммутативны все диаграммы вида
7o,b°7M = 1J дъ = \ъ°Ъ,е.ЬПе = Ь, (2)
а □ (6 □ с) -^ (аПб)Пс —-^ с □ (а □ Ь)
in
7
(3)
а П (с П 6) —^- (аПс)Пб -^i. (с П а) П 6.
Этих условий достаточно (Mac Lane [1963b]), чтобы доказать
коммутативность всех таких диаграмм, в духе теоремы когерентности из § 7.2.
Моноидальные категории (В, □ , е,...), где □ обозначает категорное
произведение или копроизведение, автоматически оказываются
симметричными, если в качестве j: axb = bxa взять (канонический)
изоморфизм, коммутирующий с проекциями. Эти идеи
разрабатываются в гл. 11.
Замкнутая категория V — это симметричная моноидальная
категория, в которой для каждого функтора — □ Ъ : V —У V однозначно
задан правый сопряженный ( )ь : V —У V. Например, категория
(АЬ, О, —) замкнута; для абелевых групп А и В сопряженный имеет
вид Ав = hom(£?,A): это абелева группа всех морфизмов В —у
—У А. Аналогично, замкнута категория (If-Mod, ®к,...) для любого
коммутативного кольца К. Декартово замкнутые категории, такие
как Set или Cat, замкнуты и в новом смысле. Во всех этих случаях
функтор ( )ь : V —У V является разновидностью внутреннего hom-
функтора.
В § 1.8 АЬ-категории (в частности, абелевы категории) уже
рассматривались как категории с hom-множествами в категории АЬ.
Аналогично, можно рассмотреть категории с hom-множествами в
любой моноидальной категории В, задав для этого: множество R
объектов г, s,£; для каждой пары объектов г, s — объект R(r,s) Е В; для
каждой упорядоченной тройки — стрелку (композицию!)
R(s,t)DR(r,s) -+R(r,t)
в категории В; для каждого объекта г — стрелку е —у R(r,r)
(единицу!). При этом композиция должна удовлетворять обычным аксиомам
ассоциативности и единицы. Результат называется 5-категорией, В-
базup о ванной категорией или категорией относительно В — а
часто У-категорией (с заменой буквы В на V). Однако заметим, что
полученная структура R не является категорией в обычном смысле;
в ней существуют лишь Yiom-объекты Д(г, s), но не hom-множества.
Последние можно получить, лишь применив к hom-объектам Д(г, s)
подходящий функтор U : В —у Set, скажем U = В(е, —), который
породит hom-множества UR(r,s). Если такие hom-множества
имеются, то говорят, что объекты R(r, s) составляют обогащение обычной
категории UR.

7.8]
Компактно порожденные пространства
215
На обогащенные категории переносятся практически все основные
результаты теории категорий при условии, что исходная категория
В — не только моноидальная, но и замкнутая. Развитие в этом
направлении (см. (Dubuc [1970]) и (Kelly [1982]), а также ссылки в этих
работах) может дать мощный метод, позволяющий единообразно
рассматривать как обычные категории, так и аддитивные категории,
связанные с замкнутыми категориями цепных комплексов (для целей
алгебры относительных гомологии), а также категории, связанные
с подходящим декартово замкнутым вариантом категории Тор.
7.8. Компактно порожденные пространства
Хорошая категория топологических пространств должна быть
декартово замкнута. Категорию Set делает декартово замкнутой
известное сопряжение
Set (X xY,Z)^ Set (X, ZY), ZY = Set (У, Z), (1)
которое отображает каждую стрелку / : X х У —у Z в /# : X —У
—у Z , причем (f^x)y = f(x,y). Такое сопряжение можно
рассмотреть и для топологических пространств X, У и Z. Мы получим
топологическое пространство Сор (У, Z), введя на множестве Тор (У, Z) всех
непрерывных отображений Y —У Z компактно-открытую топологию.
Именно, пусть предбаза открытых множеств состоит из множеств
N(C,U), где С — произвольное компактное подмножество в У, U —
любое открытое подмножество в Z, и N(C, U) содержит все те
непрерывные отображения h : Y —у Z, для которых hC С U. Стандартное
рассуждение (которое нам не потребуется) показывает, что
ограничение основного сопряжения / \-у /# из (1) дает сопряжение
Тор (X xY,Z)^ Top (X, Сор (У, Z)), (2)
если пространство У локально компактно и хаусдорфово.
Было много попыток перенести эту ситуацию на более общие
пространства У, используя различные другие топологии на пространстве
функций или на пространстве произведения. Наилучший подход
состоит в таком ограничении категории топологических пространств,
когда (категорное) произведение X \-у X х У (с его собственной
топологией как произведения) всегда имеет правое сопряженное
(которое является пространством функций с однозначно определенной
топологией).
Топологическое пространство X компактно порождено, если
каждое подмножество А С X, пересекающее любой компакт С С X по
замкнутому множеству, само является замкнутым. Обозначим через
CGHaus категорию, объекты которой — все компактно порожденные
хаусдорфовы пространства (иначе называемые пространствами Кел-
ли), причем стрелками служат все непрерывные отображения X —>■

216
Моноиды
[Гл.7
Предложение 1. Подкатегория CGHaus С Haus полна и ко-
рефлективна.
Эта подкатегория полна по определению. Для каждого хасудор-
фова пространства Y можно построить компактно порожденное
пространство KY с тем же носителем (его келлификацию), считая A CY
замкнутым в KY, если и только если А П С замкнуто в Y для всех
компактов С С Y. Таким образом, все замкнутые множества из Y
замкнуты и в KY. Это пространство хаусдорфово, и тождественное
отображение г у '• KY —у Y непрерывно. Через него пропускается
любое непрерывное отображение / : X —у Y из компактно порожденного
хаусдорфова пространства X: f = ef,
(3)
где отображение /' : X —> KY поточечно совпадает с / и непрерывно,
поскольку X компактно порождено. Таким образом, стрелка г
универсальна среди стрелок из К в Y и потому является коединицей
сопряжения, которое обеспечивает требуемую корефлективность
подкатегории CGHaus С Haus.
Из определения пространства KY следует также (см. (3)), что если
g : Y —> Z — некоторое отображение в топологическое пространство
Z, то функция ge : KY —> Z непрерывна тогда и только тогда,
когда д непрерывно на всех компактных подмножествах в Y. Отметим
также, что метризуемые пространства, а также локально компактные
хасудорфовы пространства компактно порождены.
Предложение 2. Категория CGHaus полна и кополна (в
малом).
Доказательство. Категория Haus полна (предл. 2, § 5.9),
и функтор К как правый сопряженный сохраняет пределы. Поэтому
категория CGHaus полна. Как следствие, произведение (обозначим
его □) двух пространств X и Y в категории CGHaus получается из
их обычного произведения X х Y в категории Haus по формуле
XBY = K(X xY). (4)
Иначе говоря, □ -произведение пространств Келли — это
произведение их носителей с келлификацией обычной топологии произведения.
Кополнота следует отсюда непосредственно. Поскольку любое ко-
произведение (т. е. дизъюнктное объединение) компактно
порожденных пространств в категории Haus также компактно порождено, то
достаточно построить коуравнитель параллельной пары f,g:X^X

7.8]
Компактно порожденные пространства
217
в категории CGHaus. Возьмем ее коуравнитель р : X —у Q в
категории Haus (предл. 2, § 5.9) и построим объект KQ:
f
У =1
9
Так как стрелка г : KQ —> Q универсальна, то существует
единственное отображение р' : X —>• A"Q, для которого ер' = р и р'f = p'g.
Поскольку р' является стрелкой и в категории Haus, где р служит
коуравнителем для / и д, то существует непрерывное отображение
t : Q ^ KQ такое, что р' = £р. Тогда р = ер' = etp, поэтому at = 1
и ete = г. Но г является мономорфизмом (в категории Haus), поэтому
te = 1, и в действительности г — изоморфизм. Значит, коуравнитель
пары в категории Haus лежит и в CGHaus. □
Например, если А — подмножества компактно порожденного хаус-
дорфова пространства X, то пространство отождествления X//А
является коуравнителем в категории CGHaus (сожмем в этой
категории все А в точку). Это наибольшее хаусдорфово факторпространство
для Х/А (в категории Тор); его топология автоматически является
компактно порожденной.
Теорема 1. Категория CGHaus декартово замкнута.
Если X и У — компактно порожденные хаусдорфовы
пространства, то пусть
XY =K(Cop(Y,X)) (5)
— пространство функций с келлификацией компактно-открытой
топологии. Определим е : XY \JY —у X как отображение оценки:
(fiV) ^ fy- Мы утверждаем, что е непрерывно. В действительности
достаточно доказать, что отображение е:ХухУ-^Х непрерывно на
компактах. Поскольку компактное подмножество произведения
содержится в произведении своих проекций, то достаточно показать, что е
непрерывно на множествах вида D х С, где D — компакт в Сор (У, X),
а С — компакт в Y. Пусть (/, у) G D х С, a U — открытое множество
в X, содержащее fy. Поскольку / : Y —У X непрерывно, то существует
окрестность М точки у в С такая, что fM С U. Но множество
N{M,U) входит в предбазу для Сор (У, X) (см. ее определение
перед формулой (2)), поэтому множество [N(M,U) П D] х М открыто
в D х С; оно содержит (f,y) и под действием е отображается в U.
Следовательно, е непрерывно.
Осталось показать, что е универсально среди отображений из
-DF в X. Рассмотрим любое отображение h : Z\JY —>• X из
категории CGHaus. Определим k : Z —>- Set (У, X) по формуле к =
= hfr, т. е. (kz)y = h(z,y) при всех z G Z и у Е Y. Непосредственно

218
Моноиды
[Гл.7
проверяется, что отображение kz : Y —У X непрерывно; поэтому kz Е
Е XY. Теперь покажем, что непрерывно отображение Z —У XY :
z |—У kz. Поскольку Z компактно порождено, то достаточно показать,
что непрерывно отображение Z —у Сор (У, X). Пусть теперь N(C, U) —
одно из открытых множеств в предбазе компактно-открытой
топологии, причем kz e N{C, U); тогда (h{z} x С) С U. Так как U открыто,
С компактно, a h непрерывно, то существует окрестность V точки
z, такая что h(V x С) С U. Отсюда вытекает, что kV С N(C,U).
Следовательно, к непрерывно.
Имеется коммутативная диаграмма
XYUY^-^X
kUl
zuy ;
в силу сопряженности в категории Set существует не более одного к,
для которого e(feDl) = /i, и только что мы показали, что к
непрерывно. Поэтому е универсально и определяет искомую сопряженность
CGHaus (Z □ У, X) ^ CGHaus (Z, XY). (6)
Но □ обозначает произведение в категории CGHaus, поэтому она
декартово замкнута. □
Сопряжение (6) является биекцией множеств. Хотелось бы
получить и соответствующий гомеоморфизм пространств функций
XZUY - (XY)Z.
Но он вытекает из сопряженности (6) по категорным соображениям
(упр. 3, § 4.6).
Таковы основные свойства категории CGHaus. Дальнейшие
исследования (Steenrod [1967] и др.) показывают, что эта категория
весьма полезна для топологов; в работе (Dubic, Porta [1971])
продемонстрирована ее полезность для топологической алгебры (в связи
с обобщениями двойственности Гельфанда). Все изложенное означает,
что в категории Тор мы имели дело с неправильно выбранными
математическими объектами.
Правильные объекты — это пространства из CGHaus.
Упражнения
1. Покажите, что если пространство Y хаусдорфово, то KY является
копределом (в Haus) его компактных подпространств, упорядоченных по
включению.
2. Докажите, что замкнутое (или открытое) подмножество пространства
X G CGHaus с топологией подпространства также принадлежит CGHaus.
3. Докажите, что вложение CGHaus —у Haus создает копределы.

7.9]
Петли и надстройки
219
4. Пусть Z — локально компактное хаусдорфово пространство, X Е
Е CGHaus. Докажите, что ZBX = Z х X.
5. Докажите, что категория CGHaus эквивалентна следующей:
объекты — все хаусдорфовы пространства; стрелки f : X —> Y — все функции,
непрерывные на компактах.
7.9. Петли и надстройки
В теории гомотопии мы рассматриваем категорию CGHaus
компактно порожденных хаусдорфовых пространств с отмеченной
точкой, объектами которой являются пространства X Е CGHaus с
выбранной точкой *х, а стрелками — непрерывные отображения,
сохраняющие отмеченную точку. Пусть подпространство Х^ в XY
состоит из всех таких отображений. Поскольку это подпространство
замкнуто, то оно компактно порождено. В нем естественно
определяется отмеченная точка (непрерывная функция, отображающая все Y
в *х)- Имеется стандартное сопряжение / \—у /#:
CGHaus (ZDY,X) ^ CGHaus (Z,Xy),
U U
CGHaus*(Z,X) ^ CGHaus* (Z,X(*)y).
Рассмотрим подмножество в правой части, состоящее из тех /# : Z —>
—у Х^*)¥, которые сохраняют отмеченную точку. Тогда (f^z)*Y = *х
и (f^*z)y = *х, т. е. при всех z E Z,y Е У выполнено равенство
/О,*) = * = /(*, 2/).
Это в точности те непрерывные функции /, которые сжимают клин
Z У Y = (Z □ *) U (* U Y) в точку. Соответствующее пространство
отождествления называется стянутым произведением
(Z □ Y)//[(Z П *) U (* П У)] = Z Л Y
(иногда оно обозначается Z#Y). Получаем сопряжение
CGHaus* (Z Л У, X) £* CGHaus* (Z, X^Y). (1)
Окружность 51 можно получить из единичного отрезка / =
= {t | 0 ^ t ^ 1} как пространство отождествления S1 = ///{0,1};
рассмотрим его как пространство с отмеченной точкой 0 = +1.
Определим функторы Е (стянутая надстройка) и П (пространство
петель) из CGHaus* в CGHaus*, положив
T,X = XAS1, SlX = X(*)sl;
ввиду упомянутой биекции П является правым сопряженным для Е.
Точки из CtX — это петли в X при отмеченной точке, т. е. непрерывные

220
Моноиды
[Гл.7
отображения f : I —> X, для которых /(0) = /(1) = *х- С другой
стороны, £Х — это цилиндр 1х/,в котором основания Jx{+1}, Хх
х {0} и образующая * х / сжаты в точку, которая является (новой)
отмеченной. Другими словами, это двойной конус над X (т. е.
множество X х /, в котором верхнее и нижнее основания сжаты в точку),
причем образующая, проходящая через *, также сжата в точку (см.
рис.).
Например, Е51 = S1 Л S1 — это двумерная сфера, Еп5: — это
n-мерная сфера. Единица сопряжения X —> ПЕХ отображает х Е X
в функцию (ж, —) : / —> EX. Ее можно изобразить весьма наглядно:
каждая точка х Е X отображается в ту образующую конуса, которая
через нее проходит; эта образующая является точкой в ПЕХ,
поскольку это петля, соединяющая северный полюс и (отождествленный
с ним) южный.
По индукции получаем, что Еп является левым сопряженным для
Пп : CGHaus* —> CGHaus*; это сопряжение имеет единицу X —>
—у ППЕПХ, которую можно записать как композицию
X -► ПЕХ -^^> ППЕЕХ -► ...
Функтор П, как правый сопряженный, сохраняет произведения:
ПП(ХПУ) = ППХПППУ. Эти и подобные факты можно получить
как прямым топологическим рассуждением, так и используя свойства
сопряжений.
Упражнения
1. Постройте левый сопряженный для функтора Set*(Sf, —) : Set* —>-
-> Set*.
2. Покажите, что стянутое произведение в категории CGHaus*
коммутативно и ассоциативно с точностью до естественных изоморфизмов,
которые превращают CGHaus* в симметричную моноидальную категорию,
причем единицей служит пространство из двух точек.
3. Покажите, что в категории Тор^ функтор — х Y не имеет правого
сопряженного (поскольку не сохраняет копроизведения).
4. Функтор пространства путей Р : CGHaus —»■ CGHaus определяется
по формуле РХ = Х^7, где отмеченной точкой отрезка / является 0. Если
/ G РХ, то соответствие / \-ь /(1) определяет естественное преобразование
7г : Р -Ц-Id. Покажите, что Q можно получить из коуниверсального квадрата
для диаграммы P^»Id^> *. (В классической терминологии QX называется
«слоем» отображения 7Гх : РХ —> X.)

7.9]
Петли и надстройки
221
5. Опишите коединицу сопряжения между Е и Q.
Замечания
Понятие моноидальной категории было явно сформулировано Бенабу
(Benabou [1963, 1964]), который называл их categories avec multiplication
(категории с умножением), и Маклейном (Mac Lane [1963b]), который их
называл соответственно categories with multiplication; современное название
принадлежит Эйленбергу. Первые теоремы когерентности появились в
работе (Stasheff [1963]), посвященной высшим гомотопиям, а также в работах
(Mac Lane [1963b]) и (Epstein [1966]); в последнем случае когерентность
потребовалась, чтобы дать общее определение операций Стинрода. Теоремы
когерентности стали предметом активной деятельности; Ламбек (Lambek
[1968]) нашел здесь замечательные связи с теоремами об устранении
сечения в генценовской теории доказательств; на основе его идей в работе
(Kelly, Mac Lane [1971]) была доказана теорема когерентности для
замкнутых категорий. Симплициальная категория в течение долгого времени
присутствовала неявно в формулах для границ в алгебраической топологии;
она появилась в явном виде в контексте пространств Эйленберга-Маклейна
и теоремы Эйленберга-Зильбера около 1950 г. и затем сыграла роль в
развитии гомологической алгебры (см. замечания к гл. 6). Наше обсуждение
монад и когомологии затрагивает лишь пролог к позднейшему бурному
развитию концептуальных схем гомологической алгебры.
Компактно порожденные пространства впервые появились в 1955 г.
в книге Джона Келли по общей топологии; их полезность выявилась в
работах (Steenrod [1967], Gabriel-Zisman [1967]) и др. В топологии с успехом
применяются и другие типы замкнутых категорий, в особенности
квазитопологические пространства, введенные Спеньером.
Надстройка Е над топологическим пространством долго применялась
в теории гомотопии. Картан и Серр в своей атаке (около 1951 г.) на трудную
задачу вычисления гомотопических групп сфер существенно использовали
пространства петель и надстройки. Вначале эти конструкции выглядели
как чисто геометрические, и естественное преобразование X —»■ QEX было
введено на основе топологической интуиции. Теперь оно определяется в
абстрактных терминах — как единица сопряжения.

Глава 8
АБЕЛЕВЫ КАТЕГОРИИ
Предмет этой главы составляют специфические свойства,
присущие таким категориям, как Ab, i?-Mod, Mod-i? ий- Mod — S. Все
они являются Аб-категориями (hom-множества представляют собой
абелевы группы, причем композиция билинейна), всегда существуют
конечные пределы и копределы, и эти пределы хорошо себя ведут —
в особенности ядро и коядро. Отсюда возникает совокупность аксиом,
описывающих абелеву категорию. Этих аксиом достаточно, чтобы
установить все факты о коммутативности диаграмм и связях между
морфизмами, которые в теории абелевых групп доказываются в
терминах элементов. Мы доводим изложение до этого места, оставляя
последующие вопросы гомологической алгебры для более
специального рассмотрения.
8.1. Ядра и коядра
Напомним (§ 1.5), что нулевой объект z — это объект категории
С, являющийся одновременно начальным и терминальным. Если С
имеет нулевой объект, то для любых а, Ъ Е С единственные стрелки
а —>• z и z —>• Ъ имеют произведение 0 = 0^ : а —>• 6, которое называется
нулевой стрелкой из а в Ъ. Как следствие, если один из множителей
в некотором произведении стрелок — нулевой, то и все произведение
нулевое. Нулевой объект единствен с точностью до изоморфизма,
и понятие нулевой стрелки не зависит от конкретного выбора нулевого
объекта.
Пусть категория С имеет нулевой объект. Ядро стрелки / : а —>
—> Ъ — это, по определению, уравнитель стрелок /, 0 : а =4 Ь. В более
явном виде: стрелка k : s —>■ а служит ядром для / : а —> Ь, если
fk = 0n любая стрелка h со свойством fh = 0 единственным образом
пропускается через к (в виде h = kh')\
Таким образом, если в категории всегда существуют уравнители (или,
более общо, коуниверсальные квадраты, или конечные пределы),

8Л]
Ядра и коядра
223
а также нулевой объект, то в категории существует и ядро k : s —>
—> а для любой стрелки /, причем оно единственно с точностью до
изоморфизма объекта s. Как и любой уравнитель, ядро к обязательно
мономорфно (из kg' = кЫ следует д' = Ы ввиду требования
единственности в определении). Поэтому бывает удобно считать ядро к : s —>■ а
подобъектом в а — т. е. классом эквивалентных мономорфизмов s —>
-»• а.
Приведем пример. В категории Grp нулевым объектом является
группа I из одного элемента (единицы), и для любых двух групп
нулевой морфизм G —>- Н — это единственный морфизм, который
отображает G в единицу группы Н. Ядро произвольного морфизма
групп / : G —>- Н — это вложение N —у G ядра в обычном смысле
(состоящего из всех х Е G, для которых fx = 1). Отметим, что
N — нормальная подгруппа в G, так что любое ядро в категории
Grp мономорфно, но имеются мономорфизмы, которые не являются
ядрами.
В категории множеств с отмеченной точкой Set* (§ 1.7) нулевым
объектом является одноточечное множество, а нулевое отображение
Р —» Q — это функция, отображающая все множество Р в отмеченную
точку *q G Q. Если / : Р —» Q — морфизм множеств с отмеченной
точкой, то его ядро S —> Р — это вложение совокупности S тех х G Р,
для которых fx = *q; при этом в Р и в S отмечена одна и та же точка.
Похожим образом описываются ядра в категории Тор^. В категории
Grp эпиморфизм определяется (с точностью до изоморфизма) своим
ядром, но далеко не так обстоит дело в категориях Set* и Тор^.
В любой АЪ-категории А все уравнители являются ядрами.
Действительно, в такой категории каждое hom-множество А(Ь, с) является
абелевой группой. Поэтому если дана параллельная пара /, д : Ъ —> с,
то третья стрелка h : а —>■ Ъ удовлетворяет условию fh = gh, если
и только если f(g — h) = 0. Поэтому стрелка /i, универсальная с таким
свойством, может быть описана либо как уравнитель для / и д, либо
как ядро для f — д. По этой причине в категориях Л-Mod, АЪ и т. п.
обычно имеют дело с ядрами, а не с уравнителями.
Двойственное понятие коядра уже было введено в § 3.3.
Теперь предположим, что в категории С имеется нулевой объект
z и существуют ядра и коядра для всех стрелок. Если с G С, то
множество Рс всех стрелок / с кообластью с можно превратить в пред-
порядок, считая, что д ^ / в том случае, когда д пропускается через /
(т. е. д = fg' для некоторой стрелки д'). Рефлексивное и транзитивное
отношение ^ определяет, как обычно, отношение эквивалентности =
=: / = д означает, что / ^ д и д ^ /. Классы эквивалентности
стрелок / G Рс по этому отношению образуют частично
упорядоченное множество, которое содержит частично упорядоченное множество
подобъектов из с (если рассматривать только мономорфные /, то
отношение д ^ / — это отношение вложения, которое было определено
для подобъектов в § 5.7).

224
Абелевы категории
[Гл.8
Двойственно, на множестве Qd всех стрелок и с областью d имеется
отношение предпорядка: и ^ v, если v пропускается через и (v = v'u
для некоторой стрелки v').
Выберем теперь ядро для каждой стрелки и с областью d и коядро
для каждой стрелки / с кообластью d. Согласно определениям ядра
и коядра,
/ ^ кети <£> uf = 0 <£> coker/ ^ и. (1)
Эти логические эквивалентности означают, что функции
ker : Qd -> Pd, coker : Pd -> Qd
устанавливают соответствие Галуа между предпорядками Qd и Pd
в смысле определения из § 4.5. Как и для любого такого соответствия,
треугольные тождества имеют вид
ker (coker (ker и)) = ker и, coker (ker (coker /)) = coker /.
При этом д является ядром тогда и только тогда, когда д =
= ker (coker g). Эти факты также выводятся непосредственно из
определений.
Если в категории С существуют нулевой объект, ядра и коядра, то
каждая стрелка / из С имеет каноническое разложение
/ = mq, m = ker (coker/).
(2)
Лемма 1. Если при этом f = m'q', где т' является ядром, то
коммутативный квадрат
t /
(3)
можно дополнить {единственной) диагональной стрелкой £, для
которой т = m't и q' = tq. Если при этом в категории С существуют
уравнители, а каждый мономорфизм является ядром, то стрелка q
эпиморфна.
Доказательство. По предположению т' = ker//, где р' =
= coker m':
V Л

8.2]
Аддитивные категории
225
положим также р = cokerm = coker/. Тогда р'т' = 0, поэтому р' f =
= p'm'q = 0, и р' пропускается через р по формуле р' = pw для
некоторого w. Тогда р'т = wpm = 0, поэтому m пропускается через
т' = kerp' по формуле т = m't для единственного мономорфизма t.
При этом m'q' = m't^ и стрелка т' мономорфна, и потому g' = tq.
Отсюда получаем диаграмму (3).
Чтобы доказать теперь, что стрелка q эпиморфна, рассмотрим
параллельную пару стрелок
re = se,
q' I ' \ *'
.^ rq = sq,
r, s, где rg = sg. Тогда g пропускается через уравнитель e стрелок г
и s по формуле q = eg' для некоторого q', и / = mg = ше^'. Так как
стрелка т' = ттге мономорфна, то она по предположению является
ядром, и согласно первому утверждению леммы имеется стрелка £,
для которой т = m't = met и потому 1 = et. Таким образом,
мономорфизм е имеет правый обратный и, следовательно, является
изоморфизмом. Но в качестве е был выбран уравнитель для г и s,
поэтому г = s. Значит, g является эпиморфизмом.
Таким образом, формула (2) дает разложение стрелки / на
эпиморфизм и мономорфизм. □
8.2. Аддитивные категории
Согласно определению из § 1.8, категория А является АЪ-
категорией, если в ней каждое hom-множество А(Ь, с) является
аддитивной абелевой группой (не обязательно малой) и умножение
стрелок билинейно относительно такого сложения. Каждая абелева
группа А(Ь, с) содержит нулевой элемент 0 : Ъ —> с, который
называется пулевой стрелкой (даже если А не имеет нулевого объекта
в прежнем смысле). При этом умножение на нулевую стрелку дает
нулевую стрелку, поскольку умножение дистрибутивно относительно
сложения.
Предложение1. Следующие свойства объекта z в АЪ-
категории А равпосильпы: 1) объект z является начальным;
2) объект z является терминальным; 3) lz = 0 : z —> z; 4) абелева
группа A(z,z) состоит только из нуля. Как следствие, любой
начальный (и любой терминальный) объект в А является нулевым.
Доказательство. Если объект z является начальным, то
существует единственная стрелка z —> z, поэтому lz = 0 и A(z,z) = 0.
Если lz = 0, то для любой стрелки / : Ъ —>■ z имеем / = lzf = 0/ =
= 0 : Ъ —> z, т. е. существует единственная стрелка из Ъ в z, а именно

226
Абелевы категории
[Гл.8
О, и поэтому объект z терминален. Остальные утверждения верны по
двойственности. □
Если в АЪ-категории А имеется нулевой (т. е. начальный и
терминальный) объект z, то единственные стрелки Ъ —У z и z —У с
являются нулевыми элементами в A(b,z) и A(z,c) соответственно.
Поэтому композиция Ъ —У z —У с, которая равна нулевому морфизму
О : Ъ —У с в смысле § 8.1, также является нулевым элементом в абелевой
группе А(Ь, с).
Теперь рассмотрим произведения и копроизведения в АЪ-
категории А.
Определение. Диаграмма прямой суммы х) для объектов а, Ъ Е
Е А — это диаграмма
h г2
где стрелки pi, р2, ii, i2 удовлетворяют равенствам
РхН = 1а, p2i2 = U, iiPi + i2P2 = 1С. (2)
Теорема 2. Объекты а и Ъ в АЪ-категории А имеют
произведение в А, если и только если они имеют прямую сумму. Именно,
если дана диаграмма прямой суммы (1), то объект с и проекции р\
и р2 определяют произведение объектов а иЪ. Двойственно, объект
с и инъекции i\ и г2 определяют их копроизведение. Как следствие,
два объекта а иЪ имеют произведение в категории А, если и только
если они имеют копр оиз ведение.
Доказательство. Предположим сначала, что дана диаграмма
прямой суммы (1), удовлетворяющая условиям (2). Тогда
P\i2 =Pi (iiPi +i2P2)i2 = 1орхг2 +Pii2 о 1 =pii2 +Pii2.
После вычитания получаем р\%2 — 0; по симметрии p2ii = 0. (Эти
уравнения хорошо известны для случая прямой суммы модулей.)
h h
Рассмотрим теперь какую-либо диаграмму вида а —у d —у Ъ. Если
^ - u/i + ^2/2 : б? —>- с, то pih = fi. Обратно, если р{Ы — fi (i = 1, 2)
для некоторой стрелки Ы : d —У с, то
ft' = (iiPi + i2P2)ti = hpiti + 12Р2Ы = hfi + i2/2
и потому Ы — h. Это означает, что существует единственная стрелка
h : d —у с, для которой pih = fi при г = 1,2. Потому диаграмма
х) В подлиннике употребляется термин biproduct (бипроизведение). В
литературе на русском языке принят термин прямая сумма. — Прим. ред. пер.

8.2]
Аддитивные категории
227
Vi Vi
a i— с —> Ь действительно отвечает произведению. Соответствие
h \-> (Л,/2) определяет изоморфизм абелевых групп
A(d,c) S*A(d,a) ®A(d,b),
в котором знак 0 в правой части означает прямую сумму абелевых
групп.
r\r V\ 7 Vi 7
Обратно, если дана диаграмма произведения а <— а х о —у 6, то
в силу его определения существует единственная стрелка i\ : а —у axb
с компонентами piii = 1а, p2ii = 0 и единственная стрелка г2 : Ь —>
—> а х Ъ с компонентами pii2 = О, р2г2 — 1&- Тогда
Pi(npi + ^2) = Pi + 0р2 = pi, Pi(hpi + np2) = P2,
и потому iipi + i2p2 : axb^-axb — единственная стрелка с
компонентами р\ и р2- Значит, это единичная стрелка 1ах&- Таким образом,
данная диаграмма произведения действительно определяет прямую
сумму (1), (2). □
В некоторых категориях, например в АЬ и i?-Mod, бипроизве-
дение часто называют прямой суммой г). Отметим, что диаграмма
прямой суммы описывается внутренним образом, в терминах
объектов а,Ь,с и стрелок между ними, тогда как стандартное категорное
описание произведения (и копроизведения) является внешним: оно
предполагает, что заданы стрелки во всей категории.
Для данных объектов а, Ъ Е А диаграмма прямой суммы (1), если
она существует, определена однозначно с точностью до изоморфизма
объекта с. Если всегда существует прямая сумма, то ее конкретный
выбор с = афЬ для каждой пары (а, Ь) определяет бифунктор 0 : А х
х А —> А, причем Д 0 Д для стрелок Д : а —> а' и Д : Ь —> Ь'
определяется либо уравнениями
p'iUi®h) = fjPj, * = i.2, (з)
т. е. определяется как для произведения х = 0, либо уравнениями
(Л © h)h = i'kfk, к = 1,2, (4)
те. определяется как для копроизведения 0 = II; здесь i[,i2 —
инъекции второго копроизведения 2). Действительно, первая пара
уравнений (3) однозначно определяет Д 0 Д как стрелку с
компонентами Д, Д; ввиду уравнений, определяющих второе копроизведение,
и равенства p[i2 = 0 получаем
(Д 0 f2)ik = (i'iP[ + *2Р2)(Л Ф f2)ik = i'kfk,
что соответствует второй паре уравнений. Обратное верно по
двойственности.
х) См. предыдущую сноску. — Прим. пер.
2) A p'i,p2 — проекции второго произведения. — Прим. пер.

228
Абелевы категории
[Гл.8
Результат можно также сформулировать следующим образом:
соответствие между функтором произведения а х Ъ с функцией стрелок
(3) и функтором копроизведения а II Ъ с функцией стрелок (4)
является естественным изоморфизмом.
Итерирование описанной конструкции при данных а\,..., ап Е
Е А определяет прямую сумму (BjCtj, которая характеризуется (с
точностью до изоморфизма в категории А) диаграммой
CLj —> ®jaj * ак-> 3i & — 15 • • • 1 П
и уравнениями
zipi+ ... + гпрп = 1, w, = d*, = < . (5)
[ 1? к — J-
При этом для данных ci,..., cm G -А имеется изоморфизм абелевых
групп
3,к
где J^ обозначает итерированную прямую сумму абелевых групп.
Как следствие, каждая стрелка / : ©fcC/. —> ©jO? определяется п х
х m-матрицей своих компонент fkj = Pkfij '• Uj —* Ck- При этом
композиция стрелок соответствует обычному умножению матриц
компонент. Иначе говоря, в уравнениях (5) содержится хорошо известное
матричное исчисление (см.§ 3.5).
Аддитивная категория — это, по определению, Аб-категория, в
которой имеется нулевой объект 0 и прямая сумма любой пары объектов.
Предложение 3. Пусть в аддитивной категории А даны
параллельные стрелки f,f':a—>b. Тогда
/ + /' = Hf © /% :а^Ь, (6)
где 6а : а —>■ а х а — диагональное отображение, Sb : &0б = 5115ч
—>• Ъ — кодиагональ.
Здесь диагональ определена условием р\8а = 1а = Р2^а, а
кодиагональ — условием Sbii = lb = 8bi2. Доказательство сводится
к непосредственному вычислению:
Sb(f ® f')Sa = Sb(f Ф f)(ilPl + i2P2)Sa =
= Sb(f © Г)Ч + 6*(f © f')i2 = frhf + SH2f = / + /'.
Это предложение означает, что аддитивная структура категории
А определяется прямой суммой (см. упр. 4).

8.2]
Аддитивные категории
229
Пусть А и В — две АЪ-категории. Аддитивный функтор Т : А —у
—» В — это функтор из А в 5 такой, что
T(f + f)=Tf + Tf (7)
для любой параллельной пары стрелок /,/' : 6 ч с из категории
А. Как следствие, ТО = 0. Поскольку аддитивная структура может
быть определена в терминах прямой суммы, то условие (7) можно
сформулировать следующим образом:
Предложение 4. Пусть А и В — две АЪ-категории, причем
в А всегда существуют прямые суммы. Тогда функтор Т : А —у
—у В аддитивен в том и только том случае, когда любой диаграмме
прямой суммы в А он ставит в соответствие диаграмму прямой
суммы в В.
Доказательство. Каждое из равенств piii = 1,^2*2 — lniij92 +
+ 22Р2 = 1? описывающих прямую сумму в терминах ее инъекций
ij и проекций pj, сохраняется при действии аддитивного функтора;
следовательно, он сохраняет прямые суммы.
Обратно, предположим, что Т сохраняет все бинарные прямые
суммы. Тогда для любой параллельной пары стрелок Д, /2 : а —у
->■ а' имеем: T(/i Ф /2) = ТД Ш Г/2. Равенство Г(Л + /2) = ТД + Т/2
теперь вытекает из формулы (6) и равенств T(Sa) = #та, Т(йа) =
= 5Та, которые непосредственно следуют из определений диагонали 5
и ко диагонали 5 в терминах произведения и копроизведения. □
Доказанному предложению можно придать и такой вид: функтор
Т аддитивен, если и только если Т сопоставляет каждой
диаграмме бинарного произведения в категории А диаграмму произведения
в категории В, или: если и только если он сопоставляет каждому
бинарному произведению в категории А копроизведение в категории В.
Многие известные функторы между АЪ-категориями аддитивны.
Например, если в А существуют малые hom-множества, то аддитивен
каждый hom-функтор
А(а, -):А-> АЬ, А(-, а) : Аор -у АЪ.
Если А и В являются АЬ-категориями, то это верно и для А х В,
и проекции этого произведения Ах В —у А, А х В —^ В являются
аддитивными функторами. Тензорное произведение абелевых групп —
это функтор АЬ х АЬ —у АЬ, аддитивный по каждому из аргументов.
То же верно для периодического произведения.
Упражнения
1. Покажите, что в любой аддитивной категории А каноническое
отображение
к : а\ П ... П ап —у а\ х ... х ап
(определенное в § 3.5) является изоморфизмом. (По существу это
переформулировка теоремы 2.)

230
Абелевы категории
[Гл.8
2. Определите аналогичное каноническое отображение к, бесконечного
копроизведения в соответствующее бесконечное произведение. Покажите
на примере, что это отображение не обязательно является изоморфизмом
в произвольной аддитивной категории.
3. Покажите, что прямая сумма в аддитивной категории ассоциативна
и коммутативна (с точностью до естественного изоморфизма).
4. (Альтернативное определение сложения стрелок, также приводящее
к аддитивной категории.)
а) Пусть А — категория с нулевым объектом, конечными
произведениями и конечными копроизведениями, в которой каноническое отображение
из копроизведения в произведение ai Па2 —»■ ai xa2 (§ 3.5) всегда является
изоморфизмом. Для /, f : а —»■ Ъ положим / + f = Sb(f x /') 8a- Докажите,
что такое сложение превращает каждое множество А (а, Ъ) в коммутативный
моноид, причем композиция стрелок дистрибутивна относительно
сложения.
б) Пусть при этом для каждого а £ А существует такая стрелка va : а —»■
—»■ а, что va + la = 0 : а —>- а. Докажите, что каждое множество A (a, b)
является группой относительно сложения, определенного выше, и, таким
образом, это сложение определяет на А структуру аддитивной категории
(Мае Lane [1950]).
5. (Свободная Аб-категория над категорией С.) По данной категории
С постройте Аб-категорию А и функтор С —> А, универсальный среди
функторов из С в Аб-категории. (Подсказка: объекты в категории А те же,
что в С, a A(b,c) = Z(C(6, с)) — свободная абелева группа над множеством
С(Ь,с).)
6. (Свободная аддитивная категория.)
а) По данной Аб-категории А постройте аддитивную категорию Add (A)
и аддитивный функтор А —»■ Add (А), универсальный среди функторов из
А в аддитивные категории. (Подсказка: объекты в Add (A) — всевозможные
гг-ки объектов из А, где п = 0,1,...; стрелками служат матрицы стрелок из
А.)
б) Пусть А — коммутативное кольцо К, рассматриваемое как
аддитивная категория с одним объектом. Покажите, что Add (К) совпадает
с категорией матриц Matrx, описанной в § 1.2. (Подсказка: покажите, что
Matrк обладает соответствующим свойством универсальности.)
8.3. Абелевы категории
Определение. Абелева категория — это АЪ-категория А,
которая удовлетворяет следующим условиям:
1) А имеет пулевой объект]
2) в А всегда существуют бинарные прямые суммы;
3) каждая стрелка в А имеет ядро и коядро;
4) каждый мономорфизм является ядром, а каждый
эпиморфизм — коядром.
Первые два условия означают, что А является аддитивной
категорией в смысле § 8.2. Ввиду предложения 1, § 8.2 достаточно
потребовать в условии 1) наличия не нулевого, а начального или
терминального объекта. Вместо существования прямых сумм а 0 Ъ
можно потребовать наличия всех произведений а х Ъ или всех
бинарных копроизведений.

8.3]
Абелевы категории
231
С учетом условий 1) и 2) существование ядер (условие 3)) влечет
существование всех конечных пределов. Действительно, уравнитель
пары /, д : а —У Ъ можно получить как ядро разности f — д, конечные
произведения существуют в силу 1) и 2), а наличие конечных
произведений и уравнителей гарантирует существование всех конечных
пределов. Двойственно, существование коядер влечет существование
всех конечных копределов.
Условие 4) — чрезвычайно сильное. Например, из него следует,
что если стрелка / одновременно мономорфна и эпиморфна, то она
является изоморфизмом. Действительно, если / : а —У Ъ является
мономорфизмом, то / = кет д для некоторой стрелки д, и потому
gf = 0 = 0/. Но стрелка / эпиморфна; сократив на нее, получаем:
д = 0 : Ъ —У с. Ядро нулевого морфизма д эквивалентно единичной
стрелке объекта Ъ и, следовательно, является изоморфизмом.
Категории i?-Mod, Mod-i?, Ab (и многие другие) являются абеле-
выми, с обычными ядрами и коядрами. Если категория А абелева, то
это верно и для категории функторов AJ с произвольной категорией J.
Более подробно, если даны два функтора 5, Т : J —у А, то множество
Nat (5, Т) = AJ(S, Т) всех естественных преобразований а,/? : S -^ Т
является абелевой группой, в которой сложение определено
покомпонентно: (а + f5)j = а3; + f5j : Sj —У Tj для каждого j G J. Функтор
N : J —у А, единственным значением которого является нулевой
объект в А, — это нулевой объект в категории А3. Прямая сумма
5©Т двух функторов определяется поточечно как (S(BT)a = Sa®Ta.
Ядро К естественного преобразования а : S -^ Т также определяется
поточечно: если j G J, то Kj —у Sj является ядром морфизма ctj. Для
AJ выполнены все аксиомы абелевой категории.
Предложение!. В абелевой категории А любая стрелка f
представляется в виде f = me, где стрелка т мономорфна, а е
эпиморфна] при этом
т = ker (coker /), е = coker (ker /). (1)
Если имеется другое разложение вида f = mV, где стрелка т'
мономорфна, а е' эпиморфна и коммутативен левый квадрат на
следующей диаграмме:
f
е
е
-^- • —
1
1 к
Y
>•
>-
т
т'
>■
Г
то существует единственная стрелка к, для которой e'g = ke'\
т'к = hm (т. е. коммутативны квадраты справа).

232
Абелевы категории
[Гл.8
Доказательство. Чтобы построить указанное представление
для /, положим т = ker (coker/). Поскольку (сокег/) о / = 0, то
/ имеет вид / = те для единственной стрелки е, которая эпиморфна
по лемме 1 из § 8.1. Но стрелка т мономорфна, и если определена
композиция ft, то она равна нулю тогда и только тогда, когда et = 0.
Следовательно, ker/ = kere. При этом стрелка е эпиморфна, поэтому
е = coker (kere) = coker (ker/). Соотношения (1) доказаны.
Рассмотрим теперь / и /' как объекты в категории стрелок А2.
Тогда морфизм (g,h) : f —У f — не что иное, как левый
коммутативный квадрат из (2). Рассмотрим представления / = те, /' = т'е'
и положим и = ker/ = kere. Тогда 0 = hfu = т'е'ди, поэтому е'ди =
= 0 и стрелка е'д пропускается через е = coker и по формуле е'д = ке
для единственной стрелки к. Далее, т'ке = т'е'д = hme, поэтому
т/к = hm, и в прямоугольнике из (2) оба квадрата коммутативны.
Доказательство завершено. Его вторая часть показывает, что
любой морфизм (g,h) : / —у f переводит представление для / в
представление для /', т. е. это представление является функторным. Для
случая единичного морфизма (1,1) : / —У / это означает, что любые
два разложения стрелки / на мономорфизм и эпиморфизм
изоморфны (изоморфизм к построен выше).
Это разложение позволяет (стандартно) определить образ и кооб-
раз стрелки / = те : а —у Ъ с точностью до изоморфизма по формулам
т = im/, е = coim/. (3)
Таким образом, образ т стрелки / является подобъектом ее кообла-
сти Ъ, а кообраз — факторобъектом области а. Вообще, если / = mitei,
ГДе TTli — МОНОМОрфиЗМ, t — ИЗОМОрфиЗМ И е — ЭПИМОрфиЗМ, ТО TTli =
= im/, ei = coim/, at — (стандартный) изоморфизм между кообразом
и образом. Так устроены известные конкретные категории типа АЬ.
Пусть теперь / : В —у С — морфизм в категории АЬ, ядром которого
является подгруппа К С В, образом — подгруппа S С С. Тогда /
представляется в виде композиции
где е\ — проекция на факторгруппу, т\ — вложение, а, и — очевидный
изоморфизм между кообразом В/К и образом S. Это разложение
основано на том, что каждый факторобъект В /К имеет каноническое
представление (в виде множества смежных классов).
В любой абелевой категории можно определить понятие точной
последовательности (с обычными свойствами).
Определение. Перемножаемая пара стрелок
• А ь 4 • (4)
точна в 6, если im/ = kerg {эквивалентность подобъектов из Ъ) —
или, что то же самое, coker/ = coimg.

8.3]
Абелевы категории
233
Заметим, что im/ ^ kerg, если и только если gf = 0, а / ^
^ kerg, если и только если любая стрелка к со свойством дк = О
имеет вид & = т&', где т — мономорфизм из разложения (1). Это
двоякое определение точной последовательности на самом деле
сводится к условию, хорошо известному, скажем, для случая категории
АЬ: последовательность (/, д) точна, если произведение gf равно О
и любой элемент, переходящий в 0 при отображении д, содержится
в образе отображения /.
Определение. Диаграмма
0чаА54сч0 (5)
{где 0 обозначает нулевой объект) называется короткой точной
последовательностью, если она точна в а,Ъ и с.
Поскольку стрелка 0 —у а — нулевая, то точность в а означает
мономорфность стрелки /; двойственно, точность в с означает ее
эпиморфность. Ввиду сказанного выше, условие (5) равносильно
следующим:
f = kerg, # = coker/. (6)
Аналогично, условие h = coker/ соответствует утверждению, что
последовательность
аАбЛс^О (7)
точна в Ъ и с. Классическое название для (7) — короткая правая
точная последовательность. Аналогично, условие k = ker/ выражается
короткой левой точной последовательностью.
Разложение произвольной стрелки / на мономорфизм и
эпиморфизм / = те определяет две короткие точные последовательности,
которые появляются (без нулей по краям) наверху и внизу следующей
диаграммы:
ker / coim/
. ^ . ^ .
im/
coker/
Функтор Т : А —» В между абелевыми категориями А и В по
определению называется точным, если он сохраняет все конечные
пределы и все конечные копределы. В частности, точный функтор
сохраняет ядра и коядра:
ker (Г/) = T(ker/), coker (Г/) = T(coker/). (9)
Он сохраняет также образы, кообразы и переводит точные
последовательности в точные. С учетом известного нам построения пределов

234
Абелевы категории
[Гл.8
из произведений и уравнителей, а также двойственной конструкции
получаем, что функтор Т : А —» В точен тогда и только тогда, когда
он аддитивен и сохраняет ядра и коядра.
Функтор Т точен слева, если он сохраняет все конечные
пределы. Иначе говоря, Т точен слева, если и только если он аддитивен
и ker (Tf) = T(ker/) для всех /. Последнее условие равносильно
требованию, чтобы Т сохранял короткие левые точные
последовательности.
Существует и более экономное описание абелевых категорий, не
использующее структуру абелевой группы на каждом hom-множестве.
Именно, пусть А — произвольная категория, удовлетворяющая
условиям (1), (2'), (3) и (4), т. е. аксиома (2) заменена на следующую:
(2') В категории А всегда существуют бинарные произведения
и копроизведения.
Тогда на каждом hom-множестве А (а, Ь) можно ввести сложение с
помощью формулы (2.6), и при этом А превращается в абелеву
категорию. Довольно кропотливое доказательство (Freyd [1964], Schubert
[1970]) здесь опущено: оно малополезно для приложений, поскольку
сложение в каждом из множеств А (а, Ь) обычно бывает задано
изначально.
Упражнения
1. Пусть А, В — абелевы категории, Т : А —>- В — аддитивный функтор.
Покажите, что Т точен тогда и только тогда, когда он переводит все
короткие точные последовательности в короткие точные последовательности.
2. Докажите, что если категории А л В абелевы, то и категория А х В
абелева.
3. Покажите, что категория всех свободных абелевых групп неабелева.
4. Покажите, что категория всех конечных абелевых групп (где
стрелками являются все морфизмы групп) абелева.
5. Пусть кольцо R нетерово слева. Покажите, что категория всех
конечно порожденных левых Я-модулей (стрелки — все морфизмы модулей)
абелева.
6. Пусть и ^ v — подобъекты объекта а в абелевой категории.
Определите факторобъект v/u (согласовав это определение с обычным). Докажите,
что если gf = 0, то объект kerg/im/ изоморфен двойственному объекту
coimg/coker /.
8.4. Леммы о диаграммах
Цепной комплекс в абелевой категории А — это
последовательность перемножаемых стрелок
> Сп+1 > Сп У Сп-\ -> '" , (1)
где dndn+i = 0 при всех п. Эта последовательность не обязательно
точна в сп; отклонение от точности измеряется n-м гомологическим
объектом
Нпс = Кег (дп : сп —У cn_i)/Im (dn-\-i '. cn+i —У сп) (2)

8.4]
Леммы о диаграммах
235
(о понятии факторобъекта в данном смысле см. упр. 6, § 8.3). Вначале
цепные комплексы использовались в алгебраической топологии,
причем только в категориях АЬ и К — Mod (особенно для случая, когда
К — поле вычетов целых чисел по простому модулю). Однако в более
общих вопросах теории пучков и гомологической алгебры
используются цепные комплексы во многих абелевых категориях. Определение
гомологии (2) применимо в любой абелевой категории; исследование
ее свойств требует работы с точными последовательностями, и в
теории абелевых групп при этом обычно используются элементы. Но
мы сейчас покажем, что некоторые основные леммы о диаграммах
выполнены в любой (фиксированной) абелевой категории А.
Морфизм коротких точных последовательностей (т,е) —у (т',е' )
(в категории А) — это, по определению, тройка стрелок (f,g,h) в
категории А, делающая коммутативной диаграмму
О-
О-
те
— ^0
Y Y Y
—г5 г^ *-0.
(3)
т е
Короткие точные последовательности с такими морфизмами
составляют категорию Ses А; очевидным образом она превращается в
аддитивную. Первая основная лемма состоит в следующем:
Лемма 1 (короткая лемма о пяти морфизмах). Если в
коммутативной диаграмме вида (3) строки являются короткими
точными последовательностями, то из мономорфности (соответственно
эпиморфности) f uh следует мономорфность (соответственно эпи-
морфность) д.
В случае категории АЬ возьмем элемент х Е кет д. Тогда д(х) = 0:
х'\-
■х\-
■е(х)
h
0 !->• f(x') I ^ 0^0 = he(x)
и потому he(x) = 0, е(х) = 0. Поскольку первая строка точна, то
существует элемент х', для которого т(х') = х. Поскольку вторая
строка также точна, то f(x') = 0, откуда х' = 0и потому х = 0. Это
рассуждение построено как прогон элемента х (diagram chase with x).
Такое же рассуждение можно провести в любой абелевой
категории, не используя элементов. Положим k = kerg. Тогда hek =
= е'дк = 0; поскольку h — мономорфизм, то ек = 0. Следовательно,
к пропускается через т = kere по формуле к = тк. Но при этом
0 = дк = дтк' = т' fk'\ и так как т' и / мономорфны, то к = 0.
Поскольку к = kerg, то д является мономорфизмом.

236
Абелевы категории
[Гл.8
Двойственно доказывается, что д является эпиморфизмом.
В категории АЬ мономорфизму (соответственно эпиморфизму)
отвечает в коуниверсальном квадрате мономорфизм (соответственно
эпиморфизм). Это верно для мономорфизмов в любой категории
(лемма 1, § 5.7), а для эпиморфизмов — в любой абелевой категории, что
мы и покажем.
Предложение2. Пусть в абелевой категории дан коунивер-
сальный квадрат (на диаграмме — правый).
Если при этом f является эпиморфизмом, то это верно и для /',
причем ядро к стрелки f можно представить в виде k = g'k', где
к' — ядро для f'.
Как следствие, если дана короткая точная последовательность а —у
—у Ь —У с, то любая стрелка g : d —у с порождает с помощью коуни-
версального квадрата короткую точную последовательность а —У s —У
—У d. Эта операция (а также двойственная к ней) позволяет описать
Ext (с, а) (множество всех коротких точных последовательностей из а
в с) как бифунктор на абелевой категории (Mac Lane [1963a], ch. III).
Доказательство. Коуниверсальный квадрат с вершиной s (как
и всякий коуниверсальный квадрат в абелевой категории) строится из
произведений и уравнителей следующим образом. Возьмем прямую
сумму Ъ 0 d с проекциями р\ и pi, образуем левую точную
последовательность
(таким образом, т является ядром) и положим д' = р1т, f = р2т.
Здесь стрелка jp\ — др2 эпиморфна. Действительно, пусть h(fpi —
~ 9Р2) — 0 для некоторого h. Тогда, используя инъекцию прямой
суммы ii, получаем
О = h (fp± - др2) Ч = hfpxH = ft/,
и так как / — эпиморфизм, то h = 0.
Пусть теперь uf = 0 для некоторого и. Так как /; = р2т, то
ир2пг = 0 и ир2 пропускается через jp\ — др2 = cokerm по формуле
ир2 = u'(fpi - др2). Но р2Н = 0, откуда
0 = ир2Н = u'(fpi - др2) h = и'fpiii = u'f.
Поскольку / — эпиморфизм, то и' = 0; значит, / — эпиморфизм, что
и требовалось.

8.4] Леммы о диаграммах 237
Наконец, рассмотрим к = ker/. Для пары стрелок к : а —>• Ъ
и 0 : а —> d выполнены равенства fk = 0 = #0. Согласно
определению коуниверсального квадрата существует единственная стрелка
к' : а —>• s, для которой д'к' = к и f'k' = 0. Поскольку стрелка к
мономорфна, то это верно и для к'. Покажем, что к' — ядро для /'.
Рассмотрим любую стрелку v, для которой f'v = 0. Тогда fg'v =
— 9f'v = 0, и g'v пропускается через к = ker/ по формуле g'v =
= kv' с некоторым г;'. Отсюда g'v = g'(k'v) и /'г; = 0 = f'(k'v'). Из
требования единственности в определении коуниверсального квадрата
получаем, что v = /с7'?;7. Следовательно, к' = ker/'. D
Ввиду этого предложения, в абелевой категории можно работать
с диаграммами, используя члены объектов (категории А) вместо
элементов (как делается в теории абелевых групп). Стрелку х с ко-
областью a Е А будем называть членом объекта а и применять
обозначение х Gm а. Если ж, у — члены объекта а, то положим х = у,
если существуют такие эпиморфизмы u,v, что хи — yv. Ясно, что это
отношение рефлексивно и симметрично. Докажем его транзитивность.
Пусть у w = zr для эпиморфизмов war. Образуем коуниверсальный
квадрат, показанный в верхнем углу диаграммы:
w' и
W '
Г
Т
• ^ а.
Z
Согласно предложению 2 v' и w' — эпиморфизмы, поэтому х = z. Как
следствие, можно считать, что член объекта а — это класс
эквивалентности (для отношения =) стрелок с кообластью а. Поскольку каждая
стрелка х имеет разложение х = те, то каждому члену объекта а
соответствует его подобъект (мономорфизм т), но нам этот факт
не потребуется. В каждом объекте а имеется нулевой член — класс
эквивалентности нулевой стрелки 0 —> а. Для каждого члена х Gma
существует противоположный член —х.
Для каждой стрелки / : а —>■ Ь каждый член х G т а порождает
член fx G ш Ь, причем из х = у в а следует, что /х = увЬ. Таким
образом, каждая стрелка из а в Ъ переводит члены объекта а в члены
объекта Ъ — как если бы это были элементы множеств.
ТеоремаЗ (элементарные правила работы с диаграммами). Для
членов объектов в абелевой категории выполнено следующее:
1) стрелка f : а —>■ Ъ мономорфна, если и только если для всех
х ет а из fx = 0 следует х = 0;
2) стрелка f : а —>■ Ъ мономорфна, если и только если для всех
ж, х' ет а из fx = fx' следует х = х';
3) стрелка g : Ъ —>• с эпиморфна, если и только если для каждого
z Gm с существует у ЕтЬ, для которого gy = z;
'-. П
У

238
Абелевы категории
[Гл.8
4) стрелка h : г —>• s является нулевой, если и только если hx = О
при всех х Gm r;
5) последовательность а —> Ъ —> с точна в Ь, если и только если
gf = О и для каэюдого у ет Ь из ду = О следует существование такого
х ет а, что fx = у;
6) {вычитание) для любых g : b ^ с и х,у Gm Ъ таких, что дх =
= ду, существует z ет Ь, для которого gz = 0; если при этом fx = 0
для некоторого f : b —> d, то fy = fz, и если hy = О для h : b —>• а, то
/ix = —hz.
Доказательство. Правила 1) и 2) — это просто определение
мономорфизма. Докажем правило 3). Если g — эпиморфизм, то искомый
у Е т b со свойством gy = z строится с помощью коуниверсального
квадрата (с учетом предложения 2). Обратно, если д не является
эпиморфизмом, то член 1с Gm с не имеет вида ду = 1с ни для какого
у Gm b. Правило 4) очевидно.
Докажем правило 5). Рассмотрим стандартное разложение / = те
и вначале предположим, что данная последовательность точна в Ь, так
что т = kerg. Если ду = 0, то у = myi для некоторого у\. Образуем
коуниверсальный квадрат, показанный на диаграмме слева:
е
. ^ . =
I I
Y Y
• >- • 5
Поскольку уе' = теу[ = fy[ и стрелка е' эпиморфна, то у = /yi, что
и требуется. Обратно, пусть рассматриваемое условие выполнено для
всех у Gm b. Положим k = кет д; тогда к Gm b и дк = 0 (для объекта с).
Поэтому имеется член х Gm а, для которого /ж = &, т. е. to = mexv
для соответствующих эпиморфизмов и и v. Но из этого равенства
вытекает, что мономорфизм к пропускается через т и потому im/ ^
^ kerg. С учетом равенства gf = 0 получаем, что рассматриваемая
последовательность точна.
Смысл правила 6) в том, чтобы заменить вычитание элементов
в абелевой группе. Если дх = ду, то существуют эпиморфизмы u,v,
для которых дхи = gyv, и правило 6) выполнено, если положить z =
= yv — xu Gm b. □
Приведем пример работы с диаграммой на основе этих правил.
Лемма 4 (лемма о пяти морфизмах). Если в коммутативной
диаграмме
91 91 9з 9а
CL\ >- 0-2 >■ О&з >■ G-4 ^" й5
/2
/3
и
h (4)
bi —->• b2 ——>• b3 ——>• b4 ——>• h
hi ti2 пз На
строки точны, a fi, f2, f±, fs являются изоморфизмами, то и /з
является изоморфизмом.

8.4]
Леммы о диаграммах
239
Доказательство. С учетом двойственности достаточно
доказать, что /з является мономорфизмом. В теории абелевых групп для
этого был бы использован элемент х Е ker /3. Вместо этого рассмотрим
некоторый член х Етаз, для которого fox = 0. Тогда f^x = 0;
поскольку стрелка /4 мономорфна, то д<$х = 0:
z
т
/ll
Y
у'
hv
•х\-
-^дзх
-^ О н> О = ^дзх.
Поскольку верхняя строка точна в аз, то в силу правила 5) существует
У £т а2, для которого д2у = х. Тогда 0 = f3x = hg2y = h2f2y; так как
нижняя строка точна в Ь2, то существует у' Em bi, для которого h\y' =
= f2y. Поскольку стрелка Д эпиморфна, то существует ж Gm ai, для
которого h\j\z = /2У, откуда /2^1^ = /2У- Но стрелка Д мономорфна,
и по правилу 2) giz = у и ж = д2у = g2g\z = 0. Поскольку из /зж = 0
всегда следует х = т0, то /з является мономорфизмом. П
В качестве второй иллюстрации рассмотрим морфизм (f,g,h)
коротких точных последовательностей из диаграммы (3); добавив ядра
и коядра стрелок /, д и /i, получим следующую диаграмму:
„ ran .,-г en
0 *■ Kef ?■■> ATefif ° ■>- Jfe/i
(5)
где Kef — область стрелки ker/, С of — кообласть стрелки coker/
и т. д. Столбцы этой диаграммы (с добавлением нулей вверху и внизу)
точны по построению, а средние строки — по условию. В силу
определений ядра и коядра существуют единственные стрелки т§, во,
добавление которых в верхнюю строку создает коммутативные квадраты,
и аналогично существуют единственные стрелки mi, е\ для нижней
строки. Правила из теоремы 3 позволяют без труда показать, что
первая строка точна в Kef и Кед] двойственно, последняя строка
точна в Сод и С oh. Однако первая строка не обязательно является
короткой точной последовательностью, так как стрелка во может
не быть эпиморфной. Это происходит как раз в тех случаях, когда

240
Абелевы категории
[Гл.8
стрелка mi не мономорфна. Приведем простой пример этого явления
(в категории Ab; g ф 0):
Z —
9
т
Z —
—*-z-
1
'
-^0 —
>-
>-
Потеря точности возмещается следующей неожиданной леммой,
согласно которой диаграмму (3) можно дополнить некоторой стрелкой
S, которая называется связывающим гомоморфизмом — в первую
очередь он используется в контексте относительной гомологии (комплекс
по модулю подкомплекса) и для установления соотношений между
производными функторами в гомологической алгебре.
Л е м м а 5 (лемма о ker-coker-последовательности или змеевидная
лемма). Пусть дан морфизм коротких точных последовательностей
(/, g, h) {см. (3)). Тогда существует стрелка 8 : Keh —> Cof, которая
делает точной последовательность
0 -> Kef ^ Keg ^ Keh 4 Cof
Cog
Coh -+ 0.
(6)
Доказательство. Исходя из морфизма коротких точных
последовательностей, построим диаграмму, показанную в (7) слева,
х етс0
(?)
'I >kx
z i >- ду I ^ о
zx.
Здесь со = Keh; d порождает коуниверсальный квадрат для е и к =
= ker/i; соответственно, и является эпиморфизмом с ядром s, как
в предложении 2; двойственно, d! порождает универсальный квадрат
для р = coker/ и т' с коядром s', как показано на диаграмме.
Вертикальная стрелка посредине — это композиция So = р'дк' : d —>■
—> d', причем s'So = hku = 0 и Sos = u'pf = 0. Поскольку и' = leers'
и и = cokers, то Sq имеет единственное разложение вида
Sq = u'Su : d —> cq —> а\
d'.

8.4]
Леммы о диаграммах
241
В середине находится искомая связывающая стрелка 5 : со —У а±.
Действие этой стрелки S на член х объекта со можно показать
с помощью лесенки в правой части диаграммы (7). Именно, ввиду
эпиморфности стрелки е существует у Е m Ь, для которого еу =
= кх. Тогда e'gy = hey = hkx = 0 и (поскольку левая диаграмма
точна) найдется z Gmfl', для которого m'z = ду. Мы утверждаем,
что тогда 5х совпадает с z\ — pz Gm а\. Действительно, d является
вершиной коуниверсального квадрата, и потому существует хо Em<i,
для которого ихо = х,к'хо = у. Отсюда
u'Sx = u'Suxo = SoXo = р' ду = гл'^;
поскольку и' является мономорфизмом, то 8х = z\. Это рассуждение
показывает также, что класс эквивалентности, содержащий zi, не
зависит от конкретного варианта построения лесенки (7). Именно
в соответствии с этой лесенкой обычно описывается действие
связывающего морфизма 5 на элементы абелевых групп.
С помощью лесенки мы теперь можем доказать, что ker-coker-
последовательность (6) точна — скажем, в К eh. Покажем сначала,
что 5ео = 0. Для этого достаточно проверить равенство 8e$w = 0 для
произвольного w Gm bo = Кед. Но если х = e$w Gm со, то кх = ke$w =
= ejw, где j = kerg, как на диаграмме (5). Поэтому в лесенке (7)
можно взять у = jw. Тогда ду = gjw = 0, откуда 5ео = 0. С другой
стороны, рассмотрим х Gmco, для которого 8х = 0. Тогда в лесенке
получаем z\ = 0. Из точности диаграммы (7) следует, что существует
z^ Gma с условием jz^ = z. Это означает, что gmz2 = ду. Образуем
теперь разность у0 = у — mz2 £ ш Ь. Ввиду правила 6) выполнены
равенства еуо = еу = кх и дуо = 0. Но j : bo —> b — это kerg, поэтому
существует х0 ет ^о, для которого jx0 = Уо-
х0\ ^ е0х0 х
т
\з
Y e
Уо l ^ кх = /еж
0.
Тогда кеоХо = еуо = кх и к является мономорфизмом, откуда ео^о =
= х. Мы показали, что если 6х = 0, то ж имеет вид х = ео^о и,
следовательно, лежит в образе морфизма во- Тем самым доказано,
что последовательность (6) точна; на самом деле наше доказательство
в точности соответствует обычному, в котором используются
настоящие элементы настоящих абелевых групп. □
Упражнения
1. В лемме о пяти морфизмах найдите минимальные условия (только на
/i, /2 и /4), при которых /з является мономорфизмом.

242
Абелевы категории
[Гл.8
2. В лемме о пяти морфизмах докажите эпиморфность /з, используя
члены объектов (а не двойственное понятие). (Подсказка: в таком
доказательстве требуется правило 6) из теоремы 3.)
3. Завершите доказательство того, что ker-coker-последовательность
точна.
4. Покажите, что связывающий морфизм S естествен, т. е. что это
естественное преобразование между некоторыми двумя функторами,
определенными на категории, объектами которой являются морфизмы (3)
коротких точных последовательностей.
5. 3 х 3-диаграмма имеет следующий вид (по краям стоят нули):
■>- • >- •
• >- • >- •
а) Дайте прямое доказательство 3 х 3-леммы: если 3 х 3-диаграмма
коммутативна, причем все три столбца и две последние строки — короткие
точные последовательности, то это верно и для первой строки.
б) Покажите, что эта лемма следует также из теоремы о ker-coker-
последовате льности.
в) Докажите, что если 3 х 3-диаграмма коммутативна и все три столбца,
а также первая и третья строки — короткие точные последовательности, то
это верно и для средней строки.
6. Докажите, что для произвольных стрелок / : а ^ b и д : Ъ ^ с точна
последовательность
О -► Kef -► Kegf -► Кед -► Cof -► Cogf -► Cog -► 0.
7. Покажите непосредственно, что категория Ses (А) в общем случае не
является абелевой.
Замечания
Вскоре после введения понятия категории Эйленберг и Стинрод (Eilen-
berg, Steenrod [1952]) показали, что с помощью языка категорий и
функторов можно дать аксиоматическое описание гомологии и когомологии
в топологическом пространстве. В свою очередь это привело к вопросу об
описании категорий, в которых могут лежать значения таких гомологии.
После обсуждения с Эйленбергом такое описание было дано Маклейном
(Mac Lane [1948, 1950]). Его понятие абелевой бикатегории выглядело
громоздким, и тема оказалась на заднем плане. Затем появилось
аксиоматическое исследование Бухсбаума (Buchsbaum [1955]) и было обнаружено, что
категории пучков (абелевых групп) над топологическими пространствами
абелевы, но не являются категориями модулей (Grotendieck [1957]), а также
что гомологическая алгебра в этих категориях необходима для полного
исследования когомологии пучков (Godement [1958]). Под влиянием этих
открытий абелевы категории вошли в приличное общество.
Эта глава содержит лишь элементарную теорию абелевых категорий —
вывод стандартных лемм о диаграммах непосредственно из аксиом. Наш

8.4]
Леммы о диаграммах
243
метод прогона по диаграмме основан на методе из книги (Mac Lane [1963a],
ch. XII). Ключевую роль здесь играет змеевидная лемма, которая
позволяет построить стрелку. Первые доказательства этой леммы для
абелевых категорий были неясными; здесь приведен вариант, принадлежащий
М. Андре (М. Andre, частное сообщение). Можно также доказать эти леммы
о диаграммах для произвольных абелевых категорий, исходя из случая R-
модулей и применяя подходящие теоремы вложения (Lubkin, Наг on, Freyd,
Mitchell). В этих замечательных теоремах для любой малой абелевой
категории А строятся унивалентные и точные функторы А —>- АЬ и А —>-
—>- Я-Mod (где R — подходящее кольцо), причем второй из них полон
(full). Доказательства см. в книгах (Mitchell [1965]), (Freyd [1964]) и (Pareigis
[1970]).
В этих источниках можно найти сведения и о дальнейших красивых
результатах по абелевым категориям — таких, как теорема Крулля-Ремака-
Шмидта, двойственность Мориты, построение инъективных оболочек в
подходящих абелевых категориях, структура категорий Гротендика и локально
нетеровы категории (Gabriel [1962]).

Глава 9
СПЕЦИАЛЬНЫЕ ПРЕДЕЛЫ
В этой главе изучаются два полезных типа пределов (и
копределов): фильтрованные пределы, т.е. пределы по направленным пред-
порядкам (и, в более общем случае, по определенным фильтрованным
категориям), и концы, которые порождаются определенными
бифункторами и в некотором смысле ведут себя подобно интегралам.
9.1. Фильтрованные пределы
Предпорядок Р называется направленным, если для двух любых
элементов p,q Е Р существует [общая] верхняя грань в Р, т. е. такой
элемент г, что р ^ г и q ^ r (его единственность не требуется). Как
следствие, любое конечное множество элементов из Р имеет верхнюю
грань. Направленный предпорядок называется также направленным
или фильтрованным множеством.
Это понятие обобщается и на категории (под другим названием).
Категория J называется фильтрованной, если она непуста и
выполнено следующее:
а) для каждых двух объектов j, jf G J существуют объект к Е J
и стрелки j —>• к, j' —>• к:
б) для любых двух параллельных стрелок u,v : i —> j из J
существуют к G J и стрелка w : j —>■ к такая, что wu = wv, как
в следующем коммутативном ромбе:
Условие а) означает, что дискретная диаграмма {j,j'} является
основанием конуса с вершиной к, а условие б) — что пара г =4 j также
служит основанием некоторого конуса. Как следствие, любая
конечная диаграмма в фильтрованной категории J является основанием
хотя бы одного конуса с вершиной к G J.

9Л]
Фильтрованные пределы
245
Отметим, что терминология для двойственных понятий здесь не
устоялась. В некоторых работах, например, (Mac Lane, Moerdijk
[1992]) описанная категория J называется кофилътрованной.
Фильтрованный копредел — это, по определению, копредел
функтора F : J —> С, определенного на фильтрованной категории J.
В классическом случае копределы определялись только над
направленными предпорядками (или даже над направленными
порядками). Это формальное ограничение оказалось бесполезным. На самом
деле существенны лишь формулы перестановки для фильтрованных
копределов (§ 9.2) и возможность получить все копределы из
конечных копроизведений, коуравнителей и копределов над
направленными предпорядками. Поскольку мы уже знаем, что все копределы
можно получить из (бесконечных) копроизведений и коуравнителей
(факт, двойственный к теореме 1, § 5.2), то указанная возможность
вытекает уже из следующего факта.
Теорема 1. В категории С с конечными копроизведениями и
копределами над всеми (малыми) направленными предпорядками
существуют все (малые) копроиз ведения.
Доказательство. Мы хотим построить копредел для функтора
F : J —> С, где J — некоторое множество (дискретная категория).
Пусть J+ — предпорядок, объекты которого — все конечные
подмножества S С J, упорядоченные по включению; ясно, что J+ —
фильтрованная категория. Пусть функтор F+ сопоставляет каждому
конечному подмножеству S копроизведение UFs, взятое по всем s Е
Е S. Если вложение S С Т является стрелкой и : S —>- Т в категории
J+, то возьмем в качестве F+u единственную (прерывистую) стрелку,
которая при любом s G S делает коммутативной диаграмму
F+5 = UFs ^ UFt = F+T
А А
Fs = Fs,
где г, г' — инъекции копроизведений. Ясно, что F+ — функтор J+ —>■
—у С, согласованный на J с данным функтором F, если категория
J вложена в J+ путем отождествления любого j с одноэлементным
множеством {j}.
Рассмотрим теперь естественное преобразование в : F+ -^ G, где
G — любой другой функтор J+ —> С. При любом s E S коммутативна
диаграмма
F+S = UFs- -s- >GS
\is ]G({s}cS)
Fs--e-^G{s}.
В силу определения копроизведения это означает, что в полностью
задано своими значениями 6S на Fs. Как следствие, каждый конус

246
Специальные пределы
[Гл.9
г/+ : F+ —у с над F+ полностью определяется своими значениями на
J, которые образуют конус v : F -^ с над F. При этом г/+ является
предельным конусом, если и только если это верно для v. Значит, мы
можем вычислить искомое копроизведение IIFj, являющееся
копределом функтора F, как копредел функтора F+. Он существует в силу
того, что категория J+ фильтрована. □
В качестве типичного приложения построим копределы в
категории Grp.
Предложение 2. Забывающий функтор Grp —у Set создает
фильтрованные копределы.
Доказательство. Пусть даны фильтрованная категория J
и функтор G : J —У Grp; стрелкам j —У к он сопоставляет групповые
морфизмы Gj —У Gk- Далее Gj обозначает и группу, и ее носитель.
Пусть дан также предельный конус \i для композиции функторов J —у
—У Grp —у Set с вершиной в некотором множестве S; он сопоставляет
каждому j G J функцию \ij : Gj —У S. Вначале покажем, что на
множестве S имеется единственная групповая структура, при которой
все функции \ij являются морфизмами групп. Во-первых, заметим,
что для каждого s G S существует хотя бы один индекс j такой, что
для соответствующего элемента группы выполнено равенство \ijQj —
— s. В противном случае мы могли бы удалить s из S и получить
конус с вершиной в меньшем множестве S': очевидное противоречие
с универсальностью множества S (найдутся две функции S =4 S,
дающие одинаковую композицию с /л).
Определим теперь произведение двух произвольных элементов
s, t G S. Для некоторых j, к G J выполнены равенства s = \ijQj и t =
= 1Лк9к] так как категория J фильтрована, то в ней имеется конус над
j, к с некоторой вершиной г:
Его образ при действии функтора G имеет вид Gj —У Gi «— Gk- Это
значит, что s и t соответствуют элементам группы Gi. Их
произведение в S положим равным результату применения \±i к их
произведению в Gi. Такое произведение не зависит от выбора г, поскольку
для любого другого г' имеется конус Gi —У Gm —У Gi>, состоящий из
морфизмов групп. Произведение трех множителей г, s, t ассоциативно,
поскольку можно выбрать Gi так, чтобы все они соответствовали ее

9Л]
Фильтрованные пределы
247
элементам, и воспользоваться ассоциативностью умножения в G{. Во
всех группах G{ имеются единицы, и отображения Gj —> Gk их
сохраняют. Общий образ этих единиц является единицей для умножения
в S. Аналогично строятся обратные элементы.
Мы нашли (единственную) групповую структуру на 5, при
которой /ij : Gj —>■ S является морфизмом групп. Это означает, что \i
является конусом в категории Grp с основанием G и вершиной S,
причем универсальным конусом. Действительно, если v : G -^ Т —
другой конус в категории Grp, то он остается конусом и в Set, поэтому
существует единственное отображение множеств / : S —> Т, для
которого j\i — v. Как и выше, можно проверить, что оно является
морфизмом групп. □
Ясно, что это рассуждение применимо не только в категории Grp,
но и в любой категории Algr алгебр фиксированного типа т
(который определяется системой операций и тождествами, см. § 5.6). Это
замечание относится и к следующему результату.
Следствие 3. В категории Grp всегда существуют (малые)
копределы.
Доказательство. Прежде всего, одноэлементная группа
является в категории Grp начальным объектом. Далее, для любых двух
групп G и Н существует копроизведение G * Н. В самом деле, любая
пара гомоморфизмов G —>■ L, Н —» L в третью группу L пропускается
через подгруппу в L, порожденную образами групп G и Н.
Мощность этой подгруппы ограничена; как следствие, выполнено условие
существования разрешающего множества. По теореме о сопряженном
функторе существует копроизведение G * Н.
Из этих двух замечаний следует, что в категории Grp
существуют все конечные копроизведения. Согласно предложению 2, в ней
существуют все фильтрованные копределы. Ввиду теоремы 1 в ней
существуют все малые копроизведения. Чтобы получить все малые
копределы, нужны лишь коуравнители. Но коуравнитель двух
гомоморфизмов u,v : G —>• Н — это проекция Н —>• H/N на факторгруппу
по наименьшей нормальной подгруппе N, содержащей все элементы
(ug^vg)-1, где g G G. □
Это доказательство позволяет явно описать копроизведение групп.
Его обычно называют свободным произведением] оно состоит из
конечных слов (gi,hi,g2,h2,... ,gn,h"n), содержащих символы gi G G
и hi G Н. Умножение слов состоит в их приписывании друг к другу,
а равенство устанавливается последовательными сокращениями (если
hi = 1 в группе Н, то удалим hi и перемножим gi и д^\ в группе F,
и т.д.). Доказать ассоциативность исходя из такого определения —
довольно кропотливое дело. Ввиду следствия 3 можно получить
бесконечное копроизведение UiGi групп Gi путем склеивания
всевозможных конечных копроизведений
Gix *Gi2 * • • • * Gih,
которые вкладываются как подгруппы в копроизведения большего
числа множителей. В итоге UiGi является объединением всех этих

248
Специальные пределы
[Гл.9
конечных копроизведении, отождествляемых с помощью таких
вложений.
Упражнения
1. С помощью теоремы о сопряженном функторе докажите в один шаг,
что в категории Grp всегда существуют малые копределы.
2. Докажите, что в категории Algr, описанной в § 5.6, всегда существуют
малые копределы; в частности, опишите начальный объект (в каком случае
он пуст?).
9.2. Перестановка пределов
Рассмотрим бифунктор F : Р х J —у X в кополную категорию X.
Для значений р Е Р параметра р копределы функтора F(p, —) : J —У
—>• X определяют функторы р \-> Colinij F(p,j), причем копредельные
конусы
»рj : F(p,j) -+ Colinij F(p,j) (1)
у
естественны по р (теорема 1, § 5.3). Можно непосредственно показать
(см. ниже § 9.8), что
Colimp Colinij F(p, j) ^ Colinij Colimp F(p, j) (2)
у > у у
с каноническим отображением в качестве изоморфизма. Двойственно,
пределы также коммутируют. Но пределы не обязательно
коммутируют с копределами, поскольку каноническое отображение
к, : Colinij Linip F(p,j) —У Limp Colinij F(p,j) (3)
может не быть изоморфизмом.
Это каноническое отображение определено, когда существуют все
пределы и копределы в формуле (3). Оно строится с помощью
следующей диаграммы:
F(p, j) * — LimP F(P> J) - >■ Colinij Limp F(p, j)
У У
Colinij F(p,j) < Vp Linip Colinij F(p,j) = Limp Colinij F(p,j).
(4)
Здесь v и i/-j для каждого j — предельные конусы, a /i,/ip?_ для
каждого р — копредельные конусы. Поскольку v является конусом
относительно р, а \± естественно по р, то композиция fipjiSpj с
фиксированным j является конусом относительно р. Так как конус v
универсален, то существуют стрелки olj для всех j, делающие левый квадрат

9.2]
Перестановка пределов
249
коммутативным. Поскольку /ip,- — конус относительно j, то это верно
и для а; так как конус \i универсален, то существует отображение
&, делающее правый квадрат коммутативным. Это и есть искомое
каноническое отображение.
Оно не обязательно является изоморфизмом. Рассмотрим,
например, ситуацию, когда Р — {1,2} и J — {1,2} — дискретные категории
с двумя объектами. Если существует каноническое отображение
к:(АгХ Вг) II (А2 х В2) -> (Аг II А2) х (Вг II В2)
(смысл обозначений очевиден), то оно имеет две компоненты а± и«2,
где, например, а\ определяется диаграммой
А1 -< А1 х В1 >- В1
А1 II А2 -*?— (Аг II А2) х (Вг II В2) —^ В1 U В2.
Очевидно, что в категории АЬ отображ:ение к является
изоморфизмом, а в категории Set — нет: его область — дизъюнктное объединение
двух множеств, а кообласть — дизъюнктное объединение четырех
декартовых произведений:
(Аг х Вг) U (Аг х В2) U (А2 х Вг) U (А2 х В2).
Рассмотрим теперь условия, при которых к заведомо является
изоморфизмом.
Теорема1. Пусть Р — конечная категория, J — малая
фильтрованная категория. Тогда для любого бифунктора F : Р х J —> Set
каноническая стрелка
к : Colinij Linip F(p,j) —> Limp Colinij F(p,j)
вида (З) является изоморфизмом.
Это означает, что конечные пределы в категории Set коммутируют
с фильтрованными копределами.
Доказательство. По построению копределов в терминах ко-
произведений и коуравнителей (двойственный факт к теореме 2, § 5.2
для случая фильтрованной категории J) имеется равенство
Co]unjF(p,j) = UF(p,j)/E, (5)
у J
где YLj — дизъюнктное объединение, а Е — отношение
эквивалентности на нем: именно, если х G F(p,j), x' G F(p, j'), то хЕх' в том
и только том случае, если существуют стрелки и : j —>■ fc, и' : j; —>■ fc,
для которых F(p,u)x = F(p,u')x'. Класс эквивалентности элемента

250
Специальные пределы
[Гл.9
х е F(p,j) обозначим (ж, j). Категория J фильтрована, и из условия а)
в определении таких категорий вытекает, что любой список таких
элементов (xi, ji),..., (xm,jm) можно представить как список (yi,k),...
... , (ут, к) с одинаковым вторым индексом к. Из условия б) в том же
определении следует, что любое равенство между элементами такого
списка можно реализовать, применяя одну и ту же стрелку w : к —>- к''.
Для любого функтора G : Р —> Set выполнено равенство
Linip Gp = Cone(*,G); правая часть обозначает множество конусов г
с основанием G и вершиной в точке *. Если Gp = Colinij F(p, j)
у
и категория Р конечна, то каждый такой конус состоит из
конечного числа элементов из Colinij F(p,j). Условия, делающие его
>
конусом, сводятся к конечной совокупности равенств между этими
элементами. Поскольку категория J является направленной, то ввиду
сказанного выше каждый конус т состоит из элементов тр = (ур,к')
с фиксированным к', причем ур G F(p,k') уже составляют конус
у : * -^ F(—, к'). Этот конус у является элементом из Limp F(p, к'); его
класс эквивалентности — элемент из Colinij Limp. Отображение
т ь->- (у, kf) G Colinij Linip F(p, j),
не зависящее от сделанного выбора элементов в классах
эквивалентности, и есть искомое (двустороннее) обратное для канонического
отображения к. □
Упражнения
1. Покажите, что отображение и из формулы (3) является естественным
на стрелках а : F ^ F' из XPxJ.
2. (Verdier.) Категория J называется псевдофильтр о в аннощ если она
удовлетворяет условию б) для фильтрованных категорий и следующему
условию а'): любые две стрелки i —»■ j, i —»■ f с общей областью можно
включить в коммутативный ромб
Докажите, что категория J фильтрована, если и только если она связна
и псевдофильтрована. Докажите, что категория псевдофильтрована, если
и только если ее связные компоненты фильтрованы.
3. Покажите, что в категории Set копроизведения коммутируют с ко-
универсальными квадратами.
4. С помощью упр. 2 и 3 покажите, что в категории Set псевдофильтро-
ванные копределы коммутируют с коуниверсальными квадратами.

9.3] Финальные функторы 251
9.3. Финальные функторы
Копредел часто можно вычислить, рассматривая лишь некоторую
подкатегорию. Например, если N — линейно упорядоченное
множество натуральных чисел, то копредел функтора F : N —У Cat явно
совпадает с пределом его ограничения на любое бесконечное
подмножество S С N (т. е. на любую подкатегорию, в которой для
каждого объекта из N найдется больший). В классической терминологии
такое подмножество S называется кофинальным с N; сегодня было
бы желательно отбросить ко, как не связанное с двойственностью.
Мы заменим подмножество S сначала функтором вложения S —У N,
а затем произвольным функтором.
Функтор L : J' —у J называется финальным, если для каждого k Е
Е J категория запятой (к I L) непуста и связна. Это значит, что для
каждого к имеется объект j' Е J' и стрелка к —У Lj', причем любые две
такие стрелки можно связать посредством конечной коммутативной
диаграммы вида
к = к
l |
l
у Y
Подкатегория называется финальной, если финален соответствующий
функтор вложения. Например, если J — линейный порядок, J' С J,
a L — соответствующее вложение, то его финальность означает
просто, что для каждого к G J существует такой объект jf G J, что к ^ jf.
Функторам L : J' —>■ J и F : J —>■ X соответствует каноническое
отображение
h : Colim FL -+ Colim F, (1)
которое определено при условии существования обоих копределов;
если /i' : FL -^ Colim FL и \i — копредельные конусы, то h — един-
У
ственная стрелка из X, для которой h/i'-, = /jlj' при всех j' G J'.
Теперь сформулируем основной результат:
Теорема1. Если функтор L : J' —>• J финален, а для функтора
F : J —» X существует х = Colim FL, mo существует и Colim F,
У У
причем каноническое отображение (1) является изоморфизмом.
Доказательство. По данному копредельному конусу \i : FL ^>
-^ Colim FL = х построим стрелки т/. : Fk —У х для каждого k G J,
выбрав стрелку и : к ^ Ljf и взяв в качестве т^ композицию
Fk —У FLf —у х.
Поскольку \i — конус, а категория (к ^ L) связна, то приведенная выше
диаграмма финальности показывает, что т\~ не зависит от выбора и
Lj'
Lfi
Lf2

252
Специальные пределы
[Гл.9
и j7. Значит, т : F —> х является конусом с вершиной х и основанием
F. С другой стороны, если Л : F -^ у — другой конус с тем же
основанием F, то XL : FL -1» у — конус с основанием FL. Ввиду
универсальности конуса \± существует единственная стрелка / : х —>
—> у, для которой j\i — /А. Так как А/. = \^у о Fu, то /т = Л.
Следовательно, т — предельный конус, и потому х — Colim F. Ясно,
что тогда каноническое отображение h является изоморфизмом. □
Условие финальности функтора L является необходимым для
справедливости этой теоремы (см. упр. 5). При рассмотрении
пределов полезен двойственный результат (двойственным к понятию
финального функтора является понятие инициального функтора).
Упражнения
1. Пусть j G J, причем {j} — дискретная подкатегория в J с одним
объектом j. Покажите, что вложение {j} —»■ J финально, если и только
если объект j терминален в J. Что при этом можно сказать о копределах
и терминальных объектах?
2. Докажите, что композиция финальных функторов финальна.
3. Пусть J — фильтрованная категория, функтор L : J' —ь J полон (full)
и каждая из категорий (k I L) (к Е J) непуста. Докажите, что функтор L
финален.
4. Для ковариантного hom-функтора J(&, —) : J —»■ Set докажите
с помощью леммы Ионеды, что Colim J(&, —) — одноточечное множество.
5. (Обращение теоремы 1.) Пусть категории J' и J имеют малые hom-
множества, L : J' —ь J — некоторый функтор, причем для каждого
функтора F : J^Xb кополную категорию каноническое отображение Colim FL —»■
У
—> Colim F является изоморфизмом. Докажите, что L финален. (Подсказка:
рассмотрите пример F = J (к, —), X = Set и используйте упр. 4.)
9.4. Диагональная естественность
Теперь мы рассмотрим обобщение понятия естественности. Пусть
даны категории С, В и функторы 5, Т : Сор х С —>■ В. Диесте-
ственное (dinatural) преобразование а : S -^ Т — это функция а,
сопоставляющая каждому объекту с Е С стрелку ас : S(с, с) —>■ Т(с, с)
в категории 5, которая называется компонентой преобразования а
в объекте с, причем для каждой стрелки / : с —у с из С коммутативна
шестиугольная диаграмма
5(с,с)^^Т(с,с)
•s(/,i)^ \т(1,я
S(c',c) Т(с,с'). (1)
5(1,/)^ „ , /Т(/,1)
S(c',c')^T(C',c')

9.4]
Диагональная естественность
253
Заметим, что при построении стрелок 5(/, 1) и Т(/, 1) на этой
диаграмме использована контравариантность функторов S и Т по
первому аргументу.
Каждое естественное преобразование т : S -^ Т между
бифункторами S и Т с компонентами тс?с/ : S(c,c') —>■ Т(с,с') определяет
диестественное преобразование а : S —ь Т между теми же
бифункторами, причем его компонентами служат диагональные
компоненты преобразования т; таким образом, ас = тс?с. Более интересные
примеры связаны с функторами, фиктивными по одному или более
переменным. Например, бифунктор Т : Сор х С —>■ В фиктивен по
первому переменному, если он является композицией
где Q — проекция на второй множитель, а То — некоторый функтор
(от одного переменного). Иначе говоря, каждый функтор от одного
переменного То : С —>■ В можно рассматривать как бифунктор Сор х
х С —>■ В, фиктивный по первому переменному. Бифунктор,
фиктивный по обоим переменным, — это просто объект Ъ Е В, причем
Т(с, с') = Ъ для всех объектов c,c'gCh Т(/, /') = 1& для всех стрелок
/,/'изС.
Здесь появляются диестественные преобразования S -^ Т
следующих типов. Если бифунктор S фиктивен по второму переменному, а Т
по первому, то диестественное преобразование а : S -^ Т переводит
функтор So : Сор 4Бв ковариантный функтор Т0 : С —>• Б, причем
компоненты ас : 5qc —>- Tqc делают коммутативными диаграммы
5
So/
эс —
-^Т0с
1
То/
(2)
S0c' —с-> Т0с'
для каждой стрелки / : с —> с' из С. Такое преобразование можно
было бы назвать естественным преобразованием контравариантного
функтора So в ковариантный функтор Tq. (Двойственно, — ковари-
антного функтора в контравариантный.)
Если бифунктор Т = Ъ : Сор х С —>• В фиктивен по обоим
переменным, то диестественное преобразование а : S —> b состоит из
компонент ас : S(c, с) —> 6, которые делают коммутативной диаграмму
S(c',c)^ls(c',c')
s(f,i)
5(с>с) ——*ъ
(3)

254
Специальные пределы
[Гл.9
при всех / : с —> с'. (Правая часть шестиугольника (1) склеилась
в один объект Ь.) Такое преобразование а : S -^ Ь называется
суперъестественным (extranatural, supernatural) или клином из S
в Ъ. Аналогичная терминология применяется в связи с двойственным
преобразованием /3 : Ъ -^ Т, компоненты которого /?с : Ъ —у Т{с,с)
делают коммутативным любой квадрат вида
6 ^^Г(с,с)
0с-
Пи) (4)
TfcV) ^Т(с,с')
T(/,l) V ' У
(Здесь склеилась левая часть шестиугольника (1).)
Приведем пример преобразования каждого типа. Напомним, что
евклидово пространство Е — это векторное пространство над
полем вещественных чисел R, наделенное скалярным произведением
( , ) : Е х Е —> R, которое билинейно, симмметрично и положительно
определено. Такие пространства являются объектами категории
Euclid, стрелками которой служат линейные преобразования,
сохраняющие скалярное произведение. Рассмотрим два функтора в категорию
вещественных векторных пространств:
U : Euclid -+ Vctij, * : (Euclid)op -+ Vct^.
(Ковариантный) забывающий функтор U забывает скалярное
произведение, а контравариантный функтор * переходит к двойственному
пространству. Если теперь Е — любое евклидово пространство, то
соответствие е \-у (в,—), е Е Е, определяет линейную функцию
к>е '• Е —у Е*; такие функции ке являются компонентами диестествен-
ного преобразования к : U —> * ( случай, двойственный к типу (2)).
Этот факт широко используется в римановой геометрии г): каждое
евклидово пространство естественно изоморфно своему
двойственному 2). С помощью понятия диестественности мы смогли выразить
этот факт в категорных терминах.
Отображение оценки. Если X — (малое) множество, то
отображение Vx берет значение каждой функции h : X —у А при каждом
значении аргумента х Е X. Зафиксировав (малое) множество А, мы
можем рассматривать Vx как функцию
Vx : hom (X, А) х X -у A, (h, х) н> hx,
определенную на каждом объекте X Е Set. Если X, Y — два малых
множества, то hom (X, А) х Y является функцией объектов функтора
х) Как и в других разделах математики. — Прим. ред. пер.
2) Нужно потребовать конечномерность пространства. — Прим. ред. пер.

9.4]
Диагональная естественность
255
Setop x Set —У Set. Очевидно, что для любой стрелки / : Y —У
—У X выполнено равенство h(fx) = (hf)x. Поэтому квадраты вида
(3) всегда коммутативны, и функции Vx служат компонентами
суперъестественного преобразования
V:hom(-,A) x (-) ^ А.
При этом V естественно (в обычном смысле) по аргументу А] мы
говорим, что отображение оценки hom (X, А) х X —У А диестественно
(и суперъестественно) по X и естественно по А.
Коединицы. Пусть даны функторы F : X х Р ^ Аи G : Рор хЛч
—У X. Биекция
A(F(x,p),a)**X(x,G(p,a)) (5)
естественна по ж,р, и а является сопряжением с параметром р
(теорема 3, § 4.7). Его коединицу можно получить, положив х = G(p,a)
в формуле (5); получаем совокупность компонент
£(Р,а) :F(G(p,a)) -+a, (6)
естественную по а и диестественную (=суперъестественную) по р.
Сюда включается и рассмотренный случай отображения оценки.
Вот пример диестественного преобразования двойственного типа.
В произвольной категории С каждому объекту с соответствует
единичная стрелка 1С : с —У с, которую можно рассматривать как элемент
lc Е hom (с, с) или как стрелку 1С : * —>• hom (с, с), где * обозначает
одноточечное множество. При этом hom (с, с') — функция объектов
функтора Сор хС-У Set. Для любой стрелки f : с —> с' выполнено
очевидное условие /о 1с = 1с/ о/, которое в наших терминах означает
диестественность преобразования
1 : * -^ hom(—, —).
Все три типа диестественных преобразований встречаются
совместно с естественными преобразованиями в прежнем смысле (и мы
часто будем называть их также естественными, употребляя ди лишь
там, где это существенно). Таким образом, если даны категории
и функторы
S :Сор хС хА^у В, Т : А х Dop x D -+ В,
то естественное преобразование 7 : S —> Т — это функция,
сопоставляющая каждой тройке объектов с Е С, aGi, d G D стрелку
7(c, a, d) : 5(c, c, a) —>• T(a, d, d)
категории В, причем: 1) при фиксированных cud преобразование
7(с, — ,d) естественно по а в обычном смысле; 2) при фиксированных
and преобразование ^(с, а, —) диестественно по с; 3) при
фиксированных сна преобразование j(c, a, —) диестественно по d. В этом

256
Специальные пределы
[Гл.9
определении можно заменить любую из категорий А, В, С
произведением нескольких категорий, и при этом естественность по аргументу
с Е С = С х С" можно заменить на естественность по каждому
аргументу в паре (с', с"), когда другой аргумент фиксирован (см. ниже
упр. 3). Например, в любой категории операция композиции
hom (6, с) х hom (a, b) —>• hom (а, с)
естественна. Это значит, что она естественна по а, диестественна по Ъ
и естественна по с.
Композиция двух диестественных преобразований вполне может
не быть диестественной, но любое диестественное преобразование
а : S -^ Т можно умножать с каждой стороны на преобразования,
естественные по обоим аргументам. Если а : S' -^ S и т : Т —> Т' —
естественные преобразования, то произведения стрелок
S'(c, с) ^ 5(с, с) ^ Г(с, с) ^> Г'(с, с)
являются компонентами диестественного преобразования S' ^} Т.
Более интересен (хотя легко доказывается) следующий случай.
Предложение!. Пусть даны функторы
R:C^B, S:C х Сор хС -+В, Т:С -+В
и функции {для всех c,d Е С)
q{c, d) : R(с) -+ 5(с, d, d), <r(d, с) : S(d, d, с) -^ Г(с),
естественные по с и диестественные по d. Тогда функция,
сопоставляющая каждому с е С произведение стрелок
R{c)lM>s(c,c,c)^T(c),
определяет естественное преобразование R^T.
Упражнения
1. Докажите, что единица цх : ж —»■ G(p,F(x,p)) сопряжения с
параметром диестественна по р, причем это свойство равносильно тому, что
само сопряжение естественно по р (см. § 4.7, упр. 2). Сформулируйте
двойственный факт.
2. Сформулируйте треугольные тождества для сопряжения с
параметром.
3. (Естественность при разделении переменных.) Пусть даны: объект
Ъ G В, функтор
5 : (С х £>)ор хС xD^B
и функция /9, сопоставляющая произвольным объектам с £ C,d £ D стрелку
/3c,d : 5(c, d, c,d) ^ b

9.5]
Концы
257
из категории В. Покажите, что преобразование (3 : S -^ Ь диестественно
в том и только том случае, если оно диестественно по с (при каждом
фиксированном d) и диестественно по d (при каждом фиксированном с).
Сформулируйте двойственный результат.
4. Распространите правило композиции из предложения 1 на случай,
когда S — это функтор С х Сор х С х Сор хС ^ В. Проделайте то же самое
для любого нечетного числа множителей С.
5. Пусть даны S : Сор х С ^ В и b,b' G 5. Покажите, что для дие-
стественных преобразований ЬЛ^иб'^бв общем случае не существует
корректно определенной композиции Ъ —>- 6 .
6. Обобщив упр. 3 и 4, найдите общее правило перемножения
естественных преобразований от многих переменных.
9.5. Концы
Конец — это особый (и особенно полезный) тип предела, который
определяется в терминах универсальных клиньев вместо
универсальных конусов.
Определение. Конец функтора S : Сор х С —> X — это
универсальное диестественное преобразование константы е в
функтор S; иначе говоря, это пара (e,cj), где е — объект категории X,
а и : S -^ S — клин (диестественное преобразование) с тем
свойством, что для каждого клина /3 : х -^ S существует единственная
стрелка h : х —>• е в категории В такая, что f3a = ujah при всех
аеС.
Таким образом, для каждой стрелки / : Ъ —> с категории С имеется
диаграмма
Ръ
5(6, Ь)
S(c,c)
5(6, с), (1)
в которой коммутативны оба четырехугольника (это условия дие-
стественности). Универсальность клина и означает, что существует
единственная стрелка h, для которой коммутативны оба треугольника
слева.
Свойство единственности, присущее любой универсальной
конструкции, в данном случае означает, что если (e,cj) и (е',сУ) — два
конца функтора 5, то существует единственный изоморфизм и : е —>
—> е', для которого и' о и = и (т. е. и'с о и = ис для каждого с G
G С). Будем называть и концевым клином или универсальным клином
с компонентами иос. Сам объект е называют концом функтора S
и записывают со знаком интеграла:
\S(c,c)
Ends'.

258
Специальные пределы
[Гл.9
Отметим, что переменное интегрирования с появляется под знаком
интеграла дважды (один раз контравариантно и один раз ковариант-
но) и связано знаком интеграла в том смысле, что результат больше не
зависит от с и не меняется при замене с на любое другое обозначение
объекта категории С. Это похоже на свойства символа х в обычном
интеграле J f(x) dx.
Один из примеров концов связан с естественными
преобразованиями. Два функтора U, V : С —> X определяют функтор
homx(U—,V—) : Сор хСч Set. Если Y — произвольное множество,
то клин т : Y -^ homx(U—, У—) с компонентами
тс : Y -у homx(Uc, Vc), с е С,
сопоставляет каждому у Е Y и каждому с Е С стрелку тс?у : Uc —>■
—>■ Ус из X, такую что для каждой стрелки / : Ъ —> с выполнено
условие клина Vf о т&?2/ = тс?у о U f. Но это условие равносильно
коммутативности квадрата
Ub—L^Vb
и A \vf
Uc^-^Vc,
которая означает, что т_?у при фиксированном у является
естественным преобразованием т_?у : U^V. Пусть Nat (U, V) обозначает
множество всех таких естественных преобразований. Соответствие
у \-> Т-^у — это единственная функция Y —у Nat (С/, У), для которой
коммутативна следующая диаграмма:
Y >■ hom (Uc, Vc)
l
I II
Y
Nat (U, У) -^ hom (Uc, Vc).
Здесь ujc сопоставляет каждому естественному преобразованию
Л : U -^ V его компоненту Лс : Uc —У Vc. Это в точности означает, что
uj — универсальный клин. Следовательно,
Nat (U,V)=lhom (Uc, Vc); U,V :C -> X. (2)
с
Ясно, что конец всегда является пределом, а именно пределом
соответствующей диаграммы в категории X, которая составлена из
кусков вида S(b, b) —у S(b, с) —у S(c, с), по одному для каждой стрелки
/ из С, фигурирующей в диаграмме (1) при определении концов.
Этот факт можно формализовать путем построения по категории

9.5]
Концы
259
С следующей категории С§ (которая используется только в этом
параграфе). Объекты категории С§ — это всевозможные символы с§
и /§, где с — объект, а / — стрелка из С (отметим, что с§ и (1С)^ —
различные объекты). Стрелки категории С§ — это единичные стрелки
для таких объектов и еще по две стрелки
6§ -^ /§ <- с§
для каждой стрелки / : Ъ —у с из С. Произведения полученных
стрелок определены лишь тогда, когда одна из стрелок — единичная.
Тем самым построена категория С§, которая называется категорией
разбиения для С.
Каждый функтор S : Сор хСчХ определяет функтор S§ : С§ —>
—>■ X, как показано ниже для произвольной стрелки / : 6 —у с из С
(отображения направлены сверху вниз):
С§
5§
X
5(М)
5(ь,/)
/§
■5(6, с)
S(/,c)
■5(с,с).
Из этого чертежа видно, что конус г : х -^ S§ — то же самое, что клин
uj : х ^ S. Как следствие, предел в категории S^ является концом
в категории S в следующем смысле.
Предложение 1. Для каждого функтора S : Сор х С —> X
и соответствующего функтора S§ : С* —У X, определенного выше,
имеется изоморфизм
в: [s(c,c)^Lim[S§ : С§ -+X].
(3)
Более подробно: если существует либо указанный конец, либо
указанный функтор, то существуют они оба, причем имеется
единственная стрелка в в категории X, делающая коммутативной диаграмму
С
в
Lim 5§ _h
S(c,c)
II
-SHc)
для любого с е С; здесь и — концевой клин, а А
При этом стрелка в является изоморфизмом.
предельный конус.

260
Специальные пределы
[Гл.9
Следствие 2. Пусть категория X полна в малом, а категория
С мала. Тогда каснсдый функтор S : Сор х С —> X имеет конец
в категории X.
Предложение 1 показывает, что концы определяются пределами.
Обратное доказывается проще: каждый предел можно рассматривать
как конец!
ПредложениеЗ. Пусть Т : С —>■ X — некоторый функтор, S —
композиция
Сор хС %С ^> X,
где Q — вторая проекция произведения: {с, с') и-» с'. Тогда пара
(е,т : е^> Т) является пределом для Т в X, если и только если
(г, т : е -^ S) является концом для S в X.
Доказательство. Компоненты тс конуса е -^ Т делают
коммутативным треугольник тс = Тf о ть (в силу естественности!) для
каждой стрелки / : Ъ —у с из С. Это означает, что коммутативен
каждый квадрат вида
е ^Tb = S(b,b)
S(lJ)=T(f)
Тс = S(c, с) >■ Тс = S(b, с)
(бифунктор S(—, —) фиктивен по первому переменному). В свою
очередь это значит, что т : е -^ S является клином. Как следствие, конус
т универсален, если и только если он универсален как клин. □
Этот результат означает, что имеется изоморфизм
\S(с, с) = [ Тс ^Lim Г,
с с
если существует указанный конец или предел, причем концевой клин
переходит в предельный конус; поэтому в наших обозначениях можно
записать любой предел как интеграл (конец), не указывая фиктивное
переменное (первое переменное в S).
Мы говорим, что функтор Н : X —>• Y сохраняет конец функтора
S : Сор х С —> X, если из того, что и : е -^ S является концом для S
в категории X, всегда следует, что Ни : Не -^ HS является концом
для HS; в наших обозначениях:
H\s(c,c) = [#S(c,c).
с с
Аналогично, Н создает конец для 5, если для каждого конца
v : у -^ HS существует единственный клин и : е -^ S такой,

9.6]
Ко-концы
261
что Huj = г/, и этот клин со является концом для S. Поскольку
конец (функтора S) — то же самое, что предел (соответствующего
5§), то полученные результаты относительно сохранения пределов
переносятся на случай сохранения концов. Например, hom-функторы
сохраняют (и обращают, см. § 9.6) концы:
x(x,\s(c,c)\=\x(x,S(c,c)), (4)
С С
x(\S(c,c),x\=JX(S(c,c),x). (5)
9.6. Ко-концы
Определение ко-конца функтора S : Сор х С —>• X двойственно
к определению конца. Ко-конец S — это пара (d,( '• S -^ d),
состоящая из объекта d Е X и диестественного преобразования £ (клина),
универсального среди диестественных преобразований между S и
константой. Если объект d существует, то он единствен с точностью до
изоморфизма; обычно мы будем его обозначать знаком интеграла и
связанным переменным с в качестве нижнего индекса:
с
S(c,c) ^ \s(c,c)=d.
Формальные свойства ко-концов двойственны свойствам концов.
Ко-концы нередко встречаются под другими названиями.
Например, тензорное произведение модулей над кольцом R является ко-
концом. Более подробно, кольцо R можно рассматривать как АЪ-
категорию с одним объектом (который мы также обозначим R) и
элементами г G Rb качестве стрелок, причем композиция стрелок
совпадает с их произведением в R. Левый Л-модуль В — это аддитивный
функтор R —у АЬ, который отображает (единственный) объект R
в абелеву группу В, а каждую стрелку г из R — в отображение
(скалярное умножение) г* : Ъ \-> rb в этой группе. Аналогично, правый
Л-модуль А — это аддитивный функтор Rop —> АЬ (контравариант-
ный по R). Если О — тензорное произведение в категории АЬ, то
соответствие R \-^ А ® В определяет бифунктор Rop x R —> АЬ. При
этом конец
R
Ia®b = a®rb
совпадает с обычным тензорным произведением над R.
Действительно, клин £ из бифунктора А 0 В в абелеву группу М совпадает

262
Специальные пределы
[Гл.9
с (единственным) морфизмом g : А (8) В —у М абелевых групп,
делающим коммутативной диаграмму
А (8) Б ^ А® В
r*<g)lB Q
т Y
А (8) Б ^-^М
для любой стрелки г из R. Если модули интерпретируются как
функторы, то это означает, что для любых элементов a Е A,b Е В
выполнено равенство
g(ar (8) Ь) = £>(а (8) гб).
Следовательно, М является концом, если и только если М совпадает
с А ® В с точностью до элементов вида аг (8) Ъ — а (8) rb, и это
соответствует обычному определению тензорного произведения М =
= A®RB.
Смысл этих рассуждений не в том, чтобы свести известное к
неизвестному (тензорные произведения к ко-концам), а в обобщении
известного, с тем чтобы охватить гораздо больше случаев. Если В —
моноидальная категория с умножением □ (см. гл. 7), то для любых
двух функторов Т : Рор —> В и S : Р —> В их тензорное произведение
р
ГПР5=|(Гр)П(5р)
— это объект из В. Симплициальная категория Л из § 7.5 наделена
функтором А : Л —> Тор (каждый ординал п + 1 реализуется как
n-мерный аффинный симплекс); функторы S : Лор —у Set
называются симплициальными множествами. Ко-степень S • X (множество S
в степени пространства X) совпадает с П^Х, т. е. дизъюнктным
объединением S экземпляров множества X. Следовательно, соответствие
(п, тп) н-» Sn • Am определяет функтор Лор х Л —> Тор. В этом случае
ко-конец
п
USn) - An
есть не что иное, как обычная геометрическая реализация (Lamotke
[1968], р. 34; May [1967], р. 55) симплициального множества S.
Формула ко-конца описывает геометрическую реализацию очень просто:
возьмем дизъюнктное объединение аффинных n-симплексов, по
одному для каждого t Е Sn, и склеим их посредством данных операций
перехода к грани и вырождения (т. е. стрелок из Л). Существует
аналогичное эффективное описание классифицирующих пространств
(Stasheff, Milgram) топологических поноидов (наиболее удобное в
случае категории CGHaus из § 7.8); см. (Mac Lane [1970]).

9.7]
Концы с параметрами
263
Упражнения
1. Пусть дан бифунктор S : Сор хСч Set. Докажите, что множество
Wedge (*, $) всех клиньев ш : * -4- 5 из одноточечного множества * в X
является концом для $, причем концевой клин имеет вид ии н->- о;с(*) G
G S(c,c). Сопоставьте этот факт с явным описанием предела в категории
Set как множества конусов.
2. Покажите непосредственно (не используя пределы), что в категории
X с малыми произведениями и уравнителями всегда существуют малые
концы (см. соответствующее доказательство для пределов в § 5.2).
3. Каждой категории С соответствует категория закрученных стрелок
Сф, объектами которой являются стрелки / : а —»■ Ъ из С, а стрелками
(h, к) : / —>- f — стрелки h : а' —> а (обратите внимание на закручивание!)
л к : Ъ —> Ъ', для которых f = kfh. Тогда соответствие / : (а —»■ Ь) н-»-
—»■ (а, 6) является функтором К : С# —»■ Сор х С. Докажите, что для любого
функтора S : Сор х С ^ В конусы е ^> 5Х соответствуют клиньям е -^> 5,
и с помощью этого факта докажите другим способом, что концы сводятся
к пределам (предложение 1, § 9.5).
4. Пусть Fin обозначает скелет категории непустых конечных множеств.
Его объекты — конечные ненулевые ординалы гг, а стрелки — все функции
п —>- т. Если X — некоторое множество, то соответствие п н->■ Хп определяет
функцию объектов функтора (Fin)op —>- Set. Для кольца R соответствие
п н->" Rn становится ковариантным функтором Щ ) : Fin —»■ Я-Mod, если
при этом каждая функция / : п —»■ 7?г (стрелка из Fin) отображает набор
ao,...,an_i в 6o,---,bm-i G Ят, где bj = X^aj (сумма берется по всем
тем j G гг, для которых /j G г). Докажите, что свободный Я-модуль,
порож:денный множ:еством X, — это ко-конец
п
Хп • Щп).
Покажите, что эта формула по существу соответствует обычному описанию
элементов свободного модуля как формальных конечных сумм ^ж^, г =
= 1,...,п.
5. Если категория D кополна, то можно определить тензорное произве-
с
дение функторов S : Сор —»■ Set и Т : С —>- (7 —>- £> как ко-конец /(5*с) •
• (Тс), где • обозначает ко-степень. Покажите, что тензорное произведение
является функтором D x Set —»■ D.
9.7. Концы с параметрами
По своим основным формальным свойствам концы весьма
напоминают интегралы. Все эти свойства присущи в равной мере и пределам
(если рассматривать их как концы с фиктивным переменным).
Предложение 1 (конец или предел естественного
преобразования). Пусть дано естественное преобразование j : S -^ S' между
функторами S,S' : Сор х С 4 I, которые имеют концы (e,uj)
и (е',и/) соответственно. Тогда существует единственная стрелка
9 = J 7с,с : е ^ е' в категории X, при любом с G С делающая
с

264
Специальные пределы
[Гл.9
коммутативной следующую диаграмму:
\S(c,c)-
i i
9=Slc,c '
S'(c,c)
■S(c,c)
(1)
S'(c,c).
Доказательство. Композиции 7C?C о ujc определяют клин.
Поэтому стрелка g существует и единственна в силу универсальности
клина и/.
Будем называть стрелку g концом естественного
преобразования 7-
При умножении преобразования 7 на другое естественное
преобразование У : S' -^ S" концы подчиняются правилу
|(У-7)с,с = |7с,с ° ИТс,
(2)
С учетом этого правила можно показать, что предел (или конец),
зависящий от параметра р (в некоторой категории Р), действует на
этот параметр как функтор в следующем смысле.
Теорема2 (теорема о параметре для концов и пределов). Пусть
дан функтор Т : Р х Сор х С —У X, причем функтор Т(р, —, —)
любого объекта р е Р имеет конец
ип
Г(р,с,с)^Г(р,-,-)
(3)
в категории X. Тогда существует единственный функтор U : Р —У
—>■ X с функцией объектов Up = J*T(p, с, с), дл«я которой компоненты
с
клина (3) дл«я каждого с Е С определяют преобразование (шр)с : СТр —>■
—> Т(р, с, с), естественное по р.
Доказательство. Каждая стрелка s : р —у q из Р определяет
естественное преобразование 7 = T(s, —, —) : Т(р, —, —) -^ T(q, —, —).
Поэтому в обозначениях диаграммы (1) функцию стрелок искомого
функтора U можно записать как Us = §T(s,c,c). С учетом правила
с
умножения (2) мы получаем функтор U : Р —У X. □
Мы будем записывать функтор U как С/ = § Т(—,с,с). Таким
образом,
|г(-,с,с)р = |г(р,с,с), Ит(-,с,с) s = JT(s,c,c). (4)

9.7]
Концы с параметрами
265
Такие обозначения подразумевают, что сам функтор U является
концом. В самом деле, рассмотрим JT(—, с, с) как объект в категории
с
функторов Хр и представим Т : Р х Сор х С —> X как функтор
Т# : Сор х С —У Хр', который действует на стрелки (и объекты) /, /'
из С по формуле
T*(f,n=T(-J,f):P^X.
Иначе говоря, Т и Т# связаны стандартным сопряжением
Cat (Р х Сор х С, X) ^ Cat (Сор х С, Хр).
ТеоремаЗ (теорема о параметре, продолжение). При тех же
условиях на Т функтор Т# имеет конец
оо*:\т(-,с,с)^Т#,
С
где (uif)p = (bjp)c при всех р Е Р и с Е С.
Доказательство. Конец J*T(—,c,c) является объектом в Хр,
с
а функтор Т# имеет кообласть Хр. По предыдущей теореме стрелки
(ujp)c из X определяют для каждого с стрелку в Хр (естественное
преобразование)
и* :|г(-,с,с)^Г(-,с,с):
с
его компонента в р равна (oof)p = (шр)с. Если с переменно, то ио^
становится клином J*T(—,c,c) -^ Т^. Этот клин универсален. Дей-
с
ствительно, для любого объекта F Е Хр и любого клина (3 : F ^ Т^
каждая компонента /Зс единственным образом пропускается через
соответствующую компоненту ир. Значит, /3 единственным образом
пропускается через uj^ . Тем самым определен конец для Т^. □
Эту теорему можно сформулировать полностью в терминах
категории функторов Хр, как было сделано для пределов в теореме 1,
§5.3.
Упражнения
1. (Dubuc.) Постройте категорию функторов Хр и функтор Т : С —»■ Хр,
который имеет предел, но не поточечный предел. (Указание: возьмите С =
= 2.)
2. Сформулируйте и докажите теорему о параметре для ко-концов.
3. Пусть категория X полна в малом, а С мала. С помощью предложения
1 докажите, что Lim : X —>- X является функтором (см. упр. 3, § 5.2).

266
Специальные пределы
[Гл.9
4. Покажите для произвольных категорий X и Р, что функтор X —>-
—>- Х'р', индуцированный вложением (дискретной подкатегории |Р|),
создает концы и ко-концы (см. теорему 2, § 5.3).
9.8. Повторные концы и пределы
Теперь выясним, при каких условиях двойной интеграл можно
получить как повторный (Фубини!)
Предложение. Пусть дан функтор S : Рор хРх Сор хСчХ,
причем конец J* S(p, q, с, с) существует для всех пар (р, д) объектов из
с
Р; в соответствии с теоремой о параметре будем рассматривать
эти концы как бифунктор Рор х Р —> X, a S как бифунктор (Р х
х С)ор х [Р х С) —>• X. Тогда имеется изоморфизм
в: | S(p,c,p,c)<* | MS(p,p,c,c)
<р,с> Р с
В действительности двойной конец в левой части существует
тогда и только тогда, когда существует конец J* в правой части,
р
и тогда имеется единственная стрелка 0 в категории X, делающая
коммутативной диаграмму
| 5(р,р,с,с)
£(р,с)
(р,с)
| |5(р, р, с, с) —^->- jS(p, p, с, (
р с
II
£S(p,p,c,c),
где горизонтальные стрелки {;, g ии — это универсальные клинья для
соответствующих концов. Стрелка в на этой диаграмме является
изоморфизмом.
Доказательство. Для каждой пары (p,q) Е Р х Р имеется
конец
ujp^q : \S(p,q,c,c) -^ S(p,q,-,-).
с
Для каждого х Е X каждое семейство стрелок £>р : ж —> J* S(p,p, с, с)
с
в категории X с индексами из Р определяет семейство £р?с с индексами
из Р х С, состоящее из композиций
£Р,с : х ^\S(p,p,c,c) Шр,Р,с) S(p,p,c,c).
Ясно, что £(р,_) с фиксированным р является клином относительно
с. Обратно, поскольку конец ир^р универсален, то каждое семейство

9.8]
Повторные концы и пределы
267
с индексами из Р х С, естественное по с при каждом р, является
композицией указанного вида для единственного семейства д. Семейство
д или £ суперъестественно по р (последнее — при некотором с), если
и только если соответствующий квадрат:
Qp
■Js(p,p,c,c)
$ S(p,s,c,c)
Sp,c
Uc
\S(q, q, c, c) j_' [SO, 9, c, c), S(q, q, c, c) >■ S(p, <?, c,
J с J S{s,q,c,c)
S(p,p,c,c)
S(p,s,c,c)
коммутативен для каждой стрелки s : р —>■ q из Р. При этом первый
квадрат коммутативен, если и только если он остается коммутативным
после умножения на стрелки cjp?g?c для всех объектов с. Образуем
кубическую диаграмму, в которой эти два квадрата служат передней
и задней гранями и их соединяют ребра 1Ж, cjp?p?c
^ю
и uq^c (идущие
в направлении от читателя). С учетом предыдущего, четыре боковые
грани коммутативны. Поэтому передняя грань коммутативна в том
и только том случае, если задняя грань коммутативна при всех с.
Следовательно, д является клином относительно р, если и только
если £ является клином относительно (р, с). Таким образом, клинья
из х в J* S(—, —, с, с) взаимно однозначно соответствуют клиньям из ж
с
в S. Поскольку конец — это универсальный клин, а универсальность
определена с точностью до изоморфизма, то мы получаем искомый
изоморфизм в. □
Отметим один существенный пункт: это предложение сводит
двойной интеграл к повторному при условии, что внутренний интеграл
/5(р, g, с, с) существует для всех пар (p,q) (а не только при р = q).
с
В случае пределов эта тонкость не возникает.
Сводя двойной интеграл к повторному двумя способами, получаем
известный результат об изменении порядка интегрирования.
Следствие. Пусть дан функтор S : Рор х Р х Сор х С —>• X,
причем концы J* 5(p, q, с, с) и J* S(p,p, b, с) существуют при всех p,q Е
с р
е Р и b,c e С. С учетом теоремы о параметре рассмотрим эти
концы как бифункторы (относительно p,q и b,c соответственно)]
тогда имеется изоморфизм
° ' I }5(Р'Р'С'С) - j |5(Р>Р>С>С)
В действительности левая часть существует тогда и только
тогда, когда существует правая, и изоморфизм в — это единственная

268
Специальные пределы
[Гл.9
стрелка в категории X, которая делает коммутативными
диаграммы
J J SO, р, с, с) ^ J SO, р, с, с) ^ SO, P, с, с)
юс1 с
10 II
Y
J J SO, Р, с, с) ^ J SO, Р, с, с) ^ SO, P, с, с)
с р р
при всех р Е Р и с Е С; здесь горизонтальные стрелки — это
соответствующие компоненты универсальных клиньев для
рассматриваемых интегралов.
Из этих результатов вытекают соответствующие факты для
пределов и копределов. Именно, пусть дан функтор F : Р х С —>■ X, где
Р и С — малые, а X — полная категория. С учетом предложения 3,
§9.5 получаем
Linip Limc F(p, с) = Lim^c> F(p, с) = Limc Limp F(p, c).
Соответствующая формула верна и для копределов.
Замечания
Систематическое исследование всех возможных свойств пределов
содержалось в рукописи Шевалле по теории категорий; к сожалению, эта
рукопись была утрачена некоей пароходной компанией.
Суперъестественные преобразования (и все правила их перемножения)
были открыты в статье (Eilenberg, Kelly [1966b]), а диагонально
естественные преобразования — в работе (Dubuc, Street [1970]). Первое определение
тензорного произведения функторов принадлежит Кану (Кап [1958], § 14);
далее эти произведения исследовались в неопубликованной работе Ф. Ул-
мера и Аллена Кларка.
Идея понятия конца была найдена Ионедой (Yoneda [I960]) и
эффективно применена в работе (Day, Kelly [1969]); эти авторы заметили, что
понятие конца существенно для категорий, связанных не с Set, а с другими
замкнутыми категориями. См. также (Kelly [1982]).

Глава 10
РАСШИРЕНИЯ КАНА
Пусть М — некоторое подмножество в категории С. Любую
функцию t : М —У А в непустое множество А можно продолжить на С
многими способами, и среди них нельзя выбрать какой-то
канонический или единственный. Однако если М — подкатегория в С, то для
каждого функтора Т : М —У А в принципе имеется два канонических
(или крайних) способа продолжить его до функторов L,R : С —У А.
Они характеризуются универсальностью соответствующих
естественных преобразований. В общем случае последних может и не быть, но
они обязательно существуют при условии, что категория М мала, а А
полна или кополна, и тогда они реализуются как определенные
пределы или концы. Это расширения Кана, которые являются важнейшим
понятием теории категорий. Изучая их, мы еще раз убеждаемся, что
каждое из основных понятий можно выразить через другие. В начале
этой главы мы выразим сопряженные функторы как пределы,а
закончим тем, что выразим все через расширения Кана.
10.1. Сопряженные функторы и пределы
Если для всех функторов J —у С существуют пределы и
копределы, то они определяют соответственно правый и левый сопряженный
для диагонального функтора А:
Lim
С
CJ
Lim (= правый сопряженный для Л). (1)
Обратно, левые сопряженные можно интерпретировать как пределы.
Вначале заметим, что начальный объект в любой категории С
является пределом:
Начальный объект С = Colim (0 -у С) = Lim (Id: С -У С), (2)
где 0 обозначает пустую категорию (ординал 0), а 0 —у С — пустой
функтор. Определение начального объекта е в точности означает,
что это копредел пустого функтора. При этом стрелки \ic : е —>■
—У с, единственные для каждого с, определяют конус е -^ Idc. Если
Л : d^ Idc — конус с другой вершиной, то существует единственная
стрелка / : d —У е, такая что /icf = Лс для всех с; действительно,

270
Расширения Кана
[Гл. 10
положив с = е, получаем / = Ае, а для этой стрелки выполнено
уравнение /icXe = Хс, поскольку Л — конус над Idc. Это показывает,
что е = Limldc. Обратный факт (любой предел для Id — начальный
объект) является частным случаем следующей леммы:
Лемма 1. Пусть А : d^-ldc — конус над тождественным
функтором, а для функтора F : J —» С конус XF : d^- F является
предельным. Тогда d — начальный объект в категории С.
Доказательство. Поскольку Л — конус, то треугольники
d d d
d *~Fi, d *~Fi, d :—^c
коммутативны для каждого г G J и каждой стрелки /из С. Но конус
XF — предельный, и с учетом двух первых треугольников получаем,
что Xd = 1. Тогда третий треугольник показывает, что / = Ас.
Значит, из б? в каждый объект с ведет единственная стрелка, т. е. d —
начальный объект. □
Таким образом, начальные объекты сводятся к пределам. Далее,
функтор G : А —> X имеет левый сопряженный в точности тогда,
когда для каждого объекта х категория запятой (х I G), состоящая
из всех пар (д : х —> Ga, а) имеет начальный объект. Это позволяет
выразить левые сопряженные через пределы. Напомним, что
соответствие (д,а) ь-)> а определяет (вторую) проекцию Q : (ж I G) —>• А
категории запятой.
Теорема2 (формальный критерий существования
сопряженного). Функтор G : А —» X имеет левый сопряженный, если и только
если выполнены следующие два условия:
1) G сохраняет все пределы, существующие в А;
2) для каждого х G X в категории А существует
Lim(Q :(xlG) -+A).
В этом случае левый сопряженный действует на каждый объект
х G X по формуле
Fx = Lim (Q : (ж | G) -+ А), (3)
а каждую стрелку g : х —>• Ga переводит в компоненту Xg : Fx —>•
—> Qg = а предельного конуса X для предела (3).
Доказательство. Условие 1) необходимо, поскольку правые
сопряженные сохраняют все пределы. Если функтор F сопряжен
слева с G, то каждая пара (т]х : х —> GFx, Fx) является начальным
объектом в категории (х ^ G). Поэтому каждый функтор из этой
категории запятой имеет предел (а именно, свое значение на этом
начальном объекте). Значит, условие 2) также необходимо.

10.1]
Сопряженные функторы и пределы
271
Отсюда усматривается и обратный факт. Согласно условию 2),
композиция функторов
(ylG)^(ylG)%A (4)
имеет предел в А при любом у Е X. Согласно условию 1), G сохраняет
все пределы; в силу леммы из § 5.6 Q создает все пределы.
Следовательно, Id имеет в (у I G) предел, который ввиду (2) является
начальным объектом — скажем, у —> Ga. Но тогда а является значением
а = Fy левого сопряженного F, откуда
Fy = Q [Lim (у 1 G) -»■ (у 1 G)] = Lim (Q : (у 1 G) -»• А)
(поскольку Q сохраняет этот предел, который им же и создан!).
Получена искомая формула; из нее непосредственно вытекает правило
построения левых сопряженных. □
Упражнения
1. Сформулируйте утверждение, двойственное к теореме 2.
2. (Формальный критерий представимости, Benabou.) Пусть категория
С имеет малые hom-множества, а * обозначает одноточечное множество.
Докажите, что функтор К : С —»■ Set представим, если и только если
выполнены два условия: 1) К сохраняет все пределы, существующие в категории
(7; 2) проекция категории запятой Q : (* 4- К) —> С имеет предел в С.
В этом случае предельный конус этой проекции Л : г —> Q сопоставляет
каждому объекту h Е Кс стрелку Л^ : г —»■ с, и это соответствие является
представлением К = С(г,—).
3. (Формальный критерий универсальности стрелки.) Пусть X
имеет малые hom-множества. Докажите, что универсальная стрелка из х Е
Е X в G : А —ь X существует, если и только если : 1) функтор
X(x,G—) : А —»■ Set сохраняет все пределы; 2) в категории А существует
LimQ : ((х I G) -> А).
4. (Усовершенствования формальных критериев существования.)
а) Покажите, что условие 1) в теореме 2 можно заменить на следующее:
G сохраняет все пределы, существование которых требуется в условии 2).
б) Покажите, что условие 1) в упр. 2 можно заменить на следующее: К
сохраняет предел функтора Q.
5. (Представимые и сопряженные функторы, Benabou.) Пусть С имеет
малые hom-множества. Построим для произвольного функтора К : С —»■
—>- Set категорию Gk, присоединив к С один новый объект оо и новые
hom-множества Ск(оо,с) = Кс, Ск(оо,оо) = * (одноточечное
множество), С к (с, оо) = 0 (пустое множество), с очевидным умножением. Пусть
J к : С —>- С к — функтор вложения. Докажите, что К представим, если
и только если J к имеет левый сопряженный.

272
Расширения Кана
[Гл. 10
10.2. Слабая универсальность
Пусть дан функтор (?:й-у!и объект х Е X. Слабо
универсальная стрелка из х в G — это пара (r,w : х —у Gr), состоящая из объекта
г Е А и указанной стрелки ш из I, причем для каждой стрелки
/ : х —У Ga существует стрелка f : г —У а такая, что / = Gf о w. Это
совпадает с определением универсальной стрелки с тем исключением,
что не предполагается единственность стрелки /'. По той же схеме
(Freyd) можно модифицировать всевозможные типы универсальных
объектов, определив слабые произведения, слабые пределы, слабые
копроизведения (в каждом случае предполагая существование, но не
единственность).
В качестве приложения дадим новое доказательство теоремы
Фрейда о существовании начального объекта (теорема 1, § 5.6).
Теорема 1. Пусть категория D полна в малом и имеет малые
hom-мноэюества. Тогда в D существует начальный объект, если
и только если существует малое мноэюество 5, которое является
слабо начальным, т. е. для каждого d Е D существует стрелка s —>■
—У d, где s G S.
Доказательство. Полную (full) подкатегорию в D с объектами
из S будем также обозначать S. Поскольку D имеет hom-множества,
то категория S мала; так как D полна в малом (small-complete), то
функтор вложения F : S —>■ D имеет предельный конус \i : v -^ F.
Покажем, что v = LimF служит начальным объектом в D.
Прежде всего выберем для каждого d G D стрелку s —> d и
определим 7d как композицию jd : v -4 s —> d. Мы утверждаем, что 7 : у —>
—> Ыв является конусом. Действительно, возьмем стрелку / : d —>■ d'
и образуем диаграмму
d ^d'.
Поскольку категория S полна в малом, то существует коуниверсаль-
ный квадрат для s —> d! и s' —у d' с вершиной р. Поскольку множество
S слабо начально, то имеется стрелка v —^ s" —у р. Так как
подкатегория S полна (full), то обе композиции s" —у р —у s и s" —у р —у
—У s' содержатся в 5, и два верхних четырехугольника коммутативны

10.3]
Расширение Кана
273
(/i является конусом). Далее, пятиугольник коммутативен, поскольку
р служит вершиной коуниверсального квадрата. Следовательно, 7
является конусом.
Если, определяя конус гу, мы выберем v —> s —> s в качестве fis,
то композиция jF : v -^ F определит предельный конус \i. Ввиду
леммы 1, § 10.1 v является начальным объектом в S. □
Анализ этого рассуждения показывает, что оно основывается на
доказательстве теоремы 1, § 5.6; но в том случае мы сначала
рассматривали произведение Yl s (чтобы получить единственный слабо
начальный объект), а затем — подходящий уравнитель. На этот раз
обе операции объединены в одну — взятие предела для F : S С D.
10.3. Расширение Кана
Пусть дан функтор К : М —> С, а также категория А. Рассмотрим
категорию функторов Ас, в которой объектами служат функторы
S : С —> А, а стрелками — естественные преобразования а : S —У S'.
Определим функтор Ак : Ас —у Ам, положив
(а : S^ S') ^ (аК : SK^S'K).
Построить расширение Кана — значит найти левый и правый
сопряженный для Ак. Рассмотрим эту задачу сначала для правого
сопряженного.
Определение. Пусть даны функторы К : М —У С и Т : М —У
—У А. Правое расширение Кана для Т по К — это пара R, г : RK -^ Т,
состоящая из функтора R Е Ас и естественного преобразования е,
универсального среди стрелок из Ак : Ас —у Ам в Т Е Ам.
Как всегда, свойство универсальности определяет функтор R =
= Ran^T единственным образом с точностью до естественного
изоморфизма. Более подробно, универсальность здесь означает, что для
каждой пары S, а : SK -^ T имеется единственное естественное
преобразование а : S -^ R такое, что а = г • а К : SK -^ Т. Ему отвечает
диаграмма
С \
t \xV
к\ iV4 s.RK^T. (1)
I £-\ X
M—-^A,
т
Соответствие а \-y г • o~K определяет биекцию
Nat (S, Ran^T) ^ Nat (SK, T), (2)
естественную по S; с другой стороны, эта биекция определяет Ran^T,
исходя из К и Т. Это расширение Кана называется правым, поскольку
в обозначении hom-множества Nat оно стоит справа. (Впрочем,
отметим, что некоторые авторы называют R левым расширением Кана.)

274
Расширения Кана
[Гл. 10
Универсальные стрелки из функтора Ак во все объекты Т вместе
образуют левый сопряженный функтор для Ак. Из этого общего
факта вытекает, что если каждый функтор Т Е Ам имеет правое
расширение Кана (R,£t '• RK ^ Т), то соответствие Т \-У R служит
функцией объектов правого сопряженного функтора для Ак ,причем
г является единицей этого сопряжения. В дальнейшем мы построим
правые расширения Кана для некоторых функторов Т, которые
могут существовать и в том случае, когда правый сопряженный к Ак
(в целом) не существует.
На практике бывает важен случай, когда М — подкатегория в С,
а К : М —у С — вложение М С С. Тогда Ак — это операция,
ограничивающая область функтора S : С —У А на подкатегорию
М. Обратно, для данного Т : М —у А рассмотрим его продолжения
Е : С —У А на категорию С. Тогда для любого Ее Е А и любой
стрелки / : с —у m из С существует стрелка Ef : Ее —>• Гш из А,
и такие стрелки составляют конус с вершиной Ее и основанием Т,
если рассматривать Т как функтор на категории стрелок / : с —> m
(где с фиксировано, a m меняется). Стрелки / являются объектами
категории запятой (с \. К), поэтому в качестве Ее естественно выбрать
предел (с предельным конусом Ef) функтора Т : (с \. К) —> А:
m >■ m' >■ m", Tm >■ Tm' >■ Tm".
Эта процедура (см. (1.3)) применима и в общем случае. Для
каждого с G С объектами категории запятой (с ^ К) служат объекты
(/, га) (или для краткости /), где стрелка / : с —> Km принадлежит
С, а соответствие (/, тп) \-у m является функцией объектов функтора
проекции Q : (с I К) —У М.
Теорема 1 (правое расширение Кана как поточечный предел).
Пусть даны функторы К : М —у С и Т : М —у А, причем композиция
(с I К) —у М —У А при каждом с G С имеет предел в категории А
с предельным конусом Л, который мы запишем в виде
Re = Lim ((с1К)Я М ^уА)= Lim/ Гш, / G (с | К). (3)
Каждая стрелка g : с —у с' индуцирует единственную стрелку
Rg : Lim TQ -+ Lim TQ'\ (4)
коммутирующую с предельными конусами. Эти формулы
определяют функтор R : С —У А, и для каждого п G М компоненты
предельных конусов \iKn — £п определяют естественное преобразование

10.3]
Расширение Кана
275
г : RK -^ Т. Пара R,s является правым расширением Кана для Т
по К.
Доказательство. Прежде всего, Rg в формуле (4)
определяется тем фактом, что предел является функтором относительно (с ^ К),
а потому и относительно с. Именно, если дана стрелка g : с —> с'
и проекция Q' : (с' I К) —> А, то каждая стрелка f : с' —> Km
определяет стрелку f'g : с —у Km Е (с J, if), и компоненты А//р : Re —>■
—>■ Тттг образуют конус из Лс. Поскольку конус А' универсален, то
существует единственная стрелка Rg, которая делает диаграмму
Rc = LimTQ Л/\ Тт
Y
Дс' = Lim TQ'
л',,
(5)
Гш
коммутативной при всех /'. (Действительно, соответствие /' \-> f'g
определяет функтор (д I К) : (с' I К) —> (с I К), при этом TQ' =
= TQ о (д ^ К), и Дд служит каноническим сравнением — вспомним
финальные функторы.) Если Rg выбрано таким образом, то R,
очевидно, становится функтором.
Если п Е М, то 1кп является объектом в (Кп ^ К), и предельный
конус А имеет компоненту XiKn : RKn —> Тп, обозначаемую еп. Для
каждой стрелки h : n —>■ п' построим диаграмму
Т/г
(б)
нижний треугольник коммутативен в силу определения Дд (положим
g = Kh), а верхний коммутативен, поскольку А — конус. Поэтому
коммутативен и квадрат; это означает, что преобразование е : RK —>Т
естественно.
Пусть теперь S : С —> А — другой функтор, а : SK —> Т —
естественное преобразование. Построим ас : Sc —>■ Дс, исходя из
/ : с —> Km, с помощью диаграммы
Тт-
Th
^Тт'
SKm —f S&'.
(7)

276
Расширения Кана
[Гл. 10
Для каждой стрелки h : (/, m) —>• (f ,m') категории (с I К), где /' =
= Kh о /, правый квадрат коммутативен, поскольку а естественно.
Значит, диагональные стрелки ат о Sf : Sc —>■ Тттг образуют конус
с вершиной 5с и существует единственная стрелка сгс, делающая
коммутативной диаграмму (7). Докажем, что преобразование а
естественно. Возьмем д : с —> с' и образуем диаграмму
Яс >■ Дс' >■ Гш
? ^с
5с —^ 5с' —-^ 5Кш
I «Ьр Ь/
(8)
S(f'og)
для каждой стрелки f : с' —> Km из (с' .J, If). Правый и внешний
квадраты коммутируют в силу определения сг, а верхний
прямоугольник — в силу диаграммы (5), определяющей Rg. Как следствие,
левый (внутренний) квадрат становится коммутативным, если обе
вертикальные стрелки умножить на А'., для любой из стрелок /;. Но
А; — предельный конус, поэтому и сам левый квадрат коммутативен.
Значит, преобразование а естественно.
В определении (7) для а положим с = Кп, / = 1^п, ттг = п. Мы
видим, что ап = \iKn°~Km откуда а = г • К. Таким образом, любое а
получается из г : RK —>Т по формуле а = е-аК с некоторым а. В силу
диаграммы (8) преобразование а с таким свойством единственно.
Действительно, это свойство определяет его компоненты о~кп] чтобы
определить остальные компоненты, положим на диаграмме (8) с' =
= Кп, f = 1кп, гп = п. Если а естественно, то левый квадрат
коммутативен, и тогда Хд о ас определено для всех д : с —>■ Кп. Но
А — предельный конус, поэтому определено и ос. Это означает, что г
универсально. □
Следствие 2. Пусть категория М мала, а категория А полна.
Тогда любой функтор Т : М —>• А имеет правое расширение Кана по
любому К : М —>• С, и функтор Ак имеет правый сопряженный.
В частности, это относится к случаю А = Set; он был изучен
первым в работе Кап [1958].
Следствие 3. Пусть функтор К в теореме 1 полон (full) и уни-
валентен. Тогда универсальная стрелка г : RK -^ T для расширения
Кана R функтора Т по К является естественным изоморфизмом
e:RKS*T.
Доказательство. Если п G М, то RKn получается из предела
над категорией запятой (с \, К) при с = Кп. Поскольку К полон
и унивалентен, то каждый объект / : Кп —> Km в категории запятой

10.3]
Расширение Кана
277
можно записать как / = Kh для единственной стрелки h : п —> т.
Это означает, что 1 : Кп —> Кп является начальным объектом в
категории запятой и потому RKn = Limj TQ можно найти, применив TQ
к этому начальному объекту. Следовательно, RKn = Тп, en = 1. □
Здесь содержится случай, когда расширение Кана в буквальном
смысле является расширением.
Следствие 4. Пусть М — полная подкатегория в категории С,
а Т : М —>• А — некоторый функтор, причем любая композиция
(с I К) —> М —> А имеет предел в А. Тогда существует такой
функтор R : С —>• А, что RK = Т (m. e. R служит продолжением
для Т) и тождественое естественное преобразование 1 : RK -^ Т
делает R правым расширением Кана для Т по вложению К : М —>
->С.
Доказательство. Применим следствие 3 к вложению М —>
->С. □
Левое расширение Кана L = Lan^T определяется аналогично, как
пара L, т] : Т -^ LK, где т\ универсально среди преобразований между
Т и Ак. Отсюда получаем биекцию
Nat (Lan^T, S) ^ Nat (Г, SK), (9)
естественную по S G А . Если существуют соответствующие
копределы, то L определяется по формуле
Lc = Colim ((К I с) 4 М 4 А), (10)
где Р — проекция (m, Km —> с) ^ т.
Упражнения
В упр. 1-4 используются функторы
К : М -Л С, Т : М -► А
из расширения Кана.
1. Пусть А — категория стрелок 2, а М и С — некоторые множества.
Тогда функтор Т : М —»■ 2 можно рассматривать как подмножество в М.
Покажите, что 2м — это контравариантная булева степень ?М, a Lan^T
является образом функтора Г С М по К. Опишите Ran^T.
2. (Расширения Кана представимых функторов.) Пусть А = Set,
а категории М и С имеют малые hom-множества. Покажите, что
левое расширение Кана для М(т, —) имеет вид С (Km, —) с единицей
г] : М(т, —) —ь С (Km, К—), которая определяется условием пц = 1кт-
3. Пусть М, С и А — некоторые множества, причем А содержит не менее
двух элементов, а отображение К не сюръективно. Докажите, что ни Lanx,
ни Rarix не существует.
4. (Ulmer.) Покажите, что следствие 3 остается верным, если условие «К
полон и унивалентен» заменить на «К полон и столь же унивалентен, как
и Т». Последнее означает, что для любых стрелок h,h' : т —»■ п категории
М из Kh = Kh' следует Th = Tti.

278
Расширения Кана
[Гл. 10
5. Пусть М — любая категория, а категория М^ получается
добавлением к М одного нового объекта оо, терминального в Моо. Докажите
(исходя из определений), что копредельный конус функтора Т : М —>- А
является левым расширением Кана для Т по функтору вложения М С М^,
и обратно.
10.4. Расширения Кана как ко-концы
Исчисление ко-концов дает изящную формулу для расширений
Кана; рассмотрим для разнообразия левое расширение.
Теорема 1. Пусть даны функторы К : М —>• С и Т : М —>• А,
причем для всех m,m' Е М и всех с Е С в категории А существуют
костепени С (Km', с) • Тт. Тогда Т имеет левое расширение Кана
L = Lan^T no К, если для каэюдого с G С существует следующий
ко-конец, и тогда он совпадает с функтором из L:
т
Lc = (LanKT)c = [ С (Km, с) • Гш, се С. (1)
Доказательство. По теореме о параметре можно
рассматривать указанный ко-конец как функтор относительно с. Сравним его
с каким-нибудь другим функтором S : С —У А. По лемме Ионеды
А(Тт, SKm) ^ Nat (С(Km, -),A(Tm, S-)) ^
^ \Ens(C(Km,c),A(Tm,Sc)), (2)
с
так как множество естественных преобразований можно представить
как конец (в достаточно большой полной (full) категории множеств
Ens). Имеется следующая последовательность изоморфизмов:
Nat(L, S) — A(Lc, Sc) (формула конца для Nat),
т
- \А{\ с(Кт, с) • Тт, Scj (определение (1) для L),
с
А(С(Кт, с) • Тт, Sc) (непрерывность функтора
A(-,Sc)),
ii/ns (С (Km, с), A(l m, be)) (определение костепеней),
Ens (С(Km, с), A(Tm,Sc)) (фубини)
- J A(Tm,SKm) (п0 формуле (2)),
т
= Nat (T, SK) (формула конца для Nat).

10.4]
Расширения Кана как ко-концы
279
Здесь применима теорема Фубини (перестановка концов), поскольку
оба конца J и J существуют. Категория множеств Ens должна быть
га с
достаточно велика (чтобы содержать все hom-множества категорий А
и С и множества Nat (L, 5), Nat (Т, SK) для всех S : С —>• А).
Поскольку каждый переход естествен по S, то результирующий изоморфизм
также естествен по 5, и потому L = Lan^T. □
Отметим, что обратное не утверждается: если расширение Lan^T
существует, то оно не обязано для каждого с иметь вид ко-конца (1).
Мы получим единицу г) построенного расширения Кана, если
положим S = L и применим цепочку изоморфизмов. Сформулируем
результат.
Теорема2 (расширения Кана как ко-концы, продолжение).
Пусть дано расширение Кана (1). Тогда универсальная стрелка
Т] : Т -^ LK при каэюдом п Е М является композицией инъекции
%\Кп костепени (для f = 1кп '• Кп —>• Кп) с компонентой концевого
клина ш\
Тп —^ С(Кп, Кп) • Тп
\с(Кгп,Кп) • Ттп = (ЬсЖКТ)(Кп).
Таким образом, левое расширение Кана можно представить
двояко: по формуле (1) как ко-конец, а по формуле (3.10) как копредел.
Эти формулы тесно связаны и в действительности дают два способа
представления одной и той же информации о копределах (см. ниже
упр. 1). Следствия § 10.3 можно вывести из обеих формул.
Аналогично, для правых расширений Кана имеется формула
(RanKT)c= \Ттпс^Кш\ (3)
га
верная при условии существования указанной степени и ее ко-конца
(здесь степень X означает соответствие а н-» ах в А).
Рассмотрим теперь аддитивные расширения Кана. Пусть М, С и А
являются АЪ-категориями, а оба данных функтора К и Т
аддитивны. Тогда можно описать правое Ab-Kan-расширение функтора Т по
К как аддитивный функтор В! : С —>■ А с естественной биекцией
(3.2) для аддитивных функторов S. Этот функтор R' не обязательно
согласован с обычным правым расширением Кана Ran^T, которое
получается, если забыть, что К, Т (и S) аддитивны. Однако В! по-
прежнему можно выразить как конец по формуле (3), заменив
соответствующую костепень ас (где a G А, С G АЬ) на котензор ас,
который определяется сопряжением
А(Ъ,сс) 9*АЪ(С,А(Ъ,с))
(4)

280
Расширения Кана
[Гл. 10
для всех Ъ е А (см. Day, Kelly [1969], Dubuc [1970]). Наример, если
А = Л-Mod, то получаем ас = АЬ(С, а) с очевидной структурой R-
модуля (перенесенной с a Е i?-Mod).
Производные функторы — пример на ту же тему. Пусть функтор
Т : i?-Mod —> Ab точен справа. Тогда его левые производные
функторы Тп : i?-Mod —> Ab можно наделить связывающими морфизмами,
которые превращают их в т. н. связную последовательность
функторов (Mac Lane [1963a]; Cartan, Eilenberg [1956]). Приведем основной
пример: если А — правый Л-модуль, то левые производные функторы
тензорного произведения А ®# — : i?-Mod —> Ab — периодические
произведения Тотп(А, —) : R-M.od —>• Ab.
Левые производные функторы Тп для Т можно охарактеризовать
следующим свойством универсальности: То = Т, и если Sn —
любая связная последовательность (аддитивных) функторов, то любое
естественное преобразование So -^ ХЬ продолжается до единственного
морфизма связных последовательностей функторов {Sn \ п ^ 0} —>■
-> {Тп | п > 0}.
Это свойство можно также сформулировать следующим образом.
Вложим Л-Mod в большую Ab-категорию Е с объектами (С, п), где
С — некоторый Л-модуль, п — неотрицательное целое число, и hom-
группами вида Е((С,п), (B,m)) = Ext^Tm(C, В) с композицией,
определяемой произведением Ионеды. Тогда соответствие С \-> (С, 0)
определяет функтор К : i?-Mod —> Е. В этом случае связная
последовательность аддитивных функторов {Тп | п ^ 0} — то же
самое, что один аддитивный функтор Т* : Е —>■ Ab со свойством
Т*(С,п) = ТП(С), который переводит морфизмы изЕв связывающие
морфизмы. Свойство универсальности, сформулированное выше
применительно к последовательности Т* левых производных функторов
для Т, теперь выглядит следующим образом:
Nat(S*K,T)^Nat(S*,T*).
Это в точности означает, что Т* является правым Ab-Kan-
расширением для Т = То по К : i?-Mod —у Е (и что его единицей
г : Т*К -^ Т служит тождественное преобразование).
Детали см. в работах (Cartan, Eilenberg [1956]) или (Mac Lane
[1963а]) (где категория Е определяется другим, но эквивалентным
способом — как градуированная Ab-категория).
Упражнения
1. Докажите, что если ко-концы из теоремы 1 существуют, то они
определяют копределы из формулы (3.10) для Lan^.
2. При фиксированном К опишите Lan^T и Ran^T (когда они
существуют) как функторы в Т.
3. (Dubuc.) Пусть существует Ran^T. Пусть также L : С —»■ D —
некоторый функтор. Докажите, что Ran^^T существует, если и только
если существует RanbRanxT, и тогда эти функторы (и их универсальные
стрелки) совпадают.

10.5]
Поточечные расширения Кана
281
4. (Ulmer; Day, Kelly; расширение Кана как ко-конец в категории
функторов А .) Пусть С(Кт' ,с) • Тт существует для всех mf,m E Ми всех
с Е С. Покажите, что соответствие (т',т) \-> С (Km', —) • Тт является
функцией объектов функтора Мор х М —»■ Ас. Докажите, что Т имеет
левое расширение Кана по К, если и только если этот бифунктор имеет
ко-конец, и тогда этот ко-конец является расширением Кана
т
LanxT = f C(Km, -) • Тт.
Опишите универсальную стрелку для Lan^T в терминах ко-конца.
5. (Ulmer.) Аналогично упр. 4, получите необходимое и достаточное
условие для существования Ran^T в терминах пределов в категории А .
10.5. Поточечные расширения Кана
Пусть даны функторы
С <^ М ^А^Х (1)
и правое расширение Кана Ran^T с коединицей г : (Ran^T)if ^» Т.
Будем говорить, что G сохраняет это правое расширение Кана, если
G о Ran^T является правым расширением Кана для GT по К с
коединицей Ge : G(Ran^T)i^^> GT. Это влечет (но сильнее, чем)
изоморфизм
GoRanKT^RanK(GT).
Мы уже знаем, что правые сопряженные функторы G сохраняют
пределы. Покажем теперь, что они сохраняют и расширения Кана.
Теорема 1. Если функтор G : А —» X имеет правый
сопряженный F, то G сохраняет все правые расширения Кана, которые
существуют в А.
Доказательство. Вначале рассмотрим сопряжение
A(Fx, a) ^ X(x, Ga), x е X, a G А.
Если вместо х подставить функтор Я : С —> X, а вместо а — функтор
L : С —> А, то применение этого сопряжения к каждому Lc и Не дает
биекцию
Nat (FH, L) ^ Nat (Я, GL). (2)
(Как обычно, сопряжение связывает F слева и G справа.)
Пусть теперь для функторов К и Т : М —> А имеется
сопряжение и правое расширение Кана Ran^T. Тогда для любого функтора
Я : С —>- X мы имеем следующие биекции:
Nat (Я, G о Ran^T) ^ Nat (FH, Ran^T) ^
^ Nat (Ftftf, Г) ^ Nat (ЯК, GT),

282
Расширения Кана
[Гл. 10
естественные по Н; первая и третья — это частные случаи формулы
(2), а вторая — определение правого расширения Кана. Композиция
биекций (для всех Н) показывает, что G о Ran^T является правым
расширением Кана Ran^GT. Чтобы найти его коединицу, положим
Н = G о Ran^T и возьмем образ единичной стрелки. Получаем Ge,
где г : (Ran^T) —ь Т — коединица данного расширения Кана. □
Следствие 2. Пусть R,г : RK —> Т — правое расширение Кана.
Пусть при этом категория А имеет малые hom-множества и
малые костепени. Тогда при каждом a Е А функтор A{a,R—) : С —>•
—> Set определяет правое расширение Кана для А(а, Т—) : М —> Set
с коединицей А(а,е—).
Доказательство. Левым сопряженным функтором для
А(а, —) :А —> Set является костепень X \-> X • а. □
к т
Определение. Пусть даны функторы С <— М —>• А, где
категория А имеет малые hom-множества. Правое расширение Кана
R называется поточечным, если его сохраняют все представимые
функторы А{а, —) : А —>• Set, где a Е А.
Теорема 3. Функтор Т : М —» А имеет поточечное правое
расширение Кана по К : М —>• С, если и только если при всех с
существует предел для (с I К) —>• М —>• А. В этом случае Ran^T
определяется формулами из теоремы 1, § 10.3.
Доказательство. Поскольку А(а,—) сохраняет пределы, то
любое расширение Кана, построенное по формуле предела, является
поточечным.
Обратно, пусть для каждого a Е А функтор А(а, Т-) : М —>• Set
имеет правое расширение Кана Ra = A(a,R—), как на следующей
диаграмме:
С
А
К
М
I А(а,-)
Тогда для каждого функтора V (см. диаграмму) имеется биекция
Nat (У, Ra) ** Nat (VK, А(а, Г-)),
естественная по У. В частности, это выполнено, когда V = С (с, —)
для некоторого с Е С:
Nat (С(с, -),А(а, R-)) = Nat (С(с, К-),А(а, Г-)).
Преобразовав левую часть по лемме Ионеды, а правую — по
нижеприведенной лемме, получаем (здесь Q — проекция (с I К) —> М):
^Set.
А(а, Re) ^ Cone (a, TQ : (с i К) ^ А).

10.6]
Плотность
283
Это означает, что множество конусов представимо и потому предел
для TQ существует. □
Здесь использована
Лемма. Для функтора К : М —» С всегда имеется биекция
Cone (а, (с | К) -+ М -+ С) £* Nat (C(c, K-), А(а, Г-)).
Доказательство. Конус г : a -^TQ сопоставляет каждой
стрелке / : с —>■ Хттг стрелку г(/, ш) : а —>■ Тттг, подчиненную условиям
конуса; для каждой стрелки h : тп ^ тп' имеем
r(Mo/,m') = Tftor(/,m).
Естественное преобразование /? : С(с, К—) -1» А(а, Т—) сопоставляет
любым m Е М и / : с —>■ Хттг стрелку /?ш/ : а —> Ттп, подчиненную
условию естественности: для каждой стрелки h : m' —> m имеем
pm,(Kh°f)=Thopmf.
Биекция т «->■ (3 теперь очевидна. □
Из доказательства теоремы вытекает также
Следствие 4. Расширение Кана R,e : RK-^ Т для Т является
поточечным, если и только если для всех a Е А и с Е С отображение
А(а, Re) -+ Nat (С(с, К-),А(а, Г-)),
переводящее g : а —>■ R в преобразование с компонентой для т Е М
С(с,Кт) A A(Rc,RKm) Л{9'£т\ А(а,Тт),
является биекцией.
Упражнение
1. В ситуации (1) пусть существуют Ran^T и Ran^GT с коединицами
е и е'. Докажите, что имеется единственное естественное преобразование
(каноническое отображение) w : G о Ran^T -^ HslUrGT такое, что е' • wK =
= Gs. Докажите также, что G сохраняет Ran^T, если и только если w
является изоморфизмом.
10.6. Плотность
Подкатегория М С С называется плотной в С, если каждый
объект из С является копределом объектов из М; более точно —
копределом канонического вида, для которого копредельныи конус
состоит из всех стрелок т —> с в объект с из объектов т Е М. Более
общо, плотность можно определить не только для вложения М С С,

284
Расширения Кана
[Гл. 10
но и для любого функтора К : М —У С. При этом стрелки т —у
—У с заменяются на объекты (т, / : Km —у с) категории запятой
(К ^ С). Напомним, что проекции PC,QC категории запятой имеют
вид Pc(m,f) = m, Qc(m,f) = /; отметим, что (функция объектов)
Qc может рассматриваться и как конус Qc : КРС —у с.
Определение. Функтор К : М —у С называется плотным,
если для каждого с Е С верна формула
Colim ((К|с)^>М^С) = с, (1)
причем копредельным конусом здесь является канонический конус
Qc. В частности, подкатегория М С С плотна в С, когда функтор
вложения плотен в только что определенном смысле.
Иногда определение (1) выражают следующим образом:
«Каноническое отображение ColimKPC —у с является изоморфизмом»;
здесь каноническое отображение — это единственная стрелка
к : Colim КРС —у с, которая переводит копредельный конус в Qc.
Например, одноточечное множество * плотно в категории Set.
В самом деле, для каждого множества X категория запятой (* \, X) —
это множество (дискретная категория) элементов из X, каждый из
которых рассматривается как функция х : * —у X. При этом (1)
превращается в утверждение, что каждое X является копроизведением
Их своих элементов (т. е. что функция / с областью X однозначно
определена, если задано ее значение fx для каждого х G X).
Двойственно, функтор К : М —у С называется коплотным, если
для каждого с G С верна формула
Lim ((с | К) % М ^ С) = с, (2)
причем предельным конусом служит канонический конус, который
отображает (/ : с —у Кт,т) в /. Но это как раз тот предел, который
фигурирует в определении Ran^T. Отсюда вытекает
Предложение 1. Функтор К : М —у С коплотен, если и только
если Ыс и тождественное естественное преобразование Id к '• К -^К
определяют поточечное правое расширение Кана для К по К.
В следствии 4, § 10.5 преобразование г в этом случае является
тождественным, и полученная биекция сводится к соответствию
между произвольной стрелкой / : а —У с и естественным преобразованием
f*=C(f,K-):C(c,K-)^C(a,K-) (3)
(преобразование /* — это умножение на / справа). Отсюда вытекает
Предложение2. Функтор К : М —у С коплотен, если и только
если указанное выше соответствие f ь^ С(/, К—) является при всех
а и с е С биекцией
С(а, с) ^ Nat (C(c, К-),С(а, К-)),
(4)

10.6]
Плотность
285
если и только если функтор Сор —У Ens вида
с ^ С (с, К-) : М -+ EnsM (5)
полон (full) и унивалентен; предполагается, что hom-множества
категории М лежат в Ens.
Следствие 3. Если hom-множества категории М лежат
в полной (full) категории множеств Ens, то вложение Ионеды
Y : М —у (EnsM)op, имеющее вид Ym = М(т, —), является
коплотным.
Доказательство. Непосредственно из леммы Ионеды
вытекает, что для каждого функтора F : М —У Ens выполнена формула
(EnsM)op(F,Fm) = EnsM(Fm,F) ^ Fm.
Если теперь в биекции (4) положить С = (EnsM)op, a = F и с = G,
то ее правая часть примет вид
Nat(G,F) = (EnsM)op(F,G) = C(F,G),
и (4) превращается в тождество. □
Этот результат часто формулируют следующим образом: любой
функтор М —у Ens является каноническим пределом представимых
функторов.
Факт, двойственный к предложению 2, состоит в том, что функтор
К : М —>- С плотен, если и только если соответствие с н->- С(К—,с)
определяет полный (full) и унивалентный функтор С —У Ens
В качестве приложения покажем, что полная подкатегория конечно
порожденных абелевых групп плотна в АЬ. Нужно лишь показать,
что для любых двух абелевых групп А и В отображение
АЬ (А, В) -+ Nat (Ab (K-, A), Ab (K-, В))
является биекцией. Во-первых, оно взаимно однозначно: два
гомоморфизма f,g : А —У В, совпадающие на циклических подгруппах
в А, совпадают всюду. Далее, оно сюръективно. В самом деле, если
дано естественное преобразование г : АЪ(К—,А)-^ АЪ(К—,В), то
можно определить функцию f : А —У В, взяв в качестве fa для
любого a G А значение т на отображении Z —у А, переводящем 1 в а.
Поскольку группа Z 0 Z конечно порождена, то эта функция должна
быть гомоморфизмом. Ее образ при рассматриваемом отображении
совпадает с г; доказательство завершено. Отметим, что фактически
доказано больше: полная подкатегория с одним объектом Z 0 Z плотна
в АЬ. (Требуются два слагаемых вида Z, поскольку абелевы группы
определяются в терминах бинарной операции.)

286
Расширения Кана
[Гл. 10
Упражнения
1. Покажите, что в категории .R-Mod полная подкатегория с одним
объектом R(& R плотна.
2. Покажите, что полная подкатегория с одним объектом Z не является
плотной в АЬ.
3. Пусть категория образов КМ для функтора К : М —»> С — это
подкатегория в С, объекты которой имеют вид Km для всевозможных т Е
Е М, а стрелки имеют вид Kh для h из М. Докажите, что если К полон,
то подкатегория КМ плотна в С.
4. Докажите, что объекты подкатегории М порождают С, если и только
если унивалентен функтор С —»■ EnsM , заданный соответствием с н-»-
^С(К-,с).
5. Пусть в категории С существуют все костепени С(Кт , с) • Km.
Докажите, что функтор К : М —»■ С плотен, если и только если каждый
объект с Е С является ко-концом вида
т
с= \с(Кт,с)-Кт
с ко-концевым клином ои^ : С (Km, с) • Хттг —>- с, который действует на
инъекции костепени по формуле и^г/ = / : Km —»■ с.
10.7. Все категорные понятия являются
расширениями Кана
Понятие расширения Кана охватывает все другие основные
понятия теории категорий.
Теорема 1. Функтор Т : М —>• А имеет копредел, если и только
если он имеет левое расширение Кана по (единственному) функтору
К\ : М —>• 1, и тогда ColimT является значением Lan^T на
единственном объекте категории 1.
Доказательство. Функтор S : 1 —> А — это просто объект
a G А, а естественное преобразование а : Т -^ SK\ — это конус
с основанием Т и вершиной а. Поскольку левое расширение Кана
L = Lan^х Т включает универсальное преобразование г\ : Т -^ LK\,
то оно порождает универсальный конус с основанием Т, а значит
и копредел для Т. □
Двойственно, правые расширения Кана по тому же функтору К\
порождают пределы.
Теорема2 (формальный критерий существования сопряженного
функтора). Функтор G : А —» X имеет левый сопряэюенный, если
и только если правое расширение Кана Ran^lA : X —>• А существует
и сохраняется под действием G; в этом случае правое расширение
Кана — это левый сопряэюенный F = Ran^l^ для G, и коединица
расширения Кана г : (Ran^lA)G^> 1a совпадает с коединицей
сопряжения г : FG -^ 1.
Доказательство. Пусть G имеет левый сопряженный F с
единицей Т] : 1х —> GF и коединицей г : FG -^ 1а- Тогда для всех

10.7] Все категорные понятия являются расширениями Кана 287
функторов Я : А —у С (в частности, для тождественного функтора
1^) мы можем построить биекцию
Nat (5, HF) = Nat (SG, Я), (1)
естественную по S : X —> С. Для этого положим
{а : S ^ HF} ^ {SG ^ HFG ^ Я},
{г : SG ^ Я} ^ {S ^ SGF ^ HF}.
Композиция первого и второго преобразования дает тождественное:
сг I—>- сг, поскольку диаграмма
S —>■ HF = HF
Sr]\ IhFt] И
SGF -^- HFGF -—*■ HF
HsF
коммутативна (первый квадрат выражает двумя способами
горизонтальное произведение ат\, а второй — применение функтора Я к
одному из двух треугольных тождеств для г) и г). Аналогичная
диаграмма показывает, что композиция в обратном порядке также дает
тождественное преобразование. Получена искомая биекция, очевидно
естественная по S. Если взять Я = 1^, то биекция показывает, что
F = Ran^l^; единица этого расширения является образом для а —
— \р и потому равна е. Если взять Я = G, то биекция показывает, что
GF — Ran^G, и единица этого расширения равна Ge. Таким образом,
G сохраняет правое расширение Кана Ran^l^- Мы доказали первую
половину теоремы.
Мы доказали и больше: для каждого Я выполнено равенство
HF = К&поН с единицей Не. Таким образом, Ran^l^ сохраняется
при действии любого функтора (это абсолютное расширение Кана).
Сформулируем этот факт как
Предложение 3. Пусть функтор G : А —>• X имеет левый
сопряженный F с коединицей е : FG —> 1. Тогда Ran^l^ существует,
равняется F с коединицей е и сохраняется при действии любого
функтора.
Обратно, предположим, что 1а имеет правое расширение Кана R
по G, причем G сохраняет это расширение. Тогда имеются биекции
<p = <ps: Nat (S, R) ** Nat (SG, 1A), <p(S 4 R) = e • gG,
ф = фн: Nat (Я, GR) ^ Nat (HG, G), ф(Н Л GR) = Ge • uG,
естественные no S : X —> А и Н : X —> X, с коединицами <^д1 =
= e : RG 4Ц и ^grX — Ge : GRG -^ G. Определим r\ : 1 -^ GR как
^(1 : G ^ G). Тогда ^ = 1и
Ge-r]G = 1G.

288
Расширения Кана
[Гл. 10
Это одно из двух треугольных тождеств для предполагаемого
сопряжения е : RG -^ 1а, V '• 1х —> Gi2. Второе имеет вид sR • Rt] = 1r.
Применив биекцию срл, заменим его на cp(eR • Rrj) = е. Учитывая
определение биекции ср в терминах е, нужно доказать
коммутативность квадрата
Rr]G
RG -< RGRG
RGe I
\eRG
I a -<—!— RG.
Добавим наверху прерывистую стрелку; поскольку для R уже
установлено треугольное тождество Ge • rjG = 1, то коммутативность
квадрата сводится к эквивалентности двух выражений для ее : RGRG —>■
—У 1, что и требовалось доказать. □
До сих пор в этом параграфе не использовались формулы для
расширений Кана. Теперь выясним смысл этих формул в простом
случае расширений Кана по тождественному функтору I : С —> С.
Из свойства универсальности, которое определяет эти расширения,
непосредственно вытекает, что для любого Т : С —> А верны равенства
Lan/T = Г, Ran/T = Г.
Рассмотрим, например, функтор Т : С —> Set и предположим, что
С имеет малые hom-множества. Тогда в формуле, выражающей Ran/
как конец, существуют все необходимые степени, и потому для
каждого с G С имеем
Tc=(Ran/T)c= \Tmc^m\
т
Но в категории Set выполнено равенство XY = Set (У, X), и ввиду
(2) из § 9.5 конец сводится к множеству естественных преобразований
Тс = [ Set (С(с, т),Тт) ^ Nat (С(с, -), Г).
В результате получаем лемму Йонеды.
Упражнения
1. Покажите, что биекция (1) (так же как и (2), § 10.5) является частным
случаем биекции в квадрате сопряжений (упр. 4, § 4.7):
Nat (HG, G'K) ^ Nat (F'tf, KG).
2. Выведите лемму Йонеды из формулы, выражающей Ran^T через
предел. (Получаем независимое доказательство леммы Йонеды, которая не
использовалась в доказательстве из § 10.3.)

10.7] Все категорные понятия являются расширениями Кана 289
3. а) Пусть К : М —»■ С имеет правое расширение Кана по себе R,
и пусть дана биекция (р : Nat (5, R) = Nat (SK, К). Докажите, что (Я, т/, /i)
является монадой в С; здесь т/ = <^_1(Ык), // = (p~1(s-Rs). (Это т. н. монада
коплотности в категории К.)
б) Покажите, что функтор К коплотен, если и только если г\ является
изоморфизмом.
в) Если G : А —>- X имеет левый сопряженный .Р : X —>- А с единицей
т/ : Id -^GF и коединицей е : .PG -Ц-Id, то его монада коплотности существует
и имеет вид (GF, т/, GeF) (т. е. монада определяется сопряжением).
Замечания
Формальные критерии сопряженности принадлежат Бенабу (Benabou
[1965]). Построение расширений Кана как пределов и копределов было
осуществлено в работе (Кап [1958]) для важнейшего случая, когда категорией-
кообластью служит А = Set. Значение этой конструкции осознавалось
лишь постепенно. В 1963 г. Ловер применил эти расширения в функторной
семантике. Улмер понял их важность и в неопубликованной статье вывел
формулу ко-концов (не употребляя термин ко-конец) для Lan^T. Бенабу
(не опубликовано) описал расширения Кана в относительных категориях
(включая АЬ-категории); это сделано и в работе (Day, Kelly [1969]). Дальше
эта идея развита в работе (Dubuc [1970]); здесь формула, выражающая
расширения Кана через ко-концы, играет главную роль.
Как отмечено в § 10.4, первым и важнейшим примером расширения
Кана явилось понятие производного функтора, введенное Картаном и Эй-
ленбергом. Изящную форму для такой интерпретации производных
функторов нашел Вердье, используя вложение произвольной абелевой категории
в подходящую производную категорию. См. обзор в работе (Quillen [1967]).
В основополагающей статье (Isbell [I960]) функтор К : М —»> С
называется адекватным слева, если соответствие с н->■ С(К—,с) полно (full)
и унивалентно. Это функтор из формулировки утверждения,
двойственного к предложению 2, § 10.6; как следствие, понятия адекватный слева
и коплотный совпадают. Развивая эти идеи, Избелл получил характериза-
цию категорий алгебр (Isbell [1964]).
Расширения Кана входили в обиход постепенно; многое из содержания
этой главы мне сообщил мой студент Эдуардо Дюбюк; в свою очередь,
Максу Келли принадлежат значительные усовершенствования, в особенности
использование поточечных расширений Кана.

Глава 11
СИММЕТРИЯ И ЗАУЗЛИВАНИЕ
В МОНОИДАЛЬНЫХ КАТЕГОРИЯХ
Моноидальная категория, согласно определению из гл. 7, — это
категория с бинарными тензорными произведениями,
ассоциативными с точностью до естественного изоморфизма а. Главный результат
относительно этих категорий состоит в теореме когерентности: если
коммутативна определенная пятиугольная диаграмма, включающая
а ((5), § 7.1), то коммутативны и все диаграммы, включающие это а.
Рассмотрим теперь различные обобщения этого результата.
Во-первых, заметим, что эта теорема когерентности фактически
сводится к утверждению, что моноидальная категория эквивалентна
строгой, т. е. такой категории, в которой отображение
ассоциативности всегда тождественно, так же как и отображения Аир для
единичного объекта. Далее, симметричная моноидальная категория
(§ 7.7) характеризуется тем, что тензорное произведение не
только ассоциативно, но и коммутативно с точностью до подходящего
естественного изоморфизма 7 : а П 6 = ЬПа. Кроме того,
выполнена теорема когерентности, а именно коммутативны все диаграммы,
включающие а и 75 однако не всегда можно сделать изоморфизм
7 тождественным (т.е. получить строго моноидальную категорию).
8 симметричных моноидальных категориях j2 = 1 (т. е. 7
совпадает со своим обратным), но существуют и впечатляющие примеры
моноидальных категорий с закрученным 7 (т2 Ф !)• Это категории
кос (§ 11.4), которые возникают в приложениях к квантовой физике
и теории узлов.
11.1. Симметричные моноидальные категории
Моноидальная категория М — это категория с бифунктором ®
или □ :
□ : М х М -+ М,
который для объектов а, Ъ в М записывается разными способами как
произведение:
(a,&)4aDfe, a 0 Ъ или afr,
ассоциативен с точностью до естественного изоморфизма
а : а(Ъс) ^ (ab)c (1)
и при этом некоторый элемент е является единицей с точностью до
естественных изоморфизмов
Л : еа = a, p : ае = а. (2)

11.1] Симметричные моноидальные категории 291
Эти отображения должны удовлетворять определенным требованиям
коммутативности: для а это пятиугольная диаграмма
a(b(cd)) —^ (ab)(cd) —^ ((ab)c)d
la
a((bc)d)
Oil
(a(bc)d),
(3)
см. (5), § 7.1, а для Аир- две коммутативности
а{(
IX
1
1С) —
'
—>-
[Ш
1
i)C
pi
ас
ас,
А = р : ее —> е.
(4)
Стандартным примером моноидальной категории М служит
категория всех векторных пространств над данным полем F с обычным
тензорным произведением ® в качестве произведения □ и с
одномерным векторным пространством F в качестве единицы; вот почему
моноидальные категории часто называют тензорными категориями.
Коммутативности (3) и (4) обеспечивают (как в следствии из
теоремы 1, § 7.2) коммутативность каждой диаграммы, состоящей из а,
X и р. Именно, для любого слова w в алфавите а, Ъ, е,... существует
единственная композиция стрелок а, Аир, которая все скобки в слове
w передвигает влево и устраняет все вхождения элемента е.
(Например, в (4) любое из них можно удалить до или после применения
отображения а — с одинаковым результатом.)
Примеры, приведенные ниже, подсказывают идею заузливания
(braiding).
Заузливание в моноидальной категории М представляет собой
семейство изоморфизмов
7а,ъ : a\Jb = b\Ja,
(5)
которые естественны по а и b Е М, удовлетворяют условию
коммутативности
аПе >■ еПа
(6)

292 Симметрия и заузливание в моноидалъных категориях [Гл. 11
и вместе с изоморфизмом ассоциативности а делают коммутативными
следующие две шестиугольные диаграммы (где опущен символ □ ):
(ab)c >• c(ab)
а(Ьс) (са)Ь
1-7
7-1
a(cb) >■ (ас)Ь,
а(Ьс)
7-1
(be) a
(ab)c b(ca)
1-7
(Ьа)с >■ Ь(ас).
(7)
Заметим, что первая диаграмма заменяет каждую стрелку 7аб,с с
произведением ab в качестве первого индекса на две стрелки 7 с
одинарными индексами, а вторая делает то же самое со стрелками 7а, Ьс?
где произведение присутствует во втором индексе. Заметим, что из
первого шестиугольника в (7) для 7 следует второй для 7-1 и
наоборот. Поэтому если 7 является заузливанием в М, то и гу~1 также.
Симметричная моноидальная категория, которая уже была
определена в § 7.7, — это категория с заузливанием 7, в которой
коммутативна любая диаграмма вида
7а, Ъ
ab >■ Ьа
ab.
(8)
В этом случае из каждого шестиугольника в (7) следует другой.
Теорема когерентности для моноидальных категорий, доказанная в гл. 7,
теперь будет распространена на симметричный случай с помощью
симметрической группы Sn степени п. Как и в § 7.2, будем
рассматривать □ -слова w из п букв, а также перестановки т из Sn. В каждой
симметричной моноидальной категории М перестановочному слову
wr соответствует функтор (шт)м '• Мп —у М, который определяется
перестановкой т аргументов слова w:
(W)M(ai,...,an) = w(aTl,...,aTn), a* E M.
Теорема!.. В каждой симметричной моноидальной категории
М имеется функция, которая сопоставляет каждой паре (vo~, wr)
перестановочных слов одинаковой длины п (единственный)
естественный изоморфизм
canM(W,wr) : (vg)m -»• (wt)m • Мп -»> М (9)

11.1] Симметричные моноидальные категории 293
{каноническое отображение из va в wr), причем так, что единица
в М и все реализации изоморфизмов a wy являются каноническими.
То же верно для композиции и □ -произведения канонических
отображений.
Доказательство. Между двумя различными
перестановочными словами всегда имеется хотя бы одно отображение, так как можно
использовать реализации изоморфизма а для изменения расстановки
скобок, а реализации изоморфизма 7 ~~ Для транспозиции соседних
аргументов. Это дает любую нужную перестановку аргументов, так
как все перестановки в симметрической группе получаются из
последовательных транспозиций. Тождества (7) показывают, что
перестановку индивидуального аргумента а с произведением аргументов
всегда можно заменить последовательными перестановками
индивидуальных аргументов.
Остается показать, что любые две такие композиции (пути из
(vo~)m в (wt)m) равны. Из теоремы о моноидальной когерентности
(§ 7.2) для ассоциативности мы уже знаем, что равны любые две
последовательности применений ассоциативности а, переводящие (vo~)m
в (wt)m- Поэтому можно считать, что произведение □ строго
ассоциативно и а тождественно. В этом случае шестиугольники (7) можно
заменить двумя треугольниками
abc >■ cab abc >■ bca
acb, bac.
Эти тождества показывают, что достаточно рассматривать
последовательные перестановки соседних букв а, Ь. Но симметрическая
группа Sn порождается транспозициями Т{ = (г, г + 1)
последовательных букв (г = 1,... ,п — 1). И любой замкнутый путь, состоящий из
таких транспозиций, соответствует соотношению между
образующими Т{. Известно, что все такие соотношения являются произведениями
сопряженных к определяющим соотношениям группы Sn, в качестве
которых можно взять
т? = 1, г = 1,...,п-1,
(т^+1)3 = 1, г = 1,...,п-2, (10)
TiTj = TjTi, l ^i < j -1 ^п-2.
Поэтому для доказательства когерентности достаточно показать, что
для каждого из этих соотношений коммутативна соответствующая
диаграмма путей.
Первое соотношение rf = 1 выражает свойство 72 — 1 из (8),
выполненное по предположению. Третье обеспечивается
естественностью изоморфизма 7- В случае второго соотношения (т^)3 = 1

294 Симметрия и заузливание в моноидалъных категориях [Гл. 11
естественность изоморфизма 7а,ь и ДВУХ треугольников (7а) после
перемены обозначений дает коммутативную диаграмму
7-1
аЬс >■ Ьас
1-7
т
асЪ
7-1
т
^ сЪа
По периметру получаем Т\Т2Т\ — т^тхт^^ что и требуется для (10). □
Эту теорему когерентности можно обобщить, использовав
отображения Л и р вместо единиц. Благодаря допущению (6) любую из
единиц можно удалить до или после применения изоморфизма 7?
и мы уже знаем соответствующий факт для а. Точная формулировка
полученной теоремы предоставляется читателю; потребуется
рассматривать слова от более чем п аргументов, причем некоторые из них
равны единице. Отметим также, что для формулировки следствия
в § 7.2 подобным же способом используются слова, включающие е.
Результат снова выражает тот факт, что коммутативны все
формальные диаграммы в терминах изоморфизмов а, А, р и j.
11.2. Моноидальные функторы
Если категория обладает дополнительной структурой, то следует
определить соответствующую структуру на функторах и
естественных преобразованиях. Здесь мы вновь рассмотрим случай моноидаль-
ной категории (§ 7.1).
Моноидальный функтор (F, F2,Fq) : М —> М' между моноидаль-
ными категориями М и М' включает следующие три компоненты:
1) (обычный) функтор между категориями F : М —у Мг;
2) для объектов а, Ъ в М — морфизмы в М'
F2(a,b) :F(a)UF(b) -У F(aUb), (l)
естественные по а и Ь;
3) для единиц еие'- морфизм в М'
Ъса (И)
F0 : е' -* Fe.
(2)

11.2]
Моноидалъные функторы
295
При этом в М' должны коммутировать следующие три диаграммы,
включающие структурные отображения а, А, р:
F(a) П (F(b) П F(c)) -^U- (F(a) □ F(b)) П F(c)
1 □ F2 \f2 D 1
Y Y
F(a) П (F(b П c)) (F(a П b) П F(c))
f2
F(aD(6Dc))
F(a)
F2
■F((oD6)Dc),
(3)
F(b)De'-
lDFo
F(6)DF(e)
-F2
■F(6)
\F(p)
■F(bDe),
e' П F(6)
F0D1
■F(b)
\FW
F(e)nF(b) ^F(eDb).
F2
(4)
Очевидная композиция моноидальных функторов также будет моно-
идальной.
Моноидальный функтор называется сильным (strong), если Fq
и все i*2(a, Ь) являются изоморфизмами, и строгим, если они тожде-
ственны (напомним, что моноидальная категория является строгой,
если тождественны а, А и р).
Моноидальное естественное преобразование в : (F, F2,F0) —>•
—У (G,G2,Go) : М —У М' между двумя моноидальными
функторами — это естественное преобразование между соответствующими
обычными функторами в : F —У G, такое что в М' коммутативны все
диаграммы вида
F(a)UF(b)
F2
F(aUb)
ОаПвъ
(5)
G(a)UG(b) —^ G(aUb)
(6)
Очевидная композиция двух моноидальных естественных
преобразований также будет естественной.

296 Симметрия и заузливание в моноидалъных категориях [Гл. 11
Если F — моноидальный функтор, то отображения F^ для
произведения и Fq для единицы можно продолжить до функторов,
определяемых произвольными тензорными словами v из п букв (которые
были введены в § 7.2). Для каждого такого функтора v получаем
преобразование
Fv : v(Fau...,Fan) -> Fv{au ..., an),
(?)
естественное по ai,..., an, причем F\j = F<i и Fe = Fq. Действительно,
слова определяются по индукции как тензорные произведения v\3v'
более коротких слов, и в качестве Fv\jv> мы берем F2(FV DFV/). При
таком определении очевидно, что все диаграммы из таких
естественных преобразований коммутируют. А именно, если v и w — два таких
□ -слова из п букв, то теорема когерентности дает единственное
естественное преобразование г\ : v —>■ w, построенное из отображений а,р
и Л. Тогда в силу индукции коммутативна диаграмма
v(Fa!,..., Fan) v-+ Fvfa,..., an)
Fr]
w(Fab ..., Fan) > Fw(ab ..., an).
F w
(8)
(Это не что иное, как распространение условий (3) и (4) на
произвольные слова.) Далее, для любого слова v и любого моноидального
естественного преобразования в : F —>■ G между двумя моноидальны-
ми функторами коммутативна диаграмма
v(Fa!,..., Fan) v-+ Fv(alj..., an)
v(eai,
9v(ai,...,an)
(9)
v(Gai,...,Gan) > Gv(ai,...,an);
это условие обобщает условия (5) и (6).
Если В, В' — категории с заузливанием (например, симметричные
моноидальные категории), то заузленным (braided) является такой
моноидальный функтор (F, F2,Fq) : В —» В', который коммутирует
с заузливаниями 7 и У в следующем смысле:
FaUFb-
\F2
■FbUFa
\f2
(10)
F(a\Jb)-^^F(b\Ja);

11.3]
Строго моноидалъные категории
297
здесь 7 и У — заузливания в В и В' соответственно. Заузленные моно-
идальные функторы служат морфизмами в категории моноидальных
категорий с заузливанием.
11.3. Строго моноидальные категории
Теорема 1. Любая моноидальпал категория М категорно
эквивалентна некоторой строго моноидальной категории S посредством
сильных моноидальных функторов G : М —» S и F : S —>■ М.
(Напомним, что моноидальная категория называется строго
моноидальной, если структурные отображения a,j и р — тождественные.)
Доказательство. В силу теоремы когерентности существуют
однозначно определенные канонические отображения между
словами; отсюда возникает идея вложить данную категорию М в строго
моноидальную категорию 5, состоящую из итерированных
формальных произведений элементов из М (где все пары скобок начинаются
в начале слова).
В качестве S возьмем свободный моноид, порожденный
элементами из М. А именно, пусть объектами в S являются все конечные
строки s = [Ьъ ..., б*;] объектов из М, включая пустую строку 0.
Произведение sDt строк s и t определяется как их конкатенация s • t.
Такое произведение ассоциативно, поэтому отображение
ассоциативности а в S можно взять тождественным. Далее, пустая строка 0 при
таком умножении действует как единица, поэтому отображения р и Л
в S также можно взять тождественными. При таких соглашениях S
становится моноидом, но еще не моноидальной категорией.
Определим теперь на строках из S отображение F : S —> М,
положив
F(0) = e,
F(s) = F[h,..., bk] = (... (bi □ b2) П b3)...) □ bk), (1)
где все пары скобок в правой части начинаются в начале слова.
В качестве стрелок s —>■ t между строками s и t из S возьмем все
стрелки между соответствующими объектами в М:
F(s) -> F(t) (l')
с тем же умножением, что и в М. Ясно, что это соглашение
превращает S в категорию. Далее, умножение-конкатенацию s • и можно
продолжить до умножения / • g стрелок / : s ^ t и g : и ^ v, где и
и v, подобно snt,- конечные строки объектов из М. Конкретно это
означает, что мы определяем / • g как следующую композицию в М:
F(s • и) >■ F(s) □ F(u) ^—i F{t) U F(v) >■ F(t • v);
здесь две внешние стрелки — канонические отображения из М'. Если
h : w —>■ у — еще одно отображение стрелок, то итерация этого
определения дает в качестве тройного произведения (/ • g) -h композицию
канонических отображений, следовательно также каноническое
отображение. Из теоремы когерентности для моноидальных категорий тогда

298 Симметрия и заузливание в моноидальных категориях [Гл. 11
следует, что произведение стрелок f-g строго ассоциативно. Значит, S
является строго моноидальной категорией. Далее, F станет сильным
моноидальным функтором, если в качестве Fq взять тождественное
отображение е —У е, а в качестве i*2(s? t) — единственное каноническое
отображение (все скобки сдвинуты влево)
F2(s,t):F(s)DF(t)^F(s-t). (2)
Условия (3) и (4) § 11.2 для моноидального функтора вытекают при
таком определении из теоремы когерентности для моноидальной
категории М.
Чтобы определить строго моноидальный функтор обратного
направления G : М —У S с условием G(b) = [Ь], заметим, что если Ь, с Е
Е М, то G(b) • G{c) = [b][c] = [Ь,с], и положим
G(b) = [b], G(/) = /,
Go = 1 : 0 -> е, (3)
С2(Ь,с) = 1:[Ь,с]->[ЬПс].
Здесь последнее отображение равно 1, поскольку в силу определения
(1) отображение строк [Ь, с] —> [ЬПс] — это в точности отображение
ЬПс—> ЬПс из М. Тогда для G выполнены условия (3), (4) из § 11.2.
В случае (3) заметим, что отображение Gi □ 1 равно
(G(a) • G(b)) • G(c) ^^ G(a□ b) • G(c),
[a, 6, c] i—> [a □ 6, c]
и как отображение из 5 должно в силу определения (1) совпадать
с отображением а : аП(6Пс) —У (а П 6) П с из 5; внизу диаграммы
(3) § 11.2 получаем отображение G(a), тогда как наверху а' = 1.
Произведение функторов FG : М —>■ М является тождественным
функтором, а произведение GF ему естественно изоморфно.
Следовательно, моноидальная категория М действительно категорно
эквивалентна (посредством моноидальных функторов) строго моноидальной
категории 5, как и утверждалось. □
Обратно, из эквивалентности в утверждении этой теоремы легко
вытекает теорема когерентности.
Теорема2. Если моноидальная категория М эквивалентна
строго моноидальной категории S посредством сильного
моноидального функтора G : М —>■ 5, то для ассоциативности тензорного
произведения □ в М когерентность имеет место.
Доказательство. Пусть v и w — два тензорных слова из к
букв, & 6 и 6' : v —У w — два естественных преобразования между
соответствующими функторами, причем оба построены применением
преобразования ассоциативности ав М. Используем теперь
естественные преобразования Gv и Gw, построенные как в (7), § 11.2 из G2 и Gq.

11.4]
Группы кос Вп и категория кос
299
Аналогично (8), § 11.2, коммутативна диаграмма
п
v(Ga1,...,Gan) —*-^ w(Gau ...,Gan)
\gw
СИ
Gv(au..., an) ^ Gw{ax,..., an),
как и соответствующая диаграмма для О'. Здесь 6S — сокращение от
0(Gai,..., Gan), а 6ш — от 0(ai,..., ап). Но поскольку моноидальная
категория S с G : М —>■ S является строго моноидальной, а в и в'
построены из а, то в = в' в S. Сопоставляя предыдущие диаграммы
для в и в' и зная, что Gv и Gw — изоморфизмы, мы находим, что
GOm — G6'M. Но G — эквивалентность категорий, поэтому существует
и функтор F : S —> М в обратном направлении с FG = 1. При этом
FG0M = FG6'M. Так как FG = 1, то это влечет равенство в = в' в М.
Иначе говоря, в М для ассоциативности (и аналогично для р и Л)
имеет место когерентность, как и утверждалось. □
Упражнения
1. Покажите, что если С — любая категория, то категория функторов С
с композицией в качестве тензорного умножения и с 1с в качестве единицы
является строго моноидальной категорией.
2. Покажите, что если в упр. 1 С = М — моноидальная категория, то
существует сильный моноидальный функтор (Т, Тг,То) : М —>- М такой,
что при а,Ъ,с G М
Г(а) = аП-,
Г2(а,Ь) =аа,&,с : аП(6Пс) -> (аПб)Пс,
(Т0)а = А(а)-1 : а-^еПа.
При этом обратите внимание, что условия (3) и (4), § 11.2 для этого монои-
дального функтора Т превращаются в условия (5), (7) и (9) из определения
моноидальной категории в § 7.1.
3. С помощью предыдущих результатов дайте другое доказательство
теоремы 1, не зависящее от теоремы когерентности. Обратите внимание,
что это дает независимое доказательство когерентности из теоремы 2.
11.4. Группы кос Вп и категория кос
Теперь, как было обещано, реально введем косы и
соответствующую категорию кос.

300 Симметрия и заузливание в моноидалъных категориях [Гл. 11
Коса из трех нитей, такая как показана здесь, образуется путем
перекручивания нитей в пространстве без разрывов и связывания.
Одну такую косу можно умножить на другую, отождествляя правые
концы нитей первой косы (в заданном порядке) с левыми концами
нитей второй косы. Две косы называются равными, если первую
можно деформировать во вторую без пересечения или разрыва нитей.
Вот некоторые примеры кос из трех нитей, где представлены два их
произведения и обратная коса (см. метки):
СТ1СТ2СТ1 СТ2СТ1СТ2
Очевидная деформация последней диаграммы в предыдущую
доказывает равенство
G\G2Cf\ — <J2<JiG2- (l)
Ясно, что такое умножение кос ассоциативно, имеет единицу (три
неперекрученные нити) и обратный элемент. Отсюда получаем
определение артиновой группы кос В%. Она порождается элементами о\
и $2, подчиненными только соотношению (1). Аналогично
описывается группа кос из п нитей Вп.
Более формально, можно определить группу кос Вп как
фундаментальную группу соответствующего пространства Тп, элементами
которого служат наборы из п различных точек. Действительно, пусть
Р — евклидова плоскость, а пространство Тп — множество всех
наборов из п различных точек плоскости Р с очевидной топологией.
Тогда артинову группу кос Вп можно формально определить как
фундаментальную группу такого пространства Тп.
Ясно, что группа кос Вп порождается п — 1 косами &i, которые по
одному разу перекручивают г-ю нить с (г + 1)-й. Выше указан
обратный элемент а^1 с соответствующей деформацией g\G2(J\ в g^oi^i-
Эти образующие 0{ группы Вп подчинены определяющим
соотношениям следующего вида:
ViCTi+iCTi = (Ti+i(Ti(Ti+i,
■3\Ф1-
(2)
(3)
Группа кос В<2 — это просто бесконечная циклическая группа с
(единственным) образующим а±. Группа кос В\ состоит только из
единицы.
Каждая коса из п нитей определяет перестановку п их концов и
соответствующий гомоморфизм Вп —у Sn на симметрическую группу
Sn степени п. Напомним, что Sn порождается п — 1 транспозициями

11.4]
Группы кос Вп и категория кос
301
Тг = (г, г + 1), которые переставляют элементы г и г + 1, причем
определяющие соотношения для них имеют вид
т* = 1, ПЪ = TjTh \i - j\ ф 1, (4)
ПП+1П = П+1ПП+1, г = 1,...,п-1. (5)
Отсюда снова очевиден гомоморфизм ai —> Ti группы Вп на Sn.
Из всех групп кос можно составить категорию кос В. Ее объектами
являются все неотрицательные целые числа п = 0,1,2,..., а
стрелками — косы п —> щ при п ф m стрелки п —> m отсутствуют, и имеется
лишь единичная стрелка 0 —> 0. Этим определяется моноидальная
категория, в которой роль тензорного произведения □ : В х В —» В
играет сложение □ = +; здесь сумма двух объектов (чисел) тип —
это их сумма в обычном смысле, а при операции сложения кос они
кладутся рядом:
Ясно, что эта операция (строго) ассоциативна, а пустая коса на
объекте 0 служит единицей. Поэтому категория кос В с операцией +
является строго моноидальной категорией. Она почти симметричная;
сложение объектов т + п коммутативно, и можно определить
преобразование 7а,ъ '• т + п —>• n + m, пересекая т нитей с другими п
нитями, как на следующем чертеже (для т = 3,п = 2):
Это преобразование 7 естественно по т и п, что можно наглядно
видеть (Joyal, Street, [1993]) для кос ^ : т —> т и Т] : п —У п на

302 Симметрия и заузливание в моноидалъных категориях [Гл. 11
следующей схематической диаграмме:
Требование симметрии 72 — 1 нарушается, но оба шестиугольника
коммутативны, в чем убеждает следующая диаграмма (где, конечно,
не видна ассоциативность):
Реализация кос перекрученными нитями непосредственно
указывает на значение категорий с заузливанием для теории струн в
теоретической физике.
11.5. Когерентность в категориях с заузливанием
Как мы видели в § 1, в симметричной моноидальной категории
имеет место когерентность; коммутативны все формальные
диаграммы, включающие лишь ассоциативность а и коммутативность 7- Это
никоим образом не так в моноидальной категории с заузливанием В;
для двух данных объектов а и Ъ в В может найтись бесконечное
количество канонических автоморфизмов произведения а □ 6, а именно:
1П\1\...П-\1-\...:аПЬ^аПЬ. (1)
Таким образом, на аПЬ действует подгруппа группы кос Вп; как
следствие, диаграммы с участием 7 могут не коммутировать.
В общем случае ситуация аналогична и описывается следующей
теоремой когерентности из (Joyal, Street [1993]):
Теорема1. Пусть В — категория кос, М — моноидальная
категория с заузливанием, Mq — соответствующая обычная категория.

11.5] Когерентность в категориях с заузливанием 303
Тогда существует эквивалентность категорий
homBMc(£,M) ^М0, (2)
где honiBMC обозначает категорию сильных моноидальных заузлен-
ных функторов F : В —>• М. Эквивалентность (2) получается,
если сопоставить каждому функтору F : В —» М его значение на
объекте 1 категории кос В.
Доказательство. По теореме 1, § 11.3 моноидальная категория
М сильно эквивалентна строго моноидальной категории S. Заузли-
вание j в М при этой эквивалентности непосредственно переходит
в заузливание в 5, так что эквивалентность М —> S является сильным
морфизмом категорий с заузливанием. Поэтому достаточно доказать
теорему, заменив М на строго моноидальную категорию S. Для этого
покажем, что имеется изоморфизм категорий
homBMs(B,S)^S0, (3)
где honiBMS состоит из заузленных строго моноидальных функторов
F, а изоморфизм получается, если вновь взять их значения на объекте
1 Е В. Соответствие (3) переводит каждый такой функтор F в объект
F(l) Е S. Обратно, по данному объекту а в S мы хотим определить
заузленный строго моноидальный функтор F = Fa : В —> S с F(l) =
= а. Если функтор F строгий, то он сохраняет произведение, поэтому
положим F(n) = ап. Отображения п —> п в категории кос В должны
перейти в отображения ап —> ап в категории S. Эти отображения
п —>■ п — в точности элементы n-й группы кос Вп, порожденной
стандартными отображениями сг^, i = l,...,n —1.B частности, а : 2 —>
—> 2 должно перейти в
F(o-) = 7а,а : а2 -+ а2 в S.
Отображение Oi в категории В (закручивание нити i вокруг нити i +
+ 1) можно записать как сумму (т. е. □ -произведение)
Gi = l;_i + СГ1 + 1п-г-Ь ^ "^ ^'•
Поэтому мы должны положить (что и делаем)
F((Ti) = U-! + 7а,а + ln-г-Ь ^ "^ «П-
Теперь нужно проверить, что F сохраняет определяющие
соотношения группы кос Вп. Соотношения
Gia- = G.Gu \i - j\ > 1
очевидны, а соотношение
OiOi+\Oi — Oi+\OiOi+\

304 Симметрия и заузливание в моноидалъных категориях [Гл. 11
вытекает из двух коммутативных шестиугольников для 7, показанных
на диаграмме (11) § 11.1 для случая г = 1.
Чтобы завершить определение моноидального функтора F =
= (F, F2, Fq), нужно еще построить подходящее отображение Fq, а
также отображение
F2(m,n) :F(m)\JF(n) -+ F(m + n),
естественное по т и п. Оно должно иметь вид
ашПап ^аш+п
для данного а = F(l). Но поскольку сложение кос т —> т и п —> п
сводится к размещению их рядом, то это отображение можно взять
тождественным.
Нам также требуется отображение F0 : е' —>• Fe; здесь е' —
единичный объект категории 5, тогда как е = 0 и потому F(e) =
= е'; поэтому можно взять в качестве Fq тож:дественное отображ:ение;
при таком выборе функтор F действительно оказывается строгим.
Наконец, докажем, что операция взятие значения на объекте 1 из
(3) является эквивалентностью категорий. Для этого покажем, что
она полна и точна. В самом деле, пусть даны два строгих моноидаль-
ных функтора F, G : В —> S и отображение / : F(l) —> G(l) между
их образами (значениями на объекте 1) в категории So. Мы хотим
найти естественное преобразование в : F —>■ G, значением которого на
объекте 1 является данное отображение /. Но объект п в категории
В равен n-кратному произведению объектов 1, a S является строго
моноидальной категорией и потому обладает n-кратными
степенями относительно умножения □ . Если w — некоторое □ -слово от п
переменных, то строго моноидальный функтор F дает изоморфизм
Fw : F(l)n —у F(n); если положить все переменные равными а, то это
же слово дает n-ю степень от а в категориях В и S. Значит, искомое
естественное преобразование в : F —>• G с условием 6(1) = / должно
делать коммутативной следующую диаграмму:
F(l)n-
^
F(
Fw
п)-
-^G(l)r
ir»G(
G
п)
поэтому нам следует определить вп как GwfnF~1. Из свойств
отображений Fw и Gw вытекает, что при таком определении в будет
естественным преобразованием. □
Замечание. Это доказательство следует рассуждению из
препринта (Joyal, Street [1986]); оно не включено в опубликованную позже
статью (Joyal, Street [1993]).

11.6]
Перспективы
305
В результате получаем теорему когерентности, но не в обычном
смысле. Она не утверждает, что коммутирует любая диаграмма,
составленная из основных отображений а, Л, р и 7, но служит для
описания всех композиций этих отображений, а также всех
порожденных ими эндоморфизмов итерированного тензорного произведения.
Каждому из этих отображений соответствует некоторая коса, как
например:
(аПб)Пс а Ь ^ с
7
сП(аПб),
Эта коса определяет попарные соответствия переменных при
отображении 7, рассматриваемом как естественное преобразование. Можно
неформально выразить результат следующим образом (Joyal, Street
[1993]): две композиции из а,А,р и 7 равны, если им соответствуют
одинаковые косы.
В итоге теорема когерентности формулируется следующим
образом:
Теорема2. Каждая композиция канонических отображений,
действующих на п-кратном произведении в моноидальной
категории с заузливанием М, индуцирует некоторое заузливание (элемент
группы кос). Две такие композиции совпадают на всей категории М,
если и только если они дают один и тот же элемент в Вп.
11.6. Перспективы
Изучение категорий с заузливанием имеет много связей с
другими областями математики, так же как и с некоторыми разделами
квантовой теории поля в физике. В частности, такие связи возникают
в теории струн. Там косу могут образовать переплетающиеся
траектории элементарных частиц — и более того, нити могут
соединяться и разделяться, как на фейнмановских диаграммах, описывающих
столкновения и распад элементарных частиц; здесь мы рассматриваем
косу как состоящую из траекторий (которые принадлежат не
движущимся точкам, а движущимся струнам, например осциллирующим
кольцевым струнам). Наши траектории (выше названные нитями)
тогда заменяются трубками с (топологически) круговым поперечным
сечением. Совокупность конечного числа таких трубок может
рассматриваться как морфизм (путь) в категории с заузливанием. Каждой из
этих трубок можно придать конформную структуру, и то же верно
для столкновений, точнее для их представления на фейнмановских
диаграммах (см. MacLane [1991]). Такие конструкции играют также
роль в двойственности Танака компактных топологических групп (см.
Doplicher, Roberts [1989]).
С другой стороны, одномерные нити в какой-либо косе можно
заменить лентами, а ленты закрутить один или много раз, по или против

306 Симметрия и заузливание в моноидалъных категориях [Гл. 11
часовой стрелки (о категориях лент см. Shum [1994]). Здесь имеются
существенные связи с теорией узлов (Kauffman [1991] [1993]) и снова
с физикой. Нити в косе можно заменить на клубки. В клубке нить
может начаться на нижнем уровне, закрутиться вокруг различных
других нитей, а затем вернуться в другую точку исходной прямой,
как например на следующей диаграмме:
ж
Наконец, есть впечатляющие связи с алгебрами Хопфа и
квантовыми группами (которые представляют собой обобщенные алгебры
Хопфа). Обширная библиография приведена в монографии (Schnider,
Sternberg [1993]) х).
также (*Montgomery [1993], ch. X.) — Прим. ред. пер.

Глава 12
СТРУКТУРЫ В КАТЕГОРИЯХ
В этой главе мы рассмотрим несколько новых понятий,
появившихся в теории категорий. Мы начнем с идеи внутренней категории,
которая описывается диаграммами в объемлющей категории. Затем
исследуем последовательности перемножаемых стрелок — они составляют
нерв категории, который окажется симплициальным множеством.
После этого мы рассмотрим категории высших размерностей —
сначала 2-категории, в которых имеются объекты, стрелки и 2-клетки
между стрелками, а затем категории с 3-клетками и так далее.
12.1. Внутренние категории
В этом параграфе мы работаем внутри объемлющей категории Е,
которая конечно полна, т. е. в ней существуют все конечные
произведения, коуниверсальные квадраты и терминальный объект. Как уже
отмечено во введении, внутри Е можно определить моноиды, группы,
графы и алгебраические объекты других типов. Следуя этому пути,
можно определить внутри Е и категорию; она называется категорным
объектом в Е или внутренней категорией в Е.
Такая внутренняя категория С — (Co,C\,i,do,di) должна состоять
из двух объектов Со и С\ категории Е, которые называются
соответственно объектом объектов и объектом стрелок, а также четырех
стрелок категории Е:
г:Со->Сь d0, dx : d -+ С0, 7 : Ci x c0Ci -+ Сх\ (1)
стрелка г называется единицей, do — областью, d\ — кообластью, 7 —
композицией или умножением. При этом область отображения 7 —
это вершина следующего коуниверсального квадрата:
С\ х с0 Ci ^ С\
dl (2)
С, ^ : Со,
которую в случае Е = Set можно рассматривать как множество
всех пар перемножаемых стрелок. Четыре отображения (1)
подчинены следующим четырем условиям коммутативности, которые просто
выражают стандартные аксиомы категорий. Так, формула
d0i = 1 = d\i : Co —>• Со
(3)

308
Структуры в категориях
[Гл. 12
определяет область и кообласть единичных стрелок, диаграмма
гх1 1хг
Со х с0 С\ >■ С\ х с0 С\ •< С\ х Со Со
2 7
(4)
Сг
Сг
Сг
указывает их действие при умножении 7, диаграмма
^1 S~1 S1 ^2
Сг
Сг
di
Со
d0
■ С\ X Со С\
7
Сг
определяет область и кообласть композиции, а
7X1
do
(5)
Со
С\ х c0Ci x c0Ci
1x7
Сi x c0Ci
^ Сi х Со С\
7
т
-Сг
(6)
выражает ассоциативность композиции в терминах (заведомо
ассоциативного) предела С\ х С\ х С\. Это определение по существу
совпадает с тем, которое дано в диаграмме (3), § 2.7.
Поскольку эти диаграммы выражают аксиомы категорий, то кате-
горный объект в Set — не что иное, как обычная малая категория.
Категорный объект в Grp — это категория, в которой множество
объектов Со и множество стрелок С\ являются группами, причем
все структурные отображения i,do,di и 7 являются гомоморфизмами
групп. Для случаев г и do это означает, что коммутативны диаграммы
Со х Со
С г у-С г
Со
Сг,
Сг xCi
d0xdo
Со х Со
■Сг
■ Со,
где то и TTii — умножение в группах Со и С\ соответственно. Но Со х
х Со и С\ х С\ определяют категорию-произведение С х С; поэтому
указанные диаграммы означают также, что групповые операции то
и TTii вместе определяют морфизм категорий, т. е. функтор тп : С х
х С —>■ С, который ассоциативен и имеет обратный. Таким образом,
категорный объект в Grp — то же самое, что групповой объект в Cat.
Подобная перестановка алгебраических структур возможна и в
общем случае: категория Х-объектов в категории У-объектов является
и категорией У-объектов в категории Х-объектов.

12.1]
Внутренние категории
309
Внутренний функтор f : С —>■ D между двумя внутренними
категориями С и D в общей объемлющей категории Е — это, по
определению, пара отображений fo : Со ^ Dq и fi : С\ -У Di из
Е, которые в качестве функции объектов и функции стрелок делают
коммутативными следующие очевидные диаграммы:
fiXf:
Сг х CoCi ^^ D± х d^ d Г Со —^ d
Сг
Du
D1^^Do^-^D1.
(7)
Столь же очевидно описываются внутренние естественные
преобразования между двумя внутренними функторами из С в D.
Эти внутренние функторы, однако, идут из С в другую
внутреннюю категорию D, а не в универсум Е; не существует внутренней
категории, которая бы соответствовала универсуму. Так, внутренние
функторы в категории Set не включают функторов Н : С —>■ Set
(таких, как вездесущие hom-функторы). Это заставляет по-новому
сформулировать понятие внутреннего функтора. Поскольку
множество объектов Со мало, а категория множеств кополна, то можно
заменить функцию объектов Но : Со —> Set копроизведением множеств
и его проекцией в множество Со'.
тг:Я0 = U Н0с -> С0.
сес0
(8)
Действие стрелок / : с —у с' в совокупности определяет отображения
«действия»:
С\ х с0Но ->• Но.
Таким образом, если дана внутренняя категория С в категории
Е, то нам приходится рассматривать объекты из Е над Со, такие
как 7г : Н —У Со, do : С\ —> Со. При этом левый Co-объект из Е
определяется как объект 7г : Н —У Со над Со вместе с отображением
действия
fjtidx СоН^ Я, (9)
причем здесь С\ является объектом над Со с отображением области
do '. С\ —> Со. Это отображение действия /i обязано быть
отображением над Со в том смысле, что коммутативна следующая диаграмма,
где р\ является проекцией на первый множитель:
CiXCoff-
Pi
Y
Су —
н
(10)
■ Со]

310
Структуры в категориях
[Гл. 12
оно должно напоминать о действии группы на множестве в том
отношении, что должны выполняться аксиомы единицы и
ассоциативности, а именно:
Ci х СоН
Ci х СоН
Ci х c0Ci x CoH —^ d х СоН
7X1
т
d х СоЯ э- Я.
(П)
Левый С-объект такого рода называется также внутренней
диаграммой во внутренней категории С или (следуя Борсо) внутренним
функтором со значениями в базе (internal base-valued functor). Здесь важно
отметить, что в случае Е = Set введенное понятие как раз охватывает
известные функторы из внутренней категории в объемлющую
категорию Set.
Морфизм Н —» К таких (левых) С-объектов — это просто морфизм
ф : Н —у К из Е, сохраняющий введенную структуру, т. е. делающий
коммутативными обе диаграммы
Н
Со
^К
'■ Со,
dx^^tftxc/
Н
/1
к.
(12)
Для обычных функторов Н и К со значениями в категории
множеств это соответствует определению естественного преобразования;
первая диаграмма утверждает, что ф всегда отображает Н(с) в К (с),
а вторая — что это отображение коммутирует с композицией (в чем
и состоит естественность).
Категорные объекты в категории групп изучаются в § 12.8.
12.2. Нерв категории
Пусть дана категория С (в категории Set). Рассмотренный выше
предел (72 = С\ х с0 С\ состоит из всех перемножаемых пар стрелок из
С. Можно также рассмотреть, как в (5), § 2.7, перемножаемые строки

12.2]
Нерв категории
311
из п стрелок, где
difi = d0/2, • • •, di/n_i = d0fn- (1)
Они содержатся в итерированном пределе
Сп = С\ х CqC\ x cQ ''' х CqC\ (n множителей) . (2)
Добавив Со, мы превратим последовательность множеств
Со, Ci,..., Сп,...
в симплициальное множество (в смысле § 7.5). При п = 1 нам уже
даны операторы грани do,di : С\ —>• Со. При п > 1 операторы
грани di = Сп —>■ Cn_i, г = 0,1,...,п определяются удалением или
композицией соответствующих стрелок, а именно:
^0(Л, • • • ,/п) = (/2, • • • ,/п),
di(/i,...,/n) = (/i,...,/j/j+i,...,/n), j = l,...,n-1, (3)
dn(/i, • • • ,/n) = (Л, • • • ,/n-i)-
Операторы вырождения Sj определяются добавлением подходящих
единичных отображений id0f B подходящих местах, а именно:
So(/l, ... ,/п) = (^0/i,/l,/2, • • • ,/п),
Sj(fi,-..,fn) = (Л,...,Л',^1Л-,Л'+1,...,/п) (4)
при j = 1,..., п. В результате снова получаем перемножаемые строки
из стрелок. Без труда проверяются тождества для операторов грани
и вырождения, установленные в (11)—(13), § 7.5. Можно
проиллюстрировать их геометрический смысл, представив стрелки fi как ребра
симплексов с очевидной композицией, например:
Аналогично, нерв внутренней категории в Е — это симплициаль-
ный объект в Е.
Упражнение
1. Для случая нерва категории проверьте тождества операторов грани
и вырождения, приведенные выше.

312
Структуры в категориях
[Гл. 12
12.3. 2-категории
Термин 2-категория обозначает систему из 2-клеток или
отображений, которые можно перемножать двумя различными, но
коммутирующими способами.
В первом примере (см. § 2.5) роль отображений играют
естественные преобразования. Пусть даны три функтора
R,S,T:C ^В
и естественные преобразования а : R^- S и г : S ^ Т. В § 2.4 мы
определили вертикальное произведение естественных преобразований
г • а : R —>■ Т по формуле (г • а) (с) = тс о ас для каждого объекта
с Е С. При этом сначала выполняется преобразование а, а затем г:
С
В,
С
в.
Но имеется и горизонтальное умножение естественных
преобразований, согласованное с композицией функторов (§ 2.5), как на
следующей диаграмме:
R'oR
С
А.
S'oS
Здесь (а' о а)с = a'Sc о R'ac для каждого объекта с Е С. Оба
умножения ассоциативны, и они коммутируют между собой (теорема 1,
§ 2.5).
Аналогично, имеется два коммутирующих способа умножения го-
мотопий между непрерывными отображениями. Вспомним
топологию: гомотопия 6 : f ~ g между непрерывными отображениями /
и д пространства X в пространство Y — это непрерывная
деформация отображения / в д. Иначе говоря, это непрерывное отображение
О : X х / —у У, где / — отрезок с концами 0 и 1, причем для каждой
точки х е X выполнены тождества 6(х, 0) = f(x) и в(х, 1) = д(х). Если
<р = д ~ h — другая гомотопия, то можно образовать вертикальное

12.3]
2-категории
313
произведение <р • в : / ~ h (см. ниже). С другой стороны, если даны
отображения f',g':Y—^Zn гомотопия в' : /' —> Ы между ними, то
можно образовать горизонтальное произведение в' о в : /' о / ~ д' о д,
которое является гомотопией между произведениями отображений.
Однако вертикальное произведение двух гомотопий if в, в котором О
используется при 0 < t < 1/2, з> ср при 1/2 < t < 1, оказывается
неассоциативным. Чтобы получить категорию, мы должны использовать
в качестве 2-клеток классы гомотопий гомотопий! Горизонтальное
умножение при этом коммутирует с вертикальным.
Эти (и другие) примеры приводят к общему понятию 2-категории
как структуры, состоящей из объектов, стрелок между объектами и 2-
клеток между стрелками, причем 2-клетки можно перемножать двумя
способами, горизонтальным и вертикальным.
Рассмотрим обычную категорию С с объектами а, Ь,... и
горизонтальными стрелками / : а —> Ъ. В 2-категории П на С дополнительно
имеются 2-клетки а : / => д с областью / и кообластью д, где / и д —
параллельные стрелки в (7, скажем из а в Ь, что можно выразить
формулой
a:f^g:a^b (1)
и изобразить (по вертикали) следующим образом:
а Ъ,
(2)
Для 2-клеток имеется два различных умножения. Во-первых, если
дана другая 2-клетка
а' : /' => д' : Ъ -+ с,
то имеется горизонтальное произведение а' о а:
(3)
/ /'
/'о/
(4)

314
Структуры в категориях
[Гл. 12
согласованное (вверху и внизу) с композицией стрелок. Потребуем,
чтобы 2-клетки составляли категорию относительно этого
горизонтального умножения. В частности, это означает, что для любого
объекта Ъ имеется единичная 2-клетка 1 : 1 => 1 : Ъ —у 6, которая является
двусторонней единицей относительно такого умножения. При этом
область а \-> f и кообласть а \-> д являются функторами из
горизонтальной категории 2-клеток в горизонтальную категорию стрелок.
Одновременно для каждой пары объектов а, Ъ 2-клетки из а в Ъ
служат стрелками категории с вертикальным умножением:
равно
Pool
Ь,
(5)
которое будет обозначаться жирной точкой. Для такого умножения
также существуют вертикальные единичные 2-клетки If : / => /.
Две дополнительные аксиомы связывают горизонтальное с
вертикальным. Во-первых, потребуем, чтобы горизонтальное произведение
двух вертикальных единиц также было вертикальной единицей, как
на диаграмме
а
Р\
^ h
а'
N
Р'\
N
>-
1f'f = !/' olf-
(6)
/ Г f'of
Далее, если дан набор 2-клеток
а : / => д : а —>• 6, а' : /' => д' : Ъ —>• с,
Р : д=> h:a->b, ft' : д' => Ы : Ь -)► с,
то произведения, показанные ниже:
(7)
(8)

12.3]
2-категории
315
должны удовлетворять равенству
(/?'о/3).(а'оа) = (/?'.а')о(/?.а):/'о/
h! о h : а —>
(9)
Здесь (и в других местах) вертикальное умножение обозначается
жирной точкой •, а горизонтальное умножение — кружком о (или
просто приписыванием одного множителя к другому). Аксиома (9)
называется обменом в середине четверки (middle four exchange), так
как здесь меняются местами средние два аргумента в
последовательности четырех 2-клеток /?', ft, <У, а.
Отметим, что в этой структуре возможно и горизонтальное
умножение 2-клетки на 1-клетку: нужно просто умножить 2-клетку с
любой стороны на вертикальную единицу 1-клетки. Например,
произведение f о а имеет вид
/'
/7
L/' с = а
f'oa С.
(10)
9 Г f'g
Его можно записать и так (приставив ус /' к 2-клетке а):
f
—>-
а а
->- с.
(11)
Такое определение 2-категории охватывает примеры, приведенные
выше: во-первых, 2-категорию топологических пространств,
непрерывных отображений и классов гомотопий; во-вторых, 2-категорию
Cat малых категорий, функторов и естественных преобразований.
Вертикальную категорию на объектах а и Ъ будет удобно
обозначить Т(а,Ь). Тогда правило перестановки (9) и правило (6) для
вертикальных единиц вместе означают, что горизонтальное умножение
является бифунктором между вертикальными категориями:
КаАс:Т(Ъ,с) хГ(о,6)4Г(о,с).
(12)
Кроме того, операция Ua, отображающая каждый объект а в его
единичную стрелку 1а : а —> а, является функтором из терминальной
категории 1 (с одним объектом и одной стрелкой):
Ua:l^T(a,a).
(13)
Этих двух операций достаточно, чтобы описать 2-категорию в
терминах ее вертикальных hom-категорий Т(а,Ь) — аналогично тому, как
описывается обычная категория в терминах hom-множеств (§ 1.8).
Таким образом, чтобы задать 2-категорию, нужны следующие данные:

316 Структуры в категориях [Гл. 12
1) множество объектов а, 6, с,...;
2) функция, которая сопоставляет каждой упорядоченной
паре объектов (а, Ь) категорию Т(а,Ь);
3) для каждой упорядоченной тройки объектов (а, Ь, с) —
функтор (12), который называется умножением
(композицией) ;
4) для каждого объекта а — функтор Ua вида (13).
При этом умножение 3) должно удовлетворять закону
ассоциативности, а функтор Uа — определять левую и правую единицу для
такого умножения.
Эта совокупность аксиом для 2-категорий равносильна
предыдущей. Она вполне аналогична определению категории в терминах
hom-множеств, которые здесь заменены hom-объектами Т(а,Ь). Эти
объекты — не множества, а категории (т. е. объекты категории всех
(малых) категорий Cat); можно сказать, что это обогащенные hom-
множества. Их конструкция использует тот факт, что Cat имеет
произведения и терминальный объект. Часто бывает полезно обобщить
и эту ситуацию: использовать вместо Cat моноидальную категорию
V и рассматривать категории, обогащенные в У, — с объектами из V
в качестве hom-объектов и с умножением и единицами,
определенными как выше. (См. также § 7.7 и замечание в § 1.8 о АЪ-категориях.)
Такие обогащенные категории систематически изучаются в
монографии (Kelly [1982]); см. также работу (Dubuc [1970]).
12.4. Операции в 2-категориях
Многие свойства функторов, установленные для случая Cat,
непосредственно переносятся и на другие 2-категории. Примером может
служить сопряжение. Пусть в 2-категории даны две 1-клетки между
одними и теми же объектами, направленные противоположно:
/
9
Они называются сопряженными (/ слева, д справа), если существуют
2-клетки г) и г (единица и коединица):
г] : 1 => gf :а-> а, г : fg => 1Ь : Ъ -+ Ъ, (1)
для которых выполнены следующие равенства:
ief) • (ffl) = lf:f=>fgf=>f:a^b, (2)
(де) • (ад) = 1д :д^ gfg^ g:b^a. (3)
На самом деле в 2-категории Cat эти два равенства в точности
выражают два треугольных тождества для единицы т] и коединицы

12.4]
Операции в 2-категориях
317
г (обычного сопряжения между функторами (9), § 4.1). В первом
равенстве ef фактически означает горизонтальное произведение elf,
так что формула (2) в точности соответствует следующей диаграмме:
+ Ъ
+ Ъ.
(4)
Здесь в левой части представлены два горизонтальных умножения 2-
клеток, за которыми следует вертикальное умножение результатов.
Это можно схематически изобразить следующим образом, опустив If
внизу слева:
^Ь.
(5)
Аналогично, левая часть равенства (3) включает следующие
вертикальные произведения:
ъ —^ъ.
Эта диаграмма выражает тот факт, что горизонтальное произведение
де склеивается вдоль / с горизонтальным произведением щ и в
результате получается единичная клетка из д в д.
Сходным образом можно поднять в 2-категории понятие (правого)
расширения Кана (§ 10.3). Именно, пусть в 2- категории даны объекты

318
Структуры в категориях
[Гл. 12
ттг, с, а и стрелки &, t в следующей конфигурации:
m ■
-^ а.
(в)
Тогда правое расширение Кана для t по к — это стрелка г и 2-клетка
е : гк => £
m
(7)
такие, что любая другая 2-клетка а, имеющая вид а : sk => t для
некоторой стрелки s : с —>- а, является произведением 2-клетки г
и однозначно определенной 2-клетки ст, см. ниже:
-^ а,
(8)
Иначе говоря, гиг универсальны как дополнение диаграммы (6) до
треугольника. Разумеется, это та же конфигурация, которая
использовалась в § 10.3 при описании правых расширений Кана обычных
функторов. Как и для любых алгебраических объектов, нужно определить
морфизмы между 2-категориями. Они называются 2-функторами. По
определению, 2-функтор
F :T -+U
между 2-категориями Т и £/ — это тройка функций, переводящих
объекты, стрелки и 2-клетки из Т в соответствующие компоненты из U,
причем сохраняются все категорные структуры (области, кообласти,
единицы и произведения). Если G — другой такой функтор G : Т —»
—у U между теми же 2-категориями, то 2-естественное преобразование
в : F -^ G — это функция, отображающая каждый объект a G Т
в стрелку в а : Fa —> Ga из U, причем для каждой 2-клетки а : / => д

12.4]
Операции в 2-категориях
319
из Т выполнено следующее равенство (между 2-клетками с усами):
Ff Gf
Fa f<*
Fb^^Gb = Fa^^Ga
/« Gb. (9)
Fg
Gg
В частности, применительно к ребрам (1-клеткам) это означает, что в
является (обычным) естественным преобразованием между
соответствующими обычными функторами F и G. Читатель может
проверить, что 2-категории, 2-функторы и 2-естественные преобразования
между ними служат объектами, стрелками и 2-клетками некоторой
2-категории! Ее часто обозначают 2-Cat.
Но теперь можно сделать шаг в следующую размерность. Если
даны 2-естественные преобразования в : F —>- G и (^ : F —» G между
одними и теми же 2-функторами F и G, то между этими
преобразованиями также имеются определенные отображения \± : в —>- ср,
которые называются модификациями. Именно, такая модификация \i
должна сопоставлять каждому объекту a Е Т 2-клетку /ia : ва => ipa,
такую что следующие 2-произведения совпадают для любой 2-клетки
a: f =>g:
Ff
Fa
Fa Fb
Ga Gb. (10)
Fg fb Va Gg
В трехмерном виде это можно представить следующим образом:
Ga
Передняя, задняя, нижняя и верхняя грани куба — это соответственно
Fa, Ga, /ib и /ia. Правая и левая грани коммутируют (поскольку
преобразования в и ср естественны). Равенство (10) означает, что
последовательное применение передней грани, а затем нижней, дает
тот же результат, что и применение верхней и задней грани.

320
Структуры в категориях
[Гл. 12
Сказанное подразумевает, что модификация \i рассматривается
как 3-клетка /л : 0 => (р. Если при этом в качестве 2-клеток взять 2-
естественные преобразования, в качестве стрелок 2-функторы, а в
качестве объектов — объекты, то мы получим 3-категорию. Как мы
увидим в следующем параграфе, подобно тому как 2-категорию
можно определить как категорию с hom-множествами, обогащенными за
счет перехода в Cat, можно формально определить и 3-категорию
как категорию с hom-множествами, обогащенными за счет перехода в
2-Cat.
12.5. Категория как одно множество
Обычно категорию рассматривают как структуру, состоящую из
двух множеств — множества объектов и множества стрелок 0 . Но
можно дать определение категории, использующее лишь множество
стрелок, если рассматривать объекты как стрелки особого рода,
а именно единичные. Такое определение уже было приведено в § 1.1.
Здесь мы дадим другое определение категории в терминах стрелок,
которое дальше применяется к n-категориям. Именно, категория —
это множество стрелок С с двумя функциями s,t : С —>■ С, которые
называются источник и цель, и (не всюду определенной) бинарной
операцией #, которая называется композицией; при этом для всех
x,y,z Е С должны выполняться следующие аксиомы.
Операция хфу определена, если и только если sx = ty, и в этом
случае
s(x#y)=sy, t(x#y)=tx; (l)
х# sx = х, tx#x = x; (2)
(хфу)ф z = х ф {у ф z\ если все выражения определены; (3)
ttx — tx — stx. (4)
Стрелка х является единичной, если и только если х = sx или,
эквивалентно, х — tx.
В этих терминах, функтор F : С —^ D — это просто функция из
множества С в множество D, такая что
sF = Fs, tF = Ft:C -+ D (5)
F(x#y)=Fx#Fy, (6)
если определено х # у (а тогда ввиду (5) определено и Fx # Fy).
Ясно, что такое определение категории и функтора равносильно
стандартному определению в терминах множества объектов и
множества стрелок.
х) В буквальном смысле это верно лишь для малых категорий; в общем
случае нужно вместо множеств говорить о классах. — Прим. ред. пер.

12.5]
Категория как одно множество
321
Аналогично, 2-категорию можно рассматривать как одно
множество X, состоящее из 2-клеток (например, естественных
преобразований). Тогда прежние 1-клетки (стрелки) и 0-клетки (объекты)
становятся особыми вырожденными 2-клетками. На множестве 2-клеток X
имеются две категорные структуры, горизонтальная (#о5 so,to) и
вертикальная (#i,si,ti). Каждая из них удовлетворяет приведенным
выше аксиомам категории, а также следующим условиям:
1) каждая единица для О-структуры является единицей и для 1-
структуры;
2) обе категорные структуры коммутируют между собой.
Разумеется, условие 2) означает, что
S0Sx = SiSq, Ml = Mo, *0«1 = Sit0, t0ti = Mo, (?)
и если a, /3 = 0,1 или 1,0, то для всех x,y,u,v выполнены равенства
ta(x#py) = (tax)#0(tay),
sa(x#py) = (sax)#p(say),
если обе части определены.
Поскольку Sox и tox в 0-структуре являются единицами, то они
остаются единицами и в 1-структуре в силу условия (1).
Следовательно,
Sls0 = s0, hso = so, sit0 = t0, tito=t0. (9)
С учетом условия (7) получаем также:
s0si = so, soh = so, t0si = t0, toh = t0. (10)
Эти правила вместе с (4) позволяют вычислить любое произведение,
составленное из s и t. Результаты согласуются с интуитивной
картиной ребер 2-клетки, а именно:
Sl = SiSi = tiSb
S0S± = S0ti = SqSq = tiSQ = So • • t0 = t0Si = t0ti = Sit0 = tit0,
Siti.
После этих приготовлений мы готовы к тому, чтобы дать
определение 3-категории и вообще n-категории для любого натурального
числа п. Последняя представляет собой множество X с п различными
категорными структурами (#i5Si,ti) для г = 0, ...,п — 1, которые
коммутируют между собой, причем каждая единица структуры i
является единицей и для структур j при j > i. Иначе говоря, каждая
пара #i5#j5 где j > г, составляет 2-категорию. Это непосредственно
приводит к определению полезного понятия cj-категории: i = 0,1, 2,...

322 Структуры в категориях [Гл. 12
12.6. Бикатегории
Иногда умножение морфизмов в предполагаемой категории
оказывается ассоциативным лишь с точностью до изоморфизма. Это
приводит нас к понятию бикатегории г), которая напоминает 2-категорию,
но умножение стрелок в ней ассоциативно лишь с точностью до
изоморфизма, определяемого некоторой 2-клеткой. Формально бика-
тегория В состоит из 0-клеток а,6,..., 1-клеток /, д,... и 2-клеток
/я, сг,...; соотношение между их областями и кообластями показано на
следующей диаграмме:
f 9 h
>- >- >-
г d, (1)
>- >■ >-
Г 9 Ы
где 1-клетки действуют по горизонтали, а 2-клетки по вертикали.
Более подробно, каждой 1-клетке / соответствуют 0-клетки а и Ъ
в качестве области и кообласти (/ : а —> Ь), а областью и кообластью 2-
клетки р служат параллельные 1-клетки / и /'. При этом каждой паре
0-клеток (а, Ъ) соответствует (обычная) категория В (а, 6), в которой
объектами служат все 1-клетки /, /',... из а в Ь, а стрелками являются
2-клетки между этими 1-клетками. В категории В(а,Ь) вертикальное
умножение 2-клеток ассоциативно (разумеется), и для каждого
объекта / : а —>■ Ъ имеется 2-клетка 1/ : / => /, играющая роль единицы
относительно такого умножения. Вертикальное умножение
обозначается кружком о или приписыванием одного множителя к другому.
Далее, для каждой упорядоченной тройки 0-клеток а,Ь,с имеется
бифунктор
* : В{Ь, с) х В(а, Ъ) -+ В(Ь, с), (2)
который называется горизонтальным умножением и обозначается *.
Таким образом, для 2- и 1-клеток на диаграмме (1) определены
произведения а * р, г * а и д * / следующего вида:
9*f h*g
>- >-
™ d. (3)
— >- >■
g'*f h'*g'
книге (*Цаленко, Шульгейфер [1974]), гл. 1, § 8, с. 48 термин бикате-
гория имеет другой смысл. — Прим. ред. пер.
а*р С,

12.6]
Бикатегории
323
Кроме того, для каждой 0-клетки а имеется единичная 1-клетка
1а : а —> а (которая настоящей единицей не является; см. ниже).
Это горизонтальное умножение *, хотя и записанное как обычное
умножение в категории, не является строго ассоциативным; оно
ассоциативно лишь с точностью до естественного изоморфизма а между
функторами итерированного умножения, а именно:
B(c,d) х В(Ь,с) х В(а,Ь)
1х*
*xl
B{c,d) х В(а,с)
B(b,d) хВ(а,Ъ)
' B(a,d).'
(4)
Чтобы а было естественным преобразованием функторов, требуется
коммутативность следующей диаграммы из 2-клеток, показанных на
диаграмме (1):
h*(g*f) ^—^ (h*g)*f
т*(а*р)
(т*а)*р
(5)
Л'*($'*/')-гг* С*'* 5')*'/'-
Предполагаемые единичные стрелки 1а обязаны действовать как
единицы относительно горизонтального умножения лишь с точностью до
следующих изоморфизмов Аир, естественных по / Е В (а, Ь):
Ра,Ъ I / * 1а => /, К,Ъ : h * / => /•
(6)
Тройка естественных преобразований а, А, р подчинена
следующим двум аксиомам когерентности. Возьмем упоминавшиеся стрелки
f,g и ft, а также k : d —>- е. Тогда должен быть коммутативен
следующий пятиугольник, скопированный из аксиом моноидальной
категории ((5), § 7.1):
k*(h*(g*f))
к*а
k*((h*g) */)
(k*h)*(g* f)
•((k*h)*g)*f
«*/ (7)
Y
(fc* (ft *#))*/.
Для Аир, аналогично случаю моноидальной категории ((7), § 7.1),
требуется коммутативность следующей диаграммы (левых и правых

324
Структуры в категориях
[Гл. 12
единиц):
1*Л
p*i (8)
0 * / = 0 * /•
В обычной категории С обращение всех стрелок позволяет перейти
к двойственной категории Сор (§ 2.2). Для бикатегории (как и для 2-
категории) возможны два способа дуализации: один — путем
обращения стрелок, другой — путем обращения 2-клеток!
Имеется и соответствующее определение функтора (т. е. морфиз-
ма) между бикатегориями. Предоставляем читателю дать свое
собственное определение или обратиться к литературе (см., например,
Benabou [1967]).
12.7. Примеры бикатегории
В качестве первого примера отметим, что любая моноидальная
категория М является и бикатегорией В с одной 0-клеткой.
Действительно, возьмем ее объекты а, 6,... в качестве 1-клеток, тензорное
произведение — в качестве композиции, а стрелки из М — в качестве
2-клеток. Тогда естественные изоморфизмы а, А и р из определения
моноидальной категории подходят и для построения бикатегории,
поскольку удовлетворяют тем же тождествам, выраженным в
пятиугольнике (7), § 12.6 и квадрате (8), § 12.6. Обратно, бикатегория В
с единственной 0-клеткой является по той же причине моноидальной
категорией. Как следствие, теорема когерентности для моноидальных
категорий распространяется и на отображения р,Хиав бикатегориях.
Следующим примером служит категория колец — точнее,
бикатегория, в которой:
0-клетки — кольца R, 5, Т;
1-клетки — бимодули sAr : R —>■ S;
2-клетки — гомоморфизмы бимодулей А —> А'.
Введем умножение 1-клеток. Пусть tBs обозначает бимодуль, левый
по Т, правый по S. Элементами обычного тензорного произведения
модулей В ®s А служат суммы произведений 6(8>а, где b Е В, a Е А;
при этом bs 0 а = b 0 sa {s G S) и т. д. Ясно, что такое тензорное
произведение является бимодулем, левым по Т и правым по R. Если
теперь иСт — бимодуль, правый по Т и левый по U, то хорошо
известная ассоциативность тензорного умножения модулей:
С 0т (В (g)5 А') = (С 0т В) 05 А' (1)
позволяет взять его и в качестве горизонтального умножения.
Вертикальным умножением служит обычное умножение гомоморфизмов
бимодулей А -» А' -» А"'.
Теперь опишем бикатегорию распорок. В исходной категории С
должны существовать все коуниверсальные квадраты. Для каждой

12.7]
Примеры бикатегорий
325
пары стрелок s,£ из С с общей кообластью Ъ выберем коуниверсаль-
ный квадрат, который назовем каноническим:
(2)
Распорка (span) от а к Ь в исходной категории С — это, по
определению, пара стрелок из некоторой общей вершины v с концами в а и в Ь:
(з)
Бикатегория Span (С) имеет следующие компоненты:
0-клетки — объекты данной категории С;
1-клетки — распорки из С;
2-клетки между двумя распорками из а в Ъ — те 1-клетки х : v —> с'
из С, которые делают коммутативными следующие треугольники:
Ъ.
/
(4)
Вертикальное произведение двух таких 2-клеток соответствует
произведению (в С) серединных стрелок х. Горизонтальное произведение
распорок между а и Ь и между Ь и с определяется (выбранным
ранее) каноническим коуниверсальным квадратом для двух серединных
стрелок:
А''
(5)
С.
Чтобы доказать ассоциативность такого умножения, рассмотрим три
последовательные распорки, связывающие а, Ь, с и d, к которым
добавлены сверху три (канонических) коуниверсальных квадрата, см.
диаграмму:
z
У
W
(6)
d.

326
Структуры в категориях
[Гл. 12
Поскольку квадраты коуниверсальны, то и составленные из них
прямоугольники тоже коуниверсальны. Поэтому каждое из тройных
произведений данных распорок соответствует коуниверсальному
квадрату с вершиной в верхней 0-клетке z. Поскольку коуниверсальный
квадрат каждой диаграммы единствен с точностью до
изоморфизма, то мы получаем требуемый естественный изоморфизм а между
тройными произведениями. Отсюда видно также, что коммутативна
пятиугольная диаграмма для а. Тождественная распорка на 0-клетке
а состоит из двух единичных стрелок из а в а (в категории С). Взяв
другую распорку из а в Ь и построив коуниверсальный квадрат:
а с (7)
V Ч1 /f \
а а Ь,
получаем искомое естественное преобразование Л для этого
произведения. Проверка остальных аксиом предоставляется читателю.
Бикатегории также называются слабыми 2-категориями. Такое
название подразумевает, что возможно понятие слабой п-категории.
Это действительно так, и n-категории с различными определениями
появляются в вопросах теоретической физики (см. Baez с соавторами
[1995], [1996]).
12.8. Скрещенные модули и категории в Grp
Вернемся к примерам категорных объектов. Оказывается, кате-
горные объекты в Grp — по существу то же самое, что скрещенные
модули, которые появляются в теории гомотопии. Приведем здесь
доказательство этого замечательного результата, сообщенное мне
Георгием Джанелидзе.
Скрещенный модуль задан, если задана пара групп Н и Р, причем
Р действует на Н, а также гомоморфизм ос: Н —у Р, согласованный
с этим действием. Это означает, если действие элемента р Е Р на
элемент h обозначено /ip, что для h,k Е Н и p,q G Р выполнены
равенства h1 = h,
(hp)q = hpq, (hk)p = WW, oc (hp) = p((x h)p~\
Скрещенные модули появляются в теории гомотопии.
Вспомним теперь (см. § 12.1), что внутренняя категория в
категории Grp состоит из двух групп Со и С\ и четырех гомоморфизмов
групп
d С0, Со -^-^ Си 7 : Ci х CoCi -)• Сь (1)
d0

12.8]
Скрещенные модули и категории в Grp
327
для которых выполнены соответствующие условия. Мы утверждаем,
во-первых, что в этой системе можно забыть о категорном умножении
7- Система полностью определяется диаграммой групп и
гомоморфизмов
di
С\ ^ ^Со, Со ^Ci, (2)
где
d0i = 1 = d\i (3)
и коммутаторная подгруппа, порожденная ядрами гомоморфизмов do
и d\, состоит только из единицы:
[kerdo, kerdi] = 1. (4)
Проверим, что гомоморфизмы групп d§,d\ и г, вместе взятые,
действительно помнят умножение 7- Запишем произведение
перемножаемой пары морфизмов
Л г, ^
а —> о —> с
в виде g о f. Это гомоморфизм групп, умножение в которых будем
записывать просто gi#2- Поэтому
(9i92) ° (/1/2) = (9i ° Л)(02 ° Л),
если определены оба произведения справа (снова закон обмена в
середине четверки) 1). Применив этот результат к единице 1& объекта
Ь, получаем
gof = (Ы^М/!^) = (l^^l-^l"1)^^) = /(l^ol-V (5)
Положив / = g = 1^, получаем
и = ы^1 о 1-%,
откуда
Это вытекает и из того факта, что отображение ( )-1 : С —> С, где
С — групповой объект, является функтором.
Подстановка в (5) дает равенство
9°f = f419-
Иначе говоря, категорное умножение 7 определяется групповой
структурой на С. С другой стороны,
g о / = {gl-llb) о (U1,"1/) = (9 ° h)(4l ° l^XU ° /) = дЦЧ-
1) См. § 12.3. — Прим. пер.

328
Структуры в категориях
[Гл. 12
Поэтому групповое умножение удовлетворяет условию
fl^g = gl^f.
Если объект Ъ Е Со является единицей группы Со, то 1& = i(b)
является единицей в С\, поэтому fg = gf. Но если Ъ является единицей
группы Со, то категорная стрелка д с областью Ъ лежит в kerdo,
и аналогично / лежит в kerdi. Поэтому равенство fg = gf означает,
что коммутант (4) сводится к единице.
Обратно, пусть дана диаграмма (2) в категории Grp,
удовлетворяющая условиям (3) и (4). Тогда мы можем определить категорное
умножение 7 : С\ х с0 С\ —> С\ •> положив
i(gj) = Щхд или gi^f.
Непосредственно проверяется, что 7 служит умножением в некоторой
внутренней категории для Grp.
Далее, соотношения (2), (3) и (4) в категории Grp определяют
скрещенный модуль а : Н —» Р. Именно, положим
Я = кег^0, Р = С0-
Тогда ограничение d[ отображения d\ на ker do является
гомоморфизмом
а : Н -> Р.
В самом деле, имеется короткая точная последовательность
1^ ker d0 -► Ci -^> Co -► 1,
которая стандартным образом определяет действие группы Со на Н =
= keido'. выберем в С\ по представителю для каждого элемента из
Со и трансформируем каждый элемент из ker do выбранным
представителем. Заметим, что для отображения i : Со —У С\ выполнено
равенство doi = 1, так что г расщепляет указанную короткую точную
последовательность. Обратно, читатель может показать, что
скрещенный модуль а : Н —>■ Р определяет расщепленную точную
последовательность групп. Эти взаимно обратные конструкции показывают, что
категория скрещенных модулей эквивалентна категории диаграмм (2)
в Grp с условиями (3) и (4).

Дополнение. Основания теории категорий
329
Дополнение. Основания теории категорий
Мы определили категорию в терминах множеств: как множество
объектов и множество стрелок г). Однако категории можно
определить и непосредственно — и, возможно, использовать их как
основание всей математики, не применяя теоретико-множественные аксиомы
Цермело-Френкеля. Приведем это прямое описание.
1. Объекты и стрелки. Категория состоит из объектов а, Ь, с и
стрелок f,g,h. В категории множеств объектами являются
множества, а стрелками — функции.
2. Область. Для каждой стрелки / некоторый объект а является ее
областью, а некоторый объект Ъ — кообластью; в этом случае мы
пишем / : а —>■ Ъ.
3. Композиция. Если даны стрелки / : а —У Ь и д : Ь —У с, то их
композиция или произведение — это некоторая стрелка д о f : а —>■ с.
4. Ассоциативность. Если, кроме того, имеется стрелка h : с —> d, то
тройное произведение ассоциативно:
h о (д о /) = (h о д) о / : а -> d.
5. Единицы. Каждый объект Ъ имеет единичную стрелку 1^ : Ъ —у Ъ.
Если имеется стрелка f : а —> Ь, то 1& о / = /. Если дана стрелка
g : Ъ -у с, то g о \ь = д.
Элементарный топос — это категория, в которой имеется
дополнительная структура: терминальный объект, коуниверсальные
квадраты, отображение истина, классификатор подобъектов, булевы степени
(множества подмножеств). Эта дополнительная структура должна
удовлетворять следующим аксиомам.
6. Терминальный объект. Имеется терминальный объект 1, в
который из каждого объекта а ведет ровно одна стрелка а —> 1.
7. Коуниверсальные квадраты. Для каждой пары стрелок / : а —>•
—>■ Ъ «— с : g с общей кообластью Ъ существует коуниверсальный
квадрат, определенный согласно § 3.4:
(1)
В частности (положим 6=1), для любых двух объектов а и с
существует произведение а х с.
:) См. сноску в гл. 12, с. 320. — Прим. ред. пер.

330
Дополнение. Основания теории категорий
8. Истина. Существует объект П (объект истинностных значений) г)
и мономорфизм t : 1 —> П, который называется истиной; для
каждого мономорфизма т : а —>- Ъ существует единственная
стрелка ф : Ь —> П, для которой следующий квадрат является
коуниверсальным:
а >■ 1
гр
9. Булевы степени. Каждому объекту Ъ сопоставляется объект РЪ и
стрелка еь : Ь х Р6 —>> П, такая что для каждой стрелки / : Ь х
х а —у П существует единственная стрелка д : а —у РЬ, делающая
коммутативной следующую диаграмму:
Ъ х а >■ Q
1х9\ (3)
т
Ь х РЬ—г^П.
Чтобы понять смысл этих аксиом, применим их к общеизвестной
категории всех множеств. Любое одноэлементное множество может
служить в этой категории терминальным объектом, поскольку на
каждом множестве а имеется единственная функция а —> 1. Если
даны два множества а и Ь, то коуниверсальный квадрат для двух
стрелок а —> 1 «— Ъ — это теоретико-множественное произведение и
его проекции на множители а и Ъ.
В качестве объекта истинностных значений П возьмем какое-либо
множество 2, состоящее из двух объектов 1 и 0, а в качестве
мономорфизма t : 1 —у 2 — очевидное включение. Тогда мономорфизм т : а —>
—> Ъ из аксиомы 8 соответствует подмножеству а С Ъ. Это
подмножество имеет, как известно, характеристическую функцию ф : Ъ —> 2,
которая равна 1 или 0 в зависимости от того, принадлежит или нет
элемент у G Ъ подмножеству а. Отсюда возникает коуниверсальный
квадрат (2).
Аксиома 9 описывает РЬ, множество всех подмножеств s С fr,
которое часто называют булевой степенью. Положим Sb(x,s) равным
0, если элемент х G Ъ принадлежит подмножеству s, и равным 1 в
противном случае. В результате получим коуниверсальный квадрат (3).
Итак, перечисленные аксиомы топоса выполняются в категории
множеств. Из них вытекают многие сильные утверждения. Например,
х) В книге (*Goldblatt [1979]) объект Q называется классифицирующим
объектом, а вместе со стрелкой истина — классификатором подобъектов. —
Прим. пер.

Дополнение. Основания теории категорий
331
эти аксиомы гарантируют существование всех конечных категорных
произведений и коуниверсальных квадратов, а также всех конечных
копроизведений, включая начальный объект, которым служит пустое
множество 0. Из них вытекает существование правого сопряженного
к произведению а х Ъ как функтору относительно а; это экспоненциал
с6, для которого (см. §4.6)
hom(a xb,c) = (a,cb).
Теперь категорию множеств можно описать как элементарный то-
пос, определенный выше, с тремя дополнительными свойствами:
(a) он вполне разделим;
(b) в нем выполнена аксиома выбора (АС);
(c) в нем имеется объект натуральных чисел (NNO).
При рассмотрении этих свойств полезно представлять себе объекты
как множества, а стрелки — как функции.
Утверждение, что топос вполне разделим, означает, что если даны
две различные стрелки /, g : а —У Ь, то найдется стрелка р : 1 —у а, для
которой fp ф др. Мотивировка состоит в том, что если функции / и
д различны, то они должны различаться в некоторой точке р, т. е. на
некотором элементе р множества а.
Аксиома выбора (АС) требует, чтобы для каждой сюръекции
/ : а —у Ъ существовало правое обратное отображение т : Ъ —у а,
для которого, таким образом, jот — 1&. Отображение т выбирает для
каждой точки р : 1 —у Ъ множества Ъ некоторую точку в а, а именно
произведение тр, которое под действием / отображается на р.
Объект натуральных чисел (NNO) можно описать как множество
N с начальным объектом О : 1 —У N и функцией следования s : N —У
—у N, в терминах которой функции / : N —у X можно определить
рекурсивно, указав /(0) и композицию / о s. Иначе говоря, NNO-
объект N — это диаграмма
1 4 7V 4 7V,
состоящая из точки О в N и такого отображения s, что для любых
стрелок 1 —у Ъ —У Ъ найдется единственная стрел
делает следующую диаграмму коммутативной:
стрелок 1 —у Ъ —У Ъ найдется единственная стрелка / : N —у Ь, которая
1 ^Ъ >Ъ.
При обычной записи функций это означает, что
/О = h, fs = kf,

332 Дополнение. Основания теории категорий
т. е. можно определить /, указав f(0) и выразив f(n + 1) через f(n).
Таким образом, категория множеств может быть описана как
вполне разделимый топос, в котором выполнена аксиома аксиома
выбора и имеется объект натуральных чисел. Эта совокупность
аксиом слабо совместна с некоторым вариантом аксиом Цермело (т. н.
ограниченный Цермело; см. (Mac Lane, Moerdijk [1992])). Впервые она
появилась в работе (Lawvere [1964]), где названа элементарной теорией
категории множеств . Один из примеров элементарного топоса —
пучки на топологическом пространстве; (см. Mac Lane, Moerdijk [1992]).
В этих аксиомах часто принимается, что классифицирующий
объект П имеет ровно два элемента. Это превращает его в булеву алгебру.

Указатель обозначений
333
Указатель обозначений
АЬ
АС
Adj
Alg
Bool
CAb
CAT
CGHaus
CRng
Cat
Cat/
Colim
Colim
у
Comp Bool
Comp Haus
Compmet
Cone
Cop
can
Л
Dom
ETAC
End^
Ens
Ensv
Euclid
Fin
Finord
Fid
GLn(K)
Grp
Grph
Haus
Абелевы группы, с.23
с. 331
Малые категории и сопряжения, с. 123
<, Е >-алгебры
Булевы алгебры
Коммутативные компактные топологические
группы, с. 112
Категории и функторы
Компактно порожденные хаусдорфовы
пространства, с. 215
Коммутативные кольца и гомоморфизмы, с. 23
с. 23
с. 48
с. 81
с. 248
Полные булевы алгебры, с. 145
Компактные хаусдорфовы пространства, с. 147,
154
с. 105
с. 84
с. 45
с. 197
с. 79, 81
с. 70
с. 43
Конец функтора £, с. 258
с. 22
Множества и функции в рамках универсума У,
с. 21-22
Евклидовы пространства векторов и
ортогональные преобразования, с. 254
Скелет категории конечных множеств, с. 263
Конечные ординалы и все отображения между
ними как между множествами, с. 22
с. 105
с. 24
Группы и их гомоморфизмы, с. 23
Ориентированные графы и их морфизмы, с. 62
Хаусдорфовы пространства и непрерывные
отображения, с. 159

334
Указатель обозначений
Id
K-Alg
K-Mod
Lan
L conn
Lim
Lim
Lim
Matrx
Met
Mod
Mod-R
Mon
MonB
Moncat
Nat
NNO
Open(X)
Ord
Preord
R-Mod
R-Mod-S
Ractc
Ran
Rel
Rng
SAFT
Ses-A
Set
Set*
oet^;
Smgrp
Span(C)
Top
с 269
с. 105
if-модули и их морфизмы, с. 23
Левое расширение Кана, с. 277
Локально связные топологические пространства,
с. 160
с. 83
с. 83
с. 81
Натуральные числа и прямоугольные матрицы
в качестве морфизмов, с. 21
с. 70
с. 48
Правые i^-модули, где R — некоторое кольцо, с. 23
Моноиды и их морфизмы, с. 23
с. 199
Моноидальные категории и строгие морфизмы,
с. 191
с. 53
с. 331
с. 47
Упорядоченные множества и отображения,
сохраняющие порядок, с. 145
с. ПО
Левые i^-модули и их морфизмы, с. 23
с. 37
с. 203
Правое расширение Кана, с. 273
с. 38
Кольца и их гомоморфизмы, с. 23
с. 161
Короткие точные последовательности А-модулей
Все малые множества и их отображения, с. 23
Множества с отмеченной точкой, с. 23
с. 22
Полугруппы и их морфизмы, с. 170
с. 325
Топологические пространства и непрерывные
Toph
Vet
VctF
z(n)07
отображения, с. 23
Топологические пространства и классы
гомотопных отображений, с. 23
Векторные пространства и линейные отображения
с. 37
с. 212

Указатель обозначений
335
0
1
2
3
(П,Е)
(#г,вг,*г)
(Cat- 4. -С)
biC
С la
Т IS
la
стт
С -± А
О - Grph
РТТ
Т = {Т^Ф)
VTT
#
•
о
cod
и
^
dom
hom (Ь, с)
ida
№,с)
(5, П , е, а, Л, £>)
(Б, П,е>
(F,G,r/,e> :Х-> А
(F,G,^):X^A
<Х,Т,тЫ
А
^>
0
cLact
аП6
оПЬ
а0Ь
а х b
Пустая категория, с. 21
Категория с одним объектом, с. 21
Два объекта, с. 21
Три объекта, с. 21
Универсальные алгебры типа т, с. 147, 177
с. 321
с. 136
Объекты под b при действии функтора С, с. 58
Объекты над а при действии функтора С, с. 59
Категория запятой, с. 60
с. 17
с. 181
с. 111
с. 63
с. 181
Монада, с. 162
с. 181
с. 320
Вертикальное умножение естественных
преобразований, с. 312
Горизонтальное умножение естественных
преобразований, с. 312
с. 17
с. 79
с. 252
с. 17
с. 20
с. 17
с. 258
Моноидальная категория, с. 189
Строго моноидальная категория, с. 188
Сопряжение, с. 100
Сопряжение, с. 96
с. 163
с. 22
с. 27
с. 41
с. 202
с. 76
с. 84
с. 227
с. 84

336
Терминология
Терминология
В этой книге В других источниках
стрелка отображение (Е & М), морфизм
(Gr)
область (domain) источник (source) (Ehr)
кообласть (codomain), об- цель (target) (Ehr)
ласть значений
граф предкатегория, схема диаграмм
(Mil)
естественное преобразова- морфизм функторов (Gr),
ние
функториальное отображение
(G-Z)
естественный изоморфизм естественная эквивалентность
(Е& М)
теперь неупотребительно)
мономорфизм (monic) monomorphism
эпиморфизм (epi) epimorphism, epic
идемпотент проектор (Gr)
противоположный двойственный
копроизведение сумма
уравнитель ядро, ядро разности
коуниверсальный квадрат расслоенное произведение (Gr),
декартов квадрат
универсальный квадрат кодекартов квадрат (comeet)
универсальная стрелка левое свободное отображение
(G-Z)
предел существует предел представим (Gr)
предел проективный предел, обратный
предел
копредел индуктивный предел, прямой
предел
конус к функтору проективный конус, обратный ко-
нус (G-Z)
конус от функтора индуктивный конус, ко-конус (со-
сопе)
левый сопряженный косопряженный (Mit),
сопряженный
правый сопряженный сопряженный (Mit),
косопряженный
морфизм сопряжения (unit adjunction morphism (G-Z)
of adjunction)

Терминология
337
треугольные тождества
монада
бипроизведение (в АЬ-
категориях)
АЬ-категория
г квази-обратен к ц (G-Z)
тройка
прямая сумма
предаддитивная категория
(устаревшее)
Gr = Grothendieck (Гротендик)
Ehr = Ehresmann (Эресман)
Mit = Mitchell (Митчелл)
E & M = Eilenberg & Mac Lane (Эйленберг и Маклейн)
G-Z = Gabriel-Zisman (Габриэль-Цисман)

338
Список литературы
Список литературы
Adamek, J., Herrlich, H., Strecker, G. E. [1990]: Abstract and concrete
categories. New York: John Wiley & Sons 1990.
Andre, Michel [1967]: Methode simpliciale en algebre homologique et algebre
commutative IV. Lecture Notes in Mathematics, Vol. 32. Berlin-Heidelberg-
New York: Springer 1967.
— [1970]: Homology of simplicial objects. Proceeding of the AMS symposium
in Pure Mathematics on Applications of Categorical Algebra, pp. 15-36.
Providence: American Mathematical Society 1970.
Baez, J., Dolan, J. [1995]: Higher dimensional algebra and topological quantum
field theory. J. Math. Phys. 36, 60-105 (1995).
Baez, J., Neuchli, M. [1996]: Higher dimensional algebra, braided monoidal 2-
algebras. Adv. Math. 121, 196-244 (1996).
Barr, M., Beck, J. [1966]: Acyclic models and triples. Proceedings of the
Conference on Categorical Algebra, La Jolla, 1965, pp. 336-344. New York:
Springer 1966.
— [1969]: Homology and standard constructions. Seminar on Triples and
Categorical Homology Theory, pp. 245-336. Vol. 80. Lecture Notes in Mathematics.
Berlin-Heidelberg-New York: Springer 1969.
Barr, M., Wells, С [1985]: Toposes, triples, and theories. Vol. 278. Grundlehren
der Math. Berlin: Springer 1985.
— [1990]: Category theory for computing science. Englewood Cliffs, NJ:
Prentice-Hall 1990.
Bass, Hyman [1968]: Algebraic K-theory. Mathematics Lecture Note Series. New
York-Amsterdam: W.A. Benjamin, Inc. 1968. (Перевод: Басе Х.
Алгебраическая К-теория. М.: Мир, 1973.)
ВепаЪои, J. [1964]: Algebre elementaire dans les categories avec multiplication.
// C.R. Acad. Sci. Paris 258, 771-774 (1964).
Benabou, Jean [1963]: Categories avec multiplication. // C.R. Acad. Sci. Paris
256, 1887-1890 (1963).
— [1965]: Criteres de representabilite des foncteurs. C.R. Acad. Sci. Paris 260,
752-755 (1965).
— [1967]: Introduction to bicategories, pp. 1-77. Vol. 40. Springer Lecture Notes
in Mathematics. Berlin: Springer 1967.
Birkhoff, Garrett [1967]: Lattice theory. AMS Colloquium Publications, Vol. 25,
3rd Ed. Providence: American Mathematical Society 1967. (Перевод: Биркгоф
Г. Теория решеток. М.: Наука, 1984.)
Borceux, F. [1994]: Handbook of categorical algebra; vol. 1, Basic category
theory. Vol. 2, Categories and structures, Vol. 3, Categories of sheaves.
Encyclopedia of mathematics and its applications, Vols. 50, 51, and 52. Cambridge:
Cambridge University Press 1994.
Bourbaki, N. [1948]: Elements de mathematique, Vol. VII. Algebre, Livre II,
Algebre multilineaire, ch. 3. Actualites scientifiques et industrielles, 1044. Paris:
Hermann 1948. (Перевод: содержится в кн.: Бурбаки Н. Алгебра.
Алгебраические структуры. Линейная и полилинейная алгебра. М.: Наука, 1986.)

Список литературы
339
— [1957]. Elements de mathematique, Vol. XXII, Theorie des ensembles, Livre I,
Structures, ch. 4. Actualites scientifiques et industrielles, 1258. Paris: Hermann
1957. (Перевод: Бурбаки H. Теория множеств. М.: Мир, 1965.)
Brown, Ronald [1964]. Function spaces and product topologies. Quart. J. Math.
15, 238-250 (1964).
Buchsbaum, David A. [1955]: Exact categories and duality. Trans. Am. Math.
Soc. 80, 1-34 (1955).
Bucur, I.jDeleanu, A. [1968]: Introduction to the theory of categories and
functors. London-New York-Sydney: John Wiley and Sons, Ltd. 1968. (Перевод:
By кур И., Деляну А. Введение в теорию категорий и функторов. М.: Мир,
1972.)
Cartan, Я., Eilenberg, S. [1956]: Homological algebra. Princeton: Princeton
University Press 1956. 4th ed.: 1965. (Перевод: Картан А., Эйленберг С.
Гомологическая алгебра. — М.: ИЛ, 1960.)
Cassels, J. W. S., Frohlich, A., Edrs. [1967]: Algebraic number theory. London:
Academic Press 1967. (Перевод: Алгебраическая теория чисел (ред. Касселс
Дж., Фрелих А. М.: Мир, 1969))
Cohen, Paul J. [1966]: Set theory and the continuum hypothesis. New York-
Amsterdam: W. A. Benjamin 1966. (Перевод: Коэн П. Дж. Теория множеств
и континуум-гипотеза. М.: Мир, 1969.)
Cohn, P. М. [1965]: Universal algebra. New York-Evanston-London: Harper and
Row 1965. (Перевод: Кон П. Универсальная алгебра. М.: Мир, 1968.)
Day, В. J., Kelly, G. М. [1969]: Enriched functor categories. Reports of the
Midwest Category Seminar, Vol. Ill, pp. 178-191, Vol. 106, Lecture Notes in
Mathematics. Berlin-Heidelberg-New York: Springer 1969.
Doplicher, S., Roberts, J. E. [1989]: A new duality for compact groups. Invent.
Math. 98, 157-221 (1989).
Dubuc, E. J. [1970]: Kan extensions in enriched category theory. Lecture Notes
in Mathematics, Vol. 145. Berlin-Heidelberg-New York: Springer 1970.
Dubuc, E. J., Porta, H. [1971]: Convenient categories of topological algebras,
and their duality theory. J. Pure Appl. Algebra. 1, 281-316 (1971).
Dubuc, E. J., Street, R. [1970]: Dinatural transformations. Reports of the
Midwest Category Seminar, Vol. IV, pp. 126-138, Vol. 137, Lecture Notes in
Mathematics. Berlin-Heidelberg-New York: Springer 1970.
Ehresmann, Ch. [1965]: Categories et structures. Paris: Dunod 1965.
Eilenberg, S., Elgot, S. E. [1970]: Recursiveness. New York-London: Academic
Press 1970.
Eilenberg, S., Kelly, G. M. [1966a]: Closed categories. Proceedings of the
Conference on Categorical Algebra, La Jolla, 1965, 421-562. New York: Springer
1966.
— [1966b]: A generalization of the functorial calculus. J. Algebra 3, 366-375
(1966).
Eilenberg, S., Mac Lane, S. [1942a]: Group extensions and homology. Ann.
Math. 43, 757-831 (1942).
— [1942b]: Natural isomorphisms in group theory. Proc. Nat. Acad. Sci. U.S.A.
28, 537-543 (1942).
— [1943]: Relations between homology and homotopy groups. Proc. Nat. Acad.
Sci. U.S.A. 29, 155-158 (1943).

340
Список литературы
— [1945]: General theory of natural equivalences. Trans. Am. Math. Soc. 58,
231-294 (1945).
— [1947]: Cohomology theory in abstract groups I. Ann. Math. 48, 51-78 (1947).
Eilenberg, S., Moore, J. C. [1965]: Adjoint functors and triples. Illinois J. Math.
9, 381-398 (1965).
Eilenberg, S., Steenrod, N. E. [1952]: Foundations of algebraic topology.
Princeton: Princeton University Press 1952. (Перевод: Эйленберг С, Стинрод Н.
Основания алгебраической топологии. М.: Физматгиз, 1958.)
Epstein, D. В. А. [1966]: Functors between tensored categories. Inventiones
Math. 1, 221-228 (1966).
Fox, R. H. [1943]: Natural systems of homomorphisms. Preliminary Report.
Bull. Am. Math. Soc. 49, 373 (1943).
Freyd, P. [1964]: Abelian categories: An introduction to the theory of functors.
New York: Harper and Row 1964.
— [1972]: Aspects of topoi. Bull. Austral. Math. Soc. 7, 1-72, 467-481 (1972).
Freyd, P. J., Scedrov, A. [1993]: Categories, allegories. Amsterdam: North-
Holland 1993.
Freyd, P. J., Yetter, D. [1990]: Braided compact monoidal categories with
applications to low dimensional topology. Adv. Math. 77, 1950-1982 (1990).
Gabriel, P. [1962]: Des categories abeliennes. Bull. Soc. Math. France 90, 323-
448 (1962).
Gabriel, P., Ulmer, F. [1971]: Lokal Praesentierbare Kategorien. Vol. 221.
Springer Lecture Notes in Mathematics. Berlin: Springer 1971.
Gabriel, P., Zisman, M. [1967]: Calculus of fractions and homotopy theory.
Ergebnisse der Mathematik, Vol. 35. Berlin-Heidelberg-New York: Springer
1967. (Перевод: Габриэль П., Цисман М. Категория частных и теория
гомотопий. М.: Мир, 1971.)
Godement, R. [1958]: Theorie des faisceaux. Paris: Hermann 1958. (Перевод:
Годеман Р. Алгебраическая топология и теория пучков. М.: ИЛ, 1961.)
Godel, К. [1940]: The consistency of the continuum hypothesis. Studies, Ann.
of Math., No. 3. Princeton: Princeton University 1940.
Goguen, J. A. [1971]: Realization is universal. Math. Syst. Theory 6, 359-374
(1971).
Gratzer, G. [1968]: Universal algebra. Princeton: Van Nostrand and Co. Inc.
1968.
Grothendieck, A. [1957]: Sur quelques points d'algebre homologique. Tohoku
Math. J. 9, 119-221 (1957). (Перевод: Гротендик А. О некоторых вопросах
гомологической алгебры. М.: ИЛ, 1961.)
Hatcher, W. S. [1968]: Foundations of mathematics. Philadelphia-London-
Toronto: W. B. Saunders Co. 1968.
Herrlich, H. [1968]: Topologische Reflexionen und Coreflexionen. Lecture Notes
in Mathematics, Vol. 78. Berlin-Heidelberg-New York: Springer 1968.
Ruber, P. J. [1961]: Homotopy theory in general categories. Math. Ann. 144,
361-385 (1961).
— [1962]: Standard Constructions in abelian categories. Math. Ann. 146, 321-
325 (1962).

Список литературы
341
Hurewicz, W. [1941]: On duality theorems. Bull. Am. Math. Soc. 47, 562-563
(1941).
Hurewicz, W.j Steenrod, N. E. [1941]: Homotopy relations in fibre spaces. //
Proc. Nat. Acad. Sci. USA, 1941, v. 27, N 1, p. 60-64.
Isbell, J. R. [I960]: Adequate subcategories. Illinois J. Math. 4, 541-552 (1960).
— [1964]: Subobjects, adequacy completeness and categories of algebras,
Rozprawy Mat. 36, 3-33 (1964).
— [1968]: Small subcategories and completeness. Math. Syst. Theory 2, 27-50
(1968).
Johnstone, P. T. [1977]: Topos theory. LMS Math. Monographs. New York:
Academic Press 1977. (Перевод: Дэюонстон П. Теория топосов. М.: Наука,
1986.)
— [1982]: Stone spaces. Vol. 3. Cambridge Studies in Advanced Mathematics.
Cambridge: Cambridge University Press 1982.
Johnstone, P. Т., Pare, P. [1978]: Indexed categories and their applications.
Vol. 661. Lecture Notes in Mathematics. Berlin: Springer 1978.
Joyal, A., Street, R. [1991]: Tortile Yang-Baxter operators in tensor categories.
Adv. Math. 71, 43-51 (1991).
— [1991]: The geometry of tensor calculus I. Adv. Math. 88, 55-112 (1991).
— [1986]: Braided monoidal categories, revised. Macquarie Math. Reports no.
86081, Macquarie University, Australia.
— [1993]: Braided tensor categories. Adv. Math. 102, 20-78 (1993).
Joyal, A., Tiemey, M. [1984]: An extension of the Galois theory of Grothendieck,
Mem. Am. Math. Soc. 390 (1984).
Kan, D. M. [1958]. Adjoint functors. Trans. Am. Math. Soc. 87, 294-329 (1958).
Kapranov, M., Voevodsky, V. [1994]: Braided monoidal 2-categories and Manin-
Schechtmann higher braid groups. Journal of Pure and Applied Algebra 92,
241-267 (1994).
— [1994]: Braided monoidal 2-categories, 2-vector spaces and Zamolodchikov
tetrahedral equations. Symposia in Pure Mathematics, Vol. 56, part 2, pp. 177-
260. Providence, RI: American Mathematical Society 1994.
Kauffman, L. [1991]: Knots and physics. Singapore: World Scientific 1991.
— [1993]: Knots and physics, 2nd edition. Riveredge, NJ: World Scientific 1993.
Kelly, G. M. [1964]: On Mac Lane's condition for coherence of natural
associativities. J. Algebra 1, 397-402 (1964).
— [1982]: Basic concepts of enriched category theory. LMS Lecture Notes.
Cambridge: Cambridge University Press 1982.
Kelly, G. M., MacLane, S. [1971]: Coherence in closed categories. // J. Pure
Appl. Algebra, 1971, v. 1, N 1, p. 97-140. Erratum: J. Pure Appl. Algebra, 1971,
v. 1, N 2, p. 219.
Kelly, G. M., Street, R. [1974]: Review of the elements of 2-categories, pp. 75-
103. Vol. 420. Springer Lecture Notes in Mathematics. Berlin: Springer 1974.
Kleisli, H. [1962]: Homotopy theory in abelian categories. Canad. J. Math. 14,
139-169 (1962).
— [1965]: Every standard construction is induced by a pair of adjoint functors.
Proc. Am. Math. Soc. 16, 544-546 (1965).

342
Список литературы
Lambek, J. [1968]: Deductive systems and categories I. Math. Syst. Theory 2,
287-318 (1968).
Lambeck, J., Scott, P. J. [1986]: Introduction to higher order categorical logic.
Cambridge: Cambridge University Press 1986.
Lamotke, K. [1968]: Semisimpliziale algebraische Topologie. Berlin-Heidelberg-
New York: Springer 1968.
Lawvere, F. W. [1963]: Functorial semantics of algebraic theories. Proc. Nat.
Acad. Sci. U.S.A. 50, 869-873 (1963).
— [1964]: An elementary theory of the category of sets. Proc. Nat. Acad. Sci.
U.S.A. 52, 1506-1511 (1964).
— [1966]: The category of categories as a foundation for mathematics.
Proceedings of the Conference on Categorical Algebra, La Jolla, 1965, pp. 1-21. New
York: Springer 1966.
— [1970]: Quantifiers and sheaves, pp. 329-334. Nice: Actes du congres
International des Mathematiciens 1970.
Linton, F. E. J. [1966]: Some aspects of equational categories. Proceedings of
the Conference on Categorical Algebra, La Jolla, 1965, pp. 84-95. New York:
Springer 1966.
Mac Lane, S. [1948]: Groups, categories, and duality, Proc. Nat. Acad. Sci.
U.S.A. 34, 263-267 (1948).
— [1950]: Duality for groups. Bull. Am. Math. Soc. 56, 485-516 (1950).
— [1956]: Homologie des anneaux et des modules. Colloque de topologie al-
gebrique, Louvain 1956, pp. 55-80.
— [1963a]: Homology. Berlin-Gottingen-Heidelberg: Springer 1963. (Перевод:
Маклейн С. Гомология. М.: Мир, 1966.)
— [1963b]: Natural associativity and commutativity. Rice Univ. Studies 49, 28-
46 (1963).
— [1965]: Categorical algebra. Bull. Am. Math. Soc. 71, 40-106 (1965).
— [1969]: One universe as a foundation for category theory. Reports of the
Midwest Category Seminar, Vol. Ill, pp. 192-201. Lecture Notes in Mathematics,
Vol. 106. Berlin-Heidelberg-New York: Springer 1969.
— [1970]: The Milgram bar construction as a tensor product of functors; стр. 135-
152 в: Steenrod Algebra and its Applications, Lecture Notes in Mathematics,
Vol. 168. Berlin-Heidelberg-New York: Springer 1970.
— [1991]: Coherence theorems and conformal field theory, pp. 321-328.
Category theory. 1991. Proceedings of an International Summer Category Theory
Meeting. CMS Conference Proceedings Vol. 13. Providence, RI: American
Mathematical Society 1991.
— [1995]: Categories in geometry. Algebra Logic, pp. 169-178 in Mathematica
Japonica Vol. 42.
— [1996]: The development and prospects for category theory. Appl. Categor.
Struct. 4, 129-136 (1996).
Mac Lane, S., Birkhoff, G. [1967]: Algebra. New York: Macmillan 1967. 3rd
edition. New York: Chelsea 1988.
Mac Lane, S., Moerdijk, I. [1992]: Sheaves in geometry and logic. A first
introduction to topos theory. New York: Springer-Verlag 1992.

Список литературы
343
Makkai, М., Pare, R. [1989]: Accessible categories: The foundations of
categorical model theory, Contemporary Math. 104. Providence, RI: American
Mathematical Society 1989.
Makkai, M., Reyes, G. E. [1977]: First order categorical logic. Vol. 611. Lecture
Notes in Mathematics. Berlin, Springer.
Manes, E. [1969]. A triple-theoretic construction of compact algebras. Seminar
on Triples and Categorical Homology Theory, pp. 91-119. Lecture Notes in
Mathematics, Vol. 80. Berlin-Heidelberg-New York: Springer 1969.
May, J. P. [ 1967]: Simplicial objects in algebraic topology. Princeton: Van
Nostrand Co., Inc. 1967.
McLarty, C. [1992]: Elementary categories, elementary toposes. Oxford:
Clarendon 1992.
Mitchell, B. [1965]: Theory of categories. New York-London: Academic Press
1965.
Negrepontis, J. W. [1971]: Duality in analysis from the point of view of triples.
J. Algebra 19, 228-253 (1971).
— [1971a]: On absolute colimits. J. Algebra 19, 80-95 (1971).
Pare, R. [1971]: On absolute colimits. J. Algebra 19, 80-95.
Pareigis, B. [1970]: Categories and functors. New York: Academic Press 1970.
Quillen, D. G. [1967]: Homotopical algebra. Lecture Notes in Mathematics, Vol.
43. Berlin-Heidelberg-New York: Springer 1967.
Samuel, P. [1948]: On universal mappings and free topological groups. Bull.
Am. Math. Soc. 54, 591-598 (1948).
Schnider, S., Sternberg, S. [1993]: Quantum groups: from coalgebras to Drinfeld
algebras, Boston: International Press, Inc. 1993.
Schubert, H. [1970a and b]: Kategorien, Vols. I and II. Berlin-Heidelberg-New
York: Springer 1970. (Английский перевод: Schubert H. [1972]: Categories. —
Berlin: Springer, 1972.)
Shum, M. C. [1994]: Tortile tensor categories. J. Pure Appl. Algebra 43, 57-110
(1994).
Solovay, R. M. [1966]: New proof of a theorem of Gaifman and Hales. Bull. Am.
Math. Soc. 72, 282-284 (1966).
Stasheff, J. D. [1963]: Homotopy associativity of H-spaces, I. Trans. Am. Math.
Soc. 108, 275-292 (1963).
Steenrod, N. E. [1940]: Regular cycles of compact metric spaces. Ann. Math.
41, 833-851 (1940).
— [1967]: A convenient category of topological spaces. Michigan Math. J. 14,
133-152 (1967).
Swan, R. G. [1968]: Algebraic K-theory. Lecture Notes in Mathematics, Vol.
76. Berlin-Heidelberg-New York: Springer 1968.
Tierney, M. [1972]: Sheaf theory and the continuum hypothesis, pp. 13-42. Vol.
274. Lecture Notes in Mathematics. Berlin: Springer 1972.
Ulmer, F. [1967a]: Properties of dense and relative adjoint functors. J. Algebra
8, 77-95 (1967).
— [1967b]: Representable functors with values in arbitrary categories. J. Algebra
8, 96-129 (1967).

344
Список дополнительной литературы
Watts, С. Е. [I960]: Intrinsic characterizations of some additive functors. Proc.
Am. Math. Soc. 11, 5-8 (1960).
Yoneda, N. [1954]: On the homology theory of modules. J. Fac. Sci. Tokyo, Sec.
I. 7, 193-227 (1954).
— [I960]: On ext and exact sequences. J. Fac. Sci. Tokyo, Sec. I, 8, 507-526
(1960).
Список дополнительной литературы
Андреев П. В., Бунина Е. П., Захаров В. К., Михалев А. В. [2002]:
Основания теории категорий в рамках локальной теории множеств. В кн.
Международная алгебраическая конференция. Тезисы докладов. С.-Пб., 2002,
с. 10-11.
Артамонов В. А. [1991]: Универсальные алгебры. В кн. Общая алгебра.
Т. 2. Под ред. Л. А. Скорнякова. — М.: Наука, 1991, с. 295-367.
Гельфанд С. П., Манин Ю. И. [1998]: Методы гомологической алгебры. Т. 1.
Введение в теорию когомологий и производные категории. М.: Наука, 1988.
Захаров В. К., Михалев А. В. [2002]: Локальная теория классов и множеств
как основание для теории категорий. В кн. Математические методы и
приложения. Труды девятых математических чтений МГСУ. М.: МГСУ, 2002,
с. 91-94.
Кацов Е. Б. [1978]: Тензорное произведение модулей// Сиб. матем. ж., т. 19,
№2, 318-327 (1978).
Кашу А. И. [1997]: Функторы и кручения в категориях модулей. Кишинев:
Академия Наук республики Молдова. Институт математики, 1997.
Курош А. Г., Лившиц А. X., Шульгейфер Е. Г. [I960]: Основы теории
категорий// Успехи мат. наук, 1960, т. 15, №6, с. 3-52.
Лившиц А. X., Цаленко М. Ш., Шульгейфер Е. Г. [1962]: Теория категорий.
Алгебра. Топология. Итоги науки. М.: ВИНИТИ, 1962, с. 90-106.
Мальцев А. И. [1970]: Алгебраические системы. М.: Наука, 1970.
Плоткин Б. И. [1991]: Универсальная алгебра, алгебраическая логика и
базы данных. М.: Наука, 1991.
Полин С. В. [1973]: Категории функторов в многобразии универсальных
алгебр. В сб. Матем. исследования. Кишинев, т. 8, вып. 1(27), Штиинца,
1973, с. 130-140.
Полин С. В. [1974]: Морита-эквивалентность категорий// Вестник Москов.
ун-та, сер. матем., 1974, №2, с. 41-45.
Цаленко М. Ш. [1989]: Моделирование семантики в базах данных. М.:
Наука, 1989.
Цаленко М. П., Шульгейфер Е. Г. [1967]: Категории. Алгебра. Топология.
Геометрия, 1967. Итоги науки. М.: ВИНИТИ, 1969, с. 9-57.
Цаленко М. П., Шульгейфер Е. Г. [1974]: Основы теории категорий. М.:
Наука, 1974.
Цаленко М. П., Шульгейфер Е. Г. [1975]: Категории. Алгебра. Топология.
Геометрия. Итоги науки и техники. М.: ВИНИТИ, 1975, с. 51-147.
Шульгейфер Е. Г. [1972]: Категория функторов над многообразием
универсальных алгебр// Изв. АН СССР, сер. матем., 1972, 36, №2, с. 386-400.

Список дополнительной литературы
345
Шульгейфер Е. Г. [1991]: Категории. В кн. Общая алгебра, т. 2. Под ред.
Л. А. Скорнякова. — М.: Наука, 1991, с. 368-460.
Шульгейфер Е. Г. [1993]: О проективности свободных объектов// Успехи
матем. наук, 1993, 48, №5, с. 187-188.
Шульгейфер Е. Г. [1996]: О категорной эквивалентности многообразий
многосортных алгебр многообразиям односортных алгебр// Фунд. и приклад,
матем., 1996, 2, №1, с. 279-288. (Исправление к статье «О категорной
эквивалентности многообразий многосортных алгебр многообразиям
односортных алгебр» (1996, т. 2, №1, с. 279-288)// Фунд. и приклад, матем.,
1998, 4, №1, с. 477).
Adamek, J., Rosickii, J. [1994]: Locally presentable and accessible categories.
London Mathematical Society Lecture Note Series, 189. Cambridge University
Press, Cambridge, 1994. xiv+316 pp.
Applications of categories in computer science. [1991]: Papers from the London
Mathematical Society Symposium held at the University of Durham, Durham,
July 20-30, 1991. Edited by M. P. Fourman, P. T. Johnstone and A. M. Pitts.
London Mathematical Society Lecture Note Series, 177. Cambridge University
Press, Cambridge, 1992. viii+339 pp
Berrick, A. J.; Keating, M. E. [2000]: Categories and modules with K-theory in
view. Cambridge Studies in Advanced Mathematics, 67. Cambridge University
Press, Cambridge, 2000. xviii+361 pp.
Borceux, Francis, Janelidze, George. [2001]: Galois theories. Cambridge Studies
in Advanced Mathematics, 72. Cambridge University Press, Cambridge, 2001.
xiv+341 pp.
Бур баки Н. [1987]: Гомологическая алгебра. М.: Наука, 1987.
Brown К. С. [1994]: Cohomology of groups. N.Y. etc.: Springer, 1994. (Русский
перевод с изд. 1982 г.: Браун К. С. Когомологии групп. М.: Наука, 1987.)
Calenko M. S., Grisin V. В., Raikov D. А. [1984]: Ordered categories with
involution. Rozpr. mat., 1984. 227, 115 pp.
Cameron, Peter J. [1999]: Sets, logic and categories. Springer Undergraduate
Mathematics Series. Springer-Verlag London, Ltd., London, 1999. x+180 pp.
Category theory 1999. Selected papers from the conference (CT99) held in
honour of the 90th birthday of Saunders Mac Lane in Coimbra, July 19-24,
1999. Edited by J. Adamek, P. T. Johnstone and M. Sobral. J. Pure Appl.
Algebra 168 (2002), no. 2-3. North-Holland Publishing Co., Amsterdam, 2002.
pp. i-iv and 125-437.
Faith С Algebra: Rings, Modules and Categories. Berlin etc.: Springer. I. 1973;
II. 1976. (Перевод: Фейс К. Алгебра: кольца, модули и категории. Т. 1. М.:
Мир, 1977; Т. 2. М.: Мир, 1979.)
Goldblatt R. [1979]: Topoi. The categorical analysis of logic. Amsterdam etc.:
North-Holland Publ. Сотр. 1979. (Перевод: Голдблатт Р. Топосы. Категор-
ный анализ логики. М.: Мир, 1983.)
Grillet, Pierre Antoine. [1999]: Algebra. Pure and Applied Mathematics. A
Wiley-Interscience Publication. John Wiley & Sons, Inc., New York, 1999.
xxii+676 pp.
Hatcher W. S. [1982]: The logical foundations of mathematics. Oxford: Perga-
mon Press, 1982.
Helemsky A. Ya. [1989]: The Homology of Banach and topological Algebras.
Kluwer, 1989.

346
Список дополнительной литературы
Helemsky A. У а. [2000]: Homology for the Algebras of Analysis. In the book:
Handbook of Algebra, v. 3. Ed. M. Hazenwinkel. Amsterdam: Elsevier Science
B. V., 2000, p. 151-274.
Herrlich H., Strecker G. [1979]: Category theory. An introduction. Berlin:
Heldermann Verl., 1979.
Higher category theory. [1997]: Papers from the Workshop on Higher Category
Theory and Physics held at Northwestern University, Evanston, IL, March 28-
30, 1997. Edited by Ezra Getzler and Mikhail Kapranov. Contemporary
Mathematics, 230. American Mathematical Society, Providence, RI, 1998. x+134 pp.
Hilton, P. J., Stammbach, U. [1997]: A course in homological algebra. Second
edition. Graduate Texts in Mathematics, 4. Springer-Verlag, New York, 1997.
xii+364 pp.
Hilton P. J., Wylie S. [1962]: Homology theory. Cambridge Univ. Press, 1962.
(Перевод: Хилтон П, Уайли С. Теория гомологии. М.: Мир, 1966.)
Johnstone Peter Т. [2003]: Sketches of an Elephant: A Topos Theory
Compendium — 2 Volume Set, Oxford Logic Guides, Oxford University Press,
London, (should appear in 2003).
Joyal, A., Moerdijk, I. [1995]: Algebraic set theory. London Mathematical
Society Lecture Note Series, 220. Cambridge University Press, Cambridge, 1995.
viii+123 pp.
Y. Katsov. [1997a]: Tensor products and injective envelopes of semimodules
over additively regular semirings, Algebra Colloquium 4:2 (1997) 121-131.
Y. Katsov. [1997b]: Model Theory of Functors: Axiomatizability Problems,
Journal of Pure and Applied Algebra, 119, 1997, 285-296.
Y. Katsov. [2000]: On diagrams and flatness of functors, J. Pure Appl. Algebra
154 (2000) 247-256
Kilp, M., Knauer, U., Mikhalev, A. V. [2000]: Monoids, Acts and Categories
with applications to wreath products and Graphs. Walter de Gruyter, Berlin -
N.Y., 2000.
Lawvere, F. William, Schanuel, Stephen H. [1997]: Conceptual mathematics.
A first introduction to categories. Reprint of the 1991 original. Cambridge
University Press, Cambridge, 1997. xvi+358 pp.
Massey W. S. [1978]: Homology and Cohomology Theory. Marcel Dekker inc.
N. Y. and Basel: 1978. (Перевод: Масси У. Теория гомологии и когомологий.
М.: Мир, 1981.)
Moerdijk, I. [1995]: Classifying spaces and classifying topoi. Lecture Notes in
Mathematics, 1616. Springer-Verlag, Berlin, 1995. vi+94 pp.
Moerdijk, I., Vermeulen, J. J. C. [2000]: Proper maps of toposes. Mem. Amer.
Math. Soc. 148 (2000), no. 705, x+108 pp.
Montgomery S. [1993]: Hopf algebras and their actions on rings, Regional Conf.
Ser. Math. Amer. Math. Soc, Providence RI, 1993.
Osborne, M. Scott. [2000]: Basic homological algebra. Graduate Texts in
Mathematics, 196. Springer-Verlag, New York, 2000. x+395 pp.
Plotkin B. I. [2000]: Algebra, Categories and Databases. In the book: Handbook
of Algebra, v. 3. Ed. M. Hazenwinkel, Amsterdam: Elsevier Science B. V., 2000,
79-148.
Scott P. J. [2000]: Some aspects of Categories in computer science. In the book
: Handbook of Algebra, v. 3. Ed. M. Hazenwinkel, Amsterdam: Elsevier Science
B. V., 2000, 3-77.

Список дополнительной литературы 347
Serve J. P. [1965]: Cohomologie Galoisenne. Berlin: Springer, 1965. (Перевод:
Cepp Ж. 77. Когомологии Галуа. М.: Мир, 1968.)
Sonner T. [1962]: The formal definition of categories// Math. Zeit. 1962, 80,
№8, 163-176.
The Concise Handbook of Algebra. [2002]: Ed. by A. V. Mikhalev and G. F.
Pilz, Dordrecht: Kluwer Acad. Publ., 2002. Ch. H.
Weibel, Charles A. [1994]: An introduction to homological algebra. Cambridge
Studies in Advanced Mathematics, 38. Cambridge University Press, Cambridge,
1994. xiv+450 pp.

348
Предметный указатель
Предметный указатель
1-клетка сопряженная 316
2-категория 57, 313
2-клетка 313
2-функтор 318
— фундаментальная 32
Группоид 31
— связный 32
— фундаментальный 31
АЬ-категория 40
В-категория 214
Setsc 125
hom-функтор
— ковариантный 46
— контравариантный 46
Абсолютный коуравнитель 175
Аксиома замещения 35
Аксиомы
— Геделя-Бернсайда 35
— Цермело-Френкеля 34
Алгебра над монадой 165
Алгебраическая система 146
Арность 146
Ассоциативность 18
Бикатегория 322
Бинарное слово 193
Бипроизведение 226
Бифунктор 49
Векторное пространство, базис 69
Вилка 174
— расщепленная 175
Вложение 19, 26
Гомологический объект 234
Гомоморфизм
— границы 208
— связывающий 240
Граф
— направленный 20
— ориентированный 62
Группа 14, 21
— в категории 90
— кос 299
артинова 300
— малая 34
Двойственность 43, 67
Действие
— моноида 202
— моноида на множестве 16
— оператора 146
Диагональная стрелка 103
Диагональное отображение 88
Диаграмма 12, 65, 86
— коммутативная 12, 18
Диаграммная схема 62
Единица 17
— сопряжения 99
Естественное преобразование 27
универсальное 52
сопряженное 118
Закон чередования 56, 57
Замыкание на предпорядке 166
Заузливание 291
Змеевидная лемма 240
Идемпотент 31
— расщепляемый 31
Изоморфизм 31
— естественный 27
— категорий 25, 110
Истина 124, 330
Категория 12, 20
— базированная 214
— абелева 230
— аддитивная 228
— большая 35
— внутренняя 307
— двойная 57
— двойственная 45
— декартово замкнутая 116
— дискретная 21
— замкнутая 214
— запятой 60
, проекции 61
— конечно полная 132
— конкретная 39

Предметный указатель
349
— кос 299
— локально малая слева (малая в
смысле подобъектов) 154
— локально малая справа (малая в
смысле факторобъектов) 154
— множеств 19
— моноидальная симметричная 213, 292
— обогащенная 41
— объектов над а 59
— объектов под b 58
— объектов под b относительно S 59
— полная в малом 129
— предаддитивная 40
—, произведение 48
— псевдофильтрованная 250
— разбиения 259
— расслоенная 48
— с конечными произведениями 88
— свободная 63
— свободная над графом 69
— связная 104
— связная компонента 107
— симплициальная 22
— скелетная 111
— сопряжений 120
— стрелок 53
— строго моноидальная 188
— тензорная 291
— фильтрованная 244
— функторов 53
Квадрат
— декартов 86
— коуниверсальный 86
— сопряжений (adjoint square) 122
— универсальный 80
Класс 35
— собственный 35
Классификатор подобъектов 124, 330
Клин 254
— концевой 257
— универсальный 257
Ко-конец 261
Коединица сопряжения 99
Кокомпонента 89
Кольцо малое 37
Коммутант 25
Композиция
— стрелок 17
— функторов 25
Компонента
— естественного преобразования 27
— преобразования 252
— стрелки 84, 228
Компоненты 85
Конгруэнтность 66
Конец
— естественного преобразования 264
— функтора 257
Конус 82, 83, 86
— предельный 82, 83
— универсальный 82
Кообласть 17
Кообраз 232
Копорождающее множество 150
Копредел 81
— фильтрованный 245
Копроизведение 76
—, диаграмма 76
—, инъекции 76
—, объект 76
Короткая точная последовательность
233
Коса 299
Костепень 78
Коуравнитель 78, 175
— расщепленный 176
Коядро 78
Лемма Ионеды 74
Метаграф 17
Метакатегория 17
— стрелок 19
Метрическое пространство полное 70
Многообразие 147
Множества базированные 38
Множество 23
— малое 23, 34
с отмеченной точкой 38
— с отмеченной точкой 23
Модификация 319
Монада 162
— коплотности 289
Моноид 13, 21
— (в категории) 90
— в моноидальной категории 198
Моноидальная категория 189
Мономорфизм 31
— расщепляющий 31
Морфизм 15, 19
— графов 62
— моноидальных категорий, строгий
191
— функторов 27
Наибольшая нижняя грань 134
Наименьшая верхняя грань 134
Носитель алгебры 147, 165

350
Предметный указатель
Область 17
Образ 232
Образующие и соотношения (в
категории) 66
Объединение (наименьшая верхняя
грань) 149
Объект 17
— инъективный 139
— истинностных значений 330
— категорный 307
— начальный (инициальный) 31
— нулевой 31, 222
— представляющий 73
— проективный 139
— терминальный 31
Объекты изоморфные 31
Оператор сплетающий 54
Ординал 22
Отображение
— тождественное 19
— включения 19
— непрерывное 184
— оценки 117, 254
— сопряжений 117
Пара 19
— коядерная 81
— параллельная сжимаемая 177
— стрелок перемножаемая 19
— ядерная 86
Параллельные стрелки 21
Пересечение (наибольшая нижняя
грань) 149
Подгруппа коммутаторная 25
Подкатегория 26
— корефлективная
— плотная 283
— полная (full) 26
— рефлективная 108
— финальная 251 109
Подобъект 149
Поле частных 69
Пополнение объекта 208
Пополненный симплициальный объект
208
Порождающее множество 150
Порядковое число 22
Порядок частичный 22
линейный 22
Предел 83
— индуктивный 81
— конечный 134
— обратный 83
— проективный 83
— прямой 81
Предкатегория 62
Предложение 43
Предпорядок 22
— направленный 244
Предпучок 93
Преобразование диестественное 252
— естественное 27, 51
— суперъестественное 254
Принцип двойственности 44
Проекция произведения 48
Произведение 84
— проекции 84
— прямое 84
— стрелок 17
— функторов 25
Пространство петель 219
Прямая сумма 226, 227
Путь, композиция 32
Пучок ростков функций 47
Ранг слова 194
Распорка (span) 325
Расширение Кана
абсолютное 287
поточечное 282
правое 273
Ретракция 31
Свободная Т-алгебра 166
Свободное произведение 151, 247
Свойство универсальности 12
Сечение 31
Симплициальный объект 208
Сингулярная гомология 209
Сингулярный цепной комплекс 209
Скелет 110
Соленоид, р-адический 131
Соответствие Галуа 114
Сопряжение 96
— с параметром 120
Сопряжение-эквивалентность (adjoint
equivalence) 111
Сопряженность
— слева 13
— справа 13
Специальная теорема о начальном
объекте 152
Специальная теорема о сопряженном
функторе 152
Сравнение 179
Степень 85
Стрелка 12, 17
— левая обратная 31
— нулевая 31, 89, 222

Предметный указатель
351
— нулевая (в АЬ-категории) 225
— обратимая 30
— охватывает объект 150
— правая обратная 31
— регулярная 32
— слабо универсальная 272
— сократимая слева 31
— сократимая справа 31
— универсальная 68, 71
Структурное отображение алгебры 165
Стянутая надстройка 219
Стянутое произведение 219
Схема диаграммная 20
Теорема о параметре 264, 265
Теорема о представимости 145
Теорема Фрейда о сопряженном
функторе 143
Тождество 146
Топологическое пространство
компактно порожденное 215
Топос
— элементарный 126, 329
вполне разделимый 331
Точная последовательность 232
Треугольные тождества 101
"Умножение 2-клеток
вертикальное 315, 321
горизонтальное 313-315, 321
Умножение гомотопий горизонтальное
313
Умножение естественных
преобразований
вертикальное 55
горизонтальное 55, 58, 123, 162
Умножение стрелок 17
Универсальная алгебра 146
Универсум 22, 33
Уравнитель 85
Утверждение
— атомарное 43
— двойственное 43
Факторобъект 149
Функтор 23
— Йонеды 75
— аддитивный 41, 228
— булевой степени 46
— вложения 26
— внутренний 309
— диагональный 104
— забывающий 25
— инициальный 252
— ковариантный 46
— контравариантный 45
— коплотный 284
— левый сопряженный 51, 97
— монадический 169
— моноидальный 294
— моноидальный сильный 295
— непрерывный 137
— обратный 25
— отражает копределы 181
— плотный 284
— полный 26
— правый сопряженный 97
— представимый 73
—, представление 73
— создает конец 260
— создает пределы 132
— сопряженный и обратный слева 112
— сохраняет конец 260
— сохраняет пределы 137
— строгий 295
— точный 233
— точный слева 234
— унивалентный 26
— финальный 251
Функция
— малая 34
— сложная 19
Функция объектов 23
Функция стрелок 24
Характеристическая функция 124
Цепной комплекс 234
Чередование 56, 57
Член объекта 237
Эквивалентность категорий 29, 110
Эквивалентные категории 110
Элемент универсальный 70
Эпиморфизм 31
— расщепляющий 31
Ядро 222
— разности 85

Научное издание
MA КЛЕЙН Саундерс
КАТЕГОРИИ ДЛЯ РАБОТАЮЩЕГО МАТЕМАТИКА
Перевод под редакцией В.А. Артамонова
Редактор О. В. Салецкая
Оригинал-макет: Н.Ю. Савченко
Оформление переплета: А.Ю. Алехина
ЛР №071930 от 06.07.99. Подписано в печать 21.10.03.
Формат 60x90/16. Бумага офсетная. Печать офсетная.
Усл. печ. л. 22. Уч.-изд. л. 25. Тираж: 300 экз. Заказ №
Издательская фирма «Физико-математическая литература»
МАИК «Наука/Интерпериодика»
117997 Москва, ул. Профсоюзная, 90
E-mail: fizmat@maik.ru
Отпечатано с готовых диапозитивов в ПФ «Полиграфист»
160001, г. Вологда, ул. Челюскинцев, 3
Тел.: (8172) 72-55-31, 72-61-75, факс: (8172) 72-60-72
E-mail: form.pfp@votel.ru http://www.vologda/~pfpv