Цена 10 коп.
ПОПУЛЯРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ
Вып I. А. И. Маркушевич. Возвратные последовательности
Вып. S И, И. Натансон. Простейшие задачи на максимум и минимум
Вып 3 Н. С Сомннскнй. Метод математической индукции.
Вып 4 А Н Мариушевич. Замечательные кривы*
Вып 6 П П Коровник, Неравенства
Вып 6. Н. И. Воробьев. Числа Фибоначчи
Вып 7. А Г. Курош Алгебраические уравнения произвольных степеней.
Вып в А. О. Гсльфонд. Решение уравнений и целых числах
Вып. 0 А Н Маркущсаич. Площади и логарифмы
Вып 10 А С. Смогоржевский. Метод координат
Вып II Я. С. Дубнов Ошибка в геометрических доказательствах
Вып IS H. П. Нвтансви. Суммирование бесконечно малых величин.
Вып 13 А. И Мариушевич. Комплексные числа к конформные
отображении
Выл. 14 А И Фетисва. о доказательствах в геометрии
Вып 16. И Р Шафаревич О решении уравнений высших степеней.
Вып 16. В Г. Шсрватов Гиперболические функции
Вып 17 В. Г. Болтянский. Что такое дифференцирование
Вып. 18. Г. м Миракьин. Прямой круговой цнлнндр.
Вып 19 Л. А Люстсриим. Кратчайшие линии
Вып SO. A. M. Лвишиц. Вычисление площадей ориентированных Фигур
Выл. 21 Л. Н. Головина и И, М. Яглом. Индукции в геометрии.
Вып. 23. В Г. Болтянский. Равновеликие и равносоставленные фигуры
Вып. 23. А. С Смогоржевский. О геометрии Лобачевского
Вып 24. В. И Аргунов и Л. А. Скорняков. Конфигурационные теоремы
Вып. 26. А. С Смогоржевский. Линейка а геометрических построениях
Вып 26. Б. А Трахтснброт. Алгоритмы и машинное решение эедач. •
Вып 27. В. А Успенский. Некоторые приложения механика к мата*
матнке
Вып SO. И. А. Архангельский н Б. И. Зайцев Автоматические оифро*
вые машины
Вып. 29 А. И Костоаекий. Геометрические построения одним циркулем
Вып. 30 Г Е, Шилов Кик строить графики
Вып 31 А. Г Дорфмви. Оптика конических сечений
Вып 32 Е. С Вситцедь, Элементы теории игр
Вып 33 А. С. Барсов Что такое линейное программирование *
Вып 34 Б. Е Маргулнс. Системы линейных уравнений
Вып 3S. Н. Я Виленкин Метод последовательных приближений »
Вып 3S. В. Г Болтянский Огибающая
Вып 37 Г. Е Шилов. Простая гамме (устройство музыкальной шкалы),.
Вып 38 Ю. А Шрейдер. Что такое расстояние?
Вып 39. Н. Н- Воробьев. Признаки делимости
Вып 40 С В Фомин Системы счисления г
Вып 41 Б. Ю. Коган Приложение механики к геометрии
Вып 42. Ю. И. Лгобич и Л. А. Шор. Кинематический метод а геомет-
Бнческнх оадачах
. А. Успенский, треугольник Паскаля
Вып 44 И. Я Бакельмви. Инверсии
Вып 45 Н М. Яглом Необыкновенная алгебра *
Вып 46. Н. М Соболь. Метод Моктс Карло *
Вып 47 Л А Калужинн. Основная теорема арифметики
Вып 48 А. С Солодовников Системы линейных неряленств
Вып 49. Г. Е Шилов. МатемвтнчвскяЙ аиалиа в области рациональных
функция
Вып 60. В. Г Болтянский н Н Ц. Гохберг Разбиение фигур на мень
шне части
Вып. 61 И М Бескнн. Изображения пространственных фигур
Вып 62, Н. М. Бескнн Деление отрезка в данпом отношении
Вып 63. Б. А. Розенфельд и Н. Д. Сергеева. Стереографическая проех*
цня.
I
I
■
ЛТопилярные лекции
ПО МАТЕМАТИКЕ
И.М.СОБОЛЬ
)
<
МЕТОД
МОНТЕ-КАРЛО

ПОПУЛЯРНЫЕ ЛЕКЦИИ ПО МАТЕМАТИКЕ
ВЫПУСК 46
И. М. СОБОЛЬ
МЕТОД
МОНТЕ-КАРЛО
ИЗДАНИЕ ТРЕТЬЕ.
ДОПОЛНЕННОЕ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
19 7 8

517.8 818
С 54
I АННОТАЦИЯ
В книжке изложены 'Основные приемы
метода Монте-Карло (метода статистических
испытаний). Приведены примеры
разнообразных задач, решаемых этим методом.
Предназначена для инженеров,
конструкторов, исследователей и других
специалистов, работающих в различных отраслях
народного хозяйства (в науке, тгехнике,
промышленности, медицине* экон * е, сельском
хозяйстве, торговое ктркК.». !зкже для всех,
кто желает впервые познакомиться с
методом Мб1ие*Кя||л©1 ®i чюгщгеля т^еб-уется
умение диффёрйш'« = • в>^ иятетptfosafь
• (I курс втуза).
Первое издание вышло в 1968 г. • ■•>
Книжка ! удой • - - почетной грамоты
Всесоюзного койм^реа на- лучшие учебные
пособия для народных университетов в
1971 г. ф третье издйнйё включено описание
наиболее распространенных
псевдослучайных чисел!
Илья Меерович Соболь
МЕТОД МОНТЕ-КАРЛО
(Серия: «Популярные лекции по математик»)
М., 1978 г., 64 стр. с илл.
Редактор И. М. Овчинникова Технический редактор В. Н. Кондакова
Корректоры Г. В. Подеольская, Л. С. Сомова
ИБ К» 11054
Сдано в набор 21.10.77. Подписано к печати 20.02.78. Бумага 84X108!/si, тип. № 2,
Литературная гарнитура" Высокая печать. Условн. печ. л. 3,36. Уч.-изд. л. 3,14.
Тираж 60 000 экз. Заказ N» 801. Цена книги 10 коп.
Издательство «Наука>
Главная редакция физикогматематической литературы
117071, Москва, В-71, Ленинский проспект, 1ё
Ордена Трудового Красного Знамен» Ленинградская типография № 2
имени Евгении Соколовой Союзполиграфщкдаа при Государственном комитете
Совета Министров СССР п© делам издательств,
полиграфии и книжной торговли."
198052, Ленинград, Л-52, Измайдовеквй проспект, 2S
@ ! -я редакции
физико-математической* литературы
издательства «Наука», 1978, с изменениями
-, 2020V-05Q
С ~ w 79-78
053(02)-78
*•»©' ■ . ; i ...: ., .4 '■„ л ,; ■..■■»,-« ...
• • •
5**еаеиие . . » . . .
, ; >§ 1. Общее лцаедстяякленяе о методе . . ... .
Г**** 1. Мядед -,.':-.. ■■__' .' ■_■:■' .Ц величие ,. . »
§ 2. Случайные величины . . . ...... я
н$ 3. Педуяение .слунайнызс величин ш Э1Ш , :л
J§ 4. П^еойразошания случайны* величия ... ',. .'.*
Га ала 2. Пример п ния метода Монте-К d
;| В. Расчет системы! массового ОШлужйва-
| '6. Расчет качества и надежности иЦ&и# . .
J J- Расчет 'аир©*©жд«н*я *гёйт|йшнв «вйозь ',
§ & Вызд* v.vbb шредфе - » интеррала .'■■'.'■ .
***•••*••«•
• •
| |- Яок«»атеяьства нёкот&^щ;' 'п^ёйлож-ен^й
§ 10.-О ксвадабсяунаймы-х числах . . .- >. . .
Таблицы
• '• • . • " • « * •

ПРЕДИСЛОВИЕ
Основная цель настоящей книжки — подсказать
специалистам самых различных направлений, что в их
области деятельности встречаются задачи, которые можно
решать методом Монте-Карло. Читателям, не
изучавшим теорию вероятностей, предназначен § 2, о котором
необходимо сказать несколько слов.
Каждому человеку приходилось употреблять слова
«вероятность» и «случайная величина». Интуитивное
представление о вероятности (как о частоте). более или
менее соответствует истинному смыслу этого понятия.
Но интуитивное представление о случайной величине,
как правило,, весьма далеко от математического
определения. Поэтому в § 2 понятие вероятности
предполагается известным и разъясняется только более сложное
понятие случайной величины. Этот параграф не может
заменить курса теории вероятностей: изложение здесь
упрощенное и без доказательств. Но он дает некоторое
представление о случайных величинах, достаточное для
понимания простейших приемов метода Монте-Карло.
Задачи, рассмотренные в тексте, весьма
разнообразны. Но, конечно, они не могли охватить всех областей
применения метода. Например, в книжке ни слова нет
о медицине. Однако методы § 7 позволяют рассчитывать
дозы облучения при лучевой терапии.
В третьем издании сделано несколько небольших
вставок, переработано изложение § 3 и добавлен § 10»
содержащий описание наиболее распространенного сткн
соба получения псевдослучайных чисел на современны^
ЭВМ.
Москва, 1978 г.
И. Соболь
ВВЕДЕНИЕ
§ 1. Общее представление о методе
Метод Монте-Карло — это численный метод решения
математических задач при помощи моделирования
случайных величин.
-1.1. Происхождение метода
Монте-Карло. Датой рождения метода Монте-Карло принято
считать 1949 год, когда появилась статья под названием
«The Monte Carlo method» *). Создателями этого метода
считают американских математиков Дж. Неймана и
С. Улама. В Советском Союзе первые статьи о методе
Монте-Карло были опубликованы в 1955—1956 годах **).
Любопытно, что теоретическая основа метода была
известна уже давно. Более того, некоторые задачи
статистики рассчитывались иногда с помощью случайных
выборок, т. е. фактически методом Монте-Карло.
Однако до появления электронных вычислительных машин
(ЭВМ) этот метод не мог найти сколько-нибудь
широкого применения, ибо моделировать случайные величины
вручную — очень трудоемкая работа. Таким образом,
возникновение метода Монте-Карло как весьма
универсального численного метода стало возможным только
благодаря появлению ЭВМ.
Само название «Монте-Карло» происходит от города
Монте-Карло в княжестве Монако, знаменитого своим
игорным домом. Дело в том, что одним из простейших
механических приборов для получения случайных
■*ш ' - ■ — I
*) Metropolis N., Шага S., The Monte Carlo method, J.
Amer. statistical assoc, 1949, 44, № 247, 335—341.
•■■■'**) Это были статьи В. В. Чавчанидзе, Ю. А. Шрейдера,
В. С. Владимирова.
5

величин является... рулетка. Об этом_ речь пойдет в § 3>
Здесь же, пожалуй, стоит ответить на часто задаваемый
вопрос: «Помогает ли метод Монте-Карло выигрывать
в рулетку?» Нет, не помогает. И даже не занимается
этим.
1.2. Пример. Для того чтобы читателю было более
понятно, о чем пойдет речь, рассмотрим весьма простой
пример. Предположим, что нам нужно вычислить
площадь плоской фигуры S. Это может быть совсем произ*
вольная фигура с
криволинейной границей, заданная^.
гр афически или ан алитиче-
■<ош, связная или состоящая
из нескольких кусков Пусть
это будет фигура,ч изобра-
зкенная на рис. 1, и преддай
ложим, что она вея раснол^
жена внутри единичного
квадрата.
©ыЗерем внутри квадра*
та N случайных точек. Oik);*
значим 1?ерез Nf число т©>
чек, тюпавших при этом
внутрь 5. Геометрически
очевидно, что площадь S
прнб о равнаотношенвдо N'fN. Щет Щяьшъ сбудет
А', тем больше вудет точность этой ;©це»ки.
В примере, «зобр«женном на рис. 1, выбраны JV = 40
точек. Из н*гх ffl = If точек оказались внутри S. Отно-
щение Щ'0ъ?= 1^4©==^';'*, в то время как истинная
гоЮщадь S нравна 0,В§"*). '-■-_■
iM. Две о согбен ностн метода Менте*
Кар>ло. Первая осе*,- ость метода-—простая струк*
тура вычислительного алгоритма. Как правило,
составляется программа для осуществления одного случайного
*) На rn.fi • для вы .• - .ия, шющади плоской фигуры «*«-
тод Монфв^ардо не используют: .для.. этого есть другие метода^
котя и более сложные, но зато обеспечивающие гораздо большую
точность; v ■.-;■•■■■ _ . ?
Однако указанный, в нашем примере метод Монте-Карло ттозво»;
ляет сжоль те просто вычислять «мнегомерйый 'объем» тела <в
многомерном пространстве. И » ^tOM случае меаюд \Монще-Карло чаш*
оказывается единственным <шсаКяным "методом, дающим возмож*
ность решить задачу.
/ Л
Рис. 1.
€
тшташт {в примере из- it* Х*& надо вы%ать е - v / *
точку ;в квадрате и п •> г р!#ть, принадлежит -д&, она Щ.-
7-З&тем ^ш^вспыташие повторяется -N раз, причем катщл^
оиытне зависит от всех остальных, и результаты тещ
шдаов осредйяштся. . .
■ Поэтому иногда метод Монте-Карло называют жег®-
*кмст@тис?ищсшх испытаний, . . ■.■■-,.
Вторая осо#екшстыметода,:; ощийка в- \шй, КЩ'
правило, пропорциональна *>JDJN, где D -?- некоторая
постоянная, а iV-^число испытаний. Из этой формулы
видно, что для того, чтобы уменьшить ошибку в 10 раз
(иначе говоря, чтобы получить в ответе еще один верг
^десятичный знак)1, нужно увеличить N (т. ё. объем
работы) в 'WB-paar. - ; ; :
' jicHO; что^Ч»» ься высокой; точности таким путем
невозможно. Поэтому обычно говорят, что метод Монте-
Карло';0Ci«-- о эффективен при решении тех задач, ;в
которых результат нужен с небольшой точностью (5—
Однако одну и ту же задачу можно решать
различными в-ариантадаи метода Мднте-Карло*), которым
отвечают разлитые значения D. Во многих задачах
удается значительно увеличить точность, выбрав способ
расчета, которому соответствует значительно меньшее
значение В.
^:1Ж Задачи, р'ешаемые методом Менте-
Карло. Вочзервых, метод Монте-Карло' а -«ляет
модулировать любой процесс, на протекание которого
влияют случайные факторы. Во-вторых, даш многих
математических задач, не связанных с какимйчяибо
случайностями, можно искусственно придумать
вероятностную модель (и даже не одну), позволяющую решать
зги задачи. Собственно говоря, это и было сделано в
примере из п. 1.2.
Таким образом, можно говорить о методе Монте-
Карло как об универсальное методе решения
математических зада»!.:
Особенноинтересно; чтов некоторых случаях выгодно
отказаться от моделирования-, истинного случайного
.*) В ииоеврщитой л«1%^агруре теперь.чащевпишут о дает од ах
М^нте-Ка-рло (b<j мвожественно» часяе}, яме» в вадшу, что одну и ту
ж» задачу можно' считать нрн *".--■; м »©дели$»©:; ия рвздаичйьис
случайных величин. - ' .'
1

процесса и вместо этого использовать искусственную
модель. Такая ситуация рассмотрена в § 7.
1.5. Еще о п р и м ер е. Вернемся к примеру из
п. 1.2. Для расчета нам нужно было выбирать
случайные точки в единичном квадрате. Как это сделать
физически?
Представим такой эксперимент. Рис. 1 (в
увеличенном масштабе) с фигурой 5 и квадратом повешен на
стену в качестве мишени.
Стрелок, находящийся на
некотором расстоянии от
стены, стреляет N раз,
целясь в центр квадрата.
Конечно, все пули не
будут- ложиться точно в.
центр: они пробьют на
. мишени N случайных
точек*). Можно ли по
этим точкам оценить
площадь S?
- Результат такого
опыта изображен на рис. 2.
Рис.2. В этом опыте N = 40,
N' — 24 и отношение
N'/N = 0,60, что превышает истинное значение площади
(0,35) почти в два раза. Впрочем, и так ясно, что при
очень высокой квалификации стрелка результат опыта
будет очень плохим, так как Почти все пули будут
ложиться вблизи центра и попадут в 5**).
Нетрудно сообразить, что наш метод вычисления
площади будет справедлив только тогда, когда случайные
точки будут не «просто случайными», а еще и «равно-*
мерно разбросанными» по всему квадрату. Чтобы
придать этим словам точный смысл, необходимо
познакомиться с определением случайных величин и некоторыми
их свойствами. Эти сведения изложены в § 2 без
доказательств. Читатель, знакомый с любым курсом теории
вероятностей, может пропустить весь § 2, кроме п. 2.5«
*) Мы предполагаем, что стрелок не является чемпионом мира
и удален на достаточно большое расстояние от мишени.
**) О том, как выбирались случайные точки на рис. 1 и 2,
будет сказано в п, 4.5. Оценка погрешности для этого примера
приведена в п. 9,7. ■■•'■■..
/
. I I Й ,
Л
•I—. • О
^» о •
•I " •'" '•
• ••
I % •
fjIABAJ
МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН i
. § 2. Случайные величины
Мы считаем, что понятие веррятндсть читателю более
или менее известно, и переходим Прямо к понятию
'случайная величина.
Слова «случайная величина» в обыденном смысле
употребляют тогда, когда хотят подчеркнуть, что
неизвестно, каким будет конкретное значение этой величины.
Причем иногда за этими словами скрывается просто
незнание, какова эта величина.
Однако математик употребляет эти же слова
«случайная величина», вкладывая в них вполне определен^
ное * содержание. Действительно, говорит он, мы не
знаем, какое значение примет эта величина в данном
конкретном случае, но мы знаем, какие значения она
может принимать, и знаем, каковы вероятности тех или
иных значений. На основании этих данных мы не можем
точно предсказать результат одного испытания,
связанного с этой случайной величиной, но можем весьма
надежно предсказать совокупность результатов большого
числа испытаний. Чем больше испытаний (как говорят,
чем больше статистика), тем точнее будут наши
предсказания.
Итак, чтобы задать случайную величину, надо
указать,, какие значения она может принимать и каковы
вероятности этих значений.
2.1. Дискретные/случайные величины.
Случайная величина £ называется дискретной, если она
9

шйкег принимать дискретное множество' значений х\,
хь'"*■ '' х *\ ч.. - ■■ ;- : -
'Дискретная случайная величина I определяется
таблицей ь ■''"'">'
V__/*i Х2 ... '*я\ ''' (Т)
. \pi Рг ••• Рп /'
где Хи х2, .... хп — возможные значения величины £, а
ри р2, •••> Рп—соответствующие им вероятности.
Точнее говоря, вероятность того, что случайная величина £
примет значение х< (обозначим ее через Р{£ =
х»}.),^равна рг:
Таблица (Т) й; - гж^щ распределением случайно^
величины. . ../ >.'.... ;
Числа У1, ii, ..., х„ могут быть, вообще говоря,
любыми. Однаш; вероятности ри Pi> ..., ph должны уж»*'
летворять двум условиям:"
а) все -pi положительны:
■ ■ ■'
' б) сумма всех pi равна"!:
Р1 + Р2+ ...+Рн=;=Ь (2)
Последнее условие означает, что £ о*б яз а н а в каэкь
дом случае принять одно из значений *1,дг2, ...', хп.
М&тематтеским ожиданием случайной величины f
называется число
m^ExiPi. Щ
Чтобы?* выяснить физический смысл этой величину
запишем ее в следующем виде:
п J п
*) В теория вероятностей рассматриваются также дяофетные;,.
случайные величины, которые могут .принимать бесконечнее чиса%г,
значений.
10
£)$€1©д# видноу что Щ'*т- ато среднее ъпщрнщувтттцы
|, причем более вероятные значения я* ътщт в сумму
■ &4&{№ъщ ■■ ».• весами*)'. ..
- Отметим основные свойства математическою ©шида*
ншгс если с— какая-нибудь не случайная величина, то
М(| + ^) = М|-Ьс, (4)
Ц(ф-сЩ^ (5)
тёш:\ :И .-ди- две любые сяучфят тмтты^ ш
.:\;-\щ^)^щ^Щу ■■■■ '.'■-.'.'■ (б);
Дисперсией случайной ^величины | называется число
0|г=М^^|(||)2]. (7)
^лзщоват^льно, дисперсия Of—это математическое
^(Ш^двние квадрата- отклонения случайной величины I
;0т ее среднего значения М|. Очевидно, всегда О|>0.
Математическое ожидание и дисперсия — важнейшие
числовые характеристики случайной величины |. Каково
их практическое значение? •
Если мм будем наблюдать величину | много раз и
ЗШгучада задания |ь ■■$$, ;■;_., |& (каждое
из-которых^будет равно одному из чисел хих2, ...,хп), то среднее
арифметическое от этих значений будетГблизко к М£:
-jr(h + h+ ,.. +.Ы«М£. (8)
А;щст^ст .Q£ характеризует р^брре этих значений
... около среднего Щ.
формулу (7)дт дисперсии можно преобразовать с
помощью формул (4) — (6):
D| = М [|2 - 2Щ -I + (М£)2]» М (£2) - 2М| • М| + (М|)2,
:ишуда
v -•:•■■'■■- ■ DE = M(|2)-(M|)2. Щ
*) Осреднение с весами очень часто встречается в самых
различных областях науки. Например, в механике: если в точках хи
%*„,,., Лп (да оси Ох) расположены массы ти /п&,..,., /га«, то-абс-~
цвеёао*ентра тяжести этой системы вычисляется по,формуле
-, п ■ ■ _'.п-
... k*1 "\ , »=1
I^bhi s 9 в эиш сяуяае^умма -, ; :м^сяе; обярааа равняться
единице, - ■' ..<:■■'
и

Вычислять дисперсию по формуле (9) обычно проще,
чем; по формуле (7).
Отметим основные свойства дисперсии: если с —
какая-нибудь не случайная величина, то
D(£ + c) = D|, (10)
D(c£) = c2D£. V (11)
Важную роль в теории вероятностей играет понятие
независимости случайных величин. В действитель*
ности это — довольно сложное понятие, но в простейших
случаях оно весьма очевидно *).
Для независимых случайных величин \ и х\ справед*
ливы следующие соотношения:
М(^) = М|-Мл, (12)
Dte + iO-'Dfc + Dti. (13)
Пример. Рассмотрим случайную величину к с распределением
__'/ 1 2 3 4 5 6 \
к_\1/б 1/6 1/6 1/6 1/6 1/6; •
Очевидно, реализацией этой величины можно считать число очков,
выпадающих на игральной кости: любое значение одинаково
вероятно. Вычислим математическое ожидание и дисперсию к. По фор*,
муле (3)
Мх ==?!•-£--f- ••• +6'-jr==3,5.
По формуле (9)
DK = M(K2)-(M*)2 = l2.-i-}-;... + б2- ^- (3,5)2 = 2,917.
Пример. Рассмотрим 'случайную величину 8 с распределением
e==(l/2 1/2)'
Реализацией этой величины можно считать игру в орлянку с
условием,- что, например, орел — это 3 очка, а решетка1-^-4 очка. В этом
случае
N16 = 0,5-3 + 0.5-4 = 3,5;
D9 = 0,5 (З2 + 42) - (3,5)2 = 0,25.
Мы видим, что М6=Мл, но D0<Dx Последнее можно было
легко предвидеть, так как значения 6 могут отличаться от 3,5 только
на ±0,5, в то время как в значениях к разброс может достигать ±2,5,
• *) Допустим, что кроме величины £ мы наблюдаем еще за од*
ной случайной величиной rj. Если распределение величины | не меч
няется от того, что нам уже известно значение, которое приняла ве*
личина т], то естественно считать, что | от rj не зависит.
12
Рис. 3.
2,2. Непрерывные случай н ые величины.
Предположим, что на плоскости в начале координат
расположено некоторе количество радия. При распаде
каждого атома радия из него вылетает а-частица.
Направление ее будем характеризовать углом \р (рис. 3). Так
как и теоретически, и пр*актически
возможны любые направления
вылета, то эта случайная
величина может принимать любое
значение от 0 до 2зт.
Мы будем называть
случайную величину I непрерывной, если
она может принимать любое
значение из некоторого интервала
(а,Ь).
Непрерывная случайная
величина £ определяется заданием
интервала (a, ft), содержащего возможные значения этой
величины, и функции р{х), которая называется
плотностью вероятностей случайной величины | (или
плотностью распределения £).
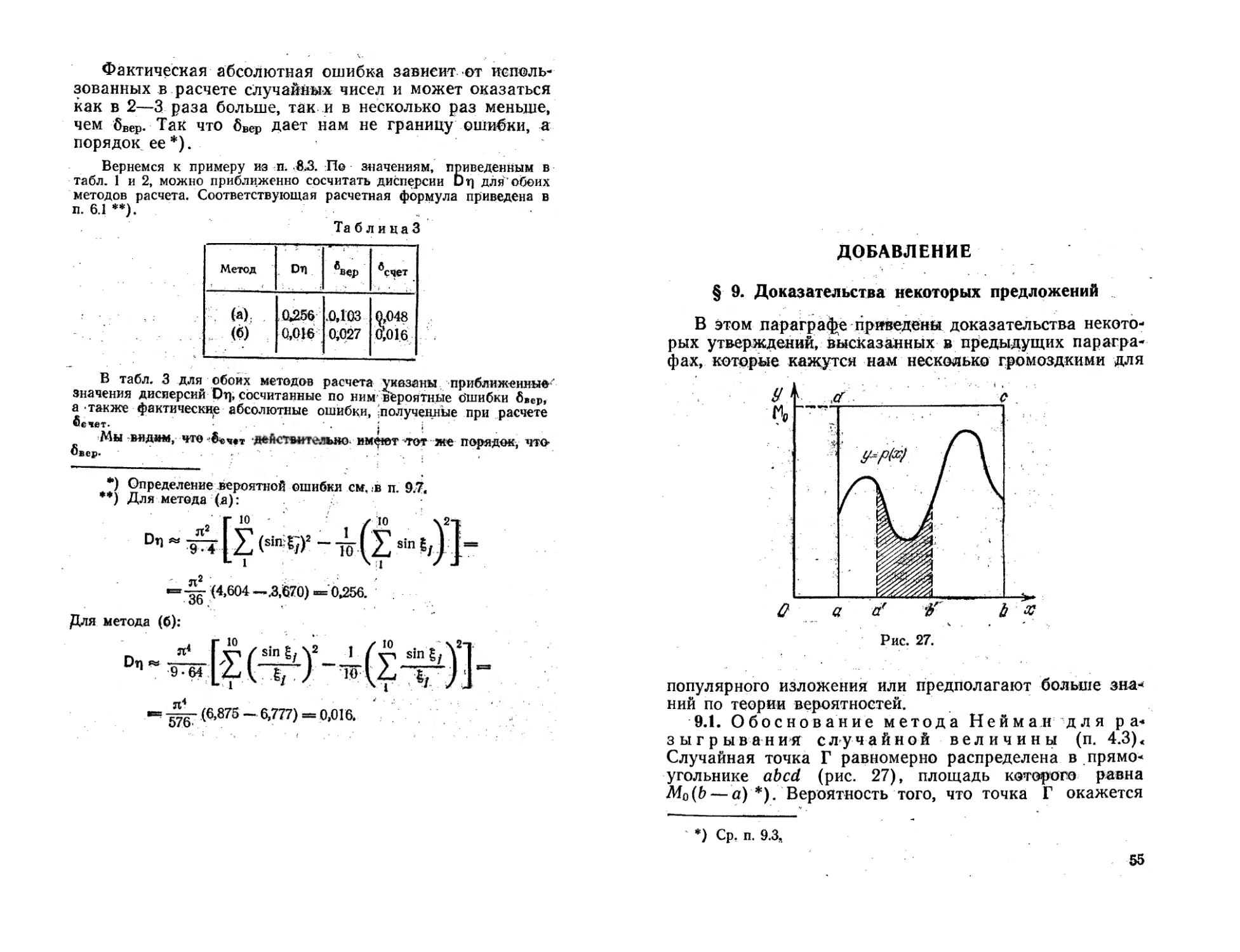
Физический смысл р(х) следующий: пусть (a't b')—^
произвольный интервал, содержащийся в (а, Ь) (т. е.
а <^ а', Ь' < 6). Тогда
вероятность того, что £
окажется в интервале (а', Ь'),
равна интегралу
v
P{a'<t<b'} = \p(x)dx.
а'
(14)
На рис, 4 з'аштрихован-
~2Г*х ная площадь равна
значению интеграла (14).
Множество значений \
может быть любым
интервалом. Возможен даже случай а == — со, а также
Ь = со. Однако, плотность р(х) должна удовлетворять
двум условиям, аналогичным условиям (1) и (2) для
дискретных величин:
а) плотность р(х) положительна:
р{х)>0; {15)
Рис. 4.
13

1б) интеграл ®т плотности р{х) -*яо модему иц 'nu/pgi
{a,b) равен 1:
ь ■':'■;
\ p(x)dx = 1.
Математическим ожиданием непрерывной случайней
величины называется число
Щ*=^хр&№х- О7)
Смысл этой -характеристики таш« >зке, как is сщщ&
дискретной случайной величины. В самом деле, тмш;
М|= J xp(x)'dx \ p(x)dx,
то легко видеть, что это есть среднее значение |: ведь
значением Д .может бь1ть любое число х из интервала
(а, Ь), которое входит в интеграл с весом /?(■*) *).
Все изложенное в п.2.1 от формулы (4) и до
формулы (13) включительно справедливо также для нёпре^
рывных случайных величин: и определение дисперсии
(7), и формула (9) для ее вычисления, и все свойства
М£ и Dg. Повторять мы их не будем **).
Укажем только еще одну формулу для
математического ожидания ^функций От ;£. Пусть по-прежнему слу*
чайная величина | имеет плотность вероятности р(х)*
Выберем произвольную непрерывную функцию/(лг) и
*) И в этом случаеможио указать на -аналогичную формулу из
механики: если линейная плотность стержня а ^ *^ & равна р.(х)»
то абсцисса центра тяжести стержня вычисляется по; формуле
Ь Ъ
■=== V дгр {x)dx/ \ р (х)Мх.
-а
**) В теории вероятностей рассматриваются также болы-м»№в
непрерывные случайные ведичиы, у которых р{х) ^ 0. Встречаются;
случайные величины, для которых М§ не" существует. Возможен слу4>
чай Dg = оо. '■"
14
о-
\\ mm~[mptx)<bc.
fmcMwjmmслучайнуювеличину и\ *=*■■■/ (|). Можй® -д©ка-
ШЩ ЧТ€К ' ь
а
Подчеркнем, что*вообще говоря* М/ШФ /(МБ).
Случайная величина у, определенная в
интервала (О, 1)"..« имеющая; плотность р(х) = 1, называется
*■■■* -омщщ® распределенной. & ial-
(О, 1) (рис.5). ■**-
В самом деле, какой бы
интервал (а', Ь') внутри (0,1)
мы ни взяли, вероятность того,
что у попадет в (a/tb,)1 равна
\ р (х) dx = Ь' — а'%
«
Рис. 5.
т. е. длине этого интервала. В частности, если мы
раздадим (0, 1) на любре^ число интервалов равной длины,
то вероятность попадания -у в.любой из этих интервалов
будет одна и та же.
Легко вычислить, что
МV. *= J хр (х) dx — [ xdx =>2 *,
о о
....-■ .1 .- '
Dy - J x*pШх~Щ>== 4- - • ~ ^ -~.
■■■©-■• - - ,
Со*случ&инч>й величиной у мы еще не раз встречмся
в* дальнейшем.
: 2.3. Нормальные с л у ч айн ы е в« л и ч швы.
Нормальной (или гауссовской) случайной^ величийойша-
аываётся случайная величина ^определенная на всей
оси (— оо, оо) и имеющая плотность
р{х)
г
2а*
Г№& и о >,G—числовые, параметры-*)v
(19)
*) а—^эт-о числе, а , не- случайз»а»г величина* Мы использовали
греческую букву, так как это обозначение общепринят^
15

Параметр а не влияет на форму кривой р(х):
изменение его приводит лишь к сдвигу кривой вдоль оси х.
Одйако, при изменении а форма кривой меняется. В
самом деле, легко видеть, что
max р{х) = р (а) = —п==-.
Если уменьшать а, то тахр(х) будет возрастать.
Однако, вся площадь под кривой р(х) по условию (16)
-з -я -/ о г г з л.
Рис. 6.
равна 1. Поэтому кривая "будет вытягиваться вверх в
окрестности х = а, но убывать при всех достаточно
больших значениях х. На рис. 6 построены две
нормальные плотности, соответствующие а = О, а — 1 и а = О,
а = 0,5. (Еще одна нормальная плотность построена наг
рис. 21, см. ниже, стр. 42).
Можно доказать, что
М£ = а, D£=c2.
Нормальные случайные величины очень часто
встречаются при исследовании самых различных по своей
природе вопросов. О причине этого будет сказано
несколько ниже. Например, ошибка измерения б, как пра«
вило, представляет собой нормальную случайную вели*!
чину.
16
: Если систематической ошибки измерения нет, то а ==
== Мб ess 0. А величина а я V D°, называемая • с р е д-
ней йв а д р а т и ч и о й погреши оеть ю,
характеризует погрешность метода измерения.
Правило «трех сигм». Нетрудно вычислить,
что, каковы бы ни были а и о в (19),
c+3ff .
Из (14) вытекает, что
Вероятность 0,997,настолько близка к 1, что иногда
последнюю формулу интерпретируют так: при одном
;иеп;ыт|^нии практически невозможно
полупить значение & отличающееся от Щ
б о д* ш е ч е м н а Зо.
^ДО/.Ц-еятр..а'льн&я:' предельная теорема
т е о р и и в е роят нр с т ё й, Эта замечательная теорема
была впервые сформулирована Лапласом. Обобщением
этой теоремы занимались многие выдающиеся
математики! в том числе П. Л. Чебышёв, А. А. Марков и
А.'$$. Ляпунов. Доказательство ее достаточно сложно.
.Рассмотрим N одинаковых независимых случайных
величин |ь Ы ...... Sjv, так что распределения
вероятностей этих величин совпадают. Следовательно, их
математические ожидания и дисперсии также совпадают.
Величины эти могут быть как непрерывными, так и
дискретными, т
^Обозначим ^:,
Обозначим через pN сумму йсех этих величин:
Из формул (6) и (13) следует4 что
Мрлг^М^ + Ег-Ь ... -f tN) = Nm,
Dp^^D^-f^-f ... НтЫ^да.
. 2 ' И. М» Соболь "|7.:',

Расширим те&еръ нормальнуюсдучвЫ^тшщ ••■■;■:
&v с такими же параметрами: а = Nm, о2 = Nb*.
В дентальной предельной теореме утверждается, я/ГО
для любого интервала (а\Ъ') при больших W
■' - ъ' '■ ' '
.'■ . - *'■= '-'.-...
Физический смыслзтойтеоремы очевиден: сумма р#
большого числа одинаковых случайных величин
приблизительно нормальна (pfiN(x)^Ръ^Щ}-
На самом деле эта теорема справедлива при гЬрадя©
более широких у • s - •■. i • все, слагаемые |ц, {* .'-; *■'» ■ Jfr
не обязаны быть одинаковыми ,и» независимыми; суы*е>
ста.---' *--fomidcOft-.-чгвв0л»:-сиг• *. ./"v "^даии» ■■•■"- :>.|Ш;«грййг
Ймв»1иг'.аг№.-.^«*»';'_|1а >'»:;•:/.' -•'--. 'г;|ючжму, -.»'■•'■:'■. • '/.'*;';
случайные величины тщ часто BcrrY даотся в .V >«>.'■;/':
В самом деле, каждый раз, ."когда*-жт '~&&жтш&кЫ
' суммарным воздействием _*_• ьш* »-::чвсяагйезшчнШ1Ь«'
вых /случа* - =' - фан?©ро», ■■ рс&дацн • л * '< *»:. - • -. ■>''■■.. •; иа#*
вшч> : ©иаз* ^.- рж.во» ,'.;»;':. : * "'.-- л .-■■•■
Например, - 'V*- -'/.«г■'■афт'-*■-■'»: ■ ч^.шЬ;.д#
' цел» ■ йочти' всегда ш - ':• етхя .■ щ^малшшй.. еяуча "\'у
■вели*' '• vt^;-i£*k^^ ' '•_'■ ;'е\Адг
условий на Г'Л\/-;;''*2^агпц»'-;,;.'::-- -т»р«Иу:.».'■«». ■'■■'--VihBt-
"'2.5*- Ou|^a*^cb^it#V;j|te^-iB^a" M;e»;T^R;arpg*j»*
чайную величину |, чтобы КЩв т. Пусть ирн:.!= •■''»■"".
Рассмотрим Л/ случайных незавнсимыд величин ^,
Ь» •••» 'i**расиред ^ , ; ко^ЬрыУ совпадалатД
распределением |. Если-Ж--йШфтт. = о, то согласно
теореме из п, 2Л^ш^ф^шщ^.суммы-$яфЩHH^-t-.i
• •'■ -htN будет '*'■'•. зителад© но^шл. • с парамет|
рами а зав' Mm, • ^яш-ЩР.:. И& iM) следует,. что
^ Если мы р /-'.■■.- ш$®-: .'■ ..зяиЬ^е'=.»■■;'" •:/ 'ж Л _■:/ нойскоб?
'ке, на N, т иелучм* эквввашеЛаеие f ^ во а в«^
1;соотн0ш«н«е йередяшем а шештш} ином
виде:
IX^-^^}^9-997-
(21)
Это — ч>;'-■'"-'Y;> а®«о;-.важиоё для метода Монте-Карло
-V ея«е, 0№9 »#№ «ам и метод расчета т, и оцен-
В::-тиШ'~шзт';"«'..■ 4 Af значений случайной велй^
•7ii:f)u:!it* ^t) видио, что среднее арифметическое
Лишений %щет ярйближеяно рашю т. С большой
U тйосшю ©шиб^а, шкот© приближения не;-а]юдосх^
ШШшшшЫ/^0^ ОчевиднОг эта ошибка стремится
■|с5%лк)-с--и"..•.«•'^■Av-1-•'■'■' ■ ."'"v,:'
' ; ' ■ v . > ' - - ' \ " " ■ !
§ 3. Получение случайных величии на ЭВМ;
;г Сама шст^ювка вопроса «получение случайных ве-
•:"[" л»«да'-'Э&Ш» и '»' {а вызывает недоумение: ведь все,
■Щ$*щёк&& Шижп&> должно #ыть заранее щт •« ;• -'* ми-
?i( Г( * • от«уда же щ)жет тшявиться сйучайиоЬть? ■
й':;'^ё ётом^ 1Шрос^ и в- самом деле есть ;rOTOpi*e'"f^ylt*
«ости, «© они шиосятся скорее к философии, так ч^о -шк
: Йа всякий случай заметим только, что случайнее
^^йчйны, о которш шла4 речь^ в §; % — это .идеальные
дЙатёматические понятия! Вопрос о том, можно ли с Ах
шмощью описать какое-либо явление природы, ревиает»
■Щ он&тОм; ТаШе описание ^*егда являетсяТ1ри^|Бйсен-
ш^^'Вол^, тогб, с^щймай"ийййчйна, котбрд^^йвшне
удОвл^в^й¥ел>но Шясывае^'Какую-то фнзи * -' * *" вё-
№ч*Щ ъ одном |срутё" явлейи; мОж^т ШМзйтьШ щбж&й
^ха^Ш'е^с^кЩ: ^^тШ'^е^велйчййы' Щт ^йселедовШии
|фугих 'шшШ:'¥:^'::;1: v;1;" ;'' -■''''' ''*".:''/" -v-':;"' ;'* ""',>:
*) Все равно, накоДШъ' ли одий ра^ по одйЪму значению каждой
щ величин |i, |jt, ,,.„ |у или mMti N значений одной величины £,
^««iciEK'scfe ШиёяучаЙнмё : • ^ ■ ШШ- '*'• • £( *тод«д и то же
Зраепредёяенне); - ;г* .ч-^-' -=^"г?-"| >^5' ;— \ ; • ; •■■-- ■'■ :•,
^ W

о , Точно так те дорога, хотррую ца карте страны мозк«
но считать прямой (идеальной математической.,дрщЩ
«без ширины»), становится полосой с sизгибами на
Крупномасштабном плане населенного-пункта...^ ; ^ .^
Обычно различают три способа получения сЛуча^Ы^
величин; таблицы случайных чисел, генераторы случаД?
ных чисел и метод псевдослучайных чисел....•';„..,:,,...,-:Х±
3.1, Т а б л и ц ы ел уча й н ы х ни сел. Продела^
следующий опыт. Напишем на девяти одинаковых бу?
; мажках цифры О, 1, 2, .►,
;...!."*».,' 9. Положим эт»Л
мажки .в шапку, переде*
шаем и будем извлекать
оттуда по одной бумажке^
.. каждый раз возвращая ее
назад И; снова
перемешивая все б^мажжи. П<щ*
ченные таким образам
цифры з апишем в виде
таблицы, подобной
таблице А в конце книги на
стр. 64 (в; таблице А
цифры для удобства
объединены в группы ?tio 5 штук).
Такая таблица называется таблицей случайных щ-с
сел, хотя правильнее было бы, назвать ее таблицей
случайных цифр. Можно ввести ее в запоминающее
устройство ЭВМ. И в ходе расчета, когда нам пона*
добится, значение случайной величины с распределением^
Л'ш ci од ^'; o,i)» -Щ\.
мы будем брать очереднуюцифру из этой Таблицы.
Самая большая из опубликованцых таблиц случай*
ных чисел содержит I 000000 цифр *)л Конечно, она
составлялась с помощью более современной' техники, чем
шапка: была сконструирована специальная рулетка с ш>
пользованием электроники/ПрЬстейшаяг схема такси ру-*
летки приведена на рис. 7 (вращайпШйёя диск резко
*) RAND Corporation, А тШ1ой random digits with lOOOQ^nor*
mal deviates, Glencoe, The Free Press, 1955.
£0
останавливается W выбирается та цифра, «а которую
^ка^ёает неподвижная стрелка)* -'
- Необходимо заметить, что составить хорошую таб*
лицу случайных чисел не так просто* как может
показаться; Любой реальный физический прибор
вырабатывает случайные величины с распределением, несколько
отличающимей от идеального распределений (22) .К тому
Щ в ходе опыта возможны ошибки (например, одна из
бумажек на некоторое время может пристать к под-
кладке). Пбэтомусоставленные таблицы тщательно
проверяются с помощью специальных статистических
тестев: не противоречат ли те или иные свойства группц
Зиёел гипотезе о том, что эти числа —значения случай*
йби величины (22).
Г приведем один из простейших тестов. Рассмотрим
таШйцу* содержащую N цифр. Пусть число нулей в
этой таблице v0, число единиц vi, число двоек V2 и т. д.
Вычислим сумму ~
.'■--. I (v< - 0.1А02. л
Теория вероятностей позволяет предсказать, в каких
пределах может лежать эта сумма: она не должна быть
слишком большой (так как математическое ожидание
каждого из v* равно 0,1 ЛГ), но не должна быть и
слишком-малой (так как это означало бы «слишком
закономерное» распределение значений).
Таблицы случайных чисел используются только при
расчетах по методу Монте-Карло вручную. Дело в том,
что все ЭВМ обладают сравнительно малой внутренней
памятью, и большая таблица туда не помещается.
Хранение же таблицы во внешней памяти и постоянное
обращение к Л ней за числами очень замедляет счет.
Однако не исключено, что со временем возможности
памяти у ЭВМ резко вырастут, и тогда таблицы
случайных чисел станут весьма практичными.
3.2; Генераторы случайных чисел.
Казалось бы, что упоминавшуюся в 3.1; рулетку можно
присоединить к вычислительной машине и по мере
надобности вырабатывать случайные числа. Однако любой
механический прибор будет слишком медленным для ЭВМ*
Поэтому в качестве генераторов случайных величин
чаще всего используют шумы в электронных лампах
2\

r#»c<$}: е$ди> «который фиксированный промеж *
времени At уровень шума превысил заданный порот
четное число раз, W записывается »уль,ш**слй . • ■ ое>
здсшо раз, то записывается единица *).
На первый взгляд это очень удо&шй способ. Пусть,
ш таких генераторов работают : i - е • *, работают (
веегвремя и засылают ;случайяыену#и»гедниицы во ■
двоичные разряды специальной ячейки; Каждый такт ~-
©дно >я-разрядное число. Ш любой момент счета можно
±г
Рис. 8.
обратиться к этой «ячейке и ©зять«оттуда ттШтя«эд^
чайной величины у, равномерно распределенной в ин-
.-те*.s - е (О,\Щ конечно, значение щфьбтттнт, г
писанное в форме m-разр- » -/г:* . *Д^.-.зйдо$*
О, 0(1)СЦ2) ... a<mj, где v /. • ш :>- у ~ ■щ$яши&%$&
■'. %цшко и ^от ■ ■' »'■ Лек' ':"*•• • енот ^недоетшков;::йо*
первых, зрудяо^'.»■• * рить.V; - нэ» вь^йб^шы: -ешйэг
чисел, Проверки .щтттгщ .шмат* лщр^ю&тфт, .-ми!
■»ак*вэгза{-•■'.■ <.^лша-^. - ' г».'■:.осге!г^щ^Л}^^нШй^ть■■
так Называемой и %г »'^^шред^яения* ^Ме^вдат ^
едшщцы в дшк^шяибо H^jsaaptflj^ ct^hJt ,'»' •; тьея
не* о* '•' • • •во^ж^/'Вдоюдо
"ЭВМ др»: # j vT;>i ^.зйд^^тсШы.-,.... •* .'•■•_';звь<..йоз'1.« ;. * v'^
сщуч^йяога сбоя, йо - * ^♦oязak^т^жeш • , v»»c-
ла v ■ ^» ожно, mm а&,"аю ходу ;л«етач ее йЗАаддошь
*> Сувдвтутж
£2
'^о^ади,г^:;:-."; ■.-.,■-'.."'.;--■_:■. :.'•■■.*•■ г-' ".';ч"л'. ■'
> '-да n i ^тякогогтягш; йесошишно^ --о«ажугси^яюя&-
•»г jto^#u когща будут строиться :с : р**, «e
^р№длде~»« задач ме1чэдщ! Мош^Ш{ШО*.^дшя
« ■''._''*'»■ V |ймш;ЭВМ>, на которых расчёты с шлшщыо
/Фйу^йййьш-:! - п;«jmtcjt * .■ изредка» содержать
.*Шсцар '.'.».«'•.; ь^ с^щ»аяьше устройст:воз кроете^ ее
экономично, Лучше^использовать так называемые пет*
':'/-•$&■ ->Пад»в'дго«л^ч;а;Ф«'»№---^чшсщт- ■ Поскольку
^шчеетво** используемых случайных^ чисеа1 продедоетси
с помощью специальных тестоа,; можноз не
^интересоваться тем, как эти %сла/ ПФ#учейы:^лишь бы они
удовлетворяли принятой системе тестов. Можно даже попытать-
4С^1ы^йшять их по-заданной формуле. rib, конечно* это
'дЩйш быть весьма.хитрая формдоа. :
%с«а^ поугучаемые по какой-либо формуле и имитн-
рук>щие значения случайной величины у, называются
цсёвд@сл$чайкыми числимы. Под словом «имитирующие»
;> подразумевается, что эти числа удовлетворяют ряжу,
тестов так, как если бы они были значениями этой слу«
^&кй величины; - ;;•..-■
кПёрвый алгоритм для -получения псевдослучайных
|йй:ел' был предложен Дж. Нейманом, Он называется
;^№дом середины квадратов4- Поясним его на примере.
S% :*Йусть задано 4-значное число; ?о=*да87р*. Возведем
его з квадрат.; Получим 8-значно^ число Щ===
;?== 0,97535376. Выберем четыре средние цифры этого-
Числа и положим yi ES= 0,5353.
Затем возведем yi в квадрат (^? == 0,2$6546р9|ч) и
^дова извлечем четыре средине цифры. Получим
\ Но^ этот алгоритм не, оправдал себя: пол^ч^лось
Шл;ь1а1е чем нужно малы» значений; Поэтому^ |^ными
■до^теяям^абыл» р; »;ботаны Дру|?йе Шф&ршяш.
fir *§льшее patnpoe »'.• не*щшущт s&^ofmu, штл-
ШШш$гметб&ш сфиттай. @н нзлокен ш ^ 10: f'
Достоинства/метод а^псевдослучайных чисел доволь^
но очевидней Во*й- * • у над шяучтж каждого числа
23

«затрачивается всего несколько'простых операций, тахЙчто
скорость генерирования случайных чисел имеет тед^же,
порядок, что и скорость работыi9BM» Во-вторых»:про*
грамма занимает всего несколько ячеек накопителя.
В-третьих, Любое из чисел ул может быть легко
воспроизведено. В-четвертых, нужно лишь один раз проверить
«качество» такой последовательности, затем ее можно
много раз безбоязненно использовать при расчете сходу
ных задач. ;-\ '. :•; ;,..' '.
Единственный недостаток метода —- ограниченность
количества псевдослучайных чисел, ибо если посяедова?
у тельность чисел у0,уь • •!«; ys, ... вычисляется ла ЭВМ
С по формуле вида , ?а:
, то она обязательно периодическая *);. Впрочем, .дця^
наиболее распространенных псевдослучайных чисел период
; столь велик, что превосходит любые практические
^потребности. ; ""
Подавляющее большинство расчетов по методу
Монте-Карло осуществляется с использованием
псевдослучайных чисел.
3.4. Замечание. Необходимо предостеречь
вычислителей: встречаются статьи* книги, стандартные
Программы, в которых указаны плохие алгоритмы
для^получения псевдослучайных чисел. Получаемые по этим
алгоритмам числа удовлетворяют только простейшим
тестам (см. выше,п. 3.1). Использование таких чисел
для-расчета достаточно сложных задач приводит к
ошибочным результатам.
§ 4. Преобразования случайных величин
При решении различных задач приходится
моделировать различные случайные величины. На ранних этапах
использования метода Монте-Карло некоторые вычисли-
*) В самом деле, в коде ЭВМ можно записать лишь конечное
число различных ^чисел. Следовательно, раньше или позже однд и$
чисел, например yL, совпадает с одним из лредыДущих чисел,
например yi- Тогда из формулы вытекает, что yz,+i =? Yi+ь Yt+a «*
= Yi+2, ..., т. е. в последовательности имеется период длины Р =
«Запас» псевдослучайных чисел обычио характеризуют
величиной L, которую называют длиной отрезка апериодичности. , ~Л
24 " . ~. ■" ■'
теля пытались для нахождения каждой случайной
величины стоить свою рулетку. Например, чтобы находить
значения случайной величины с распределением
'.(Хх
40,5
х2
0,25
0,125
0,125 )'
(22')
Рис. 9.
можно использовать рулетку, изображенную; на рис. 9,
действующую точно так же, как рулетка, изображенная
на рис. 7, но с
неравномерными делениями, про-*
иорцйональными pf,
;г Однако эта оказалось
совершенно не , нужным:
значения любой
случайной величины можно
поручить путем
преобразования Значений Одной
какой-либо (так сказать
«стандартной»)
случайной величины. Обычно
роль такой величины
играет случайная величина
у, равномерно
распределенная в "(й, 1). Как Получать значения у, мы уже
знаем. ; к' -
Условимся процесс нахождения значения какой-либо
случайной величины | путем преобразования одного или
нескольких значений у называть разыгрыванием
случайной величины |.'
4.1. Разыгрывание дискретной
случайной величины. Допустим, что нам нужно получать
значения случайной величины | с распределением
х2
Р% '■••'• -Ри
Рассмотрим интервал 0<*/<1 и разобьем его на
п интервалов, длины которых равныг рь р% ••., Рп*
Координатами точек деления* очевидно, будут у === Рь
iy*tas_ p,*f р2, у •«* plЦ- р2 -|- р8,.... • •» i/ = Pi"■+• Pi "Г" • • •
... -j-Pn-i. Полученные интервалы занумеруем цифрами
I, 2, ...'," п (рис. 10). На этом приготовления к
розыгрышу I заканчиваются. Каждый раз* когда нам надо
будет «поставить опыт» и разыграть значение & мы
26
\Рл

эта точка тошадет # ижервал>чь Hoarepw i, то f
тать, 4T€Tf *== Xf (в sfO№ottBtTet;
Доказать законность тайои и^оцед^ру совсем легко*
В самом деле, так ка« смтЩт величина у равно*
мерло распределена в (0,1), то вероятность того, что
f '2' <*'./• " ' "--;„ /if"^: -".....^.".
j - ■ - --.. . "-»---~--'-f■■"■■■'-■ —■. ,.р—- -I | --у~-
о A /m .^ Ptww- --:^тг f ^
- Рис. .Mi*. ;:\ , ;.
у окажется bv некотором интершше» ра»и&лддтт этого
интервалам Значит,
Pfo+/H- *....-+j9«^i<V.<l).^rflK*
Согласно нашей■=• процедуре ';|«^-:шгда^1Шгда;~
рд + р%4- ... +р£-1 <y<pi-kp2+ -*- Фт,:
" . " ' Л. - .- *
а вероятность этого равна р*.
Конечно^на *#ЙЩ '■ иойсп«<-(е1<Ь>11спкя»).-без.. pnees i 10;* ^Щред«'-
полошш, 4fo ' & x{i ■*& ..-.., я* расположи .Vg^irieft*.
ках накоштел* тшрЩ,' mi^p&mmM^iip%,pi^p2,rp^ФГ
■ [+■ Рг + P3t *.»» 1 — тоже подряд. Блок-схема подпрф*
граммы» №&рШЩиша%шр1ШЩ№ашрши*
. Прим ер. Разыграть 40 -sHafeHttfi^случайной величины0 с
распределением" .'■"' ?(■-■•
6^VO^i^0,42r
В качестве значений увЫбе» п^рй щи»р из таблицы А на
стр. 64; y*md : ■' ■. fta Ода**ф. v'tle* у "*«* fy: »ь0,8*гХ№0$fpO«9&
0,66j0,15; ВД; Й64;?0^. -" ^ . Ч '.\;\
— i , и ...тг-' -. . ' !■■■;■'■!•■■.
*) Так как в этом примере pi заданы с двумя десят • •. и
знаками, то вполне достаточно -братй; зн^чщие у^с двумя десяти*»
ним» знаками. При тщ^тхрШШштт-я * случай -у « 0,58,
которшй надо■ о» . » со с^учйем^у >и^58 {пёо звачение у=**
«<0,Щ возможно* а зйааднйе? у^ЩО*<-«■ ■..«.=. * «^ При эдспользв-
вании' многозначных у случай, paaejKCTBa *у*да pi мало, ве^юятеа ж ^
можно относить к любому изне^а&^нств: \<; ':*''"' •
26 ■-■'..'•■■:.-
чйют*значений в== 3, агзначениям у ^ 0,58 —значения 0 == 4.
Следователе©^ му получим значения; в-h~ 4; 3; 4; 3; 4; 4; 3; 3; 4; 3.
... Заметим, что порядок «умерации значений хъ х&'■-«.-*
з,.м *« в распределений £ может быть произвольным, од-
$адо шложжен^ыть фиксирован до тчдШ$оз1№$ыт&*
. _
^'
- . " . 'f
'
•
■"-
■:.■■■ ■.
1
''
. Находим у
'-■ 'л-*,:,. ■ "■'"■" ""чг
У<р1?
■. 1
'
и^мртваем
на A adpteca ячеек,
из KOtgpbix
берутся #1 и дс(
1
' '■ ■'"'■'■ ;~
»
л
(
^
да
. .._
'.'■ ■ \
ПоАЫгаем
:. ■'.■:?■ - - ■'
Восстанавливаем
адреса pi и Х\
■■:--|-v--
■
■ ■
■ '. :
'■■'■;:
vr
в»с. li.
г
4.2. f^aabfrpы ванне не пребыв »о"й сл^^Ш-
н о й в ел и чин ы. Доп 1!еп«4)ь, что нам «ну^о
получать значения случайной величины £, распредеаенной
>&' ''■'-■ *:\>;> ^ф/*)^:^ЛЩ ' V- шф&). ■•;;'■ >v"y::;..
Докажем, что значения/! можно находитф^т ■» ■»
нения ."'''-.-."' "'■
РЗ)
т. е., выбрав очередное значение у, надо реишть урав^
нение (Щшт:- ■ *тщ \■-*:;."■■".-.;■• »е#^'

Для доказательства рассмотрим, функцию
х
М= ) р{х)4х.
а
Из общих свойств плотности (15) и (16) следует* что*
0(а) = О, Ш*=Х?:-
a
0'(*)=== Р (х) > О-
Значит, функция у(х) монотонно возрастает от О
до 1 (рис. 12). Й любая прямая у = у, где 0<у<1»
/
7Y- -,
-
Jf\ •
1
1
1
У
*' ; ■
Рис 12»
/
;■ V \~ .- . ■•
Г !■ !
0 а а' У 1
-..-■ Рис. 13.
г Л
.-....,•■"
пересекает график у == у(х) в бдной-единственной
точке, абсциссу которой мы и принимаем за £. Таким
образом, уравнение (23) всегда имеет одно и только одно
решение.
Выберем теперь произвольный интервал (а', Ь'),
содержащийся внутри (a, by. Точкам этого интервала
отвечают ординаты кривой y — yix), удовлетворяющие
неравенству ^
у¥Ху<уШ
Поэтому если g принадлежит интервалу а' < х < Ъ*\ то
Y принадлежит интервалу у (а*) < у <; у (&'), и наоборот
(рис. 13). Значит,
Р{а? <I <Ь'} =*Р\у(я')<\<У{Ь%
28
Так как V равномерно распределена в (0, 1), то '
v
РШ)<У<у{Ь'Ъ~ут--У\а,)~ \ p[x)dx.
Итак,
о'
а, это как раз и означает, что случайная величина £,
являющаяся корнем уравнения (23), имеет плотность
вероятностей р{х). •
Прим € р. Случайная величина tj называется равномерно
распределенной в интервале (a,b)i если ее плотность постоянна в этом
интервале:
Чтобы разыгрывать значения ть составим уравнение (23):
и
а
dx
Интеграл легко вычисляется:
т) - а
Ъ-а
Отсюда получается явное выражение для т£
1 ъ=*а + у(Ь~а). (24)
Другие примеры применения формулы (23)
приведены в пп. 5.2 и 8.3.'
4.3. Метод Неймана; Для разыгрывания
непрерывной случайной величины. Может
оказаться, что разрешить ураёнение (23) относительно
| весьма трудно. Например, в случаях, когда -интеграл
от р(х) не выражается через элементарные функции или
кргда плотность р(х\ задана графически.
^предположим, что случайная величина | определена
на конечной интервале (я, Ь) я йлЬтность ее ограничена
ipHc. 14): -
р(ж)^Мв.
29

"'Размгршйа¥ь/|н:'> • -; :'£.;"-'*:'т сдедуШ|йяг м-'»■ -Jx-'i-
1) выбираем два значения v' и у" случайной; веди:*
чины -.у й строим случайную точку V(r\'; ц") с коёфдийа*
тами
ц'^а + у'ф-а). rf^y^M^
2) если точка Г лежит под кривой у ±=b/»(jc|,то -ltd*
слагаем | = г\', если же точка г ГЛ иенвит над кривой
Рис. 14.
у = р(х), то пару (у'.У') отбрасываем и выбираем но^
вую пару значений (y'.y"). ■ \ -. ■
Обоснование этого метода приведено в п. 9.1.v
4.4. О разыгрпаваяш! аор^^льнам к й*,ел»*
чин. Существует много весьма разнообразных приемов,
для разыгрывания различных случайных величин; Мы
не будем здесь ма ш ойтяШвдиватъся, Они
используются обычно лишь тогда/когда тфяёакы m£ C2 и 4*3
оказываются мадаэффезйтиввм^и; . ,v .. -. -:;{■ ,, ;-'"'!,
В «асшостда, w- * случайимеетмесшдля]ффшажь+'
ной случайной ^величины ;£» тЬк как^фшйеда^
в *i * виде неразрешимо, а интервал возможных зна>
чений £ бесконечен. -
В таблице Б в конце книги '{на стр. 64) приведены
значения (уже разыгранные) нормальной случайной ве-
30
дичины $ с математическим ожиданием М£==0 и с дйо
п^шей Ь| == *• Нетрудно доказать*), что случайная
величина
: : - X^a + dt (25)
будет также нормальной, причем из (10) и (11)
следует, что,, г.
■ T^vfW :-.:• Щ = а< D£'«=a2.
Таким образом, формула (25) позволяет с помощью
таблицы Б разыгрывать значения любых нормальных.
величин.
4JS. Снова a ;* р и м € ре из п. 1.% Теперь можно
объяснить, как выбирались случайные точки на рис. 1
-' й: 2.М& i:-' *;1 1юсйф<мт/-тт№£--ж« *,»дииатами
Значения y* » v'1 мйивляяиеЬ' не пятеркам вди;: • яэтаб»
' »=f$6434sf т. Д; ...
Мошш^^ доказать **),что так к#ка^щссм»ордвматы
нашиж точек > ,то :»** * ь и©аадания
такой точки в йюбую область внутри ква / гага равна нлос
щади этой ©бяастж й»аче говоря, точки равн* - з »
распределены в квадрате.
причем значения £* и ^ :. а -.».. лчсь'-и» таблицы Ш под*
|#v . " -.... г. ■-;■ '■'■■■- -
*^,S+0,2.(-0,007*), .;* -.'.."''.'>
- Одаа я» то^ек, о - . • "::-№-~мт. «•■^■*а»..©х« »'.•..'.• :-
'■■-"'"Щ:^«..|'»1фа!1..(2^' следует, что/а^ецаеемв,»i'V'/.-.m
.'■вйл.яй^'-оде^ .:;.*-/.'■ ■ ч;.; ■: •.
,^ешя!Ш1Л-5св-свед«шш^я=г%5-Л-сди. '«-«;, •*§» w «s'flyWL
, i Vi ■ ...т., i
•-'<*) Доказательств) приведено в п. 9.2,
**} Доказательство приведено в в, 9.3.

•-/ ГЛАВА2
ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДА МОНТЕ-КАРЛО
§ 5. Расчет системы массового обслуживания ■
5.1. Описание задач и. Рассмотрим одну из
самых простых систем массового- обслуживания, Система;
эта состоит из п линий (или каналов, или пунктов об^
служивания), каждый из которых может «обслуживать
потребителей». В систему поступают заявки, причем
моменты их поступления случайные. Каждая заявка
поступает на линию номер 1. Если в момейг поступления
fe-й заявки (назовем его 7\) эта линия свободна,; то она
приступает к. обслуживанию заявки, что, продолжается
/3 минут (t3—время занятости линии).Если в момент Тц
линия номер 1 занята, то заявка мгновенно передаётся
на линию номер 2. И так далее...
Наконец, если все я линий в момент 7V заняты, то
система выдает отказ.
Требуется определить, сколько (в среднем^ заявок
обслужит система за время Т и сколько отказов она
даст? -' . ' . "■.
Ясно, что задачи такого типа встречаются при
исследовании организации работы любых предприятий, а не
только предприятий бытового обслуживания. В
некоторых очень частных случаях удается найти аналитические
решения. Однако в сложных случаях (о них будет
сказано ниже) метод Монте-Карло оказывается единствен-;
ным методом расчета.
5.2. П р о с т ей ш и й пот о к заявок. Первый
вопрос, возникающий при рассмотрении такой систему:
что представляет собой потоклоступающих заявок? Этот
вопрос решается опытом, путем достаточно длительного
32
наблюдения за заявками. Изучение потоков заявок в
различных условиях позволило выделить некоторые
достаточно часто встречающиеся случаи.
Простейшим потоком (или потоком Пуассона)
называется такой поток заявок,
когда промежуток времени У
т между двумя
последовательными заявками есть
случайная величина,
распределенная в интервале (0, оо)
с плотностью
р Щ =* ае~ах.
(26)
Закон (26) называют так- .-
же экспоненциальным
распределением (см. рисл 15,
где достроены плотности
.{26) при 0= 1 и а==2).
Легко вычислить математическое ожидание т:
' op eto
Мт = \ хр{x)dx =ss\ xde~axdx.
После интегрирования по частям (и === х, dv = ае~ахёх)
получим
Мт
-Hxe-% + fe--^^^-^[°===i,
Параметр а называется плотностью потока заявок.
Формулу для розыгрыша т легко получить из
уравнения (23), которое в нашем случае запишется так:
Выяислив интеграл, стоящий слева, получим еоотноше*
ние
откуда
355

-.:■.- Впрочем»■.: «-■; ин&1—~y pa^W J' : * точно тшь-же*.
л*ак ^ к шщтому можйо вместо последней фор1^*ь ие^
пользовать формулу .,/...._. .
5.3. Схема р а с ч е т а. И*ар, рас - 7» т работу,
системы из п. 5.1 в случае дрес - .*■/. » * а а * * *
Каждой линии поставимте** .; ствие мчеищ ■ ;':..-,
треннего накопителя ЭВМ, в которую * i заяиж - ,
момент, когда эта линия освобождается.'• • • s■...■ .-ж ж&:
мент освобождения Ш линии через U, За начальный мо*
мент расчета выберем момент поступления первой
заявки 7i m 0. Можно считать, что - т этш мо т все ^
равны Ti; все линии свободны. В»; ■ тшшяатт 'psm
чета Тжда — Т\ + 7. Y
Первая заявка,поступает :»& лдашо номер 1. Значитf
в течение 4 линия эта будет задана. Поэтому мы* д* v
ны заменять h»а новоеэитйшш (i$:, == Г|4г% •■•'*'<--
вить единицу к счетчику выполненных заявок и перейти
к рассмотрению второй заявки*
Предположим, что k заявок уже рассмотрены. Тогда
надо разыграть момент поступление (Л+1)-й заявки.
Дляз этого вмбираем: ©череднае зц&чщше -у н по формуле
(27) вычисляем очерёдное значение т. = т^ А затем;
вычисляем момент'поступления
" -■%*&??*$■* + %•
Свободна ли в этот момент первая линия? Для уста-
НОВЛЙЯ* . -* --г^- '©*'-»■ ».'*'?■" **"."■'■'. ■:. у<<-чу -
" ■'■■;'■■'■ ';".' "■ ■ ;-^Cpfe*l^.'_. $8)
Если это условие выполнено, то зшчит, к моменту Тш
линия уже освободилас!* жщщ&ш ©бслужить эту заявку*
Мы должны заменить 4% на Tfc+i-|-Ys, добавить единицу
к счетчику выполненных заявок и перейти к следующей
Если условие (2&) не выполнено, то это значит, щпт
первая линия в момешТщ*: ' та. Тогда мы провес
ряем, свободна ли вторая линия:
V ШШ&- Л : ■ : Щ
$<Ш'$сАо&№ (Щ выполнено* тб мы заменяем 12 на
Тш Ц-%, добавляем ежйниду к сшетчику выполненных
заявок и переходим к еле* * и • > заявке.
Если же условие (2f) не ^ыталнено, то переходим
к проверке условия
Может он-: .-ться; что при-всех'4 от 1 дом гл'Л
т; е. все линии в момент Тин заийтщ. Тогда .надо
добавить: единицу в счетчик отказов и йотом перейти к рас-
смотреник> следующей заявки.
Каждый раз, вычислив Тй+1, надо проверять еще
условие окончания опыта ■ ■.', I...
Когда эт© ycл0^виe окажется выполненным, опыт
заканчивается. В счетчике вьшолнедаьиь заявок м & хаетшке
отказов будут стоять числа, рыт и Цотк.
Такой опыт повторяется N раз (с использованием,
различных у), й результа-ш всех отлтрв усредняются:
-.'.-".'■;.■ ',;.'■ ..: - .• аг . .■■ = /:■ . -.-..;;.
ч' *; '"' .-'-■' "". м ;'. 7 ■ ' -, ' ' \ ■■
'_"/■ .._■' . -'/-I v ■ .•■.'■-.■;
где |iBbrn(i) и роиед-у- значения рввщ и vft^wK, полученные
в /-м опыте.
На рис. 16 приведена блок-схема программы, осуще*
?ствляющей такой расчет (в случае необходимости мож*
?т •получить' значения рвыпо) и рбткш для отдельдаах ис*
нытанйй:» блоке «конец::опытш^.
■■'■;ч^;'7Во1Д*е--сл>ж'Н'Ы-е:"-*-^да:чи*,<3?1ень'.-- * « по*
ШзатЬу что этот же эдетод позволяет р • -т не*
срабненно более сложные системы. Йапримергвеличина
Шз может быть ш тгостояннайу а случайной и различной
для разяичйШ' ливни (что ^ответствует различному
оборудованию или различной •«; фикации* юбелужи-
'дающего лерсонала). Схема расчета останется в
основном такой же, но значения^ придется каждый раз

Ввод данных
/=' |
. \
Т|й0; *,' ■— fc «■ . „•.' — f„мС;"' * '= 1
-
да
Конец опыта
л
' /ябв =* /ст+1
1 :
/нов<# ?
.-'
не?
' ■ -
'■'■_. нет
-
!
л '■■
•-■4
^*<Ткон?
|аа
i=l
*.... .
#
. - - -
'
■
■ -. ч< - -■
0а
■
кез
- V
• :; ;*. . ■ -'.:■■:.. -';л
■ ■- > ■ ■■■ ■-■ '■■ -М
! - ' ' "
1 . •-.■■
г
аа
' ' " '
Добавляем
I к счетчику
выполненных
заявок
Шдсчет
результатов, ■
выдача, конец
задачи
■ ч
i
4
/
• ..
' .
.„ - . -.- ■• ' ■
■ tdazlt
' ■
*■
1нет
^нов*=яг/ст+J
Добавляем
1 к счетчику
отказов"
4
- г 1 .-■■ .--.-■.
."• -. ■■•..:- -л-*;..-.- ^:-
Ъ+1«Уа+>
у-: ,;4г--; .-■:-. .:.-,-■.
"HOBt==«CT+ *
■>...
■•
г *";;;
-..- .
ч
'
::-
'
•." ■
■ ■ ■' '-■
г'.". :-
.*
Рис. 16.
разыгрывать, и формула разыгрывания для каждой
линии будет своя.
Можно рассматривать так называемые системы с
ожиданием, в которых отказ выдается не сразу: заявка
хранится в течение некоторого времени tn (время
пребывания заявки в системе), и если за это время какая-^
нибудь линия освободится, то она обслужит эту заявку.
Можно рассматривать системы, в которых очередную
заявку принимает та линия, которая раньше всех
освободилась. Можно учесть случайный выход из строя
отдельных линий и случайное время ремонта каждой из
них. Можно учесть изменения плотности потока заявок
во времени. И многое, многое другое.
Конечно, расчеты таких систем не даются даром.
Чтобы получить результаты, имеющие практическую
ценность, надо выбрать хорошую модель. Для этого
приходится достаточно .тщательно изучать
действительные потоки заявок, проводить хронометраж работы
отдельных узлов и т. п.
Вообще надо знать вероятностные законы
функционирования отдельных частей системы. Тогда метод
Монте-Карло позволяет вычислить вероятностные законы
работы всей системы, как бы сложна она ни была.
Такие методы расчета чрезвычайно полезны при
планировании предприятий: вместо дорогостоящего (а
иногда просто невозможного) эксперимента в натуре мы
можем экспериментировать на ЭВМ, моделируя разные
варианты организации работы или использования
оборудования^
§ 6. Расчет качества и надежности изделий
: 6.1. П р о с т е й ш а я с х е м а расчета к а ч е с т в а.
Рассмотрим изделие--5, состоящее из некоторого (может
быть, большого) числа элементов. Например, если S
представляет собой электрический прибор, то
элементами его могут быть сопротивления ($(Л)), емкости
(Aft))» лампы и т. п. Предположим, что качество
изделия определяется значением одного выходного
параметра Ui которое можно вычислить, зная параметры
всех элементов
£/==/(jR(i), /?(2), ...*, C(i>, С(2>, ...;...). (30)

22ШХШ
Если, например, 1/--этр:' напряжение, щ-Л*./**« .■;.-.*■
участке электрическрй цепи, то по заковамг0м^Л« *'.'*■ JJ-
составить уравнения для цепи и, редааядех,\«айтй^.\^>''
В действительности, однако, параметры элтшш&^ящ*
равны в точности указанным «значениям. Например, *#ич
противление, изображенное s на дас. 17, шож^шаз&шф*
любым в интервале от Щ9 до ,23*1 Л2.
Возникает вопрос: как -аовлйяют «шшрения
параметров всех элементов-от номинальных «а .шаченне-ifffe.
Ложно подщтшт^еясщевить^#$ш
делы изменения £/, выбирая <щя-
«верх ■ элешнтшз; «худшие» awa*eH«ilf
шЁрйаметровл Шйако далеко «е feei^
Рис 17. да ишесшо, каши набора параше
^ров будет Худшим»; К тому шеу
если числом элементов велико, то>щкая8 оценка ок. /
сильно за«ышши&й: «а; самом делечмаловерояадо, =чн*Йф
все параметры одновременно шашли^ьншхупдоимя.
Поэтому разумнее считать параметры>веех^шщщгф^
и «саму величину £Лслучайными величинами и допытать*
от оценить математическое ожидание «Ш/ ? и даснеревдо
Ши, Величина ^£/~-это^ -t-.i..- ■ значение:.$ для леей,
партии изделий, а величина £Ш показывает, какие от-:
клонения U от«Ш/ гбудут встреадтд*ся на практике. ,
Напомним с (обэтом «Ьыло ^т^зштп ЖЩ^ ЩО;
UU Ф№А%№<1 МШт,.. tjW% Жт* ... *» S * *>).■--■
Вычислить аналитически распределение £/ «pi .шщг
ной функции /невозможно:Иногда этр можно сделать
-ЭKCПep;^V^TйУ№^,^%^M0tpiB^sJ ■ •; ..jjN»,- •< * :ККГ0ТОВЫХ
изделий. Но: это возможно далеко ле всегда, а на ста*;
дии лроектиро .... я -^шх©ЕДа*
■ ' Дояр*»' ь.' ,iipiHM№fi&Wf№
■ -.щтжЛ^'^ттъь*'-. !■'•■-?/ »'.'''. - е^;Шрш^€рИ€т^«.;,:.;• ^.;;
•''; • '- *»,;£) хШЯТЬЙфу .' :..'. • :->f г (ЗПЮве^у-"<;";_. <Ш .''" ' '■'. :
■ Ч^НШД «>V.4|-Oi' ■ :«'*:. ММ:- ./ %" -НЦП№
■ 'Шерея ;'-.v .- ?чрл-■. »*;'** ;" ..■*>»'■; ■-•■^■Л ;•*.; лдш.;шй&*-
таЛьно, путем просмотра большой партии таких
тов. Весьма часто это распределение оказывается нор*
•ным, Поэтаму !«вогш;лесл *• я ^наступаю*
т
сЛед$едйм§
М'4 -
/датздтгфойр^йодндо
элементе, йзббражшвето>. т^ рш W, ищтштмШ елу*
чайной величиной' р с матеШтическим ожиданием
Щр=± 22 п с Зо== 1,1 (напомним, что получить в одном
бпыте значение р, откложющееш о¥ Щ* бшшвечемна
За, практически невозйожно, см. (20)). v
Схема расчета оказывается очень простой: Для5^
каждого элементе р1азыгр1>шаетсязн^че1Ш параметра;^
затем Ш.ф^з^ШМК(0) вычисляется зйшение Z/. Повторив,
этот опыт N раз и получив значения
жем п|&&Шйеннсг ЭДтаТь, что
4,:UL
Upr, мо-
ш
Ш/«?
V&.
: hi***"-- "•■'
Рйс. 18.
ги- больших; i^' в последней' формуя^4 можно з*-
меййть мйбЖйтель 'iJKxV ^-1) на 1/iV, и тогд^ этаг фо>-
мул^;0Кажется^йрс^1Ъ1Мсл^ст№ем^^^ и*
& ма*ём^т^ескоЙ<
статистике доказывается, что
при небольших N лучше
сохранить множитель
1/(ЛГ-~Ш
6^. ihpim&pui
расчета йжд еж наст и.
Пусть Ml* хотим оценить
срёдйее время безоткаа-
*йШра^тш йздел«я^ првед-
шжшащ что дааестйы* х«*
ракТеристики; б©зопш*
" н^й работы^ Шждого и®
^элё^ейшв;^-- ■■'■"■-•.■■■■
ЕШ^ считать, чтовре^
м# Шзйткшиой рабошы
каждого эле ; и^^фшеировш^
'чзю№№уврсш!> безотка&ной рабош- i изделия не
составит труда; Например, для изделия, схематически" --изо«
6^Шешюгй>нагрй& 18г»йкоторО№ выхода из^строя одного
эяём^гта' #1ёч[ет за «собой выход? m ст^я- всего изделия»
Рис. 19,
W

"А для изделия, схематически изображенного^ на ^й&;$9».
в котором один из элементов Дублирован,
так как если, например, элемент 3 выйдет из строя, то
изделие будет продолжать работать на одном
элементе 4. ;
В действительности время безотказной работь?
любого элемента представляет собой случайную величину
0(fe). Когда мы говорим, что срок службы электрический
лампочки равен 1000 часов, то это лишь среднее
значение MG величины G: всем известно, что одна лампочка"
перегорает быстрее, а другая (в точности такая же)
горит дольше. ~ -у».;.-. -^
Если известны плотности распределений 0(ь>, для
каждого из элементов изделия» то Мб можно сосчитать
методом Монте-Карло в точности Так же, как это
Делалось в п. 6.1. В самом деле, для каждого элемента (
можно разыграть значение величины 0(й), пусть это
будет t(h). Затем по соответствующей'формуле (31) или
(32) можно вычислить значение t случайной величины
в. Повторив этот опыт достаточно много (N) раз,
можем считать, что
где tj — значение t, полученное в /-м опыте.
Необходимо заметить, что вопрос о распределении
времени жизни &&) для отдельных элементов не так уж
прост: для наиболее долговечных элементов организация
эксперимента затруднительна, так как нужно
дождаться, пока выйдет из строя достаточно много элементов,
6.3. Дальнейшие возможности метода.
Приведенные примеры показывают, что методика
расчета качества проектируемых изделий' весьма проста по.
идее. Нужно знать вероятностные характеристики всех
элементов изделия и уметь вычислить интересующую
нас величину, как функцию от-параметров этих
элементов. Тогда случайность параметров можно учесть путем
моделирования. ' - <
При моделировании можно получить гораздо
больше полезной информации а не только математическое
ожидание и дисперсию интересующей йас величины.
40
11усш наоример!, мы получили, большое число N
значений l/'i, tJ2t ..,.,„ Un с^н^йтйvвеличины & По этим
значениям можно построить приближенную плотность
распределения V. Вопрос этот относится, по существу, к
статистике, так как речь идет об обработке результатов
экспериментов (Только проведены они На ЭВМ)*
Поэтому ограничимся лишь конкретным примером.
Допустим, что мы получили всего N ■==. 120 значений
-Vyt' V% ... ^ I/120 случайной величины С/, и все они
заключены в пределах
l:Z*:~: ;' v;i<^<6,5. ' : ■
Разобьем интервал 1 <х<.6,5 на И (любое число,
не слишком большое и не слишком малое) равных
интервалов длиной-/Ах«р о,5 и сосчитаем, сколько
значений V) Попали в каждый интервал. Числа попаданий
приведены на рис. 20.
В 0 1 15 24 32 1Г 19 7 1,2
» ..Л'. I ' I .■ L. f- L—-j ' Ц f-
4 5 6 7 X
Рис. 20.
Частота попадания в какой-либо ийтервал
получается делением числа попаданий на N = 120. В нашем
примере частоты равны: 0,017; 0; 0,008; 0,12; Ч),20; 0,27;
0,14; 0,16; 0,06; 0,008; 0,017.
Над каждым, из интервалов разбиения построим
прямоугольник, площадь которого равна частоте
попадания Uj в этот интервал (рис. 21). Иначе говоря,
высота каждого прямоугольника равна частоте, деленной
на Ах Полученную ступенчатую линию называют
гистограммой. ■■ .-. s
Тистограм'ма служит приближением к неизвестной
плотности случайной величины U, Поэтому, например,
площадь гистограммы, заключенная между х — 2,5 и
jc==5s5, дает нам приближенное значение вероятности
Р (2,5 < £7 < 5,5)^0,95.
Следовательно, на основании проведенного расчета
(опыта) можно считать, что с вероятностью,
приблизительно равной 0,95, величина V заключена в интервале:
2»5<{/<5Д , ......
41

На "рте 21* №ш ерсавнейш; иттр&ешй п№Ш№Ж-эщь*
ышшнШ (Щчш§тШтяЕШШ^ с; параметрами««» * \
0У=&Щ1 I s ЕСЙШП©ЭТОЙ* ЙЛОТН0СТИ ВМЧ
.;. * I
■ . ■ . t.
того, что t'- заключена в интервале 2Д-< ^<5Д тЬпр*
лучим. довольнвАо^1изж>е значениеJQjSr*)^'-'.
•) Ход взы «йс%%«ий. Согяаево (ЩШцкит*
В ин$еграле сделаем замену переменной *■— й ар #& Тогдаь ц«
Р&5<£'<5,5}
,.. -.iff. -.;. **::.:
2л ^ -.* ,
"*
:. ' 2|5~а " ',-.■' .
l^8i>3ffa«eHi^\ послед-
эд>;-*а
неро интеграла шшШШтея с ш «V йю-":тайяи^*«с ш-. авишрй'йй^
теграла вероятностей*<Щх), в которых приведены,значений ф^даищ
^шШт^
Получим
42-
Р {2,5 <£'< 5,5}*= 0,5 [Ф (1,88) + Ф (1,54#**
\
-6.4^ ^а менада и^е, К ^mmmmo^ фяещ^и , такого
■шйа пока проводят федшх В чем главная причина
этого--^трудно сказать Скорее всего да тш, ^то worn
структоры и проектировщики не знают^о такси;
возможности,
К тому же, прежде чем ^сёчитывать таким; методом
какие-л«бо изделия, надо изучить вероятностные
характеристики,всех элементов, входящих в эти изделия. Это
немалая работа. Правда, зная эти характеристики,г
можно оценивать ячество любых изделий, состоящих из
этих элементов. Можно ^оценивать изменение качества
при замене одних элементов другими. v
Нужно ^надеяться, чтов^&пижайщие годы такие
расчеты станут привычным делом, А вероятностные
характеристики элементов будут всегда выдаваться предприя^
тиямй, лх изготовляющими. -
§ 7. Расчет прохождения нейтронов сквозь. пластинку
Вероятностные законы взаимодействия -отдельной
элеменгариЬйчастшы (нейтрона, фотона, мезона и др.)
с веществом известны. Обычно требуется найти
макроскопические характеристики процессов, в которых уча-
"C*i^^:-oir^c^eecfe '-tDomfveeerBo -ггаигах^яастю^'ПйртнЬсти^'^б-
токи ж т. п. Эта ситуация похожа на ту, с которой мы
сталкивались в §§5 и 6, и весьма у * > «на^^для
использования метода Монте-ЗСарло.
Пожалуй, чаще всего :1*етсщ Монте-Карло исполь-
зуется в нейтронной физике. Мы рассмотрим
простейший вариант задачи о прохождении «ейтрояов сквозь
пяасташеу.: "^ '
74. Постановка задачи. Пусть на однородную *
бесконечную пластинку 0.^ х «s: h надает поток-н#|ро-
нов с энергией Е0, Угол падения 90°. пПри столкновении
с атомами вещества, из*•_"'**# ,* состоит пластинка,
нейтроны могут упруго рассеиваться или поглощаться*
Предположим для простоты» что энергия ней1^напри
рассеянии йё; меняется < и любое направление «отскока»
нейтрона от атома одинаково вероятно (последнее иног*
да, !."• еддиво в веществах с • • ; »..■■■ атомами). На
рис. 22 изображены .различные ^судьбы м^щромт:
нейтрон (я) лП|ша^ пдастлш^,.дйщ:ррн ,(£) логло*
-вдается, ш^Шщт ,{$) t * • - -адастдащой*
ча

Требуется вычислить "вефоятнЬстй прохождения ::Йе**г
т||она сквозь пластинку р+, вероятность отра^ни^нШ^
тррна пластинкой >- й вероятность поглощения нен/fjpo-/
на в пластинке р°. v e
Взаимодействие нейтронов с веществом
характеризуется в рассматриваемом случае двумя постояннымиv
2С и 2Sj которые называются
сечением поглощения и сече-
нием рассеяния. Индексы 'с и
s — это первые буквы англий^
ских слов capture (захват) й ■
scattering (рассеяние). "■
Сумма этих сечений:
-—с~Х— /ГТа? называется полным сечением:
>< V Физический смысл сечений
^ -*— \ ? следующий: при столкновений
Г V нейтрона с (атомом веществе
вероятность поглощения рав-
; Рис.22. . j на 2с/2, а вероятность
рассеяния равна 2в/2. -:■■:'■
Длина свободного пробега нейтрона/к (т. е- щина
пути от столкновения до столкновения) — это случайная'
величина. Она может принимать любые положительные
значения с плотностью вероятностей
v. . .У-.^р{х)ет1е-т**т:;,:
Нетрудно заметить, что эта плотность величины 1\
совпадает с плотностью (26) случайной величины т для
простейшего потока заявок. По аналогии с п. 5.2 мы
можем сразу написать выражение для средней длины
свободного пробега ,~
и формулу для разыгрывания Я: • ;
Остается еще выяснить, тсак выбирать случайное
направление нейтрона после рассеяния. Так как задача
симметрична относительно оси х, то направление вполне
определяется одним углом ф между направлением ско-
44
а -*■
N
рости нейтрона и осью Ох. Можно доказать *),
что-требование равной вероятности любого направления в этом
случае равносильно требованию, чтобц косинус этого
угла iA = cosq) был равномерно распределен в
интервале \r-r\y I). Из формулы (24) при а==—1, Ь '=— i
следует формула для разыгрывания ja:
7.2. Схема расчета путем
моделирования истинных т р а е к т 6 р и й.; Предположим, что
нейтрон испытал k-e рассеяние внутри пластинки в
точке с абсциссой xh и после этого ч
начал двигаться в.
направлении Цй. '
Разыграем длину
свободного пробега
"Я*:-?.-— (\jty\ny
и^ вычислим абсциссу
следующего столкновения (рис. 23) о
Проверим условие
прохождения сквозь пластинку:
Если это условие выполнено, то счет траектории
нейтрона заканчивается и добавляется единица к счетчику
прошедших частиц. В противном случае проверяем условие
отражения:, г
'-.": .-■■ xk+i <0. .. -....
Если это условие выполнено, то счет траекторий
заканчивается и добавляется единица к счетчику отражённых,
частиц. Если же и это условие не выполнено, т. е.
О <; xft+i ^ А, то, значит, нейтрон испытал (k 4-1) -e
столкновение внутри пластинки, й надо разыграть
«судьбу» нейтрона при столкновении.
Согласно п. 4.1 выбираем очередное значение у и
проверяем условие поглощения:
; ;*) Доказательство приведено в n.94s ,
46
: у
*-к/ У
У\Р !
Г 1
ч
h <9

|«н зшс;;- ■ ■-; ."■■ ся и ;i-.« * гвляетш'.- *.-# и№--*-Г : ■ .
тшоШоодешшх частиц. В -противном сяучае V ' • ,
ч*э нейтрон иснв1тая |>шж ' в точке « * v..
*ftii. Тогда -разнгр. ..ем «овое направление %ц
нейтрона ; ,
я зате» ад©вт^яемкв«с* щшИ1 U * * «(ни,? •* ечяо^ужё
•едругааш ияыи^. v.. --..'•■.-
©ее^«. - -'.цы^Штт-i:- *<* 4:шкш«--.': *: яв;
что каждое значение у иск* vyewai;.всегоГ*« ; де&'
расчета одного звена траек * * ■ ■ нужны ^ внач-
Начальные значения для каждой траектории:
После того *&к будут сосчитаныШ траекторий, ока*
жется, что N+ нейтронов прошли сквозь пластинку, Ж~г
нейтронов, отразились от нее, a W нейтроновЩыш
поглощены. Очевидно» искомы© вероятности ирибшж *
равны отношениям:
На рис. 24 приведена блок-схема программы для
расчета этой задачи; Индекс / — это номер траектории, инч
жекс % -^иомер «йвлкноэеяня (вдоль тржекторй»!.
Такая штоддаа расчета ттп и -очень еетес - :), ]Ш1
нееовер i ■ .. j . 4$ маетности, таким методом трудно вш-^
числить вероятность р+, когд)а она очень маа«, Д с та*§
ким случаем как раз приходится сталкиваться при рас*
чете защиты от излучений.
Существуют более «хитрые» разновидности шетода-
'Монте-Карло, позволяющие рассчитывать й шкие сйу-*
чаи. Остановимся корожо на одном-из простейшщ *ам
риантов расчета с помощью так называемых «весон»^
7.3. Схема расчета с истголь^оватШ^ «е^
сов, заменяющих >иоглощ$йие5 Рассмотри*! ту
же задачу о прохождении «е^грО!Ш.П^ ято
вдоль одной и той же траектории движется «пажёт>, gov
стоящий из большого ч«сла -щ одинаковых нейтронов*
При столкновении в точке с абсциссой ^ Шличест^о и®«
глощенных нейтронов из «шкета» в •' / м равно
т
^ Шш1дуд>
:*Г&
Ь==М л%«ф f%*=l-
I
> A*,s
.2.
In у
±
XkArl ^ Ш-^^Ы^кТ
b
Xk+l > &%
1
* я&т '-et,
"И
^.■■■■'#*Р
IT*"*
■ню
**+.,. <4)?
*лЛВ*-^«*ь|
ч««-
да
F
у у
:*-,
|:';'- /***<» ■-§■
'ЖЙР.
.№*
>*;-jrv
*
Выдача результатов, конец задачи
..- 1В</ЗД'?-' '.-■
вшт '-.■
.-*<
:H*»v
j
S-- ■ ■
j '■ |t*+r«*2¥—t '
'«>
К
■■ ' ■*-• .^-,,
<: Дшя^'^^ ^ ;
W«t. 24»

©а(2с/2), а количествоl нейтронов, йепыташиих ршсст?
ниё» в среднем равно и>б(2а/3!,).
Добавим величину ш0(2с/2) к счетчику гюгловдщйнх;
частиц, а за движением рассеянного «пакета* будем
следить Дальше, предположив, что весь ©ставшийся
«пакет» рассеялся в одном направлении.
Все формулы счета, приведенные в п. 7.2, остаются
прежними. Только при каждом столки*: ни«
количество нейтронов в «пакете» будет уменад&тъея:
wk+l = wk{2J2),
так как часть «пакета», содержащая;:'&*(£«/£)
нейтронов, будет поглощаться. И траектория теперь не может
закончиться поглощением.
Величину W& обычно называют весом нейт^онй й
вместо того, чтобы говорить о «пакете», Состоящем йЗ
wu нейтронов^ говорят об одном нейтроне с весом «0*.
Начальный вес w0 обычно полагают равным 1. Это т
противоречит нашим рассуждениям о «бол,ьшомг пакете»,
ибо нетрудно заметить, что все шл, получающиеся при
расчете одной траектории, содержат ie>o общим
множителем. ' ^ г-" ■ . ': -;<'
блок-схема программы для реализаций такого
расчета приведена на рис. 25. Очевидно, она ничуть «е
сложнее* чем блок-схема, изображенная на р«с. 24. Одйако
можно доказать.1*), что расчет р+ методом, настоящего
пункта всегда выгоднее, чем расчет по методу п. 7.2,-
7.4. За м е чан и е. Существует довольно много
разнообразных способов расчета, использующих различные
веса. Мы не можем здесь на них останавливаться.
Отметим только, что метод Монте-Карло позволяет
решать гораздо более сложные задачи об элементарных
частицах: исследуемая среда может состоять из
различных веществ и иметь любую геометрическую структуру;
энергия частицы при каждом столкновении может
меняться. Можно учитывать много друщх ядерньш ушэо?
цессов (например, возможность деления атома при
столкновении, с нейтроном и образование при зтом
новых нейтронов); Можно рассчитать условие вознйкнове?
ния и поддерживания цепной реакции ит1*
*) Доказательство приведено в il Ш>.
48
I
1
Ввод данных
1
. /-1
k = 0, д:0 = 0, ц0 —1, ш0=1
"нов *'ст > *"!>
Яй = — -^-lnv
1
Xfc+l—Xk+hkVk
1
Xfe+i > h?
да
нет
^
; Xk+i < 0 ?
^HOB^^CT+^ft
да
нет
/нов — Уст "г 1
4>
/нов < N ?
да
Wk+i = wu (2s/2)
I
<о* = КЛ*>ь№)
1
^+1=2^—1
\
"нов — ^ст Т *
нет
Вычисление р+, р~, р
Выдача результатов конец задачи
Рис. 25.
49

"'-.' § 8; Вычисление определенного интеграла
Задачи, рассмотренные в §§5, 6, 7,были вероятност-
ными'по своей природе, и использование метода Монте-
Карло для их решения казалось довольно естественным.
Здесь, рассматривается прост©- математическая задача:
приближенное вычисление определенного интеграла.
Так как вычисление определенных интегралов
равносильно вычислению площадей;, то можно было бы
использовать метод примера 1.2. Вместо этого мы
изложим другой, более эффективный метод, позволяющий
строить разные вероятностные модели для решения этой^
задачи методом Мште-?Карло, и укажем, как среди них
выбирать модели «получше», ■,
8.1. Метод. вычисл:ени;я. ^Рассмотрим функцию»
g(x), заданную на интервале а . <С х <; Ь% Требуется
приближенно вычислить, интеграл!
&--■
Выберем »« :«льнукэи плотность распределенияv
Ръ(х), определённую на интервале (а,Ъ), (т. е..произ«*
вольную функцию р\(х), удовлетворяющую условиям'
(15)-и- (16)).
Наряду со случайной величиной |, определенной в-
интервале {Щ-Щ е-гш#тностью р\(х), нам понадобится
случайная- вешйвдм-'
Согласно (18)
ь ■■-<■_■ ■• * .
а •:
Рассмотрим теперь W одинаковых независимых
случайных величин щ,у\2, ..., tin и применим к;их сумме
центральную предельную теорему ш 2.4; Формула (21) в
этом случае запишется так:
{| ■ ы ч
l-jft,*-1 <"Зл/^-Г»0*997- -(34)-
№
Последнее соотношение означает, чт@ если ты
выберем N значений £ь |г. ••., In, то при достаточно боль-
шом.М ■'•■■■■" ■ ■-■' ■ ■ ■■ - - ■' •
-'.-'■■ ^VMLmJ. <35)
"-■ЬПШ . >■■■:■■
Оно шкаанязег также, ичто « мшть боэгыаюй дя ? *тно-
стьк» ошибш ■■•бушжеяня ($5) не т :■« шшт
Ъ*ЩЩ, ''■'
8.2. К а к в ыТ&и р а т ь схем у р ас чет а. Мы
видели, что яШ расчета интеграла (33) модою
использовать любую случайную величину £, определенную в
интервале (а, Ь). В любом случае
Однако дисперсия Drj, а с ней и оценка погрешности
формулы (35) зависят от того, какую величину £ мы
используем. В самом деле,
ъ
а
Можно доказать *), что это выражение будет
минимальным ;товда* когда Ръ(х) пропорциональна \g{x) \.
Конечно, шлбирать очень сложные р\$х) нельзя, так
как процедура разыгрывания значений | станет доемь
трудоемкой. Но руководствоваться этой рекомендацией
при выборе р\{х) можно (см. пример п. €.3).
На практике интегралы вида (33) методом Монтё-
Карло не вычисляют: для этого есть более точные ме«
тоды — квадратурные формулы. Однако при переходе к
.-многократным интегралам положение меняется: *ю.дра«
турные формулы становятся очень сложными, -а «етод
Монте-Карло остается почти без изменений.
&3. Чвхл^явы-й пря-й-ер. ° ■ ; едашв» » '"■'*■ *;л
4S/2 ',•'"/"..„'
3D
*) Доказательство приведено в п. 9.6, .,
61

Точное значение этого интеграла известно:
я/2
\ sin х dx = [— cos х]%/2 = 1.
О
Мы используем для вычисления две различные случайные
величины |: с постоянной плотностью р*(л:)=2/я (т. е. g равномерно
распределена в интервале (0,я/2)) и с линейной плотностью
Pg (x) = 8#/я2. Обе эти плотности вместе с подынтегральной
функцией sin* построены на рис. 26. Из этого рисунка видно, что
линейная плотность более соответствует рекомендации п. 8.2 о том, что
Рис. 26.
желательна пропорциональность р* (х) и sin*. Поэтому нужно
ожидать, что второй способ вычисления даст лучший результат.
(а) Пусть pg(#)s=2/:rt на интервале (0,я/2). Формула для
разыгрывания | может быть получена из формулы (24) при о = 0и
Ь = я/2:
6 —яу/2.
А формула (35) примет вид
N
wZsin|/-
/-1
Пусть N — 10. В качестве значений у используем тройки чисел
из таблицы А (умноженные на 0,001). Промежуточные результаты
сведены в табл. 1.
Таблица I
/ | t 2 j 3 4 j 5 | 6 | 7 | 8 9
Y/
If
sin lj
0,865
1,359
0,978
0,159
0,250
0,247
0,079
0,124
0,124
0,566
0,889
0,776
0,155
0,243
0,241
0,664
1,043
0',864
0,345
0,542
0,516
0,655
1,029
0,857
0,812
1,275
0,957
10
0,332
0,521
0,498
52
Результат вычисления:
/ ** 0,952.
(б) Пусть теперь pg (#) = 8х/л2. Для разыгрывания | используем
уравнение (23)
-■' I
\ (8*/я2) dx = у»
о
откуда после несложных вычислений получим
Я /—
I=tVy.
Формула (35) примет такой вид:
я2 ж-ч sjn ё/
/=i 7
Пусть N = 10. Числа у .выберем те же, что в случае (а).
Промежуточные результаты сведены в табл. 2,
Т а б л и ц а 2
/ | I | 2 3 | 4 | 5. 6 . 7 j 8 | 9 10
Y/
6/
sing/
1/
0,865
1,461
0,680
0,159
0,626
0,936
0,079
0,442
,0,968
0,566
1,182
0,783
0,155
0,618
0,937
0,664
1,280
0,748
0,345
0,923
0,863
0,655
1,271
0,751
0,812
1,415
0,698
0,332
0,905
0,868
Результат вычисления:
/ « 1,016.
Как мы и предполагали, второй способ "вычисления дал более
точный результат.
8.4. Об оценке ошибки. В п. 8.2 уже отмечалось,
что абсолютная ошибка при вычислении интеграла /
по формуле (35) практически не может превысить
величины 3VDri/iV. Однако в действительности ошибка,
как правило, оказывается заметно меньше этой
величины. Поэтому для характеристики ошибки на практике
часто используют другую величину —так называемую
вероятную ошибку
бвер = 0,675 УЩ/ЛГ.
53

Фактическая абсолютная ошибка зависит от ихшоль-
зованных в расчете случайных чисел и может оказаться
как в 2—3 раза больше, так и в несколько раз меньше,
чем бвер. Так что 6Вер дает нам не границу ошибки, а
порядок^ ее*).
Вернемся к примеру из п. В,3. По значениям, приведенным в
табл. 1 и 2, можно приближенно сосчитать дисперсии Ьц для обеих
методов расчета. Соответствующая расчетная формула приведена в
п. 6.1 **).
Та б л и ц а 3
Метод
(а);
... - <0)
Dn
,0*256
0,016
<W
.0,103
0,027
счет
0,048
o;oi6
В табл. 3 для обоих методов расчета указаны приближенные"'
значения дисперсий От], сосчитанные по ним- вероятные о'шибки бвер,
а также фактические абсолютные ошибки, лолучещше при расчете
бе-чет. ; ; ■'
Мы ВИДИМ, ЧТО Н&>еч«т
Jeep.
" ЬЯО »Mfi©T-TOT ЭКС ПОрЯДОД ЧТО/
*) Определение вероятной ошибки см. :В п. 9.7,
**) Для метода (а):
2 Г 10 / 10 V":
JV
■^ (4,604 —.3,670) «=0,256.
Для метода (б):
Dtj
я*
9-64
|Ш°-4(£Ш
я*
.шт -^- (6,875 ~6,777) = 0,016.
ДОБАВЛЕНИЕ
§ 9. Доказательства некоторых предложений
В этом параграфе приведены доказательства
некоторых утверждений, высказанных в предыдущих
параграфах, которые кажутся нам несколько громоздкими для
У
Рис. 27.
популярного изложения или предполагают больше зна*
ний по теории вероятностей.
9.1. Обоснование метода Нейман для р а*
зыгрывания случайной величины (п. 4.3)«
Случайная точка Г равномерно распределена в прямо*
угольнике abed (рис. 27), площадь которого рявна
М0 (Ь — а)*). Вероятность того, что точка Г окажется
*) Ср. п. 9.3S
55

под кривой у = р (х) и не будет отброшена, равна
отношению площадей
ъ •
\ р (х) dx
2 1
М0 {Ь - а) М0 (Ь-а)'
А вероятность того, что точка Г окажется под
кривой у = р(х) на интервале а' < х < &', также равна
отношению площадей .
v
\ р (х) dx
tf_
M0{b-a) '
Следовательно, среди всех отобранных нами значе^
ний g доля значений, попавших в интервал (а',6-'),.
равна частному
ъ' '■.'■'.[■■
J p(x)dx v
Mo{b-a) l M0(b-a) ~ ) P(x)dx*
что и требовалось доказать.
9.2. Плотность распределения величины
£' —a-f-a£ (п. 4,4). Предполагается, что величина £
нормальна с математическим ожиданием М£ = 0 и дис«
переией D£ — 1, так что ее плотность
Чтобы вычислить плотность распределения величины
£', выберем два произвольных числа Х\ <C х2 и вычислим
вероятность ,
Р (*i < £' < х2] =*= Р {*, < а + оС < *2} =
Следовательно,
(*г-а)/о
Р {*i < £' < х2} = -L- \ е-™ dx.
^2я
(хх-а)Ю
66
В последнем интеграле сделаем замену переменной, xf ==*.
■=:а-}-ох. Получим
х*
Р {*, < С < *2} = -т4=- t <г<*'-<да <**',
откуда следует (ср. (14)) нормальность величины Zf c
параметрами Mf = d, DX* =в2-
9.3. Равномерное распределение точек
(Y',y") в квадрате (п. 4.5). Так как координаты
точки (y', y") независимы, то плотность ее р (х, у) равна
произведению плотностей
р(х, y) = pY(x)pY,(y).
Каждая из этих плотностей тождественно равна. 1.
Значит, p(x,y)zs£ 1 (при 0 < х < 1 и 0 <# < 1). А это и
означает равномерность
распределения точки (y'>
y") в единичном
квадрате.
9.4. Выбору
случайного напр а в л е-
ния (п. 7.1). Условимся
задавать направление '
единичным вектором,
выходящим из начала
координат. Концы таких
векторов расположены на
поверхности единичной
сферы. Слова «любое
направление одинаково ве- Рис. 28.
роятно» означают, что
конец вектора представляет собой случайную точку Q,
равномерно распределенную на поверхности этой сферы:
вероятность того, что Покажется в любом элементе
поверхности dS, равна dS/(4n).
Выберем на поверхности сферы сферические
координаты (ф,-ф) с полярной осью Ох (рис. 28): Тогда
dS — sin q>d(p dty, (36)
причем 0<ф<л, 0,<]ф<2я.
57

ОФтшчтм чщк&э p(tyt f) нлотность случайной точки
(ф, ф). Из требования
р (Ф,-ф) rfq) rf-ф == rf5/(4jt)
и соотношения (36) вытекает, что
р(ф, ^) = (зн1Ф)/(4я). (37)
По совместной плотности ф и-. "ф" нетрудш вычислить
плотности этих величин;
%(#=^=5 p(q>;#< Vsifff^ Ш
о '■.■-,■
Равенство р(ф#^%(ф^ру# шжазыаает, чт©щ:■'*ф
независимы. Очевидно, -ф равномерно распределена
в интервале (0,2л) и формула для разыгрывания ф araiM-
шется так:
i|> = 2jty. .-..-, W
Формулу для разыгрывания ^р найдем при помощи
уравнения (23);
• ■ ■ ^ ф ■<
•j \smxdx = yf
_откуда
со$Ф=1— 2у. (41)
Формулы (40) и (41) позволяют нам выбирять
(разыгрывать) случайное направление. Конечно, значения
у в этих формулах должны быть "разными.
Формула (41) отличается от последней формулы
п. 7.1 только тем, что вместо у & ней стоит 1 — у,. а эти
величины имеют.одинаковое распределение.
9:5. Преимущес т в о способ а р а с ч е т а с
весами (п. 7.3). Введем случайные величины v и v7,
равные количеству (весу) прошедших сквозь пластинку
нейтронов, полученному при расчете одной траектории
методом п. 7.2 и методом п. 7.3.
По физическому смыслу задачи - \ ' -г
58
(Строгое доказательство этого' утверждения имеется
в книге [3].) ' ■
Так как v может принимать только два значения, о
.и 1, то распределение у задается таблицей
Приняв во внимание, что v2 = v, нетрудно
вычислить, что Dv = р+ — (р+)К
Легко видеть, что величина V может принимать
бесконечное число значений-: щ= 1, w\, w2) ..-, Wk> •••> а
также значение 0. Поэтому ее распределение задается
таблицей
Значения q\ нас интересовать не будут, так как в любом
случае можно записать выражение для дисперсии
со
Заметив, что все-ufe^l и что £ ^<7л=гМу' = р+,
получим неравенство Dv' ^ p+ — (р4)2 = Dv.
Тот факт, что диеиередя V всегда *шньше, чем
дисперсия у, показывает; что .метод п. 7.3. для расчета р+
всегда лучше, чем метод п. 7.2.
Такой же »»• s * i можно сделать о расчете р~, а при
не слишком большом поглощении — и о расчете р°.
9.6. Наилучший выбор | (и. 8.2). В п.Ь.2
получено даьфаженме для дисперсии ©ц. Чтобы найти
минимум этого шражендапрж всевозможных выборах
Рь(х), воспользуемся хорошо извествьш в анализе
неравенством -
[Ъ -»2 Ъ Ъ '
\ | и (х) v {х) 1 dxl <; \ м2'(ж) dx • \ t»2 {x) dx.
а ^ а с.
Положим и — g (x)/<yjpt{x), a li =/^/p|,(^); чогда из этого
неравенства получим
ua- J в » «
69

Значит.
Оч>Ш я (*)!<&] -P. (42)
Остается доказать, что нижняя граница достигается
тогда, когда р\{х) пропорциональна |g(x)|•
Пусть
Pe(*)=Jg(x)l ■ ' (43)
I
g (x) | dx
Нетрудно вычислить, что при такой плотности рЛх)
и дисперсия Dr\ действительно равна правой части (42);
Заметим, что выбрать «наилучшую» плотность (43)
для расчета практически невозможно: для этого нужно
знать значение интеграла \|g(*) J dx. А вычисление
HOGS
следнего интеграла представляет собой задачу,
равноценную стоящей перед нами задаче о вычислении инте-
ъ
грала V g (x) dx. Поэтому мы ограничились рекоменДа-
а .
цией, указанной в. п. 8.2.
9.7. Определение вероятной ошибки
(п.. 8.4). Пусть £ — нормальная случайная величина,
определенная в п. 2.3. Нетрудно вычислить, что, каковы
бы ни были а и а при г = 0,675 6у 1
а+г' , , ' "
\ р&(х) dx — 0,5.
Отсюда вытекает, что
Р{|£-а|<г} = Р{|£-а|>г} = 0,5,
те. отклонение большее, чем г, и отклонение меньшее,
чем г, одинаково вероятны. Поэтому величина г назьь
вается вероятной ошибкой случайной величины £.
60
В п. 8.1 мы вычисляем приближенно нормальную
величину р = (1/W) (111 + 112+ .,. + v)n) . Ее
математическое ожидание а =; Мр =7, а дисперсия а2-^ Dp =
= Dr\/N. Поэтому вероятная ошибка величины р
приближенно равна 0,675 <\/Dr\/N.
В п. 1.2 мы также имели дело с приближенно
нормальной случайной величиной, ибо
; = 1
где lj = 1, если /-я точка оказалась внутри 5, и £j = 0
в противном случае. Обозначив площадь области 5 той
же буквой S, можем записать распределение, общее
для всех величин £_,-:
fe VS 1-SJ'
Отсюда следует, что М| = 5, M|2 = S, D£ = S — S2.
Дисперсия величины N'jN равна
<? вз D {N'/N) = &£/# = 5(1- S)/N,
а вероятная ошибка приближенно равна
0,6750 = 0,675 У5(1 -S)/N.
При 5=^0,35 и N = 40 получаем значение 0,051, кото*
рое практически совпадает с ошибкой эксперимента,
описанного в п. 1.2. ^
§ 10. О псевдослучайных числах
Большинство алгоритмов для получения
псевдослучайных чисел имеют вид
. yk+i = F{\k). (4*>
Если начальное число \о задано, то все последующие
числа Yi» Y2» ••• вычисляются по одной и той же
формуле (44) при k = Q, 1, ... Метод середины квадратов
в п. 3.3 также имеет вид (44), но вместо аналитического
задания функции у = F (х) была указана совокупность
операций, которые надо проделать над аргументом х,
чтобы получить значение у.
61

10.1. К а к#?й щ&ётть бщ ш^ь ф у и к ц щ я F(j^. Cjjjet
дующий пример позволяет «оняшь, в чем шстода
из основныхтрудшстей прттшбщъ c/^v
^:j£
Рис. 29.
Л
Пример. Докажем, что фужщ«ю у — ^(*). график которой
изображен на .рис. 29, нельзя йспфиьзовй'гь яда падучёвия -- >-»''■ >■
. «§исел «9 формуле i(44)4
В самом деле, ра л .;
в единичном квадрате 0 <х<1^
.0 < у < 1 точки с декартов
выми координатами К
(Yb Y2). (Уз. Y<)' (Y6. Ye)>■•••.;.
т"ак как здесь уг=*Р(уд, %Ц*
^^Ys)* Щ^РЩ). • • •. та*вс$
"эфи & ' -раскали • ;■ ■■•*ш-щж--г
вой y=>=lF(3ir), Й*ф® ётжшт «*., -
ибо настоящие случайные точки
должны равномерно заполнять;
весь квадрат (см. п. 9.3).
Из расемотренного^рй- -
мера следует, чт
рассчитывать на успешное нс-
ЙОЛЬёвгз ' фуНКЦИЙ #==«
== jF(лг) в формуле (44)
можно только тогда, когда график этой функции
достаточно плотно зшшшгет весь <#св -«*#т! .. ?
Таким свойством обладает, например, функция
:::.}'и=№,: :' да
где g— очень большое число, .а , {г} означает дробнуй*
часть числа г. На рис. 30 построен график функции (45)
при g= 21. Читатель мг се€е представить, как этот
график выглядит при g — 517.
10.2. МетФД ер а** я ечк/нй (метод, 1нч ет^о в),.'.;:
Наиболее распространенный алгоритм для иолучен»я
псевдослучайных чисел 4ыл предложен Д. Лемером.
В основе этого алгоритма лежит функция (45), однако
для удобства реализация на ЭВМ шгщьшм аффтщ
несколько ийа-че,
Определяется ноежедшательносЕь цедмжчшсом /%, в
которой начальное шбло т®=1 зайаш, ш все жоеяе-
душцме числа wm, т2, ... вычисляются н© шш&к ж шй,;
mft+l=5l7m* [тойГ*)
146)
при k == 0, I, 2, ... Ш числам mfc вычисляются
псевдослучайные чдасла
ъ^Г*мк. \Я)
Формула (46) означает, что число ть+i равно
остатку, полученному при делении 517 т* на 2*°. В теории
сравнений (см. любой
учебник по теории; чи- М'
сел) такой- остаток; йа~ f
зывают наименьшим
положительным
вычетом по модулю 240.
Отсюда п^йеходят оба.
на|ва нйй1: алгоритма —~
метод[сравнений или ';
мещд■ фычётов.
Формулы (46) и (47) /
оч€ШЬ л«еко; • реализе-
вть на ЭВМ
работающих, с 40-разрядным»г , д
числами, при помощи
команды, умножения с Рис. 30.
удвоенным количест- ;,.--...-.-
вом фазрядш: надо использовать младцще дифрм произ*;
ведения., _:■-/.. .':. .-, ■ •
В ЭВМ, работающих с 3€-разрядными числами,
©мест®; 517 и 24Q в (46) и (47) используют 515 и 236.
"''Мая указанных последовательностей Mo, «i, тг, ... периоды сов*
пада-ют с ©т»• зкамн лпернодичностн.: Длины их равдш соответственно
Менять произвольно множители 517 й 5lS или; начальное
значение да© === 1 нельзя, так как при других значениях псевдослучайные
числа? могут оказаться плохими:
ЛШ1РАТУР&
1. Н. П. Бгусле-нкб и др. (под редакцией Ю. А. трейдера),
Метод статистических испытаний (метод Монте-Карло), СМБ,; М.,
Фвзматгиз, 1962. ..'■.-. ; -
2. €. М. Е рм а к о в, Метод Монте-Карло, и смежные вопросы, М.,
«Каука», 1971.
3. й. М. Се^'оль, Численные методы Монте-Карло, М., «Наука»,
1973. ' ■'•;.■ ,■•-..-
4. С. М. Ермаков, Г. А. Михайлов, Курс статистического
моделирования, М., «Наукам 1976. : .,
и
ж
ё
мм
л

<Mt^t--co~-t--™-4t<-tfco
OtOO —(OlOOON^O
ooootoeocnt^—«tNOO)
h-«3000NtOO(0(N
Ю«— OCniONtO —N1*
Ь~тГО — 00CN00O5<Mt^
"t •-CO (N ■* Ю (О О N СП
<моо-*<мооою —юсо
СОЮСО00СМ—CNOcNOO
nistooioM'iatocotN
<мсо<мсУ5СУ50(^1Л-*а>
JS
«=3
<
ООЮ — ООСОО^^ЩОО
ЮЮОО^ООИПОЬ"
ЮСЛ—CNlO--<SC7?C7)(N
cooocot^t^cnioiocnio
LO 00 CO tO est-» CN"*1 —' —
о.
•е-
s
sr
a
»s
a*
>>
4
о
о
о
,-i ■*т)<SlNtOЮNOO^,
^ сосмео-^ — со-*смсчоэ
_ ■* <N ОТ СО ■* ОЭ ■* — Ю СМ
га со со оо от оо ео со ю ■* ■*
tf COCRCOOOt-^OOCOt^tNCO
я
ч
\о
га
^"н ю ем-^ о> оо со со t^ со см
ЮОООЮСО^Ю-' tO СО
—ilo —осососчсооо —
со<мюоослсо(^оюоо
сотгоооооососмоотгсо
юсосо — оспсо^оосо
ОЭОЭЮГ^ОО>СЧСО(^ —
SW'-r-iO'*W'-'StD
OcocMt^cocMt^<NTj«t^
оо-^-^сл^споооою
юсососм^смсоюсо'*
•—'ООООСМООЮГ^СМ — Ю
со оэ —. со cs см to -* t^ -чр
00 to ■* 00 t"~ ЮЬ О 00 00
*
«
a
я
в*
s
4
V
Ю
2
в
л
ч
о,
о
Я
00
со
и
га
Я
ч
га
сооососо—соь--*сосоо .
сосмсо-^со-^-^оо — оа
ооою-^оооосоеоеоооо
oo^cqcooo^-^csi^-ii>oo
Mi I I I I
COe0.eMcOO«5Cr>t--COt--0
осо—-оснем—'Юсооосо
00 О- О О СО •—i —' Ю О СМ СО
— О CD СМ С? -^ © О О —^ -^
МИ II 1
СИ О СО 00 СМ СО СО «-« СО ■* СО
■* en t~~ «мюспазсооюсо
СХЭ^СМ^СОС^ОЮт£ — 00
«odo- .—. о о о —« о
CO00t^O5-*tOCNtNCO СОЮ
<N"-*t-~cOh-cNt^-*^-iCO
■* 00 — СОСОШОЮСПЮ —
ооо- tOTf«Mtqo-*cx3i.--
оосооососоююснсо^-*
3~ <о■*оо--otNcntow
oiqio -*-*оо lf5'-;co -*ю
О O^OOO 0~ — О О
I" I
t^CO-*05-*t^CMOO--000
soiooioionffi'teoo
О00 0100 00ЮОО-00 01
ОЮОСМ00Ю»-<Ю CO 00 00
о 7 о'гн' n о о odo"d
III I
woiacooo^otMocft
CNd^tDONCntDOONN
ОСОСМОО^ЮОЭЮОЭСМСО
^cocDC4t^oocniqt--^-*t^
<-ooo-fddd~do"
юо-^юсососмоо-^сно
О О СО CM — CO N. CM CM —"00
OttlOO^lOOOlO^rocON
CM —Ю —СРЮ —-^COOOCTS
o —oooo—"©ocTo""
CO
II
X
s
та
о.
f-
<u
s
та
r>.
A
с
■ cj
•8
4 >>
ф 4
4"
«■> —
&*a
и о
£ *
сз о
с га
°§
a &
К «I
sab
В"
£*
4 о
ч
«а с-
сз О
ч*
° as
Sg
<ч »
>>
f- О.
ц
к
s3
as за
ag
5 М
a *
к -а
*з 5
в 2
ег Я
>>&
ч о
ид
I I I