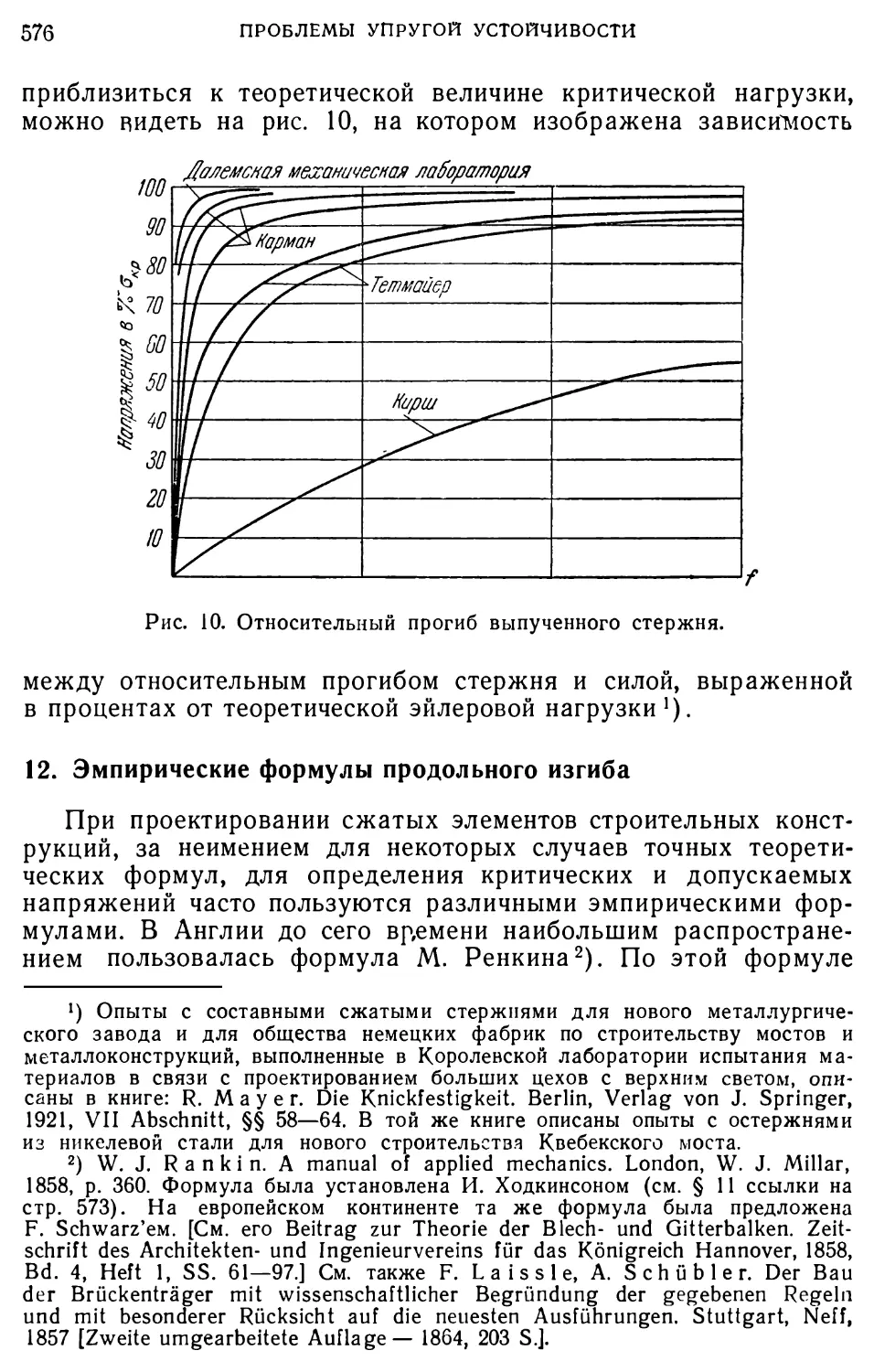
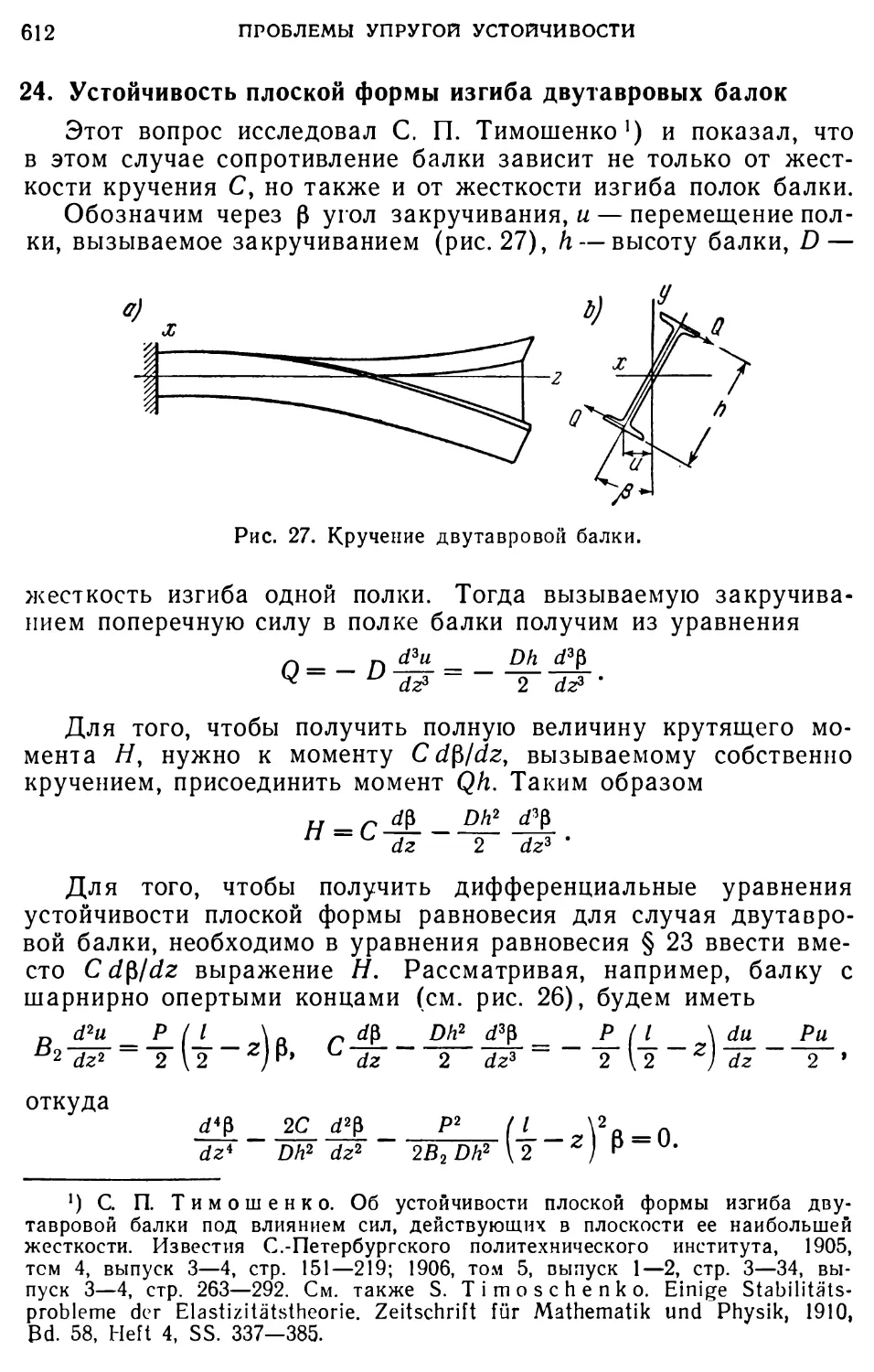
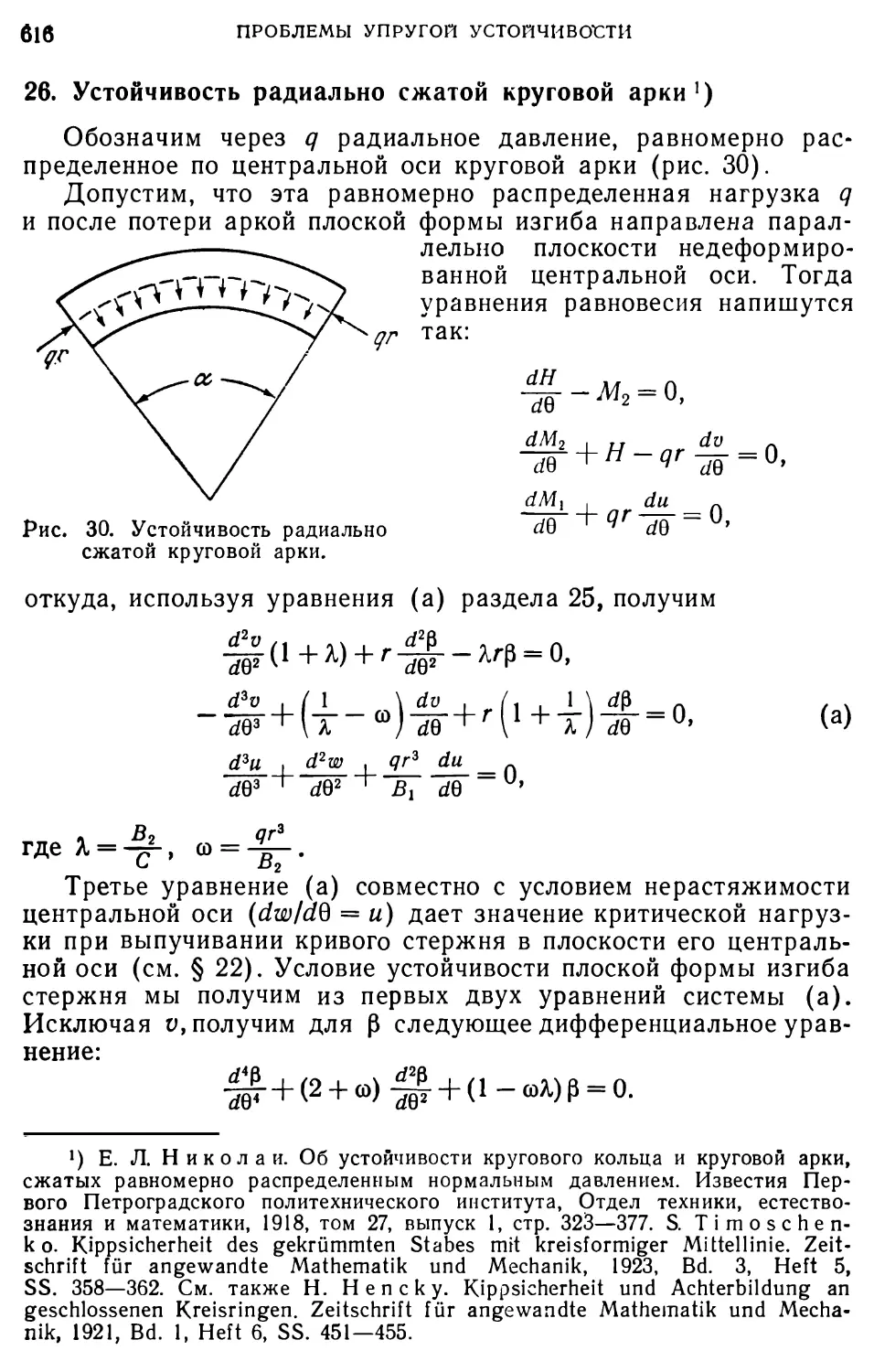
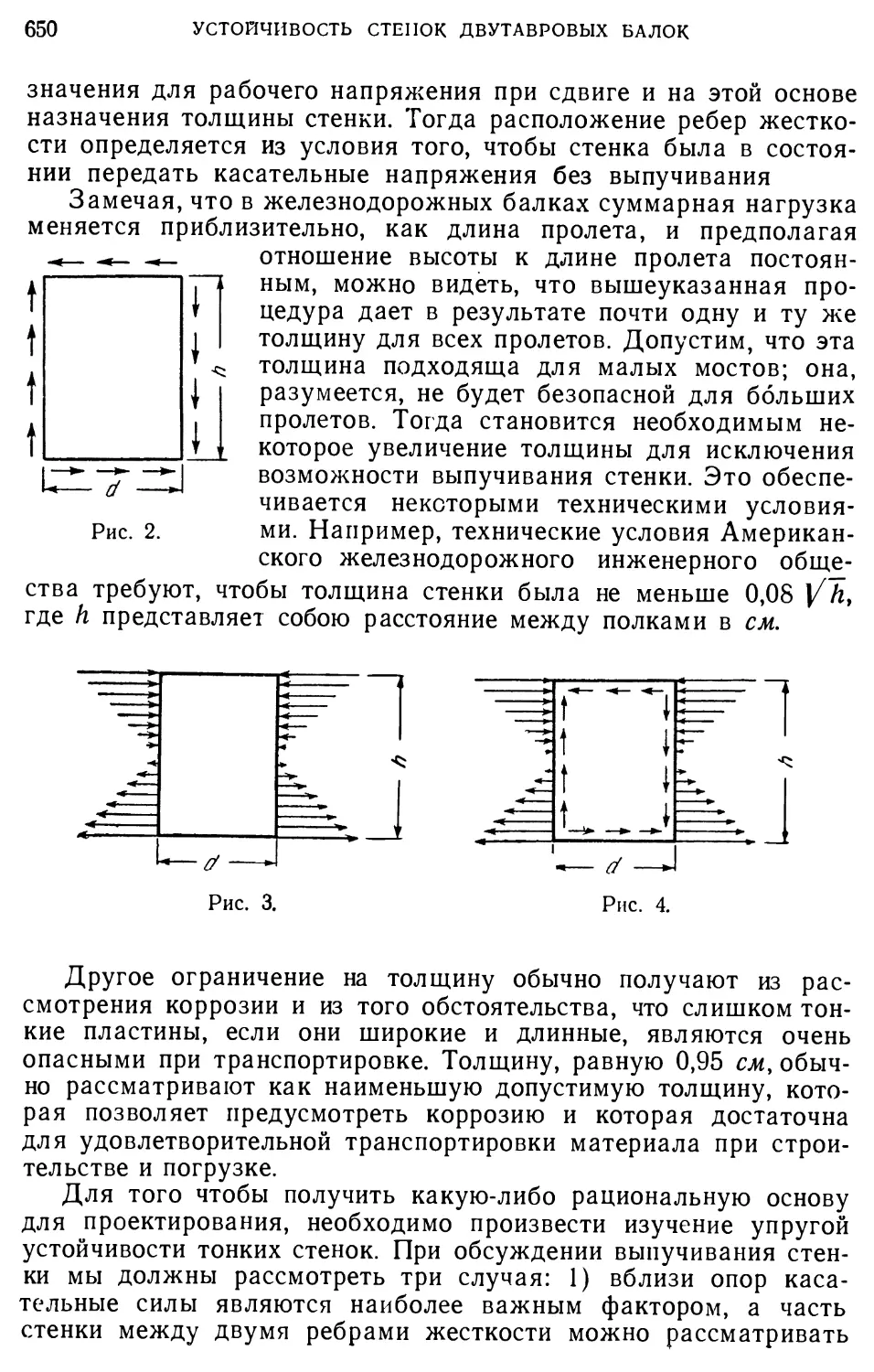
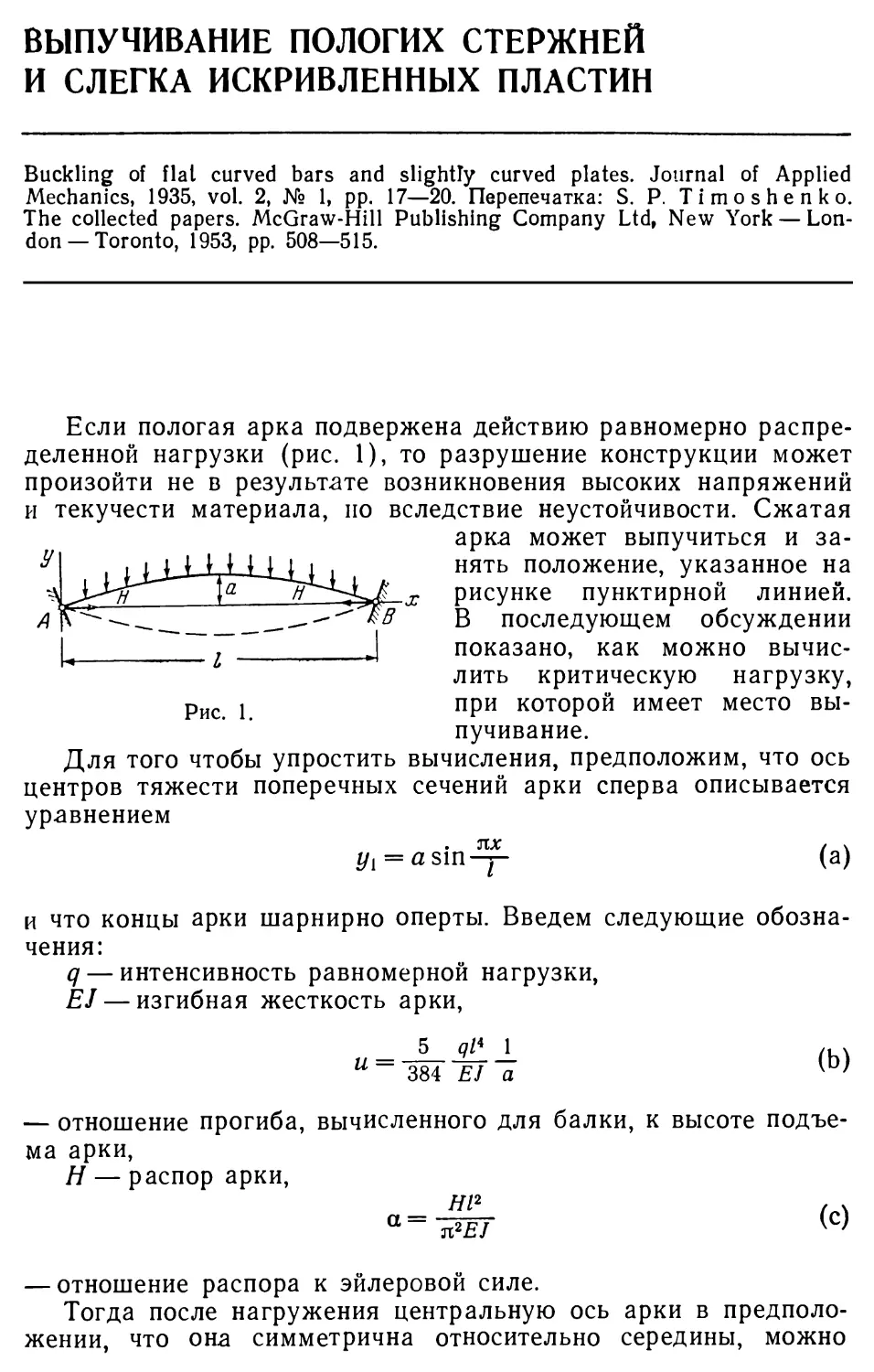
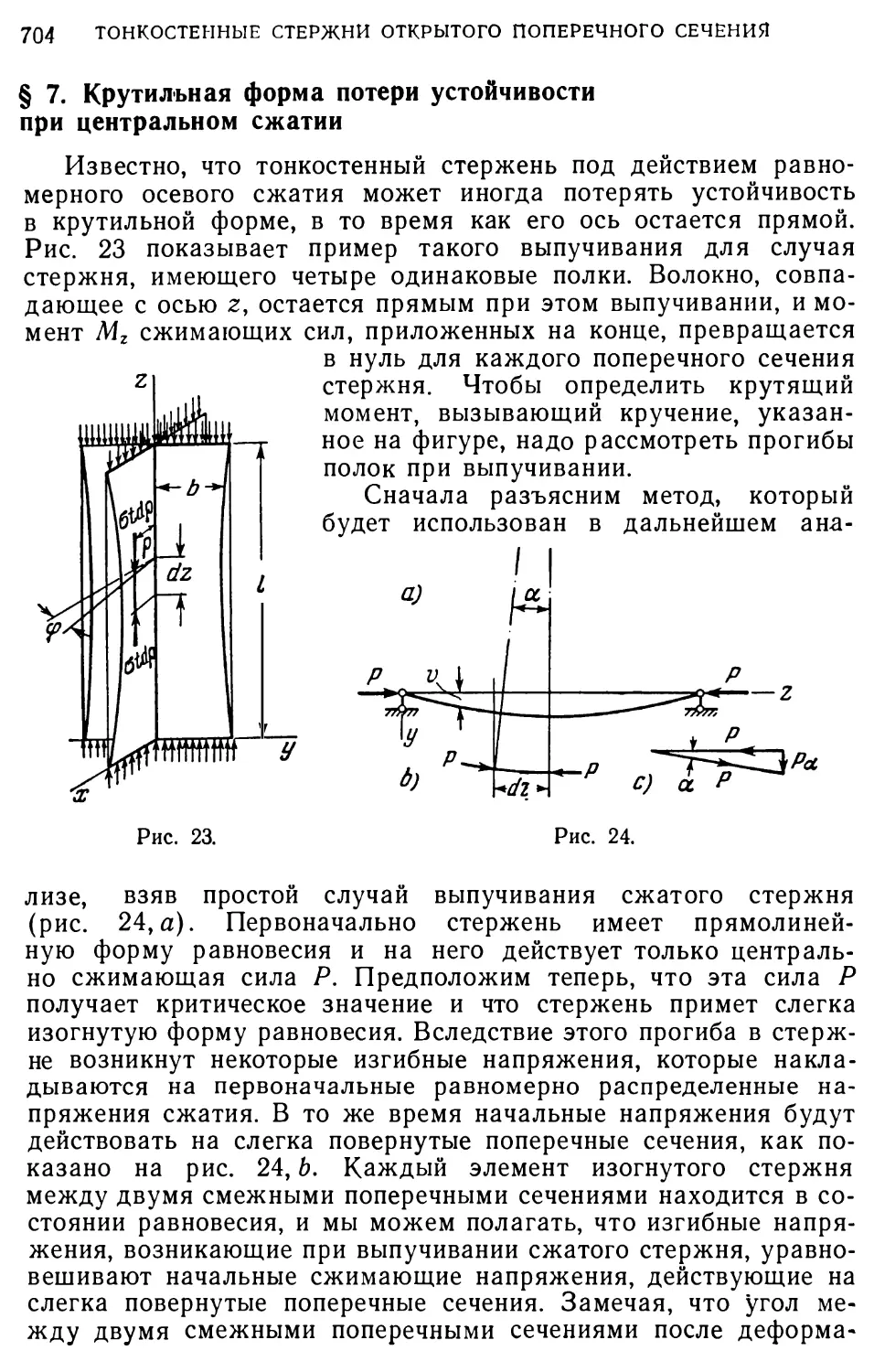
Author: Тимошенко С.П.
Tags: механика деформируемых тел упругость деформация физика строительство инженерия
Year: 1971
Text
С. П. ТИМОШЕНКО
С. П. ТИМОШЕНКО
УСТОЙЧИВОСТЬ СТЕРЖНЕЙ, ПЛАСТИН И ОБОЛОЧЕК
4
ПРЕДИСЛОВИЕ АВТОРА
Представленные здесь работы тесно связаны с развитием строительства промышленных и гражданских сооружений, а также с судостроением в России в период, предшествовавший революции.
В прилагаемой к сборнику статье профессора Э. И. Григолюка отмечено место и значение результатов, полученных мною в последующих исследованиях.
В заключение приношу глубокую благодарность профессору Э. И. Григолюку за выполненную им огромную работу по собиранию моих статей, опубликованных в различных журналах, и по проверке относящейся к ним библиографии.
Март, 1967
С. П. ТИМОШЕНКО
ОТ РЕДАКТОРА
Степан Прокофьевич Тимошенко известен широкому кругу инженеров и ученых различного профиля и разных поколений своими оригинальными исследованиями и написанными в блистательной манере книгами по сопротивлению материалов, теории сооружений, теории колебаний, теории устойчивости, теории пластин и оболочек. В каждой из этих книг, отличающихся изяществом и подкупающей простотой изложения, рассматриваемая область представлена в свете современных исследований. На этих книгах воспитывались поколения инженеров многих стран.
Исполняя должность профессора Киевского политехнического института и Петербургского института инженеров путей сообщения, С. П. Тимошенко был связан с важнейшими инженерными проблемами, волновавшими нашу страну, и сумел еще в начале текущего столетия поставить и дать решение проблем, оказавшихся особенно важными в настоящее время. Расчет сложных конструкций и сооружений С. П. Тимошенко всегда удавалось приводить к простейшим схемам, построением которых он обязан своему неповторимому инженерному чутью. '
С. П. Тимошенко внес вклад в самые различные области теории расчета на прочность сооружений и конструкций.
Сформулированные им методы и приемы расчета широко используются в настоящее время в строительном деле, в судостроении, авиастроении и в других многочисленных областях инженерного дела.
В предлагаемый вниманию читателя сборник включены семнадцать работ С. П. Тимошенко, написанных им. в период с 1905 по 1945 год и посвященных исключительно устойчивости деформируемых сред. В этих работах рассмотрена устойчивость сплошных и решетчатых прямых стержней, стержней, покоящихся на упругом основании, устойчивость плоской формы изгиба прямых двутавровых балок, плоской формы изгиба криволинейных балок. Изложена также общая теория изгиба, кручения и устойчивости тонскостенных стержней произвольного
6
ОТ РЕДАКТОРА
открытого контура. Исследована устойчивость однородных прямоугольных пластин при различных граничных условиях для ряда случаев внешнего нагружения, а также пластин, подкрепленных ребрами. Рассмотрена устойчивость цилиндрической круговой оболочки и части ее при сжатии вдоль образующей. Изучены проблемы прощелкивания биметаллических полос при изменении температуры, а также пологих стержней и пластин при внешних воздействиях. Дана теория неоднородных конструкций, в которой разбирается устойчивость пластин, балок и оболочек как в пределах, так и за пределом упругости. Наряду с точными решениями приводятся решения тех же (и многих других) задач энергетическим методом, известным ныне как метод Тимошенко. Все эти результаты в настоящее время являются уже классическими и составляют сокровищницу отечественной и мировой науки.
Каждая из включенных в сборник работ С. П. Тимошенко представляет интерес не только сама по себе, но и в совокупности с остальными работами, позволяя проследить, как менялся взгляд автора и его подход к одной и той же проблеме на протяжении некоторого периода.
Была проверена вся библиография и, по возможности, приводимые формулы. Всюду в сборнике принята метрическая система мер. Все примечания редактора даны в квадратных скобках. Редактор счел нецелесообразным вводить единую систему обозначений по всему сборнику.
Нет сомнений, что сборник оригинальных работ С. П. Тимошенко по устойчивости упругих систем будет с одинаковым интересом принят и инженерно-техническими работниками, и студентами, и начинающими научными работниками, и специалистами в области механики.
В дальнейшем предполагается выпустить сборник статей С. П. Тимошенко, посвященный прочности и колебаниям конструкций.
Э. И. Григолюк
Москва, 1970
РОДИНЕ МОЕЙ И РУССКОМУ ИНЖЕНЕРНОМУ ГЕНИЮ
ПОСВЯЩАЮ СВОЕ СОБРАНИЕ
ПРЕДИСЛОВИЕ АВТОРА
Я весьма признателен руководству Академии наук СССР, предпринявшему издание моих исследований. В этих исследованиях отражена вся моя научная деятельность. Мне хотелось бы многое сказать читателю, но я представляю себе, что автору трудно устанавливать значение своих трудов и в личном и в общественном плане.
В этой книге собраны семнадцать моих статей по устойчивости стержней, пластин и оболочек. Основная и наиболее важная часть работ была выполнена мной в период 1905—1914 годов и была опубликована в ныне труднодоступных изданиях Петербургского и Киевского политехнических институтов, Киевского университета,, Петербургского электротехнического института и Института инженеров путей сообщения. Труды, написанные мною в разное время на английском, немецком и французском языках, были изданы в 1953 году моими учениками и сотрудниками в США. Лишь два из них в свое время вышли в переводе на русский язык.
Разумеется, в той или иной форме результаты моих исследований вошли в книги, написанные мною впоследствии, в частности во второй том «Курса теории упругости» (Петроград, 1916) и в монографию «Теория упругой устойчивости» (1936, русский перевод—1946, 1955).
Содержащиеся в сборнике работы объединяет некоторый общий метод представления решений исходных уравнений задачи в форме тригонометрических рядов с последующим вычислением коэффициентов этих рядов из условий минимума суммарной энергии системы. Этот метод получил распространение в теории устойчивости деформируемых систем и известен как энергетический метод.
с. П. ТИМОШЕНКО
УСТОЙЧИВОСТЬ СТЕРЖНЕЙ ПЛАСТИН И ОБОЛОЧЕК
Избранные работы под редакцией Э. И. ГРИГОЛЮКА
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ МОСКВА 19 7 1
531 Т 41
УДК 539.30
2-4-2
ИЙ-71
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ ПОД ВЛИЯНИЕМ СИЛ, ДЕЙСТВУЮЩИХ В плоскости ЕЕ НАИБОЛЬШЕЙ ЖЕСТКОСТИ
Известия С.-Петербургского политехнического института, 1905, том 4, выпуск 3—4, §§ 1 —10, стр. 151—219; 1906, том 5, выпуск 1—2, §§ 11—15, стр. 3—34, том 5, выпуск 3—4, §§ 1—6, стр. 263—292. Отд. оттиск, С.-Петербург, 1906, 132 стр.
ТЕОРИЯ § 1. Введение
При проектировании инженерных сооружений три условия должны быть выполнены: 1) условие прочности, 2) условие
жесткости, 3) условие устойчивости. Назначая размеры инженерных сооружений таким образом, чтобы напряжения материала нигде не превосходили некоторых определенных значений, мы всегда можем удовлетворить условию первому. Второе условие требует таких соотношений между размерами проектируемых частей, при которых изменения формы конструкций под действием внешних сил не превосходили бы некоторых определенных норм. Не всегда бывает достаточно удовлетворить только этим двум условиям, и приходится исследовать также вопрос об устойчивости тех форм равновесия проектируемых частей, которые положены в основание расчетов.
Возьмем, например, случай сжатия цилиндрического стержня силами, действующими по оси его. Не всегда является достаточным произвести поверку на сжатие. Как известно, при значительной длине прямолинейная форма деформированного стержня может оказаться неустойчивой, стержень может изогнуться. В силу этого размеры сжимаемых по оси стержней приходится назначать не по величине допускаемых на сжатие напряжений, а по величине тех критических нагрузок, при которых прямолинейная форма равновесия перестает быть устойчивой.
Тот же вопрос об устойчивости деформации приходится задавать себе и в случае тонких пластинок, подверженных действию системы внешних сил, лежащих в срединной плоскости пластинки. За некоторыми пределами плоская форма перестает быть устойчивой, и пластинка может выпучиться.
Настоящая работа посвящена исследованию вопроса об устойчивости плоской формы изгиба двутавровых баок. Что
ю ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
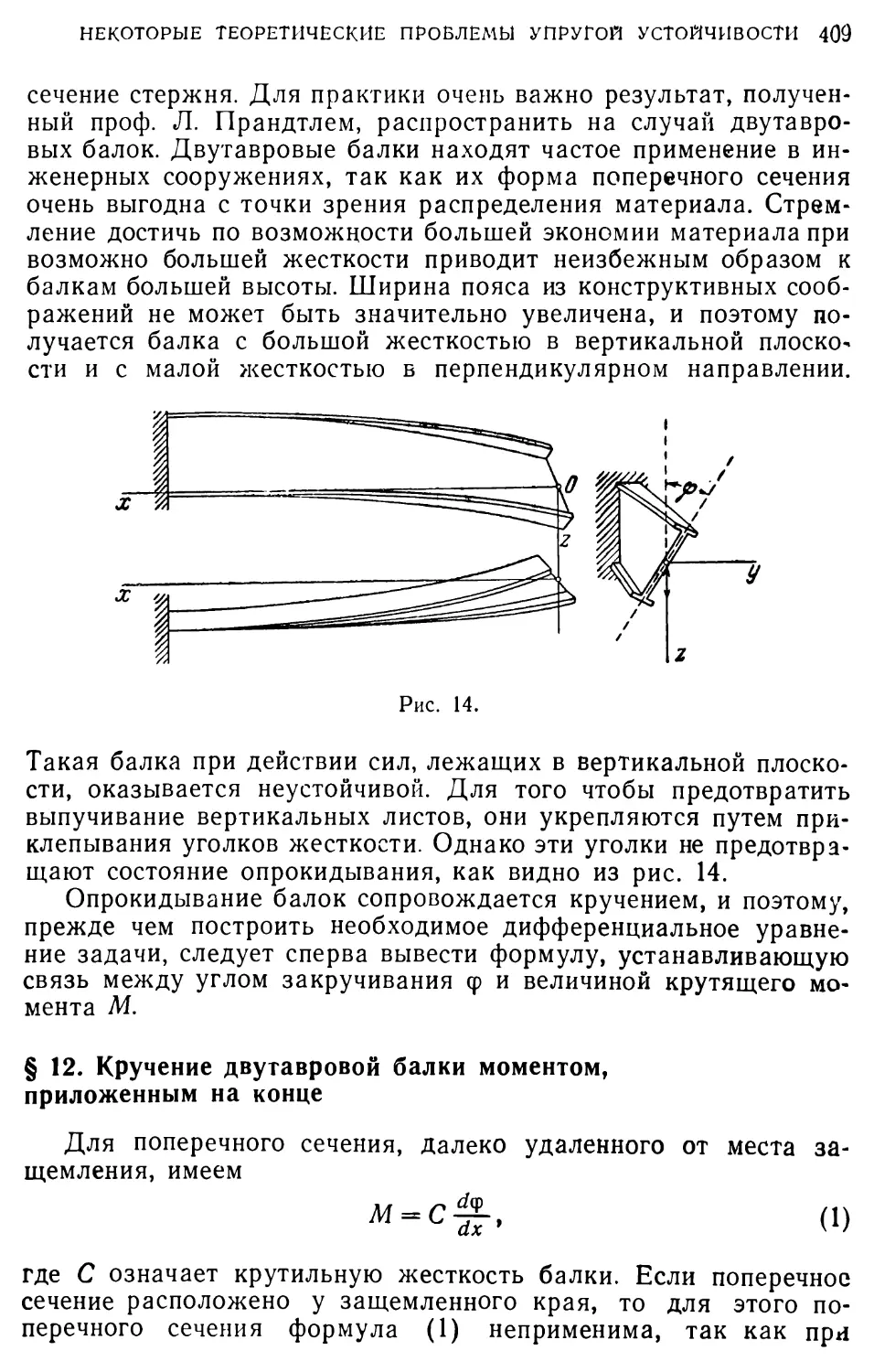
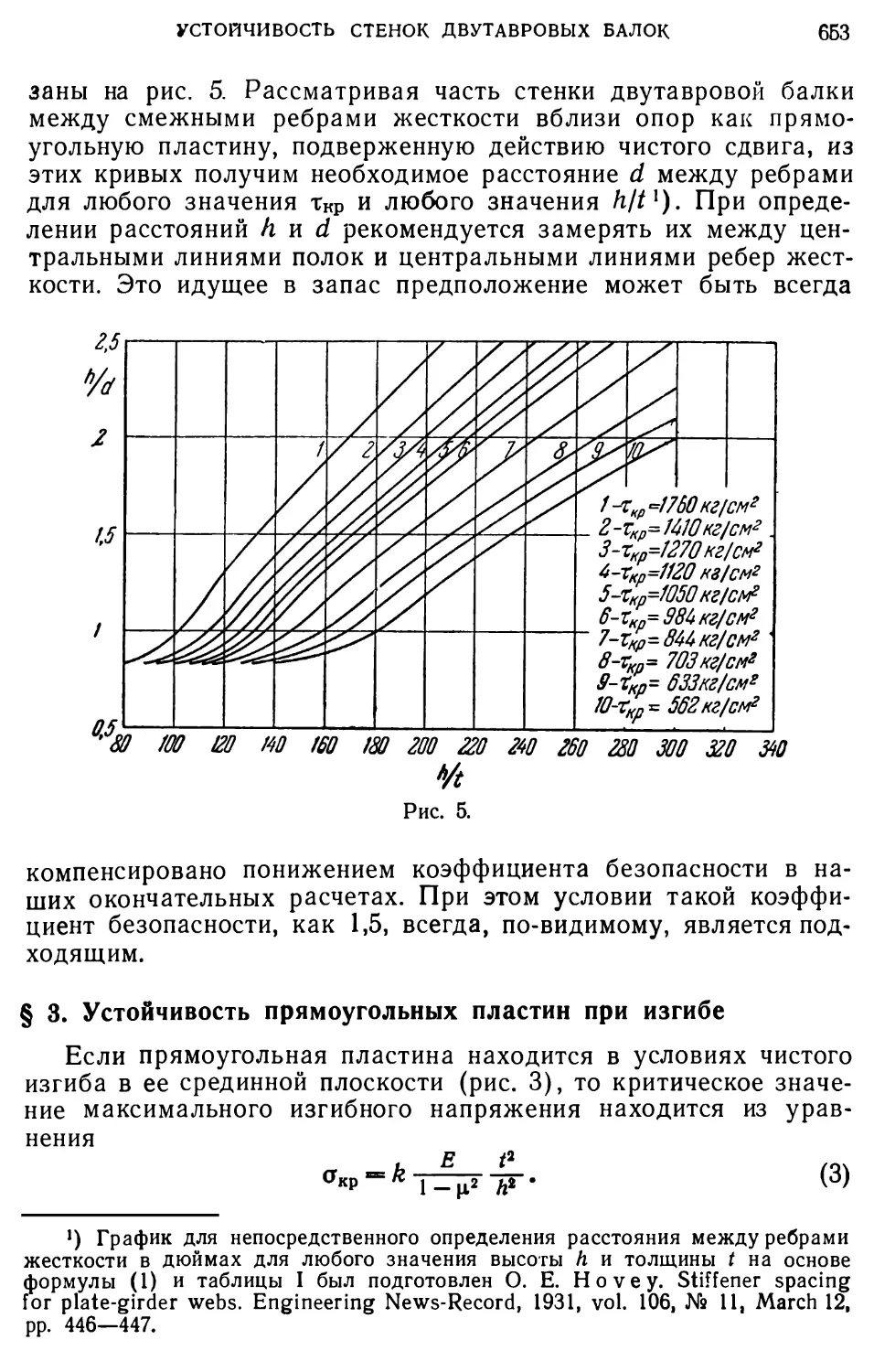
двутавровые высокие балки с тонкой вертикальной стенкой под влиянием сил, действующих в плоскости наибольшей жесткости, могут оказаться неустойчивыми — это факт общеизвестный. Мы будем различать два рода искривленных форм равновесия.
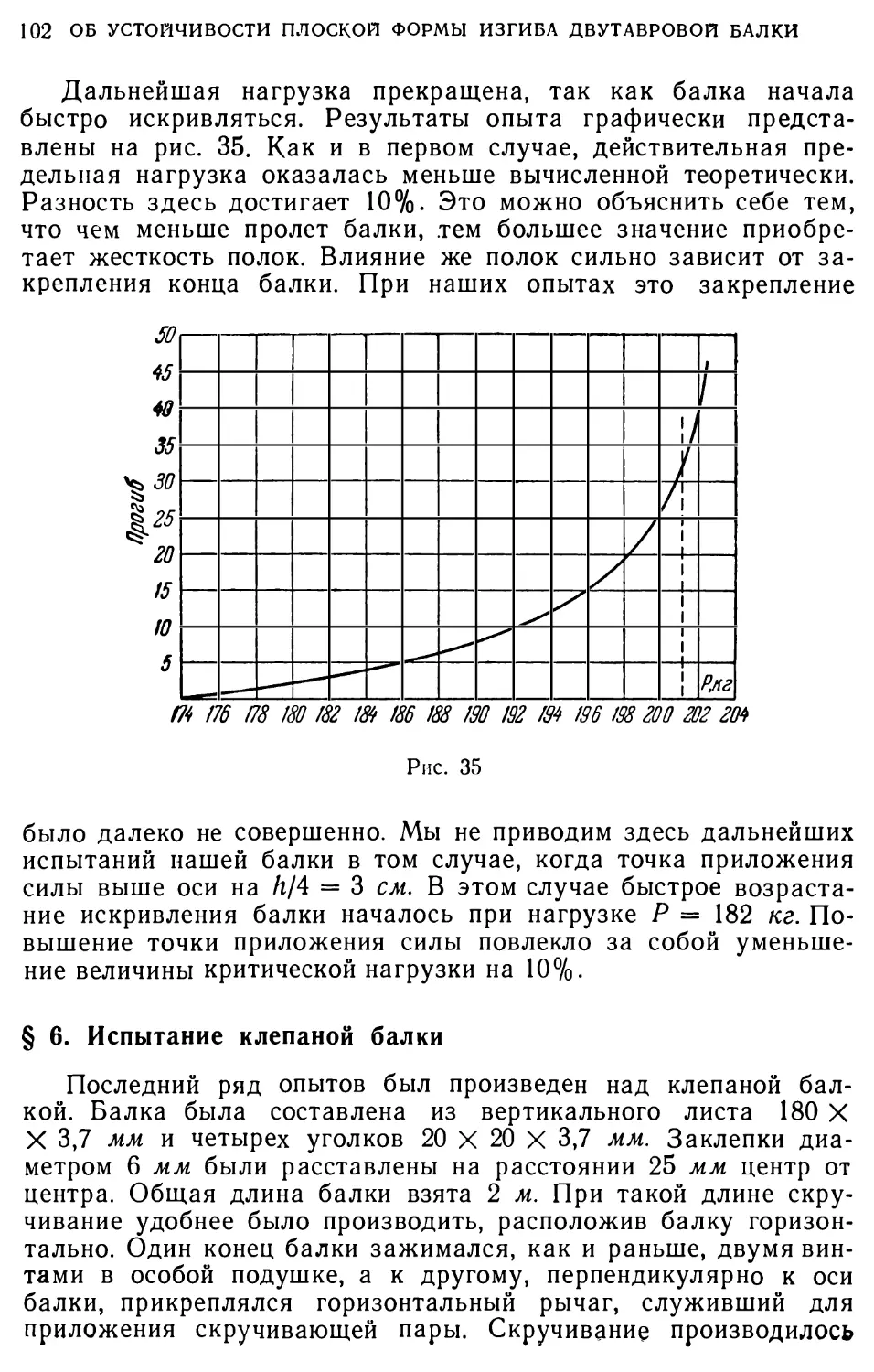
В первом случае выпучивается вертикальная стенка балки, и первоначально двутавровое сечение получает вид, представленный на рис. 1.
Рис. 1.
Насколько нам известно, теоретически этот случай нигде не разработан. Практически, для обеспечения устойчивости в этом направлении, задача решается тем, что к балке приклепывают ряд так называемых уголков жесткости. Размеры этих уголков и расстояния между ними определяются на основании совершено произвольных допущений. Обыкновенно этих уголков вполне достаточно, чтобы устранить возможность выпучивания
вертикальной стенки, но они не обеспечивают устойчивости плоской формы изгиба, так как вполне возможны искривления формы равновесия, при которых не происходит выпучивания вертикальной стенки, и изгиб балки сопровождается скручиванием ее, как это показано на рис. 2.
Возможность подобной формы равновесия может иногда наступить раньше, нежели формы указанной на рис. 1, и уголки жесткости нисколько не меняют сущности этого явления.
До сих пор нет экспериментальных исследований, которые могли бы дать эмпирические формулы для определения величины
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ Ц
тех критических нагрузок, при которых подобные формы равновесия становятся возможными. Единственные) известные нам опыты, произведенные над изгибом высоких двутавровых балок, принадлежат Л. Тетмайеру. Способ приложения внешней силы при производстве этих опытов устранял возможность свободного вращения поперечных сечений балки относительно ее оси2), вследствие чего получался вид разрушения, показанный на рис. 3. Если бы кручение балок при этих опытах не было затруднено, то для некоторых из них (самых высоких) плоская форма изгиба была бы неустойчива при напряжениях ниже предела упругости железа.
Что касается теоретического исследования интересующего пас вопроса, то здесь нам известны две работы, принадлежащие Л. Прандтлю3) и А. Мичеллу4) и появившиеся почти одновременно в 1899 году. Результаты, полученные ими, не могут быть непосредственно приложены к поверке устойчивости двутавровых балок употребительных в технике размеров.
Л. Прандтль при своих выводах пренебрегает жесткостью полок балки,
А. Мичелл же, чтобы устранить влияние полок, предполагает балки очень длин- Рис. 3.
ными. Так как в употребляемых на практике балках нельзя считать длину их очень большой по сравнению с высотой, то пренебрегать влиянием жесткости полок никак нельзя.
) А. Е. G и у. Experiments on the flexure of beams, resulting in the discovery of new lows of failure by buckling. New York, D. van Nostrand Co.; London, Cosly Fockwood and son, 1903, 122 pp.
2) Опыты производились на машине Werder’a; подробности можно найти в статье: L. Tetmajer. Die Gesetze der Knickungsfestigkeit der technisch wichtigsten Baustoffe. Mitteilungen der Materialprufungs-Anstalt am schweizerische Polytechnikum in Zurich, 1896, Heft 8, SS. 67—74.
3) Ludwig Prandtl. Kipp’-Erscheinungen. Ein Fall von instabilem elastischem Gleichgewicht. Dissertation der Universitat Miinchen, 1899, November. Nurnberg, 1900, SS. 1—75. Перепечатка: L. Prandtl. Gesammelte Abhandlungen zur angewandte Mechanik, Hydro- und Aerodynamik. Erster Teil. Springer-Verlag, Berlin — Gottingen — Heidelberg, 1961, SS. 10—74.
4) A. G. M i с h e 11. On the elastic stability of long beams under transverse forces. Philosophical Magazine afid Journal of Sciences, London — Edinburg — Dublin, Series 5, 1899, vol. 48, № 292, pp. 298—309.
12 ов УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ ВАЛКИ
В настоящей работе мы поставили себе задачу ввести при определении величины критических нагрузок влияние жесткости полок и таким образом получить формулы, по которым можно было бы производить проверку устойчивости балок в конкретных случаях, например при расчете продольных и поперечных балок мостов или длинных двутавровых балок мостовых кранов.
Так как в рассматриваемых формах равновесия существенную роль играет кручение, то нашу работу придется начать с задачи о кручении двутавровых балок.
§ 2. Скручивание двутавровой балки, один конец которой заделан неподвижно
Под скручиванием стержней подразумевают такой вид деформации, при котором в поперечных сечениях стержня будут иметь место только сдвигающие напряжения. При этом только в случаях кругового и кольцевого поперечных сечений эти сечения и после скручивания остаются плоскими; во всех других случаях отдельные точки, лежащие в одном и том же сечении, перемещаются при скручивании не только в плоскости сечения, но и по направлению оси стержня, причем это последнее перемещение различно для различных точек поперечного сечения.
Если мы скручиваемый стержень подчиним тому условию, чтобы одно или несколько поперечных сечений оставались плоскими и после деформации, то ясно, что это повлечет за собой перераспределение напряжений по поперечным сечениям. Кроме напряжений сдвигающих должны будут появиться также и нормальные. В таких случаях уже нельзя будет, вообще говоря, пользоваться для определения угла закручивания обыкновенными формулами сопротивления материалов, не оценив предварительно, насколько сильно влияние закреплений отдельных поперечных сечений.
Если мы обозначим через М скручивающий момент, через Ф угол закручивания, через С жесткость при кручении1), то для определения угла закручивания стержней со свободными концами или стержней, поперечные размеры которых малы по сравнению с длиной, мы можем пользоваться известной формулой строительной механики2)
M Cq. (1)
) А. Е. М. Love. A treatise on the mathematical theory of elasticity. 2 edition, Cambridge, University Press, 1906, vol. 2, p. 66.
2) Здесь и далее в статье штрихом обозначена производная по продольной координате х: М Cdydx.
ОВ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 13
В случае балки двутаврового поперечного сечения влияние закрепления значительно; оно сильно возрастает с увеличением ширины полок.
Непосредственно пользоваться формулой (1) в этом случае нельзя, и мы постараемся ввести еще добавочный член с таким расчетом, чтобы хотя бы приблизительно было учтено влияние жесткости полок.
Для определения этого добавочного члена мы займемся наиболее простым случаем: балка одним концом закреплена неподвижно, а к другому концу приложен скручивающий момент.
Введем обозначения, которыми мы будем пользоваться в дальнейшем нашем изложении. Обозначим через В и В2 величины EJ1 и EJ2 (главные изгибные жесткости), где Е — модуль
упругости материала, а и 2 — наибольший и наименьший моменты инерции поперечного сечения балки, через D — величинуУ3, где з — наибольший момент инерции поперечного сечения одной полки.
Начало координат поместим в центр тяжести поперечного сечения, соответствующего свободному концу балки, ось Jt-ов направим по оси балки, расположенной горизонтально, ось г-ов вертикально вниз, а ось у-ов перпендикулярно к плоскости хг в направлении, указанном на рис. 4. В таком случае система координатных осей xyz будет составлять правовинтовую систему.
Пусть скручивание осуществляется парой сил, направление которой указано на чертеже. Под действием этой пары отдельные поперечные сечения балки повернутся на некоторый переменный угол ф. Так как другой конец балки предполагается заделанным, то скручивание сопровождается изгибом полок. При малых углах закручивания ф (на практике это всегда имеет место) изгиб полок в плоскости xz мал по сравнению с изгибом их в плоскости ху, и потому в дальнейшем будем принимать в расчет только этот последний.
Прогибы срединной линии каждой полки очень просто выражаются через угол закручивания и высоту балки.
Рис. 4,
14 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Из рис. 4 видно, что
h.
YsincP’
или при малых углах ф можем синус заменить дугой, тогда будем иметь
И
У -2ф-
Изгибу полок соответствует появление сдвигающих напряжений в плоскостях поперечных сечений полок. Для определения равнодействующей Q всех сдвигающих напряжений в каком-либо поперечном сечении полки будем иметь на основании теоремы Шведлера 4)
или, подставляя вместо у его выражение через ф, получим
С -тф'.
Перерезывающие силы Q дадут пару, момент которой, очевидно, будет
Mx Qh р'2). (2)
Момент внешних сил М, скручивающий балку, должен в каждом поперечном сечении уравновешиваться моментом внутренних сил упругости. Этот последний составится из момента Mi, являющегося результатом изгиба полок, и из момента М2, получающегося от скручивания. Для определения М2 можем пользоваться формулой
М2 ч— СФ'. (Г)
Знак минус в правой части взят потому, что при нашем расположении координатных осей с возрастанием х убывает угол ф.
На основании формул (Г) и (2) для момента внешних сил М будем иметь
м-с ф' -ф'. (3)
F. W. S с h w е d 1 е г. Theorie der Bruckenbalkensysteme. Zeitschrift fur Bauwesen, 1851, Berlin, Bd. 1, Heft 4, SS. 114—123; Heft 6, SS. 162—173; Heft 9, SS. 265—278.
2) Точнее, нужно было бы написать Мх Q(h — 6), где б— толщина полки, но так как практически б мало по сравнению с ht то мы можем им пренебречь.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 5
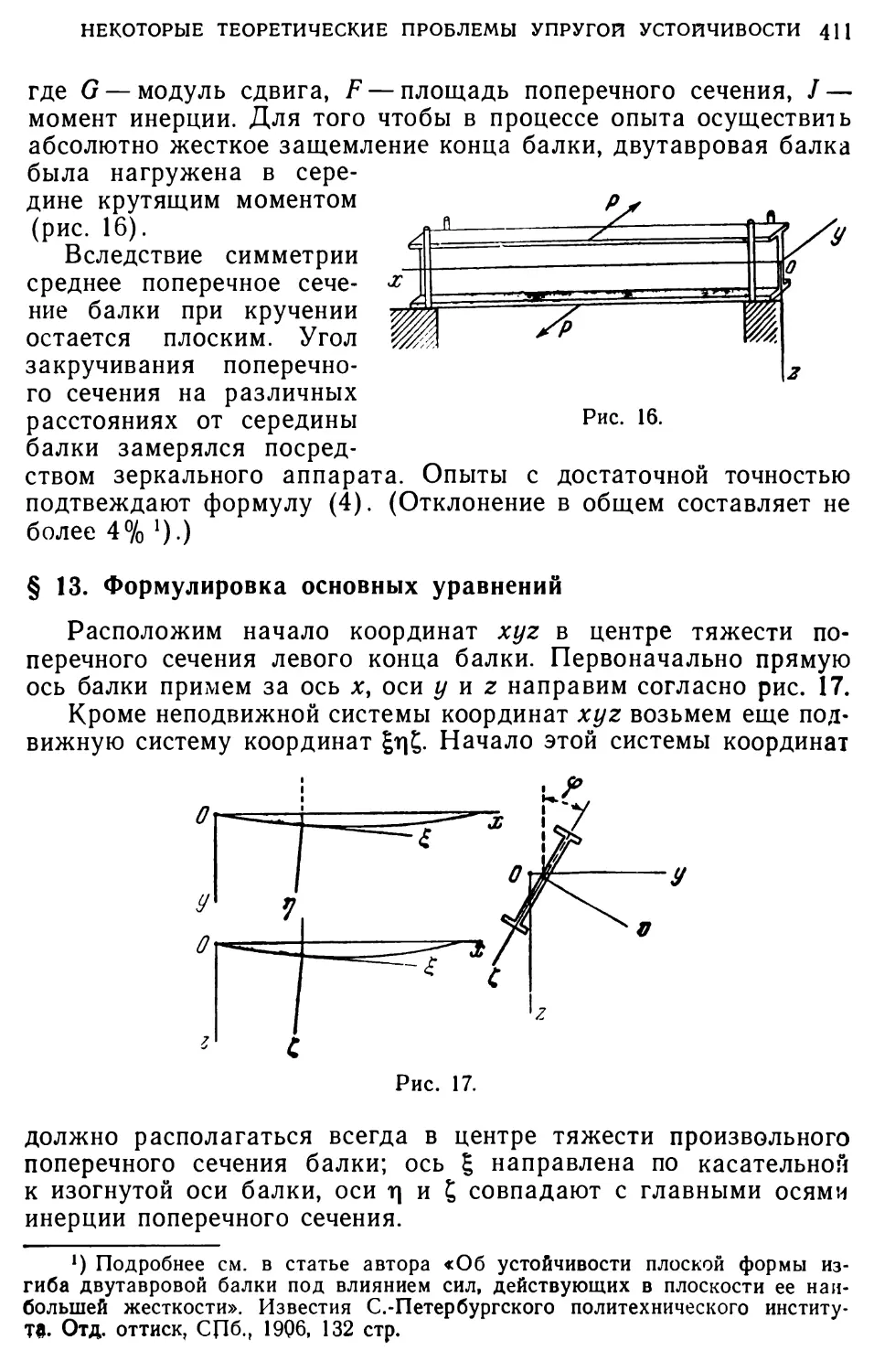
Полученная формула (3) будет положена в основание дальнейших выводов. Насколько точно она учитывает влияние жесткости полок, можно будет сказать только на основании опытов. Для осуществления заделки поперечного сечения балки я при производстве опытов пользуюсь расположением, указанным на рис. 5. Концы балки А и В не имеют возможности вращаться вокруг горизонтальной оси, пара сил прикладывается к срединному поперечному сечению. Ясно, что при скручивании это сечение в силу симметрии должно остаться плоским и его можно считать заделанным.
Т-П.
п
Y9
X I
1 1
W
Z
Рис. 5.
Перейдем теперь к определению угла закручивания балки при расположении, указанном на рис. 4. Для этого придется интегрировать уравнение (3). Для упрощения выкладок введем одно обозначение, которым будем и дальше пользоваться, именно положим
2 С _ 1
Dh2 а2 '
Нетрудно видеть, что а имеет измерение длины. Уравнение (3) перепишется так:
1 2М л о
р -(p-w 0- 3)
Решение соответствующего уравнения без последнего члена, очевидно, будет
V Qsh Wch- P,
где Q, N, Р — произвольные постоянные.
Частное решение уравнения (3') будет
На основании этого получим полный интеграл уравнения (3'):
Ф Q sh — --N ch — — х Р. a a L
(4)
16 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Произвольные постоянные могут быть определены на основании следующих условий закрепления концов:
I) При х ф 0, так как сечение, соответствующее плоскости заделки, не может повернуться.
II) При х I ф' 0. Так как полки изгибаются так, что касательные к их срединным линиям плоскости заделки парал¬
лельны оси -ов, то, следовательно,
АФ' .
III) При х 0 ф 0. Это можно написать на основании того, что на свободном конце балки приложены силы, лежащие в плоскости поперечного сечения, и нет сил, нормальных к этому сечению, следовательно,
d2y h f.
-
Из общего интеграла (4) дифференцированием находим
f Q , х , N и х М гч
Р chT TshT--C-‘ (S)
p 4-sh-4-ch-, (6)
Y а2 а а2 а 9 v J
ф' 4-сЬ - 4sh-. (7)
Y а3 а а а w
Из выражения (6) на основании третьего условия заключаем, что N 0.
Постоянную Q определим из выражения (5) на основании условия II:
п- аМ 1 с , ch — а
Подставляя найденные для Q и N значения в выражение (4), мы на основании первого условия будем иметь для величины Р значение
Определив таким образом значения всех произвольных постоянных, мы для вычисления угла закручивания в любом сечении будем иметь формулу
м f 1 „ . а „и х „tu 1
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 17
Выписываем здесь же значения производных от ср:
(9)
Ф
При х О, т. е. для сечения, соответствующего свободному концу балки, угол закручивания qp будет иметь значение
Если бы мы не приняли во внимание жесткости полок, то на основании формулы (1) имели бы для угла закручивания значение
Добавочный член в правой части формулы (10) дает нам величину уменьшения угла закручивания, и эта величина тем больше, чем больше D — жесткость при изгибе каждой полки.
Всякое увеличение ширины полок увеличивает D и, следовательно, уменьшает угол закручивания, что и нужно было ожидать заранее. В тех случаях, когда отношение а в несколько раз больше единицы, th(a) можно с достаточной точностью положить равным единице, и тогда формула (10) перепишется так:
т. е. угол закручивания балки с одним заделанным концом равняется углу закручивания балки со свободными концами, но меньшей длины. Это уменьшение длины а меняется с изменением жесткости полок.
В тех случаях, когда мало по сравнению с а, т. е. когда рассматриваются сечения, близкие к заделанному концу, мы можем th (Iа) разложить в ряд по возрастающим степеням а и для вычисления угла ср0 будем иметь выражение
(Ю)
(10')
Г ±_1Ш_1Ш5
Ml , а 3 а ) т 15 а ) Фо - с 1 — I
а
18 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
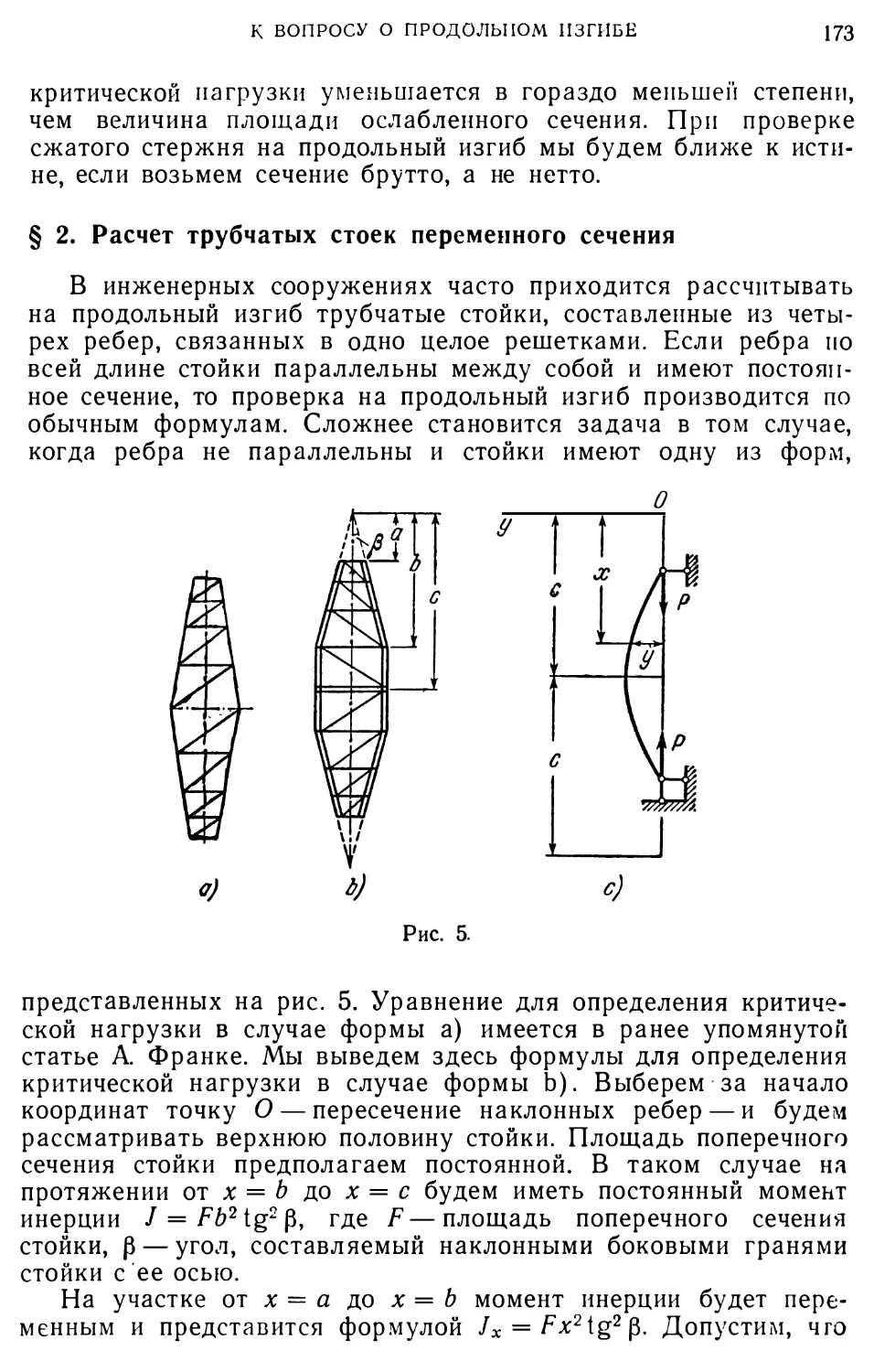
Чтобы наглядно представить, как при заданном поперечном сечении балки и заданном скручивающем моменте меняется угол закручивания в зависимости от длины, можно воспользоваться графическим построением. Для этого по оси х-ов будем откладывать длины , а по оси ординат соответствующие углы закручивания ф. Пока оба конца балки свободны, диаграмма представится в виде наклонной прямой ОЛ, проходящей через начало координат; см. рис. 6.
В случае одного заделанного конца мы вместо прямой х получим некоторую кривую линию, касательную к оси лг-ов в начале координат и асимптотически приближающуюся к прямой ВС. Относительно построения этой прямой заметим, что она параллельна ОА и пересекает ось -ов в точке В так, что
О В а.
Рис. 6.
Уравнение прямой, следовательно, будет
М , ч Ф --(-а),
что соответствует полученной нами выше формуле (10').
При производстве опытов, а также и в дальнейшем нашем изложении понадобятся некоторые численные значения множителя 1—(al)th(la) при различных значениях lа, и потому мы приводим их здесь в отдельной таблице.
Рассмотрим теперь, как меняется кручение ф' по длине балки. Пока оба конца свободны, ф' — величина постоянная, равная — МС. В случае закрепленного конца ф' величина переменная, как это видно из вышеполученной нами формулы
(9). Наибольшее значение ф' получает у свободного конца, где на основании (9)
Гиперболический косинус очень быстро растет с величиной а, и потому при значительных длинах и при малом а ф' очень
JL
а2
-±th-L
1 а
I2
а2
1 —у ih —
1 а
1
0,238
16
0,750
2
0,372
24
0,796
4
0,518
32
0,823
8
0,648
40
0,842
12
0,711
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 19
близко к величине — МС, т. е. заделка мало влияет на величину кручения свободного конца. Если мы будем брать сечения, близкие к заделанному концу, то р' на основании той же формулы (9) приближается к нулю, и, следовательно, силы упругости, действующие в этих сечениях и уравновешивающие момент внешних сил, являются следствием изгиба полок, а не кручения.
Этим мы закончим общее рассмотрение вопроса о кручении двутавровых балок и перейдем к численному определению величин С и а по заданным поперечным размерам балки.
§ 3. Вычисление величины С
В предыдущие формулы, а также и в выражения для критических нагрузок, которые нами будут ниже получены, входит величина С — жесткость балки при кручении. Опытным путем определить эту величину с достаточной точностью не трудно; но при проектировании, когда имеются только геометрические размеры конструкции, необходимо иметь способы определять величину С аналитически. Теория упругости в настоящее время дает возможность решить точно эту задачу только для нескольких наиболее простых видов поперечного сечения, как, например, прямоугольник, эллипс и др. Для двутаврового сечения точного решения пока нет, и придется для вычисления интересующей нас величины употребить какой-либо приближенный прием.
Мы для этого воспользуемся известной гидродинамической аналогией и дальнейшим ее развитием, недавно опубликованным профессором Гёттингенского университета Л. Прандтлем1).
Если через txy и txz обозначим составляющие сдвигающих напряжений при кручении и положим
. _ _ , _ d)
то задача о кручении приведется к решению уравнения
где G — модуль упругости при сдвиге, а ф' имеет прежнее значение. JI. Прандтль заметил полную аналогию между этим уравнением и уравнением поверхности, по которой прогибается мембрана, натянутая с некоторым постоянным напряжением S и нагруженная постоянной нагрузкой р на единицу площади.
х) L. Р г a n d 11. Eine neue Darstellung der Torsionspannungen bei prismatischen Staben von beliebigem Querschnitt. Jahresberichte der deutschen Mathematiker-Vereinigung, 1904, Bd. 13, Heft 1, SS. 31—36. Перепечатка: L. P г a n d 11. Gesammelte Anhandlungen. Erster Teil, 1961, SS. 81—86.J
20 ов устойчивости плоской формы изгиба двутавровой валки
Если через и обозначим ординаты этой поверхности, то уравние ее напишется так:
Л оч
dy2 ' dz2 S ' w
Для полного совпадения необходимо положить
ф ku,
где
2Gq'S Р
На основании этой аналогии J1. Прандтль вывел следующего рода зависимость между распределением напряжений по поперечному сечению и поверхностью, образуемой мембраной.
I. Если мембрана, натянутая на контур, соответствующий поперечному сечению скручиваемого стержня, выпучится благодаря равномерно распределенному по ней давлению, то линии сечения полученной таким образом кривой поверхности плоскостями, параллельными плоскости контура, будут представлять собой линии напряжений, т. е. такие линии, касательные к которым в любой точке дают направление напряжения в соответствующей точке поперечного сечения.
Вычертив систему таких Рис. 7. линий, можно получить на¬
глядную картину распределения напряжений по сечению. На рис. 7 представлен вид этих линий в случае прямоугольного поперечного сечения.
II. Величина напряжения в любой точке пропорциональна углу, составляемому линией наибольшего ската с плоскостью контура в соответствующей точке кривой поверхности, или, что то же, пропорциональна густоте линий напряжений.
III. Объем V, заключающийся между плоскостью контура и поверхностью мембраны, пропорционален жесткости стержня С. Именно
C iF. (3)
Эти три положения дают возможность экспериментальным путем установить закон распределения напряжений при самых разнообразных контурах поперечного сечения. В случае тонкостенных балок этими положениями можно воспользоваться для приближенного вычисления жесткости С. Начнем с простейшего случая, когда поперечное сечение представляет собой прямо¬
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИВА ДВУТАВРОВОЙ ВАЛКИ J1
угольник, ширина которого b мала по сравнению с длиной h. Объем V в данном случае с достаточной точностью можно заменить объемом параболического цилиндра, площадь основания которого будет bh и наибольшая ордината
рь2 и Hs'
Следовательно,
и величина будет
т 2 рь2 ии
У ” 3 8S ’
С на основании положения III
С jhb3G.
(4)
Если принять во внимание влияние коротких сторон поперечного сечения, которые слегка уменьшают объем между мембраной и контуром, то придется в формулу (4) внести поправку и представить ее в таком виде:
(5)
C ±b3(h-ab)G.
О
Рис. 8.
Коэффициент а по сравнению с точной формулой оказывается равным 0,63. Формула (5) показывает, что в тех случаях, когда
b мало по сравнению с Л, поправ кой можно пренебречь и пользоваться формулой (4).
Переходя к двутавровому поперечному сечению, представленному на рис. 8, заметим, что и в этом случае кривую поверхность мембраны в местах, удаленных от краев полки и от точек О, О, можно считать за поверхность параболического цилиндра.
В точках О, О, соответствующих местам соединения полок со стенкой двутавровой балки, ординаты поверхности мембраны имеют наибольшее значение, а у краев полок — наименьшее. Пока толщина стенки и полок b невелика, мы с достаточной точностью можем вычислить величину С, применяя формулу (4) отдельно к поперечным сечениям стенки и полок.
Рис. 9.
22 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Когда приходится иметь дело с клепаными двутавровыми балками, то тогда вычисление С возможно со значительно меньшей точностью. Мы будем считать, что трение между составными частями балки, обусловленное заклепочными соединениями, настолько значительно, что составное сечение можно считать сплошным, как то показано на рис. 9.
Тогда для приблизительной оценки величины С можно сечение разбить на ряд прямоугольников, как то пунктиром показано на рис. 9, и к каждому прямоугольнику применить формулу (4). Насколько близок будет полученный таким образом результат к истине, можно судить только на основании опытов, которые должны быть произведены над скручиванием двутавровых клепаных балок.
§ 4. Вывод основных уравнений
Переходя теперь к главной нашей задаче, именно к вопросу об устойчивости плоского изгиба двутавровой балки, выясним прежде всего, когда этот вопрос должен ставиться и может иметь практическое значение. Ясно, что в таких случаях, когда заданной системе внешних сил может соответствовать только одна форма равновесия, эта форма будет устойчивой. Если какие-либо посторонние причины произведут малые изменения формы, то, предоставленная самой себе, система вернется в свое первоначальное положение, так как это положение по предположению есть единственная возможная форма равновесия. Иное дело, когда одной и той же системе внешних сил могут соответствовать несколько форм равновесия. В таком случае система даже при незначительном отклонении от положения равновесия может к нему не вернуться, а принять другую возможную форму равновесия. Для определения, какая из возможных форм равновесия будет устойчивой, нужно только выяснить, которой из них соответствует минимум потенциальной энергии. Этим совершенно общим принципом бывает иногда трудно воспользоваться; в таких случаях при решении вопроса об устойчивости можно руководствоваться следующим признаком: если имеются две возможные формы равновесия тела, то та из них, которая мало отличается от формы, соответствующей ненапряженному состоянию, будет неустойчивой1). Таким образом, неустойчивыми будут прямолинейная форма сжимаемого цилиндрического стержня, плоская форма пластинки, сжимаемой силами, действующими в ее плоскости, и др.
При каких же условиях может возникнуть возможность появления нескольких форм равновесия Пока все измерения де-
‘) См. указанную на стр. 13 книгу А. Е. Н. Love, р. 291.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 23
формируемого тела суть величины одного порядка, малым деформациям, которые только и рассматриваются в теории упругости, будут соответствовать малые изменения формы тела, а следовательно, и малые перемещения точек приложения внешних сил. Вследствие этого можно пренебречь разностью между системами сил до и после деформации и доказать, как то сделал Кирхгоф, однозначность решения уравнений упругости, а следовательно, и невозможность появления нескольких форм равновесия в подобных случаях.
Дело обстоит иначе, когда малым деформациям могут соответствовать весьма значительные изменения формы, как то имеет место в случае тонких пластинок и стержней. Уравнения равновесия напишутся различно в зависимости от того, берем ли мы систему внешних сил, соответствующую недеформированному или деформированному состоянию тела.
Все то, что сказано относительно тонких пластинок, при некоторых условиях может быть отнесено и к двутавровым балкам самых употребительных в технике поперечных сечений. Дело в том, что стремление получить экономию в весе балки заставляет главную массу материала относить возможно дальше от оси балки. Получаются балки с большой высотой вертикальной стенки; ширина же полок балки по конструктивным соображениям не может быть значительно изменена. Вследствие этого один из главных моментов инерции поперечного сечения во много раз превосходит по величине другой. Если мы сохраним прежнее наше обозначение Вi и В2 для главных жесткостей балки при изгибе и С для жесткости при кручении, то в случае мостовых балок нередко, например, бывает, что
J5a 1 С
J3, 100 И 3000
При таких условиях прогиб балки в направлении, перпендикулярном к плоскости вертикальной стенки, при одних и тех же напряжениях может во много раз превосходить прогиб в плоскости стенки, и, следовательно, имеются налицо те условия, при которых становится возможным появление нескольких форм равновесия. Замечу здесь, что даже в том случае, когда В и В2 — величины одного порядка, возможна неустойчивость плоской формы изгиба, если только С мало по сравнению сi и В2. (Это возможно было бы осуществить, придав полкам балки значительную ширину при малой толщине как полок, так и вертикальной стенки.)
Переходя теперь к определению возможных форм равновесия двутавровой балки, изгибаемой силами, действующими в плоскости вертикальной стенки, заметим, что одна из этих форм
24 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
для нас известна вполне — это форма плоского изгиба. Так как длина балки не очень велика по сравнению с высотой (на практике '7 “g’ 4’lk) то эта известная нам форма равновесия будет при малых деформациях весьма мало отличаться от первоначальной формы балки в ее ненапряженном состоянии и, следовательно, на основании вышеприведенного признака будет формой неустойчивой. Каковы возможные искривленные формы изгиба, нам пока неизвестно, но во всяком случае они могут весьма значительно отличаться от первоначальной ненапряженной формы балки. Определить их мы постараемся, исходя из того общего положения, что возможность появления нескольких форм равновесия наступает только при вполне определенной зависимости между размерами балки и величинами действующих сил.
Пусть а определяет эту зависимость, и пока а меньше неизвестного нам еще предела ао, плоская форма изгиба есть единственная и потому устойчивая форма равновесия. В тех же случаях, когда а ао, возможны по крайней мере две формы равновесия — плоский изгиб и неплоская форма изгиба, сопровождаемая кручением. Первая из них неустойчива, а вторая устойчива. Величину ао мы найдем из следующих соображений. При аао возможно существование неплоской формы изгиба, и в уравнения, определяющие эту форму, величина а войдет как параметр. Непрерывно меняя эту величину, мы будем непрерывно изменять и вид неплоской формы изгиба балки. Чем ближе а к ао, тем меньше отличается неплоская форма от плоской, и в пределе эти две формы сливаются в одну критическую форму. Если наше предположение относительно возможности появления неплоской формы изгиба верно, то для величины ао мы должны из уравнений, определяющих неплоскую форму, получить вполне определенное решение.
При выводе основных уравнений мы будем предполагать ось балки горизонтальной и стенку балки расположенной в вертикальной плоскости. За начало координат примем центр тяжести левого концевого поперечного сечения. Оси х, у, z направим, как показано на рис. 10. Кроме неподвижной системы координат ху уу z мы построим еще подвижную систему, ц,, которая меняется при переходе от одного поперечного сечения балки к другому. Начало координат этой системы всегда совпадает с центром тяжести выбранного поперечного сечения, оси rj и совпадают с главными осями инерции сечения, ось I направлена по касательной к изогнутой оси балки 1)-
1) При малых изменениях формы можно пренебречь искажением поперечного сечения и считать все три направления взаимно перпендикулярными.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДЁУТАВРОВОЙ БАЛКИ 25
Расположение координатных осей, вид изогнутой оси балки (в случае двух опор) и одно из промежуточных поперечных сечений представлены на рис. 10.
Величина внешних сил всегда может быть подобрана таким образом, чтобы прогибы балки в плоскостях ху и xz были малыми величинами одного порядка. Что касается угла поворота поперечных сечений ф, то он будет также величиной малой,
если В2 и С малы по сравнению с В. Если же В2 не может считаться малым по сравнению с В и только С мало, то тогда угол ф может быть и не малым при малых прогибах балки.
В обоих этих случаях для кривизны изогнутой оси балки в плоскостяхг и можно пользоваться приближенными формулами
и _ у — d
к d2 ' л d2
Кривизну кривой можно себе представить в виде вектора1), отложенного по бинормали. Тогда кривизна проекции кривой на любую плоскость, проходящую через касательную к кривой, получится как проекция вектора кривизны на нормаль к этой плоскости.
Если воспользоваться этим представлением и пренебречь малым углом наклона между касательной к изогнутой оси балки
1 См. указанную на стр. 13 книгу А. Е. Н. Love, р. 60.
26 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
и осью х-ов, то на основании рис. 10 легко можно получить такие соотношения:
d2x _ d2y - d2z d2 x d2t _ d2z _ d2y dl2 dx2 dx2
Если мы через M, Мл, обозначим моменты внешних сил, действующих на левую отсеченную часть балки, относительно осей, г, то на основании известных формул сопротивления материалов можем написать
(2)
Выражение для момента М получим на основании формулы (3) § 2:
Мб Сф'—2-ф'. (3)
Уравнениями (2) и (3) мы будем пользоваться при рассмотрении частных случаев изгиба.
При составлении моментов Мц, Mi нужно знать углы, составляемые осями, г, с неподвижными осями ху уу г. Пока угол ф мал, а мы дальше и будем рассматривать только такие случаи, можно пользоваться следующей таблицей девяти косинусов:
1
Tl
1
dy
dz
X
I
dx
dx
У
dy_
dx
1
-Ф
Z
dz
dx
Ф
1
(4)
§ 5. Случай изгиба балки парами сил
В том случае, когда двутавровая балка изгибается парами сил, приложенными по концам и действующими в срединной плоскости вертикальной стенки балки, наша задача приводится
) В этих выражениях вместо cos ф взято 1 и ф вместо sin ф, что будет точно до 12 при углах, не превосходящих 110.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 27
к решению обыкновенных дифференциальных уравнений, линейных и с постоянными коэффициентами, вследствие чего на этом частном примере, может быть не имеющем большого практического значения, легче всего познакомиться с сущностью интересующего нас явления и сделать некоторые заключения, которые' в дальнейшем помогут нам при рассмотрении случаев более сложных и трудноразрешимых.
Общее расположение представлено на рис. 11. Концы балки лредполагаются закрепленными таким образом, что концевые поперечные сечения не могут вращаться вокруг оси -ов. Направления, в которых действуют изгибающие пары, показаны на
1 У
Рис. 11.
рисунке стрелками. Под действием означенных пар балка изгибается в плоскости zx. Постепенно увеличивая момент М изгибающих пар, мы можем достичь такой величины его Мкр, при которой кроме плоской формы изгиба является возможной и другая, неплоская форма равновесия. Для определения величины М19 придется рассмотреть условия равновесия неплоской формы изгиба.
Возьмем произвольное поперечное сечение балки на расстоянии х от начала координат (рис. И). Моменты Мл, получим проектированием линейного момента М пары сил на оси , г,. Если воспользоваться таблицей (4) предыдущего параграфа, то нетрудно получить для этих моментов следующие значения:
М1 М1Т' МчМ М-МФ. (1)
На основании общих уравнений (2) и (3) предыдущего параграфа мы получим, выбрав надлежащим образом знаки, систему уравнений, определяющих неплоскую форму изгиба:
м dy_ r dtp Dh2 йъФ
Ш dx dx 2 dx3 ’
28 ОВ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
В эти три уравнения входят три неизвестных: у, z и ф. Левые части наших уравнений написаны в том предположении, что ф
мало, и, следовательно, в правой части члены с ф могут быть
отброшены1). Тогда второе из уравнений (2) дает нам
dv м а,
1F-b7p
Дифференцируя первое уравнение системы (2) и принимая во внимание (3), получим уравнение, содержащее только ф и его производные:
М2ф _ р d2ф Dh2 d4ф ,
И v2 о W
(5)
В2 dx2 2 dx4
Для удобства мы введем следующие обозначения:
2 С 1 2 М2 1
Dh2 “ а2 9 B2Dh2 d4 ‘
Тогда уравнение (4) перепишется таким образом:
d_±d_ 10 (4')
dx4 a2 dx2 d« ф U Характеристическое уравнение, соответствующее (4'), дает нам два действительных и два мнимых корня. Корни эти будут
at
Ha основании этого общий интеграл уравнения (4') напишется так:
Ф A sin ах В cos ах Свх Dex. (6)
Значения произвольных постоянных могут быть определены на основании условий на концах балки. Так как концевые сечения не могут поворачиваться вокруг оси х-ов, то I) Ф 0 при х 0 и II) ф 0 при х — I.
Другую пару условий мы найдем, приняв во внимание, что на концах балки нет моментов, которые бы изгибали полки балки в плоскостях, параллельных плоскости ху следовательно, III) ф 0 при х 0 и IV) ф 0 при х.
) А. Мичелл в своей работе (стр. 11) не отбрасывает этих членов и при решении уравнений (2) пренебрегает только членами, содержащими ф2. Таким образом, для ф он получает уравнение
М2 ф
ВП d2ф Dh2 dф
bJ“ dx2 2 dx4
Гак как практический интерес имеют только те случаи, где B2Bi мало, то, пренебрегая этой величиной, получим наше уравнение (4).
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 29
На основании условий I и III будем иметь
В Сх D 0, Ва2 Сх Р2 D2 0. (7)
Чтобы удовлетворить этим уравнениям, необходимо положить
В 0, Cj — Z)j.
На основании этого мы можем решение (6) представить в таком виде:
Ф A sin ах Cl sh х.
Для определения А и С мы воспользуемся условиями II и IV, которые нам дадут
A sin а С sh 8 0,
(8)
— Ла2 sin а Ср2 sh р 0.
Условиям (8) можно удовлетворить, положив А 0 и С 0.
Но тогда все произвольные постоянные интеграла (6) будут
d2y
нулями и, следовательно, ф и будут равны нулю по всей
длине балки, т. е. мы будем иметь случай плоского изгиба. Чтобы была возможна другая неплоская форма изгиба, необходимо, чтобы уравнения (8) допускали для Л и С решения, отличные от нуля. Для этого необходимо определитель уравнения (8) приравнять нулю, т. е. положить
(x2 p2)sina 0. (9)
На основании наших обозначений мы имеем
2 , р2 1 2С
а2 Р2 и потому первый множитель (9) не может быть нулем, следовательно, для возможности появления неплоской формы изгиба
необходимо положить sin аI 0.
Таким образом, можно найти бесконечное множество значений а, а следовательно и Мкр, при которых становится возможной неплоская форма изгиба. Для этого нужно только положить
а шт, (10)
где п — целое число.
Чтобы представить себе, какой вид имеют различные формы неплоского изгиба, заметим, что на основании условий (8) и
(10) С 0, следовательно,
Ф A sin ca. (11)
30 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
ь)
Положив в условии (10) п равным единице, получим наименьшее значение для а, а следовательно, и для М, при котором плоская форма изгиба будет неустойчива. Появляющаяся неплоская форма изгиба характеризуется тем, что угол ср по всей длине будет одного знака. Максимального значения он достигает при х 2, когда sin ах 1.
Проекцией изогнутой оси балки на плоскость ху будет кривая без точек перегиба, так как сохраняет свой знак по
всей длине балки, что е' видно из уравнения (3)
В общем эта форма из гиба будет соответство вать рис. 11, взятому на ми при выводе уравнения Если в условии (10) положить п 2, то тогда Ф переменит свой знак при х 2 и ось балки изогнется, как показано на рис. 12, а. Рис. 12,6 дает вид изгиба при п 3. Чем большее, тем больше а и тем больший нужен момент, чтобы осуществить соответствующую форму изгиба.
Для практических целей особенно важно значение Л1кр, при котором становится возможной первая неплоская форма изгиба. Для этого случая должна быть составлена таблица, которой можно было бы пользоваться так, как, например, таблицей проф. Ф. С. Ясинского в случае продольного изгиба.
Для сравнения получаемых нами здесь результатов с результатами других случаев нагрузки мы введем такие обозначения:
_ _2С_ _ _1_
а2 D h2 “ V2 9
V_
d
пт2
B,Dh2
(12)
где W2 и lV2 суть отвлеченные числа. Заметим, что 1V2 зависит только от размеров балки, в выражение же для W2 входит также и изгибающий момент М. На основании (12), очевидно,
r2F. (13)
Величина W2y соответствующая заданным размерам балки, определится из условия (10), которое на основании новых обозначений перепишется при п 1 так:
I 1 2 , ТГ2
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 31
Ход расчета при определении критического изгибающего момента, очевидно, должен быть следующим. По геометрическим размерам балки, задавшись значениями модулей упругости Е и G, вычисляем величину 1V2. Тогда уравнение (14) дает нам возможность вычислить величину W2 и, следовательно, W2V2. Пусть определенное таким образом W2V2 будет равно k2, тогда
на основании (13) kVВ2С
Мкр (15)
Полученная нами формула имеет сходство с формулой Эйлера в случае продольного изгиба. Величина множителя k меняется в зависимости от размеров балки и определяет собой
влияние жесткости полок. Чем меньше D и больше длина
балки , тем менее сказывается влияние изгиба полок, тем меньше величина k. В пределе, когда D 0 и двутавровая балка состоит из одной вертикальной стенки, мы будем иметь V2 О, а на основании уравнения (14) W2V2 я2.
Следовательно, наименьшее значение для переменного множителя будет k я, и для этого случая формула (15) перепишется так: МКр Vf'C. (16)
Заметим, что к тому же самому результату мы могли бы прийти, положив в основном нашем уравнении (4) D 0. Тогда задача приведется к решению уравнения второго порядка
Общий интеграл этого уравнения будет
л М , D М
’-AsmVWK BmsTWx-
Чтобы удовлетворить условиям на концах, придется положить
on Ml
s ” ТШпя-
откуда сейчас же получается вышеприведенная нами формула (16).
Чтобы наглядно показать закон изменения k2 в зависимости от 1 V72, мы воспользуемся графическим построением. Откладывая по оси -ов величины V2 и по оси у-оп соответствующие значения W2V2, получим искомую кривую. На основании уравнения (14) нетрудно видеть, что это кривая будет гиперболой; асимптотами ее будут ось у-ов и прямая, параллельная оси лг-ов, проведенная на расстоянии я2 от нее, как это показано на рис. 13.
32 0 УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
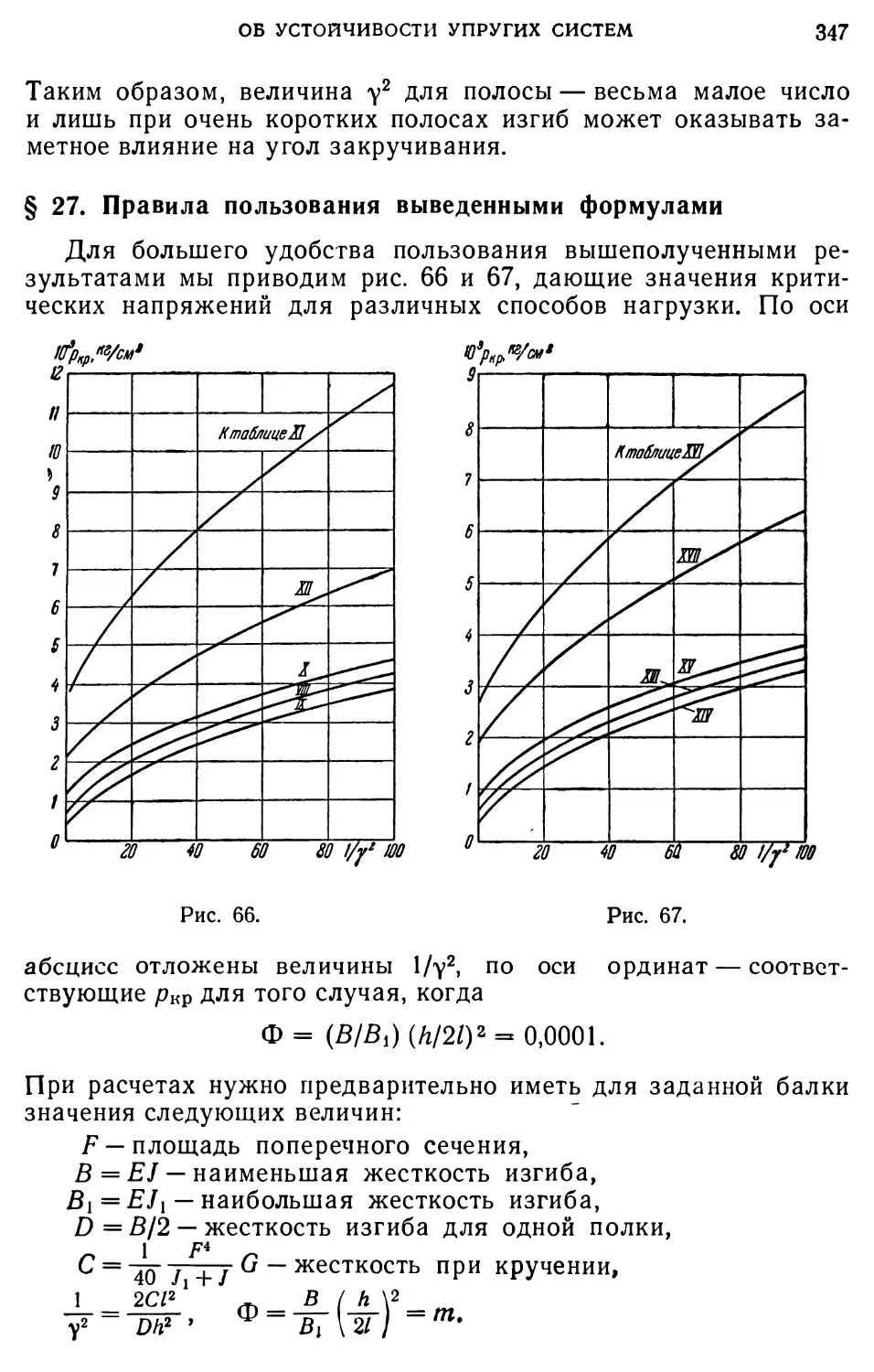
В приведенной ниже таблице А мы даем ряд численных значений k2.
Таблица А1)
1
V2
W2
W2V2 k2
кр’ кгсм2
1
V2
W
W2V2-k2
Якр, кгсм2
0,1
98,4
984
495
16
255,3
16,0
800
2
117,2
58,6
540
20
294,8
14,7
860
4
136,9
34,2
585
24
334,3
13,9
915
6
156,6
26,1
625
28
373,8
13,4
965
8
176,4
22,1
665
32
413,3
12,9
1015
10
196,1
19,6
700
36
425,7
12,6
1065
12
215,9
18,0
735
40
492,2
12,3
1110
п
B2Bi
1 Значение критического напряжения кр кгсм2 вычислено при 0,01; г 0,1; 2- Ю6 кгсм2.
Пользуясь таблицей А, нетрудно для всякого 1К2 найги соответствующее значение коэффициента к, а следовательно, и критического изгибающего момента Мкр; см. также рис. 13.
Изеиб бални со свободными
Рис. 13.
Для большего удобства пользования нужно составить таблицы напряжений, соответствующих критическим значениям изгибающего момента. Обыкновеная формула сопротивления материалов для определения наибольших нормальных напряжений R дает нам
г _ Mh __ МНЕ Н 2, 2В,
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 33
Если вместо М подставим значение критического момента из формулы (15), то для величины опасного напряжения будем
иметь n VВЕ h (7
КР 2Вх I ' '
В формуле этой возможны дальнейшие упрощения. Для этого заметим, что при малой толщине вертикальной стенки с достаточной точностью можно положить D В22. Тогда на основании наших обозначений (12)
г _ в2 1 к2
4 V2 I2 9
Подставляя это в формулу (17), окончательно будем иметь
кр -j WE (у). (18)
Как видно, опасные напряжения при одном и том же W будут пропорциональны отношению между главными моментами инерции поперечного сечения балки и квадрату отношения высоты балки к ее пролету. Следовательно, при составлении таблицы достаточно вычислить опасные напряжения для какого-либо определенного значения отношения B2Bi и hl.
В таблице А приведены значения опасных напряжений в кгсм2, соответствующие
В2 _ 1 h 2 1
В, 100 I ) 100
Модуль упругости взят равным Е 2 10е кгсм2. Если бы при заданных размерах балки отношения эти были равны
В2 _ 1 (A2 _L
В, т 9 I ) п'
то для получения опасных напряжений пришлось бы число, поставленное в таблице, умножить на 104mn.
При вычислениях 1К2 никаких затруднений встретиться не может, так как отношение hl всегда известно с большой точностью. D может быть вычислено на основании поперечных размеров балки, если только известен модуль упругости материала. Что касается С, то оно может быть вычислено на основании приемов, приведенных в § 3. Вычисления эти, конечно, будут очень неточными, но, как видно из рассмотрения таблицы А, даже большие ошибки в определении V2 не сильно повлияют на определяемую величину опасных напряжений.
Формулы, полученные нами для балок со свободными концами, легко распространить на случай балок, одним концом заделанных неподвижно. В случае первой неплоской формы
34 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
изгиба среднее поперечное сечение балки в силу симметрии остается плоским, и, следовательно, в задаче нашей ничто не изменится, если мы будем считать его неподвижно заделанным. Пара, приложенная к свободному концу, должна быть подчинена тому условию, что плоскость ее во время деформации заключает в себе главную ось инерции концевого поперечного сечения и ось jc-ob. Величина критического момента, очевидно, должна остаться прежней, длина же балки будет k 2. Следовательно,
Мк п
kV в2с
кр 2, Когда балка состоит из одной вертикальной стенки, мы будем иметь
я VВ2С
кР 2,
§ 6. Изгиб балки с заделанными концами
Положим, что концевые сечения балки закреплены таким образом, что устранена возможность вращения не только вокруг оси лт-ов, но и вокруг вертикальной оси г-ов. Вращение концевых сечений вокруг оси у-ов мы предполагаем возможными,
X —
0
р
р я
Z
-«—«Г —
0
0 ч
V—- —
)х
М,
Рис. 14.
так как при значительной жесткости балки в плоскости ее стенки невозможно обеспечить неподвижность в этом направлении. Положим, что рис. 14 представляет одну из возможных в этом случае неплоских форм изгиба.
Ясно, что для устранения вращения вокруг оси г-ов к концевым поперечным сечениям необходимо приложить некоторые моменты М0, действующие в плоскостиг и вращающие в сторону, указанную на рисунке стрелками.
Величина момента пока остается неопределенной и впоследствии может быть вычислена на основании тою, что касатель¬
ОБ УСТОЙЧИВОСТИ ПЛОСКОП ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 35
ная к изогнутой оси балки на концах должна лежать в плоскости zx, т. е. при х О и при х I 0.
Чтобы составить основные уравнения в этом случае, возьмем опять произвольное сечение на расстоянии х от начала координат и составим выражения для моментов внешних сил относительно осей, г, z взятого сечения. Пользуясь таблицей (4) § 4, получим
Mj M-g- M0g, Мц М М0р, Мг Мф М0. (1)
Пользуясь основными уравнениями § 4 и считая ср малым, будем иметь
dx ® dx dx 2 dx3
Мф-М0-В2-§, м--В.
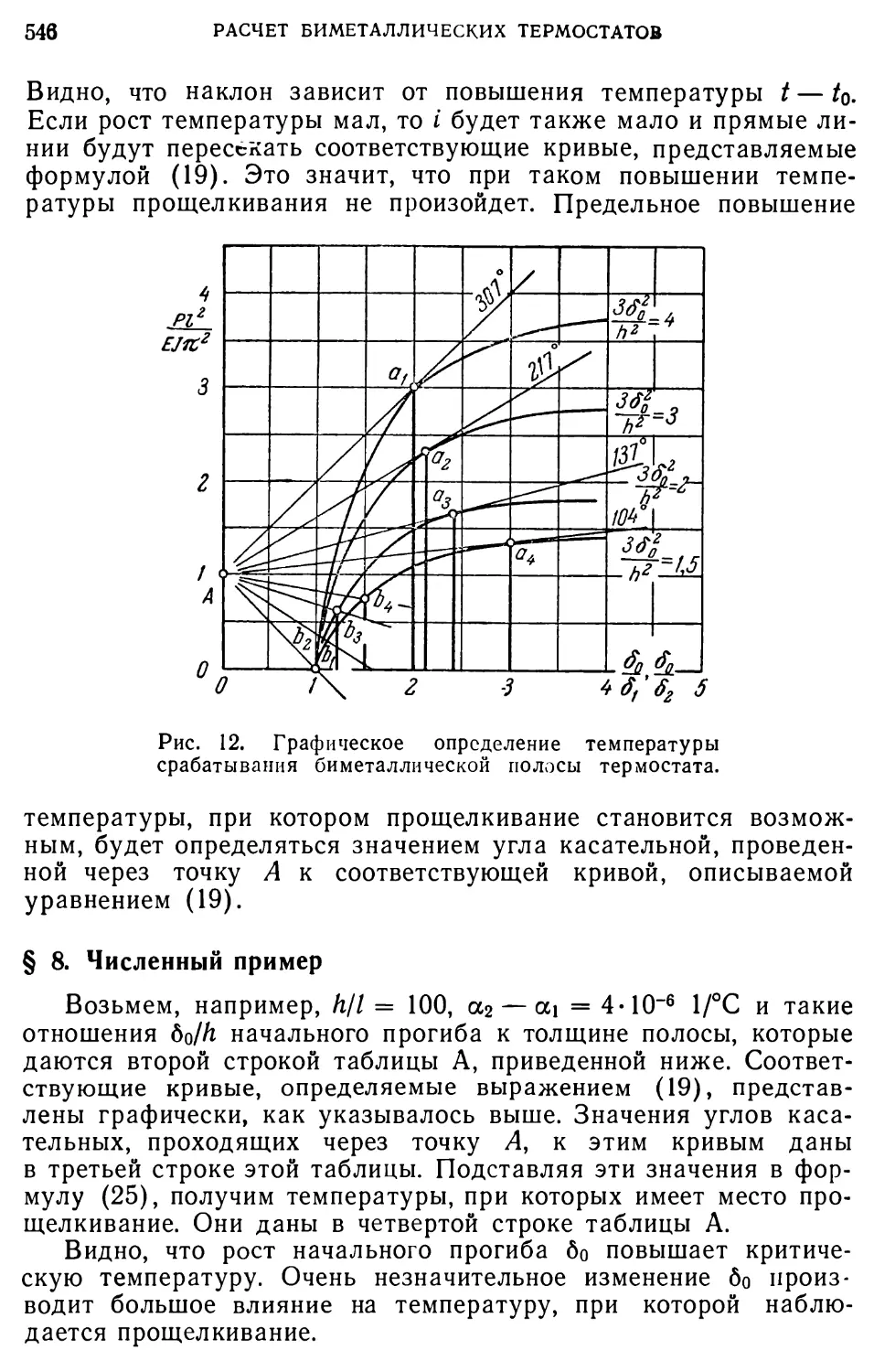
Членом Л10ф во втором из уравнений (1) мы пренебрегли, как величиной малой по сравнению с М.
Из уравнений (2) нетрудно исключить переменные у и г, для этого первое из них дифференцируем по х и вместо у и г подставляет их значения из уравнений второго и третьего, тогда получим
-(Мф-Мо)-- Сф''-ф'У. (3)
Разделив это на коэффициент при ф1У и пользуясь обозначениями предыдущего параграфа, будем иметь
(4)
В дальнейшем мы будем пренебрегать величиной по
сравнению с единицей. Полный интеграл уравнения (4) мы получим, если к рассмотренному в предыдущем параграфе интегралу уравнения без последнего члена прибавим частное решение уравнения (4), тогда
Ф A sin ах В cos ах Сех Dxex . (5)
Произвольные постоянные Л, 5, Сi, D4 и неизвестная пока величина М0 определятся из условий на концах балки.
Условия эти будут следующие:
I) при х 0 ф 0, II) при х 1 ф 0.
36 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Кроме того, момент внешних сил относительно оси подсчитанный для концевых поперечных сечений, будет нулем; следовательно,
III) ср' —-jjr р' 0 при х 0 и IV) ф — -гф' 0 при х I.
Условия I и II дают нам
(а)
A sin al B cos al C1 D -jf. (b)
Условия III и IV представятся в таком виде:
- А (а» -) С, (р - А)D, (-(f i) О,
— A cos а а3 -р-J В sin а (а3 (р3 - i) Dfi-V (- p3 о.
Эти два условия можно значительно упростить, если разделить их на коэффициент при А и принять во внимание, что
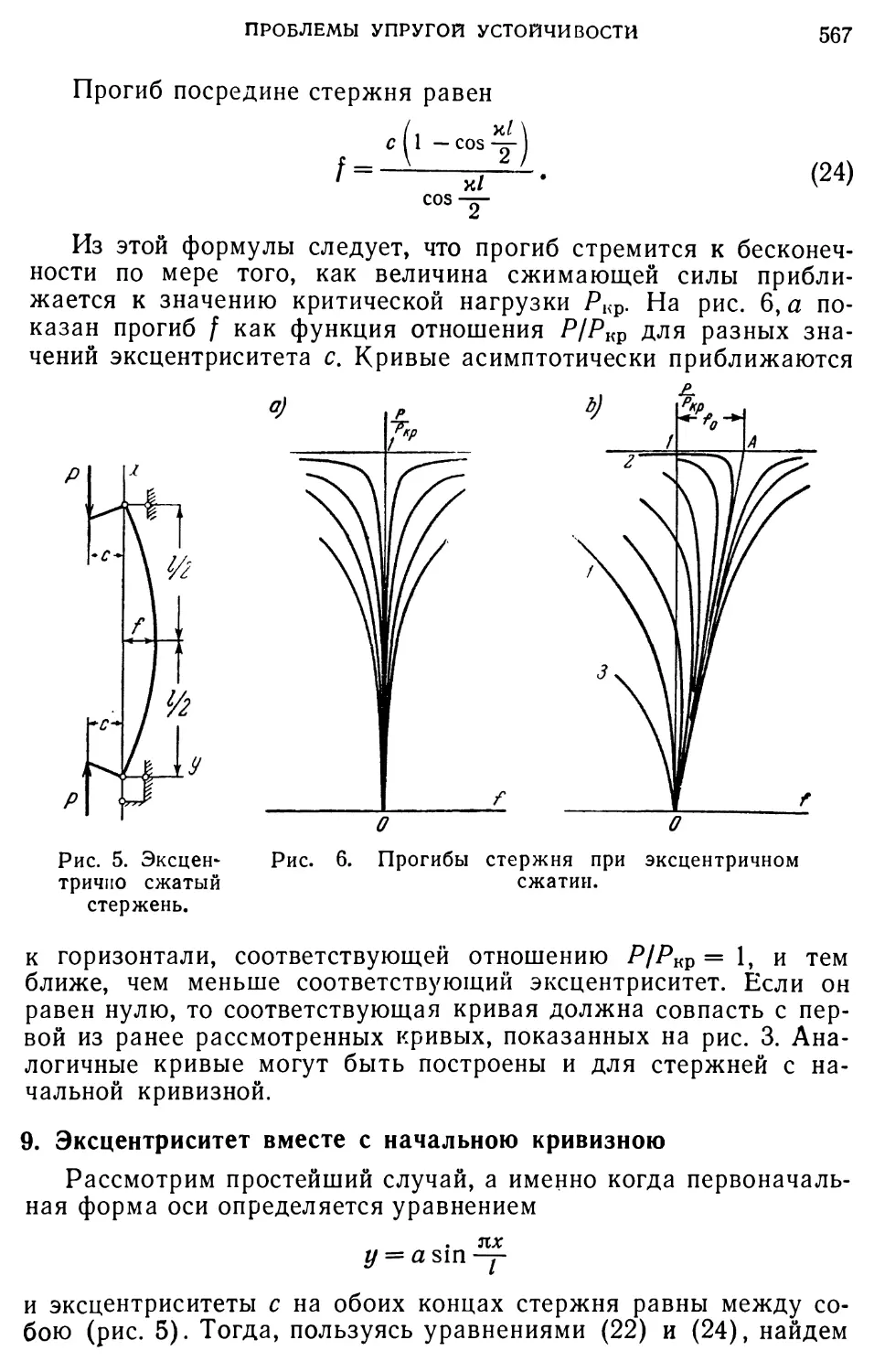
в3 —в2 —
Р L l 1 , , а ос о. 1
а3 —т а2 -f—5
а1 а2
тогда получим
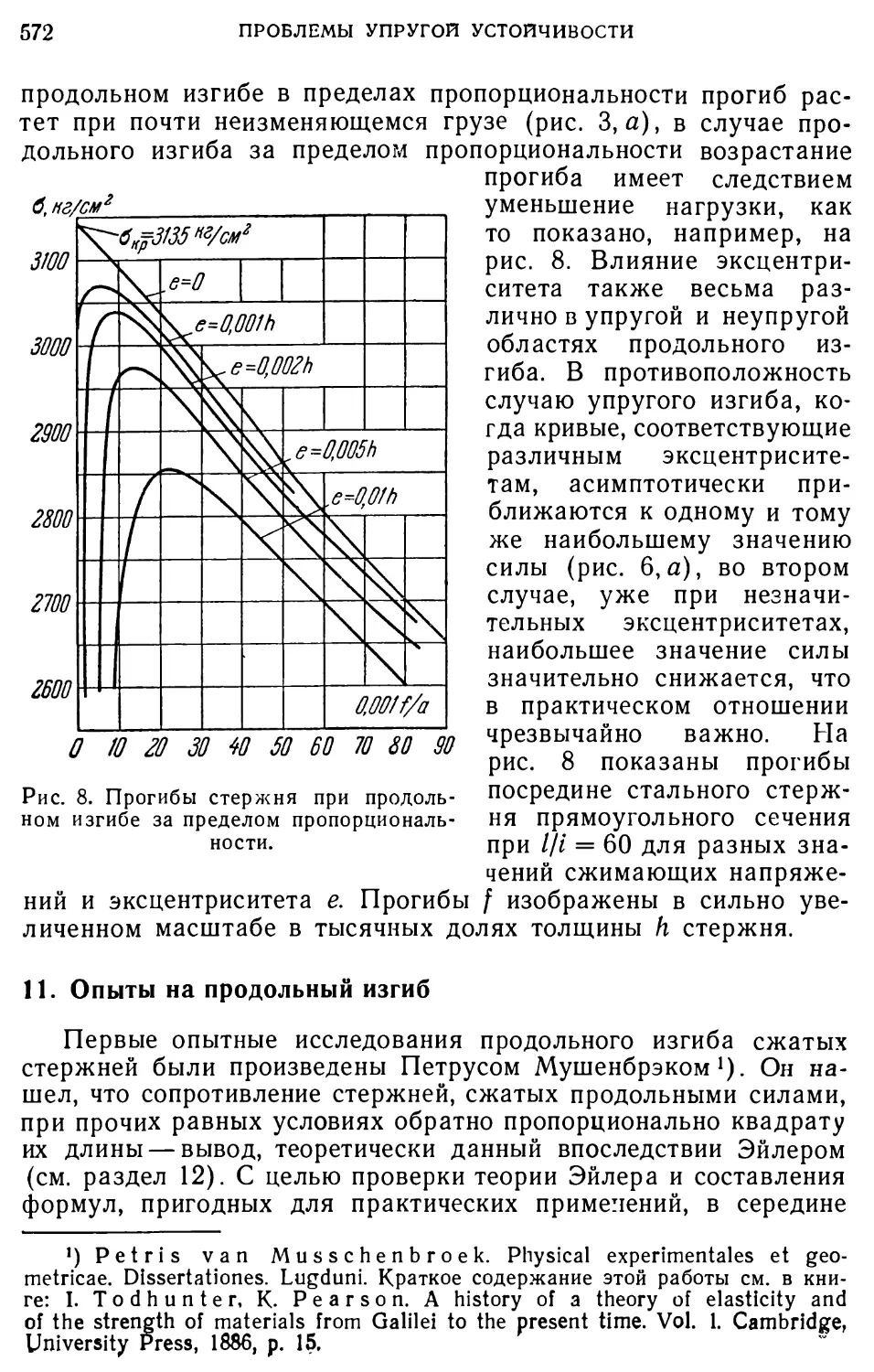
(с)
- cosaZ fisinaZ jC'- jDxeV 0. (d)
Из условий (а) и (с) можем выразить произвольные постоянные Ci и D1 через Л и Б:
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 37
Те же постоянные из условий (Ь) и (d) выразятся таким образом:
о
-sin а — cos а а
в
а
cos а — sin а а
1 м0
-
еы J
2
J
2 Меы '
л
Г ft -
sin а Н cos а
а
В
Г ft “1
sin а cos а
а
1 ма
2
L
2
2 Ме
Из сравнения (6) и (7) получим
1 -
(7)
— cos а I — sin а а
' cos а I sin а
В_
2
cos аН sin а
а
--Uo,
в_
2
cos а — — sin а а
(8)
_ Мо
2 М1 е-Ы)
Условиям (8), конечно, можно было бы удовлетворить, положив
А В М0 О,
но тогда Ci и Di также будут нулями и решение будет соответствовать случаю плоского изгиба. Чтобы неплоская форма изгиба была возможна, необходимо, чтобы условия (8) давали для произвольных постоянных решения, отличные от нуля. Нетрудно видеть, что мы удовлетворяем условиям (8), положив
А 0, cos а - sin а 1, cos а — sin а 1. (9)
Тогда будем иметь М0 — ВМ, а из условий (6) С, О, Di 0.
Для определения угла поворота ф будем иметь
Ф В (cos ах — 1). (10)
Чтобы судить о том, каков вид неплоской формы равновесия, обратимся к условиям (9). Для того чтобы они были удовлетворены, необходимо положить cosal, sina 0. Следовательно, а 2тя, где т — произвольное целое число.
Первая возможная форма, соответствующая наименьшему значению а, а следовательно и наименьшему изгибающему
38 ОБ УСТОЙЧИВОСТИ плоской ФОРМЫ ИЗГИБА двутавровой балки
моменту М, очевидно, получится, если мы положим
а 2я. (11)
В этом случае угол р все время будет одного знака и наибольшей своей величины достигнет при х 2.
Проекцией изогнутой оси балки на плоскость ху будет кри¬
вая с двумя точками перегиба, которые будут соответствовать тем сечениям балки, где Мф — М0 0, что нетрудно видеть из второго уравнения системы (2).
То же уравнение дает нам выражение для у
, _ MB I sin ах. М0х
у 57 й хГвТ'
Нетрудно видеть, что у' обращается в нуль при х 0 и при х I.
В общем неплоская форма изгиба будет иметь вид, представленный на рис. 14.
Для вычисления критического значения изгибающего момента Мкр воспользуемся обозначениями (12) предыдущего параграфа. Тогда на основании условия (11) будем иметь
Y (2ГГ2--24л2' 12
По известным размерам балки, задаваясь величиной модуля упругости, вычисляем 112, потом из (12) определим соответствующее значение W2 и, обозначая произведение W2V2 через k2 окончательно для определения критического значения Мкр будем иметь
мк p -fef2C-, (13)
Формула это совершенно совпадает с тем, что мы получили для балки со свободными концами, только, конечно, коэффициент k будет иметь другое значение. Если мы графически представим зависимость между 1У2 и 2, то, поступая так же, как и в предыдущем параграфе, получим гиперболу, асимптотами которой будут ось у-ов и прямая, параллельная оси х-ов и проведенная на расстоянии 4я2 от нее.
Величина k будет меняться в зависимости от жесткости полок балки. Если уменьшать жесткость D, то вместе с тем уменьшается и k. Когда полок совсем нет, т. е. D — О и V2 0, мы на основании (12) будем иметь
k2 W2V2 4я2
и, следовательно, формула для вычисления Мк перепишется §
ОВ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
этом случае таким образом:
ЛТ 2л VВ2С 1Ч
М Кр j , (14)
т. е. критический изгибающий момент как раз вдвое больше, нежели в случае балки со свободными концами. Заметим, что заделанной балку можно считать только в том случае, если конструкция закрепления концов такова, что действительно обеспечена полная неподвижность в известном направлении.
Возьмем для примера продольную балку моста. Ясное дело, что ее придется считать, как балку со свободными концами, так как обычно употребляемая конструкция сопряжения продольной балки с поперечными мало затрудняет возможность вращения концевых поперечных сечений вокруг вертикальных осей.
Укажем теперь, что формулу (14) для балки, состоящей из одной стенки, можно получить и из основного нашего уравнения (3), положив в нем D 0. Тогда будем иметь
„ , М2 М2 Мо
ф В2С ф В2С М
Общий интеграл этого уравнения будет
а М , г» М , М0
qp A sin г х В cos г х Н .
Y Vв2с Y в2с м
Условия на концах, очевидно, будут
I, II) при х 0 ф0 0, ф0' 0,
III, IV) при х 1 ф; 0, ф; 0.
На основании условий I, II будем иметь А 0 и В — Следовательно,
М0 1Л М ф —- 1 — COS -.X.
м Vb2c I
На основании условий III, IV будем иметь М0 М
Чтобы удовлетворить этим условиям, придется положить С(
Следовательно,
11 м Л л м0 м . м , Л
1 — cos г 0, —- f.: sin — 1 0.
Vb2c m Vв2с Yв2с
М 1 1 м л
ТИЗг smYW‘0-
м 1 о
I 2 тя.
Vb2c
Первая неплоская форма возможна, если
2я VВ2с
40 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Ниже мы приводим таблицу В, в которой для различных значений 1IV2 вычислены соответствующие значения коэффициента k2y а также значения опасных напряжений в предполо жении, что
в2 1 h _ 1
By юо и i ю
На рис. 15 представлена зависимость критических напряжений
Изгиб бажи с заделанными концами
2600
2400
2200
Vj
2000
1800
1600
1
1400
s
1200
1
1000
800
600
400
200
т:;;г
Крик
1
;НЫХ »
а прял
.-
2
'К
к
440
400
360
320
280
240
200
60
120
80
4тСг
0 2 4 6 8 10 12 4 16 18 20
1у
Рис. 15.
и величины k2 от 1V2 для балки с обоими заделанными концами по данным табл. В.
Таблица В1)
1
V»
W2
VPV - k2
RKp, кгсм2
l
V2
W2
W2V2 k2
Якр, кгсм2
од
1 563
15 630
1 980
14
2 112
151
2 300
1
1598
1 598
2 000
16
2 191
138
2 345
2
1 638
819
2 025
20
2 349
117
2 425
4
1 717
429
2 070
24
2 507
104
2 505
6
1 795
299
2 120
28
2 664
95,2
2 580
8
1 874
234
2 165
32
2 822
88,2
10
1 954
195
2210
36
2 980
82,8
2 730
12
2 033
169
2 255
40
3 138
78,5
2 800
) Значение критического — «опасного» — напряжения RKp кгсм2 вычислено при В2Вj-0,01; А 0,1; 2106 кгсм2.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 41
§ 7. Случай изгиба балки эксцентрично приложенными сжимающими силами
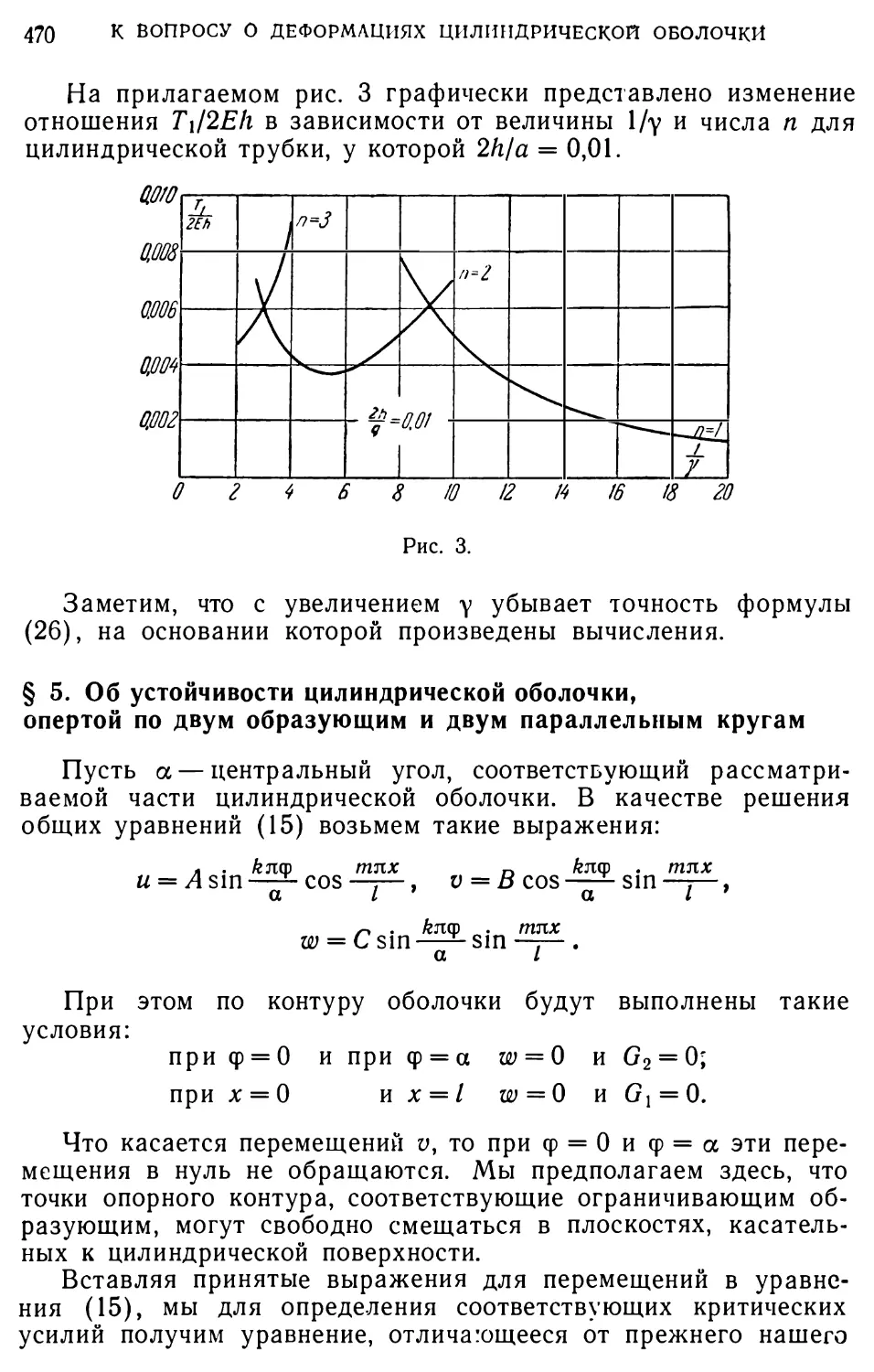
Рассмотрим теперь случай балки, сжимаемой двумя взаимно противоположными силами, линия действия которых параллельна оси балки и лежит в срединной плоскости вертикальной стенки балки. Обшее расположение видно на рис. 16.
Прикладывая к центрам тяжести концевых поперечных сечений по две взаимно противоположные силы, равные и параллельные силам Р, мы приведем систему внешних сил к двум парам сил с моментами М Ра и к двум силам Р, действующим по оси балки и сжимающим ее.
При определении величины критического момента будем идти прежним путем и начнем с вычисления Мь MVr М, соответствующих взятому нами поперечному сечению с абсциссой х.
Составляющие этих моментов, получающиеся от пары сил с моментом Af, мы можем взять из первого рассмотренного нами случая (см. (1) § 5).
Что касается моментов, получающихся от продольной силы, действующей по оси х-ов, предварительно составим их в общем виде и потом уже отбросим малые члены:
Проекции действующей силы Р на оси г, при малом ср, оче видно, будут
Координаты точки приложения силы Р относительно тех же осей будут
Р
Р
Рис. 16.
(2)
(3)
, dz ,
42 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Подставляя (2) и (3) в выражения (1) для моментов и отбрасывая малые величины второго порядка, мы получим
Мг 0, MPz, Mt-Py. (4)
Присоединяя сюда моменты от пары сил, получим систему урав¬
нений
г Жр_ __ Dh2 dz Ф
т dx dx 2 dx3 ’ гч
d2z d2u
M Pz-B, Mp Py-B2jg.
Для большей ясности начнем с рассмотрения того частного случая, когда балка состоит из одной вертикальной стенки и, следовательно, D 0. Уравнения первое и третье системы (5) перепишутся таким образом:
му' Сф', мФ р-в2;
исключая из них у, будем иметь
, М2 Р ф В2С В J ф “ - Для р' можно сразу написать решение:
ф' A sin ах В cos ах,
где
, , М2. Р А , В. , „
аУСв7’ Ф-тс08са Т51Па с-
Для определения произвольных постоянных воспользуемся условиями на концах балки. Положим, что опоры устроены таким образом, что не допускают вращения вокруг оси jc-ob. Вокруг осей у-ов и г-ов вращение может происходить свободно. Тогда будем иметь
I) ф 0 при х 0 и II) ф 0 при х 1,
откуда получаем
С — и — (1 — cos a) — sin а 0. (а)
a a v ’ a 4 J
Из условия симметрии следует, что ф ± ф, следовательно, В ± (A sin а Н- В cos а). (Ь)
Из условий (а) и (Ь) заключаем, что Л 0 и cqs а,1 ±1,
откуда а тл.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 43
Угол поворота любого поперечного сечения будет
в.
Ф — sin ах,
Y а
(7)
Наименьшее значение а, а следовательно и изгибающего момента, при котором становится возможной неплоская форма изгиба, получится, если положим
Изменения угла поворота ф по длине балки и вид изогнутой оси будут соответствовать рис. 11, соответствующему изгибу балки со свободными концами парами сил.
Величина силы Я, при которой плоская форма изгиба перестает быть устойчивой, определится из условия
Формула (9) представляет интерес, так как из нее видна связь между изучаемыми нами вопросами устойчивости плоской формы изгиба, с одной стороны, и другим, уже подробно исследованным видом неустойчивого равновесия, именно продольным изгибом — с другой. В самом деле, если мы, не изменяя величины силы, будем уменьшать плечо а, то первый член в левой части формулы (9) будет уменьшаться, и, когда а станет равным нулю, мы будем иметь Р хорошо известную фор¬
мулу продольного изгиба для случая стержня со свободными концами.
Из формулы (9) следует, что при действии продольных сжимающих сил всякий эксцентриситет в направлении наибольшего радиуса инерции поперечного сечения будет уменьшать величину критической нагрузки. Нетрудно показать, что это влияние мало; для этого представим формулу (9) в таком виде:
Мы предполагали, что поперечное сечение балки есть прямоугольник, одна сторона которого b велика по сравнению с другой б. В таком случае на основании § 3 мы можем написать С з6б3С, где G — модуль упругости при сдвиге.
Если положим эксцентриситет а равным тб, то формула (10) перепишется таким образом:
а я.
(8)
(Ю)
44 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ где R — напряжение материала от сжатия. Так как R обыкновенно очень мало по сравнению с G, то влияние малых эксцентриситетов на величину критической нагрузки ничтожно.
Рассмотрим теперь другой крайний случай, именно будем увеличивать плечо силы а до бесконечности, величину же силы беспредельно уменьшать таким образом, чтобы момент сохранял конечную величину; тогда формула (9) нам даст
Af„n ПВгС
кр I т. е. как раз то же самое, что мы имели в первом разобранном нами случае см. (16) § 5.
Познакомившись на этом частном примере с сущностью явления, перейдем к случаю двутавровой балки, т. е. к случаю, когда D в уравнении (5) отлично от нуля.
Исключая из первого и третьего уравнений системы (5) у, получим для определения ср следующее уравнение:
v 2С Р пг ( 2М2 , 2РС , п П1ч
ф DI2 В2)Ч B2Dh2 B2Dh2)y ’ или, введя обозначения
1 2 С Р 1 2 М2 , 2 PC
1
будем иметь
2 Dh2 В2 ’ d B2Dh2 B2Dh2 ’
Ф 2ф -тгФ 0.
а “1
Для ф' можно написать сразу решение:
ф' А sin ах -f В cos ах Сех Dex,
где
Интегрированием получаем
Ф A sin ах -I- В cos ах -I- С2ех D2ex Е2. (12)
Условия на концах балки будут следующими:
I, II) ф 0 при х 0 и при х 1
III, IV) ф 0 при 0 и при х 1.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 45
На основании условии I и III будем иметь
В С2 D2 Ь В2 —
— Во “Ь С2 Ь -2 О
(а)
Условия II и IV дадут нам
A sin al В cos al С2е1 D2el Е2 О,
- A J- sin al - В -р- cos а D2eV 0.
(b)
Вычитая второе из первого, будем иметь
А (I sin al В (1 -p-j cos a I Е2 0.
Мы удовлетворим написанным условиям и условию симметрии, если положим
В С2 D2 Е2 0 и sin al 0.
Тогда для угла поворота будем иметь ф A sin ах.
Первая неплоская форма изгиба становится возможной при
Рассмотрим два предельных случая.
I случай. Сжимающая сила бесконечно мала, но плечо силы велико, и изгибающий момент М есть величина конечная. В основном уравнении (И) придется Р положить равным нулю, и тогда уравнение будет тождественно с разобранным нами уравнением (4) § 5.
II случай. Плечо силы уменьшается, и в пределе точка приложения силы совпадает с центром концевого поперечного сечения. В уравнении (11) в таком случае нужно положить М 0, и оно перепишется тогда в таком виде:
Следовательно, первая неплоская форма изгиба наступит, когда
Таким образом, мы опять пришли к известной формуле продольного изгиба.
al я.
В данном случае
2 Р п2
а вГ -р-’
т. е. когда
л2В2
-—72—-
46 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
§ 8. Случай изгиба балки эксцентрично приложенными растягивающими силами
В этом случае в уравнениях предыдущего параграфа вместо Р везде придется подставить —Р. Уравнение (6) § 7, выведенное нами для случая балки, состоящей из одной вертикальной стенки, перепишется так:
Коэффициент при q будет величиной положительной, а следова тельно, ф' и ф выразятся через тригонометрические функции. Полагая
Величина момента Мкр, при которой становится возможной первая неплоская форма изгиба, определится из уравнения
Из этого уравнения видно, что всякая растягивающая сила увеличивает величину критического изгибающего момента, тогда как сжимающие силы уменьшают его. Увеличивая плечо силы беспредельно, мы придем к формуле (16) § 5 изгиба балки парами сил.
II случай
Чтобы удовлетворить условиям на концах, необходимо положить А В С 1 0. Следовательно, в данном случае возможна только форма плоского изгиба. Полагая М 0, получим случай простого растяжения.
(1)
Здесь придется рассмотреть два различных случая.
I случай
м2. Р
п Г R
будем иметь
Ф A sin ах.
М2 Р л2
(2)
В2С В2 I2
Р М2
В2 В2С
Полагая
будем иметь
Ф Аех Вех Сх.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 47
Р М2
При вс УРавнение (1) перепишется так:
ф7 0, ф ' Ах Ву ф —g—-Вх Сх.
Чтобы удовлетворить условиям на концах, придется положить А В Сi 0, т. е. и в данном случае возможна только форма плоского изгиба.
Уравнение, соответствующее двутавровой балке, напишется для случая растягивающих сил так:
Подробно разбирать это уравнение не будем, так как оно не дает ничего нового; заметим только, что, пока
плоский изгиб является единственной возможной формой равновесия.
§ 9. Влияние первоначальной кривизны оси балки
До сих пор мы предполагали, что ось балки совершенно пря мая и что плоскость изгибающих моментов точно совпадает с срединной плоскостью стенки балки. Посмотрим, какие изменения внесет в изучаемое нами явление незначительная первоначальная кривизна оси балки в плоскости ху. Для простоты положим, что ось в этом направлении согнута по кругу радиуса R.
Если балка изгибается парами сил, приложенными так, как в случае § 5, то основные уравнения напишутся таким образом:
B2Dh2 B2Dh2
2М2 2PC -
ГМ,2 О П-.2
возможны будут неплоские формы изгиба. При
B2Dh2 B2Dh2
Исключая из них неизвестное у, будем иметь
или, вводя прежние наши обозначения,
IV 1 1 1 В2
а2 ф d4 ф Ф МЦ
(2)
48 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Частным решением этого уравнения будет
--ж- (3
Заметим, что величина B2MR будет малой, так как B2R есть не что иное, как величина момента Ми который мог бы первоначальной прямой оси балки придать кривизну 1R. Так как мы считаем первоначальную кривизну малой и В2 мало по сравнению с Ви то и будет мало по сравнению с М, и, следовательно, величина ср, определяемая из (3), будет малой.
Полный интеграл уравнения (2) будет
Ф A sin ах В cos ах Схех Dex — . (4)
Условия на концах дадут нам следующие уравнения для определения произвольных постоянных:
B C1 D1-y 0, -Bc C DO,
A sin al В cos al Cel De1 — y 0, (5)
— A a2 sin al — Ba2 cos al Сф2е1 Dfi2e1 0.
В этих уравнениях через у обозначена малая величина ММ. Решая уравнения (5) относительно произвольных постоянных, получим
л Р2 vffTa Р—
П “ a2 Р2 Y 2 1 D а2 р2 ’
п _ а2 1 n _ а2 1
L‘- а2 р2 V ,еР. и1 а2 р2 Y (е_р
Подставляя их в общий интеграл (4), будем иметь
Ф „ ftg — sin a cos ал:)
о2 p2 V 2 I
, a2 ( ex , ePx C4
a2 p2 1eV 1e-W ) Y ( )
Так как уравнения (5) допускают для произвольных постоянных вполне определенные решения при всяком изгибающем моменте, то, следовательно, отдельные поперечные сечения начинают поворачиваться, и балка искривляется при самых малых нагрузках. Мы не будем подробно рассматривать закон, по которому идет изменение ф, заметим только, что сначала возрастание углов поворота и искривление балки идет медленно, но с приближением изгибающего момента к вычисленному нами для прямой балки критическому значению AfKp изменения формы делаются сразу весьма значительными. Это можно показать на основании формулы (6). Когда изгибающий момент по ве¬
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 49
личине близок к критическому, величина у будет мала, множители
а2 1 ех ех
_г_ JL - I 1
а2р2 2 ’ 1вР 1в-Р Следовательно, нам нужно разобрать только первое слагаемое
ф1 аг р2 if Sin аХ C0S “) ’
Наибольшего значения эта величина достигает при х 2. В этом случае ф можно представить таким образом:
Yp2 1
Pi —
а2 р2 а cos —
В2
Так как ц2 всегда 1, то быстрое возрастание начнется
тогда, когда cos(a2) будет приближаться к нулю, а значит, аI — к величине я, т. е. к величине, определяющей критический изгибающий момент в случае балки с прямолинейной осью.
Случай, когда ось балки прямая, но плоскость изгибающего момента не совпадает со срединной плоскостью вертикальной стенки, легко можно привести к только что разобранному. Положим, что плоскость изгибающей пары М проходит через ось балки и составляет малый угол фо с вертикальной плоскостью. Разложим момент М на составляющие Ми действующий в плоскости стенки балки, и М2, действующий в плоскости, ей перпендикулярной. Тогда отношение М2М4 будет играть ту же роль, что у в предыдущем случае, и, следовательно, при малых углах наклонения ф0 искривление оси балки начнет быстро расти с приближением М к величине критического изгибающего момента.
§ 10. Изгиб балки сосредоточенной нагрузкой, приложенной на конце
Исследование вопроса об устойчивости плоской формы изгиба балок в случае действия сосредоточенных поперечных нагрузок мы начнем с балки, одним концом полностью заделанной. Стенка балки лежит в вертикальной плоскости, и ось ее горизонтальна. Сосредоточенная нагрузка Р приложена к центру тяжести свободного концевого поперечного сечения и направлена вертикально вниз. Под действием силы Р балка изогнется, и при нашем способе заделки изгиб будет происходить в вертикальной плоскости, так как направление действующей слы
50 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
совпадает с одной из главных осей инерции поперечного сечении балки. Теперь задача наша сводится к тому, чтобы определить, при каком значении силы Р плоская форма перестает быть устойчивой. Применяя прежний метод исследования, допустим, что при некотором значении изгибающей силы балка приняла неплоскую форму изгиба, представленную на рис. 17.
Поместим начало координат в точке приложения силы Р. Ось х-ов направим параллельно первоначальному положению оси балки, ось г-ов направлена вертикально вниз, а ось у-ов перпендикулярна плоскости zx и направлена в сторону закручивания балки, как это показано на нашем рисунке.
Возьмем теперь какое-нибудь поперечное сечение балки с абсциссой х и построим для него систему координат g, rj, совершенно так же, как мы это делали в ранее нами разобранных случаях. Моменты Мь МЦу М составим в общем виде и потом уже отбросим малые члены. Координаты точки приложения силы Р относительно осей, т, при малых углах поворота ф на основании таблицы косинусов (§ 4) представятся таким образом:
Р
z
Рис. 17.
(1)
л- wf--0-»p,
du - dz ,
±-у-гъ Z x yf-z.
Проекциями силы P на те же оси координат будут
рч-ръ ъ-р-.
(2)
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 51
Выражения для моментов получатся следующими:
Пользуясь основными уравнениями равновесия (§ 4) и вы бирая соответствующим образом знаки, можем написать
Исключая из них неизвестные у и г, будем иметь для определения ф следующее уравнение:
Проф. Л. Прандтль в своей работе) имел в виду изгиб тонких пластинок и потому мог пренебречь изгибом полок, который при кручении является следствием неподвижного закрепления конца балки. Чтобы из нашего общего уравнения (6) получить этот частный случай, стоит только положить D 0. Для определения ф будем иметь
Уравнение это решается в функциях Бесселя, и интеграл его
Для того чтобы неплоская форма изгиба была возможна, необходима следующая зависимость между величиной силы Р и размерами балки:
Щ ( УЧ г) - Р (дс - у - гр),
Отбрасывая малые члены, получим
М Р (y-x-fj, Мп-Рх, Mi Pxф. (4)
B24jPxф, BllF-Px.
(5)
(6)
ф ж2(р 0-
(6')
будет
(7)
) См. § 1.
52 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Зависимость (7) установлена Л. Прандтлем и соответствует первой возможной неплоской форме изгиба. Увеличивая непрерывно Р, возможно получить целый ряд неплоских форм, как в случае изгиба парами сил, но эти формы не имеют особого практического интереса.
Переходя к случаю двутавровой балки, можно сказать заранее, что благодаря большей жесткости балка будет устойчивее и потому в выражении зависимости между силой Р и размерами балки мы должны получить число большее, нежели 4,013. Разность между нашими результатами и результатами Л. Прандтля, очевидно, будет тем большая, чем значительнее влияние оказывают полки, т. е. чем больше D и чем меньше длина балки I
Вычислить влияние полок, очевидно, можно будет только найдя интеграл уравнения (6). Нам неизвестно решение этого уравнения в замкнутой форме, и потому мы попробуем найти его, пользуясь бесконечными рядами.
Для упрощения выкладок введем такие обозначения:
2С _ 1 2Р2 _ 1
Dh2 а2 9 DB2H2 6е КО)
Нетрудно видеть, что введенные нами величина а и Ъ имеют размерность длины. Уравнение (6) перепишется тогда в следующем виде:
Ф1У-ГФ—р 0. (9)
Общий интеграл его будем искать в форме ряда
Ф А0 Ахх А2х2 А3х3 . (10)
И если этот ряд будет сходящимся, то он и представит собой
искомый интеграл нашего уравнения (9).
Для определения коэффициентов А0у Аи А2,. подставляем выражение для ф в уравнение (9) и из сравнения коэффициентов получаем
4 3 2 1 Л4 - 4г 2 1 Л2 0, 5.4-3-2-Л5 — ---3.2. Л3 0,
6-5-4-3. Л6 —--4-3 А4-гА0 0 п(п- 1)(п — 2)(п — 3) Ап—-- (п — 2)(п — 3) Л„_2- Л„_6 0,.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 53
откуда получаем для определения коэффициентов такую формулу:
Ап—2 I А
п—6
п п(п—)а2 п (п — 1) (п — 2) (п — 3) Ь6
Пользуясь ею, мы выразим коэффициенты ряда (10) через величины А0у Аи А2, Л3, которые и будут произвольными постоянными полного интеграла нашего дифференциального уравнения. В результате получим
Ф A0(M) Alx(N) A2x2(Q) A3x3(P). (11)
Здесь большими буквами М, N, Q, Р обозначены ряды, расположенные по возрастающим степеням х2.
Мы здесь не выписываем этих рядов, так как в дальнейшем пользуемся ими только в преобразованном виде. При преобразованиях для удобства вычисления нами были выбраны аргументами величины, имеющие измерение отвлеченного числа. Величины эти следующие:
х2 х2 2С I хв х62Р2 2
22 h2 D v ’ bQ h2B2D
Wi. (12)
Нетрудно видеть, что V и W2 суть отвлеченные числа, вполне определенные для каждого поперечного сечения балки. Первое из них зависит только от размера балки, и раз балка задана, то оно может быть вычислено. Что касается второго, то в него входит также и величина действующей силы. Когда мы положим х равным , т. е. рассмотрим заданный конец балки, то значения V и Wi совершенно совпадают с V и W, которыми мы пользовались в случае изгиба балки парами сил. В дальнейшем нам понадобятся значения функций (М), (N), (Р) для х I, и потому мы их выписываем ниже1):
М) 1 , W2 I -J — ,
6. 3 12.96.3 18. 1512.96.3 уг 8. 3 W 14. 11 8. 3 14. 9-6. 3 )
Г«(:
20. 17-14. 11-8. 3 ' 20. 17-14. 9-6. 3
1 1 . . Г W2
). yr-
20. 15-12.9-6. 3jJ ' 1 У4ЦО.З
4(l6. 13- 10. 3-1- 16. 11 8. 3 16. 9-6. з)
) В тех случаях, когда имеется ряд множителей, идущих в порядке чисел, для сокращения будем писать только крайние множители, заменяя промежуточные точками.
54 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
В общем виде ряд может быть представлен так:
v®T.
где
причем
п 0, 1, 2, п 0, 1, 2,.,
аоо 1
1 -2-7-8 - 13- 14. (6т-5) (6т-4)
а,п0 6т ’
а0п 0.
Далее, атп составляется из ат_,,„ и из ат„_ по формуле
1
атп (6т 2л - 3) (6т 2л - 2) (6т 2л - 1) (6т 2л) ати п
(6т 21- 1) (6т 2л) flm-
Подобным же образом составляются и два других ряда (N)t и (P)t:
(т , Г. IT4 W
М)1 1 7 . 4 13 . 10-7 . 4 19 . 16- 13. 10-7. 4 ’ _L_rF 4( 1 I т V2 L 9. 4 и 15. 12-9. 4 15. 107 . 4
W 6 ( I 1-
т 21. 18-15. 12-9.4 21 . 18-15. 10 7. 4
) l -Lr_Z_
т 21. 16- 13. 10-7. 4 ) т Jt у I 11. 4 т 4( 17. 14- 11. 4 17. 12-9. 4 17. 10 7. 4 ) I 1 Г Г2 1,
К6 L 13.4 JT
W2 W4 W6
P)i 1 9 _ Q 15. 129. 6 21. 18- 15. 129. 6 . -72--5Т4 й(ц. 854 11.б)
l4(l7. 14- 11. 8-5-417. 14 11. 6 17. 12-9. б)
V 7. 4 W2 (l3. 10-7. 4 13. 85-4“ 13. б) Тэ. 4
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 55
На основании приведенного нетрудно себе представить закон образования последовательных членов каждого ряда и показать, что ряды сходящиеся. При малых значениях V2 и W1 приходится вычислять очень немного членов, чтобы получить достаточную точность, с возрастанием же 1V2 и W2 вычисление (M)iy (N)i и (Р) делается все затруднительнее.
В дальнейшем нам понадобится также значение ф'. Мы его можем получить непосредственным дифференцированием выражения (11):
ф' 7 A (R) Л, (S) А2х (U) А3Х2 (Т).
Буквами (), (Т) обозначены ряды, расположенные по
восходящим степеням х2. Нам в дальнейшем понадобятся численные значения (), (S), (Т) при х , и потому мы ниже даем выражения для них, преобразованные на основании обо значений (12):
W2 W4 ws
5-4-3 11 - 10-9-6 . 3 17- 16- 15- 12. 9-6. 3 j L Г _1_ ша I I I
i у2 L 7. 3 V 13. 12. 11.8. 3 13. 9-6. 3
w( - w 19- 18- 17- 14. И -8. ;
1
19- 18- 17- 14. 9-6. 3
1 __Г_
19. 15 - 12. 9 6. 3 ‘“V К4 L9.3
4(l5-14-13-10. 315. 11-8. 3 15. 9-6. з) I 1 Г I U
к6 L11-.3 -
W2 W4 W6
(S)i 1 б.5.4 12. 11. 10-7. 4 18- 17- 16- 13. 10-7. 4 ‘ ’
—Г El w4 ( I I
. -г уг L 8. 4 w 14 - 13 - 12 - 9. 4 14. 10 - 7. 4 )
( 20- 19- 18- 15. 12-9. 4 20- 19- 18- 15. 10-7 . 4 1
7. 4 j у4 L Ю.
20. 16 -13. ю 7. 4; ' ‘ J 1 V4 L Ю. 4 1 (l6- 15- 14- 11. 4 16. 12-9. 4 16. 10-7. 4) l Г W2 12. 4 J
66 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
m 3 1 I W4 1 II ,
п т g. 7. 6 -г 14. 13 12 9. 6 20 19 18 15. 12 9. 6
1гг4 Ю.д.8-5.4 Ю.б)
4(l6- 15 14-11. 8-5-4 16-15. 14-11. 616. 12-9. б) 77б-5-4 (l2 11 10-7. 4 12. 8-5-4 12. б) 8 - 7 - 6 - 5 - 4 ’
Переходя к общему интегралу (11) нашего уравнения, постараемся определить произвольные постоянные в зависимости от условий на концах балки. Обозначим через ф0, ф', ф'', ф' значения угла поворота и последовательных производных его на свободном конце балки, т. е. при х 0. Тогда нетрудно на основании (И) показать, что
Ао 2 Фо» 2 V2 Фо 7б Фо
Так как мы полагаем, что к свободному концу балки не приложено сил, которые сообщали бы полкам некоторую начальную кривизну в плоскости ху, то, следовательно, ф' должно равняться нулю, откуда
I) А2 0;
ф' и ф' не являются совершенно произвольными величинами; они связаны между собой условием Dh2
II) — СфН—2“ Фо' 0, выражающим то обстоятельство, что
скручивающий момент на свободном конце балки равен нулю.
В заключение у нас остается две произвольных постоянных, для определения которых мы воспользуемся условиями закрепления для заделанного конца балки. Так как поперечное сечение, соответствующее плоскости заделки, не может повернуться, то, следовательно,
III) ф 0.
Касательные к изогнутым осям полок двутавровой балки у заделанного конца будут перпендикулярны к плоскости заделки и параллельны оси х-ов. Следовательно,
IV) ф 0. Окончательно для определения произвольных постоянных мы будем иметь два уравнения:
Ф0 (M)i Фо (N)i Чо' (P)i lz 0,
. р (13)
тФ„(Я)1 Ф0'(5) 1гФГ ( 0.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 5
Если мы примем во внимание условие II и наши обозначения (12), то условия (13) перепишутся таким образом:
ф0(м), ф(лО,1-(Р)1 о,
ill 14) (S)-7rtf 0.
Здесь М)и (А). обозначают значения функций (М), (jV),. при х.
Если мы положим
Фо 0. Фо 0.
то, очевидно, условия (14) будут выполнены, но в таком случае
Ф 0 и о,
т. е. мы будем иметь плоскую форму изгиба. Для возможности неплоской формы изгиба необходимо, чтобы уравнения (14) допускали для ф0 и ф' решения, отличные от нуля. Следовательно, определитель уравнений (14) должен быть нулем:
(M),(S)Z -i-r (Г), - т (), i-pr (), 0. (15)
Полученное уравнение дает нам зависимость между величинами W2 и 1У2, при которой становится возможной неплоская форма изгиба. Как мы видели раньше, величина 1У2 всегда может быть вычислена, если известны размеры балки и модуль упругости материала; в таком случае уравнение (15) даст нам соответствующую величину W2, а следовательно, и величину силы Я, при которой возможно искривление балки. Обозначая W2V2 через k2, мы на основании обозначений (12) будем иметь
-- k2 В2С к ’
или ркр А (16)
— формулу, аналогичную полученной нами раньше в случае изгиба балки парами сил и совпадающую с результатами Л. Прандтля (7), если положить k 4,013.
Чтобы полученная нами формула имела практическое значение, необходимо составить таблицы, пользуясь которыми можно было бы легко по заданному значению 1У2 определять величину W2, а следовательно, и коэффициент k. В противном
Ss об устойчивости плоской формы изгиба двутавровой балки
случае пришлось бы каждый раз решать уравнение (15), что гребует большой работы.
Приступая к составлению такой таблицы, необходимо прежде всего выяснить ту точность, с которой должны быть определены числа этой таблицы. Как мы ниже увидим, наибольшие напряжения, соответствующие критическому значению изгибающей силы, определяются из формулы
Поэтому, если мы при вычислении W2 достигнем точности в 1, то допущенная нами при этом погрешность изменит не более чем на 12 величину опасных напряжений. Так как другие величины, входящие в формулу (17), обыкновенно известны нам с гораздо меньшей точностью, то ясно, что точность в 1 при определении W2 можно считать вполне достаточной. Нами при составлении таблицы W2 везде вычислялось с тремя значащими цифрами, т. е. с значительно большей точностью, чем это нужно для практики.
Определять величину W2, соответствующую какому-либо определенному значению 1У2, приходится путем последовательных проб. Сначала наугад задаемся какой-либо величиной W2, но ней вычисляем значения (М)и N)u. и полученные результаты подставляем в уравнение (15). Сразу, конечно, не удается получить W2 с достаточной точностью, но по результату подстановки можно судить, в какую сторону нужно изменить W2. После двух-трех подстановок можно уже получить интересующую нас величину с желаемой степенью точности, т. е. с тремя значащими цифрами. Величины (М)и (N)i приходится вычислять с четырьмя десятичными знаками при 1У2 12 и с тремя для 1У2 12. Заметим, что при больших значениях 1У2, а следовательно и W2, вычисления становятся довольно затруднительными, и нам в этом случае много помогало пользование арифмометром. Особенно трудно получить первые дватри решения уравнения (15), пока не выяснился закон изменения W2 в зависимости от 1У2.
Дальше нам очень помогло графическое построение. Откладывая 1У2 по оси абсцисс, а соответствующие значения W2 по оси ординат, мы получили кривую, кривизна которой все убывала с возрастанием 1У2. В силу этого практически оказывалось совершенно излишним вычисление большого количества промежуточных точек кривой. Мы могли ограничиться только восемью точками, по которым была построена кривая (рис. 18) и значения W2 для промежуточных значений 1У2 уже взяты прямо из рисунка. Это мы могли сделать с тем большим правом, что величины 1У2 практически можно вычислять с очень не¬
(17)
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 59
большой точностью. Кроме изменения величины W2 на том же рис. 18 представлено изменение V2W2 k2. Эта кривая асимптотически приближается к оси у при приближении 1V2 к нулю; другой асимптотой будет прямая, параллельная оси х-ов и проведенная на расстоянии (4,013)2 от нее. Величина (4,013)2,
кнл
как мы видели, соответствует случаю, когда V2 обращается в бесконечность и 0 0, разобранному Л. Прандтлем. Ниже мы приводим таблицу С, в которой даны некоторые численные значения интересующих нас величин.
Таблица С1)
1
V2
W2
W2V2
Якр, кгсм,2
1
V2
W2
p2y2
кр’ кгм2
0,1
196
1960
700
10
575
57,5
1200
1
247
247
785
12
623
51,9
1250
2
296
148
860
14
678
48,4
1300
3
342
114
925
16
725
45,3
1345
4
381
95,3
975
24
918
38,3
1515
6
453
75,5
1065
32
1100
34,4
1660
8
516
64,5
1140
) Значение критического напряжения RKD кгсм2 вычислено при
0,01; hl -0,1; Е 2 10б кгсм2.
Вычисление таблицы доведено до 1V2 32, что оказалось вполне достаточным для тех численных примеров, которые нам приходилось разбирать. Если бы пришлось вычислять W2 для
60 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
значений 1У2, больших 32, то мы полагали бы возможным пользоваться такой формулой:
W2v2 k2 (18)
Получена эта формула на основании таких соображений: когда нам приходилось определять угол закручивания двутавровой балки, заделанной одним концом, то оказалось, что влияние жесткости полок может быть учтено очень просто — нужно только в обыкновенную формулу (не принимающую в расчет жесткости полок) вставить вместо действительной длины балки некоторую фиктивную длину (см. § 2)
или, в случае больших значений 1У2,
,(1-У).
Так как в рассматриваемом нами теперь случае неплоской формы изгиба жесткость полок влияет главным образом на кручение, то применим и здесь ранее выведенные заключения, именно положим, что для определения величины критической нагрузки Р можно пользоваться формулой (7), в которой не принята во внимание жесткость полок, но только вместо действительной длины балки I введем длину 1. Тогда будем иметь
р _ 4,013 УВ
кр 1 2
2('-™Тг)
Отсюда при больших значениях 1У2 непосредственно получается приведенная нами выше формула (18) для вычисления к2.
Величины г2, вычисленные на основании этой формулы, тем ближе к действительным значениям 2, определенным на основании уравнения (15), чем больше величина 1У2. При 1У2, равном 32, разность меньше 2. С возрастанием 1У2 до бесконечности величина г2, определяемая из (18), приближается асимптотически к (4,013)2.
Относительно вычисления опасных напряжений заметим, что если в формулу, служащую для определения наибольших нормальных напряжений, т. е.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 61
подставим вместо М его значение из (16) и примем во внимание, что на практике можно всегда с достаточной точностью положить D В22, то для вычисления опасных напряжений будем иметь
Как и в случае изгиба балок парами сил, оказывается возможным составить таблицу для одного какого-либо определенного соотношения B2Bi и А. Величины напряжений приВ2В1 1100 и А 110 помещены в таблице С. Чтобы показать закон их изменения в зависимости от величины 112, на рис. 18 вычерчена кривая опасных напряжений.
§11. Влияние внецентренно приложенной нагрузки
До сих пор мы рассматривали идеальный случай, когда точка приложения вертикальной силы совершенно совпадает с центром тяжести концевого поперечного сечения и стенка двутавровой балки расположена в вертикальной плоскости. На основании этих условий нами и было получено уравнение (15). В действительности при самой точной постановке опыта возможны малые отклонения от идеального случая, и нам нужно выяснить влияние этих отдельных отклонений.
Пусть опорное концевое поперечное сечение стенки балки заделано, но допускает поворот относительно продольной оси и малый угол, составляемый ею с вертикальной плоскостью, пусть будет cpi а. Предположим также, что точка приложения силы перемещена от центра поперечного сечения по горизонтальному направлению на малую величину а. Тогда условия II и III (см. § 10), очевидно, перепишутся таким образом:
Уравнения для определения произвольных постоянных суть
Мы видим, что уравнения (2) допускают для произвольных постоянных ф0 и ф' решения, отличные от нуля при всяких значениях изгибающей силы, и, следовательно, самая незначительная нагрузка Р уже будет вызывать искривление оси балки в плоскости ху.
-Сф' --ф' Ра, Ф а.
(1)
Фо т Фо тTW а - т-к1 ’
Фо (R)i Фо (5)г 7Г (Л —yrl(T)i “.
62 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Угол поворота концевого поперечного сечения легко найти из уравнений (2). Он будет равен
Буквой А мы обозначили довольно сложное выражение, в которое множителями входят величины а и а. При малых отклонениях от идеального случая числитель формулы (3) будет величиной малой, а следовательно, и фо будет мало, раз знаменатель— величина конечная. В тех случаях, когда величина изгибающей силы такова, что знаменатель в формуле (3) близок к нулю, угол поворота быстро возрастает. Так как знаменатель этот представляет собой не что иное, как левую часть уравнения (15) § 10, то мы можем заключить, что, когда имеются нами рассмотренные отклонения от идеального случая, искривление и кручение балки начинают быстро возрастать и могут достигнуть опасных размеров, если величина изгибающей силы приближается к критической нагрузке соответствующего идеального случая.
Заметим, что величины а и а, входящие в выражение А числителя (3), могут быть подобраны таким образом, что А обратится в нуль, тогда влияния отдельных отклонений взаимно уничтожатся и явление будет протекать так же, как и в идеальном случае.
Рассмотрим теперь влияние перемещения точки приложения силы Р по вертикальному направлению. Обозначим через d величину этого перемещения, тогда скручивающий момент у свободного конца балки, при условии появления кручения, очевидно, будет Мi Рф0б.
II условие предыдущего параграфа напишется так:
Если принять во внимание, что на практике всегда с достаточной точностью можно положить D Б22 и что на основании (12) § 10
-Сф' --ф' Ау,
(4)
откуда
Фо “ 22 Фо Qftz а.
(5)
то выражение (5) можно представить в более удобном для вычислений виде:
1 W 2d
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 63
На основании этого уравнения определяющие произвольные постоянные напишутся таким образом:
откуда для возможности появления неплоской формы изгиба получим такое условие:
(Af), 1 (Ph WЦ. (S), 4- ± (Г), -
- () j w -г Wh i-W - (8
Нетрудно видеть, что при малых перемещениях d влияние их на величину критической нагрузки, определенной для идеального случая, будет невелико. Если же d нельзя считать малым
по сравнению с высотой балки h и способ приложения изгибающей силы имеет вид, представленный на рис. 19, то тогда критическая нагрузка должна быть определена на основании уравнения (8).
Когда точка приложения внешней силы будет совпадать с верхней или нижней гранью балки, то d ±hj2 и условие (8) перепишется в таком виде:
(М), ± (Р), w (5), i уг (Г), -
- (), ± (Г), г(Л0; -(Р)г 0. (8')
Знак « » придется брать в том случае, когда точка приложения силы лежит над осью балки, и знак «—», когда она лежи г под осью. Заметим, что с повышением точки приложения силы устойчивость системы быстро уменьшается. Понижение же этой точки влияет в противоположном направлении.
(М)г (Р), Г Щ Фо (N), (), lfo 0,
(),1 (Г), W Ц- Фо (S),4 тт -
X
р
р
Рис. 19.
64 ов устойчивости плоской формы изгиба двутавровой балки
Рассмотрим теперь, как повлияет на наши выводы малое отклонение действующей силы от вертикального направления. Положим, что действующая сила, оставаясь в вертикальной плоскости yz, повернулась на малый угол а, и пусть Р и Q — вертикальная и горизонтальная составляющие этой силы. Основные уравнения для данного случая напишутся таким образом:
Исключая из этих уравнений у и z и принимая во внимание, что QВ 1 мало по сравнению с QB2 получим
Это уравнение отличается от уравнения (6) предыдущего параграфа только тем, что вместо угла ср вошел угол ф QP. Если бы мы силу оставили в ее вертикальном направлении, а повернули стенку балки на угол QР вокруг оси, то, очевидно, явление было бы то же самое. Если мы обозначим ф QР через э, то условия для определения произвольных постоянных будут такими:
Искривление оси балки в плоскости ху начинается при самых малых нагрузках. Но если угол отклонения силы d QР очень
служило нам для вычисления критических нагрузок, должно иметь бесчисленное множество корней и каждому корню соответствует своя форма неплоского изгиба. Мы до сих пор говорили о наименьшем корне этого уравнения, так как он имеет практический интерес и соответствует первой возможной неплоской форме изгиба, представленной на рис. 14. Если бы мы вычислили второй корень, то ему соответствовала бы форма рис. 20, и т. д. Все формы, кроме первой, будут неустойчивы.
- СФ' ф' P(xtf - у) Q(z-z'x
В2У (Ф Q) х Bz Рх.
(9)
Ч0 (М) Фо т т уг (р)' т
(R)i ¥o(S)tjyr(T)t 0.
(10)
мал, то искривления оси будут малы, пока величина нагрузки
л не станет приближаться к критическому значению, определенному для идеального случая.
Рис. 20,
В заключение заметим, что уравнение (15) § 10, которое
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 65
§ 12. Случай балки, лежащей на двух опорах
Пусть АВ представляет собой двутавровую балку с пролетом 21. Внешняя сила величины 2Р приложена в середине пролета таким образом, что точка приложения ее совпадает с центром тяжести срединного поперечного сечения балки. Ось балки горизонтальна, и стенка лежит в вертикальной плоскости. Концы закреплены таким образом, что устранена возможность вращения концевых поперечных сечений вокруг оси хху совпадающей с осью балки в недеформированном состоянии. Под влиянием
и 1
Ч 1 0 J
I—
t-
12Р ;
JC
ь 'о
внешней силы 2Р балка изгибается, и так как направление силы совпадает с направлением одной из главных осей инерции поперечного сечения, то изгиб будет происходить в вертикальной плоскости. Постепенно увеличивая нагрузку, мы можем достигнуть такого напряженного состояния, при котором плоская форма изгиба становится неустойчивой. Тогда ось балки может изогнуться в горизонтальной плоскости, и мы получим неплоскую форму равновесия, изображенную на рис. 21.
Стрелку прогиба оси балки в горизонтальной плоскости обозначим через d, тогда опорные реакции будут состоять из вертикальных, действующих снизу вверх сил Ру приложенных в центрах тяжести концевых поперечных сечений, и из моментов, действующих в плоскостях поперечных сечений и равных по величине Pd. Срединное поперечное сечение 00 балки в силу симметрии остается плоским, и потому мы можем настоящую задачу легко свести к ранее разобранному нами случаю балки, один конец которой заделан неподвижно. В самом деле, если мы представим себе срединное поперечное сечение балки заделанным, а к концевому сечению приложим вертикальную силу Р, проходящую в расстоянии d от центра тяжести сечения, то мы ничем не изменим условий нашей задачи и из рассмотрения условий равновесия полученной таким образом балки с одним заделанным концом должны получить искомую величину критической нагрузки для балки, лежащей на двух опорах.
66 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Возьмем левую половину балки и построим для нее систему координатных осей х, у, z, начало которой поместим на горизонтальной оси симметрии левого концевого поперечного сечения на расстоянии d от его центра тяжести. В таком случае действующая сила всегда будет проходить через начало координат. Оси направим так же, как и в ранее разобранном нами случае балки с одним заделанным концом; тогда мы можем воспользоваться уже выведенными раньше уравнениями (5) § 10 и сразу написать выражения угла поворота и его первой производной для какого-либо сечения балки:
Ф Фо (М) ф' (N) х ф' (Р) х3,
1 1
ф' Фо (Ю — Фо (5) -g Фо (Т) X2.
(2)
В настоящем случае, чтобы воспользоваться условиями на концах, необходимо еще составить выражения для у и его производной.
На основании второго из основных уравнений (5) § 10 будем иметь
В2у Рх Фо (М) q'(N)x - Ф' (Р) х3.
Отсюда интегрированием получаем
f -щ- X2 W Фо (L) Фо -g- (Е) ф'3 у',
У-Щ-х3 (7) Фо (Я) Фо Т У'оХ Уо-
При этом через (С),., (G) обозначены некоторые ряды, расположенные по возрастающим степеням х2. Если мы воспользуемся прежними нашими обозначениями, то при х ряды эти могут быть представлены таким образом:
m 1 , Е ,
VA; 2 j I 8-6.3 14 - 12.9-6.3 20 18.15 - 12.96.3 -рГ Ю-8.3 ( 16- 14.11 -8.3 16- 14.9-6.з)
г«(т 1,1.
20.17-14.11-8.3 1 22-20.17-14.96.3
W2
12 10.3
22 20. 15 12.9 6.3 ) у4 '
( 18 16 13-10-3 18-16.11-8.318-16.9-6-5-4-з) “
TrirS.-.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 67
(L)r
W2
W6
9-7.4 15- 13. 10«7.4 21-19.16-13.10-7.4
. 12 п.9. 4 4 ( 17. 15. 12-9. 4 17 15. 10 7.4 )
Ы
23 -21. 16- 13
21. 18 15. 12 9.4 1 23-21.18-15.107.4
Т
. 10 7.4 Vм L 13- 11.
4( 19-17.14-11.4. 19-17.12-9.419-17.10-7.4) ”
J _Г L 1.
F6 L 15- I3.4 - ‘
(E)i-
W2
w
11-9 6 19- 15.12-9.6
V2
Г—
L-7 5 '
( 13 11.8 5 4 13 11.6 ) ('
19-17.14-11.8-5-4
1
19- 17.14- 11.6 1 19-17
ТтЬГ2 (TIT
1
()
1
1 15-13 W2
13.10-7.4
15- 13.8-5-4 1
11 -9.4
--
W4
3-2-1 1 9-8-6.3 1 15-14-12.9-6.3
, I Г .Г4 ( I- ' Vs L 11 10-8.3 17-16-14. 11 -8.3 17-16-14.9-6.3jT
6( 23-22-20. 17-14.
.3 1 23-22-20.17-14.9-6.3
W2
23 22 20. 15 12.9 6.3 ) V V(-WW'
16.13- 10.3
19- 18-16.11 -8.3
3
13- 12- 10.3 19- 18- 16.9-6.з) V6 15- 14- 12.3 ’
W2
W4
W)l 4-3 10- 9 -7. 4 1 16- 15- 13. 10-7. 4
jL_r 1_ j4 ( V2 L J2-11-9.4 ' 18- 17- 15. .12-9.
18- 17. 15.10-7.4 КТ-
1
13. 11.4
W4 (
20-19.17.10-7.4) - Te l6T
20 19- 17. 14- 11. 4 20- 19- 17. 12-9.4
W2
15. 13.4
68 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
ГЧ 1 У I
б-б1- 12- 11 -9.6 г 18 17 15. 12 9.6 '
i2-s. 7-5-4 ( 14 13 11.8-5-4 14. 13 11.6 )
W4 ( 1- h
w 20 - 19 - 17. 14 11.85 4 20 19 17. 14 11.6
20-19- 17. 12 9.6 ) ’ - 17г ю.97.4
W2 (l6-15-13.10-7.416-l5-13.8-5-4 16-15-13.б) w 12- 11 -9.4 ‘ В выражения (1) и (2) входят пять произвольных постоянных, и для их определения имеем следующие пять условий:
I) при х 0 ф фо 0, так как закрепление концов не допускает вращения относительно оси х-ов
II) при х I у yi 0;
III) при х у у'1 0, так как касательная в этой точке параллельна оси х-ов;
IV) при х 1 ф' ф' 0;
V) Ру0 Сф' - Dh22) ф' (у0 очевидно, равно d).
Пользуясь условиями III и V, можем выразить произвольные постоянные у0 и у'0 через ф' и ф; подставляя их в условие IV, получим уравнение, заключающее только ф' и ф':
- (H)iI (L)i14- ();(G)f I6 ФГ 0. (3)
Для удобства вычисления сделаем некоторые преобразования. На основании обозначений (12) § 10 будет иметь
В2С _ 4 Dh2B2 _ 6
р2 w2V2 9 2Р2 W2
Следовательно, (3) представится в таком виде:
(L)t - (H)t - ф;()«-(0)». -г iyQ 0. (4)
Присоединяем сюда условие IV, которое нам дает
Ф ФГОЪ-О. (5)
Для определения произвольных постоянных ф' и ф получили два уравнения (4), (5). Чтобы кроме плоского изгиба возможна
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 69
была и неплоская форма равновесия, необходимо, чтобы определитель уравнений (4) и (5) обращался в нуль:
ц, - (Я), - Dl - 2Lzk_ (Sh _ о.
(6)
Для определения величины критической нагрузки придется идти прежним путем. По размерам балки и модулю упругости материала вычисляем величину 1У2, а потом путем последовательных проб определяем величину W2 таким образом, чтобы
Мзгиб балки, лежащей на двух опорах
12 к 16 18 20 22 24 26 28 30 32 34 36 38 40
Рис. 22.
V
было удовлетворено уравнение (6). Обозначая, как и прежде, W2V2 через k2f будем иметь для определения нагрузки Р1) уравнение
k гЩс
Р
1 кр
2
(7)
Если бы мы пренебрегли жесткостью полок и положили в основном уравнении D 0, то для определения критической нагрузки имели бы формулу, полученную Л. Прандтлем:
_ 2,115 УВ
кр — 12 Множитель k в формуле (7) будет величиной переменной и тем меньшей, чем меньше жесткость полок и чем больше длина балки. Чтобы можно было нашими выводами пользоваться, составлена таблица D. Восемь точек этой таблицы получены непосредственным вычислением. По ним построена кривая (рис. 22), дающая зависимость между 1У2 и W2. Кривая эта
l) Р в данном случае равно половине критической нагрузкц,
70 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
оказалась очень близкой к прямой линии, и потому не было никакой надобности вычислять многие промежуточные точки. Имея значения W2, можно было построить также кривую, дающую изменения k2 в зависимости от 1V2.
Кривая эта, с одной стороны, асимптотически приближается к оси у-ов, с другой — к прямой, параллельной оси л:-ов и проведенной на расстоянии (2,115)2 от нее, как того и нужно было ожидать на основании формулы (8) JI. Прандтля. Что касается самих вычислений, то они в данном случае несравненно проще, чем вычисления, относящиеся к случаю балки, заделанной одним концом в стену, так как ряды (К)и Щи сходятся очень быстро.
Таблица D1)
1
V2
W2
w2v2
RKр, кгсм
I
V2
W2
w2v2
кр, кгсм2
0,1
11,7
117
680
12
65,9
5,60
1620
1
15,9
15,9
800
16
84,0
5,25
1830
2
20,5
10,25
910
20
102
5,10
2020
4
29,7
7,43
1090
24
120
5,00
2190
6
38,8
6,47
1250
32
156
4,88
2500
8
47,8
5,98
1380
40
192
4,80
2770
) Значение критического напряжения RKD кгсм2 вычислено при
ВгВъ
0,01; г2 0,1;
’ 2 10‘5 кгсм2.
Мы вычисление таблицы довели до значений 1 V72 40, так как за этим пределом без больших погрешностей можно считать k постоянным, равным 2,115 1). Что касается вычисления
опасных напряжений, то для них, очевидно, остается в силе прежняя формула
-р-т»'тг(т),-
Заметим только, что будет в данном случае равно половине пролета балки. В таблице D приведены величины опасных напряжений для
В_ __ _J_ h _ 1
100 И 21 10 Модуль упругости Е принят равным 2 - 106 кгсм2.
) При 1У2 40 ошибка в определении опасных напряжений, если пдложить k 2,115, будет около 3.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 71
§ 13. Точка приложения силы не лежит на оси балки
Рассмотрим здесь, какое влияние на величину критической нагрузки будут оказывать различные отступления от только что разобранного нами случая. Положим, что точка приложения силы не точно совпадает с центром тяжести срединного поперечного сечения, а перемещена на малую величину а в направлении оси у-ов; кроме того, пусть стенка балки составляет с вертикальной плоскостью малый угол а. Тогда условия I и II предыдущего параграфа придется изменить таким образом:
Фо а У1 — а. (1)
Уравнения (4) и (5) § 12, служащие для определения произвольных постоянных qpQ и ср', перепишутся так:
Г(L)t - (Я), --1 ф' Г()(0)1 1 2ф' А,
1 (2)
где А и В — некоторые величины, зависящие от размеров балки и от малых величин а и а. Система уравнений (2) допускает для qpQ и р' решения, отличные от нуля при всяких значениях изгибающей силы. Когда определитель системы уравнений (2) приближается к нулю, то искривление балки в плоскости ху и сопровождающее его скручивание начинают быстро возрастать.
Если бы мы предположили, что действующая сила не вертикальна, а слегка наклонна, то получили бы ту же картину явления, т. е. уже при малых значениях действующей силы начались бы искривление и скручивание балки. Мы не будем на этом больше останавливаться, так как все это уже было раз подробно разобрано в случае балки с одним заделанным концом.
Перейдем теперь к вопросу, имеющему большой практический интерес, именно выясним, как влияет на устойчивость системы перемещение точки приложения внешней силы по вертикальному направлению. В случае, разобранном нами в предыдущем параграфе, точка приложения силы лежала на оси, между тем на практике точка приложения силы чаще всего совпадает с верхней или нижней гранью балки, и нужно ожидать, что это оказывает большое влияние на величину критической нагрузки.
Уравнения (1) и (2) предыдущего параграфа, очевидно, останутся в силе, и придется только изменить условия на концах. Если мы через Н обозначим перемещение точки приложения силы по вертикальному направлению, то условие II предыдущего параграфа должно быть видоизменено таким образом:
У1- нф.
(3)
72 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Соответственно этому изменятся и уравнения (4) и (5) § 12, определяющие произвольные постоянные у'0 и р':
(.), - (Я), - - Ф' Гiikziokф- - .
1 (4) ф'(5) (7’);2ф 0.
Если мы примем во внимание, что
ФФоМ'фПА'3.
то для определения величины критической нагрузки будем иметь такое условие:
-да4 аы4 №( T)tP-
-pwiэ-пгWi 0- (б)
Dh2B б
Если принять во внимание, что -ypil и положить
D В22, то при Я ±г2 условие (5) перепишется таким образом:
- (Я) (L), - ± -
_i5)i-(G)L_l_±(p)j(s)z 0_ (5)
Знак « » придется, очевидно, брать в том случае, когда точка приложения силы совпадает с верхней гранью балки. Определить величину критической нагрузки для какой-либо определенной балки можно, конечно, только решив уравнение (5').
Для того случая, когда точка приложения силы совпадает с верхней гранью (практически это наиболее часто встречающийся случай), нами составлена таблица F, где для ряда значений 1V2 приведены величины соответствующих значений W72, W2V2y а также величины опасных напряжений, вычисленных для того случая, когда
-- Тоо» 2Г То” и Е 2 Ю6 кгсм2.
Кроме того, на рис. 23 представлена графически зависимость между 1У2, с одной стороны, и величинами W2 и RKр, с другой.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 73
Таблица F1)
1
V2
W2
кр, кгсм2
1
V2
ЯГ
wv2
1
Якр, кгсм2
0,1
4,13
41,3
405
8
27,7
3,46
1050
1
6,36
6,36
505
10
34,3
3,43
1170
2
9,05
4,53
600
12
41,2
3,43
1280
3
11,9
3,97
690
16
55,3
3,46
1485
4
14,9
3,73
770
24
84,8
3,53
1840
6
21,1
3,52
920
32
114,4
3,58
2135
) Значение критического напряжения RKD кгсм2 вычислено при
ВгВх
0,01; г2 0,1, Е
' 2 - 106 кгсм2.
Сравнивая таблицы D и F, мы видим, что повышение точки приложения груза сильно влияет на устойчивость системы и это влияние тем больше, чем меньше 1V2, т. е. чем меньше длина балки при прочих равных условиях.
2400
Изгиб балпи, лежащей на дВух опорах
Сличай Л
8 Ю 12 14 16
Рис. 23.
20 22 24 26 28 30 32 Уг-
В заключение заметим, что все, что было сказано в двух последних параграфах о величине критической нагрузки, относится к первой возможной неплоской форме изгиба и при вычислениях мы пользовались наименьшим корнем уравнения (6) § 12. Но это уравнение должно иметь бесчисленное множество корней, и каждому из них соответствует своя возможная форма равновесия; все эти формы, кроме первой, будут неустойчивы. На рис. 24 изображен в плане примерный вид изогнутой оси балки, соответствующий 2-му и 3-му корням уравнения (6) § 12.
Все эти формы будут совершенно симметричны относительно срединного сечения 00, так как условие симметрии было положено в основание самого вывода уравнения (6) § 12. В сил этого уравнение (6) § 12 не заключает в себе всех возможных
74 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
форм равновесия балки, нагруженной посредине. Мы остановимся теперь на рассмотрении формы рис. 25, как имеющей практическое значение.
Если под действием нагрузки 2Я, приложенной к центру тяжести срединного поперечного сечения балки, балка изогнется, как это показано на рис. 25, то кроме опорных вертикальных реакций, равных Р и проходящих через центры тяжести концевых поперечных сечений, должны проявиться опорные моменты М0, мешающие концам балки вращаться около оси хх.
Условия равновесия не нарушатся, если мы представим себе, что опорные реакции состоят только из вертикальных противодействий Р, приложенных в точках А и В так, что величины УоР как раз соответствуют опорным моментам М0. Если мы те перь возьмем половину балки, построим для нее систему координат xyz так, чтобы начало ее совпадало с точкой А, то тогда
можно пользоваться ранее выведенными основными уравнениями и для получения величины критической нагрузки придется только изменить условия на концах. Для данного случая условия будут такие:
I) при л: 0 Фо 0;
II) при х 1 ф 0;
III) У1 Уо
Выписываем значения для ф, ф', у, у которые у нас были получены раньше:
Рис. 24.
Рис. 25.
v) - piy' рУо- сФ; Ц-
q (M) xp'(N) jXq'(P),
p'±(R) Po(S) -rX2(p'(T),
--- 3Фо(Л Фо(Я) () У0х 00»
г' - — л:2 (К) 3Фо (L) -g-jc р' () г'.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 75
Нам понадобится еще выражение для ф'. Мы его можем получить, дважды продифференцировав ф'. Тогда будем иметь
У' Фо (Q -2 Фо М) ФГ (В)
где Л, В, С суть ряды, расположенные по восходящим степеням х2.
На основании условий I и И получим
фо(П''зфо(п- (б)
Условие III дает нам
(7)
Величину г' можно выразить на основании условий IV и V через ф и ф'. Подставляя полученное таким образом значение для у'0 в (7), будем иметь
Фо'(5), - 1 - V2(A W2V2((L - (Н)
'l2
(П 6V2 - (В), V2 W2V2 ((Е), - (G)t) 0. (8)
Из уравнений (6) и (8), определяющих значения произвольных постоянных ф' и Фо, сейчас же получаем условие для определения величины критической нагрузки:
(Р)г l(S)i — I — V2 (A)t W2V2 ((L)i - (Я),) -
- (N (T 6V2 — V (B)J WV ((), - (G),) 0. (9)
§ 14. Изгиб балки сплошной нагрузкой
Рассмотрим наиболее простой случай балки, одним концом заделанной неподвижно. Ось балки предполагаем горизонтальной, стенка балки лежит в вертикальной плоскости. Нагрузка распределена равномерно по оси балки, и пусть р обозначает нагрузку, приходящуюся на единицу длины. Оставляя прежний метод рассуждений, положим, что рис. 26 в двух проекциях представляет вид изогнутой оси балки, соответствующий первой возможной неплоской форме изгиба. Положим, что начало координат Ху у, 2 совпадает с центром тяжести свободного концевого сечения балки. Возьмем какое-либо сечение балки с абсциссой ху для него построим систему координат, ц, и составим выражения моментов А, М.
76 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Сила, действующая на левую отсеченную часть балки, по величине будет равна рх, по направлению вертикальна, точка приложения ее Л, очевидно, совпадает с центром тяжести левой бтсеченной части упругой линии.
Координаты точки Л, отнесенные к осям ху уу z, очевидно, при малых прогибах выразятся таким образом:
У dx г dx
(О
Нетрудно составить теперь выражения для координат той же точки А в системе, г,. Пользуясь таблицей косинусов § 4, будем иметь
х dy ,
(2)
На основании этого, отбрасывая величины малые высших порядков, получим следующие выражения для моментов:
х
jydx
Ух)
Мг-Рх
dy_ А о_
2 dx
Мц - рх -у, М2 - рх
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 77
откуда, пользуясь основными уравнениями (см. § 3), будем иметь
х
I lydx
х dy , о I г, dф , Dh2 dzф
РХ 2 dx х У) Cdx2dxr’ (3)
D d2y _ рх2 „
й d2 2 ’ 2 dx2 “ 2 ф-
Дифференцируя первое из этих уравнений по х и подставляя в полученное таким образом выражение вместо у его значение из уравнения третьего, получим для определения р следующее уравнение:
-57 (--)--cp -fV, (4)
или, вводя обозначения')
2 ( jEL2
' _ 2С 1 _ V 2 ) (к,
а2 Dh2 ’ 6» - 2г2 ’ W
будем иметь
Ф1У-гФ--гФ 0. (40
Общий интеграл этого уравнения будем искать в форме ряда Ф А0 Ах А2х2 Агхг.
Для определения неопределенных коэффициентов будем иметь соотношения
4-3-2 - 1-Л4---Л2 0, 7-6-5.4.Л7 —0,
5-4-3-2-Л5---Л3 0, 8-7-6-5-Ай--А6—-0, (6)
6-5-4-3. Л6--Л4 0,
пп —)п — 2)п — д) Ап —— 2)Jn 3) Лп_2 - 0,
откуда получаем такую общую формулу:
АпАп-2 п(п-)а2 Ап-а п(п-)(п2)(п-3)Ьь ' рх2 1 2 М2
) Если принять во внимание, что Мх, то «
78 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Пользуясь этим, можно все неопределенные коэффициенты выразить через Л0, Аи А2, Л3, которые и будут произвольными постоянными общего интеграла уравнения (4). Угол поворота какого-либо поперечного сечения представится тогда таким образом:
ср А0 (т) Ахх (п) А2х2 (q) А3х3 (р), (8)
а кручение, соответствующее этому сечению, будет
ф' А0 (г) y Ai (5) А2 («) з2 (t). (9)
В выражениях (8) и (9) буквы т, п,., t обозначают ряды, расположенные по восходящим степеням х2. Так как в дальнейшем нам понадобятся значения функций т,., t при х , то мы их даем здесь, предварительно введя такие обозначения:
— 1 и — — W2 (1 п
а2 V2 Ь8 2h2B2D 9 '
и )
, 1 W2 , W4 , W6 .
m)i т- 8.5 16. 13. 8.5 24.21 16. 13 8.5 1
V2 10.5 ( 18. 15- 10.5 18. 13-8.5 ) V4 L 12.5 ‘ 20.
.17- 12.5 1 20.15- 10.5 1
20.13-8.5) В общем виде ряд может быть представлен так:
-35Г,
, 2т
V
где т 0, 1, 2, п 0, 1, 2, причем
) 1,
_ 1 2-3-4-9 - 10- II 12. (8т-7) (8т - 6) (8т - 5) (8т - 4) ат0 - gm
ао п 0
Далее, атп составляется из атип и ат,п-, по формуле amn (8т 2п - 3) (8т 2я - 2) (8т 2п - 1) (8т 2п) ат-'- п
I 1 (8т 2n-1) (8т 2я) ат.п-
) В тех случаях, когда имеется ряд множителей, идущих в порядке чисел, мы для сокращения письма пишем только крайние множители, заменяя промежуточные точками.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 79
Подобным же образом составляются и другие ряды (n)t и (p)t W2 , W1 , W6
(n)i - 1
9.6П 17.14-9.6 1 25.22- 17.14-9.6
I J_r W2 l деч ( 1 li
' ’ V2 L 11.6 ' 19. 16- 11. 6 19.14 9.6 J i
_Lrj 4 i i V4 L 13.6 ' 21. 18 13.6 T 21. 16 11.6
1.14-9.б) T«'lT6 .(p)1 1 1 11.8 1 19. 16- 11. 8 1 27.24-19. 16-11.8 1 j L_—I 1 —
V2 L 5 4 13. 10 5 4 13. 8 V
(21. 18-13.10-5-421.18-13.8 2I.16-11.8) T7.4 2 ( 15.12-7.4 15. 10-5. 4 15.8 ) lM'94 ’
, «74 We .
V1 7-6-5 15 - 14 - 13-8.5 23-22-21 16.13- 8.5 ’ ' -
1 1 I
f V2 9.5 17 16 15-10.5 17. 13 8.5 ' ’ ’J
-f —Г.El 1-W4( — ' 1
' V4 L 11.5 I 19-18-17-
12.5 1 19.15- 10.5
19.13.8.б) T:riT .
v _. j Ei I w I u
S)l- 876 16- 15 149. 6 ' 24 23-22- 17. 14-9. 6 ’
“p2- 10.6 ( 18- 17- 16- 11.6 “”'18.14-9-б)“ ' ' '
J-J-W ( l- b b
TK4Ll2.6 20 19 18 13.6 ' 20. 16 11.6 '
1 ) Trl46 ’
20.14-9.6
(П -3 1 I w I E 4.
— 10-9-8 18 - 17 - 16 - 11.8 26-25-24- 19.16-11.8
-y2 -4 W2 ( 12- 11 - 10-5-4 12 8 )
20-19-18-13.10-5-420-19-18-13.820.16-11.8 ibrbw2(-
1
14 13 12-7.4 1 14.105-4
80 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Если мы величину угла поворота свободного конца балки обозначим через фо, то нетрудно на основании (8) и (9) получить
Ф Ф0(т) ф'(п)х ф(7) x2 jф'(р) х
1 1 1 ()
ф' Фо (О 7 Фо («) 2 Vo' (u)x -q Ро (0 х2-
Для определения произвольных постоянных у нас будут такие условия на концах:
I и II) при 0 Фо' 0, Сфд — фо 0;
III и IV) при х1 ФО, ф;' 0,
которые дают нам следующие два уравнения:
Фо (т ф ((«),-§- (р),) о,
2 (12)
Фо (О, Pol ((sb (0,) о.
Для возможности искривления оси балки в плоскости ху должно быть удовлетворено условие
(m)i ((s), (0i) - (r)i ((n) j rL- (p),j 0. (13)
Ход расчета при определении величины критической нагрузки остается прежний. По заданным размерам балки и свойству материала вычисляем величину 1V2, а потом из уравнения (13) определяем соответствующую величину W2. Обозначая величину W2V2 через к2, будем на основании обозначений (10) иметь
К В2С
Величина (pl2)2l2 есть не что иное, как значение квадрата изгибающего момента в плоскости заделки балки. Обозначая его через М, получим уже знакомую нам формулу
Лf В2С 1 4 Мкр J (И)
§ 15. Пределы применимости выведенных формул
Формулы строительной механики, которыми мы пользовались при выводе основных уравнений, приложимы к совершенно упругим телам, и потому все результаты, относящиеся к величине критических изгибающих моментов, имеют действительное
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 81
значение лишь до тех пор, пока соответствующие им напряжения не превзошли предела упругости данного материала. За пределами упругости вычисленные по нашим формулам значения критических изгибающих моментов, вообще говоря, не имеют никакого реального значения, и ими можно пользоваться только временно, пока в интересующей нас области не имеется достаточного количества научно поставленных опытных исследований.
Так как за пределами упругости деформации растут быстрее напряжений, то надо полагать, что в таких случаях вычисленные по нашим формулам значения критических изгибающих моментов будут преувеличены, и, следовательно, проверяемые на устойчивость балки будут на деле в более опасных условиях, чем то следует из теоретически выведенных формул.
Особенно сомнительными в смысле устойчивости являются балки таких поперечных сечений, при которых отношение В2В очень мало, т. е. высокие балки, склепанные из тонких железных листов, как, например, балки мостовые. Что касается прокатных балок, то здесь приходится говорить только об устойчивости наиболее высоких из них; балки небольшой высоты имеют такие поперечные сечения, при которых можно считать устойчивость всегда обеспеченной.
Заметим, что стремление достигнуть как можно большей экономии в весе балок приводит иногда к не совсем удачным типам поперечных сечений. Для примера укажем на данные нового немецкого сортамента1).
Если принимать во внимание отношение веса погонной единицы балки к моменту сопротивления поперечного сечения, то новый сортамент представляет по сравнению со старым значительные выгоды. Но мы должны будем прийти к совершенно иным заключениям, если сравним достоинства обоих сортаментов с точки зрения устойчивости.
Экономия в весе балки достигнута благодаря тому, что взята значительно меньшая толщина стенки и ширина полок, вследствие этого жесткость балки при кручении С и отношение главных жесткостей при изгибе В2В значительно уменьшились и балка стала менее устойчивой. Сделаем примерные вычисления для наиболее высокого поперечного сечения. Данные сортамента таковы:
высота h 600 мм ширина полок Ъ 180 мм толщина стенки d 14,6 мм толщина полок t 27,2 мм.
На основании этих размеров будем иметь отношение главных жесткостей при изгибе В2В « 138.
) См. Kommisionsbericht. Zeitschrift des Vereines deutscher Ingenieure, 1905, Bd. 49, № 36, SS. 1491—1497.
82 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Жесткость балки при кручении на основании приближенных приемов, изложенных в § 3, будет
С « 12 (2,72)3 20 (1,46)3 G « 303G кгсм2. Наибольшая жесткость одной полки при изгибе будет) 2,722183. « 1320.
Полагая коэффициент поперечного сжатия для железа равным 14, получим GE 12,5. Тогда
2С 2-303 G юл
T W0-184-
Имея величину этого соотношения, уже легко вычислить для всякого пролета балки как значения 1У2, так и значения опасных напряжений, соответствующих какому-либо определенному роду нагрузки.
Положим, что балка рассматриваемого нами поперечного сечения лежит на двух опорах и нагружена посредине сосредоточенной силой 2Р, приложенной к верхнему канту балки. Пусть г2 112; тогда
т -7г(т)2 ’184-36 6’6-
На основании вычисленной нами таблицы F для полученного нами значения величины 1У2 опасные напряжения будут Rkр 960 кгсм2.
Если мы примем во внимание, что таблица F вычислена для
В, А JL
Вх 100 и 21 10
то нетрудно сейчас же получить величину опасных напряжений, соответствующую нашему случаю:
'р з1ТГ 1750 кгсм
Если бы мы задались меньшим пролетом балки и положили бы, например, г2 110, то тогда соответствующие напряжения таблицы F были бы при yj 0,184 25 « 4,6, равны
кР 735 кгсм2.
Для нашей балки мы бы получили такие опасные напряжения:
п, 735 -100 1 пол 2
R'р —38— 1930 кгсм2.
Как и нужно было ожидать, с уменьшением пролета балка становится устойчивее, но все-таки опасные напряжения остаются гораздо ниже разрушающих напряжений для железа,
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 83
Если мы возьмем наиболее высокую прокатную балку американского сортамента, то ее устойчивость оказывается еще менее обеспеченной. Размеры сечения будут:
высота h 610лш; толгцина стенки Ь 12,6 иш; ширина полок d 177,8 мм толщина полок t 22,7 мм.
Для рассматриваемой балки будем иметь В2В 142 л
2CD « 17,5.
Если положим отношение Л2 112, то у-. 36 4,8
и на основании таблицы F 1ф 830 кгсм2.
Отсюда сейчас же получаем опасные напряжения для нашего случая:
КР 83042Т44100- 1375 КгСм2-
Возьмем теперь пример клепаной двутавровой балки. Балка 1) состоит из вертикальной стенки 70 X 0,8 см и четырех
уголков 7 X 7 X 0,8 см. Свободная длина балки 21 3,25 м.
Вычисления дают нам
в 59 140 кгсм2, В2 446Е кгсм2,
B2Bi« 1133 и D 223.
(Здесь мы взяли D В22 если бы мы приняли во внимание жесткость одних уголков, то получили бы величину на 12 меньшую.)
Величину С определяем на основании приближенных формул § 3: С 72 G, откуда 2CD 0,257 и, следовательно,
F-f-Ш’-0-257 ®)2-1-38-
Для случая нагрузки, приложенной к верхнему канту балкк посредине пролета, таблица F дает нам величину опасных на пряжений 1ф 540 кгсм2, относящихся к случаю B2Bi 1100 и 12 110.
В нашем случае для величины опасных напряжений будем иметь
у» 540 104 1 оол 2
кр “ 1зз-21,б кгсм.
И здесь мы получили для опасных напряжений величину значительно меньшую, нежели разрушающие напряжения для железа. Как показывают приведенные примеры, поверка
) Это поперечное сечение соответствует продольной балке из проекта моста через Русановский проток Днепра у Киева (см. проект II. А. БелелюОского и Г. Г. Кривошеина).
84 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ft3ГИБЛ ДВУТАВРОВОЙ БАЛКИ
устойчивости балки по заданным размерам производится очень просто. На получаемые этим путем величины критических напряжений нужно смотреть как на тот опасный предел, который ни в коем случае не должен быть допускаем в сооружении. Для определения величины допустимых напряжений мы будем исходить из того положения, что при достижении напряжениями величины вычисленных критических напряжений сооружению угрожает опасность в той же мере, как, например, при растяжении достижение временного сопротивления разрыву. Следовательно, допускаемые напряжения при изгибе двутавровых балок должны быть во столько раз меньше вычисленных критических напряжений, во сколько раз допускаемое напряжение на разрыв меньше временного сопротивления разрыву.
ОПЫТЫ
§ 1. Постановка задачи
В начале настоящей статьи были получены некоторые формулы, относящиеся к скручиванию двутавровой балки с одним заделанным концом. Так как этими формулами мы пользовались в дальнейших выводах при определении величин критических нагрузок, то проверка их опытным путем является очень важной. Особенно удобна для такой проверки формула )
дающая угол закручивания для любого поперечного сечения балки. Здесь I — длина балки, х — расстояние выбранного сечения от свободного конца, М — скручивающий момент, С — жесткость при кручении в случае свободных концов и
где h — высота и D — наибольшая жесткость при изгибе каждой полки.
Проверку формулы (1) приходится начать рядом предварительных опытов по определению величин С w D.
Балки, над которыми производились опыты, были изготовлены в механической мастерской института. Для получения поперечных сечений, по возможности соответствующих теоретиче¬
1) См. формулу (8) § 2.
М Г , а , х ,,
Ф -тг- 1 — хЛ - sh a th —
Y С ,1а а
ch — а
(О
об устойчивости плоской формы Изгиба двутавровой балки 85
ски разобранному случаю, обыкновенная двутавровая балка высотой 12,7 см подвергалась остружке.
Толщина стенки и полок была доведена до 3 мм и высота до 119 мм. Для ширины полок брались величины 40 мм, 30 мм и 20 мм. Радиус окружности, сопрягающей полки с вертикальной стенкой балки, взят был очень малым, чтобы влияние закругления на величину жесткости было невелико. Относительно размеров поперечного сечения заметим, что желательно было бы иметь меньшую толщину стенки и полок, так как тогда выведенные формулы возможно было бы прилагать с большей точностью и явления неустойчивости при изгибе были бы резче выражены. К сожалению, при малой толщине балка сильно гнется во время остружки и работа становится неточной.
§ 2. Определение величины С
Так как при выбранных нами поперечных сечениях балки
величина С невелика, определение же ее должно быть сделано
как можно точнее, то пришлось отказаться от производства опыта на имеющейся в лаборатории института машине и произвести скручивание непосредственной нагрузкой.
Для этого балка была установлена в вертикальном положении. Нижний конец ее стальным острием опирается на особую подушку тп (рис. 27) и зажат двумя винтами А и В так, что концевые поперечные сечения полок остаются свободными.
К верхнему концу балки прикреплен рычаг MN, представленный на рис. 28. Концы рычагов тпит'п очерченные по дугам круга радиуса 25 см у огибаются тонкими нитями, натяжением которых и производится
скручивание балки. Чтобы достигнуть равенства натяжений обеих нитей, концы их перекинуты через блоки и понизу соединены горизонтальным стержнем. Нагрузка прилагается не к каждой нити отдельно, а ставится на общую чашку, подвешенную к средине горизонтального стержня. Этим приемом достигается и равенство натяжений, и одновременность приложения условий к обеим нитям. Таким образом осуществляется скручивающая балку пара сил. Величина ее определяется по величине поставленного на чашку груза и по длине рычага MN. В нашем случае эта длина равнялась 50 см, и потому груз в 1 кгу поставленный на чашку, давал пару, равную 0,25 кгм.
Для установки балки и прикрепления блоков мы пользовались рамой машины Амслера для изгиба.
86 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Жесткость балки определялась по углу закручивания, который измерялся зеркальным прибором. На определенном расстоянии одна от другой на балке закреплялись зажимными винтами две рамочки с зеркалами. Устанавливая на некотором расстоянии от зеркал горизонтальные шкалы и делая по ним отсчеты во время скручивания, можно определить угол закручивания с большой точностью. При наших опытах расстояние до шкалы бралось от 1,5 м до 2 м9 что при точности отсчетов по шкале до 14 деления давало возможность измерять углы закручивания до 112 ООО -116 ООО.
Ниже мы приводим результаты испытаний всех трех балок на скручивание и вычисленные по этим данным величины С.
Балка № 1. Ширина полок 40 мм. Расстояние между зеркалами I 50 см. Расстояние от зеркала до шкалы 1,5 м.
Величииа скручивающего момента в кгм
Отсчеты
верхнее
зеркало
разности
нижнее
зеркало
разности
0
252
276
36
15
0,25
216
261
36
14,5
0,50
180
246,5
35
14,5
0,75
145
232
36
14
1,00
109
218
71
28,5
0,50
180
246,5
72
29
0
252
275,5
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 87
Вычисленная на основании этих данных жесткость
С т- 177 10- кг см2.
Дф
Балка № 2. Ширина полок 30 мм. Расстояние между зеркалами 80 см. Расстояние от зеркала до шкалы 2 м.
Величина скручивающего момента в кгм
Отсчеты
верхнее
зеркало
разности
н ижнее зеркало
разности
0
65
115
62
15
0,25
127
100
63
14,5
0,50
190
85,5
62,5
14,5
0,25
127,5
100
62,5
15
0
65
115
Вычисленная на основании этих данных жесткость С 168 103 кгсм2.
Балка № 3. Ширина полок 20 см. Расстояние между зеркалами 60 см.
Расстояние от зеркала до шкалы 2 м.
Взличина скручивающего момента в кгм
Отсчеты
верхнее
зеркало
разности
нижнее
зеркало
разности
0
29,5
193
57,5
17
0,25
87
176
57,5
17
0,50
144,5
159
57,5
17
0,75
202
142
56
16,5
0,50
143
158,5
58
16,5
0,25
88
175
58
18
0
30
193
88 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Повторные испытания для той же балки, но при меньшей нагрузке, дали:
Величина скручивающего момента в кгм
Отсчеты
верхнее
зеркало
разности 1
нижнее
зеркало
разности
0
29,5
193
28,5
8,5
0,125
58
184,5
29
8,5
0,25
87
176
57,5
17
0,50
144,5
159
57,5
17
0,25
87
176
28,5
8
0,125
58,5
184
29
9
0
29,6
193
Вычисленная на основании этих данных жесткость балки С 148-103 кгсм2.
Наибольшие погрешности в приведенных опытах получаются благодаря неточности отсчетов по шкале. Так как для вычисления угла закручивания приходится сделать четыре отсчета, то погрешность может достигать 1.
Что касается погрешностей от неточности определения расстояния между зеркалами и расстояния от зеркала до плоскости шкалы, то они могут быть сделаны очень малыми. Трение в блоках, через которые перекинуты нити, также оказывает влияние на результаты. Чтобы определить погрешности, происходящие от этого трения, блоки были предварительно испытаны таким образом: через блок перекидывалась нить, к концам которой прикреплялись гири равного веса, и потом определялась величина той добавочной нагрузки, при которой одна из гирь начинает перевешивать другую.
При опытах с балкой № 1 трение не превосходило 0,1 нагрузки на блок. Столь малое трение получалось благодаря тому, что блоки взяты были малого веса (сделаны из алюминия), диаметры осей сделаны были равными 0,75 мм и концы их опирались на камни из часового механизма. При дальнейших испытаниях от больших нагрузок камни лопнули, и их пришлось заменить подшипниками из закаленной стали. Трение повысилось до 0,3,
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 89
§ 3. Определение жесткости балки при изгибе
Чтобы определить величину D (жесткость полки двутавровой балки), балка должна быть подвергнута изгибу в плоскости ее наименьшей жесткости. Наиболее удобным оказалось расположить балку на двух опорах и изгибать сосредоточенной нагрузкой, приложенной посредине пролета. Способ приложения нагрузки и устройство опор видны на прилагаемой фотографии (рис. 29). Жесткость при изгибе может быть вычислена
Рис. 29.
на основании измерения стрелки прогиба посредине пролета. Чтобы достигнуть большей точности измерения, мы воспользовались зеркальным прибором Мартенса, обыкновенно употребляемым при измерении удлинений. Расположение прибора видно на приложенной фотографии (рис. 29) и на рис. 30.
Концы пластинок тп и т'п' остриями своими т и т' вдавлены в полки испытуемой двутавровой балки. В точках пип' пластинки прижаты к стальным призмам, составляющим одно целое с зеркалами аа и ЬЬ.
При изгибе балки пластинки тп и т'п' опускаются и заставляют вращаться призмы, опирающиеся на неподвижные уголки Л и В. С призмами вращаются зеркала, направленные на шкалу MN.
Делая при помощи зрительной трубы отсчеты на шкале с точностью до 14 деления, мы можем определить стрелку прогиба с точностью до 13—14.
Погрешности, происходящие от неточного определения пролета балки и расстояния от плоскости зеркала до шкалы, могут быть сделаны очень малыми.
90 об УСТОЙЧИВОСТИ плоской формы изгиба двутавровой балки
При некоторых опытах зеркальные приборы устанавливались также и на концах балки для определения осадки опор. Отсчеты по этим зеркалам при наших нагрузках были всегда меньше 14 деления, и потому мы их нигде не принимаем в расчет.
Приводим теперь результаты, полученные при некоторых опытах, и вычисленные по этим данным жесткости балок при изгибе.
Балка № 1. Пролет балки 1196 мм. Увеличение зеркального прибора 430.
Величина нагрузки в кг
Отсчеты
зеркало 1
разности
зеркало 2
разности
0
215,5
60
10,5
11
0,5
205,0
71
11
И
1,0
194,0
82,0
10,75
11,75
1,5
183,25
93,75
11,25
11,5
2,0
172
105,25
22
23
3,0
150
128,25
22
23,75
4,0
128
152
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 91
Через пять минут было приступлено к разгрузке балки и получены такие отсчеты:
Величина нагрузки в кг
1
Отсчеты
зеркало 1
разности
зеркало 2
разности
4,0
127,75
152,0
21,75
23
3,0
149,5
129,0
21,5
23
2,0
171,0
106,0
11
11,5
1,5
182,0
94,5
11
11,5
1,0
193,0
83,0
11,25
11,75
0,5
204,25
71,25
10,75
11
0
215
60,25
Отсчеты по зеркалам, установленным на опорах, все время остаются меньше 14 деления, и потому мы их вовсе не приводим.
Определенная по среднему значению стрелки прогиба величина жесткости балки равна В2 Р348 684104 кгсм2.
Балка № 2. Пролет I 80 см. Расстояние от шкалы до плоскости зеркала 1628 мм. При этом увеличение прибора 500.
Величина нагрузки в кг
Отсчеты
зеркало 1
разности
зеркало 2
разности
0
439,5
294
18,25
19
1,0
421,25
313
18,25
18,75
2,0
403,0
331,75
37
38,5
4,0
366,0
370,25
37,5
38,75
6,0
328,5
409
92 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
При разгрузке через пять минут получены такие отсчеты:
Величина нагрузки в кг
Отсчеты
зеркало 1
разности
зеркало 2
разности
6,0
328,25
410
36,5
38
4,0
364,75
372
36,5
38
2,0
401,25
334
19,25
20
1,0
420,5
314
18,75
19,75
0
439,25
294,25
Величина жесткости при изгибе, определенная по среднему значению стрелки прогиба, будет В2 283-104 кгсм2.
Балка № 3. Пролет I 80 см. Расстояние от шкалы до зеркала 1628 мм. Увеличение прибора 500.
Величина нагрузки в кг
Отсчеты
зеркало 1
разности
зеркало 2
разности
0
285
499,5
59
57,5
1
345
442
61
61
2
403
381
60,5
62
3
466,5
39
61
62
4
527,5
257
При разгрузке через пять минут получены отсчеты:
Величина нагрузки в кг
Отсчеты
зеркало 1
разности
зеркало 2
разности
4
528
257
60,5
62
3
467,5
319
59,5
60,5
2
408
379,5
60
59,5
1
348
439
62
60,5
0
286
499,5
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 93
Вычисленная по среднему значению стрелки прогиба величина жесткости балки будет В2 883-103 кгсм2.
На основании полученных из опытов величин В2 нетрудно определить и соответствующие значения D — нужно только по геометрическим размерам балки, задавшись модулем упругости, вычислить жесткость стенки1), вычесть ее из соответствующего значения В2 и разность разделить пополам. Определенные таким образом величины для наших балок имеют следующие значения:
Балка № 1 D 339-104 кгсм2.
Балка №2 D 139-104 кгсм2.
Балка № 3 D — 439-103 кгсм2.
§ 4. Скручивание балки моментом, приложенным посредине пролета
Если скручивающий момент приложен посредине пролета балки и концы балки удерживаются, то в силу симметрии среднее сечение должно оставаться плоским. В таком случае к каждой половине балки может быть приложена формула (1) и по ней вычислен угол поворота любого сечения балки относительно ее среднего сечения. Тот же угол поворота может быть получен и опытным путем. Сравнение двух результатов покажет, насколько близка к истине формула (1).
Из прилагаемой фотографии (рис. 31) видно, что осуществлялось скручивание. Рычаг MN с помощью двух винтов закреплен посредине высоты балки. Нити, огибающие концы рычага, перекинуты через блоки А и В и соединены понизу рычагом CD Нагрузка подвешена к точке О — середине рычага CD.
Углы поворота отдельных сечений измерялись зеркальным прибором. Одно из зеркал, ш, прикреплено к рычагу MN и дает поворот среднего сечения. Кроме того, два зеркала помещены на равных расстояниях от середины балки, по ним возможно
) Эта величина мала по сравнению е жесткостью полок, и даже значительные погрешности при ее определении не окажут существенного влияния на величину D,
Рис. 31.
94 ОБ УСТОЙЧИВОСТИ плоской формы изгиба двутавровой балки
определять углы поворота, соответствующие выбранным сечениям. Результаты, полученные из опыта, приводим ниже.
Балка № 1. Зеркала помещены на расстоянии 50 см от среднего сечения балки. Расстояние от шкалы до плоскости зеркала 150 см. Длина балки между верхними и нижними зажимными винтами равна 127 см.
Величина скручивающего момента в кгм
Отсчеты
верхнее
зеркало
среднее
зеркало
нижнее
зеркало
0
124
252,5
119
1,25
114,5
219,5
110
2,0
108,5
200
104
1,25
114
219
109,5
0
124
252,5
119
Зеркала помещены на расстоянии 40 см от среднего сечения.
Величина скручивающего момента в кгм
Отсчеты
верхнее
зеркало
среднее
зеркало
нижнее
зеркало
0
144
267
116
1,25
128
234,5
100
2,0
118
214,5
90
1,25
126,5
234,5
100
0
143
267
116
Зеркала помещены на расстоянии 30 см от среднего сечения.
Величина скручивающего момента в кгм
Отсчеты
верхнее
зеркало
среднее
зеркало
нижнее
зеркало
0
209
267
192
1,25
186,5
234
214,5
2
173
214,5
228
1,25
186
234
214,5
0
208,5
267
192
Для большей наглядности мы приводим в следующей отдельной таблице величины углов поворота, полученные из опыта и вычисленные аналитически по формуле (1). В четвертом столбце приведены углы закручивания, которые получились бы,
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ QS
если бы мы пренебрегали изгибом полок и применили обычную формулу кручения.
Расстояние сечения от середины балки в см
Углы, полученные из опыта
Углы, вычисленные по формуле (1)
Углы, вычисленные по обы той формуле
50
0,0125
0,0114
0,0285
40
0,0088
0,0080
0,0228
30
0,0053
0,0049
0,0171
Балка № 2. Расстояние от плоскости зеркал до шкал 2 м. Длина балки между верхними и нижними зажимными винтами равна 127 см. Зеркала закреплены на расстоянии 50 см от среднего сечения балки.
Величина скручивающего момента в кгм
Отсчеты
верхнее
зеркало
среднее
зеркало
нижнее
зеркало
0
115
64,5
202
2
86
164
173,5
0
115
64,5
202
Зеркала закреплены в 40 см от среднего сечения балки.
Величина скручивающего момента в кгм
Отсчеты
верхнее
зеркало
среднее
зеркало
нижнее
зеркало
0
123
27,5
67,5
1,25
92,5
90
36,5
2
74
127
18,5
1,25
92
91
36
0
122,5
28
68
помещены
в 30 см от
среднего
сечения
Величина
Отсчеты
скручиваю¬
щего момен¬
верхнее
среднее
нижнее
та в кгм
зеркало
зеркало
зеркало
0
179,5
28
90
2
112
127,5
22,5
0
179,5
28
90
Ofe УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Результаты опытов и вычислений для балки № 2 приведены в следующей таблице.
Расстояние сечения от середины балки в см
Углы, полученные из опыта
Углы, вычисленные по формуле (1)
Углы, вычисленные по обычной формуле
50
0,0177
0,0167
0,0298
40
0,0126
0,0119
0,0238
30
0,0080
0,0075
0,0179
Балка № 3. Углы закручивания были измерены только для сечений, отстоящих на 50 см от середины балки. Расстояние от плоскости зеркала до шкалы 2 м. Длина балки между верхними и нижними зажимными винтами равна 127 см.
Величина скручивающего момента в кгм
Отсчеты
верхнее
зеркало
среднее
зеркало
нижнее
зеркало
0
127,5
136,5
248,75
0,25
122,75
154,5
244
0,50
118
172
239
0,75
113
190
234
1,25
103
226
224
0,75
112,5
191
233,5
0,50
117,5
173
238,75
0,25
122,5
155
244
0
127,5
136,5
248,75
Вычисленный на основании этих наблюдений угол закручи-
66
вания будет Дф 0,0165. Тот же угол, вычисленный по
формуле (1), равен Д'ф 0,0152.
Сравнивая результаты, полученные для всех трех балок, мы видим, что наша формула дает для величины жесткости значения несколько преувеличенные. Разность между данными опытов и вычисленными по формуле (1) значениями углов закручивания колеблется в пределах от 6 до 8.
Результаты вычислений по формуле (1) еще ближе совпадут с данными опытов, если вместо высоты балки h ввести расстояние между центрами тяжести поперечных сечений полок. Мы попробовали ввести эту поправку для балки № 2 и тогда
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 97
получили разность между данными опыта и результатами формулы (1) всего в 3,5.
На основании этих результатов можно считать, что основная формула кручения, которой мы пользуемся при определении критических значений нагрузок, опытами подтверждается.
§ 5. Изгиб балки в плоскости ее наибольшей жесткости
Для наблюдения над явлением искривления плоской формы изгиба двутавровой балки выбран был случай балки, заделанной одним концом. Такой способ закрепления наиболее просто осуществляется 1) — нужно только зажать конец балки между двумя точно пристроганными поверхностями. Этому же случаю соответствуют наименьшие значения критических изгибающих моментов, а значит, и наименьшие напряжения.
Из трех ранее испытанных нами балок для дальнейших опытов служила балка № 3, так как по расчету только для нее величина критических напря-
формаций, зажатый конец
был усилен двумя железными накладками, плотно пригнанными к полкам и стенке двутавровой балки. Для приложения изгибающей нагрузки на свободном конце балки было сделано приспособление, представленное на рис. 32. Благодаря ему точка приложения изгибающей силы довольно точно может быть приведена к совпадению с осью балки.
При вполне точной постановке опыта, при идеально правильной форме балки изгиб должен оставаться плоским все время, пока нагрузка не достигла критического значения. За этими пределами начинается неплоский изгиб балки, который, вообще говоря, быстро возрастает с возрастанием нагрузки. Влияние неточности установки и некоторой первоначальной кривизны оси балки сказывается в том, что искривление начинается при самых малых нагрузках. С возрастанием нагрузки это искривление растет сначала медленно, потом, с приближением нагрузки
) В случае балки на двух опорах закрепление концов должно быть устроено таким образом, чтобы сохранилась возможность свободного вращения концевых поперечных сечений балки относительно их главных осей инерции.
гиба балок сосредоточенными грузами. Чтобы при изгибе избежать местных де-
жений оказалась меньше предела упругости железа.
Для закрепления конца балки мы воспользовались машиной Амслера для из-
Рис. 32.
98 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
к ее критическому значению, возрастание кривизны идет очень быстро.
Для наблюдения этого явления мы при предварительных опытах пользовались зеркальным прибором Баушингера. Расположение зеркал и способ их прикрепления видны из приложенной фотографии (рис. 33). С помощью зрительной трубы довольно точно можно определять горизонтальные перемещения верхнего и нижнего края концевого поперечного сечения балки и по полученным перемещениям вычислять прогиб балки в горизонтальной плоскости и угол закручивания. При дальнейших опытах мы отказались от этого способа измерений, так как оказалось, что даже незначительное трение зеркального прибора
Рис. 33.
сказывается на величине появляющихся искривлений. Чтобы избежать трения, мы воспользовались микроскопом с микрометрическим винтом. Он дает возможность мерить прогибы балки с точностью до 0,01 мм, и при этом конец балки остается совершенно свободным от горизонтальных усилий.
Общий ход испытания был таков. Сначала, по выведенным ранее формулам, выяснялась величина критической нагрузки. На чашку весов, подвешенную к серьге А (см. рис. 33), устанавливалась нагрузка на 30—40 кг меньше вычисленной. Дальнейшее нагружение производилось постепенно, и при этом делались отсчеты по микроскопу или шкале зеркального прибора через каждые два килограмма. Чтобы избежать толчков и сотрясений, нагрузка производилась водой. Для этой цели на чашке с грузами устанавливался резервуар, в который осторожно приливали воду по два килограмма. В некоторых случаях, когда вес воды, помещающейся в резервуаре, оказывался недостаточным, пользовались для нагрузки мелкой дробью.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ 99
Первые опыты были произведены при пролете балки ИЗ см, считая от плоскости закрепления до точки приложения изгибающей силы. Величина критической нагрузки вычислена по следующим данным:
2С
V2 h2 D ои,в Коэффициент k определяется по формуле
_4г013__Б 28
К (1 _ У2 “ 0,0.
Значение критического изгибающего момента будет МКр 16900 кг см.
Следовательно, величина критической изгибающей силы равна
Рр 150 При взятых нами размерах балки этой нагрузке будут соответствовать напряжения, величина которых в опасном сечении не превосходит 1110 кгсм2. Следовательно, потеря плоской формы изгиба будет происходить в пределах упругости.
Раньше, нежели приступить к измерениям, на чашку была положена предварительная нагрузка, которая вместе с весом самой чашки и резервуара для воды составила 125 кг.
Дальнейшее нагружение производилось водой, измерения искривлений велись микроскопом, и полученные отсчеты приведены ниже.
Величина
нагрузки
Отсчеты
Разности
Примечания
в кг
125
22
0,70
126
21,30
1,40
128
19,90
1,70
130
18,20
2,20
132
16,00
2,85
134
13,15
3,85
136
9,30
3,90
5,40
прибор перестав¬
138
лен
100 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Величина
нагрузки
В КЗ
Отсчеты
Разности
Примечания
138
139
140
13,86
10,30
5,68
3,56
4,62
прибор
лен
перестав-
140
141
14,35
5,26
9,09
прибор
лен
перестав-
141
141,8
18,40 — 4
22,68
Дальнейшее нагружение было прекращено, так как балка начала быстро искривляться. Результаты опыта представлены для большей наглядности графически на рис. 34 сплошной линией. По оси абсцисс отложены нагрузки, а по оси ординат — соответствующие им искривления. С приближением нагрузки
1
I
1
1
i
2
fa
'i
J
122 123 № 125 126 127 128 123 130 131 132 133 № 135 136 137 138139 М 14 г.
Ш
Рис. 34.
к 142 кг искривление идет очень быстро — дальнейшее нагружение невозможно. Действительная предельная нагрузка оказалась меньше вычисленной, и разность составляет около 5.
Следующий опыт был произведен над той же балкой при прежнем пролете, но точка приложения изгибающей силы была помещена выше оси балки на величину ft4 3 см. Теоретически было показано, что всякое повышение точки приложения силы влечет за собой уменьшение критической нагрузки — опы¬
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ Ю1
том это подтвердилось. Уже при нагрузке 130 кг балка начала быстро искривляться, и дальнейшее нагружение пришлось прекратить. Получены следующие отсчеты:
Величина нагрузки в кг
От¬
счеты
Раз¬
ности
Величина нагрузки в кг
От¬
счеты
Раз¬
ности
120
30,20
126
28,70
0,24
1,62
122
29,96
128
27,08
0,46
9,48
124
29,50
130
17,60
0,80
Графически возрастание искривления с нагрузкой показано на рис. 34 пунктиром. Дальнейшие опыты произведены над той же балкой при пролете 95,2 см, т. е. при г 8. Для этого случая будем иметь
Величина критического изгибающего момента М1ф 21 150 кгсм, а следовательно, критическая нагрузка
Р«рг222
соответствующее значение наибольших напряжений будет приблизительно 1390 кгсм2. Предварительная нагрузка взята 174 кг. При дальнейшем нагружении искривление измерялось микроскопом. Полученные отсчеты приводим ниже.
Величина нагрузки в кг
От¬
счеты
Раз¬
ности
Величина нагрузки в кг
От¬
счеты
Раз¬
ности
174
0,40
190
8,00
0,50
1,76
176
0,90
192
9,76
0,60
2,28
178
1,50
194
12,04
0,80
3,04
180
2,30
196
15,08
0,76
4,12
182
3,06
198
19,20
0,94
6,55
184
4,00
200
25,75
1,15
6,25
186
5,15
201
32,00
1,15
7,80
188
6,30
202
39,80
1,70
102 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Дальнейшая нагрузка прекращена, так как балка начала быстро искривляться. Результаты опыта графически представлены на рис. 35. Как и в первом случае, действительная предельная нагрузка оказалась меньше вычисленной теоретически. Разность здесь достигает 10. Это можно объяснить себе тем, что чем меньше пролет балки, тем большее значение приобретает жесткость полок. Влияние же полок сильно зависит от закрепления конца балки. При наших опытах это закрепление
Рис. 35
было далеко не совершенно. Мы не приводим здесь дальнейших испытаний нашей балки в том случае, когда точка приложения силы выше оси на г4 3 см. В этом случае быстрое возрастание искривления балки началось при нагрузке Р 182 кг. Повышение точки приложения силы повлекло за собой уменьшение величины критической нагрузки на 10.
§ 6. Испытание клепаной балки
Последний ряд опытов был произведен над клепаной балкой. Балка была составлена из вертикального листа 180 X X 3,7 мм и четырех уголков 20 X 20 X 3,7 мм. Заклепки диаметром 6 мм были расставлены на расстоянии 25 мм центр от центра. Общая длина балки взята 2 м. При такой длине скручивание удобнее было производить, расположив балку горизонтально. Один конец балки зажимался, как и раньше, двумя винтами в особой подушке, а к другому, перпендикулярно к оси балки, прикреплялся горизонтальный рычаг, служивший для приложения скручивающей пары. Скручивание производилось
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА двутавровой БАЛКИ 103
непосредственной нагрузкой. С помощью ранее описанного приспособления достигалась одновременность и равномерность передачи нагрузки на две нити, прикрепленные к концам вышеупомянутого рычага. Длина рычага взята 1 му и потому нагрузка в 1 кг дает скручивающую пару, равную 0,5 кгм.
Угол закручивания измерялся зеркальным прибором. Для этого в двух поперечных сечениях балки, отстоящих на расстоянии 80 см одно от другого, были закреплены зеркала. Углы поворота выбранных сечений определялись на основании отсчетов по вертикально поставленным шкалам. Расстояние от шкал до плоскости зеркал взято было равным 150 см.
Величины скручивающих моментов в кгм и соответствующие им отсчеты приводим ниже.
Скручивающие моменты в кгм
Отсчеты
зеркало 1
разности
зеркало 2
разности
0
215,5
341
26,25
61,25
0,5
241,75
402,25
26,25
62,75
1,0
268
465
26,5
63
1,5
294,5
528
25,75
61,5
1,0
268,75
466,5
26,75
63,5
0,5
242
403
26,5
62
0
215,5
341
Вычисленная по этим данным жесткость балки С — 333 103 кгсм2,
Дф
Заметим, что жесткость получилась несравненно меньше той, которую можно было бы ожидать на основании вычислений по приближенной формуле, приведенной в § 3.
Для определения величины D мы подвергли балку изгибу в плоскости, перпендикулярной к плоскости стенки. Устройство опор и расположение приборов не отличалось ничем от ранее описанной установки, и потому ограничимся приведением результатов.
Пролет балки взят равным 160 см. Шкалы были установлены на таком расстоянии, что увеличение зеркального прибора равно 500.
104 ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ
Зеркала 1-е и 2-е установлены посредине пролета, 3-е и 4-е — у опор. Величины нагрузок в кг и полученные по шкалам отсчеты были следующими:
Величина нагрузки в кг
Отсчеты
зеркало 1
раз¬
ности
зеркало 2
раз¬
ности
зеркало 3
зеркало 4
0
374,25
320,5
187
240
36,75
37,5
1
337,5
358
187
240
36,75
38
2
300,75
396
187
240
37,25
37,5
3
263,5
433,5
187
240
75
75,5
5
188,5
509
187,25
240,25
76
77
7
112,5
586
187,25
240,25
75,5
76
5
188
510
187,25
240,25
75
75
3
263
435
187
240
37,25
38
2
300,25
397
187
240
37,25
38
1
337,5
359
187
240
36,75
38,5
0
374,25
320,5
187
240
Вычисленная по этим данным жесткость балки при изгибе В2 1140-104 кгсм2.
Вычитая из В2 жесткость стенки балки и деля разность пополам, получим величину D 565 104 кгсм2.
Определив опытным путем величины С и D, мы приступили к изгибу балки в плоскости ее наибольшей жесткости. Закрепление конца и способ приложения нагрузки остались прежние. Пролет балки, считая от плоскости заделки до точки приложения нагрузки, был взят равным 180 см. Следовательно,
h 1 Ю
Для вычисления величины критической нагрузки имеем
Соответствующее значение коэффициента k 7,2.
И следовательно, величина критической нагрузки будет
Якр kVC 433 кг.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ Ю5
Этому соответствуют наибольшие напряжения в опасном сечении Якр — 1300 кг)см2.
Следовательно, явление искривления плоской формы изгиба балки будет происходить в пределах упругости. На балку была положена первоначальная нагрузка 388 сг, и при этом заметного искривления не произошло. Дальнейшая нагрузка производилась постепенно и сопровождалась измерением угла закручивания концевого поперечного сечения балки.
Ниже мы приводим величины нагрузки в кг и соответствующие отсчеты, полученные с помощью зеркального прибора. Чтобы получить угол закручивания, нужно величину разности отсчетов делить на 200.
Нагрузка в кг
Отсчеты
Разности
388
200
14
398
186
28
405
158
53
410
105
412
Балка сразу сильно
искривилась
Вторичный опыт дал такие результаты:
Нагрузка в кг
Отсчеты
Разности
388
228,5
6,5
398
235,0
1,9
405
254,0
410
Балка сразу сильно
искривилась
В первом опыте при 412 кг, во втором при 410 кг начинается такое сильное искривление балки, что дальнейшая нагрузка становится невозможной. Полученная опытным путем предельная нагрузка и в этом случае меньше вычисленной. Разность составляет приблизительно 5.
О ПРОДОЛЬНОМ ИЗГИБЕ СТЕРЖНЕЙ В УПРУГОЙ СРЕДЕ
Известия С.-Петербургского политехнического института, 1907, том 7, Отдел техники, естествознания и математики, выпуск 1, стр. 145—157. Отд. оттиск, С.-Петербург, типо-литография Шредера, 1907, 13 стр.
§ 1. Определение критической силы из дифференциального уравнения
Положим, что призматический стержень АВ сжат действующими по оси его силами Р (рис. 1). Боковому выпучиванию стержня в случае продольного изгиба противодействует упругая среда, так что всякое выпучивание сопровождается появлением поперечных сил, непрерывно распределенных по длине
стержня. Величина этих сил в любом поперечном сечении тп стержня пропорциональна прогибу в этом сечении. Коэффициент пропорциональности есть величина, зависящая от упругих свойств среды.
При выбранном нами расположении координатных осей дифференциальное уравнение упругой линии выпучившегося стержня будет
i
EJ-Py-jfiy(t)(t-x)dt
(t — х) А. (1)
Здесь EJ — наименьшая жесткость стержня при изгибе, р — постоянный коэфРис. 1. фициент, характеризующий упругие свой¬
ства среды, А — реакция верхней опоры стержня. Тогда правая часть уравнения (1) представит собой величину изгибающего момента в сечении тп.
Дифференцируя дважды уравнение (1), получаем
ИЛИ
yiv 2 а2у к у 0.
(2)
О ПРОДОЛЬНОМ ИЗГИБЕ СТЕРЖНЕЙ В УПРУГОЙ СРЕДЕ Ю7
Здесь введены для упрощения такие обозначения:
2 -Х. (3)
Корни характеристического уравнения, соответствующего уравнению (2), будут г ± V — а2 ± У a4 — k4. (4)
Начнем с рассмотрения случая, когда а4— k4 0. Тогда все
четыре корня (4) — мнимые и общий интеграл уравнения (2) представится в такой форме:
у A sin рх В cos рх С sin qx D cos qx. (5)
Здесь А, В, С и D — произвольные постоянные величины, а
р Vа2 V а4 — k4 , q Vа2 — Y а4 — k4. (6)
Для определения произвольных постоянных решения (5) имеем следующие условия на концах:
1,2) при 0 у 0, 0;
3, 4) при х 1 у 0, Jjr 0.
Первые два условия дают нам следующее:
В D 0, Bp2 Dq2 0.
Так как р не равно q, то, следовательно, Б D 0.
Условия 3, 4) приводят нас к уравнениям
A sin pi С sin ql 0, Ар2 sin pi Cq2 sin ql 0. (7)
Уравнениям этим можно удовлетворить, положив А С 0.
Но в таком случае у 0, и мы приходим к прямолинейной форме стержня АВ. Чтобы была возможна и искривленная форма равновесия, необходимо, чтобы уравнения (7) давали хотя бы для одной из произвольных постоянных решение, отличное от нуля. В таком случае, как известно, определитель уравнений (7) должен обращаться в нуль. Следовательно, для возможности появления искривленной формы равновесия необходимо выполнение условия
q2 sin pi sin ql — p2 sin pi sin ql 0,
которое распадается на два самостоятельных условия:
sin р 0 и sin 0. (8)
Раз одно из этих условий выполнено, искривленная форма равновесия становится возможной. Величина соответствующей
108 о ПРОДОЛЬНОМ ИЗГИБЕ стержней в упругой среде
сжимающей силы определяется одной из двух следующих формул, написанных на основании условий (8) и обозначений (6):
а22 У аЧ4 — кЧ4 т2я2, а22 — У аЧ4 — fe44 п2 я2. (9)
Здесь тип — произвольные целые числа. Легко показать, что эти формулы сохраняют свое значение и при k4 а4.
Дальнейшая задача заключается в том, чтобы при заданных размерах стержня и заданном коэффициенте упругости среды р найти наименьшее значение а212, а следовательно, и сжимающей силы Я, при котором одно из условий (9) удовлетворено.
При k2 0, т. е. при отсутствии бокового сопротивления, первая из формул (9) дает нам
2 а22 л2я2.
Или на основании наших обозначений (3) получим
m2n2EJ
Р-
I2
т. е. имеем обычную формулу продольного изгиба.
Если сопротивление среды и длина стержня таковы, что k2l2 т2я2, то тогда обе формулы (9) дают одно и то же значение для величины сжимающей силы, соответствующей первой возможной искривленной форме равновесия, именно а22 т2я2, а следовательно,
п _ m2n2EJ 0
г J2 А
т. е. величина критической нагрузки в этом случае вдвое больше, нежели это получается для той же формы при отсутствии бокового сопротивления.
В общем случае, когда m2n2k2l2 (т 1)2я2, наименьшее значение а22, удовлетворяющее условиям (9), заключено в тех же пределах. Полагая
k2l2 т2п2 а, (10)
где 0 а (2т 1)я2, представим формулы (9) в таком виде: а212 У аЧА — (т2 я2 а)2 (т I)2 я2, а22 — У аЧ4 — (т2я2 а)2 т2я2, откуда получаем
22 _ (я2я2 а)2 (т I)4 я4 Ul “ 2 (т I)2 я2
или (11)
22 _ (т2п2 02 ап4я4 й1 2mW
О ПРОДОЛЬНОМ ИЗГИБЕ СТЕРЖНЕЙ В УПРУГОЙ СРЕДЕ 109
Если известны упругие свойства среды, то правые части формул (11) представляют собой известные величины и, следовательно, определение критического значения сжимающей силы не представляет никаких затруднений. Нетрудно показать, что при а тл2 вторая из формул (11) дает для критического значения нагрузки меньшие величины, нежели первая1), и, следовательно, расчет должен вестись по второй формуле; при тл2 а (2т 1)я2 расчет следует вести по первой формуле. В первом случае имеем т полуволн, во втором т 1.
Если размеры стержня и упругие свойства среды таковы, что т получается очень большим, мы можем пренебречь величиной а по сравнению с т2л2 и тогда получаем следующие интересные выводы:
1) Величина критической нагрузки не зависит от длины стержня и определяется поперечными размерами стержня и упругими свойствами стержня и среды. В самом деле, в этом случае
а22 k2l2 т2 л2
и, следовательно,
Р 2а2 2т™ 2 VEJ. (12)
2) Длина полуволн, на которые при выпучивании подразделяется стержень, с возрастанием числа т приближается к известному пределу, не зависящему от длины стержня. Мы имеем
k2l2 т2л2.
Принимая во внимание, что длина полуволны 5 равна Цт, будем иметь я2я2 к2, откуда
71 I4 f ю
k л V р
Сравнивая формулы (12) и (13), получаем для определения критического значения сжимающей силы такое выражение:
р 2 n2EJ
S2
Эти формулы возможно применить, например, к случаю спаянных рельсов, втопленных в асфальт или бетон мостовой одежды. При повышении температуры такой рельс подвергается
) Знак разности (аЧ2)—(а22)2 определяется знаком разности
(1i)2_(1 w)2-
110
О ПРОДОЛЬНОМ ИЗГИБЕ СТЕРЖНЕЙ В УПРУГОЙ СРЕДЕ
продольному сжатию и находится в условиях, аналогичных только что рассмотренным.
До сих пор мы полагали, что а4 А4. Покажем, что при а4 А4 невозможна искривленная форма равновесия.
Введем обозначение
k4 — а4 Ь4. (14)
Тогда корни характеристического уравнения, соответствующего уравнению (2), будут: г ± Yо2 ± b2i. Общий интеграл уравнения (2) представится в такой форме:
у Схетх cos пх С2етх sin пх С3етх cos пх С4етх sin пх. Здесь для сокращения письма нами введены такие обозначения: -iVtfTТ4 а2 УТ-а2
V 2 т Г 2 п-
Условия на концах стержня остаются прежними. Первые два из них, относящиеся к концу х 0, дают нам для определения произвольных постоянных два следующих уравнения:
Cj С3 0, (т2 — п2) Cj (т2 — п2) С3 2тпС2 — 2тпС4 0,
откуда следует:
С — С3, С2 — С4.
Два других условия, относящиеся к концу х , приводят нас к следующим двум уравнениям:
Ci (m2 — г2) cos nl sh ml — 2run sin nl ch ml
C2 (m2 — n2) sin nl ch ml 2mti cos nl sh ml 0, Ci cos nl sh ml C2 sin nl ch ml 0.
Для возможности появления искривленной формы равновесия необходимо, чтобы полученные уравнения давали для произвольных постоянных решения, отличные от нуля. Следовательно, определитель этих уравнений должен обращаться в нуль, т. е.
2тп (sin nl ch ml)2 2mn (cos nl sh ml)2 0,
что невозможно, так как sin nl и cos nl не могут обращаться в нуль одновременно.
§ 2. Применение теоремы о минимуме потенциальной энергии
К тем же результатам можно прийти, применив иной метод исследования устойчивости деформации сжатого стержня. Применим общеизвестную теорему: система находится в устойчивом равновесии, если ее потенциальная энергия является минималь¬
О ПРОДОЛЬНОМ ИЗГИБЕ СТЕРЖНЕЙ В УПРУГОЙ СРЕДЕ
111
ной. При малой сжимающей силе прямолинейная форма равновесия устойчива, потому что при всяком искривлении уменьшение потенциальной энергии сжатия мало по сравнению с появляющейся потенциальной энергией изгиба и энергией деформации упругой среды. Если мы, постепенно увеличивая продольную сжимающую силу, достигнем такого предела, когда уменьшение, при искривлении, потенциальной энергии сжатия как раз равно потенциальной энергии изгиба, сложенной с потенциальной энергией деформации среды, то с этого момента становится возможным появление второй, искривленной формы равновесия.
Если мы составим выражения для различных видов потенциальной энергии и напишем высказанное выше условие, то получим уравнение для определения критического значения сжимающей силы.
Потенциальная энергия сжатия при всяком выпучивании уменьшается, так как отдельные элементы стержня удлиняются. Нетрудно составить выражение этого удлинения. В самом деле, для длины ds любого элемента можем написать
шение потенциальной энергии сжатия при выпучивании будет
Потенциальная энергия деформации упругой среды будет
Уравнение для определения критической величины сжимающей силы представится в такой форме:
ds2 dx2 dу2 dx2 dx2 »
откуда
Искомое удлинение
И следовательно, умень-
о
Потенциальная энергия изгиба будет
о
о
Sp-§-fdxEjJ(S)2dxdx‘ (о
о
9
9
112 о ПРОДОЛЬНОМ ИЗГИБЕ СТЕРЖНЕЙ В УПРУГОЙ СРЕДЕ
В самом общем виде мы мажем представить уравнение упругой линии после выпучивания в такой форме:
тоо
V1 а тпх ГЧ
У 2а т j (2)
т-1
Подставляя это значение у в уравнение (1) и производя интегрирование, получим
(3)
Положим, что при выпучивании искривление произошло по синусоиде и
Лгпл
т sm J
тлх
Тогда из (3) получаем для определения критической нагрузки
Р _ (т2л2)2 44 ( ,
EJ 12т2к2 W
Здесь kA имеет прежнее значение. Нетрудно видеть, что полученная формула легко может быть приведена в совпадение со второй из формул (11) (§1).
Практически важно получить первую возможную искривленную форму, т. е. подобрать в формуле (4) такое число т, которому соответствует наименьшее значение сжимающей силы.
Наибольшей длиной стержня , для которой первая искривленная форма равновесия состоит из т полуволн, очевидно, будет та, при которой формула (4) дает одно и то же значение для Р независимо от того, подразделяется ли стержень на т
или на т 1 полуволн. Следовательно, для определения I2
имеем
(т2я2)2 44 _ (т I)2 я22 k4l4 12т2к2 2(т1)2я2 или
г22 я2 (т 1) т.
При очень большом т можно написать
fe22 ,
: т2я2 (5)
или
(3 EJ.
Эту формулу мы уже получили иным путем в § 1.
О ПРОДОЛЬНОМ ИЗГИБЕ СТЕРЖНЕЙ В УПРУГОЙ СРЕДЕ ЦЗ
При т оо мы можем тот же результат получить из формулы (4). Полагая, как и прежде, m2l2 1s2, имеем из (4)
Р _ я2 J k4S2
беря производную по 5 и приравнивая ее нулю, получим
Эта формула совпадает с формулой (13) § 1.
До сих пор мы полагали, что искривление стержня происходит по синусоиде, и мы подобрали число полуволн синусоиды т так, что соответствующая сжимающая сила Р является минимальной. Покажем, что для всякой другой искривленной формы нужна большая сжимающая сила Pi1). В самом деле, разность между критической нагрузкой, соответствующей любой форме искривления, и выбранной нами будет
если вместо р подставить его значение р ш4, то интересующая нас разность представится в таком виде:
и, следовательно, будет всегда положительна.
Найденное нами значение Р критической сжимающей силы будет наименьшим, при котором возможна искривленная форма равновесия.
) Нижеследующее доказательство принадлежит студенту Политехнического института А. А. Г о р е в у, любезно согласившемуся просмотреть и прокорректировать настоящую статью.
i Знак этой разности определится знаком числителя. Если для краткости обозначим
я2
р, -jq,
то числитель может быть представлен в таком виде:
wAW S ли' (Iй -»п- 2 Л(г- ,»г);
И (f)'А»’ ((’-»)
114
О ПРОДОЛЬНОМ ИЗГИБЕ СТЕРЖНЕЙ В УПРУГОЙ СРЕДЕ
§ 3. Случай вращающихся валов
До сих пор мы полагали, что коэффициент р, характеризующий упругие свойства среды, есть величина положительная и, следовательно, при выпучивании стержня появляются поперечные силы, противодействующие этому выпучиванию. Рассмотрим теперь случай, когда коэффициент р отрицательный, т. е. положим, что всякое искривление сопровождается появлением поперечных сил, стремящихся увеличить деформацию. На практике подобные условия встречаются в случае быстровращающихся валов. Если какая-либо посторонняя причина вызовет искривление вала, то сейчас же появляются центробежные силы; они действуют как непрерывная нагрузка, пропорциональная в каждом сечении прогибу. Нагрузка эта стремится увеличить произведенное искривление. Пока скорость вращения невелика, центробежные силы, пропорциональные квадрату угловой скорости, недостаточны для того, чтобы преодолеть силы упругости вала, и вал устойчиво сохраняет свою прямолинейную форму. Увеличивая угловую скорость вращения, можно всегда достигнуть предела, за которым прямолинейная форма перестает быть
устойчивой и ничтожная внешняя причина может вызвать сильное искривление вала.
Дифференциальное уравнение в этом случае, очевидно, будет
у™ 2а2у - k4y 0. (1)
Общий интеграл его
у A sh тх В ch тх С sin пх D cos пх, (2)
где
т У — а2 У а4 к4
, , , (3)
п Vа2 Уа4 к4.
Условия на концах остаются прежними. Первые два из них дают нам В D 0.
Два других приводят к уравнениям
Л sh ml С sin nl 0,
Am2 sh ml — Cn2 sin nl 0.
Чтобы хотя бы одна из произвольных постоянных была отлична от нуля, необходимо положить sin rtl 0.
Прямолинейная форма перестает быть устойчивой, когда
а2 V a4 k4 -рг
(4)
б ПРОДОЛЬНОМ ИЗГИБЕ СТЕРЖНЕЙ В УПРУГОЙ СРЕДЕ
115
Принимая во внимание, что получим из (4)
2а2 — и kA — ,
P lllL№r, (5)
В случае вращающегося вала центробежная сила, приходящаяся на элемент длины dx, будет q ш2 dx, где х — масса вала, приходящаяся на единицу длины, со — угловая скорость. Следовательно, р —ко2. На основании этого получим из формулы (5)
р _ EJn2 JLKO22
г — t2 Л2 w
Мы видим, что критическое значение продольной сжимающей силы в этом случае меньше, нежели в обычном случае продольного изгиба. Постепенно увеличивая угловую скорость, мы можем дойти до такого значения оз, при котором правая часть формулы (6) обращается в нуль и, следовательно, прямолинейная форма будет неустойчива даже при отсутствии продольной сжимающей силы. Этот случай, собственно, и имеет место на практике. Критическая угловая скорость, следовательно, будет
ГЫ (7)
— лГ1-
2 У
Интересно заметить, что эта угловая скорость как раз равна частоте поперечных колебаний вала, рассматриваемого как балка, свободно лежащая на двух опорах.
В самом деле, для свободных поперечных колебаний имеем уравнение
„ JUl - ftIL q
dt2 EJ dx4 ‘
Для колебаний, соответствующих основному тону, имеем решение
Л. , . пх
у A sin at sin —.
Подставляя это решение в уравнение (8), получаем формулу
л2 ГеТ
а т-у it
тождественную с формулой (7). Следовательно, прямолинейная форма вращающегося цилиндрического вала становится неустойчивой, если число оборотов в минуту равняется числу собственных поперечных колебаний вала за тот же промежуток времени.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
Известия Киевского политехнического института, 1907, год 7, книга 2, стр. 35—94. Отд. оттиск, Киев, тип. С. В. Кульженко, 1907, 60 стр.
§ 1. Введение
В виде составной части железных конструкций в инженерных сооружениях нередко употребляют железные листы. Толщина листов обыкновенно бывает малой по сравнению с другими их размерами, и потому к листам применимы с достаточной точностью все выводы теории упругости, относящиеся к тонким пластинкам. Известно, что тонкие пластинки, как и тонкие стержни, под действием внешних сил могут оказаться неустойчивыми.
Если, например, имеется пластинка, сжимаемая силами, лежащими в ее срединной плоскости, то, постепенно увеличивая сжимающие силы, можно достиг- а j е
нуть предела, за которым пло- - р
ПГ -1Г
Рис. L
с
Рис. 2.
ская форма сжатой пластинки перестает быть устойчивой и пластинка выпучивается. Это обстоятельство требует в случае сжатых листов или конструкций из листов составленных, кроме обычных расчетов, произвести еще отдельную проверку на устойчивость. Практически этот вопрос об устойчивости решается до сих пор на основании старой эмпирической формулы, выведенной из опытов И. Ходкинсона 1). По этой формуле определяется предельная ширина прямоугольного листа, сжатого силами, параллельными длине листа и равномерно распределенными по его поперечным сторонам, как показано на рис. 1.
Все четыре стороны листа считаются закрепленными по контуру. В таких приблизительно условиях будет находиться горизонтальный лист de в сжатом мостовом поясе коробчатого сечения (рис. 2).
) См. JI. Д. Проскуряков. Строительная механика, Часть 1, С.-Петербург, тип. Бенке, 1902, стр. 206.
к ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
117
Величина безопасного сжимающего напряжения по формуле И. Ходкинсона выражается так:
Здесь б обозначает толщину листа; Ь — его ширина; А — постоянный коэффициент, зависящий от упругих свойств материала.
На основании приведенной формулы нужно было бы заключить, что критическое значение сжимающего напряжения пропорционально корню квадратному из отношения толщины листа к его ширине; между тем точное решение вопроса об устойчивости указывает, что такое заключение совершенно не соответствует действительности и интересующее нас критическое значение сжимающего напряжения пропорционально квадрату отношения толщины листа к его ширине, если только сжатие не превосходит предела упругости материала. Надо полагать, что в опытах И. Ходкинсона выпучивание происходило при напряжениях, превосходящих предел упругости; к таким случаям выводы теории упругости, очевидно, совершенно неприложимы.
В случае сжатого листа, одна из продольных сторон которого свободна, как, например, в случае вертикального листа ab таврового сечения или листов cdy ef коробчатого сечения (рис. 2), полагают, что предельная ширина, при которой можно еще не опасаться выпучивания, вчетверо меньше, нежели в случае листа, всеми сторонами опертого на контур. В мостах для этого случая установлена предельная ширина листа в 350 мм.
Перечисленными указаниями и пользуются проектирующие при решении вопроса об устойчивости. Чтобы достигнуть достаточной жесткости, конструктор усиливает свободные края сжатых листов уголками, в коробчатых поясах ставит диафрагмы и соединяет вертикальные листы понизу решеткой. Хотя таким способом обыкновенно достигается достаточная жесткость, но все же были случаи крушения мостов, при которых листы поясов после разрушения носили ясные признаки выпучивания1). Вследствие этого исследование вопроса об устойчивости сжатых листов может иметь не только теоретическое, но также и большое практическое значение.
В настоящей работе мы приводим решение задачи в нескольких простейших случаях. Изложение начинаем с изложения
l) Das Eisenbahnungliick bei Monchenstein. Schweizerische Bauzeitung, 1891, Bd. 17, № 25, SS. 155—160; G. Mantel. Zum Einsturz der Monchensteiner Briicke. Там же, № 26, SS. 161—165; W. Ritter, L. Tetmajer. Bericht iiber die Monchensteiner Brucken-Katastrophe. Dem Vorteher Schweiz. Post- und Eisenbahndepartements erstattet von dem technischen Expert. Там же, Bd. 18, № 26, 18 SS,
118
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
задачи, решенной Дж. Брайаном1) и относящейся к прямоугольному листу, опертому всеми сторонами на контур. Остальные приведенные здесь задачи относятся к случаю прямоугольного листа, одна из продольных сторон которого остается свободной. Что касается другой продольной стороны, то задача разобрана в трех различных предположениях:
1) Продольная сторона оперта на контур;
2) Продольная сторона заделана абсолютно;
3) Продольная сторона заделана упруго.
Поперечные стороны во всех этих случаях предполагаются опертыми. Для пояснения того, что мы считаем опертым и что
стинки, как это делает в своем курсе А. Ляв2). Таким путем проще получить решение, чем, например, исследуя общее выражение для потенциальной энергии деформирующейся пластинки, как это сделано в выше цитированной работе Дж. Брайана, но зато остается недоказанным, будет ли устойчива исследуемая форма равновесия выпучившейся пластинки и будет ли ей действительно соответствовать наименьшее значение сжимающей силы.
§ 2. Принятые обозначения
В изложении мы будем пользоваться обозначениями курса А. Лява. Срединную плоскость пластинки примем за плоскость ху, ось г-ов направим нормально к пластинке. Толщину пластинки обозначим через б, а длину и ширину—буквами а и Ь. Помещая начало координат в углу пластинки, направляем оси х и у так, что уравнениями сторон прямоугольного контура будут х 0, х а, у 0, у Ь.
Двумя парами плоскостей, параллельных координатным плоскостям zx и гу, выделим прямоугольный элемент пластинки со сторонами dx и dy. Внутренние силы, распределенные по каждой из сторон выделенного элемента, согласно теории Густава Кирхгофа заменяем равнодействующими силами и парами. Как
) G. Н. В г у a n. On the stability of a plane plate under trusts in its own plane, with applications to the «buckling» of the sides of a ship. Proceedings of the London Mathematical Society, 1891, vol. 22, pp. 54—67.
2) A. E. H. Love. A treatise on the mathematical theory of elasticity. Cambridge, University Press, vol. 2, 1893, pp. 304—307.
заделанным краем, приведен рис. 3.
Опертый прой
Рис. 3.
Заделанный край
При решении перечисленных здесь задач мы будем исходить из дифференциального уравнения равновесия выпучившейся пла-
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
119
равнодействующие, так и моменты пар разложим на три составляющие, параллельные координатным осям. Обозначения этих составляющих сил и моментов, отнесенных к единице длины сторон выделенного прямоугольного элемента, приведены на рис. 4. Рис. а) дает обозначения составляющих сил, рис. Ь)—обозначения моментов.
Прогибы пластинки при выпучивании обозначим через до; тогда кривизна поверхности, по которой выпучивается пластинка, определяется величинами
k
d2w
ko
d2w
4 - dx2 ’ 2 dif ' X dxdy
Изгибающие моменты G и G2 и скручивающий момент Н выразятся такими формулами:
G — C(k ok2), G2 C(k2 oki), H C(l —o)x. (2)
Здесь через С обозначена цилиндрическая жесткость пластинки; выражение ее будет
с-пптг 3
Через а обозначено пуассоново отношение. При вычислениях мы будем принимать его равным 14.
Из условия равновесия выделенного элемента получаем следующие уравнения1):
дР 1 dU2 т и та» п dU f dPjt
d2w
(i)
дх
дТ
ду
дТ2
дх
И
ду
-Txkx-T2k2-0, дх , ду -f- Рk Pt2 (U t2) f о
— Ti х — T2k2 0,
дН
дх
за.
ду
Т2 0,
двх дН _ _п
дГ df
(4)
(5)
‘) См. указанную па стр. 118 книгу А. Ц. Н. Uove, р. 304.
120
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
§ 3. Прямоугольная пластинка всем периметром оперта на контур )
Обозначим через Р величину сжимающего усилия, приходящуюся на единицу длины поперечных сторон пластинки. Никаких других внешних сил к пластинке не приложено. Пока Р мало, плоская форма пластинки есть единственная и потому устойчивая форма равновесия. Увеличивая Р, мы можем достигнуть некоторой критической величины сжимающего напряжения, при которой, кроме плоской, возможна и искривленная форма равновесия. При дальнейшем возрастании Р пластинка выпучивается, но пока Р превосходит критическое значение сжимающего усилия на малую величину, искривленная форма равновесия пластинки мало отклоняется от плоской формы. В таком случае величины k, k2 и т, определяющие кривизну выпучившейся пластинки, суть величины малые, и в уравнениях равновесия (4) некоторые члены могут быть отброшены. В самом деле, перерезывающие усилия Т и Г2, как видно из уравнении моментов (5), суть величины того же порядка, что и моменты или величины ku k2, т; следовательно, такие члены, как Tku Т2, Тт, T2k2y суть величины второго порядка малости и могут быть опущены в общих уравнениях (4). Полученной таким образом системе уравнений мы можем удовлетворить, положив U U2 P2 0.
Величину же Рi примем за постоянную, равную —Р. Тогда из уравнений (5) и третьего уравнения системы (4) получаем такое дифференциальное уравнение для поверхности выпучиьшейся пластинки:
c( W-) -«- »’
Возьмем частное решение этого уравнения в такой форме:
л. пгтсх. пки ,_ч
w A sin - а -sin—у-. (2)
Очевидно, это решение удовлетворяет заданным условиям закрепления:
при х 0 и х a w 0 и G, 0;
при у 0 и y b w 0 и G2 0.
1) См. указанную на стр. 118 книгу А. Е. Н. Love, р. 304.
2) Это частный случай задачи Дж. Брайана (см. выше § 1). G. Н. Bryan при выводе идет иным путем: он пользуется общими теоремами об устойчивости, подробно разобранными в его интересной работе «On the stability of elastic systems». Proceedings of the Cambridge Philosophical Society, mathematical and physical sciences, 1889, vol. 6, pp. 199—210.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
121
Кроме того, удовлетворены условия для напряжений на контуре:
Л -я, и1 и2 р2 0.
Относительно величин Т и Т2 никаких условий на контуре не поставлено, и они могут быть определены из уравнений (5) § 2.
Взятое нами частное решение (2) представляет одну из возможных искривленных форм равновесия выпучившейся пластинки. Подставляя это решение в дифференциальное уравнение (1), найдем то значение сжимающего усилия Я, при котором взятая нами форма равновесия становится возможной. Результат подстановки будет
2 т1 п2 2
( т2к2 , п2п2 2 ( tnz , п2 X
I а2 62 _ 2 УЖ Ь2 )
а
Из всех возможных форм равновесия интересно найти ту, которой соответствует наименьшее значение Р для этого нужно числа тип подобрать так, чтобы правая часть (3) была минимумом. Очевидно, п нужно положить равным единице. Для определения же числа ш, т. е. числа полуволн, на которые подразделится при выпучивании пластинка, нужно дополнительное исследование. Обозначим через К длину полуволны; тогда а2т2 № и уравнение (3) перепишется так:
f——V8
Р Сл2 , 62 '. (3')
Если длина пластинки велика, то изменению числа полуволн т на единицу соответствует малое изменение длины В таком случае мы можем положить, что X изменяется непрерывно, и обычным путем найти значение А, обращающее правую часть (3') в минимум. Легко видеть, что это будет при X Ь. Следовательно, первой возможной искривленной формой равновесия будет та, при которой выпучившаяся пластинка узловыми линиями подразделяется на квадраты. Если длина пластинки невелика, то тогда число полуволн т определяется на основании таких рассуждений. Положим, что при некоторой длине пластинки первая искривленная форма равновесия имеет т полуволн. Увеличивая длину, можем достигнуть такого предела, при котором пластинка может подразделиться и на т и на т -К 1 полуволн под действием одного и того же сжимающего
122
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
усилия Р. Длина пластинки, соответствующая этому предельному состоянию, определится на основании (3) из уравнения
( п2я2 , я2 2 Г (tn I)2 я2 , я212
а2 Ь2 ) L а2 b2 J
п2я2 (tn I)2 я2 ’
а2 а2
откуда а Ъ У т (т 1). (4)
Из приведенной формулы получается предельная длина а, при которой первая искривленная форма равновесия состоит из т полуволн. Одну полуволну будем иметь при длинах от а 0 до а b Г2. Две полуволны — при длинах от а Ь 2 до а b Уб и т. д.
Формулы (3') и (4) вполне решают вопрос об устойчивости, и ими нужно пользоваться вместо приведенной вначале формулы И. Ходкинсона. Безопасное сжимающее напряжение следует брать во столько раз меньше критического напряжения, получаемого из формулы (3'), во сколько раз безопасное сопротивление при простом растяжении берется меньше временного сопротивления разрыву. Величины Я, получающиеся из формулы (3'), очевидно, имеют смысл только до тех пор, пока они не превосходят предела упругости материала.
Чтобы показать, как зависит критическая величина сжимающего напряжения от толщины пластинки, и связать полученные результаты с дальнейшим, введем одно новое обозначение, положим
РЪ2 _ 2РЬ2 (1 — о2) _ г,
С “ 63 Ut
Принимая во внимание, что Р6 R, где R — величина сжимающего напряжения, будем иметь
u-XSlfri»()’. ,50
Из формулы (3) при ti 1 имеем
б
Следовательно, при заданном соотношении между длиной и шириной пластинки величина U постоянна, и следовательно см. (5'), „р пропорционально квадрату отношения 66.
Для наглядного представления изменения U, а следовательно, и Кр в зависимости от соотношения между длиной и шириной пластинки построим диаграмму (рис. 5). По оси абсцисс
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
123
отложим отношение а6, а по оси ординат соответствующие значения U, пропорциональные критическому напряжению R. Таким образом, получим систему кривых — каждая из них соответствует определенному числу полуволн т. Нижние части этих кривых, показанные утолщенными линиями, определят собой при каждом заданном отношении а6 величину U, а следовательно, и RKV, соответствующие первой возможной искривленной форме
равновесия. С возрастанием длины U стремится к постоянному пределу, соответствующему подразделению пластинки на ряд квадратов. В этом случае из формулы (6) имеем U 4л2 и критическое сжимающее напряже¬
ние будет
Якр
Таблица А
4п2Е
12 (т)21-)’
а
ъ
и
кр, кгсм2
а
Ъ
и
кр,
кгсм2
0,5
61,7
1097
1,1
39,9
709
0,6
50,6
900
1,2
40,8
725
0,7
44,7
795
1,3
42,2
750
0,75
42,8
761
—
_
0,8
41,5
738
1,4
44,1
784
0,9
39,9
709
1,5
46,3
823
1
39,5
702
1,6
48,9
869
Ниже мы приводим ряд численных значений U для случая т 1; отношение аb изменяется от 0,5 до 1,6. Этих чисел достаточно, чтобы с практически нужной точностью определить величину U для любого соотношения а6. Рядом приведены величины критических напряжений, вычисленные в предположении 66 100, 2106 кгсм2 и а 14. Если действительное соотношение 66 п, то для получения критических напряжений нужно числа
таблицы помножить на Возьмем численный пример. Железный лист, находящийся в условиях, соответствующих разобранной задаче, имеет длину
124
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
а 522 см, ширину b 60 см, толщину 61 см. Найти величину критического сжимающего напряжения. Как мы видели, пластинка при выпучивании подразделяется на части, возможно менее отличающиеся от квадратов. Следовательно, в нашем примере лист подразделится на восемь или на девять полуволн. Наибольшая длина а' листа, которой соответствует первая искривленная форма с восемью полуволнами, определится из формулы (4):
а' 60 уЧПГ 509,1 см.
Так как полученная величина а' меньше длины нашего листа, то, следовательно, наш лист при выпучивании подразделится на девять частей. Длина каждой части будет 5229 58 см. Соотношение между длиной и шириной равно 5860 0,97. Со¬
ответствующее U получаем из таблицы интерполированием:
U 39,6 и кр « 700 (-у-)2 1940 кгсм2.
Следовательно, при четверном запасе прочности в данном случае возможно допустить сжимающее напряжение в 490 кгсм2. Мы предполагали края листа опертыми, в действительности края листа бывают приклепаны и жесткость листа больше, нежели то получается из вышеприведенных формул. Влияние приклепывания тем, очевидно, больше, чем меньше ширина листа.
§ 4. Случай прямоугольной пластинки, выпучивающейся по цилиндрической поверхности
Положим, что в прямоугольной пластинке оперты только поперечные стороны х 0 и х а, по которым равномерно распределены продольные сжимающие усилия. Величину их, отнесенную к единице длины, обозначим, как и раньше, через Р. По продольным сторонам при выпучивании появляются непрерывно распределенные усилия, обеспечивающие искривленной пластинке цилиндрическую форму. Дифференциальное уравнение поверхности будет то же, что и раньше:
c(4-)pJ-0- 0)
Частное решение уравнения возьмем в этом случае в такой
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
125
Подстановкой этого решения в уравнение (1) получим величину критической нагрузки, соответствующую выбранной форме равновесия:
р р т2л2 __ Е63 т2к2 ,о
И а2 12(1 -а2) а2 '
Полученное для Р значение отличается от результата обычной формулы продольного изгиба множителем (1—а2). Такое увеличение жесткости получилось вследствие того, что пластинка выпучивается по цилиндрической, а не по антикластической поверхности.
Первая возможная искривленная форма равновесия будет л2
при т 1 Р С—j-, или, вводя величину U, получим
TI РЬ2 2 Ь2
f_3t2_ (4)
И здесь величина U вполне определяется соотношением между длиной и шириной пластинки. Если прибегнуть к графическому построению, аналогичному построению предыдущего параграфа, то для U получим кривую, имеющую своими асимптотами оси л;-ов и у-ов.
Для вычисления величины критического напряжения будем иметь прежнюю формулу:
п кр 12(1 - а2) (Ь6)2
§ 5. Прямоугольная пластинка тремя сторонами оперта на контур. Случай 1-й
Пусть опертыми сторонами будут стороны х 0, х а, у 0. Сжимающие усилия Р равномерно распределены по сторонам х 0 и х а. Основным уравнениям равновесия (4) § 2 удовлетворим, положив
Р — Р, Р2 С1 2 0.
Дифференциальное уравнение искривленной при выпучивании поверхности пластинки будет прежнего вида:
c(-2wf)'-Sl-0- Всякое решение этого уравнения, удовлетворяющее условиям закрепления на контуре, определит одну из возможных форм равновесия. Подстановкой взятого решения в уравнение (1) получаем величину сжимающих усилий Р, соответствующую вобранной форме равновесия.
126 К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
Возьмем решение уравнения в таком виде:
л тпх п
w Ay sm——. (2)
Вид искривленной поверхности, представленной этим решением, таков, что всякое сечение ее плоскостями, параллельными плоскости zy, дает прямую линию, проходящую через ось х-ов, и, следовательно, выпучивание пластинки сопровождается скручиванием. Сжимающее усилие Я, соответствующее выбранной нами форме равновесия, будет
Р С(3)
т. е. то же самое, что и в случае пластинки, выпучивающейся по цилиндрической поверхности.
Нетрудно видеть, что взятое решение удовлетворяет условиям закрепления:
при х 0 и х a w О, G 0;
при у 0 до 0, G2 0.
Что касается четвертой, неопертой стороны у 6, то по ней, для возможности выбранной нами формы равновесия, должны
быть распределены по известному закону усилия Т2 и моменты G2 и Н. Эти усилия вместе с напряжениями по опертой
продольной стороне и производят скручивание пластинки. Под¬
считаем величину скручивающего момента, приходящуюся на единицу длины пластинки. Усилия и моменты, отнесенные к еди нице длины на стороне у Ь, будут
С2 С (k2 afe,) - ACab-- sin (4)
H C(l-a)x AC(l-a) -cos-, (5)
rj, dH dG2 An m2n2. ткх
Т -ж1 АС—5т—- 6
Г. Кирхгоф показал1), что момент Я может быть заменен перерезывающим усилием Г2, распределенным по закону
и2тг2
т' on лг т“л . ткх _ч
7’2--ж-ЛС(1-а)—r-sin—(7)
) Lord Kelvin (W. Thomson). Treatise on natural philosophy. Vol. 2, Cambridge, University Press, 1888, p. 645. G. К i г с h h о f f. Uber das Gleichgewicht und die Bewegung einer elastischen Scheibe. Journal fur die reine und angewandte Mathematik (Crelle), 1850, Bd. 40, № 1, SS. 51—88. Gs sammelte Abhandlungen, 1883, Leipzig, B. G. Teubner, SS. 234—279.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
127
На опертой стороне момент G2 О, а перерезывающие усилия Т2 и Г2 имеют значения (7) и (6). Отнесенный к единице длины момент этих усилий относительно оси л;-ов будет
М (т2ть G2 A2b-a)C-sn--. (8)
Мы остановились на вычислении скручивающего момента М, чтобы показать, что к тому же результату можно прийти элементарным путем. Пусть АВ (рис. 6) представляет собой сечение выпучившейся пластинки плоскостью, параллельной плоскости zy. Угол вращения ср взятого поперечного сечения относительно оси х-ов может быть выражен через ширину пластинки b и прогиб на неопертом крае
DiO Л и тКХ
ВС Abs in :
очевидно,
ВС л. тпх
Ф Г5 A sin т АВ а
Кручение пластинки выразится через первую рИс. 6.
производную от угла ф по х, а изменение величины кручения, обусловленное непрерывным распределением скручивающего момента, — второй производной от того же угла. Обозначая буквой К величину жесткости пластинки при кручении, получим для скручивающего момента, отнесенного к единице длины, такое выражение:
М--К-АК
-sin-
ткх
(9)
Сравнивая полученный результат с формулой (8), видим, что формулы эти разнятся только тем, что вместо множителя 2b( 1—а) С входит множитель К. Нетрудно показать, что эти множители одинаковы. Подставляя вместо С его значение, будем иметь
“«-ic-WTsr ‘)
Для жесткости при кручении К с достаточной точностью можем взять 1)
K jb6G,
) См. нашу работу «Об устойчивости плоской формы изгиба двутавровой балки под влиянием сил, действующих в плоскости ее наибольшей жесткости». Известия С.-Петербургского политехнического института. Отд. оттиск, С.-Петербург, 1906, 132 стр.
128
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
где G — модуль упругости материала при сдвиге. Подставляя вместо G его выражение через Е, получим
— формулу, тождественную с формулой (10).
Таким образом, элементарное рассмотрение приводит к тем же результатам, что и точная теория. Этим элементарным приемом мы воспользуемся в следующей задаче.
§ 6. Прямоугольная пластинка тремя сторонами оперта на контур. Случай 2-й
Взятое в предыдущем параграфе решение (2) привело нас к заключению, что по продольной неопертой стороне должны быть непрерывно распределены усилия Г2, Г2, G2. Такое решение не может иметь практического значения, и мы им воспользовались, чтобы на простейшем примере показать элементарный прием для определения распределения усилий. Теперь мы ставим своей задачей отыскать такое решение основного дифференциального уравнения, при котором продольная неопертая сторона пластинки являлась бы свободной от всяких усилий.
Можно заранее сказать, что в этом случае критическое значение сжимающей силы будет большее, нежели для пластинки, обе продольные стороны которой свободны. Увеличение жесткости пластинки получается благодаря появлению реакций по опертой стороне, противодействующих выпучиванию пластинки. На рис. 7 представлено одно из поперечных сечений пластинки после выпучивания. Линия АВ будет, очевидно, уже не прямая, как в ранее рассмотренном случае, а искривленная, как показано на рисунке. Реакции по опертой стороне имеют направление, указанное стрелкой.
Как закон распределения этих реакций, так и критическое значение сжимающей силы попробуем предварительно найти элементарным путем. Для этого примем линию АВ за прямую; через ф обозначим угол, составляемый ею с осью у-ов. Выпучивание пластинки и в этом случае сопровождается скручиванием. Величина изменения необходимого для этого скручивающего момента, отнесенная к единице длины, выражается через угол ср, как и в предыдущем случае, формулой
ж 1 rs d2(D , 1Ч
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
129
Непрерывное изменение скручивающего момента обусловлено реакциями, появляющимися при выпучивании вдоль опертой стороны у 0 пластинки. Если величину реакции, отнесенную к единице длины, обозначим через q, то будем иметь
q dx М dx fС dx,
откуда
2 rr d2р _ 4 „ d2w
q Т А Ь2 А
(2)
В полученной формуле мы обозначили через w прогибы пластинки по срединной линии, соединяющей центры поперечных сечений. Заменим каждое элементарное усилие q dx, приложенное у края пластинки, равным и параллельным ему усилием в центре поперечного сечения О и парой сил y q dx. Так как скручивающие пары не меняют величины критической нагрузки, то наша задача теперь сведена к случаю продольного изгиба стержня (рис. 8), выпучиванию которого противодей- m — ствуют поперечные реакции, распределенные по закону, представленному формулой (2).
Эту задачу продольного изгиба мы решим таким образом.
Пусть Q — сжимающая сила, при которой произошло выпучивание стержня. Если эта сила мало отличается от критической нагрузки, то полученная искривленная форма рав новесия стержня мало отличается от прямолинейной, и мы для выражения кривизны можем пользоваться обычным приближенным выражением. Возьмем произвольное сечение тп с абсциссой х и напишем уравнение равновесия верхней отсеченной части:
а а2
EJ--Qw j q(l-x)di-(l-x)j qdl
(3)
Последовательным дифференцированием получаем
а а2
г-i г d4w d2w
EJ -т-т- — Q-
dx4
dx2
130 К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
Вставляя вместо q его значение (2), получаем дифференциальное уравнение изогнутой оси стержня в такой форме:
«—(«-) «
Общий интеграл уравнения (4) будет ш Л sin (q - -K Bcos-7-(2-г)
Чтобы удовлетворить условиям на концах стержня, необходимо положить в-о.
Следовательно, критическое значение сжимающей силы будет
r EJn2. 4С с
Полученная формула дает возможность сделать такое заключение. Удерживание на контуре одной из продольных сторон пластинки увеличивает ее жесткость. Величина возрастания критической нагрузки определяется членом 4С62 и, следовательно, пропорциональна К и обратно пропорциональна квадрату ширины. Чем больше ширина пластинки, тем меньшее влияние на величину критической нагрузки оказывает удержание одной из продольных сторон на контуре. Это общее заключение, сделанное на основании элементарного решения, совершенно верно. Численное же значение добавочного члена оказывается, как это мы увидим из точного решения, преувеличенным приблизительно на 25. Это преувеличение жесткости является результатом нашего предположения, что поперечное сечение АВ после выпучивания остается прямолинейным. Если принять вышеуказанную поправку, то формула (5) дает возможность легко вычислять величину критической нагрузки для пластинки, тремя сторонами опертой на контур.
§ 7. Точное решение предыдущей задачи
Исходим из ранее полученного дифференциального уравнения для поверхности выпучившейся пластинки:
r( dw I О dw -Ё1Е р 1
С дх2 ду2 ду ) Г дх2 и- 1)
Возьмем решение этого уравнения в такой форме:
w Asin-f(y).
к ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК 131
Тогда условия закрепления на поперечных опертых сторонах пластинки х 0 и х а будут удовлетворены. В самом деле,
при х 0 w 0, Gj 0;
при х a w 0, Gj0.
Неизвестная пока функция f(y) должна быть так подобрана, чтобы было удовлетворено уравнение (1) и условия на продольных сторонах пластинки. Подставляя решение (2) в дифференциальное уравнение (1), получим для определения f(y) такое уравнение:
Г ») - 2 (;) Г ») () - (-) Г (. - о. (3)
Общий интеграл этого уравнения может быть представлен в такой форме:
f (у) СеаУ С2еаУ С3 cos fiy С4 sin pz, (4)
где аир имеют значения
«- W(“)’♦(“)'
Заметим, что р есть число вещественное, т. е.
В самом деле, если бы то тогда величина крити¬
ческой сжимающей силы рассматриваемого случая равнялась бы эйлеровой нагрузке или была бы меньше ее, между тем как удерживание одной из продольных сторон пластинки наверное увеличивает ее жесткость, и, следовательно, должно иметь место неравенство (6). Произвольные постоянные Сi,., С4 общего интеграла должны быть подобраны таким образом, чтобы были удовлетворены условия на продольных сторонах пластинки. По опертой продольной стороне у 0 должны быть выполнены два следующих условия:
I) при у 0 w 0;
II) при у 0 G2 C у зг) “ 0.
Что касается неопертой продольной стороны у — Ь, то она
должна быть свободна от всяких усилий. Следовательно,
III) О » 0 при у » Ь,
132 К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
Условия относительно перерезывающих усилий Г2 и моментов Я, как уже ранее было упомянуто (см. § 5), могут быть сведены к одному условию такого вида:
'г дН л -
Т2 0 при у Ь.
Если мы примем во внимание одно из основных уравнений равновесия (5) § 2, то последнее условие может быть представлено в таком виде:
IV) 2-0 при у-Ь.
Итак, для определения четырех произвольных постоянных общего интеграла (4) имеем такое же число условий на продольных сторонах пластинки.
Условия I и II дают нам два таких уравнения:
Сх С2 С3 0, (V С2а2 - С3р2 0;
так как а ф р, то полученным уравнениям можно удовлетворить, положив С3 0 и Ci —С2.
В таком случае неизвестная функция f(y) должна иметь форму
(у) A sh ay В sin ру.
Условия III и IV приводят нас к уравнениям А а - о (-)’ sh «» - Б jf 0 () sin р». 0,
а-2()4о (--)а»- (7)
- Bf ( 2 (-f - о (.) cos р - 0.
Этим уравнениям мы можем удовлетворить, положив А В 0.
Но в таком случае и f(y) 0, следовательно, пластинка сохраняет свою первоначальную плоскую форму. Для возможности выпучивания пластинки необходимо, чтобы уравнения (7) допускали для А и В решения, отличные от нуля. Это, очевидно, может иметь место лишь в том случае, когда определитель этих уравнений обращается в нуль, т. е. когда
- а р а (-)’ а - 2 (Ь)’ or (L)’ tg cth аб - 0.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
133
Полученное уравнение мы можем упростить, если примем во внимание следующие равенства:
Р 2(-)-о и а’-2
вытекающие из обозначений (5).
Окончательное условие, при котором становится возможным выпучивание пластинки, перепишется в такой форме:
Ра2-сгНг)2ihab а аИг)2'
Число т, входящее в это уравнение, обозначает, на сколько полуволн подразделяется пластинка при выпучивании. Меняя т, получаем различные возможные формы равновесия и соответствующие им критические значения сжимающего усилия Я. Р . Дальнейшие вычисления по- jrP Х
кажут, что наименьшее значение Я получается при т 1, у
т. е. когда выпучившаяся пластинка имеет вид, представлен- Рис. 9.
ный на рис. 9.
Уравнение, определяющее возможность выпучивания в этом частном случае, будет
p(a2-cr-)2tha6 a(p2 a-)2tgp6. (9)
Сюда входят как размеры пластинки а, 6, б, так и соответствующие значения Я. Чтобы яснее была видна зависимость между размерами пластинки и Я, введем наше прежнее обозначение РЬ2С U и, кроме того, положим
л262а2 V. (10)
Тогда уравнение (9) представится в таком виде:
VyW-V -o)VVTrv2ih(VVuV v ) VVuV VVuv (-a)v2tgVyuv-v). (ii)
Из двух величин, входящих в уравнение (11), величина V зависит только от отношения ширины пластинки к ее длине. Раз это отношение задано, мы, решая уравнение (11), находим соответствующее значение U. Решение уравнения в каждом частном случае требует довольно длинных арифметических вычислений, так как корни приходится подбирать последовательными пробами. Это подбирание решений можно значительно себе облегчить, если воспользоваться элементарным решением,
134
К ВОПРОСУ ОБ УСТОПЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
изложенным в § 6. Для критического значения сжимающей силы нами была получена формула
EJn2 , 4С
Здесь EJ — наименьшая жесткость пластинки при изгибе, К — жесткость при кручении.
Принимая во внимание, что
Q-Pb, С,
63
12(1 -а2)
и полагая EJ ЬСУ будем иметь
РЪ2 п2Ь2
f 6
или, вводя наши обозначения U и V, получим
U V 6.
(12)
Это и есть результат, полученный элементарным путем.
Уже ранее было замечено (см. § 6), что второй член в правой части выражения (12) преувеличен и что это преувеличение можно оценить в 25. Убедиться в этом можно таким образом. Пусть длина пластинки возрастает беспредельно. Величина V при этом, очевидно, стремится к нулю, а следовательно, U стремится к некоторому постоянному пределу. Для нахождения этого предела возьмем уравнение (9) и представим его в таком виде:
ja tgpfr р thab
a2
(13)
При очень большой длине величины аb и рb будут малы. Мы можем разложить tgfib и th ab в ряды и сохранить только по два первых члена этих рядов; тогда левая часть (13) преобразуется так:
.teW 'Ч»»
Р th ab ,_.(a6)2
Если вместо аир ввести их значения и воспользоваться обозначениями U, 1, то нетрудно получить
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК 135
Правая часть (13) может быть преобразована таким же способом:
Г 2 Я1
(X — (Т —5
а2
2
1 »,. “ 4 а V Р
2
тг2
--Hl I f _ 4 а V Р
-'н
Подставляя полученные результаты в уравнение (13), будем для определения предельного значения U иметь
i±vm13-,
откуда U 4,5, т. е. действительно на 25 меньше того, что дает элементарное решение. Введя эту поправку, будем иметь для определения U, при различных соотношениях между длиной и шириной пластинки, такую формулу:
7 4,5. (14)
Результаты, которые получаются для U из этой формулы, очень близки к корням уравнения (И). При отношении аb от
а
Ь
О 2 4 6 S Ш 12
Рис. 10.
1 до 2 разности немного больше 1; с возрастанием же длины пластинки эти разности быстро уменьшаются, и уже при аb 10 разность меньше 15. Следовательно, на практике всегда можно пользоваться формулой (14) для определения величины критического сжимающего усилия. Кроме того, ряд значений U вычислен нами из уравнения (11). Результаты помещены в таблице В и изображены графически на диаграмме (рис. 10). По оси
136 К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
абсцисс отложены значения отношения а6, а по оси ординат — соответствующие значения U. Полученная кривая асимптотически приближается к прямой у 4,5.
Таблица В
а
Ь
и
Якр, кгсм2 при-- 100
а
Ь
и
Якр, кгсм2
прн 100 о
1
14,21
252,6
2,5
6,02
107,0
1,2
11,20
199,1
3
5,56
98,9
1,4
9,40
167,1
4
5,09
90,5
1,6
8,24
146,5
5
4,88
86,8
1,8
7,45
132,5
8
4,64
82,5
2
6,89
122,5
10
4,59
81,6
. Раз для известного соотношения между длиной а и шириной b пластинки величина U определена, то величина соответствующего сжимающего напряжения RKр найдется так
р _ Р _ EU62 Kkv 6 “ 12(1 -о)Ь2 ’
и, следовательно, для всякого U величина Кр обратно пропорциональна квадрату отношения ширины пластинки b к толщине ее б. С возрастанием толщины и уменьшением ширины пластинки жесткость ее быстро возрастает. В таблице В приведены числовые значения RKр, полученные в предположении
у 100, а -j, Е 2 106 кгсм2.
Когда приходится определять RKр для пластинки, у которой, например, Ь8 п то числа таблицы нужно, очевидно, умножить на число (100п)2. Если мы за среднее значение предела упругости для железа возьмем 2000 кгсм2, то нетрудно убедиться вычислением, что при длинных пластинках, уже начиная с Ь8 20, величина критического значения сжимающего напряжения Кр меньше предела упругости и быстро уменьшается с увеличением Ьб, так что при Ь8 100 уже RKр 80 кгсм2. Короткие пластинки, конечно, более жестки.
Возьмем численный пример.
Положим, железный лист имеет длину а 1,60 м, ширину Ь 40 см, толщину б 1 см. При у 4 величина U бу¬
дет U 5,09. При этом значении U и при Ь8 100 значение критического сжимающего напряжения по таблице В будет Rkр 90,5 кгсм2 так как в нашем случае Ь8 40, то искомую
к ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
137
величину критического сжимающего напряжения получим, умножая число таблицы на 6,25; следовательно,
кР 90,5 X 6,25 566 кгсм2.
В условиях, аналогичных рассмотренному нами случаю сжатой пластинки, находятся полки уголка, сжатого силами, равномерно распределенными по концам (рис. 11). Если ребра АВ, АС, DE и DF удерживаются неподвижно и полки уголка имеют значительную ширину, то сжатый уголок не выпучивается, как стержень, и к нему неприложимы формулы продольного изгиба. Каждую полку уголка нужно рассматривать как пластинку, тремя сторонами опертую на контур. Раз сжимающие усилия достигнут критического значения, определяемого по вышеприведенным формулам, обе полки уголка начинают выпучиваться в одну и ту же сторону. Ребро AD при этом остается прямолинейным, а отдельные поперечные сечения уголка, сохраняя свой вид, поворачиваются около ребра АВ. Если только нижние ребра DF и DE удерживать неподвижно, а верхние оставить свободными, то значение критического сжимающего напряжения уменьшается. Оно будет такое же, как для пластинки, опертой тремя сторонами, но имеющей длину вдвое
большую, нежели длина AD уголка.
В заключение скажем еще несколько слов о значении первоначальной кривизны пластинки. Особенно важное значение имеет первоначальная кривизна в плоскости zx. Если эта кривизна не нуль, то правые части уравнений (7) отличаются от нуля, и из них можно получить для произвольных постоянных А и В определенные решения при всяком значении сжимающего усилия Р. Следовательно, при самых малых нагрузках уже начинается искривление пластинки; но, пока первоначальная кривизна невелика и определитель уравнений (7) не близок к нулю, возрастание кривизны идет медленно. С приближением определителя к нулю значения произвольных постоянных А и В начинают быстро возрастать, а вместе с тем быстро растет и искривление пластинки. Если бы мы картину явления представили
188
к ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
графически, откладывая по оси абсцисс величину сжимающего усилия, а по оси ординат соответствующие ему искривления, то получили бы приблизительно кривую, представленную на рис. 12.
Кривая асимптотически приближается к прямой АВ, параллельной оси у-ов и проведенной на расстоянии Ркр от нее. Здесь ЯКр вычисляется по формулам, относящимся к первоначально плоским пластинкам.
§ 8. Прямоугольная пластинка с абсолютно заделанной продольной стороной
Сохраняя прежнее расположение координат, положим, что
стороны 0 их а оперты и по ним равномерно распределены
сжимающие усилия Р кг на единицу длины стороны. Сторона у 0 абсолютно заделана, и сторона у b свободна от всяких усилий. Дифференциальное уравнение равновесия выпучившейся пластинки остается прежним:
cf dw I о dw I d4g, I P — л m
bdx дхду dy)±y dx2 U
Решение этого уравнения возьмем в прежней форме:
w Asin--f(y). (2)
Оно удовлетворяет условиям на поперечных опертых сторонах х 0 и х а:
при х 0 w 0 и G 0;
при х a w 0 и G 0.
Для определения f(y) из (1) будем иметь прежнее линейное уравнение с постоянными коэффициентами. Интеграл его будет
f (У) СеаУ С2еаУ С3 cos у С4 sin ру, где а и р, как и раньше, имеют значения
«-7ЩГМ'
Условия по заделанной продольной стороне у 0 будут:
I) при у 0 w 0;
К ВОПРОСУ ОВ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК 139
По свободной продольной стороне у b условия остаются прежние:
III) при у Ь G2 0;
IV) при у Ь l 2-f-O.
Условия I и II приводят нас к уравнениям
С С2 С3 0, (С С2) (х 0,
откуда
г _ _ аС3 РС4 аС8 - рС4
Cl 2а 9 С2 2а
Подставляя эти величины в общий интеграл, можем представить f(y) в такой форме:
f(y) A (cos р( - ch ay) В (sin у - sh ay.
Подставляя полученное значение f(y) в условия III и IV и производя некоторые преобразования, получим два таких уравнения:
А р2 0 (гГ cos 2 ” Иг)2ch ab
В р2 0 ()2 sin рб -§ а2 - а (-)2 sh ab 0,
X - р а - а (S-)’ sin (Ь ар а ()’ sh ab В р а2 - а (--)2 COS р Р р2 а (-—)2 ch ab j 0.
Уравнения эти могут дать для А и В определенные решения, отличные от нуля, только в том случае, если определитель их обращается в нуль, т. е. когда
р2а ()2 cos рб а2 - а (-)2 ch аб р а2 - а (-)2 cos рЬ р р2 а (-)2 ch ab р2 а (-)2 sin рЬ
ча2- Hr) sh аб - р а2 - а (-)2 sin Р6
ap2 tx(-)2sha J-. (5)
Введя временно обозначения
п9. ( ттс 2 , о ( ттс 2
Р al—) a al—) s-
140
к ВОПРОСУ Ofc УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
можем уравнение (5) представить в более простом виде:
«22 _ Д2С2
2ts (s2 t2) cos pb chab — sin sh aft. (6)
Число m, входящее в уравнения (5) и (6), обозначает число полуволн, на которое пластинка подразделяется при выпучивании. Задаваясь числом т и размерами пластинки, мы можем из уравнения (6) определить то значение продольного сжимающего усилия Я, при котором выбранная форма равновесия выпучившейся пластинки становится возможной. В дальнейшем мы будем вычислять критические значения сжимающего усилия Р в предположении, что т 1. Имея числа для этого случая, мы можем определить РКр для любого другого числа т.
Для вычисления корней трансцендентного уравнения (6) при различных размерах пластинки мы введем наши прежние обозначения
тогда уравнение (6) может быть после ряда преобразований представлено в виде
JL у — U (—г V U j cos V-v Vuv chVv Vvu
(±VuvW-ySfw)x
X snV - V уш shV V VTjV. (7)
Задаваясь различными соотношениями между длиной и шириной пластинки, а следовательно, различными значениями V, определяем из уравнения (7) соответствующие значения U. Ряд вычисленных значений U приведен в нижепомещенной таблице С.
Таблица С
а
b
и
RKn, кгсм2 Ь
при -100
а
Ъ
и
RKn, кгсм2 Р L при 100
1
16,76
298,0
1,8
13,24
235,4
1,1
15,41
274,0
1,9
13,43
238,8
1,2
14,47
257,3
2,0
13,67
243,1
1,3
13,88
246,8
2,1
14,01
249,1
1,4
13,45
239,1
2,2
14,35
255,1
1,5
13,20
234,7
2,3
14,76
262,4
1,6
13,13
233,5
2,4
15,21
270,4
1,635
13,11
233,1
—
—
—
1,7
13,15
233,8
2,5
15,73
279,7
к ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК 141
Рассматривая приведенные в таблице С численные значения U, мы видим, что сначала с возрастанием длины пластинки U убывает и между аЬ 1,6 и аЬ 1,7 достигает своего наименьшего значения. (Ниже будет показано, что U имеет минимум при аЬ 1,635.) При дальнейшем возрастании отношения ab U начинает увеличиваться, сначала медленно, а потом все быстрее.
На основании этого сейчас же можно сделать заключение, что выбранная нами форма равновесия, состоящая из одной полуволны, не всегда будет первой возможной искривленной формой равновесия; иногда искривленная форма с двумя, тремя и т. д. полуволнами может соответствовать наименьшему сжимающему напряжению. Чем длиннее пластинка, тем на большее число полуволн она подразделится при выпучивании. Заметим, что при подразделении пластинки на несколько полуволн, каждая часть пластинки, соответствующая одной полуволне, находится совершенно в таких же условиях, как отдельная пластинка, длина которой равна длине полуволны. Отсюда ясно, что длинная пластинка стремится подразделиться на такое число полуволн, чтобы для каждой полуволны отношение между длиной ее и шириной пластинки было как можно ближе к 1,635, т. е. к тому пределу, которому соответствует наименьшее значение сжимающего напряжения. Для большей наглядности мы представим изменения величины U графически. Для этого по оси х-ов отложим значения отношения а6, а по оси у-ов соответствующие значения U. Наметив значения U, приведенные в таблице С, мы можем построить кривую для того случая, когда искривленная форма равновесия состоит из одной полуволны. Чтобы получить кривые для случая двух, трех и т. д. полуволн, нужно повторить прежние значения Uy увеличивая абсциссы в два, в три и т. д. раз. Таким образом получена система кривых, представленная на рис. 13. Кривые эти пересекаются между собой, и нижние их части, вычерченные утолщенной линией, определяют собой те значения , которые соответствуют первой возможной форме равновесия. С возрастанием длины пластинки утолщенная линия диаграммы все меньше и меньше отклоняется от прямой, параллельной оси х-ов и соответствующей U 13,11.
Следовательно, при расчете пластинок значительной длины без большой погрешности можно принять U 13,11. Раз величина U для заданной пластинки определена, мы можем вычислить величину критического сжимающего напряжения кр по формуле
р _ Ркр __
кр 6 12 (1 — а2) Ь2
142
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
Относительно величины RKр здесь можно сделать те же заключения, что и в случае пластинки, тремя сторонами опертой на контур, именно: при заданном отношении аb величина критического напряжения прямо пропорциональна квадрату толщины пластинки и обратно пропорциональна квадрату ее ширины.
В таблице С приведен ряд значений кр. Величины эти вычислены в предположении
Е 2- 10 кгсм, т 4 j 100.
Если в рассчитываемой пластинке Ь8 м, то числа таблицы, очевидно, придется помножить на число (100п)2.
Возьмем численный пример. Положим, имеется лист, длина которого а 3,00 м, ширина Ь 0,50 м, толщина б 0,01 м. Продольная сторона заделана, поперечные оперты; под действием сжимающих усилий лист подразделится на три или на четыре полуволны. В случае трех полуволн отношение длины полуволны к ширине пластинки будет равно двум, соответствующее значение U будет U 13,67.
В случае подразделения пластинки на четыре полуволны длина каждого участка будет 75 см. Отношение длины полуволны к ширине пластинки будет 1,5, и соответствующее U 13,20. Следовательно, первая возможная искривленная форма равновесия будет состоять из четырех полуволн. Величина критического напряжения по таблице RKр 234,7 кгсм2.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
143
10,210,21,27 50,7-1,27
В нашем примере отношение ширины к толщине bJ8 50. Следовательно, число таблицы нужно помножить на (10050)2 4:
кР 234,7 X 4 938,8 кгсм2.
Возьмем еще пример из мостовых конструкций. Проверим на устойчивость вертикальный лист таврового сжатого пояса в двухраскосной ферме, рассчитанной Е. О. Патоном1). Сечение в панели 5—7 имеет размеры, указан- 7архлпаг
ные на рис. 14. Будем считать, что - ' '
вертикальный лист абсолютно заделан по линии поясных заклепок; тогда расчетная ширина листа будет b 45,7 см, отношение ширины и толщины Ь6 36.
Длина панели, а следовательно, и расчетная длина вертикального листа равна 4,5 м. При такой длине мы без больших погрешностей мо- Рис. 14.
жем положить U 13,11.
Критическое сжимающее напряжение по таблице С будет кр 233,1 кгсм2. Чтобы получить значение критического напряжения для нашего случая, нужно число таблицы помножить на число (10036)2.
Будем иметь
Якр 233,1 (-)2 1800 кгсм1.
Получаем напряжение, не превосходящее среднего значения предела упругости для железа. При четырехкратном запасе прочности возможно было бы в данном случае допустить не больше 450 кгсм2. В действительности основное напряжение в этой панели достигает величины 684 кгсм2. Кроме того, имеются еще значительные дополнительные напряжения. Влияние дополнительных напряжений особенно неблагоприятно в том случае, если они повышают сжимающие напряжения у свободного продольного края листа.
Выше нами приведено то соотношение между длиной и шириной пластинки, которому соответствует наименьшее значение критического сжимающего напряжения. Отыскание величины этого соотношения приводит к разысканию значения У, которому соответствует минимум U. Величины U и V связаны между собой уравнением (7), которое имеет вид
Ф (U, 10 0.
) Е. О. Па тон. Расчет сквозных ферм с жесткими углами. М., типолитография В. Рихтера, 1901.
144
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
Составим производную dy(U,V)dV и приравняем ее нулю. Полученное таким образом уравнение совместно с уравнением (7) определяют собой искомые величины U и V. Путем последовательных пробных подстановок находим для U и V следующие значения: U 13,11; V 3,69, откуда искомое соотношение
§ 9. Прямоугольная пластинка с упруго заделанной продольной стороной
Нами рассмотрены два крайних случая закрепления продольной стороны пластинки. В первом случае продольная сторона оперта. Закрепление допускает свободное вращение, и моменты (G2)vо обращаются в нуль. Во втором случае продольная сторона абсолютно заделана, исключена всякая возможность вращения и, следовательно, производная (dwdy)v0 обращается в
Рис. 15.
нуль. На практике имеет место обыкновенно некоторый средний случай, несвободный продольный край листа рядом заклепок приклепывается к другим частям конструкции. Такое закрепление по своим свойствам может приближаться то к одному, то к другому из ранее рассмотренных случаев в зависимости от жесткости тех частей, к которым край листа приклепан. Если эти части очень жестки, край можно считать абсолютно заделанным; если же они гибки, податливы, то свойства закрепления приблизительно те же, что и в случае опертого края. Чтобы численно оценить влияние упругости заделки на величину критического сжимающего усилия, мы разберем тот простейший случай, когда при выпучивании пластинки по заделанному краю
появляются моменты G2, распределенные по закону
п dw 1
С2 а--. (1)
Подобное распределение можно представить себе осуществленным таким образом. Положим, имеются два вертикальных листа ABCD и EFGH (рис. 15), соединенных между собой ря¬
к ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК 145
дом лежащих одна возле другой пластинок, образующих собой плоскость ABFE. Полученная таким образом конструкция коробчатого поперечного сечения подвергается действию сжимающих усилий, равномерно распределенных по краям AD, ВС, FG и ЕН вертикальных листов. Раз сжимающие усилия превосходят известный предел, вертикальные листы могут начать выпучиваться; при этом первоначально коробчатое сечение искривляется и принимает вид, представленный на рис. 16.
Моменты G2j которые появятся по верхним краям выпучившихся вертикальных листов, очевидно, будут в каждом поперечном сечении пропорциональны углу т (см. рис. 16).
Если вместо ряда отдельных полосок взять сплошной горизонтальный лист, то закон распределения момента G2, конечно, изменится, но пока длина листа достаточно велика по сравнению с его шириной, можно считать, что формула (1) дает и в этом случае для моментов G2 значения, близкие к действительности. Величина коэффициента а в формуле (1) очень просто выражается через размеры горизонтального листа. Если взять направление координатных осей, как показано на рис. 15, обозначить через С' цилиндрическую жесткость горизонтального листа, через d ширину того же листа, то кривизна горизонтального листа в плоскости zy будет почти постоянна и равна
Здесь через w мы обозначим прогибы одного из вертикальных листов при выпучивании. Для момента G2 получим выражение
Установив такой закон распределения изгибающего момента по закрепленному краю вертикального листа, мы можем каждый из вертикальных листов рассматривать как отдельную пластинку, две стороны которой х 0 и х а оперты, сторона у о упруго заделана и сторона у b свободная от всяких
Рис. 16.
2 dw
(2)
(3)
146 К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК ’
усилий. Здесь а и b обозначают размеры вертикального листа., Если эта пластинка под действием сжимающих усилий выпучится, то для искривленной формы равновесия будем иметь прежнее дифференциальное уравнение. Решение этого уравнения опять-таки можем взять в прежней форме и только для отыскания произвольных постоянных функции'
f (у) Сеау C2eav С3 cos §у С4 sin рг
будем иметь несколько иные условия на продольных сторонах пластинки.
По заделанному краю пластинки условия будут следующие: I) при у 0 w 0;
II) при 0 G2 C'4.
Условие II может быть представлено в иной форме. Принимая во внимание, что вдоль заделанной стороны
где С — цилиндрическая жесткость вертикального листа, перепишем условие II в таком виде:
тт. (d2w С' 2 (dw (dw ,л.
“ Ы»_,- (4
Условия по свободной продольной стороне будут прежние:
III) при y b G2 0;
IV) при ,_ “L2-g--0.
Условия I и II приводят нас к таким уравнениям:
Ci С2 С3 0,
Са2 С2а2 — С3р2 х (Са — С2а С4р),
откуда получаем
г с3 (а2 р2 ца) С4 р г _ С3 (а2 р2-сцх) , С4 р
1 2ца 2 а 9 2 2ац 2 а
Следовательно, функция f(y) в данном случае может быть представлена в таком виде:
(у) A (cos р у - sh а у - ch а у) В (sin ру - - sh ay). (5)
Заметим, что при х оо, т. е. в случае бесконечно жесткого горизонтального листа, выражение (5) совпадает с тем, что мы имели для f(y) при абсолютно заделанной продольной стороне (см. § 8). Если найденное выражение (5) для f(y) подставить
к ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК 147
в условия III и IV для свободного края пластинки, то после ряда преобразований получаются два таких уравнения:
л (р2 )cos Р6 (2 -а )ch ab(“2 )sh ab
В (р2 ст--j sinрб (а2 - а sh аб О,
А — р (а2 — а sin р а (р2 ст-j sh ab
а2 1
-а (р2 ст-г)сЬа
В р (а2 — а -2) cos р р (р2 а“г) ch ab j 0.
Здесь предположено, что искривленная форма равновесия со стоит из одной полуволны, т. е. в общем решении уравнения положено т 1.
Чтобы упростить уравнения (6), введем такие обозначения:
02. Я2 , 2 я2 2 Р2 7
Р2 г ', a2-r-s, - 9- (7)
Тогда будем иметь
А (t cos рб 5 ch ab qs sh ab) В sin p 5 sh ab j 0,
A( — ps sinp6 at shaft qatchab) B(s cosp6 pcha6) 0.
Искривленная форма равновесия становится возможной, когда определитель уравнений (6') обращается в нуль. Это условие можно представить в таком виде:
2st (s2 t2) cos рb ch ab —
” 1 S sin pb sh ab — 2qs2 sh ab cos pfe 2q t2 ch ab sin pb. (8)
Полученное нами условие (8) для возможности выпучивания пластинки отличается от такого же условия (6) предыдущего параграфа только двумя последними членами правой части, имеющими множителем q. При бесконечно жестком горизонтальном листе А оо, q обращается в нуль, и тогда оба условия совпадают.
Для того, чтобы вывести какие-либо заключения относительно влияния упругости заделки, нужно решить уравнение (8) для различных частных предположений относительно величины ц, определяющей жесткость заделки.
148
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
Введем наши прежние обозначения:
РЪ2 тг я 2Ь2
и -
Тогда после некоторых преобразований уравнение (8) представится в таком виде:
V — U V U j cos Vyuv - V ch VYuv V
(1 yuv-v sin Vyuv-v sh VyWv Vuv
Vib
shyvymcosVyW-
VVuvv
Vuv giJ-Ch Vyuv V smVyuV - V
yyuv-v
(9)
Чтобы ясно представлять себе величину входящего в уравнение (9) множителя ib, определяющего жесткость заделки, заметим, что согласно обозначению (4)
цЬ
2Ь_
С d
(Ю)
Если мы предположим, что горизонтальный лист имеет те же размеры, что и вертикальный, то С С b d и, следовательно, лЬ 2. Если горизонтальный лист имеет двойную толщину, то lib 16.
Мы вычислили ряд корней уравнения (9) в двух предположениях: при ib 2 и xb 8.
Результаты вычислений приведены в таблицах D и Е и, кроме того, представлены графически на рисунках 17 и 18.
Таблица D (ib 2)
Таблица Е (лЬ — 8)
а
Ъ
и
RKn, кгсм2 Ъ
при -100
а
Ъ
и
RKn, кгсм2 Ъ
при -—100
а
Ь
и
RKr., кгсм2
Р L при -ф100
а
Ъ
и
ЯКр» кгсм2 при — — 100
1
14,75
262,3
2,5
8,93
158,8
1
15,57
276,8
2,3
11,63
206,8
1,3
11,12
197,7
2,7
9,15
162,7
1,3
12,31
218,9
2,5
12,17
216,4
1,5
9,95
176,9
2,9
9,45
168,0
1,5
11,41
202,9
2,7
12,83
228,1
1,6
9,57
170,2
3,0
9,63
171,2
1,8
10,99
195,4
3
14,03
249,5
1,8
9,08
161,4
3,1
9,81
174,4
2
11,10
197,4
4
19,45
345,8
2,0
8,84
157,2
3,5
10,69
190,1
2,3
8,81
156,6
4
12,06
214,4
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ пластинок 149
Приведенные в таблицах D и Е корни уравнения (9) вычислены путем последовательных пробных подстановок. Подстановки приходилось повторять по нескольку раз, чтобы получить
решения с тремя верными знаками. Работа значительно облегчается, если принять во внимание, что функция VYUV — V изменяется приблизительно по линейному закону, и вычислять промежуточные ее значения интерполированием.
160 К ВОПРОСУ ов устойчивости сжатых пластинок
Величина критического сжимающего напряжения вычисляется по прежней формуле:
п __ ЕЦ 62 акр- 12 (1 — а2) Ь2
В таблицах D и Е приведены значения ьр, вычисленные в предположении Ь6 100. Если в рассчитываемой пластинке
Ь6 п, то числа таблицы, оче45,720,953 видно, придется помножить на (100лг)2
—8,898,890,953 для примера проверим на
устойчивость вертикальные листы
— 45,720,953 сжатого мостового пояса1). По¬
перечное сечение пояса представ-25г4— лено на рис. 19.
Будем считать, что вертикальные листы упруго заделаны Рис. 19. по линии поясных заклепок. Сле¬
довательно, расчетная ширина 8 89
пластинки будет 6 45,72 — 41,28, отношение между
Ь 41,28 „0 0
ширинои и толщинои пластинки при этом равно -Q 953 43,3.
Расчетная длина пластинки равна длине панели « 386 см.
Вычислим теперь жесткость заделки. Если бы вертикальные листы были непосредственно соединены с горизонтальными листами, то на основании формулы (10) имели бы xb 2 6,5.
Соединительные уголки увеличивают жесткость заделки, и это увеличение тем больше, чем на большее число полуволн подразделяется вертикальный лист при выпучивании. Выпучивание вертикальных листов, очевидно, сопровождается скручиванием уголков. Если принять во внимание, что прогибы выпучившегося листа выражаются формулой
- . тпх с ч
w A sin —— (у),
то угол поворота для любого поперечного сечения уголка будет ЁЕ. - л тпх д (у)
' -v 1 О 1 1 1 ду а ду
Кручение т уголка в любом поперечном сечении, очевидно,
выразится формулой
d2w _ л тп п тпх df (у)
Т д COS з.
ду дх а а ду
1) Пример взят из книги Е. О. П а т о н а «Расчет сквозных ферм с жесткими углами», М., типолитография В. Рихтера, 1901, стр. 64.
к ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК 151
Это кручение не постоянно по длине уголка; оно непрерывно меняется благодаря непрерывно распределенным по заделанному краю вертикального листа моментам — G2. Если через К обозначим жесткость уголка при кручении, то будем иметь
G2dx-Kdx K-dx, (11)
и, следовательно, условие по заделанному краю в случае одного уголка будет таким:
d2w _ т2п2 dw _ „ dw ,
ду2 С а2 ду ду Коэффициент жесткости заделки в данном случае будет
jzJL. (13)
Из формул (12) и (13) видим, что влияние уголков на жесткость заделки выражается таким же образом, как и влияние изгиба горизонтальных листов. Следовательно, для получения полной жесткости заделки нужно только просуммировать коэффициенты жесткости, полученные по формулам (4) и (13) для отдельных частей. Заметим еще, что коэффициент жесткости, определяемый формулой (13), зависит от числа полуволн т: чем это число больше, тем больше и жесткость заделки.
Возвращаясь к нашему численному примеру, положим, что при выпучивании вертикальный лист подразделится на четыре полуволны. Тогда коэффициент жесткости, обусловленный наличием двух уголков, будет
V- О А с а2 ,
или, подставляя численные значения размеров, получим цЬ — 2,33.
Здесь для определения жесткости уголка при кручении К мы пользовались приближенной формулой
tf i-(2c)63G,
где с — ширина полки уголка, б — его толщина, G —
модуль упругости при сдвиге.
Полная жесткость заделки, следовательно, будет
IхЪ х'Ь хЬ 6,5 2,33 8,83.
Для определения величины критического сжимающего напряжения мы без больших погрешностей можем воспользоваться числами таблицы Е, вычисленной для iЪ 8.
152
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
Соотношение между длиной полуволны и расчетной шириной о 386
листа будет 4 41 28 2,34. Такому соотношению по таблице Е соответствует U « 11,8. Следовательно,
KP 'l2(fS) 1120 кгсм2.
Если бы мы предположили, что при выпучивании лист подразделится на пять полуволн, то тогда соотношение между длиной полуволны и расчетной шириной листа было бы более невыгодно, но зато возросла бы жесткость заделки, именно:
„и 2,33 -52 0
цЬ 42 3,66,
и, следовательно, цб 6,5 3,66 10,16.
Чтобы окончательно решить, которое из двух предположений более невыгодно, необходимо иметь таблицу значений U при IлЬ 10,16.
Все расчеты мы произвели в предположении, что нет диафрагм, соединяющих вертикальные листы коробчатого сечения,
и нет уголков, окаймляющих вертикаль-
ные листы понизу. На практике устрой-
и
—ством диафрагм и наклепыванием угол-
157,5 ков по низу вертикальных листов обеспечивают достаточную жесткость пояса при
37ж коробчатом сечении. Этого нельзя ска¬
зать относительно поясов таврового сечения.
Для примера разберем вопрос об устойчивости вертикального сжатого листа пояса таврового сечения. Размеры в сантиметрах указаны на рис. 20. Длину панели примем равной 3 м и положим, Рис- 20- что при выпучивании вертикального ли¬
ста получается три полуволны. Рассмотрим, какова будет в данном случае жесткость заделки xb. Если пренебречь трением, которое имеет место между уголками и горизонтальным листом благодаря заклепочным соединениям, и считать, что уголки и горизонтальный лист при кручении работают независимо друг от друга, то жесткость кручения К будет
К G I3 (20 28) 16G кгсм2.
Жесткость изгиба вертикального листа С будет
I3 Е 4
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК 153
Жесткость заделки по формуле (13) будет
При определении критического сжимающего напряжения без значительной погрешности можно воспользоваться таблицей D, ib 2. Если лист считать заделанным по линии поясных заклепок, то Ь 33 см. При подразделении листа на три полуволны аЬ » 3, Якр 171 X 9 1 539 кгсм2.
Если бы мы считали край листа абсолютно заделанным, то тогда лист при выпучивании должен был бы подразделиться на четыре полуволны и
§ 10. Влияние изгибающего момента на величину критического сжимающего усилия
До сих пор мы рассматривали случаи сжатия пластинки силами, равномерно распределенными по поперечным сторонам. Если к такому сжатию прибавляется еще изгиб пластинки в ее плоскости, то усилия на поперечных сторонах распределятся по линейному закону, как это представлено, например, на рис. 21.
Подобная комбинация сжатия и изгиба нередко встречается на практике, например, в сжатых мостовых поясах при наличии дополнительных напряжений, обусловленных жесткостью узлов.
Вопрос об устойчивости пластинки, находящейся в подобных условиях, решим элементарным путем. Положим, что три стороны пластинки (рис. 21) х 0, х а, у 0 оперты, четвертая сторона свободна от всяких усилий. Усилия по поперечным сторонам приводим к одной равнодействующей Q, действующей по срединной линии 00 пластинки, и к паре сил Му направление вращения которой указано на рисунке стрелкой. Если под влиянием действующих сил пластинка выпучится, то по опертой продольной стороне пластинки появятся непрерывно распределенные реакции q. Пусть на рис. 22 АВ представляет одно из поперечных сечений пластинки плоскостью параллельной плоскости zy.
аЬ 7533 2,3, RK » 260. 9 2340 кгсм'
м
Рис. 21.
Рис. 22.
154
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
Будем считать, что АВ— прямая, и пусть ф — угол, составляемый этой прямой с осью у. Перенеся реакции q параллельно самим себе на срединную линию 00 пластинки, мы, как и в § 6, сводим задачу об устойчивости пластинки к вопросу об устойчивости стержня, подвергающегося сжатию Q и изгибу в плоскости своей наибольшей жесткости. Выпучиванию стержня в направлении наименьшей жесткости противодействуют силы q, непрерывно распределенные по некоторому неизвестному нам закону. Задача эта подобна той, которая была нами ранее разобрана в статье «Об устойчивости плоской формы изгиба двутавровой балки» ).
Возьмем произвольное поперечное сечение тп стержня с абсциссой х и составим
2 для него выражение изгибающего момента в плоскости xz (рис. 23).
Если принять во внимание, что форма выпучившейся пластинки мало отличается от плоской формы и жесткость пластинки при изгибе в ее плоскости во много раз превосходит жесткость в направлении перпендикулярном, то можно написать такое дифференциальное уравнение:
l-х Ц2
EJS--Qzi tidl (l-x)jqdi-Mp.
Q
X
1 KS
' N
‘
1
а
Г
ш
г м
сьс-
Дифференцируя это уравнение дважды по х, получим гг d4z d2z d2(p
(1)
Здесь EJ — наименьшая жесткость пластинки при изгибе, следовательно,
EJ СЬ. (2)
Второе дифференциальное уравнение составим, приняв во внимание скручивание стержня. Если через К обозначим жесткость пластинки при кручении, то момент внутренних сил упругости относительно касательной к оси стержня в каком-либо сечении с абсциссой х будет
к
(3)
lJ См. сноску на стр. 127.
к ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК 155
Момент внешних сил относительно той же оси напишется так:
12 1-Х
-J «§-И' w)
о о
или,сравнивая (3) и (4), получим
12 1-х
о О
Дифференцируя по х, получим уравнение
Из уравнений (1) и (5) можем исключить неизвестные нам реакции q. Если мы, кроме того, вместо р подставим его выражение через прогибы стержня
2z
ф — ь
то будем иметь дифференциальное уравнение, определяющее искривленную форму равновесия:
или
dz. 1 (п Ш 4К dz _
rfFTlQ _6 W) w
Чтобы удовлетворить условиям на концах стержня, возьмем решение этого уравнения в форме
z AsmY4rQT-Щ
так как при х z 0, то для возможности появления искривленной формы равновесия необходимо положить
т f __L (п _l _ 4С _ тл
V EJ Ъ Ь2 ) I
Для величины критической сжимающей силы и момента получаем условие
„Ш,Е« « (7)
Сравнивая полученное выражение с формулой (5) § б, видим, что момент выбранного нами направления (см. рис. 21)
156
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
уменьшает устойчивость сжатой пластинки. Момент противоположного знака, разгружая волокна, лежащие у свободного края листа, увеличивает жесткость. Если положить М Qa, где a — эксцентриситет сжимающей силы, то
«--М-Т Тг)- (8)
ъ
Значение а нужно брать со знаком « » или «—», смотря по тому, откладывается ли оно от оси пластинки в сторону положительных или отрицательных у-ов.
Если нет продольной сжимающей силы и, следовательно, пластинка подвергается чистому изгибу, то критическое значение изгибающего момента получим из формулы (7), положив Q 0:
EJn2 b , К _ СЬ2 я2. К М I2 4 Ъ I2 4 Г
§ 11. Прямоугольная пласгинка сжимается силами, равномерно распределенными по продольным сторонам
Положим, что поперечные стороны пластинки (рис. 24) х 0 и х а оперты; продольные стороны у 0 и у b свободны; по ним равномерно распределены сжимающие усилия Р на единицу длины стороны. Пока сжимающие усилия не превзошли
А
ншипи
X
1
0
г
ttttt 1 т тt ff
а ►
'
У
В
У
Рис. 24. Рис. 25.
некоторого определенного предела, плоская форма есть единственная возможная форма равновесия пластинки. За этим пределом пластинка под влиянием сжимающих сил может скручиваться. Пусть АВ (рис. 25) представляет собой одно из поперечных сечений пластинки после скручивания. Усилия Ру при которых скручивание становится возможным, определятся на основании элементарных соображений. Если через К обозначим жесткость пластинки при кручении и через ср угол поворота сечения АВ, то изменение момента внутренних сил упругости отно¬
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
157
сительно оси 00 при переходе от одного сечения к другому, бесконечно близкому, будет К
Приравнивая это изменению момента внешних сил, получим уравнение
ЬцР dx K--dx, (1)
откуда получаем для ср выражение
у Asm у -у х В cos у --х.
Чтобы удовлетворить условиям на опертых сторонах пластинки, нужно положить В 0 и
т-- 2
Первую возможную искривленную форму получим при сжимающих усилиях
pif- О)
Так как при тонких пластинках величина К пропорциональна ширине пластинки, то, следовательно, величина критического сжимающего усилия в данном случае не зависит от ширины пластинки Ь. Принимая во внимание, что
К у 663G 1,5ЬС,
получим из (3)
1,6-5-С. (4)
Критическое значение сжимающего усилия в данном случае в полтора раза больше, нежели в ранее рассмотренном нами случае (см. § 4) выпучивания пластинки по цилиндрической поверхности.
Если, кроме поперечных, одна из продольных сторон пластинки, например сторона у 0, оперта, то жесткость пластинки возрастет. Величину критического сжимающего усилия Р можно также определить элементарным путем.
Пусть АВ представляет одно из поперечных сечений пластинки после выпучивания, ср — угол его поворота. Если через z обозначим величину прогибов пластинки по срединной линии 00, то для реакций q, появляющихся при выпучивании вдоль опертой продольной стороны, будем иметь
пт dz
-EJ4Z'
где EJ — жесткость пластинки при изгибе в плоскости zx.
158 К ВОПРОСУ ОБ устойчивости сжатых пластинок
Дифференциальное уравнение кручения пластинки будет «
Или, вставляя вместо ср его выражение через прогибы р ,
получим
zv _ К _1_ — -i z Г 0
EJb2 EJb W
Общий интеграл уравнения (5) напишем в таком виде:
z Сеах С2еах С3 cos х С4 sin х. (6)
Здесь
л лг( К 2 2 р 4 . к 2
а г К 62) EJ Ь EJ Ь2 9
г г — Р “ Г У EJ Ь2 ) EJ Ъ EJ Ь2
Произвольные постоянные Сь., С4 общего интеграла (6)
определим на основании условий на концах:
I) При х 0 z 0. II) При х 0 z 0.
III) При х a z 0. IV) При х а г 0.
Из условий I и II имеем
Cj С2 С3 0, (Cj С2) а2 — С3р2 » 0,
откуда С3 0, Ci - С2.
Следовательно, решение г может быть представлено в такой форме:
z Л sh а В sin р.
Условия III и IV приводят к уравнениям
A sh al В sin р I 0, Аа2 sh а I — Bp2 sin р I 0.
Чтобы полученные уравнения допускали для А и В решения, отличные от нуля, должен обращаться в нуль их определитель. Следовательно, sin рI 0.
Для определения критического значения сжимающих усилий Р будем иметь
АР 2 К л
EJb EJb2 а
откуда
р-7Ти7Т'' »)
к ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
159
Если положить EJ ЬС, К 1,56С, то формула (8) может быть представлена в таком виде:
-c(i,5 4).
(9)
Сравнивая полученную формулу с формулой (4), видим, что возрастание жесткости пластинки за счет удерживания одной из
продольных сторон, выражается членом -С. Жесткость
пластинки возрастает с увеличением отношения Ьа.
Р
Рис. 26.
Рис. 27.
Если бы мы и другую продольную сторону пластинки удерживали, то имели бы случай, разобранный Дж. Брайаном (см. § 3). Величина критического сжимающего усилия в этом случае будет
pc(i -) (10)
При Ь2а2 1,013 формула (10) дает для Р значения меньшие, нежели формула (9); следовательно, пластинке легче выпучиться, как показано на рис. 27, нежели скрутиться, как представлено на рис. 26.
Предыдущую задачу можно решить также, исходя из общего дифференциального уравнения
r dw
d4w
d4w
дх4
дх2 ду2 ду‘
г) Р
d2w
ду2
0.
(П)
Полагая w A sin -f(y), будем иметь
(у) Cea« С2еау С3еу С4е4
160
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ пластинок
Здесь аир имеют значения
§ 12. Случай прямоугольной пластинки, обе продольные стороны которой заделаны, поперечные стороны оперты
Пластинка сжимается силами, равномерно распределенными по поперечным сторонам. Дифференциальное уравнение выпучившейся пластинки остается прежним:
При этом удовлетворяются условия на опертых поперечных сторонах пластинки х 0, х а. Неизвестная пока функция f(y) должна быть подобрана таким образом, чтобы были удовлетворены условия на продольных заделанных сторонах у 0 и у Ь.
Чтобы было удовлетворено уравнение (1), функция f(y) должна иметь форму
Для определения С3 и С4 принимаем во внимание условия на
(и
Решение берем в прежней форме:
„ . тпх р ч
w A Sin — f(y).
f(y)-
(2)
f (у) СеаУ С2еау С3 cos р у С4 sin р у.
При у 0 имеем условия: I) w 0 и II) -- 0; следовательно,
С С2 — 0, (Сх С2) сх С4р — 0,
откуда
Искомая функция f(y) имеет вид
f (у) с4 (cos ру - ch ay) С3 (sin p - sh cu).
стороне у b, где должно быть III) w 0 и IV) - 0;
С4 (cos рb — ch ab) С3 (sin рб — - sh ab j 0,
С4 (р sin рб a sh ab) С3 (р cos рб — р ch ab) 0.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК 161
Для возможности появления выпучивания необходимо положить, что вышенаписанные уравнения допускают для С3 и С4 решения, отличные от нуля, что возможно лишь при условии
(cos рb — ch ab) (р cos р — р ch ab)
— sinрб — --sh a(р sin рб а sh ab)
или
(cospb — ch ab)2 — sinpb — --shabj sinpb sha. (3)
Здесь аир имеют те же значения, что и в ранее разобранных задачах:
7IW(W' e- vV-(™)4™)-
Вводим наши прежние обозначения:
™-и - v-
Г U » п2 V »
тогда условие (3) может быть представлено в таком виде (при т 1):
(cos V-V yuV-ch У V Vuv)2
- (sin V-v VuV —sh y_ v yjjy x
V Vv Vvu j
x(sinlf-V VW Yv u_ sh Vv Wu), (4)
V V-v Vuv или, выполняя указанные действия, получим
1
1
COS V- V Vuv ch Vv Vuv
Vuv-v2
tg V- V Vvu th Vv Vuv. (4')
Задаваясь каким-либо соотношением между длиной и шириной пластинки, мы этим самым определяем величину V; тогда величина V определится из уравнения (4'). Ряд решений этого уравнения мы приводим в нижеследующей таблице F. Заметим, что при аb 1 можно вместо уравнения (4') решать более простое уравнение
tg V- v Vuv uyv у2,
102 К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
так как th Vv Y'UV весьма мало отличается от единицы,
a ch VV VUV — большое число.
Наиболее невыгодное соотношение между размерами пластинки лежит в пределах
0,6 - 0,7. (5)
При сжатии очень длинных пластинок они, очевидно, будут при выпучивании подразделяться на участки, удовлетворяющие условию (5), и для вычисления критического сжимающего напряжения можно с достаточной точностью положить U 69.
При выводе мы полагали продольные стороны пластинки абсолютно заделанными. Без особого затруднения можно разобрать случаи упруго заделанных продольных сторон— придется только несколько изменить условия на контуре и положить, что при
у 0 и у b w 0
d2w dw
и -чг а.
ду2 ду
Коэффициент а характеризует степень жесткости заделки: при а оо мы имеем абсолютно заделанный край, при а 0— опертый край. Величина критических сжимающих напряжений в зависимости от коэффициента а будет занимать одно из промежуточных значений между числами таблиц А и F.
Заметим еще, что с возрастанием ширины пластинки, следо-
вательно с убыванием отношения а6, величина V — V UV определяемая уравнением (4'), стремится к пределу я, откуда получаем
и V у- 2п2.
Следовательно, величина критического сжимающего напряжения в этом случае та же, что и при опертых продольных сторонах (см. (6) § 3); так как V в данном случае очень большое число, то членами n4V и 2я2 можно пренебречь. Окончательно получим U V или, подставляя значения U и V, найдем я2 С
Р—2 обычная формула Эйлера для стержня с опертыми
концами.
Таблица F1)
а
Т
и
КР‘
кгсм2
а
b
и
кр-
кгсм2
0,4
0,5
0,6
0,7
93,2
75,9
69,6
69,1
1657
1350
1237
1229
0,8
0,9
1,0
1,5
72,0
77,3
84,6
141
1280
1374
1504
2507
) Значение критического напряжения кр кгсм2 вычислено при 66100; Е 2 103 кгсм2.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК 163
§ 13. Случай прямоугольной пластинки, обе продольные стороны которой оперты, поперечные стороны заделаны
Частное решение основного дифференциального уравнения возьмем в форме
w Af(x) sin--. (1)
Взятое решение удовлетворяет условиям на продольных опертых сторонах, так как при у О и y b w О и дтду2 0. Неизвестная функция f(x) должна удовлетворять уравнению
Г () (_ 2 -) () - () о
и, следовательно, может быть представлена в виде f (х) Аеах Веах Сех Dex,
где
-л я2 Р , f П‘ « V ьТ--2СУ -р
ri± -±- if- d.
Р V b2 2С у b2
Jt2
p 1
1 P2
b2
с 1
1 4C2
TC2
U2
p
n
1
1 ЛГ 2
(2)
Произвольные постоянные А, В,. должны быть подобраны таким образом, чтобы были выполнены условия на поперечных заделанных сторонах х 0 и х а:
I) f(x) 0 при х 0;
II) Г 00 0 при х 0
III) f(x) 0 при х а;
IV) '() 0 при х а.
Из условий I и II заключаем, что f(x) должна иметь форму
f х) С (ch ах sh ах D (ch а — sh а е.
Чтобы выполнить условия III и IV, нужно удовлетворить уравнениям
С (ch аа у sh аа е D (ch аа — у sh a а 0,
С (a sh aa р ch аа pePa) D (a sh aa — p ch aa — pePa) 0.
164 К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
Для произвольных постоянных С и D возможны решения, отличные от нуля, только в том случае, если выполнено условие
(ch аа — sh аа еа (a sh аа — р ch а а — р6а)
ach а а — sh а а — (a sh аа р ch аа рра).
После ряда сокращений настоящее условие может быть пред ставлено в виде
a gqp sh аа sh pa ch аа ch pa 1. (3)
Введем наши прежние обозначения:
РЪ2 _ тт к2Ь2 „
п » гЛ тогда выражения для аа и pa после некоторых преобразований могут быть представлены в таком виде:
аа
pa
(4)
При заделанных поперечных сторонах критическое сжимающее напряжение, очевидно, должно быть больше, нежели в том случае, когда все четыре стороны пластинки оперты; следовательно, в рассматриваемом случае (см. § 3) U 4я2 и величины аа и pa всегда мнимые. В таком случае условие (3) может быть представлено в виде
2л2;
где
1 — -2-) sin sinp cs7 cosp 1, (5)
Чтобы найти значение критического сжимающего усилия для пластинки с заданным соотношением aб, нужно вычислить V и потом из уравнения (5) найти соответствующее значение U. Из бесчисленного множества корней, которое нам дает уравнение (5), очевидно, нужно взять наименьший — он будет соответствовать первой возможной искривленной форме равновесия.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК 165
Нами вычислено значение U для квадратной пластинки — в этом случае V jt2 и U 56,0.
Задачу о выпучивании сжатой прямоугольной пластинки возможно было бы решить еще для некоторых частных случаев закрепления. Например, для того случая, когда одна из продольных сторон заделана, а другая оперта, при опертых поперечных сторонах, или для случая, когда обе продольные стороны и одна из поперечных оперты, другая же поперечная сторона заделана. Так как эти задачи не имеют особого практического значения и решаются тем же приемом, что и выше разобранные случаи, то останавливаться на них не приходится.
Разобранные в настоящей статье задачи являются с математической стороны наиболее простыми и далеко не исчерпывают всех случаев, с которыми приходится встречаться при расчетах. Большое значение могло бы, например, иметь решение вопроса
о выпучивании пластинки, сжатой сосредоточенными силами. Попытку решения простейшей из этих задач мы встречаем в работе А. Зоммерфельда ). К сожалению, положенные им в основание уравнения не выражают действительного явления и потому все дальнейшие выводы ошибочны. В настоящее время мы заняты экспериментальной проверкой результатов работы А. Зоммерфельда.
Не меньший интерес представляет вопрос о выпучивании сжатой пластинки в том случае, когда сжимающие напряжения изменяются по длине, например возрастают от концов к середине пластинки. В таких примерно условиях будут горизонтальные листы трубчатых балок прямоугольного поперечного сечения. Эта задача особых трудностей не представляет, и мы к ней надеемся вернуться в следующей статье.
) A. Sommerfeld. Ober die Knicksicherheit der Stege von Walzwerkprofilen. Zeischrift fur Mathematik und Physik, 1907, Bd. 54, Heft 2, SS. 113—153.
К ВОПРОСУ о ПРОДОЛЬНОМ ИЗГИБЕ
Известия Киевского политехнического института, 1908, год 8, книга 2, стр. 181—212. Отд. оттиск, Киев, тип. С. В. Кульженко, 1908, 32 стр.
§ 1. О продольном изгибе стержней переменного сечения
При определении критического значения сжимающей силы Р приходится исходить из основного дифференциального уравнения упругой линии (рис. 1)
Е1Чг-рУ- W
При постоянном поперечном сечении уравнение (1) дает нам известную формулу Эйлера. Если поперечное сечение переменное и величина момента инерции J можег быть представлена по всей длине стержня одной какой-либо функцией от х, то задача сводится к интегрированию линейного уравнения второго порядка.
Ряд простейших случаев этого рода, именно случаи конического стержня и стержня, ограниченного поверхностью параболоида вращения, разрешены еще Эйлером1). Случай стержня, ограниченного какой угодно поверхностью вращения второго порядка, разобран Лагранжем. Несколько задач того же рода разобрано в недавно вышедшей статье А. Франке2).
В том случае, когда момент инерции J не может быть представлен по всей длине стержня одной функцией от х, приходится стержень подразделить на отдельные участки, для каждого участка составить свое выражение для J и написать свое дифференциальное уравнение изогнутой оси. При определении произвольных постоянных интегри¬
) L. Е u 1 е г. Sur la force des colonnes. Histoire de l’Academie Royale des sciences et belles-lettres avec lcs Memoires, tires der Registres de cette Academie. 1759, tome 13, pp. 252—282.
2) A. F г a n k e. Knicksiecherheit bei entspechender Zunahme des Fragheitsmoments des Stabquerschnittes. Zeitschrift fur Architektur und Ingenieurwesen, Hannover, 1907, Bd. 53(12), SS. 471—482. '
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
167
рования придется принять во внимание, что в сечениях, разделяющих два какие-либо участка, отрезки упругой линии обоих участков имеют общую ординату и общую касательную. Присоединяя к этому условия на концах стержня, будем иметь достаточно уравнений для исключения произвольных постоянных и определения критического значения сжимающей силы.
Применим эти общие соображения к простейшему случаю. Положим, что стержень составлен из двух цилиндрических частей различного поперечного сечения, но имеющих одну общую ось (рис. 2). Обозначая через А и 2 моменты инерции поперечных сечений верхнего и нижнего участков и располагая координатные оси по рис. 1, получим следующие уравнения:
(2)
EJX ” РУ Для верхнего участка;
EJ2l — РУ2 для нижнего участка. Вводя обозначения
177 7 02 получим общие интегралы уравнений (2) в форме
ух Сх sin Qx С2 cos Qxy
у2 С3 sin Q2x С4 cos Q2x. (4)
i
1 ШШ Рис. 2.
Для определения произвольных постоянных и критической нагрузки имеем условия:
I) У 0 при х I
II) у'2 0 при х О
III) У У2 при х а
IV) г' ПРИ х а.
(5)
Подставляя в эти условия значения у и у2 из (4), получим четыре уравнения, линейных относительно произвольных постоянных Ci, С2,. Уравнениям этим можно удовлетворить, положив все произвольные постоянные равными нулю, но тогда :тержень не получает никакого искривления. Такое решение указывает, что прямолинейная форма равновесия есть одна из зозможных форм. Чтобы была возможна искривленная форма равновесия, необходимо, чтобы уравнения (5) допускали для величин Сь. решения, отличные от нуля, что возможно лишь
i том случае, если определитель уравнений (5) обращается
168
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
в нуль. Составляя этот определитель и приравнивая его нулю, получаем уравнение
(6)
1авнение
g _ 62 sin 62fl sin 9ifl 4- 6i cos 9 cos 02a ® 1 02 cos 0a sin 02a — 0i cos 02a sin 0 -477
из которого можно определить величину критическои сжимающей силы, если заданы величины , a, 01 и 02 ).
Возьмем такой частный случай: а 2, 01 202 (т. е. момент инерции поперечного сечения в нижней части стержня
в четыре раза больше, нежели момент инерции сечения в верхней части).
Пользуясь тригонометрическими таблицами, легко подобрать решение уравнения (6). В данном случае получим 0j 2,466, или на основании обозначений (3)
Ркр 6,08--.
Если верхнюю часть сделать более жесткой, чем нижнюю, и положить 01 022, то получим
о оо EJ2
кр 2 I
sssss sdsss
а) Ь) с) d)
Рис. 3.
Пользуясь полученными числами, интересно сравнить величины критической нагрузки для четырех случаев, представленных на рис. 3.
Критические нагрузки будут иметь значения:
a) Лер Щг 2,47; с) Ркр 6,08;
b) Ркр Ц- 2,83; d) ЯКр тг- 9,87.
Из этого можно сделать заключение, что ослабление сечения у свободного конца имеет гораздо меньшее влияние на величину критической нагрузки, чем такое же ослабление у за¬
деланного конца.
Особенно просто решается трансцендентное уравнение (6) в том случае, когда один из участков стержня мал, т. е. когда длина а или длина Ь мала по сравнению с длиной стержня I.
) Е. Л. Николаи указал нам на статью A. Franke «Die Tragkraft der Saulen bei veranderlichen Querschnitb (Zeitschrift ftir Mathematik und Physik, 1901, Bd. 46, Heft 4, SS. 419—434), где уравнение (6) представлено в более простом виде. Если подставить вместо 01 а величину 0i(—6), то уравнение (6) может быть представлено так: tg0i6 tg 02а 0i : 02.
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
169
Положим, например, что а — малая величина и 02 0i, другими словами, определим, как изменится величина критической нагрузки, если у закрепленного конца стержня ослабить сечение на небольшом протяжении. Вследствие этого ослабления величина критической нагрузки уменьшится, и мы будем иметь 0i я2.
Пока а — малая величина и 02 не очень велико по сравнению с 0i, изменения в величине критической нагрузки невелики и 0i близко к я2. Можно к длине стержня прибавить малую величину б, так что
0i( 6) -. (7)
Тогда влияние удлинения стержня 61 на величину критической нагрузки будет такое же, как и ослабление сечения на протяжении а. Величина б определяется без особого затруднения. Принимая во внимание, что 0б — малая величина, получим на основании равенства (7)
М5Г5Г-
Подставляя это в уравнение (6) и отбрасывая малые ве личины высших порядков, получим
1 _ е,
0J 6 а (02 - е2)
или, внося вместо 01 и 02 их значения (3), получим
6 а--‘7г. (8)
J2
Влияние ослабления сечения на величину критической нагрузки таково, как если бы сечение оставалось неизменным, а длина стержня возросла на величину, определяемую формулой (8). К тому же результату опытным путем пришел и проф. А. Фёппль ).
Если ослабить сечение стержня у свободного конца на малом протяжении 6, то влияние этого ослабления на величину критической нагрузки будет малой величиной высшего порядка. Убедиться в этом можно таким путем. В уравнение (6) вместо а поставим величину — b и примем во внимание, что Ь
) A. F б р р I. Vorlesungen iiber technische Mechanik. Dritter Band. Festigkeitslehre. Leipzig, Druck und Verlag von B. G. Teubner, 1897, S. 373. Перевод на русский язык: Aug. F б p p 1. Теория сопротивления материалов и теория упругости. С.-Петербург, скоропечатня П- О. Яблонского, 1901, стр. 335.
170
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
мало. Тогда, отбрасывая малые величины высших порядков, представим уравнение (6) в такой форме:
9 18ТЛЪ 0161 tg 0l 01 Ы tg2 0’
откуда 6 0.
Мы видим, что влияние ослабления сечения зависит от места, в котором это ослабление сделано. Чем ближе ослабленное место к заделанному концу, тем влияние его У на величину критической нагрузки больше.
Мы разобрали два крайних случая: случаи ослабления сечения у закрепленного и у свободного конца. Чтобы вычислить влияние ослабления в каком-либо промежуточном сечении, нужно решить задачу о продольном изгибе стержня, состоящего из трех участков (рис. 4). Для каждого участка нужно составить свое дифференциальное уравнение. Общие интегралы полученных таким образом уравнений будут
I
1
I,
М
I,
I,
Рис. 4.
у Сх sin 0jЛГ С2 COS 0, С3 sin 02JC С4 cos 02,
уП „
г2
С3 sin 02х С4 cos Q2x,
С5 sin 03 х С6 cos 03л:.
Для исключения произвольных постоянных и для определения критического значения сжимающей силы будем иметь шесть условий:
(9)
Положим, что 01 0з 0 и 2 — малая величина, т. е. возьмем стержень постоянного поперечного сечения и на небольшом протяжении 2, на расстоянии 3 от закрепленного конца, сделаем вырез (см. рис. 4). Вследствие этого величина критической нагрузки уменьшится, и мы будем иметь
е(, 2 3) е-.
Так как мы предполагаем ослабление на небольшом протяжении, то изменение критической нагрузки будет невелико,
I)
У'г
0
при
х 0;
И)
Уг
яУз
при
х 3;
III)
У2
У
при
х 12 3;
IV)
У
0
при
х 1 2 Ь
V)
У 2
-Уз
при
х 13
VI)
У 2
-У
при
х h
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ 171
и мы можем подобрать малую длину 61 так, что 0( б) я2.
Величина критической нагрузки для надрезанного стержня будет такая же, как и для цельного стержня, но удлиненного на величину б. Для определения б воспользуемся уравнениями (9). Принимая во внимание, что 06 и 02— малые величины, можем представить уравнения (9) в такой форме:
I) С5 0;
II) С6 cos 03 С3 sin 023 С4 cos 023;
III) С3 sin 023 022 cos 023 С4 cos 0J3 — 022 sin 023
С sin 03 02 cos 03 С2 cos 03 — 02 sin 03;
IV) Сх С20 б 0;
V) — С60 sin 03 С302 cos 023 — С402 sin 023;
VI) С302 cos 023 — 022 sin 02з С402 sin 02з Ч- 022 cos 023
Cj0 cos 03 — 02 sin 03 — С20 sin 03 02 cos 03.
Пользуясь уравнениями I, IV и V, исключаем из уравнений III и VI величины Си С2 и С3; получаем
— С6 cos 03 С602 sin 03
С2 б 0 sin 03 02 cos 03 — С2 cos 03 — 02 sin 03э С60 sin 03 С602 cos 03
С2 б 02 cos 03 — 02 sin 03 С20 sin 03 02 cos 03,
откуда для определения б получаем уравнение
02 sin 03 — cos 03 _ 0 sin 03 (б 2) — cos 03
0 sin 03 022 cos 03 02 cos 03 (б 2) 0 sin 03
Это уравнение может быть представлено так:
Ь-ТГЕТвГ Ы 1, 1
е tg е3 е tg е3
, , , , е(б 2)
е tg е3 tg е3
Для всех сечений, не очень близких к закрепленному концу,
022 0 Ш L)
величины Q tg-ез и —— малы, и потому, отбрасывая ма¬
лые величины высших порядков, можем представить уравнение для определения б в таком виде:
б 0-02 _ J-J,
U 02
COS2 03 - COS2 03. (10)
J 2
Из этой формулы видно, как меняется влияние ослабления в зависимости от положения ослабленного сечения.
172
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
Если на стержне имеется несколько ослабленных мест и общее протяжение ослабленных участков мало по сравнению с длиной стержня, то влияния отдельных ослаблений на величину критической нагрузки можно сложить между собой. Если bi — длина какого-либо ослабленного участка и аг- — его расстояние от закрепленного конца, то
1п
б bt Ji-cos2 0а. (11)
i
Очень просто определить влияние ослаблений на критическую нагрузку з том случае, когда эти ослабления одинаковы и расположены на равных расстояниях одно от другого. В таком случае Ь Ь2. Ьп, 2. Jп и, следовательно,
1п
б ь 2 cos2 00, » Щ-. (12)
1 1 1 1
Пользуясь этим, можно сделать некоторые заключения относительно влияния заклепочных отверстий на величину критической сжимающей силы. Возьмем такой численный пример. Равнобокий уголок 75 X 75 X 10 мм ослаблен заклепочными отверстиями диаметра 2 см, отстоящими на 30 см одно от другого. Насколько уменьшится величина критической нагрузки по сравнению с цельным уголком
Благодаря заклепочному отверстию площадь сечения и его
момент инерции уменьшается примерно на 15:
— , 1 nb I
А 6 ’ 2 30 Подставляя это в формулу (12), найдем 6180. Следовательно, влияние отверстий на величину критической нагрузки несколько больше 1.
В настоящем выводе мы заменили круглые заклепочные отверстия квадратными вырезами, сторону квадрата приняли равной диаметру отверстия, предположили, что части стержня, непосредственно прилегающие к ослабленному участку, работают полным сечением. На самом деле явление, конечно, гораздо сложнее, и только путем опыта возможно установить более точно, как велико влияние заклепочных отверстий на величину критической нагрузки. Вышеприведенный вывод позволяет сделать только такое заключение: при ослаблении стержней на небольшом протяжении отверстиями или надрезами величина
к ВОПРОСУ о ПРОДОЛЫЮМ ИЗГИБЕ
173
критической нагрузки уменьшается в гораздо меньшей степени, чем величина площади ослабленного сечения. При проверке сжатого стержня на продольный изгиб мы будем ближе к истине, если возьмем сечение брутто, а не нетто.
§ 2. Расчет трубчатых стоек переменного сечения
В инженерных сооружениях часто приходится рассчитывать на продольный изгиб трубчатые стойки, составленные из четырех ребер, связанных в одно целое решетками. Если ребра по всей длине стойки параллельны между собой и имеют постоянное сечение, то проверка на продольный изгиб производится по обычным формулам. Сложнее становится задача в том случае, когда ребра не параллельны и стойки имеют одну из форм,
представленных на рис. 5. Уравнение для определения критической нагрузки в случае формы а) имеется в ранее упомянутой статье А. Франке. Мы выведем здесь формулы для определения критической нагрузки в случае формы Ь). Выберем за начало координат точку О — пересечение наклонных ребер — и будем рассматривать верхнюю половину стойки. Площадь поперечного сечения стойки предполагаем постоянной. В таком случае на протяжении от х Ь до х с будем иметь постоянный момент инерции J Fb2tg2, где F—площадь поперечного сечения стойки, р — угол, составляемый наклонными боковыми гранями стойки с ее осью.
На участке от х а до х Ъ момент инерции будет переменным и представится формулой Jx Fx2 tg2p. Допустим, чго
О
Рис. 5.
174
К ВОПРОСУ О ПРОДОЛЫЮМ ИЗГИБЕ
стойка под действием сжимающей силы Р несколько искривилась, и напишем дифференциальные уравнения равновесия для каждого участка. Уравнения получатся такие:
и общий интеграл первого из уравнений (1) имеет форму
Общий интеграл второго из уравнений (1) будет в обоих случаях иметь форму
I случай.
Для определения произвольных постоянных и нахождения величины критической нагрузки мы имеем два условия на концах (см. рис. 5):
I) у 0 при х а, II) у'2 0 при х су и два условия в месте сопряжения двух участков:
I) от л: а до х b EF х2 tg2 р - Pyt;
II) от х Ь до х с EF b2 tg2p — Pt2.
(1)
Придется отдельно рассмотреть два случая. В первом случае
У1 V ct sin ( In --) Ca cos ( In --). (2)
где
Во втором случае
(4)
г2 Ai sin Qx cos 0x,
где
(5)
III) Ijl y2 при a; b, IV) tj y'2 при x b.
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ 175
Принимая во внимание условия I и II, представим решения уравнений (1) в таком виде:
У1
Сх Ух sin (ц In j, у2 cos 0 (с — х),
где — величина наибольшего прогиба искривленного стержня. Условие III дает нам
f cos 0 (с — b)
с,
Наконец, условие IV приводит нас к уравнению для определения критической нагрузки:
tg0(c-ft) 2je l 2ictg(iln-)- (6)
В том случае, когда с 6, т. е. когда стойка состоит из двух сложенных основаниями пирамид, уравнение (6) принимает более простой вид:
tg (м'1п4)
Пользуясь тригонометрическими таблицами, можно без особых затруднений решать уравнения (6) и (7), последовательно подбирая соответствующее х. Имея ji, находим и величину критической нагрузки, так как на основании обозначения (3)
р 2 1 EF tg2 р М- 4
II случай.
Условия на концах и в месте сопряжения двух участков остаются прежние, и потому решения уравнений (1) представятся в таком виде:
у Ci (хк1 — ak'k2xk2), у2 cos 0 (с — х).
Принимая во внимание условия в месте сопряжения двух участков, приходим к такому уравнению для определения критической нагрузки:
Ч)
1 k.2
tg Q(c-b) -
Qb
(4Г-ШТ
(8)
Уравнение это для заданных размеров стойки может быть разрешено путем последовательного подбора. В том случае, когда Ьа 1, т. е. когда мы имеем призматическую стойку, уравнение (8) получает форму tg0(c — Ь) оо, следовательно,
0(с — Ь) п2у т. е. получим формулу Эйлера.
176
К ВОПРОСУ о ПРОДОЛЬНОМ ИЗГИБЕ
Переходим теперь к предельному случаю, когда PEF tg2 р 14.
Уравнения (6) и (8) в этом случае могут быть приведены к совпадению. В самом деле, полагаем в уравнении (6) jli О, тогда 0 126 и, следовательно,
ini'
а
(9)
В уравнении (8) для предельного случая нужно, на основании обозначений (4), положить k k2 12; тогда будем иметь
10
Неопределенность раскроем, полагая
k Ct, k2 2 и приближая а беспредельно к нулю; получим
1. (If-41)1.
1Ш-Ч1-И
.“(4Г-Ш11 ,
“(4Г-
kl 2 —
а0
(l2anA) (а а_.
06 1 2а In — 1 j
а 0
так как для предельного случая 1206 1, то, следовательно, Таблица I уравнения (10) и (9) тожде¬
ственны.
Для определения критической нагрузки приходится пользоваться или уравнением (6), или уравнением (8). При помощи уравнения (9) можно установить границы применения этих уравнений. Для этого задаемся рядом значений для отношения 6а и из уравне¬
ния (9) вычислим соответствующие значения для (с — 6)6. Ряд таких значений помещен в таблице I.
Если мы от предельного случая PEF tg2p 14 отклонимся
в область применения уравнения (6), т. е. положим
ь_
а
с — Ь Ъ
Ъ
а
с — Ъ Ъ
1
3,142
20
2,061
2
2,638
40
1,992
5
2,304
100
1,924
10
2,159
оо
1,571
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
177
PEF tg2 р 14, то 0 возрастает, правая часть уравнения (6) начинает убывать и для сохранения равенства необходимо, чтобы величина (с — Ь)Ь тоже убывала. При отклонении в область применения уравнения (8) 0 убывает, правая часть уравнения (8) возрастает и для сохранения равенства необходимо, чтобы отношение (с — Ь)Ь тоже возрастало. При расчете стойки нужно найти величину bа для данной стойки и посмотреть, какое значение (с — Ь)Ь соответствует этой величине по таблице I. Если действительное значение (с — Ь)Ь меньше, нежели то, что мы найдем в таблице, то придется для определения критической нагрузки пользоваться уравнением (6). В противном случае решаем уравнение (8).
Решим численный пример: положим са 16, bа 12. При таких отношениях получим (с — Ь)Ь 13, т. е. величину меньше той, что дает таблица I. Следовательно, для нахождения величины критической нагрузки придется пользоваться уравнением (6). Уравнению этому мы удовлетворим, положив х 0,765. В таком случае
WF 2 T 0-835-
Мы видим, что критическое сжимающее напряжение пропорционально tg2 р. Если мы примем Е 2 106 кгсм2 и tg2p 0,001, то критическое напряжение будет Р PvvF 1670 кгсм2.
Так как в основание всех выводов положено допущение, что явление продольного изгиба происходит в пределах упругости, то ясно, что получающиеся в результате вычислении значения критических напряжений только тогда соответствуют действительности, если они не превосходят предела упругости. В противном случае они никакого реального значения не имеют и для нахождения критической нагрузки нужно прибегнуть к опытным данным. Можно, например, воспользоваться таблицей Ф. С. Ясинского, составленной на основании опытов Л. Тетмайера и И. Баушингера. В этой таблице даны величины критических напряжений для призматических стержней в зависимости от отношения г, где — длина стержня, г — наименьший радиус инерции. Если для заданной стойки критическое напряжение 1ф, определяемое из уравнения (6) или (8), получится большим предела упругости, то мы подыскиваем призматический стержень с таким соотношением г, чтобы для него формула Эйлера давала такое же значение р1ф. Критическое напряжение, соответствующее этому отношению 1г по таблице Ф. С. Ясинского, примем за критическое напряжение для рассчитываемой трубчатой сквозной стойки.
178
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
Положим, что в вышеразобранном численном примере tg2p 1500, тогда критическое напряжение будет к р 3340 кгсм2 напряжение это превосходит предел упругости железа.
Подыскиваем призматический стержень таких размеров, чтобы для него по формуле Эйлера получилось то же критическое напряжение. Для этого воспользуемся формулой
Ркр п2Е у)2.
Для критического напряжения 3340 кгсм2 получим г 77. Этому соотношению по таблице Ф. С. Ясинского соответствует критическое напряжение — 2245 кгсм2 для литого железа. Заметим еще, что уравнения (6) и (8) значительно упрощаются
в том случае, когда отношение bа близко к единице в та¬
ком случае малая величина). Положим --1а, где а — ма1 Ь
лая величина; тогда In — а.
Уравнение (6) представится в виде
ige‘-‘ w(1 )-
Для уравнения (8) получим такое выражение:
tgei-»)--яг (“, )
§ 3. О влиянии тангенциальных напряжений на величину критической нагрузки
При определении величины критической нагрузки мы исходили из дифференциального уравнения изогнутой оси стержня:
Здесь не принято во внимание влияние перерезывающей силы на величину прогиба; перерезывающая сила увеличивает прогиб и потому уменьшает величину критической нагрузки.
Для оценки влияния перерезывающей силы будем исходить цз того основного положения, что устойчивой формой равновесия является та, которой соответствует минимум потенциальной энергии. Пусть призматический брусок АВ сжат между двумя плоскостями силой Р (рис. 6). Концы стержня предполагаем свободно вращающимися. Если всякое искривление стержня сопровождается увеличением потенциальной энергии, то прямолиней¬
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
179
ная форма устойчива. В противном случае она неустойчива, и мы будем иметь явление продольного изгиба. Пока форма стержня прямолинейна, мы будем иметь потенциальную энергию только от сжатия. При искривлении стержня потенциальная энергия сжатия уменьшается, так как каждый элемент тп принимает некоторую большую длину т'пно зато в стержне накапливается энергия от изгиба и от сдвига.
Критическим значением сжимающей силы, очевидно, будет то, при котором уменьшение энергии от сжатия будет как раз равно энергии от изгиба и сдвига. При дальнейшем возрастании сжимающей силы прямолинейная форма равновесия становится неустойчивой.
В случае свободных концов искривленная ось стержня в самом общем случае может быть представлена таким уравнением:
тоо
( Jimsin. (1)
т-1
Приращение длины dx какого-либо элемента тп при искривлении стержня будет
т'п' — тп У dx2 dy2 — dx у dx. (2)
Соответствующее уменьшение потенциальной энергии от сжатия в элементе тп будет
(3)
Уменьшение 6ii энергии сжатия во всем стержне определится интегрированием элементарных выражений (3):
в0‘“тйг)2-
о
Или, подставив вместо у его общее выражение (1), найдем
О
-4-2 А тпл2 гп. тях сп- плх И у -
I 2 COS COS С1Х —
р V л- тп2 I PI X ,2 (тп
t2jM“T) у— hM—)
Рис. 6.
180
К ВОПРОСУ о ПРОДОЛЬНОМ ИЗГИБЕ
Потенциальная энергия от изгиба в элементе тп будет
М2 dx Р2у2 dx 2ЁТ 2EJ 9
(5)
Полная энергия 6v2 от изгиба получится суммированием элементарных выражений (5):
о о
. г» V1 А А т71Х ппх 1 P2l V1 2 пч
2 AmAn sin j sin j dx m (®)
Для составления выражения потенциальной энергии от сдвига заметим, что перерезывающая сила Q в каком-либо сечении
определяется формулой Q P--. Соответствующий угол сдвига у будет у kQGF, где F — площадь поперечного сечения,
G — модуль сдвига, k — коэффициент больший единицы, зави¬
сящий от формы сечения. Для прямоугольного сечения k 65, для двутаврового k 22,4. Потенциальная энергия от сдвига в каком-либо элементе длиной dx будет
'щ-dx. (7)
Полная энергия от сдвига 8v3 определится суммированием элементарных выражений (7):
i
Г kQ kP2 Г (dy. kP2l V л2 (тп2 04
6Уз J 2GF X 2GF J 1 dx) 4GF 2d m I ) ' 0 0
Критической сжимающей силой будет наименьшее значение Я, удовлетворяющее условию 6ii 62 бз или
Pt л ( тя2_ РЧ V «2 , kPH V 12 (тк
4 ДЛт I ) 4EJ IGF Zj ЛтТ) ’
откуда
IX (Т)2
р
-L.y А2 (не)2
ej GF Li m i j
J_V Л2 , folly Л2т2 2 К
EJ GF 2J Лт —T JT,2 2 —
л mni GF
Наименьшее значение для P получим, очевидно, тогда, когда дробь 2 т2 тяг2 получает свое наибольшее значение, т. е.
к ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
181
когда из сумм взят только один первый член и, следовательно. т 1.
В таком случае стержень искривляется по синусоиде
- . пх
у А sin —
и критическая сжимающая сила определяется формулой1)
Лф р 1 k (9)
EJn2 GF
Второй член в знаменателе представляет собой результат влияния перерезывающей силы на величину критической нагрузки. Полагая этот член равным нулю, мы придем к обычной формуле Эйлера.
Если через г обозначим наименьший радиус инерции сечения и отношение модулей Е : G положим равным 2,6, то формула (9) может быть представлена в таком виде:
Лер ——jr . (2')
л2 72 26k
В случае железных стержней формула Эйлера может быть применена к вычислению критической нагрузки при г 100, следовательно, в пределах применимости формулы (2х) - -
1 I2 1
-V-у юоо. „ „
л2 г2 Рис. 7.
Обыкновенно можно считать 2,6 k 10, откуда заключаем, что влияние тангенциальных напряжений на величину критической нагрузки меньше 1.
Все предыдущие рассуждения относятся к тому случаю, когда сдвиг может быть выражен формулой у kQGF, и потому неприменимы к расчету составных стержней. Положим, мы имеем трубчатую стойку квадратного поперечного сечения, составленную из четырех ребер, связанных решеткой (рис. 7). При
) Подобная формула недавно получена инженером F. Nussbaum’oM: см. его статью «Die genaue Saulenknicklast». Zeitschrift fur Mathematik und Physik, 1907, Bd. 55, Heft 1—2, SS. 134—138. Вывод Ф. Нуссбаума построен на рассмотрении дифференциального уравнения изогнутой оси и сложнее нашего. В применении к численному примеру Ф. Нуссбаум делает ошибку и на основании ошибочного результата заключает, что влияние тангенциальных напряжений на величину критической нагрузки может достигать 10. С этим мы не можем согласиться и покажем, что в пределах применимости формулы (9) влияние тангенциальных напряжений меньше 1.
182
К ВОПРОСУ о ПРОДОЛЬНОМ ИЗГИБЕ
расчетах полагают, что решетка вполне обеспечивает неподвижность одного ребра относительно другого, и потому пользуются формулой Эйлера, выведенной для цельных стержней. В действительности при слабой решетке возможен сдвиг одного ребра относительно другого. Эта возможность сдвига может значительно уменьшить величину критической нагрузки.
Если представить себе диагонали решетки легко растяжимыми, то, очевидно, каждое из ребер стойки будет работать самостоятельно, и вместо определения критической нагрузки для стойки как одного целого придется рассчитывать на про-
ствием поперечной силы Q (рис. 8). Допустим, что диагонали работают только на растяжение и что сечение диагоналей невелико по сравнению с сечением ребер; в таком случае можно пренебречь сжатием ребер при перекашивании, и выделенный элемент решетки примет под действием силы Q форму параллелограмма ab'c'd. Угол перекашивания у легко определится, если мы найдем удлинение диагонали б. Пусть Fd — площадь поперечного сечения диагонали, а — длина выделенной панели, а — угол между диагональю решетки и ребром стойки; тогда
Если бы мы допустили, что диагонали решетки работают не только на растяжение, но и па сжатие, и пренебрегли растяжением распорок, то получили бы угол перекашивания вдвое меньшим, чем то следует из формулы (10). В разбираемом нами случае стойки квадратного поперечного сечения придется принять
дое ребро. Чтобы оценить влия-
дольный изгиб отдельно каж-
о
а
Рис. 8.
d
ние растяжимости диагоналей на величину критической нагрузки для составной стойки, воспользуемся формулой (9). Для этого нужно добавочному члену в знаменателе придать другое выражение. Выделим одну из панелей составной стойки и рассмотрим, каков будет угол перекашивания у выделенной панели под дей-
6 -- sin a EFd cos а
Следовательно, угол сдвига
6
Q
(Ю)
a sin а
EFd sin2 а cos а
К ВОПРОСУ о ПРОДОЛЬНОМ ИЗГИБЕ
183
во внимание две решетки. Тогда для угла перекашивания найдем выражение
V лги Л (10')
1 Athj sin2 a cos а v 7
Сравнивая полученную формулу с формулой для у при сплошном сечении, легко видеть, как должен быть преобразован добавочный член в знаменателе формулы (9), чтобы ее возможно было применить к случаю трубчатой стойки. Если ввести обозначения 4EFd sin2 a cos а Pd, EJn2jl2 Ре (зйлерова критическая нагрузка), то критическая нагрузка для нашей трубчатой стойки определится из формулы1)
Р ed . (ID
'“Р Pe d' К '
Ре Pd
Мы видим, что для нахождения истинного значения критической нагрузки приходится величину Ре, определяемую по формуле Эйлера в предположении, что трубчатая стойка работает как цельный стержень, помножить на коэффициент уменьшения
f-pTtk- (12
Обыкновенно Pd очень велико по сравнению с Ре и коэффициент ф близок к единице. При малом сечении диагоналей уменьшение критической нагрузки может получиться весьма значительным. Л. Прандтль приводит пример сжатого стержня из Квебекского моста. Площадь сечения стержня F 4950 см2, площадь сечения диагоналей Fd 64 см2, момент инерции сечения 129- 105 сму Е 2,1 106 кгсм2, а 45. При этих данных Ре 88 ООО Ту Pd 47 500 т. На основании формулы (5) коэффициент уменьшения ф 0,35. Критическая сжимающая сила
будет
Ркр 0,35Р 31 200 т.
Соответствующее напряжение
Ркр -у- 6300 кгсм2.
Так как полученное напряжение превосходит предел упругости, то непосредственно им руководствоваться нельзя и придется
) К подобной формуле на основании совершенно иных соображений пришел проф. L. Р г a n d 11. Knicksicherheit von Gitterstaben. Zeitschrift des Vereines deutscher Ingenieure, 1907, Bd. 51, № 47, SS. 1867—1869. Перепечатка: L: P г a n d 11. Gesammelte Abhandlungen zur angewandte Mechanik, Hydround Aerodynamik. Erster Teil, Berlin — Gottingen — Heidelberg, Springer-Verlag, 1961, SS. 87—93.
184
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
воспользоваться опытными данными. На основании формулы
Ркр Еп2 (у)2
подберем цельный стержень с таким соотношением г, чтобы для него по формуле Эйлера получалось то же напряжение, что и для взятого нами составного стержня. Будем иметь
— я л— 57.
Г У Ркп
Р кр
Для такого соотношения по таблице Ф. С. Ясинского находим критическое напряжение ркр 2540 кгсм2. Наибольшее напряжение, допущенное в этом стержне, равнялось 1460 кгсм2. Следовательно, коэффициент безопасности равен 1,7.
§ 4. О продольном изгибе стержней с упруго заделанными концами
При проверке сжатых стержней на продольный изгиб мы предполагаем концы или свободно вращающимися, или абсолютно заделанными. В действительности приходится обыкновенно иметь дело с некоторым промежуточным случаем: концы стержня приклепаны к другим стержням и поэтому не могут свободно поворачиваться, но в то же время их нельзя считать и абсолютно заде» ланными. Под действием внешних сил концы эти будут поворачиваться, и, пока явление происходит в пределах упругости, углы поворота пропорциональны действующему моменту. Пусть АВ представляет искривленную ось сжатого стержня, а и р— углы, составляемые концевыми касательными с осью х (рис. 9). Тогда моменты М и М2, появляющиеся на концах стержня при выпучивании, будут
ЬА kdy 2у
где k и k2— коэффициенты, определяемые упругими свойствами заделки.
Уравнение изогнутой оси представится в таком виде:
jPJ р п — Mi ( х) М2х т
dx2 У I I »
общий интеграл его будет
у A sin 0jc В cos 0jc — —1 (1)
IP
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
185
Принимая во внимание условия на концах
I) у 0 при х О, II) у 0 при х , представляет уравнение упругой линии в таком виде:
и — ( Mi Ml 51П0г-4_-1 cos 0 х—Мх (2)
Р sin 0 Ptgf)J Р C0SdX IP ip '
Принимая во внимание, что
А-о-«-г и
получим для определения Мt и М2 два уравнения:
«.(' tf ттр») м‘ (таг - w) - »
Mi _ )(_м_ _ i _ i) о.
(3)
Чтобы было возможно искривление стержня, необходимо, чтобы написанные уравнения допускали для М и М2 решения, отличные от нуля. Для этого нужно, чтобы определитель уравнений (3) обращался в нуль. Таким образом, для нахождения величины критической нагрузки получаем трансцендентное уравнение
( л. kl fel9 ( k20 k — Л —
А WP Ptg0JPtg0 PI l)
-(h- U b®. -1 0 (4)
Pl P sin 0 ) P sin 0 Pi) u- W
Особенно просто решается уравнение (4) в том случае, когда концы стержня находятся в одинаковых условиях и, следовательно, ki k2 k. Уравнение (4) в данном случае представится в таком виде:
60 , 60 2k Л ( 60
PI Р sin 0 Р tg 0 U-
Приравнивая каждый из множителей нулю, мы получим два условия для возможности выпучивания. Легко показать, что первая возможная искривленная форма равновесия будет определяться из условия
kQ k9 kQ tg'
Р sin 0 Р tg 0 Из него находим
1—й—10.
1 w р
186
К ВОПРОСУ о ПРОДОЛЬНОМ ИЗГИБЕ
Первый корень полученного уравнения лежит между я2 и я Если жесткость заделки уменьшать и приближать k к нулю, правая часть уравнения (5) беспредельно возрастает. При k О, т. е. при свободно вращающихся концах, будем иметь
. 0
tg-y - оо,
5L р ,
2 2 9 КР
я2
2
При ft оо, т. е. при абсолютной заделке концов, получаем
, 0 п 0 п 4я2
tgy 0, РКр—2—
Если бы мы для определения критической нагрузки воспользовались вторым условием, т. е. положили
kO , кв
Р sin 0
_ __ 1 О
р tg 0 PI 1
то после некоторых преобразований получили бы
0
2 2 4 ’ к
, 0
(6)
Корни этого уравнения будут лежать в пределах 0
т я
для k 0 и
f-4,49
для k оош
Определяемые уравнением (6) искривленные формы равновесия будут иметь точку перегиба, соответствующие им сжимающие силы будут больше сил, определяемых уравнением (5).
Если условия заделки концов стержня различны и kx не равно k2, то нужно для определения критической нагрузки решать уравнение (4). Положим, например, k 0 и k2 оо, т. е. возьмем стержень с одним заделанным и одним свободно вращающимся концом. Разделим уравнение (4) на k2, при этом получим (0P)tg0—lPl О, или tg 0 0, откуда 0 4,49.
В виде численного примера разберем такой случай. Квадрат, составленный из стержней одинакового поперечного сечения, сжимается силами Р (рис. 10). Определим то значение сил Р, при котором становится возможным искривление, указанное на рисунке пунктиром; стержни ab и cd можно считать упруго заделанными; вращению их концов мешают распорки Ьс и ad. Что¬
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
187
бы повернуть концы этих распорок на угол ср нужно приложить по концам моменты
2EJ М ф —.
Следовательно, коэффициенты заделки будут
, - 2 EJ
kl k2 -J-.
Критическая сжимающая сила определится из уравнения (5):
, Ql _ Pi
g 2 2EJQ '
отсюда, принимая во внимание значение 9, получим
. 0 Ы
Т-ТПервый корень этого уравнения будет
Лер 16,46
Ц- 2,029,
EJ
I2
Если бы мы считали концы совершенно свободными, то получили бы Ркр 9,87 -(EJl2).
При абсолютно заделанных концах РКр 39,48 -(EJP).
§ 5. О продольном изгибе мноюпролетных стержней
Иногда приходится на продольный изгиб рассчитывать стержни, опертые больше, нежели в двух точках. Положим, у нас имеется стержень ABC с промежуточной опорой В, допускающей свободное вращение (рис. 11).
Критическая сжимающая сила для стержня ABC при постоянном поперечном сечении будет занимать некоторое среднее значение между критической сжимающей силой для стержня длины 1 и критической силой для стержня длины 2. Более короткий участок, очевидно, будет подкреплять участок более длинный. Если через М обозначим изгибающий момент в сечении В и примем во внимание, что в В оба участка искривленного стержня имеет общую касательную, то величина критической нагрузки легко находится из уравнения
упругой линии. Введем обозначения: Ql р. дЛЯ верхнего
г EJ
участка, 02 j-щ- для нижнего,
188
к ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
Уравнение упругой линии, если принять во внимание условия закрепления концов, будет
Af sin 0ja: , Мх
h
М sin 02л; М cos 00 , M(l2 — x)
у p tg e22 p f l2p для нижнего участка.
Принимая во внимание, что в точке В оба участка имеют общую касательную, приходим к уравнению
Af0, - М М0 2 м m
Ptg0ii , Ptg022 Р12'
которое может быть представлено в таком виде:
01 j 022 П (011 Ь 02) (011 22) Sin 11 Sin 022 (2)
Зная размеры стержня и пользуясь тригонометрическими таблицами, легко путем подбора решить уравнение (2), а следовательно, найти и соответствующее значение критической сжимающей силы.
При 0ii 02Ь оба участка нашего стержня независимо друг от друга должны были бы выпучиться при одной и той же сжимающей силе. Уравнению (2) можно в этом случае v, удовлетворить, положив 0ii ©22 Jill- Если нижний участок стержня сделать бесконечно
жестким, т. е. положить 022 0, то тогда уравнеs ’ ние (1) представится в виде
-Ц — tg 0ji 0ii,
Q 1
т. e. получим то же уравнение, что и в случае стерж1г ня с одним заделанным и другим свободно вращающимся концом.
При Oji у 022 уравнение (2) принимает вид 9 з 0ТКУДа 0ii 1,93, или рк р
Рис 12 Я,-Э,72 г 14,88
,2 ,2
М 2
Настоящий вывод легко обобщить на тот случай, когда в промежуточной опоре приложена продольная сила, как это обыкновенно бывает в многопролетных стойках (рис. 12). Обозначим через Q силу, приложенную в промежуточной опоре, и положим 02 f Р; тогда уравнение (1) примет вид
M0J. М М0 2 М ПЧ
р tg 0,, Plx - (P Q) tg 022 (Р Q) 2 w
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
189
или
- 0, ctg е,, 02ctg 022 у-
J_
h
(3')
В случае трехпролетного стержня весь вывод делается более длинным, но ход расчета остается прежним. Пусть ь 2, з — длины пролетов (рис. 13). Введем обозначения:
0
-Y-k- ж- е»-
Р
EJ3
Тогда, принимая во внимание условия на опорах, напишем уравнения упругой линии так:
М sin 01. Мхх
у-
и
Р sin 0ij
Ml
Ph
м2
P tg 022 P sin 022
для I участка, sin 02л: — cos 02л:
M2x , Afj (l2 — x)
1
, I
и
'
V.
'чх '
С
г'
л t
р
сз Ж UP
UP
для II участка,
У
M2 sin 02а: М2 cos 03х , М2(13 — х)
Ptg033 Р
кР
для III участка.
Рис. 13.
Здесь через Mi и М, обозначены изгибающие моменты, соответствующие промежуточным опорам В и С.
Если принять во внимание, что в В и С смежные участки имеют общие касательные, то можно написать два таких уравнения:
М
01
09
tg 0ii tg 02i м (тг - infer) м2 (
у у-) М2 (у г-)0,
2 1 12) l2 Sin 022 03
tg 022
L о
tg е3;3 h h 1
(4)
Условие для возможности выпучивания получим, если приравняем нулю определитель уравнений (4). Будем иметь
02 1 1 ( 02 03
h
01
. tg 0i tg 022
tg 022 tg 9.
h 12 U
-(J- )2 0
l2 sin 022
(5)
Из полученного условия в каждом частном случае может быть найдена величина критической сжимающей силы.
Если крайние участки имеют одинаковое поперечное сечение и равные длины, то уравнение (5) представится в виде разности двух квадратов и может быть разложено на два множителя.
190
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
Выпучивание возможно, когда один из этих множителей обращается в нуль. Для определения величины критической нагрузки придется пользоваться одним из таких двух уравнений:
Ql I 02 L П
tg0ii tg022 sin 022 j 1
01 , 02 1 2 , 02
1 pin A tg 0ii ' tg022 lx l2 л sin 022
Если стержень постоянного сечения, т. е. 01 02 0, то уравнения (6) могут быть представлены в более простом виде:
cos (0 -y-j - sin 0j cos -у- 0,
sin (eI-.)-(_j-JL) sine, sin - 0. ()
При определении критической нагрузки придется пользоваться тем из этих уравнений, которое дает наименьший корень.
Если 1 2, т. е. когда все три пролета одинаковой длины, го на основании первого из уравнений (7) будем иметь
0i я.
Если 1 и k приближать к нулю, оставляя средний участок конечным, то мы в пределе придем к стержню с заделанными концами. Первое из уравнений (7) при сохранении малых первого порядка представится в таком виде:
02. 02 02 cos y — 0 sin cos Y'
02
Для возможности выпучивания необходимо, чтобы я, 4Е1л2
откуда Ркр —j2— т е- получим то же выражение для критической силы, что и для стержня с заделанными концами.
Настоящий вывод без всяких затруднений может быть распространен на тот случай, когда сжимающие силы приложены и в промежуточных точках.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Известия Киевского политехнического института, 1910, год 10, Отдел инжв' нерной механики, книга 2, стр. 147—167. Отд. оттиск, Киев, 1910, 21 стр.
I. СЖАТИЕ ПРЯМОУГОЛЬНОЙ ПЛАСТИНКИ ДВУМЯ ВЗАИМНО ПРОТИВОПОЛОЖНЫМИ СИЛАМИ
В одной из предыдущих своих работ1) мы рассмотрели несколько случаев выпучивания прямоугольной пластинки под действием усилий, равномерно распределенных по краям. В случае сосредоточенных сил задача становится несравненно более сложной, так как в основном уравнении
’ d4w , n d4w , d4w rp d2w d2w л
1 Их zdy2 “ U
с(-
дх4 1 дх2 ду2 1 ду4
коэффициенты будут переменными.
Здесь мы приведем приблизительное решение для одного частного случая, исследованного проф. А. Зоммерфельдом2). Прямоугольная пластинка, опертая по краям, сжимается двумя взаим но противоположными силами Р, приложенными в серединах продольных сторон пластинки (рис. 1).
Когда силы Р достигнут известного предела, плоская форма равновесия пластинки перестает быть устойчивой, пластинка выпучивается. Величину критической нагрузки приблизительно можно найти из таких соображений. При выпучивании пластинки точки приложения сил Р несколько сблизятся, и благодаря этому силы Р совершат некоторую
работу. В то же самое время изменится и величина потенциальной энергии деформированной пластинки. Это изменение
Рис. 1.
1) См. нашу работу «К вопросу об устойчивости сжатых пластинок». Известия Киевского политехнического института, 1907, год 7, книга 2, стр. 35—94.
2) A. S о m m е г f е 1 d. Ober die Knicksicherheit der Stege von Walzwerk-
profilen. Zeitschrift fur Mathematik und Physik, 1907, Bd. 54, Heft 2,
SS. 113—153.
192
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
главным образом будет заключаться в энергии изгиба. Если приравнять работу сил Р энергии изгиба выпучившейся пластинки, то получим уравнение для нахождения Ркр. Если бы изменение потенциальной энергии пластинки заключалось лишь в энергии изгиба, то получаемое таким путем значение Р1ф было бы совершенно точным. В действительности задача значительно сложнее, так как, кроме изгиба, выпучивание пластинки сопровождается изменением растяжений.
Условиям на опертых сторонах пластинки мы удовлетворим, положив
пи - тпх 1Ч
w sm-f- 2а а ’ М
т 1, 3, 5,.
Потенциальная энергия изгиба выпучившейся пластинки будет
(2)
Сближение бb точек приложения сил Р найдется из следующей формулы:
«- () V» -(Л Л
Соответствующая этому сближению работа внешних сил будет
gLiAl-A3 A5-.)2.
Приравнивая эту работу потенциальной энергии изгиба (2), приходим к уравнению для определения критического значения сжимающей силы Р:
fg-(A,-A, As- 3
Нужно отыскать такое соотношение между коэффициентами Аи Аз,., чтобы определяемое из уравнения (3) значение Ркг имело наименьшее значение; другими словами, нужно найти м. нимум выражения
Y(«i_LW
Cn2ab2 Lk а2 Ь2 ) т 2 (Л,-А3 Л5-.)2‘
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
193
Составляя производную от этого выражения по какому-либо коэффициенту Ат и приравнивая ее нулю, найдем
уЛ2 (mL _L2 я Ат U2 Ь ) Q _
т л л ч ( т2 1 2 ( т2 1 2 (Л,-Л3 Л5- )Т-г Здесь Q — величина постоянная для всякого т, и потому выра¬
жение (5) даст нам нужное соотношение между коэффициентами льА3,А,. 1
Вставляя значение Ат в выражение (4) для критической силы, найдем
р _ Cn2ab2 1
кР - 2 V 1 Вводя для отношения длины пластинки к ее ширине обозначение ц, аb, найдем
р _ Ск2 с
КР 2Ь S J I 2 ' W
ЪVj
Для нахождения критической нагрузки нужно лишь найти стоящую в знаменателе сумму бесконечного ряда1).
Возьмем разложение ch-- в бесконечное произведение
Яг Яг
е 2 е 2
-(1 z2)(l т) t1 'ж)
Логарифмируя это выражение и составляя от него производную, найдем
Т2 г ( 1 z2 9 Z2 25 Z2 -) S m 3 Составляя производную от обеих частей полученного выражения, найдем
я2 1 у 1_ _ у 2г2
8 2 nz m2 z2 Za (m2 z2)2
ch —
Или, умножая на г и принимая во внимание равенство (7), получим
3 V 1 - я fth яг яг2 1 о
Lk (m2 z2)2 8 L 2 ch2 (яг2) J ‘ w
) Изложенный ниже прием суммирования принадлежит проф. В. П. Ермакову.
194 К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Пользуясь таблицами гиперболических функций, легко можно вычислять значения для Ркр при различных значениях Я.
Заметим, что с возрастанием длины пластинки сумма
очень быстро приближается к своему пределу я8 и критическая сила — к пределу
Ркр (9)
зт
Для (I ajb 2 означенная сумма будет 0,973 -g-.
Надо помнить, что вычисляемое по формуле (6) значение критической нагрузки будет меньше действительного и разность между действительной и истинной величиной ЛФ будет более значительной для коротких пластинок. Насколько близка к истине полученная формула, можно судить лишь на основании опытов.
Мы пришли к решению, взяв для w выражение (1). Если для w взять самое общее выражение
VI V1 л пшх пщ
W7l J Ащп Sin - Sin ;
то можно показать, что наименьшее значение для критической сжимающей силы получаем, беря одно определенное значение для п. При аЬ примем значение п 1.
Мы предполагали края пластинки свободно поворачивающимися, но величину критической силы можно приблизительно определить и при заделанных продольных сторонах пластинки. В этом случае
ш 0; -- 0 при у 0 и при у Ь.
Условию этому мы удовлетворим, положив
Потенциальная энергия изгиба для этого случая выразится так:
т _ n4abC X ( т2 , 4 2 л2
V- в-JjVo5 ь2) т'
к ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
195
Сближение сжимающих сил при выпучивании пластинки будет
(ж)'Л.- )'
о
Приравнивая работу сил Р потенциальной энергии изгиба, придем к уравнению
Рп2(Ах - Л3 А,-.)2 _ л41
Соотношение между отдельными коэффициентами будет
nnoMUQQ 1Я ПГк’ТГкЛЛЛГ
Заметим, что полученная нами 2 2
формула (9) была бы совершенно
точна, если бы сжимающие усилия 1.
передавались лишь бесконечно уз- Рис. 2.
кой полоске АВ и задача состояла
в том, чтобы найти критическую сжимающую силу для этой полоски при условии, что ее выпучиванию препятствуют незаштрихованные части пластинки (рис. 2).
II. ОБ УСТОЙЧИВОСТИ ЦИЛИНДРИЧЕСКОЙ ТРУБКИ ПРИ ПРОДОЛЬНОМ СЖАТИИ1)
§ 1. Исходные уравнения
Если по краям цилиндра кругового поперечного сечения (рис. 3) радиуса а приложены равномерно распределенные сжимающие усилия (Р — величина усилия, отнесенная к единице длины края), то они вызовут укорочение цилиндра, равное lP2hE; здесь — длина цилиндра, 2h — толщина стенки. Увеличивая постепенно сжимающие усилия, можно достигнуть предела, когда цилиндрическая форма равновесия перестает быть
Ъ
) Здесь и далее под цилиндрической трубкой понимается тонкая круговая цилиндрическая оболочка.
196
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
устойчивой, стенки цилиндра выпучиваются. Величина критичехкого значения сжимающих усилий Р может быть найдена как из уравнений равновесия, так и из рассмотрения изменений потенциальной энергии при искривлении. Будем обозначать через и, v и w компоненты перемещений точки Р по направлениям оси цилиндра, касательной к круговому сечению и нормали, направленной внутрь цилиндра. Деформация срединной поверхности определится выражениями относительных линейных деформаций
dv w
е2 ди dx 9
ад ф
и относительным сдвигом dv , ди
со
дх
ад ср
(1)
и изменениями кривизны d2w
дх2
х
-it
-±(
d2w ,
d2w. dv гд)
дф
dv
дх дф
дх
(2)
Рис. 3.
ф — угол между плоскостью ху и плоскостью UW.
Потенциальная энергия, отнесенная к единице поверхности цилиндра, составится из части
Eh
1
(в, вг)2 - 2 (1 - а) (е,е2 - ш2),
(3)
(4)
зависящей от величин ei, ег и со, а также части
J С (и, х2)2 - 2 (1 - а) - т2),
2 Eh3
зависящей от изгиба, где С у .
Дифференциальные уравнения равновесия для данного случая напишутся так (обозначения А. Лява1)):
дТх
дх
dN
dS:
дф
дЫ2
дх
дф
2 0,
Та
dSx
дТо
дх d2w ,
дНj dG2 , АТ
a-ar--WN О’
Н2 Н” (5 Н“ S2) а — 0.
дх2 1 2 dGi
а
дф То о,
дН
-м2 о,
дх
дф
- Nxa 0,
(5)
(6)
) А. Е. Love. Lehrbuch der Elastizitat. Autorisierte deutsche Ausgabe. Ubersetzt von A. Timpe. Leipzig und Berlin, Druck und Verlag von B. G. Teub-
ner, 1907, S. 610. Далее A. E. H. Love —A. Timpe.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
197
Величины моментов Gи. через перемещения и, v, w выразятся такими формулами:
G — C(xj OK2)t Go — С(и2 ctkj), 1 — H2 С (I — а) т. (7)
Что касается усилий 7, Г2, Si и S2, то они с достаточной точностью определятся формулами
В том случае, когда растяжения) срединной поверхности малы, для определения Гь. приходится пользоваться более точными формулами. Для кругового цилиндра радиуса а формулы эти будут2)
Определение критического значения сжимающего усилия Р —Т покажем на нескольких простейших примерах.
§ 2. Форма, симметричная относительно оси цилиндра
Положим, что края концевых поперечных сечений оперты. Тогда, увеличивая постепенно груз Q можно достигнуть состояния, когда начинается выпучивание стенок, представленное на рис. 4.
Пока образующие цилиндра остаются прямолинейными, деформация заключается в продольном сжатии. Величина относительного удлинения будет
Оно сопровождается поперечным расширением —сгео.
Потенциальная энергия, соответствующая этому напряженному состоянию, будет
При выпучивании стенок цилиндра потенциальная энергия его возрастет, так как к сжатию в продольном направлении
) Относительные деформации и сдвиги срединной поверхности.
2) А. Е. Н. Love — A. Timpe, S. 621.
ТС сге2) т2 с--(е, ае,) -
2 — 2ог — Зет2 к 1 _ 2сг а2 к2 2 (1 — а) а 2 (1 — а) а
а 2сг2 2 ст х2 1
2(1— сг) а 2(1— а) а у
.
(9)
VQ 4nalEhz.
(Ю)
198
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
присоединится растяжение по направлению касательной к круговому поперечному сечению и изгиб стенок. Очевидно, это приращение потенциальной энергии б V может получиться лишь за счет работы 6Т сжимающего груза Q, который при выпучивании стенок цилиндра несколько опустится. Величина критического значения сжимающей силы определится из
условия
6V8 Т. (11)
Положим
Л. ffZTCX л sin —j—, а 0. (12)
Что касается и, то оно определяется из того условия, что усилие Т остается при выпучивании постоянным и, следовательно,
Рис. 4. 6l 02 ео '
T2e0.
На основании формул (1) и (2) будем иметь
ei ео — — sm-
1 - . тях : — Л sin — сге0, со 0,
, л тяг. тях Л——у— Sin
х2 0, т 0.
2 ош
Подставляя эти величины в выражения (3) и (4), найдем величину потенциальной энергии цилиндра после выпучивания:
i i j
J (81 е2)2 2 (1 - а) е1е2 — -j co2j j dx у J кdx j
Eh
3(1 - а2) 1ап
I
V0 - 2hEoeo J -jsin 2nadx АЧп А2
о
откуда
6У -2гстео Г — sin 2nadx EhA2 — А2 2,1ал. (13)
j cl I а з v — о ) I
о
Опускание груза Q при выпучивании цилиндра определится так:
i i
, Г а. тях . 1 Г dw 2 1
6rJ -jsin — dx jj dx 0 0
44
. тях , А2 т2я2
Sin —7— dx —A ;—
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 199
Соответствующая этому опусканию работа груза Q равна
6Т 2паР
Г А. пглх , А2 т2п2
J Т5Ш—'dx 4 Г
(14)
Сравнивая (13) и (14), получим
р _ 2l2Eh 2 Eh3 m2Ji2
Гкр “ а2т2л2 3 (1 -a2)
Задаваясь различными значениями m, мы из формулы (15) найдем соответствующее значение Ркр. Практически интересно найти то число т, которому соответствует наименьшее значение сжимающей силы. Это может быть сделано так же, как в случае продольного изгиба стержня в упругой среде. Очевидно, наибольшей длиной , при которой первая искривленная форма имеет m полуволн, будет та, для которой формула (15) даст одно и то же значение РКр независимо от того, подразделяется ли поверхность при выпучивании на m или на m 1 полуволн.
Для нахождения получим уравнение
2l2Eh 2Ehz т2я2 _ 2l2Eh , 2Eh3 (m l)2jt2
а2пг2л2 ' 3 (1 — a2) I2 a2 (m 1 )2 n2 3(1— a2) 2 откуда Уmm )--У ah—. (16)
3(1 - a2)
Предельная длина, при которой искривленная форма состоит из одной полуволны, будет
I 2nah 3(43 Гай.
3(1-а2)
Для двух полуволн предельная длина будет
I fonдА 5(93 уш.
3(1 —а2)
При значительной длине цилиндра число m получается большим. Для этого случая длину одной полуволны X Ijm можно, на основании формулы (16), с достаточной точностью положить
_ _l_ _ п Vah
ш 4 3(1 -a2)
То же значение для длины полуволны мы могли бы получить и из формулы (15), заменяя в правой части 2т2 на X2 и
PKp -P. (17)
200 К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
приравнивая производную по X нулю. Если найденное значение подставить в выражение для РКр, то получим
4 Eh2 aV3(1 -а2) '
Соответствующее сжимающее напряжение будет
РкР 4rr —- —г—(18) И р 2Л а 3(1 _а2) Чтобы явление выпучивания происходило в пределах упругости, необходимо, чтобы толщина стенки 2h была весьма мала по сравнению с радиусом П. Например, для железа должно быть соблюдено условие
— г 1 0,001. а 3(1 -а2)
За пределами упругости формулы (17) и (18), конечно, неприменимы. Найденное нами значение Ркр может быть определено и из дифференциальных уравнений равновесия (5) и (6). В рассматриваемом случае
С1 -Сщ -С, 02-Сощ-Со-, , - Я 2 0, 5, - S2 0, Г, const - Р, T2--j 2Eh.
Первое и второе уравнения системы (6) дают нам N2 о, Ы,а-аС.
Вставляя это в уравнение третье системы (5), получим d4w , n d2w , w Л
dx4 dx2 а
или, вводя обозначения
__Ол2 2Ez _3 (1 — о2) ,4
С а2С a2h2 К ’
приходим к уравнению
2а2до й4до 0.
Принимая во внимание, что при 0 ш 0 и найдем
иу A sin рх В sin qx9
где
р V а2 V а4 — ft4, q Va2 — a4 — kA.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 201
Для возможности выпучивания необходимо, чтобы
a4-fe4 0.
Так как при х I имеем те же условия закрепления, что и при х 0, то, следовательно,
A sin pi В sin ql 0, Ар2 sin pi Bq2 sin ql 0.
Для возможности выпучивания необходимо, чтобы определитель написанных уравнений обращался в нуль, т. е. чтобы
sinp 0 или sing7 0,
откуда для определения ЯКр имеем
а212 УаЧ'-kH4 т2я2, а212 - VаЧ - k44 п2л2, (19)
где т и п — любые целые числа.
При большой длине стержня можно положить
г22 т2л2,
где т — целое число.
В этом случае оба условия (19) приводят к одному и тому же результату аЧ2 т2л2, или
2Ст2я2 22 2С3(1 -а2) Eh2
р _ _ кр 2 ah aV3(-o2)
что совершенно совпадает с ранее полученным значением (17). Интересно полученное значение для Ркр сравнить с тем, что в применении к нашему цилиндру дает формула Эйлера
0 EJn2
271CL Ркр J2
Здесь — момент инерции поперечного сечения.
В случае тонкостенного цилиндра можно положить
j 2па32Н
J 2
Следовательно, для возможности продольного изгиба нужно, чтобы
(20)
Ркр Ркр в том случае, если
4Аг Ena2h
аУ3(1 — а1) 12 ’
откуда находим такое соотношение между размерами цилиндра: А я2 3(1 -а2) а2 „ , „ а2 _ d
202
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
При меньшем значении отношения ha цилиндр, раньше чем изогнуться подобно стержню, получит искривление стенок, представленное на рисунке 4 (стр. 198). При выводе формулы (17) мы предполагали края цилиндра свободно поворачивающимися. При длинных цилиндрах способ закрепления концов не играет роли, и потому формула (17) может быть применена и в случае цилиндров с заделанными краями.
§ 3. Искривления, не сопровождающиеся растяжением
Если края сжатого цилиндра не только могут свободно поворачиваться. но и отдельные точки их могут перемещаться, то цилиндр при некотором значении сжимающих усилий может принять новую форму равновесия, причем переход к этой форме равновесия не будет сопровождаться изменением растяжения срединной поверхности. Перемещения, соответствующие этому изменению формы, могут быть представлены так1):
и - J Вп sin (йф р„); v Впх cos (йф р„);
Vi , 21)
W - 2j tiBnx sin (йф Р„).
При этом изменении формы потенциальная энергия цилиндра увеличится, так как к энергии сжатия присоединится энергия изгиба, определяемая такими изменениями кривизны:
1 d2w , dv пъ — п D. , .
«i 0; х2 -jr 15Г) 2j — в»х Sln W Эя);
т “ -J JLr Вп cos (n(V
Это увеличение потенциальной энергии получается за счет работы внешних сжимающих сил. Работу эту 6Т можно найти из таких соображений. Образующие цилиндра при рассматриваемом изменении формы остаются прямолинейными и наклоняются на угол
Y У 2 вп cos (йф р„)2 2 пвп cos (йф р„)12.
Этому наклону соответствует работа
2Л
бT Plj f у2аdq -J-alP JBn(1 n) (22)
0
J) См. указанную на стр. 196 книгу А. Е. Н. Love — A. Timpe, S. 575.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
203
Условия для нахождения критического значения сжимающих усилий Р найдем, приравнивая работу ЬТ потенциальной энергии изгиба ):
6V Cnl 2 Вп у nt2 (1 - а) а2; (23)
получим
„ 9Г Ул'гг-)гВппЧ 2(-о)аЛ
Р Li I (ОЛ
кр — 4 2 , , 2 . V
а 2jBn nf
При п 1 получаем перемещения цилиндра как твердого тела. При п 2
Рр у у 2 2 (1 — a) a2 j. (25)
Если длина цилиндра значительна по сравнению с его диаметром, то критическое сжимающее усилие с достаточной точностью будет
р _ 24 С ,2 _ I® Eh2 h 2
Гкр“ 5 а4 5 а(-о2) а а2 ' Сравнивая этот результат с формулой (17) § 2, находим2)
р _ п 43 Л2
КР “ КР с Г “Т
5 у 1 — а2 а а2
Легко показать, что принятое нами изменение формы без изменения растяжений не удовлетворяет основным уравнениям равновесия (5) и (6) § 1. Для этого достаточно сравнить выражение
Г2-27 Xе’ (27)
получаемое из формул (9) § 1, с тем, что дает третье уравнение системы (5) § 1, если в него вместо Ni и N2 подставить их значения из уравнений системы (6) § 1.
Из этого уравнения имеем
„ dNx дЫ2 rp „ d2w С д2х ооч
Т-ад-х WTiaWTW (28)
Вставляя вместо хг его значение, получим из (27) и (28) такие значения:
т2- To-g) § S ВпХ sin (гф Р»)»
Т2 - sin («Ф Pn)-
) См. указанную на стр. 196 книгу А. Е. Н. Love — A. Timpe, S. 583.
2) где Р'кр определяется выражением (17).
204
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Оба значения для Т2 различны, и потому взятые нами перемещения (1) не удовлетворяют уравнениям равновесия. Для удовлетворения уравнений равновесия к изгибу нужно присоединить еще растяжение.
Не удовлетворяют выбранные перемещения и условиям на концах. При х 0 и х I должны быть выполнены условия
G, 0, ЛГ.-iL»-Р-.
1 9 1 а дф дх
Между тем при перемещениях (1) Gi является линейной функцией х и не обращается в нуль при х.
Следовательно, для удовлетворения дифференциальным уравнениям равновесия нужно к выбранным перемещениям (1) присоединить еще растяжения и некоторые усилия, распределенные по краям.
Решения некоторых задач, относящихся к деформации цилиндрических трубок1), дают основание полагать, что потенциальная энергия, которая получается от добавочных растяжений и от усилий по краям, мала по сравнению с потенциальной энергией изгиба; поэтому формула (5) может служить для определения критического значения сжимающей силы.
Мы рассмотрели простейший случай, когда цилиндр подвергается равномерному продольному сжатию, усилие Р постоянно по всему поперечному сечению. Практически интересен также случай, когда усилие меняется по закону соэф, т. е. Ti Р соэф, В этом случае цилиндр подвергается действию изгибающих моментов по концам, и, пока эти моменты не превзошли известного предела, цилиндр гнется, как стержень. При возрастании усилий может произойти выпучивание стенки цилиндра со стороны сжатых образующих.
Интересна также задача об устойчивости части цилиндра, ограниченной двумя образующими и двумя круговыми поперечными сечениями и сжатой усилиями Я, параллельными образующей.
III. ОБ УСТОЙЧИВОСТИ ИЗГИБА ПОЛОСЫ С КРУГОВОЙ ОСЬЮ
Пусть ВАВ' — ось полосы, имеющая форму дуги круга радиуса а. А расположено в среднем сечении полосы (рис. 5). Длина полосы равна 2аа. Поперечное сечение полосы — вытянутый прямоугольник, длинные стороны которого параллельны плоскости кривизны ОВВ Обозначим через Л и В наибольшую
J) См. указанную на стр. 196 книгу А. Е. Н. Love — A. Timpe, S. 626.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ упругих систем
205
и наименьшую жесткости полосы при изгибе; тогда В EJi и А EJ2j где i и 2— наибольший и наименьший моменты инерции поперечного сечения. Мы будем предполагать, что Л велико по сравнению с 2. Если полосу изгибать двумя парами сил М, лежащими в плоскости ВОВ', то полоса, очевидно, будет изгибаться в той же плоскости. Мы будем иметь плоскую форму изгиба. Постепенно увеличивая М, можно достигнуть предела, когда плоская форма перестает быть устойчивой, полоса выпучивается, ось ее изгибается по линии двоякой кривизны. Величину момента Мкр, при которой плоская форма изгиба перестает быть устойчивой, можно легко найти из дифференциальных уравнений равновесия Предположим, что выпу чивание полосы произо шло, но перемещения от дельных точек малы В таком случае деформацию возможно определить следующим образом. Пусть Р — одна из точек на оси полосы. Положение ее до деформации определяется углом 0. Построим систему координатных осей х0, у0, z0, направления которых совпадают с направлениями радиуса, касательной и перпендикуляра к плоскости кривизны ОВВ'. При выпучивании полосы точка Р переместится. Пусть и, v и w — перемещения в направлении осей х0, у0 и z0. Поперечное сечение полосы, соответствующее точке Я, при выпучивании несколько повернется, и плоскость наибольшей жесткости составит с плоскостью ОВВ' угол р. За положительный будем принимать поворот в направлении от х0 к у0. Для концов полосы будем иметь v 0 и р 0. Обозначим через х и у направления главных осей инерции поперечного сечения полосы после выпучивания и через z направление касательной выпучившейся оси полосы в точке Р. Тогда моменты G, Gu Н относительно х, у п z выразятся через перемещения и, v, w и р так ):
G a a2dQ2) В а2 дЭ2 а2 дО)9 Н CUd0 a2de)‘
Здесь через С обозначена жесткость кручения.
) Формулы эти можно получить из общих выражений, полученных в указанной на стр. 196 книге А. Е. Н. Love —A. Timpe (S. 513), полагая в них 120 0.
206 К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Те же величины легко можно выразить через момент внешних сил М. Принимая во внимание малость перемещений,
получим
G Mp, Gt M, (2)
Вставляя эти значения G и Н в уравнение (1), найдем
(-4)3-о. 45И4-)- (3)
Исключая из полученных уравнений величину р, найдем
d3v. « Ма(, Ма dv А )Ч
Полагая
(l--)(l- Щ к (5)
получим из уравнения (4)
D sin kQ cos kQ.
Если форма выпучившейся пластинки симметрична относительно середины, то должно быть выполнено равенство ЗиД30 О при 0 0.
Следовательно,
g- D sin kQ.
На концах полосы G 0 и р 0. Следовательно,
d2vdQ2 0.
Условие это будет выполнено, если
и С г, 22 -Ь 1
cos fta 0, т. е. когда ka ——я-
Принимая во внимание равенство (5), получим уравнение для определения Л1кр:
if, 6
откуда при г 0
м„ - ± (Wf-(7)
Здесь I 2аа обозначает длину полосы.
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 207
Отметим несколько частных случаев. Если ось полосы прямолинейна, а оо. Для критического значения момента получаем выражение
Мкр ± i У АС. (8)
Эта формула совпадает с тем, что было получено нами1).
Если ось полосы слегка искривлена, т. е. если а велико по сравнению с , Мкр можно вычислять по формуле
- Чг ± Т
Знак « » соответствует направлению моментов, взятому на рисунке, знак «—» — моментам противоположного направления. Если ось полосы представляет собой полукруг, то ая, формула (7) дает нам
Значение Мкр, соответствующее знаку « », будет в этом случае А С
равно 2 2значение Мкр, соответствующее знаку «—», об¬
ращается в нуль. Подобный результат объясняется тем, что в данном случае полоса может вращаться без деформации относительно диаметра, соединяющего концы В и В'. При этом вращении р и v равны нулю на концах полосы.
Мы рассмотрели случай п 0. Полагая и 1, 2, 3,., получим серию различных форм равновесия, симметричных относительно середины А. Полагая dvdQ Dcos 0, получим ряд возможных форм равновесия, не симметричных относительно середины.
Если положить на концах полосы дидд 0, то найдем выражение для Мкр в случае полосы с заделанными концами.
) С. П. Тимошенко. Об устойчивости плоской формы изгиба двутавровой балки под влияиием сил, действующих в плоскости ее наибольшей жесткости. Известия С.-Петербургского политехнического института. Отд. оттиск, СПб., 1906, стр. 30, формула (16).
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ. ПРИМЕНЕНИЕ НОВОЙ МЕТОДЫ К ИССЛЕДОВАНИЮ
устойчивости НЕКОТОРЫХ мостовых
КОНСТРУКЦИЙ.')
Известия Киевского политехнического института, 1910, год 10, Отдел инженерной механики, книга 4, стр. 375—560. Отд. оттиск, Киев, тип. С. В. Кульженко, 1910, 188 стр. То же, 1911. Перевод на французский язык: Sur la stabilite des systemes elastiques. Application d’une nouvelle methode a la recherche de la stabilite de certaines parties constitutives des ponts. Annales des ponts et chausees, 9th series, 1913, tome 15, vol. 3, Mai —Juin, № 24, pp. 496—566; tome 16, vol. 4, Juillet — Aout, № 39, pp. 73—132; tome 17, vol. 5, Septembre — Octobre, № 50, pp. 372—412; Paris, A. Dumas. 1914. 174 p. Перепечатка: S. P. Timoshenko. The collected papers. McGraw-Hill Publishing Company Ltd, New York — London — Toronto, 1953, pp. 92—224.
ВВЕДЕНИЕ
Повышение качеств строительных материалов и усовершенствование конструкций в современных инженерных сооружениях приводят к тому, что значение теоретического расчета при проектировании все возрастает. Чем выше качества материала и чем совершеннее конструкция, тем лучше могут быть выполнены условия, которые обыкновенно кладутся в основание выводов строительной механики и теории упругости, тем с большим основанием можно переходить от грубых, приближенных формул к более точным теоретическим исследованиям.
До недавнего времени исключительное внимание при расчетах обращали на вычисления напряжений; меркой прочности являлось отношение допущенных напряжений к временному сопротивлению материала. Ряд крупных катастроф показал, что такого расчета для современных инженерных сооружений далеко не достаточно, принятые нормы допускаемых напряжений не всегда обеспечивают надлежащую прочность, необходимы дополнительные исследования относительно устойчивости как отдельных частей, так и всего проектируемого сооружения. Важность проверки на устойчивость в настоящее время сознается всеми, но вследствие недостатка в теоретической разработке вопросу устойчивости и в строительной механике, и в технических расчетах отводят лишь весьма скромное место, обыкновенно ограничиваются только проверкой на продольный изгиб сжатых стержней. Но в таких же условиях неустойчивого равновесия,
) Сочинение удостоено Институтом инженеров путей сообщения премии инженера путей сообщения Д. И. Журавского,
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
209
как сжатый стержень, может оказаться и сжатый лист, и изгибаемая балка, и сжимаемая внешним давлением цилиндрическая трубка и т. д. К сожалению, для этих более сложных задач далеко не всегда имеется надлежащее решение, которое инженер мог бы применить непосредственно к расчету; иногда же решения эти получены столь сложным путем, что для сознательного их применения необходима гораздо большая математическая подготовка, чем того можно требовать от инженера-конструктора.
Приступая к составлению настоящей работы, мы поставили себе целью не только собрать и упростить решения уже исследованных вопросов устойчивости, но также получить и новые решения для задач, имеющих практическое значение. Это нам в некоторых случаях удалось выполнить благодаря применению особой методы, к изложению которой мы теперь и переходим.
Пока все размеры упругого тела одного порядка, малым деформациям соответствуют и малые перемещения отдельных точек. В таком случае можно считать, что система внешних сил при деформации не меняется; это является необходимым условием для однозначности решения уравнений теории упругости. В том случае, если два или по крайней мере один из размеров мал, т. е. еслч мы имеем дело с тонким стержнем или тонкой пластинкой, малым деформациям могут соответствовать конечные перемещения. При этом условии1) одной и той же системе сил могут соответствовать несколько различных форм равновесия, и возникает вопрос об устойчивости этих форм. Рассчитываемая конструкция, очевидно, будет прочной лишь в том случае, если положенная в основание расчета форма равновесия устойчива. Для практических приложений необходимо знать то наименьшее значение внешних нагрузок, при котором становится возможным несколько форм равновесия. Значение это в дальнейшем будем называть «критическим». Пока нагрузка меньше критической, возможна лишь одна-единственная форма равновесия, и эта форма, очевидно, будет устойчивой. При нагрузках, больших критической, возможны по крайней мере две формы равновесия. Устойчивой формой будет та, которой соответствует минимум потенциальной энергии. Для определения критического значения нагрузки пользуются обыкновенно таким приемом. Рассматривают возможные формы равновесия, удовлетворяющие условиям на поверхности и весьма мало отличающиеся от той формы равновесия, которая соответствует нагрузкам, меньшим «критической». Для этих возможных форм равновесия составляют дифференциальные уравнения равновесия и отыскивают
) G. Н. В г у а п. On the stability of elastic systems. Proceedings of the Cambridge Philosophical Society, mathematical and physical sciences, 1889, vol. 6, pp. 199—210.
210
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
те значения внешних сил, при которых эти дифференциальные уравнения допускают решения, удовлетворяющие условиям на контуре. Наименьшее из этих значений и будет критическим. Для критического значения нагрузки получается бесчисленное множество возможных форм равновесия, так как решение дифференциальных уравнений заключает в себе произвольный постоянный множитель. Это указывает на неопределенность формы равновесия для нагрузок, равных критической. Неопределенность эту легко демонстрировать при испытании стержней на продольный изгиб или при испытании на изгиб высоких двутавровых балок. Таким образом, отыскание критических значений нагрузок сводится к решению дифференциальных уравнений при заданных условиях на контуре. При исследовании устойчивости сжатых стержней мы будем иметь дело с одним обыкновенным дифференциальным уравнением. Для случая изгиба полос и двутавровых балок придется решать систему из двух обыкновенных дифференциальных уравнений. При расчете сжатых пластинок задача сводится к интегрированию линейного дифференциального уравнения в частных производных. Таким образом, наиболее простыми являются задачи, относящиеся к устойчивости сжатых стержней. В случае сжимающих сил, приложенных по концам, задача приводится к линейному уравнению с постоянными коэффициентами. При сжатии стержня силами, равномерно распределенными по длине, получаем уравнение, решаемое в бесселевых функциях. Для более сложных случаев нагрузки приходится иметь дело с уравнениями, для которых неизвестны интегралы в замкнутой форме; тогда ищут решение в форме бесконечного ряда. Отыскание критической нагрузки сводится к суммированию иногда весьма сложных и медленно сходящихся рядов. Работа эта практически часто является настолько сложной, что приходится отказываться от дальнейшего решения задачи. Задачи об устойчивости изгиба полос и двутавровых балок являются более сложными. В этом нам пришлось убедиться при исследовании устойчивости плоской формы изгиба двутавровых балок1). Для решения задачи при простейших способах нагрузки пришлось на вычисления затратить несколько месяцев. Попытки решить ту же задачу для условий, более близких к действительности, привели к столь сложным вычислениям, что работу пришлось оставить. Решение задачи об устойчивости пластинок удалось получить лишь для простейших случаев нагрузки и то далеко не для всех способов закрепления по контуру пластинки.
) С. П. Т и м о ш е н к о. Об устойчивости плоской формы изгиба двутавровой балки под влияиием сил, действующих в плоскости ее наибольшей жесткости. Известия С.-Петербургского политехнического института. Отд. оттиск, СПб., 1906, 132 стр.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
211
Перечисленные затруднения при интегрировании уравнений заставляют искать другие методы для решения вопросов устойчивости, такие, которые давали бы возможность находить величины критических нагрузок непосредственно, не прибегая к интегрированию дифференциальных уравнений равновесия. Наиболее естественно обратиться в данном случае к рассмотрению выражения для энергии системы. Нам обыкновенно известна форма равновесия, соответствующая нагрузкам, меньшим критической. Без затруднений возможно составить выражение для изменения энергии системы при малом отклонении от этой формы равновесия. Если при всяком возможном отклонении потенциальная энергия системы возрастает, рассматриваемая форма равновесия будет устойчива; в противном случае она будет неустойчива. Критическим будет то значение нагрузки, при котором изменение энергии системы для какого-либо возможного отклонения обращается в нуль. Обозначим через V измененче энергии внутренних сил упругости системы и через Т работу внешних сил при отклонении от рассматриваемой формы равновесия, тогда критическое значение нагрузки найдется из уравнения
T V. (1)
Очевидно, из всех возможных отклонений нужно выбрать то, при котором уравнение (1) дает для внешних сил наименьшее значение. Подобный способ определения критического значения нагрузок был предложен Дж. Брайаном1). Он применил этот способ к нахождению критической нагрузки для сжатого стержня со свободно поворачивающимися концами и для решения вопроса об устойчивости прямоугольной сжатой пластинки с опертыми краями. В обоих этих случаях легко написать общее выражение для отклоненной формы равновесия и найти значения для V и Т. Вставляя их в уравнение (1), получим критическое значение для внешних сил. Подобным путем легко получить критическое значение сжимающей силы для призматического стержня в упругой среде2) и для прямоугольной пластинки, сжимаемой двумя взаимно противоположными силами3). Однако в большинстве случаев задача об определении критической
1) См. цит. на стр. 209 работу, а также статью: G. Н. В г у а n. On the stability of a plane plate under thrusts in its own plane, with applications to the «buckling» of the sides of a ship. Proceedings of the London Mathematical Society, Series 1, 1891, vol. 22, pp. 54—67.
2) См. нашу работу «О продольном изгибе стержней в упругой среде». Известия С.-Петербургского политехнического института, 1907, том 7, Отдел техники, естествознания и математики, выпуск 1, стр. 145—157.
3) См. нашу работу «К вопросу об устойчивости упругих систем». Известия Киевского политехнического института, 1910, год 10, Отдел инженерной механики, книга 2, стр. 147—167,
212
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
нагрузки является более сложной, так как общее выражение для отклоненной формы равновесия неизвестно и его нужно разыскать. Для этого мы можем воспользоваться таким приемом: на основании опытных данных и принимая во внимание условия на контуре, задаемся подходящей формой равновесия и для этой формы составляем выражения для V и Т; вставляя эти выражения в уравнение (1), найдем критическую нагрузку. Конечно, выбранная произвольно форма равновесия не будет, вообще говоря, удовлетворять уравнениям равновесия, но если условия на контуре выполнены, то из уравнения (1) можно довольно точно найти критическую нагрузку. Прием этот аналогичен тому, который был применен лордом Рэлеем для изучения колебаний упругих систем. Мы пользовались этим приемом для исследования изгиба стержней и пластинок1). При выборе отклоненной формы равновесия мы можем ее представить в виде функции от ряда параметров и потом эти параметры выбрать так, чтобы определяемая из уравнения (1) величина критической нагрузки имела минимальное значение. Возьмем, например, тот случай, когда отклоненная форма определяется функцией одной переменной, как то имеет место в случае выпучивания сжатых стержней. Искривленная форма стержня может быть представлена так:
w а1у1 (х) а2 ср2 (х) а3ф3 (х). (2)
Здесь через w обозначаем прогиб стержня в сечении, определяемом координатой х. Каждую из функций (pi(), фг()». выбираем так, чтобы они удовлетворяли заданным условиям на концах и чтобы ряд (2) мог представить с достаточной точностью ожидаемую искривленную форму равновесия. Имея выражение (2) для отклоненной формы, можно найти величины
V и Т они представятся в виде функций от параметров аи а2, а3, г. Выражение для критической нагрузки получится из уравнения (1) и тоже будет зависеть от величин аи ci2, остается эти величины подобрать так, чтобы для критической нагрузки получить наименьшее значение. Таким образом, задача об определении критической нагрузки сводится к нахождению минимума известного выражения. Увеличивая число параметров аи ai,., мы будем получать все большую точность; в пределе получаем точное решение. Поясним все сказанное примером. Положим, требуется найти критическое значение сжимающей силы для стержня, заделанного нижним концом (рис. 1). Пусть
1) См. нашу работу «Применение нормальных координат к исследованию изгиба стержней и пластинок». Известия Киевского политехнического института, 1910, год 10, Отдел инженерной механики, книга 1, Отд. оттиск, Киев, 1910, 49 стр.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 213
под действием сжимающей силы Р произошло искривление стержня. Дифференциальное уравнение равновесия для искривленной формы будет
EJPy О, (3)
откуда у б COS ej xj
Чтобы было выполнено условие у верхнего конца, нужно положить
1‘ (2дг 1) я
V EJ 21
Следовательно, критическое значение нагрузки будет
п _ __ 2,4674
42 2
К тому же результату легко прийти, пользуясь приемом Дж. Брайана.
Изменение потенциальной энергии деформации при искривлении стержня будет
г- to-
о
Работа внешних сил при искривлении стержня представится произведением из силы Р на величину опускания верхнего конца стержня. Опускание это, очевидно, равно разности между длиной дуги, по которой искривился стержень, и длиной ее проекции на вертикальное направление и может быть представлено формулой
т Ш'йх-
о
Уравнение (1) дает нам для критического значения нагрузки формулу
е,1 Ш
Р w I . (4)
() о
214 ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Общее выражение для искривленной формы можно в данном случае представить в форме такого тригонометрического ряда:
„ ТСХ - Зях ,
у A0cos-y-A cos-y-.
Вставляя это в выражение для Ркр, найдем
Р'р '
Наименьшее значение для Рнр, совпадающее с вышенайденной величиной, получим, полагая все коэффициенты, кроме Л0, равными нулю, т. е. вставляя вместо у его значение, определяемое из уравнения (3).
Применим теперь к разбираемому случаю намеченный выше приближенный метод. Представим себе искривленную форму так:
у — 6 ахх2 а2х4.
При этом условия у закрепленного конца, очевидно, будут выполнены:
при 0 У— S и 0.
Для простоты вычислений мы ограничиваемся тремя первыми членами степенного ряда. Для потенциальной энергии внутренних сил упругости при изгибе получаем выражение
i
У Ц- J (2а 2a2x2)2dx.
о
Работа внешних сил при искривлении стержня представится формулой
Г 4 J (2аХ 4а2хг)2 dx.
о
Вставляя это в уравнение (1) и вводя обозначение а2а z, мы получим для критической нагрузки выражение
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
215
Разыскание наименьшего значения для Рьр приводит нас к квадратному уравнению
608z24 640z2 0.
Корнями этого уравнения будут
0,1749 0,8777
I2 9 2
Вставляя значение Z в выражение для РКр, получим
п _ 2,4697 кр 2
Найденное приближенное значение для РКр отличается от точного меньше чем на 0,1. Таким образом, три первых члена степенного ряда обеспечивают в данном случае точность большую, чем то требуется для практических приложений. Увеличивая число членов в выражении для прогиба, мы будем увеличивать и точность результата. Заметим, что вычисление дальнейших приближений требует значительно большей затраты времени и практически является излишним. К нему следовало бы прибегнуть лишь в том случае, если бы мы хотели получить значения нагрузок, соответствующих формам равновесия с одной или несколькими точками перегиба. Эти формы равновесия, как известно, неустойчивы и не имеют практического значения.
Заметим здесь, что при вычислении критического значения нагрузок по описанному способу мы всегда для них будем находить величины большие действительных. Получается это потому, что, задаваясь формой изгиба, мы как бы вводим в нашу систему дополнительные связи, благодаря чему не все возможные отклонения действительной системы будут возможными и для нашей фиктивной системы с дополнительными связями. Такое уменьшение числа степеней свободы системы ни в каком случае не может сопровождаться уменьшением жесткости. Жесткость лишь в исключительных случаях и для некоторых определенных форм равновесия может остаться неизменной, вообще же она возрастет, а следовательно, возрастет и величина критической нагрузки.
Недостатком описанного приближенного метода следует считать то, что мы при вычислении не можем указать степени точности получаемого результата. О погрешности можно судить лишь сравнивая последовательные приближения. Заметим, однако, что и в тех случаях, когда задача решается путем интегрирования соответствующих уравнений, далеко не всегда может быть установлена строго степень точности результата, так как приходится обыкновенно иметь дело с суммированием сложных рядов и с решением трансцендентных уравнений, связывающие суммы этих рядов.
216
ОБ УСТОЙЧИВОСТИ упругих систем
Мы на частном примере выяснили ход решения задачи в том случае, когда отклоненная форма равновесия является функцией одной переменной. Метод без всяких изменений может быть применен и в том случае, когда приходится иметь дело с функцией нескольких переменных (при исследовании устойчивости пластинок имеем две переменные) и когда, следовательно, задача об устойчивости сводится к интегрированию уравнения в частных производных. Во всех случаях вместо интегрирования уравнений придется выполнить ряд квадратур и потом найти минимум некоторого выражения, зависящего от параметров а, a2l а3,. Получаемое при этом приближенное выражение для отклоненной формы представляет собой приближенное значение интеграла соответствующего дифференциального уравнения, и тогда описанный метод можно рассматривать как приближенный прием интегрирования дифференциальных уравнений. Связь между операциями, выполняемыми при приближенном вычислении критической нагрузки, и интегрированием соответствующего дифференциального уравнения выясним на вышеразобранном простейшем случае продольного изгиба.
Задача, как мы видели, свелась к нахождению минимума такого выражения:
i
о
Минимум этот будет иметь место в том случае, когда
J ж)21хЬ J(S)2- J (ffdxb J (ж)21х0-
0 0 0 0
Или, принимая во внимание выражение (4), найдем
0
т. е. задача сводится к нахождению минимума такого интеграла:
s- (-§-)’-(SOI (5)
о
что равносильно интегрированию дифференциального уравнения
EJz Pz О,
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
217
где z dydx. Интеграл этого уравнения совпадает с интегралом уравнения (3).
Таким образом, разыскание минимума интеграла (5) равносильно интегрированию уравнения (3). При пользовании приближенным методом мы вместо задачи вариационного исчисления решаем задачу о нахождении минимума выражения
в котором вместо у вставлено его значение в форме степенного ряда.
На математической стороне этого вопроса мы больше останавливаться не будем; этому предмету посвящена замечательная работа швейцарского ученого Вальтера Ритца ). Сводя интегрирование уравнений к нахождению минимума интегралов, В. Ритц показал, что для обширного класса задач мы, увеличивая число параметров аи а2, а3, , получим сходящийся процесс и в пределе придем к точному решению задачи. Для того цикла задач, которыми мы в дальнейшем будем заниматься, такого доказательства не имеется, но приложения приближенного метода к задачам, для которых уже имеется точное решение, показывают, что метод этот даст очень хорошие результаты и практически не приходится искать больше двух приближений. Схема вычислений по В. Ритцу отличается от вышеописанной. Для примера проделаем по В. Ритцу вышеразобранный пример. Задача, как мы видели, свелась к интегрированию уравнения (3). Интегрирование это равносильно разысканию минимума интеграла2)
) W. R i t z. Ober eine neue Methode zur Losung gewisser Variationsprobleme der mathematischen Physik. Journal fur die reine und angewandte Mathematik, 1909, Bd. 135, SS. 1—61. Перепечатка: W. R i t z. Gesammelte Werke. Oeuvres publiees par la Societe Suisse de Physique, Paris, Gauthier-Villars, 1911, SS. 192—250.
2) Чтобы при нашем способе вычислений прийти к такому же интегралу, как у В. Ритца, нужно выражение для потенциальной энергии изгиба взять в такой форме:
о
(6)
о
о
о
Вводя соответствующие изменения в выражение (4), мы в заключение придем к результату В. Ритца.
218
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Вставляем вместо у его выражение в виде степенного ряда и подбираем величины аь а2, а3,. так, чтобы 5 приобретало значение минимума, т. е. полагаем
dS0 __ гл dS0 __ л dS0 q. да да2 да3 и’
чтобы эта система линейных уравнений имела решение, необходимо, чтобы ее определитель обращался в нуль. Составляя этот определитель и приравнивая его нулю, получим уравнение для нахождения РКр-
Мы в дальнейшем будем пользоваться ранее описанной схемой вычислений. Схема эта у нас выработалась постепенно при разработке отдельных вопросов устойчивости.
Пользуясь описанным приближенным методом, мы могли получить как решения уже исследованных вопросов, так и новых задач, для которых интегрирование соответствующих уравнений не было до сих пор выполнено. Новые результаты нам удалось получить при исследовании устойчивости сжатых поясов открытых мостов и сжатых составных стержней, а также при рассмотрении устойчивости плоской формы изгиба балок и устойчивости пластинок. Для большей полноты работы и для выяснения точности принятого метода мы приводим не только новые результаты, но также и решения некоторых уже ранее исследованных задач. Таким путем получилось довольно полное собрание задач устойчивости, могущих иметь практическое значение. Работа распадается на следующие отделы:
I. О продольном изгибе сжатых стержней.
И. Об устойчивости плоской формы равновесия изгибаемых стержней.
III. Устойчивость сжатых пластинок.
Отдел первый
О ПРОДОЛЬНОМ ИЗГИБЕ СЖАТЫХ СТЕРЖНЕЙ
§ 1. Элементарные случаи продольного изгиба
Задача о продольном изгибе призматического стержня с одним заделанным и другим свободным концом нами уже была решена при изложении общего метода. Введением вместо кривизны ее приближенного значения d2ydx2 задача привелась к линейному дифференциальному уравнению с постоянными коэффициентами. По поводу такого упрощения задачи в свое
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
219
время делалось немало возражений. Некоторые 1) находили возможным даже утверждать, что получение верного значения для критической нагрузки при сделанном допущении является просто счастливой случайностью. В настоящее время, после трудов проф. Ф. С. Ясинского, можно считать вопрос о допустимости введения приближенного выражения для кривизны окончательно решенным, и никто не станет считать получение верного результата из упрощенного уравнения счастливой случайностью. Кроме принципиальных возражений по поводу решения Эйлера, к его формуле делались еще различные поправки, цель которых была — учесть влияние укорочения стержня под действием продольной сжимающей силы. Поправки эти очень малы, и мы на них не будем останавливаться2).
От случая продольного изгиба стержня с одним заделанным концом легко перейти к изгибу стержня с двумя опертыми или заделанными концами. Для них получаются известные значения критической нагрузки:
р _ EJn2 р _ 4я2 кр 12 кр Jz
Первый из этих случаев является основным, и в дальнейших задачах мы критическую нагрузку будем представлять в такой форме:
FJk2
w- (7)
(li — называют коэффициентом длины; jxl — приведенной длиной стержня.
Остановимся несколько подробнее на такой задаче. Найти критическое значение нагрузок для стержня АВ (рис. 2),
1) А. С 1 е b s с h. Theorie de lelasticite des corps solides. Traduit par Barre de Saint-Venant et A. Flamant. Paris, Dunod, 1883, p. 864. Перевод с немецкого книги: А. С 1 е b s с h. Theorie der Elastizitat fester Korper. Leipzig, B. G. Teubner, 1862.
2) Одна из поправок имеется в новом издании известной книги: А. Е. Н. L о v е. Lehrbuch der Elastizitat. Deutsche Ausgabe von A. Timpe, Leipzig—Berlin, B. G. Teubner, 1907, S. 468 перевод с английского: A. E. Love. A treatise on the mathematical theory of elasticity. 2 edition, Cambridge, University Press, 1906. Вместо длины стержня в формулу Эйлера входит величина
1 пг,
где г — радиус инерции поперечного сечения. Поправка весьма малая, не имеющая практического значения, и, как нам кажется, является результатом пропуска, допущенного А. Лявом.
220
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
к которому кроме сил по концам приложена еще сила Р2 в среднем сечении С. Для большей общности будем считать, что верхняя и нижняя половины стержня имеют разные жесткости EJ
иУ2. Введем обозначения:
Рг ь — v Л ’ , V.
Применим к нахождению критического значения Рi Р2 новую методику. Потенциальная энергия изгиба при отклонении стержня от прямолинейной формы равновесия представится такой формулой 1):
I 12
V —y2dx - J y2dx.
12 0
Работа грузов Pi и P2, опускающихся при искривлении стержня, будет
I 12
Р2
' -у У'2 dx J УП dx
Прямолинейная форма перестает быть устойчивой в тот момент, когда
2
I 12 I 12
L J у''2 dx Щ1 j у2 dx -у- t2dx J t2 dx,
112 0 0 0
Для работы опускающегося груза при искривлении оси стержня А. Ляв берет выражение
R — J cos 0 ds j,
где R — величина сжимающего стержень груза, — длина стержня, 0 — угол, составляемый касательной к искривленной оси стержня с направлением R. К этому выражению следовало бы прибавить величину
- Jcos20rfs
представляющую работу груза R при опускании от продольного сжатия стержня. Если сделать такое добавление к выражению работы груза, то поправка, введенная А. Лявом, пропадает.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 221
откуда, пользуясь введенными выше обозначениями, получим
( Ш 1 J y2dx± J ydx I
Vo 12 '
ej2
(Pi P2)кр т (8)
T Sy'2dx ПТ I у'Ых
Если бы точное значение для у нам было известно, то, вставляя его в уравнение (8), мы нашли бы точное значение для (Pi Л)кр- В самом общем виде для заданных условий на концах прогиб у может быть представлен в виде такого тригонометрического ряда:
-. пх , - . 2ях , - . Зя ,
у A sin — А sin —j—hsin—-—-.
Для получения приближенного значения критической нагрузки ограничимся лишь первыми двумя членами разложения. Вставляя полученное таким образом значение для у в уравнение (8), найдем
Bl k v-H-Hv-ilg-z-HvO'fe’
' 1 (9)
оЯ
Здесь через z обозначено отношение А : А. Теперь остается для каждой пары значений k и у подобрать z таким образом, чтобы Р Рч приобретало минимальное значение.
Заметим, что в тех случаях, когда y не сильно отклоняется
от единицы, можно ограничиваться первым приближением, т. е.
полагать в выражении (9) z 0. Тогда
(р j р __ (Y1) EJ2n2 jчч
кр - у(Л1) 2— UO)
Положим, например, у 1 и дадим k ряд значений: fe-1; 1,25; 1,50; 1,75; 2; 3.
Тогда определяемые по формуле (10) значения критической нагрузки будут
п n _ BJ2n2 EJ2tl2 EJ2k2
Ul r2)KV — 2 , (0,952 ’ (0,91 )2’
72я2 У2я2 2я2
(0,89)2 » (0,87)2 » (0,82)2 Результат этот совершенно совпадает с тем, что было получено проф. Ф. С. Ясинским путем интегрирования соответствующих
222
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
дифференциальных уравнений. Такое же совпадение мы получим и для у 125. При дальнейшем увеличении y Уже появляются разности между точным и приближенным решениями, большие 1; нужно прибегнуть здесь ко второму приближению.
§ 2. Продольный изгиб стержня под действием собственного веса
В качестве более сложного случая рассмотрим искривление стержня под действием собственного веса. Пусть q — вес единицы длины стержня; тогда сжимающая сила у нижнего конца стержня будет ql Задача наша — найти для стержня данной жесткости EJ то наименьшее значенине ql, при котором возможно искривление, представленное на рис. 3. Дифференциальное уравнение равновесия в этом случае будет
(II)
Интеграл этого уравнения может быть представлен в бесселевых функциях. Для критической силы получим 4)
_ BJn2
W)КР “ (1,Ц. )2
Рис з Применим теперь к этому случаю при¬
ближенный метод, представим у в виде степенного ряда. В самом общем случае четная функция от х, удовлетворяющая условиям на концах, будет
у (I2 — х2) (а0 ахх2 а2л4 -Ь.).
Потенциальная энергия изгиба при искривлении стержня будет
()'
о
Работа силы тяжести, соответствующая тому же искривлению, представится формулой
г-'-№
Л) См. цитируемую на стр. 219 книгу А. Е. Н. Love, S. 488.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
223
Критическое значение веса определится из уравнения
о о
откуда
ql
о
(12)
I
О
Остается для коэффициентов а0, аь а2,. в общем выражении для у подобрать такие величины, чтобы ql, определяемое из уравнения (12), имело наименьшее значение. Ограничимся тремя членами и положим
у (12 — х2) (а0 ах2) 12а0 (Рах — а0) л:2 — ах4 Ь0 Ьх2 Ь2х4.
Вставляя это в выражение (12) для критической силы, получим
Здесь введено обозначение z b2b.
Разыскание наименьшего значения для ql)Kр приводит нас к такому квадратному уравнению:
Сравнивая этот результат с точным решением, находим, что в данном случае погрешность меньше 2.
При решении задачи мы приняли для у выражение в форме степенного ряда, но можно, конечно, представить у и иначе; нужно только, чтобы были выполнены условия, высказанные
1 4 zl2 -z2l о
откуда
0,2200 1 12-
1,3478
22 “ J2
Вставляя Z в выражение для ()Кр, найдем , А 8,15 EJzt2
ч О) Юь J CJJI
Ч1)кр -р (1,10)2
224 ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
при изложении метода. Возьмем, например, у в виде тригоно¬
метрического ряда. Чтобы удовлетворить условиям на концах, нужно положить
лх Злх , 5лх ,
У d COS г 2 cos 2J Г a COS 2 i Ограничиваясь двумя членами и вставляя полученное таким образом у в выражение для (ql) кр, найдем
, п _ Е1л2 18г2
КЧЧкр 82 0,1487 0,6078-г 2,148722
Здесь z обозначает отношение а2: а
Разыскание наименьшего значения для (ql) кр приводит нас к квадратному уравнению
z2 0,4020z-0,01235 0, корнями которого будут
Zi 0,0286, z2 —0,4306.
Вставляя Z в выражение для (ql) кр, получим
( i _ _ В1л2
Whv - 2582 - (1,12)2
Мы получили, таким образом, для критического значения
нагрузки величину меньшую, чем та, что дана в курсе А. Лява. Следовательно, ближе к истине то значение для ()кр, которое дает Ф. С. Ясинский ). Им получена величина
(70кр 7Цг. (13)
Результат этот совпадает с нашим, погрешность лежит за пределами той точности, с которой произведены вычисления Ф. С. Ясинского. Таким образом, представление у в виде тригонометрического ряда является для данной задачи более выгодным. Заметим, что если положить в выражении для (0кр z 0, что равносильно оставлению лишь одного первого члена в разложении для уу то мы получим
EJл2
КЯчкр — (119)2
т. е. погрешность составляет 5.
) Ф. С. Ясинский. Собрание сочинений. Редактор Н. Н. Митинский, том 1, С.-Петербург, 1902, Сборник Института инженеров путей сообщения, выпуск 5, стр. 179.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
225
Покажем на этом примере связь между интегрированием дифференциального уравнения (И) и вычислением (ql)uv по приближенному способу. Приближенный метод привел нас к разысканию минимума выражения (12), а это равносильно разысканию минимума интеграла МНЬ «-()
Полагая z S, найдем
dyldx и составляя вариацию EJz ql-x)z 0.
А
Л
1
Л
1
'
Уравнение это совпадает с уравнением (11).
Заметим в заключение, что результаты, полученные нами здесь, могут быть распространены на тот случай, когда стержень АВ Рис. 4.
со свободно поворачивающимися концами подвержен действию продольных сжимающих усилий, равномерно распределенных вдоль оси и направленных от концов к середине (рис. 4). В этом случае каждая половина стержня находится в условиях, принятых в вышеразобранной задаче.
§ 3. Продольный изгиб стержня под действием распределенных сжимающих усилий, меняющихся от концов к середине стержня по линейному закону
Концы стержня АВ (рис. 5) считаем свободно поворачивающимися. Закон изменения сжимающих усилий представлен диаграммой Ь). Пусть q dx — усилие, приходящееся на
элемент dx на расстоянии х от нижнего конца. Наибольшее значение сжимающее усилие, а значит, и сжимающие напряжения приобретают в сечении О. Величина этого усилия будет, как легко видеть из рис. 5, 6, равна ql2j8. Найдем, пользуясь новой методой, то значение qy при котором становится возможной искривленная форма, представленная на рисунке 5, а.
Потенциальная энергия при отклонении стержня от прямолинейной формы равновесия возрастает на величину
i
У y2dx.
о
Для составления выражения работы сжимающих сил при искривлении стержня выделим два элемента, симметрично
226
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
расположенных относительно середины О; х и I — х — расстояния этих элементов от нижнего конца стержня. При искривлении стержня выделенные элементы сблизятся на величину
X
При этом приложенные к выделенным элементам усилия совершат работу
(±-x)dxj (H-Jdi.
X
Полная работа сжимающих сил при искривлении оси стержня будет
2 1—х
т-т (-)« J(-sr)'
О х
или, если выполнить интегрирование по частям, найдем
2
Т -j J х (I — х) у'2 dx.
Сравнивая Т и V, получим уравнение для определения qlv.
Изображенную на рис. 5 форму изгиба можно представить так:
- . лх , л. Зпх , „ . 5лх ,
у A sin — Ах sin —j—- Л2 sin ——-.
Ограничиваясь лишь двумя первыми членами этого разложения и вставляя полученное таким образом значение прогиба в формулы для Т и V, найдем
Т-f ЛЬгг-ткг)' (1 -ш)- ЛА (44--т)
ЕЫ (Л2 81Л).
V 43
Сравнивая полученные значения Т и V и обозначая через z отношение Ах : Л, найдем
ql2_ 8
EJti2
1 81z2
42
(14)
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 227
Остается для z подобрать такое значение, чтобы ql28 было минимальным. Разыскание этого минимума приводит нас к такому квадратному уравнению:
z2 — 0,5205г — 0,012 0;
корни этого уравнения будут zx — 0,0226, z2 0,5430.
Вставляя Z в выражение (14) и производя вычисления, найдем
ql2 _ EJn2 8 0,48162 Следовательно, коэффициент длины в данном случае будет
ц 0,4816 0,694,
что совершенно совпадает с результатом проф. Ф. С. Ясинского, полученным путем интегрирования дифференциального уравнения бесконечными рядами. Заметим, что, ограничиваясь лишь первым приближением, т. е. полагая в выражении (14) z равным нулю, мы получим
I 0,682,
т. е. в определении х сделаем ошибку, меньшую 2.
Остановимся теперь на математической стороне вопроса. Сравнение выражений для Т и V приводит нас к такому уравнению:
Г 1
J X ( - х) i2 dx Ц-1 у2 dx, (15)
о о
и нам приходится разыскивать минимум дроби
i
J у2 dx
J х (I — х) yf2 dx
о
Это равносильно такому уравнению:
i iii J х (I — х) if2 dx 6 J у2 dx— j у2 dx 6 j x (I — x) y'2 dx 0,
0 0 0 0
или, принимая во внимание равенство (15), получим
(16)
б J7 у2 — х1 — х) у'2 j dx 0.
228
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Обозначая у' через z и составляя вариацию интеграла, найдем
EJz zx(l-x) О
или
EJt ±y'x(l-x) 0. (17)
Следовательно, разыскание минимума дроби (16) равносильно интегрированию уравнения (17), которое, как легко видеть, представляет собой дифференциальное уравнение равновесия для искривленной формы, представленной на рис. 5.
Пользуясь новой методой, можно без всяких затруднений разрешить вопрос об устойчивости сжатого стержня при более сложных законах распределения нагрузок, но мы ограничимся лишь вышеразобранными примерами — их вполне достаточно, чтобы видеть ясно все преимущества новой методы. Интегрирование дифференциального уравнения, требующее суммирования сложных рядов, заменяется несколькими простыми квадратурами.
I
dx
§ 4. Продольный изгиб стержня с опертыми концами в упругой среде
Положим, призматический стержень АВ сжимается двумя взаимно противоположными силами Р. Всякому искривлению стержня препятствуют реакции упругой среды. Предположим, что реактивное усилие, приходящееся на элемент тп (рис. 6), про-
tпopциoнaльнo длине элемента и величине прогиба стержня в сечении, соответствую-
1. щем выделенному элементу. Эти условия
можно считать приблизительно выполненными в целом ряде технических задач. При отыскании Ркр новым методом придется принять во внимание не только энергию деформации стержня, но также и упругой среды. Для энергии изгиба стержня и для работы сжимающих сил Р при искривлении стержня можем пользоваться прежними общими выражениями. Что касается энергии деформации среды, то выражение для нее может быть составлено так. Пусть р — коэффициент, характеризующий жесткость среды; тогда в силу сделанных предположений реакция среды, приходящаяся на элемент тп, представится формулой у dx. Так как в каждый момент реакция пропорциональна прогибу,
В
-у
Рис. 6.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
229
то работа реактивной силы будет (p2)y2dx, а следовательно, вся энергия деформированной среды может быть представлена формулой
1JV
dx.
Возможность искривления стержня наступает тогда, когда работа сил Р при искривлении стержня равна энергии изгиба стержня, сложенной с энергией деформации среды, т. е. когда будет выполнено условие
i i i
-у J у'2 dx Ц- J у2 dx 1- J if dx. (18)
ООО
Для рассматриваемого случая самый общий вид изогнутой оси стержня может быть представлен так:
тоо
ттсх
Am sin —j—.
m-1
Вставляя это в уравнение (18) и выполняя интегрирование, найдем
Р SR-’)2 '
Легко видеть, что наименьшее значение Р приобретает тогда, когда все Ат1 кроме одного, обращаются в нуль; следовательно, первой возможной искривленной формой равновесия будет синусоида. В отличие от ранее разобранных случаев, здесь первая форма может иметь несколько точек перегиба, число их будет зависеть от величины коэффициента р, характеризующего жесткость среды.
Положим, что первая форма состоит из т полуволн; тогда
- . тих
y Amsm—r.
Из формулы (19) получим
р _ EJ («я)( р4 ГкР 2«2я2
Введем одно обозначение, которым будем пользоваться в дальнейших задачах, именно положим
p i67Bi. (20)
230
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
тогда
Ея2 (тг —
т2я4
кр 12
Следовательно, коэффициент длины в данном случае равен
ц Л 1 (21)
_ 2J 16В2 ’
У m w
Пока среда обладает малой сопротивляемостью, т. е. пока мал коэффициент р, вполне естественно положить, что первая искривленная форма равновесия будет без точек перегиба. Увеличивая р или, что все равно, увеличивая В2, мы достигнем предела, когда стержню выгоднее изогнуться по кривой с двумя полуволнами, далее с тремя, с четырьмя и т. д. полуволнами.
Пусть первая искривленная форма имеет т полуволн и мы по¬
степенно увеличиваем В2; спрашивается, при каком значении В2 стержень примет форму с т 1 полуволнами Очевидно, форма с т 1 полуволнами явится первой искривленной формой равновесия при том значении В2, когда коэффициент длины ji, определяемый по формуле (21), уменьшится от замены т на т 1. Интересующее нас значение В2 найдется из уравнения
1 1
16В2
(т I)2 я4 откуда
В2 тЦт 1)2. (22)
Для т 1 получим В2 24,35; следовательно, пока В2 24,35, первая форма равновесия не имеет точки перегиба. Подставляя вместо т в выражение (22) числа 2, 3, 4,., получим ряд значений В2, при которых совершается переход от одной формы к другой с большим числом полуволн. Значения эти приведены ниже в таблице. Верхний ряд чисел дает число полуволн для первой искривленной формы, а нижний — предельные значения Б2, при которых эта форма может получаться.
т
1
2
3
4
5
6
7
В2
24,35
219,2
876,7
2 435
5 479
10 739
19 091
Коэффициенты длины х в пределах первых шести форм равновесия помещены в нижеследующей таблице I. Изменение коэффициента длины в зависимости от величины В2 предстазлено графически на рис. 7,
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Таблица I
231
в2
в2
и
В2
и
т
1
т
4
0
1
3
5
1
0,9268
0,8185
0,7410
40
50
75
100
0,4210
0,4064
0,3758
0,3512
1 ООО
1 500
2 000 2 435
0,1951
0,1785
0,1654
0,1562
10
15
0,6152
0,5373
200
219,2
0,2862
0,2774
т
5
20
0,4831
3 000
0,1494
24,35
0,4472
4 000
0,1396
т
3
5 000
0,1315
5 479
0,1280
т
2
300
500
0,2628
0,2349
т
6
25
0,4460
700
0,2143
8 000
0,1174
30
0,4372
876,7
0,2000
10 000
0,1097
10 739
0,1085
232
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Для вычисления коэффициента длины ц в случае очень больших значений В2 можно пользоваться упрощенной формулой. В самом деле, при больших В2 число полуволн т велико, и потому вместо формулы (22) можно написать такую:
Б2 т;
определяя отсюда т2 и вставляя его в формулу (21), получим
А —
2 V2 f В2
Для В2 — 10 000 упрощенная формула дает х 0,1107; точное решение, как видно из таблицы I, будет х 0,1097, следовательно, разница меньше 1. С дальнейшим увеличением В2 разница между точной и приближенной формулами еще меньше, и потому можно считать, что х убывает обратно пропорцио-
4
нально yg2
§ 5. Продольный изгиб в упругой среде стержня со свободными концами
Предположим, что концы сжатого стержня АВ не только могут свободно поворачиваться, но также и перемещаться в направлении, перпендикулярном к оси стержня. При отсутствии
Рис. 8.
упругой среды стержень будет, конечно, в неустойчивом равновесии. С возрастанием жесткости среды устойчивость стержня будет расти, нужно прикладывать все большие и большие силы Р, чтобы получить искривленные формы равновесия. Не-
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
233
Рис. 9.
сколько первых форм представлено на рис. 8, а, 6, с, d. Разысканием критических значений сжимающей силы для этого случая занимался Г. Циммерман1). К решению задачи он подходил, рассматривая изгиб стержня, лежащего на упругом основании и сжимаемого двумя эксцентрично приложенными силами (рис. 9). Постепенно уменьшая эксцентриситет, Г. Циммерман в пределе приходит к форме, представленной на рис. 8, Ъ. При такой постановке вопроса заранее являются исключенными из рассмотрения формы, несимметричные относительно середины стержня, как, например, формы, представленные на рис. 8, а и на рис. 8, с.
Интегрирование дифференциального уравнения равновесия для изгиба стержня, представленного на рис. 9, не представляет никаких
принципиальных затруднений, но вычисление Ркр и исследование различных форм равновесия является делом довольно сложным. Г. Циммерман ограничивается лишь рядом значений Ркр для первой симметричной формы равновесия (рис. 8,6). Пользуясь новой методой, можно без затруднения вычислить РКр для целого ряда форм равновесия. Такого общего решения, как мы нашли в предыдущей задаче, здесь не получится. Дело в том, что разложение по синусам кратных дуг для предыдущей задачи является разложением по нормальным функциям. Выражение для потенциальной энергии системы заключает лишь квадраты коэффициентов разложения, и потому каждая форма равновесия определяется лишь одним членом разложения.
Если в настоящей задаче взять для прогиба у общее выражение, то для возможности получения из него целого ряда форм равновесия придется ввести много параметров, что должно сильно затруднить вычисления. Мы значительно упростим дело, если каждую из возможных форм равновесия рассмотрим особо.
Мы будем, как и в предыдущей задаче, постепенно увеличивать жесткость среды и рассмотрим, как при этом будет изменяться первая искривленная форма равновесия. В случае весьма податливой среды первой искривленной формой равновесия будет форма, мало отличающаяся от прямолинейной. Она представлена на рис. 8, а. Ограничиваясь вторым приближением, представим уравнение изогнутой оси стержня так:
у ах A sin (2nxl).
) Н. Zimmermann. Knickfestigkeit eines Stabes mit elastischer Quer§lytzung. Zentralblatt der Bauverwaltung, 1906, 3d. 26, № 40, S. 251—255
234 ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Приравнивая работу внешних сил энергии изгиба и деформации среды, получим уравнение для определения РКр в такой форме:
4 JV2rf -T-.f ydx tf (y-dx.
ООО
Здесь р — коэффициент, характеризующий жесткость среды, al
у 2— прогиб стержня. Вставляя вместо у принятое выраже¬
ние и пользуясь обозначениями
а I 0 16 EJB2
zx и Р——
получим по выполнении квадратур
16В 1 г г2 р EJn2 л2 2 я 12 I Ея2 ооч
кр- t2 z2 2n2 и22 W
Остается для каждого частного значения В2 разыскать такую величину для г, чтобы ЯКр было минимумом. Задача эта сводится к решению такого квадратного уравнения:
z2 (7,1938 - —z - 19,739 0.
Изменение коэффициента длины х в зависимости от В2 представлено на рис. 10. Для В2 — 0 корни квадратного уравнения будут
2, 0, Z2 0О.
Для первого из корней формула (23) дает Ркр и, сле¬
довательно, i 0,5. Для второго корня получим Ркр 0, следовательно, х оо.
Первый результат соответствует выпучиванию стержня по двум полуволнам, а второй относится к вращению стержня как твердого тела.
Второй по порядку является форма, представленная на рис. 8, Ь. Прогиб для этого случая с достаточной точностью можно представить в такой форме:
Л 9 I 1 А
sin —г A j sin — о.
Постоянная величина 6 должна быть определена так, чтобы сумма проекций реакций упругой среды на ось у-ов равнялась нулю, следовательно, должно быть выполнено условие г
у dx 0, откуда б (л у-).
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
235
Уравнение для определения Ркр будет иметь вид -у у'2 dx Щ-1 у2 dx у2 dx.
Полагая At : А г, получим
Р -
г кр
19 22
EJn2 i2l2
(24)
Разыскание минимума приводит нас к квадратному уравнению
22 4- ( — ill 4- 2 - О
z 16В2 3 27) z 9
Изменение коэффициента длины х в зависимости от В2 представлено на рис. 10 особой кривой для каждого т. Пересечение
кривой для т 2 с кривой, построенной для первой формы, определяет значение В2, при котором совершается переход от первой формы ко второй. Для В2 0 корни нашего квадратного
236
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
уравнения будут 0 и оо, соответственно этому (24) дает нам р EJn2 р 9EJk2
г Кр 2 П Г Кр 2 Форма, представленная на рис. 8, с, получается из формы рис. 8, а при больших значениях В2. Точно так же форма, представленная на рис. 8, d, получается из формы 8,6. В заключение приводим таблицу значений для х. Для каждого значения В2 взята та форма равновесия, которой соответствует наибольшее х.
Таблица II
в2
В2
В2
0
оо
22,8
0,7678
300
0,372
1
2,738
36
0,6929
403
0,342
5
1,038
56,5
0,6125
500
0,324
10
0,9140
я4
0,5178
600
0,310
15
0,8275
150
0,451
750
0,292
20
0,7878
200
0,414
1000
0,270
Для небольших значений В2 (0 В2 200) величины ja, помещенные в таблицу II, определены с большой точностью; сравнение с результатами Г. Циммермана дает четыре верных знака. С возрастанием В2 точность понижается, и увеличить ее можно было бы лишь при помощи дальнейших приближений, т. е. при более сложных выражениях для высших искривленных форм. Это, конечно, потребовало бы значительной работы, между тем как практическое значение полученных таким путем результатов невелико, так как с возрастанием В2 величины jo, приближаются к тем, что были выше получены для несмещающихся концов.
§ 6. Задача проф. Ф. С. Ясинского
Интересуясь вопросом устойчивости сжатых поясов открытых мостов, Ф. С. Ясинский исследовал задачу о продольном изгибе призматического стержня в упругой среде при условии, что сжимающие усилия распределены по длине стержня по закону, представленному на рис. 5 и рассмотренному в § 3. Одно неверное заключение привело Ф. С. Ясинского к ошибочным значениям коэффициента длины jli для некоторых частных значений величины В2, характеризующей жесткость среды. Составленной Ф. С. Ясинским таблицей коэффициентов длины jli у нас в России пользуются при расчете открытых мостов. Ввиду такого практического значения таблицы всякие поправки к ней приобретают большой интерес. Найдем эти поправки при помощи новой методы.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
237
В каждой точке стержня действуют направленные к середине О сжимающие усилия интенсивности (Рис- И»)-
Выпучиванию стержня препятствует упругая среда, жесткость которой, как и прежде, будем характеризовать величиной В2
р416.
Нами уже было составлено выражение для работы сжимающих сил при искривлении оси стержня (см. § 3). Путем интегрирования по частям выражение это может быть представлено так:
12
Т у J х (I — х) у'2 dx
Т (-) l2dx.
Рис. 11.
Сохраняя для потенциальной энергии изгиба стержня и деформации среды прежние выражения, получим уравнение для
определения критического значения q в такой форме:
i
J л: ( - л:) tf2 dx Щ- J у2 dx J у2 dx, (25)
откуда
i
EJ J у2 dx р J tf dx
О о
I
J у'2 х (I — х) dx
(26)
Задача сводится к разысканию минимума дроби (26). Прежде чем останавливаться на приближенном вычислении этого минимума, установим связь между принятым здесь методом и тем способом решения задачи, которому следовал Ф. С. Ясинский. Разыскание минимума дроби (26) равносильно выполнению условия
ill
EJ J у2 dx р J ус1х-у'2х1-х) dx
ООО
Составляя вариацию и принимая во внимание условия на концах:
0.
238
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
а) у 0, у 0 при х 0; Ь) у 0, у 0 при х , получим
0IV Ух ( - jc) (I - 2х) у' Ру 0. (27)
Уравнение это совпадает с тем, которое Ф. С. Ясинский интегрировал посредством бесконечных рядов1). Общий интеграл его может быть написан в такой форме:
у С,Ф, () С2ф2 () Сзфз (ж) с4ф4 (х).
Здесь ф1 (х) ,.ф4 (х) представляют собой бесконечные ряды, расположенные по степеням х. В выражения для коэффициентов этих рядов входят величины q и В2. Принимая во внимание условия на концах, можно составить трансцендентное уравнение, связывающее значения q и В2. Из него и определяются те значения q, при которых возможно искривление оси стержня.
Ф. С. Ясинский при составлении трансцендентного уравнения сделал предположение, что первой искривленной формой равновесия будет кривая без перегибов и симметричная относительно середины. Таким образом, из рассмотрения исключены были формы с четным числом полуволн; между тем при некоторых значениях величины В2 именно эти формы явятся первыми возможными искривленными формами. Это обстоятельство послужило причиной того, что некоторые из значений коэффициента длины (Li, помещенных в таблице Ф. С. Ясинского, меньше действительных, а следовательно, определяемая по таблице степень устойчивости стержня является преувеличенной. Интегрирование уравнения (27) при надлежащих условиях на концах будет изложено в другом месте2), здесь же составим таблицу значений коэффициента длины х при помощи новой методы, где вместо суммирования сложных рядов и решения трансцендентного уравнения придется выполнить лишь ряд простых квадратур3).
) В сочинении Ф. С. Ясинского приняты несколько иные обозначения. Чтобы уравнение Ф. С. Ясинского (см. цитируемую на стр. 224 книгу, стр. 167, уравнение (h)) привести к полному совпадению с уравнением (27), нужно положить в нем
6 х — 2, р V — 2, у 6 — у, q р.
2) Это исследование войдет в исполняемую под моим руководством дипломную работу студента инженерного отделения П. Е. Добровольского.
3) Относительно бесконечных рядов и составленного из них трансцендентного уравнения Ф. С. Ясинский пишет: «при больших значениях В2 при ходится определять до 28 членов каждого основного и производного рядов; это до такой степени усложняет вычисления, что непосредственное применение формулы к практическим расчетам становится совершенно немыслимым». Наш опыт показал, что разыскание одного корня трансцендентного уравнения требует нескольких дней усиленной работы с арифмометром. При этом нет уверенности, что найден действительно наименьший корень. Установить степень точности при этих вычислениях весьма затруднительно.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
239
Чтобы упростить вычисления, мы не будем брать общего выражения для у, из которого можно было бы получить ряд возможных форм равновесия, а исследуем каждую из этих форм отдельно. Ясно, что при малых значениях В2, т. е. в случае весьма податливой среды, первой искривленной формой будет,
Рис. 12.
как то предполагал Ф. С. Ясинский, кривая без перегибов, изображенная на рис. 11. Форма эта с достаточной для практики точностью может быть представлена так:
Зя
у A sin — А sin -у-
Вставляя это в выражение (26) и выполняя указанные интегрирования, получим для наибольшего значения сжимающего усилия формулу
18122-(122)
I EJk2 q 8 12
(28)
Здесь z А : А.
Задача о критическом значении сжимающих усилий сводится к разысканию минимума дроби (28), для чего нужно решить квадратное уравнение
1 0,16426В2
2 15,909 — 0,43802В2
Z - -П-ПРР, , П 1СЛ Ос'Р2 2 р,3798 (81 0,16426В2) 81 0,16426В2
0.
240
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Для случая В2 0 приходим к результату, полученному раньше (см. § 3). Ряд значений коэффициента длины вычислен, и изменение этой величины в зависимости от В2 представлено на рис. 12 в виде особой кривой.
Постепенно увеличивая жесткость среды, мы достигаем наконец предела, когда первой формой явится кривая с одной точкой перегиба (рис. 13). Подсчеты показали, что эта форма появляется, начиная с В2 ж 18.
Для значений В2 22,8; 56,5; 162,8, приведенных в таблице Ф. С. Ясинского, мы будем иметь кривую с одной точкой перегиба. Возможность такого рода кривой Ф. С. Ясинским как раз и была исключена, поэтому для этих значений В2 получаются существенные отклонения в величинах коэффициента длины (Li. Изображенную на рис. 13 форму можно с достаточной точностью представить так:
у A sin
2тсх
Т
Ai sin
4тсх
П
Вставляя это в выражение (26) и выполняя интегрирование, получим
I2 EJn2 1 -(1 Z2) 1622 7Я2
1
8я2
_ 2Л_Ц 2 (А L.) (Л
я2 9 ) 3 8л2 )
(29)
Разыскание минимума полученного выражения приводит нас к квадратному уравнению
-0,2251 (l6 J)z2(3,622 --)z 0,2251 (l-g-) 0. (30)
Вставляя для каждого значения В2 значение надлежащего корня уравнения (30) в выражение (29), получим ряд значений коэффициента длины х. Значения эти представлены на диаграмме особой кривой для каждого т. Пересечение кривой для т 2 с кривой, полученной для первой формы равновесия, определит то значение В2, с которого начинают появляться формы с точками перегиба.
Третья форма равновесия будет иметь две точки перегиба, подразделяющие искривленную ось стержня на три участка. Так как сжимающее усилие не остается постоянным по длине стержня, то средняя полуволна искривленной формы не равна
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
241
по длине крайним. Мы удовлетворим этим условиям, положив
- . Злх , - . Ълх
у A sin—j—b А sin —j-.
Вставляя это в выражение (26) и выполняя интегрирование, получим
qT Определяя для каждого частного значения В2 то значение z,
2
которому соответствует минимум q-t можем составить закон
изменения ц в зависимости от В2; закон этот представлен на рис. 12 особой кривой для каждого т.
Исследовав таким путем три первые формы равновесия, мы можем составить таблицу III значений х. Конечно, для каждого В2 пришлось брать ту форму равновесия, которой соответствует наибольшее х.
Таблица III
в2
и
Результаты Ф. С.
Ясин¬
ского
В2
и
Результаты Ф. С. Ясинского
В2
И
0
0,694
0,694
22,8
0,363
0,351
200
0,245
5
0,524
—
56,5
0,324
0,287
300
0,224
10
0,443
—
100
0,289
—
500
0,204
15
0,394
162,8
0,257
0,248
1000
0,174
Для сравнения в таблице приведены также и результаты Ф. С. Ясинского. Наибольшее отклонение получилось для 2-й формы равновесия.
Для больших значений2(2 1000) можно вычислять ц, считая, что эта величина меняется обратно пропорционально
ГВ (см. § 4).
Чтобы судить о точности результатов, полученных новой методой, было вычислено значение для В2 56,5 путем интегрирования уравнения бесконечными рядами, причем было принято во внимание вышеупомянутое изменение условий на концах. Полученный таким путем результат для ц совпал в трех первых знаках с тем, что помещено в таблице III. Отличие от результата Ф. С. Ясинского— 11, что дает изменение р на 23t
242
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
§ 7. Задача Ф. С. Ясинского при условии смещающихся концов
Оставим то же распределение сжимающих усилий, что и в предыдущей задаче, но предположим, что концы сжимаемого стержня не только могут свободно поворачиваться, но также и перемещаться в направлении, перпендикулярном к оси стержня. При отсутствии упругой среды такой стержень, очевидно, будет в неустойчивом равновесии. Степень устойчивости будет возрастать с увеличением жесткости среды, характеризуемой величиной коэффициента В2.
Основное уравнение для определения критического значения сжимающих усилий будет такое же, как и в предыдущем пара-
же мы применим новую методу. Как и в § 4, будем рассматривать каждую из возможных форм равновесия особо.
Пока мы имеем дело с весьма податливой упругой средой, т. е. при малых значениях В2, первой отклоненной формой равновесия будет форма, представленная на рис. 14. Стержень АВ остается прямолинейным и только поворачивается на некоторый угол а, следовательно,
Легко видеть, что это значение у удовлетворяет дифференциальному уравнению (27) при условии р q. К тому же результату мы придем, приравнивая работу внешних сил энергии деформации среды. В самом деле, работа внешних сил будет
графе. Задача сведется к интегрированию того же дифференциального уравнения (27), придется изменить лишь условия на концах. При принятом способе закрепления, очевидно, изгибающий момент и перерезывающая сила у каждого из концов обращаются в нуль, следовательно,
Рис. 14.
для некоторых частных значений В2 было
выполнено в вышеупомянутой работе; здесь
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 243
Для энергии деформации среды получим выражение
о
Сравнивая выражения для V и Т, найдем, что форма, представленная на рис. 14, является возможной формой равновесия при
условии р q. Наибольшее значение сжимающего усилия, соответствующее середине стержня, будет
ql2 РI2 Ел2 2В2
8 8 I2 л2
Следовательно, коэффициент длины в этом случае будет
л
— У 2 у w ‘
Изменение i в зависимости от В2 представлено на рис. 15 особой кривой для каждого т.
Постепенно увеличивая жесткость среды, мы можем достигнуть такого значения для В2, когда первая искривленная форма
244
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
равновесия будет иметь вид, представленный на рис. 16. Для прогиба у мы можем взять такое выражение:
Л. пх , - . 3пх .
у A sin — А sin — б.
i
Величина б определится из условия J ydx 0, откуда б
Jr)
Вставляя значение у в выражение (26) и выполняя интегрирование, получим
Я'я
7я2
К-- (-)-
EJ я2
Ы)2
(31)
где z Ai :А. Разыскание минимума для q приводит нас
к такому квадратному уравнению:
_2 3076,76- 11,658В2 _ 74,022 0,29718В2 _Л
2 -5995,78 14,875В2 2 - 5995,78 14,875В2 “ U
Вставляя надлежащий корень этого уравнения в формулу (31), можем для ряда значений В2 вычислить соответствующие х
Рис. 16.
величины коэффициента длины х. Изменение i в зависимости от В2 представлено кривой на рис. 15. Пересечение этой кривой с кривой, соответствующей первой форме, дает то значение В2(В2 «15), с которого появляется форма, представленная на рис. 16.
Следующей формой равновесия будет кривая с точкой перегиба посредине (рис. 17). Прогиб в этом случае можно
Об УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 245
представить так:
, „. 2лх
у ах A sin-j-.
Приравнивая работу внешних сил изменению потенциальной энергии системы, получим
z2SL(22_i1)
I ЕЫ лМ я 6 J EJn2
12я2 я3 16 8я2
8 12 _1 _Z_ _i_ ,2 J L_ I2
Легко показать, что минимум для q -g- получается при z я6. Следовательно, на основании (32)
Г 1 з_
п_- 6 8я2 я4 _ 0,35100
11 У J _Bfj _ 1 0,004025В2
Соответствующая кривая для х вычерчена на рис. 15.
Следующая форма равновесия будет иметь две точки перегиба. Прогиб для этого случая можно взять в такой форме:
-. Зял; , - . 5ял; 2 (А , А
у Л sin — л, sin (т -б-)
Для критического значения сжимающей силы получим выражение
Остается для каждого частного значения В2 найти такую величину г, чтобы q-g- было минимумом. Изменение коэффициента длины х в зависимости от В2 представлено на рис. 15. Ограничиваясь рассмотренными формами равновесия, составляем таблицу IV значений коэффициента длины р,. Для каждого В2 выбрана та форма равновесия, которой соответствует наибольшее я, следовательно, наименьшее значение критической силы.
С возрастанием В2 числа таблицы IV, как и нужно было ожидать, приближаются к результатам, помещенным в таблице III. Для некоторого суждения о точности полученных выше значений х было вычислено jx для В2 100 путем интегрирования
246
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Таблица IV
Ba
B2
M- J
В2
0
OO
15
0,574
200
0,261
1
2,221
20
0,542
300
0,236
3
1,283
50
0,431
500
0,206
5
0,993
100
0,340
1000
0,176
10
0,703
150
0,277
дифференциального уравнения. Расчет показал, что три первых знака в выражении для х при обоих способах расчета одинаковы.
х
§ 8. Практические приложения полученных результатов
Мы уже отмечали, что случаи продольного изгиба, рассмотренные в двух последних параграфах, приобретают практическое значение в связи с расчетом сжатых поясов открытых мостов. Мосты без верхних горизонтальных связей не нашли у нас в России большого распространения, но в некоторых государствах
Западной Европы их строят довольно часто, и в последнее время вопросу устойчивости таких мостов посвящено немало
журнальных статей ). Работы эти в теоретическом отношении не идут
дальше старых работ
Ф. Энгессера, и следует пожалеть, что такое исследование, как работа нашего проф. Ф. С. Ясинского, осталось малоизвестным на Западе. Введя некоторые поправки в таблицу Ф. С. Ясинского, мы остановимся также на тех упрощениях, которые могут быть допущены при расчетах.
Предположим, что фермы открытого моста —раскосного типа (рис. 18). В таком случае при равномерно распределенной нагрузке и при большом числе панелей можно считать, что усилия в раскосах растут по линейному закону в направлении от середины пролета к опорам. Стержень АВ, являющийся сжатым
верхним поясом фермы, будет подвергаться действию сжимающих усилий, распределенных примерно по такому закону, как предполагалось в последних двух параграфах. Величина q ха¬
) Н. К а у s е г. Die Knicksicherheit der Druckgurte offener Brucken. Zentralblatt der Bauverwaltung, 1909, Bd. 29, № 94, SS. 611—612.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
247
рактеризующая интенсивность сжимающих усилий, определится из формулы
7 1. (33)
где Q — сплошная нагрузка, приходящаяся на одну ферму, — пролет и h — высота фермы. Результат этот получается так: растягивающее усилие в раскосе, соответствующем сечению тпу при большом числе панелей будет
2 sin а
Следовательно, сжимающее усилие, передаваемое от раскоса поясу, равно
О М cos а
IV 2 sin а
Разделив это выражение на длину панели а, найдем интенсивность сжимающих усилий в сечении пт в такой форме:
Q I cos а _ ( 2 )
1 2) a sin а lh
Сравнивая это с принятым в предыдущих исследованиях законом распределения сжимающих усилий q — ), придем к
результату (33).
Выпучиванию стержня в направлении, перпендикулярном к плоскости фермы, будут препятствовать стойки и раскосы фермы, которые при изгибе верхнего пояса окажут в соответствующих узлах реактивные давления, пропорциональные прогибам. При значительном числе стоек можно без большой погрешности считать реактивные усилия непрерывно распределенными по длине стержня.
Чтобы свести задачу к случаям, разобранным в §§ 6 и 7, делают два следующих предположения. Во-первых, считают, что верхний пояс имеет постоянное поперечное сечение, во-вторых, что все стойки обладают одинаковой «отпорностью», т. е. оказывают одно и то же сопротивление изгибу. Очевидно, в запас прочности придется взять наименее отпорную стойку и то сечение пояса, которому соответствует наибольшее значение ilr.
Для пользования таблицами, полученными в предыдущих параграфах, остается лишь вычислить в каждом частном случае величину р и связанную с ней величину В2.
Пусть ABCD (рис. 19) —поперечное сечение моста. В запас прочности предположим, что стойки соединены с верхним
248 ОБ УСТОЙЧИВОСТИ УПРУГИХ систем
поясом шаровыми шарнирами, тогда при изгибе они окажутся в условиях балки с одним заделанным концом. Реактивная сила Р будет пропорциональна прогибу у. Если сила, сжимающая стойку, мала по сравнению с соответствующей эйлеровой нагрузкой, то связь между Р и у будет такой: у Pb33EJU где Ъ — длина
стойки и EJ 1 — жесткость изгиба для нее.
Чтобы учесть влияние продольной силы на прогиб стойки, удобнее всего воспользоваться нлшими приближенными формулами).
Пусть S — сжимающее усилие в стойке фермы. Соответствующая эйлерова нагрузка будет7iJt2(2)2. Введем обозначение
« EJxn2
Рис. 19. : (2ьу
а2.
Тогда прогиб у будет связан с реактивной силой Р такой формулой:
У
РЪ3 1
3EJX 1 - а
2
откуда
р _ 3EJi (1 - а2) у г ьъ '
и, следовательно, искомый коэффициент р будет
SEJi (1 — а2)
Р — ьъа ’
где а — длина панели. При расчетах, как уже мы упоминали, приходится брать ту стойку, которой соответствует наименьшее значение р.
При составлении формулы (34) мы совершенно не приняли во внимание деформации поперечной балки. Жесткость ее обыкновенно велика по сравнению с жесткостью стоек, а потому влияние ее деформации ничтожно. Если бы мы это влияние хотели учесть, то для прогиба у нужно было бы взять выражение
_ РЬ 1 . P(b h)2d
У 3EJi 1 - а2 ' 2EJ2
и соответственно изменить р. Имея значение р, вычисляем В2 по формуле
16Е.
2
1) См. нэшу работу, указанную на стр. 212,
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
249
Если опорные стойки настолько жестки, что их прогибом можно пренебречь, то следует для вычисления jl пользоваться таблицей § 6, в противном случае считаем концы свободно перемещающимися и применяем результаты § 7. С возрастанием В2 растет число полуволн, на которые сжатый пояс подразделяется при выпучивании, и разность между коэффициентами длины х, вычисленными по таблицам §§ 6 и 7, убывает.
В качестве примера возьмем случай, приведенный в сочинении Ф. С. Ясинского1). Потерпевший крушение мост через реку Кевду имел следующие размеры:
33,53 м, d 3,56 му h 3,56 м,
6 195,6 см, а 2,134 му J 212 см4,
2 6490 см4у г 6,71 сму
где г — радиус инерции для поперечного сечения пояса.
Сжимающее усилие S для наименее отпорной стойки в момент крушения было равно 22180 кг. Полагая Е 1,93 106 кгсм2у найдем а2 0,835. Тогда на основании формулы (34)
0 3 1,93 Ю3. 212 (1 — 0,835) _ Л 107 кг
195,63 213,4 ( СМ2-
Следовательно,
п2 _ 0,127 (3353)4 _ ЛП
D 16 1,93 103 6490
Коэффициент длины при условии абсолютно жестких опорных стоек будет i 0,303 (см. рис. 12),
_ 3353 0,303 _ 1СО
С V I lOZ.
г 6,71
Критическое напряжение будет рКр 854 кгсм2 (для сварочного железа по таблицам Ф. С. Ясинского).
При вычисленном значении В2 сжатый пояс в случае выпучивания должен был изогнуться по кривой с одной точкой перегиба2). Считая, что кривая должна быть без перегибов, Ф. С. Ясинский получил в рассмотренном случае для критического напряжения преувеличенное значение, именно ркр 1007 кгсм2у т. е. величину, на 18 большую вышенайденной.
Для приблизительной поверки на устойчивость сжатого пояса открытого моста мы сделали ряд допущений. Некоторые допущения, как, например, предположения непрерывного распределения сжимающих усилий и упругих реакций, не влекут за собой значительных погрешностей при определении критических
1) См. указанную на стр. 224 книгу Ф. С. Ясинского, стр. 223.
2) Форма с двумя полуволнами ясно видна на фотографии, снятой после
крушения. См. Ф. С. Ясинский, там же, стр. 223.
250
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
напряжении, так как число стоек, приходящееся на каждую полуволну выпучившегося пояса, обыкновенно не менее трех. Значительно большие погрешности могут получиться от наших предположений относительно закона распределения сжимающих усилий по длине пояса, а также от введения в расчет жесткости наименее отпорной стойки и наименьшего значения xl: г для пояса. Эти допущения сделаны в запас прочности, и потому, рассчитывая по таблицам §§ 6, 7, мы получим всегда запас устойчивости, больший расчетного. Если из конструктивных или экономических соображений излишний запас в устойчивости является невыгодным, то тогда нужно остановиться на более точном определении критических напряжений. Вычисление этих напряжений при помощи интегрирования соответствующего дифференциального уравнения является, как мы уже упоминали, делом весьма сложным. Применение же в каждом частном случае новой методы может быть выполнено без всяких затруднений. Рассмотрим на частном примере, как влияет на величину критических напряжений закон распределения сжимающих усилий по длине пояса. Мы исходили из предположения равномерного распределения нагрузки по пролету моста и, как следствие, получили линейный закон возрастания сжимающих усилий в направлении от середины к концам.
Если предположить другой крайний случай — сосредоточенную силу Q посредине пролета, то усилия во всех раскосах фермы, представленной на рис. 18, будут одинаковы. Верхний пояс будет сжат равномерно распределенными по длине усилиями, направленными от конца к середине пролета. Усилие, приходящее на единицу длины сжатого пояса, будет q Q2h.
Если пренебречь сопротивлением стоек изгибу и рассматривать верхний пояс как стержень, свободный по длине, то будем иметь случай, разобранный в § 2. Критическое сжимающее усилие определится из формулы
ql _ EJn2
2 (0,56)2 (35)
При тех же самых предположениях, но при условии равномерного распределения нагрузки по пролету моста будем иметь для критического значения сжимающего усилия (см. § 3)
ql2 _ EJn2 Oft
8 “ (0,694)2 V
Сравнивая формулы (35) и (36), находим, что при отсутствии боковых сопротивлений второе предположение дает для критических напряжений значения, меньшие в отношении
( 0,56 2
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
251
При наличии боковых сопротивлений разность критических напряжений, вычисленных при вышеуказанных двух предположениях, будет меняться в зависимости от жесткости среды. Надо полагать, что эта разность будет убывать с возрастанием В2, а следовательно, и с увеличением числа полуволн, на которое подразделяется стержень при выпучивании.
Для примера возьмем случай, когда искривленнная ось стержня имеет одну точку перегиба. При нагрузке, равномерно распределенной по пролету моста, мы имеем закон изменения коэффициента длины х в зависимости от В2 (см. рис. 12). Посмотрим, как изменится х с переходом к сосредоточенной силе Верхний пояс будет в таких же условиях, как стержень ЛВ, представленный на рис. 20. Сжимающие усилия q направлены к середине О и равномерно распределены по длине стержня. Наибольшее сжимающее усилие будет в сечении О, оно, очевидно, равно ql2. Основное уравнение для определения (ql2)кр напишется так:
72 I 1
q J х t2dx -у J y”2dx у J у2 dx.
(37)
Левая часть уравнения представляет собой работу сжимающих усилий q при искривлении оси стержня. Правая часть — изменение потенциальной энергии системы. Ограничиваясь вторым приближением, мы можем для формы, представленной на рис. 20, взять выражение
- . 2пх , л. 4пх у A sin —j—b A j sin —j—.
Вставляя это в уравнение (37) и выполняя интегрирование, получим
lql_ EJn2
2 кр I2
1 16г2 - (1 г2)
1,1, 20 8 2 г 9л2
EJn2
(.и)2
(38)
Остается для каждого частного значения В2 отыскать то г, которому соответствует минимум ql2.
252
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Если ограничиться лишь первым приближением и положить z 0, то из сравнения выражений (38) и (29) заключаем, что коэффициенты длины х, вычисленные при двух крайних предположениях (сосредоточенная посредине сила или равномерно распределенная нагрузка), относятся между собой, как
Не производя дальнейших вычислений, выскажем такие положения.
1) С увеличением числа полуволн, на которое стержень подразделяется при выпучивании, разность между критическими напряжениями, определяемыми при двух крайних предположениях, убывает.
2) Производя расчет в предположении равномерно распределенной нагрузки, мы делаем погрешность в запас прочности.
Остановимся теперь на тех погрешностях, которые мы допускаем при вычислении критических напряжений, вводя в расчет наименее отпорную стойку и наименьшее значение itfr для пояса. Очевидно, что обе эти погрешности идут на повышение коэффициента безопасности. Величина погрешностей тем меньше, чем меньше меняется по длине моста сечение пояса и «отпорность» стоек. Чтобы найти точное значение для критического напряжения, нужно знать закон изменения сечения пояса и «отпорности» стоек. Ход расчета покажем на частном примере.
Положим, что сечение пояса и «отпорность» стоек меняются по параболическому закону. В таком случае можно положить
Наименьшая жесткость пояса, равная7о, будет по концам (при х 0 и х ); наименьшая отпорность стоек соответствует середине пролета и определится величиной
Критические же напряжения будут
относиться, как
7 701 т2х(1 — ), Р Р0 1 — тх(1 — х).
Рассмотрим первую форму равновесия для случая, разобранного в § 6. Основное уравнение для определения критического значения сжимающего усилия напишется так:
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
253
Если ограничиться первым приближением и положить у Asinj-, то из уравнения (39) найдем
1 ЫЧ (“Гг 1) Т l 2ml2 (l7 1-)
UjKP- 4м i
6 2п3)
где В 16EJ0 ‘
Предположим, что жесткость пояса посредине пролета вдвое больше, а «отпорность» стоек вдвое меньше, чем на концах; тогда
9 4 9 2
Ml J2 9 tTL р у
. , 1,87 —0,565
V 8 кр I2 4М 6 2л2)
Если бы мы произвели расчет в предположении постоянной жесткости пояса EJ0 и постоянной «отпорности» стоек, определяемой величиной Ро2, то получили бы такой результат:
Ш _ Е10л2
I в кр I2
1--0,565
jnnx- 41)
6 2л2)
Из сравнения результатов (40) и (41) заключаем, что в тех случаях, где изогнутая ось стержня представляет собою кривую без перегибов, мы вычислим критические напряжения с большой точностью, если введем в расчет наибольшую жесткость пояса и наименьшую «отпорность» стоек. Результат будет тем точнее, чем меньше меняется жесткость пояса по длине пролета. Относительно высших форм равновесия можно заранее сказать, что введение в расчет наибольшей жесткости пояса даст для сжимающих усилий преувеличенное значение.
Мы пока ограничились первым приближением при решении уравнения (39). В качестве второго приближения возьмем
254
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
тогда получим
ql2 _ EJ0n2 8 I2
1812 m22 tШ 8г2 (I w) Ш z
L 6 2я2 4я2 2 2л2
)
В каждом частном случае нужно подобрать г так, чтобы ql28 получило минимальное значение. Для В2 0, т212 4, т11 2
найдем
(ql2 _ EJ0n2
8 кр (0,502)2 ‘
Вычисления, проделанные нами для первой формы равновесия, должны быть повторены и для высших форм. Только на основании такого подробного исследования возможно в каждом
О частном случае оценить
влияние на величину критической нагрузки изменения сечения пояса и «отпорности» стоек по длине пролета.
Пользуясь результатами § 7, можно вывести некоторые общие заключения относительно
параллельными поясами. Устойчивость
К
-г —
—ЩВ
-лплтппПППТ
Рис. 21.
устойчивости мостов с эта будет зависеть от главных пропорций моста и от жесткости опорных рам.
Предположим, что мост не имеет поперечных связей и усилия, воспринимаемые верхними горизонтальными связями, передаются опорам через посредство опорных рам. Верхние горизонтальные связи представлены на рис. 21. В случае равномерно распределенной нагрузки горизонтальная ферма АВВ'А' подвергается действию сжимающих усилий, направленных к середине пролета ОО и возрастающих по линейному закону в направлении от середины к опорам. Всю ферму АВВ'А' мы можем рассматривать как один весьма жесткий стержень. Применяя новую методу, легко найти то критическое значение сжимающей силы
(Q — нагрузка, распределенная по мосту), при кото¬
ром стержень, оставаясь прямым, повернется на некоторый угол а. Повороту этому будут препятствовать стойки главных
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
255
мостовых ферм и опорные рамы. Реакции, оказываемые стойками, можно считать непрерывно распределенными по пролету моста; величину их определим, как и раньше, при помощи коэффициента жесткости р.
Реакции опорных рам будут приложены к концам стержня. Величина реакций Р пропорциональна прогибу и может быть представлена формулой
рр'4- 42
Сжатый стержень перестает быть устойчивым, если работа сжимающих сил при повороте стержня на угол а превосходит изменение потенциальной энергии системы. Работа внешних сил в этом случае может быть представлена так:
т -ТТ (см- § 7)-
Энергия изгиба стоек будет
v4 J yldx: -2
JL
12
Рис. 22.
Энергия деформации рам на основании обозначения (42) представится так:
Основное уравнение для определения критических напряжений будет
3L iL-JU2Z, a' (SL2
4 6 2 12 Р 2 откуда критическое значение сжимающего усилия получится в такой форме:
(fl-TT- ОТ
Коэффициент р вычисляется так же, как и в случае открытых мостов (изгибом верхней распорки пренебрегаем). Нужно лишь удвоить величину, получаемую по формуле (34); тогда
D _ 67, (1 -а2) ,ллх
Р Wa (44
Здесь а, и а имеют те же значения, что и в формуле (34).
Что касается коэффициента р', то величина его будет зависеть от устройства опорных рам. Если взять случай, представленный на рис. 22, то прогиб у при действии в плоскости рамы
256 ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
горизонтальной силы Р будет
Р h3 , Р h2a
У
2 33(1-а) 2 Ш2 откуда на основании обозначения (42) получим
1
Р' -
Л3 ah2
63(l-a) 12 EJ2
Здесь a2 обозначает отношение продольной сжимающей силы к эйлеровой нагрузке для стойки рамы. Вставляя это в формулу (43), получим
gl2 ЪЕХ12( -а2) . 3 8 4Ь3а 2h3 ah2
оч т (45)
373(l-a) 3 EJ2
В том случае, когда b h и з h, получаем ql2 _ EJn2 г 31 (1 — a2) J,. 3I3 J2
8 I3 J 4ji2 ab3 J л2 J 2b3 ab2
Kp 1 —r. 5Г ' 3(l-a) 3
(46)
Здесь через EJ обозначена жесткость при изгибе в горизонтальной плоскости фермы АВВ'А', представленной на рис. 21.
Приблизительно можно положить J — где F — пло¬
щадь поперечного сечения верхнего пояса. Коэффициент длины для этого случая будет
“ г 31 (1 — а2) , 313 J2 1 ' 4я2 ab3 I л2 J 2Ь3 ад2
3(1-а) 3
В тех случаях, где i и 1 весьма малы по сравнению с , коэффициент длины получается большим; верхняя горизонтальная ферма может оказаться в неустойчивом равновесии. Из формул (46) и (47) ясно видно, что на устойчивость особенно влияет высота ферм. С увеличением высоты запас устойчивости быстро падает.
Полученные результаты могут дать некоторые указания относительно надлежащего выбора жесткости опорных рам, обыкновенно рассчитываемых лишь на действие ветра.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
257
§ 9. О продольном изгибе составных стержней
Предыдущие выводы сделаны при условии сплошного стержня, для которого дифференциальное уравнение изогнутой оси может быть с достаточной точностью представлено в таком виде:
-§- М. (48)
На практике очень часто применяют составные стержни, склепанные из нескольких частей, соединенных решетками, и возникает вопрос о поверке на устойчивость таких стержней. Задача эта привлекла всеобщее внимание после известной катастрофы при постройке Квебекского виадука. Появился целый ряд теоретических работ и опытных исследований, но полного согласия между опытом и теорией нет еще и до сих пор, главным образом потому, что при опытах часто остаются невыполненными условия, принятые при теоретических исследованиях. Особенно трудно обеспечить надлежащее закрепление концов сжимаемого стержня.
Пользуясь принятым в настоящей статье методом, мы дадим простое решение задачи об устойчивости составных стержней и в заключение приведем результаты одного опыта, с достаточной точностью подтверждающего некоторые из полученных нами формул.
До сих пор при исследовании устойчивости мы принимали во внимание лишь энергию изгиба выпучившегося стержня и не вводили в расчет влияние поперечной силы, которая появляется при искривлении оси стержня. Влияние это оказывается ничтожным в случае сплошного стержня, но при составном стержне поперечная сила может иногда вызвать значительное уменьшение критической нагрузки.
Пусть стержень АВ (рис. 23) искривился в плоскости ху под действием сжимающих сил Р. Перерезывающая сила в каком-
либо сечении тп будет равна Q P-у. Если принять во внимание влияние этой силы на изгиб, то мы не придем к простому уравнению (48). На составлении нового уравнения и на его интегрировании мы не останавливаемся1) и переходим к рассмотрению энергии системы.
) Работа эта сделана инженером Нуссбаумом: F. Nussbaum. Die genaue Saulenknicklast. Zeitschrift fur Machemalik und Physik, 1907, Bd. 55, Heft 1—2, SS. 134—138.
258 ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Общее выражение для работы сжимающих сил Р при искривлении стержня у нас имеется. Энергия изгиба напишется в данном случае так:
Составим теперь выражение для энергии сдвига. Угол сдвига в каком-либо сечении пт вычисляется по формуле
kQ_kP_dy_ .
Y GF GF dx
Здесь F — площадь поперечного сечения, G — модуль сдвига, k — коэффициент, зависящий от формы сечения. (Для прямоугольного сечения k 65, для двутаврового k меняется в пределах от 2 до 2,4.) Энергия сдвига представится так:
i i
Г AQL ах ±Е1_ Щ2йх
J 2GF йХ 2GF J dx) '
о о
Приравнивая работу внешних сил изменению энергии деформации, получим уравнение для определения Рир:
i i i yj y'2dx
ООО
Общее выражение для прогиба стержня в случае свободно поворачивающихся концов может быть записано так:
тоо
ч - тпх
У 2j mSin —.
m 1
Вставляя это в уравнение (50) и выполняя интегрирование, получим
2 У.9 , Ьл у EJ jQ т GFU
Наименьшее значение для Р получим, очевидно, полагая все коэффициенты Ат, кроме А, равными нулю; тогда
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
259
Обозначая
получим
11-Р и GF - П
2 — И k di
Р PePL__ Ф Р
р J_. -L Ф (52)
Р Так как величина фициент ф будет
В
z
7
И
л
7
IZ
У
Н-
Рис. 24.
Pd весьма велика по сравнению с Ре, то коэфблизок к единице. Влияние перерезывающей силы в случае сплошного стержня ничтожно.
Переходя к расчету составных стержней, отметим прежде всего, что добавочный член kGF в знаменателе формулы (51) есть не что иное, как тот множитель, на который приходится множить поперечную силу Q для получения угла сдвига Y- Это обстоятельство дает возможность сразу написать выражение для РКр в случае некоторых типов составных стержней, нужно только в каждом частном случае установить зависи¬
мость между углом перекашивания y и поперечной силой Q. Возьмем стержень, представленный на рис. 24, состоящий из поясов АВ и АВ и соединительной решетки. Выпучивание свободно может происходить в плоскости ху, следовательно, в обычную формулу Эйлера войдет момент инерции 0 относительно оси z. При определении влияния поперечной силы будем считать число панелей решетки весьма большим и найдем угол перекашивания yi из рассмотрения одной панели (рис. 25). Обозначим через Fa — поперечное сечение диагонали, Fg — поперечное сечение пояса, Fp — поперечное сечение распорок.
Если величина Fa мала по сравнению с Fg и FPi то можно считать, что перекашивание, изображенное пунктиром на рис. 25,
260 ОБ устойчивости упругих систем
является результатом растяжения диагонали. Удлинение диагонали будет
б Qa
cosaEFrfsina 9
абсолютный сдвиг тп найдется из Л тпр:
б Qa
тп -
cos a cos2 a sin aEFd
Угол перекашивания будет
Yl Q , , (53)
11 a EFdcos a sin a 4 7
Вставляя в формулу (51) вместо величины kGF множитель при Q в выражении (53), получим значение критической нагрузки для стержня, представленного на рис. 24:
р1 Гкр 12 , 1 (54)
EJqTI2 EFd cos2 a sin a
Легко видеть из полученного результата, что влияние поперечной силы может быть значительным лишь в том случае, когда Fd весьма мало по сравнению с сечением поясов.
Введем обозначение EFd cos2 a sin a Pd, тогда формула (54) перепишется так:
Ркр Ре Ре Pd фе'
Для разрушившегося стержня из Квебекского моста имеем Ре 88-103 г, Ра 47,5 103 г, следовательно, ф 0,35.
Если при составлении угла перекашивания принять во внимание сжатие распорок решетки, то, пользуясь рис. 25, найдем
Y2:
Q , Qb _ Q ( 1 . 1 ра Е Fd sin a cos2 a Fp tg a ’
EFd sin a cos2 a EF(
Вставляя получившийся при Q множитель в формулу (51), получим
рп кр 12 , 1 , 1 (55)
EJ0n2 EFd sin a cos2 a EFP tg a
В том случае, когда FP Fd Fy формула (55) перепишется так:
«p Р 1 cos3 a (56)
7qji2 F sin a cos2 a
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
261
рп -
кр
2
1
Если соединительная решетка имеет двойные диагонали (рис. 26), то формула (55) перепишется так:
1
т _ ‘ (55')
EJQn2 2EFd sin a cos2 a EFP tg a
Для стержня трубчатого сечения, представленного на рис. 27, придется принять во внимание две соединительные решетки. Для критической нагрузки получим
J i (55)
Ри
кр —
2
EJ0я2 4EFd sin a cos2 а 2EFP tg а
Предполагается, конечно, что по длине стержня имеется ряд поперечных диафрагм или связей, устраняющих возможность
искажения сечения.
Для решетки, представленной на рис. 28, можно пользоваться формулой (54).
Во всех разобранных случаях влияние поперечной силы на Ркр может быть значительным лишь при весьма слабой решетке, как то имело место в сжатых стержнях Квебекского виадука (в нем площадь сечения диагоналей примерно составляла 1750 сечения поясов). С подобными условиями мы встречаемся при поверке на устойчивость верхних горизон-
Рис. 26.
г н
л
в
i
а
—
о
в,
Рис. 28.
Рис. 29.
тальных связей моста с параллельными поясами (рис. 29). Если опорные рамы, расположенные в плоскостях АА и ВВ, настолько жестки, что неподвижность концов можно считать обеспеченной, то тогда приходится проверить, не может ли горизонтальная ферма АВВА под действием сжимающих усилий изогнуться в своей плоскости. Пренебрегая изгибом стоек главных ферм моста, можно всю ферму АВВАХ рассматривать как стержень, находящийся в условиях, принятых в § 3.
262
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Тогда критическое значение сжимающей силы в сечении 00 будет
(q± EJ0n2
8 кр (0,694 If ф
Здесь о 2F (а2)2 ф можно положить равным РаРе Ра) или же, принимая во внимание деформацию распорок, вычислить на основании формулы (55). Такое приближенное решение
вопроса дает некоторые указания относительно надлежащего выбора размеров для верхних горизонтальных связей.
Перейдем теперь к случаю, когда пояса составного стержня соединены между собой лишь рядом поперечных планок (рис. 30). Такого рода конструкция нашла за последнее время
х
т т п
Щ 1П
а2
а2
L
Г
Рис. 30.
широкое распространение в сжатых мостовых элементах. Положим, что при сжатии составной стержень может выпучиться в плоскости ху. Обозначим через 0 момент инерции всего сечения относительно оси г-ов, через J момент инерции поперечного сечения одного пояса, через 2 момент инерции соединительной планки. Мы опять можем воспользоваться формулой (51). Для этого установим связь между углом перекашивания уз и поперечной силой Q. Выделим из стержня (рис. 30) сечениями тп и тП элемент длиной а.
Перекашивание его под действием поперечной силы Q представлено на рис. 31. Легко видеть, что
(6, б2) 2
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
263
Предполагая, что точки перегиба поясов совпадают с сечениями тп и тПи получим
Qa3
2-8-EJ
следовательно,
_ Q ( ab. a1 Y3_ E I 12h 24У (57)
Вставляя величину 257г) вместо §pr в форму¬
лу (51), получим
pin Кр “ 2
ЯоЯ2 122 2AEJ
(58)
Результаты, получаемые по этой формуле, будут вполне удовлетворительны, пока Ркр2 мало по сравнению с EJxn2a2, т. е. пока сжимающее усилие, приходящееся на каждый пояс, мало по сравнению с критической нагрузкой, вычисленной для элемента пояса между двумя поперечными планками. В противном случае опреде-
J2 o
кр
22.
EJf
I
Рис. 32.
ляемые по формуле (58) значения Р будут несколько преувеличенными и действительная устойчивость стержня будет менее расчетной. Изменяя расстояние b между поясами и жесткость планок, мы можем, оставляя постоянной величину Ju беспредельно увеличивать 0 и 2. В таком случае два первых члена в знаменателе формулы (58) будут стремить ся к нулю, и мы в пределе получим Ркр 247ia2, т. е. значение критической нагрузки получится большим, чем для одной рамы с бесконечно жесткими распорками (рис. 32). Для рамы критическая нагрузка будет 2EJn2la2.
Такой результат можно объяснить тем, что при исследовании перекашивания элемента, представленного на рис. 31, мы не приняли во внимание влияние продольной сжимающей силы на величину прогиба. Влиянием этим можно пренебречь лишь в том случае, когда Ркр2 мало по сравнению с EJn2a2, как это обыкновенно и бывает на практике.
Если принять во внимание продольную силу, то прогиб 62 (см. рис. 31) будет
1
Q а3 Т 8i 1 - а2
где а-
кр
EJ л2
264
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
и формула для определения критической нагрузки напишется так:
piv _ 1
KD —
КР 12 , ab а2 1 ’ (59)
EJ0я2 122 24j 1 - а2
При расчетах по формуле (59) следует поступать так. В качестве первого приближения определить Ркр из (58) и на основании полученного результата вычислить а2. Вставляя а2 в (59), найдем второе приближение для Ркр, на основании которого
можно более точно определить а2 и повторить вычисление Ркр. Конечно, эти вычисления приходится проделывать лишь в том случае, если а2 не мало. На практике почти всегда можно ограничиться формулой (58).
Возьмем часто встречающееся на практике поперечное сечение, составленное из двух швеллеров, соединенРис зз ных планками (рис. 33). Чтобы состав¬
ной стержень был равнопрочным при продольном изгибе как в направлении оси х, так и в направлении уу необходимо, чтобы Jy Jx.
Если мы можем свободно распоряжаться величиной 6, то надлежащее соотношение между у и Jx можно установить так. Зная продольную силу, подбираем по обычному способу величину Jx и таким образом устанавливаем величины Якр и J. Задаваясь теперь расстоянием между планками а и жесткостью планок EJ2, можно из формулы (58) или (59) найти необходимый размер Ь. Если величину b нельзя менять из конструктивных соображений, то, выбрав Jx обычным способом, тем самым определяем и величину Jy тогда уравнения (58) и (59) дают зависимость между а и 2. Задаваясь жесткостью планок, находим надлежащее между ними расстояние. Действительное решение получим, очевидно, лишь в том случае, если при выбранных размерах Jx Jy.
Все выводы, конечно, относятся к тому случаю, когда критические напряжения не превосходят предела упругости материала. В противном случае формулы (58) и (59), конечно, дадут для Ркр преувеличенные значения. Ввиду значительного практического интереса формулы (59) мы предполагаем ее подвергнуть опытной проверке в механической лаборатории Киевского политехникума. В настоящее время приводим результаты нескольких предварительных опытов с деревянным стержнем. Дерево, конечно, далеко не совершенный материал для проверки теоретических формул, и мы на нем остановились лишь по¬
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
265
тому, что не располагали надлежащими машинами и опыт весь вели с помощью самых простых приспособлений.
Обыкновенно при опытах на продольный изгиб сжимают стержень, два конца которого снабжены остриями и потому могут свободно поворачиваться 1). Чтобы уменьшить влияние трения, а главное, чтобы получить искривление при меньших нагрузках, мы решили испытывать на продольный изгиб стержень с одним заделанным и другим свободным концом. Нижний конец стержня А (рис. 34) вертикально защемляется в особых тисках, к верхнему концу Ву снабженному особым наконечником, прикладывается через посредство особой рамы С вертикальная нагрузка D. Чтобы избежать толчков и вредных сотрясений, мы в качестве нагрузки пользовались водой, подводя ее из калиброванного сосуда с помощью сифонной трубки F.
Опыт ведется в таком порядке: предварительно с помощью уровня устанавливается в вертикальном положении стержень АВу и потом навешивается на него рама С и сосуд для воды D. Центральная передача силы достигается с помощью особого приспособления у верхнего конца стержня (рис. 34, с). С помощью винтиков М и N можно слегка перемещать подкладку О, а вместе с тем и призму рамы С до тех пор, пока не достигнем точной установки. О точности можно судить, наблюдая с помощью зрительной трубы К и шкалы
) Наиболее точно поставленные опыты в этой области принадлежат Th. К а г m а п ’ у. Untersuchungen iiber Knickfestigkeit. Gottingen, Dissertation, 1909. Эта работа опубликована под тем же названием в «Mitteilungen tiber Forschungsarbeiten», herausgegeben vom Verein deutscher Ingenieure. 1910, Heft 81, 44 SS. Перепечатка: Th. К а г m a n, Collected works. Butterworths scientific publication, London, 1956, vol. 1, pp. 90—140. Наконечники, снабженные твердыми трехгранными призмами, обеспечивали свободное поворачивание концов. В известных опытах JL Тетмайера благодаря коническим наконечникам трение было значительно большим, что влекло за собой погрешности в величине Ркр.
40с
АЁ
266
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
отклонения конца В при нагрузке стержня (точность отсчетов 0,01 мм). Мы при опытах старались добиться такой установки, чтобы нагрузка, равная примерно половине критической, не вызывала заметных искривлений.
Стержень для опытов был составлен из двух линеек, склеенных между собой особыми брусками, расставленными на 7 см
Поперечный разрез 25
2Я 1,75
Вид сбону
-5,5-
7
Размеры в сантиметрах Рис. 35.
ш
ось от оси (рис. 35). Свободная длина стержня взята равной 140 см. Жесткость распорок настолько значительна, что их деформацией можно пренебречь; тогда формула (59) перепишется так:
EJqU2 1
(60)
Р
г кр
2
1
24 , 42 1 - а2
Чтобы воспользоваться формулой, выведенной для стержня с опертыми концами, нужно взять, конечно, длину равной 21 Величины о и ь входящие в формулу (60), были найдены из предварительных опытов. Для нахождения 1 линейки перед
склеиванием были испытаны на из-
I 1 гиб. Из этих опытов найдено EJi
500 кгсм2. Величина EJ0 найдена
из изгиба составного стержня. ЧтоРис. 36. бы исключить влияние перекашива¬
ния отдельных элементов, нагрузка располагалась, как показано на рис. 36. При этих условиях средняя часть стержня испытывает чистый изгиб и Eh может быть найдено измерением прогиба посредине пролета. Из опыта было найдено:У0 1,8- 105 кгсм2.
Следовательно, критическая нагрузка, вычисленная по обычной формуле, будет Р1ф 70л242 22,6 кг. Критическая нагрузка для одного элемента пояса между двумя распорками равна EJin2a2 500л2(5,5)2 165 кг. Следовательно, а2 0,06. Вставляя эти величины в формулу (60), найдем
Р
-Г кр
22,6
5,52
21,3 кг.
1 24 360 4. 14Q2 0,94
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
267
Результаты произведенных двух опытов представлены на рис. 37. По оси абсцисс отложены нагрузки, по оси ординат — прогиб верхнего конца стержня. В обоих случаях при нагрузках, больших 20,4 кг, произошли сильные искривления. Величины
прогибов верхнего конца стержня в мм приведены в таблицах отсчетов с точностью до 0,01 мм.
Для исследования влияния расстояния между распорками на величину Р1ф мы распилили распорки через одну и получили таким образом расстояние а 2 X 5,5 1,5 12,5 см. Критическая нагрузка для одного элемента пояса будет EJn2a2 32 кг; так как критическую нагрузку Ркр можно было ожидать равной 16 сг, то, следовательно,
а2 8 : 32 0,25.
26Й
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
1-ый опыт 2-ой опыт
Р, кг
Отсчет,
мм
Прогиб,
мм
9.4
11.4
13.4
15.4
17.4
18.4
19.4 19,9
20.4
27.38
27.38 27,36 27,53 27,80 28,05 28,65 29,10
0
0
-0,02 0,15 0,42 0,67 1,27 1,72
Сильное искривление
Р, кг
Отсчет,
мм
Прогиб,
мм
9,4
13.4
15.4
17.4
19.4
20.4
При да, нагрузки
8.05
8.05 8,00
7.50 5,86
2.50
льнейшем во: - сильное ис
0
0
0,05
0,55
2,19
5,55
зрастании
кривление
Вставляя это в формулу (60), получим
22,6
360
1
12,52 4 1402 0,75
16,2 КЗ.
3 - ий опыт
Здесь благодаря влиянию перекашивания элементов стержня получается уменьшение нагрузки на 28. При испытании стержень сильно искривился, когда нагрузка достигла величины
16,4 кг. Результаты опыта приведены в таблице отсчетов. Изменение прогибов с увеличением нагрузки представлено графически на рис. 37.
Из диаграммы видно, что результаты опыта близко совпадают с теоретическими данными.
В дальнейшем мы еще распилили распорки через одну и оставили, таким образом, лишь три промежуточные распорки. В этом случае а 12,5 X 1,5 26,5 см. Критическая нагрузка для элемента пояса между двумя распорками будет EJn2la2 7 кг. Формула (60) дает для Ркр значение около 6,5 кг.
Из опыта мы нашли для критической нагрузки значение 8,4 кг. Следовательно, здесь стержень оказался более жестким, чем то следует из теоретических формул. Объяснить это можно отчасти тем, что при выводе формулы предполагалось большое число распорок, мы же имели лишь три промежуточные распорки. Кроме того, последний опыт производился при значительно меньших напряжениях, в этом случае величина Е могла быть несколько больше расчетной.
Р, кг
Отсчет,
мм
Прогиб,
мм
4,4
10,44
0
6,4
10,60
0,16
8,4
10,75
0,31
10,4
11,0
0,56
12,4
11,40
0,96
14,4
12,28
1,84
15,4
13,97
3,53
16,4
Сильное искривление
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
269
Конечно, приведенных здесь опытных данных далеко не достаточно, их желательно распространить на такие материалы, как сталь и железо, и вести исследование не только в пределах упругости, но также и при более высоких напряжениях. Принятая здесь постановка обеспечивает с большой точностью принятые условия на концах.
§ 10. О продольном изгибе криволинейных стержней
Вопрос об устойчивости стержней с криволинейной осью приобретает интерес в связи с расчетом сводов, толщина которых мала по сравнению с пролетом. Выделяя из свода элемент шириной единица, считая по образующей свода, можем рассчитывать его, как брусок, ось которого совпадает с осью свода. Жесткость изгиба такого стержня в плоскости оси, очевидно, будет
Eh3 12(1-а2)
где h — толщина свода, а — коэффициент Пуассона.
Мы здесь рассмотрим тот случай, когда толщина б постоянна, ось свода представляет дугу круга и нагрузка имеет характер гидростатического давления, т. е. интенсивность постоянна и направление нормально к оси в каждом поперечном сечении стержня.
Пусть стержень ADB (рис.
38) с круговой осью длиной аа находится в равновесии под действием равномерно распределенных нормальных давлений интенсивности р и реакций Т ра, направленных по касательным к оси стержня в точках А и В. Очевидно, Т представляет собой постоянное по длине стержня сжимающее усилие. Соответствующее ему сжимающее напряжение будет TF paF, где F — площадь поперечного сечения стержня. Постепенно увеличивая давление , мы можем достигнуть предела, когда дуга круга перестает быть устойчивой формой равновесия для оси стержня. Стержень искривится, кроме продольного сжатия получится еще изгиб. Мы здесь будем рассматривать лишь те случаи, когда искривление происходит в плоскости оси стержня. При рассмотрении устойчивости прямолинейных стержней мы видели, что работа внешних сил, соответствующая малым отклонениям от первоначальной формы равновесия, представляется величиной второго порядка малости.
270
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Поэтому вопрос об устойчивости возникает лишь тогда, когда изменения потенциальной энергии, соответствующие каким-либо отклонениям от первоначальной формы, также представятся величинами того же порядка. Переходя к рассмотрению устойчивости криволинейного стержня ADB, нам придется остановиться на тех отклонениях от первоначальной формы равновесия, для которых удлинения оси являются величинами второго порядка малости. Будем обозначать через w и v радиальное и касательное перемещения какой-либо точки Р при выпучивании стержня, тогда относительное удлинение элемента стержня представится такой формулой ’):
е-2aw)Jrw )-vl' (61)
Чтобы удлинение было величиной второго порядка малости, должно быть выполнено условие
w-. (62)
Предположим в точках А и В шарниры, тогда должны быть выполнены условия:
v w — 0 при 0 0; v w 0 при 0 а.
Положим
V Л, (l coSj Aj(l -cos--j Л3 (l — cos--j
(63)
тогда на основании (62) получим
dv „ 2я. 2л0. „ 4л. 4л0 , п
да Ж Л-51П— Л2 —sin —. (64)
Задавшись, таким образом, искривленной формой равновесия, найдем величину критической нагрузки принятым в настоящей статье методом. При выпучивании стержня внешние давления совершат некоторую работу, кроме того, освободится часть энергии сжатия, так как отдельные элементы получат дополнительное удлинение еу определяемое по формуле (61). За счет этого появится энергия изгиба. Круговая форма равновесия перестает быть устойчивой, когда работа внешних давлений, сложенная с уменьшением энергии сжатия, как раз равняется энергии изгиба. Изменение кривизны стержня при выпучивании может быть представлено известной формулой
) См. стр. 37 нашей работы, указанной на стр. 212.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
271
Поэтому выражение для потенциальной энергии изгиба будет
_а п — оо
т С Г 1 ( d2w , 2 С а V л2 Г 2ап 2а1лз-2
f- tJ -(.-ш)ай0т 1 —(—)J
п 1
Здесь вместо а; поставлено его значение (64).
Дополнительное удлинение, которое испытывает каждый элемент стержня при выпучивании, на основании (61) и (62) будет
1 Idw 2
Вследствие этого потенциальная энергия сжатия уменьшится на величину
(wvYadQ
о
1 00 2 1 00
s Л s (¥)-
4 п1 ' п
Вопрос о работе внешних сил при искривлении был нами исследован в другом месте1), и мы воспользуемся готовым выражением
а
Т Г w2 dw v2 ,Q
т J (aw-—-v4e---r)dQ
о
п — оо лоо 2 г оо
Т Sr-т S. -т2
г1 ' г 1 ' п 1
Вставляя полученные выражения в уравнение баланса энергии, получим
п оо 2 00 2 г оо 1
т2)л(¥Г-т(2)-т21я
г-1 t 1 г-1 J
г оо 2 г со л
(Su).iS(¥)'-r -
г 1 г1 J
1 00
а V1 2 Г 2гя 2azjc з 12
-т 2И»Ьт-Ьг) J (65)
С а
г1
) См. стр. 41 нашей работы, указанной на стр. 212.
272
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
откуда находим критическое значение давления
. (66)
Наименьшее значение для 1ф получим, полагая в выражении (66) все коэффициенты Ап, кроме первого, равными нулю. Тогда
При а 2я, т. е. когда кривой брусок представляет собой полное кольцо, формула (67) дает для критического давления
значение нуль. Результат этот объясняется тем, что в случае полного коль-
Последнее выражение совпадает с результатом, полученным для сплошного кольца Морисом Леви1). Первая искривленная форма для кольца представлена на рис. 39.
Пользуясь формулой (68), можно поверять на устойчивость цилиндрические трубки, подвергающиеся внешнему гидростатическому давлению. Задача эта может иметь практическое значение в связи с расчетом жаровых труб в котле.
) М. Levy. Memoire sur un nouveau cas integrable du probleme de l’elastique et l’une de ses applications. Journal de mathmatique pures et appliqu6es,
3 serie, 1884, vol. 10, pp. 5—42.
(67)
ца оба шарнира совпадают и кольцо может около общего шарнира совершать вращение без деформации.
Чтобы получить критическое давление для полного кольца, нужно в выражении (66) положить все Лп, кроме А2, равными нулю; тогда
(68)
Рис. 39.
ОБ УСТОЙЧИВОСТИ упругих систем
273
В случае весьма малого угла а первый член в правой части формулы (67) играет преобладающую роль и величина критической сжимающей силы Т будет
где s — длина дуги. Результат этот совпадает с тем, что получается для второй искривленной формы (с одной точкой перегиба) в случае прямого стержня. То обстоятельство, что мы здесь сразу приходим ко второй форме, объясняется тем, что именно для этой формы удлинения оси представятся малой величиной второго порядка. Характер искривления указан на рис. 38 пунктиром 4). Формулой (67) можно пользоваться не только в случае круга, но и при других пологих кривых и таким образом поверять на устойчивость двухшарнирные и трехшарнирные арки. При а я результат формулы (67) совпадает с тем, что получается для сплошного кольца по формуле (68). Этого результата и нужно было ожидать, так как каждая половина кольца, представленного на рис. 39, находится в одних и тех же условиях, и ничто не изменится, если в точках А и В или С и D поместить шарниры.
Мы рассмотрели здесь те случаи, когда выпучивание происходит в плоскости оси стержня. В случае выпучивания в направлении, перпендикулярном к плоскости оси, изгиб будет сопровождаться кручением. Придется иметь дело с более сложной задачей. Задача эта приобретает большой практический интерес в связи с расчетом криволинейных сжатых поясов открытых мостов, и мы надеемся к ней вернуться в ближайшем будущем2).
§ 11. Об устойчивости стержневых систем
Новая метода с успехом может быть применена к исследованию устойчивости не только отдельных стержней, но также и систем, из стержней составленных. В качестве примера разберем вопрос об устойчивости сжатых раскосов решетчатой фермы с параллельными поясами.
) Вопросом об устойчивости криволинейных стержней под действием гидростатического давления занимался К. Federhofer. Zur Festigkeit radial belasteter Kreisbogen. Sitzungsberichte der Akademie der Wissenschaften. Wien, 1909, Bd. 118, Heft 7, Abteilung Ha, SS. 1101—1128. К сожалению, автор рассматривает форму равновесия, симметричную относительно середины, и потому получает для РКр преувеличенное значение. Вместо формулы (67) он приходит к такому результату:
2) Один элементарный случай решен в нашей статье: см. сноску 3) на стр. 211.
274
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Рис. 40.
Положим, имеется система сжатых параллельных раскосов ап-1, Ьп2 (рис. 40). Все раскосы имеют одинаковую длину, одинаковую жесткость изгиба Е в направлении, перпендикулярном к плоскости фермы, и сжаты одной и той же силой Р. Каждый из сжатых раскосов пересекается в нескольких равноудаленных точках с системой параллельных растянутых раскосов,
имеющих ту же длину , жесткость изгиба EJ2 и растянутых одной и той же силой Q. Будем исходить из предположения, сделанного Ф. С. Ясинским, что при выпучивании оси всех раскосов каждого ряда, оставаясь параллельными, выгнутся по одинаковым плоским симметричным кривым1). При выпучивании сжимающие силы Р совершат некоторую работу Г, а растягивающие силы Q — отрицательную работу —Т. Система становится неустойчивой, когда Т—Т1 сделается равным изменению энергии деформации системы. Это изменение равно энергии изгиба сжатых и вытянутых стержней. Основное уравнение для определения РКр напишется так:
о о
»
о о
Так как сжатые и вытянутые раскосы при выпучивании имеют ряд общих точек, то можно принять кривые изгиба совпадающими и положить
„ . пх
У1 У2 А sin —.
Вставляя это в уравнение (70), получим
Ркр Q
2
(Ч)-
(71)
Результат этот совершенно совпадает с тем, что получено Ф. С. Ясинским путем интегрирования соответствующих диффе-
) Предположение это оставлено Ф. С. Ясинским без доказательства, вероятно, потому, что он во всех случаях считал кривую без перегибов первой возможной искривленной формой равновесия.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
275
ренциальных уравнений1). В том случае, когда длина растянутых раскосов отличается от длины А сжатых раскосов, основное уравнение (70) перепишется так:
о о
- 11 ifrb-(72)
о о
Так как прогибы раскосов в местах пересечения одинаковы, то можно положить
„ . ПХ Л . пх
Ух А Sin—, у2 A Sin--.
Вставляя это в уравнение (72) и вводя обозначение k:h m, получим2)
(73)
Формулы эти получены в предположении, что имеется весьма большое число общих точек у сжатого и растянутого раскосов. Ф. С. Ясинский исследовал вопрос, насколько применимы формулы (71) и (73) в случае одного или двух пересечений, и нашел, что в пределах 021,5ь OCQ.P2 погрешность практически ничтожна.
Мы не будем останавливаться на подробностях этого исследования, отметим только, что выводы могут быть значительно упрощены, если пользоваться приближенными формулами для прогибов стержня, испытывающего продольные сжимающие или растягивающие усилия3).
§ 12. Пределы применимости полученных формул
Во всех рассмотренных нами случаях продольного изгиба задача сводится к нахождению коэффициента длины jm. Величина критической нагрузки может быть определена по формуле для основного случая, если в нее вместо действительной длины вставить приведенную длину jы. Получим
р _ EJn2 КР (ц)2 ’
) См. указанную на стр. 224 книгу Ф. С. Ясинского, стр. 177.
2) Ф. С. Ясинский, там же, стр. 183.
3) См нашу работу, указанную на стр. 212,
276
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
откуда
Ркр —
(74)
г — наименьший радиус инерции поперечного сечения стержня.
Формула (74) выведена в том предположении, что Е — величина постоянная, поэтому вычисляемые по ней значения ркр соответствуют действительности лишь в том случае, если они не превосходят предела упругости материала, т. е. при сравнительно длинных стержнях.
Полагая, например, для железа' 2-106 кгсм2 и предел упругости равным 2-103 кгсм2, найдем, что формула (74) применима лишь для г 100. На практике весьма часто приходится иметь дело с более короткими стержнями, и возникает вопрос об их расчете на продольный изгиб. Начнем с основного случая, как наиболее изученного и теоретически, и экспериментально. За пределом упругости главным образом пользуются эмпирическими формулами. Из большого количества имеющихся формул предпочтение следует отдать формуле JI. Тетмайера. Она наиболее проста и построена на основании многочисленных удовлетворительно поставленных опытов. Критическое напряжение по JI. Тетмайеру представится так:
где аир для определенного материала являются постоянными величинами, определяемыми из опыта.
Новейшие, более точные исследования1) показали, что формула (75) дает для ркр значения меньшие действительных. Объясняется это тем, что при опытах, положенных в основание этой формулы, не всегда было обеспечено точное центрирование. Влияние эксцентриситета тем большее, чем меньше величина г, поэтому для сравнительно коротких стержней (для Иг 40) погрешности в формуле Л. Тетмайера особенно значительны. У нас в России нашла значительное распространение таблица критических напряжений, составленная Ф. С. Ясинским. Пользуясь опытами Л. Тетмайера и отчасти М. Консидера, Ф. С. Ясинский вычислил по способу наименьших квадратов значения коэффициентов аир, входящих в формулу (75), и составил таблицу значения для ркр в пределах от Ijr 20 до 250 2). Для г 40 таблица эта дает для ркр величины, значительно меньшие действительных, но, пока нет достаточного количества опыт¬
) См. указанную на стр. 265 работу Th. Karman’a.
2) Непонятно, зачем при составлении таблицы все вычисления исполнены
с шестью знаками, раз определяемые величины при самой тщательной постановке опытов находятся с точностью, не большей 5—10.
(75)
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
277
ных данных, ею приходится пользоваться. Получаемые при этом погрешности, очевидно, идут в запас прочности.
Кроме чисто эмпирических формул возможно для определения кр за пределами упругости посторить и аналитическую формулу, аналогичную формуле Эйлера (74). Нужно только для материала стержня знать зависимость между деформациями и напряжениями при сжатии за пределами упругости. Мы остановимся несколько на этом способе вычисления р1ф, так как он поможет нам выяснить вопрос о критических напряжениях в более сложных случаях продольного изгиба, например, при выпучивании стержней в упругой среде и при Еыпучивании составных стержней.
Предварительным испытанием на сжатие устанавливается зависимость между напряжениями и деформациями. В пределах упругости отношение приращения напряжения к приращению деформации есть величина постоянная, равная модулю упругости материала Е. За пределами упругости деформации растут быстрее напряжений, и отношение приращения напряжения к приращению деформации будет некоторой функцией от напряжения. Обозначим ее через Е Для исследования изгиба стержня за пределами упругости примем два таких положения 4). 1) Допустим, что при изгибе стержня за пределами упругости поперечные сечения остаются плоскими и 2) что зависимость между напряжениями и деформациями при изгибе такая же, как при простом растяжении или сжатии. После этих предварительных замечаний переходим к явлению продольного изгиба. Предположим, что стержень прямоугольного поперечного сечения сжат за пределом упругости. Рассмотрим, как изменится распределение напряжений по плоскости поперечного сечения MN (рис. 41), если оси стержня дать незначительное искривление в плоскости рисунка. В силу первого допущения в плоскости MN должна быть линия А (нейтральная), перпендикулярная к плоскости рисунка, по которой не произойдет при изгибе никаких изменений в величине напряжений. По одну сторону этой линии произойдет увеличение, а по другую — уменьшение напряжений. При увеличении напряжений зависимость между приращением напряжения и сжатия определится соответствующей величиной ЕВ местах уменьшения напряжений будем
) Положения с достаточной точностью подтверждаются опытами Е. Меуег’а; см. его статью «Die Berechnung der Durchbiegung von Staben, deren Material dem Hookeschen Gesetze nicht folgt». Physikalische Zeitschrift, 1907, Jahrgang 8, JSfe 22, SS. 827—831.
278 ОБ УСТОЙЧИВОСТИ УПРУГИХ систем
иметь лишь упругую деформацию, связь между напряжениями и деформациями определится модулем упругости Е. Если через 1р обозначим кривизну оси стержня в сечении MN, то, пользуясь обозначениями рис. 41, найдем такие выражения для наибольших напряжений, вызванных изгибом:
h гу „ 2 Z7
Pi- Р2 -у-
Положение нейтральной оси определится из того условия, что сумма напряжений изгиба должна равняться нулю, следовательно, h2E' l:lE. Принимая во внимание, что h h2 h, находим _ и УЁ 1 и V Е' 1
h — —.— г— Ну Н2 — ,— ,— Н,
V Е' V Е VE' VE
Момент напряжений изгиба будет
АЛ b U1 , и Л bh 4ЕЕ' I
3(Vi V2) 12 yY VWf р‘
Здесь b — ширина сечения. Как и в случае изгиба в пределах
упругости, момент оказывается пропорциональным кривизне.
Отличие только в том, что вместо модуля упругости Е входит величина 4EEfj(rE YW)2 у зависящая от Е а следовательно, и от продольных сжимающих напряжений.
Назовем величину эту «приведенным модулем» упругости и обозначим через Я; тогда
М — HJ
р ах2
Зависимость Н от сжимающих напряжений находится из предварительного опыта на сжатие. Раз момент пропорционален кривизне, то сейчас же можем написать и выражение для критической нагрузки:
Ркр и ркр Яя2(у)2; (76)
так как величина Н весьма мало зависит от формы поперечного сечения, то, следовательно, и за пределами упругости ркр зависит лишь от величины отношения г. Для проверки формулы
(76) были произведены опыты ) с мартеновской сталью (временное сопротивление разрыву 6800 кгсм2у удлинение 16,7, модуль упругости 2,17-106 кгсм2). В пределах упругости опыты с большой точностью подтвердили формулу Эйлера, за этими пределами опыты хорошо согласуются с результатами формулы (76).
См. указанную на стр. 265 работу Th. Karman’a.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
279
За пределами текучести, т. е. для г 40, величина рЩ) начинает сильно возрастать, и в пределе мы должны получить временное сопротивление сжатию.
Итак, опыты показывают, что и за пределами упругости можно для основного случая пользоваться формулой Эйлера, нужно только вместо Е вставить Я, что равносильно уменьшению жесткости изгиба в отношении Н : Е. От основного случая легко перейти и к другим, где сжимающая сила постоянна по длине и коэффициент длины jm зависит только от способа закрепления концов. Здесь также придется первоначальную жесткость изгиба заменить величиной ; коэффициент длины от этого, очевидно, не меняется, и мы можем пользоваться формулой Л. Тетмайера или таблицей Ф. С. Ясинского. Влияние закрепления концов за пределами упругости, конечно, будет значительно меньшим, чем то следует из обычной формулы Эйлера. Для примера выпишем ряд значений ркр для основного случая и для случая заделанных концов 1).
1
г
р'р, кгсм2
ркр. кгЮм
Ркр
ркр
свободные
концы
заделанные
концы
200
532
1904
3,58
150
946
2275
2,40
100
1904
2646
1,39
50
2646
3016
1,15
Эта таблица лишний раз подтверждает то правило, что в случае жестких узловых соединений все же следует считать концы сжатых стержней свободно поворачивающимися.
Если сжимающее напряжение не постоянно по длине, то с переходом за пределы упругости коэффициент длины jm меняется в зависимости от напряжений. Возьмем, например, продольный изгиб от собственного веса. Если за пределами упругости не менять i, то это равносильно предположению, что жесткость изгиба по всей длине стержня уменьшается в отношении Н :, где Н — приведенный модуль, вычисленный для нижнего сечения, соответствующего наибольшим напряжениям. В действительности только часть стержня будет сжата за пределом упругости, и только для этой части необходимо уменьшить жесткость изгиба. Ясно, что, оставляя за пределом упругости коэффициент длины х без изменения, мы будем получать для критических напряжений величины, меньшие действительных.
) Числа взяты из таблицы Ф. С. Ясинского.
280
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Еще большие изменения коэффициента длины за пределом упругости получаются в случае выпучивания стержня в упругой среде. Величина х в этом случае зависит от В2, где В2 р416. С переходом за пределы упругости р не меняется, жесткость же изгиба уменьшается в отношении Н : Е, следовательно, Б2, а вместе с тем и 1jm возрастают. Пользуясь таблицами § 6 и § 7, возрастание это может быть отчасти учтено. Покажем это на численном примере. Положим, что, пользуясь вышенаписанной формулой для В2 и рис. 12, мы для рассчитываемого стержня нашли, что В2 80, i 0,303 и jiljr 60.
Для отношения 1г 60 критическое напряжение по таблице Ф. С. Ясинского будет приблизительно равно 2500 кгсм2. Так как напряжение это превосходит предел упругости железа, то жесткость изгиба стержня будет меньше EJ, и во столько раз меньше, во сколько раз 2500 меньше критического напряжения, вычисляемого по обычной формуле Эйлера. Полагая Е 2 106 кгсм2, найдем, что жесткость изгиба при напряжениях
2 106л2 5
2500 кгсм2 уменьшится в отношении 2500 : — jf
В таком же отношении должно возрасти В2 необходимо, следовательно, произвести повторный расчет. Для В2 176
ixl 252
по рис. 12 находим х 0,252. В таком случае 303 50.
По таблице Ф. С. Ясинского находим соответствующее ркр 2646 кгсм2.
Дальнейшие приближения будем получать, повторяя расчет в прежнем порядке. Для напряжения 2646 кгсм2 уменьшение
2 Ю6 я2
жесткости изгиба будет 2646 : —— 033; соответствующее
В2 будет равно 80:0,33 240, коэффициент длины по рис. 12 будет равен 0,233, следовательно, ilr 46 и соответственно кр 2704 кгсм2.
Дальнейшие повторения вычислений уже не внесут существенных изменений в величину ркр. Мы при расчете предполагали уменьшение жесткости изгиба постоянным по всей длине стержня, в действительности при заданном распределении внешних сил сжимающее усилие меняется по длине, и в то время, как в средней части стержня материал будет сжат за пределом упругости, концы стержня еще не получат достаточных деформаций, их жесткость изгиба не изменится. В силу этого обстоятельства вычисленное выше значение для ркр все же будет несколько меньше действительного, мы получим погрешность, идущую в запас прочности.
Аналогичным способом можно учесть влияние изменения ц за пределами упругости и в случае составных стержней. Возьмем, например, формулу (58), выведенную в предположении
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
281
соединения поясов стержня одними поперечными планками. Выражение для критической силы может быть представлено в таком виде:
Р EJ рЛ2 1 КР 2 Jt2 ab EJ0 Jt2 a2 EJ0 12 2 EJ2 24 2
Следовательно,
2 1 j ЗТ2 EJq I ТС Q EJq уу
“ 1 7 177 1м T2 Ш' '
Положим, что, вычисляя х по формуле (77) и пользуясь таблицей Ф. С. Ясинского, мы получили в заключение для р1ф значение, большее предела упругости. В таком случае жесткость изгиба как всего стержняУ0, так и каждого из поясов EJ уменьшается в отношении Н : Е, жесткость же планок, не испытывающих при продольном сжатии никаких напряжений, остается без изменения. Благодаря этому второй член в выражении
(77) для i2 уменьшается, а вместе с тем уменьшается и х. Если это обстоятельство принять во внимание, то повторным расчетом можно внести поправку в величину ркр. При желании, конечно, можно получать и дальнейшие приближения.
Мы остановились на задаче о продольном изгибе за пределами упругости, чтобы отчасти выяснить вопрос об изменениях коэффициента длины х. Из предыдущего ясно, что обычно делаемое предположение относительно постоянства коэффициента длины х 2) правильно лишь в некоторых случаях. Обыкновенно х с переходом за предел упругости меняется в зависимости от напряжений. В некоторых случаях влияние этого изменения на величину ркр может быть вычислено без особых затруднений. Если пренебречь изменениями л, то получаемые от этого погрешности идут в запас прочности. Этим можно оправдать обычный способ расчета, при котором для х берется одно и то же значение независимо от величины напряжений.
Отдел второй
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ РАВНОВЕСИЯ ИЗГИБАЕМЫХ СТЕРЖНЕЙ
§ 13. Постановка задачи
В этом отделе мы займемся теми случаями неустойчивого равновесия, которые возникают иногда при изгибе стержней в плоскости их наибольшей жесткости. Если одна из главных жесткостей изгиба мала по сравнению с другой, то, изгибая стержень в плоскости наибольшей жесткости, можно, постепенно
) См. книгу Ф. С. Ясинского, указанную на стр. 224, стр. 208.
232
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
увеличивая изгибающие силы, прийти к пределу, когда плоская форма изгиба перестает быть устойчивой, ось стержня искривляется в направлении наименьшей жесткости, причем отдельные поперечные сечения стержня поворачиваются. Вместо плоского изгиба мы будем иметь изгиб в двух плоскостях, сопровождающийся кручением. Явление это проще всего демонстрировать на изгибе обыкновенной линейки. Изгибая руками линейку в плоскости ее наибольшей жесткости, легко можно почувствовать то предельное значение изгибающего момента, при котором плоская форма перестает быть устойчивой.
Явление неустойчивости возможно при различных формах поперечного сечения.
Мы рассмотрим случай прямоугольного сечения, как то имеет место при изгибе линейки или железной полосы, и случай двутаврового поперечного сечения. Двутавровое сечение весьма часто встречается на практике, и потому вопрос об устойчивости плоской формы изгиба двутавровых балок имеет большое практическое значение.
Стремление получить возможно большую экономию в материале и желание достигнуть возможно большей жесткости в плоскости действия сил заставляют конструктора увеличивать высоту двутавровой балки. Ширина поясов при этом из конструктивных соображений не может быть значительно увеличена. В заключение получается поперечное сечение, один из главных моментов инерции которого во много раз больше другого. Балка имеет в направлении, перпендикулярном к плоскости действия сил, недостаточную жесткость, становится возможным явление неустойчивости.
Обыкновенно в инженерных сооружениях этот недостаток жесткости устраняется дополнительными связями, но иногда эти связи не могут быть поставлены из конструктивных соображений, иногда связей недостаточно, в обоих случаях балка может оказаться значительно менее прочной, чем то следует из обычных расчетов, заключающихся в вычислении наибольших напряжений.
При исследовании устойчивости плоской формы изгиба мы будем предполагать, что искривление в направлении наименьшей жесткости сопровождается лишь поворотом отдельных поперечных сечений балки, форма же сечений остается неискаженной ). Такие явления, как выпучивание вертикальной стенки балки или выпучивание горизонтальных сжатых листов, мы рассмотрим ниже при исследовании устойчивости пластинок.
1) Мы пренебрегаем малыми искажениями сечения, сопровождающими явления обычного изгиба и кручения.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
283
Некоторые из задач, которыми мы займемся в этом отделе, уже были разрешены раньше1). Решения эти получены путем интегрирования соответствующих дифференциальных уравнений равновесия. Даже в простейших случаях действия внешних сил уравнения получаются весьма сложными. Интегралы выражаются в виде бесконечных рядов. Суммы этих рядов входят в трансцендентные уравнения, которые приходится в каждом частном случае решать для определения критической нагрузки. Нахождение корней этих уравнений требует огромного количества вычислений, при которых легко можно ошибиться. Здесь мы применим для отыскания критических значений нагрузки новую методу.
Для задач, ранее решенных, результаты, полученные иным методом, являются надежной проверкой. Для новых задач приближенная метода дает решения, точность которых вполне достаточна для практических приложений. При желании в каждом частном случае точность может быть повышена до желаемой степени.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА полос ПРЯМОУГОЛЬНОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
§ 14. Основные уравнения
При выводе основных уравнений мы будем предполагать ось стержня горизонтальной и плоскость наибольшей жесткости расположенной в вертикальной плоскости. За начало координат будем принимать или центр тяжести левого концевого сечения, или (в случае симметрии) центр тяжести срединного сечения. Ось х-ов направим по оси стержня, ось у-ов — перпендикулярно к плоскости наибольшей жесткости, ось г-ов — вертикально вниз. Кроме главной системы координат ху уу z мы при выводе основных уравнений для искривленной формы равновесия будем пользоваться еще вспомогательной системой , т,.
Начало этой системы будем располагать в центре тяжести рассматриваемого поперечного сечения. Оси ц и направим но главным осям инерции поперечного сечения, ось совпадает
1) См. работу: L. Р г a n d 11. Kipp-Erscheinungen. Ein Fall von instabilem elastischem Gleichgewicht. Dissertation der Universitat Munchen, 1899, November, Nurnberg, 1900, SS. 1—75 Перепечатка: L. P r a n d 11. Gesammelte Abhandlungen zur angewandte Mechanik, Hydro- und Aerodynamik. Erster Teil. Springer-Verlag, Berlin — Gottingen — Heidelberg, 1961, SS. 10—74, и нашу работу, указанную на стр. 210.
284
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
с направлением касательной к искривленной оси стержня. Расположение координат показано на рис. 42.
В дальнейшем будем пользоваться следующими обозначениями: В EJ — наименьшая жесткость изгиба, В EJX — наибольшая жесткость изгиба, С — жесткость стержня при кручении, ф — угол поворота какого-либо поперечного сечения при выпучивании изгибаемого стержня.
Вычисление величин В и В не встречает затруднений, так как значением Е можно всегда задаться или определить опытным путем. Величины и J находятся по размерам сечения.
Что касается величины С, то, как показали произведенные нами опыты, для определения ее можно пользоваться приближенной формулой Сен-Венана:
где F — площадь поперечного сечения, р — полярный момент инерции поперечного сечения, G — модуль упругости при сдвиге.
В случае сплошного стержня приведенная формула дает вполне удовлетворительные результаты для уголкового, таврового или двутаврового сечения. Для составных, склепанных стержней вычисленная по формуле жесткость С является несколько преувеличенной, так как заклепки не могут вполне устранить относительных перемещений отдельных составных частей стержня при его скручивании.
При составлении уравнений равновесия необходимо знать выражения для косинусов углов, составляемых осями, т), с осями х, у, z,
в
Рис. 42.
ОВ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
285
Значения этих величин при малых искривлениях могут быть представлены такой таблицей:
1
С
1
dy
dz
X
1
dx
dx
У
ах
1
-Ф
dz
г
dx
Ф
1
Рассекая стержень на две части и составляя уравнения равновесия для одной половины, получим )
М-Сф',
Здесь через Af, Мц, Мg обозначены моменты внешних сил относительно соответствующих осей. Так как мы рассматриваем лишь малые искривления и полагаем, что отношение ВВ — малая величина, то входящие в уравнения члены с множителем р можно пропустить. Тогда задача об отыскании критических значений изгибающих сил сведется к интегрированию двух таких дифференциальных уравнений:
Af6 Cp't Mi By. (78)
Для каждого частного случая действия внешних сил остается лишь подставить соответствующие значения М и Мg. Величина критической нагрузки не будет зависеть от Ви наибольшей жесткости изгиба.
Только при изгибе стержня двумя взаимно противоположными парами сил написанные уравнения допускают элементарное решение в круговых функциях. При изгибе сосредоточенными силами приходим к уравнениям, решения которых выражаются в функциях Бесселя. В случае распределенных нагрузок и переменного сечения решения получаются в виде бесконечных рядов.
) Здесь не принято во внимание то обстоятельство, что направления I, г) и меняются при перемещении по оси стержня.
286
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
§ 15. Чистый изгиб
Предположим, что полоса прямоугольного поперечного сечения изгибается двумя взаимно противоположными парами сил М, действующими в плоскости наибольшей жесткости хг. Концы закреплены так, что вращение их относительно оси х невозможно. Относительно осей, параллельных у и z, возможно свободное поворачивание.
При изгибе плоская форма равновесия будет устойчивой, пока М не достигнет известного критического значения Мкр. Начиная с этого момента, кроме плоской, возможна искривленная форма равновесия,
1 М представленная на рис.
м ‘ —г х 43. Величину AfKp можно
ТУ найти или решая уравне-
7 ния равновесия (78) для
искривленной формы, или исследуя изменения потенциальной энергии и работу внешних сил при переходе от плоской к искривленной форме. В рассматриваемом случае чистого изгиба приводим оба решения.
Рассекая стержень на две части и рассматривая равновесие одной из них, найдем
Mi — Мф.
(79)
Уравнения равновесия (78) напишутся так:
Mtf Сф', АГф - В у.
Исключая из них у, получим
ф (М2С)ф 0. (80)
Полученное уравнение совершенно совпадает с тем, что мы имели для случая продольного изгиба стержня с опертыми концами. Так как по условию закрепления ф равно нулю при х 0 и при х , то для определения Л1кр получаем то же уравнение, что и в вышеупомянутом случае продольного изгиба, именно
sin УЩСВ ) 0.
Первая неплоская форма равновесия становится возможной при условии
I УМ21ВС л,
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
287
откуда
(81)
Формула эта имеет такое же значение, как и формула Эйлера для продольного изгиба призматических стержней. Пока М Мкр, плоская форма есть единственная возможная, а потому и устойчивая форма равновесия. При М Мкр плоская форма неустойчива, возможны сильные искривления полосы в направлении легчайшего изгиба.
Постараемся теперь найти выражение для Мьр из рассмотрения выражения для потенциальной энергии системы.
Пока всякое отклонение от плоской формы изгиба, возможное при заданном способе закрепления концов, сопровождается увеличением потенциальной энергии системы, форма эта будет устойчива. Чтобы искривить полосу в направлении легчайшего изгиба, необходимо приложить внешние силы. По удалении этих сил полоса опять возвращается к первоначальной форме равновесия. Если значение изгибающих моментов таково, что отклонения от плоской формы изгиба сопровождаются уменьшением энергии, плоская форма перестает быть устойчивой. Величину Мкр найдем из того условия, что при малых отклонениях от плоской формы изгиба изменение энергии системы равно нулю.
Остается теперь высказанное положение представить в виде уравнения. При отклонении от плоской формы равновесия к энергии изгиба в плоскости наибольшей жесткости присоединяется еще энергия изгиба в плоскости, ей перпендикулярной (в плоскости ху), и энергия кручения. Таким образом, энергия деформации возрастает. При этом внешние силы, изгибающие пары, совершают некоторую работу, так как при выпучивании полосы концевые сечения несколько поворачиваются в направлении действия моментов. Величину Мкр получим, приравнивая работу моментов увеличению энергии деформации.
При наших обозначениях энергия V изгиба в плоскости ху и энергия V2 кручения представятся такими формулами:
Работу внешних сил найдем из таких соображений. Вследствие изгиба в плоскости ху концы оси стержня сблизятся на
поворачивание поперечных сечений на угол р, то сближение 6Z
о
о
величину
Если принять во внимание также и
о
288
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
двух точек, лежащих в концевых поперечных сечениях на расстоянии z от оси, представится формулой
Вставляя вместо ф' его значение из уравнений равновесия (79) и принимая линейный закон распределения напряжений по плоскости концевых сечений, получим для работы внешних сил при искривлении такое выражение:
Здесь через b обозначена ширина поперечного сечения и через h — его высота.
Основное уравнение для определения Мкр напишется так:
Из решения дифференциального уравнения (80) мы знаем, что в данном случае у и ф меняются по закону синуса. Пола-
должны взять ф (МЛС) sin (пх1).
Вставляя эти значения в уравнение (82) и выполняя интегрирование, получим для Мкр прежнее значение. В данном случае мы заранее знали искривленную форму и потому из уравнения (82) получили точное значение для Мкр. Если бы форма заранее не была известна, то, пользуясь тем же уравнением, можно было бы найти для критического значения момента приближенное значение так.
Задаемся выражением для у, например, в форме степенного ряда
Из дифференциальных уравнений равновесия определяем соответствующее значение для ф так, чтобы были удовлетворены условия на концах. После этого значения ф и у подставляем в основное уравнение (82) и выполняем интегрирование. Для Л4кр получим выражение, в которое войдут коэффициенты аь
о
Л2
А 2 I I
I y'dX j y'dx.
I I I
J y'2 dx -- J y2 dx Y j Ф'2 dx-
(82)
0
0
0
гая у i4sin-y-, мы, как видно из уравнений равновесия (79),
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
289
а2, Яз,. Остается между этими коэффициентами выбрать такие соотношения, чтобы Мкр получало наименьшее значение. Увеличивая число коэффициентов аи. мы будем получать все более точное значение для Мкр. Мы здесь не будем останавливаться на приближенном решении задачи и перейдем к иным условиям закрепления на концах. Положим, что концевые сечения не могут поворачиваться относительно осей, параллельных осям х и г. В таком случае на концах не только ф и у, но также и их первые производные ф' и у' обращаются в нуль. Для определения Мкр воспользуемся основным уравнением (82). Выражение для у берем в такой форме:
У а — cos--j.
Форма эта, очевидно, удовлетворяет условиям закрепления на концах. Из дифференциальных уравнений равновесия (79) находим
МА (« 2лх
’“с I1-005—)-
Вставляя эти значения для ф и у в основное уравнение и выполняя интегрирование, получим
Мкр 2яДС. (83)
Таким образом, устранив возможность вращения концевых поперечных сечений относительно вертикальных осей, мы тем самым вдвое увеличили устойчивость полосы. Без особых затруднений можно было бы рассмотреть и другие способы закрепления концов. Каждый раз для Мкр мы будем получать формулу вида Мкр—(84)
Величина коэффициента k будет меняться в зависимости от условий на концах.
Для большего удобства в приложениях перейдем от выражения для М1ф к формулам, дающим непосредственно величину критического напряжения. При изгибе парами сил величина наибольшего нормального напряжения, соответствующая Мкр,
будет MKph _ kE VBC h
Рк E Ж 1 вГ T
В случае прямоугольного сечения шириной b и высотой Л полученная формула может быть представлена в более простом
290
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
виде. Величина С выражается формулой
C jb3A(l - 0,63-) G
ИЛИ
для малых значений отношения b : h.
Для найме
Следовательно,
Для наименьшей жесткости изгиба В имеем В hbE.
С В j 54
Е 1 -f о А,м
Вставляя это в вышеполученную формулу для ркр и пользуясь в дальнейшем обозначением
(84')
получим
Ркр 0,62 kEQ. (85)
Пользуясь выражением для изменения энергии системы при отклонении полосы от плоской формы равновесия, мы можем без затруднений оценить влияние продольной силы Р на величину Мкр. Если по концам изгибаемой полосы приложить действующие вдоль оси сжимающие силы, то они, очевидно, будут уменьшать значение Мкр. Растягивающие силы окажут противоположное действие. Объясняется это тем, что при отклонении полосы от плоской формы равновесия сжимающие силы Р будут производить положительную работу, растягивающие — отрицательную. Присоединяя к правой части основного уравнения (82) эту работу с соответствующим знаком, получим
iiii J y'2dx J y'2dx Y J q'2dx± — J i2 dx. (86)
oooo
Если концы могут свободно поворачиваться относительно осей, параллельных у и z, то для у и ф берем выражения
„. пх МА. пх
у Asm —, ф y-sin —.
Вставляя их в вышеполученное уравнение, найдем
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
291
Верхний знак соответствует сжимающим, нижний — растягивающим силам Р. При Р 0 получаем для М1ф прежнее значение, при Мкр 0 форму-
л а обращается в обыч- х т
ную формулу продольно- z го изгиба. Если через а2 2
обозначить отношение Рис. 44.
продольной силы Р к
эйлеровой нагрузке Вя22, то формула (87) может быть представлена так:
Мкр с VTW. (88)
Когда концы стержня не могут поворачиваться относительно вертикальной оси, нужно положить
- (1 2тсх МА (л 2пх у A -cos-y-J, ф - COS — j.
Вставляя это в уравнение (86), получим
ML 47i2B 2п VBC Г -±Р -или Л4кр 1±х (89)
Формулы (88) и (89) решают при принятых условиях на концах вопрос об устойчивости полосы, подвергающейся действию эксцентрично приложенных растягивающих или сжимающих сил (рис. 44).
§ 16. Изгиб полосы силой, приложенной на конце
Предположим, что высота прямоугольного поперечного сечения полосы, представленной на рис. 45, велика по сравнению с шириной; тогда, постепенно увеличивая изгибающую силу Р9 можно достигнуть предела, когда кроме плоской формы равновесия становится возможной и искривленная форма. Ось полосы искривляется при этом в плоскости ху, как представлено на рис. 45. Для какого-либо поперечного сечения с абсциссой х будем иметь
Af Р Л-y-if (-), Mt P(l-x) Ф.
Вставляя это в дифференциальные уравнения равновесия (78), получим
СФ' Р Л--'(-), Р(1-х)р Ву. (90)
Исключая отсюда у, придем к уравнению
Р2
292
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Интеграл этого уравнения может быть представлен в замкнутой форме через функции Бесселя:
Таблицы для соответствующих функций составлены проф. Л. Прандтлем1). Если воспользоваться условиями на концах:
Ф 0 при х 0 ф' 0 при х 1,
то для определения РКр получим трансцендентное уравнение,
наименьший корень которого даст
ш
Кр 2 (91)
Применим теперь к определению Ркр приближенную методу. Плоская шХ форма изгиба будет устойчива, пока всякое отклонение от нее сопровождается увеличением энергии системы, другими словами, пока энерРис. 45. гия кручения и энергия изгиба в
плоскости ху при всяком отклонении от плоской формы будут в сумме меньше работы силыР при том же отклонении. Для энергии кручения и изгиба сохраняются в силе прежние формулы:
i i
Fi4jV2rf. у24 JV-
Для вычисления работы силы Р необходимо определить опускание точки приложения силы при любом отклонении от плоской формы равновесия. Легко видеть, что опускание силы Р от деформации элемента стержня dxy выделенного на расстоянии х от заделанного конца, будет равно y(l — х)у dx.
Суммируя влияния деформаций отдельных элементов на перемещение точки приложения силы Р, найдем для работы этой силы выражение
i
Г Р J фy(l-x)dx.
) Эти таблицы приведены в весьма ценной для инженеров книге: Е. J a h пk е, F. Е m d е. Funktionentafeln mit Formeln und Kurven. Leipzig und Ber¬
lin, B. G. Teubner, 1909. Перевод на русский язык: Е. Янке, Ф. Эмде, Таблицы функций с формулами и кривыми. Харьков — Киев, ДНТВУ, 1934.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 293
Очевидно, плоская форма изгиба перестает быть устойчивой, когда
i i i
Р J фу I - х) dx -у у2 dx Y§ ф'2 dx. (92)
О 0 0
Если для первой возможной неплоской формы равновесия известны точные выражения у и р через х, то, вставляя их в полученное уравнение, найдем точное выражение для Ркр. Для приближенного решения задачи зададимся прогибом у так, чтобы были удовлетворены условия на концах, тогда ф определится из уравнений равновесия. Полученные таким образом значения ф и у вставляем в наше уравнение (92). В виде первого
приближения положим
У а- cos).
Эта форма удовлетворит условиям на концах, так как у у' 0 при х 0; у 0 при х.
Из уравнений равновесия (90) находим
откуда
, РА Г лх л п ч . лх 1
ф' — cos )sm ж,
РА Г 41 . лх , у ч лх Л
С я Sin 21 х) C0S 21 Произвольная постоянная интегрирования выбрана так, чтобы было выполнено условие у закрепленного конца: ф 0 при
х 0.
Вычисление РКр может быть значительно упрощено путем следующих преобразований:
i г 1
у J ф'2 dx у (фф')' - фф dx
0 L о
Из уравнений равновесия имеем
СФ-у'(-).
Кроме того, из условий на концах стержня следует, что
фф'' о.
Окончательно энергия кручения представится в такой форме:
t I
У J (f'2dx фу ( - х) dx,
294 ОБ УСТОЙЧИВОСТИ УПРУГИХ систем
и уравнение для определения Ркр перепишется так:
i i Р уу ( — л:) dx В J у2 dx. (93)
о о
Вставляя вместо ф и у их значения, получим
i
„ я4 Г 2 пх.
BCwJcos wdx
pL -
Кр “ I
П2
4
я2 Г Г 4. пх , п ч ял: Лг . пх .
iFj irsinlr (-x)cos-r-J(-x)cosirrf
ВСяа
откуда
п _ 4,34 VВС
Кр “ 2
Таким образом, первое приближение дает нам для Ркр величину, отличающуюся от действительной критической нагрузки на 8. Полученная точность является вполне достаточной для практических приложений. Покажем на этом примере, как возможно, пользуясь основным методом, получить дальнейшие приближения. В виде второго приближения возьмем
S-l-cosf l-cosiSL).
Эта форма изгиба, как легко видеть, удовлетворяет условиям на концах. Из уравнений равновесия находим
Р ( л пх I Зя п ч Ал. пх , ЗЛ,я . 3ялг ф — с A COS 2l jCOS 2l (I х) 2i sn 21 21 Sln 21 )j Интегрируя и выбирая надлежащим образом произвольную постоянную, получим
Р ( 4А1. лх , у ч - ял: , ААХ1.
Ф -с I —s,n 1Г л cos 1Г -3S sin
Зял:
21
( - х) Л, cos - - А Л,).
ОВ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 295
Интегралы, входящие в основное уравнение (93), имеют следующие значения: i
Р J щ ( — х) dx
__ Р2 Г А2л2 3 3 9Ап2 3 3 ЛЛхп2 73
С 42 Т17 42 1Г 9л2 4Z2-2Я2 1“
- (о, 1613Л2 3,450л - 0.8750ЛЛ,,
В J y2dx В - у(Л2 81Л).
Подставляя эти значения в уравнение (93), получим п2 ВСя4 Л2 81Л
кр_ 324 0,1613Л2 3,450Л-0,8750ЛЛ,
Если в этом выражении положить А 0, то придем к ранее полученному первому приближению. Для отыскания второго приближения определим отношение АА z таким образом, чтобы Ркр приобретало минимальное значение. Задача сводится к нахождению минимума такой дроби:
1 812
0,1613 3,450z2 - 0,875z '
Наименьшее значение этой дроби равно 5,60 при z — —0,0397. Вставляя это в выражение для Ркр, получим второе приближение: р 4,13 V ВС
Кр J2 отличающееся от истинного значения на 3.
Пользуясь обозначениями предыдущего параграфа, получаем формулу для определения критических напряжений:
ркр 0,62 -4,01 0 2,490 1). (94)
Если кроме поперечной изгибающей силы Р имеется продольная растягивающая или сжимающая сила Г, то основное уравнение для определения Ркр напишется так:
til
Р J Фy(lx)dx -§У2 dx -§-Jф'2dx ± j у'2dx.
о ООО (95)
) При составлении этой формулы взято точное значение для Ркр; см. формулу (91).
296
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Последний член представляет собой работу продольной силы при отклонении полосы от плоской формы равновесия. Верхний знак соответствует растягивающей, нижний — сжимающей силе.
Вставляя вместо р и у их выражения, взятые для первого приближения, мы получим для определения Ркр такую формулу:
Яр В,С' , ± , ГС , ' (96)
-(W) »(-)
Если РКр 0, то Т Вя242.
При помощи формулы (96) мы устанавливаем связь между явлением продольного изгиба и явлением выпучивания полосы под действием поперечной нагрузки Р. Этим решается задача об устойчивости полосы, закрепленной наклонно (рис. 46). Принимая во внимание, что в этом случае Р R cos а, Т R sin а, получим для определения RKp уравнение
2 го-2 п 4- RkC sin а ВСп2 - 0
Акроь а-Г о,13082 0,5234 ’
откуда
Якр 2 0,2614 cos а “ В j tg2 а 0,1307л2 j.
Таким образом, для рассматриваемого случая вопрос о величине критического значения изгибающей силы решается весьма просто. Полученная формула абсолютно точна для а 90, и погрешность ее составляет 8 при а 0. Решение рассмотренной задачи путем интегрирования соответствующего дифференциального уравнения было выполнено проф. JI. Прандтлем. При этом ему пришлось иметь дело с суммированием медленно сходящихся рядов. Сравнение нашей формулы с его результатами показывает, что для а 0 приближенное решение вполне удовлетворительно для практических приложений. Например, при а 45 погрешность составляет всего 1. Если бы понадобилась большая точность, то можно перейти ко второму приближению и т. д.
Применяя новую методу, мы задались выражением для прогиба у и потом из уравнений равновесия определили соответствующее значение ф. Еще проще и точнее можно получить значение для Ркр, если задаться выражением для ф и величину у найти из уравнений равновесия. Мы удовлетворим условиям на концах, если в рассматриваемом случае положим
ях. „ Зпх
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
297
из уравнений (90) получаем
У (I - х) A sin Л, sin.
Вставляя это в основное уравнение (92) и выполняя интегрирование, получим
р2 _ ВСп2 1 9z2
Р “ 1 1 1 2,37г2 2,326z
81 1б ”7
где z А : А. Наименьшее значение для РКр будет
р 4,03 Vbc
Кр J2
При выбранном значении ф будем иметь у заделанного конца (у)хо 0. Условие это следует из уравнений равновесия (90) и не было нами удовлетворено при первом способе нахождения Ркр.
Задача об изгибе полосы силой, приложенной на конце, не представляет особого практического значения. Такой способ нагрузки и закрепления концов интересен лишь потому, что его удобнее всего осуществить на опыте, который дает возможность проверить теорию1). При производстве опытов является необходимость в двух поправках: нужно уметь оценить влияние собственного веса полосы и влияние повышения и понижения точки приложения изгибающей силы Р. Так как здесь идет речь о малых поправках, то для их вычисления, конечно, вполне достаточно пользоваться лишь первым приближением.
Для оценки влияния собственного веса нужно к левой части уравнения (93) присоединить работу, совершаемую весом балки при ее искривлении. Пусть q — вес балки, приходящийся на единицу длины. При деформации какого-либо элемента балки, находящегося на расстоянии х от закрепленного конца (см. рис. 45), будет опускаться правая часть балки весом q(l — х). Центр тяжести этой части находится на расстоянии ( — х)2 от взятого элемента и потому опустится на величину
ty (l2X- dx.
Работа веса балки, соответствующая деформации одного элемента, напишется так:
, (1-х)2 -
qw 2 dx.
) Такие опыты были произведены проф. Л. Прандтлеад.
298
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Полная работа веса балки представится такой формулой:
Эта величина должна быть присоединена к левой части уравнения (93). Если для ф и у взять выражения, соответствующие первому приближению, то левая часть уравнения представится так:
Влияние собственного веса таково, как если бы 0,31 этого веса была сосредоточена на нагруженном конце.
Относительно влияния на величину Ркр положения точки приложения изгибающей силы можно сразу отметить, что всякое повышение точки приложения будет уменьшать Ркр и понижение будет увеличивать ее. Пусть а — возвышение точки прило. жения силы над центром тяжести поперечного сечения; в таком случае при отклонении полосы от плоской формы изгиба скручивающий момент на нагруженном конце будет отличен от нуля и равен (ф)СР. Первое из дифференциальных уравнений (90) напишется так:
Беря для у выражение, соответствующее первому приближению, найдем, что
о
РА2л2 412С
0,0664 Р 0,31Q.
Сф' Р А - у - if ( - х) а (ф),.
Энергия кручения будет
Y J ф'2 dx 1 фф'' - J фф dx
(фф')0 4 J ру (I х) dx
о
Для работы опускающегося груза получим выражение
о
откуда
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
290
Вставляя найденные значения энергии кручения и работы опускающегося груза в основное уравнение (92) и выполняя интегрирование, найдем
А2РЧ я2 f 1 1 . 4 (4-я)2 Pal ) В яМ2
2 С
( 1 1 . 4 (4 — я)2 Pal _ В яМ2 v
16 я2 я4 (С — Pal) j 2 164 2
При а О мы возвращаемся к ранее нами полученному первому приближению для РКр- При малых значениях аЦ можно упростить вычисление РКр. Для этого подставляем в третий член левой части уравнения (97) вместо Р его первое приближение, т. е. 4,34 Увсl2. Выполняя после этого вычисления и сохраняя лишь члены первого порядка относительно а, можем представить уравнение в таком виде:
А2РЧ я2 1 1 L . а , fTT В Л2я4 I
2С 4 6 п2 ) ' I V С J 2 164 2
Уравнение это отличается от того, которое мы имели для случая а О, тем, что вместоЯ2 стоит множительР2 1 2у Bcj.
Величина критической силы, следовательно, уменьшается в отношении и Ркр следует вычислять по фор¬
муле
(98)
§ 17. Изгиб заделанной одним концом полосы равномерно распределенной нагрузкой
Пусть под действием равномерно распределенной нагрузки q произошло искривление полосы в плоскости ху (рис. 47). Рассечем стержень на две части по тп и напишем условия равновесия для правой части. Скручивающий момент в сечении тп, как легко видеть из рисунка, будет
i
Сф' q J dl у -ух-у'х- ); (99)
X
здесь через у обозначен прогиб в сечении с абсциссой § и ух — прогиб в сечении тп. Дифференцируя по х и выполняя указанное интегрирование по g, получим
СФ- J q d ( - х) у - q l )2 у’
X
300
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Изгибающий момент в плоскости наименьшей жесткости будет q(l — х)2, и второе дифференциальное уравнение равновесия напишется так:
- д (1-х)2
р.
(100)
Исключая из двух таким образом полученных дифференциальных уравнений величину у, получим
Сф -
дг d-xf АВ
ф.
Интегрируя это уравнение и учитывая условия на концах, получим для критического значения изгибающей нагрузки Q
qI формулу ') 0р (101)
Определим теперь QIP из рассмотрения энергии системы.
Пока всякое отклонение полосы от плоской формы изгиба со-
т провождается увеличением энер¬
гии, форма эта устойчива. Непрерывно увеличивая нагрузку, мы, наконец, достигнем предела, когда при некотором определенном отклонении полосы от плоской формы работа нагрузки q как раз будет равняться сумме энергии кручения и энергии изгиба в плоскости ху. Соответствующая этому моменту велиРис. 47. чина нагрузки и представит собой
искомое критическое значение ее. Работа равномерно распределенной нагрузки при искривлении полосы в плоскости ху выразится, как было показано в предыдущем параграфе, такой формулой:
—J—-1 ,
2 ’ '
7 ж-
1 ФГ
(l-xf
dx,
или, вставляя вместо у весия (100), найдем
его выражение из уравнения равно-
1) Результат этот принадлежит проф. Л. Прандтлю.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 301
Для энергии изгиба и энергии кручения имеем прежние формулы:
У. 4 J У2 dx -g- J ( - xf ф2 dx, 4 J Ф'2 dx.
0 0 о
Приравнивая работу внешних сил энергии деформации, получим основное уравнение для определения критического значения нагрузки:
i
-g- j ( — х)4 ф2 dx С j ф'2 dx. (102)
о о
Для точного решения задачи нужно из всех возможных отклонений от плоской формы изгиба выбрать такое, которому соответствует наименьшее значение q. Удовлетворяющее этому условию отклонение и будет представлять собой первую возможную неплоскую форму равновесия, а соответствующая ему нагрузка будет искомой критической нагрузкой. Как и в предыдущих задачах, мы можем с любой точностью получить интересующую нас величину, идя путем последовательных приближений. Выберем для угла поворота ф функцию от х, удовлетворяю¬
щую условиям на концах. В данном случае можно положить
„. тех , л . Злх . л. 5пх ,
ф Л81П-2Г Л18т2- —ь.
Мы для простоты вычислений ограничимся лишь двумя членами. Каждый из этих членов порознь удовлетворяет условиям на концах:
Ф 0 при х 0; ф' 0 при x L
Увеличивая число членов, мы в пределе придем к точному решению задачи, так как удовлетворяющая известным условиям функция от х всегда может быть представлена в виде бесконечного ряда
Л. тех I л. 3 тех I л 5тех I
sin—р Ах sin —j—bsin—-—f-.
Ограничиваясь двумя членами, вставляем полученное таким образом значение для ф в основное уравнение (102).
Выполняя интегрирование и обозначая AJA z, ql Q, представим уравнение в таком виде:
0,5 0,2 - (п2 - 6) ± (3я2 - 22,5)г
0,5 0,2 - (9я2 - 6) г2 --(1 Эг2),
302
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
откуда
П2 _ ВСп2 1 9z2
4 0,0411 0,1462 0,158г2
Наименьшее значение для Q2 будем иметь при z 0,214. Соответствующее значение Q будет
п 13,2 Уве
Укр 12
Сравнивая это с точным решением (101), находим, что погрешность меньше 3. Таким образом, путем самых элементарных вычислений мы получили решение весьма сложной задачи, причем точность этого решения вполне достаточна для практических приложений. Отыскивать дальнейшие приближения в данном случае нет надобности, так как имеется точное решение. Сравнивая это решение с решением (91) для случая сосредоточенной на конце силы, заключаем, что при равномерно распределенной нагрузке изгибаемая полоса является более устойчивой. Устойчивость такова, как если бы на конце была сосредоточена нагрузка, равная 4,01Q12,85 0,312Q.
Составим теперь формулу для критических напряжений. Сохраняя прежние обозначения (84), получим
Р«р ЖГ3-98Д 103
Следовательно, критические напряжения в данном случае приблизительно в полтора раза больше тех, что мы получили для случая сосредоточенной силы.
До сих пор предполагалось, что равномерная нагрузка распределена по оси полосы, как то можно считать в случае действия собственного веса. Рассмотрим, как влияет на величину QKP повышение или понижение нагрузки. Пусть нагрузка распределяется по линии, параллельной оси полосы и отстоящей от нее на расстоянии а. Благодаря изменению положения нагрузки изменится также выражение для работы внешних сил при отклонении полосы от плоской формы равновесия. К работе, обусловленной опусканием точек оси полосы, придется присоединить работу, зависящую от поворота отдельных поперечных сечений полосы. Каждый элемент нагрузки q dx, расположенный на а выше оси, совершит при повороте сечения на
угол ф работу q dx--. Следовательно, вся работа, обусловленная кручением, будет
Ц- j ф2 dx.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 303
Основное уравнение для определения Qlp перепишется так: i i i
-g- J ( — х)4 qPdx qa J ср2 dx С J q2 dx.
0 0 0
Вставляя вместо ср его приближенное значение, найдем
(0,0411 0,1462 0,158z2) (1 г2) (1 9г2).
Получим, таким образом, для определения QKp квадратное уравнение. Так как здесь речь идет лишь о небольших поправках, то вместо решения квадратного уравнения поступим так: сохраним прежнюю искривленную форму, а следовательно, и прежнее значение для z тогда левая часть нашего уравнения перепишется так:
§ (о, 0796 1,04в).
Во втором члене в скобках можно вместо Q вставить его значение, найденное выше. Тогда
4 аВ- 1,046 _ 4- 1,046 a n fB _ Л 017 а , ТГ
Q3 13,2 I V С ),6U I V С
Уравнение перепишется таким образом:
0,0796 Jgi (1 3,98 ) - 1,41.
Вследствие повышения точки приложения нагрузки в левой части уравнения получился заключенный в скобках дополнительный множитель, благодаря которому значение QKp уменьшается в отношении
1 —J.
Y i3-98ti4
При малых значениях all можно QHP вычислять по формуле
Qkp 12'85ГС (l- hrY7г)- 104)
До сих пор мы предполагали сечение полосы постоянным. Для переменного сечения точное решение задачи становится еще более сложным. Приближенный метод в этих случаях может быть применен без всяких затруднений. Возьмем простейший
304
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
пример. Прямоугольное поперечное сечение полосы имеет постоянную ширину, высота же меняется по линейному закону, как то показано на рис. 48. Определим критическое значение изгибающей силы Р. Предположим бесконечно малое отклонение полосы от плоской формы равновесия и составим уравнение, приравнивая работу силы Р тому изменению энергии деформации, которое соответствует взятому искривлению. Жесткость изгиба и кручения для сечения тп представится формулами
Рис. 48.
В
В0 (1-х) I
с
с о (1-х)
I
где В0 и Со — жесткости изгиба и кручения для заделанного сечения. Основное уравнение напишется так:
i i i J С0 --Фndx J В0 у2 dx pj ty (I - х) dx.
ООО
Из уравнения равновесия для данного случая имеем у РфВ0. Вставляя это в полученное уравнение, найдем
Р2
Во
J фЧ (I — x)dx -у- J ф'2 ( — л:) dx.
Ограничиваясь первым приближением, положим
л лх
Ф A sin —or.
2
Выполняя интегрирования, указанные в основном уравнении, найдем
2,42 VB
Ркр —
I2
(105)
§ 18. Изгиб балки силой, приложенной посредине пролета
Положим, что при значении силы, равном 2Р, становится возможной неплоская форма равновесия (рис. 49).
Располагая координатные оси, как показано на рисунке, и составляя выражения для изгибающего и скручивающего мо-
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
305
ментов в каком-либо сечении тпу мы получим такие дифференциальные уравнения для неплоской формы равновесия:
ВуГ Р ( - х) Ф, СФ' - Р у t ( - ). (106)
Предположим, что закрепление концов не допускает вращения относительно оси -ов. Относительно осей, параллельных у и z, возможно свободное поворачивание. В таком случае для угла ф будем иметь следующие условия:
Ф 0 при х ; ф' 0 при х 0.
2Р
У т.
1
Применим для нахождения критической нагрузки приближенную методу.
Для работы силы 2Р и для Рис. 49,
потенциальной энергии деформации, связанной с искривлением, будем иметь прежние формулы:
i i i T 2Pj y(l-x)dx, Vx В у2 dx, V2 C j q'2dx.
0 0 Для определения Р1ф напишем уравнение
2Р J фг ( — х) dx В J у2 dx С J ф'2 dx.
(107)
Принимая во внимание первое из уравнений равновесия (106), получим
J ( — х)2 ф2 dx С J ф'2 dx.
Представим ф в форме тригонометрического ряда
пх
2Г
- пх. л Зпх. ф A COS-07- Ах COS -757“
21
Ограничиваясь для простоты вычислений первыми двумя членами разложения и обозначая А : А z, получим из основного уравнения (107)
ВСп2 1 9 z2
Р2
84
306 ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Остается для z подобрать такое значение, чтобы Р было минимумом. Задача эта сводится к решению такого квадратного уравнения:
z2 2,105г — 0,11110.
Корнями его будут
1 0,051, z2 — 2,155.
Вставляя значение z в выражение для Ркр, найдем
п _ 2,117 VBC
Кр “ 12
Решение этой задачи путем интегрирования соответствующих уравнений было выполнено Л. Прандтлем; им получена для Ркр величина Рп,Шр-. (108)
Погрешность наших вычислений составляет, следовательно, около 0,1. Заметим, что, ограничиваясь лишь одним первым членом в выражении для у, мы получим вполне удовлетворительный результат. Для этого в формуле для Ркр положим
2 0, тогда р VBC я _ 2,146 VВС
кр “ 12 71 ГГ 12
т. е. погрешность — около 1V2 Составим теперь формулу для критических напряжений:
PKplh 2,1155с h
Ркр Е 2Вх 2В Т'
или, пользуясь обозначениями (84) и полагая С:В 1,54,
Ркр 1,3120. (109)
Рассмотрим теперь, какое влияние на Ркр будет оказывать перемещение точки приложения силы по вертикальному направлению. Пусть а обозначает возвышение этой точки над осью полосы. Вследствие такого повышения работа силы при искривлении возрастет на величину Т аРф.
Основное уравнение представится в таком виде: i i
J ( — х)2 ф2 dx аРф2 С J ф'2 dx.
о о
Для определения Ркр получаем квадратное уравнение. В случае малых значений а вычисления можно упростить таким образом:
во втором члене левой части уравнения вставим вместо Р ранее
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
307
полученное значение; тогда, ограничиваясь для ф первым приближением, найдем
Р2 3 (± , М Сп2 ал ВС _ Сл2 ( i i 7Д _а_ _Д 1
В 4 U “Т“ л2 Г 81 ГП ГГ “ 8 I 1 А, К С
'y8(i)
Влияние повышения точки приложения силы оценивается дополнительным множителем в правой части уравнения. Принимая во внимание малость величины а, получим
Лф 2,10,87-f-j-j-)' 110
При решении задачи мы задались выражением для ф и определили у из дифференциальных уравнений равновесия (106). Можно поступить иначе, задаться выражением для у и потом определить ф. Для упрощения вычислений ограничимся при этом лишь первым приближением; положим
y Al -cosf-).
Тогда второе из дифференциальных уравнений равновесия (106) дает
Сф' - АР l — cos4--f-( — х)sin
откуда, принимая во внимание условия на концах, получим
АР Г 41 . пх у пх ,. 41
Ф - — х- — sm-w-(l-x)cos-w—l(l
При заданных условиях на концах
i i i
J ф'2 dx фф'о — J фф dx -j J Фу ( — х) dx.
о оо
Следовательно, основное уравнение для определения Р1ф можно представить так:
i Р J W У — х) dx В J у2 dx.
о о
Вставляя вместо ф и у их значения и выполняя интегрирование, получим
А2Р2п21 Г 3 ,1 8(4 tl_ ВА2п4 111Ч
4С U2_t6 л2 U ) 323 ’ АА
откуда
2,22 У ВС
308
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Погрешность — около 5. Второй способ вычисления Ркр дает менее удовлетворительные приближения, чем первый.
Воспользуемся полученными результатами для оценки влияния продольной силы. Очевидно, при наличии продольной сжимающей силы Р,ф будет меньше вышевычисленного значения; растягивающая сила, наоборот, будет увеличивать устойчивость полосы. Основное уравнение в данном случае напишется так:
Второй член в левой части уравнения представляет работу ежи мающей силы Т при выпучивании полосы.
Вставляя вместо ф и у прежние значения и выполняя инте грирование, найдем
Когда Т Вя242, Ркр обращается в нуль, мы будем иметь явление продольного изгиба. Для меньших значений Т вели-
есть критическая нагрузка при отсутствии продольной силы. В случае растягивающих сил нужно только переменить знак Т.
В заключение рассмотрим еще тот случай, когда закрепление концов не допускает вращения относительно вертикальной оси. В таком случае ось полосы при искривлении должна принять форму, представленную на рис. 50. Чтобы удовлетворить условиям на концах, положим
Р J щ (I — х) dx Т J dx В J г2 dx.
о
о
о
Р2п21
АС
_8_
л2
g-ф
Тп2 В п4
8 323
(112)
Рис. 50.
чина Ркр в каждом частном случае может быть вычислена из полученного выше уравнения (112). Сравнивая уравнения (111) и (112) и пользуясь обозначением 4 Т12Вп2 а2, можем написать для критической нагрузки при наличии
продольной силы такое выражение: 2Р' 2Р Yl — а2, где 2Р
У а — cosp) 4j(l — cos 2 (1 -COS--).
Ограничимся лишь первым членом разложения; тогда
Сф' — руу' I — х) РА 11 — cosj- -у- ( — ) sin j-,
РА Г 21. пх it v пх Л ф q— х —— Sin —j— ( — X) cos — I.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
309
Уравнение для определения РКр сохранит прежний вид:
Р J фу ( — x)dx В J у2 dx.
Вставляя вместо ф и у вышенаиденные значения и выполняя ин-
Р2 Вл2
тегрирование, получим -0,4453 --, откуда
кр
3,33 Vвс
12
Благодаря дополнительному закреплению устойчивость полосы возросла примерно в полтора раза. При наличии продольной сжимающей силы Т основное уравнение напишется так: i i i
Р J фу (I — х) dx Т J jL J dx В J у2 dx,
откуда
Когда Т Вл22, то Р обращается в нуль, и мы будем иметь явление продольного изгиба для стержня с заделанными концами. В случае растягивающей силы знак у Т нужно переменить на противоположный.
§ 19. Изгиб балки равномерно распределенной нагрузкой
Предположим, что нагрузка равномерно распределена по оси полосы и условия закрепления таковы, что концы не могут поворачиваться относительно оси л:-ов. Пусть q — нагрузка, приходящаяся на единицу длины балки; тогда вся нагрузка будет равна 2Q 2ql. Постепенно увеличивая q, можно достигнуть предела, когда плоская форма равновесия перестает быть устойчивой, ось полосы искривляется, как то показано на рис. 51. Обозна-
шипгг
t л
, 1
f f
V
Г -
п
Рис. 51.
чим через прогиб оси посредине пролета. Положение точек приложения опорных реакций определяется величиной е (см, рис. 51):
i
у j if-у) dx.
310 ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Располагая координатные оси, как показано на рисунке, мы можем для какого-либо сечения тп написать такие уравнения равновесия:
By Q ( - х)р - j (I - х)2 ф (I2 - х2),
( 1 113) Ср' - Qe-f-yy'(l-x) q J yl ух-yx(l x)dl j.
Интегрирование этих уравнений может быть выполнено при помощи рядов; но мы здесь для нахождения Кр применим приближенную методу. Составим, как и прежде, выражения для работы внешних сил Т и для приращения потенциальной энергии при искривлении V. Значение критической нагрузки найдем из условия равенства этих двух величин. Пользуясь результатами § 16, можем для работы внешних сил при искривлении написать такое выражение:
i i i
Т 2Q J рг ( — х) dx — q J щ” ( — xf dx -у J pr (12 — x2) dx.
0 0 0
Для энергии кручения и изгиба остаются прежние выражения. Основное уравнение для определения критического значения нагрузки напишется так:
i i i
Я J ФУ” (Р “ х2) dx С J qp'2 dx В J у2 dx.
0 0 0
Вставляя вместо у его выражение через ф из первого дифференциального уравнения равновесия системы (113), получим
i i
J ф2 (I2 - х2)2 dx cf ф'2 dx. (114)
о о
Чтобы удовлетворить условиям на концах, возьмем ф в форме такого тригонометрического ряда:
- тех. л Злх ,
Ф A cos -гг- А cos -
21 1 1 21 ‘ В качестве первого приближения ограничимся одним первым членом в разложении для ф. Вставляя это значение ф в основное уравнение (114) и выполняя ряд простых квадратур, получим q2l2 1 1 , 1 , 12 _ Сл2
В 2 3 10 я4 J - 2 ’
откуда (ql) кр 3,56-.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
311
Чтобы иметь возможность оцепить точность полученного результата, нужно перейти ко второму приближению. Положим
„ пх , „ Зпх Ф A cos 2ГАх cos -у-.
Вставляя это значение ф в уравнение (114), найдем
tH'twtp'IH1 - т¥)г
(y-7 TV8i-Mi11-
Здесь, как и раньше, через z обозначено отношение АА. Выполняя арифметические вычисления, получим
( 1) - п 1 9г2 2 у 0,3899 0,23 Юг 0,2682-г2
Теперь остается величину z подобрать так, чтобы (ql)HV приобретало минимальное значение. Задача эта сводится к решению такого квадратного уравнения:
z2 3,113г — 0,1111 0.
Корнями уравнения будут zx 0,046, z2 —3,148. Вставляя значение Z в выражение для (ql)кр, получим
Л 3,540 У ВС 11с
(70кр 12 (115)
Сравнение найденного результата с первым приближением показывает, что в данном случае величина критической нагрузки определена с большой точностью.
Составим теперь формулу для критического напряжения:
ркр44110 (П6
где 0 имеет прежнее значение (84').
Влияние повышения линии распределения нагрузки на величину (7)кр может быть приближенно оценено таким же образом, как и в предыдущей задаче. Пусть линия распределения нагрузки расположена на величину а выше оси полосы. Опускание каждого элемента нагрузки составится из двух частей: из опускания соответствующей точки оси и из опускания от поворота соответствующего поперечного сечения балки. Это добавочное опускание можно представить формулой тр22.
Работа нагрузки, соответствующая этому дополнительному
опусканию, очевидно, будет равна J aqPqdx.
312 ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Уравнение для определения (ql)кр напишется так:
i i i -jg j Ф2 I2 — x2fdx aq J ф2 dx С J ф'2 dx.
О 0 0
Так как здесь мы имеем дело с малой поправкой, то можем ограничиться первым приближением, кроме того, во втором члене левой части уравнения можно вместо ql вставить ранее вычисленное критическое значение, тогда получим
22 п оооо - Сл2 Vй - Сп2 (л 3,56-4 а f В
4В и’уу“ 84 22 84 V я2 I V с)-
Влияние повышения нагрузки определяется дополнительным множителем в правой части. Принимая во внимание, что ajl — малая величина, можем написать
-0,77 Ж).
Вычисление критической нагрузки мы могли бы вести в несколько ином порядке. Можно задаться не углом поворота ф, а прогибом оси балки. Этот путь является более удобным, если нужно определить влияние продольной силы на величину (ql) кр. Чтобы упростить выкладки, мы ограничимся в данном случае лишь первым приближением. Положим
« Л(1-СОЗ).
Вставляя принятое выражение у во второе из дифференциальных уравнений равновесия (113) и выполняя интегрирование, найдем
Г 12 1 , пх 4 пх. х2 тех. 41
р- — l2)cosir-Ts,nrircos-2rirf-
Основное уравнение будет
i i i q J ф (2 — х2) dx С J ф'2 dx В J у2 dx.
О 0 0
Выражение для энергии кручения преобразуем следующим образом:
С j cp'2dx С I фф'о - J фф dx -f J ЧУ (Р - х2) dx.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 313
Тогда основное уравнение перепишется так:
J щ (2 -x2)dx B j у2 dx,
или, принимая во внимание значения р и у и выполняя интегрирование, получим
(qiy яЧ ( 4 34 . 1 1 Вп
8 С я;2 12 20 j 323 ’ ul'
откуда „п _ 3,61 VВС
WKp р.
Сравнивая это с ранее полученным первым приближением, находим, что второй порядок вычислений дает менее удовлетворительный результат.
Если, кроме изгибающей нагрузки, имеются продольные сжимающие силы 7 то уравнение для определения qKр напишется так:
Y J УУ (2 x2)dx Т (--)2 dx B у2 dx.
0 0 0
Вставляя вместо ф и у их прежние значения, получим
(ql)2n2l f 4 34 , 1 . 1 I ТпЧ _ Вл4 (. 0.
8С п2 я4 12 1 20 J ' 82 323 Сравнивая (117) и (118) и пользуясь прежним обозначением
ATI2 2 а2,
Вл2
можем выражение для критической нагрузки в случае действия продольной сжимающей силы переписать так:
(0кР ql ll — а2; здесь ql 3,54 У ВС I2.
Когда Т Вя242, ql)Kр 0, мы имеем явление продольного изгиба. В случае растягивающей силы, очевидно, нужно переменить знак Т.
§ 20. Изгиб балки силой, приложенной не посредине пролета
Пусть сила 2Р приложена на расстоянии а от левого конца балки. Закрепления таковы, что концевые сечения не могут вращаться относительно оси -ов. Положим, мы, постепенно увеличивая силу 2Р, достигли предела, когда становится возможной
314
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
неплоская форма равновесия. Ось балки изогнется по некоторой кривой, не симметричной относительно середины пролета (рис. 52). Решение настоящей задачи путем интегрирования соответствующих дифференциальных уравнений является еще более сложным, чем в предыдущих случаях. Нужно составить
уравнения для каждой ветви _21 изогнутой оси балки и при ин¬
тегрировании принять во внимание, кроме условий на концах, условия в месте приложе2Р ' с ния силы 2Р. Здесь обе ветви
кривой имеют общий прогиб, общую касательную и, кроме того, углы ф и ф' для обеих ветвей одинаковы. Разыскание РКр при этих условиях привело Рис. 52. бы к весьма сложному транс¬
цендентному уравнению. Приближенная метода в этом случае упрощает дело. Задача сводится к простым квадратурам и нахождению минимума некоторой дроби.
Расположим оси координат согласно рис. 52, тогда угол ф в общем виде можно представить в форме тригонометрического ряда
„ . Зях ,
2sin-
л. ях , „ . 2ях
Ф A sin 2j—г Ai sin-
21
21
Принимая во внимание значения опорных реакций
R i
2Р (21 - а)
R2
2 Ра
1 21 А2 21 можно для искривленной оси балки написать уравнения:
т D „ 2Р (21 — а)
I участок By ——— Х(Р
II участок
в у Щр (21 - х) ф.
(119)
Работа внешних сил при искривлении представится так:
Т
2Р (21 - а) 21
а и
J dx J фу (21 — х) dx.
Для потенциальной энергии кручения и изгиба в плоскости ху будем иметь прежние общие выражения.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
315
Вставляя вместо у его значения из уравнений (119), можем написать основное уравнение для определения критической нагрузки в такой форме:
Т 2Р (2 а) Г У22 dx Jr Цг J ф2 № -x)2dx C j ф'2 dx,
0 “ 0 (120)
откуда
(2РКр)2
11
ВС ф'2 dx
о
(- 21 )2 J Ч1 dx J Ф (2 )' dx
Для каждого частного значения а должны быть выполнены указанные квадратуры и потом постоянные Л, Ль Л2,. должны быть подобраны так, чтобы 2Ркр приобретало минимальное значение.
Ограничимся в разложении для ср двумя первыми членами и положим а , тогда
(2 PKpf l
72
2я2
(121)
Здесь г, как и раньше, обозначает отношение А: Л. Сразу видно, что для данного случая нужно положить 2 0. Этого нужно было и ожидать, так как мы взяли симметричную нагрузку. Величина для Р,ф получится та же, что и в § 18.
Пользуясь формулой (121), можно найти значение критической нагрузки и для высшей формы равновесия, при которой искривленная ось имеет одну точку перегиба (рис. 53).
Для этого нужно только считать коэффициент А бесконечно большим по сравнению с Л. В таком случае в выражении для Якр (121) можно пренебречь постоянными членами по сравнению с величиной z. Окончательно получим формулу
Рис. 53.
(2ЯКр)2
ВС я2 4
316
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
или, производя вычисления,
Решение, полученное для данного случая путем интегрирования дифференциального уравнения, даст нам
Р.Г-Уж. (122)
Следовательно, ограничиваясь всего одним членом, мы получаем для высшей формы равновесия критическую нагрузку с погрешностью около 6. Если взять для ф значение
то можно получить значительно большую точность. Мы здесь не будем останавливаться на вычислении дальнейших приближений и возвратимся к этой задаче при исследовании устойчивости двутавровых балок.
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВЫХ БАЛОК
§ 21. Основные уравнения равновесия
Нами были получены дифференциальные уравнения для неплоской формы равновесия полосы прямоугольного поперечного сечения (см. § 14). Рассмотрим теперь, какие изменения должны быть внесены в эти уравнения при переходе от прямоуголь-
Вопрос становится более сложным, когда мы переходим к двутавровой балке, так как здесь кручение может сопровождаться изгибом полок двутавровой балки. Если сравнить два способа скручивания, представленные на рис. 54, а и рис. 54, bt
л ях , Ф —г А.2 sin
2 пх I ’
Рис. 54.
ного к двутавровому сечению. Как уже было отмечено, искривление оси балки в направлении легчайшего изгиба сопровождается кручением. Пока мы имели дело с полосой узкого прямоугольного сечения, можно было считать, что скручивающий момент пропорционален производной от угла закручивания. Зависимость эта выражалась уравнением М Сф'.
ОБ УСТОЙЧИВОСТИ упругих систем
317
то при одних и тех же размерах балок одному и тому же скручивающему моменту будут соответствовать в обоих случаях различные углы закручивания. Балка с одним заделанным и другим свободным концом окажется более жесткой. Для нее кручение сопровождается изгибом полок. Влияние этого изгиба на величину угла закручивания может быть оценено с достаточной точностью путем самых элементарных соображений. Скручивающий момент внешних сил должен уравновешиваться моментом касательных напряжений, распределенных по плоскости поперечного сечения. При скручивании, представленном на рис. 54, by имеются касательные напряжения двух родов. Одни напряжения обусловлены собственно кручением, их момент будет М Сф'.
Другой род касательных напряжений является следствием изгиба полок. Если через у обозначим прогиб полки в ее плоскости и через D жесткость полки при изгибе в этой плоскости, то для перерезывающей силы Q, обусловленной изгибом полки, получим величину Q Dy'.
Так как другая полка балки гнется при кручении в прямопротивоположную сторону, то перерезывающие силы обеих полок в каждом поперечном сечении балки образуют пару сил с моментом М2 hDy'. Здесь через h обозначена высота двутавровой балки. Если принять во внимание, что У уф, то крутящий момент, соответствующий изгибу полок, будет
д Л h2D rrr
М2 2 Ф
Знак минус взят потому, что при принятом на рис. 54, Ъ направлении оси л:-ов у а следовательно, и ф' будут отрицательными.
Из условия равновесия внешних и внутренних сил будем иметь
М1М1 М2 Сф' - 22- ф' (123)
Видоизменив таким образом формулу кручения, мы можем нужные нам дифференциальные уравнения для неплоской формы равновесия двутавровой балки написать так:
,, п dq Dh2 d3q ,, D d2z ЛГ D d2y 1n(4
dx 2 dx3 ’ dx2 ’ dx2 9 (124)
Как и в предыдущих задачах, изгиб в плоскости наибольшей жесткости не оказывает влияния на явление выпучивания, и нам в дальнейшем придется иметь дело лишь с первым и третьим из написанных уравнений. Вставляя в каждом частном случае нагрузки значения М6 и Afj;, мы будем получать два совместных
318
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
дифференциальных уравнения, заключающих две неизвестные функции ф и у. Исключая одно из неизвестных, придем к обыкновенному дифференциальному уравнению четвертого порядка. Лишь в случае истого изгиба это будет уравнение с постоянными коэффициентами, в других же случаях придется иметь дело с более сложными уравнениями, интегралы которых приходится разыскивать в форме бесконечных рядов.
§ 22. Чистый изгиб
Положим, что закрепление концов не допускает вращения концевых сечений относительно оси х-ов. Постепенно увеличивая значения изгибающих моментов Му действующих в плоскости наибольшей жесткости, мы можем достигнуть такой величины Мкр, при которой становится возможной неплоская форма равновесия, представленная на рис. 55. Дифференциальные уравнения равновесия (124) пере-
пишутся в этом случае так:
DA2
2
ЛГ-Сф'--т-ф,
М ф — By.
х Вместо решения этих уравнений применим для наРис. 55. хождения Мкр новую методу.
Составим выражения для изменения потенциальной энергии деформации и для работы внешних сил при отклонении от плоской формы изгиба.
Потенциальная энергия, соответствующая изгибу в плоскости хуу будет
V, J У2 йх т I у 4 )2 dxт J у т ф)2 dx-
0 0 о
Первый член представляет энергию, соответствующую изгибу стенки балки, два других представляют энергию изгиба полок. После преобразований получим
ут JV2rf-TLJV2rf.
о о
Так как мы уже учли влияние изгиба полок, то энергия кручения представится так:
4JV
dx.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 319
Жесткость С с достаточной точностью может быть вычислена по приближенной формуле, приведенной в § 14. Работу моментов при искривлении можно на основании того, что было получено в § 15, представить так:
i
Т М J ty'dx.
О
Или, принимая во внимание условия на концах и выполняя интегрирование по частям:
i i J у'ф' dx (г'ф)о - фу dx,
О о
получим
I
Т — М J qpy dx J ф2 dx.
Приравнивая работу внешних сил энергии деформации, получим уравнение для определения М1р:
i i i
J y2dx С ф2с1х -Щ- Ф2dx. (125)
о
Введем обозначение:
ЩГ Y2. (126)
Величина у имеет измерение отвлеченного числа. Тогда из вышенаписанного уравнения получим
вс
mL
J ф'2 dx у2Р J ф2 dx
кр — i
Ф2 dx
i
Для принятого нами закрепления концов самое общее выражение для угла ф будет
„ . лх , „ . 2лх , - . Зях ,
Ф Ах sin —— А.2 sin —j—р sin ——Ь.
Вставляя это в выражение для Мкр, найдем
ВС л2 2 Y24 2 п4ап
320
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Наименьшее значение для Мкр получим, полагая все ЛЛ, кроме А, равными нулю; тогда
MKp -Vifn2. (127)
Сравнивая полученный результат с тем, что мы имели для чистого изгиба полосы прямоугольного поперечного сечения (см. § 15), видим разницу лишь в дополнительном, множителе, зависящем от величины у. Для всех значений у формула для Мкр будет иметь прежний вид:
но только k будет меняться в зависимости от у.
С этим обстоятельством мы встретимся и при других способах приложения внешних сил. Для определения устойчивости балки при каком-либо определенном типе нагрузки уже недостаточно одной величины, как то имело место в случае полосы прямоугольного сечения, придется приводить целую таблицу величин, зависящих от коэффициента балки у.
Рассмотренный случай может иногда иметь и практическое значение. В таких условиях, например, находится средняя часть поперечной мостовой балки, заключенная между местами прикрепления продольных балок. Для большего удобства пользования мы приводим в таблице V для ряда значений у2 соответствующие значения k. В той же таблице приведены значения k2y2. Величина эта изменяется по линейному закону, чем следует пользоваться при интерполировании.
Таблица V1)
1
Y2
Л
Y2
k
А
Y
к'см' 1
Y2
k
k
Y
Ркр, кгсм
0,1
98,4
31,4
9,92
495
16
255,3
4,00
15,97
800
1
107,3
10,36
10,36
518
20
294,8
3,83
17,17
860
2
117,2
7,66
10,83
540
24
334,3
3,73
18,28
915
4
136,9
5,85
11,70
585
28
373,8
3,66
19,33
965
6
156,6
5,11
12,51
625
32
413,3
3,59
20,33
1015
8
176,4
4,70
13,28
665
36
452,7
3,55
21,28
1065
10
196,1
4,43
14,00
700
40
492,2
3,51
22,19
1110
12
215,9
4,24
14,70
735
100
1084
3,29
32,90
1645
Ф
) Значение критического 0,0001; Е 2 106 кгсм2.
напряжения ркр кгсм2 вычислено при
При расчетах удобнее пользоваться не величиной Л1кр, а величиной соответствующих ему наибольших нормальных напряжений.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
32
Величина этих напряжений определится такой формулой:
к У ВС h Ркр-я , 2В
Пользуясь выражением для y и принимая во внимание, что для двутавровых балок с достаточной точностью можно положить В 2D, найдем
с _ Dh2 Bh2
22y2 42y2
Вставляя это в формулу для р1ф, получим
_ 1 р k В h2 Ркр - 4 Y Bl 12
или, вводя обозначение
получим
Вх12 Ф’
Ркр j y Ф. (129)
Для большей простоты вычислений в таблице V приведены значения ky, там даны также и значения ркр для Ф 0,0001 и Е 2 - 10б кгсм2. При расчете нужно по размерам балки вычислить величины lу2 и Ф. Для полученного lу2 в таблице V найдем соответствующее критическое напряжение, вычисленное в предположении Ф 110 000. Если для нашей балки Ф 1т, то придется данное в таблице критическое напряжение умножить на 10 000т; полученный таким образом результат и будет искомым критическим напряжением. (Вопрос о том, как поступать, если вычисленные напряжения превосходят предел упругости, будет рассмотрен ниже.)
Если кроме изгиба балка подвергается также и продольному сжатию, то придется к работе момента присоединить работу продольной сжимающей силы Т. Уравнение для определения Мкр напишется так:
322
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
В данном случае удобнее задаться выражением для у. Положим
Для определения р необходимо написать дифференциальное уравнение равновесия, соответствующее изгибу в плоскости ху. Если принять во внимание продольную силу, то уравнение это будет
Вставляя полученные для р и у значения в основное уравнение, найдем
Сравнивая этот результат с тем, что мы имели для случая чистого изгиба, находим разницу в добавочном множителе правой части. Если обозначить через а2 отношение продольной силы Т к эйлеровой нагрузке Вп212, то формулу для Мкр можно представить в таком виде:
Наибольшие напряжения от изгиба, соответствующие Мкр, можно в данном случае получать при помощи таблицы V, нужно
только определяемые по ней р1ф
балки должна принять форму, представленную на рис. 56. Уравнение для определения Мкр будет
Л лх
Sill-у-.
Мр Ту - By,
откуда находим
МКр —1-Vln2 Л-х2.
(130)
S х то нужно переменить знак Т и а2.
Если вместо сжимающей будем иметь растягивающую силу,
Рассмотрим теперь случай, когда закрепления концов препятствуют вращению концевых сечений около осей, параллельных оси z. При искривлении ось
умножить на У1 — а2.
Рис. 56.
ill I
М fV dx -f- J У2 dx Т J Ф'2 dx -j- J ф2 dx.
Ь оо о
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 323
Чтобы удовлетворить условиям на концах, положим
л (l-COSL),
тогда
, В ( 2л 3. 2лл:
-м(—) 5Ш —
Вставляя это в основное уравнение, получим
Mlp l(l4n2f),
откуда
мкр —--с- 2пВС у1 4у2я2. (131)
Для критических напряжений остается в силе прежняя общая формула (129). Ряд значений k и соответствующих ркр для
Ф 0,0001 приведен в таблице VI.
Таблица VI 0
1
Y3
fe2
Y2
k
А
Y
ркр, кгсм2
1
Y2
k
У2
k
А
У
Ркр. кгсм
0,1
1
1563
125
39,5
1980
16
2191
11,7
46,8
2350
1598
40,0
40,0
2000
20
2349
10,8
48,5
2430
2
1638
28,6
40,5
2025
24
2507
10,2
50,1
2510
4
1717
20,7
41,4
2070
28
2664
9,76
51,6
2580
6
1795
17,3
42,4
2120
32
2822
9,39
53,1
2660
8
1874
15,3
43,3
2170
36
2980
9,10
54,6
2730
10
1954
14,0
44,2
2210
40
3138
8,86
56,0
2800
12
2033
13,0
45,1
2260
50
3532
8,40
59,4
2970
14
2112
12,3
46,0
2300
100
5506
7,42
74,2
3710
ф
) Значение 0,0001; Е 2
критического напряжения рко кгсм2 вычислено при : 10 кгсм2.
Если кроме изгибающих моментов приложена продольная сжимающая сила, то уравнение для определения Мкр напишется так:
iiii i
М J tq' dx Y j у'2 dx J у2 dx j ф'2 dx J р2 dx.
0 0 0 0 о
324 ОБ УСТОЙЧИВОСТИ УПРУГИХ систем
Вставляя вместо у выражение у А 1 — cos-y-j и вместо ф его значение, определяемое из дифференциального уравнения равновесия Мер Ту — М0 —By (через Л10 обозначены действующие в плоскости ху моменты, препятствующие поворачиваться концевым сечениям около осей, параллельных оси г-ов), получим
4л2В ) откуда
Мкр 2nVlBC - Л 4яУ 1 - . (132)
Здесь а2 имеет прежнее значение.
Для определения наибольших напряжений от изгиба, соответствующих моменту Мкр, можно пользоваться таблицей VI, нужно только получаемые при этом значения ркр множить на
IГ
величину у 1 —j-.
Заметим, что с убыванием величины у2 выражения для Мкр и рНр, полученные нами для двутавровой балки, приближаются к величинам, найденным раньше (см. § 15, формулы (81), (83)) для полосы прямоугольного поперечного сечения. Такого результата и нужно было ожидать, так как убывание у2 соответствует или уменьшению D, или увеличению пролета. В обоих случаях значение изгиба полок убывает.
§ 23. Изгиб балки силой, приложенной на конце
нен
УА
г
Пользуясь результатами, полученными для полосы (см. уравнения (90)), мы можем сразу написать дифференциальные уравнения для неплоской формы равновесия двутавровой балки (рис. 57):
г )№ fff
Сф - —ф
PA-y-tf(l-x),
X P(l — х)р By.
Исключая из этих уравнений у, получим
у
Рис. 67. Щ- piv _ Сф - р2 (1х)г Ф 0.
Уравнение это нами было проинтегрировано при помощи бесконечных рядов1). Были вычислены значения Ркр для
) См. нашу работу, указанную на стр. 210.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
325
следующих условий на концах:
при х 0 ф 0 и ф' 0; при х 1 ф 0 и Сф' — ф' 0.
Величина критической нагрузки может быть представлена в прежней форме: Ркр k YВС I2. Ряд значений k и соответствующие значения рир для Ф 0,0001 приведены в таблице VII.
Таблица VII
1
У2
k2
У2
k
А
Y
Ркр. кгсм
1
Y2
Y2
k
k_
У
ркр, кг(см2
0,1
1
196
44,3
14,0
700
10
575
7,58
24,0
1200
247
15,7
15,7
785
12
623
7,20
25,0
1250
2
296
12,2
17,2
860
14
678
6,96
26,0
1300
3
342
10,7
18,5
925
16
725
6,73
26,9
1345
4
381
9,76
19,5
975
24
918
6,19
30,3
1515
6
453
8,69
21,3
1065
32
1100
5,87
33,2
1660
8
516
8,03
22,7
1140
40
1272
5,64
35,7
1785
Ф
) Значение 0,0001; Е 2
критического напряжения ркр кгсм2 вычислено при 10е кгсм2.
Для значений у2, больших 40, можно находить k по такой приближенной формуле:
тггу- 133)
Мы больше не останавливаемся на этом случае, так как он не имеет особого практического значения. Применение новой методы к этой задаче потребовало бы значительных вычислений. Второе приближение для малых значений lу2 дает, как показали вычисления, значительные погрешности (до 7).
§ 24. Изгиб балки силой, приложенной посредине пролета
Пусть сила 2Р приложена в центре тяжести поперечного сечения тп (рис. 58). Закрепление концов не допускает вращения концевых поперечных сечений относительно оси л;-ов. Если, постепенно увеличивая нагрузку, мы придем к неплоской форме равновесия, то условия на концах будут следующие:
при х»0 ф'»0 и — 0; при х 1 ф0
326 ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Дифференциальные уравнения для неплоской формы равновесия будут следующие (см. § 18, формула (106)):
By Р ( - ) ф, СФ' - Ф' - Р у tf (-).
Не будем останавливаться на обычном способе интегрирования этих уравнений и перейдем к применению новой методы.
77
——1 1 р
Л -J
р—1—Ар
-X
Рис. 58,.
Мы удовлетворим условиям на концах, если положим
- пх , Л Зпх , - 5пх ,
Ф Acos-r А cos -xj- A2cos-
21 1 2 1 2 I .Тогда на основании первого из уравнений равновесия y -(l-x)(Acos- AlCos.).
Уравнение для определения Ркр мы получим, приравнивая работу внешних сил при отклонении от плоской формы изгиба изменению потенциальной энергии деформации. В рассматриваемом случае уравнение это примет такой вид:
1 I 1 1
2Р J фу (I — х) dx В J y2dx С J ф2dx J ф2dx,
О ООО
или, принимая во внимание первое из дифференциальных уравнений равновесия, получим
i i -I
р J ф2 ( — x)2dx С J ф2dx у22 J ф2 dx. (134)
о Lo о J
р2 в
о
Здесь у2 определяется прежней формулой (см. формулу (126)), но обозначает половину пролета.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 327
Ограничиваясь в выражении для ср двумя первыми членами разложения и выполняя указанные в уравнении квадратуры, получим
RC 4r(l9z2) -g-Y2(l81z2)
PlTxjo, 1(и-U (135)
6 я 4я2 2(б 9я2 j 2 г, как и раньше, обозначает отношение А : А.
Если в полученной для Ркр формуле положить у2 0, другими словами, если пренебречь изгибом полок, то мы придем к формуле, выведенной для полосы (см. § 18).
Чтобы судить о точности формулы (135), вычислим значение РКр для какого-либо у2 и сравним с тем, что дает для этого у2 непосредственное интегрирование уравнения1). Положим, например, у2 1. Формула (135) дает р2 _ ВС 4,278 257,7г2
кр “ 4 0,2680 0,25332 0,1780z2 ‘
Разыскание минимума этого выражения приводит нас к квадратному уравнению
z2 2,0932 -0,016 0,
откуда z 0,008, z2 — 2,100. Вставляя значение Z в формулу для Ркр, получим п _ 15,90 VBC
Кр — 12
Если ограничиться первым приближением, то получим р _ 15,96С
кр J2
Интегрирование дифференциального уравнения при помощи бесконечных рядов дает нам
р _ 15,95С
кр 2
Сравнивая эти три результата, видим, насколько выгодно пользоваться новой методой при решении вопросов устойчивости двутавровых балок. Результаты, для вычисления которых при помощи рядов пришлось затратить несколько недель, могут быть получены в продолжение одного часа. Общий вид формулы для Ркр сохраняется:
р kVBC
Кр 12
) Для нескольких значений у2 нами вычислено ЯКр путем интегрирования дифференциального уравнения рядами (см. нашу работу, указанную на стр. 210).
328 ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Заметим, что через Р обозначена половина нагрузки и через — половина пролета. Для критических напряжений будем иметь такую формулу:
pKDlh k В h2 k ,
РпЕш,— Етт;тё-Етф- ('36)
где Ф Bh24B12.
Таблица VIII О
1
Y2
V
Y2
k
k
Y
ркр, кг;с
1
Y2
k2
Y2
k
k
Y
ркр, кг1см2
0,1
11,7
10,8
3t42
680
24
120
2,24
Го,95
2190
1
15,9
3,99
3,99
800
32
155
2,21
12,5
2500
2
20,5
3,20
4,53
910
40
192
2,19
13,9
2770
4
29,7
2,73
5,45
1090
50
237
2,18
15,4
3080
6
38,8
2,54
6,23
1250
60
282
2,17
16,8
3360
8
47,8
2,45
6,92
1380
70
327
2,16
18,1
3620
12
65,9
2,37
8,12
1620
80
371
2,15
19,3
3860
16
84,0
2,29
9,17
1830
90
416
2,15
20,4
4080
20
1
102
1
2,26
10,1
2020
100
оо
461
2,15
2,115
21,5
4300
Ф
) Значение критического напряжения pKD кгсм2 вычислено при 0,0001; Е 2 106 кгсм2.
7х 70,8
тЛ
-7ms
Для большего удобства при расчетах можно пользоваться
таблицей VIII. В ней для ряда значений у2 приведены соот¬
ветствующие значения k, ky, k2y2 и ркр для Ф 0,0001. Значения k2ly2 меняются по закону, близкому к линейному; этим
следует пользоваться при интерполирова¬
нии.
В качестве численного примера найдем с помощью таблицы VIII величину критической нагрузки и соответствующее значение критического напряжения для балки указанных на рис. 59 поперечных размеров. Пролет балки 21 3,25 м.
По таблице моментов инерции находим В 59 140 Е кгсм2, В 446 Е кгсм2. Жесткость полки D 12В 223 кгсм2. Площадь поперечного сечения F 98,24 см2. Полагая модуль при сдвиге G 8-105 кгсм2, найдем жесткость кручения С по приближенной формуле Сен-Венана:
j
j i
Рис. 59.
40 J 40 59 140 446 8 10’сгсл2 31,2 10б кгсм1.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
329
Определив по размерам балки значения жесткостей В, Si, D и С, находим
J_2C_ - В ( h2 _ 1
Y2 D г2 ’ ’ Bj 2 j 2860 '
Для найденного значения 1у2 и для Di 0,0001 по таблице VIII путем интерполирования находим р'кр 767 кгсм2. Чтобы найти р1ф для нашей балки, нужно найденную по таблицам величину помножить на отношение Ф : Di — 3,5; тогда получим ркр 767- 3,5 » 2680 кгсм2; так как найденное значение рКр превосходит предел упругости железа, то следует ожидать искривления балки при напряжениях, меньших вычисленного.
Исследуем теперь вопрос о влиянии на величину критической нагрузки повышения или понижения точки приложения внешней силы. Задача эта имеет практический интерес, так как обыкновенно нагрузка прилагается или к верхнему канту балки, как, например, в мостовых продольных балках, или к нижнему канту, как это встречается часто в мостовых подъемных кранах. Если точка приложения силы повышена на величину а над центром тяжести среднего сечения балки, то опускание ее при
искривлении балки будет больше, чем опускание соответствующей точки оси, на величину аф22 (ф0 — угол поворота среднего сечения балки). Это дополнительное опускание сопровождается дополнительной работой нашего груза 2Р. Присоединяя эту работу к левой части уравнения (134), получим уравнение для определения Ркр в таком виде:
i i i -1
J ф2 ( — х)2 dx Рф2а С J ф'2 dx уЧ2 J ф2 dx.
о Lo о J
Если точка приложения силы ниже оси балки, то а нужно
считать отрицательным. Положим ф A cos (я2). Тогда из на¬
шего уравнения, по выполнении квадратур, получим
т(т)p“-c(irvw)’
2 Dh2 Bh2
откуда, принимая во внимание, что V — 2с2 4С1Г получим
р 1Л1. -1 ” I L
кр 2 Г- 5 I Г— V1 5 —
Я2 2 Я4
8 Y 32
I.
330
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Заключенный в скобки дополнительный множитель определяет влияние повышения точки приложения силы на величину ЛФ. Если точка приложения силы совпадает с верхним или нижним кантом балки, то а ± г2 и формула для Ркр напишется так:
При у 0 множитель в скобках обращается в единицу. Такой результат объясняется тем, что при конечных С и D (если бы D обратилось в нуль, то В 2D 0, следовательно, Ркр 0)
Y может обратиться в нуль только при h 0 или оо. В этих же случаях повышение точки приложения силы на величину г2 никакого влияния на Ркр иметь не может. Величина Ркр для нескольких значений lу2 была нами вычислена путем интегрирования соответствующего уравнения при помощи бесконечных рядов. Сравним полученные там результаты с теми, что дает приближенная формула. Для у2 1 нами было получено Ркр 2,522 Увсl2.
Приближенная формула дает Ркр 2,534 Увсl2. Погрешность составляет лишь 12.
Для 1у2 32 нами было получено Ркр 1,89 У ВС 2. Приближенная формула для этого случая дает Ркр 1,92 У ВС 2; здесь погрешность составляет 172.
Во всяком случае точность нашей формулы, являющейся лишь первым приближением, вполне достаточна для практических приложений. Точность результата может быть еще повышена, если в формуле (137) ограничиться вычислением дополнительного множителя, заключенного в скобки, и на этот множитель помножить РКр, найденное с большей точностью для того случая, когда точка приложения силы совпадает с центром тяжести срединного сечения.
Для удобства расчетов мы приводим таблицы IX и X для случаев, когда приложенная посредине пролета нагрузка совпадает с верхним или нижним кантом балки.
Для случая балки, нагруженной посредине, представляет некоторый практический интерес и вторая возможная форма равновесия с двумя полуволнами. С этим случаем придется иметь
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
331
Таблица IX1)
1
Y2
ркр. кгсм2
1
Y2
fe2
Y2
ркр, кгсм2
0,1
1
2
3
4 6 8
10
12
4,13
6,36
9,05
11.9
14.9 21,1 27,7 34,3 41,2
6,42
2,52
2,13
1,99
1,93
1,88
1,86
1.85
1.85
2,03
2,52
3,01
3,45
3.86 4,59 5,26
5.86 6,42
405
505
600
690
770
920
1050
1170
1280
16
24
32
40
50
60
70
80
100
55,3
84,8
114
147
187
227
267
307
388
1,86
1,88
1,89
1.92
1.93
1.94
1.95
1.96
1.97 2,115
7,44
9,21
10.7 12,1
13.7 15,1 16,3 17,5
19.7
1490
1840
2140
2420
2740
3020
3260
3500
3940
ф:
1) Значение критического напряжения ркр кгсм2 вычислено при 0,0001; 2- 106 кгсм2.
Таблица X1)
1
Y2
k2
У2
k
k_
У
ркр, кгсм2
1
Y2
k2
У2
k
k_
У
ркр. кгсм2
0,1
33,1
18,2
5,75
1150
16
125
2,80
11,2
2240
1
39,1
6,25
6,25
1250
24
168
2,65
12,9
2580
2
45,6
4,78
6,75
1350
32
211
2,57
14,5
2900
3
51,8
4,16
7,20
1440
40
250
2,50
15,8
3160
4
58,0
3,81
7,62
1520
50
301
2,45
17,3
3460
6
70,0
3,42
8,37
1670
60
351
2,42
18,7
3740
8
81,5
3,19
9,03
1860
70
401
2,39
20,0
4000
10
92,5
3,04
9,62
1920
80
449
2,36
21,2
4240
12
103,1
2,93
10,15
2030
100
546
2,34
23,4
4680
оо
—
2,115
—
—
) Значение
критического напряжения pKP
кгсм
2 вычислено при
Ф
0,0001; 2
10е кгсм2.
дело, когда две балки АВ и CD связаны поперечными связями в плоскости тп (рис. 60).
Силы приложены в точках типи направлены перпендикулярно к плоскости ху. Основное уравнение для определения Ркр сохранит свой прежний вид:
i iii 2Р J py(t-x)dx C j у'Чх В j у2dx j p2dx.
332
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Уравнение равновесия, соответствующее изгибу в плоскости ху, будет
By Р (I — х) ф.
Условия на концах будут следующими:
при х 0 ф 0, у 0; при х 1 ф 0, у 0.
Мы удовлетворим этим условиям, положив
„. пх , „ . 2пх , „ . Зпх.
Ф A sin — Л1 sin——I- А2 sin —j—I-.
Ограничимся первыми двумя членами разложения и полученное таким образом приближенное значение для ф вставим
Рис. 60.
в основное уравнение для определения Р1ф. Заменяя у через ф с помощью вышенаписанного дифференциального уравнения равновесия и выполняя указанные квадратуры, получим
ВС
J ф'2 dx у22 J ф'2 dxj
кр
Ф2 ( — х)2 dx
п2ВС
1 4z2 зт2у2 (1 16z2)
I J Lj-JL 3 2зт2 9зт2 2 3 8я2 ) '
(138)
Здесь г, как и раньше, обозначает отношение А : А.
Чтобы оценить точность полученной формулы, положим y 0; тогда мы должны получить значение РКр для полосы прямоугольного поперечного сечения:
р2 __ п2ВС
кр —
1 4z2
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 333
Разыскание минимума Я1ф приводит к такому квадратному уравнению:
z2 l,1245z-0,2500 0;
корнями уравнения будут Z 0,1901, z2 —1,3147. Вставляя z 1 в выражение для Ркр, получим
р _ 5,58)ГВС
кр j2
Точное же решение для рассматриваемого случая дает нам
р _ 5,561ВС
Кр 2
Следовательно, погрешность меньше 0,5.
Формула для определения р1ф будет такого же вида, как и для первой формы равновесия (см. формулу (136)).
Для облегчения расчетов нами составлена при помощи формулы (138) для РКр таблица значений р1ф1 вычисленных в предположении Ф Bh2B-Al2 0,0001.
Таблица XI1)
1
Ya
k2 Ya
k
k
У
ркр, кгсм2
1
Y2
k2 У2
k
k_
У
Ркр.
0,1
339
58,2
18,4
3 680
24
1120
6,82
33,4
6 680
1
368
19,2
19,2
3 840
32
1373
6,55
37,1
7 420
2
402
14,2
20,1
4010
50
1941
6,23
44,1
8810
4
467
10,8
21,6
4 320
100
3520
5,93
59,3
11 900
8
600
8,66
24,5
4 900
оо
5,56
Ф
) Значение 0,0001; 2
критического напряжения ркр кгсм‘ 106 кгсм2.
2 вычислено при
Для исследования устойчивости двутавровой балки, изгибаемой силой, приложенной посредине пролета, важно уметь оценивать влияние продольной растягивающей или сжимающей силы. Нами было произведено определение этого влияния для нескольких частных значений у2. Вычисления привели к весьма сложным формулам, неудобным для практических приложений. Вместо этих сложных вычислений предположим, что влияние продольной силы можно с достаточной точностью оценить, пользуясь формулами, выведенными в случае чистого изгиба. Если через а2 обозначим отношение продольной силы Т к эйлеровой нагрузке, то нужно напряжения 1ф, определяемые при помощи таблиц VIII, IX и X, множить на величину У1—а2.
334
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
В случае второй формы равновесия с точкой перегиба посре-
-ii о5
дине пролета нужно ркр множить на величину у 1 —j-.
В заключение остановимся на вопросе об устойчивости двутавровой балки, концы которой не могут поворачиваться относительно осей, параллельных оси z-ов. При выпучивании ось балки должна принять форму, представленную на рис. 61.
Принимая новую методу, мы будем задаваться выражением для р; тогда выражение для у найдется из дифференциального
уравнения равновесия
By P(l-x)f-M0.
х Здесь через Мо обозначены моменты, препятствующие _ концам поворачиваться от¬
носительно вертикальных Рис- 61- осей. Величину М0 легко
найти из того условия, что у' О при х 0 и при х I. Интегрируя это уравнение и принимая во внимание высказанные условия на концах, найдем
УЛМ0
t)
У
- 1 —►
М(
-«(W)
и, следовательно,
y i(t-x)tр-(-.).
Основное уравнение для определения Ркр напишется так:
i iii
2Р J qy(l-x)dx C jp'2dx B J y2dx-f- j q2dx.
0 0 0 0
Вставляя вместо у его значение, получим
г I 1 J р2 (I - xf dx С ф'2 dx y2l2 J ф2 dx 3(t jI)'
0 Lo о J
Ограничиваясь первым приближением и полагая ср Л1 cosyj,
(139)
найдем
ВСп2 24
1 у2л
-аФГ
Для оценки точности этой формулы положим у2 0, тогда мы должны получить Ркр для случая полосы прямоугольного
ОБ УСТОЙЧИВОСТИ УПРУГИХ CI1CTLM
335
поперечного сечения. Произведя указанные вычисления, найдем РКр 3,36С2.Точное решение для полосы, как мы уже упоминали, будет Ркр 3,25 У ВС 2; таким образом, погрешность первого приближения — около 3.
Мы не останавливаемся на нахождении следующего приближения (при желании оно может быть получено без всяких затруднений) и составим таблицу XII критических напряжений по формуле (139).
Таблица XII )
I
Y2
k2 У2
к
k
У
Ркр’ кг1см2
1
Y2
k2 Y2
k
_k_
Y
Ркр, мсм2
0,1
112,5
33,5
10,6
2120
16
291
4,27
17,1
3420
1
122,7
11,1
11,1
2220
24
381
3,97
19,5
3900
2
134
8,19
11,6
2320
32
472
3,84
21,7
4340
4
157
6,27
12,5
2500
40
562
3,75
23,7
4740
6
179
5,46
13,4
2680
50
675
3,67
26,0
5200
8
202
5,02
14,2
2840
60
788
3,62
28,1
5620
10
224
4,73
15,0
3000
80
1014
3,56
31,8
6360
12
247
4,54
15,7
3140
100
1240
3,52
35,2
7040
Ф
) Значение 0,0001; Е сг
критического напряжения ркр кгсм2 вычислено при 1 106 кгсм2.
Пользоваться настоящей таблицей можно лишь в тех случаях, когда закрепление действительно не допускает никакого вращения концов балки относительно вертикальных осей.
До сих пор мы полагали, что при выпучивании балки по длине ее не появляется никаких реакций, препятствующих этому выпучиванию. Если балка выпучивается в упругой среде, то появятся усилия, пропорциональные прогибам в отдельных точках балки. Возможны и такие условия, что при выпучивании балки появляются моменты, распределенные по длине и препятствующие поворачиванию Рис. 62.
поперечных сечений балки. Какого бы типа реакции ни были, но раз они пропорциональны соответствующим перемещениям, т. е. если они носят характер упругих реакций, то новая метода дает возможность с любой точностью исследовать вопрос устойчивости такой системы. Возьмем, например, такой случай. Две параллельные двутавровые балки с опертыми концами соединены рядом поперечин. При выпучивании балок отдельные их поперечные сечения поворачиваются,
336
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
и поперечины должны изогнуться, как то представлено на рис. 62. При наличии ряда поперечин можно принять непрерывное распределение моментов, препятствующих поворачиванию сечений балок. Если через р обозначить коэффициент, характеризующий жесткость поперечин, то на единицу длины выпучивающейся двутавровой балки придется момент т рф. Основное уравнение для определения критической нагрузки напишется так:
z i
2Р J фу (I - х) dx С J ф'2 dx В J у2 dx
О 0 0
J ф2 dx -2- J ф2 dx.
i
DH2 2
о
Добавочный член в правой части представляет собой энергию деформации поперечин. При малом р влияние реактивных моментов скажется лишь в том, что несколько увеличится сила Ркр. При дальнейшем возрастании жесткости поперечин мы будем иметь такое же явление, как в случае продольного изгиба стержней в упругой среде. Окажется, что первой искривленной формой равновесия может быть форма с одной или несколькими точками перегиба. Определение Ркр при заданном значении р не представляет никаких принципиальных затруднений.
§ 25. Изгиб двутавровой балки равномерно распределенной нагрузкой
Положим, что, постепенно увеличивая нагрузку q, мы достигли предела, когда становится возможной неплоская форма равновесия, представленная на рис. 63. Сохраняя те же обозначения, что мы имели для изгиба полосы (см. § 19), представим дифференциальные уравнения равновесия в такой форме:
Ву (12-х2),
I
f у у' (I - ) q J 06 - ух- у'х(Ъ- ж) dl.
X
Вместо обычного приема интегрирования этих уравнений применим новую методу. Приравнивая работу внешних сил при искривлении балки в плоскости ху изменению потенциальной энергии, соответствующему этому искривлению, получим основное уравнение для определения критической нагрузки в такой
Сф о— ф
-Qe-
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
337
форме:
I ill
Я J ФУ (I2 — х2) dx С ф'2 dx Л- В J у2 dx J ф2 dx.
О ООО
Вставляя вместо у” его значение из первого уравнения
х
Рис. 63.
равновесия и принимая во внимание обозначение у2 Dh22Cl2, можем основное уравнение представить в таком виде:
i - i i -jg- J ф2 (12 — х2)2 dx C J ф'2 dx y2l2 J ф2 dx.
L-0
(140)
Если закрепления не допускают вращения концов лишь относительно оси х-ов, то для формы равновесия, представленной на рис. 63, самое общее выражение угла ф будет
- лх , - Злх , - 5лх ,
Ф A cos A j cos -7— А2 cos
21
Мы ограничимся первыми двумя членами разложения. Вставляя полученное таким образом приближенное значение ф в основное уравнение (140) и выполняя интегрирование, найдем
Г±_±4—LJ1. 24 Л 1 М 1 1 12 21
4В L 2 3 10 л п 16 2 3 10 8n)Z 1 02:2 (1 812)
откуда
у- СВп2 19г2 4 (181г2
21 0,3899 0,23 Юг 0,2682г2 ’
(141)
Здесь г обозначает отношение А : А. Для каждого частного значения у приходится z подбирать так, чтобы ql приобретало
338
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
минимальное значение. Общий вид формулы для критического значения нагрузки остается прежним:
, n k Уве
wOkp 12
Приступая к вычислению значений k, мы отметим прежде всего то обстоятельство, что первое приближение для ()Кр, получаемое из формулы (141) при 2 0, весьма мало отличается от второго приближения. Наибольшего значения эта разность достигает при у2 0, здесь она составляет примерно 23 от определяемой величины. Для y2 132 разность эта равна 14. С возрастанием у2 разность убывает. Такая близость первого и второго приближения указывает на высокую точность результата, получаемого приближенной методой.
Второе обстоятельство, значительно упрощающее вычисление k, следующее. Если для какого-либо значения у2 сравнить величину, определяемую по формуле (141), с соответствующим значением k для случая нагрузки посредине пролета (см. табл. VIII), то найдем, что отношение этих величин почти не меняется при изменении у. Так, например, для y 0 мы получили
Ркр 2,115 Увсl2 для сосредоточенной силы,
(7)кр 3,54 VbcP для равномерной нагрузки.
Отношение величин k будет 2,115 : 3,54 0,598.
Для у2 132 вычисления дали следующие результаты:
Ркр 2,21 УВСН2 для сосредоточенной силы,
(qI)kp 3,68 YUc IР для равномерной нагрузки.
Интересующее нас отношение будет 2,21 : 3,68 0,600.
Для y2 1 получились такие результаты:
Ркр 3,99 ВС jl2 для сосредоточенной силы,
у1)кр — 6,62 VBCl2 для равномерной нагрузки.
Здесь отношение величин k будет 3,99 : 6,62 0,602.
Следовательно, можно высказать положение, что эффект равномерно распределенной нагрузки такой же, как если бы 0,6 этой нагрузки было сосредоточено посредине пролета. Для нахождения критического значения для равномерно распределенной нагрузки нужно критическое значение сосредоточенной силы разделить на 0,6.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
839
От величины критической силы перейдем к величине критических напряжений:
Ркр Eql2h4BU или, вставляя вместо ql его критическое значение, получим
О ±feJL.
Рк р 2 Вх 21
принимая во внимание значение С Вг24уЧ2, найдем
142 По сравнению с тем, что мы имели для случая сосредоточенной силы посредине пролета, прибавился дополнительный множитель 12. Если принять во внимание вышеопределённое отношение величин k для обоих случаев нагрузки, то можно сказать, что критические напряжения в случае равномерной нагрузки при прочих равных условиях составляют 0,50,6 0,833 от критических напряжений в случае сосредоточенной силы посредине. Для большего удобства вычислений мы приводим ниже таблицу значений ркр для случая Ф 0,0001.
Таблица XIII1)
1
Y2
k2
Y2
k
k
Y
ркр. кгсм2
I
Y2
Y2
k
А
Y
РКр. кгсм2
0,1
32,3
17,9
5,68
568
24
335
3,73
18,3
1830
1
44,0
6,63
6,63
663
32
433
3,68
20,8
2080
2
56,6
5,32
7,52
752
40
538
3,65
23,2
2320
4
81,9
4,54
9,05
905
50
660
3,63
25,7
2570
6
108
4,23
10,4
1040
60
784
3,62
28,0
2800
8
132
4,08
11,5
1150
70
912
3,60
30,2
3020
12
182
3,94
13,5
1350
80
1037
3,58
32,2
3220
16
234
3,81
15,3
1530
90
1156
3,58
34,0
3400
20
282
3,76
16,8
1680
100
1282
3,58
35,8
3580
оо
—
3,54
—
—
) Значение
критического напряжения pKD кгсм2 вычислено при
Ф
0,0001
; Е Ч
106 кгсм2.
Если бы мы в качестве численного примера взяли случай, разобранный в § 24, то для критического напряжения получили бы величину 2230 кгсм2.
Если нагрузка распределена не по оси балки, а выше или ниже ее по линии z ±а, то при составлении работы внешних сил нужно принять дополнительное опускание нагрузки,
340
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
зависящее от поворота отдельных поперечных сечений балки. Основное уравнение для определения (ql)KV напишется так:
I t Г- I I
J Ф2 (12 — 2)2 dx qa j qp2 dx С J p'2 dx y2l2 J qp2 dx. о о Lo о J
(143)
Мы ограничимся лишь первым приближением и положим ср A cos (пх2). Тогда, выполняя интегрирование, найдем
2 5 1 1 , 1 , 12 , al п(п2. 2 я4
q 42 3 10 пА) У 2 8 32)
Решая это квадратное уравнение, получим
(0кР Ва
71‘
В'а , 4ВС Т г v 32
Y2-oo
.(1_± _1_ _112 J L_L 12
2 3 10 n) 2 3 10
Принимая во внимание равенство Bi24C2 y2, представим выражение для fa) кр в таком виде:
л Yl 4 У
V2P Г l_4-J-4.il
V 2 3 10 п
X Г . Уа-
144)
Дополнительный множитель, заключенный в скобки, и определяет собой влияние повышения или понижения нагрузки на величину ее критического значения.
Так как на практике чаще всего прикладывают нагрузку к верхнему или нижнему канту балки, то нами составлены таблицы XIV и XV для р1ф при а ±А2.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
341
Таблица XIV )
I
Y2
k2
Y2
k
k
Y
кр, кгсм2
1
Y2
k2
Y2
k
k_
Y
Ркр»
KafcM2
0,1
13,5
11,6
3,67
367
24
253
3,25
15,9
1590
1
20,6
4,54
4,54
454
32
339
3,26
18,4
1840
2
28,9
3,80
5,38
538
40
433
3,27
20,8
2080
4
46,8
3,43
6,84
684
50
543
3,29
23,3
2330
6
66,1
3,31
8,13
813
60
655
3,30
25,6
2560
8
85,2
3,28
9,23
923
70
767
3,30
27,7
2770
12
125
3,27
11,2
1120
80
888
3,31
29,8
2980
16
166
3,22
12,9
1290
90
999
3,32
31,6
3160
20
207
3,23
14,4
1440
100
1109
3,33
33,3
3330
оо
—
3,54
—
—
) Значение критического напряжения ркр кгсм2 вычислено при
Ф 0,0001; Е 2 10е кгсм2.
Таблица XV1)
l
Y2
k2
Y2
k
k
т
ркр» кг см2
1
Y2
k2
Y2
k
k
Y
Ркр»
кгсм.2
0,1
77,3
27,7
8,79
879
24
441
4,30
21,0
2100
1
93,5
9,77
9,67
967
32
552
4,16
23,5
2350
2
110
7,43
10,5
1050
40
671
4,08
25,9
2590
4
144
6,01
12,0
1200
50
807
4,01
28,4
2840
6
177
5,41
13,3
1330
60
942
3,96
30,7
3070
8
204
5,09
14,3
1430
70
1076
3,92
32,8
3280
12
266
4,76
16,3
1630
80
1211
3,87
34,8
3480
16
328
4,50
18,1
1810
90
1347
3,86
36,7
3670
20
384
4,38
19,6
1960
100
оо
1475
3,84
3,54
38,4
3840
) Значение критического напряжения Ф 0,0001; Е 2- 10б кгсм2.
Ркр кгсм2 вычислено при
Рассмотрим теперь вторую возможную неплоскую форму равновесия с точкой перегиба посредине пролета. Задача эта представляет некоторый практический интерес, так как иногда две параллельно идущие балки соединяют посредине пролета поперечными связями, препятствующими образованию первой неплоской формы. Основное уравнение (140) остается в силе, общее выражение для угла поворота нужно взять в такой форме:
Л. ПХ. л. 2пх , - . Зпх.
Ф A sin — Ах sin —j—A2sm—j--
342
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
При этом, очевидно, ф обращается в нуль при х 0 и при
X ± 1.
При изменении х на —х меняется знак угла ф. Искривленная форма оси балки имеет вид, представленный на рис. 64. Ограничиваясь двумя первыми членами разложения для ф и вставляя это приблизительное значение ф в основное уравнение, получим
4 В С л2 14 z2 у2я2 (1 16 z2)
тР
'4 i_2 jL _1_
3 5 т 2я
48 I, 1 , I, 2 , 1 , 3
л4 ( 81 ) 1 3 5 32я4 )'
-гг
где z А : А.
Задача теперь заключается в отыскании для каждого значения у2 такой величины 2, при которой ql получает минимальное
значение. Полагая у2 О, у получим (ql) „р для случая
полосы прямоугольного сечения. Разыскание минимума (ql) кр в этом случае сводится к решению квадратного уравнения
г2 1,7062 — 0,2500 0.
Корнями этого уравнения будут 2 j 0,1358, z2 —1,8414.
Вставляя величину Z в выражение для ()кр, найдем
8,24 VBC
Рис. 64.
т.
кр
2
(145)
Сравнивая это с тем, что мы имели для второй формы равновесия в случае силы, сосредоточенной посредине, Ркр 5,56 V ВСР, можем сказать, что для второй формы равновесия эффект распределенной нагрузки такой, как если бы 23 этой нагрузки было сосредоточено посредине пролета. Примерно то же соотношение сохраняется и в случае двутавровой балки, т. е. тогда, когда y2 не равно нулю. Для ряда значений у2 вычислены нами соответствующие значения й, а также и р1ф для Ф 0,0001. Значения эти помещены в таблице XVI.
Чтобы оценить влияние повышения или понижения нагрузки, придется воспользоваться уравнением (143). Ограничиваясь лишь первым приближением и вставляя вместо ф величину ф A sin (лхl), получим (здесь а обозначает повышение нагрузки)
2 5 1 1 , 1 , 3 , al Сп2 t о о
q 1в V2 з ПГ 4n) q Т 2Г ( Y П )
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
343
Таблица XVI 1)
1
Y2
k2
Y2
k
k
У
кр кгсм2
1
Y2
k2 У2
k
k
У
кр» кг см2
0,1
709
84,2
26,6
2660
24
2370
9,93
48,6
4860
1
767
27,7
27,7
2770
32
2920
9,55
54,0
5400
2
841
20,5
29,0
2900
50
4150
9,11
64,4
6440
4
982
15,7
31,3
3130
100
7569
8,70
86,9
8690
8
1260
12,6
35,5
3550
оо
™
8,24
—
—
) Значение критического напряжения ркр кгсм2
вычислено при
Ф 0,0001; Е 2-10е кгсм2.
Решая это квадратное уравнение относительно ql, получим (7)кР - В
I Р(l-L ±J-
2 3 10 4я4
. Г а2В2 , Ся2 (1 у2п2) 4В
1 M2i W±_± _L М
Г 2 3 10 4л4 ) Л 2 3 10 4л4)
Проделывая ряд преобразований, получаем , _ 2л V Ш VlyW
ЯЧ кр — 2 Г о j О А
У 1-тт4г
f „(1 „») (- - 1_)
ауУТ )
х), - hn
(146)
Влияние повышения нагрузки на величину ее критического значения определяется дополнительным множителем, заключенным в скобки. Пока а положительно, множитель меньше единицы. Для отрицательных а, соответствующих понижению нагрузки, множитель больше единицы. Вообще, как можно было и заранее ожидать, влияние повышения и понижения нагрузки для второй формы не так значительно, как мы имели для первой формы. Ряд значений множителя нами вычислен для того случая, когда а ± г2.
Соответствующие величины р1ф для Ф 0,0001 помещены в таблицах XVII и XVIII.
344
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Таблица XVIP)
1
Y2
k2
Y2
k
k
т
кр кгсм2
I
Y2
k2
Y2
k
k
Y
кр» кгсм2
0,1
536
73,2
23,2
2320
24
2040
9,22
45,2
4520
1
590
24,3
24,3
2430
32
2560
8,94
50,6
5060
2
655
18,1
25,6
2560
50
3720
8,62
61,0
6100
4
784
14,0
28,0
2800
100
6972
8,35
83,5
8350
8
1040
11,4
32,2
3220
оо
—
8,24
—
—
) Значение критического напряжения ркр кгсм2 Ф 0,0001; Е 2- 106 кгсм2.
вычислено при
Таблица XVIII )-
1
Y2
k2
Y2
k
k
Y
Ркр»
кгсм2
1
1
k2 Y2
k
k
T
кр
кг1см2
0,1
935
96,7
30,6
3060
24
2750
10,7
52,4
5240
1
992
31,5
31,5
3150
32
3330
10,2
57,7
5770
2
1076
23,2
32,8
3280
50
4640
9,63
68,1
6810
4
1240
17,6
35,2
3520
100
8210
9,06
90,6
9060
8
1550
13,9
39,4
3940
оо
—
8,24
—
“
В заключение рассмотрим случай, когда закрепление концов не допускает вращения относительно осей, параллельных оси г. Дифференциальное уравнение для изгиба в плоскости ху (рис. 61) напишется так:
ВуГ
_ д (2 - х2
-ф-АГ0.
Через М0 обозначены моменты, препятствующие концам вращаться около вертикальных осей. Величину М0 найдем из условий: у' 0 при х 0 и при х I. Интегрируя вышенаписанное уравнение и принимая во внимание условия на концах, получим
««-«'’(ту)-
Вставляя значение у в основное уравнение
i iii
q J щ” (I2 — х2) dx С J ф'2 dx В J у2 dx J ф2 dx,
найдем
i
r I
JV (I2 - X2)2 dx C J ф'2 dx YЧ2 J ф2 dx (i--L)2.
o Lo о J
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
345
Ограничимся первым приближением и положим ср А (1 cos пх1).
При этом условия на концах, очевидно, будут удовлетворены. По выполнении интегрирования находим из основного уравнения
(а1)2 2ВСп2 (1 у2я2) (147)
4 0,5295 1
На основании этой формулы составлена нижеследующая таблица XIX критических напряжений.
Таблица XIX1)
1
Y2
k2
Y2
k
k
У
кр» кгсм2
1
Y2
kr
Y2
k
k
У
Ркр, кгсм2
0,1
372
61,0
19,3
1930
24
1260
7,25
35,5
3550
1
404
20,1
20,1
2010
32
1560
6,98
39,5
3950
2
444
14,9
21,1
2110
50
2230
6,68
47,2
4720
4
520
11,4
22,8
2280
100
4100
6,40
64,0
6400
8
667
9,13
25,8
2580
оо
—
—
—
—
) Значение критического напряжения ркр Ф 0,0001; Е 2 106 кгсм2.
, кгсм2
вычислено при
Если кроме изгибающих сил имеются еще продольные сжимающие или растягивающие усилия Г, то влияние этих последних на величину критической нагрузки можно учесть, как и ранее, вводя дополнительный множитель У1 — а2 для первой формы равновесия и множитель 1—а24 для второй формы и для случая заделанных концов.
§ 26. Влияние изгиба на кручение полосы прямоугольного поперечного сечения
При исследовании устойчивости плоской формы изгиба полосы прямоугольного поперечного сечения мы представляли зависимость между скручивающим моментом Мь и кручением такой формулой: Mi Cqp'-
Для двутавровых балок потребовалось дополнительное исследование. Обнаружилось, что на угол кручения может оказать большое влияние жесткость изгиба полок. Влияние этого изгиба было учтено нами при посредстве дополнительного члена, и формула кручения получилась в таком виде:
346
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
В дальнейшем при решении вопросов устойчивости двутавровых балок величина Dh22Cl2 у2 играла большую роль; с убыванием у2 критическая нагрузка для двутавровой балки приближалась по величине к соответствующей нагрузке для полосы прямоугольного поперечного сечения. В случае у2 0 формулы, выведенные для двутавровой балки, совпадают с соответствующими формулами для полосы. Попробуем элементарным путем оценить влияние изгиба на кручение полосы и определим, какова может быть погрешность от нашего предположения, что для этого случая у2 0.
Пусть левый конец полосы заделан, правый свободен. Будем через у обозначать прогибы оси полосы в плоскости ху, тогда прогиб какой-либо линии тп в той же плоскости определится формулой (рис. 65) у у фг.
т
т.
t.
id
Ъ
V
ib
Рис. 65.
Если плоскостями тп и тпи параллельными плоскости ху, выделить элемент полосы, то перерезывающая сила от изгиба для какого-либо поперечного сечения элемента будет
( )
Момент этих усилий относительно оси х-ов будет
А 2
ТГ J (' Z(P') zdz (p -h 2
Eb3 h3. ,,, Bh
12 12 ф 12
Следовательно, формулу для кручения полосы прямоугольного поперечного сечения следует написать в таком виде:
М — Сф' — р'.
Сравнивая это с формулой для двутавровой балки, находим, что при кручении полосы величина Bh2 12 играет ту же роль, что в двутавровых балках величина Dh22. Пользуясь прежними обозначениями, следует положить Bh2l2Cl2 у2- Полагая с достаточной точностью для прямоугольника С :В 1,54, найдем
1 18,52 1(ОЧ
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
347
Таким образом, величина у2 Для полосы — весьма малое число и лишь при очень коротких полосах изгиб может оказывать заметное влияние на угол закручивания.
§ 27. Правила пользования выведенными формулами
Для большего удобства пользования вышеполученными результатами мы приводим рис. 66 и 67, дающие значения критических напряжений для различных способов нагрузки. По оси
Ю9рнР,гм
Рис. 66.
Рис. 67.
абсцисс отложены величины 1у2, по оси ординат — соответствующие кр для того случая, когда
Ф (BBi) (Л2)2 0,0001.
При расчетах нужно предварительно иметь для заданной балки значения следующих величин:
У7 —площадь поперечного сечения,
В EJ — наименьшая жесткость изгиба,
Bi EJX — наибольшая жесткость изгиба,
D Вj2 — жесткость изгиба для одной полки,
1 F4
С j- j G — жесткость при кручении,
1 _ 2С21 m - в ( h V - m Y2 - oh2 ’ Bl 2l )
348
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Через обозначена половина пролета и через h — высота поперечного сечения балки ).
По вычисленному значению у2 находим из диаграммы критическое напряжение для того случая, когда Ф 0,0001. Искомое Кр будет равно табличному, умноженному на величину 04т.
Если определенное таким образом значение ркр не превосходит предела упругости материала, то расчет является законченным, коэффициент уменьшения напряжений для рассчитываемой балки будет
Ф временное сопротивление
Остановимся теперь на том случае, когда вычисленное по вышеуказанному способу кр превосходит предел упругости материала. При этом условии формулы, выведенные из уравнений теории упругости, очевидно, прямо не могут быть применены, приходится прибегнуть к данным опыта. Устойчивость двутавровых балок за пределами упругости до сих пор опытным путем не исследована, но мы можем для нашей цели воспользоваться многочисленными опытами над продольным изгибом стержней. В пределах упругости для сжимаемого стержня критическое напряжение определяется, как известно, по формуле рк р Еп2(г1)2.
Как мы уже показали (см. § 12), и за пределами упругости можно вычислять кр аналитически, но в таком случае придется
иметь дело с некоторым переменным значением модуля упру¬
гости. Формула напишется так:
ЫРЕ'п(т) (149)
где Е' — величина, меняющаяся в зависимости от р'. Для ряда значений г имеются значения р' , найденные опытным путем. Мы можем найти соответствующие значения Е' и отношение Е': Е — отношение это будет функцией от р'р.
Если мы теперь обратимся к вопросам устойчивости двутавровых балок, то здесь величина критической нагрузки всегда определяется формулой такого вида:
Лф kVjF. (150)
) Это относится к случаям, представленным на диаграммах. Для чистого изгиба и для изгиба силой, приложенной на конце, мы обозначали через весь пролет и полагали
1 2С12 В (h2
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
349
Коэффициент к, как мы видели, зависит от величины у2 Dh2l2Cl2 Bh2ACl2. Причем, вычисляя k по первому приближению, можно заметить, что для больших значений у, т. е. для малых величин 1у2, k меняется приблизительно пропорционально у, для малых же значений у или для больших значений 1у2 к меняется очень медленно, асимптотически приближаясь к значению к для полосы. На основании этих соображений можем заключить, что для малых значений 1у2 сила Якр, а следовательно, и соответствующие напряжения меняются пропорционально В, для больших же значений Iу2 сила Ркр пропорциональна У В. После этих предварительных замечаний перейдем к оценке устойчивости двутавровой балки за пределами упругости. Положим, что, производя опыт над устойчивостью балки, мы нашли, что критическое напряжение, т. е. наибольшее напряжение, соответствующее моменту отклонения балки от плоской формы изгиба, равно р'р, и пусть величина эта больше предела упругости. В таком случае мы можем утверждать, что, рассчитывая балку по нашим формулам, выведенным в предположении совершенной упругости материала, мы получили бы для критического напряжения значение кр, большее действительного '. Попробуем для каждого значения р'р установить величину отношения ркр : р'р на основании имеющихся опытов над продольным изгибом.
Как и в случае продольного изгиба, можно за пределами упругости вычислять критические напряжения по ранее выведенным формулам, но только нужно вместо постоянного модуля Е ввести переменный модуль Е зависящий от величины 'р. Раз меняется модуль, то вместе с тем меняется и В — величина, пропорциональная модулю, и к — зависящая от В. Начнем с того случая, когда изменением к можно пренебречь. Для каждого р' мы из опытов на продольный изгиб можем найти соответствующее значит, и уменьшение жесткости В. Чтобы формула (150) дала нам и за пределами упругости верные значения для критического напряжения, нужно вместо В вставить величину ВЕ'Е, другими словами, напряжения, получаемые по формулам, годным в пределах упругости, нужно помножить за пределами упругости на УЕ'Е, и, следовательно,
Пользуясь этим соотношением и таблицей Ф. С. Ясинского для критических напряжений, можно составить таблицу, где каждому значению кр, определенному по формулам, имеется
350
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
соответствующее значение р'р, т. е. действительное критическое напряжение (см. табл. XX).
Таблица XX Таблица XXI
Ркр»
кгсм
Ркр,
кгсм2
Ркр» кгсм2
Ркр,
кгсм2
Ркр»
кгсм2
ркр, кг см2
Ркр» кгсм2
Ркр,
кгсм2
2000
1900
5000
2680
2000
1860
7000
2570
2500
2120
6000
2790
2500
2020
10000
2710
3000
2290
7000
2860
3000
2140
13000
2790
3500
2420
8000
2930
3500
2230
20000
2890
4000
2530
10000
ЗОЮ
4000
2310
30000
3000
4500
2610
12000
3070
5000
2420
50000
3080
Мы считаем до сих пор k неизменяющимся. Возьмем теперь второй крайний случай, когда k изменяется пропорционально у, следовательно, пропорционально У В. В таком случае для получения действительных критических напряжений по формуле (150) нужно и k и У В уменьшить в отношении УЕ'Е, и, следовательно,
На основании этого соотношения составлена таблица XXI.
При больших значениях у2 следует пользоваться таблицей XX, так как в этом случае k мало меняется с изменением lу2. При малых величинах у2 нужно брать значение Ркр из таблицы XXI. Найдя величину р'р и исходя из определенной величины временного сопротивления, можно составить таблицу коэффициентов ср уменьшения допускаемого напряжения.
Все эти рассуждения построены на предположении, что и за пределами упругости напряжения от изгиба в полках балки могут быть определены по обычным формулам. Это будет правильно лишь при том условии, если момент инерции стенки мал по сравнению с моментом инерции полок. В противном случае мы получаем для напряжений в полках преувеличенные значения напряжений и, следовательно, действительные критические напряжения будут несколько больше вычисленных по таблице XX или XXI.
Этим мы заканчиваем исследование вопроса об устойчивости плоской формы изгиба балок. Вычисленные таблицы облегчают нахождение критических напряжений в отдельных частных случаях, и мы считаем, что в таком упрощенном виде поверка на устойчивость может быть введена в обычный расчет балок наряду с поверкой на прочность и на жесткость. Это, конечно,
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
351
должно несколько повлиять на выбор поперечных сечений балок, придется отдавать предпочтение балкам с широкими поясами. Они более устойчивы, и потому коэффициент уменьшения р допускаемого напряжения получается большим. Если по конструктивным соображениям ширина пояса не может быть увеличена, то тогда для увеличения ф придется дополнительными поперечными связями уменьшать свободную длину балки.
Отдел третий
УСТОЙЧИВОСТЬ СЖАТЫХ ПЛАСТИНОК
§ 28. Основные уравнения
Предположим, что пластинка подвергается действию сжимающих сил, расположенных в ее срединной плоскости. При увеличении этих сил можно достигнуть предела, когда плоская форма равновесия перестает быть устойчивой, пластинка выпучивается. Возможность этого явления, аналогичного продольному изгибу тонких стержней, должна быть принята во внимание при расчете конструкций, составленных из листов, например, при расчете сжатых поясов трубчатого, коробчатого и таврового поперечных сечений, при расчете толщины стенки клепаных двутавровых балок и т. д. Несмотря на всю практическую важность, вопрос об устойчивости сжатых пластинок теоретически исследован весьма мало1), а надлежаще поставленных опытов не имеется вовсе, так как весьма трудно практически осуществить заданные условия закрепления по контуру пластинки.
Инженеры-конструкторы при расчетах или пользуются неудовлетворительными эмпирическими формулами, составленными на основании старых опытов И. Ходкинсона, или же в запас прочности понижают допускаемые напряжения, как то рекомендует делать Ф. С. Ясинский. Для достижения надлежащей жесткости конструкции листы подкрепляют уголками жесткости, особыми диафрагмами и т. д.
Пользуясь новой методой, возможно несколько расширить область уже исследованных вопросов, относящихся к устойчивости пластинок, и таким образом получить некоторые практические указания относительно выбора толщины листов.
) Простейший случай выпучивания прямоугольной пластинки, опертой по контуру, разрешен G. Н. Вгуап’ом. См. его работу, цит. на стр. 211. Несколько более сложных задач исследовано в нашей работе «К вопросу об устойчивости сжатых пластинок». Известия Киевского политехнического института, 1907, год 7, книга 2, стр. 37—94.
352
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Мы ограничим наши исследования случаем прямоугольной пластинки. Длину и ширину пластинки обозначим через а и 6, толщину через б, жесткость при изгибе через С, тогда
C-Wbv 51
Координатные оси х и у будем располагать в срединной плоскости пластинки, как то показано на рис. 68. Нормальное напряжение по площадкам, перпендикулярным к оси jc-ob, обозначим чёрез Рiб. Соответствующее напряжение по площадкам, перпендикулярным к оси у-ов, будет Р2б, касательное напряжение Sб.
Если через w обозначить прогиб пластинки в какой-либо точке при выпучивании, то дифференциальное уравнение для искри-
вленной срединной поверхности напишется так:
dw. 0 d4w. dwA , d2w ,
L
п( dw I о dw. dw V дх z дх2 ду2 ду
дх2
P 2S0. (152)
Вопрос о нахождении критичеРис. 68. ского значения внешних сил сво¬
дится к интегрированию полученного уравнения. Интегрирование это было до сих пор выполнено лишь в случае, когда Р и Р2— постоянные величины и, кроме того, две взаимно противоположные стороны пластинки оперты. Если Pi и Р2 не постоянны, то уравнение (152) будет иметь переменные коэффициенты и интегрирование становится весьма сложным.
При пользовании новой методой для решения вопроса об устойчивости пластинки необходимо составить выражения изменения потенциальной энергии системы при выпучивании и работы Т внешних сил, соответствующей этому выпучиванию. Потенциальная энергия при выпучивании, очевидно, возрастет, к энергии сжатия присоединится энергия изгиба V, для которой можно воспользоваться готовым выражением
(153)
Очевидно, пока V Т при всяком возможном отклонении пластинки от плоской формы, форма эта будет устойчива. Критическое значение внешних сил найдется из уравнения Т V.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
353
§ 29. Прямоугольная пластинка с опертыми краями
Для этого случая искривленная форма равновесия может быть представлена в таком виде:
Рассмотрим случай сжатия пластинки усилиями Рь равномерно распределенными по сторонам х О и х а (случай Дж. Брайана). При выпучивании каждая пара взаимно противоположных точек, лежащих на нагруженных сторонах пластинки, сблизится на величину
и потому работа внешних сил при искривлении пластинки может быть представлена так:
Для определения Ркр нужно положить в выражении (157) п 1; что касается т, то его следует подобрать так, чтобы выражение
ш 2 S'413'11
(154)
m1 л 1
Вставляя это в выражение для V, получим
(155)
m1 п» 1
а
О
Ъ
а
(156)
О о
m1 п1
Сравнивая Т и V, получим
(157)
т1 п—1
т2 1 2
354
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
имело минимальное значение. Число т, как видно из общего выражения (154), определяет число полуволн, на которое подразделяется пластинка при выпучивании, и ат — длина одной полуволны. Пока длина пластинки мала, мы будем иметь одну полуволну, т 1, и на основании (158)
Ркр Ся2( -)2. (159)
Постепенно увеличивая длину пластинки а, мы достигаем предела, когда пластинка может принять форму с одной или двумя полуволнами при одном и том же значении Р. При дальнейшем увеличении а форма с двумя полуволнами появляется при меньших усилиях, чем форма с одной полуволной. Дальше возможны формы с тремя, четырьмя и т. д. полуволнами. Момент перехода от формы с т полуволнами к форме с т 1
полуволнами определяется равенством
т2л2 л2 2 Г (т I)2 л2 л2 2
а2 Ь2 ) а2 Ъ2 J
(т I)2 л2
откуда
а b m (m 1). (160)
Одну полуволну будем иметь при изменении а от нуля до b У 2, две полуволны — для Ъ У2 ab У6 и т. д.
При весьма большой длине пластинки т — большое число, и на основании (160) можно положить а Ьт, откуда ат К 6, т. е. длина каждой полуволны равна ширине пластинки. По заданным размерам пластинки мы, пользуясь уравне¬
нием (160), можем установить число полуволн для первой плоской формы равновесия.
Зная т, вычисляем РКр по формуле (158). Чтобы установить зависимость Ркр от отношения Ь : б, введем новую величину
РЬ2 _ 2РЬ2 (1 — о2) п п
— 53 (161)
Тогда критические напряжения представятся формулой
р- иЕ 62 Рр 6 12(1 -а2) Ь2 ‘
Принимая во внимание выражение для Ркр, заключаем, что величина U зависит лишь от соотношения между длиной и шириной пластинки, следовательно, при определенном отношении аb критические напряжения пропорциональны (66)2 (см. формулу (162)). Уменьшая в два раза толщину пластинки, мы тем самым в четыре раза уменьшаем ее сопротивление выпучиванию.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
355
Пользуясь формулами (158) и (161), мы составили нижеследующую таблицу значений U для различных аb. В таблице XXII даны также значения р1ф для случая 66100, Е 2-106 кгсм2, а 0,25.
Если в рассчитываемой пластинке Ь6 пу то для получения ркр нужно числа таблицы множить на величину Ю4п2. Для значений а больших, чем b У2, нет надобности вычислять величины U, так как при дальнейшем возрастании длины пластинка при выпучивании подразделяется на несколько полуволн. Каждая полуволна будет находиться в таких же условиях, как опертая по контуру пластинка длины X и ширины Ь.
Таблица XXII
а
Ъ
и
ркр кгсм2 при 66 100
а
т
и
кр, кгсм2 при 66 1Q0
0,5
61,7
1097
1,0
39,5
702
0,6
50,6
900
1,1
39,9
709
0,7
44,7
795
1,2
40,8
725
0,75
42,8
761
1,3
42,2
750
0,8
41,5
738
1,4
44,1
784
0,9
39,9
709
1,5
46,3
823
А
11
—г
тт
Я
Из таблицы видно, что значительным отклонениям величины ajb от единицы соответствуют малые изменения в значении 1ф; поэтому при достаточно длинных пластинках можно не определять числа полуволн m и положить, что U 39,5.
Если длинную сжатую пластинку желательно усилить приклепкой уголков жесткости, параллельных поперечным сторонам, то расстояние К между уголками нужно взять такое, чтобы Я b 2. Как видно из таблицы XXII, такое расположение уголков повышает сопротивление пластинки выпучиванию примерно на 13. Располагая уголки
наклонно или приклепывая уголок вдоль срединной оси пластинки, конечно, можно достигнуть большей жесткости.
В условиях только что рассмотренной пластинки будут находиться грани трубки квадратного поперечного сечения (рис. 69), сжатой силами, равномерно распределенными по
Рис. 69.
356
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
концам. При значительной длине а трубка будет в таких же условиях, как сжатый стежень. Критическое значение сжимающей силы найдется по формуле Эйлера
р _ EJn2 _ Ел2 2 ,я
КР — а2. а2 3 Соответствующее критическое напряжение будет
ЯкР Ел2 Ъ2
Р«р 4Ьд а2 6 Если длина трубки а не очень велика по сравнению с 6, то при малой толщине стенки 6 раньше искривления оси трубки может произойти выпучивание ее стенок. Полагая для этого случая
4 Сл2 Ел2 62
Р кр '
ЬЬ2
3(1 -а2) Ъ2
и приравнивая р значению критического напряжения, найденному из формулы Эйлера, получим такое соотношение между размерами трубки:
Ь2 62 (163)
2а2
(1 - а2) Ь2
Если 622а2 б2(1 — а2)62, то выпучивание стенок произойдет раньше искривления оси трубки.
Положим для железа предел упругости равным 2000 кгсм2, Е 2 -106 кгсм2, а 0,25; тогда предельное соотношение между
Ь и 6, при котором происходит выпучивание пластинки в пределах упругости, будет Ь8 59,2. На практике нередко приходится встречаться с случаями, когда Ь8 больше указанного предела и, следовательно, критические напряжения меньше 2000 кгсм2.
Рассмотрим теперь такую задачу. Прямоугольная пластинка с опертыми краями сжата усилиями, равномерно распределенными по срединной поверхности пластинки, параллельными оси х-ов и направленными к середине пластинки (рис. 70). Подобная задача поставлена, но не разрешена в старом издании курса А. Лява1).
Обозначим через q усилие, приходящееся на единицу
срединной поверхности пластинки; тогда дифференцильное
-а
) А. Е. Н. Love. A treatise on the mathematical theory of elasticity. Cam bridge, University Press, 1893, vol. 2, p. 306.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
357
уравнение (152) перепишется для рассматриваемого случая так ): „( d4w , п d4w. dw , d2w А Зд:4 дхду ду j дх2 0
Полагая w A sin(луb)f(x), мы придем к обыкновенному дифференциальному уравнению с переменными коэффициентами. Решить это уравнение и, следовательно, получить значение критического напряжения можно при помощи бесконечных рядов. Чтобы избежать связанных с этим длинных вычислений, применим новую методу.
При выпучивании пластинки потенциальная энергия деформации возрастает на величину V, определяемую формулой (153). Работа сжимающих сил имеет такое значение:
Ъ а2
т с хЩйхаУ-
О о
Сравнивая Т и V, получим уравнение для определения q. Как и в случае продольного изгиба, мы можем вычислить с достаточной для практики точностью величину критического напряжения, вставляя вместо общего выражения для w (см. формулу
(154)) его приближенное значение. Для упрощения выкладок ограничимся двумя первыми членами разложения и положим
oy sin-sini 1sin--). (164)
Вставляя это в выражение для V и Г, найдем
т Л2 Л2 - - Цг z2 (J- ).
Здесь через 2 обозначено отношение А : А.
Основное уравнение для определения критического напряжения напишется так:
Н±_ J__ J_2 22 (1 _УЯ
4 L 8 2я2 я2 г 2 8 2л2 J
п2СаЬ Г 1 . 1 2 2 9 , 1 21
“-8-1Ы -55-) 2 (-W-W) J
откуда величина критического сжимающего напряжения для х а2 будет
q а Сл2
W Jtf6 J 1 3_ 9_ 1_
8 2я2 я2 2 8 2я2
)
) Уравнение это доставлено для лерой половины пластинки.
358
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Для каждого частного значения alb нужно подобрать z таким образом, чтобы выражение (165) было минимумом. В случае alb 0 уравнение (165) совпадает с тем, что мы имели для продольного изгиба стержня под действием собственного веса. Этого, конечно, и нужно было ожидать, так как при 6 оо можно считать, что пластинка выпучивается по цилиндрической поверхности. Для удобства сравнения с ранее разобранным случаем (Дж. Брайана) введем обозначения:
7 _ Яа b2 _ qa __ UE б2
U 2 С ’ кр 26 12(1-а2) Т2 '
На основании (165) заключаем, что U зависит лишь от отношения длины пластинки к ее ширине и, следовательно, для
определенного значения аЬ критическое напряжение пропорционально 6262. Несколько значений для U, а также ркр для 66 100 приводим в таблице XXIII.
Взятая нами форма искривления (164) соответствует выпучиванию пластинки по одной полуволне. Увеличивая отношение а6, достигнем предела, когда первая искривленная форма равновесия будет иметь две полуволны, дальше будем получать формы с тремя, четырьмя и т. д. полуволнами. Для
двух полуволн можно искривленную форму равновесия представить так:
w sin--Л sin-. (166)
Вставляя это значение w в общие выражения для работы Т
и энергии изгиба V, получим
Г п-цЬЛг у'.
Для критического напряжения получим такое общее выражение:
с». (4 -ЙЧ16-Й’2
26 32а26 _L 4. -L 2 _ 102 '
16 4 2 9л5
Остается для каждого значения ajb подобрать z таким об¬
разом, чтобы qa26 было минимальным. В таблице XXIV при¬
Таблица XXIII
а
Ь
и
Ркр, кгсм' при Ы6100
0
оо
оо
0,5
188,4
3350
0,7
131,9
2345
1
102,6
1824
1,2
93,0
1650
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 359
водим значения U и значения критического напряжения для Ь6 100.
Таблица XXIV
ркр»
ркр,
а
и
кгсм2
а
и
кгсм2
Ъ
при
Ъ
при
66100
66-100
1
114,8
2040
1,5
74,3
1320
1.2
90,6
1610
2
64,7
1150
На рис. 71 нанесены кривые, представляющие изменения U в зависимости от отношения аb для первой и второй форм. Пересечением этих кривых определяется то соотношение между длиной и шириной пластинки (примерно аb 1,17), начиная с которого пластинка подразделяется на две полуволны. Дальнейших форм равновесия мы здесь не исследуем, опускаем также случай, когда пластинка сжимается усилиями в двух взаимно перпендикулярных направлениях; задача эта может быть исследована при помощи новой методы без особых затруднений.
Остановимся теперь на задаче, имеющей большое практическое значение: вычислим критические напряжения для прямоугольной
пластинки, опертой по контуру и изгиоаемои в плоскости контура усилиями, распределенными по поперечным сторонам (рис. 72) ). Дифференциальное уравнение равновесия (152) при этом распределении усилий напишется так:
) Для этой же задачи до сих пор имеется лишь приближенное решение, данное проф. Н. Reissner’oM (см. его статью «ОЬег die Knicksicherheit ebener Bleche». Zentralblatt der Bauverwaltung, 1909, Bd. 29, № 14, SS. 93—96). Г. Рейсснер полагает, что в случае изгиба величина наибольших напряжений, соответствующих моменту выпучивания, будет вдвое большей, чем для пластинки, имеющей вдвое меньшую ширину и находящейся в условиях задачи Дж. Брайана. Для получения критических напряжений по Г. Рейсснеру нужно числа таблицы XXII помножить на 8.
360
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
При помощи подстановки w A sin -f(y) мы приводим задачу к интегрированию дифференциального уравнения с переменными коэффициентами. Нам пришлось убедиться, что интегрирование этого уравнения способом бесконечных рядов представляет собой весьма сложную работу, так как ряды в нужных для практики пределах оказываются медленно сходящимися. Из произведенных вычислений выяснилось, что для квадратной пластинки U РЬ2С 240.
Вычислим величину критических напряжений при помощи новой методы. Положим, что длина пластинки такова, что при выпучивании получается лишь одна полуволна. На основании распределения внешних сил можно заключить, что искривленная форма будет несимметрична относительно срединной оси пластинки, параллельной оси я-ов. В качестве приближенного выражения для прогиба возьмем
Рис. 72.
w sin —р sin jSin--j.
Вставляя w в выражения для потенциальной энергии изгиба V и для работы Т внешних сил, получим
у-ЫИ±-Я(±-гП
т-т
о о
(168)
При составлении выражения для Т предположено, что усилия по поперечным сторонам пластинки распределены по закону Р( 1—yab). При а 12 будем иметь, очевидно, случай чистого изгиба; для а оо получаем равномерно распределенные сжимающие усилия (задача Дж. Брайана). Приравнивая работу внешних сил потенциальной энергии изгиба, получаем основное уравнение для определения критических напряжений
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
361
в такой форме:
Ыгт
откуда
Ся (1-Й г2(14) р а2. „ч , 1 322 9л2а
Для а оо получается результат Дж. Брайана (нужно положить z 0); для а 12 будем иметь
О»)
Теперь остается для каждого частного значения отношения аb выбрать z таким образом, чтобы РКр было минимумом. Поступая по обычным правилам нахождения минимума и максимума и обозначая для краткости ab i, найдем для Ркр выражение
PKP -L2(l(i2)(lV).
Для сравнения с предыдущими результатами будем определять вместо РКр величину U:
РкрЬ2 9л4 (1ц2)(14ц2)
С 32 ц2 Величина эта зависит лишь от соотношения между длиной и шириной пластинки.
Для наибольших напряжений, соответствующих моменту выпучивания, будем иметь такую формулу:
Р UC UE 62
Рк 6 “ Ь26 - 12(1 - а2) Ь2
При заданном соотношении аb величина критических напряжений пропорциональна квадрату отношения 8Ь. В таблице XXV мы приводим для ряда значений аb соответствующие величины U, а также рир для Ь6 100. Если рассчитываемая пластинка имеет отношение Ь6 т, то для получения ркр нужно числа таблицы XXV множить на величину 104т2; наименьшие напряжения будут соответствовать наименьшему U.
362
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Как легко видеть из формулы (170), минимум U будет при
V II V 12 0,707.
Таблица XXV
а
Ъ
и
Ркр, кгсм1 при 66 100
а
Т
и
ркр, кгсм2 при Ь6 100
0,2
826
14680
0,707
247
4390
0,4
325
5780
0,8
250
4440
0,5
274
4870
1,0
274
4870
0,6
253
4530
1,2
313
5560
Мы предполагали, что выпучивание пластинки происходит по одной полуволне. В случае значительной длины первая искривленная форма может иметь несколько полуволн, каждая из этих полуволн находится в таких же условиях, как только что рассмотренная пластинка. Чтобы упростить нахождение числа полуволн, на которое подразделяется пластинка при выпучивании, мы приводим рис. 73, в котором по оси абсцисс
отложены величины аb, по оси ординат — величины U для различного числа полуволн. При расчете, очевидно, нужно выбрать то число полуволн, которому соответствует наименьшее V. Из диаграммы видно, что с увеличением аb отклонения U от наименьшего значения U 247 все убывают, и потому для достаточно длинной пластинки можно положить
Ркр 4390 104.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
363
Выпучивание в пределах упругости возможно лишь при сравнительно тонких пластинках. Полагая для железа предел упругости равным 2000 кгсм2, найдем предельное отношение:
ъ _ inn т 4390 1AQ
6 V 2000
Рассмотрим теперь вопрос об устойчивости длинной прямоугольной пластинки, подвергающейся действию сдвигающих напряжений (рис. 74). Опыт показывает1), что и в этом случае
У
т
м
ъ 1 ♦
ГГ)
Р 7 I
I а
♦ X
—
— — -
—- А—►
Q
Рис. 74.
при увеличении касательных напряжений дальше известного предела плоская форма перестает быть устойчивой, пластинка выпучивается и при этом подразделяется узловыми линиями на ряд полуволн. Узловые лииии в данном случае уже не будут параллельны оси у, как это получалось в ранее рассмотренных задачах. Мы обозначим через а угол, составляемый этими линиями с осью х-ов.
Чтобы упростить задачу, будем считать пластинку весьма длинной. В таком случае при выборе искривленной формы равновесия придется принимать во внимание лишь условия на продольных сторонах пластинки. Для этих сторон в случае опертых краев будем иметь
Г d2W At
w 0; ду при у0 и Уь-
Если через X обозначить длину одной полуволны, то искривленную форму равновесия, получаемую опытным путем, можно аналитически2) представить так:
w A sin-y-sin (х ау). (171)
) W. Е. Lilly. Web stresses in plate girders. Engineering. 1907, vol. 83, February, pp. 136—139.
2) Мы выбираем форму так, чтобы были удовлетворены условия на контуре, и не исследуем вопроса относительно того, удовлетворяет ли выбранное значение w дифференциальному уравнению (152).
364 ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Всякое сечение этой поверхности плоскостью PQ, параллельной плоскости zx, будет представлять собой синусоиду.
Если предположить, что каждая точка срединной поверхности пластинки при выпучивании совершает лишь перемещение wt нормальное к плоскости ху, то сдвиг для какого-либо элемента тп может быть представлен формулой )
172)
Обозначим через Т6 величины сдвигающих напряжений по краям пластинки, тогда уменьшение потенциальной энергии сдвига при выпучивании можно представить так:
173
О о
Здесь через m обозначено число полуволн. Плоская форма равновесия перестает быть устойчивой, когда найденное выше уменьшение энергии сдвига как раз равно потенциальной энергии изгиба. Вставляя в общее выражение для энергии изгиба V принятое значение прогиба w и выполняя интегрирование, найдем
1'-Т5Г-6» 2 -х-1«). 174
Сравнивая V и 1Л, получим
г'--Щ6«г 2 Ж1“,)г- 075
Наименьшее значение для Т будем иметь в том случае, когда Х Ь 1 а2 и а V 2
Вставляя это в выражение для 71, найдем
Т 4 VI, U -я24 VI 55,8.
Критическое значение касательных напряжений будет
Т 62я24 У2 16 2
(Pt) кр ь22(—о2) 992 Ю4 jJ кг см2. (176)
) Результат этот получим, если в общих формулах для сдвига (см. цитируемую на стр. 219 книгу А. Лява, S. 592, 594, формулы (18) и (20;) положим перемещения и ни равными нулю.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
365
§ 30. Практические приложения полученных результатов
На основании полученных решений можно сделать некоторые заключения относительно выбора надлежащих размеров стенки клепаной двутавровой балки. Высота стенки балки обыкновенно назначается в зависимости от пролета. В мостовых продольных балках и в мостах со сплошной стенкой стремятся увеличивать высоту, чтобы этим уменьшить вес балки и увеличить ее жесткость. Уменьшение веса в данном случае является следствием принятого в настоящее время расчета. Пока не принимается во внимание устойчивость стенки, увеличение ее высоты за счет толщины дает увеличение прочности, так как при этом возрастает момент сопротивления поперечного сечения. Дальше мы увидим, что такое увеличение прочности иногда может быть только кажущимся и что на прочность существенным образом влияет отношение между высотой и толщиной стенки. Что касается жесткости балки, то ее стараются увеличивать, чтобы этим удовлетворить выставляемому обычно требованию относительно прогиба моста. Требование это объясняется желанием по возможности уменьшить влияние на напряжения динамических причин. Амплитуда колебаний, которые возникают в балке от перемещения нагрузки, будет действительно тем большая, чем меньше жесткость, чем больше максимальный статический прогиб, но вообще дополнительные напряжения, вызываемые колебаниями, невелики1), и в мостах малых пролетов ими можно пренебречь по сравнению с дополнительными напряжениями, зависящими от ударов колес о стыки и ударов изношенных бандажей. Напряжения от удара, конечно, будут тем большими, чем больше жесткость балки. Таким образом, стремление увеличивать высоту стенки является, на наш взгляд, недостаточно обоснованным, и если такое повышение балки не связывается с соответствующим утолщением стенки, то в результате получаются конструкции меньшей прочности, чем то следует из обычных расчетов. Для большей убедительности высказанного положения я приведу результаты старых опытов, произведенных бельгийским инженером М. Хуботтом в 1856— 1857 годах2). М. Хуботт изгибал клепаные двутавровые балки силой, приложенной посредине пролета, и нашел, что увеличение высоты стенки не только не повышает прочности балки, а даже уменьшает ее. Из двух балок одинакового пролета 1,5 м и с одинаковой толщиной стенки 0,5 см одна имела высоту 30 см, другая — 49 см. Момент сопротивления поперечного
) См. нашу работу «О вынужденных колебаниях призматических стержней». Известия Киевского политехнического института, 1909, год 9, книга 4, стр. 201—252.
2) М. Н о u b о 11 е. Versuche iiber die Festigkeit blecherner Trager. Der Civilingenieur, 1858, Bd. 4, SS. 98—102.
366
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
сечения более высокой балки был равен 1058 сж3, а для низкой — 524 см3. Следовательно, исходя из обычных способов расчета, нужно было ожидать, что более высокая балка будет вдвое прочнее низкой балки. Опыт дал совершенно иные результаты: высокая балка получила сильные искривления при нагрузке 24 т, низкая балка выдержала 27,5 т. Повышение стенки балки, увеличившее вдвое момент сопротивления поперечного сечения, сопровождалось в данном случае уменьшением прочности балки на 13. Как легко видеть из приведенных значений критической нагрузки, разрушение для обеих балок наступило при напряжениях значительно меньших временного сопротивления материала. Приложенные к опытам М. Хуботта рисунки изогнутых балок ясно показывают, что в данном случае материал балки не разрушился и сильное искривление явилось результатом выпучивания стенки1). Произведенных М. Хуботтом опытоп, конечно, весьма недостаточно, чтобы вывести практические заключения относительно надлежащего выбора соотношения между высотой и толщиной стенки, но все же они ясно показывают, что величина момента сопротивления недостаточно определяет прочность балки.
Остановимся теперь несколько подробнее на выборе толщины стенки. Обыкновенно при расчетах толщина стенки опре деляется путем поверки ее на наибольшие касательные напряжения. Если принять, что высота балки составляет определенную часть пролета и нагрузка пропорциональна пролету, то мы всегда будем получать для толщины стенки одну и ту же величину, и действительно для мостовых балок величина эта меняется в весьма небольших пределах: 10—12 мм. Толщину в
1 см берут и для низкой балки, и для балки высотой в 1,5 а(. Устойчивость стенки в обоих случаях будет, конечно, весьма различна. Недостаток устойчивости сравнительно тонкой стенки двутавровой балки стараются возместить на практике путем понижения допускаемых напряжений и введением дополнительных частей в виде вертикальных углов жесткости; в последнее же время замечается стремление к более полному исследованию вопроса устойчивости стенки двутавровой балки и роли уголков жесткости2).
J) Нужно отметить, что в описанных опытах стенка балок была в особенно невыгодных условиях, так как отсутствовали уголки жесткости и изгиб производился сосредоточенной силой.
2) Кроме цитированной выше работы проф. W. Е. Lilly отметим работу: Н. М. G i b b. A new method of proportioning webs and stiffeners in plate girders. Engineering, 1910, vol. 90, July 8, pp. 39—41. К сожалению, авторы эти не воспользовались работами своего соотечественника Дж. Брайана. Вместо того чтобы применить готовую формулу, проф. Ц. Лилли разыскивает величину критических напряжений для сжатой пластинки элементарным путем и приходит в заключение к неверной формуле.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
367
Если двумя вертикальными сечениями выделить часть вертикальной стенки балки у середины пролета, то при распределенной нагрузке она будет находиться в условиях, близких к случаю пластинки, изгибаемой в срединной плоскости. Величина критических напряжений может быть вычислена при помощи таблицы XXV. При езде поверху кроме изгибающих усилий, действующих по вертикальным краям выделенной части стенки, будут еще приложены некоторые давления по верхнему краю (рис. 75, а). Мы для упрощения задачи будем считать эти
усилия равномерно распределенными и обозначим через Q давление, приходящееся на единицу длины. В таком случае сжимающее напряжение по верхнему краю будет Q6. Усилия эти должны уравновеситься касательными напряжениями по вертикальным краям пластинки. Нормальные напряжения по горизонтальным площадкам будут изменяться по высоте балки; закон изменения представлен на рис. 75, Ь. Это обстоятельство делает задачу нахождения критических напряжений в данном случае весьма сложной, и мы для приблизительной оценки влияния давлений Q поступим так: приложим к нижнему краю пластинки усилия, равные и прямо противоположные усилиям Q (на рисунке усилия эти отмечены пунктиром). Это, конечно, ставит выделенную пластинку в более невыгодные условия, и вычисленные при этих условиях значения критических напряжений будут меньше действительных. Присоединением усилий по нижнему краю мы устраняем касательные напряжения и для вычисления критических напряжений можем воспользоваться формулами (168), нужно только в выражении для работы внешних сил присоединить член, соответствующий работе сил Q. При взятой для случая чистого изгиба форме выпучивания работа представится так:
ь)
И1МНМ HUHH
I I I I I I « I I I I I I I I I I I
Рис. 75.
)-жля(14г
368
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
и основное уравнение для ЯКр будет
тН1г) (1 4г
п2С “ 8
откуда
(1ц2)2 22 (14ц2)-м-4-г(1 4г2)
кР й — (177)
9л2 2
Здесь принято аЬ х и а 12 (случай чистого изгиба).
Остается для различных значений х и Qb2n2C подобрать значение z таким образом, чтобы Ркр имело минимальное значение. Предположим, что на протяжении одного метра поперечины передают стенке балки давление в Ют, тогда Q 100 кгсм и
Qb2 100 b2 12(1 - а2)
я2С 6 62 2 106я2 '
Полагая б 1 см и а 0,25, получим Q62 ft2 45 Л 1ЛЛ Q2 « от Ь 1СЛ
W теЖ8ТЖ 056 для й 100: 1с 1’27 для 'б
Вставляя это в выражение (177), найдем, что для Ь6 100
9п4С «А 0 поп 9л4С ,
кР-64а ’ ПРИ .8: Ркр -64Г17,7 при ц1.
Следовательно, соответствующие напряжения таблицы XXV придется уменьшать на 8—11,5. В случае Ь6 150
9,58 при ц 0,8 и Ркр . 14,75 при ц1,
т. е. напряжения, приведенные в таблице XXV, приходится уменьшать на 18—25.
Несмотря на весьма значительные уменьшения критических напряжений, все же величина их, как видно из таблицы, получается значительной, и потому поверку стенки на устойчивость посредине пролета придется делать лишь в случае большой высоты балки. Для упрощения задачи мы предположили равномерное распределение давлений Q. Рассмотрим теперь другой крайний случай—действие сосредоточенной силы. Некоторое
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
369
суждение о величине критическои нагрузки в этом случае можно составить на основании решения1), полученного для пластинки, сжимаемой двумя взаимно противоположными силами (рис. 76). В данном случае
п _ _ 4л62 6
'“р Ъ “ 12(1 -а2) Ь ' ио)
При толщине, равной 1 см, получим ЯКр 222-104бЬ кг.
Формула (178) выведена в предположении опертых краев. Так как стенки балки не могут свободно поворачиваться и имеется лишь одна сила Я, уравновешивающаяся касательными напряжениями по сечениям тп и т'п то надо полагать, что действительное значение РКр больше того, что мы получаем из формулы (178). Полученные результаты дают некоторое основание полагать, что в средней части пролета устойчивость стенки балки при выработанных практикой размерах является в достаточной степени обеспеченной.
В иных условиях находится часть стенки у опор. Здесь главное значение
имеют касательные напряжения, и мы для определения критического их значения можем воспользоваться результатом, полученным для случая чистого сдвига в срединной плоскости пластинки. Формула (176) выведена в предположении опертых краев и бесконечной длины пластинки. Применяя ее к поверке на устойчивость стенки балки, мы, конечно, будем получать для критических напряжений значения, меньшие действительных. Учесть это можно, понижая для данного случая коэффициент безопасности. Если допускать напряжения, равные половине (Pt) кр, получаемого из формулы (176), то для случая Ь6 100 найдем, что предельные касательные напряжения Rt 500 кгсм2 для Ь6 150 Rt 220 кгсм2.
Выше мы отмечали, что при обеспечении надлежащей устойчивости стенки двутавровой балки существенную роль играют уголки жесткости. Вес этих частей в мостах со сплошной стенкой весьма значителен2), и потому рациональное их расположение
1
- о -
а
j
г
1
А
'
Рис. 76.
’) См. работу A. Sommerfeld’a «Uber die Knicksicherheit der Stege von Walzwerkprofilen». Zeitschrift fur Mathematik und Physik, 1907, Bd. 4, Heft 2, SS. 113—153, и нашу работу «Einige Slabilitatsprobleme der Elastizitatstheorie». Zeitschrift fiir Mathematik und Physik, 1910, Bd. 58, Heft 4, SS. 337—385.
2) В американских мостах с пролетом 22 м вес уголков составляет 7з от
веса стенки. В английских мостах того же пролета вес уголков вдвое больще.
См. цитированную на стр. 336 работу Н. М. Gibb’a.
370
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
имеет большое практическое значение. Если мы возьмем среднюю часть балки, находящуюся в условиях, близких к чистому изгибу, то на основании вышесказанного можно утверждать, что вертикальные уголки жесткости не оказывают в этом месте существенного влияния на устойчивость стенки, так как пластинка при выпучивании подразделяется на участки вертикальными узловыми линиями, которые могут совпадать с линиями расположения уголков. У опор роль уголков значительно большая, но и здесь вертикальное их расположение следует признать нерациональным, гораздо выгоднее направить их перпендикулярно к тем узловым линиям, которыми пластинка подразделяется на отдельные полуволны при выпучивании под действием касательных напряжений.
Конечно, сделанных здесь заключений далеко не достаточно для полного решения вопроса о выборе размеров вертикальной стенки балок, но мы полагаем, что дальнейшие указания можно получить лишь путем опытного исследования изгиба клепаных балок. Несколько опытов, имеющих своей целью выяснение роли уголков жесткости, подготовляется в настоящее время в механической лаборатории Киевского политехникума.
§ 31. Прямоугольная пластинка с одним свободным краем
Предположим, что поперечные стороны пластинки (л; 0, х а) оперты, продольная сторона у b совершенно свободна от усилий (рис. 77). Что касается стороны у 0, то рассмотрим
задачу в трех предположениях: 1) сторона у 0 оперта, 2) сторона у 0 абсолютно заделана, и 3) сторона у 0 упруго заделана. Все эти задачи имеют некоторое практическое значение в связи с расчетом сжатых поясов таврового и коробчатого сечений. Сжимающие усилия будем Рис. 77. считать распределенными по по¬
перечным сторонам пластинки. При выпучивании пластинки эти усилия совершат некоторую работу Т. Величина критических напряжений найдется из того условия, что Т должно равняться изменению потенциальной энергии деформации V.
Начнем с того случая, когда продольная сторона у 0 оперта; тогда прогиб w и d2wdy2 должны быть равны нулю при
у 0. Относительно интенсивности Р сжимающих усилий, рас¬
пределенных по сторонам х 0 и а, предположим, 4TQ
У
1
ъ
1
1
а
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
371
она меняется по линейному закону и может быть представлена так:
При а оо получим равномерное распределение сжимающих усилий, полагая а 12, будем иметь случай чистого изгиба. Мы удовлетворим условиям на опертых сторонах, если положим wAysmnxla. Это равносильно предположению, что деформация пластинки состоит в поворачивании сечений х const относительно оси л:-ов.
Потенциальная энергия изгиба для выбранной формы равновесия получится из формулы (153):
Приравнивая Т вышенайденному значению потенциальной энергии, получим
Второй член в полученном для Р0 выражении не зависит от а, т. е. от длины пластинки; что касается первого, то он убывает с возрастанием длины. На основании этого можем сделать заключение, что при взятых условиях на контуре первая искривленная форма имеет одну полуволну. Вместо Pq введем прежнюю величину U:
Величина эта зависит лишь от отношений а6, и потому для заданного отношения ajb критические напряжения Ркр Р06
) Результат этот совершенно совпадает с тем, что было нами ранее получено путем интегрирования уравнения (152). См. формулу (14) на стр. 25 нашей работы, цитируемой на стр. 351,
Работа сжимающих сил при искривлении будет
а b
О О
Полагая а оо, найдем
(180)
372
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
будут пропорциональны 62Ь2. Ряд значений U и соответствующие Кр для случая Ь6 100 помещены в таблице XXVI.
Таблица XXVI
а
Ь
и
ркр, кгсм1
при Ы6 100
а
Ъ
и
Ркр. кгсм
при Ьб 100
1
14,21
252,6
2,5
6,02
107,0
1,2
11,20
199,1
3
5,56
98,9
1,4
9,40
167,1
4
5,09
90,5
1,6
8,24
146,5
5
4,88
86,8
1,8
7,45
132,5
8
4,64
82,5
2
6,89
122,5
10
4,59
81,6
—
—
—
сю
4,50
80,0
В таких условиях, как только что рассмотренная пластинка, находятся полки сжатого уголка BACEDF (рис. 78).
Постепенно увеличивая сжимающие усилия, равномерно распределенные по концам уголка, мы можем достигнуть предела,
когда плоская форма для полок уголка iU-U перестает быть устойчивой. Нетрудно
установить, при каком соотношении между размерами уголка а, Ь и б выпучивание полок произойдет ранее, нежели ilex' и кривление оси уголка.
Эйлерова нагрузка для уголка опре¬
делится по формуле
Ел2 6Ь3
F
—Ь
т
ъ
La
откуда
Рис. 78.
кр
Р кр
КР ш
12
Ел2 Ь2 аГ2Л
Приравнивая это результату, полученному выше для пластинки, мы при значительной длине а найдем
6С п v Ел2 Ь2 6 Ь
-гтг (1 — а) —5“ или -г —.
Ъ26 ' 1 а2 24 1 b а
Для 6Ь bа искривление уголка, как стержня, наступи ранее выпучивания полок.
Мы остановились на частном случае равномерного распределения сжимающих сил, чтобы путем сравнения с точным решением установить, насколько удовлетворительно выбрана нами искривленная форма равновесия.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
373
Сохраняя обозначение Ро для случая равномерного распределения сжимающих усилий, мы из уравнения (179) для более общего закона распределения найдем
' (181)
Р'о Ро
(Pf0 — интенсивность усилий и Р'сд — критическое напряжение для точки у 0.) На рис. 79 графически представлены распределения усилий для нескольких значений а.
Край
сбободен
Край Край свободен сдободен
Рп I Рп
Край
сдободен
Край Край Край
сдободен сдободен сдободен
Край оперт
ocJU I сс I Край оперт Край оперт
„. oc j J сс I ос0 I ос-1
Праи оперт Край оперт Край оперт Край оперт
Рис. 79.
В случае чистого изгиба критические напряжения Р'0д в два раза превосходят величину, полученную для равномерно распределенных сжимающих усилий. Для а 34 Р'0 оо — пластинка будет устойчива при всякой величине напряжений.
В большинстве технических задач продольная сторона пластинки, которую мы считали до сих пор опертой, соединена обыкновенно при помощи заклепок с другими частями конструкции. Хотя такое соединение и допускает некоторый поворот края пластинки, но все же свободное поворачивание затруднено. Появятся усилия, момент которых в каждой точке контура можно считать пропорциональным углу поворота. Обозначая через а коэффициент пропорциональности, получим
таШ,.л- 182
где т — момент усилий, приходящихся на единицу длины приклепанного края пластинки. Коэффициент а имеет различное значение в зависимости от способов закрепления. Рассмотрим здесь два наиболее часто встречающихся случая, именно случаи таврового и коробчатого сечений (рис. 80).
Край ВВ' свободен от всяких усилий; что же касается края ААто он склепан с поясными уголками. При выпучивании
374
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
вертикального листа таврового сечения (рис. 80, а) поясные уголки работают на кручение. Угол поворота ср какого-либо поперечного сечения уголков будет ср dwdy)y0. Следовательно, скручивающий момент в любом сечении может быть представлен формулой
Здесь через К обозначена жесткость кручения поясных уголков. При вычислении К можно пользоваться формулой, данной в § 14, к площади уголков следует присоединить и площадь зажатой между ними части вертикального листа. Дальше мы увидим, что
даже значительные погрешности в определении величины К не имеют существенного влияния на величину критических напряжений. Имея выражение для скручивающего момента М, находим момент т усилий, приходящихся на единицу края АА' пластинки. Очевидно,
В дальнейшем нам понадобится выражение для энергии кручения уголков Vi. Имея выражение для М, получим
а а
При выпучивании вертикальных листов коробчатого сечения поворачиванию приклепанного края листов будет препятствовать не только сопротивление кручению поясных уголков, но также и сопротивление изгибу горизонтальных листов АС. Выражение для момента усилий, соответствующих кручению, уже нами найдено выше; что же касается момента т от изгиба листа ЛС,
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 375
то, обозначая через С жесткость изгиба листа, через d расстояние между вертикальными листами и предполагая изгиб по цилиндрической поверхности, найдем
(184)
Следовательно, момент усилий, приходящихся на единицу приклепанного края пластинки, будет
„ dw . 2С, (dw
171 Шх дх2ду)ушо d ду)у-о’
и энергия деформации, соответствующая моменту заделки, будет
а
Vijr J (m ml)pdx
О
-«185
о
После этих предварительных замечаний переходим к исследованию устойчивости сжатой прямоугольной пластинки, одна из продольных сторон которой упруго заделана, другая свободна от всяких усилий. Положим, что при выпучивании пластинки получается одна полуволна, и возьмем для искривленной формы такое выражение:
w Ау Ах - cos(186)
При А 0 мы получим ранее рассмотренную форму равновесия, соответствующую опертому краю пластинки. При увеличении жесткости заделки увеличивается и значение отношения А:А. Момент усилий, приходящихся на единицу заделанного края, будет
( Ктс2. 2СЛ (dw , ( Кп2 , 2 С,. пх
m rrii (—-) (w)y_o А (— -) sin —.
Соответствующая энергия деформации определится формулой
а
А(Кл2 , 2С, ( „.„г ях Ага (Клг , 2С, Аа
У1 -2-1——JJ 5Ш ——(- —) —Y.
О
где y — величина, определяющая жесткость заделки.
Для случая таврового сечения придется положить С О, следовательно, у Кп2а2.
Для определения критического значения сжимающих усилий будем пользоваться прежним методом. Составим выражение для
376 ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
потенциальной энергии изгиба пластинки V и выражение для работы внешних сил при выпучивании Т. Основное уравнение для определения РКр напишется так:
T V Vj. (187)
Вставляя в общее выражение для потенциальной энергии изогнутой пластинки взятое нами выражение для w, найдем
4- A2J-(±-±)-I Ъ Iх н Ь. (1 — г) 1 ,
т Ча42 ab W я) 324 аЧ2л V
АА' it)1 4)
Работа сжимающих усилий Ркр, равномерно распределен¬
ных по поперечным сторонам, представится так:
а Ь
тA’b (-I)2АА‘ьг (т - 1Ш
О о
_ Рк2 4 а
Вставляя полученные результаты в основное уравнение (187) и вводя обозначения: ААЪ z, ab jlx, получим для критического значения сжимающих усилий Ркр такую формулу:
1 , 2(1-а) р _ Сл2 3
Ркр — а2
juEl „ 22 (А_ 1 jii_
л2 2 л 4 л 32 .
y2(1_4)22 (т-)
(188)
Для каждого частного значения х и у нужно выбрать z таким образом, чтобы Ркр получило минимальное значение.
Возьмем, например, случай квадратной пластинки (ji 1) и положим, что степень закрепления характеризуется величиной у bС 2; тогда получим
р Сл2 0,0205 0,4853 0,4285z2 0,8123z а2 0,3333 0,5372z 0,2268г2
Наименьшее значение для Р1ф будет
Якр -р-1.517, откуда С-- я2 1,517 14,97,
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
377
Точное решение задачи для данного случая дает ) U 14,75, следовательно, погрешность составляет около 1,5. Для jli 2 U 9,03, тогда как точное решение для этого случая дает U 8,84 — погрешность около 2.
Дальнейшие вычисления показали, что при малой жесткости закрепления для значений ybC 2 можно при определении Р1ф ограничиваться первым приближением и положить в общей формуле (188) 2 0; тогда
р -Сп2 I 1 9 ЧЬ Л
кр a2 L я2 С J
С увеличением жесткости заделки точность общей формулы понижается. Например, для ybC 8 получаем для пластинки с отношением аЬ 2 U 11,77; точное решение для этого случая U 11,10; погрешность составляет уже 6. Ниже мы приводим таблицы значений U и соответствующих критических напряжений для железных пластинок (Е 2 106 кгсм2, о 0,25),
Таблица XXVII (7 2)
а
и
ркр, кгсм2 при Ьб 100
и
РКр» кгсм
при Ыб 100
1
14,75
262,3
2,5
8,93
158,8
1,3
11,12
197,7
2,7
9,15
162,7
1,5
9,95
176,9
2,9
9,45
168,0
1,6
9,57
170,2
3,0
9,63
171,2
1,8
9,08
161,4
3,1
9,81
174,4
2,0
8,84
157,2
3,5
10,69
190,1
2,3
8,81
156,6
4
12,06
214,4
Таблица
XXVIII
и
РКР кг'см2
и —
и
Ркр. кгсм
ъ
при Ьб » ЮО
ь
при Ыб 100
1
15,57
276,8
2,3
11,63
206,8
1,3
12,31
218,9
2,5
12,17
216,4
1,5
11,41
202,9
2,7
12,83
228,1
1,8
10,99
195,4
3
14,03
249,5
2
11,10
197,4
4
19,45
345,8
1) См. таблицу II нашей работы, цитируемой на стр. 351.
за
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
у которых 66 100. Если у рассчитываемой пластинки Ь6 — т, то критические напряжения, приведенные в таблицах, должны быть помножены на 104 (66)2.
Из приведенных таблиц видно, что наименьшего значения критические напряжения достигают при вполне определенном соотношении между длиной и шириной пластинки. Длинная пластинка при выпучивании подразделится на несколько полуволн, и каждая полуволна будет в таких же условиях, как только что рассмотренная пластинка. Длина X одной полуволны будет зависеть от жесткости закрепления. Чем меньше величина ybС, тем X больше, и при ybC 0, т. е. при опертом краеД равно длине пластинки. При ybC 2 пластинка стремится разделиться на полуволны длиной X 2,26, так как этому соотношению соответствует наименьшее значение критического напряжения. Точно так же для ybС 8 наиболее невыгодный случай будет, когда X 1,8Ь.
Постепенно увеличивая жесткость заделки, мы в пределе получим пластинку с абсолютно заделанной продольной стороной. Эта задача также может быть исследована при помощи новой методы. Вполне удовлетворительные результаты получаются, если взять для прогиба выражение
w a (l-cos Ц) Л,(1-С08
Мы не приводим дальнейших выкладок и даем лишь окончательную таблицу значений U и кр для 66 100 ).
Таблица XXIX
а
и
ркр, кгсм2 при bб 100
и ь
и
Ркр. кгсм1 при ЬЬ — 100
1
16,76
298,0
1,8
13,24
235,4
1,1
15,41
274,0
1,9
13,43
238,8
1,2
14,47
257,3
2,0
13,67
243,1
1,3
13,88
246,8
2,1
14,01
249,1
1,4
13,45
239,1
2,2
14,35
255,1
1,5
13,20
234,7
2,3
14,76
262,4
1.6
13,13
233,5
2,4
15,21
270,4
1,635
13,11
233,1
2,5
15,73
279,7
1,7
13,15
233,8
Самое невыгодное соотношение между длиной и шириной пластинки, как видно из таблицы XXIX, будет а6 1,635. В случае большой длины пластинка стремится подразделиться на такое число полуволн, чтобы Хb 1,635. Заметим, что при изме¬
1) Таблица взята из нашей статьи, указанной на стр. 351.
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
379
нении ybC от 8 и до оо величина наименьшего значения U меняется от 10,99 до 13,11, т. е. за известными пределами изменения в жесткости заделки не оказывают существенного влияния на величину ркр.
Пользуясь полученными результатами, можно сделать некоторые практические заключения относительно устойчивости сжатых вертикальных листов тавровых и коробчатых поясов. Для тавровых поясов принято брать свободную ширину листа не больше 350 мм. При большей ширине лис.та свободный край его окаймляется особым уголком жесткости. Приняв толщину вертикального листа равной 10 мм, найдем, что предельное отношение Ь6 35. Что касается жесткости заделки, то в тавровых поясах обыкновенно у ЬС 81). В таком случае, как легко видеть из таблицы XXVIII, критическое напряжение для длинной пластинки будет ркр 195 104352 1590 кгсм2.
Если принять во внимание, что кроме основных напряжений в поясах моста возможны значительные дополнительные напряжения, обусловленные жесткостью узлов, то нужно признать, что общепринятыми расчетами далеко не всегда обеспечен надлежащий запас устойчивости тавровых поясов. Окаймляющие уголки, приклепываемые по нижнему свободному краю сжатого вертикального листа, обыкновенно не рассчитываются, между тем при недостаточных размерах влияние их на жесткость может оказаться незначительным, и вся конструкция получится неустойчивой. Для обеспечения надлежащей устойчивости следовало бы окаймляющий уголок с прилежащей к нему частью вертикального листа отдельно проверять на продольный изгиб.
Коробчатые пояса благодаря наличию диафрагм, окаймляющих уголков и соединительной решетки, связывающей нижние края сжатых вертикальных листов, обыкновенно значительно устойчивее тавровых.
Выясним отдельно роль каждой из этих связей. Диафрагмы ставятся обыкновенно на расстоянии от 2 до 3 метров, они связывают вертикальные листы, но на устойчивость их сами по себе могут влиять лишь в слабой степени. В самом деле, вертикальные листы на протяжении одной панели при выпучивании подразделяются на несколько полуволн. Если узловые линии этой искривленной поверхности случайно совпадут с сечениями, где предполагается поставить диафрагмы, то тогда диафрагмы не окажут на величину критического напряжения никакого влияния.
Обыкновенно же диафрагмы влияют на соотношение между длиной и шириной полуволн и этим повышают несколько критическое напряжение, но повышение это, как можно видеть из
) См. стр. 44 нашей статьи, указанной на стр. 351,
380
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
таблиц XXVII, XXVIII, XXIX, невелико. Значение диафрагм выясняется в связи с устойчивостью окаймляющих уголков. Чем диафрагмы расставлены чаще, тем меньше свободная длина уголка, тем больший запас устойчивости мы будем иметь. Рассчитывая окаймляющий уголок с прилежащей к нему частью вертикального листа на продольный изгиб, мы можем установить надлежащую связь между размерами уголка и расстоянием диафрагм друг от друга.
Относительно соединительной решетки заметим, что в тех случаях, когда она состоит лишь из распорок, поставленных на одну заклепку, влияние ее на устойчивость невелико, поясные уголки могут выпучиваться независимо один от другого. Решетка может иметь существенное значение и будет в состоянии отчасти заменять действие диафрагм лишь в том случае, когда кроме распорок имеются и раскосы, т. е. когда окаймляющие уголки с решеткой составляют одну жесткую систему.
Укрепив надежным образом нижний край сжатых вертикальных листов, мы их можем в дальнейшем проверять на устойчивость при помощи таблицы XXII, т. е. рассчитывать их, как пластинку с опертыми краями.
§ 32. Пластинка с заделанными продольными сторонами
Постепенно увеличивая жесткость закрепления верхнего и нижнего краев, мы в пределе придем к пластинке с абсолютно заделанными продольными сторонами. Поперечные стороны будем считать опертыми.
Сохраняя прежнее расположение координатных осей, получим такие условия на контуре:
w 0 и 4 0 ПРИ 0 и у Ь
л d2w А Л
w 0 и 0 при х 0 и х а.
Мы удовлетворим этим условиям, взяв для искривленной формы равновесия такое выражение:
w 1 — cos Л — cos-jjsin-.
Вставляя это в выражение для потенциальной энергии V и в выражение для работы внешних сил Г, мы из уравнения V Т
с большой точностью можем определить величину критических напряжений. Мы не приводим здесь дальнейших вычислений, так как для рассматриваемого случая нами ранее уже была со¬
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ 381
ставлена таблица значений U и р1ф. Результаты эти помещены в таблице XXX.
Таблица XXX
а
Т
и
рк р. кгсм при bб 100
а
Ъ
и
ркр, кгсм при Ы6 - 100
0,4
93,2
1657
0,8
72,0
1280
0,5
75,9
1350
0,9
77,3
1374
0,6
69,6
1237
1,0
84,6
1504
0,7
69,1
1229
1,5
141
2507
1
Наиболее невыгодное соотношение между длиной и шириной пластинки лежит в таких пределах: 0,6 аb 0,7. Длинная пластинка при сжатии стремится подразделиться на полуволны такой длины X, чтобы отношение Кb удовлетворяло вышенаписанному неравенству.
Отметим здесь результат, ясно видный из полученных до сих пор таблиц: чем жестче закрепления, тем большую величину имеют критические напряжения, и тем меньше длина волн, на которые подразделяется пластинка при выпучивании.
§ 33. Об устойчивости пластинок, сжатых за пределы упругости
Полученными выше таблицами можно пользоваться непосредственно лишь до тех пор, пока вычисляемые по ним напряжения рКр не превосходят предела упругости материала. За этими пределами вычисляемые по таблицам р1ф будут иметь преувеличенные значения, и их придется уменьшать. С такого рода уменьшением напряжений мы уже имели дело при расчете на продольный изгиб призматических стержней (см. § 12). За пределом упругости для получения критических напряжений приходилось в формуле Эйлера вместо первоначальной жесткости изгиба В вставлять уменьшенную жесткость В причем
В Ркр
Здесь 'р — действительные критические напряжения, определенные из опыта (мы пользовались таблицей Ф. С. Ясинского), рир — критические напряжения, определяемые по формуле Эйлера. Аналогичное явление мы будем иметь и при выпучивании пластинок. Положим, прямоугольная пластинка сжата за пределы упругости равномерно распределенными по поперечным сторонам усилиями Я, параллельными оси х-ов. Если эту пластинку начать гнуть по цилиндрической поверхности, образующие
382
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
которой перпендикулярны к оси х-ов, то жесткость изгиба окажется уменьшенной в отношении С С В'В р'ркр. При изгибе пластинки по цилиндрической поверхности, образующие которой параллельны оси х-ов, жесткость изгиба окажется неизмененной, равной С. В общем случае изгиба пластинки кривизна как в плоскости xz, так и в плоскости yz будет отлична от нуля, и при расчете следовало бы вместо жесткости изгиба вставить некоторое значение, среднее между С и С'. Во всех исследованных случаях выпучивания пластинок величина критического напряжения представляется такой формулой:
В силу вышевысказанных соображений будем пользоваться этой формулой и за пределами упругости, вставив вместо С под одним из радикалов величину С' тогда
и, следовательно,
Такое соотношение между действительным критическим напряжением и напряжением, вычисленным по формулам, приложимым в пределах упругости, мы уже получали при исследовании устойчивости двутавровых балок. Во втором отделе была приведена таблица XX, которой можно пользоваться и здесь для нахождения р'р. Конечно, такой способ вычисления можно рассматривать лишь как первое приближение. Для точного решения вопроса нужно исследовать задачу об устойчивости пластинки, жесткость которой меняется с изменением направления плоскости изгиба.
ЗАКЛЮЧЕНИЕ
Этим мы заканчиваем наше исследование по устойчивости упругих систем. Хотя собрание решенных задач получилось довольно обширным, но все же работа не может претендовать на полноту и не представляет собой исчерпывающего исследования по трактуемому вопросу. Некоторые задачи были нами только намечены и остались нерешенными. Целый ряд практически важных вопросов совсем не затронут в нашей работе. Несмотря на это, мы все же надеемся, что примененный нами метод исследования несколько облегчит дальнейшую работу и поможет в от¬
ис _ и У с V с Ркр ь2б ь26
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
т
дельных частных случаях найти удовлетворительные решения, годные для применения к практическим расчетам. Как новые результаты в нашем исследовании мы можем отметить:
В отделе I:
a) Таблица коэффициентов длины х для расчета сжатых поясов открытых мостов.
b) Исследование влияния смещения концов сжатых поясов при недостаточно жестких опорных стойках.
c) Расчетные формулы для проверки на продольный изгиб составных стержней.
d) Формула для проверки на продольный изгиб стержня с круговой осью.
В отделе II: Помещен ряд новых таблиц, облегчающих разыскание критических напряжений для двутавровых балок, изгибаемых в плоскости вертикальной стенки.
В отделе III:
a) Решена задача об устойчивости прямоугольной пластинки, сжимаемой силами, равномерно распределенными по срединной плоскости.
b) Исследован вопрос об устойчивости прямоугольной пластинки, изгибаемой в ее срединной плоскости.
c) Дана формула для проверки на устойчивость пластинки, испытывающей чистый сдвиг.
Для многих задач приведены таблицы критических напряжений, облегчающие применение полученных результатов к расчетам.
При составлении таблиц мне много помогал студент П. Е. Добровольский, за что считаю своим приятным долгом принести ему здесь глубокую благодарность.
Предлагая вниманию инженеров новые результаты, остается только пожелать, чтобы полученные формулы нашли применение в технических расчетах и, таким образом, способствовали выработке более рациональных конструкций.
Август, 1910 г.
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Einige Stabilitatsprobleme der Elastizitatstheorie. Zeitschrift fur Mathematik und Physik, 1910, Bd. 58, Heft 4, SS. 337—385. Sonderdruck: Leipzig, B. G. Teubner, 1910, 49 S. Перепечатка: S. P. Timoshenko. The collected papers. McGraw-Hill Publishing Company Ltd, New York—London—Toronto, 1953, pp. 1—50.
В инженерных сооружениях очень часто в качестве важных частей железных конструкций находят применение длинные призматические стержни и пластины. Толщина стенки пластин и размеры поперечного сечения стержней по отношению к длине являются малыми, и вследствие этого, как известно, некоторые формы упругого равновесия могут в результате оказаться неустойчивыми. Прямой стержень может искривиться именно под действием продольно направленной сжимающей силы, а пластина, нагруженная в срединной плоскости сжимающими силами, может выпучиться. При расчете важно заранее знать те значения внешних сил, которых они должны достичь для того, чтобы форма равновесия стала неустойчивой. И лишь после решения этого вопроса можно выносить правильное суждение
о степени безопасности конструкции.
В настоящей статье дается решение некоторых задач устойчивости; она распадается на следующие главы:
I глава: Продольный изгиб.
II глава: Об устойчивости прямоугольной пластины, нагруженной в своей плоскости сжимающими силами.
III глава: Устойчивость плоской формы равновесия двутавровых балок.
IV глава: Устойчивость цилиндрической оболочки, подверженной сжатию в направлении образующих.
Эти исследования были опубликованы на русском языке в 1905—1908 годах 1).
) С. П. Тимошенко. Об устойчивости плоской формы изгиба двутавровой балки под влиянием сил, действующих в плоскости ее наибольшей жесткости. Известия С.-Петербургского политехнического института, 1905, том 4, выпуск 3—4, стр. 151—219; 1906, том 5, выпуск 1—2, стр. 3—34, выпуск 3—4, стр. 263—292. С. П. Тимошенко. О продольном изгибе стержней в упругой среде. Там же, 1907, том 7, выпуск 1, стр. 145—157. С. П. Т имошенко. К вопросу об устойчивости сжатых пластииок. Известия Киевского политехнического института, 1907, год 7, книга 2, стр. 35—94. С. П. Тимошенко. К вопросу о продольном изгибе. Там же, 1908, год 8, книга 2, стр. 181—212.
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 385
I. ПРОДОЛЬНЫЙ ИЗГИБ
§ 1. Эйлерова критическая нагрузка
Если призматический стержень сжат между двумя плоскими поверхностями, то вопрос об устойчивости прямолинейной формы равновесия решается путем исследования выражения потенциальной энергии для прямолинейной и изогнутой форм равновесия. Расстояние между двумя концами стержня остается постоянным; тогда ось стержня должна при изгибе удлиняться, и, следовательно, энергия сжатия уменьшится. Если уменьшение этой энергии больше той энергии, которая соответствует изгибу стержня, то прямолинейная форма равновесия стержня неустойчива. Величина критической нагрузки будет определена, когда мы предположим, что энергия изгиба будет равна уменьшению энергии сжатия.
Обозначим через Е модуль Юнга, J — момент инерции, i — соответствующий радиус инерции и F — площадь поперечного сечения стержня.
Направим координатные оси согласно рис. 1 и обозначим через у прогиб стержня в некотором сечении тп тогда получим удлинение оси стержня при изгибе
Если Р — величина сжимающей силы, то уменьшение энергии сжатия при изгибе равно
4 V, P6l-ij()‘dx. (1)
Потенциальная энергия изгиба будет
«'-тгг-w»’'- 2
о е
В случае, когда оба конца свободно оперты, можно уравнение изогнутой оси написать в следующей форме:
т
J
' п -47'
в
S'
Рис. 1.
т оо
VI л 71JCJC
Zi т ®т 1 ♦
У т1
386 НЁКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Подставляя эту величину в выражения для 6Vi и бК2, получим
(3)
4
Полагая 6V 6V2, найдем критическую силу
EJ
р„- 2 (5)
Наименьшее значение критической силы получается, если взять первый член суммы (tn 1). В таком случае имеем
р _ EJn2
Кр — 2 (6)
Таким образом, мы пришли к известной формуле Эйлера.
Выше предполагалось, что концы стержня при изгибе друг по отношению к другу не сближаются. В этом случае изгиб влер чет за собой уменьшение продольно напра-
д вленной сжимающей силы Р. Последняя
А fa У формула также сохраняет силу, когда сжи мающая сила считается постоянной и пред-
I j полагается, что изгиб оси стержня приво-
I дит к сближению концов (рис. 2).
р Сближение концов 6 при малом изгибе
ь ь получается из формулы
61 Т J Ш dx 2FF Ш dx
Рис. 2. оо
Работа внешних сил, которая соответствует этому сближению концов стержня, равна
о о
Уменьшение потенциальной энергии сжатия при изгибе будет
w'-w)’
о
Потенциальная энергия изгиба будет определяться из формулы (2).
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 387
Для нахождения критической силы мы должны теперь составить следующее уравнение:
6T 6V2-6Vlt
или
тж)2(1х -ту’-1х’ 8
О о
откуда получается то же самое выражение для критической силы (6).
§ 2. Влияние поперечной силы. Устойчивость решетчатых стержней
При выводе формулы (6) поперечной силой Q Р dydx пренебрегалось. Для того чтобы при вычислении учесть поперечную силу, мы должны к правой части уравнения (8) добавить потенциальную энергию сдвига
i
Т Г kQ2 dx
aF J 2GT-
0
Здесь G — модуль сдвига, к — числовой коэффициент, который зависит от формы поперечного сечения. Уравнение для определения критической силы теперь мы должны записать в следующем виде:
т Ш dx -mi y2dx wl Щ dx (9)
о оо
Для случая свободно опертых концов полагаем у Ат sin , тогда для критической силы получим выражение
Р
-L А2 — У A2 (—Y ' EJ GF Z4 т I )
Наименьшее значение Р получается, когда под знаком суммы 2 оставляется только один член; в таком случае имеем
Ркр 12 „ 1 2 ' 7я2 GF я2 j2 ’
Для железа формула Эйлера применима только до тех пор,
когда li 100 или когда 2л22 1000. Так как 2,6х 10, то
388 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
влияние поперечной силы на величину критической нагрузки в случае сплошного стержня меньше 1.
Для решетчатого стержня влияние поперечной силы может быть много значительнее, и оно зависит от площади поперечного
сечения диагонали. На рис. 3, а показан решетчатый стержень квадратного поперечного сечения, а на рисунке
а)
Рис. 3.
3,6 — одна панель стержня. При воздействии поперечной силы Q образуется угол перекоса у прямоугольника ABCD:
(п)
АЁРЛ
I'd sirr a cos а
Здесь Fd означает площадь поперечного сечения диагонали. Полученное выражение для угла сдвига v следует подставить в формулу (10) вместо величины kQGF. Обозначая, далее,
4EFd sin2 a cos а Pd
и
и-р
мы должны записать формулу (10) следующим образом '):
кр
PePd Pe Pd
(12)
) Эта формула выведена проф. Л. Прандглем другим путем. См. L. Р г a n d 11. Knicksicherheit von Gitterstaben. Zeitschrifi des Vereines deutscher Ingenieure, 1907, Bd. 51, № 47, SS. 1867—1869. Перепечатка: L. P r a n d 11. Gesammelte Abhandlungen zur angewandten Mechanik, Hydro- und Aerodynamik. Springer-Verlag, Berlin—Gftttingen—Heidelberg, Erster Tei4, 1961,
SS. 87—93.)
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 389
§ 3. Устойчивость в упругой среде
Мы можем определить величину критической силы и формы выпучивания сжатого стержня, когда при изгибе появляются поперечные силы, которые непрерывно распределены по всей длине и в каждом поперечном сечении пропорциональны прогибу этого сечения. Если р — коэффициент пропорциональности, то поперечная сила на элемент dx стержня равна (рис. 4) ру dx.
Изменение потенциальной энергии, которое соответствует работе поперечных сил. будет
674
I
y2dx.
Потенциальная энергия изгиба равна
Уменьшение потенциальной энергии сжатия, когда расстояние между концами остается постоянным, таково:
V
Г ( dlJ У
2 J dx )
dx.
Для определения критической силы получим тогда следующее уравнение:
6VX-6V2 6VA.
. тлх Лт Sin Полагая для свободно опертых концов » Ап
-)4эЦ«
имеем
Р
(14)
Дальше будет показано, что наименьшее значение Р получается, когда стержень изгибается по синусоиде. В этом случае мы должны в формуле (14) под знаком суммы 2 оставить только один член. Примем еще, что первая форма выпучивания имеет т полуволн; тогда получим
р р г (tn27i2)2 k4l4
FhJ 22 (15)
где 4 р7.
Наибольшая длина стержня, при которой первая равновесная форма выпучивания состоит из т полуволн, будет,
399 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
разумеется, такой, при которой формула (15) дает одно и тоже значение Ркр независимо от того, разделяется стержень на т или на т 1 полуволн. Для определения нужно составить следующее уравнение:
(т2я2)2 k4A _ (т -f I)2 я22 kAlA 12т2я2 12(т )2 я2
откуда
2 -(т1)п. (16)
Если длина стержня велика, то число полуволн т также велико и длина одной полуволны с достаточной точностью может быть определена из следующей формулы:
I я Яу4
5«т яЫ (17)
Подставляя полученное значение lт в формулу (15), имеем
PK2EJk2Y4rEJ M¥-- (18
Вместо выпучивания по синусоиде примем общее выражение для выпученной оси; тогда соответствующее значение продольно направленной сжимающей силы Р будет всегда больше найденного значения ЯКр. В таком случае
1 (™f До сих пор мы молчаливо принимали, что р положительно. Если р отрицательно, то, беря под знаком суммы S только первый член, из формулы (14) получим наименьшее значение Р:
-§-. (19)
Эта формула может быть использована при вычислении критической угловой скорости волны, которая подвержена действию продольно направленных сжимающих сил. Обозначим через л массу единицы длины волны, тогда мы должны в формуле (19) вместо р ввести выражение —лй2, где Q — угловая скорость. Тогда получим
D Е1я2 о9 2
Ркр— п2
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 391
Выпучивание при отсутствии продольно направленных сжимающих сил возможно только тогда, когда
Из этого уравнения следует формула для критической угловой скорости:
Это значит, что критическая угловая скорость равна частоте поперечных колебаний волны.
Если вместо сжимающей силы действует продольно направленная растягивающая сила, то критическая угловая скорость увеличивается.
Формулы (17) и (18) могут быть использованы для расчета спаянных рельсов (продольно направленная сжимающая сила возникает в них при повышении температуры) и для расчета сжатых стержней, которые покоятся на упругом основании.
II. ОБ УСТОЙЧИВОСТИ ПРЯМОУГОЛЬНОЙ ПЛАСТИНЫ, НАГРУЖЕННОЙ В СВОЕЙ ПЛОСКОСТИ СЖИМАЮЩИМИ СИЛАМИ1)
§ 4. Дифференциальное уравнение задачи
До тех пор, пока сжимающие силы малы, плоская форма пластины является единственной и, следовательно, устойчивой формой равновесия. При возрастании сжимающих сил может быть достигнут предел, при котором возможна, кроме плоской, еще изогнутая форма равновесия пластины. Величина критической силы будет определена с помощью дифференциального уравнения изогнутой пластины. Срединную плоскость пластины примем за плоскость ху. Оси хну направим так, чтобы края пластины определялись прямыми х 0, х а, у 0, у Ь. Пусть 7 S и N — удельные силы (рис. 5, a) a G и Н — удельные моменты2) (рис. 5,6). Обозначая через w прогиб пластины
) Результаты, содержащиеся в §§ 6 и 7, совпадают в основном с теми, которые проф. Н. Reissner, конечно, независимо от этой статьи, основанной на русских работах автора, получил в статье «ОЬег die Knicksicherheit ebener Bleche». Zentralblatt der Bauverwaltung, 1909, Bd. 29, № 14, SS. 93—96.
2) Приняты обозначения A. E. H. Love. A treatise on the mathematical theory of elasticity. 2 edition, Cambridge, University Press, 1906. Перевод на немецкий язык в серии В. G. Teubner. Sammlung von Lehrbuchern auf dem Gebiete der mathematischen Wissenschaften (Bd. 25). A. E. H. Love. Lehrbuch der Elastizitat. Deutsche Ausgabe. Obersetzt von A. Timpe. Leipzig und Berlin, B. G. Teubner. 1907. Далее A. E. H. Love — A. Timpe.
(20)
392 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
и через С 6312(1 — а2) жесткость пластины (цилиндрмче ская жесткость), где б — толщина пластины, а а — коэффициент
Пуассона, для удельных моментов получим следующие выражения:
-с(.
d2w d2w дх2 а ду2 ) 1
п. _ п( dw , _ d2w
и2- с -г а
дх2 )
Ну — Н2 С — а)
d2w
дхЩ'
Состояние равновесия описывается следующими уравнениями:
дТх dS2
дх ду дх2 iV 1 дх ду дТ2 d2w d2w
d2w-Nl-4N2 X' 0,
dSi
дх
dNx
ду
dN2
дх
ду
(-
дх ду 1 1
d2w
Их2 S.
Ni-tN2 Y' о,
(-
ду
7'. s
дНх
дх
G
dGo
ду
, дх ду
n2 o, дх
ду2
2) 2' 0,
(1)
ду
-Nl 0,
d2w дх ду
— Go
d2w
дх ду
ы d2w , и d2w
ду2
Si S2 0.
(2)
Пренебрегаем членами, содержащими произведение частных производных от w тогда из системы уравнений (2) получим
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 393
Первые два уравнения системы (1) приближенно удовлетворяются, если положить
S S2 Т2 0. (4)
Что касается Ти то будем рассматривать задачу в предположении, что
Тх const - Р, X' Y' Z' 0. (5)
Тогда пластина будет сжата силами, которые равномерно распределены на сторонах х 0 и х а. Введем выражения для N и N2 согласно (3) в третье уравнение системы (1), тогда с учетом (4) и (5) получим следующее уравнение:
d4w 0 d4w d4w Ti d2w _
1 dx2dy2 C dxr U W
Для определения критической силы мы должны решить уравнение (6).
Будем различать следующие условия на краях:
I. На свободно опертом крае
w
Край параллелен оси у.
II. На защемленном крае
л dw л
w 0, ж0. S)
Край параллелен оси у.
III. На свободном крае
nld2w d2w_ дг. дН2 . ч
2 - дх2 а ду2 ) ’ 2 дх 0
Край параллелен оси х.
Последнее условие на основе первого уравнения системы (2) заменено следующим:
2 0. О')
§ 5. Пластина на всех краях оперта и сжата силами Р —Ти
равномерно распределенными на сторонах х 0, х а1)
В этом случае уравнение (6) следует записать так:
d4w 9 d4w. dAw. Р d2w _п ( дх4 Z дх2 ду2 ду4 С дх2 '
) G. Н. Bryan. On the stability of a plane plate under thrusts in its own plane, with application to the «buckling» of the side of a ship. Proceedings of the London Mathematical Society, Series 1, 1891, vol. 22, pp. 54—67-
394 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Условия на краях пластины будут удовлетворены, если примем, что
- . тлх . пли
уАтп
Внося это выражение в уравнение (6'), имеем
2 2
т2 п2 2
Р Сл2 —2 2 - -. v Ю)
Практически важно найти наименьшее значение Я, при котором возможно выпучивание. Для этого, естественно, полагаем п 1; что касается значения ш, то оно определяется с помощью следующих рассуждений. Примем, что при некоторой длине первая выпученная форма равновесия имеет т полуволн. Увеличивая длину а, мы можем достигнуть предела, при котором пластина будет подразделяться на т полуволн и т 1 полуволну. Длина пластины, которой соответствует это предельное состояние, находится из следующего уравнения:
(т2л2 л2 2 Г(т1)2я2 я22
1а» ЬЧ I а2 Ь2
т2л2 (т 1 )2 л2 9
откуда а Ъ У т т 1).
Эта формула определяет наибольшую длину, при которой первая выпученная форма равновесия имеет т полуволн. Мы будем иметь одну полуволну, когда длина находится в пределах от а 0 до а Ъ У2, две полуволны, когда длина оказывается в пределах от а ЬУ2 до а ЬУ, и т. д.
Если длина пластины велика, то т также является большим числом, и поэтому с достаточной точностью можно положить а Ьт.
При выпучивании пластина стремится разбиться на квадраты. Критическая сила определяется из уравнения (10), в котором принимается а Ьт и п 1,
Ркр Щг- (11)
Соответствующее этой критической силе напряжение равно
Ркр Ел2 62
Ркр 3 (1 - а2) Ь2 '
Именно при таких же условиях, как исследуемая пластина, будет находиться также каждая сторона трубы квадратного поперечного сечения (рис. 6).
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 395
Для длинной трубы интересно найти то отношение толщины
стенки б и ширины трубы 6, при котором выпучивание стенки
начинается раньше продольного изгиба трубы как стержня. Эйлерова критическая сила для стержня квадратного поперечного сечения длиной равна
р - т - . 2 дм
Г е 2 J 12 3 Соответствующее напряжение будет
р Ел2 г2
Ре 4Ь6 I2 6 Сравнивая это выражение с установленной прежде формулой (11'), получим
1 т
Если у —- “ q2) » Т0 спеРва наступает выпучивание
стенки трубы, а не продольный изгиб оси трубы.
Если желательно увеличить устойчивость трубы с помощью поперечной диафрагмы (что очень целесообразно), то следует взять расстояние между ними равным h b 12.
§ 6. Три края пластины оперты, сжимающие силы параллельны свободному краю
Края 0, х а и у 0 оперты, край у Ъ является свободным. Пластина на сторонах х 0 и х а сжата равномерно
распределенными силами (рис. 7). Для этого случая применимо также уравнение (6).
Граничные условия суть
л d2w d2w л л
W ’ дхтадуг при 0 И Х а (1и И); ay0; 4pL alF' 0 ПРИ У 0 (III и IV);
d2w d2w л д (d2w d2w , 01 ч d3w
W ater0, W adr) 2(1o)WMr:0
при yb (V и VI).
Условия I и II удовлетворяются выражением
f
Л ПТЛХ с - (у).
(12)
896 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Из уравнения (6') получим дифференциальное уравнение для определения f(y):
,,v to) - 2 (EL) ш (S.)' _ ()г f (,) _ 0. (,3,
Произвольные константы в общем интеграле этого уравнения
находятся из условий III, IV и V, VI на краях у 0 и у Ь. Условия III и IV дают С3 0, С — С2. Следовательно,
(у) A sh ay В sin у.
Из условий V и VI получим следующие уравнения:
Эти уравнения будут удовлетворены, если положить А В 0, но в этом случае для всей пластины f(y) 0, и мы получим плоскую форму равновесия. Для того чтобы было возможно выпучивание, необходимо детерминант системы уравнений (15)
Расчет показывает, что наименьшее значение сжимающей нагрузки, при котором имеет место выпучивание, получается при т 1, т. е. когда форма выпученной пластины представляется рис. 7. Внося в уравнение (16) вместо а и р их значения, полученные в предположении, что т 1, и обозначая
f (У) Се-аУ С2еаУ С3 cos §у С4 sin ру
(14)
Аа2 — сг sh ab — В р2 а sin рb 0, А,.(.)ch-
- р’ 2 (-)’-с (-)’ cos р» 0.
(15)
О
приравнять нулю, т. е. должно
выполняться следующее урав-
Р х нение:
Рис. 7.
а
p2r()2tgp. (16)
(17)
получим следующее уравнение:
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 397
Из этого уравнения в предположении произвольного значения Vy т. е. для произвольного отношения между а и Ьу получим различные значения U и, следовательно, ркр:
Ркр тт Е б2 — и 12(1-a2) (18)
Критическое напряжение при одном и том же отношении аЬ пропорционально отношению (8Ь)2. В приведенной дальше таблице А вычислены значения U и кр в предположении, что 66 0,01; при другом отношении между шириной и толщиной данные в таблице значения кр нужно умножить на коэффициент 10026262.
Таблица А
а
Ь
и
Ркр, кг1см (66 100)
а
b
и
ркр, кгсм2 (66 100)
1
14,21
252,6
2,5
6,02
107,0
1,2
11,20
199,1
3
5,56
98,9
1,4
9,40
167,1
4
5,09
90,5
1,6
8,24
146,5
5
4,88
86,8
1,8
7,45
132,5
8
4,64
82,5
2
6,89
122,5
10
4,59
81,6
С увеличением длины пластины отношение bа уменьшается и величина U достигает предельного значения 4,5. Это предельное значение легко находится из уравнения (16). Значение U может быть получено с достаточной точностью из следующей формулы: U V 4,5. Стороны сжатого железного уголка находятся в подобных условиях, как и исследованная выше пластина, когда края ЛС, АВ,
DE и DF (рис. 8) свободно оперты.
Легко установить соотношения между длиной и размерами Ь и б, при которых сопротивление пластин уголка выпучиванию равно сопротивлению всего уголка по отношению к продольному изгибу.
Эйлерова критическая сила уголка равна
р Ел2 663 Ге- 2 12 »
соответствующее критическое напряжение будет Рр Ел2 Ъ2
Реа
е
2ЬЬ
I2 24
Полагая величину ре равной величине кр, которую определяем из формулы (18) в предположении, что U 4,5, найдем Ь8 ЦЬ.
398 П 1лКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
§ 7. Края х 0 и х а оперты, край у О защемлен, край у b свободен
Сжимающие силы Ti — Р равномерно распределены на краях х 0 и х а. Основное уравнение и условия I, II на
краях х 0 и х а, а также условия V, VI на крае у Ь
остаются теми же самыми; для края у 0 мы должны положить w 0 и dwdy 0. Примем для w прежнее выражение, тогда на основе вышеприведенного условия на крае у — 0 для произвольных констант общего интеграла (14) получим выражения
г _ аС3 рС4 п аС3 — Р4
2а 9 2 2а
Функция f(y) может быть выражена в следующей форме:
f (у) A (cos P - ch ay) В (sin 0г - sh ay.
Из условий V и VI на крае у Ь следуют уравнения
А р2 а (-)2 cos рb а2 - а (-)2 ch аб
В р2 а (-)2 sin рб 1 а2 - а (-)2 sh ab 0,
А - Ь а2 - а ()2 sin рб а р2 а (L)2 sh ab вр а2 - от (-)2 cospft р р2 a ch ab 0.
Для того чтобы была возможна выпученная форма равновесия пластины, детерминант этих уравнений должен быть равен нулю; и если это так, то имеем необходимое условие для определения критических значений сжимающей силы. Если
. 0о , тл 2 о ттс 2
'Ра1—) и а-(—)
то детерминант можно представить в следующей форме:
2ts (s2 rf2)cos,pcha6 1 s- - sinpft shaft. (19)
При m 1 и различных значениях отношения bа из уравнения (19) можно определить соответствующие значения U и, следовательно, рКр (см формулу (18)). Ряд корней уравнения (19), так же как и значения кр при 6Ь 0,01, приведены в таблице В; при других отношениях между толщиной и шириной пластины нужно числа таблицы В умножить на коэффициент 10026262.
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 399
Таблица В
а
Ъ
и
ркр, кгсм2 (дб - 100)
а
Ъ
и
ркр, кгсм (М-100)
1
16,76
298,0
1,8
13,24
235,4
1,1
15,41
274,0
1,9
13,43
238,8
1,2
14,47
257,3
2,0
13,67
243,1
1,3
13,88
246,8
2,1
14,01
249,1
1,4
13,45
239,1
2,2
14,35
255,1
1,5
13,20
234,7
2,3
14,76
262,4
1,6
13,13
233,5
2,4
15,21
270,4
1,635
13,11
233,1
—
—
_
1,7
13,15
233,8
2,5
15,73
279,7
Расчеты показывают, что наименьшее значение критического напряжения соответствует отношению аb 1,635; из этого следует, что длинная сжатая пластина стремится разделиться на такое число волн, чтобы отношение между длиной полуволны и шириной пластины по возможности было бы близко к значению 1,635. Система кривых т 1, т
2,. на рисунке ) (диаграмма к таблице В) изображает зависимость между длиной полуволны, числом т и значением U. Нижняя часть кривой т определяет значение критического напряжения при произвольном отношении аb. Из рисунка легко видно, что с ростом аb значение U все меньше отличается от 13,11.
В условиях, подобных только что рассмотренной пластине, находится стенка железного тавра сжатого пояса моста (рис. 9). Здесь 6Ь 140; тогда длина пластины велика по сравнению с шириной, так что в этом случае можно принять с достаточной точностью, что U 13,11. Согласно таблице В критическое напряжение равно тогда Кр 233« ЮО2 1402 1460 кгсм2. Для того чтобы увеличить сопротивление выпучиванию, необходимо, чтобы вертикальная пластина была подкреплена на свободных краях при помощи уголкового железа.
§ 8. Влияние упругого защемления на крае у 0
В предшествующей задаче мы принимали, что край пластины у 0 абсолютно защемлен и поэтому (dwdy)y 0 0. В практике, однако, нельзя найти абсолютно жесткого защемления, но
п
,ОЛЩО ,
0,2 0,2 1,27
-50,71,27 Рис. 9.
х) Этот рисунок в опубликованной работе не приведен.
400 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
наблюдается нечто среднее между опертым и защемленным краями. Длинный край пластины (несвободный) будет посредством рядов заклепок присоединен к другой части конструкции. Такой род соединения может быть принят по своей природе то опертым, то защемленным, в зависимости от жесткости части, к которой приклепывается край пластины. Если эта часть очень жесткая, то можно рассматривать край пластины как защемленный; если же она податливая, то характер этого соединения примерно такой же самый, как в случае опертых краев. Для того чтобы оценить влияние упругого защемления, рассмотрим простейший случай, когда при выпучивании пластины момент G2, возникающий на защемленном крае, изменяется по закону G2 a(dwdy). Это позволяет реализовать следующий способ рассуждений.
Две вертикальные пластины ABCD и EFGH соединены друг с другом расположенной посредине полосой, которая изображена плоскостью ABFE (рис. 10, а). Сжимающие силы равномерно распределены на свободно опертых краях AD, ВС, ЕН
и FG. Когда сжимающие силы превышают известный предел, то вертикальные пластины могут выпучиться и П-образное поперечное сечение деформируется, как показано на рис. 10,6. На краях АВ и FE выпученной вертикальной пластины появляются моменты G2, которые в каждом поперечном сечении пропорциональны углу т. Обозначая через d расстояние между вертикальными пластинами и через С изгибную жесткость полосы пластины, которая связывает вертикальные пластины, получим тогда для момента G2 следующее выражение:
При определении критического напряжения необходимы уравнение (6 ) и прежнее выражение (12) для w.
Условия I и II на краях х 0 и х а, а также условия V и VI на крае у b остаются такими же, как и в § 7. Для края у 0 имеют место условия
Рис. 10.
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 401
откуда
2
где ы — постоянная.
На основе условия на крае у 0 для произвольных постоянных общего решения (14) получим следующие соотношения:
Г — Сз (а2 Р2 Иа) _ с с Сз Р2 Ев) I с
1 2р,а 2а ’ 23 2ца 2а Следовательно,
f (у) A cos Р - а sh ay - ch а г В sin 0г sh си.
Полагая ы оо, получим для f(y) выражение предыдущего параграфа. Для свободного края у b имеют место два следующих уравнения:
А (t cos fib 5 ch ab 4- qs sh ab) В (t sin fib - s sh ab'j « 0,
A (— fis sin p sh ab qat ch ab В (fis cos fib pt ch ab) 0.
Здесь введены обозначения:
, 4 q2 , it2 2 я2 a2 82
P2 a —;г, 5 a2 — a —г, q .
1 a2 a2 ’ ap,
Выпучивание может иметь место только тогда, когда детерминант этих уравнений равен нулю. Это условие служит для определения критического напряжения.
Мы вычислили ряд значений U для различных величин отношения аb для Ь 2 и xb 8. Эти результаты представлены в таблицах С и D; там даны также значения критического напряжения для случая 6Ь 0,01. Из таблиц видно, как с увеличением коэффициента защемления jli значение U и, следовательно, также Кр приближаются к значениям таблицы В для пластины с абсолютно защемленным краем.
Таблица С (jj, 2)
а
Ъ
и
РКУ кгсм (Ь6 100)
а
Ь
и
ркр, кг 1см2 (Ь6 100)
1
14,75
262,3
2,5
8,93
158,8
1,3
11,12
197,7
2,7
9,15
162,7
1,5
9,95
176,9
2,9
9,45
168,0
1,6
9,57
170,2
3
9,63
171,2
1,8
9,08
161,4
3,1
9,81
174,4
2
8,84
157,2
3,4
10,69
190,1
2,3
8,81
156,6
4
12,06
214,4
402 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Таблица D (х.Ь 8)
а
Ъ
и
ркр. кгсм2 (Ьб - 100)
а
Ъ
и
ркр. кгЮм1 (bб - 100)
1
15,57
276,8
2,3
11,63
206,8
1,3
12,31
218,9
2,5
12,17
216,4
1,5
11,41
202,9
2,7
12,83
228,1
1,8
10,99
195,4
3
14,03
249,5
2
11,10
197,4
4
19,45
345,8
Именно в условиях, подобных рассмотренным, находятся вертикальные пластины сжатого пояса моста, поперечное сечение которого представлено на рис. 11. Длина пластины равна 386 см.
Жесткость защемления, с одной 45720,953 стороны, зависит от жесткости
' ' горизонтальных пластин и, с дру¬
гой стороны, от жесткости же'8,898,890953 лезных уголков. Для горизонталь¬
ных пластин соответствующий '45,720,953 коэффициент жесткости i' опре¬
деляется на основе формулы (20):
пг пг
-25,4-
, С’ 2
I сЧ'
Рис. п. Когда горизонтальные пластины
имеют ту же толщину, как и вертикальные пластины, можно полагать С' 2С, и х'Ь 2 2 «7,2. Соединительные железные уголки увеличивают жесткость защемления, поэтому выпучивание вертикальных пластин сопровождается кручением уголков. Момент G2, который зависит от жесткости уголка, пропорционален dwdy. В самом деле, угол закручивания железного уголка в произвольном поперечном сечении определяется по формуле
г-(
d2w
дх ду Jyie0
Величина Т изменяется по длине уголка, это изменение обусловливает существование момента G2- Если К — жесткость уголка на кручение, то
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 403
Коэффициент защемления, обусловленный жесткостью уголка, равен
К т2п2 гмч
Ц2 -с—. (21)
Согласно приближенной формуле Сен-Венана в предположении, что вертикальные пластины при выпучивании разделяются на четыре полуволны, получим jli 2,33Ь. Суммарный коэффициент
защемления равен ы р jj 9,5Ь. Из таблицы D для ab 3864-45,7 2,1 принимаем
TJ 11 о 200-1002 (0,953)2 , «
f 11,3 И Ркр (45 7)2 870 кгсм
Истинное значение ркр несколько больше, потому что таблица D вычислена для xb 8.
§ 9. Края х 0 и х а оперты; края у 0 и у Ь защемлены
Сжимающие силы Т — Р распределены равномерно по краям х 0 и х а.
Уравнение (6') применимо также и в этом случае; условия на краях х 0 и х а остаются прежними. Что касается краеа у 0 и у Ь, то для них имеют место условия w 0, dwdy 0.
Для определения критического напряжения необходимо определить корни трансцендентного уравнения
(cos р b — ch ab)2 — (sin рб — sh ab j (sin p j sh ab j. (22)
Мы нашли несколько корней для различных значений аЬ они указаны в таблице Е; там даны также значения р1ф, соответствующие отношению 6Ь 0,01.
Таблица Е1)
а
Ъ
и
ркр, кгсм2
а
Ъ
и
Ркр. кгсм2
0,4
93,2
1657
0,8
72,0
1280
0,5
75,9
1350
0,9
77,3
1374
0,6
69,6
1237
1
84,6
1504
0,7
69,1
1229
1,5
141
2507
) Значение критического напряжения ркр кгсм2 вычислено при 66100: Е
2
106 кгсм2.
404 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Из таблицы видно, что самое неблагоприятное соотношение alb между размерами пластины расположено в пределах от 0,6 до 0,7:
0,6 у 0,7. (23)
При выпучивании удлиненные сжатые пластины будут разделяться, очевидно, на полуволны так, чтобы условие (23) удовлетворялось. Критическое напряжение можно получить с достаточной точностью, полагая приближенно U равным 69.
§ 10. Устойчивость прямоугольной пластины, сжатой сосредоточенными силами
Мы уже исследовали некоторые случаи выпучивания прямоугольных пластин под действием равномерно распределенной на краях нагрузки. Однако когда пластина сжата сосредоточенными силами, то задача много сложнее, так как удельные усилия для различных точек пластины не остаются постоянными
и уравнение (6) будет иметь переменные коэффициенты. Здесь мы хотим привести приближенное решение для одного специального случая, который был исследован профессором А. Зоммерфельдом ).
Прямоугольная пластина, опертая на краях, сжата дву-
У мя противоположными, прилорис 12. женными в середине длинных
сторон, силами Р (рис. 12). Как только силы Р достигают определенной границы, плоская форма равновесия пластины становится неустойчивой, и пластина выпучивается. Величина критической нагрузки может быть приближенно определена из следующих соображений. При выпучивании пластины точки приложения сил Р будут несколько сближаться и, следовательно, силы Р будут производить определенную работу. Одновременно и величина потенциальной энергии деформированной пластины также изменяется. Это изменение касается главным образом энергии изгиба. Полагая работу сил Р равной энергии изгиба выпученной
l) A. Sommerfeld. Ober die Knicksicherheit der Stege von Walzwerkprofilen. Zeitschrift fur Mathematik und Physik, 1906, Bd. 54, Heft 2, SS. 113— 153. См. также A. Sommerfeld. Nachtrag und Berichtigung zu der Abhandlung: Ober die Knicksicherheit der Stege von Walzwerkprofilen. Там же, 1906, Bd. 54, Heft 3, SS. 318—324.
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 405
пластины, получим в результате уравнение для определения РКрСчитая изменение потенциальной энергии пластины равным только энергии изгиба, получим таким путем некоторое достаточно точное значение Ркр. В действительности, однако, задача много сложнее, так как выпучивание пластины, наряду с изгибом, сопровождается изменением деформаций и сдвигов срединной поверхности.
Условия на опертых краях удовлетворяются следующим выражением:
щ Y1 А тпх А w-sm-f 2j т (А)
т 1, 3, б,.
Потенциальная энергия изгиба выпученной пластины равна
Взаимное сближение 66 точек приложения сил Р определяется из следующей формулы:
- Т (lrL« аа -. у.
Соответствующая работа на этом перемещении равна Рп2
4 Ь
(Л,-Лз Л5-
Приравнивая эту работу потенциальной энергии изгиба (24), получим уравнение для определения критической силы Р:
Рп2
4 Ъ
Отсюда следует:
(A,-A, As- (25)
СпЧЬ' St'T' 'F') А’“
2 (Ai — Л3 А5 —. )2
Ркр 2 (А, — А, А-.— . Л2 (26)
Для того чтобы это выражение имело минимум, произвольные коэффициенты Ат должны иметь вид
V л2 (- -L2 А.-(-1 Г — ,1V I г- (27)
406 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Подставляя величину Ат согласно (27) в выражение (26), получим критическую силу
Ся2аЬ2 1
Р,
КР 2 V 1
Обозначая через отношение длины пластины к ее ширине, найдем х аb. Тогда имеем
-ТГ X- ' . (28)
(ц2 т2)2
т»1, 3, 5,.
Для определения критической силы мы должны также найти сумму бесконечного ряда в знаменателе1). Разложим ch яг2 в бесконечное произведение:
После логарифмирования этого выражения и дифференцирования следует:
4thlT 2(l z2 9 г2 25 г2 )3
1
JmJ т2 г2
m-1,3, 5,.
Дифференцируя обе части этого уравнения, найдем л2 1 VI 1 2z2
(29)
® ch2 — т2 z2 Ашк (т2 z2)2
2 1,3,5. т1,3,5,.
После умножения на г, принимая во внимание выражение (29), получим
(30)
Посредством таблиц гиперболических функций легко, пользуясь формулой (30), вычислить значение Рир при различных jli. Заметим, что сумма
S.
(ц2 т2)2
т1, 3, 5,.
) Способ суммирования был указан мне проф. В. П. Ермаковым.
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 407
с ростом длины пластины очень быстро приближается к своему предельному значению я8, а критическая сила — к своему предельному значению, равному Ркр Для ji alb 2 указанная сумма равна 0,973 я8.
Вычисленное по формуле (28) значение критической силы будет, вероятно, меньше действительного, и разница между вычисленным и действительным значениями Ркр для более коротких пластин будет более значительной. Насколько близко отражает полученная формула действительное положение, можно судить только на основе эксперимента. (Ряд таких опытов недавно производился в механической лаборатории Высшей технической школы в Киеве1).)
Мы решили задачу, принимая для w выражение (А). Выберем для w общее выражение
w
, sin
sin
rrny
aV
8p
-та
J
Рис. 13.
Можно доказать, что наименьшее значение критической силы получается при определенном значении п когда аЬу то п 1.
Мы предположим, что все края пластины свободно оперты; значение критической силы может быть также приближенно вычислено, когда удлиненные края пластины защемлены. Для этого случая
и при у Ь.
Эти условия удовлетворены, когда w 1 — cos
2яг V л гппх
—2j Am sin —
b I 44 m'
m-1, 3,5,.
Потенциальная энергия изгиба в этом случае равна т n4abC V т2. 4 2 „2
8 L lirftS’j Am-
т-1, 3, 5,.
Сближение сжимающих сил при выпучивании пластины равно
бb.JfAt-A3 As-.)2.
1) Киевский политехнический институт.
408 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
S (I
Полагая работу сил Р равной потенциальной энергии изгиба, получим следующее уравнение:
Ря (А — ;43 А5 —.)2 _ пАаЬС Ъ 8
m-I, 3, 5,.
Соотношение между отдельными коэффициентами Ат остается тем же самым, и поэтому
о _ Си2 кр “Г (2)2 у г 1 V
2и L т2 (2ц)2 J
т-1, 3, 5,.
При значительной длине на основе (30) получим
п _ Ся2 8 _ 8яС 01Ч
Ь я Ъ ' Заметим, что формула (28) вполне точна, когда сжимающие силы действуют только на бесконечно узкую полосу; в таком случае задача заключается в том, чтобы определить критическую нагрузку для этой полосы при условии, что незаштрихованная часть (рис. 13) препятствует выпучиванию полосы.
III. УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ РАВНОВЕСИЯ ДВУТАВРОВЫХ БАЛОК1)
§11. Введение
Термином «опрокидывание» проф. Л. Прандтль характеризует явление неустойчивости, которое наступает у стержней, поперечное сечение которых обладает двумя весьма различными главными моментами инерции, когда эти стержни подвергаются действию поперечных нагрузок в направлении наибольшей жесткости. Следует отметить, что в этом случае отклонение стержня вбок всегда связано с закручиванием его.
Проф. Л. Прандтль определил значение критической нагрузки при опрокидывании для одного специального случая действия сил2), при этом было рассмотрено прямоугольное поперечное
) Здесь я хотел бы выразить сердечную благодарность проф. Л. Прандтлю зв многообразную помощь при решении задачи об устойчивости двутавровых балок.
2) L. Prandtl. Kipperscheinungen. Ein Fall von instabilem elastischem Gleichgewicht. Dissertation der Universitat Munchen, 1899. Niirenberg, 1900, SS. 1—75. Перепечатка: L. Prandtl. Gesammelte Abhandlungen zur angewandte Mechanik, Hydro- und Aerodynamik. Erster Teil. Springer-Verlag, Berjn — Gottingen — Heidelberg, 1961, SS. 10—74.
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 409
сечение стержня. Для практики очень важно результат, полученный проф. Л. Прандтлем, распространить на случай двутавровых балок. Двутавровые балки находят частое применение в инженерных сооружениях, так как их форма поперечного сечения очень выгодна с точки зрения распределения материала. Стремление достичь по возможности большей экономии материала при возможно большей жесткости приводит неизбежным образом к балкам большей высоты. Ширина пояса из конструктивных соображений не может быть значительно увеличена, и поэтому получается балка с большой жесткостью в вертикальной плоскости и с малой жесткостью в перпендикулярном направлении.
Такая балка при действии сил, лежащих в вертикальной плоскости, оказывается неустойчивой. Для того чтобы предотвратить выпучивание вертикальных листов, они укрепляются путем приклепывания уголков жесткости. Однако эти уголки не предотвращают состояние опрокидывания, как видно из рис. 14.
Опрокидывание балок сопровождается кручением, и поэтому, прежде чем построить необходимое дифференциальное уравнение задачи, следует сперва вывести формулу, устанавливающую связь между углом закручивания ф и величиной крутящего момента М.
§ 12. Кручение двутавровой балки моментом, приложенным на конце
Для поперечного сечения, далеко удаленного от места защемления, имеем
М-С, (1)
где С означает крутильную жесткость балки. Если поперечное сечение расположено у защемленного края, то для этого поперечного сечения формула (1) неприменима, так как при
410 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
кручении полки претерпевают изгиб. Влияние изгиба можно принять в расчет следующим образом. Пусть у— прогиб полки в направлении, параллельном плоскости ху (рис. 15). Тогда у (Л2)ф, а поперечная сила в произвольном поперечном сечении полки вычисляется по формуле
Q dM —) dy — D 3(P
45 J-Я О
dx3
dx3
(2)
где D означает изгибную жесткость полки в плоскости ху.
Добавим к моменту чистого кручения момент поперечных сил, тогда для определения угла закручивания получим уравнение
d(p , Dh2 dф
м — С
dx
dx3
(3)
2 С
Вводя обозначение и принимая во внимание условия
на концах балки:
при х 0 ф 0 и р' 0,
при х I ф 0,
получим решение уравнения (3) в следующей форме:
(4)
Для х 0 имеем ф0 — а th—j. Второй член в скобках
характеризует влияние изгиба полок на величину угла закручи¬
вания. Вообще, если отношение а значительно больше единицы, то можно также с достаточной точностью принять
Влияние защемления конца является таким, как если бы балка имела вместо длины длину — а.
Формула (4) проверена опытом. Сначала констатируем, что при определении С для практических целей с достаточной точностью применима формула Сен-Венана 1)
г- GF4 U “ 4л2 ’
) А. Е. Н. Love — A. Timpe, книга, указанная на стр. 391, S. 376.
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 411
где G — модуль сдвига, F — площадь поперечного сечения, J — момент инерции. Для того чтобы в процессе опыта осуществить абсолютно жесткое защемление конца балки, двутавровая балка была нагружена в середине крутящим моментом (рис. 16).
Вследствие симметрии среднее поперечное сечение балки при кручении остается плоским. Угол закручивания поперечного сечения на различных расстояниях от середины балки замерялся посредством зеркального аппарата. Опыты с достаточной точностью подтвеждают формулу (4). (Отклонение в общем составляет не более 4 ))
§ 13. Формулировка основных уравнений
Расположим начало координат xyz в центре тяжести поперечного сечения левого конца балки. Первоначально прямую ось балки примем за ось х, оси у и z направим согласно рис. 17.
Кроме неподвижной системы координат xyz возьмем еще подвижную систему координатт. Начало этой системы координат
должно располагаться всегда в центре тяжести произвольного поперечного сечения балки; ось g направлена по касательной к изогнутой оси балки, оси ц и совпадают с главными осями инерции поперечного сечения.
1) Подробнее см. в статье автора «Об устойчивости плоской формы изгиба двутавровой балки под влиянием сил, действующих в плоскости ее наибольшей жесткости». Известия С.-Петербургского политехнического института. Отд. оттиск, СПб., 19Q6, 132 стр.
412 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСРИ
Кривизны оси балки в плоскостях gr и будут определяться по формулам
. d
W'
dl2'
При малых деформациях кривизны в плоскостях ху и хг будут определяться из выражений
d2r
W'
d2y , d2z
, u_, __
T ,1 r2 ctlz dy2
d2z
dx2
d2y
dx2
Обозначим через Мл, моменты внешних сил относительно осей, г,; эти моменты действуют на левую часть балки. Тогда получим следующие уравнения:
о и и j d2z
2 dl2 2 dx2 ‘ db
Mi в2 45- Rn (Х м -
ф)»
(6)
Здесь через Вi и Вг обозначена изгибная жесткость в плоскостях г и. При выводе принималось, что В2 и С малы по сравнению е В.
В дальнейшем мы используем уравнения (5), когда вместо. введвм их значения.
§ 14. Изгиб парой сил
Балка изгибается по концам приложенными парами сил М М Ph в плоскости ж (рис. 18). Концы балки закреплены так, что они свободно поворачиваются относительно осей ц и; тогда
—1
Р
п
т
h
V
Р
Рис. 18.
при увеличении М достигается предел, при котором, кроме плоской изогнутой формы равновесия, возможна пространственно искривленная форма равновесия, как видно из рис, 18,
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 413
В уравнения (5) введем следующие значения моментов:
Тогда получим следующие уравнения:
-»)
Так как отношение B2Bi является малой величиной, то, вводя обозначения
2С 1 2М 1
Dh2 ' а2 ’ DB2h2 d4 ’ W
получим дифференциальное уравнение для определения р:
1 „ 1
Ф,у-4-Ф,,-гФ 0,
откуда
Ф » A sin ах В cos ах Се С2“Рдс» (7)
где Произвольные постоянные Л, В, Сь С2 находятся из условий на концах балки:
при х 0 ф 0, ф 0; при ф 0, ф 0.
Из условий при л: 0 следует: В 0, Ci С2. Из условий при х I вытекают уравнения
A sin al С sh р — 0, — Аа2 sin а Ср2 sh р — 0.
Эти уравнения удовлетворяются, когда А С 0. В этом случае, однако, для всех сечений балки ф 0 и она имеет плоскую форму равновесия. Для того чтобы была возможна искривленная пространственная форма равновесия, необходимо, чтобы детерминант вышеупомянутого уравнения был равен нулю, или sin al 0. Следовательно, а I tin, где п — целое число. Первая возможная неплоская искривленная форма равновесия соответствует случаю, для которого искривленная ось балки не имеет точки перегиба, т. е. когда п 1.
Если вместо а ввести ее величину, то получим уравнение для определения критического значения изгибающего момента:
--Й- т7 у-'Л (8)
414 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Отношение 2а2 зависит только от размеров балки и упругих свойств материала и может быть вычислено для данной балки на основе выражений (6). (Значение С определяется по приближенной формуле Сен-Венана.) Затем выписываем значение 44, которое зависит от изгибающего момента; в результате из уравнения (8) определяем изгибающий момент.
Полагаем отношение (lAd4):(l2a2) равным k. Тогда на основе
соотношений (6) получим kVB_ (g)
Af,
кр '
Для определения Мкр удобно в каждом частном случае пользоваться таблицей А, в которой даны значения k для различных значений 2а2.
Таблица А1)
JL
a
I
d
PKp, кгсм
1а а2
1« d
k:
Ркр, кгсм2
0,1
98,4
984
495
16
255,3
16,0
800
2
117,2
58,6
540
20
294,8
14,7
860
4
136,9
34,2
585
24
334,3
13,9
915
6
156,6
26,1
625
28
373,8
13,4
935
8
176,4
22,1
665
32
413,3
12,9
1015
10
196,1
19,6
700
36
452,7
12,6
1065
12
215,9
18,0
735
40
492,2
12,3
1110
) Значение
критического напряжения ркр кгсм2
вычислено при B2Bi 0,01; hl 0,1; E
: 2 10® кгсм2.
— 0,01;
Е 2. 106 кгсм2.
В таблице А указаны также значения наибольших растягивающих (сжимающих) напряжений кр, соответствующих Мкр. Эти напряжения вычислены для частного случая, когда
В2
В1
Значение ркр при других соотношениях между размерами балки легко определяется. В самом деле,
MKph k h
pKP ITT 27; г
Вводим вместо С ее значение из формулы (б) и учитываем, что для двутавровой балки имеет место приближенная зависимость EJ 1
D —2 2 82- Тогда формулу для ркр можно представить в следующей форме:
у 0,1;
Ркр :
kE I 4
I J2 (hy а , W ) 9
(10)
ИЁКОТОРЫЁ ТЕОРЕТИЧЁСКИЕ ПРОБЛЁМЫ УПРУГОЙ УСТОЙЧИВОСТИ 415
т. е. для определенного значения 1а и, следовательно, также значения k напряжение ркр пропорционально отношению 21 и квадрату отношения hl. Если для некоторой балки 21 1т и (hl)2 1я, то, умножая числа таблицы А на (100т) (100я), получим ркр. Было принято, что концы балки при изгибе могут
поворачиваться вокруг оси I. Если это не так, то для определе¬
ния произвольных констант общего интеграла (7) служат следующие условия:
при х 0 ф 0, ф' 0;
при х 1 ф 0, ф' 0.
Эти условия определяют, как и в прежнем случае, значение JVKp. Первая неплоская искривленная форма равновесия следует из уравнения а 2я. Теперь придем к следующей формуле:
Ряд значений kr и р' дан в таблице В.
Таблица В1)
JL
а2
d
Л'2
р'кр, кгсм
2
аа
1 d4
k'2
Ркр, кгсм2
0,1
1 563
15 630
1 980
14
2 112
151
2 300
1
1 598
1 598
2 000
16
2 191
138
2 345
2
1 638
819
2 025
20
2 349
117
2 425
4
1 717
429
2 070
24
2 507
104
2 505
6
1 795
299
2 120
28
2 664
95,2
2 580
8
1 874
234
2 165
32
2 822
88,2
2 655
10
1 954
195
2210
36
2 980
82,8
2 730
12
2 033
169
2 255
40
3 138
78,5
2 800
Значение
критического напряжения р' кгсм2
вычислено при 52В1 0,01; hl 0,1; Е
:2 Ю6 кгсм2.
Заметим, что, если положить D 0, т. е. если под балкой подразумевать только вертикальную стенку, справедливо следующее уравнение:
и критическое значение изгибающего момента определяется из следующих формул:
416 НЁКОТОРЫЁ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
для свободно опертых краев
м
кр
nV вгс
I
для защемленных краев
МКр
2я V В2С
I
Точно так же просто, как и при изгибе парами сил, решить задачу об изгибе балки под действием двух противоположно направленных растягивающих или сжимающих сил, параллельных оси балки.
§ 15. Балка, заделанная на одном конце и нагруженная сосредоточенной силой на другом
Точка приложения поперечной силы Р совпадает с центром тяжести поперечного сечения. Сила действует в срединной плоскости вертикального листа и направлена перпендикулярно к оси балки. Начало координат хуг перенесем в точку приложения силы, ось х направим прямо по оси балки, а ось г вдоль силы Я,
При постепенном увеличении силы Р можно достигнуть границы, при которой плоская форма равновесия перестает быть устойчивой, балка опрокидывается, как видно из рис. 19. Далее выберем вспомогательную систему координат g, rj,, тогда для произвольного поперечного сечения балки в случае малых кривизн существуют зависимости
м1р(ух)' Мп-Рх, Mt Px ф.
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 41
Внося эти выражения в уравнения (5), имеем
Вг-РЩ. В-Рх.
Отсюда получим уравнение для определения р:
Р2х2 „ . Dh2 IV 10Ч
-g—ф-Сф —PIV. (12)
Полагая в этом уравнении D 0, т. е. пренебрегая изгибом полок, придем к случаю, изученному проф. Л. Прандтлем, об изгибе стержня прямоугольного поперечного сечения. Если уравнение (12) разделить на коэффициент при ф1У, то получим
ф1у--ф--ф 0, (12')
где
J_ _2C_ _2Р2 _1_
a2 Dh2 ’ DB2h2 Ь
Решение уравнения (12) будем проводить в форме бесконечного ряда
Ф А0 АХ А2Х2.
Вводя это выражение в уравнение (12'), найдем зависимость между коэффициентами Л0, Аи.общий интеграл уравнения (12) представим в следующей форме:
Ф Фо Щ Фо N ± ф2 Q Фо'3 Р, (14)
где ф0, фр,. — значения угла закручивания и производных от него по х при х 0; М, N,. — бесконечные ряды, располо женные по возрастающим степеням х2.
Первая производная по хот выражения (14) будет
Ф' ТФо m Фо S J Фо' t1 l 'х2 Т.
Произвольные постоянные ф0 и ф определяются из условий на концах балки.
Так как на правом конце (х 0) изгибающий и крутящий моменты отсутствуют, то
Ф 0, -Сф0' ф'-0.
Для защемленного конца балки (х I) имеют место следующие условия:
Ф в Ф 0-
418 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Эти условия с учетом условий при х 0 позволяют теперь записать:
фо'фщт-Ь0-
(15)
ф0Пч5;-5-т,о.
Вышеупомянутые уравнения удовлетворяются, если положить Ф0 Фо 0; однако тогда для всей балки ф 0, и мы получим, таким образом, плоскую форму равновесия. Для того чтобы была возможна неплоская искривленная форма равновесия, необходимо детерминант уравнений (15) положить равным нулю, т. е. должно быть
Mt St Г - , n 0. (16)
Заметим, что бесконечные ряды М,, Nh. содержат только различные степени 2а2 и 666. Из формул (13) можно для заданной балки заранее вычислить величину 12а2. Тогда величина 666, которая зависит от поперечной силы Р и, следовательно, также и от критического значения РНр, определяется путем решения трансцендентного уравнения (16). Обозначая (l6b6): (l2a2) k, с учетом (13) найдем
Лф kVC (17)
Для вычисления Ркр составлена таблица С, в которой для ряда значений Ра2 даны соответствующие значения k2.
Таблица С1)
JL
а3
6 Ъ8
k2
Ркр. кгсм
JL
а2
в
ь
k2
РКр, кгсм2
0,1
196
1960
700
10
575
57,5
1200
1
247
247
785
12
623
51,9
1250
2
296
148
860
14
678
48,4
1300
3
342
114
925
16
725
45,3
1345
4
381
95,3
975
24
918
38,3
1515
6
453
75,5
1065
32
1100
34,4
1660
8
516
64,5
1140
) Значение
критического напряжения рк0 кгсм2
вычислено при В21ВХ — 0У01; Л 0,1;
2- Юб кгсм2.
Числовой пример. С помощью таблицы С определим критическую нагрузку балки из листового железа длиной
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 419
5 м и поперечного сечения, изображенного ниже. Имеем (рис. 20)
Ji 27 900 см4, 2 287 см4, р ( 2 28 200 см4,
F 76,1 см2,
QF 8 105 (76,1)4 ) п EJ2 Р 4С Р -
40Jp 40 282 102 ’ 2 ’ a2 EJ2 А2
Для этого значения 2а2 таблица С дает р'кр 1350 кгсм2. Критическое напряжение балки равно
Ркр РкР ' 100 100 77 (т)2 1390 кгсм2-
Для значений, лежащих вне пределов таблицы С, величину k можно с достаточной точностью определять по приближенной формуле
‘-ttSf- о» НГ,
Эта формула основана на следующих соображениях. Для балки прямоугольного поперечного сечения проф. JI. Прандтль нашел
и a mo W 4,013 У ВС
k 4,013 и РКр j2— 6 6 0,3 — 500,8
JL
Для того чтобы принять во внимание жесткость полок, мы должны использовать формулу (4') Рис. 20.
и вместо действительной длины балки ввести фиктивную длину — а. При этой длине балка со свободными концами имеет тот же самый угол закручивания, который наблюдается в балке с одним защемленным концом (см. § И), Так как длина в этой формуле для критической нагрузки входит во второй степени, то приходим, таким образом, к формуле (18). Стоит заметить, что формула (17) неприменима, когда точка приложения силы не совпадает с центром тяжести поперечного сечения. При повышении точки приложения нагрузки критическое значение нагрузки Ркр уменьшается, при понижении точки приложения — увеличивается.
§16. Балка, нагруженная сосредоточенной силой в середине пролета
Точка приложения сосредоточенной силы расположена в центре тяжести поперечного сечения посредине пролета, а сила стремится изогнуть балку в плоскости ее наибольшей жесткости. При увеличении силы 2Р может быть достигнуто такое предельное
) Опыты, проведенные на клепаной балке из листового железа, показывают, что в этом случае приближенная формула Сен-Венана также применима.
420 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
состояние, когда плоская изогнутая форма равновесия перестает быть устойчивой и балка должна опрокинуться (рис. 21).
Проведем оси координат xyz согласно рис. 21 и рассмотрим левую половину балки; тогда для нее можно использовать
Г 1
9-. Л,
2Р 1 Я
1
о
1, 1 -1
о л
Рис. 21.
вышеустановленное общее решение (14). При определении произвольных констант необходимо вывести выражение для прогиба балки у и его производной у'. Из второго уравнения (И) следует, что
В2у - Рх р0 М ф' N -g- ф' 3 Р j-.
Это выражение интегрируем дважды:
у'х Фо ft ¥ох Чох3 у о,
У - - Фо 11 ф И ТФо3 ху'о У О-
Здесь С,., G — бесконечные ряды, расположенные по возрастающим степеням х2.
Для определения постоянных интегрирования имеем следующие условия:
при х 0 1) ф0 0; 2)y0d; 3) Яу0 Сф'---ф';
при » 4) 0; б) у 0; 6) ФО.
Значения у0 и у'0 можно из условий 3) и 5) выразить через ф' и фо; если эти значения ввести в условие 4), то найдем
- Щ I, — ф ЕЬ - ф Q,
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 421
Добавляя еще условие 6), которое может быть написано следующим образом:
Ф уЧЛП-о,
получим два уравнения с двумя неизвестными и (р'0. Для того чтобы было возможно опрокидывание, необходимо детерминант этих уравнений приравнять нулю; следовательно,
0Ь -ffiSlrQ. (19)
В вышеупомянутом уравнении имеются только следующие величины:
I2 2 С 2 РЧ2
а2 Dh2 И 6е “ DBh1 '
Величину 12а2 можно для данной балки вычислить заранее, тогда уравнение (19) будет служить для вычисления 16Ьв. Если ввести обозначение (l6b6): (Ра2) k2, то получим, что
„ _ kVec
Кр J2.
Заметим, что здесь Я1ф есть половина поперечной сосредоточенной силы и — половина длины балки.
В таблице D представлены значения k2 для различных значений 2а2 и значения кр для В2В 0,01 и Л2 0,1. При других отношениях между этими величинами табличные данные
следует умножить на 100-100тг, где 1m J2IJ1 и 1лг (Л2)2 соответствуют заданной балке.
Таблица D1)
а»
в
ь
k
ркр. кгсм2
2
а
il
ь
ркр, кгсм
0,1
11,7
117
680
12
65,9
5,60
1620
1
15,9
15,9
800
16
84,0
5,25
1830
2
20,5
10,25
910
20
102
5,10
2020
4
29,7
7,43
1090
24
120
5,00
2190
6
38,8
6,47
1250
32
156
4,88
2500
8
47,8
5,98
1380
40
192
4,80
2770
) Значение
критического напряжения ркр кгсм2
вычислено при В21Вх — 0,01; г2 0,1; Е «
- 2 10е кгсм2.
422 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
С увеличением 12а2 величина k стремится к предельному значению 2,12 (это значение определил проф. JI. Прандтль для
Таблица Е1)
л
а2
Ь8
k2
Ркр. кгсм2
л
а2
Is
ъ8
k
Ркр. кгсм2
0,1
4,13
41,3
405
8
27,7
3,46
1050
1
6,36
6,36
505
10
34,3
3,43
1170
2
9,05
4,53
600
12
41,2
3,43
1280
3
11,9
3,97
690
16
55,3
3,46
1485
4
14,9
3,73
770
24
84,8
3,53
1840
6
21,1
3,52
920
32
114,4
3,58
2135
) Значение критического
напряжения pKD кгсм2 вычислено при В2В1—0,01;
Л2 -0,1;-2.10® кгсм2.
2Р
стержня прямоугольного поперечного сечения). Если точка приложения поперечной силы лежит выше центра тяжести среднего
поперечного сечения, то критические напряжения будут меньше соответствующих зна770,8 чений, приведенных в табли700,8 Де D. Мы исследовали слуL чай, когда точка приложения
силы совпадает с верхней поверхностью полки балки. Для Рис. 22. этого случая составлена таб¬
лица Е.
С помощью таблицы Е легко определить значение критического напряжения балки, схематически представленной на рис. 22. Имеем
-325см
х 59 100 см Jp 59 500 см41
С
GF4
8 105 (98,2)4 40-595- 102 ’
J — 446 см4у F 98,2 см2у
I2 2 С12
а2 '
0,75.
40 40-595-102’ a2 Dh2
Согласно таблице Е с запасом имеем Ркр 480 кгсм2.
Для нашей балки найдем
ркр 480 100 100- (-)2 1670 кгсм2.
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 423
Наконец, заметим еще, что формулы для определения значения 7Кр выведены в предположении, что все явление происходит в пределах упругости. Вычисленные по этим формулам напряжения, превышающие предел упругости материала, не соответствуют действительным критическим напряжениям. В этом случае опрокидывание наступает раньше, чем это должно быть на основании вычислений.
При выводе, кроме того, ранее принималось, что ось балки является прямой и сила действует в средней плоскости вертикального листа. В практике, однако, всегда встречается отклонение от этого предположения, и поэтому балка начинает изгибаться в плоскости, перпендикулярной к вертикальному листу. Однако изгиб остается малым до тех пор, пока поперечная сила Р значительно отличается от теоретического значения Якр, Опыты1) на сплошной клепаной балке полностью подтверждают результаты, приведенные в таблице С (отклонение не превосходит приблизительно 5). Для балки с опертыми концами опыты показывают значительное отклонение от результатов вычислений. Объяснение этого несоответствия состоит в том, что принятое в вышеупомянутом рассмотрении закрепление концов для этого случая очень затруднительно реализовать.
IV. УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКОЙ оболочки, ПОДВЕРЖЕННОЙ СЖАТИЮ В НАПРАВЛЕНИИ ОБРАЗУЮЩИХ
§ 17. Общие соотношения
Действие на края круговой цилиндрической оболочки радиуса а равномерно распределенных сжимающих сил (Р — величина сжимающей силы, отнесенная к единице длины края) вызывает укорочение цилиндра, равное Pl2hE. Здесь — длина цилиндрической оболочки, 2h — толщина стенки. При постепенном приращении сжимающих сил может быть достигнут предел, при котором цилиндрическая форма равновесия не будет больше устойчивой и цилиндрическая стенка выпучится. Величина критического удельного усилия РКр может быть определена как с помощью уравнения равновесия, так и путем исследования изменения потенциальной энергии при выпучивании. Обозначим через и, v, w компоненты перемещения точки R в направлениях: оси цилиндрической оболочки, касательной к круговому поперечному сечению и внутренней нормали к цилиндру (рис. 23).
) См. работу автора, указанную на стр. 411.
424 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Деформации срединной поверхности определяются посредством выражений: удлинения
е,
ди
дх
е2
1 ди а др
w
а
(О
сдвиг
dv . 1 ди
со —з— ,
дх ' адф ’
изменения кривизн
d2w 1 d2w i dv 1 d2w. dv
dx2 9 a2 дф2 дф J T — a дх дф ' dx ) 9 ' '
где ф — угол между плоскостью ху и плоскостью uw.
Энергия деформации, отнесенная к едиг. нице поверхности, состоит из части, зависящей от величин удлинений ei и ег и сдви¬
га со:
L
7-(в1 в2)2-2(1 -a)(e,e2--J- со2), (3)
01 и из части, зависящей от изгиба и кручения:
С (хг щ — 2(1 —а) (х - т2). (4)
2 Eh8
Рис. 23.
3 1 -а2
Дифференциальные уравнения равновесия для этого случая имеют вид
дх
дф
дх
dG.MU _ дх дф iV 1
ГГ, d2W , ГТУ Л
Тй х2 Т2
N2a О, Nxa О,
(5)
дф
Н2 ”Н (Si 4” S2) cl — 0.
(6)
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 425
Обозначения для удельных сил и удельных моментов приняты согласно Ляву ).
Удельные моменты Gi, G2 могут быть следующим образом выражены через перемещения ut v и w:
Gj — С(щ ок2), G2 — С(к2 ок), Нх — 2 С(1 —от)т. (7)
Что касается удельных усилий Ту Т2, Si и S2, то они в случае, когда деформация существенно характеризуется удлинениями и сдвигом, с достаточной точностью определяются следующими формулами:
ТуЛъоъ), 7’2 1-2(е2 те1), 5, e_S2 JjL®. (8)
Когда величины удлинений и сдвига срединной поверхности малы, то для определения Т,. следует пользоваться более точными формулами.
Для круговой цилиндрической оболочки радиуса а эти формулы, согласно Ляву2), имеют вид
-Г 3 . Ч , 2 - 2а - За2 х, 2а аг х2
1 W' 1 2) 2(1-а) Г“ 2(i-a) TJ’
гр л Г 3 , т 2а2 К 2 —q 21 л
2 — г2 2 (1 — а) а 2(1 — a) aj (9)
S,-§(-а)« . Следующий простой пример показывает, как определяется критическое значение сжимающей силы Р —Т.
§ 18. Осесимметричная форма выпучивания цилиндрической оболочки
Круговые края цилиндрической оболочки шарнирно оперты. При постепенном приращении нагрузки Q может быть достигнуто состояние, при котором начинается выпучивание (рис. 24), До тех пор, пока образующая цилиндрической оболочки остается прямой, имеет место деформация продольного сжатия. Величина удлинения равна
- Q 1 - 1 Тг
2я а 2hE 2hE
) А. Е. Н. Love — A. Timpe, книга, указанная на стр. 391, S. 610.
2) А. Е. Н. Love — A. Timpe, книга, указанная на стр. 391, S 621.
426 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Эта деформация сопровождается поперечным удлинением, равным —сгео. Потенциальная энергия, соответствующая этому напряженному состоянию, равна
К0 2я alEhzl (10)
При выпучивании оболочки потенциальная энергия увеличивается, так как к энергии сжатия в продольном направлении прибавляется энергия растяжения в направлении касательной к поперечному сечению и энергия изгиба стенок оболочки. Очевидно, можно показать, что это приращение потенциальной энергии 6V происходит за счет работы 6Т сжимающей нагрузки Q, которая при выпучивании стенок облочки немного опускается. Величина критической сжимающей силы определяется из условия
67 6 Г.
Пусть
w — A sin
тлх
Т
v 0.
(И)
(12)
Что касается перемещения и, то оно определяется из условия постоянства удельного усилия Т при выпучивании; следовательно,
8j сге2 — (78q.
Принимая во внимание формулы (1) и (2), найдем
е, е0-а — sin
„ m2n2.
А—2—sin
тлх
Т
тлх
I
1 -. тлх
е2 А sin— ае0,
х2 0, т 0.
0 0,
Внося эти значения в выражения (3) и (4), получим величину потенциальной энергии цилиндрической оболочки после выпучивания:
VQ 6V
2n а
Eh
J tel e2)2 — 2 (1 — a) (e,e2 - -j o2) dx у J dx j
I
V0 - 2hEo0 J 4 sin 2яа dx AHn A2 3(ffff2) Ina.
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 427
Отсюда
61 — 2hEoe0 J sin - 2па dx
ЕкА2Щ- А2 з (ffg2) mf Ыа. (13)
Величина опускания нагрузки Q при выпучивании оболочки равна
Г А. штлс , , 1 Г (dw2 Г Л. тялс , . Л2 т2я2
6 J Tsin— tJ Ы dxJ Tsin—'—-—
0 0 0
Работа нагрузки Q, соответствующая этому опусканию, будет
бТ 2лаР а sin dx -1. (14)
- о J
Приравнивая выражения (13) и (14), найдем
р _ 2l2Eh , 2Eh3 m2 л2 п-.
КР“ а2т2л2 3(1-а2) 2 в
Из формулы (15) для различных значений m получим соответствующие значения Ркр. Для практики важно определить то значение т, при котором получается наименьшее значение сжимающей силы. Его можно найти тем же способом, как и при исследовании продольного изгиба стержня в упругой среде (см. § 3). Наибольшая длина , при которой первая выпученная форма имеет m полуволн, очевидно, та, для которой фор¬
мула (15) дает одно и то же значение РКр независимо от того, разделяется ли поверхность при выпучивании на m полуволн или на m 1 полуволн.
Для определения предельного значения I имеет место следующее уравнение:
2l2Eh. 2Eh m2n2 __ 2l2Eh. 2Eh (т1)2я2
a2m2n2 3(1— a2) I2 a2 (tn l)2 я2 3 (1 - a2) Z2 ’
откуда Vm(m 1)—пГаН „. (16)
r v ' 3(l-a2)v v '
Предельная длина, при которой выпученная форма соответствует одной полуволне, равна
УТпУШ ЗАЗуш.
3(l-a2)v г
428 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
При двух полуволнах предельная длина будет
3(1 — a2)v‘ ’ v
При значительной длине цилиндрической оболочки число т также велико; в этом случае можно, с достаточной точностью, для длины полуволны X 1т на основе формулы (16) при нять выражение
J__ nVah
т 3(1— a2) '
То же значение длины полуволны можно было бы получить из формулы (15), если в правой части величину 12т2 заменить на К2 и приравнять нулю первую частную производную от Ркр по Я. Подставляя найденное значение X в выражение для Якр, найдем
Р 4-2 П7)
кр a3(1 -a2)' U)
Соответствующее сжимающее напряжение равно
А о 2h 1
Ркр — Е . . (18)
H v 2h а 3(1 -a2) ;
Для того чтобы выпучивание происходило в пределах упругости, необходимо, чтобы толщина стенки 2h была достаточно мала по отношению к радиусу а. Например, для железа должно выполняться условие
—-i o,ooi.
а 3(1-02)
За пределом упругости формулы (17) и (18), конечно, неприменимы.
Определенное выше значение РКр может быть также найдено из дифференциальных уравнений равновесия (5) и (6). Для рассмотренного случая существуют соотношения
G-Cx-C-g-, Gs--Cac1--Cr-g.,
Я, Я2 0, S, - — S2 О, Г, const - Р, Т2 - - 2Eh.
Первое и второе уравнения системы (6) дают
N3 0, JV,a-aC-g-.
Внося эти результаты в третье уравнение системы (5), получим dw , n d2w и» npt л
aC4F aP Т2А“
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 429
или, вводя обозначения
2г2 2Eh - „М
IT zr ’ а2С а2Л2 ’
придем к следующему уравнению:
sylv 2 r2w t4w 0.
Тогда, для краевых условий при х 0, w 0 и d2wfdx2 0, отсюда следует:
w — A sin рх В sin qx, где р Vr2 (г4 - t)'h, q - Vr'-ir'-t)1,.
Для того чтобы выпучивание было возможным, необходимо, чтобы гА — 0. При х I существуют те же самые краевые
условия, что и при х 0, следовательно,
A sin pl В sin ql 0, Ар2 sin pi sin ql 0.
Для того чтобы имело место выпучивание, необходимо детерминант этих уравнений приравнять нулю, т. е. sin pi 0 и sin ql 0, откуда для определения Якр получим уравнения
гЧ2 Vrl-tl т2я2, гЧ2 - г44-44 п2л2, (19)
где тип суть произвольные целые числа. Если длина цилиндрической оболочки велика, то можно положить t2l2 т2р2у где т — целое число.
В этом случае оба условия (19) приводят к одному и тому же результату: г22 т2я2 или
р 2Ст2я2 9Г2 2С3(1 -g2) 4 Eh2
кр 2 ah “ aV3(1 -а2)
что полностью соответствует ранее полученному значению (17). Интересно только что установленное значение Ркр сравнить со значением, которое дает формула Эйлера; применительно к нашей цилиндрической оболочке имеем
0 п' EJn2 2тсаР кр — j2
Здесь J — момент инерции поперечного сечения. Для тонкостенного цилиндра можно принять, что
j _ 2па3 2h J 2
Для того чтобы выпучивание могло иметь место, необходимо, чтобы
(20)
430 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ Если р'р ркр, ТО
4 Eh2 En2a2h
aV3(1— (Т2) I2
Отсюда получим следующее соотношение между размерами цилиндрической оболочки:
h _ к23(1 -а2) д» 1 а 42 2 Если отношение iа меньше этого значения, то цилиндрическая оболочка, прежде чем выпучиться, как стержень, будет претерпевать местное выпучивание стенок, как указано на рис. 24.
Было принято, что края цилиндрической оболочки шарнирно оперты. Для длинного цилиндра вид краевого закрепления не имеет никакого значения, и формула (17) может быть, следовательно, применена также и для цилиндра с защемленными краями.
§19. Деформация цилиндрической оболочки при отсутствии удлинений и сдвигов
Если края сжатой цилиндрической оболочки могут не только свободно поворачиваться, но и свободно перемещаться, то цилиндрическая оболочка может при определенной величине критической силы принять некоторую форму равновесия, причем переход к этой форме равновесия происходит без какого-либо изменения удлинений и сдвигов срединной поверхности. Перемещения, соответствующие этому типу деформации, могут быть выражены следующим образом1):
И - У вп sin (тр р„), v У Впх cos (шр р„),
(21)
ш — 2j пВпх sin (шр р„).
Потенциальная энергия цилиндрической оболочки при этом изменении формы будет увеличиваться, так как к энергии сжатия добавляется энергия изгиба. Последняя определяется следующими изменениями кривизн:
п 1 d2w . v п3 — п . , п
— 0» К2 — а2 ду2 ду)- 2л а2 Sin (Яф Pl) т “ 2 cos Р»)
1 А. Е. Н. Love — A. Timpe, книга, указанная на стр. 391, S. 545.
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 431
Приращение потенциальной энергии получается путем вычисления работы внешних сил. Эта работа должна определяться из следующих соображений. При рассматриваемом типе деформации образующие цилиндрической оболочки остаются прямолинейными и наклоняются на угол
Y V'2iBn cos (шр Р„)2 2 пвп cos (п ф р„)2.
Этот наклон соответствует работе
2Я
бr yPJ i2ady aalp'SiBl п (22)
О
Величина удельного усилия Ркр будет определена, если приравнять работу ЬТ потенциальной энергии изгиба )
6V Cnl J (3— Bl п212 2(1- а) а2. (23)
Отсюда следует:
п„ 2С 22-)2 В2п ‘Зи22 2(1 — сг) а2
КР а4 2в2(1«2) ‘ ( )
При п 1 получим перемещение цилиндрической оболочки как жесткого тела. При п 2 имеем
Ркр - 4 2 (i - т) а2. (25)
Если длина цилиндрической оболочки велика по сравнению с диаметром, то с достаточной точностью найдем
п 24 С 12 16 Eh2 hi2 ГСЧ
Р«р-Г1Г1 5 а (1 — q2) (26)
Из сравнения этого результата с формулой (17) § 18 следует,
что
п п 4УТ А Р
кр-кр 5(1_а2) а а2.
Легко доказать, что если принять деформацию оболочки такой, что растяжение и сдвиг срединной поверхности отсутствуют, то
А. Е. Н. Love — A. Timpe, книга, указанная на стр. 391, S. 583.
432 НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
основные уравнения равновесия (5) и (6) не удовлетворяются. Для этого достаточно выражение
Г -ЖЙГ:1ГС’ (27)
которое следует из формулы (9) сравнить с тем, которое дает
третье уравнение системы (5), когда вместо N и N2 вводятся их
значения из системы уравнений (6). Из третьего уравнения системы (5) следует:
(28)
Если вместо ввести его значение, то из (27) и (28) получим следующие значения:
т- т S в»х sin р»),
- § S tt2 sin (up ft,).
Эти значения Т2 различаются, и, следовательно, принятые выражения для перемещений не удовлетворяют уравнениям равновесия. Для того чтобы эти уравнения удовлетворялись, необходимо одновременно с рассмотрением изгиба учесть и деформацию срединной поверхности.
Принятые выражения для перемещений не удовлетворяют также граничным условиям. Для х О и х должны выпол няться условия:
G О,
дг 1 дН __ р dw
yVl FdT-
Между тем как, когда перемещения заданы выражениями (21), G оказывается линейной функцией х и не становится равной нулю при х 0. Для удовлетворения дифференциальных уравнений равновесия необходимо наряду с выбранными перемещениями (21) учесть еще также удлинение и некоторые напряжения на круговых краях.
Решение некоторых задач о деформации цилиндрических оболочек (см. А. Ляв )) дает повод утверждать, что потенциальная энергия, которая накапливается вследствие дополнительного удлинения и напряжения краев, мала по сравнению с потен¬
) А. Е. Н. Love — A. Timpe, книга, указанная на стр. 391, S. 626.
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 433
циальной энергией изгиба, и поэтому формула (25) может служить для определения критической нагрузки.
Мы рассмотрели простейший случай, когда цилиндрическая оболочка, сопротивляющаяся выпучиванию, равномерно нагружена и удельное усилие по всему поперечному сечению постоянно. Для практики имеет значение случай, когда удельное усилие изменяется по закону cosqp, т. е. Т —Р cos ср.
В этом случае цилиндрическая оболочка испытывает действие изгибающих моментов, которые приложены по концам, и до тех пор, пока эти моменты не превзойдут некоторой границы, оболочка изгибается, как стержень.
При дальнейшем приращении сил может иметь место выпучивание стенок оболочки на той стороне, где,образующие сжаты.
Интересна также задача об устойчивости части оболочки, ограниченной двумя образующими и двумя круговыми поперечными сечениями, которая сжата силами Я, параллельными образующим.
Киев, 1909 г.
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Университетские известия, Киев, 1911, год 52, № 7. Отд. оттиск, Киев, тип. университета Св. Владимира, 1911, 25 стр.
§ 1. Новый метод определения критических сил
Повышение качеств строительных материалов и усовершенствование конструкций в современных инженерных сооружениях приводят к тому, что значение теоретического расчета при проектировании все возрастает. Чем выше качества материала и чем совершеннее конструкция, тем лучше могут быть выполнены условия, которые обыкновенно кладутся в основание выводов строительной механики и теории упругости, тем с большим основанием можно переходить от грубых приближенных формул к более точным теоретическим исследованиям.
До недавнего времени исключительное внимание при расчетах обращали на вычисления напряжений; мерой прочности являлось отношение допущенных напряжений к временному сопротивлению материала. Ряд крупных катастроф показал, что такого расчета для современных инженерных сооружений далеко не достаточно, принятые нормы допускаемых напряжений не всегда обеспечивают надлежащую прочность, необходимы дополнительные исследования относительно устойчивости как отдельных частей, так и всего проектируемого сооружения. Важность проверки на устойчивость в настоящее время сознается всеми, но вследствие недостатка в теоретической разработке вопросу устойчивости и в строительной механике, и в технических расчетах отводят лишь весьма скромное место, обыкновенно ограничиваются только проверкой на продольный изгиб сжатых стержней. Но в таких же условиях неустойчивого равновесия, как сжатый стержень, может оказаться и сжатый лист, и изгибаемая балка, и сжимаемая внешним давлением цилиндрическая трубка, и т. д. К сожалению, для этих более сложных задач далеко не всегда имеется надлежащее решение, которое инженер мог бы применить непосредственно к расчету; иногда же решения эти получены столь сложным путем, что для сознательного их применения необходима гораздо большая математическая подготовка, чем того можно требовать от инженераконструктора. В настоящей заметке мы предлагаем новый метод, значительно упрощающий решение вопросов устойчивости и в
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ 435
сложных случаях дающий возможность получения приблизительного решения задачи.
Пока все размеры упругого тела одного порядка, малым деформациям соответствуют и малые перемещения отдельных точек. В таком случае можно считать, что система внешних сил при деформации не меняется; это является необходимым условием для однозначности решения уравнений теории упругости. В том случае, если два или по крайней мере один из размеров мал, т. е. если мы имеем дело с тонким стержнем или тонкой пластинкой, малым деформациям могут соответствовать конечные перемещения. При этом условии ) одной и той же системе сил могут соответствовать несколько различных форм равновесия, и возникает вопрос об устойчивости этих форм. Рассчитываемая конструкция, очевидно, будет прочной лишь в том случае, если используемая при расчете форма равновесия устойчива. Для практических приложений необходимо знать то наименьшее значение внешних нагрузок, при котором становится возможным несколько форм равновесия. Значение это в дальнейшем будем называть «критическим». Пока нагрузка меньше критической, возможна лишь одна-единственная форма равновесия, и эта форма, очевидно, будет устойчивой. При нагрузках больших критической возможны по крайней мере две формы равновесия. Устойчивой формой будет та, которой соответствует минимум потенциальной энергии. Для определения критического значения нагрузки пользуются обыкновенно таким приемом. Рассматривают возможные формы равновесия, удовлетворяющие условиям на поверхности и весьма мало отличающиеся от той формы равновесия, которая соответствует нагрузкам, меньшим «критической». Для этих возможных форм равновесия составляют дифференциальные уравнения равновесия и отыскивают те значения внешних сил, при которых эти дифференциальные уравнения допускают решения, удовлетворяющие условиям на контуре. Наименьшее из этих значений и будет критическим. Для критического значения нагрузки получается бесчисленное множество возможных форм равновесия, так как решение дифференциальных уравнений заключает в себе произвольный постоянный множитель. Это указывает на неопределенность формы равновесия для нагрузок, равных критической. Неопределенность эту легко демонстрировать при испытании стержней на продольный изгиб или при испытании на изгиб высоких двутавровых балок. Таким образом, отыскание критических значений нагрузок сводится к решению дифференциальных уравнений при
) См. G. Н. Bryan. On the stability of elastic systems. Proceedings of the Cambridge Philosophical Society, mathematical and physical sciences, 1889, vol. 6, pp. 199—210.
436 ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
заданных условиях на контуре. При исследовании устойчивости сжатых стержней мы будем иметь дело с одним обыкновенным дифференциальным уравнением. Для случая изгиба полос и двутавровых балок придется решать систему из двух обыкновенных дифференциальных уравнений. При расчете сжатых пластинок задача сводится к интегрированию линейного дифференциального уравнения в частных производных. Таким образом, наиболее простыми являются задачи, относящиеся к устойчивости сжатых стержней. В случае сжимающих сил, приложенных по концам, задача приводится к линейному уравнению с постоянными коэффициентами. При сжатии стержня силами, равномерно распределенными по длине, получаем уравнение, решаемое в бесселевых функциях. Для более сложных случаев нагрузки приходится иметь дело с уравнениями, для которых неизвестны интегралы в замкнутой форме; тогда ищут решение в форме бесконечного ряда. Отыскание критической нагрузки сводится к суммированию иногда весьма сложных и медленно сходящихся рядов. Работа эта практически часто является настолько сложной, что приходится отказываться от дальнейшего решения задачи. Задачи об устойчивости изгиба полос и двутавровых балок являются более сложными. В этом нам пришлось убедиться при исследовании устойчивости плоской формы изгиба двутавровых балок1). Для решения задачи при простей- ших способах нагрузки пришлось на вычисления затратить несколько месяцев. Попытки решить ту же задачу для условий, более близких к действительности, привели к столь сложным вычислениям, что работу пришлось оставить. Решение задачи об устойчивости пластинок удалось получить лишь для простейших случаев нагрузки и то далеко не для всех способов закрепления по контуру пластинки.
Перечисленные затруднения при интегрировании уравнений заставляют искать другие методы для решения вопросов устой чивости, такие, которые давали бы возможность находить величины критических нагрузок непосредственно, не прибегая к интегрированию дифференциальных уравнений равновесия Наиболее естественно обратиться в данном случае к рассмотрению выражения для энергии системы. Нам обыкновенно известна форма равновесия, соответствующая нагрузкам, меньшим критической. Без затруднений возможно составить выражение для изменения энергии системы при малом отклонении от этой формы равновесия. Если при всяком возможном отклонении по¬
) См. нашу работу «Об устойчивости плоской формы изгиба двутавровой балки под влиянием сил, действующих в плоскости ее наибольшей жесткости». Известия С.-Петербургского политехнического института. Отд. оттиск. СПб., 1906, 132 стр.
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ 437
тенциальная энергия системы возрастает, рассматриваемая форма равновесия будет устойчива; в противном случае она будет неустойчива. Критическим будет то значение нагрузки, при котором изменение энергии системы для какого-либо возможного отклонения обращается в нуль. Обозначим через V изменение энергии внутренних сил упругости системы и через Т работу внешних сил при отклонении от рассматриваемой формы равновесия, тогда критическое значение нагрузки найдется из уравнения
Г V. (1)
Очевидно, из всех возможных отклонений нужно выбрать то, при котором уравнение (1) дает для внешних сил наименьшее значение. Подобный способ определения критического значения нагрузок был предложен Дж. Брайаном1). Он применил этот способ к нахождению критической нагрузки для сжатого стержня со свободно поворачивающимися концами и для решения вопроса об устойчивости прямоугольной сжатой пластинки с опертыми краями. В обоих этих случаях легко написать общее выражение для отклоненной формы равновесия и найти значения для V и для Т. Вставляя их в уравнение (1), получим критическое значение для внешних сил. Подобным путем легко получить критическое значение сжимающей силы для призматического стержня в упругой среде2) и для прямоугольной пластинки, сжимаемой двумя взаимно противоположными силами3). Однако в большинстве случаев задача об определении критической нагрузки является более сложной, так как общее выражение для отклоненной формы равновесия неизвестно и его нужно разыскать. Для этого мы можем воспользоваться таким приемом. На основании опытных данных и принимая во внимание условия на контуре, задаемся подходящей формой равновесия и для этой формы составляем выражения для V и Т. Вставляя эти выражения в уравнение (1), найдем критическую нагрузку. Конечно, выбранная произвольно форма равновесия не будет, вообще говоря, удовлетворять уравнениям равновесия, но если условия на контуре выполнены, то из уравнения (1) можно довольно точно найти критическую нагрузку.
) См. цитируемую на стр. 435 работу, а также его статью «On the stability of a plane plate under thrusts in its own plane, with application to the «buckling» of the sides of a ship». Proceedings of the London Mathematical Society, 1891, Series 1, vol. 22, pp. 54—67.
2) См. нашу работу «О продольном изгибе стержней в упругой среде». Известия С.-Петербургского политехнического института, 1907, том 7, выпуск 1, стр. 145—157.
8) См. нашу работу «К вопросу об устойчивости упругих систем». Известия Киевского политехнического института, 1910, год 10, книга 2, стр. 147—167.
438 ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
Прием этот аналогичен тому, который был применен лордом Рэлеем для изучения колебаний упругих систем. Мы пользовались этим приемом для исследования изгиба стержней и пластинок1). При выборе отклоненной формы равновесия можно ее представить в виде функции от ряда параметров и потом эти параметры найти так, чтобы определяемая из уравнения (1) величина критической нагрузки имела значение минимума. Возьмем, например, тот случай, когда отклоненная форма опре-
для критической нагрузки получить наименьшее значение. Таким образом, задача об определении критической нагрузки сводится к нахождению минимума известного выражения. Увеличивая число параметров а, 2, , мы будем получать все большую точность; в пределе получаем точное решение. Поясним все сказанное примером. Положим, требуется найти критическое значение сжимающей силы для стержня, заделанного нижним концом (рис. 1). Пусть под действием сжимающей силы Р произошло искривление стержня. Дифференциальное уравнение равновесия для искривленной формы будет
1) См. нашу работу «Применение нормальных координат к исследованию изгиба стержней и пластинок». Известия Киевского политехнического института, 1910, год 10, книга 1.
X
деляется функцией одной переменной, как то имеет место в случае выпучивания сжатых стержней. Искривленная форма стержня может быть представлена так:
Р
w ау (х) а2 ф2 () а3ф3 (). (2)
Здесь через w обозначаем прогиб стержня в сечении, определяемом координатой х. Каждую из функций ф1(л:), ф2(), выбираем так, чтобы ряд (2) мог представить с достаточной точностью ожидаемую искривленную форму равновесия. Имея выражение (2) для отклоненной формы, можно найти величины V
Ш1'
У и Г; они представятся в виде функций от параметров аь а2, а3,. Выражение для критической нагрузки получится из уравнения (1) и тоже будет зависеть от величин аи 2,. ; остается эти величины подобрать так, чтобы
Рис. 1.
Е11ру
(3)
откуда
Чтобы было выполнено условие у
верхнего конца, нужно положить
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ 439
Следовательно, критическое значение нагрузки будет
р _ EJn2 _ 2,4674
42 “ 2
К тому же результату легко прийти, пользуясь приемом Дж. Брайана. Изменение потенциальной энергии деформации
i
при искривлении стержня будет V Щ- J (Уг)2 dx или
о
i i т Г NPdx Р2 Г о ,
V J 2EJ 2EJ J У '
О о
Работа внешних сил при искривлении стержня представится произведением из силы Р на величину опускания верхнего конца стержня. Опускание это, очевидно, равно разности между длиной дуги, по которой искривился стержень, и длиной ее проекции на вертикальное направление и может быть представлено формулой
2 dx.
Уравнение (1) дает нам для критического значения нагрузки формулу
е’ Ш
Ркр i (4а)
dx
я
dy_V
или
, dx )
о
I
EJ I 1-Л2 dx
т
Р., V- 4Ь)
J У2 dx
о
Общее выражение для искривленной формы можно в данном случае представить в форме такого тригонометрического ряда:
„ пх. я Злх , у Aq cos -nj - А cos
2 21
440
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
Вставляя это в первое из выражений для РКр, найдем
Наименьшее значение для РКр, совпадающее с вышенайденной величиной, получим, полагая все коэффициенты, кроме Л0, равными нулю, т. е. вставляя вместо у его значение, определяемое из уравнения (3).
Применим теперь к разбираемому случаю вышенамеченную приближенную методу. Представим искривленную форму в виде степенного ряда
При этом условия у закрепленного конца, очевидно, будут выполнены:
Для простоты вычислений мы ограничиваемся тремя первыми членами степенного ряда. Для потенциальной энергии внутренних сил упругости при изгибе получаем выражение
Работа внешних сил при искривлении стержня представится формулой
Вставляя это в уравнение (1) и вводя обозначение а2а z, мы получим для критической нагрузки выражение
Разыскание наименьшего значения для РКр приводит нас к квадратному уравнению
при х 0 у и -- 0.
J iwf dx Ц J (2ai 12а22)2 dx.
0
о
о
608г24 640г2 0,
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ 44)
Корнями этого уравнения будут
0,1749 0,8777
I2 9 2
Вставляя значение Z в выражение для РКр, получим р _ 2,469 EJ
Кр р
Найденное приближенное значение для Якр отличается от точного меньше чем на 0,1. Таким образом, три первых члена степенного ряда обеспечивают в данном случае точность большую, чем то требуется для практических приложений. Увеличивая число членов в выражении для прогиба, мы будем увеличивать и точность результата. Заметим, что вычисление дальнейших приближений требует значительно большей затраты времени и практически является излишним. К нему следовало бы прибегнуть лишь в том случае, если бы мы хотели получить значения нагрузок, соответствующих формам равновесия с одной или несколькими точкаАми перегиба. Эти формы равновесия, как известно, неустойчивы и не имеют практического значения.
Заметим здесь, что при вычислении критического значения нагрузок по описанному способу мы всегда для них будем находить величины, большие действительных. Получается это потому, что, задаваясь формой изгиба, мы как бы вводим в нашу систему дополнительные связи, благодаря чему не все возможные отклонения действительной системы будут возможными и для нашей фиктивной системы с дополнительными связями. Такое уменьшение числа степеней свободы системы ни в каком случае не может сопровождаться уменьшением жесткости. Жесткость лишь в исключительных случаях и для некоторых определенных форм равновесия может остаться неизменной, вообще же она возрастает, а следовательно, возрастет и величина критической нагрузки.
Недостатком описанного приближенного метода следует считать то, что мы при вычислении не можем указать степени точности получаемого результата. О погрешности можно судить, лишь сравнивая последовательные приближения. Заметим, однако, что и в тех случаях, когда задача решается путем интегрирования соответствующих уравнений, далеко не всегда может быть установлена строго степень точности результата, так как приходится обыкновенно иметь дело с суммированием сложных рядов и с решением трансцендентных уравнений, связывающих суммы этих рядов.
Мы на частном примере выяснили ход решения задачи в том случае, когда отклоненная форма равновесия является функцией одной переменной. Метода без всяких изменений может быть
442 ПРИБЛИЖЁННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
применена и в том случае, когда приходится иметь дело с функцией нескольких переменных (при исследовании устойчивости пластинок имеем две переменные) и когда, следовательно, задача об устойчивости сводится к интегрированию уравнения в частных производных. Во всех случаях вместо интегрирования уравнений придется выполнить ряд квадратур и потом найти минимум некоторого выражения, зависящего от параметров аи а2, а3,. Получаемое при этом приближенное выражение для отклоненной формы представляет собой приближенное значение интеграла соответствующего дифференциального уравнения, и тогда описанный метод можно рассматривать как приближенный прием интегрирования дифференциальных уравнений. Связь между операциями, выполняемыми при приближенном вычислении критической нагрузки, и интегрированием соответствующего дифференциального уравнения выясним на вышеразобранном простейшем случае продольного изгиба. При пользовании приближенным методом задача о нахождении критического значения нагрузки могла быть сведена к нахождению минимума такого выражения (см. формулу (4Ь)):
о
I
У2 dx
о
Минимум этот будет иметь место в том случае, когда
fy2dx8i шах ж)2(1хьу21хо
0 0 о о
или, принимая во внимание (4Ь), когда 4fa'
о
т. е. задача сводится к нахождению минимума такого интеграла:
(5)
о
что равносильно интегрированию уравнения
EJy Py 0, совпадающего с уравнением (3).
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ 443
При пользовании приближенным методом мы, вместо задачи вариационного исчисления, решаем задачу о нахождении минимума выражения
О
в котором вместо у вставлено его значение в форме степенного ряда.
На математической стороне этого вопроса мы больше останавливаться не будем; этому предмету посвящена замечательная работа швейцарского ученого Вальтера Ритца 1). Сводя интегрирование уравнений к нахождению минимума интегралов, В. Ритц показал, что для обширного класса задач мы, увеличивая число параметров аи а2, а3,., получим сходящийся процесс и в пределе придем к точному решению задачи. Для того цикла задач, которыми мы в дальнейшем будем заниматься, такого доказательства не имеется, но приложения приближенного метода к задачам, для которых уже ранее получено точное решение, показывают, что метод этот дает очень хорошие результаты и практически не приходится искать больше двух приближений.
Пользуясь описанной приближенной методой, мы могли получить2) как решения уже исследованных вопросов, так и новых задач, для которых интегрирование соответствующих уравнений не было до сих пор выполнено. Новые результаты нам удалось получить при исследовании устойчивости сжатых поясов открытых мостов и сжатых составных стержней, а также при рассмотрении устойчивости плоской формы изгиба балок и устойчивости пластинок.
§ 2. Продольный изгиб стержня под действием собственного веса
В качестве примера рассмотрим искривление стержня под действием собственного веса. Пусть q — вес единицы длины стержня, тогда сжимающая сила у нижнего конца стержня будет ql. Задача наша заключается в том, чтобы найти для стержня данной жесткости EJ то наименьшее значение ql, при котором возможно искривление, представленное на рис. 2. Дифференциальное уравнение равновесия в этом случае будет
Е'-§-ч«-)ж-о- «)
J) W. Ritz. Uber eine neue Methode zur Losung gewisser Variationsprobleme der mathematischen Physik. Journal fur die reine und angewandte Mathematik, 1909, Bd. 135, SS. 1—61.
2) См. нашу работу «Об устойчивости упругих систем». Известия Киевского политехнического института, 1910, год 10, книга 4, стр. 375—560.
444
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
Интеграл уравнения этого может быть представлен в бесселевых функциях. Для критической силы получим )
(ql) к
EJn2 (1,12)3
Применим теперь к этому случаю приближенную метбду, представим у в виде степенного ряда. В самом общем случае четная функция от х, удовлетворяющая условиям на концах, будет
у (Р — х2) (а0 ах2 а2х4.).
Потенциальная энергия изгиба при искривлении стержня будет
О
Работа силы тяжести, соответствующая тому же искривлению, представится формулой
Рис. 2.
Критическое значение веса определится из уравнения
i i
откуда
J Ш2йхЧг J (-802dx’
ql-
ЕЛ
(
«-(
2 dx
(7)
Остается для коэффициентов а0, аи a2i. в общем выражении для у подобрать такие величины, чтобы ql, определяемое
Ч См. А. Е. Н. L о v в. Lehrbuch der ElastizitSt. Deutsche Ausgabe von A. Timpe, Leipzig — Berlin, B. G. Teubner, 1907, S. 488 (перевод с английского: A. E. H. Love. A treatise on the mathematical theory of elasticity.
2 edition, 1906, Cambridge, University Press) и Ф. С. Ясинский. Собрание
сочинений. Ред. Н. Н. Митинский. Том I, С.-Петербург, 1902. Сборник Инсти¬
тута инженеров путей сообщения, выпуск 5§, стр. 179,
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ 445
из уравнения (7), имело наименьшее значение. Ограничимся тремя членами и положим
у (I2 — х2) (а0 ахх2) 12а0 (12а — а0) х2 — ахА b0 6ja:2 fe24-
Вставляя это в выражение (7) для критической силы, получим
рг 14 zl -z4
(90кр jt 4 — l20zl2l4z4t
Здесь введено обозначение z Ъ2Ь.
Разыскание наименьшего значения для ()кР приводит нас к такому квадратному уравнению:
откуда
0,2200 1,3478
1 j2— 2 J2
Вставляя Zi в выражение для ()кР, найдем
, п _ 8,15EJ _ EJn2 vWkP — 2 — (,10)2 ‘
Сравнивая этот результат с точным решением, находим, что в данном случае погрешность меньше 2.
При решении задачи мы приняли для у выражение в форме степенного ряда, но можно, конечно, представить у и иначе; нужно только, чтобы были выполнены условия, высказанные при изложении метода. Возьмем, например, у в виде тригонометрического ряда. Чтобы удовлетворить условиям на концах, нужно положить
пх , Зя , 5я ,
у а cos -gj- а2 cos аъ cos —-.
Ограничиваясь двумя членами и вставляя полученное таким образом у в выражение для ()кр, найдем
, -v EJn2 l8lz2
WKP - 82 0,1487 0,60782 2,1487z2
Как и раньше, 2 обозначает отношение а2: а.
Разыскание наименьшего значения для (ql)р приводит над К квадратному уравнению
22 0,4020 - 0,01235 — 0,
446 ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
корнями которого будут Z 0,0286, z2 — 0,4306. Вставляя Z в выражение для получим
n EJzt2 EJzt2 Ш)к
;кР 1,258I2 (1,12J2 '
Результат этот совпадает с ранее приведенным решением, погрешность лежит за пределами той точности, с которой произведены вычисления Ф. С. Ясинского.
Таким образом, представление у в виде тригонометрического ряда является для данной задачи более выгодным. Заметим, что если положить в выражении для (ql)Kv 2 0, что равносильно оставлению лишь одного первого члена в разложении для у, то мы получим
, -v Езп2
WKP в 1192
Погрешность составляет 5.
Покажем на этом примере связь между интегрированием дифференциального уравнения (6) и вычислением ()Кр по приближенному способу.
Приближенная метода привела нас к разысканию минимума выражения (7), а это равносильно разысканию минимума интеграла
s I EJ Ш -ЧУ-) dx-
Полагая z dydx и составляя вариацию S, найдем
EJz ql-x)z 0.
Уравнение это совпадает с уравнением (6).
Заметим в заключение, что результаты, полученные нами здесь, могут быть распространены на тот случай, когда стержень АВ со свободно поворачивающимися концами подвержен действию продольных сжимающих усилий, равномерно распределенных вдоль осй и направленных от концов к середине. В этом случае каждая половина стержня находится в условиях, принятых в вышерассмотренной задаче.
Таким же приемом может быть решена более сложная задача о выпучивании стержня в упругой среде при действии на него сплошной нагрузки, меняющейся по закону, представленному на рис. 4, Ь. Вопрос этот представляет большой практический интерес, с ним приходится встречаться при расчете откры¬
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
44
тых мостов. При искривлении на каждый элемент стержня будет действовать реакция среды §у dx, пропорциональная прогибу стержня у. Коэффициент пропорциональности р зависит от
степени податливости среды. Работа сжимающих сил при искривлении стержня равна
12 I
Т J X ( - X) (-g-)2 dx J X ( - X) (-g-)2 dx.
0 0
Основное уравнение (1) получит вид
i i
откуда
i J (ж-)2 dx if J (ST i JV
0 0 0
EI J(-S-)2rfxpJ
_
2
(8)
) dx
Разыскание минимума этой дроби равносильно выполнению условия
448 ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
Составляя вариации и принимая во внимание условия на концах:
d2u
-JL. у 0 При JC О И При Х 1у
получим
4’“ 2 а: ( — а:) “Уг ( “ 2) У 0. (9)
Вместо интегрирования этого уравнения, мы можем критическое значение сжимающей силы найти приближенным методом. Для этого нужно только в выражение (8) вместо у вставить подходящую форму искривления. Например, в случае податливости среды стержень изогнется по кривой без перегибов и можно положить
„. пх , - . Злх
у A sin — А sin -j-.
Этих двух членов ряда достаточно, чтобы определить значение критической силы с тремя верными знаками1).
§ 3. Об устойчивости плоской формы изгиба балки
Здесь мы рассмотрим один из тех случаев неустойчивого равновесия, которые возникают иногда при изгибе стержней в плоскости их наибольшей жесткости. Если одна из главных жесткостей изгиба мала по сравнению с другой, то, изгибая стержень в плоскости наибольшей жесткости, можно, постепенно увеличивая изгибающие силы, прийти к пределу, когда плоская форма изгиба перестает быть устойчивой, ось стержня искривляется в направлении наименьшей жесткости, причем отдельные поперечные сечения стержня поворачиваются. Вместо плоского изгиба мы будем иметь изгиб в двух плоскостях, сопровождающийся кручением. Явление это проще всего демонстрировать на изгибе обыкновенной линейки. Изгибая линейку руками в плоскости ее наибольшей жесткости, легко можно почувствовать то предельное значение изгибающего момента, при котором плоская форма перестает быть устойчивой. Явление неустойчивости возможно при различных формах поперечного сечения. Мы рассмотрим случай прямоугольного и двутаврового поперечных сечений. Предположим, что полоса АВ с опертыми концами изгибается в плоскости наибольшей жесткости силой, приложенной посредине пролета. Найдем значение силы 2Р, при котором становится возможной неплоская форма равновесия (рис. 5). Рас¬
) См. цитированную на стр. 443 нашу работу
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ 449
полагая координатные оси, как показано на рисунке, и составляя выражения для изгибающего и скручивающего моментов в каком-либо сечении mг, мы получим такие дифференциальные уравнения для неплоской формы равновесия:
By Р(1-х) ф, Сф' - Р у tf (I - ),
где В — жесткость изгиба, а С Ф — угол поворота сечения тп.
(Ю)
жесткость при кручении и
2Р
77
-Х‘
П
Рис. 5.
Предположим, что закрепление концов не допускает вращения относительно оси х-ов. Относительно осей, параллельных у и г, возможно свободное поворачивание. В таком случае для угла ф будем иметь следующие условия:
Ф 0 при х ; ф' 0 при х 0.
Применим к нахождению критической нагрузки приближенную методу. Для работы силы 2Р и для потенциальной энергии деформации, связанной с искривлением, будем иметь формулы
i i i Т 2Р j фy(l-x)dx, V B J y2dx С J у'Чх.
0 0 0
Для определения ЯКр напишем уравнение
i i i
2Р J Фy(l-x)dx Bj у2dx С J фndx. (11)
0 0 0
Принимая во внимание первое из уравнений равновесия (10), получим
-Q- J ( — х2) ф2 dx С J ф'2dx.
450 Приближенный метод исследования устойчивости Представим ф в форме тригонометрического ряда:
ЗХХ I ц I
ф Azos-Ax cos —h.
Ограничиваясь для простоты вычислений первыми двумя членами разложения и обозначая А:А г, мы получим из основного уравнения (11)
ВС л2 1 9 z2
Р2.
2л2 6 9я2)
Остается для -г подобрать такое значение, чтобы Р было минимумом. Задача эта сводится к решению такого квадратного уравнения:
z2 2,105-0,1111 0.
Корнями его будут z 0,051, z2 —2,155.
Вставляя значение z в выражение для Р1ф, найдем
ЛсР 2Л17ГС- 12
Решение этой задачи путем интегрирования соответствующих уравнений было выполнено Л. Прандтлем; им получена для Якр величина
р _ 2,115яс
кр 12
Погрешность наших вычислений составляет, следовательно, около 0,1. Заметим, что, ограничиваясь лишь одним первым членом в выражении для у, мы получим вполне удовлетворительный результат. Для этого в формуле для Ркр положим
2 0, тогда р _ VBC я _ 2,146 VBC
кр - I2 ГТ ГГ “ I2 ’
8Й Т)
т. е. погрешность — около 172.
Чтобы от изгиба полосы прямоугольного поперечного сечения перейти к изгибу двутавровой балки, нужно принять в расчет деформацию полок балки. При отклонении балки от плоской формы изгиба полки балки гнутся в плоскости наибольшей своей жесткости. Величина прогиба, обусловленная поворачиванием какого-либо сечения на угол ф, будет равна (г2) ф, где h — высота балки.
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ 451
Потенциальная энергия деформации балки будет равна
i i i v bJ у2 dx С J y'2dx -9f- j cp2dx,
0 0 о
где через D обозначена наибольшая жесткость изгиба одной полки балки. Основное уравнение (1) для определения критического значения изгибающей силы 2Р напишется так:
i iii 2Р фу (I- x)dx В J у2 dx С JV2 dx Dh2 J ф2 dx,
0 ООО
или, принимая во внимание первое из уравнений (10), получим
Р2
В
1 I 1 1 J ф2 ( - х)2 d С J ф2 dx Y22 J ф2 dx), (13)
о 'о о где для упрощения введено обозначение
Полагая
2 Dh2
V2 w
- пх , л Зпх Ф A cos Ах cos -
2 1 21 и вставляя в уравнение (13), найдем
ВС 8‘(1 922) 32'г(181г2)
Р KD
КР 4 1
где -г, как и раньше, обозначает отношение Ах : А.
Для у 0 мы получим тот же результат, что и для полосы (формула (12)).
Задаваясь различными значениями у2, можно составить таблицу для значений Ркр при различных поперечных сечениях и различных пролетах двутавровой балки. Сравнение с результатами, полученными путем интегрирования соответствующих дифференциальных уравнений, показывает, что и в данном случае приближенная метода дает вполне удовлетворительные результаты 1).
) См. указанную на стр. 443 нашу работу.
452 ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
§ 4. Об устойчивости прямоугольной пластинки, сжатой двумя взаимно противоположными силами
В качестве последнего примера рассмотрим вопрос об устойчивости пластинки, представленной на рис. 6. Решение этой задачи путем интегрирования соответствующего дифференциального уравнения принадлежит проф. А. Зоммерфельду 1).
Прямоугольная пластинка, опертая по краям, сжимается двумя взаимно противоположными силами Р, приложенными
личина потенциальной энергии деформированной пластинки. Это изменение главным образом будет заключаться в энергии изгиба. Если приравнять работу сил Р энергии изгиба выпучившейся пластинки, то получим уравнение для нахождения Ркр. Если бы изменение потенциальной энергии пластинки заключалось лишь в энергии изгиба, то получаемое таким путем значение РКр было бы совершенно точным. В действительности задача значительно сложнее, так как кроме изгиба выпучивание пластинки сопровождается изменением относительных удлинений.
Условиям на опертых сторонах пластинки мы удовлетворим, положив
Потенциальная энергия изгиба выпучившейся пластинки будет
стает быть устойчивой, пластинка
в серединах продольных сторон пластинки. Когда силы Р достигнут известного предела, плоская форма равновесия пластинки пере-
V 1 W4 V X V X J V 1 Ж Л XXX Лш ЧУ X X X X V X WX X X X X X 1IV4
j выпучивается. Величину критиче-
j
ской нагрузки приблизительно можно найти из таких соображений. При выпучивании пластинки точки приложения сил Р несколько сблизятся, и благодаря этому силы Р совершат некоторую работу. В то же самое время изменится и ве-
а
г
Рис. 6.
W sin
,4msin
тпх
l) A. S о in m e г f с 1 d. Obcr die Knicksiclierhcit der Stege von Walzwerkprofilen. Zeitschrift fiir Mathematik und Physik, 1907, Bd. 54, Heft 2, 113-153.
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ 453
Сближение 66 точек приложения сил Р найдется из следующей формулы:
M'S (жЫ
0 ' х— а2
Соответствующая этому сближению работа внешних сил будет
--(А-Лз Л,-.J.
Приравнивая эту работу потенциальной энергии изгиба (15), приходим к уравнению для определения критического значения сжимающей силы Р:
a,-a, a,- (16)
Нужно отыскать такое соотношение между коэффициентами Аи Аг,. чтобы определяемое из уравнения (16) значение РКр было наименьшим; другими словами, нужно найти минимум выражения
Сл2аЬ2 Zu а2 b2 I
2 (А — i43 Л5 —. )2 (17)
Составляя производную от этого выражения по какому-либо коэффициенту Ат и приравнивая ее нулю, найдем
S-o (т
т a2 b2 ) О
А»± Д, П2 ± ГОТ2 Q М2. (18)
Ах-А3 Аь- (“Н5- -ьг)
Здесь Q — величина постоянная для всякого т, и потому выражение (18) даст нам нужное соотношение между коэффициентами Аи Аг, Л5,.
Вставляя значение Ат в выражение (17) для критической силы, найдем
р _ Сп2аЪ2 1
КР “ 2 v 1
454 ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
Вводя для отношения длины пластинки к ее ширине обозначение х аb, найдем
р Сл2 (19)
Для нахождения критической нагрузки нужно лишь найти стоящую в знаменателе сумму бесконечного ряда1).
Возьмем разложение ch-- в бесконечное произведение
Яг Яг
е е
Логарифмируя это выражение и составляя от него производную, найдем
Т 2 2 ( 1 z2 9 z2 25 z2 ) S т2 z2
Составляя производную от обеих частей полученного выражения, найдем
я2 1 VI 1 V 2г2
8 и2 712 т2 z2 мЛ (т2 г2)2
с 2
Или, умножая на г и принимая во внимание равенство (20), получим
2)
Пользуясь таблицами гиперболических функций, легко можно вычислять значения для Рир при различных значениях jli. Заметим, что с возрастанием длины пластинки сумма
2-(гЫ‘
очень быстро приближается к своему пределу я8 и критическая
) Изложенный ниже прием суммирования принадлежит проф. В. П. Ер макору.
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ 45§
сила — к пределу
Р
1 кр
4л С
(Для х ajb 2 означенная сумма будет 0,973 j
Надо помнить, что вычисляемое по формуле (19) значение критической нагрузки будет меньше действительного и разность между действительной и истинной величиной РКр будет более значительной для коротких пластинок. Насколько близка к истине полученная формула, можно судить лишь на основании опытов.
Мы пришли к решению, взяв для w выражение (14). Если для w взять самое общее выражение
w
22
тлх. пли , Sin Sin —т
то можно показать, что наименьшее значение для критической сжимающей силы получаем, беря одно определенное значение для пу и при а b будет п 1.
Мы предполагали края пластинки свободно поворачивающимися, но величину критической силы можно приблизительно определить и при заделанных продольных сторонах пластинки. В этом случае
п dw w 0; 0 при у 0 и при
у ь.
Условию этому мы удовлетворим, положив
W
(l -cos-)2 An sin
Рис. 7.
Потенциальная энергия изгиба для этого случая выразится
так:
я4 аЬС 8
Сближение сжимающих сил при выпучивании пластинки будет
ь
6 Ъ
456 ПРИБЛИЖЁННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
Приравнивая работу сил Р потенциальной энергии изгиба, придем к уравнению
Рп(Ах-Аг Аь-.)2 я4,
Соотношение между отдельными коэффициентами будет прежнее, и потому
при значительной длине на основании (21)
Заметим, что полученная нами формула (22) была бы совершенно точна, если бы сжимающие усилия передавались лишь бесконечно узкой полоске АВ (рис. 7) и задача состояла бы в том, чтобы найти критическую сжимающую силу для этой полоски при условии, что ее выпучиванию препятствуют незаштрихованные части пластинки.
Ь
КР Ь (2х)3
S т2 (2ц)2
1 12
К ВОПРОСУ о ДЕФОРМАЦИЯХ И УСТОЙЧИВОСТИ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
Известия Электротехнического института, Петроград, 1914, том И, стр. 267— 287. Отд. оттиск, Пг., тип. А. Э. Коллинса, 1914, 23 стр. Вестник общества технологов, 1914, том 21, № 21, 1 ноября, стр. 785—792.
С вопросом о деформациях и напряжениях, возникающих в цилиндрических трубках и оболочках с цилиндрической срединной поверхностью, приходится довольно часто встречаться в различных отделах строительной механики, но, несмотря на всю практическую важность этих задач, теоретическому разрешению их до сих пор уделялось сравнительно мало внимания. В настоящий момент можно считать вполне разработанным лишь вопрос о деформациях цилиндрической оболочки, не сопровождающихся растяжением срединной поверхности1), и вопрос об устойчивости цилиндрической трубки, подвергающейся действию равномерного наружного давления2). В настоящей заметке мы намечаем общий ход решения задачи об определении деформаций цилиндрической оболочки и подробно останавливаемся на вопросе об устойчивости цилиндрической оболочки, подвергающейся равномерному сжатию вдоль образующих цилиндра. В заключение приводим формулу, позволяющую оценивать влияние на устойчивость пластин искривления их по цилиндрической поверхности.
§ 1. Уравнения равновесия
На рис. 1 представлен элемент цилиндрической оболочки, вырезанный двумя меридиональными плоскостями и двумя поперечными сечениями, перпендикулярными к образующим цилиндра. При составлении уравнений равновесия мы будем пользоваться обозначениями, принятыми в курсе теории упругости
) J. W. S. Rayleigh. Theory of sound. 2 edition. New York, Macmillan Co., 1896, vol. 2, p. 395.
2) Cm. R. Lorenz. Die nicht achsensymmetrische Knickung dunnwandiger Hohlzylinder. Physikalische Zeitschrift, 1911, Bd. 12, № 7, SS. 241—260. Дальнейшая разработка этого же вопроса имеется в статьях: R. V. Southwell. On the collapse of tubes by external pressure. Phylosophical Magazine and Journal of Science, 1913, Series 6, vol. 25, № 149, pp. 687—698; vol. 26, № 153, pp. 502—511 и R. M i s e s. Der kritische Auflendruck zylindrischer Rohre. Zeitschrift des Vereines deutscher Ingenieure. 1914. Bd. 58, N 19, SS. 750-755.
458 К ВОПРОСУ О ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
А. Лява1). На рис. ,а указаны положительные направления усилий Ть Т2у отнесенных к единице длины сечения срединной поверхности. На рис. 1,6 отмечены положительные направления моментов. Направляя в каждой точке срединной поверхности ось -ов вдоль образующей цилиндра, ось у в направлении касательной к параллельному кругу в сторону возрастания
угла ф, ось z-ов в радиальном направлении и обозначая через и, v и w соответствующие перемещения точек срединной поверхности при деформации, мы на основании общих уравнений равновесия1) можем в случае цилиндрической оболочки написать такую систему уравнений:
д_
дх
dS
dS2
дф
— Sta
d2v
дх2
ТА
д2у дх дф
at d2w 1
дТ2
дх
dN
дф
d2w
dv
дх дф дх
dw
дх )
)-М'Т7)
дх
дф
аТ,
а
G,
S Ы dtf,
d2w
дх2
dv
дх
дх
дф
rp d2v с d2v dw л Т1адх2 2 ( дх дер дГ)-'
q ( d2w , dv ,
2 дх дф ' дх )'
дх
aG
(о
) См. А. Е. Love. Lehrbuch der Elaslizitat. Deutsche Ausgabe von Al. Timpe, Leipzig — Berlin, B. G. Teubner, 1907, SS. 612, 613. В дальнейшем: A. E. H. Love — A. Timpe.J
К ВОПРОСУ о ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
459
Уравнения эти написаны в том предположении, что на оболочку действует лишь нагрузка, нормальная к поверхности. Интенсивность ее, представляющаяся некоторой функцией от х и ф, обозначена у нас через р.
В тех случаях, когда усилия Ти Т2 и S далеки от тех критических значений, при которых приходится считаться с вопросом устойчивости, мы можем в уравнениях (1) пропустить члены, где Ту Т2у. множатся на различные производные от малых перемещений и, v и w.
Тогда, исключая из этих уравнений величины Vi и N2y придем к такой системе:
адТ1_дЪ0
дх 9р
а --4- 0, (2)
д2Н2 d2Hi. 1 d2G2
дх
Т2 а
dep
дЮ1
дх2
дх dep дх дер а дер2
ар 0.
Все входящие в эти уравнения величины Т,.» Н2 могут быть выражены через составляющие перемещений иу v и w, для чего нужно воспользоваться известными зависимостями между перемещениями, деформациями и усилиями1). Деформация срединной поверхности определяется двумя растяжениями и сдвигом, которые могут быть найдены из формул ди dv w
е -
дх 9 е2 адф а w дх
Соответствующие усилия будут равны
Т — 27г ди , a dv w
1 1 — о2 дх а дф G а )
2Eh j ди , _dv w
1 — а2 дх а дер а ) 9
dv , 1 ди
(D - .
я а дер
q q Eh (dv , 1 ди 1 2 1 а д а дф '
О)
(4)
Здесь через 2h обозначена толщина оболочки.
Изменения кривизны срединной поверхности определяются величинами
d2w , dv 1 d2w
и _ d2w , __ 1 d2w dv _ 1 1 dx2 9 2 a2 dep2 ‘ дф J T “ a dv
dep2 1 dep )9 ' a dx dep 1 dx
Соответствующие значения моментов Gi,. выразятся такз Gj — С (k -f- ok2), G2 — — С (k2 -f
Я1 -Я2 С(1-а)т.
(6)
l) A. E. H. Love —A. Timpe, книга, указанная на стр. 458, SS. 594, 597, 604, 605.
460 К ВОПРОСУ О ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
Здесь С 27i33(l—а2) представляет собой цилиндрическую жесткость оболочки.
Вставляя значения усилий и моментов в уравнения (2), придем к такой системе дифференциальных уравнений:
д2и , 1—а I д2и , 1сг 1 d2v а dw q
дх2 1
1 -f- O’
2
д2и
а2 дф2 1 2
1 — а д2а
дх дф 1 dw а дф
а
а д дф u. d2v _ л2 а дф2
дл:
2 дл:2 h2 1 — а д3ш
д2а
(Т 3 1о
а
d3w
дл:2 дф 1 d3w
)
дл:2 1 d2v
дх2 дф
да . 1 dv __ w __ h2 (
дх ' а дф а 3 дх
д3у 2h2 1 — а ( d4w
а3 дф3 dAw ,
дф2
и
1 d4w
а
3 а
дх2 дф д4оу
2г2 1 - or j 3 а V
а дф2 дх2 д3и
1 d4w
дх2 дф2 ' а3 дф4
дл:2 дф2 1
.L 4-
а3 дф3
)-
дл:2 дф ар (1 — а2) 27г
«0.
(7)
Для определения деформации цилиндрической оболочки приходится в каждом частном случае разыскивать такие решения уравнений (7), которые удовлетворяли бы условиям на краях.
§ 2. Цилиндрическая трубка со свободными краями
Если края цилиндрической трубки свободны, то можно с большой точностью положить, что срединная поверхность трубки при деформациях под действием давлений р не испытывает ни удлинений срединной поверхности, ни ее сдвигов1). В таком случае на основании (3) будем иметь
dv w __ о до ди
п ifL o
дх и’
0.
а дф а дх а дф
Самые общие выражения для перемещений, удовлетворяющие написанным уравнениям, могут быть представлены в таком виде:
U — -B„sin(rt(p p„),
v 2 Ап cos (пср а„) Впх cos (mp р„), w — nlAnsin(npan)Bnxsin(nq
Подобными решениями можно воспользоваться и в том случае, когда мы имеем дело не с цельной трубкой, а с частью
(8)
) См. А. Е. Н. Love — A. Timpe, книга, указанная на стр. 458, S. 619.
к ВОПРОСУ о ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 461
ее, вырезанной двумя меридиональными сечениями (рис. 2). Если края оболочки, соответствующие образующим цилиндрической поверхности, оперты1), то для перемещений можно принять такие выражения:
Saa D. глср
— Вп sin-f-,
V 2 (Л«
W
При этом, конечно, не будут удовлетворены условия на краях х1, х —. При взятых нами перемещениях здесь появятся моменты Н1 и G, отличные от нуля, но соответствующие им напряжения будут иметь характер местных напряжений и не окажут существенного влияния на общую деформацию оболочки.
При определении коэффициентов Ап и ВПу входящих в выражения для перемещений (8), проще всего воспользоваться свойствами нормальных координат. Потенциальная энергия деформации, соответствующая выражениям (8), при длине цилиндра 21 представится так:
V Cnl п231У nAl n2l2 2 (1 - a) a2 B2n. (9)
Для разыскания коэффициентов An и Bn мы можем составить группу таких уравнений:
дУ р» 10
Рис. 2.
дЛп
Здесь Рп и Qn — обобщенные силы, соответствующие координатам Ап и Вп. Выражения для обобщенных сил легко написать, если принять во внимание, что произведения PndAn и QndBn представляют работу, производимую внешними силами на перемещениях, соответствующих приращениям координат dAn и dBn 2).
) Под опертым краем будем подразумевать такой, для которого w О и 0 ( 1, 2).
2) Примеры решения задачи таким путем имеются в нашей статье «При¬
менение нормальных координат к исследованию изгиба стержней и пласти¬
нок». Известия Киевского политехнического института, 1910, год 10, книга I.
Отд. оттиск, Киев, 1910, 49 стр.
462 К ВОПРОСУ о деформациях цилиндрической оболочки
Тем же выражением (9) для потенциальной энергии мы можем воспользоваться и в случае цилиндрической оболочки, пред- ставленной на рис. 2. Нужно только вместо п везде поставить ппа и окончательный результат разделить на 2яа.
§ 3. Цилиндрическая трубка с опертыми краями
В этом случае деформации трубки будут сопровождаться растяжениями и сдвигами в срединной поверхности, и потому формулы (8) не могут здесь служить приближенными выражениями для перемещений. Чтобы найти эти перемещения, нужно обратиться к общим уравнениям (7). Мы можем удовлетворить этим уравнениям и условиям на опертых краях, если положим
V1 V1 л тПХ
и 2а 2а Лтsin Л(Рcos Г
V1 V1 г» тпх
v 2u2u Втп cos Я(р sin т
V1 тпх
w 2j 2u Стп sin Л(р sin —i—
(id
Здесь через I обозначена длина трубки. Начало координат расположено так, что на концах трубки х О и х L Легко видеть, что при выбранных выражениях для перемещений w yl G обращаются в нуль при х 0 и х. Теперь остается только подобрать постоянные Атп,. так, чтобы были удовлетворены дифференциальные уравнения (7). Представляя интенсивность сплошной нагрузки в виде ряда
Р 2 2 Dmn sin Л(р sin (12)
и вставляя (И) и (12) в уравнения (7), получим для каждых трех коэффициентов Атп, Втп и Стп три таких уравнения:
л ( тя 2 , 1 — а п2. р 1 а п пт , „ а тя _ тп I ) -Г 2 а2 V mn 2 a I I ’
„ 1 а тп . п Г I — т tnn 2. п2.
Ашп-2-n-j- Втп а—) —
, h2 1 — а (mn 2. h2 п21 , п Г п . h2 п ( тп 2 , h2 п3 1 п
- атп. D Г п h2 п3 , 0 ч h2 п (тп 21.
Атп-нВ - тг (2-ст)т--(—) J
, „ Г 1 I А2 (тп , 2г2 г2 (тп 2 , А2 га4 п а(1-ст2) А
Стга- -з-а(— — — (— --Dmn 2Eh 0.
К ВОПРОСУ О ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
463
Вводя обозначения атп1 уту ha р, получим
(Y2m 1 а
1 — а
Я2)
1 СГ
' nYm тпаут
0,
ttYm mn -Ц- Y п2 -(1-а) У2т п2
я3) 0,
Cm„ n -y-nY„ -
,n x(2-a)«Y -x«3
(13)
Л av В
ttiti m 1 л
P2 4 2p2 9 P2 4 _ a2( 1-cr2)
СтД1 TYm — П Vm -Tn)- Ш n
При помощи этих уравнений коэффициенты Атп,. могут быть выражены через известную величину Dmny и если полученные таким путем ряды (И) будут сходящимися, то они и представят собой искомые перемещения точек цилиндрической оболочки.
Если вместо цельной трубки мы будем иметь лишь часть ее, ограниченную двумя образующими, то в случае опертых краев мы можем воспользоваться для перемещений прежними выражениями (11). Нужно только везде вместо п вставить величину ппа, где а — центральный угол, соответствующий выделенной части цилиндрической оболочки. Решение это будет соответствовать известному решению Навье для прямоугольной пластинки с опертыми краями.
Если мы будем беспредельно увеличивать радиус ау сохраняя ширину выделяемой из цилиндра полоски конечной, и введем обозначения аа by аср уу то из (12) и из третьего уравнения системы (13) найдем
3 1 СТ2 Dmn
. пли . тлх
Р Dmnsm sin — ,
Следовательно,
W3 1 - a2
W 2u 2j 2 Eh3л4
С tnn
2 Eh3я4
m2 пГ2 2 b2 j
_ . тлх . пли
Dmn sin —:— sin - ----
(m2 пУ 2 I2 b2 J
что совершенно совпадает с вышеупомянутым решением Навье.
§ 4. Об устойчивости цилиндрической трубки
Если тонкостенная цилиндрическая трубка подвергается действию равномерного наружного давления или испытывает рав номерное сжатие вдоль оси цилиндра, то при увеличении внешних сил можно достигнуть предела, когда цилиндрическая форма
464 К ВОПРОСУ О ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
равновесия сжатой трубки перестает быть устойчивой. Для определения критических значений внешних сил и соответствующих им критических напряжений необходимо обратиться к дифференциальным уравнениям (1). Если нас интересует величина критического наружного давления, при котором трубка сплющивается, то в уравнениях (1) должны быть сохранены кроме конечных членов также и малые члены, имеющие множителем величину Г2. При определении критических значений усилий, вызывающих продольное сжатие трубки, необходимо сохранить члены с множителем Т. Наконец, при разыскании критического значения скручивающих моментов, которые могут быть приложены по концам трубки, нужно оставить члены, имеющие множителем 51 и S2. Мы остановимся здесь на случае продольного; сжатия трубки ).
Исключая из уравнений (1) величины N и N2 и сохраняя лишь те малые члены, которые включают множителем Тi, мы придем к такой системе уравнений:
а
дх
dS,
дТ2
дНх
дх
дф
дх
rjy d2w I rp , d2G 1 a 1 dx2 2 a dx2
1 dG2 , ad p , d2.
rp d2v n 1a dx2 — ’
дх дф дх дф а дф
1 d2GJ__()
,2
(14)
l) Частный случай этой задачи, когда выпучившаяся поверхность трубки симметрична относительно оси трубки, рассмотрен нами в работе «Einige Stabilitatsprobleme der Elastizitatstheorie». Zeitschrift fur Mathematik und Physik, 1910, Bd. 58, Heft 4, SS. 337—385. Там же разобран простейший случай деформации, несимметричной относительно оси, именно тот случай, когда перемещения не сопровождаются растяжениями срединной поверхности. Дальнейшее исследование этого вопроса принадлежит Р. Лоренцу (R. Lorenz). См. его статью «Die nichtachsensymmetrische Knickung diinnwandiger Hohlzylinder». Physikalische Zeitschrift, 1911, Bd. 12, № 7, SS. 241—260. Так как P. Лоренц для упрощения решения пренебрег перемещениями ы, то полученные нм результаты могли внушать некоторое сомнение, что и заставило нас еще раз обратиться к решению того же вопроса. В самое последнее время мы познакомились с весьма ценной работой Р. Саусвелла (R. V. Southwell. On the general theory of elastic stability. Philosophical Transactions of the Royal Society of London, 1913, Scries A, vol. 213, pp. 187—244). В ней автор дает общую теорию устойчивости упругих систем и в качестве одного из примеров приводит цилиндрическую трубку, испытывающую продольное сжатие. Р. Саусвелл освобождает задачу от ограничений, наложенных на перемещения Р. Лоренцем, и получает систему уравнений, близкую к системе, найденной нами. Результаты, полученные им для весьма длинной трубки, вполне правильны, но одно ошибочное заключение помешало ему распространить решение на случай коротких трубок, от которых легко перейти к практически важной задаче об устойчивости части цилиндрической оболочки, заключенной между двумя образующими.
к ВОПРОСУ О ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 465
Выражая при помощи (4) и (6) усилия через перемещения, придем к таким уравнениям:
д2и , 1а d2v a dw. 1 — сг д2и
дх2 1 1 (Т
2а
д2и
дх дер а дх 1 — а d2v
дх дф
а
2
d2v
а дф'4
0,
н2
2
1 — а
дх2 Г d3w
а дф2
1 dw.
ад ф
к2
I
а
d3w
d2v дх2 d3w , 1 d2v
_ дх2 дф дх2 J
1
дх2 дф
а3 дф3 ' а1 , Тй d2v
1 2Eh дх2 ди , dv
3 дф2 (1 — а2) 0,
2 Eh
h2 Г
—га
d4w
дх 1 d4w
а дф I сг
w
а
д3и
дх4
а дх2 дф2 d4w
а дх2 дф 1 d3v
-
2z2 п ,Г1 Л ,1 d3v Л 3 1 аЧ а дх2 р2 ф а дх2 9р J
dw , 1 d4w , 1 d3v 1 _ л
Л2 Га 3 L а ;
(15)
дх2дф2 1 а3 дф4
Мы удовлетворим этим уравнениям, положив
л ди w ,
v 0, 0-5— — const,
аде а
Это решение соответствует цилиндрической форме равновесия сжатой трубки.
Чтобы получить критические усилия, соответствующие выпучиванию трубки по поверхности, симметричной относительно оси, положим, что v 0, и и w представляют собой функции х.
В таком случае система уравнений (15) сведется к двум таким уравнениям:
ди а
w о,
дх а 9
аТ j
2Eh
(1 -or2)
d2w дхт
ди ___ w дх а
h2 d4w Л
-з-а- 0’
откуда находим
dw 3 Г, (1 — a2) d2w. 3(1-а2) _
дх 2 Ш3 дх2 ЛР W 0
Мы удовлетворим этому уравнению, положив
л тях л . TLX
w — A sin —j— A sin.
(16)
456
К ВОПРОСУ о ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
Здесь через X обозначена длина волн, на которые подразделяется цилиндрическая трубка при выпучивании. Вставляя выражение w в уравнение (16), получим для критического значения усилий Т1 такой результат:
Длинная трубка при выпучивании подразделится на большое число волн, и мы можем с большой точностью считать, что длина волны X как раз будет та, которой соответствует минимум выражения (17). В таком случае критическое напряжение будет равно
В случае очень короткой трубки выпучивание произойдет по поверхности с одной полуволной. Постепенно увеличивая длину, мы последовательно будем получать две, три и т. д. полуволн. Длина, при которой совершается переход от формы равновесия с m полуволнами к форме с m 1 полуволнами, определится из того условия, что формула (17) дает при этом для кр одно и то же значение независимо от того, вставим ли мы вместо X I I величину — или —. Таким путем получается соотношение
Следовательно, две полуволны получаются, начиная с длины
(7,)кр
(17)
(18)
Полагая а 0,3 и Е 2,2 106 кгсм2, найдем
ркр — 1,33 Ю® — кгсм2.
(19)
При этом легко видеть, что
± 15(1-о),- 0,578.
а
2 h
а
(20)
3(1 — а2)
Для получения трех полуволн длина должна быть не меньше
к ВОПРОСУ О ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
467
и т. д. Характер явления совершенно такой же, как и при выпучивании сжатой прямоугольной пластинки с опертыми краями. Все это относится, конечно, лишь к формам равновесия, симметричным относительно оси.
Для получения критических напряжений, соответствующих формам равновесия, несимметричным относительно оси трубки, необходимо обратиться к уравнениям (15). Возьмем для перемещений такие выражения:
и A sinmp cos-
v В cos шр sin
. . тпх
w С sin Яф sin —j—.
Вставляя их в уравнения (15) и пользуясь обозначениями га р, атя Y- придем к такой системе уравнений:
A (v2 g—п2) Д Л2 пу Соу О,
В 1 а у2 гг2 -j- (1 - а)у2
а 1 4 ст
А —тг- пу
2 Eh
Аау В п -у пг 2 3 р2п2
с V 11V4 РW f « - 0.
Критическое значение сжимающих усилий найдется из условия равенства нулю определителя уравнений (21). Вводя обозначение у Тi(l—o2)2Eh, получим для у такое уравнение второй степени:
(21)
1
1 — а п2
1 а п
2 у
1 а п
а_
Y
1 — сг
г
Р2(1 -а)
I Р2 п2 I
у2 3 y2 3
y i-y2
0.
(22)
468 к ВОПРОСУ о ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
Практически важен лишь тот случай, когда у — малая величина, так как только при этом условии явление выпучивания произойдет при напряжениях, не выходящих из пределов упругости. Мы можем поэтому в уравнении (22) отбросить член, заключающий у2. Отбрасывая также члены, имеющие своим множителем величину (Р23)2, придем к такому результату:
- У О “ 2) Y4 (я2 Y2)4 “ (2 а)(3 - о) у4п2 2y4(1 - сг2)-
— у2п4 (7 а) (3 о) у2п2 п4— 2п6 :
: y2(«2 Y2)2 t4f (y2 -Ця2) l Ц- (п2 Y2)2 -
Рассмотрим сначала случай, когда длина трубки мала или когда трубка при выпучивании подразделяется на большое число коротких волн. При таком условии у2 — большое число, и мы, ограничиваясь в решении (23) самыми главными членами, получим
Если положить п О, то придем к полученному выше результату (17) для симметричной относительно оси деформации. Наименьшее значение критических напряжений, определяемых формулой (24), будет то же, что дает формула (18). При этом соотношение между длиной продольных волн и числом п волн, образующихся по окружности цилиндрической трубки, найдется из условия
Пока длина трубки или одной полуволны настолько мала, что
у2 У3(1 — а мы будем иметь деформацию, симметричную
относительно оси трубки. С убыванием у будут появляться две, три и т. д. волны по окружности цилиндра, но величина критических напряжений при этом будет мало отличаться от того, что дает формула (18).
Рассмотрим теперь второй предельный случай, когда величина у, входящая в выражение (23), мала, т. е. когда длина продольных волн, на которые подразделяется трубка при выпучивании, велика по сравнению с радиусом трубки. Сюда, между прочим, относится эйлеров случай продольного изгиба.
К ВОПРОСУ О ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
469
При малом значении у мы можем сохранить в числителе выражения (23) лишь члены, не содержащие у и члены порядка ру и у4- В знаменателе удерживаем лишь члены порядка у2. Тогда из (23) получаем
(1 - а2) у4 -у- («4 - га2)2 Y2 4«6 - (7 а) п (3 а) п)
У V2 («4 Я2) ' Для получения эйлерова случая нужно положить п 1, тогда
г, . тпх „ . . тпх
V В COS ф Sin—J—, W В Sin ф sin -у—.
Каждая точка какого-либо поперечного сечения совершает в плоскости этого сечения в направлении ф я2 одно и то же
D. тпх ,-г
перемещение, равноеsin ——. При этом, конечно, сплющивания трубки не происходит. Из выражения (25) при п 1 получаем
(1—а2) о
У 2 ИЛИ
Тх п2а2
1ППГ212
что совершенно совпадает с формулой Эйлера для случая стержня с опертыми концами, так как а22 есть не что иное, как квадрат радиуса инерции поперечного сечения тонкостенной трубки.
Для п 1 мы можем, опуская малые величины высших порядков, написать
(1 - а2) V2 Р2 п2(п2- I)2
у п2(п2 1) 3 у2(п2) Наименьшее значение г, порученное из этой формулы, будет равно — 2р У — а2 (п2 — 1)1 (п2 ) При этом
_7j_ 2h 1 я2 - 1
2Eh а 3(1 -а2) п2 1 ‘
Соответствующая длина волны определяется соотношением
9 рп2(п2- 1)
3(1-а2) ’
откуда
2h п Vп2 — 1
470 К ВОПРОСУ 0 ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
На прилагаемом рис. 3 графически представлено изменение отношения Т2Е1г в зависимости от величины lу и числа п для цилиндрической трубки, у которой 2ha 0,01.
Рис. з.
Заметим, что с увеличением у убывает точность формулы (26), на основании которой произведены вычисления.
§ 5. Об устойчивости цилиндрической оболочки,
опертой по двум образующим и двум параллельным кругам
Пусть а — центральный угол, соответствующий рассматриваемой части цилиндрической оболочки. В качестве решения общих уравнений (15) возьмем такие выражения:
- .яср тпх г»яф . тлх
и A Sin — COS —7— , V В COS Sin 7—,
a I 9 a I 9
.яф. тлх W С sin—— Sin —Т—. а При этом по контуру оболочки будут выполнены такие условия:
при ср 0 и при ф а w 0 и G2 0;
при х 0 и x l w 0 и Gj 0.
Что касается перемещений vy то при ф 0 и ф а эти перемещения в нуль не обращаются. Мы предполагаем здесь, что точки опорного контура, соответствующие ограничивающим образующим, могут свободно смещаться в плоскостях, касательных к цилиндрической поверхности.
Вставляя принятые выражения для перемещений в уравнения (15), мы для определения соответствующих критических усилий получим уравнение, отличающееся от прежнего нашего
К ВОПРОСУ О ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ 471
уравнения (22) только тем, что вместо п будет стоять число knla. Как и в случае цельной трубки, будем различать здесь искривленные формы с короткими волнами (у — большое число) и формы с длинными волнами. При большом у мы на основании (24) будем иметь
В» I a YJ , (1 — а2) у2 ы
у 3 Y2 2я2 , 2 Ы')
Если в этой формуле перейти от цилиндрической поверхности к пластинке, то второй член пропадает, и мы при k 1 будем иметь
Наименьшее значение сжимающих усилий получим при
Y2 . (с)
Обозначая через Ъ величину а а (ширину пластинки), найдем п2а2К2 п2а2Ь2, откуда К Ь.
Пластинка стремится при выпучивании подразделиться на квадраты. Вставляя значение (с) для у в формулу (Ь), придем к известному результату Дж. Брайана1):
_ р2 4я2а2 _ h2 4я2
У-Ъ W W9
откуда
т _ 2 Eh3 4я2 _ 4я2С 1 1 3 1 - а2 Ь2 “ Ъ2
Возвращаемся теперь к общей формуле (а). Наименьшее значение критических усилий, определяемых по этой формуле, представится так:
ТЛ-. ——- (d')
2Eh а 3(1-а2) V
причем должно быть соблюдено условие
(е)
Я‘
l) G. Н. Bryan. On the stability of a plane plate under thrusts in it own plane, with application to the «buckling» of the sides of a ship. Proceedings of the London Mathematical Society, 1891, Series 1, vol. 22, p. 61 (формулы (18) и (19)).
472 к ВОПРОСУ О ДЕФОРМАЦИЯХ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
Если угол а не мал, т. е. рассматриваемая часть цилиндрической оболочки не является весьма пологой, то при малом значении р мы получим для у большое число, и, следовательно, будет соблюдено условие, при котором формула (d') имеет место. Если угол а настолько мал, что
я2 3 (1 —а2) аг 40 то уравнение (е) дает для у мнимую величину. Мы должны в таком случае обратиться при определении критических напряжений к формуле (а). Полагая в ней k 1, найдем то значение у» ПРИ котором критические усилия приобретают наименьшее значение. Для этого составим производную по у2 и приравняем эту производную нулю. Тогда получим у2 я2а2. При таком значении у формула (а) дает нам
4 п9 я2 , 1 9 а2
-у
Или, обозначая через Ъ ширину полоски, равную аа, будем иметь
Г, _ 4 h2n2. b2 2Eh 3 Ь2( -о2) 4я2а2
(27)
Результат этот может быть написан в несколько ином виде, если принять во внимание, что при малом значении а между а,
Ъ и стрелкой f имеет место такое соотношение: 624 2а. Сле¬
довательно,
Тх 4 n2h2.24 я2 h2 Л f2 ( ,
2Eh 3 62(1-а2) я2 а 3 1-а2 62 1 0,448 4Л2 ’ 27 '
Первый член в этой формуле определяет величину критического усилия, соответствующего пластинке ширины Ь. Второй член дает нам увеличение жесткости, обусловленное изгибом пластинки по цилиндрической поверхности со стрелкой f.
Подобным же образом может быть рассмотрена задача при условии появления на выпучившейся поверхности длинных волн. Мы здесь на этом вопросе не будем останавливаться, так как он, как нам кажется, не может иметь особого практического значения.
Поступила в редакцию 18 октября 1914 года
ОБ УСТОЙЧИВОСТИ ПЛАСТИНОК, ПОДКРЕПЛЕННЫХ ЖЕСТКИМИ РЕБРАМИ
Сборник Института инженеров путей сообщения, Петроград, 1915, выпуск 89. Отд. оттиск, Пг., тип. А. Э. Коллинса, 1914, 31 стр.
§ 1. Подкрепление сжатой прямоугольной пластинки ребрами, параллельными направлению сжатия
При решении вопроса об устойчивости сжатых пластинок, подкрепленных жесткими ребрами, будем пользоваться общим приемом, который мы применяли при исследовании устойчивости стержней, двутавровых балок и тонких пластинок1).
Предположим, что прямоугольная пластинка сжимается силами, равномерно распределенными по сторонам, параллельным оси у (рис. 1). Пусть
Р — усилие, отнесенное к л
единице длины контура пластинки и р Ph (h— толщина пластинки) — соответствующее сжимающее напряжение. Если края пластинки оперты, то критическое значение сжимающих напряжений, при котором плоская форма пластинки перестает быть устойчивой, при аЬУ2 определяется формулой
Рис. 1.
Р кр;
Ся2 (1Р2)2 b2h р2
(1)
где через С обозначена цилиндрическая жесткость пластинки,
0 ,и равная 12 __а2 , и через р — величина отношения ая.
При большой длине выпучивание пластинки происходит по волнообразной поверхности. Узловыми линиями, перпендикулярными к направлению сжатия, пластинка разделяется на ряд прямоугольников, длина которых А,, равная длине полуволны
) См. нашу работу «Об устойчивости упругих систем». Известия Киевского политехнического института, 1910, год 10, книга 4, стр. 375—560. Отд. оттиск, Киев, тип. С. В. Кульженко, 1910. 188 стр.
474 ПЛАСТИНКИ, ПОДКРЕПЛЁННЫЙ ЖЕСТКИМИ РЁБРАМИ
выпучившейся поверхности пластинки, должна быть вставлена в формулу (1) вместо а а рб для получения критического напряжения.
Величина Я, а следовательно, и число полуволн, на которые подразделяется пластинка при выпучивании, должны быть выбраны так, чтобы 1ф, определяемое по формуле (1), имело минимальное значение. Предположим теперь, что для увеличения жесткости пластинки мы ее подкрепили ребрами, параллельными направлению сжатия. Обозначим через В жесткость изгиба каждого из этих ребер, через F — площадь его поперечного сечения, через Р — величину сжимающей силы, приходящейся на одно подкрепляющее ребро. (Мы будем предполагать, что ребра и пластинка испытывают одно и то же сжатие. В таком случае сила Р получится умножением сжимающих напряжений в пластинке на величину площади F.)
В самом общем случае выпучившаяся поверхность прямоугольной пластинки с опертыми краями может быть представлена таким бесконечным рядом:
оо оо
SV „ . тпх. пли
2j Атп sin - sin.
т 1 гг 1
Соответствующая этому искривлению потенциальная энергия изгиба выпучившейся пластинки будет равна
-4 J I№жГ'I'1-о)W--Ш»-
О О
_ С ab V V 2 (т2л2 , п2л2 2
ТТ Za 2л Ятп а2 Ь2 )
т 1 п 1
Если подкрепляющее ребро расположено на расстоянии С от оси лг-ов, то потенциальная энергия изгиба этого ребра при выпучивании его вместе с пластинкой представится так:
4isr т4 (misin- m2sini Am3sinp-.)2.
m-1
Рассмотрим теперь, какую работу совершат сжимающие силы при выпучивании пласгинки. Усилия Р, приложенные
ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ 475
непосредственно к пластинке, совершат работу
r-f-»()2 2 ».
т 1 гг1
Работа силы Pi, сжимающей подкрепляющее ребро, представится такой формулой:
r-(L -
оо
Р, я2 а V о 1л пс 1 , „ . 2tcci , л. Зяс1 , 2
rtf2 2i 1 ml Sin ь Ат2 Sin Ат3 sin —.).
m 1
Если имеется k подкрепляющих ребер, си с2, — рас¬
стояния их от оси х, Р1, Рг, Рк — соответствующие значения сжимающих сил и Ви В2, Bk — соответствующие жесткости изгиба, то полная потенциальная энергия изгиба ребер представится суммой
S V‘ T S Bi i m4(Amlsin Am2sin2-
i l i 1 m -1
, л 3ncl 2
Am3sin--.J
Для полной работы соответствующих сжимающих сил при искривлении ребер получаем такое выражение:
ИTi 2Рг S т2 (Лт sin Лт2 sin г
i l i 1 т» 1
. л. ЗЛС, 2
m3sin—-.j.
Критическое значение сжимающих напряжений получим, приравнивая потенциальную энергию изгиба системы при выпучивании работе сжимающих сил. Таким образом получается
уравнение
у 2 vt т 2 г,. (2)
Вставляя в это уравнение найденные выше выражения для потенциальной энергии и для работы сжимающих сил и вводя обозначения
а
ЪС yi’ РЬ bh 0ii
476
ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
получим для критических напряжений такое выражение:
I т» 1 п 1
2 2 2 m4mlsinm2sin--.) X
i-1 т-1 J
xSS m2Amn ш sin
I m “1 я1 i 1 m 1
2лс. VI1
Am2 S 'm l “) Теперь остается подобрать коэффициенты Атп таким образом, чтобы выражение (3) для кр получало минимальное значение. Приравнивая нулю производную от выражения (3) по каждому из коэффициентов Атп и принимая во внимание уравнение (2), получим для нахождения коэффициентов систему бесконечно большого числа линейных уравнений такого вида:
ik пкс
-гг I Атп (т2 п2Р2)2 V sin m4 X
I 1
X Ащх sin Am2 sin
ППС.
m2Amn 2 2j sin-j- m2 X г-i
„ tic. 2tic. Л
X Aml sin -jf- Am sin —. j j 0. (4)
Здесь для сокращения письма введено обозначение р0
Cn2lb2h.
Эти уравнения допускают для коэффициентов Атп решения, отличные от нуля лишь в том случае, если их определитель обращается в нуль. Составление этого определителя мы упростим, если примем во внимание, что каждое из уравнений вида (4) -заключает не все коэффициенты Лтп, а лишь те, у которых первый значок является общим. Соответственно этому мы можем разбить все наши уравнения на группы и искать условия равенства нулю определителя одной из этих групп. Мы можем
ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ 477
ограничиться первой группой, заключающей уравнения вида -( Л,„(1 «2р2)2 2 YfSin-p- X
I 1
X (y4„siny-l)2sin-- )-
Если мы возьмем какую-либо другую группу уравнений из общей системы, то делением этих уравнений на число т4 получим систему уравнений такого вида:
Уравнения эти отличаются от группы уравнений (4') лишь тем, что вместо числа р входит число рm, что соответствует возможности подразделения пластинки при выпучивании на т полуволн.
Следовательно, как и в случае неподкрепленных пластинок, мы можем в настоящей задаче ограничиться рассмотрением лишь тех искривлений пластинки, которым соответствует выпучивание по одной полуволне. Соответствующие критические напряжения найдутся из условия равенства нулю определителя уравнений (4). Величина их может быть вычислена с любой степенью точности путем увеличения числа членов в ряде
sinSsini (5)
представляющем форму выпучивания пластинки по одной полуволне. В первом приближении можно ограничиться первым членом выражения (5); тогда вместо системы уравнений (4') получим уравнение
478 ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
откуда
(6)
В случае нескольких равноудаленных ребер одинаковой жесткости это первое приближение даст вполне удовлетворительные результаты. При наличии одного или двух подкрепляющих ребер приходится в некоторых случаях для обеспечения надлежащей точности переходить к вычислению дальнейших приближений.
§ 2. Случай одного подкрепляющего ребра, проходящего посредине пластинки
В этом случае ксЬ я2. Принимая выпучивание по одной полуволне (формула (5)), представим уравнения (4') в таком виде 1):
Уравнения, заключающие четные коэффициенты, дают для р1ф такие значения, как в случае нсподкрепленной пластинки, имеющей ширину 62. Наименьшее из этих значений, определяемое из второго уравнения системы (7), равно
Соответствующие этим решениям поверхности искривления пластинки имеют вдоль подкрепляющего ребра узловую линию.
) Первый значок при коэффициентах, общий для всех коэффициентов, мы здесь пропускаем.
-р-(1 Л, 2y (л,-л3 л5-
Ркр А 26 (Ai — Л3 Л5 —.) О,
-р-(1 42)2 Л2 — рк,Л2 0,
f (1 9р2)2 Л3 — 2 (Л, — Л3 Л5 —. )—
— V (А — 26 (л — А А ) о.
(7)
-р-(1 16р2)2 Л4 — ркрЛ4 о,
-р- (1 25р2)2 А2y (Л, — Л3 А — ) —
— Ркр Л5 26 (Л — Л3 Л5 —.) 0,
pKp fH 14Р2)2.
(8)
ПЛАСТИНКИ, ПОДКРЕПЛЁННЫЕ ЖЕСТКИМИ РЕБРАМИ 479
Если подкрепляющее ребро обладает большой жесткостью, то при условии 2р У2 формула (8) дает наименьшее значение для критического напряжения. Влияние подкрепления равносильно в этом случае уменьшению расчетной ширины пластинки вдвое.
Обратимся теперь к тем из уравнений (7), которые заключают нечетные коэффициенты. Увеличивая число коэффициентов в выражении (5), а следовательно, и число уравнений (7), мы будем получать все более точное значение для соответствующего р,ф.
Если ограничиться двумя нечетными коэффициентами, то соответствующие уравнения системы (7) напишутся так:
Л, р (1 Р2)2 2у Ркр (1 26) 2Л 3 у рКр б) О,
2 Л, Ркрб) Л3 f- (1 9р2)2 2у - Ркр (1 26) 0.
Явление выпучивания может иметь место лишь в том случае, если написанные уравнения допускают для А и А3 решения, отличные от нуля. Для этого необходимым условием язляется равенство нулю соответствующего определителя. Составляя его и приравнивая нулю, найдем второе приближение для р1ф из уравнения
()2 (14б) (12б) (аb) 8y6ab4у2- (9'
Здесь для сокращения письма мы ввели обозначения
(1 Р2)2 2у а, (1 9р2)2 2у Ь.
Для получения третьего приближения берем три нечетных коэффициента в выражении (5). Соответствующая система уравнений (7) представится в таком виде:
А, ff (1 Р2)2 2у - Ркр (1 26) 2А3 Y РкРб)
2Л5 (-fY-pKp6) 0,
2А, Y РкРб) Л3 f- (1 9р2)2 2у - ркр (1 26)
2(Y P«p6) 0,
2Л, (г Y “ Ркрб) 2Л3 y ркрб)
A5f (1 25р2)2 2у - ркр (1 26) 0.
480 ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЁСТКИМИ РЁБРАМИ
Приравнивая нулю определитель этих уравнений, получим для нахождения третьего приближения Кр такое кубическое уравнение:
“ (гТ 6б (-гТ (1 46) (а 6 с) - 24Y6
(РкРр- )— (1 26)(а6 ас 6с) 86у(а 6 с) 12у2 (1 —2б)-Ь
abc — 4y2 (а Ъ с) 16у3 0. (10)
Здесь для сокращения письма введено обозначение
(1 25р2)2 2у с.
Этим путем можно получать и дальнейшие приближения для Ркр, но практически с ними не приходится иметь дела, так как третье приближение всегда обеспечивает надлежащую точность. Мы всегда можем представить критическое напряжение такой формулой:
Ркр kpQ,
где коэффициент k будет зависеть от соотношения между жесткостями и между площадями поперечных сечений листа и подкрепляющего ребра.
Ряд значений этого коэффициента для различных у и б приведен в таблице А.
При вычислении мы пользовались в случае коротких пластинок вторым приближением. Для длинных пластинок (р 2) первое приближение дает вполне удовлетворительные результаты, и мы им и ограничивались. Из таблицы видно, что для каждого у и 6 имеется свое значение р, которому соответствует Amin, причем это р возрастает с увеличением жесткости подкрепляющего ребра. Следовательно, в случае длинных пластинок мы получим при выпучивании ряд полуволн. Длина их будет больше, чем для неподкрепленной пластинки, и тем больше, чем жестче подкрепляющее ребро. Если ограничиться первым приближением и положить
n _ п (1р2)2 2у
Ркр-Ро р2(126) ’
то легко показать, что наименьшее значение критического напряжения получается при р2 У 2у и равняется
2(1 ГТ2у ) п
1 26 Р9
Этими формулами решается вопрос о числе полуволн, на которое подразделяется длинная пластинка при выпучивании.
Таблица
ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ 481
С4
in
00
о
in
,
,
Г--
со
l
СО
СО
1
со
in
со
п
CD
CD
CD
со
со
со
со
см
—Г
—Г
см
со
со
II
«о
ю
о
in
оо
О
in
_
4
см
in
00
СО
сОл
1
со
Tf
см
И
CD
СО
CD
со
со
со
со
in
со
со
со
со
in
in
«о
ю
-
in
00
О
ю
1—1
см
о
о
00
00
(N
со
см
о
II
CD
CD4
CD
со
со
со
со
со
in
in
in
in
со
со
U
«о
(N
in
00
О
in
т«
СО
сОл
05
СО
СО
00
,
со
СО
СО
II
ссГ
со
CD
со
со
см
о
о
о
о
см
II
ю
й
о
in
00
О
in
г—1
г—1
Tt«
Tt
Tf«
СО
о
in
сч
II
CD
со
со
со
со
со
со
см
см“
см
см
со
со
со
«о
' 1
,“н
s
ю
00
О
ю
,
,
l
со
05
ю
ю
,
0
05
СО
н
CD
CD
CD
со
со
со
ю
со
со
со
со
in
rf
0
о
о
in
г.
со
in
о
in
oo
О
in
СО
00
in
00
со
ю
00
со
05
in
00
II
CD
CD4
CD
со
со
—Г
о
05
05
стГ
оГ
стГ
о
о
о
оГ
«о
о
in
00
О
in
СО
СМ
©
05
г—1
in
о
см
12
II
CD
CD
со
со
ю
со
См
—г
—Г
о
—Г
см
см
см
«о
ю
о
1П
00
о
in
см
о
1
in
05
СМл
Tt
CD
CD
со
со
со
со
см
см
—Г
см
см
со
оо
со
см
1
о
(N
ю
ю
со
СГ
ю
00
01
in
in
со
о
Ю
00
00
Tt
со
о
со
о
05
05
in
о
со
о
п
ссГ
со
in
См
о
стГ
оо
оо
tsT
оо
оо
00
оГ
05
оо
оо
ю
-
о
ю
о
05
со
о
ю
о
о
ю
00
см
о
ю
со
со
Tt
00
г—
in
со
II
со
CD
СО
См
о'
о
05
05-
оГ
стГ
о
о
05
05
«о
о
in
00
ео
о
Tf«
СО
см
СМ
Tf
00
Tf«
о
Tf
СО
см
о
в
СО
CD
со
ю
См
о
о
о
о
о
см
о
о
в
о
СМ
00
см
см
СО
Tt
о
,
00
со
см
СО
Tt«
о
ю
О
00
00
со
см
in
О)
см
со
in
со
см
I
CD
со
оГ
tc
со
со
со
со
со
со
t
со
со
со
со
со
о
-
со
,
95
05
о
00
со
о
,
см
00
05
05
1П
CO_
о
05
со
см
in
о
in
05
СО
со
—
см
1Л
п
CD4
оГ
ь.
1г
гС
ь.
(С
оо
оо
tsT
Ь.
nT
tc
ts.
«о
8
со
СМ
,
т«
СО
00
05
г.
см
,
СО
Ю
о
00
СО
о
00
05
CM
см
СО
со
о
00
05
CD
1П
см
оГ
оо
оо
N.
tsT
00
оо
05
оо
оо
оо
гС
h-
ю
S
CD
00
о
см
С0Л
00
о
CM
СО
00
о
см
СО
o'
o
—Г
см
см
см
см
см
со
со
etf
Tt
оа
482 ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
и вопрос об определении той жесткости, которую нужно придать подкрепляющему ребру в случае длинной пластинки, чтобы иметь право уменьшить расчетную ширину пластинки вдвое.
1) В качестве примера рассмотрим стальную пластинку, для которой а 120 см, Ь 200 см, h 1,4 см, Е 2,2 106 кгсм2, 1 — а2 0,9. В этом случае
р0 ig- 98,5 кгсм2, СЬ 50,8 кг см2.
При отсутствии подкреплений критическое напряжение на
1 362
основании формулы (1) будет ркр Ро сГзб“ 506 кгсм2.
Наибольшее критическое напряжение соответствует тому случаю, когда подкрепляющее ребро можно считать абсолютно жестким и, следовательно, можно принять расчетную ширину пластинки равной 12Ь. При этом условии
о 442
Ркр 4р0 -Щ- 16,54р0 1627 кгсм2.
Рассмотрим, каковы должны быть поперечные размеры подкрепляющего ребра, если желательно обеспечить наибольшее значение ркр. Из таблицы А видно, что при заданном соотношении между сторонами пластинки (р 0,6) надлежащая жесткость ребра будет вполне обеспечена, если мы примем у 5, т. е. возьмем ребро, жесткость которого при изгибе равна 254 Е кгсм2. В случае корытообразного поперечного сечения подкрепляющего ребра ближайшим подходящим размером будет швеллер № 8. Соответствующий ему наибольший главный момент инерции равен 114 см4, и площадь равна 11,9 см2.
Склепывая этот швеллер с широким листом, мы для приближенного вычисления жесткости получаемого таким путем ребра можем брать момент инерции сечения швеллера относительно оси, лежащей в плоскости соприкасания швеллера с листом ). В таком случае для швеллера № 8 будем иметь
В (114 11,9 42) 304 кгсм2.
) Если обозначим через f площадь поперечного сечения швеллера, через h его высоту, через U площадь сечения листа и через б его толщину, то, считая малыми отношения ffi а и б(г 26) р, мы, ограничиваясь малыми первого порядка, можем положить
о (-)2(12р-а),
где 0 — момент инерции сечения относительно оси, проходящей через центр тяжести.
ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ 483
Соответствующее y 6 и б 0,042. Надлежащая жесткость ребра является, таким образом, вполне обеспеченной. Заметим, что в случае материала высокого качества (предел упругости 3000 кгсм2) при выбранных нами поперечных размерах подкрепляющего ребра пластинка может быть подвергнута действию довольно значительной равномерно распределенной нагрузки без риска вызвать в подкрепляющем ребре остаточные деформации.
Возьмем, например, давление на пластинку 0,8 атм. Считая подкрепляющее ребро абсолютно жестким, найдем, что на него
передается усилие 0,8 120 100 — _8 5600 кг.
Предположив распределение давлений вдоль ребра по параболическому закону и приняв для момента сопротивления швеллера, склепанного с широким листом, величину, на 30 большую момента сопротивления одного швеллера, найдем, что при выбранном нами давлении наибольшее напряжение в подкрепляющем ребре равно 2840 кгсм2.
2) Рассмотрим теперь пластинку с прежними размерами сторон, но толщиной 2 см. В этом случае р0 201 кг)см2, СЬ 148Е кгсм2. При отсутствии подкреплений критическое напряжение для пластинки определится по формуле (1). Оно будет равно 1033 кгсм2.
Если пластинку подкрепить швеллером № 8, то будем иметь
Y--2,05, 6 0,0296.
Из уравнения (9) находим в таком случае ркр 14,8р0 2975 кгсм2.
3) Рассмотрим теперь пластинку вдвое большей длины:
а 240 см, Ь 200 см, h 1,4 см,
Е 2,2 10б кгсм2, 1 - а2 0,9.
Из таблицы А видно, что для обеспечения той жесткости подкрепляющего ребра, при которой возможно положить расчетную ширину пластинки равной 0,56, необходимо, чтобы у было больше 10. Возьмем в качестве подкрепляющего ребра швеллер № 10. В таком случае
213 13,9-25 560 см Y -gll,0, 6 0,05.
Уравнение (9) дает для критического напряжения ркр » 16,4р0 1615 кгсм2, что почти совпадает с ранее найденным (пример 1) критическим напряжением для неподкрепленной пла стинки со сторонами а 240 см, Ь 100 см.
484 ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
§ 3. Случай двух ребер равной жесткости, делящих пластинку на три равные части
Уравнения (4') представятся в этом случае так:
рНА (1 Р2)2 3 (Л, — Л5 Л7 — Ап.)-
“ Ркр А 36 — А5 А7 — Ап.) О,
НЛ2( 1 4р2)2 3у(А2-А4 А8 - А10.)-
— Ркр А2 36 (А2 — А4 Л8 — А10.) О, Л3(19р2)2-ркИз 0,
§-М4 (1 16Р2)2 - 3Y (А2 -A4 As-A10.)-
Ркр А4 — 36 (А2 — А4 Л8 — А10.) О,
ргМбО 25р2)2 — 3(Л, — Л5 Л7 — Лп (11)
— Ркр As — 36 (Л — Аъ Л7 — Ап.) О,
§-Л6(1 Збр2)2-ркрЛ60,
НЛ7(149р2)2 Зу(А-Л5 Л7-Лп
— Ркр.Aj 36 (А1 А5 Л7 — Лц.) О, Л8 (1 64р2)2 3Y (А2 - Л4 Л8 - Л,о.) -
— Ркр Л8 36 (А2 — А4 Л8 — А10.) О,
Уравнения, заключающие коэффициенты Л3, Л6, Л9,., дадут для ркр такие же значения, как и в случае неподкрепленной пластинки. Узловые линии соответствующих искривленных поверхностей будут совпадать с линиями подкрепляющих ребер. Наличие весьма жестких ребер сводит, таким образом, нашу задачу к расчету неподкрепленной пластинки втрое меньшей ширины.
Рассмотрим теперь систему уравнений, заключающих коэффициенты Аи Л5, Л7,. Соответствующие им формы искривления будут симметричны относительно линии у 62. Первое приближение для р1ф получим, ограничиваясь одним коэффициентом А. Тогда первое из уравнений (11) дает нам
Ро (1P2)2 3y
ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ 485
Для получения второго приближения возьмем коэффициенты А и Л5. Тогда соответствующие уравнения системы (11) напишутся так:
А f (1 Р2)2 Зу - Ркр (1 36) зА5 Y Ркрб) о,
ЗЛ, Y Ркрб) Ай (1 25р2)2 3Y - Ркр (1 36) 0.
Приравнивая нулю определитель этих уравнений, получим для разыскания второго приближения р1ф уравнение
_РкрЭ2(1 _ Рк_ (1 36) _ j ab_ 9y2 Q
Р о Р о
Здесь для сокращения письма введены такие обозначения:
(1 Р2)2 3 у а, (1 25р2)2 3 у Ь.
Таким же путем можно получить и дальнейшие приближения. Мы на них здесь не останавливаемся, так как практически второе приближение всегда обеспечивает достаточную точность.
Как и в случае подкрепления пластинки одним ребром, мы можем получать значения ркр умножением р0 на коэффициент k, величина которого будет зависеть от значений р, у и 6. Несколько значений этого коэффициента для различных р дано в таблице В.
Таблица В
Y
10
3
5
20
3
10
3 N.
б - 0,05
6-0,1
б - 0,05
6 0,1
б - 0,05
6-0,1
б - 0,05
6-0,1
0,6
26,8
24,1
36,4
33,2
36,4
36,4
36,4
36,4
0,8
16,9
15,0
23,3
20,7
29,4
26,3
37,2
37,1
1,0
12,1
10,7
16,3
14,5
20,5
18,2
28,7
25,6
1,2
9,61
8,51
12,6
11,2
15,5
13,8
21,4
19,0
1,4
8,32
7,36
10,5
9,32
12,7
11,3
17,2
15,2
1,6
7,70
6,81
9,40
8,31
11,1
9,82
14,5
12,8
1,8
7,51
6,64
8,85
7,83
10,2
9,02
12,9
11,4
2,0
7,61
6,73
8,70
7,69
9,78
8,65
11,9
10,6
При вычислении этой таблицы мы пользовались вторым приближением лишь при малых значениях р. Для р больше 1,2 первое приближение дает достаточную для практических расчетов точность.
Длинная пластинка при выпучивании будет подразделяться на полуволны, причем длина одной полуволны будет тем большая, чем жестче подкрепляющие ребра. Если ограничиться первым приближением, то легко показать, что наименьшее значение
486 ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
рКр при заданных у и б соответствует р2У1 Зу и равняется 2(1 1 3у ) г, 135— Ро- Отсюда легко может быть найдена та жесткость ребер, подкрепляющих длинную пластинку, при которой можно принять расчетную ширину пластинки равной У3Ь.
Мы пока рассмотрели те уравнения системы (11), которые заключают коэффициенты Ль Л5, Л7,. Если бы мы обратились к уравнениям, в которые входят коэффициенты Л2, Л4, Л8,. с четными значками, то, составляя соответствующий определитель и приравнивая его нулю, нашли бы для ркр значения, большие тех, которые были найдены выше из первой группы уравнений.
Подкрепляя пластинку двумя жесткими ребрами, мы можем, конечно, обеспечить значительно большую устойчивость, чем в случае одного подкрепляющего ребра, так как при надлежащем выборе жесткости ребер можно уменьшить расчетную ширину пластинки в три раза.
В качестве примера возьмем пластинку с прежними параметрами:
а 120 см, Ь 200 см, h 1,4 см, Е 2,2 106 кгсм2,
1 — а2 0,9, р0 98,5 кгсм2, СЬ 50,8Е кгсм2.
Из таблицы В видно, что при у 5 подкрепляющие ребра можно считать абсолютно жесткими. Следовательно, подкрепив
пластинку двумя швеллерами № 8, мы можем вычислить критические напряжения по формуле (1), вставив вместо Ъ величину 7з и вместо р величину 0,9. Таким путем мы найдем, что
Ркр 3587 кгсм2.
Если бы, сохраняя все другие размеры, мы увеличили длину
пластинки вдвое, то для обеспечения полной жесткости подкрепляющих ребер нужно было бы остановиться на швеллере № 12.
В случае большого числа равномерно распределенных подкрепляющих ребер мы можем пользоваться первым приближением и вычислять критические напряжения по формулам (6).
Возьмем в качестве примера пластинку с такими размерами: а 1100 см, b 550 см, h 3,75 см — и положим Е 2,2 X X Юб кгсм2, 1 — о2 0,9.
Найдем критическое значение наиряжсиий в предположении, что пластинка подкреплена пятыо равноудаленными ребрами. Поперечное сечение ребер представлено на рис. 2. Вычисляя mq-
ПЛАСТИНКИ, ПОДКРЕПЛЁННЫЕ ЖЁСТКИМИ РЕБРАМИ 48
мент инерции поперечного сечения ребра относительно оси тп, найдем
42 000 см4, СЪ Е 269 кгсм2, y 15,7, 6 0,062.
Вставляя это в формулу (6), получим ьр о-21,7 2030 кгсм2.
Если бы мы при проверке подкрепленной пластинки на устойчивость разделили ее соответственно ребрам на пять продольных полосок и применили к каждой такой полоске формулу Эйлера, то получили бы для критического напряжения величину, приблизительно равную 1400 кгсм2у т. е. значительно меньшую найденного выше ркр.
§ 4. Пластинка, подкрепленная поперечными ребрами
Предположим, что прямоугольная пластинка, сжатая равно мерно распределенными усилиями р (рис. 3), параллельными оси х, подкреплена системой жестких ребер, перпендикулярных к направлению сжатия. Предполагая края пластинки опертыми, мы можем искривленную форму пластинки, получающуюся при выпучивании, представить прежней формулой
W
тоо я-оо
j 2 л,
т1 п 1
тпх. ппи. Sin Sin —7—
1
1 :
р
.4
7
(а)
Рис. 3.
В таком случае для потенциальной энергии изгиба пластинки получим
т — оо п »оо
V-ТЪ ь
m 1 п-1
Работа сжимающих сил при выпучивании пластинки пред ставится так:
тоо лоо
Т_ _P_ab_ V V 2Л2 а2 2 4 m mn' m 1 г — 1
Выпучивание пластинки сопровождается искривлением подкрепляющих ребер. Возьмем одно из этих ребер, отстоящее от оси у на величину с. Искривление его на основании (а) может быть представлено так:
т—оо я»оо
Wi '
2 2 л
т1 л-1
sin
sin
ппу
488 ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
Если мы через Вг обозначим жесткость ребра при изгибе, то потенциальная энергия искривленного ребра будет равна
о
В, Ь я4 ”vi „ - яг, „ 2яс, л Зяс, 2
727 2 (i«sin “T' Ansin-L A„sin-.J.
Я-1
Для полной энергии всех ребер, число которых обозначим через k, получим выражение
i-k
-1
k ВЯ4 A A . nCl , . 2nci , - . 3jtCl , V
463 ylrtin—- “Л2Л81П - -Лзбш J
i-1 Л-1
Значение критического напряжения найдем из уравнения
T V VX. (с)
Вставляя вместо Т, V и V найденные выше выражения и пользуясь обозначениями
Bt п2С a q
'cF Vi 'W Pot J р’
придем к такому результату:
т — ОО П.ВШОО
Ркр Ж I S S тп (т2 2Р2)2
I т-1 п-1
П-оо
So VI м I nct. . . X.
2ViP Ч Irt SU1 « 2n Sm “в Зп Sm
Зя с, L
i-1 л-1
тоо п—оо
71 00 п “ ОО ч
(d)
т1 w»l J
Напишем теперь условия, при которых полученное для рКр выражение приобретает минимальное значение.
Приравнивая нулю производную от этого выражения по каждому из коэффициентов Атп, мы придем к системе уравнений
ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ 459
такого вида: р-Атпт±пГ
ik , л
. тле, , лс, 2пс,
2;Р я Sin — (4,„sin -±- А2п sin —
-1
3 лс. 3„sin—-.)-ркрт2Атп 0. (е)
Все эти уравнения могут быть разбиты на группы, причем в каждую группу войдут лишь коэффициенты с одним определенным значением п.
Легко видеть из общего выражения (d), что наименьшее значение критических напряжений получается при п 1. Это соответствует тому случаю, когда выпучившаяся пластинка не имеет узловых линий, параллельных оси х. В дальнейшем нам придется рассмотреть лишь группу уравнений такого вида:
tk
VI « тле, ( л лс. „ 2лс,
Ат (т2 р2)2 2j 2YP3 sm — (Л, sin -J- A2sin i-1
43sin-p. — Xm2Am 0. (f)
Здесь мы для упрощения письма отбросили второй общий для всех коэффициентов значок и ввели обозначение АфР2Ро X.
Величина критических напряжений найдется, как и в ранее рассмотренных случаях, из условия равенства нулю определителя системы уравнений (f).
Особенно просто решается задача в том случае, когда имеется большое число одинаковых, равномерно и весьма густо ) распределенных поперечных ребер. При этом условии можно положить
ik tk
Sn тле. и тле. плс,
sin2 тг, , sin sin 0.
а 2 Jmd а а
i- -1
В таком случае система уравнений (f) распадается на отдельные уравнения, в каждое из которых будет входить лишь один коэффициент. Вид этих уравнений будет такой:
Ат т2 Р2)2 YP3 “ Ят2 0.
) Расстояние между ребрами весьма мало по сравнению с шириной пластинки Ь.
490 ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
Приравнивая нулю множитель при Ат, получим для критических напряжений формулу
(m p2)2 feyp3 (Ъ
Ркр — Р0 p2m2 VАС
Число полуволн т, на которое подразделяется пластинка при выпучивании, должно быть определено таким образом, чтобы выражение (13) давало для pKP наименьшее значение. С возрастанием р возрастает и число т. Переход от формы с т полуволнами к форме с т 1 полуволнами соответствует тому значению р, при котором
(т2 р2)2 feyp3 __ Цт 1)2 р22 уР3
р2ет2 Р2 (m l)2 ’
откуда получаем т2(т I)2 р4 уР3. Полагая т 1,2, 3,., можно при известных у и k найти соответствующие предельные значения для р. Если т велико, то можно положить
4 т УР4 yP3 При у 0 получаем т р. Неподкрепленная длинная пластинка стремится при выпучивании подразделиться узловыми линиями на квадраты.
С возрастанием у увеличивается т, следовательно, убывает длина волн, на которые подразделяется пластинка. Если при пользовании формулой (13) мы получим для т такое значение, при котором на каждую полуволну придется не менее трех подкрепляющих ребер, то найденное таким способом ркр будет довольно близко к действительности.
При малом числе ребер или при большой их жесткости необходимо при определении ркр перейти к общим уравнениям (f). Ниже мы рассматриваем несколько частных случаев.
§ 5. Сжатая пластинка, подкрепленная посредине одним поперечным ребром
В этом случае уравнения (f) представятся в таком виде:
Л 1(1 P2)2 2yP3-X 2yP3(- Л3 Л5-Л7.) 0,
Л2(4 Р2)2-4Я 0,
Л3 (9 р2)2 2vP3 - 9А. 2ур3 (- Л, - Л5 А.) 0,
Л4(16 р2)2- 161 0,
А5 (25 р2)2 2Р3 - 25Л 2Yp3 (А, - А3 - А7.) 0,
(14)
Уравнения, заключающие коэффициенты с четными значками, дают критические напряжения, соответствующие тем фор¬
ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЁБРАМИ 491
мам выпучивания, при которых подкрепляющее ребро не искривляется вовсе — оно располагается вдоль узловой линии выпучившейся пластинки. Получаемые при этом результаты, конечно, будут совпадать с тем, что найдено для неподкрепленной пластинки, имеющей длину 0,5а и ширину Ь.
Займемся теперь уравнениями, заключающими коэффициенты с нечетными значками. Предположим, что длина пластинки удовлетворяет-условию р У2. В таком случае при отсутствии подкреплений пластинка выпучится по одной полуволне и критическое напряжение определится из формулы (1). Если жесткость подкрепляющего ребра невелика, то мы получим значение ркр с достаточной точностью, если ограничимся первым приближением и сохраним лишь коэффициент А. Первое из уравнений
(14) даст нам в таком случае
Чтобы получить второе приближение, нужно взять коэффициенты A j и Л3. Первое и третье уравнения системы (14) напишутся так:
Критические напряжения найдутся из условия равенства нулю определителя этих уравнений. После некоторых сокращений уравнение для определения X напишется так:
9А2 - А (9 р2)2 9(1 р2)2 20YP3 (1 Р2)2 (9 р2)2
2YP3 (1 Р2)2 (9 р2)2 0. (17)
Отсюда могут быть найдены значения нр при заданных y и р. Возьмем, например, квадратную пластинку и положим у 1. В таком случае первое приближение дает нам р1ф 6р0. Из уравнения (17) в качестве второго приближения получаем ркр 5,920. Разница между первым и вторым приближением столь незначительна, что вычислять дальнейшие приближения нет никакой надобности.
Возьмем теперь более короткую пластинку с более жестким ребром. Положим, например, р 0,5 и у 10. В таком случае для первого и второго приближения получаем следующие значения: Ркр 16,25 ро и кр 15,78 р0-
(1 р2)2 2yP3 — Я 0,
откуда
(15)
(1 Р2)2 2yP3 - Я - 2УР3Л3 0,
- A j2yP3 А3 (9 р2)2 2ур3 - 9Я 0.
(16)
492 ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
Разница между двумя последовательными приближениями несколько больше 3, следовательно, и в этом случае можно ограничиться вторым приближением.
На практике иногда приходится решать такую задачу: какой жесткости необходимо взять поперечное подкрепляющее ребро, чтобы иметь право считать его абсолютно жестким Решим этот вопрос, пользуясь найденным выше вторым приближением. Если мы в уравнении (17) будем увеличивать значение у, то вместе с ним возрастут А и кр.
Искомое значение у, соответствующее условиям абсолютно жесткого ребра, мы найдем, приравнивая значение А, получаемое из уравнения (17), тому значению, которое получается из второго уравнения системы (14). Таким путем приходим к уравнению
(4 р2)2 (9 р2)2 9 (4 р2)2 (1 Р2)2 -4(1 р2)2 (9 Р2)2 - 2,25 (4 р2)
Y 8р3 (1 Р2)2 8р3 (9 р2)2 — 20р3 (4 Р2)2
(18)
Несколько значений у для различных р приведено в нижеследующей таблице.
р
0,5
0,6
0,7
0,8
0,9
1,0
1,2
1,41
Y
12,6
7,18
4,39
2,80
1,82
1,26
0,433
0
а
6,86
6,96
7,17
7,53
8,14
8,57
14,4
оо
Связь между размерами пластинки и моментом инерции поперечного сечения подкрепляющего ребра, устанавливаемая равенством (18), может быть представлена в таком виде: (ha)3b4 а. Значения а даны в вышеприведенной таблице.
§ 6. Сжатая пластинка, подкрепленная тремя равноудаленными поперечными ребрами
Если ограничиться первыми семью членами в ряде, представляющем искривленную поверхность пластинки, то первые семь уравнений системы (f) (стр. 489) представятся в таком виде
ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
493
(рис. 4):
А (1 Р2)2 4yP3 — Л — 4YPM7 О,
Л2 (4 р2)2 4yP3 - Щ - 4YpM6 О,
А3 (9 р2)2 4yP3 - 9Я - 4YpM5 О,
А4 (16 р2)2 — 16Я 0,
А5 (25 р2)2 4yP3 - 25А - 4yPM3 О, Aq (36 р2)2 4yP3 - 36А - 4YpM2 О, А7 (49 р2)2 4yP3 - Ш - 4yP3 0.
(19)
Четвертое из этих уравнений соответствует выпучиванию пластинки по четырем полуволнам. При этом подкрепляющие ребра не искривляются — они располагаются вдоль узловых линий. В случае малой_ жесткости ребер прямоугольная пластинка, для
Повышая жесткость подкреплений, мы получим две полуволны, дальше три и, наконец, четыре полуволны.
Чтобы определить критическое напряжение для того случая, когда первая искривленная форма имеет одну полуволну, придется воспользоваться уравнениями первым и седьмым системы
(19). Ограничиваясь первым приближением, мы из уравнения первого получим X (1 Р2)2 4уР3.
Для получения второго приближения приравниваем нулю определитель уравнений первого и седьмого. Для нахождения X получаем уравнение
49А2 - Л 49 (1 р2)2 (49 р2)2 200yP3
(49 р2)2 (1 р2)2 4Yp3 (49 р2)2 (1 р2)2 0. (20)
Уже при сравнительно малых значениях у (например, для квадратной пластинки при y 912) первая искривленная форма будет иметь две полуволны, и нам для определения критических напряжений необходимо обратиться к уравнениям
которой р У2 , выпучится по одной полуволне.
а
'Р
Рис. 4.
494 ПЛАСТИПКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
второму и шестому системы (19). Если ограничиться первым приближением, то из уравнения второго получим
(4 p2)2 4Yp3 4 Для получения второго приближения приравняем нулю определитель уравнений второго и шестого, тогда для X получается такое уравнение:
144А,2 — Я 4 (36 р2)2 36 (4 р2)2 160yP3
(36 р2)2 (4 р2)2 4уР3 (36 р2)2 (4 р2)2 0. (21)
Заметим, что уравнения (21) и (20) дают для К значения, весьма близкие к соответствующим первым приближениям, и практически можно ограничиваться первыми приближениями.
При дальнейшем увеличении жесткости подкрепляющих ребер пластинка при выпучивании будет подразделяться на три полуволны. Соответствующие критические напряжения определятся из уравнений третьего и пятого системы (19). В качестве первого приближения получаем
- (9 р2)2 4ур3
9
Уравнение для определения второго приближения напишется так:
225А2 — Я 9 (25 р2)2 25 (9 р2)2 136YP3
(9 р2)2 (25 р2)2 4yP3 (25 р2)2 (9 р2)2 0. (22)
Практически иногда представляет интерес подобрать y та‘ ким образом, чтобы подкрепляющие ребра при выпучивании пластинки не искривлялись. Для получения соответствующей жесткости ребер приравняем значение Я, определяемое из уравнения (22), выражению X (16 р2)216, получаемому из уравнения четвертого системы (19). Тогда для у получаем значение
оок
16(25 Р2)2 (9 Р2)2 - (16 р2)2 9 (25 р2)223 (9 р2)2 jg- (16 р2)
Y 136Р3 (16 р2)2 - 64р3 25 р2)2 (9 Р2)2 Необходимая жесткость ребер получается тем большей, чем меньше р. Несколько значений у приведено в нижеследующей таблице.
р
0,6
0,8
1,0
1,2
1,4
Y
101
42,6
21,7
12,4
7,71
ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ 495
§ 7. Об устойчивости прямоугольной пластинки, подвергающейся действию касательных напряжений1)
В случае пластинки с опертыми краями мы можем принять для выпучившейся поверхности уравнение
W
тпх. ппи sin sin —
()
Потенциальная энергия изгиба пластинки будет иметь значение ,, С ab V V л2 (п2к2. я2я22 .f t li b)
m l n»l
При выпучивании пластинки отдельные элементы ее срединной
плоскости испытывают сдвиг, величина которого определяет- i п —i-—«в
ся формулой
dw dw 00ч
шлГГ- 23
Если мы через pt обозначим величину равномерно распределенного касательного усилия, приходящегося на единицу длины контура пластинки,
то соответствующее приращение энергии сдвига будет равно
а b
t
1 t
1
у
J
Рис. 5.
О О
Вставляя вместо w его значение (а) и принимая во внимание, что
а
J
. тпх рпх j л sin cos -— dx О,
если т ±р
четное число, и
а
I
тпх sin COS
рпх 1 2 а
-— dx —
) Приближенное решение этой задачи для случая весьма длинного прямоугольника было дано нами (см. стр. 161 нашей работы, указанной на стр. 473). Прямоугольная пластинка с конечным соотношением сторон рассмотрена И. Г. Бубновым («Строительная механика корабля», том 2, 1914, С.-Петербург, тип. морского министерства, стр. 528). Вследствие пропуска некоторых членов критические напряжения, полученные И. Г. Бубновым, имеют несколько преувеличенные значения. Здесь мы приводим таблицу критических напряжений в исправленном виде.
496 ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
если т ±р — число нечетное, найдем для V выражение такого вида:
1 2 ЛтпАрч (От2 _ р2) 2 _ П2)
Здесь т ± р и п ± q — нечетные числа.
Величину критического значения pt найдем из уравнения
V Vi 0. (с)
Вставляя вместо V и V их значения, будем иметь
С ab V V 12 I m2jl2 n2jl2 2
2 4 Li Zu А™ a2 b2 j
(Р)кр
mnpq
AmnApq (m2 _ p2) ((2 _ n2)
(24)
Приравнивая нулю производную от pt по каждому из коэффициентов Атп и принимая во внимание уравнение (с), получим систему уравнений, линейных относительно Атп, Apqy.
Уравнения эти можно разбить на две группы. В одну из них войдут коэффициенты с четной суммой значков и в другую — с нечетной. Введя обозначения
а -ft Т-Р’
Ск2
b2h Р И
Сп2 л2 b
- я,
ь Г’ b2h го ЬЦр,)кр 32 а
можем представить первую из этих групп в таком виде:
П
22
13
31
33
42
24
44
Л 22
Вц
¥
д В22
О
о
о и '25
8_
45
8_
45
16
225
О
О
Аз
31
33
42
А24
Л44
0
0
0
' 45
-
45
—
225
. 0,
4
5
4
5
,36
25
0
0
0
. 0,
Bis
0
0
24
75
-
21
— 105
. 0,
0
Вп
0
21
24
75
— 105
. 0,
0
0
Взз
72
35
72
35
, 144 49
. 0,
24
75
П 21
72
35
В 42
0
0
. 0,
21
24
75
72
35
0
В2
0
. 0,
i 105
105
, 144 49
0
0
В 44
. 0,
(d)
ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ 497
М1Р2)2 о , 1бЛ(1р2)2 р _ , (t 9Э2)2 Л где Ви — рг » -22—I р 1з— Н jp »
(9 р2)2 Я „ (9 9(i2)2 X D _ , (16 4- 4р2)2 Л.
31 р2 33 р2 9 D 42 Г р2 , (416(52)2А D _ , (1616P2)2A
24 — I рг 9 пи ”” ' р2 Величина (pi) ир определится из условия равенства нулю определителя этих уравнений.
Первое приближение, довольно близкое к точному решению при р, близком к единице, мы получим, ограничиваясь двумя первыми строками и двумя первыми колонками написанной выше системы уравнений.
В таком случае для X получаем такое уравнение:
16Я2(1 р2)4 _ 16 р4 81 1
откуда
_ 1 Р2
± 9 (1 р2)2
Соответствующее значение pi)Кр равно
1 _ 2 Ь _ _ 9я2 (1 р2)2 _
X р0 32 а 32 р3 р0'
При а Ь получаем в качестве первого приближения
(pt) кР ± 11,1 Ре-
В качестве второго приближения возьмем первые пять строк и пять колонок системы (d). Соответствующий определитель приводит нас после некоторых сокращений к такому результату: Р4 Г« , 81 (1р2)2. 81 (1 р2)2. 81 2 (1 р2)2
Л 81 (1 Р2)4 L 25 (1 9р2)2 ' 25 (9 Р2)2 25 (99p2)2J
(25)
Для квадратной пластинки эта формула дает (pt)nр — 9,43 роПолученный результат отличается от первого приближения на 15. Это обстоятельство, а также вычисления дальнейших приближений дают основание считать формулу (25) достаточно точной для вычисления критических напряжений в случаях пластинок, близких к квадратным. С возрастанием отношения р точность формулы убывает. Объясняется это тем обстоятельством, что длинная пластинка при сдвиге, как и при продольном сжатии, подразделяется на ряд полуволн.
Величина критических напряжений в таком случае будет за известными пределами мало меняться от изменений длины, но
498 ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
форма искривления пластинки получается весьма сложной, — нужно брать много членов в общем выражении для прогибов (а), чтобы обеспечить надлежащую точность результата. С возрастанием длины а возрастает значение членов ряда (а), соответствующих большим значениям значка ту поэтому в качестве следующего приближения можно взять первые шесть строк и шесть колонок системы (d). Вводя обозначение
— ( т2П2)
(т2 1232)2 ут п '
мы можем после некоторых сокращений представить уравнение для определения следующего приближения в таком виде:
- (И-)2 (4 4) (э -9)41-(4 4) (9 - 1)i(I 9)4-4)
(1 1)(4 4) (-)2(16 4) (1 1) (-)2(1 9) (16 4)
()2(9. 1)(16-4) (--)2(9.9)(16-4)я2 1,3696(1. 1) X
X (4-4) (9-9) (16-4) 0,42270 (4-4) (1 1)(9- 1) (16 - 4)
4,4373 (4 4) (1 - 9) (9 9) (16 4)
1,3696(4.4)0 9) (9 1) (16 4) 0. (26)
Определяемое из этого уравнения значение (pt)Кр отличается в случае квадратной пластинки от вышеприведенного второго приближения лишь в четвертом знаке. При р 2 разность между вторым и третьим приближением достигает 2. Для р 3 эта разность равна 9,5.
Несколько значений коэффициента k, на который следует множить величину р0, чтобы получить соответствующие значения (pt) кр, приведены в нижеследующей таблице.
р
1
1,2
1,4
1,5
1,6
1,8
2,0
2,5
3
k
9,42
8,0
7,3
7,1
7,0
6,8
6,6
6,3
6,1
При вычислениях мы получаем из уравнений (25) и (26) при наибольшем по численному значению корне два знака, что соответствует двум различным направлениям сдвигающих напряжений.
Системы уравнений, аналогичной системе (d) и заключающей коэффициенты Атп с нечетной суммой значков, мы здесь не рассматриваем. Соответствующие ей наибольшие значения Л получаются меньшими, чем из системы (d).
ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ 499
В случае весьма длинной пластинки влияние поперечных сторон на обстоятельства изгиба ничтожно, и мы можем для приблизительной оценки величины критических напряжений задаться подходящей формой искривления так, чтобы в отношении прогибов были удовлетворены условия на продольных сторонах пластинки. Мы получим форму искривления, подходящую к той, которую дает опыт, если положим
w A sin -у sin у (х ау). (е)
Этому выражению соответствует выпучивание пластинки по ряду волн длины 5 ), причем узловые линии составляют с осью х-ов угол а.
Вставляя выражение (е) в уравнение (с), получим
(Мер ба2 2 (1 а2)2.
Наименьшее значение критического напряжения получим, полагая s bY 1а2 и а—12. Этому соответствует
(р)кр Ро 5,7.
Полученный результат довольно близок к тому, что мы нашли раньше для пластинки с отношением сторон 0 3.
§ 8. Подкрепление пластинки, подвергающейся действию касательных усилий
Рассмотрим предварительно случай прямоугольной пластинки неограниченной длины, подкрепленной системой ребер, параллельных длине пластинки.
Для искривленной поверхности пластинки в случае выпучивания мы можем воспользоваться приближенным выражением
(е) предыдущего параграфа. Полагая
w A sin -у- sin у ( ау),
мы найдем для искривленной формы подкрепляющего ребра, расположенного на расстоянии с от оси х, выражение
wt A sin sin у (х ас).
Соответствующее значение потенциальной энергии равно
а
JhC Wl. _ ,2 я Bta 2 ci
Vi 2 J dx2 X s 4 Sln b ’
0
) Is — длина полуволны.
500 ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
Потенциальная энергия всей совокупности подкрепляющих ребер представится так:
У S Л2 -gJr mBt sin2.
i l
Здесь через т обозначено число полуволн, на которое пластинка подразделяется при выпучивании.
Потенциальная энергия выпучившейся пластинки на основании общей формулы (см. § 1) представится в таком виде:
F A2fTbi 2 60(2 --- V 2)2-
Приравнивая полную потенциальную энергию V V работе касательных сил при выпучивании, определяемой формулой
а Ъ
Идт dw j 1
-Wdfdxdy
о о
найдем для критического значения касательных напряжений такое выражение:
(л) кр -g- 2 6а2 4 1- Y. (1 а2)2 (27)
Здесь ро имеет прежнее значение, через у обозначена сумма
j 2Bi sin2 f-1
Cb
При большом числе одинаковых и равноудаленных ребер эта сумма равна приблизительно отношению суммы жесткостей ребер к жесткости листа.
Теперь остается в выражении (27) подобрать а и s таким образом, чтобы (pt)кр получило минимальное значение. Составляя условия минимума, найдем
s b Vvi 0 a2)2,
6а2 VYi (1 2)2 - 2 Yi (l «2)2 -
- 2 у, (1 а2)2 4а2 (1 а2) 0.
Каждому значению у будет соответствовать свое а и s, соответственно этому будет меняться и (р)Кр-
В нижеприведенной таблице имеется ряд значений коэффициента А, на который нужно множить ро, чтобы получить соот¬
Пластинки, подкрепленные жесткими ребрами 501
ветствующее значение (pt)Кр. При уь равном нулю, этот коэффициент равняется 5,7, дальше он возрастает вместе с уь
Yi
5
10
20
30
40
50
60
70
80
90
100
6,98
7,70
8,67
9,36
9,90
10,4
10,8
11,1
11,4
11,7
12,0
В качестве численного примера рассмотрим такой случай. Стальной лист шириной 180 см и толщиной 1 см подкреплен тремя равноудаленными ребрами, швеллерами № 8. Сохраняя прежние значения величин, характеризующих упругие свойства материалов, найдем
р0 62 кгсм2, СЬ ЪЕ кг см2, Yi 80.
Из вышеприведенной таблицы находим k 11,4, следовательно, Ркр 707 кгсм2.
Если стальной лист утолстить до 1,2 см, то получим
р0 89,3 кгсм29 Yi 46, k 10,2, ркр 911 кгсм2.
Если длина и ширина пластинки одного порядка, то выражение для искривленной поверхности пластинки нужно взять в общем виде:
т-»оо л оо
SV л тпх ппу 2j Атп sin —sin —у-;
т—1 п—1
искривленная форма подкрепляющего ребра, находящегося на расстоянии Ci от оси х-ов, представится так:
т—оо оо
- . тпх. tinci
2и in Sm “ Sin у-.
т-1 г—1
Для потенциальной энергии всех изогнувшихся ребер получим выражение
— ft m oo
2 тх 1 m-1
X (mlsin-m2sin-- m3sin-
502 ПЛАСТИНКИ, ПОДКРЕПЛЕННЫЕ ЖЕСТКИМИ РЕБРАМИ
Если имеется большое число равномерно распределенных ребер одинакового сечения, то вышенаписанное выражение для V можно заменить таким:
т' kn4В VI V1 4 а2
У1 “ ga3 т Атп
В отличие от того, что мы имели в предыдущем параграфе для случая неподкрепленной пластинки (см. формулу (Ь)), получим для пластинки, подкрепленной большим числом одинаковых и равноудаленных ребер, такое выражение для полной энергии деформации:
v -Т Т 2 2л”« № яW х.
Здесь через yi обозначено отношение kBCb.
Что касается работы скалывающих напряжений при выпучивании пластинки, то она представится таким же выражением, как и в случае неподкрепленной пластинки. Поэтому в системе уравнений (d) предыдущего параграфа нам придется при переходе к подкрепленной пластинке изменить лишь значения членов, расположенных по диагонали. Везде вместо (пг2 п2р2)2 нужно поставить (пг2 п2р2)2 т4у.
В таком случае для первого приближения получаем
1 Р2
Л 9 (1P2)2 Yi ’
Второе приближение для X определится такой формулой:
,4 1 Р4 Г, . 81 (1 р2)2 Yi ,
А 81 (1 P2)2 Yi2 L 25 (9 Р2)2 81 Yi Г
, 81 (1 Р2)2 У , 812 (1 Р2)2 Yi 25 (1 9P2)2 yi 25 ) (9 9P2)2 81yiJ‘
Без особых затруднений может быть составлено и третье приближение, которым мы пользовались в случае неподкрепленной пластинки при р 2.
Заметим, что получаемые таким путем приближенные формулы будут годиться также для случаев двух и трех равноудаленных подкрепляющих ребер; нужно только под yi пРи Двух ребрах подразумевать величину ЗВCb и при трех ребрах величину 4 ВСЬ.
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
Uber die Stabilitat versteifter Platten. Der Eisenbau, 1921, Bd. 12, № 5—6, SS. 147—163. Перепечатка: S. P. Timoshenko. The collected papers. McGraw-Hill Publishing Company Ltd, New York — London — Toronto, 1953, pp. 264—287.
Постоянное улучшение строительных материалов и соответствующее увеличение допускаемых нагрузок приводит в железных конструкциях к применению пластин все меньшей толщины. В связи с этим вопрос об устойчивости пластин при действии сил в их срединной плоскости имеет непрерывно возрастающее практическое значение. Простейшее удавшееся решение задачи относится к устойчивости всесторонне опертой прямоугольной пластины под действием равномерных сжимающих сил, распределенных на двух противолежащих сторонах.
Без особых трудностей получается решение задачи также в случае, когда пластина на сторонах, на которых действуют сжимающие силы, оперта, а на остальных сторонах закреплена произвольным образом.
Во всех рассмотренных случаях критическое напряжение зависит не только от отношения сторон, но также и от толщины пластины. Для заданного отношения сторон критическое напряжение пропорционально квадрату толщины и может поэтому при соответствующем увеличении толщины обеспечить необходимую устойчивость пластины. Но такое решение не всегда экономично. Во многих случаях достигается лучшее использование материала, когда сохраняется первоначальная толщина пластины, а для обеспечения устойчивости вводятся соответствующие ребра жесткости. Этот способ выполнения находит применение в судостроении, в балках со стенками, выполненными целиком из железных листов, и т. д. При назначении поперечного сечения ребра жесткости и определении расположения этого ребра обычно руководствуются практическими соображениями.
В этой работе дан приближенный способ решения этой задачи и показано его применение к расчету всесторонне опертой подкрепленной пластины для следующих случаев:
1. Пластина находится под действием сжимающих сил, которые равномерно распределены на двух противоположных сторонах.
2. Пластина нагружена равномерно по периметру касательными силами.
504
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
3. Пластина в своей срединной плоскости подвержена чистому изгибу или изгибу со сжатием.
Для этих случаев представлены числовые таблицы, которые облегчают применение использованного метода для практических расчетов.
§ 1. Постановка задачи и метод решения
Приближенный способ, применение которого мы покажем, основан на рассмотрении потенциальной энергии системы1).
Плоская форма равновесия пластины, которая подвержена действию сил в своей срединной плоскости, является устойчивой,
когда при каждом отклонении от плоской формы равновесия
потенциальная энергия пластины
5Р я растет. В противном случае рав-
7 новесное состояние пластины ока-
г-6 зывается неустойчивым. Этот
ZZ- общий критерий применим к про-
стейшей задаче, а именно к всесторонне опертой пластине при У действии простого сжатия
Рис. 1. (рис. 1). При выходе элемента
пластины из плоской формы равновесия накапливается потенциальная энергия изгиба V и одновременно несколько уменьшается потенциальная энергия сжатия. Предположим, что точки опоры пластины не могут перемещаться, каждый прогиб пластины связан с удлинением волокна тп и это обусловливает уменьшение потенциальной энергии сжатия. Пусть V и составляет указанное уменьшение энергии. В том случае, если V Vu прогиб пластины связан с увеличением потенциальной энергии, вследствие этого плоская форма равновесия устойчива. В случае V V плоская форма равновесия неустойчива. Критическое значение сжимающего напряжения вытекает из условия
V Vt. (1)
При определении потенциальной энергии изгиба пластины применим следующую известную формулу:
а Ь
т 1 п Г С U d2w , d2w2 0 п ЧГ d2w d2w ( d2w 2“П , ,
V 2 J J 1 дх2 ду2 ) 2 V4 дх2 ду2 Ydxdy) dx dy’
о о
(2)
Изложение этого метода и его применение к решению различных задач устойчивости двутавровых балок и пластин содержатся в книге автора «Об устойчивости упругих систем». Киев, 1910.
ОБ УСТОЙЧИВОСТИ подкрепленных ПЛАСТИН 505
где до —прогиб пластины, v—коэффициент Пуассона; D Eh2(—v2) означает изгибную жесткость пластины. Удлинение элемента тп при выпучивании пластины равно
а
2 J (dwdxf dx, а соответствующее уменьшение потенциальной
и
энергии сжатия будет
(4;-)’ 3
О О
В случае пластины, опертой на всех сторонах, прогиб при выпучивании можно представить в следующей форме:
V4 V4 А. тпх. ппи лч
w 2л 2и . (4)
m« 1 Л“ 1
Подстановка этого выражения в формулы (2) и (3) дает
б)
т» 1 1
(6)
т1 П“1
Из основного уравнения (1) получим в этом случае для критического значения сжимающего напряжения следующее выражение:
у у л2 (at2
_ n2D а2 Ь2 )
акР h Y Y 2 т
Zk тп а2
где коэффициенты Атп выбираются так, чтобы а1ф согласно выражению (7) обращалось в минимум. Легко понять, что нужно сохранить только тот член, который соответствует п 1. Далее из свойств числителя и знаменателя в (7), которые представляют суммы исключительно положительных членов, следует, что для минимума как в числителе, так и в знаменателе все члены, кроме одного, необходимо положить равными нулю. Таким способом получим
Dn2 I mb
b2h
506
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
Этому соответствует выпучивание пластины по следующей поверхности:
(Ь)
„ . тях . яу
w Aml sin — sin -jj-
Отсюда вытекает, что пластина при выпучивании разделяется на т полуволн с помощью узловых линий, параллельных оси у. Теперь остается только выбрать соответствующее значение т. Полагаем т 1 и обозначаем )
Dr2 ч
(с)
ое
b2h
тогда получим
KP Oe( j)2koe.
(8)
Некоторые значения k в зависимости от отношения ajb представлены в таблице I.
Таблица I
а
b
k
акр, кгсм1 при h 0,01 b
а
Ъ
k
акр, кгсм2 при h 0,01 Ъ
0,3
13,2
2620
1
4,00
795
0,4
8,41
1670
1,1
4,04
803
0,5
6,25
1240
1,2
4,13
821
0,6
5,14
1020
1,3
4,28
851
0,7
4,53
901
1,4
4,47
889
0,8
4,20
835
1,41
4,49
893
0,9
4,04
803
Отсюда видно, что для а Ъ коэффициент k принимает наименьшее значение. Следовательно, бесконечно длинная пластина разделяется на квадраты, в то время как пластина конечной длины распадается на прямоугольники с таким отношением сторон, которому соответствует минимум аКр. Вопрос о числе волн может быть легко решен из вышеупомянутого сопоставления. Для этого можно воспользоваться также общей формулой (а). Переход от волнового числа т к числу га 1 имеет место тогда, когда правая часть формулы (а) не изменяет своего значения при замене га на га 1; таким образом, получим
Ъ ,1а , 1ч Ь , 1 а
Ш г— (tn Ь 1) :—;—т)
а 1 т b v a,ml,
откуда
-т- Ym(m 1).
Величина ае есть эйлерово критическое напряжение для полосы дли ной bt толщиной h и шириной, равной 1 см.
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
507
Переход от одной к двум полуволнам происходит при аЬ У 2, от двух к трем полуволнам — при а6 У6 и т.д. После определения волнового числа и соответствующего ему k значение акр может быть вычислено без затруднений. В третьем столбце таблицы I даны значения а1ф, которые вычислены в предположении, что Л 0,016, v 0,3, Е 2,2 Ю6 кгсм2. При другом отношении Л6 табличные значения нужно только умножить на (Л262)- 104.
§ 2. Жесткость ребер при равномерном продольном сжатии
Из предыдущего следует, что критическое напряжение при малом отношении Л6 может оказаться меньше напряжения, которое пластина при достаточной жесткости в состоянии воспринять. Вообще выпучивание пластины не приводит к разрушению, однако все же имеет своим следствием нежелательные явления. Та часть сжимающей силы, которая при недостаточной жесткости пластины не может быть воспринята, передается более жесткой части конструкции, которая составляет опору пластины. Следствие этого явления состоит в перенапряжении более жесткой части конструкции. Можно, не изменяя толщины пластины, увеличить ее жесткость введением ребер жесткости и воспрепятствовать нежелательному выпучиванию. Таким образом можно, например, путем введения одного ребра (которое делит пополам ширину пластины и которое простирается параллельно направлению сжатия) жесткость длинной пластины поднять примерно в четыре раза. Дальнейшее увеличение жесткости может быть достигнуто посредством соответствующего увеличения числа ребер. При этом возникает как вопрос о связи между жесткостью ребра и устойчивостью подкрепленной пластины, так и, кроме того, вопрос о том, какой жесткостью ребро со своей стороны должно обладать для того, чтобы выпучивание пластины не причинило бы никакого изгиба ребра. На эти вопросы могут быть даны ответы на основе вышеупомянутого способа.
Пусть дан ряд ребер, параллельных оси jc-ob (рис. 1);
си С2, — расстояния ребер от этой оси; Fu F2y. и Ви В2.—
соответственно площади поперечных сечений и изгибные жесткости ребер; Рь Р2,. — сжимающие силы, пропорциональные площадям поперечных сечений FUF2. Прогиб при выпучивании подкрепленной пластины можно представить формулой (4). Вообще прогиб пластины при выпучивании связан с изгибом ребра. Потенциальная энергия i-го ребра будет
Л оо
1 в‘ I Ши 2 » (Л-‘ sm
О т-1
508 ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
Для суммарной энергии изгиба подкрепленной пластины получим выражение
оо оо
тг _ V V 2 т2 f п2 2
V Za Za Лтп'¥') “Г
m 1 я- 1
ST1S',('4-siT-4sl“ir- )
Уменьшение потенциальной энергии сжатия i-то ребра вследствие изгиба равно
0 т-1
Для суммарного уменьшения потенциальной энергии сжатия при выпучивании подкрепленной пластины получим формулу
Т7 _ axh ab V1 V i 2 гп2л2 ,
Vi— 2 Li mn а2
m— 1 л-1
Етг 21 ™5K.sinyl„smiS
I m-1
Подставим выражения для V и Vi в уравнение (1) и введем обозначения
й-v. т5г-Й-’ т-е- о)
Тогда получим следующее выражение для критического напряжения:
оо оо оо
‘ ЛС
кр -р- S j4w № ”22 2 1 У S m (AmI Sitl
( т—1 п—1 i т—1
,msSi„ia.):;;тм™
' I т—1 n—1
2 б; т2 (Лт-. sin Ащ2 sin -5L -- (d)
i т1
в котором коэффициенты Атп выбираются так, чтобы выражение стало минимальным.
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
509
Если при выводе формулы (d) оставим отличным от нуля только коэффициент Атп и примем во внимание условие (1), то получим систему линейных уравнений следующего вида;
ji4mn (т2 n2p2)2 2 2 у sin-- m4 a„i sin y-
Am2 sin )- P2crKp tn2Amn
2 blsnJm2iAmsn-Am2njL. ) (). (e)
i
Эта система уравнений может быть удовлетворена, если мы положим все коэффициенты Атп равными нулю, что соответствует плоской форме равновесия подкрепленной пластины. Для того чтобы была возможна выпученная форма равновесия подкрепленной пластины, необходимо, чтобы детерминант уравнений (е) был равен нулю. Это условие мы используем при вычислении критического напряжения. Расчеты показывают, что мы получим удовлетворительное приближенное значение для акр, если ограничимся лишь небольшим числом уравнений бесконечной системы (е) и, соответственно этому, числом коэффициентов. Покажем способ расчета на простых примерах. В качестве первого примера возьмем случай одного ребра, которое делит ширину пластины пополам. Было показано (§ 1), что можно ограничиться при наших расчетах случаем выпучивания по одной полуволне. Тогда систему уравнений (е) можно представить следующим образом:
-(1Р2)2Л2у(А-Лз Л5-.)-
— кр А 1 26 (Л1 — А3 А5—.) 0,
-р-(1 4р2)2 А2 — сгкрЛ2 О,
L(l9P)A3-2y(Al-A3 A5-.)- f)
— (Хкр Из — 26 (A j — А3 А5 —.) 0,
-р-(1 1бр2)2 А4 — окрА4 О,
Уравнения, которые содержат коэффициенты Ап с четными пу соответствуют такой форме выпучивания, при которой ребро жесткости совпадает с узловой линией и поэтому при выпучивании оно не испытывает изгиба. Из этих уравнении существенно только уравнение с коэффициентом А2. Соответствующее напряжение акр имеет такое же значение, как и в случае
510
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
неподкрепленной пластины шириной 12Ь. При недостаточной жесткости ребра возможно, что пластина выпучится при напряжении меньшем, чем упомянутое выше, и что при этом ребро
недостаточной жесткости изогнется.
Для определения критического напряжения, соответствующего такой форме выпучивания, необходимо рассмотреть уравнения системы (f), содержащие коэффициенты Ап с нечетными п. Если ограничиться только одним уравнением и соответственно этому одним коэффициентом Ль то в первом приближении получим
(1 Р2)2 2у nm
р2(126) КШ)
В случае длинных пластин ((3 2) это первое приближение дает необходимую точность. Для более коротких пластин необходимо отыскивать следующие приближения. Если принять во внимание два уравнения системы (f) и соответственно этому два коэффициента А и А3 и приравнять нулю соответствующий детерминант, то получим следующее уравнение:
(ftp2)2 (1 46) -р2 (1 26) (с d) - 8Y6 cd- 4Y2 0, (g)
где
k , c ( 1P2)2 2y, d ( 1 9p2)2 2Y.
Возьмем три уравнения и соответственно три коэффициента А, Л3 и Л5 и покажем, что в этом случае имеет место лишь незначительное отклонение от результатов, основанных на уравнении (g); поэтому мы можем с достаточной точностью использовать при вычислении аКр уравнение (g). Соответствующие значения коэффициентов k даны в таблице II.
В тех случаях, когда значение k оказывается больше соответствующего значения k для неподкрепленной пластины шириной V26, последние следует сопоставить. Длинная пластина при выпучивании разделяется на ряд полуволн. Волновое число легко определяется из условия, что k должно принимать наименьшее значение.
Применим вышеупомянутые результаты к расчету пластины со следующими параметрами:
а 120 см, b 200 см, h 1,4 см, Е 2,2-106 кгсм2,
1 — v2 0,9.
В этом случае
щ- 98,5 кгсм Db 50,8 2,2 Ю6 кгсм2м аЬ 0,6,
Таблица II
ОВ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
511
Ю 00 О ю Ю- со
CD CD CD 0 CD CD CO N W CO CO
II
-
LO 00 О Ю 00 CO 0 Ф CO S 0 0 0 0 0 0 0 Ю CO CO CO CO Ю lO
Ю 00 О CM О » — 00 00 CN CD N Э
0 0 0 0 0 0 01 0 Ю Ю lO Ю 0 0
in ОО О Ю 0 0_ 0_ 0 00к 0 0 0
CD CD CO CD CD Tf CM —o o O CD S S c S
8
n
-
UO 00 О —I CO © lO ь-
CD CD CD CD CD CO rf CO CM CM Cm Cm CO CO rf CO
ЮОООЮ—'СПСОСПЮЮЬ-ООСПСО CO CD CD CO CO CCT LO CO CO CO CO ю
О Ю Г» СО Ю Ю 00 CD ЮСОООЮООСОЮООСО СП 00
со cd со cd со о сп сп сп сп сп о о о сп
I
Ю 00 О Ю h. СО CM тр О СЛ Ю 3 СМ
ссГ со со со ю со of —— о См См См Ю 00 0 Ю — t4 (N 05 W Tf
со со со со со Tt СО см См CM СМ СО 00 со см
ю Ю со о со
СОСПЮООт«СМЮЮСО О О) -н т05ЮОС0О
ю с» С»
со со ю См о О) 00 00 t оо оо оо сп О) оо оо
I
-
о
иэ 00 О W о ю
со СО СО СМ О О) О) сп О)
Ю О СП СО СО СО Tf 00
о ю н Ю S со
О) О -нI о О) О)
lO » © СО СП CD (N (N тр ОЭ Tf CD СО со СО Ift CM о о о о о СМ со см о о
СМ 00 CM CM CD Tf
Ю О N ® 00 со — СМ
CD со“ оГ S 0” 0“ 0 0 со со s со 0 со со
I
8000а00ср0—'СМ
осо—.смюоюосо
0“
® щ.
СП N N N N N оо ОО N tT tT
COCM-H30OOO)NW-H-HTt0
Ю тр 00_ СОж О 00 № CM CM CD со о оо ол
со Ю см О) оо оо 1Г tC оо оо сгГ оо оо оо NT 1Г
COOOOCMTfCOOOOCMTfCOOOOCMCOO
©сГсмсмсмсмсмсооос»5‘;
512
ОВ УСТОЙЧИВОСТИ ПОДКРЕПЛЁННЫХ ПЛАСТИН
Для неподкрепленной пластины на основе формулы (8) получим аКр 506 кгсм2. Наибольшее значение критического напряжения, которого можно достичь в случае одного ребра жесткости, находится также из формулы (8), если в этой формуле вместо Ь ввести 12Ь. Таким способом получим аКр 1627 кгсм2. С этим значением мы можем считаться только в том случае, если ребро имеет достаточную жесткость и при выпучивании пластины не изгибается. Возьмем, например, в качестве ребра жесткости швеллерное железо № 8 и примем во внимание, что центр тяжести соединения швеллера с широкой пластиной располагается почти в плоскости соприкосновения швеллера с пластиной; поэтому при расчете жесткости момент инерции поперечного сечения можно определять по отношению к оси, лежащей в плоскости соприкосновения. В этом случае
Б (114 11,9 42) 304 2,2 106 кгсм2;
тогда получим у BbD « 6, б 0,042.
На основе таблицы II заключаем, что в этом случае выбранное ребро жесткости можно рассматривать как абсолютно жесткое. Повышая толщину пластины до 2 см, получим
ае 201 кгсм2, Db 148 2,2 106 кг см2.
Тогда для подкрепленной пластины имеем акр 1033 кгсм2. Если эта пластина подкреплена швеллерным железом № 8, то
найдем, что y 7 2,05, 6 0,03.
Значения у и б оказались такими, что таблица II не может быть использована; поэтому, решая непосредственно уравнение (g), получим k 14,8, аКр кое 2975 кгсм2. Отсюда заключаем, что в этом случае выпучивание пластины сопряжено с изгибом ребра жесткости. Для того чтобы этот изгиб предотвратить, необходимо увеличить жесткость ребра. Жесткость ребра нужно также увеличить с ростом длины пластины. Например,
а 240 см, b 200 см, h 1,4 см,
2,2 106 кгсм2, 1 - v2 0,9.
При отсутствии ребра жесткости имеем критическое напряжение, равное акр 407 кгсм2.
Из таблицы II для заданного отношения сторон (р 1,2) следует значение у которое должно быть больше 10 в том случае, если при выпучивании пластины можно избежать изгиба ребра. Если в качестве ребра жесткости выбрать швеллерное железо № 10, то
В (213 13,9- 25) 560 - 2,2- 106 кгсм2, YH0, 6 0,05. Уравнение (g) дает
k 16,4, акр kae 16,4 98,5 1615 кгсм2.
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
513
Найденное значение k приближается к значению, соответствующему абсолютно жесткому ребру.
Способ, который был использован для одного ребра, может быть обобщен на случай нескольких ребер. Для случая двух одинаковых ребер жесткости, которые разделяют пластину на три равные поля по ширине, в первом приближении (при использовании прежних обозначений) получим
_ (1 Р2)2 Зу _ и ,1П
кр Ge р2(1__35) кае, (II;
Несколько соответствующих значений k приведены в таблице III.
Таблица III
Y-
юз
Y-5
Y-:
203
Y-
10
р
б - 0,05
6-0,1
6 - 0,05
6-0,1
6 - 0,05
6-0,1
6 - 0,05
6-0,1
0,6
26,8
24,1
36,4
33,2
36,4
36,4
36,4
36,4
0,8
16,9
15,0
23,3
20,7
29,4
26,3
37,2
37,1
1
12,1
10,7
16,3
14,5
20,5
18,2
28,7
25,6
1,2
9,61
8,51
12,6
11,2
15,5
13,8
21,4
19,0
1,4
8,32
7,36
10,5
9,32
12,7
11,3
17,2
15,2
1,6
7,70
6,81
9,40
8,31
11,1
9,82
14,5
12,8
1,8
7,51
6,64
8,85
7,83
10,2
9,02
12,9
11,4
2
7,61
6,73
8,70
7,69
9,78
8,65
11,9
10,6
В тех случаях, когда формула (И) дает для k значения, большие, чем соответствующие k для неподкрепленной пластины шириной 7зЪ, вводим в вышеупомянутую зависимость последнее из двух чисел. Тогда получим случай абсолютно жесткого ребра.
При большем числе ребер жесткости можно приближенные
значения критического напряжения определять по следующей
формуле:
(1 Р2)2 2 yi sin2“y
акр af Y пег
1 2 6 sin2 -у-
i
Примем, например, следующие размеры пластины 1): а 1100 см, Ъ 550 см, А 3,75 см,
Е 2,2 106 кгсм2, 1 - v2 0,9,
) Как в этом, так и в предыдущих примерах вычислеиия относятся к подкрепленным стальным листам, которые находят применение в военном судостроении.
514
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
и вычислим критическое напряжение в случае пяти равноудаленных ребер, для которых
В 42. 103 2,2. 106 кгсм2, у 15,7, 6 0,062.
Тогда из формулы (12) получим, что аКр 2030 кгсм2. Найденное напряжение меньше соответствующего значения для пластины шириной, равной V6. Это показывает, что выпучивание пластин сопровождается изгибом ребер.
Способ, использованный в случае продольного подкрепления, может также найти применение в случае поперечных ребер. Когда неподкрепленная пластина при выпучивании разделяется на ряд полуволн, ясно, что расположение ребер жесткости в соответствующих узловых линиях не оказывает никакого влияния
Рис. 2. Рис. 3.
на критическое напряжение. Постановка поперечных ребер имеет только тогда смысл, когда благодаря этому изменяется отношение между длиной волны и шириной пластины.
Ограничимся здесь приведением окончательных результатов для случаев, представленных на рис. 2 и 3. Практически важно знать наименьшую жесткость ребра, при которой в случае выпучивания пластины ребра не прогибаются. Тогда ребра можно рассматривать как абсолютно жесткие и расчетную длину пластины в случае рис. 2 полагать равной 72а, а в случае рис. 3 — 4а.
В таблице IV даны соответствующие значения у BbD в случае поперечного ребра.
Таблица IV
р
0,5
0,6
0,7
0,8
0,9
1
1,2
1,41
Y
12,6
7,18
4,39
2,80
1,82
1,26
0,433
0
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
515
Отсюда следует, что с увеличением длины пластины необходимая жесткость ребра уменьшается. При р 1,41 у равно
Таблица V
р
0,6
0,8
1
1,2
1,4
Y
101
42,6
21,7
12,4
7,71
нулю, так как при этом отношении сторон неподкрепленная пластина делится на две полуволны. В таблице V даны некоторые предельные значения y BbD в случае трех поперечных ребер жесткости (рис. 3).
§ 3. Чистый сдвиг
В этом параграфе мы исследуем вопрос об устойчивости всесторонне опертой прямоугольной пластины, нагруженной по
всему периметру касательными силами (рис. 4). Задача этого
рода встречается при расчете стенок поперечных переборок
в судостроении и при расчете
толщины металлических листов балок со сплошной стенкой. При определении критического значения касательного t напряжения используем наш метод. До тех пор пока пластина остается плоской, накапливается только потенциальная энергия сдвига. При выпучивании появляется потенциальная энергия изгиба V,
причем потенциальная энергия сдвига несколько уменьшается. Обозначим это уменьшение энергии через V, тогда для определения критического касательного напряжения получим при этом также прежнее основное уравнение (1):
и a ►
'С
И
1
i
й-v
V
Рис. 4.
v vx.
(1')
Когда пластина оперта на всех сторонах, мы можем для прогиба при выпучивании пластины использовать представление (4) и при вычислении потенциальной энергии изгиба воспользоваться формулой (5). Следовательно, остается только определить уменьшение потенциальной энергии сдвига. Угол сдвига, который образуется вследствие прогиба w пластины, равен
516
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
dw dw rp
Ъ»—5J W Тогда V.—
о о
Введем сюда общее выражение (4) и примем во внимание формулы интегрирования
а
Г. тпх рлх г, .
sin —— cos -i-j- ах 0, когда т р — четное число;
о
а
С. тшс рях 1 2а tn
sin cos-—dx--о 5 когда т р — нечетное число.
J й а я я — р о
Тогда получим
оо оо оо оо
mnpq
Р4 (т2 — p2)(q2 — п2)
mnpq
причем т'’р и м 7 представляют собою нечетные числа. Выражения V и V вносим в уравнение (1), тогда получим формулу для критического напряжения
Dab m l ng 1 кр б 4г оо оо оо оо AnnApq (m2 _ p2)2 _ „2) mnpq
Коэффициенты Лтп и выбираются так, чтобы ткр было минимальным. Это приводит, как и прежде, к системе линейных уравнений. С помощью обозначений
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
517
эту систему можно представить следующим образом1):
Aw
М1Р2)2
Р2
4
Т о
о
45
Ая
4
¥ 16М1 Р2)2 Р2
_4
5
__4_
5 36 25
О
- —
Ли
О
__4_
5
Я(1952)а
Р2
О
24
75
Ati
О
__4
5
О
Я (9Э2)2 Р2
О
. 24
Лзз
О
25
Я (9902)а
Аа
Р2 72 ' 35
0
75
21 72
35
, Я(164р’)» _ ра -О,
-О,
-О,
-О,
О,
-О,
(к)
Величины касательных напряжений, при которых возможно выпучивание пластины, находятся из условия, что детерминант системы уравнений (к) равен нулю. Как и прежде, мы можем найти последовательные приближения для ткр, если будем принимать во внимание все большее число уравнений (к), соответственно этому все большее число коэффициентов Атпл Ограничимся двумя первыми уравнениями системы (к), соответственно коэффициентами Лц, Л2, тогда в качестве первого приближения получим
Л - 9 (1р2)2 или с учетом обозначений (13) имеем 2)
__ 9я2 (1р2)2
ТКр 4- 32 рз е (14)
Точность этого приближения в случае квадратной пластины приблизительно равна 15. С увеличением р растет также и ошибка решения (14). Для того чтобы достичь большей точности, необходимы дальнейшие приближения. Если приндть во внимание пять первых уравнений системы (к) и соответственно пять коэффициентов Ац,., Л33, то получим
р4 Г1 81 .81 (1Р2)2 , 81 (1р2)2
81 (1р2)4 L 625 25 JTTWy 25 (9 р2)2
Я2 -
г. (15)
1) Для упрощения мы записываем только коэффициенты при величинах Атп, которые стоят в первой строке. Наша система заключает в себе только величны Атп, для которых сумма индексов m п равна четному числу. Уравнения, которые содержат Атп при т п нечетных, приводят к более высоким значениям ткр. Поэтому нет необходимости принимать их во внимание.
2) Двойной знак соответствует двум различным возможным направлю
ниям касательного напряжения,
518
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
Мы вычислим также третье приближение с шестью уравнениями системы (к). В случае квадратной пластины разница между вторым и третьим приближением заметна только в четвертом десятичном знаке. С увеличением длины пластины растет также и соответствующая разница. При р 2 это различие равно 2. При р 3 оно равно 9,6. На основе этих результатов можно заключить, что наше третье приближение имеет достаточную для практических целей точность. Как и прежде, можно значение критического напряжения представить в форме тКр koe. Ряд значений коэффициента k дан в таблице VI.
Таблица VI
р
1
1,2
1А
1,5
1,6
1,8
2
2,5
3
k
9,42
8,0
7,3
7,1
7,0
6,8
6,6
6,3
6,1
ткр, кгсм2 при h 0,016
1870
1590
1450
1410
1390
1350
1310
1250
1210
С увеличением отношения р значение k уменьшается. Как можно видеть из числового ряда, это уменьшение происходит все более медленно. Величина k стремится к предельному значению, соответствующему случаю бесконечно длинной пластины. Приближенно это предельное значение k можно найти на основе следующих соображений: в случае длинной пластины характер подкрепления на поперечных сторонах не имеет особого влияния на величину k поэтому при выборе формы прогиба при выпучивании руководствуются условиями на продольных сторонах пластины. Мы можем, например, прогиб при выпучивании длинной пластины представить приближенным образом в форме
w A sin -у sin у (х — ay). (1)
При этом пластина выпучивается с образованием ряда полуволн по длине s. Соответствующие узловые линии образуют с осью ц угол, тангенс которого равен а; выражение (1), введенное в основное уравнение (1), дает
ткр ба2 2 - --(1а2)2. (16)
Наименьшее значение тКр соответствует условию s b У а2 И а 1V2. Тогда получим значение xKp — 5,7at, которое близке
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
519
к значению, найденному для случая р 3. В третьей строке таблицы VI даны значения ТкР для случая
2,2 106 кгсм1, v 0,3, h 0,016.
§ 4. Приложение к расчету металлических балок со сплошной стенкой
Вышеуказанные результаты имеют практическое значение при расчете толщины металлических листов клепаных балок со сплошной стенкой. Обычный прикладной метод, который принимает во внимание только распределение касательных напряжений, очень часто дает неподходящие размеры. Учет устойчивости приводит к повышению толщины стенки. Так как для вытекающего отсюда подкрепления не существует бесспорных теоретических оснований, то получится конструкция с весьма различным запасом устойчивости.
В качестве примера рассмотрим два следующих моста из американской практики1).
1. Балка со сплошной стенкой Нью-йоркской железнодорожной ветки с верхним расположением рельсовых путей пролетом около 30 м железный лист стенки имеет размеры 300 X 1,6 480 см2 расстояние между вертикальными ребрами вблизи концов балки Ь « 160 см. Максимальная поперечная сила равна Q 152 тоннам. Действующее касательное напряжение равно т 152 000480 316 кгсм2.
Если лист стенки между двумя ребрами жесткости рассматривать как опертую пластину с размерами а 300 см, Ъ 160 см, h 1,6 см, то на основе таблицы VI найдем тКр 1340 кгсм2. Существующий запас устойчивости равен п тнрт 4,25. Подкрепление листа стенки в поясе даст в результате еще дальнейшее повышение коэффициента запаса п.
2. Балка пролетом I 34,4 м из листового железа Канадской тихоокеанской железной дороги с расположенными наверху рельсовыми путями. Максимальная поперечная сила будет Q 150 т. Металлический лист стенки имеет размер 305 X X 1,11 см2 338 см2 на расстоянии до 3,6 м от опоры, в противном случае размер листа будет только 305 X 0,95 см2 290 см2. Длина концевой панели листа Ъ 168 см. Действующее касательное напряжение составляет т 150 000338 444 кгсм2. Критическое напряжение в случае, когда а — 305 см, Ь 168 см, Л 1,11 см, будет тир 590 кгсм2.
) Примеры взяты из статьи: Н. Rode. Beitrag zur Theorie der Knickerscheinungen. Der Eisenbau, 1916, Bd. 7, Heft 9, S. 217.
520
ОБ УСТОЙЧИВОСТИ подкрепленных пластин
Следовательно, существующий запас устойчивости равен п ТТкр 590444 1,32.
Мы видим, что обе балки со сплошными стенками, которые удовлетворяют американским нормам1), имеют весьма различный запас устойчивости. Для балок со сплошными стенками большого пролета ( 15 м) запас устойчивости обыкновенно уменьшается с увеличением высоты балок, потому что расстояние между ребрами жесткости и толщина стенки металлического листа очень часто остаются неизменными. Поэтому ясно, что для такой балки исследование запаса устойчивости может иметь особенное практическое значение.
Хотя выпучивание стенок не влечет за собой непосредственно опасности разрушения, оно несет, однако, нежелательное изменение в распределении сил между отдельными частями сооружения. Выпученная стенка при последующем приращении поперечной силы не будет больше в состоянии воспринять соответствующее приращение касательного напряжения.
В таком случае стенка действует между двумя ребрами как растянутая диагональ фермы. В таком положении будет часть стенки вдоль воображаемой диагонали, которая при удлинении более всего нагружает здесь расположенные заклепки. Это явление не прошло мимо внимания инженеров. В свое время был дан способ расчета балок со сплошными стенками2), в котором учтено то обстоятельство, что после превышения определенной нагрузки балка со сплошными стенками ведет себя так же, как раскосная ферма. Допущение выпучивания стенки, по нашему мнению, недозволительно из-за возникающих при этом дополнительных напряжений, которые не могут быть вычислены с достаточной точностью. Выпучивание стенки точно так же следует считать недопустимым, как, например, появление остаточных деформаций при переходе предела упругости конструкционного материала. Если мы при растяжении или сжатии пояса в качестве допускаемого напряжения принимаем половину предела упругости, тогда для коэффициента безопасности, само собой разумеется, по отношению к устойчивости следует выбирать также значение, равное 2. Для того чтобы показать, что это требование не приводит ни к какому чрезмерному значению толщины стенки, дадим в таблице VII значения допускаемых напряжений т V2TKp в кгсм2 для толщин стенки, которые заимствованы для балок со сплошными стенками из американской строительной практики с расстоянием между ребрами жесткости Ь 150 см, и с различной высотой стенки а.
) См. Н. A. L. Waddell. Bridge engineering. First edition, John Wiley. 1916, p. 1670.
2) Cm. W. E. Lilly. The design of plate girders and column. London, Chapman and Hall, 1908. См. также упомянутую на стр. 519 работу Н. Rode.
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
Таблица VII
521
Двукратный запас по отношению к устойчивости для обоих вышеупомянутых американских мостов будет достигнут, если толщину стенки выбрать равной — 1,25 см. При уменьшении высоты балки согласно таблице VII допускаемое напряжение уве личивается. Следовательно, для мостов меньшего пролета следует уменьшить толщину стенки.
В дальнейшем мы перейдем к размерам ребер жесткости. Рассмотрим простейший случай, когда пластина разделяется с помощью одного ребра пополам (рис. 5). Применим прежний способ решения и представим форму выпучивания с помощью выражения (4), тогда на основайии уравнения (1) можно получить выражение для ткр в случае подкрепленной пластины. Определение минимума этого выражения для тКр приводит к следующей системе линейных уравнений:
t
♦
1
д
itr
1
♦
1
t
- с У
Рис. 5.
Ац Aii
2VP2 Т 16М1Р2)2
—2yP2A, О
Р2
Дзз
О
36
25
Ац
-2yP8X
4
5
i
—2,81 y32A.
Л09Р2)2
к—
Аъ
0.
. -0,
Т
. «0,
-2,81.
. -0,
0.
.0,
2,81 YP2
. -0,
(s)
Здесь введены обозначения:
522
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
Тогда, ограничиваясь двумя первыми уравнениями, соответственно этому первыми двумя коэффициентами Ли, Л22, и полагая детерминант этих уравнений равным нулю, получим
Р2 Г. 2уР4 Г'А “ 9(1 р2)2 L (1 р2)2 J 1
откуда в качестве первого приближения найдем
9я2 (1 р2)2 Г1 2Vp т,
Ткр 32р3 L1 “Г (1р2)2 J 1)
Этот результат отличается от результата, полученного для неподкрепленной пластины (формула (14)), только за счет последнего члена, который передает влияние ребра жесткости на устойчивость пластины. Если повысить жесткость В ребра (соответственно у) то значение тнр увеличится. Предельным критическим напряжением будет то, которое соответствует непод¬
крепленной пластине с размерами b X 7гя. Дальнейшее повышение жесткости ребра не оказывает никакого влияния на тКр. Для каждого значения р можно также определить то наибольшее значение ткр, которое можно достичь введением одного ребра. При уменьшении р влияние ребра жесткости растет, одновременно растет также то значение у, которому соответствует абсолютно жесткое ребро.
Некоторые предельные значения y определенные из четырех уравнений системы (s), даны в таблице VIII.
В том случае, если у длинной, подкрепленной несколькими ребрами пластины принять во внимание три смежных ребра и среднее из них рассчитать на основе таблицы VIII, то следует ожидать недостаточную жесткость. Здесь можно заметить то же самое явление, как в случае сжатой пластины с поперечными ребрами жесткости. Сравнивая значения таблицы V при Р 1; 1,2; 1,4 со значениями таблицы IV при р 0,5; 0,6; 0,7, обнаружим в результате, что при равной ширине и равном расстоянии между ребрами жесткости в случае трех ребер величина y должна быть в 1,75 раза больше выбранного значения. Поэтому в случае длинной, подкрепленной многими ребрами и нагруженной касательными напряжениями пластины следует в качестве приближенного значения y вводить вдвое большее значение, нежели то, которое было получено в случае одного ребра жесткости (таблица VIII). Таким способом при расстоянии между ребрами 7гЯ 152 см и для различных значений высоты стенки b получим приведенные в таблице IX значения у.
Таблица VIII
р
2
1,5
1,25
1
Y
0,83
2,9
6,3
15
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН 623
Таблица IX
b, cm
152
203
244
305
alb
2
1,5
1,25
1
Y
1,7
5,8
12,6
30
h 1 cm
48
160
360
850
, CMA
h 1,1 cm
64
220
480
1130
h 1,2 cm
83
280
620
1470
В этой же таблице указаны также необходимые моменты инерции ребра жесткости для трех различных толщин стенки. Из конструктивных соображений величины, приведенные для b 152 см, следует повысить. По нашему мнению, остальные результаты можно принять во внимание при назначении размеров ребер жесткости. В американской практике поперечное сечение ребра жесткости выбирается обычно больше, чем это необходимо в соответствии с таблицей IX. Для высоты, большей 275 см, обычно выбирают ребро, у которого J 2500 см4 (2 X 15,24 см X 8,89 см X 0,953 см) ); для меньшей высоты поперечное сечение выбирается в зависимости от ширины пояса; момент инерции изменяется в пределах от 1450 смА до 320 смА. Заметим здесь, что в Америке при расчете металлических стенок на сдвиг в случае никелевой стали принимается повышенное напряжение, равное приблизительно 1125 кгсм2. Видно, что вследствие условий устойчивости такие напряжения могут быть использованы.
Иногда длинная, нагруженная касательными силами пластина подкреплена продольными ребрами жесткости. В этом случае для оценки необходимой жесткости можно использовать приближенное решение (1). Складывая энергию изгиба пластины с энергией изгиба ребер жесткости, из уравнения (1) получим следующий результат:
тр-it 6а22 t(1а2)2 19
где
2Bi sin2
’) См. Н. A. L. Waddell. Bridge engineering. First edition, John Wiley, 1916, p. 1670.
524
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
Здесь Bi — жесткость ребра, с — расстояние ребра от продольного края пластины. Для каждого yi из формулы (1) следует выбрать те значения а и s, которые соответствуют наименьшему значению ткр. В следующей таблице приведены значения k в формуле тКр koe.
Таблица X
1
Yi
i
5
10
20
30
40
50
60
70
80
90
100
k
6,98
7,70
8,67
9,36
9,90
10,4
10,8
11,1
11,4
11,7
12,0
Для примера возьмем стальную пластину (с Ъ 180 см, h 1 см), которая подкреплена на равном расстоянии швеллерным железом № 8. Тогда имеем ое 62 кгсм2, Db 15 X X 2,2 X Ю6 кгсм2, yi 80. Из таблицы X найдем k 11,4, следовательно, тКр 11,4 X 62 707 кгсм2. Если толщину пластины увеличить до 1,2 см, то в результате получим ае 89,3 кгсм2, Yi « 46, k 10,2, тКр 911 кг)см2.
§ 5. Эксцентричное сжатие
В случае эксцентричного сжатия или растяжения пластины распределение нормального напряжения можно представить с помощью следующей формулы1) (рис. 6):
В случае а 0,5 имеем чистый изгиб, при а 0,5 — эксцентж ричное сжатие, при а 0,5 — экс¬
центричное растяжение.
Для определения критического значения максимального сжимающего напряжения oq применим прежний метод. Предполагая пластину всесторонне опер-
той, мы можем сохранить преж-
Рис- ние выражения для прогиба пла¬
стины при выпучивании (4) и для потенциальной энергии изгиба (5). Уменьшение потенциальной энергии сжатия можно представить следующей формулой:
--)()'dx.
: Г'“
J
t 1.
Г01
Sj HTTP
t7
у
-
a
) Сжимающее напряжение считается положительным.
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
525
Если для w ввести его выражение согласно (4) и принять во внимание формулы интегрирования
и
Г. iny. ту j
у sin -у- sin dy
ь_
4
О,
при — ,
если i — четное число,
4 Ъ2
я2 2-_ jiy » если i — нечетное число,
то получим
оо оо
т mj0 ab V1 V л2 m2jc2 “Т а2
т 1 1 1
гсг0 а
2 2аЬ
S 62 V 12 8i у у «лт„лт, 1
а2 4 ” Я2 Lk (П2 - »2)2 '
т1 L п 1 л-1 i J
Вводя выражения У и Vi в основное уравнение (1), найдем
(о)кр
л4
т1 n-1
V V -2 т2я2 1 V т2п2 Г V «2 32 V V 4iAmnAmi 1
тп а2 2а а2 тя п2 Zl Li (п2-12)2
т—1 г1 т1 L j n-1 I J
(t)
Рассмотрим случай изгиба пластины по одной полуволне. Из условия минимума (t) получим систему линейных уравнений следующего вида:
Ч(-±)НгМ
i
где п i — нечетные числа.
Приравнивая нулю детерминант этой системы уравнений, по« лучим выражение для определения (сто)кр- Первое приближение, которому соответствует первое уравнение системы (и), имеет вид
(20)
(о)кр е ( а b ) j _ 1
2а
Эта формула дает достаточную точность для больших значений а. (Например, при а 1,5 в случае квадратной пластины
526
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
ошибка равна 4.) Если принять во внимание два уравнения системы (и) и соответствующий детерминант приравнять нулю, то получим следующее уравнение для определения критического напряжения во втором приближении:
«тГ-о-
Вычисление критических значений напряжения в последующих приближениях показывает, что для а 0,75 второе приближение имеет достаточную для практических целей точность. В случае чистого изгиба приходится искать дальнейшее приближение, принимая во внимание три уравнения системы (и). Как и прежде, можно результат нашего вычисления представить в форме (схо)кр k(je- Несколько значений коэффициента k приведены в следующей таблице XI.
Таблица XI
Для каждого значения а можно найти отношение а6, при котором коэффициент k принимает наименьшее значение. В случае чистого изгиба (а 0,5) наименьшее значение k соответствует отношению аЬу приблизительно равному 23.
Следовательно, в этом случае длинная пластина при выпучивании разделяется на ряд полуволн, длина которых соответствует найденным выше наиболее неблагоприятным значениям отношения аb. Из сопоставления значений таблицы XI легко установить, что достаточно большое отклонение наиболее неблагоприятного значения отношения аb имеет лишь незначительное влияние на величину k. Из этого можно заключить, что вертикальное ребро жесткости в средней части пролета балки со сплошными стенками не имеет никакого значительного влияния на запас устойчивости вертикальной стенки. Этот запас устойчивости обычно уменьшается, если высота балки растет.
В рассмотренном выше случае балки со сплошными стенками Канадской тихоокеанской железной дороги в средней части пролета имеется вертикальный металлический лист раз¬
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕПНЫХ ПЛАСТИН
527
мерами 305 см X 0,953 см. Следовательно, ое Dn2b2h 19,6 кгсм2. Принимая часть металлической стенки между двумя ребрами жесткости в качестве пласПГины, опертой по периметру, получим b -- 305 см, а 152 см. Следовательно, на основе таблицы XI найдем, что k 25,6. Критическое значение напряжения будет (ао)Кр 25,6 19,6 500 кгсм2.
Несмотря на то, что критическое напряжение вследствие заделки вертикальной стенки в полке несколько повышается, следует все-таки ожидать, что выпучивание пластины в середине балок происходит при обычных условиях нагружения. Прогиб при этом выпучивании может остаться незаметным вследствие его малости, однако, несмотря на это, он имеет влияние на распределение напряжения. Стенка передает напряжения только до критического предельного значения. При дальнейшем росте изгибающих моментов напряжения в стенке остаются неизменными и приращение моментов будет получаться только за счет полки, напряжения в которой вследствие этого растут. Заметим, что при достижении критического нормального напряжения вертикальная стенка не способна воспринять касательные напряжения. Стенка ведет себя частично как растягиваемая диагональ в решетчатой балке, вертикальная стойка которой представляет собою ребро жесткости балки со сплошными стенками. Мы уже отмечали, что такое перераспределение напряжений сопряжено с перенапряжениями некоторых заклепок и во всяком случае должно быть нежелательным в конструкции.
Повышая толщину стенки до 1,25 см, мы уменьшим прогиб при употребительных размерах листа. Каждое дальнейшее повышение устойчивости посредством равномерного подкрепления стенки неэкономно. Целесообразно установить горизонтальное ребро жесткости в средней части пролета балки. Это ребро жесткости может быть установлено приблизительно на расстоянии одной четвертой высоты стенки от сжатого края. Значения таблицы II показывают, что таким образом без особой расточительности материала можно достичь значительного увеличения жесткости. Постановка горизонтального ребра жесткости с вертикальным ребром жесткости не сопровождается никаким особым усилением, так как значение вертикального ребра жесткости в средней части пролета балки имеет второстепенный характер.
УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА КРИВЫХ СТЕРЖНЕЙ С ЦЕНТРАЛЬНОЙ ОСЬЮ В ФОРМЕ КРУГА
Kippsicherheit des gekrummten Stabes mit kreisformiger Mittellinie. Zeitschrift fur angewandte Mathematik und Mechanik, 1923, Bd. 3, Heft 5, SS. 358—362. Перепечатка: S. P. Timoshenko. The collected papers, McGraw-Hill Publishing Company Ltd. New York — London — Toronto, 1953, pp. 371—376.
К решению поставленной задачи применим известные дифференциальные уравнения равновесия криволинейных стержней1). В случае стержня, который вдоль его центральной оси, образованной дугой круга, сжат равномерно распределенной и
направленной к центру (рис. 1) нагрузкой, эти уравнения принимают особенно простой вид. Решение этих уравнений даст нам величину искомой критической нагрузки2).
) А. Е. Н. Love. A treatise on the mathematical theory of elasticity. Cambridge, University Press. Third edition, 1920, pp. 403, 453.
2) Решение задачи об устойчивости плоской формы изгиба стержней с центральной осью в форме дуги круга в случае чистого изгиба дано автором («К вопросу об устойчивости упругих систем». Известия Киевского политехнического института, 1910, год 10, книга 2, стр. 147—167). Некоторые задачи
о потере устойчивости плоской формы изгиба кривых стержней были обсуждены проф. Е. Николаи («Об устойчивости кругового кольца и круговой арки, сжатых равномерно распределенным нормальным давлением». Известия Первого Петроградского политехнического института, Отдел техники, естествознания и математики, 1918, том 27, выпуск 1, стр. 323—377). Перепечатка: Е. J1. Николаи. Труды по механике М., Гостехиздат, 1955,
стр. 278—328.
УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА КРИВЫХ СТЕРЖНЕЙ 529
§ 1. Вывод дифференциального уравнения
Перемещения в направлении подвижных осей х, у, z (рис. 2) обозначим через и, и, w, а угол закручивания — через р. Тогда
для изгибающих моментов G, G и для крутящего момента Н получим известные выражения:
п В ( Q d2v п Вх (d2u. dw JJ С dv. dp 1ч
G a2 (a 02 ) ’ 1 a2 W92 9 ) ’ a2 W9 a e) ’
где В и B означают главные изгибные жесткости, С — крутильная жесткость, а — радиус центральной линии стержня. Вводя эти выражения в уравнения равновесия1)
dH л л dG. г j dv л dG dti « г
dQ ’()adQ ’ 10 1_а'Ж 0, получим
-§-(1Я) а-5--Яар0,
-4F 4r(r-co) a-50 ( x) 0 (3)
d3u - d2w - qa3 du _ d03
где
“ (4)
Третье уравнение (3) вместе с условием нерастяжимости центральной оси dwdQ и дает известную критическую нагрузку при выпучивании кривого стержня в плоскости центральной оси2).
х) Мы принимаем, что равномерно распределенная нагрузка q после деформации направлена параллельно плоскости недеформированной центральной оси.
2) См. мою работу, цитированную на стр. 52Q,
530 УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА КРИВЫХ СТЕРЖНЕЙ
Условие устойчивости плоской формы изгиба стержней получим из двух первых уравнений системы (3). Исключая v, получим тогда для р следующее дифференциальное уравнение:
(2 ю) (1 — соЯ) р 0. (5)
Решение этого уравнения имеет вид
Р A sin k6 В cos9 CshM DchM, (6)
где k-V ,-1,
1 V-1y (I±)2 coX- 1.
§ 2. Случай свободных концов
В качестве простейшего примера рассмотрим случай, когда на концах стержня G и р равны нулю (рис. 1). Эти концевые условия выполняются, если положить в решении (6) постоянные В, С, D равными нулю, а
А-Т-
Из (7) получим
(я2 - а2)2 со —
а2 (я2 Аа2)
Критическая сила стержня равна
сol
ТКР — qa — а2 В случае ос 7гя получим
т _ па _ (я2 а2)2 о
i КР а2 а2 а2 (Я2 Яа2) W
Т — — (Q)
кр а2 4 А, ' W
Это решение соответствует образованию восьми волн в замкнутом круговом кольце, когда силы q при потере устойчивости плоской формы изгиба сохраняют свое направление. Случай, когда эти силы при опрокидывании всегда направлены к центру кольца, мы рассмотрим дальше.
Когда угол а является очень малым, из (8) получим известную формулу Эйлера Гкр Вя22, где а а обозначает длину кривого стержня. При а я формула (8) дает Гкр 0, что соответствует возможности вращения как жесткого тела вокруг диаметра полукольца. Для k ппа получим формы равновесия более высокого порядка с числом полуволн, равным п. Пола¬
УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА КРИВЫХ СТЕРЖНЕЙ 531
гаем а тп, тогда представим критическую нагрузку согласно формуле (8) следующим образом:
Т _ (п2 - пг2)2 пч
кр а2 пг2 'km2 п2) ' '
Переход от формы равновесия с одной полуволной к форме с двумя полуволнами соответствует случаю (Г1ф)п1 (ГКр)п«2 или, согласно (8),
(1-т2)2 (4-т2)2 Ят2 1 Ат2 4
Это дает пг 1,48 и а 1,48я. Это означает, что при 1,48я а 2я первая выпученная форма равновесия будет состоять из двух полуволн.
В случае а 2я этой форме соответствует Гкр 0, т. е. круговое кольцо может свободно вращаться вокруг диаметра. Первая выпученная форма равновесия замкнутого кругового кольца будет состоять из четырех полуволн.
§ 3. Заделанные концы
С помощью общего решения (6) мы можем исследовать устойчивость плоской формы изгиба круговых стержней также и при других условиях на концах. Примем, например, что на концах стержней р и ddQ равны нулю (заделанные концы); тогда из (6) получим следующее уравнение для вычисления нагрузки, при которой происходит потеря устойчивости плоской формы изгиба стержня:
Пусть а очень мало, тогда мы можем величину kia рассматривать как очень малую величину и пренебрегать k по сравнению с k. Это позволит в таком случае условия равновесия (10) представить в следующей форме:
Это уравнение удовлетворяется при k 2яа. При этом получим
(4я2 — а2)2 ® “ а2 (4д2 Ла2)
Это значит, что критическая сила стержня равна
k-k2
2 Н sin ka sh kYa — 2 cos ka ch ka 0.
(10)
2 — ka sin ka — 2 cos ka 0.
(11)
(13)
Этот результат теряет силу в предельном случае эйлеровой критической нагрузки (а 0).
532 УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ изгиба кривых стержней
Для больших значений а мы вычислили некоторые значения критической нагрузки из уравнения (10) ). Соответствующие значения о даны в следующей числовой таблице:
0,250л
0,500л
1,00 л
1,063л
1,Юл
1,24л
1,50л
2л
60,1
12,6
1,85
1,538
1,40
1,00
0,69
0,60
При стремлении а к величине 2nV 2 1Я уравнение (10) снова переходит в уравнение (11), и мы получим характеристическое число со 1А,. Сравнивая результаты расчетов по формуле (12) с данными числовой таблицы, мы можем заключить, что эта приближенная формула дает хорошие значения для со также при очень больших значениях углов а. При вс lUn ошибка составляет 2,2. При а 7гя ошибка равна
7,1. § 4. Вывод выражения для критической нагрузки с помощью потенциальной энергии
Каким образом можно найти критическую нагрузку плоской формы изгиба стержня из рассмотрения потенциальной энергии системы, мы хотим показать на простейшем примере, для которого G и р на концах стержня равны нулю (рис. 1).
В случае плоской формы равновесия потенциальная энергия стержня состоит только из энергии сжатия. Допустим теперь, что стержень выпучился, благодаря этому накапливается потенциальная энергия изгиба и кручения, но в то же самое время потенциальная энергия сжатия будет несколько уменьшаться. Когда сумма потенциальной энергии изгиба VB и энергии кручения Vr оказывается больше уменьшения потенциальной энергии сжатия VD, плоская форма равновесия стержня будет устойчивой. В противоположном случае эта форма неустойчива. Критическую нагрузку можно найти из уравнения
VB V7
(14)
Примем, что p vsin
я0
dv
W-Y
тогда первое уравнение (3) дает аа А, л2а2 я0
1 А
cos-
) При вычислениях мы принимали коэффициент Пуассона а 0,3 и К « 0,65, что соответствует узкому прямоугольному поперечному сечению стержня.
УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА КРИВЫХ СТЕРЖНЕЙ
533
Вводя эти величины р и dvdQ в формулы (1) для моментов, получим для потенциальной энергии следующие выражения:
О
а
vn -
dv V
a dO
2 9 qa2а3 Л я2а2 2
) аМ у214-(-тг-)
1 gvaj
Внося эти выражения в уравнение (14), имеем для критической нагрузки Гкр прежнюю формулу (8).
§ 5. Нагрузка, непрерывно направленная к центру
В качестве второго примера мы хотим рассмотреть случай, когда силы q при выпучивании всегда направлены к центру кольца (рис. 3). При составлении уравнения для вычисления нагрузки, при которой происходит потеря плоской формы изгиба, мы должны теперь привлечь к рассмотрению работу компонентов внешних сил q в направлении перемещения V. Эта работа равна
a v
л Г ja Г QV j 2 Qa2 а4 а Я я2а2 2
О о
Уравнение для вычисления критической нагрузки будет
Vb Vt Vd A.
(15)
Из этого уравнения при а я имеем
Вп2
кр Яа а2 а2 (а2 Л2 )
При а V2Jt формула (16) дает
Т
1 кр
В 12
а2 Л 4’
Рис. 3.
что согласуется с результатом расчетов Г. Хенки1) для замкнутого кругового кольца.
) Н. Hencky. Kippsicherheit und Achterbildung an geschlossenen Kreisringen. Zeitschrift fur angewandte Mathematik und Mechanik, 1921, Bd. 1, Heft 6, SS. 451—455.
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
Analysis of bi-metal thermostats. Journal of the Optical Society of America and Review of Scientific Instruments, 1925, vol. 11, № 3, pp. 233—255. Перепечатка: S. P. Timoshenko, The collected papers. McGraw-Hill Publishing Company Ltd, New York — London — Toronto; 1953, pp. 403—421.
ВВЕДЕНИЕ
Последующее исследование содержит общую теорию изгиба биметаллической полосы, подверженной равномерному нагреванию. Эта теория применяется к анализу работы биметаллической полосы термостатов. Получены выражения для вычисления температуры, при которой происходит прощелкивание, полного перемещения при прощелкивании и температуры, соответствующей прощелкиванию в обратном направлении. С помощью этих выражений могут быть вычислены размеры термостата для данной температуры срабатывания и заданного полного диапазона температуры. Полученные результаты основаны на некоторых идеальных условиях. Например, предполагается, что разность коэффициентов линейного температурного расширения при нагревании остается постоянной, что трением в опорах можно пренебречь и что ширину полосы можно считать очень малой. Существует мнение, что эти предположения не так далеки от реальных условий и что результаты, полученные с помощью приведенной теории, могут быть полезными при выборе размеров термостата и анализе напряжений, возникающих в биметаллических полосах при их работе.
§ 1. Прогибы равномерно нагретой биметаллической полосы
Пусть узкая полоса, состоящая из двух металлов, сваренных вместе, равномерно нагревается от температуры tQ до t С. Если коэффициент линейного температурного расширения этих металлов различен, то нагревание сопровождается изгибом полосы.
Пусть ai и а2 означают коэффициенты линейного температурного расширения металлов 1 и 2 (рис. 1), Е и Е2 означают модули упругости этих металлов, а и а2— их толщины, h — толщина полосы. Примем ширину полосы равной единице. Последующий анализ проведен в предположении, что первоначально плоское и перпендикулярное к оси поперечное сечение полосы в процессе изгиба остается плоским и перпендикулярным к искривленной оси полосы. Рассмотрим элемент, вырезанный из
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
535
полосы двумя поперечными сечениями тп и тП если а2 oti, то изгиб полосы происходит выпуклостью вниз, как показано на рис. 1, с. Все силы, возникающие в поперечном сечении металла 1 на вогнутой стороне полосы, могут быть представлены осевой растягивающей силой Р и изгибающим моментом М. Для металла 2 на выпуклой стороне полосы все силы, действующие в поперечном сечении, могут быть сведены к продольной сжимающей силе Р2 и изгибающему моменту М2. Вследствие того что к полосе не при- 0) ' ложено внешних нагрузок, (77
все силы, возникающие в 1-4 1 любом поперечном сечении полосы, должны взаимно уравновешиваться; поэтому
PI P2 P, (1)
J- pfi М, М2. (2) Рис- 1 Прогиб равномерно нагретой
2 биметаллической полосы.
Обозначая через р радиус кривизны полосы, EJ — изгибную жесткость металла , Е22 — изгибную жесткость металла 2, получим, что
EJ Д Я
М2.
о Р
Подставляя эти выражения в (2), имеем
1 Ph giy» . (3)
Другое уравнение для вычисления Р и р получим из рассмотрения деформации. На поверхности соединения обоих металлов относительные удлинения продольных волокон металлов 1 и 2 должны быть равны, следовательно,
или, используя (1) и (3), найдем
h I 2 EJ
2р ' гр
1 (а2 — ai) (t — 0)
21ВДВД). _ ai)(( _ Wi
откуда
(-Д-Л-)'
,a, Eza)
536
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
Полагая а1а2 пи ЕЕ2 п и помня, что, aj12, 2 а12, получим общее выражение для кривизны биметаллической полосы:
1 _ 6(q2-gl)(-o)(l m)2
р г 3 (1 т)2 (1 тл) (т2 1тг)
Если толщины обоих металлов равны, то ai
1 _ 24 (q2- а,)(- 0)
Яг, m 1 и
г (14 п 1 п)
(4)
(5)
Кривизна пропорциональна разности удлинений обоих металлов и обратно пропорциональна толщине полосы. Очевидно, что величина отношения EJE2 п не оказывает какого-либо заметного влияния на кривизну полосы. Примем, например, п 1, тогда
1 _ 3 (а2 — ai) ( — 0) р 2 h
(6)
При п У2 или п 2
_1_ _ 48 (аг — cti) (t — i0) р 33 h
(7)
Рис. 2. Прогиб шарнирно опер той биметаллической полосы.
между выражениями составляет только око-
Различие (6) и (7) ло 3.
Когда кривизна 1р получена, то прогиб б полосы может быть легко вычислен. Например, пусть биметаллическая полоса АВ, шарнирно опертая по концам, изгибается вследствие равномерного нагревания, как показано на рис. 2. Тогда ввиду того, что кривая АСВ представляет собою дугу окружности радиуса р, следует, что б(2р— 6) (2)2. Или, вспоминая, что прогиб б мал по сравнению с радиусом кривизны, имеем 2рб 24, откуда
б 28р. (8)
§ 2. Напряжения, возникающие в биметаллической полосе при нагревании
Максимальное нормальное напряжение биметалла при нагревании возникает в волокнах на поверхности соединения обоих металлов. Это напряжение состоит из двух частей: а) из напряжения, обусловленного осевой силой, и б) из напряжения, вызванного изгибом. Для металла 1 это напряжение будет определяться из выражения
_ Р I Ртах - а, 2р »
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
537
или, используя (3), найдем
Ртах 7 -7 (Я1 ВД Т1-
В простейшем случае Е Е2 Е, a, a2 yi и Ртах
l) или используя (6), имеем
Ртах Е (2 l) ( “ ) (9)
Полагая Е 1,9 106 кг)см2, а2 — ос 4-10-6 1С, — to 200 С, получим ь результате ртах 759 кгсм2.
AE(oc2-oc,)(t-t0)
Рис. 3. Распределение нормальных напряжений по произвольному поперечному сечению биметаллической полосы при равномерном нагреве.
Распределение нормального напряжения по поперечному сечению полосы показано на рис. 3. Легко видеть, что напряжения, распределенные по всему поперечному сечению, взаимно уравновешиваются. Они могут быть сведены к двум одинаковым противоположно направленным парам сил.
Предыдущее обсуждение неизменно касалось поперечных сечений, удаленных от концов. Вблизи концов картина распределения напряжений более сложная. В простейшем случае двух металлов, имеющих равные толщины и равные модули упругости, при нагревании вблизи концов появляются касательные напряжения между двумя металлами, как показано на рис. 4. Для каждого материала нормальные напряжения могут быть сведены к центральной силе Р использованной в предыдущих расчетах, и к паре xUPh. Напряжения, вызываемые этими силами, показаны выше на рис. 3. Распределение касательного напряжения вдоль поверхности соединения металлов не может быть определено элементарным путем, и можно лишь считать, что оно носит «локальный» характер и что касательные напряжения сосредоточены вблизи концов полосы на расстоянии,
Рис. 4. Касательные напряжения, возникающие вблизи концов биметаллической полосы.
538
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
величина которого имеет тот же порядок, что и толщина h полосы. Это показывает, что максимальная интенсивность этих напряжений может быть того же самого порядка, что и вычисленные выше нормальные напряжения. Такое заключение может оказаться до некоторой степени важным при анализе упругих свойств материала, используемого для сварки обоих металлов.
Если модули и толщины двух металлов различны, то вдоль поверхности соединения металлов вблизи концов полосы при нагревании возникают не только касательные, но также и нормальные напряжения. Эти напряжения также носят местный характер и могут быть сведены к двум равным и противоположным парам сил такой величины, которая нужна для того, чтобы вместе с парами lUPa и 'UPa2, рассмотренными ранее, произвести в обоих металлах кривизну 1р.
§ 3. Изгиб, вызванный внешними силами
В настоящем обсуждении будет использовано предыдущее предположение о том, что первоначально плоское поперечное сечение остается при изгибе по-прежнему плоским. Задача об изгибе стержня, состоящего из двух материалов, сваренных между
собою, может быть решена следующим образом.
Допустим, что Е2Е (рис. 1). Это обстоятельство можно принять во внимание, рассматривая изгиб полосы из однородного материала, но с поперечным сечением, показанным на рис. 5. Уменьшение ширины металла, соответствующее менее жесткому материалу, должно быть взято в отношении ЕЕ2, если жесткость полос остается той же самой. Распределение напряжения при изгибе будет зависеть от положения нейтральной оси, проходящей через центр тяжести О поперечного сечения. Пусть с определяет положение центра тяжести; тогда, используя предыдущие обозначения EJE2 п, аа2 т, получим
_ V2(ai а2)2 2а(1 - 1я)
ах а2п
В случае, когда а а2 l2h,
h Т“
Рис. 5. Эквивалентное поперечное сечение однородной полосы.
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
539
Момент инерции поперечного сечения относительно нейтральной оси будет
Если оба материала имеют один и тот же модуль упругости, то п 1 и из (11) получим
Интересно сравнить эти результаты с результатами, полученными для изгибной жесткости полосы, считая ее однородной и принимая для модуля упругости среднее значение Е 12(Е Е2). В этом случае
Полученное значение находится в очень хорошем соответствии с формулой (12).
Для п 2
Сравнение с выражением (13) дает разницу около 9.
Отсюда можно заключить, что при вычислениях изгибной жесткости биметаллической полосы может быть использована формула для однородного стержня, если в нее ввести вместо модуля упругости среднее значение модулей упругости слоев полосы. Если п близко к единице (в случае монель-металла 1) и никелевой стали п 10,85), этот метод вычислений оказы вается достаточно точным.
') Медно-никелезый сплав.
В случае, когда ах а2 l2h,
(п)
Для п 10,85
Для п 2
г3 (0,2896 - 0,2128) 0,0768г3. 0,0573г3.
(12)
(13)
Eh3 1 п 12 2п'
(14)
Для п 10,85 выражение (14) дает
0,0772Eh
EJ . 1 0,0625Eth
540
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
Используя приведенную формулировку, можно легко получить напряжения, вызванные в закрепленной биметаллической
полосе при нагревании. Рас-
ъ. Мо
) I
Рис. 6. Биметаллическая полоса с защемленными концами.
смотрим сперва биметаллическую полосу с защемленными концами (рис. 6). При равномерном нагревании на концах полосы возникают пары М0. Величина этих пар должна быть такой, чтобы ликвидировать кривизну 1р, обусловленную нагреванием (рис. 6). Уравнение для вычисления М0 примет вид
Мр _ J_ __ 3 (g2-ai)(t — t0)
EJ p 2 h
Здесь
i(1 2), Л3.
Соответствующее максимальное изгибное напряжение равно
6М0 6 3 р j (ctg cci) (t ip) 3 п (г rt d i
P U2 U2 ' о EJ . 4 E (a2 CCj)( ()
Комбинируя изгибные напряжения, обусловленные М0, с напряжениями в свободной биметаллической полосе от нагревания (рис. 6), получим распределение напряжений, показанное на рис. 7.
»
Рис. 7. Распределение нормальных напряжений в биметаллической полосе с защемленными концами.
I
р
- ж
» О
Рис. 8. Изгиб биметаллической полосы с одним заделанным и одним шарнирно опертым концом.
В случае биметаллической полосы, заделанной на конце А и имеющей сосредоточенную опору на конце В (рис. 8), реактивная сила R в опоре В должна быть такой, чтобы уничтожить прогиб б, который был бы произведен на конце В нагреванием свободной полосы. Используя выражение (6) и формулу
I2 R12
для прогиба консольной балки, имеем '2z5fT' откуда
3 EJ
R-
3EJ 1
9 EJ
(a2 - a,) t - t0).
21 р 4 hi
Максимальный изгибающий момент в заделанном конце балки
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
541
примет вид
Мщах RI (а2 — а,) ( — 0),
и соответствующее максимальное изгибное напряжение равно
Ртах -ШДГ (а2 - а,) ( - t0).
Это напряжение на 50 выше, чем напряжение для полосы с двумя защемленными концами, которое было найдено выше.
§ 4. Изгиб равномерно нагретой биметаллической пластины
В отличие от узкой полосы, при нагреве биметаллической пластины следует рассмотреть кривизны в двух различных направлениях. Для малых изгибов и равномерного нагрева эти кривизны будут равны и постоянны по всей поверхности пластины, так что пластина принимает сферическую форму.
Радиус кривизны р может быть получен точно таким же образом, как и выше для случая узкой полосы. Необходимо только принять во внимание, что слои, параллельные нейтральной поверхности, будут претерпевать вследствие сферического изгиба равные удлинения или укорочения в обоих перпендикулярных направлениях. Вследствие этого обстоятельства в этом случае могут быть также использованы соотношения § 1. Необходимо только вместо Еi и Е2 соответственно ввестиУ( 1 — о) и Е2(1—а), где а означает коэффициент Пуассона, который считается для обоих металлов одинаковым. Ввиду того, что окончательные формулы (4) и (6) содержат только отношение ЕЕи их нужно оставить без изменения, и они могут быть использованы при вычислении кривизны при изгибе пластин.
Ясно, что изгиб пластины по сферической поверхности невозможен без некоторой деформации срединной поверхности пластины. Если прогибы малы, скажем меньше половины толщины пластины, то этой деформацией срединной поверхности пластины без какой-либо существенной ошибки можно пренебречь, но с увеличением прогиба влияние этой деформации становится все более и более явным, и она должна быть принята во внимание.
РАСЧЁТ ПОЛОСЫ ТИПА БИМЕТАЛЛИЧЕСКОГО ТЕРМОСТАТА
§ б. Свободный изгиб биметаллической полосы
Пусть полоса биметалла имеет начальную кривизну, равную 1ро, начальный прогиб б0 (рис. 9) и изгибается таким образом, что материал с большим коэффициентом линейного температурного расширения находится на вогнутой стороне. При нагревании такой полосы кривизна будет постепенно уменьшаться, и
542
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
при некоторой температуре полоса минует плоскую форму и потом изогнется вниз, как показано пунктирной линией на рис. 9. Изменение кривизны получается из выражения (6):
I
A
1 , 1 3 (а2 - at) (t -10)
P0 P; 2 h (I5)
Соответствующий прогиб находится из выражений (8) и (15):
Рис. 9. Изгиб криволинейной биметаллической полосы.
12
б 8
_ Р ГЗ (а2- а,) (t-t,,) 1 1
8 L 2 h p„J
-T(a2-aW-'o)-6. (16)
Для термостата существенно не постепенное изменение кривизны, а скачкообразное ее изменение путем прощелкивания, и для того, чтобы получить этот эффект, необходимо закрепить концы полосы.
§ 6. Искривленная биметаллическая полоса в жесткой рамке
Рассмотрим здесь простейший случай термостата в виде искривленной биметаллической полосы, закрепленной между фиксированными опорами А и В в жесткой рамке (рис. 10). Предположим, что температурные расширения рамки и центральной оси полосы равны и что при начальной температуре давление полосы на опоры отсутствует. Пусть — длина полосы. Ширину полосы примем равной единице. Кроме того, обозначим через
ро — начальный радиус кривизны,
60 — начальный прогиб полосы ),
F 1 h — площадь поперечного сечения полосы,
-jy3 — момент инерции поперечного сечения,
Е (Е Е2) — средний модуль упругости,
б — прогиб вниз полосы после нагревания для случая «свободных концов» (см. формулу (16)),
61 — измеряемый вверх прогиб, при котором начинается прощелкивание полосы,
) Точнее, амплитуда, начального прогиба полосы.
Рис. 10. Биметаллическая криволинейная полоса в жесткой рамке.
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
543
62 — направленный вниз прогиб полосы после прощелкивания, to— начальная температура полосы,
t — температура, при которой происходит прощелкивание, ti — температура, при которой имеет место прощелкивание в обратном направлении;
Дt t — t — диапазоны изменения температуры, h — температура, при которой прогиб в случае «свободных концов» равен 6о.
Деформацию полосы при нагревании можно разделить на две стадии: во-первых, постепенное уменьшение прогиба от начального значения 6о до некоторого значения 61 и, во-вторых, прощелкивание вниз, как изображено пунктирной линией на рис. 10. В процессе постепенного уменьшения начальной кривизны полосы происходит продольное сжатие полосы. Соответствующая сжимающая сила Р стремится воспрепятствовать выпучиванию и может предотвратить его при условии, что рост температуры не будет достаточно большим.
Температура, при которой происходит потеря устойчивости путем прощелкивания, и прогиб 61, от которого оно начинается, могут быть найдены, если определить следующие два выражения:
1. Выражение, определяющее силу Р в функции уменьшения прогиба полосы при нагревании.
2. Выражение для сжимающих сил Р, необходимых для предотвращения прощелкивания полосы, когда заданы и температура и прогиб.
Для того чтобы получить увеличение сжимающей силы, обусловленное уменьшением прогиба, предположим, что центральная ось изогнутой полосы является плоской кривой. Тогда разница между длиной кривой и длиной хорды будет равна
Без какой-либо существенной ошибки можно считать, что кривая начального прогиба полосы есть синусоида. Тогда имеем у 6osin я- Подставляя это выражение в (17), найдем
Когда в процессе нагревания прогиб полосы уменьшается от 6о до 61, соответствующее укорочение полосы согласно формуле (18) станет
(17)
о
6qJ12 62я2
4 4 ’
544
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
а сжимающая сила будет равна
или
Р
4
62я2
4
Р1
EJn2
7
г2
4
1 -
(19)
Это выражение дает зависимость силы Р от отношения 6160.
При вычислении силы, необходимой для предотвращения прощелкивания полосы, сначала примем, что опоры А и В (см. рис. 10) удалены и полоса свободна; тогда при нагревании форма полосы будет иметь вид, указанный линией АСВ. Соответствующий прогиб б может быть найден из формулы (16). g Допустим теперь, что эта полоса
1 изгибается выпуклостью вверх,
ч как изображено пунктирной ли-
нией на рис. 11, и удерживается
в этом изогнутом состоянии с помощью сжимающих сил Р.
Ясно, что величина сил Р будет зависеть от величины бь Для того чтобы получить зависимость между 6i и Р, примем, что первоначально линия АСВ (рис. 11) представляет собою сину-
тех
сойду б sin —. Тогда перемещения в направлении у, происходящие в процессе изгиба от формы АСВ до формы АСВ, суть у б sin ял:, а дифференциальное уравнение кривой прогибов АСВ будет
EJy bsnf)-Py,
Рис. 11. Кривая прогибов биметаллической полосы.
откуда
d2y Р 6л2 . тех
ЁТу sin —.
dx2
(20)
Используя обозначение
имеем
EJ
у A sin kx В cos kx -22 sln —
я 1
(21)
(22)
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
545
где А и В являются произвольными постоянными интегрирования. Исключая случай, когда kln является целым числом1), из условий на концах можно заключить, что А В 0. Поэтому
л 6
01 кЧ2 , ’
ИЛИ
wiL 23)
Подстановка сюда выражения для 6 согласно (16) дает
“eTit5 тё- лб7 “2 ) 1 б7 1' Это выражение определяет силу, необходимую для удержания полосы АСВ в состоянии АСВ выпуклостью вверх, показанном на рис. И пунктирной линией. Видно, что величина Р возрастает с уменьшением прогиба 6ь
Выражения (24) и (19) дают полное решение задачи о прощелкивании полосы. Если значение силы, вычисленной из (24), всегда больше значения, даваемого формулой (19), то это означает, что реакции Р в опорах А и В (рис. 10) не в состоянии предотвратить прощелкивание. С другой стороны, если для некоторого значения отношения 6061 величина силы Р, вычисленная из (24), становится меньше величины силы, полученной из формулы (19), то реакции Р рамки предотвратят прощелкивание полосы.
§ 7. Графическое решение
Для того чтобы определить предел увеличения температуры t — to, который именно необходим для прощелкивания полосы, можно использовать следующий графический метод.
Сначала, используя формулу (19), строим кривые, представляющие Pl2EJл2 в функции 606ь Несколько кривых такого рода, соответствующих различным значениям отношения 36ог2, показаны на рис. 12. Эти кривые имеют своими асимптотами горизонтальные прямые, отстоящие на Због2 от оси абсцисс.
Кроме того, формула (24) может быть представлена графически прямыми, проходящими через точку 1 (рис. 12), имеющую координаты х 0, у Pl2EJn2. Наклон этих линий определяется выражением
, (25)
) Соответствующее значение Р определяется известной формулой Эйлера для сжатого стержня.
546
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
Видно, что наклон зависит от повышения температуры t — to. Если рост температуры мал, то i будет также мало и прямые линии будут пересекать соответствующие кривые, представляемые формулой (19). Это значит, что при таком повышении температуры прощелкивания не произойдет. Предельное повышение
Рис. 12. Графическое определение температуры срабатывания биметаллической полосы термостата.
температуры, при котором прощелкивание становится возможным, будет определяться значением угла касательной, проведенной через точку А к соответствующей кривой, описываемой уравнением (19).
§ 8. Численный пример
Возьмем, например, hjl 100, а2 — ai 4 -10-6 1С и такие отношения боh начального прогиба к толщине полосы, которые даются второй строкой таблицы А, приведенной ниже. Соответствующие кривые, определяемые выражением (19), представлены графически, как указывалось выше. Значения углов касательных, проходящих через точку Л, к этим кривым даны в третьей строке этой таблицы. Подставляя эти значения в формулу (25), получим температуры, при которых имеет место прощелкивание. Они даны в четвертой строке таблицы А.
Видно, что рост начального прогиба 6о повышает критическую температуру. Очень незначительное изменение 6о производит большое влияние на температуру, при которой наблюдается прощелкивание.
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
Таблица А
547
з«ол2
1,6
60h
0,707
0,814
1,000
i
0,111
0,272
0,628
t -10, C 6i60
104
137
217
0,333
0,408
0,472
6260
0,667
0,813
0,940
ti - to, c
83
79
50
А, C
21
58
167
1,154
1,00
307
0,500
1
0
307
Абсциссы точек касания аи я2, 0з и а4 (см. рис. 12) представляют значения отношений бобь при которых начинается прощелкивание полос. Соответствующие значения 6160 даны в пятой строке таблицы.
§ 9. Аналитическое решение
То же самое решение может быть найдено также аналитическим путем. Используя обозначения
Рг
У
ху
оЗ.-„ №
16 гб0 из выражений (10) и (24) имеем
У а( --L),
у гх 1.
Наклон касательной к кривой (19') равен
dy _ 2а dx х3
Подставляя в (24') выражения (26) и (19') для i и у, получим следующее выражение для абсцисс точек касания:
(190
(24')
(26)
За а— 1
(27)
Подставляя в эту формулу а 1,5; 2; 3 и 4, имеем соответствующие числа пятой строки таблицы А. Из (26) и (27) получим выражение для наклона касательной
i 2a
За
(28)
548 РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
Внося это в формулу (25), имеем
'4(
t-to з u' . (29)
А2 3 9 62 ,
16 hb
(a2ai)
Из этой формулы может быть вычислена критическая температура.
§ 10. Прогибы полосы после прощелкивания
Из анализа, изложенного выше, видно, что во время нагревания прогиб полосы, первоначально равный 6о, постепенно уменьшается. Когда он достигнет величины бь определяемой формулой (27), происходит прощелкивание, и полоса, первоначально имевшая выпуклость вверх (рис. 10), приобретает выпуклость, направленную вниз. Дифференциальное уравнение функции прогиба после прощелкивания будет таким же, как уравнение (20), но прогиб теперь имеет направление вниз и его величина дается уравнением
а
2“‘
Вместо формул (23) и (24) будем иметь
я2 EJn2 1 62 ’ PI2 1 Г 3 I2 , w, п Лба
(24'
EJn2
Вместо уравнения (19) будем иметь Р2 Зб2 6
(19')
EJn2 h2 V б2
Очень простое графическое решение уравнений (19') и (24') показано на рис. 12. Для того чтобы получить величину 6062, необходимо только провести через точку 1 линии 1Ьи 1Ь2,. с наклоном, равным
1 16 гбо 2 а1 '
Тогда абсциссы точек Ь, 62,. дают значения 6062 и ординаты, соответствующие значениям P12EJtc2. Это решение дает нам возможность очень легко вычислить перемещения полосы
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
549
при прощелкивании. Возьмем, например, числовой пример, разобранный выше, и примем Због2 2. В этом случае из рис. 12 и таблицы А видно, что прощелкивание начинается, когда
6i 0,408 6о. Направленный вниз прогиб после прощелкивания равен 62 0,813 бо. Полное перемещение в процессе прощелкивания будет равно
Si 62 1,22 бо-
§11. Температура, при которой происходит прощелкивание в обратном направлении
Если после прощелкивания полосы начинается охлаждение, то может быть установлен некоторый предел t понижения температуры, при котором полоса становится неустойчивой и прощелкивает в обратном направлении, так что температура, контролируемая термостатом, будет изменяться в пределах от t до t. Диапазон температуры At t — t имеет практическое значение и может быть легко вычислен следующим образом.
Пусть t2 означает температуру, необходимую для того, чтобы вызвать в полосе со «свободными концами» прогиб б, равный бо (см. формулу (16)). При такой температуре потерявшая устойчивость путем прощелкивания полоса не будет оказывать давление на опоры А и В рамки, т. е. условия будут теми же самыми, как и в начальном невыпученном состоянии. Однако теперь материал с более высоким коэффициентом линейного температурного расширения расположен на выпуклой стороне. Вследствие этого охлаждение произведет над прощелкнутой полосой тот же эффект, что и нагревание для полосы в ее первоначальной форме. Понижение температуры t2— t, необходимое для того, чтобы произвести прощелкивание в обратном направлении, будет равно повышению температуры t —10, вычисленной выше (см. таблицу А). Поэтому критическая температура t термостата при прощелкивании в обратном направлении находится из уравнения t — t t — tQy из которого имеем
tl t2-(t-t0). (30)
Здесь 2 определяется из выражения
4-Ж(Х2-а,)('2о) 2- (31)
Используя выражения (30) и (31), получим числа в двух последних строках таблицы А. Из этой таблицы видно, что с понижением критической температуры диапазон температур
уменьшается, т. е. термостат становится более чувствительным
изменению температуры,
650
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
Из (25) и (31) получим
Wo -nr,(-'o).
Подставляя отсюда t2 в (30), имеем
'.-'о (-'о).
(32)
Для того чтобы получить большую чувствительность, величину i следует взять очень малой, т. е. величина ЗбоЛ2 должна быть близка к единице, а бо — близко к 0,577Л. Практически невозможно иметь достаточную точность при таком малом начальном прогибе, и для того, чтобы получить достаточно чувствительный термостат с большими начальными прогибами, становится необходимым применение податливых рамок.
§12. Искривленная биметаллическая полоса в податливой рамке
Допустим, что благодаря податливости рамки реактивные силы Р (см. рис. 10) производят увеличение Д расстояния между опорами А и В. Тогда укорочение полосы, произведенное этими силами при нагревании, будет
Для того чтобы получить величину А податливости рамки, необходимо принять во внимание следующее. Допустим, что эта податливость эквивалентна податливости растягиваемой полосы, имеющей длину и поперечное сечение F. Тогда Д PIEF Подставляя это выражение в (а), получим
41 41 Д’
а соответствующая сжимающая сила равна
где
(33)
Вместо формулы (19) имеем
Р12 36л 6
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
551
Выражение (24) остается без изменения. Теперь из (34) и (24) критическая температура может быть получена точно таким же путем, как объяснено выше в случае жесткой рамки. Может быть использован тот же графический метод, что и показанный на рис. 12, необходимо только принять ординаты кривых равными не 36ог2, a k 36оЛ2. Возьмем, например, k 16 и 60 2ft, тогда k ЗбоЛ2. Наклон линии 1аъ на рис. 12 будет определять критическую температуру. Величина наклона согласно таблице А равна 0,272, и выражение (25) примет вид
Подставляя сюда предыдущие данные, имеем t — t0 338 С. Температура, при которой происходит прощелкивание в обратном направлении, согласно формуле (32) будет
Легко видеть, что большая чувствительность может быть получена увеличением податливости рамки, т. е. уменьшением наклона L
Используя выражения (24), (32) и (34), можно вычислить размеры полосы и таким образом получить, теоретически говоря, любую заданную чувствительность и любую заданную температуру срабатывания термостата. При использовании обозначений § 8 соответствующие выражения имеют вид
-w(a2-ct,)('o) 1,272-
t — to _ 1 — i
t-t0 1 I '
(32')
(19)
(24)
у — ix l.
Из (19) найдем
dy _ 2k a dx x3
(a)
Подставляя (а) и (19) в (24), имеем
Отсюда
(35)
Внося это выражение в (а), получим
(36)
552 РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
Следовательно,
12М1зУ32
t-h—3-4 (37)
16 г60
(a2-ai)
Допустим, например, что термостат должен иметь температуру срабатывания t — to 300 и иметь такую чувствительность, чтобы прощелкивание в обратном направлении происходило, когда понижение температуры становится равным 10 от температуры срабатывания термостата; тогда из (32') имеем (1—0(1 0 0,9, или 0,053. Внося это значение в (36), найдем
62
ka k 3 -jp 1,29 (b)
Теперь из (37) получим
I2 _ 1 1,053 _ 4 1,053» 104
М -i--300-4-1Гв 9
Принимая, например, Ijh 200, имеем Из (35) имеем
-W8’55''
3,65. (с)
Из уравнений
y-ix- 1, у ka — 4) определяем прогиб 62 полосы после прощелкивания; имеем
-Г 1,70. (d)
2
Диапазон полного прогиба полосы при срабатывании равен
61 62 60 (зд-- -уо) 0,8660. (е)
Видно, что с ростом отношения ft начальный прогиб и диапа¬
зон прогиба (е) может быть увеличен.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Stabilitatsprobleme der Elastizitat. Handbuch der physikalischen und technischen Mechanik, Bd. IV, Lieferung 1, Leipzig, Verlag von Johann Barth, 1929, SS. 81 — 145.
Перевод на русский язык: Вопросы устойчивости упругих систем. JL, Кубуч, 1935, 117 стр.
1. Введение
Первые исследования в области устойчивости упругих систем принадлежат Леонарду Эйлеру и Жозефу Лагранжу. Эйлер первый классифицировал ) различные формы упругой линии призматических стержней. Он показал2), что прямой, достаточной длины стержень может выпучиться под влиянием силы, действующей вдоль его оси. Позже он исследовал задачу о равновесии вертикального стержня под влиянием собственного веса3). Ж. Лагранж разработал теорию Эйлера, распространив ее на стержни переменного сечения, и применил ее для выяснения наиболее устойчивой формы сжатых стержней4).
С вопросами упругого равновесия приходится встречаться и во многих других случаях. Так, например, Морис Леви5) и Жорж Альфан6) исследовали устойчивость круговых колец,
) L. Е u 1 е г о. Methodus inveniendi lineas curvas maximi minimive proprietate gaudentas, sive solutio problematis isoperimetrici lattissimo sensu accepti. Lausannae et Genevae. Apid Marcum-Michaelum. Bousquet et Socios. Additamentum I: De curvis elasticis. 1744, pp. 245—310. Перевод на русский язык: JI. Эйлер. Метод нахождения кривых линий, обладающих свойствами максимума или минимума, или Решение изопериметрической задачи, взятой в самом широком смысле. Приложение I: Об упругих кривых. Серия «Классики естествознания». М.—JL, ГТТИ, 1934, стр. 447—572.
2) L. Euler. Sur la force des colonnes. Memoire de Г Academie Royale des sciences et belles-lettres avec les Memoires, tires des Registres de cette Academie, Berlin, 1759, vol. 13, pp. 252—282.
3) L. Eulero. De altitudine columnarum sub proprio pondere corruetium. Acta Academia Scientiarum Imperialis Petropolitanae (1778, tom II, pars I). 1780, pp. 163—193.
4) J. L. Lagrange. Sur la figure des colonnes. Miscellanea Taurinensia, Royal Society of Turin, 1770—1773, vol. 5, p. 123. Перепечатка: Oeuvres. Ed. Serret. Paris, Gauthier-Villars, 1862, pp. 125—170.
5) M. Levy. Memoire sur un nouveau cas integrable du probleme de l’elastique et l’une de ses applications. Journal de mathematiques pures et appliquees (Liouville Journal), Series 3, Paris, 1884, vol. 10, pp. 5—42.
6) G. H. H a 1 p h e n. Sur une courbe elastique. Comptes rendus des sances de 1’Academie des sciences, 1884, vol. 98, N2 7, pp. 422—423.
554
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
находящихся под действием равномерного радиального давления. J1. Прандтль1) и А. Мичелл2) произвели исследование устойчивости изогнутой полосы. Устойчивость прямоугольной сжатой пластинки была рассмотрена Дж. Брайаном3). За последние годы разрешено много других задач этого рода, связанных главным образом с различными вопросами строительной техники.
Первая попытка систематизировать эти отдельные вопросы и создать общую объединяющую их теорию принадлежит Дж. Брайану4). Он выяснил, что теорема Густава Кирхгофа5) об однозначности решений уравнений теории упругости не может быть применена для некоторых тел, как, например, в случаях исследования длинных стержней, тонких пластинок и оболочек. Для тел, все размеры которых являются величинами одного порядка, явление потери устойчивости может иметь место только в том случае, если предел пропорциональности данного материала не мал по сравнению с модулем упругости (как, например, для резины, желатина и пр.) и компоненты деформации не малы по сравнению с единицей. При этом исследовании им было принято за основное положение, что устойчивое равновесие при произвольной форме тела обусловливается тем, что потенциальная энергия при этом случае нагружения имеет минимальное значение. Исходя из этого принципа, он имел возможность получить не только уже известные решения для сжатых стержней и круговых колец6), но также и некоторые новые результаты по устойчивости прямоугольных пластинок.
) L. Prandtl. Kipperscheinungen. Ein Fall von instabilem elastischem Gleichgewicht. Dissertation der Universitat Miinchen, 1899. Nurnberg, 1900, SS. 1—75. Перепечатка: L. Prandtl. Gesammelte Abhandlungen. Erster Teil, Berlin — Gottingen — Heidelberg, Springer-Verlag, 1961, SS. 10—74.
2) A. G. М. M i с h e 11. On the elastic stability of long beams under transverse forces. Philosophical Magazine and Journal of Sciences, London— Edinburgh—Dublin, Series 5, 1899, vol. 48, № 292, pp. 298—309.
3) G. H. Bryan. On the stability of a plane plate under thrusts in its own plane, with applications to the «buckling» of the sides of a ship. Proceedings of the London Mathematical Society, 1891, vol. 22, pp. 54—67; G. H. Bryan. On the buckling and wrinkling of plating when supported on parallel ribs or on a rectangular framework. Там же, 1894, vol. 25, pp. 141—150.
4) G. H. Bryan. On the stability of elastic systems. Proceedings of the Cambridge Philosophical Society, Mathematical and Physical Sciences, 1889,
vol. 6, pp. 199—210.
6) G. Kirchhoff. Uber das Gleichgewicht und die Bewegung eines unendlich dunnen elastischen Stabes. Journal fur die reine und angewandte Mathematik, 1859, Bd. 56, SS, 285—313. См. также A. Korn. Allgemeine Theorie der Elastizitat. Handbuch der physikalischen und technischen Mechanik, Bd. 3, Leipzig, J. A. Barth, 1927, SS. 1—52.
e) G. H. Bryan. Application of the energy test to the collapse of a thin long pipe under external pressure. Proceedings of the Cambridge Philosophical Society, 1888, vol. 6, pp. 287—292.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
655
Р. Саусвелл ) работал над дальнейшим развитием этой теории. Он рассматривал идеальный абсолютно прочный материал, разрушение которого возможно только при потере устойчивости; в этом случае вопрос не ограничивается только тонкими стержнями, тонкими пластинками и оболочками. Он составил общие уравнения безразличного равновесия, выражающие критерии неустойчивости данной формы при условии, что компоненты деформации не малы по сравнению с единицей.
Благодаря применению этих уравнений, Р. Саусвелл пришел к заключению, что известные решения вопросов, устойчивости, полученные на основании приближенных теорий тонких стержней и пластинок, правильны как первые приближения общих решений, получаемых на основании уравнений безразличного равновесия.
Над общими вопросами упругой устойчивости работал и Р. Мизес2). Он рассматривал систему точек, соединенных между собою упругими стержнями и находящихся иод действием внешних сил. На основании своих рассуждений он пришел к следующему выводу, касающемуся любой упругой системы, обладающей при отсутствии внешних нагрузок определенным естественным состоянием: «Если нагрузки, приложенные к упругой системе точек, заданы только до некоторого численного значения X, то среди этих значений имеется такое, отличное от нуля, значение Хо (оно может быть равно и бесконечности), что для всех X с абсолютной величиной, меньшей Х0, существуют однозначные устойчивые состояния равновесия. Когда X приближается к нулю, то эти состояния беспрерывно приближаются к естественному состоянию. Для значений X, больших Я0, задача равновесия может иметь несколько решений». Это положение, выведенное для упругой системы точек, справедливо и для любого упругого тела. Значение критического предела Хо зависит от формы тела, рода нагрузки и величины модуля упругости, причем более тонким телам и меньшему модулю упругости соответствуют меньшие значения Хо. В действительности строительные материалы имеют конечное значение предела текучести. Они начинают течь или разрушаться при напряжениях, которые очень малы по сравнению с модулем упругости. Из этого следует, что на практике для таких строительных материалов вопрос об упругой устойчивости имеет значение только в случаях тонких стержней, пластинок и оболочек.
) R. V. Southwell. On the general theory of elastic stability. Philosophical Transactions of the Royal Society of London, Series A, 1913, vol. 213, pp. 187—244.
2) R. M i s e s. Uber die Stabilitatsprobleme der Elastizitatstheorie. Zeitschrift fur angewandte Mathematik und Mechanik, 1923, Bd. 3, Heft 6, SS. 406—422.
556
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
При исследовании специальных задач упругой устойчивости в большинстве случаев применяется один из следующих двух методов.
а) Статический метод. Сущность этого метода заключается в следующем: полагают, что система получила весьма малое отклонение от начального положения, устойчивость которого исследуется, и составляют условия равновесия для этого отклоненного состояния тела под действием заданной системы сил. Пренебрегая членами с высшими степенями перемещений, приходят, таким образом, к системе линейных дифференциальных уравнений, в которые величины внешних сил входят как параметры. Значения нагрузок, при которых система может иметь более одного положения равновесия, определяются характеристическими числами этих линейных уравнений, т. е. такими величинами параметров, при которых линейные дифференциальные уравнения могут иметь бесконечно много решений, удовлетворяющих тем же условиям на поверхности1). Следовательно, исследование проблемы устойчивости этим методом сводится к проблеме краевых значений.
б) Энергетический метод. Потенциальная энергия системы в положении равновесия, упругая устойчивость которого исследуется, сравнивается с энергией той же системы при ее незначительном отклонении от положения равновесия. В соответствии с условиями устойчивости потенциальная энергия системы в положении устойчивого равновесия должна иметь минимальное значение.
При применении энергетического метода без труда получаются приближенные решения для критических значений нагрузок2), если только задаться подходящей кривой изгиба или формой выпучивания, отвечающей условиям краев или концов. Тогда приближенное вычисление критических значений еще заключается в том, что для выпученной формы принимается конечный ряд функций, которые приблизительно соответствуют ожидаемой форме потери устойчивости, а коэффициенты этого ряда посредством обычного исследования на минимум определяются так, чтобы значения внешних нагрузок были минимальными.
1) См. R. Mises. Die Differential- und Integralgleichungen der Mechanik und Physik als 7 Auflage von Riemann — Webers Partiellen Differentialgleichungen der mathematischen Physik, herausgegeben von R. Mises. Bd. 1. Braunschweig, Viegweg und Sohn, 1925.
2) С. П. Тимошенко. Об устойчивости упругих систем. Применение новой методы к исследованию устойчивости некоторых мостовых конструкций. Известия Киевского политехнического института, 1910, год 10, книга 4, стр. 375—560. Отд. оттиск, Киев, 1910, 188 стр. См. также Н. М. Westerg а а г d. Buckling of elastic structures. Proceedings of the American Society of Givil Engineers, 1921, vol. 47, № 9, pp. 453—533. Discussion: Там же, 1922, vol. 48, pp. 1265—1271.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
557
1. УСТОЙЧИВОСТЬ ПРЯМЫХ И КРИВЫХ СТЕРЖНЕЙ
2. Призматический стержень. Различные случаи выпучивания
Если Р — сжимающая сила, направленная по оси стержня, a EJV и EJZ — жесткости стержня в главных плоскостях, то система дифференциальных уравнений искривленной оси имеет следующий вид:
сРг , л (1)
Е1гРу О,
EJa
dx2
Pz 0.
На рис. 1 показаны различные возможные случаи закрепления концов стержня. Критическое значение сжимающей силы,
Рис. 1. Различные случаи выпучивания.
при которой прямолинейная форма сжатого стержня становится неустойчивой и происходит его выпучивание, определяется наименьшим значением Ркр параметра Р: исходя из этого, можно найти отличное от тривиального у 0, 2 0 решение системы уравнений (1), которое удовлетворяло бы условиям закрепления концов стержня. Если допустить, что EJZ EJy, то из уравнений (1) в случае стержня с шарнирно опертыми концами (рис. 1 у а) имеем
Elz2 (2)
Р. Г кр
2
То же значение критической силы мы получим для случая, показанного на рис. 1, d. Для случаев, показанных на рис. 1,6 и ,ct значения критических сил определяются формулами
Р
г кр
EJzn2
412
Р
г кр
4 EJzn2
(3)
558
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Если один конец стержня жестко заделан, а другой закреплен шарнирно (рис. 2: у у' 0 при х 0; у 0 при х ), то дифференциальное уравнение оси имеет следующий вид:
EJz Py Qlx). (4)
Наименьшее значение РКр сжимающей силы Р, удовлетворяющей условиям закрепления концов, получается из следующего тригонометрического уравнения:
откуда
смещается вдоль оси.
n 2,046zjx2 _ 20,19EJZ сч
'SzЖ 2 “ 2 W
Рис. 2. Один
конец стержня Если условия на концах сжимаемого стержня
заделан, другой в обеих главных плоскостях инерции различны, конец свободно то для определения критической силы необходи-
PUDTTTQOTPa 11 .
мо произвести сравнительные вычисления в обеих плоскостях.
Если у стержня с шарнирно опертыми концами ось вращения шарниров не совпадает ни с одной из главных осей инерции поперечного сечения, то решение вопроса о продольном изгибе такого стержня осложняется тем, что его изогнутая ось не будет плоскою кривой. Практический интерес может представить случай стержня из равнобокого углового железа, когда оба его конца опираются на призмы, параллельные между собою и параллельные одной из полок уголка. В этом случае критическую силу можно записать следующим образом:
Ркр 0,87я2 EJ12, (7)
где J — момент инерции поперечного сечения относительно оси, направленной под углом в 45 к главным осям инерции1).
3. Исследование призматического стержня энергетическим методом
Применяя энергетический метод к исследованию, например, продольного изгиба стержня с шарнирно опертыми концами, рассмотрим незначительное отклонение этого стержня от пря¬
l) P. F i 11 u n g е г. Ober die Knickung von Staben mit Schneidenlagerung. Verhandlung des zweiten internationalen Kongresses fiir technische Mechanik, Zurich, 1926. Zurich und Leipzig, Fiissli, 1927, SS. 379—382. См. также P. Fil lunger, Ober die Eulerschen Knickbedingungen fiir Stabe mit Schneidenlagerung. Zeitschrift fiir angewandte Mathematik und Mechanik, 1926,
Bd. 6, Heft 4, SS. 294—308.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
559
молинейной формы равновесия (рис. 1, а). Потенциальная энергия изгиба равна
Изменение расстояния между шарнирами вследствие искривления оси равно
а соответственное уменьшение энергии сжатия при искривлении стержня равно
Если для произвольного прогиба, удовлетворяющего условиям закрепления концов, V V2, то прямолинейная форма равновесия сжатого стержня устойчива. Если V V2, то прямолинейная форма равновесия стержня неустойчива. Значение критической силы найдем из уравнения
Для стержня с обоими шарнирно опертыми концами уравнение изогнутой оси можно представить в форме следующего тригонометрического ряда:
Если взять только первый член ряда, то получим наименьшее значение Р, соответствующее критической силе Ркр согласно формуле (2).
Применяя энергетический метод, можно легко получить приближенные решения для РКр, если вместо общего выражения согласно уравнению (12J задаться другим подходящим уравнением кривой прогиба, удовлетворяющим условиям закрепления концов стержня. Если, например, воспользоваться кривой
(8)
о
о
(9)
о
(10)
о
к, v2.
(П)
S. inx
a, sin —.
(12)
Подставляя это значение в уравнение (11), найдем
Р
560
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
прогибов балки, нагруженной посредине сосредоточенной силой, то, обозначив вызванный этой силой посредине пролета прогиб через , согласно уравнению (11) будем иметь
12 Pf2 _ 24EJzf2 5 I “ 3
откудя
р ЮEJZ
КР — 2 Отклонение от точного решения, даваемого формулой (2), меньше чем на 1,5. Если в рассматриваемом случае допустить, что выпучивание произошло по кривой, по которой изгибается балка под влиянием равномерно распределенной по всему пролету нагрузки ), то с ошибкой менее 0,1 будем иметь
р _ 9,882EJZ
Кр 2
Еще более точное решение задачи об устойчивости стержня можно получить, написав соответствующее уравнение кривой прогиба в виде ряда
tj alfl(x) aj.i(x) a3f3x) (13)
где каждая функция f(x), Ы),. должна удовлетворять условиям закрепления концов стержня. Этот ряд подставляют в уравнение (11) и подбирают параметры аи a2l а3,. так, чтобы получить для Р1ф наименьшее значение2).
4. Учет больших прогибов
Если пользоваться уравнением (1), то прогиб стержня при выпучивании получается неопределенным. Для его определения необходимо вместо приближенного значения кривизны d2ydx2 принять ее точное значение. Принимая за независимую переменную длину дуги 5 кривой изгиба и обозначая через т (рис. 1 у а) угол, образуемый касательной с осью стержня, получим точное дифференциальное уравнение упругой линии:
-g- --C0ST . (14)
1) При этом прогиб равен
_ 16 , (к 0 X3 X4
у 5 lz I4 )
2) С. П. Тимошенко, статья, указанная на стр. 556.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
561
Решение этого уравнения в некоторых частных случаях можно найти у Л. Заальшютца ), К. Кримлера2), Ж. Альфана 3) и М. Борна 4).
Рассматривая случай малых прогибов стержня с шарнирно опертыми концами (рис. 1, а), можно определить приближенно величину прогиба, подставив в уравнение (14) значение
« 1 Я2С2 о яs
COS Т 1 2” —J2 COS j ,
в предположении, что кривая прогиба представляет плоскую
синусоиду, уравнение которой у с sin (us). Тогда уравне¬
ние (14) преобразуется так:
d2y , Р с2 п2 Р о ns
у2 1гш ycos Т
Подставляя в правую часть этого уравнения я22 вместо PEJ и с sin (nsl) вместо г, получим
d2y , Р с3 я4. Я5 , . ЗяяХ
1- -ЁТУ Т1г(5т-Г 5т—)-
Решение этого уравнения, удовлетворяющее условиям на концах, дает
71S I. 3jts
у csm — -- Ci sin—у-,
где _ «)
В случае пологих кривых, для которых нагрузка Р мало отличается от критической нагрузки РКр, величина сх мала по сравнению с с и уравнение (15) дает достаточное приближение для прогиба посредине стержня5). Из уравнения видно, что
) L. S а а 1 s с h u t z. Der belaste Stab unter Einwirkung einer seitlichen Kraft. Auf Grundlage des strengen Ausdrucks fur den Krummungsradius. Leipzig, B. G. Teubner, 1880, 247 SS.
2) C. J. К r i e m 1 e r. Labile und stabile Gleichgewichtsfiguren vollkommen elastischer auf Biegung beanspruchter Stabe mit besonderer Berucksichtigung der Knickvorgange. Karlsruhe, Druck der G. Braunschen Hofbuchdruckerei, 190:2.
3) G. H. H a 1 p f e n. Traite des fonctions elliptiques et de leurs applications. Vol. 2, Paris, Gauthier-Villars, 1888, p. 192.
4) M. Born. Untersuchungen tiber die Stabilitat der elastischen Linie in Ebene und Raum unter verschiedenen Grenzbedingungen. Gottingen, Preisschrift,
1906.
6) R. M i s e s. Ausbiegung eines auf Knicken beanspruchten Stabes. Zeitschrift fiir angewandte Mathematik und Mechanik, 1924, Bd. 4, Heft 5 SS. 435—436. См. также О. D о m k e. Die Ausbiegung eines Druckstabes bei Uberschreitung der Knicklast. Die Bautechnik, 1926, Bd. 4, Heft 51, SS. 747— 748 и R. W. Burges. The comparison of a certain case of the elastic curve with its approximation. The Physical Review, Series 2, 1917, vol. 9, № 3. pp. 192-197.
562 ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
возрастание прогиба при переходе границы устойчивости идет очень быстро. Если нагрузка будет только на 1 больше критической, то прогиб, вычисленный по уравнению (15), составит уже 9 от длины стержня.
5. Устойчивые и неустойчивые формы равновесия
Дифференциальные уравнения (1) имеют решения, удовлетворяющие условиям закрепления концов, только при определенных значениях нагрузки Р. Возьмем, для примера, случай стержня с жестко заделанным нижним концом (рис. 1,6); в этом случае общее решение уравнения имеет вид
у С, sin УХ С2 COS У X.
Условия на концах будут удовлетворены только в том случае, когда Cj 0 и cos YpEJz I 0. Таким образом, задача разрешима лишь для тех значений параметра У РЕ Jz для которых У ТП1 Т я (« 0,1,2,.).
Нагрузки, при которых возможно равновесие стержня в искривленном состоянии, могут быть представлены в следующей форме:
Р ,(2я И1)я (« 0,1,2,.). (16)
Это уравнение определяет точки раздвоения формы равновесия. Если воспользоваться теперь изложенным выше приближенным методом, то можно рассчитать прогибы с2 для значений нагрузок несколько больших, чем те, которые даются уравнением (16), и получить кривые, представленные на рис. 3, а 1). Очевидно, используя линейные дифференциальные уравнения (1), можно получить только касательные к этим кривым в точках пересечения кривых с осью абсцисс. Для больших прогибов следует применить общее решение уравнения (14), и тогда будут иметь место кривые, изображенные на рис. 3, Ь. Если нагрузка Р такова, что для нее
2п -Ь 1 _ Р 2п 1 1 о q 2 Ё1 2 )»
го кроме неустойчивой прямолинейной формы равновесия возможны п форм с 1, 3,.,2 п—1 полуволнами и с 0, 1, 2,.
Ч R. MUes, работа, указанная на стр. 556.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
563
., п — 1 точками перегиба. На рис. 4, например, показаны три формы равновесия, которые возможны, если величина Р больше, чем (94) EJzn2jl2.
а)
(. V
2
25112
4
При исследовании устойчивости различных форм равновесия необходимо принять во внимание потенциальную энергию
о)
с)
системы.
Устойчивыми формами равновесия будут те, для которых потенциальная энергия системы имеет минимальное значение. Произведенные в этом направлении исследования привели к следующему заключению ): при значениях нагрузок, меньших первой критической силы Р 72я242, устойчива только прямолинейная форма равновесия; при больших — только искривленная без точек перегиба. Это однако, не решает вопроса об устойчивости или неустойчивости какой-либо особой формы равновесия, при которой ось стержня выходит из своей плоскости.
стержня.
l) А. Е. Н. Love. A treatise on the mathematical theory of elasticity. 4th edition, Cambridge, University Press, 1927, p. 411 Перевод на русский язык: А. Ляв. Математическая теория упругости. М.—Л., ОНТИ, 1935, стр. 429, М. Born, статья, указанная на стр. 561. R. Mises, статья, указанная на стр. 555.
564
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
в. Влияние поперечной силы
Для того чтобы учесть влияние поперечной силы на величину критической нагрузки, напишем дифференциальное уравнение упругой линии стержня в следующем виде:
d2y _ М. к d2M .„ч
ETZ GF dx9 'J
Здесь F — площадь поперечного сечения, G — модуль сдвига, и — коэффициент, зависящий от формы поперечного сечения и неравномерного распределения касательных напряжений по площади поперечного сечения. Так, например, для прямоугольного поперечного сечения вычисления дают к 1,50, а для сечения круговой формы х 1,33. Рассматривая, например, стержень с шарнирно опертыми концами (рис. 1, а) и подставляя в уравнение (17) Ру вместо М, получим в результате
«4‘--)S-p»-0-
Критическое значение силы Р равно 1)
р — Elz7- (1й)
КР 2 xEJ z7l2
GFl2
Если принять во внимание, что выражение EJzn2Fl2, согласно уравнению (2), представляет собою критическое напряжение, которое не может превосходить предела упругости материала, а также что величина G, как правило, велика по сравнению с пределом упругости данного материала, то можно прийти к заключению, что влияние поперечной силы для сплошных стержней практически не имеет значения. Для составных стержней, как мы увидим из дальнейшего (см раздел 17), уже нельзя пренебрегать влиянием поперечной силы на величину критической нагрузки.
При применении энергетического метода необходимо- в левой части уравнения (11) учесть потенциальную энергию сдвига
у‘-1ш (§)’dx
о
Тогда
V VZ V2. (19)
J) Это выражение впервые дал F. Engesser. Die Knickfestigkeit gerader Stabe. Zentralblatt der Bauverwaltung, 1891, Bd. 11, № 49, SS. 483—486. См. также F. Nussbaum. Die genaue Saulen Knicklast. Zeilschrift fur Mathematik und Physik, 1907, Bd. 55, Heft 1—2, SS. 134—138.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 565
Принимая для стержня с шарнирно опертыми концами
1 00
. tot х At sm —,
i 1
получим согласно уравнению (19) следующее выражение для критической нагрузки:
Если под каждым знаком суммы взять только первый член, то для величины критической силы получим значение, даваемое уравнением (18).
7. Стержни с начальной малой кривизной
Рассмотрим стержень длиною , с шарнирно опертыми концами, первоначальная форма оси которого в плоскости наименьшей жесткости определяется следующим рядом:
. пх I . 2пх I. Зпх ллуч
ух ах sin — а2 sm -у- а3 sin -у-. (20)
Под действием сжимающей продольной силы Р появляется добавочное искривление стержня, которое можно представить следующим рядом:
. пх I . 2пх I - 1
y2blsin — b2sin ——Ь. (21)
Для определения коэффициентов этого ряда воспользуемся началом возможных перемещений1). Потенциальная энергия изгиба стержня равна
О 1
Сближение концов стержня, вызываемое изгибом, составляет
О
) С. Г1. Тимошенко. Теория упругости. Издание Института инженеров путей сообщения. Часть 2, СПб., тип. А. Э. Коллинса. 1916, стр. 62. См. также S. P. Timoschenko. Ober die Biegung von Staben, die eine kleine anfangliche Kriirnmung haben. Beitrage zur technischen Mechanik und technischen Physik. August Foppl zum siebzigsten Geburtstag. Berlin, Verlag von J. Springer, 1924, SS. 74—81.
566 ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
или, используя выражения (20) и (21), найдем
“ОО
eair2(6i 2aA)-
Если мы имеем малый прогиб, соответствующий возрастанию коэффициентов Ь в выражении (21), то уравнение возможных перемещений получит следующий вид:
откуда найдем
bi
EJn2. .2 ркр
— 1 г —г-
2Р
Подставляя найденные значения в выражение (21), получим формулу для прогиба, вызываемого сжимающей силой:
а. лх , а2 . 2лх , а3. Злх ,
У2 -рЛ Sin-y рг Sin-т-Н ТГ Sin j h.
JjL _ 1 02JJiL _ 1 42 _H. _ 1
1 2 p 1 P 1 (22)
Как легко видеть, прогиб, определяемый первым членом ряда (22), бесконечно возрастает при приближении сжимающей силы Р к критическому значению РКр-
8. Влияние эксцентриситета точки приложения силы
Примем, что эксцентриситеты приложения сил на обоих концах стержня равны между собою по величине и направлению и лежат в плоскости его наименьшей жесткости. В таком случае дифференциальное уравнение прогиба стержня с шарнирно опертыми концами (рис. 5) имеет вид
Е1 Ру--Рс,
где с — величина эксцентриситета. Решение этого уравнения при выполнении условий закрепления концов имеет вид
У с
cos y ( — 2х) к1
- 1
(23)
где х У PEJ.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
567
Прогиб посредине стержня равен
( cost)
х
(24)
Из этой формулы следует, что прогиб стремится к бесконечности по мере того, как величина сжимающей силы приближается к значению критической нагрузки Р1ф. На рис. 6, а показан прогиб f как функция отношения РРкр для разных значений эксцентриситета с. Кривые асимптотически приближаются
Рис. 5. Эксцентрично сжатый стержень.
Рис. 6. Прогибы стержня при эксцентричном сжатии.
к горизонтали, соответствующей отношению РРкр 1, и тем ближе, чем меньше соответствующий эксцентриситет. Если он равен нулю, то соответствующая кривая должна совпасть с первой из ранее рассмотренных кривых, показанных на рис. 3. Аналогичные кривые могут быть построены и для стержней с начальной кривизной.
9. Эксцентриситет вместе с начальною кривизною
Рассмотрим простейший случай, а именно когда первоначальная форма оси определяется уравнением
пх
у asm —
и эксцентриситеты с на обоих концах стержня равны между собою (рис. 5). Тогда, пользуясь уравнениями (22) и (24), найдем
558
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
прогиб , вызванный сжимающей силою Р:
(25)
Если эксцентриситет имеет такое направление, что соответствующий изгибающий момент Р с стремится увеличить начальную кривизну, то величины а и с в выражении (25) имеют одинаковые знаки, и при возрастании нагрузки Р прогиб будет беспрерывно расти. Это возрастание прогиба при разных значениях эксцентриситета с и различных начальных прогибах а можно получить как функцию отношения РРкр из кривых, расположенных справа от линии ОА на рис. 6, Ь. Иначе обстоит дело, когда изгибающий момент Р с стремится уменьшить начальную кривизну. Тогда величины а и с в формуле (25) имеют разные знаки и направление прогиба зависит от отношения са. Соответствующие условия прогиба для определенных значений отношения са представлены на рис. 6, b кривыми слева от линии ОА. Как видно, некоторые из этих кривых пересекают вертикальную ось РРнр. Это значит, что прогибы, направленные в начале загружения вправо (рис. 5), при некоторых значениях нагрузки Р меняют свое направление, и разрушение, вследствие прогибов, происходит влево. Величины отношений РРкр, соответствующих вышеупомянутым точкам пересечений оси, получим из выражения (25), положив f равным нулю. Тогда будем иметь
Условия, представленные на рис. 6, b кривою , касающейся вертикальной оси, можно получить из уравнения (26), допустив, что РРир очень мало. Тогда
Если эксцентриситет с численно больше, чем следует из формулы (27), и направлен так, что может вызвать прогиб, противоположный начальному а, то увеличение прогиба f от нагрузки Р можно представить кривою, подобной кривой 3 на рис. 6, Ь, показывающей, что уже в начале нагружения направление прогиба противоположно начальному прогибу а.
а
с
(26)
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
569
Если принять, что в формуле (26) 1—(РР,ф)—очень малая положительная величина, то получим
ас —4я. (28)
Соответствующие условия представлены на рис. 6, b кривою 2, точка пересечения которой с вертикальной осью приближается к точке РРкр 1. Прогиб для этого предельного случая находим при помощи выражения (25), подставляя в него ас —4я и рассматривая 1—(РРкр) как малую величину. Таким образом, получим
0 а. (29)
Для всех значений отношения ас, лежащих в границах, определяемых выражениями (27) и (28), направление прогиба меняется при определенных значениях Р, и соответствующие кривые на рис. 6, Ь пересекают вертикальную ось. Эти явления изменения направления прогиба имеют место также в случаях сложных начальных форм слегка искривленных стержней1), и существование их можно установить опытами 2).
10. Продольный изгиб стержней за пределом пропорциональности
В основу вывода дифференциальных уравнений (1) изогнутой оси стержня положено условие, что материал стержня следует закону Гука. Вследствие этого выведенные из этих уравнений формулы для критических нагрузок дают значения, соответствующие действительности только до тех пор, пока вызываемые ими сжимающие напряжения не превосходят предела пропорциональности. Теорию продольного изгиба за пределом пропорциональности разработал Ф. Энгессер. Величина критического напряжения на основании формулы (2) будет
_ я2Е
ар Щ)2 (30)
где i JF — наименьший радиус инерции поперечного сечения. В этом уравнении коэффициент Е есть отношение между напряжением и относительным укорочением в пределах пропорциональности ор. Это отношение нарушается, как только предел пропорциональности оР перейден. Фридрих Энгессер
) Н. Zimmermann. Die Knickfcstigkeit von Staben mit nicht gerader Achse. Eine Erweiterung der Eulerschen Knicktheorie. Sitzungsberiohte der Preussischen Akademie der Wissenscnaften. Sitzung der physikalisch-mathematischen Klasse, 1923, Bd. 25, 18 Oktober, SS. 262—281.
2) K. Memmler. Neuere experimented Beitrage zur Frage der Knickfestigkeit. Verhandlung des zweiten internationalen Kongresses fur technische Mechanik, Zurich, 1926. Zurich und Leipzig, Fussli, 1927, SS. 357—363.
570
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
показал1), что это может быть учтено, если в выражение (30) вместо Е подставить отношение dods, представляющее тангенс угла наклона диаграммы сжатия, который с переходом за предел пропорциональности непрерывно становится меньше Е. Ф. С. Ясинский указал 2), что это соображение пригодно только для таких напряжений, которые растут при малых прогибах. На выпуклой стороне стержня, где имеет место уменьшение сжатия, появляются вновь лишь упругие деформации, и для нее
dodE Е. В своих позднейших работах Ф. Энгессер принял это во внимание3) и дал для критического напряжения более точную формулу
Оч-щг, (31)
в которой Е заменено через Е' (приведенный модуль) 4) —величину, ле жащую между значениями dode и и зависящую от величины напряжения акр, так и от формы поперечного сечения. Рассмотрим, например, случай прямоугольного попереченого сечения высотою h (рис. 7) и допустим, что под действием критической нагрузки РНр имеет место небольшой изгиб стержня и что поперечные сечения выпученного стержня остаются плоскими; тогда помимо равномерного сжимающего напряжения акр появляются еще дополнительные напряжения, распределение которых показано на рис. 7 заштрихованными площадями. Если R — радиус кривизны осевой линии стержня в поперечном сечении тп, а Е dod есть тангенс угла наклона касательной к диаграмме сжатия для напряжения аКр ор, то согласно рисунку
_ Exhx , _ Eh2 al R ’ 2 R
Рис. 7. Распределение дополнительных напряжений при продольном изгибе за пределом пропорциональности.
Из условия равновесия можно заключить, что алгебраическая сумма заштрихованных площадей на рис. 7 должна быть
) F. Engesser. Ober die Knickfestigkeit gerader Stabe. Zeitschrift fiir Architektur und Ingenieurwesen zu Hannover, 1889, Bd. 35, SS. 455—462.
2) F. J a s i n s k i. Noch ein Wort zu den «Knickfragen». Schweizerische Bauzeitung, 1895, Bd. 25, № 24, SS. 172—175. Перевод на русский язык: Ф. С. Ясинский. Избранные работы по устойчивости сжатых стержней. М. — Л., Гостехиздат, 1952, стр. 202—211.
3) F. Engesser. Ober Knickfragen. Schweizerische Bauzeitung, 1895. Bd. 26, № 4, SS. 24—26 и F. Engesser. Widerstandsmomente und Kernfiguren bei beliebigem Formanderungsgesetz (Spannungsgesetz). Zeitschrift des Vereines deutscher Ingenieure, 1898, Bd. 42, № 34, SS. 927—931.
4) У автора «модуль продольного изгиба».
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
571
равна нулю. Из этого следует, что
h И 1ц Ё
Принимая во внимание, что h h2 h, получим в результате
hVE , hVT,
rl — - г , П2 — '
Ve VEi ’ VI VEi
Обозначим через b ширину поперечного сечения; тогда изгибающий момент в сечении, равный моменту внутренних сил, изображенных на рис. 7 заштрихованными площадями, составит
М Н-1Г -И —. (32)
где J bh3l2 и
Е' (33)
(,) ’
Выражение (32) имеет такую же форму, как и обычное уравнение кривизны стержня; следует только вместо модуля упругости Е поставить величину Е'—приведенного модуля для стержня прямоугольного сечения. Величины Е и Е определяются на основании испытаний соответствующих материалов на сжатие. Тогда, пользуясь формулой (33), можно определить Е' как функцию (ткр. Подставив Е7 в выражение (31), найдем соответственные значения. Отсюда можно определить значение акр как функцию отношения li для определенного материала. На основании изложенного можно заключить, что критические напряжения в области неупругих деформаций зависят не только от гибкости стержня, т. е. от отношения , но также и от формы его поперечного сечения. Влияние последней, однако, незначительно.
Дальнейшую разработку теории продольного изгиба за пределом пропорциональности дал Т. Карман1). Он вывел выражение (31) независимо от Ф. Энгессера и дал графический метод определения изогнутой оси искривленного стержня за пределом пропорциональности. Применяя этот метод, он показал, что очертания осевых линий отклоняются от синусоидальной формы в том отношении, что меняется кривизна посредине стержня. Это явление проявляется еще резче при уменьшении гибкости стержня li. Он показал также, что, в то время как при
) Th. К arm а п. Untersuchungen iiber Knickfestigkeit. Forschungsarbeiten auf dem Gebiete des Ingenieurwesens. Verein deutscher Ingenieure, Forschungsheft, Berlin, 1910, Heft 81, 44 S. Перепечатка: Th. К a г m a n. Collected works. Vol. 1 London, Butterworths scientific publication, 1956, vol. 1, pp. 90—140. См. также R. V. Southwell, статья, указанная на стр. 555.
572
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
продольном изгибе в пределах пропорциональности прогиб растет при почти неизменяющемся грузе (рис. 3, а), в случае продольного изгиба за пределом пропорциональности возрастание
прогиба имеет следствием
б. мгсм2 уменьшение нагрузки, как
то показано, например, на рис. 8. Влияние эксцентриситета также весьма различно в упругой и неупругой областях продольного изгиба. В противоположность случаю упругого изгиба, когда кривые, соответствующие различным эксцентриситетам, асимптотически приближаются к одному и тому же наибольшему значению силы (рис. 6, а), во втором случае, уже при незначительных эксцентриситетах, наибольшее значение силы значительно снижается, что в практическом отношении чрезвычайно важно. На рис. 8 показаны прогибы посредине стального стержня прямоугольного сечения при 60 для разных значений сжимающих напряжений и эксцентриситета е. Прогибы f изображены в сильно увеличенном масштабе в тысячных долях толщины h стержня.
3100
3000
2900
2800
2700
2600
Рис. 8. Прогибы стержня при продольном изгибе за пределом пропорциональности.
11. Опыты на продольный изгиб
Первые опытные исследования продольного изгиба сжатых стержней были произведены Петрусом Мушенбрэком ). Он нашел, что сопротивление стержней, сжатых продольными силами, при прочих равных условиях обратно пропорционально квадрату их длины — вывод, теоретически данный впоследствии Эйлером (см. раздел 12). С целью проверки теории Эйлера и составления формул, пригодных для практических применений, в середине
) Petris van Musschenbroek. Physical experimentales et geometricae. Dissertationes. Lugduni. Краткое содержание этой работы см. в книге: I. T о d h u n t e г, K. Pearson. A history of a theory of elasticity and of the strength of materials from Galilei to the present time. Vol. 1. Cambridge, University Press, 1886, p. 15.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
573
XIX столетия Итоном Ходкинсоном) было произведено очень подробное исследование работы сжатых колонн. В его исследованиях были применены чугунные колонны с закругленными и плоскими концами. Эти условия закрепления концов отличались от тех, которые положены в основу теории Эйлера, и потому результаты опытов не совпадали с выводами этой теории.
На основании своих опытов И. Ходкинсон дал эмпирическую формулу, обычно приписываемую Л. Гордону или М. Ренкину (см. раздел 12) и нашедшую впоследствии большое применение при проектировании сжатых элементов в инженерных конструкциях. Е. Ламарль2) первый указал на то, что теория Эйлера пригодна только для определения напряжений, не превышающих предела пропорциональности, и дает удовлетворительные результаты при стойках достаточно большой длины. В последующих опытах, произведенных Иоганном Баушингером3) и Людвигом Тетмайером4), были применены заостренные опоры, и таким образом, концы стержней были поставлены в условия, значительно более близкие к теоретическим предположениям, чем это делалось раньше. Эти опыты показали, что для длинных стержней, для которых а1ф не превосходит предела пропорциональности, теория Эйлера дает точные значения критических нагрузок. В дальнейшем, при более точно поставленных опытах по исследованию продольного изгиба стержней, были применены опорные закрепления, обеспечивающие совмещение линии действия сил с осью стержня5).
Применяя вместо заостренных опор поддающиеся регулированию опорные призмы, Т. Карману6) удалось показать, что формула Эйлера дает значения критической нагрузки с ошибкою менее 1Опыты производились им со стальными стержнями прямоугольного сечения при различных значениях гибкости 1L
) Е a t о n Hodgkinson. Experimental research on the strength of pillars of cast iron and other materials. Philosophical Transactions of the Royal Society of London, Series A, Part 2, 1840, vol. 130, pp. 385—456. Cm. также E. Hodgkinson. Experimental research on the strength of pillars of cast iron from various parts of the Kingdom. Там же, 1857, vol. 147, pp. 851—899.
2) E. L a m a r 1 e. Memoire sur la flexion du bois. Annales des travaux publics de Belgique, Series 1, Bruxelles, 1845, vol. 3, pp. 5—64; 1846, vol. 4, pp. 5—36.
3) I. Bauschinger. Zerknickungs-Versuche. Mitteilungen aus dem mechanischen-technischen Laboratorium der technischen Hochschule in Munchen, Munchen, Th. Ackermann, 1887, Heft 15, SS. 11-57.
4) L. T e t m a j e r. Die Gesetze der Knickungs- und der zusammengesetzten Druckfestigkeit der technisch wichtigsten Baustoffe. 3 Auflage, Leipzig und Wien, F. Deuticke, 1903, 211 S.
5) A. C. Consider. Resistance des pieces comprimees. Les Comptes Rendus du Congres international des procdes de construction, 1889. Paris, Baudry, 1891, vol. 3, pp. 371—397.
e) Th. Каплап, работа, указанная на стр. 571.
574
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Результаты этих опытов приведены на рис. 9, где величина акр показана как функция li. Верхняя кривая, переходящая при 88 в гиперболу Эйлера, дает значения акр, вычисленные на основании формул (31) и (33). Нижняя кривая дает значения наибольших напряжений, соответствующих эксцентриситету, равному 1200 толщины стержня (см. § 10, рис. 8). За исключением одного случая, все полученные опытным путем значения не
сиг
Рис. 9. Критические напряжения стержня при различных значениях гибкости.
выходят из границ, очерченных этими кривыми. Видно, что обе характерные для поведения материала стержней границы — предел упругости и предел текучести — делят кривую критических напряжений на три части. На основании этого подвергающиеся продольному изгибу стержни можно подразделить на очень длинные, средней длины и короткие. На основании опытов над очень длинными стержнями Т. Карман пришел к следующему выводу: «. результаты опытов на продольный изгиб таких стержней весьма точно совпадают с данными теории Эйлера. Теоретическое требование совершенной упругости — увеличения прогиба при постоянном значении силы — хорошо удовлетворяется при длинных стержнях. Чем стержень короче, т. е. чем больше значение критического напряжения, тем скорее наступает падение нагрузки».
Опыты над стержнями средней длины (82 li 47) показали, «что начальный эксцентриситет приложения силы не только ускоряет явление прогиба, но также значительно уменьшает максимальную нагрузку. После того, как будет достигнута максимальная нагрузка, у большинства стержней появляется внезапный прогиб».
При опытах с короткими стержнями (387ь22) «главным образом имеет значение поведение стержня при напряжениях,
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
675
близких к пределу текучести. Предел текучести, собственно говоря, и является причиною неустойчивости стержня, так как отношение delete становится чрезвычайно малым; но эта неустойчивость имеет временный характер, так как сопротивляемость материала восстанавливается, и стержень получает способность снова выдерживать большую нагрузку». Теория продольного изгиба за пределом пропорциональности Энгессера — Кармана в дальнейшем была применена М. Рошем и И. Бруннером к продольному изгибу сжатых стержней двутаврового сечения1). При этом гибкости испытываемых стержней были следующие:
У 18,6; 20; 28; 45; 65; 82; 100; 120; 160,
и для каждой гибкости мерою эксцентриситета были: т 0 (центрально приложенная сила), т 1 (сила, приложенная на границе ядра сечения), т 3 (сила, приложенная на расстоянии, равном утроенному расстоянию до границы ядра). При этих опытах обнаружилось более сильное падение сопротивления с ростом эксцентриситета и очень хорошее совпадение стрел прогиба с теоретически вычисленными в момент выпучивания.
Незадолго перед этим в Берлин-Далемской механической лаборатории были произведены опыты над продольным изгибом стержней с усовершенствованными опорными призмами на концах2). Эти опыты дали следующие результаты:
a) Кривая Эйлера пригодна в тех пределах, где напряжения, соответствующие эйлеровым значениям, вызывают чисто упругие или преимущественно упругие деформации.
b) Критическое напряжение для чистого продольного изгиба до гибкостей 1Ц 30-7-40 не переходит за предел текучести материала стержня.
c) Кривая перехода от линии Эйлера к прямой предела текучести зависит от свойств материала между пределами пропорциональности и текучести. Эта кривая тем ближе подходит к точке пересечения обеих главных линий, чем меньше пластическая деформация материала при напряжениях, меньших предела текучести, и в наивыгоднейшем случае — чисто упругой деформации до предела текучести — она отсутствует.
d) Стержень с начальной кривизной может в упругой области достичь эйлеровой нагрузки, как и однородный прямой стержень, когда сжимающая нагрузка прикладывается посредством рычага. Точность, с которой разным исследователям удалось
) М. R о s, J. Brunner. Die Knicksicherheit von an beiden Enden gelenkig gelagerten Staben aus Konstruktionsstahl. Bericht № 13 der Eidgenossischen Materialpriifungsanstalt an der Eidgenossisohen Technischen Hochschule, Zurich, August, 1926.
2) K- Memmler, статья, указанная на стр. 569.
576
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
приблизиться к теоретической величине критической нагрузки, можно видеть на рис. 10, на котором изображена зависимость
между относительным прогибом стержня и силой, выраженной в процентах от теоретической эйлеровой нагрузки1).
12. Эмпирические формулы продольного изгиба
При проектировании сжатых элементов строительных конструкций, за неимением для некоторых случаев точных теоретических формул, для определения критических и допускаемых напряжений часто пользуются различными эмпирическими формулами. В Англии до сего времени наибольшим распространением пользовалась формула М. Ренкина2). По этой формуле
1) Опыты с составными сжатыми стержнями для нового металлургического завода и для общества немецких фабрик по строительству мостов и металлоконструкций, выполненные в Королевской лаборатории испытания материалов в связи с проектированием больших цехов с верхним светом, описаны в книге: R. Mayer. Die Knickfestigkeit. Berlin, Verlag von J. Springer, 1921, VII Abschnitt, §§ 58—64. В той же книге описаны опыты с остержнями из никелевой стали для нового строительства Квебекского моста.
2) W. J. R a n k i n. A manual of applied mechanics. London, W. J. Millar, 1858, p. 360. Формула была установлена И. Ходкинсоном (см. § 11 ссылки на стр. 573). На европейском континенте та же формула была предложена F. Schwarz’eM. См. его Beitrag zur Theorie der Blech- und Gitterbalken. Zeitschrift des Architekten- und Ingenieurvereins fur das Konigreich Hannover, 1858, Bd. 4, Heft 1, SS. 61—97. См. также F. L a i s s 1 e, A. Schiibler. Der Bau der Briickentrager mit wissenschaftlicher Begriindung der gegebenen Regeln und mit besonderer Riicksicht auf die neuesten Ausfuhrungen. Stuttgart, Neff, 1857 Zweite umgearbeitete Auflage— 1864, 203 S.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
577
допускаемое напряжение с учетом продольного изгиба стержня с шарнирно опертыми концами равно
0ДОП 7772 (34)
.и(7)
где а — допускаемое напряжение материала на растяжение и изгиб, р — постоянная величина (для литого железа равная 0,000077). На европейском континенте применяют главным образом линейные зависимости Л. Тетмайера. Из опытов Л. Тетмайера над стержнями с шарнирно опертыми концами (см. § 11) выяснилось, что формулу Эйлера можно применять в тех случаях, когда 80 (чугун), 105 (литое железо), 90 (литая сталь), 86 (никелевая сталь с 5 никеля), 100 (дерево). При меньших значениях гибкости акр в кгсм2 могут быть определены по формулам, приведенным ниже.
Чугун
тКр 7760
1 — 0,0155 у 0,00007 (у)2.
Литое железо
огКр3100(
1 — 0,00368 у).
Литая сталь
хкр 3350 (
l-0,00185у). (35)
Никелевая сталь
О
О
11
о.
Jl- 0,00490 у).
Дерево
сгкр 2931
(l- 0,00662 у).
Согласно нормам для железных конструкций германских го-
сударственных железных дорог, не допускается применение стержней при гибкости 150. Кривая Эйлера применима для в пределах от 150 до 100. При гибкостях в пределах от 100 до 60 значения аКр даются прямою, которая при 60 достигает предела текучести материала. При 60 значения аКр принимаются равными пределу текучести.
В Америке для определения допускаемых напряжений при продольном изгибе также часто пользуются линейными зависимостями, Американское общество по строительству мостов, например, пользуется следующими формулами:
(Тдоп 1340 — 7 () для значений 120 60, 1 о’доп920 кгсм2 для значений 60. J
В американской практике применяются и параболические зависимости. Дж. Джонсон1) для определения критического на¬
) J. В. J о h n s о п. Cast — iron strength resilience tests and specifications. Transactions of the American Society of Civil Engineers, 1890, vol. 22, pp. 91— 134. См. также стр. 148 кииги J. В. Johnson, С. W. Bryan, F. C. Turneaure. The theory and practice of modern framed structures. New York, John Wiley and Sons, 1893, 527 p.
578
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
пряжения в стержнях из литого железа предложил следующую формулу ):
Для назначения допускаемого напряжения при продольном изгибе иногда принимают2), что сжимающая сила связана с определенным эксцентриситетом, и считают эту силу опасной тогда, когда она вызывает в наиболее сжатых волокнах напряжения, соответствующие пределу текучести материала. Так как при этих вычислениях величина начального эксцентриситета в большинстве случаев берется произвольно, то этот способ не дает большей точности, чем несравненно более простое вычисление сопротивления продольному изгибу при центральном сжатии3).
13. Устойчивость призматического стержня при переменной вдоль оси сжимающей силе
Первая задача этого рода, а именно исследование продольного изгиба стержня под действием собственного веса, была подвергнута анализу Эйлером4), но его работа, сама по себе крайне интересная, не получила удовлетворительной обработки.
1) См. С. Е. Fuller, W. A. Johnson. Applied Mechanics. Vol. 2. Strength of materials. New York, J. Wiley and Son, London, Chapman and Hall, 1919, d. 360.
2) A. О s t e n f e 1 d. Exzentrische und zentrische Knickfestigkeit mit besonderer Beriicksichtigung der fur schmiedbares Eisen vorliegenden Versuchsergebnisse. Zeitschrift des Vereines deutscher Ingenieure, 1898, Bd. 42, N 53, SS. 1462—1470 и A. О s t e n f e 1 d. Einige Bemerkungen iiber die Bestimmung der Abmessungen exzentrisch und zentrisch beanspruchter Saulen. Там же, 1962, Bd. 46, № 49, SS. 1858—1861. См. также В. Kirsch. Ergebnisse von Versuchen iiber die Knickfestigkeit von Saulen mit fest eingespannten Enden. Там же, 1905, Bd. 49, № 22, SS. 907—915. R. Kochi in. Berechnung eines auf exzentrischen Druck beanspruchten Stabes. Schweizerische Bauzeitung, 1899, Bd. 33, N9 18, SS. 159—160.
3) Th. К a r m a n. Festigkeitsprobleme in Maschinenbau. Encyklopadie der mathematischen Wissenschaften, Bd. 4, Teilband 4, Heft 3, § 27, S. 375, Leipzig, B. G. Teubner, 1910. Перепечатка: Th. Karman. Collected works. Vol. 1. London, Butterworths scientific publication, 1956, p. 198.
4) L. Euler. Determinatio onerum, qual columnae gestare valent (pp. 121 —145. Examen insiqnis paradoxi in theorie columnarum occurentis (pp. 146—162). De altitudine columnarum sub proprio pondere corruentium (pp. 163—193). Acta Academia Scientiarum Imperialis Petropolitanae (1778, tom II, pars I), 1780, pp. 121—193. См. также I. Todhunter, K. Pearson. A history of the theory of elasticity and of the strength of materials from Galilei to the present time. Vol. 1, Cambridge, University Press, 1886, pp. 44—49.
(37)
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
579
Полное решение этого вопроса дал А. Гринхил1). Для призматического стержня с заделанным нижним концом и свободным верхним, как показано на рис. 11, дифференциальное уравнение изогнутой оси имеет следующий вид:
dy dx
(а)
где q — равномерная нагрузка на единицу длины стержня (в частном случае — собственный вес стержня на единицу длины). Если ввести новую независимую переменную, определяемую соотношением z 2з VqEJ (I “ )82 и положить dydz vf то уравнение (а) можно переписать в виде
d2v , 1 dv , Л 1 п rfj l1 ” 9)о 0-
Общее решение этого уравнения имеет следующий вид:
dx
— яГ( х)'к А1,г) В1ч(z)-
где Л и 5 — произвольные постоянные.
Для того чтобы d2ydx2 0 при х постоянную А необходимо приравнять нулю, и чтобы dydx 0 при х 0, необходимо при
z у У-jj иметь _1, (г) 0. Тогда величину критической нагрузки мы получим
Наименьший корень этого уравнения равен2)
(ql)K р 7,83
EJ
I2
Рис. 11. Продольный изгиб при действии собственного веса.
из уравнения
(38)
А. Гринхил исследовал также различные случаи сжатых стержней переменного сечения, как, например, продольный изгиб кругового конуса под действием собственного веса, а также стержней, имеющих форму параболоида вращения. Он установил, что во всех случаях, когда величина переменного момента
) A. G. Greenhill. Determination of the greatest height consistent with stability that a vertical nole or mast can be made, and of the greatest height to which a tree of given proportions can grow Proceedings of the Cambridge Philosophical Society, Mathematical and Physical Scienccs, 1881, vol 4 pp. 65—73. ’ '
2) S. P. Timoshenko. Sur la stabilite des systemes elastiques. Annales des ponts et chaussees. 1. Partie, 9 serie, 1913, tome 15, vol. 3, Mai —Juin № 24, p. 514.
580 ПРОБЛЕМЫ УПРУГОЙ устойчивости
II —х т
инерции определяется выражением 01—j—1 , а интенсивность распределенной по оси стержня нагрузки — формулой
(I я
—j—1 , соответствующее дифференциальное уравнение
изогнутой оси может быть решено при помощи функций Бесселя.
i
Критическое значение нагрузки Q J q dx всегда можно
о
EJ
представить в виде QKpK“jr- Численные значения коэффициента х для некоторых частных случаев были вычислены А. Динником1) и даны в таблице I.
Таблица I
n. т п
0
1
2
3
4
0
7,87
5,78
3,67
1
16,1
13,0
9,87
6,59
—
2
27,3
23,1
18,9
14,7
10,2
3
41,3
36,1
30,9
25,7
20,2
4
52,1
45,8
39,5
33,0
Ф. С. Ясинский2) исследовал случай сжатого стержня постоянного поперечного сечения, находящегося под действием распределенной нагрузки, заданной в форме (расположение оси
X
показано на рис. 12) 7д0у- В этом случае критическая нагрузка определяется выражением:
QKp - 5,125-. (38')
Для определения приближенного значения критической нагрузки весьма полезным оказывается использование энергетического метода. Рассматривая, например, случай одновременного действия сжимающей силы Я, приложенной к верхнему концу
) А. Н. Д и н н и к. О продольном изгибе при распределенной нагрузке. Известия Екатеринославского горного института, 1915, том И, выпуск 1, стр. 1—19. Перепечатка:.А. Н. Динник. Избранные труды. Том 3. Киев, Изд-во АН УССР, 1956, стр. 187—201. См. также Akinasa О п о. On the stability of long struts of variable section. Memoirs of the Fukuoka College of Engineering, Kyushu University, Fukuoka, Japan, 1919, vol. 1, № 5, pp. 39b—406.
2) F. J a s i n s k i. Recherches sur la flexion des pieces comprimes. Annales des ponts et chausses, Series 7, 1894, vol. 8, pp. 233—364. Перевод на русский язык: Ф. С. Ясинский. Избранные работы по устойчивости сжатых стержней. М.—Л., Гостехиздат, 1952, стр. И—137. См. также Ф. С. Я с и нс к и й. Собрание сочинений. Том 1. СПб., Издание Института инженеров путей сообщения, 1902.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
581
стержня, и равномерно распределенной нагрузки q (рис. 12) и допуская, что изогнутая ось определяется выражением
ТСХ
y f cos__ найдем, что потенциальная энергия изгиба равна
21
2. Работа действующих при изгибе стержня сил
,7 EJn4 v бйг равна
г - Т Ш 41()’ V--.,- 1 (4 -1) р.
о о
Полагая Т V, получим
Отсюда следует, что для того, чтобы принять во внимание влияние собственного веса стержня на критическую нагрузку, следует допустить, что 0,3 этого веса приложено к верхнему концу стержня. Если представить уравнение изогнутой оси в виде
пх , Злх.
У f COS - COS —уд b.
и подобрать коэффициенты fu 2, з,. из того условия, чтобы энергия системы имела минимум, то можно еще точнее определить величину критической нагрузки ).
В случае стержня с шарнирно опертыми концами при действии на него осевой силы Р и рав- Рис- 12 Д0Вре- Рис. 13. Про-
г менное действие дольный изгиб HOMepHO распределенной нагрузки собственного веса стержня с шарq (рис. 13) приближенное значе- и сжимающей си- нирно опертыние критической СИЛЫ можно лы. Один конец ми концами при получить ИЗ выражения стержня заделан, действии соб-
J г другой — свободен ственного веса
n2EJ ql огл от связей. и сжимающей
а jf- силы.
кр '
Применяя энергетический метод, можно получить еще более точное приближение. Если привести формулу для определения
) С. П. Тимошенко, статья, упомянутая на стр. 556. Решение подобной задачи с применением функций Бесселя было дано А. Н. Д и н н и к о м в «Приложении функций Бесселя к задачам теории упругости». Известия Донского политехнического института, Новочеркасск, 1913, том 2, стр. 219—366. Перепечатка: А. Н. Д и н и и к. Избранные труды. Трм 2. Киев, Изд-во АН УССР, 1955, стр. 7—122.J
582
ПРОБЛЕМЫ УПРУГОЙ устойчивости
критической нагрузки к виду Ркр kEJ12, то величина коэффициента х будет зависеть от отношения m qlP. Некоторые численные значения коэффициента х приведены в таблице И1).
Таблица II
m
0
0,25
0,50
0,75
1,0
2
3
4
5
10
X
n2
8,64
7,40
6,17
4,94
0
-4,94
-9,87
-14,8
-39,5
Отрицательные значения коэффициента х дают наибольшие значения растягивающих усилий, при которых может наступить выпучивание. Эти данные могут иметь практическое значение в тех случаях, когда речь идет о стержнях большой гибкости,
как, например, о штангах, применяемых при бурении очень глу¬
боких скважин. Для того чтобы устранить возможность выпучивания таких стержней, к их верхнему концу необходимо приложить значительную растягивающую силу.
Продольный изгиб призматических стержней под влиянием сжимающих сил, приложенных как по концам, так и в промежуточных точках, был исследован Ф. С. Ясинским 2).
14. Продольный изгиб стержней переменного поперечного сечения
Задача определения критической нагрузки в этом случае приводит к решению дифференциального уравнения второго порядка с переменными коэффициентами. Это уравнение было составлено Ж. Лагранжем3) при определении критической силы для стержней, имевших форму конуса и параболоида вращения.
Случай, имеющий практическое значение, приведен на рис. 14. Стержень симметричен относительно своего среднего сечения,постоянного поперечного сечения с моментом инерции Jo. Переменные моменты инерции поперечного сечения 1 концевых частей стержня меняются по закону J J0(xa)m. Моменты
Рис. 14. Продольный изгиб стержня переменного поперечного сечения.
) Эти расчеты даны Н. П. Гришковой в статье «Влияние собственного веса на продольный изгиб стержней». Вестник инженеров, 1928, № 3, стр. 149—152.
2) Ф. С. Ясинский, работа, указанная на стр. 580.
3) J. L. Lagrange. Sur la figure des colonnes. Miscellanea Taurinensia, Royal Society of Turin, 1770—1773, vol 5.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
583
инерции концевых поперечных сечений равны Л 0(6а)т. Для случаев, когда т 2 и т 4, дифференциальные уравнения изогнутой оси могут быть решены при помощи элементарных функций; когда т 1 и т 3, решение уравнений может быть получено при помощи функций Бесселя. Выражение для критической нагрузки может быть представлено в таком виде:
р — х —I
г кр л J2
где коэффициент х зависит от отношений А и io, так же как и от показателя т. Численные значения коэффициента х, вычисленные при различных значениях hjl и JiJ0 А. Динником приведены в таблице III.
Таблица III
o
0
0,2
0,4
0,6
0,8
l.o
1
f m 1
6,48
7,58
8,68
9,46
9,82
Я2
01
m 2
5,40
6,67
8,08
9,25
9,79
Jt2
U,1 i
j m 3
5,01
6,32
7,84
9,14
9,77
JI2
I m 4
4,81
6,11
7,68
9,08
.9,77
JI2
( m 1
7,01
7,99
8,91
9,63
9,82
JI2
0,2
m 2
6,37
7,49
8,61
9,44
9,81
n2
m 3
6,14
7,31
8,49
9,39
9,81
Я2
m 4
6,02
7,20
8,42
9,38
9,80
n2
f m 1
7,87
8,60
9,19
9,70
9,84
JI2
0,4
m 2
7,61
8,42
9,15
9,63
9,84
JI2
m 3
7,52
8,38
9,10
9,63
9,84
JI2
1
m 4
7,48
8,33
9,10
9,62
9,84
JI2
m 1
8,60
9,12
9,55
9,74
9,85
7l2
0,6
1 m 2
8,51
9,03
9,48
9,74
9,85
Я2
I m 3
8,50
9,02
9,47
9,74
9,85
JI2
1
m 4
8,47
9,01
9,45
9,74
9,85
JI2
j
m 1
9,27
9,54
9,69
9,83
9,86
JI2
0,8
m 2
9,24
9,50
9,69
9,82
9,86
JI2
m 3
9,23
9,50
9,69
9,81
9,86
JI2
1
m 4
9,23
9,49
9,69
9,81
9,86
JI2
1,0
ji2
я2
n2
я2
я2
JT2
Исследованием вопроса об определении наивыгоднейшей формы стержня, который при равной длине и одинаковом сопро¬
) А. Н. Д и н н и к. О расчете сжатых стоек переменного сечения. Вестник инженеров, 1927, № 8, стр. 333—335. Перепечатка: А. Н. Д и н н и к. Избранные труды. Том 3. Киев, Изд-во АН УССР, 1956, стр. 202—210. См. также A. F г а n k е, Knicksicherheit bei entsprechender Zunahme des Tragheitsmoments des Stabquerschnittes. Zeitschrift fur Architektur und Ingenieurwesen, Hannover, 1907, Bd. 53 (Bd. 12 der neuen Folge), SS. 471—482.
584
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
тивлении выпучиванию имел бы наименьший объем, занимался еще Ж. Лагранж1), но решение этого вопроса было получено значительно позднее Т. Клаузеном2) и Е. Николаи3). При этом было показано, что при одинаковой длине стержня и одинаковой величине критической нагрузки объем стержня переменного сечения будет менее объема стержня постоянного сечения в отношении У32. А. Франке4) исследовал продольный изгиб стоек, состоящий из нескольких частей призматической формы. И. Дондорф5) исследовал условия продольного изгиба для большого числа случаев при непрерывном и прерывном изменении осевой силы и поперечного сечения стержня. При решении таких задач можно пользоваться графическим методом, предложенным J1. Вианелло6). Эрих Трефтц7) указал на сходимость этого метода. Для определения влияния частичного ослабления поперечного сечения стержня на величину критической нагрузки можно воспользоваться энергетическим методом. Соответствующее исследование показывает, что для призматического стержня с шарнирно опертыми концами уменьшение площади поперечного сечения на протяжении небольшого участка d на расстоянии с от середины стержня вызывает такое же уменьшение критической нагрузки, какое вызвало бы увеличение длины стержня I на величину б. Эта величина б определяется уравнением
6 d-l- cos -j-, (40)
) J. L. Lagrange, статья, указанная на стр. 582.
2) Th. Clause n. Ober die Form architektonischer Saulen. Bulletin physico-math. de l’Academie de St.-Petersbourg, 1851, vol. 9, pp. 369—380.
3) E. Jl. Николаи. Задача Лагранжа о наивыгодиейшем очертании колонн. Известия С.-Петербургского политехнического института, Отделение техники, естествознания и математики, 1907, том 8, выпуск 1, стр. 255—288 Перепечатка: Е. Л. Николаи. Труды по механике. М., Гостехиздат, 1955, стр. 9—44 и Н. В 1 a s i u s. Trager kleinster durch Biegung und Stabe grosster Knickfestigkeit bei gegebenen Materialverbrauch. Zeitschrift fur Mathematik und Physik, 1913, Bd. 62, Heft 2, SS. 182—197.
4) A. Franke. Die Tragkraft der Saulen bei veranderlichem Querschnitt. Zeitschrift fur Mathematik und Physik, 1901, Bd. 46, Heft 4, SS. 419—434. Knicksicherheit bei entsprechender Zunahme des Tragheitsmoments des Stabquerschnittes. Zeitschrift fur Architektur und Ingenieurwesen, Hannover, 1907,
Bd. 53 (Bd. 12 der neuen Folge), SS. 471—482.
6) J. Dondorff. Die Knickfestigkeit des geraden Stabes mit veranderlichem Querschnitt und veranderlichem Druck. Dissertation, Dusseldorf, 1907.
6) L. V i a n e 11 o. Graphische Untersuchung der Knickfestigkeit gerader Stabe. Zeitschrift des Vereines deutscher Ingenieure, 1898, Bd. 42, № 52, SS. 1436—1443. См. также F. Engesser. Ober die Berechnung auf Knickfestigkeit beanspruchter Stabe aus Schweifi- und Flufieisen. Zeitschrift des Osterreichischen Ingenieur- und Architekten-Vereins, 1893, Bd. 45, № 38, SS. 506—508.
7) E. Trefftz. Allgemeine Theorie der Knickung des geraden Stabes. Zeitschrift fur angewandte Mathematik und Mechanik, 1923, Bd. 3, Heft 4, SS. 272—275.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
585
где — момент инерции поперечного сечения стержня, J — момент инерции ослабленного поперечного сечения на участке d. Как можно видеть, влияние ослабления поперечного сечения на критическую нагрузку тем больше, чем ближе ослабление сечения к среднему сечению стержня. Из этого можно заключить, что частичное ослабление поперечного сечения, как, например, от заклепочных отверстий, незначительно влияет на величину критической нагрузки; при этом предполагается, что гибкость стержня достаточно велика, чтобы явление продольного изгиба происходило в пределах пропорциональности1).
15. Продольный изгиб неразрезных стержней
Для исследования этого вопроса рассмотрим сначала изгиб сжатого стержня, к концам которого приложены два момента Mi и М2. В этом случае диффе-
ренциальное уравнение изогнутой » р х
оси имеет вид
9
Решив ЭТО уравнение И введя Рис. 15. Изгиб сжатого стержня, обозначение а2 Р27, найдем
для углов поворота концевых сечений 0j и 02 следующие значения (рис. 15):
01 Шг ф1 W ф2 02 W ф2 W ф1
где
Ф1
(а) 3 р), ф2 (а) 6 (—I .
' а2 а tg а ' 7 а sin а а2 Из уравнений (41) получим величину критической нагрузки стержня с упруго опертыми концами. Подставив в эти уравнения 0i —М1т, 02 —М2т2, где т и т2 — постоянные, зависящие от жесткости закрепления, будем иметь
(шф1 mr) 'W Ч‘ьЕ' “
МчМ Мг -О.
) A. F б р р 1. Mitteilungen aus dem mechanischen-technischen Laboratorium der technischen Hochschule in Miinchen. 1897, Heft 25, Munchen. Th. Ackermann. С. П. Тимошенко. К вопросу о продольном изгибе. Известия Киевского политехнического института, 1908, год 8, книга 2. стр. 181-212.
586 ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Критическое значение сжимающей силы Р найдем, приравняв нулю определитель этих двух уравнений. Отсюда получим следующее уравнение для вычисления критической силы1):
1 -pf(l “ m2) —p2rl j2 mm2 0. (42)
На рис. 2 изображен случай, когда mi оо и т2 0. Критическую силу получаем в этом случае из уравнения а tg а. Если гп оо, а т2 Ф 0, то из уравнения (42) получим
tg (а2) а2 EJ
а 1т2
tg а
Если mi оо и тг оо, то получим следующее уравнение для определения критической нагрузки:
tg (ct2)
- 22--0.
1--
tga
Выпучивание стержня может произойти при 1 а 2пп или
о i a a 2 tg-g -g.
Первое условие соответствует симметричным, а второе — несимметричным формам изогнутой оси искривленного стержня с заделанными концами.
Рассмотрим случай неразрезной балки, находящейся под действием сжимающих сил. Обозначим через 1у 12. длины следующих друг за другом пролетов, Ри Рч, — соответствующие силы, рассматриваемые как постоянные в каждом пролете, Мь М2,. — последовательные опорные моменты. Тогда из условий непрерывности можно составить уравнения трех моментов, аналогичные известным уравнениям Клапейрона. Положив
РА , РЛ
о 11 о
а -F7- , ей
EJi 9 2 EJ2
и пользуясь равенствами (41), получим уравнение трех моментов в таком виде:
Мп1п
6EJп ' ос, j fi он j fij
jf-Ф2(a„) Мп1 (зтФ. (a„) -3-EJn; ф1 (а )
Мп2 б' ФгСоп 1) 0 (43)
) См. Н. Zimmerman n. Zur Berechnung der Knickfestigkeit von Staben mit mehreren Feldem. Zentralblatt der Bauverwaltung, 1922, Bd. 42, № 65
SS. 389—393.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
587
Число этих уравнений равно числу промежуточных опор, а при свободно опертых концах — числу неизвестных опорных моментов М1). В этом случае критическая нагрузка определяется из того условия, что определитель системы уравнений (43) равен нулю.
Для балки, лежащей на трех опорах, уравнение (43) принимает вид
17Гф1 (“»зЙгГ4’»(ct2) 0,
и для определения критической нагрузки будем иметь уравнение
—(— Х-— —— (— о. (44)
EJ1 а2 ai tg otj EJ2 a a2 tg a2
Развитый выше метод можно применять и к стержням постоянного сечения на упругих опорах2), однако в случае стержней постоянного сечения, ежа- д
тых одинаковыми усилиями по всей длине, при наличии толь- р х
ко упругих промежуточных
опор проще принять за лиш- 1у
ние неизвестные опорные ре- С т, -
v рис Изгиб поперечной силои
акции, а не моменты. Для этого сжатого стержня,
первоначально рассмотрим изгиб сжатого стержня под влиянием поперечной силы (рис. 16). Если положить, как и ранее, а2 Р27, то уравнение изогнутой оси участка стержня, лежащего слева от точки приложения силы Q, будет иметь следующий вид:
гм ас
Ql sm г п
I . ах Qcx , v
У —5 : Sin—j 57— (а)
v Ра sin a I PI 47
Уравнение для участка стержня справа от точки приложения силы Q получим, заменив в уравнении (а) х на ( — х) и с на ( — с). В случае неразрезной балки с упругими промежуточными опорами обозначим через Ru R2,. опорные реакции, а через mRy m22, . соответствующие прогибы на этих опорах. Применив теперь уравнение (а) и приняв во внимание
) Если концы стержней заделаны, то к уравнениям (43) нужно добавлять два уравнения, выражающие условия задепки концов.
2) Н. Zimmerman n. Der gerade Stab auf elastischen Einzelstiitzen
mit Belastung durch langsgerichtete Krafte. Sitzungsberichte der Preussischen Akademie der Wissenschaften. Sitzung der physikalisch-mathematischen Klasse,
Berlin, 1907, erster Halbband, 7 Marz, SS. 235—244.
588
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
действие всех поперечных сил Ru 2, получим для г-й промежуточной опоры следующее уравнение:
lsin3r V. ai хг V
pasna 2uSn I PI Zuii
i-r i-r
IП—-7-— 'Vi ('-«,) lr 'v'
„J. - S 'sl-Ч-—ТГ ('-«) «) -1 -1
Здесь — полная длина стержня, с2,., сп — расстояния между последовательными опорами, считая от.правого конца стержня, и xr I — сг. Число уравнений типа (45) равно числу промежуточных опор. Если приравнять определитель этой системы уравнений нулю, то Рис. 17. Балка на трех опорах. получим уравнение для опре¬
деления критической нагрузки. Как пример рассмотрим балку, лежащую на трех опорах (рис. 17). Для этого случая получим уравнение
. ai. а2 п ”Sin —т—
-Rm R- — 1 llh R
Pa sin a PI 9
или
. alt. aU. (lil 2 Pm
Sin Sin -у- д sin a I —I. (46)
Если m 0, т. e. промежуточная опора жесткая, уравнение (46) имеет вид, тождественный уравнению (44). Если же т оо, то будем иметь балку на двух опорах, и уравнение (46) для определения критической нагрузки получит вид sin a 0 (т. е. a я), откуда получим известное эйлерово значение критической силы. Для всех промежуточных значений т (0 m 00) величины Р1р лежат между названными пределами. Наипростейший случай имеем при 1 2 2; уравнение (46) принимает вид
sin-2acos j(- —-)-siny 0. (b)
Наибольшего значения Р1ф достигает при т 0, т. е. когда промежуточная опора абсолютно жесткая. В этом случае каждая половина стержня будет находиться в условиях стержня с шарнирно опертыми концами и для вычисления Р1р будем иметь а2 я. При т оо средняя опорная точка не оказывает никакого сопротивления выпучиванию и для вычисления Ркр имеем a я. Для всех промежуточных значений т 2я a я.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
589
В этих границах sin (а2) 0 и cos (а2) 0. Стоящее в прямых скобках выражение в уравнении (Ь) равно нулю только при
Рт ч
—т- с)
Для всех значений т, меньших тех, что даются соотношением
(с), стоящий в прямых скобках член всегда будет отрицателен, а величина Ркр определится из условия а2 я и будет точно такая же, как и при совершенно жесткой промежуточной опоре. Для величин пг больших, чем те, которые определяются соотношением (с), критическую нагрузку можно найти, приравняв
нулю выражение, стоящее в уравнении (Ь) в прямых скобках.
Наименьшая жесткость, при которой во время выпучивания стержня можно считать опору абсолютно жесткой, определяется из зависимости (с). Она равна
1 3
пг
4кр 4 4я2 При 1Фк Лф находится из уравнения (46). Нижний предел для Ркр, соответствующий m оо, тот же, что и раньше, т. е. при а я. Верхний предел определится из условия пг 0. Соответствующее значение а должно быть менее 2я потому, что при а 2я правая часть уравнения (46) обращается в нуль, а левая часть становится отрицательной. При незначительном уменьшении значения а можно сделать обе части уравнения равными между собою. Из этого следует, что каждое смещение промежуточной опоры относительно середины вызывает соответственное уменьшение устойчивости стержня.
Если стержень имеет несколько равноудаленных друг от друга промежуточных опор одинаковой жесткости, определяемой коэффициентом п, то предельное значение силы, при которой опорные точки при выпучивании стержня не оседают, можно оп-
Р . 1
ределить из уравнения пг р—, гдег 1 —число пролетов,
П 1; кр
EJn(n)2
Кр 12
и р — числа, приведенные в таблице IV1).
Таблица IV
rt1
2
3
4
5
6
7
9
11
р
0,500
0,333
0,293
0,276
0,268
0,263
0,258
0,255
) И. Г. Бубнов. Строительная механика корабля. Часть 1. С.-Петербург, тип. морского министерства, 1912, стр. 259.
690
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
16. Сопротивление продольному изгибу сжатого стержня, лежащего на упругом основании
Этот вопрос представляет практический интерес в связи с расчетом сжатых поясов открытых мостов; для случая шарнирно опертых стержней он был исследован Ф. Энгессером1) и Ф. С. Ясинским2). При помощи энергетического метода можно весьма просто определить величину критической нагрузки3). Общее выражение для изогнутой оси можно в этом случае написать в следующем виде:
. пх. . 2пх. . Зпх , v
t a1sin—j—bflsin—р a3sin—. (a)
Потенциальная энергия деформации состоит из двух частей: энергии изгиба стержня и энергии деформации упругого основания. Допуская, что реакция основания пропорциональна прогибу у, и обозначая через ру величину этой реакции на единицу длины стержня, получим следующее выражение для энергии деформации:
у-Ч- (Ь)
О О
Если приравнять это выражение работе сжимающих сил Я, приложенных к концам стержня, то в результате получим
Чг I чЯ dx 2 у2'йх т (1г)2 dx с
О 0 0
или, подставляя вместо у его значение из выражения (а),
1) F. Engesser. Die Zusatzkrafte und Nebenspannungen eisener Fachwerksbriicke. Berlin, Verlag von Julius Springer, 1893.
2) Ф. С. Ясинский, работа, указанная на стр. 580.
8) С. П. Тимошенко. О продольном изгибе стержней в упругой среде. Известия С.-Петербургского политехнического института, 1907, том 7, вып. 1, стр. 145—157 и С. П. Тимошенко, статья, указанная на стр. 556.
Рис. 18. Продольно сжатый шарнирно опертый стержень, лежащий на упругом основании.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
591
найдем
ГС«о п оо
2 2 п4а2п Y 2
Р р „-со nl (d)
п
где
V-W- 47
Определим минимум величины Ркр с помощью выражения
(d). Это выражение будет иметь минимум, когда все коэффициенты аПу кроме одного, обратятся в нуль, а соответствующая форма выпученной оси представляет синусоиду у ansin(nuxl). Подставляя это выражение в соотношение (с), получим
Лф (п2 ). (48)
Число п в этом уравнении нужно выбрать так, чтобы правая часть уравнения обращалась в минимум. Если у— малая величина, то п нужно положить равным единице. Увеличивая постепенно у можно дойти до такого состояния, когда выпученная ось стержня с одной полуволной перейдет в кривую с двумя полуволнами, и тогда п 2. Соответствующее значение у получается из уравнения 1 у1 22 у22, откуда у 4. Продолжая наши вычисления, найдем то значение у, при котором кри¬
вая изгиба с п полуволнами переходит в кривую с п 1 полуволнами. Оно определится из уравнения
п2 - (п1)2 (п1)2 ,
откуда
у п2(п)2. (49)
Пользуясь этим уравнением, можно легко определить число п для любых значений у и при помощи уравнения (48) вычислить соответствующее значение Р,ф. Если у очень велико, то число п тоже велико, и уравнение (49) в этом случае можно заменить уравнением у пА. Подставив последнее выражение в формулу (48), найдем
р 2EJn2. (grn
''кр (г)2 КОЮ)
или, пользуясь уравнением (47),
Ркр 2 УЩ.
(51)
592
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
При этом длинный стержень при искривлении подразделяет
4
ся на короткие полуволны длиною ln nYEJр, и величина Лф будет вдвое больше эйлеровой критической нагрузки для шарнирно опертого стержня длиною я.
Если мы имеем сжатый стержень, свободно лежащий на упругом основании без опор на концах, то задача определения РКр является более сложной. Г. Циммерман ) исследовал частный случай, когда искривленная ось располагается симметрично относительно среднего сечения стержня. С. П. Тимошенко2) с помощью энергетического метода определил Ркр для несимметричных форм. Полное исследование этого вопроса дал Е. Хвалла3). Он показал, что для сжатого стержня, свободно лежащего на упругом основании, значение Р1ф можно вычислить из следующего трансцендентного уравнения:
1 — За2 sh (wa) ДЛЯ симметричной формы,
sin w ± -z—-2 — . (52)
о — я я )— для несимметричнои формы,
где
0 УЩ 2(г1) 1-
Произведенные вычисления показывают, что для возрастающих значений w число п приближается к предельному значению 2, соответствующему величине Ркр VEJ. Сравнивая это выражение с формулой (51), можно вывести, что для больших значений у, когда выпученный стержень подразделяется на большое число волн, шарнирное закрепление концов лежащего на упругом основании стержня может поднять величину критической нагрузки на 100. Исследование случая шарнирно опертого призматического стержня, лежащего на упругом основании под действием переменного по длине усилия, было произведено Ф. С. Ясинским4) и развито С. Г1. Тимошенко5). При распределении усилий по закону, представленному на рис. 19 штриховкою, критическое значение сжимающей силы q
) Н. Z i m m е г m a n n. Die Knickfestigkeit eines Slabes mit elastischer Quersliitzung. Berlin, W. Ernst und Sohn, 1906.
2) С. П. Тимошенко, статья, указанная на стр. 556.
3) Е. С h w а 11 a. Die Stabilitat eines elastisch gebetteten Druckstabes. Zeitschrift fiir angewandte Mathematik und Mechanik, 1927, Bd. 7, Heft 4, SS. 276—284.
4) Ф. С. Ясинский, работа, указанная на стр. 580. См. также Ф. С. Ясинский. Собрание сочинений. Том 2. С.-Петербург, Сборник Института инженеров путей сообщения, 1902, выпуск 58, § 11, стр. 17—20.
®) С. П. Тимошенко, статья, указанная на стр. 556.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
593
определяется выражением
(f)Kp - (53)
Коэффициенты к даны в таблице V.
Таблица V
уя4
16
0
5
10
15
22,8
56,5
1Q0
162,8
200
300
500
1000
и
‘20,5
35,9
50,3
63,6
74,9
94,0
118
149
164
197
237
326
Таблица VI
уя4
Тб
0
1
3
5
10
15
20
50
100
150
200
300
500
1000
и
0
2,00
6,02
10,0
20,0
29,9
33,6
53,1
85,3
129
145
177
233
319
Зависимость (53) можно применять и в случае сжатого стержня, свободно лежащего на упругом основании и нагруженного согласно рис. 19. Соответствующие значения коэффициента к приведены в таблице VI.
И. Дондорф1) исследовал продольный изгиб лежащего на упругом основании сжатого стержня переменного поперечного сечения. Обе таблицы V и VI применимы для расчета сжатых поясов открытых мостов. В этом случае, вместо непрерывного упругого основания, мы имеем отдельные упругие поперечные опоры. Если число этих опор значительно и они имеют одинаковую жесткость, то их влияние на критическую нагрузку можно заменить влиянием сплошного основания, жесткость которого определяется постоянной величиной р Way где W — величина силы, которую нужно приложить к верхнему концу стойки (упругой поперечной опоры), чтобы вызвать перемещение этого конца, равное единице, а — длина панели. Если
1) J. Dondorff, работа, указанная на стр, 584.
Рис. 19. Выпучивание шарнирно опертого
стержня под действием сжимающей силы, изменяющейся вдоль оси.
594
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
подобрать длину а так, чтобы вычисленная при этой длине критическая эйлерова сила была бы не менее чем втрое больше критической силы подпертого сбоку стержня, то при замене отдельных поперечных опор сплошной упругой средой не произойдет большой неточности в вычислении критической нагрузки ).
При применении энергетического метода можно определить боковую устойчивость сжатых поясов открытых мостов при допущении отсутствия непрерывного распределения боковых реакций и при переменном поперечном сечении, что соответствует действительным условиям решетчатых мостов2).
Для расчета сжатых поясов открытых мостов можно, как указал Г. Мюллер-Бреслау3), применить теорию неразрезных балок на упругом основании (см. § 10). Однако во многих случаях она приводит к очень громоздким вычислениям.
17. Продольный изгиб составных сжатых стержней
Для составных стержней величина критической сжимающей силы зависит не только от момента инерции поперечного сечения , но также и от жесткости соединительной решетки. Если эта решетка недостаточно жестка, то величина Ркр может оказаться значительно меньше, чем для сплошного стержня при одинаковом моменте инерции поперечного сечения. Это уменьшение критической силы происходит главным образом под влиянием поперечной силы, и это влияние значительно больше для составных стержней, чем для сплошных. При приближенных вычислениях критической силы для составных стержней можно пользоваться формулой (18), выведенной для сплошных стержней. При этом надо только учесть, что входящий в это уравнение множитель кGF имеет следующее значение: умножив его на величину поперечной силы, получим угол сдвига у нейтральной оси сплошного стержня. Для составного стержня величина vcGF должна быть заменена равнозначным выражением, выведенным отдельно для каждого типа решетки путем исследования деформации, вызываемой поперечной силой. Рассмотрим, например, стержень, представленный на рис. 20, а, где решетка составлена
) Это было доказано очень интересными опытами F. Engesser’a (см. Versuche und Untersuchungen uber den Knickwiderstand des seitlich gestutzten Stabes. Der Eisenbau, 1918, Bd. 9, № 2, SS. 28—34).
2) W. W i e r z b i с k i. О statecznosci pasow sciskanych w mostach otwartych. Sprawozdania i prace. Warszawskiego Towarzystwa Politechnicznego, Warszawa, 1922, tom 1, zcszyt 4, str. 28—39. См. также S. Kasarnowsky, D. Zetterholm. Zur Theorie der seiten Steifigkeit der Druckquere offener Fachwerkbrucken. Der Bauingenieur, 1927, Bd. 8, Heft 42, SS. 763—769.
3) H. Muller-Breslau. Die graphische Statik der Baukonstruktionen. Bd. 2, 2 Abteilung. Leipzig, Baumgartner А. Кгбпег, 1908, S. 309.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
595
из простых раскосов (диагоналей) и распорок, и исследуем деформацию одной панели, изображенной на рис. 20, Ь. Допустив, что стержни решетки имеют в узлах идеальные шарниры, найдем, что боковое перемещение ааь вызванное поперечной силою Q, состоит из двух частей: из перемещения, происходящего
d)
н
н
п
-2
Рис. 20. Выпучивание составного сжатого стержня.
от сжатия распорки СВ, и из перемещения, вызываемого удлинением диагонали ас.
Обозначив через Fa и Fp площади поперечных сечений диагонали и распорки, найдем
и угол сдвига равен
Qh , Qd о aUl EFP EFd Se ф’
q Qh. Qd sec2 ф
p p aEFa
Если в формулу (18) вместо кGF подставить выражение
h - d sec2 ф aEFd ’
596
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
то получим 1)
(54)
где
(55)
Из этого следует, что если площади поперечных сечений Fd и Fp очень малы по сравнению с площадью поперечного сечения поясов, то критическая нагрузка будет значительно меньше той, которая определяется формулой Эйлера. Формулу (55) можно применять и для расчета составного стержня с одними диагоналями без распорок, как то показано на рис. 20, с. Для этого нужно подставить в формулу (55) значение угла ср, отмеченного на рисунке, и исключить из выражения (55) член, содержащий величину Fp. При перекрестных диагоналях следует удвоить значение Fd в выражении (55) и отбросить член, содержащий величину Fp. В составных стержнях с перекрестными диагоналями и распорками в последних не возникают напряжения от поперечной силы. Критическую силу для таких стержней вычисляют так же, как и для стержней с пересекающимися диагоналями без распорок.
Изложенным выше способом может быть определена и критическая нагрузка для составного стержня, соединенного планками. Допустим, что точки перегиба поясов, изгибаемых в виде буквы S, лежат посредине панелей, и рассмотрим элемент, заключенный между двумя смежными точками перегиба (20, с). Легко видеть, что боковое перемещение аа, слагается из двух частей: из перемещения 6i Qa2h24EJP, вызываемого изгибом планки, и перемещения 62 Qa348EJq, вызываемого изгибом поясов. Угол сдвига равен
) Это решение было найдено сначала F. Engesser’oM. Die Knickfestigkeit gerader Stabe. Zentralblatt der Bauverwaltung, 1891, Bd. 11, № 49, SS. 483—486; Ober die Berechnung statisch unbestimmter Systeme. Там же, 1907, Bd. 27, № 93, SS. 606—607; Knicksicherheit von Gitterstaben. Zeitschrift des Vereines deutscher Ingenieure, 1908, Bd. 52, № 9, SS. 359—360. См. также L. Prandtl. Knicksicherheit von Gitterstaben. Zeitschrift des Vereines deutscher Ingenieure, 1907, Bd. 51, № 47, SS. 1867—1869 перепечатка:
L. Prandtl. Gesammelte Abhandlungen zur angewandten Mechanik, Hydround Aerodynamik. Erster Teil. Berlin, Springer-Verlag, 1961, SS. 87—93 и С. П. Тимошенко. К вопросу о продольном изгибе. Известия Киевского политехнического института, 1908, год 8, книга 2, стр. 181—212.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
697
Подставляя в формулу (18) вместо кQF выражение ah2EJp a22AEJq,
найдем, что коэффициент а соотношения (54) имеет в этом случае следующее значение:
При выводе этой формулы мы пренебрегали влиянием сжимающей силы на величину прогиба поясов 62. Если сжимающая сила Р2 не мала по сравнению с величиной n2EJqa2, то этим влиянием сжимающей силы на прогиб поясов пренебрегать нельзя, и выражение (56) нужно тогда заменить следующим ):
Выведенные на основании элементарных соображений зависимости (55), (56) и (57) дают вполне удовлетворительные решения, пока число панелей стержня п lа достаточно велико. В противном случае необходимо детальнее рассмотреть форму продольного изгиба составного стержня. Такие исследования составных стержней с простыми диагоналями (рис. 20, с) произвели Г. Мюллер-Бреслау2) и К. Люнберг3). Полное решение этого вопроса дал Р. Мизес4) в своей общей теории продольного изгиба стержневых систем. Его формула для критических нагрузок РКр при слабых диагоналях и большом числе панелей дает результаты, вполне совпадающие с выводами вышеприведенной элементарной теории. Для общего случая он приводит
) Эта формула дает результаты, вполне согласующиеся с опытами. См. С. П. Тимошенко, работа, указанная на стр. 556.
2) Н. Miiller-Breslau. Die neueren Methoden der Festigkeitslehre und der Statik der Baukonstruktionen. 4 Auflage. Leipzig, Alfred Kroner, 1913, S. 415.
3) K. L j u n b e r g. Auf Knickung beanspruchter Gitterstabe. Der Eisenbau, 1922, Bd. 13, № 1, SS. 100—105.
4) R. M i s e s. Ober die Stabilitatsprobleme der Elastizitatstheorie. Zeitschrift fur angewandte Mathematik und Mechanik, 1923, Bd. 3, Heft 6, SS. 406—422. См. также R. Mises, J. Ratzerdorfer. Die Knicksicherheit vcn Fachwerken. Zeitschrift fur angewandte Mathematik und Mechanik, 1925, Bd. 5, Heft 3, SS. 218—235.
(56)
(57)
PKp TC2EJg где P — :-p-
598
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
следующее выражение (рис. 20, с):
n2EJ х 1Лр’ где
K2 (±izltg я 2 п ±.
К я lg 41-2) ’ п а ’
I Л Jt 2 Fj 1
I2 g 4я — 2 C0S2n) Р 77 2 sin3 ф
Коэффициенты к2 и Я для некоторых значений я даны в таблице VII.
Таблица VII
n
2
3
4
5
10
oo
X2
1,216
1,070
1,035
1,020
1,004
1
X
0,6667
0,3167
0,1778
0,1125
0,0269
0
Дальнейшие исследования по теории стержней, соединенных планками, произвели Г. Мюллер-Бреслауl), JI. Манн2) и М. Грюнинг3). Последний дает для значения критической нагрузки следующую формулу (обозначения см. на рис. 20, е):
(59)
где
t n2EJ (ah. а2
К “ 2 I 12р 24р j
2лг2 Л jx
СО —5” 1 — cos—. л2 п )
Для больших значений п величину со можно приравнять к единице, и формула М. Грюнинга становится идентичной с формулой (56). Общую теорию устойчивости ферм разработал Р. Мизес4).
)' Н. М й 11 е г - В г е s 1 а и. Die neueren Methoden der Festigkeitslehre und der Statik der Baukonstruktionen. 4 Auflage. Leipzig, Alfred Kroner, 1913, S. 380.
2) L. Mann. Statische Berechnung steifer Vierecknetze. Zeitschrift fur Bauwesen, 1909, Bd. 59, Heft 10—11, SS. 539—568.
3) M. G runing. Die Statik des ebenen Tragwerkes. Berlin, Verlag von Julius Springer, 1925.
4) R. Mises, статья, указанная на стр. 555 и R. М i s е s, J. R a t z е rd о r f e r. Die Knicksicherheit von Rahmentragwerken. Zeitschrift fiir angewandte Mathematik und Mechanik, 1926, Bd. 6, Heft 3, SS. 181—199. Cm. также H. Muller-Breslau. Zur Berechnung der Knicklast des Rahmenstabes. Zeitschrift fiir angewandte Mathematik und Mechanik, 1924, Bd. 4, Heft 6, SS. 487—490.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
599
18. Устойчивость ферм
Теорию упругой устойчивости ферм разработал Р. Мизес1)В дальнейшем приводятся некоторые результаты его исследований. Рассмотрим плоскую ферму с k узлами, связанными между собою 5 прямыми стержнями, и имеющую т опорных закреплений. Предположим, что система находится в «естественном» состоянии, при котором на нее не действуют никакие внешние или внутренние силы. Обозначим через I естественную длину стержня, а через а длину стержня при каком-либо напряженном состоянии системы. Тогда действующая на стержень сила равна SEF(a — ). Для каждого деформированного состояния имеется только одна система сил, при которой ферма находится в равновесии. Для определения этих сил располагаем находящуюся в равновесии ферму в декартовой системе координат х и у, причем координаты k-vo узла обозначим Xh и , а через atk — угол между осью х и стержнем tk, лежащим между узлами Т и К. Угол будем отсчитывать от положительной оси х до стержня против направления часовой стрелки. Составляющие Xh и Yh внешней силы, приложенной к k-ыу узлу, определяются из следующих уравнений равновесия:
где суммирование распространено на все стержни, примыкающие к узлу k. Для выяснения устойчивости какого-либо определенного деформированного состояния Р. Мизес рассматривает потенциальную энергию системы. Состояние равновесия будет устойчивым, если потенциальная энергия имеет минимальное значение, т. е. если любому бесконечно малому перемещению при заданных опорных условиях соответствует положительная затрата работы. Потенциальная энергия деформации фермы равна
t t
или
t
t
tk
а работа внешних сил будет
L — 2 Xkxk Y kyk).
k
l) R. Mises, статья, указанная на стр. 555.
600 ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Отсюда выражение для полной энергии системы напишется так:
и i 2 -Т- а - 01, - 2 ( (Ь)
tk k
Функцию надо понимать как функцию от 2k— т независимых координат х и у, которые связывают а и а следующими геометрическими зависимостями:
ат (Л - xtf yk - ytf atk (yk - vi) ' (xk - xt)-
Для исследования устойчивости равновесия данного состояния системы дадим каждому узлу, насколько это позволяют опорные условия, бесконечно малые перемещения 6х, 6 у. Тогда
6atk 6(xk- xt) cos atk 6 (yk- yt) sin aik,
atk - 6 (xk - xt) sin atk 6 (yk- yt) cos atk
и на основании начала возможных перемещений dU
(с)
S -у- (а - 1) C0S a(fe - хк 0.
дуь 2(а-05та-Г,0.
дх k t
dU
(a')
Такой же вид имеют уравнения равновесия (а), выведенные выше на основании статических соображений. Работа, затраченная на переход к смежному состоянию, равна
dU я , dU ,
бижгб1 жбг1
, 1 Г U. , , д2и. , , 0 д2и. , 1 ,
jbXiybyi2;bXibyi (d)
На основании равенств (а') совокупность членов первого порядка в уравнении (d) равна нулю; для того чтобы определить знак бU, надо рассмотреть члены второго порядка. Эти члены, отбрасывая коэффициент 12, можно переписать в таком виде:
д г dU х , dU х , dU Л , 1 ,
1 дх, дх, 1 ду, дх2 2 J
I . (е)
причем знак дифференцирования перед каждой скобкой относится только к первым множителям каждого слагаемого, а не
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
601
к 8х, б у. Все члены суммы (е) представляют собою однородные выражения второй степени относительно перемещений 6, б у. Обозначая для сокращения элементы суммы (е), или вторые производные от U, через схи С2, схъ, , с2и 22, , сзи с32, приходим к такому вопросу: когда выражение
спЬх 2с2Ьх1Ьу1 с1ъЬххЬх2. (f)
будет давать только положительные значения, чтобы U с учетом только членов второго порядка обращалось в минимум Основываясь на теории квадратичных форм, Р. Мизес установил для положительных значений выражения (f) следующие условия:
1. Необходимо (но еще недостаточно), 'гобы определитель коэффициентов с был положителен.
2. Если считать с переменным, т. е. рассматривать различные формы равновесия, то переход из устойчивых форм равновесия в неустойчивые формы будет характеризоваться тем, что определитель, составленный из коэффициентов с, обращается в нуль (без того, однако, чтобы имела место инверсия; переход точки, для которой детерминант равен нулю, не должен еще неминуемо приводить ее в неустойчивую область).
3. Для устойчивости необходимо и достаточно, чтобы был положительным не только определитель в целом, но и каждый определитель, который мы получаем от общего, отбрасывая в нем последние ряды и столбцы, был положителен, т. е.
с с2
сп
С2
С13
о,
С2
с22
С23
С21 с22
С3
С32
сгз
Для практического применения особенно важно второе из вышеприведенных условий: устойчивые формы равновесия всегда отделены от неустойчивых такой формой, для которой определитель коэффициентов с обращается в нуль. Приравненный нулю определитель с Мизес называет «уравнением неустойчивости» и приходит в конечном итоге к следующим заключениям: если имеет место ненапряженное состояние, то оно всегда устойчиво; действительно, если все а равны , то U 0; кроме того, U, как сумма квадратов, имеет только положительные значения, поэтому каждое изменение формы, если оно вообще вызывает напряжения, нуждается в положительной затрате работы. Рассмотрим ряд форм равновесия, при которых внешние силы отличаются между собою общим коэффициентом К и изменяются пропорционально этому коэффициенту. Если в уравнение неустойчивости подставить XX, XY, то получим уравнение относительно X, и
602
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
нужно только найти для него минимум. Для всех Л, меньших этой величины, имеем устойчивое состояние системы, так как переход от устойчивого- положения при нулевых напряжениях к неустойчивому должен произойти через положение, соответствующее уравнению неустойчивости. Если, кроме того, известно, что эта величина К есть простой корень уравнения неустойчивости, то его левая часть, т. е. определитель величин с, меняет свой знак. Для больших значений К имеем неустойчивое положение равновесия.
Применение этих общих положений можно найти в оригинальной работе Р. Мизеса.
19. Продольный изгиб винтовых пружин
Если винтовая пружина подвергается осевому сжатию, то при достижении сжимающей силой определенной границы пружина может выпучиться. Это значение сжимающей силы является критической силой пружины. Эта задача была исследована Е. Хурльбринком ), Р. Граммелем2), а также К. Бицено и Я. Кохом3). Установив законы поперечного изгиба винтовой пружины, можно затем определить значение критической нагрузки, пользуясь тем же методом, что и для призматических стержней. При этом необходимо принять во внимание также сжатие пружины, так как здесь оно значительно и им нельзя пренебрегать, как то делается при исследовании устойчивости стержней. Влияние поперечной силы также значительно, поэтому нужно исходить из выражения, аналогичного формуле (18). Пусть а — диаметр стержня пружины, г—радиус винтовой линии, п — число витков, h0 — высота шага витка, 0 nh0 — первоначальная высота пружины. Обычное приближенное уравнение для вычисления осадки пружины имеет вид
б OqPIo, (а)
где cto 4r3a4h0G.
Жесткость на изгиб винтовой пружины с большим числом витков равна
О EG и
р“ 2nr E 2G W
) Е. Hurlbrink. Berechnung zylindrischer Druckfedern auf Sicherheit
gegen seitliches Ausknicken. Zeitschrift des Vereines deutscher Ingenieure,
1910, Bd. 54, No 4, SS. 133—137; № 5, SS. 181 — 184.
2) R. G r a m m e 1. Die Knickung von Schraubenfedern. Zeitschrift fur angewandte Mathematik und Mechanik, 1924, Bd. 4, Heft 5, SS. 384—389.
3) С. В. В i e z e n o, J. J. Koch. Die Knickung von Schraubenfedern
Zeitschrift fur angewandte Mathematik und Mechanik, 1925, Bd. 5, Heft 3,
SS. 279—280.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
603
Величина, характеризующая жесткость пружины по отношению к поперечной силе (соответствующая величина для стержня сплошного сечения) составляет
4пг3 , ч
Yo_ ЕаН0
Если пружина сжата до новой высоты I, то она становится тем более податливой по отношению к изгибу и сдвигу, чем
Ркр К, h
0,8 i 0,7 0.6 0,5 0,4 0,3 02 Ш
V
л
ч
ч
—-г
10
Рис. 21. Критическая сила продольно сжатой винтовой пружины.
больше будет иметь витков на единицу длины. Поэтому вместо формул (Ь) и (с) будем использовать следующие:
„ а40 EG I 4пг3 10
Р 2пГ 20 77’ Y Еа4 Т ‘
Вводя в выражение (18) Р и у вместо EJ и xG7, получим
п Ро ГкР “ И о
1 2 PoYo
Подставляя1) вместо Ркр значение (о— 1)а010 и полагая z 0, получим следующее уравнение для вычисления г:
Z3 - г2 К- (PoYo РоОо) 2 - 0.
12о
(d)
Это уравнение имеет только один вещественный, а именно положительный, корень, который определяет осадку, при которой наступает явление продольного изгиба. Соответствующая критическая нагрузка может быть легко вычислена с помощью выражения (а). Зависимость ЯКраоо от отношения 0г по вычислениям К. Бицено и Я. Коха приведена на рис. 21.
1 На основании равенства (а).
604
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
20. Устойчивость вала при кручении
Как известно, длинный вал, скручиваемый парами сил, может потерять устойчивость: его ось начнет искривляться. При вычислении критического значения крутящего момента Мкр исходят из того, что призматический стержень с одинаковой изгибной жесткостью под действием двух на концах приложенных крутящих пар обнаруживает винтообразную форму равновесия ’).
Положим, что — длина стержня, (я2) — а — угол между осью цилиндра и касательной к винтовой линии, г — радиус цилиндра, на котором лежит искривившаяся по винтовой линии ось бруса. Кривизна и угол закручивания кривой соответственно при этом равны
1 cos2 а
7
sin а cos а
т .
г
Обозначая через М крутящий момент и через В жесткость при изгибе, получим
В cos2 а ,,
—-— - М cos а,
или (а)
,, В cos а
М .
г
Если величина крутящего момента М достаточна для того, чтобы удержать стержень от смещения концов, и осевая линия вала при искривлении образует как раз полный виток винтовой линии, причем радиус ее очень мал, то угол а винтовой линии с большим приближением можно принять равным я2. Тогда cos а 2яг, и из уравнения (а) получим
Мкр --. (60)
А. Гринхил2) рассмотрел случай стержня, одновременно подвергающегося действию осевой сжимающей силы Р и крутящего
) G. R. Kirchhoff. Ober das Gleichgewicht und die Bewegung eines unendlich diinnen elastischen Stabes. Journal fur die reine und angewandte Mathematik (Crelles), 1859, Bd. 56, SS. 285—313 или G. R. Kirchhoff. Vorlesungen iiber mathematische Physik. Bd. 1. Vorlesungen iiber Mechanik. 3 Auflage. Leipzig, B. G. Teubner, 1883, 455 S. Перевод на русский язык
с 4-го издания 1897 года: Г. Кирхгоф. Механика. Лекции по математиче¬
ской физике. М., Изд-во АН СССР, 1962, 402 стр.
2) A. G. G г е е n h i 11. On the strength of shafting when exposed both to
torsion and to end thrust. Proceedings of the Institution of Mechanical Bnffl-
neer», 1883, pp. 182-209,
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
605
момента М. Для вычисления критической величины сил, действующих на вал, он дал следующее уравнение:
Р. М2 _ тс2 (
В 4В2 I2
При Р 0 это выражение совпадает с формулой (60). Для случая М 0 имеем эйлерово значение критической нагрузки.
Р. Граммель1) исследовал продольный изгиб вала переменной жесткости.
Устойчивость винтовой линии изогнутого и закругленного стержня исследовал Е. Л. Николаи2).
21. Устойчивость замкнутого кругового кольца при действии равномерного внешнего нормального давления
Положим, что под действием внешнего давления круговое кольцо сплющилось и приняло форму эллипса3), как это показано на рис. 22. Обозначим через г радиус центральной оси кольца; р — внешнее нормальное давление на единицу длины; EJ — жесткость кольца при изгибе; и — радиальное перемещение при сплющивании; 0 — угол после изгиба, отсчитываемый от горизонтальной оси АВ
М0 и S0—изгибающий момент и продольное сжимающее усилие в поперечном сечении А
Uo — радиальное перемещение в том же сечении. Тогда
S0 Р (г - «о).
Рассматривая перемещения и как величины малые и пренебрегая малыми величинами высшего порядка, получим изгибающий момент М в каком-либо поперечном сечении С:
М М0 — рг (щ — и).
) R. Grammel. Das kritische Drillungsmoment von Wellen. Zeitschrift iur angewandte Mathematik und Mechanik, 1923, Bd. 3, Heft 4, SS. 262—271.
2) E. JI. Николаи. К задаче упругой линии двоякой кривизны. Дис¬
сертация. Петроград, 1916. Перепечатка: Е. И. Николаи. Труды по ме¬
ханике. М., Гостехиздат, 1955, стр. 45—277. Е. L. Nicolai. Uber die
Stabilitat des zu einer Schraubenlinie gebogenen und gedrillten Stabes.
Zeitschrift fur angewandte Mathematik und Mechanik, 1926, Bd. 6, Heft 1,
SS. 30—43.
8) Мы рассматриваем здесь только перемещения в плоскости центральной оси стержня. Выпучивание кривого стержня из своей плоскости рассматривается в § 25.
Рис. 22. Выпучивание замкнутого кругового кольца.
606
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Дифференциальное уравнение равновесия1) изогнутой центральной оси стержня напишется так:
l “) “ Мй рг(щ-и). (а)
Общее решение этого уравнения будет
и сх sin kQ с2 cos kQ где c и C2 — произвольные постоянные, а
2 i-. (Ь)
Для удовлетворения условий симметрии (§)0_о т ® необ-
ходимо, чтобы sin(tt2) 0. Наименьший корень этого уравнения, дающий критическую величину внешнего давления, равен k 2; тогда из уравнения (Ь) получим
3 EJ соч
Ркр “ Г3 (62)
Это известная формула М. Леви2). К такому же результату придем, если представим перемещения в виде тригонометрического ряда и применим энергетический метод3). Согласно уравнению (а) при давлении большем кр, деформация кольца ста¬
новится неопределенной. В этом случае для вычисления прогиба необходимо вместо приближенного уравнения (а) применить точное. Ж- Альфан4) и А. Гринхил5) с помощью эллиптических функций дали точное решение задачи. К. Федерхофер6) дал приближенное решение для деформаций сжатого кольца.
) Дифференциальное уравнение деформации кругового кольца установил J. Boussinesq. Resistance d’un anneau a la flexion, quand sa surface exterieure supporte une pression normale, constante par unite de longueur de sa fibre. Comptes rendus des seances de l’Academie des sciences, 1883, vol. 97, № 15, pp. 842—848.
2) M. Levy. Memoire sur un nouveau cas integrable du probleme de l’elastique et l’une de ses applications. Journal de mathematiques pures et appliquees (Liouville Journal), Series 3, Paris, 1884, tome 10, pp. 5—42.
3) G. H. Bryan. Application of the energy test to the collapse of a thin long pipe under external pressure. Proceedings of the Cambridge Philosophical Society, 1888, vol. 6, pp. 287—292.
4) G. H. H a 1 p h e n. Sur une courbe elastique. Comptes rendus des seances de l’Academie des sciences, 1884, vol. 98, № 7, pp. 422—428. См. также G. H. H a 1 p h e n. Traite des fonctions elliptique et de leurs applications. Part 2. Paris, Gauthier-Villars, 1888.
5) A. G. Greenhill. The elastic curve under uniform normal pressure. Mathemalische Annalen, 1899, Bd. 52, SS. 465—500.
6) K. Federhofer. Ober die Berechnung der Einbeulung des gleichmaflig gedruckten Kreisringes. Verhandlungen des zweiten internationalen Kongresses fur technische Mechanik, Zurich, 1926. Zurich und Leipzig, Fussli, 1927, SS. 388—392.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
607
22. Круговая арка под равномерным нормальным давлением
Устойчивость круговой арки любого пролета исследовали Е. Хурльбринк ), С. П. Тимошенко2), Р. Майер3) и Е. JI. Николаи4). Для того, чтобы длина центральной линии при изгибе оставалась неизменной, необходимо допустить, что кривая изгиба имеет несимметричную форму (рис. 23). Соответствующее дифференциальное уравнение получим из уравнения (а) § 21, подставляя в него и0 М0 0.
Тогда и С sin kQ с2 cos kQ. Для того, чтобы удовлетворялись условия (и) е0, еа 0, необходимо, чтобы С2 0 и ka я. Последнее условие дает
Ркр- г3 а2 AJ-
Рис. 23 Выпучивание круговой арки при равномерном давлении.
Если а я2, формула (63) совпадает с выражением (62).
Если а мало, то в скобках зависимости (63) можно пренебречь единицею, и тогда получим
с 47я2 ,ал.
кр — ркрг — (2га)2
Критическая нагрузка та же, что и для призматического
стержня с жестко заделанными концами длиною, равною длине оси
т,. лмтт арки. В случае очень малой
Таблица VIII J
величины а, т. е. для очень
пологих арок, сжатие арки оказывает заметное влияние на критическую нагрузку, и потому оно должно быть принято во внимание. Опыты Р. Майера5) с равномерно нагруженными арками подтверждают вышеизложенную
a
30
60
90
120
150
180
ni
8,62
4,38
3
2,36
2,07
2
) Е. Н и г 1 b г i n k. Festigkeits-Berechnung von rohrenartigen Кбгрегп, die unter ausserem Drucke stehen. Schiffbau, 19071908, Bd. 9, JSTs 14, SS. 517—523.
2) С. П. Тимошенко. Об устойчивости упругих систем. Известия Киевского политехнического института, 1910, год 10, книга 4, стр. 375—560. Отд. оттиск, Киев, тип. С. В. Кульженко, 1910, 188 стр.
3) R. М а у е г. Ober Elastizitat und Stabilitat des geschlossenen und offenen Kreisbogens. Zeitschrift fiir angewandte Mathematik und Physik, 1912, Bd. 61, Heft 3, SS. 246—320 и R. Mayer. Die Knickfestigkeit. Berlin, Verlag von Julius Springer, 1921, S. 127.
4) E. L. Nicolai. Stabilitatsprobleme der Elastizitatstheorie. Zeitschrift
fiir angewandte Mathematik und Mechanik, 1923, Bd. 3, Heft 3, SS. 227—229.
6) R. Mayer. Die Knicksicherheit in sich versteiften Hangebriicken, sowie des Zwei- und Dreigelenkbogens innerhalb der Tragwandebene. Der Eisenbau.
1913, Bd. 4, № 12, SS. 423—428.
608
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
теорию. Для случая заделанных концов1) имеем
РкР тЙт2-1), (65)
где т — ближайший к единице корень уравнения
т a ctg та a ctg а.
Для некоторых значений угла а в таблице VIII приведены соответствующие величины т.
Задача об устойчивости кривого стержня, составленного из двух полос разного материала, и его деформации при нагревании вследствие разницы между коэффициентами линейного температурного расширения этих материалов была обсуждена С. П. Тимошенко2).
II. УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА
23. Устойчивость плоской формы изгиба стержней с очень узким прямоугольным поперечным сечением
Хорошо известно, что стержень с весьма различными по величине моментами инерции поперечного сечения относительно главных осей при изгибе его в плоскости наибольшей жесткости может потерять устойчивость и выпучиться. Первые задачи этого рода были обсуждены Людвигом Прандтлем 3) и А. Мичеллом 4), которые исследовали случай очень узкого прямоугольного поперечного сечения.
а) Чистый изгиб. Рассмотрим стержень длиною I с узким прямоугольным поперечным сечением, изгибаемый двумя парами сил, приложенными по концам и действующими в плоскости наибольшей жесткости. Когда изгибающие моменты достигнут некоторого критического значения Мкр, произойдет боковое выпучивание оси стержня. Если считать, что концы стержня могут свободно поворачиваться относительно главных осей х и у, но что вращению концов вокруг оси стержня z пре¬
) Е. Л. Н и к о л а и, статья, указанная на стр. 607.
2) S. Timoshenko. Analysis of bi-metal thermostat. Journal of the
Optical Society of America and Review of Scientific Instruments, 1925, vol. 11,
№ 3, pp. 233—255.
3) L. P r a n d 11. Kipperscheinungen. Ein Fall von instabilem elastischem Gleichgewicht. Dissertation der Universitat Munchen, 1899. Niirnberg, 1900, SS. 1—75. Перепечатка: L. P r a n d 11. Gesammelte Abhandlungen zur angewandten Mechanik, Hydro- und Aerodynamik. Erster Teil. Berlin — Gottingen — Heidelberg, Springer-Verlag, 1961, SS. 10—74.
4) A. G. M. Michel 1. On the elastic stability of long beams under transverse forces. Philosophical Magazine and Journal of Sciences, London — Edinburgh — Dublin, series 5, 1899, vol. 48, № 292, pp. 298—309.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
609
пятствуют закрепления, то искривленная форма стержня будет иметь вид, показанный на рис. 24. Боковое выпучивание стержня связано, как видно, с его кручением.
Рис. 24. Устойчивость плоской формы в случае чистого изгиба.
Рис. 25. Устойчивость плоской формы изгиба в случае консольного стержня.
Если В и В2 — главные жесткости стержня при изгибе, С — жесткость его при кручении, то получим следующие дифференциальные уравнения равновесия (рис. 25):
M № В2, М-с. (а)
Критическое значение момента для стержня с шарнирно опертыми концами равно Мкр. (66)
Соответственно для стержня с заделанными концами будем
иметь Мкр 2kVB_' (67)
Оба выражения аналогичны формуле продольного изгиба
Эйлера. Критический момент не зависит от наибольшей жест
610
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
кости изгиба В ). Он пропорционален VВ2С и обратно пропорционален длине стержня. Формулы дают удовлетворительные результаты до тех пор, пока соответствующие напряжения изгиба ниже предела пропорциональности материала.
В основу этой теории легли приближенные соотношения (а). Они достаточны для вычисления критической величины изгибающего момента, но деформации остаются неопределенными. Их можно вычислить, только применяя точные дифференциальные уравнения2).
Рис. 26. Устойчивость плоской формы изгиба в случае стержня, нагруженного в середине.
Ь) Стержень с одним заделанным концом, нагруженный силой Р на свободном конце. Располагая координатные оси, как показано на рис. 25, и применяя прежние обозначения, получим критическую силу
Ркр 4,013-. (68)
с) Стержень, нагруженный сосредоточенною силою Р посредине. В этом случае (рис. 26) критическая нагрузка равна
16,93 В2С
кр
(69)
Если точка приложения силы Р находится над центральной осью стержня, то критическое значение нагрузки уменьшается.
2) Это связано с допущениями, сделанными при выводе уравнения (а). Они равнозначны предположению, что В с». Ср. Н. К е i s s n e г. Ober die Stabilitat der Biegung. Sitzungsberichte der Berliner mathematischen Gesellschaft (Beilage zum «Archiv der Mathematik und Physik»), 1904, Bd. 3, SS. 53—56.
2) K. Federhoffer. Berechnung der Auslenkung beim Kippen gerader Stabe. Zeitschrift fur angewandte Mathematik und Mechanik, 1926, Bd. 6, Heft 1, SS. 43—48.
ПРОБЛЕМЫ упругой устойчивости 611
Обозначая через а расстояние точки приложения силы от оси, найдем ) Ркр (l - 1,74у i-) (70)
А. П. Коробов2) и А. Н. Динник3) исследовали случай, при котором сила Р приложена не посредине длины стержня. Критическую нагрузку при любом положении точки приложения силы по длине стержня можно вычислить по формуле
р у-Ус
кр 12 9
где коэффициент х изменяется в зависимости от расстояния с — точки приложения силы — от ближайшей опоры; значения его приведены в таблице IX.
Таблица IX
с
1
0,50
0,45
0,40
0,35
0,30
0,25
0,20
0,15
0,10
0,05
X
16,93
17,15
17,82
19,04
21,01
24,10
29,11
37,88
56,01
111,6
d) Другие случаи нагрузки. В случае стержня, опертого обоими концами, критическое значение равномерно распределенной вдоль оси нагрузки равно
, А 28,3 VbC ,_1Ч
(70кР р-2— (71)
Для стержня с заделанными концами, нагруженного посредине, имеем Якр -26С'. (72)
Для равномерно нагруженного стержня с одним заделанным концом
Мкр- 12’85ЛС (73)
1) Этот результат выведен в предположении, что а мало по отношению к. Более полное исследование этого вопроса было выполнено А. П. Коробовым: Устойчивость плоской формы изгиба полосы. Известия Киевского политехнического института, 1911, год И, книга 4, стр. 247—264.
2) А. П. Коробов, см. указанное выше исследование.
8) А. Н. Динник. Об устойчивости плоской формы изгиба. Известия Донского политехнического института. Новочеркасск, 1913, часть 2, отд. 2, стр. 47—78. Перепечатка: А. Н. Динник. Избранные труды. Том 1. Киев, Изд-во АН УССР, 1952, стр. 115—141.
612 ПРОБЛЕМЫ УПРУГОЙ устойчивости
24. Устойчивость плоской формы изгиба двутавровых балок
Этот вопрос исследовал С. П. Тимошенко1) и показал, что в этом случае сопротивление балки зависит не только от жесткости кручения С, но также и от жесткости изгиба полок балки.
Обозначим через р угол закручивания, и — перемещение полки, вызываемое закручиванием (рис. 27), h — высоту балки, D —
Рис. 27. Кручение двутавровой балки.
жесткость изгиба одной полки. Тогда вызываемую закручиванием поперечную силу в полке балки получим из уравнения
У U dz3 2 dz3 '
Для того, чтобы получить полную величину крутящего момента Я, нужно к моменту Cddzy вызываемому собственно кручением, присоединить момент Qh. Таким образом
и -г At - Dh2 Л.
п dz 2 dz3 '
Для того, чтобы получить дифференциальные уравнения устойчивости плоской формы равновесия для случая двутавровой балки, необходимо в уравнения равновесия § 23 ввести вместо С ddz выражение Н. Рассматривая, например, балку с шарнирно опертыми концами (см. рис. 26), будем иметь
R d2u _ Р ( I р r Dh2 d3 _ Р ( I du Ри
dz2 2 2 Z)С dz 2 dz3 2 2 Z) dz 2 9
откуда
d'fi 2С d2 Р2 (I 2о_0 dz4 Dh2 dz2 2B2 Dh2 2 P
) С. П. Тимошенко. Об устойчивости плоской формы изгиба двутавровой балки под влиянием сил, действующих в плоскости ее наибольшей жесткости. Известия С.-Петербургского политехнического института, 1905, тем 4, выпуск 3—4, стр. 151—219; 1906, том 5, выпуск 1—2, стр. 3—34, выпуск 3—4, стр. 263—292. См. также S. Timoschenko. Einige Stabilitatsprobleme der Elastizitatstheorie. Zeitschrift fur Mathematik und Physik, 1910, Bd. 58, Heft 4, SS. 337—385.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
613
Интегрируя это уравнение, находим критическую силу
kVBC
Р
г кр
I2
(74)
где коэффициент k зависит от величины т2 2Cl2Dh2. Некоторые значения коэффициента k приведены в таблице X. Соответствующее критическое напряжение равно
oK PKplEh8B (75)
или, если подставить В2 2D,
__km_ р В2 h2 ар 16 Bi I2
В третьей строке таблицы X критические напряжения вычислены при следующих данных:
Е 2 10е кгсм2 и (В2В,) (Л22) (Г4-
Таблица X
т2
0,4
4
8
16
24
32
48
64
80
96
160
240
320
400
k
кр
86,4
680
31,9
800
25,6
910
21,8
1090
20,3
1250
19,6
1380
19,0
1620
18,3
1830
18,1
2020
17,9
2190
17,5
2770
17,4
3360
17,2
3860
17,2
4300
4
405
505
600
770
920
1050
1280
1490
1670
1840
2420
3020
3500
3940
1150
1250
1350
1520
1670
1860
2030
2240
2420
2580
3160
3740
4240
4680
При расчетах этой таблицы принято, что точка приложения силы лежит на оси балки. Смещение точки приложения силы вверх уменьшает, а вниз — увеличивает значение PKV и акр. Приведенные в четвертой и пятой строках таблицы X величины а' и а''р дают критические напряжения для тех случаев, когда точка приложения силы совпадает с верхней или нижней полкой балки.
В случае равномерно распределенной нагрузки величина (7)нр находится также по формуле (74). Соответствующие значения коэффициента k и критические напряжения для трех разных способов приложения нагрузки приведены в таблице XI.
Таблица X
т3
0,4
4
8
16
24
32
48
61
80
128
2Э0
280
360
400
k
7кр
143
568
53,3
663
42,6
752
36,3
905
33,8
1040
32,6
1150
31,5
1350
30,5
1530
30,1
1680
29,0
2080
29,0
2570
28,8
3020
28,6
3400
28,6
3580
4
367
454
538
684
813
923
1120
1290
1440
1840
2330
2770
3160
3330
кр
879
967
1050
1200
1330
1430
1630
1810
1960
2350
2840
3280
3670
3840
614
ПРОБЛЕМЫ УПРУГОЙ устойчивости
С. П. Тимошенко1), используя энергетический метод, рассмотрел ряд других случаев устойчивости плоской формы равновесия двутавровых балок. Им произведены также исследования устойчивости при напряжениях выше предела пропорциональности материала2).
25. Устойчивость плоской формы изгиба кривых стержней и колец
Для решения этого вопроса используем известные дифференциальные уравнения равновесия криволинейных стержней3). Введем подвижную систему координат xyz ось z направим по
касательной к деформированной оси стержня, а оси х и у — по главным осям поперечных сечений. Составляющие перемещения по направлениям подвижных осей обозначим через и, v, w, а угол закручивания — через р (рис. 28). Рассмотрим стержень с круговой центральной осью и обозначим через 0 центральный угол, который будем отсчитывать от неподвиж-
Рис. 28. Изгиб элемента криволинейного стержня.
ного радиуса-вектора. Тогда для изгибающих моментов Afi и М2 и для крутящего момента Н (рис. 28) будем иметь следующие выражения:
dw
dQ
)
dQ2
н-(ж '-§)-
(«)
где B и B2 представляют собою главные жесткости при изгибе, С — жесткость при кручении, г — радиус центральной оси.
Чистый изгиб4). Если круговой стержень узкого прямоугольного сечения изогнут парами сил М, приложенными по концам
1) С. П. Тимошенко, работа, указанная на стр. 556.
2) S. P. Timoshenko. Beams without lateral support. Transactions of the American Society of Civil Engineers, 1924, vol. 87, paper № 1549, pp. 1247—1262.
3) См. A. E. H. L о v e. A treatise on the mathematical theory qf elasticity. Third edition. Cambridge, University Press, 1920, p. 403, p. 453,
4) С. П. Тимошенко, работа, указанная на стр. 556,
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
615
(рис. 29), то уравнения (а) можно представить в следующем
виде:
М
_ Я, (d2u _ г2.
dw
)
г2 dQ2 1 dQ
1 dv С I dv сф
MTd§ -Ыгж)
р м
(а')
Из второго и третьего уравнений получим
Une-o,
где
к2--
(-)(—f)
ВоС
(Ь)
(с)
Принимая, что концевые поперечные сечения стержня не поворачиваются вокруг касательных к его центральной оси, будем иметь условия (Р)ео 0, (Р)0а О. Из решения уравнения (Ь) получим для вычисления критического значенияУИ дальнейшее условие а я, откуда на основании выражения (с) получаем
М,
кр
2 С
2 г
(77)
Рис. 29. Устойчивость плоской формы при изгибе кругового стержня.
Положительный знак в уравнении (77) соответствует указанному на рисунке направлению М. Для г оо и га I выражение (77) совпадает с формулой (66) для прямых стержней При малых значениях а отношение я2а2 будет большой величиной, и мы получим
АГ,
В2 С и у В2С
кр
2 г “
га
Это указывает на влияние незначительной кривизны стержня на величину Мкр.
616
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
26. Устойчивость радиально сжатой круговой арки1)
Обозначим через q радиальное давление, равномерно распределенное по центральной оси круговой арки (рис. 30).
Допустим, что эта равномерно распределенная нагрузка q и после потери аркой плоской формы изгиба направлена параллельно плоскости недеформированной центральной оси. Тогда
Третье уравнение (а) совместно с условием нерастяжимости центральной оси (dwdQ и) дает значение критической нагрузки при выпучивании кривого стержня в плоскости его центральной оси (см. § 22). Условие устойчивости плоской формы изгиба стержня мы получим из первых двух уравнений системы (а). Исключая v, получим для р следующее дифференциальное уравнение:
) Е. JI. Н и к о л а и. Об устойчивости кругового кольца и круговой арки, сжатых равномерно распределенным нормальным давлением. Известия Первого Петроградского политехнического института, Отдел техники, естествознания и математики, 1918, том 27, выпуск 1, стр. 323—377. S. Timoschenko. Kippsicherheit des gekriimmten Stabes mit kreisformiger Mittellinie. Zeitschrift fiir angewandte Mathematik und Mechanik, 1923, Bd. 3, Heft 5,
SS. 358—362. См. также H. H e n с k y. Kippsicherheit und Achterbildung an geschlossenen Kreisringen. Zeitschrift fiir angewandte Mathematik und Mechanik, 1921, Bd. 1, Heft 6, SS. 451—455.
уравнения равновесия напишутся qp так:
Рис. 30. Устойчивость радиально сжатой круговой арки.
откуда, используя уравнения (а) раздела 25, получим
-(1А) гЦ--Агр 0,
d3u , d2w qr3 du
dP1- dW 'ВГ M
(2 G)-g- (l-coA)p 0.
где
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ 617
Решение этого уравнения таково:
Р A sin kQ В cos kQ С sh kQ D ch kQ, (b)
-1±±(1руТГ7.
Если M2 и p на концах стержня равны нулю (при шарнирно опертых концах), то получим
г _ (оВ2 _ (я2-а2)2 В2 (-0v
WHkp Г2 “ а2(л;2 Яа2) г2
В случае а я2
(7г)кр 4 тг (79)
Это решение соответствует образованию восьмерки при сплющивании замкнутого кругового кольца, когда при потере плоской формы равновесия силы q сохраняют свое направление. Если же эти силы все время имеют направление к центру кольца, то
(80)
Если угол а очень мал, то из выражения (78) получим известную формулу Эйлера. При а я согласно формуле (78) имеем (дт)1ф 0, что соответствует возможности поворота арки как твердого тела вокруг диаметра полукольца. Для 1,48я а 2я первая форма равновесия после выпучивания будет состоять из двух полуволн.
В случае заделанных концов стержня из уравнения (Ь) для определения значения критической нагрузки получим
k-k2
2 Н—— sin ka sh ka — 2 cos ka ch a 0.
Для некоторых значений а соответственные со приведены в табл. XII.
Таблица XII
а
0,25я
0,5я
я
1,063л,
1, 1я
1,24я
1,5я
2я
(D
60,1
12,6
1,85
1,538
1,80
1,00
0,69
0,60
618
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
При малых значениях а для вычисления со можно пользоваться формулой
_ (4л2 — а2)2
а2 (4л2 Аа2)
Также рассмотрен случай круговой арки, лежащей на упругом основании таком, что каждое перемещение у, нормальное плоскости кольца, вызывает упругое сопротивление, пропорциональное у1). Симметричное опрокидывание кругового кольца при равномерно распределенном внутреннем и внешнем давлении и потеря устойчивости плоской формы изгиба, вызванная собственными напряжениями, были исследованы Р. Граммелем 2).
III. УСТОЙЧИВОСТЬ ПЛАСТИН И ОБОЛОЧЕК
27. Дифференциальные уравнения выпученной пластинки и энергетический критерий устойчивости
Тонкая пластинка под действием сжимающих и касательных сил, действующих в срединной ее плоскости, может потерять устойчивость и выпучиться. Возможность этого явления имеет большое практическое значение и должна учитываться при проектировании стальных конструкций. Первые опытные исследования выпучивания сжатых стальных пластинок были произведены Итоном Ходкинсоном3) в связи с проектированием знаменитых трубчатых мостов «Британия» и «Конуэй». Некоторые данные его опытных исследований применяются и теперь в мостостроении для определения толщины сжатых пластинок и полок. В дальнейшем для решения специальных задач устойчивости тонких пластинок будем применять два метода, а именно: 1) метод интегрирования дифференциального уравнения равновесия выпученной пластинки и 2) энергетический метод.
Рассмотрим плоскую пластинку малой толщины 2Л, жесткость на изгиб которой равна B 2Eh33( — ji2). Срединную плоскость пластинки примем за плоскость координатных осей
М Е. Л. Николаи, статья, указанная на стр. 616.
2) R. G г а ш ш е 1. Das Umstiilpen und Umkippen von elastischen Ringen. Zeitschrift fur angewandte Mathematik und Mechanik, 1923, Bd. 3, Heft 6, SS. 429—441 и R. Gramme 1. Die Kipperscheinungen bei elastichen Ringen.
Там же, 1927, Bd. 7, Heft 3, SS. 198—210.
3) Описание этих очень интересных опытов можно найти в книге:
Edwin Clark. The Britania and Conway tubular bridges with general
inquires on beams and on the properties of materials used in constructions.
London, Day and Son, vol. 1, 2, 185Q.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
619
ху и обозначим, как обычно1), через
h h Л
Т J cf dz, Т2 “ J (7 dz, 5 J ху dz -л -л -л
равнодействующие напряжений, взятых по всей толщине пластинки и отнесенных к единице длины ее срединной плоскости.
Величины Ти Т2 и S принимаются такими, чтобы под их действием пластинка имела лишь весьма малый прогиб. Тогда дифференциальное уравнение равновесия выпученной пластинки напишется так:
81
Это уравнение выведено Барре Сен-Венаном 2), и вывод его можно найти в работе Т. Кармана3). Определение критических значений действующих сил ведет к нахождению таких решений уравнения (81), которые удовлетворяют заданным условиям закреплений контура пластинки.
При применении энергетического метода критические значения усилий, приложенных по контуру или по всему объему пластинки и действующих в срединной плоскости пластинки, определяются из того условия, что работа А этих сил, затрачиваемая на изгиб пластинки, должна быть равна соответствующему приращению потенциальной энергии пластинки. Если uy v и w — бесконечно малые дополнительные перемещения при выпучивании пластинки, то соответствующие удлинения и сдвиг равны _ ди. 1 dw 2 _ ди. 1 dw 2
Сдс дх Т Тх) ВУ ду 12ду)
_du.dv.dw dw Уху “ dy dx ' dx dy 9
и мы получим для работы деформации продольных усилий и изгиба соответственно следующие выражения:
J (Т1ех Т2гу Syxy)dF
1) См. статью: J. W. Geckeler. Biegung. Handbuch der physikalischen und technischen Mechanik. Bd. 3. Leipzig, Johann A. Barth, 1927, SS. 130—198.
2) B. S a i n t - V e n a n t. См. его примечание 8 к § 73 в книге, переведенной с немецкого (A. Clebsch. Theorie der Elastizitat fester Кбгрег. Leipzig, В. G. Teubner, 1862) на французский язык: Theorie de l’elasticite des corps solides. Paris, Dunod, 1883, pp. 702—704.
3) Th. К arm an. Festigkeitsprobleme in Maschinenbau. Encyklopadie der
mathematischen Wissenschaften. Bd. IV, Teilband 4, Heft 3, b 27, Punkt 8.
Ebene Platten, Leipzig, B. G. Teubner, 1910. SS. 348—352.
620
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Критерий возможности выпучивания имеет вид
A-J7, 7, SY„) dF i В -
Это уравнение можно упростить, если воспользоваться следующей ) второй фиктивной вспомогательной системой: «вспомогательная система должна быть плоской и подобной заданной пластинке, но испытывать только фиктивные удлинения и сдвиг ди dv да , dv
дх9 ду и дудх9 а также удовлетворять действительным
перемещениям и и v краев. Для этой системы равенство между внешней и внутренней работой будет иметь следующий вид:
W'-.'-.s()R
Если это вспомогательное соотношение отнять от действительного выражения работы (а), то получим уравнение следующего вида:
ШЧ-§)2Ыж)54‘г';
(82)
Это уравнение было применено Дж. Брайаном2) и С. П. Тимошенко3) при решении различных вопросов устойчивости пластинок.
Если действующие на пластинку внешние силы отличаются друг от друга одним общим коэффициентом А,, то величины Т1, Г2 и 5 имеют тот же множитель. Вычисление критического значения внешних сил приводит тогда к отысканию той функции w f(x,y), которая сответствует минимуму коэффициента.
) Этот метод вывода уравнения (82) дал Н. R е i s s n e г. Energiekriterium der Knicksicherheit. Zeitschrift ftir angewandte Mathematik und Mechanik, 1925, Bd. 5, Heft 6, SS. 475—478.
2) G. H. Bryan. On the stability of a plane plate under thrusts in its own plane, with applications to the «buckling» of sides of a ship. Proceedings of the London Mathematical Society, Series 1, 1891, vol. 22, pp. 54—67.
3) С. П. Тимошенко. Об устойчивости упругих систем. Известия Киевского политехнического института, 1910, год 10, книга 4, стр. 375—560. См. также S. P. Timoschenko. Ober die Stabilitat versteifter Platten. Der Eisenbau, 1921, Bd. 12, № 5—6, SS. 147—163.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
621
28. Устойчивость прямоугольной пластинки с опертыми краями при действии сжимающих сил, лежащих в срединной плоскости )
В этом случае уравнение выпученной поверхности может быть представлено в следующем виде (рис. 31):
w
ml n 1
тпх. ппи. Sin Sin —-г—
(а)
Если допустить, что сжимающие силы распределены равномерно ВДОЛЬ СТОрОН ПЛаСТИНКИ, И ПОЛОЖИТЬ Qi —0Ху 02 —Оу, то, подставив выражение (а) в уравнение (82), получим
2 2 татп
О2
оо оо 22 г» 9 9 9
2 тт
т 1 п1
m l Ai-1
ai S
т 1 п1
(Ь)
Простейший случай получим при о2 0, т. е. при равномерном сжатии пластинки в направлении оси х. Тогда из уравнения (Ь) находим
а, п2В т 1 1 1
2Л
m1 п 1
2 2
(с)
о »
ИМИ
b
L
t t t м ♦ 1
У
Рис. 31. Прямоугольная пластинка, сжатая в своей плоскости.
Легко видеть, что следует взять только те члены, которые соответствуют величине п 1. Далее, из того обстоятельства, что числитель и знаменатель выражения (с) представляются суммами положительных членов, следует, что для получения минимума все члены, кроме одного, как в числителе, так в знаменателе должны быть приравнены к нулю. Таким образом, получим
ч п2В ( b. 1 а2 л.
Ыкр - 2Й2Л т а т Т) ’
откуда следует, что пластинка выпучивается так, что в направлении оси х она разделяется на m полуволн. Теперь остается
только найти соответствующее значение для величины т. Для малых а полагаем, т 1 и
п2В
о
2 b2h
(83)
) G. Н. Вгуап, статья, указанная на стр. 620.
622 ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
где ое—критическое напряжение по Эйлеру для полос длиной Ь, толщиной 2h и шириной 1 см. Тогда получим
(а1)кР ае(4 )2. (84)
Из этого следует, что (ai)Kp при a6 1 имеет наименьшее значение. Следовательно, бесконечно длинная пластинка подразделяется при выпучивании на квадраты, в то время как пластинка конечной длины делится на прямоугольники с таким соотношением сторон, которое соответствует минимуму для (ai)Kp. Вопрос о числе полуволн может быть легко разрешен. Переход от т полуволн к т 1 происходит тогда, когда правая часть формулы (d) при замене т на т 1 не изменяет своей величины. Отсюда имеем
b I 1 а I 1 b I I л
Ш Г(т I) ;—:—г,
а ' tn b х 7 a ' m I 6 ’
или ajb т Ут I).
Перевод от одной полуволны к двум имеет место при ab Y_2. Переход от двух полуволн к трем имеет место при аb У6. Если 02 не равно нулю, то также можно заключить, что для минимума все члены сумм в правой и левой частях выражения (Ь), кроме одного, должны быть равны нулю. Таким образом, получим
ctjп2 а2п2 -2се т2 п2. (е)
Если о 02 а, то из уравнения (е) найдем
кр “.(-). (85)
Для всякого другого соотношения между о и 02 необходимо в уравнении (е) найти такие значения тип, чтобы эти напряжения стали бы минимальными. Полное исследование этого вопроса опубликовано И. Г. Бубновым l).
29. Пластинки с тремя опертыми краями под действием сжимающих сил, параллельных свободной стороне
Пусть края 0, х а и у 0 (рис. 31) оперты, а край у Ь свободен. Решение дифференциального уравнения равно-
) И. Бубнов. Строительная механика корабля. Часть 2. СПб., тип. морского министерства, 1914, § 21, стр. 492—514.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
623
весия (81) в этом случае представится в виде1)
w sin —— (С sh ay D sin ру),
w sin
(a)
где
Р-
2hO т2я2 В а2 1
(Ti 7.
При этом будут удовлетворены условия на опертых краях пластинки. На свободном крае будем иметь условия
с « - р)' sh ab - D f „ (-)2 sin 06 - 0,
Co of - (2 - Rl -f ch ab - Dp fi- (2 - ц) (--) cos f№ - 0.
Выпучивание будет возможно, если определитель этих уравнений будет равен нулю, т. е. если будет удовлетворено следующее уравнение:
Вычисления показывают, что наименьшая величина сжимающей силы, при действии которой может иметь место выпучивание, получается при т 1. Пользуясь выражением (83), можно представить критическое напряжение в таком виде:
В нижеприведенной таблице XIII даны значения k и (Ji)Kp для различных соотношений аb при 2 h 0,01 b и Е 2,2 106 кгсм2. При другом соотношении между шириной и толщиной приведенные в таблице для (ai)Kp значения должны быть умножены на коэффициент 1002(2Л)262.
) См. С. П. Тимошенко. К вопросу об устойчивости сжатых пластинок. Известия Киевского политехнического института, 1907, год 7, книга 2, стр. 35—94. См. также S. P. Timoschenko. Einige Stabilitatsprobleme der Elastizitatstheorie. Zeitschrift fur Mathematik und Physik, 1910, Bd. 58, Heft 4, SS. 337—385 и H. Reissner. Ober Knicksicherheit ebener Bleche. Zentralklatt der Bauverwaltung, 1909, Bd. 29, № 14, SS. 93—9§,
И
откуда
P « -1. p-)7 th ab - a e p (-ff tg P6. (b)
()кр kee.
(86)
624
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Т а б л и ц а XIII
а
Ъ
0,5
1
1,2
1,4
1,6
1,8
2
2,5
3
4
5
k
4,40
1,440
1,135
0,952
0,835
0,755
0,698
0,610
0,564
0,516
0,503
(сг,)кр.
кгсм2
855
280
221
185
162
147
133
119
110
100
S8.4
В вышеприведенном решении принято, что сжимающие напряжения распределяются равномерно. Если приложенная к пластинке сжимающая сила имеет некоторый эксцентриситет с такой, что сжимающие напряжения у свободного края увеличиваются, то критическая величина сжимающей нагрузки, при которой наступает выпучивание, уменьшается. Соответствующая величина среднего сжимающего напряжения может быть вычислена по следующей приближенной формуле1):
(7')кР TT4F ( 456) 87
30. Края х 0 и х а оперты,
край у 0 заделан, край у Ь свободен
Если считать, что сжимающие напряжения о —ох распределены равномерно по краям х 0 и х а, то, поступая, как и прежде, удается для определения критических напряжений получить следующее уравнение:
25 (s2 t2) cos рб ch ab а 1 s sin sh ab, (a)
где
, n9 , т2я2 9 m2n2
P s a2-x-jr-.
Для m 1 и для разных значений отношения аb можно при помощи уравнения (а) вычислить соответствующие значения коэффициента k в формуле (86). Результаты вычислений приведены в таблице XIV.
Таблица XIV
alb
1
1,1
1,2
1,3
1,4
1.5
1,6
1,7
1,8
1,9
2,0
2,2
2,4
k
1,70
1,56
1,47
1,41
1,36
1,34
1,33
1,33
1,34
1,36
1,38
1,45
1,47
(1 )кр, кг см2
328
301
283
271
263
258
257
257
258
263
267
281
283
1) С. П. Тимошенко, статья, указанная на стр. 623.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
625
В этой таблице приведены также значения (ai)Kp, подсчитанные при 2г6 0,01. Вычисления показывают, что наименьшая величина критического напряжения соответствует отношению аb 1,635. Из этого следует, что длинная сжатая пластинка стремится разделиться на такое число полуволн, чтобы отношение между длиною одной полуволны и шириною пластинки было возможно ближе к величине 1,635.
31. Влияние упругой заделки края у 0)
Выше мы допускали, что сторона пластинки заделана, и потому использовали условие (dwdy)yo 0. Часто имеет место промежуточный случай между свободно опертым и жестко заделанным краями. Чтобы учесть влияние упругой заделки, рассмотрим наипростейший случай, а именно когда при выпучивании пластинки на заделанном крае возникает момент, пропор-
dw гг,
циональныи углу поворота края, иначе, величина с-Тогда условия закрепленного края у 0 напишутся так:
(») сМг-) ,
ду2 у-о ду )у—о
где с — постоянная величина. Соответствующее уравнение определителя может быть составлено так же, как и раньше, и критическое напряжение для различных значений коэффициента с может быть вычислено по формуле (86). Значения коэффициента k для случаев, когда сЪ 2 и cb 8, приведены в таблице XV.
Таблица XV
аЬ cb Nw
1
1,3
1,5
1,8
2
2,3
2.5
2,7
3
4
2
1,49
1,13
1,01
0,92
0,90
0,89
0,90
0,93
0,98
0,90
8
1,58
1,25
1,16
1,11
1,12
1.18
1,23
1,30
1,16
1,12
Из таблицы видно, что с увеличением коэффициента заделки с величины k и (сп)кр приближаются к величинам, имеющим место для пластинки с абсолютно заделанным краем.
32. Края х 0 и х а оперты, края у 0 и у Ъ заделаны )
Сжимающие силы распределены равномерно по краям л: 0 и х а. Поступая, как и ранее, найдем тогда, что критическое напряжение может быть представлено той же формулой (86).
) С. Г1- Тимошенко, статья, указанная на стр. 623,
626 ПРОБЛЕМЫ упругой устойчивости
Соответствующие значения коэффициента k даны в табли це XVI.
Таблица XVI
ab
0,4
0,5
0,6
0,7
0,8
0,9
1
k
9,44
7,69
7,05
7,00
7,29
7,83
7,69
Из этой таблицы видно, что самое неблагоприятное соотношение между размерами пластинки лежит в пределах 0,6
а6 0,7. Длинные сжатые пластинки при выпучивании, очевидно, будут подразделяться на полуволны, удовлетворяющие вышеприведенному условию. Случай, когда продольные края сжатой пластинки подкреплены упругими балками, которые при выпучивании пластинки изгибаются, имеет практическое значение при проектировании конструкций мостов и судов и исследован К. А. Малышевым1) и В. Раком2).
Устойчивость прямоугольной пластинки, сжатой двумя противоположными силами, приложенными к серединам длинных сторон, исследована А. Зоммерфельдом 3) и С. П. Тимошенко4).
33. Устойчивость прямоугольной пластинки при действии касательных сил в срединной плоскости
Задачи такого рода встречаются при расчете стенок поперечных переборок в кораблестроении и при определении толщины вертикального листа балки со сплошными стенками. В этом случае необходимо исследовать вопрос об устойчивости опертой по всему контуру прямоугольной пластинки, находящейся под действием касательных усилий, равномерно распределенных по всем ее сторонам5). При определении критического значения
) К. Ч а л ы ш е в. К вопросу о расчете пластинок, лежащих на упругом контуре. Известия С.-Петербургского института инженеров путей сообщения, 1914, выпуск 87. Отд. оттиск, СПб., 1914, 22 стр.
2) В. Ра к. Об устойчивости сжатой прямоугольной пластины, подкрепленной по краю уголком жесткости. Известия Института инженеров путей сообщения, Петроград, 1916. Отд. оттиск, Петроград, 1916, 15 стр.
3) A. S о m m е г f е 1 d. Ober die Knicksicherheit der Stege von Walzwerkprofilen. Zeitschrift fur Mathematik und Physik, 1906, Bd. 54, Heft 2, SS. 113—153.
4) С. П. Тимошенко, статья, указанная на стр. 623.
5) С. П. Тимошенко. Об устойчивости пластинок, подкрепленных жесткими ребрами. Сборник Института инженеров путей сообщения, Петроград, 1915, выпуск 89. Отд. оттиск, Петроград, тип. А. Э. Коллинса, 1914, 31 стр. и S. P. Timoschenko, Ober die Stabilitat versteifter Platten. Per Eisenbau, J921, Bd. 12, № 5—6, SS. 147—163.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
627
касательных напряжений применимо уравнение (82), принимающее в этом случае вид (рис. 31)
а Ь а Ъ
d2W 2
При этом выпученную форму пластинки можно представить следующим выражением:
оо оо
V1 V1 тпх ппУ
о» 2и 2j ®тп ® a sn
m 1 n»l
Подставляя это выражение в уравнение (а), найдем для критического напряжения формулу
««‘SSid F)'
m 1 п 1
Т-кр
«-SEES—,5лтто'
(Ь)
где п р и п q — нечетные числа. Коэффициенты атп и аРЯ нужно подобрать так, чтобы тнр имело наименьшее значение. Это приводит к системе линейных уравнений, которые, пользуясь обозначениями
о а
р-т
Вл2
Л2
ае
ое —
2b2h 9 Л
32Р
Ткр
можно представить в таком виде ):
ап
ап
а и
Ал
fls s
а«
Я (1 Р2)2
е
4
9
0
0
0
8
45
.4
9
16М1Р2)2 pj
4
5
4
“ 5
JL
25
0
.0
4 М19Р2)’ ”5 02
0
0
24
75
.п
4
о
М9 Р2)2
о
и
5
2
21
л
о
о
М9 9Р2)2
72
и
25
02
35
8
0
24
2-
72
1
Я, (16 4Р2)2
1-
45
75
21
35
т
Р2
“ т -о
-о
о -о
) Для упрощения написаны только коэффициенты величин атПу стоящих в первом ряду. Система содержит только величины атп, при которых т п есть четное число. Уравнения, содержащие атп с нечетными т п, приводят к большим значениям тКр, и нет необходимости их здесь учитывать.
628
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Величина касательных напряжений, при которой возможно выпучивание пластинки, находится из условия равенства нулю определителя составленной системы уравнений. Последовательные приближения для значения тьр находим, принимая во внимание все большее количество уравнений и соответственно коэффициентов атп. Величину критического напряжения можно, как и раньше, представить в форме ткр kae. В таблице XVII дан ряд значений коэффициента k, определенных с помощью шести уравнений вышеприведенной системы.
Таблица XVII
ab
1
1,2
1,4
1,5
1,6
1,8
2
2,5
3
k
9,42
8,0
7,3
7,1
7,0
6,8
6,6
6,3
6,1
ткр, кгсм2
1870
1590
1450
1410
1390
1350
1310
1250
1210
В третьей строке этой таблицы приведены значения ткр, подсчитанные для случая 2z 0,016; jli 0,3; 2,2-10б кгсм2. С увеличением отношения аЬ коэффициент k уменьшается и стремится к предельному значению, соответствующему бесконечно длинной пластинке. Величину этого предельного значения k можно найти следующим приближенным способом: в случае весьма длинной пластинки способ закрепления поперечных краев не имеет особого влияния на величину коэффициента k можно, задавшись подходящей формой выпучивания, определить величину k из условий на продольных краях пластинки. Например, уравнение выпученной поверхности пластинки можно приближенно написать в таком виде:
w A sin — sin (х — ау).
При этом пластинка выпучивается, образуя ряд полуволн длиною s. Соответственные узловые линии образуют с осью у угол, тангенс которого равен а. Если подставить выражение w в основное уравнение (82), то получим ткр 5,7ае, что соответствует условиям s b У 1,5 и а Подробнее этот вопрос
исследовали Р. Саусвелл и Сильвия Скан1). Для пластинки бесконечной длины с опертыми краями они нашли тир 5,35at., а для пластинки с заделанными краями — ткр 8,98сге. Выше¬
) R. V. Southwell, S. W. S к а n. On the stability under shearing forces of a flat elastic strip. Proceedings of the Royal Society of London, Series A, 1924, vol. 105, № 733, pp. 582—607.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
620
приведенные результаты имеют практическое значение при определении толщины вертикального листа клепаной балки со сплошной стенкой. Обычно применяемый метод, учитывающий только касательные напряжения, очень часто дает недостаточные размеры. Из соображений устойчивости толщину стенки балки увеличивают. Так как это увеличение делается без теоретического обоснования, то получаются конструкции с весьма различными сопротивлениями выпучиванию. Хотя выпучивание стенки и не представляет непосредственной опасности разрушения, тем не менее получаются нежелательные изменения в распределении напряжений между отдельными частями конструкции. При дальнейшем возрастании поперечной силы выпученная стенка не будет более в состоянии воспринимать соответствующее возрастание касательных напряжений. Стенка работает тогда между обоими поясами балки как диагональ ферменной конструкции. При этом большая часть нагрузки придется на часть стенки, лежащую вдоль означенной диагонали, и на расставленные по ее направлению заклепки, что не ускользнуло от внимания инженеров1).
34. Устойчивость прямоугольной пластинки, изгибаемой в срединной плоскости
При одновременном сжатии и изгибе прямоугольной пластинки распределение напряжений по краям (рис. 32) можно представить следующим
УРа _г
При Х оо убудет иметь рИс. 32. Прямоугольная пластинка при место случаи равномер- одновременном действии сжатия и изгиба, ного распределения сжимающих напряжений. Случай а 0,5 представляет собой чистый изгиб. При а 0,5 имеем внецентренное сжатие, а при а 0,5 — внецентренное растяжение. Для определения критической величины максимального сжимающего напряжения a i
l) W. Е. Lilly. The design of plate girders and columns. London, Chapman and Hall, 1908 и W. E. Lilly. Web stresses in plate girders. Engineering, 1907, vol. 83, February, pp. 136—139. См. также H. H. Rode. Beitrag zur Theorie der Knickerscheinungen. Der Eisenbau, 1916, Bd. 7, № 9, SS. 210— 218 (cm. S. 217) третья часть статьи.
где
маь
постоянная величина, зависящая от положения нейтрального волокна.
X
а
630 ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
можно применить уравнение (82). Предполагая, что пластинка оперта по всему контуру, можно написать прогиб при выпучивании в форме
2 атп sin — sm
т 1 п1
Рассмотрим случай выпучивания пластинки по одной полуволне (т 1). Исходя из того условия, что (aj)Kp должно быть минимумом, получим следующего вида систему линейных уравнений ):
.(I)Г--(1-- i)- if fSif-0. (а)
1
где n 1 — нечетное число, а ое n2B2b2h. Если определитель этих уравнений приравнять нулю, то получим уравнение для определения (ai)Kp. Первое приближение, соответствующее форме выпучивания w аи (sin nxa)»(sn луb), дает
Юкр Ое (“ у) Ц— (88)
1 “ 2а
Эта формула дает достаточную точность при больших значениях а (например, при a 1,5 ошибка для квадратной пластинки составляет около 4). Если взять два уравнения системы (а) и приравнять нулю соответствующий определитель, то для критического напряжения во втором приближении получим следующее уравнение:
Х(1Тг) (14-г) (12-)2(14-Нг)20-
Определение численных значений при последующих приближениях показывает, что для a 0,75 второе приближение дает достаточную для практических- применений точность. В случае чистого изгиба (a V2) следует брать дальнейшее приближение и принять во внимание три уравнения системы (а). Как и прежде, результаты вычислений можно написать в форме (cji)кР kae. Некоторые значения коэффициента k приведены в таблице XVIII.
тпх. ппу
') С. П. Т имошенко. Теория упругости. Часть 2. Стержни и пластинки. С.-Петербург, тип. А. Э. Коллинса, 1916, стр. 329. См. также И. Г. Бубнов. Строительная механика корабля. Часть 2. СПб., тип. морского министерства, 1914, стр. 517.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
631
Таблица XVIII
fl6
а
0,4
0,5
0,6
0,667
0,75
0,8
0,9
1
1.5
0,50
29,1
25,6
24,1
23,9
24,1
24,4
25,6
25,6
24,1
0,75
18,7
—
12,9
—
11,5
11,2
_
11,0
11,5
1,00
15,1
—
9,7
—
8,4
8,1
—
7,8
8,4
1,25
13,3
—
8,3
—
7,1
6,9
—
6,6
7,1
1,50
10,8
7,1
6,1
6,0
5,8
6,1
Для каждой величины а можно найти такое отношение а6, при котором коэффициент k имеет наименьшую величину. Например, при чистом изгибе наименьшая величина k соответствует отношению а6 23. Следовательно, в этом случае длинная пластинка при выпучивании делится на ряд полуволн, длина которых соответствует упомянутому выше невыгоднейшему отношению а6.
Из таблицы XVIII ясно видно, что довольно значительные отклонения от невыгоднейшего значения отношения а6 имеют лишь незначительное влияние на величину коэффициента k. Из этого следует заключить, что вертикальные подкрепления в средней части пролета балок со сплошными стенками не имеют никакого влияния на устойчивость вертикальных листов.
35. Устойчивость подкрепленных пластинок
Во всех вышеразобранных случаях выпучивания пластинок критическое напряжение зависело не только от соотношения сторон, но также и от толщины пластинки. При заданном соотношении сторон величина критического напряжения пропорциональна квадрату толщины пластинки; соответствующим увеличением толщины пластинки можно обеспечить необходимую устойчивость. Однако такое решение не всегда рационально. Во многих случаях можно получить лучшее использование материала, если, сохраняя первоначальную толщину пластинки, для обеспечения ее устойчивости ввести соответствующие ребра жесткости. Такой способ применяется в кораблестроении при проектировании металлических балок со сплошными стенками. Например, путем введения ребра жесткости, параллельного сжимающей силе и подразделяющего ширину сжатой пластинки на две части, можно увеличить жесткость длинной пластинки примерно в четыре раза (рис. 31). Дальнейшего увели чения жесткости можно добиться путем соответствующего увеличения числа ребер жесткости. При этом возникает вопрос о зависимости между жесткостью ребер и устойчивостью
632
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
подкрепленной пластинки с тем, чтобы при выпучивании пластинки не происходило изгиба ребер. Этот вопрос можно разрешить на основании общего энергетического критерия устойчивости, данного в разделе 21х).
Пусть дан ряд ребер жесткости, параллельных оси х (рис. 31), и С, с2,. — расстояния их от этой оси, Fи F2,.— площади их поперечных сечений, Ви В2,. — соответствующие жесткости при изгибе, Рь Р2,. — сжимающие силы в ребрах, пропорциональные площадям поперечных сечений. При
V V1 тпх . ппц
w 2j2j аsin 5 sin ь
выражение для потенциальной энергии ребра i напишется так:
л 00
В Г d2w 1 Bin4 V 4 ( nci I 2яci. 2
-Г J -d)dx-iarAm K.sm — am2s.n—.).
О m1
Энергия изгиба пластинки равна
п4В ab X V о (т2. п2 2 ——2л 2иатпЪ-р)
т1 п1
оо
, VI Bin4 4 . net . . 2nci , 2
2иаГ 2d т ат sm-- «m2sm—g h.J.
m»l
Допустим, что пластинка находится под влиянием равномерного сжатия в направлении оси х, и обозначим сжимающее напряжение через о —ах. Тогда из уравнения (82) при условии, что а 1 имеет минимальное значение, получим систему однородных линейных уравнений следующего вида:
ое атп (гп2 п2р2)2
2YiSin-m4 (aml siny- am2sin-.
I
— р2сг, т2атп 2 6, sin-jp- т2 X
x(amlsin- am2sin.) О, (а)
где
. Pi __ Pj __ s. д _ p
6Я 2Afor, 2bh ’ b p
) S. P. T i m о s с h e n k o. Ober die Stabilitat versteifter Platten. Der pisenbau, 1921, Bd. 12, № 5—6, SS. 147—163,
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
633
В случае одного жесткого подкрепляющего ребра, делящего ширину пластинки пополам, и выпучивания по одной полуволне (т 1) систему уравнений (а) можно представить следующим образом 1):
р- (1 -- Р2)2 «1 2 (а, — а3 -Ь а5 —.)- 1
- ЫкР «1 26 (а, - а3 а5 -.) О,
г (1 4Р2)2 2 Юкр 02 О»
-f (1 9р2)2 а3 - 2у(а, - а3 аъ -.)- - (i)kp «з - 26 (а, - а3 а5 -.) О,
-р- (1 1бр2)2 а4 - (Ti)Kp а4 О,
Уравнения, содержащие коэффициент ап с четным г, соответствуют тем формам выпучивания, при которых подкрепляющее ребро совпадает с узловой линией и поэтому при выпучивании не изгибается. Из этих уравнений практическое значение имеет то, которое содержит коэффициент а2. Соответствующее значение напряжения (cri)Kp имеет такое же значение, как и в случае неподкрепленной пластинки шириною 62. При недостаточной жесткости подкрепляющего ребра может случить ся, что пластинка выпучится при меньшем напряжении, чем указано выше; при этом изогнется и ребро. Для определения критической нагрузки, соответствующей этой форме выпучивания, следует применить систему уравнений (Ь) с нечетными ап. Если мы примем во внимание только два уравнения системы (Ь)
и, соответственно, два коэффициента а и я3 и приравняем определитель этих уравнений нулю, то получим
(2)2 (1 46) - kp (1 26) (с d) - 8Y6 cd - 4y2 0, (с)
где
a i)kL с (1p2)2 2Y rf (l 902)2 2y.
и е
Пользуясь тремя уравнениями, содержащими три коэффициента ау а3, я5, получим лишь незначительные отклонения от результатов, соответствующих уравнению (с). Поэтому значения (ai)Kp с достаточной точностью можно вычислить, пользуясь уравнением (с). Ряд значений коэффициента k приведен в таблице XIX (при 6 0,1).
Индекс т 1 в коэффициентах атп опускается.
634
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Таблица XIX
р Y
0,6
0,8
1
1,2
1.4
1.6
1.8
2
5
16,5
14,6
11.1
9,06
7,91
7,38
7,19
7,29
10
16,5
16,8
16,0
14,2
12,0
10,5
9,70
9,35
15
16,5
16,8
16,0
16,5
15,7
13,6
12,2
11,4
20
16,5
16,8
16,0
16,5
16,1
16,1
14,7
13,4
25
16,5
16,8
16,0
16,5
16,1
16,1
16,2
15,4
р Y
2,2
2,4
2,6
2,8
3
3,2
3,6
4
5
7,58
8,06
8,50
7,91
7,62
7,38
7,19
7,29
10
9,30
9,49
9,86
10,4
11,1
10,5
9,70
9,35
15
11,0
10,9
11,1
11,5
12,0
12,7
12,2
11,4
20
12,7
12,4
12,4
12,6
13,0
13,5
14,7
13,4
25
14,5
13,8
13,6
13,6
13,9
14,3
15,7
15,4
Случаи, когда коэффициент k больше соответствующих значений для неподкрепленной пластинки шириной 62 (уравнение (84)), выпадают из рассмотрения; здесь нужно использовать значения k для неподкрепленной пластинки.
Длинная пластинка при выпучивании подразделяется на ряд полуволн. Их число легко определяется из условия, что коэффициент k должен принимать наименьшую величину.
Примененный при одном подкрепляющем ребре метод может быть распространен и на случай нескольких ребер. В случае двух одинаковых ребер, делящих пластинку на три равные части, получим, используя старые обозначения, в качестве первого приближения выражение
(а ) — (1 Р2)2 3V а
ValKP “ р2 ( 35)
При большем числе ребер жесткости приближенное значение критического напряжения определяется по следующей формуле:
(1 р2)2 2 Y sin2-2
Метод, примененный к случаю продольных ребер, может быть распространен и на случай поперечных ребер жесткости. Так как неподкрепленная пластинка при выпучивании подразде¬
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
635
ляется на ряд полуволн, то ясно, что распределение ребер жесткости в соответствующих узловых линиях не оказывает влияния на критическое напряжение. Постановка поперечных ребер жесткости имеет только тогда смысл, когда от этого изменяется отношение между длиной волны и шириной пластинки1). Этот же метод можно применить к случаю подкрепленной пластинки, подвергающейся действию касательных усилий.
36. Устойчивость круговых пластинок
Устойчивость равномерно сжатой круговой пластинки исследовал Дж. Брайан2). Другие случаи были рассмотрены А. Динником3) и А. Надаи4). Допустим, что пластинка выпучивается симметрично по отношению к ее центру. Обозначим через г расстояние от центра пластинки, а — радиус пластины, w — прогиб, ф dwdr — угол наклона касательной к упругой поверхности в меридиональном сечении, р — равномерно распределенное давление на единицу наружного контура пластинки, В — изгибную жесткость пластинки. Тогда дифференциальное уравнение равновесия выпученной пластинки имеет вид
или, вводя новую переменную х г у получим
1)(Р 0 (а)
что представляет дифференциальное уравнение Бесселя с параметром, равным единице. Ограничиваясь случаем сплошной круговой пластинки, можно написать решение уравнения (а) в виде
Ф-с.М-Т--ТТгТГ- )
) Некоторые числовые результаты см. в указанной на стр. 632 статье С. П. Тимошенко.
2) G. Н. Bryan. On the stability of a plane plate under thrusts in its own plane, with applications to the «buckling» of the sides of a ship. Proceedings of the London Mathematical Society, 1891, vol. 22, pp. 54—67.
8) A. H. Д и н н и к. Приложение функции Бесселя к задачам теории упругости. Часть 1. Статика. Известия Донского политехнического института, Новочеркасск, 1913, том 2, отд. 2, стр. 219—366. Перепечатка: А. Н. Д и ня и к. Избранные труды. Том 2. Киев, Изд-во АН УССР, 1955, стр. 7—124.
4) А. N a d a i. Uber das Ausbeulen von kreisformigen Platten. Zeitschrift des Vereines deutscher Ingenieure, 1915, Bd. 59, N 9, SS. 169—174; JSfe 11,
636
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
Если контур г а защемлен, то qp cJ (а У рВ) 0, откуда
14,68В .
Р Кр — а2 '
(91)
В случае свободного края имеем
Из этого следует, что при полном защемлении контура критическое напряжение в 32 раза больше, чем при свободном контуре. Задача о выпучивании круговой пластинки под влиянием меняющейся вдоль радиуса температуры, изученная А. Надаи1), показывает, что некоторые случаи потери устойчивости при радиально симметричном распределении температуры могут быть решены без особых затруднений.
Упругая устойчивость кольцевой пластинки под действием равномерно распределенных по контуру касательных усилий была исследована В. Дином2). Он показал, что необходимые уравнения для решения задачи о бесконечно длинной полосе можно вывести в качестве предельного случая из уравнений, полученных при решении задачи о кольцевой пластинке.
37. Устойчивость цилиндрической оболочки при равномерном наружном давлении
Если длина оболочки весьма велика по сравнению с ее диа метром, то краевые условия не оказывают заметного влияния на величину критического давления. В этом случае можно пользоваться формулой (62), выведенной для кругового кольца. Если из трубы вырезать кольцо длиною, равною единице, то изгибную жесткость этого кольца следует принять равной
и выражение для критического давления (62) принимает вид
где а — радиус цилиндрической оболочки, а 2h — толщина ее.
) A. Nadai, статья, указанная на стр. 635.
2) W. R. Dean. The elastic stability of an annular plate. Proceedings of the Royal Society, London, Series A, Mathematical and Physical Sciences, 1924, vol. 106, No 737, pp. 268—284.
_ 3 В Чкр- аз
(93)
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
637
Исследование устойчивости длинной цилиндрической оболочки за пределом упругости может быть произведено1) при помощи того же метода, который был применен для случая призматического стержня прямоугольного поперечного сечения (§ 10). Опыты по устойчивости цилиндрических труб были поставлены А. Карманом2), Р. Стюартом3) и Г. Куком4).
Случай выпучивания сравнительно короткой цилиндрической оболочки, при котором должны быть приняты во внимание условия на концах и деформация срединной поверхности, был впервые рассмотрен Рудольфом Лоренцем5) при упрощающих предположениях. На основе теории тонких оболочек Р. Саусвелл6) и Р. Мизес7) исследовали случай цилиндра конечной длины.
Положим, I — длина цилиндра, а — радиус срединной поверхности, ф— угол между плоскостью, проходящей через точку Р срединной поверхности и ось цилиндра, и неподвижной плоскостью. Координаты точки Р показаны на рис. 33. Перемещение этой точки разлагаем на составляющие: и — параллельно образующей (ось х)у v — вдоль касательной к контуру поперечного сечения (ось у), w — по направлению внутренней нормали к поверхности. За положительные направления удельных усилий
) R. V. Southwell. On the collapse of tubes by external pressure. Philosophical Magazine and Journal of Sciences London — Edinburgh — Dublin, Series 6, Part I, 1913, vol. 25, May, JVb 149, pp. 687—698; Part II,
1913, vol. 26, September, № 153, pp. 502—511; Part III, 1915, vol. 29, January, No. 169, pp. 67-77.
2) A. P. Carman, M. L. Car. Resistance of tubes to collapse. Urbana, University of Illinois, Engineering Experiment Station, 1906, Bulletin № 5, 25 pp.
3) R. T. S t e w a r t. Collapsing pressure of bessemer steel lapwelded tubes, three to ten inches in diameter. American Society of Mechanical Engineers, Transactions, 1906, vol. 27, № 1116, pp. 730—820 (discussion: pp. 820—821).
4) G. Cook. The collapse of short tubes by external pressure. Philosophical Magazine and Journal of Sciences, London — Edinburgh — Dublin, Series 6,
1914, vol. 28, № 163, pp. 51—56; 1925, vol. 50, № 298, pp. 844—848. Библиографию по этому предмету того же автора см.: G. Cook. The resistance of tubes to collapse. British Association for the advancement of science. Report of the eighty-third meeting, Birmingham, 1913, September. London. J. Murray, 1914, pp. 213—224.
6) R. Lorenz. Achsensymmetrische Verzerrungen in dunnwandigen Hohlzylindern. Zeitschrift des Vereines deutscher Ingenieure, 1908, Bd. 52, №43, SS. 1706—1713.
6) R. V. Southwell, вышеуказанная статья, стр. 687.
7) R. M i s e s. Der kritische Aussendruck zylindrischer Rohre. Zeitschrift des Vereines deutscher Ingenieure, 1914, Bd. 58, № 19, SS. 750—755.
Рис. 33. Устойчивость трубы.
638
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
и моментов принимаем показанные на рис. 34, а и 34,6. Для этого случая будем иметь следующие дифференциальные уравнения равновесия1):
KJ1 I 1 dS2 I А
лГТ“лГг2 0,
д
дх
as,
дф
дТ2
дх
д2Мх
дх2
дф
д2Я,
дЯ,
1 дМ2
дх а 1 д2М2
о,
дх дф
дф
- p2(lsl)q
-j- (1 С) (1 вг) q — 0,
(а)
где q — наружное давление, а
_ d2p dw Г1 дх дф дх 9
1 dv
В этих уравнениях вместо удельных усилий и моментов нужно подставить следующие выражения:
2Eh Г ди. ц ( dv 2Eh f ди , 1 (dv )
Т1Г 71-Э5Г-®)Ь
Eh f dv. 1 ди , h2 ( d2w , dv )
1 i dx а дф ' 3a2 dx дф dx j j Eh f dv 1 du h2 ( d2w . dv )
1 p, I dx а дф 3a2 dx дф ' dx j ) 9
_ 2 Eh3 f d2w. i ( d2w , dv )
3 1 — M-2 I dx2 a2 дф2 дф j
2 Eh3 f d2w . 1 (d2w . dc;)
3 1 — Ц2 ( длс2 ' a2 дф2 дф j J
2 Eh I t d2w. dv
3 1 fi a dx дф ' dx )
Перемещения могут быть выражены так:
и U cosmjtsinmp, у К sinmjtcosmp, (b)
я W sin mx sin шр.
Т i 72 5, 52
М2 Я,
) А. Е. Н. Love, книга, указанная на стр. 563, р. 572 стр. 599 русского перевода.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
639
Для случая т nil на обоих краях цилиндра х О и х I должны быть удовлетворены условия Т 0, v 0, w 0. Обозначив
а (1 — х2)
У ЕЙ—
(с)
и пренебрегая членами порядка выше первого в величинах U, V, W, перепишем уравнения (а) следующим образом:
w м , l- и о , п
TU 2mS
1 — x A2
(т
,2 I 2
З-ц h2
m
За2
(d)
M-m »r , я I 2 u Л2 n Л2 o T» a U3 ппзгГ (-Jr
Л2 — 1
2h2 m2n2
n4)w 0.
Полагая определитель этих уравнений равным нулю, найдем критическое значение q. Исключая члены порядка if2, фЛ, А4
Рис. 34. Удельные силы и удельные моменты в цилиндрической
оболочке.
и ft2m, получим следующее дифференциальное уравнение:
-ф (п - 1) (-jj- n2)2-f шl4-
(l-ц2)m4.г„4(,г2-l)20,
откуда приближенно имеем
л2
За2
п‘' (п2 — 1)
640
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
или, с помощью формулы (с), получим выражение
_ 2Eh f (n2-)h2 , тАаА (Q„
кр а ( 3 (1 — ji2) а2 г4 (г2 — 1) J ' Для очень длинного цилиндра выражение г4а4 я4а44 очень мало, и эта формула примет вид
2ЕНЪ п2 - 1 3(1-Х2) а3 '
Полагая п 2, приходим к ранее полученному выражению (93), показывающему, что очень длинная цилиндрическая оболочка выпучивается так, что ее поперечное сечение принимает эллиптическую форму. Для более короткой цилиндрической оболочки может происходить выпучивание по форме с п 3 и при величине q меньшей той, которая соответствует случаю п 2. Это, впрочем, справедливо только при не очень значительной степени т. При увеличении т величина q при п 4 будет меньше, чем при п 3. Поэтому при увеличении т, т. е. при уменьшении длины цилиндра, число п возрастает.
38. Устойчивость цилиндрической оболочки под действием продольных сжимающих сил
Эта задача была исследована Р. Саусвеллом1) и С. П. Тимошенко2). Если выпученная форма равновесия симметрична по отношению к оси цилиндра, то, аналогично уравнениям (а) (раздела 37), получим следующие дифференциальные уравнения равновесия (рис. 35):
ди и л
H-W о,
дх а ’
откуда
аГ 1 ох д2т ди w ah2 dw х 2Eh 11 ' дх2 дх а 3 дх4 “ и
2 Eh3 dw „ d2w. 2Eh л
T -w-Ti -w0-
Это то же самое уравнение, которое было получено для стержня на упругом основании (раздел 16). Подставляя в вы-
2 Eh 2Eh
ражение (51) вместо EJ rf р соответственно
3 1 — I2
и
) R. V. Southwell, статья, указанная на стр. 637.
2) С. П. Тимошенко. К вопросу о деформациях и устойчивости ци¬
линдрической оболочки. Известия Электротехнического института, Петроград,
1914, том 11, стр. 267—287.
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
641
и обозначая о оболочки найдем
'Г
gjr, для случая длинной цилиндрической
2 Eh
-'кр
я3(1-и)
(95)
В общем случае выпучивания равномерно сжатой цилиндрической оболочки необходимо воспользоваться выражениями (Ь) раздела 37 для перемещений. Для короткой оболочки приходим для сгкр к значениям, даваемым (95). В случае длинной цилиндрической оболочки получим следующее выражение для критического сжимающего напряжения:
Е v
г2
X
а4т4 (1 — ц2) т2“ К4 “ д2)2 a2fn2 (4гб — (7 i) г4 (3 ц) п2
Если П 1 Еп2а2
Окп ого Т.
a2m2 (л п2)
и т я, то из выражения е. критическое напряжение
(а)
(а) находим
кр 22
Эйлера.
Для п 1 из формулы (е) имеем приближенно
Г (1 — i2) а2т2 - h2 п2 (п2 — I)2 1 кр 1-2 L л2(л21) h За2 а2п2 («21) J ' '
Наименьшее значение акр получим при
г2 (г2 — 1).
а2т2
тогда
а 3(1-1) ’
2Eh 1 п2 -1
-’кр'
(96)
X
Рис. 35. Осесимметричное выпучивание цилиндриче¬
ской оболочки.
х 3(1 -ц2) п2 1 '
Это показывает, что для длинной цилиндрической оболочки критическое напряжение меньше, чем найденное выше для случая симметричного выпучивания.
Если отдельные точки концов могут перемещаться, то при известной величине сжимающих сил цилиндрическая оболочка может принять такую форму равновесия, что переход к ней не будет сопровождаться деформациями и сдвигами срединной поверхности1). Соответствующие этому характеру деформации
) S. P. Timoschenko. Einige Stabilitatsprobleme der Elastizitatstheorie. Zeitschrift ffir Mathematik und Physik, 1910, Bd. 58, Heft 4, SS. 337—385.
642
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
перемещения имеют следующий вид1):
и — А у sin 2р, v Ах cos 2р, w — 2Л sin 2р.
Применяя энергетический метод, получим для этого случая следующее значение критического напряжения:
Для короткой цилиндрической оболочки эта величина будет меньше критических значений, даваемых формулами (95) и (96).
39. Устойчивость тонкостенной цилиндрической оболочки при кручении
Этот вопрос разрабатывал Е. Шверин2). Для вычисления критических касательных напряжений он дал следующую приближенную формулу:
40. Устойчивость тонкостенной сферической оболочки при равномерном радиальном наружном давлении
Этот случай в предположении симметричного выпучивания рассмотрели Р. Цолли3) и Е. Шверин4). Обозначив через а радиус срединной поверхности и через 2h толщину стенки, получим критическую величину сжимающего напряжения в оболочке шара из выражения
выведенного при условии, что величина
)) А. Е. Love, книга, указанная на стр. 638, п. 506 стр. 529 русского перевода.
2) Е. Schwerin. Die Torsionstabilitat des diinnwandigen Rohres. Zeitschrift fur angewandte Mathematik und Mechanik, 1925, Bd. 5, Heft 3, SS. 235—243.
8) R. Z б 11 y. Uber ein Knickungsproblem an der Kugelschale. Promotionsarbeit. Ziirich, Technische Hochschule, 1915.
4) E. Schwerin. Zur Stabilitat der dunnwandigen Hohlkugel unter gleichmafiigen Aussendruck. Zeitschrift fiir angewandte Mathematik und Mechanik, 1922, Bd. 2, Heft 2, SS. 81—91.
(97)
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
643
является нечетным целым числом, равным или большим трех. Если W не имеет указанных значений, то следует определить
величины
5 - W 5 - W
С1 4 с2 4 »
соответствующие ближайшим целым числам Wi 3 2п или
W2 3 2п2 и сравнить сжимающие напряжения
где
л Зд2 1 2
л - -дг (1 -Ц2).
Меньшее из этих двух значений и будет искомым критическим
сжимающим напряжением.
ОБЩАЯ ЛИТЕРАТУРА
Ф. Ясинский. Собрание сочинений. Ред. Н. Н. Митинский. Том 1. СПб., 1902. Сборник Института инженеров путей сообщения, 1902, выпуск 56, 320 стр.
Th. К а г m а n. Festigkeitsprobleme im Maschinenbau. Encyklopadie der mathe.matischen Wissenschaften, Bd. 4. Mechanik, Teilband 4, Heft 3, § 27. Leipzig, B. G. Teubner, 1910, SS. 311—385. Перепечатка: Th. К a r m a n. Collected works. London, Butterworths scientific publication, 1956, vol. 1, pp. 141—207.
A. E. H. Love. A treatise on the mathematical theory of elasticity. Fourth edition. Cambridge, University Press, 1927, 643 p. Перевод на русский язык: А. Л я в. Математическая теория упругости. М. — Л., ОНТИ, 1935.
R Mayer. Die Knickfestigkeit. Berlin, Verlag von Julius Springer, 1921.
R. Mises: Die Differential und Integralgleichungen der Mechanik und Physik als 7 Auflage von Riemann — Webers partiellen Differentialgleichungen der mathematischen Physik. Hrsg. von R. Mises. Bd. 1. Braunschwieg, Viegweg und Sohn, 1925.
L. Tetmayer. Die Gesetze der Knickungs- und der zusammengesetzten Druckfestigkeit der technisch wichtigsten Baustoffe. 3 Auflage. Leipzig und Wien, Franz Deuticke, 1903, 211 S.
С. П. Тимошенко. Курс теории упругости. Часть 1. Издание Института инженеров путей сообщения. СПб., тип А. Э. Коллинса, 1914. Часть 2. 1916, то же.
С. П. Тимошенко. Сопротивление материалов. 3-е издание. Киев, Л. Идзиковский, 1916, 475 стр.
I. Todhunter, К. Pearson. A history of the theory of elasticity and of the strength of materials from Galilei to the present time. Vol. 1, Galilei to Saint-Venant, 1639—1850. Cambridge, University Press, 1886. Vol. 2, Saint-Venant to lord Kelvin, part 1, 1893; vol. 2, part 2, 1893.
B. Saint-Venant. См. его примечания к переводу с немецкого книги: А. С 1 е b s с h. Theorie der Elastizitat fester Korper. Leipzig, B. G. Teubner, 1862, 424 SS. в «Theorie de lelasticite des corps solides». Paris, Dunod, 1883, 900 pp.
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
The stability of the webs of plate girders. Engineering, 1934, vol. 138, № 3580, pp. 207—209. Перепечатка: S. P. Timoshenko. The collected papers. McGraw-Hill Publishing Company Ltd, New York —London—Toronto, 1953, pp. 493—507.
В настоящее время назначение габаритов двутавровых балок основано в большой степени на эмпирических правилах. Будучи следствием длительного опыта, эти правила обычно дают удовлетворительные размеры и в то же самое время являются достаточно гибкими, так что они оставляют значительную свободу для индивидуального решения. В результате этого мы имеем множество размеров двутавровых балок, спроектированных для одного и того же пролета и одной и той же нагрузки. Сравнивая, например, двутавровые балки пролетом 30,5 м и высотой 3,05 м, мы найдем, что толщина стенки изменяется от 1,11 см до 1,59 см1). Сравнение 2) двух двутавровых балок пролетом 27,4 м, одной для американской железной дороги, а другой для британской железной дороги, показывает, что в американском типе ребра жесткости содержится 25, а в британском 40 общего количества материала, заключенного в стенке и в ребрах жесткости.
Такое разнообразие размеров указывает, что старая проблема выбора габаритов двутавровых балок не может считаться полностью решенной. Если это справедливо для двутавровых балок обычных размеров, то это должно быть существенно более верным при проектировании двутавровых балок исключительно больших габаритов, для которых обширный опыт отсутствует. В течение последних лет было сооружено значительное число двутавровых балок большого пролета, достигающего иногда 91,4 ж3). При проектировании таких балок надлежащий выбор толщины стенки и расположения ребер жесткости стано¬
) Н. Н. Rode. Beitrag zur Theorie der Knickerscheinungen. Der Eisenbau, 1916, Bd. 7, № 6, SS. 121—136; № 7, SS. 157—167; № 9, SS. 210—218; № 10, SS. 239—246; № 12, SS. 295—299. Cm. S. 217.
2) H. M. G i b b. A new method of proportioning webs and stiffeners in plate girders. Engineering, 1910, vol. XC, pp. 39—41.
3) Описание отдельных больших двутавровых балок можно найти в статье: L. К а г n е г. Solid web girders bridges of large span in steel. Publications of the International Association for Bridge and Structural Engineering, 1932, vol. I, pp. 297—313,
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
645
вится важной проблемой, которая может быть удовлетворительно решена только на основе рациональной теории или с помощью модельных испытаний.
Проблема определения правильной толщины стенки и подкрепления стенки является, в сущности, проблемой устойчивости.
Хорошо известно, что стенка, если она недостаточно толста или неудовлетворительно подкреплена, может выпучиться вбок и вести себя как связь, в то время как ребра жесткости будут работать как стойки. Для того, чтобы принять во внимание возможность такого выпучивания, некоторые инженеры ) рекомендуют узкую полосу стенки, составляющую угол 45 с продольной осью балки, рассматривать как стержень, воспринимающий сжимающие напряжения по своему поперечному сечению, равные касательным напряжениям у нейтральной оси. Длина такого сжатого стержня принимается равной h У 2 , где h — неподкрепленная высота стенки, а концы стержня считаются заделанными. Такое предположение, как мы увидим позднее, значительно недооценивает устойчивость неподкрепленных стенок.
Для того, чтобы получить более надежное заключение с точки зрения устойчивости стенки, должна быть привлечена теория выпучивания тонкой пластины, нагруженной нормальными и касательными напряжениями в ее плоскости. Различные задачи этого рода были обсуждены автором много лет назад2), и в то время предполагалось, что при проектировании двутавровых балок должна быть использована рациональная теория. В течение последнего года автор имел удобный случай вернуться к исследованию той же самой проблемы и получить некоторые новые решения задачи устойчивости, относящиеся к проектированию двутавровых балок.
1) См., например, статью: F. Е. Т и г п е а и г е. Experimental determinatipn of stresses in web plates and stiffeners of plate girxlers. Journal of the Western Society of Engineers, 1907, vol. 12, Na 6, pp. 788—819.
2) С. П. Тимошенко. Об устойчивости упругих систем. Применение
новой методы к исследованию устойчивости некоторых мостовых конструкций. Известия Киевского политехнического института, 1910, год 10, Отдел инженерной механики, книга 4, стр. 375—560. См. французский перевод этой статьи: Sur la stabilite des 8уз1ётез lastiques. Application d’une nouvelle methode a la recherche de la stabilite de certaines parties constitutives des
ponts. Annales des ponts et chaussees. 9 series, 1913, tome 15, vol. 3,
pp. 496—566, tome 16, vol. 4, pp. 73—132, tome 17, vol. 5, pp. 372—412.
См. также статьи автора «Uber die Stabilitat versteifter Platten». Eisenbau, 1921, Bd. XII, № 5—6, SS. 147—163 и «Problems concerning elastic stability in structures». Transactions of the American Society of Civil Engineers, 1930,
vol. 94, Paper № 1749, pp. 1000—1020 (discussion: 1021—1033; author’s reply; 1033—1035),
646
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
Цель настоящей статьи состоит в том, чтобы собрать воедино существующие сведения об устойчивости стенки, как тонкой пластины, и показать с помощью нескольких примеров, как результаты теоретических исследований могут быть использованы при проектировании двутавровых балок.
§ 1. Эксперименты
Первые эксперименты с выпучиванием тонких стенок, передающих касательные и изгибные напряжения, были проведены
В. Фёйрбёрном в связи со строительством известных трубчатых мостов Британия и Конуэй. Даже в наше время эти классические эксперименты1) имеют большой интерес для инженерного дела, связанного с тонкостенными конструкциями. Мост Британия представляет собою трубчатый тип моста и имеет прямоугольное поперечное сечение. Большие трубы имеют пролет 137,2 м и размеры поперечного сечения 8,23 м на 4,88 м. Так как этот мост для того времени представлял необычно большую конструкцию, то было решено провести эксперименты на моделях для того, чтобы определить безопасные размеры трубы и наиболее благоприятное распределение Материала. После значительного числа предварительных экспериментов было решено испытать большие модели в одну шестую линейных размеров намеченного моста. Стенки этих моделей труб состояли из листов 1,14 ж высотой и только 0,254 см толщиной. Первые эксперименты показали, что при сравнительно небольшой нагрузке появляется волнистость стенок, при этом длина волны формируется под углом приблизительно 45 с осью основания. «Из этих экспериментов ясно, что растяжение на всем протяжении днища и сжатие вдоль верхней части находятся в той же связи с действием и противодействием друг другу; при деформации стенок образуются диагонали, являющиеся средством связи». «Диагональная волна складкообразования ясно вырисовывает линию сильнейшей деформации. Очевидно, что стенки выявляют неблагоприятную деформацию от изменения формы, как следствие тенденции верхней и нижней частей трубы деформироваться совместно; пластины будут достаточно жестки, если они в состоянии сохранить свою форму, и, следовательно, жесткость определяется в этом эксперименте с целью видоизменения конструкции стенок. Это было сделано путем добавления стоек из уголкового железа на всем протяжении и по всей высоте стенок,
) Wm. F a i г b a i г n. An account of the constructions of the Britannia and Conway tubular bridges with a complete history of their progress. London, J. Weale, New York, Putnam, 1849,
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
64
приклепывания стоек к стенкам с целью увеличения жесткости стенок и в то же время с тем, чтобы верхняя и нижняя части трубы оставались на месте. Они были прототипами тавровых железных стоек в больших трубах.» Дальнейшие эксперименты иллюстрируют важность стоек, прикрепленных к стенкам; они показывают, как с помощью небольшого добавления металла к весу трубы верхняя и нижняя части ее остаются точно такими же, как и прежде, в то время как предельная прочность значительно повышается. Из этих экспериментов узнают, что «когда высота стенки увеличивается, то предосторожности, необходимые для поддержания формы стенок, становятся весьма трудно преодолимыми». Тавровое железо, косынки и пластины жесткости, использованные для этой цели в одной из труб моста Британия, весили 215 т, или свыше одной трети всего веса стенок.
Экспериментальные трубы были нагружены сосредоточенной силой в середине, тогда поперечная сила была постоянной вдоль длины пролета. При проектировании реального моста было принято во внимание, что максимальное поперечное усилие уменьшается к середине пролета, а толщина стенки в средней части равняется 1,27 см и 1,59 см на концах.
В то время были выполнены также некоторые экспериментальные работы по двутавровым балкам ). Толщина стенки модели балки повсюду равнялась 0,635 см габаритная высота была 3,05 м в центре и 1,83 м на концах, а расстояние между опорами было 20,1 м. Балка разрушалась вследствие выпучивания стенки. Позднее балка была отремонтирована, а вертикальная стенка подкреплена путем добавления стоек из уголкового железа в каждом соединении вертикальных пластин стенки. Таким путем прочность балки была значительно увеличена, и, наконец, она вышла из строя при большей нагрузке путем совместного разрушения верхней и нижней частей.
Дальнейшие опыты с двутавровыми балками были проведены бельгийским инженером М. Хуботтом2). Были испытаны две двутавровые балки длиной пролета 1,5 м, 0,5 см толщиной стенки и соответственно 30 см и 49 см высотой. Нагруженные посредине пролета, обе балки разрушались вследствие выпучивания стенки, которая не имела ребер жесткости. Балка большей высоты сломалась при меньшей нагрузке, хотя ее момент сопротивления в два с лишним раза больше момента сопротивления балки меньшей высоты.
1) Е. Clark. The Britannia and Conway tubular bridges with general inquiries on beams and on the properties of materials used in constructions. Vol. 1, 2. London, Day and son, 1850.
2) M. Houbotte. Versuche uber die Festigkeit blecherner Trager. Der Civilingenieur, 1858, Bd. IV, SS. 98—102.
648
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
В более недавние времена некоторая работа с двутавровыми балками была выполнена профессором В. Лилли1). Была сконструирована двутавровая балка следующих размеров: высота 24,1 см, длина 1,60 м. Полки были сделаны из двух пластин (5,08 см X 0,95 см) и двух уголков (3,17 см X 3,17 см 3,17 см X X 0,64 см). Каркас балки был выполнен из отдельных половин, которые были приболчены к стенке. Эта конструкция разрешала в эксперименте использовать различные толщины стенки. Поэтому было проведено большое число опытов со стенкой различной толщины и при различном расположении подкрепляющих элементов.
Прикладывая нагрузку посредине пролета, получим волнообразование в стенке. «Было найдено, что длина волны выпучины почти не зависит от толщины, если ребра жесткости значительно прочнее стенки. Угол наклона волны зависит от расстояния между ребрами жесткости и от высоты балки. Ребра
Рис. 1.
жесткости предотвращают образование волн, но вокруг концов ребер возникают высокие местные напряжения, вызывающие сморщивание этой части стенки». Фотография, воспроизведенная на рис. 1, представляет волнообразование в случае, когда стенка подкреплена только в середине, где приложена нагрузка.
Эксперименты с двутавровыми балками большого размера были проведены в Соединенных Штатах Америки профессором Ф. Турнором2). Основные заключения этих опытов следующие: 1) напряжения в стыке пластин с подкрепляющими ребрами при нагружении в пределах упругости хорошо согласуются с теоретическими значениями напряжений; в качестве неизбежного результата обнаружилось, что осевые напряжения в вертикальных ребрах, не подверженных действию местных нагрузок, практически равны нулю; 2) предел упругого сопротивления стенки без ребер жесткости примерно вдвое больше предельного значения, определяемого для стержня формулой Эйлера, которая
) W. Е. Lilly. Web stresses in plate girders. Engineering, 1907, vol. 83, February, pp. 136—139. См. также книгу профессора В. Лилли: The design of columns and struts. The economic design of columns. Web stresses in plate girders with plate. London, Chapman and Hall, 1908. Cm. W. E. Lilly. The design of plate girders. London, Chapman and Hall, 1904, 130 pp.
2) Статья, указанная на стр. 645.
устойчивость стенок двутавровых балок 649
применялась к диагональному элементу, как было определено выше.
Серия опытов с прокатанными и составными двутавровыми балками проводилась Муром и Уилсоном1). Эти экспериментаторы пришли к заключению, «что способность сопротивлению выпучивания тонких стенок без промежуточных ребер жесткости недооценивается» и «что можно с уверенностью построить балку без промежуточных ребер жесткости, если отношение неподкрепленной ширины к толщине стенки больше 60. Однако необходимо понизить рабочие напряжения, допускаемые в стенке, если это отношение оказывается больше».
Из проведенных экспериментов можно видеть, что двутавровая балка может передавать поперечную силу опорам двумя путями: 1) если нагрузка недостаточна для того, чтобы вызвать образование волн, то стенка балки передает поперечную силу, работая на сдвиг; 2) в случае больших нагрузок, которые приводят к волнообразованию, одна часть поперечных сил передается касательными напряжениями в стенке, как прежде, а другая часть — как в ферме, в которой стенка-пластина работает как связь, а ребра жесткости — как стойки. Величина нагрузки, при которой начинается образование волн, зависит от толщины стенки и от расположения и размеров ребер жесткости. В случае стенки достаточной толщины и удовлетворительного подкрепления двутавровая балка может нести общую нагрузку, при которой она спроектирована, без какой-либо потери устойчивости стенки. Такие соотношения мы обычно имеем в мостах. С другой стороны, имеются конструкции с очень тонкими стенками, которые выпучиваются в самом начале нагружения, и в них суммарная нагрузка практически передается, как в ферме.
Мы имеем примеры такого рода балок2) в самолетных конструкциях.
Хотя выпучивание стенки не означает непосредственного разрушения балки, размеры в случае мостов выбираются обычно так, чтобы исключить выпучивание при эксплуатационных условиях. Обычная процедура состоит в выборе некоторого
) Н. F. Moore. Strength of I-beams in flexur_e. Engineering Experiment Station of the University of Illinois Bulletin. 1913, Nv 68, 40 pp.; H. F. Moore, W. M. Wilson. Strength of webs of I-beams and girders. Engineering Experiment Station of the University of Illinois Bulletin, 1916, № 86, 50 pp.
2) H. Wagner. Ebene BlechwandtrSger mit sehr dflnnem Stegblech. Zeitschrift fur Flugtechnik und Motorluftschiffahrt, 1929, Bd. 20, Heft 8, SS. 200— 207; Heft 9, SS. 227—233; Heft 10, SS. 256—262; Heft 11, SS. 279—284; Heft 12, SS. 306—314. См. также A. W. В u e 1, C. A. Turner, J. M. Wilson. Spacing stiffeners in plate girders. Engineering News, 1898, vol. XL, N 10, pp. 154—156; F. G. S h i n n e r, C. A. P. Turner. Spacing striffeners In plate girders. Engineering News, 1898, vol. XL, Mb 25, pp. 399—400.
650
УСТОЙЧИВОСТЬ СТЕПОК ДВУТАВРОВЫХ БАЛОК
значения для рабочего напряжения при сдвиге и на этой основе назначения толщины стенки. Тогда расположение ребер жесткости определяется из условия того, чтобы стенка была в состоянии передать касательные напряжения без выпучивания
Замечая, что в железнодорожных балках суммарная нагрузка меняется приблизительно, как длина пролета, и предполагая отношение высоты к длине пролета постоянным, можно видеть, что вышеуказанная процедура дает в результате почти одну и ту же толщину для всех пролетов. Допустим, что эта толщина подходяща для малых мостов; она, разумеется, не будет безопасной для больших пролетов. Тогда становится необходимым некоторое увеличение толщины для исключения возможности выпучивания стенки. Это обеспечивается некоторыми техническими условиями. Например, технические условия Американского железнодорожного инженерного общества требуют, чтобы толщина стенки была не меньше 0,08 г, где h представляет собою расстояние между полками в см.
1'
1
г
1,
Рис. 2.
1
J
Другое ограничение на толщину обычно получают из рассмотрения коррозии и из того обстоятельства, что слишком тонкие пластины, если они широкие и длинные, являются очень опасными при транспортировке. Толщину, равную 0,95 см, обычно рассматривают как наименьшую допустимую толщину, которая позволяет предусмотреть коррозию и которая достаточна для удовлетворительной транспортировки материала при строительстве и погрузке.
Для того чтобы получить какую-либо рациональную основу для проектирования, необходимо произвести изучение упругой устойчивости тонких стенок. При обсуждении выпучивания стенки мы должны рассмотреть три случая: 1) вблизи опор касательные силы являются наиболее важным фактором, а часть стенки между двумя ребрами жесткости можно рассматривать
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
651
как прямоугольную пластину, подверженную действию равномерного сдвига (рис. 2); 2) посредине пролета касательными напряжениями можно пренебречь по сравнению с нормальными напряжениями; тогда часть стенки между ребрами жесткости находится в условиях чистого изгиба, представленного на рис. 3; 3) в промежуточных поперечных сечениях существует комбинация нормальных и касательных сил, как показано на рис. 4.
Эти три случая обсуждаются ниже.
§ 2. Устойчивость прямоугольных пластин при чистом сдвиге
Исследование устойчивости прямоугольных пластин при действии касательных сил (рис. 2) показывает, что критическое значение касательного напряжения, при котором происходит выпучивание, может быть представлено следующей формулой:
_и Е 2 П
ТкР“ 1Ц2 rf2 » W
где k — числовой коэффициент, зависящий от способа закрепления краев пластины и от отношения hjd между сторонами прямоугольника, Е — модуль упругости материала, ji — коэффициент Пуассона материала, at — толщина пластины.
Если h велико по сравнению d, как, например, в трубчатом мосте Британия, упомянутом выше, то коэффициент k практически зависит только от граничных условий вдоль длинных сторон прямоугольника. Для пластины, свободно опертой вдоль длинных сторон, k 4,40; в случае, когда продольные стороны заделаны, k 7,36 1).
Следует заметить, что длинные вертикальные ребра жесткости обычно недостаточно жестки для того, чтобы удовлетворить предположение о том, что вертикальные края заделаны, и мы обезопасим себя, если будем считать эти края свободно опертыми.
Если длины сторон прямоугольника имеют один и тот же порядок, то вычисление k становится более сложным2). Некоторые приближенные значения этого коэффициента для случая свободно опертых краев даны в таблице I. Предположено, что
) R. V, Southwell, S. W. S k а n. On the stability under shearing forces of a flat elastic strip. Proceedings of the Royal Society of London, Series A, 1924, vol. 105, № 733, pp. 582—607. R. V. Southwell. Note on the stability of laminar shearing motion in a viscous incompessible fluide. Phylosophical Magazine and Journal of Sciences, Series 6, 1924, vol. 43, № 285, pp. 540—553.
2) См. С. Тимошенко, статья, указанная на стр. 645.
652
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
h больше d. Если имеет место обратный случай, то в таблице I мы должны читать не hd, a dh и в формулу (1) ввести вместо d величину h.
Таблица I
Значения коэффициента k в уравнении (1) для прямоугольных пластин со свободно опертыми краями
hd
1,0
1,2
1,4
1,5
1,6
1,8
2,0
2,5
3,0
оо
k
7,75
6,6
6,0
5,8
5,7
5,6
5,4
5,2
5,0
4,4
Из формулы (1) можно видеть, что устойчивость пластины быстро уменьшается с уменьшением толщины пластины. Используя выражение (1) для случая, когда h велико по сравнению с d, и предполагая, что материал пластины есть сталь, для которой 2,1 X Ю6 кгсм2 и х 0,3 найдем, что критическое напряжение равно )
ткр 4,83 Е. (2)
Это значение приблизительно в три раза больше, чем значение, полученное путем применения формулы критического напряжения для сжатого стержня к узкой полосе стенки, наклоненной под углом 45 к продольной оси балки. Если некоторые эксперименты2) показывают, что заметное выпучивание имеет место при напряжениях приблизительно вдвое больших, чем это дает формула для сжатого стержня, то это можно объяснить тем обстоятельством, что экспериментальные образцы двутавровых балок имеют очень тонкие стенки, для которых возможная начальная кривизна может иметь много больший эффект, чем в случае двутавровой балки обычных габаритов.
Полагая для строительной стали предел текучести при сдвиге равным 1400 кгсм2 и подставляя это значение в формулу (2) для тКр, найдем, что соответствующее значение отношения djt приблизительно равно 85. Следовательно, если значение отношения высоты балки к толщине стенки не больше 85, то оправдано иметь ребра жесткости только в местах приложения сосредоточенных сил.
Используя формулу (1) и таблицу I, можно для данного значения ткр представить зависимость между отношениями hjt и hd посредством кривой. Несколько кривых этого рода пока¬
) Формула (2) справедлива для любого значения модуля упругости Е, когда ц ОД
2) F. Е. Turneaure, статья, указанная на стр. 645.
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
6БЗ
заны на рис. 5. Рассматривая часть стенки двутавровой балки между смежными ребрами жесткости вблизи опор как прямоугольную пластину, подверженную действию чистого сдвига, из этих кривых получим необходимое расстояние d между ребрами для любого значения ткр и любого значения htl). При определении расстояний h и d рекомендуется замерять их между центральными линиями полок и центральными линиями ребер жесткости. Это идущее в запас предположение может быть всегда
15 hd 2
1,5
'80 ЮО 120 140 00 J80 200 220 240 260 280 300 220 340
Vt
Рис. 5.
компенсировано понижением коэффициента безопасности в наших окончательных расчетах. При этом условии такой коэффициент безопасности, как 1,5, всегда, по-видимому, является подходящим.
§ 3. Устойчивость прямоугольных пластин при изгибе
Если прямоугольная пластина находится в условиях чистого изгиба в ее срединной плоскости (рис. 3), то критическое значение максимального изгибного напряжения находится из уравнения
акр “ k J _ 2 (3)
х) График для непосредственного определения расстояния между ребрами жесткости в дюймах для любого значения высоты h и толщины t на основе формулы (1) и таблицы I был подготовлен О. Е. Hove у. Stiffener spacing for plate-girder webs. Engineering News-Record, 1931, vol. 106, № 11, March 12, pp. 446—447.
654
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
Значения числового коэффициента ky вычисленные ) в предположении, что края пластины свободно оперты, даны в таб« лице II.
Таблица II
Значения коэффициента k в уравнении (3) для свободно опертых прямоугольных пластин при чистом изгибе
dh
0,4
0,5
0,6
0,67
0,75
0,8
0,9
1,0
1,5
2,0
3,0
оо
k
23,9
21,1
19,8
19,7
19,8
20,1
21,1
21,1
19,8
19,7
19,8
19,7
Видно, что если d больше й, то с увеличением d наблюдается только очень небольшое изменение коэффициента k и этот коэффициент достигает минимального значения 19,7, полученного для отношения dh 0,67. Это обстоятельство объясняется тем, что прямоугольная пластина, имеющая большой размер d выпучивается по нескольким волнам (рис. 6) с вертикальными
-
j . ; i
—-r ' '
III i i i i
F“ f
t h
b-,1
hr-
d Рис. 6.
узловыми линиями и отношение длины волны к высоте h оказывается равным 0,67. Например, для случая djh 2 получаются три волны и каждая волна находится в тех же самых условиях, что и пластина с отношением djh 0,67. Когда djh 3, получаются четыре волны с отношением длины волны к высоте, равным 0,75. Отсюда можно видеть, что вертикальные ребра жесткости несущественно влияют на устойчивость стенки. Рассматривая балку из строительной стали, спроектированную на основе растягивающего напряжения, равного 1120 кгсм2, полагая, как и прежде, коэффициент безопасности равный 1,5 и подставляя эти значения в формулу (3), получим акр 1,5 X X 1120 1680 кгсм2 с учетом k 19,7 найдем ht 165. Сле-
) См. статью автора, указанную на стр. 645; см. также И. Бубнов. Строительная механика корабля. Часть II. СПб., тип. морского министерства, 1914, стр. 525.
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
655
дует отметить, что при определении этого отношения были сделаны наиболее неблагоприятные предположения. Влияние вертикальных ребер жесткости было опущено, и, кроме того, пренебрегалось жесткостью краев стенки вблизи полок. В случае изгиба выпучивание стенки происходит при сжатии полки, а эффект жесткости края вдоль этой полки должен иметь большее влияние на критическое напряжение, чем в случае, который был обсужден выше. Принимая во внимание также, что выпучивание стенки при изгибе не представляет непосредственной опасности для балки, но просто указывает, что стенка больше не принимает полного участия в передаче сжимающих изгибных напряжений, по-видимому, более логично в этом случае понижать коэффициент безопасности по сравнению со случаем сдвига и брать его равным 1,25, что поднимает отношение lift до 180.
Учитывая вертикальные ребра жесткости и используя значение k из таблицы И, можно иногда уверенно полагать А равным 200 и выше.
В больших двутавровых балках иногда используются горизонтальные ребра жесткости1). В таких случаях верхняя часть стенки (рис. 7) может рассматриваться как горизонтальная пластина d а, подверженная комбинированному действию изгиба и сжатия. Распределение сжимающих напряжений по ширине пластины а в случае выпучивания может быть представлено формулой
CT CT«p(1-)- (4) Посредством изменения коэффициента а могут быть получены различные условия распределения напряжения. Принимая, например, а 1, получим случай, когда сжимающее напряжение вдоль одного края пластины равно а1ф и равно нулю вдоль другого. Такое условие мы имеем на рис. 7, беря а V2Л. Если а 7г, то напряжение, определяемое формулой (4), изменяется от акр до —сгКр. Это случай чистого изгиба. На рис. 7 получим этот вариант при а А. Условие а оо дает случай равномерно сжатой пластины.
Критическое значение сжимающего напряжения акр в случае комбинированного действия изгиба и сжатия находится из той же формулы (3), как и прежде.
х) L. Кагпег, статья, указанная на стр. 644.
656
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
Значения коэффициентов k для нескольких значений а даны в таблице III.
Используя приведенную выше таблицу, можно получить критические значения сжимающего напряжения для различных
Таблица III
Значения коэффициента k в формуле (3) для свободно опертых прямоугольных пластин, подверженных совместному действию изгиба и сжатия
da
а
0,4
0,6
0,75
0,8
1,0
1,5
0,75
15,4
10,6
9,5
9,2
9,0
9,5
1,00
12,4
8,0
6,9
6,7
6,4
6,9
1,25
10,9
6,8
5,8
5,7
5,4
5,8
1,50
8,9
5,8
5,0
4,9
4,8
5,0
оо
6,92
4,23
3,60
3,45
3,29
3,60
положений горизонтального ребра жесткости АВ (рис. 7). Можно видеть, что такое ребро жесткости является более эффективным подкреплением стенки двутавровой балки, чем вертикальное ребро жесткости.
§ 4. Устойчивость прямоугольных пластин при комбинированном действии изгиба и сдвига
В случае комбинированного действия изгиба и сдвига (рис. 4) может быть использован тот же самый метод вычисления критического значения напряжений, что и в случае одного сдвига. Результаты таких вычислений1), выполненные для трех различных значений отношения dй, представлены на рис. 8.
Кривые У, 2, 3 этого рисунка получены при условии, что по оси абсцисс откладываются значения отношения действительного касательного напряжения к критическому касательному напряжению, определяемому из формулы (1). Для того, чтобы получить критическую величину максимального изгибного напряжения, следует ввести в формулу (3) значения коэффициента k, которые принимаются за ординаты. Видно, что для малых значений т, скажем тткр 0,4, влияние касательного напряжения на критическое значение изгибающего напряжения мало. Таким образом, оказывается оправданным определение толщины стенок двутавровых балок из рассмотрения средней части пролета балки в условиях чистого изгиба.
) Эти расчеты были выполнены Stewart’oM Way’eM, аспирантом Мичиганского университета.
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
657
Когда тткр приближается к единице, кривые 1, 2, 3 становятся очень крутыми; это указывает, что к напряжениям чистого сдвига могут быть добавлены значительные изгибные напряжения, не вызывающие заметного уменьшения критических значений касательного напряжения. Это оправдывает рассмотрение части стенки вблизи опор как пластины, подверженной действию чистого сдвига. Кривая 4 рис. 8 построена для двутавровой балки постоянного поперечного сечения, несущей равномерно распределенную поперечную нагрузку, в предположении, что dh 0,5. Поперечное сечение имеет такие размеры, что максимальное изгибное напряжение в середине пролета, представленное точкой А кривой, и максимальное касательное напряжение на опоре, изображенное точкой В, достигаются одновременно.
25 А 20
5 к
Ю
5
0 О 0,1 0J 0,3 0,4 0,5 0,8 0,7 0,8 0 Vtv
Рис. 8.
Тогда для любого промежуточного поперечного сечения соответствующее значение максимального изгибного напряжения дается ординатой параболической кривой АВ, так как изменение изгибных напряжений вдоль пролета следует параболическому закону. Видно, что парабола АВ всегда ниже кривой 1. Таким образом, если толщина стенки и положение ребра жесткости выбраны так, чтобы удовлетворить условиям устойчивости в середине пролета и на опорах, то во всех промежуточных поперечных сечениях устойчивость также будет обеспечена.
В случае двутавровой балки переменного поперечного сечения иногда необходимо проверить устойчивость стенки там, где имеет место внезапное изменение поперечного сечения. Такие дополнительные расчеты могут быть также проведены посредством кривых, представленных на рис. 8.
658
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
§ 5. Приложения
Полученные выше результаты, относящиеся к устойчивости прямоугольных пластин, могут быть следующим образом использованы для выбора размеров двутавровых балок. Сначала определим необходимую толщину стенки в середине пролета для того, чтобы предотвратить выпучивание стенки при действии изгибающих напряжений. Тогда, принимая наиболее неблагоприятное предположение и коэффициент безопасности равным 1,25, получим отношение ht 180.
Когда толщина стенки выбрана, то расположение ребер жесткости мы должны определить таким образом, чтобы стенка имела возможность передавать касательные напряжения без выпучивания. Для этой цели могут быть использованы кривые рис. 5, откуда для любого требуемого значения касательного напряжения получается необходимое отношение djt шага ребра жесткости к толщине стенки. Коэффициент безопасности в этом случае может быть выбран равным 1,5.
В качестве примера рассмотрим теперь двутавровые балки высотой 1,83 м и 3,05 м. В случае h 1,83 м и считая ht 180, найдем, что t 1,02 см принимаем толщину стенки равной 1,11 см.
Принимая рабочее напряжение при сдвиге равным 703 кгсм2, а коэффициент безопасности 1,5, мы используем на рис. 5 кривую для ткр 1050сгсл2. Для ht 180 X 1,02 : 1,11 165 находим, что hd 1,44 и d 127 см. Для ткр 703 кгсм2 находим hjd 1,06 и d 173 см.
Используя в данном случае технические условия Американского железнодорожного инженерного общества, найдем, что
t 0,08 h 1,08 см.
Примем t 1,11 см. Расстояние между ребрами для рабочего напряжения т 703 кгсм2 равно
d 1 (1050 - т) 0,356 (1050 — т) 50 56 см.
Для рабочего напряжения
т 2з X 703 кгсм2 d 133 147 см.
Тогда предложенный способ выбора размеров двутавровых балок дает ту же самую толщину стенки и до некоторой степени большее расстояние между ребрами жесткости, чем это получается, если использовать технические условия Американского железнодорожного инженерного общества.
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
659
В случае 1г 3,05 м и при t ft180 1,70 см получим t 1,75 см. Расстояние между ребрами жесткости для ткр 703 кгсм2 согласно рис. 5 равно d 150 t 262 см. Технические условия Американского железнодорожного инженерного общества в этом случае для толщины стенки t дают значение, равное 1,43 см, а для расстояния между ребрами жесткости d значение, равное 1,83 м. Таким образом, мы получили до некоторой степени большую толщину стенки и большее расстояние между ребрами жесткости, чем это дается техническими условиями Американского железнодорожного инженерного общества.
§ 6. Ребра жесткости
Рассматривая часть стенки между двумя последовательными ребрами, мы предполагали в нашем обсуждении, что ребра жесткости имеют достаточную изгибную жесткость и когда стенка выпучивается, они остаются прямыми. Если эта жесткость недостаточна, то наклоненные волны выпученной стенки пересекают ребра жесткости и выпучивание стенки сопровождается изгибом ребер жесткости. Такой изгиб был, очевидно, например, в некоторых эксперимен- т
тах В. Фёйрбёрна, обсужденных выше. Для того, чтобы определить необходимую жесткость, достаточную для предотвращения изгиба ребер жесткости во время выпучивания стенки, рассмотрим случай, представленный на рис. 9: прямоугольная пластина длиной 2d и шириной ft свободно оперта на краях и подвержена чистому сдвигу. Для того чтобы предотвратить боковое выпучивание, пластина подкреплена стойкой АВ. Если изгибная жесткость стойки мала, то ее влияние на величину критического касательного напряжения будет также малым. Волны выпученной пластины будут пересекать стойку, и будет происходить изгиб стойки. Последовательно увеличивая жесткость стойки, мы можем в конце концов достичь условий, при которых каждая половина пластины будет выпучиваться, как свободно опертая прямоугольная пластина с размерами в плане ft X dt а стойка будет оставаться прямой. Соответствующая предельная величина EJ изгибной жесткости стойки может быть найдена из рассмотрения энергии деформации изгиба пластины и стойки 1). Несколько
С
A F
tt
1 D
§ G
d
1Г71
— У —J
Рис. 9.
) С. Тимошенко, статья, указанная на стр. 645.
660
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
значений отношения yi этой жесткости к жесткости dEt12(1—jli2) одной панели стенки, если она изгибается по цилиндрической поверхности, даны в таблице IV.
Таблица IV Таблица V
Отношения Yi Отношения Ya
dh
1
34
58
12
Yi
1,66
6,8
12,6
30
dh
1
56
23
12
25
Y2
1,92
4,11
10,6
32,1
67,8
При вычислении этой таблицы предполагалось, что только стойка АВ на рис. 9 является гибкой, а стойки CD и FG являются абсолютно жесткими.
Другая серия расчетов была выполнена в случае трех панелей и двух гибких промежуточных ребер жесткости. Поступая,
как в предыдущем случае, и обозначая через Y2 отношение изгибной жесткости ребра жесткости к изгибной жесткости одной панели, мы получим значения, приведенные в таблице V ).
Значения yi и у2 представлены кривыми на рис. 10. Видно, что в случае трех панелей требуемая жесткость двух промежуточных ребер жесткости больше, чем в случае двух панелей; эта жесткость должна до некоторой степени возрастать с увеличением числа панелей. Допуская, что во всех практических случаях жесткость ребер жесткости не будет 0,5 Q6 0,7 0,8 0,9 1 1,1 1,2 больше, чем удвоенная жест-
’ dti кость, даваемая таблицей IV,
получим при этих значениях Рис. 10. данные таблицы VI — тре¬
буемые моменты инерции поперечного сечения ребер жесткости для разных высот и толщин стенки при интервале между ребрами жесткости, равном d 1,52 м.
I
L
a)
'Щ
. _ ea(-u) ' act3 rr_Mjtf2
b)
L , , —
h i
ipeb,
pucb
;pa
N
x
Рф
ocmatt
'О Ж6С 1ПСЯ fy
muocm
1ЯМЫМ
и
и
06.
fuca
ipo
1
4
1
) Эта таблица была вычислена Stewart’oM Way’eM.
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
661
Видно, что для меньшей высоты вычисленный момент инерции поперечного сечения много меньше, чем то значение его, которое действительно назначается. Для ббльшей высоты вычисленные значения J достигают обычных размеров. Например, в случае h 3,05 см ребро жесткости согласно американским
Таблица VI Требуемый момент инерции ребер жесткости
h, cm
162
203
244
305
dh
1
34
58
12
Y 2Yi
3,30
11,6
25,2
60
t 0,95
CM
2,51
8,53
18,5
44,2
J л.4
1,11
CM
3,96
13,6
29,5
70,1
J, CM
t 1,27
CM
5,97
20,3
44,2
105
t 1,43
CM
8,53
29,2
63,5
151
техническим условиям) состоит из двух уголков 15,2 см X X 8,89 см X 0,95 см. Момент инерции для такого ребра жесткости для t 1,43 см равен 159 см4, что близко к значению 151 см4, данному в таблице VI.
) Н. A. L. Waddell. Bridge Engineering. First edition. New York, John Wiley, 1916, p. 1670.
ВЫПУЧИВАНИЕ ПОЛОГИХ СТЕРЖНЕЙ И СЛЕГКА ИСКРИВЛЕННЫХ ПЛАСТИН
Buckling of flat curved bars and slightly curved plates. Journal of Applied Mechanics, 1935, vol. 2, № 1, pp. 17—20. Перепечатка: S. P. Timoshenko. The collected papers. McGraw-Hill Publishing Company Ltd, New York — London— Toronto, 1953, pp. 508—515.
Если пологая арка подвержена действию равномерно распределенной нагрузки (рис. 1), то разрушение конструкции может произойти не в результате возникновения высоких напряжений и текучести материала, но вследствие неустойчивости. Сжатая
Для того чтобы упростить вычисления, предположим, что ось центров тяжести поперечных сечений арки сперва описывается уравнением
и что концы арки шарнирно оперты. Введем следующие обозначения:
q — интенсивность равномерной нагрузки,
EJ — изгибная жесткость арки,
_ 5 ql 1 ,м
U 384 EJ а — отношение прогиба, вычисленного для балки, к высоте подъема арки,
Н — распор арки,
Рис. 1.
L
арка может выпучиться и занять положение, указанное на рисунке пунктирной линией. В последующем обсуждении показано, как можно вычислить критическую нагрузку, при которой имеет место выпучивание.
пх
tji a sin—г-
(а)
(с)
— отношение распора к эйлеровой силе.
Тогда после нагружения центральную ось арки в предположении, что оня симметрична относительно середины, можно
ВЫПУЧИВАНИЕ ПОЛОГИХ СТЕРЖНЕЙ И ИСКРИВЛЕННЫХ ПЛАСТИН 663
с достаточной точностью представить следующим уравнением1):
а (1 — и). их , ,ч
1 - a sin Т
Это уравнение может быть использовано не только при и 1, но также и при и 1, т. е. в тех случаях, где прогиб искривленного стержня, вычисленный, как для простой балки, больше первоначальной высоты подъема арки. Величина а также может быть больше единицы, но она должна быть меньше четырех, поскольку при а 4 выпучивание арки происходит с точкой перегиба в среднем сечении арки и предположение, заключенное в уравнении (d), о том, что арка остается симметричной по отношению к середине, больше не выполняется.
Допуская сначала, что и С 1, из уравнения (d) мы найдем, что прогиб у2 положителен, если а 1, и отрицателен, когда а 1. Это означает, что арка имеет форму, показанную на рис. 1 сплошной линией, если распор меньше эйлеровой силы для стержня с опертыми концами, и что та же арка может изогнуться вниз, как показано на рисунке пунктирной линией, если распор больше эйлеровой силы. Когда и 1, то прогиб у2 положителен при а 1 и становится отрицательным при а 1.
Действительная форма арки после нагружения может быть определена, когда величина а, и, следовательно, распор Я, известны. Уравнение для вычисления распора Я получается приравниванием изменения длины пролета, обусловленного прогибом, укорочению стержня от распора. Считая, что для пологой кривой сжимающая сила постоянна по длине стержня и равна Я, получим уравнение
жт №)'« о о
в котором F есть площадь поперечного сечения стержня. Вводя вместо у и у2 их выражения по формулам (а) и (d) и интегрируя, получим
(1 _ )2 (1 — met) (1 — ct)2, (f)
где
4 , ч
Для данной арки величина т легко вычисляется, и если нагрузка q задана, то величина J может быть определена из
) См. книгу автора «Strength of materials». Part 2. London, Macmillan and Co., 1931, p. 422. Перевод на русский язык: С. П. Тимошенко. Сопротивление материалов. Часть 2. Л.—М., ГТТИ, 1934, стр. 81.
664 ВЫПУЧИВАНИЕ ПОЛОГИХ СТЕРЖНЕЙ И ИСКРИВЛЕННЫХ ПЛАСТИН
уравнения (Ь). Тогда соответствующие значения а и распора Н получаются из уравнения (f). Поскольку это уравнение является нелинейным, то для а при некоторых условиях можно получить более чем один действительный корень; последнее означает, что существует несколько возможных форм равновесия и что устойчивость этих форм должна быть исследована.
Рассматривая правую часть уравнения (f) как функцию а, найдем, что при т с 1 эта функция имеет минимум, равный нулю при а 1, и максимум при а (2 m)3mf Величина этого максимума будет
4 (l-m)3
27 т2 №)
На рис. 2 правая часть уравнения (f) представлена графически для случая т V2. Для этого значения т максимум наблюдается при а 5з, а величина этого максимума согласно выражению (h) равна 2г7 Если нагрузка q такова, что левая часть уравнения (f) больше этого максимума, то получим только одно действительное решение для а, которое указывает, что возможна только одна форма равновесия, следовательно, такое равновесие является устойчивым. Если левая часть уравнения (f) меньше величины, определяемой выражением (h), то для а получим три решения, соответствующих точкам пересечения s, г и t на рис. 2, и необходимо рассмотреть вопрос об устойчивости соответствующих форм равновесия. Используя эти заключения в только что разобранном числовом примере, найдем, что равновесие арки всегда устойчиво, если (1 — w)2 2г7 что эквивалентно условиям
ы1-227, « 1 227. (i)
Первое из этих условий соответствует форме равновесия, выпуклой вверх, как показано на рис. 1 сплошной линией, а второе условие — форме, выпуклой вниз, как обозначено на рисунке пунктирной линией.
Для любого значения т, меньшего единицы, условия устойчивости, эквивалентные условиям (i), будут
Рис. 2.
и 1
4 (1-т)3
27 т2
и 1
4 (1 — т)3
W т2
0)
ВЫПУЧИВАНИЕ ПОЛОГИХ СТЕРЖНЕЙ И ИСКРИВЛЕННЫХ ПЛАСТИН 665
Следовательно, условия, делающие возможным существование более чем одной формы равновесия (здесь необходимо исследовать устойчивость этих форм равновесия), суть
«1-у
4 (1 — т)3
27
и 1
W
(1 -т)3
(к)
Если 1, то уравнение (f) имеет только один действи¬
тельный корень, как можно видеть из рис. 3, на котором кривые представляют собой правую часть уравнения (f) при т 2 и т 1. Видно, что для любого положительного значения величины (1—и)2 мы получим только одно значение а, которое меньше единицы. Следовательно, для 1 существует только одна возможная форма равновесия, которая будет устойчивой. Вопрос о неустойчивости возникнет, только если т 1 и нагрузка находится в пределах, указанных условиями (к).
При исследовании устойчивости выгодно представить графически подъем арки в функции нагрузки или в функции величины и. С помощью уравнения (d) найдем этот подъем:
а (1 — и)
(1)
Принимая в каждом частном случае серию значений а, можно из уравнения (f) вычислить соответствующие значения и, а из уравнения (1) — подъем at. На рис. 4 значения aja изображены в зависимости от и. Сплошная линия относится к случаю, для которого т V2, а две пунктирные линии — к случаям m 1Д и т 1. Рассматривая график для случая т 7г, видим, что прогиб постепенно возрастает с увеличением нагрузки вплоть до точки Л, которая соответствует максимуму (при а 5з) на кривой, изображенной на рис. 2. Начиная с этой точки, дальнейшее изменение прогибов происходит при уменьшении иу т. е. при падении нагрузки q. Это обстоятельство означает, что в точке Л, т. е. при (1 — и)2 227» форма равновесия арки, изображенная на рис. 1 сплошной линией, становится неустойчивой, и арка выпучивается вниз, как показано пунктирной кривой. Стрела прогиба этой новой формы равновесия определяется положе¬
666 ВЫПУЧИВАНИЕ ПОЛОГИХ СТЕРЖНЕЙ И ИСКРИВЛЕННЫХ ПЛАСТИН
нием точки В рис. 4. Эта новая форма равновесия является устойчивой, и любое последующее увеличение нагрузки приводит к постепенному росту прогибов, как это иллюстрирует часть ВС кривой рис. 4. Распор Н во время этого нагружения уменьшается. Он становится равным нулю в точке С и оказывается отрицательным при дальнейшем увеличении нагрузки. Если, отправляясь от точки Bf мы. начнем убавлять нагрузку, то прогибы арки постепенно уменьшатся вплоть до точки D. В этой точке нагрузка становится недостаточной для того, чтобы удерживать арку, изогнутую выпуклостью вниз, и она выпучивается вверх в положение, определяемое точкой Е на рис. 4. Из этого обсуждения видно, что существует возможность иметь более чем одну форму равновесия в области, ограниченной вертикальными линиями ED и АВ, которые соответствуют условиям (i). В общем случае эта область определяется условиями (к), и мы может заключить, что критическая нагрузка, при которой арка будет выпучиваться выпуклостью вниз, находится из уравнения
, , f 4 (1 - m)3 1Ч
М-1 27 От2 (1)
Из кривых, представленных на рис. 4, можно видеть, что область, в которой возможно существование более чем одной формы равновесия, становится меньше и меньше с увеличением т и когда т становится равным единице, оба предела, определяемые (к), совпадают; следовательно, начиная с этого значения 72, возможна только одна форма равновесия.
В предыдущем обсуждении предполагалось, что арка подвержена равномерно распределенной нагрузке; однако полученные результаты можно использовать во всех случаях, в которых прогиб арки, рассматриваемой как балка, может быть представлен с достаточной точностью синусоидой. Предполагая, например, что арка в среднем сечении нагружена сосредоточенной
ВЫПУЧИВАНИЕ ПОЛОГИХ СТЕРЖНЕЙ И ИСКРИВЛЕННЫХ ПЛАСТИН 667
вертикальной силой Р, из уравнения (I)1) получим критическое значение этой силы; необходимо только в это уравнение ввести выражение
Р1г
и 4817а
Аналогичным способом можно также решить задачу, если сила Р приложена не в среднем сечении, а в другом. Необходимо только подставить в выражение (ш) вместо Р348У соответствующий прогиб в среднем сечении балки.
Результаты предыдущего обсуждения можно использовать при исследовании выпучивания биметаллических полос, подверженных изменению температуры. Такие полосы используются как элементы приборов (термостатов), служащих для регулирования температуры. Простое рассмотрение показывает, что вследствие разницы коэффициентов линейного температурного расширения двух металлов прямолинейная биметаллическая полоса при изменении температуры искривляется. Кривизна ее может быть вычислена из уравнения2)
1 _ 3 (в2 — 8i) (t —10) , .
Р 2 h 9 W
в котором ei и 62 суть коэффициенты линейного температурного расширения (предполагается, что 62 61), h — толщина полосы, a t —10 — повышение температуры. Таким образом, кривизна биметаллической полосы, вызванная нагревом, пропорциональна повышению температуры и разности двух коэффициентов линейного расширения и обратно пропорциональна толщине полосы. Выражение (2), выведенное для двух металлов с равными модулями упругости, может быть также с достаточной степенью точности использовано в случае, когда материалы имеют
) Эта частная задача обсуждалась С. L. М. Н. Navier, Resume des lemons donnees a l’ecole des ponts et chaussees, sur l’application de la mechanique a l’etablissement des constructions et des machines. 1 Partie. Deuxieme edition. Paris, Cher Carilian-Goeury, 1833, p. 273. См. также С. В. В i e z e n о. Uber eine Stabilitatsfrage beim gelenkig gelagerten, schwach gekrummten Stabe. Proceedings Koninklijke Akademie van Wetenschappen te Amsterdam, 1929, vol. 32, № 7, pp. 990—994. См. также С. В. В i e z e n о. Das Durchschlagen eines schwach gekrummten Stabes. Zeitschrift ftir angewandte Mathematik und Mechanik, 1938, Bd. 18, Heft 1, SS. 21—30. Случай, когда центральная ось арки не является пологой кривой, рассматривался А. N a d a i. Labile Gleichgewichtslagen stark gebogenen Stabe. Technische Blatter. Zeitschrift des deutschen polytechnischen Vereins in Bohmen, Prague, 1915, Jahrgang 47, Jsfe 3 und 4, SS. 137—145.
2) См. книгу автора «Strength of materials». Part 1. London, Macmillan and Co., 1931, p. 245. Перевод на русский язык: С. П. Тимошенко, Сопротивление материалов. Часть 1. Л.—М., ГТТИ, 1934, стр. 222.
668 ВЫПУЧИВАНИЕ ПОЛОГИХ СТЕРЖНЕЙ И ИСКРИВЛЕННЫХ ПЛАСТИН
несколько различные модули упругости, как, например, в случае монель-металла и никелевой стали1).
Зная кривизну, найдем прогиб среднего сечения полосы, опертой по обоим концам, обусловленный повышением температуры на — toy как для пологой дуги круга; он равен
где — длина полосы, а р — радиус кривизны, определяемый выражением (2).
Теперь рассмотрим биметаллическую полосу, которая имеет небольшую начальную кривизну, и допустим, что концы полосы шарнирно оперты, как показано на рис. 1 сплошной линией. Если металл на вогнутой стороне имеет больший коэффициент линейного температурного расширения, чем металл на выпуклой стороне, то полоса при нагревании прогибается вниз, и как результат этого прогиба будет возникать распор Н. При некоторой температуре, зависящей от размеров полосы и от разницы коэффициентов линейного температурного расширения обоих металлов, форма полосы, изображенная на рис. 1 сплошной линией, становится неустойчивой, и полоса внезапно выпучивается вниз, как указано пунктирной линией. В термостате источник нагревания в момент выпучивания полосы отключается и начинается охлаждение, которое в конечном счете приводит к выпучиванию полосы в направлении вверх; таким образом источник нагревания снова включается. Это явление аналогично случаю выпучивания плоской арки при нагружении и разгрузке, который был только что обсужден. Для того чтобы определить температуру, при которой происходит выпучивание, необходимо только использовать вместо прогиба, вызванного нагрузкой, прогиб (п), обусловленный температурой. Тогда уравнение (1) примет вид
Используя выражение (2) для кривизны, получим, что температура ti, при которой происходит выпучивание полосы в направлении вниз, вычисляется из уравнения
Температура t2l при которой полоса выпучивается в направлении вверх после охлаждения, получается из первого неравенства
) Более общее использование изгиба и выпучивания биметаллических полос дано автором в статье «Analysis of bi-metal thermostats». Journal of the Optical Society of America and Review of Scientific Instruments, 1925, vol. 11, № 3, pp. 233—255.
ВЫПУЧИВАНИЕ ПОЛОГИХ СТЕРЖНЕЙ И ИСКРИВЛЕННЫХ ПЛАСТИН 669
(к). Следовательно, Возьмем, например, lh 100, 82 — ei 4 10_e 1 С, а значения т. h23a такими, как это указано в первой строке таблицы I, отношения первоначальной стрелы подъема а полосы к ее толщине h — в соответствии со второй строкой этой таблицы. Значения (ti — 0), вычисленные из уравнения (3), и значения (2 — to)у найденные из уравнения (4), представлены соответственно третьей и четвертой строкой таблицы.
Числовые данные о выпучивании биметаллических полос
т
23
12
13
14
alh
ti-to, С 2 — 0 С
0,707
104
83
0,814
137
79
1,000
217
50
1,154
307
0
Из таблицы видно, что температура выпучивания 11 увеличивается с ростом первоначальной кривизны и что в то же самое время температура t2 уменьшается, так что чувствительность термостата, определяемая разностью 11 — 2, быстро понижается с увеличением критической температуры ti. Это положение может быть улучшено введением упругих опор для биметаллической полосы.
Если при действии распора Я расстояние между опорами возрастает на некоторую величину ЗЯ, пропорциональную Я, то уравнение для вычисления распора Я имеет вид
о о
и вместо уравнения (f) получим
(1 — и)2 (1 — та) (1 — а)2; (о)
здесь
(р)
Очевидно, что поведение -биметаллической полосы с упругими опорами может быть исследовано тем же самым способом, как и прежде.
Необходимо только вместо величины т ввести новую величину ти зависящую от упругости опор. Посредством подходящего регулирования упругости опоры может быть получена требуемая чувствительность термостата1).
1) См. указанную на стр. 66 статью авторе,
ТЕОРИЯ ИЗГИБА, КРУЧЕНИЯ И УСТОЙЧИВОСТИ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Theory of bending, torsion and buckling of thin-walled members of open crosssection. Journal of the Franklin Institute, 1945, vol. 239, Part 1 (§§ 1—3), № 3, pp. 201—219; Part 2 (§§ 4—7), № 4, pp. 249—268; Part 3 (§§ 8—10), № 5, pp. 343—361. Перепечатка: S. P. Timoshenko. The collected papers. New York — London — Toronto, McGraw-Hill Publishing Company Ltd, 1953,
pp. 559—609. Перевод на французский язык: Theorie de la flexion, torsion et
flambage des barres a parois minces et a section ouverte. L’ossature mtallique,
1947, vol. 12, № 7—8, pp. 328—341; № 9, pp. 376—388. Перевод И. К. Снитко
на русский язык: Добавление к книге С. П. Тимошенко «Устойчивость упругих систем», 2-е изд., М.—Л., Гостехиздат, 1955, стр. 502—561.
Введение
Первые задачи о неустойчивости тонкостенных стержней были решены около полувека тому назад, но наибольшие достижения в этой области были достигнуты за последнее время, преимущественно в связи с разработкой конструкций самолетов. Требования экономии веса ведут к широкому использованию тонкостенных стержней, и анализ деформаций и потери устойчивости таких конструктивных элементов приобретает огромное практическое значение. В этой работе мы начинаем с изучения теории изгиба тонкостенных стержней открытого постоянного поперечного сечения и вводим понятие о центре сдвига. Затем, используя теорему взаимности Максвелла, переходим к изучению кручения и устанавливаем тождественность центра сдвига и центра кручения. После обсуждения задачи о совместном изгибе и кручении мы переходим к проблеме неустойчивости и обсуждаем задачи крутильной формы потери устойчивости и бокового выпучивания стержней. Очевидно, при такой последовательности изучения получается значительное упрощение в построении теории тонкостенных систем и достигается лучшее понимание явления крутильной потери устойчивости.
§ 1. Чистый изгиб призматических стержней
Рассмотрим призматический стержень произвольного поперечного сечения. Предположим, что нагрузки приложены на его концах и сводятся к двум равным и противоположно направленным моментам, действующим в плоскости продольной оси стержня. В этом случае наблюдается чистый изгиб стержня. Поперечные сечения стержня в процессе чистого изгиба остаются
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 671
плоскими и только вращаются относительно нейтральных осей, которые проходят через центры тяжести попереченых сечений. Принимаем начало координат в центре тяжести С одного из поперечных сечений, направляем ось z по продольной оси стержня, ось х по нейтральной оси и выбираем направление оси у таким образом, чтобы получить правую систему координат, представленную на рис. 1. Выберем положительные направления моментов Мх, Му (а также углы поворота
поперечных сечений) в соответствии с правилом правой системы, как показано на рис. 1, обозначив через гх радиус кривизны в плоскости yz, взятый со знаком плюс в том случае, если угол поворота поперечных сечений увеличивается по мере увеличения z получим
ог --у, Мх J ozydF , My-jozxdF
EJ
ху
(i)
Очевидно, плоскость, в которой действует изгибающий момент, совпадает с плоскостью упругой оси стержня только в том случае, когда Jxy 0, т. е. если изгибающий момент находится в одной из главных плоскостей стержня.
Подобное же рассуждение можно повторить для случая, когда нейтральные оси становятся параллельными оси у и, исходя из принятого правила знаков, мы получим
х, Мх J ozydF —
F
EJ
ху
(2)
На основании этих двух частных случаев мы можем, пользуясь принципом наложения, исследовать изгиб стержня от действия моментов, лежащих в любой осевой плоскости. Рассмотрим, например, изгиб от пары сил, действующей в плоскости yz. В этом случае Му обращается в нуль. Чтобы выполнить это условие, пользуясь уравнениями (1) и (2), мы должны положить
EJ
ху
EJU
0,
откуда
Jx у
672 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Снова используя принцип наложения, получим
EJX EJxy _(лл4) 1
откуда
Мх - , ,
х гх гу Jy гх
1 MxJy 1 Mxjxy
6)
’ ry EJJyJly) '
Имея эти выражения для кривизн в плоскостях yz и xzt мы можем вычислить изгибные напряжения по уравнению
0 г —У - — Х - -2- (JylJ-J Хух). (4)
Гх ry J xJ у J ху
Эти напряжения обращаются в нуль, если выражение, взятое
в скобки, равняется нулю. Отсюда мы получим уравнение Jvy —
— JxyX 0 для определения нейтральной оси. Подобным же образом, если пара сил Му действует в плоскости xzt находим
1 _ 1 _ MyJx
г ExJy-Jly) ’ ry EJxJy-Jly) '
. -2 UхуУ Xх)' )
JxJу Jху
Полученные результаты могут быть, строго говоря, применены только в том случае, когда напряжения распределены по концам стержня таким же образом, как и в любом промежуточном поперечном сечении. Однако применение этих формул обычно распространяется и на другие случаи распределения напряжений; при этом предполагается, что замещение одной системы усилий на концах другой, статически эквивалентной, вызывает только местные изменения напряжений вблизи концов и не оказывает
существенного влияния на деформацию стержня, если размеры
его поперечного сечения малы в сравнении с длиной. Пределы применимости этого принципа, впервые сформулированного Сен-Венаном, для случая тонкостенных стержней открытого поперечного сечения будут более подробно обсуждены ниже.
§ 2. Поперечный изгиб призматических стержней
Предположим, что изгиб однородного стержня вызывается системой сил, параллельных оси у и действующих в плоскости, параллельной плоскости yz (рис. 1), на таком расстоянии от этой плоскости, что имеет место только изгиб без кручения; другими словами, поперечные сечения стержня поворачиваются при деформации лишь относительно осей х и у, но не относительно
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 673
оси z. Пусть величинами изгибающего момента и поперечной силы в любом поперечном сечении будут Мх и Qy соответственно. Тогда, рассматривая равновесие элемента стержня, выделенного двумя смежными поперечными сечениями (рис. 2), получим следующие уравнения:
dMjc
dz
dz — Qydz О,
dQy
dTqydz 0
что дает
dMx
dz
Q
dQy
dz
- Qy
(5)
Здесь qy — интенсивность распределенной нагрузки. Подобным же образом, рассматривая поперечные нагрузки, параллельные плоскости xz (рис. 3), получим
dQx _ дч
Qx dz Ух ' '
dMy
dz
Возвращаясь к случаю, представленному на рис. 2, допустим, что изгибающий момент Мх вызывает изгиб оси согласно
шин
, 11 х
1
у А
dz
мх
Рис. 2.
dz
г
4ri
V
Е
dz
rf 9
Рис. 3.
формулам (3) и изгибные напряжения1), определяемые выражением (4). Поперечные силы Qy вызывают касательные напряжения. Вычисление этих напряжений представляет сложную задачу, которая точно разрешается только для немногих видов поперечного сечения. Если стержень имеет одну осевую плоскость симметрии и нагрузка приложена в этой плоскости, на основании свойств симметрии мы заключаем, что такая нагрузка вызывает только изгиб в плоскости симметрии, но не кручение. Если имеются две плоскости симметрии, мы можем разложить любую поперечную нагрузку, проходящую через ось стержня, на две составляющие, действующие в плоскостях симметрии, и отсюда заключить, что такая нагрузка не вызывает кручения.
1) Строгие выводы теории упругости показывают правильность этого допущения.
674 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
В общем же случае мы найдем, что касательные напряжения, вызванные поперечной силой Qy, дают результирующую, которая обычно не проходит через центр тяжести поперечного сечения. Это указывает на то, что нагрузка должна действовать на некотором расстоянии от осевой плоскости yz для того, чтобы вызвать только изгиб без кручения. Например, в случае консоли полукруглого поперечного сечения (рис. 4) для осуществления изгиба, при котором вертикальная сторона поперечного сечения
не поворачивается, сила Р должна проходить через точку О, расстояние которой от вертикальной стороны поперечного сечения составляет1)
где а есть радиус поперечного сечения и ji — коэффициент Пуассона материала стержня. Это расстояние всегда больше, чем расстояние между центром тяжести С и вертикальной стороной поперечного сечения.
Перемещение плоскости действия поперечной нагрузки, требуемое для того, чтобы исключить кручение, имеет большое практическое значение при применении тонкостенных стержней открытого поперечного сечения (рис. 5). Для этого случая может быть легко получено приближенное решение2). В случае тонкостенных стержней можно допустить, что касательные напряжения т равномерно распределены по толщине t и параллельны соответствующей касательной к средней линии поперечного сечения. Вдоль этой линии они меняются в зависимости от
) Эта задача была обсуждена автором. См. его статью «Применение функции напряжений к исследованию изгиба и кручения призматических стержней». Сборник Института инженеров путей сообщения, СПб, 1913, выпуск 82, стр. 1—21.
2) Это приближенное решение получил и его практическое значение разъяснил Р. Майларт: R. М a i 11 а г t. Zur Frage der Biegung. Schweizerische Bauzeitung, 1921, Bd. 77, № 17, SS. 196—197 и Ober Drehung und Bie gung. Там же, 1922, Bd. 79, № 20, SS. 254—257.
x
Рис. 4.
Рис. 5.
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 676
расстояния s от края1) (рис. 5) и могут быть вычислены с помощью уравнения равновесия бесконечно малого элемента стержня, показанного на рис. 5; там же представлены положительно направленные напряжения. Проектируя все силы, действующие на этот элемент, на ось z и допуская, что толщина стенки t может меняться в зависимости от s, но не зависит от г, получим уравнение
dsdz t dz ds О,
в котором az означает нормальное напряжение в любой точке средней линии поперечного сечения. Из этого уравнения следует:
дЫ) _ _ , да2 т
ds 1 dz
Подставляя вместо oz его выражение (4) и используя уравнение (5), получим
ds J J —J2 уУ хуХ
иь х у ху
Интегрируя это уравнение и замечая, что у края (при s 0) касательное напряжение равно нулю, поскольку не имеется касательных сил, действующих на поверхности стержня, находим
xt , ув ;2- ( f У ds - Jxy (xt ds). (8)
JxJy-Jxy 5 Эта величина, представляющая собой касательную силу на единицу длины средней линии поперечного сечения, называется потоком касательных усилий. Интегралы правой части представляют собою моменты относительно осей х и у соответственно той части площади поперечного сечения, которая заштрихована на рис. 5. Эти моменты можно легко вычислить в каждом частном случае, и мы получим тогда значения xt для каждого зна¬
чения величины 5. В частном случае, когда х и у являются главными осями поперечного сечения, имеем Jxy 0, и формула (8) дает
S
х t —j— J yt ds. (9)
х) Согласно правилу правовинтового вращения s имеет ноложитель вый знак.
676 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
bht
Возьмем, например, швеллерное сечение стержня постоянной толщины tx) (рис. 6). Выбирая оси координат, как показано на рисунке, из формулы (9) вычислим величину т. Результат этого вычисления отмечен на рис. 6 штриховкой. Можно видеть, что вдоль полок поток касательных усилий меняется по линейному закону, в то время как вдоль стенки — по параболе. Касательные напряжения в стенке дают вертикальную равнодействующую, представленную площадью соответствующей заштрихованной фигуры, равную
Qyh bht 2 h2t -7r(—T-r)Qy
Касательные напряжения в полках дают пару сил, момент которых составляет Qyb2h4AJx. Разделив этот момент на QVt находим расстояние
Qu bht
Jx ' 2
d
b2h2t
(10)
Рис. 6.
определяющее положение результирующей поперечной силы Qy, статически эквивалентной вычисленной системе касательных напряжений.
Для того, чтобы вызвать изгиб швеллера без кручения в случае действия поперечной нагрузки, параллельной стенке швеллера, плоскость действия этой нагрузки, очевидно, должна находиться на расстоянии d от срединной плоскости стенки.
Поперечная нагрузка, перпендикулярная к стенке, не вызо вет кручения, если она действует в плоскости симметрии хг. Линия пересечения этой плоскости с ранее найденной плоскостью нагрузки, параллельной стенке, называется осью центров сдвига, а ее пересечение с плоскостью ху дает центр сдвига поперечного сечения. Из этого рассуждения ясно, что любые поперечные внешние силы, распределенные вдоль оси центров сдвига, вызовут только изгиб без кручения, поскольку каждая из этих сил может быть разложена на две составляющие, действующие в двух вышенайденных плоскостях и вызывающие только изгиб.
В качестве второго примера рассмотрим поперечное сечение, средняя линия которого есть дуга круга (рис. 7). Снова имеем одну ось симметрии, которую принимаем за ось х; для вычисле¬
1) Предполагается, что толщина очень мала и что поперечное сечение представляется только его средней линией.
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 677
ния потока касательных усилий используем формулу (9). Пусть толщина стенки t будет постоянной. Тогда, обозначая через а радиус средней линии и через ср угол, определяющий положение текущей точки на средней линии, мы имеем
ds a dy, у — a sin (а — р).
Подставляя эти значения в формулу (9), получим ф
Qy f Qy
тt —г- аЧ sin (а — p) dq -7- аЧ cos (а — р) — cos а.
Jjc J Jx
о
Мы видим, что поток касательных усилий равен нулю при р О и ф 2а. При ф а он имеет наибольшее значение
Qy
(тОтах ”7 1 COS (х).
J х
Вследствие симметрии мы заключаем, что центр сдвига находится на оси х. Его расстояние е от центра круга можно
получить, разделив на Qy момент касательных усилий, вычисленный относительно центра круга. Отсюда
а
2а Г , , Л sin:a — a cos a ,« «ч
e 7— xt ds 2a : . (11)
Qy J a —sin a cos a v '
о
В частном случае, когда a я, т. е. когда стержень представляет собой тонкую кольцевую трубку с продольной прорезью, получим е 2а. Центр сдвига находится вне трубы в направлении, противоположном прорези, и на расстоянии а от срединной поверхности трубы.
В общем случае, когда центральные оси х и у не являются главными осями (рис. 8) и нагрузка, вызывающая толькр изгиб.
678 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
действует в плоскости, параллельной плоскости yz, для вычисления потока касательных усилий воспользуемся формулой (8). Чтобы вычислить расстояние х0 плоскости нагрузки от центра тяжести сечения С, найдем относительно С момент касательных усилий, определяемых формулой (8), и разделим его на Qy. Тогда требуемое расстояние составит
т
Xq — j тtr ds
(ms т 8 — Ju rds ytds Jxu rds xtds. (12)
oJ I yJo 0J J
Здесь m означает всю длину средней линии поперечного сечения, а г есть расстояние от центра С до касательной к произвольной точке средней линии поперечного сечения, как показано на рис. 8. Последнее имеет положительный знак, если вектор, совпадающий с касательной и имеющий направление, по которому 5 возрастает, дает положительный момент относительно С.
Подобный же анализ можно проделать в случае, если силы действуют в плоскости, параллельной плоскости xz. Нормальные напряжения в этом случае определяются формулой (4'). Подставляя ее в соотношение (7), можно получить выражение для потока касательных усилий
xt J rQx ,2 (jXy( ytds-Jx xtds). (13)
JxJy Jxy J0 о Беря момент этих усилий относительно центра тяжести и замечая, что положительному значению этого момента соответствует перемещение плоскости нагрузки в направлении отрицательного у, получим
т
Уо i Ixtr ds
О
т s т s -—5— х rds xtds — Jxu rds ytdsI. (14)
II I i J
Выражения (12) и (14) дают нам координаты центра сдвига для общего случая.
Эти формулы могут быть написаны в более простой форме, дош мы заметим, что rds представляет собой удвоенную плр
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 679
щадь элементарного треугольника, заштрихованную на рис. 8, и если введем обозначение
jrds
(Ос
для удвоенной площади сектора, описываемого радиусом-вектором, когда расстояние вдоль средней линии возрастает от 5 О до s. Используя это обозначение и интегрируя по частям, получим для первого члена, заключенного в скобки, выражения (12):
J г ds J yt ds J das J yt ds cos J yt ds — J юsyt ds.
0 0 0 0 о 0 0
Замечая, что интеграл первого члена правой части равен нулю для обоих пределов, получим
т t т
J г ds J yt ds — J (osyt ds.
0 0 0
Подобным же образом мы можем преобразовать другие члены выражений (12) и (14), заключенные в скобки, и получим
Уо
(т т Jу I ds JХу I (оsxt ds J (12 )
о о (т т J х ds J ху I ds J. (14 )
о о Когда х и у — главные оси поперечного сечения, то Jxy 0. Тогда получим
т т
х0 -J- J сад ds, ih — у- J (isxt ds.
х о у о
Если средняя линия поперечного сечения состоит из нескольких прямых отрезков, то вычисление координат центра сдвига часто может быть значительно упрощено. Возьмем, например, швеллер постоянной толщины, но с неодинаковыми полками (рис. 9). Если силы действуют в плоскости, параллельной плоскости yz, то результирующая касательных напряжений, действующих по стенке, равна Qv, а горизонтальные касательные
680 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
напряжения в полках приводятся к паре сил. Рассматривая только нижнюю полку, используя формулу (8) и подставляя в нее у —с, х —(b— d — 5), находим
it j Qy_j2 IJyCts Jxyt ds - .
Результирующее касательное усилие в полке равно
xtds jxQjyy-iiy Ьт Мт'т)-
Умножая это выражение на Л и прибавляя момент Qyd от касательных напряжений в стенке, найдем относительно центра
тяжести момент, создаваемый всеми касательными напряжениями,
—т распределенными по поперечному
сечению. Разделив этот момент на
l Qy, получим
bht
J J — J2
J xJ у Jxy
к— Л
ху
(4-т):
d.
—I Для того, чтобы вычислить коорди-
- нату го, допустим, что нагрузка при-
Рис 9 ложена в плоскости, параллельной
плоскости xz. Поперечная сила Qx воспринимается только полками. Поток касательных усилий нижней полки можно получить из формулы (13), что дает
т' ‘ 7 т)
Касательное усилие в нижней полке равно ъх
'4х
Г QJt Г с (Ъх d
STtds jxjy-jly Г
Умножая эту силу на h и деля на Qx, получим расстояние результирующей касательной силы Qx от верхней полки; вторая же координата центра сдвига будет
Уо h — с —
ьЬ
J J — J2
JxJу Jху
hy2xl 2).
В случае зетового сечения (рис. 10), когда нагрузка параллельна плоскости yz, используя формулу (8), найдем, что каса-
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 681
тельное усилие в нижней полке отсутствует. Оно должно отсутствовать и в верхней полке, следовательно, х0 0. Считая теперь, что нагрузка параллельна плоскости xz, и используя формулу (13), найдем, что касательное усилие в полке равно Q2, откуда следует, что центр тяжести поперечного сечения С должен находиться в плоскости нагрузки. Значит, у0 0 и центр сдвига в этом случае совпадает с центром тяжести.
Если все полки стержня пересекаются по одной оси, как показано на рис. И, то касательное усилие также проходит через
эту же ось, и она, очевидно, является осью центров сдвига.
Для вычисления перемещений, вызванных в стержне какой-
Рио. 11.
либо поперечной нагрузкой, распределенной вдоль оси центров сдвига, разлагаем эту нагрузку на две составляющие, параллельные осям х и г, и вычисляем изгибающие моменты Мх и Му в плоскостях yz и xz соответственно. Тогда, применяя зависимостй (3) и (3'), получим следующие выражения для кривизнг
гх Е (j ху ху)
_1_ _ 1 гу Е ('Л “ ху)
(MXJ у MyJ Ху),
(MXJ ху MyJx).
(IS)
Если х и у являются главными осями, эти выражения сводятся к
1
мх
EJ „
1
Му
EJ
(16)
Обозначим перемещения в направлениях х и у через и и v. Тогда, применяя правило знаков, установленное в § 1, для малых перемещений получим
6,82 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
и соотношения (16) дают
EJX-MX, EJy My. (17)
Дифференцируя эти зависимости дважды по z и используя уравнения (5) и (6), получим
EJyrq,. (18)
Если поперечная нагрузка не проходит через ось центров сдвига, то она вызывает не только изгиб, но и кручение стержня. При решении подобной задачи мы заменяем каждую силу, которая не проходит через ось центров сдвига, параллельной силой, проходящей через эту ось, и парой сил, действующих в плоскости, перпендикулярной к оси стержня. При таком методе рассуждений задача разделяется на две части: 1) исследование изгиба, вызванного силами, распределенными вдоль оси центров сдвига, и 2) исследование кручения парами сил, действующими в плоскостях, перпендикулярных к оси стержня. Первая часть задачи уже рассмотрена. Часть, имеющая отношение к кручению, будет рассмотрена в следующем параграфе.
§ 3. Чистое кручение тонкостенных стержней открытого поперечного сечения
Если стержень подвергнут кручению парами сил, приложенными к торцам в плоскостях, перпендикулярных к оси стержня, и концы свободно могут депланировать, то имеем деформацию чистого кручения. В этом случае будут возникать только касательные напряжения в каждом поперечном сечении стержня. Закон распределения этих напряжений зависит от формы поперечного сечения и одинаков для всех поперечных сечений стержня. В случае тонкостенных открытых поперечных сечений можно допустить с достаточной точностью, что касательное напряжение в любой точке направлено параллельно соответствующей касательной к средней линии поперечного сечения и пропорционально расстоянию от этой линии. Угол кручения на единицу длины равен
e f, (19)
где через Т обозначен крутящий момент, а С есть крутильная жесткость стержня. В случае тонкостенного открытого поперечного сечения постоянной толщины t с достаточной точностью можно принять, что
CmtQ, (20)
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 683
где т есть длина средней линии поперечного сечения, a G — модуль сдвига. Если поперечное сечение состоит из нескольких элементов различной толщины, можно принять, что
(21)
Продольные волокна стержня принимают вследствие кручения форму спиралей, которые при малом угле кручения могут рассматриваться как прямые линии, наклонные к оси вращения. Если через р обозначить расстояние волокна от оси вращения, то угол наклона волокна к оси составит р0.
Депланация поперечного сечения ) в случае тонкостенного открытого сечения может быть наглядно представлена, если заметить, что вдоль средней линии поперечного сечения отсутствует касательное напряжение; это указывает на то, что элементы средней линии остаются нормальными к продольным волокнам, превращающимся в спирали при кручении. На рис. 12, например,
показана депланация поперечного сечения скрученного двутаврового стержня. При повороте относительно центральной продольной оси стержня центральные продольные волокна полок, находящиеся на расстоянии г2 от оси вращения, становятся наклонными и составляют с этой осью угол 0г2. Средние линии поперечных сечений полок составляют тот же угол с осью х, как показано на рисунке.
В общем случае (рис. 13, а), допуская, что при кручении поперечные сечения стержня поворачиваются относительно оси, параллельной оси центров тяжести и проходящей через точку Л, получим, что любое продольное волокно N в срединной поверхности стенки, определенное расстоянием s, взятым вдоль средней линии поперечного сечения, становится наклонным к оси вращения на угол р0. Отрезок касательной к средней линии в точке N остается перпендикулярным к волокну и образует с плоскостью ху после кручения небольшой угол р0 cos а г0 (где г — расстояние касательной оси вращения), взятый со
1) Или искажение поперечного сечения — перемещение точек поперечного сечения в осевом направлении, связанное с неплоским распределением перемещений по поперечному сечению.
684 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
знаком плюс, если вектор, направленный по касательной в сторону возрастающего s, дает положительный момент относительно оси вращения. Пусть через w обозначено перемещение в направлении z точек средней линии поперечного сечения. Тогда для по¬
ложительного угла кручения имеем
4г--е. (22)
После интегрирования получим
s
w w0 — 0 J г ds, (23)
о
где через w0 обозначено перемещение в направлении z точки, от которой измерено расстояние 5. Интеграл правой части этого
выражения представляет собой, как мы уже видели, удвоенную площадь сектора, которая описывается радиусом р по мере того, как мы продвигаемся вдоль средней линии поперечного сечения от конца (5 0) до точки N. Секториальная площадь является положительной, когда радиус р поворачивается в положительном направлении, т. е. от х к у, и отрицательной при вращении в противоположном направлении. Значение интеграла для s т в таком случае будет выражено удвоенной алгебраической суммой трех площадей, заштрихованных на рис. 13, Ь.
В предыдущем рассуждении мы предположили поворот поперечного сечения относительно произвольно выбранной точки А. Рассмотрим теперь, какое действие оказывает на депла-
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
685
нацию изменение центра вращения. Допустим, что центр вращения смещен из точки А в точку В (рис. 14). Рассматривая элемент ds средней линии и обозначая через х, у координаты точки N, а через хау уа координаты центра поворота Л, мы из рисунка видим, что
г ds dx уа — у) — dy (ха - х).
Если переместить центр вращения из Л в Б, следует принять ха с и уа b за координаты нового центра вращения.
Тогда
rds rds bdx — c dy.
Чтобы вычислить депланацию, вызванную поворотом сечения вокруг В, мы должны подставить r ds вместо г ds в выражение (23), тогда получим
5 S S S
J r ds J г ds J b dx — с dy) J г ds bx — су const. (24)
Отсюда видно, что результатом перемены положения центра вращения в дополнение к ранее вычисленным перемещениям (23) является перемещение Ьх — су
const, которое в качестве линейной функции х и у не требует никакой дополнительной деформации стержня и которое достигается только путем перемещения стержня как абсолютно твердого тела. Это указывает на то, что в случае чистого кручения стержня со свободными концами выбор оси вращения несуществен и что любая линия, параллельная центру тяжести стержня, может быть принята за ось вращения.
Используя выражение (23), можно вычислить среднее значение депланации wa в следующем виде:
Рис. 14.
т ms
wa ± j wds-Wo-j ds j rds.
(25)
Вычитая это значение из ранее вычисленного значения пере¬
686 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЁЧЁНИЯ
мещения (23), получим депланацию поперечного сечения относительно плоскости, соответствующей среднеарифметическому w. Продолжая применять обозначение w для перемещений относительно вновь принятой плоскости, получим
Первый член в скобках есть постоянная, зависящая от геометрических размеров средней линии поперечного сечения, в то время как второй член представляет удвоенную е 1 площадь сектооа. соответствующую дуге s
мем дугу окружности (рис. 15) с углом 2а. Принимая центр сдвига О за центр вращения, получим
и депланация, представленная выражением (28), равна
(26)
Применим это выражение к вычислениям депланации в нескольких простых случаях. В качестве первого примера возь-
(27)
(28)
Рис. 15.
г а — в cos (а — ф), ds a d-ф,
S
Ф
J г ds a J а — е cos (а — гз) ds а а-ф е sin (а — )
о о
т 8 2а
J ds J rds D -j аг e sin (а — -ф) Ар а2 а,
оо о
w 0а а (а — гз) — е sin (а — гз).
Мы видим, что депланация антисимметрична относительно оси симметрии поперечного сечения и равна нулю при г) а.
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 687
В качестве второго примера рассмотрим швеллер (рис. 16). Изучая поворот относительно центра сдвига О, найдем следующие
выражения для удвоенных площадей секторов трех участков поперечного сечения:
688 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Используя эти формулы, получим
2 b h s
—2ьТн о о
Подставляя это значение в выражение (28), получим следующие значения для депланации:
т Вт(Ь — d — s) при sb,
ay 0—Y — bd dsj при b s b h,
w Q-(d h b — s) при sb h.
Изменение w вдоль средней линии поперечного сечения при 0 1 показано заштрихованными площадями на рис. 16.
При вычислении депланации полезно использовать аналогию с балкой. Вообразим среднюю линию поперечного сечения выпрямленной и рассмотрим ее как балку длиной п, на которую действует фиктивная нагрузка интенсивности г. В этом случае cos
представляет площадь нагрузки
s
на участке 5 от конца; J соSds
о
есть момент этой нагрузки для той же точки, а величина D представляет опорную реакцию балки. Таким образом, величина D — G)s есть касательная сила в балке. Возьмем для примера поперечное сечение, показанное на рис. 17, а. Рассматривая поворот его вокруг центра сдвига О, найдем, что г h2 для нижней полки, г 0 для стенки и г —г2для верхней полки. Соответствующая фиктивная нагрузка будет такой, как показано на рис. 17, Ь. Реакция на левом конце будет
п — h h b
Рис. 17. 2 0 h 2b Значения касательных усилий соответствуют заштрихованным площадям на рис. 17, Ь. Будучи умножены на 0, они дают депланацию данного поперечного сечения.
а)
Ь)
I
hZ
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 689
В случае поперечных сечений, все элементы которых пересекаются в одной точке (рис. 11), г равно нулю для всех точек средней линии; следовательно, при кручении не будет происходить депланации этой линии.
§ 4. Неравномерное закручивание тонкостенных стержней
В предыдущем обсуждении предполагалось, что крутящий момент приложен к концам стержня и что поперечные сечения стержня могут свободно депланировать. В таком случае депланация одинакова для всех поперечных сечений и происходит при полном отсутствии осевых деформаций продольных волокон. Задача становится более сложной, если поперечные сечения не могут свободно депланировать или если крутящий момент изменяется вдоль длины стержня. Депланация в таких случаях изменяется вдоль стержня и кручение сопровождается растяжением или сжатием продольных волокон. Скорость изменения угла закручивания вдоль оси стержня также изменяется; назовем этот случай неравномерным4) кручением.
Начнем обсуждение этого рода задач с простого случая кручения двутавровой балки, поперечное сечение которой
имеет две оси симметрии. Допустим, что один конец заделан и не может депланировать. Крутящий момент Т приложен на другом конце (рис. 18). Очевидно, заделывая конец балки и устраняя депланацию, которая представлена на рис. 12, мы увеличиваем сопротивление балки кручению. Кручение в этом случае сопровождается изгибом полок. Крутящий момент Т уравновесится частично касательными напряжениями, рассмотренными в предыдущем параграфе, и частично сопротивлением полок изгибу. Первую часть крутящего момента обозначим через Тх. Она пропорциональна скорости изменения угла закручивания вдоль оси балки. Обозначая этот угол через ф, используя формулу (19) и отмечая штрихами производные по г, получим
Т СФ'.
(29)
Вторая часть крутящего момента будет найдена путем рассмотрения изгиба полок. Из симметрии можно заключить, что в данном случае кручения поперечные сечения балки поворачиваются
) или стесненным кручением.
690 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
относительно оси центров тяжести и прогиб верхней полки балки равен и cpi2. Используя теперь уравнения (17) и (6), заключаем, что поперечная сила в полке будет
Qx
dMy
dz
- EJ
d3u
У dz3
EJyh
Ф
где Jv есть момент инерции поперечного сечения одной полки. Поперечная сила в нижней полке будет равна поперечной силе в верхней полке и противоположно направлена. Эта пара сил составит вторую часть крутящего момента
EJyh2
Ф
(30)
Тогда уравнение для вычисления угла закручивания примет вид
Е1Л2
Т Тх Т2 Сф'
Ф
(31)
Интегрированием этого уравнения мы займемся позже. Пока констатируем только, что когда ср найдено, можно вычислить обе
части крутящего момента 7 и Т2 и найти напряжения в балке, вызванные каждой из этих частей.
Мы видим, что проблема неравномерного кручения решена в предположении изменения угла закручивания вдоль оси стержня и путем деления крутящего момента на две части, из которых одна представляет чистое кручение, определяемое соотношением (29), другая же зависит от изгиба полок. Зная расположение оси вращения и угол закручивания, мы находим кривые прогибов полок. Из этих кривых прогибов могут быть найдены вызванные изгибом поперечные силы, с помощью которых определяется вторая часть крутящего момента. Следует отметить, что при анализе изгиба полок мы использовали уравнение (17), в котором кривизна пропорциональна изгибающему моменту. Это означает, что рассматривалось только влияние нормальных напряжений ог на кривизну балки, а влиянием касательных напряжений пренебрегалось, что обычно и практикуется при анализе изгиба балок.
Применим теперь вышеописанный метод решения к рассмотрению неравномерного кручения тонкостенного стержня любого открытого поперечного сечения. Допустим (рис. 19), что у стержня один конец, z 0, заделан, в то время как к другому концу, z , приложен крутящий момент Т. Имея в виду рассуждения,
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 6И
изложенные в § 2, ясно, что поперечная сила, приложенная в центре сдвига А концевого нагруженного поперечного сечения, вызывает только изгиб стержня, но не закручивание. Таким образом, на основании теоремы взаимности заключаем, что крутящий момент Т, приложенный к концу, не вызовет никакого прогиба точки А и ось центров сдвига ААХ останется прямой линией, в то время как поперечные сечения стержня при кручении поворачиваются относительно этой оси. Обозначая через р угол поворота любого поперечного сечения, найдем, что часть Т1 крутящего момента, вызывающая напряжения чистого кручения, дается выражением (29). Для вычисления второй части Т2 крутящего момента (соответствующей изгибу полок в случае двутавровой балки) мы поступаем, как и раньше, и пренебрегаем влиянием касательных напряжений на деформацию срединной поверхности стенки. Тогда осевые перемещения w, определяющие депланацию поперечных сечений, будут найдены тем же способом, как и в случае чистого кручения (см. выражение (28)). Заметим только, что кручение теперь является неравномерным, и заменяем постоянную 0 переменной величиной ф' относительного угла кручения. Тогда
Поскольку ф' изменяется вдоль длины стержня, смежные поперечные сечения будут депланировать неодинаково, следствием чего является осевое удлинение е2 продольных волокон стержня. Замечая, что D и cos в выражении (32) не зависят от г, получим
Предполагая теперь, что волокна не оказывают друг на друга бокового давления, получим нормальные напряжения, вызванные неравномерным кручением, в следующем виде:
Таким образом, видно, что нормальные напряжения в данном поперечном сечении пропорциональны соответствующим осевым перемещениям w. Следовательно, диаграммы предыдущего параграфа, изображающие депланации поперечных сечений, дают одновременно картину распределения нормальных напряжений oz, возникших при неравномерном кручении.
Можно видеть, что результирующая сила и моменты Мх и Му от напряжений, распределенных в соответствии с выражением (33), равны нулю. Чтобы доказать это, используем теорему взаимности. Допустим, что нормальные напряжения величиной р равномерно распределены по концевому поперечному сечению стержня на рис. 19. Подобные напряжения, конечно, не
w f'(D- со,).
(32)
аг Ец (D — cos).
(33)
692 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
вызывают никакого поворота конца, и действующий крутящий момент Т не производит никакой работы. Тогда на основании теоремы взаимности работа, выполненная напряжениями р на перемещениях w, вызванных крутящим моментом, должна быть равна нулю, и мы получим
m m
J wpt ds pqp' J (D — cd5) t ds 0.
о о
Отсюда
m
J (D — cos) tds 0, (34)
о
и результирующая напряжений (33) превращается в нуль. Приложим теперь к концу стержня напряжения изгиба ру, пропорциональные расстоянию от оси х1). Такие напряжения вызывают чистый изгиб, но не вызывают никакого поворота конца относительно оси z. Крутящий момент не совершает работы при этом изгибе. Следовательно, работа изгибающих напряжений при кручении должна быть равна нулю, и мы получим
m пг
J w pyt ds рф' J (D — cos) yt ds 0. о о
Это показывает, что момент относительно оси х напряжений (33) исчезает. Подобным же образом можно доказать, что момент Му при этом также равен нулю.
Имея выражение (33) для нормальных напряжений, мы можем теперь вычислить соответствующие касательные напряжения, которые аналогичны напряжениям, рассмотренным нами при обсуждении вопроса об изгибе полок двутавровой балки, и благодаря которым составляется вторая часть Т2 крутящего момента. С этой целью используем уравнение равновесия (7). Подставляя в это уравнение выражение (33) для az, получим
Интегрируя это последнее выражение и отмечая, что ф не зависит от s и что т при 5 0 равно нулю, получим
s
тt — Еср' J (D — ©s) t ds. (35)
о
1) Через р обозначено в данном случае напряжение, возникающее на расстоянии, равном единице, от оси х.
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧПОГО СЕЧЕНИЯ 693
Часть Т2 крутящего момента получается тогда суммированием вдоль средней линии моментов, создаваемых элементарными касательными силами (тt)ds относительно центра сдвига, что дает
т ms
Т2 J (t) г ds — Е(р' j rds J (D-as)t ds. (36)
О 0 0
Эта формула может быть упрощена, если заметить, что из выра¬
жений (27) следует соотношение
rds _d(D-lds
as
Отсюда
ms m s
J rds j (D-as)tds - J rf(0rfas) ds J (D-as)tds.
0 0 о 0
Интегрируя выражение правой стороны по частям и используя соотношение (34), получим
ms m
г ds J (D — (os) t ds J (D — cds)2 t ds.
оо о
Подставляя это в формулу (36), находим следующее выражение для Г2:
m
Т2 -cp' J (D - со,)21 ds. (37)
о
В предыдущем параграфе было показано несколько случаев вычисления величины D — cos, меняющейся вдоль средней линии поперечного сечения. Суммируя квадраты этой величины вдоль средней линии, получим интеграл правой части формулы (37). Примеры таких вычислений будут даны ниже. Поскольку D и
o)s имеют размеры длин, возведенные в квадрат, интеграл будет
иметь размер длины в шестой степени. Вводя обозначение
m
Е (D — asf t ds Си (38)
о
перепишем формулу (37) в следующей форме:
Т2 - С1ф' (39)
Это выражение представляет часть крутящего момента, обусловленную неравномерностью закручивания и неравномерностью депланации. При дальнейшем рассмотрении мы назовем ее
694 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
крутящим моментом депланации1), а постоянную Сi— жесткостью депланации. Складывая выражения (29) и (39), получим дифференциальное уравнение неравномерного кручения тонкостенных стержней открытого поперечного сечения2):
Т Сф' - С,ф' (40)
Ранее полученное уравнение (31) является только частным случаем уравнения (40). Когда уравнение (40) решено и выражение для угла закручивания ф найдено, получим Т и Т2 соответственно из выражений (29) и (32). Напряжения, вызванные Ть можно тогда вычислить как напряжения чистого кручения. Нормальные и касательные напряжения, вызванные моментом Г2, можно найти соответственно из выражений (33) и (35).
Определение жесткости депланации требует, как мы уже видели, вычисления интеграла левой части формулы (38). В § 3 было рассмотрено несколько случаев определения выражений D — cos. Используя их, мы без большого труда можем получить выражение для Сь Возьмем, например, поперечное сечение в форме дуги круга (рис. 15). Тогда
D — os а а (а — ф) — е sin (а — ф).
Подставляя это выражение в формулу (38) и интегрируя, получим для постоянной толщины t
2а
С Eta31 а (а — )) — е sin (а — -ф)2 dty, о
где по формуле (11)
sin а — а cos а Л
е : 2а.
а — sin а cos а
После интегрирования получим
С, -гEta5 а3 — 6 (sin аcos а)2 I.
1 3 L а — sin а cos а J
‘) Употребляется также термин «изгибно-крутящий момент».
2) Это уравнение было выведено автором для частного случая двутаврового сечения; см. его статью «Об устойчивости плоской формы изгиба двутавровой балки под влиянием сил, действующих в плоскости ее наибольшей жесткости». Известия С.-Петербургского политехнического института,
1905, том 4, выпуск 3—4, стр. 151—219; 1906, том 5, выпуск 1—2, стр. 3—34.
Распространение этого уравнения на сечения с неодинаковыми полками было сделано К. Вебером: С. Weber. Ubertragung des Drehmoments in Balken mit doppelflanschigen Querschnitt. Zeitschrift fur angewandte Mathematik und Mechanik, 1926, Bd. 6, № 2, SS. 85—97. Дальнейшее распространение этого уравнения на случай тонкостенных открытых поперечных сечений произвольного вида принадлежит Г. Вагнеру: Н. Wagner. Verdrehung und Knickung von offenen Profilen. Festschrift «Funfundzwanzig Jahre Technische Hochschule
Danzig». 1929, SS. 329—343.
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 695
Для случая швеллера величины D — cos показаны на рис. 16. Значение интеграла в формуле (38) равно
Ъ b h
2t(b-d-sfds d4 — b s J ds
0 b
d2h 2b3 - 6db (b - d).
Подставляя вместо d его значение из формулы (10), получим r р МЬ. ЗА
Wh)-
Подобным же образом для зетового сечения, представленного на рис. 17, находим
r р tb3h2 4b3 12b2h Ш2 2h3
12 8b3 2b2h 6bh2 h3
В случае, если имеем поперечные сечения, все полки которых пересекаются вдоль одной оси (рис. И), значение D — cos превращается в нуль и жесткость депланации также равна нулю.
§ 5. Вычисление угла закручивания
Чтобы получить угол закручивания, мы должны интегрировать уравнение (40). Вводя обозначение СС — k2y придаем
уравнению (40) вид
Общим решением этого уравнения будет
Ф -jff А А sh kz А2 ch kz. (41)
Постоянные интегрирования находятся из условий на концах стержня. В случае, представленном на рис. 19, ф и ф' равны нулю на заделанном конце (z 0), поскольку поворот этого поперечного сечения и его депланация, определяемая формулой (32), в данном случае исключены. На конце z I мы предполагаем отсутствие нормальных напряжений. Тогда, как видно из выражения (33), ф равно нулю при z I. Чтобы удовлетворить всем этим условиям, мы должны принять
“ cTF ’ А — А2 » — Ci3 th kl.
Подставляя это в выражение (41) для ф, получим
Ф -з- kz — sh kz th kl (ch kz — 1). (42)
696 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
гг
Для конца стержня z получим
irihkl)-
Второй член в скобках представляет влияние, оказываемое на угол закручивания жесткостью депланации стержня. Очевидно, это влияние уменьшается по мере того, как увеличивается длина стержня.
Формула, полученная для угла закручивания, хорошо согласуется с опытами. Чтобы реализовать экспериментально условия,
теоретически допущенные для за-
s ' деланного конца стержня, круче-
Г ние вызывали парой сил, прило¬
женной посредине, в то время как
« - концы стержня не могли повора-
pZ чиваться, но могли свободно де-
планировать (рис. 20). Принимая Рис. 20. во внимание условия симметрии,
ясно, что среднее поперечное сечение остается плоским и каждая половина стержня находится в положении, принятом при выводе только что указанной формулы для угла закручивания. Измеряя угол закручивания на различных расстояниях от середины, можно проверить полученную теоретическим путем формулу1).
Производя анализ, мы здесь предполагали, что нормальные напряжениям на конце z l отсутствуют. Если они имеются и распределяются согласно формуле (33), то производная p на конце не равна нулю и будет иметь место дополнительное кручение, вызванное напряжениями аг, распределенными у конца2). Чтобы установить связь между р и этими нормальными напряжениями Oz, умножим обе части выражения (33) на (D — о)3)tds и проинтегрируем по всей длине т средней линии поперечного сечения. Таким способом получим
т т
J azD — s) t ds J (D — cos)21 ds Сдо,
) Такие опыты при использовании двутавровых балок с различными соотношениями ширины полок и высоты балки были проделаны автором. См. его статью «Об устойчивости плоской формы изгиба двутавровой балки под влиянием сил, действующих в плоскости ее наибольшей жесткости». Известия
С.-Петербургского политехнического института, 1906, том 5, выпуск 3—4, стр. 263—292.
2) Подобное кручение, вызванное продольными напряжениями, было впервые обсуждено В. 3. Власовым. См. его книгу «Тонкостенные упругие стержни», М. — Л., Стройиздат Наркомстроя, 1940, стр. 94.
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 697
ИЛИ
т
ср J g2(D — сos) t ds. (43)
1 о
Подставляя вместо аг значения нормальных напряжений у конца г , находим на основании выражения (43) значение ф. Используя это значение вместо нуля в нашем предыдущем решении, находим, что угол закручивания ф можно получить путем прибавления к вышенайденному выражению для ф величины
-Аыкг-).
Эта величина определяет угол закручивания, вызванной нормальными напряжениями, приложенными на конце стержня. Подставляя вместо ф его значение (43) и учитывая, что2 ССи получим для этого угла выражение
т
ф С ch kl (Ch kz ) J z 1 ds
0
Это решение предполагает, что напряжения az распределены вдоль поперечного сечения в соответствии с выражением (33), которое устанавливает, что нормальные напряжения пропорциональны депланации w, как представлено на рис. 16 и 17.
Результирующая сила и результирующий момент для таких распределений напряжений равны нулю, как это показано в § 4.
Исходя из принципа СенВенана, можно заключить, что подобные силы могут вызвать только местный эффект, но в случае тонкостенных открытых сечений это влияние может стать практически важным и должно быть поэтому принято во внимание. Например, сравнивая зетобразное сечение, стенка которого нагружена равномерно распределенными растягивающими усилиями (рис. 21,а), с плоской пластиной, на которую действует местная нагрузка, как представлено на рис. 21,6, можно установить, что
У
777)W
Т77Л7.
а)
Ь)
Рис. 21.
698 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
распределение напряжений в обоих случаях будет различным. В случае пластины мы можем допустить, что распределение напряжений по поперечным сечениям быстро приближается к равномерному по мере того, как увеличивается расстояние от нагруженного конца. В случае зетобразного сечения условия осложняются; вследствие растяжения стенок будут возникать изгиб полок и закручивание стержня зетобразного профиля. Соответствующие неправильности в распределении напряжений не уменьшаются так быстро с увеличением расстояния от конца стержня, как мы наблюдаем в случае плоской пластины. В этом примере напряжения, приложенные к концу, не находятся в согласии с выражением (33), но кажется разумным предположить, что будет иметь место только локальное возмущение в распределении напряжений и что на коротком расстоянии от конца будут действовать равномерные растягивающие напряжения в сочетании с напряжениями, определяемыми выражением (33) ). Это оправдает применение зависимости (44) и в случаях, подобных представленному на рис. 21, а.
Поскольку закон распределения нормальных напряжений на конце установлен, подставляем соответствующее выражение для ог в выражение (44) и вычисляем р. Зная ср, мы можем вычислить напряжения, вызванные кручением, используя выражения (29), (33) и (35). Если имеются продольные сосредоточенные силы, приложенные на конце, то интегрирование в формуле (44) должно быть заменено суммированием, и мы получим
ф cOT(ch2“iSp(D“®) 45)
Возьмем в качестве примера случай, представленный на рис. 21, с. Результирующая сила и моменты Мх, Му четырех сил Р, приложенных к концу, равны нулю. Значения D — со3 для зетобразного сечения даны на рис. 17, а. Используя эти значения, получим
2 Р, № - ш.) - 2PD 2Р (о - Щ - Р.
Подставляя это выражение в зависимость (45), получим формулу для угла закручивания. Из данного обсуждения видно, что продольные силы не вызывают кручения в том только случае, если они приложены к точкам, для которых величина D — cos, определяющая перемещения от депланации w, равна нулю. Положения таких точек для швеллера и зетобразного сечения показаны на рис. 16 и 17, а. Этот вывод может быть получен также на основе теоремы взаимности. Если кручение вызывает
) По-видимому, желательно данное положение проверить опытами.
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 699
депланацию концевого поперечного сечення, т. е. перемещения точек на конце стержня в направлении оси 2, то силы, параллельные оси z, приложенные к тому же концу, должны вызвать закручивание. Из рис. 17, а заключаем, что продольная сила, приложенная к любой точке стенки зетобразного сечения, вызывает всегда одинаковое закручивание, в то время как в случае швеллера угол закручивания будет зависеть от положения точки приложения силы, как можно видеть из рис. 16.
§ 6. Комбинированное действие изгиба и кручения
Рассмотрим теперь общий случай деформации тонкостенного стержня, находящегося под действием произвольных поперечных сил. Каждая сила может быть заменена параллельной силой, проходящей через ось центров сдвига, и крутящим моментом. Таким образом, получим стержень, нагруженный вдоль оси его центров сдвига и подверженный действию крутящих моментов, приложенных в нескольких поперечных сечениях. Поперечные силы, приложенные к оси центров сдвига, вызывают только изгиб. Соответствующие прогибы и напряжения могут быть вычислены, как указано в § 2. Рассматривая кручение, используем результаты, полученные в предыдущем параграфе. Возьмем начало координат на конце стержня и обозначим через Го крутящий момент на том же конце. Тогда угол закручивания части стержня между концом и первой поперечной силой на основании выражения (41) равен
Ф -р-г-- А A j sh kz А2 ch kz. (46)
Подобное же уравнение может быть написано для каждого участка стержня, расположенного между двумя последовательными поперечными силами. Необходимо только заменить Т0 значением крутящего момента в начале этого участка. Тогда постоянные интегрирования должны определяться из условий непрерывности в точках приложения сил. Вычисления могут значительно упроститься, если вместо постоянных выражения (46), т. е. Л, Аи Л2, мы введем величины, определяющие условия на конце z 0 стержня1). Дифференцируя уравнение (46) и подставляя z 0, получим
Фо Л Л2, фоЛ262,
) Этот метод был развит А. Н. Крыловым в связи с анализом изгиба балок, лежащих на упругом основании. См. его книгу «О расчете балок, лежащих на упругом основании», изданную Академией наук СССР. 3-е издание. Ленинград, 1931,
700 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
где индексы 0 левой стороны уравнений указывают, что величины относятся к концу 2 0 стержня. Решая эти уравнения относительно постоянных Ау Аи А2 и подставляя их значения в уравнение (46), получим
Ф Фо-Фо8ЬЬ -р-ф(chfcz- l) -p-(z- jshег). (47)
Здесь угол закручивания любого поперечного сечения первого
участка стержня выражен через параметры qp0, ср, ф, Т0 на
конце 2 0. Дифференцируя уравнение (47), получим
1 т
ф' ф' ch kz у ф sh kz (1 “ ch kz)
T 1 (48)
ф йф' sh kz Фо ch kz —sh kz.
Уравнения (47) и (48) применимы при значении z между 0 и а, где а определяет положение первой поперечной силы. Рассматривая теперь второй участок стержня и принимая, что 2 а, следует учесть крутящий момент, приложенный в поперечном сечении 2 а. Пусть через Тi обозначен этот крутящий момент. Выражение для угла закручивания на втором участке стержня теперь можно получить путем прибавления угла закручивания, вызванного моментом 7 к предыдущему выражению (47). Таким образом получим при 2 а
Ф Фо у Фо sh kz -2 Фо' (ch kz - 1)
Wc7z T z) Fc7.za T (2 a) Последний член правой части уравнения представляет угол, вызванный моментом 7Y Он получен из первого члена уравнения (47) после подстановки Т вместо Т0и z — а вместо 2, поскольку теперь расстояние момента Тi до рассматриваемого поперечного сечения составляет 2 — а.
Подобным же образом можно поступить и с третьим участком стержня и так далее, вплоть до последнего. Выражения для Ф во всех участках стержня содержат те же постоянные ф0, Фо, Фо и Т0. Все эти постоянные могут теперь быть определены из условий на двух концах стержня.
Для иллюстрации этого метода рассмотрим несколько простых примеров. Начнем со случая, когда стержень закручен под действием крутящих моментов, приложенных по концам, и когда в то же время концы так закреплены, что депланация совершенно исключена. Поскольку не имеется сил, приложенных р пролете стержня, уравнение (47) может быть использовано по
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 701
всей длине стержня. Предполагая, что конец г 0 неподвижен, и отмечая, что депланация исключена, мы должны подставить в уравнение (47) ро 0, Фо 0, что дает
Ф р-Фо(chkz-l) -j(z- -j-shftz),
j, (50)
ф' -j Фо' sh kz -pjSr- (1 — ch kz).
Так как депланация на другом конце стержня (z I) также устранена, имеем
Ф -j уд sh kl (1 — ch kl) 0,
откуда
„ Т0 1 — ch kl
ф0 1с7 sh kl
Подставляя это выражение в первое из уравнений (50), получим угол закручивания
Ф - kdishIi(chkz
Полагая z , получим поворот конца z I стержня на угол
Т01 (. 2 ,, kl р iH1-irthir)-
В этой формуле второй член в скобках отражает влияние ограничения по отношению к депланации на концах стержня на величину угла закручивания.
В качестве второго примера рассмотрим случай, представленный на рис. 22. Стержень, опертый на концах, находится под действием внецентренной поперечной силы, приложенной на расстоянии а от левого конца. Обозначая через е расстояние силы от оси центров сдвига, сводим поставленную задачу к задаче об изгибе Рис. 22.
стержня силой Р, сопровождающемся закручиванием, вызванным крутящим моментом Ре, приложенным на расстоянии а от левого конца стержня. Предположим сначала, что концы стержня не могут поворачиваться относительно оси г, но свободны для депланации. В таком случае
ф ф о при 2 0 и z U
702 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Для части стержня от 20 до 2а, используем уравнение (47). Подставляя в него фо сро 0, получим
ф уфЬ2 -г-(2- jSh Ц.
Для правой части стержня, z а, используем уравнение (49), которое при ф0 фо 0, 7 Ре дает
P T9oShb 7(z-shfe) r2-a-sh(3-a),
ф ky'0 sh kz — -щ- sh kz — -щ- sh kz — a).
Замечая, что на конце z — I ф, ф 0, получим следующие уравнения для вычисления постоянных фц и Т0:
Т 4)0 kbl ( — Т — РсГ I — а Т — а) ’
Фо sh — -j-shkl --sh k(l — а).
Решая эти уравнения, получим
Подставляя эти значения в выражения для ф, получим углы закручивания для обеих частей стержня. Используя их в выражениях (29), (33) и (35), мы можем вычислить нормальные и касательные напряжения, вызванные крутящим моментом Ре.
Если концы стержня, представленного на рис. 22, заделаны и не могут депланировать, то концевые условия будут
ф ф' 0 при 2 0 и 2 1.
Подставляя ф0 ф 0 в уравнение (49), получим при za
ф-р-ф(сЬг- х)тг ishfe)
й2с, 2 — а Т (z а ’
Применяя это уравнение для конца z , получим для вычисления постоянных Фо' и Т0 следующие уравнения:
ргФ(с1kl- 1) р-( - j-sh6) - - a-jshk(l-a),
уФр sbkl -j(l — chkl) — — chA( —a).
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 703
С помощью этих уравнений для каждого частного случая могут быть вычислены постоянные р'' и Т0. Подставляя их в выра жения для ф, мы опять имеем полное решение задачи. Решив задачу для одной сосредоточенной силы, как показано на рис. 22, мы можем с помощью метода наложения найти решение для любого числа сосредоточенных сил.
Случай распределенной нагрузки может быть также решен без затруднений. В качестве примера возьмем опять стержень, представленный на рис. 22, и предположим, что вместо силы Р мы имеем распределенную нагрузку постоянной интенсивности q, приложенную вдоль линии, параллельной оси z, на расстоянии е от оси центров сдвига. Крутящий момент в любом поперечном сечении равен Т Т0 qez. Подставляя это значение в уравнение (40) и решая его, как и раньше, получим
Ф Ф0 Фо sh 2 -2 ф (ch kz — 1) р-(г- -j-shftz)-
2 k2Ct
Допустим, что оба конца стержня заделаны, т. е. ф ф' 0 при z 0 и z I. Тогда, подставляя ф0 ф 0 в вышеприведенное выражение для ф, получим
2 k2Ci
Используя это уравнение для конца z I и замечая, что исходя из условий симметрии Т0 —qel2, получим следующее уравнение:
р-Фо (h kt— 1)“ 2k2Cl 2k2Cx откуда
_ Qd sh kl
'Ро и 2kC, ch kl - 1 '
Подставляя это значение в выражение для ф, находим
Р - Sol -щгт(Qhkz -- 2г (z - тshkz)жг
Это выражение может быть упрощено и представлено в следующем виде:
qe Г k(z2 — lz). I и kz и k ( — z) 1
Ф 2 irsh-2-sh-2 ’
Мы видим, что решение уравнения (40) в частных случаях не представляет трудностей.
704 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
§ 7. Крутильная форма потери устойчивости при центральном сжатии
Известно, что тонкостенный стержень под действием равномерного осевого сжатия может иногда потерять устойчивость в крутильной форме, в то время как его ось остается прямой. Рис. 23 показывает пример такого выпучивания для случая стержня, имеющего четыре одинаковые полки. Волокно, совпадающее с осью z, остается прямым при этом выпучивании, и момент Мг сжимающих сил, приложенных на конце, превращается
в нуль для каждого поперечного сечения стержня. Чтобы определить крутящий момент, вызывающий кручение, указанное на фигуре, надо рассмотреть прогибы полок при выпучивании.
Сначала разъясним метод, который будет использован в дальнейшем ана-
Рис. 23.
лизе, взяв простой случай выпучивания сжатого стержня (рис. 24, а). Первоначально стержень имеет прямолинейную форму равновесия и на него действует только центрально сжимающая сила Р. Предположим теперь, что эта сила Р получает критическое значение и что стержень примет слегка изогнутую форму равновесия. Вследствие этого прогиба в стержне возникнут некоторые изгибные напряжения, которые накладываются на первоначальные равномерно распределенные напряжения сжатия. В то же время начальные напряжения будут действовать на слегка повернутые поперечные сечения, как показано на рис. 24, Ь. Каждый элемент изогнутого стержня между двумя смежными поперечными сечениями находится в состоянии равновесия, и мы можем полагать, что изгибные напряжения, возникающие при выпучивании сжатого стержня, уравновешивают начальные сжимающие напряжения, действующие на слегка повернутые поперечные сечения. Замечая, что угол между двумя смежными поперечными сечениями после деформа¬
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 705
ции (рис. 24УЬ) равен а —(d2vdz2)dz, мы заключаем, что действие сжимающих сил Р на повернутые поперечные сечения эквивалентно действию поперечной нагрузки на каждый элемент стержня (рис. 24, с), имеющей величину —Р (d2vdz2)dz. Отсюда ясно, что упругая ось стержня и соответствующие изгибные напряжения могут быть найдены при допущении, что стержень находится под действием фиктивной нагрузки интенсивностью
—Р d2vdz2. Дифференциальное уравнение упругой оси (18) в этом случае имеет вид
FJ — р d2v
nJx dz4 r dz2 '
Из этого уравнения можно получить обычным путем известное критическое значение сжимающей силы Ркр.
Возвращаясь теперь к задаче о крутильной форме потери устойчивости, показанной на рис. 23, мы можем констатировать, что в критическом состоянии потерявшая устойчивость форма равновесия поддерживается продольными сжимающими напряжениями, действующими на повернутые сечения волокон. Предполагая, что толщина t полок мала, и принимая, что площадка поперечного сечения t dp находится на расстоянии р от оси, мы видим, что вследствие крутильного выпучивания ее прогиб равен v рф. Возьмем элемент полосы, заключенный между двумя смежными поперечными сечениями, находящимися на расстоянии dz учитывая действие начальной сжимающей силы ot dp на слегка повернутые поперечные сечения полосы (рис. 23), получим силу
- (ot dp) dz- (at dp) p -0- dz.
Ее момент относительно оси z равен —o(d2ydz2)dz-t-p2 dp. Складывая эти моменты и распространяя суммирование на все поперечное сечение, мы получим крутящий момент, действующий на элемент выпученного стержня, заключенный между двумя смежными поперечными сечениями. Используя обозначение т2 для крутящего момента на единицу длины стержня, получим
т-4а 0 J -а13- 7о
о
где о есть полярный момент инерции поперечного сечения стержня относительно центра сдвига, совпадающего в данном случае с центром тяжести поперечного сечения. Чтобы вывести теперь уравнение для стержня, потерявшего устойчивость, используем уравнение (40). Дифференцируя это уравнение по z и
706 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
замечая, что по правилу знаков тг —dTdzt найдем
Cjq)IV — Cqp mz. (51)
Подставляя вместо тх полученное выше его значение, найдем СтФ1У — (С — oJ0) ф 0. (52)
На основании этого уравнения можно теперь вычислить критическое значение сжимающего напряжения а.
В случае, представленном па рис. 23, средние линии всех полок пересекаются в одной точке и жесткость депланации С равна нулю. Отсюда
(С-а0) р 0.
Это уравнение удовлетворяется в предположении, что величина в скобках равна нулю, что дает
с ¥ыю ffp XJl -F- 53)
0 4 ьч 0
о
Мы нашли, что критическое значение сжимающего напряжения не зависит от длины стержня и от формы потери устойчивости, определяемой углом ф. Такой результат получается потому, что при выводе уравнения (40) мы пренебрегли всяким сопротивлением полок изгибу в направлении, перпендикулярном к полке. Для того, чтобы учесть его, мы должны рассматривать каждую полку как равномерно сжатую пластину, шарнирно опертую вдоль трех сторон и полностью свободную для выпучивания по четвертой стороне. Такое более точное допущение показывает, что критическое напряжение равно )
(п лы , Ь2 Gt2
сгКр (0,456 2 j 6(1 ь2.
Второй член в скобках дает влияние на критическое напряжение длины стержня. Для стержней значительной длины этим членом можно пренебречь. Тогда получим
_ 0,75Gt2 акР (1 -ц)62
При х 0,3 это значение больше, чем вычисленное выше, приблизительно на 7.
) Это решение было получено автором; см. «К вопросу об устойчивости сжатых пластинок», Известия Киевского политехнического института, 1907, год 7, книга 2, стр. 35—94 и «Einige Stabilitatsprobleme der Elastizitatstheorie». Zeitschrift fur Mathematik und Physik, 1910, Bd. 58, Heft 4, SS. 337—385.
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 707
Уравнение (52) справедливо также в случаях, когда С не равно нулю и при несимметричных поперечных сечениях, если только ось стержня остается прямой во время потери устойчивости. Это требует, как мы позже увидим, чтобы ось центров сдвига совпадала с осью центров тяжести подобно тому, как это происходит в случае зетобразного сечения. Во всех таких случаях критическое сжимающее напряжение получается.из решения уравнения (52). Вводя обозначение k2 (ао — С)Си мы находим, что таким решением будет
Ф A sin kz А1 cos kz A2z Л3. (54)
Если концы сжатого стержня не могут поворачиваться, но свободны для депланации, мы имеем следующие условия на концах:
ф ф о при z 0 и z l;
отсюда следует:
Ах Аъ 0, Л, 0, А 0, kt--nn.
Подставляя вместо k его значение, получим
ао-С -С,.
Наименьшее значение а, удовлетворяющее этому условию, равно ')
ткр--(с (55)
Если концы стержня заделаны и не могут депланировать, концевые условия будут
ф ф' 0 при 2 0 и z 1.
Чтобы удовлетворить этим условиям, мы должны принять, что
А -f Л3 0, А Л2 0, kl 2пп.
Критическое сжимающее напряжение в этом случае составит
Надо отметить, что решение (53), ранее найденное при С 0, может быть также получено из уравнения (52) при Си
) Это решение было получено Г. Вагнером (Н. Wagner); см. его статью «Verdrehung und Knickung von offenen Profilen» в юбилейном выпуске «Fiinfundzwanzig Jahre Technische Hochschule Danzig». 1929, SS. 329—343.
708 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
не равном нулю, если только концы стержня могут свободно поворачиваться друг относительно друга, так что можно принять ф' за постоянную величину. В этом случае в общем решении уравнения (54) полагаем, что А А А3 0, и принимаем ср A2z. Чтобы найти крутящий момент, вызывающий закручивание в этом случае, мы 1 разлагаем внешние сжимающие силы ot ds,
I действующие на каждую продольную поло-
I су и параллельные оси zy на две составляю-
, щие: одну в направлении наклона волокон
I и другую, параллельную плоскости ху, как
показано на рис. 25 в точке N верхнего по-
I перечного сечения. Эта вторая составляю-
I щая способствует появлению крутящего мо-
мента. Если через р обозначено расстоя-
j ние полосы от оси поворота, то угол накло-
— на к оси z составит рф' и только что упо¬
мянутая горизонтальная составляющая сжимающей силы ot ds даст момент отноРис. 25. сительно оси zy равный ot ds р2ф'. Суммируя
эти моменты и распространяя результат на все поперечное сечение, получим Т аф'0. Когда а достигает своего критического значения (53), найдем
Т СФ'.
Этот крутящий момент, как видим, достаточен, чтобы поддерживать скрученную форму равновесия стержня.
§ 8. Потеря устойчивости вследствие изгиба и кручения при центральном сжатии
Рассмотрим общий случай потери устойчивости, когда при центральном сжатии происходит не только закручивание, но и изгиб оси сжатого стержня. Примем, что х и у — главные центральные оси поперечного сечения стержня, а х0 и у0 — координаты центра сдвига. Прогибы оси центров сдвига в направлениях х и у обозначим соответственно через и и v и, как и раньше, через ф — углы закручивания поперечных сечений вокруг оси центров сдвига. Тогда прогибы центральной оси при выпучивании, как видно из рис. 26, будут и оФ и v — х0ф. Полагая для случая шарнирно опертого стержня, что на его концах действует только сжимающая сила Я, найдем изгибающие моменты относительно главных осей в любом поперечном сечении:
MxP(v- л;0ф), Му — Р(и yQq).
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 709
Дифференциальными уравнениями (17) упругой кривой оси центров сдвига будут
d2u
d2v
у dz2 Ь УоФ) EJX — Р (v 0ф). (56)
dz2
Для того, чтобы написать уравнение угла закручивания ф, поступим, как и в предыдущем параграфе. Возьмем элемент поперечного сечения t ds, определяемый координатами х и у в плоскости поперечного сечения. Составляющие его прогиба в направлениях х и у при выпучивании будут соответственно равны
и (Уо - у) Ф
И
v — (х0 — х) ф.
Беря вторые производные этих выражений по z и рассматривая элемент dz волокна, найдем, как и раньше, что сжимающие усилия ot ds, действующие на слегка повернутое сечение элемента dz, дают следующие составляющие усилий в направлениях х и у:
— at ds -5- и (г0 - у) ф dz, - at ds--v - (х0 - х) ф dz.
Обозначая, как и раньше, штрихами производные по z и беря моменты найденных составляющих сил относительно оси центров сдвига, получим для элемента t ds следующее крутящее усилие на единицу длины стержня:
dm2 - сг ds и(у0 - у) ф (Уо — y) ot ds v - (х0 - х) ф (х0 — х). Интегрируя по всему поперечному сечению и замечая, что a J t ds Р, J yt ds 0, J xt ds 0,
получим
где
J уЧ ds Jx, J x4 ds Jy,
p p
mz-x0v”-yQu)P-rlP4,
9 9 . 9 . '8-2 Уо —7—
710 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
есть квадрат радиуса инерции поперечного сечения относительно его центра сдвига. Подставляя вычисленное значение mz в уравнение (51), получим
с,ptv — С — гР) ф - Р (x0v - у0и) 0. (57)
Это уравнение вместе с уравнениями (56) теперь будет использовано для определения критического значения сжимающей силы Р 1).
Как видно, угол поворота ср входит во все три уравнения; отсюда следует, что в общем случае крутильная форма потери устойчивости сопровождается изгибом оси, и мы имеем комбинацию крутильной и изгибной форм потери устойчивости. В частном случае, когда х0 у о 0, т. е. когда ось центров сдвига совпадает с осью центров тяжести, каждое из уравнений (56) и (57) содержит только одно неизвестное и может рассматриваться самостоятельно. Уравнения (56) дают тогда два значения критической силы, соответствующие потере устойчивости в двух главных плоскостях по Эйлеру. Уравнение (57) содержит в этом случае только одно неизвестное ф и дает нам критическую силу для чистого крутильного выпучивания, уже рассмотренного в предыдущем параграфе. Из трех значений критической силы для практического использования будет приниматься, конечно, наименьшее.
Возвращаясь к общему случаю, предположим, что концы сжатого стержня не могут поворачиваться относительно оси z (рис. 23), но свободны как в отношении депланации, так и в смысле поворота вокруг осей х и у. В этом случае концевые условия будут
и 0 ф О; и v” ф 0 при 2 0 и 2.
Все эти условия будут удовлетворены, если принять решение уравнений (56) и (57) в виде
Л. JXZ л. JXZ л , 3XZ г s-w
jSin —, v A2s in — , ф Л3 sin —у-. (58)
Подставляя эти выражения в уравнения (56) и (57), получим следующие уравнения для вычисления постоянных Аи А2 и Лз:
(р - EJy Л, Ру0А3 0, (Р - EJX - J.) Л2 - Рх0А3 0,
V (59)
РгоЛ, - Рх0А2 (- С, ±г - С г20Р Л3 0.
) Система уравнений, эквивалентных уравнениям (56) и (57), была впервые получена Робертом Каппусом: R. К а р р u s. Drillknicken von Staben mit offenem Profil. Jahrbuch 1937 der deutschen Luftfahrtforschung. Bd. 1, SS. 409—413 и Drillknickungen zentriscn gedriickter Stabe mit offenem Profil im elastischen Bereich. Luftfahrtforschung, 1937, Bd. 14, JNTs 9, SS. 444—457,
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 711
Эти уравнения удовлетворяются, если принять А А2 Л3 0, что соответствует прямой форме равновесия сжатого стержня. Чтобы иметь выпученную форму равновесия, уравнения (59) должны давать для Ль А2 и А3 решения, отличные от нуля, что возможно только в том случае, если детерминант системы уравнений (59) обращается в нуль. Для упрощения написания введем обозначения:
n2EJy n2EJx
Л—2
p3-L(c c,-), (60)
где Р1 и Рг — эйлеровы силы при выпучивании в двух главных плоскостях, а Рз определяет критическую силу для чисто крутильной формы потери устойчивости, как это дано уравнением (54). Тогда, приравнивая нулю детерминант уравнений (59), получим
Р-Р1 0 у0Р
0 Р — Р2 — х0Р 0,
УоР хор го(рр3)
что после раскрытия дает следующее кубическое уравнение для вычисления величины критической силы Р:
(- rl х§ yl) Я (, р2 рз) rl - ХР, - У1Р2 Р -
- гЦР.Р, Р2Р3 P,P3) Р PxP2P,rl 0. (61)
Это уравнение позволяет сделать следующее важное заключение. Предположим, что Р Р2, т. е. что меньшая эйлерова критическая сила соответствует изгибу в плоскости xz, и исследуем при этом знак левой части уравнения (61) для различных значений Р. Если значение Р очень мало, то можно пренебречь всеми членами, содержащими Р, и левая часть уравнения (61) сведется к величине РР2Рг1у которая является положительной. Предположим теперь, что Р принимает значение Р тогда левая часть уравнения (61) обратится в vlP(P 2) и так как Р1 P2t выражение это будет отрицательным. Это указывает на то, что корень уравнения (61) меньше Р и что, допустив возможность кручения при выпучивании, мы всегда получим критическую силу, меньшую эйлеровой.
Чтобы найти критическую силу для частного случая, вычислим, пользуясь обозначениями (60), численные значения коэффициентов уравнения (61) и затем решим это кубическое уравнение1). Мы получим три значения Р, из которых практически
) Это решение может быть значительно упрощено использованием номограмм, как показано в упомянутой на стр. 710 статье Р. Каппуса.
712 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
используется наименьшее. Подставим эти значения в уравнения 59), найдем для каждого возможного вида критической силы отношения А : А3 и А2:А3. Эти отношения, устанавливая зависимость между углом закручивания и перемещением поперечного сечения, определяют для каждой критической формы положение оси, параллельной оси стержня, вокруг которой поворачивается поперечное сечение при выпучивании.
Если стержень имеет очень тонкую стенку и малую длину , то Р3 может стать меньше Р и Р2. В этом случае наименьший корень уравнения (61) приближается к величине Яз. Подставляя его в уравнения (59), найдем, что линейные перемещения А и А2 малы в сравнении с углом закручивания; это указывает на то, что форма выпучивания приближается к чисто крутильной форме потери устойчивости, рассмотренной в предыдущем параграфе. В том случае, если стержень имеет толстую стенку и значительную длину , Р3 обычно больше, чем Р и Р2у а наименьший корень уравнения (61) приближается к значению Рь Влияние кручения на критическую силу будет незначительным в этом случае, и обычная формула для сжатого стержня дает тогда удовлетворительные результаты.
Если поперечное сечение имеет ось симметрии, вычисление РКр упрощается. Пусть ось х есть ось симметрии, тогда у0 О и член, содержащий ф в первом из уравнений (56), пропадает. Потеря устойчивости стержня в плоскости симметрии независима от кручения, и соответствующая критическая сила определяется формулой Эйлера. Мы должны считаться только с выпучиванием, происходящим перпендикулярно к плоскости симметрии, и с кручением. Соответствующие уравнения имеют вид
Поступая, как раньше, и используя решение (58), получим для вычисления критической силы условие
Это квадратное уравнение имеет два решения, которые совместно с эйлеровой силой для выпучивания в плоскости симметрии определяют три критических значения силы Р, из которых для практического приложения должно использоваться наименьшее. Рассматривая левую часть уравнения (62), видим, что при очень малых значениях Р она переходит в величину гР2Ръ, которая является положительной. Мы видим также, что она отрицательна при Р Р2 и при Р Р3, поскольку обращается тогда в
EJxv -P(v- оФ), Сyv - (С - г20Р) р Px,v.
что дает
Р — Р2 — х0Р -х0Р гЦР-Рг) 0
rl(P-P2)(P-P3)-xlP 0.
(62)
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 713
— хР2. Она отрицательна также при всех значениях Р между р р2 и Р Р3, поскольку первый член в ней становится отрицательным, а второй — всегда отрицателен. Из этого рассуждения заключаем, что один корень уравнения (62) меньше, чем Р2 или Яз, в то время как другой больше каждого из них. Меньший из этих корней — эйлерова сила для выпучивания в плоскости симметрии — дает нам требуемую критическую силу.
Все сделанные выше выводы основаны на решении в форме (58). Без какого-либо осложнения можно взять решение в более общей форме, приняв
Это соответствует предположению, что при выпучивании стержень подразделяется на п полуволн. Наши предыдущие заключения будут иметь силу также и в этом случае; надо только подставить в выражение (60) значения п2п212 вместо я22. Соответствующие критические значения нагрузки будут, естественно, большими, чем те, которые получаются при выпучивании по одной полуволне, и представляют практический интерес только в том случае, если стержень имеет промежуточные равноотстоящие боковые опоры.
Если концы стержня защемлены, то концевые условия будут
и v qp 0, и' v' ф' 0 при 2 0 и z l.
Поскольку при выпучивании возникнут концевые моменты, мы будем иметь вместо уравнений (56) следующие:
Эти уравнения совместно с уравнением (57)1) определят теперь форму выпучивания стержня и соответствующие критические силы. Все эти уравнения и концевые условия будут удовлетворяться, если взять
Подставляя эти выражения в уравнения (57) и (64), получим для вычисления критических сил те же уравнения (61). Надо только в обозначения (60) ввести 4я22 вместо я22.
- . nnz л. nnz л. nnz пп
и Asm ——, u i42sm——, ф Л38т——. (63)
nnz
) Уравнение (57) было выведено при рассмотрении элемента стержня, лежащего между двумя смежными поперечными сечениями, причем на него не влияют изменения концевых условий.
714
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
§ 9. Выпучивание при кручении и изгибе стержня, находящегося в упругой среде
Рассмотрим устойчивость центрально сжатого стержня, если во время выпучивания возникают поперечные реакции, пропорциональные его прогибам. Предположим, что эти реакции распределены вдоль оси N, параллельной оси стержня и определяющейся координатами hx и hy (рис. 27). Обозначая, как и раньше, составляющие прогиба оси центров сдвига через и и v, а угол
поворота относительно этой оси через ф, найдем, что составляющие прогиба оси N, вдоль которой распределены реакции, равны
х и (Уо hy) qp и v (х0 - 1гх) ф.
Соответствующие реакции на единицу длины будут
-kxu (Уо - hy) ф
И
-kyv-(xo-hx)q,
где kx и ky — постоянные, определяющие жесткость упругой среды. К этим реакциям мы прибавим боковые усилия, получающиеся от действия начальных сжимающих усилий на слегка повернувшиеся поперечные сечения. Эти ранее рассмотренные силы (см. § 8) составляют на единицу длины
— J ot ds и (у0 — у) ф и — J otds v — (xQ — х) q.
Интегрируя и складывая результаты с вычисленными упругими реакциями, мы в конечном итоге получим следующие выражения для интенсивностей распределенных поперечных нагрузок:
Qx-kx и (у0 - hy) ф - Р (и г0ф)
Я у “ ky lv (о - hx) ф - Р (v - 0Ф). Подставляя это в уравнения (18), получим
EJyuV Р (и у0ф) kx и (у0 - hy) ф 0, EJxvlv Р (v — х0ф) ky v — (xQ — hx) ф 0.
(66)
(67)
К этим уравнениям упругой оси мы должны прибавить уравнения для угла закручивания ф. Поскольку реакции распределены вдоль оси N, которая не совпадает с осью центров сдвига, они будут вызывать крутящие моменты, распределенные вдоль
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 715
стержня. Величина этих крутящих моментов на единицу длины будет равна
-kxu (го - hy) ф (го - hy) kyv- (х0 - hx) ф (х0 - hx).
Упругая среда может сопротивляться кручению также и в случае, когда ось N совпадает с осью центров сдвига. Это действие на стержень может быть представлено непрерывно распределенным крутящим усилием, интенсивность которого пропорциональна углу закручивания и может быть выражена в виде—фф, гдеф есть также постоянная, зависящая от жесткости среды. Складывая эти два компонента интенсивности распределенного крутящего момента с интенсивностью, ранее полученной от действия начальных сжимающих сил на повернутые поперечные сечения волокон (см. § 8), получим
тг (ХЬV У0U) Р ФФ kx « Оо - ky) Ф (У0 Ну)
kyv- (о - hx) ф (х0 - hx) - фф. (68)
По этому значению т2 мы находим вместо уравнения (57), данного в предыдущем параграфе, следующее уравнение для угла закручивания:
cyv -(С- гР) ф - Р (x0v - IJ0U) kxu (у0 - hy) ф (г0 - hy)
(0 hx) ф (х0 Ь-х) рФ ()
Это уравнение вместе с уравнениями (67) определяет формы выпучивания стержня в упругой среде и соответствующие значения критических сил1).
Если концы стержня не могут поворачиваться, но свободны для депланации, то выбираем решение этих уравнений в форме (63), причем вычисление критической силы потребует, как и раньше, решения кубического уравнения. В некоторых частных случаях вычисление можно значительно упростить. Возьмем простой пример стержня с двумя плоскостями симметрии. В этом случае ось центров сдвига совпадает с осью центров тяжести и мы будем иметь х0 г0 0. Полагая, что упругие реакции распределены вдоль оси центров тяжести, мы одновременно получим hx hy 0, и уравнения (67), (69) обратятся в следующие:
EJyulv Ри kxu 0, EJxvw Pv kyv 0,
С,ф-(С-г§Я)ф фф 0.
Отсюда видно, что в этом случае выпучивание стержня в плоскостях симметрии не зависит от кручения и что можно
) Эти уравнения были впервые получены В. 3. Власовым в его книге «Тонкостенные упругие стержни», М. — Л., Стройиздат Наркомстроя, 1940, стр. 411.
716 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
рассматривать отдельно все три формы выпучивания. Первые два уравнения дают известную уже критическую силу для изгиба в плоскостях симметрии. Последнее уравнение дает критическую нагрузку для крутильного выпучивания. Принимая решение в форме (63),для последней критической силы найдем выражение
С.- с ф
ЛР -5— (70)
г0
В каждом частном случае, зная С и гф, выберем для п такое значение, которое придаст выражению (70) минимальное значение. Когда йф 0, мы должны принять п 1, и критическая сила (70) становится равной критической силе, ранее полученной из формулы (55).
Рассмотрим теперь случай, когда поперечное сечение стержня имеет одну ось симметрии, которую мы примем за ось х. Тогда уо 0. Предположим также, что упругие реакции распределены вдоль оси центров сдвига. Тогда hy 0, hx 0 и уравнения (67) и (69) дадут
EJyuw Ри kxu 0,
EJxvw Pv kyv — Рх0 cp 0,
Cyv - СФ kфФ Рф - Px0v 0.
Следовательно, выпучивание в плоскости симметрии не зависит от закручивания и может рассматриваться отдельно. Выпучивание в направлении, перпендикулярном к плоскости симметрии, связано с кручением, и мы должны рассматривать последние два из вышеприведенных уравнений одновременно. Выбирая решение этих уравнений в форме (63), для вычисления постоянных А2 и Аз получим
— P- kf) Px0--A3 0,
a2(ejxЦ-
АгРч С, (С - гР) ft, Л3 0.
Критическое значение нагрузки можно найти, приравнивая нулю детерминант двух уравнений. Таким путем мы получим квадратное уравнение для Ркр, из которого в каждом частном случае можно вычислить величину критической силы. Если ф 0, мы должны принять, что п 1, и получим для Ркр уравнение, которое совпадает с ранее полученным уравнением (62).
Используя уравнения (67) и (69), можно исследовать выпучивание стержня в случае, когда ось, вокруг которой поворачиваются при выпучивании поперечные сечения, не смещается.
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 717
Чтобы получить такую ось вращения, нам остается только при¬
нять, что kx kv оо. Тогда ось N на рис. 25 остается прямой во время выпучивания и поперечные сечения будут поворачиваться вокруг этой оси. Уравнения (67) в этом случае дадут
И (го - fly) ф 0, v-(x0-hx) Ф 0,
и мы получим
гг (го hy) Ф. » (х0 - hx) ф.
Из уравнения (67) мы также имеем, что
kx и (Уо - hy) ф EJyU™ - Р (и гоф). ky v - (хо - hx) ф - EJxv™ - Р (v - ж0ф).
После подстановки в уравнение (69) получим PIV Сх (Уо - hyf EJy (хо - hxf EJX - СФ
ф fro “ (4 Уо) К; Щ фФ 0- (7)
Выбирая решение в форме (63), можно вычислить на основании этого уравнения в каждом частном случае критическую силу.
В том частном случае, когда стержень имеет две плоскости
симметрии, имеем х0 у0 0. Подставляя ф в урав¬
нение (71), получим
(С, AJE7, 4;7. ) С JL к,
— т
В каждом частном случае для п следует принять такое значение, чтобы сделать выражение (72) минимальным.
Если ось центров сдвига принять за ось вращения, имеем hx х0, hy уо и уравнение (71) дает
П2ТС.2 2
С'Т С Ч
Лф -7- (73)
г0
Когда равно нулю, мы должны принять п 1, и выражение (73) дает для РКр то же значение, что и уравнение (55), как этого и надо ожидать.
Принимая, что ось вращения бесконечно удалена от стержня, и полагая, например, что hy оо, из уравнения (71) получим
Ф1У„ Яф-0,
что дает для РКр известную эйлерову силу при выпучивании стержня в плоскости xz.
718 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Иногда вместо неподвижной оси вращения может быть взята плоскость, параллельно которой некоторые волокна стержня будут перемещаться при выпучивании. Если, например, стержень приварен к тонкому листу (рис. 28), волокна стержня, совпадающие с поверхностью яя, при выпучивании не могут перемещаться в плоскости листа, но будут перемещаться в направлении, перпендикулярном к этой плоскости. При решении такой задачи целесообразно взять центральные оси х, у параллельными и перпендикулярными листу. Обычно оси не будут больше являться главными осями и надо будет изменить соответствующие дифференциальные уравнения изгиба оси стержня. Из выражений (1) и (2) в общем случае имеем
х
У
Рис. 28.
Мх — EJ xv — EJ xyti'‘ Му Е Jyu” EJxyv.
Дифференцируя эти уравнения дважды по z и используя уравнения (5) и (6), получим
qy EJxvlv EJ
ху“
IV
EJyulv EJxyv
IV
(74)
Рассматривая произвольную форму поперечного сечения (рис. 29), примем, что волокно N с координатами hXt hv не может смещаться в направлении х.
Обозначая, как и раньше, через и и v прогибы оси центров сдвига О в направлении х и у, находим для прогибов волокна N следующие выражения:
Ч Ф (Уо - hy) V - Ф (0 - hx).
Из условий закрепления волокна N заключаем, что
и Ф (Уо hy) 0. (75)
Вследствие такого закрепления возникнут реакции, параллельные оси х
и непрерывно распределенные вдоль волокна N. Пусть будет интенсивностью этой распределенной нагрузки. Тогда величины qx и qv в уравнениях можно получить путем подстановки kx ky 0 в выражения (66) и сложения qo с первым из этих уравнений. Таким образом, находим
Чх - Р (« У№) Яо Яу-Р (v - оф)
С
X
¥
t х
Н ' Уо
У
Рис. 29.
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
719
Подставляя это в уравнения (74), получим
q0 Р (и у0ф) EJyulv EJxyv
IV
EJxvlv EJxyulv P v - 0ф) 0.
(76)
Второе из этих уравнений после подстановки вместо и его значения из уравнения (75) дает следующее уравнение, содержащее только v и ф:
EJxvlv Pv - EJху (у0 - hy) ф1У - Рх0ф 0.
(77)
ТТУ
У о Ji О
у
Рис. 30.
Второе уравнение для v и ф получается в результате рассмотрения кручения стержня. Для этого используем уравнение (69). Подставляя в это уравнение А‘ф ky 0,
—kxu (Уо — hy) ф 7о, получим С1ф.У_(С-г§Р)ф -
- р (x0v - у0и) - q0 (у0 - hy) 0.
Подставляя в это уравнение значение и из уравнения (75) и значение qQ из первого уравнения (76), находим
С EJy (о — hy)2 cpiv — Сф
РГ ('§ h2 — у2) - EJxy у, - hy) v™ -
- Рхр 0. (78)
Уравнения (77) и (78) теперь будут использованы для вычисления критических нагрузок1). Принимая, что концевые условия будут ф ф v 0 при г 0 и при г , выбираем решение уравнений (77) и (78) в форме (58) и после подстановки получим
( -р)а2- (у0 - hy) - Рх о А3 0,
- _EJxy (го -hy)- Pxq А2
С, Еу (у0 - hy С - Р(г§ Л - Л3 0.
Приравнивая нулю детерминант этих уравнений, получим, как и раньше, квадратное уравнение для Р, из которого может быть вычислена критическая нагрузка в каждом частном случае.
Если стержень симметричен относительно оси у, как в случае швеллера (рис. 30), то оси х и у являются главными осями;
1) Эти уравнения были получены Дж. Гудиром: J. N. G о о d i е г. Buckling of compressed bars by torsion and flexure. Cornell University, Engineering Experiment Station, Bulletin № 27, 1941, 32 pp.
720 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
следовательно, JXy 0, хо 0 и выше приведенные уравнения превращаются в такие:
(1-р)л2о,
С, EJy (у0 hyf С - Р (г А - Д, 0.
Из первого уравнения мы получим эйлерову нагрузку для выпучивания в плоскости симметрии. На основании второго уравнения получим критическую силу кручения при оси вращения в плоскости листа:
С, Е1у(1Л-ку)Ц- С
Ркр 2 h2 _ 2 (79)
г0 ' Пу У о
Тот же результат получится из уравнения (71) после подстановки
TIZ
Хо hx kff 0, ф А3sin —.
§ 10. Устойчивость тонкостенных стержней при изгибе и сжатии
Известно, что балки, изогнутые в плоскости их максимальной жесткости, могут терять устойчивость из-за бокового выпучивания, сопровождающегося кручением1). Рассмотрим случай, когда стержень подвержен действию центрально сжимающей силы Р и изгибающих моментов Mi и М2, приложенных к концам (рис. 31). Предположим, что влиянием силы Р на величину изгибных напряжений можно пренебречь. В таком случае нормальное напряжение в любой точке не зависит от г и может быть выражено уравнением
) Этот вид выпучивания стержней с узким прямоугольным поперечным сечением был исследован Л. Прандтлем (L. Prandtl) (см. его диссертацию «Kipperscheinungen. Ein Fall von instabilcm elastischem Gleichgewicht». Dissertation der Universitat Munchen, 1899, Niirnberg, 1900) и А. Мичеллом (A. G. Michell. Elastic stability of long beams under transverse forces. Philosophical Magazine and Journal of Sciences, Series 5, 1899, vol. 48, № 292, pp. 298—309). Случай двутавровой балки был рассмотрен автором в упомянутой на стр. 694 статье. Распространение этой теории на стержни с любым тонкостенным открытым поперечным сечением было сделано В. 3. Власовым в упомянутой на стр. 715 книге. Некоторые случаи исследованы также Дж. Гудиром (J. N. Goodier. Flexural-torsional buckling of bars of open section. Cornell University, Engineering Experiment Station, Bulletin Jsfo 28, 1942 i6 pp.).
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 721
в котором х и у являются главными центральными осями поперечного сечения. Начальный прогиб стержня, вызванный моментами Mi и М2, принимаем очень малым. Исследуя устойчивость этой изогнутой формы равновесия, мы поступаем, как и раньше. Предполагая, что возникли дополнительные прогибы и и v оси центров сдвига одновременно с поворотом ф относительно этой оси, пишем уравнения равновесия для этой новой формы, слегка отличной от первоначально изогнутой формы, получившейся от действия моментов Мг и М2. Составляя эти уравнения, мы пренебрегаем малыми начальными прогибами и поступаем, как и в предыдущем случае, когда ось стержня была вначале прямой. Тогда составляющие прогиба любого продольного волокна стержня, определенного координатами х и уу будут
« (Уо У) Ф и v - (лг0 - х) ф.
Интенсивности фиктивных поперечных нагрузок и распределенных крутящих моментов, возникших в результате действия начальных сжимающих сил в волокнах на их слегка повернутые поперечные сечения, можно получить, как и раньше (см. § 8), и представить в виде уравнений
Ях — otds и (г0 - у) Ф,
F
qu- j otds v - (х0 - х) ф,
F
mz - j otds и (г0 - у)ф (г0 - у)
F
otds v — (х0 — х) ф (х0 — х).
F
Подставляя выражение (80) вместо о и интегрируя, получим qx- Pu-(PyQ Mt)t, qy — Pv (Px о - M2) ф,
mz - (Py0 Af,) и (Pxо - M2) v (M,p, - Af2p2 - Pr§ ф,
где введены следующие обозначения:
J у3 dF J x2y dF J xdF J xy2 dF
pl 77 2y' p8“ 7 2x' 81
p
Г' м
I
Xt 7
Ml у
Jry
p,
и x
M,
Рис. 31.
722 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Уравнения (18) и (51) тогда дают Elytis Ри (Ру0 М,) ф О,
EJxv™ Pv - (Рхо - М2) ф О,
С,ф _ (С М,Р, - М2 - Рг) ф (82)
(Ру0 Мх) и - Рхо - М2) v 0.
Эти уравнения являются общими уравнениями равновесия для выпученной формы стержня. Пользуясь этими уравнениями, можно вычислить критические значения внешних сил при любом данном концевом условии.
Начнем со случая внецентренного сжатия. Если через ех и еу обозначить координаты точки приложения сжимающей силы Р, то имеем
Мх — Реу, М2 Рех.
Подставляя это в уравнения (82), получим:
EJyU,™ Ри Р(у0- еу) р 0,
EJxvIV Pv -Р(х о- ех) ф 0,
Cyv _ (С - Реур, - Рехр2 - Prl) Ф (83)
Р(Уо- еу) и -Р(х0- ех) v 0.
В случае шарнирно опертых концов имеем следующие концевые условия:
u v ф 0, u v ф 0 при 2 0 и z , которым можно удовлетворить, принимая
Л 3XZ а 3XZ 1 TtZ
I sin — , v A2sm —, ф Л381п —.
Подставляя эти выражения в уравнения (83), получим
EJy - Р) А, - Р (у0 - еу) А3 0,
(ех - р) Л2 Р (х0 - ех) А3 0,
“ Р (Уо еу) Р (о ех) А2
(с, С - РеуР, - РехР2 - Prl) А3 0.
(84)
Приравнивая нулю детерминант уравнений (84), получим, как и раньше, кубическое уравнение для вычисления Ркр.
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 723
В частном случае, когда сжимающая сила Р действует вдоль оси центров сдвига, имеем ех дс0, еу у0 и уравнения (83) значительно упрощаются, поскольку каждое из них содержит только одну переменную величину. Боковые выпучивания в двух главных плоскостях не зависят друг от друга и не зависят от кручения. Мы получим три критических значения Р, из которых два определяются формулами Эйлера, а одно соответствует крутильному выпучиванию.
Если точка приложения сжимающей силы не совпадает с центром сдвига, то.три уравнения (83) взаимно связаны и прогиб стержня во время выпучивания связан с кручением. Задача значительно упрощается, если стержень имеет одну ось симметрии. Предположим, что плоскость yz есть плоскость симметрии и что сжимающая сила Р действует в этой плоскости. Тогда х0 ех 0 и уравнения (84) превращаются в следующие:
(еу4-- р)а1-Р (Уо - еа) Л3 0, (eJxр)а2 О,
(85)
-Р(Уо- еу) Л, (с, С — Реир, - Рг§ Аг 0.
Из второго уравнения мы видим, что выпучивание в плоскости симметрии не зависит от кручения и что соответствующая критическая нагрузка равна эйлеровой. Выпучивание в плоскости xz и кручение взаимно связаны, и соответствующие критические силы можно получить, приравнивая нулю детерминант первого и третьего из уравнений (85). Это дает
EJyjr — Р -Р(Уо-еу)
-Р(Уоеу) C C-Pefr-Pr
0.
Используя выражения (60) и вычисляя детерминант, получим для определения критических сил следующее квадратное уравнение:
(Л - Р) Р-Л -Р(г2о М - Р2 (Уо - еу)2 0. (86)
При очень малых значениях Р левая часть этого уравнения положительна. Когда Р Pi, она отрицательна. Следовательно, уравнение (86) имеет корень меньший, чем Pi, т. е. меньший, чем эйлерова нагрузка для выпучивания в плоскости xz.
Если еу уо, то сжимающая сила приложена в центре сдвига и уравнение (86) дает
724 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Два решения этого уравнения будут иметь вид Р Ри Р -
Рз
Первое из них соответствует выпучиванию от изгиба в плоскости xzt второе — чисто крутильному выпучиванию.
Поскольку левая часть уравнения (86) положительна, когда Р — малая величина, и постепенно уменьшается по мере увеличения Я, мы заключаем, что наименьший корень уравнения увеличится, если в последнем члене приравнять нулю выражение, заключенное в скобки, т. е. если принять, что еу у0. Следовательно, критическая нагрузка достигает максимального значения, если сжимающая сила приложена к центру сдвига. Если еу 0, то уравнение (86) представится таким же, как уравнение (62), ранее полученное для центрального сжатия. Если поперечное сечение имеет две оси симметрии, имеем у0 Pi 0 и уравнение (86) принимает вид
(Р1-Р)(Р3-Р)г2-Р2е2 0,
или
Р2 (г2 -el)-P (Р3 Pi)r20 P.P.2 о. i87)
Из этого уравнения находим
Pl P3±V(P3- Я,)2 4Р1Р3еЦг2 (88)
Ч)
Видно, что если еу г0, то имеются два положительных корня, которые приближаются к значениям Р и Р3 по мере того, как еу приближается к нулю. Если еу г0, тогда один корень будет положительным, другой отрицательным; последнее указывает на то, что при больших эксцентриситетах нагрузки стержень может потерять устойчивость под действием эксцентричного растяжения. Когда еу г0, на основании уравнения (87) видно, что один корень равен
РхР'
другой корень приближается к бесконечности.
Мы обсудили случай стержня со свободно опертыми концами. Если концы заделаны, то концевые условия будут
и v ф 0, и' v' ф' 0 при 2 0 и z ,
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 725
условия на концах удовлетворяются, если возьмем
и —j4j (1 — COS-pj,
v » А2 (l — cos-j,
Ф А3 (l cosjj
Подставляя эти выражения в уравнения (83), получим для вычисления критических нагрузок уравнение, подобное тому, которое уже выведено для свободно опертых концов. Разница состоит только в том, что появляется величина 4я22 вместо значения я22, которое было раньше.
Теперь рассмотрим случай, когда стержень подвергается действию чистого изгиба. Подставляя Р О в уравнения (82), получим
EJyUF Af 1ф 0, EJxv™ М2 р О,
C,PIV - (С Af ,Р, - М2р2) ф М,и M2v 0. (89)
Принимая для ut v и ф тригонометрические выражения, которые мы ранее использовали, можно легко вывести уравнение для вычисления критических значений изгибающих моментов.
Особый интерес представляет случай, когда стержень обладает изгибной жесткостью в одной из главных плоскостей, во много раз большей, чем в другой плоскости, и изогнут в плоскости большей жесткости. Предположим, например, что плоскость yz есть плоскость наибольшей жесткости и что стержень изогнут в этой плоскости под действием моментов М. Чтобы определить критическое значение Ми при котором происходит боковое выпучивание, используем первое и последнее из уравнений (89). Предполагая, что концы свободно оперты, подставляем в эти уравнения выражения
„ . П2
и з А sin — ,
Ф А3 sin,
М2 0,
тогда получим
ЕЛ.-ЛМ з 0,
— МхА С С Аг 0.
Приравнивая нулю детерминант этих уравнений и используя
726 ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
обозначения (60), для вычисления критических значений М получим уравнение
M2_PipiMi_jPiP3r2 0i
откуда
м1кр -р
о. Р Р 2
—л Ь PiPsro
(90)
В частном случае, когда поперечное сечение имеет две оси симметрии, Pi равно нулю, и мы получим
М
1кр
Vp1pA уEJy (с, с).
(91)
В случае обратной симметрии, как на рис. 32, a, 3i также равно нулю, и формула (91) остается в силе. То же уравнение действительно и в случае, когда поперечное сечение имеет одну ось симметрии, если изгибающие моменты действуют в плоско-
—х
Ь)
с)
Рис. 32.
сти, перпендикулярной к оси симметрии, как на рис. 32,6, так как Pi также и в этом случае равно нулю. Если изгибающий момент М действует в плоскости симметрии, как представлено на рис. 32, с, то pi не равно нулю и следует использовать формулу (90) для вычисления MiKp. В вышеприведенном рассуждении предполагалось, что EJy мало в сравнении с EJX. Если С и Ci также малы, то выпучивание произойдет при малых значениях Mi, т. е. при малых изгибных напряжениях в стержне.
Если EJX имеет такой же порядок, как и EJyi то боковое выпучивание произойдет при малых напряжениях только при условии, если С и Ci очень малы. Это условие может быть выполнено, если поперечное сечение подобно представленному на рис. 23. Здесь Ci равно нулю, а С очень мало, если толщина полки незначительна.
ТОНКОСТЕННЫЕ СТЕРЖНИ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ 7 27
Мы обсудили здесь изгиб стержня под действием моментов, приложенных на концах. Только в этом случае нормальные напряжения (80) не зависят от г, вследствие чего мы получаем уравнение (32) с постоянными коэффициентами. Если стержень изогнут под действием поперечной нагрузки, то изгибные напряжения изменяются вдоль 2 и вместо уравнений (82) получим систему линейных уравнений с переменными коэффициентами. Вычисление критических значений поперечной нагрузки тогда становится более сложным. Несколько случаев неустойчивости такого рода обсуждены автором в упомянутой выше статье (см. стр. 696)).
1) См. также книгу автора «Theory of elastic stability». New York —London, McGraw-Hill book company, 1936, p. 239 перевод на русский язык: «Устойчивость упругих систем». М.—Л., Гостехиздат, 1946; 2-е изд., 1955, стр. 275.
ПЕРЕЧЕНЬ РАБОТ С. П. ТИМОШЕНКО ПО УСТОЙЧИВОСТИ, НЕ ВКЛЮЧЕННЫХ В НАСТОЯЩИЙ СБОРНИК
1. О выпучивании высоких балок. On the buckling of deep beams. Philosophical Magazine and Journal of Sciences, Scries 6, 1922, vol. 43, № 257, pp. 1023—1024.
2. Балки без боковых опор. Beams without lateral support. Transactions of the American Society of Civil Engineers, 1924, vol. 87, Paper N 1549, pp. 1247—1262 (discussion: pp. 1263—1270; author’s reply: pp. 1270—1272).
3. Проблемы, связанные с упругой устойчивостью конструкций. Problems concerning elastic stability in structures. Transactions of the American Society of Civil Engineers, 1930, vol. 94, Paper N 1749, pp. 1000—1020 (discussion:
pp. 1021 — 1033; author’s reply: pp. 1033—1035). См. также Proceedings of the American Society of Civil Engineers, 1929, vol. 55, N 4, pp. 855—875 (discussion: там же, 1929, vol. 55, № 7, pp. 1889—1898; author’s reply: там же, 1930, vol. 56, N 4, pp. 779—781).
4. Устойчивость и прочность тонкостенных конструкций. Stability and strength of thin-walled constructions. Proceedings of the third international congress for applied mechanics, Stockholm, 24—29 August, 1930. Ab. Sveriges Litografiska Tryckerier, Stockholm, vol. 3, 1930, pp. 3—15.
5. Рабочие напряжения для сжатых стержней и тонкостенных конструкций. Working stresses for columns and thin-walled structures. New York, 1932,
4 pp. (American Society of Mechanical Engineers — Advance Paper № 47, Meeting December 5—9, 1932). Transactions of the American Society of Mechanical Engineers, 1933, October — December, vol. 55, № 4, pp. 173—177; discussion: pp. 177—183, author’s closure: pp. 182—183 (ARM-55-20).
6. Устойчивость двутавровых балок при изгибе. Stability of plate girders subjected io bending. International Association for Bridge and Structural Engineering. First congress. Paris, 19—25 May, 1932. Preliminary publication. Zurich, general secretariat, 1932, pp. 129—147.
7. Устойчивость двутавровых балок при изгибе. Stability of plate girders subjected to bending. International Association for Bridge and Structural Engineering. First congress. Paris, 19—25 May, 1932. Final report. Zurich, general secretariat, 1932, p. 150.
8. Устойчивость стенок двутавровых балок. Stability of web of plate girders. New York, 1933, 6 pp. American Society of Mechanical Engineers—Advance Paper. Meeting, June 26—30.
Э. И. ГРИГОЛЮК
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ В ОБЛАСТИ УСТОЙЧИВОСТИ ДЕФОРМИРУЕМЫХ СИСТЕМ
Всем строем мысли и душевных качеств ты обязан Родине. Она дала тебе жизнь и талант. Талант есть сокровище, окупленное историческим опытом и мукой многих поколений. На любой общечеловеческой ценности лежит неистребимая печать нации, где она родилась.
Л. М. Леонов
Имя Степана Прокофьевича Тимошенко известно многим поколениям инженеров и специалистов в различных областях механики. Поэтому автору этих строк казалось небезынтересным привести и некоторые биографические сведения об этом человеке, оставившем неизгладимый след в механике деформируемых сред, являющемся мировым авторитетом в своей области, нашем соотечественнике. Для молодежи важно знать, как же вырастают титаны, откуда проистекает живой источник мысли и таланта, как он формируется, что способствует и что заглушает спонтанное развитие человеческого гения.
1. КРАТКИЙ БИОГРАФИЧЕСКИЙ ОЧЕРК
В селе Шпотовке, расположенном в 30 верстах от украинского города Конотопа Черниговской губернии, в семье землемера Прокофия Тимофеевича Тимошенко 22 декабря 1878 года родился сын Степан. От своего отца он унаследовал огромную трудоспособность. Отец (1847—1932) был сыном крепостного крестьянина, воспитывался вместе с детьми помещика, окончил харьковские курсы землемеров и с 20 лет начал работу землемера, особенно важную в те пореформенные годы, когда произошло в России освобождение от крепостной зависимости крестьян; он разделял либеральные взгляды, был против ограничения земств, против искусственного сохранения дворянских землевладений.
Мать — Юзефина Яковлевна Сарнавская (1854—1920) — дочь отставного военного. Она окончила женскую Фундуклеевскую гимназию в Киеве. Свой мягкий характер, любовь к труду, склонность к чтению, образность и легкость письма она передала своему старшему сыну—Степану.
Детство Степана протекало в старой помещичьей усадьбе Базиловке, имении Скоропадских, которое в 1880 году арендовал отец.
732
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
С пяти лет начались занятия с матерью, а с восьми лет с учительницей. Еще через год был приглашен репетитор Михаил Михайлович Коваленко для подготовки Степана в реальное училище города Ромны, расположенного в 30 верстах от Базиловки. Через два года, в 1889 году, он сдал вступительный экзамен в училище. Воспоминания о Ромнах, городке, посаженном у крутых берегов реки Сулы, с благоухающими рощами, Степан Прокофьевич пронес через всю свою жизнь, и те, кто встречался с ним в позднюю пору его жизни, знают, что Ромны — это самая любимая тема его разговоров: они всплывают неизбежно, с чего бы ни начался разговор.
Домашнюю подготовку к урокам в училище Степан выполнял очень серьезно и тщательно и всегда был подготовлен, тем не менее напряженность на уроке из-за возможного вызова оставалась. Эта нелюбовь к классным занятиям у него сохранилась, хотя и был он первым учеником. Суббота посвящалась чтению художественных произведений, стал вырабатываться круг чтения. Появились товарищи, с которыми придется много работать в зрелые годы (А. Ф. Иоффе). Незабываемы будут уроки географии Владимира Ивановича Тимофеева и уроки математики Льва Львовича Ижицкого.
В училище проявилась любовь Степана к обсуждениям математических доказательств. Здесь же возникла мечта о поступлении в одно из лучших высших учебных заведений того времени (не только в России)—Петербургский институт инженеров путей сообщения. Пришлось много времени уделить решению конкурсных задач и остаться в дополнительном классе в основном для подготовки к конкурсным экзаменам по математике и русскому языку.
В 1896 году Степан окончил училище и поехал в Петербург для сдачи вступительных экзаменов. Условия конкурса в путейский институт были особенно тяжелыми, требования были очень высокими, экзаменаторы — строгими и, чтобы не остаться за бортом, он одновременно стал сдавать в Институт гражданских инженеров, чтобы в крайнем случае стать архитектором. Но конкурс он выдержал в оба института и, разумеется, предпочтя путейский, Степан стал студентом этого выдающегося учебного заведения России.
Первые два года отводились общеинженерным, а следующие три — специальным техническим предметам. Раньше в этом институте читали сопротивление материалов и теорию сооружений Г. Ламе и Б. Клайперон, которые организовали лабораторию испытаний, позднее здесь работал Д. И. Журавский, крупнейший строитель мостов. При С. П. Тимошенко математику читал Д. А. Граве, механику — автор трехтомной монографии Д. К. Бобылев, проектирование мостов — Н. А. Белелюбскии и J1. Ф. Ни¬
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
733
колаи, статику сооружений — Ф. С. Ясинский. Последний оставил самое сильное впечатление у С. П. Тимошенко.
Чувствовалось отсутствие рационально поставленных практических занятий по читаемым курсам и впоследствии Степан Прокофьевич в своей 53-летней педагогической деятельности во многих высших школах Петербурга, Киева, Мичигана и Стенфорда уделит семинарским занятиям со студентами особое внимание.
На пятом курсе он выполнил четыре дипломных проекта (по мостам, по железным дорогам, по портовым сооружениям, по паровым машинам) и сдал выпускной экзамен; за описание Виордского виадука, где С. П. Тимошенко был практикантом, им была получена премия.
После окончания института в 1901 году — год службы в армии сапером в качестве вольноопределяющегося. Любовь к преподаванию сказалась и здесь — он организовал вечерние занятия по арифметике и геометрии с солдатами. Вечерами много занимался анализом, аналитической геометрией, эллиптическими интегралами, посещал заседания Петербургского математического общества, а также состоял экзаменатором по математике на репетициях абитуриентов путейского института.
После службы в армии он был принят лаборантом в механическую лабораторию путейского института, которой ведал Н. А. Белелюбский. Здесь проводились испытания цементов для русских цементных заводов, прочности и твердости рельсов; участие в этих работах дало глубокое знакомство и с устройством самих испытательных машин, и с методами испытаний. Ощущая недостаточность математической подготовки, он слушал лекции в институте по дифференциальным уравнениям в частных производных и высшей алгебре, курс Д. К. Бобылева по высшей математике, в котором в виде приложения рассматривалась проблема кручения стержней и действие движущейся динамической нагрузки на мосты. Зачислился вольнослушателем в университет, посещал заседания Физического общества; доклады А. Н. Крылова на заседаниях этого общества оставили сильное впечатление и характером постановки инженерной задачи, и методом ее решения. «Скоро появилась и практическая возможность начать работу в направлении использования математики в решении инженерных вопросов. Эту возможность мне дал Петербургский политехникум. Атмосфера этой школы оказала огромное влияние на все мое дальнейшее развитие, на мою судьбу».
В марте 1903 года профессор кафедры сопротивления материалов Петербургского политехнического института в Сосновке С. И. Дружинин пригласил Степана Прокофьевича лаборантом в механическую лабораторию, и он дал согласие. В отличие от
734
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
путейского института здесь предполагалось, кроме лекций, устроить семинарские занятия с небольшими группами студентов. Эти занятия по сопротивлению материалов (по курсу С. И. Дружинина) и по теоретической механике (вслед за И. В. Мещерским) и пришлось вести С. П. Тимошенко. Свободное время посвящалось изучению недавно переведенной книги Августа Фёппля по сопротивлению материалов, переводу первого тома известного курса А. Лява по теории упругости, штудированию курсов Г. Ламе и А. Клебша, монографии Г. Римана «Дифференциальные уравнения в частных производных» (1869). Слушал также курс теории упругости И. Г. Бубнова, посещал основанный в 1903 году механический кружок В. Л. Кирпичева, организатора Киевского политехнического и Харьковского технологического институтов. Между тем приходили из Швейцарии испытательные машины фирмы «Амслер — Лаффон»; сборке машин и изучению принципов их работы нужно было также уделять время.
Летом 1904 года — поездка за границу (третья по счету) для ознакомления с немецкими высшими техническими школами: посещение Берлинского политехникума, политехникума в Мюнхене и, в частности, лекций и лаборатории А. Фёппля, основанной еще И. Баушингером. Результат этой поездки — реферативная статья «Формулы сложного сопротивления с точки зрения различных гипотез прочности» в «Известиях Петербургского политехнического института» (1905).
При изучении книги Рэлея «Теория звука» Степана Прокофьевича увлекла идея приближенного расчета частот колебаний, и в развитие работы В. Фрама (1902) о колебаниях однородного судового вала с двумя дисками на концах он учел методом Рэлея влияние массы вала на частоту колебаний, а также показал, как развить решение на случай нескольких дисков. Это была его первая печатная работа «К вопросу о явлениях резонанса в валах», опубликованная в «Известиях Политехнического института» за 1905 год. «В дальнейшем я не раз пользовался методами Рэлея, и его книга оказала на мою последующую работу очень большое влияние».
После нового 1905 года из-за революционных событий и связанных с ними студенческих волнений вузы закрылись; они были закрыты и большую часть 1906 года. Степан Прокофьевич, не связанный преподавательской работой, решил поехать в Гёттингенский университет, на философском факультете которого открыли институт математики во главе с К. Рунге и институт прикладной механики во главе с Людвигом Прандтлем. Здесь он посещал лекции В. Фойгта по проблемам механики, лабораторные занятия по сопротивлению материалов Л. Прандтля, лекции Макса Абрахама по дифференциальным уравнениям в част¬
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
735
ных производных, а также семинар по прикладной математике и механике Феликса Клейна. В институте Л. Прандтля он начал заниматься исследованием устойчивости двутавровой балки, предварительно впервые показав, что в задаче кручения такой балки принцип Сен-Венана несправедлив.
С осеннего семестра 1905 года уже в Петербургском политехникуме он продолжил решение начатой задачи об устойчивости двутавровой балки и поставил соответствующие опыты. Остальное время уходило на слушание лекций И. В. Мещерского по уравнениям Лагранжа, И. И. Иванова по эллиптическим функциям, И. В. Станевича по теории вероятностей, университетских лекций А. Н. Крылова по приближенным вычислениям, а также домашних «Бесед по механике» В. Л. Кирпичева. «Если впоследствии я оказался неплохим преподавателем, то этим в большой степени обязан Кирпичеву».
«Вспоминая теперь о деятельности механического кружка В. Л. Кирпичева, ясно видно, что он не только содействовал научной работе участников, но им в свое время была выполнена важная работа по введению в жизнь нового метода преподавания механики, оказавшегося плодотворным и принятого теперь не только в России, но и далеко за ее пределами. Во всей этой работе руководство и указания В. Л. Кирпичева сыграли важную роль» («Кружок имени В. Л. Кирпичева», Mimchen, 1958,
11 стр.).
В начале 1906 года вышла статья «Об устойчивости двутавровых балок», и С. П. Тимошенко направил ее и еще три опубликованные работы по совету и с представлением В. Л. Кирпичева в Киевский политехнический институт в связи с замещением кафедры сопротивления материалов, на которую он в конце 1906 года был избран в возрасте 28 лет, не прочитав еще ни одной лекции. После избрания он тотчас переехал в Киев. Летнее время 1906 года он вновь провел в Гёттингене; посещал лекции Е. Зермело по теории потенциала и В. Фойгта по термодинамике. В это время он начал свою работу по устойчивости прямоугольных равномерно сжатых пластин и в «Известиях Киевского политехнического института» за 1907 год опубликовал статью «К вопросу об устойчивости сжатых пластинок». Характерно отношение самого автора к этой работе: «Эта работа является, пожалуй, наиболее существенной из всего, что мною сделано в области устойчивости деформаций».
В Киевском политехническом институте он поставил свой курс сопротивления материалов, написав этот курс (1908, 1909, литографированное издание; 1911, окончательный вариант), и составил задачник по курсу (1910). Построив курс от простого к сложному, сформулировав гипотезы, связанные с рассматриваемой задачей, он заново перестроил весь курс сопротивления
736
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
материалов. То традиционное изложение предмета, которое принято в настоящее время, обязано С. П. Тимошенко. Одновременно он ряд лет читал курс теории упругости, литографированное издание которого вышло в 1909 году на русском языке.
Лето 1907 года было посвящено изучению переведенного на немецкий язык курса теории упругости Артура Лява (Ляв — Тимпе), пятого тома технической механики А. Фёппля и первого тома «Теории звука» Дж. Рэлея. Он решил задачу устойчивости составного стержня и проблему о сжатии кольца противоположными силами. В следующем году он стал готовить работу по устойчивости для немецкого журнала математики и физики, представляющую итоги опубликованных им результатов в русских изданиях.
Весна 1909 года — вновь Гёттинген. Это лекции Ф. Клейна по теории упругости, В. Фойгта по гидродинамике, Л. Прандтля по аэродинамике. Получены результаты по применению метода нормальных координат к изгибу стержней и пластин. Кроме того, метод Рэлея был использован в проблеме о вынужденных продольных и поперечных колебаниях стержней и колебаний балки от движущейся поперечной силы.
С осеннего семестра 1908 года он был назначен сперва секретарем, а затем в 1909 году деканом инженерно-строительного отделения. Следующий год 19091910 был посвящен применению энергетического метода к проблеме устойчивости и написанию монографии «Об устойчивости упругих систем» (1910). Представление решений с помощью тригонометрических рядов и вычисление коэффициентов этих рядов из условия минимума энергии позволило ему рассмотреть широкий класс трудных проблем устойчивости и ввести энергетический метод в практику инженерных исследований. Об использовании этого метода в проблеме теории колебаний говорилось выше. В феврале 1911 года С. П. Тимошенко за противодействие правительственной политике управления учебными заведениями был отстранен от государственной службы и все время вплоть до переезда в августе в Петербург посвятил подготовке к изданию курса сопротивления материалов, продажа права издания которого позволила получить ему средства для существования. Одновременно он подал свою работу «Об устойчивости упругих систем» на соискание присуждаемой раз в десять лег премии имени Дмитрия Ивановича Журавского, равной годовому профессорскому окладу. Это было первое и последнее присуждение премии имени Д. И. Журавского. Ею в июле 1911 года была отмечена представленная работа и статья «Об устойчивости плоской формы изгиба двутавровых балок» согласно отзывам И. Г. Бубнова, Н. А. Белелюбского, С. И. Белзецкого, В. Л. Киргшчева, Г. В. Ко¬
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
737
лосова, Г. Н. Соловьева, жюри в составе М. А. Ляхницкого, Г. К. Мерчинга, Н. Н. Митинского, А. И. Прилежаева, Г. Н. Соловьева. Отзывы И. Г. Бубнова, С. И. Белзецкого, В. Л. Кирпичева, Г. В. Колосова были опубликованы в 1913 году в «Сборнике Института инженеров путей сообщения». 1913 год считается годом рождения известного общего метода решения дифференциальных уравнений — метода Бубнова. В действительности этот метод был сформулирован на два года раньше и поводом к этому явилась работа С. П. Тимошенко. В письме к автору этих строк от 22 сентября 1969 года С. П. Тимошенко написал, что отзыв И. Г. Бубнова, представленный в жюри в 1911 году, тождественен тому, который был опубликован в 1913 году.
Вследствие увольнения с государственной службы С. П. Тимошенко вел в первое время почасовые занятия в петербургских вузах (Электротехническом и Политехническом институтах). В это время он подготовил статью «О действии поперечного удара на балку» (1912) и «О влиянии касательных напряжений на поперечные колебания балок», опубликованную спустя 10 лет (1921). В 1912 году в связи с проектированием новых дредноутов он по рекомендации А. Н. Крылова был приглашен консультантом военно-морского флота по прочности на судостроительные заводы; он провел в Электротехническом институте опыты с моделями поперечных переборок. Работы его по устойчивости и изгибу пластин были использованы при проектировании больших линейных кораблей. Здесь хотелось бы отметить, что творцом строительной механики корабля, как научной дисциплины, безусловно, является И. Г. Бубнов: его основополагающий курс, работа по определению напряжений в обшивке судов, метод редукционных коэффициентов, решение различных проблем изгиба и устойчивости пластин, его известный метод решения дифференциальных уравнений, исследования по вибрации судов, проектирование и расчеты прочности линейных кораблей типа «Севастополь» представляют собою огромное и важное наследие. С. П. Тимошенко после ухода И. Г. Бубнова в 1914 году, будучи главой кафедры строительной механики кораблестроительного факультета Петербургского политехнического института, провел дальнейшее формирование этой научной дисциплины, введя в нее энергетические методы и методы теории упругости.
Работа в Обществе технологов и доклады на его заседаниях привели к написанию статьи «Вопросы прочности в паровых турбинах» (1912).
Участие в 1912 году на математическом конгрессе в Кембридже привело к знакомству с Артуром Лявом, Хорасом Лэмбом, Леви-Чивита.
738
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
А. Н. Крылов отказался от профессорской должности в С.-Петербургском Институте инженеров путей сообщения в пользу С. П. Тимошенко, и в результате, когда в январе 1913 года опала была снята, С. П. Тимошенко удалось получить должность профессора по теоретической механике; лекции по этому курсу впоследствии были опубликованы в расширенном изложении. Впоследствии он получил кафедру теоретической механики. Затем он был зачислен и в Электротехнический институт. Времени стало больше, и ему удалось решить ряд новых задач. Он распространил мембранную аналогию Прандтля на случай изгиба, исследовал изгиб балки сечением полукруга при поперечной силе, параллельной диаметру, и показал, что изгиб не сопровождается кручением, когда сила приложена не в центре тяжести, а в отстоящем от нее на некотором расстоянии центре сдвига. Затем он изучил неосесимметричную потерю устойчивости цилиндрической оболочки. В конце 1913 года он закончил первый том своего курса теории упругости, который отличался от известных в то время отечественных курсов Д. К. Бобылева (1886), Ф. С. Ясинского (1897, 1903), И. Г. Бубнова (1909).
В связи с наступившей в августе 1914 года первой мировой войной возникли проблемы увеличения пропускной способности железных дорог, следовательно, состава поездов, веса паровозов. Важным было и то обстоятельство, что во многих случаях на железных дорогах были использованы легкие рельсы (26,8 кгм). Кроме того, необходимо было усилить и мосты, и верхние строения путей. Несколько раньше С. П. Тимошенко был назначен членом мостовой комиссии инженерного совета Министерства путей сообщения, и естественно, что эта работа и была предложена ему. В отличие от исследования Н. П. Петрова, известного своей гидродинамической теорией трения в подшипниках, в котором рельс представлялся как упругая однородная балка на упругих опорах, по которой движется груз, он упругие опоры заменил сплошным упругим основанием и получил обозримые результаты. Эти результаты были опубликованы в виде четырех статей: «К вопросу о прочности рельс» (1915), «К вопросу о вибрациях рельс» (1915), «О динамических напряжениях в рельсах» (1915), «Влияние начальной осадки шпалы на условия изгиба рельс» (1916).
Летом 1915 года главным образом по ранее опубликованным работам С. П. Тимошенко составил вторую часть курса теории упругости (1916). Эти две части составили фундамент последующих, опубликованных сперва на английском языке монографий по теории упругости, по теории пластин и оболочек, по устойчивости деформируемых систем. Военные заказы ученым все возрастали. Степан Прокофьевич получил предложение от военно-инженерного совета быть экспертом по строительной ме¬
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
739
ханике и от ведомства воздушного флота — экспертом по прочности аэропланов.
Летом 1917 года он начал писать «Статику сооружений».
После революции в конце декабря 1917 года С. П. Тимошенко на время зимних каникул поехал в Киев повидать семью. Вернуться в Петроград ему не пришлось. Летом ему удалось стать профессором Киевского политехнического института; здесь он принял участие в комиссии академика В. И. Вернадского по организации Украинской Академии наук и представил записку об организации отдела механики академии, опубликованную в ее трудах. Летом 1918 года он начал писать книгу по расчету арок, которая в 1922 году вышла на французском языке.
В 1920 году С. П. Тимошенко уехал из России. В марте 1920 года он переехал в Югославию и занял место заведующего кафедрой сопротивления материалов в политехникуме Загреба. Начались мучительные годы жизни вне родины, жизни эмигранта, жизни на грани нищеты. Окруженная почетом и вниманием жизнь русского профессора осталась позади и больше никогда не вернется. Нужно теперь каждый раз бороться за самого себя. Наступает несколько лет перерыва в научной работе. В связи с организацией лаборатории испытаний материалов в политехникуме была предпринята поездка в Германию, Францию, Англию. Чтение курса сопротивления материалов и графостатики, устройство жизни почти не оставляло времени для научной работы. В этот период он начал работу о подкреплении отверстий растягиваемых листов (1924).
Летом 1922 года Степан Прокофьевич переехал в Америку сотрудником фирмы по устранению вибраций. «После долгих колебаний я решил остаться в Америке,. здесь я расширил свой опыт в деле применения научного анализа к решению технических задач,. написал ряд курсов, которые нашли распространение. Но нового в Америке сделал мало». Для этой фирмы была написана работа по расчету коленчатых валов (1923), по определению модуля Юнга резины (1923).
В 1923 году он перешел на должность инженера в компанию «Вестингауз» и был прикреплен к ежедневному табельному учету. Здесь он вел деятельность консультационного характера: по применению поляризованного света и определению напряжений, по определению модуля упругости бронзы при высоких температурах, по вычислению твердости на основе частоты колебаний маятника на шлифованной поверхности образца (1923). В связи с составленной им программой работ по рельсам для американских железных дорог, он поставил опыты, о которых он сообщил в 1926 году на втором международном конгрессе по прикладной механике в Цюрихе. По вечерам он читал для инже¬
740
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
неров курс теории упругости и курс сопротивления материалов. Эти лекции составили затем первую часть книги по прикладной теории упругости, опубликованную совместно с И. М. Лессельсом (1925).
В 1927 году он окончил книгу по вибрациям «Теория колебаний в инженерном деле» (1928), взяв примеры из своей заводской практики, а теорию — из ранее опубликованных русских работ. Отметим также опубликованную в 1924 году работу «Приближенное решение плоских задач теории упругости», посвященную приложению метода Ритца к плоской задаче теории упругости. Ему принадлежит идея организации секции механики при Американском обществе инженеров-механиков (1928), при которой впоследствии был создан журнал прикладной механики. «Обдумывая причину наших достижений в компании «Вестингауз», я прихожу к заключению, что немалую роль в этом деле сыграло образование, которое дали нам русские высшие инженерные школы. Основательная подготовка в математике и в основных технических предметах давала нам громадное преимущество перед американцами, особенно при решении новых, не шаблонных задач».
С сентября 1927 года, через пять лет после приезда в Америку, он занял кафедру по исследовательской работе в области механики инженерной школы Мичиганского университета и переехал в Анн-Арбор, оставшись все же консультантом в компании «Вестингауз».
В Мичиганском университете он организовал курсы для будущих докторов наук, летнюю школу в области механики, на которой практиковались еженедельные доклады сторонних известных лекторов-механиков: Л. Прандтля, Р. Саусвелла, X. М. Вестергаарда, А. Надаи, семинар по строительной механике, испытательную лабораторию с целью постановки докторских работ по усталости, ползучести, оптическому методу изучения напряжений. Он прочитал в университете многочисленные курсы по теории колебаний, избранным задачам сопротивления материалов (написал два тома курса, 1930), теории тонких стержней и пластин, теории упругости (1933), по экспериментальному исследованию пластичности металлов (вошло в третье издание курса сопротивления материалов), динамике жесткого тела, теории упругой устойчивости (1936).
В 1930 году он сделал на третьем международном конгрессе по прикладной механике в Стокгольме реферативный доклад по устойчивости стержней, пластин и оболочек, а в 1932 году в Париже— доклад на конгрессе Международного союза инженеровстроителей по устойчивости тонкой стенки с ребрами.
С сентября 1936 года С. П. Тимошенко состоит уже профессором Калифорнийского университета в Стенфорде и переезжает
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
741
в Пало Альто. Здесь он продолжает занятия с докторантами, читает курс тонких пластин и оболочек (1940), курс механики, статики сооружений (1945), истории сопротивления материалов (1953), ведет семинар по статике сооружений и по строительной механике. Следует отметить опубликованную в это время работу «Теория висячих мостов» (1943), а также работу «Теория изгиба, кручения и выпучивания тонкостенных стержней открытого поперечного сечения» (1945), посвященную общей теории стержней открытого профиля. Он участвует в работе пятого международного конгресса по прикладной и теоретической механике в Кембридже (Массачусетс, США), представив доклад по изгибу прямоугольной пластины с защемленным краем. К его шестидесятилетию был выпущен юбилейный сборник с работами его учеников и коллег (1938).
В 1944 году, когда Степану Прокофьевичу исполнилось 65 лет, и он должен был выйти в отставку (пенсий в Америке профессорам не полагается), университет в обход существующих правил предложил ему должность преподавателя, не занимающего кафедры.
В дальнейшем он участвовал в работах Константинопольского (1952), Брюссельского (1956), Стрезского (1960), Мюнхенского (1964) международных конгрессов по прикладной и теоретической механике. В 1954 году, когда ему исполнилось 75 лет, он решил кончить с чтением лекций и готовить лишь повторные издания своих книг.
Огромные заслуги С. П. Тимошенко перед инженерным делом, техническим образованием были отмечены различными премиями и медалями, свидетельствующими о разнообразном его влиянии на инженерное дело: премия имени Салова Министерства путей сообщения России за работу «К вопросу о прочности рельс» (1915); медаль имени Ворчестера Рида Варнера за заслуги в области механики в 1935 году и медаль имени Ламме в 1939 году за заслуги в области инженерного образования выданы Американским обществом инженеров-механиков; медаль имени Левери за статью о расчете висячих мостов (Институт имени Франклина, 1948); международная медаль имени Джемса Уатта за достижения в области инженерного дела (Институт инженеров-механиков, 1947); медаль Густава Транзестера от Союза инженеров, окончивших Льежский политехникум, в 1948 году за влияние его работ на развитие прикладной механики; медаль имени Джемса Алфреда Эвинга от Общества английских гражданских инженеров (1963).
С. П. Тимошенко был выбран членом Академии наук ряда стран: Украинской Академии наук (Киев, 1918); Российской Академии наук (Ленинград, 1928, член-корреспондент технического отделения, позднее — иностранный член Академии наук
742
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
СССР); Польской Академии наук (Варшава, 1935, член-ксрреспондент); Американского философского общества (Нью-Йорк, 1939, член-корреспондент); Французской Академии наук (Париж, 1939, член-корреспондент); Американской Академии наук (Вашингтон, 1941, член-корреспондент); Лондонского королевского общества (1944, почетный член); Итальянской Академии наук (Рим, 1948, почетный член).
Почетные звания доктора наук (honoris causa) присуждены С. П. Тимошенко: Лехайским университетом (США, 1938); Мичиганским университетом (США, 1938); Цюрихским Высшим техническим институтом (Швейцария, 1947); Мюнхенским Высшим техническим институтом (Федеративная Республика Германия, 1949); Глазговским университетом (Англия, 1951); Болонским университетом (Италия, 1954); Загребским политехникумом (Югославия, 1956); Туринским политехникумом (Италия, 1960).
В 1958 году С. П. Тимошенко приехал в СССР, посетил Львов, Харьков (Технологический институт), Киев (Институт механики АН УССР), Москву (институты механики и машиноведения АН СССР, МВТУ, МГУ, Академию строительства и архитектуры), Ленинград (Политехнический институт, Институт инженеров транспорта). Рассказывая о предложении вице-президента АН СССР академика А. В. Топчиева начать вновь работу на Родине, С. П. Тимошенко заметил автору этих строк, что дело не только в том, что ему в девятый раз пришлось бы начинать все сначала, а в том, что он не смог бы оправдать оказываемое ему доверие — приближалось восьмидесятилетие. В результате этой поездки была написана книга «Инженерное образование в России» (1959), а также исторический обзор в «TheRussian Revue» (1956, vol. 15,№ 3, стр. 173—185) и в «Journal of Engineering Education» (1956, vol. 49, № 2, стр. 122—125).
В 1967 году он вновь посетил Киев, Ромны, Москву и Ленина град.
2. ЭНЕРГЕТИЧЕСКИЙ МЕТОД
Имея в виду рассмотрение поведения деформируемых систем под действием внешних сил, мы будем под устойчивостью системы понимать свойство ее сохранять исходную форму равновесия при фиксированных внешних воздействиях.
Важнейшая задача состоит в формулировании критерия устойчивости. Самым ранним, классическим критерием является статический критерий, или критерий Эйлера (1744). Он применим только к консервативным системам, и критическая нагрузка вычисляется как та наименьшая нагрузка, при которой возможно одновременное существование исходной и бесконечно
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
743
близкой к ней форм равновесия. Наибольшей общностью обладает динамический критерий, введенный Ж. Лагранжем (1788) и рассмотренный А. Пуанкаре (1881) и А. М. Ляпуновым (1892). Он может быть использован для консервативных и неконсервативных систем. В этом случае задача приводится к решению дифференциальных уравнений движения системы и изучению поведения этих решений во времени.
Энергетический критерий основан на рассмотрении потенциала всех сил, действующих на систему; он применялся Г. Кирхгофом (1850, 1859), Дж. Рэлеем (1873), Дж. Брайаном (1888), С. П. Тимошенко (1907, 1908, 1910), В. Ритцем (1908, 1909). Он базируется на принципах возможных перемещений и возможных изменений напряженного состояния. Здесь мы будем рассматривать метод решения задач устойчивости, основанный на энергетическом критерии.
Обычно проблема определения критических нагрузок требует решения дифференциальных уравнений, вид которых определяется типом конструкции и нагружением. За исключением простейших вариантов, отыскание решений этих уравнений составляет трудную проблему. В редких случаях можно получить решение в замкнутой форме. Поэтому естественно избежать прямого пути при решении дифференциальных уравнений. В теории линейных колебаний упругих систем для вычисления частоты или периода колебаний Дж. Рэлей широко использовал удовлетворяющее граничным условиям приближенное представление действительной формы колебаний. Эти результаты вошли в его замечательную книгу «Теория звука» (1877 — первое издание, 1894—1895 — второе). Метод Рэлея вычисления собственных частот колебаний упругой системы без решения дифференциальных уравнений задачи основан на равенстве кинетической и потенциальной энергии для нахождения как основной (1873), так и высшей (1899) частот. Рэлей рассмотрел колебания струн, стержней, цилиндрических, сферических и конических оболочек, используя для описания движения системы форму колебаний простейшего осциллятора.
Физик из Гёттингена Вальтер Ритц (1908, 1909) провел обоснование метода в случае собственных колебаний струны и прямоугольной пластины, описывая ее движение с помощью бесконечного ряда, и, таким образом, он имел возможность находить основную и высшие частоты, в то время как Дж. Рэлей, за исключением работы 1899 года, всюду определял только основную частоту. Первая работа В. Ритца озаглавлена «Об одном новом методе решения некоторых вариационных задач математической физики». В этой связи Дж. Рэлей (1911) пишет, что «удивительно, как он В. PhtuJ мог рассматривать метод как
744
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
новый», что в «одной из ранних работ (1899). этот метод дан в форме, почти в точности совпадающей с той, в какой он предложен Ритцем», «. я полагал, что это исследование В. Ритца ограничивается применениями метода». Возможно, что В. Ритц развил свой метод и независимо. Статья же Дж. Рэлея вышла, когда В. Ритц был уже в могиле. Интересно проведенное В. Ритцем сравнение точного и приближенного решения частоты колебаний струны, которое показало, что полином с двумя членами дает ошибку 0,01, а с пятью— 10-7. В. Ритц (1908) выбирал для прогиба пластины ряд, который удовлетворяет граничным условиям, условиям полноты и по возможности характеру деформации:
тр
w 2 wm wm (х, у). (1)
m 1
Вводя его в вариационное уравнение
ЯМ(4)’
где D Е№ 12(1 —v2) —цилиндрическая жесткость, v— коэффициент Пуассона, ху у — ортогональные координаты, h — толщина пластины, q — поперечное давление, он нашел выражение, заключающее в себе квадраты wh. Минимизируя это выражение, получим р линейных алгебраических уравнений относительно параметра wh.
Ни Дж. Рэлей, ни В. Ритц не рассматривали задач устойчивости. Это сделал Дж. Брайан в работе «Об устойчивости упругих систем» (1888), где он вводит потенциал II упругой системы в виде суммы потенциальной энергии, потенциала объемных и поверхностных сил. Начало возможных перемещений Ж. Лагранжа (1788) указывает признак равновесия как условие стационарности потенциала системы (6П 0). Согласно принципу Лежена Дирихле (1846) в устойчивом состоянии потенциал системы имеет минимум (б2П0), в неустойчивом — максимум (62П0), в безразличном — одинаков для всех состояний, смежных с исследуемым (62П 0). В упомянутой статье Дж. Брайаном впервые поставлена задача об общей устойчивости упругого тела. Автор ее говорит, что условие 62П 0 возможно при потере устойчивости стержней, пластин и оболочек лишь по чисто изгибным формам, без растяжения — сжатия и сдвигов срединной поверхности, и это вынуждает его утверждать, что, например, сферическая оболочка будет всегда устой-
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
745
чива под равномерным всестороннем давлением, так как она,
«как доказал Гаусс, не допускает чисто изгибных деформаций».
Таким образом, в трактовке критерия устойчивости б2П 0 он смешал возможное условие с необходимым.
Затем он исследует устойчивость бесконечной пластины при сжатии по краям, представляя прогиб рядом
оо
w 2 w sin rtinxl) (опертые края) (3)
или
оо
w 2 w cos тпхl) (защемленные края), (3')
о
приравнивает работу сжимающей силы потенциальной энергии изгиба
i i
и получает значение минимальной критической силы Р я2)2, где I — ширина пластины.
В статье «Применение энергетического метода к задаче о потере устойчивости длинной тонкой трубы под действием внешнего давления» (1888) Дж. Брайан приравнивает уменьшение энергии продольного сжатия потенциальной энергии изгиба и, задаваясь формой прогиба в виде ряда Фурье, получает формулу Эйлера; аналогично выводится им и формула для критического равномерного давления бесконечной трубы с нерастяжимой круговой осью (формула Ж. Бресса — Ф. Грасгофа, исправленная на общий случай коэффициента Пуассона, см. выражение (1) гл. VI настоящей статьи).
Рассмотрим теперь применение вариационного метода к проблеме устойчивости пластин конечных размеров. Составим потенциальную энергию U тонкой упругой пластины, для которой гипотезы Кирхгофа о жестком нормальном элементе имеют место. Она равна
и и0 иг и2,
где U0 — энергия докритического состояния.
Потенциальная энергия сил, лежащих в плоскости пластины, будет
а Ъ
J J 'е1 12Y dx
о о
746 с п- ТИМОШЕНКО И ЕГО РАБОТЫ
где Nь N2f N12 — удельные усилия в срединной поверхности пластины.
Но для квадратичного приближения, согласно Г. Кирхгофу,
ди. 1 dw 2
е дх Т 3F) '
dv. 1 dw 2
82 ” ду 2 I ду ) »
— du dv. dw dw dy dx dx dy
Здесь w, vy w — перемещения, обусловленные выпучиванием, x, у— ортогональные координаты срединной поверхности. Тогда
а Ъ
-15 » т () Т7 4г(f Л
О О
l NlWNl2 w)N2wdxdy-
о о
Интегрирование по частям второго интеграла дает
I (NN)dxdi-
о о
b а а Ъ
J (W,u)o dy (N 12f)o dx- j j (4 -2.) dxdy,
0 0 0 0
ll(NWNtr)dxdy
о 0
a b a b
J (N2v)b0 dxj (Nl2v) dy — J J (- -f-)dxdy.
0 0
В полученных выражениях двойные интегралы приводят к уравнениям плоского равновесия в усилиях
dN , dNX2 _ n
dx dy u’
dN2 j dN2 л
dy dx u’
а контурные интегралы составляют работу краевых сил
Ь а
U J (NiU Л,2у)о dy J (Nl2u N2v)q dx,
9 9
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ 747
Таким образом,
- J т Ш» - ж w т (тг Л “ d» u'-
00 _
и и
Потенциальная энергия изгиба равна
а Ь
1 Г Г f I d2w . (5гш 2 , 01 ЧГ д2ш 2 d2w а2гг» П , ,
U'- 2D дх di2 ) V4UiJ дх2 di,2 Л
О о
Если прогиб w получил приращение бw, то потенциальная энергия изменится на величину
ьи ШХ Ш2.
Вместе с тем изменится и положение точек приращения нагрузок и краевых сил. Приращение прогиба бw настолько мало, что изменение деформированного состояния будет происходить при постоянных значениях внешних, в том числе и краевых, сил. Приращение работы внешних сил равно
6Г-2Р60;
здесь 60 — перемещение точек приложения внешних сил в направлении самих сил.
Для каждого малого возможного перемещения бw состояние равновесия будет тогда, когда первая вариация потенциальной энергии системы равна нулю:
6П 6U - 6Л бUx 6U2 - 6Л 6UX бU2 0. (6)
В результате получим
-
_ 4 Ifт (45гЛdx dy -
о о
Введем теперь сюда выражение (1), тогда потенциал П будет однородной квадратичной функцией wk. Условие экстремума П для всех значений wk, которые удовлетворяют условию стационарности 6П 0, даст в результате П 0. Поэтому
748 с. П. ТИМОШЕНКО И ЕГО РАБОТЫ
приближенно критические силы можно определять из условия равенства нулю потенциала всех сил П 0;
п-т»Ш-)
- W- Г»т ( Л Л-
00 _
2 1 0. (7)
Критерий П 0 является необходимым, но недостаточным условием для равновесия пластины при потере устойчивости. Достаточным условием равновесия является условие экстремума 6П 0.
Так как
а Ь
6П J I Ф w’ тУ' Wxx’ Wx«' Wvv) dx dy 0 0
то с помощью уравнения Эйлера вариационной задачи
получим линейное уравнение устойчивости Сен-Венана относительно прогиба w. Пусть U 22, U2 2DJ. Тогда из условия П 2DJX — 22 0 следует D J2J.
Теперь обсудим работу Дж. Брайана «Об устойчивости плоской пластины, нагруженной в своей плоскости сжимающими силами, с применениями к «выпучиванию» бортовой обшивки корабля» (1891), где рассмотрена упругая первоначально плоская пластина, нагруженная в срединной поверхности усилиями N1, N2i N12. Он вычисляет уменьшение потенциальной энергии деформации срединной поверхности, или работу начальных усилий в этой поверхности,
-11 h т Ш«. Ж (Л
о о
и приравнивает ее потенциальной энергии изгиба пластины при
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
749
выпучивании
Следовательно, критерий Дж. Брайана имеет вид
П U — А 2JXD — 22 0, или D J2Ji. (8)
Условие максимума цилиндрической жесткости будет
6D 6-у- 2D6-1- 0. (9)
У1 УI
На основе вышеизложенного видно, что Дж. Брайан полагает, что прогиб w при потере устойчивости имеет первый порядок малости, он вычисляет работу сил Nu N2, N12 на удлинениях и сдвигах в срединной плоскости, обусловленных только прогибами w, эти удлинения и сдвиги, очевидно, имеют второй поря¬
док малости. Срединную поверхность он считает недеформируемой в своей плоскости (и v 0). Тем не менее оказалось, что учет перемещений и и v приводит к тому же выражению для критерия устойчивости D J2IJь Впоследствии Г. Рейсснер (1925), выводя уравнение устойчивости пластины
энергетическим методом, принимая во внимание перемещения и и у, был удивлен, что в результате Дж. Брайан получил «правильный конечный результат».
В дальнейшем Дж. Брайан исследует устойчивость опертой прямоугольной пластины, равномерно сжатой по сторонам усилиями N и N2, представляя прогиб в виде двойного тригонометрического ряда. Он дает также вариационный вывод (6П 0) уравнения устойчивости равномерно сжатой пластины (N N2t N2 0).
С. П. Тимошенко («Теория упругой устойчивости» (1936)) при выводе критерия (8) основывается на условии недефор-
мируемости срединной поверхности (ei 62 у 0). Тогда
согласно выражениям (5) перемещения и и v в срединной поверхности определяются через прогиб w при выпучивании следи 1 dw 2 dv (dw 2
дующими соотношениями: (-) .
du dv _ dw dw
ду dx dx dy
750
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
В дальнейшем он полагает усилия в срединной поверхности пропорциональными одному параметру а:
Nianu N2 an2t Л12 шг12, и определяет критическое значение этого параметра из формулы
а —
о о
а b
о о
—Ь
Вводим теперь сюда приближенное представление для прогиба (1), отображающее выпученную поверхность пластины и удовлетворяющее условиям на контуре ее. Условие минимума а приводит к линейной однородной системе уравнений относительно коэффициентов wm:
д, dJ2 _ n dJ 1 _ dJ2 _ n dJi _ dJ2
-a2. 0,.p. _ a -p- 0,.
dw i owi dw2 dw2 dw3 dw 3
Равенство нулю определителя этой системы уравнений дает ненулевые значения коэффициентов wm и характеристическое уравнение для вычисления минимального значения а. При решении конкретных задач С. П. Тимошенко вычислял критические значения нагрузки из условия минимума а по параметрам прогиба wm.
Первое применение С. П. Тимошенко энергетического метода содержится в работе 1907 года «О продольном изгибе стержней в упругой среде». Автор, исследуя задачу, поставленную в заголовке, пишет: «Применим общеизвестную теорему — система находится в устойчивом равновесии, если ее потенциальная энергия является минимальной. При малой сжимающей силе прямолинейная форма равновесия устойчива, потому что при всяком искривлении уменьшение потенциальной энергии сжатия мало по сравнению с появившейся энергией изгиба и энергией деформации упругой среды. Если мы, постепенно увеличивая продольную сжимающую силу, достигнем такого предела, когда уменьшение, при искривлении, потенциальной энергии сжатия как раз равно потенциальной энергии изгиба, сложенной с потенциальной энергией деформации среды, то с этого момента становится возможным появление второй, искривленной формы равновесия». Автор записывает свою формулировку в виде (р — коэф-
е. П. ТИМОШЕНКО И ЕГО работы
751
фициент постели для сплошного упругого винклерова основания)
т р (if)2 dx т (-йг) т
0 0 о
и, вводя сюда вместо прогиба выражение (3), получает формулу для критической силы.
В статье 1908 года «К вопросу о продольном изгибе» автор, вычисляя критическую силу сжатого и опертого по концам стержня с учетом поперечной силы, исходит из следующего энергетического соотношения:
тр J(-S-)2w Jw12)
0 0 0
при этом член, обусловленный изгибом (первый справа), он записывает не как раньше через вторую производную (М EJd2wdx2), а через прогиб (М Pw). Обе эти работы С. П. Тимошенко написаны и опубликованы до знаменитых мемуаров Вальтера Ритца (1908, 1909).
В представленной в 1909 году в немецкий журнал «Zeitschrift fur Mathematik und Physik» статье «Некоторые теоретические проблемы упругой устойчивости» (1910) дается энергетический вывод формулы Эйлера для свободно опертого стержня для случая, когда при потере устойчивости расстояние между концами стержня не изменяется и вследствие этого продольная сжимающая сила при выпучивании несколько уменьшается. Из-за несмещаемости концов при выпучивании ось стержня удлиняется и энергия сжатия уменьшается. Критическое состояние отыскивается из условия равенства уменьшения энергии сжатия при выпучивании потенциальной энергии изгиба:
ТР J (4гГ dxSr w2 dx- (13)
Использование представления (3) приводит к эйлеровой силе Р я22.
Другой случай может быть, если концы стержня перемещаются вдоль оси. Тогда критерий устойчивости имеет вид
_1_
2
о
т А - i № ««
о о -J о о
752
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
Член слева составляет работу силы Р на продольном перемещении концов за счет искривления оси при выпучивании, первый член справа есть потенциальная энергия изгиба, а второй — уменьшение потенциальной энергии сжатия при изгибе. С учетом М Pw из (14) следует тот же критерий устойчивости (13).
Итак, согласно С. П. Тимошенко, в критическом состоянии равновесия потенциал П равен нулю; из этого условия определяется критическая сила:
При этом, если критическая сила Р вычисляется согласно (16) через изгибающие моменты и условия равновесия в текущих сечениях стержня удовлетворяются, то формула (16) дает более точные значения критических сил, чем (15).
Вносим в выражение для Р прогиб, удовлетворяющий граничным условиям
Отсюда получаем соотношения между параметрами, которые и вводим в выражение (17), принимающее при этом минимальное значение. Это критическое значение представляет собою приближение сверху к точному значению, так как принятое выражение для прогиба накладывает дополнительные связи на упругую линию стержня и за счет этого при выпучивании некоторые возможные формы прогиба не реализуются.
(15)
О
или
р — г I
(16)
о
W 2 wm-wm (х).
: 17)
Отыскиваем минимум Р» по wm:
(18)
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
763
С. П. Тимошенко не дает доказательства сходимости решения и его единственности. Точность вычислений этим методом в общем случае оценивается лишь на основе сравнения последовательных приближений. Метод позволяет уточнять результат, используя второе, третье,. приближения. При удачном выборе формы выпучивания первое и второе приближения обычно дают практически хороший результат. Представляя форму выпученной поверхности в виде целого полинома или тригонометрического ряда, автор сводит решение к интегрированию и вычислению минимума простых функций. Итак, метод С. П. Тимошенко основывается на критерии устойчивости Дж. Брайана, соединенном с условием минимума внешней нагрузки.
Рассмотрим потенциал всех сил для продольно сжатого стержня
П - У EI (тЯ“-Tpi Ш “ (19)
О о
его вариация имеет вид
«I - (И ) РЩ Ьш Л «.--
»
где последние два члена представляют собою условия на концах. Вводя в (19) для шарнирно опертых концов w w 1 sin (ял:), получим, что потенциал П — квадратичная функция параметра Wi
тт п2 (n2EJ п 9
П 1г1-75 р)
и
Ш я2 я27 D dm я2 п2Е1 п
Условие нейтрального равновесия (6П 62П 0) соответствует cOldwi d2Udw2 0. Это дает Р Р n2EJl2. Но при этом, как указывалось выше, П 0, следовательно, критерий Дж. Брайана удовлетворяется.
Форма (20) может быть использована в процедуре Ритца — Тимошенко, о которой речь идет ниже.
С. П. Тимошенко также впервые (1910) применил способ Рэлея — Ритца к задачам устойчивости. При этом минимум
754
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
критической силы Р отыскивается из экстремума потенциала П: -0 (-1,2,8.). (21)
При этом получается однородная система линейных алгебраических уравнений. Ненулевые решения этой системы соответствуют обращению в нуль ее детерминанта. Отсюда получается уравнение для вычисления критического значения Р. Этот способ определения критических нагрузок получил название метода Ритца — Тимошенко.
Монография «Об устойчивости упругих систем» (1910), переведенная в 1913 году на французский язык, целиком построена на применении энергетического метода, основанного на процедуре (18), к многочисленным проблемам устойчивости сплошных и решетчатых стержней, устойчивости плоской формы изгиба прямоугольных полос и балок, односторонне сжатых пластин при различных условиях опирания. Подробнее эти результаты представлены в соответствующих разделах нашего послесловия. С. П. Тимошенко дал также применение своего метода к задаче об осесимметричном выпучивании продольно сжатой цилиндрической оболочки.
Всегда важно знать мнение автора о месте своих результатов в ряду других исследований. В упомянутом выше письме от 22 сентября 1969 года С. П. Тимошенко указывал: «Думаю, что единственным моим предшественником приближенного метода был Рэлейъ.
3. СТЕРЖНИ
Теоретическая постановка задачи об устойчивости центрально сжатых стержней принадлежит Леонарду Эйлеру (1744). Он получил выражение для «силы колонны» (1757; публикация: 1759): Р jt2542, где — длина консольного
стержня, нагруженного продольной силой на конце, В — изгибная жесткость. Эйлер основывался на линеаризированном уравнении устойчивости, проводя линеаризацию выражения для кривизны плоской изогнутой оси стержня, поэтому вопрос о прогибе оставался неопределенным. Это обстоятельство долгое время вызывало сомнение в корректности такого подхода, а в более позднее время приводило к заключению, что правильный результат, сопутствующий решению приближенного дифференциального уравнения задачи, случаен.
Такое отношение к результату Эйлера несправедливо. Во-первых, в то время не был создан математический аппарат для решения точного дифференциального уравнения изгиба; теория эллиптических функций была создана позднее. Во-вторых, не
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
755
был оценен именно сам линейный подход и статический критерий Эйлера, плодотворность которого в настоящее время бесспорна. Согласно этому критерию критическая нагрузка вычисляется как наименьшая нагрузка, при которой одновременно с исходной формой равновесия (в случае стержня — прямолинейной) статически возможна смежная, бесконечно близкая к ней форма равновесия (в случае стержня — изогнутая). Заметим, что современная трактовка этого критерия сформулирована Ф. С. Ясинским. Через сто лет указанной точки зрения придерживался даже известный специалист в области теории упругости А. Клебш (1862), в распоряжении которого уже были таблицы эллиптических функций.
Жозеф Лагранж (1770) решил точное уравнение задачи в рядах для случая опертого по концам стержня, получив зависимость между силой, амплитудой прогиба и длиной стержня; при амплитуде прогиба, равной нулю, из него вытекает выражение р п2п2В12. Ж- Альфан (1884) показал, что при критической силе прогиб равен нулю, и нашел выражение критической силы консоли Р n2EJ(2n 1)242 (г 0, 1, 2, 3,.); EJ — минимальная изгибная жесткость стержня. Позднее с помощью таблиц эллиптических функций было установлено, что незначительное увеличение сжимающей силы сверх критической сопровождается существенным ростом напряжения. Это, в частности, следует из решения А. Шнейдера (1901) для продольно сжатого стержня, опертого по концам:
При Л 0 сжимающая сила достигает критического значения и прогиб Wo равен нулю.
В диссертации на звание адъюнкта Института инженеров путей сообщения Ф. С. Ясинский (1894) путем перехода к пределу для точного дифференциального уравнения продольного изгиба консоли показал, что оно при прогибе, равном нулю, имеет вид линеаризированного уравнения Эйлера; отсюда ясно, почему приближенное уравнение продольного изгиба дает точное решение критической нагрузки
Рф lim
lim
-0 L (amax — w)Vl — (dwds)2
w- 0
L wmax - w
В 1892 году Ф. С. Ясинский ввел понятие приведенной длины сжатого стержня.
756
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
Что касается опытов на устойчивость, то первый эксперимент принадлежит П. Мушенбреку (1729). Опыты А. Дюкло (1820) и особенно И. Ходкинсона (1840—1857) нанесли ущерб теории Эйлера; последние послужили обильным материалом для отрицательного отношения к формуле Эйлера. Много позднее, после опытов И. Баушингера (1887), М. Консидера (1891), JI. Тетмайера (1890, 1896), стало ясно, что в обширных опытах И. Ходкинсона не соблюдались граничные условия, не соблюдались предосторожности для избежания эксцентриситета приложения нагрузки, что испытываемые образцы имели начальную кривизну и часть образцов претерпевала выпучивание за пределом упругости. По-видимому, бельгиец М. Ламарль (1846) первый объяснил расхождение теории Эйлера с экспериментом несоблюдением граничных условий и неупругостью материала. В опытах И. Баушингера, Л. Тетмайера, М. Консидера осуществлялось тщательное центрирование нагрузки. После этих опытов кончились 150 лет сомнений в теории Эйлера.
В России предшественником С. П. Тимошенко в области теории устойчивости стержней был Ф. С. Ясинский. Его работы оказали на С. П. Тимошенко огромное влияние.
В своей первой работе «О продольном изгибе стержней в упругой среде» (1907) С. П. Тимошенко приводит общее дифференциальное уравнение устойчивости стержней постоянной жесткости, сжатых концевыми силами, лежащих на сплошном упругом винклеровом основании, когда прогиб в любой точке основания пропорционален (с коэффициентом р) нормальной к основанию силе в этой точке. При свободно опертых концах даны точное и приближенное решения. Полагая, что прогиб ра-
оо
S. тлх
wmsm——, из энергетического критерия
1
т- шг1 j-
0 0 0
он получает выражение критической силы
р.— 1—
So ( тп 2 wm I )
1
и показывает, что минимальное значение критической силы достигал
гается, если выпучивание происходит по синусоиде w wm sin ——.
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
757
Тогда
(1)
Статья С. П. Тимошенко «К вопросу о продольном изгибе» (1908) посвящена разнообразным задачам устойчивости стержней и их систем. Исследуется устойчивость сжатого по концам стержня с упруго заделанными концами, сжатого стержня, опертого по концам, с упругой или жесткой посредине опорой, устойчивость консолей со ступенчатым изменением жесткости (два и три участка) и консоли, у которой на одном участке жесткость постоянна, а на другом убывает по квадратичному закону. Задача для параболоида вращения рассматривалась Эйлером (1759), для произвольной поверхности вращения второго порядка — Ж. Лагранжем (1770—1773), ступенчато-постоянные стержни — А. Франке (1901 —1907). Для ступенчато-постоянных стержней интересна полученная С. П. Тимошенко приближенная оценка влияния ослабления сечения на малом участке на критическую силу. За пределом упругости автор считает необходимым пользоваться таблицами критических напряжений Ф. С. Ясинского, составленных на основе опытов И. Баушингера и Л. Тетмайера.
Наиболее важным является раздел статьи, посвященный учету влияния сдвига на критическую силу. Автор энергетическим методом выводит формулу Ф. Нусбаума (1907) для сплошных стержней
где Pe n2EJjl2 ЯСд GFk k — коэффициент формы поперечного сечения; Р — критическая сила стержня с учетом суммарного действия изгиба и поперечного сдвига. Формула (2) выведена для стержней со свободно опертыми концами, выпучивающимися по одной полуволне; однако она справедлива и для других граничных условий, если прогиб за счет изгиба и прогиб за счет сдвига представляются в виде рядов по одним и тем же тригонометрическим функциям. При этом угол поперечного сдвига определяется по формуле у kQGF РСд, а сама поправка для сплошных стержней незначительна. Она существенна для составных стержней, которые широко использовались в гражданских сооружениях и рациональный расчет которых не был своевременно исполнен, что привело к разрушениям (например, Квебекского моста). В этой связи автором и решена задача об устойчивости раскосной фермы — двух прямых стержней — поясов, связанных жестко присоединенной решеткой (раскосов). Потеря устойчивости за счет изгиба характеризуется здесь укорочением одного пояса и удлинением другого, а за счет сдвига —
р;' P7lягд,
(2)
758
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
перекашиванием элементов соединительной решетки. При вычислении угла перекоса следует учесть растяжение и сжатие раскосов (диагоналей решетки). Если пренебречь растяжением распорок и сжатием поясов (стоек), считать площади диагоналей малыми по сравнению с площадью пояса, то угол перекоса — угол сдвига — будет у QyiEFd sin2 a cos а (а — угол между диагональю и стойкой; EFd— жесткость растяжения диагонали; х 4, так как рассматриваются двойные диагонали для квадратного трубчатого стержня).
Работа «Некоторые теоретические проблемы упругой устойчивости» (1910) содержит краткое изложение предыдущих результатов по влиянию сплошного основания на критическую силу опертого сжатого стержня и вывод Р для решетчатого стержня квадратного сечения (энергетический вывод в обоих случаях).
Наконец обсудим содержание первого отдела монографии «Об устойчивости упругих систем» (1910), основанной на энергетическом методе и содержащей исследования устойчивости прямолинейных и круговых сплошных стержней и прямых составных. В нем рассматривается выпучивание кругового шарнирно опертого стержня с несжимаемой осью при равномерном нормальном давлении. Изучается устойчивость составного опертого стержня под действием концевой и приложенной в месте изменения жесткостей продольных сил, показано, что даже в первом приближении результаты близки к точному решению Ф. С. Ясинского. Разбирается устойчивость консоли под действием собственного веса (2 приближения), устойчивость опертого стержня, когда интенсивность продольной сжимающей нагрузки изменяется от середины к концам от нуля по линейному закону. Исследуется устойчивость стержней на упругом сплошном основании с постоянным коэффициентом постели, когда концы оперты и стержень нагружен либо сжимающей силой на конце (см. работу 1907 года), либо продольные непрерывно распределенные силы меняются от нулевого значения в середине к значениям на концах по закону прямой. Эта задача была сформулирована Ф. С. Ясинским (1902), который свел к этой схеме расчет верхнего сжатого пояса открытого моста с ездой понизу, учитывая еще и продольную сжимающую силу по концам, и получил решение в бесконечных рядах, введя существенное ограничение— симметричное волнообразование. С. П. Тимошенко с помощью двух тригонометрических форм проанализировал симметричное выпучивание, выпучивание с одной и двумя точками перегиба (в последнем случае крайние полуволны не равны средней). Та же задача была разобрана и для свободных концов (симметричная форма, поворот с перегибом). Отдельно изучен при свободных концах лежащий на сплошном основании стер¬
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
759
жень под действием концевых продольных сил. Впервые были разобраны несимметричные волнообразования. Интересно отме.тить, что при податливой среде можно получить равную нулю критическую силу, соответствующую вращению стержня, и силу, равную второй эйлеровой нагрузке, отвечающей выпучиванию по двум полуволнам. Далее дан подробный анализ устойчивости составных стержней. Рассматривается безраскосная ферма — рама из двух продольных стержней с поперечными стержнями — планками. Автор считает число полей, образованных поперечинами, достаточно большим, все поля одинаковыми, оба пояса также одинаковыми и при вычислении угла перекоса у допускает, что в каждом поле пояс изгибается, как балка с точкой перегиба посредине высоты пояса. Тогда угол у будет зависеть от перемещения за счет поперечной силы пояса и от перемещения вследствие изгиба горизонтальной планки; при этом так как в действительности пояс не сжат, а сжато-изогнут, то в первый член нужно ввести поправку.
Точное решение этой задачи при п любых полях дано Р. Мизесом гораздо позже (1926); когда число полей велико, из него следует обсуждаемое решение С. П. Тимошенко.
Выпучивание раскосных (решетчатых) стержней автор изучал и в работе 1907 года; здесь он дополнительно учел сжатие распорок решетки и получил выражение для критической силы
Р РеХ Род' Р сд2 (3)
где Рсд1 nEFd cos2 a sin а; РсД2 EFV tg а; EFP — жесткость на растяжение раскоса; х 1, когда диагонали одинарные, х 2, когда они двойные, и к 4, когда диагонали двойные, а стержень — квадратная труба. Случай, когда исходящие из одного сечения диагонали наклонены к оси под разными углами, исследовал Н. П. Виноградов (1914).
За пределом упругости при выпучивании сжатых сплошных стержней в упругой среде и составных стержней используется концепция приведенного модуля.
4. ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ ОТКРЫТЫХ СТЕРЖНЕЙ И ПРОБЛЕМА ОПРОКИДЫВАНИЯ БАЛОК
Настоящей проблеме посвящены пятнадцать работ С. П. Тимошенко. Значение, которое сам автор придавал этой проблеме, видно также и из письма его в редакцию журнала «Philosophical Magazine» «О выпучивании высоких балок» (1922). Естественно, что эти вопросы включались автором в обзорные работы и в его книги по устойчивости, в том числе и в «Курс теории упругости. Часть 2. Стержни и пластинки» (1916).
760
С. П. ТИМОШЕНКО и НГО РАБОТЫ
Обратимся сперва.к первой работе «Об устойчивости плоской формы изгиба двутавровой балки» (1905—1906).
Проблема устойчивости плоской формы изгиба была поставлена практикой строительства гражданских и промышленных сооружений второй половины прошлого века. Ф. С. Ясинский (1894) дал своеобразный метод исследования устойчивости верхнего пояса открытых мостов в связи с рядом катастроф решетчатых мостов (например, моста через реку Кевду) из-за малой поперечной жесткости верхнего сжатого пояса. Он аппроксимировал этот пояс шарнирно опертым стержнем; влияние стоек свел к сплошному однородному основанию, а раскосов — к непрерывной продольной нагрузке, пропорциональной расстоянию от середины стержня. Ф. С. Ясинский указал также на важность расчета двутавровых балок. Во втором томе его собрания сочинений (1902) описано коробление тонкостенных балок и приводятся фотографии железных двутавровых балок с потерявшими устойчивость вертикальными стенками: «Несмотря на огромное значение коробления балок для правильного расчета металлических сооружений, явление это до сих пор не исследовано теоретически и опытов произведено пока еще недостаточное количество». В опытах Л. Тетмайера (1896) исключалась возможность свободного закручивания. Теоретические исследования Л. Прандтля (1899) и А. Мичелла (1899) касались плоской формы изгиба полосы, и они не решали задачи для двутавровой балки. Л. Прандтль рассмотрел консоль при чистом изгибе, при равномерной поперечной нагрузке и при сосредоточенной поперечной силе, приложенной выше центра тяжести поперечного сечения. Для случая чистого изгиба и приложения концевой сосредоточенной поперечной силы он рассмотрел вариант, когда одно концевое сечение жестко заделано, а другое лишено свободы бокового перемещения. Наконец, дал приложение теории к двухопорной балке нагруженной одной или несколькими сосредоточенными силами. Следует также отметить тщательно поставленный им эксперимент, подтвердивший расчеты автора. Уточнение результатов Л. Прандтля было выполнено А. П. Коробовым (1911). А. Мичелл исследовал устойчивость консоли с сосредоточенной силой на конце при свободном и неповорачивающемся крае, консоли со свободным краем при равномерной поперечной нагрузке, двухопорной балки со свободными концами при сосредоточенной силе посредине пролета и, наконец, устойчивость полосы при совместном действии продольной сжимающей силы и концевых моментов. Для консоли и двухопорной балки им были поставлены эксперименты (ошибка соответственно равна 2,91 и 0,24).
Из соображений повышения сопротивления изгибу или уменьшения веса двутавра выгодно увеличивать площадь поясов
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
761
и высоту вертикальной стенки. Первоначально изгиб балки происходит в плоскости наибольшей жесткости. Ему соответствует плоская форма равновесия. При достижении некоторой нагрузки плоская форма равновесия перестает быть единственно возможной и возникает изгибно-крутильная форма равновесия, происходит опрокидывание. При опрокидывании имеет место изгиб также и в плоскости наименьшей жесткости, сопровождаемый закручиванием. Если Ви В2— соответственно наибольшая и наименьшая изгибная жесткость, а С — жесткость свободного кручения, то обычно В2Вх 0,01, СВ 13000, а отношение высоты балки к длине hl 15 -s- 112. Но даже если жесткости В и В2 имеют один и тот же порядок, а жесткость С значительно меньше изгибных жесткостей балкиг то тем не менее также возможна неустойчивость плоской формы изгиба. Главный вопрос — сопротивление кручению.
Выше уже отмечалось, что результаты для тонкой полосы не могут быть непосредственно перенесены на случай двутавровых балок, поскольку имеет место принципиальное различие их сопротивлений опрокидыванию. Оно обусловлено различием сопротивлений полосы и двутавра кручению. Для полосы наблюдается чистое — сен-венаново кручение и крутящий момент Л4кр связан с углом поворота ср зависимостью
СЗх (1)
где С — жесткость чистого кручения; х — продольная координата. Как известно, в этом случае точки первоначально плоского поперечного сечения выходят из плоскости, смещаются в продольном направлении. Поперечное сечение перестает быть плоским. Как теперь говорят, оно искажается, или депланирует.
Для двутавра кручение также сопровождается депланацией поперечного сечения, при этом происходит дополнительный изгиб в плоскости наименьшей жесткости, так как продольные перемещения полок стеснены, а крутящий момент по длине балки может изменяться. Изменение крутящего момента по длине приводит к изменению по длине балки депланаций. Здесь имеет место стесненное кручение. Следовательно, лишь часть крутящего момента соответствует сен-венанову кручению. Это важный и принципиальный вопрос. Его решение привело впоследствии к созданию теории изгиба и кручения тонкостенных открытых стержней. Это впервые заметил С. П. Тимошенко, который установил, что для двутавра крутящий момент равен
(2)
здесь D — жесткость стесненного кручения. Для двутавровой
762
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
балки автор полагает ее равной D 7г22, причем EJ — наибольшая изгибная жесткость полки; г — высота балки. Для полосы D 0.
Часто ссылаются на опыты К. Баха (1910), который замерил отклонения от закона плоских сечений в балке, когда поперечная нагрузка не проходит через центр изгиба. В этом нет необходимости. Несоблюдение закона плоских сечений при опрокидывании было ясно и Л. Прандтлю, и С. П. Тимошенко. При исследовании закручивания консоли двутаврового поперечного сечения С. П. Тимошенко отмечает, что, исключая случай кругового кольца, точки поперечных сечений перемещаются и в плоскости, и вдоль оси. Если одно из сечений закрепить, то это вызовет появление нормальных напряжений. Поэтому-то формула (1) и несправедлива для двутавровых балок.
Автор, полагая, что углы поворота поперечного сечения малы (sin ф ф), ввел в рассмотрение следующие гипотезы:
1) поперечное сечение не меняет своей формы;
2) сдвиг отсутствует;
3) балка испытывает простой, а не сложный изгиб.
Первая гипотеза дает зависимость между углом поворота поперечного сечения, боковым перемещением нейтральной оси и полок. Последняя гипотеза приводит к связи между боковыми поперечными силами в полках и соответствующими им прогибами.
Интегрируя уравнение (2) для стержня, заделанного одним концом и на другом конце нагруженного только крутящим моментом, можно получить угол поворота
о)
Лф _ М Г ch (ld) 11 (АЛ
dx С Lch(ld) _Г
где d YdCI2 ; l xl; х — расстояние от свободного конца. Отсюда на свободном конце (х 0)
,5)
и, следовательно, угол закручивания тем меньше, чем больше жесткость полок на изгиб. В заделке (х ), как видно из (4), dydx 0; поэтому согласно выражению (2) внешний крутящий момент М уравновешивается за счет изгиба полок, а не кручения.
Жесткость С на кручение автор вычисляет с помощью гидродинамической аналогии, как для тонкостенной балки: объем
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
763
между поверхностью мембраны, натянутой над профилем балки, и плоскостью, рассчитанной, как параболический цилиндр, пропорционален С: С sbsG3, где b — ширина, а 5 — длина линии контура поперечного сечения балки. Поправка за счет коротких сторон для тонкой балки (b s) незначительна: С b3(s — 0,636) G3.
Далее автор рассмотрел изгиб балки концевыми моментами М и получил выражение для их критических значений
(6)
где k 1 для балок со свободными концами (нет поворота только вокруг продольной оси) и когда один конец свободен, а другой неподвижно заделан; k 2 для заделанных концов (нет поворота концевых сечений относительно продольной оси и оси, параллельной стенке; возможно вращение вокруг оси, перпендикулярной стенке). В случае свободных концов задача приводится к обыкновенному дифференциальному уравнению с постояннными коэффициентами и решение выражается в элементарных функциях. При этом автор учитывает влияние и постоянной начальной кривизны, и продольного растяжения или сжатия силой Р. Приведем окончательное выражение, когда D 0 (полоса), определяющее соотношение между критическими значениями М и Р:
М2 я2
± Р -Г 2, (7)
где знак плюс относится к сжатию, а минус — к растяжению. Отсюда при М 0 вытекает эйлеров случай для свободно опертых концов.
Затем изучается устойчивость консоли при действии поперечной силы на конце, в центре тяжести и вне его, консоли при равномерном поперечном давлении, а также двухопорной балки со свободными концами при сосредоточенной силе, приложенной в центре тяжести середины пролета. Здесь задача сводится к дифференциальному уравнению с переменными коэффициентами, и автор ищет решение для ф в форме степенного ряда по х. Например, в случае консоли, нагруженной сосредоточенной силой Р,
ркУЩ., (8)
Значения коэффициента k k(Cl2D) подсчитаны для ряда отношений Cl2D. Когда D 0, k 4,013; этот результат получен
764
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
Л. Прандтлем. При Cl2D 32 автор дает приближенную формулу представляющую собою выражение критической силы для полосы, в которую для учета жесткости полок вместо I внесена фиктивная длина l 1—dth(ld), полученная согласно первой формулы (5) в предположении, что кручение консоли в основном определяется жесткостью полок. При C2D 32 ошибка приведенной формулы составляет 2.
Заметим, что в этой работе (стр. 71) автор вводит начальные параметры р0, р', р'', ср где штрих означает производную по х.
Произведенная оценка влияния перемещения точки приложения силы по оси симметрии, которая лежит в плоскости действия нагрузки, показывает, что малые отклонения, соразмерные с высотой балки, не влияют на Я; повышение точки приложения силы понижает устойчивость, а понижение — ее увеличивает.
Для двухопорной балки в формуле (8) коэффициент k имеет другие значения. Когда D О, k 2,115 (Л. Прандтль); при этом k k(Cl2D) тем меньше, чем меньше жесткость полок и длина балки. Автор разобрал случай симметричной и несимметричной потери устойчивости.
Заметим, что при действии сосредоточенных сил уравнения задачи интегрируются в бесселевых функциях, а при распределенной нагрузке — в нетабулированных бесконечных рядах.
Автор отмечает ограниченность применимости своих результатов упругой работой материала. Интересно, что проведенные автором расчеты прокатанных балок немецкого и американского сортамента установили необеспеченность их устойчивости; рассмотренная им клепаная балка отечественного моста показала, что имеет место предельный случай. Это соответствовало практике строительства того времени. Проведенные исследования выяснили, что использование дополнительных связей для увеличения жесткости конструкции не всегда приводит к нужным результатам.
Важной частью диссертации автора «Об устойчивости плоской формы изгиба двутавровой балки» был эксперимент, в котором на специально изготовленной балке определялись жесткости С и D и угол закручивания для проверки первой формулы (5). Закручивание выполнялось парой сил посредине пролета, при этом формула для жесткости дала на 6—8 большие значения.
Предшествующее обсуждение показало, что, за исключением частных случаев, задача о боковом выпучивании балок сво¬
4,013 Ув2с
(9)
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
765
дится к вычислению корней сложных трансцендентных уравнений. Использование энергетического метода позволяет существенно упростить расчет. В монографии «Об устойчивости упругих систем» (1910) (отдел II) автор дает применение этого метода для решения задач об опрокидывании полосы и двутавровой балки. Критическая нагрузка определяется из равенства потенциальной энергии балки U работе внешних сил А на перемещениях, обусловленных выпучиванием:
U А.
Для двутавровой балки
и -1в (тй т D Ш d тс Ш (10)
0 0 о
Первые два члена представляют собою энергию изгиба, последний член — кручения. Работа А определяется в каждом частном случае. Например, при нагружении полосы концевыми моментами М и продольными силами N она равна
0
причем знак плюс соответствует сжатию, а минус — растяжению. Здесь крутильную жесткость автор определяет уже по формуле Сен-Венана С GF440JPt где р — полярный момент сопротивления, F — площадь поперечного сечения. Эта формула дает завышенные значения для клепаных балок из-за относительных перемещений составных частей.
В уравнение (10) одновременно входит и боковое перемещение оси балки w, и угол закручивания ср. Поэтому при решении задачи следует либо задаваться прогибом w, вычисляя угол поворота ф при выбранном прогибе w из уравнения равновесия, либо задавать угол поворота ф, а прогиб w находить из уравнений статики. Вычисления автора для полосы показали, что результаты будут более точными, если аппроксимировать функцию угла поворота ф. Использование тригонометрических представлений для угла поворота ф одно- или двучленного вида позволило получить результаты, близкие к точным. Например, в случае чистого изгиба полосы со свободными концами и концами, не поворачивающимися вокруг продольной оси и оси сечения, лежащей в плоскости действия момента, получается точное решение
Mt k-Vl(NNef, (12)
где ft 1 в первом и 2 во втором случае. Второе подкоренное
766
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
выражение учитывает продольную силу (минус — сжатие, плюс — растяжение), причем Nc — эйлерова критическая сила, соответствующая заданным граничным условиям и форме волнообразования. В остальных случаях учет продольной силы проводится аналогично путем умножения критического усилия, вычисленного от поперечных сил, на коэффициент
r Vl(NNe)2.
Для консольного стержня (w dwjdx 0 при х 0 и d2wdx2 0 при х ), нагруженного в центре тяжести поперечного сечения силой Р, полагая w W 1—cos (лх21), получим Р„ 4,34 Ув2С12, в то время как точное выражение, найденное Л. Прандтлем, имеет вид Р 4,01 В2С2; погрешность 8. Если же принять w wi 1 — cos (лх21) ; w2 1—cos (Зя2), то P, 4,13 YB2Cjl2 — ошибка 3. Полагая же (ф 0 при х 0 и dydx 0 при х I) ф ф1 sin (nxj2l) ф2 sin (Зяя2), можно найти Р 4,03 B2Cjl2. Связь между w и ф согласно уравнению равновесия имеет вид Р( — х)ф B2d2wdx2. Во втором случае при х 0 принято d2wdx2 0, а в первом случае d2wdx2 Ф 0.
Кроме этих задач исследована устойчивость консоли при равномерном поперечном давлении. Двучленное тригонометрическое представление для ф дает (ql), 13,2 YB2Cjl2, в то время как точный результат Л. Прандтля (ql), 12,85 УВ2С12 (погрешность менее 3)- Разобрана устойчивость консоли с линейно переменными крутильной и изгибной жесткостями при поперечной силе на конце (Р„ 2,42 У В0С012; однопараметрическое представление для ф; Во, С0 соответствуют заделке). Изучено выпучивание полосы со свободно опертыми концами, когда поперечная сила расположена посредине (в том числе и несимметричное выпучивание) или в произвольном сечении пролета либо, когда нагружение осуществляется равномерным поперечным давлением. Рассмотрен случай сосредоточенной силы посредине пролета, когда концы не поворачиваются вокруг продольной оси и оси минимальной инерции поперечного сечения полосы.
Важным в этих задачах является учет внецентренного приложения внешней силы в плоскости наибольшей жесткости (на b выше или ниже центра тяжести поперечного сечения). Например, при малых Ьl для полосы, свободно опертой по концам и нагруженной посредине силой, имеем
РР. 1-0,87-5-А),
где Р соответствует центральному приложению поперечной силы Р в плоскости наибольшей жесткости полосы. Таким обра¬
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
767
зом, автор рассмотрел также и ряд не разобранных ранее задач по устойчивости плоской формы изгиба полосы.
Перейдем к рассмотрению опрокидывания двутавровых балок. Здесь изучена устойчивость балки с обоими свободными и с обоими заделанными концами при чистом изгибе, при сосредоточенной силе посредине пролета, при равномерном поперечном давлении. Для опертых концов при действии сосредоточенной силы и равномерного давления разобрано также несимметричное выпучивание. Далее исследована консольная балка при сосредоточенной силе на конце; здесь сравнение с точным решением показывает, что при больших d2 DC12 второе приближение для угла поворота ф дает 7 ошибки. Одновременно анализируется влияние продольных сил и положения нагрузки по отношению к центру тяжести. Затем рассматривается выпучивание в упругой сплошной винклеровой среде, когда возникающие по длине балки распределенные моменты пропорциональны углу поворота. Соответствующий член, обусловленный влиянием среды, вносится в уравнение энергии.
Следует отметить специальный параграф (§ 26), посвященный влиянию изгиба на кручение полосы, и аналогию с изгибным кручением двутавра.
Многочисленные таблицы и графики критических нагрузок и критических напряжений даны в зависимости от величины DC12. За пределом упругости материала критические напряжения предлагается рассчитывать по формуле для упругого материала, а результат умножать на коэффициент YEJE, где Ек — касательный модуль; при этом принимается концепция касательного модуля. Используя таблицу Ф. С. Ясинского, автор приводит критические напряжения за пределом упругости.
В работе «Некоторые теоретические проблемы упругой устойчивости» (1910) (глава III) рассмотрено кручение двутавровой консоли, дан вывод уравнений устойчивости и приведены точные решения об опрокидывании однопролетной двутавровой балки при чистом изгибе при свободных и заделанных краях, консоли при поперечной силе в концевом сечении и двухопорной свободно опертой балки от поперечной силы в середине пролета. Эти результаты содержатся в докторской диссертации автора и обсуждались выше.
В статье «К вопросу об устойчивости упругих систем» (1910) (раздел III) путем точного интегрирования уравнения для бокового прогиба определяется критическое значение концевых изгибающих моментов, приложенных в плоскости наибольшей жесткости тонкой упругой опертой круговой полосы, при симметричном выпучивании, а также указан путь получения критического значения моментов при несимметричном волнообра¬
768
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
зовании. Здесь же поставлена та же задача для заделанных концов.
В «Курсе сопротивления материалов» (Киев, 1911, § 181, стр. 509—517) излагается энергетический анализ устойчивости опертой полосы и двутавровой балки при сосредоточенной силе посредине пролета и дан расчет критических напряжений в балке за пределом упругости.
В статье «Приближенный метод исследования устойчивости упругих систем» (1912) (§ 3) содержится решение энергетическим методом задачи об опрокидывании двутавровой балки и полосы со свободно опертыми концами при нагружении сосредоточенной силой посредине пролета. Впервые это решение приведено в монографии «Об устойчивости упругих систем» (1910).
Во второй части «Курса теории упругости» (1916) даны точные и приближенные значения критических нагрузок для семи вариантов полосы и пяти вариантов балок. В частности, даны результаты ученика автора А. П. Коробова (1911) для сосредоточенной силы в произвольном сечении свободно опертой однопролетной балки.
В статье «Устойчивость плоской формы изгиба кривых стержней с центральной осью в форме круга» (1923) в предположении о сжимаемости оси получены с помощью энергетического метода точное и приближенное решения задачи об устойчивости части кругового кольца при равномерной радиальной нагрузке, направленной и до и после деформации параллельно плоскости недеформированной оси, в случае свободно опертых и заделанных концов. Энергетическим методом исследован случай равномерного давления на круговую арку, направленного всегда к центру кольца. Случай чистого изгиба круговой арки разобран был автором ранее (1910). В 1918 году ряд задач для замкнутого кольца и арки при нормальном давлении рассмотрел Е. Л. Николаи.
Работа С. П. Тимошенко «Балки без боковых опор» (1924) содержит проектировочный расчет балок на опрокидывание на основе энергетического метода. В ней приведены таблицы и графики критических напряжений для двухопорной балки со свободно опертыми и заделанными краями при равномерной по всему пролету нагрузке и сосредоточенной силе в середине пролета. Когда концы свободно оперты, разобрана несимметричная потеря устойчивости по двум полуволнам. За пределом упругости предлагается в полученные ранее формулы вносить вместо Е приведенный модуль Эшессера Е„ 4EEk(YE VEkf.
В пятом разделе работы «Проблемы, связанные с упругой устойчивостью конструкции» (1930) приводятся выражения для
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
769
критических сил консоли, нагруженной на конце, и опертой однопролетной балки с сосредоточенной силой посредине.
Глава пятая (§§ 46—54) монографии «Теория упругой устойчивости» (1936) посвящена устойчивости плоской формы изгиба двутавровых балок и круговых колец. Заметим, что устойчивость за пределом упругости рассматривается здесь на основе концепции приведенного модуля Энгессера.
Важна в методологическом отношении заключительная статья автора по рассматриваемому кругу вопросов «Теория изгиба, кручения и устойчивости тонкостенных стержней открытого профиля» (1945). Многие тонкие вопросы теории излагаются здесь ясно и четко. В работе дано объективное рассмотрение результатов других авторов, развивавших его основополагающие исследования (К. Вебер, 1926; Г. Вагнер, 1929; Р. Каппус, 1937; В. 3. Власов, 1940; Дж. Гудир, 1941 —1942). В этой статье излагается общая теория стержней открытого профиля; на основе теоремы взаимности Максвелла показана тождественность центра сдвига и центра кручения. Сперва анализируется чистое и стесненное кручение стержней. Затем — комбинированное кручение и изгиб при произвольном нагружении, в этом случае используется метод начальных параметров И. Г. Бубнова — А. Н. Крылова. Остальная часть статьи посвящена устойчивости. На примере крестообразного с равными полками стержня изучается крутильная форма потери устойчи« вости при продольном сжатии, для балки со свободно депланирующими и свободно поворачивающимися концами рассматривается изгибно-крутильное выпучивание вследствие центрального сжатия. Обсуждается изгибно-крутильное выпучивание в упругой среде и, наконец, устойчивость тонкостенных стержней при изгибе и сжатии (полоса, двутавровая балка, произвольный профиль).
Следует отметить здесь обсуждение предела применимости принципа Сен-Венана о статической эквивалентности усилий в отдалении от зоны приложения нагрузок для стержней открытого профиля.
Работы С. П. Тимошенко явились основополагающими для разработки теории изгиба, кручения и выпучивания тонкостенных стержней. Ниже содержится перечисление ряда дальнейших результатов в этой области.
К. Вебер (1926) получил дифференциальное уравнение кручения для двутавровой балки с неодинаковыми полками. Г. Вагнер (1929) исследовал крутильную форму, совмещая центры изгиба и вращения, он ввел понятие единичного искажения.
А. Остенфельд (1931) отметил неточность результатов Г. Вагнера, обусловленную предположением о совпадении центров изгиба и вращения, и получил точные решения для уголкового,
770
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
таврового и швеллерного профилей. Ф. и Г. Блейхи (1936) энергетическим методом вывели дифференциальные уравнения стержней полигонального профиля в перемещениях. Они заметили, что обычные дифференциальные уравнения стержней верны и для сечений, не обладающих двумя осями симметрии, если вместо перемещений центра тяжести вводить перемещения центра изгиба. Они рассмотрели боковое выпучивание поперечно нагруженных и центрально сжатых стержней. Р. Каппус (1937) изучил изгиб, кручение и устойчивость профиля общего вида, также основываясь на теореме о стационарности потенциальной энергии; он же показал, что Ф. и Г. Блейхи в своих уравнениях опустили малый член, содержащий крутильную жесткость. Е. Лундквист и М. Флиг (1937) установили положение центра вращения, соответствующее минимуму критической нагрузки.
В. 3. Власов (1936, 1938, 1939, 1940) развил теорию для произвольно нагруженных тонкостенных стержней произвольного профиля. В дальнейшем удалось построить общую теорию деформации замкнутого тонкостенного стержня (А. А. Уманский, 1939). Была дана вариационная формулировка теории деформации тонкостенного профиля открытого и закрытого сечения (Г. Ю. Джанелидзе, 1943—1944). Был произведен учет сдвига (Р. А. Ададуров, 1947—1948), рассмотрены криволинейные стержни общего вида (Н. Я. Грюнберг, Г. Ю. Джанелидзе,
А. А. Уманский), разобрано действие подвижной и динамической нагрузки на тонкостенные стержни (И. И. Гольденблатт, 1947; В. Г. Александров, 1949; В. В. Болотин, 1952—1953). Построена общая теория тонкостенных стержней за пределом упругости и рассмотрена их несущая способность (А. Р. Ржаницын, 1941; Р. А. Межлумян, 1950—1953). Описаны конечные перемещения тонкостенных стержней (Л. П. Кобец; С. П. Вяземский, 1957) и изучено послекритическое их поведение (К. Федергофер, 1933; Е. Д. Томилов, 1938). В дальнейшем были разобраны неразрезные балки, балки, скрепленные упругими связями. Анализировались теоретически и экспериментально устойчивость и деформации тонкостенных стержней при ползучести. Что касается выпучивания двутавровых балок, то случай несимметричных сечений изучался П. А. Соколовым (1939); Г. Нилендер (1943) оценил влияние деформации стенки на боковое выпучивание балок, а Дж. Гудир и М. Бартон (1944) — то же на кру тильную жесткость.
Во всех этих исследованиях существенно использование предположения о неизменности формы поперечных сечений. Таким образом, изучается общая форма выпучивания в условиях депланации поперечных сечений. Что касается местной формы потери устойчивости, соответствующей искривлению поперечных сечений, то применительно к крутильному выпучиванию уголков
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
771
она была проанализирована С. П. Тимошенко (1907); рассмотрение этой задачи в предположении недеформируемости контура было произведено позднее. В общем случае может одновременно происходить и общее и местное выпучивание. Независимое рассмотрение этих форм, вообще говоря, дает лишь приближенную оценку результата.
5. ТОНКИЕ УПРУГИЕ ПЛАСТИНЫ
Леонард Эйлер (1767) первый рассмотрел проблему изгиба тонкой упругой пластины применительно к ее колебаниям, представляя поверхность пластины системой упругих ортогональных нитей, обладающих поперечной инерцией. Е. Хладни (1787, 1802, 1817) своими исследованиями в области акустики дал толчок к развитию теории колебаний пластин. Яков Бернулли (1789) исследовал малый поперечный изгиб пластины, рассматривая ее уже не как систему нитей, а как систему балок; он вычислил узловые линии колеблющихся пластин. Неудачи (1811, 1813) и успехи (1816) Софи Жермен в этой области хорошо известны. Софи Жермен (1811) в мемуаре, представленном в Парижскую Академию наук, полагала, что энергия деформации пластины пропорциональна квадрату суммы обеих кривизн срединной поверхности. Ж. Лагранж (1811) добавил недостающий член и получил уравнение малых поперечных колебаний пластины
Z)V2 где D — цилиндрическая жесткость; w— прогиб; у— удельный вес; g — ускорение силы тяжести; t — время; V2 — оператор Лапласа.
Уравнения изгиба упругих тонких пластин, нагруженных поперечной нагрузкой, с учетом растягивающих усилий в срединной поверхности выводили еще Ж. Лагранж и С. Пуассон (1814); последний рассмотрел случай, когда продольные усилия по ортогональным направлениям неодинаковы. В 1820 году Луи Навье вывел и три года спустя опубликовал уравнение
D V2 V2w N У2ш 0, (1)
которое соответствует сжатию пластины удельными силами N, равномерно распределенными по всему контуру. Предпринятая им попытка решения задачи устойчивости прямоугольной пластины, опертой в углах, оказалась безуспешной. И С. Пуассон, и Л. Навье основывались на представлении о молекулярном строении пластины, предполагая, что молекулярные силы пропорциональны изменению расстояний между молекулами. В 1829 году С. Пуассон дал полную теорию колебаний осесим¬
77 2
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
метричных круговых пластин на основе уравнений Л. Навье теории упругости. Густав Кирхгоф в статье «О равновесии и движении упругой пластины» (1850) оспорил поставленные С. Пуассоном граничные условия и с помощью принципа возможных перемещений получил дифференциальное уравнение изгиба пластины в форме Ж. Лагранжа и С. Пуассона, но с другими граничными условиями. Он нашел, что условия для поперечной силы и крутящего момента объединяются одним условием.
В частности, из его вариационного уравнения б J JjD(V2ay)2—
— qzwdx dy 0 следует уравнение DV2V2ay qz qz — поперечное давление. В. Томсон (Кельвин) и П. Тэт (1876) дали геометрическую интерпретацию результата Г. Кирхгофа, указывая, что три условия (для поперечной силы, изгибающего и крутящего моментов) С. Пуассона выполняются только для толстой пластины, а для тонкой пластины должны выполняться два условия Г. Кирхгофа (для обобщенной поперечной силы и изгибающего момента). В упомянутой статье Г. Кирхгоф дал полную теорию колебаний круговых пластин. Удельные усилия и удельные моменты в теорию пластин введены Ф. Герингом (1860), А. Клебш дал впервые условия равновесия пластины в усилиях (1862).
Теория пластин конечного «квадратичного» прогиба изложена в тридцатой лекции Г. Кирхгофа «Лекций по математической физике» (1876), ее видоизменение для мембран дано
А. Фёпплем (1907), для пластин — Т. Карманом (1910), для пологих оболочек — К. Маргерром (1938). В комментариях к книге
А. Клебша (к § 73) Б. Сен-Венан (1883) вывел уравнение изгиба пластины с учетом усилий в срединной плоскости Nu N2t N12, объемных сил в этой же плоскости qx, qv и поверхностного поперечного давления qz:
„ „ д2т , d2w . d2w . dw , dw оч
DV Vffl Af11 2Ni2d7d Чхд7 ЧуЩГ:С- W
При qz 0 отсюда следует линеаризированное уравнение устойчивости.
Пренебрегая массовыми силами, Дж. Брайан выписал энергетический критерий устойчивости для пластин, предполагая равенство потенциальной энергии, обусловленной изгибом вследствие неустойчивости, работе контурных сил (1891). Используя двойной тригонометрический ряд для w, он нашел выражение для критического напряжения в случае прямоугольной пластины со свободно опертыми четырьмя краями, равномерно сжатой неодинаковыми силами в двух направлениях. Он показал, что, например, при одностороннем сжатии при выпучивании пластина
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
773
разделяется на тп прямоугольников. Он разобрал случаи, когда Nx N2 и когда N Ф О, N2 0. В последнем случае критическое напряжение равно
Ni _ п2Е (mb , а (6 2 оч
СГ— б— 12(1— v2) а 6 ’ ' '
и при потере устойчивости аb Ут т 1). Если п» 1, то
аb т, и пластина разделяется на квадраты.
Для случая равномерно сжатой силами N сплошной круговой пластины он получает из энергетического функционала уравнение (1), которое точно — в бесселевых функциях — решает
для случая жестко защемленного и свободно опертого края, и вычисляет критические значения N, соответствующие осесимметричному волнообразованию. Формула (3) демонстрирует непригодность использовавшейся во второй половине прошлого века эмпирической формулы И. Ходкинсона (1849) сх const У 6Ь и показывает, что в его опытах напряжения были выше предела упругости.
С. П. Тимошенко исследовал выпучивание только прямоугольных пластин. Его первая работа по устойчивости пластин была опубликована в 1907 году и была связана с расчетом сжатых поясов мостов, в которых, в частности, использовались большепролетные сварные и клепаные двутавровые балки. В дальнейшем им была развита теория устойчивости подкрепленных пластин в связи с проектированием крейсеров возрождавшегося после цусимской трагедии русского морского флота.
Рассмотрим работу «К вопросу об устойчивости сжатых пластинок» (1907), опубликованную в «Известиях Киевского политехнического института». Автор находит критическую нагрузку равномерно сжатых в одном направлении пластин, когда:
1) три стороны оперты, одна свободна; нагружены противоположно опертые края, либо опертый и свободный в поперечном направлении края;
2) три стороны оперты, одна жестко либо упруго защемлена; нагружены противоположно опертые края;
3) две противоположные стороны оперты, две нагруженные свободны;
4) две противоположные стороны свободно оперты, две другие, нагруженные, жестко защемлены, либо, наоборот, нагружены свободно опертые стороны.
Все эти задачи решаются точно. Прогиб при потере устойчивости, например, для первых трех случаев представляется в виде г ч. тпх
w wj(y) sin , тогда граничные условия для опертых краев
точно удовлетворены и задача сводится к решению обыкновенного дифференциального уравнения четвертого порядка
774
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
относительно f(y). Автор находит критические усилия для отношений сторон от аb 1 до аb 10 и определяет наиболее невыгодное для пластины отношение сторон. В случае, когда одна или две стороны свободны, С. П. Тимошенко дает оригинальный прием вычисления критических сжимающих сил, рассматривая текущий элемент, параллельный сжимающим силам, как балку и составляя для него дифференциальное уравнение закручивания. Таким путем, например, в случае пластины с тремя опертыми и одной свободной стороной, сжимаемой по опертым краям, получено, что
где А 6, в то время как точное решение при а —► оо дает
Автор исследует выпучивание по цилиндрической поверхности и выпучивание свободно опертой по всем краям пластины при одностороннем сжатии. Как отмечалось выше, решение последней задачи дано Дж. Брайаном. С. П. Тимошенко считает, что решение задачи проще отыскивать непосредственным решением дифференциального уравнения Сен-Венана, чем путем исследования потенциальной энергии выпученной пластины; но при этом «остается недоказанным, будет ли устойчива исследуемая форма равновесия выпучившейся пластинки и будет ли ей действительно соответствовать наименьшее значение критической силы».
В этой же статье показано, что результат А. Зоммерфельда (1906) об устойчивости прямоугольной пластины под действием противоположных сосредоточенных сил в середине сторон, когда все стороны свободно оперты, либо когда две нагруженные жестко защемлены, а две другие оперты, ошибочен. Впоследствии (1910) С. П. Тимошенко вернется к этой задаче и даст корректное решение.
В рассматриваемой статье С. П. Тимошенко ставит задачи об устойчивости односторонне сжатых прямоугольных пластин с тремя опертыми и одной жестко защемленной стороной, когда сжимающие силы параллельны двум опертым краям, и о выпучивании при контурных усилиях, меняющихся по длине. Обсуждаемое исследование ценно не только своими результатами по устойчивости пластин. Автор проявил себя как инженер. Все разобранные им задачи нашли место в мостовых конструкциях, и это мастерски показано. Подкупает именно кажущаяся простота анализа и выбор простейших расчетных схем (см., например, случай упруго защемленного края).
Позднее Генрих Рейсснер (1909) опубликовал результаты, впервые полученные С. П. Тимошенко. Он рассмотрел
А 4,5.
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
775
одностороннее равномерное сжатие прямоугольной пластины по свободно опертым краям, когда два других края свободно оперты, свободны, защемлены или один защемлен, другой — свободен.
В § 1 работы «К вопросу об устойчивости упругих систем» (1910) энергетическим методом решена задача о выпучивании прямоугольной пластины от двух сосредоточенных противоположно направленных сил, приложенных в середине свободно опертых либо жестко защемленных сторон, когда две другие стороны свободно оперты. Работа сжимающих сил Р на взаимном перемещении точек приложения (dwdy)2dx прирав-
о
нивается потенциальной энергии изгиба и кручения за счет выпучивания; автор пренебрегает энергией вследствие изменения деформаций и сдвигов срединной поверхности. Прогиб при
выпучивании представляется в виде w (у) wmsin(rmixa)y
т 1, 3, 5
причем f(y) sin (nyb) для опертых и f(y) 1 — cos (2nyb) для защемленных нагруженных краев (b — длина пластины в направлении сжатия). В предельном случае пластины бесконечной ширины получается Р knDb здесь k 4 при опертых и k 8 при защемленных краях. Уточнение этих результатов было бы основано на учете деформации сдвига и удлинений срединной поверхности.
Монография «Об устойчивости упругих систем» (1910, отдел III) содержит приложение энергетического метода к обсуждаемому вопросу. При этом определяется минимум критической нагрузки по отношению к параметрам принятой выпученной формы пластины. Здесь вычислены критические нагрузки для свободно опертой по всем сторонам прямоугольной пластины при равномерном одностороннем сжатии, при одностороннем сжатии, когда нагрузка по контуру меняется по произвольному линейному закону (предельные случаи — равномерное сжатие и чистый изгиб), когда сжимающая сила постоянна в одном направлении и меняется от нуля по линейному закону в другом. Рассмотрен случай равномерно сжатых противоположно опертых краев и двух других жестко защемленных, а также случай совместного действия сжатия и изгиба на противоположно опертых краях, когда третий край свободен, а четвертый упруго защемлен. Кроме первого случая, используется двухпараметрические представления для прогиба. Наконец, впервые разобрано выпучивание бесконечно длинной пластины при сдвигающих силах на опертых краях. Аппроксимирующая функция выбирается так, что прогиб на контуре равен нулю, а изгибающие моменты
776
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
на контуре не равны нулю. Здесь
пи. п (х аи) ,,ч
w sm -у sin—(4)
где X — длина полуволны вдоль оси х, узловые линии наклонены к опертым краям на угол arctga. Все эти результаты применены к выбору размеров вертикальных листов двутавровых балок (высоты и толщины), и обсуждаются с точки зрения установленных данных ранее исполненные конструкции мостовых балок.
В написанной для известного немецкого «Журнала математики и физики» статье «Некоторые теоретические проблемы упругой устойчивости» (1910) даны решения пяти задач об устойчивости прямоугольной пластины, равномерно сжатой по противоположно опертым краям, когда два других края оперты или жестко защемлены, если один край оперт, другой свободен, когда один край свободен, другой защемлен абсолютно жестко либо упруго. Кроме того, изложено решение задачи о выпучивании пластины при сосредоточенных силах, приведенное также в статье «К вопросу об устойчивости упругих систем» (1910). Этот же результат представлен и в § 4 работы «Приближенный метод исследования устойчивости упругих систем» (1912).
Устойчивость сжатой в одном направлении, подкрепленной ребрами параллельно обоим краям прямоугольной пластины изучалась И. Г. Бубновым в § 12 его курса «Строительная механика корабля. Часть I» (1912), который подменил задачу устойчивости пластины задачей об устойчивости перекрестного набора, сжатого в одном направлении, — система опертых одинаковых равноудаленных -продольно сжатых стержней покоится на таком же поперечном наборе опертых стержней. Принимая за лишние неизвестные реакции поперечных балок, он в результате не смог получить точного решения задачи и рассмотрел в конечном итоге стержень, опертый на абсолютно жесткие опоры, но и эта расчетная схема оказалась непреодолимой.
С. П. Тимошенко показал, что нет смысла заменять подкрепленную пластину системой изолированных балок-полосок, как это делал И. Г. Бубнов, и что задача об устойчивости подкрепленной пластины решается энергетическим методом при любом числе ребер.
Проблеме устойчивости прямоугольных пластин, подкрепленных наделенными только изгибной жесткостью упругими ребрами, параллельными прямолинейным сторонам, посвящено две работы.
В статье «Об устойчивости пластинок, подкрепленных жесткими ребрами» (1915) энергетическим методом исследуется случай опертых краев. Прогиб при выпучивании представляется
е. П. ТИМОШЕНКО И ЕГО работы
777
в виде
т оо п оо
V1 тлх пли z-ч
ш 2j Wmn smTsn 6 w
m 1 n1
Число ребер может быть различно, как и расстояния между ними и их изгибная жесткость. Условие минимума для Р приводит к бесконечной системе алгебраических уравнений. Разбирается случай, когда ребра параллельны и перпендикулярны сжимающим силам. Например, если ребра направлены вдоль сжатия, то возможно выпучивание по одной полуволне (т 1). Хорошее приближение для критической силы Р при равноудаленных одинаковых ребрах жесткости получается при одночленном приближении (т п 1). Подробно изучается случай одного и двух одинаковых симметрично расположенных ребер. При ребрах, поставленных вдоль направления сжатия, узловые линии выпученной поверхности могут совпадать с ребрами, тогда последние не изгибаются и на устойчивость рассчитывается неподкрепленное поле пластины между ребрами. Однако наименьшая критическая нагрузка может соответствовать и случаю изгиба ребер и определяется величинами BbD (где В — изгибная жесткость ребра) и аb. Таблицы таких расчетов представлены в статье.
Устойчивость при сдвиге пластины конечной длины впервые исследовалась И. Г. Бубновым во второй части курса «Строительная механика корабля» (1914). Он решил эту задачу методом ортогонализации, который впоследствии получил его имя, используя выражение (5) в качестве аппроксимирующей функции. С. П. Тимошенко также использует это представление для прогиба при построении решения энергетическим методом. Получающаяся в результате бесконечная система алгебраических уравнений разделяется на две группы с четной и нечетной суммой индексов при wmn. Наименьшие значения дает система с четной суммой индексов при wmn система уравнений, которая содержит Wmn с нечетной суммой индексов, приводит к более высоким критическим касательным напряжениям т. Автор рассматривает три приближения, удерживая члены с Шп, w22, с WU W22, «Ms, 0зь ЯУ33 и с Wu w22, Wzu «Из» a33, 42- Для квадратной пластины (ab 1) второе приближение от первого отличается на 15, а третье от второго — в четвертой значащей цифре. При аb 2 и аЬ 3 третье приближение разнится со вторым соответственно на 2 и 9,5.
Автор изучает также выпучивание длинной пластины с поперечными ребрами при сдвиге, задаваясь формой (4) для прогиба. Частный случай длинной неподкрепленной пластины при сдвиге был разобран автором ранее, в 1910 году.
778
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
В заключительной статье «Об устойчивости подкрепленных пластин» (1921) используется энергетический метод в комбинации с представлением (5) и приводятся общие решения для подкрепленной параллельно сжатию прямоугольной пластины, для подкрепленной пластины, подверженной чистому сдвигу, и для неподкрепленной опертой пластины при эксцентричном сжатии (расчеты для первых двух приближений). Первые два случая разобраны в статье 1915 года, последний опубликован впервые. Здесь дополнительно даны числовые результаты, основанные на представлении (4). Интересны анализ размеров исполненных конструкций и проектировочные расчеты металлических листов клепаных мостовых балок со сплошной стенкой. На основе анализа предлагается практическая рекомендация: при чистом сдвиге длинной, подкрепленной многими ребрами пластины относительную жесткость BbD выбирать вдвое большей, чем в случае одного ребра, делящего пластину пополам.
Трудно воздержаться, чтобы не привести небольшую цитату из обсуждаемой статьи, показывающую, что автору остался лишь небольшой шаг, чтобы исследовать послекритическое поведение пластины и ввести понятие эффективной ширины: «Вообще выпучивание не приводит к разрушению, однако все же имеет своим следствием нежелательные явления. Та часть сжимающей силы, которая при недостаточной жесткости пластины не может быть воспринята, передается более жесткой части конструкции, которая составляет опору пластины. Следствие этого явления состоит в перенапряжении более жесткой части конструкции».
Таким образом, автором поставлены и доведены до инженерного решения многие важные задачи об устойчивости прямоугольной пластины. Изучено влияние граничных условий, различных видов нагружения, их комбинации на критическую нагрузку. Проанализированы предельные случаи (бесконечно длинная пластина). Оценено влияние ребер жесткости на характер выпучивания и критическую нагрузку.
Проблема послекритического поведения исследовалась автором гораздо позже (см. гл. 8).
6. ТОНКИЕ УПРУГИЕ ОБОЛОЧКИ
Проблема устойчивости тонких упругих оболочек — важная и трудная проблема строительной механики. В прошлом веке она ставилась в связи с расчетом трубчатых мостов, жаровых труб; в нашем веке — применительно к расчету корпуса корабля, подводной лодки, двигателя, летательного аппарата и т. п.
В середине XIX века уже обсуждалась задача об устойчивости от внешнего равномерного давления q тонкой круговой
С, П. ТИМОШЕНКО И ЕГО РАБОТЫ
779
цилиндрической оболочки. Теоретическим исследованиям предшествовал ряд опытов; особенно известны опыты В. Фёйрбёйрна (1859), поставленные в связи с проектированием трубчатых мостов Британия и Конуэй. Анализируя тридцать опытов с цилиндрическими оболочками конечной длины из сварочного листового железа с клепаным швом, он дает следующую эмпирическую формулу для поперечного критического давления:
Я k щ
где Л, , — соответственно толщина, радиус срединной поверхности и длина цилиндрической оболочки; , а 2,19 — эмпирические константы.
В первых теоретических исследованиях рассматривался только случай равномерного нормального давления, а цилиндрическая оболочка считалась неограниченно длинной; вместо нее изучалось выпучивание узкого кругового кольца, поэтому эффектом Пуассона, связанным с плоской деформацией, пренебрегалось.
Ф. Грасхоф, обсуждая результаты предыдущей работы, в 1859 году впервые получил формулу для критического нормального давления упругого кольца, превращающегося при потере устойчивости в эллипс. Ту же формулу приводит в своем курсе прикладной механики и Ж. Бресс (1859). Позднее ее выводили Ж. Буссинэ (1883), А. Гринхил (1883), М. Леви (1884).
Энергетическим методом Дж. Брайан (1888) нашел следующее выражение:
г2 — 1 Е h3 12 1 - v2 W
здесь п — число волн в окружном направлении; Е — модуль Юнга; v — коэффициент Пуассона. При п — 2 круговая труба становится эллиптической и
3D 1 Eh3 п_ Eh3 п
mln — — 4 1 _ v2з » 12 (1 -v2) '
Из (1) видна ошибочность формулы Ануина (1875) (v 0) , n2Ehs2R3.
В. Лилли (1908) экспериментально получил осесимметричную форму потери устойчивости круговой цилиндрической оболочки при равномерном продольном сжатии.
А. Маллок (1908) обратил внимание на то, что при продольном сжатии сначала возникают несимметричные складки, а при значительном уменьшении оси — симметричные, поэтому продольная сила в процессе деформации изменяется. При этом радиус трубы после потери устойчивости имеет вид
R R w0 cos Яф sin (mnxl),
780
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
где т — число полуволн вдоль оси. «Чем меньше hR, гем больше порядок гармоники». Автор полагает, что выпучивание, а также выворачивание (например, конуса), происходит при недеформируемой поверхности. Он первый высказал идею построения теории на основе изометричности деформированной поверхности исходной поверхности оболочки. При этом деформированная и исходная поверхности имеют одинаковую внутреннюю геометрию, а деформация поверхности соответствует чистому изгибанию. Эта идея получила интенсивное развитие в пятидесятых и шестидесятых годах нашего столетия.
Рассматривая равномерно сжатую вдоль оси толстостенную цилиндрическую круговую оболочку при осесимметричной деформации, Рудольф Лоренц (1908) получил уравнение устойчивости тонкой цилиндрической оболочки и нашел критическое сжимающее напряжение
для обоих свободно опертых ( 1 У3) и обоих защемленных краев (ft 213). Из (2) видно, что Р. Лоренц пренебрег поперечной сжимаемостью материала. Это учел С. П. Тимошенко, который в рамках гипотез Кирхгофа — Лява получил для критического напряжения формулу, носящую его имя:
qt г 1 (о. 0,605— при v 0,3) (3)
3(1 —v2) R R у Г
в представленной в 1909 году и опубликованной в 1910 году на немецком языке статье «Некоторые теоретические проблемы упругой устойчивости» (глава IV) и работе «К вопросу об устойчивости упругих систем» (1910, раздел II). Результаты этих работ обсудим ниже.
В докритическом состоянии оболочки стенки прямолинейны. Потенциальная энергия накапливается за счет продольного сжатия, относительное значение которого е gЕ. После выпучивания потенциальная энергия возрастает на величину dt) за счет работы б А продольной сжимающей силы 2я Rho. Критическое значение силы находится из условия б U б Л, при этом
2п I
Ш В J (е, е2)2-2 (1 - v) (е,е2 - R dydx о о
271 I
J J (к, х2)2-2(1 - v) - --jl R dp dx,
о о
I I
Т J (4я”)2 dx 7Г J wdx
о о
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
781
где еь ег, у» хь кг, К12 — относительные удлинения, сдвиг, изменения кривизны и кручения срединной поверхности, обусловленные выпучиванием; w — прогиб той же поверхности при выпучивании. Член в квадратной скобке есть опускание груза 2nRho. При этом второй член в выражении 6 А определяет работу силы 2nRho на продольном перемещении (ei — e0)dx vwdxR. Это ясно из следующего. Поскольку деформация осесимметрична, то
после потери устойчивости v 0, w w0 sin t a величина
продольного перемещения находится из условия постоянства силы 2nRho:
Ni B (е, ve2) В (е0 — v2e0) const, В -2-,
и так как е2 —ve — wR, то ei е vwR. В результате критическое напряжение равно
В случае очень короткой оболочки потеря устойчивости будет происходить по одной полуволне; при увеличении длины — по двум, трем,., т полуволнам. Существенно замечание автора, что величину т, соответствующую минимальной сжимающей силе, можно определить, как для стержня, лежащего на сплошном упругом основании. Переход от равновесия с т 1 полуволнами происходит при длине
V -4 Ут(т 1) Ут.
¥ уТ(1-v2)'
Когда длина I велика, то велико и число т, тогда длина выпучины равна
--4 УМ (±,72УМ при v 0,3), (б)
У 12(1 -V2)
а минимальное критическое напряжение вычисляется подстановкой (5) в (4) или непосредственно из условия минимума dojdm » 0. В результате получим формулу (3). Автор замечает, что для длинных оболочек характер закрепления краев не имеет значения, поэтому формула (3) применима и для защемленных краев.
В этой же статье формулы (3), (4) выведены путем решения дифференциального уравнения устойчивости
п d4w. , d2w . Eh Л
D-dah4-lw0' (6
782
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
Прогиб при этом представляется в виде
до до0 sin rx Wi sin r2x, rU2
o2t ' Eh
4D2 D2
Тогда условие до d2wdx2 0 при лг 0 удовлетворяется выбранными выражениями, а из условия до d2wdx2 0 при х I С. П. Тимошенко получает два алгебраических уравнения относительно Доо и W. Ненулевое решение их соответствует обращению в нуль определителя этих уравнений, отсюда и следует формула (3). Заметим, что из формулы для г)2 видно,
o2h2 Eh
что выпучивание возможно, когда 7)2 или когда
Постановка задачи об устойчивости продольно сжатой цилиндрической оболочки при несимметричном волнообразовании принадлежит С. П. Тимошенко. В обсуждаемой статье он рассмотрел неосесимметричное выпучивание оболочки со свободными концами в предположении, что срединная поверхность ее не претерпевает деформаций удлинений и сдвигов. Если выражения для перемещений оболочки и, и, до удовлетворяют условию недеформируемости срединной поверхности в ней самой, т. е. уравнениям
то перемещения должны быть выбраны в следующей форме:
Для опертых краев ап Рп 0, а для опертой цилиндрической панели кроме этого вместо п нужно ввести величину mta, где a — угол раствора панели. Эти выражения автор и использует, решая задачу энергетическим методом. Заметим, что при этом образующая остается прямой. Когда число окружных волн равно двум, круговое сечение переходит в эллиптическое, критическое напряжение становится минимальным, равным
т EhRV3(l -V2).
D
Ы - 2j т Un sin a
V 2 v'n cos (яф P„) vx cos (rnp „), w S яv'n s'n («Ф P„) vx sin (nq an).
a
24 Dl2 5 Rh
(7)
При l R отсюда имеем
2 E h42 23 1 l2h
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
783
где а определяется по формуле (3). Для коротких оболочек формула (7) приводит к более низким критическим напряжениям, чем формула (3). Однако для бесконечно длинной оболочки (-оо) она дает неудовлетворительный результат: а оо.
С. П. Тимошенко критически относится к своему решению, полученному в предположении, что ei 82 у 0, отмечая, что, вводя гипотезу об отсутствии растяжения и сдвига срединной поверхности и выбирая в соответствии с этим выражения для перемещений, не удается удовлетворить основным уравнениям равновесия: «Чтобы эти уравнения удовлетворялись, необходимо одновременно с рассмотрением изгиба учесть и деформацию срединной поверхности». Одновременно не удовлетворяются и некоторые граничные условия (например, меридиональный изгибающий момент при х 0).
В обсуждаемых работах автор одновременно поставил задачу об устойчивости продольно сжатой цилиндрической панели, решение которой он опубликует в 1914 году, и задачу об устойчивости круговой цилиндрической оболочки под действием концевых изгибающих моментов, которая была рассмотрена
В. Флюгге в 1932 году.
Вслед за этим, в некоторой мере освободившись от обременительной гипотезы об отсутствии удлинений и сдвигов срединной поверхности, Р. Лоренц (1911) численно проанализировал формулу (7). Сперва в случае обоих опертых концов, считая, что «СуимСи полагая
и 0, a v и0 cos mp sin (гаях), w w0 sin пер sin (mnxl) (9)
при осесимметричном волнообразовании, он нашел ст Eh3(1 — v2), а при числе п окружных волн, равном 2, получил о, EhlY3(1 — v2) R. В случае защемленных краев (w dwdx v 0 при х 0 и х — I) он, принимая v и0 exp (гаях) и w w0 exp (гаях), пришел к характеристическому уравнению задачи. Далее он разбирает случай, когда и, v, w подчиняются выражениям (10), но проводит численную оценку и расчетную формулу не получает.
Дальнейшее исследование неосесимметричного волнообразования цилиндрической оболочки выполнил С. П. Тимошенко в статье «К вопросу о деформациях и устойчивости цилиндрической оболочки» (1914), опубликованной в «Вестнике Общества технологов» и в «Известиях Петроградского электротехнического института». В этой работе представлены основанные на гипотезах Кирхгофа — Лява уравнения нейтрального равновесия круговых цилиндрических оболочек в удельных усилиях и моментах, а также в обусловленных выпучиванием перемещениях и, у, w срединной поверхности для случаев продольного сжатия и равномерного нормального давления. Эти уравнения
784
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
соответствуют безмоментному докритическому состоянию. Они впоследствии широко использовались многими авторами и известны как уравнения С. П. Тимошенко. Их подробный вывод дан в монографии «Курс теории упругости. Часть 2. Стержни и пластинки» (1916). Как и прежде, автор рассматривает случай свободно опертых краев (прогиб, изгибающий момент, окружное перемещение и приращение продольной сжимающей силы равны нулю на обоих краях: w d2wdx2 v 6Ni 0). Перемещения при потере устойчивости в форме
тпх . тпх . . тпх
U — Uq sin шр cos ——, V vQ cos шр sin ——, w w0 sin шр sin ——
(10)
при подстановке в систему дифференциальных уравнений нейтрального равновесия удовлетворяют ей и приводят к алгебраической системе уравнений относительно и0, Vo, w0. Ненулевые для Uq, v0l w0 решения отвечают равенству нулю детерминанта этой системы уравнений. Пренебрегая членами порядка (оЕ)2 и (Л)4, автор получает выражение для критического напряжения. Оно анализируется в двух предельных случаях.
1) Величина y2 (mnRl)2 является большим числом. Это будет, когда либо длина оболочки мала, либо когда при выпучивании появляется большое число волн т в продольном направлении (выпучивание с образованием коротких волн). Тогда
Е г 1 h2 (п2 у2)2 , (1 — у2) у2
1— v2 L 12 R2 у2 (г2 у2)2 ' '
Если п 0, то деформация является симметричной и мы получим формулу (3). Минимум критического продольного напряжения также соответствует формуле (3), он будет при
(Y -y)2ir 13(1 “v2b (12
Отсюда видно, что в случае большого числа т продольных волн критическое напряжение неосесимметричной потери устойчивости равно ст при осесимметричном волнообразовании. Выпучивание будет осесимметричным, если длина цилиндрической оболочки или длина одной полуволны будет настолько малой,
что у2 2R У 3(1 —v2)ft. С уменьшением у в окружном направлении возникнут две, три и т. д. волны. Но тем не менее критическое напряжение, будучи отличным от значения (2), не существенно от него отличается.
2) Когда величина у мала, то длина продольной волны значительно больше радиуса оболочки и
_ Е Г 1 — v2 2 1 А2 п2п2(п2-1)2
l-v2 L«2(«2l) Y 12 R2 у2 п2 1 г
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
785
Эта формула включает случай общей потери устойчивости оболочки как стержня. Поэтому при п 1 имеем формулу Эйлера для свободно опертых краев
Отсюда видно, что для длинной цилиндрической оболочки критическое напряжение при несимметричном выпучивании с малым числом окружных волн п меньше критического напряжения осесимметричного деформирования, например, при п 2 формула (14) дает 35 значения критического напряжения, определяемого по формуле (3). Когда число окружных волн п велико и я2 » 1, выражения (3) и (14) идентичны. Этот результат впервые был обнаружен Р. Саусвеллом (1913).
В. Флюгге (1932), подробно исследовав задачу о продольно сжатой цилиндрической оболочке, показал, что формула (3) пригодна для оболочек средней длины, когда
С. П. Тимошенко, а также многие другие позднейшие исследователи полагали, что выражения (3) и (14) применимы и для граничных условий, отличных от свободного опирания. Эти формулы основаны на предположении о безмоментности докритического напряженного состояния, состоящем в том, что до момента выпучивания оболочка за счет продольного сжатия равномерно расширяется в радиальном направлении.
Эксперименты, поставленные А. Робертсоном (1928—1929),
В. Флюгге (1932) и Е. Лундквистом (1933), установили, что критическая нагрузка на 10—60 ниже расчетной. Попытка объяснить это расхождение начальными несовершенствами формы оболочки, нереализуемыми в опыте граничными условиями привела к разработке теории для многочисленных других граничных условий для безмоментных и моментных докритических состояний и к развитию нелинейной теории устойчивости и послекритического поведения оболочек, в формулировании которой сыграли роль другие работы С. П. Тимошенко (см. главу 8). Например, было показано, что при осесимметричном выпучивании
n2ER2
2(1 -v2)2
Если
R
то
1 Eh пг-
(И)
R л21 ‘
786
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
в случае свободных краев оболочки критическое напряжение вдвое меньше, чем это определяется по формуле (3), и что это есть минимальное критическое напряжение для этой формы волнообразования. В опытах были получены ромбовидные формы выпучивания, которые в дальнейшем были использованы при решении задачи о послекритическом поведении оболочки с целью определения и верхнего и нижнего значений критической нагрузки. Эти результаты были получены также для конструктивно ортотропных и слоистых оболочек. Применение для опытных образцов материала типа майлара позволило получить в опытах весьма надежные результаты.
В обсужденной выше работе исследуется и случай равномерно сжатой вдоль образующих тонкой упругой круговой цилиндрической панели с опертыми краями. Если принять в качестве перемещений при потере устойчивости выражение (10), то удовлетворим равенству нулю прогиба и изгибающего момента на всех краях, а также равенству нулю окружных перемещений на криволинейных краях; прямолинейные края панели свободно перемещаются по касательной к окружности. Результаты для панели получаются введением вместо п величины kna, где k — число полуволн в окружном направлении, а а — угол раствора панели. Здесь также можно различить случаи длинных и коротких волн.
При больших у
а критическое напряжение сг находится по формуле (3). При этом угол а не является малым, величина же hR мала.
Когда величина угла а раствора панели мала, то можно полагать k 1 и из условия минимума доду2 0 (у2 я2а2) можно найти минимум критического напряжения
здесь f — высота подъема панели, а b — длина ее криволинейной стороны. Первый член соответствует известной формуле Дж. Брайана (1888) (см. формулу (3) главы 5) для равномерно сжатой шарнирно опертой прямоугольной пластины. Второй член учитывает влияние кривизны: чем высота подъема f выше, тем панель более устойчива.
Все полученные С. П. Тимошенко результаты по устойчивости цилиндрических оболочек обсуждаются в «Курсе теории упругости. Часть 2. Стержни и пластинки» (1916) и в монографии «Теория упругой устойчивости» (1936). В первой из этих книг ставится задача о выпучивании цилиндрической оболочки
1 к2Е h2 У 1 -V2 ¥
48(1 - у2) ‘
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
787
при кручении, которая была изучена позднее Е. Шверином (1924) и под руководством автора Л. Доннеллом (1933). Там же указан путь решения задачи об устойчивости цилиндрической оболочки при комбинированном действии равномерного поперечного давления и продольного сжатия, которая впоследствии была решена П. Ф. Папковичем (1929), Р. Мизесом (1929), Т. Токугавой (1929).
Опыты Карла Баха (1902) показали, что при действии на тонкую сферическую оболочку равномерного внешнего давления появляются впадины. С. П. Тимошенко в статье «К вопросу о расчете сферических оболочек» (1913) указал, что теоретическое решение этой задачи отсутствует, и поставил в этой работе указанную задачу.
7. УСТОЙЧИВОСТЬ ЗА ПРЕДЕЛОМ УПРУГОСТИ
Стержни. В конце XIX века были высказаны основные идеи, связанные с устойчивостью стержней за пределом упругости, и даны основные расчетные формулы. Так, в 1889 году профессор политехникума в Карлсруэ Фридрих Энгессер предложил рассчитывать критическую силу стержней за пределом упругости по формуле Эйлера с заменой модуля Юнга Е касательным модулем Eh darfe, равным тангенсу угла наклона касательной к диаграмме зависимости напряжения о от деформации 6 в точке, соответствующей критическому напряжению
о о. Тогда критическое напряжение равно (X— гибкость стержня)
Чтобы учесть технологические и конструктивные особенности, рекомендовалось Eh (1895) определять с помощью формулы Л. Тетмайера
сг а — ЬХ.
Это завершило теорию касательного модуля Энгессера, которая пренебрегает возможной разгрузкой отдельных волокон и полагает, что при потере устойчивости продольное усилие непостоянно, оно несколько возрастает.
Однако опыты И. Баушингера (1887) обнаружили на выпуклой стороне стержня, испытывающего продольный изгиб, уменьшение напряжения сжатия. Это позволило М. Консидеру (1889) и Ф. С. Ясинскому (1892, 1895) упрекнуть Ф. Энгессера в некорректности. Рассуждения здесь таковы. Возникающий при выпучивании стержня изгибающий момент у волокон, прилегающих к выпуклой стороне, вызывает деформацию растяжения. Эти волокна разгружаются, и обусловленные продольным изги¬
788
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
бом напряжения по закону Герстнера здесь, следуя закону Гука, определяются модулем Юнга Е. Волокна, примыкающие к вогнутой стороне, вследствие изгиба испытывают сжатие, следовательно, пропорциональнык, так как приращения напряжений обусловленные выпучиванием, невелики.
Ф. С. Ясинский (1895) даже вывел условие постоянства продольного усилия при потере устойчивости, уравнение границ зон догрузки и разгрузки, но окончательной расчетной формулы для а все же не дал. Ф. Энгессер согласился с отмеченной выше критикой и вывел выражение для критического напряжения
п2Е,
V ’
EKJ1 EJ2
(2)
где 1, г — соответственно моменты инерции зоны догрузки и разгрузки относительно линии их раздела; J — центральный момент инерции всего поперечного сечения относительно оси наименьшей жесткости. Здесь — двойной, или приведенный, модуль Энгессера. Таким образом, Ф. Энгессер завершил и теорию приведенного модуля. Однако инженеры были ряд лет в стороне от этой полемики, которая не оставила следа в научной литературе того времени (см., например, монографии К. Баха (1902), В. Лилли (1908)), вплоть до публикации 16 опытов Т. Кармана (1908, 1910) со свободно опертыми стержнями прямоугольного поперечного сечения, после чего теория приведенного модуля получила признание. Но последующие эксперименты показали, что теория касательного модуля лучше соответствует опыту, и лишь Ф. Шэнли (1946, 1947) привел соображения, заставившие ревизовать теорию приведенного модуля.
В своей монографии «Об устойчивости упругих систем»
(1910) (§ 12, стр. 69—75) С. П. Тимошенко вычисляет приведенный модуль для прямоугольного поперечного сечения:
р ЕЕк о
(VE VTKf'
полагая, что он может быть применен и для стержней другой формы, поскольку форма сечения мало сказывается на вычислении. Из следующей таблицы видно, что для не очень малых значений EJE это действительно так:
ЕкЕ 1 0,8 0,5 0,3 0,1
Прямоугольное сечение 1 0,892 0,685 0,501 0,231
Круг 1 0,892 0,689 0,506 0,239
Тонкое кольцо 1 0,891 0,681 0,491 0,216
Идеальный двутавр 1 0,889 0,667 0,462 0,182
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
789
Для основного случая (шарнирно опертые концы) автор ведет расчет критической силы P по теории приведенного модуля. «Влияние закрепления концов за пределами упругости будет
f J
меньшим, чем то следует из обычной формулы Эйлера Рф
За пределом упругости следует учитывать изменение коэффициента длины fx, как, например, в случае стержня, лежащего на сплошном упругом основании, стержня, подверженного действию собственного веса». Автор дает расчет Р для составного стержня. Используя таблицы Ф. С. Ясинского и свои расчетные таблицы, автор показывает, как учесть изменение х за пределом упругости. Считая же const, мы будем иметь заниженные значения критических напряжений. В расчетной процедуре Ф. Энгессера поправка в формулу Эйлера вводится только на модуль, но если используется зависимость or от гибкости К для данных граничных условий, то они объединены.
В статье «Балки без боковых опор» (1924), рассматривая устойчивость плоской формы изгиба двутавровой балки при нагрузке в плоскости стенки (равномерная поперечная нагрузка и сосредоточенная поперечная сила посредине пролета, свободно опертые и заделанные концы), автор дает расчетную модель для определения критических напряжений за пределом упругости, считая, что крутильная жесткость стержня и минимальная жесткость поперечного сечения остаются неизменными, при этом в максимальную изгибную жесткость вместо модуля Юнга Е вносится приведенный модуль Е
Позднее общая теория тонкостенных стержней открытого профиля за пределом упругости развивалась А. Р. Ржаницыным (1942, 1949), Р. А. Межлумяном (1953, 1956). Г. В. Полукаров (1948) рассмотрел упруго-пластическую потерю устойчивости полосы, Г. М. Чувикин (1954) поставил специальные опыты по изучению выпучивания двутавровых балок за пределом упругости.
Пластины. С. П. Тимошенко принадлежит первая работа по устойчивости пластин за пределом упругости. Он рассматривает эту проблему в монографии «Об устойчивости упругих систем» (1910, § 33, стр. 180—181), вычисляя критические напряжения продольно сжатой тонкой прямоугольной пластины. В случае упругого выпучивания критическое напряжение, соответствующее решению основанного на гипотезах Кирхгофа уравнения Сен-Венана, равно
(4)
причем D 7г312 (1—v2)—цилиндрическая жесткость; 6, h — соответственно ширина и толщина пластины; k — коэффициент, зависящий от граничных условий.
790
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
Определяя критическое напряжение при потере устойчивости за пределом упругости, автор умножает аупр на коэффициент
УEJE. Тогда VdYт- Р)
Эта рекомендация носит общий характер и не связана с граничными условиями задачи. Рассуждения здесь следующие. В докритическом состоянии пластина испытывает равномерное одноосное сжатие, в перпендикулярном направлении напряжения равны нулю. Пластина очень тонка, поэтому при выпучивании разгрузки не происходит и дополнительные продольные напряжения от изгиба определяются касательным модулем Ек. При потере устойчивости напряженное состояние становится плоским. Если изгиб происходит по цилиндрической поверхности, то можно считать, что в направлении образующей этой поверхности материал работает упруго и его жесткость равна Д в направлении же сжатия материал деформирован упруго-пластически и имеет жесткость DEJE. Здесь введено предположение, что коэффициент Пуассона v постоянен (такой же, как и в упругой области) и не зависит от величины продольного напряжения, и допущение о том, что деформация в продольном направлении не влияет на характеристики материала в поперечном направлении. Эти соображения позволяют представить уравнение устойчивости односторонне сжатой прямоугольной пластины с напряжением а в виде
ъ (Ек d4w , 0 d4w , д4аЛ лт d2w Л ,r f
Е дх4 дх2 ду2 ду4 ) 1 дх2 “ ’ ah где w — прогиб при потере устойчивости; х, у — ортогональные координаты. Отсюда следует та формальная операция, которая описана выше.
Автор замечает, что при выпучивании за пределом упругости по нецилиндрической поверхности следует рассчитывать критические напряжения по формуле (5), вводя вместо D среднее между D и DEJE значение жесткости. «Для более точного решения вопроса нужно исследовать задачу устойчивости пластинки, жесткость которой меняется с направлением плоскости изгиба». Эта мысль нашла отражение в последующих формальных расчетных моделях, предложенных Ф. Блейхом (1924) (анизотропная упруго-пластическая деформация, концепция касательного модуля):
гл Г d4w. 0 d4w , d4w' d2w л Ек
D dxr 2 11 дх2 dy2 dy Nl dx2 ’ 11 — E ’
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
791
М. Рошем и А. Эйхингером (1932) (изотропная упруго-пластическая деформация, концепция приведенного модуля):
Dr, V2 V -,§ - - 2Na-g. о,
„ _ (8)
Л Е (lfEJE)2 Е ’
где N, Л2, N2 — удельные усилия в плоскости пластины в докритическом состоянии; Е. Хвалла (1928):
DV-nw-Nl-N2-2Nl2- 0, (9)
К. Кольбруннером (1946):
Г 1 I Ек , _EK dw 0 dw. d4ail d2w _ ,lm
dt(-tV t)i2m-Nv0 (10)
и (уточнение гипотезы анизотропии пластической деформации)
ъ (Ек d4w. 0 d4w. d4w АГ d2w л Ек. . , 11Ч
D ( Е дх4 2т Эх2 Э2 “I д(4) 1 дх2 0, Л1- (И)
Последующие опыты на дюралевых и стальных образцах, в том числе и фундаментальные эксперименты Курта Кольбруннера в Цюрихском политехникуме (1935, 1946) (350 прямоугольных дюралевых пластин, опертых на нагруженных краях и с различными граничными условиями на ненагруженных краях), показали, что теория С. П. Тимошенко дает хорошее соответствие опыту для длинных пластин.
Другими словами, согласно указанной выше идее, подобно тому как это делал ранее Я. Бернулли при расчете поперечного изгиба упругих поверхностей, пластина представляется системой ортогональных балок-полос, взаимодействующих друг с другом. Тогда можно рассмотреть два предельных случая, когда переход напряжений за предел упругости материала в продольном направлении не влияет на упругие характеристики деформаций в поперечном направлении либо, когда переход за предел упругости в продольном направлении ведет за собою переход материала за предел упругости в поперечном направлении. Резюмируя, можно сказать, что С. П. Тимошенко ввел впервые предположение о чисто пластическом состоянии и концепцию касательного модуля при анализе потери устойчивости пластин.
Дальнейшая попытка построить теорию устойчивости неупругих пластин на основе идеи о двойном модуле принадлежит
В. Кауфману (1936), использовавшему некорректные соотношения для вариаций напряжений, и П. Бижляру (1938), не учитывавшему изменений усилий в срединной поверхности при выпучивании; последний использовал в неудачной и громоздкой
792
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
форме соотношения деформационной теории пластичности и в результате принял, что материал пластины при потере устойчивости находится целиком в пластическом состоянии. Общая теория устойчивости пластин и оболочек, учитывающая существование областей упругих, упруго-пластических и чисто-пластических деформаций для несжимаемого материала, следующего теории деформационного типа, построена А. А. Ильюшиным (1946).
Опыты не подтверждают формулы для критических напряжений, основанные на идее о двойном модуле, — они дают завышенные значения, а идея о чисто-пластическом напряженном состоянии в соединении с уравнениями пластичности деформационного типа приводит к значениям критических напряжений, согласующимся с данными экспериментов. Результаты же, основанные на соотношениях между приращениями напряжений и деформаций при выпучивании, подчиняющихся теории типа течения, не соответствуют опытам.
Для сравнения приведем уравнения устойчивости упруго-несжимаемой (v 0,5) пластины, выпучивающейся при чисто-пластическом состоянии от равномерного одностороннего сжатия:
на основе деформационной теории (Ес — секущий модуль)
Оболочки. С. П. Тимошенко изучил устойчивость только оболочки цилиндрической формы. Наиболее интересен случай равномерного продольного сжатия. Тогда критическое напряжение при упругих деформациях равно
Ech3 9
на основе теории пластического течения
а длина полуволн выпучивания будет
Если при вычислении цилиндрической жесткости D 7i312(l—v2) вместо модуля Юнга ввести приведенный модуль Энгессера (1895) для прямоугольного поперечного се-
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
793
то соответственно получим
l.-HiVRh,
(15)
где
kl
Отсюда видно, что чем менее деформирован материал за пределом упругости, тем длина выпучины будет больше, стремясь при ЕЕк 1 к величине 1,72 У Rh (v 0,3). Посмотрим, к чему приводит эта процедура, рекомендованная С. П. Тимошенко в «Курсе теории упругости» (часть 2, 1916, стр. 374) (см. также «Теорию упругой устойчивости», 1936, стр. 442; русский перевод, 1946, стр. 390) и позднее предложенная И. Геккелером (1928).
Выпишем уравнение нейтрального равновесия при осесимметричной потере устойчивости:
Здесь w — прогиб при потере устойчивости; х — осевая координата; N oh — удельное меридиональное усиление безмоментного докритического состояния; 6Afj— приращение меридионального удельного изгибающего момента вследствие выпучивания оболочки.
Из (17), (18) видно, что предложенная выше процедура предполагает, что в кольцевых сечениях, перпендикулярных сжимающим силам, материал деформирован за пределом упругости, при этом одна его часть нагружается, другая терпит разгрузку; в меридиональных же сечениях деформация остается упругой.
Если предполагать, что линии раздела упругих и упруго-пластических зон (зон нагрузки и разгрузки) в меридиональных и кольцевых сечениях расположены на одном и том же расстоянии от срединной поверхности, то получим, что критическая длина выпучины оказывается такой же, как и при выпучивании в упругой области, а критическое напряжение равно («Теория упругой устойчивости», 1936, стр. 442)
(17)
причем
(18)
3(1 —v2) (1ЕЕк)2 ’
1 4
(19)
при этом для всего диапазона ЕкЕ ku а при ЕкЕ 0 и ЕкЕ 1 k k3.
794
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
В случае бесконечно длинной трубы, подверженной равномерному поперечному давлению р, в формулу Ф. Грасхофа — Ж. Бресса
Р “ R3 4 1 - v2 R3 ' '
автор («Курс теории упругости», часть 2, 1916, стр. 369; «Теория упругой устойчивости», 1936, стр. 369) вместо модуля Юнга Е вставляет величину ЕТогда
к —Г1 г ч (21)
1 V (1к)2
и 43(1 УЕЕк)2 при v 0,5.
Полагая, что разгрузки не происходит ни в одном волокне, для несжимаемого материала получим существенно заниженные по сравнению с (21) значения: k ЕЪЕ.
В случае трубы конечной длины С. П. Тимошенко рекомендует в формуле Р. Мизеса (1914) вместо Е подставлять Е
(«Курс теории упругости», часть 2, 1916, стр. 391), отмечая, что «вопрос об устойчивости трубки за пределом упругости в рассматриваемом случае сложнее, чем при плоской деформации, так как изменению меридиональной кривизны щ должно соответствовать неизмененное значение Е и лишь изменению кольцевой кривизны х2 соответствует измененный модуль Е».
Предложенный ранее формальный учет упругой сжимаемости материала для пластин и оболочек был использован Д. Джерардом (1957) при расчете критических напряжений в цилиндрической и сферической оболочках.
Интересно отношение ряда механиков к попытке формулирования расчетных методов устойчивости за пределом упругости. Например, В. JI. Кирпичев, Г. В. Колосов, С. И. Белзецкий, высоко оценивая работы С. П. Тимошенко по упругому выпучиванию, упрекали его в своих отзывах на книгу «Об устойчивости упругих систем» за включение этих вопросов, считая, что проблема устойчивости при пластических деформациях — проблема только экспериментальных исследований.
8. НЕЛИНЕЙНЫЕ ПРОБЛЕМЫ УСТОЙЧИВОСТИ И ПОСЛЕКРИТИЧЕСКОЕ ПОВЕДЕНИЕ УПРУГИХ СИСТЕМ
В теории устойчивости тонких упругих оболочек в нелинейной постановке работы С. П. Тимошенко сыграли безусловно значительную роль, и эта роль определяется тем, что поведение оболочки в механическом смысле в ряде случаев может быть описано изогнутым по пологой кривой сжатым стержнем,
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
795
нагруженным поперечной нагрузкой. Здесь следует отметить две статьи. Статья «Расчет биметаллических термостатов» (1925) посвящена расчету биметаллических полос, искривленных по пологой кривой. Если металл с большим коэффициентом линейного температурного расширения расположить с вогнутой стороны, то при нагреве кривизна оси будет уменьшаться. Это изменение кривизны будет непрерывным, если концы полосы могут свободно перемещаться в продольном направлении. Если это свободное расширение концов воспретить, то появится продольная сила, в случае несмещающихся краев равная
N l2EF (dwdxf dxt которую можно считать постоянной по
длине полосы, но которая зависит от амплитуды прогиба или от прогиба в середине полосы, поскольку рассматривается осесимметричная деформация. Здесь Е 1г(,1 Е2), так как автор рассматривает полосу со средним модулем упругости. Центральная ось полосы считается синусоидой. Поскольку концы шарнирно оперты и изгибающий момент на концах равен нулю, автор исходит из уравнения второго порядка для прогиба
которое является линейным. В результате получается уравнение, связывающее амплитуду прогиба W с изменением температуры At. Автор дает графическое решение полученного уравнения и аналитическое решение, определяющее температуру прощелкивания в одном направлении при нагреве А и температуру прощелкивания в противоположном направлении при охлаждении At-.
Аналитическое выражение для критической температуры получается следующим образом. Если считать, что изгиб происходит по дуге круга, то радиус кривизны стержня будет
с другой стороны, раньше для нее получено выражение
Тогда критические температуры вычисляются по формуле
о
1р 32 («2 - ai) At Л, при этом амплитуда прогиба равна
W 28р,
A t.±
З2 (a2 — cti)
16 ffh
796
С, П. ТИМОШЕНКО И ЕГО РАБОТЫ
Здесь — расстояние между опорами; Н — высота подъема полосы; т 4JFh2; , F, h — соответственно момент инерции, площадь поперечного сечения и толщина полосы; аь а2 — коэффициенты линейного температурного расширения.
В работе «Выпучивание пологих кривых стержней и слегка изогнутых пластин» (1935) изучается симметричное прощелкивание синусоидального шарнирно опертого пологого стержня, концы которого либо жестко закреплены в продольном направлении, либо упруго перемещаются пропорционально продольной силе под действием равномерного поперечного давления q. Автор нашел, что параметр поперечной нагрузки при прощелкивании равен
_ (1 — т)
q± 3845Я ± к 27 mJ '
В современной терминологии и — верхняя критическая нагрузка, U- — нижняя критическая нагрузка. Отсюда ясно, что прощелкивание вообще возможно при т 1. Когда т О, критическая нагрузка бесконечно велика. Автор описал этот процесс и проанализировал его.
Величина 5384 взята как максимальный прогиб свободно опертой балки в центре. Это значение соответствует точному решению уравнения Я. Бернулли; при этом деформированная ось — парабола. Если же, как принято в решении, считать ось синусоидой, то вместо 5384 следует ввести величину 4я5. Распространение описанного решения на случай несимметричной деформации позволило установить границы применимости приведенного решения. Оказалось, что при т 211 несимметричная форма прощелкивания соответствует более низкому значению критической нагрузки. При этом сжимающая продольная сила в стержне постоянна и равна второй эйлеровой силе. Заметим, что постановка этой задачи содержится еще в работе Навье (1833), которому, однако, не удалось решить эту задачу. Для сосредоточенной силы Р в середине пролета С. П. Тимошенко рекомендует в указанную выше формулу вводить вместо 7± величину Р±48УЯ. Этот случай был изучен ранее К. Бицено (1929), который не ограничивался симметрией деформации, но вычислил только верхнюю критическую нагрузку и, следовательно, не описал всего процесса деформирования и не дал выражения для критической силы. Позднее в работе Т. Кармана и Шу Шен-цзяна (1939), посвященной осесимметричному прощелкиванию сферической оболочки, была использована модель арки — прогибы происходят вертикально, коэффициент Пуассона равен нулю — и для этой модели определены верхняя и нижняя критические нагрузки. Впоследствии аналогично удалось рассмотреть и многие другие граничные условия для одно¬
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
797
родных биметаллических и трехслойных стержней с заполнителем при статических и динамических воздействиях.
В монографии «Теория упругой устойчивости» (1936, стр. 390—395) приводится решение методом Ритца задачи о послекритическом поведении прямоугольной шарнирно опертой пластины при равномерном сжатии удельными усилиями р в одном направлении; для деформаций используются выражения Г. Кирхгофа (см. главу 30 его «Лекций по математической физике», 1876), соответствующие «квадратичной» теории А. Фёппля — Т. Кармана (1907, 1910). Для нормального w и касательных и, v перемещений принимаются выражения (сжатие вдоль оси у)
где и0, Vo, wо — постоянные; х, у — ортогональные оси, параллельные сторонам пластины; А — относительное сжатие продольного края пластины; Ь, а — длина пластины в продольном и поперечном направлении. Перемещения и на краях х 0 и х а равны нулю, а перемещения v при у 0 и у Ъ равны.
Для квадратной пластины и0 v0 A (v 0,3),
здесь h — толщина пластины.
Теперь легко вычисляются эффективная ширина 6эфф 2р( —v2)EbhA и критическое напряжение а АУ(1— v2), соответствующие равномерному двустороннему сжатию с напряжениями ау а и ах vcr.
Второе приближение автор строит, сохраняя для и и v прежние выражения, а прогиб w представляя в форме
В дальнейшем автор рассматривает случай, когда боковые края (х 0 и х а) абсолютно неподвижны:
причем х определяется из условия, что результирующая нормальных напряжений по боковым граням (х 0, х а) равна нулю.
В результате, варьируя энергию деформации по трем параметрам wо, v0, uq, для квадратной пластины (а Ь) получаются
w wQ sin — sin , v i0sin -
пх. пи
с 1 п Ч—
а
а(у--)
798
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
выражения (v 0,3)
ш0 1,133ft )---1, Д. 2,816-g-.
Найденные зависимости позволяют определить распределение напряжений в квадратной пластине в зависимости от величины Д. Задачу о приведенной ширине в линейной постановке ставил П. Ф. Папкович (1920). Т. Карман (1924), Г. Шнадель (1930) и К. Маргерр (1937) исследовали эту задачу на основе нелинейных уравнений.
9. ТЕОРИЯ НЕОДНОРОДНЫХ КОНСТРУКЦИИ
В статье «Расчет биметаллических термостатов» (1925)
С. П. Тимошенко рассматривает деформацию биметаллической полосы при действии внешних сил и изменения температуры. Проблема равномерного нагрева свободной упругой полосы восходит к И. Вилларсо (1863). В обсуждаемой статье впервые обращается внимание на касательные напряжения по поверхности спая полос у концов; эти напряжения не могут быть найдены из элементарных соображений, носят локальный характер и могут иметь такие же значения, как и нормальные напряжения. Сперва автор оценивает влияние отношения модулей упругости слоев ЕЕ2 на изгибную жесткость биметаллической полосы, когда толщины слоев одинаковы. При ЕЕ2 12 и 2 жесткость отличается на 3 от соответствующего значения при Е Е2. В дальнейшем он биметаллическую полосу подменяет полосой из однородного материала, но видоизмененного поперечного сечения: исходное прямоугольное поперечное сечение из материалов с двумя различными модулями упругости Е и Е2 заменялось им на ступенчатое однородное сечение, например с модулем упругости Еj, путем умножения ширины слоя с меньшим модулем Е2 на отношение Е2Е. После этого расчет ведется обычным путем: находится положение центра тяжести нового поперечного сечения, через которое пройдет нейтральная ось при изгибе, и вычисляется изгибная жесткость сечения относительно нейтральной оси. При равных толщинах слоев биметалла анализируется зависимость изгибной жесткости от отношения ЕЕ2 и устанавливается, что при отношениях ЕЕ2у близких к единице, при вычислении изгибной жесткости полосу можно считать однородной и вместо модуля упругости такой полосы вводить среднее его значение Х2(Е Е2). Это заключение относится к случаю, когда полоса является достаточно узкой.
Для пластины автор рекомендует считать коэффициенты Пуассона слоев одинаковыми. Это очень существенное замечание, которое неоднократно использовалось впоследствии при по¬
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
799
строении рациональных теорий слоистых и неоднородных оболочек. Теория биметаллических пластин и оболочек, которая автором настоящего обзора была развита позднее, показывает, как резко сокращаются при этом вычисления, а его первая работа (1947) по этому вопросу о расчете круговой пластины иллюстрирует сведение задачи о биметаллической пластине к задаче о расчете однородной пластины. Очевидно, получаемая погрешность при вычислении прогибов и напряжений при этом невелика. Аналогичное упрощение наблюдается и в теории трехслойных оболочек с заполнителями и, вообще, в теории многослойных оболочек.
10. ОБЩАЯ ХАРАКТЕРИСТИКА
Выше были обсуждены исследования С. П. Тимошенко в области устойчивости деформируемых систем. Его работы вызвали интенсивное развитие теории устойчивости стержневых и балочных систем, а также систем типа оболочек. Для многочисленных случаев выпучивания стержней решетчатого типа, тонкостенных балок, неподкрепленных и подкрепленных пластин им были получены расчетные формулы, таблицы и графики, которые сыграли большую роль в проектировочных работах. Построенные им дифференциальные уравнения устойчивости цилиндрических оболочек оказались эталоном для сопоставления с другими вариантами уравнений этой задачи. Предложенный им энергетический метод дал инженеру простой и доступный аппарат для решения линейных задач устойчивости. Он ставил и решал нелинейные задачи устойчивости — о прощелкивании стержней; эти его работы привели уже других исследователей к формулированию нелинейных теорий тонких оболочек. Непосредственно не занимаясь пластичностью, он дал инженерные приемы расчета на устойчивость и за пределом упругости; его предложения способствовали развитию различных подходов к расчету пластин и оболочек на устойчивость с учетом пластических деформаций. Изучение проблемы кручения, изгиба и выпучивания двутавровых балок привело в конечном итоге к созданию новой области строительной механики — теории тонкостенных стержней. Сформулированные при этом методы широко стали использоваться при расчете гражданских сооружений (зданий, мостов), конструкций башенного типа, при проектировании судов, крыльев и корпусов летательных аппаратов. Некоторые из допущений, использованные им для построения теории неоднородных стержней, основанной на гипотезе о жестком плоском поперечном сечении, впоследствии были перенесены на однородные пластины и оболочки, для которых гипотеза о недеформируемом нормальном элементе может выполняться, а может и не соблюдаться.
800
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ
Как воспринимались работы С. П. Тимошенко во время их публикации, можно судить по высказыванию выдающегося русского инженера и ученого И. Г. Бубнова по поводу монографии «Об устойчивости упругих систем»: «.работа С. П. Тимошенко кладет прочное основание для дальнейшего прогресса многих отраслей инженерного дела».
Книги С. П. Тимошенко по сопротивлению материалов, истории сопротивления материалов и теории упругости, по статике сооружений, расчету арок, технической механике, по устойчивости твердых деформируемых систем, по теории упругости, по теории колебаний, по теории пластин и оболочек сыграли неоценимую роль в развитии строительной механики в широком смысле этого слова, а также в формировании научного и технического мышления многих миллионов инженеров и у нас и за рубежом. Например, курс и задачник по сопротивлению материалов выдержали у нас свыше десяти изданий. Остальные книги издавались по нескольку раз. Все они переведены на многие языки мира и изучались многими поколениями инженеров, студентов, научных работников. Многочисленные результаты личных исследований С. П. Тимошенко разбросаны среди его книг и учебников, и это освобождало большинство читателей от изучения его оригинальных работ, напечатанных в малодоступных в наше время изданиях. Влияние его на техническое обучение огромно и у нас и во всем мире — оно основано не только на издании монографий и учебников, но и на чтении С. П. Тимошенко лекций, проведения им семинаров и курсов.
Исследования С. П. Тимошенко касались широкого круга проблем, которые, будучи поставлены еще в начале XX века, получили бурное развитие в настоящее время.
С. П. Тимошенко является человеком совершенно исключительного инженерного чутья. Его методы, его решения, его книги иллюстрируют это неоценимое качество. Он умеет схватить самое главное в рассматриваемых явлениях и решить поставленную задачу, используя минимальный математический аппарат. Трудно указать направление в области строительной механики, где бы им не были получены результаты, оставившие неизгладимый след.
С. П. Тимошенко получил инженерное воспитание и научное крещение в Петербурге и Киеве. Его учителями были такие яркие ученые, как В. Л. Кирпичев, Ф. С. Ясинский, И. Г. Бубнов. Такая фигура, как С. П. Тимошенко, могла возникнуть только в условиях крупной инженерной школы в области строительной механики, которая оформилась в России во второй половине XIX и начале XX века. Вместе с тем нельзя не отметить, что, по-видимому, ни у кого из ученых его масштаба не пострадала так, как у него, и жизнь и работа из-за эмиграции, из-за разрыва живых связей с Родиноц.
СОДЕРЖАНИЕ
Предисловие автора 3
От редактора 5
ОБ УСТОЙЧИВОСТИ ПЛОСКОЙ ФОРМЫ ИЗГИБА ДВУТАВРОВОЙ БАЛКИ ПОД ВЛИЯНИЕМ СИЛ,
ДЕЙСТВУЮЩИХ В ПЛОСКОСТИ ЕЕ НАИБОЛЬШЕЙ ЖЕСТКОСТИ
Теория 9
§ 1. Введение 9
§ 2. Скручивание двутавровой балки, один конец которой заделан неподвижно 12
§ 3. Вычисление величины С 19
§ 4. Вывод основных уравнений 22
§ 5. Случай изгиба балки парами сил 26
§ 6. Изгиб балки с заделанными концами 34
§ 7. Случай изгиба балки эксцентрично приложенными сжимающими силами 41
§ 8. Случай изгиба балки эксцентрично приложенными растягивающими
силами 46
§ 9. Влияние первоначальной кривизны оси балки 47
§ 10. Изгиб балки сосредоточенной нагрузкой, приложенной на конце . 40
§11. Влияние внецентренно приложенной нагрузки 61
§ 12. Случай балки, лежащей на двух опорах 65
§ 13. Точка приложения силы не лежит на оси балки 71
§ 14. Изгиб балки сплошной нагрузкой 75
§ 16. Пределы применимости выведенных формул 88
Опыты 84
§ 1. Постановка задачи 84
2. Определение величины С 85
§ 3. Определение жесткости балки при изгибе 89
4. Скручивание балки моментом, приложенным посредине пролета. . 93
§ 5. Изгиб балки в плоскости ее наибольшей жесткости 97
§ 6. Испытание клепаной балки 102
О ПРОДОЛЬНОМ ИЗГИБЕ СТЕРЖНЕЙ В УПРУГОЙ СРЕДЕ
§ 1. Определение критической силы из дифференциального уравнения . 106
§ 2. Применение теоремы о минимуме потенциальной энергии 110
§ 3. Случай вращающихся валов 114
802
СОДЕРЖАНИЕ
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ СЖАТЫХ ПЛАСТИНОК
§ 1. Введение 116
§ 2. Принятые обозначения 118
§ 3. Прямоугольная пластинка всем периметром оперта на контур. 120 § 4. Случай прямоугольной пластинки, выпучивающейся по цилиндрической поверхности 124
§ 5. Прямоугольная пластинка тремя сторонами оперта на контур. Случай 1 125
§ 6. Прямоугольная пластинка тремя сторонами оперта на контур. Случай 2 128
§ 7. Точное решение предыдущей задачи 130
§ 8. Прямоугольная пластинка с абсолютно заделанной продольной
стороной 138
§ 9. Прямоугольная пластинка с упруго заделанной продольной стороной 144 § 10. Влияние изгибающего момента на величину критического сжимающего усилия 153
§ 11. Прямоугольная пластинка сжимается силами, равномерно распределенными по продольным сторонам 156
§ 12. Случай прямоугольной пластинки, обе продольные стороны которой заделаны, поперечные стороны оперты 160
§ 13. Случай прямоугольной пластинки, обе продольные стороны которой оперты, поперечные стороны заделаны 163
К ВОПРОСУ О ПРОДОЛЬНОМ ИЗГИБЕ
§ 1. О продольном изгибе стержней переменного сечения 166
§ 2. Расчет трубчатых стоек переменного сечения 173
§ 3. О влиянии тангенциальных напряжений на величину критической нагрузки 178
§ 4. О продольном изгибе стержней с упруго заделанными концами . . 184
§ 5. О продольном изгибе многопролетных стержней 187
К ВОПРОСУ ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
I. Сжатие прямоугольной пластинки двумя взаимно
противоположными силами 191
II. Об устойчивости цилиндрической трубки при продольном сжатии . .195
§ 1. Исходные уравнения 195
§ 2. Форма, симметричная относительно оси цилиндра 197
§ 3. Искривление, не сопровождающееся растяжением 202
III. Об устойчивости изгиба полосы с круговой осью 204
ОБ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
Введение 208
Отдел первый. О продольном изгибе сжатых стержней 218
§ 1. Элементарные случаи продольного изгиба 218
§ 2. Продольный изгиб стержня под действием собственного веса . . . 222
§ 3. Продольный изгиб стержня под действием распределенных сжи¬
мающих усилий, меняющихся от концов к середине стержня по линейному закону 225
§ 4. Продольный изгиб стержня с опертыми конца,ми в упругой среде . 228
СОДЕРЖАНИЕ
803
§ 5. Продольный изгиб в упругой среде стержня со свободными концами 232
§ 6. Задача проф. Ф. С. Ясинского 236
§ 7. Задача Ф. С. Ясинского при условии смещающихся концов. . 242
§ 8. Практические приложения полученных результатов 246
§ 9. О продольном изгибе составных стержней 257
§ 10. О продольном изгибе криволинейных стержней 269
§ 11. Об устойчивости стержневых систем 273
§ 12. Пределы применимости полученных формул 275
Отдел второй. Об устойчивости плоской формы равновесия
изгибаемых стержней 281
§ 13. Постановка задачи 281
Об устойчивости плоской формы изгиба полос прямоугольного поперечного сечения 283
§ 14. Основные уравнения 283
§ 15. Чистый изгиб 286
§ 16. Изгиб полосы силой, приложенной на конце 291
§ 17. Изгиб заделанной одним концом полосы равномерно распределенной нагрузкой 299
§ 18. Изгиб балки силой, приложенной посредине пролета 304
§ 19. Изгиб балки равномерно распределенной нагрузкой 309
§ 20. Изгиб балки силой, приложенной не посредине пролета 313
Об устойчивости плоской формы изгиба двутавровых балок. 316
§ 21. Основные уравнения равновесия 316
§ 22. Чистый изгиб 318
§ 23. Изгиб балки силой, приложенной на конце 324
§ 24. Изгиб балки силой, приложенной посредине пролета 325
§ 25. Изгиб двутавровой балки равномерно распределенной нагрузкой . 336
§ 26. Влияние изгиба на кручение полосы прямоугольного поперечного
сечения 345
§ 27. Правила пользования выведенными формулами 347
Отдел третий. Устойчивость сжатых пластинок . . . 351
§ 28. Основные уравнения 351
§ 29. Прямоугольная пластинка с опертыми краями 353
§ 30. Практические приложения полученных результатов 365
§ 31. Прямоугольная пластинка с одним свободным краем 370
§ 32. Пластинка с заделанными продольными сторонами 380
§ 33. Об устойчивости пластинок, сжатых за пределы упругости . . .381
Заключение 382
НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
I. Продольный изгиб 385
§ 1. Эйлерова критическая нагрузка 385
§ 2. Влияние поперечной силы. Устойчивость решетчатых стержней. 387
§ 3. Устойчивость в упругой среде 389
II. Об устойчивости прямоугольной пластины, нагруженной
в своей плоскости сжимающими силами 391
§ 4. Дифференциальное уравнение задачи 391
§ 5. Пластина на всех краях оперта и сжата силами Р —Ти равномерно распределенными на сторонах х 0, х а 393
804
содержание
§ б. Три края пластины оперты, сжимающие силы параллельны свободному краю 395
§ 7. Края х 0 и х а оперты, край у 0 защемлен, край у Ъ свободен 398
§ 8. Влияние упругого защемления на крае у 0 399
§ 9. Края х 0 и х а оперты; края у 0 и у Ь защемлены. 403 § 10. Устойчивость прямоугольной пластины, сжатой сосредоточенными
силами 404
III. Устойчивость плоской формы равновесия двутавровых балок. 408
§ 11. Введение 408
§ 12. Кручение двутавровой балки моментом, приложенным на конце. 409
§ 13. Формулировка основных уравнений 411
§ 14. Изгиб парой сил 412
§ 15. Балка, заделанная на одном конце и нагруженная сосредоточенной
силон на другом 416
§ 16. Балка, нагруженная сосредоточенной силой в середине пролета.419
IV. Устойчивость цилиндрической оболочки, подверженной
сжатию в направлении образующих 423
§ 17. Общие соотношения 423
§ 18. Осесимметричная форма выпучивания цилиндрической оболочки. 425 § T9. Деформация цилиндрической оболочки при отсутствии удлинений
и сдвигов 430
ПРИБЛИЖЕННЫЙ МЕТОД ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ УПРУГИХ СИСТЕМ
§ 1. Новый метод определения критических сил 434
2. Продольный изгиб стержня под действием собственного веса . . . 443
§ 3. Об устойчивости плоской формы изгиба балки 448
§ 4. Об устойчивости прямоугольной пластинки, сжатой двумя взаимно
противоположными силами 452
К ВОПРОСУ О ДЕФОРМАЦИЯХ И УСТОЙЧИВОСТИ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ
§ 1. Уравнения равновесия 457
§ 2. Цилиндрическая трубка со свободными краями 460
§ 3. Цилиндрическая трубка с опертыми краями 462
§ 4. Об устойчивости цилиндрической трубки 463
§ 5. Об устойчивости цилиндрической оболочки, опертой по двум образующим и двум параллельным кругам 470
ОБ УСТОЙЧИВОСТИ ПЛАСТИНОК, ПОДКРЕПЛЕННЫХ ЖЕСТКИМИ РЕБРАМИ
§ 1. Подкрепление сжатой прямоугольной пластинки ребрами, параллельными направлению сжатия 473
§ 2. Случай одного подкрепляющего ребра, проходящего посредине пластинки 478
§ 3. Случай двух ребер равной жесткости, делящих пластинку на три
равные части 484
§ 4. Пластинка, подкрепленная поперечными ребрами 487
СОДЕРЖАНИЕ
805
§ 5. Сжатая пластинка, подкрепленная посредине одним поперечным
ребром 490
§ 6. Сжатая пластинка, подкрепленная тремя равноудаленными поперечными ребрами 492
§ 7. Об устойчивости прямоугольной пластинки, подвергающейся действию касательных напряжений 495
§ 8. Подкрепление пластинки, подвергающейся действию касательных
усилий 499
ОБ УСТОЙЧИВОСТИ ПОДКРЕПЛЕННЫХ ПЛАСТИН
§ 1. Постановка задачи и метод решения 504
§ 2. Жесткость ребер при равномерном продольном сжатии 507
§ 3. Чистый сдвиг 615
§ 4. Приложение к расчету металлических балок со сплошной стенкой. 519 § 5. Эксцентричное сжатие 524
УСТОЙЧИВОСТЬ ПЛОСКОЙ ФОРМЫ ИЗГИБА КРИВЫХ СТЕРЖНЕЙ С ЦЕНТРАЛЬНОЙ ОСЬЮ В ФОРМЕ КРУГА
§ 1. Вывод дифференциального уравнения 52.9
§ 2. Случай свободных концов 530
§ 3. Заделанные концы 531
§ 4. Вывод выражения для критической нагрузки с помощью потенциальной энергии 532
§ 5. Нагрузка, непрерывно направленная к центру 533
РАСЧЕТ БИМЕТАЛЛИЧЕСКИХ ТЕРМОСТАТОВ
Введение 534
§ 1. Прогибы равномерно нагретой биметаллической полосы 534
§ 2. Напряжения, возникающие в биметаллической полосе при нагревании 536
§ 3. Изгиб, вызванный внешними силами 538
§ 4. Изгиб равномерно нагретой биметаллической пластины 541
Расчет полосы типа биметаллического термостата 541
§ 5. Свободный изгиб биметаллической полосы 541
§ 6. Искривленная биметаллическая полоса в жесткой рамке. 542
§ 7. Графическое решение 545
8. Численный пример 546
§ 9. Аналитическое решение 547
§ 10. Прогибы полосы после прощелкивания 548
§ 11. Температура, при которой происходит прощелкивание в обратном
направлении 549
§ 12. Искривленная биметаллическая полоса в податливой рамке. . 550
ПРОБЛЕМЫ УПРУГОЙ УСТОЙЧИВОСТИ
1. Введение 553
1. Устойчивость прямых и кривых стержней 557
2. Призматический стержень. Различные случаи выпучивания 557
3. Исследование призматического стержня энергетическим методом. 558
4. Учет больших прогибов 560
806
СОДЕРЖАНИЕ
5. Устойчивые и неустойчивые формы равновесия 6. Влияние поперечной силы 7. Стержни с начальной малой кривизной 8. Влияние эксцентриситета точки приложения силы 9. Эксцентриситет вместе с начальною кривизною 10. Продольный изгиб стержней за пределом пропорциональности. .
И. Опыты на продольный изгиб 12. Эмпирические формулы продольного изгиба 13. Устойчивость призматического стержня при переменной вдоль оси
сжимающей силе 14. Продольный изгиб стержней переменного поперечного сечения.
15. Продольный изгиб неразрезных стержней 16. Сопротивление продольному изгибу сжатого стержня, лежащего на
упругом основании 17. Продольный изгиб составных сжатых стержней 18. Устойчивость ферм 19. Продольный изгиб винтовых пружин 20. Устойчивость вала при кручении 21. Устойчивость замкнутого кругового кольца при действии равномерного внешнего нормального давления 22. Круговая арка под равномерным нормальным давлением II. Устойчивость плоской формы изгиба 23. Устойчивость плоской формы изгиба стержней с очень узким прямоугольным поперечным сечением 24. Устойчивость плоской формы изгиба двутавровых балок 25. Устойчивость плоской формы изгиба кривых стержней и колец . .
26. Устойчивость радиально сжатой круговой арки III. Устойчивость пластин и оболочек 27. Дифференциальные уравнения выпученной пластинки и энергетический критерий устойчивости 28. Устойчивость прямоугольной пластинки с опертыми краями при действии сжимающих сил, лежащих в срединной плоскости 29. Пластинки с тремя опертыми краями под действием сжимающих сил,
параллельных свободной стороне .
30. Края х 0 и х — а оперты, край у 0 заделан, край у Ъ свободен
31. Влияние упругой заделки края у 0 32. Края х 0 и х а оперты, края у 0 и у Ъ заделаны. .33. Устойчивость прямоугольной пластинки при действии касательных
сил в срединной плоскости 34. Устойчивость прямоугольной пластинки, изгибаемой в срединной
плоскости 35. Устойчивость подкрепленных пластинок 36. Устойчивость круговых пластинок 37. Устойчивость цилиндрической оболочки при равномерном наружном
давлении 38. Устойчивость цилиндрической оболочки под действием продольных
сжимающих сил 39. Устойчивость тонкостенной цилиндрической оболочки при кручении.
40. Устойчивость тонкостенной сферической оболочки при равномерном
радиальном наружном давлении Общая литература 562
564
565
566
567
569
572
576
578
582
585
590
594
599
602
604
605
607
608
608
612
614
616
618
618
621
622
624
625
625
626
629
631
635
636
640
642
642
643
СОДЕРЖАНИЕ
807
УСТОЙЧИВОСТЬ СТЕНОК ДВУТАВРОВЫХ БАЛОК
§ 1. Эксперименты 646
§ 2. Устойчивость прямоугольных пластин при чистом сдвиге. .651
§ 3. Устойчивость прямоугольных пластин при изгибе 653
§ 4. Устойчивость прямоугольных пластин при комбинированном действии изгиба и сдвига 656
§ 5. Приложения 658
§ 6. Ребра жесткости 659
ВЫПУЧИВАНИЕ ПОЛОГИХ СТЕРЖНЕЙ И СЛЕГКА ИСКРИВЛЕННЫХ ПЛАСТИН 662
ТЕОРИЯ ИЗГИБА, КРУЧЕНИЯ И УСТОЙЧИВОСТИ ТОНКОСТЕННЫХ СТЕРЖНЕЙ ОТКРЫТОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Введение 670
§ 1. Чистый изгиб призматических стержней 670
§ 2. Поперечный изгиб призматических стержней 672
§ 3. Чистое кручение тонкостенных стержней открытого поперечного сечения 682
§ 4. Неравномерное закручивание тонкостенных стержней 689
§ 5. Вычисление угла закручивания 695
§ 6. Комбинированное действие изгиба и кручения 699
§ 7. Крутильная форма потери устойчивости при центральном сжатии. 704 § S. Потеря устойчивости вследствие изгиба и кручения при центральном сжатии 708
§ 9. Выпучивание при кручении и изгибе стержня, находящегося в упругой среде 714
§ 10. Устойчивость тонкостенных стержней при изгибе и сжатии. . 720
Перечень работ С. П. Тимошенко по устойчивости,
не включенных в настоящий сборник 728
Э. И. Григолюк
С. П. ТИМОШЕНКО И ЕГО РАБОТЫ В ОБЛАСТИ УСТОЙЧИВОСТИ ДЕФОРМИРУЕМЫХ СИСТЕМ
1. Краткий биографический очерк 731
2. Энергетический метод 742
3. Стержни 754
4. Изгиб и кручение тонкостенных открытых стержней и проблема опрокидывания балок 759
5. Тонкие упругие пластины 771
6. Тонкие упругие оболочки 778
7. Устойчивость за пределом упругости 787
8. Нелинейные проблемы устойчивости и послекритическое поведение
упругих систем 794
9. Теория неоднородных конструкций 798
10. Общая характеристика 799
Степан Прокофьевич Тимошенко
устойчивость стержней, пластин И ОБОЛОЧЕК
М., 1971 г., 808 стр. с илл.
Редактор И. К. Снитко.
Техн. редактор С. Шкляр. Корректор В. П. Сорокина.
Сдано в набор 15Х 1970 г. Подписано к печати 1811 1971 г. Бумага 60 X907ie. Физ. печ. л. 50,5 1 вкл. Условн. печ. л. 50,625. Уч.-изд. л. 49,03. Тираж 8000 экз. Т-02154. Цена книги 3 р. 73 к. Заказ № 817.
Издательство «Наукаэ.
Главная редакция
физико-математической
литературы.
Москва, В-71, Ленинский проспект, 15.
Ордена Трудового Красного Знамени Ленинградская типография № 2 имени Евгении Соколовой Главполиграфпрома Комитета по печати при Совете Министров СССР Измайловский проспект, 29,