Author: Бабаков В.В.
Tags: авиация и космонавтика летательные аппараты ракетная техника космическая техника авиация самолетостроение авиатехника
Year: 1969
Text
В.В. БАБ
ПРОЕКТИРОВАНИЕ
ПОВЕРХНОСТЕЙ
КРИВЫМИ
ВТОРОГО
ПОРЯДКА
В САМОЛЕТОСТРОЕНИИ
В. В. БАБАКОВ
ПРОЕКТИРОВАНИЕ
ПОВЕРХНОСТЕЙ
КРИВЫМИ
ВТОРОГО
ПОРЯДНА
В САМОЛЕТОСТРОЕНИИ
ИЗДАТЕЛЬСТВО
«МАШИНОСТРОЕНИЕ»
Москва 1969
УДК 629.7.01.62—408.64 : 515/516
В книге излагается метод проектирования и задания слож-
ных поверхностей кривыми второго порядка на основе теоремы
Паскаля и Брианшона, приемов графических построений, про-
ективного дискриминанта, аффинных преобразований и спосо-
бов сопряжения кривых. Дается краткое описание методов
ортогональных сечений, пропорциональных кривых, степенных
уравнений, радиусографии и др., проводится сравнение их
с методом кривых второго порядка. Практическое применение
метода кривых второго порядка проиллюстрировано на зада-
нии сложных поверхностей основного тела, надстроек на нем,
стекателей, зализов, носков рулей и закрылков, воздушных
каналов.
Книга рассчитана на инженеров-конструкторов и техноло-
гов конструкторских бюро авиационной промышленности. Она
будет также полезна для аналогичных специалистов судо-
строительной и автомобилестроительной промышленностей.
Табл. 4. Иллюстр. 87. Библ. 11 назв.
Рецензент канд. техн, наук В. А. Андреев
3-18-6
149-69
ПРЕДИСЛОВИЕ
В ряде отраслей машиностроения, таких как самолетострое-
ние, автомобилестроение, судостроение, проектирование и зада-
ние сложных поверхностей весьма распространенная инженер-
ная задача.
При решении этой задачи в силу установившихся традиций
и, возможно, недостаточного обмена опытом различные отрасли
машиностроения используют разные методы.
В отечественном и зарубежном самолетостроении метод про-
ектирования и задания сложных плавных поверхностей при по-
мощи кривых второго порядка нашел широкое применение. Не-
которые конструкторские бюро отечественной авиационной про-
мышленности давно применяют этот метод. Так, например, ряд
поверхностей агрегатов самолетов Ту-104, Ту-124, Ту-114 и мно-
гих других спроектированы при помощи метода кривых второго
порядка.
Эстетичность кривых второго порядка была давно замечена
и архитекторами. Кривые второго порядка используются ими
при задании форм различных сводов. В частности, образующая
монумента покорителям космоса в Москве является кривой вто-
рого порядка.
Метод кривых второго порядка обеспечивает наименьшую
трудоемкость по сравнению с другими методами, простоту гра-
фических построений, обусловленную математичностью задания
линий, плавность и эстетичность линий, высокую точность зада-
ния поверхности и ее воспроизведения по чертежу и возмож-
ность использования аналитического расчета.
Однако в других отраслях промышленности метод кривых
второго порядка широкого применения еще не получил. Одной
из причин этого является недостаточность информации о широ-
ких возможностях этого метода и преимуществах его использо-
вания при проектировании и задании сложных поверхностей
В отечественной литературе обобщен лишь опыт использования
метода кривых второго порядка в работах плазовых цехов и
почти не отражен опыт его применения конструктором, хотя
именно им определяется как сама форма поверхности агрегатов
самолета, так и способы ее задания и построения.
Предлагаемая читателю книга обобщает опыт использования
метода кривых второго порядка в одном из отечественных сама-
2007
3
летостроительных конструкторских бюро. В ней изложены тео-
ретические основы этого метода; описаны последовательность и
приемы, которыми пользуется конструктор, и даны некоторые
рекомендации по заданию сложных поверхнрстей, характерных
для агрегатов современного самолета, с иллюстрацией на ряде
примеров.
/Многообразие форм сложных поверхностей самолетных агре-
гатов дает основание полагать, что многолетний опыт авиацион-
лой промышленности в использовании метода кривых второго
порядка может быть с успехом использован и в других отраслях
машиностроения.
Следует заметить, что хотя метод кривых второго порядка
прочно вошел в практику самолетостроения, его возможности
изучены еще далеко не полностью. Так, например, еще недоста-
точно исследованы вопросы, связанные с сопряжением кривых,
с использованием цифровых вычислительных машин для анали-
тического расчета, станков с программным управлением и др.
Дальнейшее практическое использование и изучение метода по-
зволит более полно и по достоинству оценить его широкие воз-
можности.
Автор приносит глубокую благодарность всем товарищам,
просмотревшим рукопись книги и давшим много ценных замеча-
ний, в частности, инициатору использования метода кривых вто-
рого порядка в отечественном самолетостроении инженеру
В. П. Сахарову и канд. техн, наук В. А. Андрееву.
Глава I
МЕТОДЫ, ПРИМЕНЯЕМЫЕ
ПРИ ПРОЕКТИРОВАНИИ И ЗАДАНИИ
СЛОЖНЫХ ПОВЕРХНОСТЕЙ
При проектировании и задании сложных поверхностей конст-
руктор может пользоваться различными методами. Каждому из
них присущи свои достоинства и недостатки. С целью сравнения
существующих методов между собой рассмотрим их на примере
построения одной и той же простой поверхности.
1. МЕТОД ОРТОГОНАЛЬНЫХ СЕЧЕНИЙ
Самым старым методом проектирования плавных поверхно-
стей является метод ортогональных сечений или иначе метод
батоксов (вертикальных продольных сечений) и горизонталей
(горизонтальных продольных сечений). Он основан на примене-
нии законов начертательной геометрии. Метод появился с самого
начала развития судостроения и до сих пор успешно применяется.
Сущность этого чисто графического метода сводится к построе-
нию большого количества поперечных и продольных сечений
поверхности в трех проекциях. Контуры этих сечений взаимно
корректируются по проекциям большого количества отдельных
точек для получения плавных линий. Расстояния между плоско-
стями поперечных сечений, плоскостями батоксов и горизонталей
выбираются в зависимости от величины агрегата и кривизны его
поверхности. Чем больше сечений, тем точнее задана поверх-
ность.
Проектирование и задание поверхности производится в сле-
дующей последовательности (рис. 1):
1) при помощи лекала или гибкой рейки вычерчиваются за-
данные основные продольные линии (в данном примере главный
батокс — батокс 0 и главная горизонталь — горизонталь 0);
2) на профильной проекции откладываются координаты
исходных точек (по батоксу 0 и горизонтали 0) для выбранных
поперечных сечений и намечаются от руки обводы этих сечений;
3) на проекциях (на которых они прямые) наносятся следы
плоскостей батоксов и горизонталей;
5
4) с намеченных от руки обводов сечений снимаются коорди-
наты точек, по которым эти точки переносятся на боковую про-
екцию батоксов. Полученные точки соединяются кривыми ли-
ниями. Точно так же на горизонтальной проекции строятся кри-
вые горизонталей;
Рис. 1. Метод ортогональных сечений
5) координаты отдельных точек, выпадающих из плавных
кривых батоксов и горизонталей, корректируются до тех пор,
пока кривые батоксов, горизонталей и поперечных сечений не
станут плавными. Этот этап работы является самым трудоемким
и требует от конструктора определенного навыка;
6) через уточненные точки при помощи лекала или гибкой
рейки проводятся окончательные кривые батоксов, горизонталей
и поперечных сечений;
6
7) на сетке батоксов и горизонталей соответствующих сече-
ний производятся замеры координат точек и заполняется таб-
лица.
Метод ортогональных сечений дает наглядное представление
о поверхности, но объективной оценки плавности поверхности он
не дает, так как единственным критерием плавности является
опытный глаз конструктора. Оценка производится только ви-
зуально. Этот метод не позволяет точно воспроизвести поверх-
ность по табличным данным. В практике самолетостроения для
крупных агрегатов типа фюзеляжа самолета расстояния между
поперечными сечениями принимают равными около 500 мм,
а расстояния между плоскостями батоксов и горизонталей —
504-100 мм, при этом расхождения с оригиналом при повторном
построении по табличным данным достигают 10 мм. В отдель-
ных случаях метод ортогональных сечений применяется и сей-
час, особенно для прикидочных построений. Методики аналити-
ческого расчета он не имеет.
2. ЛУЧЕВОЙ МЕТОД
Лучевой метод [9], [10] был предложен в судостроительной
промышленности Г. Е. Павленко*. Существо метода заклю-
чается в представлении формы поверхности в виде двух семейств
пересекающихся прямых (лучей) при криволинейном проекти-
ровании элементов поверхности на плоскость. Основные сечения
(шпангоуты, горизонтали) на лучевом чертеже изображаются
прямыми линиями, что в известной степени обеспечивает плав-
ность обводов. Так как на лучевом чертеже проекции основных
сечений изображаются одновременно, то не требуется произво-
дить взаимной корректировки точек поверхности на всех трех
проекциях, как это делается в методе ортогональных сечений,
где применяется плоскопараллельное проектирование.
Для проектирования поверхности лучевым методом должны
быть заданы четыре геометрических условия. Они однозначно
определяют поверхность.
На рис. 2 показан пример задания и построения поверхности
лучевым методом. Поверхность здесь задана следующими
четырьмя условиями: горизонталью 0, батоксом 0, обводами се-
чений 1 и 2. Построение производится в следующей последова-
тельности:
1) на лучевом чертеже под произвольным углом наклона к го-
ризонтали проводится прямая, изображающая лучевую гори-
зонталь 0;
2) с горизонтали 0 на профильной проекции на лучевую го-
ризонталь 0 проектируются точки, соответствующие абсциссам
сечений 1 и 2;
* Г. Е. Павленко, Геометрический анализ и проектирование формы
корабля, Морской сборник, 1926. № 6.
7
3) через полученные точки проводятся прямые лучевых сече-
ний 1 и 2 (луч для сечения 1 горизонтален);
4) аналогичные построения делаются для остальных горизон-
талей;
5) на лучевую горизонталь 0 проектируется соответствующая
абсцисса искомого сечения Л;
6) через полученную точку проводится прямая, соответствую-
щая лучевому сечению Л;
7) абсциссы точек пересечения лучевого сечения Л с луче-
выми горизонталями есть соответствующие абсциссы искомого
сечения Л.
В случае если батокс 0 на боковой проекции перестает быть
параллельным горизонталям, построение несколько усложняется
(рис. 3). Для нахождения абсцисс сечений Б и В необходимо
через точки батокса 0, соответствующие этим сечениям, провести
дополнительные горизонтали, затем воспроизвести дополнитель-
ные горизонтали и сечения Б и В на лучевом чартеже и указан-
ным выше способом найти соответствующие абсциссы искомых
сечений Б и В.
В качестве четырех исходных данных, определяющих форму
поверхности, могут быть: батокс 0, сечение 0, кривая тангенсов
углов наклона лучевых горизонталей (tga) и кривая проекций
на плоскость батокса 0 (плоскость симметрии) вершин лучевых
шпангоутов (Г. Е. Павленко кривую tga назвал директрисой,
а кривую проекций вершин лучевых шпангоутов — радиантой).
8
Поверхность при лучевом методе может быть задана и дру-
гой комбинацией четырех исходных данных.
В случае если исходные данные удается выразить аналити-
чески, то можно составить уравнение всей поверхности и мате-
матическим путем определить любую точку поверхности.
Диапазон практического применения лучевого метода следует
считать ограниченным. Так, в ряде случаев для получения опре-
Рис. 3. Построение для случая, когда батокс 0 на боковой проекции
не параллелен горизонталям
деленной формы обводов сечений может потребоваться задание
горизонталей или сечений на лучевом чертеже не прямыми ли-
ниями, а кривыми. Это приводит к значительному усложнению
графических построений, сводящих на нет преимущество луче-
вого метода. Подобное усложнение построений наступает и в слу-
чаях, когда нулевой батокс (килевая линия) представляет со-
бой не прямую линию, параллельную горизонталям (ватерли-
ниям), а кривую линию.
В этих случаях практически не применим и аналитический
расчет из-за сложности математических выражений исходных
линий.
В силу перечисленных трудностей лучевой метод не получил
применения в самолетостроении.
3. МЕТОД ПРОПОРЦИОНАЛЬНЫХ КРИВЫХ
Частным случаем лучевого метода является метод пропор-
циональных кривых.
9
В основу метода положена «струйная теория», опубликован-
ная И. П. Алымовым *, которая использовалась для образования
подводной части судовых поверхностей [10]. Метод нашел при-
менение и в автомобилестроительной промышленности [5], [6], [7],
где и получил название «метода пропорциональных кривых».
Базируется он на пропорциональности координат соответствую-
щих точек линий и подобии фигур. Каждое последующее сече-
ние поверхности строится по тому же закону, что и исходное
сечение, т. е. соответствующие координаты сечений пропорцио-
Рис. 4. Метод пропорциональных кривых
нальны. Построение ведется при помощи «ключей пропорцио-
нальности». Такими ключами обеспечиваются плавные законо-
мерные переходы поверхности из одного сечения в другое. При
помощи метода пропорциональных кривых решаются следующие
основные задачи:
— построение сечений, подобных одному заданному (исход-
ному) сечению;
— построение промежуточных сечений между двумя задан-
ными сечениями.
Проектирование и задание поверхности производится в сле-
дующей последовательности (рис. 4):
1) при помощи лекала или гибкой рейки строятся заданные
основные контурные линии (батокс 0, горизонталь 0) и исходное
сечение (сечение А);
2) для построения искомого сечения (например, сечения В)
на профильную проекцию переносятся с боковой и горизонталь-
ной проекций точки Т батокса 0 и Т\ горизонтали 0 этого сечения;
* И. П. А л ы м о в., Очерки системы струйного образования судов, Мор-
ской сборник, 1879, № 9, 10, 12.
10
3) выбрав произвольные точки О и Оь строят ключи пропор-
циональности OCD и O\EF\
4) взяв произвольную точку на контуре исходного сечения
(например, точку Л4), проектируют ее на ключи, как это показано
на рис. 4, и получают точку Мх на контуре искомого сечения.
Таким же способом определяют положения необходимых для
построения контура искомого сечения точек и при помощи лекала
или гибкой рейки строят обвод сечения;
5) при помощи аналогичных ключей строят обводы остальных
сечений;
6) основные контурные линии (батокс 0, горизонталь 0) и
исходное сечение задаются на чертеже координатами отдельных
точек. Разбираемый пример является простейшим, так как все
сечения в нем подобны одному исходному сечению. Если же
исходными являются не одно сечение, а несколько, то построения
значительно усложняются. В ряде случаев в качестве ключей
пропорциональности приходится использовать не прямые, а кри-
вые линии. Кривизна их подбирается исходя из требуемой фор-
мы поперечных сечений. Это значительно усложняет графиче-
ские построения.
Если исходные контурные линии заданы аналитически, то
можно составить уравнение такой поверхности. Однако для
сложной поверхности оно слишком громоздко для практического
использования.
Метод пропорциональных кривых в самолетостроительной
промышленности применения не получил.
4. МЕТОД СТЕПЕННЫХ УРАВНЕНИЙ
В судостроении нашли применение для задания поверхности
судов методы с использованием параболических кривых. Наи-
большее распространение из них получили кривые, опубликован-
ные И. А. Яковлевым [9], [10], позволяющие отображать различ-
ные судовые обводы. Аналитическое выражение этих кривых
имеет вид
y=kxm(l—xn)P9
где k, т, п, р — постоянные положительные числа.
В авиационной промышленности был использован частный
случай кривых Яковлева, который был положен в основу метода,
получившего название «метода степенных уравнений» [1].
Сущность его заключается в аналитическом задании про-
дольно-лучевых сечений кривыми, преобразованные уравнения
которых имеют вид
г х (2А — х)
У Утах I 77
L J
или
и
Для задания линии степенным уравнением (рис. 5) необхо-
димы четыре исходных данных. Для первого уравнения
(рис. 5, а) —начальная точка О кривой, одна промежуточная
точка А, конечная точка В и касательная к кривой в этой точке.
Рис. 5. Данные для составления степенного урав-
нения
Для второго уравнения (рис. 5,6) —начальная и конечная точки
кривой и касательные в этих точках. Система координат выби-
рается так, чтобы начало координат проходило через начальную
точку кривой, а ось абсцисс была параллельна касательной
к кривой в конечной точке.
Рис. 6. Характер кривых в зависимости от значения
показателя степени
Изменение характера кривых в зависимости от величины
показателей степени т или п показано на рис. 6. При значениях
0<т<1 для первого уравнения и 1</1<оо для второго уравне-
ния кривые обращены выпуклостью вверх. При 0<т<1 для
первого уравнения касательная к кривой в начальной точке вер-
тикальна и совпадает с осью у (при т=\ она становится наклон-
ной, а при т>1 — горизонтальной). В частных случаях кривые
12
являются кривыми второго порядка (при т = 0,5— эллипсом,
при т= \ или п = 2 — параболами).
Тип уравнения выбирается в зависимости от исходных
данных.
Рассмотрим применение метода степенных уравнений к по-
верхности, изображенной на рис. 1 и 4. Проектирование и зада-
ние поверхности производится следующим образом (рис. 7):
1) намечаются зоны использования первого или второго
уравнений (в нашем примере в зоне I используется первое урав-
нение, а в зоне II — второе);
2) по исходным данным рассчитываются и строятся основные
продольные линии (главный батокс 0, главная горизонталь 0) и
поперечные сечения 1 и 2. Показатели степеней для определения
ординат батокса 0 находятся по следующим формулам:
для зоны I
1 , А(2В — А)
g £2
для зоны II
„ _ C-tg^
/Дт- ’ .
C-tg<pi —
Ординаты точек батокса 0 определяются по формулам:
для зоны I в сечении М
У Mi —
хм (2В хм)
В2
для зоны II в сечении L
Аналогично рассчитываются координаты горизонтали 0 и исход-
ных поперечных сечений 1 и 2\
3) производится разбивка лучей, в плоскостях которых будет
производиться расчет координат точек контуров требуемых попе-
речных сечений;
4) ординаты точек (ум) в плоскостях лучей и показатели сте-
пеней уравнений для зоны I определяются аналогично ордина-
там батокса 0 и горизонтали 0. Для определения показателей
степеней уравнений исходные размеры (ац, 6ц и т. д.) берутся
в плоскостях лучей;
5) для задания поверхности в зоне II определяются углы ф
наклона касательных продольно-лучевых сечений. В нашем при-
мере заданы <pi и ф5, т. е. углы наклона касательных для про-
дольно-лучевых сечений в плоскостях луча I (батокс 0) и луча V
(горизонталь (?). Для определения углов <р остальных продольно-
13
Рис. 7. Метод степенных уравнений
лучевых сечений задаются графиком изменения tgcp при значе-
ниях ф ОТ (£1 до ф5;
6) ординаты точек (z/L) в плоскостях лучей и показатели сте-
пеней уравнений для зоны II определяются аналогично ордина-
там батокса 0 и горизонтали 0. Для определения показателей
степеней уравнений исходные размеры (6ц, tg ф2 и т. д.) берутся
в плоскостях лучей;
7) по рассчитанным такими способами ординатам продольно-
лучевых сечений на требуемых дистанциях строятся контуры
поперечных сечений;
8) положения исходных точек основных контурных линий
(батокса 0 и горизонтали 0) и исходных поперечных сечений 7
и 2 задаются на чертеже размерами, а промежуточных попереч-
ных сечений — таблицей.
Метод степенных уравнений по существу является методом
аналитическим. Метод сложен и трудоемок, поэтому для прики-
дочных построений он мало пригоден и широкого распростране-
ния не получил.
5. МЕТОД РАДИУСОГРАФИИ
Метод радиусографии применен в авиационной промышлен-
ности (предложен инж. Д. С. Китаиновым). Сущность его заклю-
чается в построении и задании контуров основных продольных
и поперечных сечений поверхности сопряженными дугами различ-
ных окружностей. Для построения контуров поперечных сечений
задаются линии центров дуг окружностей. Хотя дуги окружно-
стей и являются кривыми второго порядка, метод радиусографии
не относится к методу кривых второго порядка, так как основан
на совершенно других принципах. В нем используется как чисто
графический способ построения, так и построение по аналитиче-
скому расчету.
На рис. 8 показано задание методом радиусографии той же
поверхности, что и на рис. 1, 4 и 7. Проектирование и задание
производится в следующей последовательности:
1) по исходным данным вычерчиваются основные продоль-
ные линии (в данном примере батокс 0) и намечаются обводы
поперечных сечений;
2) в зависимости от характера поперечных сечений с по-
мощью построений, выполняемых циркулем, определяется по-
требное количество сопряженных дуг различных окружностей,
из которых будут состоять обводы поперечных сечений (в дан-
ном примере достаточно двух дуг с радиусами г\ и г2);
3) намечаются линии положения центров дуг окружностей
вдоль поверхности, что и определяет способ построения сечений
(в данном примере линия центров для ri и величина сектора, рав-
ная 19° для радиусов г2);
15
4) для основных и вспомогательных продольных линий
(в данном примере батокс 0 и линия центров) подбираются со-
пряженные дуги окружностей. С целью уменьшения величины
радиусов дуг и их количества применяется масштабное сжатие
продольных линий. В данном примере сжаты хвостовая часть
батокса 0 и линия центров;
5) по уточненным таким образом исходным точкам оконча-
тельно строятся поперечные сечения;
6) устанавливаются размеры для линии центров и радиусов
дуг сопряженных окружностей основных продольных линий.
Один из основных недостатков метода радиусографии заклю-
чается в недостаточной плавности изменения кривизны линий
(так как они задаются сопряженными дугами различных окруж-
ностей, причем сопряжение их осуществляется только по общей
касательной). Недостаточная плавность особенно заметна на
примере овала, состоящего из сопряженных дуг окружностей.
Даже малоопытный глаз всегда отличит овал (по угловатости
его обвода) от эллипса, являющегося единой кривой второго
порядка с плавным изменением кривизны.
Графические построения обводов методом радиусографии
довольно громоздки, так как для обводов продольных линий и
поперечных сечений, как правило, требуется задание нескольких
линий центров. Необходимо добавить, что достижение высокой
точности графического построения дуги окружности большого
радиуса само по себе является довольно сложной задачей и тре-
бует создания специального инструмента.
В силу этих соображений метод радиусографии широкого
применения не получил.
6. МЕТОД КРИВЫХ ВТОРОГО ПОРЯДКА
Метод кривых второго порядка применяется в авиационной
промышленности. Сущность его состоит в задании кривыми вто-
рого порядка продольных линий, обводов поперечных сечений,
а также вспомогательных линий для построения. поверхности.
Сами линии могут быть построены графическими приемами или
рассчитаны аналитически. Как расчет,.так и способы графиче-
ских построений, основаны на свойстве кривых второго порядка,
в соответствии с которым для их определения достаточно пяти
условий. В наиболее часто встречаемом случае задаются три
точки кривой (начальная Л, промежуточная В и конечная С)
и две касательные (в начальной и конечной точках). Графиче-
ское построение кривой второго порядка по этим условиям,
основанное на теоремах проективной геометрии Паскаля и
Брианшона, осуществляется следующим способом (рис. 9):
а) проводятся основные лучи—луч I из точки А через
точку В и луч II из точки С через точку В (точка В является
промежуточной заданной точкой кривой);
2 2007
17
б) проводится произвольная прямая — луч а из точки А до
пересечения с лучом II (в точке £>);
в) из точки О (вершины) проводится прямая через точку D
до пересечения с лучом I (в точке Е);
г) из точки С проводится прямая через точку Е до пересече-
ния ее с лучом а. Точка пересечения F есть точка, принадлежа-
щая искомой кривой второго порядка.
В зависимости от потребного количества точек построение
повторяется поворотом луча а вокруг точки А в промежутке от
касательной Л О до точки В. Аналогичное построение выпол
Рис. 9. Графическое построение кривой второго
порядка
няется для определения точек правой ветви кривой ВС, для чего
произвольные лучи проводятся уже из точки С.
На рис. 10 показан пример задания методом кривых второго
порядка той же поверхности, что и на рис. 1, 4, 7, 8. Проектиро-
вание и задание производится в следующей последовательности:
1) при помощи лекала или гибкой рейки вычерчиваются пред-
варительно основные продольные линии обвода (батокс 0 и гори-
зонталь 0) и намечаются обводы требуемых поперечных сечений:
2) в зависимости от характера поперечных сечений выби-
рается способ задания их обводов кривыми второго порядка.
Для определения способа используются приемы графических по-
строений. В данном примере выбрано построение по заданной
точке (луч Л);
3) при помощи лекала или гибкой рейки намечаются вспомо-
гательные линии, необходимые для построения обводов попереч-
ных сечений (луч Л);
4) для намеченных основных и вспомогательных продольные
линий (в данном примере батокс О, горизонталь 0 и луч Л) под-
бираются кривые второго порядка. Подбор ведется при помощи
графических построений, о которых рассказано выше;
18
5) по уточнённым таким способом исходным точкам оконча-
тельно строятся обводы поперечных сечений;
6) устанавливаются размеры для необходимых точек, задаю-
щих основные и вспомогательные линии (пять условий для каж-
дой кривой).
Рис. 10. Метод кривых второго порядка
Промежуточная точка кривой второго порядка может зада-
ваться не ее координатами, а при помощи относительной вели-
чины — проективного (графического) дискриминанта f (рис. 11).
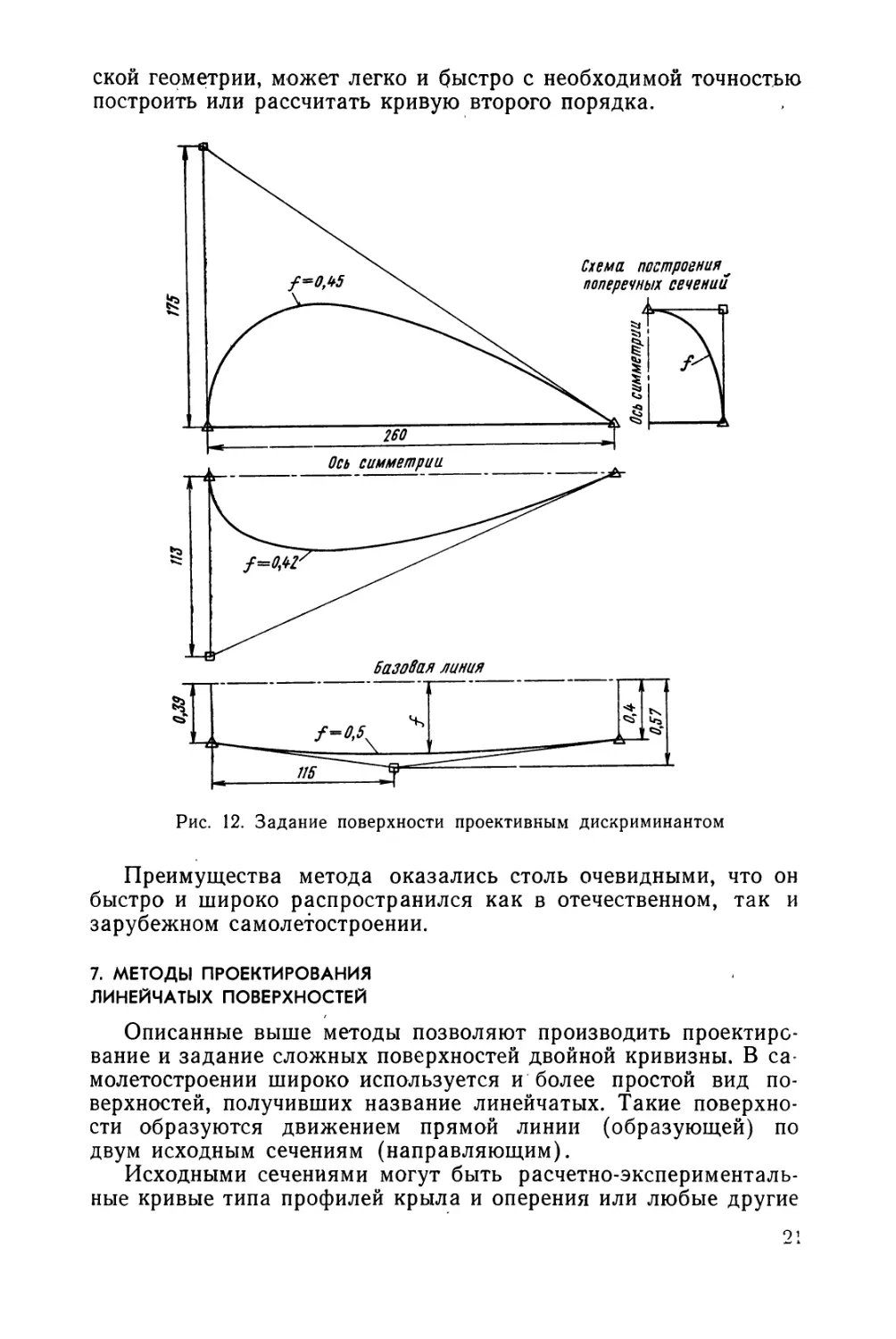
Задание той же поверхности кривыми второго порядка, что
и на рис. 10, но при помощи проективного дискриминанта пока-
2*
19
'зано на рис. 12. Здесь вместо' координат заданных промежуточ-
ных точек основные продольные линии (батокс 0 и горизон-
таль О') задаются величиной проективного дискриминанта. Для
задания и построения обводов поперечных сечений используются
-не заданные точки, определяемые лучом А, а проективный ди-
скриминант, задаваемый графиком. Сама кривая графика
дискриминантов сечений, в свою очередь, задается как кривая
второго порядка или в частном случае как прямая.
Рис. 11. Проективный дискриминант
При воспроизведении поверхностей, заданных кривыми вто-
рого порядка, совпадение их с первоисточником получается
практически полным. Точность воспроизведения определяется
главным образом точностью применяемого инструмента.
Большим достоинством метода является возможность лег-
кого и быстрого построения обводов любого количества попереч-
ных сечений путем задания небольшого количества продольных
линий, соединяющих исходные точки. Благодаря этому полу-
чается наглядное изображение на чертеже проектируемой
формы.
Свойство кривых второго порядка подчиняться аффинным
преобразованиям позволяет отказаться при больших размерах
проектируемого изделия от построения продольных линий обво-
дов поверхности в натуральную величину. Для этого строится
«сжатый контур» продольных линий, на котором все продоль-
ные линии, заданные кривыми вторюго порядка и прямыми, мас-
штабно сжимаются с сохранением натуральных величин орди-
нат. Применение «сжатого контура» позволяет сократить потреб-
ные для построений производственные площади.
Кривые второго порядка обладают исключительно эстетиче-
ским видом. Характерно, что кривая, проведенная от руки высо-
коквалифицированным проектировщиком (конструктором или
плазовиком) почти в точности совпадает с кривой второго
порядка.
Благодаря доступности кривых второго порядка технике гра-
фических построений и аналитическому расчету каждый, обла-
дающий элементарными знаниями начертательной и аналитиче-
20
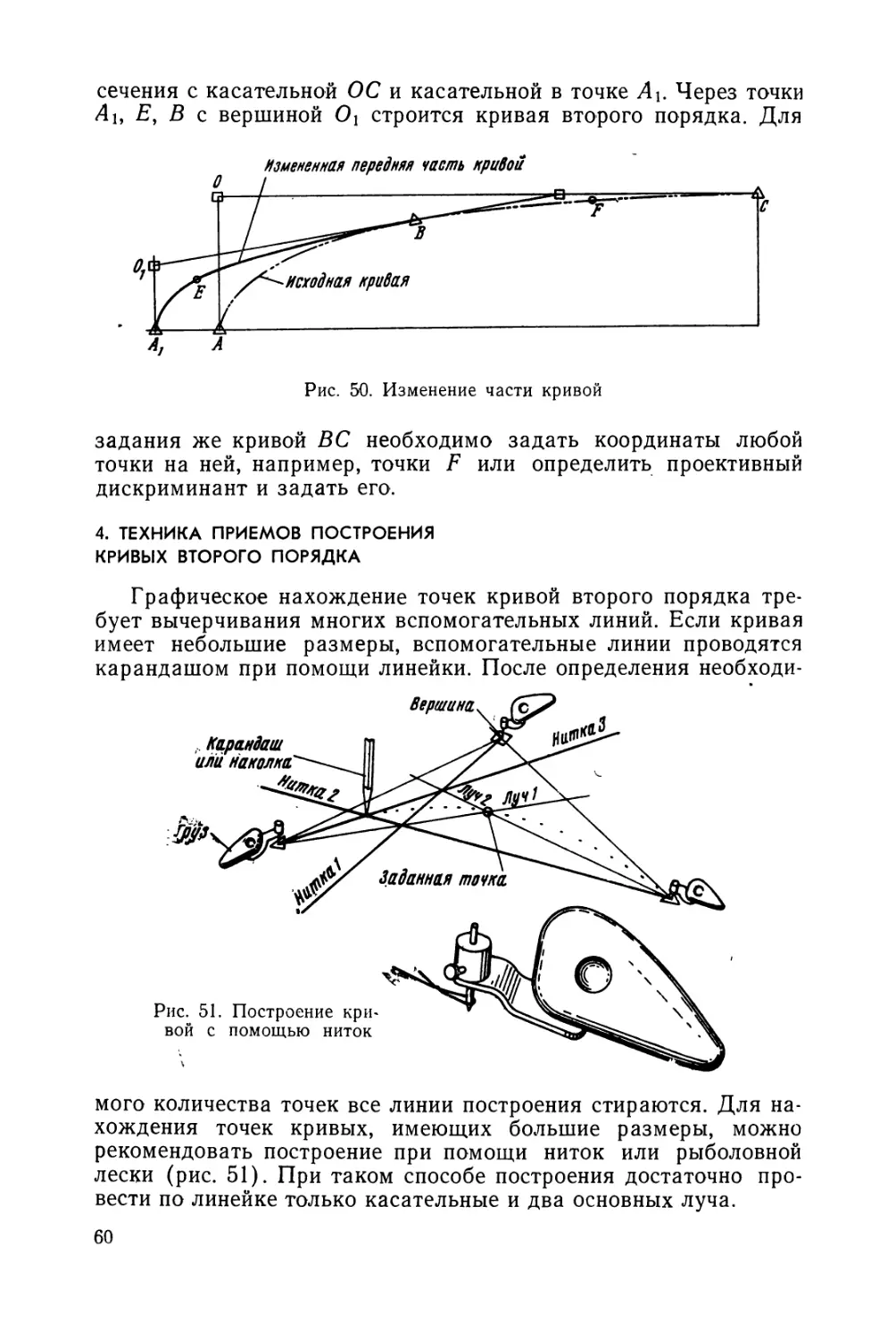
ской геометрии, может легко и быстро с необходимой точностью
построить или рассчитать кривую второго порядка.
Рис. 12. Задание поверхности проективным дискриминантом
Преимущества метода оказались столь очевидными, что он
быстро и широко распространился как в отечественном, так и
зарубежном самолетостроении.
7. МЕТОДЫ ПРОЕКТИРОВАНИЯ
ЛИНЕЙЧАТЫХ ПОВЕРХНОСТЕЙ
Описанные выше методы позволяют производить проектиро-
вание и задание сложных поверхностей двойной кривизны. В са-
молетостроении широко используется и более простой вид по-
верхностей, получивших название линейчатых. Такие поверхно-
сти образуются движением прямой линии (образующей) по
двум исходным сечениям (направляющим).
Исходными сечениями могут быть расчетно-эксперименталь-
ные кривые типа профилей крыла и оперения или любые другие
21
кривые. Они задаются в виде таблиц координат или другими
методами, в том числе и кривыми второго порядка.
Образующие могут соединять точки исходных сечений, соот-
ветствующие одинаковым долям хорд или их проекций
(рис. 13,а), или же соединять точки исходных сечений с одина-
ковыми наклонами касательных (рис. 13, б).
Рис. 13. Линейчатые поверхности
В последнем случае7 линейчатые поверхности называются
торсовыми. Особенностью торсовых поверхностей является то,
что они разворачиваются на плоскость, т. е. могут быть полу-
чены простой гибкой листового материала.
Искомые точки и сечения линейчатых поверхностей легко
находятся с помощью графических построений приемами начер-
тательной геометрии.
С целью сокращения производственных площадей и повыше-
ния точности построений разработаны аналитические методы
расчета линейчатых поверхностей [1]. Аналитический расчет по-
зволяет определять координаты любой точки поверхности, каса-
тельные в них, определять развертки и т. д., то есть аналитически
производить полную увязку линейчатой поверхности.
а СОВРЕМЕННЫЕ ТРЕБОВАНИЯ К МЕТОДАМ
ПРОЕКТИРОВАНИЯ И ЗАДАНИЯ СЛОЖНЫХ ПОВЕРХНОСТЕЙ
Поиски новых методов проектирования и задания плавных
поверхностей явились следствием все возрастающих требований,
предъявляемых к поверхностям. Основными требованиями яв-
ляются:
— наглядность изображения поверхности на чертеже, необ-
ходимая для оценки ее на начальном этапе проектирования. На
этом этапе поверхность можно оценить только визуально. Ника-
22
кие расчетные таблицы или аналитические выражения не могут
дать наглядного представления о сложной поверхности, а сле-
довательно, не позволяют и оценить ее;
— возможность применения простых приемов графических
построений, обеспечивающих наименьшую трудоемкость. Это
условие выдвигается самой сущностью проектирования поверх-
ности, которое теснейшим образом связано с конструктивной
разработкой и сводится к нахождению компромисса между ря-
дом противоречивых требований. Например, для самолетострое-
ния противоречивые требования выдвигают аэродинамика, проч-
ность, технологичность, вес и удобство эксплуатации. Так как
к такому компромиссу приходят постепенно, по мере выяснения
всех требований, то поверхность в процессе проектирования под-
вергается многократным значительным изменениям. Возмож-
ность быстрого изменения форм поверхности может обеспечить
только метод с малыми затратами труда;
— гарантированная плавность и эстетичность линий, т. е.
закономерное изменение кривизны. Гарантированную плавность
можно достичь только в случае возможности выражения кривых
с помощью уравнений, т. е. возможности аналитически прове-
рить изменение кривизны;
— возможность точного воспроизведения поверхности по
одному и тому же чертежу, определяемая условиями взаимоза-
меняемости. Из практики самолетостроения, например, известно,
что при задании поверхности методом батоксов и горизонталей
положения точек поверхности одного и того же агрегата, по-
строенного на разных заводах по одному и тому же чертежу,
отличаются на 10—15 мм. а при задании методом кривых вто-
рого порядка — всего на 0,2—0,5 мм\
— возможность аналитического задания и расчета, позво-
ляющая получить координаты точек поверхности практически
с любой точностью. Это требование сейчас становится актуаль-
ным, так как в промышленность широко внедряются электрон-
ные вычислительные машины и станки с программным управле-
нием, призванные значительно ускорить как процесс проектиро-
вания поверхности, так и изготовление изделия в целом;
— минимальные размеры производственных площадей для
расчерчивания на плазе линий, определяющих поверхность.
Это достигается заменой плазов продольных линий сжатыми
контурами и применением таких приемов графических построе-
ний, в которых вспомогательные линии построения не выходят
из размеров контуров агрегата. Экономии производственных пло-
щадей способствует и использование аналитического расчета.
Из сопоставления разобранных методов проектирования и
задания сложных плавных поверхностей видно, что наиболее
полно этим требованиям отвечает метод кривых второго порядка,
поэтому его можно считать наиболее перспективным,
Г л ава II
ОСНОВНЫЕ СВЕДЕНИЯ
ИЗ ТЕОРИИ КРИВЫХ
ВТОРОГО ПОРЯДКА
ПОНЯТИЕ О КРИВЫХ ВТОРОГО ПОРЯДКА
Всякое алгебраическое уравнение можно освободить от ра-
дикалов и дробей, если таковые имеются, после чего это урав-
нение приобретает вид многочлена. Такой многочлен сокра-
щенно можно обозначить как
где А — постоянное число;
s, t — целые положительные числа или нули.
Каждый член Axsy* многочлена имеет определенное измере-
ние, равное сумме показателей при х и у, т. е. s + Л Наивысшее из
измерений всех членов уравнения называется степенью этого
уравнения. Если алгебраическая линия изображается в декарто-
вых (прямоугольных) координатах уравнением n-й степени, то
она называется линией n-го порядка.
Линией (или кривой) второго порядка называется линия,
уравнение которой в декартовых координатах имеет вторую сте-
пень относительно текущих координат.
Общее уравнение второй степени (кривой второго порядка)
с двумя неизвестными переменными имеет вид
Ax2 + Bxy + Cy2+Dx + Ey+F = G. (1)
Доказывается, что уравнение этого вида соответствует лишь
линиям эллиптического, гиперболического и параболического ти-
пов, т. е. кривым конических сечений [8].
Кривые второго порядка называются также кривыми кониче-
ских сечений, потому что они могут быть получены пересечением
правильного кругового конуса плоскостями, не проходящими че-
рез его вершину. При пересечении получается одна из трех кри-
вых [3]: эллипс (в частном случае окружность), парабола или
гипербола (рис. 14).
Если секущая плоскость пересекает все образующие конуса,
то кривая есть эллипс (в частном случае, когда секущая плос-
24
кость перпендикулярна оси конуса, — окружность); если она
параллельна только одной образующей, то кривая — парабола,
а двум — гипербола.
Если менять в известных пределах положение секущей плос-
кости (см. рис. 14), то мы получим бесчисленное множество кри-
вых второго порядка.
Рис. 14. Конические сечения
По значениям коэффициентов в общем уравнении (1) кривой
второго порядка можно определить тип кривой (эллиптический,
гиперболический или параболический). Критерием для этого
служит величина В2—4АС, называемая аналитическим дискри-
минантом.
Если В2—4АС<0— кривая эллиптического типа,
В2—4АС>0—кривая гиперболического типа,
В2—4ЛС = 0— кривая параболического типа.
Общее уравнение кривой второго порядка (1) имеет шесть
коэффициентов (Л, В, С, D, Е, F). Коэффициент F (свободный
член) характеризует положение кривой относительно начала
координат.
Если все члены уравнения (1) разделить на F, то оно при-
мет вид
ax2 + bxy + cy2 + dx + ey + 1 =0. (2)
Из уравнения (2) видно, что кривая второго порядка опре-
деляется значением пяти коэффициентов (a, b, с, d, е), т. е. пятью
геометрическими условиями. Действительно, пусть нам известны
координаты пяти точек, принадлежащих кривой второго по-
рядка:
Л(*1, У1); ^(*2, Уг); ^з(*з, уз);
Л(*4, У4); Рб(*5, Уб).
25
Подставляя значения координат этих точек в общее уравне-
ние (2) кривой второго порядка, получим систему пяти урав-
нений:
ах* 4- Ьхг у! + сyj + dxt -\-еУ1 + 1=0,
ах2 Н" Ьх^уч + cyi, 4- dx3 -|- е у 2 ^-1 = 0,
ах23 4- Ьх3у3 4- су23 dx3 4- еу3 4-1 = 0,
' a-xl + bx^-^cyl+dx^ey^A^O,
ах23 + Ьх3у5 4- с у25 4- dx5 4- е у5 4- 1 = 0.
Решая совместно эти уравнения, мы получим такие значения
коэффициентов (a, b, с, d, е), при которых координаты каждой
из заданных пяти точек (Pi, Р2, Рз, Р-ь Р5) будут удовлетворять
уравнению (2).
Эта очень важная особенность кривых второго порядка (до-
статочность для определения кривой пяти геометрических усло-
вий) является аналитической основой разбираемых ниже графи-
ческих построений.
2. ТЕОРЕМЫ ПАСКАЛЯ И БРИАНШОНА
В разд. 1 на основе аналитической геометрии было показано,
что кривая второго порядка определяется пятью геометриче-
скими условиями (пять точек и т. д.). Достаточность пяти точек
или других пяти геометрических условий для определения кри-
вой второго порядка доказывается и проективной геометрией
в теореме Штейнера (о проективном образовании конических се-
чений), и в следствиях этой теоремы [2]. Приведем без доказа-
тельств лишь следствия теоремы Штейнера.
Следствие 1. Через пять несвязанных точек проходит одно
и только одно коническое сечение.
Следствие 2. Существует одно и только одно коническое
сечение, которое касается пяти данных несвязанных прямых.
Следствие 3. Коническое сечение однозначно опреде-
ляется заданием четырех его точек и касательной в одной из них,
а также заданием трех его точек и касательных в двух из них.
Графические построения кривых второго порядка по усло-
виям следствий теоремы Штейнера основываются на теоремах
Паскаля и Брианшона [2], [4].
Теорема Паскаля. Во всяком шестиугольнике, вписанном
в кривую второго порядка (эллиптическую кривую, параболиче-
скую, гиперболическую или окружность), точки пересечения про-
тивоположных сторон лежат на одной прямой.
По шести точкам эллипса (Л, В, С, D, Е, F) построен шести-
угольник (рис. 15). Противоположными сторонами шестиуголь-
ника являются соответственно стороны АВ и DE, ВС и EF, AF
26
и CD. Пересечения противоположных сторон дают точки L, М,
N, лежащие на одной прямой, которая называется «линиеи
Паскаля».
По шести точкам, лежащим на кривой второго порядка,
можно построить различные шестиугольники в зависимости от
порядка следования сторон. Математиком Штейнером были
доказано, что шесть точек определяют шестьдесят шестиуголь-
ников. Каждому такому шестиугольнику будет соответствовать
своя линия Паскаля. На рис. 15 в качестве примера показан
штрих-пунктирными линиями шестиугольник, вписанный в тот
же эллипс и построенный через те же точки. Там же показана
соответствующая этому шестиугольнику линия Паскаля. Иллю-
страция теоремы Паскаля применительно к параболе дана
на рис. 16.
Используем теорему Паскаля для графического построения
кривой второго порядка. Пусть известны пять точек кривой
А, В, С, D, Е, найдем шестую точку Р, принадлежащую этой
кривой. Для этого выполним следующие построения (рис. 17):
1) продолжим стороны АВ и DE, как противоположные сто-
роны шестиугольника ABCDEP, до их пересечения в точке L.
Точка L будет принадлежать линии Паскаля;
2) продолжим прямую CD и проведем из точки А произволь-
ную прямую до пересечения ее с CD в точке М;
3) проведем через точки L и М линию Паскаля до пересече-
ния ее в точке N с продолжением прямой ВС;
4) из точки N проведем через точку Е прямую до пересечения
ее с прямой AM. Точка пересечения Р будет принадлежать той
же кривой второго порядка.
27
Мы видим, что по точкам А, В, С, D, Е, Р можно построить
шестиугольник, противоположные стороны которого пересе-
каются в трех точках, лежащих на одной прямой, т. е. соблюдено
условие теоремы Паскаля.
Рис. 16. Теорема Паскаля для параболы
Аналогичным способом можно найти и точку и сколько
угодно других точек, все они будут принадлежать данной кривой
второго порядка.
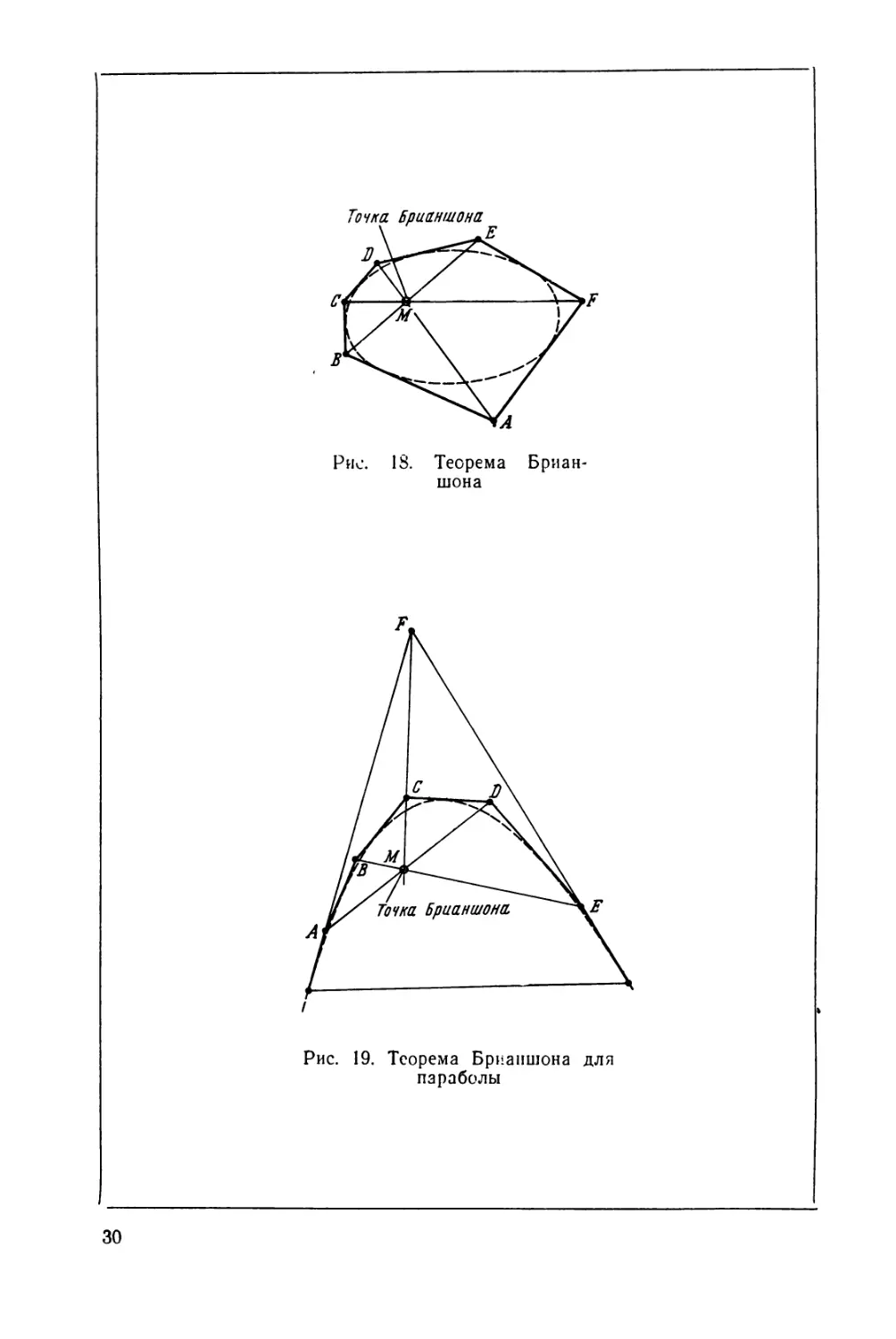
Теорема Брианшона. Прямые, соединяющие противоположные
вершины шестиугольника, описанного около кривой второго по-
рядка, пересекаются в одной точке (рис. 18).
Через шесть вершин А, В, С, D, Е, F построен описанный
около эллипса шестиугольник (каждая сторона шестиугольника
28
является касательной к эллипсу). Противоположные вершины
А и D, В и Е, С и F соединены прямыми, пересекающимися
в точке Af, которая называется точкой Брианшона. На рис. 19
показана точка Брианшона, построенная для параболы.
В частном случае теоремы Паскаля две соседние вершины
шестиугольника могут сливаться в одну точку (рис. 20). Вслед-
ствие этого соединяющая их сторона превращается в касатель-
ную. Здесь точка С слилась с точкой D, а сторона CD шести-
угольника превратилась в касательную (см. рис. 15). Этот ча-
стный случай дает возможность, используя линию Паскаля,
найти графическим построением касательную к кривой второго
порядка в данной точке.
Аналогично в частном случае теоремы Брианшона (рис. 21)
касательная EF слилась с касательной AF. Этот частный случай
дает возможность, используя точку Брианшона, найти графиче-
ским построением точку касания касательной к кривой второго
порядка.
В других частных случаях теорем Паскаля и Брианшона мо-
гут совпадать и несколько пар соседних вершин или сливаться
несколько соседних касательных.
Теоремы Паскаля и Брианшона (в том числе и частные слу-
чаи их) позволяют по пяти заданным условиям простыми гра-
фическими построениями найти кривую второго порядка, т. е.
определить любое количество точек ее и найти касательные в лю-
бой из точек.
3. ПРИЕМЫ ГРАФИЧЕСКИХ ПОСТРОЕНИЙ
Проектирование сложных поверхностей кривыми второго
порядка ведется конструктором главным образом при помощи
графических построений. Элементы аналитического расчета при-
меняются при этом редко, так как обычно конструктор не распо-
лагает временем для математического анализа построений,
а графические приемы позволяют успешно обходиться без та-
кого анализа.
Основные случаи графических построений кривых второго
порядка, основанные на теоремах Паскаля и Брианшона, в зави-
симости от различных пяти условий задания их следующие.
Случай 1. Построение (см. рис. 9) по начальной и конечной
точкам кривой, касательным в них и одной промежуточной —
заданной точке (по трем точкам и двум касательным).
Порядок построения дан в разд. 6, гл. I.
Этот случай является самым распространенным и наиболее
часто применяющимся при подборе и построении как линий про-
дольного контура, так и поперечных сечений.
Случай 2. Построение (рис. 22) по начальной и конечной точ-
кам кривой, касательной в одной из них и двум промежуточным
29
Рис. 18. Теорема Бриан-
шона
Рис. 19. Теорема Брианшона для
параболы
30
Рис. 21. Частный случай теоремы
Брианшона
31
точкам (по четырем точкам А, В, С, D и одной касательной
в точке Л).
Порядок построения:
1) из точки А через точки В и С проводятся прямые;
2) из точки D через точки В и С проводятся прямые;
Рис. 22. Построение по
четырем точкам и одной
касательной
3) через точку N, пересечения прямых АС и DB, и через
точку М, пересечения прямых АВ и DC, проводится прямая
до пересечения с касательной в точке А. Точка пересечения О
есть вершина кривой, а линия OD есть касательная в точке D;
4) пользуясь точкой В (или С) как заданной, проводится по-
строение остальных точек кривой способом, разобранным в слу-
чае 1 (см. рис. 9).
Рис. 23. Построение по
пяти точкам
Этот случай также используется довольно часто при подборе
линий продольных контуров и для определения неизвестной ка-
сательной в одной из конечных точек кривой.
Случай 3. Построение (рис. 23) по начальной и конечной точ-
кам кривой и трем промежуточным точкам (по пяти точкам
А, В, С, D, Е).
32
Порядок построения:
1) из точки А проводятся прямые через точки В, С, D\
2) из точки Е проводятся прямые через точки В, С, D\
3) через точку М, пересечения прямых АВ и ЕС, и через
точку N, пересечения прямых АС и ЕВ, проводится прямая;
4) через точку /(, пересечения прямых АВ и ED, и через
точку L, пересечения прямых AD и ЕВ, проводится прямая;
Рис. 24. Построение
двум точкам и трем
сательным
Точка О, пересечения прямых NM и LK, есть вершина иско-
мой кривой, а АО и ЕО — касательные в начальной и конечной
точках кривой;
5) пользуясь любой из точек В, С или D как заданной, прово-
дим построение остальных точек кривой способом, разобранным
в случае 1 (см. рис. 9).
Для большей точности построений следует принимать как за-
данную точку, лежащую в районе наибольшей выпуклости
кривой.
Для контроля правильности нахождения вершины О полезно
провести дополнительное построение, для чего через точку G,
пересечения прямых АС и ED, и через точку Н, пересечения пря-
мых AD и ЕС, проводится прямая, которая должна также пройти
через вершину О.
Данный случай используется для определения касательных
в начальной и конечной точках кривой, а также при подборе ли-
ний продольных контуров.
Случай 4. Построение (рис. 24) по начальной и конечной точ-
кам кривой, касательным в них и третьей касательной к кривой
(по двум точкам А и В, касательным в точках А и В и каса-
тельной EF).
Порядок построения:
1) проводятся прямые AF и ВЕ\
3 2007 33
2) через точку L, пересечения этих прямых, проводится пря-
мая OL. Точка К, пересечения прямой OL с касательной EF,
есть точка искомой кривой;
3) через точку Л, как через заданную, проводится построение
остальных точек кривой способом, разобранным в случае 1
(см. рис. 9).
Случай 5. Построение (рис. 25) по начальной точке кривой,
касательной в ней и трем касательным к кривой (по одной
точке А и четырем касательным Л, t2, t$ и /4).
Порядок построения:
Рис. 25. Построение по
одной точке и четырем
касательным
1) касательные tx и /4 продолжаются до пересечения их
в точке О;
2) соединяются прямыми точки L и N, а также точки О и Л4;
3) через точку £),. пересечения прямых LN и ОМ, и точку А
проводится прямая до пересечения ее в точке С с касательной /з-
Точка С есть точка искомой кривой;
4) соединяются прямыми точки А и N, а также точки О и С;
5) касательные и ^ продолжаются до взаимного пересече-
ния в точке G;
6) через точку Е, пересечения прямых ОС и AN, и точку G
проводится прямая до пересечения ее с касательной t4 в точке В.
Точка В есть конечная точка кривой;
7) пользуясь точкой С как заданной, проводится построение
остальных точек кривой способом, разобранным в случае 1
(см. рис. 9).
Случай 6. Построение (рис. 26) кривой по пяти заданным ка-
сательным (Л, t2, ts, t4 и /5).
Порядок построения:
1) касательные tx и /5 продолжаются до пересечения их
в точке О;
2) соединяются прямыми точки К и N, а также точки О и L;
34
3) через точку D, пересечения прямых О’ и OL, и точку М
проводится прямая до пересечения ее в точке А с касательной 6.
Точка А есть точка начала кривой;
4) проводится прямая ОМ до пересечения ее в точке Е с пря-
мой AW;
5) через точку Е, пересечения прямых КЛ’ и ОМ, и точку L
проводится прямая до пересечения ее в точке В с касательной /5.
Точка В есть точка конца кривой;
Рис. 26. Построение по пяти касательным
6) проводятся прямые КМ и LN\
7) через точку G, пересечения прямых КМ и LN, и точку О
проводится прямая OG. Точка С, пересечения прямой OG с ка-
сательной /3, есть точка касания касательной /3 к кривой;
8) через точку С, как через заданную, проводится построение
остальных точек кривой способом, разобранным в случае 1
(см. рис. 9).
Случай 7. Построение (рис. 27) по начальной и конечной точ-
кам кривой, касательным в них, которые параллельны межд>
собой, и одной промежуточной точке (по трем точкам А, В, С
и двум параллельным касательным t\ и /2). В этом случае точка
пересечения касательных (вершина) лежит в бесконечности,
Полученная таким построением кривая всегда является эллип-
сом.
Порядок построения:
1) через точку В проводятся прямые из точек Л и С до пере
сечения с заданными касательными G и /2;
2) проводится произвольная прямая DE, параллельная каса-
тельным, до пересечения ее с прямыми АВ и СВ;
3) проводится из точки А прямая АЕ;
3*
35
4) из точки С через точку D проводится прямая до пересече-
ния ее с прямой АЕ. Точка F, пересечения прямых АЕ и CD,
есть точка искомой кривой.
Аналогичное построение повторяется путем проведения ли-
ний, параллельных касатель-
Рис. 27. Построение по трем точ-
кам и двум касательным
ным и линии DE,
Приведенные построения
кажутся несколько слож-
ными только на первый
взгляд. Их легко освоить
с помощью небольшой тре-
нировки. Для успешного
проектирования и задания
сложных поверхностей кри-
выми второго порядка до-
статочно освоить графиче-
ские построения случаев 1,
2 и 3. Так как проектиров-
щик имеет известную сво-
боду в выборе условий за-
дания той или иной линии,
то можно избежать применения остальных случаев построений.
Поэтому случаи 4, 5, 6 и 7 применяются довольно редко.
4. ПРОЕКТИВНЫЙ ДИСКРИМИНАНТ
Основным случаем задания кривой второго порядка является
задание начальной и конечной точек кривой, касательных в них
и одной промежуточной (заданной точки). Промежуточная точка
кривой может быть задана и косвенно при помощи так называе-
мого проективного (графического) дискриминанта.
Проективным дискриминантом f называется отношение
отрезка медианы между основанием кривой и точкой пересече-
ния ее с кривой к длине всей медианы (см. рис. 11).
Рассмотрим, каким образом получаются кривые второго по-
рядка с различными значениями проективного дискриминанта.
Для этого удобнее всего пользоваться так называемой единич-
ной системой координат, у которой медиана и половина основа-
ния кривой равны единице, а касательные пересекаются под пря-
мым углом. Единичная система координат показана на рис. 28
Выше было показано, что если рассечь правильный круговой
конус произвольной плоскостью, то след от пересечения поверх-
ности конуса с этой плоскостью будет кривой второго порядка.
Возьмем правильный круговой конус (рис. 29) с углом при вер-
шине (/САВ), равным 90°, радиусе направляющей (основания)
и высоте, равными единице (АО = ОС = ОВ= 1). Пересечем этот
конус плоскостью Р с углом наклона а относительно основания
36
Докажем, что проективный дискриминант кривой, получае-
мой от пересечения конуса наклонной плоскостью, зависит от
угла наклона а этой плоскости.
Уравнение конической поверхности с вершиной в начале
координат имеет вид
д2 1 £2 . С2
где а и Ь —полуоси направляющего эллипса;
с — высота конуса.
Рис. 28. Проективный дискриминант кривых второго порядка в единичной
системе координат
В нашем случае а = Ь = с=1, тогда уравнение конической по-
верхности с вершиной в начале координат принимает вид
X24-Z2—«/2 = 0.
Перенесем начало координат в центр направляющей окруж-
ности и положительное направление по оси у повернем на 180°.
Уравнение такого конуса
x2+z2—(1—у)2=0
или
x2+z2—у2+2у—1 =0.
Уравнение плоскости Р, проходящей через начало координат:
z=«/-ctga.
Решая совместно уравнение конуса и секущей плоскости Р,
получим уравнение кривой ВМС в установленной системе коор-
динат:
х2 + «/2 • ctg2 a—у2 + 2у—1=0. (3)
Это уравнение является и уравнением проекции кривой ВМС
на плоскость N, т. е. является уравнением кривой BMiC. Теперь
37
докажем, что прямые, образующие конуса, АС и АВ являются
касательными к кривой BMiC в точках С и В. Так как углы АСВ
и АВС равны каждый 45°, то достаточно доказать, что наклоны
касательных к кривой ВМ[С в точках С и В также будут равны
45°. Найдем производные кривой ВМ[С, лежащей в плоскости N9
Рис. 29. Определение дискриминанта кри-
вой в единичной системе
в точках С и В, для чего продифференцируем уравнение (3)
2xdx + 2ydy • ctg2a—2ydy + 2dy = 0
или
xdx + dy(y- ctg2a—у + 1) = 0.
Отсюда
dy _____________________________x______
dx yctgiar-y + 1
В точке C x=l; z/ = 0, тогда —=---— = — 1 и </AC В = 45°.
dx 1
В точке В х =— 1; у = 0, тогда — =1 и /ЛВС = 45°.
dx
Таким образом, мы доказали, что кривая ВМ\С является кри-
вой второго порядка и касательные в точках В и С этой кривой
пересекаются под прямым углом. Проективный дискриминант
кривой ВМ\С f= 0^11- .
38
ОМ 1 = ОМ • s in а = 0C1 ~КС' • sin а=(0С1 - W1) • tg а,
cos а
но
КСХ=КМ=ОМЬ
a
ОС = ОС1 = ОЛ = 1,
тогда
ОЛ^=(1-0^) tga.
Откуда
ОМХ =----,
1 + tga
а
ОМ] __ ОЛ4Т _ tga
7 АО ~ 1 1 + tga 1
Из формулы (4) видно, что проективный дискриминант про-
екции кривой на вертикальную плоскость N зависит от угла на-
клона а секущей плоскости Р.
Меняя величину угла а, получим семейство кривых второго
порядка в единичной системе координат, симметричных относи-
тельно медианы с величиной проективного дискриминанта от О
до 1 (см. рис. 28).
Из сопоставления рис. 28 и 14 видно, что при:
0°<а<45° 0</<0,5—кривая эллиптического типа;
a = 45° / = 0,5 —кривая параболического типа;
90°>о>45° 1>/>0,5—кривая гиперболического типа;
а = 0° /=0 — кривая превращается в прямую линию;
a = 90° /=1 —кривая превращается в две пересекаю-
щиеся прямые линии.
Говоря о проективном дискриминанте, мы рассматривали
кривые второго порядка как кривые, получаемые в результате
пересечения правильного кругового конуса плоскостями. Эти
кривые (эллипс, парабола и гипербола) являются симметрич-
ными относительно медианы. В практике же проектирования
сложных поверхностей симметричные кривые используются
очень редко, а обычно применяются кривые, не симметричные
относительно медианы. Такие несимметричные кривые легко по-
лучить, проведя так называемые аффинные преобразования сим-
метричных кривых (подробно об аффинных преобразованиях
будет сказано в следующем разделе этой главы). Для примера
получения несимметричной кривой из симметричной приведем
здесь лишь аффинное преобразование, заключающееся в изме-
нении угла наклона медианы (рис. 30). В результате такого пре-
образования получена кривая, не симметричная относительно
медианы.
39
с о в
Рис. 30. Аффинное преобразование
симметричной кривой в несимметрич-
ную
Рис. 31. Изменение дискриминанта по Рис. 32. Изменение дискри-
дуге эллипса минанта по дуге окруж-
ности
40
Отдельные участки любой кривой второго порядка можно
рассматривать как кривые, полученные в результате аффинного
преобразования. На рис. 31 показаны три различных участка
эллипса, все они не симметричны относительно медианы. Следует
заметить, что проективные дискриминанты этих участков имеют
различные значения, зависящие от величины угла пересечения
касательных. Аналогично изменяется величина проективного
дискриминанта дуги окружности.
Величина проективного дискриминанта дуги окружности
в зависимости от центрального угла (рис. 32)
а
. BD __ tg ~4
OD ~ а ‘
у
Следует заметить, что для кривой эллиптического типа, каса-
тельные к начальной и конечной точкам которой пересекаются
под прямым углом (включая и частный случай эллиптической
кривой — дугу окружности), проективный дискриминант равен
0,4142. В параболе же любая ее часть имеет проективный дискри-
минант, всегда равный 0,5.
При задании кривых продольных обводов используются кри-
вые с дискриминантами, не выходящими из диапазона f = 0,3—0,7.
Кривые с дискриминантами, близкими к 0 и 1, используются
редко, так как они имеют угловатую форму из-за быстрого из-
менения величины радиуса кривизны вдоль кривой (в начальных
точках кривой при /, близком к 0, и в середине кривой при f,
близком к 1).
Кривые, образующие продольные обводы, по которым опре
деляются исходные точки для построения обводов поперечных
сечений, были стандартизированы по дискриминанту. Введейие
такой стандартизации дает возможность применить упрощенный
расчет кривых при помощи таблиц. Стандартизация сводится
к ограничению числа цифр'дискриминанта до трех после запя-
той, причем последними цифрами являются 0 или 5. Практиче-
ски вполне можно обойтись всего двухзначными (после запятой)
дискриминантами. Такое ограничение при проектировании слож-
ных поверхностей и геометрической увязке их на масштабном
чертеже совершенно незаметно. Таким образом, могут быть ре-
комендованы следующие стандартные значения проективных
дискриминантов: 0,3; 0,31; 0,32; 0,33 и т. д. до 0,7.
Построение обводов поперечных сечений может вестись не по
заданным точкам, а при помощи дискриминантов (см. рис. 12)'.
Значения величин дискриминантов поперечных сечений могут
быть постоянными или изменяющимися от сечения к сечению.
В первом случае величина дискриминанта может быть стандарт-
ной. Если же величины дискриминантов поперечных сечений из-
41
меняются, то значения их стандартизировать нельзя. Стандар-
тизация требует ступенчатого изменения значений дискриминан-
тов сечений, что неминуемо привело бы к нарушению плавности
обводов. Поэтому изменение дискриминантов сечений в таких
случаях задается в виде графика.
При задании обводов поперечных сечений дискриминантами
(постоянными или переменными) следует проверить плавность
формы с помощью контрольных продольных лучевых сечений.
Это следует сделать из-за того, что некоторые неблагоприятные
сочетания исходных для построения сечений продольных линий
даже при постоянном дискриминанте поперечных сечений могут
вызвать плавные, но нежелательные провалы или выпучивания
(подробно об этом см. разд. 5, гл. III).
5. АФФИННЫЕ ПРЕОБРАЗОВАНИЯ
Кривые второго порядка, полученные в единичной системе
координат и симметричные относительно медианы, можно пре-
вратить в несимметричные кривые любых размеров и формы.
Для этого используется свойство кривых второго порядка
аффинно преобразовываться.
Аффинное преобразование (рис. 33) заключается в любом
изменении масштаба кривой по ее осям координат, или в измене-
нии наклона одной из осей координат, или одновременно и того
и другого.
Основные положения аффинных преобразований [4J:
1) прямые линии остаются прямыми;
2) параллельные линии остаются параллельными:
AB\\CD\\EE, А2В21| C2D21| Е2Л2,
А^З II <V>3 II ^з^з*
42
3) отношения отрезков, расположенных на одной и той же
прямой (или на параллельных прямых), остаются неизменными:
АВ А2В2 А^В^
~АК~~~~ АХК^~ А9К2~~ Дз^з ’
ОК = ОХКХ О?К2 __ ОзКз
OF OXFX O2F2 O6F3 ’
4) кривая второго порядка остается кривой второго порядка,
не меняет своего типа (эллиптического, параболического или
гиперболического) и сохраняет значение проективного дискри-
минанта.
При помощи аффинных преобразований кривую единичной
системы координат с заданным значением проективного дискри-
минанта легко преобразовать в кривую, у которой касательные
к начальной и конечной точкам будут пересекаться под любым
углом. Последовательность такого преобразования показана на
рис. 34, а аналитические зависимости можно вывести приведен-
ным ниже способом.
Пусть известны ординаты кривой для соответствующих абс-
цисс в единичной системе. Проведем аффинные преобразования
кривой наклоном медианы на угол 0, вместе с медианой повер-
нутся и все точки кривой.
43
Тогда
ВМ=у,
Х=х—Ах,
но так как
Ax=t/*cos р,
то
Х=х—у-cos Р;
y=«/*sin р.
Теперь произведем аффинное преобразование по сжатию
(или растяжению) вдоль медианы.
Основываясь на свойстве аффинных преобразований сохра-
нять пропорциональность на параллельных отрезках, получим
т МВ Y Lx
п М^В Kj Д.К1 ’
откуда
ДХ1 = ДХ —,
т т
Подставляя значения Лх и У в выражения для и Уь
получим
Хг=х — кхг — х — Lx ——=х — Z/-COS 3 —— ,
т ' т
—= z/-sin0^-.
т т
Следовательно, для общего случая преобразования кривой
в единичной системе координат имеем
Хг — х — y-cos ,
т
F^zz-sinp — .
т
п
Примечание. Если угол 0<9О°, то перед членом у • cos 0 — ставится
т
знак минус, а при 0>9О°—знак плюс.
Для получения кривой с таким же проективным дискриминан-
том, углом наклона медианы и углом пересечения касательных,
но с другим размером основания кривой остается произвести
масштабное преобразование, которое показано на рис. 35.
Для улучая, когда начало кривой совпадает с началом коор-
динат, окончательные формулы аффинного преобразования
имеют вид
'X2=fx~у*cos 0—
\ т /
r2=».sinp — М,
т
44
где х, у — координаты точек кривой в единичной системе;
Х2, Т2—координаты точек искомой кривой;
М — масштаб.
Масштаб “ 2i= A
ае аО тО dO X, Г,
М принимается равным половине натуральной длины основа-
ния искомой кривой.
А
Медиана
Окончательно преобразованная
[искомая) кривая
Аффинно преобразованная кривая
единичной системы координат
Е
Натуральная длина основания
Рис. 35. Масштабное преобразование кривой
Зная координаты точек кривой второго порядка в единичной
системе координат, с помощью приведенных формул определяют
координаты ряда точек любой кривой второго порядка [1].
Используя свойства аффинных преобразований, можно еди-
ную кривую второго порядка заменить двумя кривыми, в точно-
сти лежащими на первой. Проективные дискриминанты этих но-
вых кривых в общем случае имеют другие значения, отличные
от дискриминанта единой кривой. Такое деление называется
аффинным делением кривой и может быть использовано, напри-
мер, в случае, когда кривая имеет большую длину и построение
ее затруднено. Аффинное деление кривой производится в точке,
лежащей на медиане, в которой касательная всегда будет парал-
лельна основанию кривой (рис. 36). Точные значения проектив-
ных дискриминантов участков аффинно разделенной кривой
определяются по формуле
1 +
Из формулы следует, что при делении параболы, проектив-
ный дискриминант которой равен 0,5, участки ее также будут
иметь дискриминанты, равные 0,5. Следует заметить, что у пара-
болы не только части ее, полученные аффинным делением, но
45
и любые другие всегда имеют проективный дискриминант, рав-
ный 0,5.
Рис. 36. Аффиннее деление кривой
6. СОПРЯЖЕНИЕ КРИВЫХ
Плавное сопряжение двух кривых второго порядка между
собой предусматривает соблюдение в точке сопряжения двух
условий: общая касательная и общий радиус кривизны. Сопря-
жение по общей касательной при графических построениях
не вызывает затруднений. Для сопряжения же и по общему
радиусу кривизны приходится применять элементы аналитиче-
ского расчета.
Рис. 37. Сопряжение кривых второго порядка
Одна из сопрягаемых кривых должна быть задана пятью гео-
метрическими условиями. По ним определяется радиус кривизны
в точке сопряжения со второй кривой, которая должна иметь
четыре геометрических условия задания. Пятым условием будет
радиус кривизны, найденный для первой кривой, или другое
условие, определенное с помощью этого радиуса кривизны (на-
пример, заданная точка или проективный дискриминант).
При проектировании сложных поверхностей методом кривых
второго порядка для сопряжения двух кривых наиболее удобно
пользоваться аналитической зависимостью между радиусом кри-
визны и проективным дискриминантом (рис. 37)
0 = 2/1 а1 , /2=--------1
6 (1 - /1)2 *1 1 + ] / М
И Qb2
46
На практике для сопряжения кривых можно пользоваться
графиком, приведенным на рис. 38. По известному значению /1
находится значение функции xp(fi). Далее по величине гр (Л) и
размерам а2, Ь% (см. рис. 37) путем расчета определяется
значение функции
Рис. 38. График для определения дискри-
минанта по радиусу кривизны
Затем по величине функции гр (f2) на том же графике опре-
деляется f2 [1]. Вместо графика можно пользоваться табл. 1
и той же формулой.
Таблица 1
f Ф(/) f ф <f) 7 Ф(У) / Ф7)
0,3 0,367 0,4 0,889 0,5 2 0,6 4,5
0,31 0,404 0,41 0,966 0,51 2,167 0,61 4,893
0,32 0,443 0.4142 1 0,59 2,347 0,62 5,324
0,33 0,485 0,42 1,049 . 0,53 2,543 0,63 5,798
0,34 0,531 0,43 1,138 0,51 2,756 0,64 6,321
0,35 0,58 0,44 1,235 0/5 2/87 0,65 6,898
0,36 0,633 0,45 1,339 0,56 3,240 0,65 7,536
0,37 0,69 0,46 1,452 0,'7 3,514 0,67 . 8,244
0,38 0,751 0,47 1,573 0,58 3,814 0/8 9,031
0,39 0,817 0,48 1,704 0,59 4,141 0,69 9,908
0,49 1,846 0,7 10,889
47
Проективный дискриминант одной из сопрягаемых кривых,
определенный с помощью радиуса кривизны в точке сопряжения,
в общем случае будет иметь нестандартное значение. Так как
линии продольного обвода задаются стандартными значениями
проективных дискриминантов, то определенную величину ди-
скриминанта округляют до ближайшего стандартного значения.
Рис. 39. Определение дискриминанта из условия непересекае-
мости кривых
Связь проективного дискриминанта с радиусом кривизны
используется не только для плавного сопряжения кривых про-
дольных обводов, но и в других случаях. Например, требуется
определить проективный дискриминант кривой батокса верхней
поверхности фонаря летчика так, чтобы он не выходил за кривую
батокса основного тела фюзеляжа (рис. 39). Для этого находим:
а) радиус кривизны в точке В кривой АВ
Qb v-ftfbt ;
б) дискриминант f2 кривой ВС
48
Другой пример использования этих зависимостей при под-
боре кривых поперечных сечений показан на рис. 40. Пусть дана
кривая АБ с дискриминантом f = 0,3. Если по радиусу кривизны
в точке Б кривой АБ находить дискриминанты кривых БВ с раз-
личными размерами я, то по мере увеличения размера а значе-
ния проективных дискриминантов будут уменьшаться. За счет
этого все семейство кривых БВ будет находиться внутри кривой
АБ. На этом же рис. 40 показана кривая ВГБ, проективный ди-
скриминант которой не увязан с радиусом кривизны в точке Б.
Из-за этого она пересекает кривую АБ.
Из приведенных примеров видно, как использование неслож-
ного расчета по определению проективного дискриминанта
с помощью радиуса кривизны обеспечивает выполнение условия
непересекаемости кривых, выходящих из одной и той же точки
и имеющих общую касательную в ней.
Следует заметить, что в практике проектирования сложных
поверхностей не всегда удается получить полное сопряжение по
общей касательной и радиусу кривизны в точке сопряжения.
Кривая с проективным дискриминантом, определенным по ра-
диусу кривизны, может оказаться не удовлетворяющей конструк-
тивным или иным требованиям. В этих случаях довольствуются
лишь сопряжением по общей касательной, являющимся обяза-
тельным условием для плавного сопряжения двух кривых второ-
го порядка. В частности, сопряжение кривых поперечных сече-
ний, как правило производится только по общей касательной.
Основные выводы
1. Кривые второго порядка (кривые конических сечений)
охватывают эллиптические, параболические и гиперболические
кривые, т. е. являются наиболее простыми типами кривых.
4 2007
49
2. Показателями типа кривых являются аналитический или
проективный (графический) дискриминанты.
Так, кривые, имеющие проективный дискриминант 0<f<0,5,
относятся к эллиптическим кривым, 0,5<f<l—к гиперболиче-
ским кривым и/=0,5 — ч параболическим кривым.
Часть эллипса (или окружности), заключенная между полу-
осями, пересекающимися под прямым углом, имеет проективный
дискриминант f=0,4142. У параболы любые ее отдельные части
имеют проективный дискриминант f = 0,5.
3. Кривая второго порядка определяется пятью геометриче-
скими условиями.
4. Имеются простые способы графических построений кривых
второго порядка по пяти геометрическим условиям (пять точек,
три точки и две касательные, четыре точки и одна касательная
и т. д.).
5. При помощи аффинных преобразований можно получить
кривую второго порядка любой формы и размеров.
6. Любую кривую второго порядка можно разбить на не-
сколько кривых, в точности совпадающих с исходной. Разбивку
наиболее удобно вести при помощи аффинного деления.
7. Две кривые второго порядка могут быть плавно сопряжены
между собой по общей касательной и общему радиусу кривизны
в точке сопряжения.
8. В основе всех графических построений кривых второго
порядка лежат аналитические зависимости. Поэтому, кроме чи-
сто графического метода проектирования сложных поверхностей,
могут быть применены методы аналитического расчета. Разра-
ботано несколько методов аналитического расчета координат
точек кривых второго порядка, в том числе и с использованием
цифровых вычислительных машин, позволяющих определять
координаты точек с любой степенью точности.
Г л а в a III
ПРАКТИЧЕСКИЕ ВОПРОСЫ
ПРОЕКТИРОВАНИЯ
СЛОЖНЫХ ПОВЕРХНОСТЕЙ
КРИВЫМИ ВТОРОГО ПОРЯДКА
1. ПОСЛЕДОВАТЕЛЬНОСТЬ РАБОТ
ПРИ ПРОЕКТИРОВАНИИ СЛОЖНЫХ ПОВЕРХНОСТЕЙ
Исходным материалом для проектирования поверхности
(обводов) того или иного агрегата служит общекомпоновочный
чертеж всего изделия. Для самолета это общий вид его в трех
проекциях с рядом основных сечений и разрезов. Общекомпо-
новочный чертеж для самолетов средних размеров обычно де-
лается в масштабе 1 :25.
Этот чертеж определяет деление самолета на основные агре-
гаты (фюзеляж, фонарь, гондолы двигателей, крыло, оперение
и т. д.) и габаритные размеры агрегатов. С общекомпоновочного
чертежа берутся основные размеры и предварительные контуры
каждого агрегата. Этот же чертеж определяет и место каждого
агрегата на самолете, т. е. сопряжение его с другими эле-
ментами.
Работу по созданию обводов, т. е. по проектированию поверх-
ности агрегата, можно разбить на следующие этапы:
1) предварительная конструктивная увязка или разработка
компоновочного чертежа;
2) геометрическая увязка обводов или проектирование его
поверхности;
3) масштабное моделирование;
4) плазовая теоретическая увязка;
5) натурное моделирование.
Наиболее ответственной, сложной и трудоемкой работой
в проектировании обводов является предварительная конструк-
тивная и геометрическая увязки обводов. Эта работа требует от
конструктора разносторонних знаний в области конструирова-
ния, проектирования пространственных форм, аэродинамики,
технологии и т. д., а также большой точности и аккуратности
в работе. От того, сколь правильно будет спроектирована по-
верхность агрегата и будут правильно выбраны его размеры,
зависят летные, технологические и эксплуатационные характери-
стики будущей конструкции.
4*
51
Предварительная конструктивная увязка ставит своей целью
определить компоновку агрегата, систему координат его, раз-
меры, точки и сечения, определяющие обводы, предварительные
обводы поверхности и схему конструкции.
Геометрическая увязка обводов ставит своей целью связать
.^непрерывным построением исходные (определяющие) сечения,
т. е. определить поверхность агрегата. Она завершается выпу-
ском теоретического чертежа, на котором задаются обводы, спо-
соб их построения и необходимые размеры. При геометрической
увязке в зависимости от сложности и размеров агрегата опреде-
ляется метод проектирования и задания обводов; увязка обводов
ведется параллельно с предварительной конструктивной увязкой,
при этом они корректируют друг друга.
Чертежи при предварительной конструктивной и геометриче-
ской увязках выполняются обычно в трех проекциях в масштабе
1:10 или 1 :5. Удобно выполнять их в одном и том же масштабе
для. простоты корректировки. При геометрической увязке целе-
сообразно строить и предварительный сжатый контур. Он удобен
для подбора кривых второго порядка и с него можно снять бо-
лее точно все размеры для заполнения предварительных таблиц.
Подробно о построении сжатого контура сказано в разд. 5 дан-
ной главы.
Если проектируемая поверхность является сложной, то
обычно после разработки ее на чертеже делается масштабная
модель. Такая модель позволяет выявить грубые ошибки в зада-
нии поверхности, наглядно оценить ее пригодность, отработать
поверхность сложных переходных участков и, если требуется,
подправить отдельные места с последующей коррекцией увязоч-
ного чертежа. Модель делается из дерева или пластилина, мас-
штаб ее удобнее выбирать равным масштабу увязочного чертежа.
Следующим этапом проектирования поверхности является
плазовая увязка. Основная ее цель — создание графического эта-
лона поверхности агрегата путем точного построения ее в на-
туру. Такой эталон обводов является исходным материалом для
изготовления различной технологической оснастки (шаблонов,
прессформ, болванок и т. п.) и натурной конструктивной увязки
деталей каркаса агрегата. Одновременно плазовая увязка
используется для проверки плавности обводов и, в случае необ-
ходимости, подправки и уточнения их.
При разработке конструктивных чертежей плаз теоретиче-
ских обводов является исходным материалом для конструктора,
без него невозможно создание качественных чертежей элементов
каркаса. Плаз теоретических обводов представляет собой гори-
зонтальную металлическую или фанерную панель, на которой
изображены в натуральную величину обводы агрегата в виде
системы параллельных сечений. В настоящее время панели пла-
зов делаются в основном из дуралюмйна, покрытого эмалью.
Нанесение контуров сечений производится тушью. Осевые линии
52
и координатная сетка процарапываются до металла. Расчерчи-
вание плаза требует применения специального точного чертеж-
ного и мерительного инструмента. Точность построения обводов
на плазе по данным теоретического чертежа составляет 0,1 —
0,2 мм. По плазовой теоретической увязке корректируется тео-
ретический чертеж и заполняются таблицы.
Последним этапом создания обводов является изготовление
натурной модели или болванки, которая выполняется с помощью
шаблонов, сделанных по плазу. На натурной модели произво-
дится окончательная проверка формы, доводка сложных пере-
ходных участков, которые не всегда удается отработать на чер-
теже или на масштабной модели. Для всех сложных форм на-
турные модели делаются, как правило, обязательно. В дальней-
шем они используются для технологических операций. Натурные
модели изготовляются главным образом из дерева. В случае
обнаружения на натурной модели местных нарушений плавности
обводов, модель дорабатывается по указанию конструктора,
причем плавность проверяется гибкой рейкой. С доработанных
мест модели снимаются шаблоны и обводы переносятся на плаз.
По шаблонам дорабатывается плаз и соответственно уточняется
теоретический чертеж.
2. ОБЩИЕ ПОЛОЖЕНИЯ
ПРИ ПРОЕКТИРОВАНИИ СЛОЖНЫХ ПОВЕРХНОСТЕЙ
Началу проектирования любого агрегата и его поверхности
(обводов) предшествует выбор системы координат. Для сопря-
гаемых между собой агрегатов желательна единая система ко-
ординат. Однако она не всегда оказывается приемлемой и мо-
жет привести к неоправданному усложнению технологии изго-
товления деталей и технологии сборки. Так, например (рис. 41),
для фюзеляжа самолета наиболее удобными осями координат
будут оси ОфХф, Оф*/ф, Оф£ф. Однако они оказываются неудоб-
ными для крыла, конструктивные элементы которого (лонже-
роны, нервюры) не будут лежать в какой-либо из плоскостей
проекций или в плоскостях, параллельных им. Для крыла удоб-
нее за оси координат принять оси Ок*к, Ок//к, O^zK. Так как со-
пряжения поверхностей крыла и фюзеляжа не являются плав-
ными, различие систем координат их скажется только в месте
стыка. Плоскость стыковочной нервюры крыла будет наклонной
относительно осей координат крыла.
Другим примером целесообразности использования различ-
ных систем координат могут служить фюзеляжи некоторых са-
молетов, у которых отогнута вниз передняя часть для обеспече
ния необходимого обзора из кабины. Так как передняя часть
фюзеляжа является герметической кабиной, то ей стремятся по
соображениям прочности и веса придать форму тела вращения..
Естественно, что для такой кабины удобнее иметь свою систему
координат. Если обводы такого фюзеляжа (рис. 42) проекти-.
35
руются методом кривых второго порядка, то в общем случае
косые поперечные сечения не будут линиями второго порядка.
Поэтому для плавного сопряжения обводов передней и средней
частей фюзеляжа приходится вводить переходный участок.
Образование поверхности в переходном участке ведется либо
методом ортогональных сечений, либо при помощи продольно-
лучевых сечений.
Проектирование и увязку обводов удобнее вести, строя попе-
речные сечения через равные расстояния (например, для фюзе-
ляжей и гондол двигателей через 500 мм). Такая первоначальная
разбивка сечений позволяет производить увязку обводов агре-
гата до определения мест расположения силовых элементов (на-
пример, шпангоутов в фюзеляже). Этим экономится время, так
как увязку обводов можно выполнять параллельно с разработ-
кой конструкции. Последующие же построения сечений по сило-
вым элементам при увязанных обводах будут чисто механиче-
ской работой.
После принятия системы координат производится наметка
формы агрегата. Инструментами на этом этапе работы служат
опытный глаз и рука конструктора, лекало или гибкая рейка.
Определив приблизительно обводы агрегата, выбирают «основ-
ное тело».
Основное тело служит базой для создания как самого агре-
гата, так и его обводов. Отдельные места основного тела подвер-
гаются последующим доработкам местными обжатиями, над-
стройками и вырезами (см. рис. 42). В данном примере основным
телом служит сигарообразный фюзеляж, фонарь и воздухозабор-
ники являются надстройками, в районе воздухозаборников
54
Сл
Рис. 42. Основное тело, надстройки и обжатия
имеются обжатия, а законцовка получена путем выреза поверх-
ности фюзеляжа двумя конусами, имитирующими выхлопные
струи двигателей.
Без разделения сложных поверхностей на основное тело,
надстройки и обжатия трудно получить четкие и красивые ли
нии обводов. Кроме того, такое разделение позволяет проекти-
ровать обводы одновременно нескольким конструкторам, т. е.
расширить фронт работ и сэкономить время, а также облег-
чает осуществление различных изменений обводов. Разбив
обводы агрегата на основное тело, надстройки и обжатия, начи-
нают детальную разработку обводов и задание кривыми вто-
рого порядка основных линий, определяющих эти обводы.
3. ПОДБОР КРИВОЙ ВТОРОГО ПОРЯДКА
ПОД НАМЕЧЕННУЮ КРИВУЮ
На чертеже кривая второго порядка должна быть четко за-
дана пятью условиями. В практике самолетостроения ее задают
следующими наиболее простыми и удобными условиями:
1) координаты начальной точки;
2) координаты конечной точки;
3) касательная в начальной точке;
4) касательная в конечной точке;
5) координаты промежуточной (заданной) точки или значе-
ние проективного дискриминанта кривой.
Задание кривых другой комбинацией пяти условий (напри-
мер, координаты пяти точек, координаты четырех точек и одна
касательная и т. д.), как правило, не применяется.
Для задания кривой второго порядка приняты следующие
условные обозначения (рис. 43):
начальная и конечная точки кривой — треугольник;
точка пересечения касательных (вершина) — квадрат;
заданная точка — кружок;
56
проективный дискриминант — буква f с численным значе-
нием, например, f = 0,43.
Подбор кривых второго порядка под намеченные кривые про-
изводится при помощи графических построений. Как основное
применяется построение по начальной и конечной точкам кри-
вой, касательным в них и одной промежуточной точке, так как
в начальный период проектирования обводов конструктор имеет
большую свободу в выборе условий задания кривых и может
Медиана
Кривая второго порядка
Намеченная кривая
Рис. 44. Подбор кривых второго порядка для наме-
ченной кривой
задаться положением касательных. Рассмотрим на примере спо-
собы подбора. Пусть имеется намеченная лекалом или гибкой
рейкой кривая с начальной точкой А и конечной В и нами задано
положение касательных в этих точках (рис. 44). Выбираем про-
извольную промежуточную точку С на намеченной кривой и
строим через нее, как через заданную точку, кривую второго по-
рядка. Промежуточную точку следует брать на кривой вблизи
медианы, в противном случае построение будет менее точным.
Если после построения несовмещение построенной кривой
Намеченная кривая
Рис. 45. Характер изменения
кривой при смещении заданной
точки
с намеченной можно считать допустимым, то необходимо зафик-
сировать заданную точку, определив ее размеры, или определить
по медиане проективный дискриминант и обозначить его.
В случае когда задано условие получить совмещение какой-
либо части кривой с максимальным приближением, то переме-
щая промежуточную точку вниз или вверх, повторяют построе-
ние (рис. 45). Если же отклонения от намеченной кривой полу-
57
чаются недопустимыми, то следует попытаться сдвинуть вдоль
касательных начальную или конечную точку или же разбить
кривую на несколько участков (рис. 46). При разбивке кривой
на несколько участков точку разделения следует выбирать в за-
висимости от характера кривизны. Если кривая имеет ярко вы-
раженное изменение кривизны, то точку разделения берут ближе
к месту наибольшей кривизны, а если же кривизна изменяется
нерезко, то — примерно в середине кривой (рис. 47). Касатель-
ной в точке разделения можно задаться на глаз или найти ее
графическим построением по четырем точкам и одной каса-
тельной (рис. 48).
Для такого построения две точки (начало кривой — точка А
и точка разделения В) нам известны, известна также касатель-
ная в точке А, две же дополнительные точки С и D выбираются
произвольно на намеченной кривой. Такое определение касатель-
ной обеспечивает наибольшее совпадение кривой второго поряд-
ка с намеченной на участке, где производилось определение
касательной. Все четыре точки принадлежат кривой второго по-
Рис. 47. Выбор точки разделения кривой
рядка. Для плавного сопряжения участка ACDB кривой с участ-
ком BE следует определить радиус кривизны в точке В для
участка ACDB, с помощью него найти проективный дискрими-
нант участка BE кривой и выполнить контрольное построение
участка BE. Если же на участке BE требуется выдержать какую-
нибудь точку, которая не попадет на кривую, построенную по
проективному дискриминанту, определенному с помощью ра-
диуса кривизны, то следует принять эту точку за заданную и че-
58
рез нее строить участок кривой. В этом случае участки ACDB и
BE кривой будут сопрягаться только по общей касательной.
Частным случаем при разбивке намеченной кривой на уча-
стки и подборе кривых второго порядка является использование
дуги окружности (рис. 49). Этот прием применяется довольно
часто.
Точка разделения намеченной кривой
Рис. 48. Построение касательной в точке
разделения кривой
Разбивкой намеченной кривой на участки при подборе под
нее кривых второго порядка можно получить их полное взаим-
ное совпадение.
Однако, по возможности, следует избегать такой разбивки,
так как это ведет к неоправданному нагромождению построений,
а главное при этом не всегда удается выдержать в точках раз-
бивки сопряжения кривых второго порядка по радиусу кривизны.
Кривая же, состоящая из нескольких кривых второго порядка,
не сопряженных по радиусу кривизны, теряет смысл математич-
ности задания.
Прием разбивки кривой на участки находит широкое приме-
нение при различного рода доработках обводов, когда доработ-
кам хотят придать местный характер. Например, требуется из„-
менить левую часть кривой второго порядка АВС с вершиной
в точке О, не затрагивая правой ее части, начиная от точки В
(рис. 50). Причем задана новая начальная точка кривой Ai, ка-
сательная в ней и заданная точка Е. В этом случае сперва опре-
деляется касательная в точке В. Для этого на кривой АВ произ-
вольно выбираются дополнительно две точки (касательная
в точке А известна) и графическим построением находится каса-
тельная в точке В. Касательная в точке В продлевается до пере-
59
сечения с касательной ОС и касательной в точке Аь Через точки
41, Е, В с вершиной Ох строится кривая второго порядка. Для
задания же кривой ВС необходимо задать координаты любой
точки на ней, например, точки F или определить проективный
дискриминант и задать его.
4. ТЕХНИКА ПРИЕМОВ ПОСТРОЕНИЯ
КРИВЫХ ВТОРОГО ПОРЯДКА
Графическое нахождение точек кривой второго порядка тре-
бует вычерчивания многих вспомогательных линий. Если кривая
имеет небольшие размеры, вспомогательные линии проводятся
карандашом при помощи линейки. После определения необходи-
мого количества точек все линии построения стираются. Для на-
хождения точек кривых, имеющих большие размеры, можно
рекомендовать построение при помощи ниток или рыболовной
лески (рис. 51). При таком способе построения достаточно про-
вести по линейке только касательные и два основных луча.
60
Построение нитками выполняют два человека. На чертеже
или плазе отмечаются исходные точки построения (начальная,
конечная, заданная и вершина), карандашом или смываемой
тушью проводятся касательные и основные лучи — луч 1 и луч 2.
Иглы ниткодержателей устанавливаются на начальную, конеч-
ную точки и вершину. Один человек, натягивая нитки 1 и 2, дер-
жит их перекрестие на луче 1. Второй человек, натягивая
нитку 3, держит ее на перекрестии нитки 1 и луча 2. Точка пере-
сечения нитки 3 с ниткой 2 есть точка искомой кривой, которая
отмечается карандашом или накалывается
наколкой. Первый человек передвигает пе-
рекрестие ниток 1 и 2 вдоль луча 1, вто-
рой— соответственно, передвигая нитку 3,
производит накалывание остальных точек.
Аналогичное построение проводится и для
правой части кривой. На полученные точки
накладывается гибкая рейка, которую за-
крепляют устанавливаемыми на нее гру-
зами. После этого вдоль рейки проводится
кривая, а вспомогательные линии построе-
ний стираются.
Вспомогательные построения, например
для нахождения касательных или заданных
точек (рис. 22, 23, 24, 25, 26), проводятся
при помощи линейки.
При сравнительно небольшой практике
графические построения кривых второго по-
рядка занимают немного времени. Так, на-
Рис. 52. Кривые,
использованные
для хронометража
пример, трудоемкость построения попереч-
ного сечения, состоящего из двух сопряженных кривых (рис. 52),
составляет:
1) при построении на чертеже в масштабе 1 :5 карандашом
с помощью линейки и лекала 10 мин (построение выполняет один
человек);
2) при построении на плазе в масштабе 1 : 1 тушью с по-
мощью ниток и гибкой рейки 15 мин (построение выполняют два
человека).
Распределение же времени по хронометражу следующее:
а) нанесение исходных точек для построения (начальной, ко-
нечной, вершины и заданных дискриминантом) в первом случае
2 мин, во втором — 5 мин.
б) определение промежуточных точек графическим построе-
нием (по контуру кривой через 15—20 мм на чертеже и через
50—100 мм на плазе) в первом случае 7 мин, во втором —
5 мин*,
в) проведение кривой через найденные точки (лекалом на
чертеже и рейкой на плазе) в первом случае 1 мин, во втором —
5 мин.
61
5. СЖАТЫЙ КОНТУР
При промышленном изготовлении крупногабаритных агрега-
тов со сложной поверхностью широко применяется плазово-шаб-
лонный метод [1]. При этом методе основным графическим эта-
лоном элементов поверхности является теоретический плаз.
Построение на плазе обводов крупных агрегатов (таких как
фюзеляж самолета, гондолы двигателей и шасси и т. п.) в нату-
ральную величину требует больших производственных площа-
дей. Кроме того, построение больших по длине линий технически
затруднено. Используя свойства аффинных преобразований при
проектировании поверхностей методом кривых второго порядка,
можно избежать построений продольных линий в натуральную
величину, применив сжатый контур.
Сжатый контур представляет собой чертеж, на котором по-
строены сжатые вдоль оси абсцисс основные продольные линии
(нулевые батоксы, максимальная ширина и т. п. ) и вспомога-
тельные линии (линии заданных точек или графики дискрими-
нантов сечений и т. п.), т. е. линии, определяющие исходные
точки для построения обводов поперечных сечений. Масштаб сжа-
тия обычно принимается равным 1 :5 или 1 : 10. Ординаты точек
продольных линий остаются натуральной величины (рис. 53) .
Применение сжатого контура при проектировании поверхно-
стей методом кривых второго порядка позволяет с точностью до
0,1—0,2 мм без использования аналитического расчета получить
исходные данные для построения обводов поперечных сечений.
Сжатый контур является основным геометрическим носителем
(эталоном) ординат точек основных контурных и вспомогатель-
ных линий.
На сжатом контуре удобно производить построение продоль-
ных линий, имеющих большую длину и малую кривизну, так как
на нем они становятся более выпуклыми. Удобен он и для по-
строения контрольных продольных сечений при проверке плав-
ности спроектированной поверхности. Все небольшие искажения
плавности на сжатом контуре видны более рельефно, чем на про-
дольных линиях, построенных в натуральную величину. Кроме
того, на сжатом контуре удобно вносить изменения в обводы,
которые в процессе проектирования всегда неизбежны.
На рис. 54. показан сжатый контур основного тела фюзеляжа
самолета, образование и задание обводов которого дано в разд. 1
гл. IV.
Для более быстрого получения предварительных обводов
(до точного построения их на плазе) может оказаться целесооб-
разным построение предварительного сжатого контура самим
конструктором-проектировщиком. Предварительные обводы мо-
гут потребоваться для построения деревянного макета самолета,
для развертывания работ, связанных с подготовкой производ-
ства, например, для клейки и предварительной обработки на-
62
f=0,5
Батокс
верха
Батокс
низа
полуширина
f = 0^№
I Стр.горизонталь
^~Ось симметрии
Сжатый контур
(масштаб сжатия 1‘5)
Рис. 53. Принцип построения
сжатого контура
СП
со
2
Рис .54. Сжатый контур фюзеляжа
турной болванки, для предварительной обработки шаблонов
и рубильников стапелей. Кроме того, предварительный сжатый
контур облегчает работу и самого конструктора-проектировщика
по подбору и заданию кривых второго порядка для намеченных
контуров обводов. На сжатом контуре подбор кривых произво-
дить значительно удобнее, чем на масштабном чертеже. На мас-
штабном чертеже, где нанесен весь агрегат, построения по под-
бору кривых слишком мелки и их трудно точно выполнить.
Последовательность работ при использовании сжатого кон-
тура для подбора кривых второго порядка:
а) нанести сетки осей поперечных сечений или шпангоутов
и затем основные точки, определяющие размеры агрегата;
б ) нанести точки, снятые замером с масштабного увяэочного
чертежа, по сечениям;
в) через основные точки и точки, перенесенные с масштабного
увязочного чертежа, провести при помощи лекала или гибкой
рейки продольные линии обводов;
г) произвести подбор кривых второго порядка для намечен-
ных лекалом или гибкой рейкой продольных линий.
Так как от предварительного сжатого контура не требуется
высокой точности построения, то можно вводить масштабное
сжатие и по оси ординат с тем, чтобы контур можно было разме-
стить на чертежной доске. Строится предварительный сжатый
контур на ватмане или кальке.
При масштабах сжатия по оси абсцисс 1 : 10 и оси ординат
1 :2 размеры, снятые с такого сжатого контура, отличаются от
размеров, снятых с сжатого контура, точно построенного на
плазе, на 2—3 мм.
По данным предварительного сжатого контура заполняется
таблица ординат по сечениям или шпангоутам. Такая таблица
вносится в теоретический чертеж и используется для различных
предварительных построений сечений, а также для контроля при
построении окончательного сжатого контура на плазе.
В заключение можно сформулировать основное назначение
и достоинства сжатого контура продольных сечений обводов:
1) являясь эталоном исходных размеров для всех последую-
щих построений (поперечных сечений, контуров продольных
шаблонов и т. п.), позволяет определять исходные точки с высо-
кой точностью, без использования аналитического расчета;
2) позволяет отказаться от построения плаза продольных ли-
ний в натуральную величину, чем достигается значительная эко-
номия производственных площадей;
3) удобен для проверки плавности и характера кривизны
контрольных продольных и продольно-лучевых сечений (благо-
даря сжатию все искажения плавности видны более рельефно);
4) удобен для подбора кривых второго порядка для намечен-
ных контуров продольных обводов (продольные линии большой
5 2007
65
длины благодаря сжатию становятся удобными для их графиче-
ского построения);
5) удобен для внесения в процессе проектирования изменений
в обводы.
6. ВСТРЕЧАЮЩИЕСЯ ИСКАЖЕНИЯ
ПЛАВНОСТИ ПОВЕРХНОСТИ, СПОСОБЫ ИХ ВЫЯВЛЕНИЯ И УСТРАНЕНИЯ
В основном применение метода кривых второго порядка га-
рантирует получение плавных поверхностей при построении их
на плазе по данным масштабного увязочного чертежа. Однако
в ряде случаев для получения плавной поверхности необходимо
подобрать правильное сочетание между собой основных линий
продольных обводов, являющихся исходными для построения
поперечных сечений. Характерными в этом отношении являются
три часто встречающихся при проектировании поверхностей
случая:
1) случай, когда вторая проекция главного батокса или полу-
ширины имеет S-образную форму;
2) случай, когда график дискриминантов поперечных сечений
имеет S-образную форму;
3) комбинация первых двух случаев.
В этих случаях увязки на масштабном чертеже может ока-
заться недостаточно и сочетание между собой основных линий
приходится корректировать на сжатом контуре или при построе-
нии в натуру.
Для наглядности разберем типовые случаи (рис. 55) на при-
мере построения поверхности гондолы шасси. (В разбираемом
примере умышленно не показано задание продольных линий кри-
выми второго порядка, чтобы не загромождать чертеж). Форма
определяющих сечений гондолы была выбрана, исходя из сле-
дующих соображений:
1) сравнительно большая угловатость верхней части сечений
1 и 2 определилась желанием получить наибольшую ширину
верхней панели гондолы для лучшей силовой связи ее с крылом;
2) прямолинейный участок обвода нижней части сечения 3
был продиктован, с одной стороны, желанием иметь максимально
«обжатые» обводы, а с другой — необходимостью сохранить
строительную высоту лонжерона;
3) законцовка гондолы, начиная от сечения 6, была выбрана
в виде тела вращения для обеспечения простоты технологии изго-
товления (возможности изготовления законцовки из листа на
токарно-давильном станке).
Эти соображения определили:
1) для верхней части обводов сечений:
а) величину дискриминантов сечений 1 и 2, а следовательно,
и направление графика дискриминантов от сечений /, 2 к концу
гондолы (fB) ;
66
Ъ) величину дискриминантов сечений законцовки от сечения 6
до конца гондолы (дискриминант f четверти окружности яв-
ляется величиной постоянной и равен 0,4142), а следовательно,
я направление графика дискриминантов (fB).
Плавность продольно-лучевых сечений верхней поверхности
зависит от вида кривой графика дискриминантов сечений (fB)
между сечениями 2 и 6. График fB, показанный сплошной линией,
обеспечивает плавные (без провалов) кривые продольно-лучевых
сечений (для примера показан луч Д). График же fB, показан-
ный пунктирной линией, дает провал кривой луча А. Естествен-
но, что небольшой провал на масштабном увязочном чертеже
можно не заметить. При построении же обводов на плазе даже
небольшой провал обнаружить легко. Для этого контрольные
продольно-лучевые сечения строятся на сжатом контуре. Сжатый
контур очень удобен для таких целей, так как на нем становятся
наглядными все местные искажения плавности;
2) для нижней части обводов сечений:
а) границу прямолинейных участков нижней части попереч-
ных сечений (ее принято называть границей плоской части
сечений);
б) величину дискриминанта нижней части сечения 3 (fH);
в) величину дискриминантов сечений законцовки, начиная
от сечения 6 до конца гондолы (/н=0,4142), и направление гра-
фика fH;
1 г) величины дискриминантов /н от сечения 3 вперед по на-
правлению к сечению /, которые были приняты как постоянные,
что и определило, следовательно, направление графика дискри-
минантов.
Для обеспечения плавности продольно-лучевых сечений ниж-
ней поверхности на участке от сечения 3 до сечения 6 должно
быть подобрано правильное сочетание графика ее дискриминан-
тов (fH) и границы плоского участка. График fH и граница плос-
кого участка, показанные сплошными линиями, обеспечивают
плавные (без провалов) продольно-лучевые сечения (для при-
мера показан луч Б).
График же дискриминантов fH и граница плоского участка,
показанные пунктиром, дают провал кривой луча Б.
Из разобранного примера видно, что для обеспечения плав-
ности поверхности приходится проверять ее несколькими про-
дольно-лучевыми сечениями. Плавность лучевых сечений и их
характер корректируются соответствующим подбором вели-
чины дискриминантов сечений. После того как будут подобраны
дискриминанты сечений, их наносят на график. Сам график ди
скриминантов после этого задается кривыми второго порядка.
Логичнее и лучше в подобных случаях построение поперечных
сечений задавать не графиком дискриминантов, а одним из про-
дольно-лучевых сечений, которое принято называть «лучом за-
данных точек», так как график дискриминантов по существу
68
является производным от луча заданных точек. В процессе про-
верки плавности поверхности контрольными продольно-лучевыми
сечениями следует корректировать луч заданных точек, а не гра-
фик дискриминантов. После этого луч задается кривыми второго
порядка.
Положение луча заданных точек, всегда следует выбирать
таким образом, чтобы он проходил при-
мерно через середины всех кривых попе-
речных сечений. Такое положение задан-
ных точек облегчает графические по-
строения и дает минимальные ошибки.
Если заданные точки поперечных сече-
ний будут лежать возле самого начала
кривых, то графическое построение их
может оказаться или невозможным, или
будет, затруднено и приведет к большим
ошибкам. Эти ошибки графических по-
строений сказываются в несовпадении
кривых при повторных построениях их,
хотя они будут строиться по одним и тем
Рис. 56. Выбор поло-
жения луча заданных
точек
же исходным данным.
На рис. 56 показаны правильно (луч Л4) и неправильно
(луч N) выбранные положения луча заданных точек. Луч М пе-
ресекает кривые всех поперечных сечений примерно посередине,
а луч N пересекает внешние сечения у их началу.
Необходимость в построении контрольных продольно-лучевых
сечений, их направление и количество при небольшом опыте
легко определяются характером изменения и взаимным сочета-
нием обводов поперечных сечений, совмещенных на одном и
том же чертеже или плазе.
7. ОФОРМЛЕНИЕ ТЕОРЕТИЧЕСКИХ ЧЕРТЕЖЕЙ
Поверхность (обводы) какого-либо агрегата задается систе-
мой параллельных поперечных и перпендикулярных к ним про-
дольных сечений.
Способ построения таких сечений и необходимые для этого
размеры задаются на теоретическом чертеже.
В зависимости от принятого метода задания обводов теоре-
тические чертежи оформляются по-разному.
Если обводы заданы методом ортогональных сечений
(рис. 57), то на теоретическом чертеже задаются размеры, опре-
деляющие взаимное положение сечений, и в виде таблицы —
координаты точек (по батоксам и горизонталям) для построе-
ния контуров сечений. Для построения промежуточных сечений
необходимо по заданным в теоретическом чертеже размерам
провести на чертеже или плазе линии батоксов и горизонталей,
69
замерить их для искомых сечений и по этим размерам вычер-
тить их.
При задании обводов методом кривых второго порядка на
теоретическом чертеже (рис. 58) приводятся исходные размеры
для построения линий продольного контура, вспомогательных ли-
ний построения (лучей заданных точек или графиков дискрими-
нантов и т. д.) и указывается схема построения сечений. Допол-
1 2 3-8 9 10 11 12
Бат.Оь
Баш. /в
Бат.2в
Бато^
б а гл. 1 к
Бат2к
ось сеч. а
макс, ширина.
гор. /в
Гор.2^
Гор.1 к
ГОР-2Я
Рис. 57. Теоретический чертеж фюзеляжа, заданного методом ортогональ-
ных сечений
нительно приводится и таблица координат исходных точек для
построения сечений. Она обеспечивает возможность контроля
правильности построений на плазе. Кроме того, таблица облег-
чает работу конструкторов. Например, если конструктор начи-
нает разработку конструкции шпангоута, а плазовых обводов
еще нет, то он может построить контур сечения шпангоута, поль-
зуясь данными таблицы для интерполяции.
В зависимости от назначения теоретические чертежи делятся
на предварительные и окончательные. Предварительный теоре-
70
тический чертеж выполняется конструктором-проектировщиком
в процессе увязки обводов на чертеже. Он является исходным
материалом для построения плаза. Предварительный теоретиче-
ский чертеж должен содержать в себе все данные, которые сво-
дили бы построение обводов на плазе к чисто механической ра-
боте. Кривые второго порядка позволяют добиться такой отра-
ботки обводов на масштабном увязочном чертеже (с использо-
Рис. 58. Теоретический чертеж фюзеляжа, заданного кривыми второго
порядка
занием в наиболее сложных случаях предварительного сжатого
контура). Плазовику же остается лишь повторить построения
в натуральную величину, для чего ему достаточно владеть прие-
мами графических построений кривых второго порядка. В случае
использования метода батоксов и горизонталей, из-за погреш-
ностей построения на масштабном увязочном чертеже, получить
точные данные для построения плаза не удается. В этом случае
неизбежно уточнение размеров при построении плаза. Взаимная
увязка и корректировка размеров на плазе является трудоемкой
работой, требующей от плазовика большого опыта и наметан-
ного глаза.
При задании обводов кривыми второго порядка может быть
рекомендован и другой способ увязки обводов и оформления
71
предварительного теоретического чертежа. Он заключается
в том, что подбор кривых второго порядка для исходных продоль-
ных линий производится плазовиком при построении им сжатого
контура, а продольные линии на теоретическом чертеже задаются
координатами отдельных точек в таблице. Способ построения
поперечных сечений должен быть определен и задан конструк-
тором-проектировщиком на предварительном теоретическом чер-
теже. При задании обводов таким способом необходим постоян-
ный контакт в работе плазовика и проектировщика. Этот способ
дает экономию во времени, необходимом для проектирования
обводов и их построения на плазе.
Окончательный теоретический чертеж выпускается после вы-
полнения плазовой увязки и проверки плавности на натурной
болванке. Он представляет собой скорректированный предвари-
тельный теоретический чертеж и должен обеспечивать возмож-
ность воспроизводства плаза по уже уточненным данным. На нем
дается таблица с уточненными по плазу размерами.
На предварительном теоретическом чертеже разбивка сече-
ний, как правило, выполняется через равные промежутки (обыч-
но через 500 мм). Это объясняется тем, что при создании предва-
рительного теоретического чертежа еще не известно положение
основных силовых элементов конструкции, например шпангоу-
тов. При создании окончательного теоретического чертежа поло-
жение силовых элементов бывает уже известно, поэтому на нем
показывается разбивка силовых элементов и дается таблица
исходных данных для их построения.
Довольно часто на натурной болванке выявляются отдельные
нарушения плавности обводов и болванка дорабатывается по
месту с последующим перенесением исправлений на плаз. Такие
местные исправления могут нарушать стройность задания обво-
дов на чертеже. Однако из-за этого нет смысла пересматривать
всю систему задания обводов, а достаточно на окончательном
теоретическом чертеже привести схему и размеры для местной
доработки. Наиболее часто для задания местных доработок при-
меняется метод батоксов и горизонталей.
При указании размеров на теоретических чертежах следует
руководствоваться общими правилами машиностроительного
черчения. На чертеже должен даваться лишь минимум необхо-
димых размеров. На окончательных теоретических чертежах, для
облегчения воспроизводства плазов или расчетов, допускается
ставить справочные размеры, которые являются производными
размерами от заданных. Чтобы отличить справочные размеры,
их обводят прямоугольниками. Например (рис. 59), кривая AF
пристраивается к кривой ABCDE, для чего графическим построе-
нием или расчетом по точкам А, В, Ct D, Е находится касатель-
ная в точке А. Касательная же в точке F является продолже-
нием прямой GF. Абсцисса вершины М и ордината вершины N,
лежащие на продолжении прямой GF, находятся графическими
72
построениями или расчетом. Они являются справочными разме-
рами и поэтому обводятся прямоугольниками. Если не обводить
прямоугольником справочные размеры, то из чертежа не всегда
бывает ясно, как они получились.
Положение осей сечений или шпангоутов задается от услов-
ной «нулевой дистанции». Дистанционные размеры дублируются
размерами между осями сечений или шпангоутов. За «нулевую
дистанцию» могут быть приняты носок агрегата, точка поворота
осей координат (например, в фюзеляже с передней кабиной, ко-
торая имеет свою систему координат) и т. п.
На теоретических чертежах самолетные агрегаты принято
располагать так, чтобы направление полета было справа налево.
Если же направление полета слева направо, то над боковой про-
екцией ставится стрелка, указывающая направление полета. Над
стрелкой делается надпись: «Направление полета».
В примечании к чертежу обязательно должно указываться,
как дан теоретический контур (по наружному обводу агрегата,
т. е. с учетом толщины обшивки, или по внутреннему без учета
толщины обшивки). Следует указывать также, какой показан
агрегат (левый или правый). Принято показывать правый агре-
гат. В этом случае делается надпись: «Правый показан, левый —
отраженный вид». Если же агрегат располагается несиммет-
рично, то необходимо отмечать, где он ставится, например:
«обтекатель устанавливается только с левой стороны фюзеляжа».
Такая надпись необходима для плазового цеха.
Глава IV
ПРИМЕРЫ ОБРАЗОВАНИЯ
И ЗАДАНИЯ
СЛОЖНЫХ ПОВЕРХНОСТЕЙ
1. ОСНОВНОЕ ТЕЛО
Типовым примером основного тела со сложной поверхностью
могут служить фюзеляжи самолетов.
Сложность поверхности фюзеляжа определяется назначением
самолета, его аэродинамической и конструктивной компоновкой.
Наиболее простую поверхность имеет фюзеляж пассажир-
ского самолета (рис. 60). На этом же чертеже даны необходимые
размеры для задания его обводов методом кривых второго по-
рядка.
Сечения от носка фюзеляжа до сечения В—В являются
окружностями, сечения хвостовой части — эллипсами, т. е. проек-
тивные дискриминанты всех поперечных сечений фюзеляжа
равны 0,4142. Размеры для горизонтальной проекции, обведет
ные прямоугольником, находятся с помощью графических по-
строений. Так, размер полуширины в сечении В—В определяется
после построения главных батоксов верха и низа на боковой
проекции, как полусумма ординат этих батоксов в данном сече-
нии. Ордината вершины кривой определяется путем графиче-
ского нахождения касательной к левой ветви кривой полуши-
рины, начиная от сечения В—В.
Носок фюзеляжа (фонарь кабины штурмана) представляет
собой тело вращения со срезанной нижней частью. Такая форма
обеспечивает легкость механической обработки литой рамы,
а срез делается для установки плоского обогреваемого стекла.
Верхняя часть фюзеляжа за рамой фонаря кабины штурмана
подвергается обжатию для установки фонаря кабины летчиков.
На рис. 61 показан фюзеляж с более сложной поверхностью
Чтобы не затенять сути ее образования, на чертеже не пока-
зано задание продольных линий кривыми второго порядка (за
исключением графиков изменения дискриминантов поперечных
сечений), так как оно является достаточно простой задачей
и разобрано в разд. 3 гл. III.
74
Сеч.о Сеч? Сеч.2 Сеч.З Сеч.ч Сеч.5 Сеч.6 Сеч.7 Сеч.6 Сеч.З Сеч.10 Сеч.п Сеч.12 Сеч.13 Сеч./ч Сеч.1б Сеч.гб Сеч.17 Сеч.18 Сеч.13 Сеч.2С Сеч.21 Сеч.22 Сеч.73 Сеч.14- Сеч.25 Сеч.26 Сеч.27 Сеч.28 Сеч.29
Построение сечении
от сеч.о до сеч. R-R
Построение сечений
от R-R до 6-6
Построение сечений
от 6-6 до В-В
Построение сечений
. от В-В до конца, фюзелмц
Рис. 60. Фюзеляж пассажирского самолета
f~0,WV2.
Ось центров
Стр, гор.
УслоСно
оазВернушо
Условно
развернуто
в
График дилерами
Ьазовая линия
Симметрично правой,
стороне относительно
линии А
R^-a (const)
Ян=<5 (const)
A
Стр. гор
ч। Стр, гор.
’U
Сим немрачно про-
Вий сторон? иПМй-
сстельно линии. С
Зак. 2007
!
Рис. 61. Фюзеляж со сложной поверхностью
Передняя часть фюзеляжа, являющаяся кабиной экипажа,
имеет свою систему координат, Она представляет собой тело вра-
щения, поэтому поперечные сечения ее являются окружностями.
Исходными поперечными сечениями остальной части фюзе-
ляжа являются:
сечение 7, принадлежащее кабине и представляющее собой
окружность;
сечение 5, размеры которого определяются проходящими че-
рез него воздушными каналами двигателей и центропланом
крыла (они и определили необходимость наличия плоских уча-
стков как сбоку, так и сверху);
сечение 5 (определяется габаритами двигателей) ;
сечение 7 (определяется габаритами сопел двигателей и пред-
ставляет собой две окружности, соединенные верхней и нижней
горизонтальными перемычками).
Верхняя часть фюзеляжа от сечения 2 и до сечения 7 разде-
ляется на два самостоятельных тела, соединенных между собой
перемычкой. До сечения 5 высота перемычки К совпадает с ну-
левым батоксом А верхней поверхности. От сечения 5 до сече-
ния 7 перемычка проходит ниже нулевого батокса. Сопряжение
перемычки с внутренней частью контура поперечных сечений
производится дугой постоянного радиуса /?в. Внутренний контур
сечений принят симметричным внешнему контуру относительно
линии D. В общем случае внешнюю верхнюю часть поперечных
сечений можно считать состоящей из вертикальных прямых Г и
кривых второго порядка. Дискриминанты этих кривых в сече-
нии /ив сечениях кабины равны 0,4142, так как эти сечения
являются четвертями окружностей. На участке от сечения 3 до
сечения 7 кривая принята как четверть эллипса, превращающе-
гося в сечении 7 в четверть окружности. Дискриминанты этих
сечений поэтому также равны 0,4142. На участке между сече-
ниями 1 и 3 дискриминанты уменьшаются для обжатия сечений
с целью обеспечения слива пограничного слоя между фюзеля-
жем и началом воздухозаборника.
Нижняя часть фюзеляжа разделяется на два самостоятель-
ных тела, соединенных между собой перемычкой, на участке
между сечениями 5 и 7. Сопряжение перемычки с внутренней
частью контура поперечных сечений производится дугой постоян-
ного радиуса /?н. Внутренний контур сечений принят симметрич-
ным внешнему контуру относительно линии Е, Внешние обводы
нижних частей поперечных сечений являются кривыми второго
порядка. Дискриминанты этих кривых в сечении /, в сечениях
кабины, а также в сечении 7 равны 0,4142 (они являются четвер-
тями окружностей). Между сечениями / и 7 величины дискри-
минантов сечений сначала уменьшаются, затем увеличиваются и
снова уменьшаются до величины 0,4142 в сечении 7. Такая форма
графика дискриминантов поперечных сечений нижней поверх-
ности продиктована необходимостью выполнения «правила пло-
75
щадей» самолета. «Правило площадей» для околозвуковых са-
молетов в пределах определенного диапазона скоростей полета
позволяет уменьшить сопротивление интерференции. Оно заклю-
чается в придании частям самолета такой формы, которая обес-
печивала бы по определенному закону плавное изменение по
длине самолета суммарной площади поперечных сечений всех
его частей (фюзеляжа, крыла, гондол двигателей и шасси, опе-
рения и т. д.). Стремление выдержать «правило площадей» при-
водит к проявлению на фюзеляже талии в месте сопряжения его
с крылом.
В разбираемом примере начальное 1 и конечное 7 сечения
наклонены относительно остальных сечений, являющихся нор-
мальными к строительной горизонтали фюзеляжа. При таком
даже небольшом угле наклона возле наклонного сечения нару-
шается непрерывность построения обводов нормальных попереч-
ных сечений. Это объясняется тем, что если тело двойной кри-
визны, продольные определяющие линии и нормальные попереч-
76
ные сечения которого заданы кривыми второго порядка, рассечь
наклонной плоскостью, то обводы полученного наклонного сече-
ния не будут являться кривыми второго порядка.
При необходимости построения нормальных сечений в непо-
средственной близости от заданного наклонного сечения посту-
пают следующим образом (рис. 62): строят несколько нормаль-
ных поперечных сечений; по полученным нормальным сечениям
и конечному заданному наклонному строят батоксы и горизонта-
ли или продольно-лучевые сечения. Таким образом, вводится
участок для перехода от построений поперечных сечений мето-
дом кривых второго порядка к построениям методом ортогональ-
ных сечений. По последнему методу и строятся нужные попереч-
ные сечения.,
Построение фонаря экипажа разбираемого фюзеляжа рас-
смотрено в разд. 3, а построение стекателя — в разд. 4 данной
главы.
2. ОБЖАТИЯ
На рис. 63 показано обжатие фюзеляжа для встроенного фо-
наря кабины летчиков. Увязка обводов такого обжатия произво-
дится одновременно с увязкой обводов фонаря (обжимаемый
фюзеляж показан на рис. 60, а фонарь — на рис. 66).
Построение обжатия:
1) обжимается верхняя часть фюзеляжа, основное тело кото-
рого в поперечных сечениях образовано окружностями. Центры
окружностей лежат на криволинейной оси сечений;
2) исходными сечениями обжатия являются сечения Л 6, 8.
Сечение /, представляющее собой окружность, является началом
обжатия. Граница обжатия по сечению 6 проходит через
точку И, лежащую в сечении основного тела фюзеляжа и являю-
щуюся точкой начала плоскости стекла III. Сечение 8 со стороны
задней части фюзеляжа является сечением основного тела фю-
зеляжа, а передней — последним сечением обжатия, вырождаю-
щимся в прямую линию;
3) главный батокс обжатия задан кривой второго порядка
с дискриминантом Касательной в начальной точке А кривой
обжатия является касательная к кривой основного тела фюзе-
ляжа в сечении 1. Она находится графическим построением
по кривой главного батокса основного тела фюзеляжа. Второй
касательной является продолжение оси рамы. Точка пересече-
ния касательных или вершина кривой обжатия находится графи-
чески, поэтому положение ее обозначено размером в прямо-
угольнике;
4) кривые обжатия поперечных сечений строятся по дискри-
минанту /обж, который задается графиком. Исходной точкой
графика /обж является сечение 1. Так как оно является окруж-
ностью, то /обж= 0,4142. Касательная в этой точке горизонтальна,
77
00
Сеч.1 Сеч.2 СечЛ Сеч.6 Сеч.8
О, №2
Схема построения
Рис. 63. Обжатие фюзеляжа под фонарь
так как все предыдущие сечения (перед сечением 1) являются
окружностями и, следовательно, имеют / = 0,4142. Сам график
/обж задан кривыми второго порядка;
5) граница обжатия задана кривыми второго порядка;
6) взаимная увязка кривых границы обжатия и графика ди-
скриминантов /обж производится при помощи контрольного про-
дольно-лучевого сечения — луча А, который должен быть плав-
ным и не иметь провалов. Это обеспечивает плавность и отсут-
ствие провалов для всех остальных продольно-лучевых сечений.
В теоретическом чертеже луч А не задается.
Другим примером местного обжатия может служить обжатие
фюзеляжа для заборника воздуха (рис. 64). Построение поверх-
ности обжатия здесь задано глубиной его Д, линией вершин Б
и постоянным дискриминантом сечений обжатия / = 0,5. Ширина
обжимаемой поверхности фюзеляжа определяется касательными
к поперечным сечениям поверхности, проведенными из точек
вершин Б.
Такое же обжатие можно задать границей обжатия на фюзе-
ляже, глубиной обжатия и дискриминантами сечений обжатия,
которые в общем случае могут быть переменной величины.
В этом случае линию вершин не задают, она определяется пере-
сечением горизонтальных касательных в точках глубины обжа-
тия с касательными к основному контуру сечений фюзеляжа
в точках границы обжатия.
К обжатию можно отнести и плоский срез нижней части
фюзеляжа (рис. 65) для обогреваемого стекла штурмана. Кон-
79
тур плоской части стекла задан кривыми второго порядка.
В углы поперечных сечений, получающиеся от пересечения плос-
Рис. 65. Плоский срез фонаря кабины штурмана
кости с основной поверхностью фюзеляжа, вписаны параболы
(f = 0,5). Граница парабол на фюзеляже задана кривой второго
порядка.
3. НАДСТРОЙКИ
К надстройкам относятся фонари кабин экипажа, обтека-
тели локаторов, различные воздухозаборники и т. п.
Фонари кабин экипажа с точки зрения построения обводов
разделяются на накладные и встроенные. Встроенный фонарь
требует доработки основного тела фюзеляжа путем его обжатия
(см. рис. 63). Конец встроенного фонаря, как правило, плавно
вливается в тело фюзеляжа. Накладной фонарь является само-
стоятельным телом, наложенным на фюзеляж.
Встроенный фонарь кабины экипажа показан на рис. 66. Два
летчика размещены в кабине рядом (слева и справа). Обводы
и размеры фонаря определялись из следующих условий:
а) высота — из условий обеспечения необходимого обзора
вперед и вниз и вписываемости главного батокса (батокса 0)
фонаря в главный батокс фюзеляжа;
80
б) ширина фонаря в сечении 5: по верхней раме — исходя
из допустимого зазора между конструкцией фонаря и головой
летчика, а внизу— из допустимого расстояния между штурвалом
и окантовкой фонаря;
в) переднее остекление, состоящее из шести плоских стекол
I, II и III — из условия обеспечения необходимого обзора вперед
и в стороны;
г) в сечении 8 фонарь должен плавно вписываться в основ-
ное тело фюзеляжа.
Построение фонаря:
1) плоскость стекла I задана гранями БВ и ВГ, т. е. двумя
пересекающимися линиями. Точка Б лежит на главном батоксе
обжатия и определяется при его построении. Поэтому ордината
точки Б показана в прямоугольнике. Границей плоскости
стекла / является грань ГД. Положение ее на проекции в плане
задано размером, а на боковой проекции она определяется по-
строением. Линия пересечения БД плоскости стекла / с поверх-
ностью обжатого фюзеляжа, а следовательно, и точка Д опреде-
ляются графическим построением (например, при помощи сече-
ния фюзеляжа и плоскости стекла / вертикальными продоль-
ными плоскостями);
2) плоскость стекла II задана гранями ГД и ГЕ. Границей
плоскости этого стекла является грань ЕЖ. Точка Ж находится
как точка пересечения контура сечения 4 обжатого фюзеляжа
с плоскостью стекла II. Линия пересечения ДЖ плоскости
стекла // с поверхностью обжатого фюзеляжа определяется гра-
фическим построением так же, как и линия БД\
3) плоскость стекла III задана гранями ЕЖ и ЕИ. Точка И
лежит на границе обжатия в сечении 6. Ордината ее на боковой
проекции задается, а абсцисса находится построением;
4) главным батоксом фонаря (батокс 0) от сечения 8 до
точки К является главный батокс основного тела фюзеляжа. От
точки В rq точки К главный батокс фонаря задан как кривая
второго порядка. Касательной в точке В этой кривой является
продолжение грани БВ, а касательной ’ч точке К является каса-
тельная к главному батоксу необжатого фюзеляжа (последняя
определяется графическим построением). Дискриминант j\ кри-
вой ВК следует выбирать так, чтобы кривая ВК не пересекала
главный батокс необжатого фюзеляжа Это условие будет со-
блюдено, если радиус кривизны главного батокса фюзеляжа
в точке К будет равен или больше радиуса кривизны батокса
фонаря. Для проверки можно использовать формулы определе-
ния радиуса кривизны, которые даны в разд. 6, гл. II;
5) исходными сечениями фонаря являются сечения 5 и 8.
Сечение 5 определяет необходимую ширину фонаря, а в плоско-
сти сечения 8 фонарь вливается в обвод фюзеляжа;
6) ширина фонаря в плоскости рамы между сечениями 5 и 8
задана кривой второго порядка. Точка Л этой кривой находится
6 2007
81
на контуре сечения 8 (размер г')- Для определения касательной
к точке Л следуй построить сечение необжатого фюзеляжа гори-
зонтальной плоскостью, проходящей через ось рамы. Затем гра-
фическим построением найти касательную в точке Л, принадле-
жащей этому горизонтальному сечению;
7) верхушка фонаря (выше плоскости рамы) между сече-
ниями 5 и 8 строится кривыми второго порядка. Для построения
ее сечений задаются вершины и дискриминанты кривых fB, значе-
ния которых находятся на графике. Линия вершин задана как
кривая второго порядка, причем точка М (размер Ь') находится
из построения сечения S, а касательная в точке М находится гра-
82
фическим построением.
Для этого сперва следует
определить вершины кри-
вых верхней части (ле-
жащих выше' плоскости
рамы) сечений основного*
тела фюзеляжа. Анало-
гично строится и график
дискриминантов fB верху-
шек фонаря.
Для данного случая,
когда сечения основного
тела фюзеляжа являются
окружностями, координа-
ты точек М и L, а также
дискриминант f в сече-
нии 8 легко определяют-
ся и аналитически с по-
мощью следующих соот-
ношений:
. Н
a = arcsm ;
R
„ п , 90° — а
2'=/?-cosa;
90° — а
1---
90° — а
tg—т~
Для необжатого фюзеляжа, используя эти соотношения,
можно определить точки линии пересечения фюзеляжа с пло-
скостью рамы, точки линии вершин и точки линии графика ди-
скриминантов. По полученным точкам с помощью графических
построений можно найти касательные в точках Л1, Л и для гра-
фика дискриминантов в точке, соответствующей сечению 8;
8) верхушку фонаря от начала фонаря до сечения 5 и боко-
вину фонаря от грани ЕИ до сечения 8 можно задать кривыми
второго порядка. Однако в данном случае из-за громоздкости
построений это делать нецелесообразно. Значительно проще их
задать при помощи батоксов и горизонталей (рис. 67).
На кладной фонарь кабины экипажа показан на рис. 68.
Члены экипажа размещены в кабине один за другим’
Обводы и размеры фонаря определялись из следующих
условий:
6*
83
СечА Сечда. сеч.5 Сеч.6 Сеч.7
бат.О - -
6ат.1 - —
6am. 2 — — -
6am. 3 — — —
Ось рамы
Гор. / — — —
Гор. 2 — — — —
Рис. G7. Построение верхушки и боковины фонаря
а) высота—из условия обеспечения необходимого обзора
вперед и вниз;
б) ширина: внизу — исходя из допустимого расстояния между
штурвалом и окантовкой фонаря, вверху — из допустимого рас-
стояния между конструкцией фонаря и головами членов
экипажа;
в) основные обзорные передние стекла — плоские;
г) линии AL и БВ—границы сбрасываемой крышки.
К боковому остеклению не предъявлялось специальных тре-
бований. Для простоты задания оно было выбрано конструкто-
ром как торсовая поверхность, переходящая в плоскость. Такое
задание поверхности остекления обеспечивает его простое изго-
товление из органического стекла путем гибки разогретого листа
на оправке.
Построение фонаря:
1) положение горизонтали 1 по высоте (размер в прямоуголь
нике) определяется из условия, что точка L лежит на обводе
сечения 1 фюзеляжа;
2) плоскость лобового стекла задана гранями MN и ML;
3) граница плоскости лобового стекла задана осью верхней
рамы и гранью KL;
4) горизонтальные сечения по оси верхней рамы и горизон-
таль 1 заданы соответствующими размерами от начала фонаря
до сечения 2, являющегося границей сбрасываемой крышки;
5) обводы верхушки фонаря между сечениями 1 и 2 являются
дугами окружностей;
6) поверхность остекления крышки фонаря, ограниченная
точками KLLD, строится как торсовая поверхность;.
7) поверхность остекления крышки фонаря от линии FD до
сечения 2 является плоскостью;
8) обводы поперечных сечений фонаря между сечениями 2
и 3 состоят из двух учабтков: верхняя часть каждого сечения —
дуга с радиусом /?, нижняя часть — прямая линия с наклоном
на угол а. Величины радиусов для соответствующих сечений на-
ходятся на графике /?, который задан кривой второго порядка.
Исходная точка графика для сечения 2 определяется из по-
строения сечения 2. Касательная в этой точке определяется как
касательная к кривой /?вп между сечениями 1 и 2. Величины /?вп
между сечениями 1 и 2 находятся из построений сечений. Угол
наклона а прямой сечений между сечениями 2 и 3 постоянный.
Величина угла а находится из построения сечения 2 (она по-
стоянна на участке между линией Г,Ь и сечением 2, так как этот
участок является плоскостью);
9) верхушка козырька фонаря от начала его до сечения 1
строится по батоксам и горизонталям. В чертеже фонаря должна
быть показана разбивка батоксов и горизонталей и таблица их
для дополнительных сечений.
85
Такое задание верхушки ко-
зырька фонаря показано на рис. 67.
На рис. 69 показан пример обра-
зования обводов накладного фо-
наря, изготавливаемого из органи-
ческого стекла методом формова-
ния в матрицу. После формования
передняя часть фонаря срезается
наклонной плоскостью. Срезанная
часть заменяется плоским стеклом.
Обводы фонаря представляют со-
бой тело вращения, образующая ко-
торого (главный батокс) задана
двумя кривыми второго порядка.
Поперечные . сечения являются
окружностями.
Если накладной фонарь проек-
тируется не как тело вращения, то
необходимо задавать и его горизон-
тальную проекцию. В этом случае
сечения могут быть заданы кривы-
ми второго порядка с постоянным
или переменным по длине фонаря
значением проективного дискрими-
нанта.
Обтекатель радиолокатора, рас-
положенный под фюзеляжем, пока-
зан на рис. 70. Обводы и размеры
его определялись:
а) допустимыми расстояниями
между антенной и контуром обте-
кателя;
б) положением антенны по вы-
соте, которое должно обеспечивать
необходимые углы обзора радио-
локатора вперед и вверх, назад и
вниз;
в) линией ВС пересечения обте-
кателя с фюзеляжем, которая для
создания прямого лонжерона в ме-
сте крепления обтекателя должна
быть прямой.
Построение обтекателя:
1) конечное сечение 3 обтека-
теля совпадает с контуром сечения
фюзеляжа. Контур фюзеляжа яв-
ляется кривой второго порядка, по-
этому легко найти касательную
87
к точке С и по ней размер а до вершины и дискриминант /
этого сечения;
2) горизонтальная проекция линии пересечения А'В'С' обте-
кателя с фюзеляжем находится по заданной боковой проекции
линии пересечения АВС;
3) на кривой В'С' (или Л'В') для построения линии вершин
находится касательная в точке В';
4) исходными величинами для построения графика дискри-
минантов являются дискриминант сечения 3 и дискриминант се-
чения 2, определенный из условия обеспечения необходимого за-
зора между антенной и обтекателем. Уменьшение величины
дискриминантов от сечения 2 по направлению к сечению 0 обус-
ловлено желанием придать передней части более заостренную
форму;
5) обводы поперечных сечений от начала обтекателя (сече-
ние 0) до сечения 1 строятся по дискриминантам, замеряемым
на графике для соответствующих сечений. Касательные к точ-
кам пересечения обтекателя с фюзеляжем являются верти-
калями;
6) обводы поперечных сечений от сечения 1 до конца обтека-
теля (сечение 3) строятся также по дискриминантам, замеряе-
мым на графике. Касательные к кривым сечений обтекателя
определяются линией вершин (размеры F).
Минимальный зазор между обтекателем и антенной прове-
ряется в процессе подбора и задания исходных линий путем по-
строения контрольных сечений.
88
На рис. 71 показан обтекатель антенны локатора, располо-
женного в носовой части фюзеляжа. Продолжение этого обтека-
теля использовано для размещения на нем остекления кабины
штурмана.
Размеры и обводы обтекателя определяются:
а) необходимыми зазорами между антенной и контуром
обтекателя;
б) положением антенны по высоте и длине, выбранным ис-
ходя из потребных углов обзора радиолокатора;
Сеч.о Сеч 1 Сеч.2 сеч.З исходные сечения
Рис. 70. Подфюзеляжный обтекатель радиолокатора
в) изготовлением боковых стекол кабины штурмана в виде
частей поверхности тела вращения (для простоты технологии
изготовления стекол);
г) необходимостью иметь плоское стекло на нижней над-
стройке кабины штурмана, размеры которого определяются за-
данным полем обзора визира штурмана.
Построение обтекателя:
1) исходным сечением обтекателя является сечение 2.
Его обводы состоят из:
а) прямолинейного участка, размер А которого задан шири-
ной, необходимой для размещения плоского стекла нижней над-
стройки кабины;
б) двух сопряженных окружностей (с радиусом и центром
О], радиусом и центром О2). Координаты центра Oi опреде-
89 '
Рис. 71. Носовой обтекатель радиолокатора
ляют размеры Б и D, а величина радиуса выбрана из усло-
вия касания его к контуру сечения 3. Эти условия определяют
максимальную ширину обтекателя В. Абсциссой центра О2 яв-
ляется размер А плоского участка. Ордината центра О2 опреде-
ляется из условия сопряжения дуг с радиусами и /?2;
2) участок обвода обтекателя между сечениями 2 и 3 задан
как цилиндрическая поверхность, направляющей которой служит
сечение 2 обтекателя. Линия сопряжения дуг с радиусами Ri и
/?2 на этом участке является продольной осью рамы верхнего
и нижнего стекол, а сами стекла представляют собой части по-
верхности кругового цилиндра;
3) вторым определяющим сечением обтекателя служит сече-
ние /, проходящее через центр антенны. Его обводы состоят из
плоского участка и из сопряженных между собой дуг двух окруж-
ностей. Координаты центров дуг окружностей, величина плос-
кого участка, максимальная ширина и главный батокс подо-
браны таким образом, что они обеспечивают необходимое рас-
стояние от обвода обтекателя до антенны и определяют размеры
исходных продольных линий в этом сечении и общую плавность
продольных линий;
4) исходные продольные линии, определяющие необходимые
размеры для построения любого сечения (размеры а, б, в, г, д),
подобраны как кривые второго порядка и заданы соответствую-
щими размерами начальных и конечных точек, размерами вер-
шин и дискриминантами. Вместо дискриминантов исходные про-
дольные линии построения можно было задать и размерами по
сечению 1 (как заданные точки для соответствующих продоль-
ных линий).
4. СТЕКАТЕЛИ
Стекатели применяются для законцовки фюзеляжа, в кото-
ром два реактивных двигателя расположены рядом, для сопря-
жения обводов гондол и фюзеляжа, если двигатели расположены
рядом с фюзеляжем, и т. д.
Первый тип стекателя показан на рис. 72, 73. Такие стекатели
делаются на фюзеляжах, подобных разобранному в разд. 1 дан-
ной главы (см. рис. 61). Стекатель (рис. 72) образован пересе-
чением продолженной поверхности фюзеляжа конусом с углом а
наклона образующей /?. При таком образовании поверхности
стекателя его форма и размеры определяются углом наклона
образующей конуса. \
Образование поверхности аналогичного стекателя, но с за-
данной длиной (до сечения 2) осуществляется следующим обра-
зом (рис. 73):
1)* обводы фюзеляжа продлеваются до сечения 2 (линии
4,5, Г, £>, /?н, /?в);
91
2) через точки М и N сечения 2 проводится дуга радиусом
/?1=Е + В, а через точки М и К — радиусом В2 = Ж+В;
3) линии центров дуг окружностей с радиусами Ri и /?2 про-
водятся от сечения 2 до центра окружности торцевого сечения 1
фюзеляжа;
4) для построения промежуточных сечений (между сечения-
ми 1 и 2) откладываются точки центров Е и Ж (для R\ и /?2) и
проводятся дуги с радиусами R{=E±B и Я2 = Ж+В до пересе-
чения с продолжением обвода фюзеляжа.
В этом примере поверхность стекателя образована пересече-
нием продолженной поверхности фюзеляжа двумя конусами
(7?i и Т?2).
Образование поверхности стекателя гондолы двигателя, рас-
положенной рядом с фюзеляжем (рис. 74), производится следую-
щим образом:
92
Рис. 73. Стекатель заданной длины
93
Рис. 74. Стекатель гондолы дви-
гателя
Ось симметрии.
1) продлеваются обводы гондолы (линии А, Б, В, Г, D, Е,
/н).
В данном примере обводы гондолы сведены на конус до се-
чения 4\
2) нижняя и верхняя поверхности сопряжения гондолы с фю-
зеляжем (линии Ж, И, tga, /?н, /?в, flconst) продлеваются до пере-
сечения с продолженными до сечения 6 (фиктивными) обводами
гондолы;
3) полученная поверхность вырезается конусом с углом р
наклона образующей Rc.
В приведенных примерах стекатели имеют острые ребра. При
необходимости ребра можно закруглить, как это делается при
построении зализов. Такое построение разобрано в разд. 5 дан-
ной главы (см. рис. 76).
5. ЗАЛИЗЫ
Зализы применяются для обеспечения плавного сопряжения
двух различных поверхностей, например крыла и фюзеляжа
самолета. На рис. 75 показано образование при помощи кривых
второго порядка передней части зализа крыла и гондолы дви-
гателя.
Контуры зализа на горизонтальной проекции заданы линией
касания зализа к верхней (размер Г) и нижней (размер В) по-
верхностям крыла, а на боковой проекции — линией касания
зализа к гондоле (размеры А и Б). От сечения 2 и далее к концу
зализа поперечные сечения его заданы параболами (/ = 0,5). Но-
сок зализа до сечения 2 задан радиальными сечениями, также
являющимися параболами. В общем случае сечения зализа мо-
гут быть заданы кривыми второго порядка с любыми (постоян-
ными или переменными) значениями дискриминантов.
На рис. 76 показана хвостовая часть зализа крыла и фюзе-
ляжа. Контуры зализа на боковой проекции заданы линией ка-
сания зализа к фюзеляжу, а на горизонтальной проекции —
линиями касания зализа к верхней и нижней поверхностям крыла
(задание продольных линий кривыми второго порядка условно
не показано). Контур хвостика зализа получается как линия
пересечения поперечных сечений верхней и нижней поверхностей
зализа, построенных на фиктивных продолжениях верхней и
нижней поверхностей крыла. Обводы поперечных сечений зализа
заданы кривыми второго порядка: для верхней поверхности —
дискриминантом /в, для нижней — дискриминантом /н. Измене-
ние /в и г по длине зализа задано графиками. Задаваясь раз-
личными значениями fB и /н, подбирают нужный контур хвостика
зализа Можно задаться контуром хвостика зализа, а точку хво-
стика .принимать как заданную точку кривых поперечных сече-
ний зализа Закругление сечений хвостика зализа производится
дугами окружностей. График изменения величин радиусов дуг
95
о
Рис. 75. Передняя часть зализа
2007
Рис. 76. Хвостовая часть зализа
по длине хвостика строится на развертке линии хвостиков за-
лиза. Дуги окружностей вписываются по нормалям к линии
хвостиков или в поперечных сечениях строятся эллипсы.
6. ВОЗДУШНЫЕ КАНАЛЫ
К воздушным каналам относятся воздухозаборники турбо-
реактивных двигателей, выхлопные трубы, входные и выходные
каналы радиаторов и т. п.
При проектировании их должен быть выдержан заданный
закон изменения площадей сечений по длине канала.
На рис. 77 показан входной канал радиатора. Исходными
сечениями его являются сечения 1 и 5.
Сечение 0 по передней кромке строится эквидистантно исход-
ному сечению 1.
Обводы канала заданы:
а) на боковой проекции нулевыми батоксами В для верхней и
Б для нижней поверхностей;
б) на горизонтальной проекции максимальной шириной ка-
нала А;
в) графиками дискриминантов сечений верха (fB) и низа (fH).
Требуемые площади сечений определяются характером гра-
фиков дискриминантов сечений и характером контурных линий
канала на боковой и горизонтальной проекциях.
На рис. 78 показана половина выхлопной трубы турбовинто-
вого двигателя (вторая половина симметрична ей). Исходными
сечениями трубы являются сечения 1 и 8.
Обводы выхлопной трубы заданы:
а) на боковой проекции линиями максимальных высот верх-
ней А и нижней Б частей;
б) на проекции в плане линиями максимальной ширины
В и Г;
в) осями центров сечений Д и Е\
г) линией, определяющей радиусы
д) графиками дискриминантов сечений и
е) графиками радиусов /?в.
В разбираемом примере кривые четвертей наружной части
сечений имеют одинаковые дискриминанты fi, а внутренней—f2.
В общем случае дискриминанты кривых каждой четверти
сечений могут изменяться по своему закону.
Требуемые площади сечений определяются графиками ди-
скриминантов и характером контурных линий трубы на боковой
и горизонтальной проекциях.
7. НОСКИ РУЛЕЙ И ЗАКРЫЛКОВ
Обводы носков рулей, закрылков и т. п. обычно задаются
двумя исходными сечениями и способом образования по ним
поверхности.
98
2007
CO
CO
Сеч.О Сеч.1 Сеч. 2 Сеч.З
Сеч. 4 Сеч.З
Рис. 77. Канал радиатора
о
о
4
Рис. 78. Выхлопная труба
На рис. 79 показана образование поверхности носка руля,
заданной сечениями А—А и В—В и графиком изменения дискри-
минантов сечений f. Поверхности частей подобных агрегатов мо-
гут быть заданы и как линейчатые поверхности, т. е. поверхно-
сти, образованные движением прямой линии (образующей) по
обводам двух исходных сечений (направляющим). Исходные
сечения можно задавать кривыми второго порядка, как это сде-
лано в разбираемом примере. Образующие могут соединять
точки, находящиеся на одинаковых относительных расстояниях
от начала хорд. Примером такой линейчатой поверхности может
служить крыло самолета.
Прямые (образующие) могут соединять точки исходных сече-
ний, имеющие одинаковый наклон касательных. Такие поверх-
ности называются торсовыми. Торсовые поверхности разверты-
ваются на плоскость.
На рис. 80 показано образование обводов закрылка крыла
торсовой поверхностью. Построение выполнено следующим
образом:
1) кривыми второго порядка задаются два исходных сечения,
лежащих в параллельных плоскостях (сечения АВС и Д1В1С1);
2) точки исходных сечений, имеющие одинаковый наклон ка-
сательных, соединяются прямыми линиями (AAi, BBlt СС^
и т. д.). Эти линии являются проекциями образующих;
3) точки искомого сечения (например, сечения ЛМВМСМ) нахо-
дятся путем деления длин соответствующих проекций образую-
щих на части, пропорциональные расстояниям между сечениями:
Z = AAi = ВВг = CCi .
АмА1 ВМВ\ СмС-[
7**
101
4) полученные таким делением точки на проекциях образую-
щих соединяются при помощи лекала или гибкой рейки.
Рис. 80. Торсовая поверхность
Торсовые поверхности благодаря простоте их образования
нашли широкое применение в авиационной промышленности при
задании сложных поверхностей.
Глава V
О ПРИМЕНЕНИИ
АНАЛИТИЧЕСКОГО РАСЧЕТА
Кривые второго порядка нашли широкое применение при про-
ектировании и задании сложных поверхностей прежде всего
благодаря простоте графических построений. Графический ме-
тод построения кривых второго порядка можно считать вполне
законченным и самостоятельным. Однако в ряде случаев оказы-
вается целесообразным использовать и аналитический расчет.
Он дает возможность с любой требуемой точностью определять
координаты точек линии или поверхности, удобен для построе-
ния обводов крупногабаритных агрегатов, графическое построе-
ние которых затруднено, может служить средством контроля
графических построений и т. д.
Широкое применение нашли два метода расчета:
1) чисто аналитический, основанный на использовании урав-
нения семейства (пучка) кривых второго порядка, проходящих
между точками касания^ кривой к двум пересекающимся каса-
тельным (параметрическое уравнение);
2) графо-аналитический, при котором используются таблицы
и номограмма.
Оба метода позволяют решать, основную задачу расчета —
определение ординат ‘ точек кривой при заданных абсциссах,
а также вспомогательные задачи: определение касательных, ра-
диусов кривизны в любых точках кривой и т. п.
1. МЕТОД РАСЧЕТА, ОСНОВАННЫЙ
НА ИСПОЛЬЗОВАНИИ УРАВНЕНИЯ ПУЧКА КРИВЫХ
Этот метод [11] заключается в составлении параметрического
уравнения и приведения его к виду y = f(x) или x = f(y). Под-
ставляя в уравнение линии значения абсцисс, находим соответ-
ствующие ординаты или наоборот.
Для проведения расчета по этому методу кривая должна быть
задана начальной и конечной точками, касательными в них и
третьей .(заданной) точкой на кривой (рис. 81). Если кривая за-
дана не третьей точкой, а проективным дискриминантом, то по
юз
его значению следует найти координаты заданной точки. Точка
будет находиться на медиане.
Параметрическое уравнение имеет вид
(АС)-(ВС)+й(АВ)2 = 0, • (5)
где (АС) —уравнение касательной в точке А;
(ВС) —уравнение касательной в точке В;
(АВ)—уравнение хорды АВ;
k— параметр.
Параметр k определяет данную кривую пучка и находится
с помощью координат заданной
точки D
(АС) (ВС)
Рис. 81. Задание кривой
для аналитического расчета
Для примера составим пара-,
метрическое уравнение кривой,
исходные точки которой имеют
координаты
Ах = 0, у = 0;
Вх=11, у^4\
Сх=6, у = 7\
Dx*=4, у=3. '
Для этой кривой:
уравнение касательной (АС) 6у—7х = 0,
уравнение касательной (ВС) 5у + 3х—53 = 0,
уравнение хорды (АВ) \\у—4х = 0.
Эти уравнения составляются как уравнения прямых линий,
проходящих через две точки.
Параметр k определяется подстановкой в уравнение (6) соот-
ветствующих координат заданной точки В*
__ (fy — lx) (5y 4-Зх —53) __ _ (6»3 —7»4) (5-3 4- 3-4 — 53)
' ............ — (11.3 — 4.4)2
(Иу —4х)2
= ^0,8996 « -0,9.
Зная значение параметра k, составляем уравнение кривой:
(бу—7х) (5у + Зх—53) —0,9 (11 у—4х)2 = 0.
После преобразования получим
у = 0,3942х -2,0164+/ - 0,2935х2+3,1153х + 4,0659 . (7)
Подставляя в это уравнение заданные значения абсцисс, на-
ходим ординаты точек кривой.
104
В общем случае уравнение (7) имеет вид
у - Рх + Q ± VPx2-\-Sx+T . (8)
По значению коэффициента 7? можно судить о типе кривой:
/?<0— эллиптическая, /?=0 — параболическая, /?>0 — гипер-
болическая.
В разбираемом примере R = —0,2935, следовательно, кривая,
выраженная уравнением (7), — эллиптического типа.
Знак перед квадратным корнем берется противоположным:
знаку, стоящему перед членом Q.
Для упрощения работы по составлению уравнения кривой и
расчету ординат разработаны расчетные бланки, на которых
весь расчет разделен на простейшие операции. Ниже (см.
табл. 2) дан образец бланка для составления уравнения кри-
вой, начало которой совпадает с началом координат
(см. рис. 81).
Подставив значения коэффициентов Р, Q, R, S и Т в уравне-
ние (8), получим уравнение (7) .
Этот метод может быть использован для расчета элементов
линейчатых поверхностей типа крыла или оперения самолета.
Направляющими таких поверхностей являются расчетно-экспе-
риментальные кривые, которые, как правило, задаются в виде
таблиц ординат. В этом случае следует по таблицам построить
кривые линии профиля, а затем для них подобрать кривые вто-
рого порядка.
После этого составляются уравнения кривых и производится
расчет.
Расчет позволяет определить ординаты и малки любых точек
поверхности, развертку ее и т. д.
2. ГРАФО-АНАЛИТИЧЕСКИЙ МЕТОД РАСЧЕТА
Этот метод разработан канд. техн, наук В. А. Андреевым [II
Он основан на аффинных преобразованиях с использованием
таблиц единичных координат кривых для стандартных значений
проективных дискриминантов и номограммы единичной системы
координат кривых с теми же стандартными значениями дискри-
минайтов.
Для проведения “расчета по этому методу кривая должна
быть задана начальной и конечной точками, касательными в них
и величиной проективного дискриминанта (рис. 82).
Образец таблицы единичных координат для стандартных зна-
чений проективных дискриминантов 21 точки кривой дан в при-
ложении.
Номограмма построена в единичной симметричной системе
координат (рис. 83). В такой системе хорда кривой равна двум!
единицам, ордината вершины равна одной единице, угол при
105
Исходные точки —
*в У В *с Ус *D Уй
11 4 6 7 4 3
G Н
ХОУС—УО*С
10 289
М Р
xbL+x*c—xbxc УВ^ 2 )+ус( *в \ хс~—)
м
78,8516 0,3942
R V
ръ—и УсЕ м
—0,2935 4,7050
Таблица 2‘
Е F
ХВУС—УВ*С хвУо—Ув*о
53 17
К L
(E—F—G) G Н kXB
0,8996 9,8956
Q и
ХсЕ 2Л4 кУв+Ус~УсУв м
—2,0164 0,4489
5 Т
2PQ+V
3,1153 4,0659
вершине равен 90°. На номограмме дано семейство кривых
со стандартными значениями дискриминантов.
Расчет ординат точек кривой при заданных абсциссах выпол-
няется в следующей последовательности:
1) рассчитывается коэффициент вершины (см. рис. 82)
Ч
2хС
ХВ
2) рассчитывается для каждой
сительная абсцисса
3) графическим построением
на номограмме (рис. 83) для
каждого значения относительной
абсциссы хм находятся ближай
шие табличные единичные абс-
циссы Х1таб И Х2таб, Между КОТО-
РЫМИ находится относительная
абсцисса искомой точки, для чего:
заданной абсциссы хм отно-
Рис. 82. Задание кривой
для графо-аналитического
расчета
а) на номограмме отклады-
вается величина q (точка К);
б) через точку К и вершину С
проводится прямая КС;
в) через точку с относительной
абсциссой хм проводится ли-
ния, параллельная КС, до пересечения с кривой, соответствую-
щей заданному дискриминанту /зад. Кривая, соответствующая
/"зад, строится на номограмме при помощи линейной интерполя-
ции между ближайшими кривыми со стандартными значениями
дискриминантов;
г) определяются ближайшие табличные единичные абсциссы
Е1таб> #2таб;
4) по таблице единичных координат для ближайшего мень-
шего стандартного дискриминанта по Х1Таб и х2Таб находятся
табличные единичные ординаты ^1Таб 'и ^2таб. Величины единич-
ных ординат ух и у2 для заданного дискриминанта /зад опреде-
ляются умножением единичных табличных ординат г/1таб и ^2таб
на множитель Х =/зад/f СтанД или же линейной интерполяцией —
по величине Ау, взятой из таблицы единичных координат.
Далее табличные единичные абсциссы Х1Таб и х2таб, найден-
ные для единичной симметричной системы координат, пересчи-
тываются в единичную несимметричную систему координат
(рис. 84) по формулам
*1=*1таб ±
*2=*2таб±?2(<7-1),
107
где перед вторым членом уравнения ставится знак плюс, если
и знак минус, если ?<1;
5) зная %1, х2, у\, у2, хм, линейной интерполяцией находим
77 7 । —^1) [у?, —у] ) .
Ум ~ У1 т----= = »
х2 —
6) по формуле для аффинного преобразования определяем
искомые ординаты ум t для заданных абсцисс хм
у р I У р \ —
Ум-=-у- ХМ + (Ус----J Ум •
Проиллюстрируем примером расчет ординаты ум для кривой,
показанной на рис. 82, при хм =3:
I) <? =—=1,09;
7 7 11
2) хж=-^-=0,545;
3) по номограмме (см. рис. 84) находим
*1таб = °>5 И *2таб = 0Д
108
4) по таблице (см. приложение) для ближайшего меньшего
^станд=0,36 находим
l/lTa6=0,2864 и #2таб —0,3137.
Определяем значение
к= м«__1,01,
0,36
тогда
71=0,2864 -1,01= 0,2893,
1/2=0,3137•1,01 =0,3168,
Рис. 84. Пересчет единичной симметричной системы в единичную несиммет-
ричную
х1=0,54-0,2893(1,09- 1)=0,526,
6) Ум=
х2=0,54-0,3168(1,09-1)=0,628;
5) у 0(2893 + _(0..545 - 0,526)(0,3168 - 0,2893)
’ Ум ' 1 0,628 — 0,526
7 — -Ц 0,2944= 1,237.
2 )
Для обеспечения необходимой точности расчета на практике
используются таблицы единичных координат для 201 точки кри-
вой и номограмма с относительными абсциссами и значениями
стандартных дискриминантов, нанесенных через 0,01 (0,36; 0,37
и т. д.). Применительно к габаритам агрегатов самолета такие
таблицы и номограмма обеспечивают точность расчета ординат
кривых до 0,1 мм.
8 2007
109
Для повышения точности расчета можно использовать аффин-
ное деление рассчитываемой кривой на несколько участков.
Для упрощения расчета по графо-аналитическому методу
разработаны также расчетные бланки [1].
Трудоемкость расчета по графо-аналитическому методу зна-
чительно меньше, чем при аналитическом методе, основанном на
составлении параметрического уравнения. Так, расчет 10 ординат
Рис. 85. Кривая для сравнительного хронометража
кривой по заданным абсциссам графо-аналитическим методом
занимает около 20 мин, а аналитическим — 1,5-4-2 часа. При гра-
фическом методе на построение кривой расходуется примерно
столько же труда, сколько при графо-аналитическом методе рас-
ходуется на расчет и построение.
В табл. 3 приведены сравнительные результаты хрономет-
ража графического построения на плазе сжатого контура (мас-
штаб сжатия nd оси абсцисс 1 :5) кривой (рис. 85) и такого же
построения ее с применением графо-аналитического расчета.
Таблица 3
№ опе- рации Наименование операций Время мин ‘ Число работаю- щих
рафическое построение 1 2 3 4 Отложить исходные точки для построения, найти по дискриминанту заданную точку Проделать графическое постро- ение промежуточных точек при помощи ниток Провести через точки с помощью рейки кривую Замерить ординаты в сечениях и заполнить таблицу 10 5 5 5 1 2 1 1
[—। Итого 30 человеко-минут
ПО
Продолжение
№ опе- рации Наименование операций Время мин Число работа io- щи х
эение с примене-1 графо-аналити- ского расчета 1 2 3 Рассчитать ординаты точек в сечениях и заполнить таблицу Отложить по таблице на плазе точки Провести через точки с помощью рейки кривую 20 6 5 1 1 1
си о 1—1 S о X X (U Итого 31 человеко-минута
Дальнейшим развитием графо-аналитического метода явился
интерполяционный расчет с использованием таблиц координат
в несимметричной единичной системе (для дискретных значений
коэффициента q), который позволяет рассчитывать ординаты то-
чек кривой с любым значением проективного дискриминанта.
3. ИСПОЛЬЗОВАНИЕ ТЕОРЕМЫ ПАСКАЛЯ
ДЛЯ АНАЛИТИЧЕСКОГО РАСЧЕТА
Кроме описанных методов расчета может применяться и ме-
тод, основанный на математическом описании графических по-
строений по теореме Паскаля (рис. 86). Кривая задана точками
А, Е, В и двумя касательными АС и ВС. Для определения коор-
динат любой точки кривой необходимо последовательно найти
точки пересечения трех пар прямых: BF с АЕ, СК с BE и
AM с BF.
Так, для определения координат точки N:
1) находим точку пересечения произвольно проведенной пря-
мой BF с прямой АЕ (точку К). Для этого составляем уравне-
ние прямой BF как проходящей через две точки В и F
у —У F _ х ~ XF
у В — УР Хв — Хр"
откуда
У У В (* — *f) — tip (х — хв)
ХВ —Хр
Аналогично составляется уравнение прямой АЕ
у = УЕ ~ ХА^ ~ У* (Х ~ Хе>
хЕ — хА
Решай совместно эти два уравнения прямых, находим коор-
динаты их точки пересечения К;
8* III
Рис. 86. Схема расчета по
теореме Паскаля
112
2) аналогично определяем координаты точки М, как точки
пересечения прямых СК и BE, и координаты искомой точки N,
как точки пересечения прямых AM и BF;
3) смещая точку F по прямой АС, определяем координаты не-
обходимого количества точек кривой.
Недостатком этого метода является то, что он не позволяет
найти ординату точки кривой по заданной ее абсциссе или
наоборот.
Этим методом удобно определять касательную к кривой
в какой-либо точке. Например, надо найти касательную OL
к точке О кривой, которая задана точками О, А, В, С и касатель-
ной СМ (рис. 87).
Для определения касательной OL\
1) находим координаты точки N, как точки пересечения пря-
мых О А и СВ\
2) находим координаты точки К, как точки пересечения пря-
мых ОВ и АС',
3) находим координаты точки L, как точки пересечения пря-
мых СМ и KN',
4) по координатам точек О и L составляем уравнение каса-
тельной OL
где
yL х о
—— = t°r >.
XL
ПРИЛОЖЕНИЕ
ТАБЛИЦА ЕДИНИЧНЫХ КООРДИНАТ И ПРИРАЩЕНИЙ ОРДИНАТ
/ X 1 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0
1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2
0,30 У 0,30000 0,29785 0,29136 0,28035 0,26452 0,24335 0,21616 0,18166 0,13780 0,08057 0
Ау 0,01000 0,00990 0,00958 0,00906 0,00831 0,00736 0,00614 0,00467 0,00300 0,00121 0
0,31 г 0,31000 0,30775 0,30094 0,28941 0,27283 0,25071 0,22230 0,18633 0,14080 0,08178 0
Ду 0,01000 0,00989 0,00958 0,00903 0,00827 0,00728 0,00604 0,00459 0,00290 0,00114 0
0,32 У 0,32000 0,31764 0,31052 0,29844 0,28110 0,25799 0,22834 0,19092 0,14370 0,08292 0
Ду 0,01000 0,00989 0,00955 0,00900 0,00823 0,00721 0,00596 0,00448 0,00280 0,00107 0
0,33 У 0,33000 0,32753 0,32007 0,30744 0,28933 0,26520 0,23430 0,19540 0,14650 0,08399 0
Ду 0,01000 0,00989 0,00955 0,00898 0,00817 0,00714 0,00587 0,00437 0,00269 0,00101 0
0,34 У 0,34000 0,33742 0,32962 0,31642 0,29750 0,27234 0,24017 0,19977 0,14919 0,08,^00 0
Ду 0,01000 0,00988 0,00953 0,00895 0,00813 0,00707' 0,00577 0,00426 0,00260 0,00095 0
1 1 1 1 1 1
0,35 У 0,35000 0,34730 0,33915 0,32537 0,30563 0,27941 0,24944 0,20403 0,15179 0,08595 0
Ду 0,01000 0,00988 0,00952 0,00891 0,00807 0,00699 0,00567 0,00415 0,00250 0,00090 0
0,36 у 0,36000 0,35718 0,34857 0,33428 0,31370 0,28640 0,25161 0,20818 0,15429 0,08685 0
Ду 0,01000 0,00988 0,00951 0,00888 0,00802 0,00691 0,00558 0,00405 0,00240 0,00085 0
0,37 7 0,37000 0,36706 0,35818 0,34316 0,32172 0,29331 0,25719 0,21223 0,15669 0,08770 0
Ду 0,01000 0,00987 0,00949 0,00885 0,00796 0,00683 0,00547 0,00394 0,00230 0,00079 0
0,38 7 0,38000 0,37693 0,36767 0,35201 0,32968 0,30014 0,26266 0,21617 0,15899 0,08849 0
д7 0,01000 0,00987 0,00947 0,00883 0,00790 0,00675 0,00538 0,00383 0,00222 0,00075 0
0,39 7 0,39000 0,38680 0,37714 0,36084 0,33758 0,30689 0,26804 0,22000 0,16121 0,06924 0
Ду 0,01000 0,00986 0,00945 0,00878 0,00784 0,00660 0,00527 0,00372 0,00212 0,00070 0
0,40 7 0,40000 0,39666 0,38559 0,36962 0,34542 0,31355 0,27331 0,22372 0,16333 0,08994 0
Ду 0,01000 0,00986 0,00944 0,00874 0,00778 0,00660 0,00520 0,00364 0,00206 0,00068 0
Продолжение
f X 1 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0
1,1 1,2 1,3 1,4 1,5 1,6 1.7 1,8 1,9 2
0,41 У 0,41000 0,40652 0,39603 0,37836 0,35317 0,32013 0,27849 иЮ, 22733 0,16536 0,09061 0
Ду 0,01000 0,00986 0,00942 0,00870 0,00778 0,00650 0,00508 0,00354 0,00196 0,00062 0
0,42 7 0,42000 0,41637 0,40545 0,38705 0,36092 0,32681 0,28353 0,23084 0,16730 0,09122 0
д7 0,01000 0,00984 0,00940 0,00868 0,00768 0,00544 0,00500 0,00342 0,00190 0,00060 0
0,43 7 0,43000 0,42623 0,41485 0,39572 0,36857 0,33302 0,28849 0,23423 0,16917 0,09181 0
Ду 0,01000 0,00984 0,00938 0,00862 0,00760 0,00632 0,00488 0,00332 0,00180 0,00056 0
0,44 7 0,44000 0,43607 0,42423 0,40433 0,37615 0,33931 0,29333 0,23752 0,17094 0,09236 0
Ду 0,01000 0,00982 0,00936 0,00858 0,00752 0,00624 0,00476 0,00320 0,00172 0,00052 0
0,45 7 0,45000 0,44590 0,43358 -0,41290 0,38365 0,34552 0,29807 0,24070 0,17264 0,09287 0
Ду 0,01000 0,00984 0,00934 0,00854 0,00746 0,00614 0,00464 ,0,00310 0,00164 0,00048 0
1 1 | 1 1 1
0,46 У 0,46000 0,45574 0,44291 0,42143 0,39109 0,35163 0,30268 0,24377 0,17426 0,09335 0
Ду 0,01000 0,00982 0,00932 0,00848 0,00736 0,00602 0,00454 0,00298 0,00156 0,00046 0
0,47 У 0,47000 0,46556 0,45222 0,42990 0,39844 0,35763 0,30718 0,24673 0,17580 0,09380 0
ду 0,01000 0,00982 0,00930 0,00842 0,00730 0,00592 0,00442 0,00290 0,00150 0,00044 0
0,48 У i 0,48000 0,47538 0,46151 0,43831 0,40571 0,36353 0,31157 0,24960 0,17728 0,09423 0
ду 0,01000 0,00982 0,00926 0,00840 0,00722 0,00582 0,00430 0,00276 0,00140 0,00040 0
0,49 У 0,49000 0,48520 0,47077 0,44669 0,41290 0,36932 0,31585 0,25235 0,17867 0,09463 0
Ду 0,01000 0,00980 0,00924 0,00832 0,00712 0,00570 0,00418 0,00268 0,00134 0,00038 0
0,50 У 0,50000 0,49500 0,48000 0,45500 0,42000 0,37500 0,32000 0,25500 0,18000 0,09500 0
Ду 0,01000 0,00980 0,00920 0,00826 0,00704 0,00560 0,00406 0,00258 0,00128 0,00036 0
.0,51 У 0,51000 0,50480 0,48920 0,46326 о;42701 0,38057 0,32404 0,25755 0,18126 0,09535 0
Ду 0,01000 0,00980 0,00918 0,00820 0,00694 0,00548 0,00394 0,00248 0,00122 0,00034 0
QO
продолжение
f X 1 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0
1,1 1,2 1,3 1,4 . 1,5 1,6 1,7 1,8 1,9 2
0,52 У 0,52000 0,51459' 0,49837 0,47144 0,43393 0,38602 0,32796 0,26000 0,18246 0,09568 0
Ду 0,01000 0,00978 0,00914 0,00814 0,00684 0,00536 0,00382 0,00238 0,00116 0,00030 0
0,53 Г 0,53000 0,52437 0,50750 0,47956 0,44075 0,39136 0,33175 0,26235 0,18360 0,09528 0
Ду 0,01000 0,00978 0,00912 0,00808 0,00674 0,00524 0,00372 0,00228 0,00110 0,00030 0
0,54 У 0,54000 0,53414 0,51661 0,48762 0,44747 0,39657 0,33543 0,26461 0,18468 0,09627 0
Ду 0,01000 0,00976 0,00908 0,00800 0,00664 0,00514 0,00360 0,00218 0,00104 0,00028 0
0,55 У 0,55000 0,54390 0,52568 0,49560 0,45408 0,40167 0,33899 0,26676 0,18570 0,09654 0
Ду 0,01000 0,00976 0,00904 0,00792 0,00654 0,00500 0,00348 0,00210 0,00098 0,00026 0
0,56 Г 0,56000 0,55365 0,53471 0,50352 0,46059 0,40564 0,34244 0,26884 0,18667 0,09б79 0
Ду 0,01000 0,00974 0,00898 0,00782 0,00642 0,00488 0,00334 0,00198 0,00092 0,00024 0
4
0,57 У 0,57000 0,56338 0,54368 0,51133 0,46698 0,41148 0,34576 0,27080 0,18758 0,09703 0
by 0,01000 0,00974 0,00896 0,00778 0,00632 0,00474 0,00322 0,00190 0,00088 0,00022 0
0,58 У 0,58000 0,57312 0,55263 0,51308 0.47327 0,41620 0,34896 0,27268 0,18845 0,09725 0
Ду 0,01000 0,00972 0,00890 0,00768 0,00618 0,00464 0,00312 0,00182 0,00082 0,00022 0
0,59 У 0,59000 0,58283 0,56152 0,52673 0,47943 0,42079 0,35205 0,27448 0,18926 0,09746 0
Ду 0,01000 0,00970 0,00886 0,00760 0,00606 0,00446 0,00298 0,00172 0,00078 0,00018 0
0,60 У 0,60000 0,59253 0,57037 0,53430 0,48547 0,42523 0,35501 0,27620 0,19004 0,09764 0
Ду 0,01000 0,00968 0,00879 0,00747 0,00591 0,00431 0,00286 0,00162 0,00072 0,00019 0
0,61 У 0,61000 0,60221 0,57916 0,54177 0,49138 0,42954 0,35787 0,27782 0,19076 0,09783 0
д? 0,01000 0,00967 0,00873 0,00737 0,00578 0,00419 0,00273 0,00155 0,00069 0,00018 0
0,62 У 0,62000 0,61188 0,58789 0,54914 0,49716 0,43373 0,36060 0,27937 0,19145 0,09801 0
Ду 0,01000 0,00965 0,00867 0,00726 0,00565 0,00405 0,00261 0,00146 0,00064 0,00016 0
Продолжение
f X 1 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0
1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2
0,63 У 0,63000 0,62153 0,59656 0,55640 0,50281 0,43778 0,36321 0,28083 0,19209 0,09817 0
Ду 0,01000 0,00963 0,00862 0,00715 0,00551 0,00391 0,00251 0,00139 0,00061 0,00014 0
0,64 У 0,64000 0,63116 0,60518 0,56355 0,50832 0,44169 0,36572 0,28222 0,19270 0,09831 0
Ду 0,01000 0,00961 0,00855 0,00704 9,00536 0,00376 0,00239 0,00132 0,00056 0,00013 0
0,65 У 0,65000 0,64077 0,61373 0,57059 0,51368 0,44545 0,36811 0,28354 0,19326 0,09844 0
Ду 0,01000 0,00959 0,00847 0,00691 0,00522 0,00363 0,00228 0,00126 0,00054 0,00013 0
0,66 У 0,66000 0,65036 0,62220 0,57750 0,51890 0,44908 0,37039 0,28480 0,19380 0,09857 0
Ду 0,01000 0,00957 0,00839 0,00679 0,00507 0,00348 0,00217 0,00118 0,00051 0,00012 0
0,67 У 0,67000 0,65993 0,63059 0,58429 0,52397 0,45256 0,37256 0,28598 0,19431 0,09869 0
Ду 0,01000 0,00953 0,00831 0,00665 0,00492 0,00335 0,00207 0,00110 0,00046 0,00011 0
1 1 1 1 1
0,68 ' 7 0,68000 0,66946 0,63890 0,59094 0,52889 0,45591 0,37463 0,28708 0,19477 0,09880 0
Ду 0,01000 0,00951 0,00822 0,00651 0,00476 0,00321 0,00197 0,00105 0,00044 0,00011 0
0,69 7 0,69000 0,67897 0,64712 0,59745 0,53365 0.45912 0,37660 0,28813 0,19521 0,09891 0
ду 0,01000 0,00949 0,00813 0,00636 0,00460 0,00307 0,00186 0,00099 0,00041 0,00010 0
.0,70 7 0,70000 0,68846 0,65525 0,60381 0,53825 0,46219 0,37846 0,28912 0,19562 0,09901 0
ДУ 0
ЛИТЕРАТУРА
1. Андреев В. А., Зворыкин В. А. и др., Расчет и построение кон-
туров самолета на плазе, Оборонгиз, 1960.
2. Глаголев Н. А., Проективная геометрия, Изд-во «Высшая школа»,
1963.
3. Гордон В. О. и Семенцов-Огиевский М. А., Курс начерта-
тельной геометрии, Техтеоретиздат, 1955.
4. Гуревич Г. Б., Проективная геометрия, Физматгиз, 1960.
5. Долматовский Ю. А., Автомобильные кузова, Машгиз, 1960.
6. Долматовский Ю. А., Разработка сложных поверхностей промыш-
ленных изделий, «Техническая эстетика», 1964, № 9, 10.
7. Кириллов А. Н., Сюрфасография, ОНТИ, 1937.
8. Мусхелишвили Н. И., Курс аналитической геометрии, Гостех-
издат, 1947.
9. Н о г и д Л. М., Проектирование формы судна и построение теоретиче-
ского чертежа, Л., Судпромгиз, 1962.
10. X а н о в и ч И. Г., Анализ и проектирование формы судовой поверх-
ности, Л., Госстройиздат, 1933с
11. Liming R. and Hart ге у H., Lofting Problems of Streamline
Bodies, J. Aero Digest, 1942—1945.
ОГЛАВЛЕНИЕ
Стр.
Предисловие....................................................... 3
Глава I. Методы, применяемые при проектировании и задании слож-
ных поверхностей............................................... 5
1. Метод ортогональных сечений................................ 5
2. Лучевой метод.............................................. 7
3. Метод пропорциональных кривых.............................. 9
4. Метод степенных уравнений....................................И •
5. Метод радиусографии....................................... 15
6. Метод кривых второго порядка ..............................17
7. Методы проектирования линейчатых поверхностей..............21
8. Современные требования к методам проектирования и задания
сложных поверхностей..........................................22
Глава II. Основные сведения из теории кривых второго порядка 24
1. Понятие о кривых второго порядка...........................24
2. Теоремы Паскаля и Брианшона................................26
3. Приемы графических построений..............................29
4. Проективный дискриминант...................................36
5. Аффинные преобразования..................*.................42
6. Сопряжение кривых...................i......................46
Глава III. Практические вопросы проектирования сложных поверхно-
стей кривыми второго порядка...................................51
1. Последовательность работ при проектировании сложных поверх-
ностей .......................................................51
2. Общие положения при проектировании сложных поверхностей 53
3. Подбор кривой второго порядка под намеченную кривую ... 56
4. Техника приемов построения кривых второго порядка .... 60
5. Сжатый контур..............................................62
6. Встречающиеся искажения плавности поверхности, способы их
выявления и устранения........................................66
7. Оформление теоретических чертежей..........................69
Глава IV. Примеры образования и задания сложных поверхностей 74
1. Основное тело...............................................74
2. 9бжатия....................................................77
3. Надстройки.................................................60
4. Стекатели..................................................91
5. Зализы.....................................................95
123
Стр
6. Воздушные каналы............................................98
7. Носки рулей и закрылков.....................................98
Глава V. О применении аналитического расчета.....................103
1. Метод расчета, основанный на использовании уравнения лучка
кривых.........................................................ЮЗ
2. Графо-аналитический метод расчета.........................105
3. Использование теоремы Паскаля для аналитического расчета 111
Приложение. Таблица единичных координат и приращений ординат 114
Владимир Васильевич Бабаков
ПРОЕКТИРОВАНИЕ ПОВЕРХНОСТЕЙ КРИВЫМИ ВТОРОГО ПОРЯДКА
В САМОЛЕТОСТРОЕНИИ
Редактор С. Б. Геллер Художник Е. Н. Алексеев
Технический редактор Т. С. Старых Корректор Л. Е. Хохлова
Т-00449 Сдано в набор 17/IX-1968 г. Подписано к печати 18/11-1969 г.
Формат 60X90716 Печ. л. 8,0 в т. ч. 1 вкл. Уч.-изд. л. 7,0 Бум. л. 4,0
Бумага типограф. № 2 Тираж 1700 экз. Цена 35 коп. Тем. план 1969 г. № 149
Издательство «Машиностроение», Москва, К-51, Петровка, 24. Изд. зак. 2420
Московская типография № 8 Главполиграфпрома
Комитета по печати при Совете Министров СССР,
Хохловский пер., 7. Тип. зак. 2007