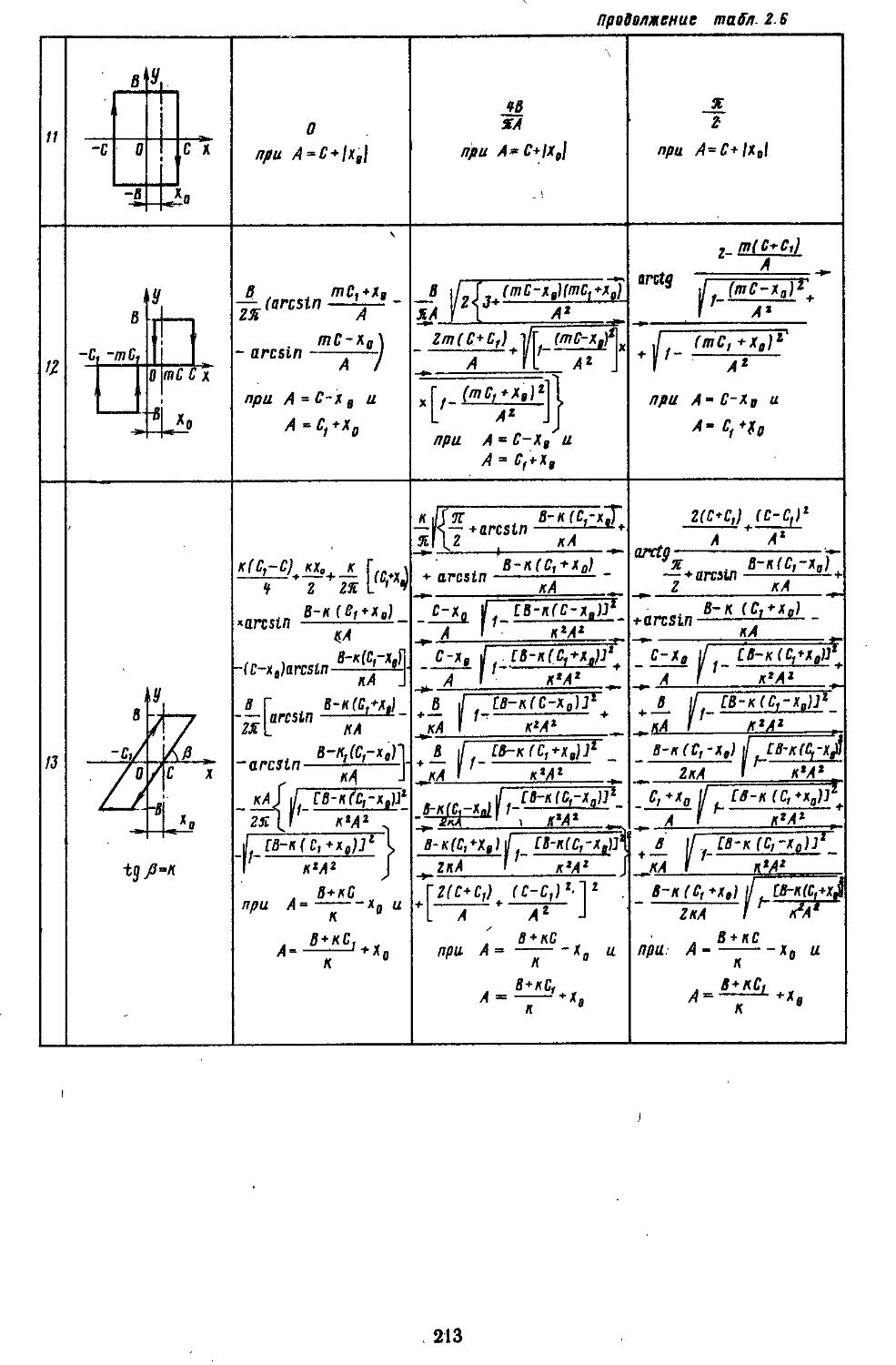
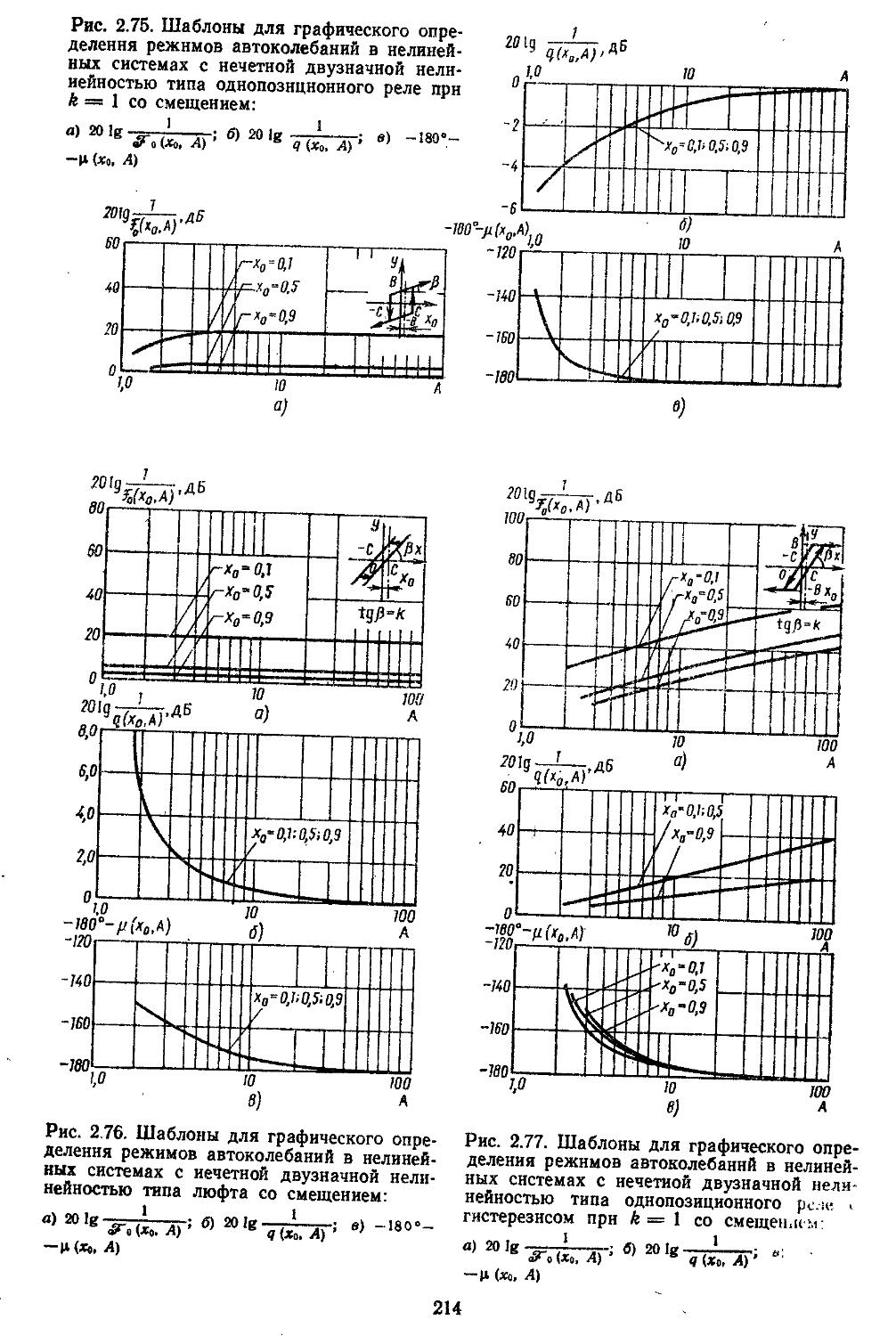
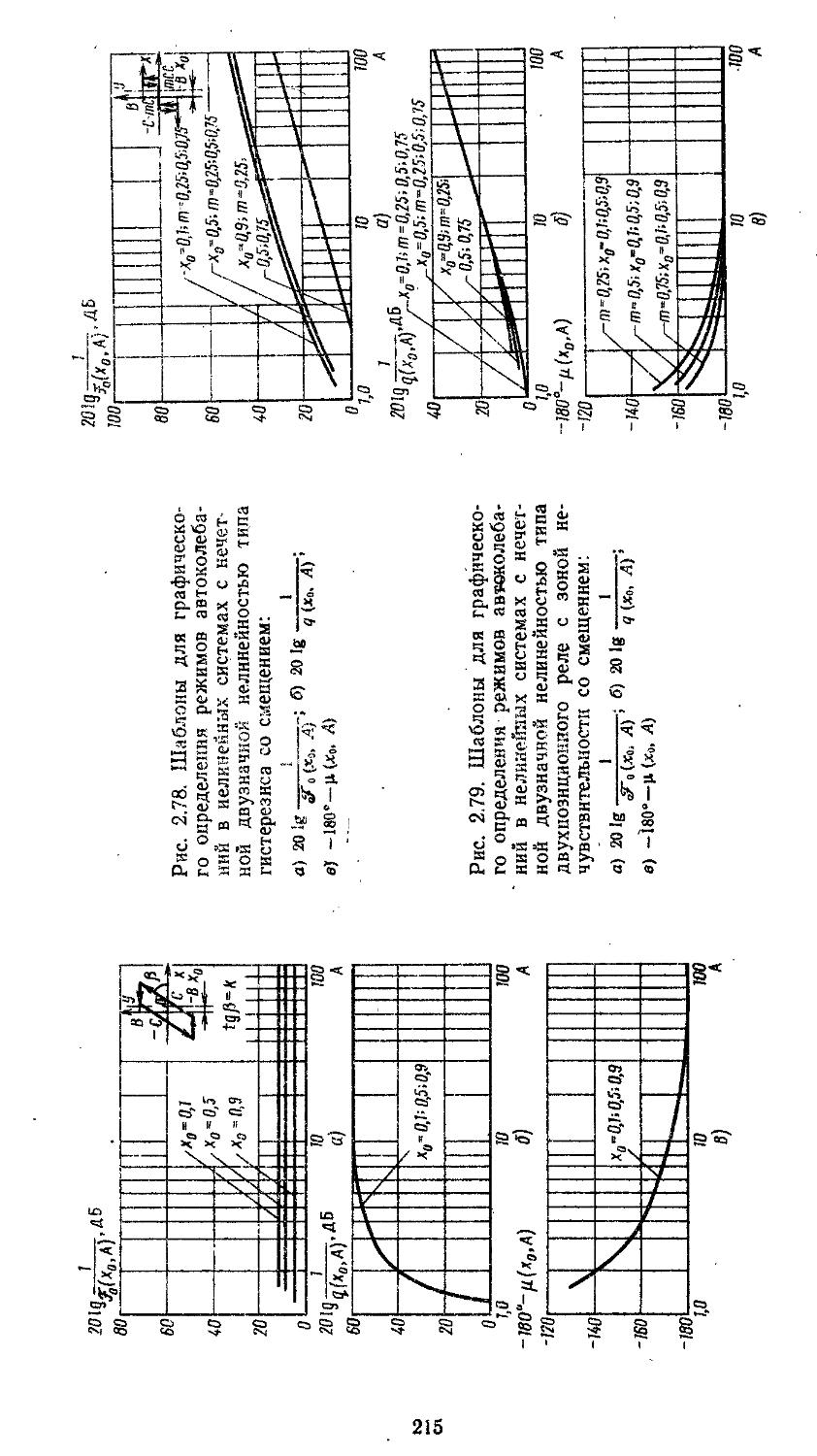
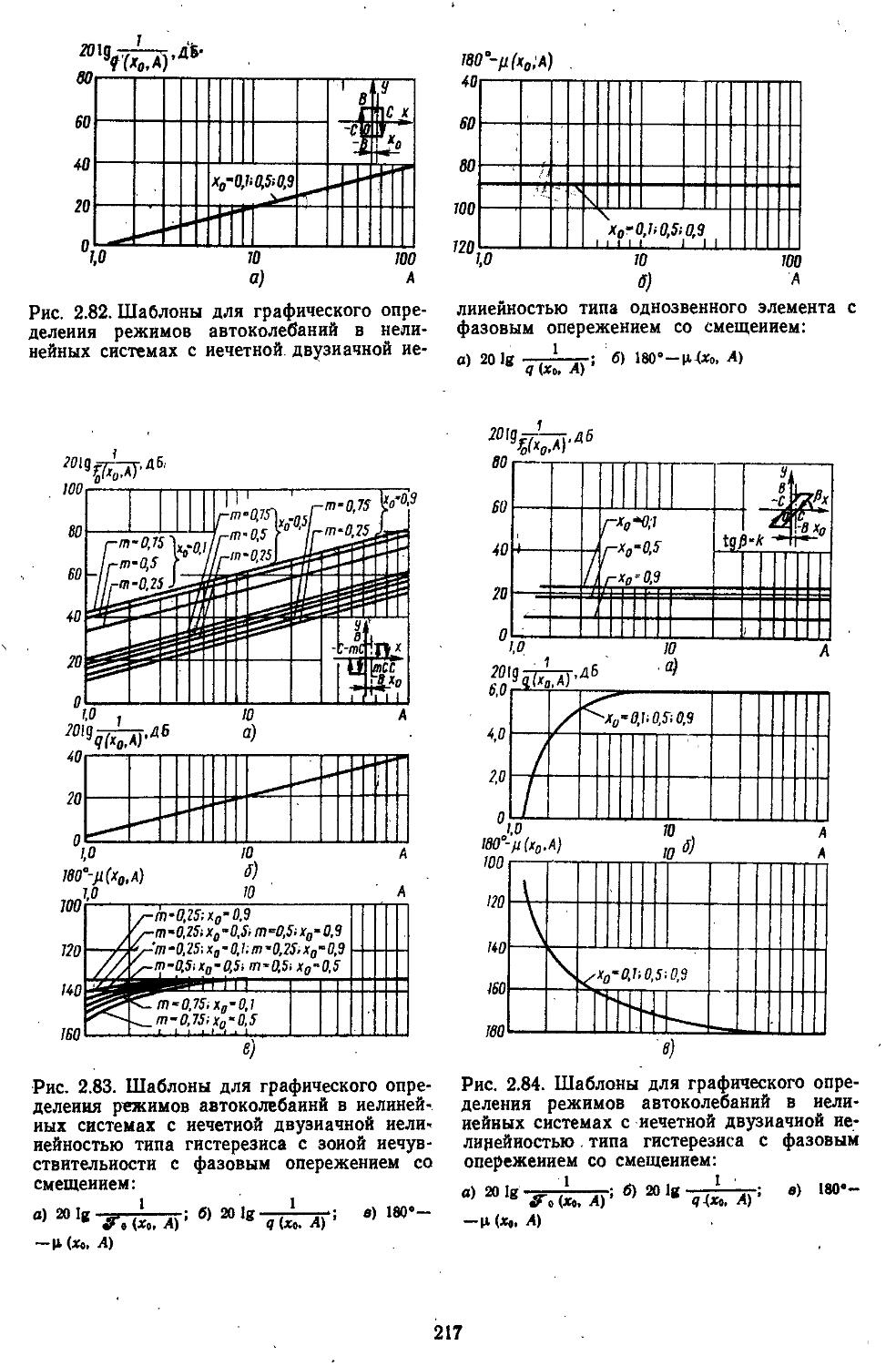
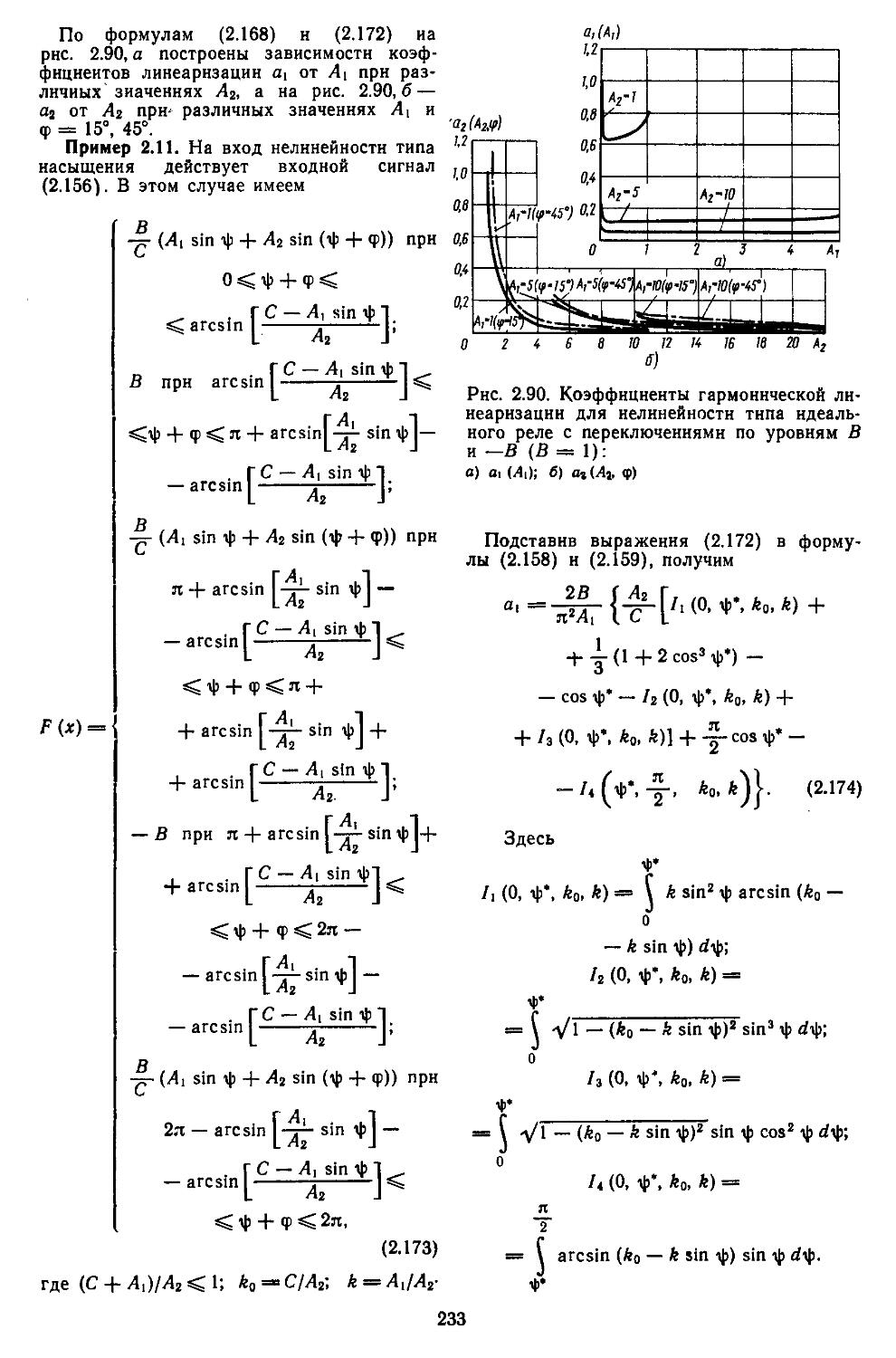
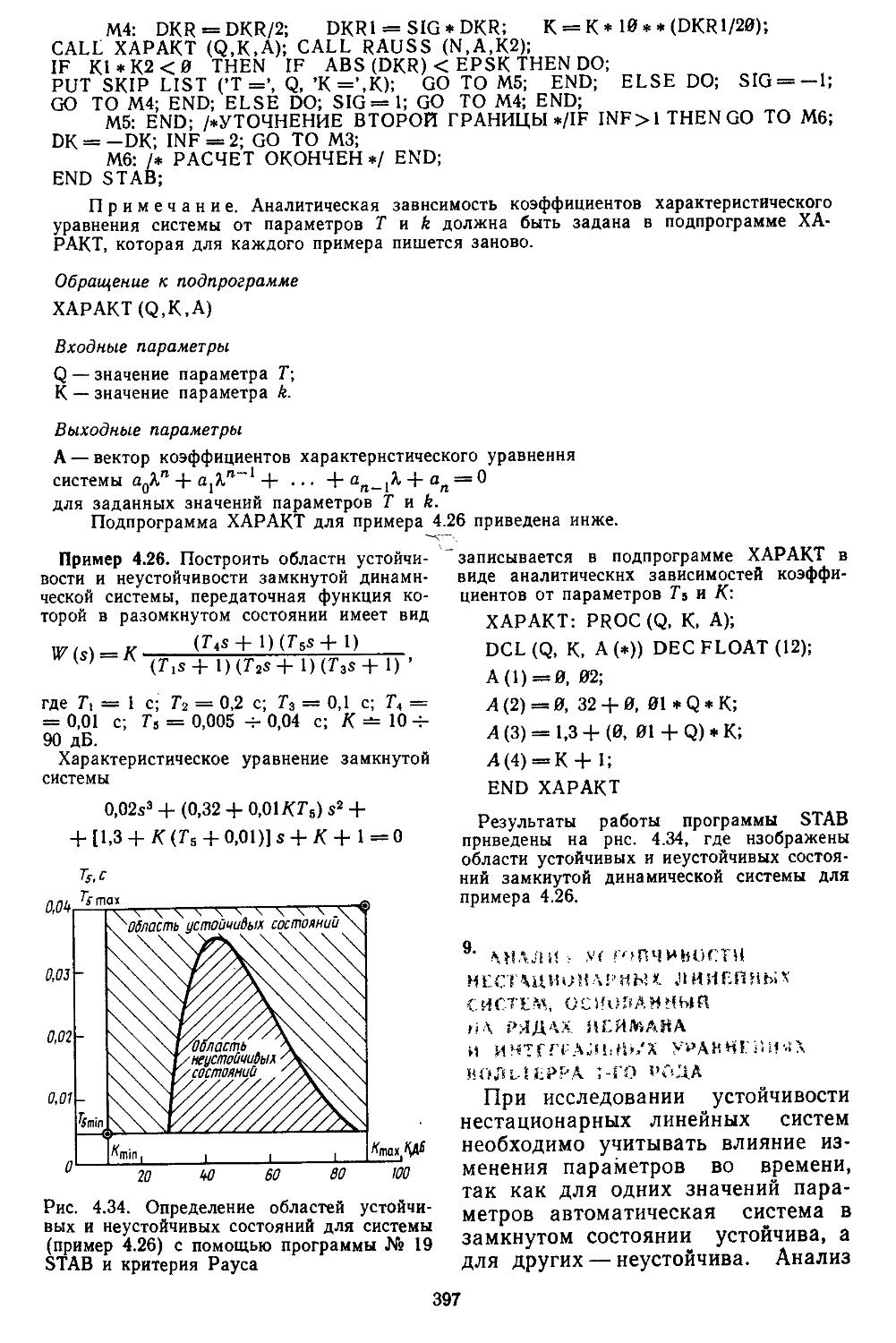
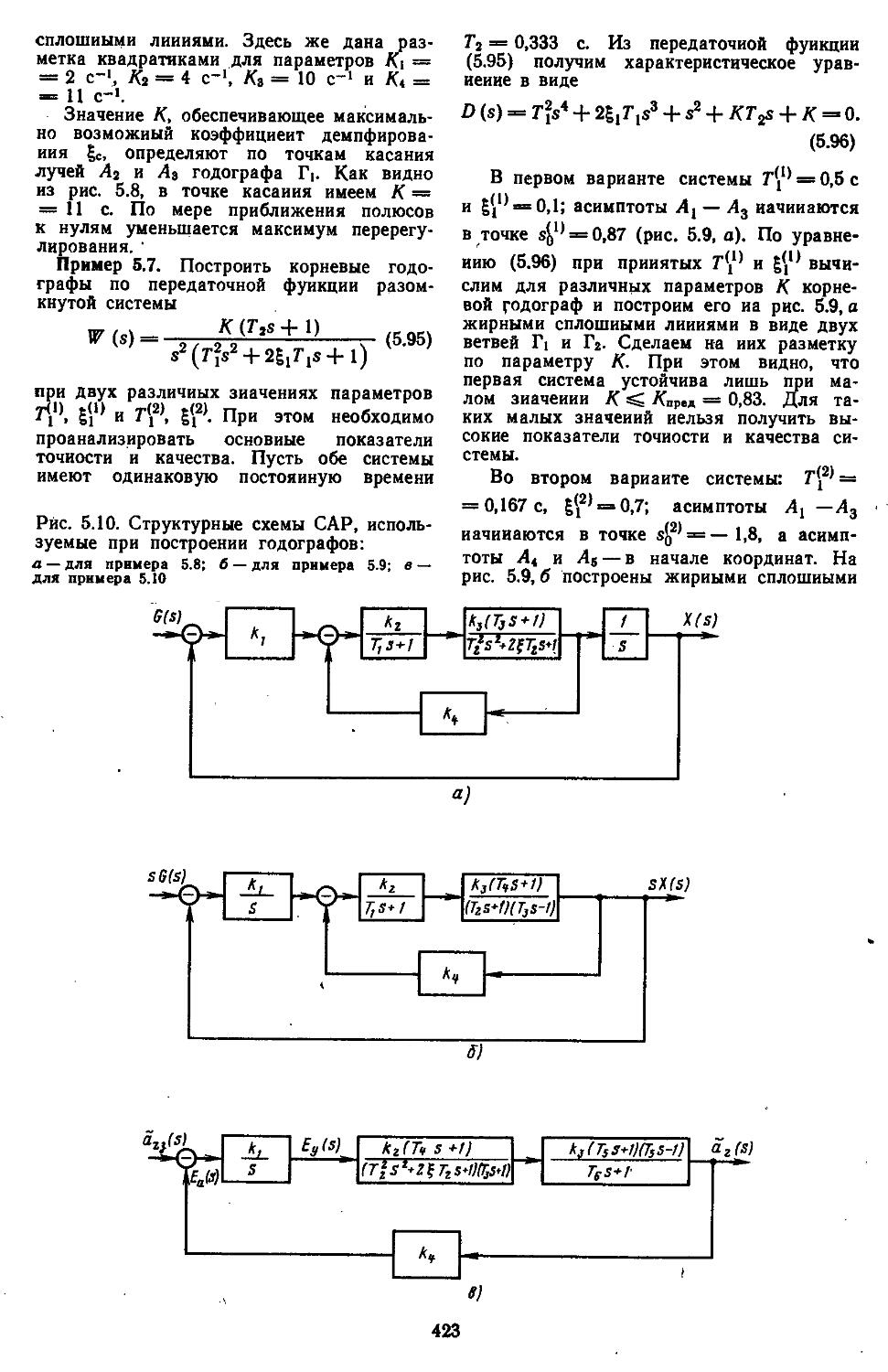
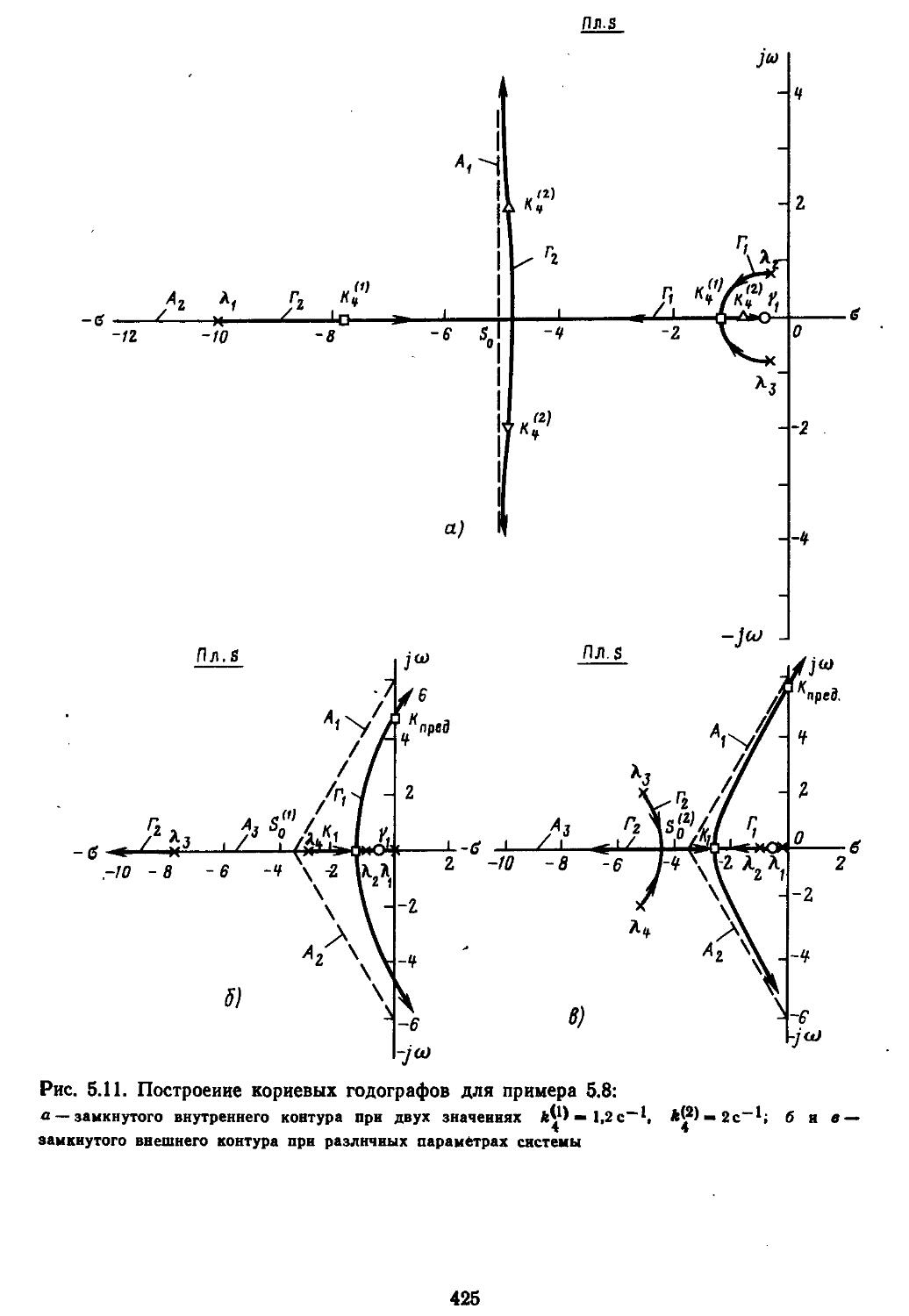
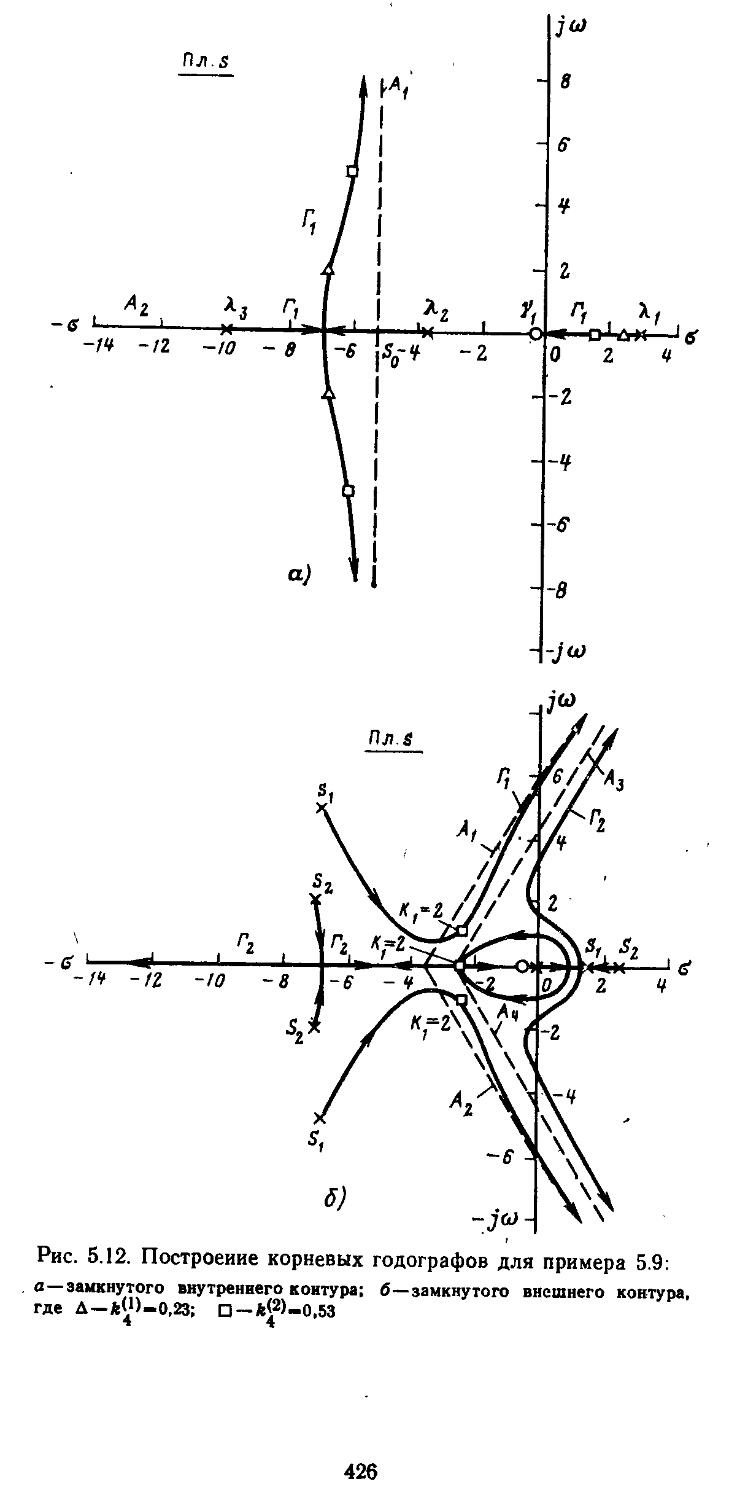
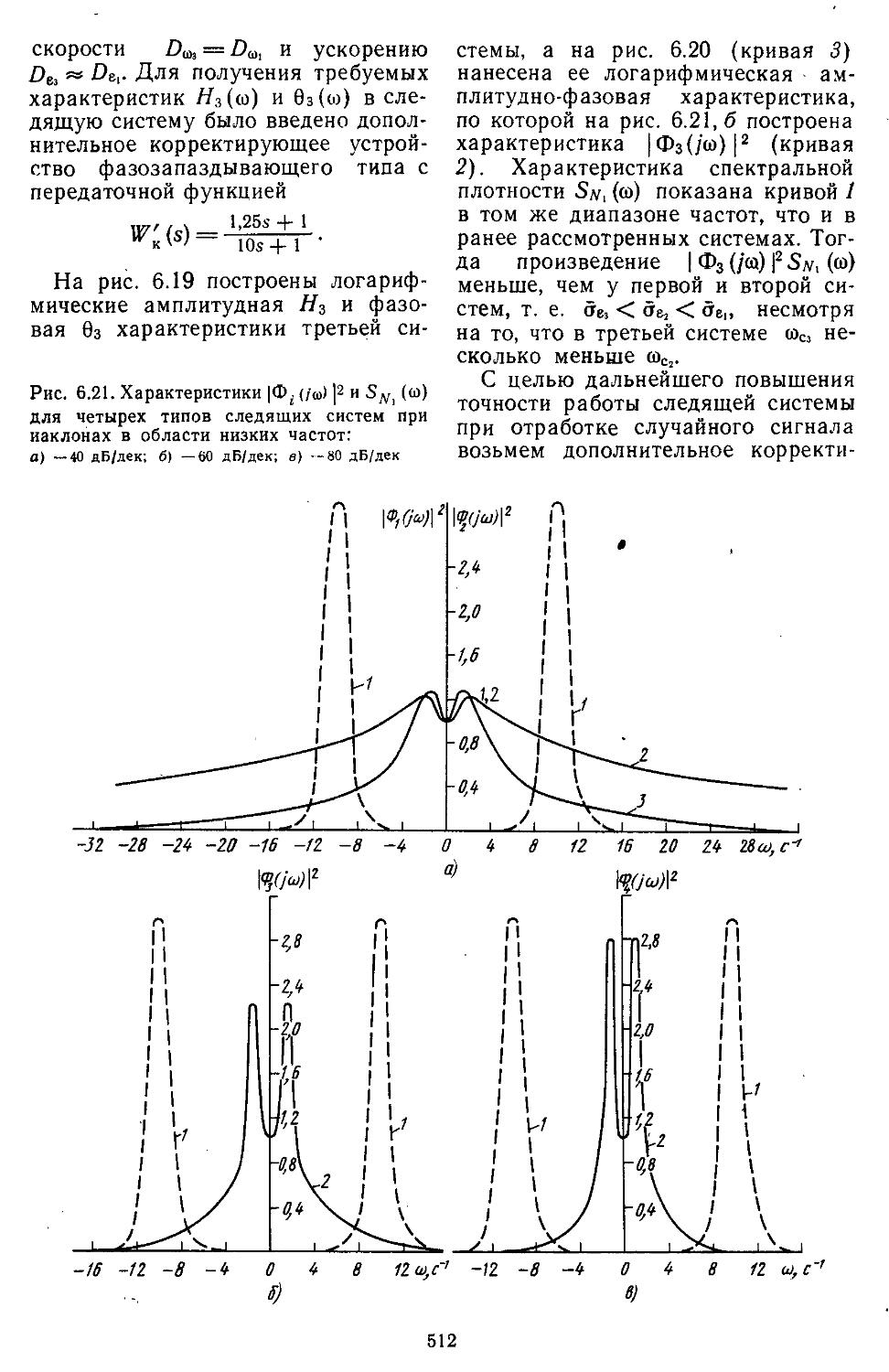
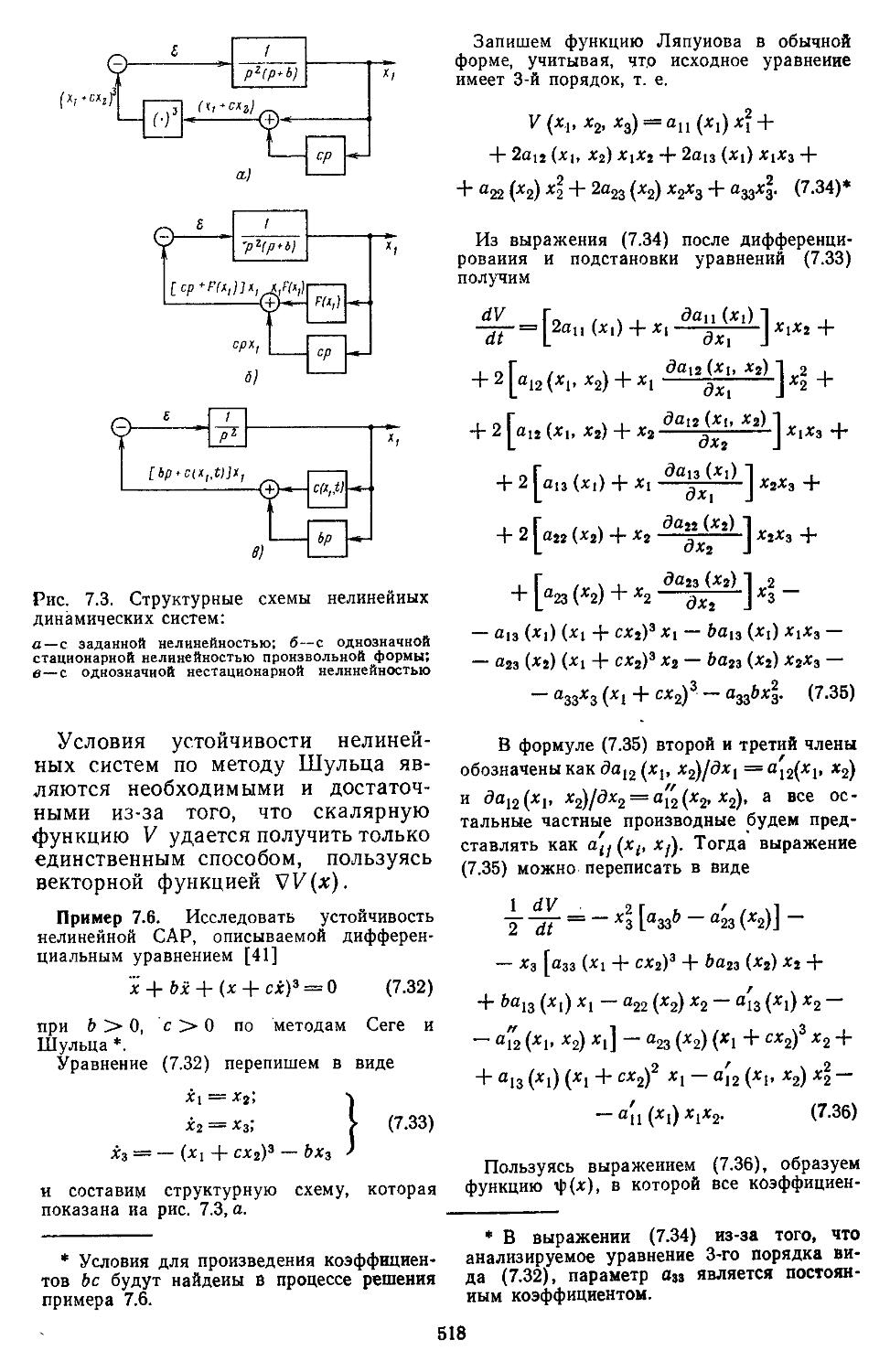
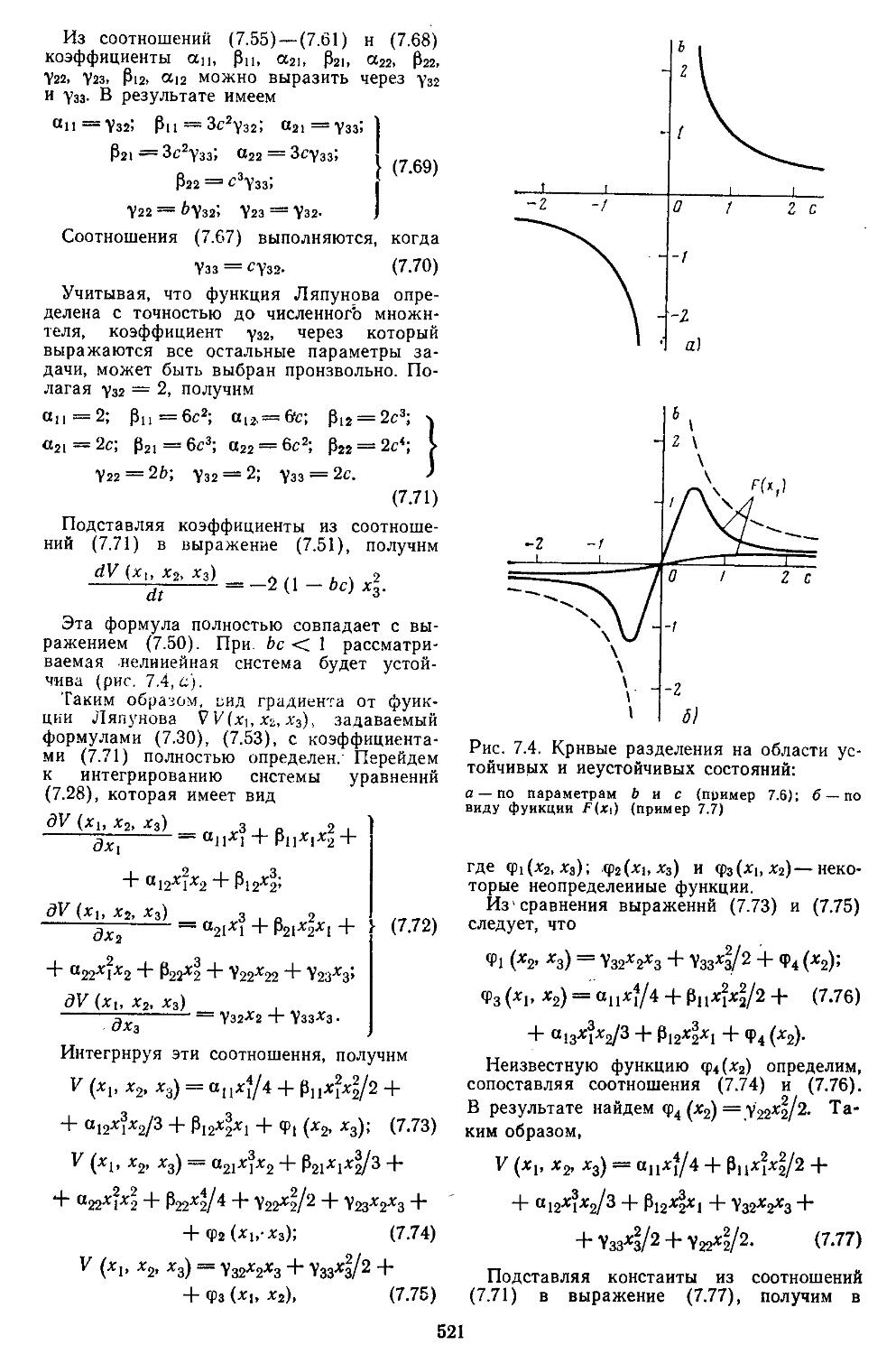
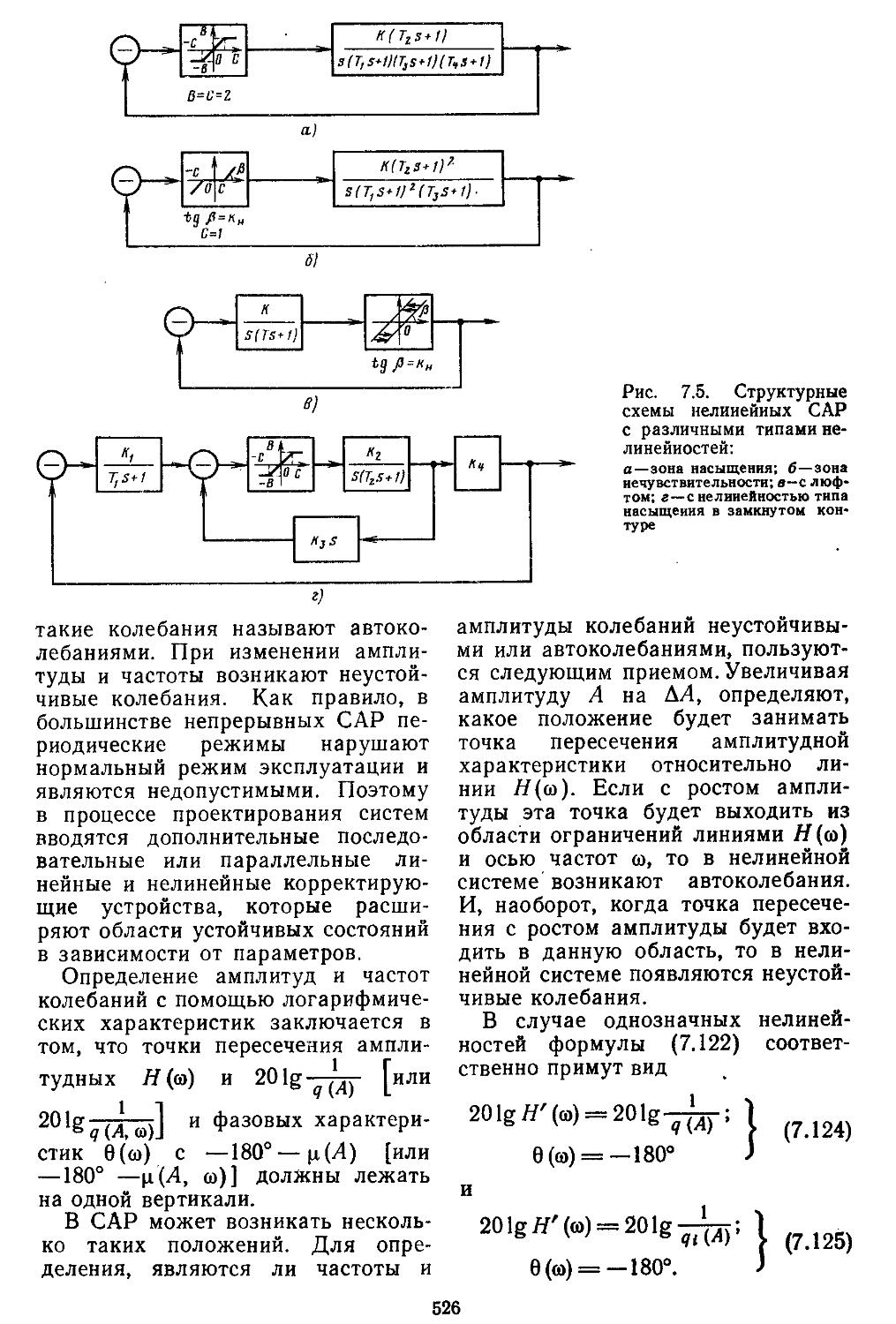
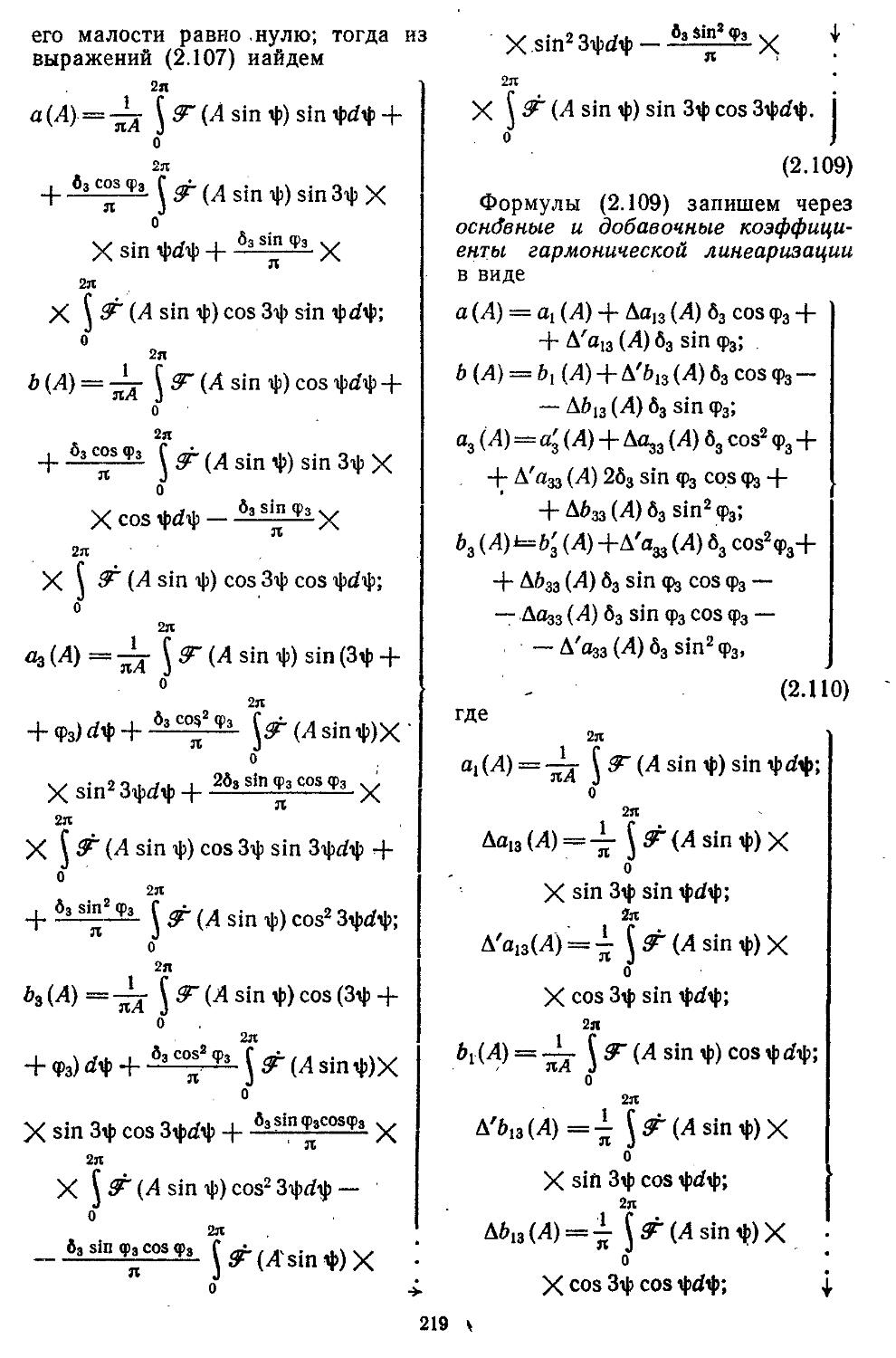Author: Топчеев Ю.И.
Tags: автоматика системы автоматического управления и регулирования интеллектуальная техника технология управления оборудование систем управления техническая кибернетика проектирование
ISBN: 5-217-00151-8
Year: 1989
Ю.И.Тм,жев
для проектирования систем
автоматического
регулирования
Ю.ИТотеев
Атлас для проектирования систем автоматического регулирования
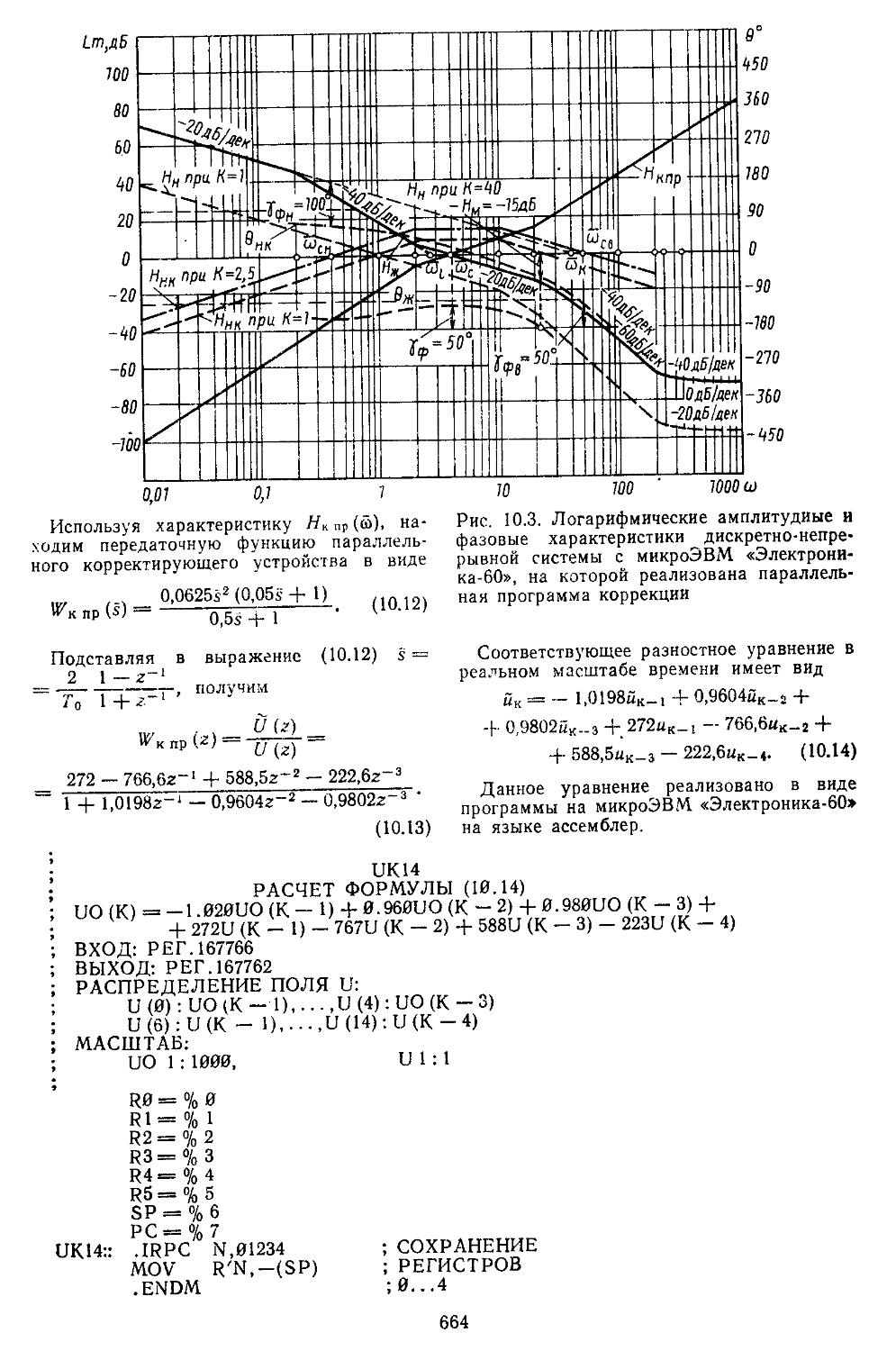
Допущено Государственным комитетом СССР по народному образованию в качестве учебного пособия для студентов высших технических учебных заведений
Scanned by LinCAD
МОСКВА «МАШИНОСТРОЕНИЕ» 1989
ББК 32.965я73
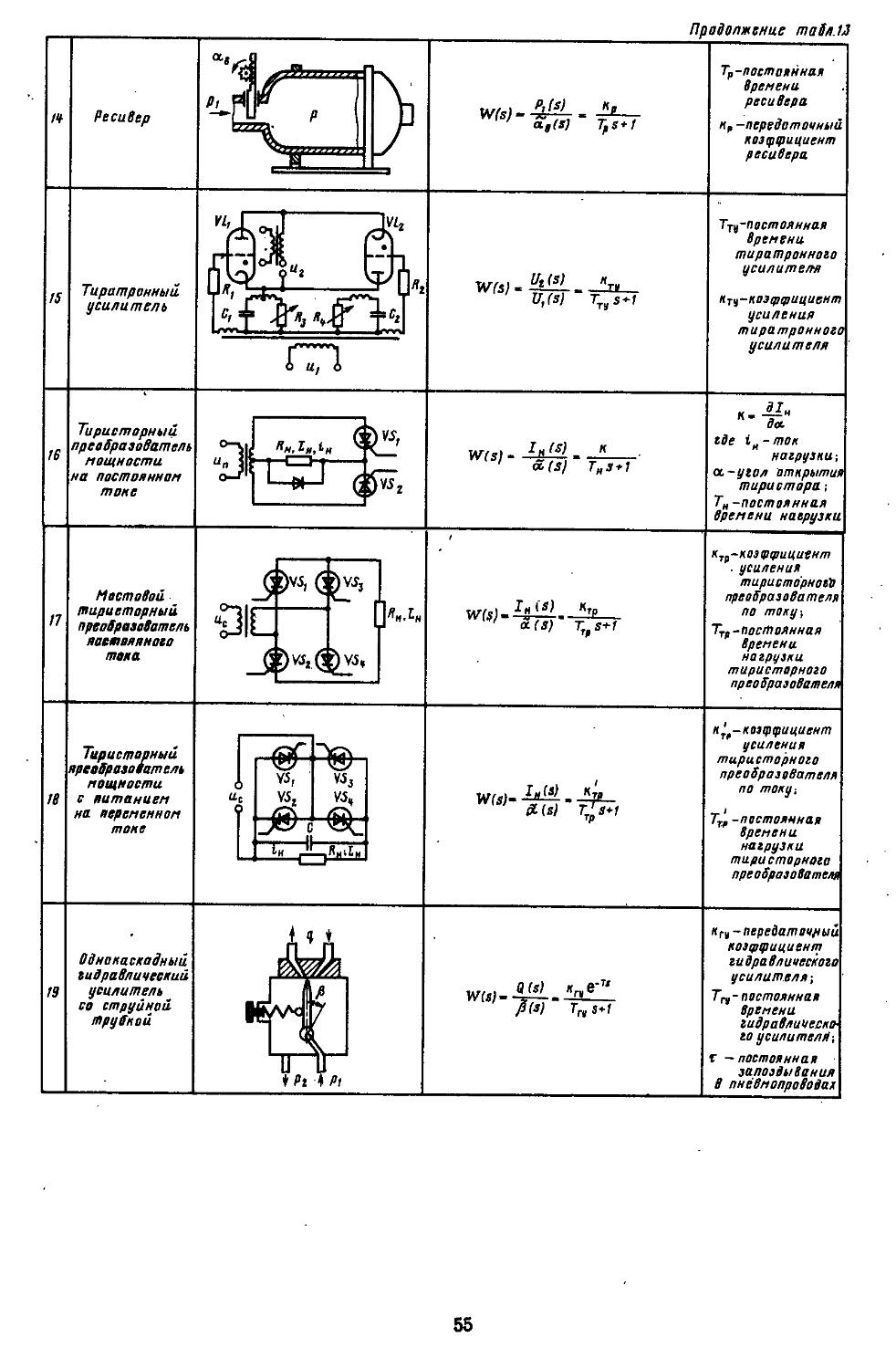
Т58
УДК 681.51.001.63(075.8)
Рецензенты: 1. Кафедра МВТУ соответствующего профиля, зав. кафедрой член-корр. АН СССР Е. П. Попов
2. Академик АН СССР А. А. Воронов
Топчеев Ю. И.
Т58 Атлас для проектирования систем автоматического регулирования: Учеб, пособие для втузов. — М.: Машиностроение, 1989.— 752 с.: ил.
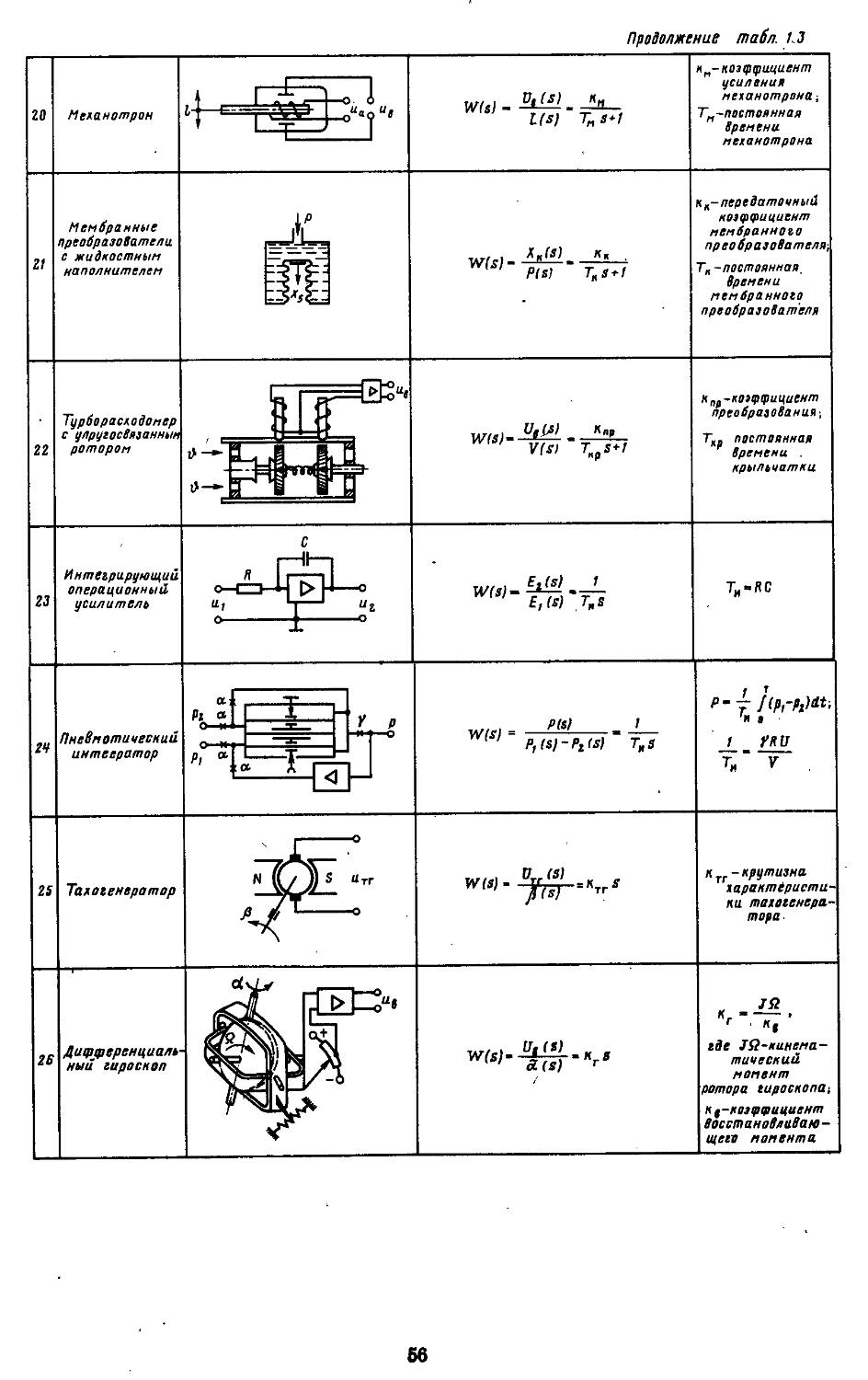
ISBN 5-217-00151-8
Приведены алгоритмы, номограммы, графики и таблицы для исследования устойчивости, показателей качества и точности различных классов систем, позволяющие решать задачи анализа и синтеза. Разработаны вычислительные процедуры и рабочие программы иа языке ПЛ/1 для проектирования автоматических систем регулирования (САР) с помощью ЕС ЭВМ в пакетном и интерактивном режимах работы. Все теоретические положения иллюстрированы многочисленными примерами выбора структур и параметров реальных систем.
Может быть полезен инженерно-техническим работникам, занимающимся расчетом и проектированием САР и управления в различных отраслях науки и техники.
Т КБ 53-83—89 ББК 32.965я73
038(01оУ
ISBN 5-217-00151-8 © Издательство «Машиностроение»,
1989
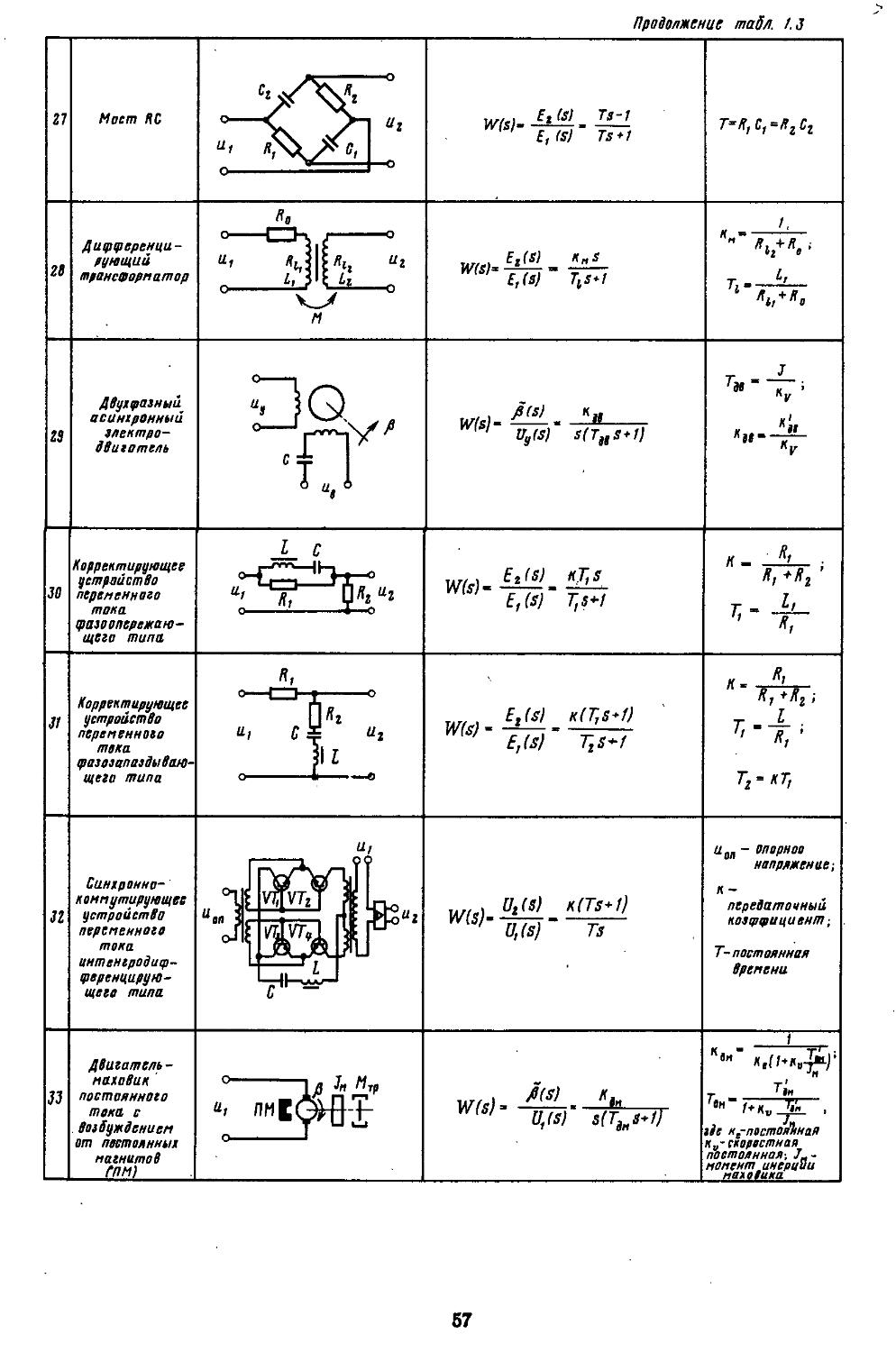
ОГЛАВЛЕНИЕ
Предисловие ..................... . 7
Введение........................... 10
РАЗДЕЛ I. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ . . . 20
Глава 1. Математические модели линейных элементов (объектов) . ..... 21
1. Векторная и покоординатная формы описания непрерывных и дискретных элементов 21
2. Методы линеаризации уравнений...............30
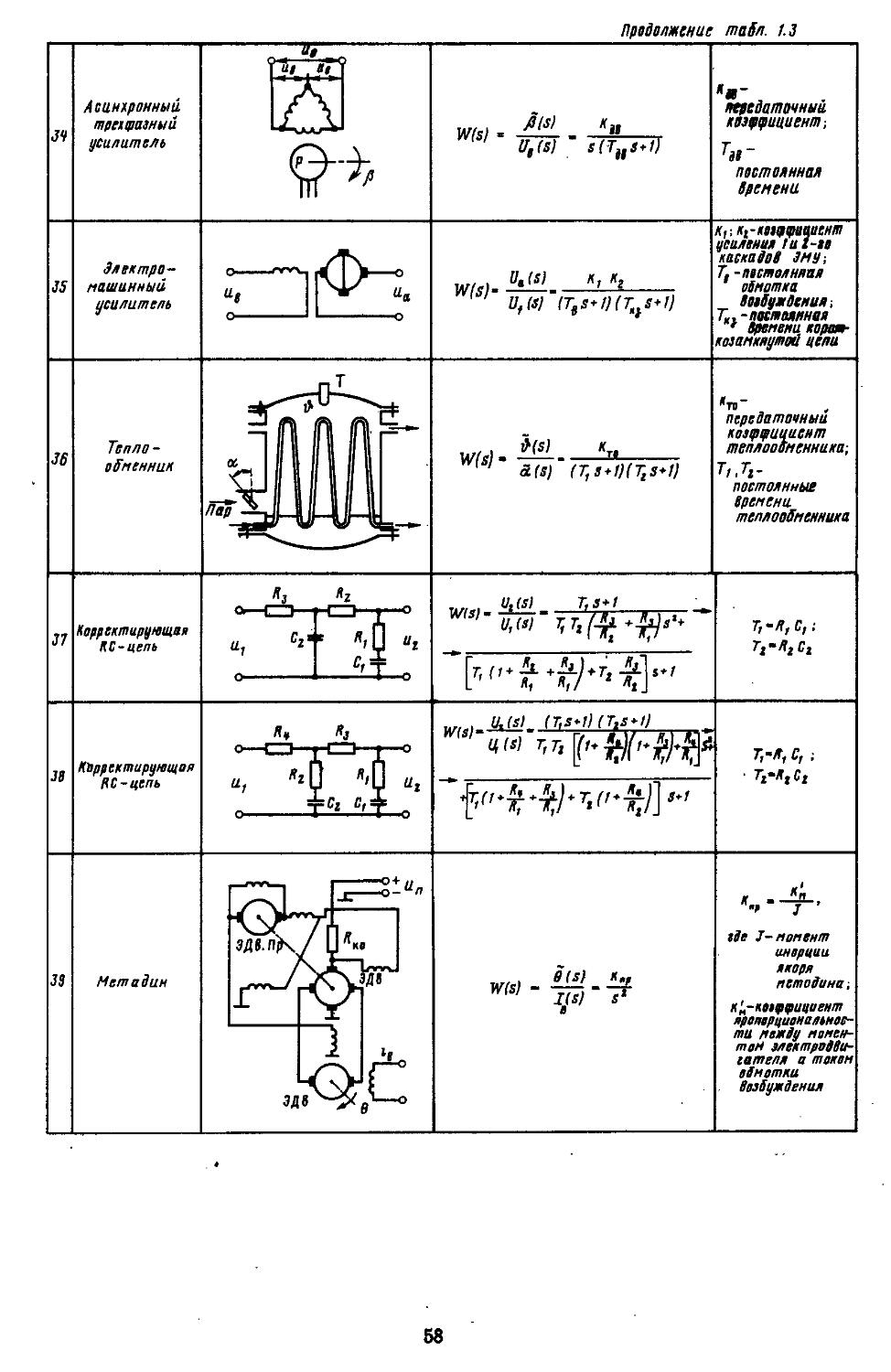
3. Типы уравнений состояния ...... 41
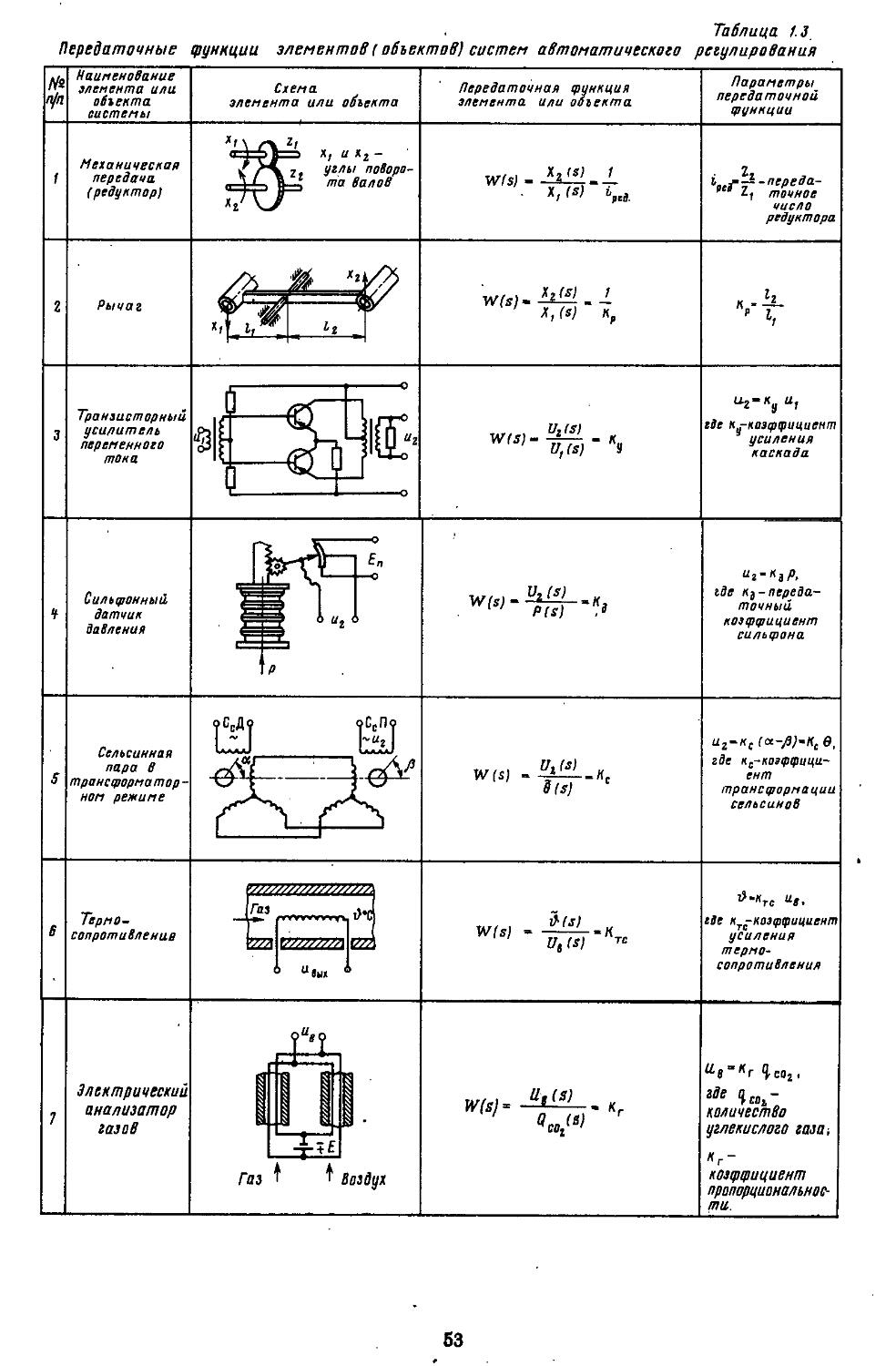
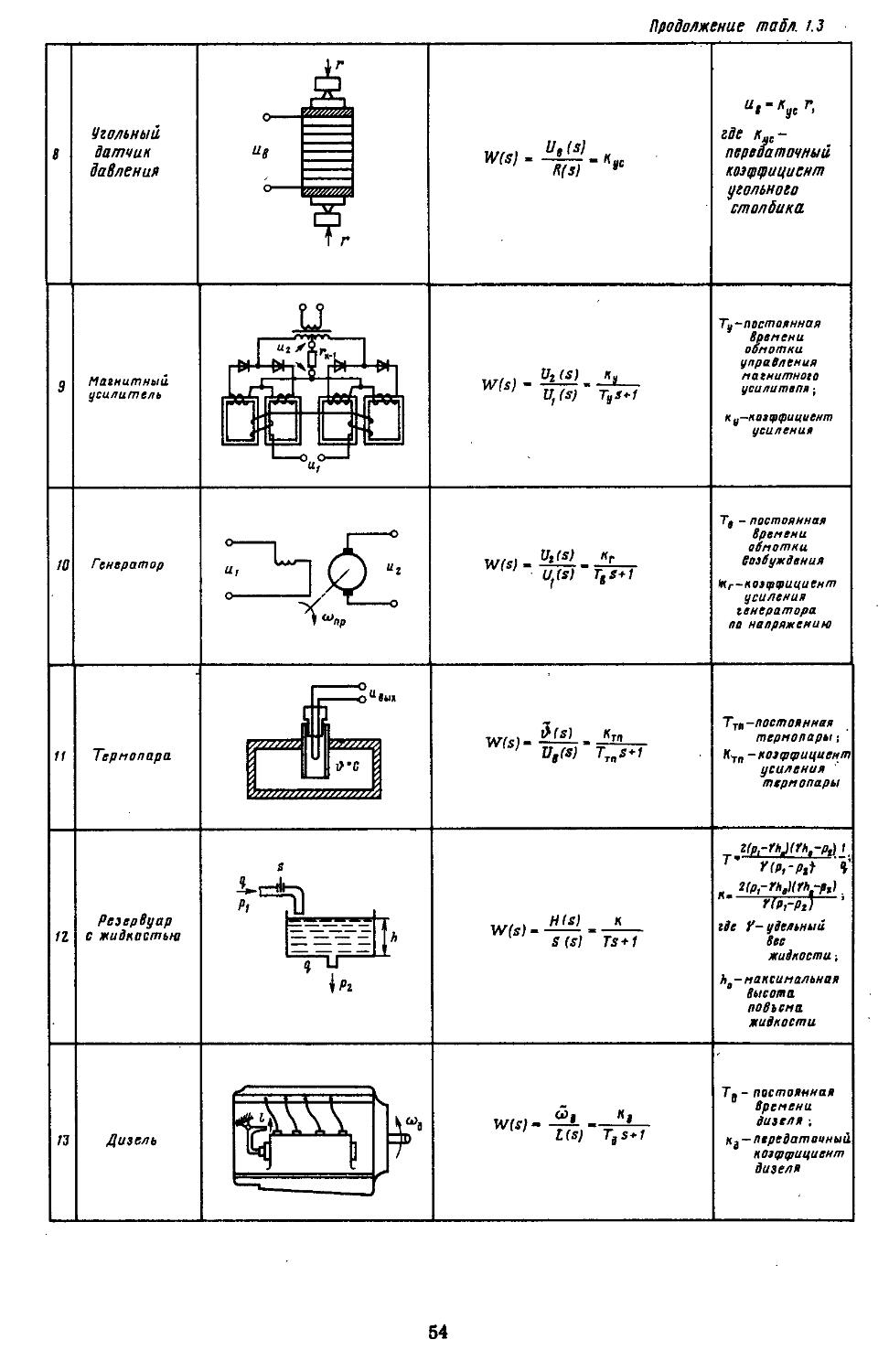
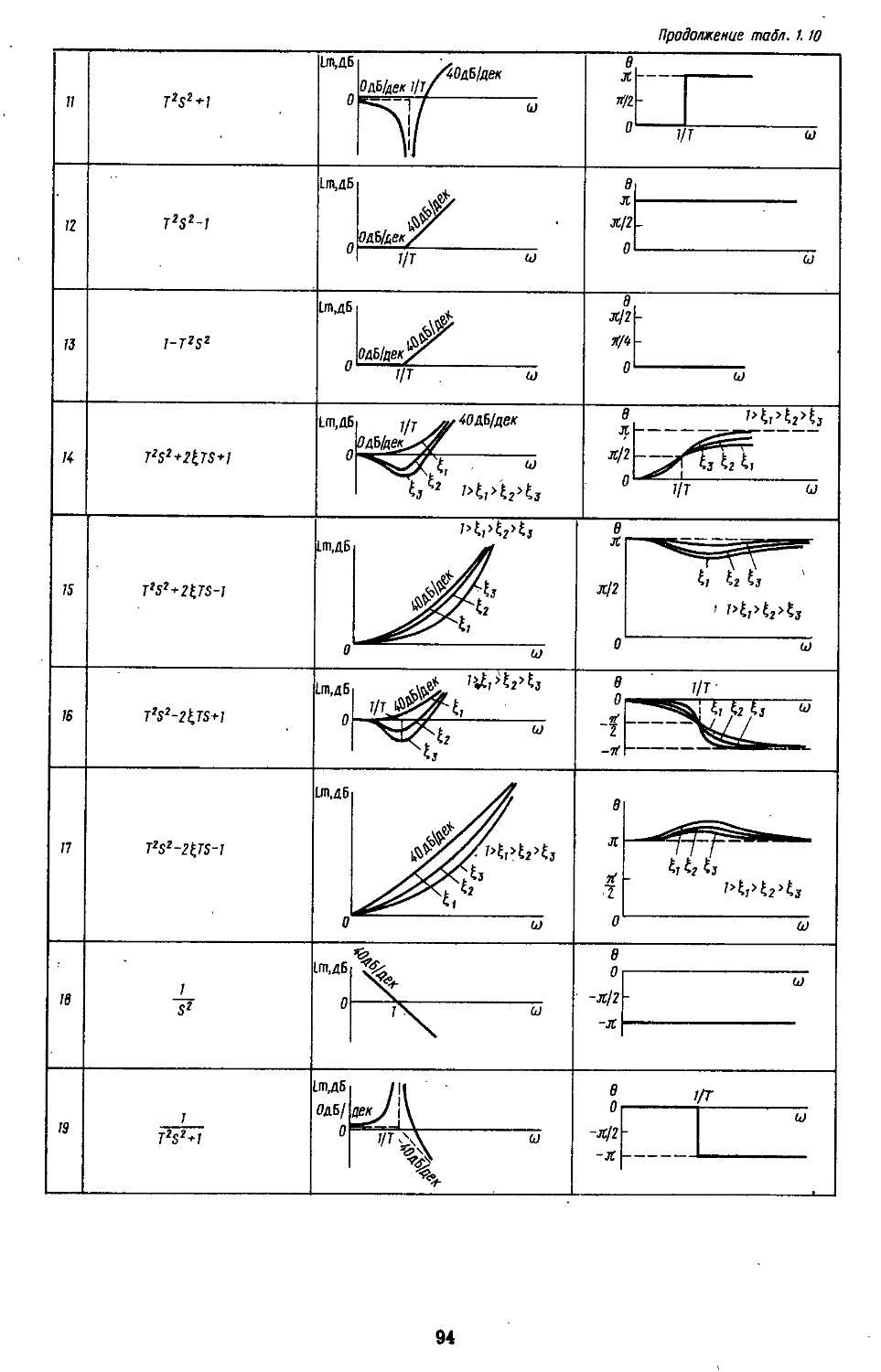
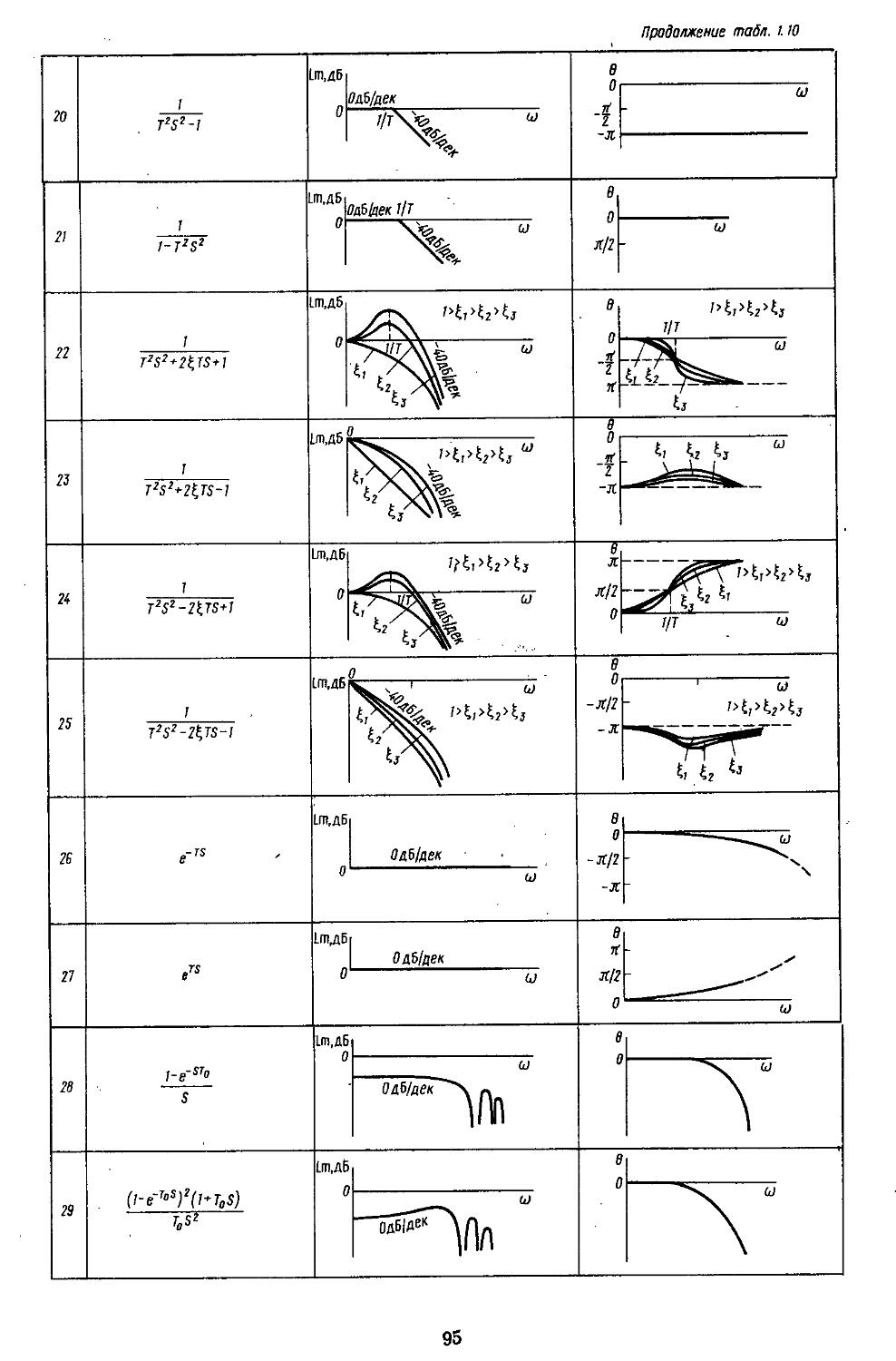
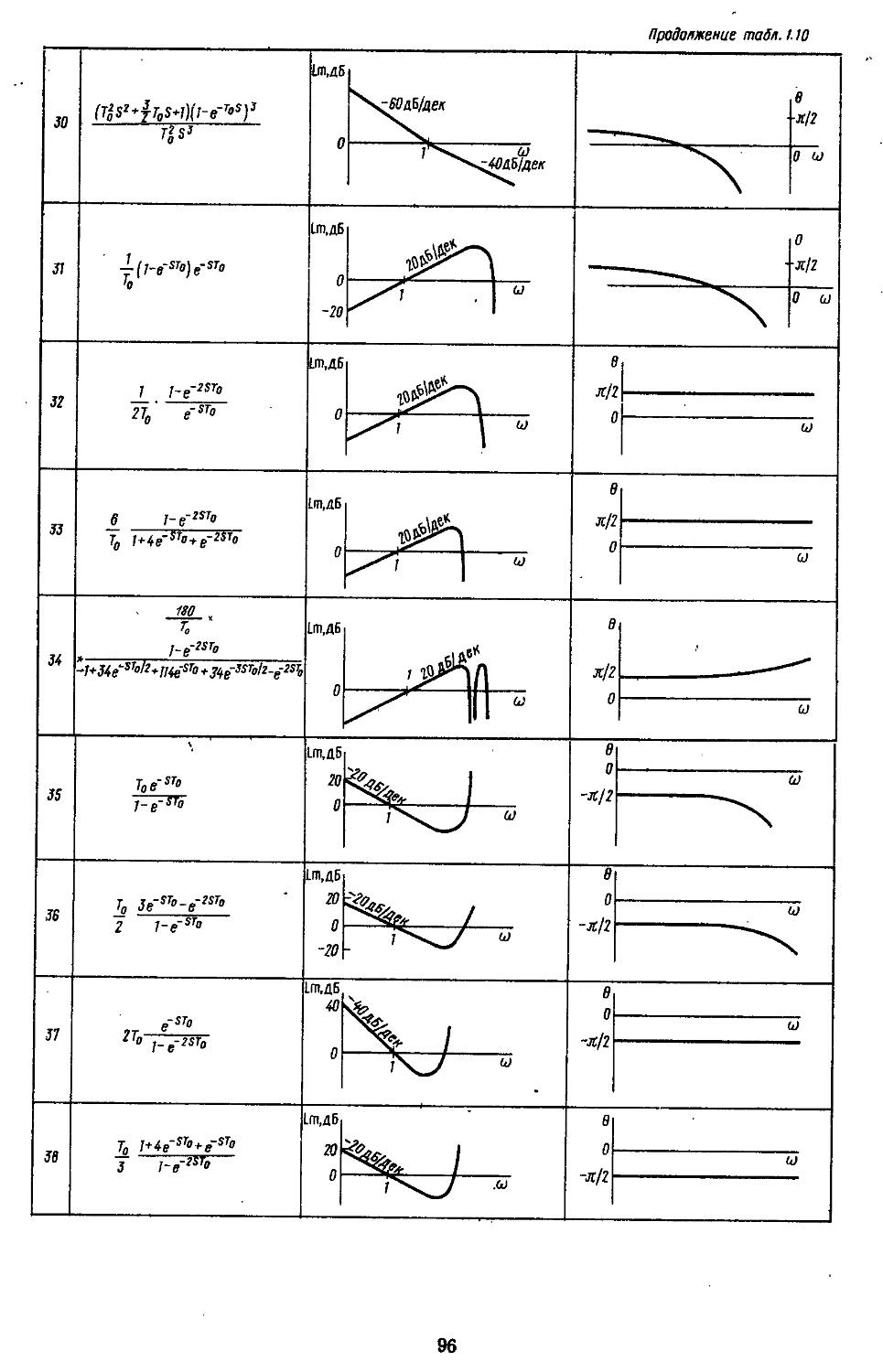
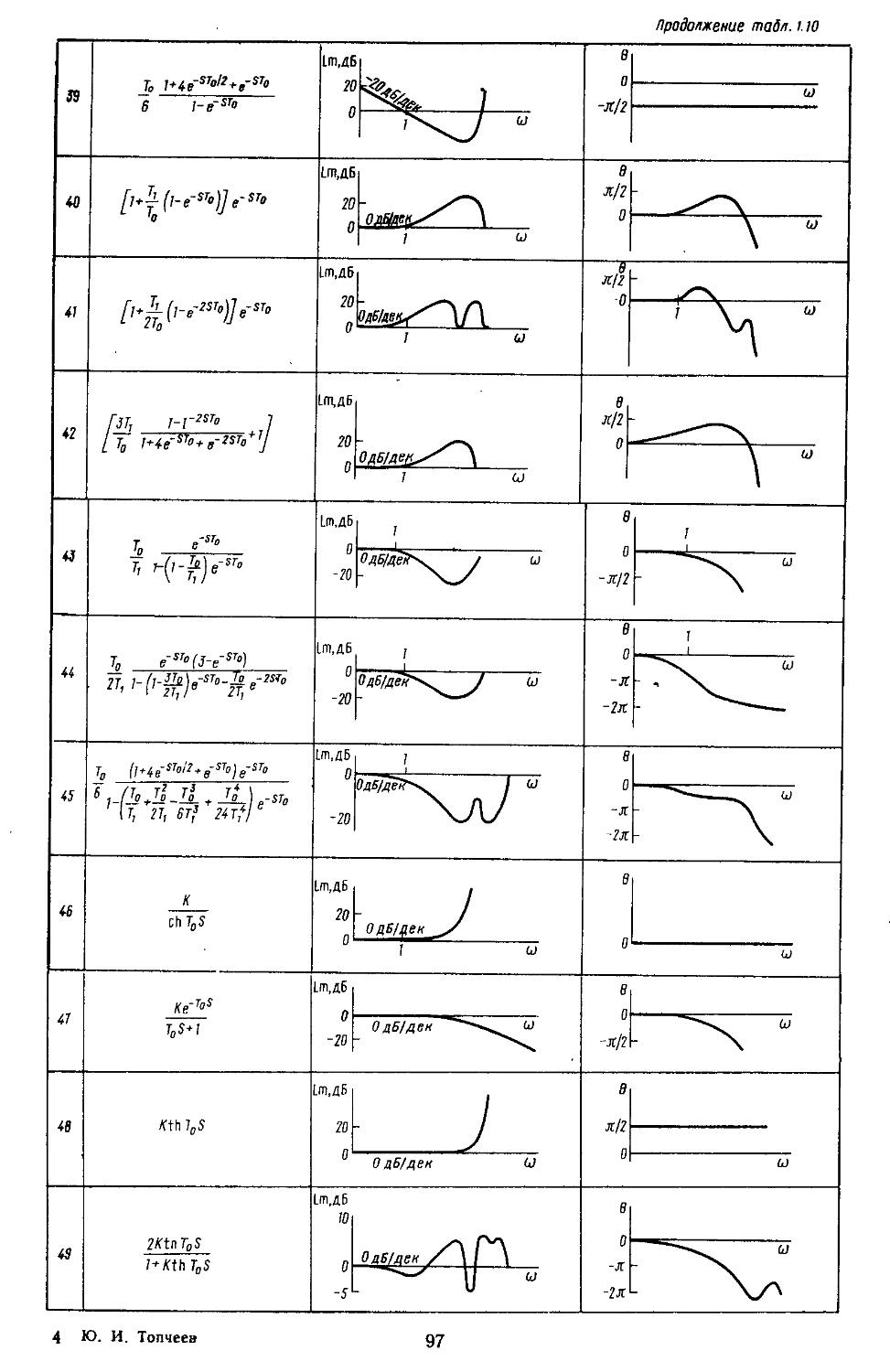
4. Передаточные функции типовых звеньев . . 46
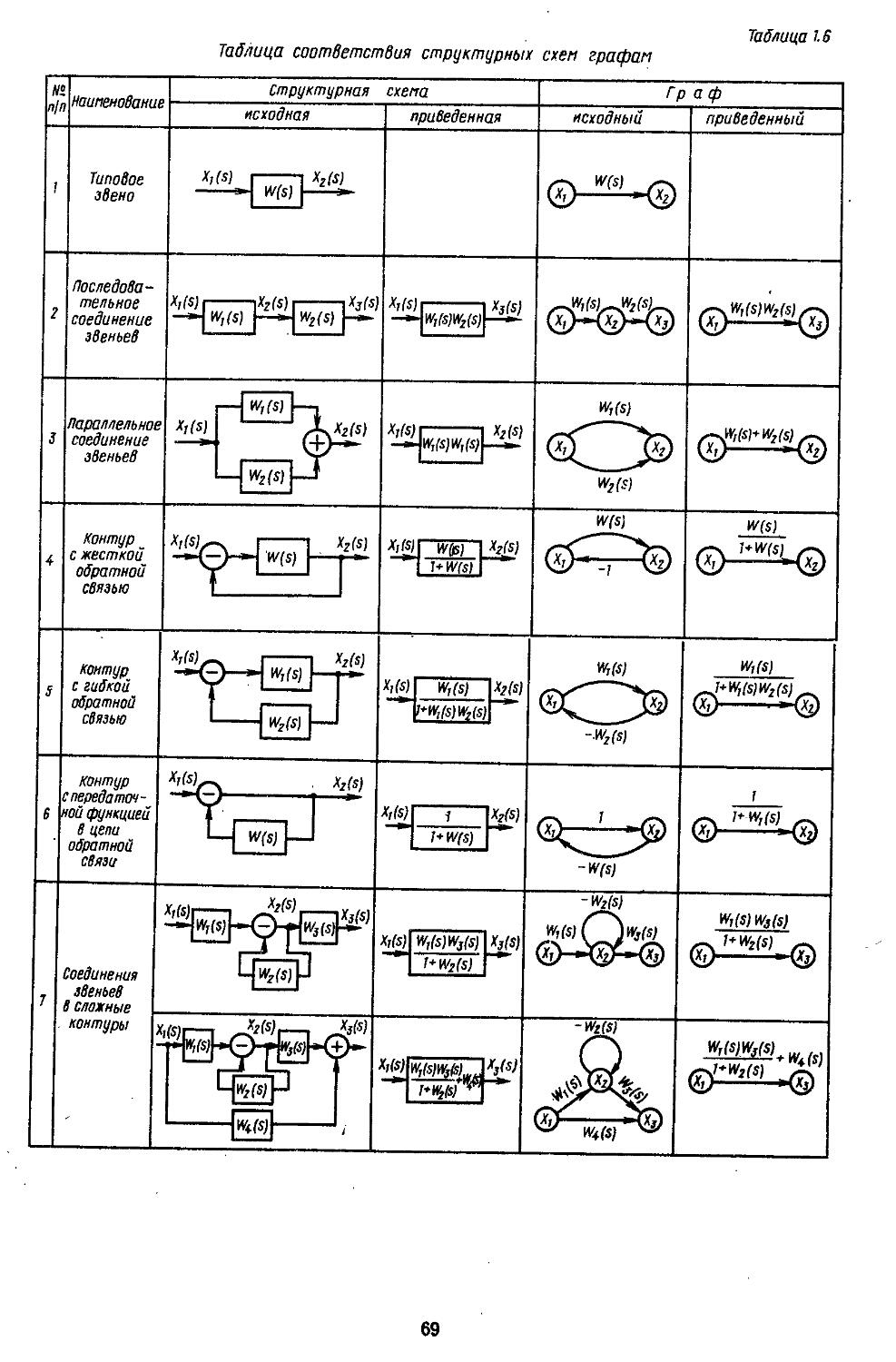
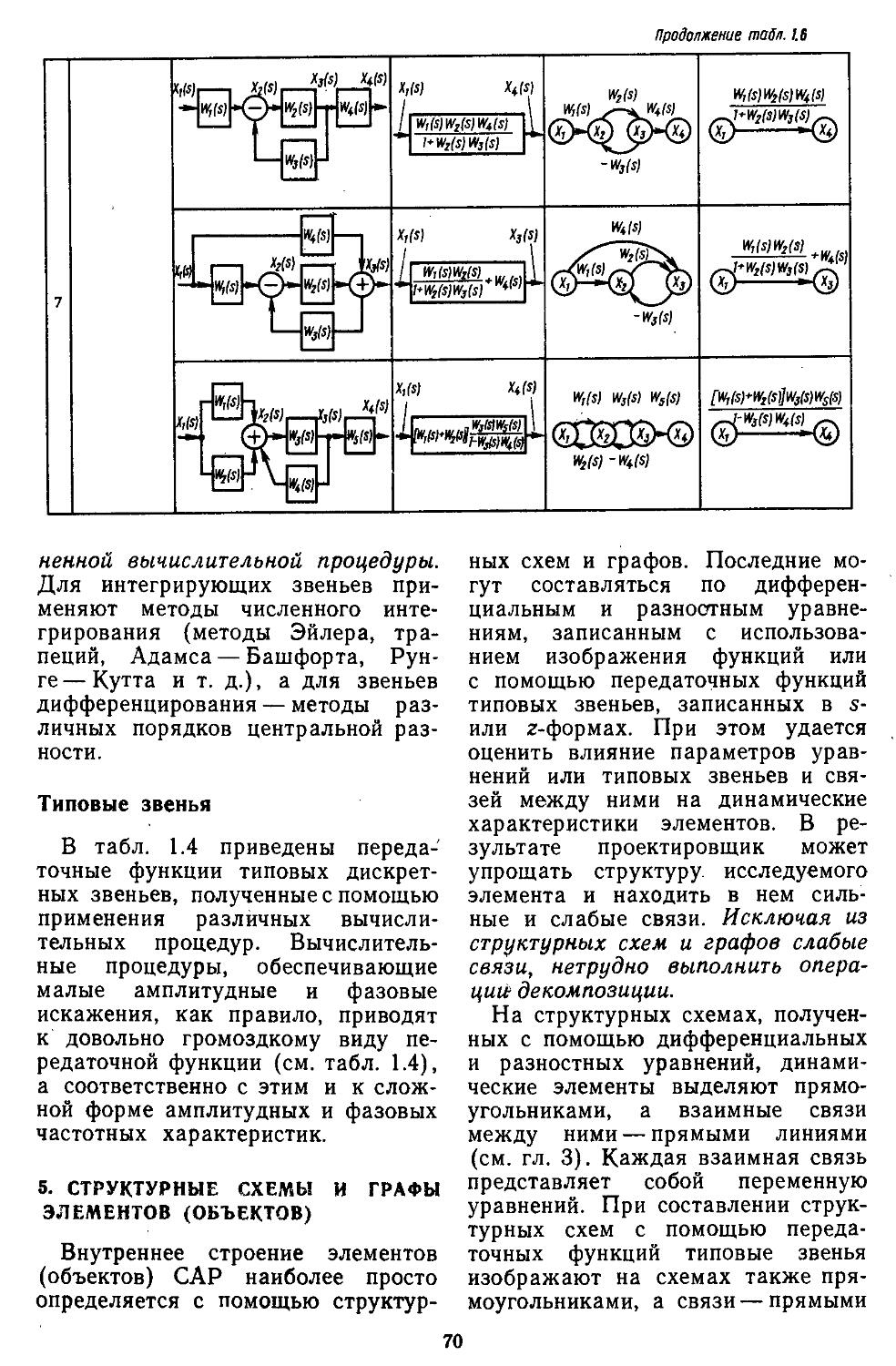
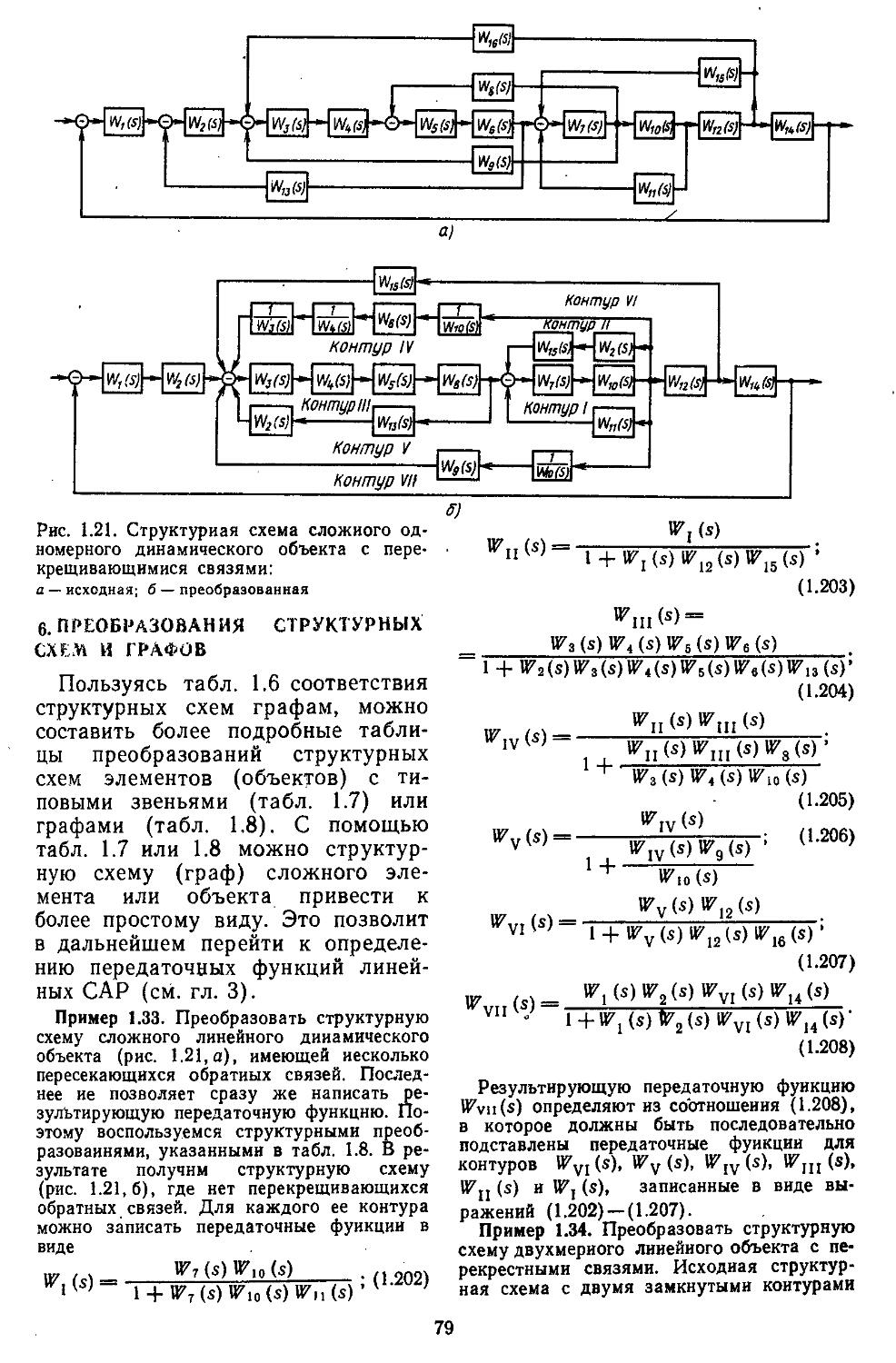
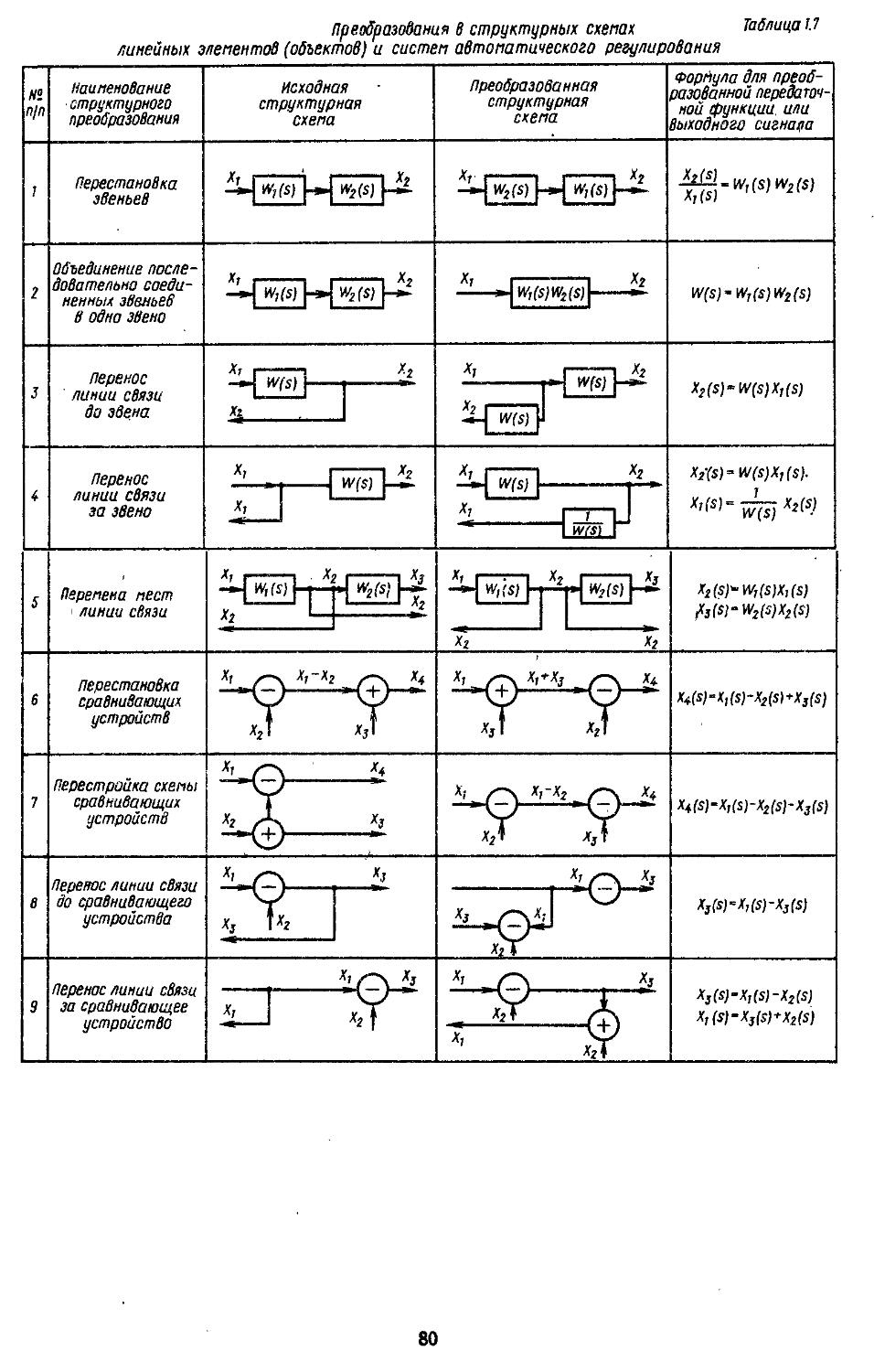
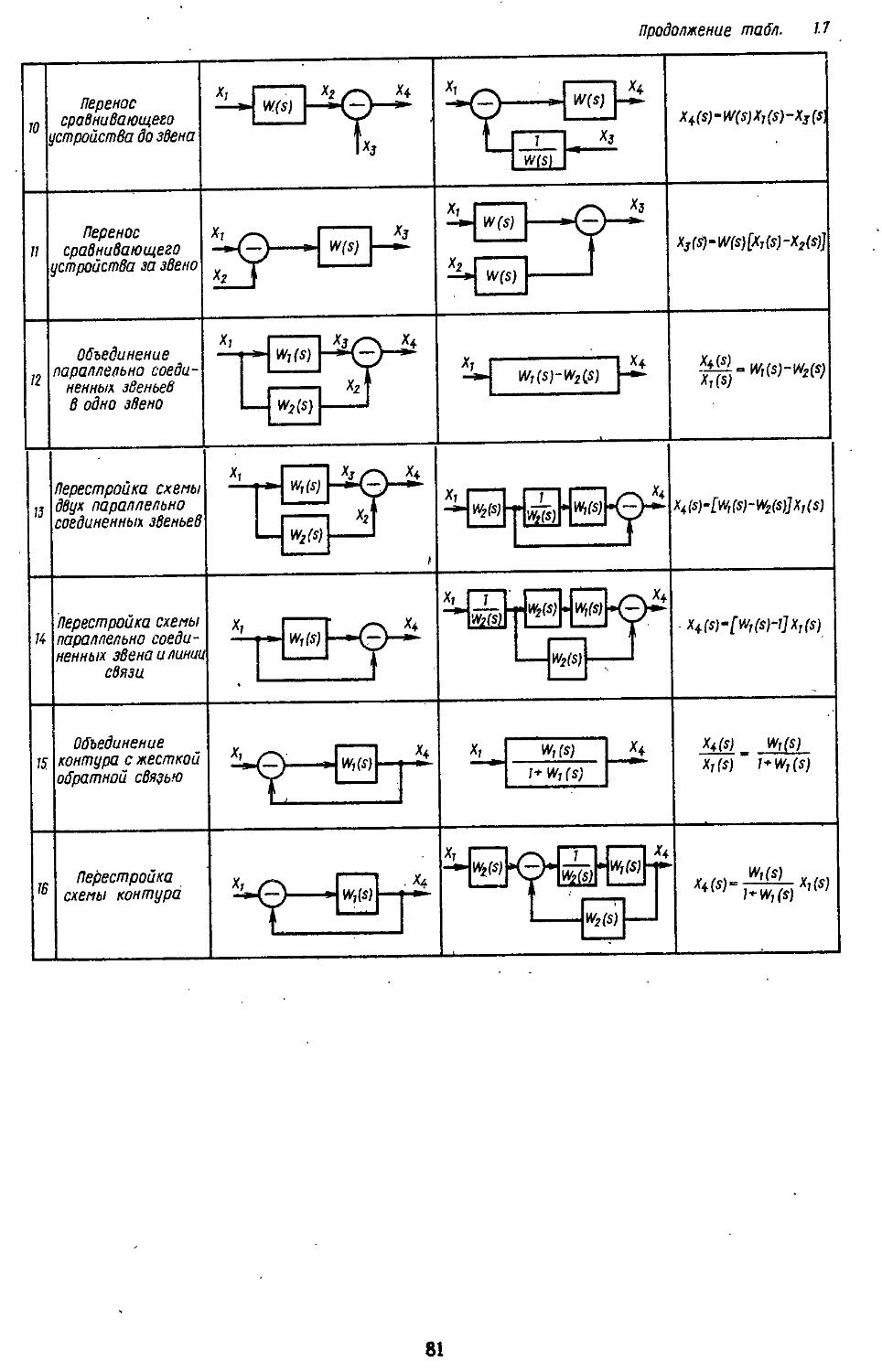
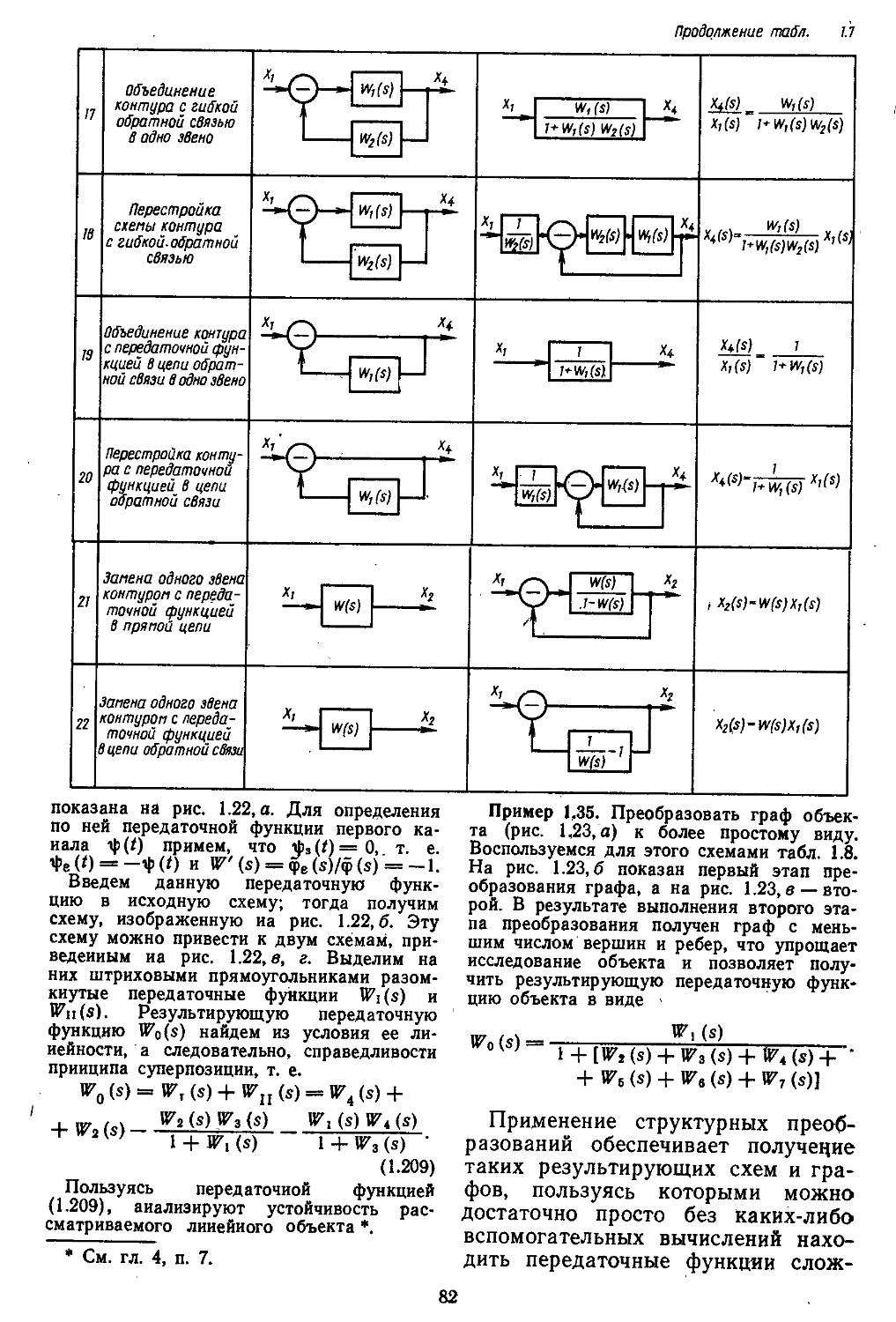
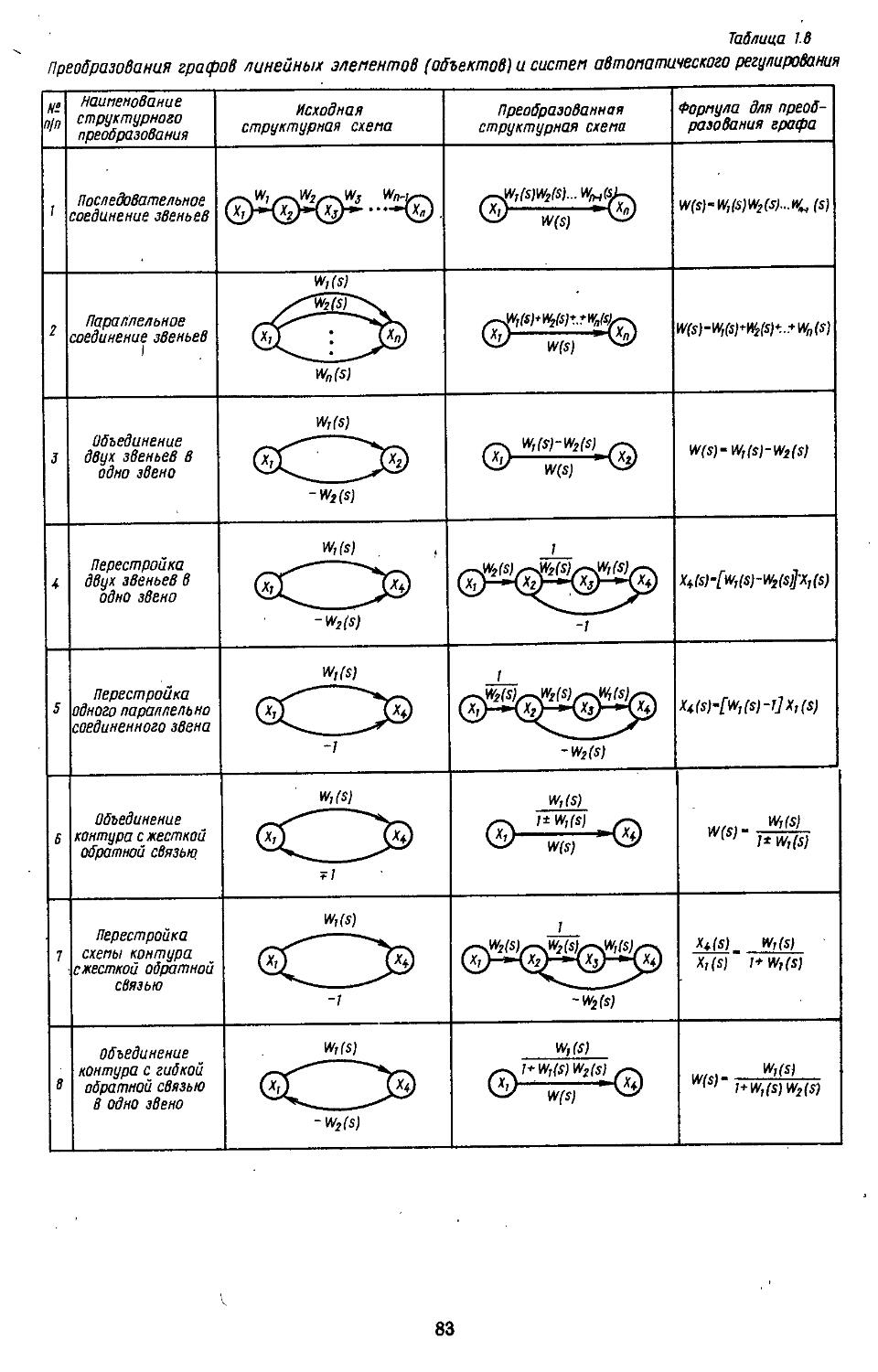
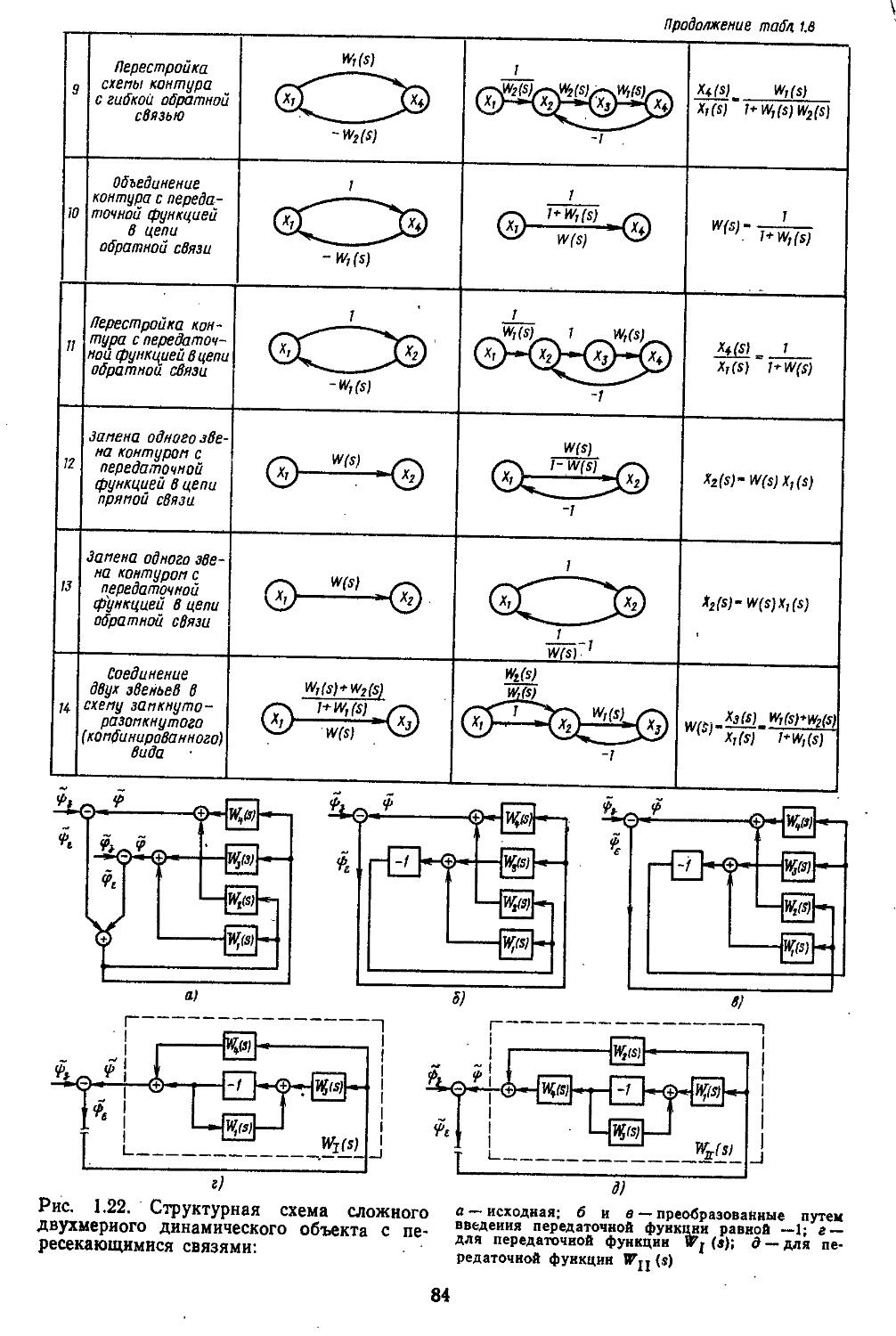
5. Структурные схемы и графы элементов (объектов) .................70
6. Преобразования структурных схем н графов 79
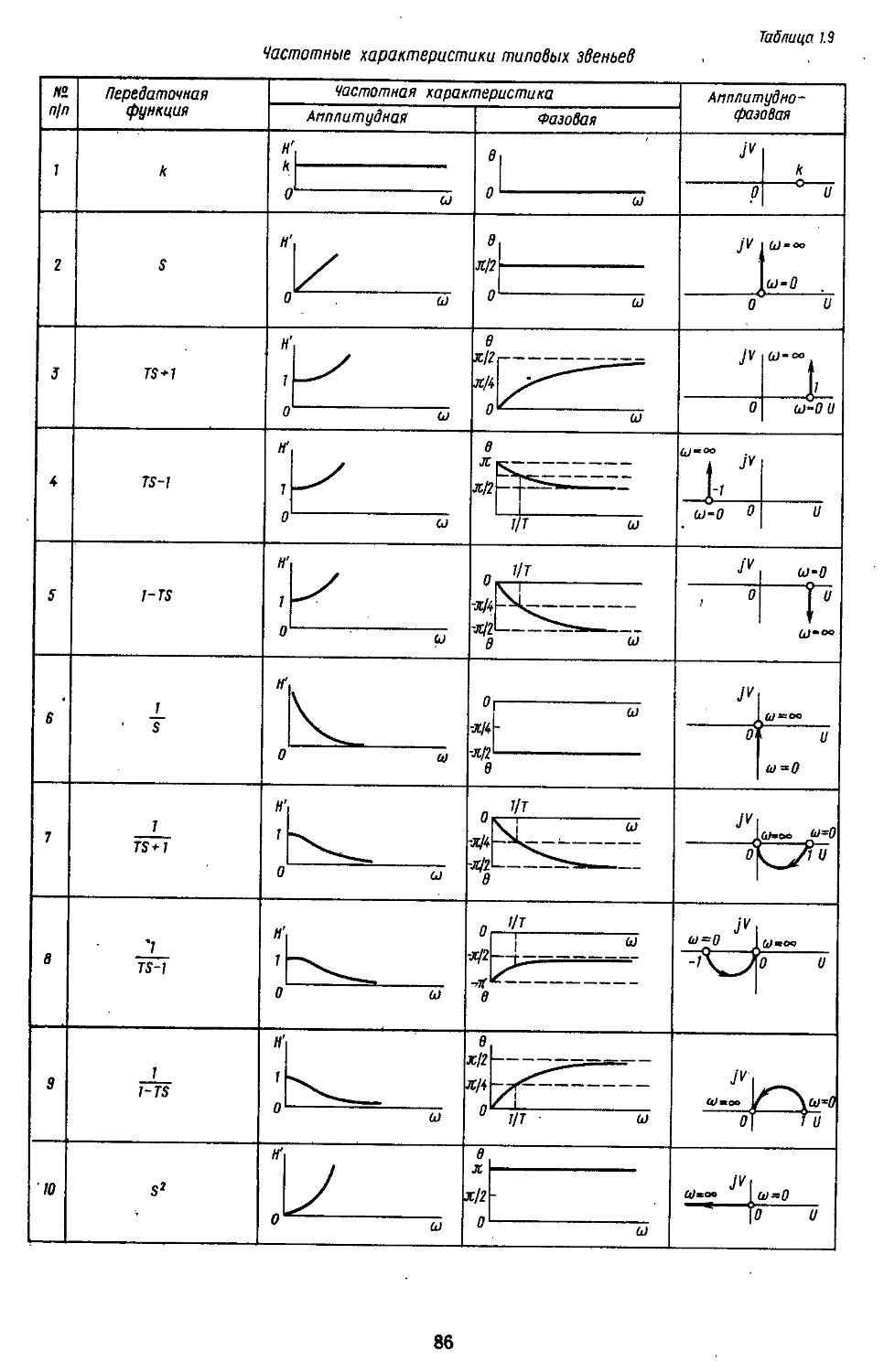
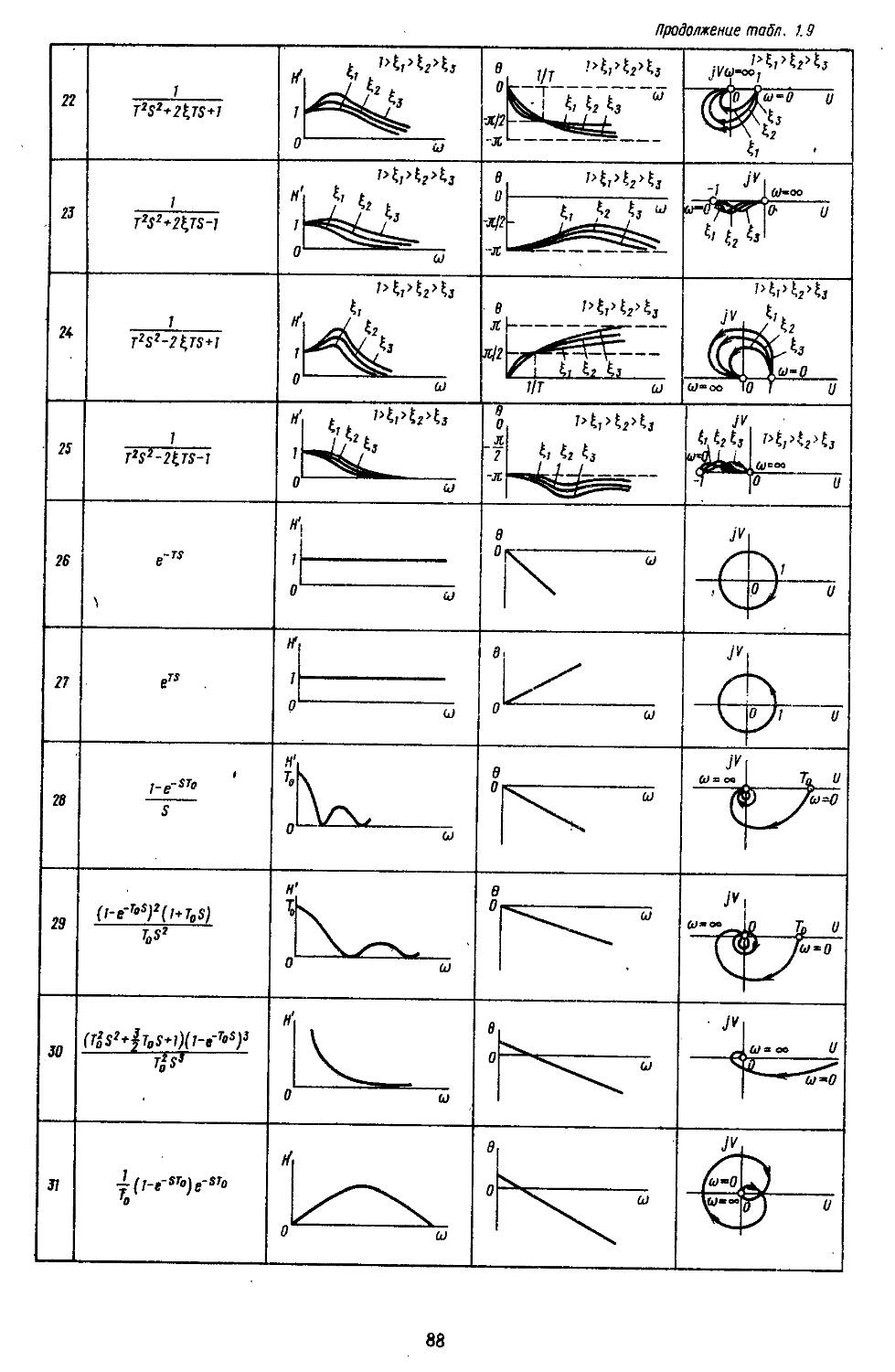
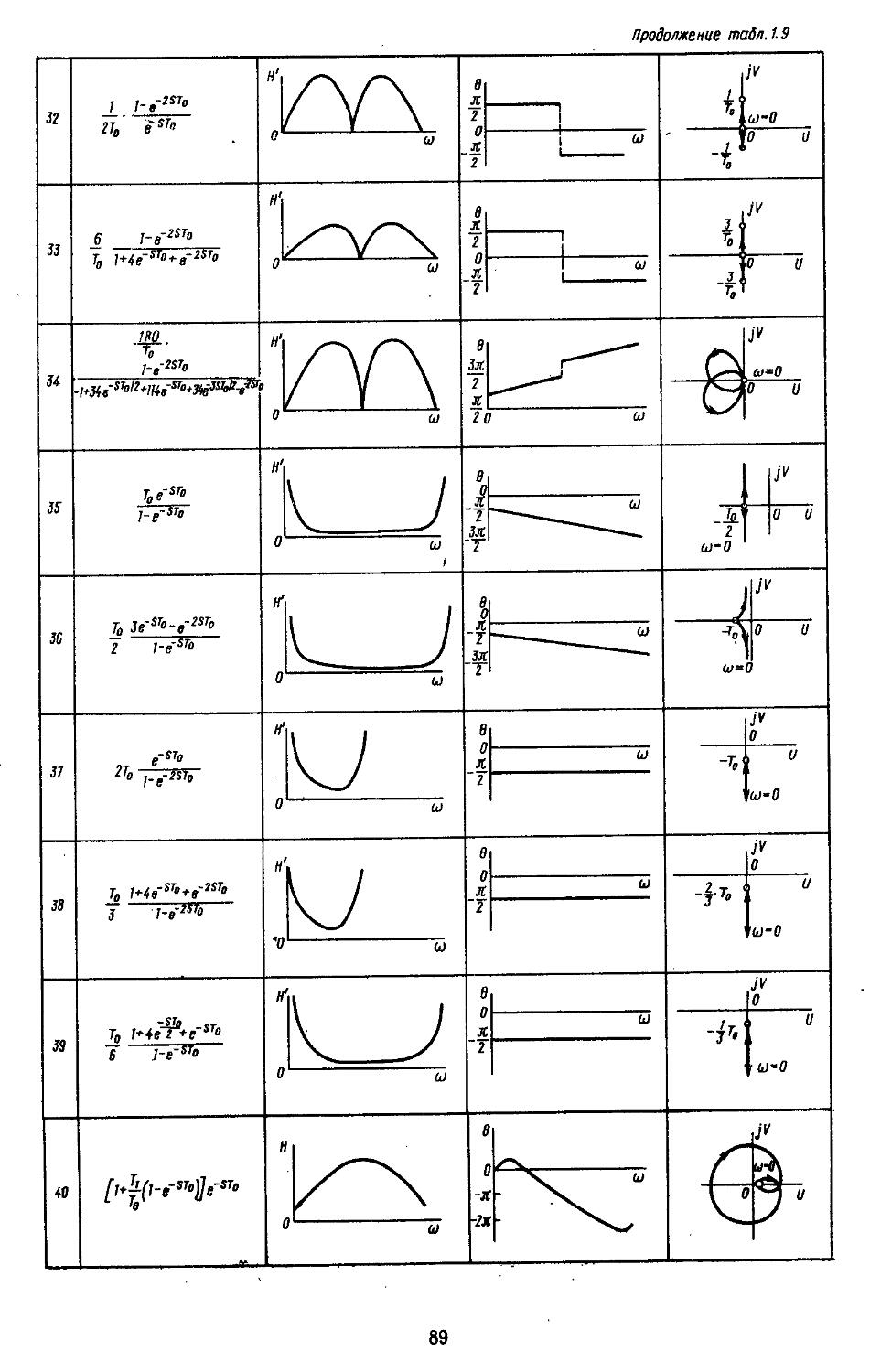
7. Частотные характеристики типовых звеньев 85
8. Применение регрессионного анализа для составления математических моделей объектов 116
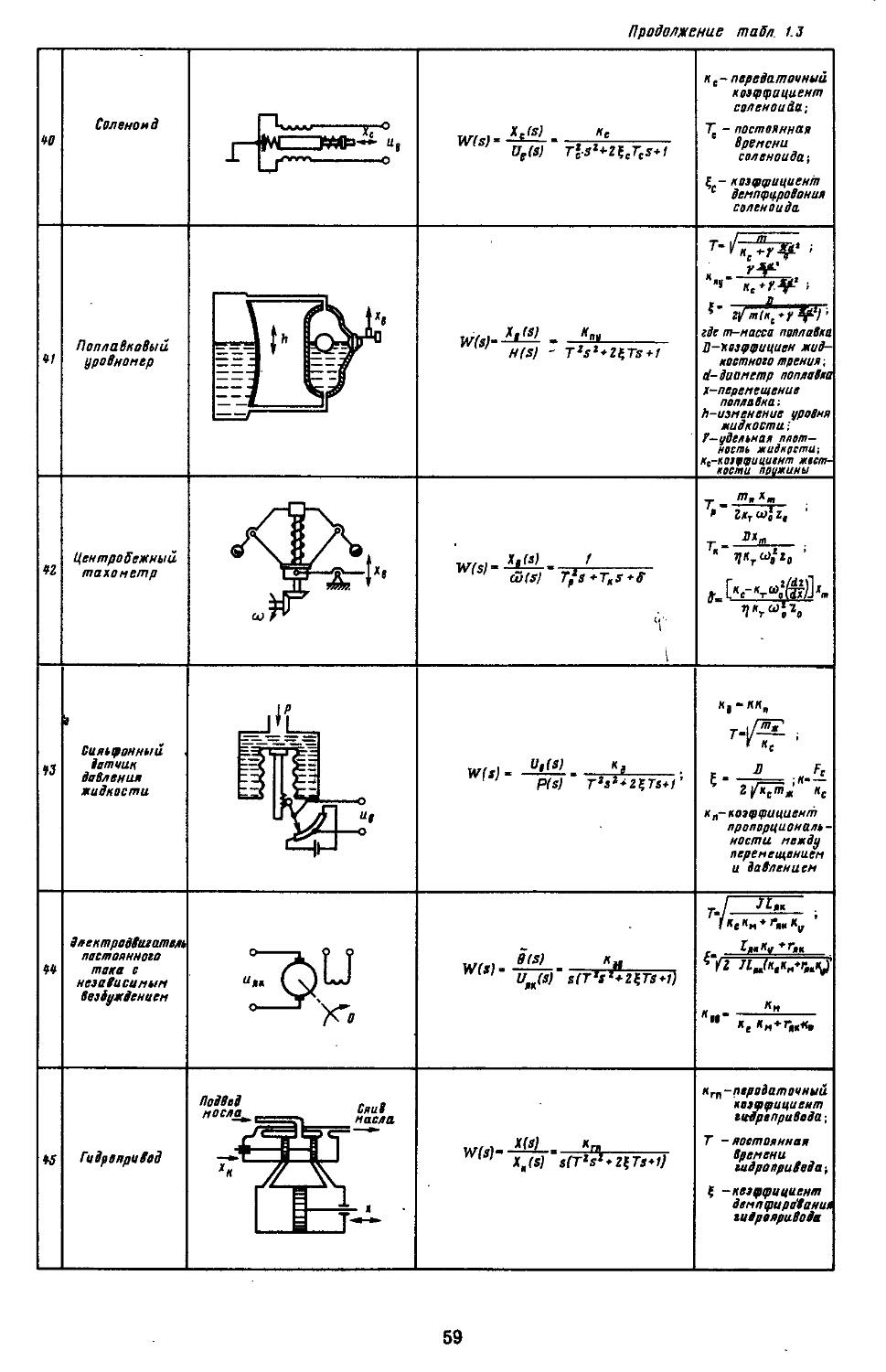
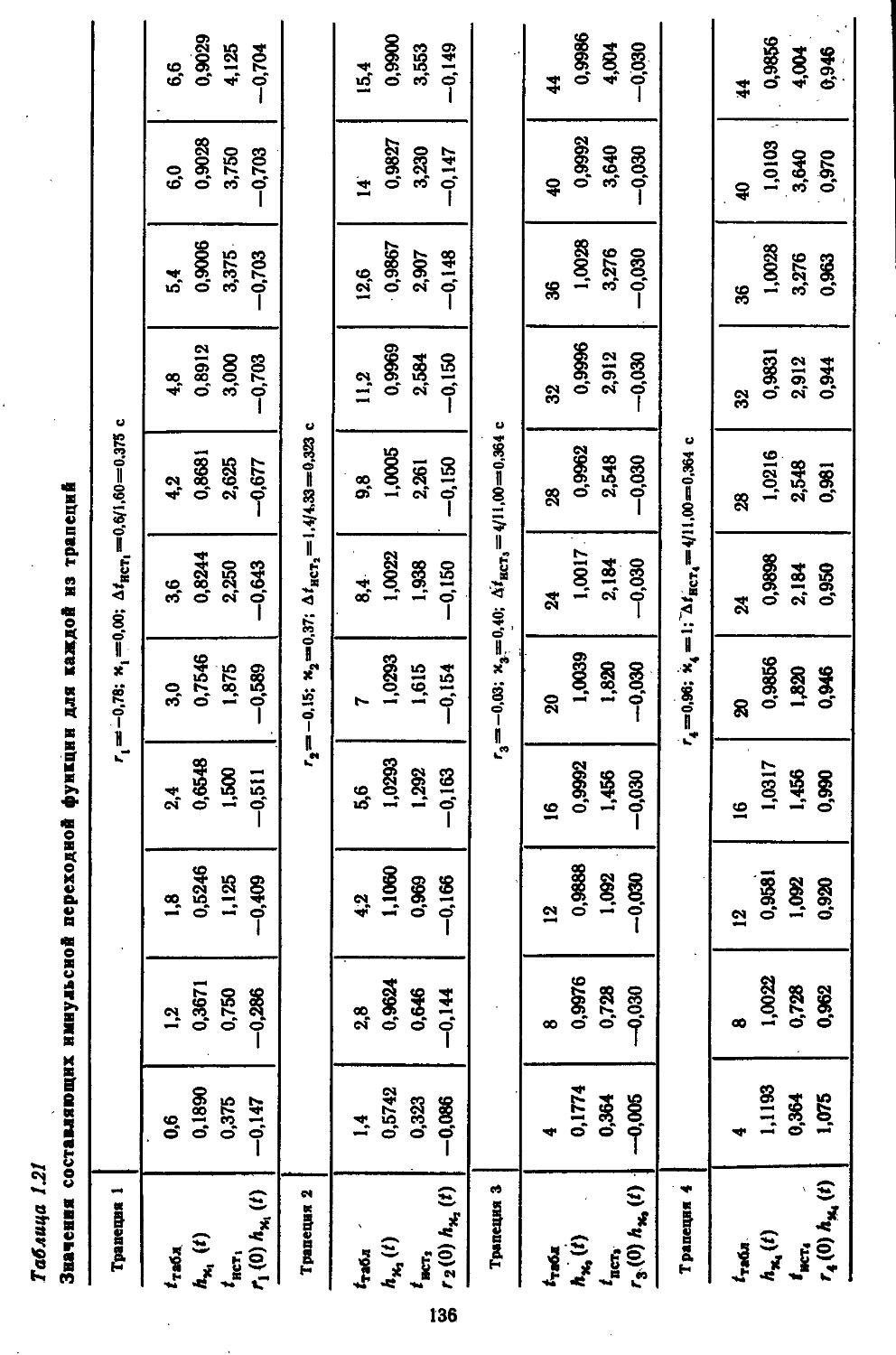
9. Импульсные переходные функции . . .128
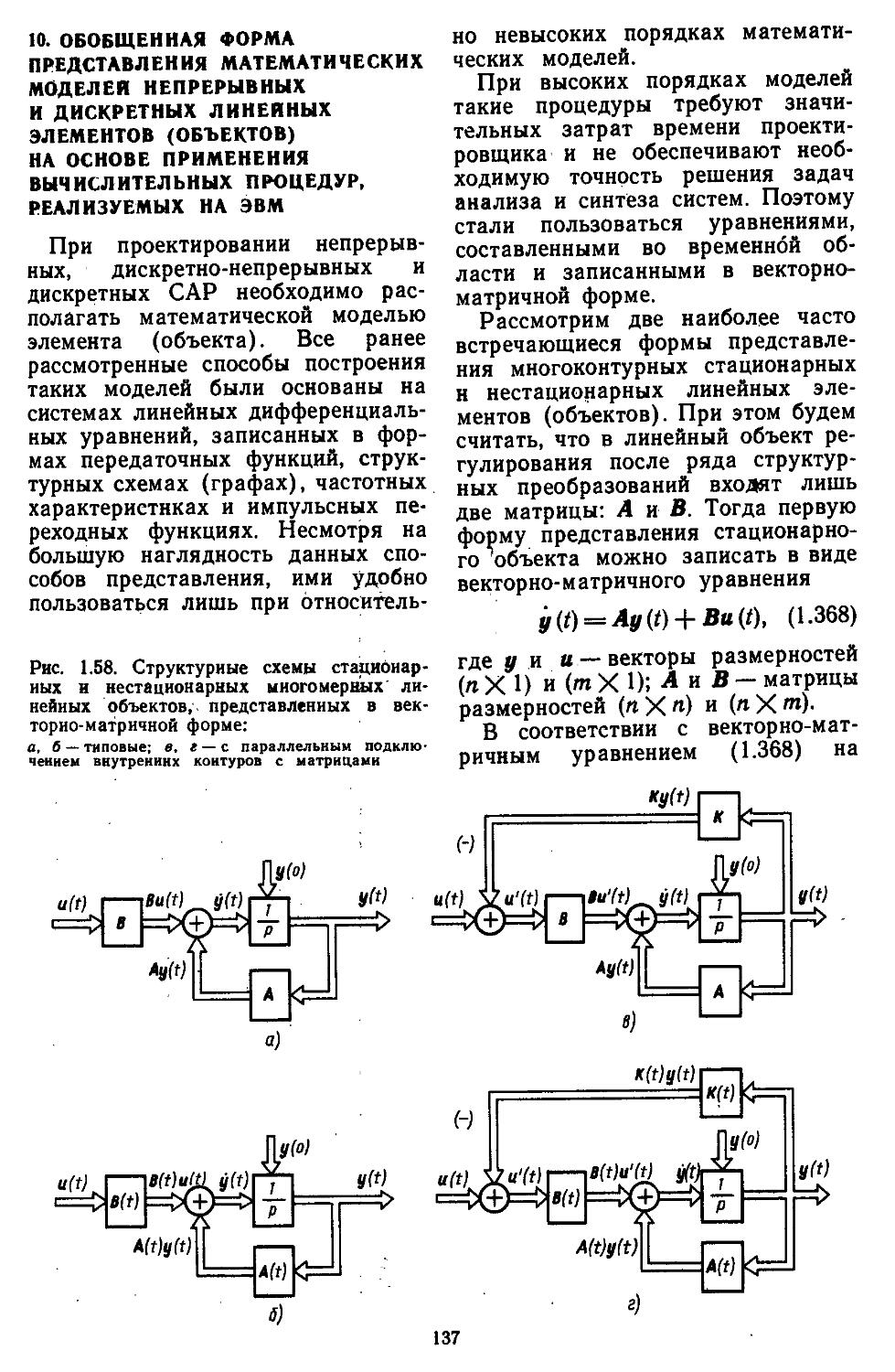
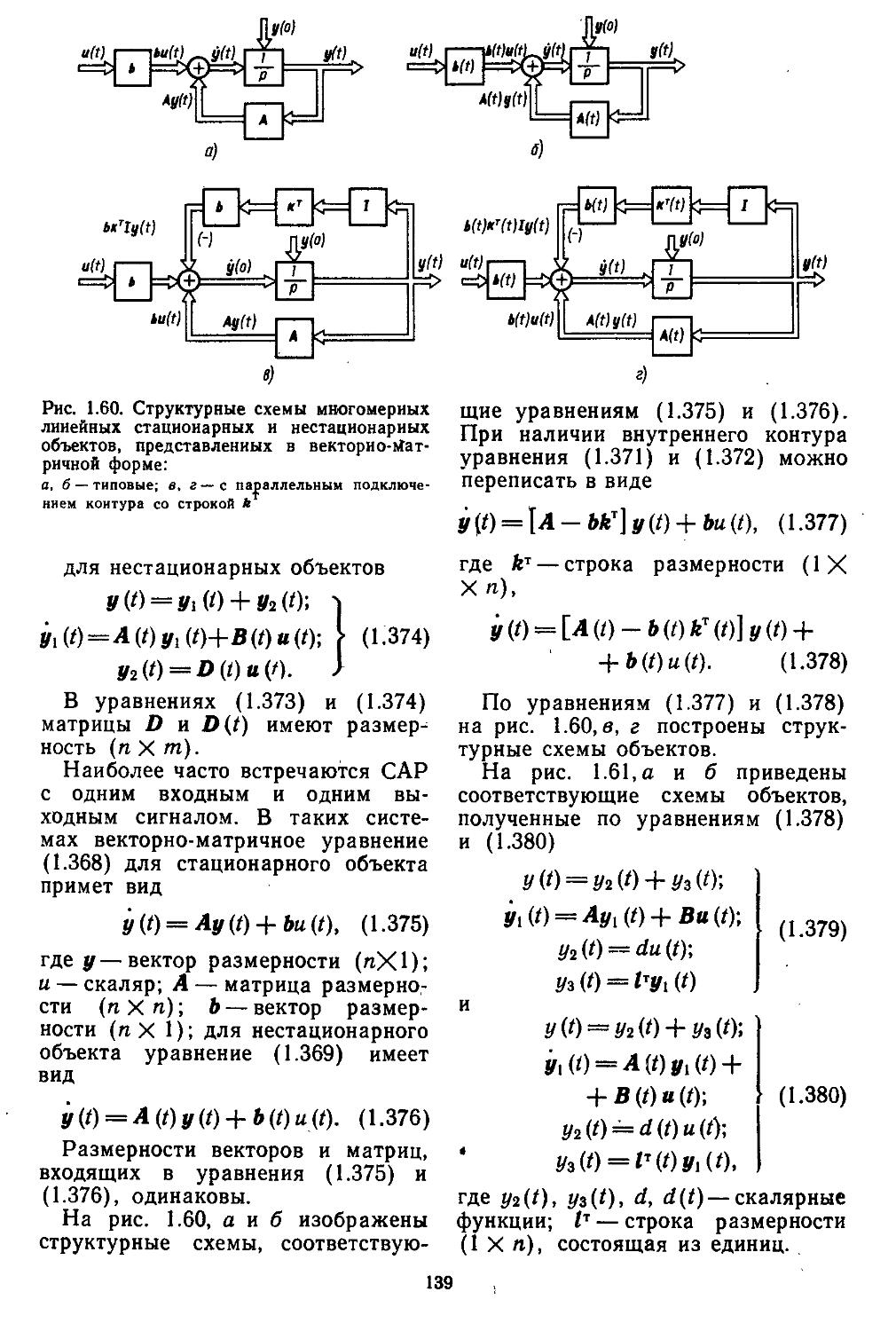
10. Обобщенная форма представления математических моделей непрерывных и дискретных линейных элементов (объектов) на основе применения вычислительных процедур, реализуемых на ЭВМ 137
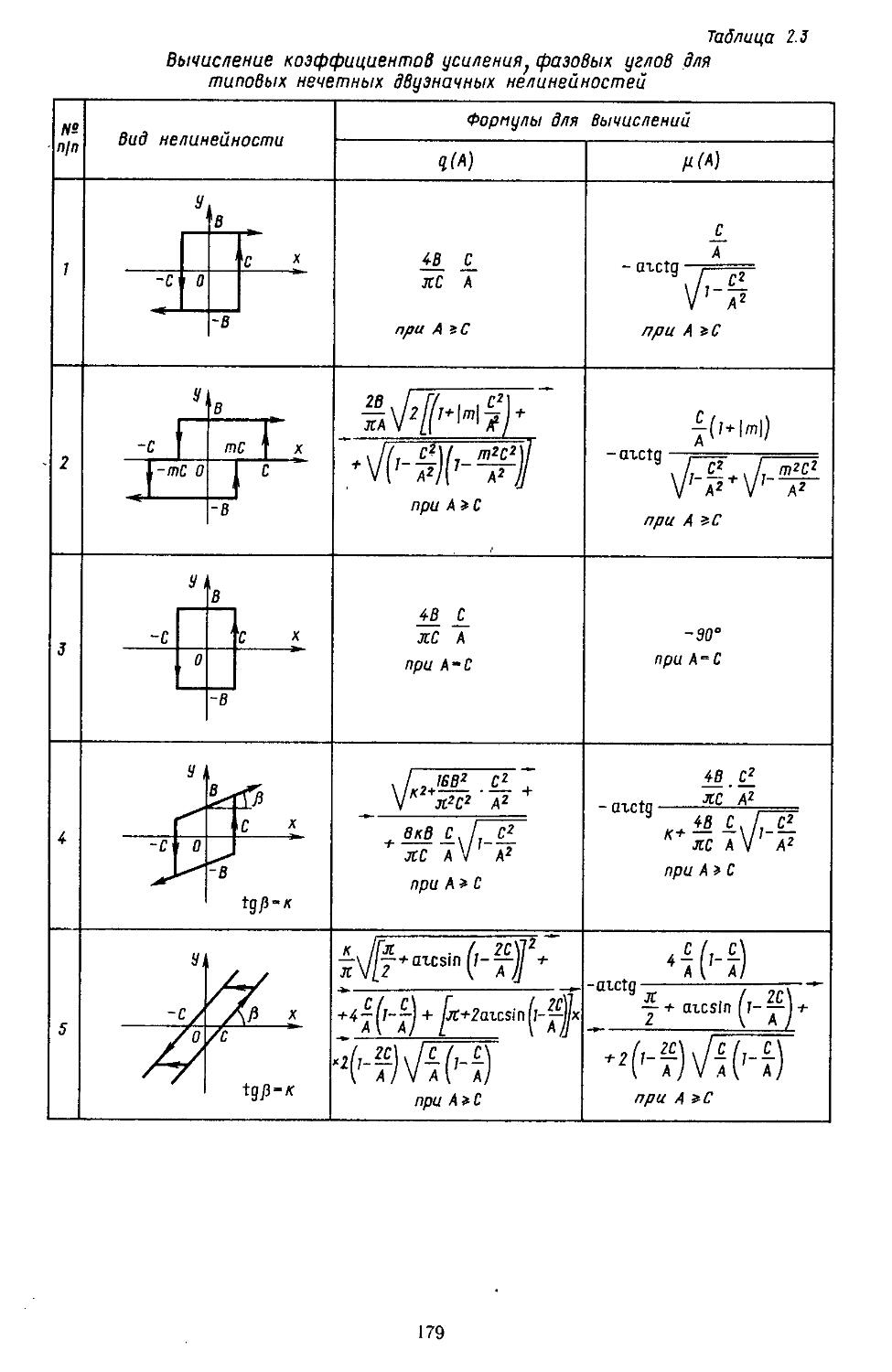
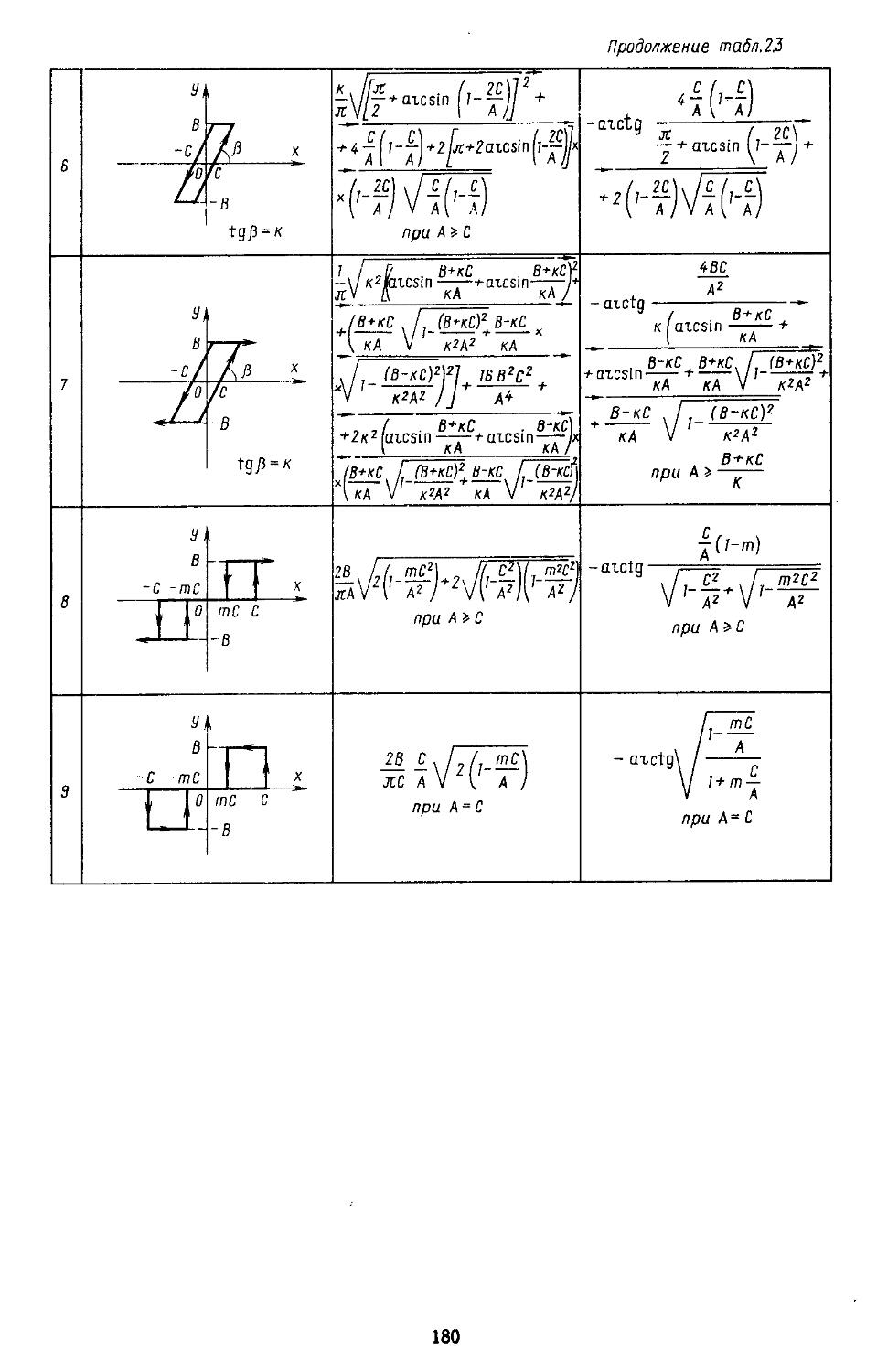
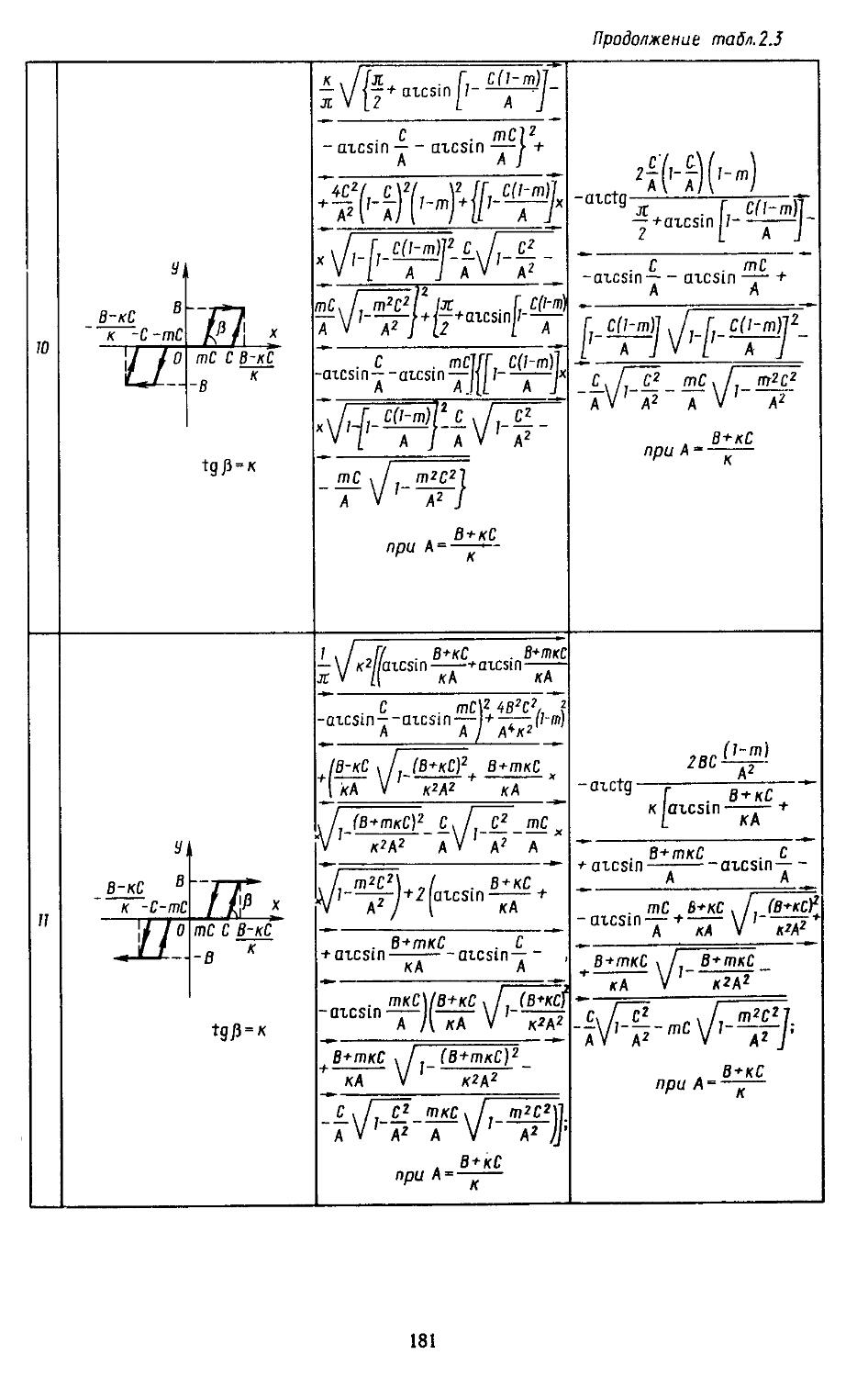
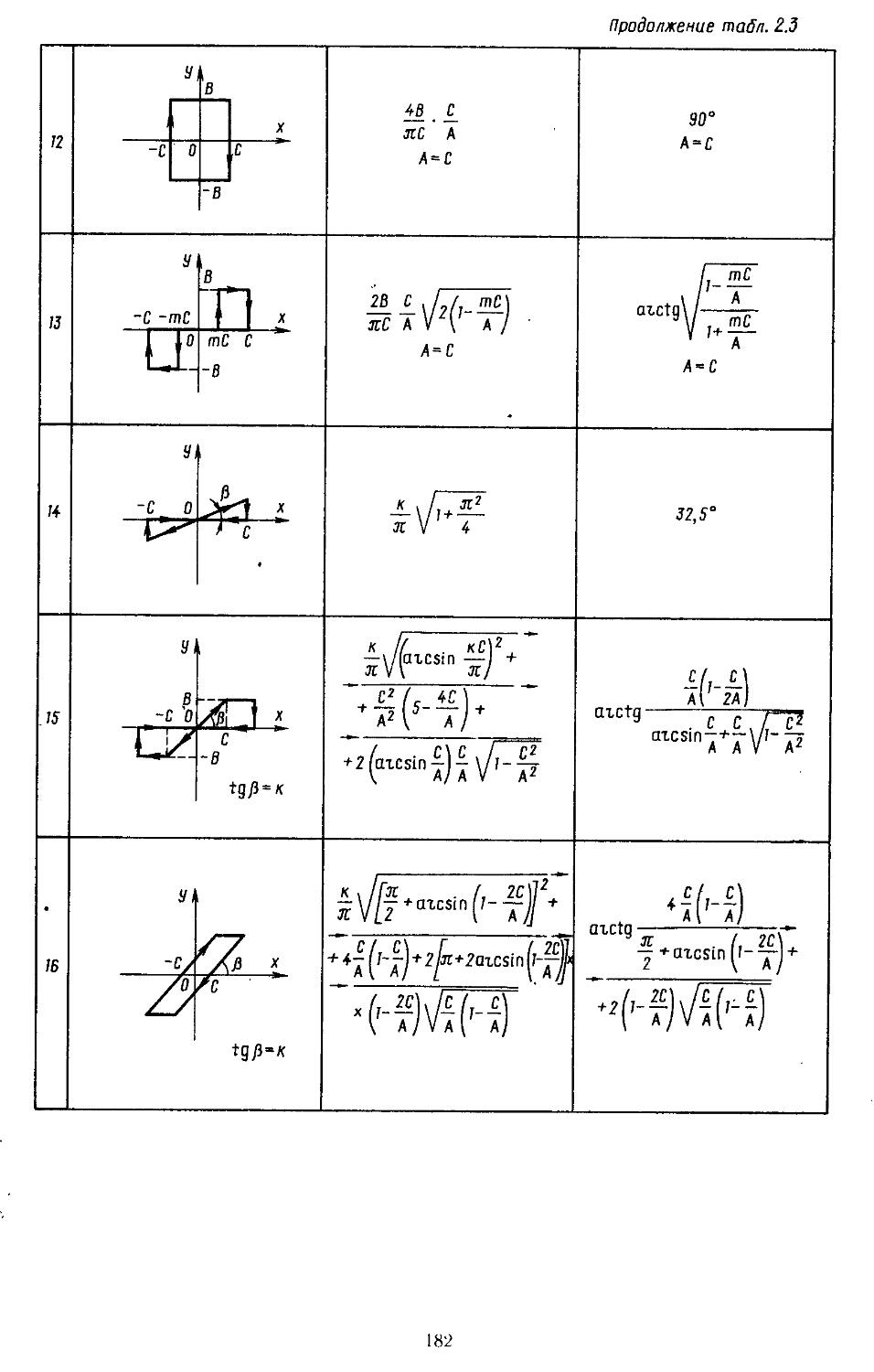
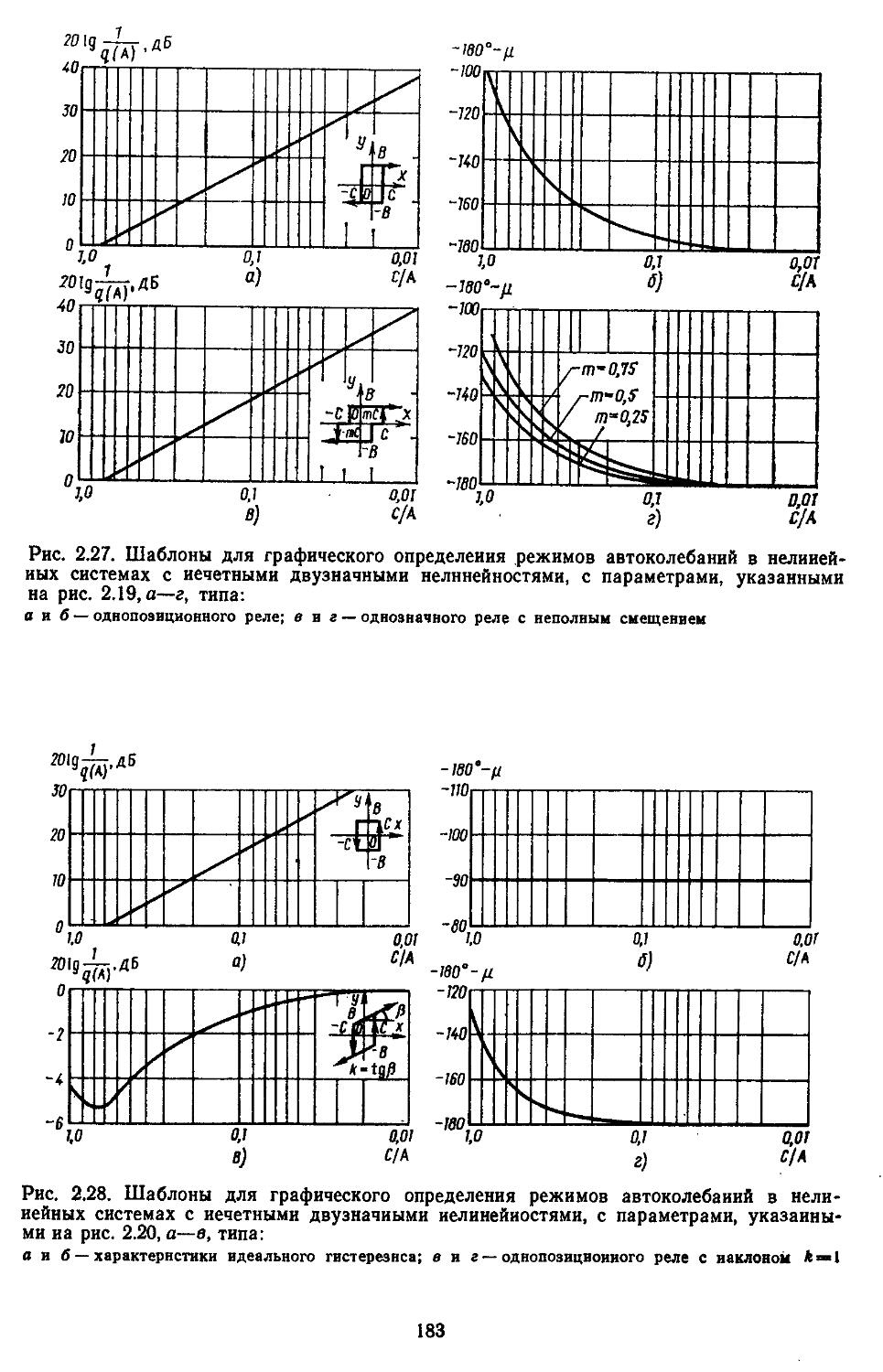
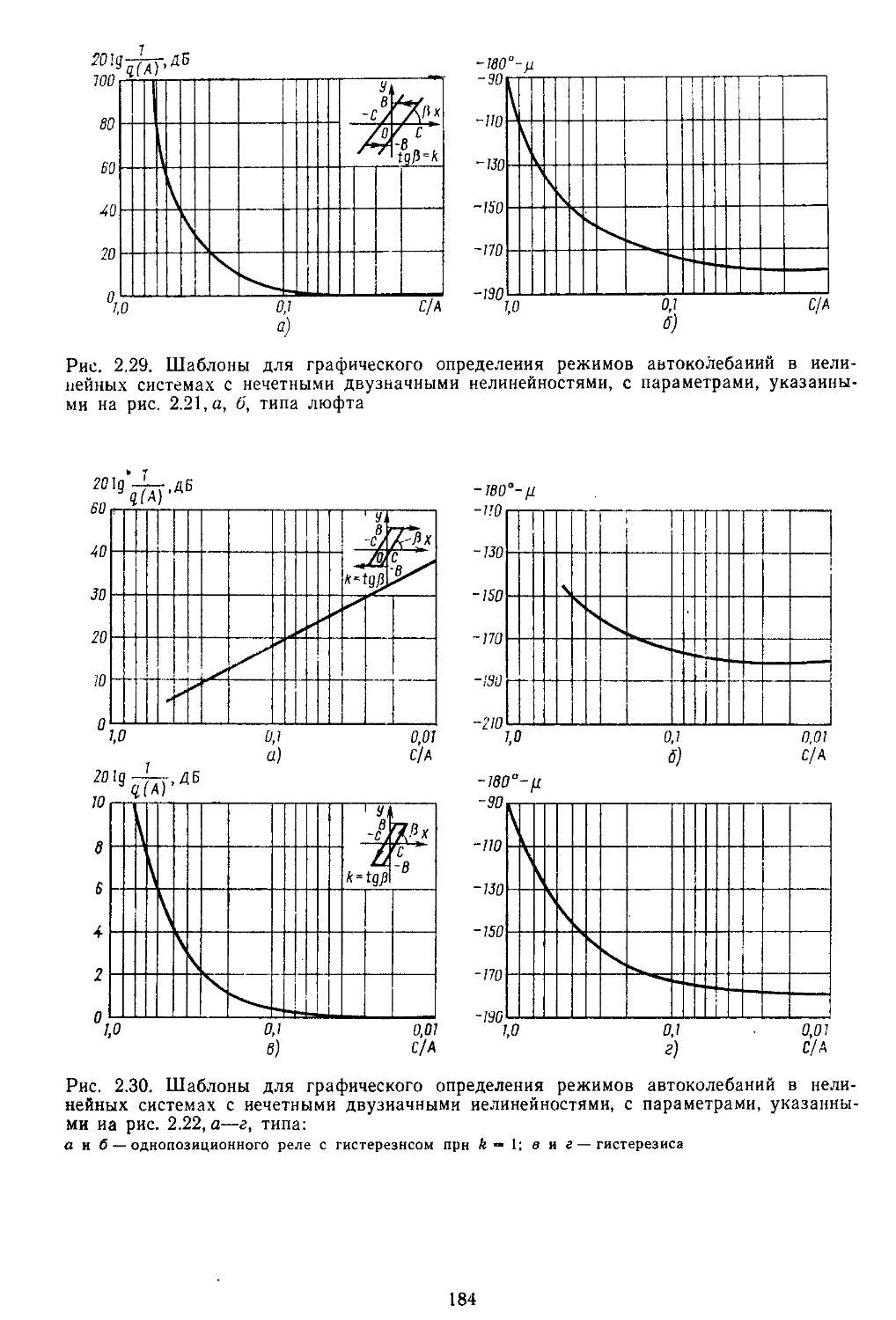
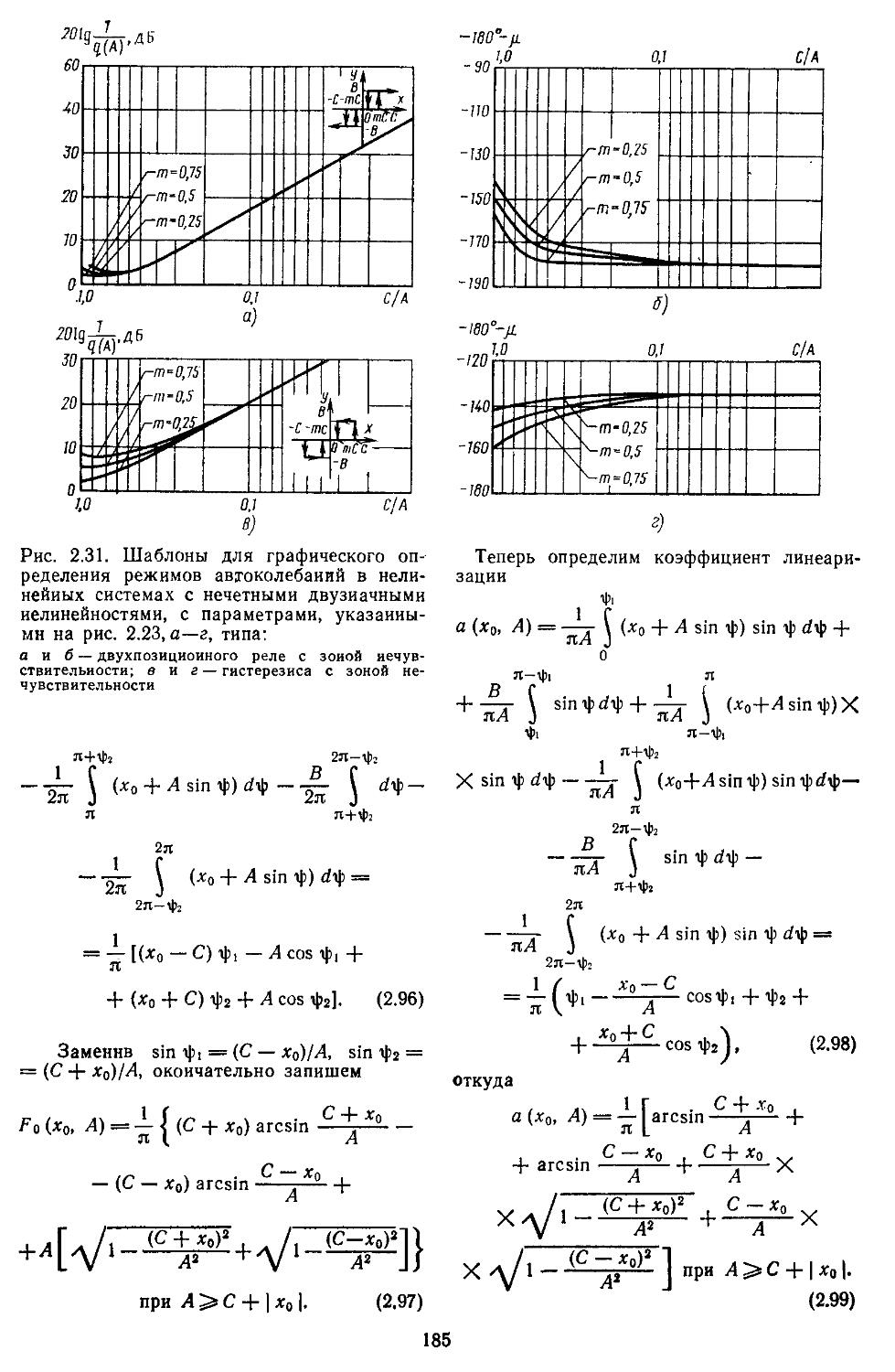
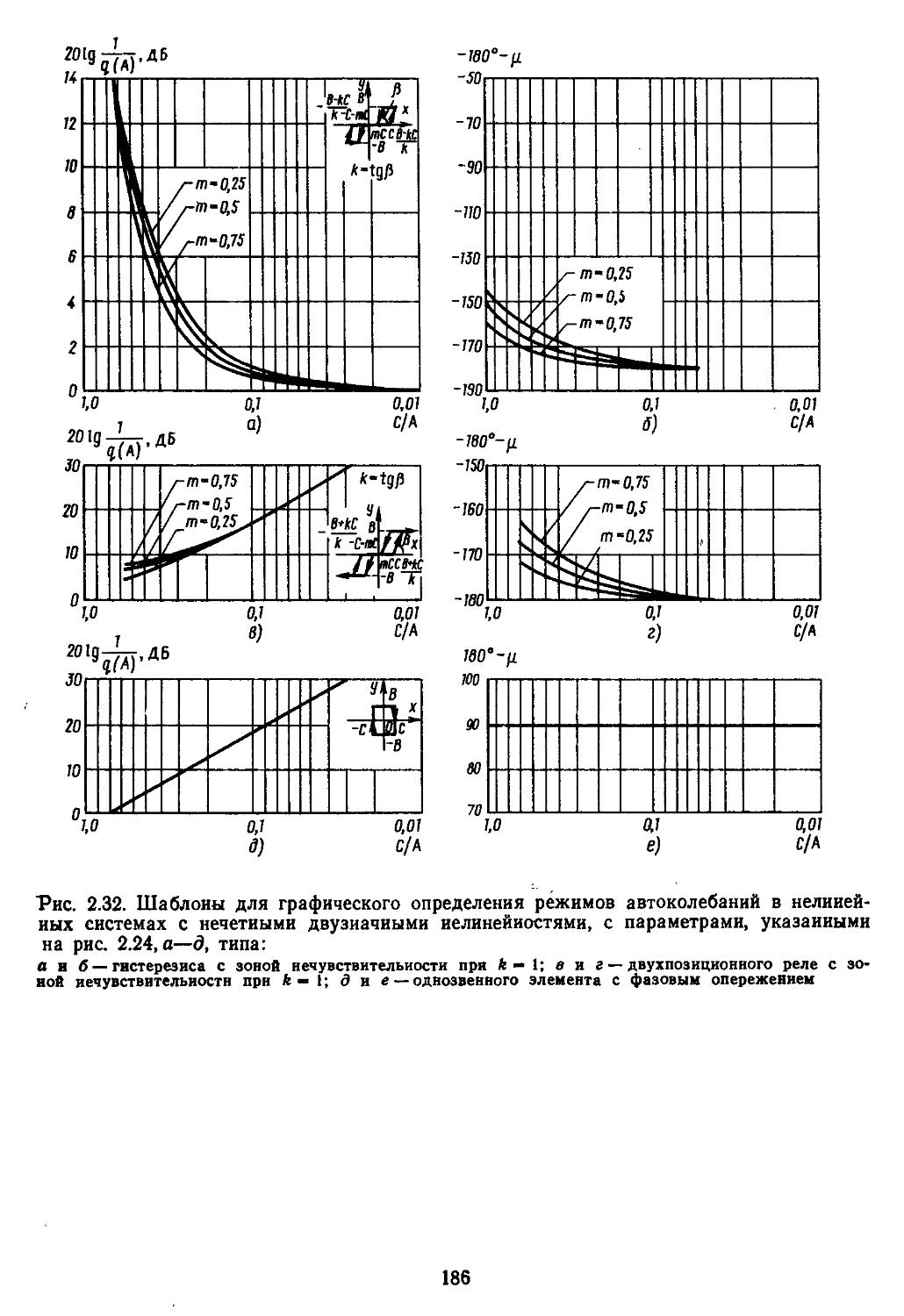
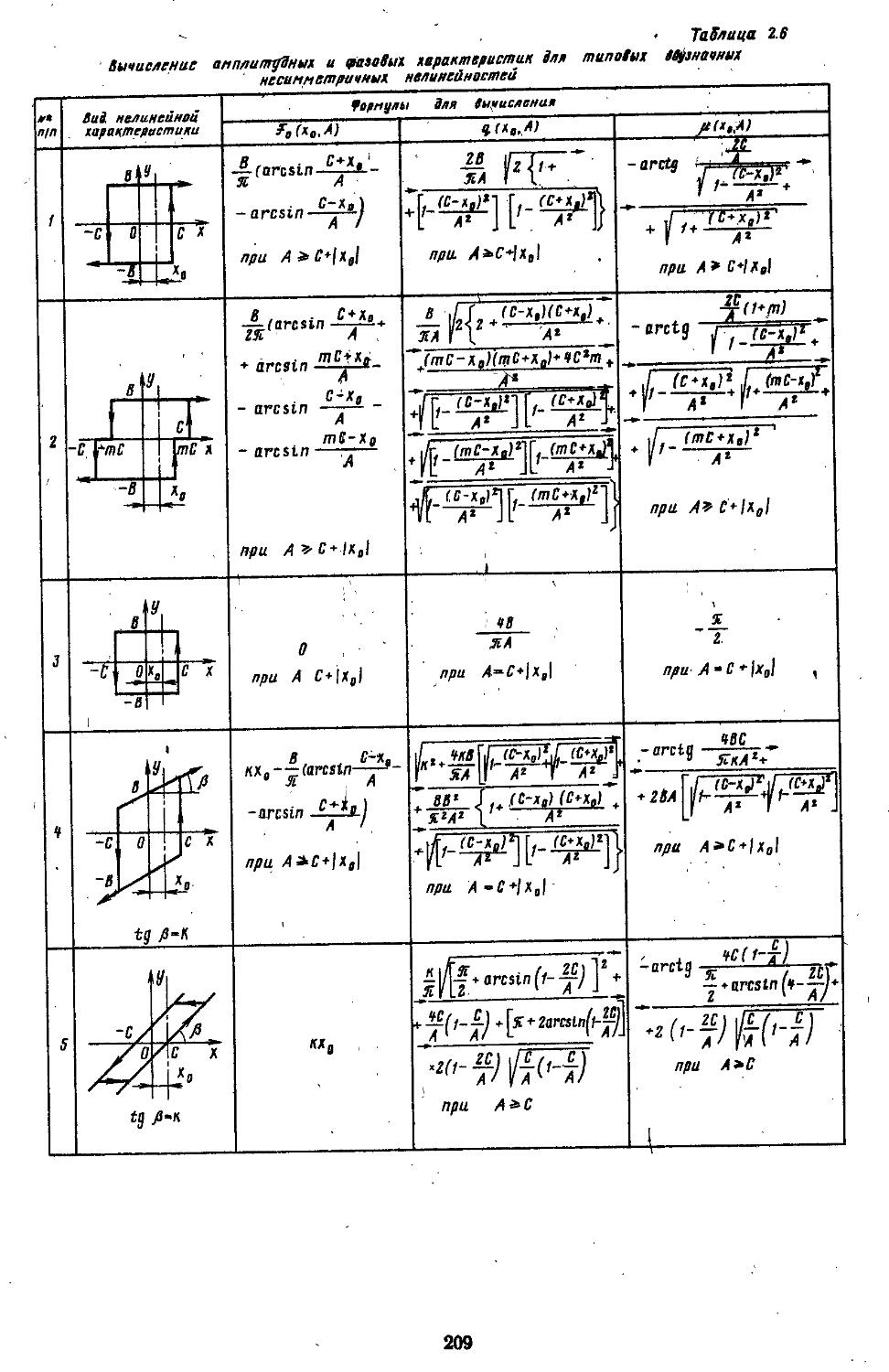
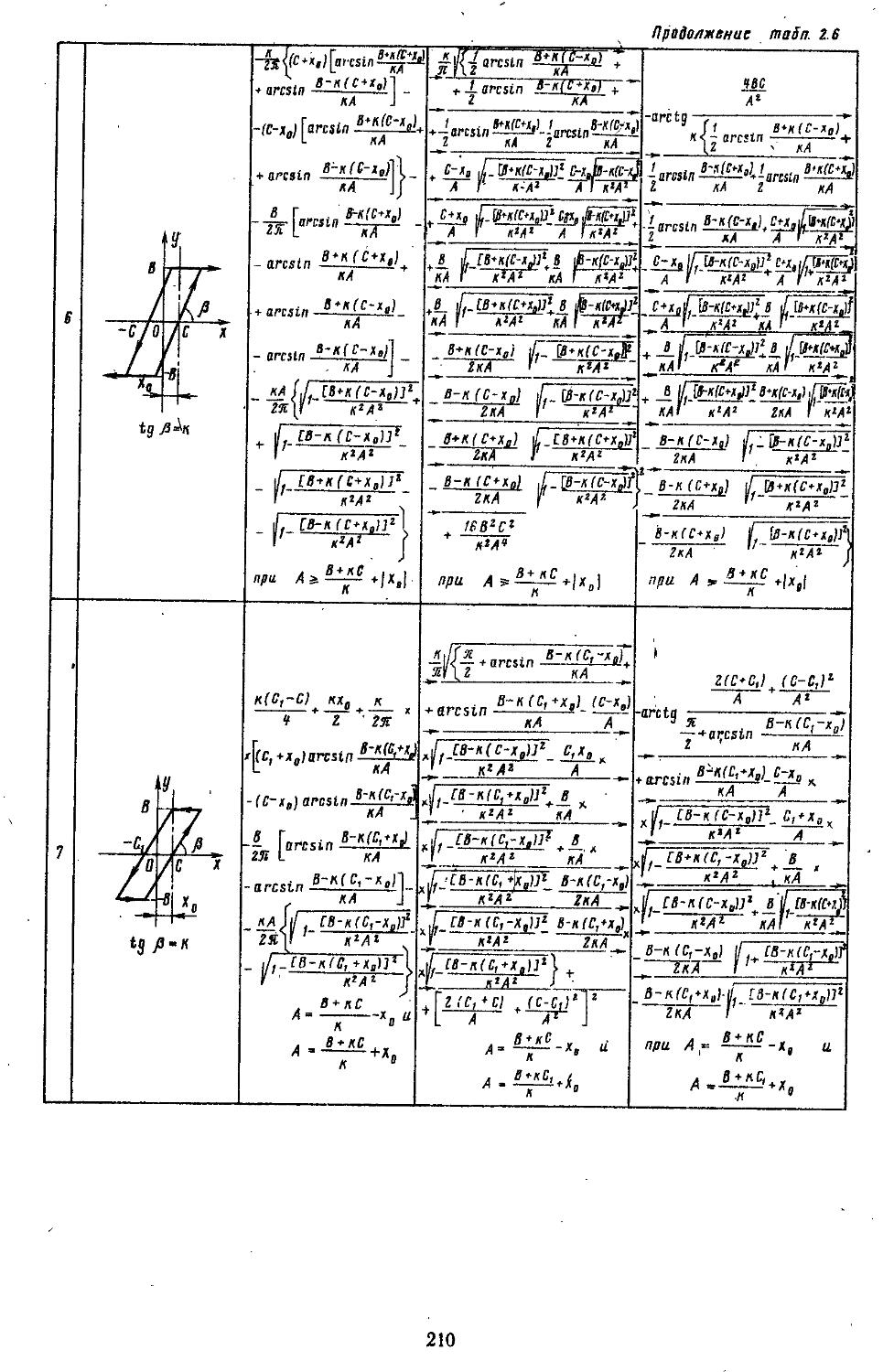
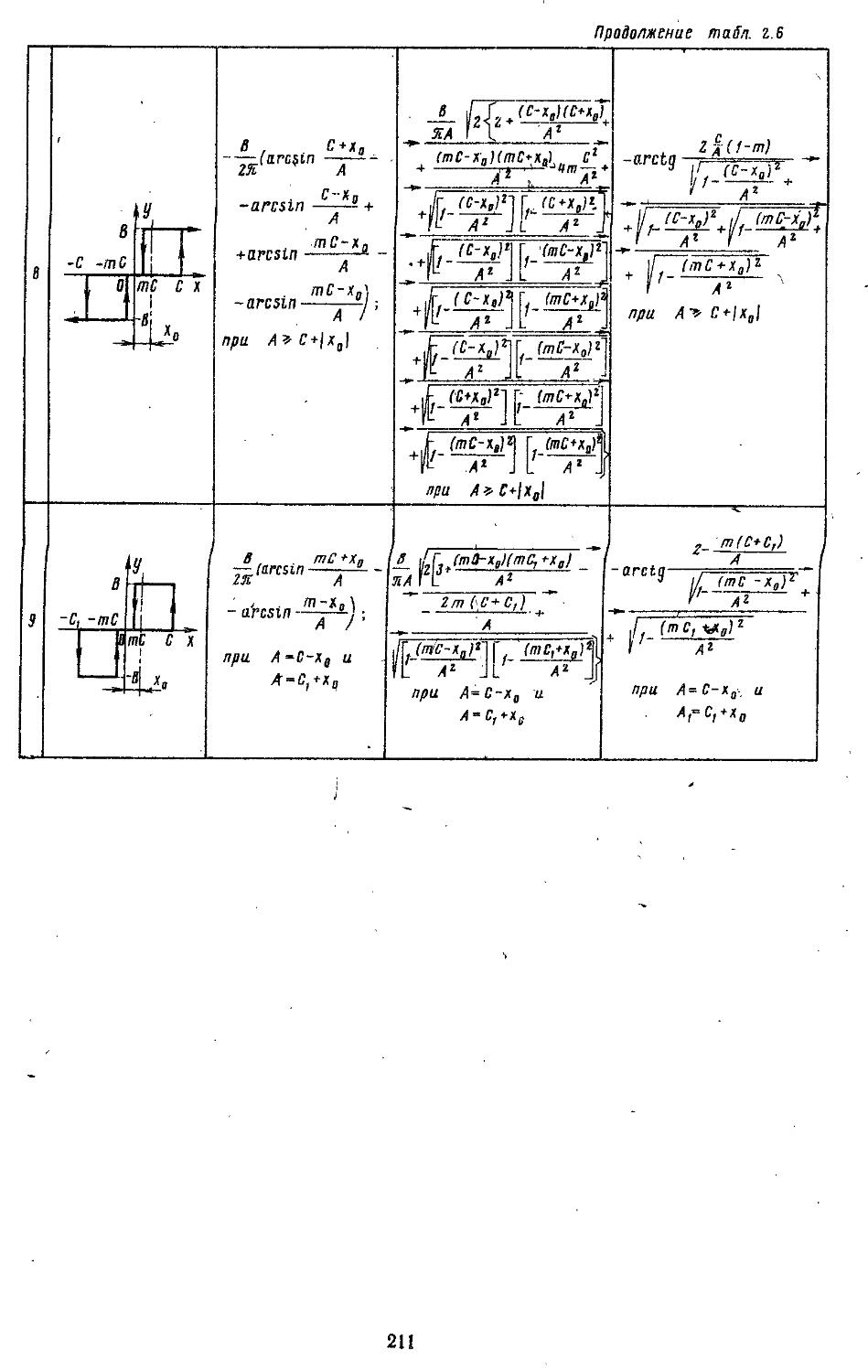
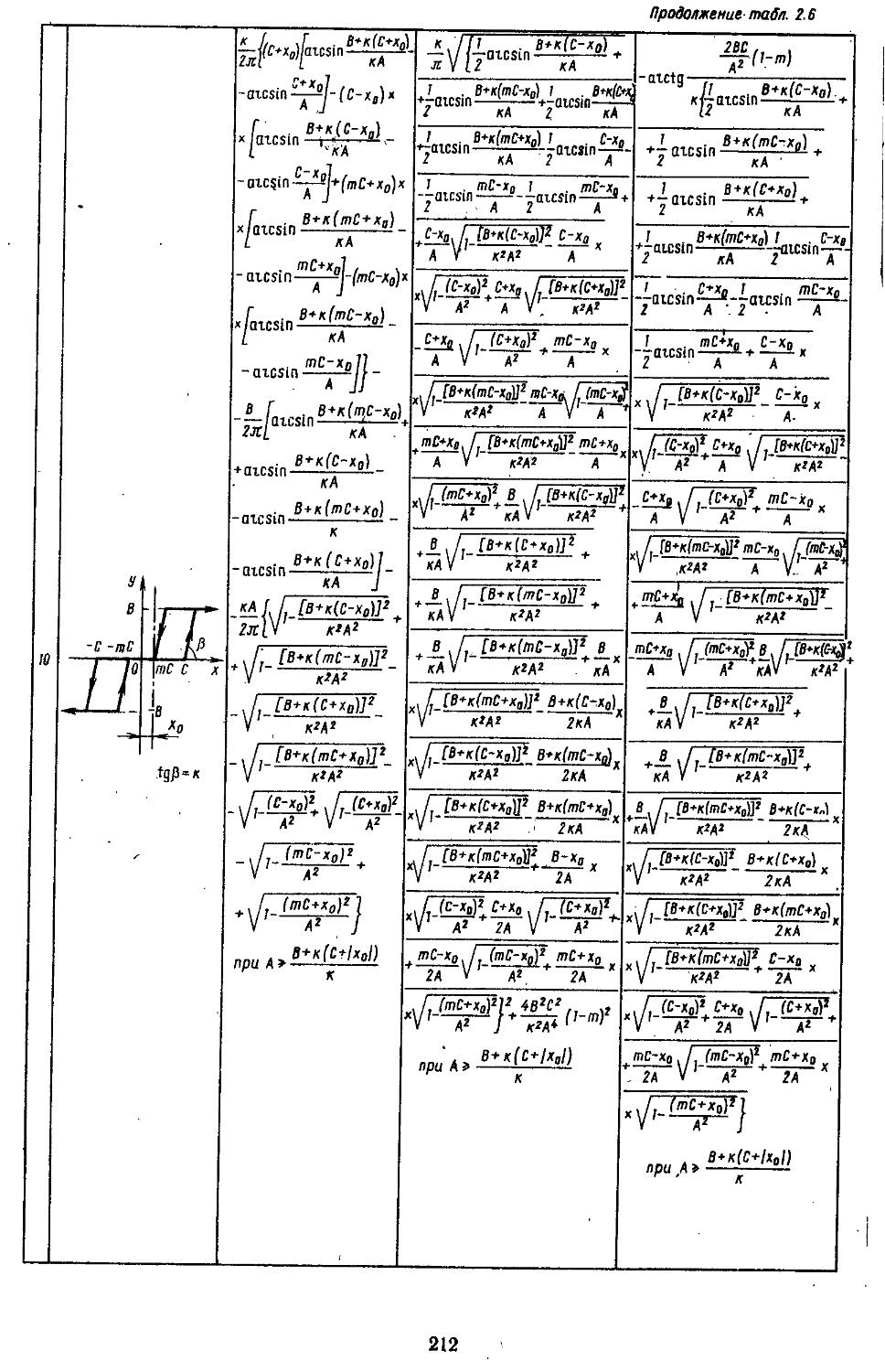
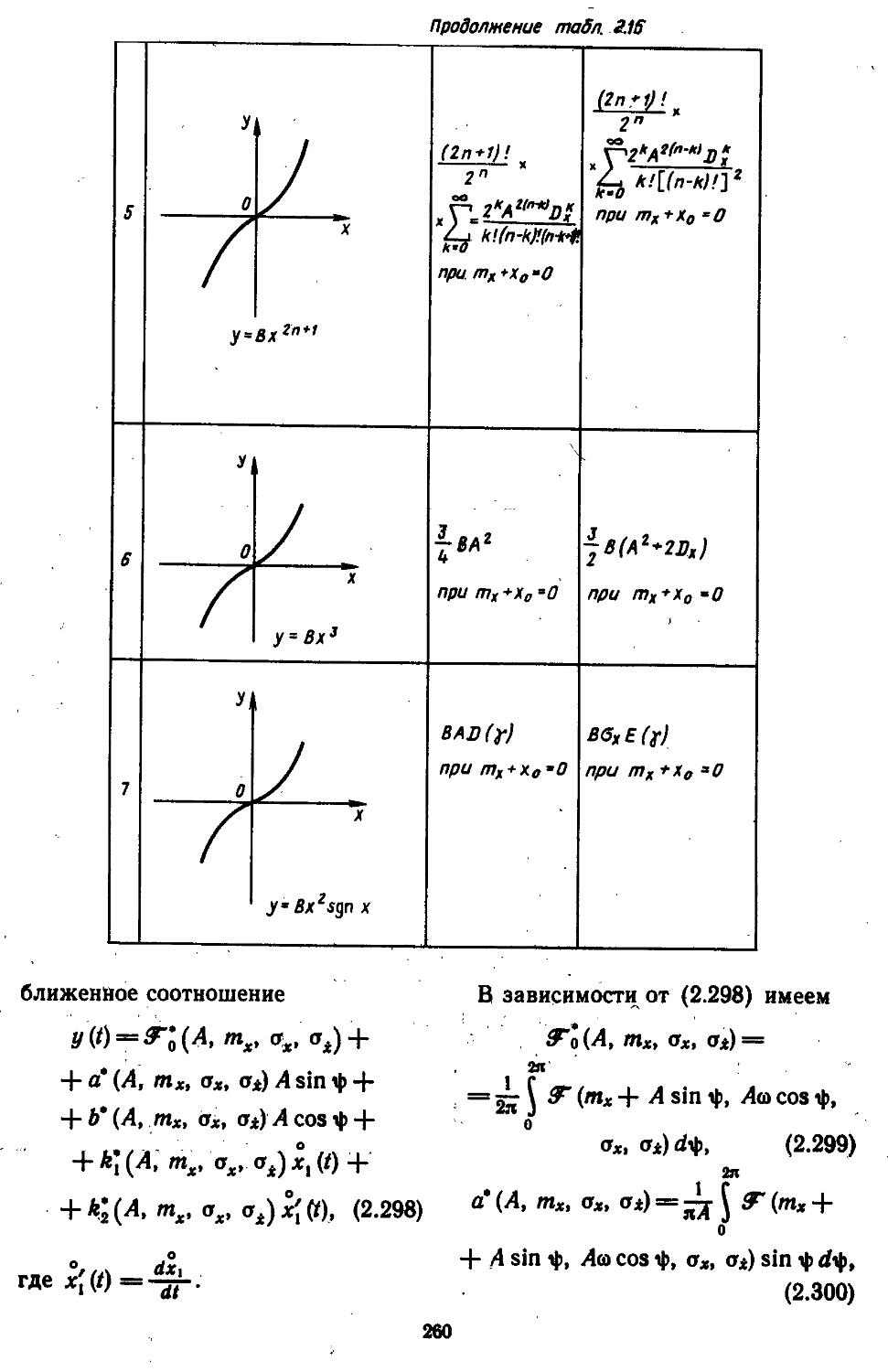
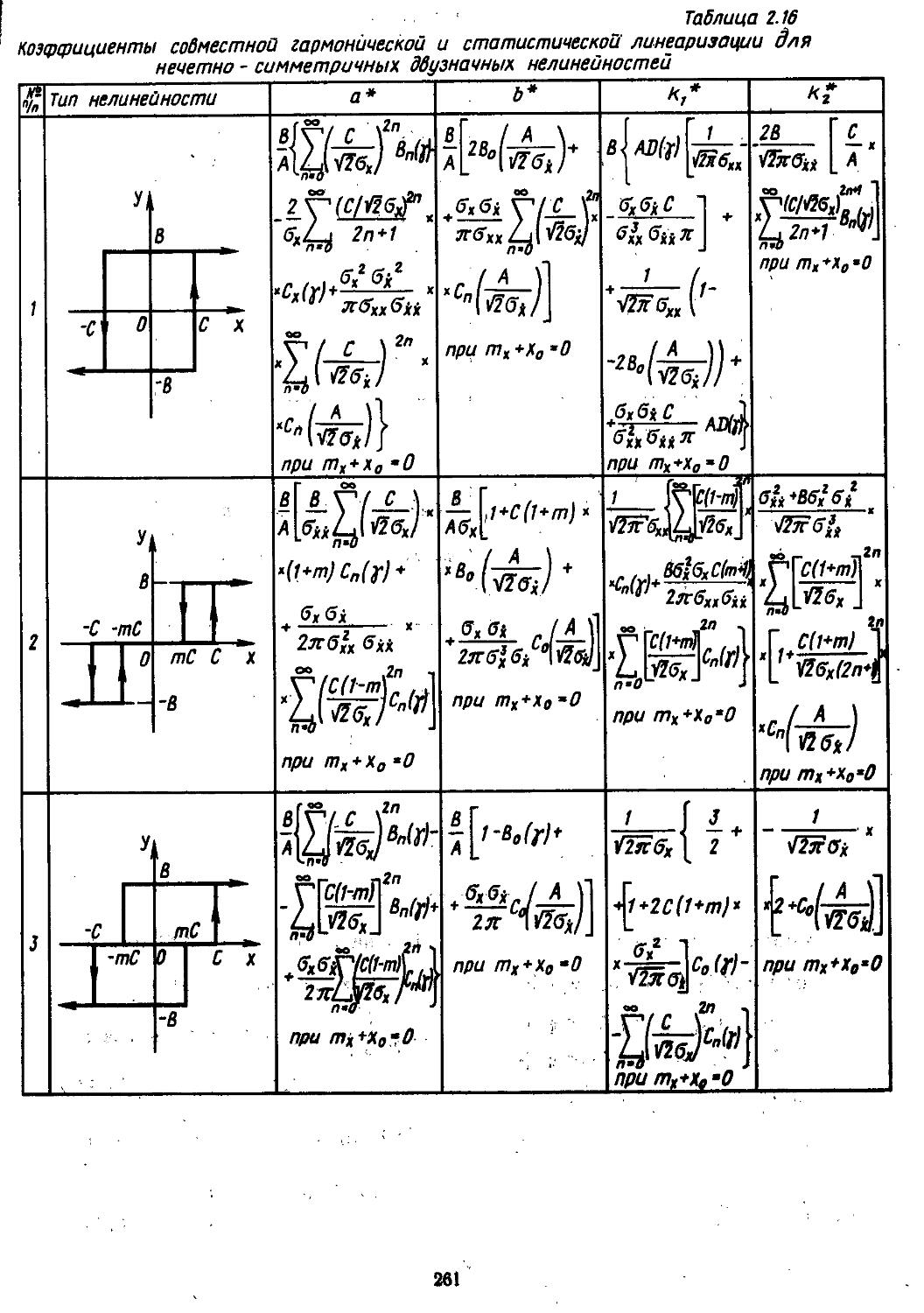
Глава 2. Математические модели не линейных элементов . . 145
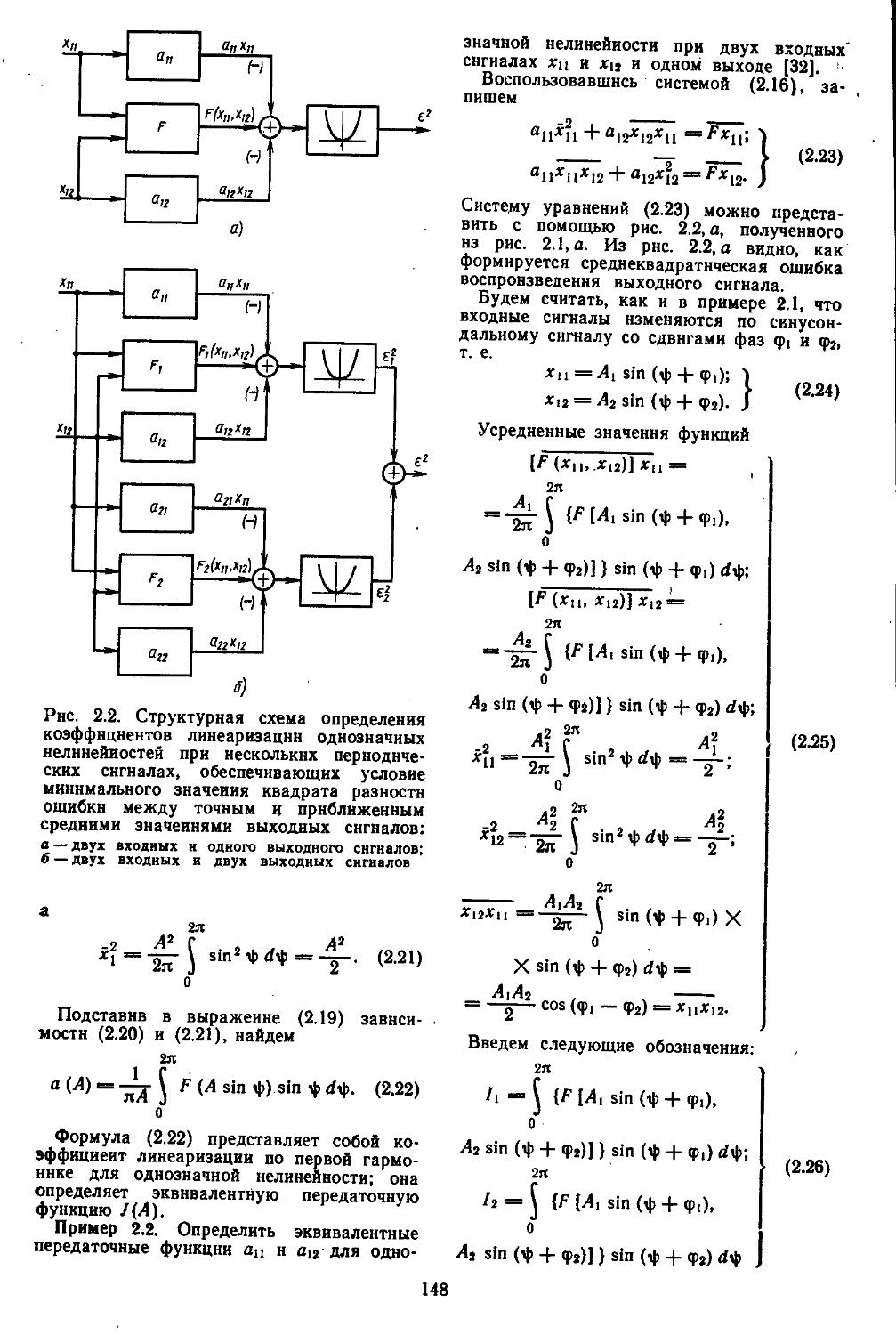
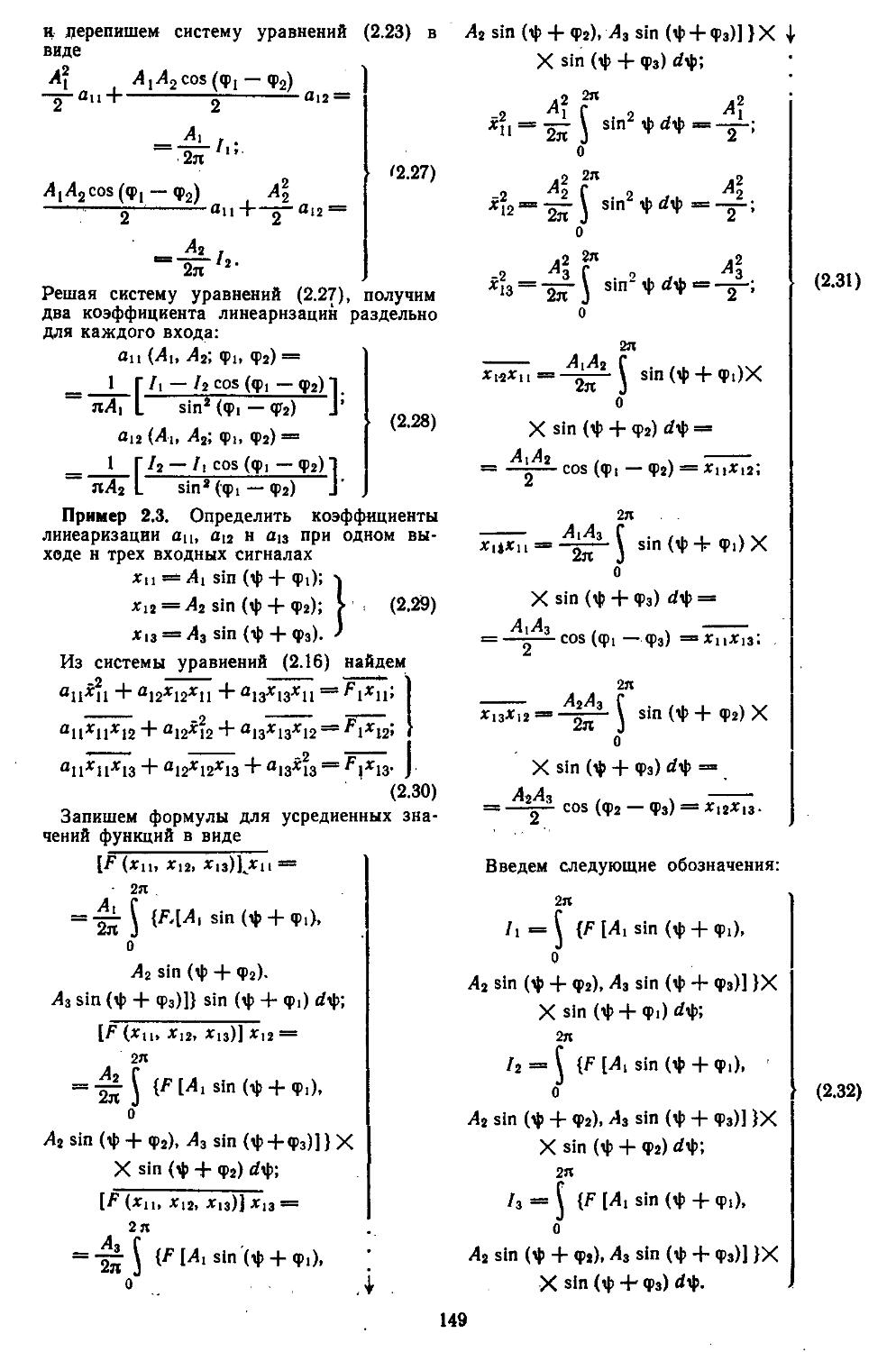
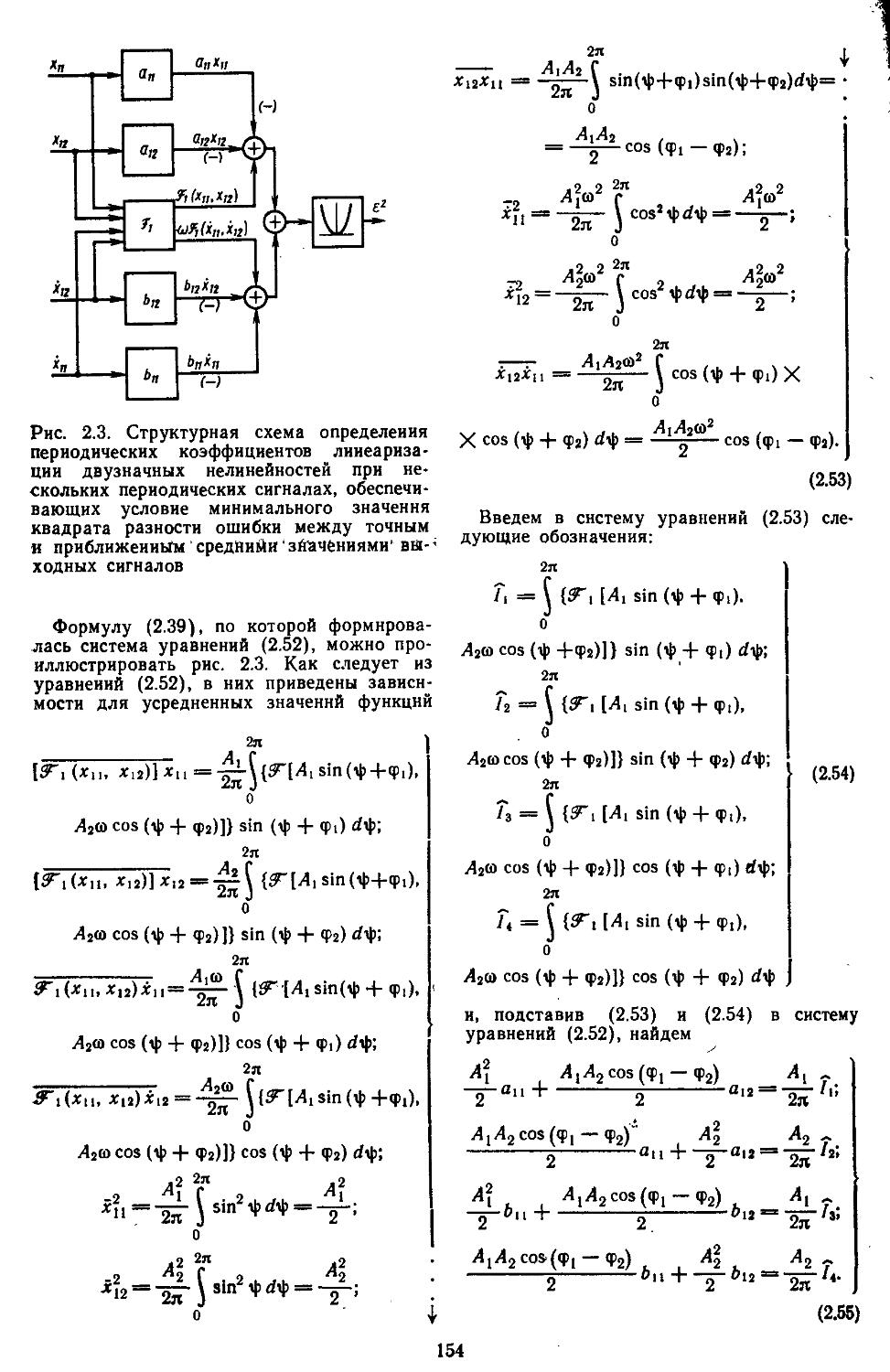
1. Общий метод описания эквивалентных передаточных функций нелинейных элементов . .145
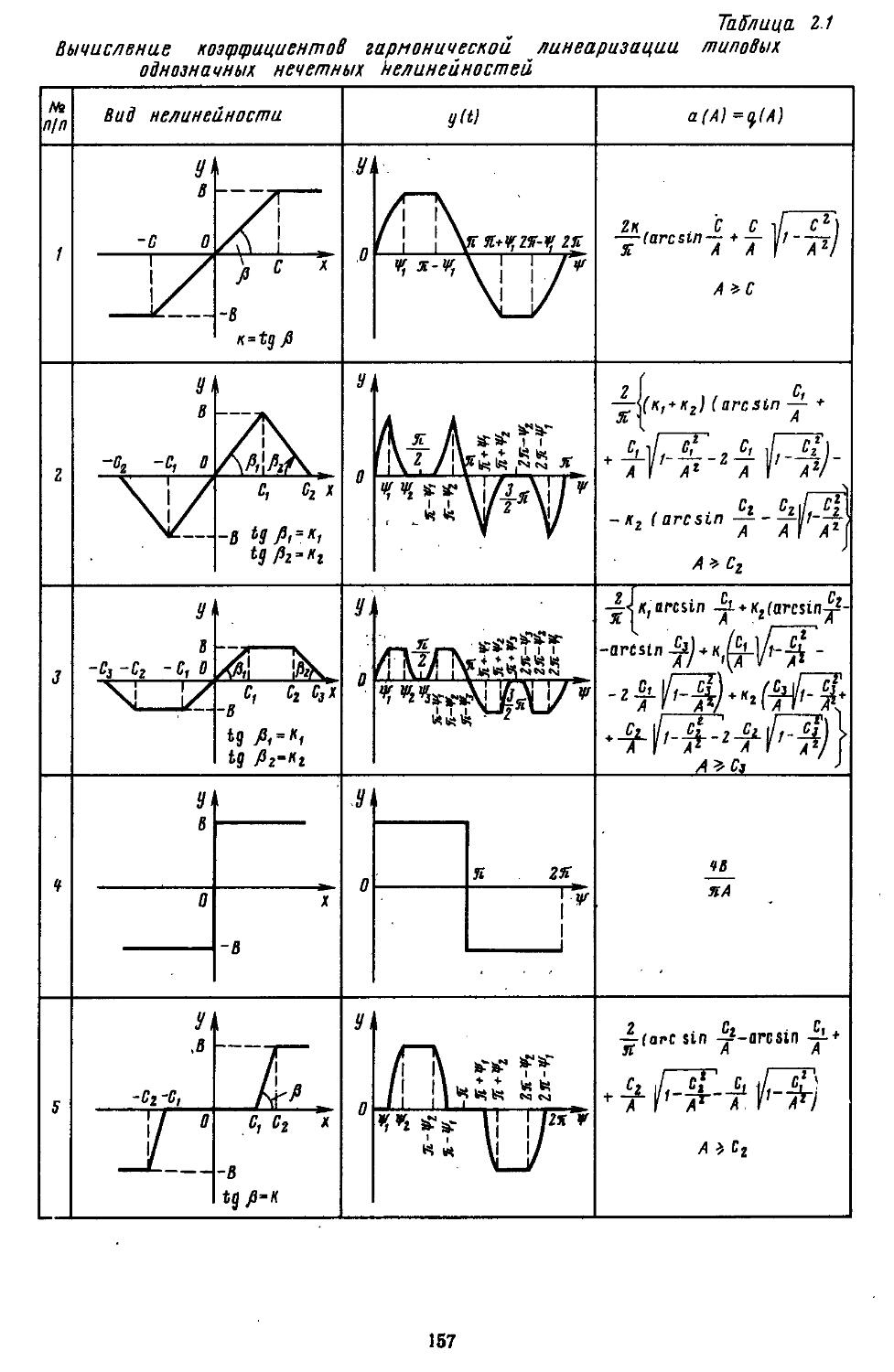
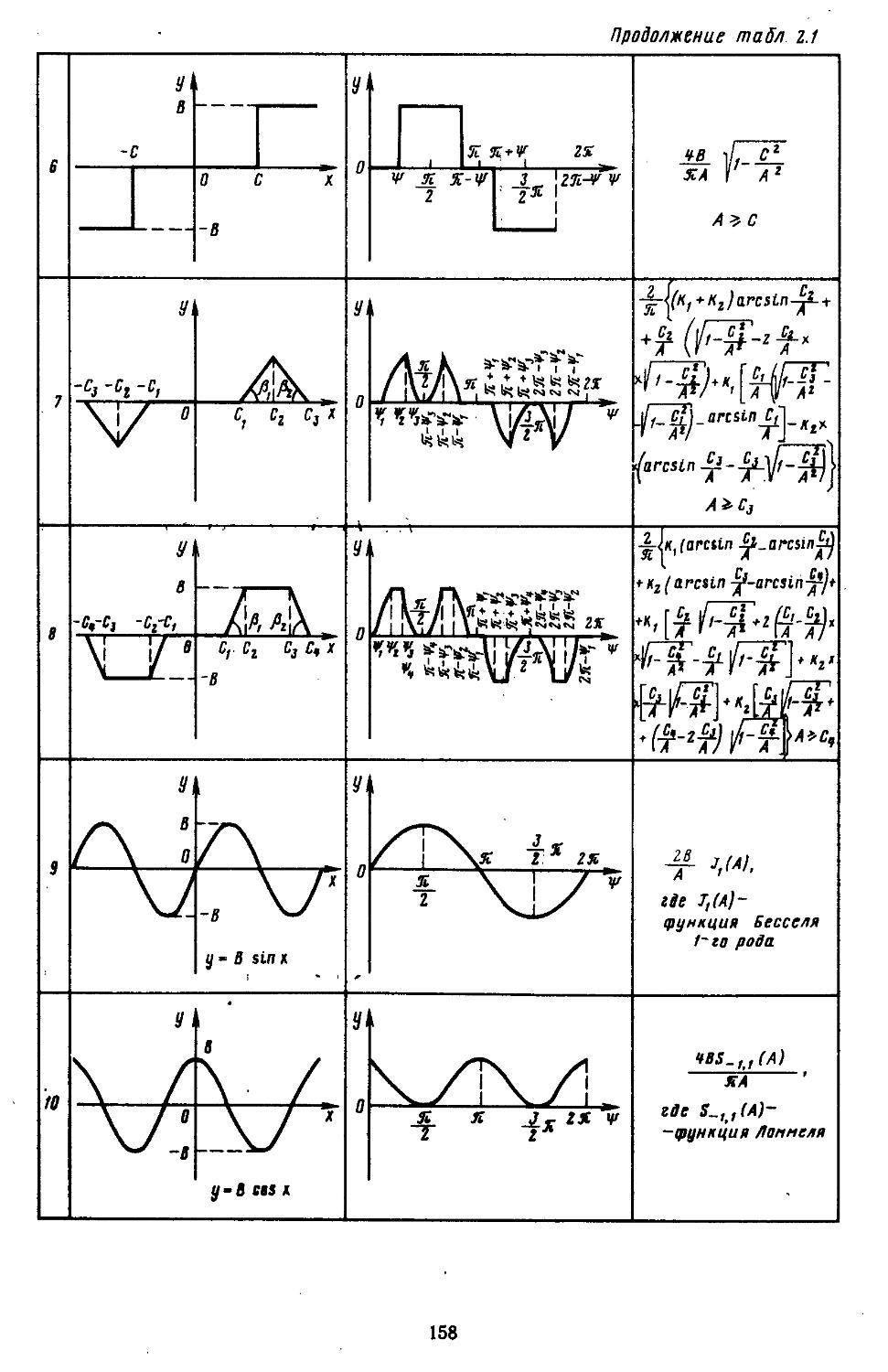
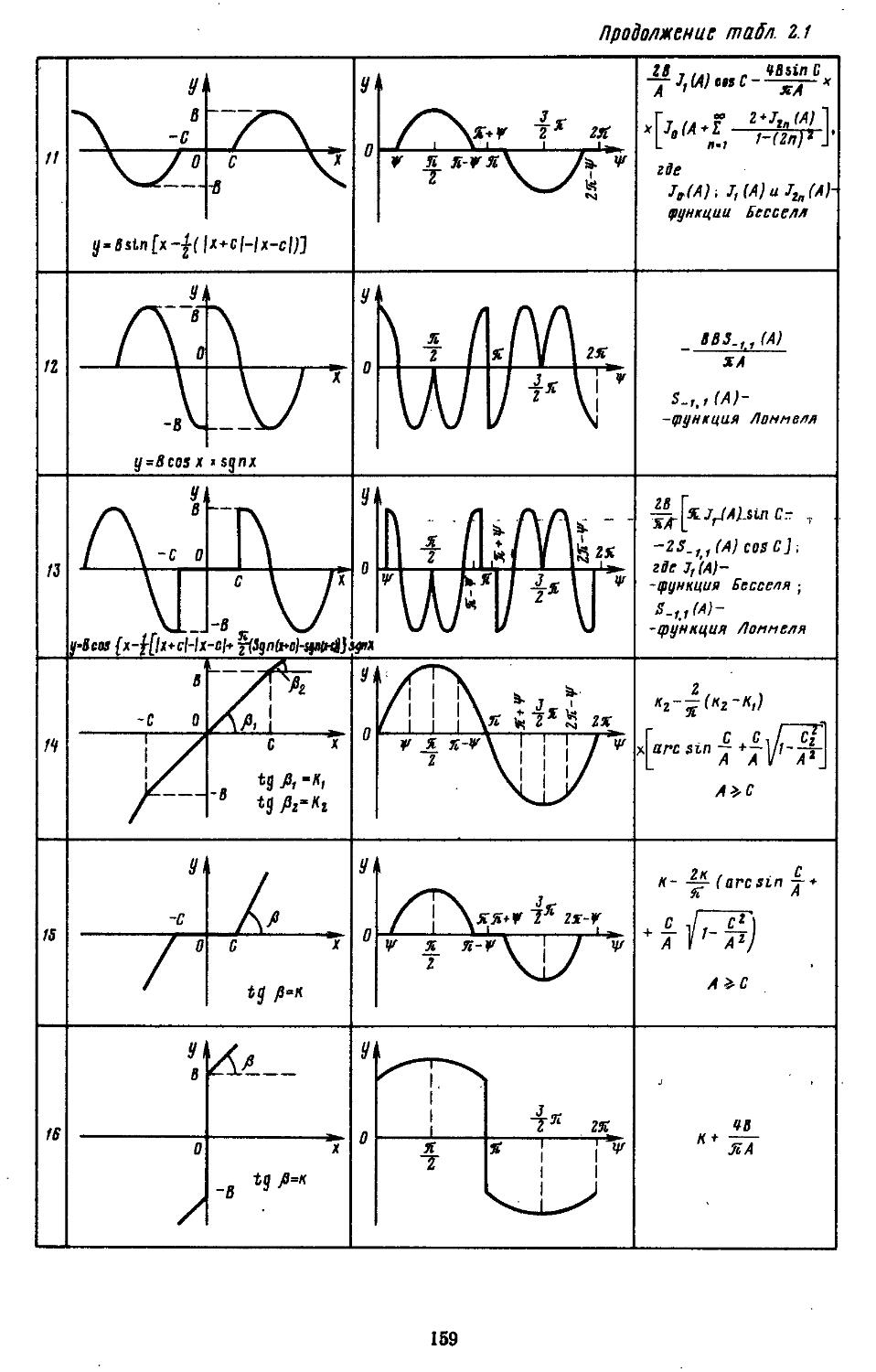
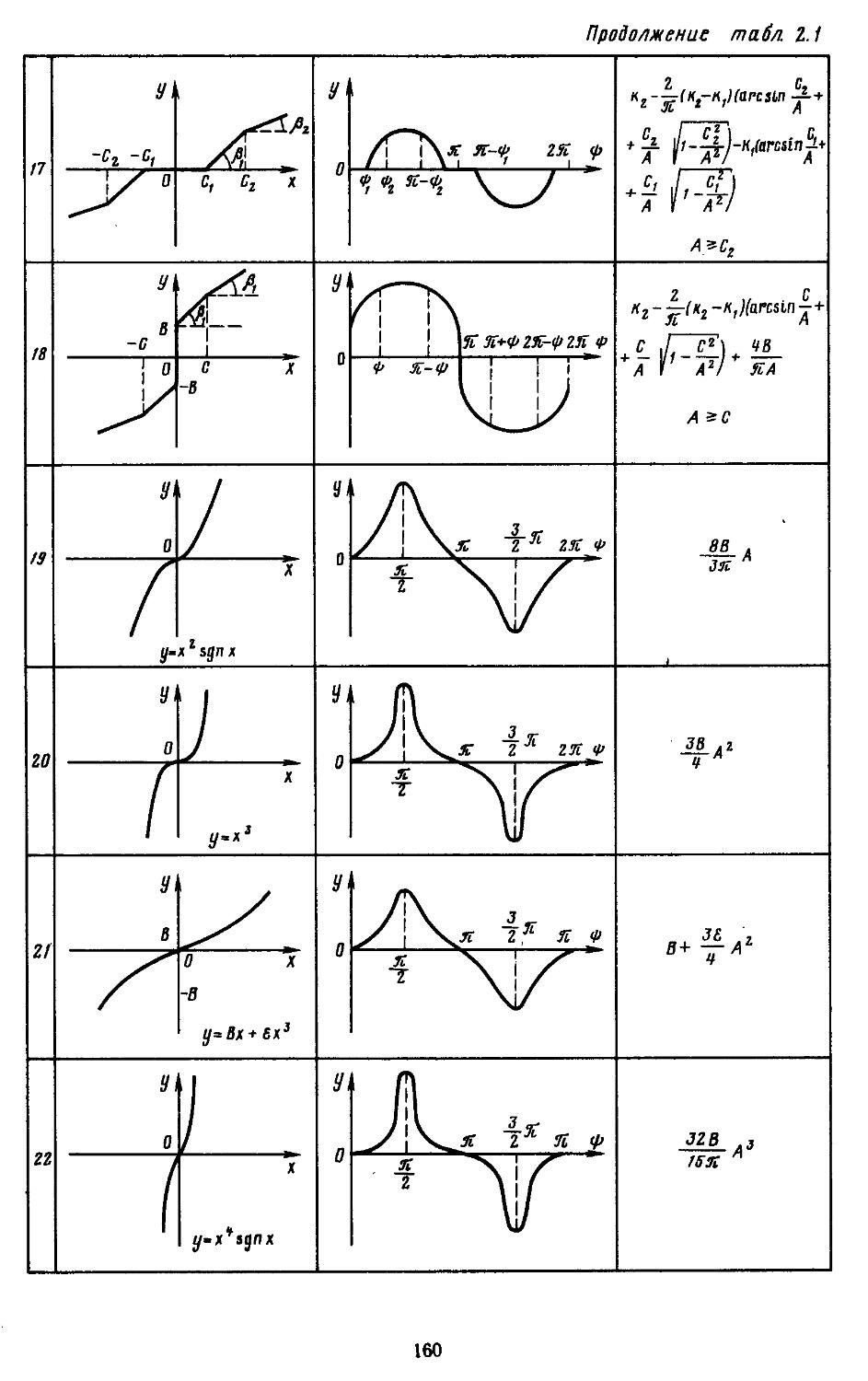
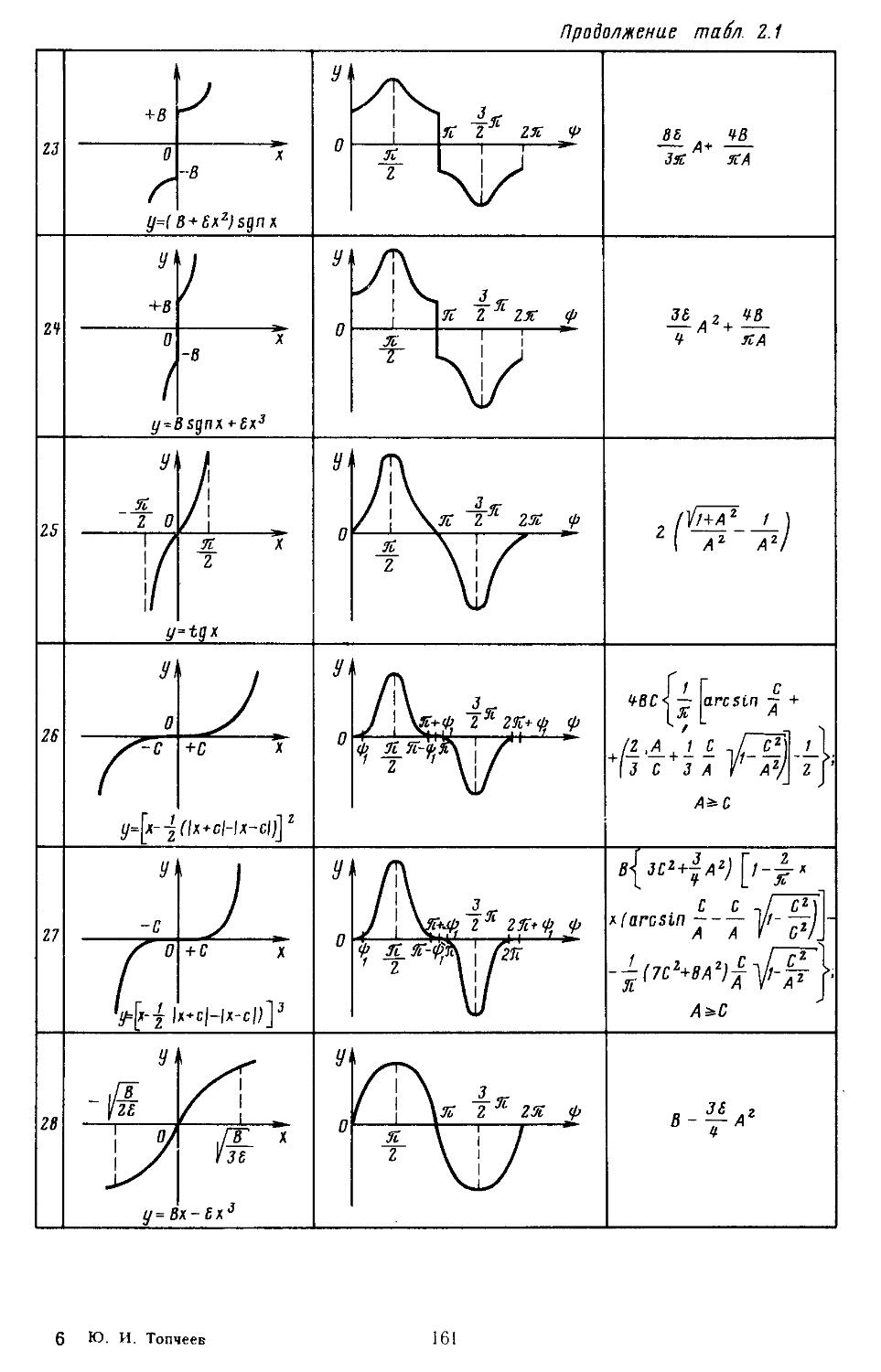
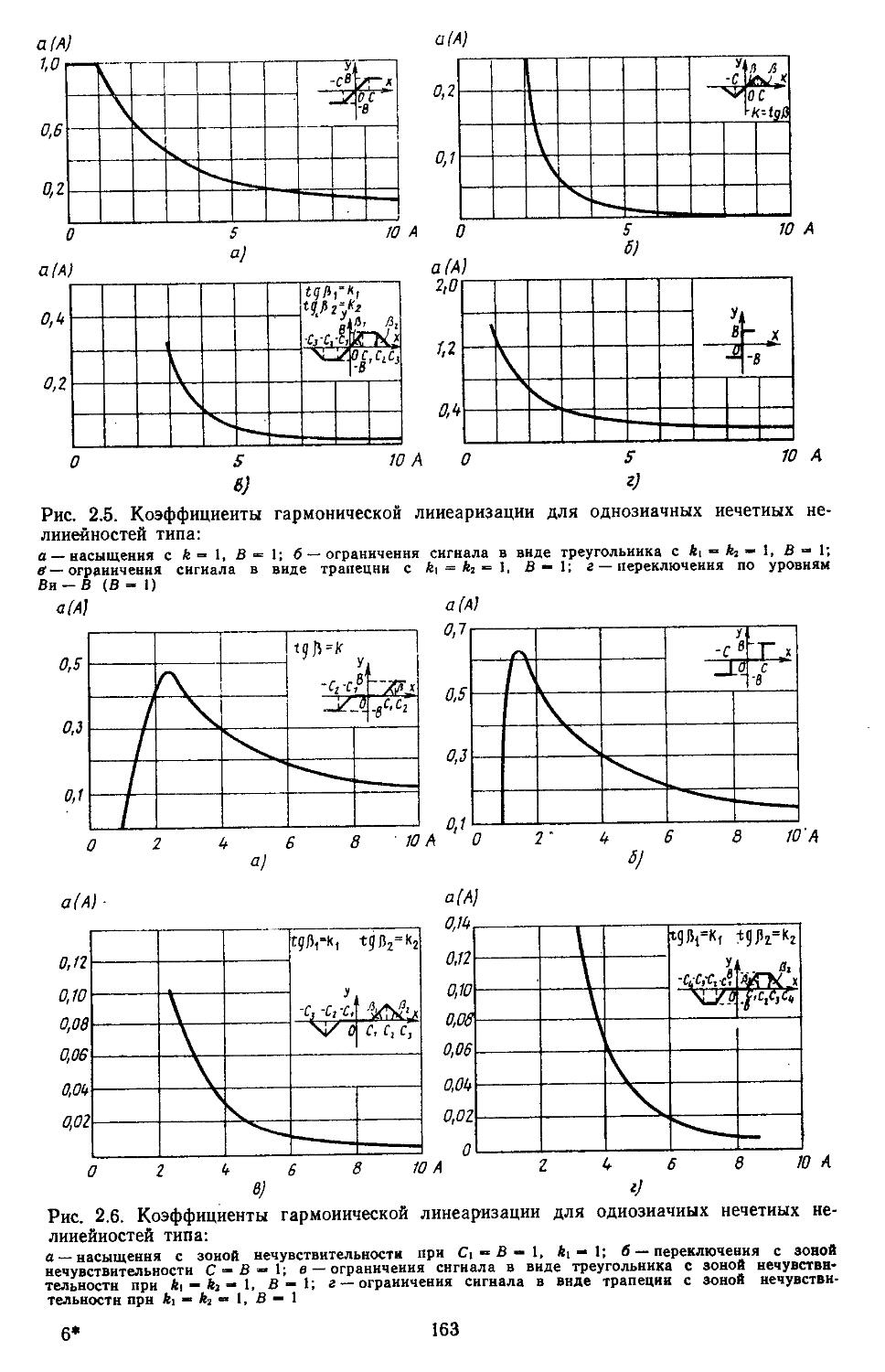
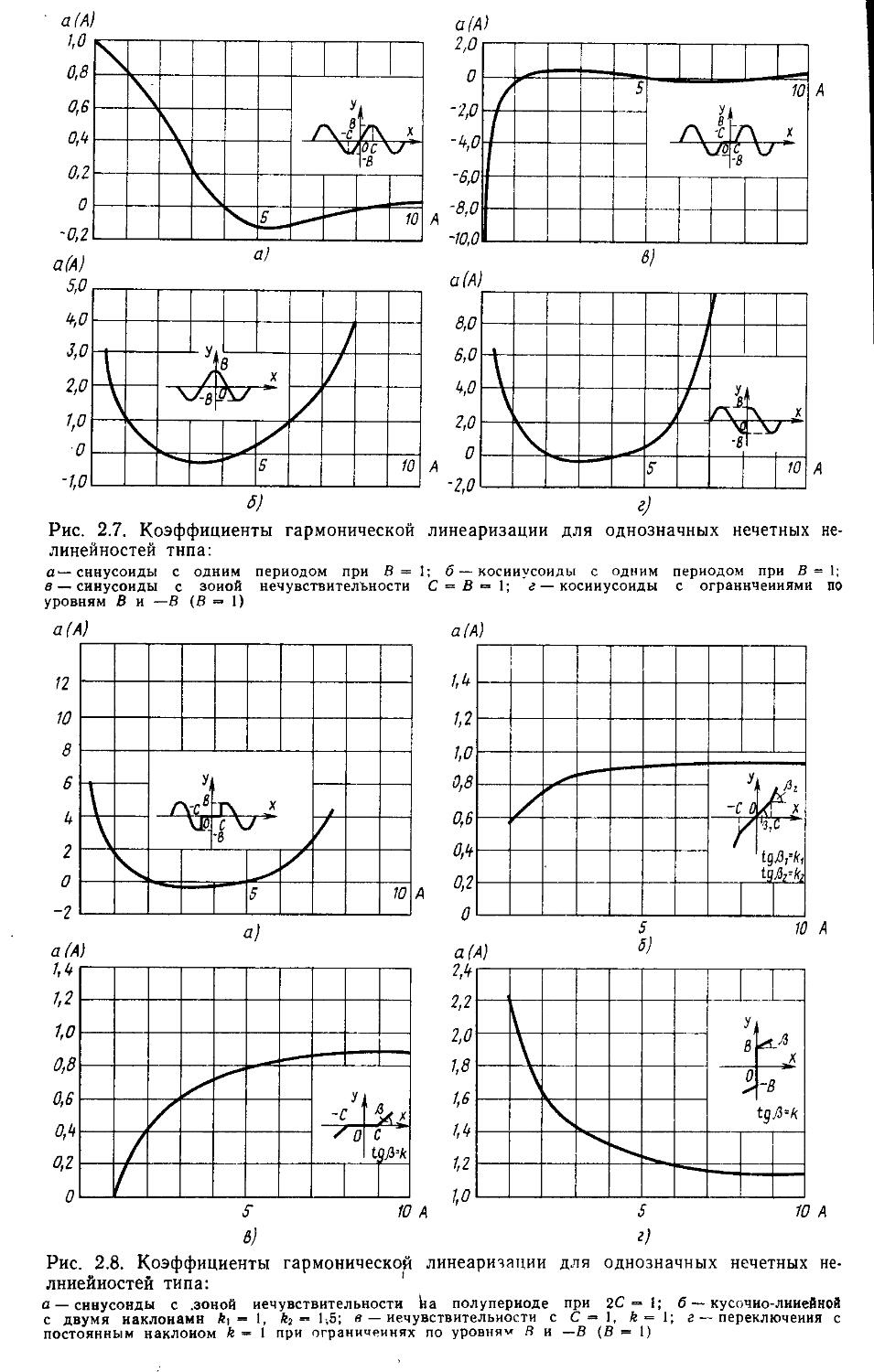
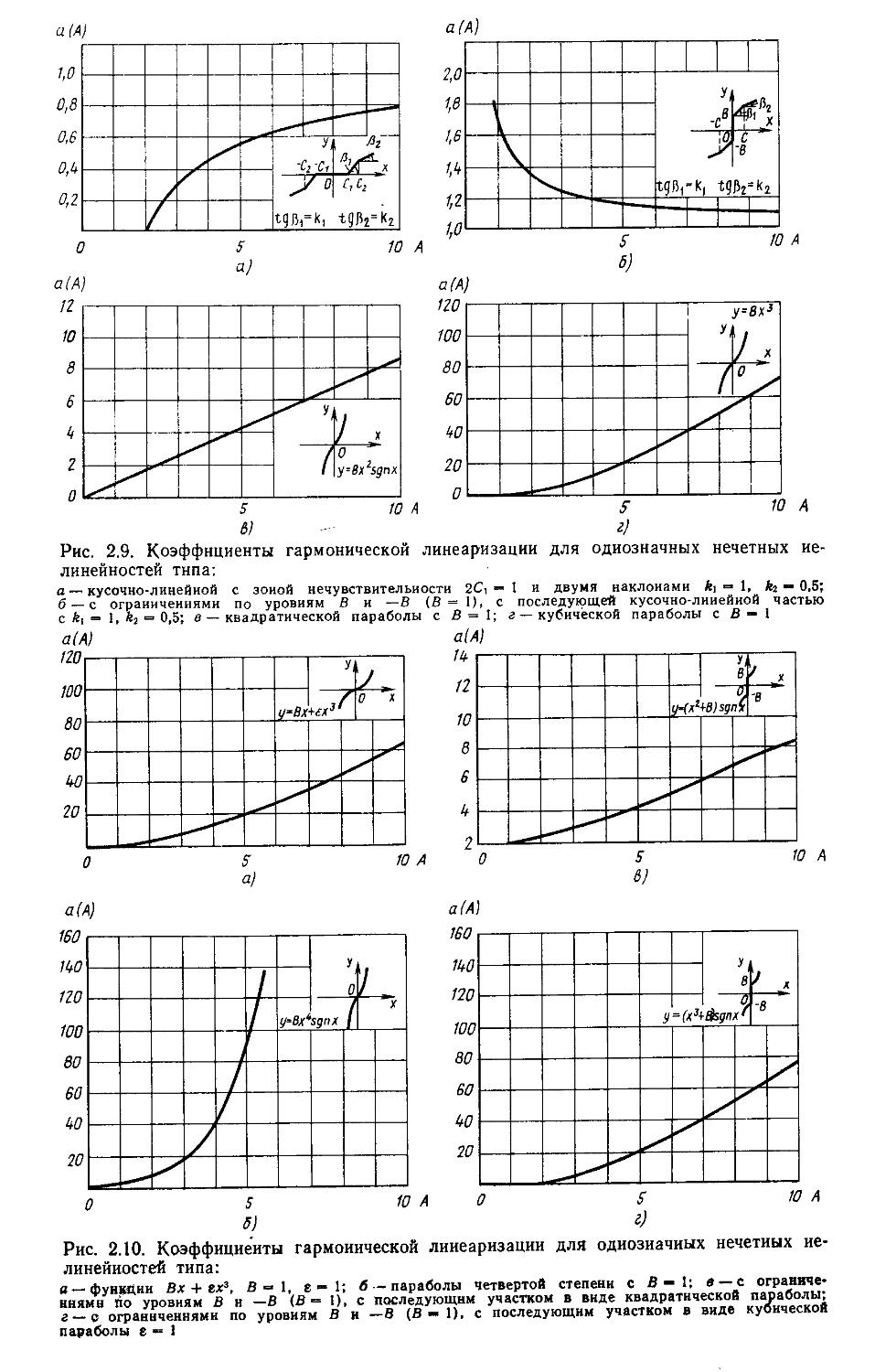
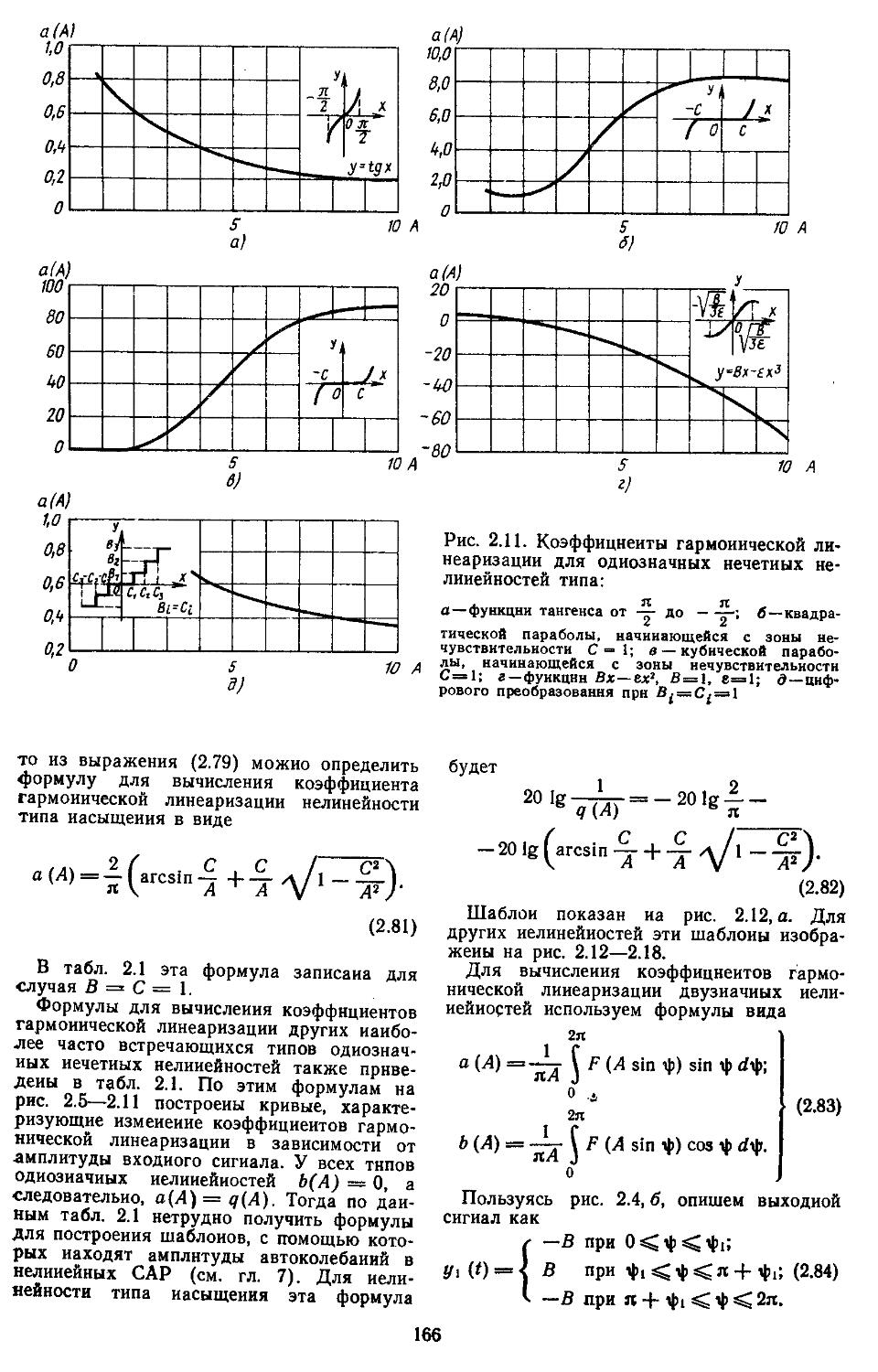
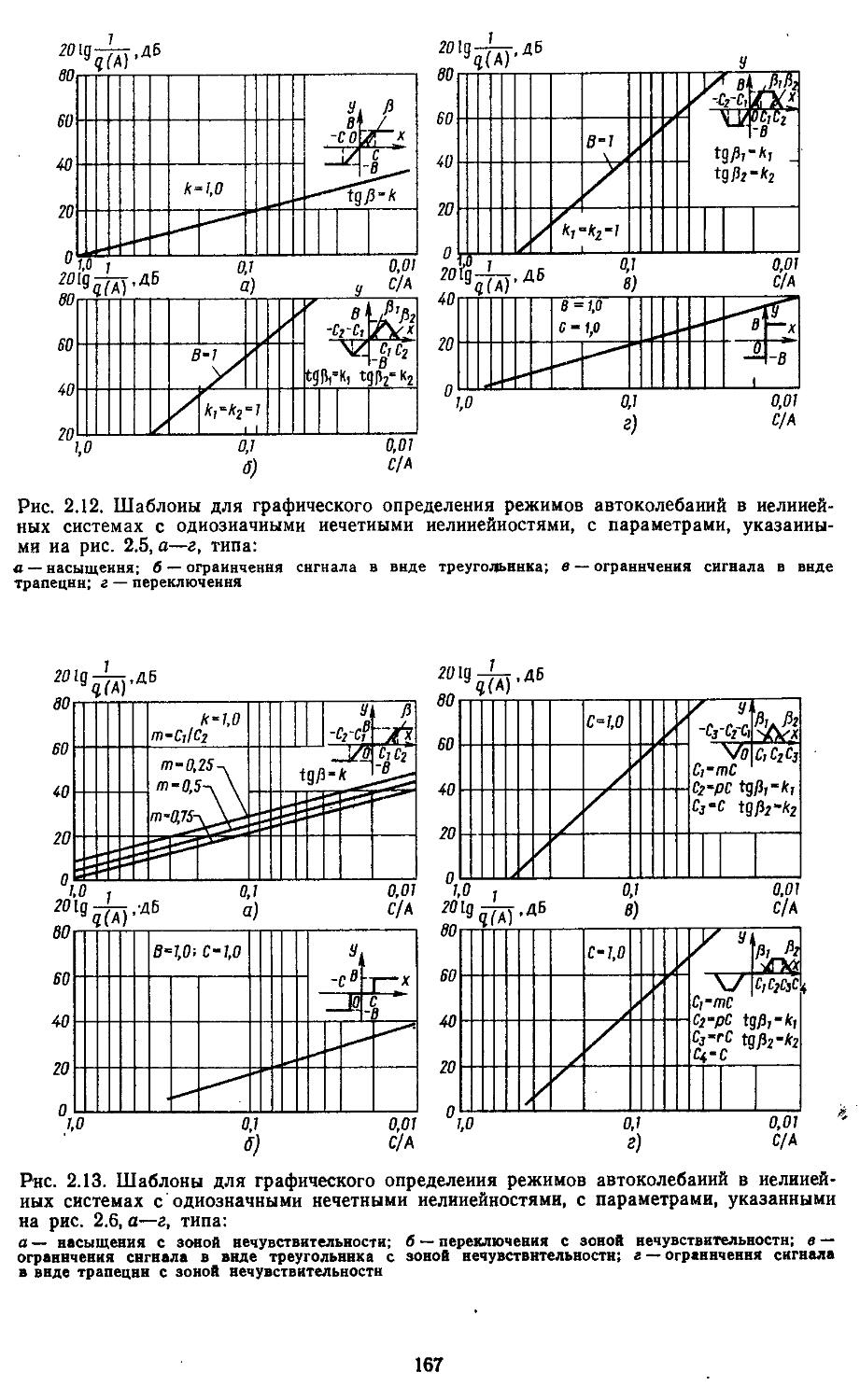
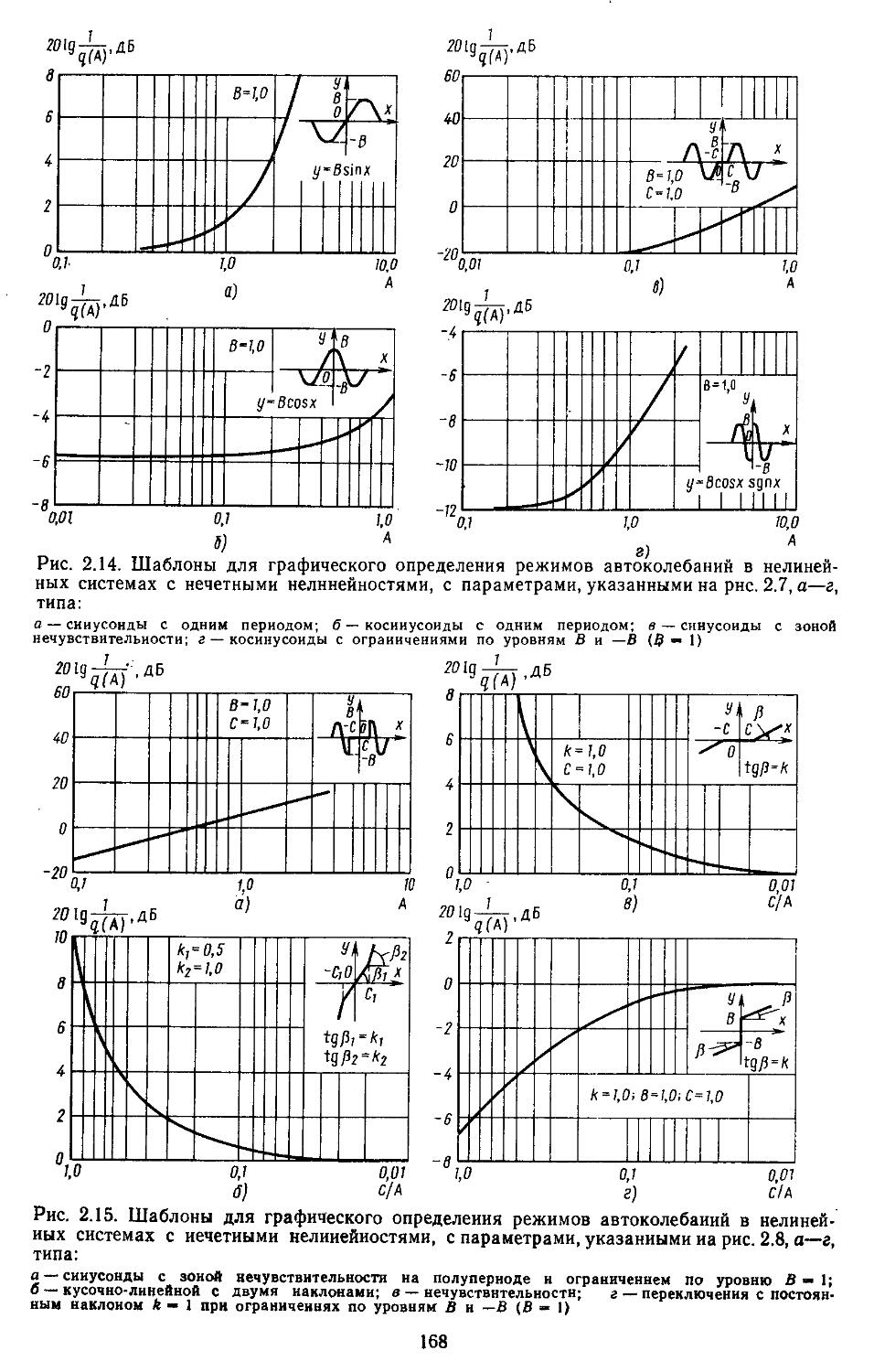
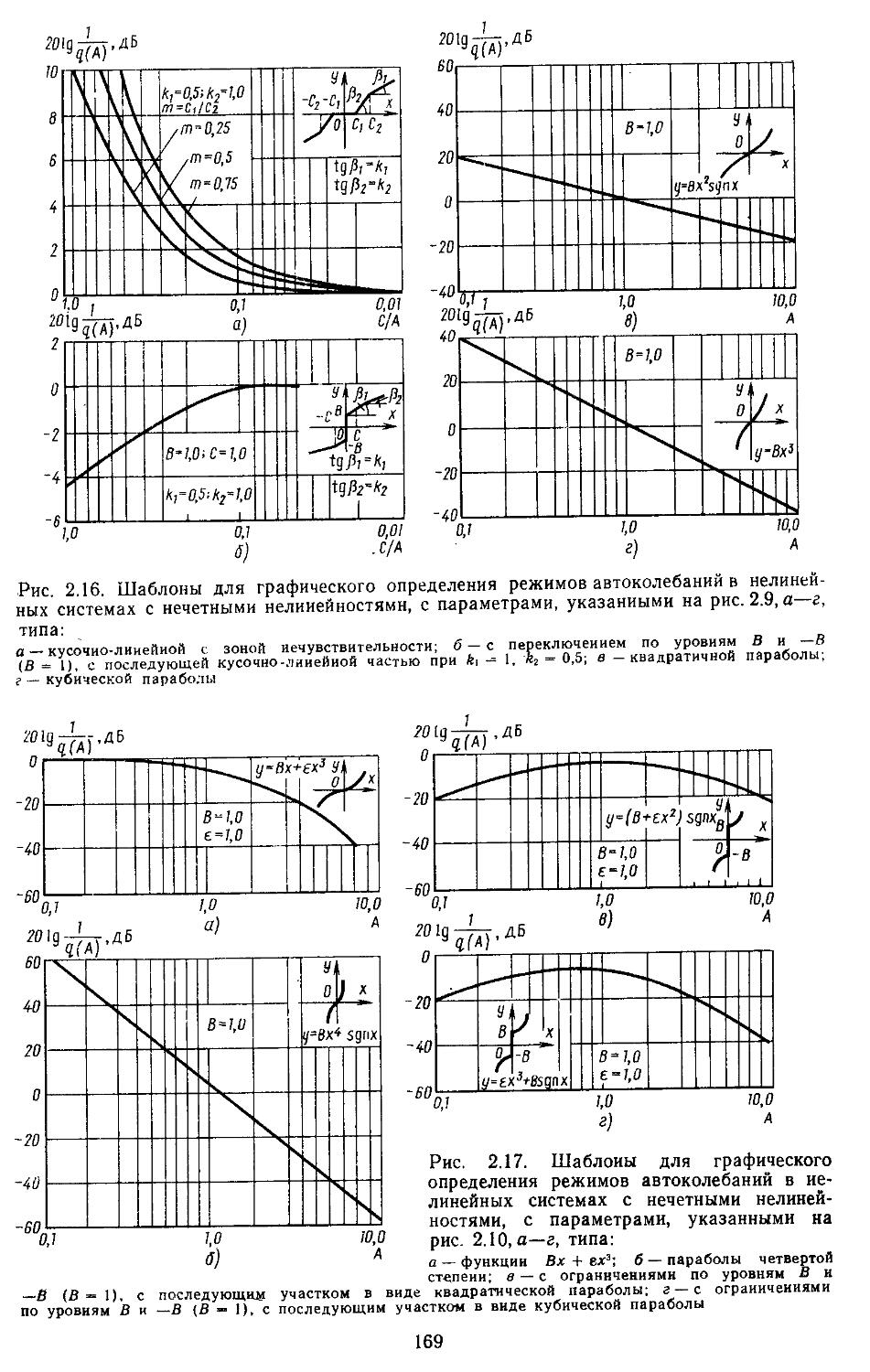
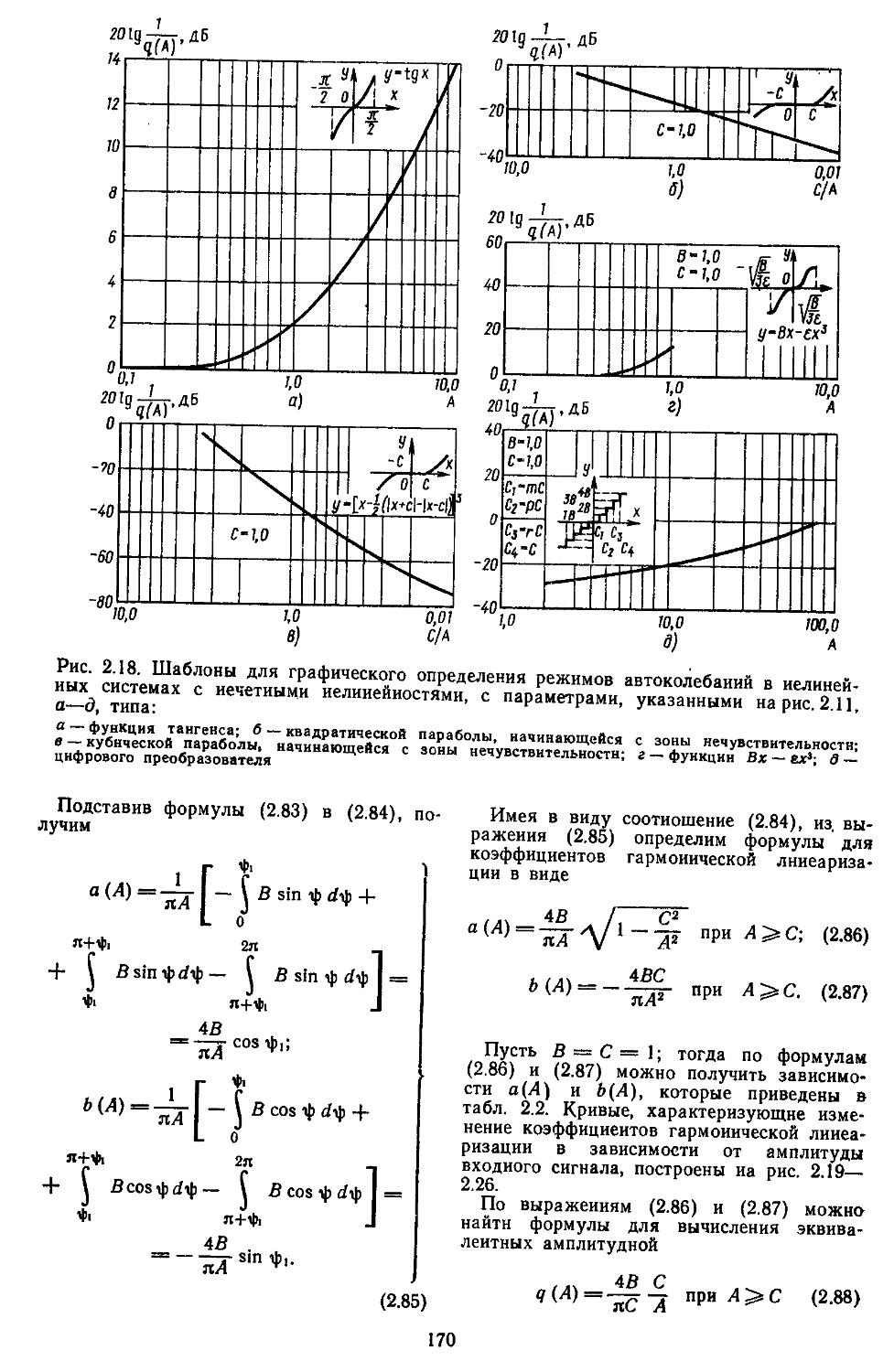
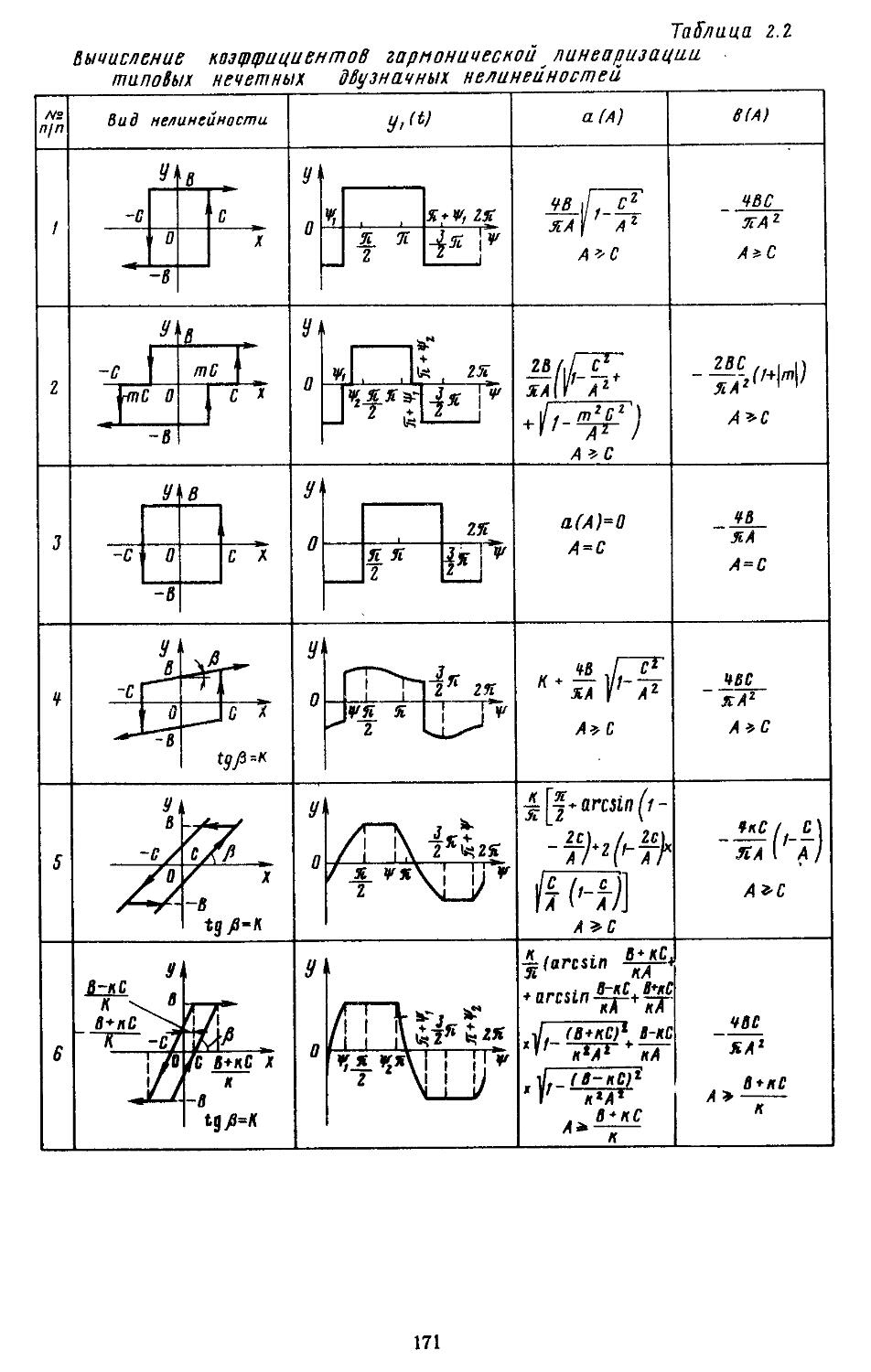
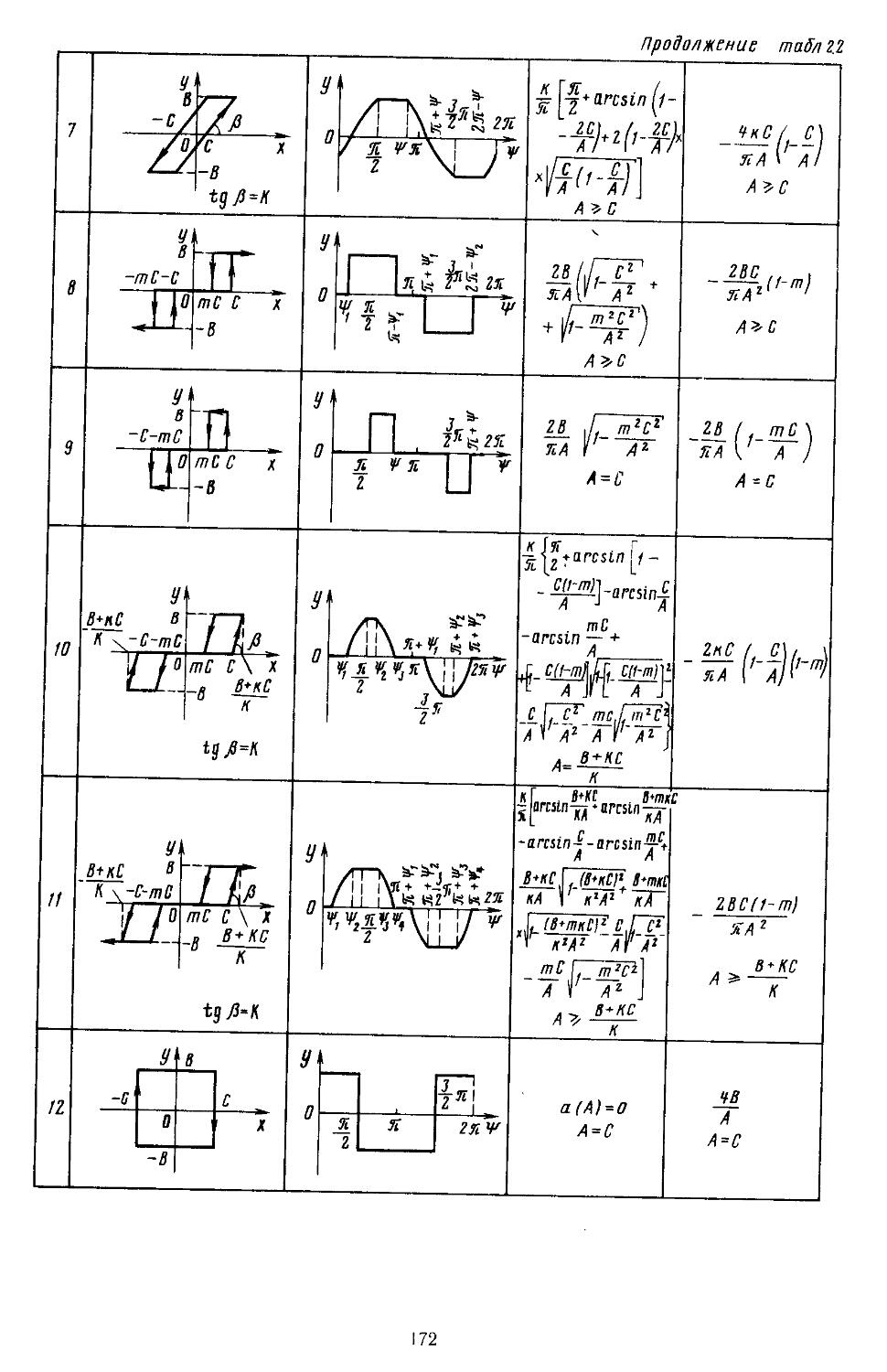
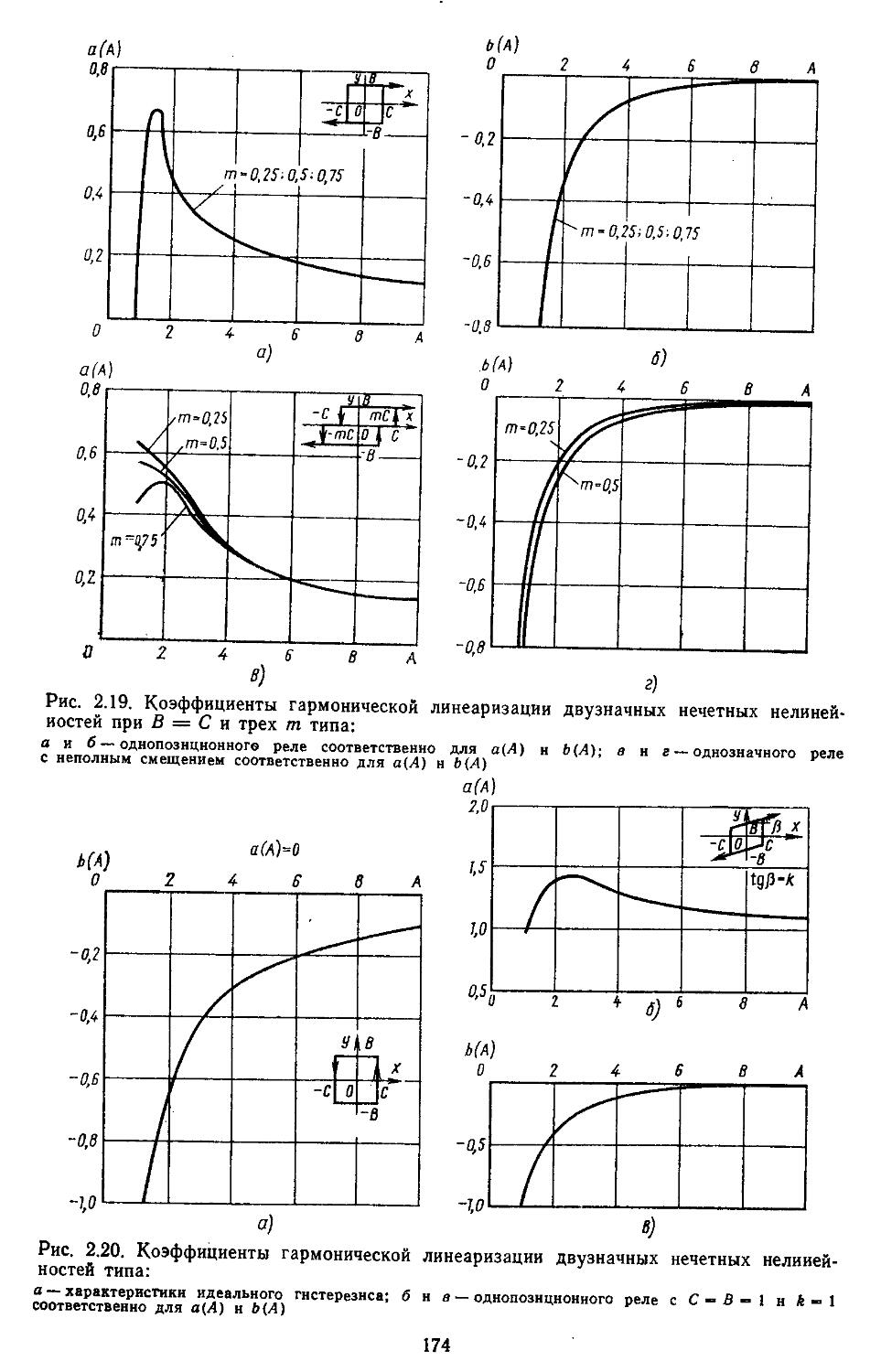
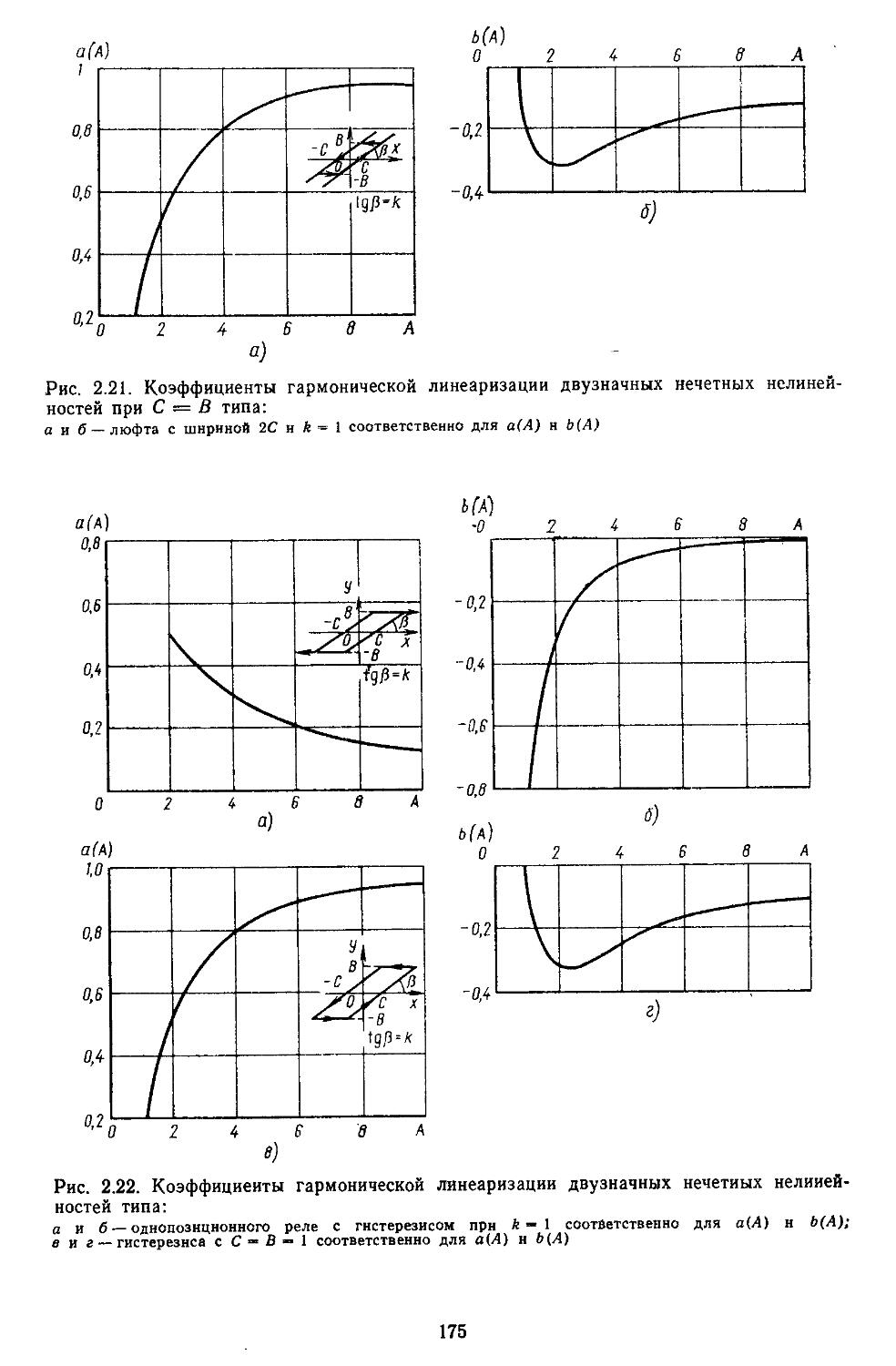
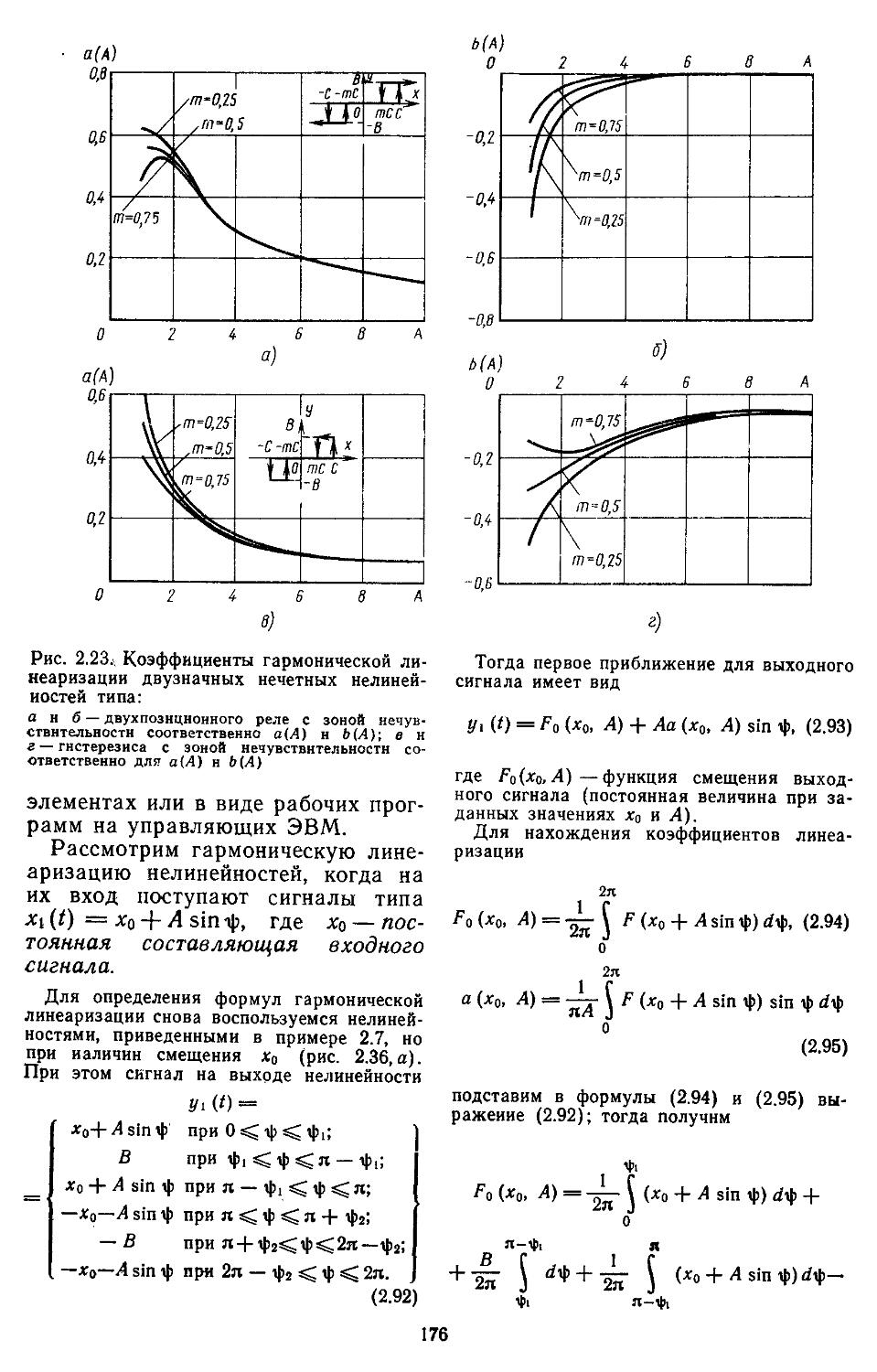
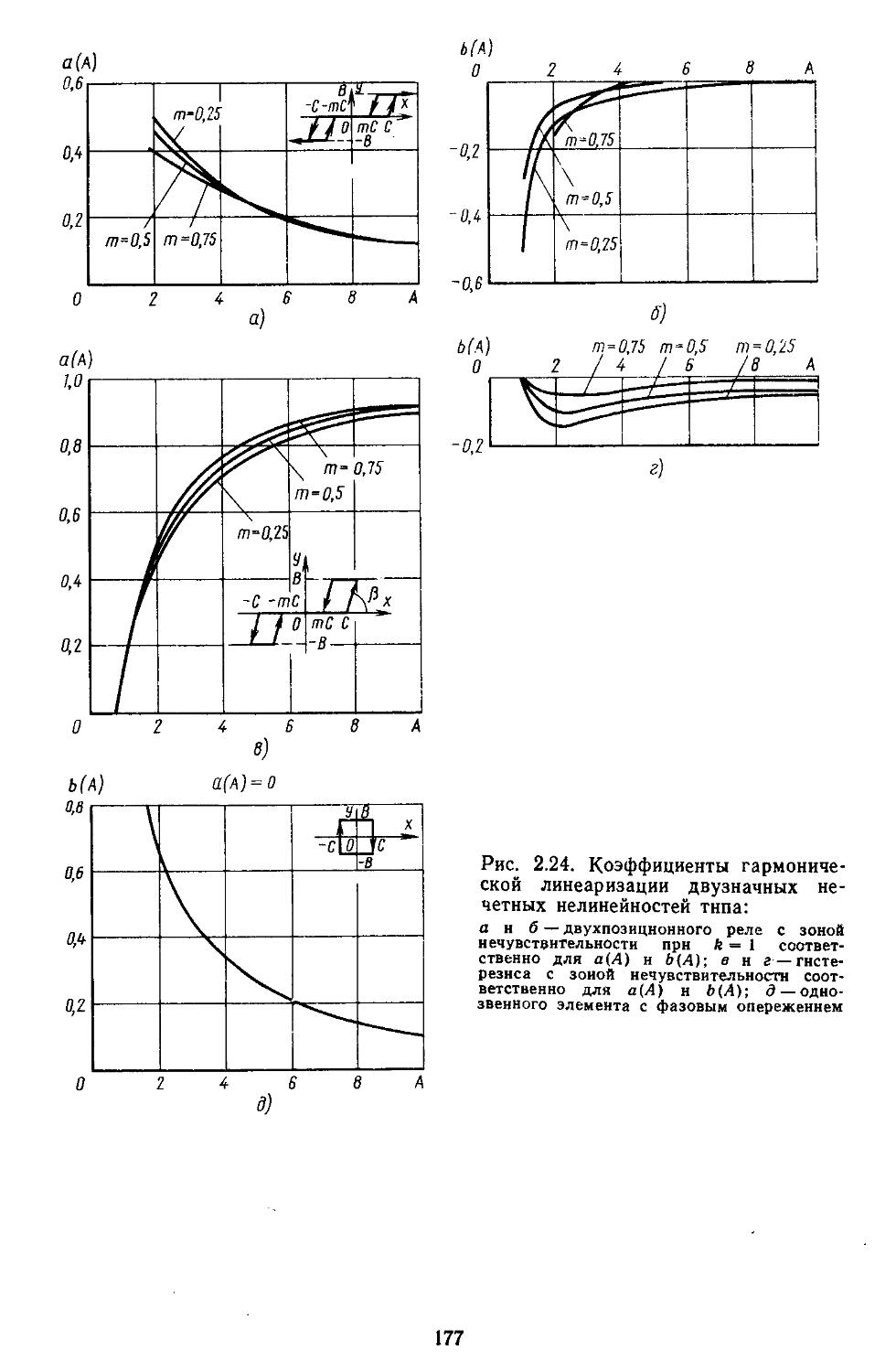
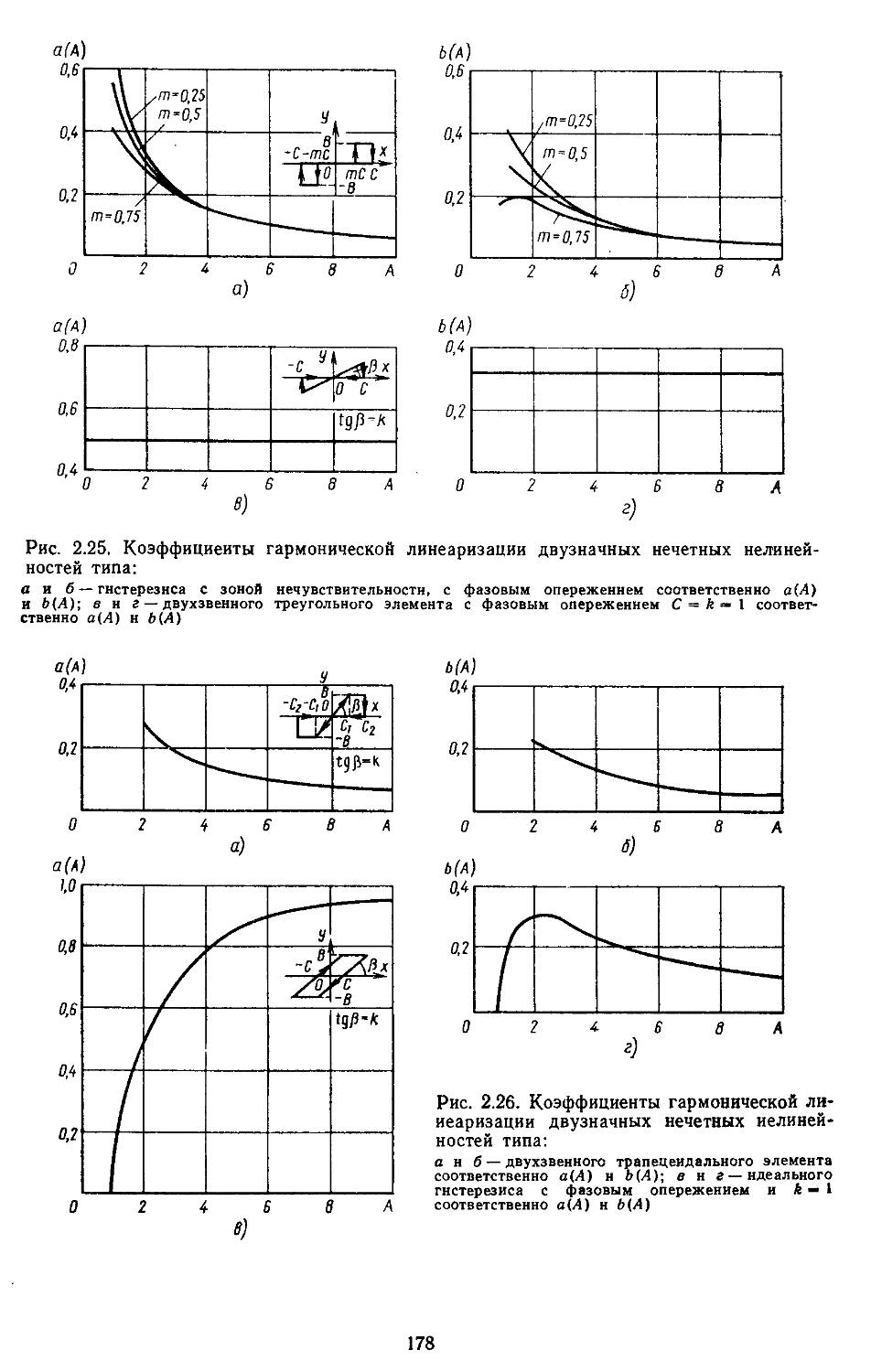
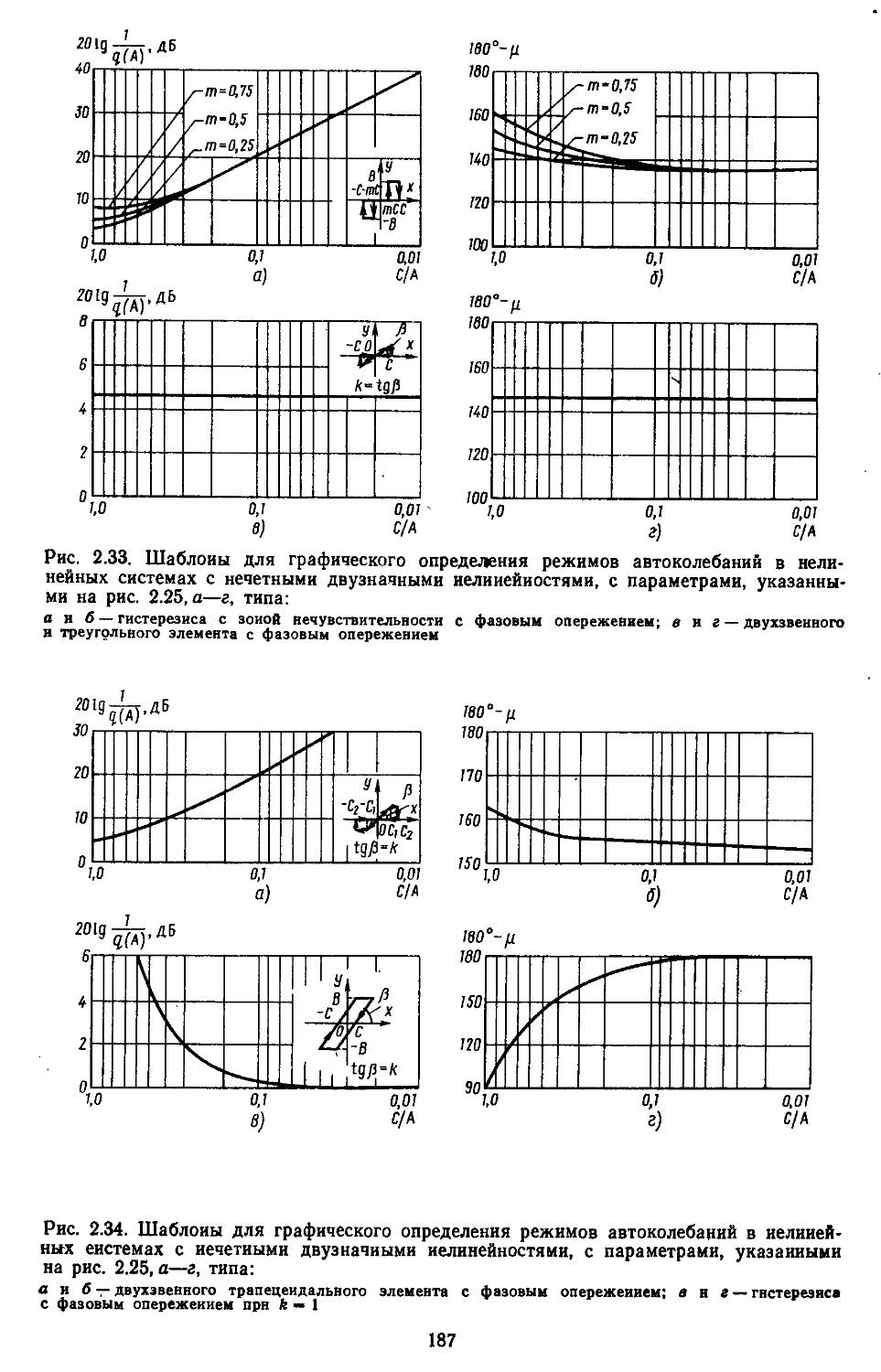
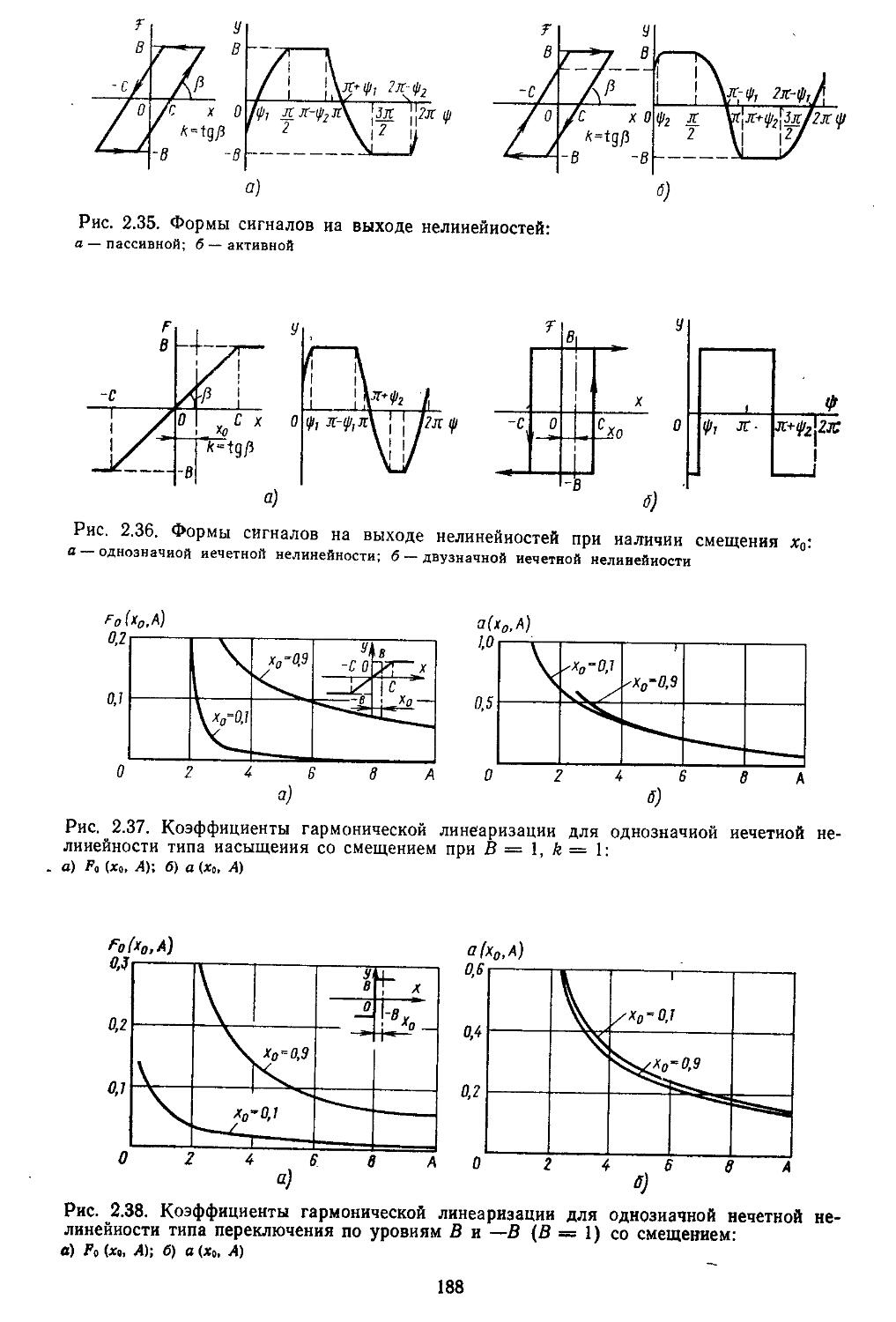
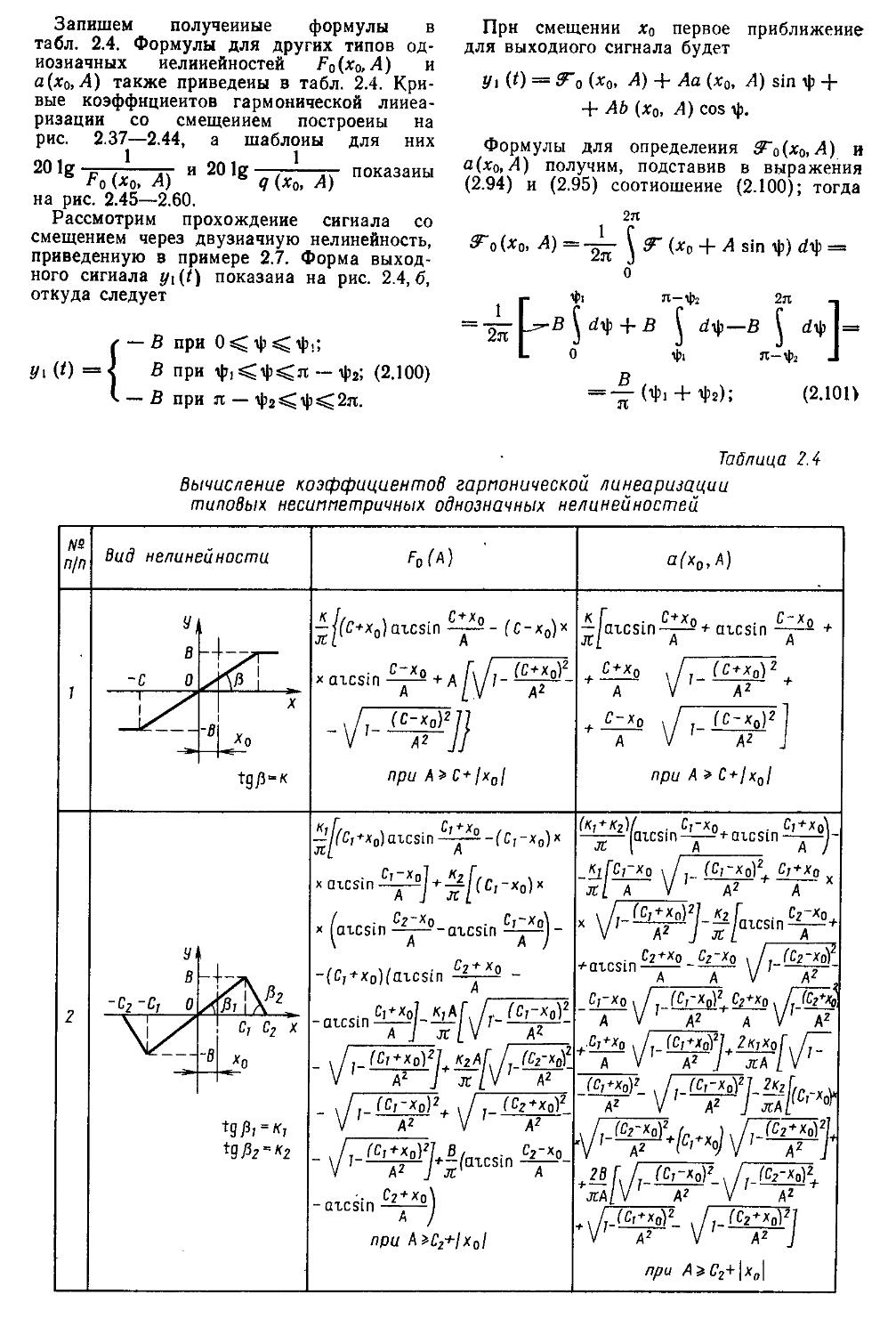
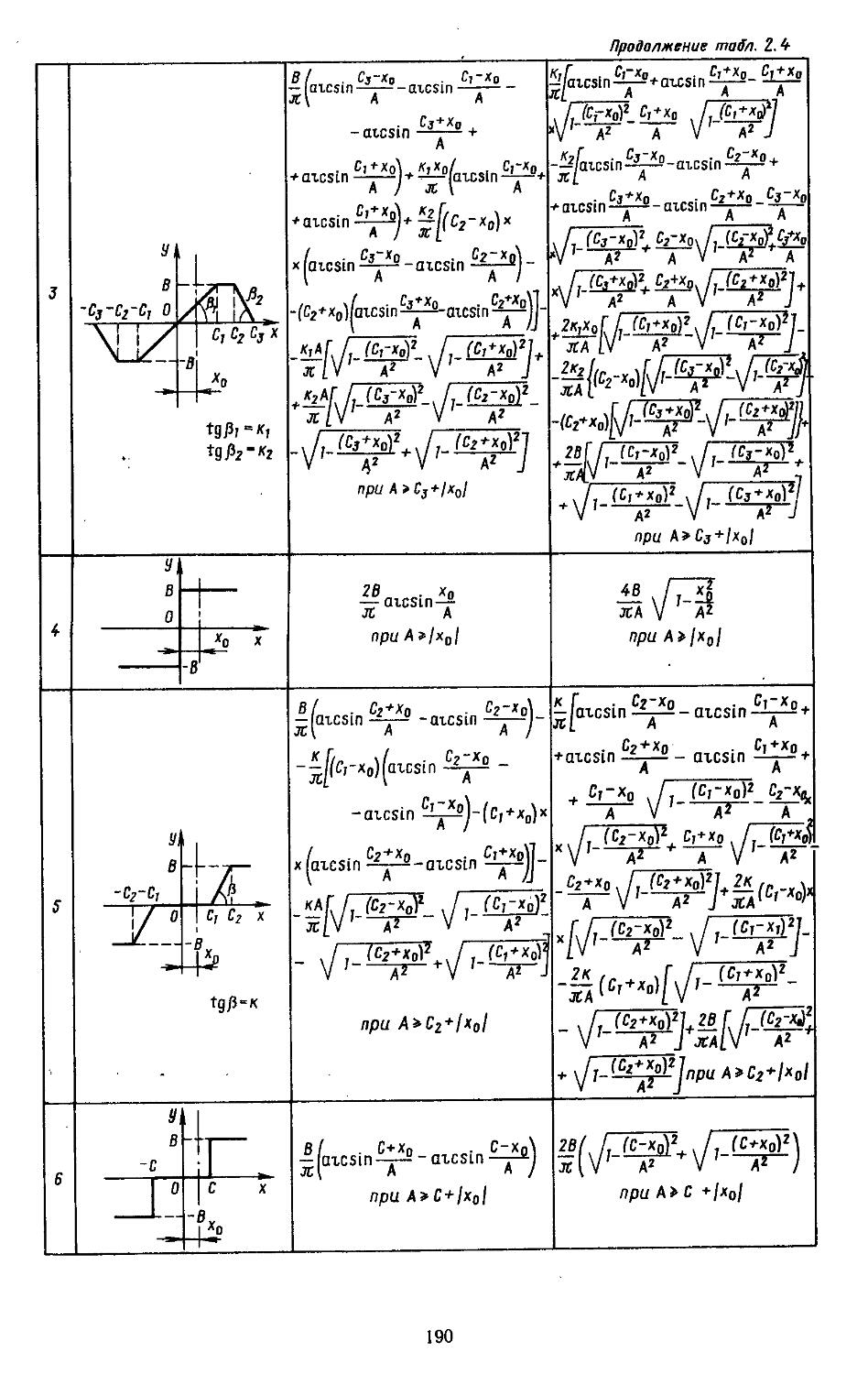
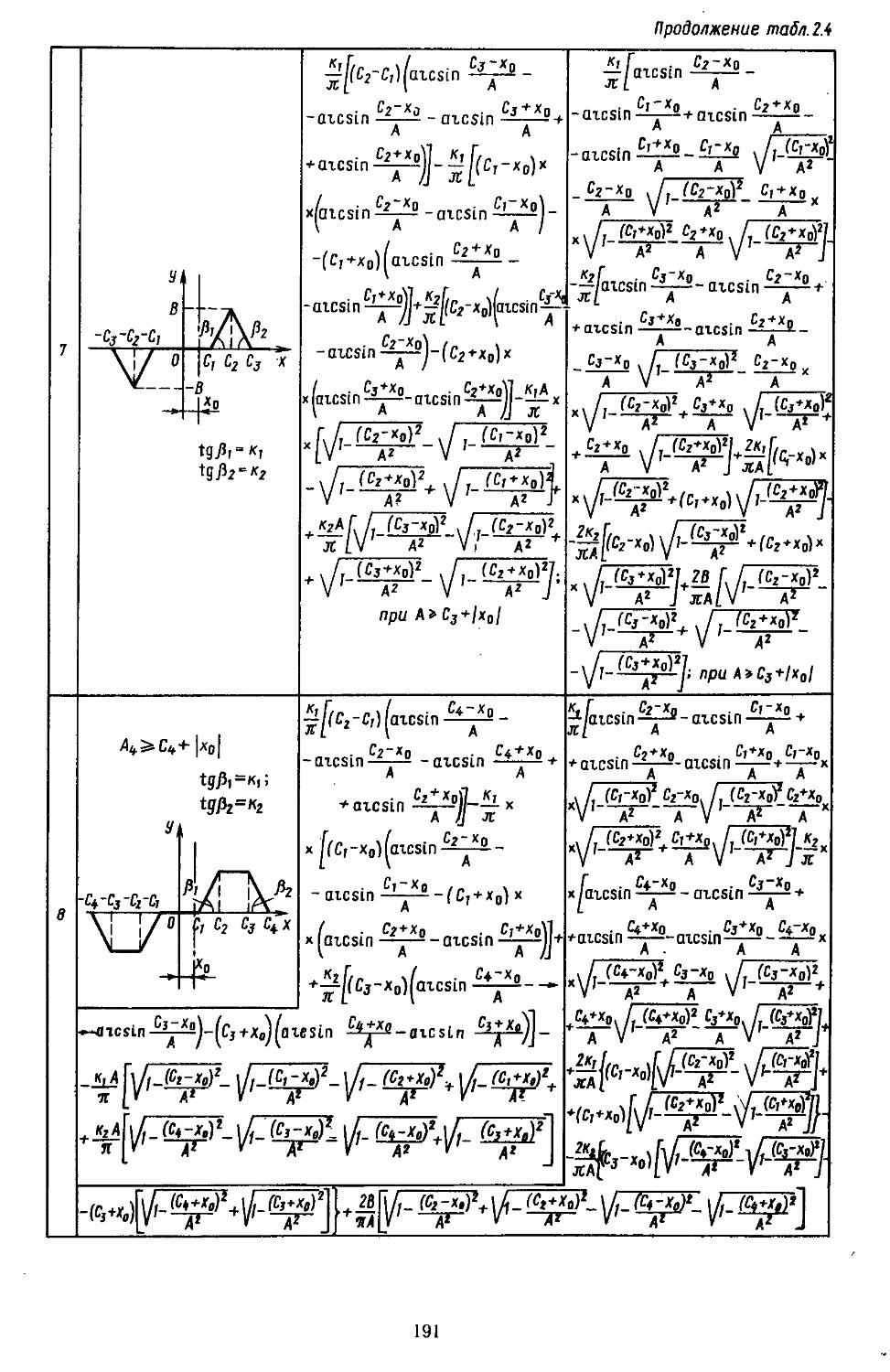
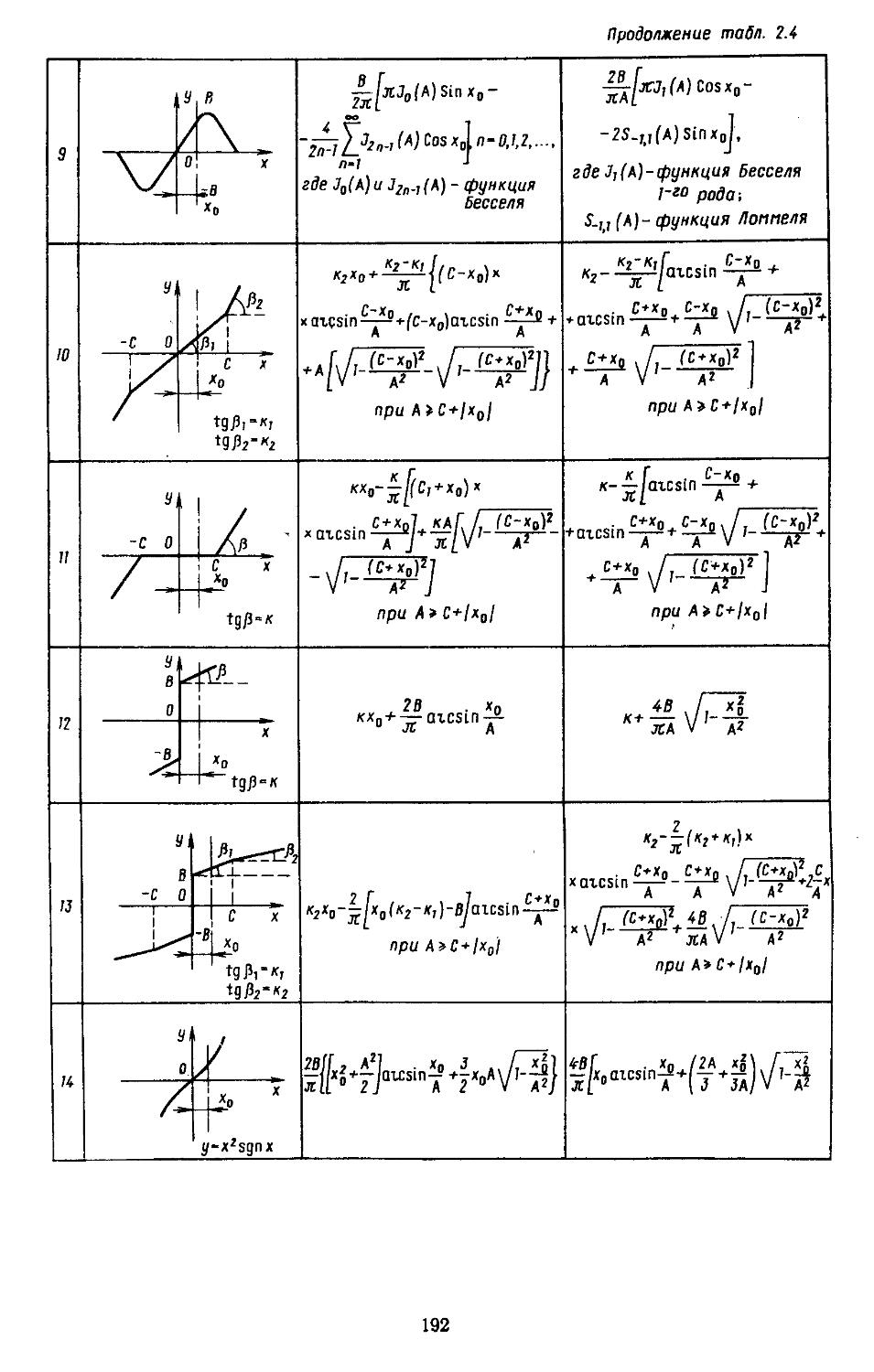
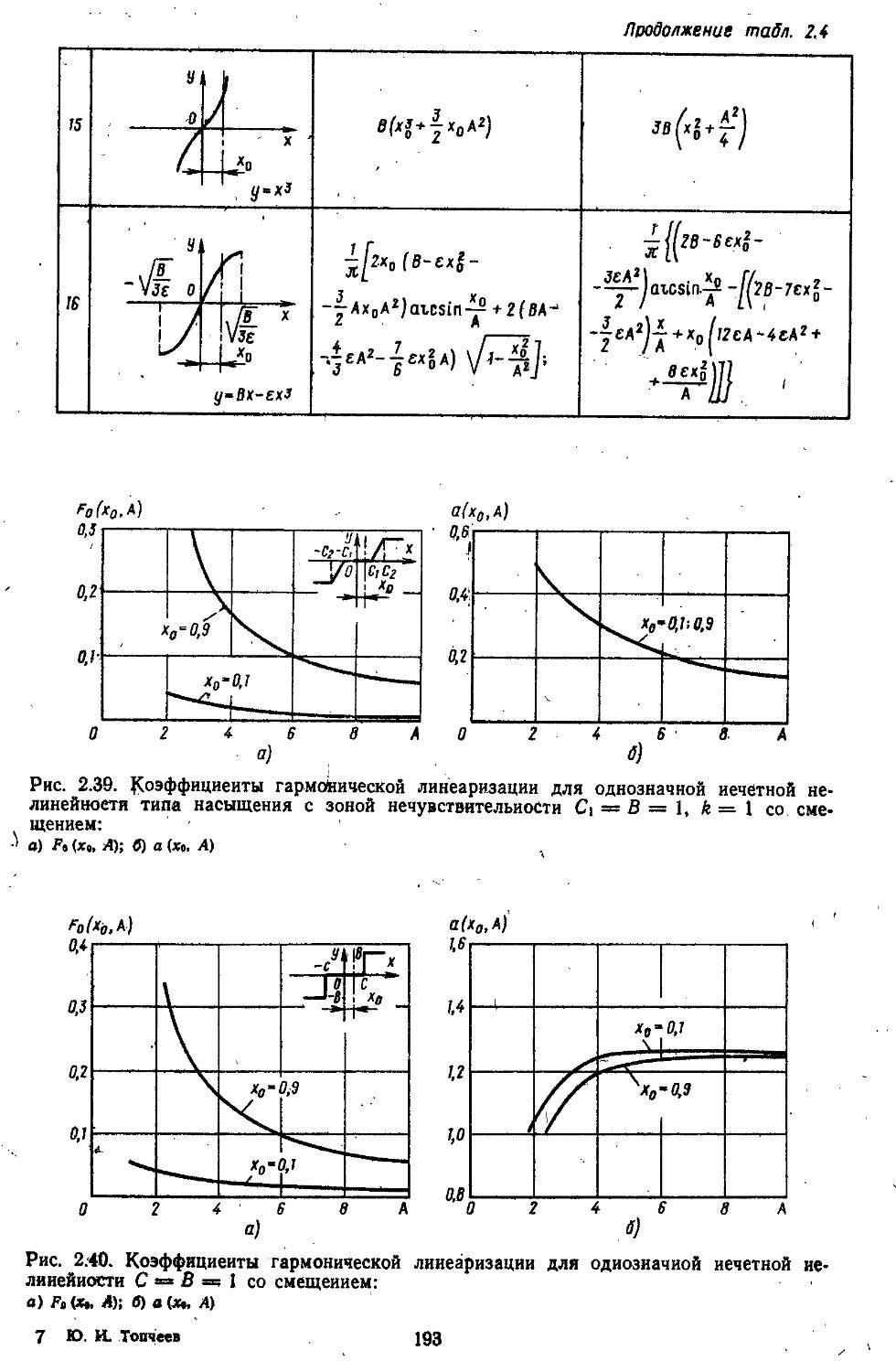
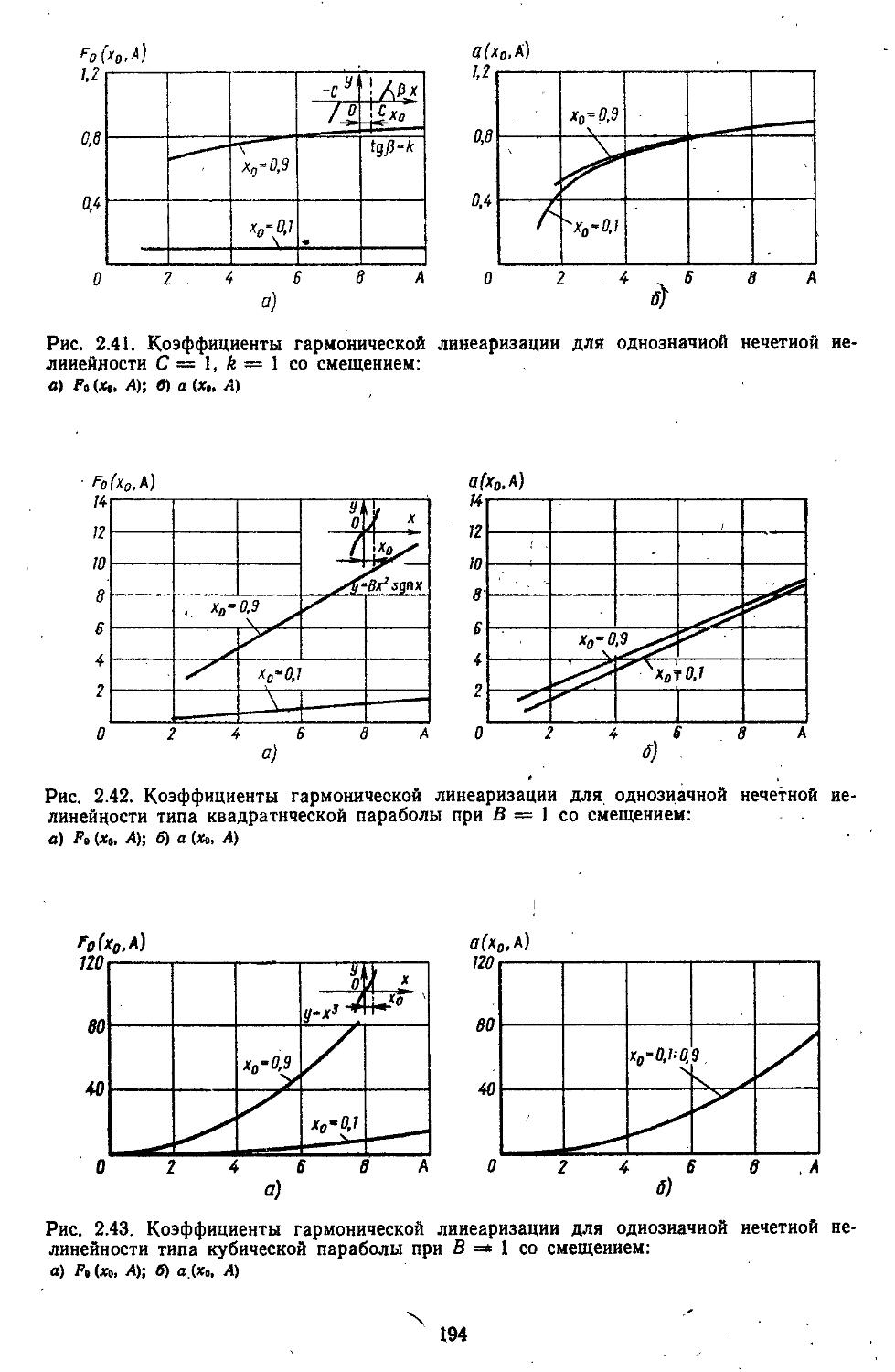
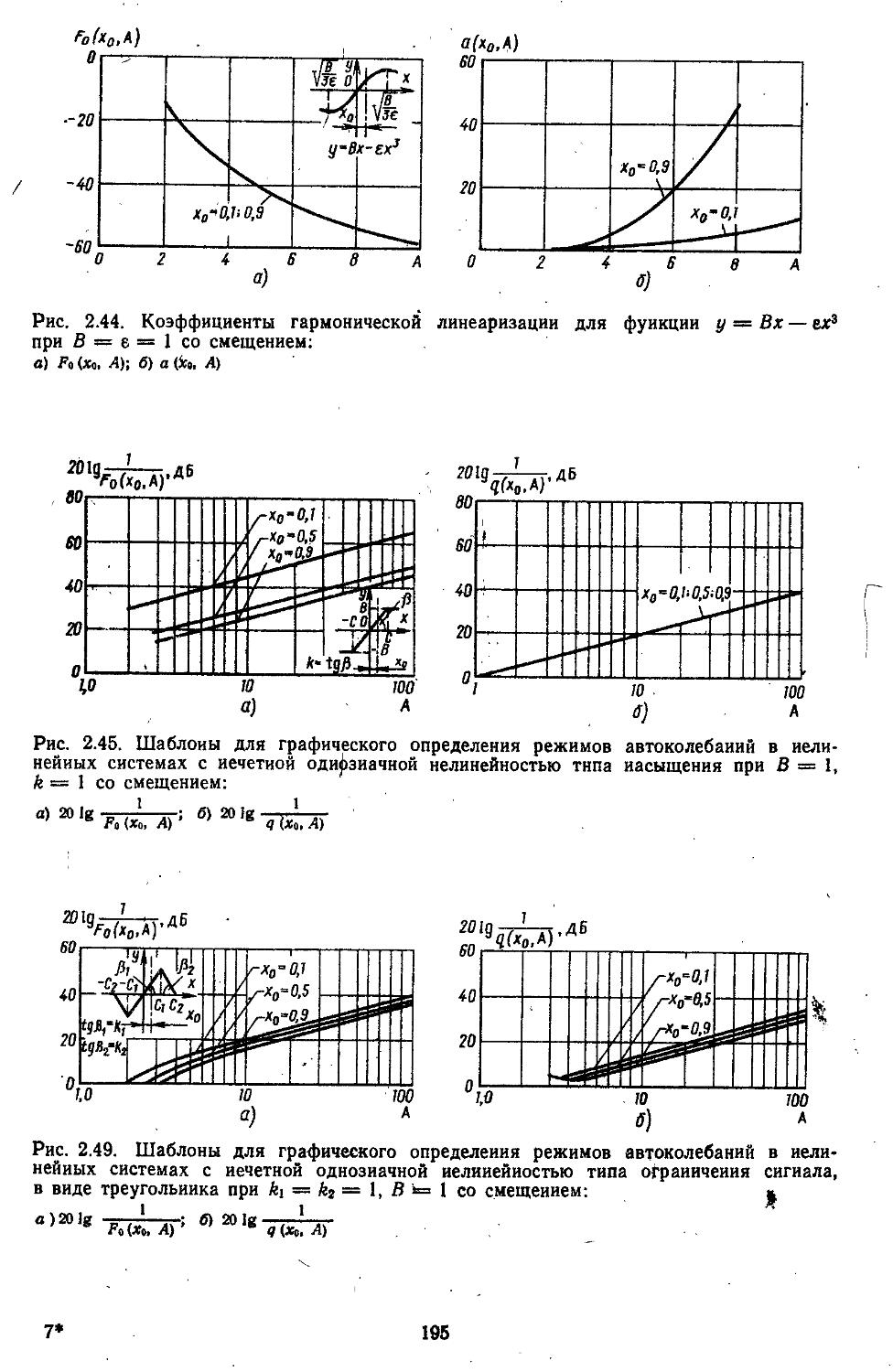
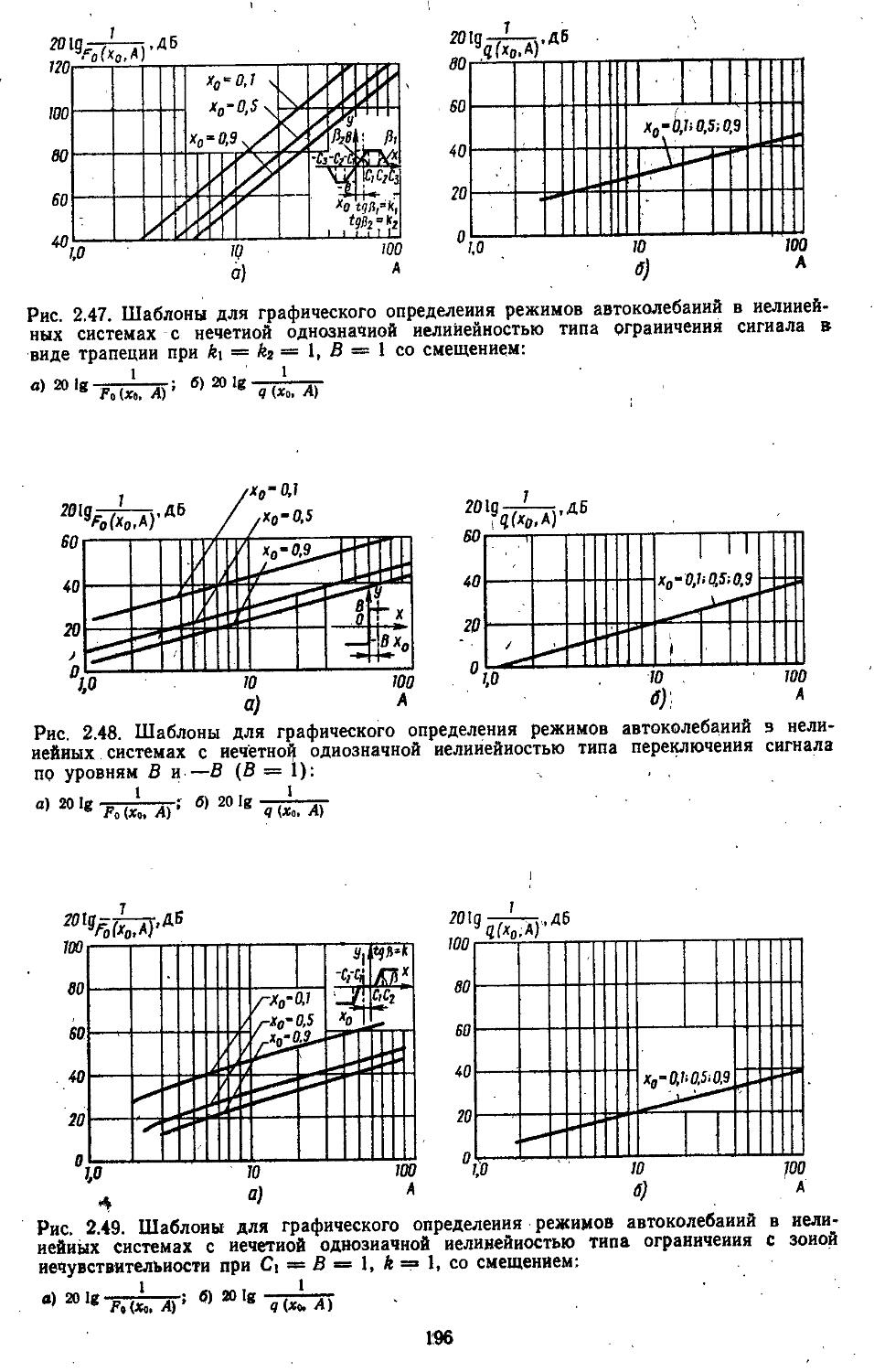
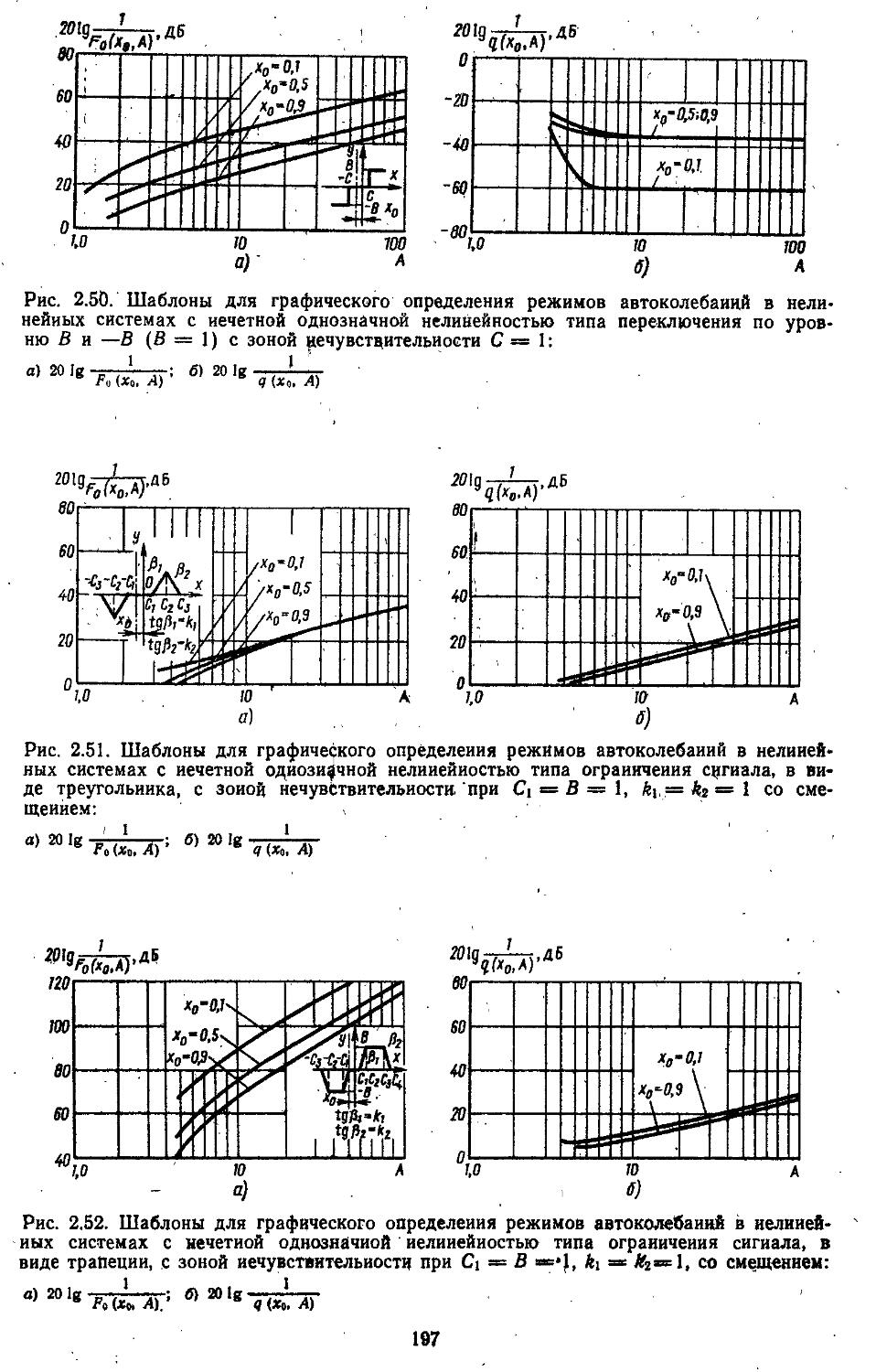
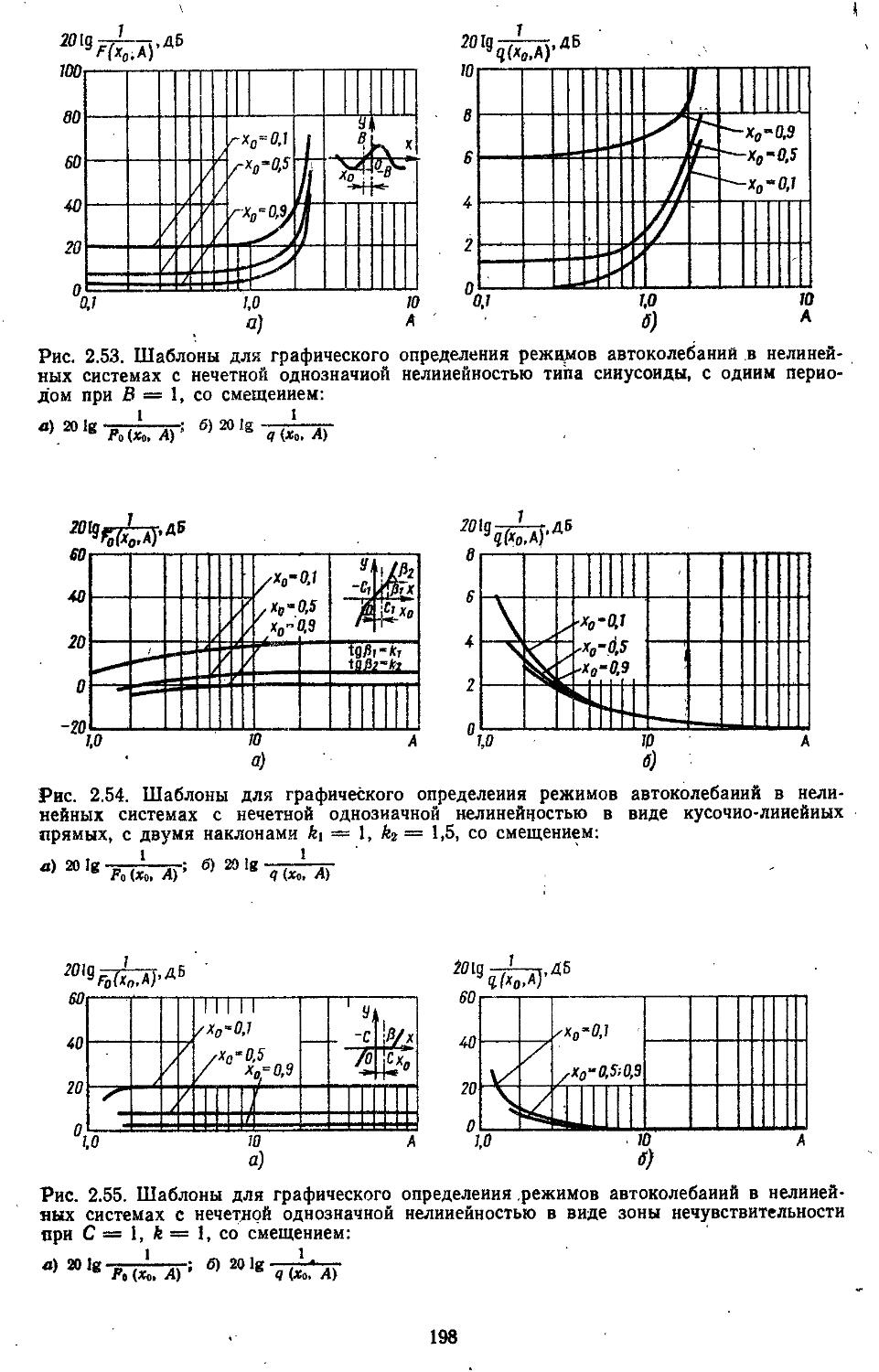
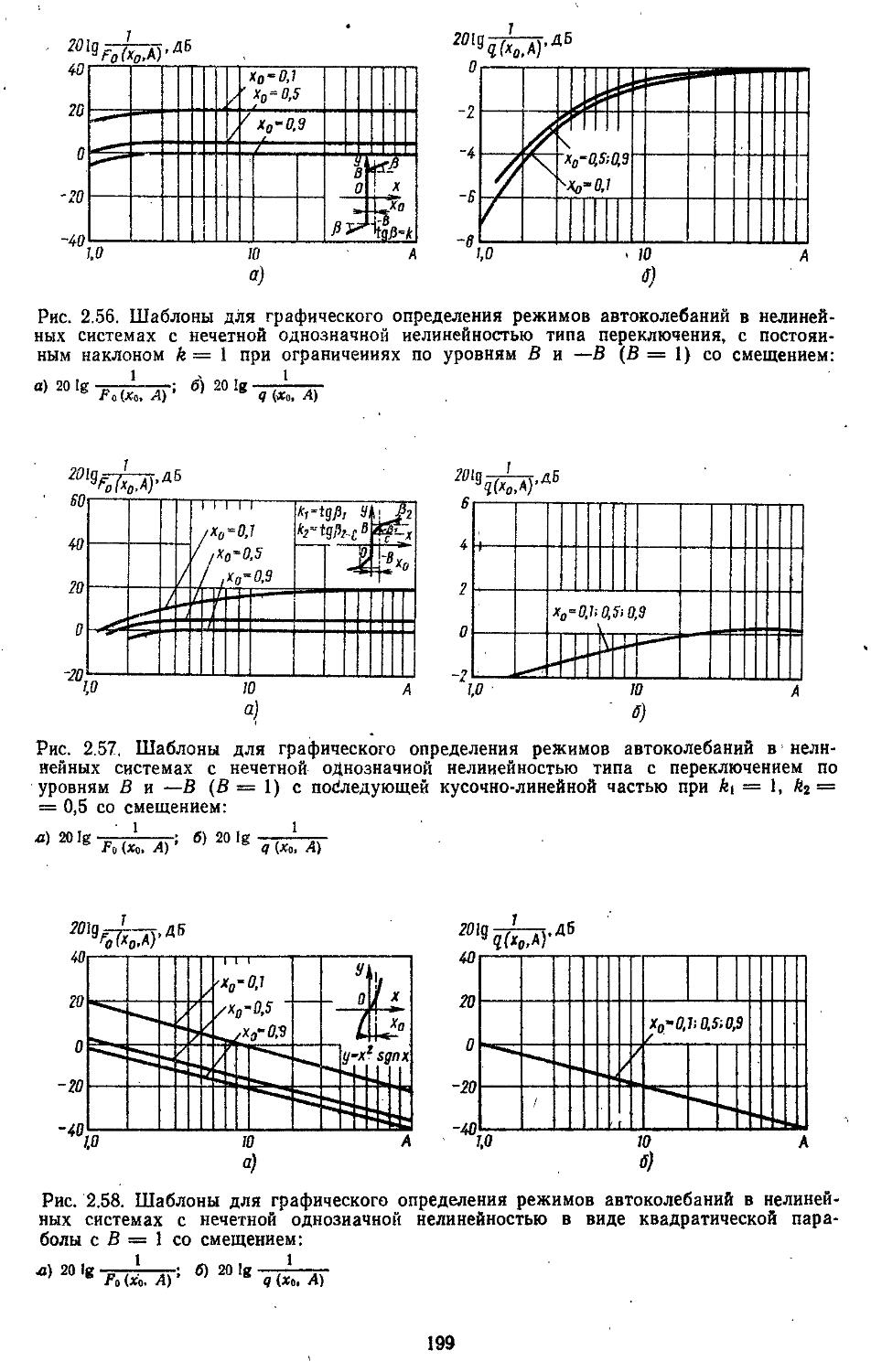
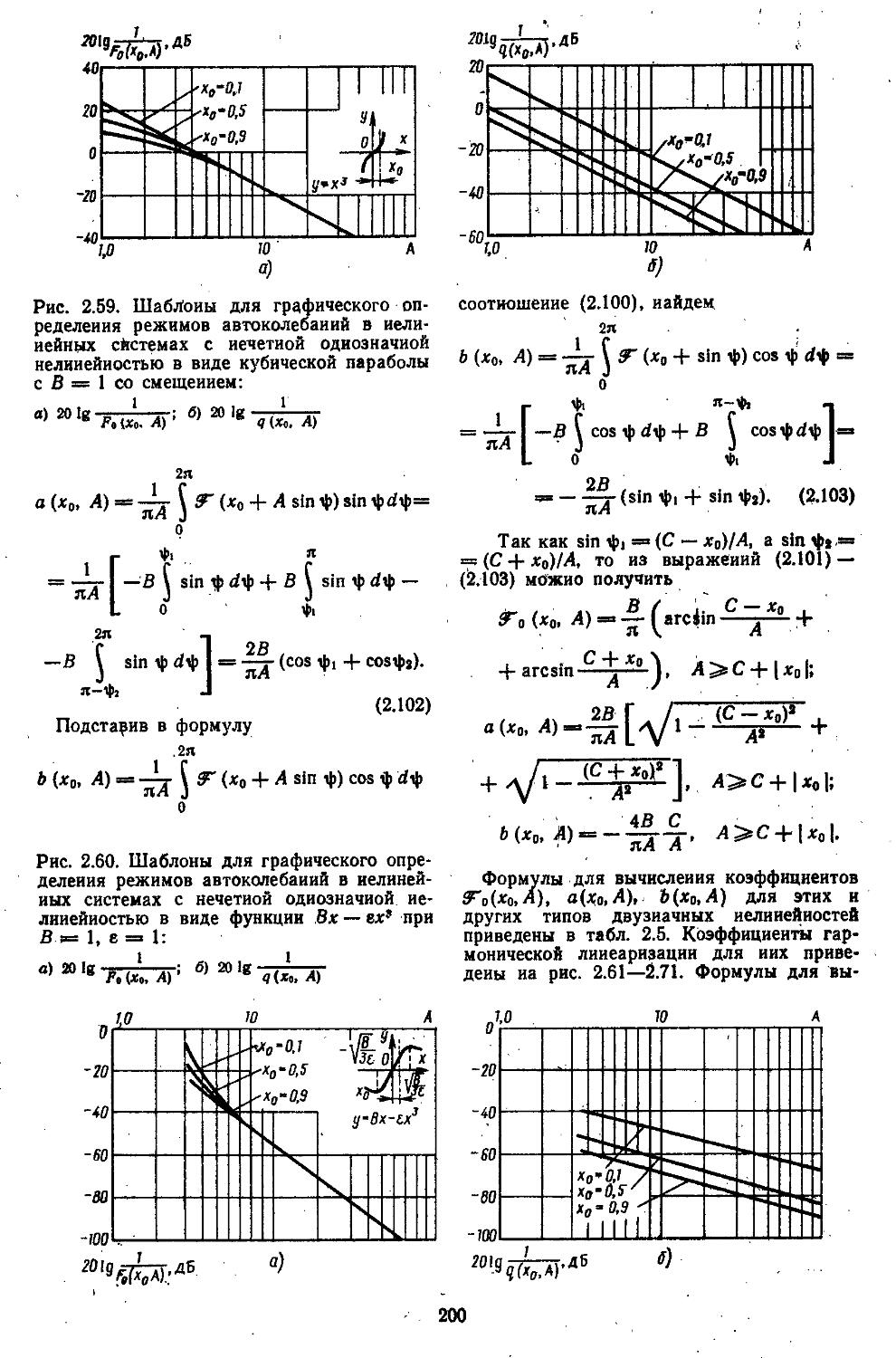
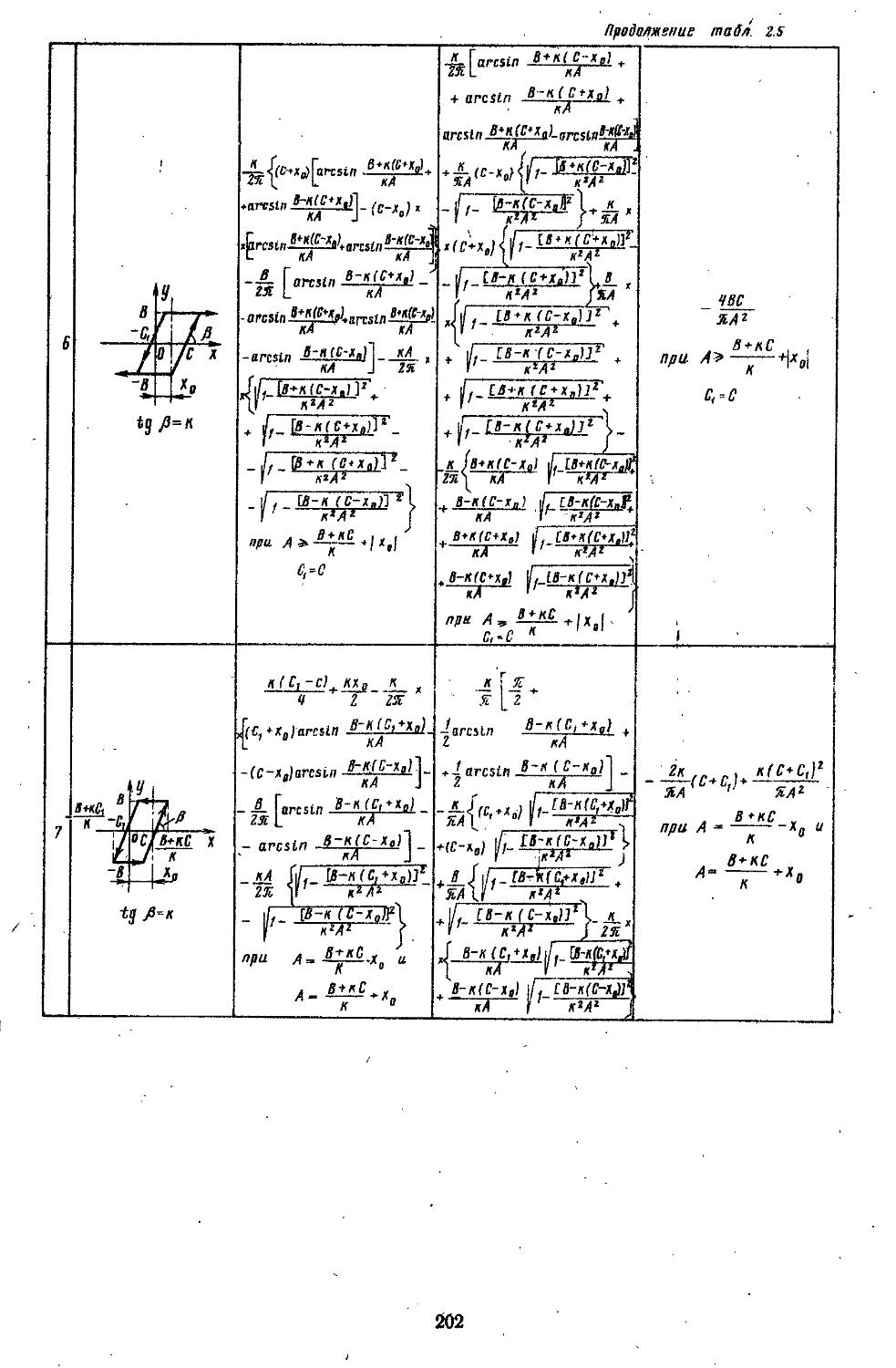
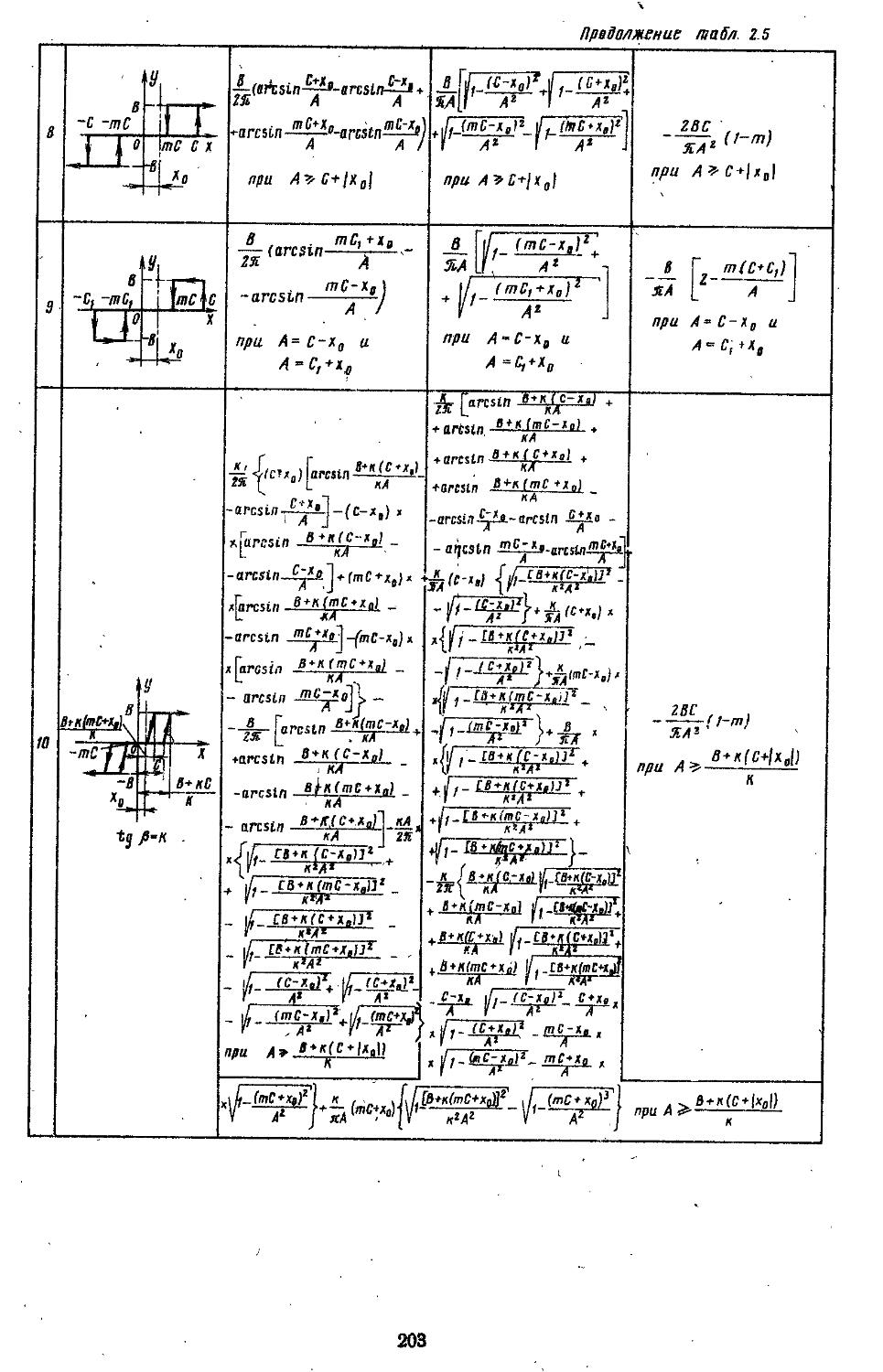
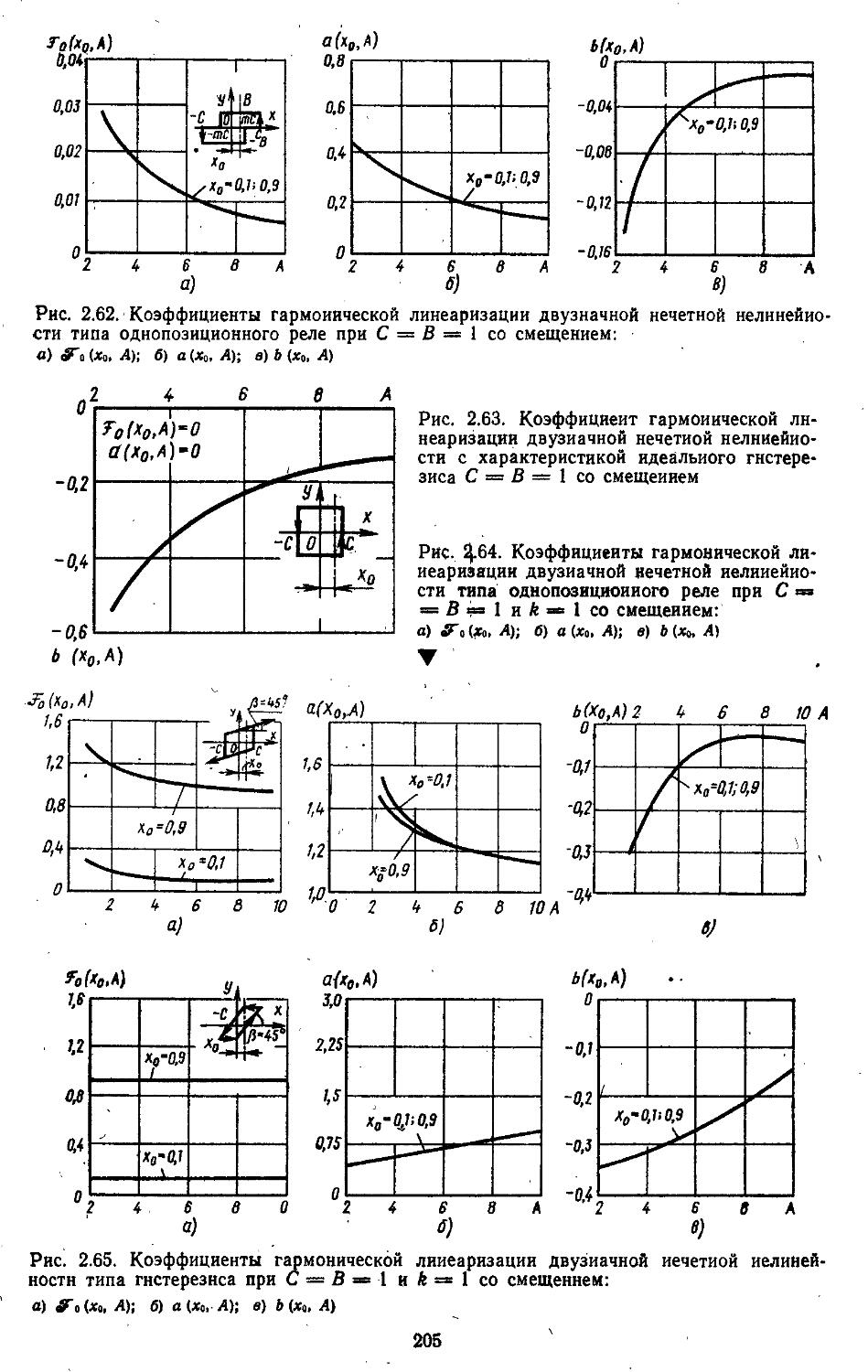
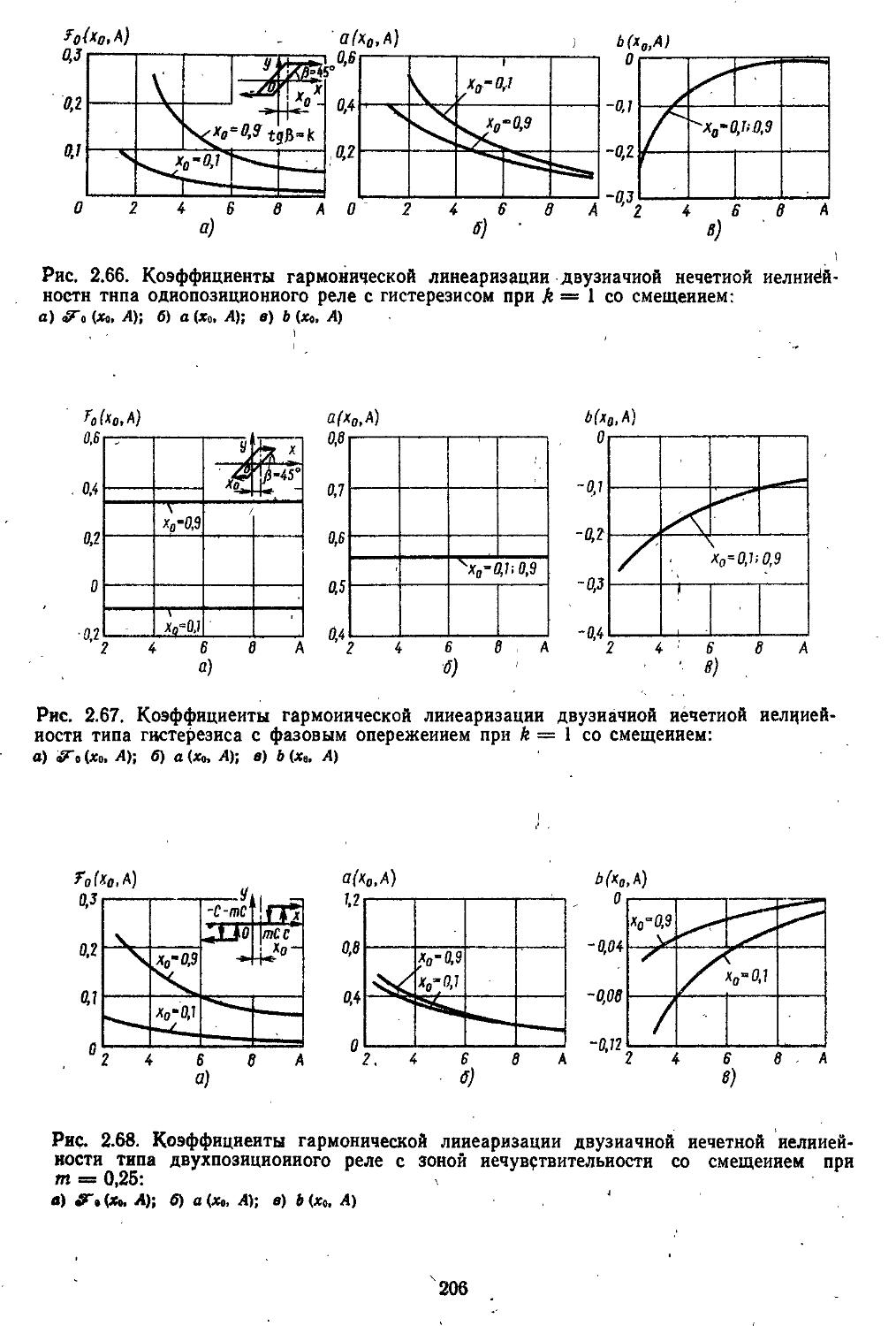
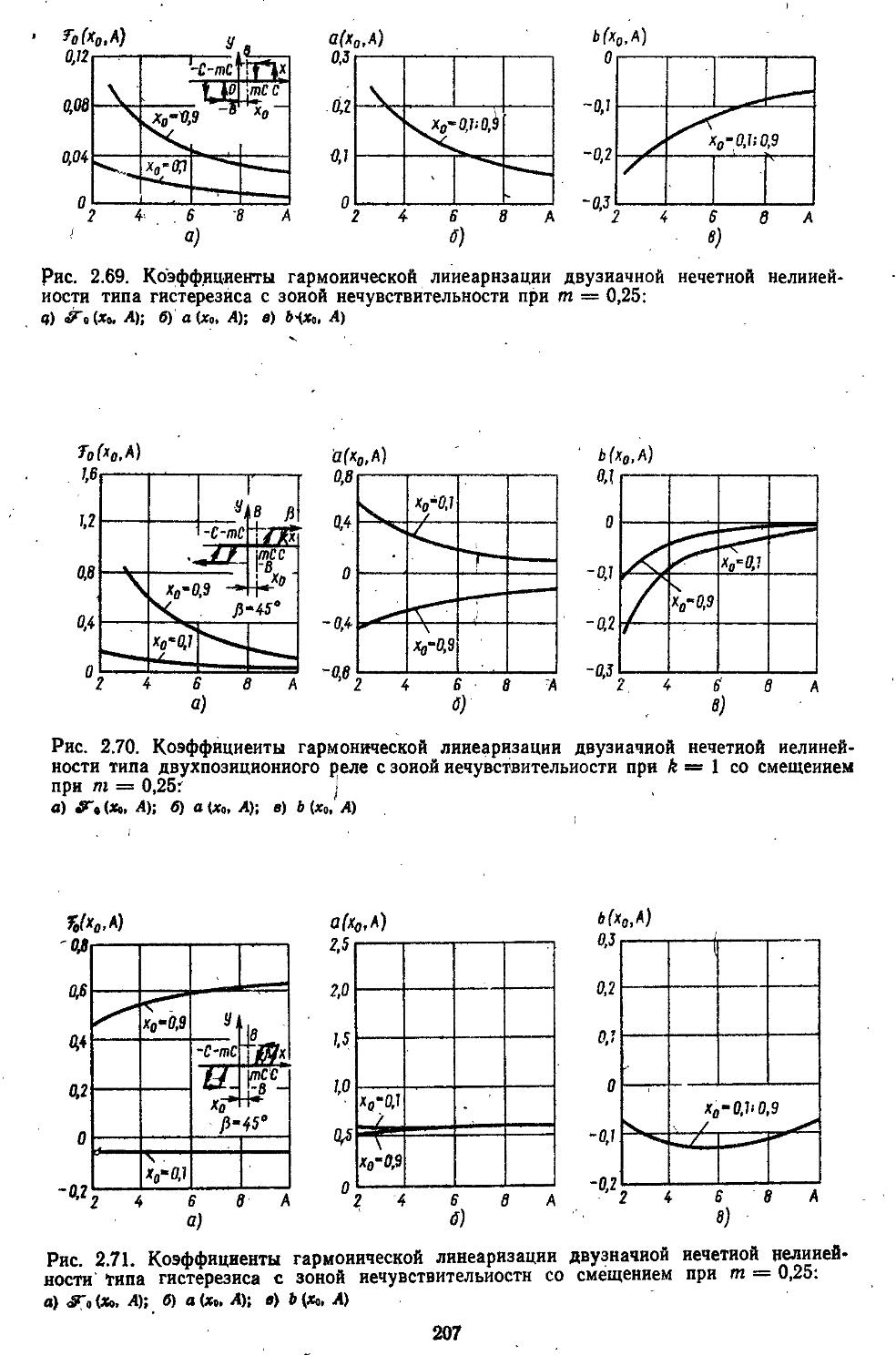
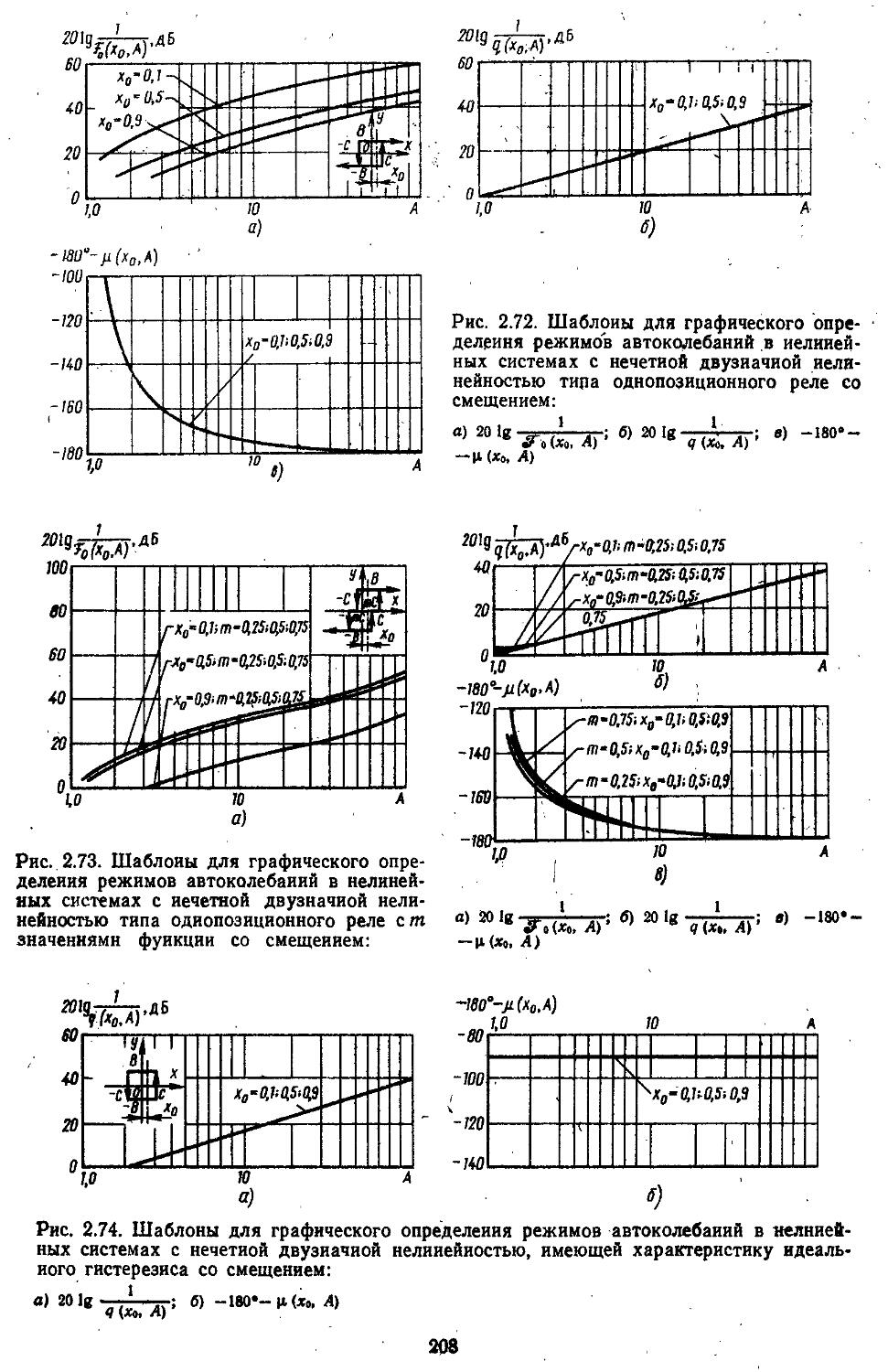
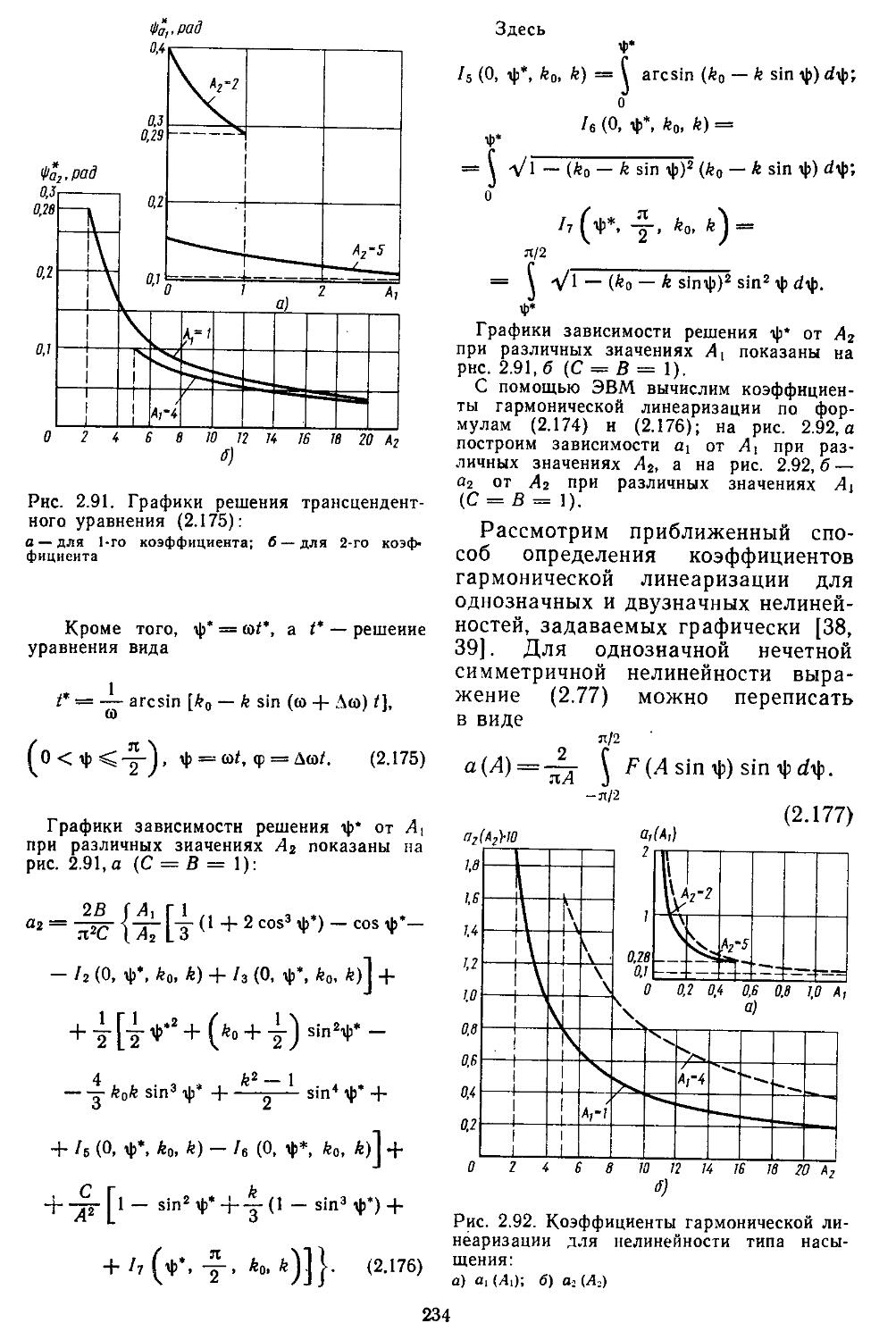
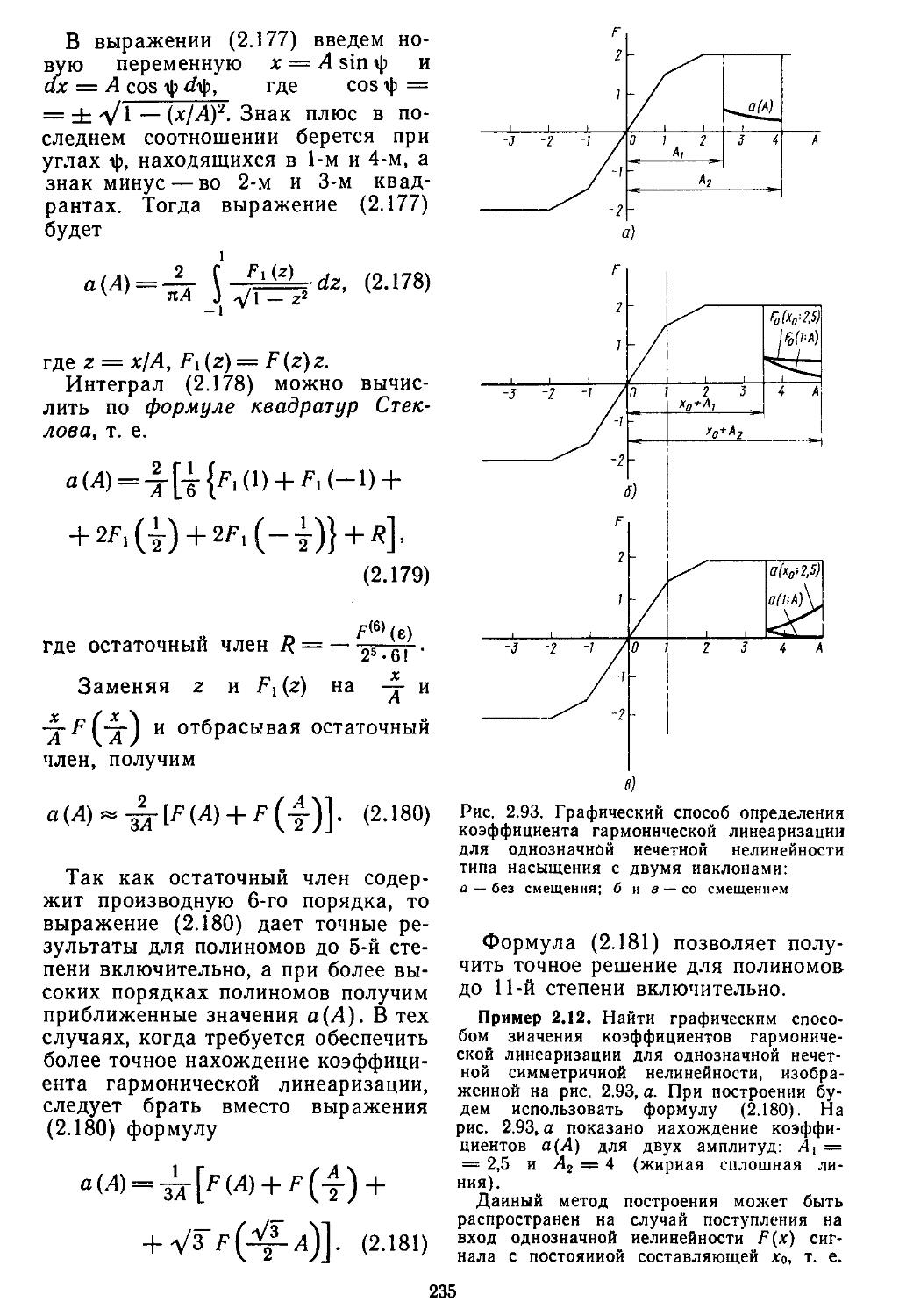
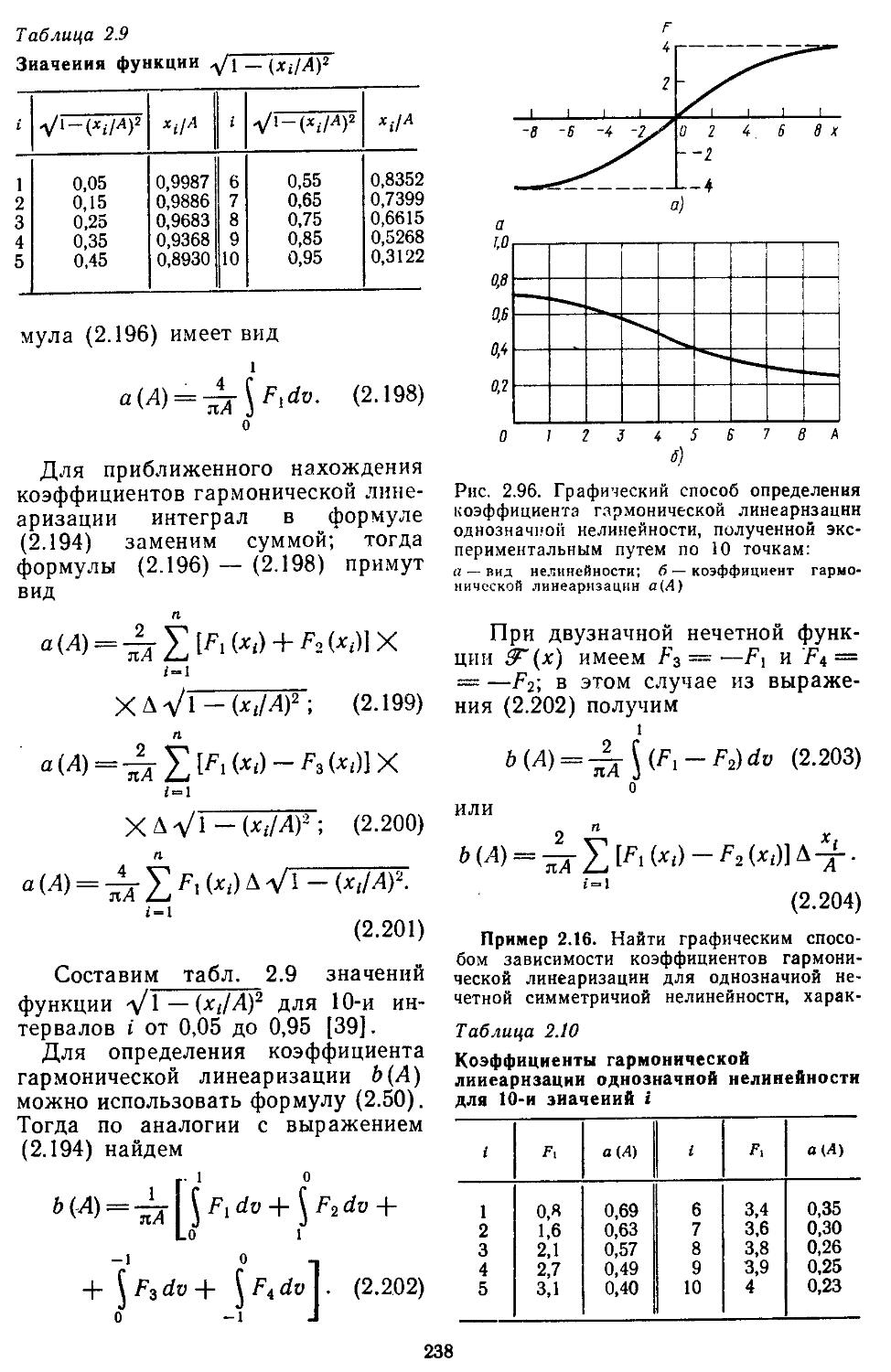
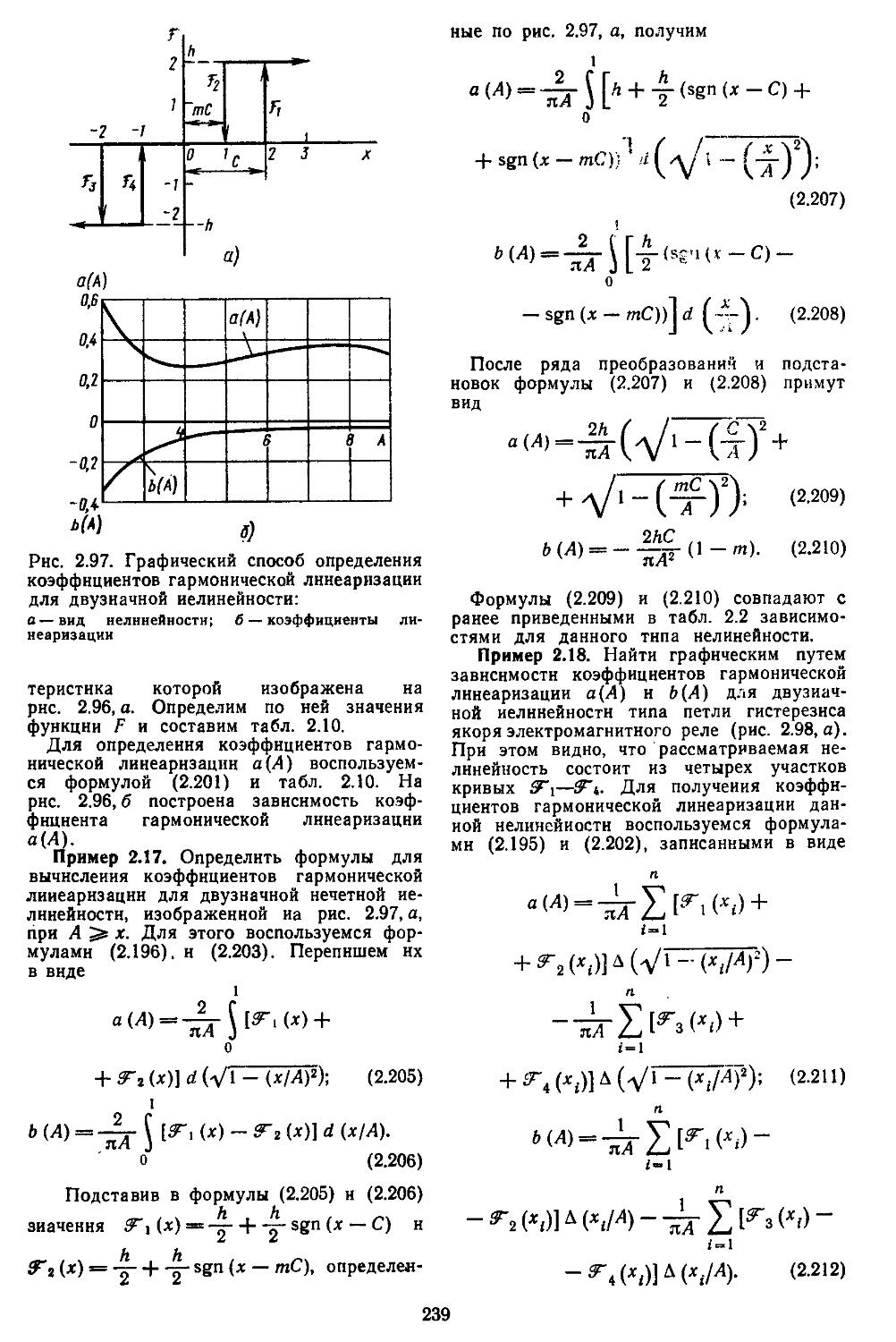
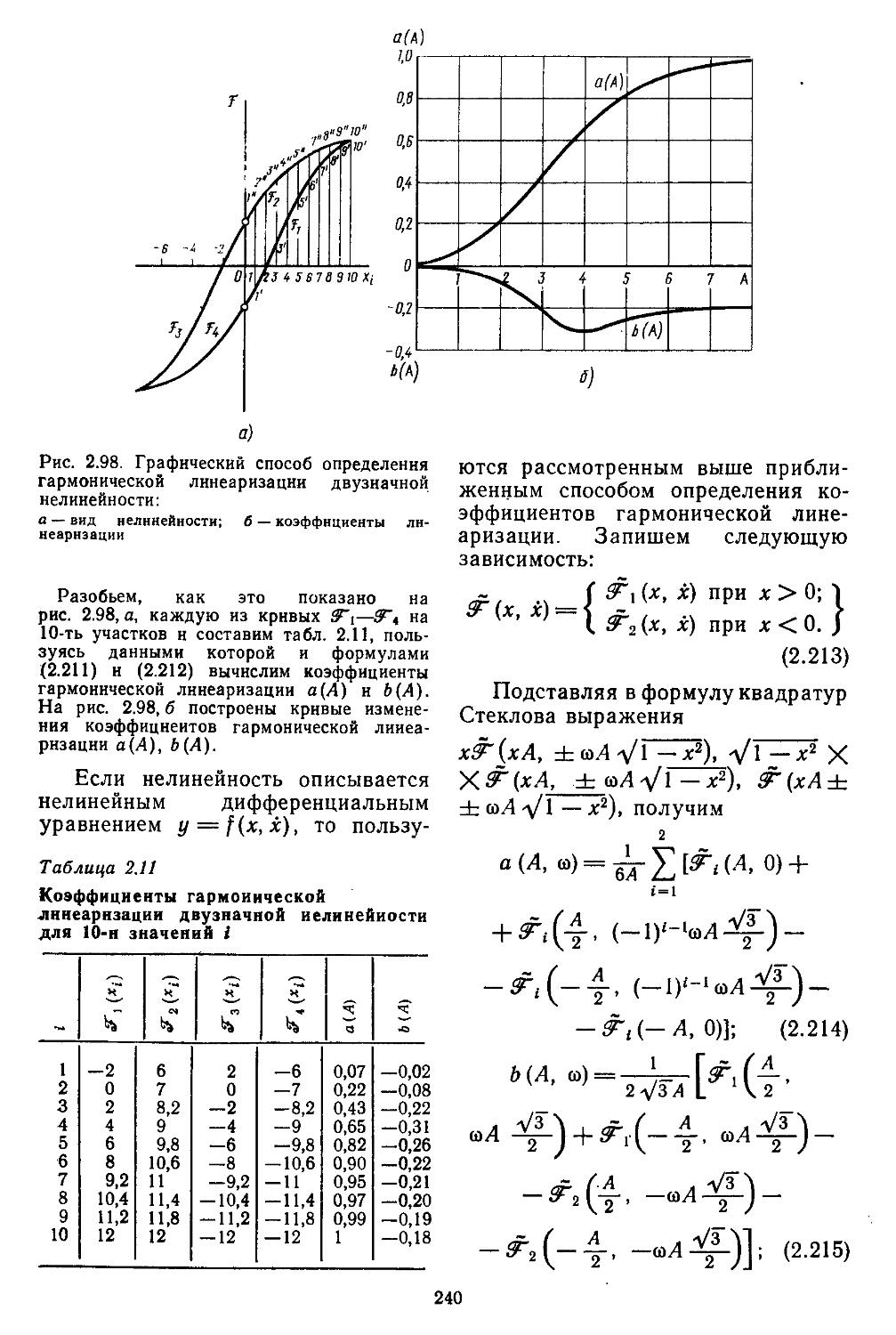
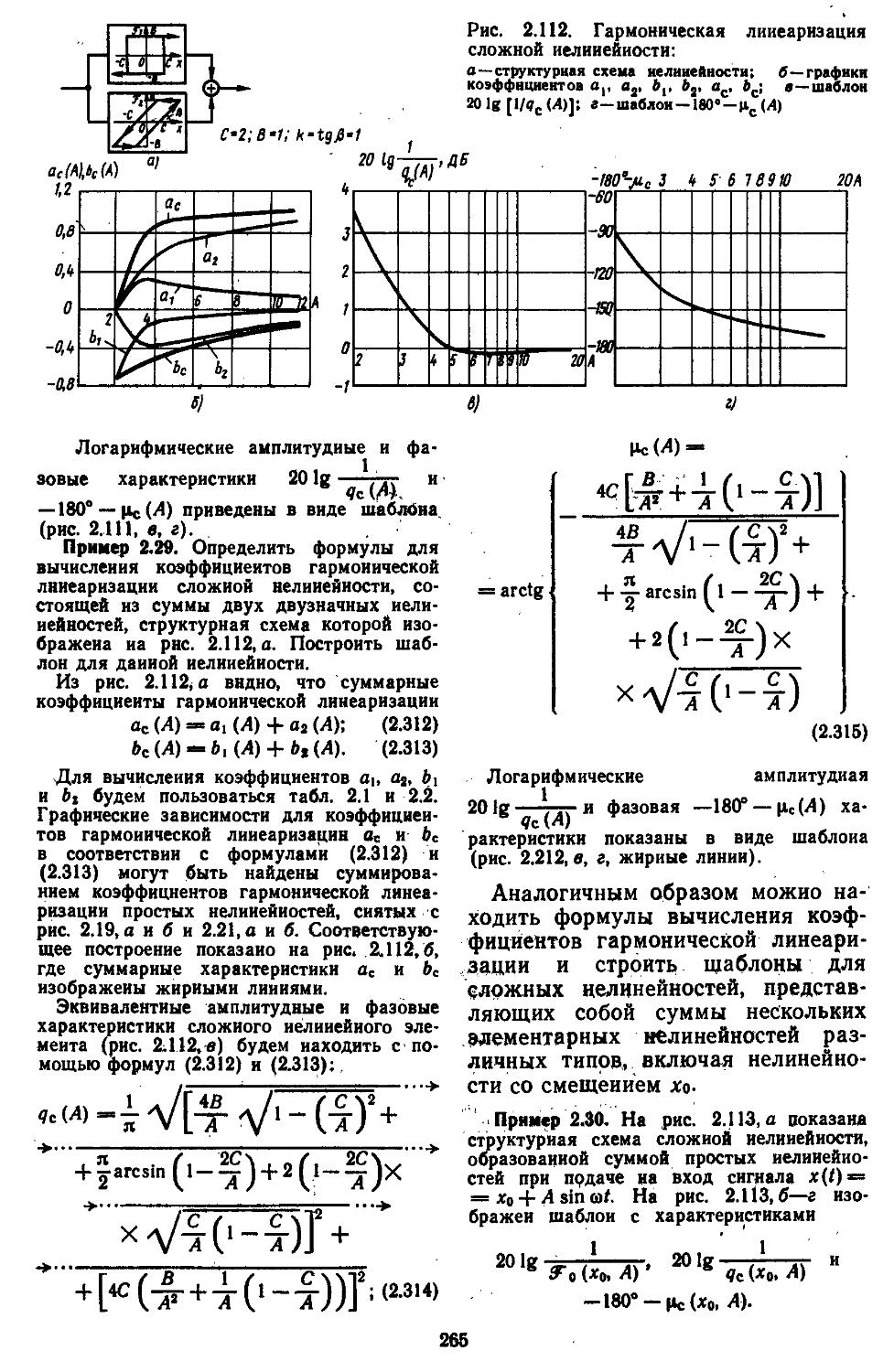
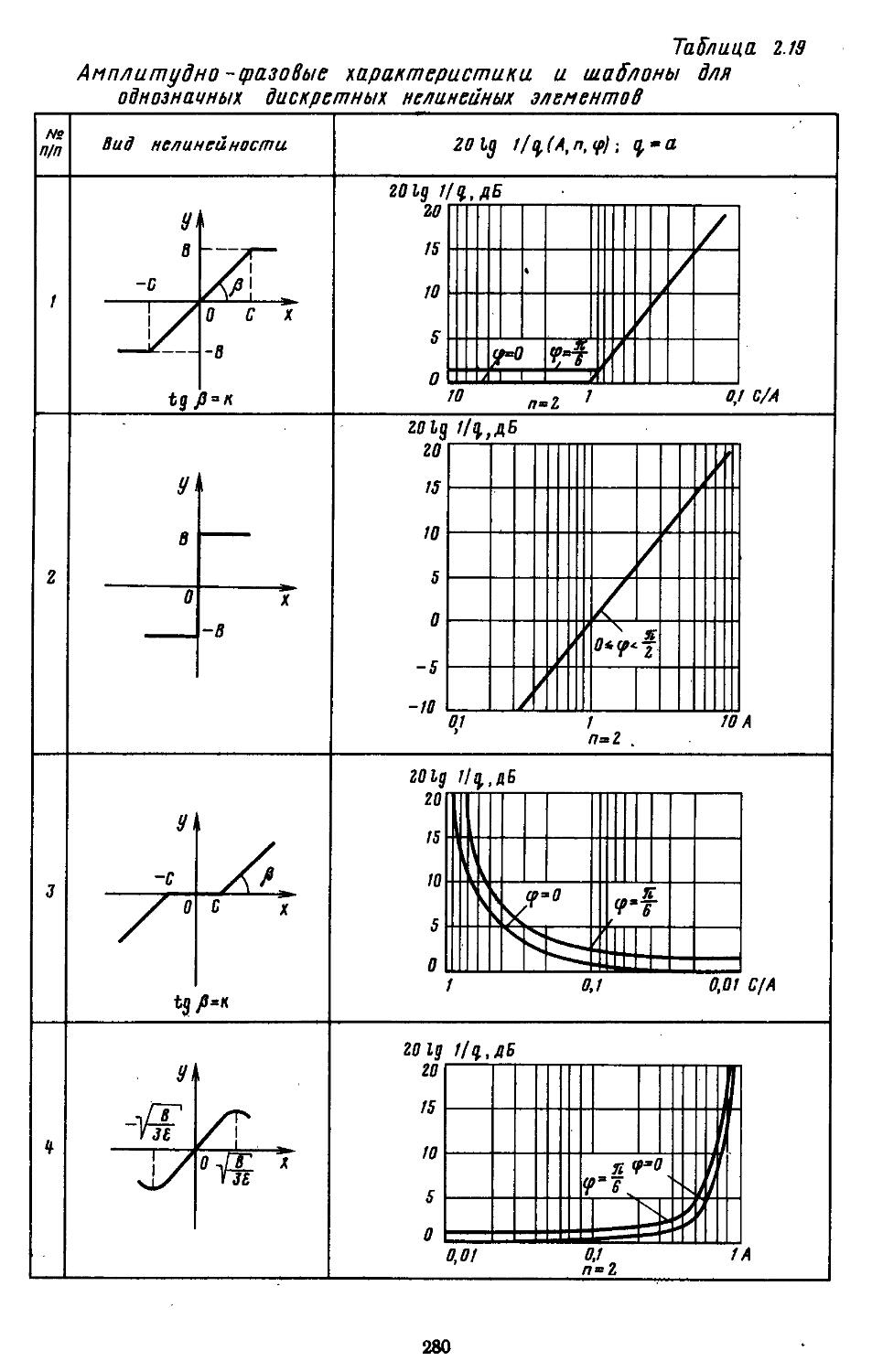
2. Гармоническая линеаризация типичных нелинейных элементов . . 155
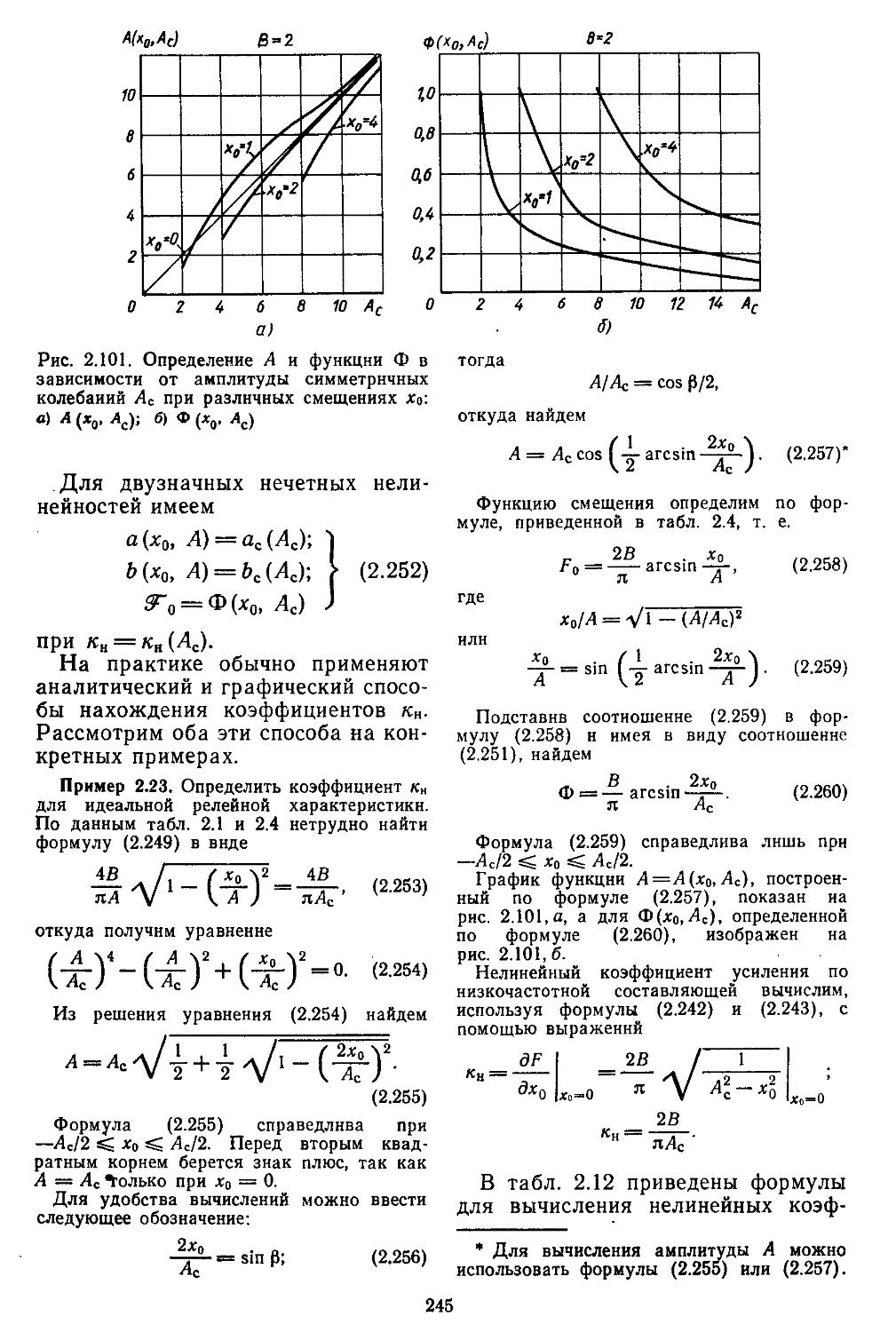
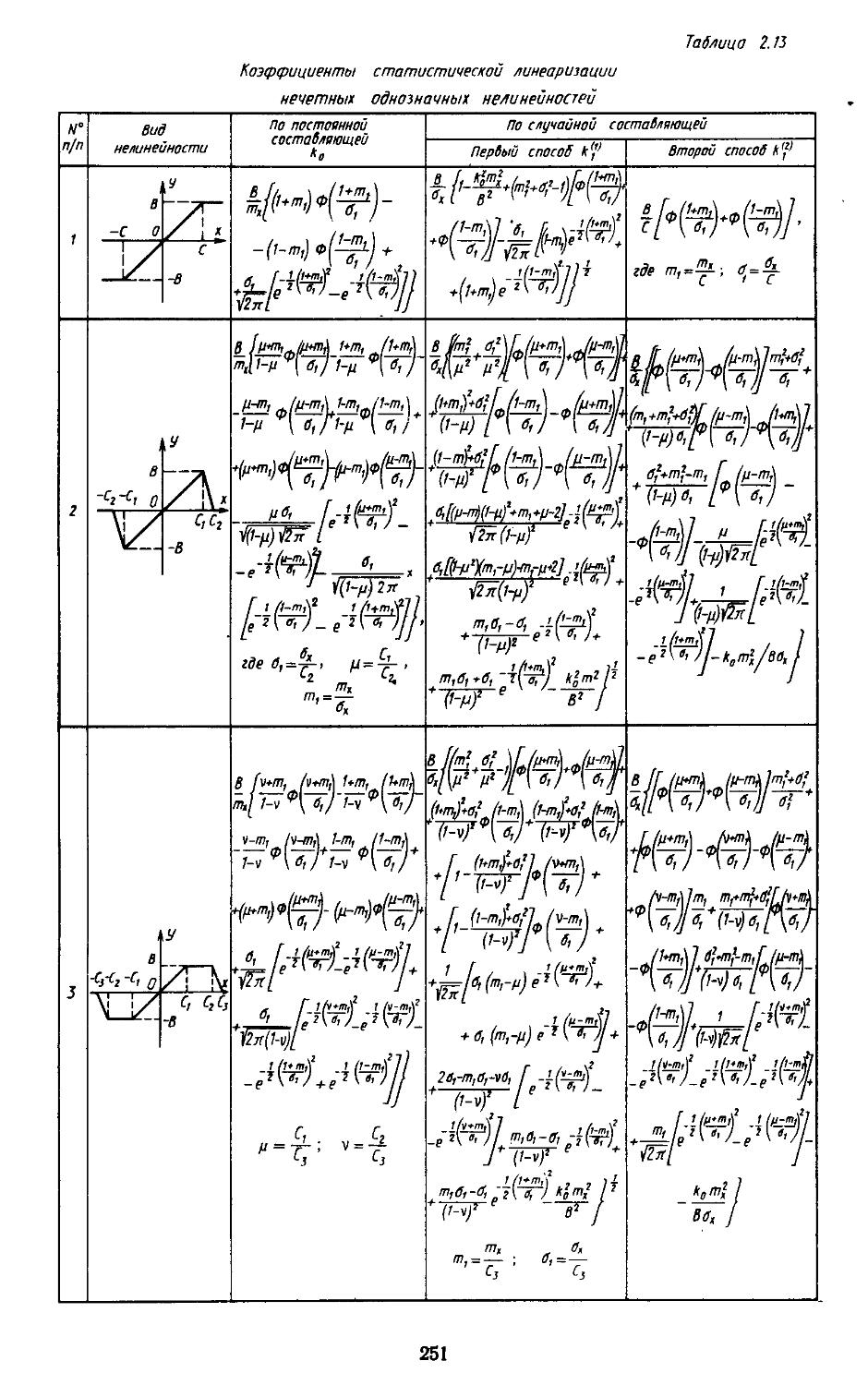
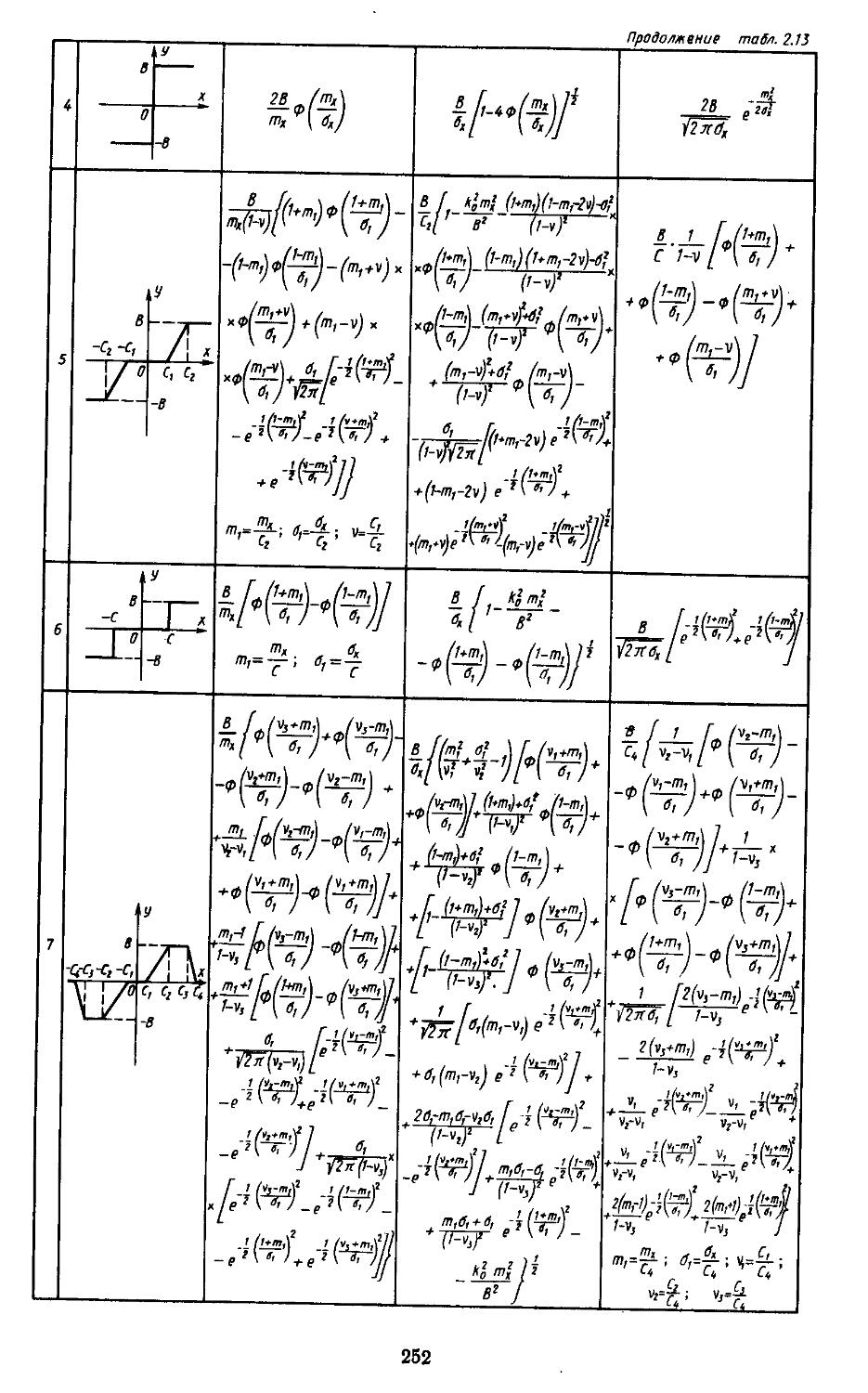
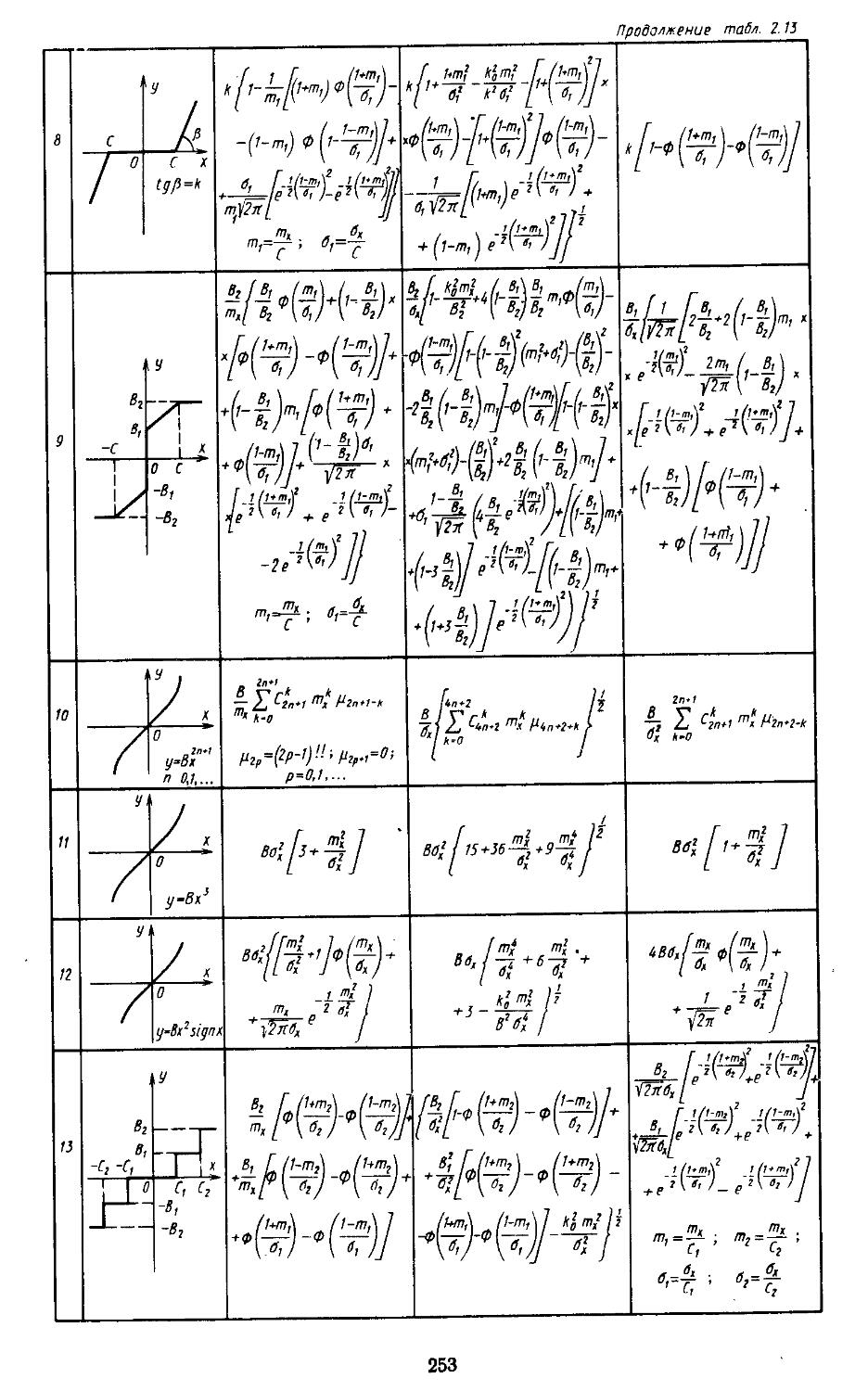
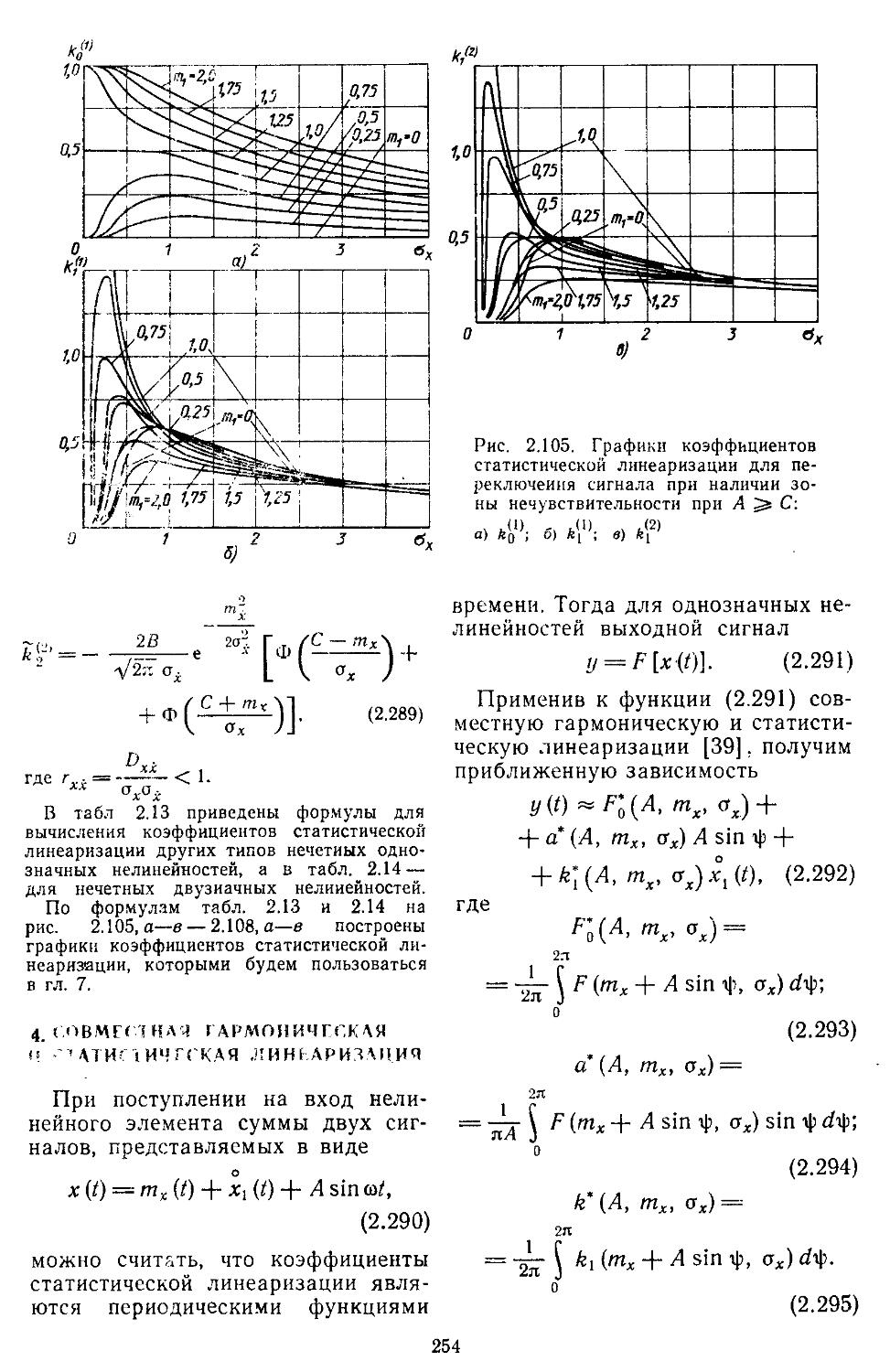
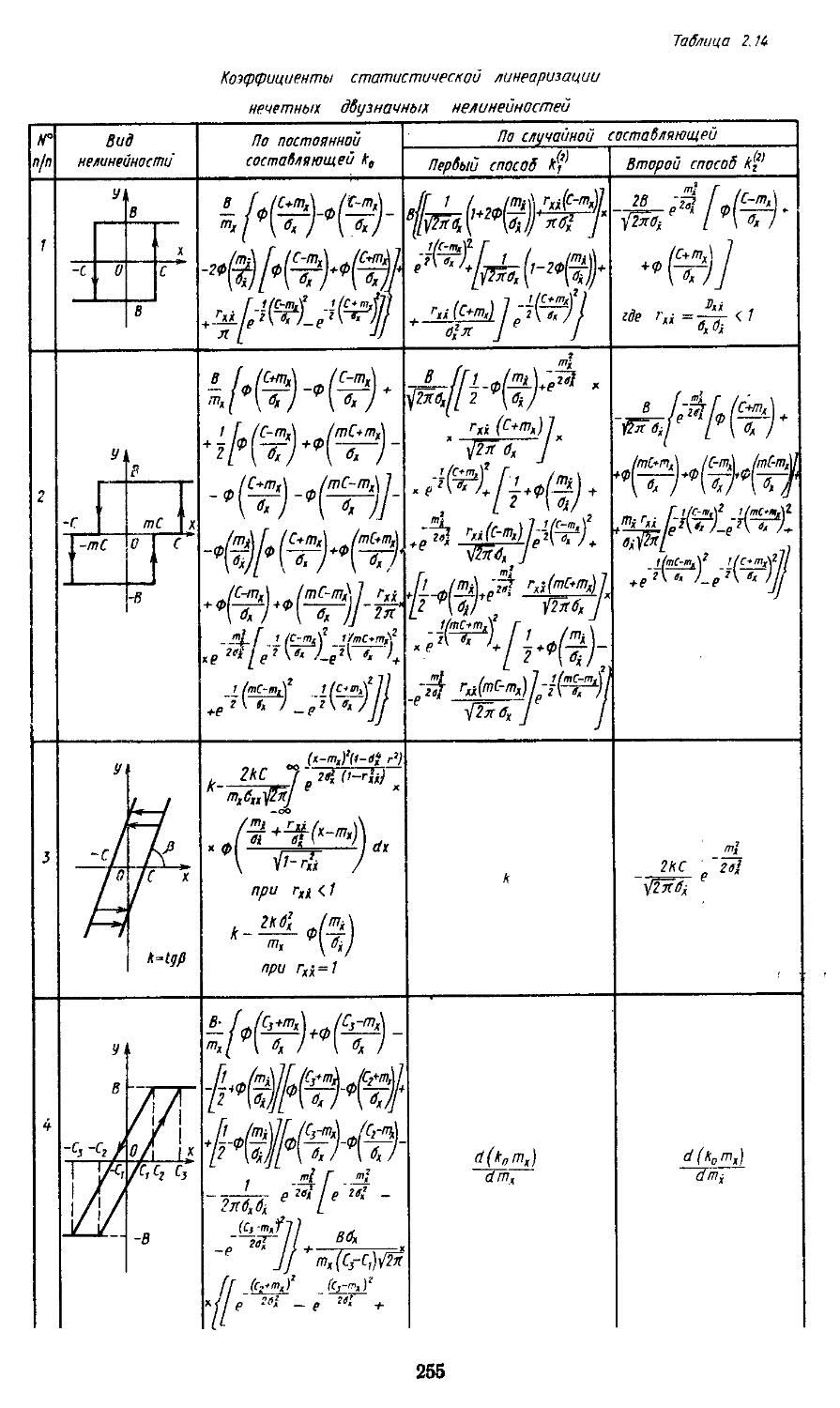
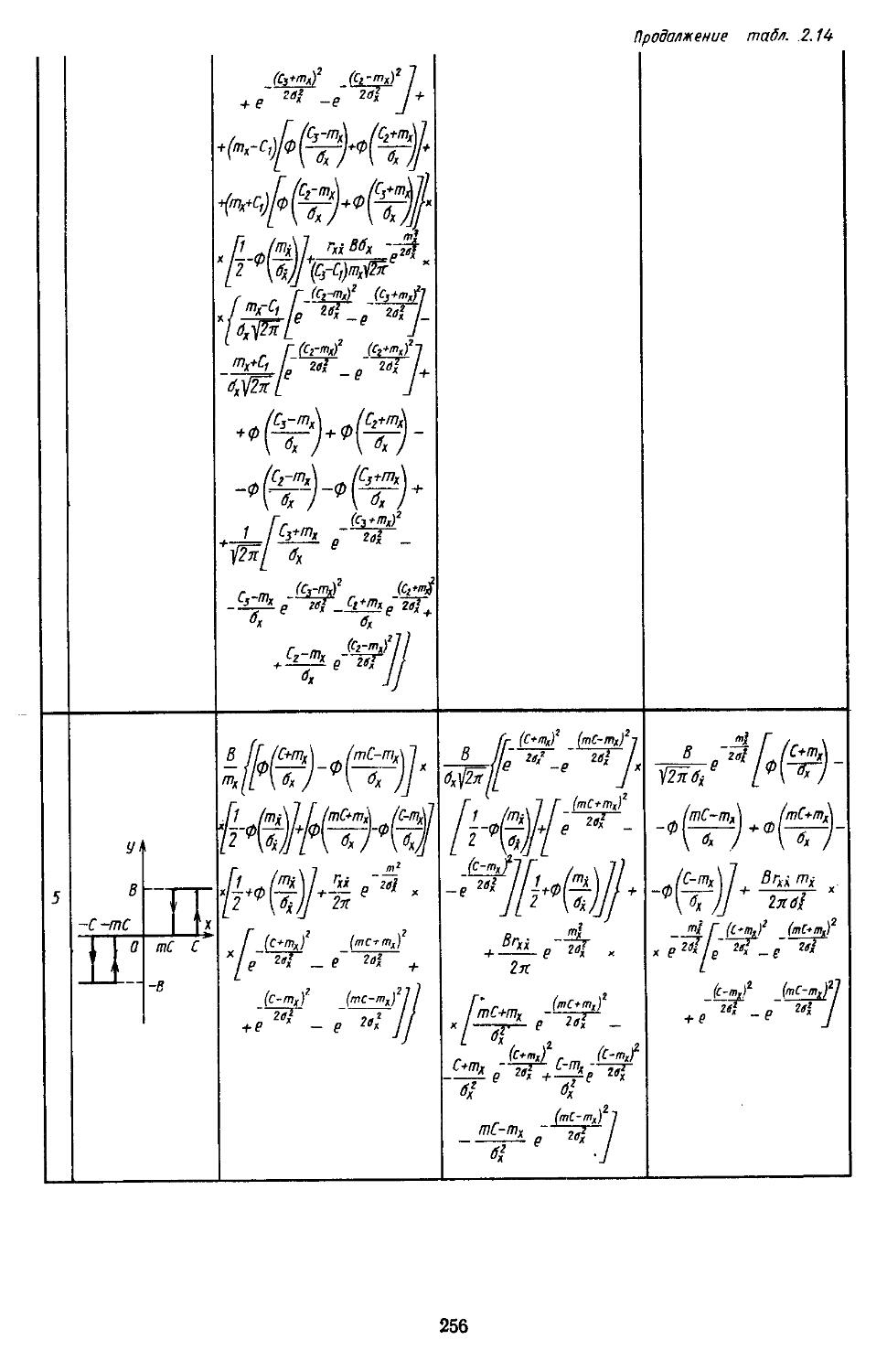
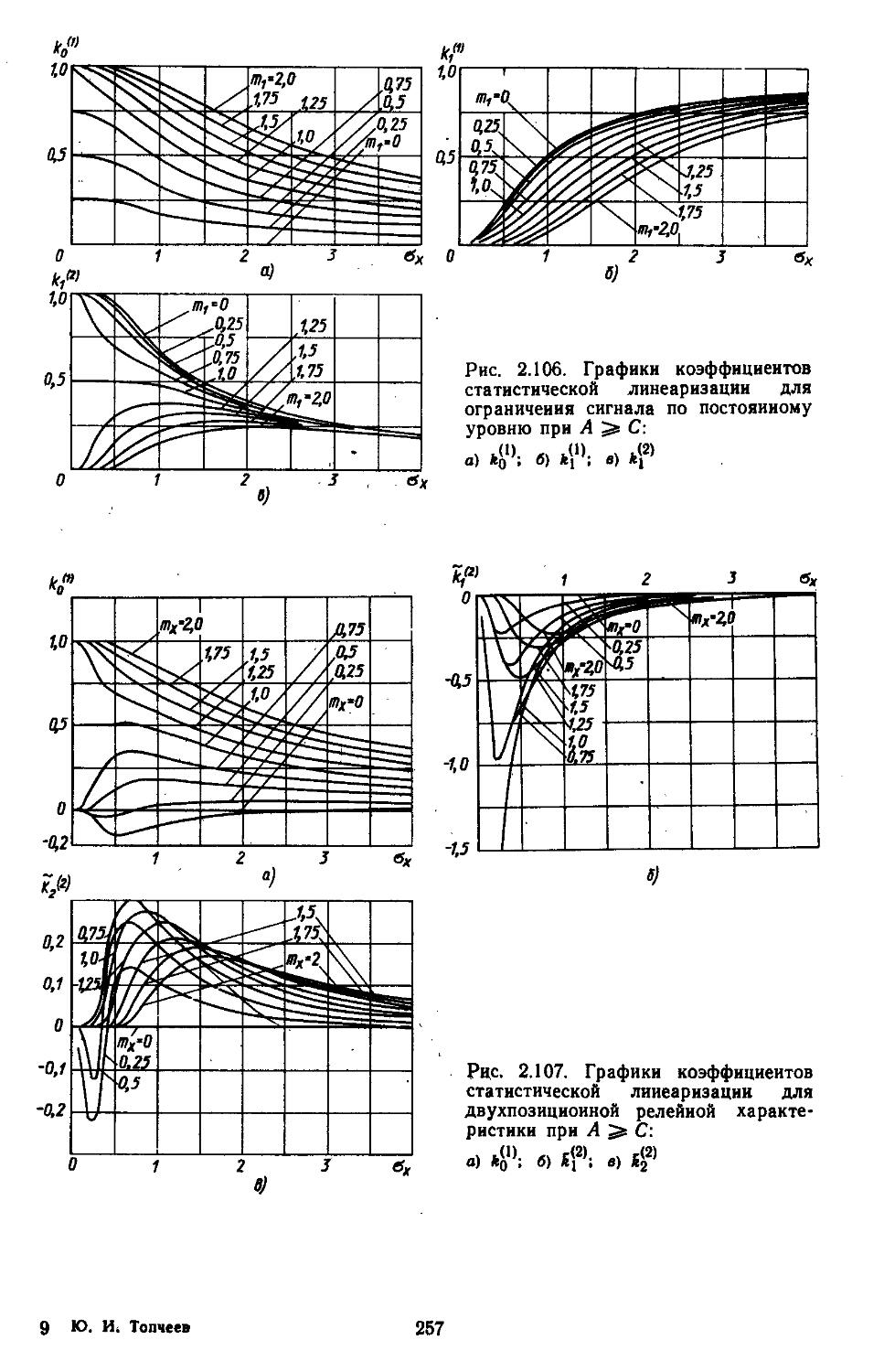
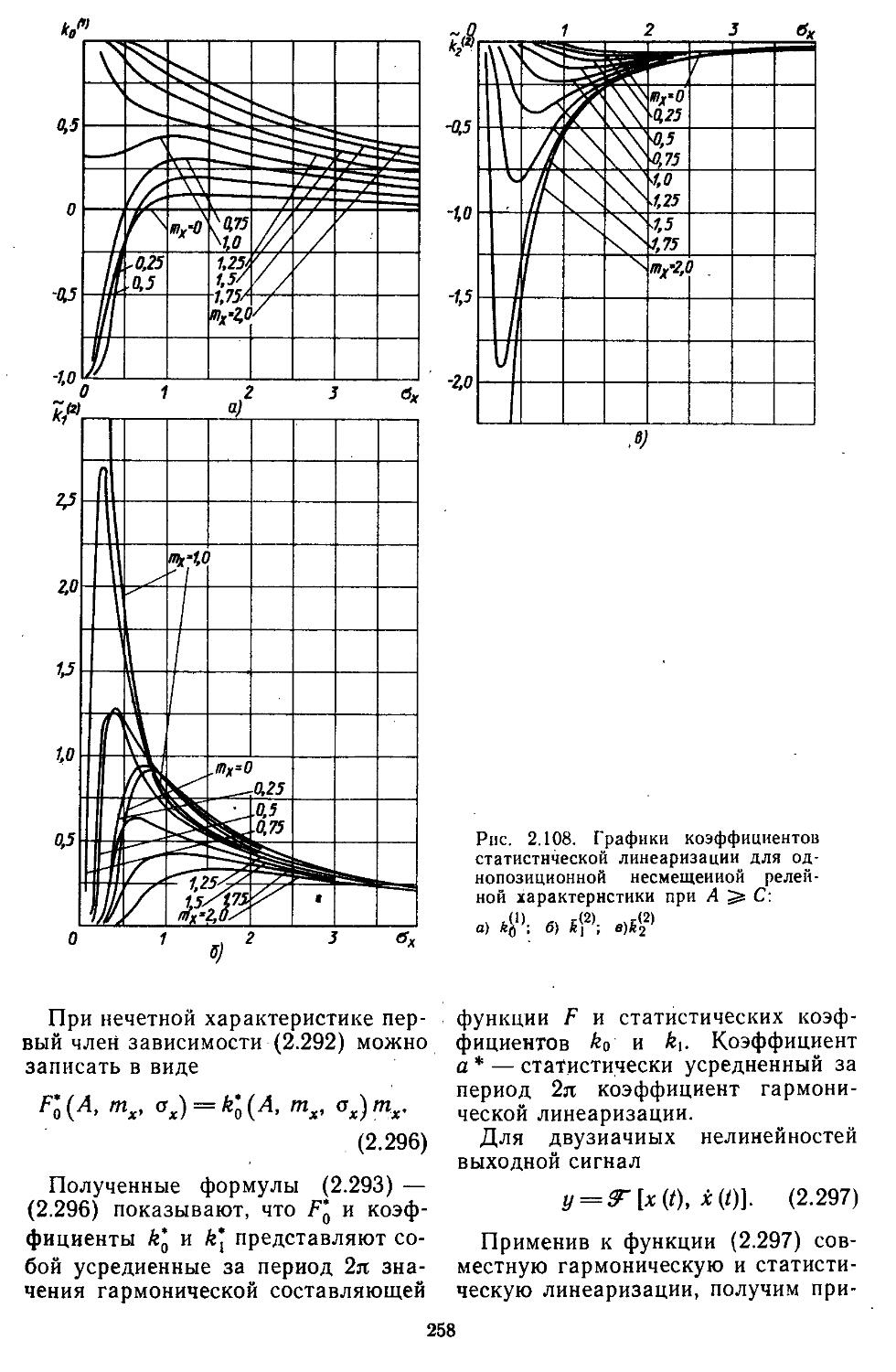
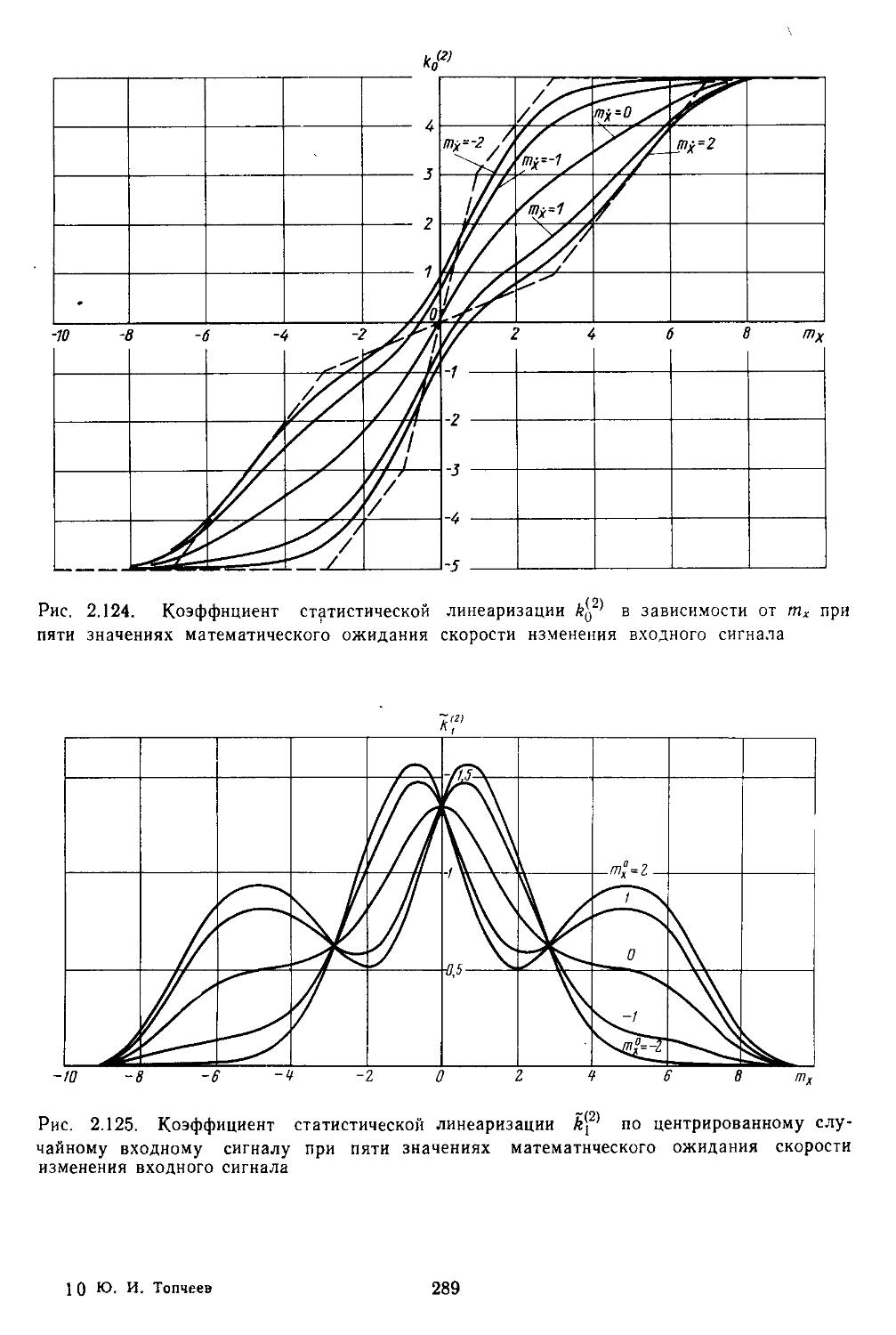
3. Статистическая линеаризация существенных нелинейных элементов . 248
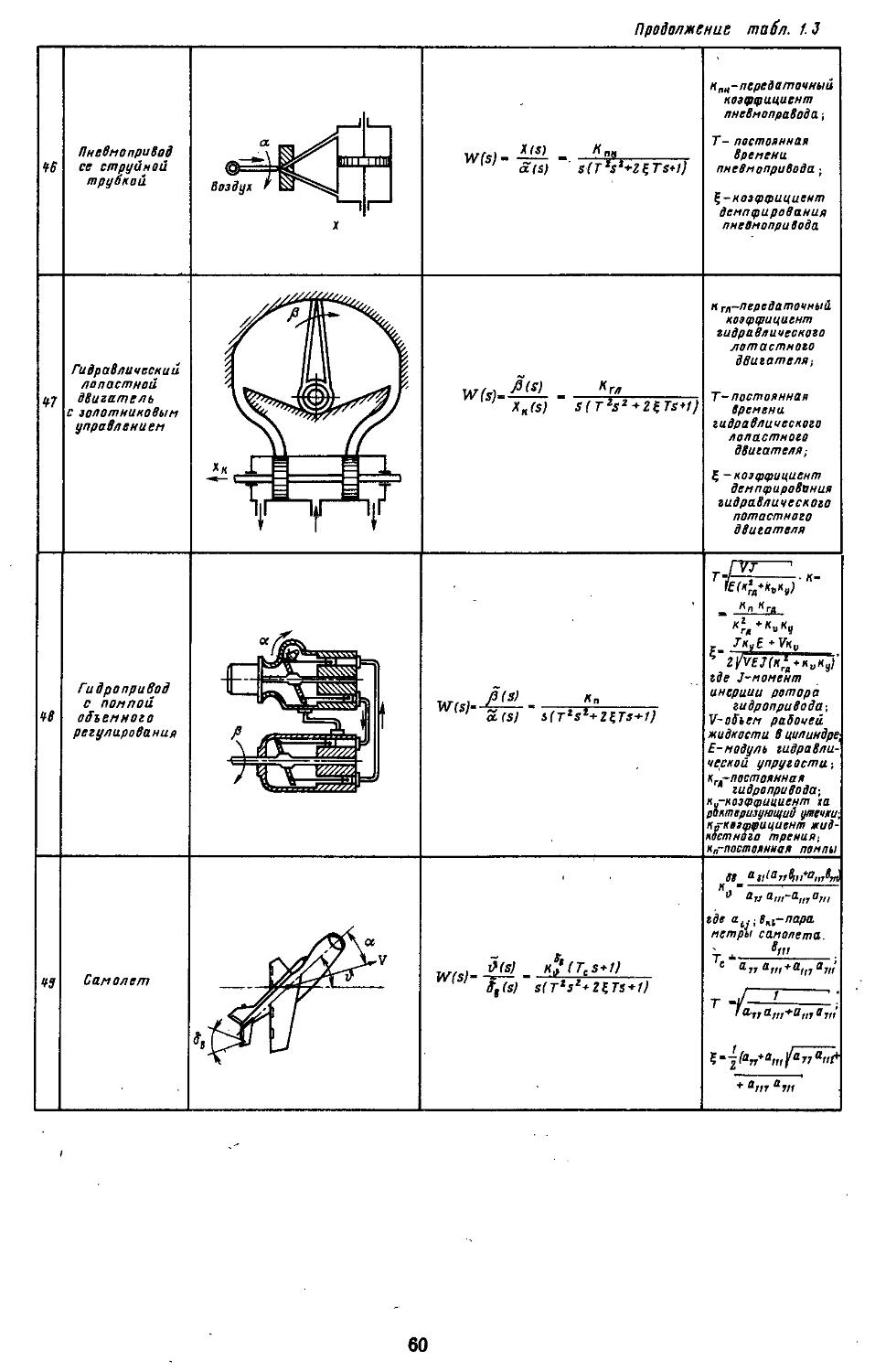
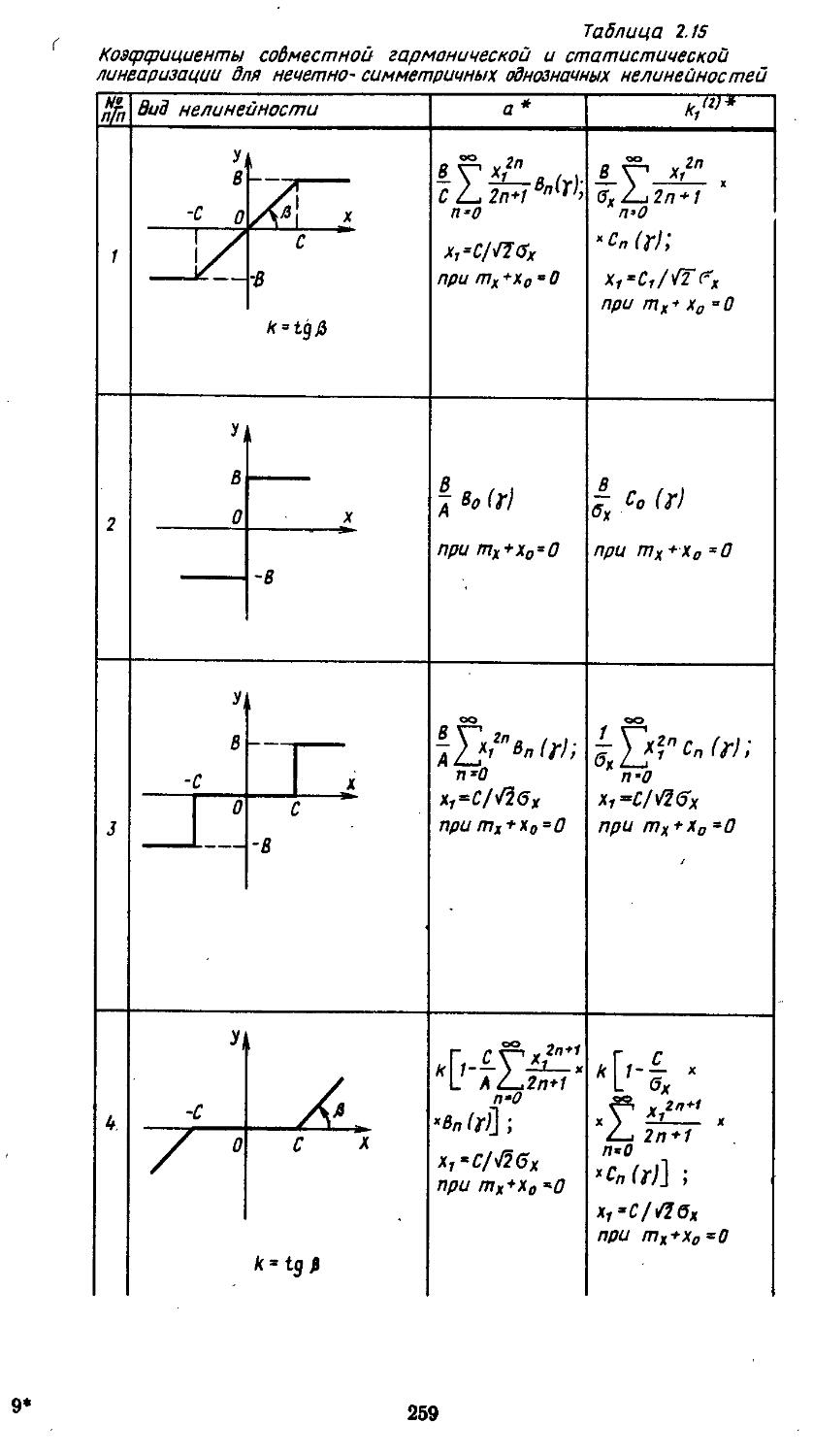
4. Совместная гармоническая и статистическая линеаризация .... 254
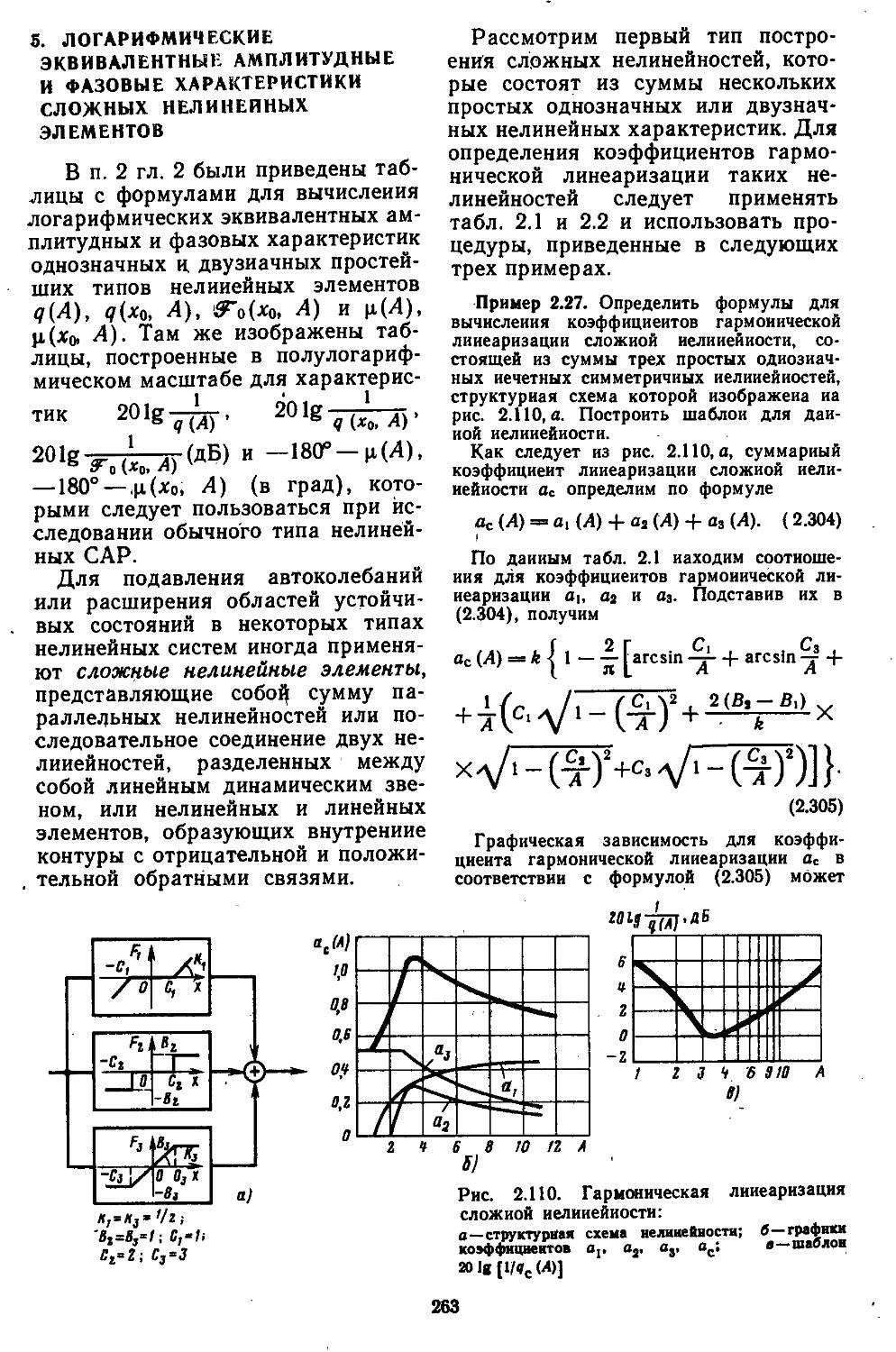
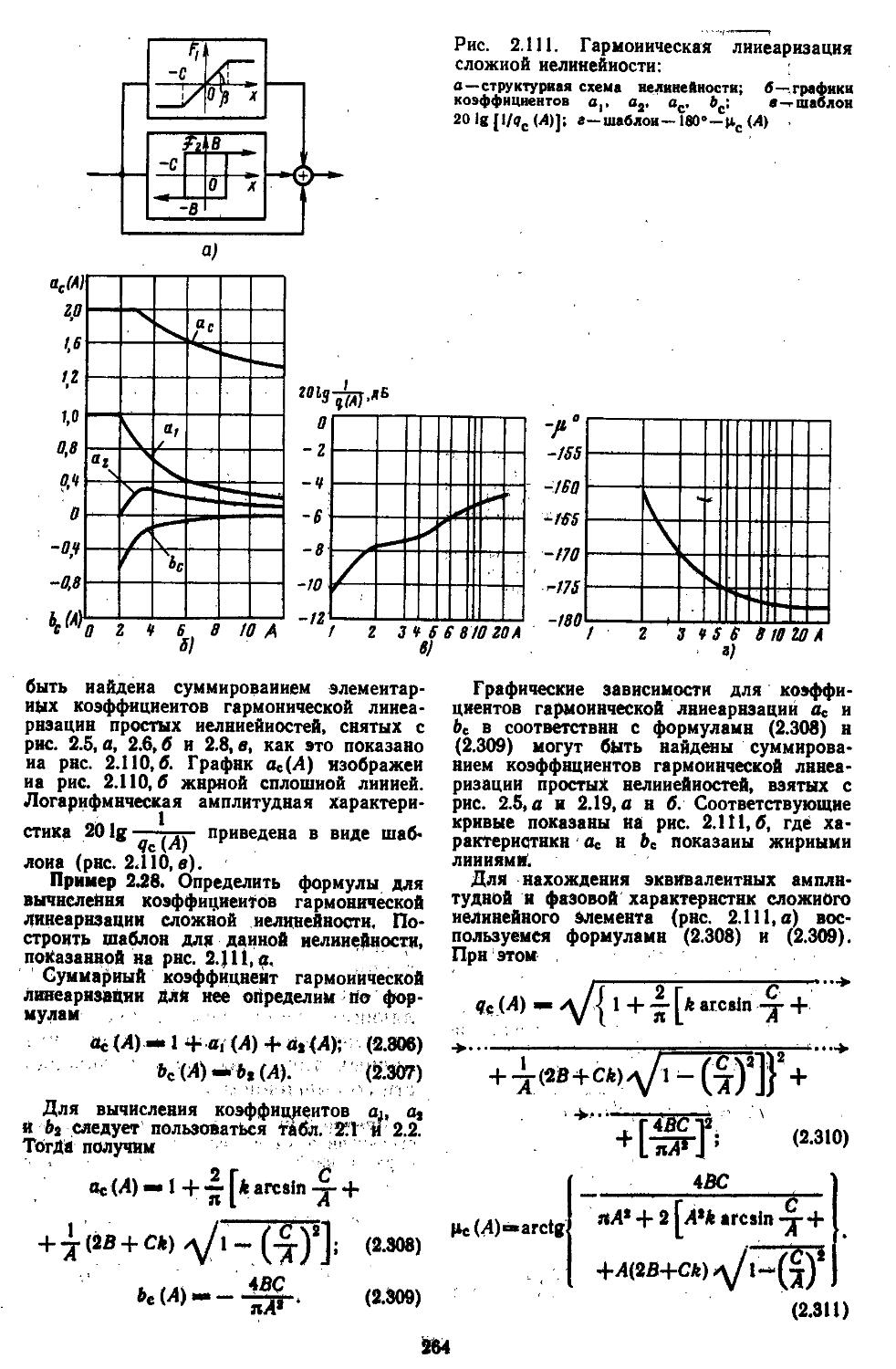
5. Логарифмические эквивалентные амплитудные и фазовые характеристики сложных нелиней-
ных элементов .... 263
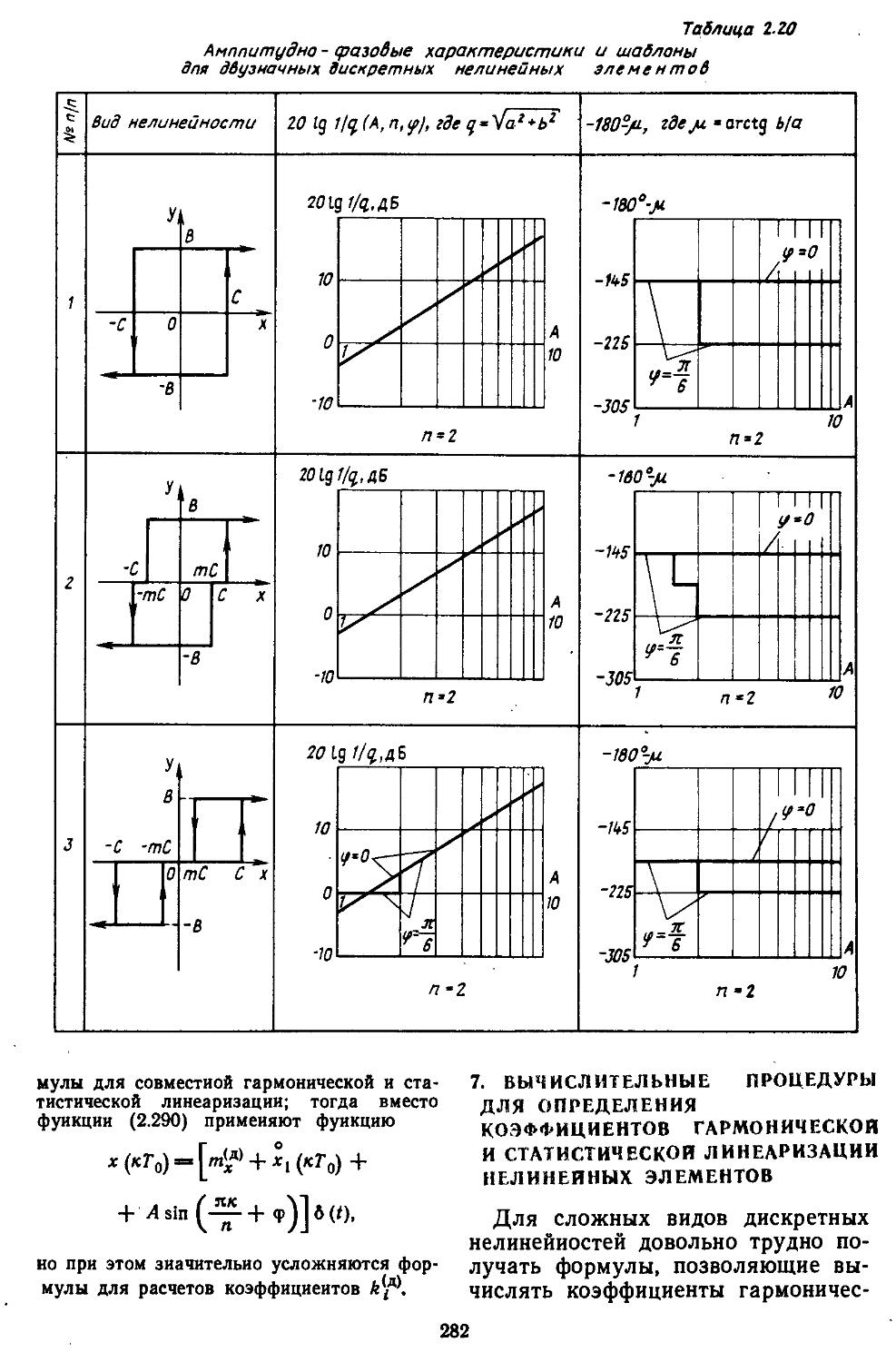
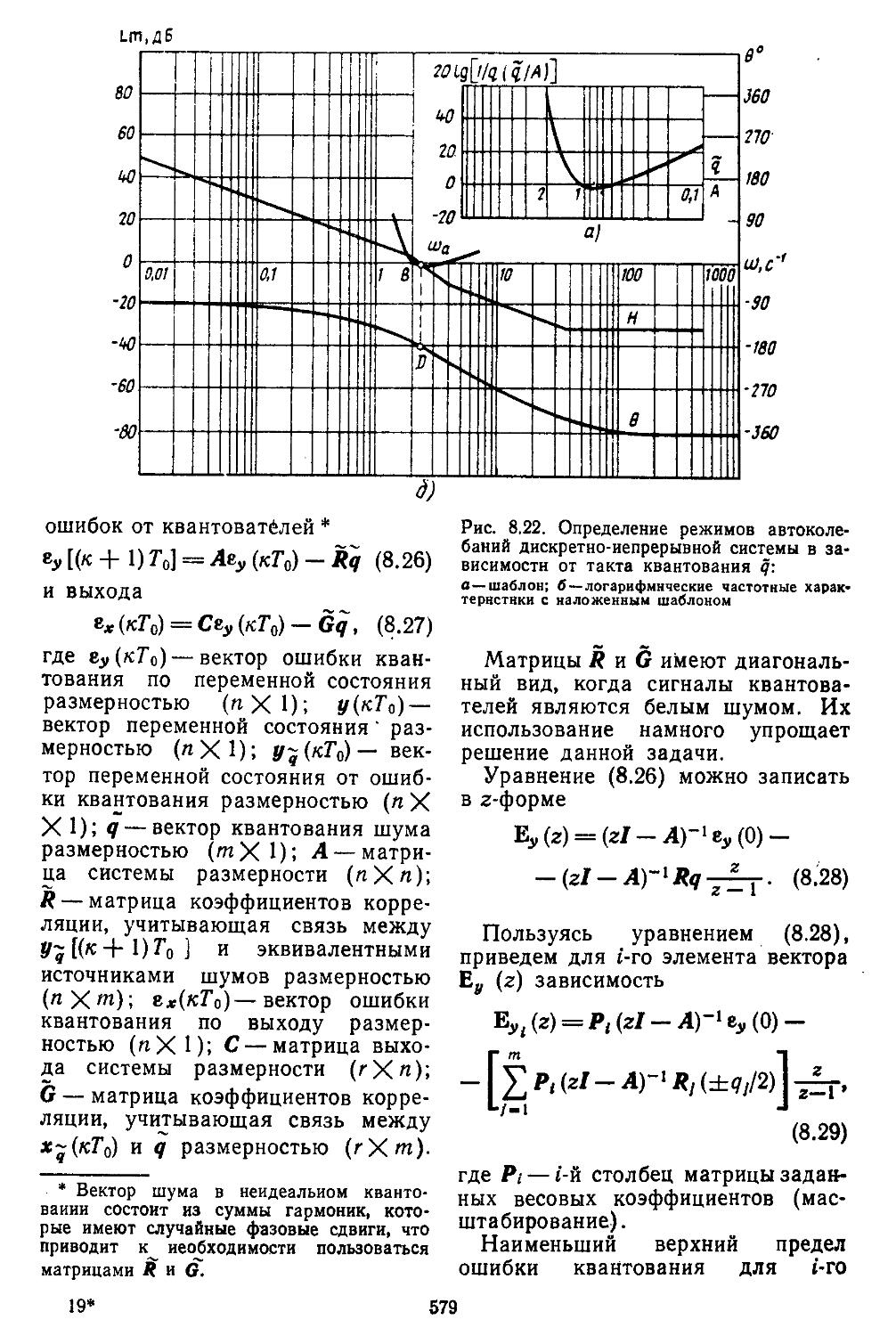
6. Статистическая линеаризация существенных дискретных нелинейных элементов . ................275
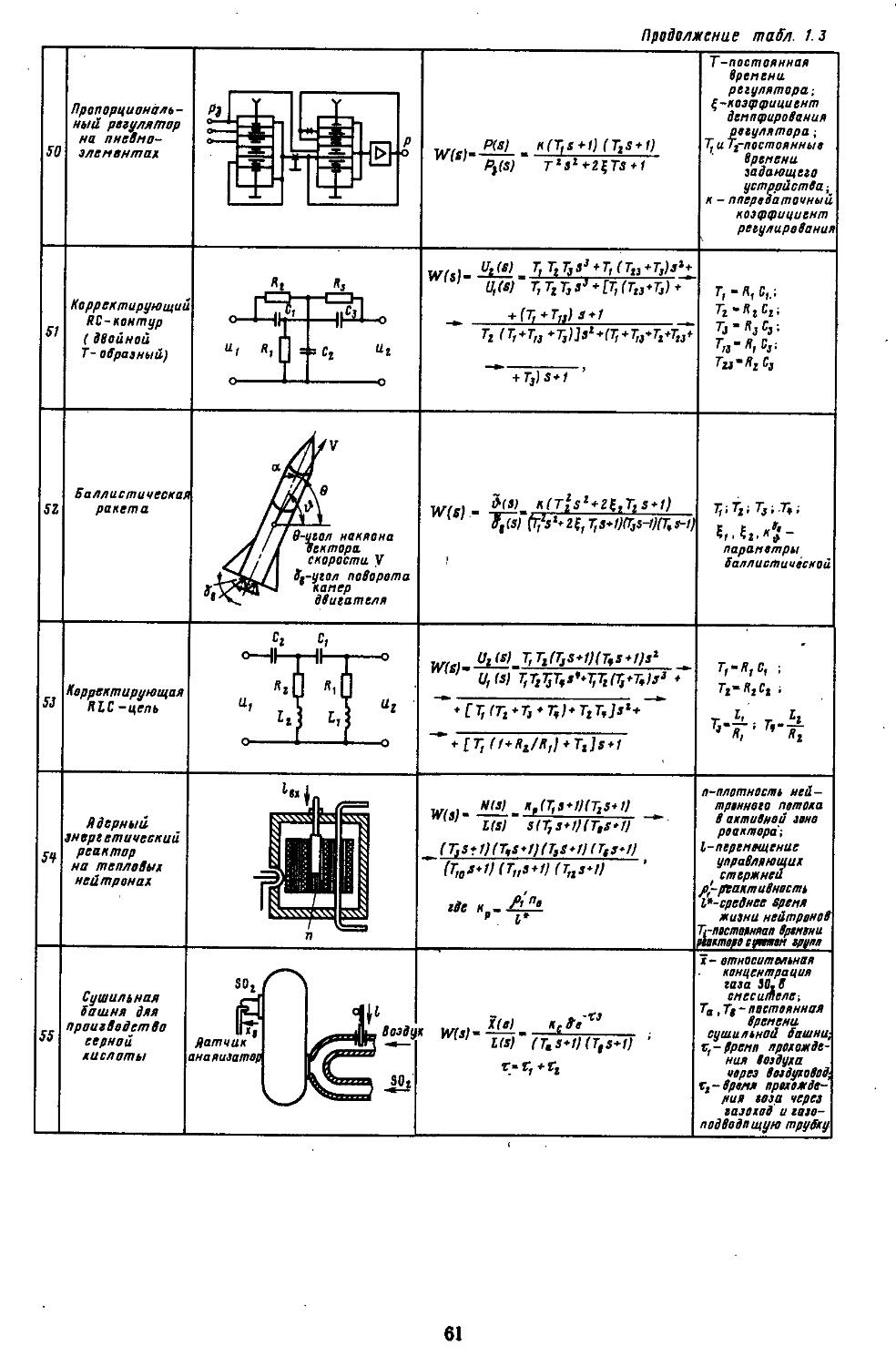
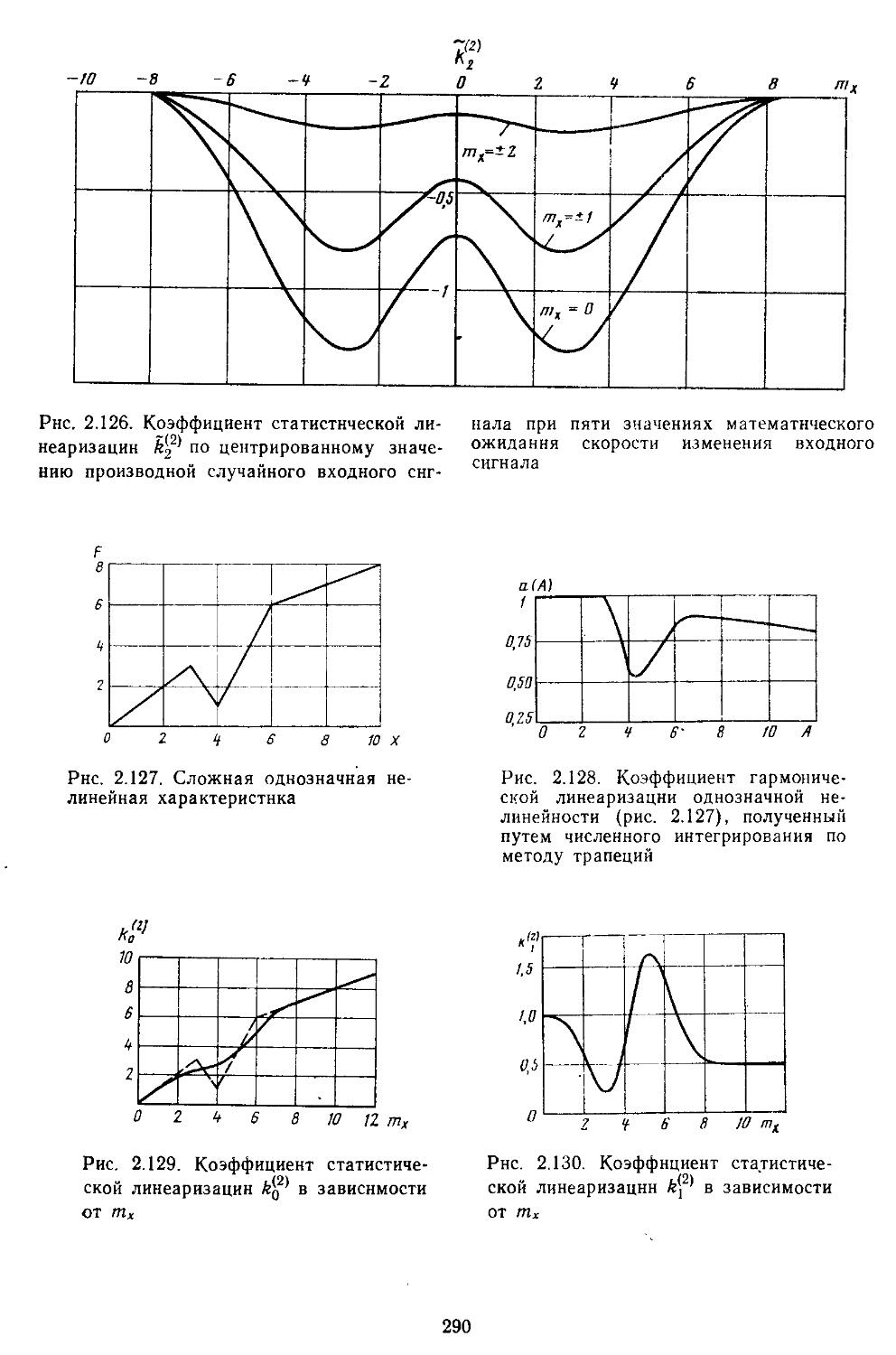
7. Вычислительные процедуры для определения коэффициентов гармонической и статистической линеаризации нелинейных элементов . . . 282
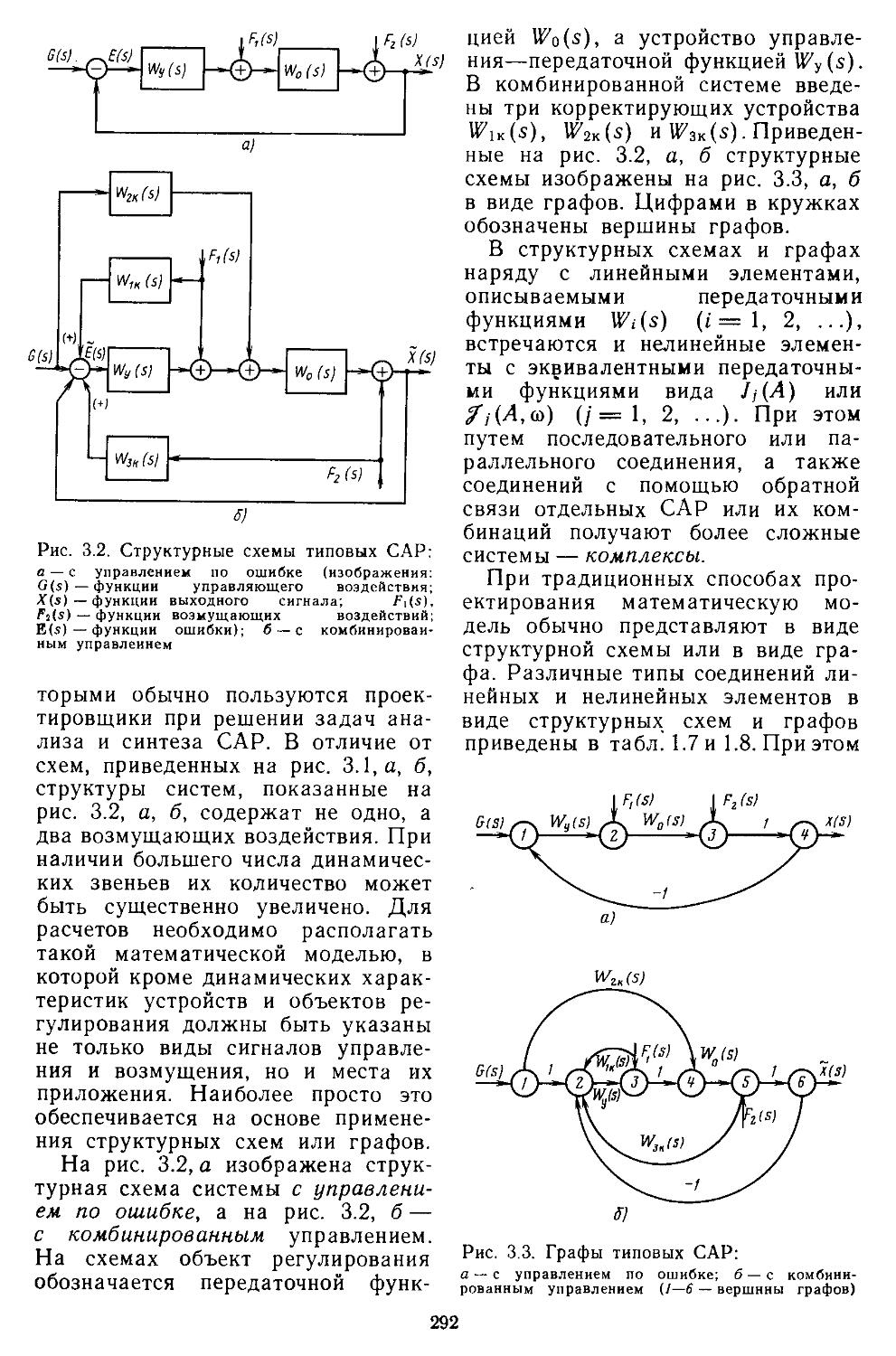
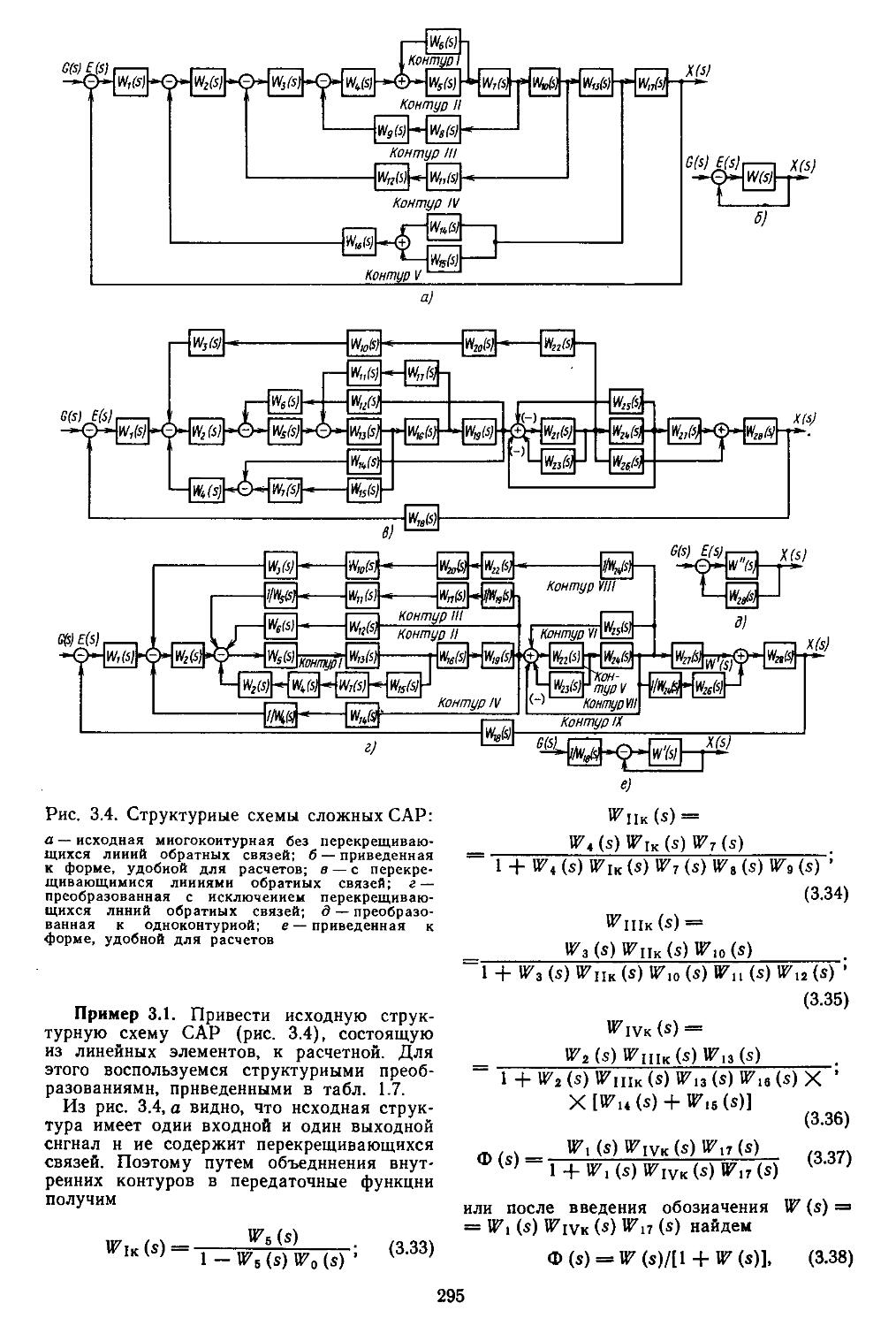
Глава 3~ Математические модели систем автоматического регулирования . ... 291
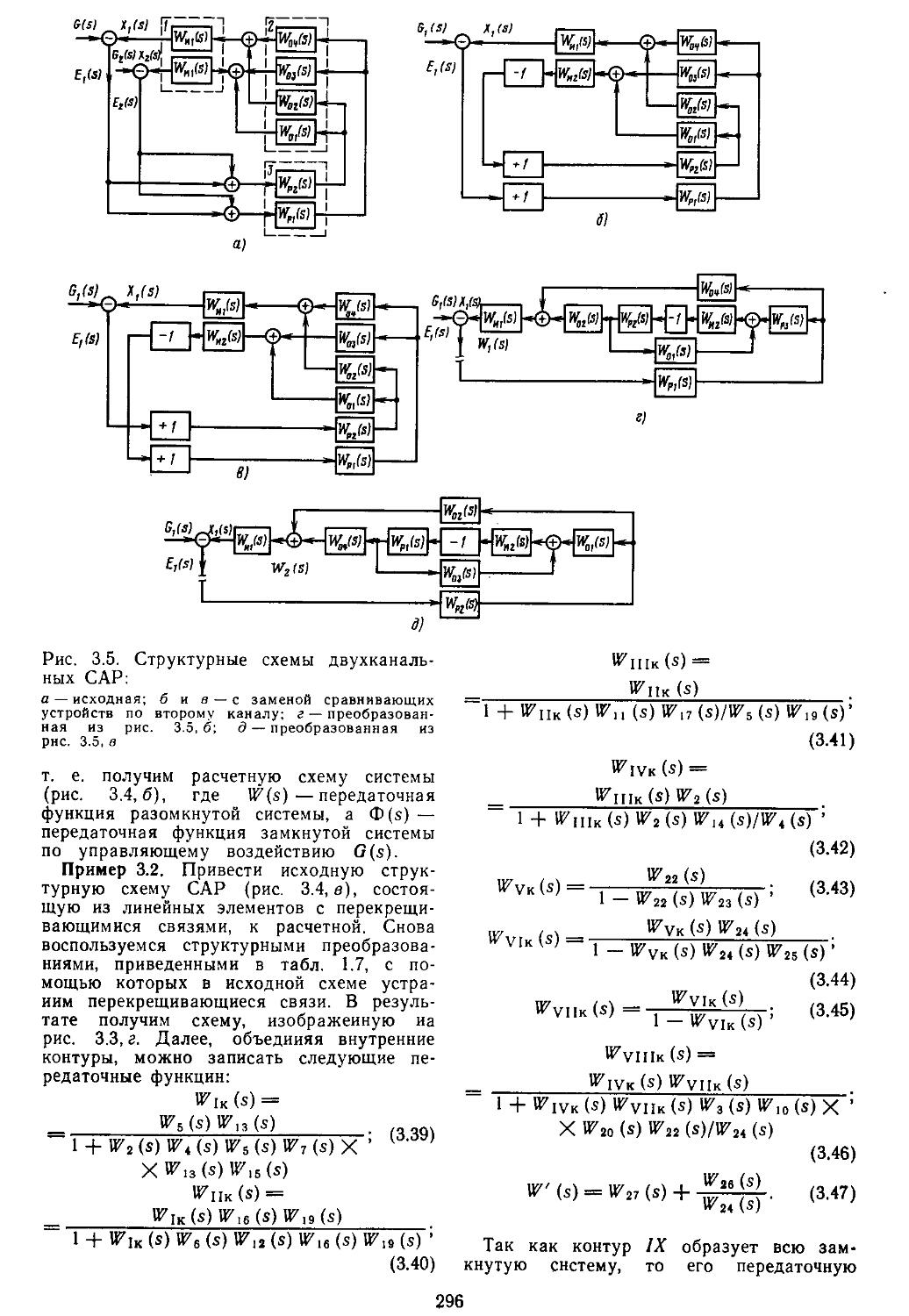
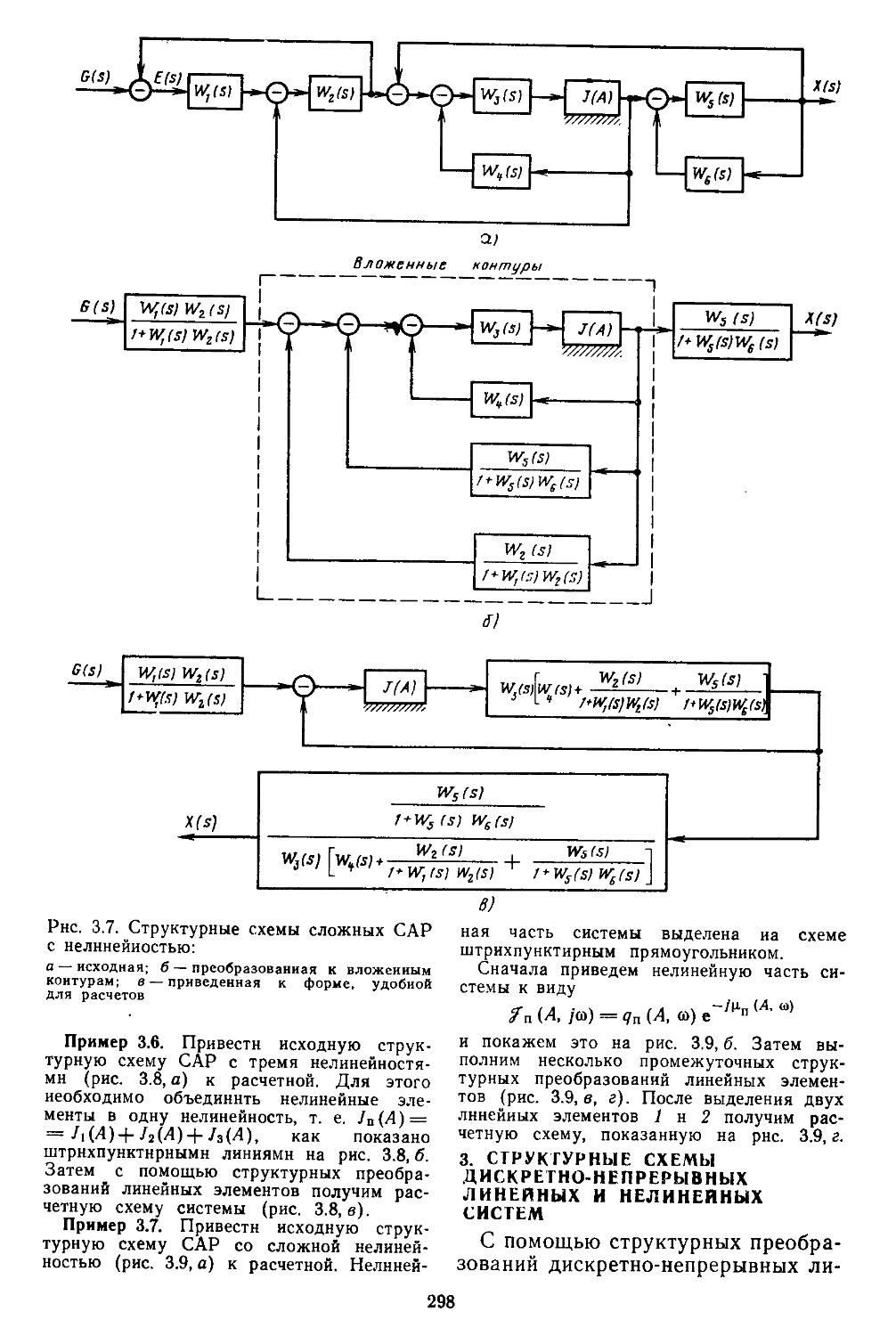
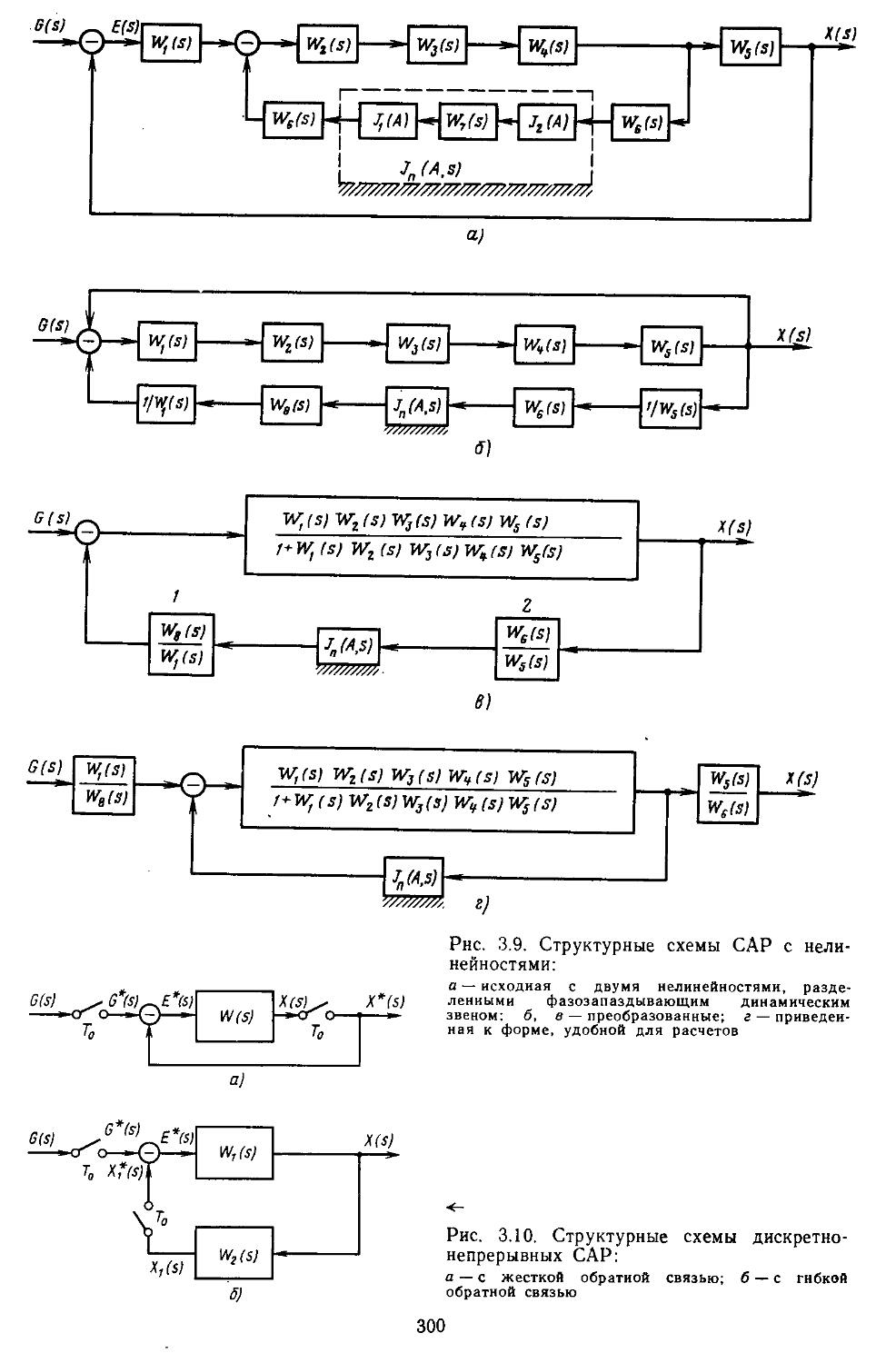
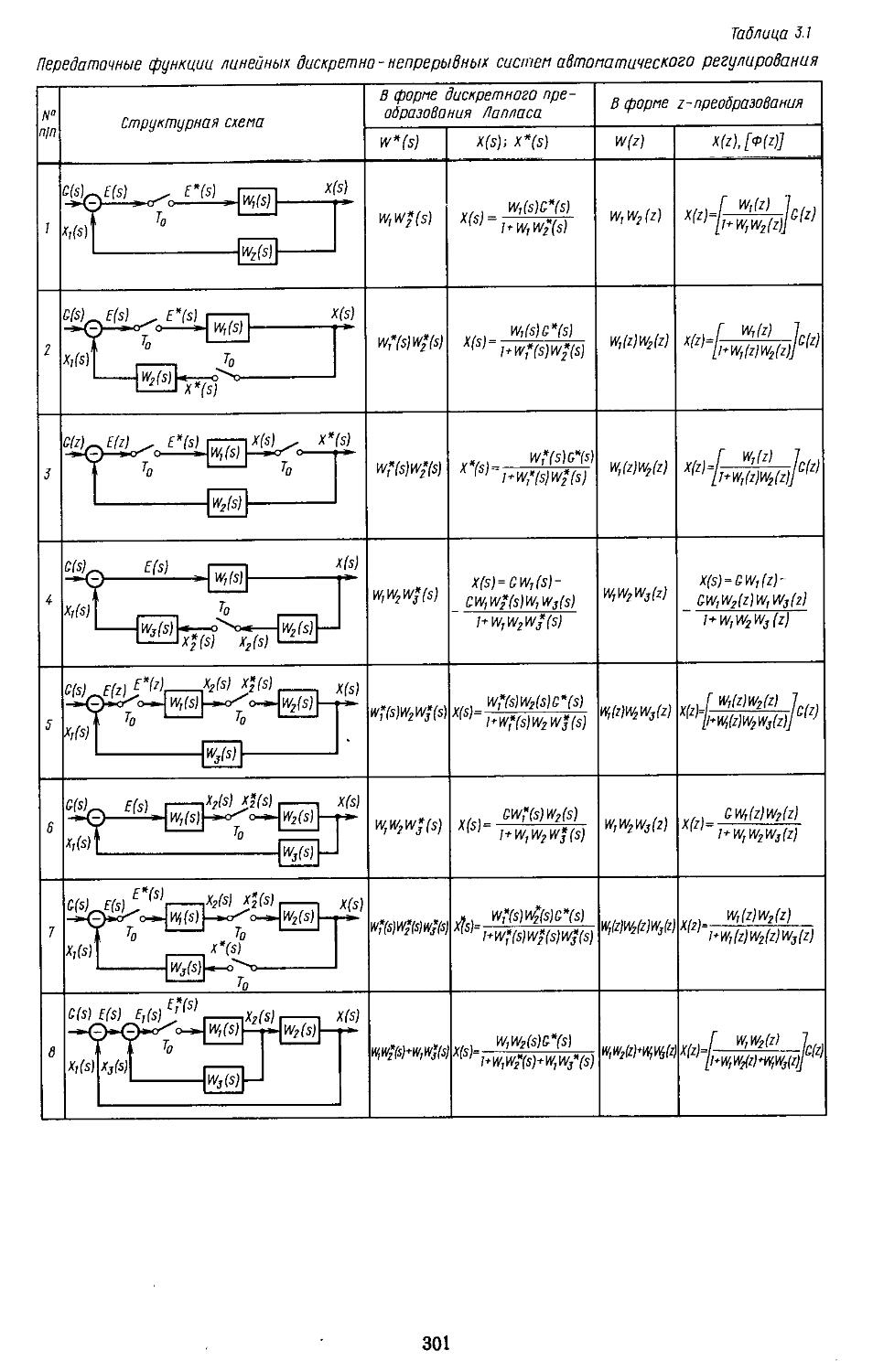
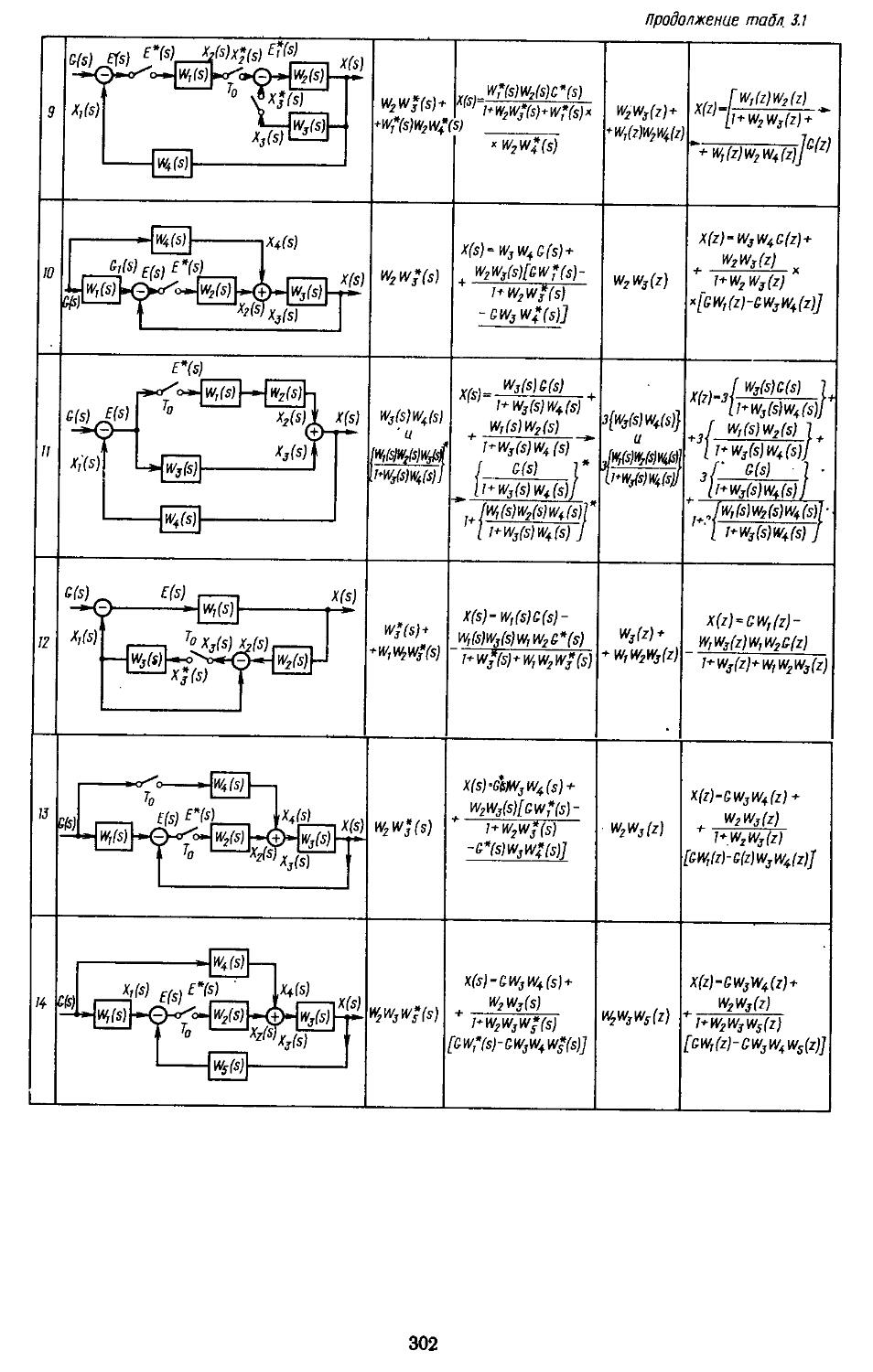
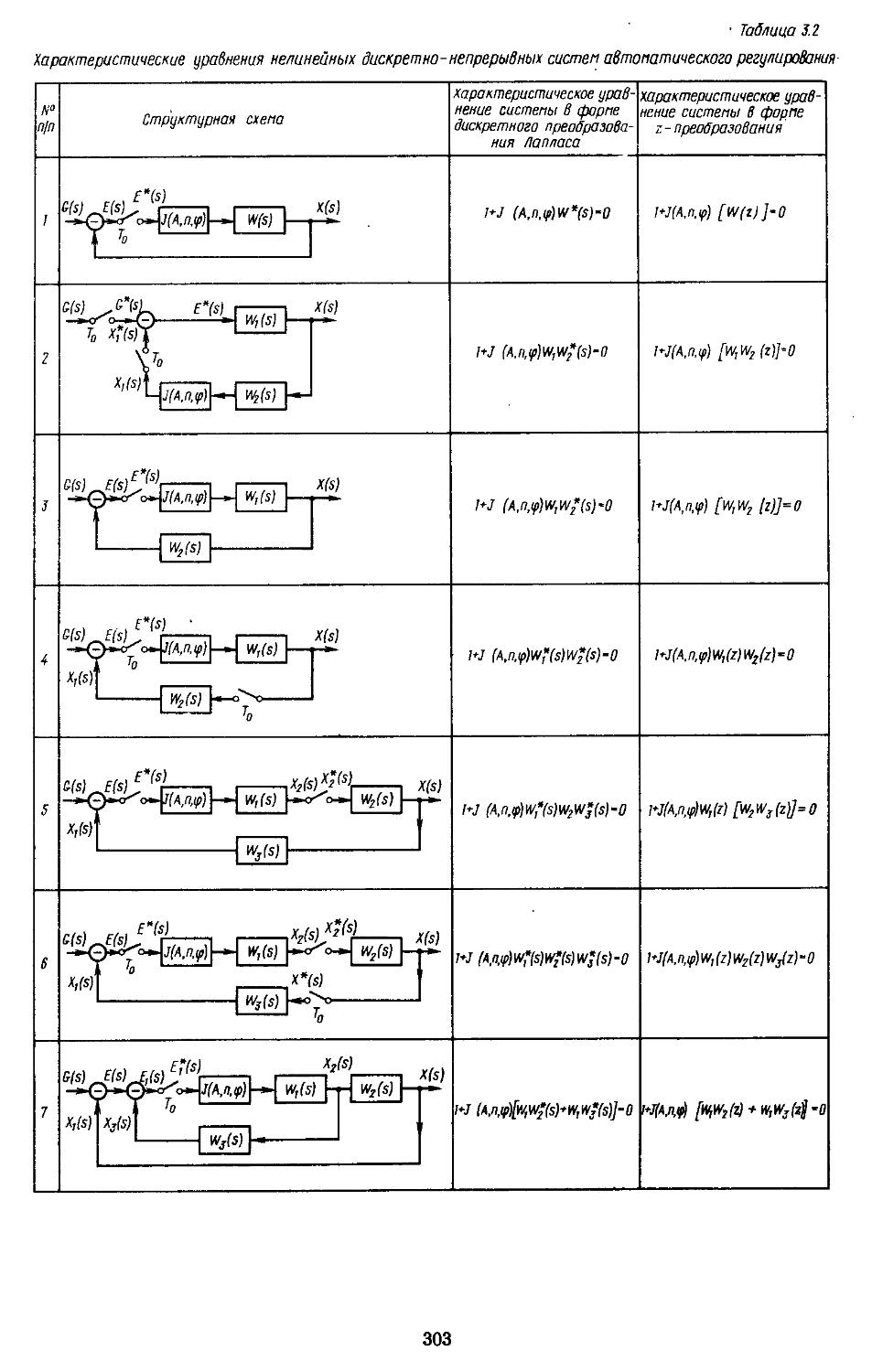
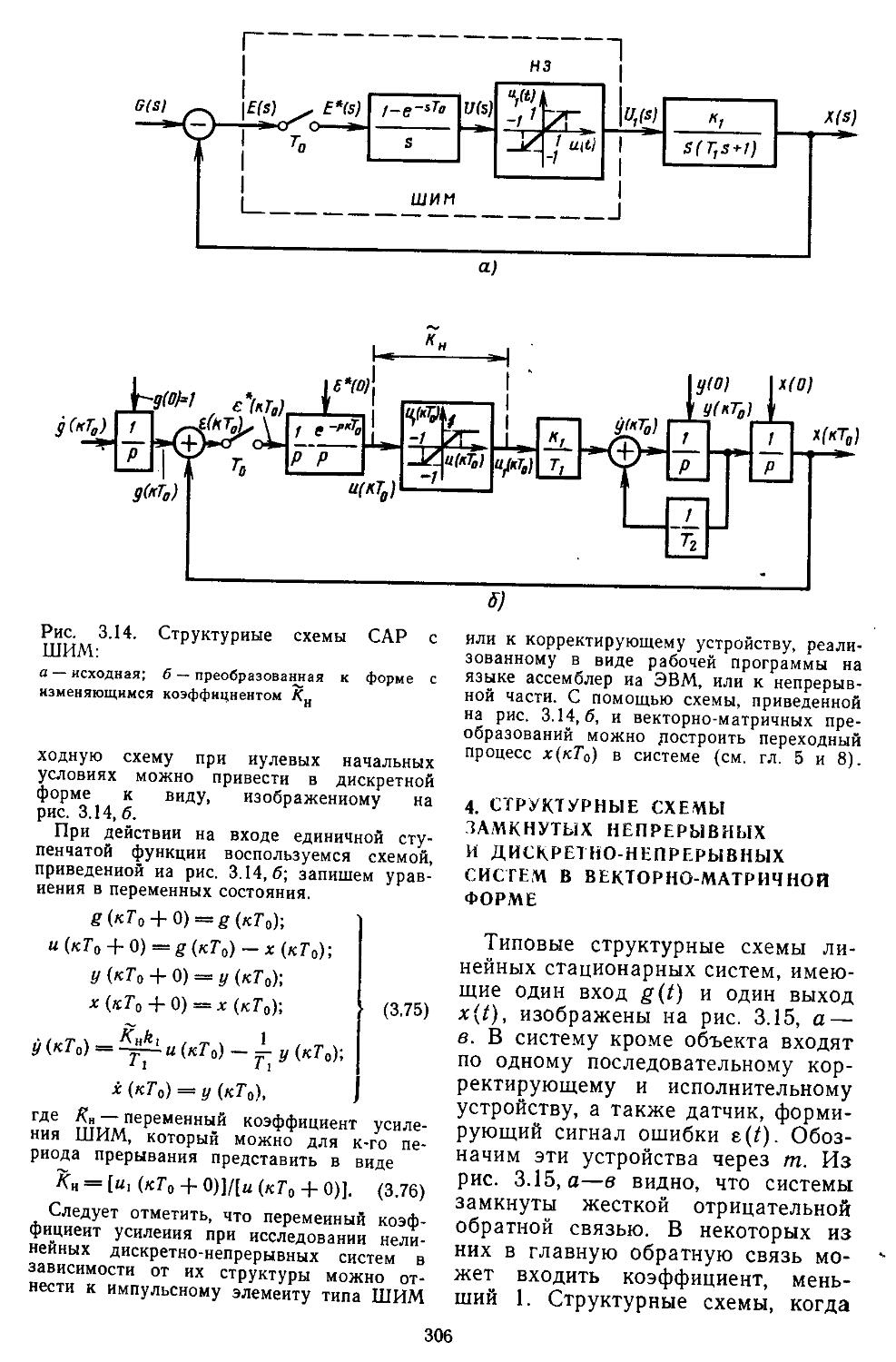
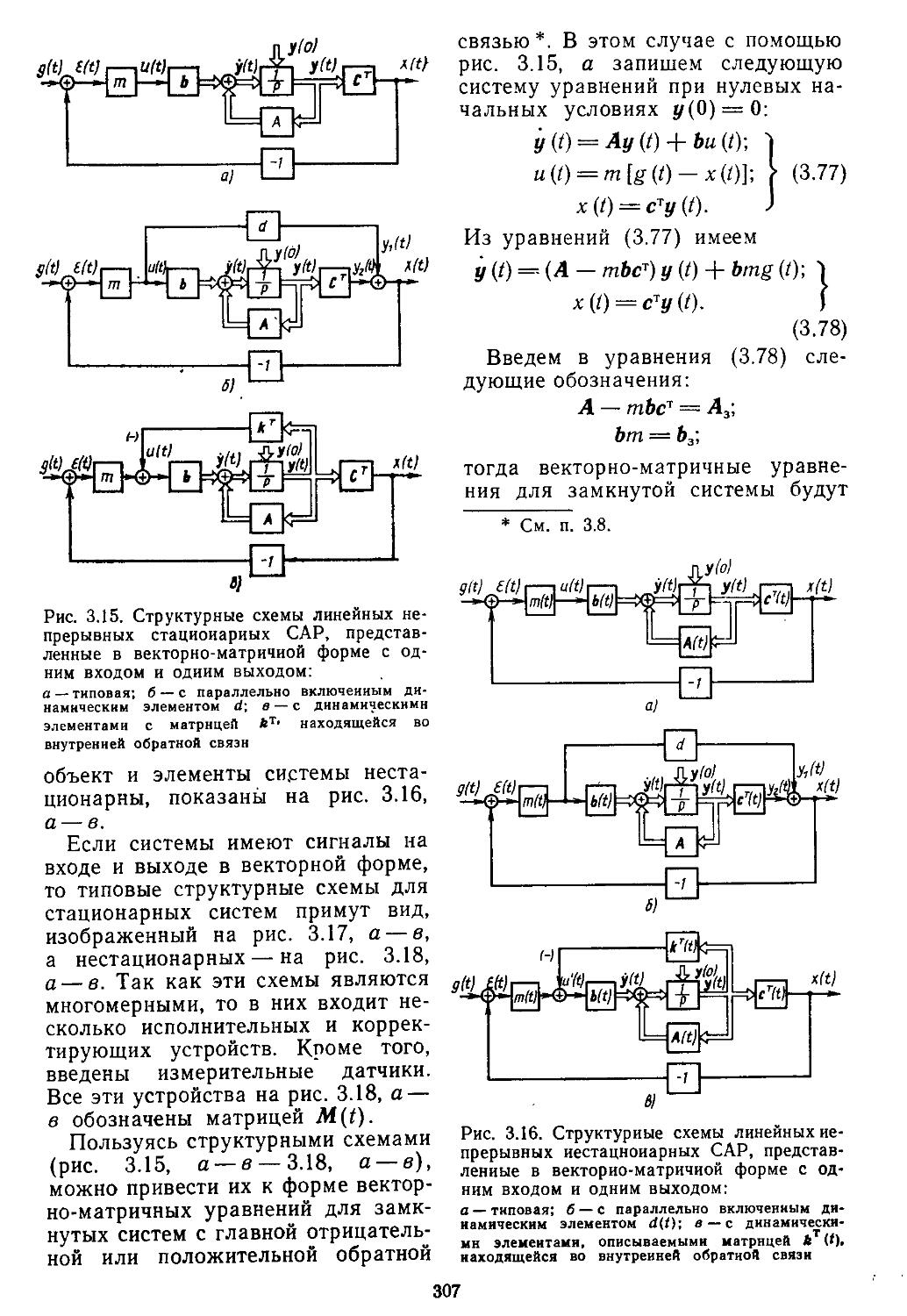
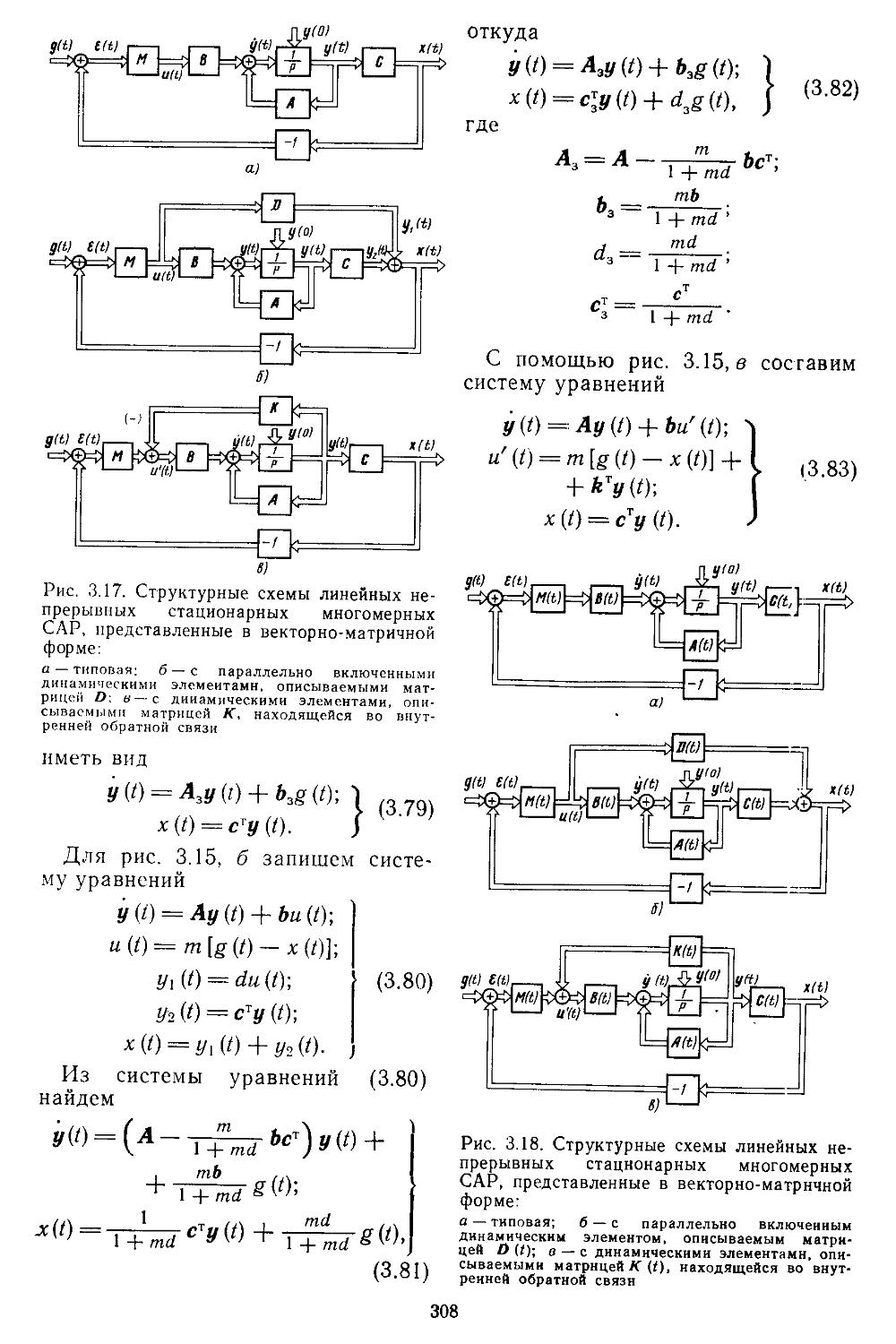
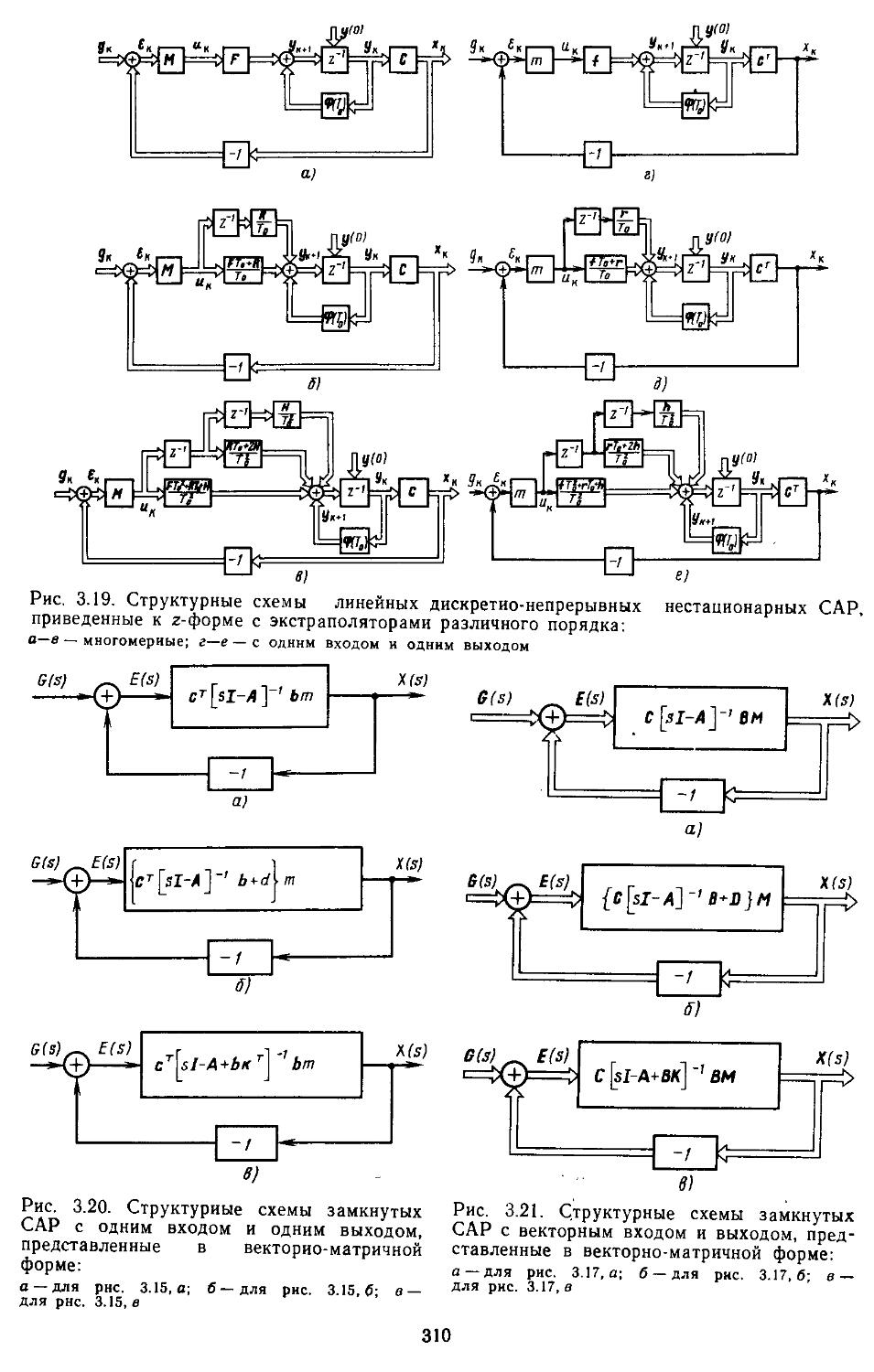
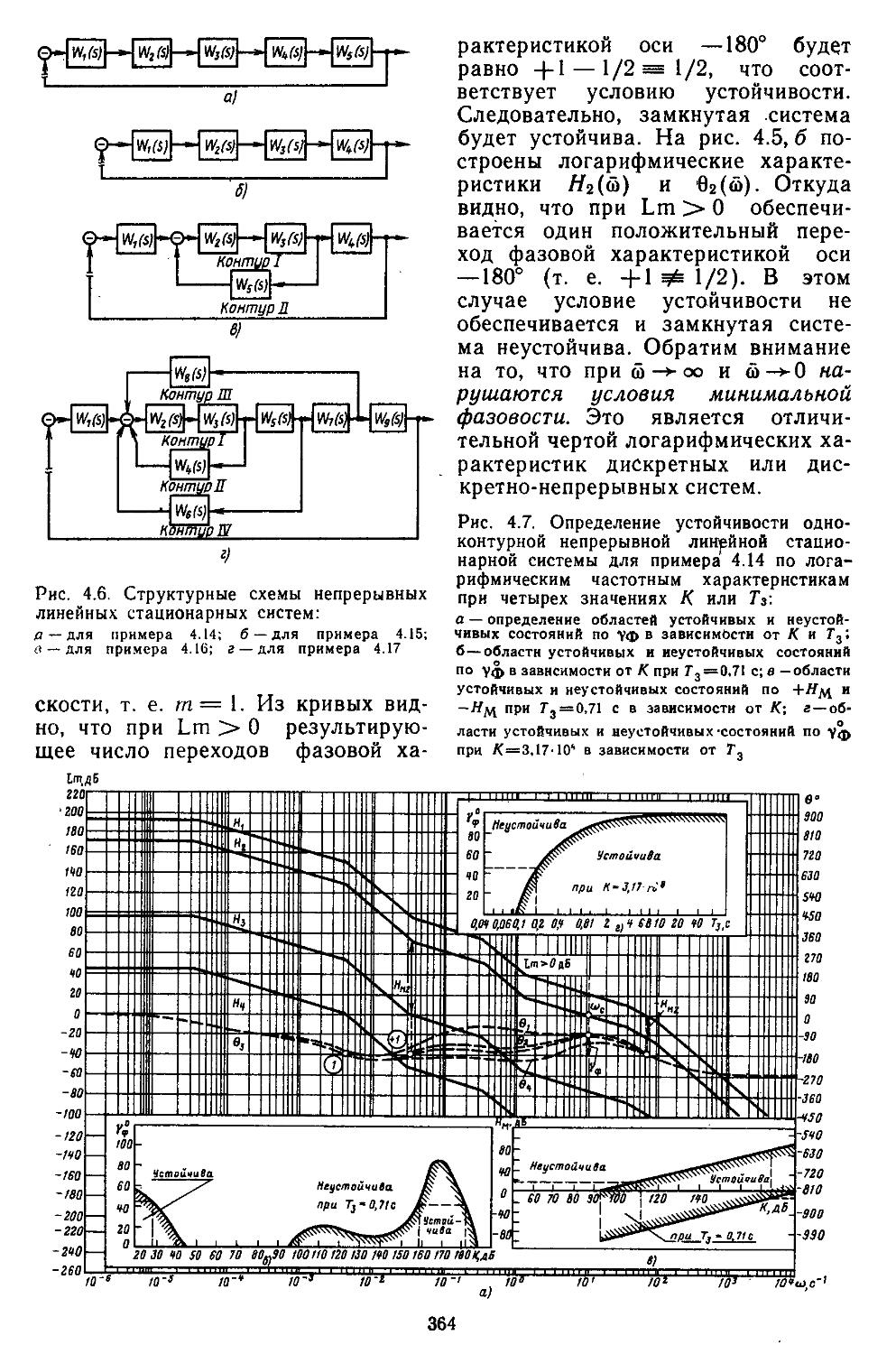
1. Структурные схемы и графы САР .... 293 2. Структурные преобразования непрерывных линейных и нелинейных систем пли их графов ....... 294 3. Структурные схемы дискретно-непрерывных линейных и нелинейных систем .... 298 4. Структурные схемы замкнутых непрерывных и дискретно-непрерывных систем в векторно-матричной форме ..................306
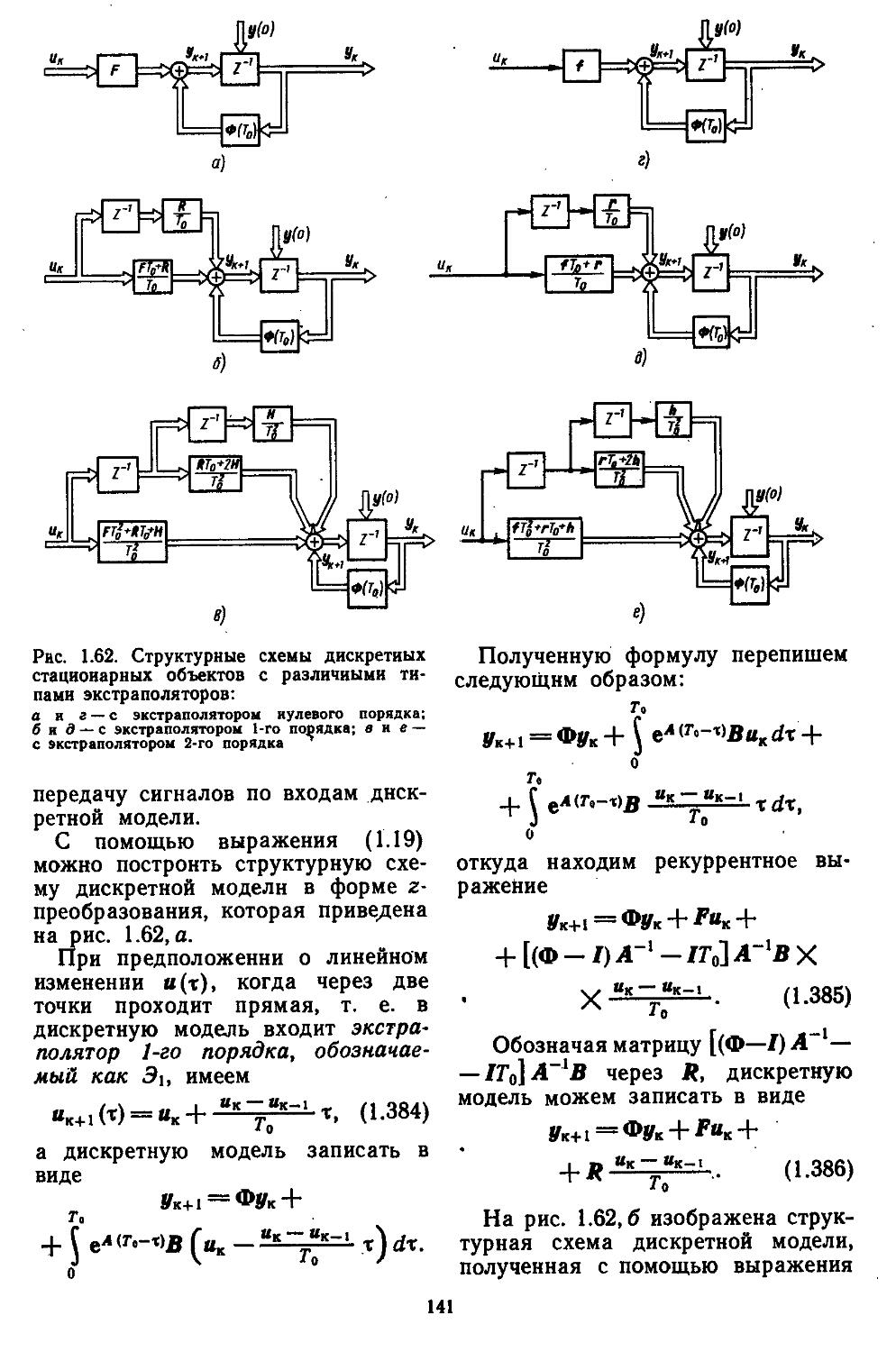
5. Спектральное разложение произвольных действительных и комплексных матриц . .311 6. Алгоритмы вычисления функций от матриц . 322 7. Дискретные модели
САР ..................326
3
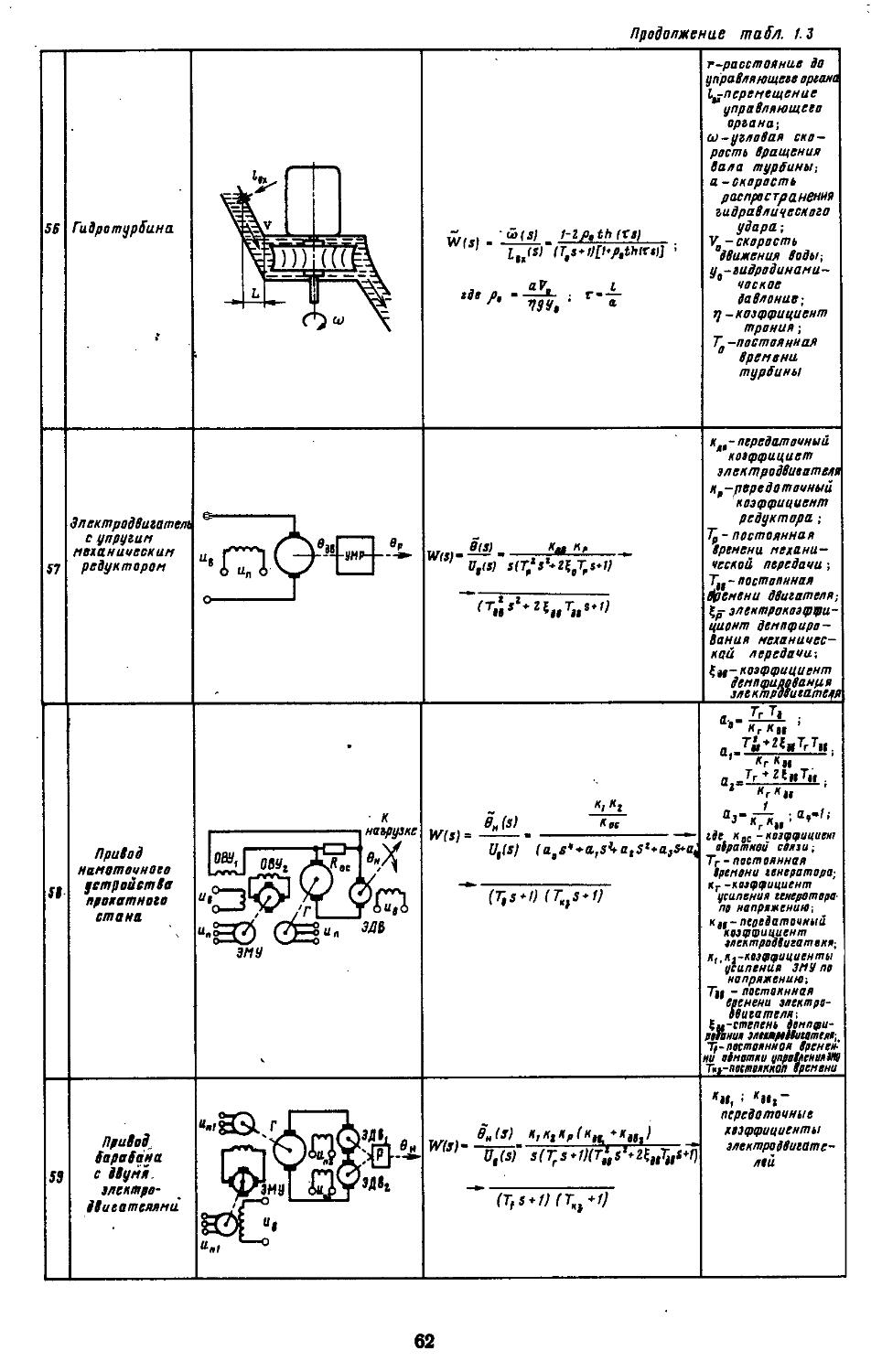
8. Управляемость и наблюдаемость .... 328
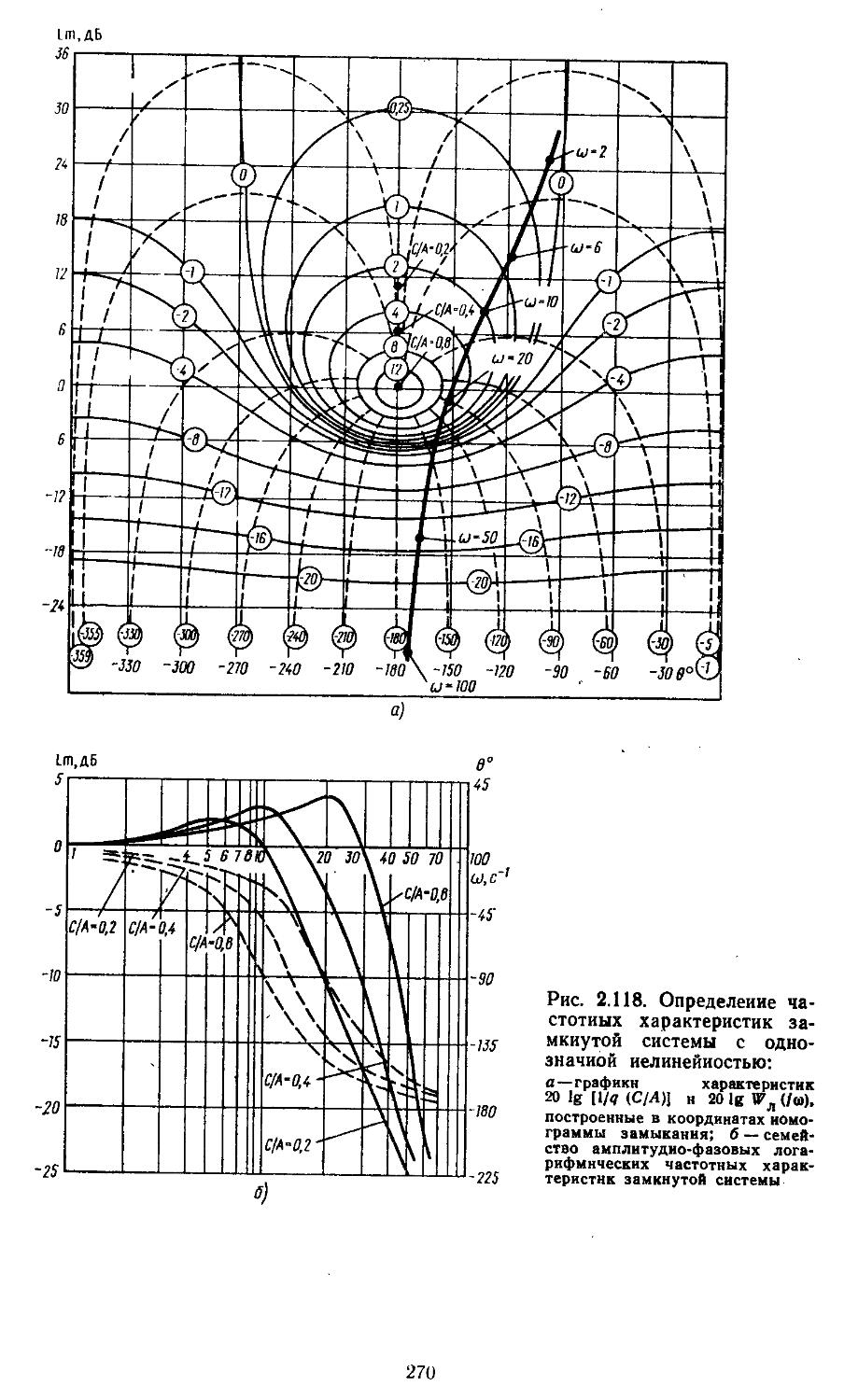
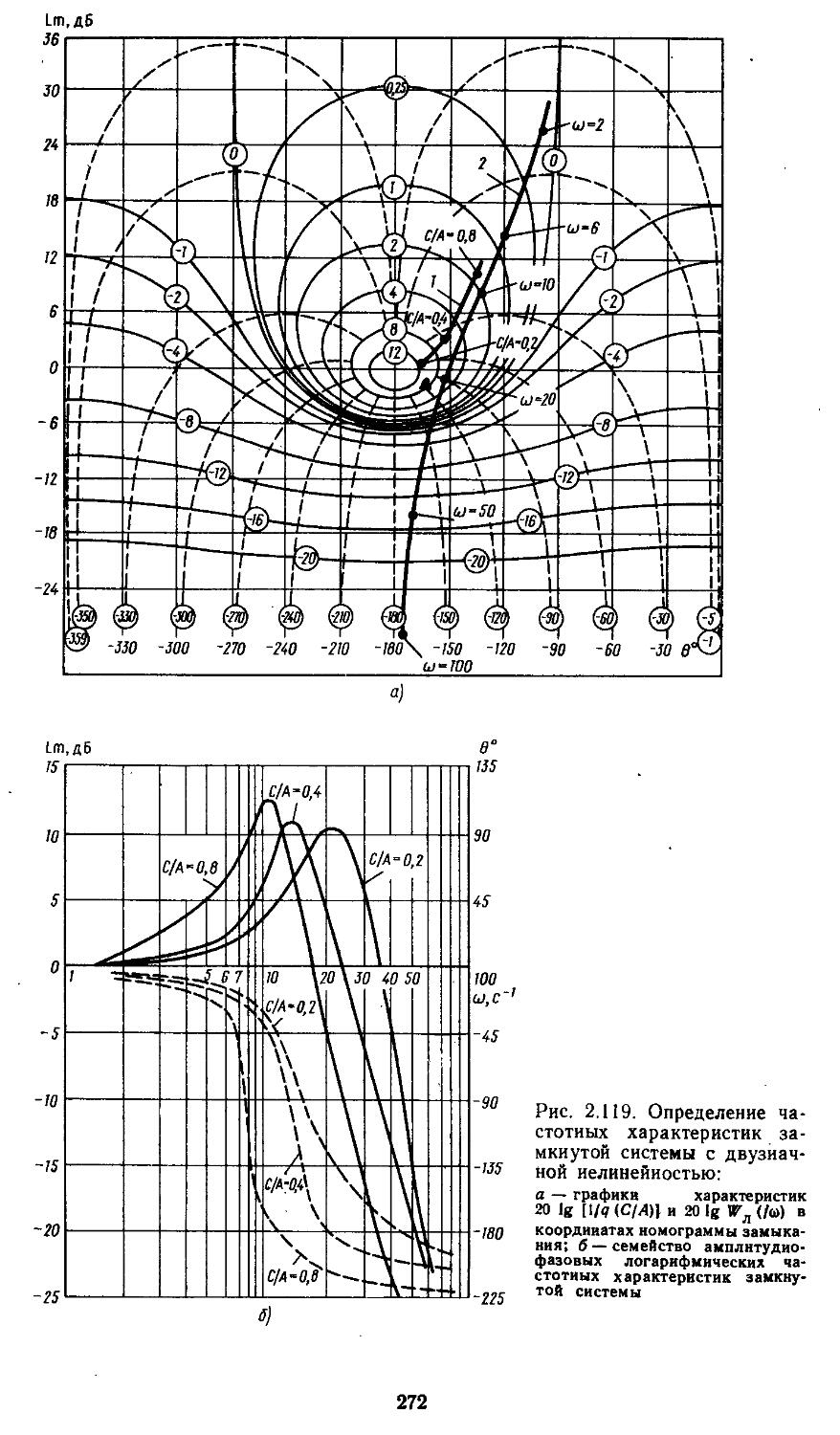
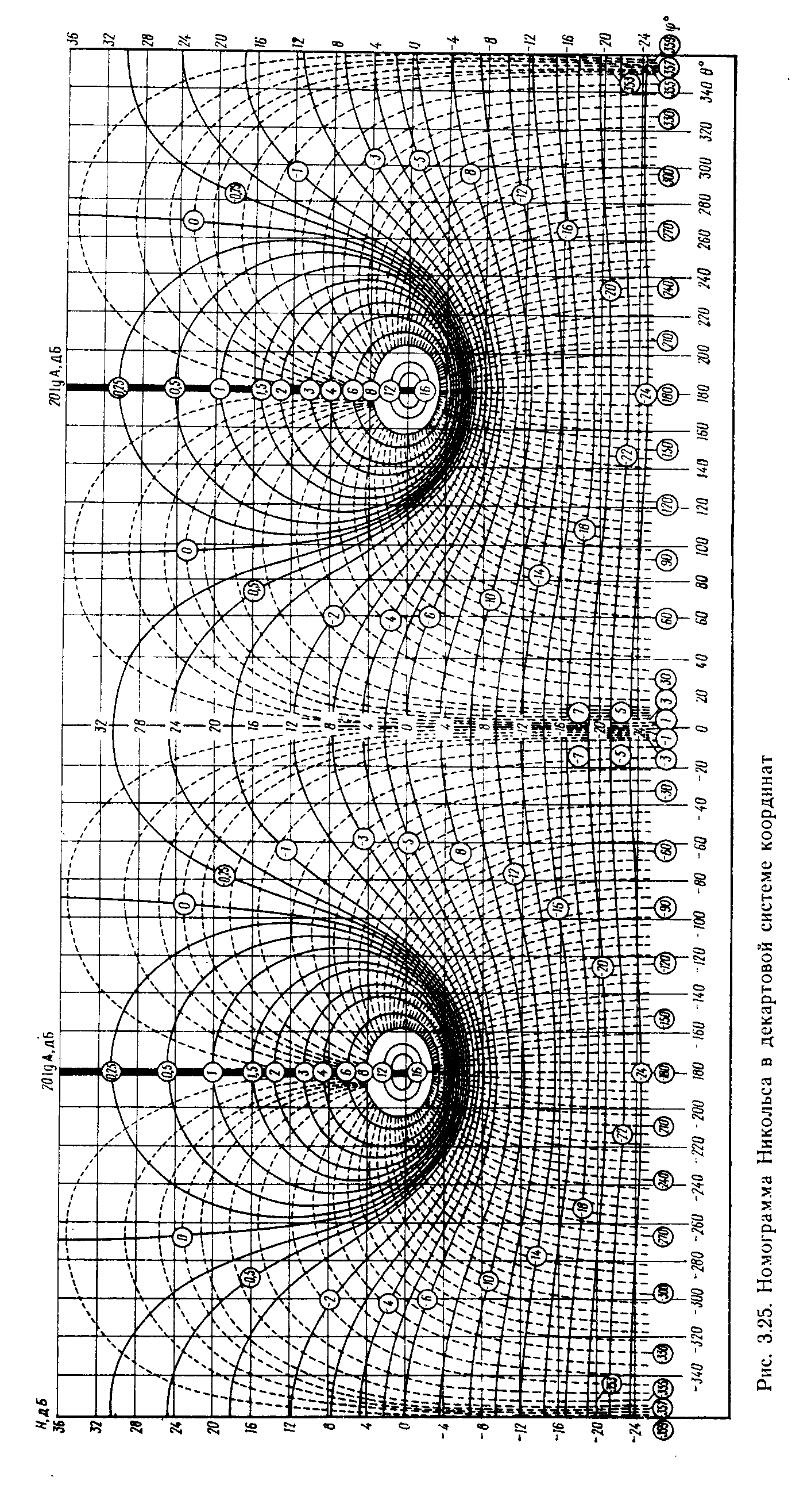
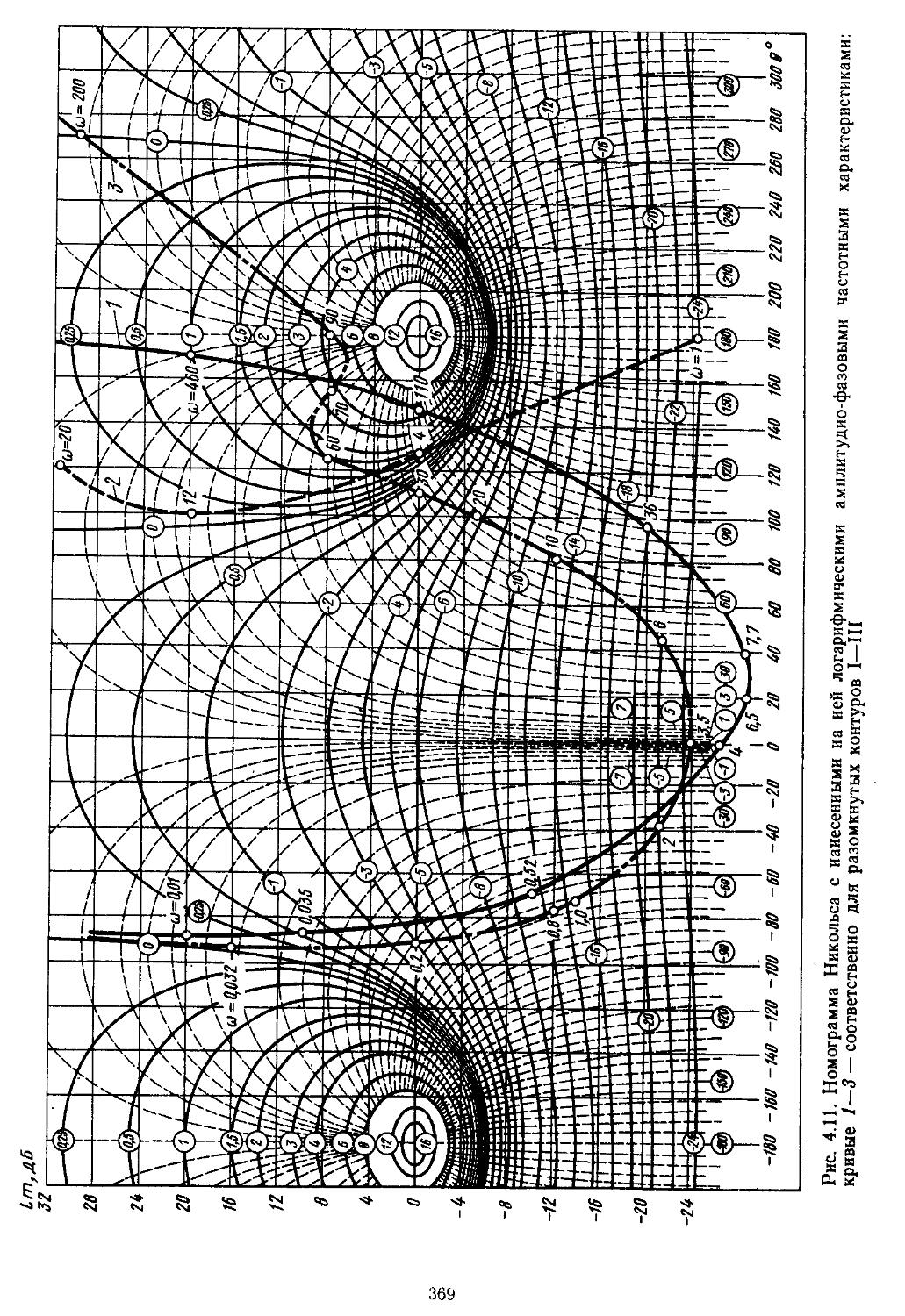
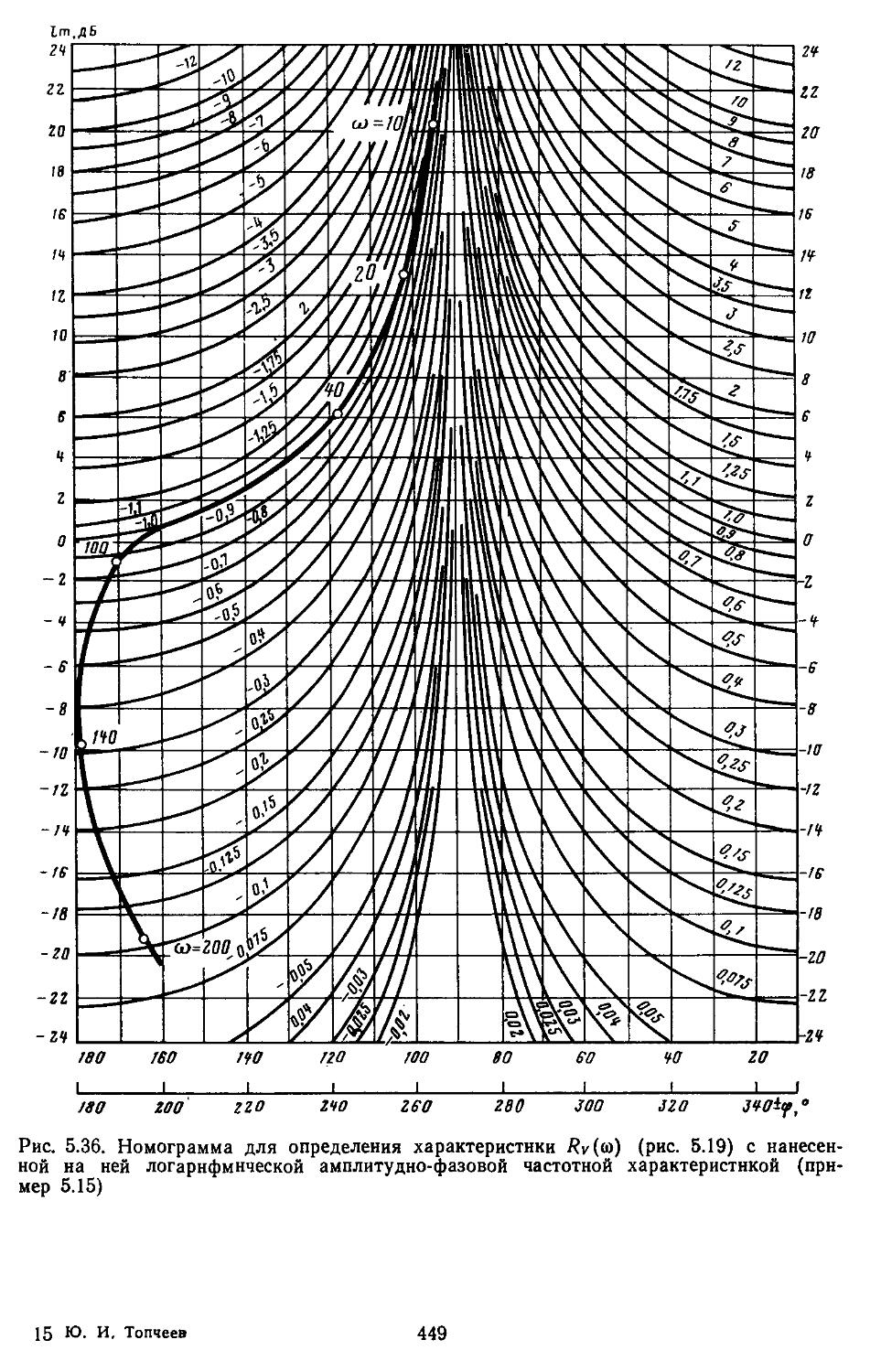
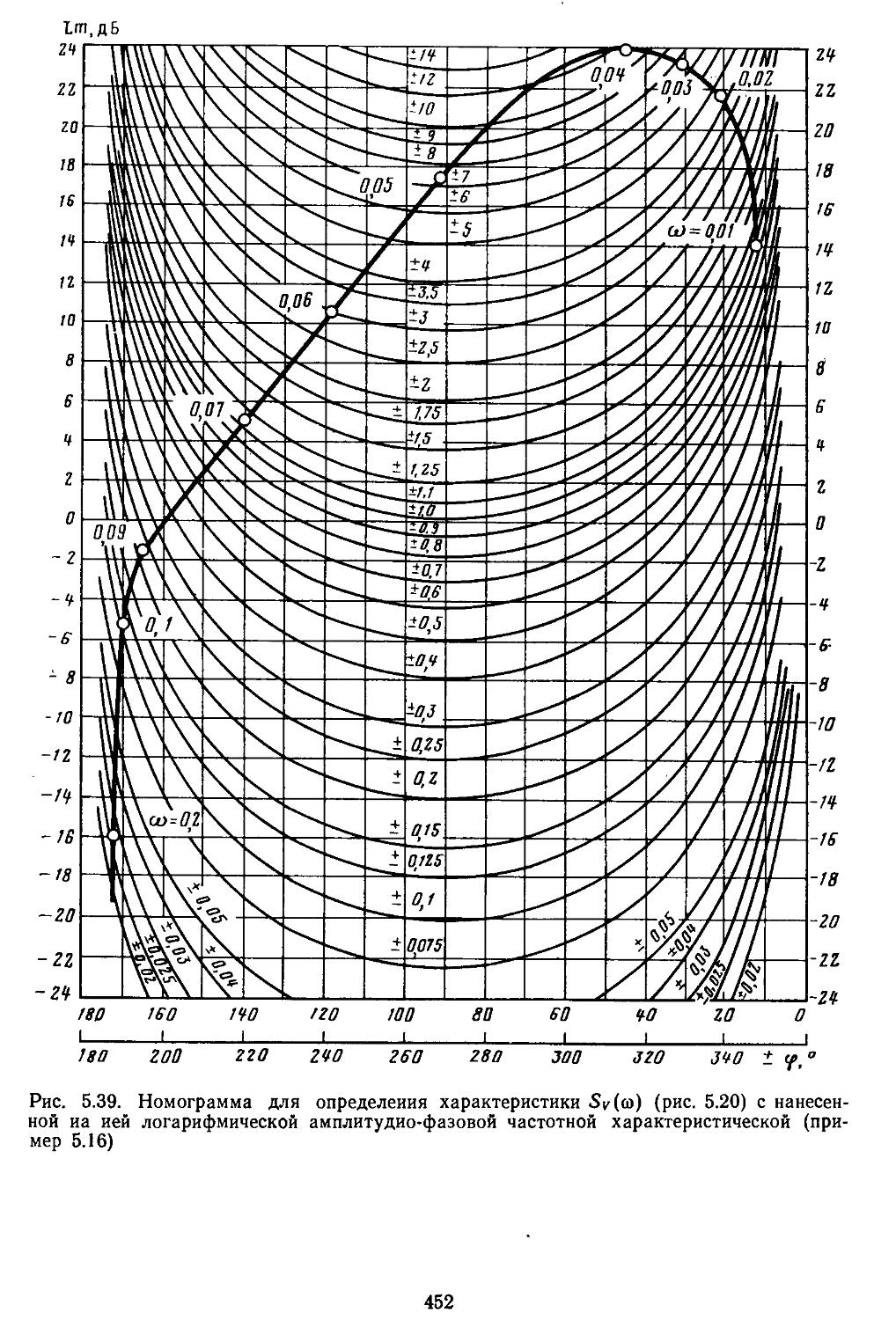
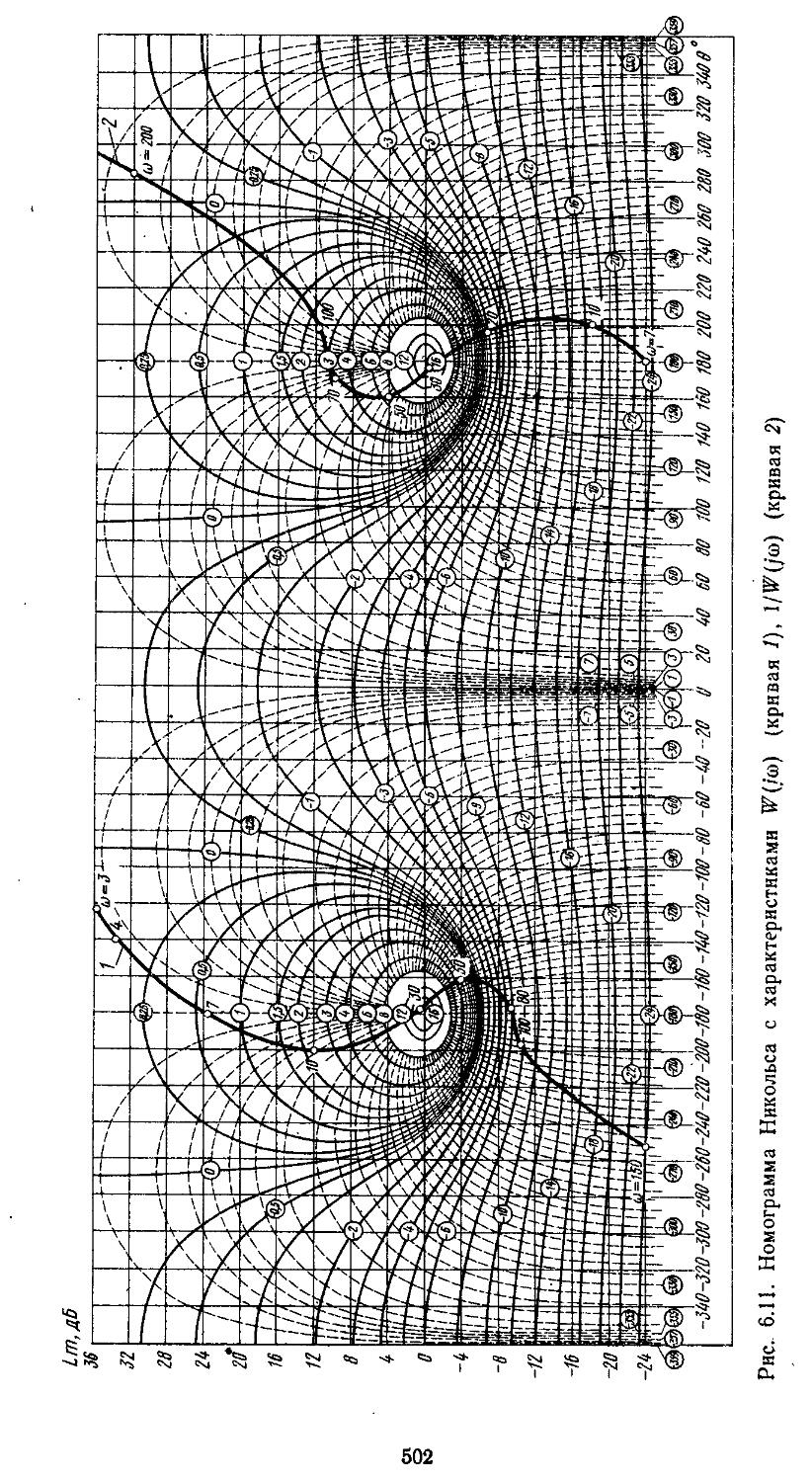
9. Номограммы и вычислительные процедуры для построения логарифмических частотных характеристик замкнутых систем .... 333
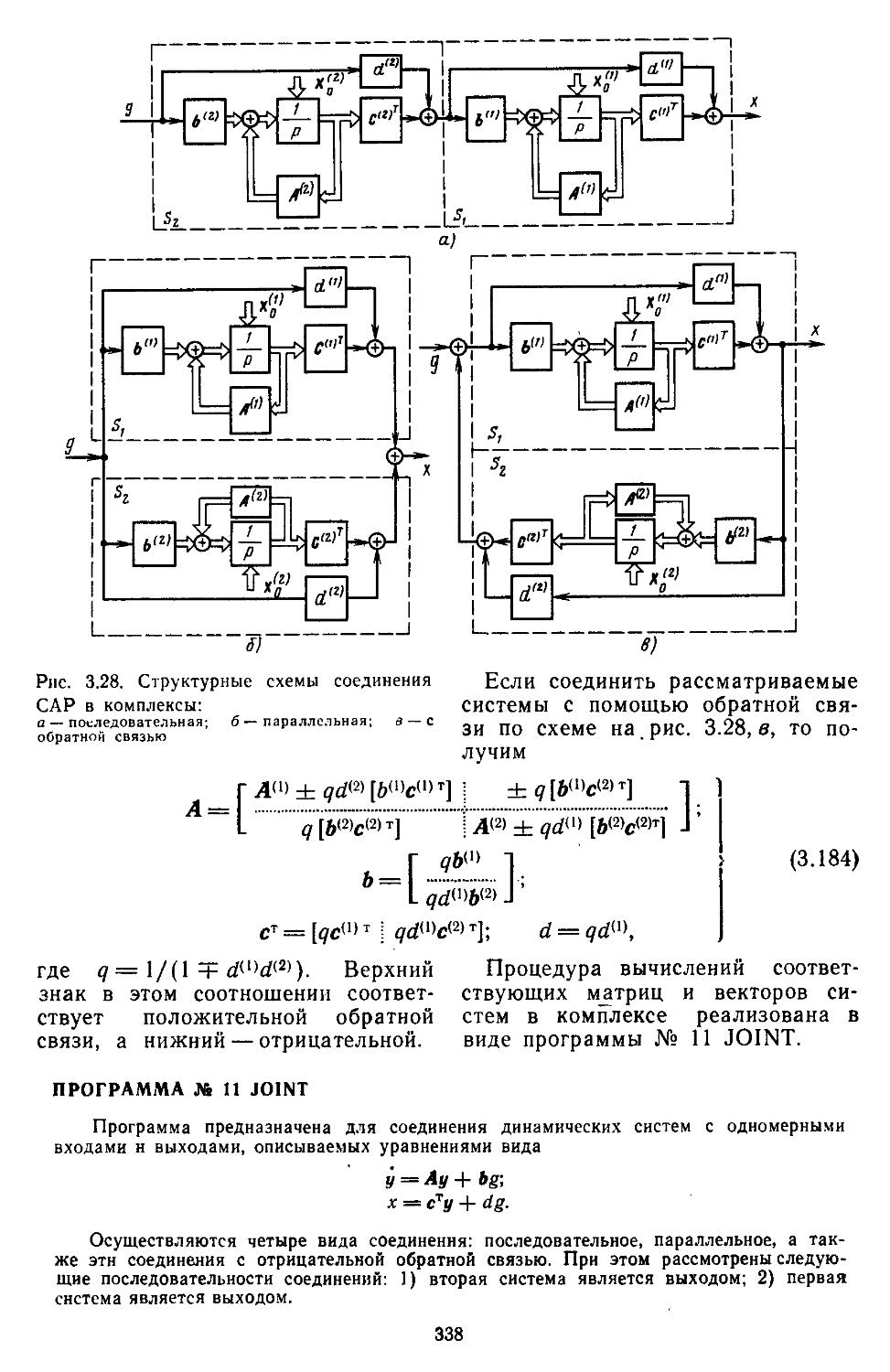
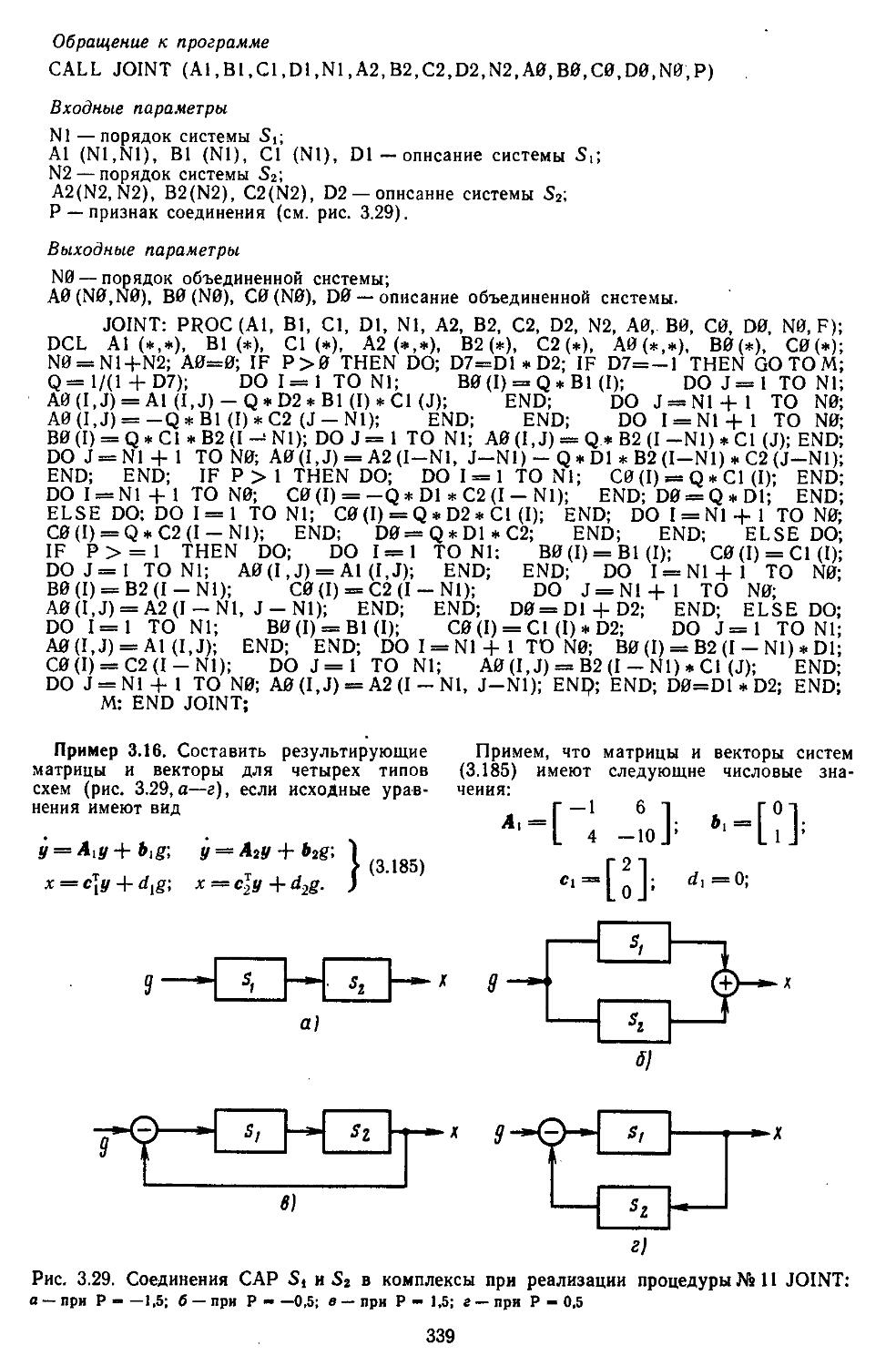
10. Соединение САР в динамические комплексы 337
11. Вычислительные процедуры для определения передаточных функций разомкнутых и замкнутых САР ..... 340
РАЗДЕЛ II. АНАЛИЗ СИСТЕМ АВТОМАТИЧЕСКОГО РЕ-
ГУЛИРОВАНИЯ . . . 343
Глава 4. Исследование устойчивости Линейных непрерывных и дискретно-непрерывных систем автоматического регулирования ........................344
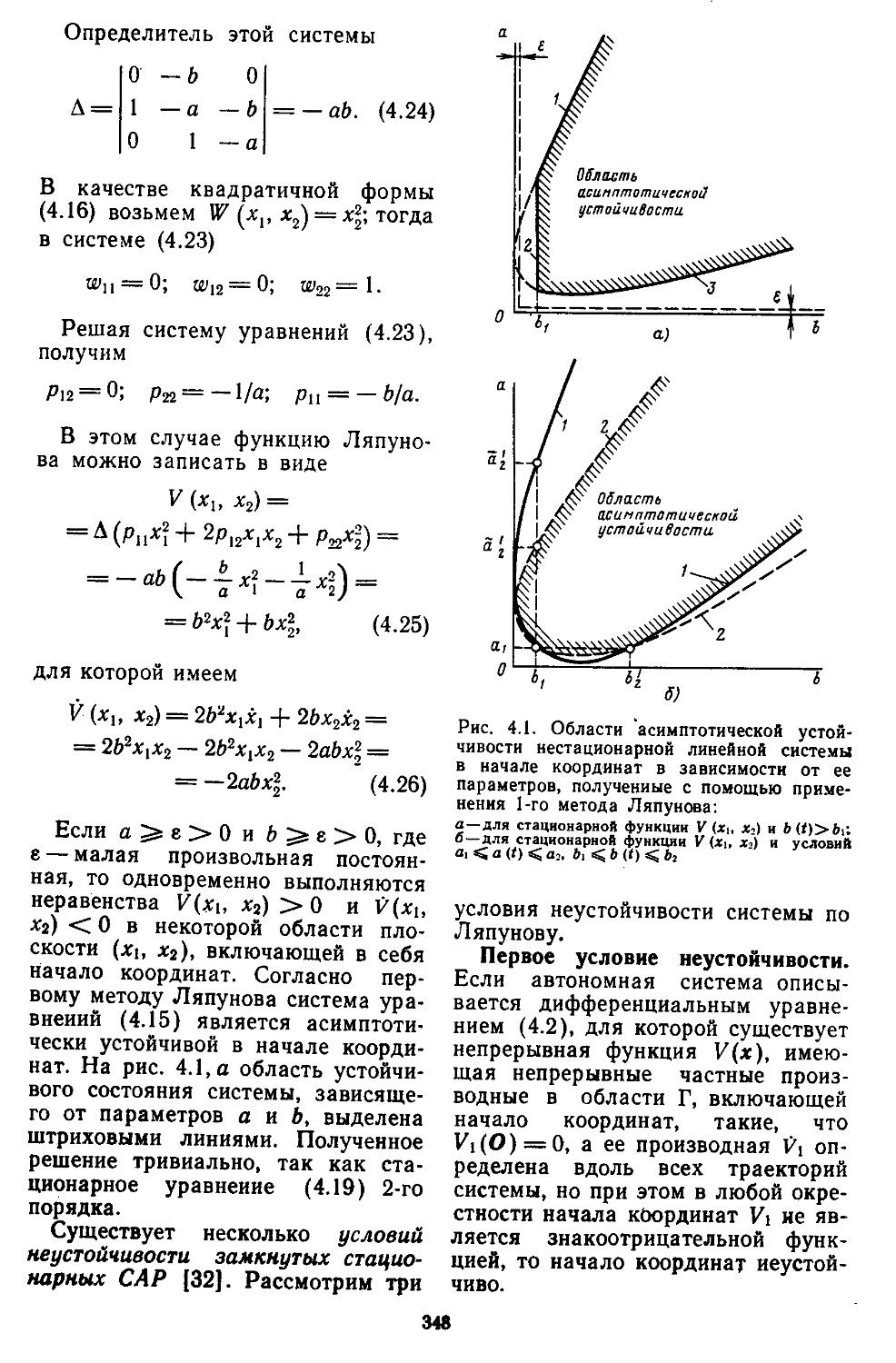
1. Устойчивость линейных систем по первому методу Ляпунова . . . 344
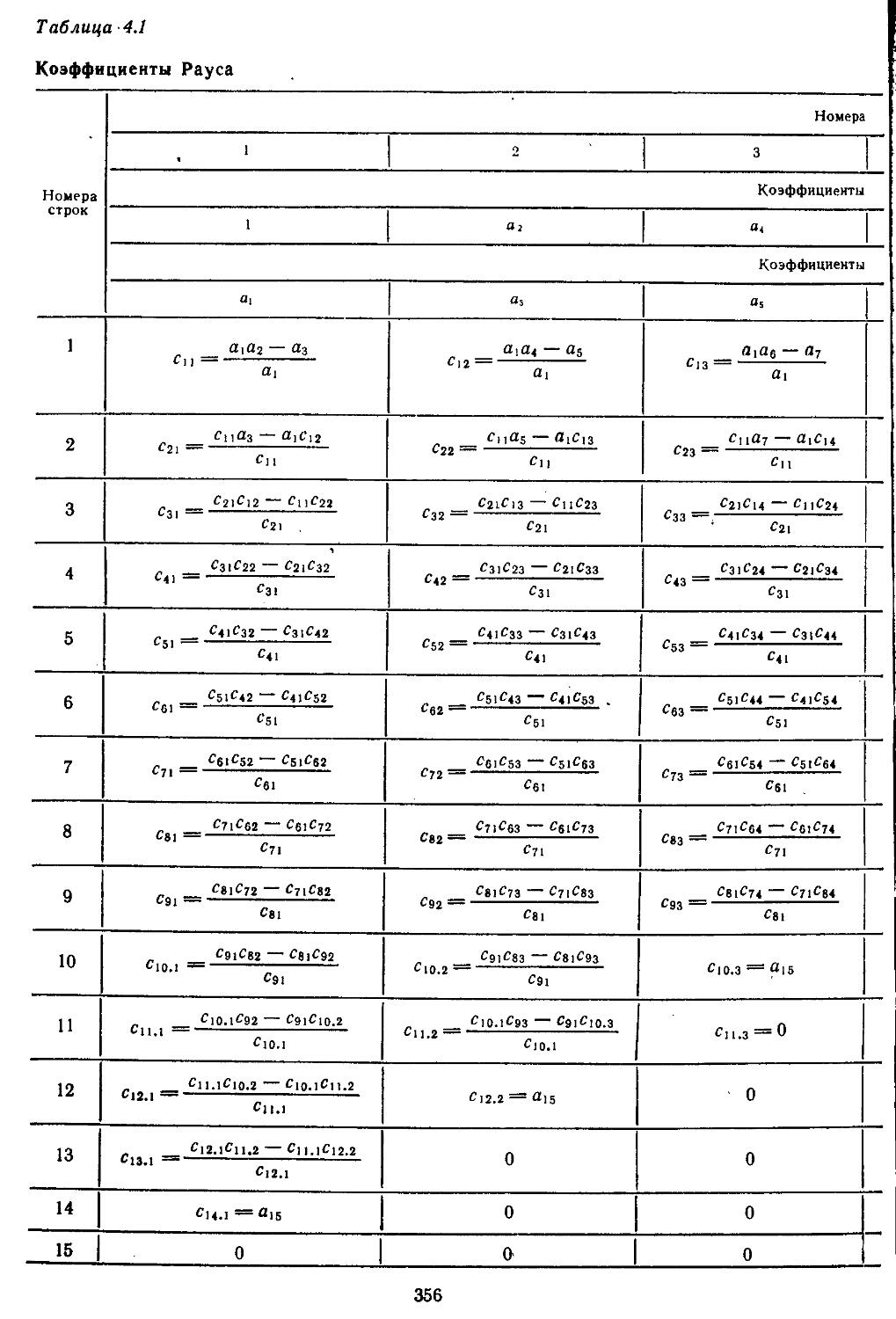
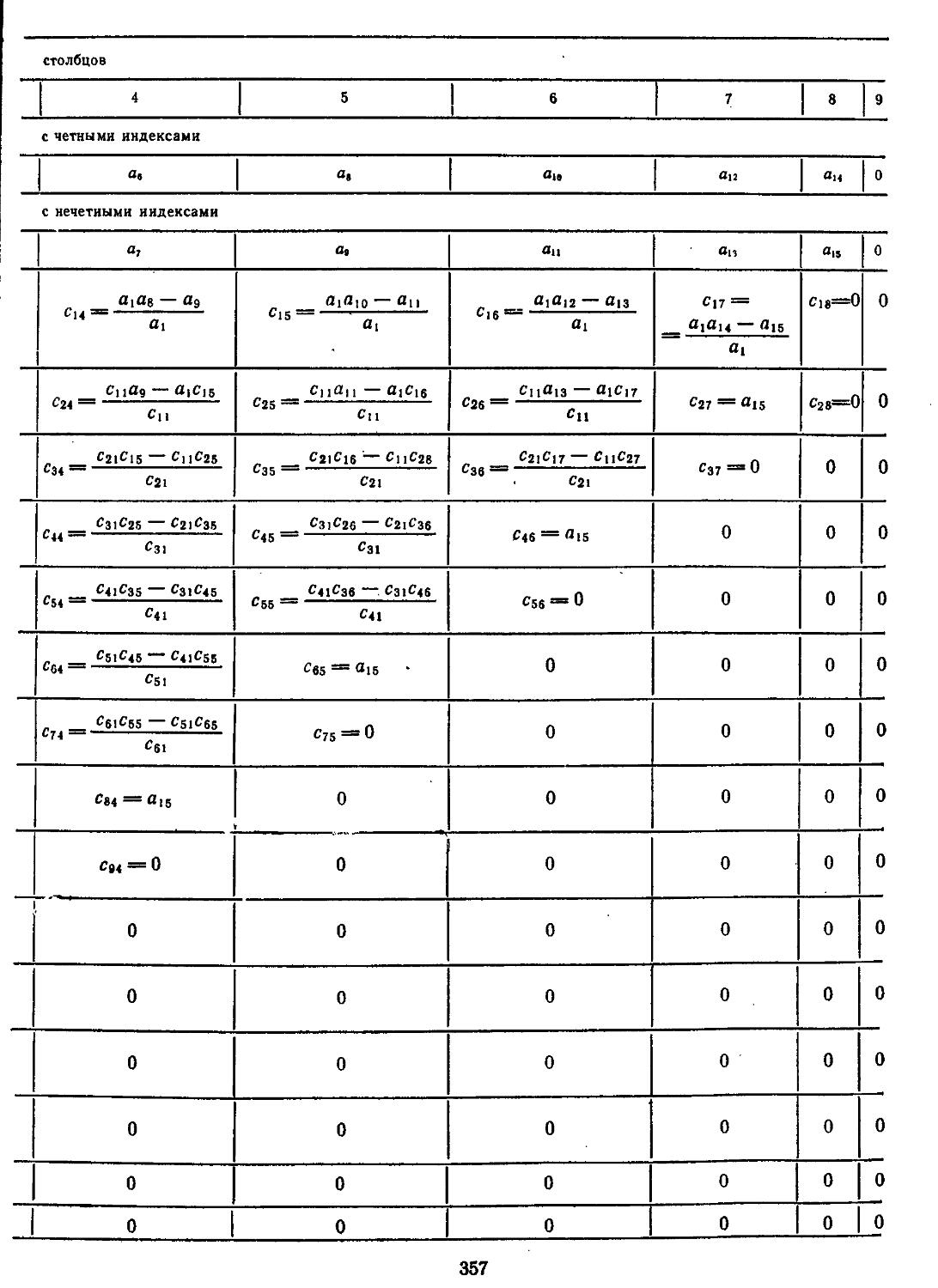
•2. Алгебраические критерии5 устойчивости Гурвица, Рауса, Льеиара — ШипЯра и Шур—Кона 353
3. Частотные критерии
' устойчивости однокон-
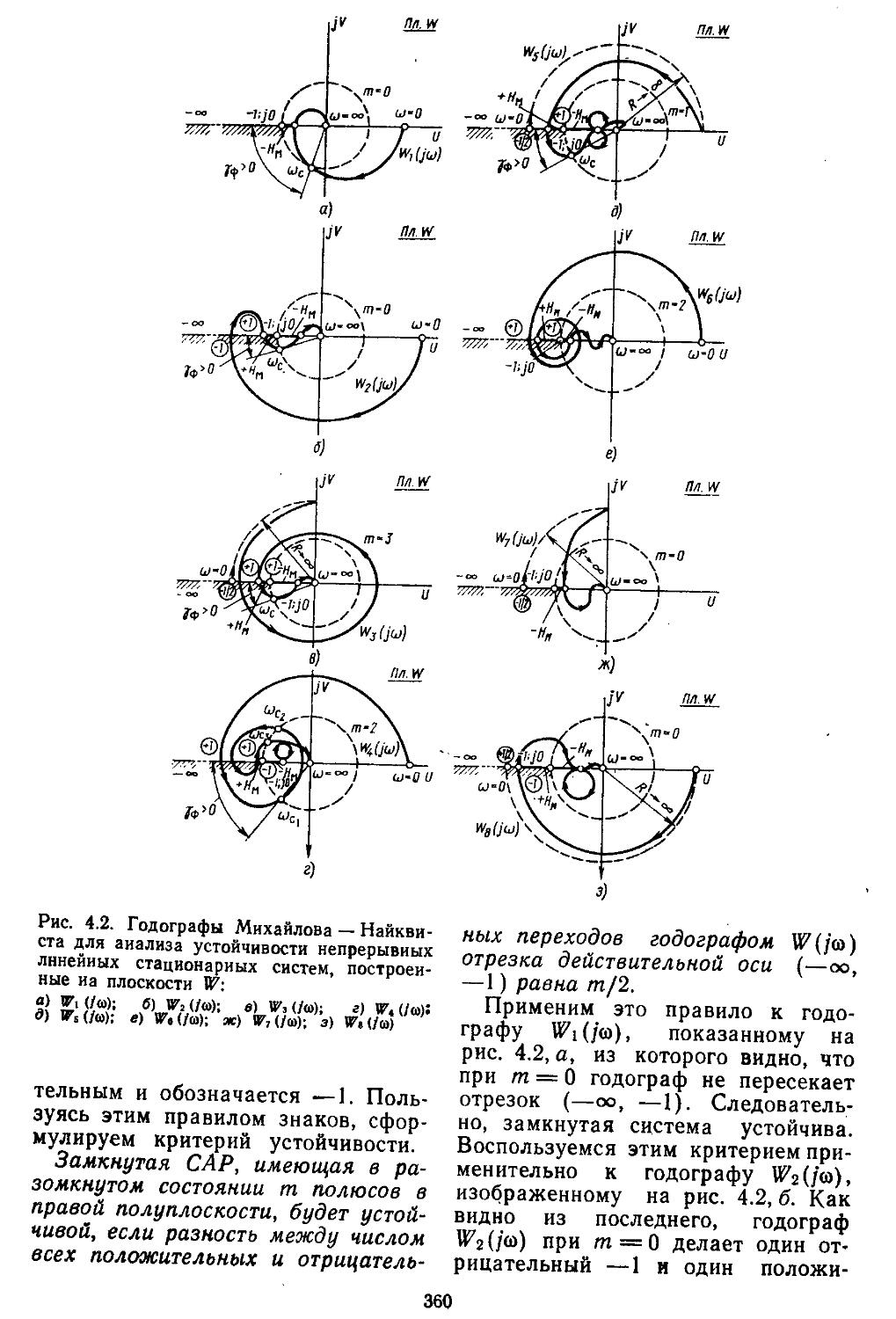
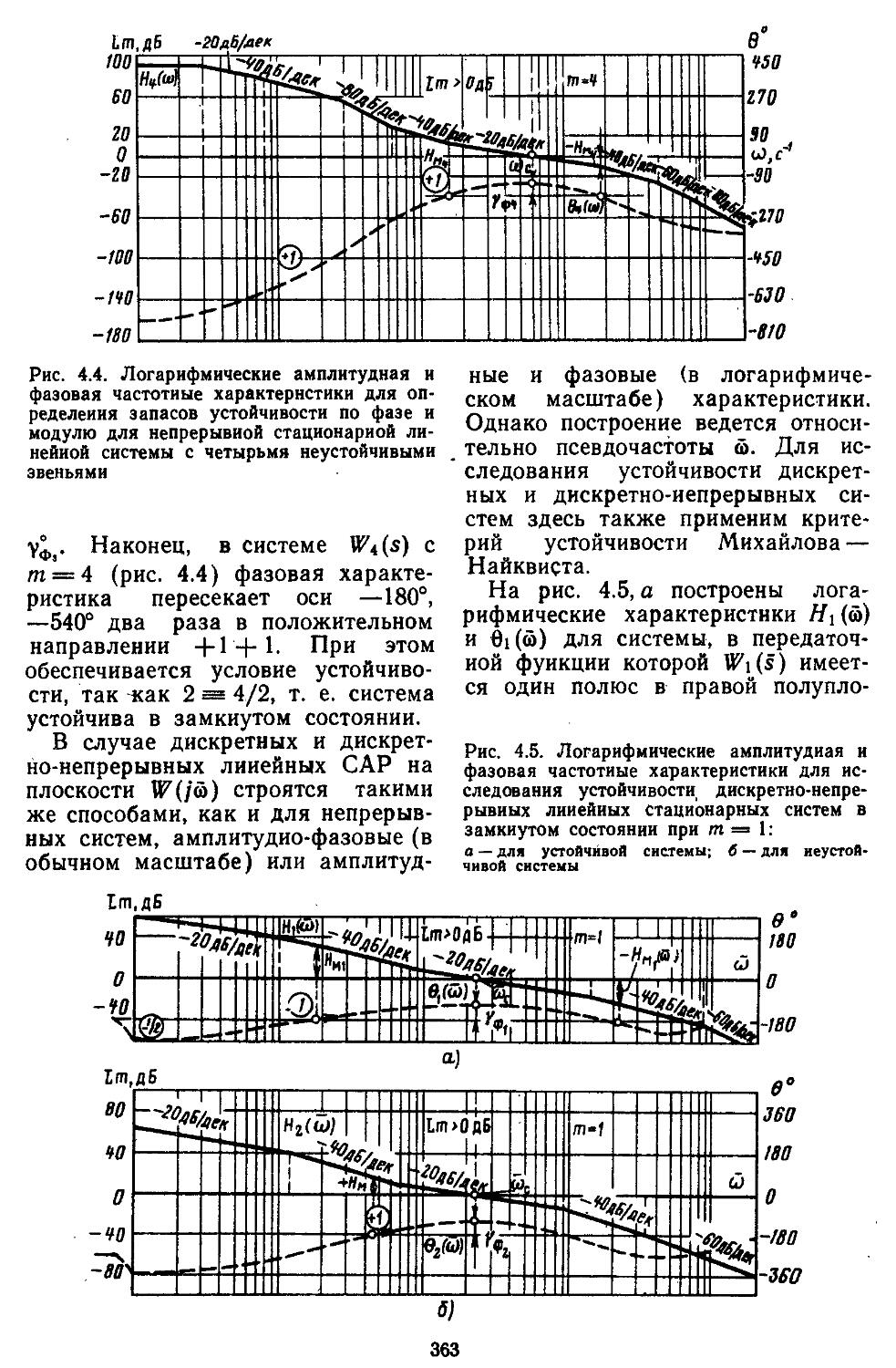
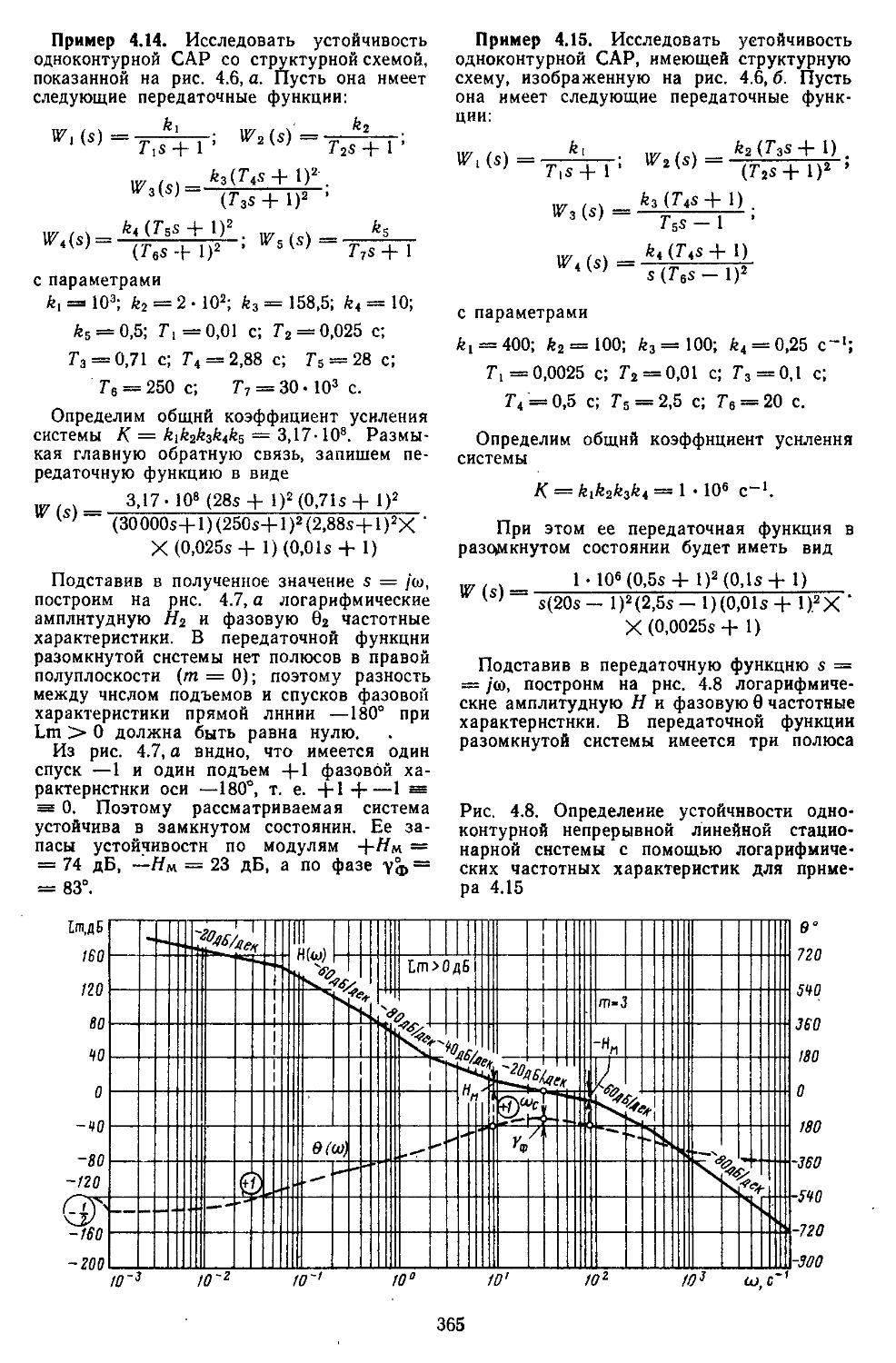
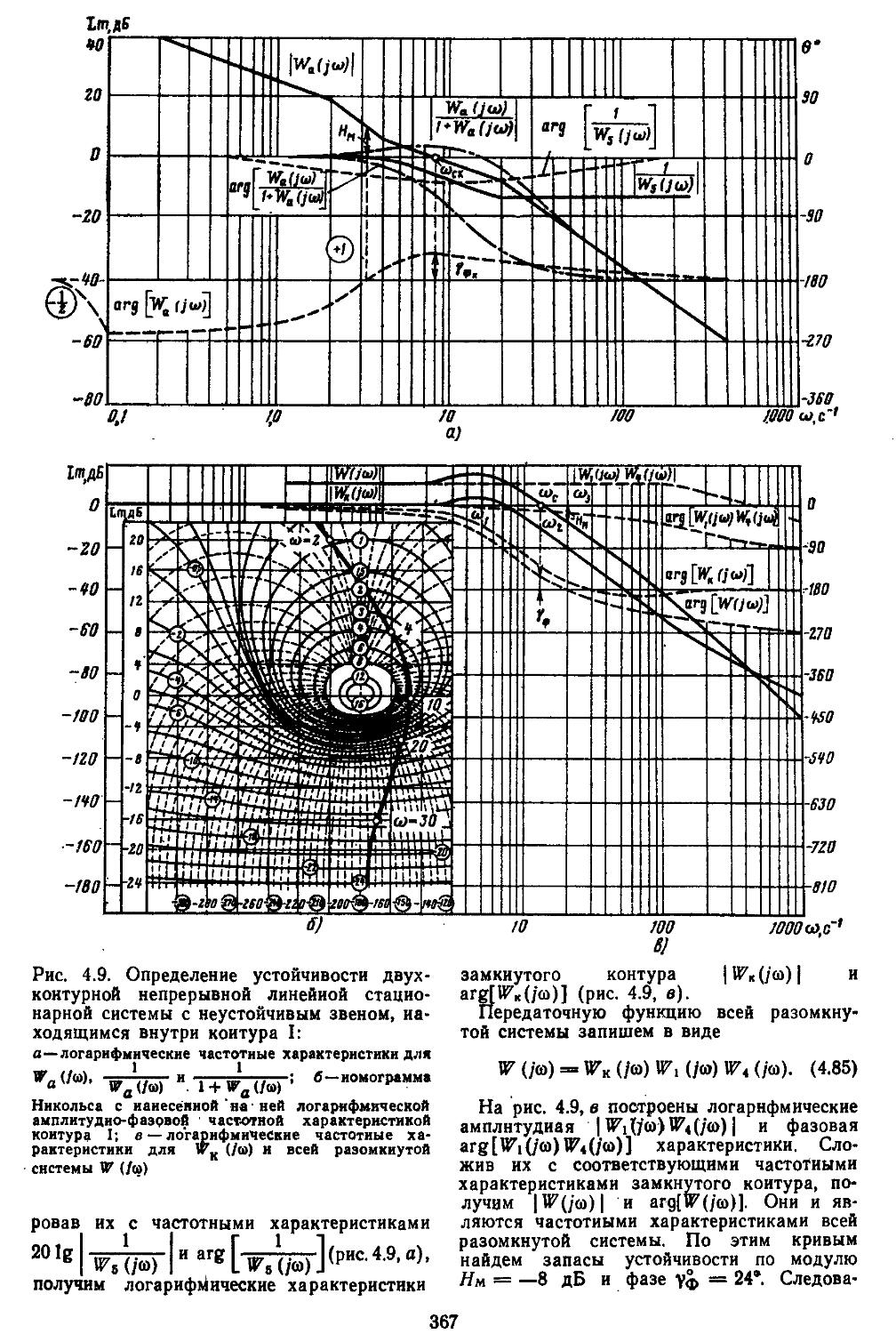
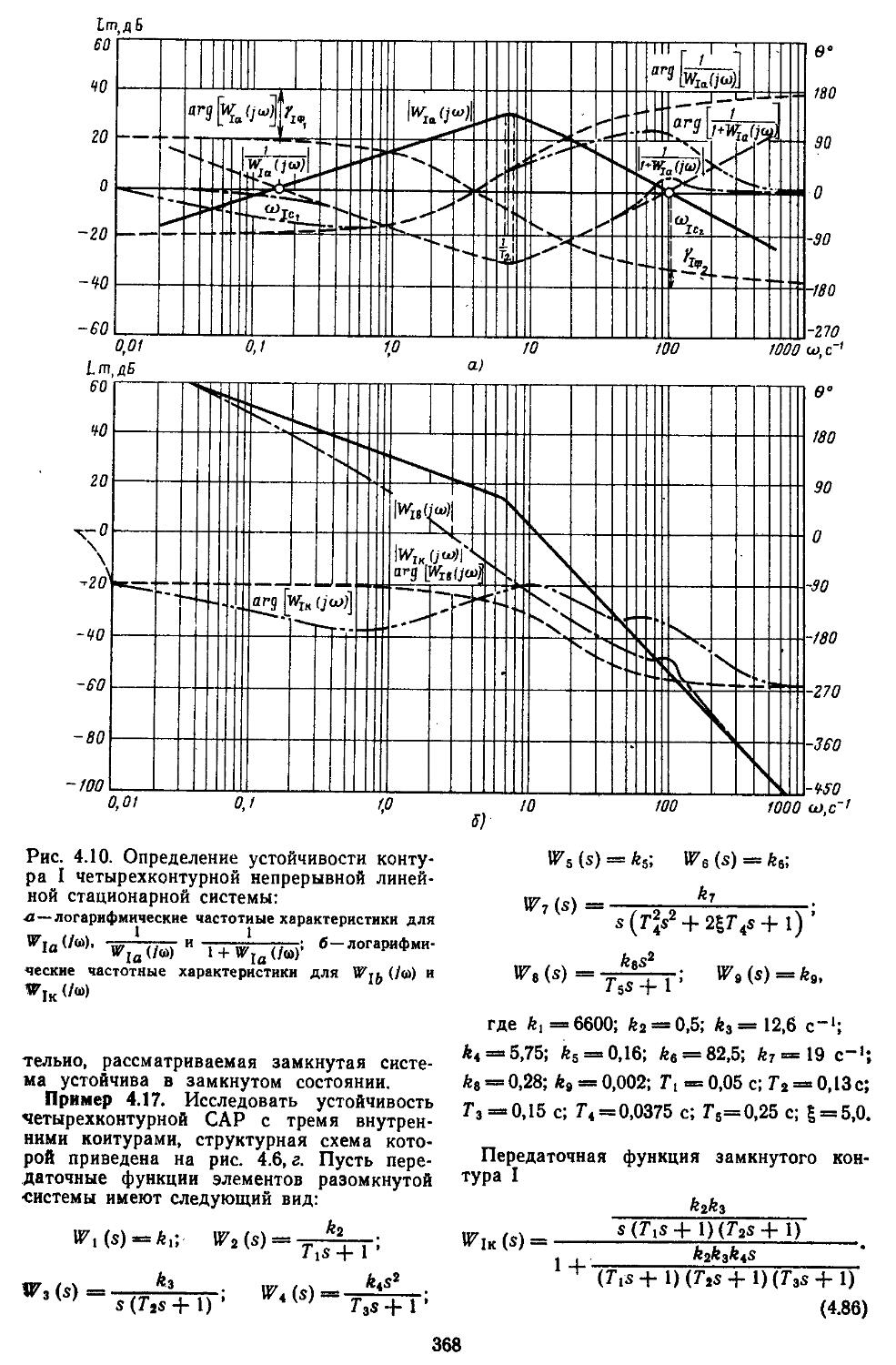
турных САР по Михайлову Найквисту .359
4. Частотные критерии устойчивости миогокон-туриых САР по Михайлову— Найквисту . . 366
5. Частотные критерии
• устойчивости САР с
трансцендентными звеньями по Михайлову —
Найквисту ............372
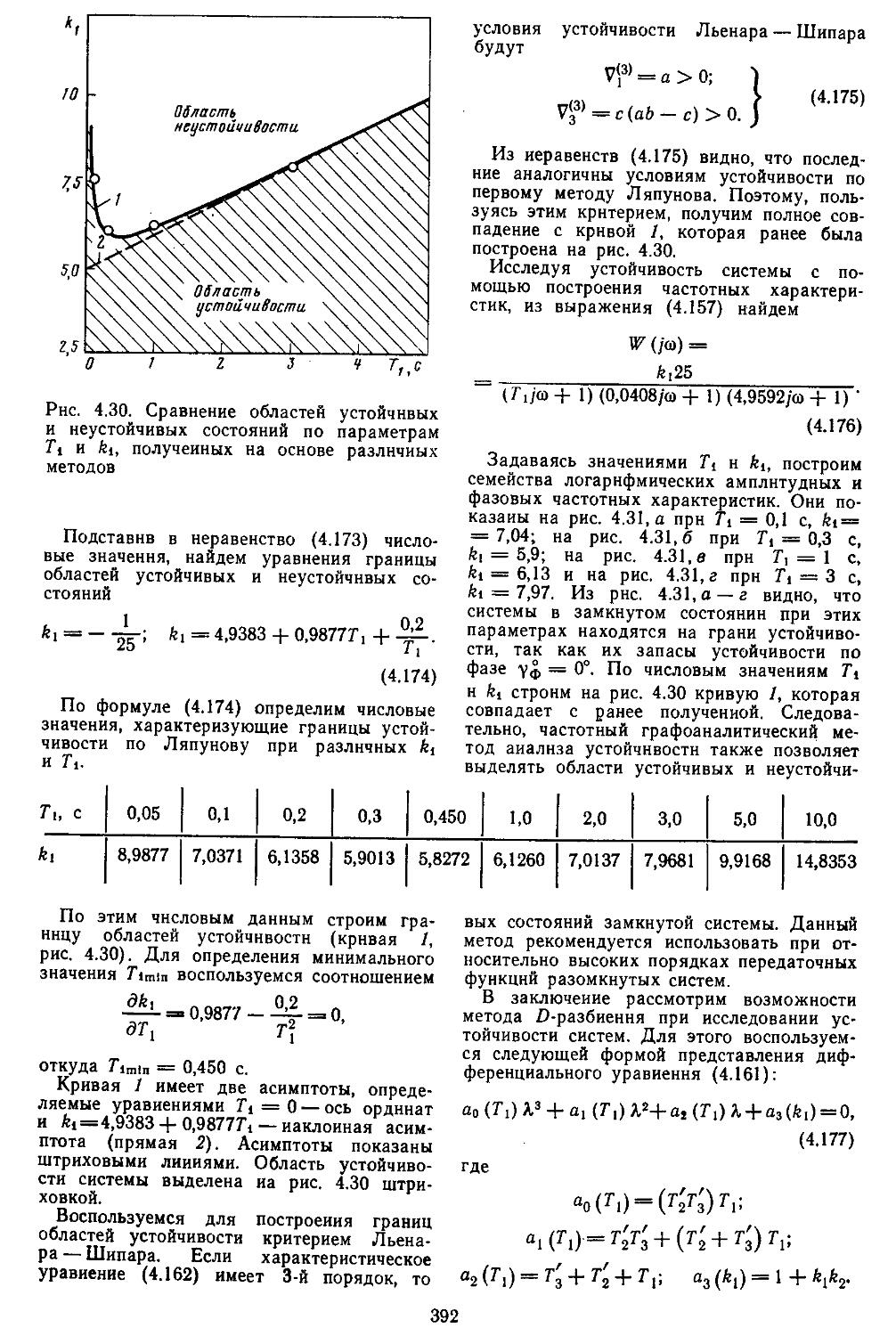
6. Выделение областей устойчивых и неустойчивых состояний и исследование устойчивости систем со слабодемпфи-роваииыми элементами 374
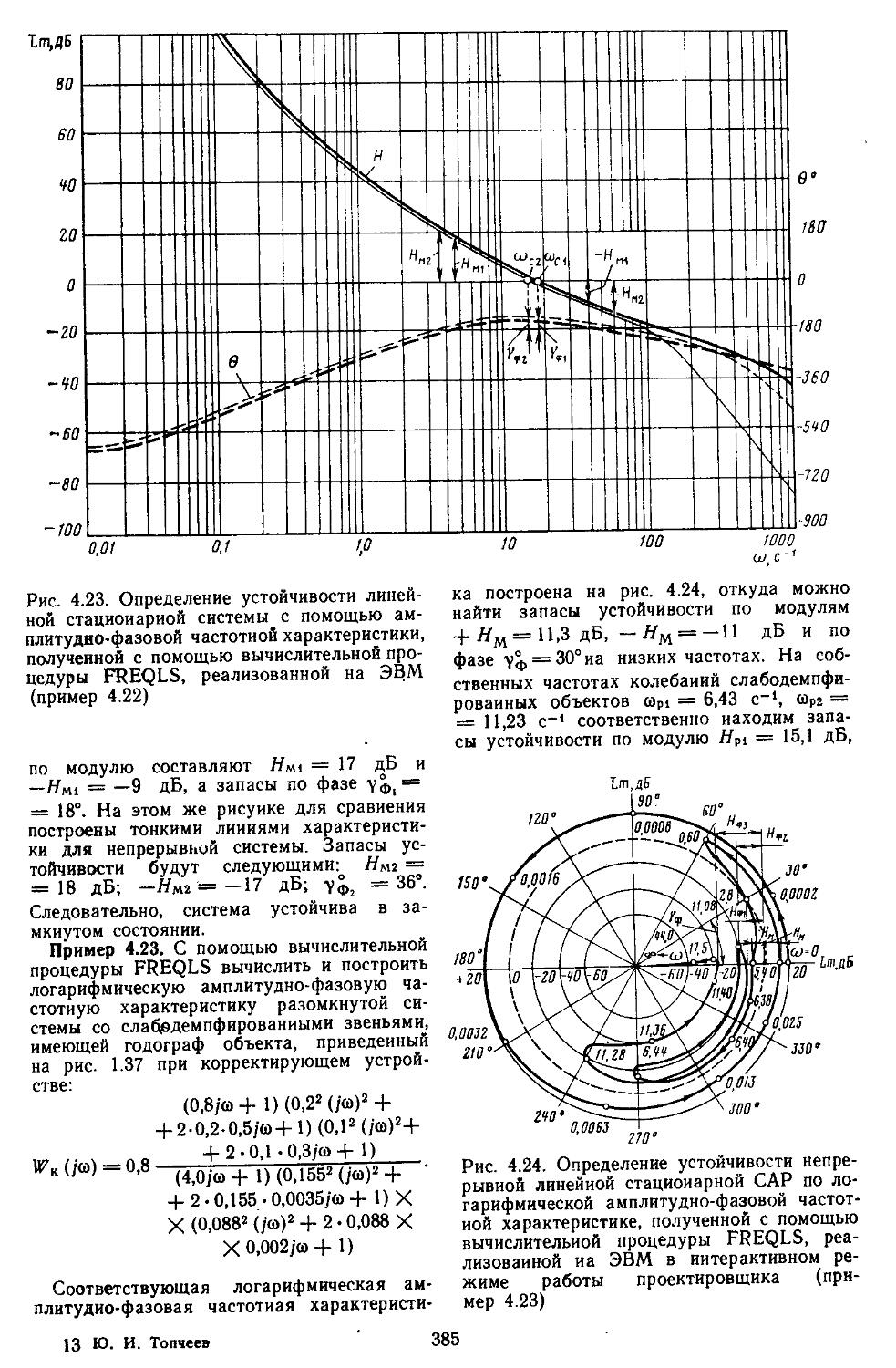
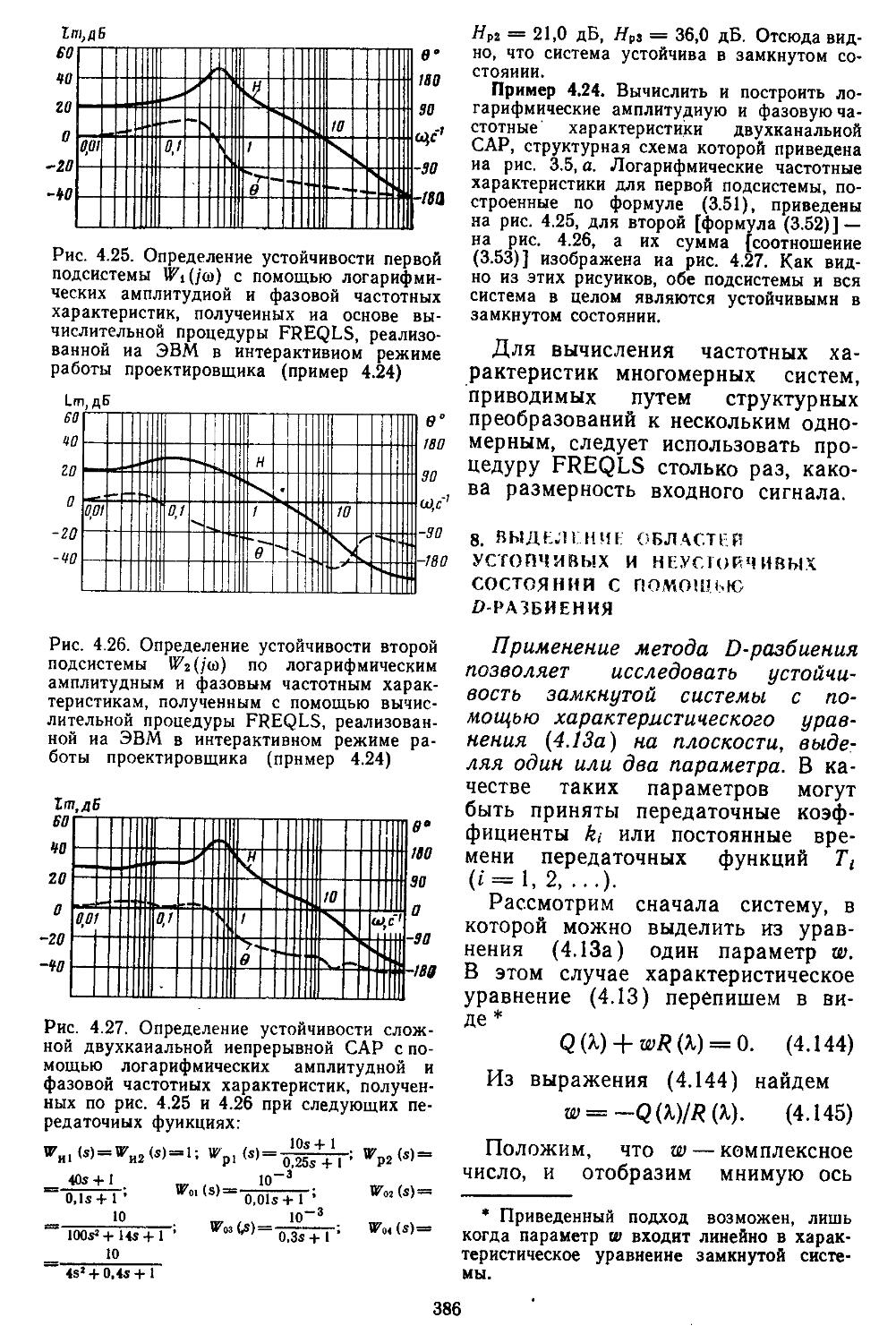
7. Вычислительные процедуры для анализа устойчивости непрерывных и дискретно-непрерывных систем частотными методами.............. 382
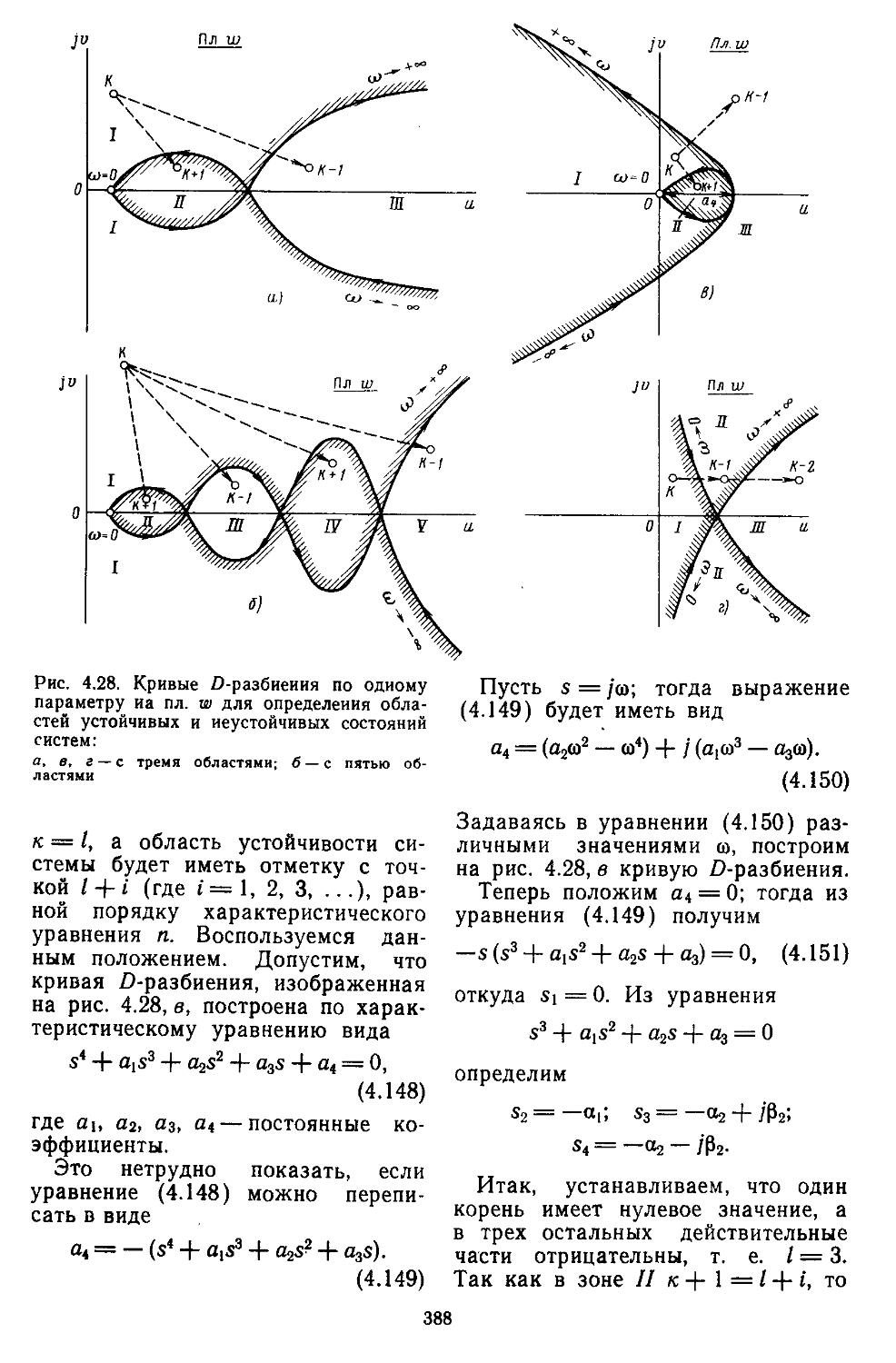
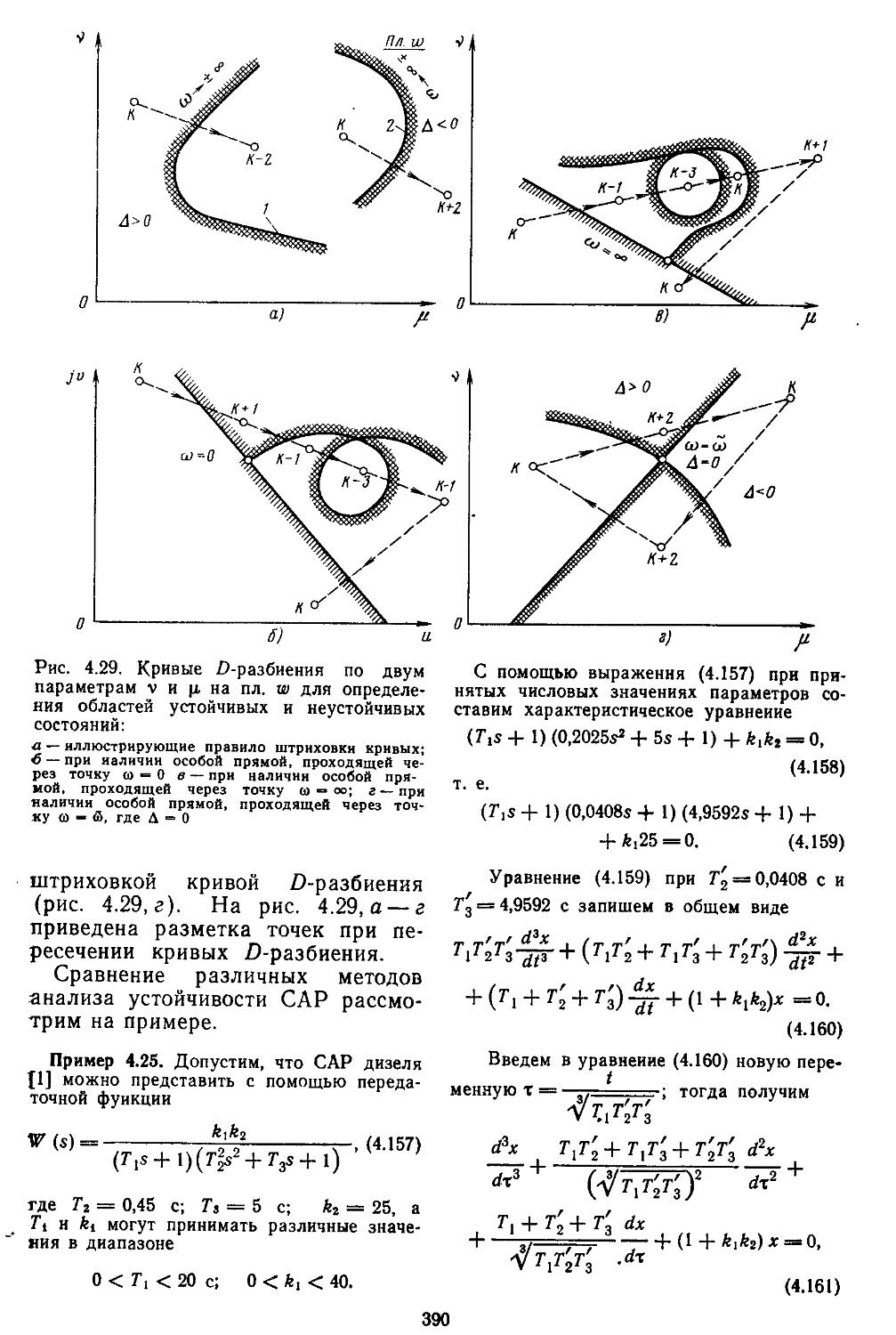
8. Выделение областей устойчивых и неустойчивых состояний с помощью D-разбиеиия . 386
9. Анализ устойчивости нестационарных линейных систем, основанный на рядах Неймаиа и интегральных уравнениях Вольтерра 1 -го рода -. 397
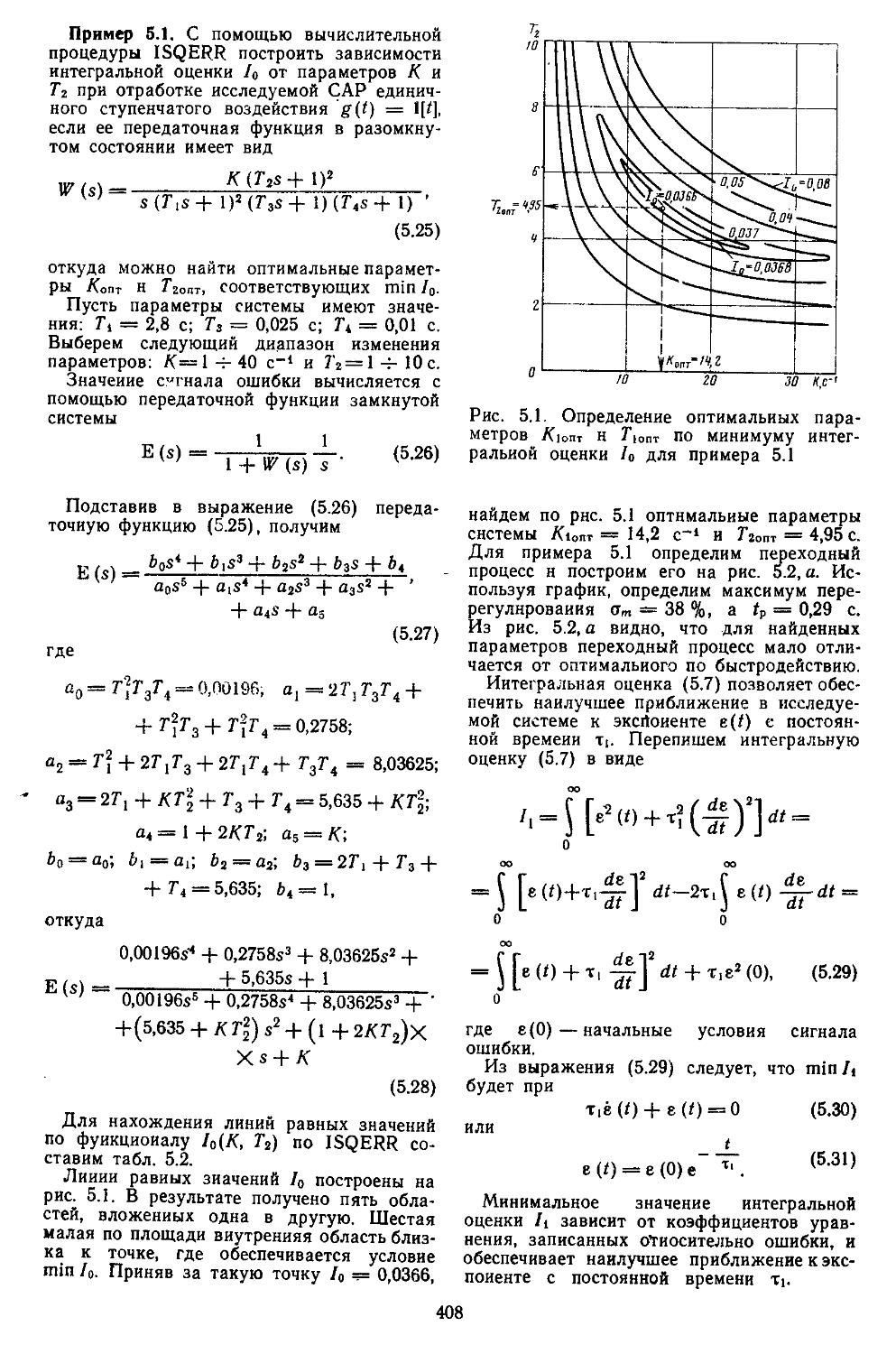
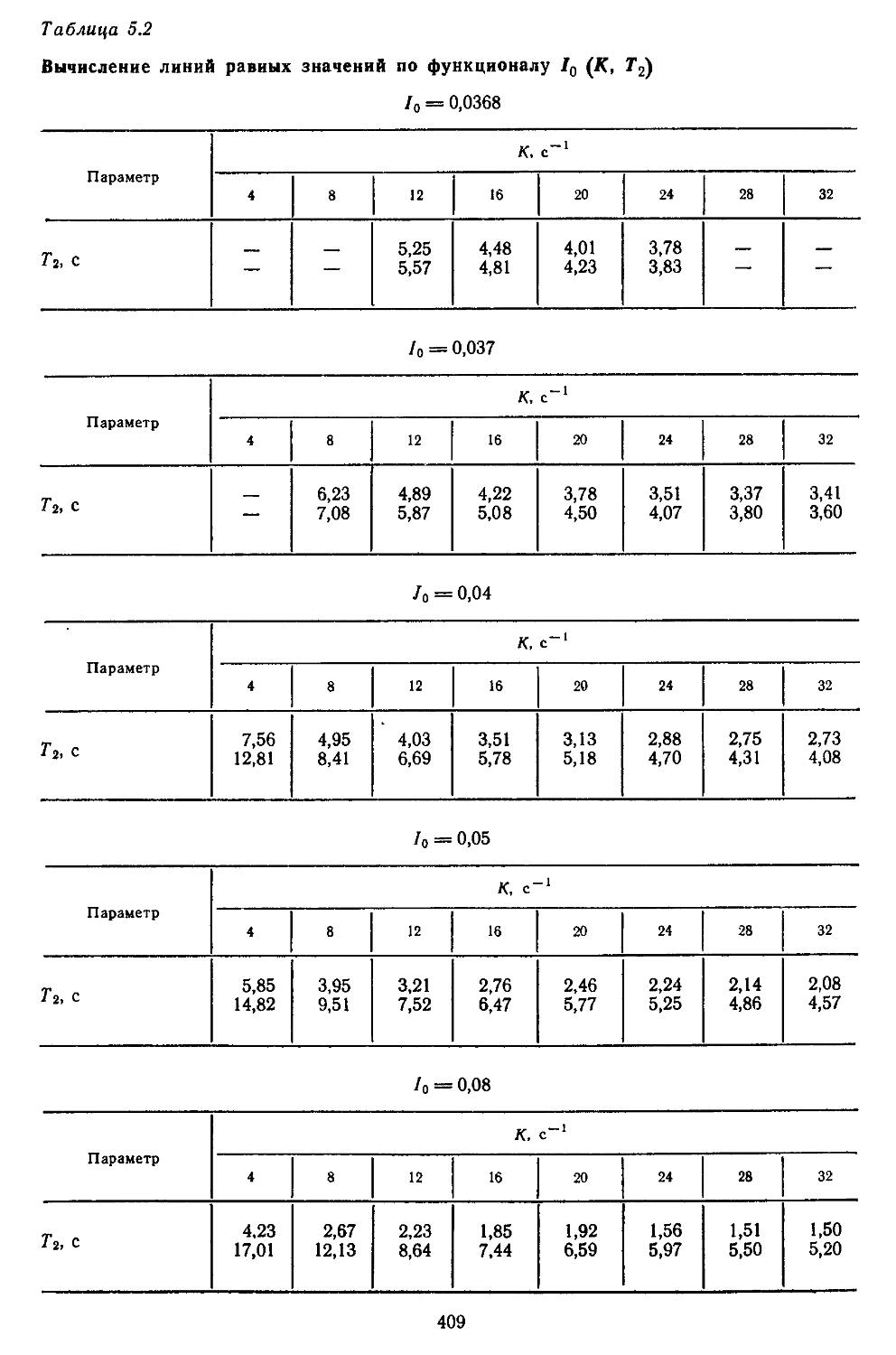
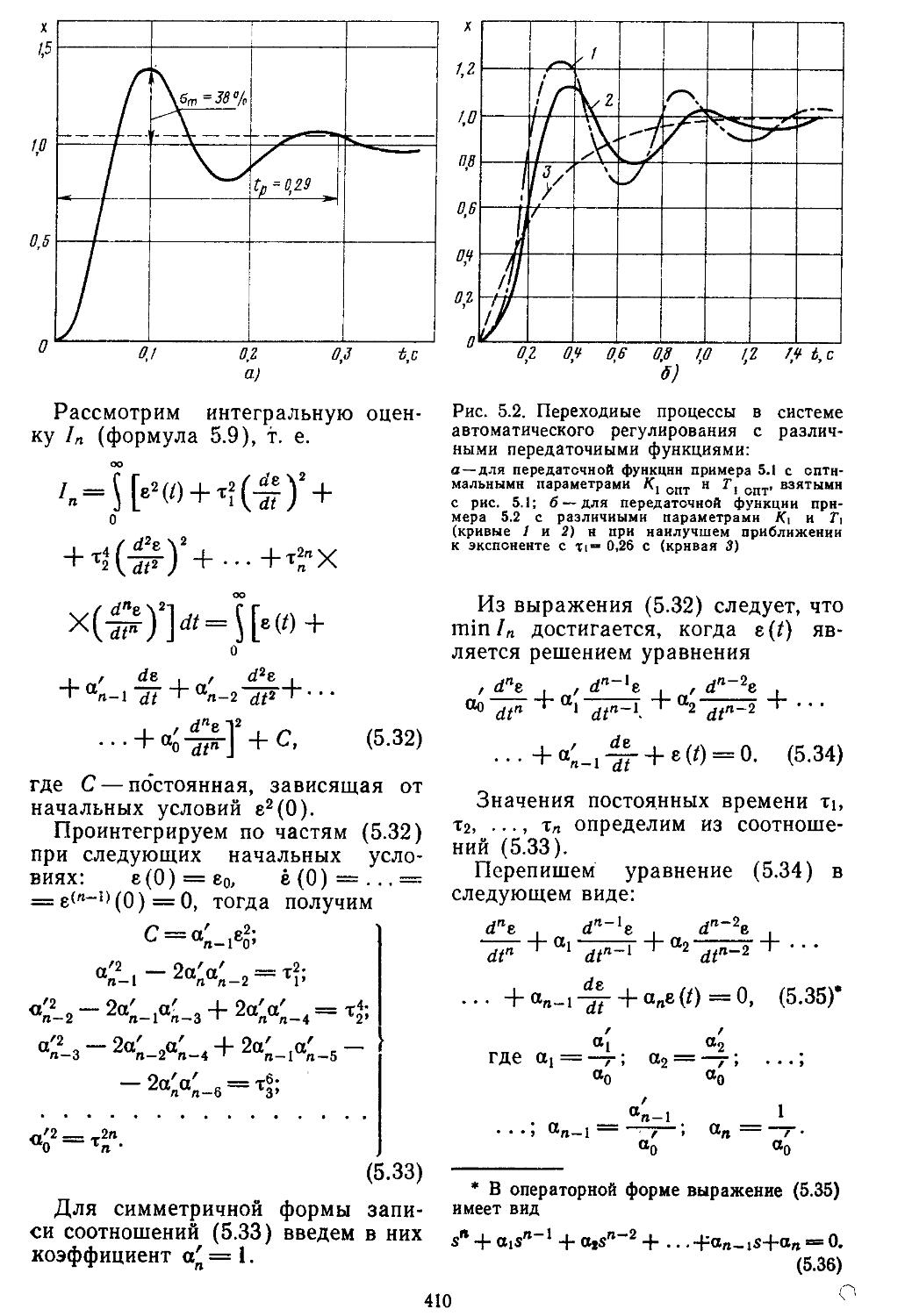
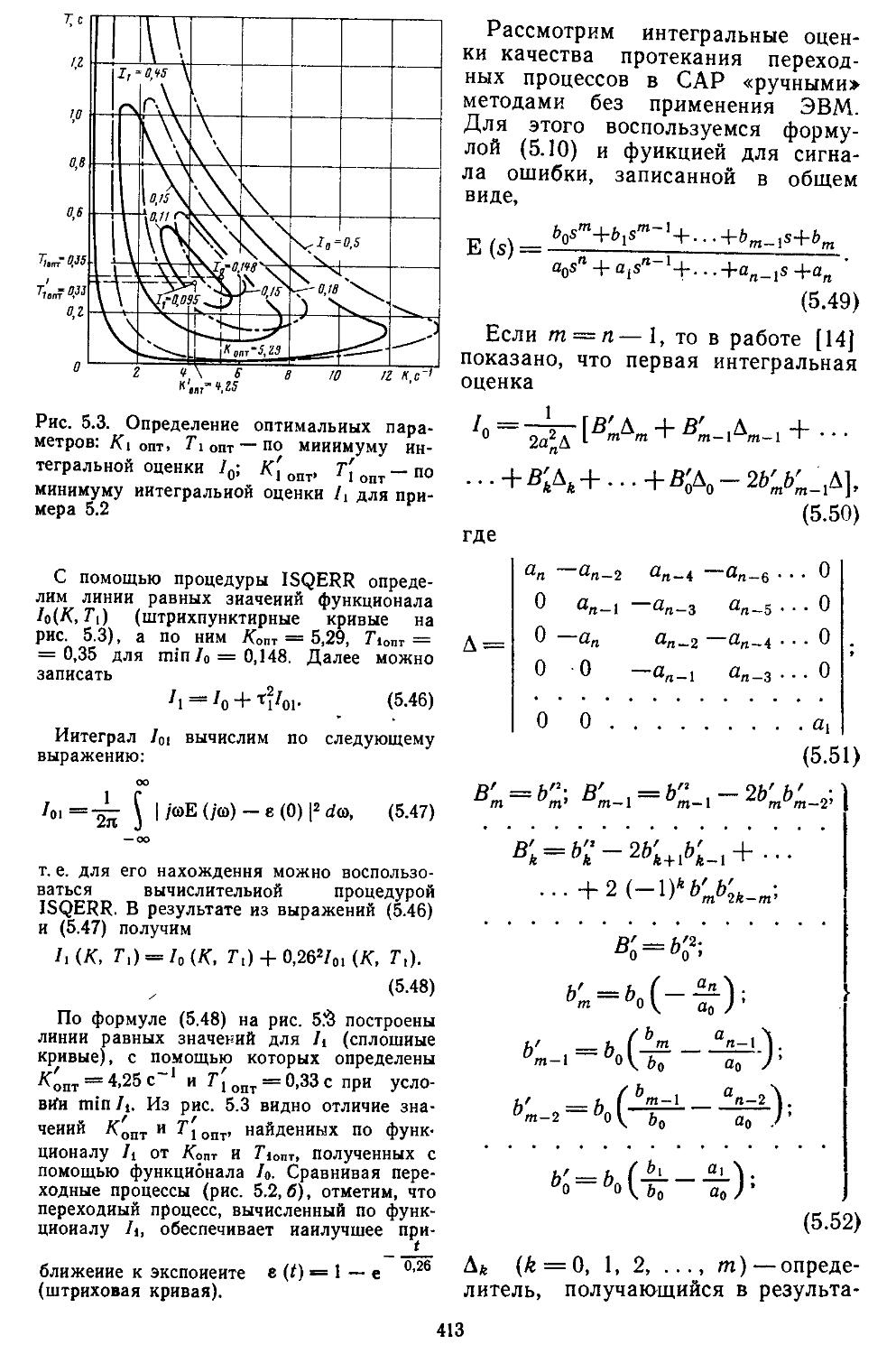
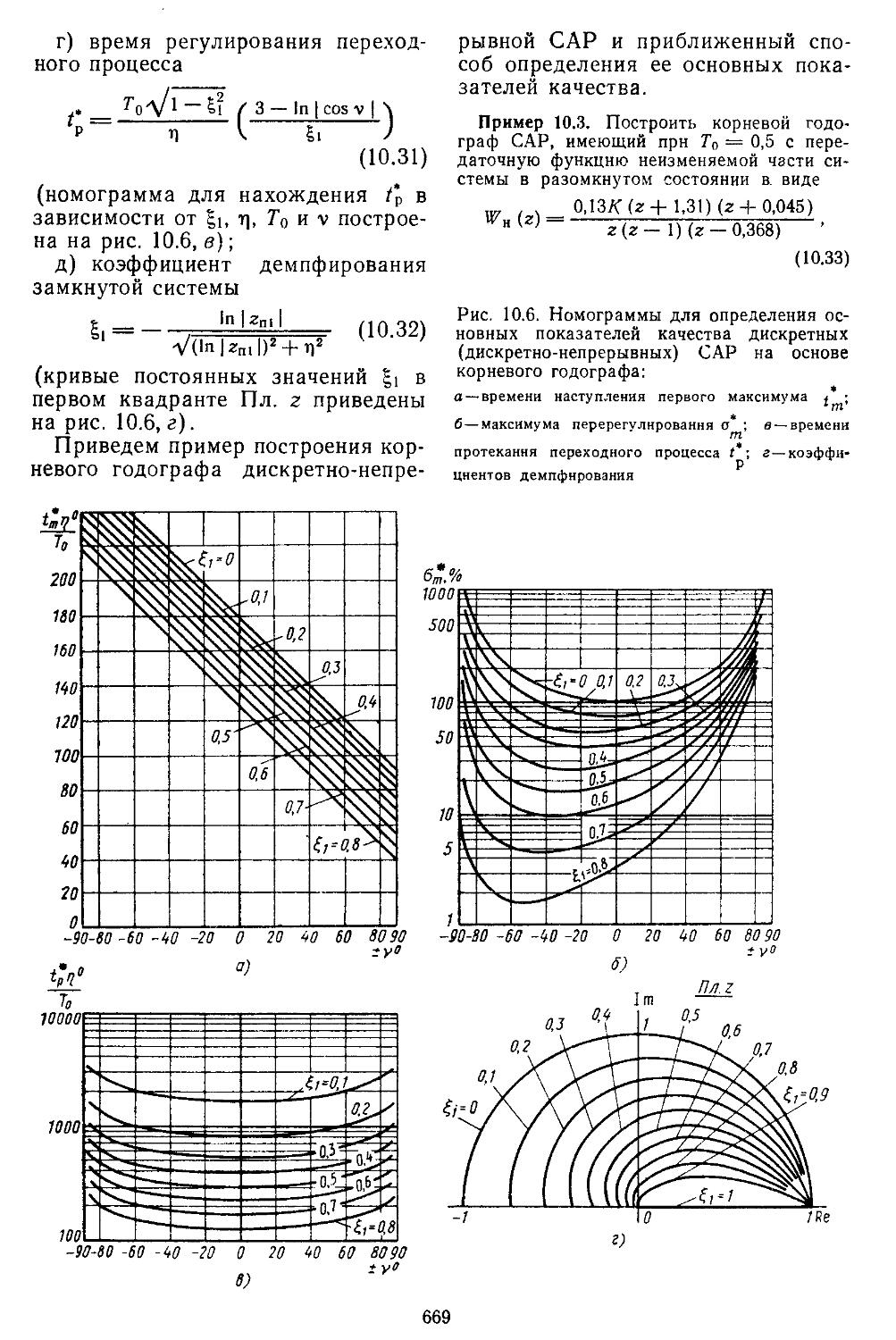
Глава 5. Исследование качества непрерывных и дискретно-непрерывных систем автоматического регулирования 403
1. Интегральные оценки качества ...... 405
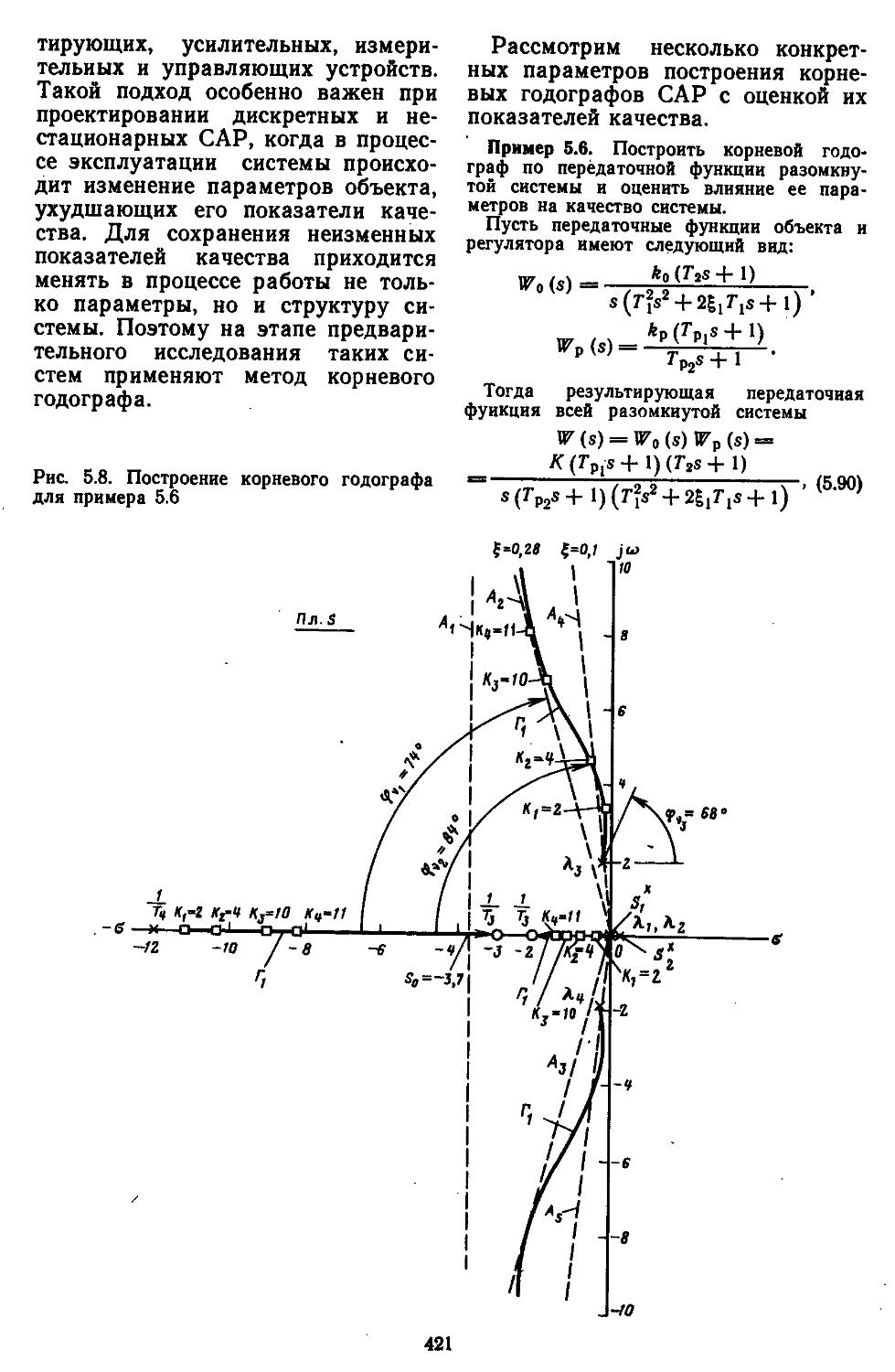
2. Метод корневого годографа ..................416
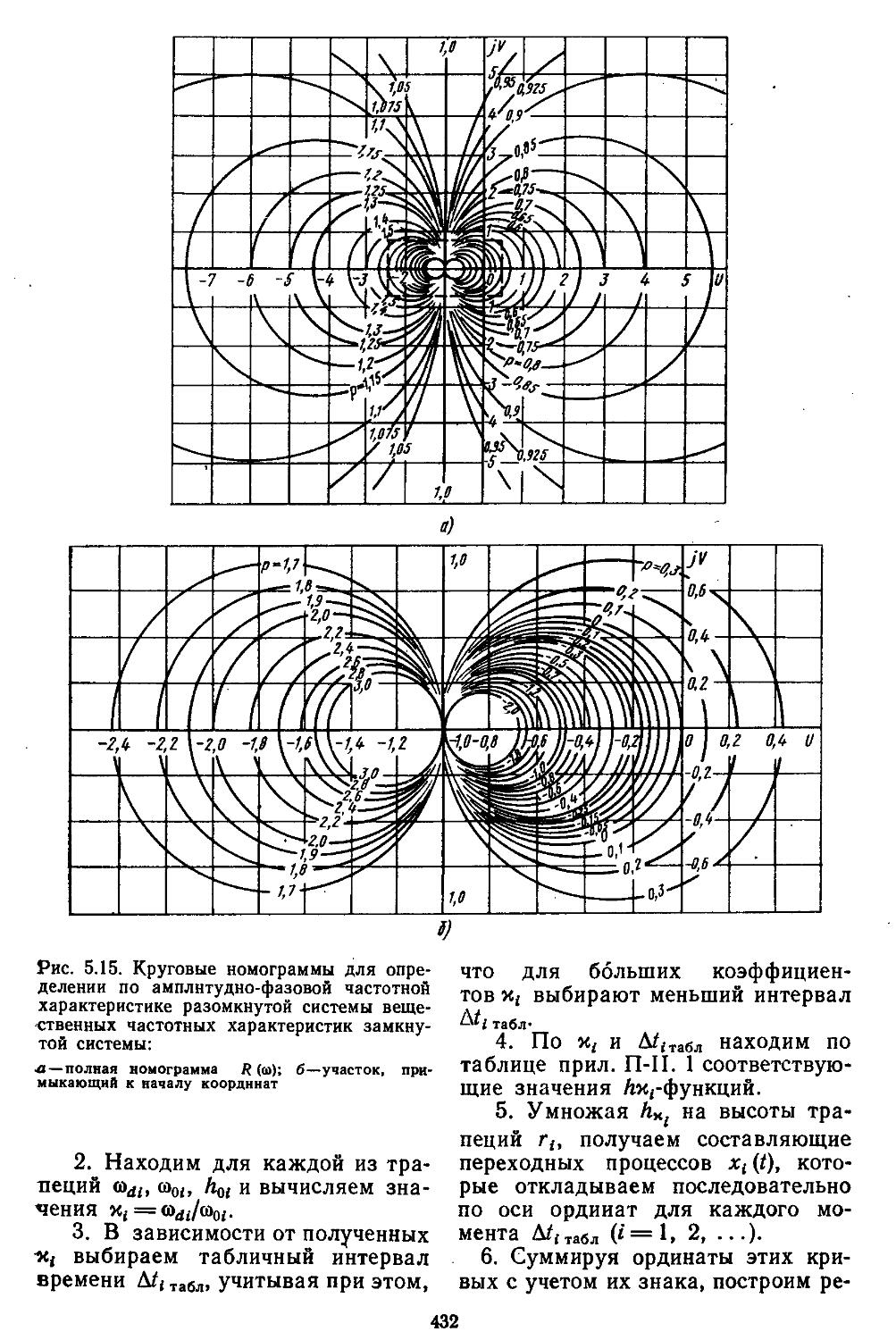
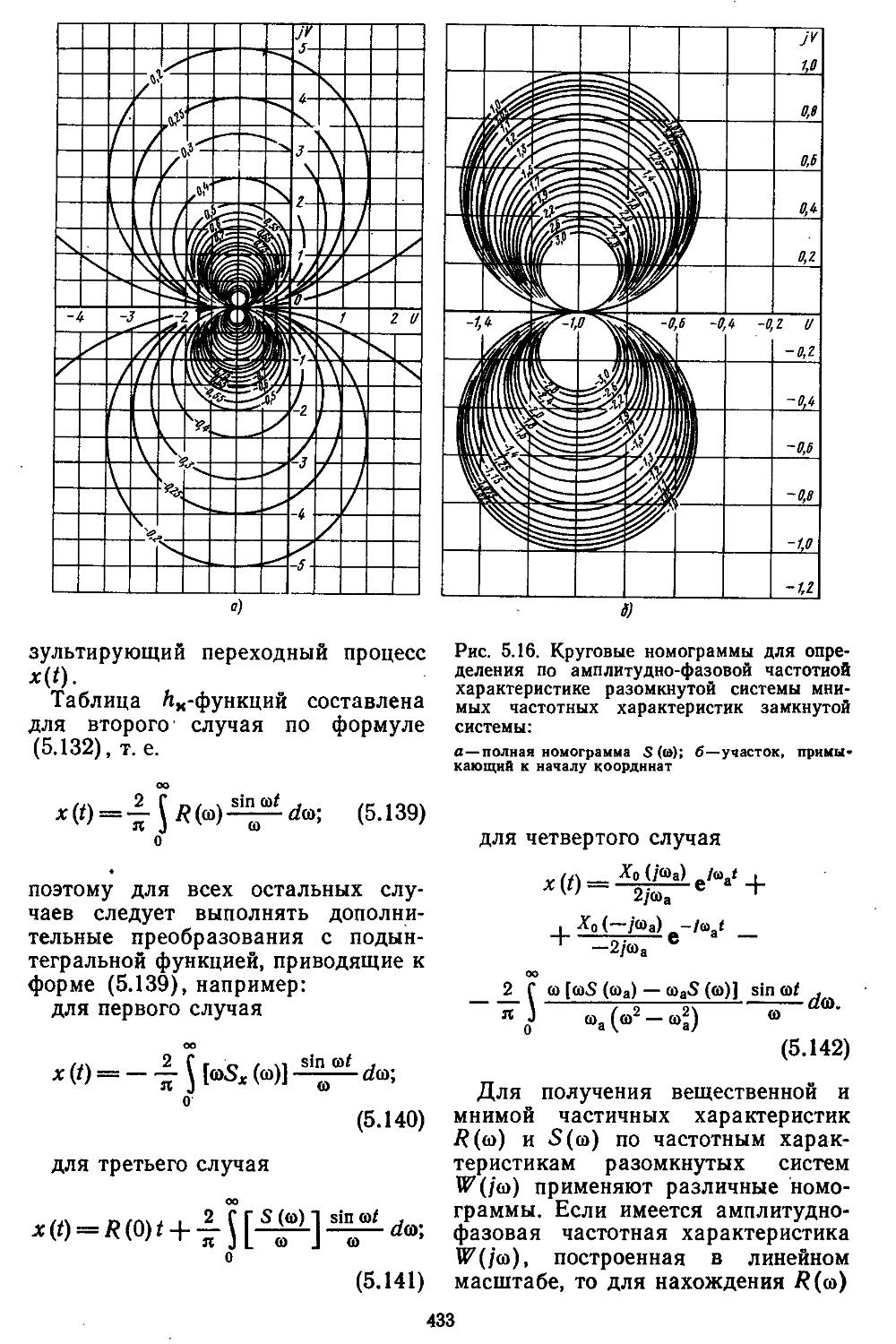
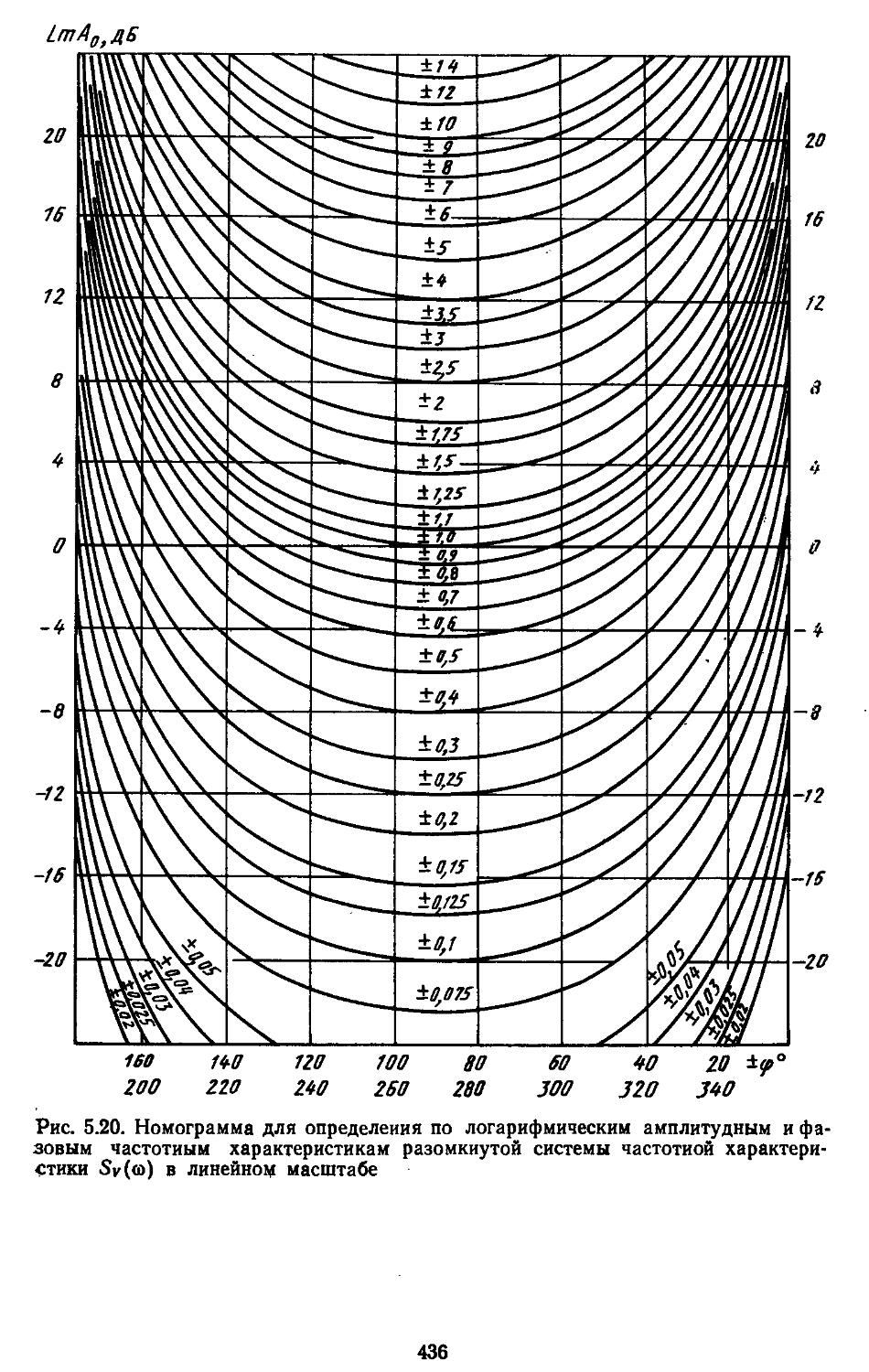
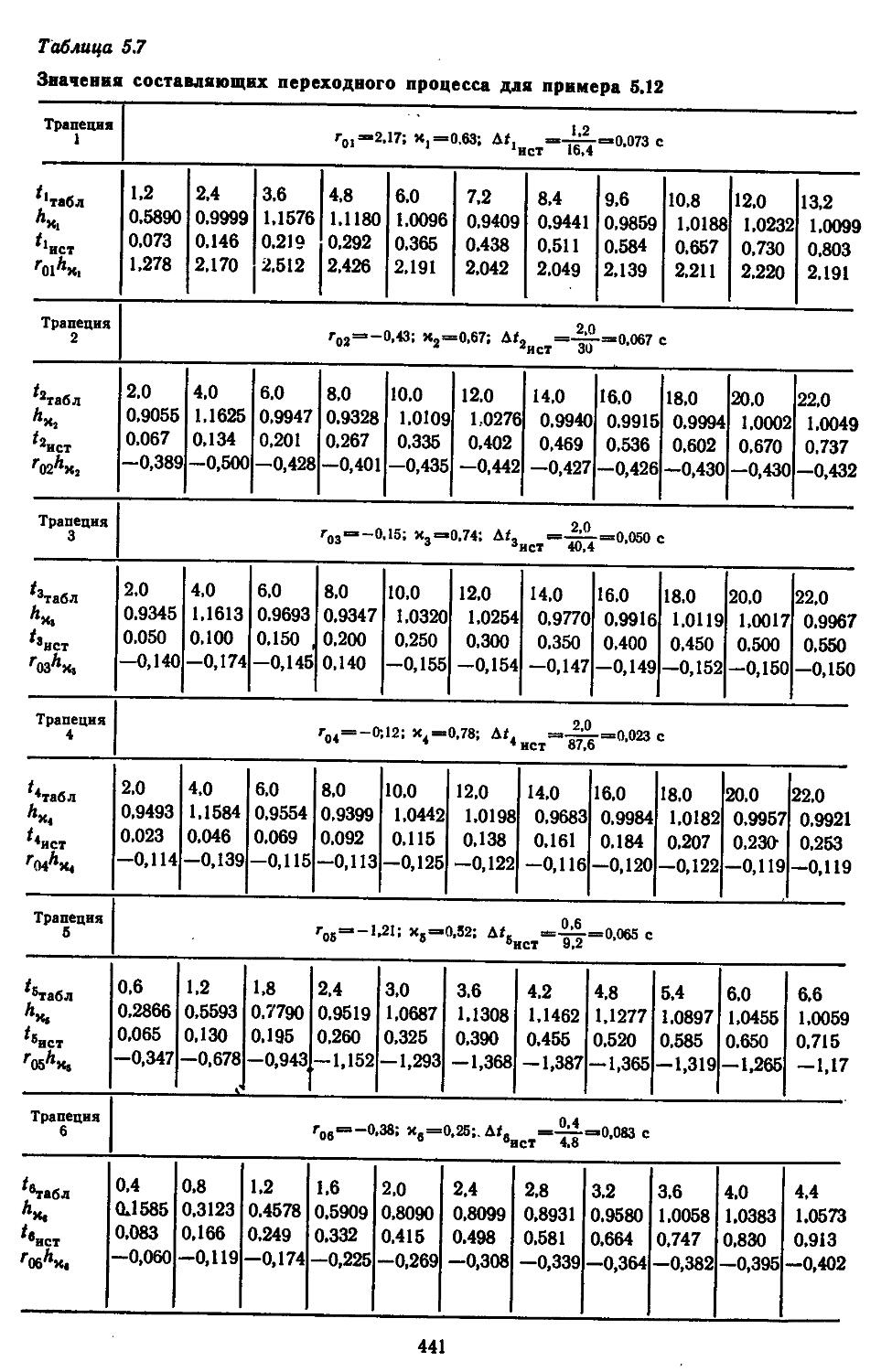
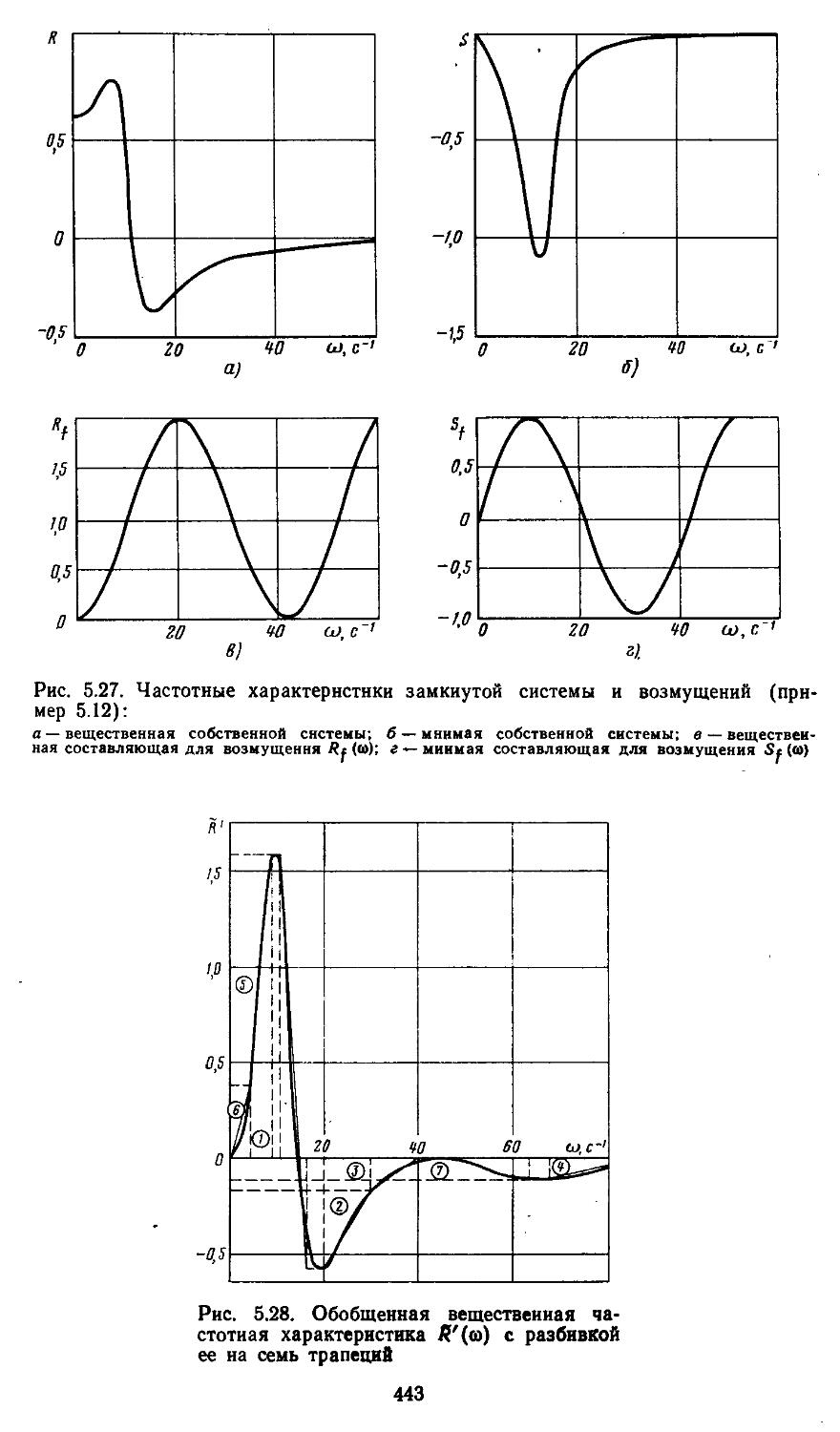
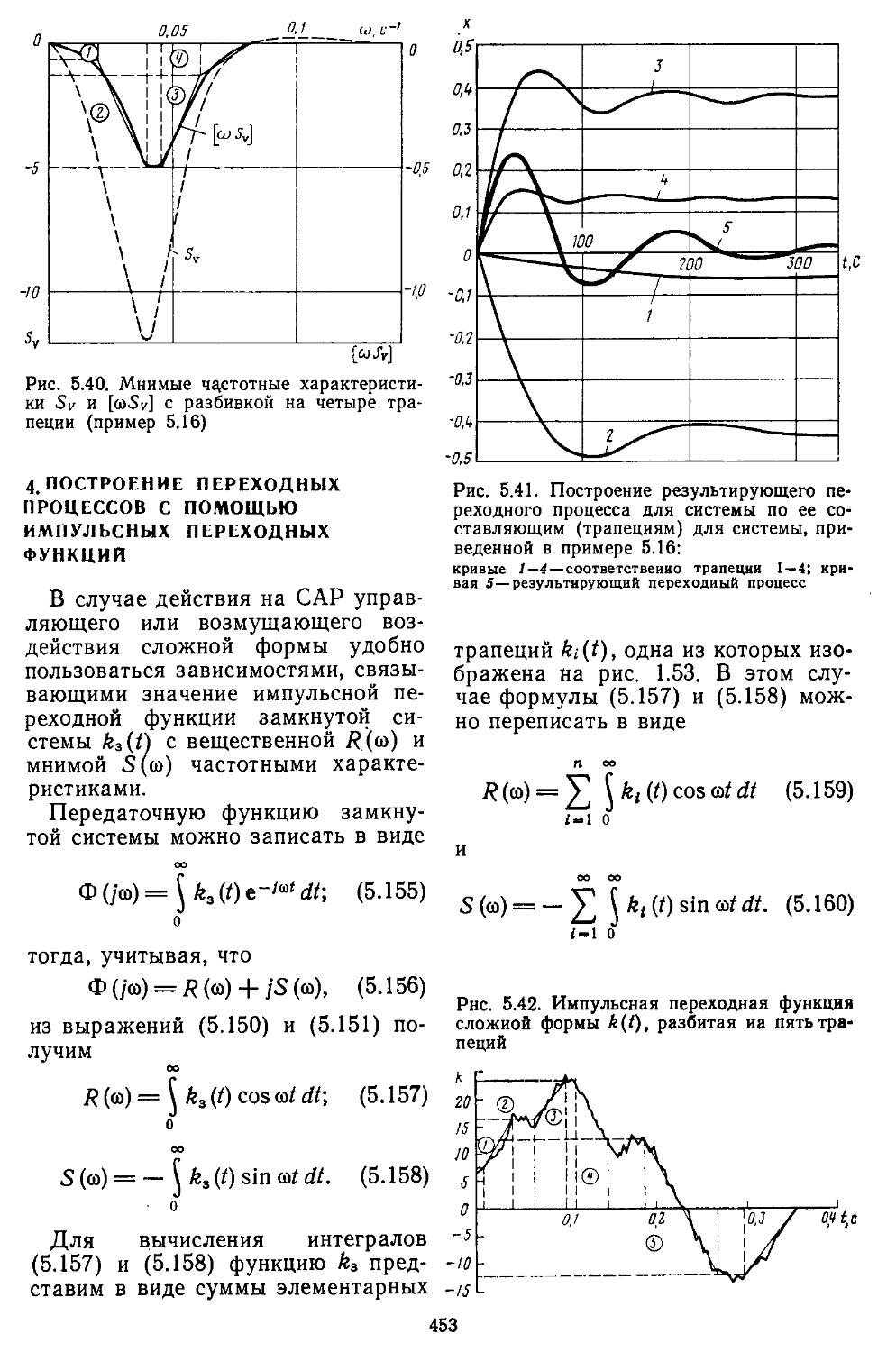
3. Построение переходных процессов с помощью вещественных или мнимых частотных характеристик замкнутых систем с помощью Лх-фуик-ций......................429
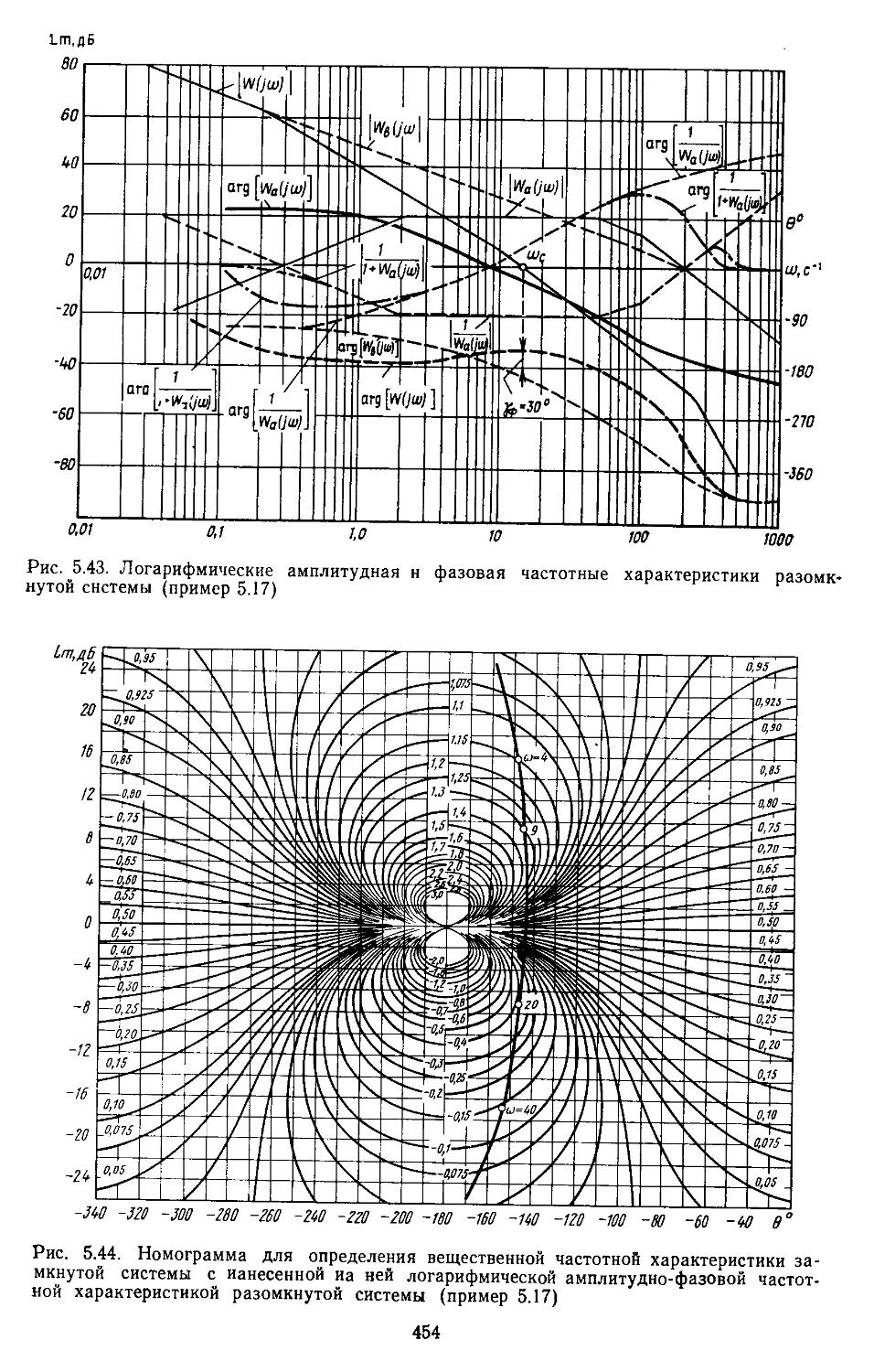
4. Построение переходных процессов с помощью импульсных переходных функций ...... 453
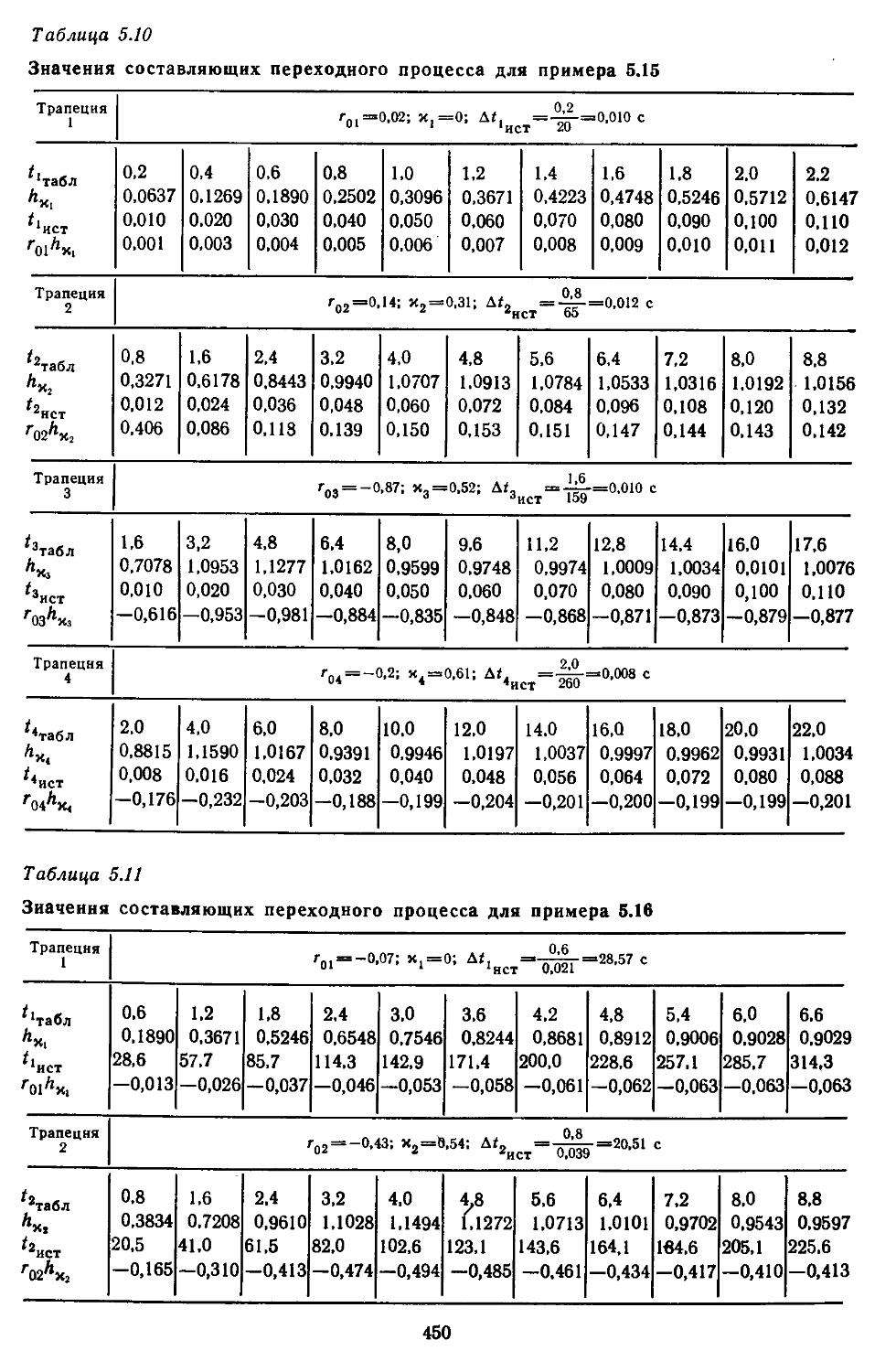
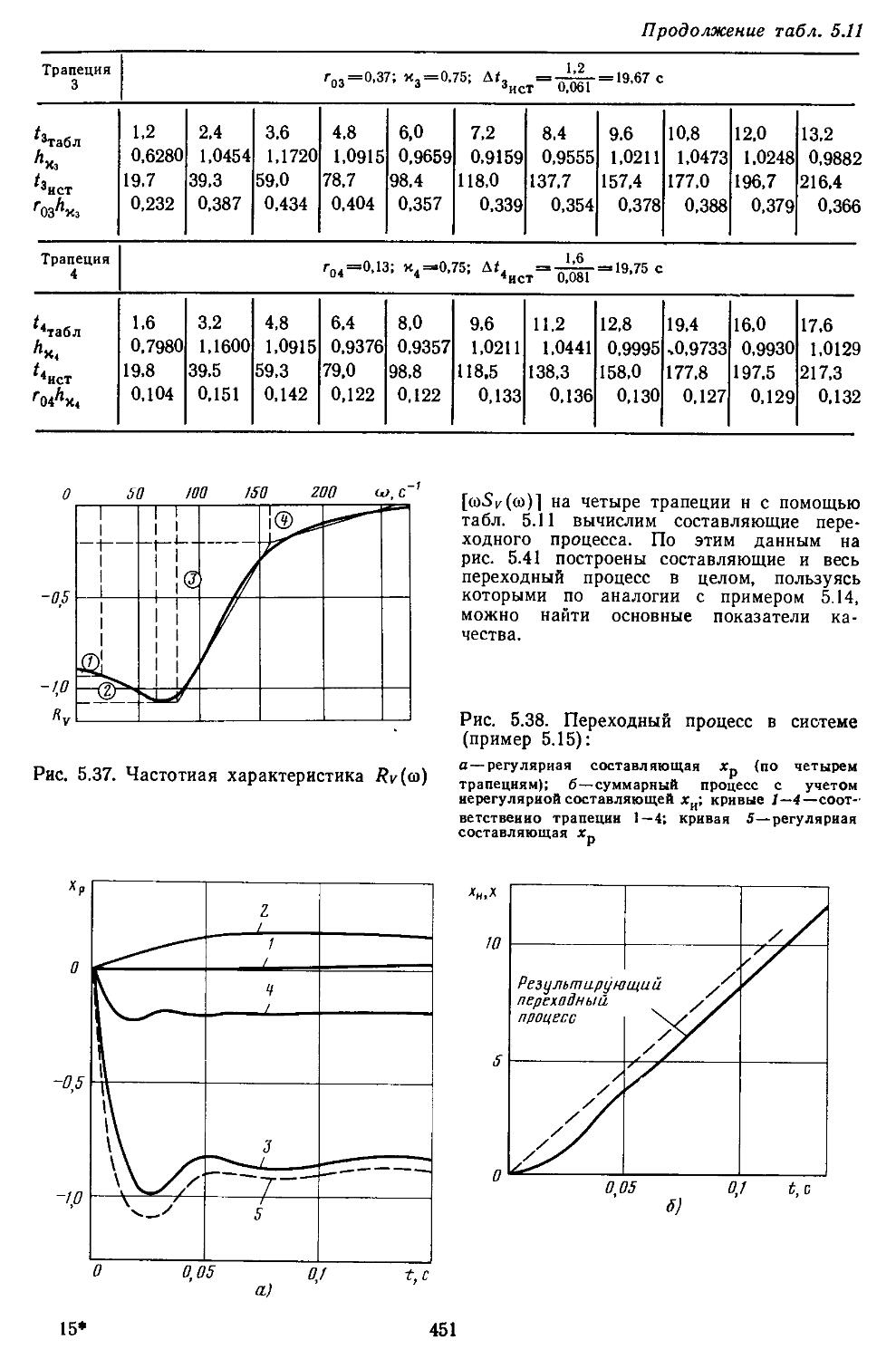
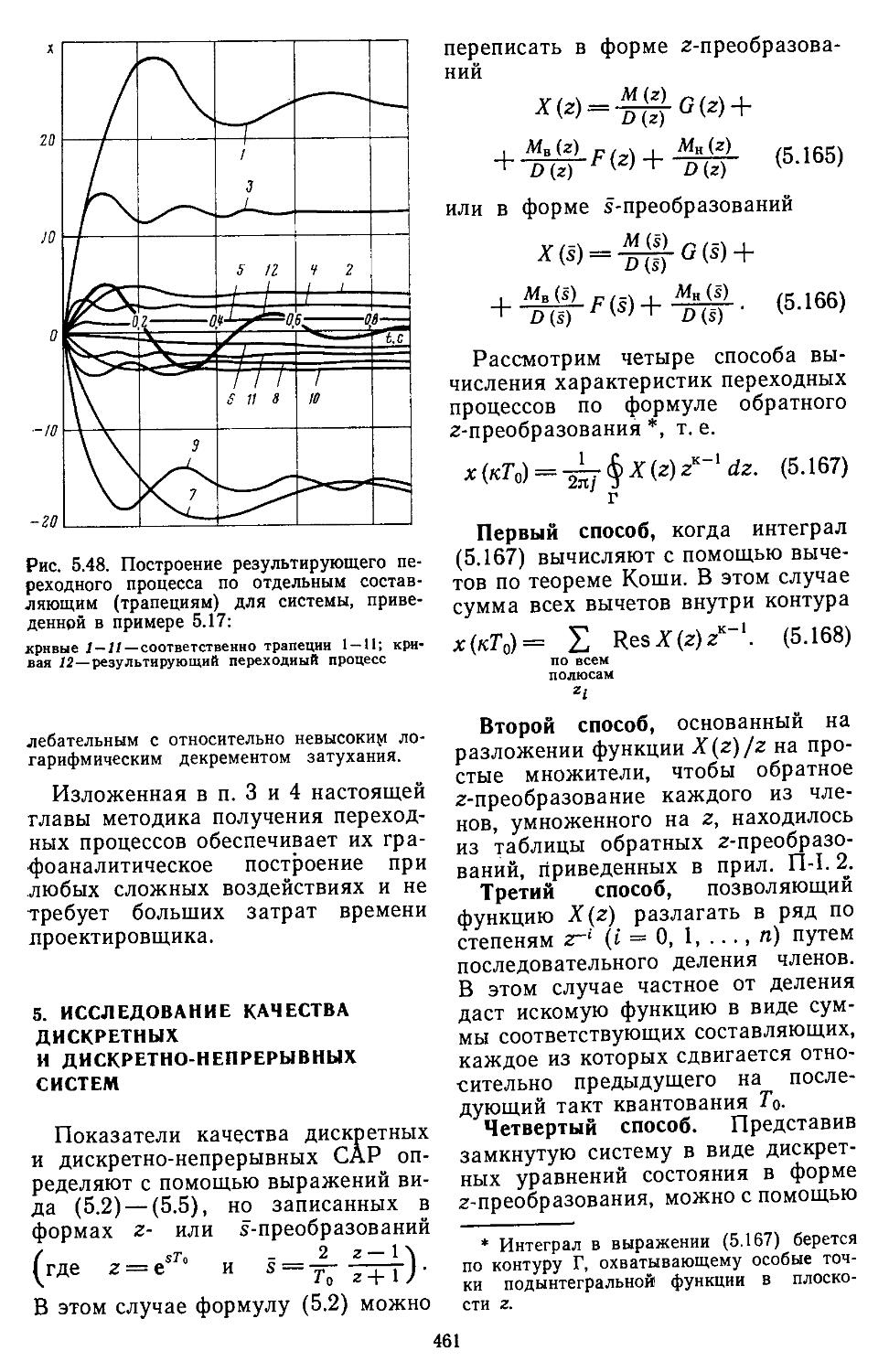
5. Исследование качества дискретных и дискретно-непрерывных систем 461
6. Определение переходных процессов нестационарных линейных САР 465
7. Построение переходных процессов в системах с помощью вычислительной процедуры, реали-
, . зоваииой иа ЭВМ . . 466
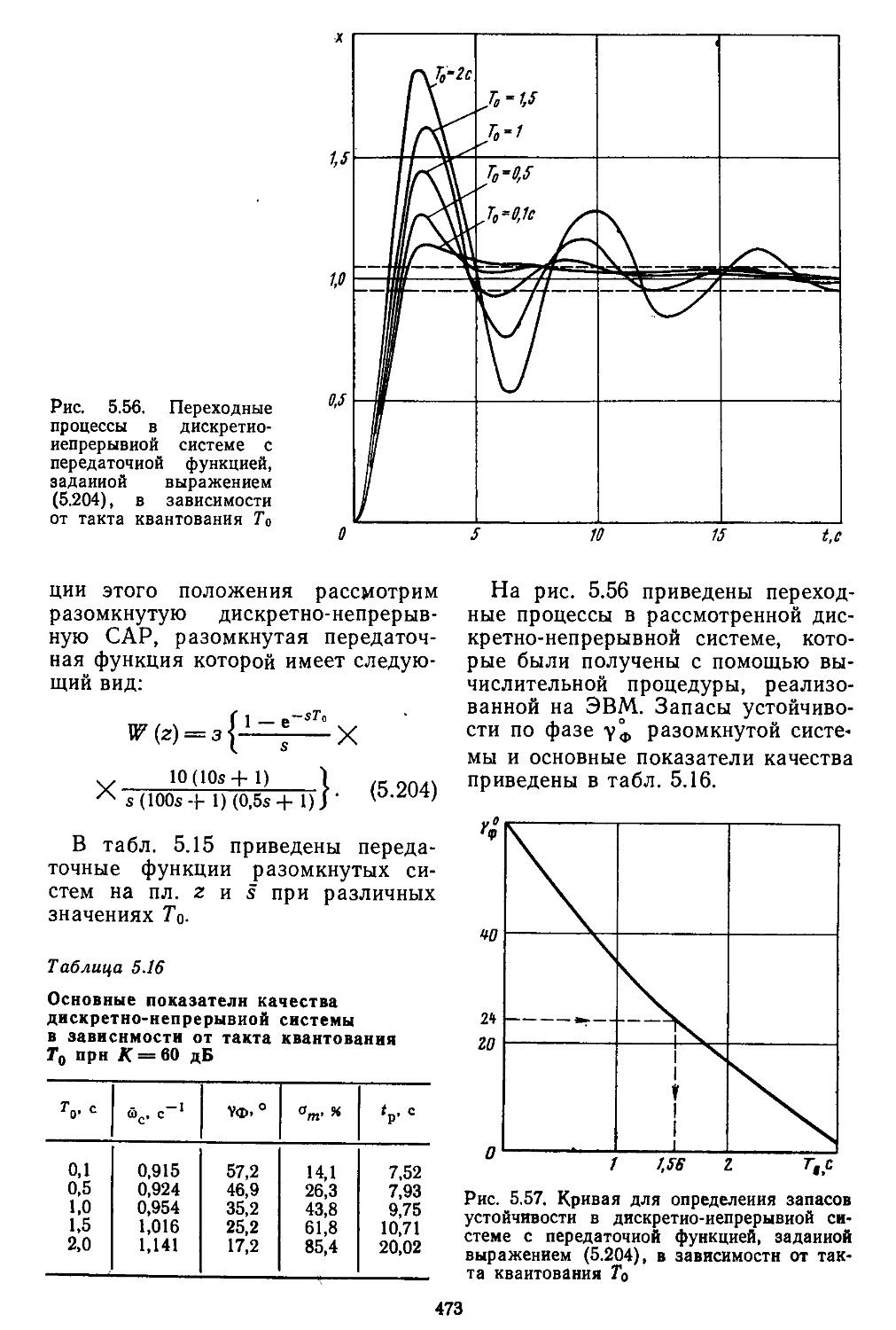
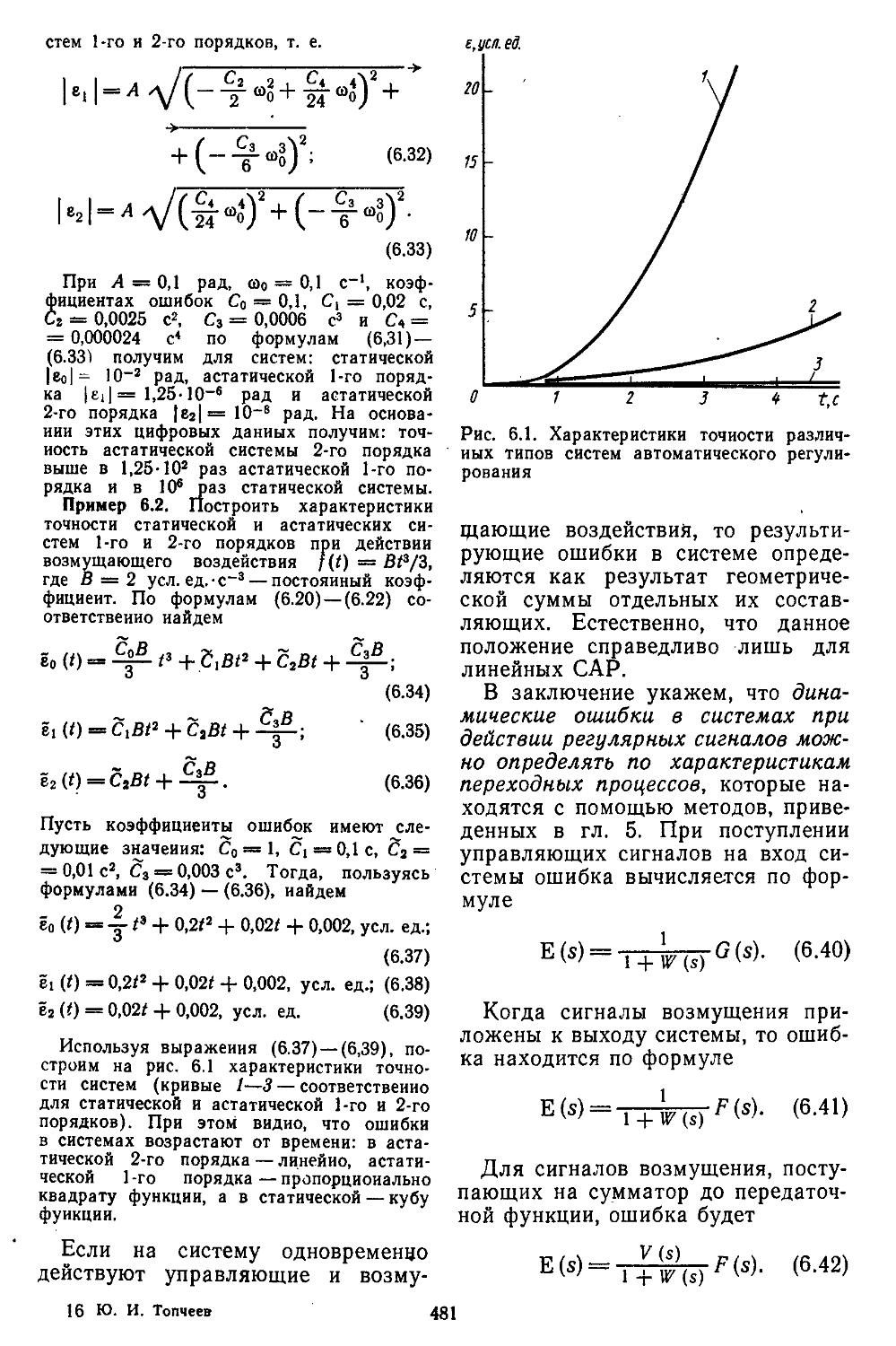
8. Сравнение . запасов устойчивости САР с основными ' показателями Качества . ’ . . . . 470
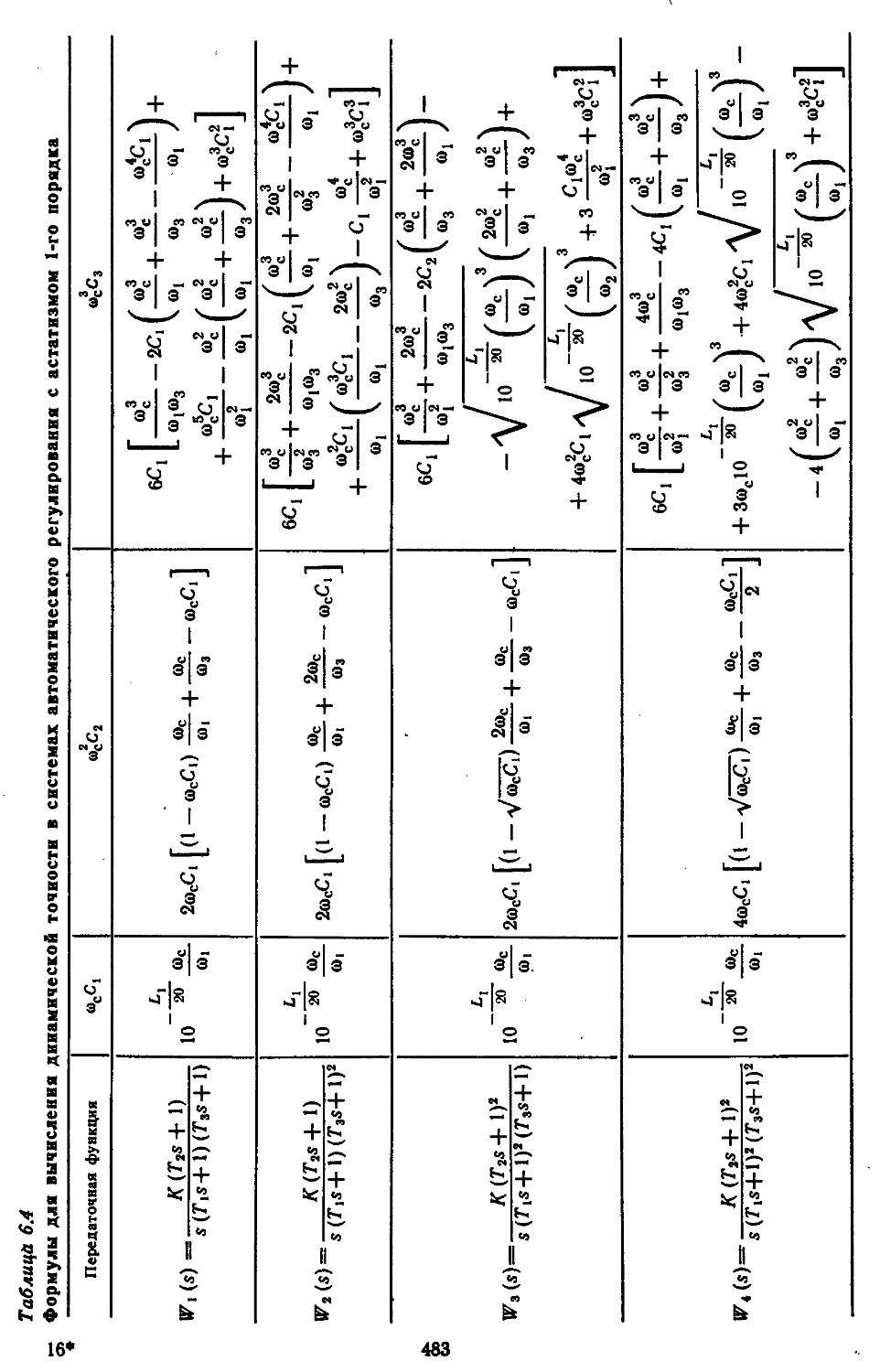
Глава 6. Исследование Динамической точности непрерывных и дискретио-иепрерывиых линейных систем автоматического регулирования . . 474
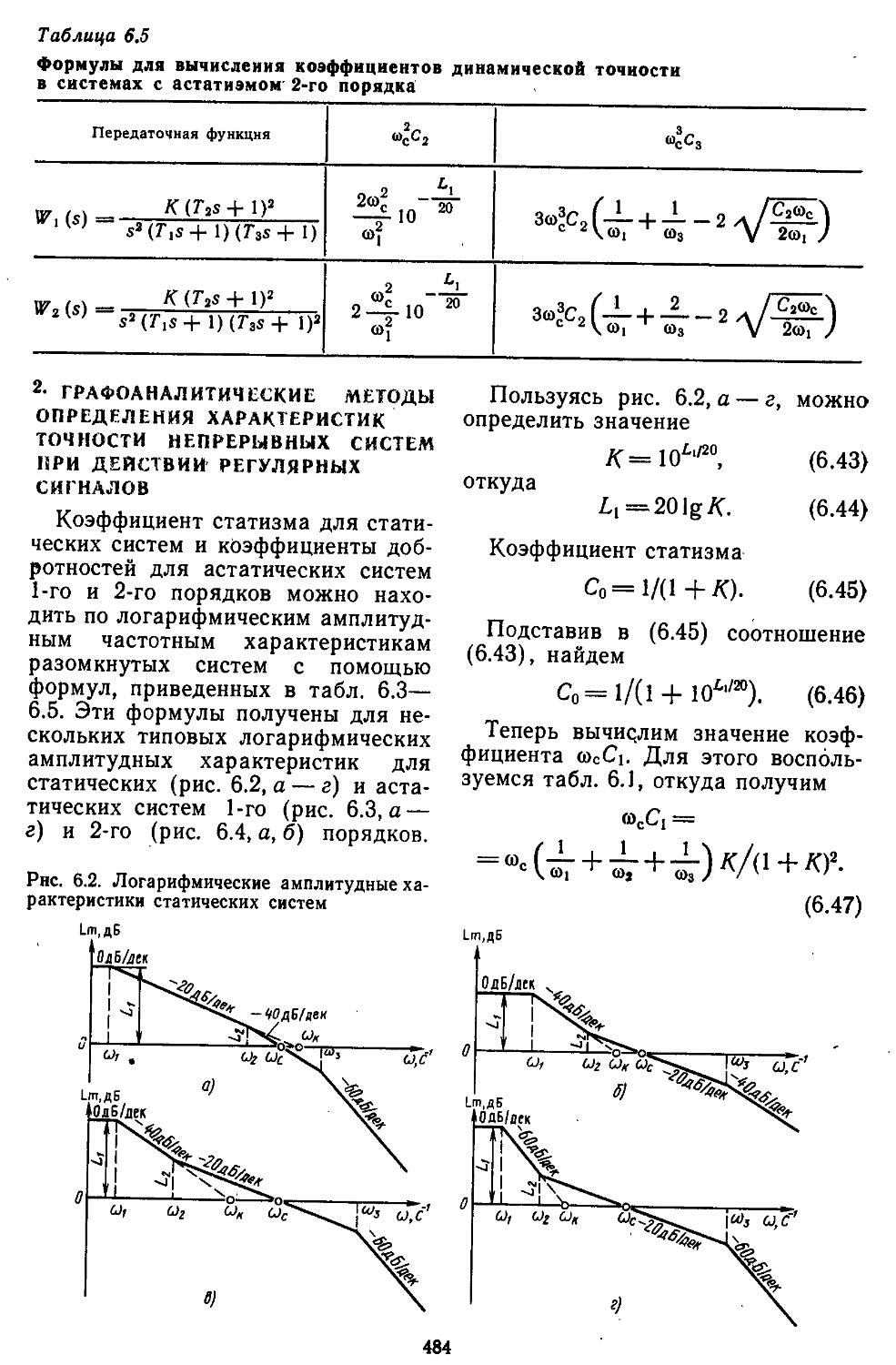
1. Характеристики точности непрерывных систем при действии регулярных сигналов .... 474
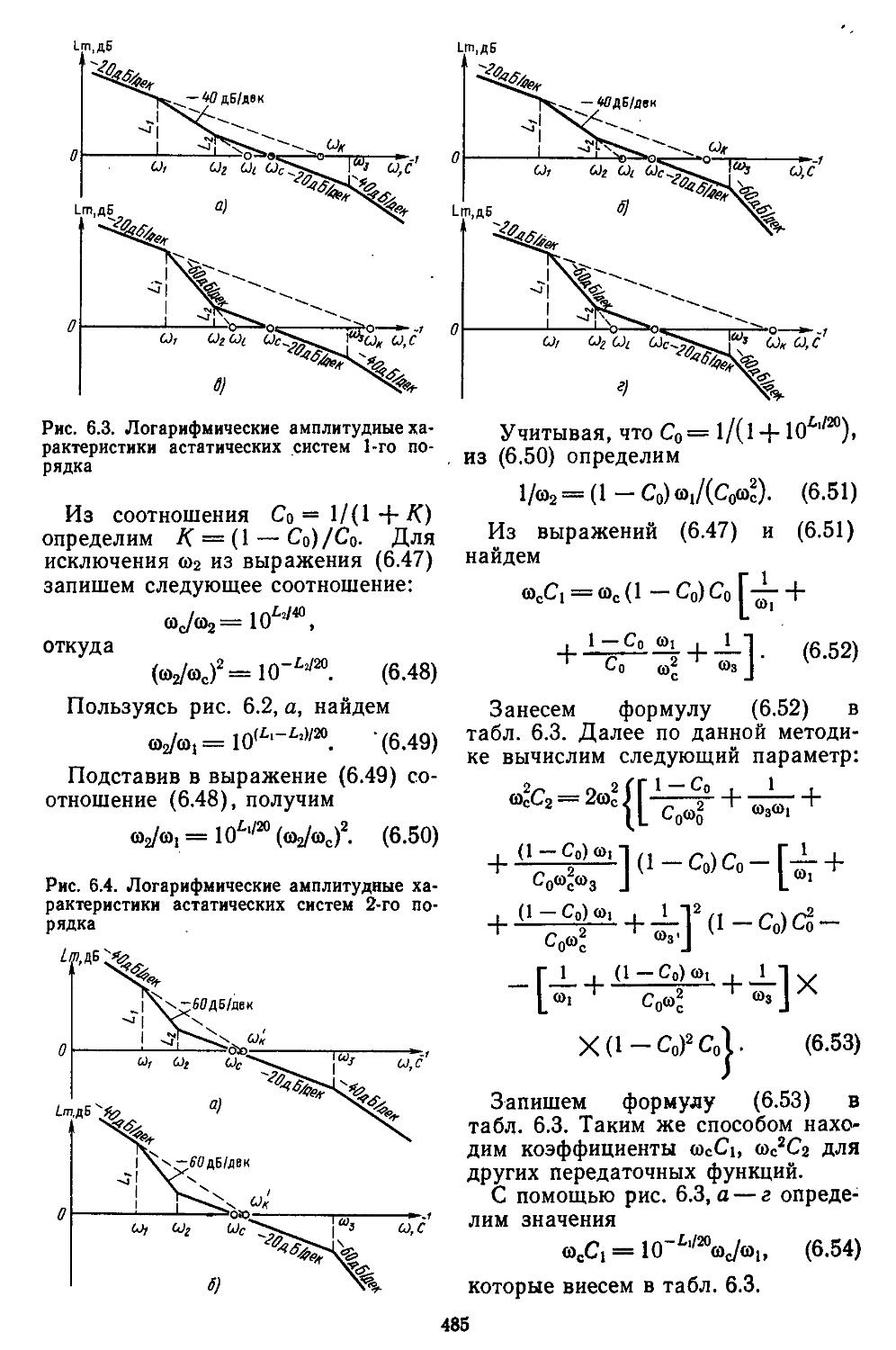
2. Графоаналитические ме-. тоды определения ха-- рактеристик точности непрерывных систем при действии регулярных сигналов.................484
3. Повышение точности систем иа основе применения принципа комбинированного управления 491
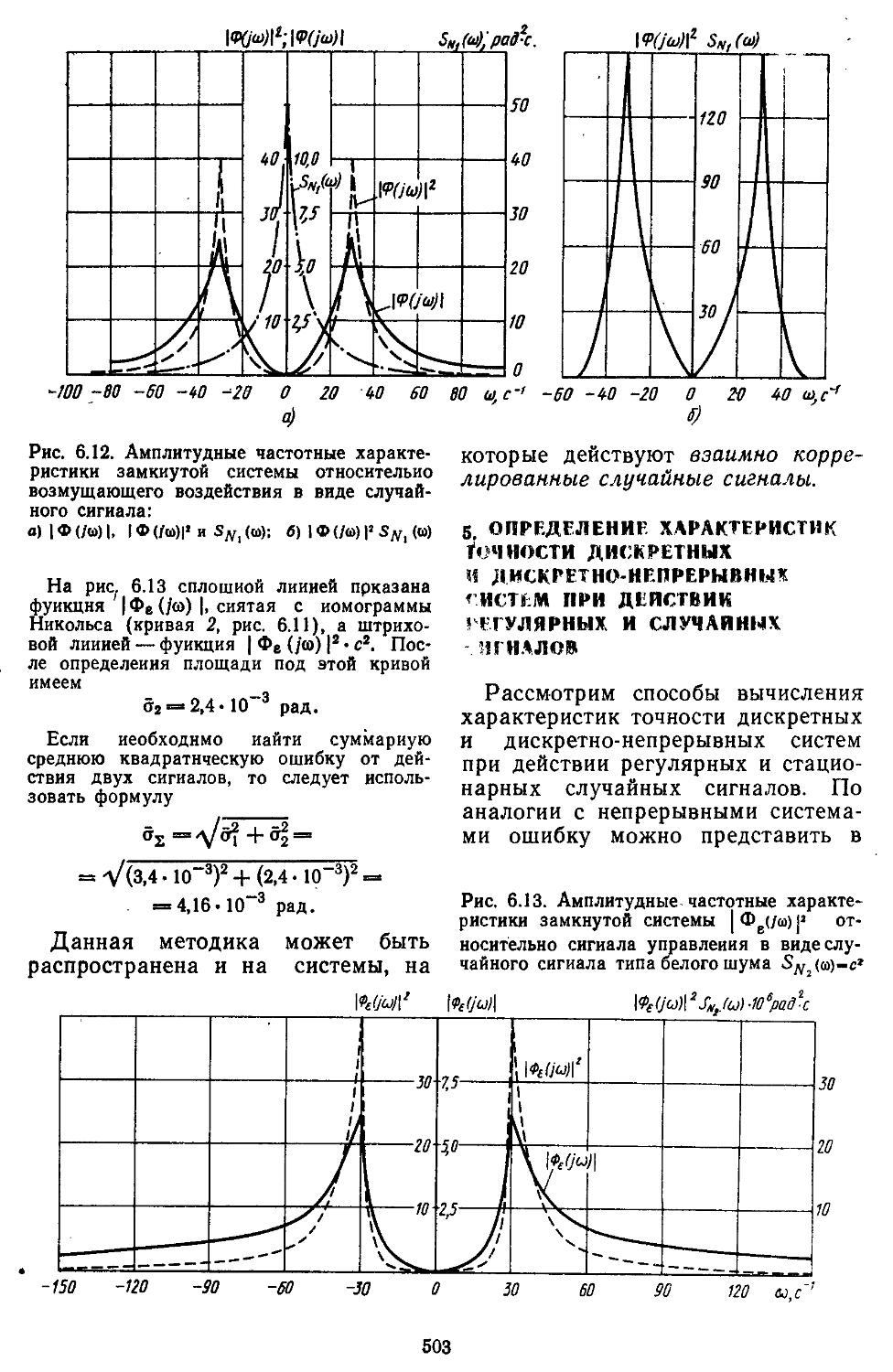
4. Определение характе-- ристик точности систем при действии стационарных случайных сигналов 496
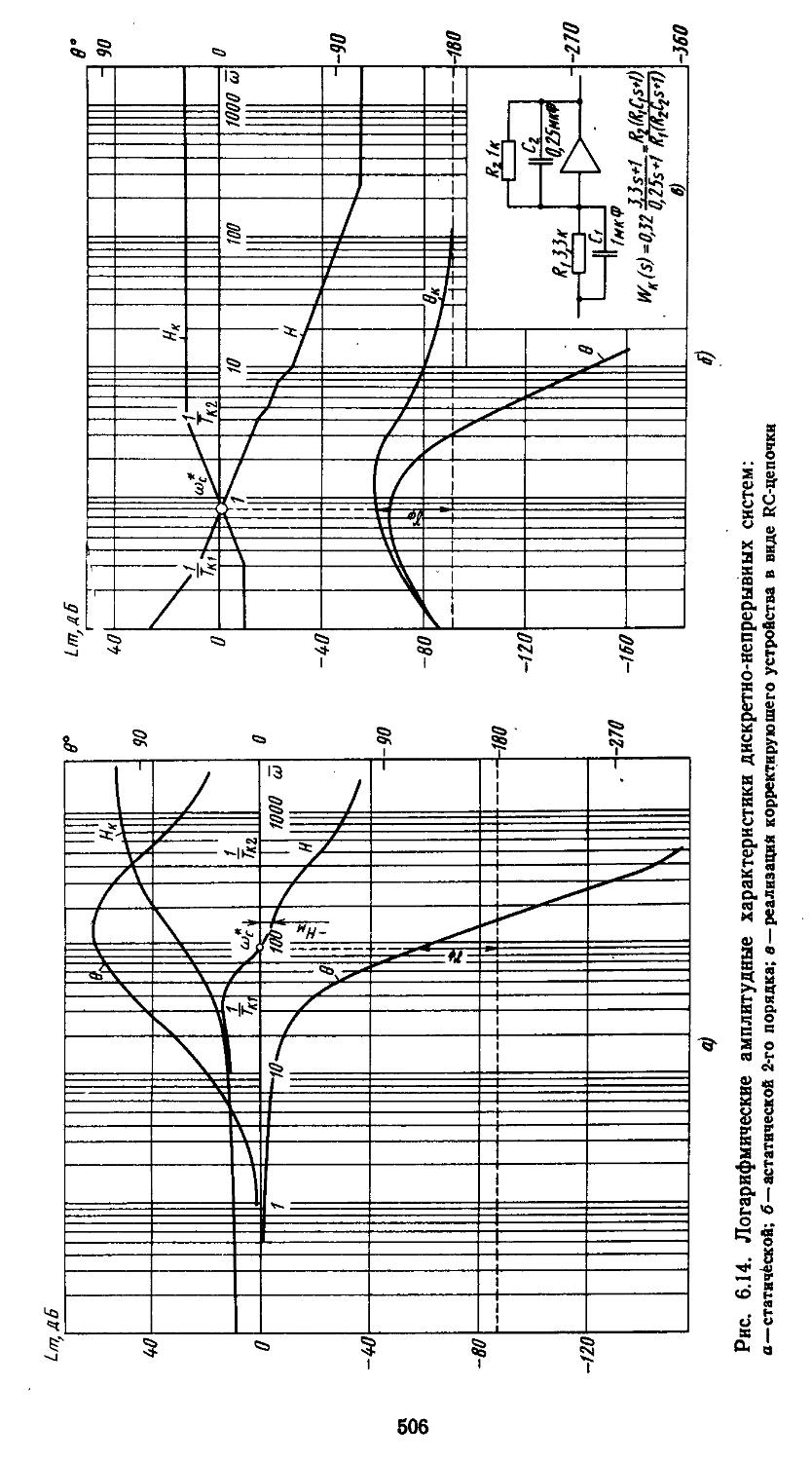
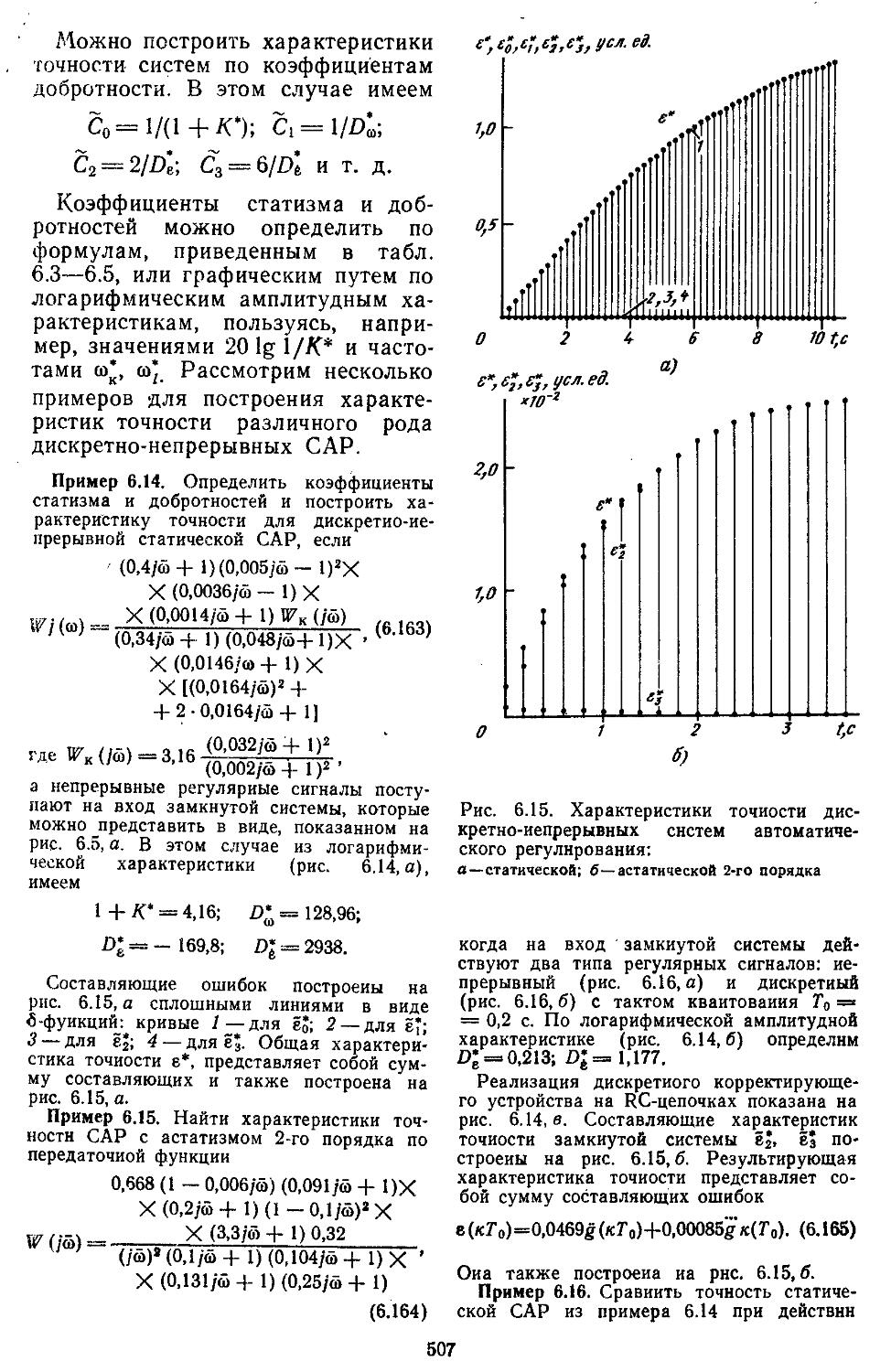
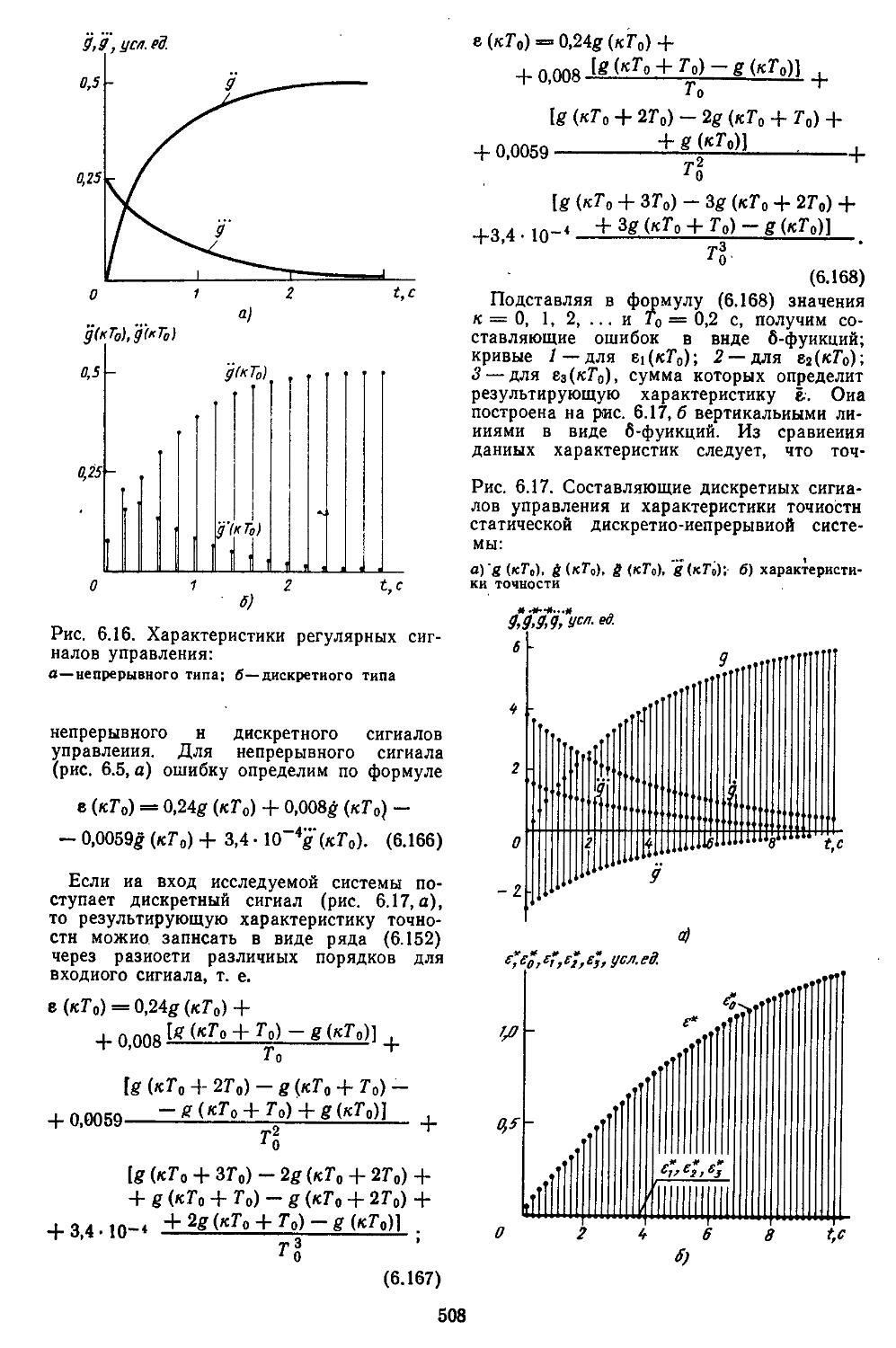
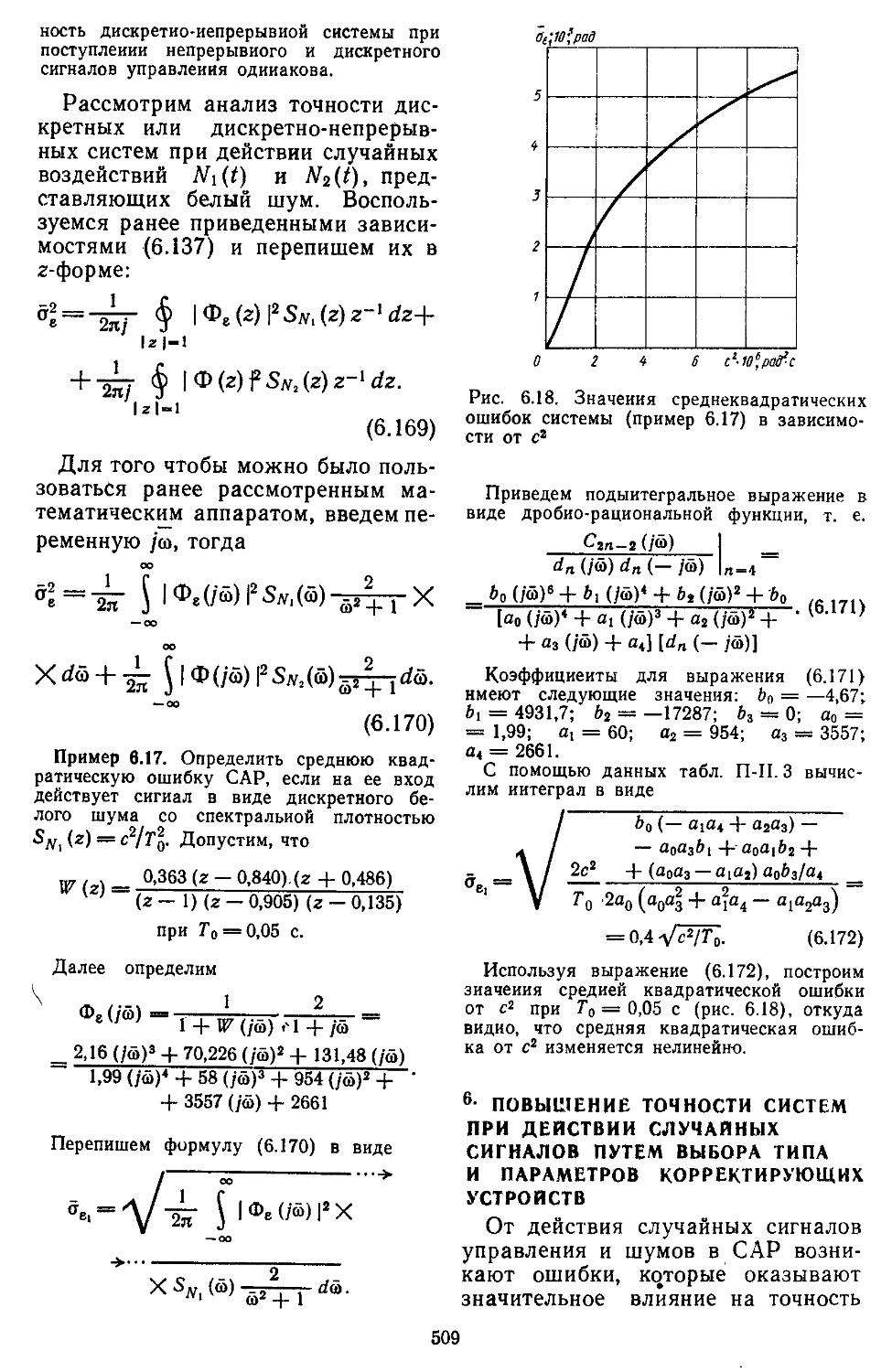
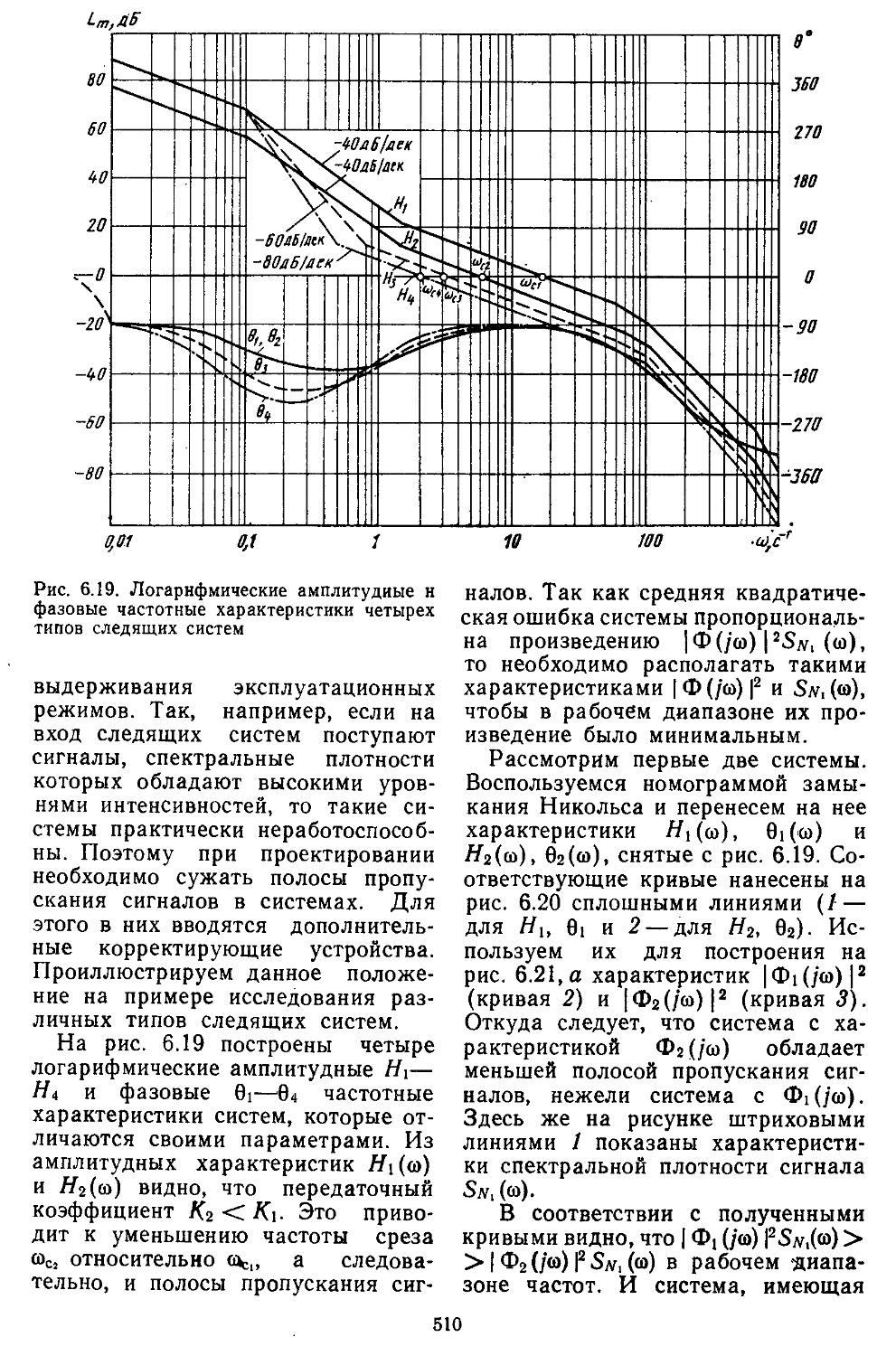
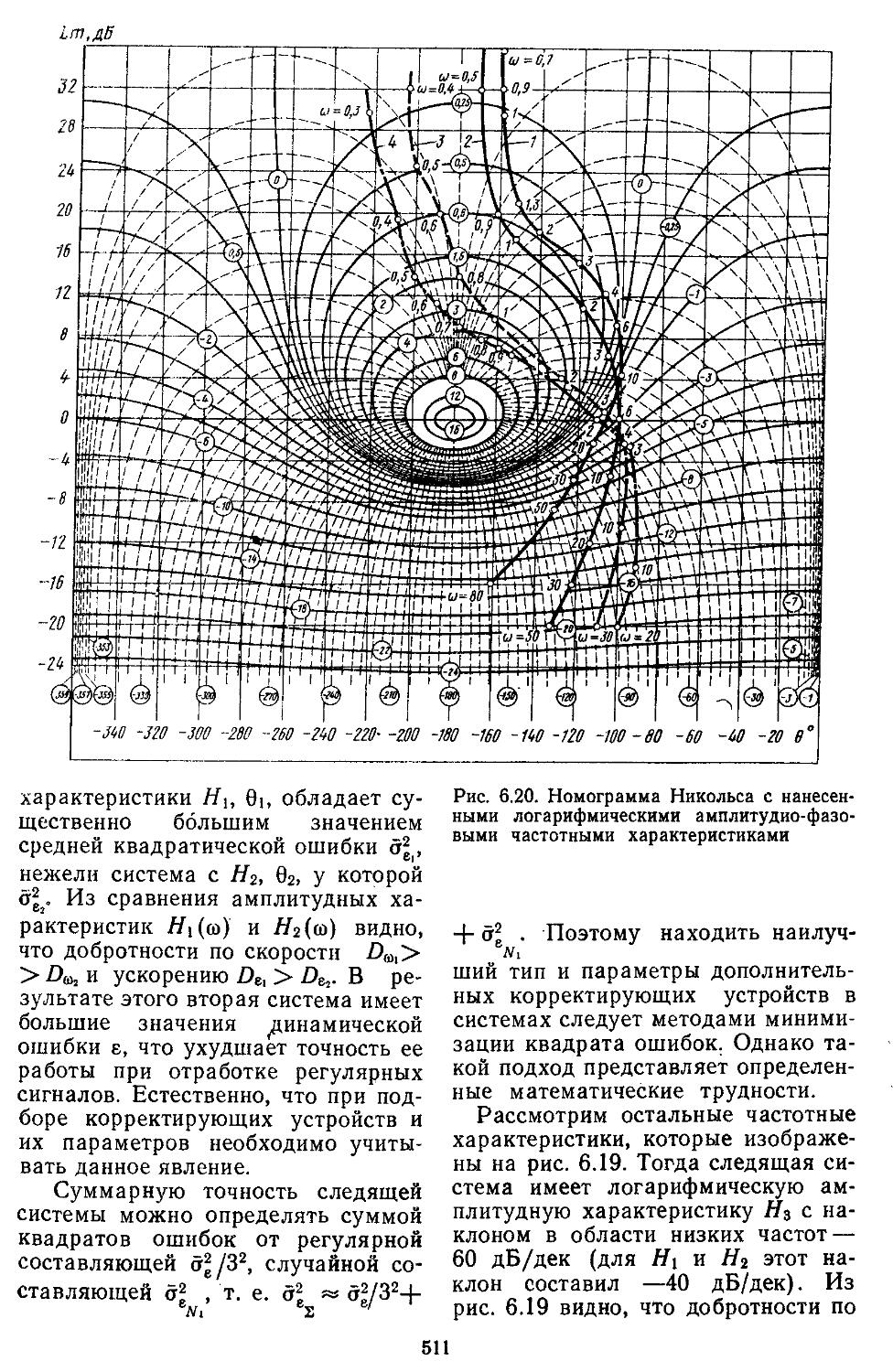
5. Определение характеристик .точности дискретных и дискретно-непрерывных сиетем при действии регулярных и случайных сигналов 503
6. Повышение точности систем при действии случайных сигналов путем "Выбора типа и парамет-
4
ров корректирующих устройств . . . . . 509
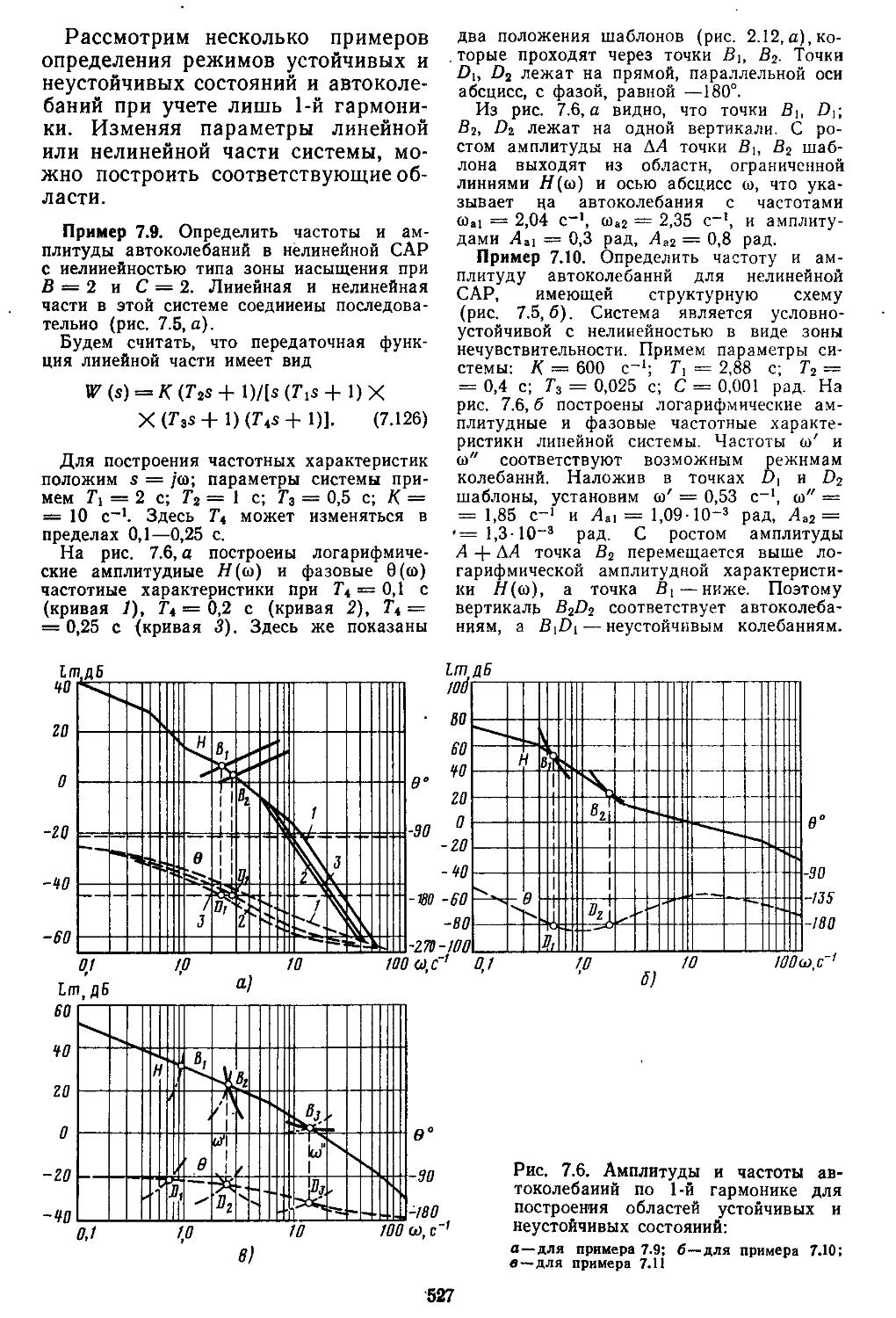
Глава 7. Нелинейные системы автоматического регулирования 513 1. Исследование устойчивости нелинейных систем по второму методу Ляпунова .... 513 2. Применение метода гармонической линеаризации для анализа устойчивости непрерывных нелинейных систем с учетом влияния 1-й гармоники . ...........................524
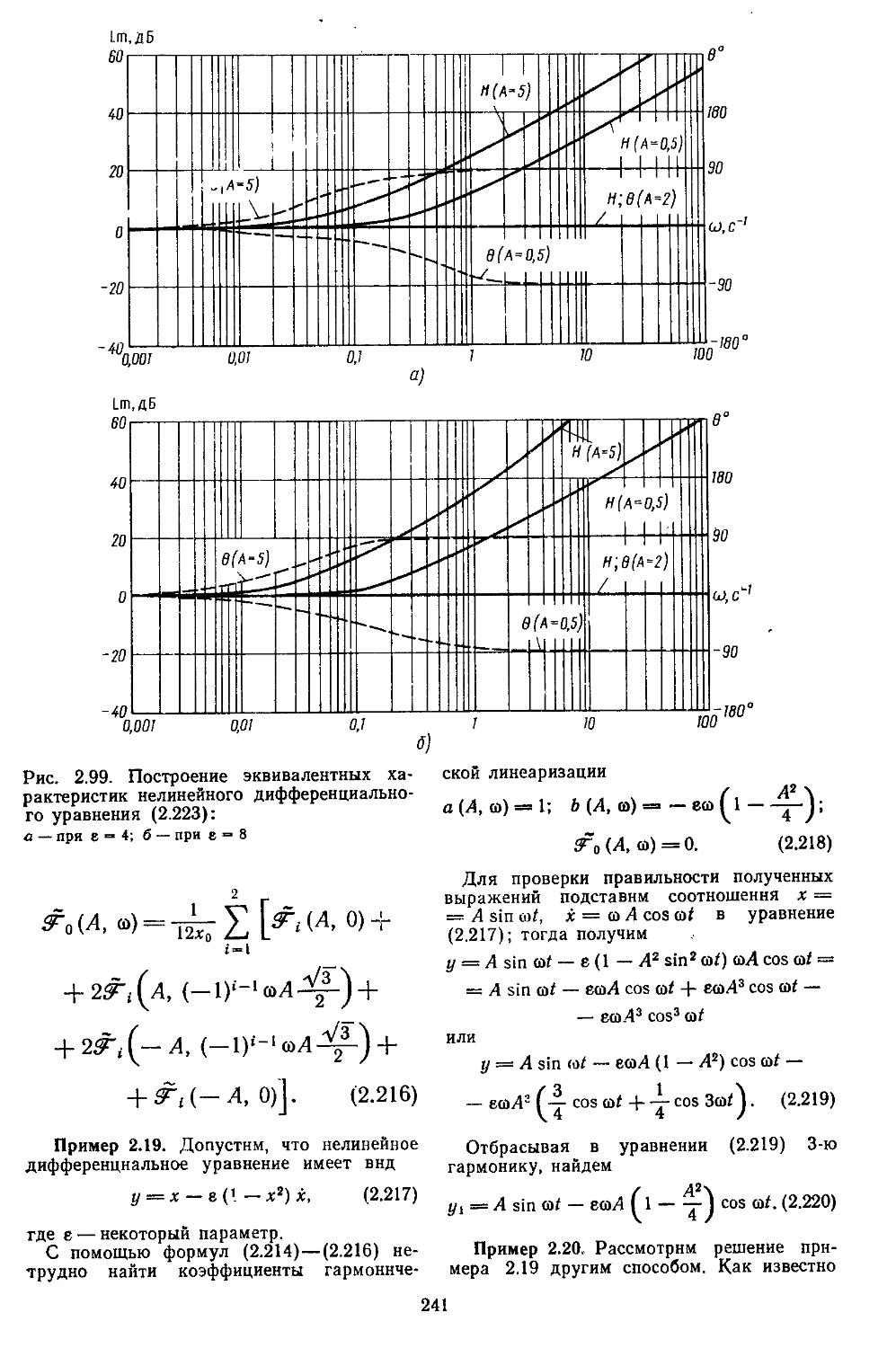
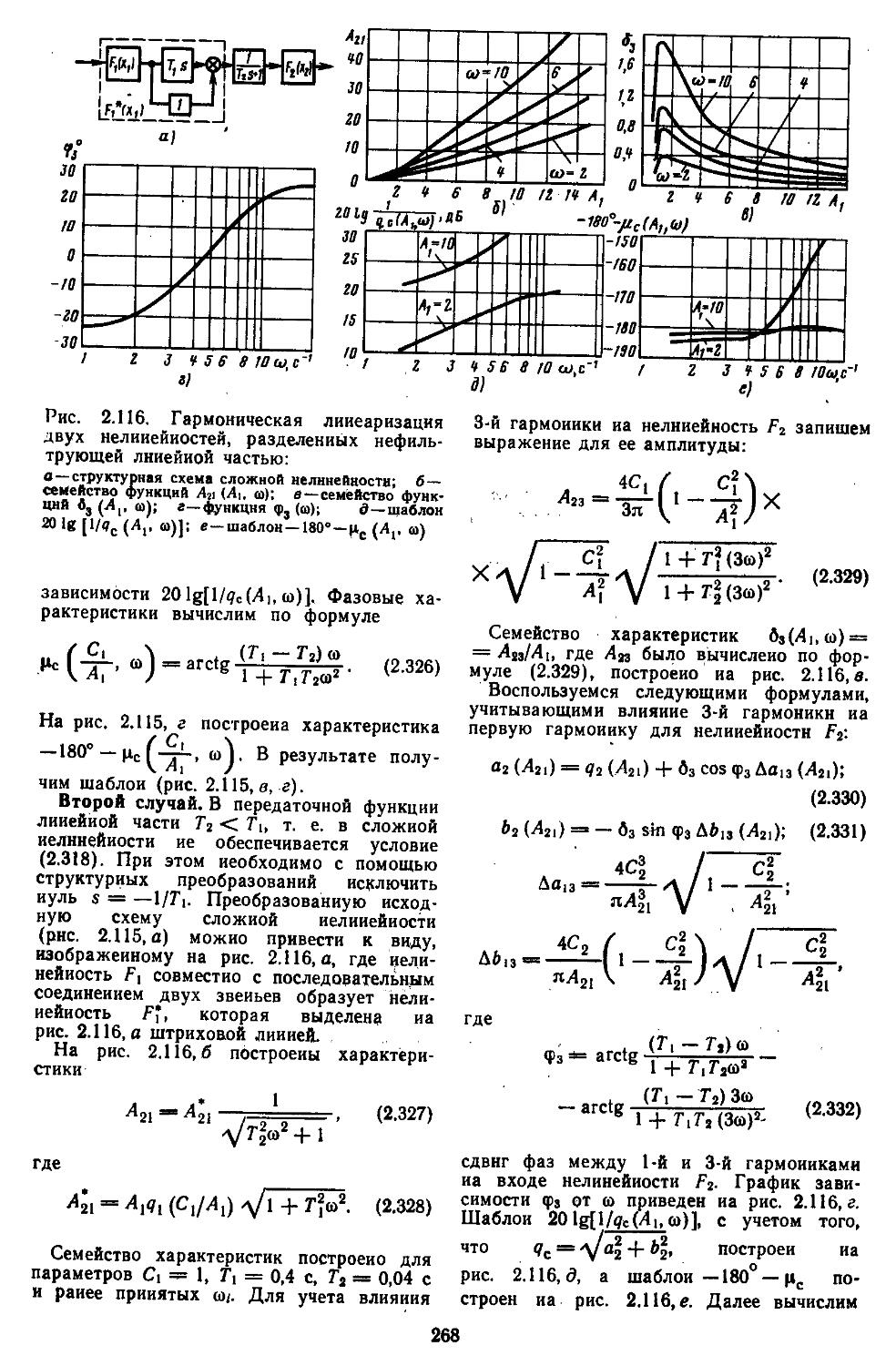
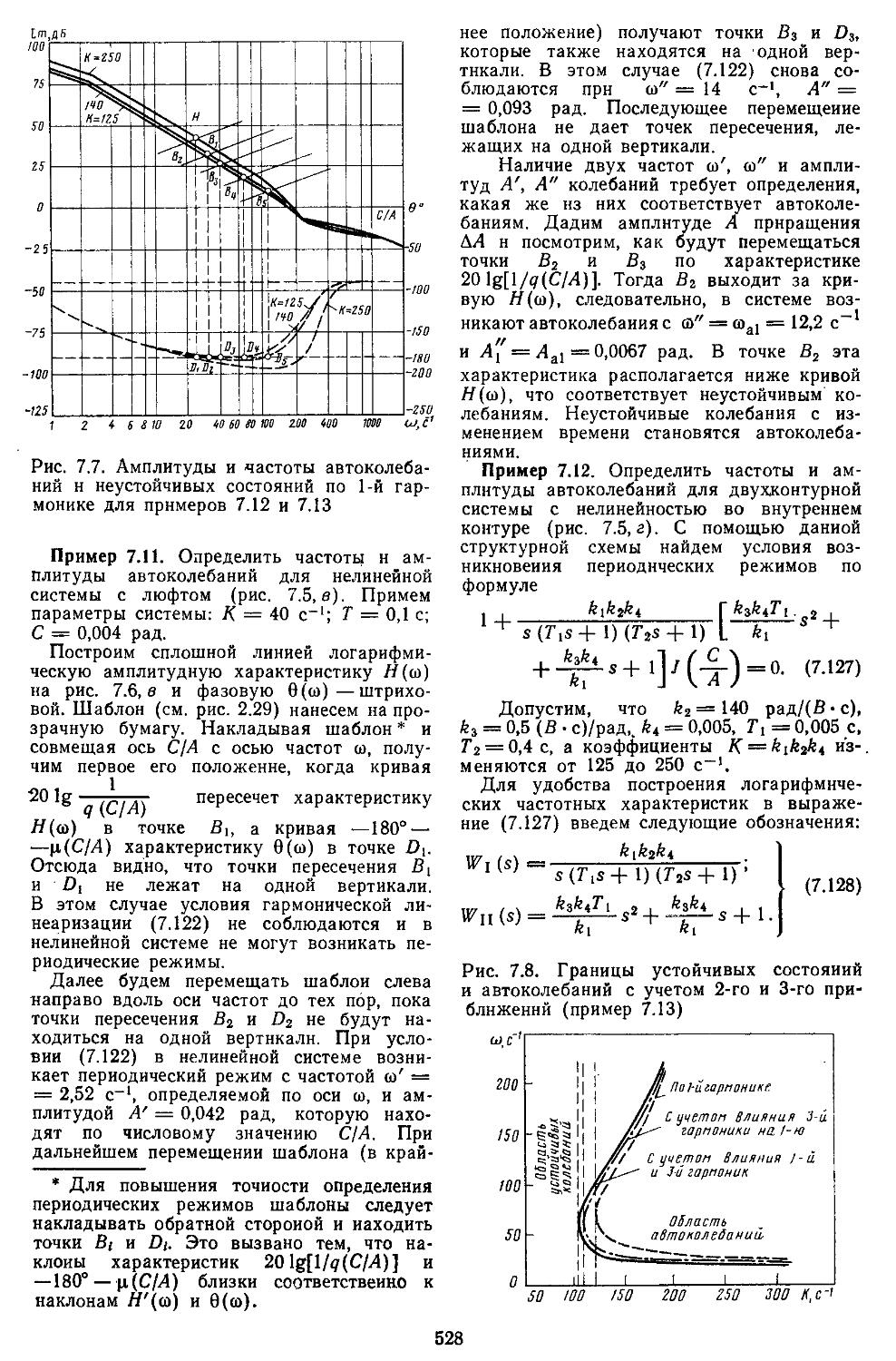
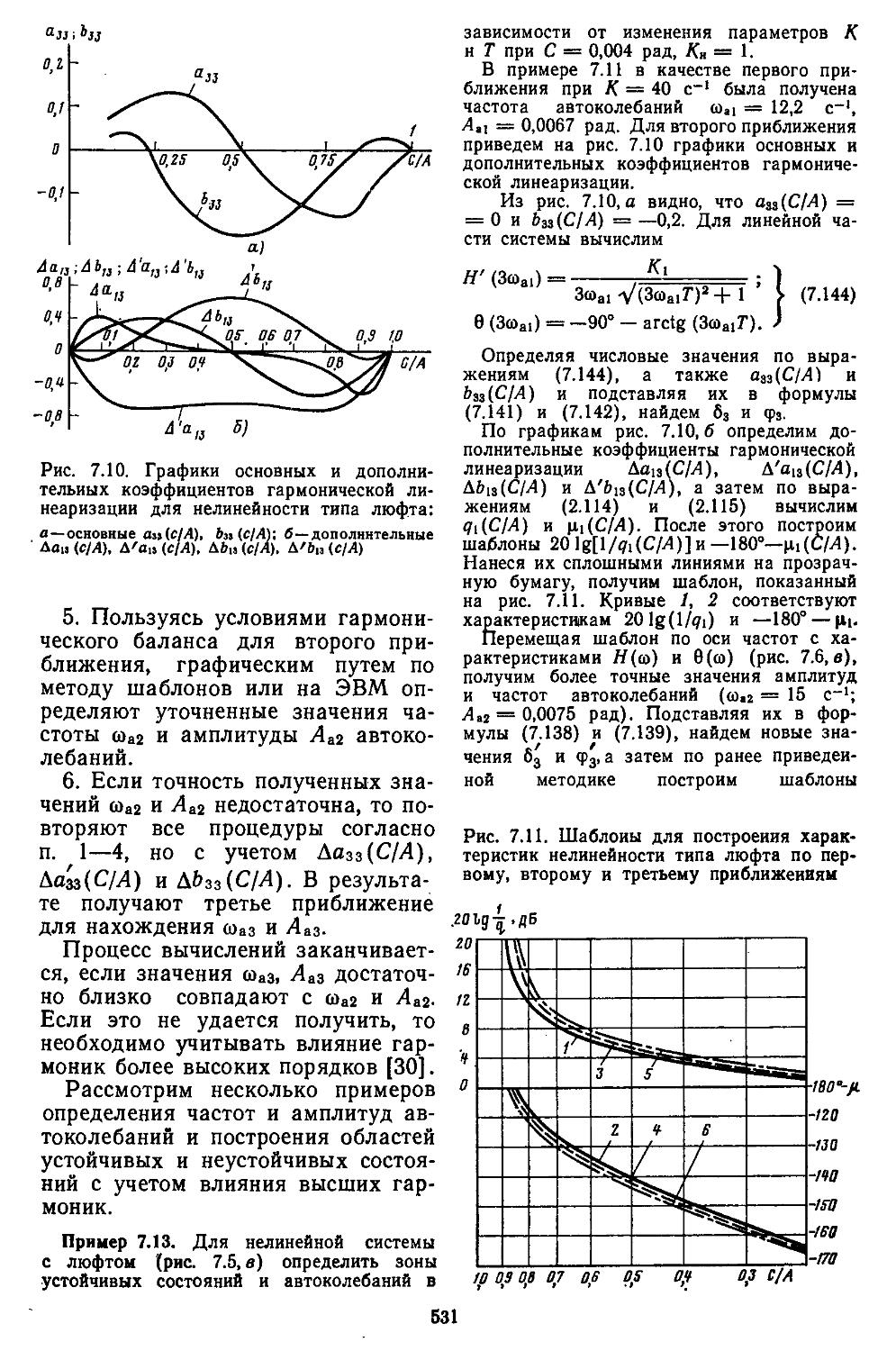
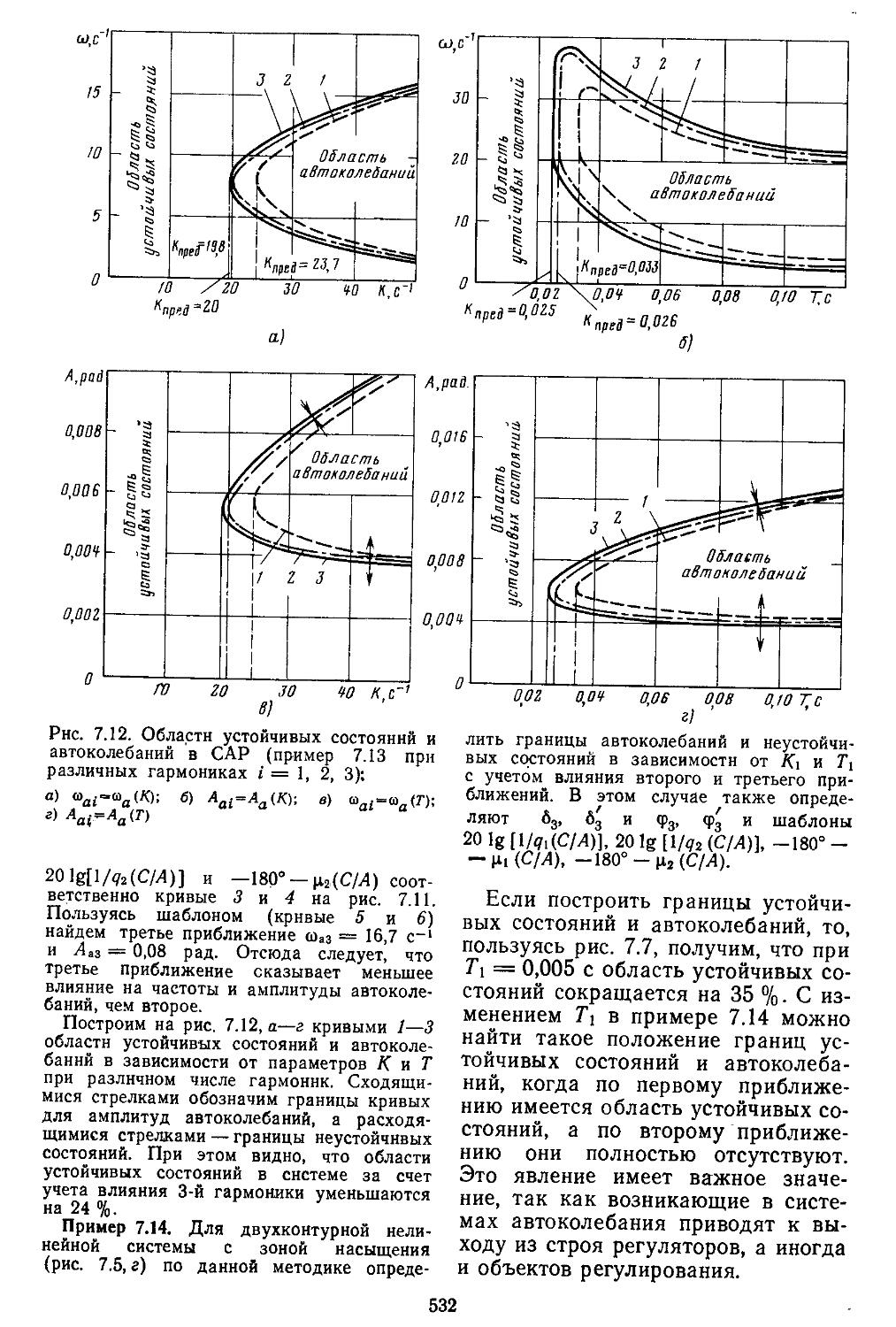
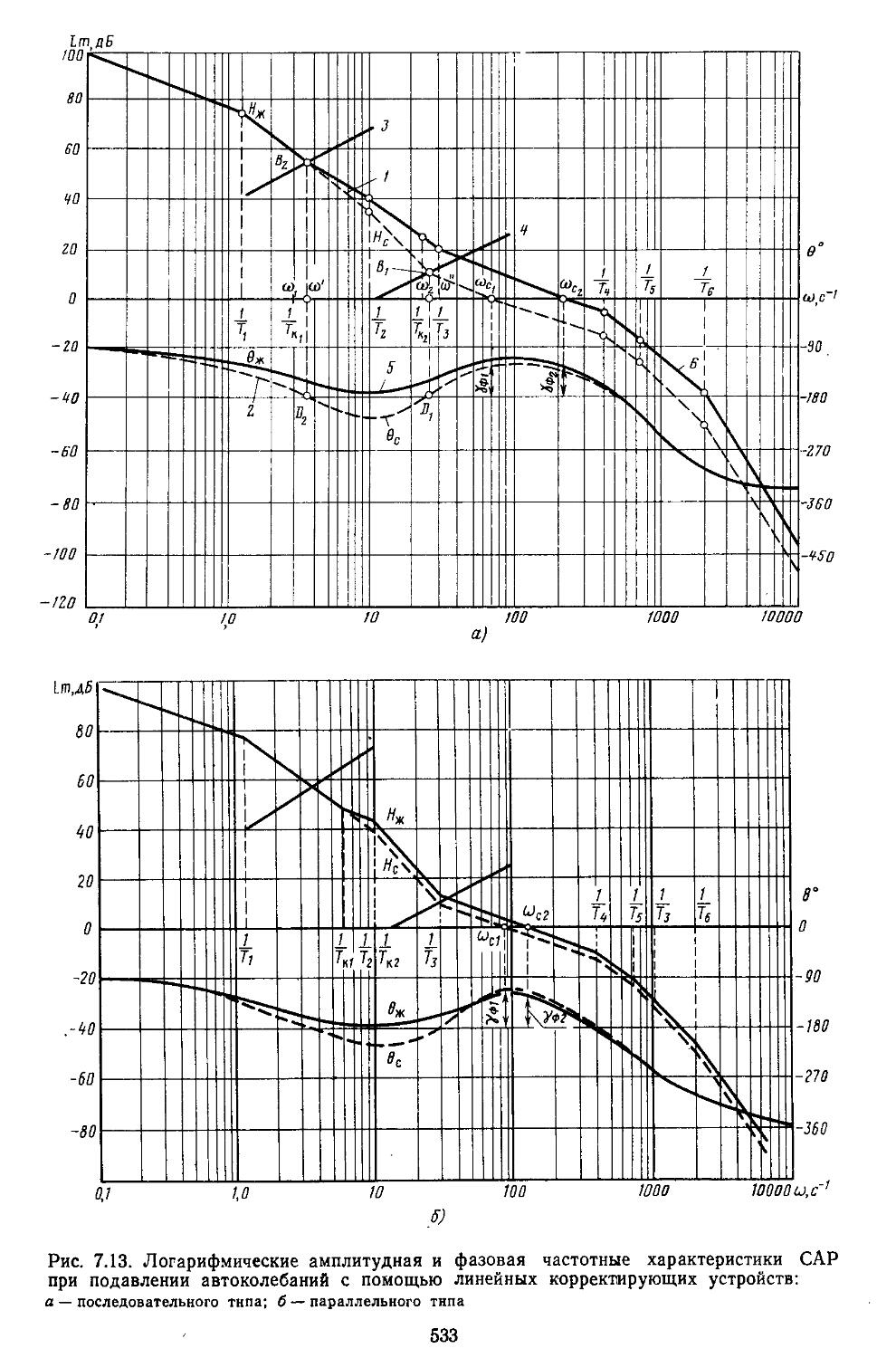
3. Применение метода гар-. ионической линеаризации при учёте высших гармонических составляющих ..................529
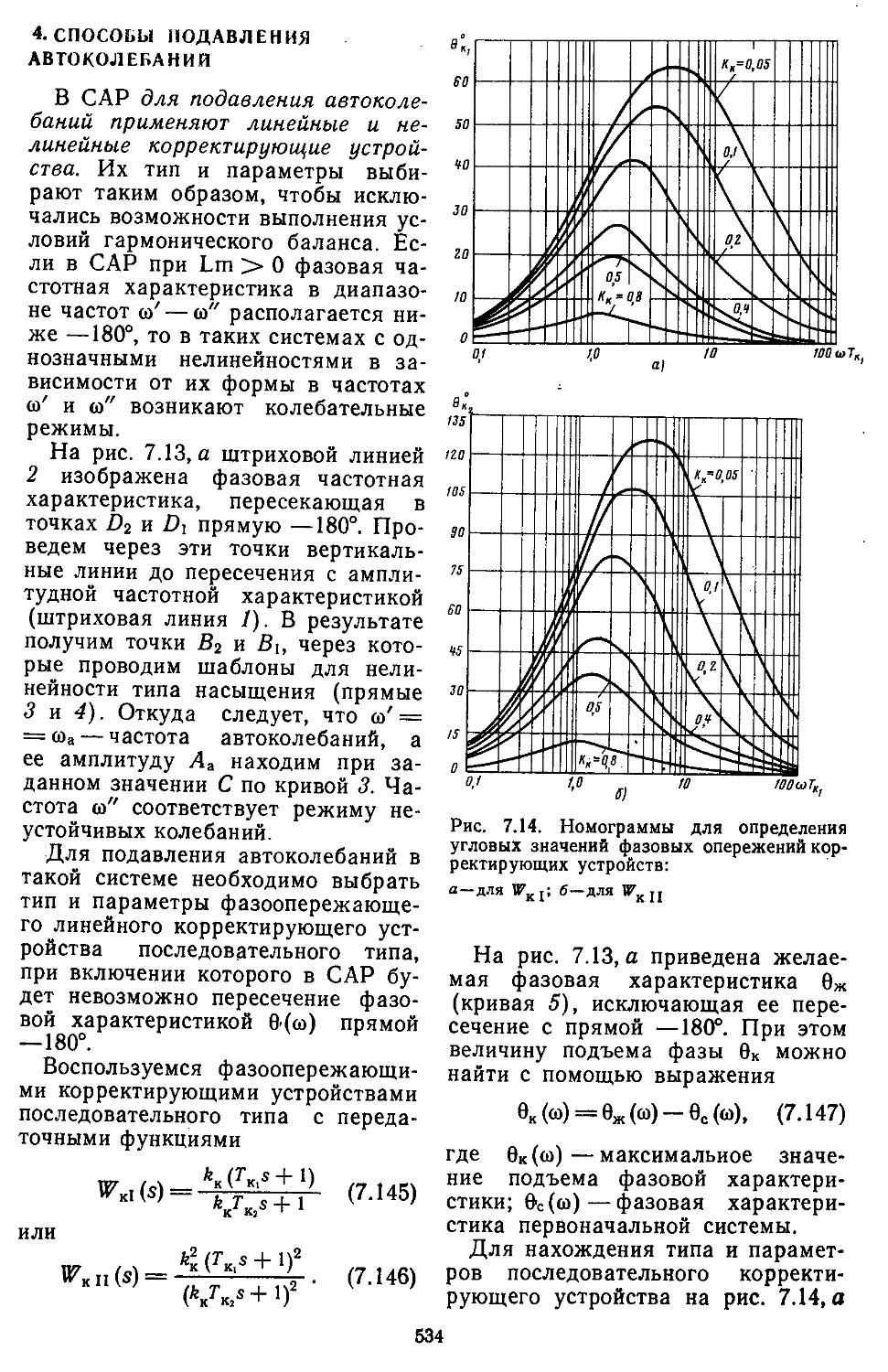
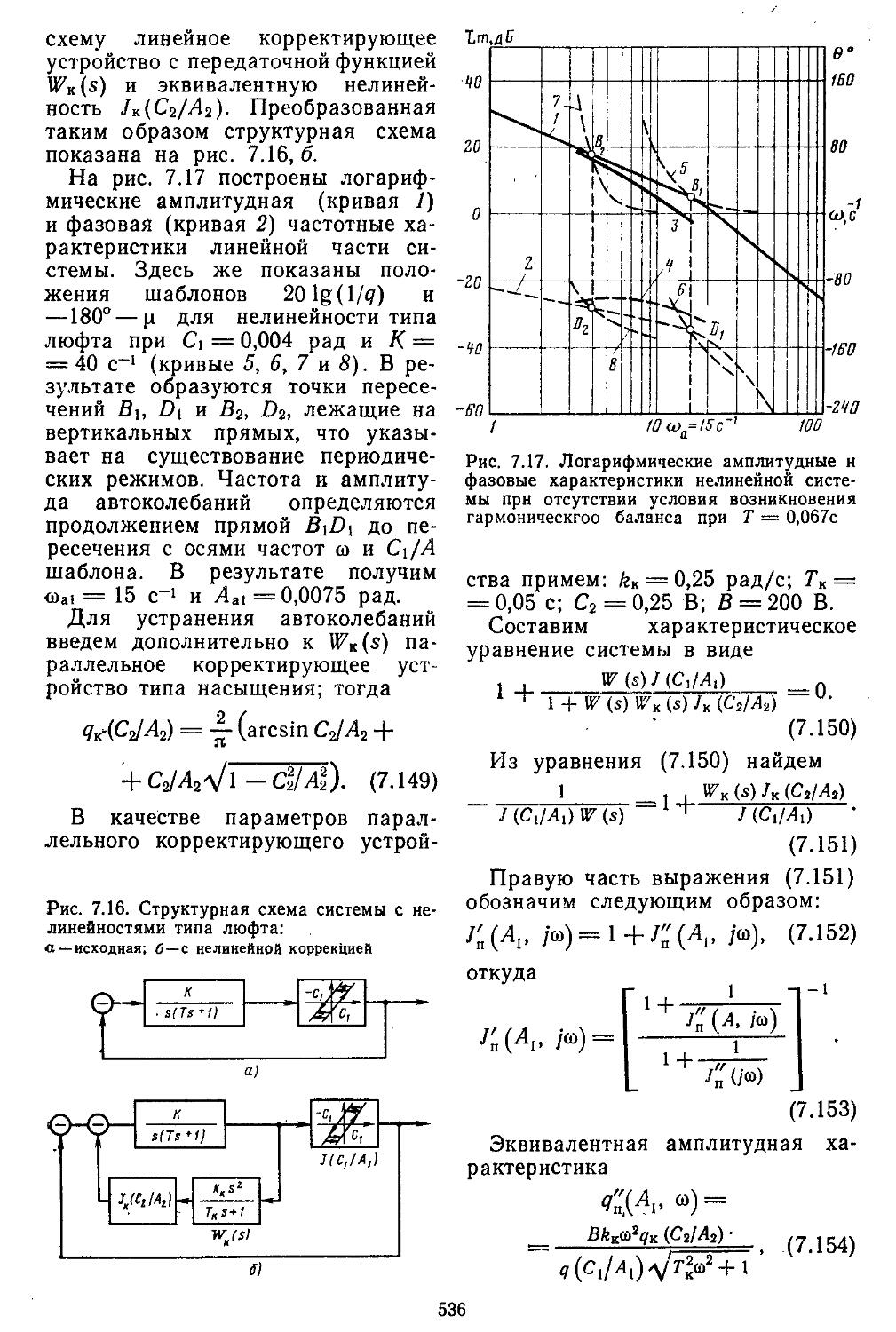
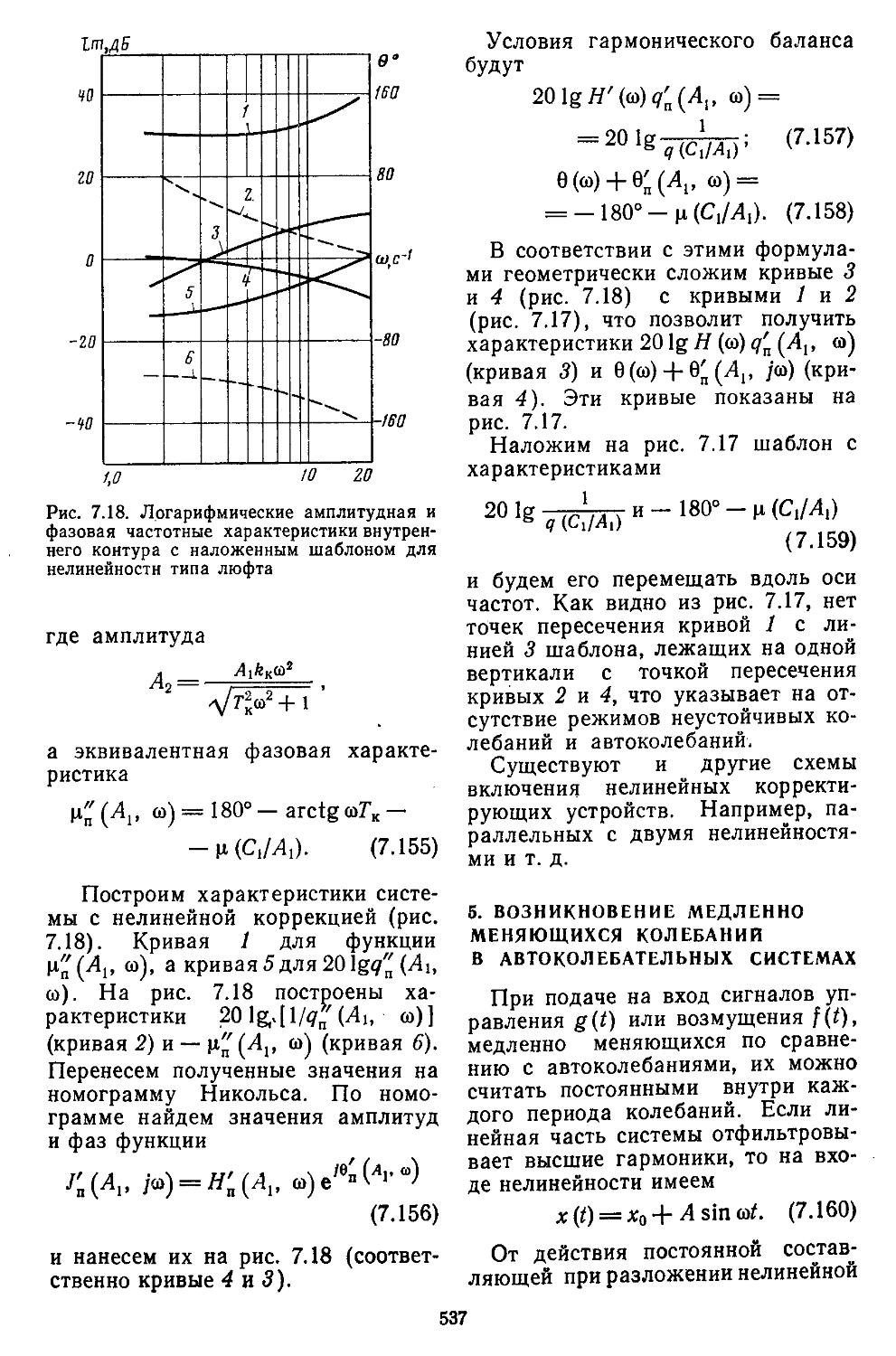
4. Способы подавления ав-
токолебаний .... 534
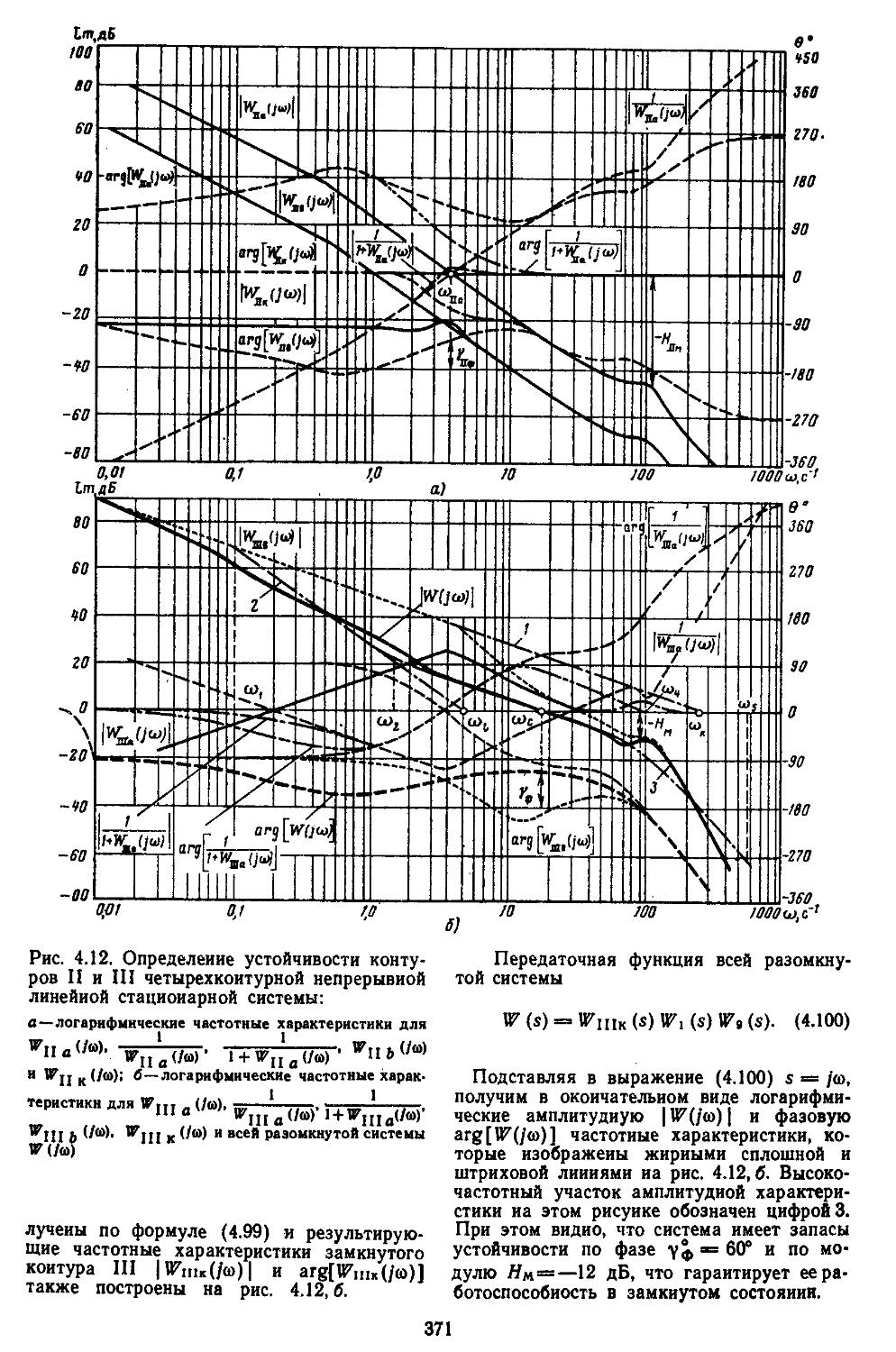
5. Возникновение медленно меняющихся колебаний в автоколебательных системах ....... 537
6. Вынужденные колебания в нелинейных системах 540 7. критерий абсолютной устойчивости нелиией-
иых систем . . . . . 543 8. Устойчивость иелиией-г иых дискретных и дискретно-непрерывных систем 551
9. Влияние случайных процессов иа нелинейные -САР .....................554
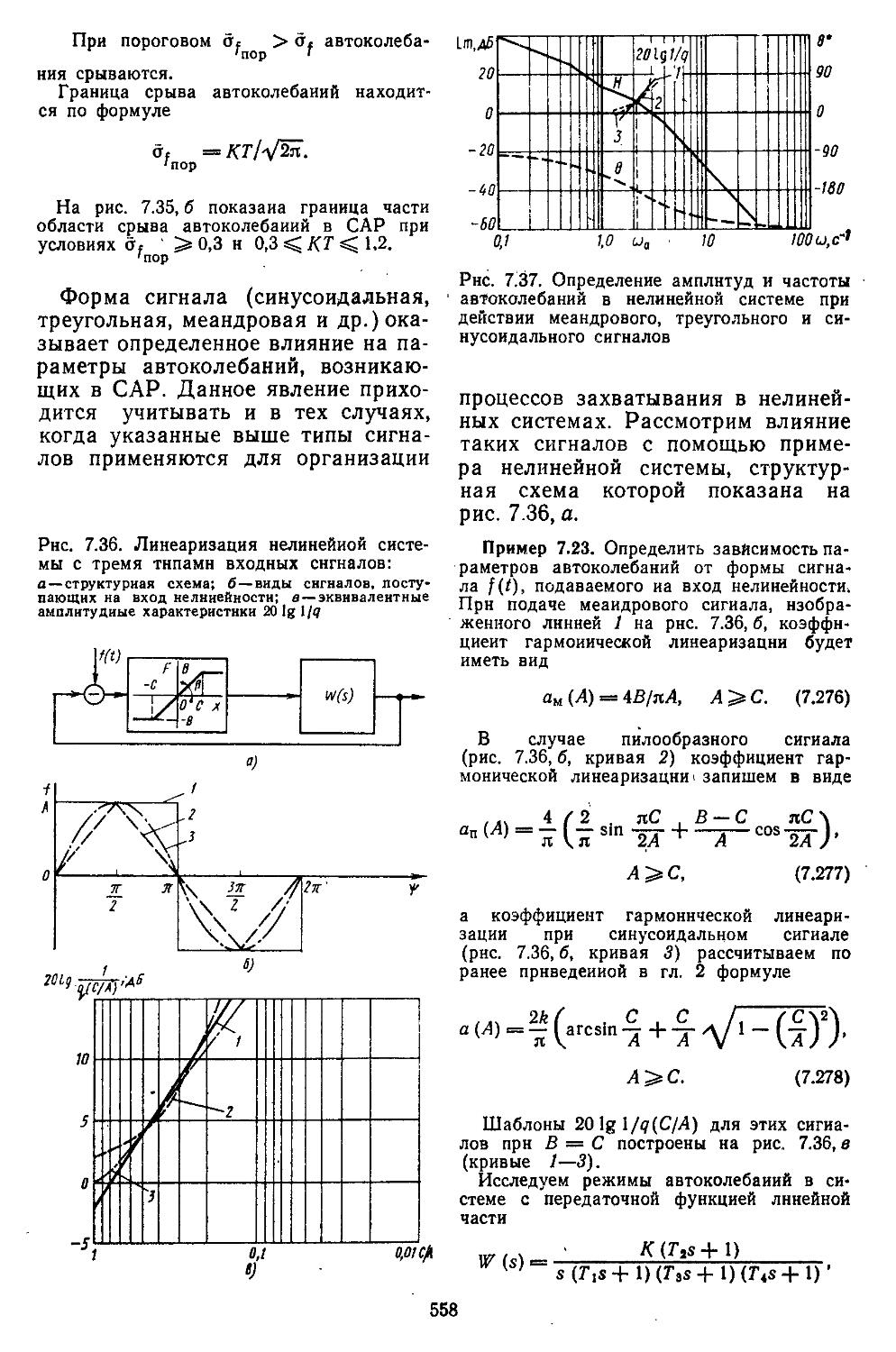
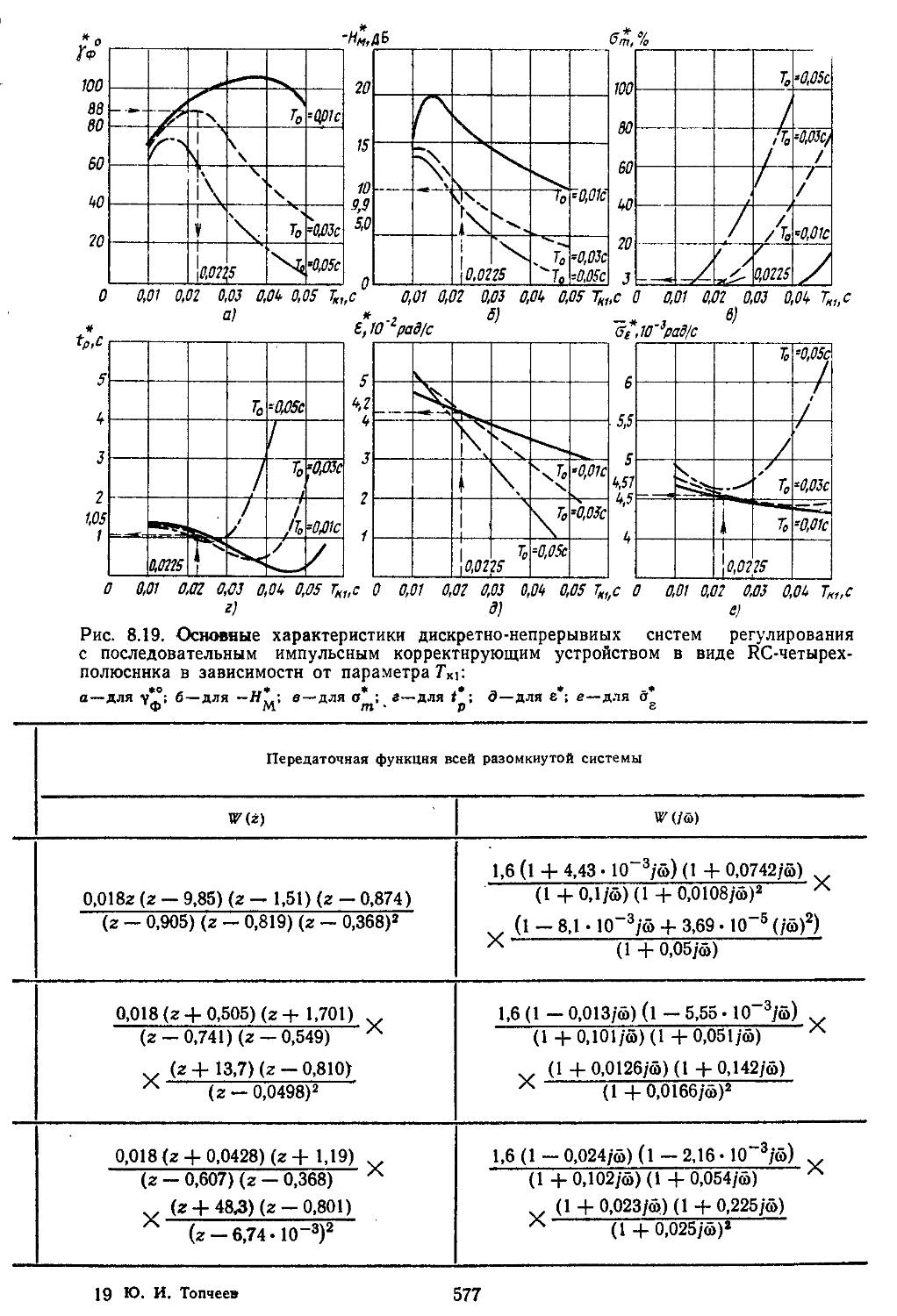
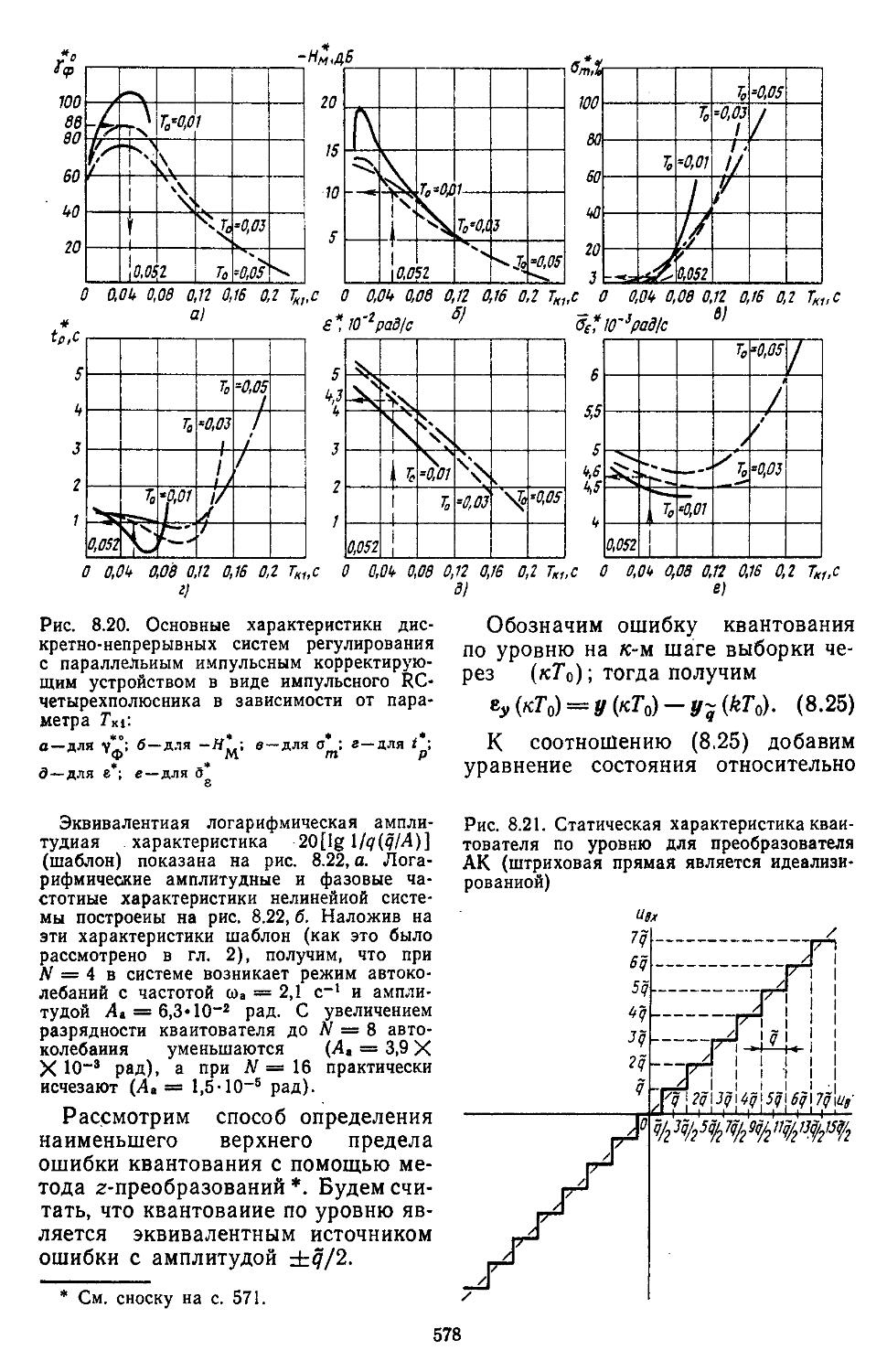
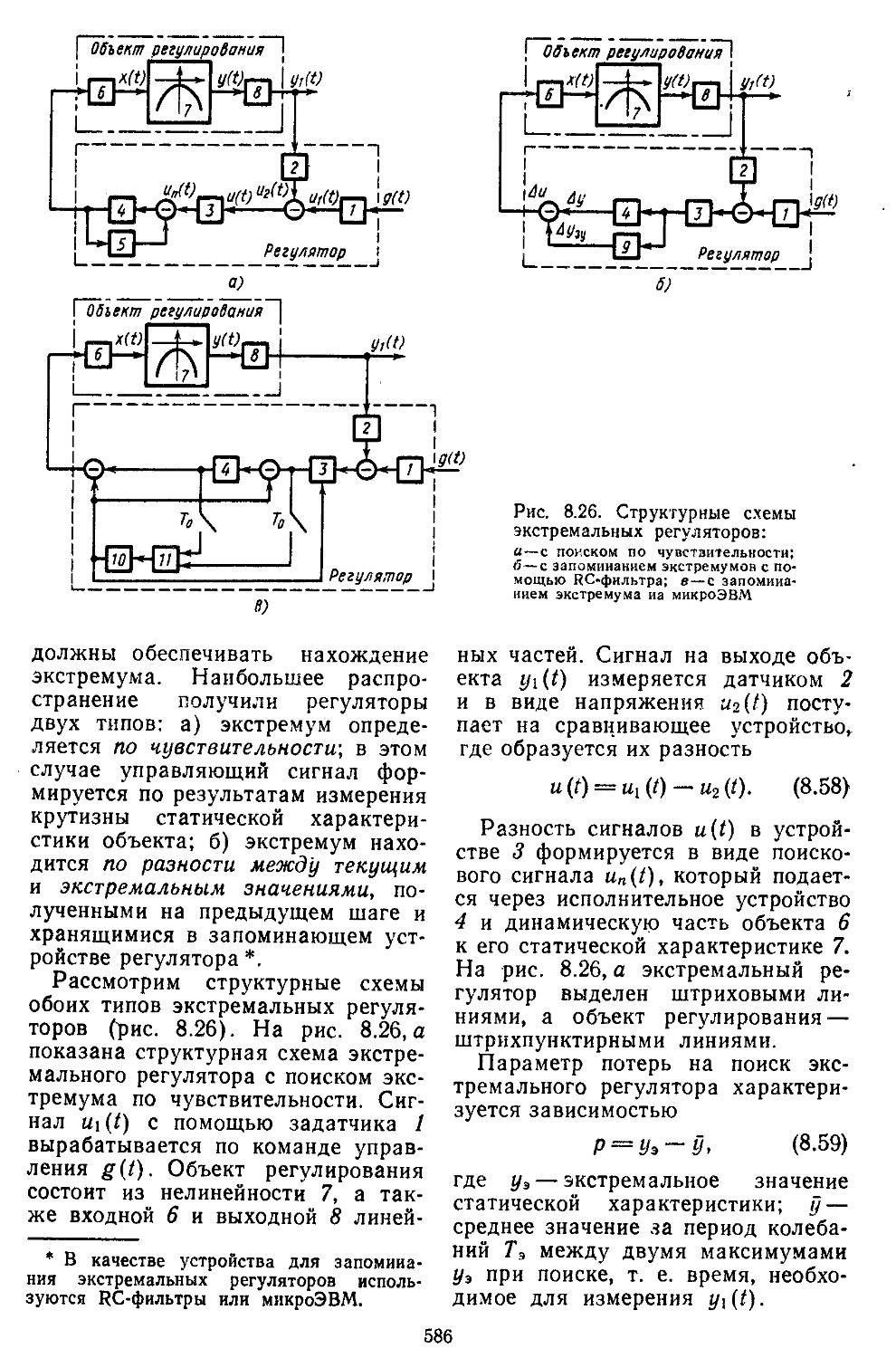
Глава 8. Проектирование систем автоматического регулирования с заданной структурой 553 1. Непрерывные линейные и нелинейные системы 558 2. Дискретно-непрерывные линейные. и нелинейные системы ............................569
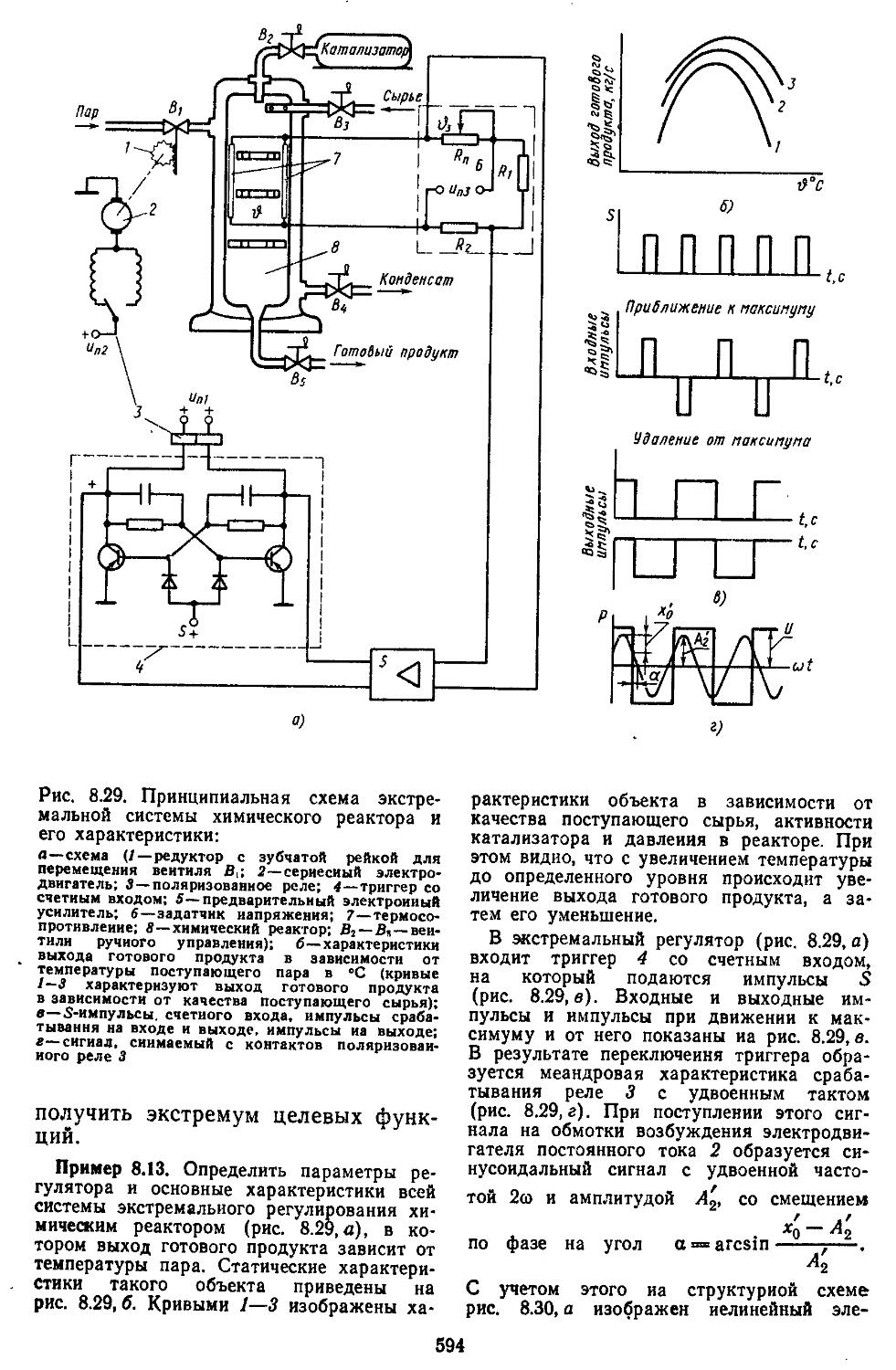
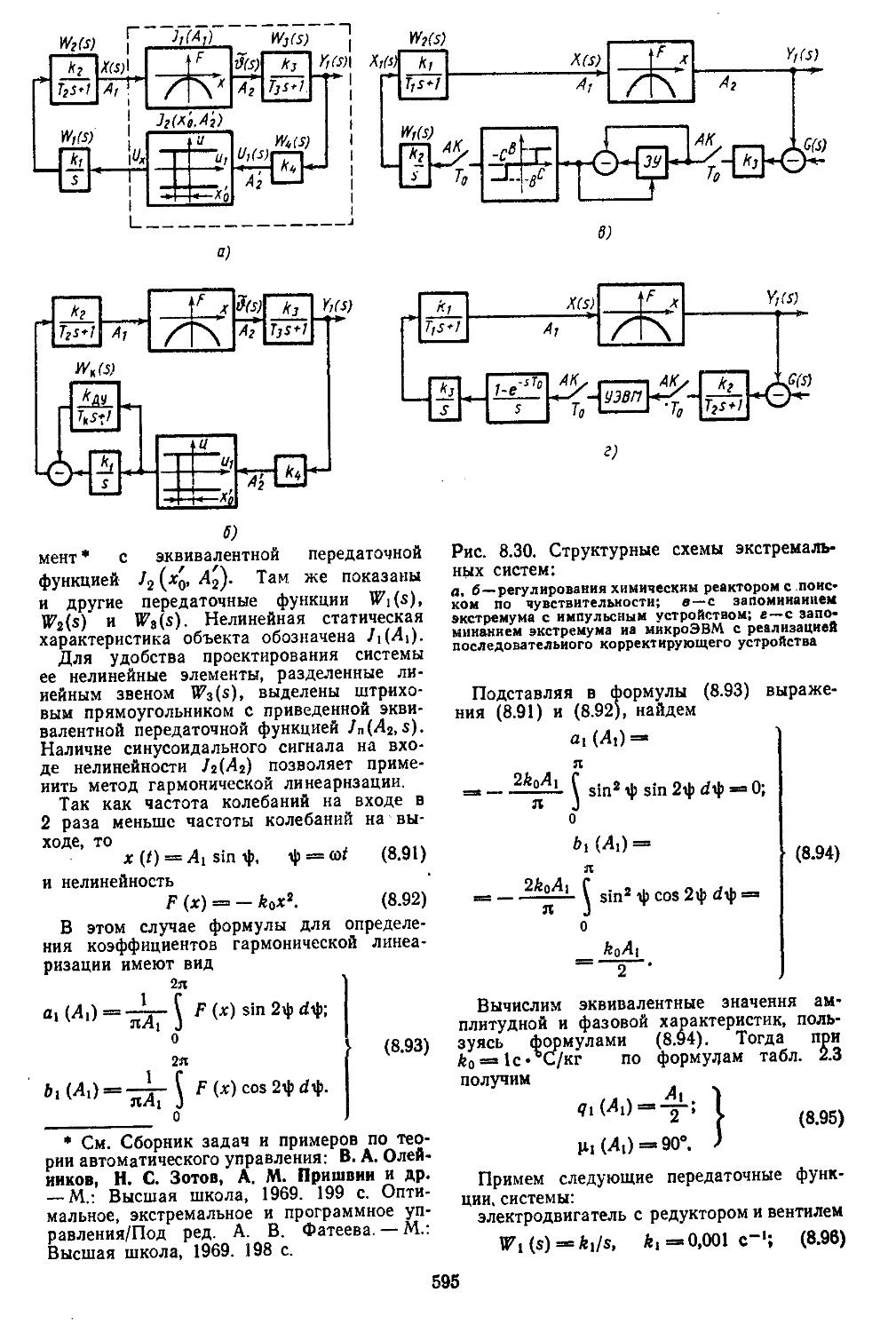
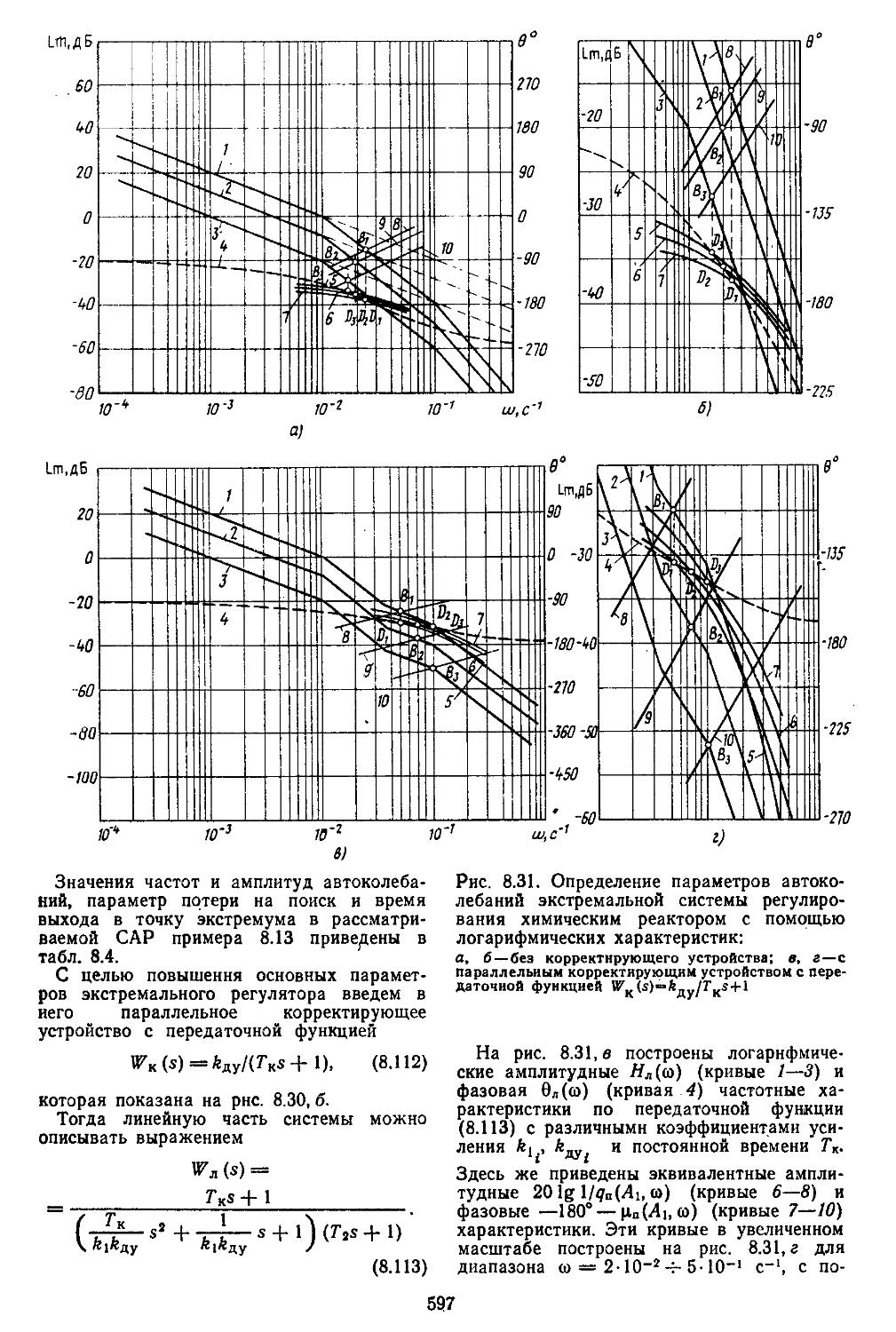
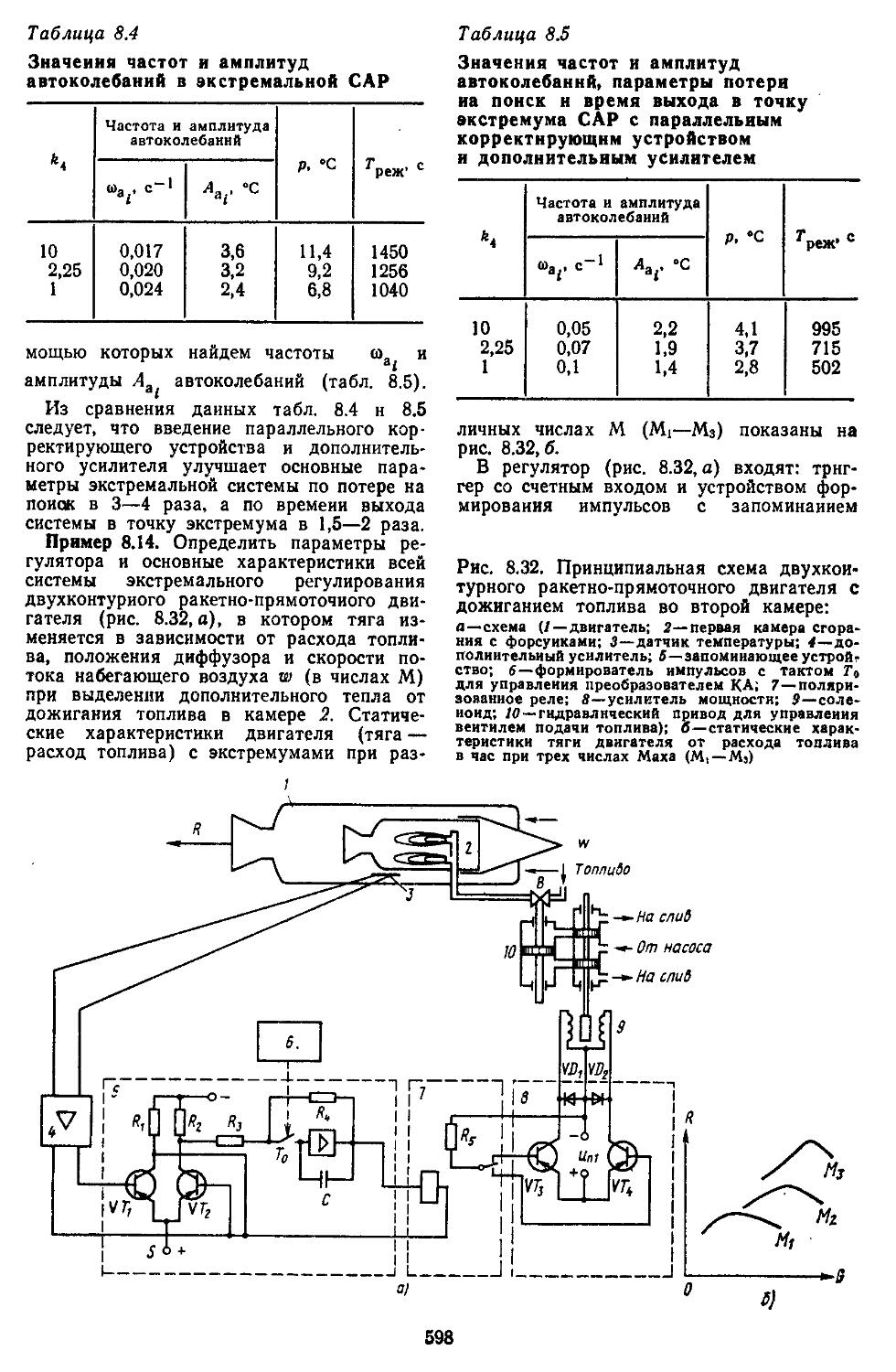
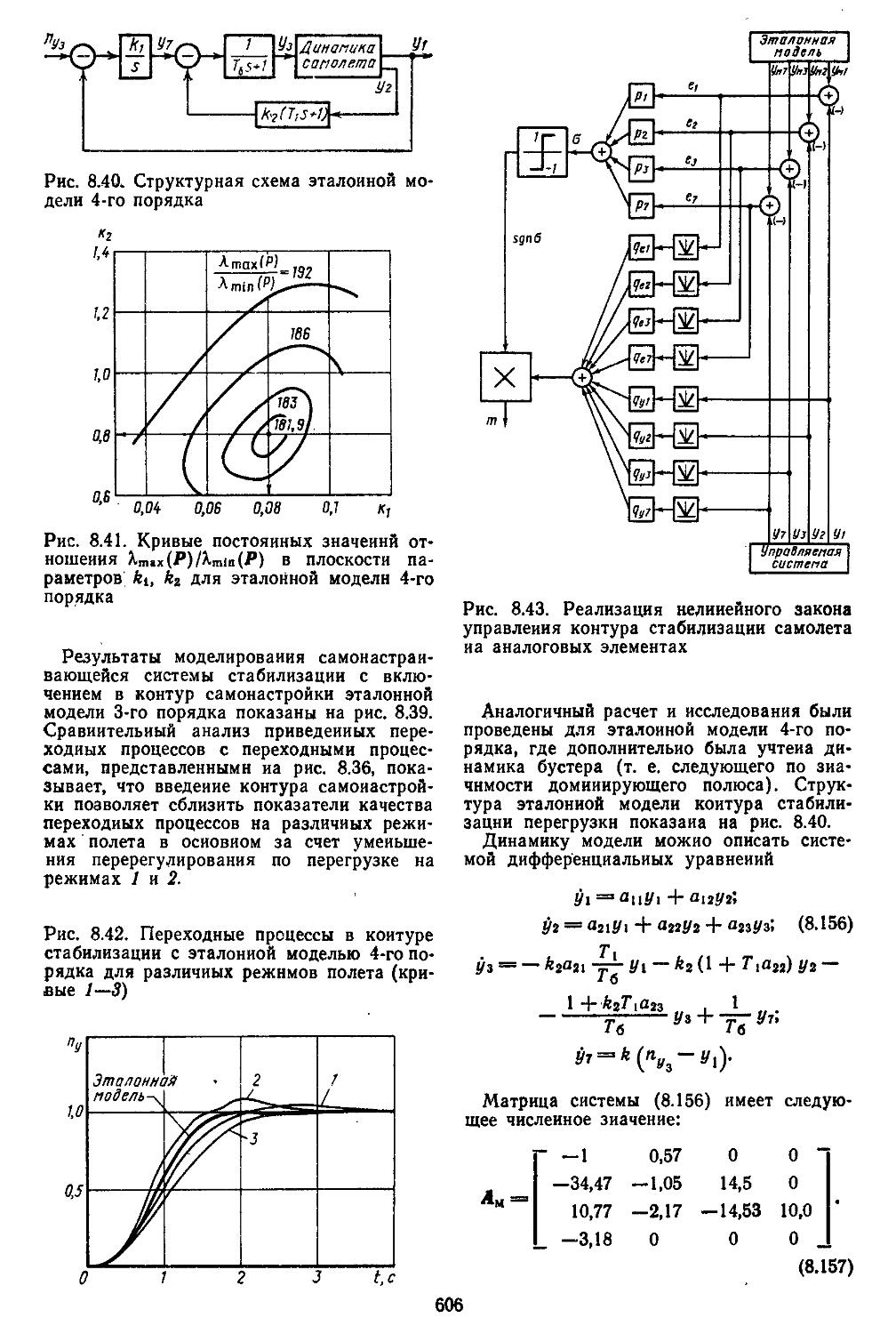
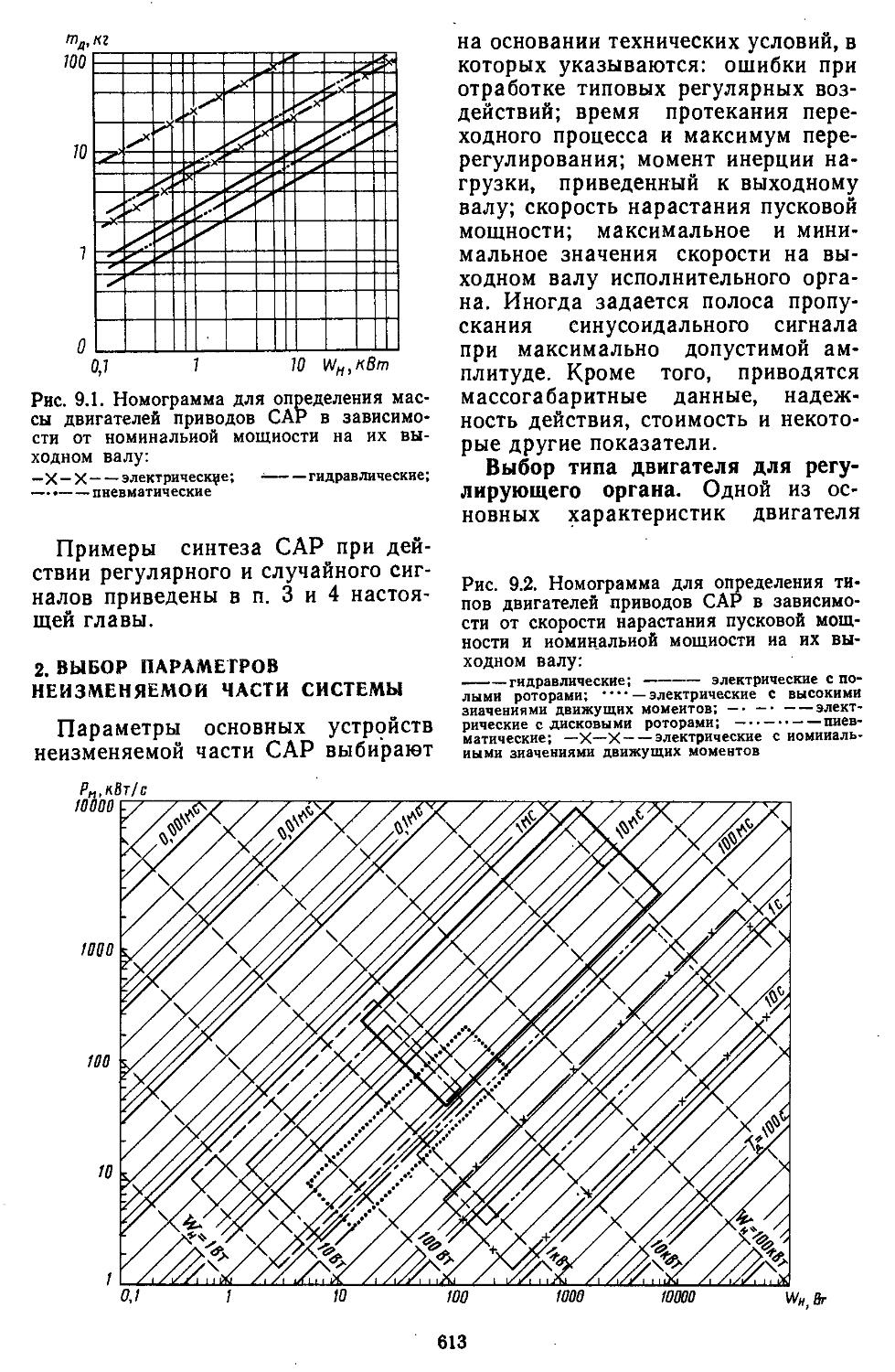
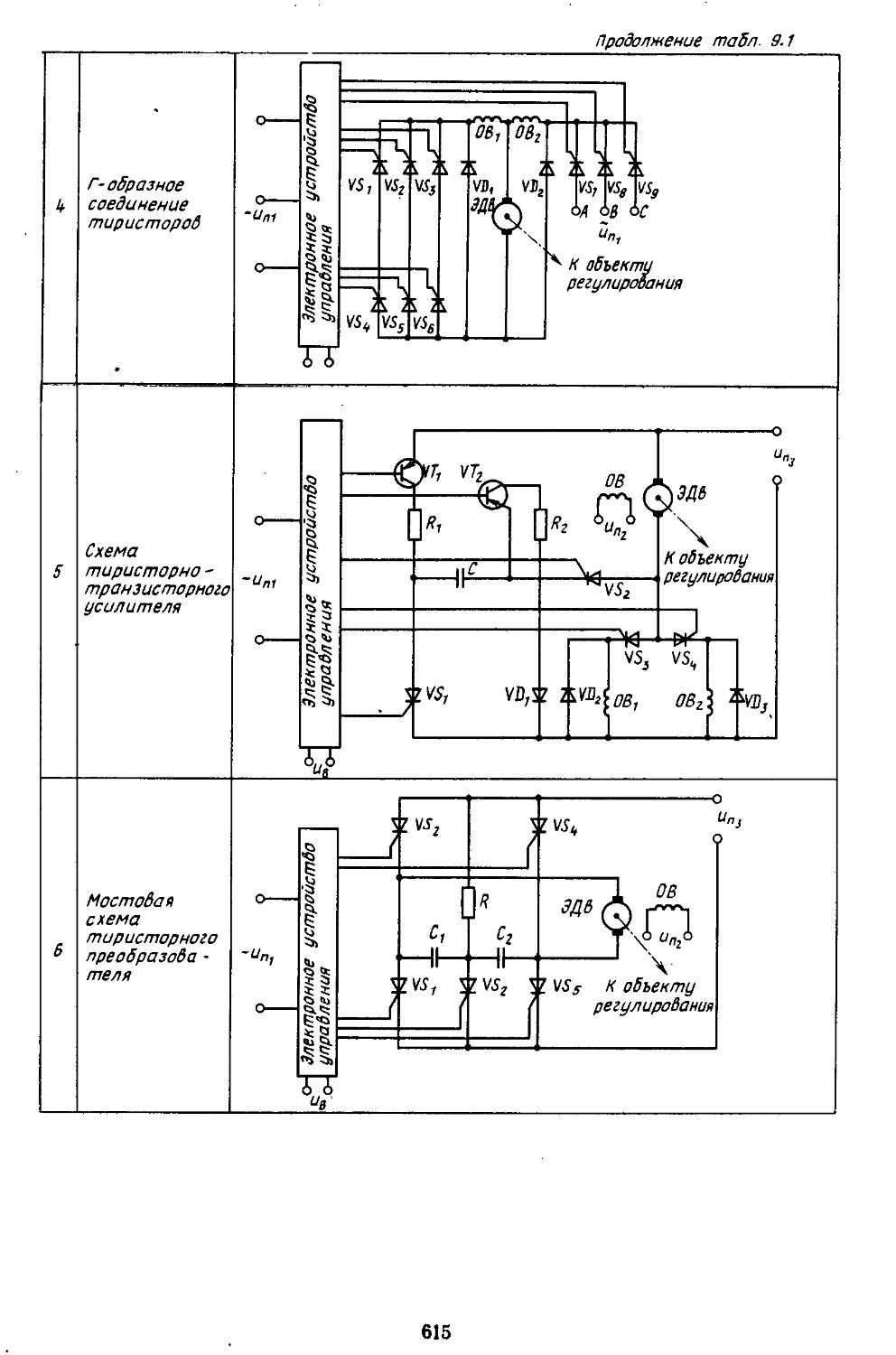
3. Экстремальные системы автоматического регулирования ...... 585 4. Расчет и исследование самонастраивающейся системы управления с эталонной моделью и сигнальной компеиса-. . 600
АВ-РЕ-. . 609
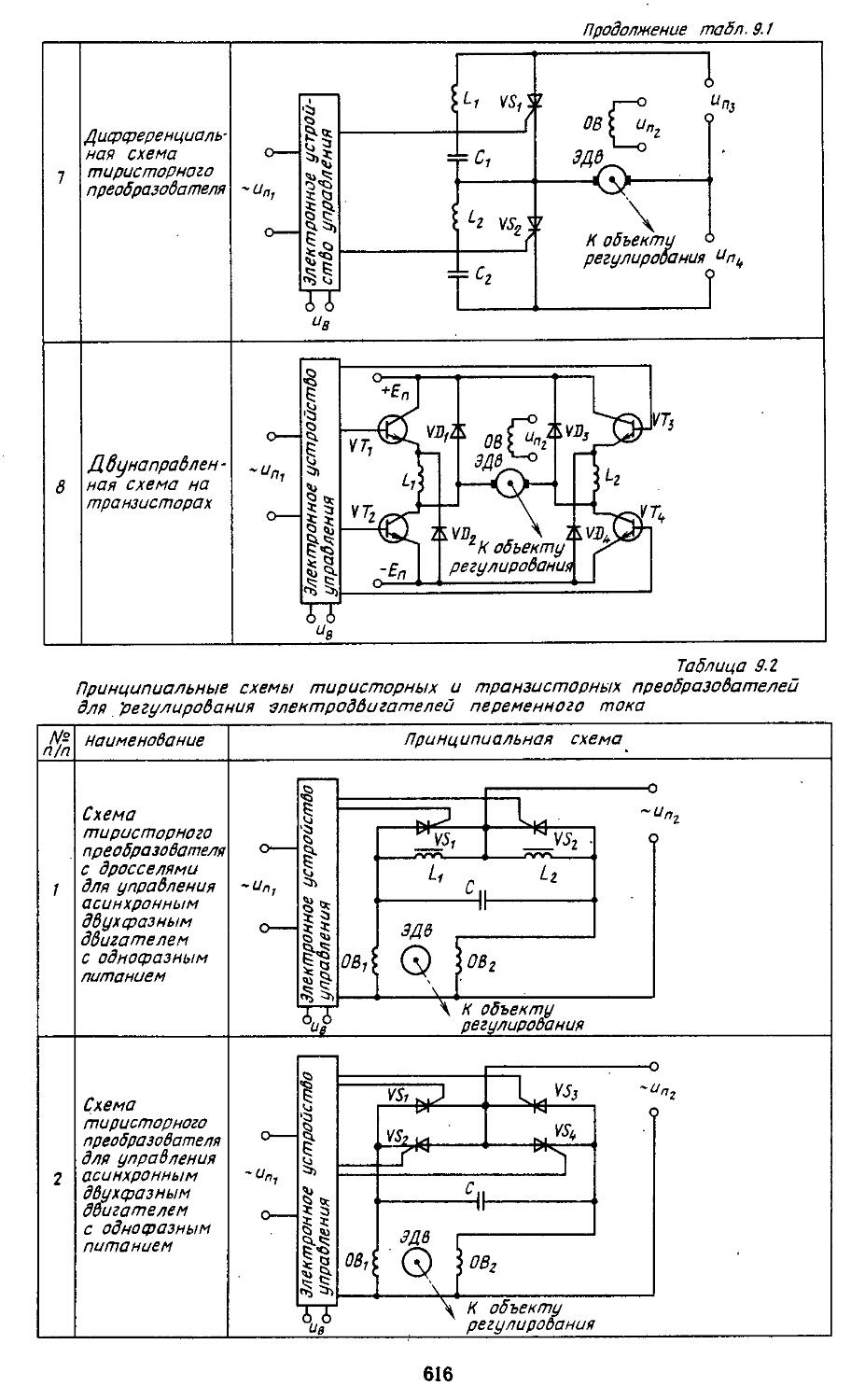
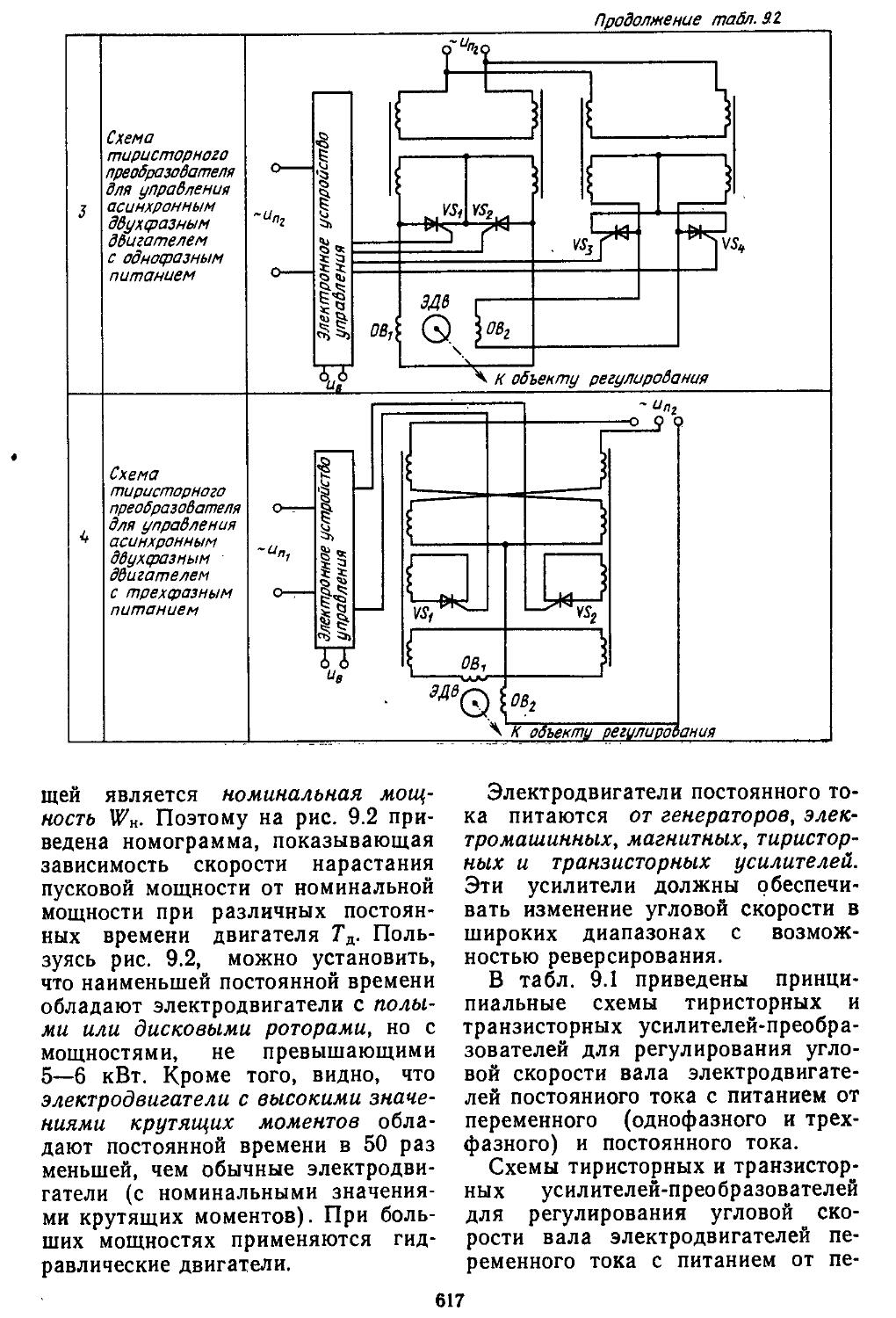
Глава 9. Синтез линейных непрерывных систем автоматического регулирования при регулярных и случайных воздействия^ ......... 609 1. Постановка задачи синтеза систем регулиррва-
РАЗДЕЛ III. СИНТЕЗ СИСТЕМ
А ТОМАТИЧЕСКОГО ГУЛ И РОВАН ИЯ
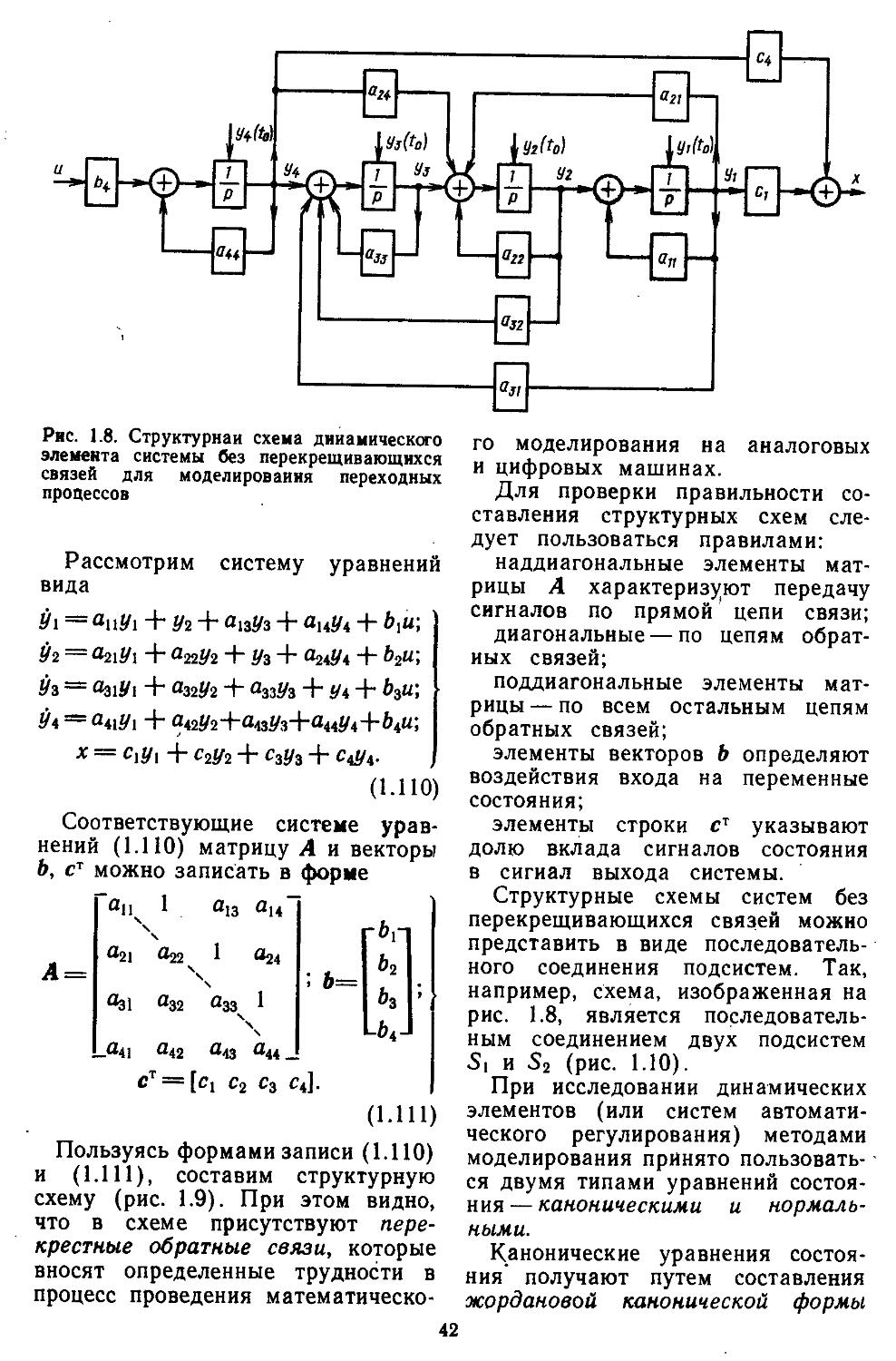
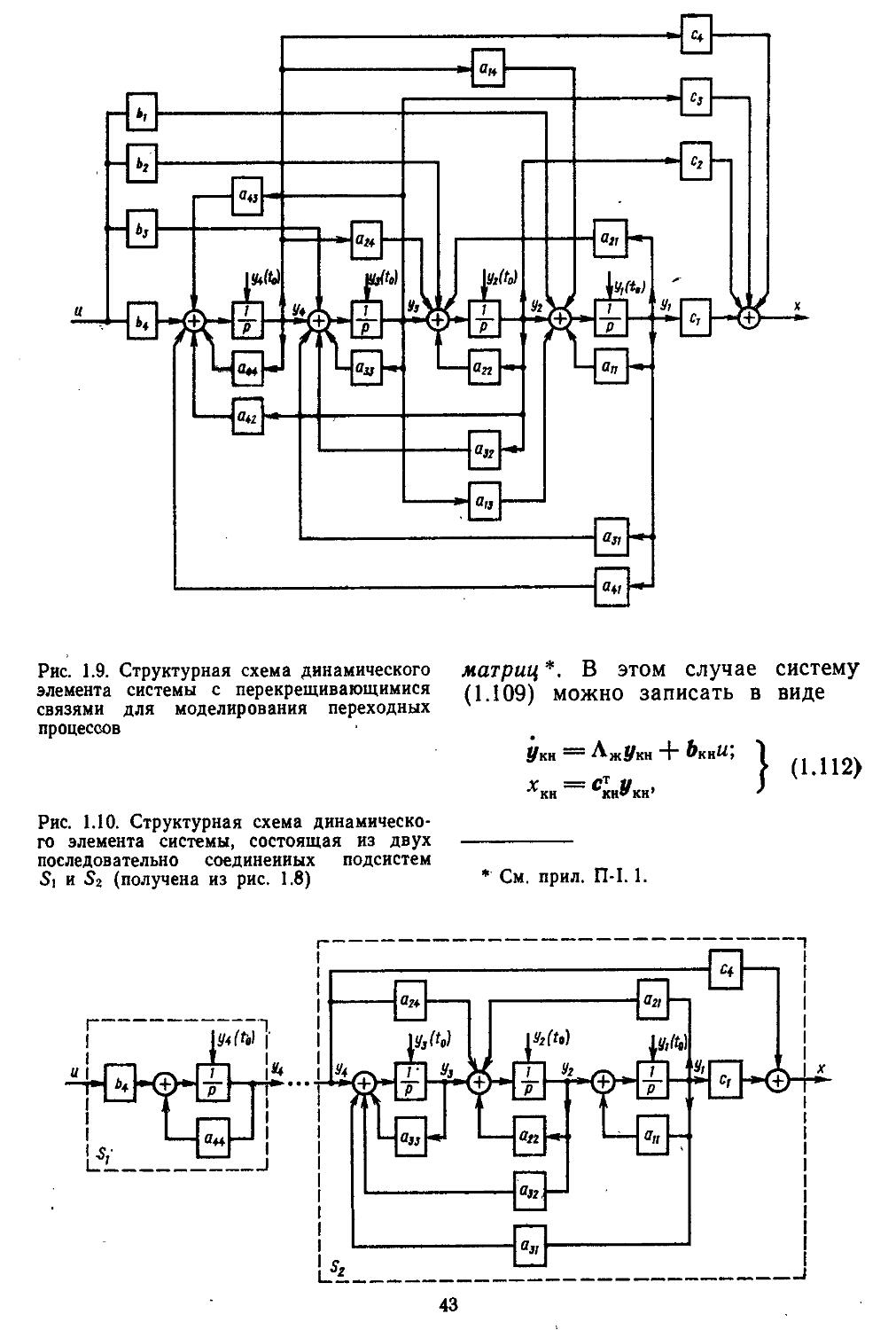
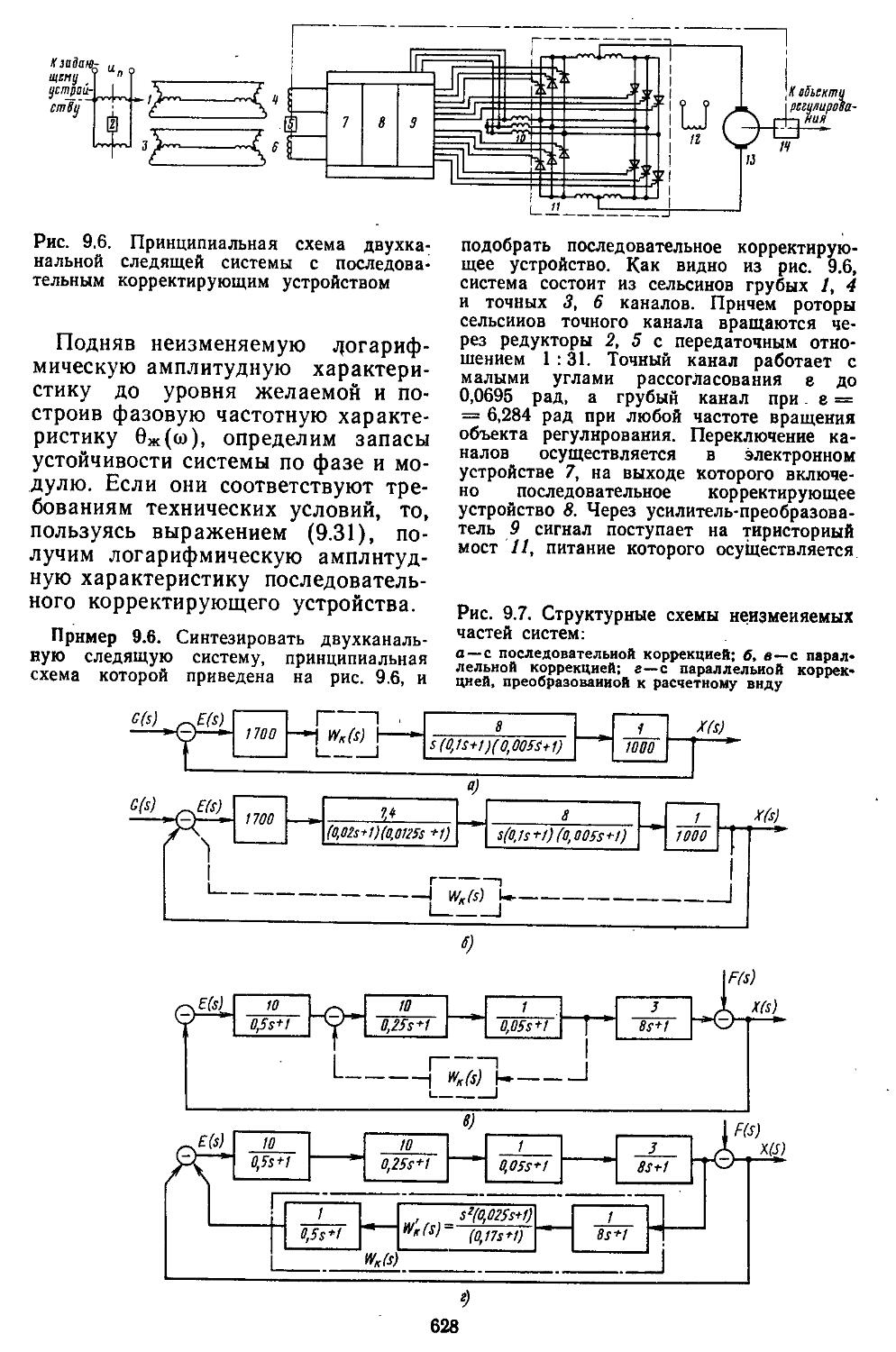
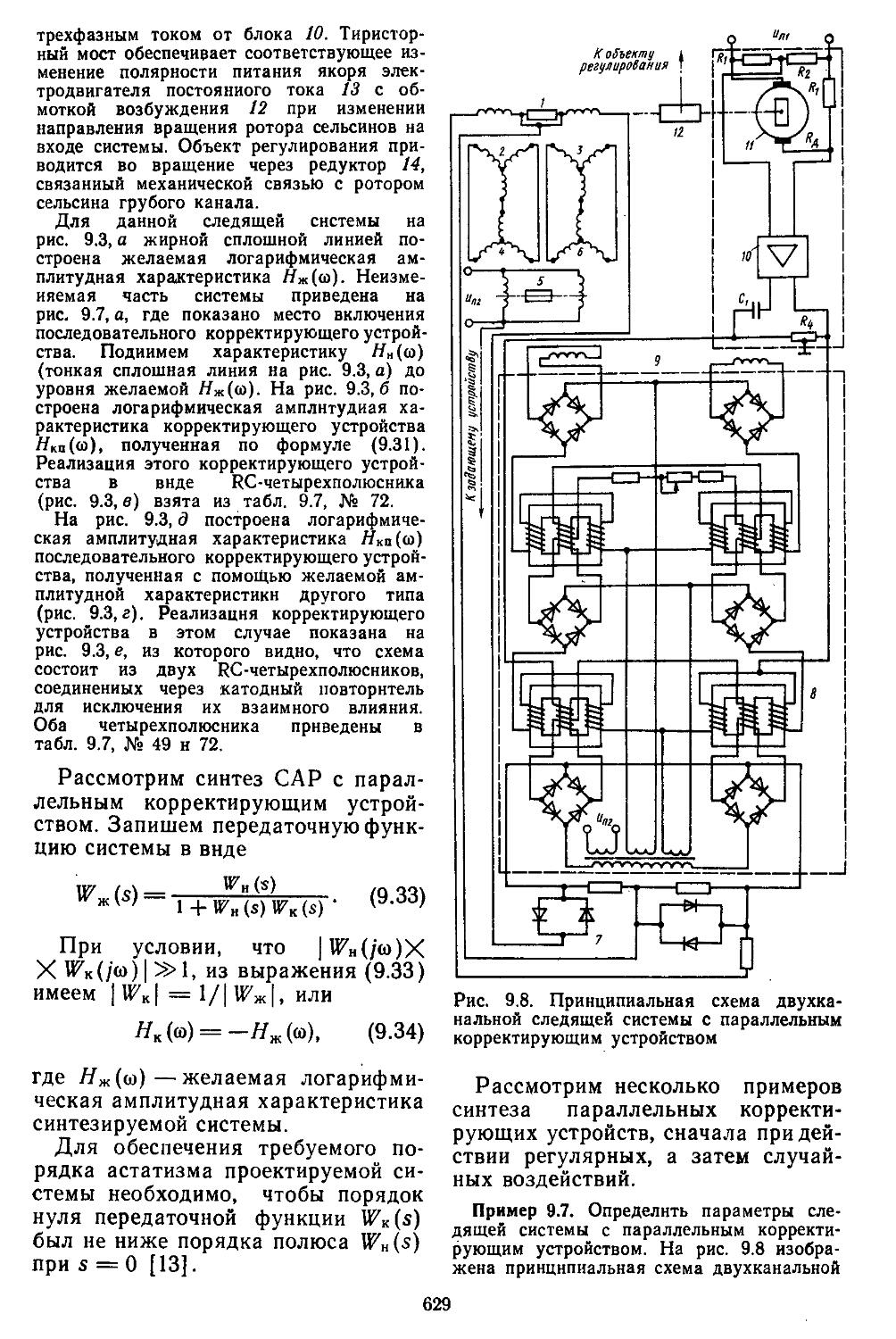
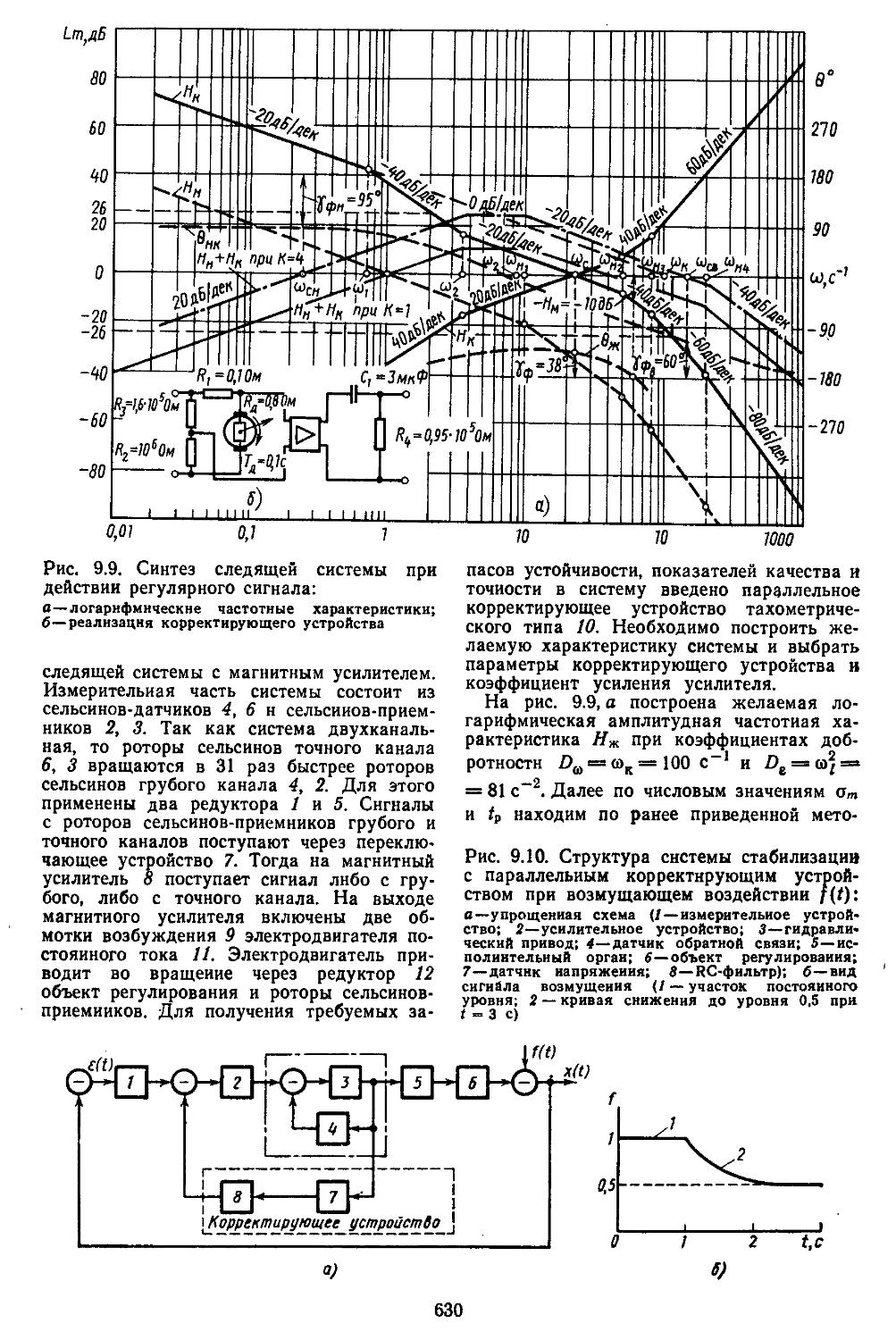
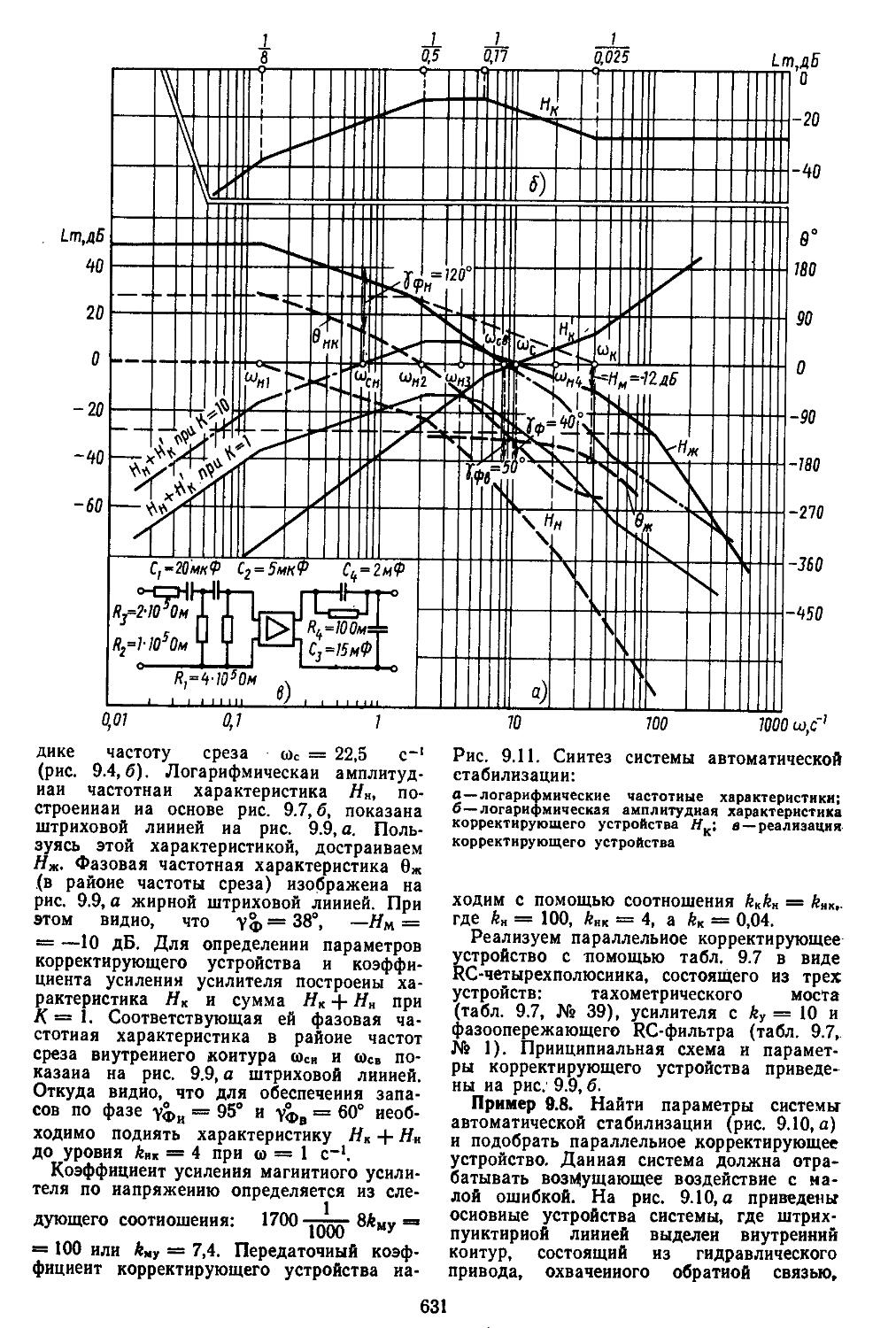
иия, основанная иа частотных методах . . . 610 2. Выбор параметров неизменяемой части системы 613 3. Построение желаемых амплитудной и фазовой частотных ' характеристик разомкнутых систем ....... 622 4. Синтез последовательных и параллельных корректирующих устройств . ................627
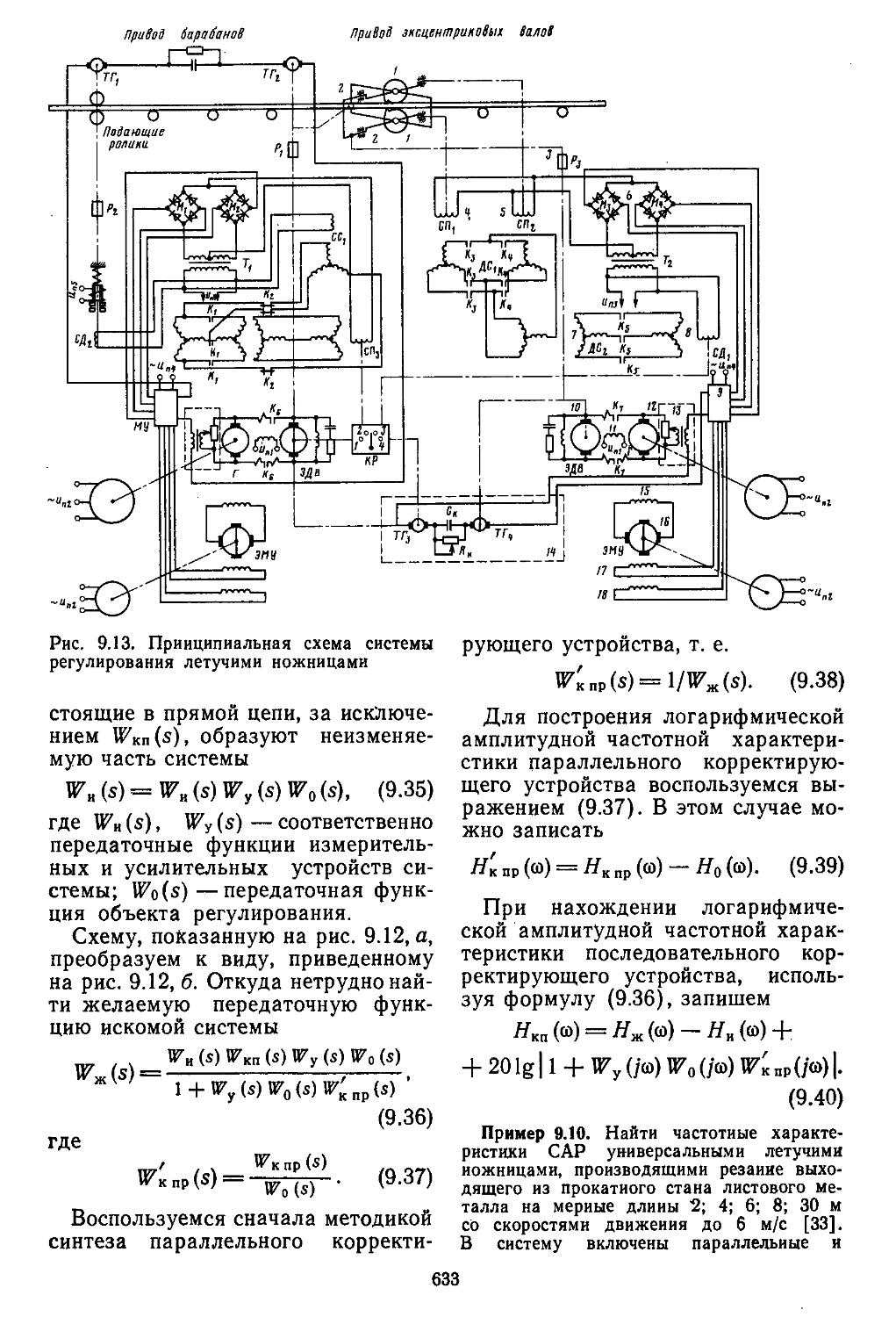
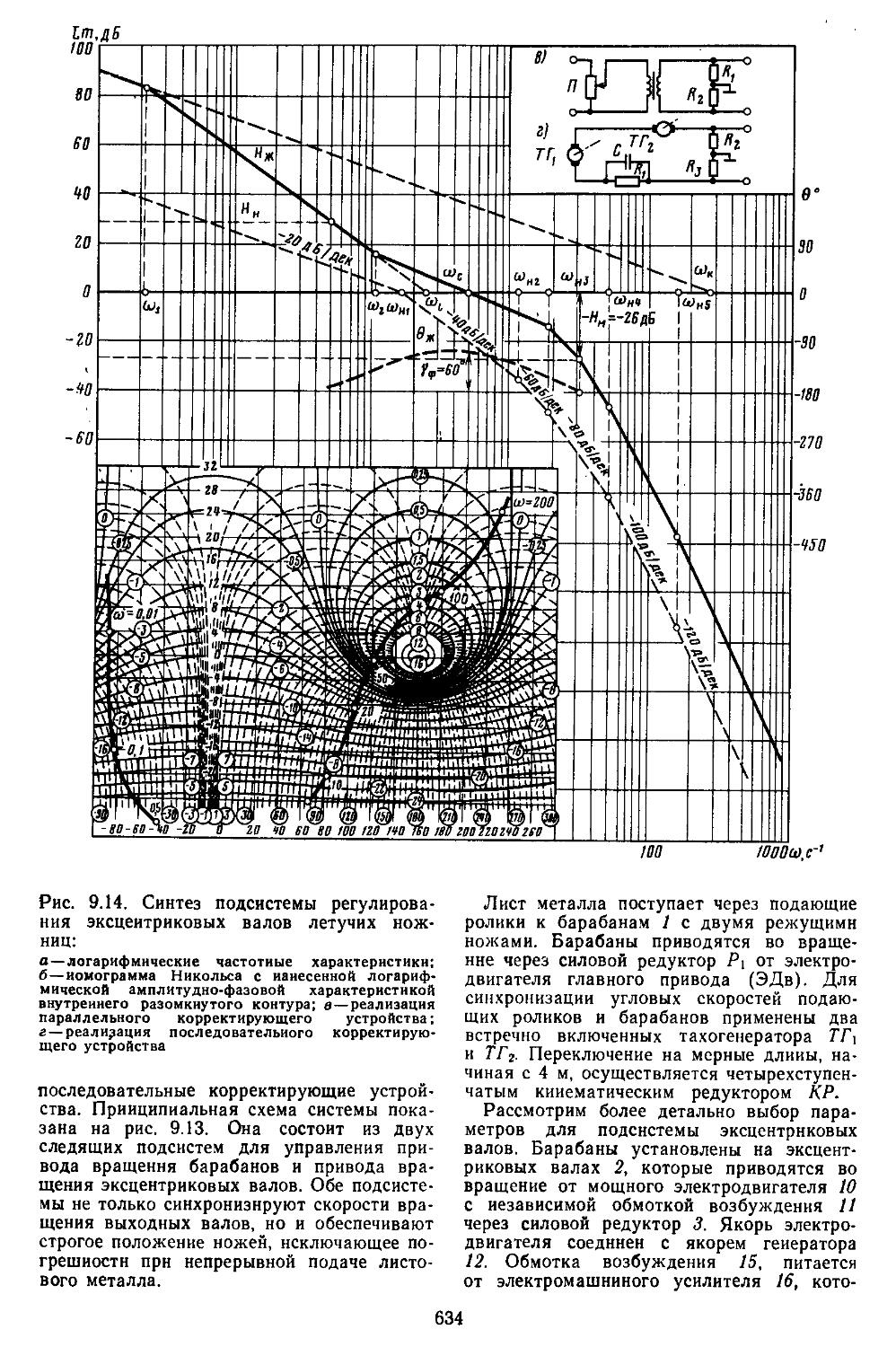
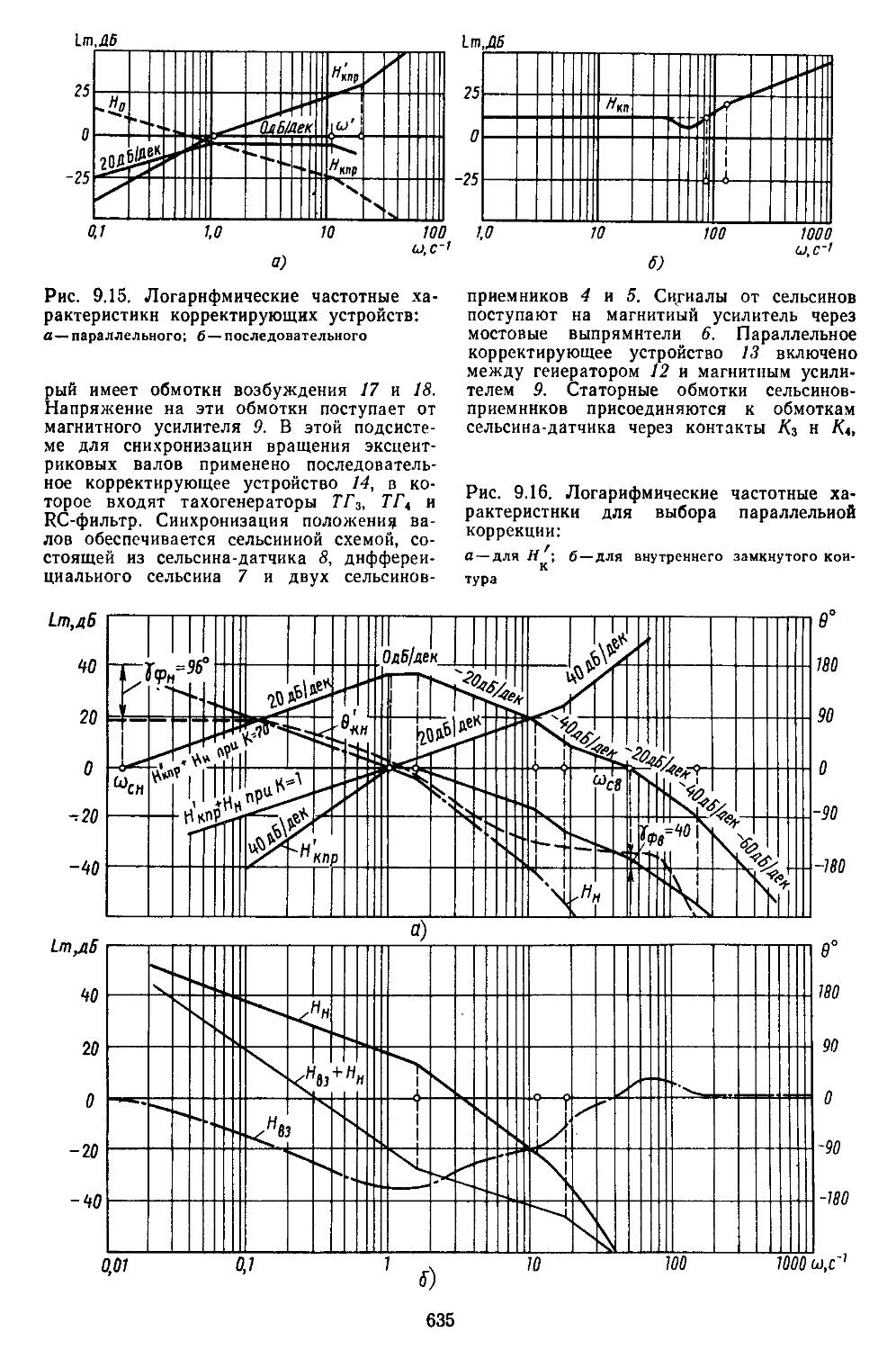
5. Синтез последовательно-параллельных корректирующих устройств . 632
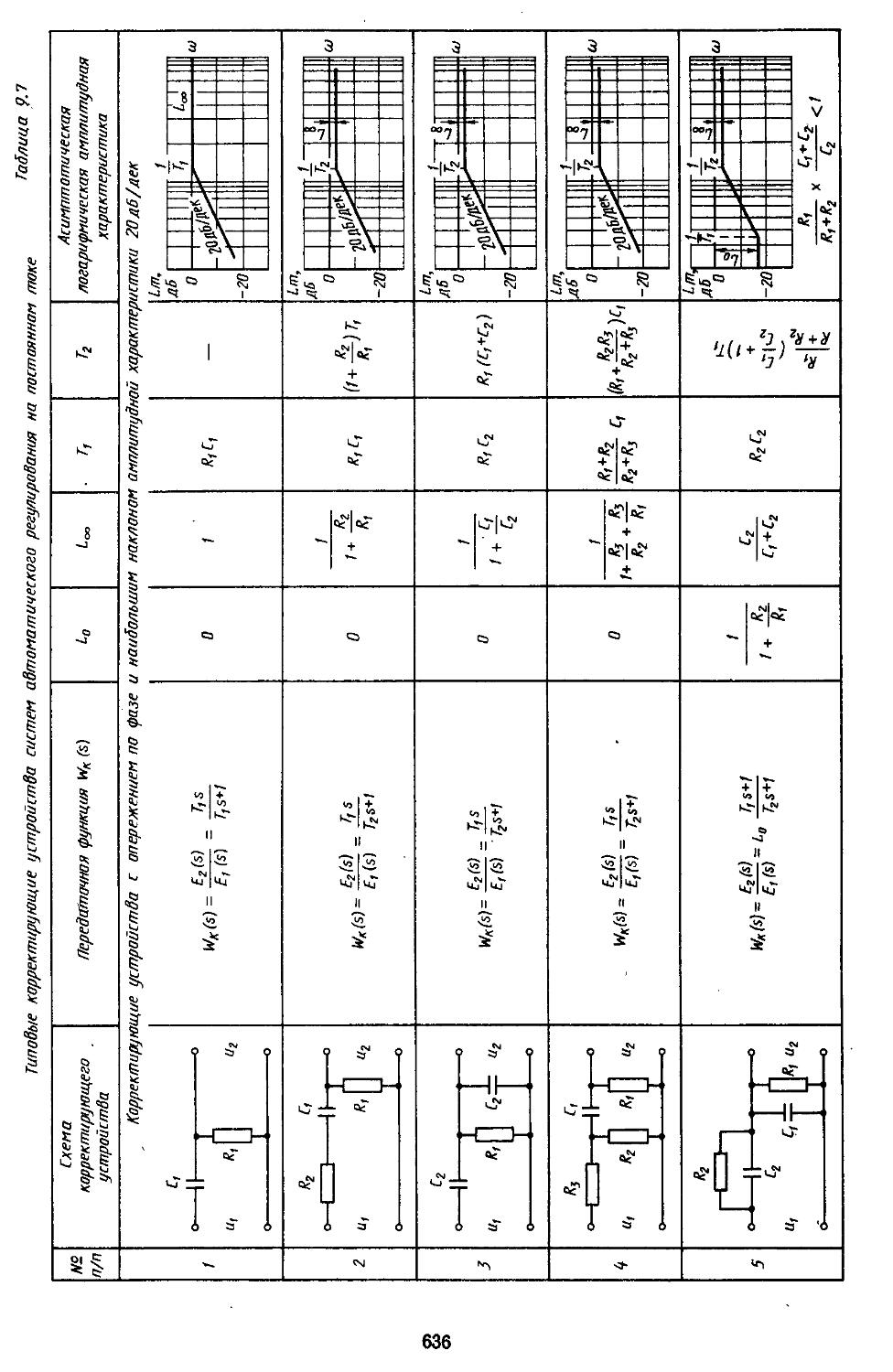
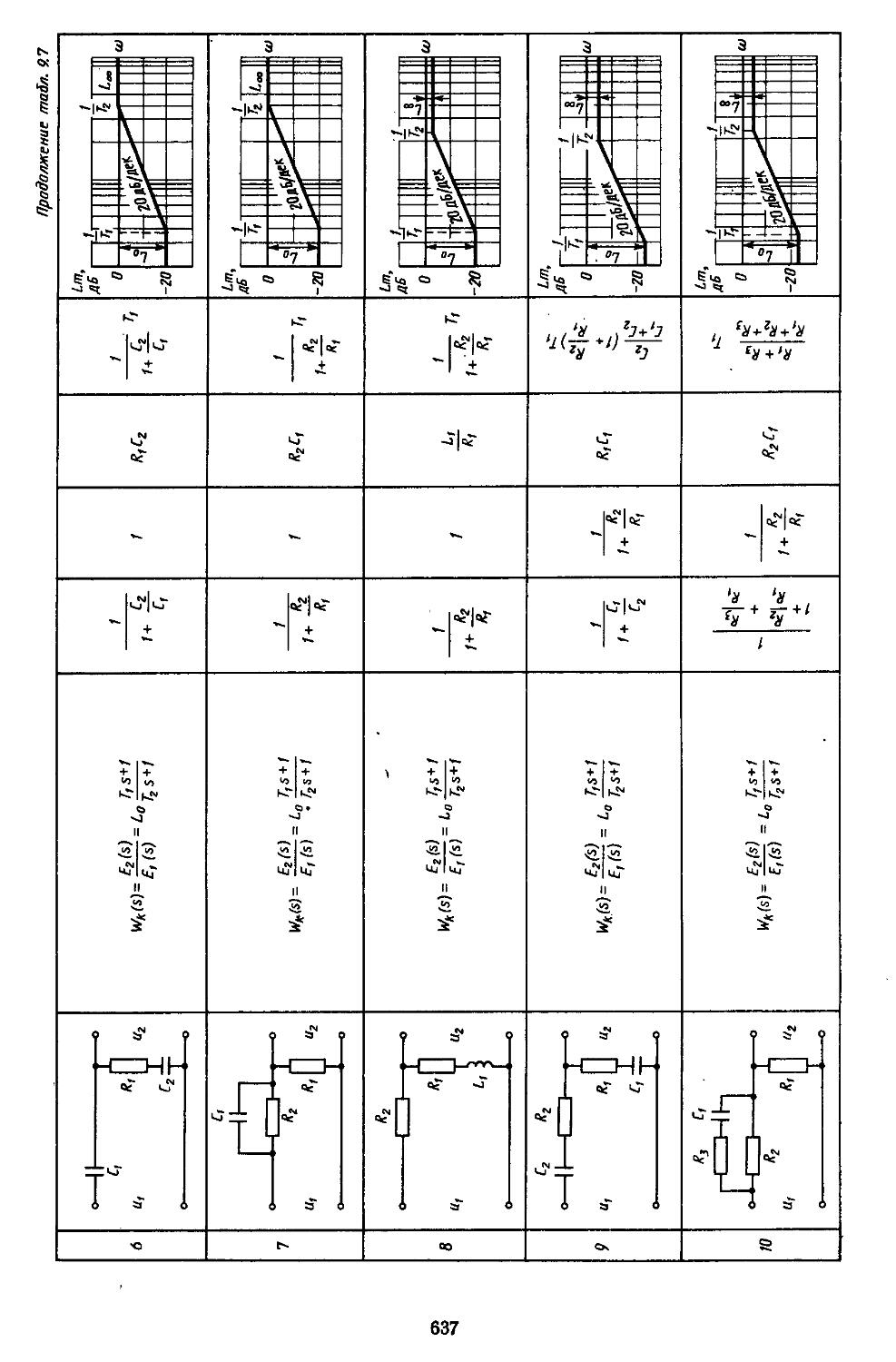
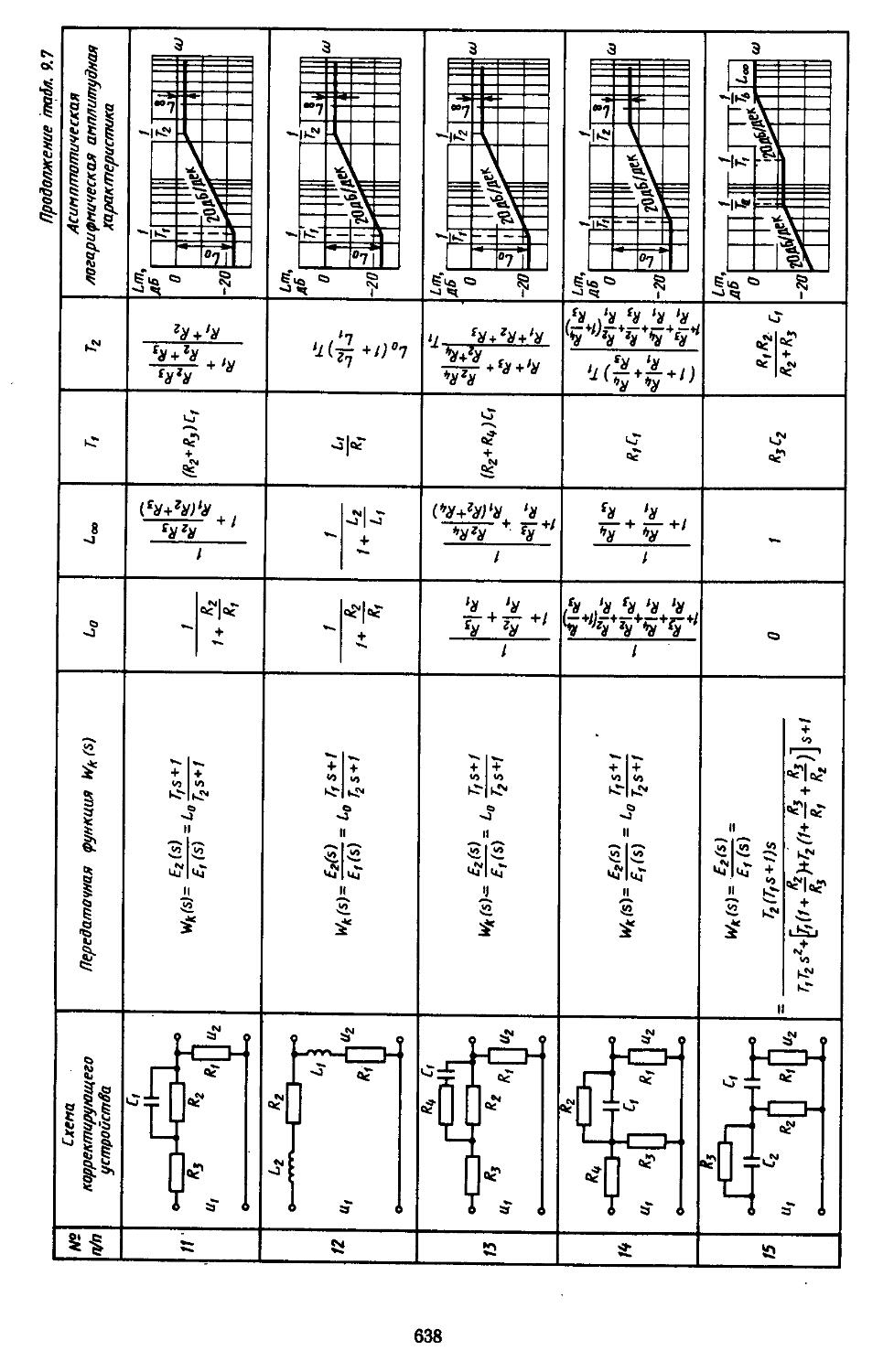
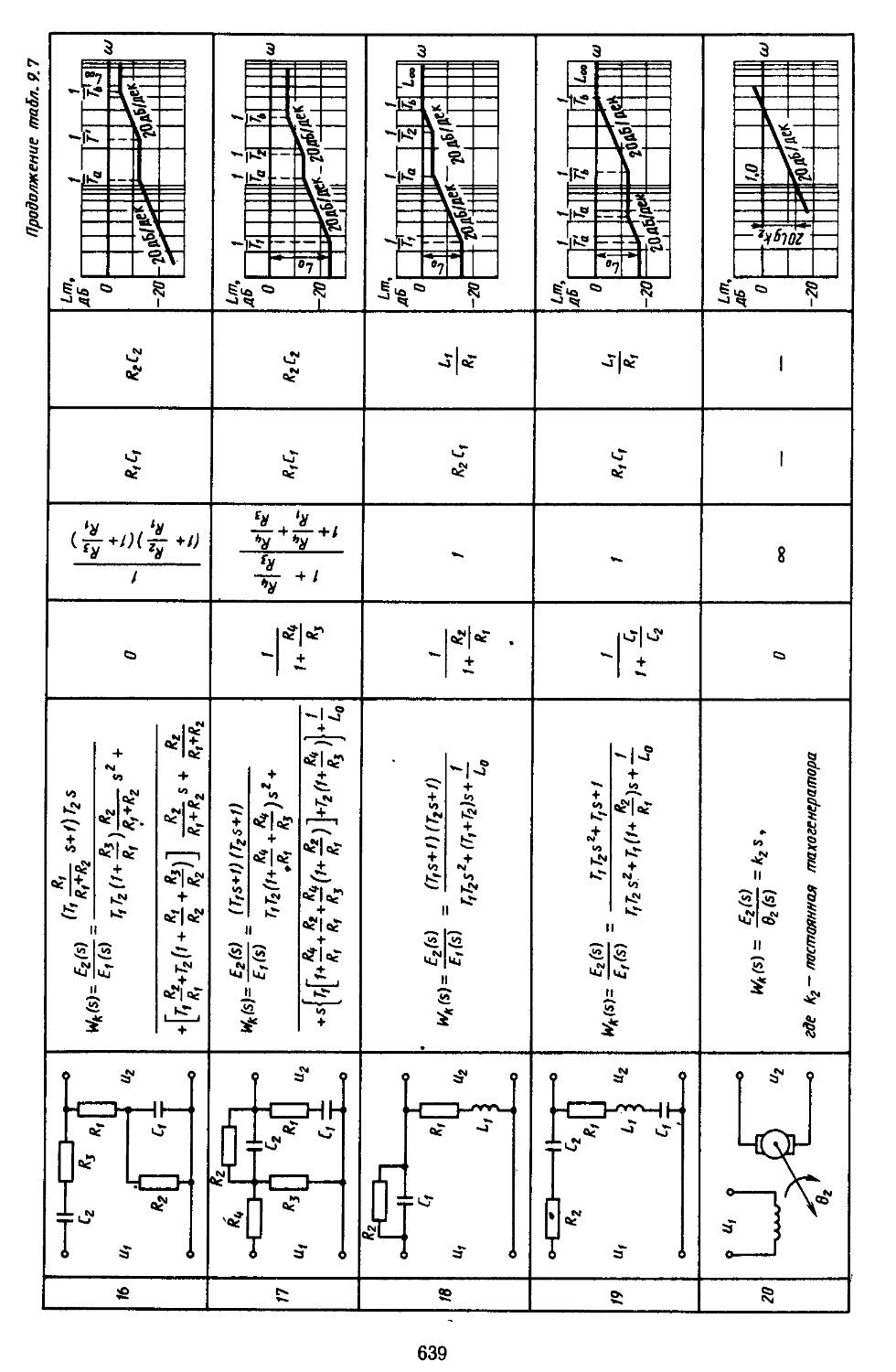
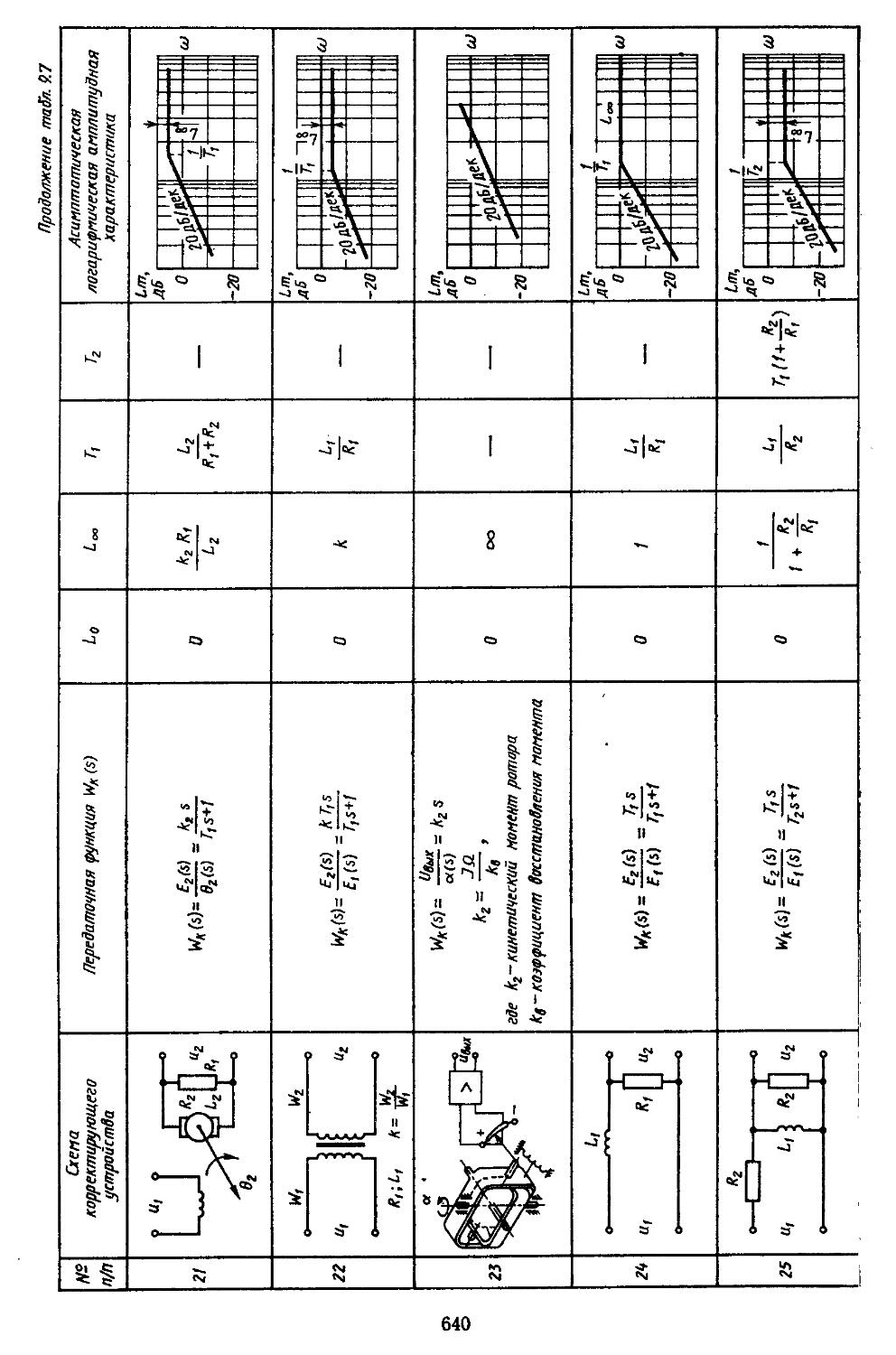
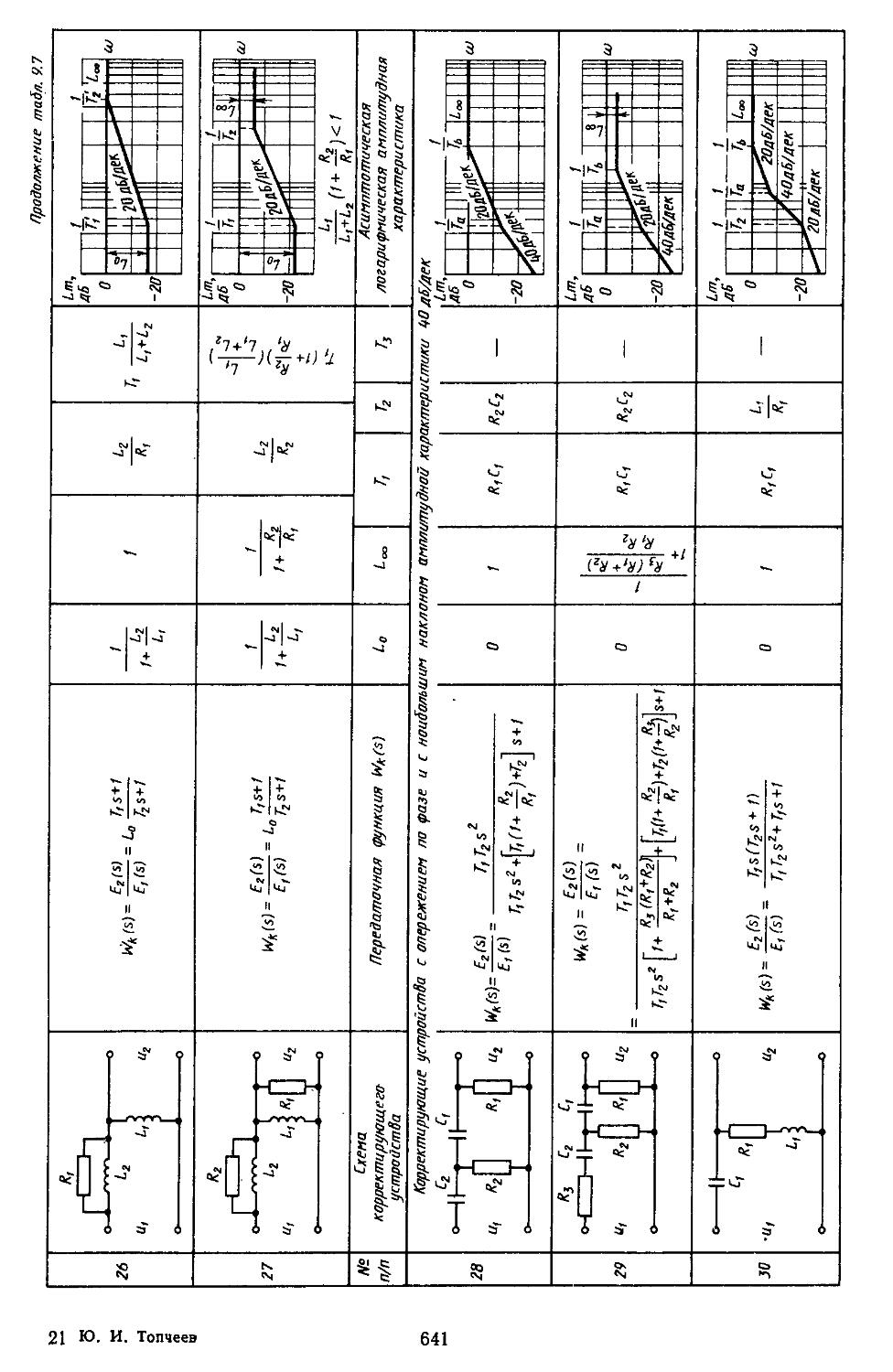
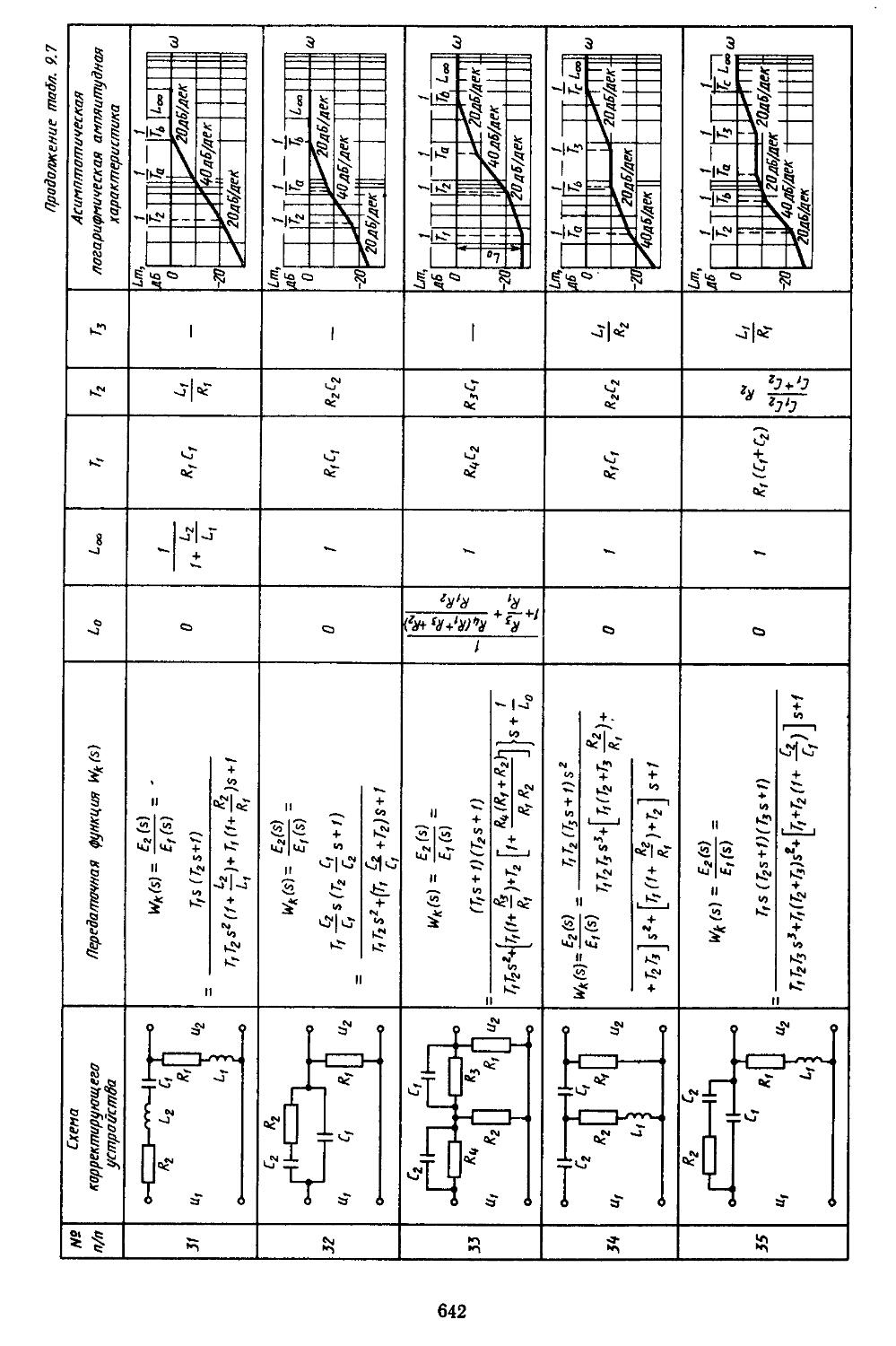
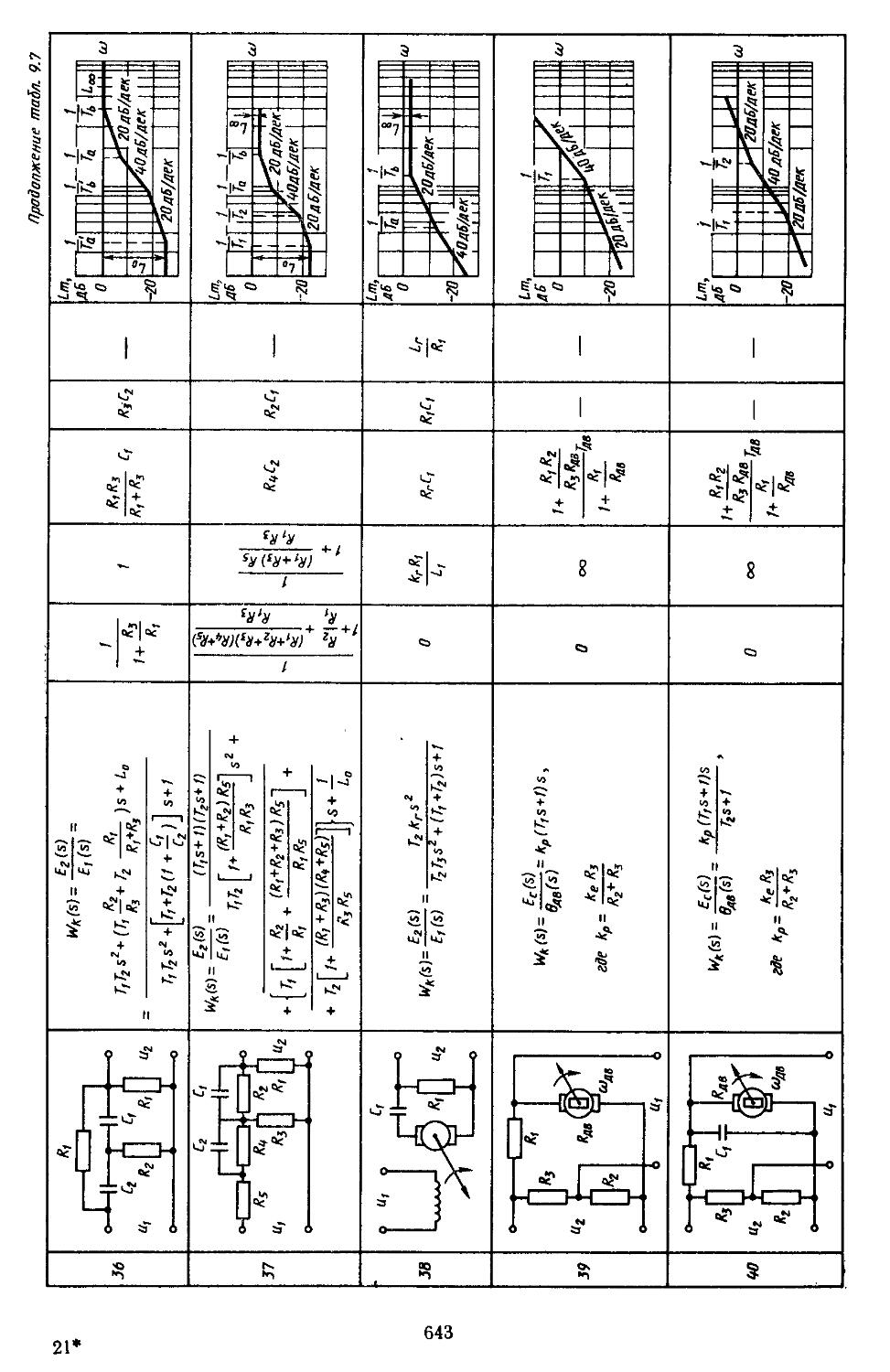
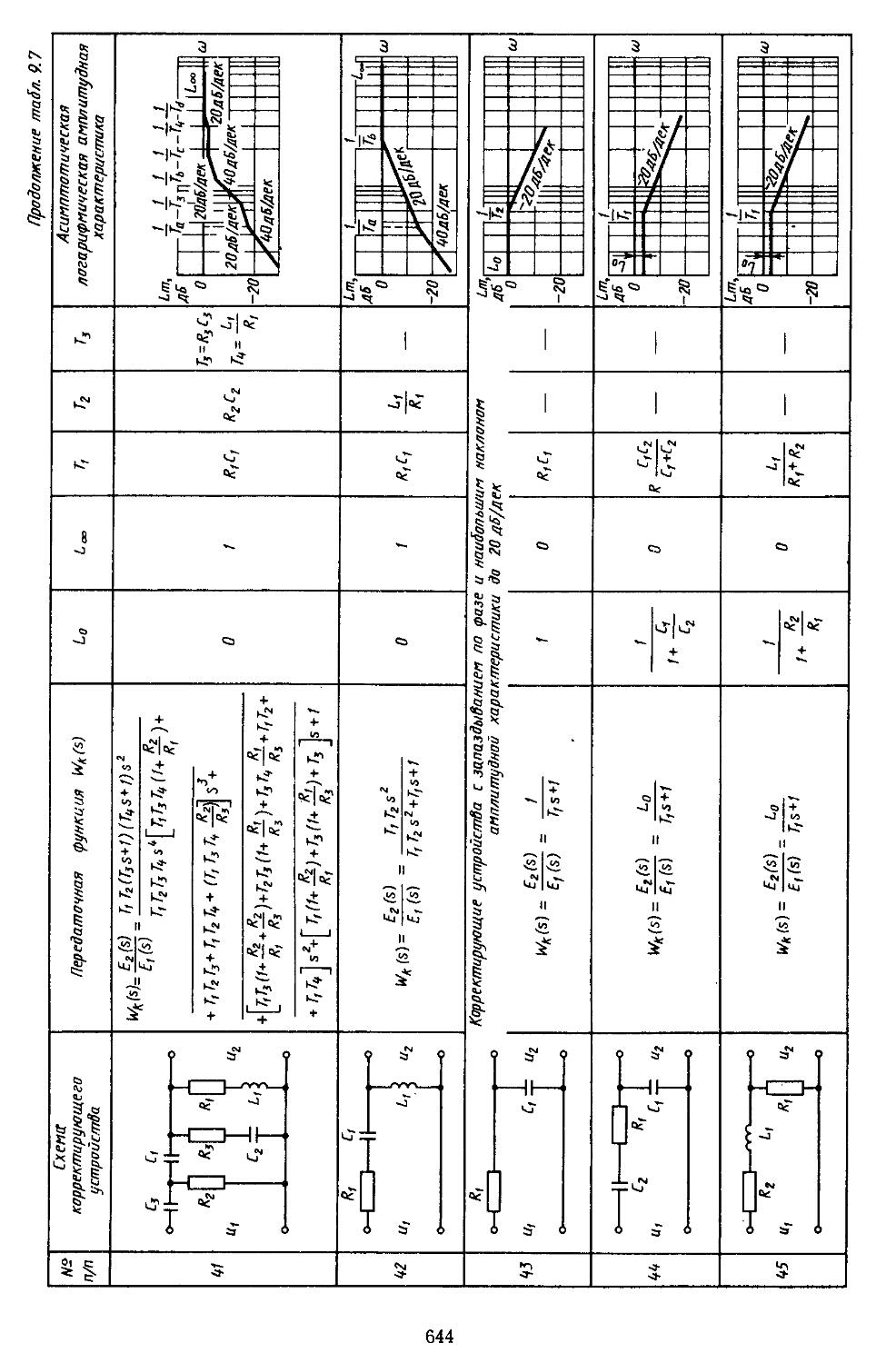
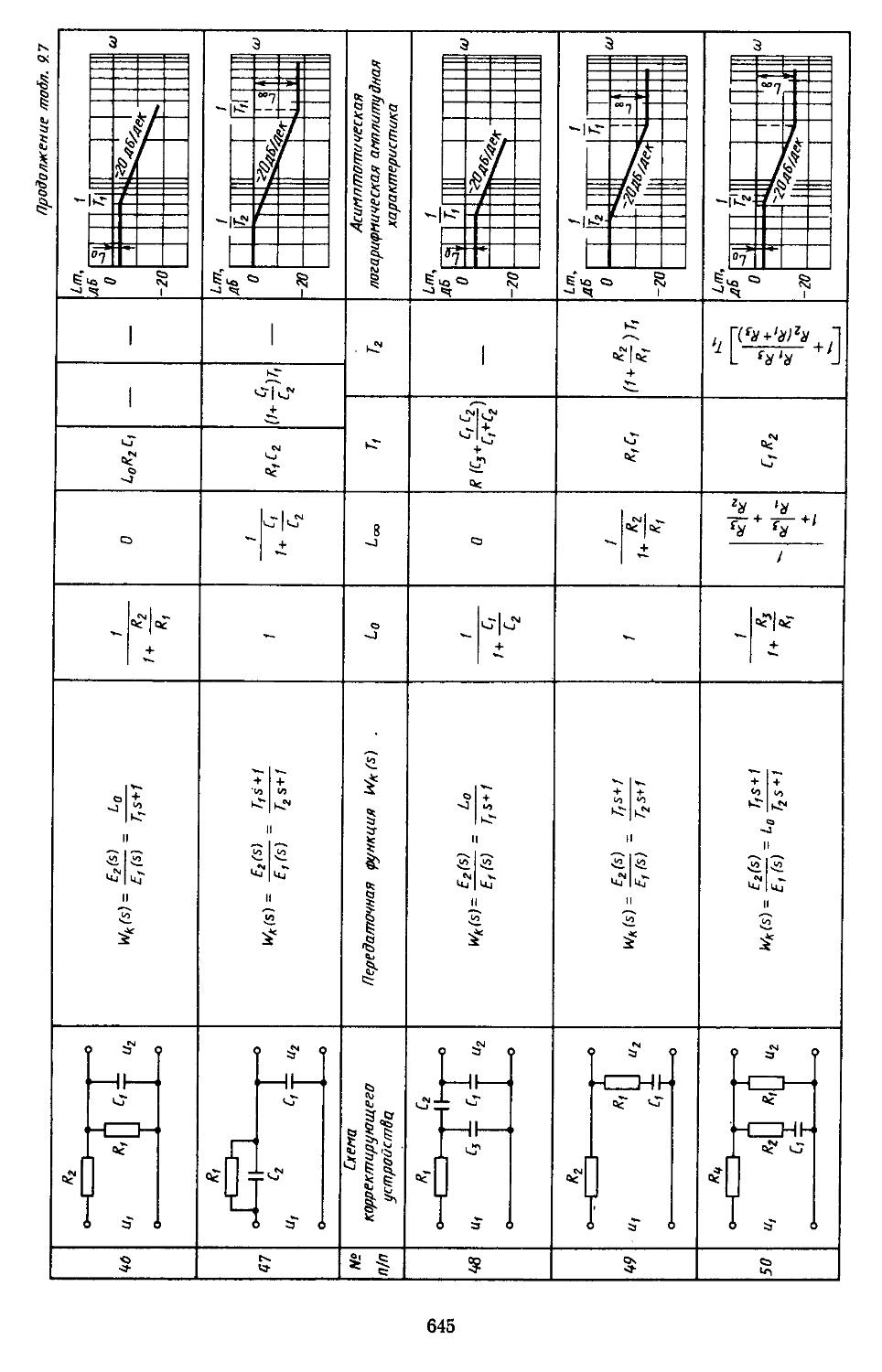
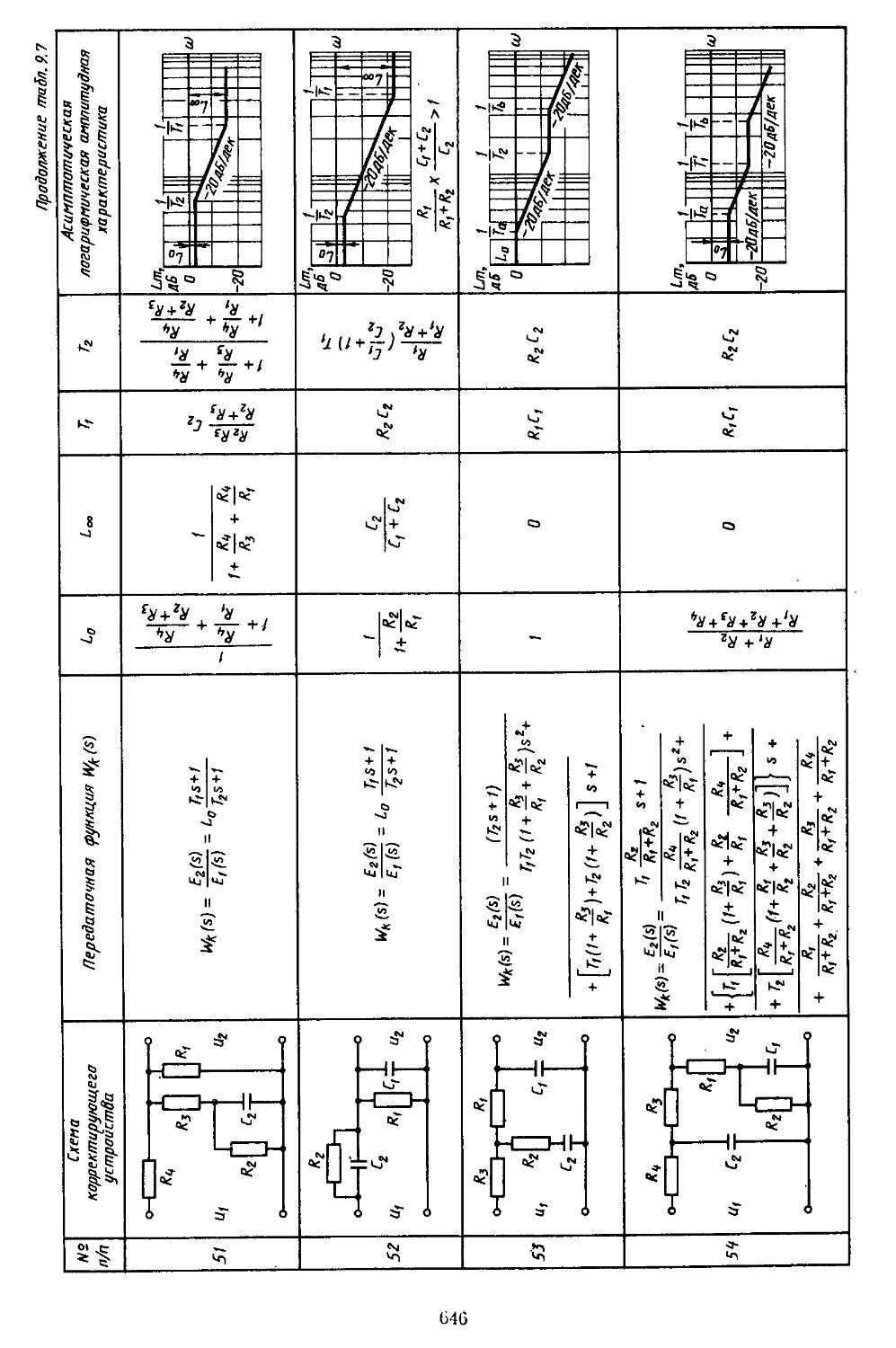
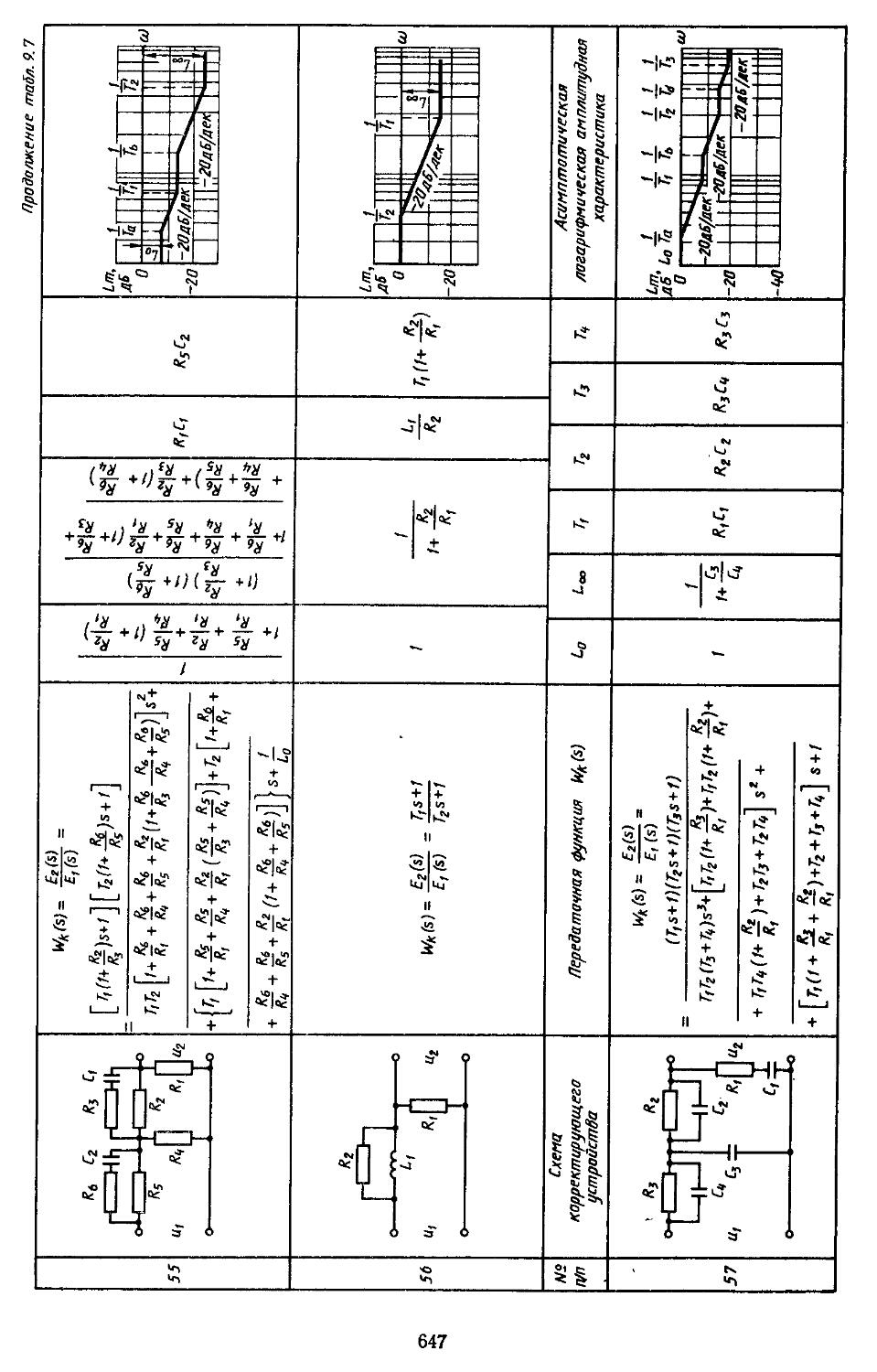
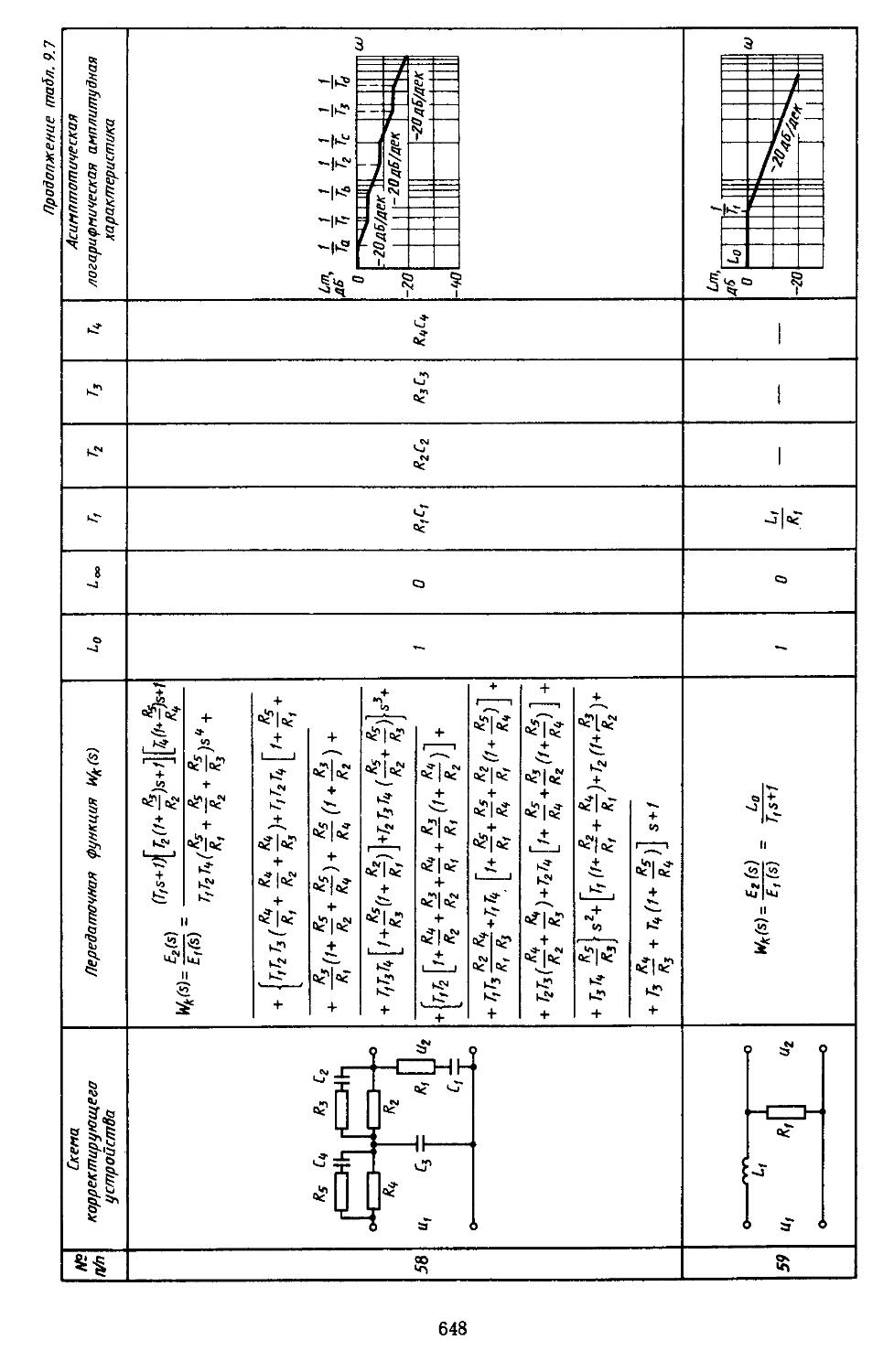
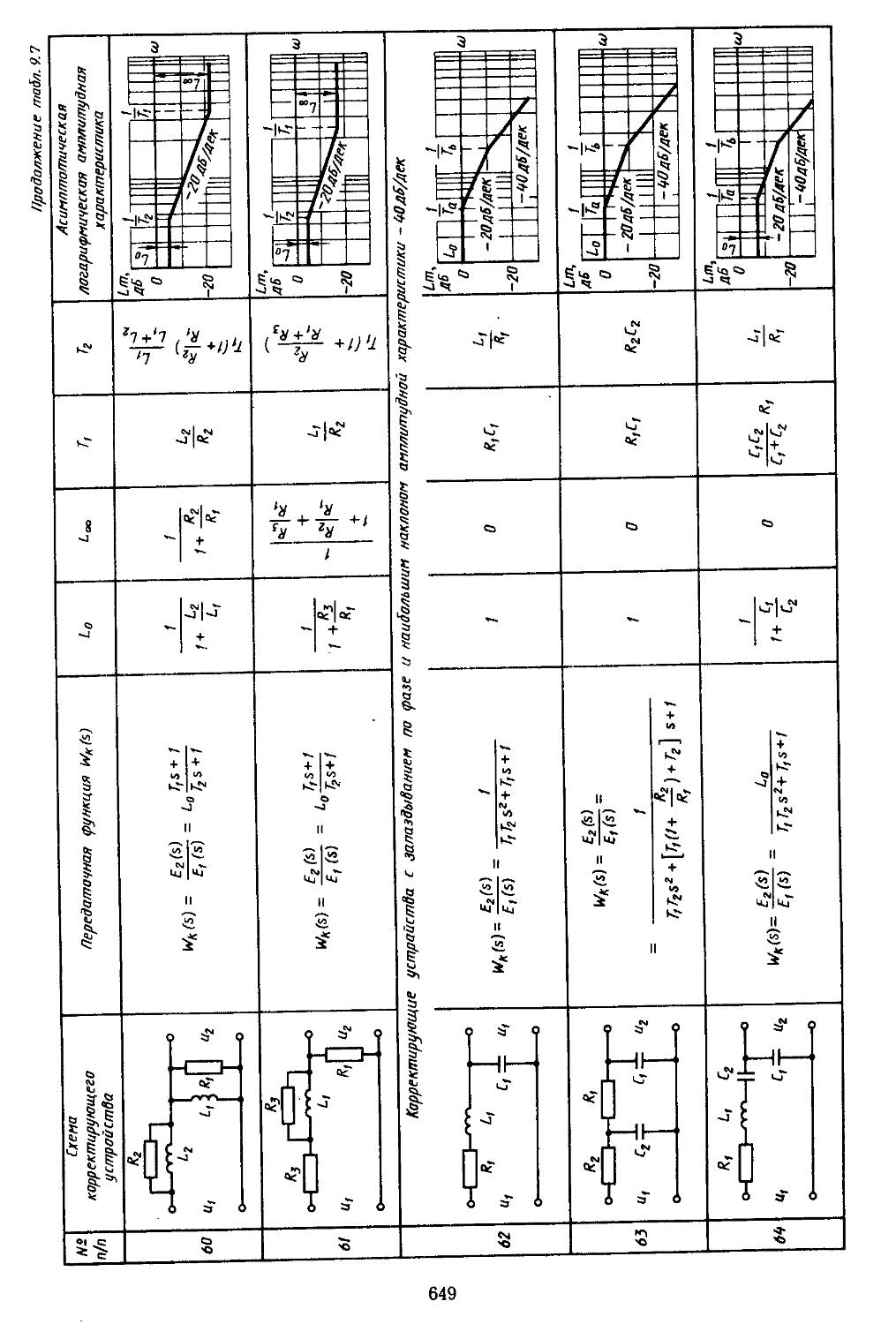
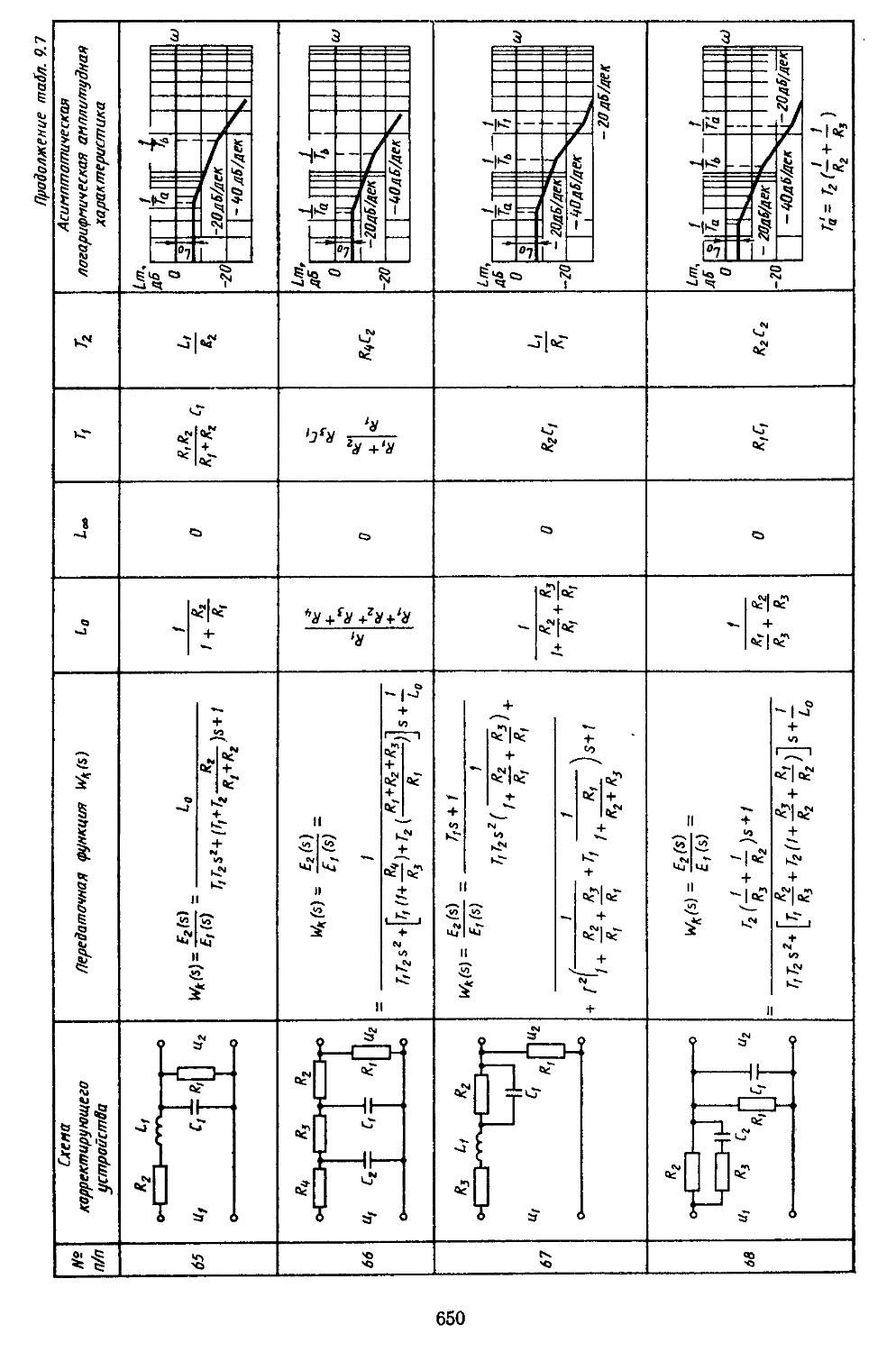
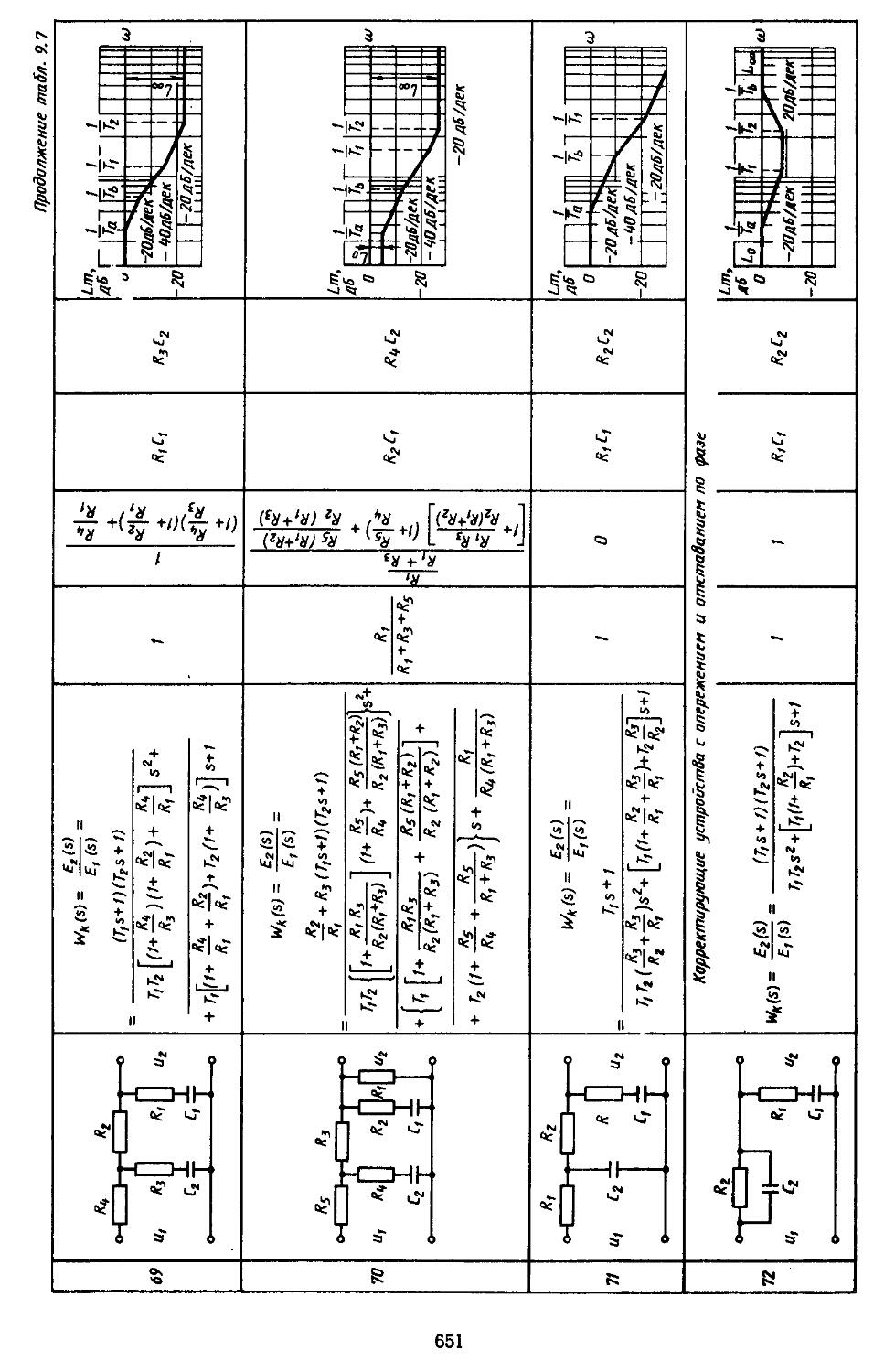
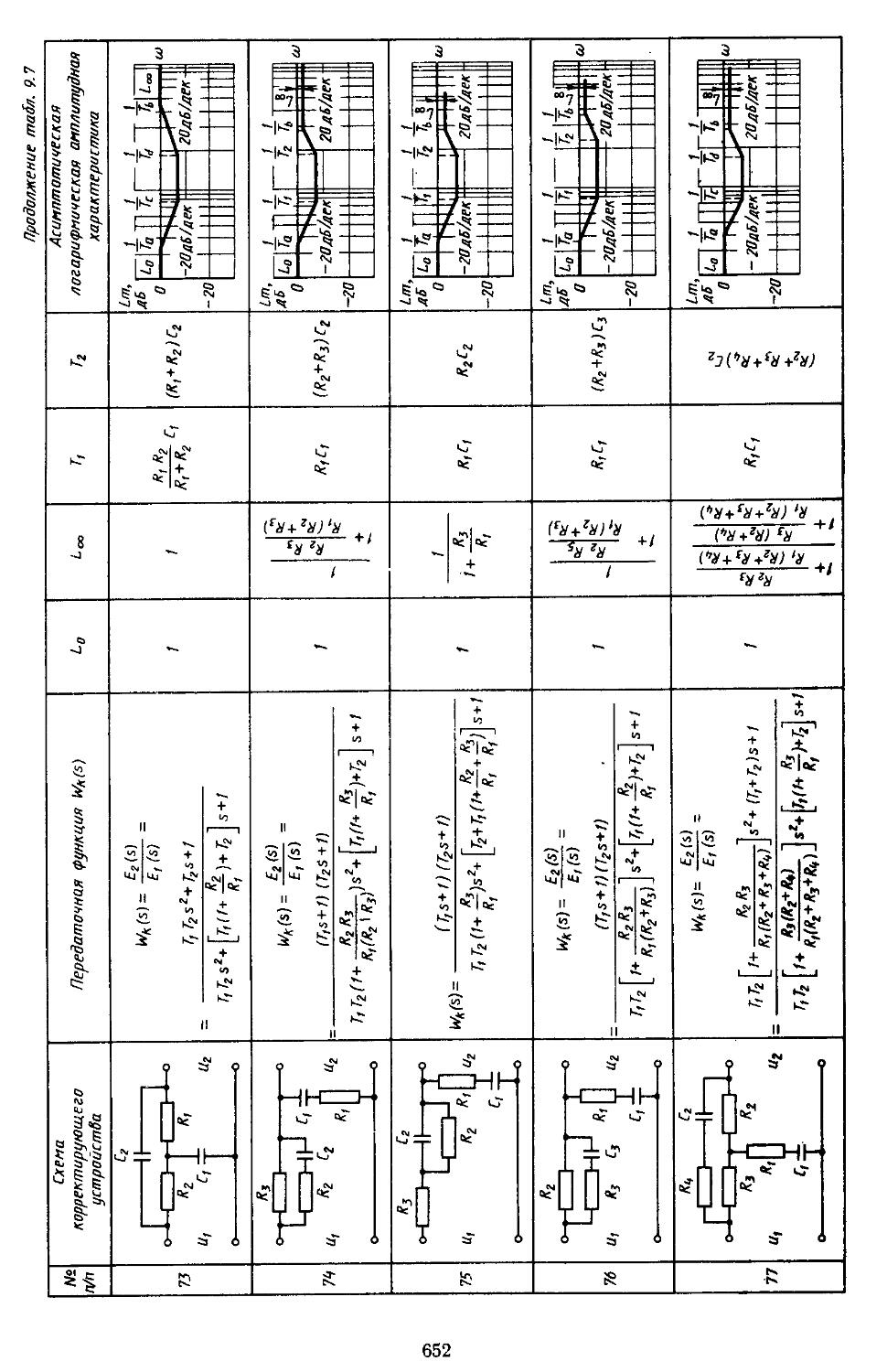
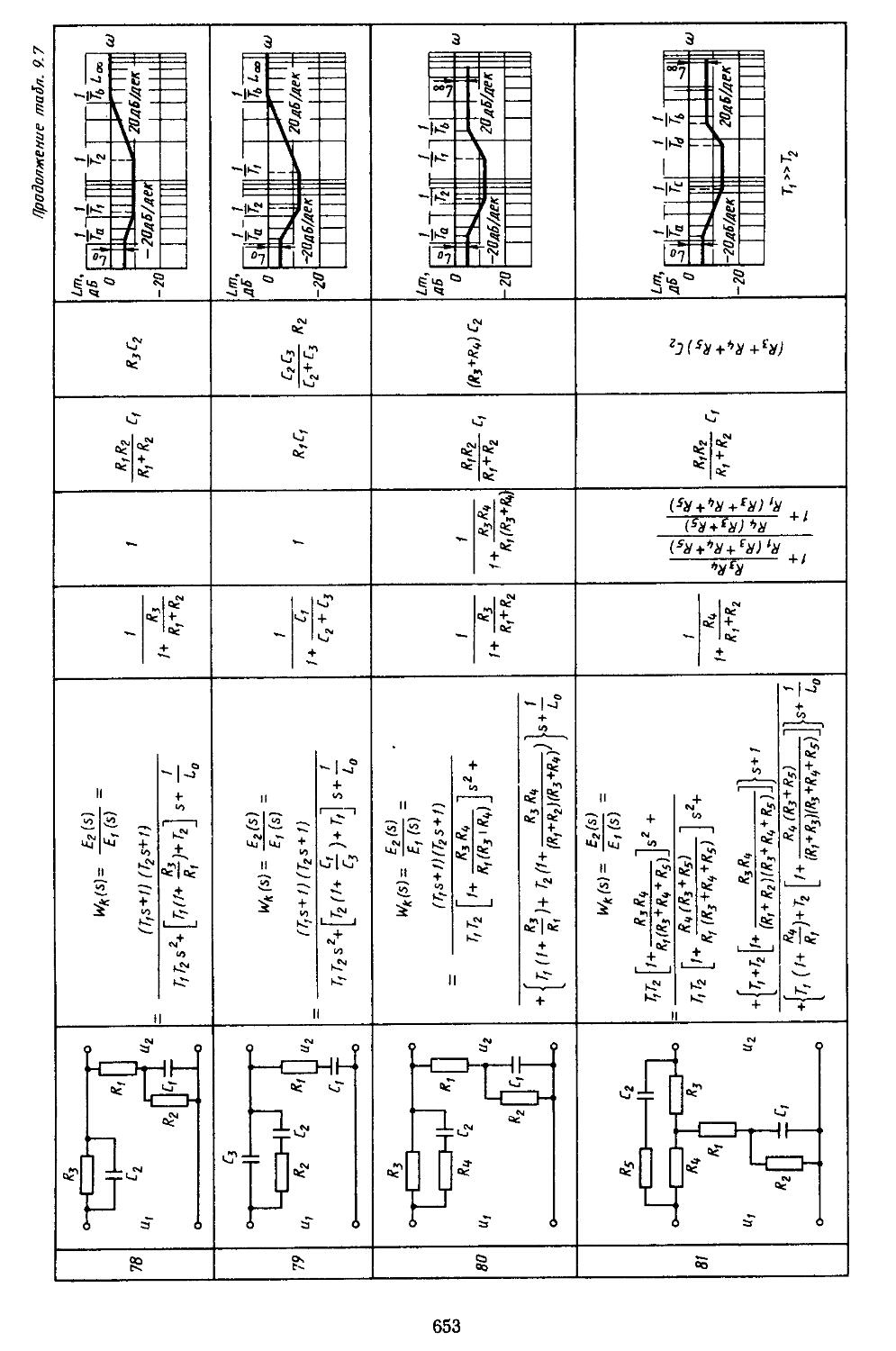
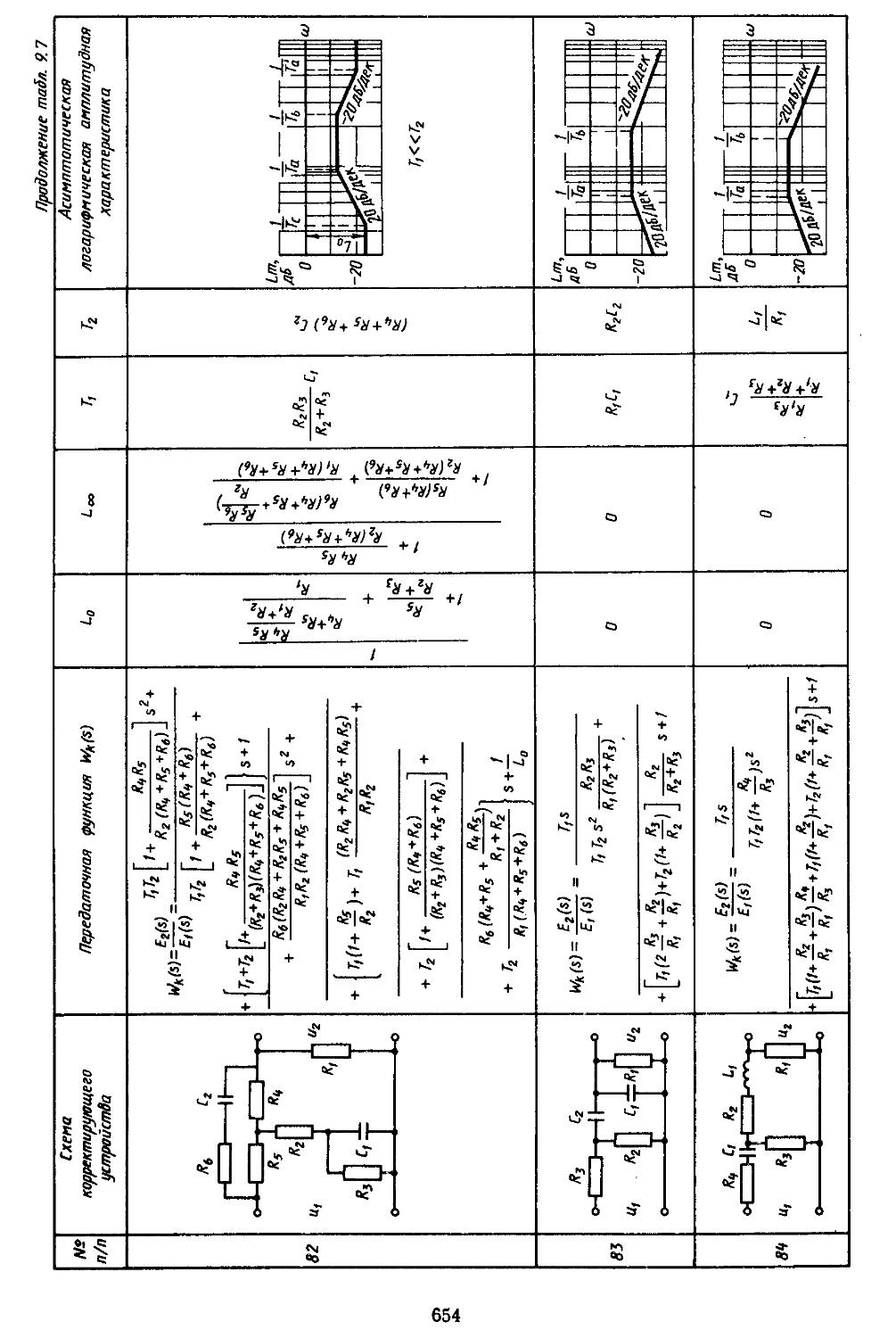
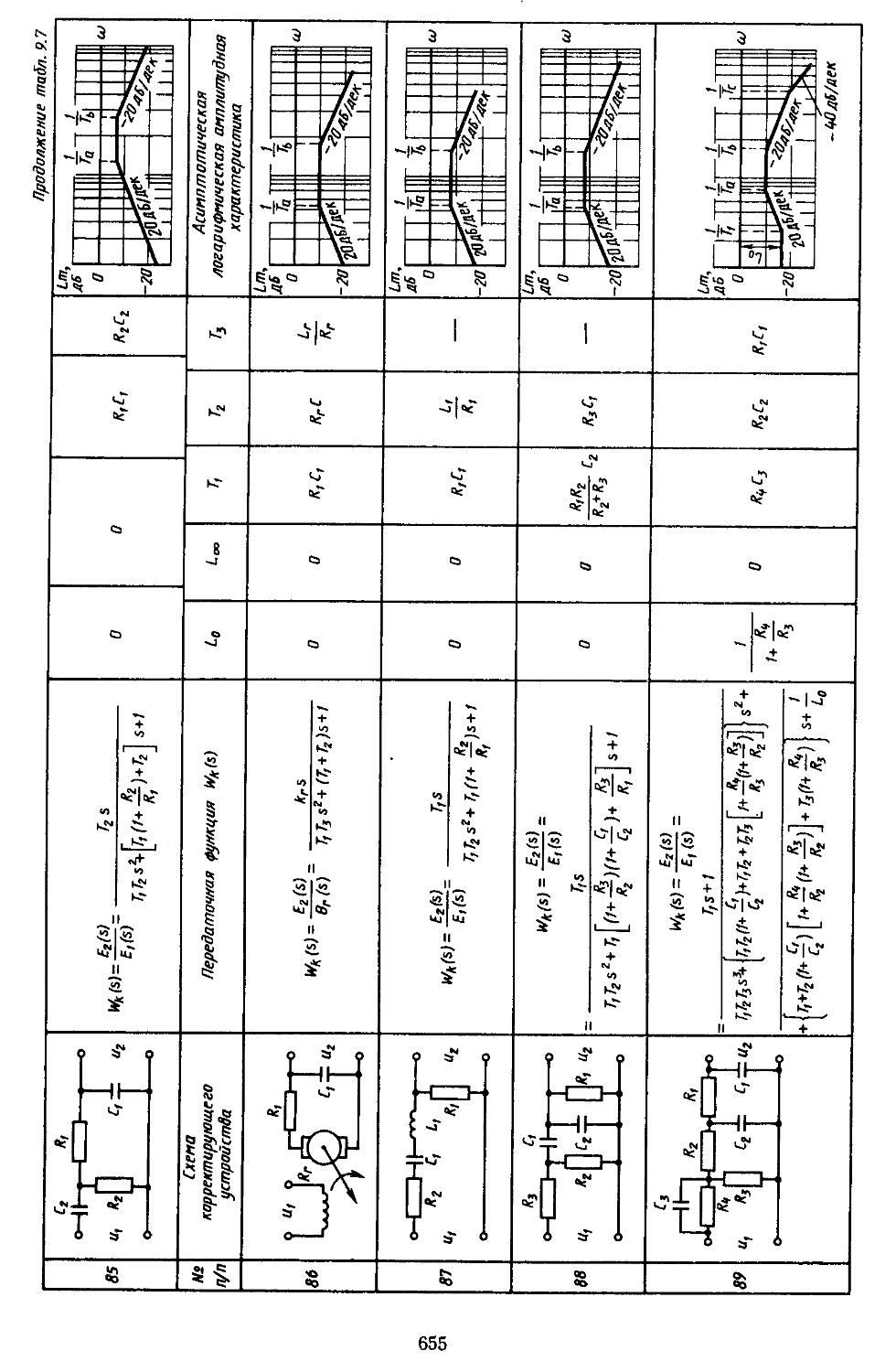
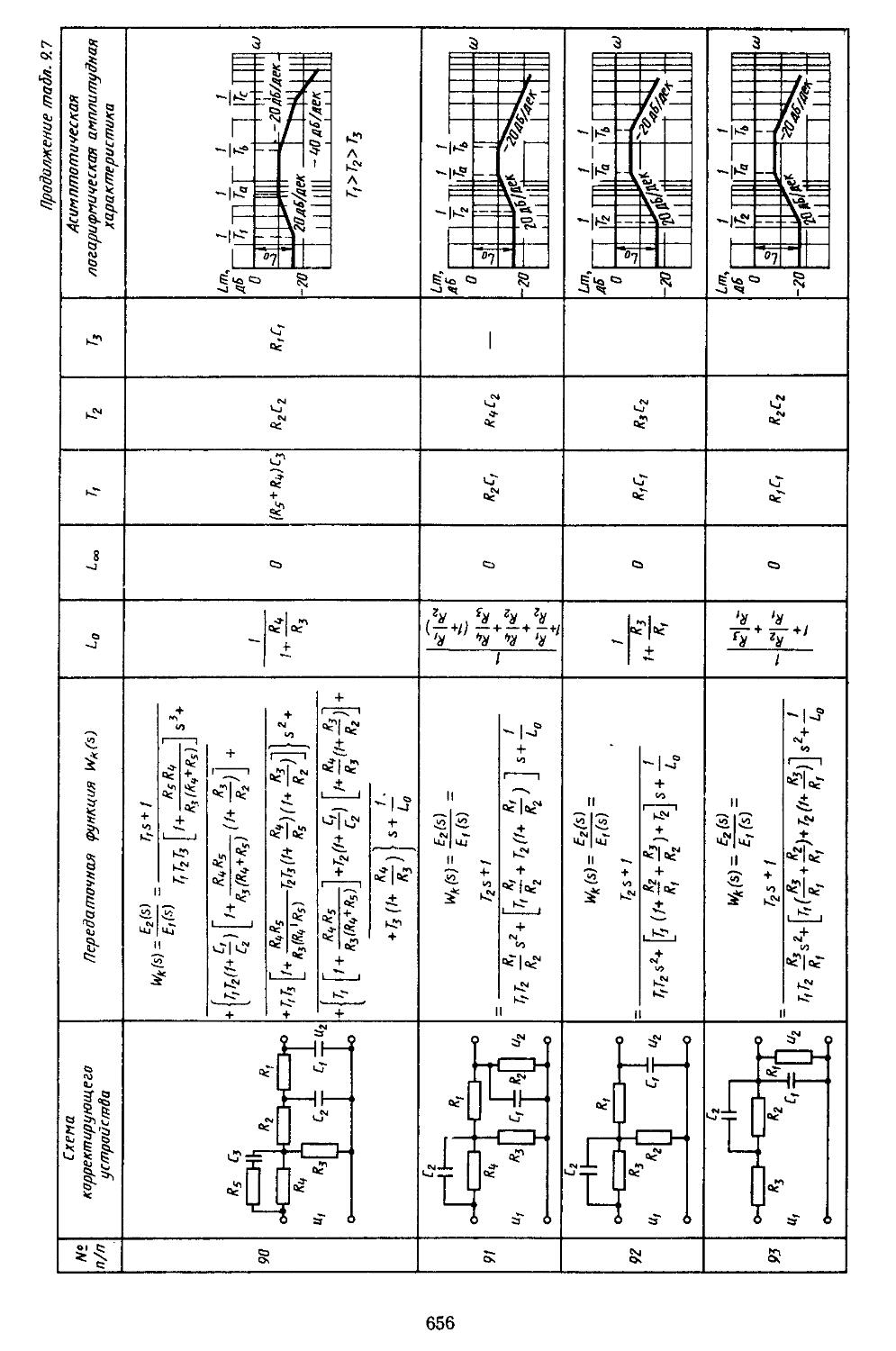
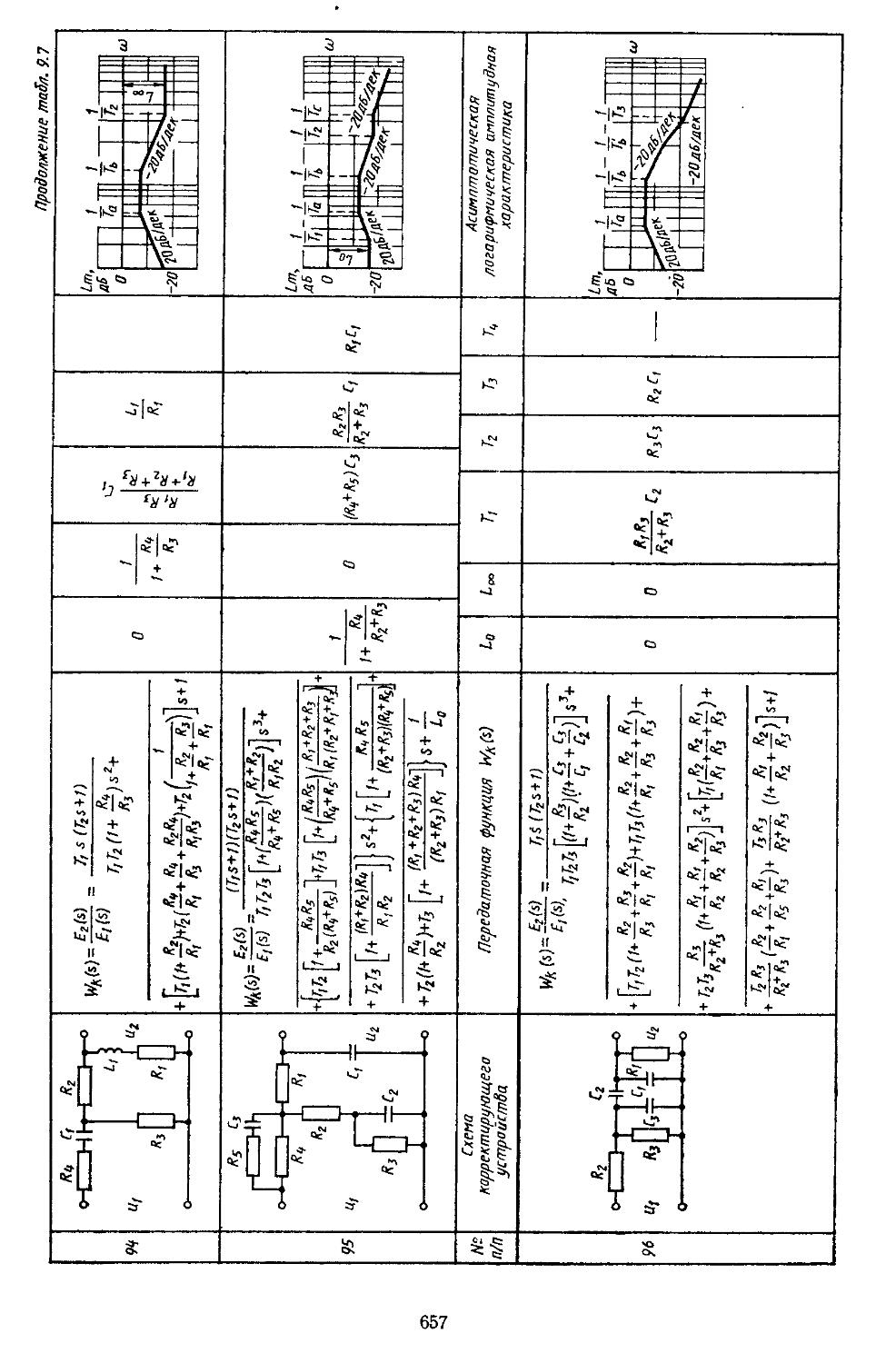
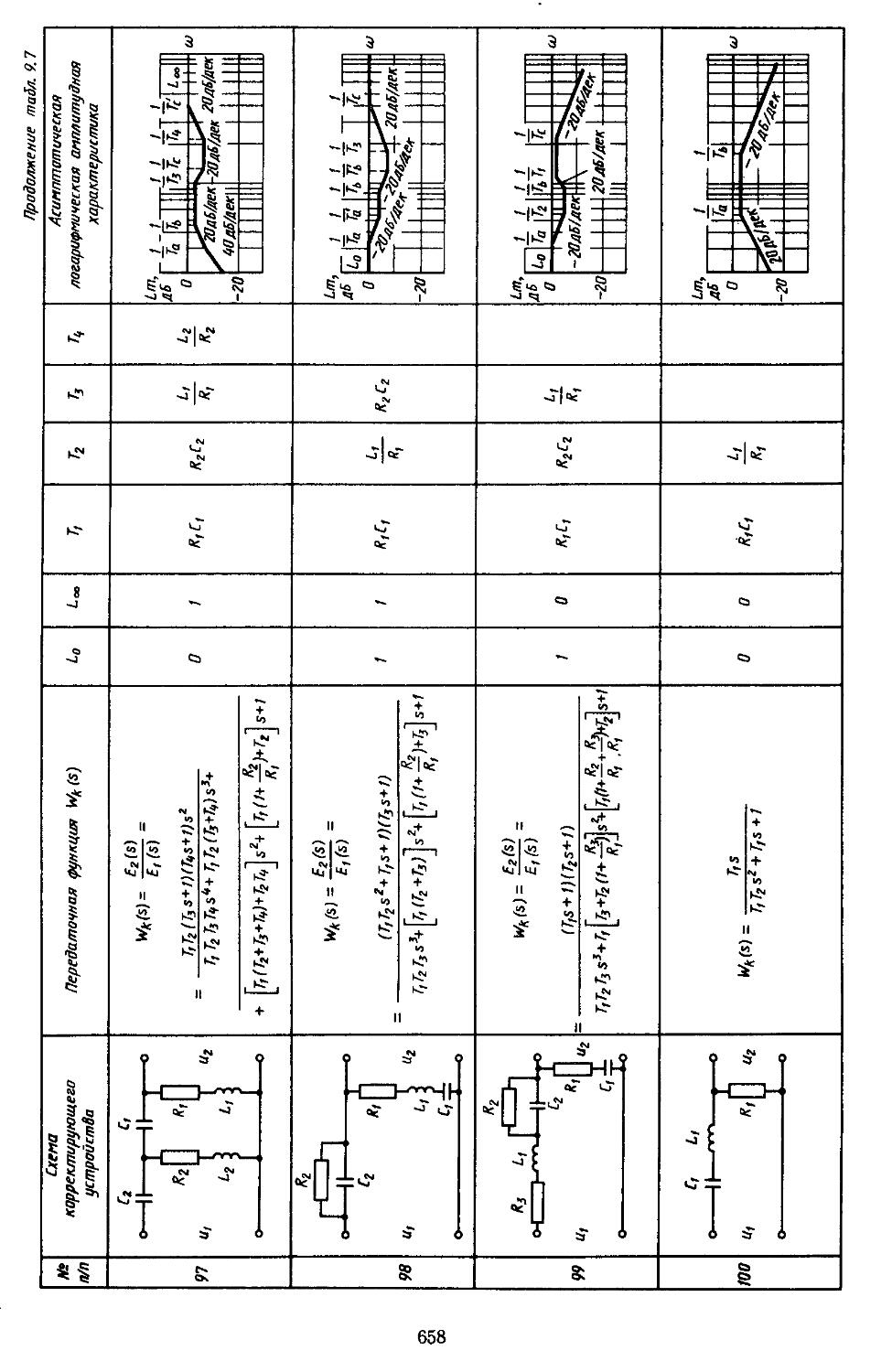
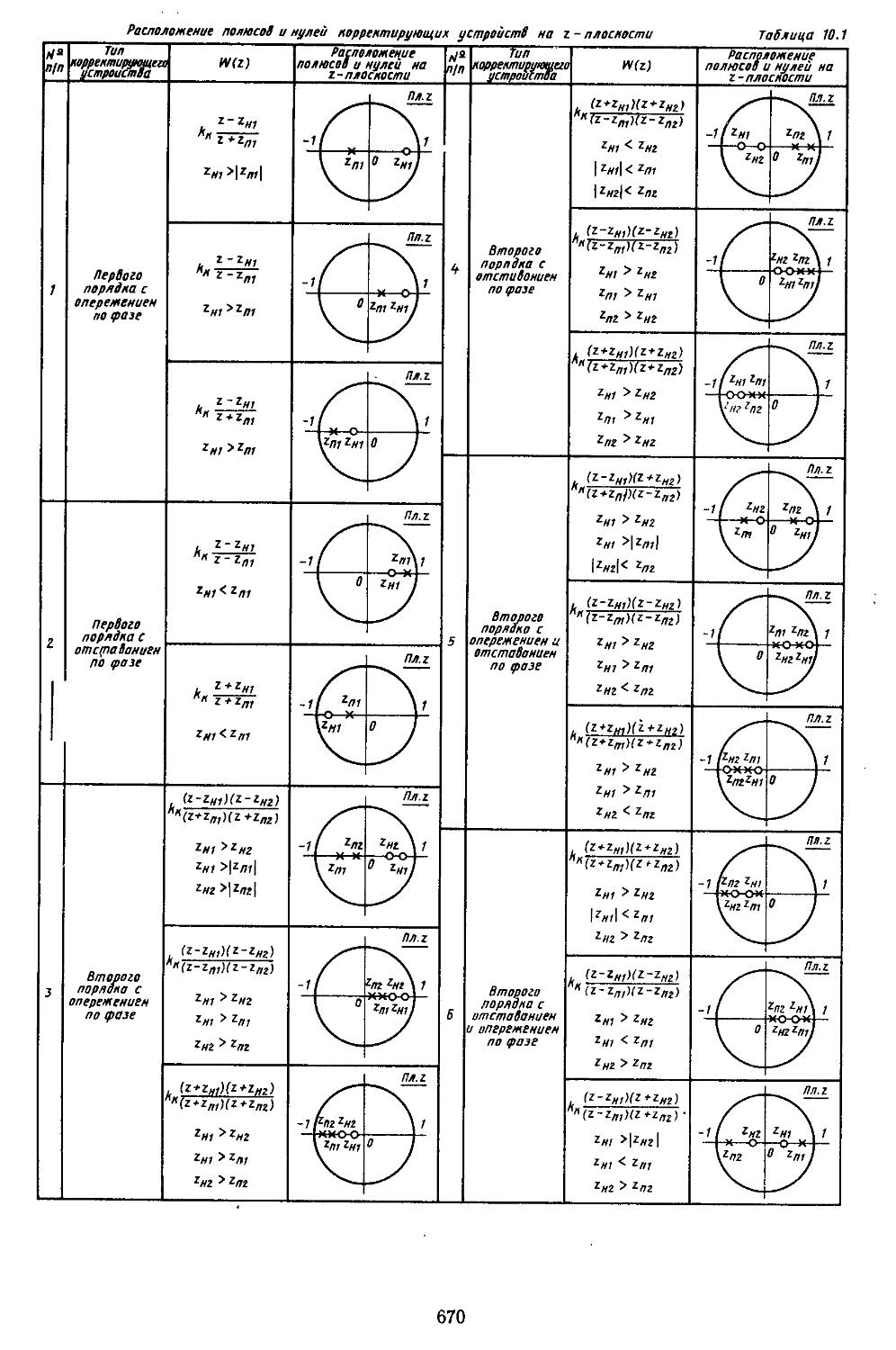
6. Таблицы пассивных корректирующих устройств 659
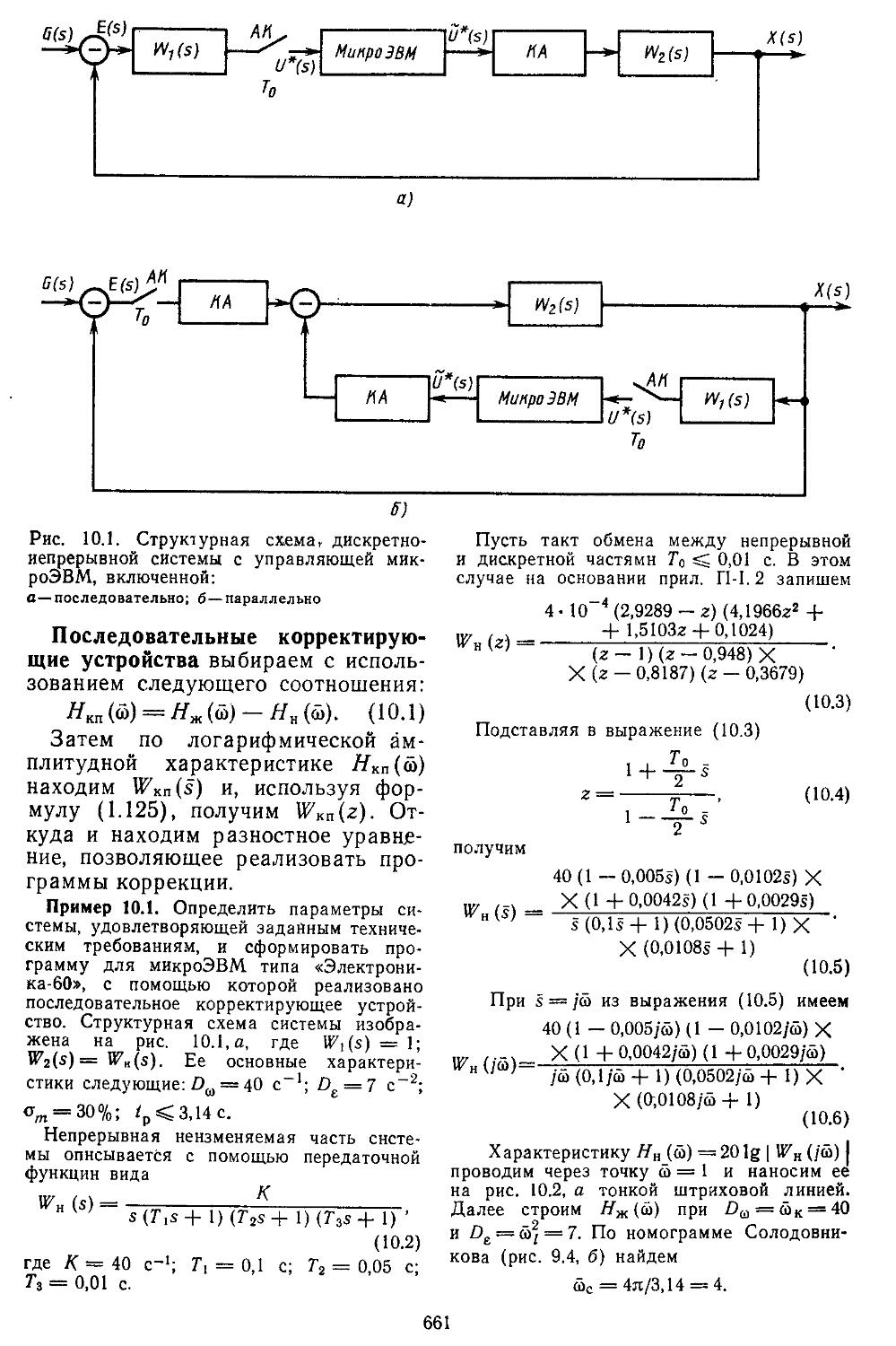
Глава 10. Синтез линейных дискретно-непрерывных систем автоматического регулирования ..............................659
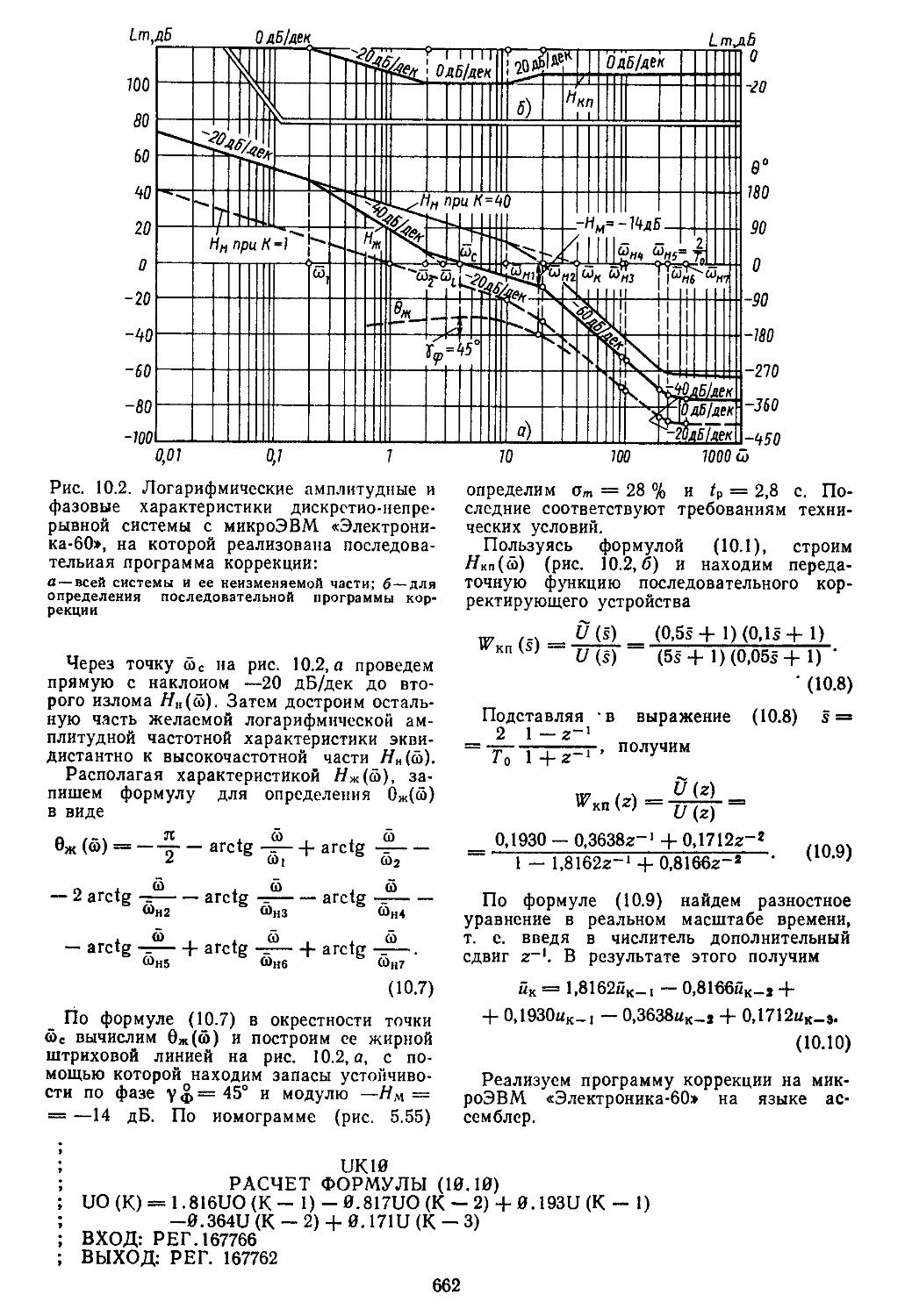
1. Методика синтеза дис-кретио-иепрерывиых систем и а основе билинейного преобразования 660 2. Синтез систем автоматического регулирования , по, методу корневого го-
i , ... дографа . . 665
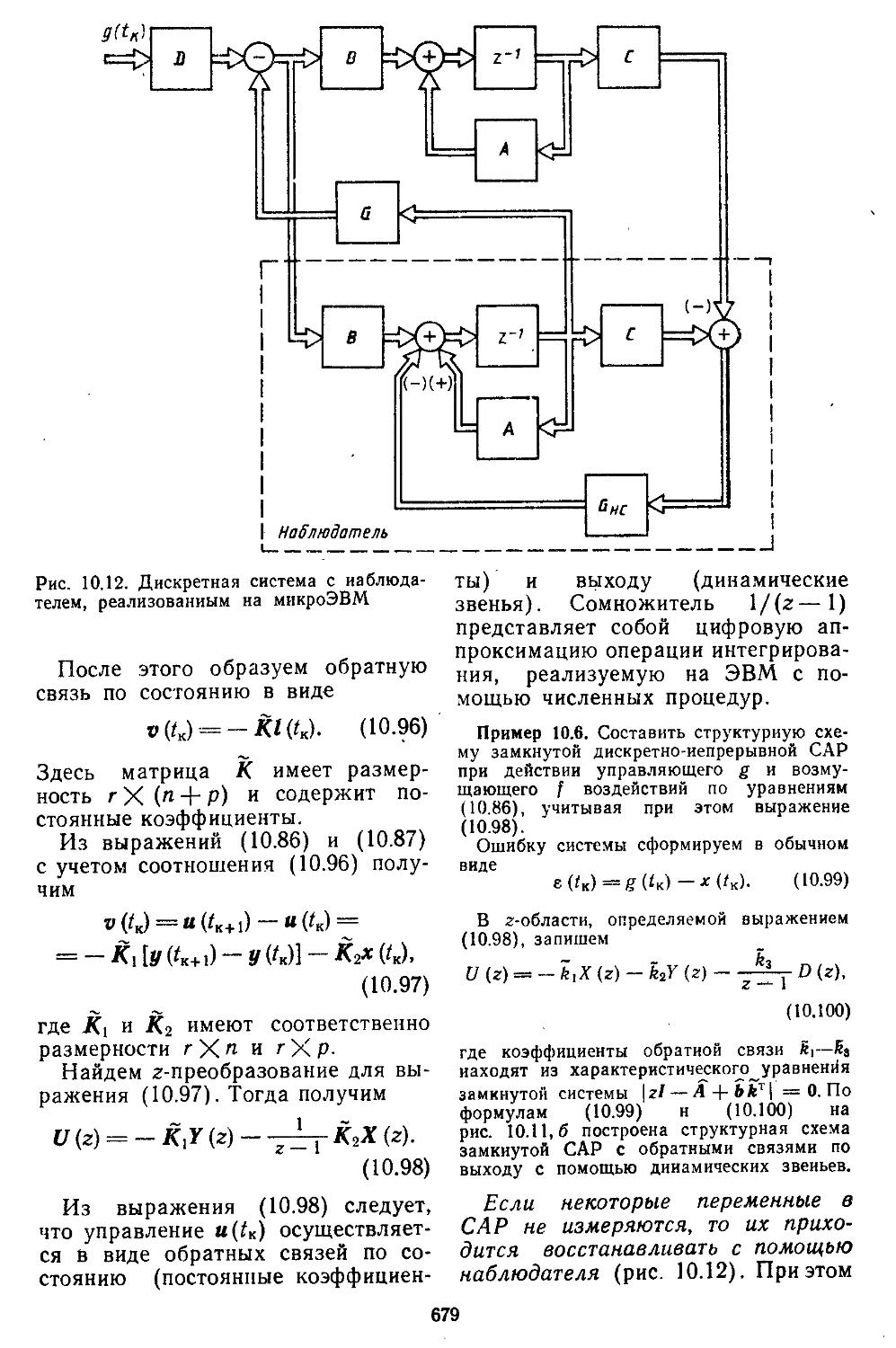
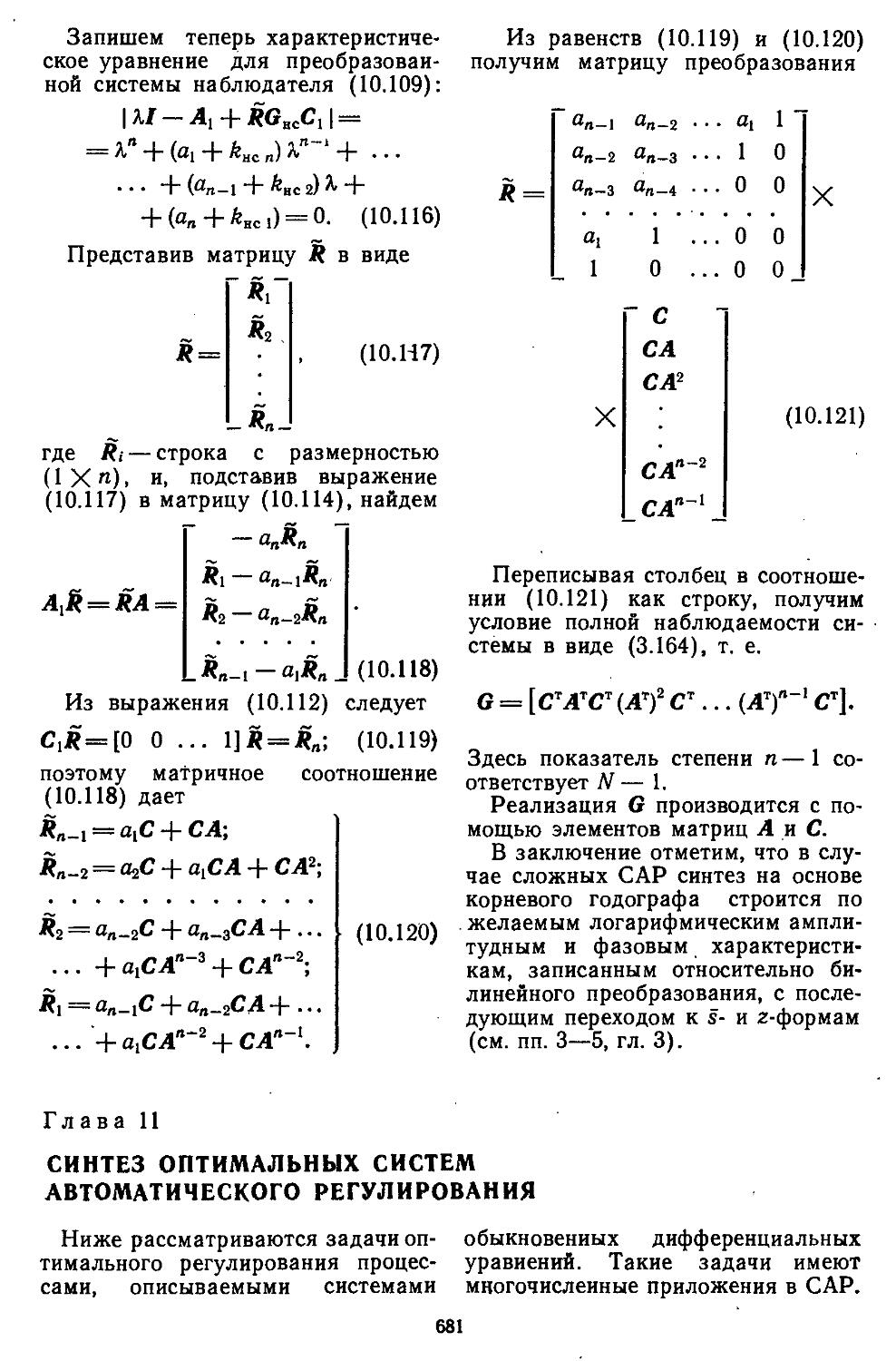
3. Синтез систем автоматического регулирования по заданному расположению иудей и полюсов с помощью введения обратной связи по состоянию и выходу . . 674
4. Реализация обратной связи по состоянию с помощью дополнительно введенных динамических звеньев .... 677
Глава И. Синтез оптимальных систем автоматического регулирования ... 681
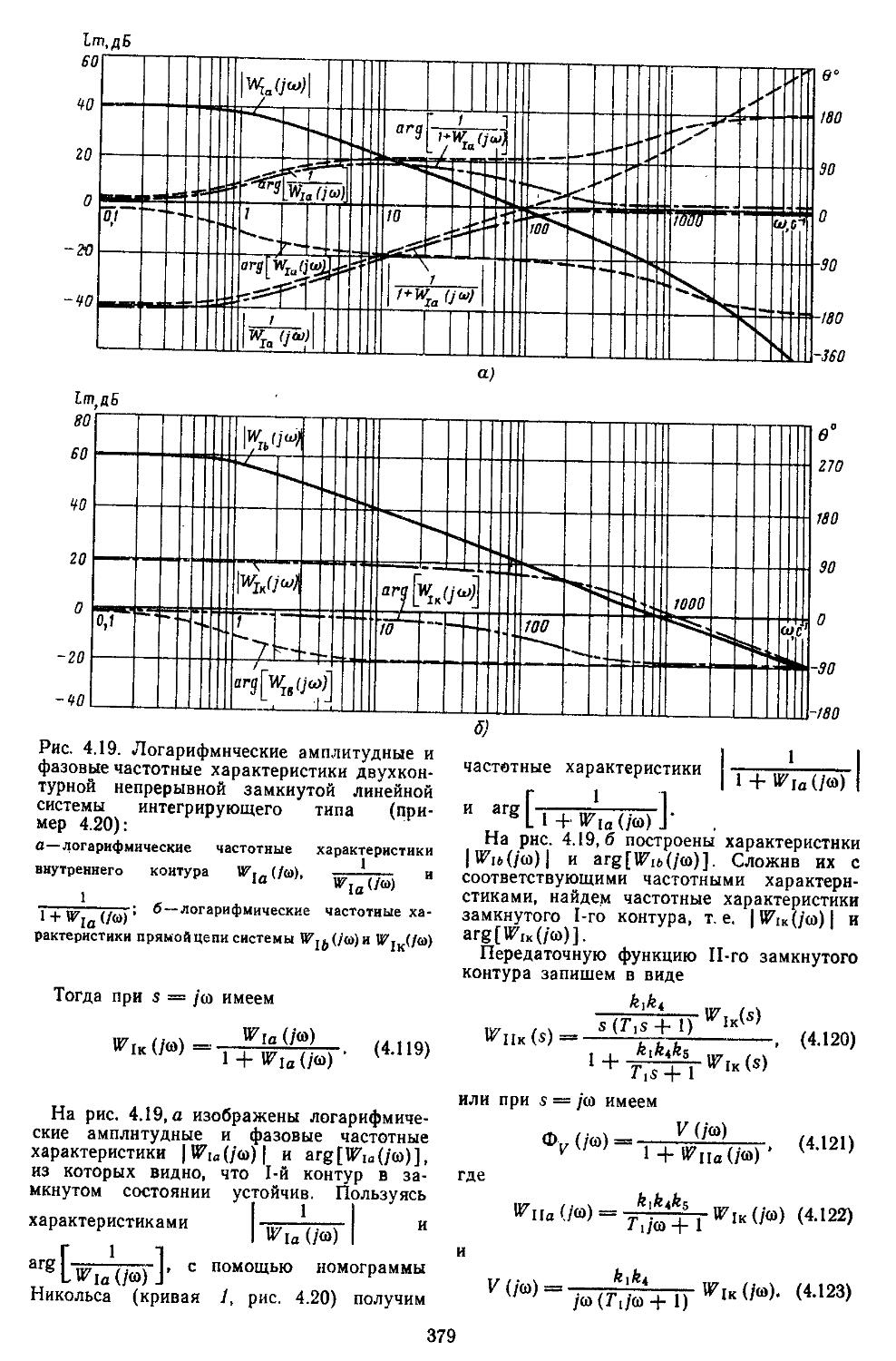
1. Принцип максимума . 682 2. Синтез систем с помощью метода динамического программирования .....................694
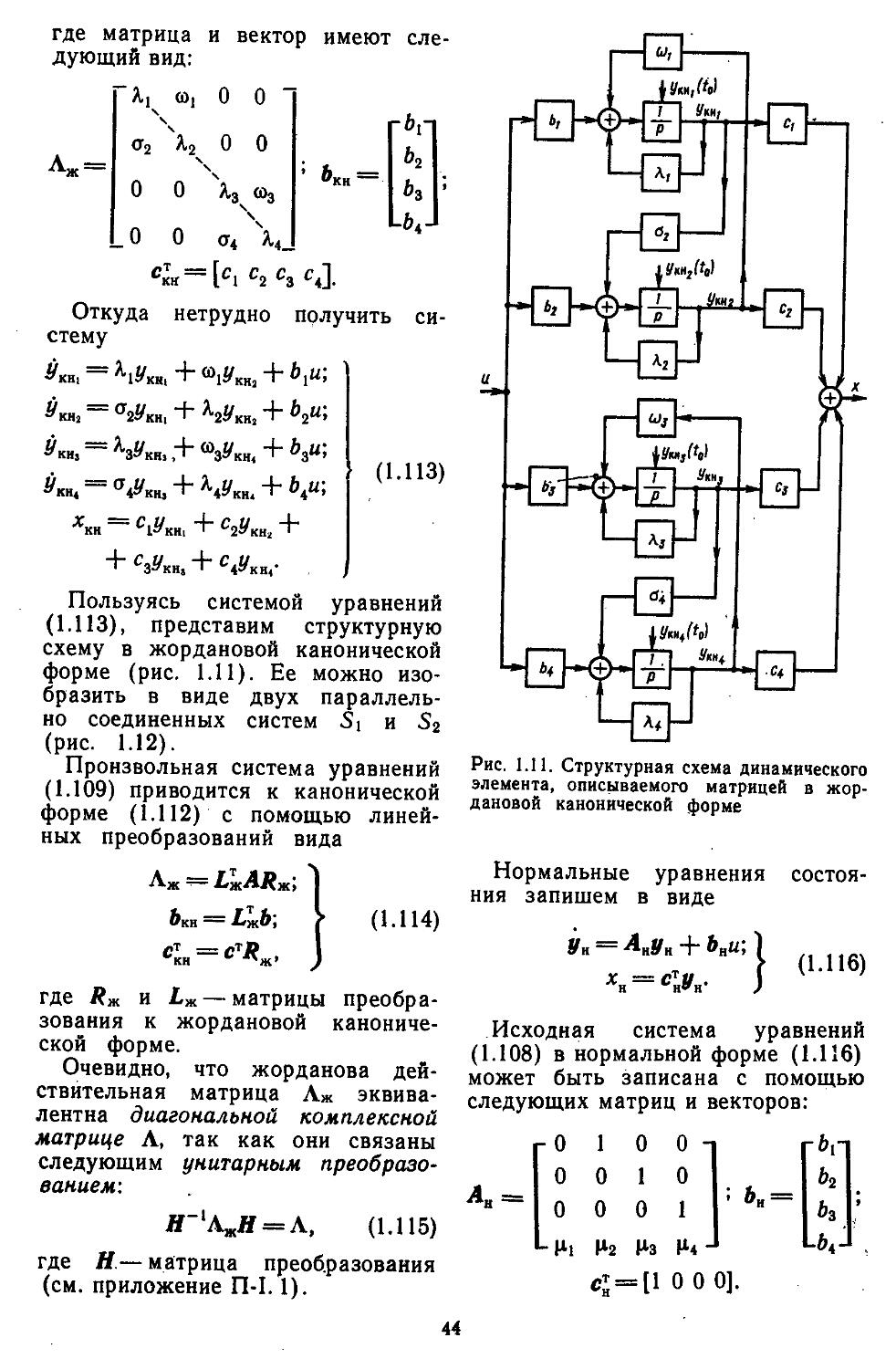
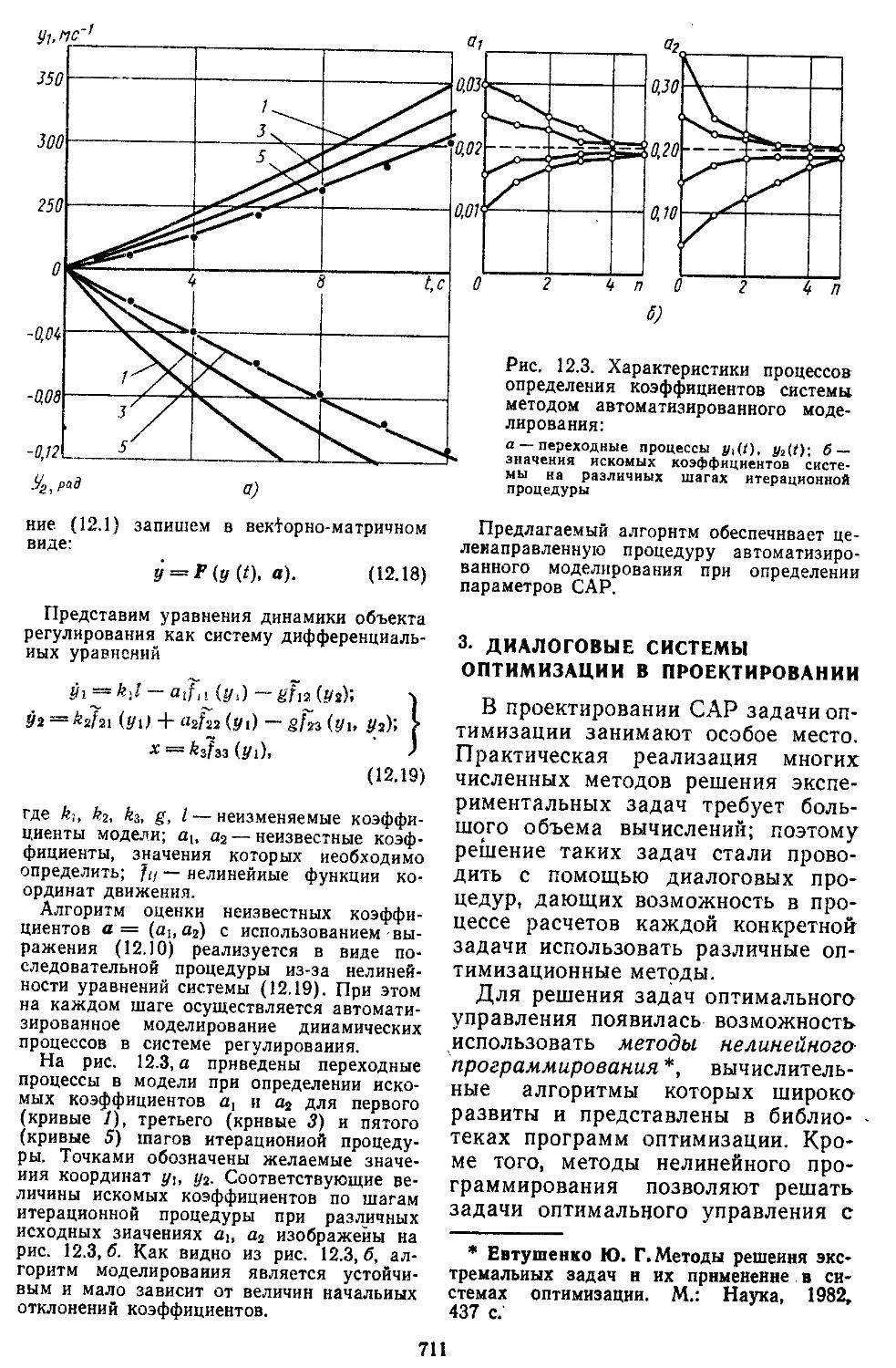
Глава 12. Автоматизированные методы моделирования и проектирования систем регулирования ..........................702
1. Системы автоматизированного моделирования и проектирования . 703 2. Автоматизация модели-
рования систем регулирования ..............706
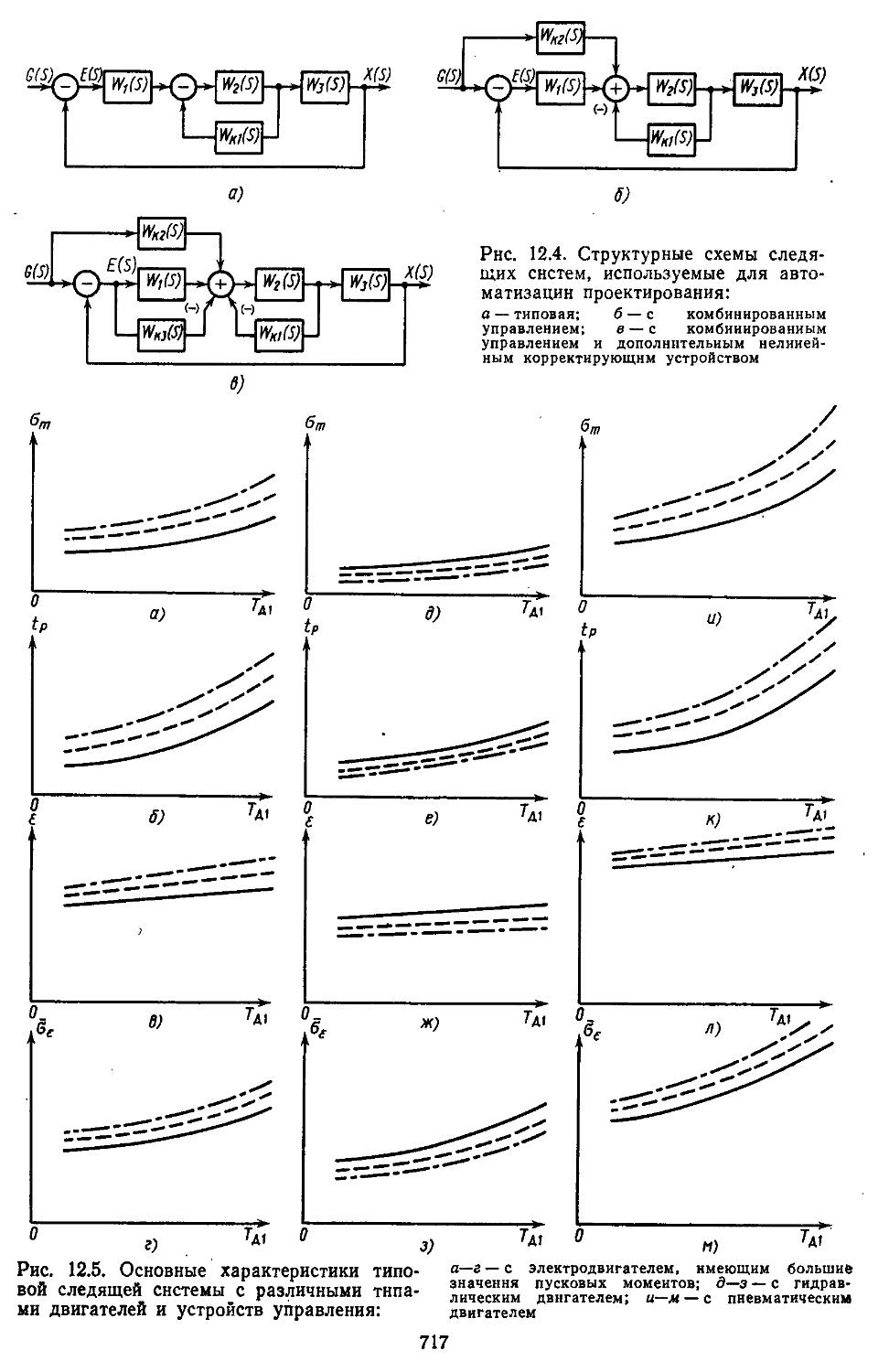
3. Диалоговая система оптимизации в проектировании ................711
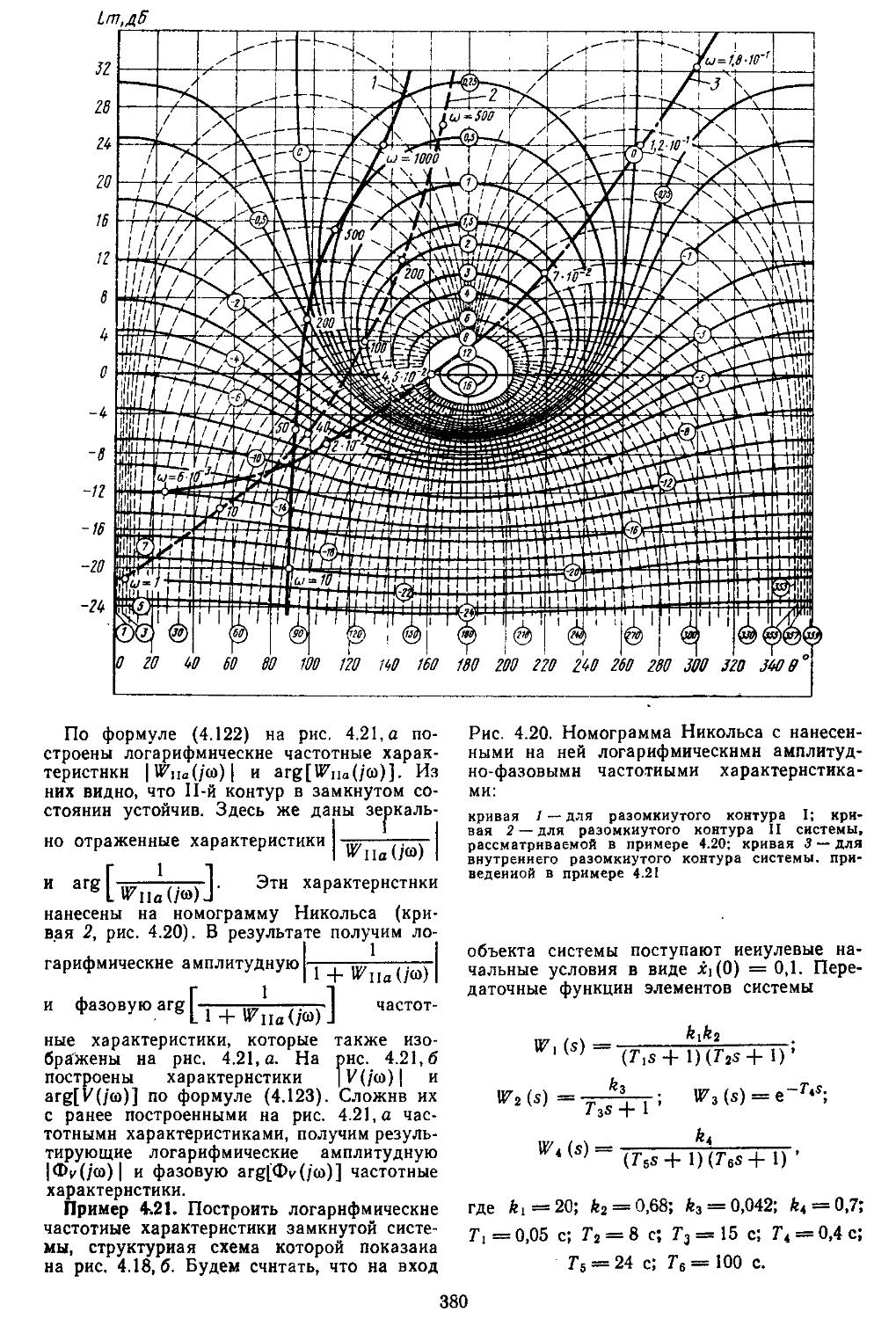
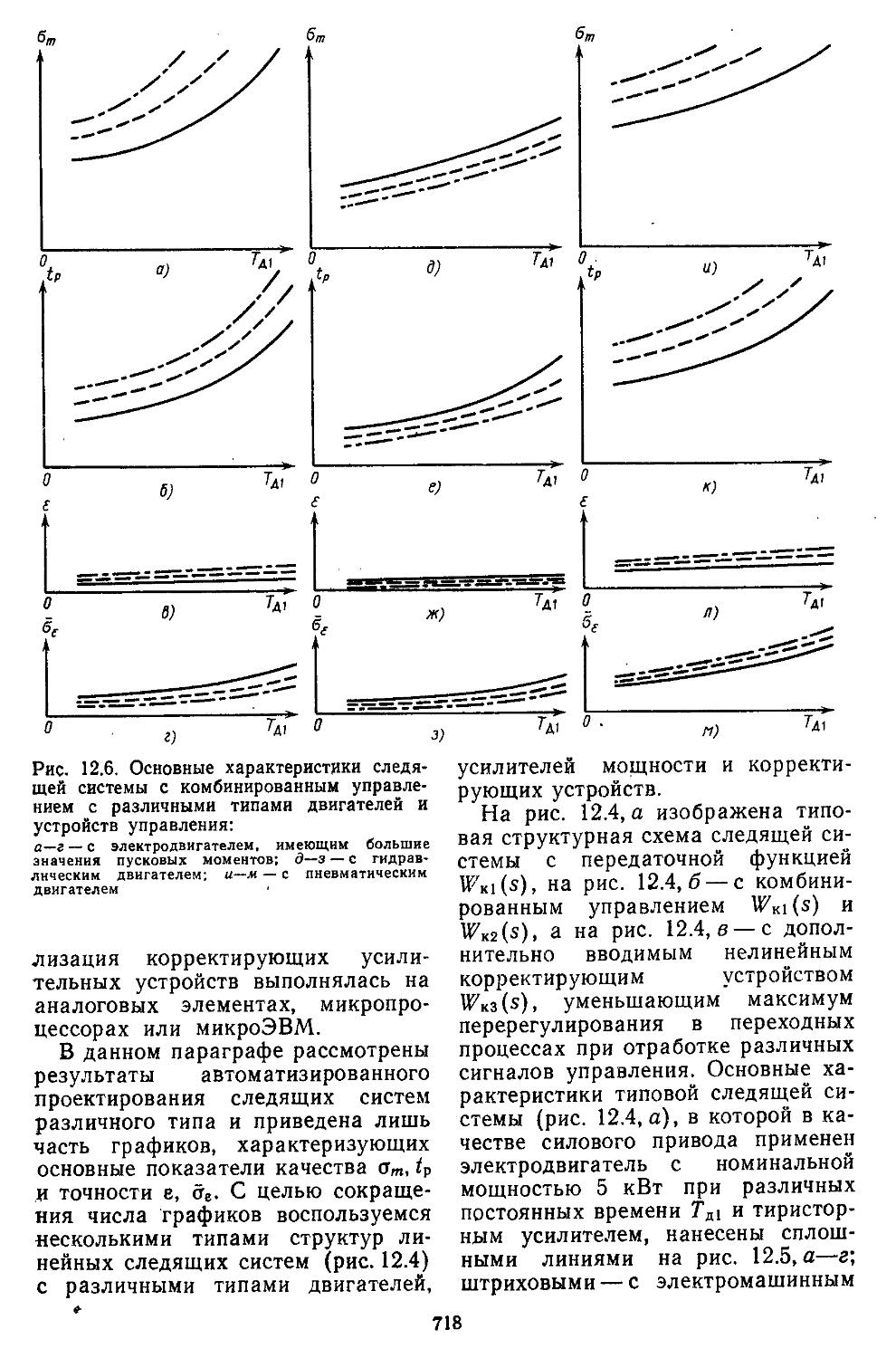
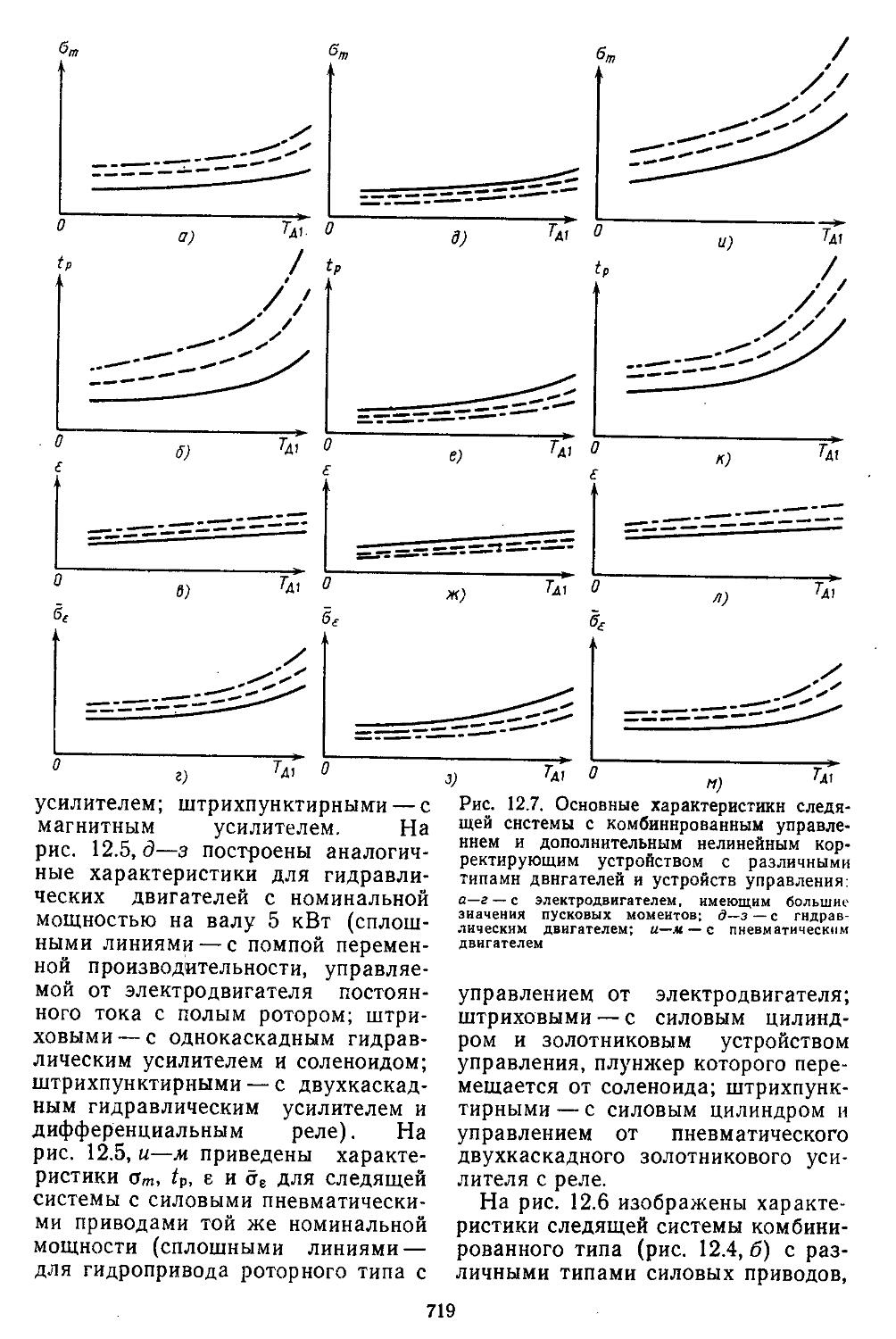
4. Автоматизация проектирования систем регулирования ...... 716
5
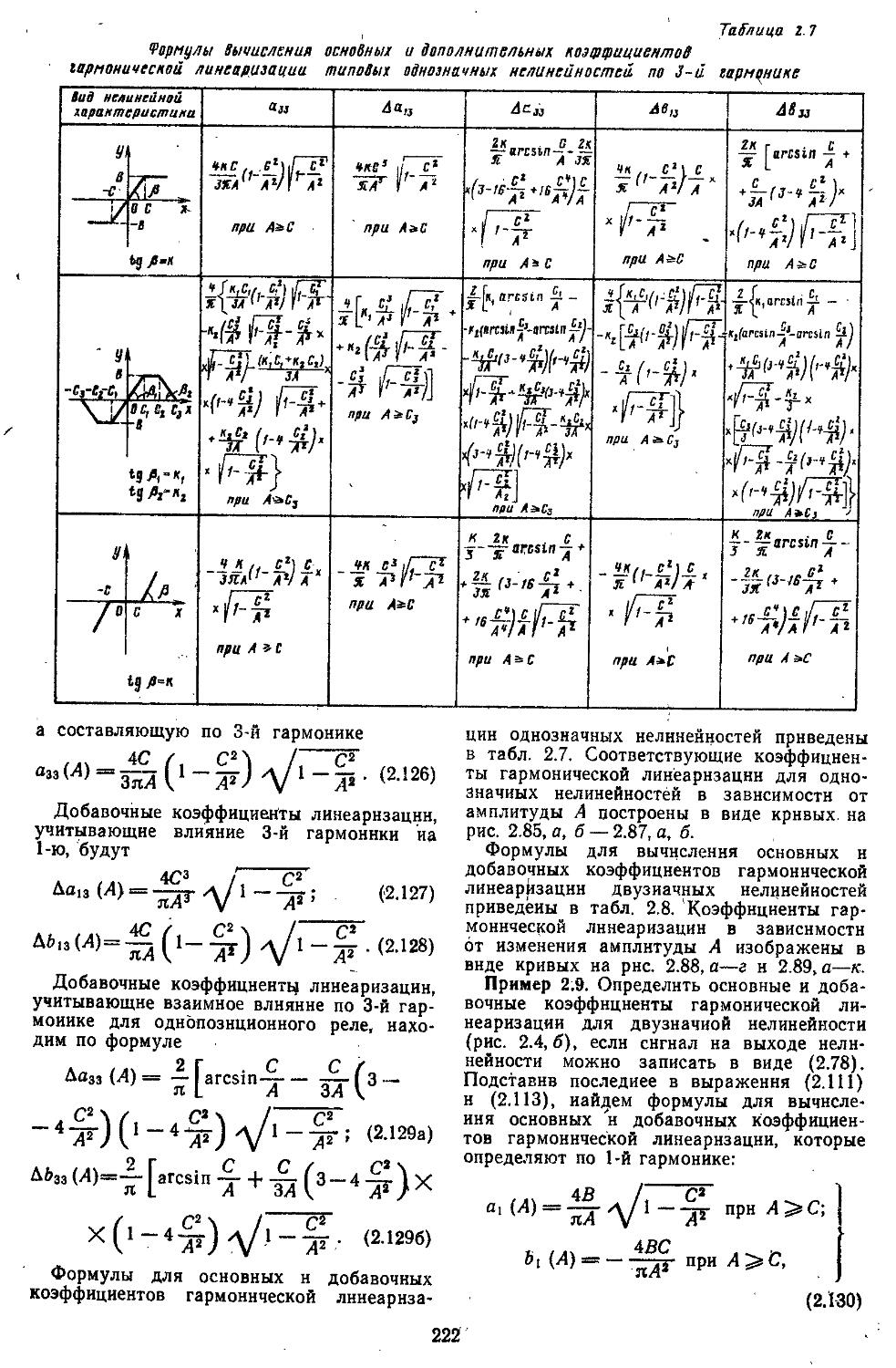
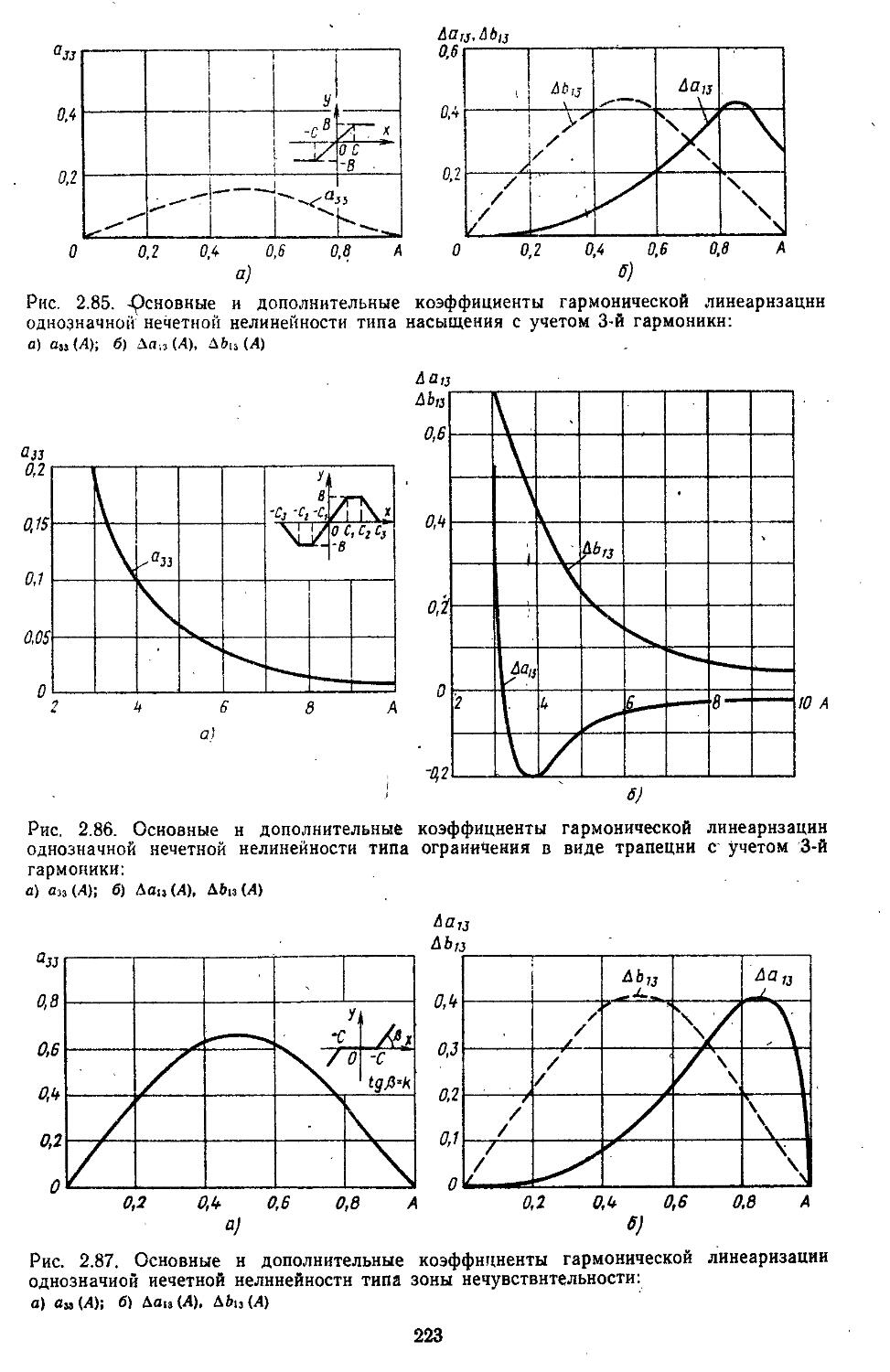
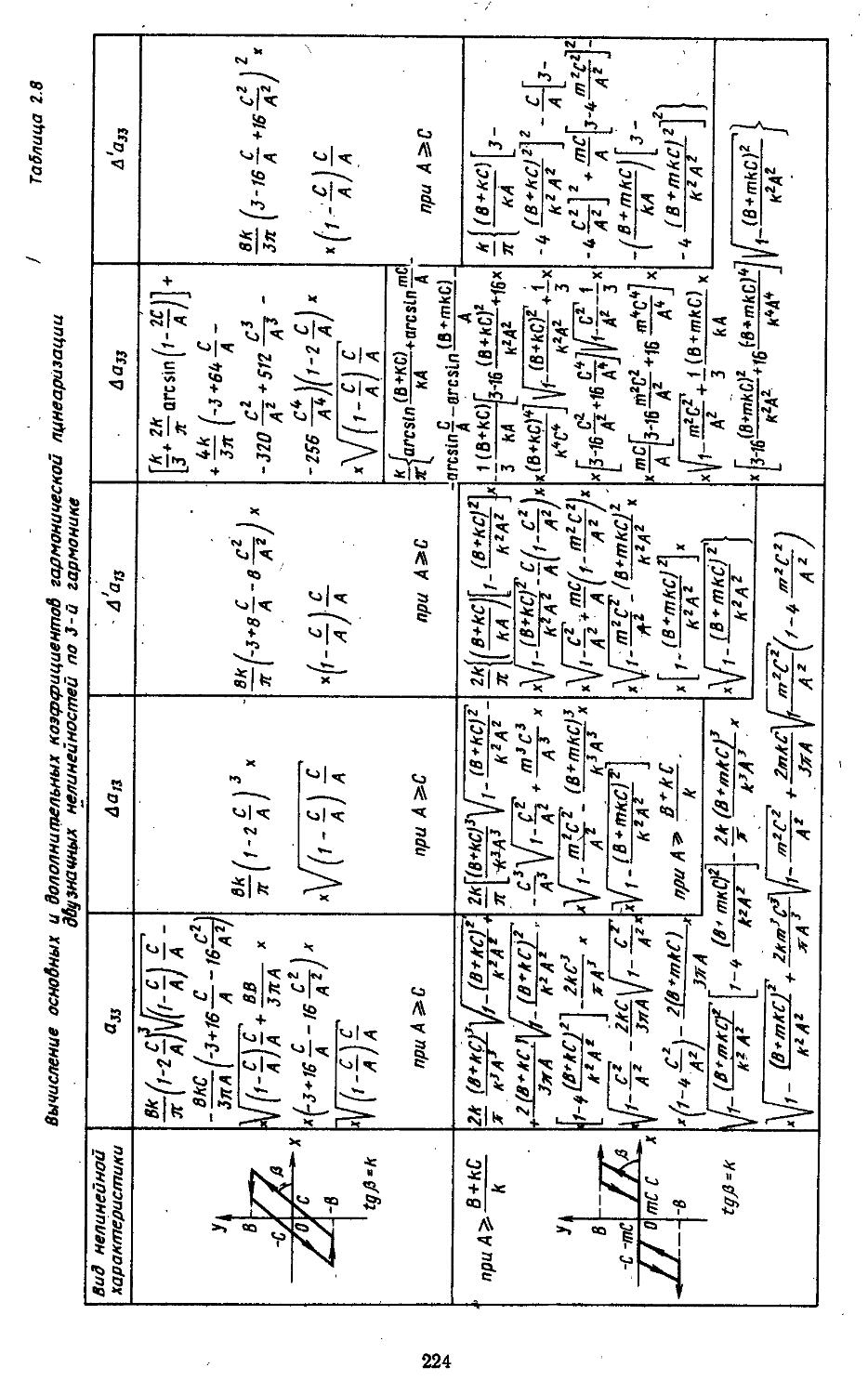
Приложения Приложение П-1.1. Основные сведения по векторно-матричному исчислению . . .721
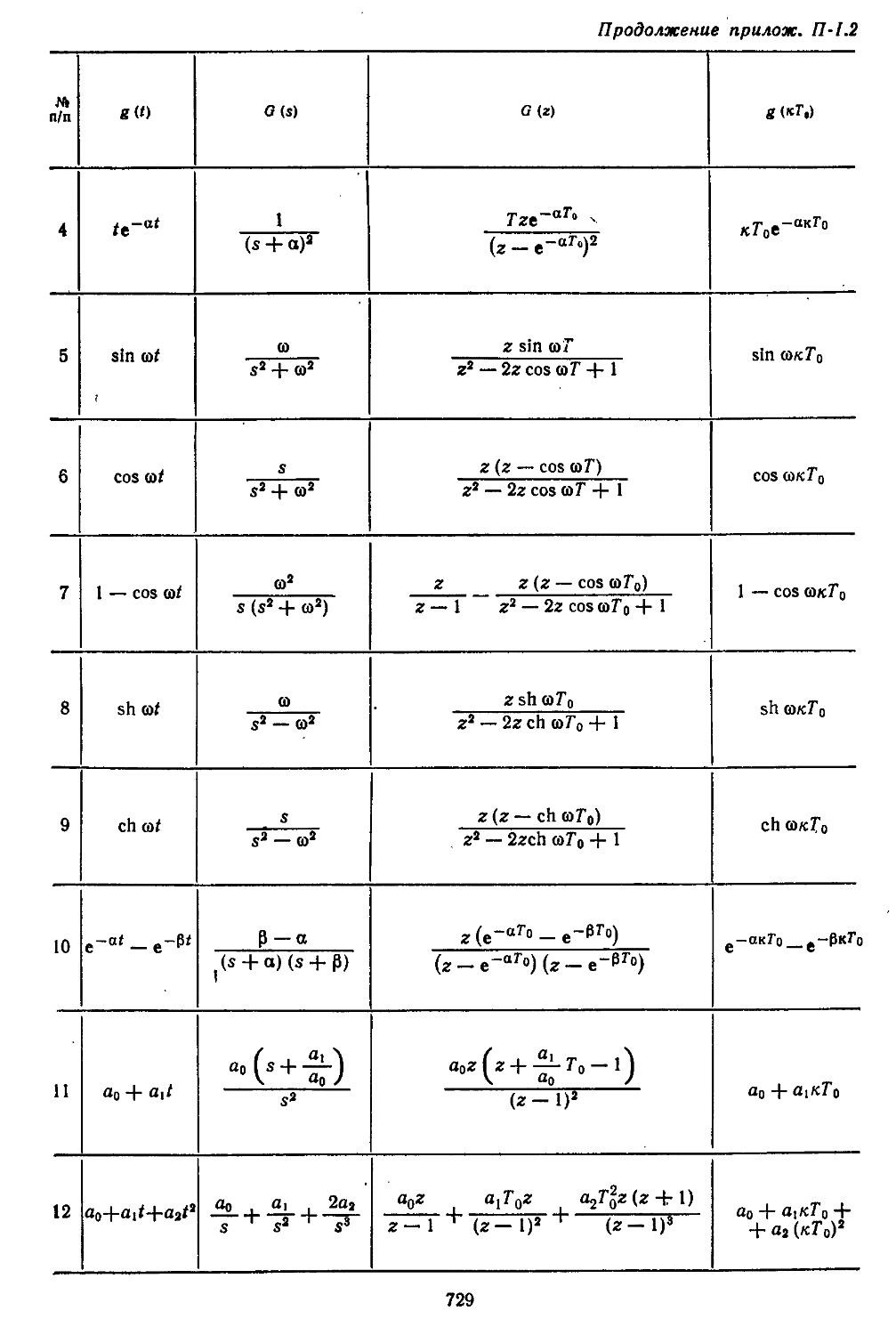
Приложение П-1.2. Таблица прямых и обратных s- и г-преобразоваиий дли сигналов возмущений . . . 728
Приложение П-1.3. Таблица z-преоб-разований для передаточных функций .............................730
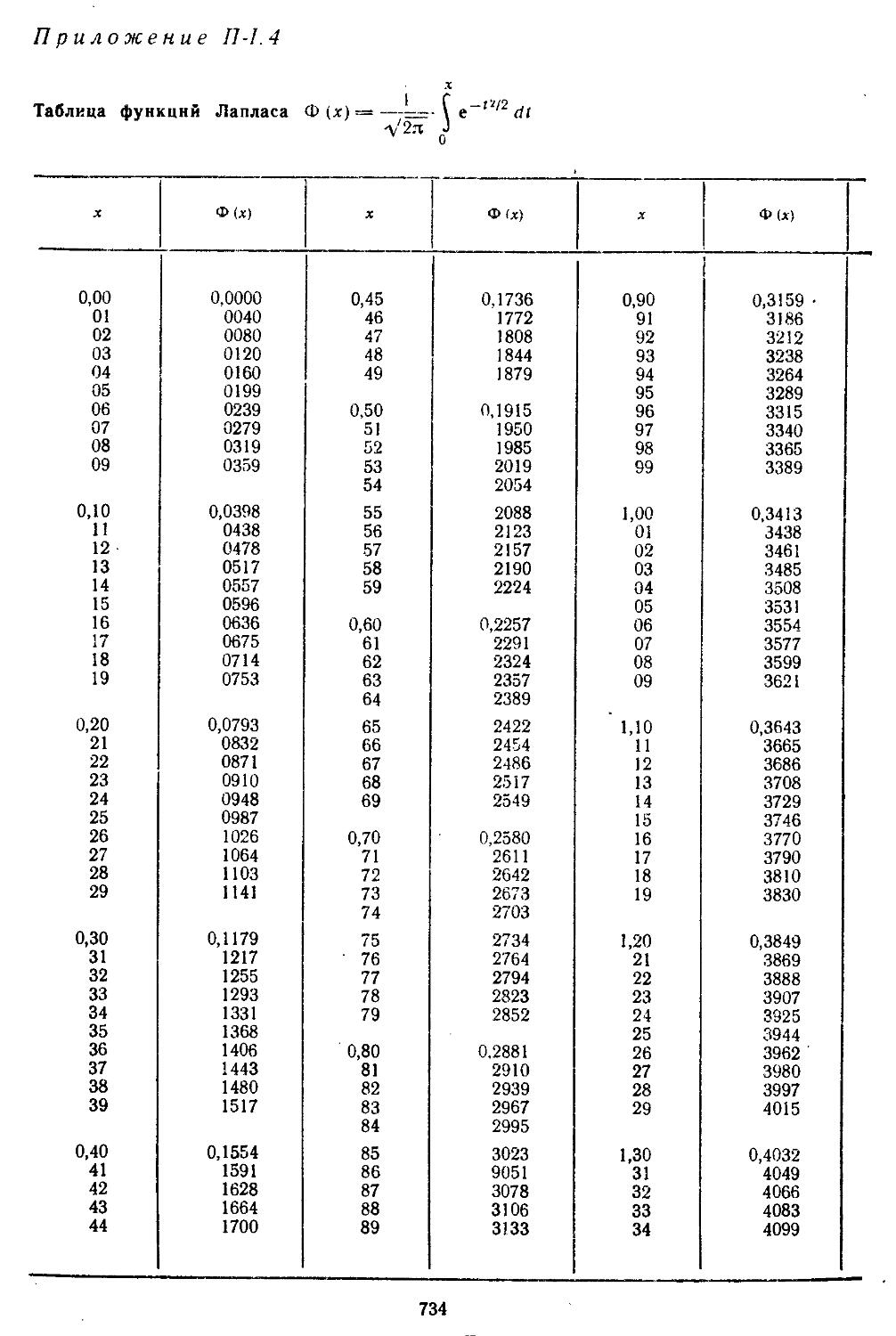
Приложение П-1.4. Значения функций
Лапласа . . 734
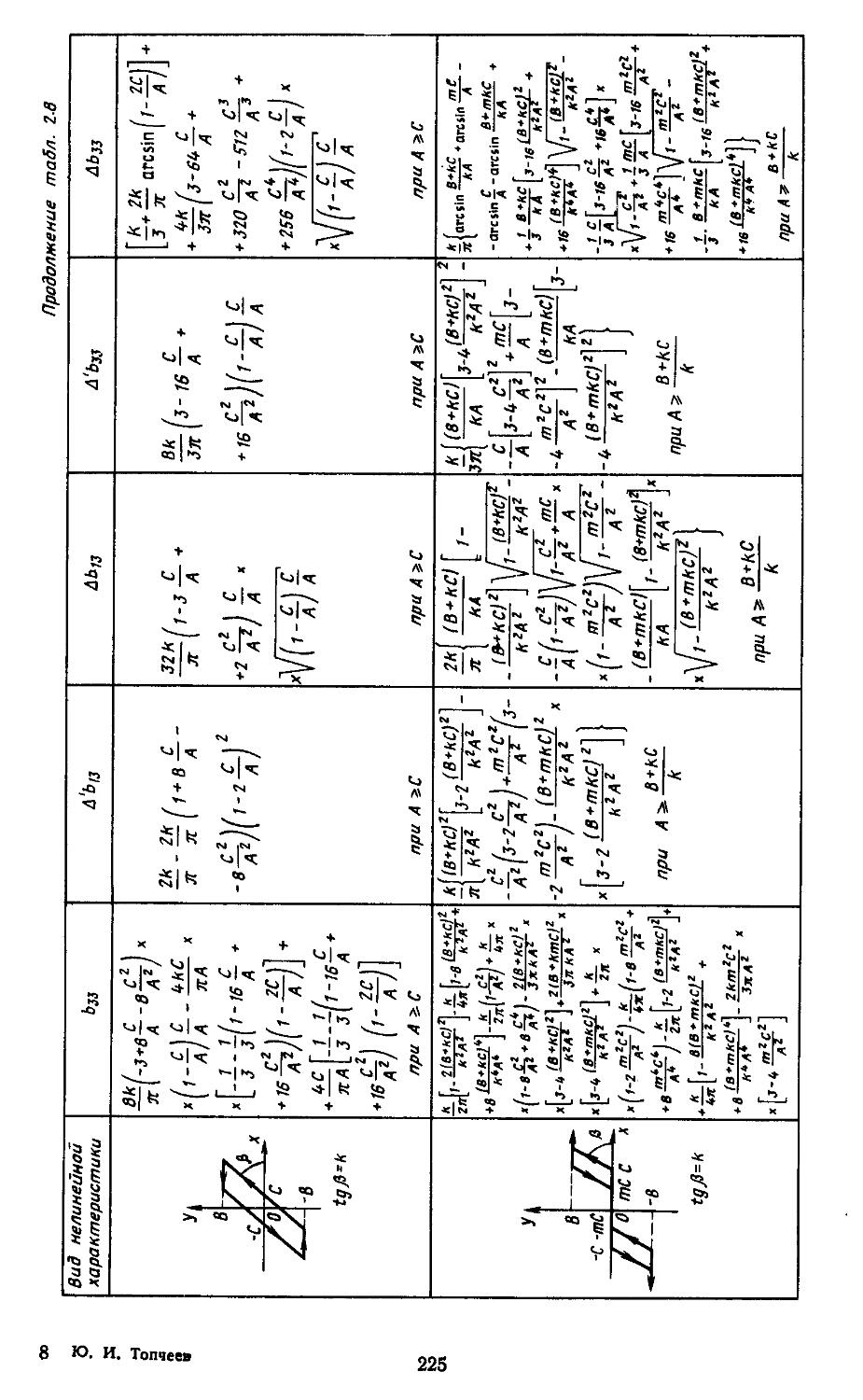
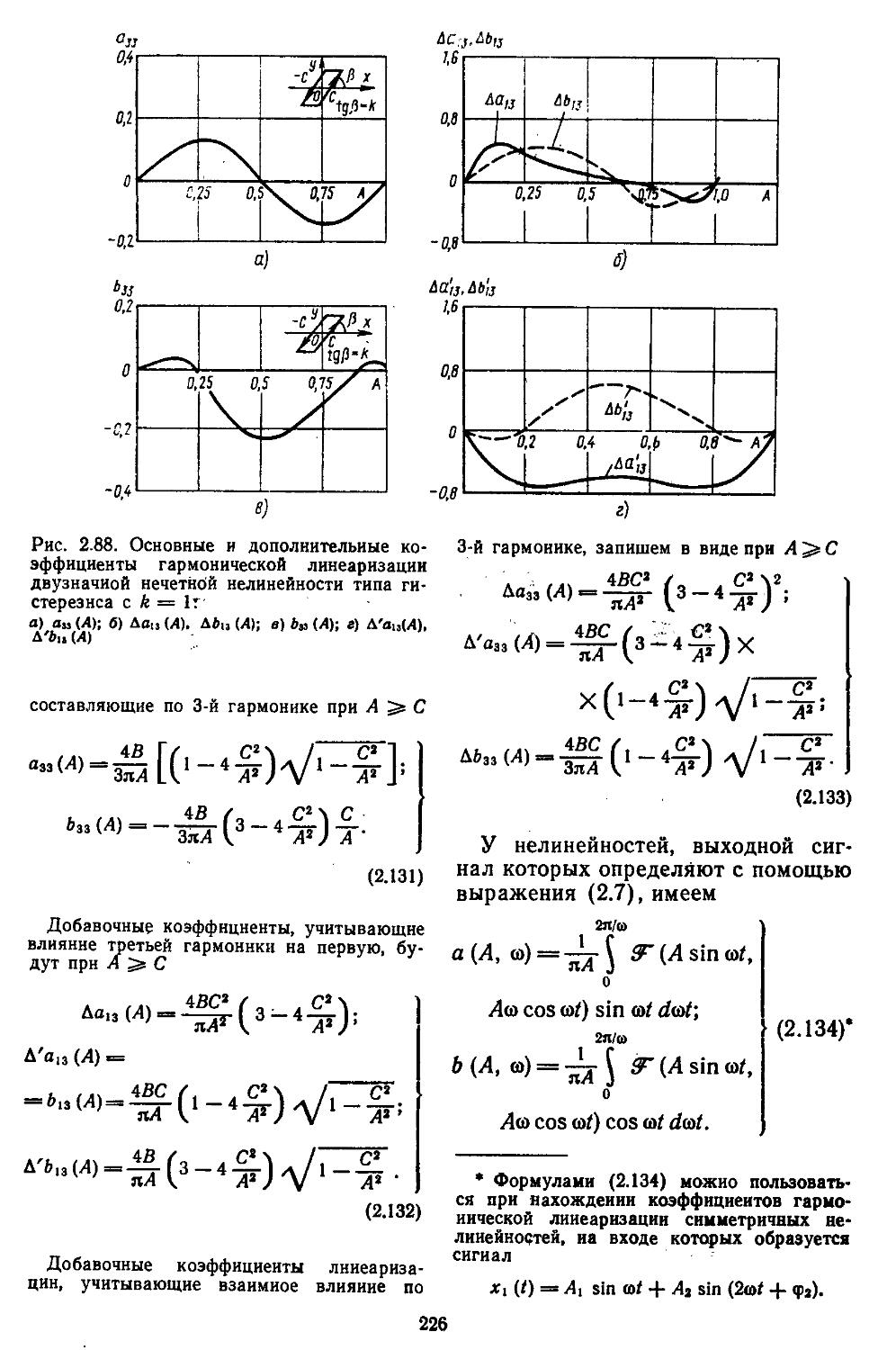
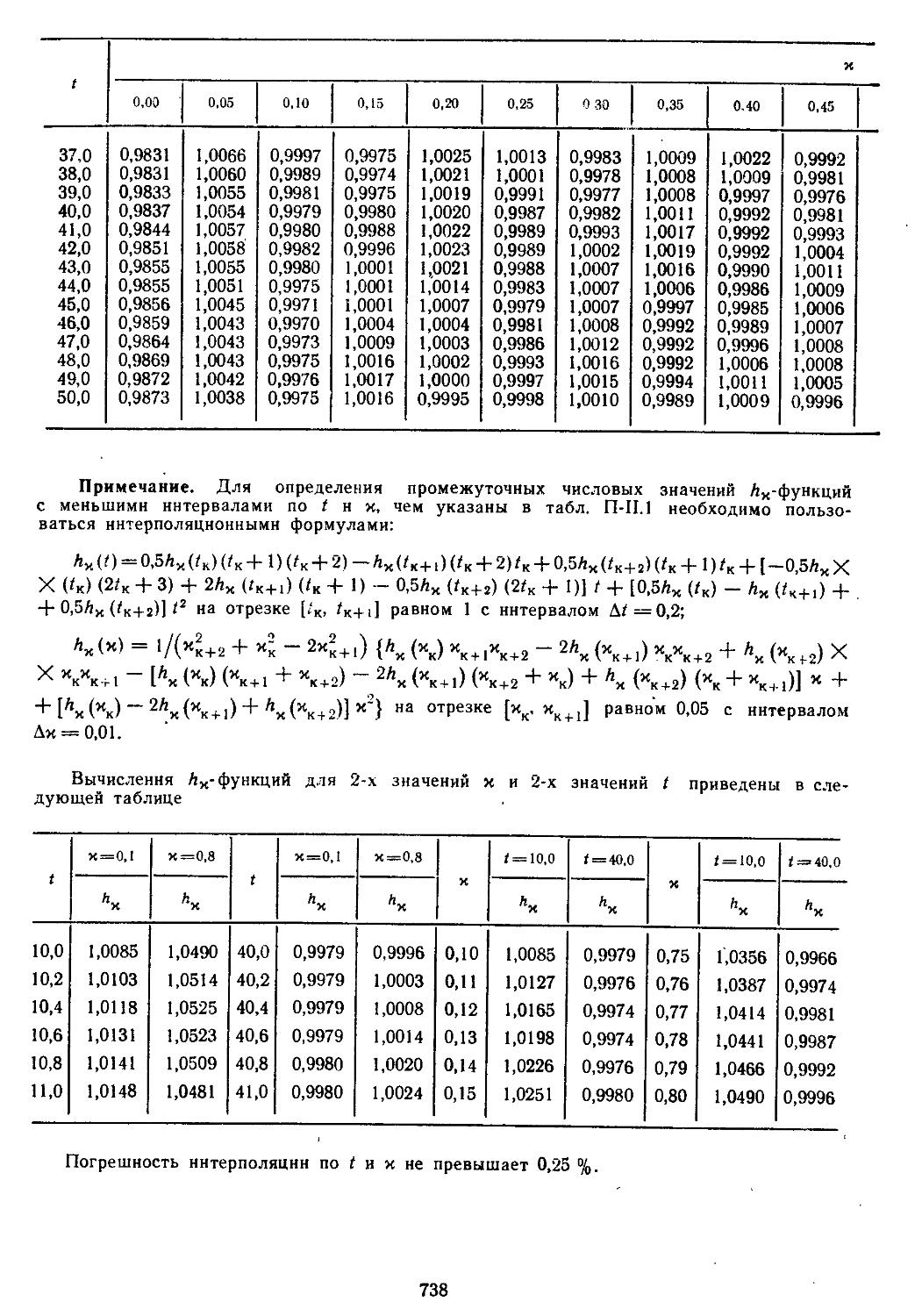
Приложение П-11.1. Таблица Лх (/)-функций .... 736
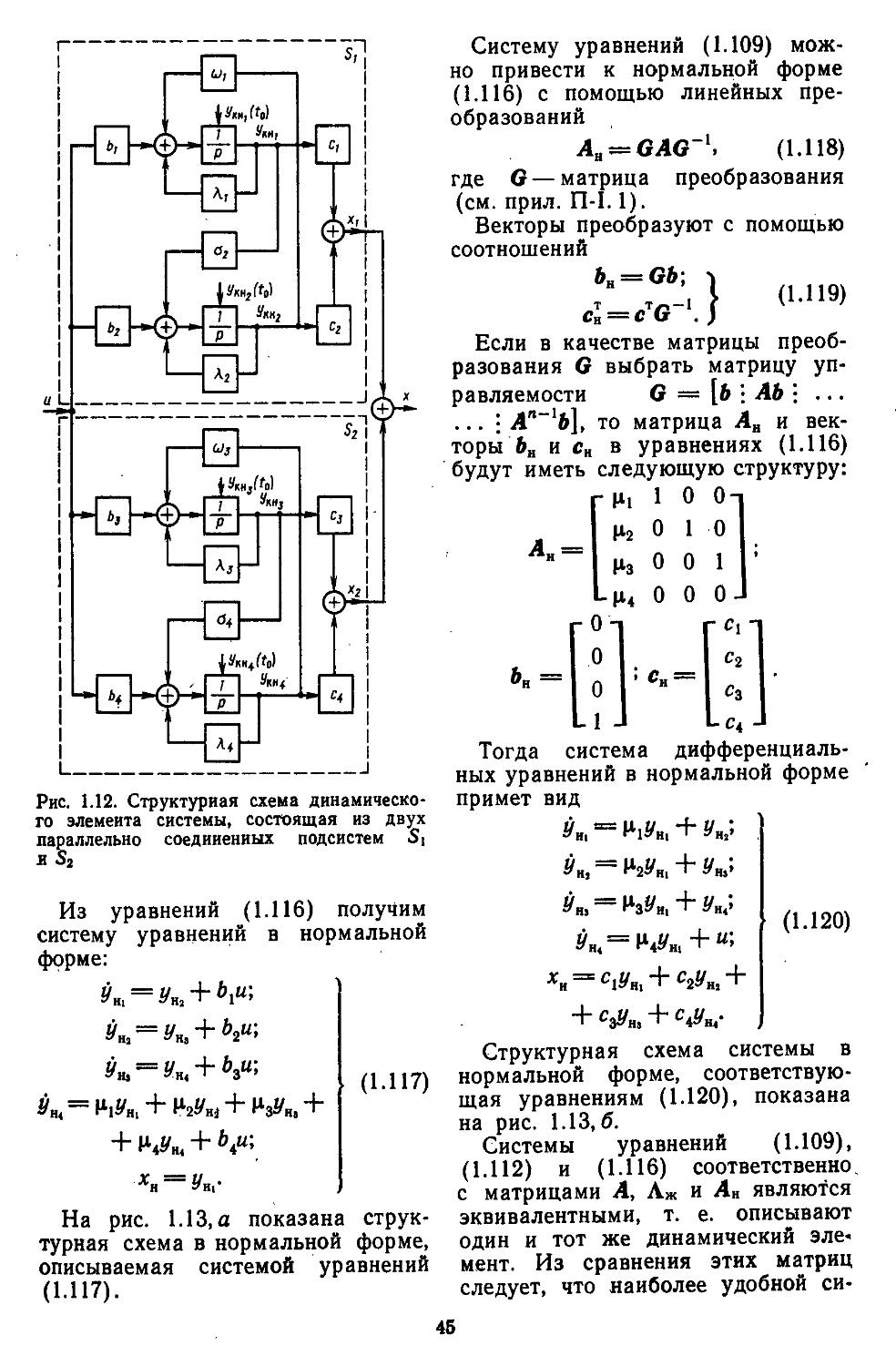
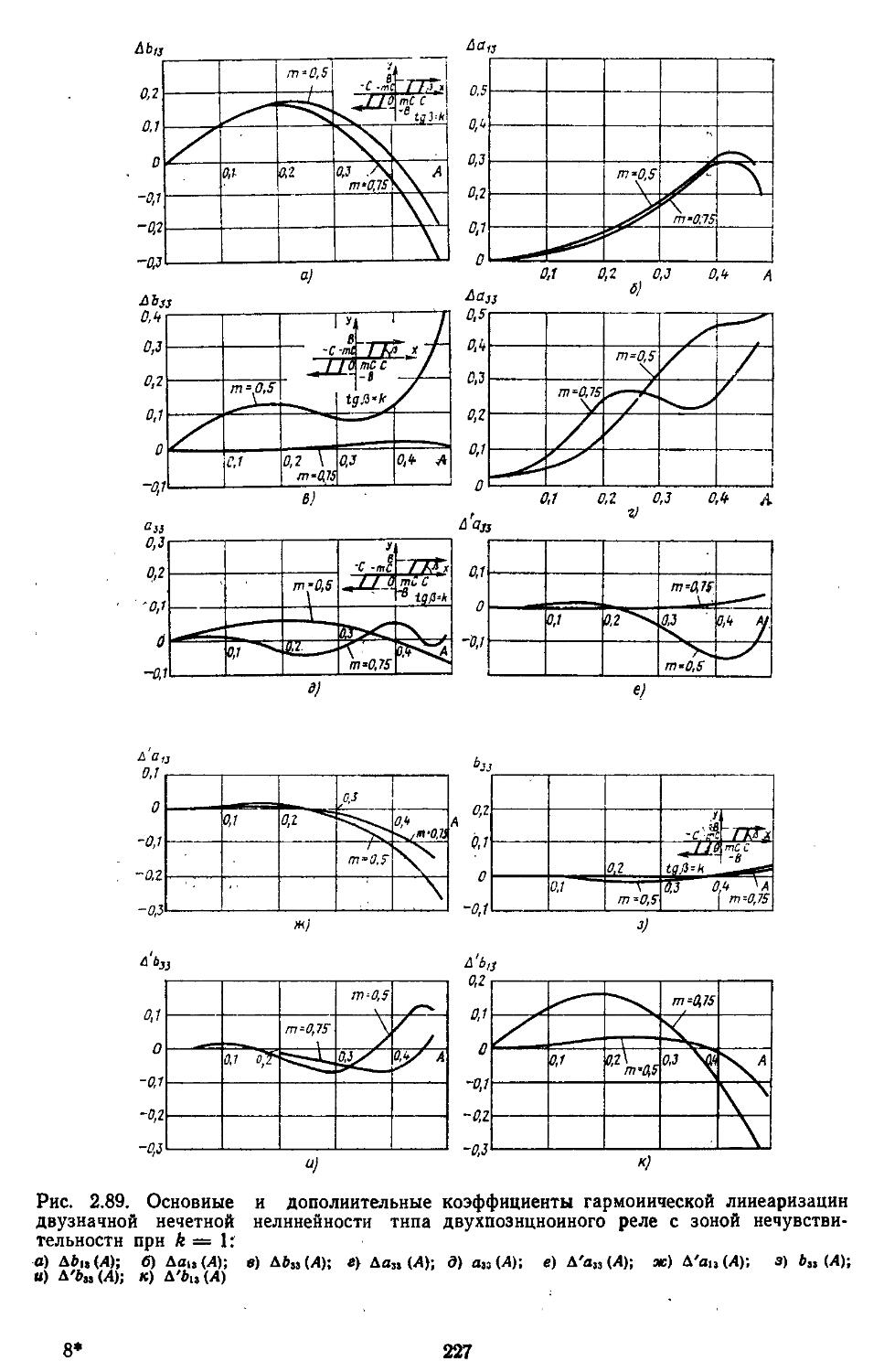
Приложение П-11.2. Назначение и состав информационно-программного обеспечения для автоматизации проектирования систем автоматического регулирования .... 738
Приложение П-11:3. Формулы для вычисления интегралов от дроб-ио-рациональиых функций . . . 740
Список литературы................ 744
Предметный указатель...............746
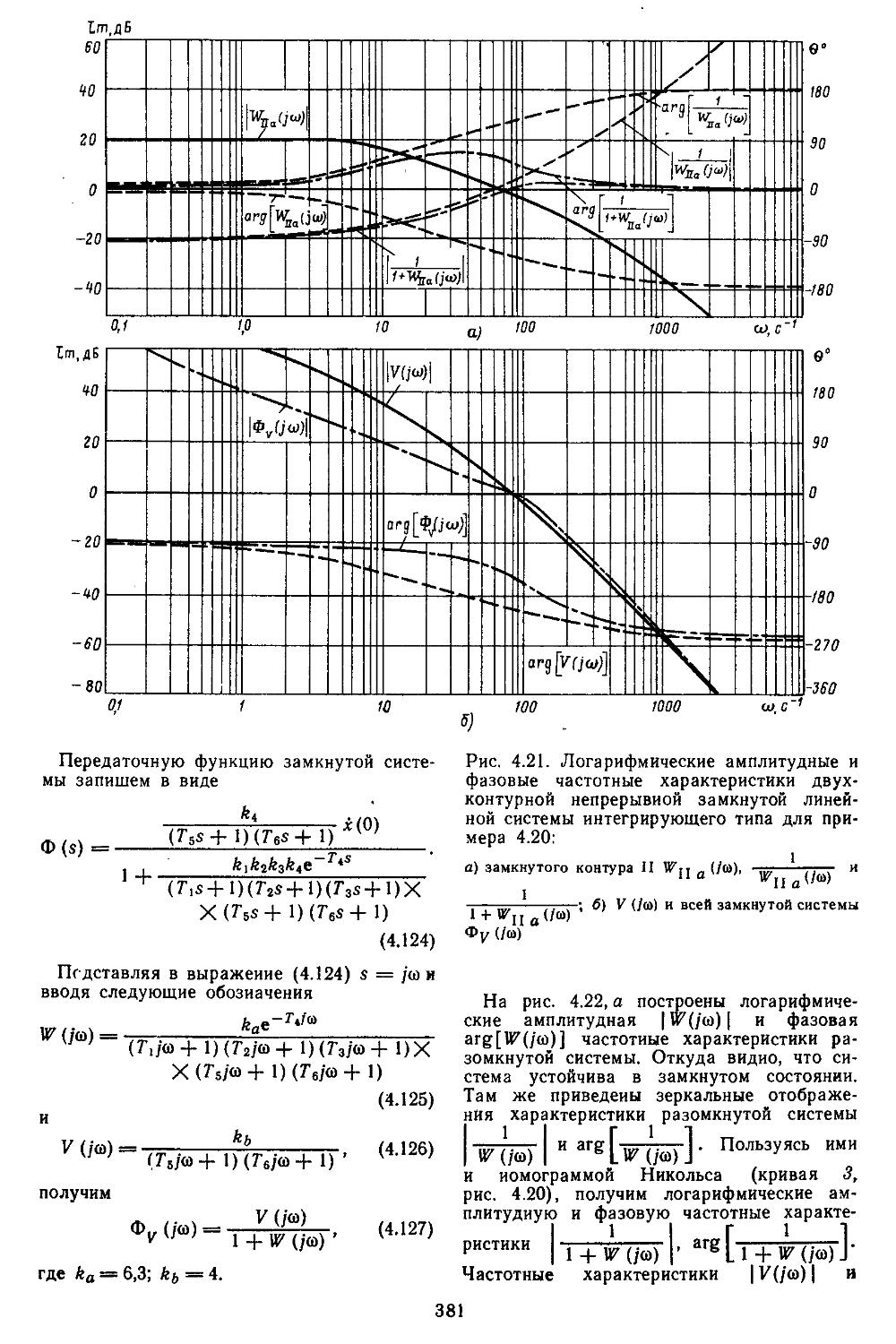
Светлой памяти талантливого организатора высшего образования Виктора Михайловича Колобашкина посвящается эта книга
ПРЕДИСЛОВИЕ
Теория автоматического регулирования изучается во всех высших технических учебных заведениях в качестве одной из базовых дисциплин. На ее основе в дальнейшем читаются такие курсы, как теория автоматического управления, автоматизированные системы переработки информации, управление технологическими и организационно-экономическими процессами, теория автоматизированного проектирования систем и их математическое обеспечение, теория принятия инженерных решений, а также целый ряд дисциплин специального назначения. Объекты и устройства систем регулирования отличаются по своей физической природе и принципам построения, поэтому проектировщику необходимо не только иметь хорошую подготовку в области механики, электротехники, электроники и вычислительной техйики, ио и уметь учитывать специфические особенности объекта. С целью овладения практическими навыками использования методов теории автоматического регулирования будущие специалисты в процессе обучения выполняют домашние задания, курсовые и дипломные работы по проектированию систем управления конкретными объектами.
Трудность выполнения проектных работ в значительной степени определяется сложностью математического аппарата, используемого при описании объектов и систем автоматического регулирования (САР). Для непрерывных объектов с сосредоточенными и распределенными
параметрами — это обыкновенные дифференциальные и интегральные уравнения и дифференциальные уравнения в частных производных соответственно; а для объектов, информация с которых снимается в дискретные моменты времени,— разностные уравнения. В такой форме описываются, в частности, и процессы в управляющих вычислительных машинах, получивших к настоящему времени весьма широкое распространение в САР.
Проектирование САР обычно выполняют либо в частотной области с применением специальных таблиц и номограмм, либо во временной области с помощью алгоритмов, реализуемых на универсальных ЭВМ. Основу математического аппарата в первом случае составляют: непрерывное и дискретное преобразования Лапласа; амплитудно-фазовые характеристики, полученные с помощью s-, z- и «-преобразований.
Случайные процессы описываются методами гармонической и статистической линеаризаций. Во временной области используется векторно-матричное описание объекта в пространстве состояний, что позволяет при применении вычислительных методов линейной алгебры создать единый математический аппарат для исследования непрерывных и дискретных систем. Оба подхода к проектированию долгое время развивались независимо друг от друга. Однако с помощью современного математического аппарата их можно объединить. Именно
7
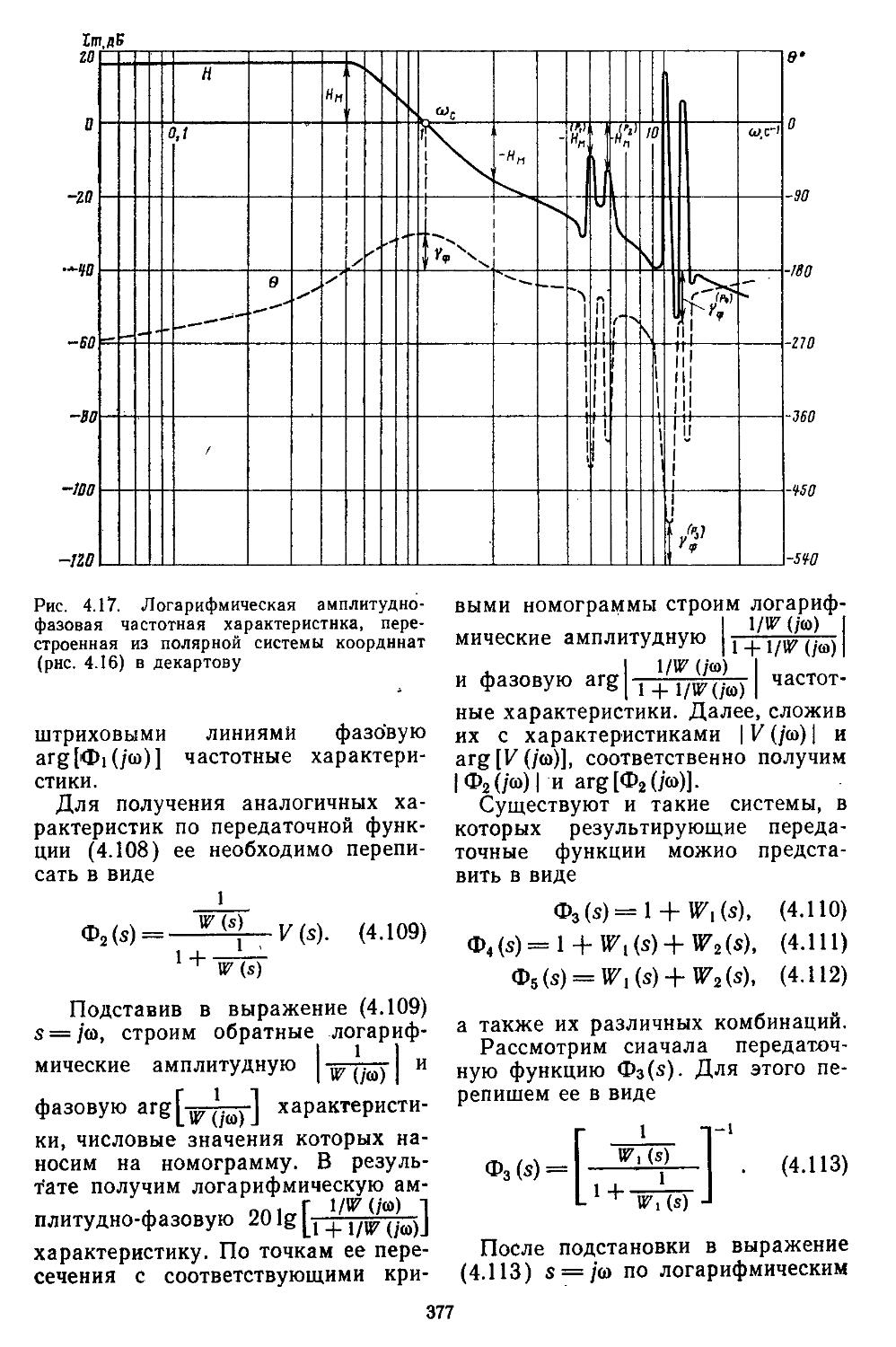
такой обобщенный подход положен в основу рассматриваемых в данной книге методов. Это привело к разработке ряда алгоритмов проектирования систем и соответствующих программ на языке ЙЛ/1. Они позволяют формировать обобщенные модели элементов в дискретной форме; вычислять коэффициенты, полюсы и нули передаточных функций; строить амплитудно-фазовые частотные характеристики (в обычном и логарифмическом масштабах), корневые годографы и переходные процессы.
Кроме того, были составлены процедуры для определения характеристик точности при действии регулярных и случайных сигналов; вычисления коэффициентов гармонической, статистической и совместной линеаризаций; выделения областей автоколебаний (по амплитуде или частоте) и устойчивых состояний.
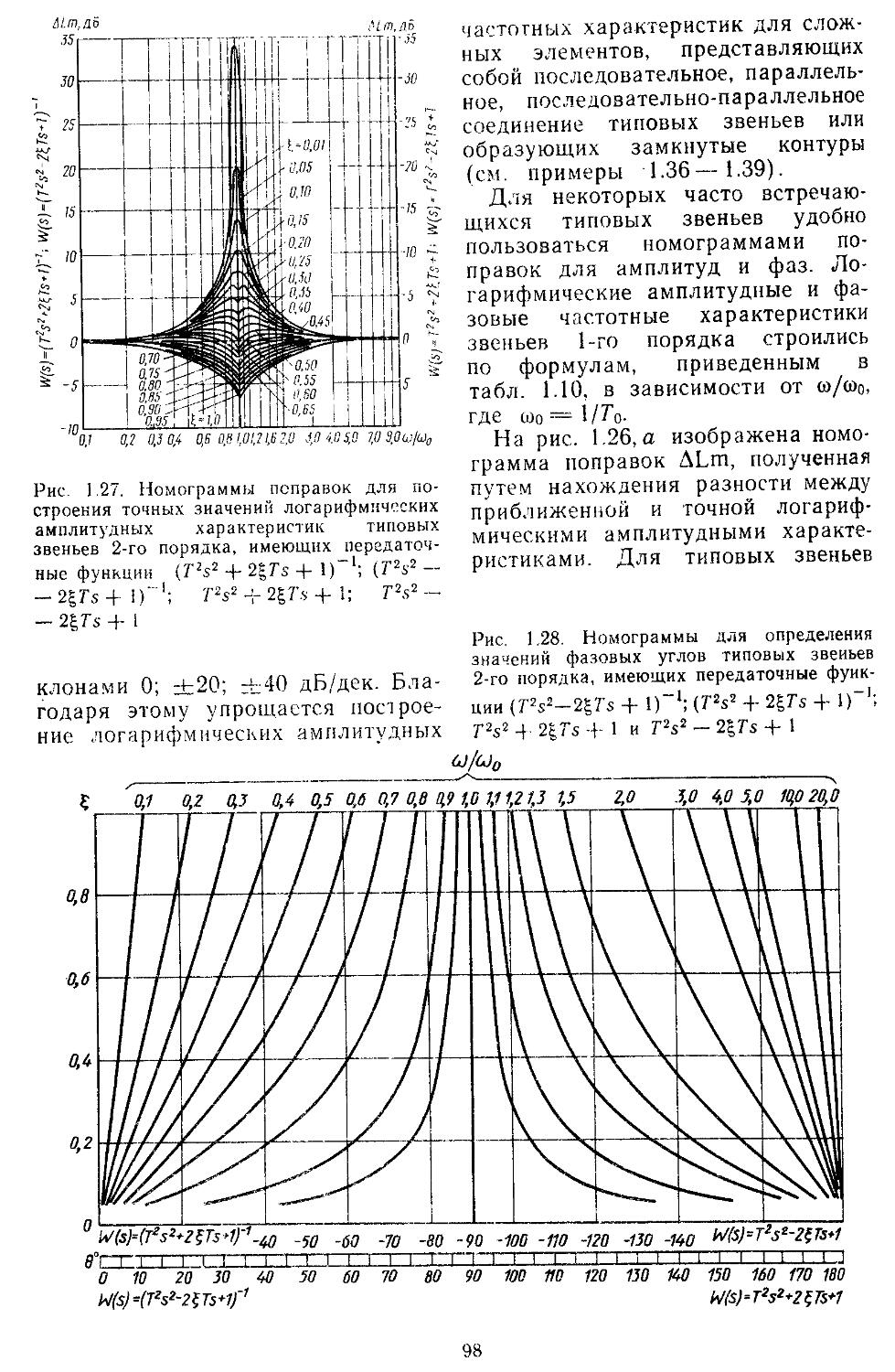
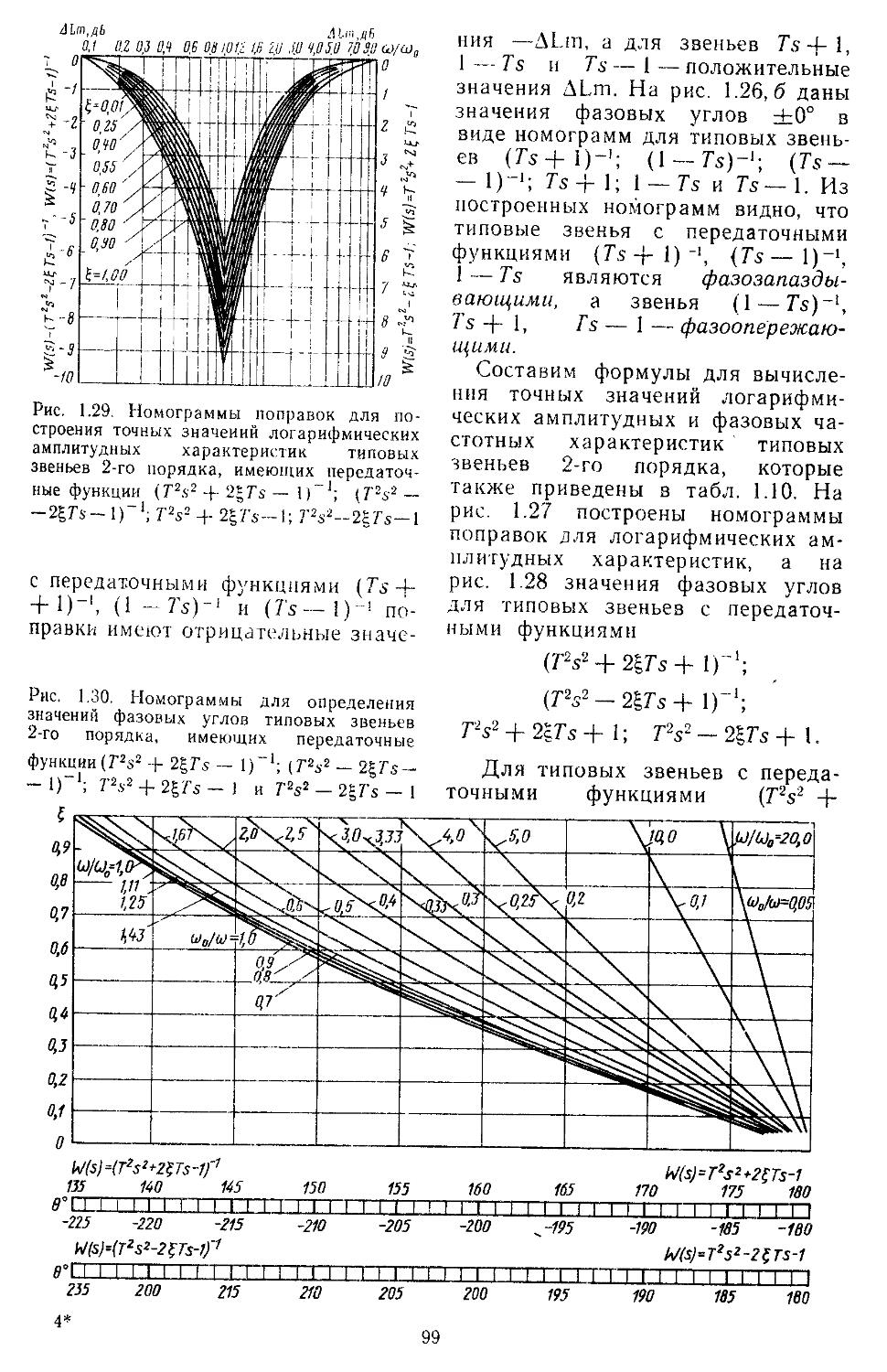
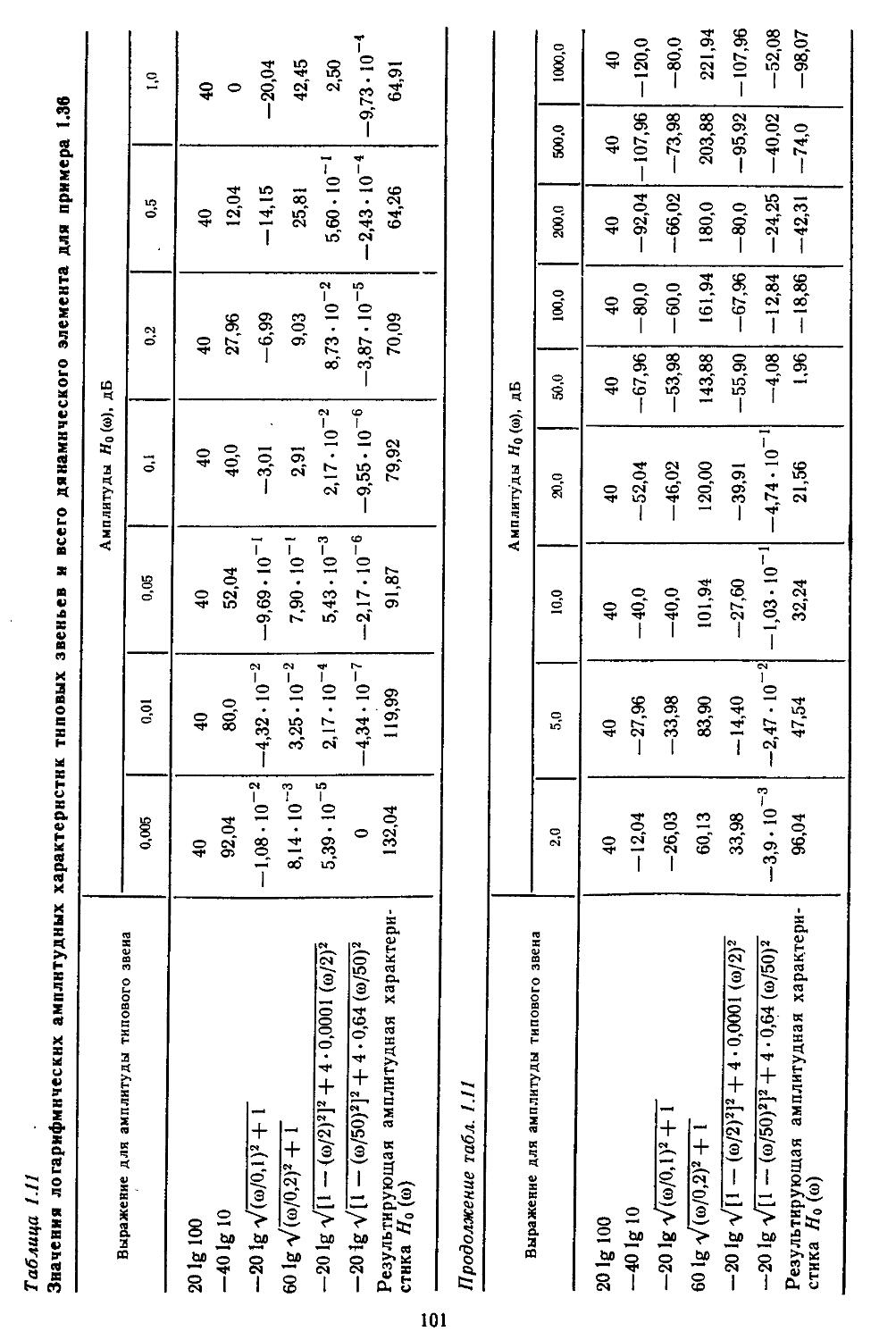
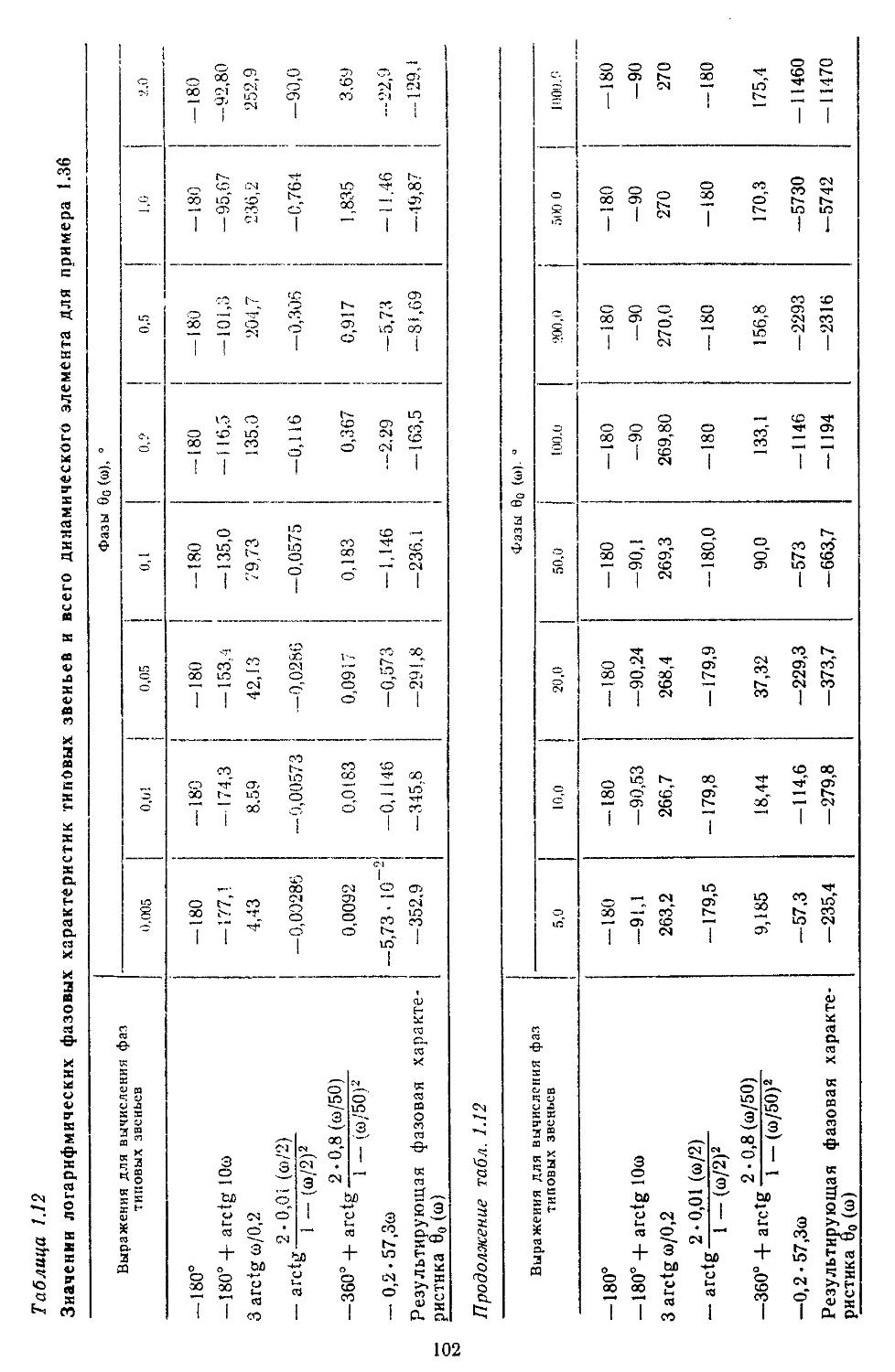
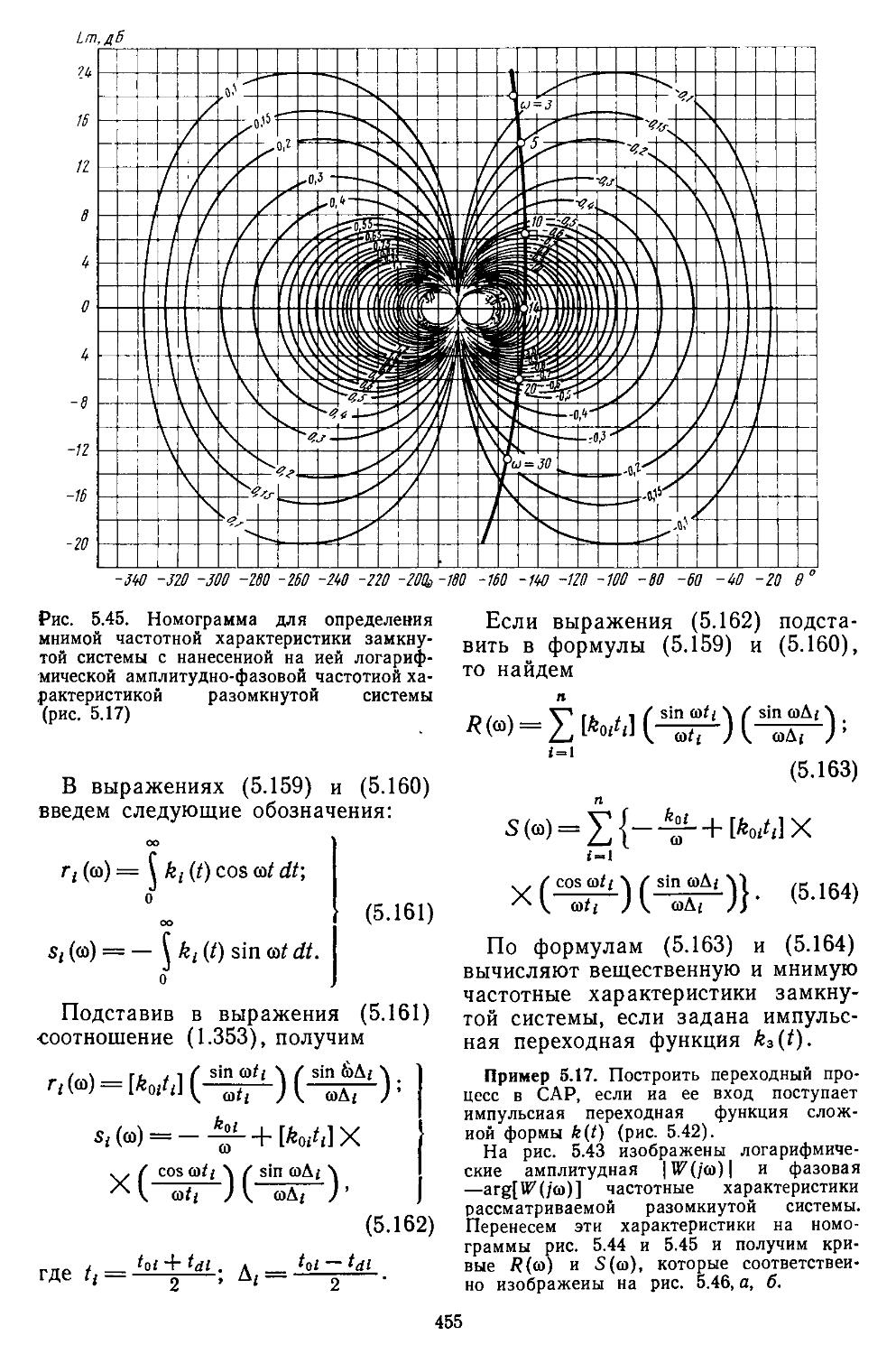
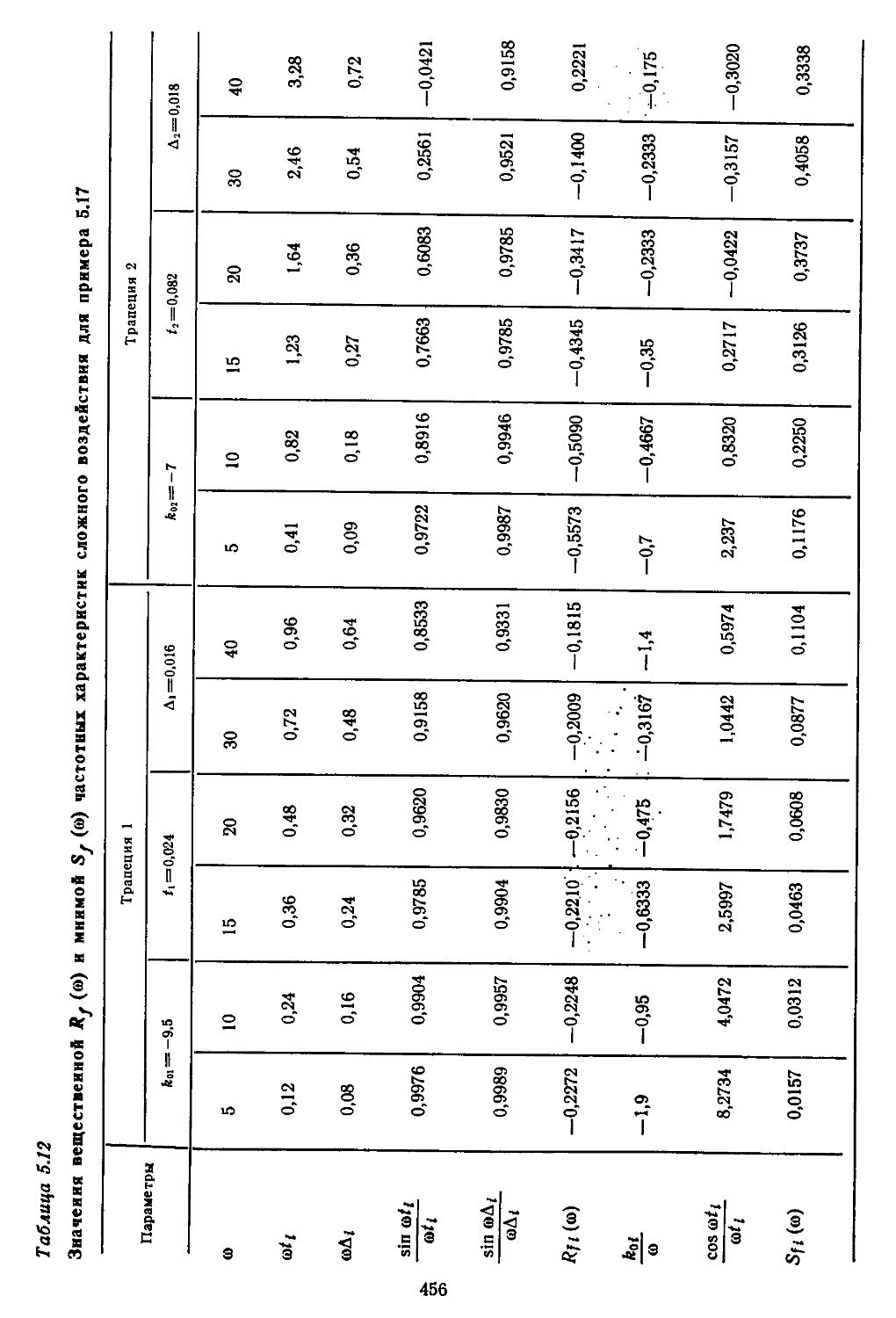
Значительное внимание уделено составлению математических зависимостей и номограмм для построения частотных характеристик разомкнутых и замкнутых систем и определения показателей качества переходных процессов и характеристик точности. Рассмотрены процедуры анализа устойчивости нелинейных систем по Ляпунову или с применением методов гармонической, статистической и совместной линеаризаций.
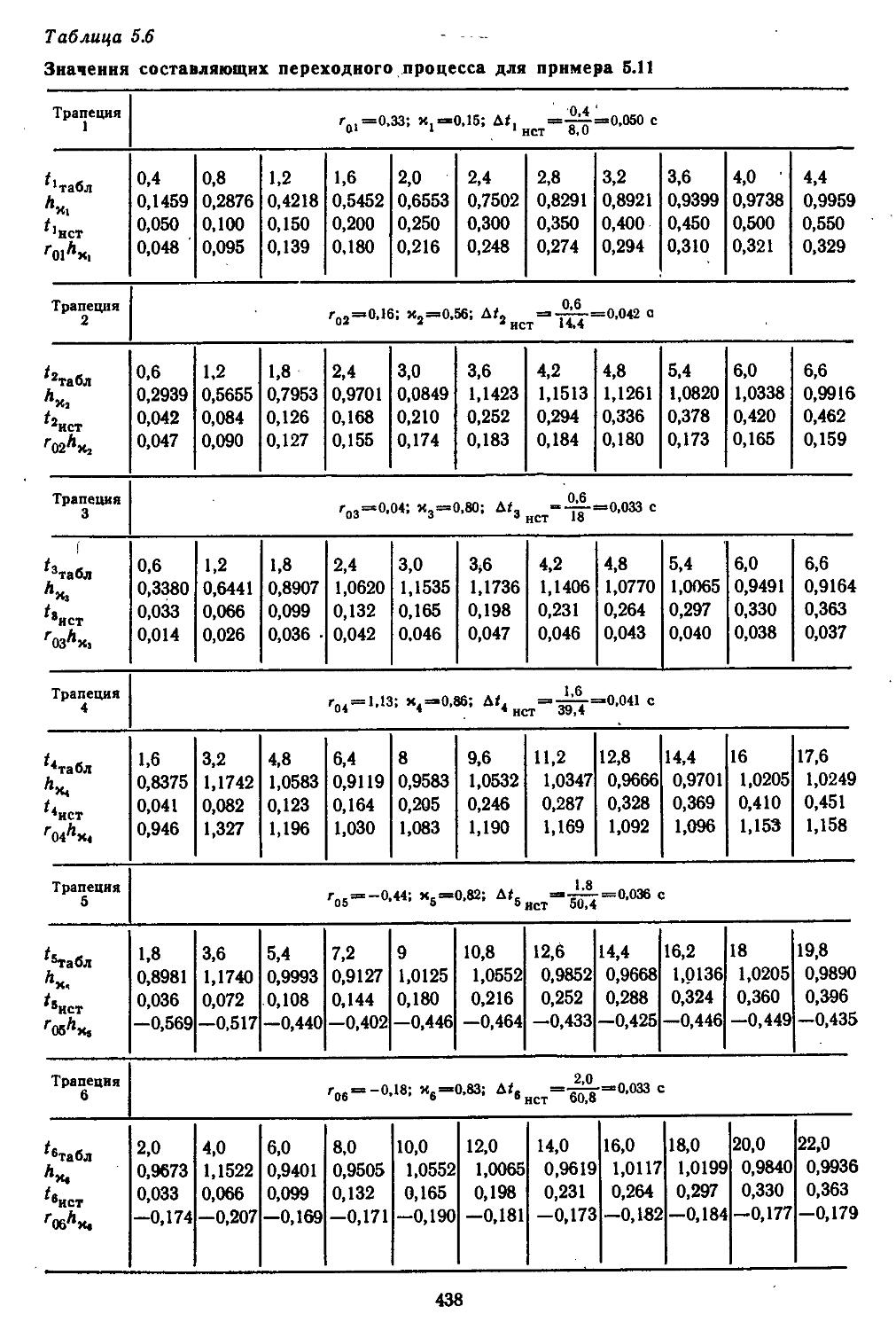
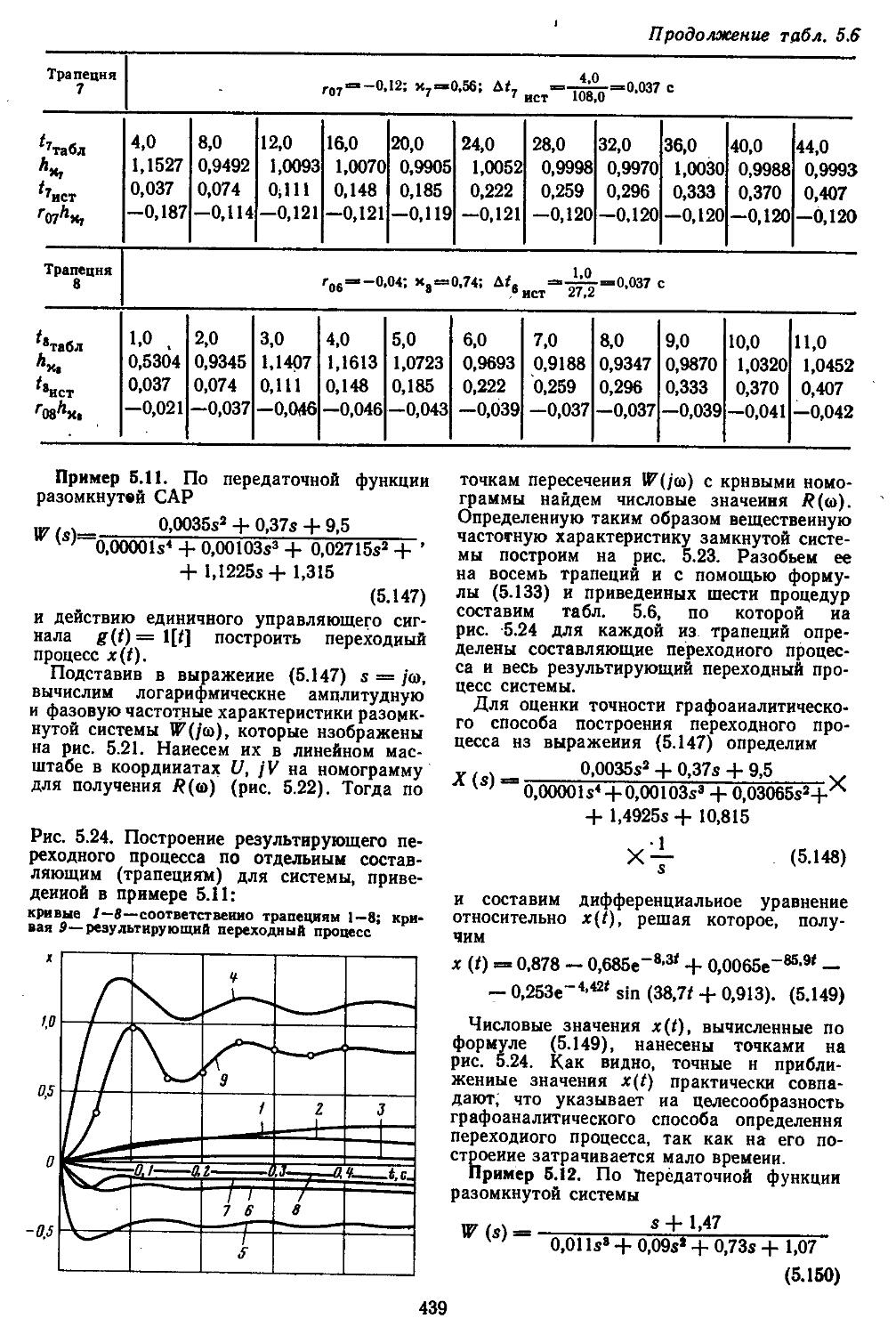
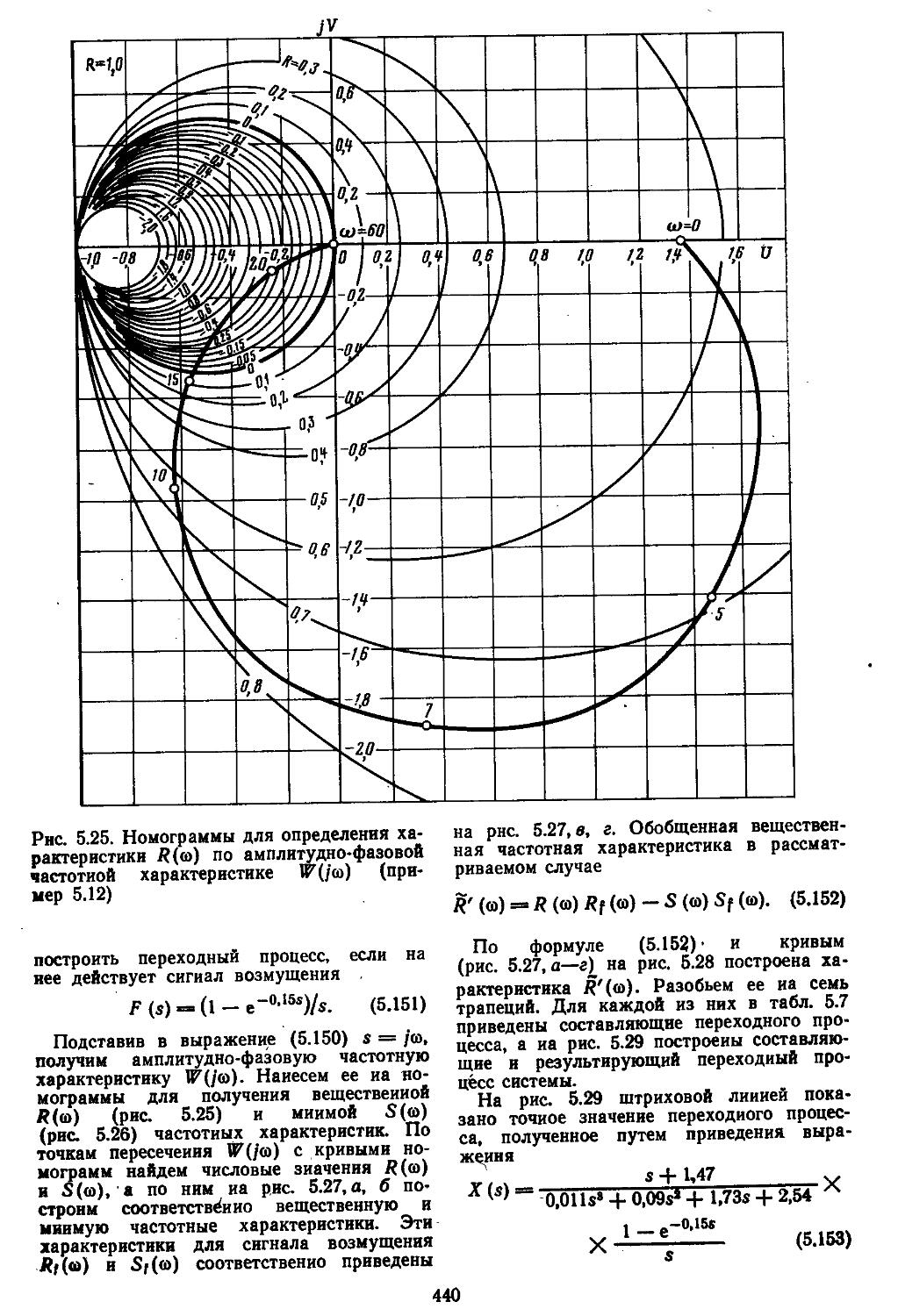
Каждая глава снабжена конкретными примерами получения амплитудно-фазовых частотных характеристик систем с отрицательными и положительными обратными связями; построения корневых годографов, вещественных и мнимых частотных характеристик замкнутых систем и нахождения по ним приближенных значений показателей качества; вычисления по трапецеидальным характеристикам и hM-функциям кривых протекания переходных процессов; определения характеристик точности систем и уменьшения в них ошибок путем
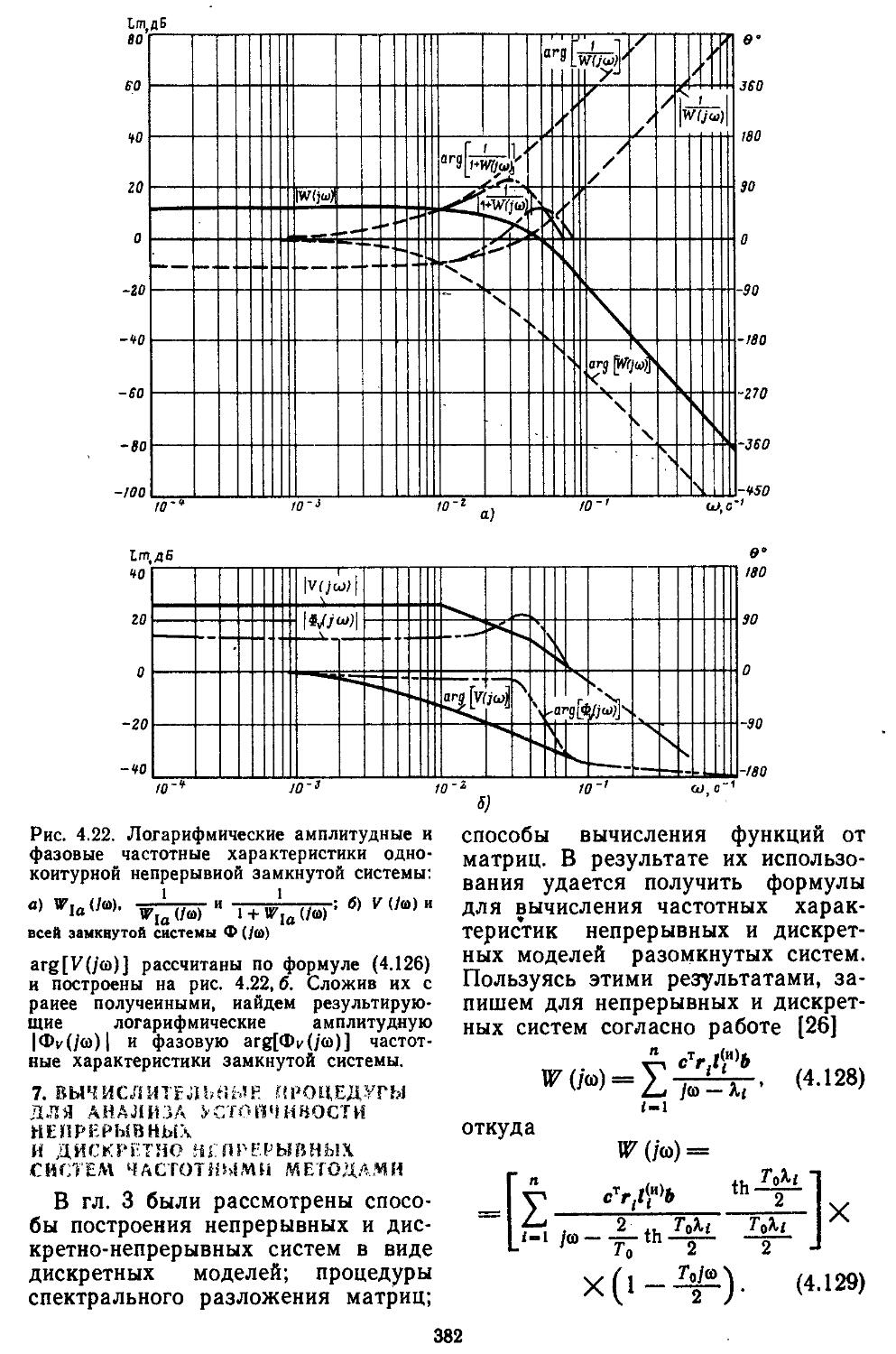
применения условий инвариантности.
Задачи синтеза САР решают двумя способами: на основе построения амплитудных частотных характеристик неизменяемых частей с последующим выбором типа и параметров последовательных, параллельных и параллельно-последбва-тельных корректирующих устройств или с применением принципа максимума Понтрягина и метода динамического программирования. Оба способа позволяют решать задачи синтеза в классе систем с заданной структурой. Однако в первом случае удается получить линейные корректирующие устройства, реализуемые в непрерывных системах в виде RC-фильтров, а в дискретных и дискретно-непрерыйных — линейных корректирующих программ для управляющих ЭВМ. Применяя второй способ синтеза, получим нелинейные корректирующие устройства, которые в непрерывных системах реализуются уже на базе активных устройств с операционными усилителями и преобразователями на диодах, а в дискретных и дискретно-непрерывных системах —в виде нелинейных корректирующих программ.
При проектировании систем могут использоваться различные методы: расчетно-теоретические, основанные на номограммах, таблицах и графиках, а также с помощью реализации вычислительных процедур На ЕС ЭВМ в пакетном или интерактивном режимах работы. Все модули прикладных программ составлены на языке ПЛ/1. Если в систему включена управляющая ЭВМ, то программы для нее пишутся на языке ассемблер, как наиболее близком к кодам команд вычислительных машин.
В конце книги приведено несколько примеров сквозного проектирования наиболее распространенных типов САР, позволяющих йе только определять структуру системы, но и строить кривые, облегчаю
8
щие нахождение наиболее рациональных значений параметров устройства управления и объекта. Все примеры относятся к конкретным промышленным системам, и их проектирование ведется на инженерном уровне. Оформление схем и графиков, полученных в процессе проектирования а также рабочих программ выполнено в соответствии с требованиями ЕСКД и ЕСПД.
При составлении Атласа для проектирования САР автор руководствовался рядом монографий и учебных пособий, список которых приведен в конце книги. Порядок изложения материала в Атласе и его содержание главным образом основаны на учебнике Н. Н. Иващенко «Автоматическое регулирование*, 4-издание, Машиностроение, 1978 г. и учебном пособии Ю. И. Топчеева и А. П. Цыплякова «Задачник по теории автоматического регулирования», Машиностроение, 1977 г.
Существенный вклад в учебное пособие внесли сотрудники кафедры «Управления комплексами» Московского инженерно-физического института С. К. Коваленко, М. А. Колывагин, А. И. Титков и Ю. Ю. Шумилов, которые предложили несколько оригинальных подходов решения ряда задач. В подготовке рукописи книги к печати приняли участие Р. С.. Кондратьева, А. И. Логинов, С. В. Осипов, Е. И. Попов, А. Г. Синевич и А. В. Чукашев, без помощи которых книга не получила бы надлежащей наглядности и доступности изложения. Улучшить содержание книги помогли ценные замечания и советы, высказанные рецензентами академиком А. А. Вороновым и членом-корреспондентом АН СССР Е. П. Поповым, за что я выражаю им самую глубокую признательность. Автор будет благодарен всем читателям за замечания по данной книге.
ВВЕДЕНИЕ
В настоящее время в промышленности и сельском хозяйстве применяются десятки тысяч различных типов систем автоматического регулирования (САР), которые обеспечивают высокую эффективность производственных процессов.
Современные САР представляют собой сложные динамические системы, обеспечивающие высокую точность отработки сигналов управления в условиях действия различных возмущений и помех. При больших величинах возмущений и уровней помех нарушаются нормальные эксплуатационные режимы, снижается точность и ухудшаются показатели качества переходных процессов в системах по сравнению с заданными техническими условиями. Проектирование таких САР представляет достаточно сложную проблему, так как в них входят устройства и объекты управления различной физической природы.
Для получения надлежащих характеристик САР проектировщику приходится находить компромиссные решения, так как требования к точности и показателям качества переходных процессов взаимоисключающие. Основной путь преодоления такого противоречия — применение в САР элементов с большими коэффициентами усиления и корректирующих устройств с перестраиваемыми во время работы параметрами. Однако с ростом коэффициентов усиления возрастает влияние нелинейностей в элементах, что приводит к нарушению принципа суперпозиции и необходимости учета при проектировании уп
равляющих и возмущающих воздействий. С их изменением в системах появляются чередующиеся режимы устойчивого, неустойчивого движений и автоколебаний.
В нелинейных системах наряду с высшими гармониками могут также возникать субгармоники, приводящие в большинстве случаев к поломке устройств управления или объектов. В области, близкой к резонансу, в слабодемпфирован-ных системах за счет нелинейностей возможно появление скачкообразных изменений алй1литуд и фаз. Существует еще целый ряд особенностей поведения нелинейных систем регулирования, которые также будут рассмотрены в книге.
Перестройка параметров корректирующих устройств может производиться непрерывно или скачкообразно. В результате нарушается стационарность процессов в элементах, динамика которых в этом случае описывается дифференциальными, интегральными или разностными уравнениями с переменными параметрами. Существует целый ряд систем с параметрами, изменяющимися случайным образом. Скачкообразный характер измене-' ния параметров по своему действию эквивалентен введению дополнительных возмущений в системе в строго определенные моменты времени. Все эти явления -крайне нежелательны, так как они приводят к снижению точности и ухудшению показателей качества. Необходимость учета влияния нелинейностей и непостоянства параметров устройств и объектов вынуждает
10
проектировщиков отказаться от традиционных методов описания динамики процессов. Приходится прибегать к таким способам линеаризации уравнений, при которых сохраняется зависимость поведения системы от амплитуды сигнала, или использовать ряды Воль-терра и Неймана [15, 21, 39].
С целью уменьшения влияния нелинейностей на поведение системы в них вводятся дополнительные нелинейные элементы компенсирующего типа или корректирующие устройства, подавляющие режимы автоколебаний. Эти способы являются наиболее эффективными и в тех случаях, когда входные сигналы изменяются в достаточно широком, диапазоне. Следует отметить, что в подобных системах введение дополнительных нелинейностей позволяет обеспечить существенное повышение коэффициентов усиления элементов при сохранении хороших показателей качества. Однако отказы средств нелинейной компенсации и коррекции в таких системах недопустимы, так как они приводят к возникновению автоколебаний с большой амплитудой и малой частотой и, как следствие, к выходу из строя автоматических регуляторов. Поэтому необходимо предусматривать . резервирование технических средств компенсации и коррекции.
Для уменьшения влияния нестационарности часто используют методы компенсации изменений параметров или создают системы, в которых обеспечиваются условия неполной инвариантности к собственным параметрам объекта и возмущениям [13]. Это может быть получено путем создания самонастраивающихся систем или введения двух-, трехканальиых корректирующих устройств псевдолиней-ного типа.
В самонастраивающихся системах определение параметров объекта может выполняться различными методами — прямыми или
косвенными. Наибольшее жё распространение получили следующие два: с подачей на вход объекта поискового сигнала и беспоисковые. Как известно, поисковый сигнал нарушает нормальный режим работы системы и вносит дополнительные возмущения, снижающие точность процесса регулирования [30], и его применение не всегда возможно. Кроме того, подача поискового сигнала ведет к уменьшению быстродействия системы из-за дополнительных затрат времени на выполнение измерительных и вычислительных операций. Этих недостатков лишены беспоисковые самонастраивающиеся системы, в которых в качестве эталонной модели используют управляющие ЭВМ. В таких системах по результатам сравнения сигналов с эталонной модели и объекта либо производят подстройку модели, либо перестраивают структуру и параметры корректирующего устройства [13, 35]. Такой способ формирования сигналов называют сигнальной компенсацией. Он нашел широкое применение в тех системах регулирования, параметры которых меняются во времени достаточно медленно. К ним относятся системы стабилизации, ориентации и управления летательных аппаратов в относительно узком диапазоне изменения высот и скоростей полета [13, 24].
В системах автоматической посадки самолетов, параметры которых обладают еще большей степенью нестационарности, аналитические методы расчета представляют значительные трудности. Поэтому проектирование систем этого класса обычно осуществляют методами математического и полунатур-иого моделирования [13, 28].
При относительно невысокой степени нестационарности объектов применяют системы регулирования с двух- или трехканальными корректирующими устройствами псев-долинейного типа, обеспечивающи
11
ми уменьшение чувствительности к изменениям собственных параметров объекта и к сигналам возмущения. Реализацию корректирующих устройств осуществляют на основе фильтров с активными элементами или в виде рабочих программ микропроцессоров. Меняя программы, удается существеиио снизить чувствительность характеристик системы к изменениям параметров и возмущениям. Такой способ уменьшения влияния нестационарности достаточно прост в аппаратном исполнении. Следует также отметить, что методика расчета систем с корректирующими устройствами псев-долииейного типа не представляет больших трудностей и может производиться во временной и частотной - областях.
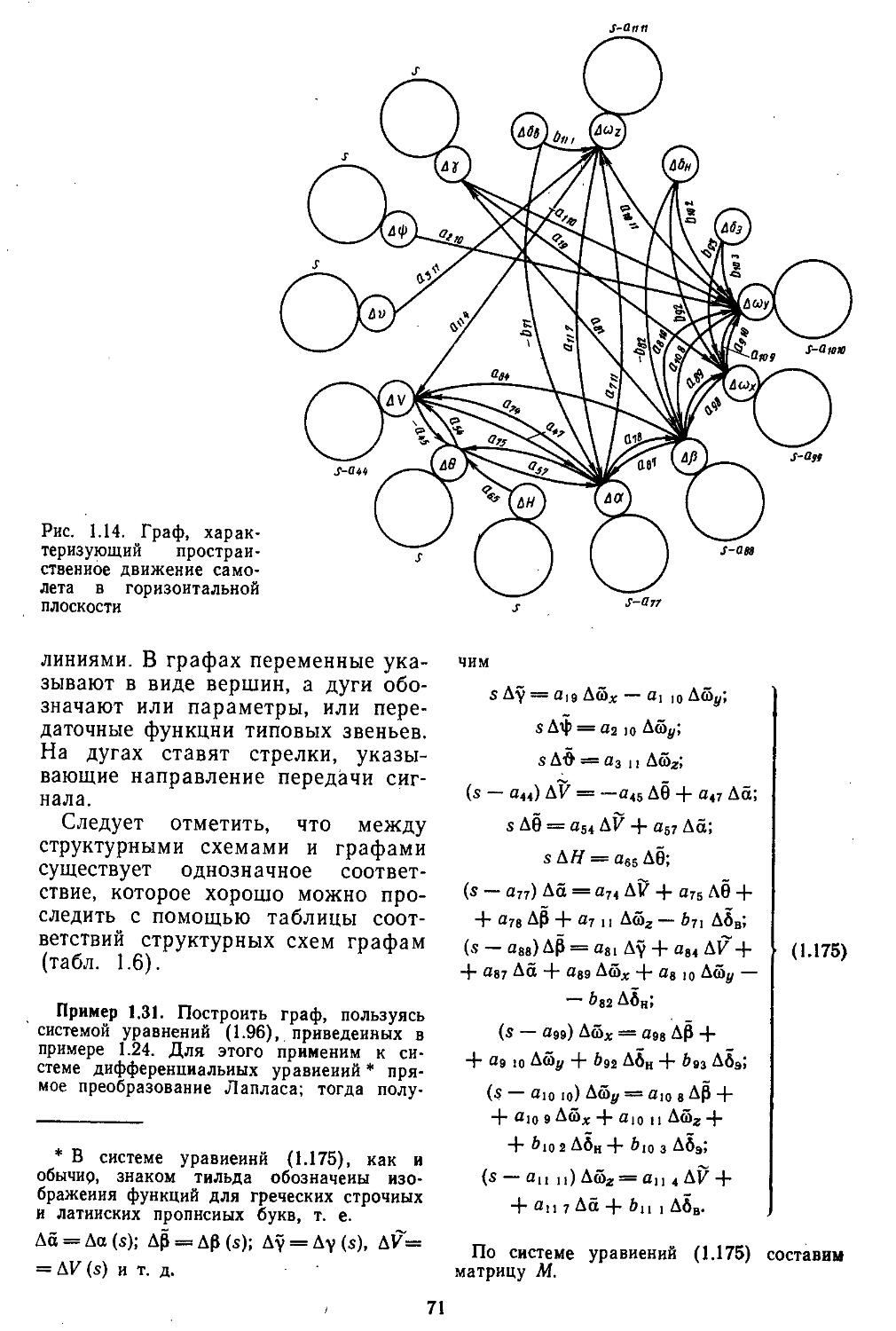
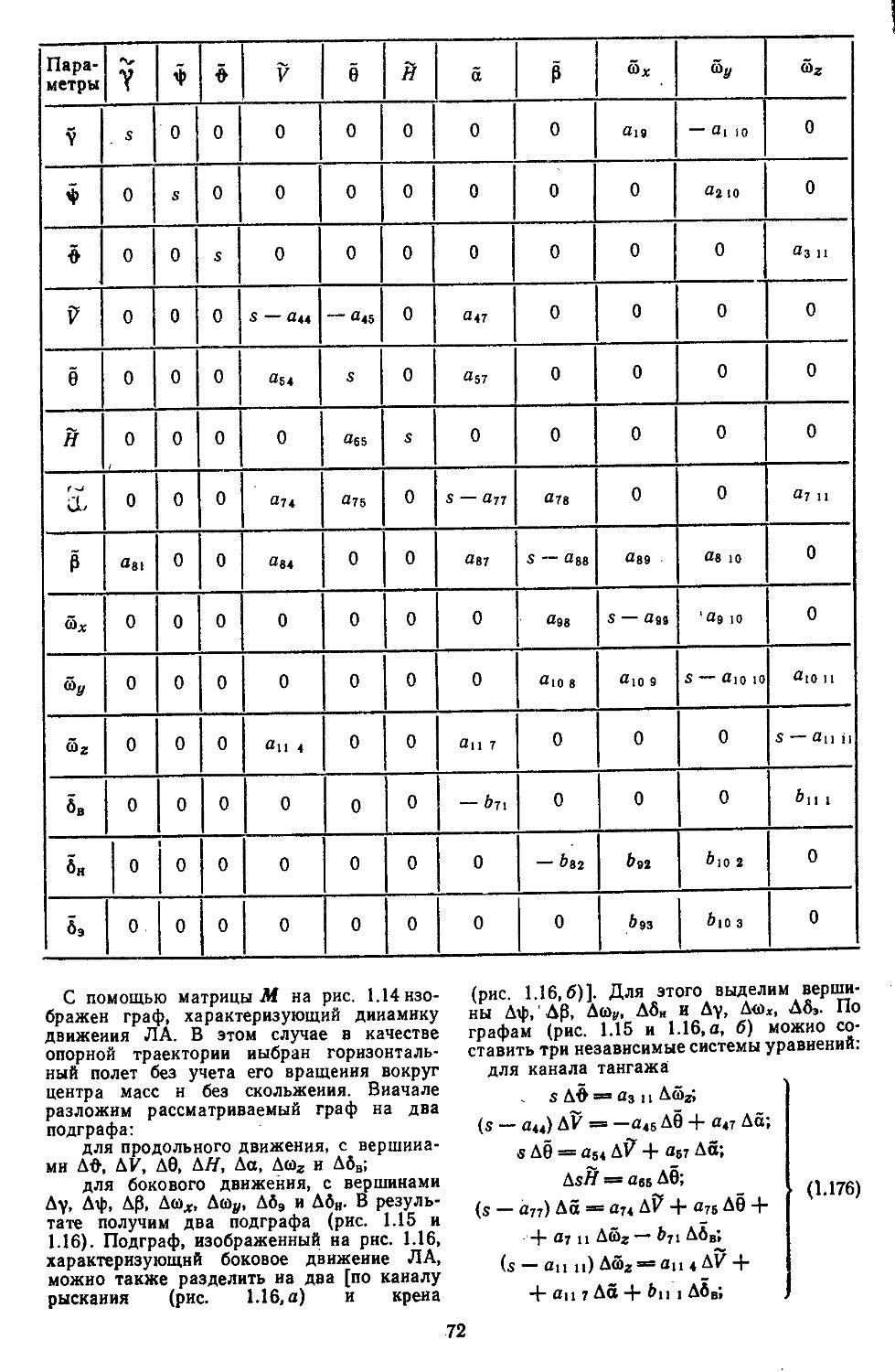
Для описания современных сложных САР наиболее удобен векторно-матричный аппарат, позволяющий создать единую компактную форму математического представления широкого класса объектов. К ним относятся непрерывные, дискретные и дискретно-непрерывные стационарные н нестационарные системы линейного типа и такие нелинейные системы, в которых нелинейная часть отделена от линейной. В системах такого рода с помощью методов теории пространства состояний и спектрального разложения матриц удается получить ее дискретную модель в форме, удобной для реализации иа ЭВМ. В этом случае исследуемые процессы зависят от времени и могут быть легко сравнимы с экспериментальными данными [11, 21, 26, 27, 32].
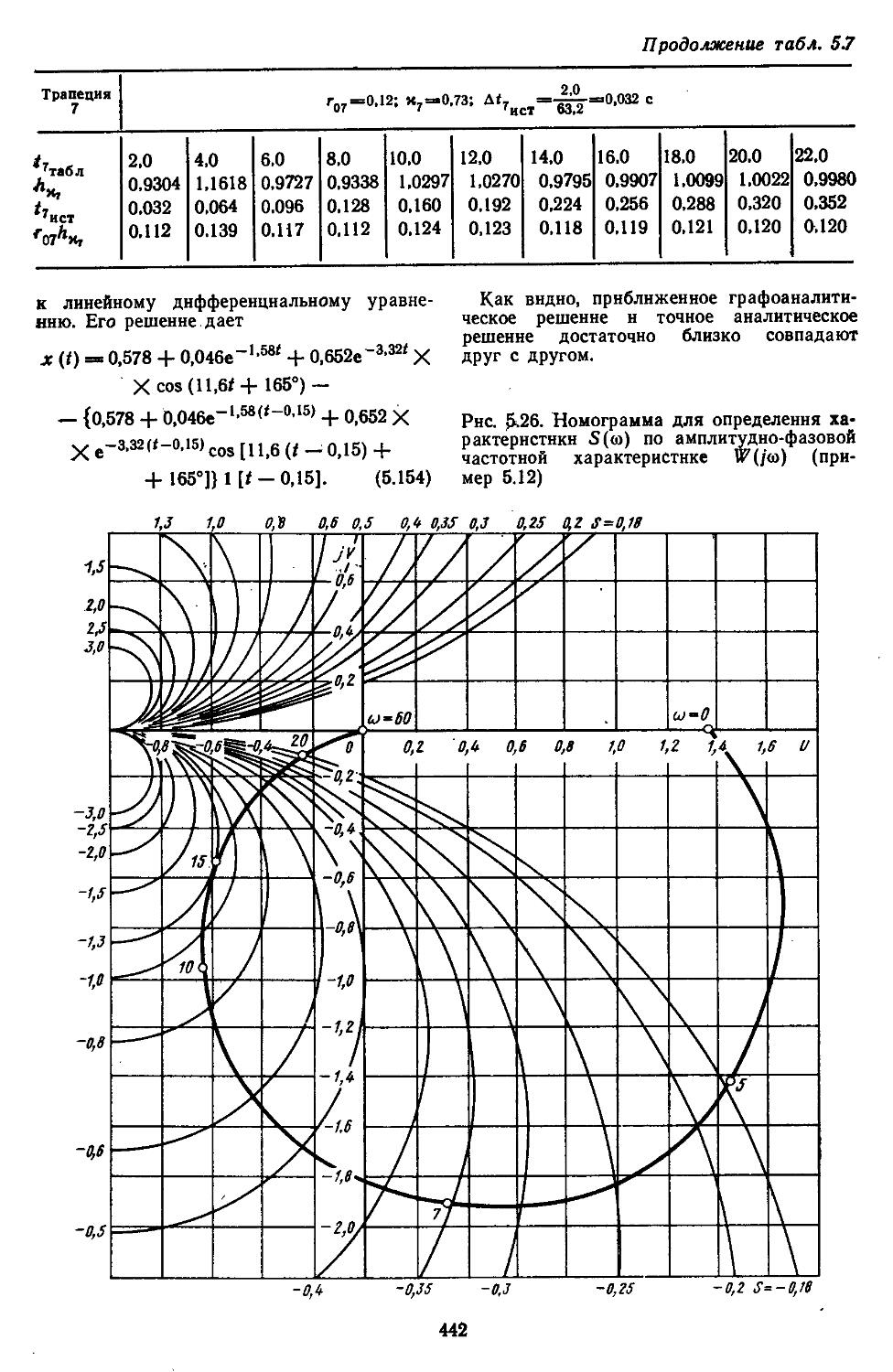
При проектировании САР довольно часто необходимо располагать амплитудно-фазовыми частотными характеристиками, по которым находят запасы устойчивости всей разомкнутой системы. Пользуясь нми, можно оценивать влияние изменений параметров элементов системы и объектов на ее устойчивость в замкнутом состоянии. Методы исследования систем в частот
ной области позволяют находить также показателя качества и характеристики точности. Такой частотный подход к анализу систем достаточно удобен при использовании номограмм и таблиц /^-функций [33, 35].
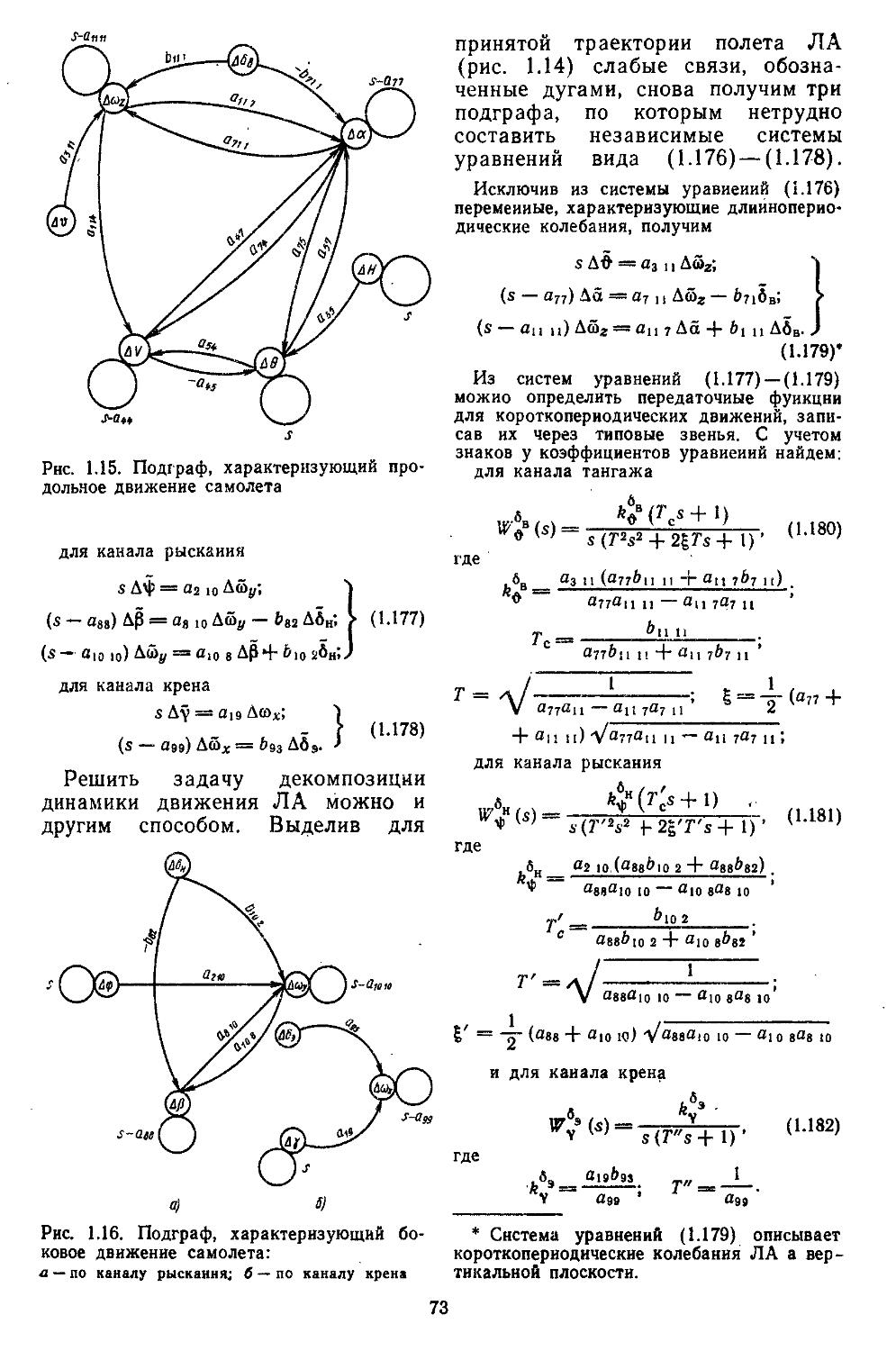
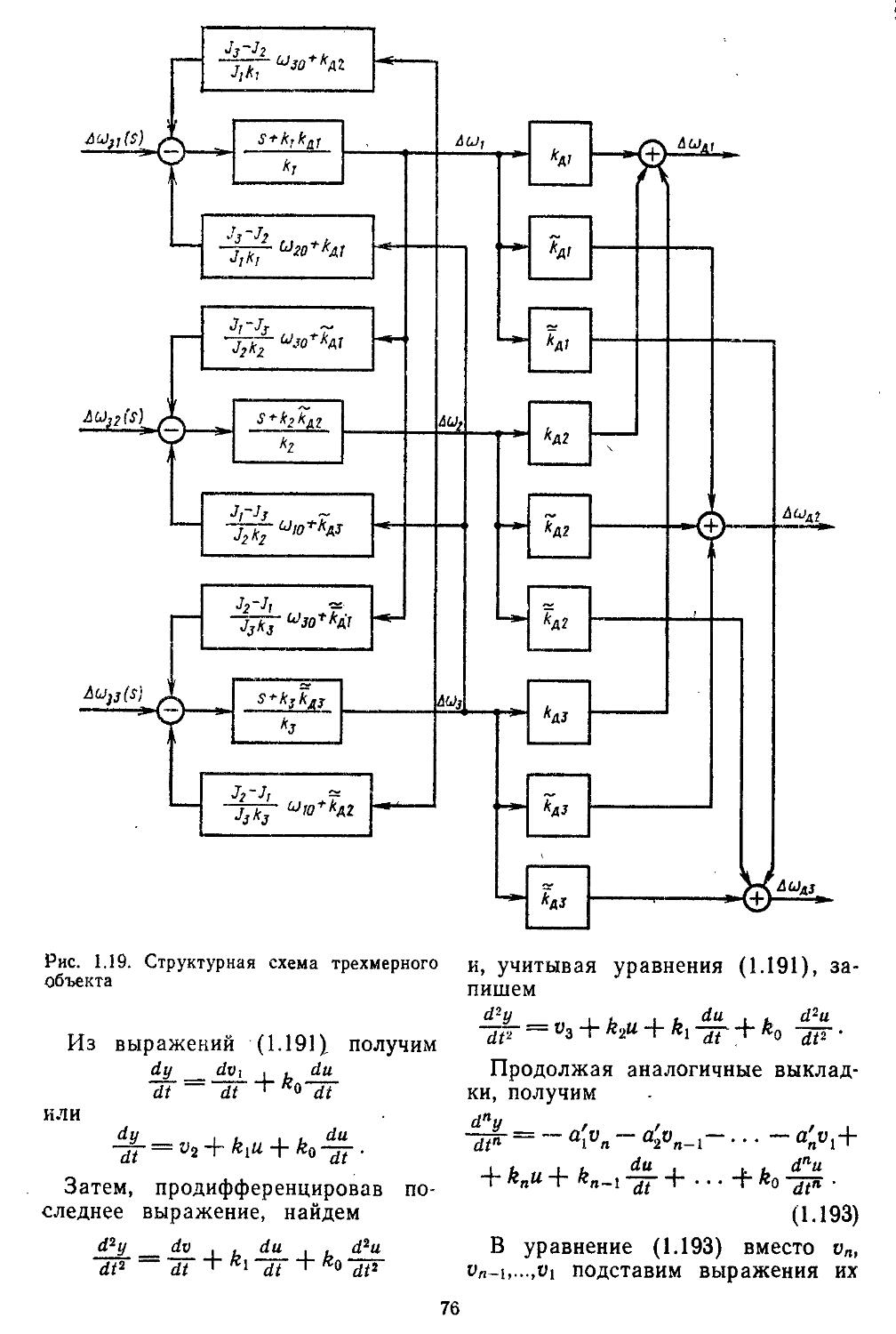
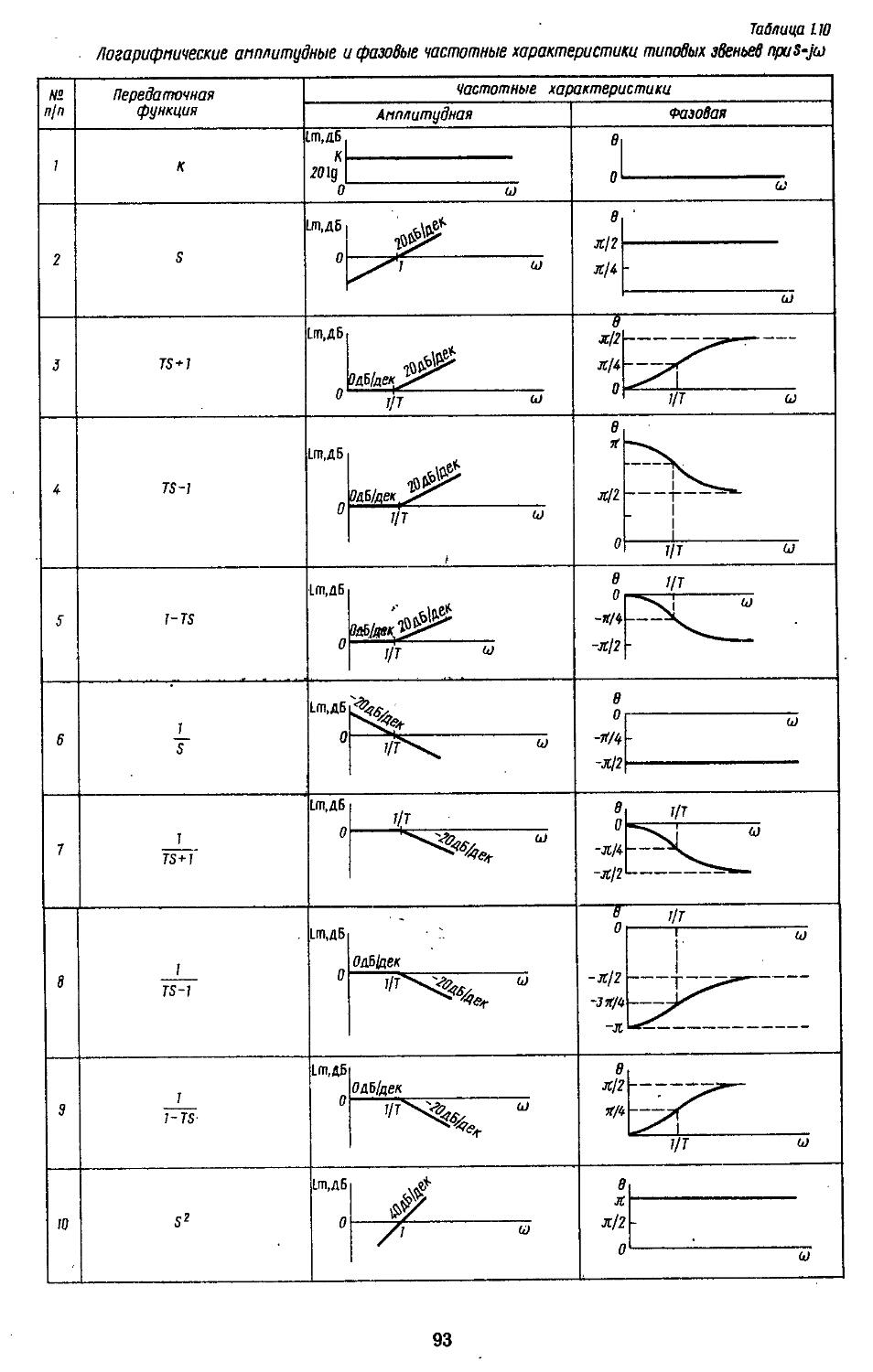
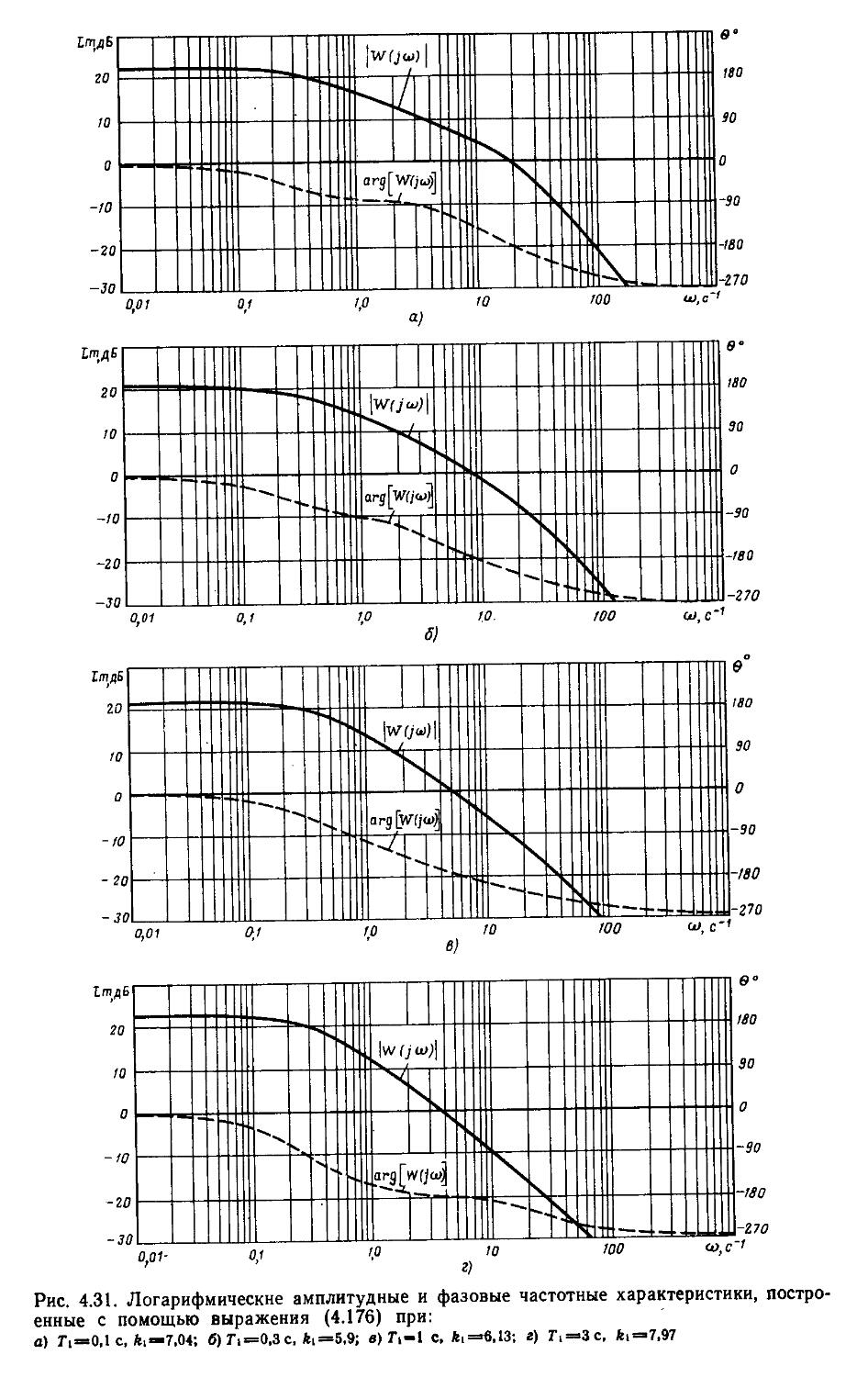
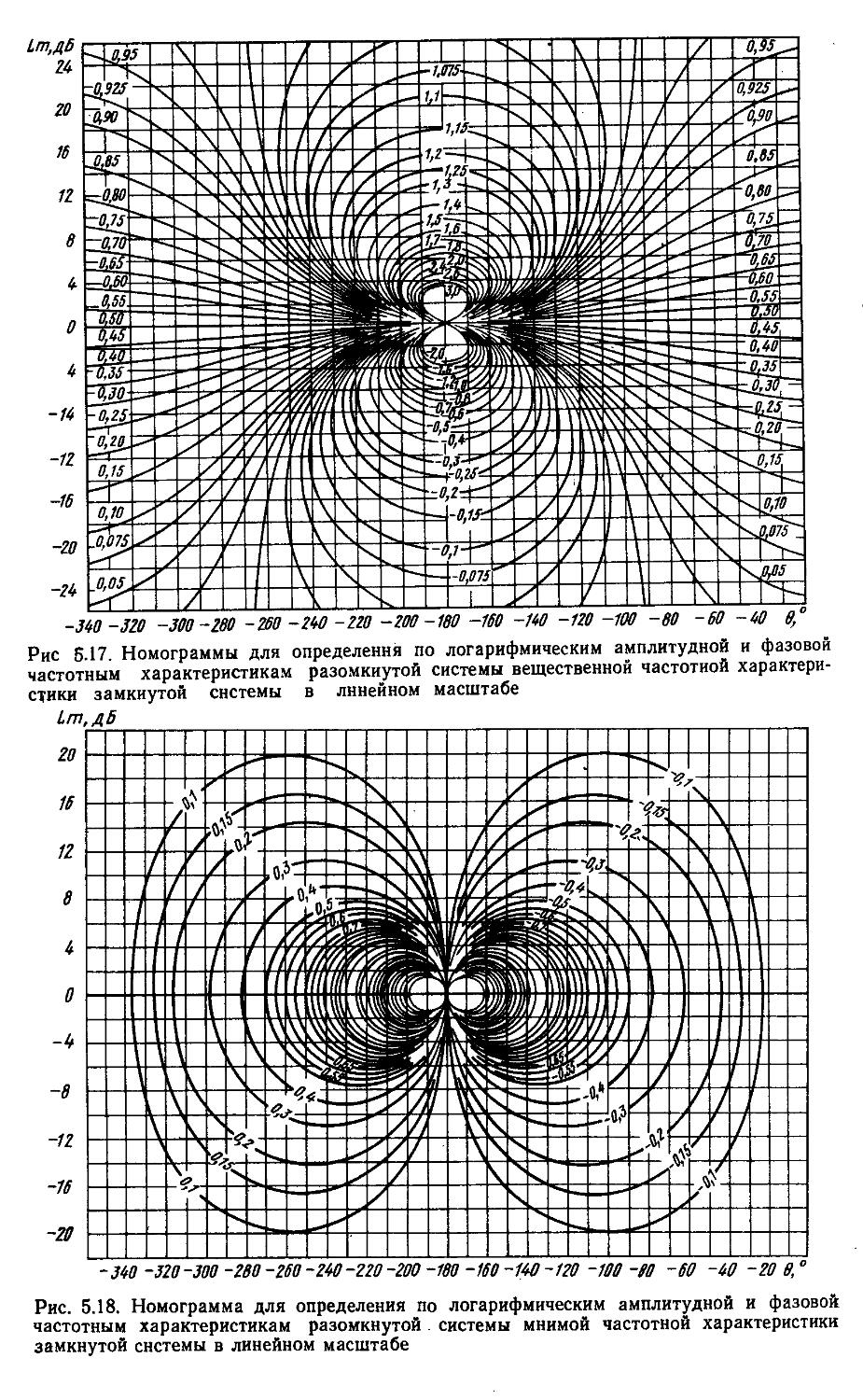
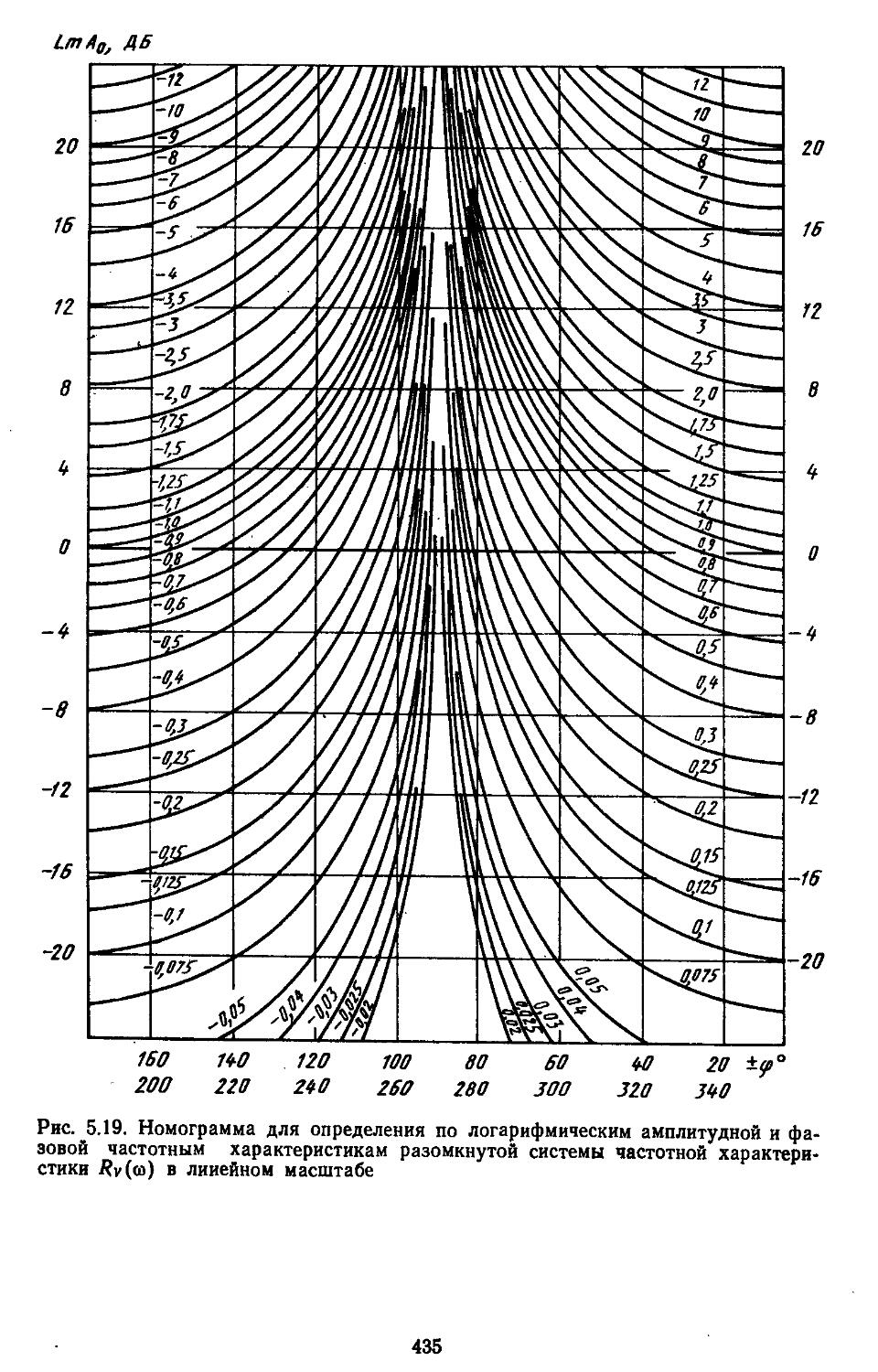
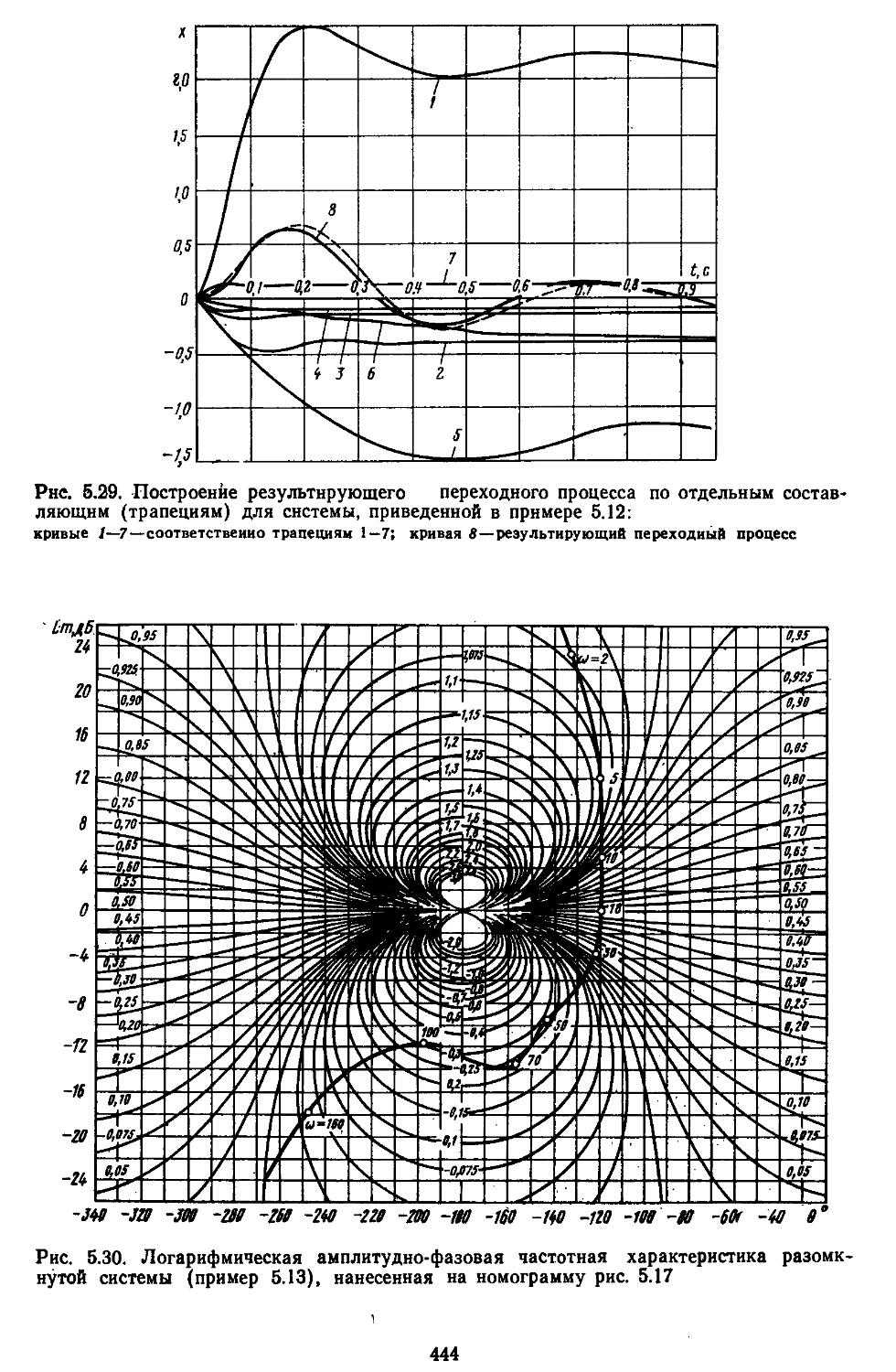
При высоких порядках дифференциальных и разностных уравнений, описывающих динамические процессы в системах, удобно применять дискретные модели, которые позволяют с помощью спектрального разложения действительных и комплексных матриц создавать алгоритмы вычисления коэффициентов передаточных функций и частотных характеристик [27, 28]. Введение специальных вычислительных процедур обеспечивает получение амплитудных н фазовых частотных характеристик на графических построителях в обычном или логарифмическом масштабе. В последнем случае проектировщики, располагая семейством логарифмических характеристик, могут достаточно быстро выбирать наиболее рациональные, для обеспечения устойчивости, параметры системы.
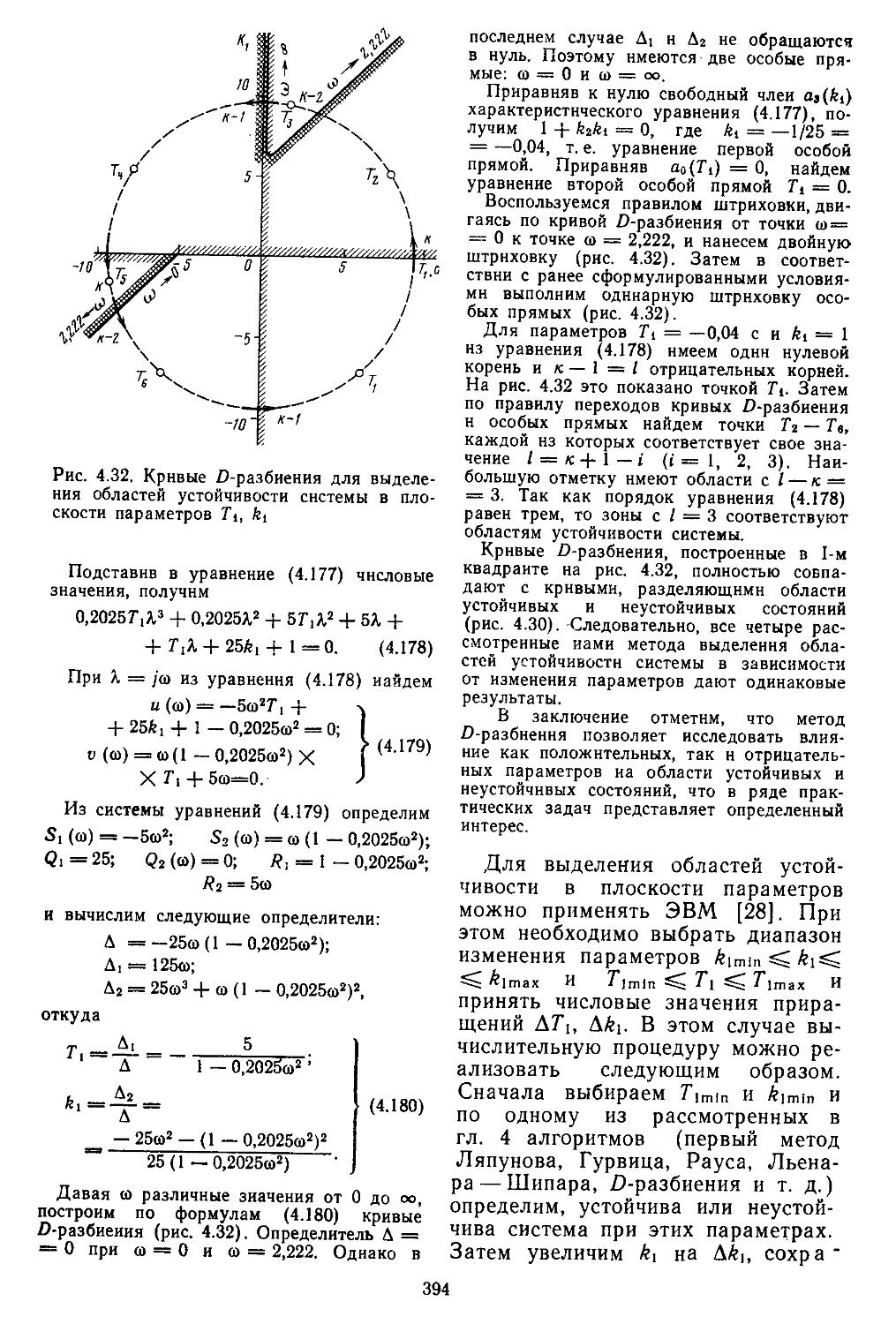
Устойчивость является необходимым, но не достаточным условием нормального функционирования САР. Наличие устойчивости свидетельствует лишь о том, что переходный процесс, вызванный действием внешнего воздействия или существованием ненулевых начальных условий, является затухающим. Но прн этом не определяются ни время затухания, ии максимальное отклонение регулируемой величины, ни число колебаний. А именно эти показатели и характеризуют качество протекания процессов регулирования [1, 6, 13, 16].
При реализации вычислительных процедур определения передаточных функций находят числовые значения их нулей и полюсов. Располагая ими, можно построить корневой : годограф замкнутой системы при различном расположении нулей и полюсов разомкнутой систе
12
мы или путем вычисления интегральных оценок качества [13, 14].
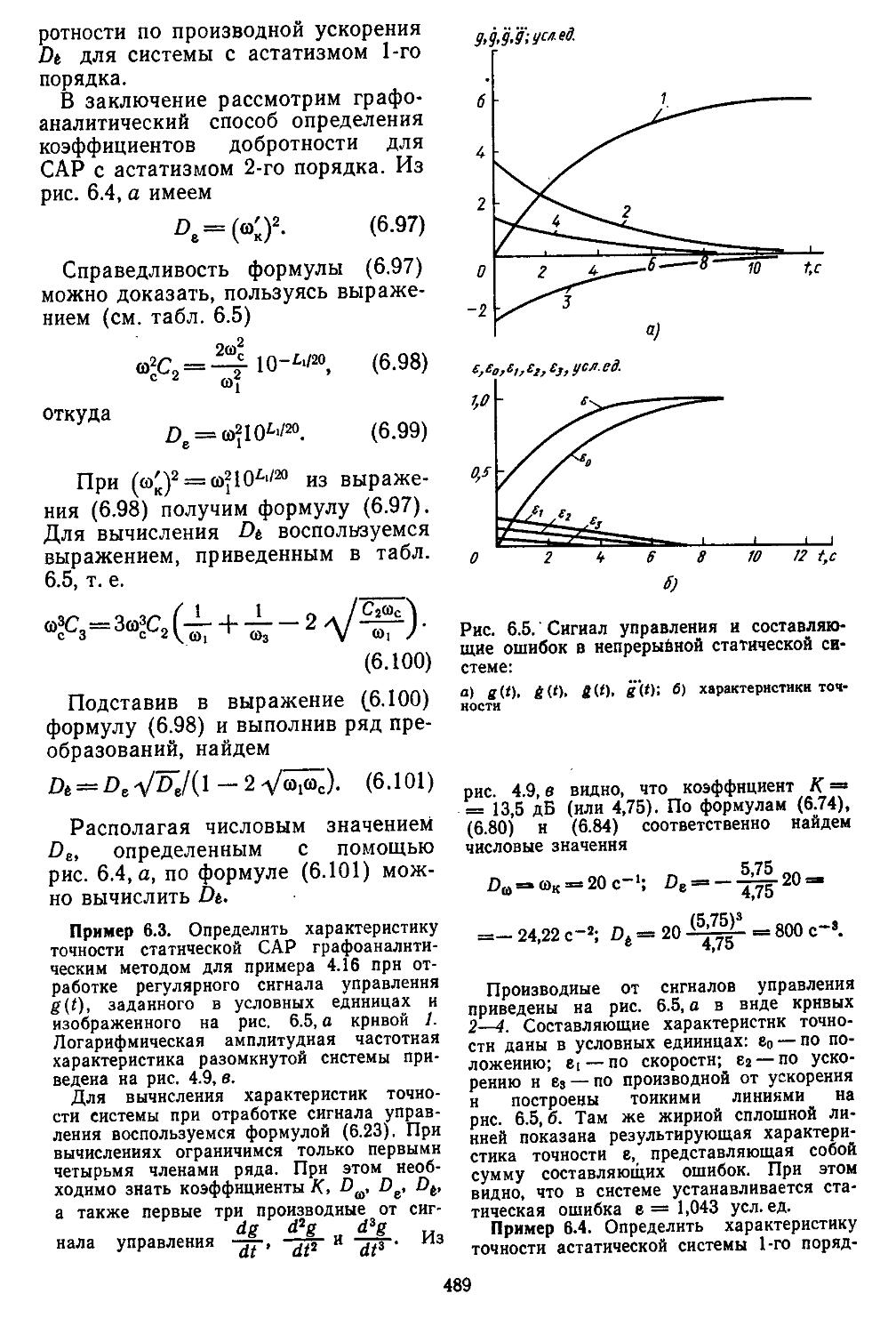
Весьма важной характеристикой САР является их динамическая точность (ошибка отработки системой управляющих нлн возмущающих регулярных и случайных воздействий). В практике проектирования динамическую точность часто определяют значениями коэффициентов добротностей по скорости и ускорению, а также полосой пропускания замкнутой системой управляющего сигнала [31]. Все эти вычислительные процедуры в данной книге реализованы в виде пакета прикладных программ [20] на алгоритмическом языке ПЛ/1 [29].
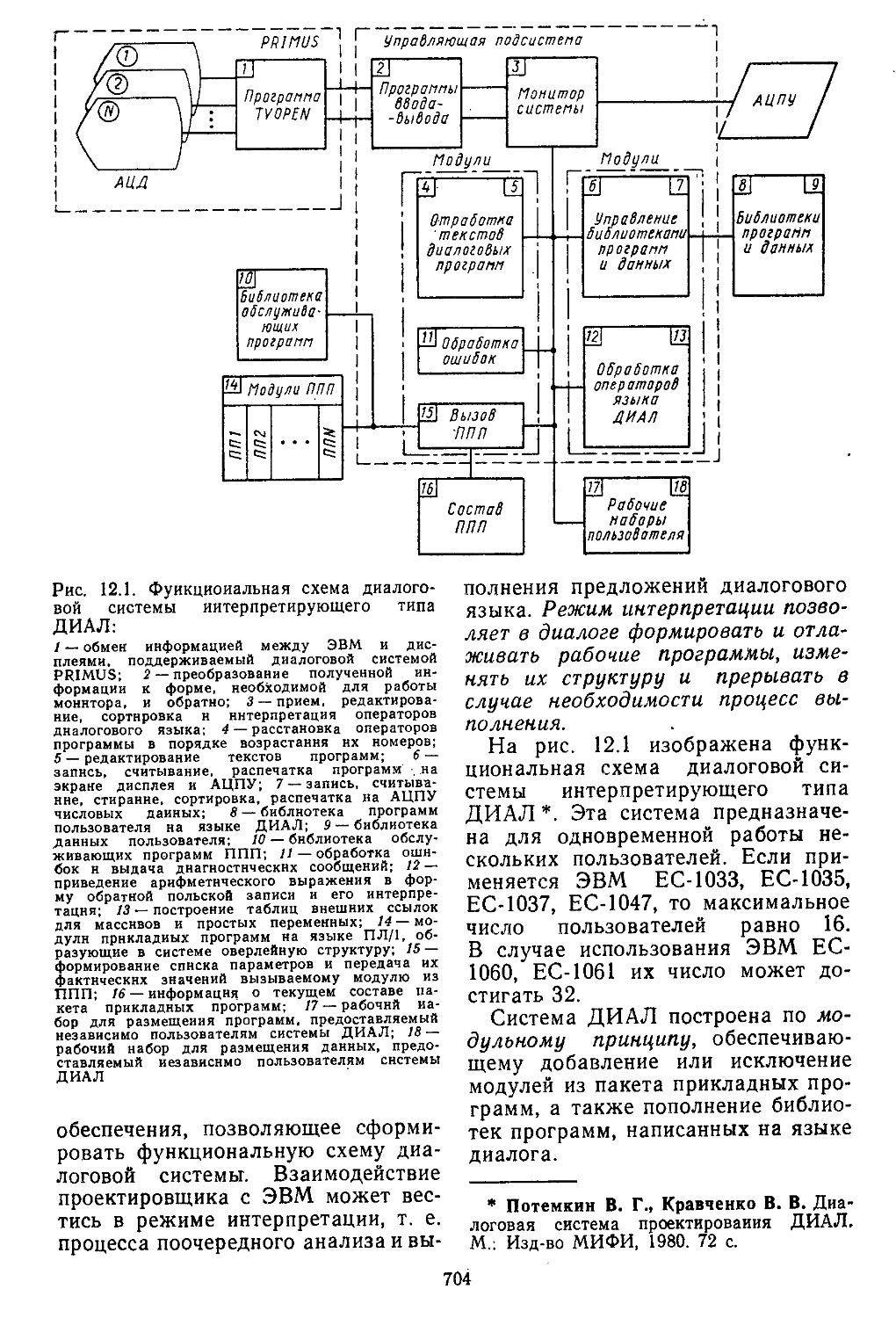
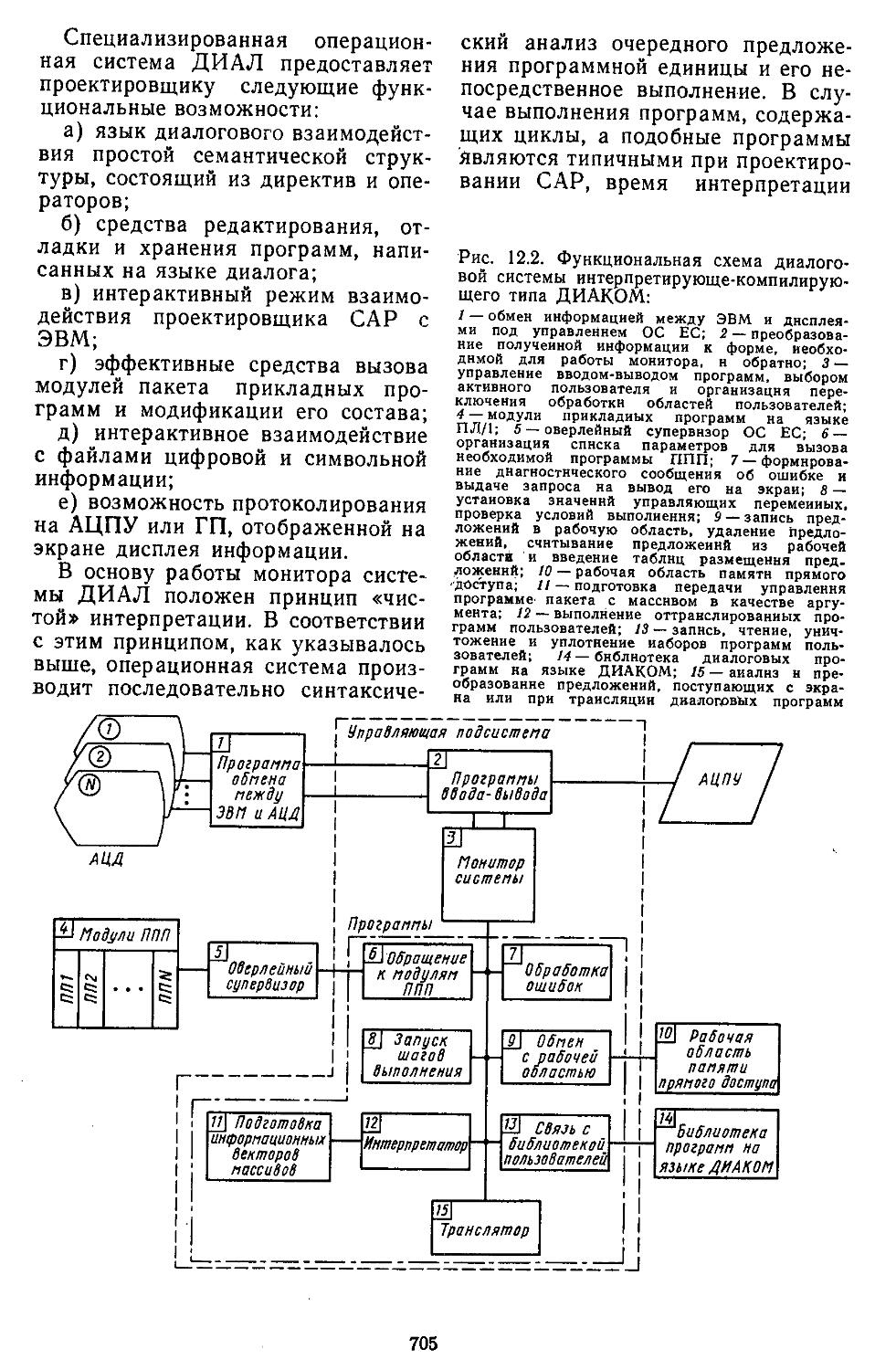
Применяя терминальные устройства для ввода и отображения символьной и графической информации, можно организовать взаимодействие пользователя с ЭВМ в диалоговом режиме [23]. В этом случае проектировщик в процессе работы будет получать текущую информацию о ходе выполнения той или иной процедуры. Такой подход позволяет анализировать большое число различных вариантов системы и выбирать из них наилучший. Организация диалогового взаимодействия пользователя с пакетами прикладных программ под управлением универсальной операционной системы ограниченных возможностей может осуществляться при наличии специализированной операционной системы интерпретирующего нли интерпрети-рующе-компилирующего типа.
Функциональные возможности специализированной операционной системы предоставляют пользователю: язык диалогового взаимодействия; средства написания, редактирования, отладки и хранения программ на языке диалога в системной библиотеке; решение задач анализа н синтеза САР в интерактивном режиме; вызов модулей пакета прикладных программ и их дальнейшее наращивание;
выдачу протоколов сеанса работы с ЭВМ [23]. Специализированные операционные системы представляют собой комплекс программных средств больших возможностей, предназначенный для одновременной работы группы инженеров в режиме автоматизированного проектирования и моделирования. При этом каждый пользователь может выполнять различные виды работ по анализу и синтезу систем независимо друг от друга. В настоящее время на автоматизированных комплексах выполняют не только расчетно-проектные, но н чертеЖ-но-графнческие работы [20, 27]. В данной книге приведены лишь два пакета прикладных программ для решения задач соответственно анализа и синтеза. Они могут быть использованы в режиме автоматизированного проектирования со специализированными операционными системами ДИАЛ [26], ДИАКОМ [23], ДИФОР, ПРАСАК и др.
Независимо от способа выполнения работ— традиционным ручным методом илн автоматизированным путем — весь процесс проектирования делится на несколько характерных этапов.
Первый этап проектирования — построение математической модели объекта регулирования. Зная физические процессы, происходящие в объекте, можно при определенных допущениях описать его поведение аналитически, обычно с помощью дифференциальных,' интегродиффе-ренциальных или разностных уравнений. Так как математическую модель составляют на основании графических или табличных экспериментальных данных, то коэффициенты уравнений (или матрицы) представляют в виде чисел. При этом проектировщик знает диапазоны изменения входных и выходных переменных. В результате он может составить структурную схему объекта регулирования с помощью матриц, передаточных функций и графов [12, 32,
13
38, 39]. Каждый из этих методов имеет свои особенности. Так, например, векторно-матричные структурные схемы не позволяют проектировщику изучать особенности внутренних связей в объектах, но их представление через переменные состояния удобно при моделировании на ЭВМ. Структурные схемы с передаточными функциями элементов являются достаточно громоздкими, но по иим можно не только выявить все внутренние связи, но и определить возможные места включения различных устройств компенсации. Данный способ представления объектов особенно часто применяют при частотных методах исследования систем регулирования. Использование графов позволяет найтн пути прохождения сигналов через элементы объектов, определить сильные и слабые связи и упростить структуры объектов за счет исключения слабых связей, что приводит к уменьшению порядка уравнений динамики и, следовательно, сокращению объема вычислительных работ. Все эти методы являются эквивалентными, и, располагая матрицами, можно получать структурные схемы или графы объектов, и наоборот.
Исходные данные об объектах часто задают в виде графиков, числовых таблиц, логарифмических амплитудных и фазовых частотных характеристик. Так как графики практически всегда являются нелинейными, то для получения линейных моделей объектов необходимо использовать линеаризацию в приращениях относительно опорной траектории движения или метод наименьших квадратов. Оба способа дают удовлетворительные результаты в том случае, если функции, описывающие нелинейные зависимости, дифференцируемы по крайней мере один раз илн достаточно хорошо аппроксимируемы в заданной области рабочих режимов касательными к
ним. При наличии ступенчатых и разрывных функций приходится применять методы гармонической, статистической или комбинированной— гармонической и статистической— линеаризаций [13, 14, 32, 33, 39].
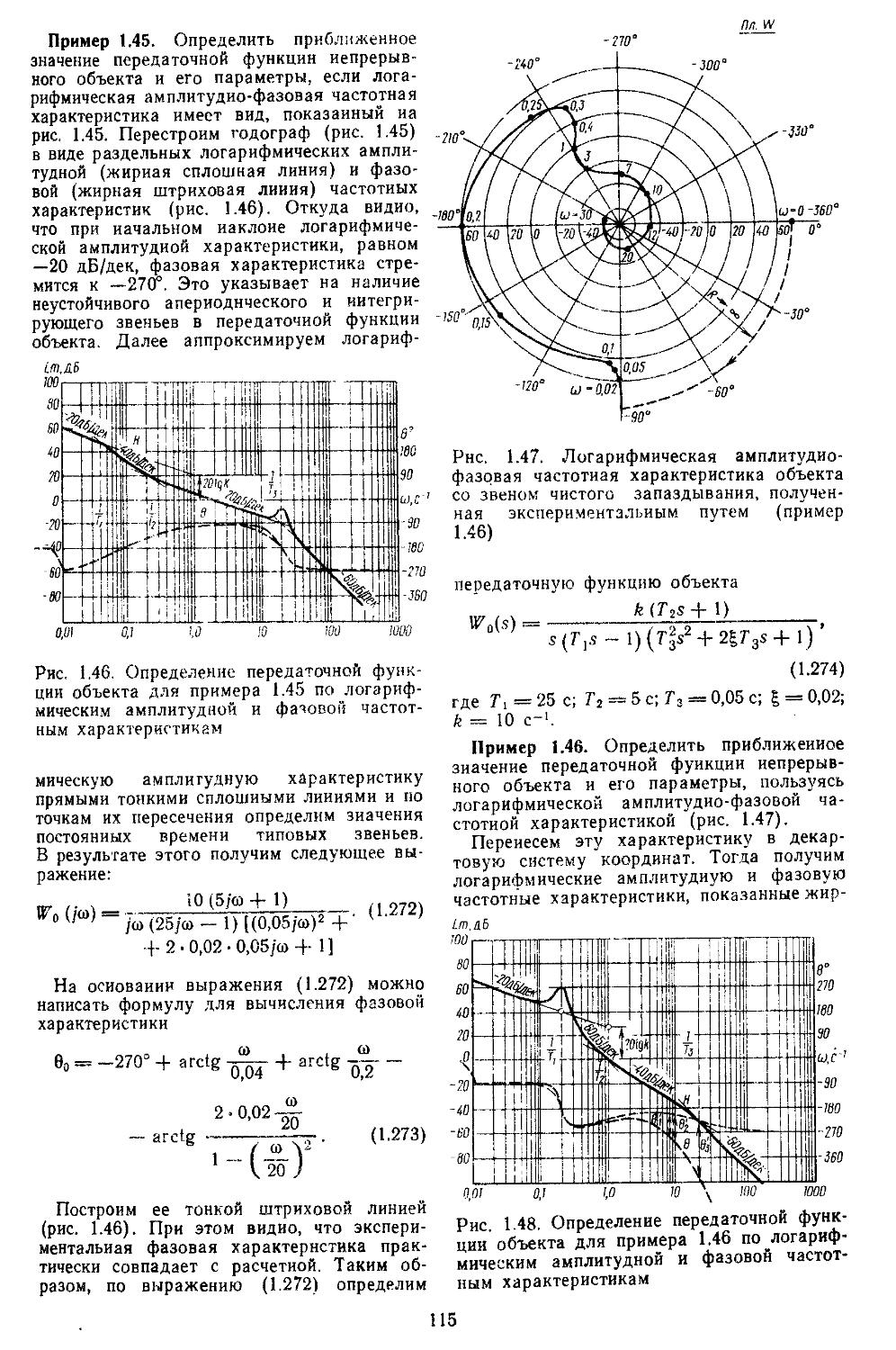
По снятым в процессе экспериментов амплитудным н фазовым частотным характеристикам реальных объектов при различных частотах и амплитудах входных сигналов можно построить упрощенную передаточную функцию объекта. Данный способ дает хорошие результаты лишь для объектов простой структуры, состоящих из набора последовательно соединенных элементов, когда возможно получение промежуточных значений амплитудных и ф'азовых характеристик после каждого из элементов.
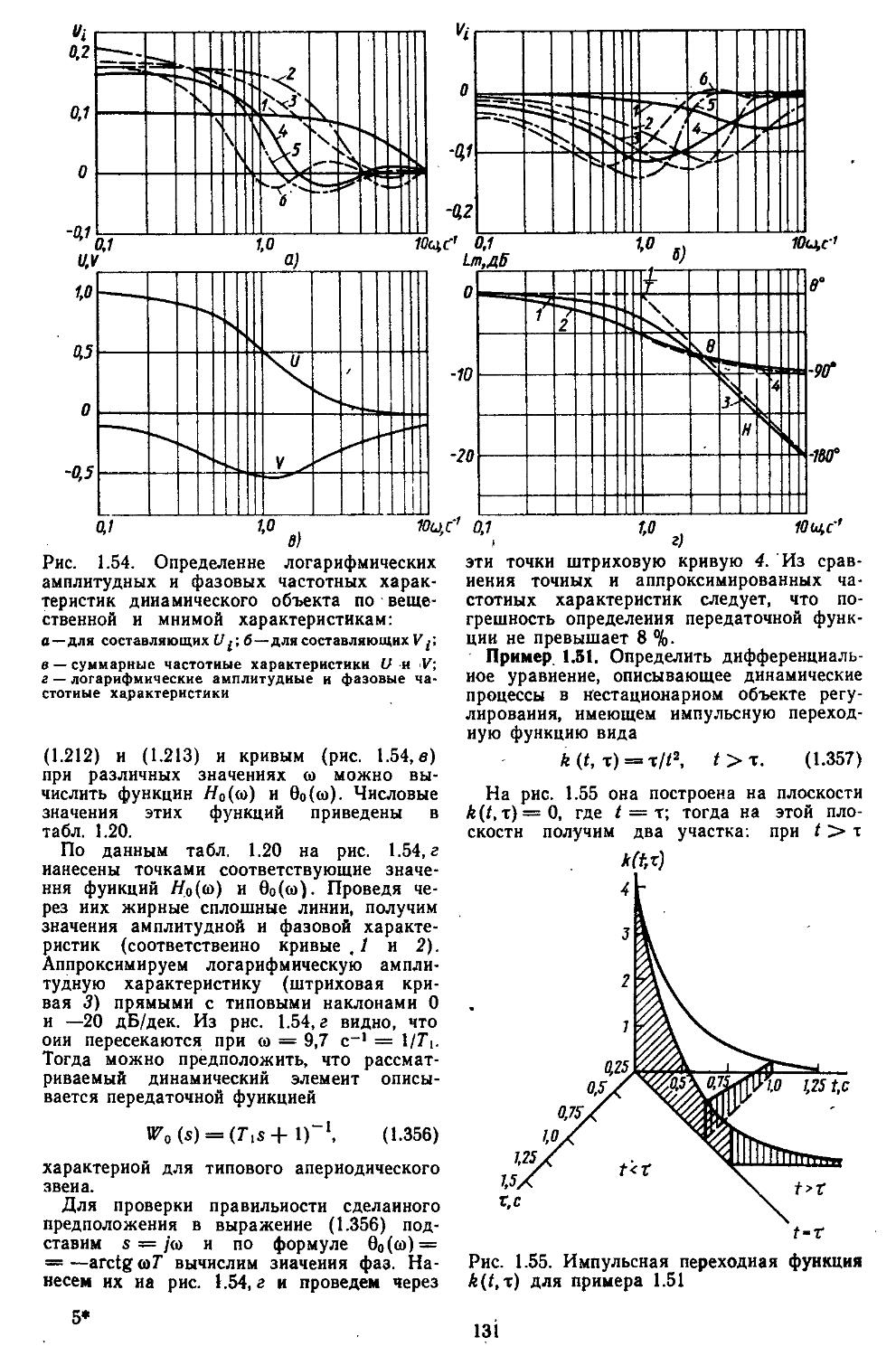
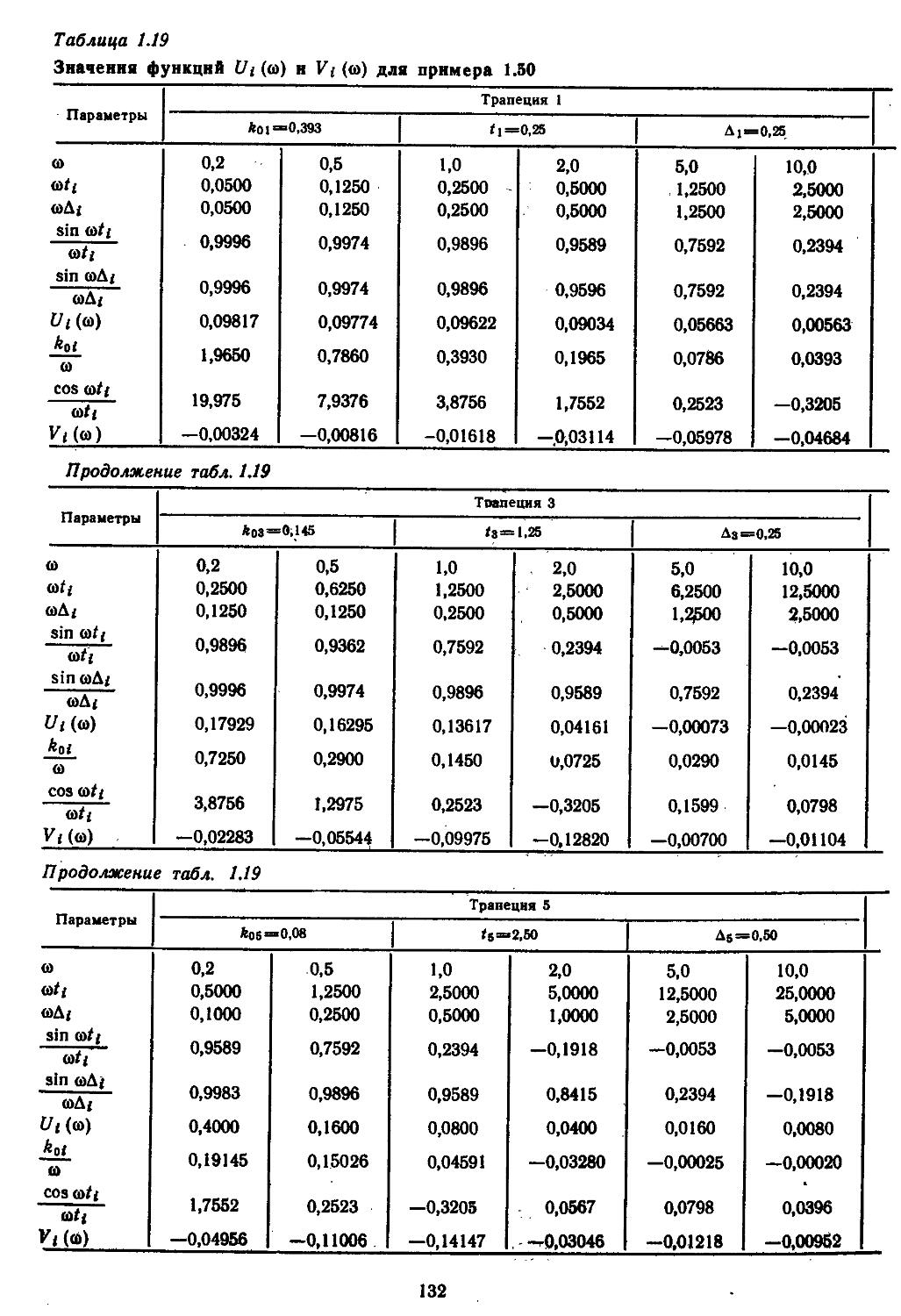
В некоторых случаях экспериментально определяется семейство переходных процессов ria выходе объекта при подаче на его вход случайных сигналов, сформированных в виде набора псевдослучайных чисел на ЭВМ. Как известно, такие переходные процессы описываются интегральным уравнением с импульсной переходной функцией, которая характеризует динамику объекта. Зная импульсную переходную функцию, можно построить вещественную и мнимую частотные характеристики и по ним определять логарифмические (амплитудную и фазовую) характеристики, после чего нетрудно найти математическую модель объекта [13, 31].
Полученные модели являются математической формализацией процессов в реальных объектах, причем один и тот же объект в зависимости от принятых допущений может быть описан в различной форме. В связи с этим возникло направление, в рамках которого разрабатываются методы определения математической модели, наилучшей в отношении приближения
14
ее частотных или временных характеристик к аналогичным характеристикам реального объекта, по данным наблюдения за входными и выходными переменными нормально функционирующего объекта. Это направление было названо идентификацией. В настоящее время достаточно полно разработаны лишь методы идентификации линейных объектов.
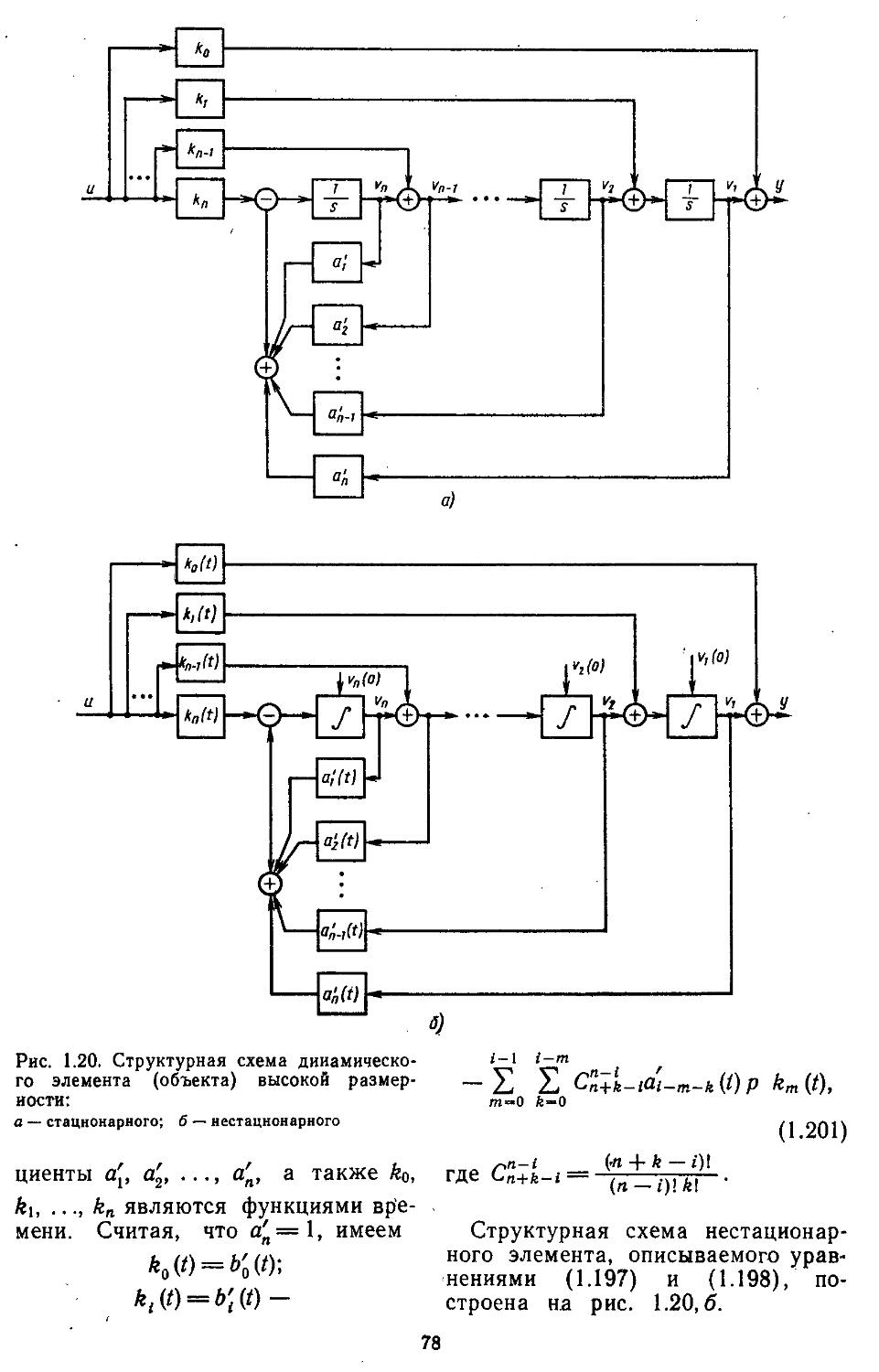
Второй этап проектирования — выбор устройств неизменяемой и изменяемой частей системы. К неизменяемой части принято относить исполнительные органы, усилители мощности и измерительные средства. Их обычно выбирают не только с учетом требований к точности и качеству процессов регулирования, ио в основном по надежности действия, массогабаритным характеристикам, стоимости, стойкости к влиянию агрессивной среды, взрывобезопасности и т. п. Существенное влияние оказывают и традиции конструкторского бюро, ведущего проектирование, а также оснащенность завода, на котором планируется серийный выпуск САР (автоматических регуляторов, следящих систем и т. д.). К изменяемой части системы относят электронные усилители, преобразователи, микропроцессоры и различные дополнительные средства компенсации сигналов, а также устройства коррекции динамических характеристик.
На втором этапе проектировщик составляет математические модели устройств управления, входящих в неизменяемую часть системы. Это обеспечивает основу для построения структуры всей САР. Если принято решение о месте включения устройств изменяемой части (т. е. полностью определена структура всей системы), дальнейшее проектирование сводится к решению задачи анализа, в противном случае — задачи синтеза. По принятой сейчас терминологии оба этапа относятся к классу задач,
решаемых для систем с заданной структурой. Но, по существу, это справедливо лишь для первого варианта, когда действительно структура системы полностью установлена и в процессе проектирования выбирают лишь типы и параметры устройств изменяемой части. Во втором случае структуру изменяемой части находят в процессе решения задачи синтеза и одновременно с ее определением выбирают наиболее рациональные параметры исследуемых устройств управления.
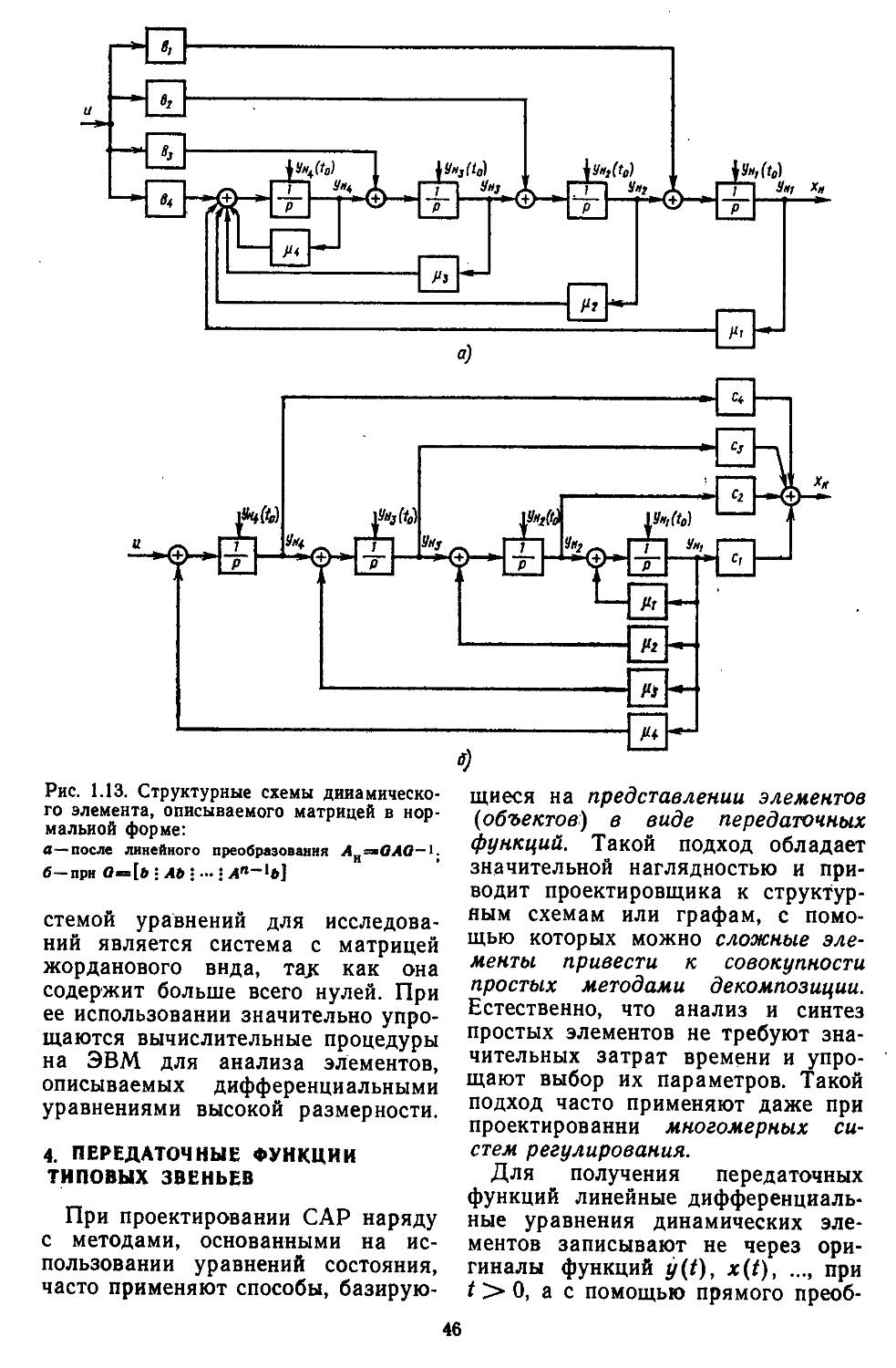
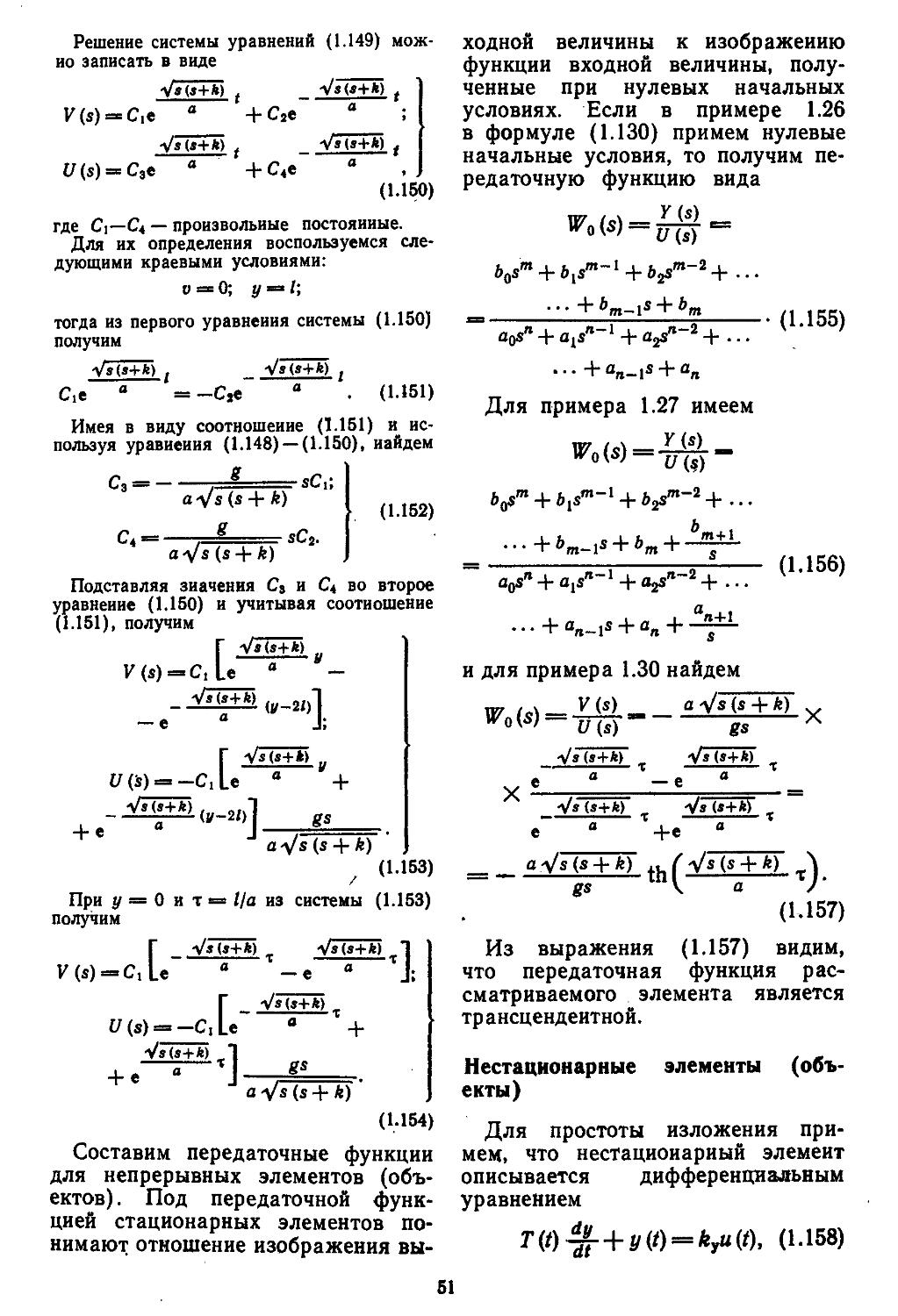
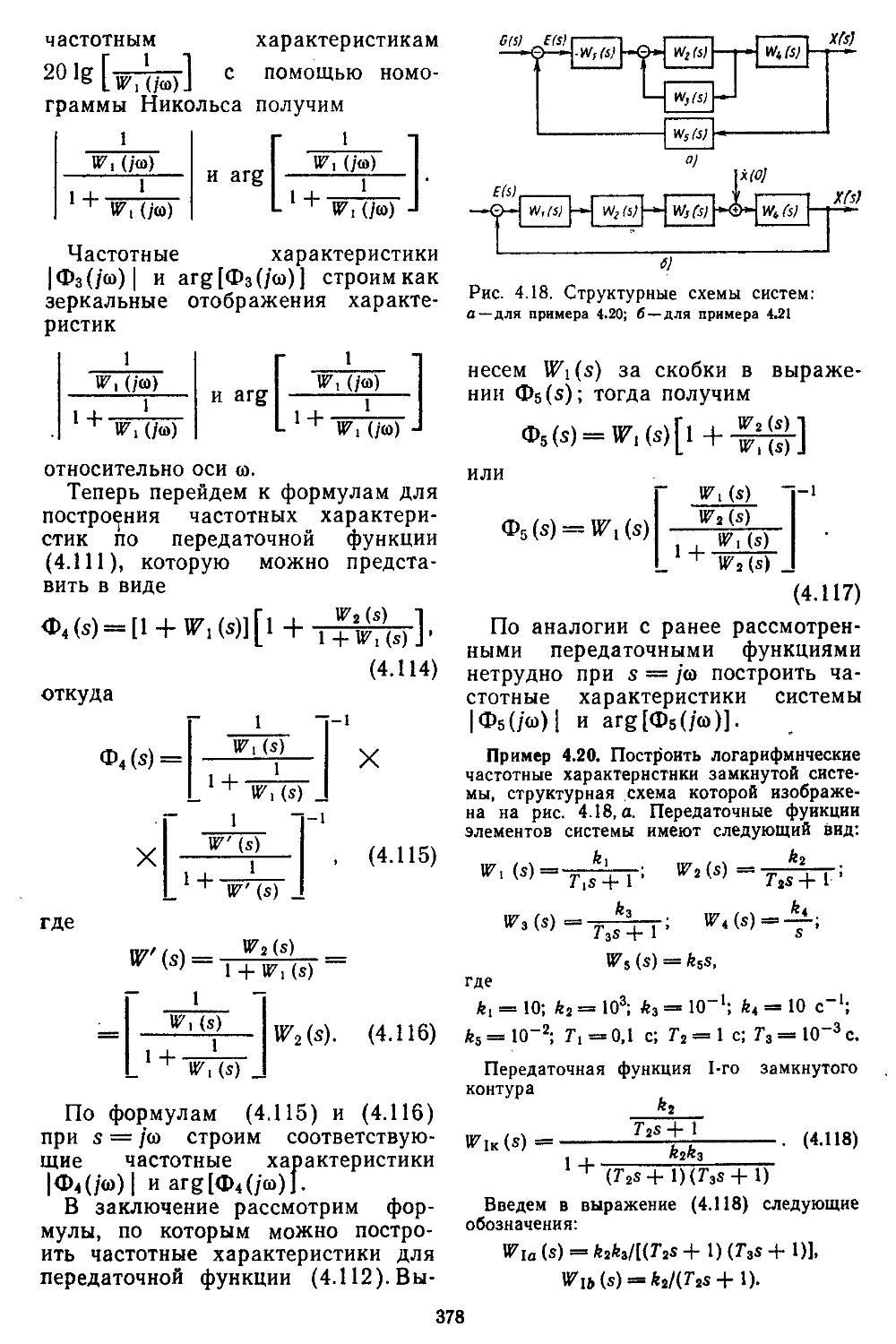
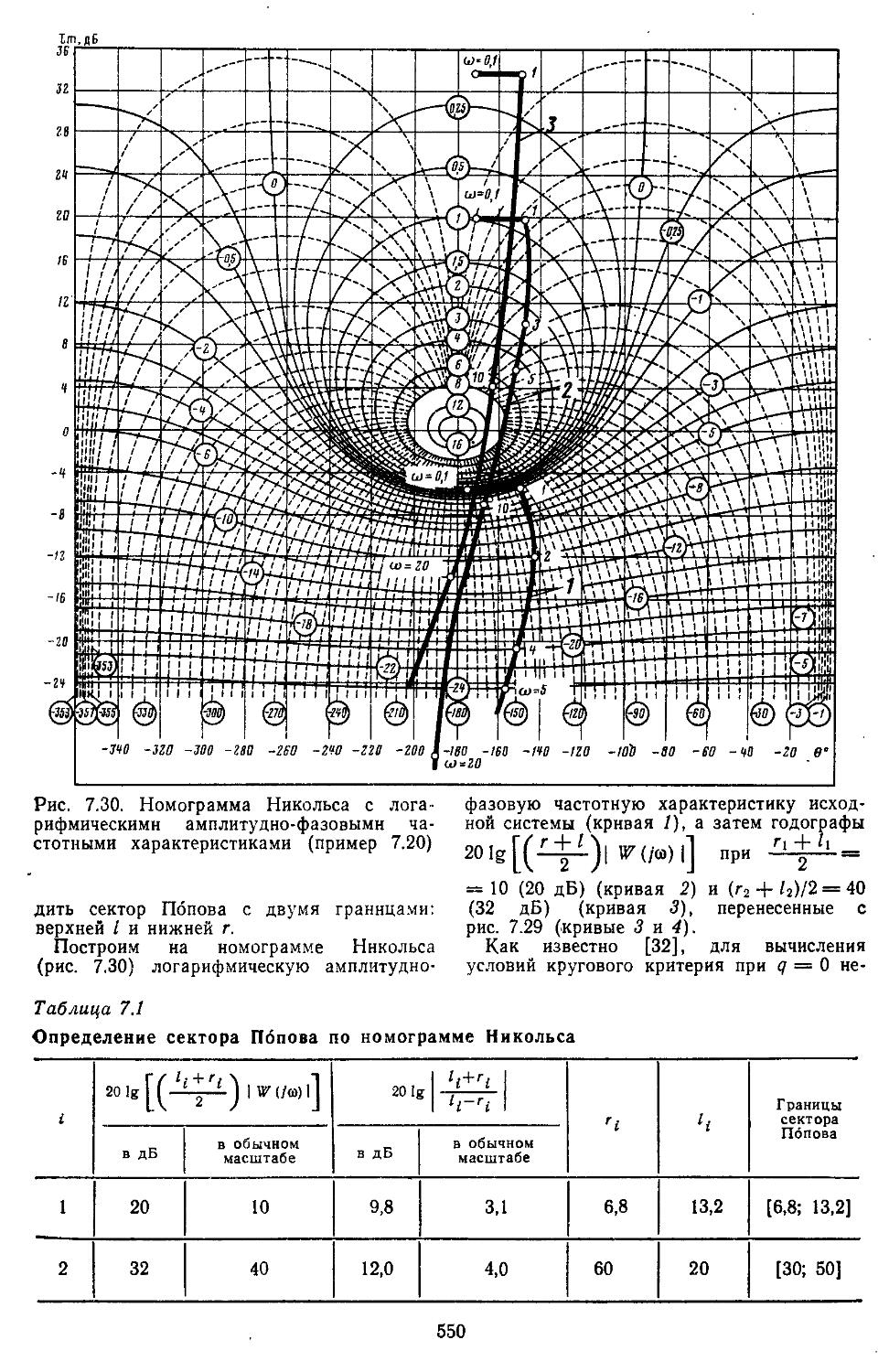
Третий этап проектирования — решение задачи анализа или синтеза. Рассмотрим методику решения первой из них. Как уже указывалось выше, в данном случае инженер располагает полной структурой системы, что намного упрощает проектирование. При этом процесс проектирования сводится к расчетно-теоретической работе, которую выполняют вручную с помощью номограмм и таблиц или автоматически — иа ЭВМ. Для применения этих методов проектировщик должен найти математические модели замкнутых и разомкнутых систем регулирования. Последние обычно являются сложными и представляют собой последовательно и параллельно соединенные группы элементов с внутренними и внешними обратными связями, для них-то и необходимо научиться находить передаточные функции. Решение подобной задачи при ручных методах наиболее просто осуществляется с помощью номограммы Никольса. Если проектирование ведется на ЭВМ, то по структурным схемам составляются уравнения состояния в жордано-вой канонической или нормальной формах [12, 27, 28, 32]. Количественно структура исследуемых систем оценивается спектральным числом обусловленности матриц.
Для упрощения указанных выше ручных и машинных операций ши
15
роко используют методы структурных преобразований, позволяющие представить многоконтурные системы в виде одноконтурных. Следует отметить, что такие преобразования существенно отличаются для линейных и нелинейных систем. Это связано с невозможностью применения принципа суперпозиции и необходимостью сохранения амплитуды сигнала на входе нелинейной части неизменной, независимо от выполняемых преобразований. Поэтому нельзя перемещать линейные передаточные функции (матрицы) за нелинейный элемент. Преобразование линейных передаточных функций (матриц), расположенных до нелинейного элемента нли за ним, выполняют обычными способами. В результате таких преобразований в большинстве случаев удается отделить нелинейную и линейную части системы друг от друга, что упрощает выполнение расчетов. Преобразование структурных схем дискретно-непрерывных систем и получение по ним соответствующих передаточных функций возможно путем введения фиктивных ключей. В дальнейшем будет показано, что существуют такие дискретно-непрерывные системы регулирования, для которых, не удается найтн передаточные функции в замкнутой форме.
Принятый порядок анализа САР состоит в последовательном выполнении следующих действий: исследование устойчивости, качества и точности. Анализ устойчивости при ручных методах проектирования определяется тнпом системы: линейная нлн нелинейная, дискретная нли непрерывная.
Устойчивость непрерывных линейных систем может исследоваться с помощью первого метода Ляпунова, а также алгебраических критериев (Гурвица, Рауса н Льенара — Ши-пара). Для дискретных систем используется критерий Шур—Кона. Основным недостатком применения
данных критериев следует считать невозможность получения при этом оценок качества и точности. Пользуясь ими для систем высокой размерности, проектировщик не может дать рекомендаций по выбору параметров,- не только обеспечивающих запасы устойчивости,/ но и удовлетворяющих требованиям к качеству и точности процессов регулирования.
Анализ устойчивости непрерывных н дискретных нелинейных систем обычно выполняют с помощью второго метода Ляпунова, гармонического баланса Крылова— Боголюбова и критерия абсолютной устойчивости Попова. Следует отметить, что на устойчивость дискретных нелинейных систем большое влияние оказывает выбор такта квантования, поэтому последнему в . книге уделено достаточно большое внимание. При использовании автоматизированных методов проектирования непрерывные, дискретно-непрерывные : линей-
ные и нелинейные системы представляют в виде дискретной мо-делн.
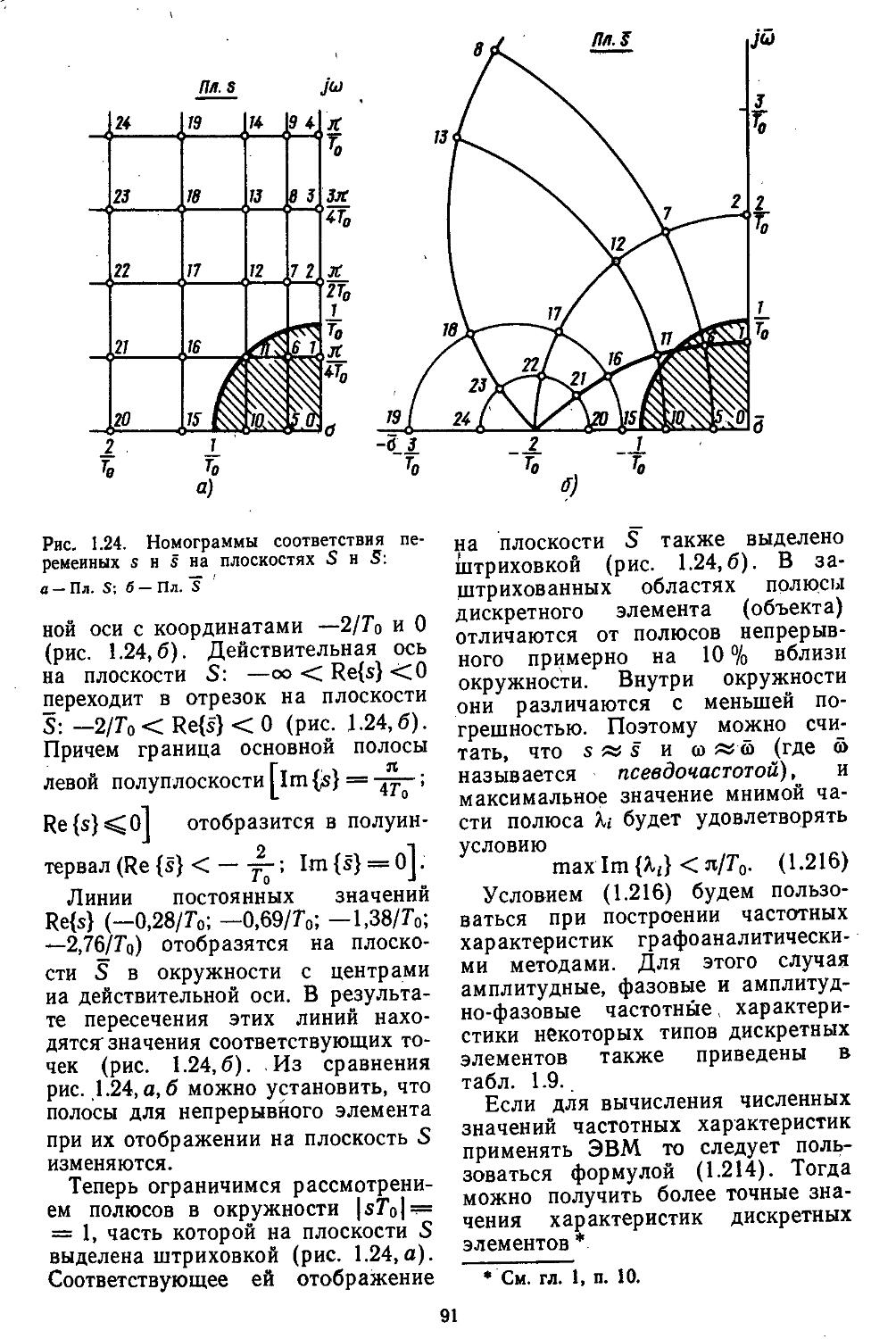
Частотные критерии устойчивости предполагают использование передаточных функций для описания системы регулирования и справедливы прн ее полной управляемости и наблюдаемости. Тогда критерий устойчивости по Ляпунову аналогичен критериям Михайлова, Михайлова — Найквиста и D-разбиения Неймарка. Эти критерии применимы к анализу как непрерывных, так и дискретных систем. Однако в первом случае они базируются на методах «-преобразований, во втором — z-преобразоваиий. Положив s = ja>, строятся частотные характеристики, по которым определяют запасы устойчивости систем регулирования по фазам и модулям н с помощью специальных номограмм оценивают показатели качества и характеристики точности. В дискретных системах вместо z-преобразования часто прибегают
16
к преобразованию s*, которое не является взаимно однозначным из-за периодичности 2л/Г0 (Т'о— такт квантования). Поэтому на плоскости s выделяют основную полосу — < Im s < уг-, для ' которой
обеспечивается взаимно однозначное соответствие и с погрешностью до 10% считается s = s, т. е. все полюсы отображаются сами в себя. Большим преимуществом частотных критериев устойчивости является возможность их распространения н на многие типы нелинейных систем [30].
Исследовать качество непрерывных и дискретных линейных систем можно, анализируя расположение нулей и полюсов передаточной функции замкнутой системы, а также по корневому годографу, интегральным оценкам, вещественным и мнимым частотным характеристикам замкнутой системы. Последний метод обладает значительными преимуществами, так как позволяет по свойствам вещественной частотной характеристики не только находить основные показатели качества, но и строить переходные процессы. При этом используют набор графиков, номограмм н рабочих программ. Построение переходных процессов в нелинейных непрерывных системах ведут с помощью методов припа-совывания или численных процедур интегрирования уравнений. Оба эти способа реализуются в виде рабочих программ для ЭВМ. В дискретных нелинейных системах применяют расширенные переходные матрицы, определенные в различные интервалы времени (которые сводятся к рекуррентным процедурам или многомерному z-преобра-зованию) [24].
* Преобразование s аналогично били-, _ 2 z — 1
нейному, т. е. s = -=——г-г- Однако здесь То 2+1
вместо s подставляют /б, где <5 —псевдочастота.
Нелинейности в замкнутых системах часто приводят к режимам автоколебаний, которые большей частью недопустимы на выходе системы регулирования. Однако во внутренних контурах иногда преднамеренно вводят автоколебания таким образом, что они уменьшают влияние залипания плунжеров в гидравлических устройствах, но не проходят на выход системы. Поэтому проектировщик должен владеть приемами, обеспечивающими возбуждение автоколебаний с требуемой амплитудой и частотой илн их подавление путем введения дополнительных корректирующих устройств. Следует отметить, что при подаче на вход нелинейных систем, находящихся в автоколебательном режиме, случайных сигналов с большим уровнем спектральной плотности может происходить срыв автоколебаний. Все эти вопросы рассматриваются в данной книге в связи с проектированием нелинейных САР.
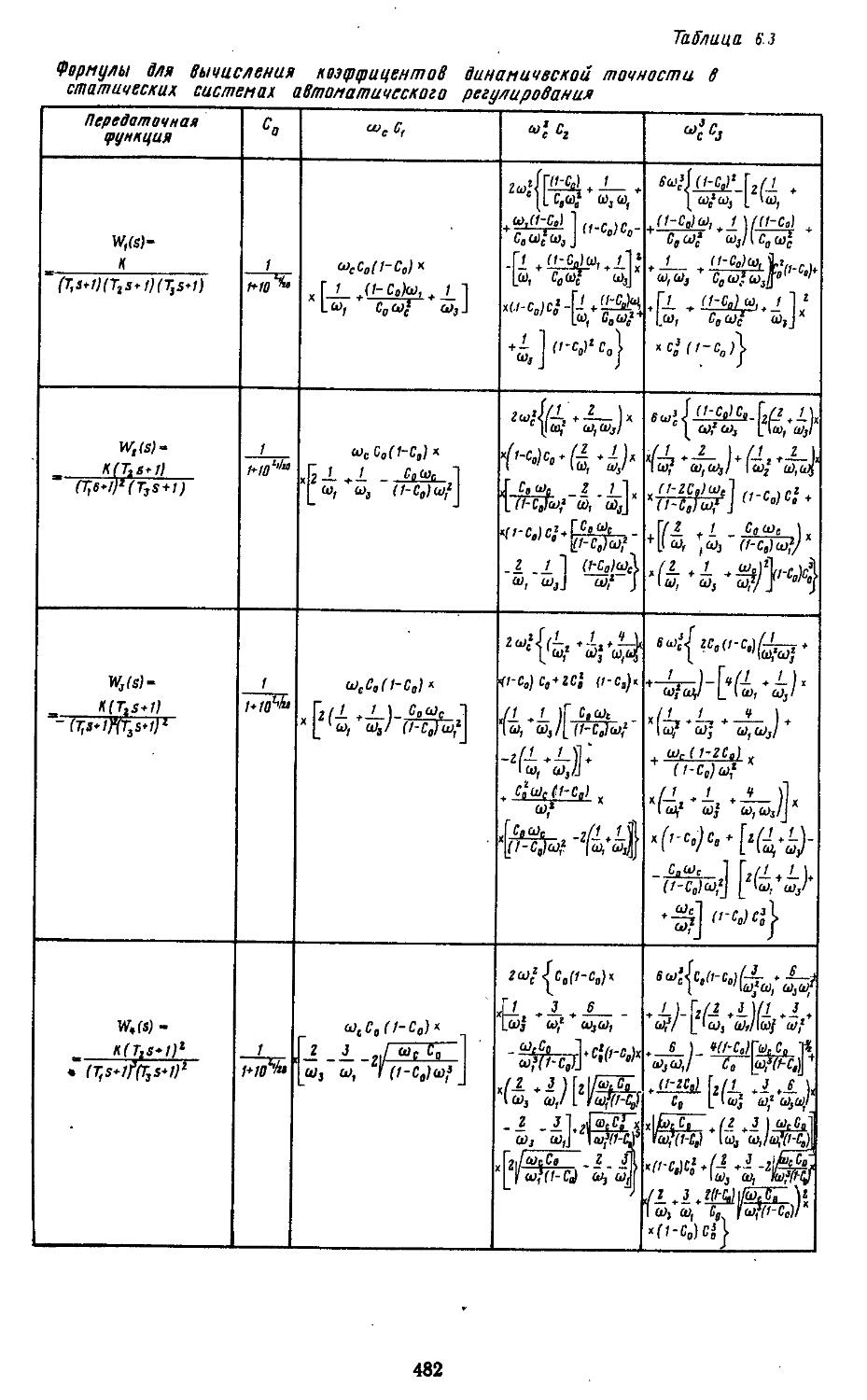
Проблема повышения динамической точности является основной, так как без ее решения невозможно обеспечить выполнение возложенных на систему регулирования задач. Иначе говоря, системы автоматической стабилизации не смогут поддерживать режимы регулирования с заданной техническими условиями точностью, системы программного управления выведут объект на недопустимые рабочие режимы, следящие системы будут воспроизводить входные сигналы с крайне большими искажениями.
На характеристики точности значительное влияние оказывают не только сигналы управления и возмущения, но и помехи, поступающие извне или образующиеся внутри системы. Поэтому при анализе точности САР учитывают два типа ошибок: регулярные и случайные. Для уменьшения регулярных ошибок необходимо увеличивать коэффициенты усиления устройств управления. Но при этом
17
следует всегда помнить, что одновременно возрастает нежелательное влияние нелинейностей на поведение системы. С ростом коэффициентов усиления увеличивается полоса пропускания системы, что приводит к возрастанию ошибкй от действия шумов. Проектировщик может, например, выбрать параметры системы таким образом, чтобы обеспечивалась минимальная сумма квадратов динамической и случайной ошибок. Возможно применение и других критериев оптимальности [31].
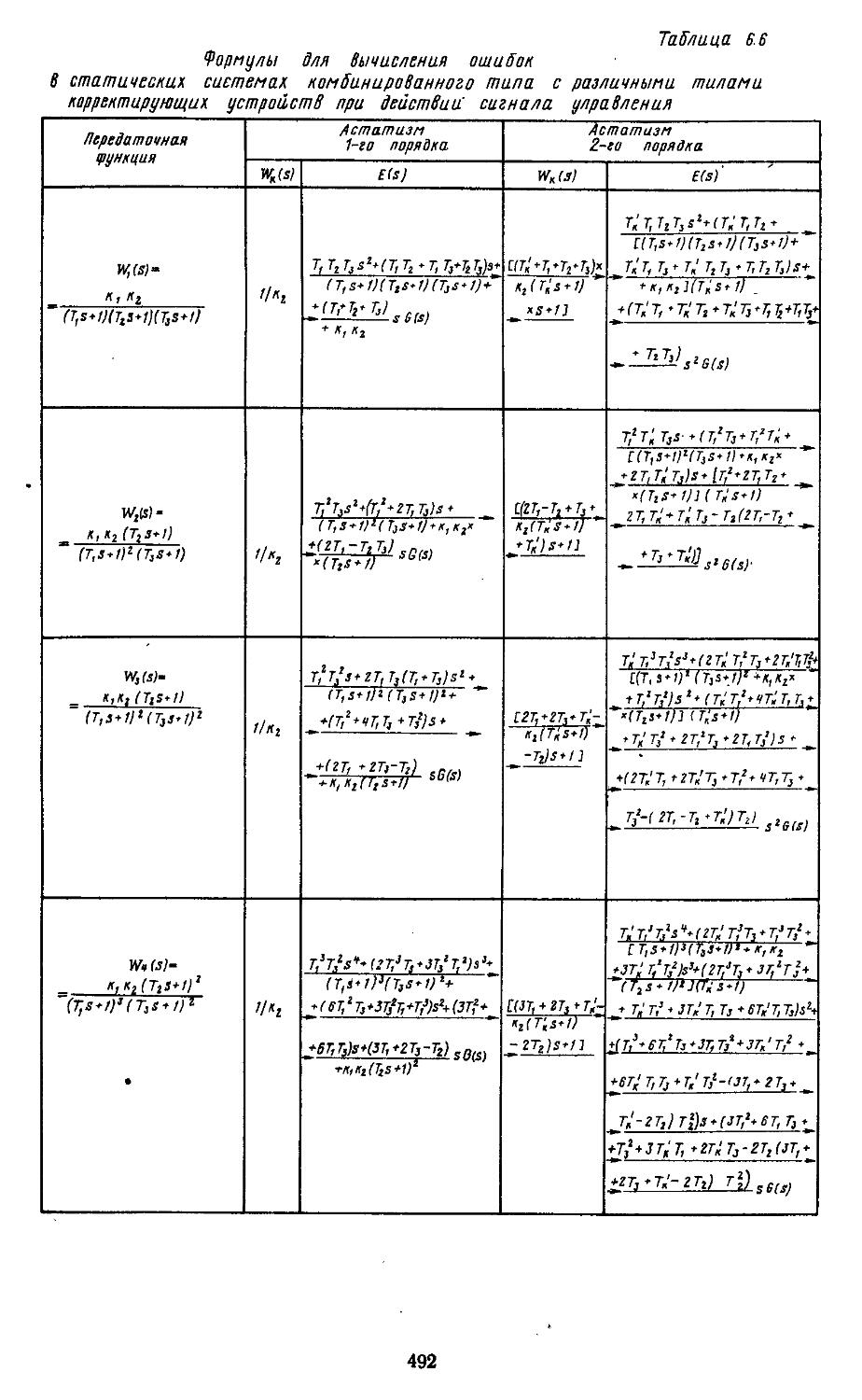
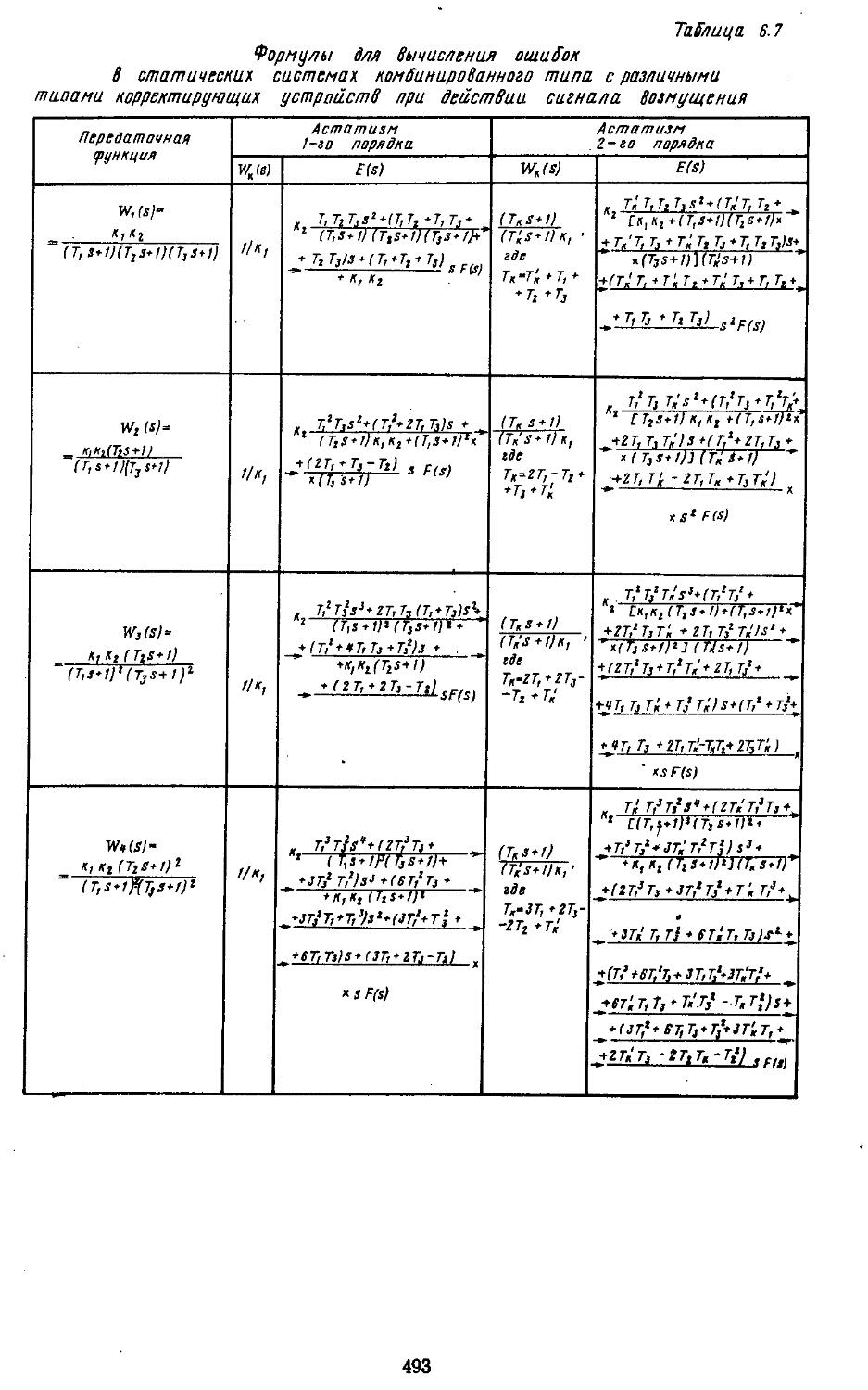
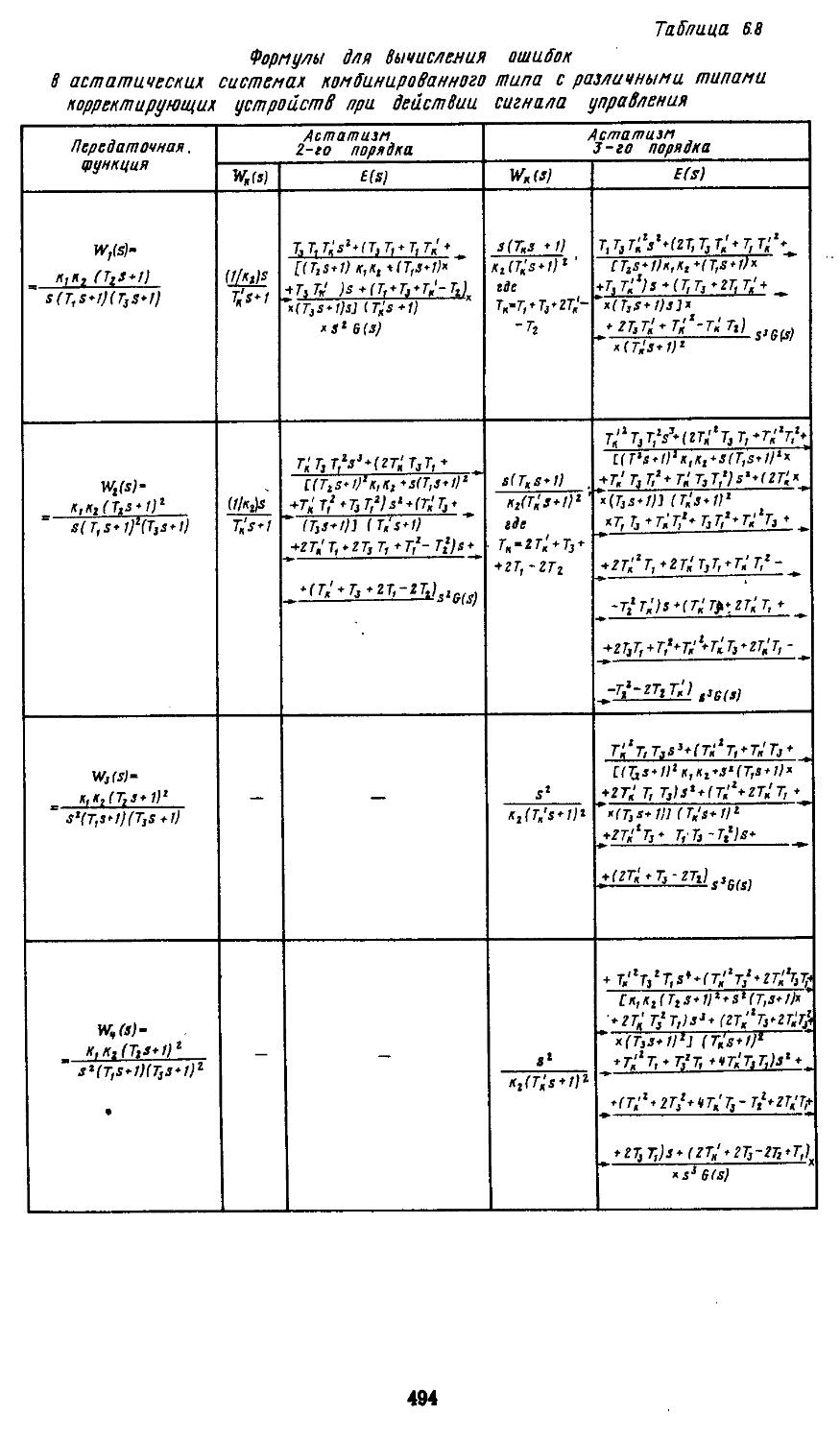
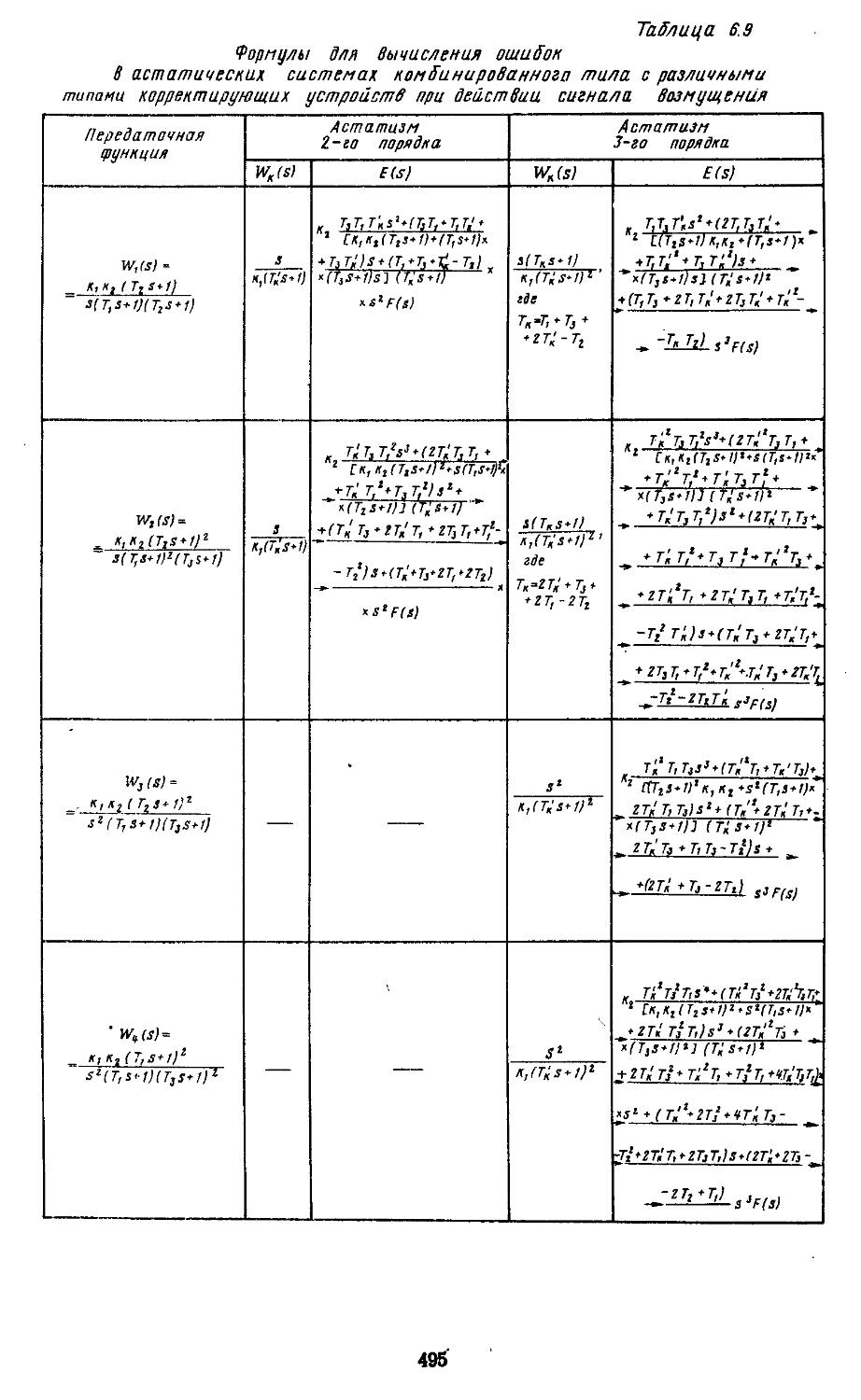
Предложенный Щипановым способ построения комбинированных САР позволяет путем подбора дополнительных корректирующих устройств повышать порядок астатиз-ма исходной системы [13]. Используя данный способ, можно создавать системы регулирования с астатизмом 2-го н 3-го порядков. Дальнейшее повышение порядка принципиально возможно, но оно приводит к значительному возрастанию влияния помех на точность систем. Ввиду этого на практике не применяются системы с порядком астатизма выше третьего.
Обратимся теперь к более сложным задачам синтеза. В самом простом случае они сводятся к выбору типа и параметров последовательных, параллельных н последовательно-параллельных корректирующих устройств, обеспечивающих наиболее точное воспроизведение регулярных сигналов управления. Возможна и более сложная постановка задачи, когда требуется определить тип и параметры корректирующего устройства, обеспечивающего минимальную среднюю квадратическую ошибку помех при заданных динамической ошибке н времени протекания переходного процесса. В результате решения задачи синтеза в обоих случаях в систему вводятся линейные корректирующие устройства. Они реализуются в виде RC-фильтров илн рабочих
программ для микропроцессоров на языке ассемблер-
При рассмотренных постановках задачи синтеза не учитывались ограничения, накладываемые на управляющие воздействия или фазовые координаты. С учетом таких ограничений задачи синтеза систем регулирования решают с использованием принципа максимума Понтрягина [5, 18, 39] или метода динамического программирования Веллмана [3, 32]. Корректирующие устройства, обеспечивающие оптимальное управление, зависят от времени, если они определяются по принципу максимума, и от фазовых координат при определении по методу динамического программирования. Вычислительные процедуры обоих методов являются сложными для задач высокой размерности и требуют больших затрат времени при расчетах на ЭВМ. Эти процедуры наиболее эффективно реализуются в рамках автоматизированных систем проектирования.
Корректирующие устройства, синтезированные по принципу максимума или методу динамического программирования, являются существенно нелинейными. В простейших задачах они реализуются в виде фильтров с операционными усилителями и набором диодных линеек, а в более сложных — в виде программ микропроцессоров. При реализации программ используют численные методы дифференцирования и интегрирования в реальном масштабе времени. Обычно применяют четыре способа программирования: прямое, последовательное, параллельное и последовательно-параллельное. Пользуясь этимн программами, можно выбрать наиболее рациональные параметры микропроцессора или мнкроЭВМ. (по длине разрядной сетки, объему памяти и быстродействию), которые входят в систему регулирования в качестве одного нз элементов.
18
Четвертый этап проектирования —математическое моделирование системы, разработанной на универсальных ЭВМ серий СМ или ЕС. Если результаты моделирования соответствуют техническим условиям, то на этом процесс проектирования заканчивается и составляется эскизный проект САР. Затем на его основании выполняют техническое проектирование и проводят испытания (полунатурные и натурные).
В книге рассмотрены все четыре этапа на примере сквозного проектирования ряда распространенных САР как традиционными способами (ручное проектирование), так и на ЭВМ в диалоговом режиме
(автоматизированное проектирование). Справочный материал, упрощающий работу инженер а -проекти-. ровщика, помещен в приложениях.
Настоящей книгой могут пользоваться студенты, прослушавшие курсы лекций по теории автоматического регулирования (управления), вычислительной технике и владеющие методами программирования на языках ПЛ/1 н ассемблер. Книга представляет собой и справочное пособие для инженеров-проектировщиков систем автоматического регулирования и управления. Программы, написанные на языке ПЛ/1, могут быть использованы при автоматизированных методах проектирования.
РАЗДЕЛ I
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Для проектирования САР инженер должен располагать общей структурой всей системы, каждый элемент которой представляется с помощью основных характеристик, определяющих его функционирование. Обычно к элементам принято относить объект регулирования и устройства управления. Происходящие в них процессы можно описывать в различной форме. Наиболее часто для этих целей применяют дифференциальные, ннтегродифференциальные и разностные уравнения, записанные в покоординатной илн в векторноматричной форме через переменные состояния. Эти переменные могут быть однородны по своей физической природе. В механических элементах это линейные иди угловые перемещения, скорости нли ускорения; в гидравлических н пневматических устройствах давления, секундные расходы жидкости или газа; в электрических-— изменения величины тока и напряжения; в химических — концентрации взаимодействующих продуктов; в физико-энергетических установках — плотности нейтронного потока, изменения реактивности и т. п.
Однако большую часть элементов не удается описать с помощью переменных, имеющих единую физическую природу. В этих случаях пользуются различными типами переменных. Например, в электродвигателях — угловой скоростью вала, величиной тока нли напря
жением на клеммах якоря; у летательных аппаратов — значением перегрузки н углом отклонения рулевых органов; в нагревательных печах — температурой и расходом горячего газд; в смесителях для производства цемента — содержанием мела и угловой скоростью крестовины.
Дифференциальные, интегроднф-ференцнальные н разностные уравнения записывают с помбщью различных упрощающих предположений. : К ннм в первую. очередь можно отиестн линеаризацию уравнений относительно программной траектории или рабочей точки, позволяющую применять непрерывное или дискретное преобразование Лапласа. Тогда при нулевых начальных условиях получают передаточные функций объектов, устройств управления и САР в s-, z- и s-формах. Пользуясь ими, создают структурные схемы нли графы, по которым находят характеристики разомкнутых и замкнутых систем в частотной области. Наряду с этим используют математический аппарат спектральной теории матриц при составлении непрерывных и дискретных моделей САР во временной области. Это дает возможность разрабатывать единые алгоритмы, а по ним н рабочие программы для проектирования систем на ЭВМ.
Многие из элементов не удается описать в виде линейных дифференциальных, интегродифференци-альных и разностных уравнений
20
из-за присутствия в них существенных нелинейностей. Тогда математические модели таких элементов составляют на основе методов гармонической, статистической или совместной линеаризаций. Эти модели позволяют учесть влияние нелинейностей на характер поведения САР, так как их коэффициенты изменяются в зависимости от величин сигналов управления (возмущения) или начальных условий. С целью повышения точности исследования нелинейных САР при
составлении коэффициентов гармонической линеаризации элементов используют высШиё /^афмЫй-ческие составляющие,; Определение коэффициентов гармонической' и статистической линеаризации ‘ елЬзк-ных нелинейностей производят с помощью рабочих программ на ЭВМ.
Пользуясь материалами раздела I, проектировщик формирует модели различного рода устройств и систем автоматического регулирования.
Г л а в а 1
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ЛИНЕЙНЫХ ЭЛЕМЕНТОВ (ОБЪЕКТОВ)
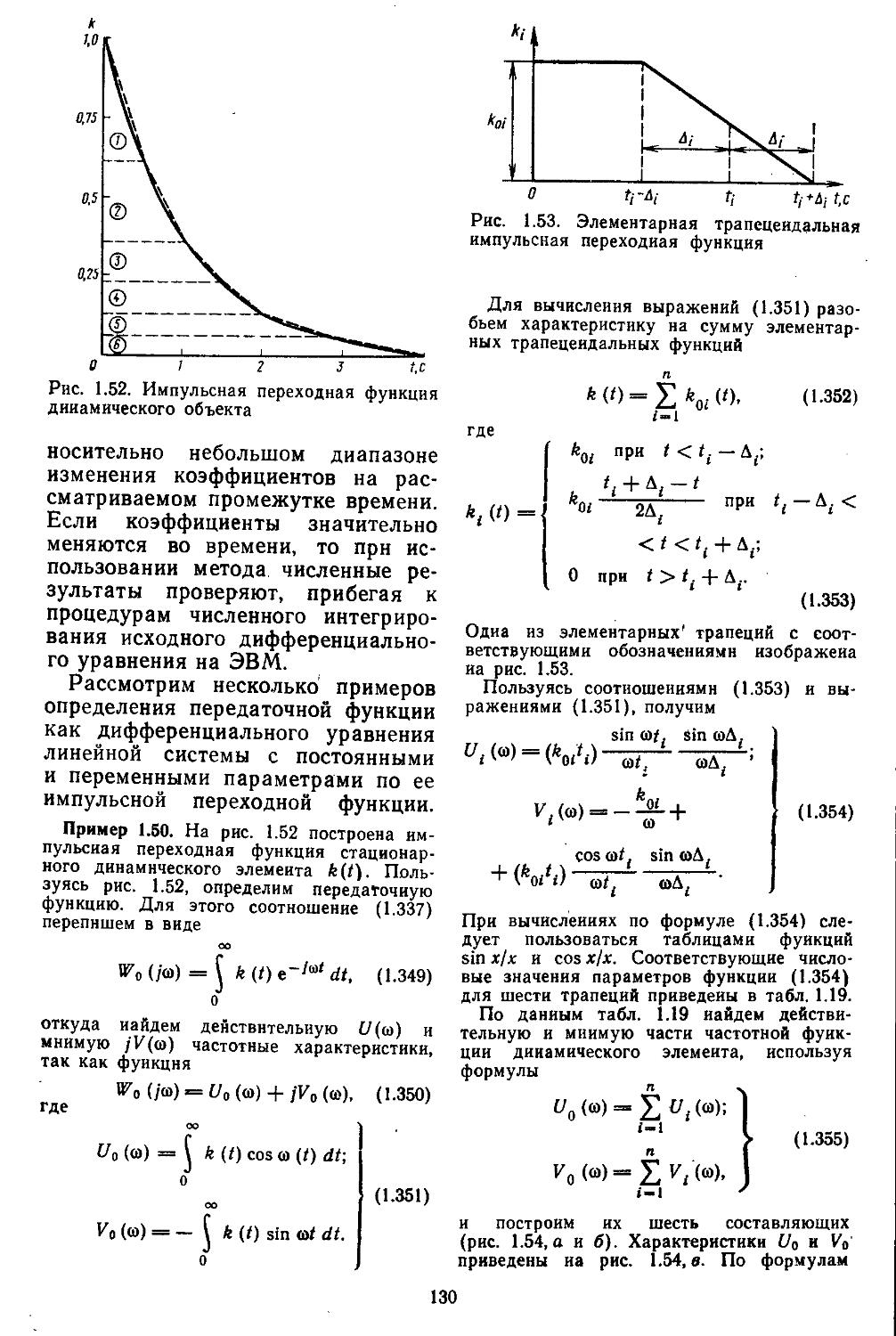
Математические модели элементов составляют в виде алгебраических, дифференциальных; интегро-дифференциальных и конечно-разностных нелинейных уравнений. Описание динамических процессов в элементах с сосредоточенными параметрами производят; с помощью обыкновенных дифференциальных уравнений, а с распределенными параметрами — уравнений в частных производных. При проектировании систем автоматического управления нелинейные уравнения обычно линеаризуют, что приводит к векторно-матричной форме их представления или к частотным функциям.
В тех случаях, когда рассматриваемые процессы в элементах не удается описать указанными выше способами, используют таблицы с числовыми значениями, характеризующими входные и выходные переменные. Применяя к ним методы регрессионного анализа, также можно получить нелинейные алгебраические Или дифференциальные уравнения. ,
1. ВЕКТОРНАЯ И ПОКООРДИНАТНАЯ ФОРМЫ ОПИСАНИЯ НЕПРЕРЫВНЫХ И ДИСКРЕТНЫХ ЭЛЕМЕНТОВ
Динамические элементы относятся к непрерывным, если рассматриваемые в них процессы и сигналы изменяются непрерывно. В дискретных же элементах процессы и сигналы имеют конечное число значений по величине и времени. Математическое описание элементов удобно выполнять через переменные состояния, и тогда их динамику можно представить в виде системы уравнений 1-го порядка относительно этих переменных. При такой форме описания элементов переменные состояния аналогичны обобщенным координатам, а пространство их изменения является фазовым. Состояние элемента в любой текущий момент времени характеризуется совокупностью фазовых координат, которые можно объединить в вектор состояния и представить их описание в векторной форме (математической модели).
21
в)
Рис. 1.1. Обобщенные схемы представления нелинейных нестационарных динамических элементов:
а, б — разомкнутого типа; в, г — замкнутого типа
уравнений (1.1) в виде схемы, воспользуемся соотношением
у (0 = (-1 )ly(t). (1.2)
Обычно при описании элементов непрерывного действия используют переменные состояния y(t), связанные с выходными x(t) и входными «(О с^гцала^ц с помощью следующих уравнений:
= u(t), 0; j
*(0==?(ff(0. «(0, 0, J
где
у (0 =
/(У(О, «(<), ') =
Г А -1
А
q (у (/). «(0. 0 =
~fn~ - <71 -<?2
•~qr
Уравнения (1.1) справедливы на интервале времени (/0, (] при заданных начальных условиях У (to), it (to). Для того чтобы представить систему векторных нелинейных
Здесь р = d/dt — символ дифференцирования; I — единичная матрица.
Обобщенные схемы нелинейных нестационарных динамических элементов могут быть представлены в виде многомерных систем, изображенных на рис. 1.1, а, б— разомкнутых типов, а на рис. 1.1, в, г— замкнутых типов.
Будем считать систему уравнений (1.1) нелинейной, если в ней переменные состояния присутствуют не только в линейной форме, но и в виде произведений, целой (дробной) степени координат и трансцендентных функций от них. Во многих элементах нелинейную зависимость часто не удается выразить в аналитической форме, тогда ее представляют графиками или в виде таблиц.
Перейдем к рассмотрению некоторых типов нелинейных непрерывных систем уравнений, описывающих поведение стационарных и нестационарных устройств и объектов регулирования.
Пример 1.1. Уравнение устройства для замера угловых скоростей выходного вала двигателя внутреннего сгорания или турбин можно записать в виде
m-^-+fe0-^-+M3 = fe<o. (1.3) гДе I — перемещение массы m устройства для замера угловых скоростей; kv — коэффициент скоростного трения; kc — коэффициент жесткости пружины; k — коэффициент пропорциональности при угловой
22
скорости выходного вала двигателя или турбины со.
В этом уравнении сила сопротивления пропорциональна третьей степени перемещения массы. На практике часто нелинейный член уравнения (1.3) представляют в виде al + 0Z3, н выражение (1.3) становится аналогичным левой Части уравнения Дуффинга. Уравнение (1.3) является стационарным, так как его параметры не зависят от времени.
Запишем уравнение (1.3) в виде системы (1.1). Для этого введем следующие обозначения: Z = Zt; /i=Zj; тогда
Л-z»;
2 т 1 т 1 т
(1.4)
Пример 1.2. Уравнение ракеты, вертикально стартующей под действием силы тяги двигателя, будет
... dtfl । ь ( dh V I и\ + feo ("тг) +тЮе =
Пример 1.4. Перемещение связанных между собой тросом тележек поточной линии можно описать следующим упрощенным уравнением:
-g-=V-fee'r(<-₽) , (1.8)
где г — расстояние между тележками; V — скорость ведущей тележки; fe, а и 0 — постоянные коэффициенты,
В уравнении (1.8) нелинейность определяется трансцендентной функцией, а его форма записи соответствует уравнению (1.1) в скалярном виде.
Пример 1.5. Рассмотрим в качестве объекта регулирования электродвигатель переменного тока. Уравнение вращения вала можно представить в виде
J + Аош + Ад®3 + Ат sgn ш = kyu, (1.9)
dm (Z) di
(1.5)
где Л —высота полета ракеты; m(t) — переменная масса ракеты; kv, k — постоянные коэффициенты; g — ускорение свободного падения.
Уравнение (1.5) является нелинейным нестационарным, так как аэродинамическое, сопротивление пропорционально квадрату скорости движения (второе слагаемое), а значение массы зависит от времени полета m(Z). При Л = Л| и Й1 — ha из уравнения (1.5) получим систему нелинейных уравнений hi = ha", Aq ,2 h
---77Г A; — g H--77TU m (Z) 2 “ m (Z)
где ® — угловая скорость вала электродвигателя; J — момент инерции якоря; А„ — коэффициент скоростного трения; Ая — ко-1 эффициеит, учитывающий нелинейность механической характеристики; момент треиия без смазки AfT имеет значения: —Ат < < МТ < Ат; ky—r передаточный коэффициент электродвигателя; и — управляющее напряжение иа клеммах якоря электродвигателя. В уравнении (1.9) нелинейность определяется механической характеристикой электродвигателя и трением без смазки. В соответствии с формулой (1.1) уравнение (1.9) можно переписать в следующем виде:
dm dt
kn k„ a
-j- Ш----j- m3 —
Ат* Ay
— — sgn ш + — и.
(1.Ю)
Пример 1.3. Уравнения углового движения искусственного спутника Земли при действии иа него моментов силы тяги e(Z) относительно его главных осей инерции можно записать в форме Эйлера
do>i Ja — J a
dt J i
data J i “ J з
~dT = Ta
dm3 J a — J \
dt J a
“i (Z) ш2а>з 4-----
, (Z)
а>з<01 -I---p2- ;
•<s тат, + ,
(1.7)
где Ji, ш/, ui (Z = 1, 2, 3) — соответственно составляющие момента инерции, угловой скорости и управляющего момента относительно одной из главных осей искусственного спутника Земли.
Система уравнений (1.7) нелинейна из-за наличия'в выражениях правых частей произведений угловых скоростей.
Пример 1.8. Составим в упрощенной форме уравнения движения летательного аппарата (ЛА) в вертикальной плоскости при относительно небольшом диапазоне изменения высоты полета [36].
Спроектируем все силы, действующие иа ЛА, иа прямую, касательную к траектории его полета; тогда найдем
dV oV2S
т -^у- = Р cos а —— Сх — mg sin 0,
(I-И)
где т — практически мало меняющаяся масса ЛА; V — скорость полета; Р — сила тяги двигателя; р — плотносА воздуха; S — площадь крыльев; Ся — коэффициент лобового сопротивления; g — ускорение свободного падения; 0 и а —углы наклона траектории и атаки (0 = О — а; здесь О — угол тангажа).
23
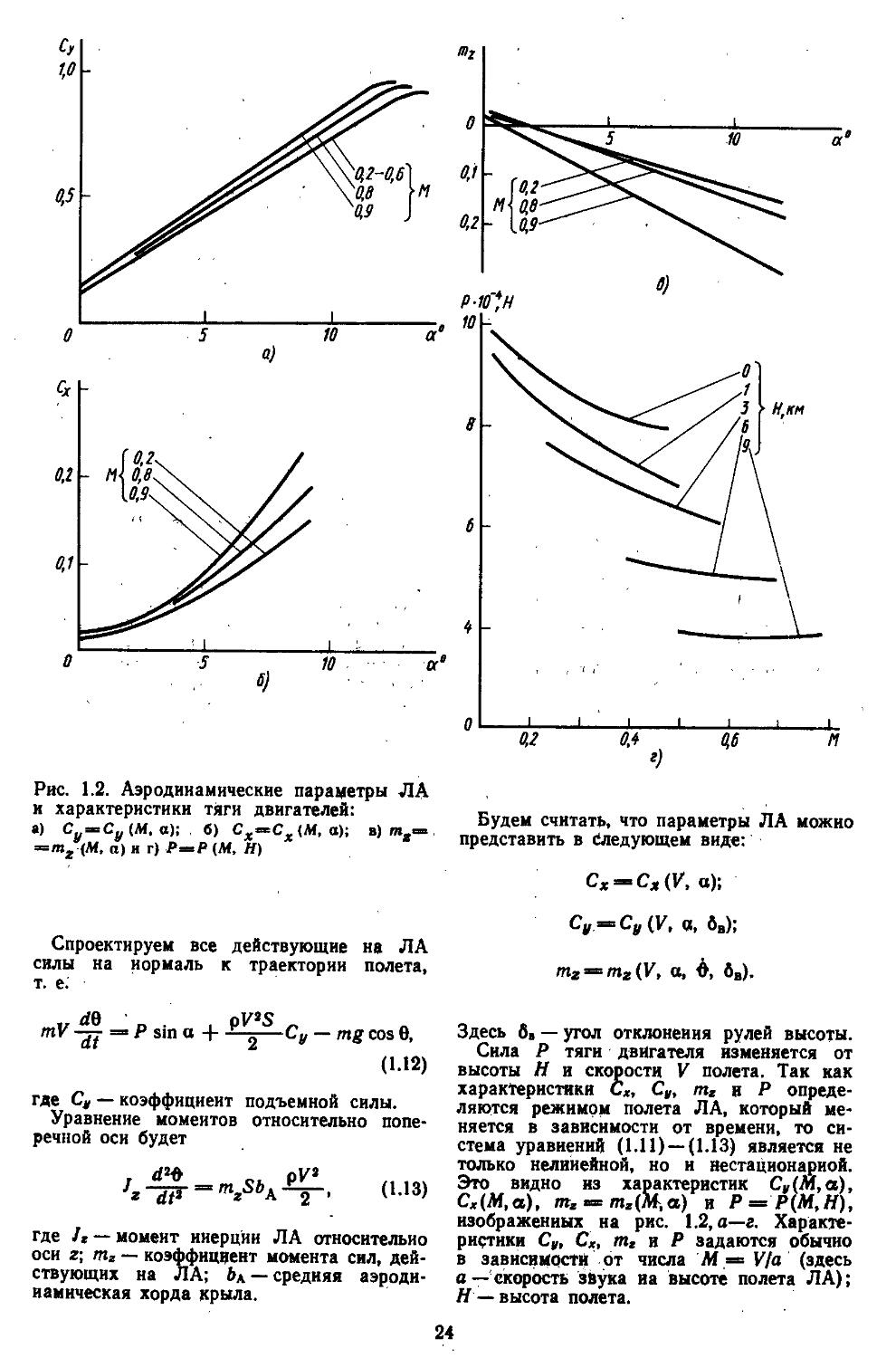
Рис. 1.2. Аэродинамические параметры ЛА и характеристики тяги двигателей: ») С =Су(М, а); б) СХ=СХ(М, а); в) =тг (М, а) и г) Р=Р (М, Н)
Будем считать, что параметры ЛА можно представить в Следующем виде:
СХ = СЯ(У. а);
Cy = Cy(V, а. бв);
Спроектируем все действующие на ЛА
силы на нормаль к траектории полета, тг = тг(У, а, Ь, ба).
т. е.
mV = Р sin а + - ъ $ Су — mg cos 0, и» л
(1.12)
где Су — коэффициент подъемной силы.
Уравнение моментов относительно поперечной оси будет
а-1з)
где Уж — момент инерции ЛА относительно оси г; тг — коэффициент момента сил, действующих на ЛА; Ьа — средняя аэродинамическая хорда крыла.
Здесь бв — угол отклонения рулей высоты.
Сила Р тяги двигателя изменяется от высоты Н и скорости V полета. Так как характеристики Сх, Су, т? и Р определяются режимом полета ЛА, который меняется в зависимости от времени, то система уравнений (1.11) —(1.13) является не только нелинейной, но и нестационарной. Это видно из характеристик Су(М, а), Cx(Af,a), тг = 7пг(М,а) и Р *= Р(М,Н), изображенных на рис. 1.2, а—г. Характеристики Су, Сх, тг и Р задаются обычно в зависимости от числа М = Via (здесь о —скорость звука на высоте полета ЛА); Я—высота полета.
24
Запишем уравнения (1.11) —(1.13) в виде системы
• Р pV2S _
V = —cos а —— Сх — т 2т
— g sin (О — а); ,
Р , pV’S „ , а = — -л— sin а — ---Су +
Vm 2т •
+ -у- cos (О — а) + <0z> . SftApVs шг-------2Ц~т*'
Ь = в>г.
(1.14)
В системе уравнений (1.15) применены следующие обозначения:
X-QCx; Y=QCy- Z = QCz; Мх = mxQl; Му = myQl;
Л = -рс =
— РеЙММ-
Q=qS, q^pV42,
(1.16)
где бет — значение углового положения рукоятки управления двигателем.
Безразмерные аэродинамические коэффициенты Сх, Су, Сх, тх, ту, mz являются нелинейными функциями параметров траектории полета самолета и величины отклонений органов управления:
Пример 1.7. Составим уравнения пространственного движения ЛА (самолета) [4:
Ь = <ог cos у + ш9 sin у;
у = шх — tg О (в>у cos у — <ог sin у);
Ф ” 'cosT COS V ~ “г sin Y):
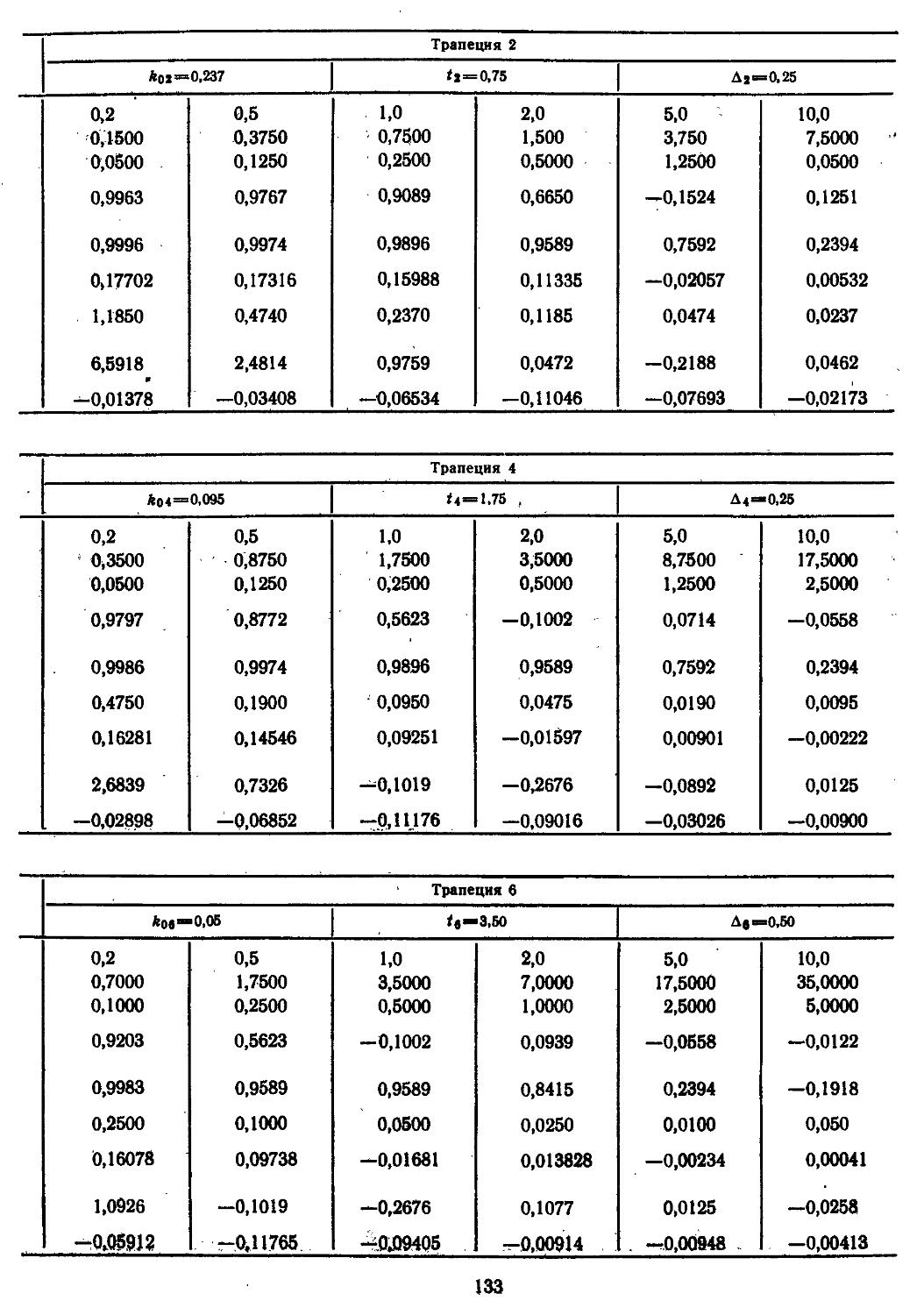
V = X {Р cos (а + фр) cos 0 — — X cos 0 + Z sin 0 — mg sin 0);
® = "mV lsin (<X + <₽p) C0S Y + + cos (а + фр) sin 0 sin y] —
— X sin 0 sin у + Y cos у — — Z cos 0 sin у — mg cos 0);
H — V sin 0; g a = шг —у- cos у;
0 = Шр + to* sin a + -p- cos 0 sin y;
®x = -ц [Mx - (Jг — Jy) Шр<ог];
[Afp — (Jx — Jг) ®x®zl;
®z= [Afz — — Jx) ®x®y]>
(1.15)
Су Су (Af, бв, а, Оз);
Сх = Сх(Су, му, СХ = СХ(М, бн, 0);
тх = тх (М, бн, б9, шх, (Ор, 0);
Шр = ту (М, бд, бэ, (Од., Шр, 0); тх тх (М, Су, бв, ©аз Р, Дхцс).
(1.17)
Здесь Р — величина тяги силовой двигательной установки; Дхцс— нелинейное измерение центровки самолета в зависимости от его массы т; б,, б,, б,— угловые положения рулей высоты, направления и Крена; as — угол установки крыла.
Из систем уравнений (1.15) —(1.17) видно, что пространственное движение самолета описывается довольно сложными нелинейными уравнениями, параметры которых зависят от многих переменных, что затрудняет их применение при проектирований систем демпфирования, стабилизации и управления. Для проектирования этих систем обычно прибегают к методам линеаризации, позволяющим разделить пространственное движение самолета на три независи- . мых: Продольное (в вертикальной плоскости), боковое (в горизонтальной плоскости) и вращение (вокруг продольной оси).
При описании элементов дискретного действия в общем виде пользуются разностными уравнениями
у(^к+i) — 7(у(^к)» ^к)>
“('к)> и. Г
где О, у. ф — соответственно углы тангажа, крена и рыскания; 0 — угол наклона траектории и курса; а, 0, у —соответственно углы атаки, скольжения, крена; ®*. ш«, Шг — проекции Вектора угловой скорости <в на связанные оси координат; /х, Jy, Л — моменты инерции самолета относительно связанных осей; ф₽ —угол установки двигателя.
где
~У\
У2 (t*)
25
Щ (tK) ~
U2 (^к)
u(tK) =
-Um(tK)_
~Xi (tK)~ x2 (/K)
_ xr (t^)_
u(tK), tK) =
q(y(tK), u(tK),
l ПК — <71K ?2k
_ ?гк _
Наиболее распространенным случаем является, когда такт квантования — постоянная величина То. При этом вместо системы (1.18) будем иметь
»К«+1)7’о] = /(у(к7’о),ч
и(кТ0), кТ0);
<119>
а(кТо), кТ0).
В дискретных элементах наряду с типовыми нелинейностями могут содержаться" нелинейные модуляторы. Если квантование осуществляется в них по уровню, то модулятор (элемент) представляет собой цифровое вычислительное устройство. При квантовании по времени элементы с широтно-импульсной и время-импульсной модуляциями, а также комбинированной модуляцией являются нелинейными. Обычно модуляторы представляют собой преобразователи, на выходе которых образуются последовательности импульсов определенной формы. Эти импульсы мож-
Рис. 1.3. Упрощенная схема дискретного элемента с широтно-нмпульсной модуляцией:
«Гу — преобразователь длительности импульсов; «Гт—устройства сиихроииой работы ключей; Нх— выходное устройство; тк—ширина импульса
но заменять эквивалентными прямоугольными (экстраполяция нулевого порядка), трапецеидальными (экстраполяция 1-го порядка) и параболами (экстраполяция 2-го порядка). С целью упрощения математического аппарата такую последовательность часто принято представлять в виде дельта-функций.
Рассмотрим несколько примеров описания дискретных элементов.
Пример 1.8. Составим обобщенное уравнение дискретного элемента, обеспечивающего широтно-импульсную модуляцию, в форме (1.18) {67]. Упрощенная схема такого устройства показана на рис. 1.3.
Если считать, что тк = У у [е (fK)l, тогда имеем
Г «max Sgn 8 (/к) при /к <
« (^к) = । f + тк; (1-20) < 0 при <к + тк С / </к+1.
Подобного рода устройство преобразует непрерывный сигнал в дискретный. Такое устройство называют преобразователем «аналог — код» (АК.).
Пример 1.9. Опишем процессы, происходящие в дискретном преобразователе «вал — цифра» (ВЦ), с помощью уравнения оо
«1(хГо)=»£ е(кТ0)а(1-кТ0), (1.21) к-о
где ’ е — входной сигнал; «1 — выходной сигнал; То — такт квантования; и — дедьта-фуикция.
Если данный преобразователь является нелинейным и имеет коэффициент гармонической или статистической линеаризации kn, то уравнение (1.19) примет вид
и1(кТ’0) = *и£ е (кТ0) и (t — кТ0). (1.22) к-о
26
Рис. 1.4. Преобразователь код—аналог1: а — принципиальная схема; б — формы входного и выходного сигналов
I
Klj (к*/)Гр
КТ0 (a*/)Tq
<9
Пример 1.10. Составим уравнение преобразователя «код — аналог» (КА), пользуясь рис. 1.4, а. При этом видно, что в схему входит ключ, операционный усилитель (ОУ), два резистора R\, Ri и конденсатор С. В таком преобразователе в момент замыкания ключа конденсатор С заряжается и «запоминает» поступившее из него напряжение, которое с течением времени уменьшается по экспоненциальной кривой. Формы входного и выходного сигналов показаны на рис. 1.4,6. Пользуясь принятыми обозначениями, запишем уравнения для напряжения в межтактовые моменты времени на выходе преобразователя в форме (1.19), т. е.
t_ «н(П = Кое Гп [«(/)-«(<-Го)]; «нЮ-Kie Гп [«(1-Го)-— «(/ —2Г0)]; (1.23)
f—кГц
«1к(/) = Кке Тп {и (t-кТо)-
-«[/-(к+1)Г0]}.
Пример 1.11. Реализовать иа бортовой цифровой вычислительной машине (БЦВМ) нелинейный закон стабилизации искусственного спутника Земли при его движении в вертикальной плоскости. Если закон стабилизации должен обеспечить быстродействие при отработке угла тангажа, то его можно описать как
„ in- ЗИ1Г4НП-1- «<01«(011
“1 опт 1*1--Sgn I V 1'1 Ч----2J------ г
(1.24)
где Ui — сигнал на выходе управляющей БЦВМ; © — угол отклонения оси спутника в вертикальной плоскости; J, — Момент инерции спутника относительно осн Ог.
Для составления рабочей программы БЦВМ выражение (1.24) следует пред
ставить в виде разностной зависимости
ОПТ (кГ0) = — sgn { О (кГ0) +
{0(кТ0)-*[(кТо)-То])Х )
4. X I»(кГр) - О[(кТр) - Гр] | | {1 25) 2/гТ* > ’
Наличие символа sgn указывает на нелинейность разностного уравнения.
Пример 1.12. Рассмотрим реализацию на БЦВМ системы уравнений в отклонениях от заданной траектории полета космического ЛА [21], представленной в виде
^. + ky(t) = a, (1.26)
где у — вектор отклонений от заданной траектории; k — постоянный параметр; а — ускорение, измеряемое акселерометрами, устрановлеиными на гидроплатформе космического ЛА.
Уравнение (1.26) является линейным, н его решение на БЦВМ реализуется с помощью метода Руиге — Кутта 4-го порядка. Для этого перепишем уравнение (1.26) в виде
где
у = «*;
w = —ky а, „
(1.27)
W = у)\
w — g(w, у).
(1.28
Тогда формулу Рунге — Кутта 4-го по-
рядка можно записать в виде
Ук+i = Ук + -g- (*i + 2А» + + 2Лз + *<);
а»к+1 = в*к Ч—o' (ti + 21s Ч"
Ч- 21з + !<)•
(1.29)
27
В соотношении (1.29) принято
*1 = t Кк, Ук, »к) = Ук, U=g (<к. У к, »к) = — fey к + ак; fes = f ^к + Ук + ~^~,
wK4--y)=wK-A^-X
X Ук + -у- «к!
Ь=<(*к4--у-> Ук + -£-> WK+
Ч—== — кУк — А ®к + Як!
Аз — f ^к Ч—Ук Ч-
Wk ч- -у) = Wk — kToyK —
— fe “У Wk Ч- 2 “к’
к — g (Jk + Ук Ч- ~2~<
WK + -у) = — fewK —
То Тп
, -fe-y WK4-fe’ -yyK-
j.2 А — ®к 4“ лк;
А4 = f (к Ч- То, УкЧ-fes, Wk-Ms) — г2 = Wk — /гТоук — -у WK +
у»з 2»з
+ Ь* у Ук fe -у Лк + Толк;
(1.30)
^4 — g (^к 4“ То, ук + Аз, Wa Ч- *з) = ” т 4 ” * ' г " Г2
= ~ Аук — feTowK Ч- fe2 ~уУк Ч-
Т2
+ А2у WK —
Т2
А у Лк Ч* вк.
Подставим значения из соотношений (1-30) в уравнения (1.29); тогда в форме (1.18) получим
Ак+1 = Ук1
+ wKl 1
AT2 fe2T4 2 + 24 АТ2\
(1-31)
1
( Т20 fe2T4\ +
“’к+1==юД1-*-Т +~24~J ~ ' ( то\ - УкА (у-1 Ч- A То Ч-
( АТоА
+Лк I1 —б2/ г°-
Соотношения (1.31) могут быть применены для составления рабочих программ, реализуемых иа БЦВМ, или определения их передаточных функций (см. п. 8).
Пример 1.13. Составим разностные уравнения в форме (1.18)'для численных процедур интегрирования и их реализации иа управляющей ЭВМ. Для этого воспользуемся уравнением
= « (О- (1-32)
at
При нулевых начальных условиях и(1о) = = 0, «1(1о)=б из уравнения (1-32)
имеем:
для метода Эйлера
И1 ,(к+1)= и1к Ч" ^оик’ (1 ’33)
для метода Адамса — Башфорта
“1(к+1) = “1(к-1)Ч-2Гоик; (1.34)
для метода Адамса — Мультвна
“1 (к+1) “ «1 (к-1) + -у (“к + 4“к-1+“к-2).
(1.35)
Рекуррентные соотношения (1.33) — (1.35) нетрудно реализрвать в виде рабочих программ на управляющей ЭВМ (cut. гл. 10).
Пример 1.14. Составим разностные уравнения в форме (1.18) численных процедур дифференцирования для их реализации на управляющей ЭВМ. Для этого воспользуемся уравнением
= «.(/)• (1-36)
at
При нулевых начальных условиях имеем: для метода первой центральной разности
“к+1-“к-1=2го“1к: (L37>
для метода второй центральной разности То
“к+1 “к-1 = 3 X
X («1 (к+1) Ч-4«1к Ч-«1 (к-1))- (1-38)
Рекуррентные соотношения (1:37) и (1.38) также реализуются в виде рабочих программ на управляющей ЭВМ (см. гл. 10). j
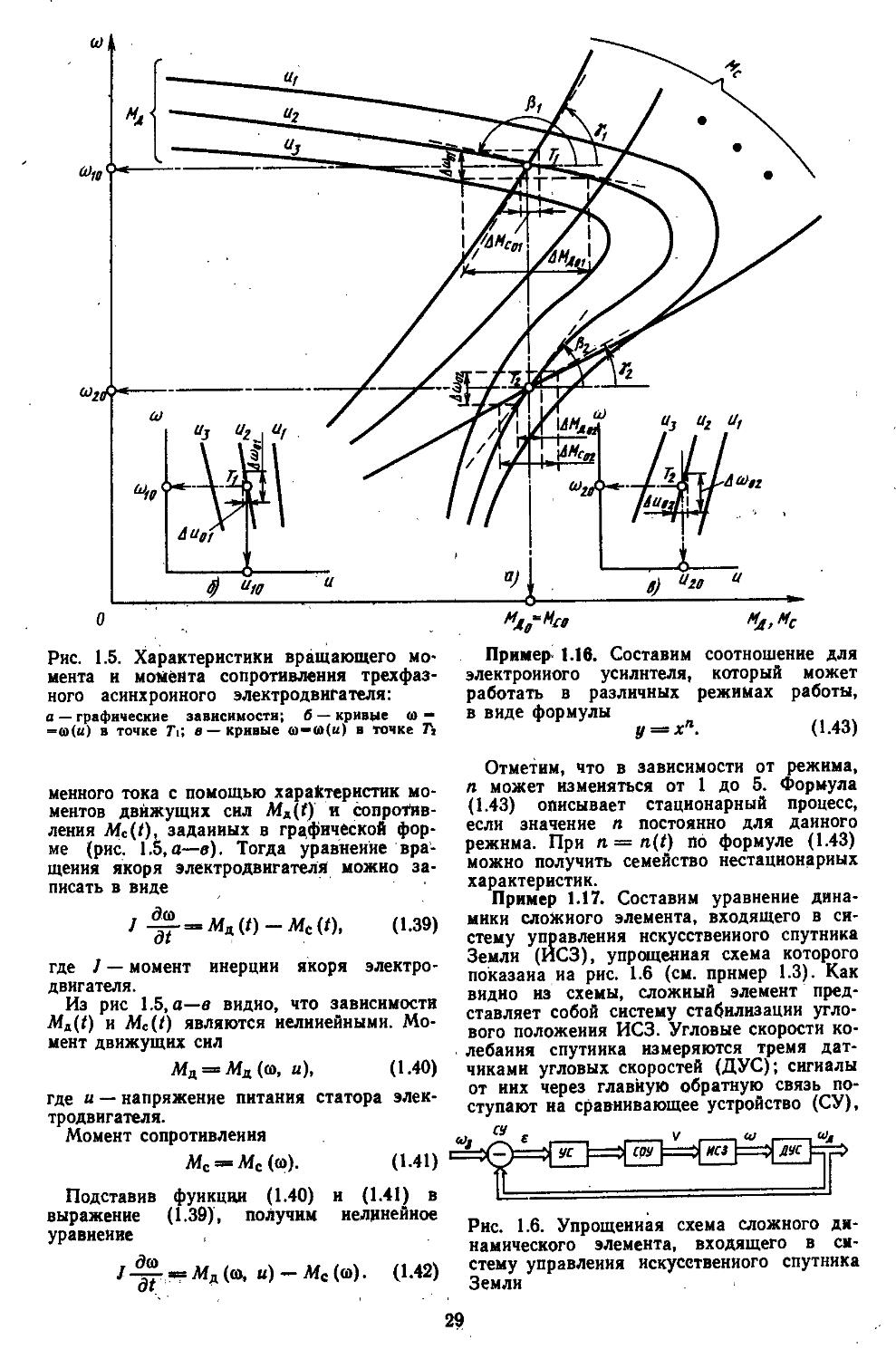
Пример 1.15.' Составим уравнение динамики асинхронного электродвигатели пере-
28
Рис. 1.5. Характеристики вращающего момента и момента сопротивления трехфазного асинхронного электродвигателя: а — графические зависимости; б — кривые ш — =(&(и) в точке Л; в —кривые (а—(й(и) в точке А
менного тока с помощью характеристик моментов движущих сил Мд(Г) и сопротивления Afc(O, заданных в графической форме (рис. 1.5,а—в). Тогда уравнение вращения якоря электродвигателя можно записать в виде
J -^- = Л4д(/)-Л4с(/), (1.39)
где J — момент инерции якоря электродвигателя.
Из рис 1.5, а—в видно, что зависимости Л4д(0 и Me(t) являются нелинейными. Момент движущих сил
Мд = Мд(ш, и), (1.40)
где и — напряжение питания статора электродвигателя.
Момент сопротивления
Мс = Мс(ш). (1.41)
Подставив функции (1.40) и (1.41) в выражение (1.39), получим нелинейное уравнение
/-^- «Мд(®, «)-Мс(<о). (1.42)
Пример* 1.16. Составим соотношение для электронного усилителя, который может работать в различных режимах работы, в виде формулы
у^хп. (1.43)
Отметим, что в зависимости от режима, п может изменяться от 1 до 5. Формула (1.43) описывает стационарный процесс, если значение п постоянно для данного режима. При п = n(t) По формуле (1.43) можно получить семейство нестационарных характеристик.
Пример 1.17. Составим уравнение динамики сложного элемента, входящего в систему управления искусственного спутника Земли (ИСЗ), упрощенная схема которого показана иа рис. 1.6 (см. пример 1.3). Как видно из схемы, сложный элемент представляет собой систему стабилизации углового положения ИСЗ. Угловые скорости колебания спутника измеряются тремя датчиками угловых скоростей (ДУС); сигналы от них через главную обратную связь поступают на сравнивающее устройство (СУ),
Рис. 1.6. Упрощенная схема сложного динамического элемента, входящего в систему управления искусственного спутника Земли
29
где и формируется ошибка системы стабилизации е. Сигнал ошибки усиливается электронным усилителем (УС) н поступает иа струйные органы управления (СОУ), уменьшая угловые колебания ИСЗ.
Обозначим через k,, k3 и k3 коэффициенты усиления электронного усилителя совместно со струйными органами управления. Тогда получим следующие соотношения:
Ui=fei(o>3i—а>д1); )
и3 = kt (ш3а — Шдз); f (1.44)
Из = k3 (Ш33 — <Одз).
Будем считать, что ДУС идеальны, но установлены с перекосом; тогда каждый гироскоп будет реагировать иа угловые скорости вокруг других осей, т. е.
ее можно разложить в ряд Тейлора. Линеаризуем первое уравнение системы (1.1) по этому методу при условии малости приращений Ду (О, Ду (О, Д«(0 относительно положения равновесия f (уе, ао)=О,т. е.
= + (1.47)
является линейным уравнением, для которого справедливы частные производные
“ JL JL df> ~ ду, ду3 ' ’ • дуп
(Од: = ka 1 со 1 + £дз<Оз + бдзШз;
<0д2 = йщШ1 4- йд»<о» + ЛдзЮз! У (1.45)
<ОдЗ = 4д 1 to I + £д2®2 + Лдз<Оз, )
где km, km, km’, km, km, km’, km, km, km— постоянные коэффициенты.
Подставим соотношение (1.44), (1 45) в (1.7); тогда получим
• /з — J? ki
<01 --------у-----Шз<0з —у- X
X (^Д1®1 + £д2®2 + ^Д3®з) + , k, + 7ГШз,:
• /1 — /3 fej .
<02 ==------т—- <0з<0! — -т- X
J2
df__ ду
dfп dfn dfn
_ ду, ду3 '‘’ <Эул_
~ df, df, ди, ди3
df, -дип
ди
dfn'
(1.48)
(1.49)
dfn dfn ___________
du, du3 ‘ ‘ dun _
X (АЁд!©! + Йд2©2 + £дЗ®з) + &2 + -у— <о32;
• ^2 — А . .
(Оз «а--------------©2©1 — X
'Э -»з
X (*Д1©1 4“ &Д2©2 + £дЗ©з) +
' + -у" <*>33.
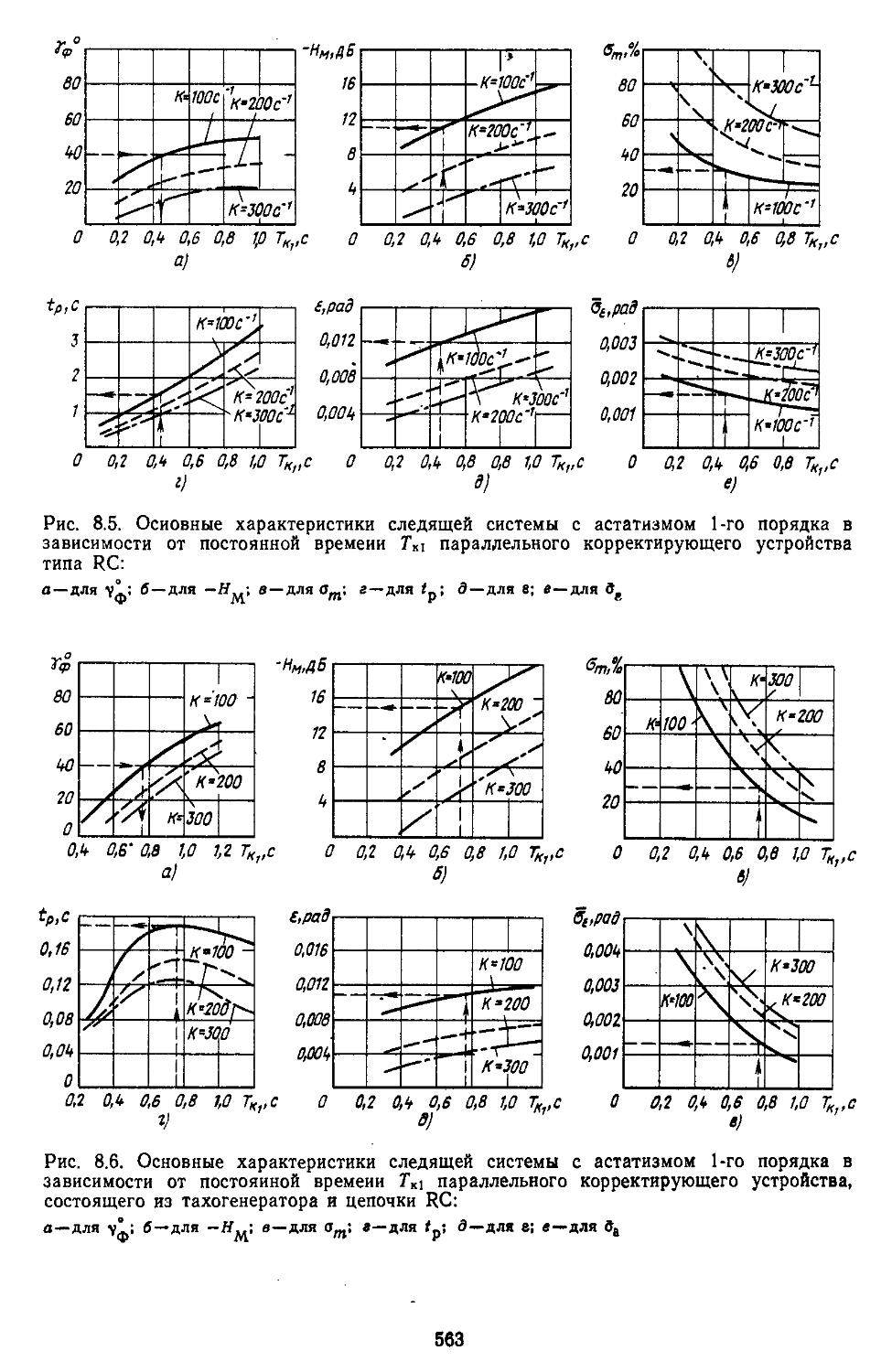
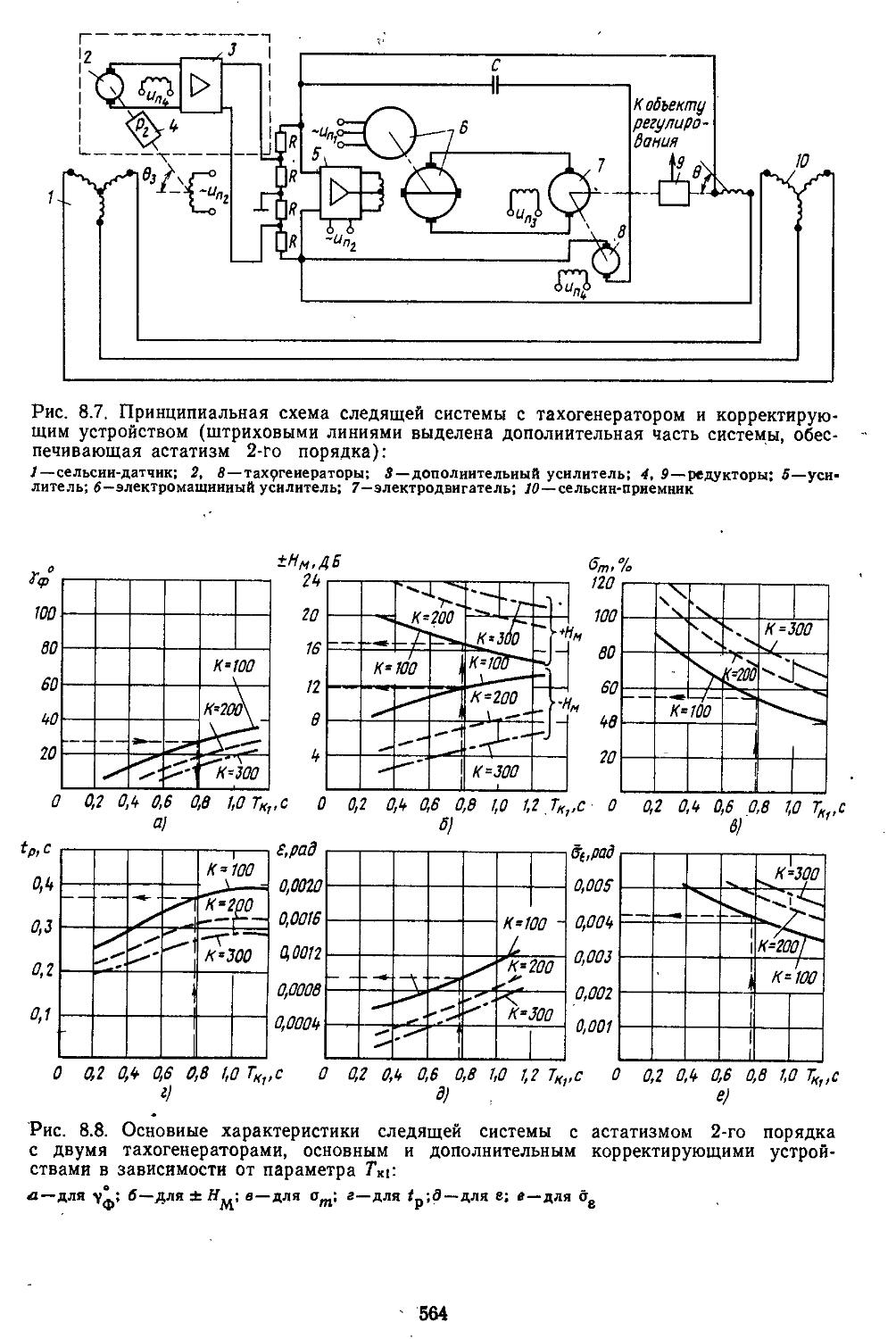
’ - Зз
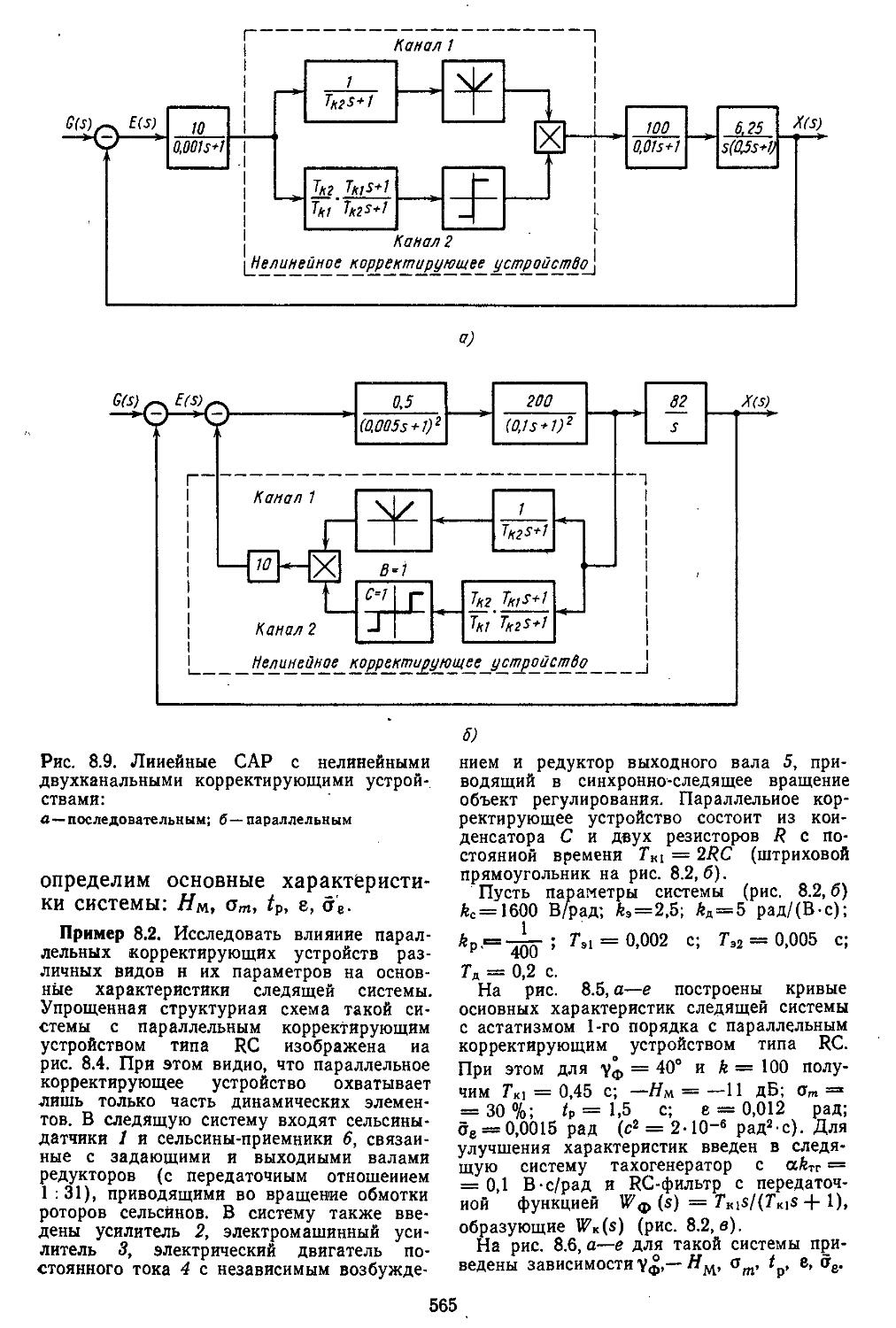
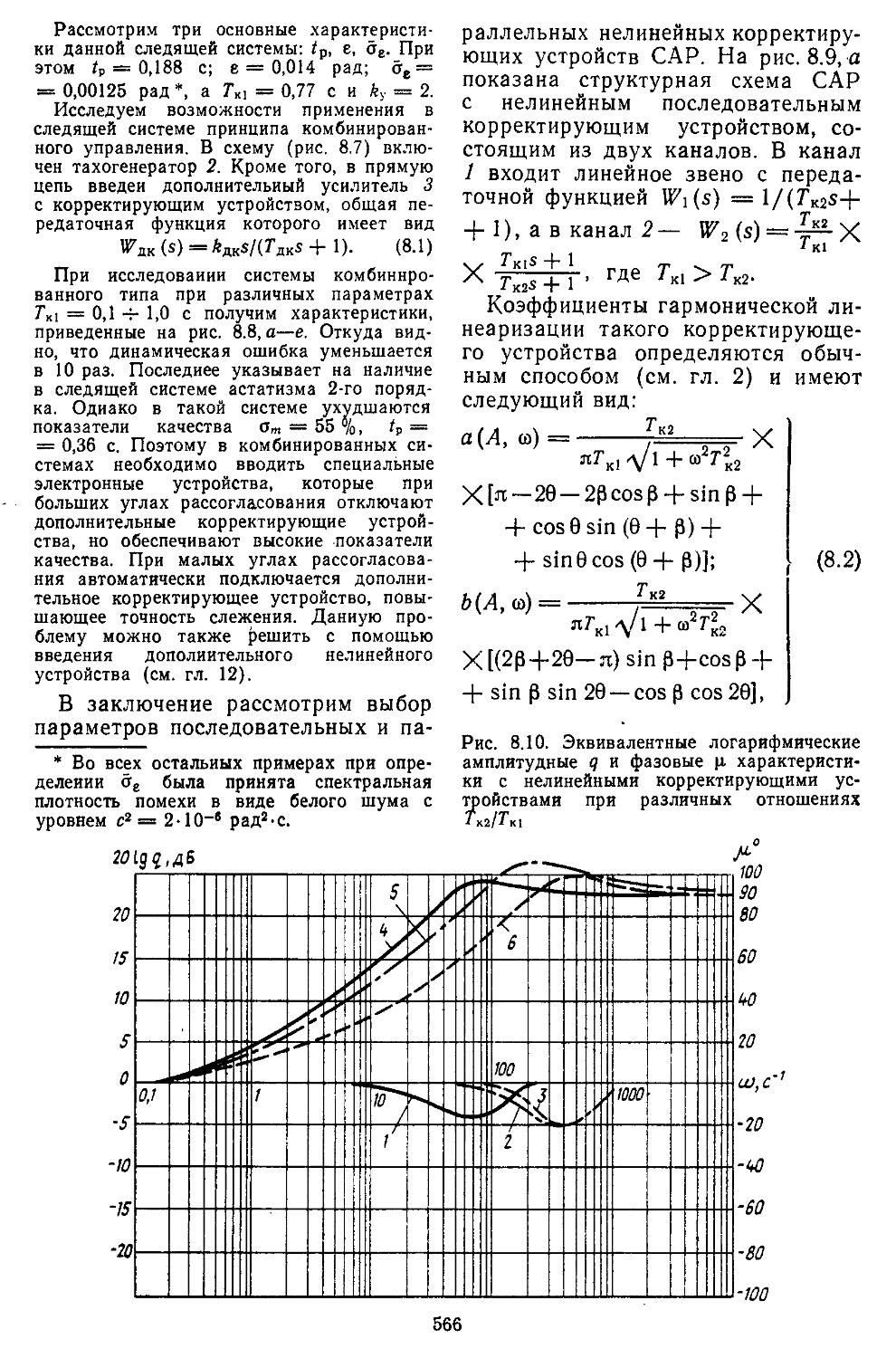
(1.46)
Здесь (1.48) и (1.49) — матрицы Якоби, а уе — положение равновесия в достаточно малой окрестности при фиксированном управлении «о и малых Да.
Из второго уравнения системы (1.1) получим также линейное уравнение
Дх = ^-Ду + -||-Ди со следующими значениями ных производных:
(1.50)
част-
Итак, сложный динамический объект описывается системами
уравнений (1.45) и (1.46).
дд, дд,
ду, ду3 '" дуп
dg,
2. МЕТОДЫ ЛИНЕАРИЗАЦИИ УРАВНЕНИИ
Существует ряд методов линеаризации уравнений. Рассмотрим четыре из них, которые наиболее часто применяют на практике.
Первый метод линеаризации. Нелинейная функция является аналитической в рабочей области, и
d<7 _ _ ду
ач_—. ди
ддп ддп
~ дд, ди.
(1.51)
___ dgn ду3 ‘ ’ дуп.
dg, dqi ~ ди3 ‘ ' дип
ддп ддп ддп _ ди, диг ’ ' ’ ди
п_
У-Уе
(1.52)
У-Уе
U-Ua
30
Уравнение равновесия q(ye,u0) = ==0.
Если провести линеаризацию относительно опорной траектории программного движения с параметрами у(/) = уп(/); *(0 = *п(0; «(0 = — «п(0, то система (1.1) примет ВИД
, , У (1.53)
Линеаризованные уравнения динамических элементов (1.47), (1.50) можно записать в векторно-матричной форме
y(t) = Ay(t) + Bu(ty 1
x(t) = Cy(t) + Du(f), J
где A = [a/Z], B = [&iz], C = [ciZ],> -О = Hi/] — постоянные матрицы соответственно типа (n X пУ (п X т)> (гХп), (гХт).
Линеаризованная система (1.53) даст
у(/) = А(0у(0 + В(/)«(0;| (1 55) x(t) = C(t)y(t) + D(t)u(t), J
где А(0 = [ао(0]; В(/) = [6г/(/)]; С (0 = к, (0]; D (/) = [d4 (/)] - переменные во времени матрицы тех же порядков, что для системы (1.54).
Если элемент имеет один входной «(/) и выходной x(t) сигналы, то уравнения (1.54) и (1.55) могут быть записаны в виде
У (0 = АУ (0 + Ьи (/); | J 56) x(t) = c'y(t) J
и
y(t) = A(t)y(t) + b(t)u(ty, j x(t) = cx (t)y(t), i
где b — столбец; ст — транспонированный по отношению к вектору с вектор.
Пример 1.18. Линеаризуем систему уравнений (1.7) из примера 1.3 с помощью
первого метода. Введем обозначения
। «1 (0 “ й>2Шз + , —
- /з о о X “» &
G)2<di
—(Й10 , W10 fa>20, U2C (*>30. изо
Составим матрицы
п Л — Ц— h'
О-------j—ш3-----у-—а>2
0
'2
(*>20 (*>30
(1.58)
~ 1 Ji 0 0
ди 0 1 Ji 0 (1.59)
0 0 1 Ji-
Пользуясь уравнением. _(Ц47), запишем уравнения (1.7) в линеаризованном виде с учетом выражений (1.58) и (1.59):
Ау =
<*>30
Г А*0! 1
X I I +
Lag)3J
31
1 Л
о о
о
Au, -1
Ли2 I (1.60)
Лиз -•
Пример 1.19. Линеаризация уравнений (1.7) дана в примере 1.18. Выполним теперь лввеаризацию системы (1.46), поль
зуясь обозначениями »а «= и, = у и <0* = X, или
[©1 *1 Г ©31 *1 Г ©Д1 "1
©2 I > U « I ©з2 I» X « I ©д2 I *
ш3 J L Шзз J L Шд3 J i
(1.61)
Имея в виду вектор (1.61), по формулам (1.48), (1.49) и (1.51) найдем матрицы
©3 “* k j А?д2
^j-A®2— ktkai
df
ду
/. - /» „ и z г - ©3 — К2Кд)
Ji
г ©2 ~ А?3Лд1 *3
— kikjn
— ©j — k3ka2
Л “ /3 „ t, z ----------- Qji — «2ЙДЗ
(1.62)
—©10
©20
©80
[kt 0 0 -|
О ki О I;
I
О 0 k3 J
(1.63)
кзкщъ
dy
" ^Д1 1!д2 ЙдЗ ‘
вд1 Йд2 ЙдЗ
- Лд1 Лд2 ЛдЗ -
(1.64)
Пользуясь матрицами (1.62) —(1.64), по формулам (1.47) и (1.50) запишем систему линеаризованных уравнений в виде
klkjll
©3 — kikjtf
®2 — 1®1^ДЗ
Д© =
©3 — &2&Д1
— ^2^Д2
©1 ^З^ДЗ
®3 —
•“ ^эЛдз
' ^Д1
Д<0д = Йд1
- *Д1
^Д2
Йд2
Лд»
^дз ‘ БдЗ ЛдЗ -
[А о>1 А®2 Д®3
A ®i
А®2 I (1.66)
А®з J
[kt О О
Полученные системы уравнений (1.65) и (1.66) являются линейными.
Второй метод линеаризации. Нелинейные характеристики ие могут быть описаны математически, а задаются в графической форме соответствующими зависимостями у = Af(x) (рис. 1.7). В этом случае производят графическую линеаризацию характеристики 2 в рабочей точке То с координатами (хо, уо), т. е. кривая заменяется касательной. Тогда вместо частных производных находят частные разности Ахо, Дуо и можно записать следующее соотношение:
* ЛМо I . Ди = ——— Дх.
Ахо |т,
(1.67)
©1 ““ А?зЛд2
©10
<1>20 Oho
характеристик элемента при режимах работы, заданных кривыми 1—3
32
Пользуясь соотношением (1.67), коэффициент усиления можно представить в виде
АМо I
Ахо |То
(1.68)
Таким образом, получим линеаризованное уравнение
Ау = ^2 Ах. (1.69)
Пример 1.20. Выполним графическую линеаризацию характеристик трехфазного асинхронного электродвигателя, пользуясь кривыми, изображенными иа рис. 1.5, а—в. При этом найдем коэффициенты усиления в точках Т] и Тг путем замены кривых касательными. На рис. 1.5, а показано также графическое определение разностей Дшо1, АЛ1д01, АЛ4Со1, АШо2| АЛ1д02, АЛТс02. Пользуясь ими, для точки Tt имеем
ЛЛГ„ д .. Дб1
Л©1 = —Г------
AcOqi
Aw,
ЛМ-Aw-----
т, Ли0,
АМСм I
= —-£«1- д<о. Ашей I?,
(1.70)
Коэффициенты уснлеиня в точке Г, обо
значим через
k ЛМд" I • ь -*,=^Г|Т1’ ka-
I
Д<о01 |Т1
ЛЛ4.
До1
Аи01
(1.71)
Учитывая соотношения (1.71), перепишем систему (1.70) в виде
Aw, = kt Aw — kt Ьи;
Aw, = k3 Aw.
(1.72)
Для точки Tt получим
AAf„ Ь(йг •£ Aw02 • Аш + 1т, АМ„ Д02- AU02 Au; т2
Дй)2 ДАС ___ Си AWq2 т2 (1.73)
Коэффициенты усиления В 7*2 будут
ь — Ди 1 AwoS 2 ^2 "“ т3 АЛ4„ Дм Д«02 1т2
Аз ДМ. 1 — CQ2 1 AWo2 Г] (1.74)
Подставив соотношения (1.74) в (1.73), получим линейные уравнения
Aw, = k, Aw — kt Au,;1
, J (1.75)
Aw2 = k3 Aw. )
Третий вид линеаризации. Вместо непосредственного определения частных про
изводных вводим переменные в исходные нелинейные уравнения. Эти переменные имеют вид
у = Уо + Ду; ч
х = х0 + Ах; I (1.76)' и = и0 + Au. J
Следует помнить, что приращения переменных всегда зависят от времени t. Все слагаемые, стоящие в правых частях полученных выше выражений, разобьем на. три группы: не содержащие прнращення Ду и Au; содержащие приращения Ду и Au в виде простых множителей; содержащие произведения или степени приращений. Полагая приращения Ду и Au малыми по сравнению с соответствующими координатами опорной траектории (у0, и0), можно считать слагаемые третьей группы практически равными нулю. Слагаемые первой группы будут определять опорное движение, а слагаемые второй — движение в отклонениях (Ду, Ди) от опорной траектории (i/о, “о)-
Пример 1.21. Линеаризуем с помощью третьего способа уравнение (1.3), подставив в него I = 1о + Л1(О и ш = wo+Aw(O. где lt> и шо — постоянные. В результате получим
d2 d
m (Z° + Д/) + kv {l° + AZ) +
+ kc (l0 + AZ)3 = k (wo + Aw). (1.77)
Из уравнения (1.77) можно получить две зависимости: для опорного движения
>1с10 = Аш0
и в приращениях
m bl + kv AZ + 3kcl3 M = k Aw. (1.78)
Уравнение (1.78) является линейным.
Пример 1.22. Линеаризуем уравнение (1.5) относительно опорной траектории вертикального взлета ЛА, т. е. m(Z) = = m0(Z)+Am(Z) и Zi(Z)—Zio(Z)+Aft(l). Подставив эти соотношения в уравнение (1.5), запишем
d2
[m0 (Z) + Am] [h0 (Z) + ДЛ] +
( d 12
+ M -£-[Ao(<)+ ДЛ] > + I at )
+ [mo (Z) + Am] g = k [m0 (Z) + Am],
(1.79)
Из уравнения (1.79) можно получить две зависимости: относительно опорной траектории
m0 (Z) Но (t) + k0 [/i0(Z)]2 +
+ т0 (Z) g = £А0 0)
2 ГО. И. Топчеев
33
и в приращениях
Ло (0 Am + т0 (t) l\h + 2й0Л0 (/) АЛ +
+ gAm = £Am. (1.80)
Уравнение (1.80) является линейным.
Пример 1.23. Перепишем уравнения (1.12), (1.13) при относительно небольшом изменении высоты полета в виде
dV n pV*S „ ... .
m — = Р cos а - Сх (V, а)-
— mg sin (О — а);
.. d (Ъ — а)
mV —-г-.—- = Р sm а + at
+ ^-Cy(V, а, бв)-
— mg cos (О — а);
(1.81)
Будем считать, что р н Р постоянны.
Для линеаризации системы нелинейных уравнений (1.81) примем
d = до + Ад;
а = а0 + Да;
У = У04-АУ;
<Oz — <*>го 4" Ао)2; бв = бво + Дбв.
(1.82)
Получим системы уравнений для координат опорного движения и приращений относительно опорной траектории.
Относительно координат опорной траектории для движения центра масс ЛА имеем
1 ГР pV0 4Z
— = -[Pcosa0-^-X
X SCX (Vo, a0) — mg sin (du — a9)J;
d (d0 — a0) 1
dt mVa
[P sin a0 +
(1.83)
Pio
4---2~ SCy(Vv, ap, 6Bp) —
— mg cos (dp — a0)].
В общем случае при определении параметров опорного движения необходимо учитывать также и вращение ЛА вокруг центра масс:
A) S64pi/g
^2 — mz (Уо. ctp, др, бвв). (1.84)
Решение задачи формирования опорной траектории движения сводится к решению системы трех приведенных выше нелинейных дифференциальных уравнений. При этом следует учитывать ограничения, которые выбирают из условий, характери
зующих режимы полета ЛА: прямолинейное горизонтальное движение, набор высоты прн неизменной скорости, разгоне или торможение на заданной высоте и т. д.
Рассмотрим пример, когда ЛА набирает высоту при постоянной скорости движения центра масс (Уо). Предположим также, что набор высоты производится с постоянной вертикальной скоростью (Vy = const). Тогда угол наклона траектории полета
Vu
Go = arctg yf- = d0 — g0. (1.85)
* 0
В этом случае уравнения (1.83) можно записать в виде
рУо Р cos a0-------— SCX (Уо, a0) —
— mg sin (d0 — a0) = 0; рУ?
P sin a0 4-----j- SCy (Уо, a0, 6B0) —
— mg cos (d0 — a0) = 0.
(1.86)
Из уравнения (1.84) при условии отсутствия вращения ЛА вокруг центра масс получим уравнения связи между координатами полета и угловым положением рулей высоты бво
тг(Уо. «о. бв0) = 0. (1.87)
Таким образом, можно записать систему нелинейных уравнений
рУ*
Р cos a0----g— scx (Уо. a0) =
= mg sin Go; рУп
P sin a0 4--SCy (Уо. a0> 6Bo)=
= mg cos Go;
mx (Vq* «о. 6Bo) = 0; d0 — a0 = 0.
Решение уравнений (1.88) при заданных значениях скорости полета Уо н наклоне траектории 60 относительно величины тяги Р, угловых координатах d0, ao и положении руля высоты бво определит систему программ изменения этих параметров, обеспечивающих набор высоты ЛА:
Р = Рпр (0;
d0 = dnp (0. go — anp (O'. бво бв пр (О-
С учетом выражений (1.89) система уравнений для приращений, записанных относительно координат опорного движения,
(1.88)
(1.89)
34
будет иметь вид pVoSCx + ^-Cy ~|ои(0 :------------------
Г Vos п
-[Р sin <хо + р —С“+ 1----------1 а.» (0 -
+ mg cos (б0 — a0)J Да — ______________[ — [mg cos (d0 — a0)] Ad;
' 013 (0.
d (Ad - Да) _ ' dt
==^k{[pV°SCHVo-°o.6Bo) +
I____________________
pv|s „1 Г pv2s n
CH AV + [/ c°s«o+-2-c£-
— 021 (Q -’ *---- 022 (0 |---
— mg sin (d0 — a0) j Aa + I
+ [mg sin (d0 — a0)J Ad +
1----- Oj3 (/) |—I
pV2S в I
+ —^-C®»A6Bj; (1.90)
— bu (0 —1
d* Ad 1 Г ...
dt2 ~ L₽^0S64mz a0' d0> 6bo) +
1-------1 031 (0 I---------------
pV2 vl pV?S6. „
+ ~ SbAmvz\ AV + да +
| o32 (0| “
IO35 (t) I I I 634 (t) *
Перепишем полученную систему уравнений в виде
AV = — Оц AV — 012 Ла — Ad;
Д<х == — G21 AV — O22 Ла — — O23 Ad — Ьц Абв + A<oz;
A d>z = a3i AV + а3з Ла + + а35 Лсо2 + 634 А6В.
(1.91)
С помощью системы уравнений (1.91) можно составлять структурные схемы в пространстве состояний (для моделирования систем во времени) или путем «замораживания» коэффициентов и применения преобразования Лапласа находить передаточные функции (для анализа систем в частотной области).
Пример 1.24. Для модели пространственного движения самолета, рассмотренного в примере 1.7 [см. выражения (1.15) — (1.17)], систему линеаризованных уравнений можно записать в виде
Oio (0
Ду = tg d0 (aya sin уо + шго cos Yo) Ay + (wzo sin y0 — cos y0) Ad + 1 Am» —
J------1 g.i (О I------------1 —IQ13 (<) I----------' —I a.» (0 |~
— tg d0 cos Yo Awy + tg d0 sin y0 А<ог;
“| Oi 10 (0 I" “ ai и (0 I"
Дф = cosec d0 (Oyo sin y0 + <ozo cos y0) Ay + (tg d0 cosec d0 (ayB cos y0 — sin y0)) Ad + ' 021 (О I ‘ ’ I 023 (01'
+ (cos Yo cosec d0) Affly — (sin y0 cosec d0) Awz;
I 0210 (0 I j 02 11 (0 |~
Ad = (Wyo cos yo — <0» sin Yo) Ay + sin Yo Ao>y + cos Yo A“z; ’ O31 (() ~ a310 (1)|_ “ Озн (t) ~
AV = m~l [CxpV0S cos £0 -|- 2pV0SCz sin 0O] AV — g cos % Л0 +
---------------- 044 (0 ------------1 " 04S (Op
2
35
+ т 1 [Р (—sin(a0 + фр))со5р0—O,5C“pV0ScosPo] Да +
| Я47 (0 | '
+ m-1 [P (— cos (a0 + <pp)) sin Po + O,5CxpV0S sin 0O + 0,5p V0SCf sin 0O +
IД43 (0
+ 0,5pV2oscz cos Po] др + (o,5m-lpVoSC*H sin Ро)лйн;
Д0 = P (mVt) * [— sin (a0 + <pp) sin y0 + cos (a0 + <pp) sin Po cos y0] — I_________________________________________________________
— O,5m-1pVoSCx sin po cos y0 — O,5m-IpVoSC“ao sin y0 —
------------1 Psi (0 I-------------------------
- 0&n~'pVQSCzcos p0 cos у0 Ду - {p (mV^)-’ [sin (a0 + <pp) cos y0 + ________________________I I_______________________________
+ cos (a0 + qpp) sin Po sin yol — 0,5m~lpSCx sin p0 sin y0 +
+ O,5m-IpSC“a0 cos y0 — 0,5m~ipSCz cos Po sin y0 + gV0 cos 00J Д V +
-------------:--------------------1 a54 (0-----------1
+ gV0 1 sin 0O Д0 + {P (mV0) 1 cos (a0 + фр) cos y0 - P (mV0) 1 sin (a0 + фр) sin p0 sin y0 —
— 0,5m *pV0SC“ sin P0 sin y0 + 0,5m 'pV0SC“ cos y0J Да +
' Д57 (0
+ {P (mV0)-1 cos (a0 + ФР) cos p0 sin y0 — 0,5m“lpV0SCx cos p0 sin y0 —
I_____________________________________________________________
— O,5m-1pV0SC^ cos Po sin y0 + О.бт-'рУдЗСг sin P0 sin y0) ДР —
| ess (01
— 0,5m-1pV0SC2H cos Po sin у0 Д6Н;
ДЯ = sin 0o AV + Vo cos 0o Д0;
L|a84(O|- ~|fl65 (Op
Да = g (V0)-1 sin Y0 Ду + {o.Sm-'CjpSao — 0,5m-1C*BpS6B0 + gV~2 cos y0 —
—I Д7. (0 |— 1-------------------------------------------
— (mV0)-1 sin a0 {CxpV0S cos p0 + 2pV0SCz sin p0) — (mV0)-2 X
X sin a0 {P cos (Oq + фр) cos p0 — mg sin 0O — 0,5p V0SCX cos Pq + 0,5p V2SCZ sin Po}} Д V +
............ Д74 (0 I” ~~~ ~~~~~ r~~~
36
+ gV^2 sin a0 cos 0O Л0 — {o,5m ’C“pV0S + (mV0) 1 sin a0 [P (— sin (a0 + <pp) cos Po) —
1---1 075 (О I-----1 1-------------------------------------------------------
— O,5C“pVoS cos Po] + (ffiV0)-1 cos a0 [p cos (a0 + <pp) cos 0O — O,5pVoSCx cos Po +
+ 0,5p VqSCz sin Po — mg sin 0O]} Да — {ой cos Po + ----------- a?? (0 | ' , '
+ (mV0)-1 sin a0[P (— cos (a0 + <pp) sin Pg) + O,5pFoSCx sin Po +
+ O.SpVgSC^ sin Po + 0,5pV^SCz cos Po] } ДР — sin Po Д<*>ж + 1 Д«2 —
---1 078 (0 | “|07»(0|“ ~| fl7 11 (0 |~
— 0,5m-'pVgSCy8 Д6В — 0,5 (тУ0)-1 sin aopVoSCzH sin Po л6н;
*—| г>7. (0 H J------1 г>78 (О I-----------1
др = cos O0 cos Yo Ду — sin O0 sin Vo ДО + I----------[ fl8i (0 |-* ----1 Oss (01---*
+ { O,5m“lpSC|po + 0,5m”'pSC*“6^ *- V^2gcos O0 sin y0 + (mVo)-1 X 1_____________;___________________________________------------------
X Sin Po [CxpV0S cos Po + 2pV0SCz sin p0] —
— (mVo)1 sin Po [P cos (a0 + <pp) cos p0 — O,5pFoscx cos p0 + O,5pVoSCz sin Po —
------------------;---------------------------------------------1 034 V)-
— mgsin0o] } Д7 — V^1 sin Pgg cos 90 Л0 + {Oxocos a0 + (m^o)-' sinPo X
X [P sin (a0 + <pp) cos Pg - O,5pVoSC“ cos Po] } Да + {o,5/n-1c!*pVos +
+ (mV0)-‘ sin Pg [P cos (a0 + q>p) sin p0 + 0,5CxPVgS sin Po + 0,5pVjjCgS sin Po + + 0,5pV|SCz cos Po] - 0,5pVgSCx cos Po (тГ0)-1 cos p0 + (mV0)~1 cos Po X
X [P cos (a0 + <pp) cos Pg + O,5pVos sin POCZ — mg sin 0O] } ДР + a88 (0
+ sin a0 Дшх + 1 Дшу — {o,5m_1pVos^zH (1 +sin2 Po) }д6н’
~|аз»(0|“ ~| 08 10 (0 |~ ' | ba (/) |
Л“х = {№₽^os/ [Фо + + 0,5VQllm&xifaVt + in*^ + фбэо] +
+ 0,25У7‘рф<[- ^o~2'«x^®x, “ Vllm^a J } ДК + ДР +
-----1 084 (0 |---:------------------- *----1 098(0 |-
37
+ 0,25 (JxV0)^pV^l2mxx Д<ож + {0,25 (ZJCV0)-|pVgS/W> - (Zz - Jy) Jx *a>4 +
--------) «99 (0 | ' | a9 10 (0 |
+ - Jy) ^>z + 0,5/-*р723/т$н Дбн + 0,5Z£*pV|SZmJ9 Дбэ;
-----1 Й9 11(0 | ' ' | 6 92 (0 | " <>93 (0 |
Ашу = {Zy’pVoSifm^ + +
I____________________________
+ О,5и0-Чт^Шж0 + mJ?690 + tn»^] + 0,5 V1 pVjjS/ [- O,5Vo'2<«^“,o “
| ^19 4(0 | "
- О,5Ко~2ХХо] } ЛV + 0,5 (Jy)~l pV§SZm* Ap + [o,25 (JyV0)~l pV2SZ2m“* -
' | «10 8 (0 | a19 9 (0 |
- {Jx - 'z) '7Ч0] A“x + 0,25 (Vo)-1 рф/2«;у M>y + Z;1(Zx-Zz) Awz + ————————— ! | 019 19 (0 | | 019 11(0 |
+ 0,5Z^lpV2SZm®H A5H + 0,5Z“lpV^SZm®9 Д6Э;
1----1 fri02(0 |—1 L—| &i9s(0 |---1
A6Z = {Z^’pVoS^ [mz (Cy) + A7C“a0 + m*» (6в0 - dM) + ОЛ^Хх]-l_____________________________________________________________________
- 0,25 (ZzV20)~‘ pVjfoXX} A V +
| 011 4 (0 “
+ ^J~lpV2SbA [т“(Су) + AxC“] Да - J,1 (Jy-Jx) <*y Дш, + Гг'(}у-1Х) Д®, +
I 011 7 (0 ------------------ '-------1 ан 9 (О I-1 1 «11 io (0 I--
+ 0,25 (ZzV0)-‘ (>V2Sb2Amzx Дшг + 0fiJ~lpV2SbAtn‘ Д6В.
--------Д.и1(0--------1 1-----1 <>i и (0 |J (1.92a)
Приведенной системе уравнений дадим порядковый номер (1.92а).
Коэффициенты системы уравнений (1.92а) зависят от текущих параметров опорного движения
(Yfl’ %- ^0’ V0> ®0’ Н(У %’ 00* “«О’ “(/О’
“го- 6во) (U926)
и в самом общем случае являются функциями времени (at/(t), bti(t)). Рассмотрим способ определения значений координат (1.926), когда в качестве опорного движения выбран прямолинейный горизонтальный полет ЛА без вращения его вокруг центра масс и без скольжения. В этом случае часть координат должны быть приняты равными нулю, т. е. у0 = Фо = 0о = Ро = = Шхв = <о»9 = <0x9 = 0. Кроме того, скорость Ко и высота Яо полета ЛА, а также масса т, как режимные характеристики,
должны быть заданы. Таким образом, задача отыскания параметров опорной траектории сводится к вычислению Фо = «о, 6>д и величины потребной тяги Р = Ро- Как видно из выражений правых частей нелинейных уравнений (1.15), для обеспечения прямолинейной горизонтальной траектории необходимо выполнение следующих условий:
V == -L {р0 cos (а0 + <рр) — X) = 0;
0 = —V {Ро sin (а0 + Фр) + Y + mg] = 0; tnv
<az — -j~ Мг = 0. ~
(1.93)
Заменив в системе уравнений (1.93) X, Y, Мг их выражениями, получим систему
38
уравнения относительно искомых параметров
Л (Ль а0, бво) == Po cos (Оо + Фр) —
Р(^о)Ф
-------2----Сх ^СУ' = °’
ft (Ро, Ио, 6во) = Po 5>п (ао + Фр) +
Р (*о) VoS
4- П_^_о_ Cs/ (Д1_ 6в01 ао_ аз) + mg = 0.
(з (Ро, Ио, 6в9) —
— тг(М, Су, бв0, Ро, Дх(т)) = 0.
(1.94)
Решение системы (1.94) может быть получено любым нз существующих методов определения корней нелинейных уравнений, а также путем минимизации функции вида з
Р = £ dfi (Ро, ао, б*,), где d{^0. (1.95) i-i
Найденные значения Ро, а0, 6в0 известны как балансировочные параметры полета ЛА и являются нелинейными функциями режимных характеристик Но, Ро, т.
Подставив значения параметров опорной траектории в выражения для коэффициентов at/ и bi/ из достаточно громоздкой системы уравнений (1.92а), получим
Ду = 019 А(Дх ~~ П1 ю Д<в^;
Дф === Од ю Асо^;
Af> = а3 11 A<oz;
ДР = а44 ДР — а45 ДО + а31 Да;
ДО = а54 ДР + а57 Да;
АЯ = ав5 ДО;
Да = O74 ДР + П75 ДО + O77 Да 4-
+ а7в ЛР + о? и Аи2 — 671 А6В;
Д^ == O31 Ду + Оз4*гДР + Пет Да +
4- Пзз ДР + Пвэ Аоож 4* Пз ю А<в^ — — 632 Дбн»
Дшх = а98 др 4- а» Дсож 4- а9 ю &®у 4-
4- 692 А6Н 4- 693 А6Э;
Дйу = ею з ДР 4" пю 9 Лфх 4" Пю ю А<о^ 4-4" Пю 11 Д<*>г 4- 610 г Л6Н 4-610 3 А6Э;
ДсЬг== П] 14 АР 4* О] 17 Да 4- Oi 1 i j Дсо2 4-4" 6i и Д6В.
(1.96)
Система дифференциальных уравнений (1.96) является линейной относительно приращений соответствующих переменных.
Четвертый метод линеаризации.
Он основан на определении коэффициентов по методу наименьших квадратов. Рассмотрим два случая.
Первый случай. Функция у = = f(x) задается таблицами. Тогда коэффициент линеаризации
Е Ау, Ах, а = -^------- прип>1 (1.97)
Е (*xi)2 i-l
и линеаризованное уравнение можно записать в виде
Ду = а Ах. ' (1.98)
Второй случай. Функция зависит от двух переменных y = f(xi,x2). Тогда коэффициенты линеаризации
z п \2
~I Е ЛХИ ЛХ2< ) \i-l /
(1.99)
В этом случае линеаризованное уравнение представим как
Ду = а Ах! + b Лх2. (1.100)
Когда нелинейная зависимость выражается аналитически, то соответствующие суммы следует заменить интегралами. Для одной переменной вместо выражения (1.97) запишем
Дхо Д/ (Лх) Дх«/ (Дх)
= ------------• (ШОП
Ax2d (Дх) — Дхо
39
Таблица 1.1
Линеаризация функции у = хп по методу наименьших квадратов
Коэффициент усиления Разложение функции в ряд Тейлора в точке хо Погрешность данного метода линеаризации
1 Ду = Дх 0
2х0 Ду = 2х0 Дх + Дх2 Дх2
3х0 + У (Дхо)2 Ду = Зхц Дх + Зх0 Дх2 + Дх3 3(х°“4) Дх2 + Дх3
4хо + -у- <Лх°)2 Ду = 4Xq Дх + бХц Дх2 + + 4х0 Дх3 + Дх4 6(х«_т) Дх2+ + 4х0 Дх3 + Дх4
5*о + 4 хо д*2 + + у(дх0)4 Ду = 5хд Дх + Юхд Дх2 + 10х2 Дх3 4-+ 5Хц Дх4 + Дх5 х2(10х0--|-) Дх2 + + lOxjj Дх3 + + (бх0 — у) Дх4 + Дх5
где Дх0 и —Дхо — предельные отклонения от рабочей точки, для которых с заданной точностью выполняется линеаризация; Дх — переменная интегрирования. Для двух переменных имеем [39]
ДХо1 Дх02
J Д[ (Дх,) Дх, х
— Дхо1 — Дхи
X Axfd (Дх,) d (Дх2) -Дхо1 ДХ02
- J j Д[ (Дх2) Дх, X — Дх«1 — Дх»2
__________X Ax|d (Ах,) d (Дх2) Дхо2 *
j Дх, Ьх22 X
— Дхы — Дхо2
X d (Дх,) d (Дх2) — [Дх01 ДХ02
j Дх, Дх2 х -Дхм — ДХ02
X d (Дхг) d (Дх2)12
Axoi Дхоз
j Д[ (Дх2) Дх2Дх2Х
- Дхо1 — ДХ02
X d (Дх,) d (Дх2) —
ДХ01 ДХоз
- j J Д((Дх,)Дх,Х
— ДХ01 ”“ДХ(>2
X Дх2 d (Дх,) d (Дх2)
Дх«1 Дхо2
j Дх2 Дх| X
— Дхо1 — Дхоз
X d (Дх,) d (Дх2) —
[Дх» Дхм
5 ' ДХ1 д*г х
— ДХ01 — ДХ«2
]2.
Пример 1.25. Линеаризуем функцию у = = х" [39] для я > 0 (см. пример 1.16) вблизи точки хь; тогда получим
Ду = лх" 1 Дх. (1.104)
По методу наименьших квадратов определим
(1.102)
40
ДУ = (х0 + дх)п - х" (1-105)
Подставив соотношения (1.104) и (1.105) в (1.101), найдем
Дх0
j [(х0 + Дх)" — х"] Axd (Дх)
— ДХо
ДХо
j (Дх)2 d (Дх)
—Дхо
(1.106)
Рассмотрим систему уравнений вида
У\ =^111/1 + Уъ
У 2 — 0211/1 + 0221/2 + Уз + О24«/4;
Уз — Оз11/1 + а321/2 + О33У3 +
1/4 = 0441/4 + 640;
х =?= Clyi + c^t.
(1.108)
После интегрирования (1.106) получим
Перепишем систему (1.108) в обычной векторно-матричной фор-
ме
а =
[^]
_ к-1
(Д*о)3
(1.107)
Пользуясь формулой (1.107), составим табл. 1.1 коэффициентов усиления при изменении п от 1 до 5, из которой видно, что по мере роста степени погрешность линеаризации по методу наименьших квадратов возрастает.
3. ТИПЫ УРАВНЕНИИ СОСТОЯНИЯ
Уравнения (1.54) —(1.57) являются уравнениями состояния динамического элемента системы автоматического регулирования, записанные в принятых проектировщиком переменных. Эти уравнения можно записать и через другие переменные; тогда при удачном их выборе получим наиболее простую форму представления элемента. Следует иметь в виду, что описания динамики системы с помощью различных наборов переменных состояния всегда однозначно связаны между собой.
Уравнения состояния применяют при математическом и аналоговом моделировании динамических элементов, результатом которого являются соответствующие переходные процессы.
у *= Ау + Ьи;
х = с*у,
(1.109)
где
~alt 1 0 0“
а21 022 ч 1 О24
O31 а32 Озз 1
_ 0 0 0 а44 _
О
О
cT = [ci 0 0 с4].
Располагая математическими зависимостями (1.108) или (1.109), нетрудно составить структурную схему системы для аналогового или цифрового моделирования динамических процессов (рис. 1.8). При этом видно, что в систему, описываемую уравнением 4-го порядка, входят переменные состояния: yi — Уа. Причем выходом каждого интегратора является одна из указанных переменных, а их нумерация возрастает справа налево. При таком представлении можно определить различные пути передачи сигналов непосредственно в матрице А, что упрощает получение обобщенной формы представления математических моделей элементов.
41
Рис. 1.8. Структурная схема динамического элемента системы без перекрещивающихся связей для моделирования переходных процессов
Рассмотрим систему уравнений вида
У 1 = апУ1 + у2 + ai3y3 + аыу4 +
# 2 = ^21 У\ + О-22.У1 4“ Уз + 4“ ^2«;
* /з = Оз1У 1 4“ йззУз 4“ а33*/з 4- «/4 4- Ъ3и\ У 4 = ацУ1 4- а42у2+а^у3+аиу4+Ь4и;
х = С1У1 4- С2у2 + С3у3 + C4Z/4.
(1.110)
Соответствующие системе уравнений (1.110) матрицу А и векторы Ь, ст можно записать в форме
Оц 1 013 а14
ч \ ч
<*21 <*22 1 ^24
<*31 <*32 <*33 1
ч
х х _<*41 <*42 а43 ^44 _
ст = [сх с2 с3 с4].
(1.111)
Пользуясь формами записи (1.110) и (1.111), составим структурную схему (рис. 1.9). При этом видно, что в схеме присутствуют перекрестные обратные связи, которые вносят определенные трудности в процесс проведения математическо
го моделирования на аналоговых и цифровых машинах.
Для проверки правильности составления структурных схем следует пользоваться правилами:
наддиагональные элементы матрицы А характеризуют передачу сигналов по прямой цепи связи;
диагональные — по цепям обратных связей;
поддиагональные элементы матрицы — по всем остальным цепям обратных связей;
элементы векторов Ь определяют воздействия входа на переменные состояния;
элементы строки ст указывают долю вклада сигналов состояния в сигнал выхода системы.
Структурные схемы систем без перекрещивающихся связей можно представить в виде последовательного соединения подсистем. Так, например, схема, изображенная на рис. 1.8, является последовательным соединением двух подсистем Si и S2 (рис. 1.10).
При исследовании динамических элементов (или систем автоматического регулирования) методами моделирования принято пользоваться двумя типами уравнений состояния— каноническими и нормальными.
Канонические уравнения состояния’ получают путем составления жордановой канонической формы
42
Рис. 1.9. Структурная схема динамического элемента системы с перекрещивающимися связями для моделирования переходных процессов
матриц *. В этом случае систему (1.109) можно записать в виде
Укя — Лжукн 6khU;
X = Ст О , кн кн»ки’
(1.112)
* См. прил. П-1.1.
Рис. 1.10. Структурная схема динамического элемента системы, состоящая из двух последовательно соединенных подсистем Si и S2 (получена из рис. 1.8)
43
где матрица и вектор имеют следующий вид:
Xj (Oj О О
\ п гМ
Л = а2 л2 о 0
Ж 0 0 \ (03 ’ 6кн== ь3 ;
_ 0 0 <т4 Л4_ 4
Скя ~ [С1 С2 С3 CJ-
Откуда нетрудно получить систему
#кн, = а-Х^кн, + МКН2 + blU>
Укн2 = C2f/KHl + ЧУкъ + Ь2и> ^киэ^^кНз.+ ^З^ + М; ^к4=стлн, + МКН1 + й4и; , ’
хкк = сЛн1 + с2г/КН2 +
+ СзУ*ъ + С^кк4-
Пользуясь системой уравнений (1.113), представим структурную схему в жордановой канонической форме (рис. 1.11). Ее можно изобразить в виде двух параллельно соединенных систем Si и S2 (рис. 1.12).
Произвольная система уравнений (1.109) приводится к канонической форме (1.112) с помощью линейных преобразований вида
Рис. 1.11. Структурная схема динамического элемента, описываемого матрицей в жордановой канонической форме
Л.ж -— 1>жАКж>
Ькя == ^„ = 0^,
(1.Н4)
где /?ж и £ж — матрицы преобразования к жордановой канонической форме.
Очевидно, что жорданона действительная матрица Лж эквивалентна диагональной комплексной матрице Л, так как они связаны следующим унитарным преобразованием:
Н1ЛЖН = Л, (1.115)
где Н.— матрица преобразования (см. приложение П-1.1).
Нормальные уравнения состоя-
ния запишем в виде
х = сти . I '
и и» и /
Исходная система уравнений (1.108) в нормальной форме (1.116) может быть записана с помощью следующих матриц и векторов:
г° 1 0 0 - гМ
0 0 1 0 £>2
Л = 0 0 0 1 : &и = *>3
-Hi Н2 Нз М-4 - Ld4J
ЙТ = сн = [1 0 0 0].
44
Рис. 1.12. Структурная схема динамического элемента системы, состоящая из двух параллельно соединенных подсистем Si и S2
Из уравнений (1.116) получим систему уравнений в нормальной форме:
г/На=уНз + М;
К — ^н< + М> (1 117)
^=1‘Л + М« + |‘зУн,+
+ Мщ +
хн = УЯ1-
На рис. 1.13, а показана структурная схема в нормальной форме, описываемая системой уравнений (1.117).
Систему уравнений (1.109) можно привести к нормальной форме (1.116) с помощью линейных преобразований
AH==GAG-1. (1.118) где G — матрица преобразования (см. прил. П-1.1).
Векторы преобразуют с помощью соотношений
&н = Gb;
Т__ тг-1 f
Сн = С О . )
(1.119)
Если в качестве матрицы преобразования G выбрать матрицу управляемости G — [б ; АЬ • ... ... • Ап-1&], то матрица Ан и векторы Ь№ и ся в уравнениях (1.116) будут иметь следующую структуру:
ГН1 1 0 О-. |х2 0 10 Из ° 0 1 - 0 0 0 -
Тогда система дифференциальных уравнений в нормальной форме
примет вид
Мн, + ^,5 ^=Мн,+^
^н.= Мн,+«'> ХИ = С1УИ1 + С2УИ1 +
+ + сЛг
(1.120)
Структурная схема системы в нормальной форме, соответствующая уравнениям (1.120), показана на рис. 1.13,6.
Системы уравнений (1.109), (1.112) и (1.116) соответственно, с матрицами А, Аж и Ан являются эквивалентными, т. е. описывают один и тот же динамический элемент. Из сравнения этих матриц следует, что наиболее удобной си-
45
Рис. 1.13. Структурные схемы динамического элемента, описываемого матрицей в нормальной форме:
а—после линейного преобразования ЛН=«ОЛО—I. б—при О=[а • ЛЬ : — • Лп~
стемой уравнений для исследований является система с матрицей жорданового вида, так как она содержит больше всего нулей. При ее использовании значительно упрощаются вычислительные процедуры на ЭВМ для анализа элементов, описываемых дифференциальными уравнениями высокой размерности.
4. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ТИПОВЫХ ЗВЕНЬЕВ
При проектировании САР наряду с методами, основанными на использовании уравнений состояния, часто применяют способы, базирую
щиеся на представлении элементов (объектов) в виде передаточных функций. Такой подход обладает значительной наглядностью и приводит проектировщика к структурным схемам или графам, с помощью которых можно сложные элементы привести к совокупности простых методами декомпозиции. Естественно, что анализ и синтез простых элементов не требуют значительных затрат времени и упрощают выбор их параметров. Такой подход часто применяют даже при проектировании многомерных систем регулирования.
Для получения передаточных функций линейные дифференциальные уравнения динамических элементов записывают не через оригиналы функций у (t), x(t). при
t > 0, а с помощью прямого преоб
46
разования Лапласа (1.121) приводят к изображениям функций У(з), X(s), которые записывают прописными буквами в виде
О©
У(«)= J e^(Od(0 = ^{y(O}, О
(1.121) или Y (з) -е- у (t), где 3? — символ прямого преобразования Лапласа-, s — оператор * *.
Наряду с прямым преобразованием Лапласа в теории автоматического регулирования применяют и обратное преобразование Лапласа **.
Разностные уравнения записывают в виде последовательности дискретных сигналов y(tK), x(tK), ..(к = 0,1, ...) или с помощью такта квантования То в видеу(кТ’о), x(kTq),... Если применить к этим переменным прямое дискретное преобразование Лапласа, тогда для у(кТ0) имеем
со
Y*(s)=Zyme-SKT‘. (1.122) к-0
Иногда дискретные сигналы записывают в виде *** y*(t), ...
Здесь у* (/) — модулированная последовательность б-фуикций, т. е.
со
/(0 = У(0Еб(/-кГо), (1.123) к-0
и соотношение (1.122) с учетом выражения (1.123) будет
СО
Y* ($) = j у* (0 e~st dt, (1.124)**** о
или
Y* (s)^-y*(t).
* При исследовании элементов и САР оператор s заменяют комплексной переменной, записываемой относительно круговой частоты <о.
** Применение обратного преобразования Лапласа описано в гл. 5, п. 3.
*** Дискретные значения оригинала н изображений обозначают звездочкой.
**** Если подставить в соотиошеиие (1.124) выражение (1.123), то получим
оа со
Г(8)«^у(кТ0) д(/-/сГо)е-*кГ<|Л,
к—0 0
откуда найдем соотношение (1.122).
При практическом применении преобразований Лапласа операции ведут не над заданными функциями, а над их изображениями. Для получения изображений необходимо пользоваться некоторыми правилами отображения (свойствами s-преобразования), наиболее важные из которых приведены в табл. 1.2.
Y(s)^-y(t)-
Y'(s)^-ty{t)\
У"($)«*-/2у(0;
(1.125)
y<»)(s)45-(-l)n tny(t),
и для интегрирования изображений
^У(а)б/а^^-. (1.126)
С помощью преобразования Лапласа можно получать передаточные функции по линейным дифференциальным уравнениям, описывающим динамические процессы в стационарных и нестационарных элементах (объектах). В стационарных элементах коэффициенты являются постоянными, поэтому передаточная функция постоянна и ее параметры не зависят от времени *. В нестационарных элементах коэффициенты меняются от времени и передаточная функция представляет собой сумму членов ряда, каждый из которых определяется характером изменения как самого параметра от времени, так и его производных. Чем выше степень нестационарности элемента (объекта), тем больше приходится брать членов ряда. Если параметры изменяются на некотором интервале времени не более чем на 20 % [12], то можно пользоваться
* В прил. П-1.2 приведены таблицы s-преобразований простейших функций.
47
Таблица 1.2
Основные свойства «-преобразования
Наименование свойства Форма представления в виде
оригинала «-преобразования
Линейность S’ {Л1У1 (t) ± а2у2 (t)} aiYt (s) ± a2Y (s)
Изменение масштаба S?{y(at)}, а>0 »|-ft 1*1 I
Дифференцирование оригинала 3?{y(n>(t)}. rty(n-l)(s)
Интегрирование оригинала 3? | У (т) dr | Y(s) s -
Сдвиг аргумента от оригинала при t^O 35 (у (t — а)}, а > 0 e~asY (s)
Свертка оригиналов 35 {yi (t) ® у2 (t)} Yt (s) Y2 (s)
Дифференцирование изображения 35 {(-l)n t*y (t)} Y(n>(s)
Интегрирование изображения У (t) 1 If J oo $ Y(s)ds 0
Сдвиг аргумента у изображения e“fy (t) Y(s-a)
Предельное соотношение ^(lim y(t, a)\ <а->а > lim Y (s, a) a + a
Так как изображение всегда является аналитической функцией, то можно записать соотношения для производных изображений.
методом «замороженных» коэффициентов. Иногда для каждого интервала времени получается своя передаточная функция с постоянными параметрами.
Стационарные элементы (объекты)
Применение преобразования Лапласа к линейным обыкновенным дифференциальным уравнениям. С помощью табл. 1.2 и соотношений (1.125) применим прямое преобразование Лапласа к некоторым ти
пам линейных дифференциальных уравнений с сосредоточенными постоянными.
Пример 1.26. Допустим, что объект САР выражен в виде однородного дифференциального уравнения
а0У(П> + “У"-0 +•••
••• +%_,«/' + %'/= °- (1-127)
Зададим произвольные начальные условия
У (to), У' (to).у(п”1) (t0);
48
тогда запишем
иием вида
аа [snr (s) — у (/о) sn-1 — у' (/0) sn 2 — ...
• - J/(n-2> (А>) s - У(п-1)(<о)1 +
+ aI[sn-1r(s)-y(/0)sn-2 -
— y' (t0) sn~3 — ... — y(n-2) (fo)l + • • ... +an-i [sK (s) — у (f0)] + anY (s)—O.
(1.128)
Если данный объект описывается в виде неоднородного дифференциального уравнения, то
аоу{п) + aty<n~l} + ... + an_ty' + апу = «= M(m> + +... + &«_!«' +
+ bmu. (1.129)
Зададим следующие начальные условия:
У (io), у'(io)..у(п-1) (М;
и (to), и'(to)..«(т-1)(<о);
тогда получим
а0 [snr (s) — у (to) sn~l — у' (to) sn~2 — ...
• •• — У(п~2) (to) s — y(n-1) (f0>] +
+ ai [s'*-* Y (s) — у (to) sn~2 —
- У' (to) sn~3 — ... - y(n~2) (to)] + • • • ... + an_t [sF (s) — у (to) + anY (s)] =
= b0 [smC7 (s)—и (t0)sm~l — u' (t0) sm~2—...
... -u'm~2>(to)s- (/„)] +
+ &. [sm-‘£/ (s) - и (to) s'”-2 -
- u' (to) sm~3 - ... - u<m-2> (t„)] + ... ... + (st/ (s) - и (to)] + bmU (s).
(1.130)
Из приведенных зависимостей примера 1.26 следует, что с помощью прямого преобразования Лапласа дифференциальные уравнения вида (1.127) н (1.128) можно привести к алгебраическим уравнениям, что значительно упрощает методы исследования объектов. В работе [17] приведены таблицы для прямого и обратного «-преобразований различных функций.
Применение преобразования Лапласа -к Интегродифференциамным уравнениям.
Пример 1.27. Допустим, что САР описывается иитегродифференциальиым уравие-
аоу(п) + ail/'* ° + ... +an-iy' + t
+ апу + a„+! j у (r) dr = bou{m} 4-c>
+ &1и*т *> + ... + bm-iy' + bmu + t
+ 6m+i и (r) dr. (1.131) о
Тогда, применив к уравнению (1.131) прямое преобразование Лапласа при нулевых начальных условиях, получим
aosnY (s) + alSn~lY (s) + ...
... + an-isY (s) + anY (s) + an+x = = basmU (s) + blSm~'V (s) + ...
.. • + bm_\sU (s) + bmU (s) + frm+1-
(1.132)
Применение преобразования Лапласа к интегральнным уравнениям. Обычно в практических задачах встречаются интегральные уравнения типа свертки: 1-го рода t
g(t)=\k(t-x)f(x)dx-, (1.133) о
2-го рода *
f (О = S (0 + $ k (t — T)f (т) dx, о
(1.134) где f(t)—искомая функция; k(t) и g(t) — заданные функции. .
Интегральные уравнения 1-го рода приводятся к «-преобразованию только в тех случаях, когда их можно преобразовать в интегральные уравнения 2-го рода.
Рассмотрим преобразование Лапласа для интегральных уравнений 2-го рода, когда интеграл абсолютно сходится. Тогда оригинал уравнения (1.134) после «-преобразования примет следующий вид:
F(s) = G(s) + K(s)F(«), (1.135) решение которого даст
49
В выражении (1.136) функция F(s) не допускает непосредственного применения обратного преобразования Лапласа. Для выполнения данной процедуры выражение (1.136) следует переписать в виде
F (s) = G (s) + G (s). (1.137)
Тогда функция
«В-гаЬ- (1138)
имеет оригинал q(t).
Решение (1.137) можно привести к оригиналу, т. е.
= + (1.139)
Имея в виду свертку q®g, из выражения (1.139) найдем
g(t) = f(t) + (~q)®g. (1-140)
Как следует из соотношения (1.140), в исходном интегральном уравнении (1.134) ядро k(t) заменено взаимным ядром —q (t), а функции fug поменялись местами.
Пример 1.28. Найдем изображение Q(s), если ядро интегрального уравнения (1.134) имеет вид
k (0 = а0 + в) (О + • • • + яп/п,
Пример 1.29. Найти изображение G(s) для интегрального уравнения
.• t
g (t) = (1 — т)~“ f (т) dx = g (/), о
0 < а < 1.
Положив f ® 1 = <р (/) и ’имея в виду, что
= (1J44)
получим следующее уравнение:
_7g) <D(s) = G(s). (1.145)
S
В формулах (1.144) и (1.145) символом Г обозначена гамма-функция.
Решением уравнения (1.145) будет
ф (S) ------!---- g (S). (U46)
Г(1—a)s“
Соотношение (1.146) представляет собой изображение функций интегрального уравнения 1-го рода.
Применение преобразования Лапласа к дифференциальным уравнениям в частных производных. Если исследуемая САР представляет собой систему с распределенными параметрами, то ее следует описывать уравнениями в частных производных.
откуда
К(«) = -7- + -^Г-+ ... +-^г- (1-141)
Пример 1.30. Допустим, что объект системы описывается системой дифференциальных уравнений в частных производных
вида
Подставив соотношение (1.141) в формулу (1.138), получим
О (si = — a°s" + Hflis"-1 + ... + д!ап sn+1— aosn — llais"-1 —... —-nl an
(1.142)
Выражение (1.142) и представляет собой изображение для интегрального уравнения £го рода.
Рассмотрим интегральное уравнение 1-го рода (1.133) при условии, что функции £(/) и g(t) дифференцируемы и k (0)^0; тогда после дифференцирования уравнения (1.133) найдем
t
k (0) f (t) + J k'(t — x)f(x) dx = g' (/), о
(1.143)
dv ду
a2
+> + ^ = 0;
ди ду
dv
dt
(1-147)
где v(f), u(t) — переменные, а g, и и а — параметры объекта.
Применим к системе уравнений (1.147) преобразование Лапласа; тогда получим
dV dy
dU dy
— sU — kU; g
g a2
sV.
(1.148)
которое можно привести к изображению вида (1.137).
Продифференцируем уравнения no t/, т. e.
d2V Г -y/s js + k) ]2
dy2 =L a J '
d2U Г Vs(s + fe) I2 dy2 “ L a J
(1.148)
. (1.149)
g
50
Решение системы уравнений (1.149) можно записать в виде
Vs(s+fc) f _ Vs(s+*> t
V(s) = C,e a +Cte a ;
Vs(s-t-ft) * _ Vs(s+fc)
£J(s) = C3e a +C4e a
(1.150)
где Ci—C< — произвольные постоянные.
Для их определения воспользуемся следующими краевыми условиями:
о=О; у = Z;
тогда из первого уравнения системы (1.150) получим
Vs(s+fe) _ Vs(s+fe)
С.е » = -С,е а . (1.151)
Имея в виду соотношение (1.151) и используя уравнения (1.148) —(1.150), найдем
С3 =--------. g :.-sCf,
a^s (s + k)
C4 . g — sCi. a^/s (s + k)
(1.152)
Подставляя значения C3 и C< во второе уравнение (1.150) и учитывая соотношение (1.151), получим
[Vs (s+*> у е “
— е “ J;
[Vs(s+*> и е ° +
j£S±E gs
a Vs (s + k) / (1.153) При у = 0 и т = l/а из системы (1.153) получим
[_ Vs(s+A) t Vs(s+*) 1 е “ - е “ J;
[Vs(s+ft) ______ е~ ° +
Vs(s+fc) _1
+ е---~ J- gs
ai/s(s + k)
(1.154)
Составим передаточные функции для непрерывных элементов (объектов). Под передаточной функцией стационарных элементов понимают отношение изображения вы
ходной величины к изображению функции входной величины, полученные при нулевых начальных условиях. Если в примере 1.26 в формуле (1.130) примем нулевые начальные условия, то получим передаточную функцию вида
пт, /а _ Z-Ш. и-£/(s)
V'n + M'n“l + M'n"2+ •••
••• +6m-ls + 6m Oqs" + ajs"-1 + a<^~2 + ... ... +a„_is + a„
(1.155)
Для примера 1.27 имеем
bgSm + blsm-1 + b2sm~2+...
+bm-ls + bm + ^-
-----n------------zzr2----- (1.156)
Oqs" + n^s + a^n 2 + ...
•••+*„-!* +*n + -^±L
и для примера 1.30 найдем
П7^_^)» ал/sd + k)
W - 7Г&-------------X
Vs (s+k) Vs (s+k) t e~ a - e a У ... -__ . . _ s=
Vs (s-t-fe) x Vs (s+k} e" a +e a
__ a*Js (s-\-k) .. f Vs (s + k) gs \ a J'
(1.157)
Из выражения (1.157) видим, что передаточная функция рассматриваемого элемента является трансцендентной.
Нестационарные элементы (объекты)
Для простоты изложения примем, что нестационарный элемент описывается дифференциальным уравнением
г(0^-+^(0=М(0. (1-158)
51
где’ Т(t)— постоянная нестационарного элемента, зависящая от времени; Лу — коэффициент усиления, не зависящий от времени.
Определим передаточную функцию данного элемента в форме Заде [12], введя для этого следующее обозначение: D(p,t) = = T(f)p-\-\, Здесь p=d/dt— символ дифференцирования. Имея это в виду, уравнение (1.58) перепишем в виде
D(p, t) у (t) = kyii (t). (1.159)
Введя импульсную переходную функцию в уравнение (1.159), получим
D(p, t)k(t, x) = kyd(t — x), (1.160) где k(t, т) — импульсная переходная функция элемента; б(/—т)— дельта-функция, приложенная в момент t = х.
Выполним преобразование Фурье для уравнения (1.160); тогда найдем
D{p,t)W0(s, f)es< = £yesf, О-161) где H5q(s, t) — передаточная функция, зависящая от времени, которая имеет вид
4-00
1Г0 (5> 0 = j k (t, х) е~s (<~тМт.
(1.162)
Разложим D(p, t)u(t)v(t) по степеням р и запишем в виде суммы двух членов, т. е.
£>(р, t)u(t)v(t) = u(t)D(p, +
(1-163)
Полагая в выражении (1.163) u(t) — W0(s, t) и v = es<, найдем
D(s, t) W0(s, i)est = W0(s, t)X
XD(p, +
(1.164)
Если в выражении (1.164) ко-жж dD(s, t)
эффициенты —относительно медленно меняются от времени, что
соответствует медленному изменению T(t) в уравнении (1.158), то решение уравнения (1.164) можно получить, пользуясь методом итераций. В этом случае, пренебрегая производными передаточной функции H70(s, t), найдем решение в виде ряда
ir0(s, 0 = ^(5, t) + W2(s, 0+ ...
...+U7„(s, П- (1-165)
Очевидно, что первое приближение Wi (s, t) даст передаточную функцию с медленно меняющимися параметрами T(t) уравнения (1.158), т. е. для «замороженного» коэффициента T(ti) в момент времени ti.
Пользуясь выражением (1.164), оценим точность метода «замороженных» коэффициентов применительно к уравнению (1.158). Для этого последнее перепихнем в виде
d[7-(/)s+l] dWe(s,t) , ds dt '
+ [T(t)s+\]W0(s,t) = ky, (1.166)
откуда найдем
Лу
(S> = Г (/) s + 1 ~
Т (t) dlT, (s, t) ]fi7.
T (/) s + 1 dt ' (l-l67)
При первом приближении из выражения (1.167) имеем
Wi (s, t) — U?! (s, t) — T s + j ,
(1.168)
где T является постоянным параметром для каждого момента времени ti.
Второй член ряда
1F2(s, /) =
-Т (о kyr (t) T(t)s+1 (Г(/)5-ЫР •
(1.169)
Тогда из выражений (1.168) и
(1.169) получим передаточную функцию второго приближения в
52
Таблица 1.3
Передаточные функции элементов! объектов) систем автоматическою регулирования
№ п/п Наименование элемента или объекта системы Схема элемента или объекта Передаточная функция элемента или объекта Параметры передаточной Функции
1 Механическая передача (редуктор) *’\ Г\г1 U-4-PJ > »«!- Z 2, углы поворо- н ) J > й—4 та валов 7\j Wfs)-*Z<!’.L *, <s> 19еГГ~переда' Zf точное число редуктора
2 Рычаг «1 г w(s)- . 2 x, (s) Kp К - г2 ' г,
3 Транзисторный усилитель переменного тока р i у I 'С glffi}2 —о ' 1 U,(s) K3 “г-\ где к-коэффициент усиления каскада
Силыронный датчик давления ТД ГД—. W(S)-I^>.K3 1 P(s) ,a “г-*аР> где Kj-передаточный коэффициент сильфона
5 Сельсинная пара в трансформатор -нот режиме 0 S ^2“яс 0. где ^-коэффициент трансформа ции сельсинов
б Термо-сопротивление |^аз VYVVYVYVY4 ^*4 У7777777Л Х777) ' “«ых 1 tSr-",. ^•кгс чв, где кТ-коэффициент усиления термосопротивления
7 Электрический анализатор газов Газ XL ц f t воздух W(sj^ -Ut<Si - Kr ^0^ ^8акг фсо2. где ^СОГ шичество увлеки слово гада, кГ-козффициент пропорциональности.
63
Продолжение та Ил. 1.3
в Угольный, ватник давления С “в с £ НН
rT2gjJ ТГ
л с-
пвродаточный
коэффициент угольного столбика.
Магнитный усилитель
W(s) -
Ut(s)
U,(s)
Ту-постаянная Времени обмотки управления магнитного усилителя;
к ^-коэффициент усиления
Wfs)
Ut(s) кг
Ut(s) ~TtS.1
T9 - постоянная Времени обмотки возбуждения
^кГ~козффициенгл усиления генератора по напряжению
Резервуар с жидкостью
Дизель
Win} - —rsi .
!> U,(s) ТпЛ.1
W(s>-
Hts)
Sts)
Ts + 1
А -
Z(s) Tas+1
Тт(1-постоянная термопары;
Ктп -позририциент усиления термопары
2!p,-rnjm-pj i T' r<p,-P,i ?
*---------------
где У- удельный дес жидкости;
Ь0-максимальная Высота подъем а жидкости
Тв - постоянная времени дизеля
к д — передаточный коэффициент дизеля
54
ПроВолжсиие mal/itJ
/* Ресивер 1 т-|- AW _ Jff Wl' i,(s} Trs+t Тр-постоянная времени ресивера к^-передоточный козрнрициент ресивера
15 Тиратронный усилитель 1 И- \г =£] W(s) - ls^ - *™ Т^-оостоянная времени тиратронного усилители к-тц-коэффициент усиления тиратронного усилителя
г -8ч "•>'0' ч ГТ71 1 U,(s) rTas*l
t6 Тиристорный преобразователь мощности на постоянном токе °""ж *н, 1ц,1н ""Лгт-1—п— j)4 W(s) - • K 11 a(s) T„3<-1 det еде 1н-ток нагрузки, ос.-угол открытия тиристора; Тн -постоянная времени нагрузки
n Настовой тиристорный преобразователь яастояяною тока ]лн.£н w(s)-h^- lP/ Л(3) TTfs+1 кТр-козффициент . усиления тиристорного преобразователя по току-, ^‘Постоянная времени нагрузки тиристорного преобразователя
£ j)w, (i
IE j)V-5.
IB Тиристорный преобразователь мощности с питанием на переменном токе Vfls)- - &- ff. is) 7Tp s*1 к*г-козф(рициеит усиления тиристорного преобразователя по току-, Trf -постоянная времени нагрузки тиристорного преобразователь
< U /ОТ \сл
1 Y5, A «3 Ю,
c 'C’V
IB Однокаскадный гидравлический усилитель со струйной трубкой 1 ) ± j /ъ up ♦ Рг Т Pi pts) Tn s*t кгу - передаточный коэффициент гидравлического усилителя-, Тп- постоянная времени гидравлического усилителя-, г —постоянная запаздывания в пневмопроводах
55
Продолжение табл. 1.3
20 Механотрон 4~~|г~~Т^а' H J. W(si - V* W _wm L(s) TMs4 кп-козффициент усиления межанотрона-, Тм~постоянная времени межанотрона
2/ Мембранные преобразователи, с жидкостным наполнителем 4, wisl- Xl,IS' - 11 PIS) T'S-rl кк-передатйчный коэффициент мембранного преобразователя-, Т„ -постоянная времени мембранного преобразователя
22 Турборасходомер с улругосвязаннын ротором t f' ——В?ц* WIS)--^^- --,<"|, V(6> T,fl4 к „^коэффициент преобразования-, Тк« постоянная времени . крыльчатки
гз Интегрирующий операционный усилитель с Я П-—J Lp_1 ц2 W(S)_£1M._L E,(s) TKs
24 Пневматический интеератор ws! , —^1 J_ P, IS)-Pits) T,s Р- Y кр,->№- Л уяи Т„~ V
а Pl at — - d_ У p
Pl а :с Г-I—
25 Тахогенератор х 1 о N S “тг “° wts!-^r-^ к гг- крутизна характеристики. тахогенератора
26 Дифференциальный гироскоп c(xJy кЖ 1)9 П vgpp zF>Tz^ q+ 1 кг-^. К9 где JQ-кинема-тический момент ротора гироскопа-, к ^-коэффициент восстанавливающего момента
66
Продолжение табл, t.3
27 Мост НС и< 1 W(s)- . IhL U Ef(Sj Ts + f T-Я, с,-яг сг
23 Дифференцирующий трансформатор к, М 0 Л : я«. "г Ui—о W(shh™.£L Ef\S) i\S*i v*, • Tl"T3T *lt+ ^o
23 Двухфазный* асинхронный электродвигатель Псе, ст О и, , , fits) K„ Uyts) S(T„S<-1) Tu " ; Л j, Ku к»-пг~ Kv
30 Корректирующее устройство переменного тока. фазоопережающего типа. 1 С Ws)-^- E,(s) T,s<-t К - ; Я/ +^2 T ~ ' Я,
31 Корректирующее устройство переменного тока фазозапаздывающего типа Я, Л Яг “г 1 W,S) E,(s) Tts4 K- — к, *яг; T< R, Тг = KT,
32 Синхронно-коммутирующее устройство переменного тока интенгродиф-фвренцирую-щего типа “l о? AC rv, —!— i4s >К“г t'W/r, 1 w P-^ Г~Г~^£| U,(s) Ts u 0„- опорное напряжение-, к - передаточный коэффициент; Т-постоянная времени
33 Двигатель -маховик постоянного тока с возбуждением от постоянных магнитов ГПМ) Qi » Wf<). *(sl - *>" W(s> U,(s) slT^t) t к’"' г TL " вн Ъ'„ t гве ке-постоАная kv-скоростная постоянная-, депонент инерции маховика
57
Продолжение табл. 1.3
34 Асинхронный тремразный усилитель < —~я— wts) - #,5> - к" If, (S) 0(Т„0*1) Кя~ HttcdamoHHuu. мз^фициенш твз~ постоянная Времени
35 Электро-каминный усилитель W(s). -'--У. 11,(3) (Т,Р*1)(ТЛ10*1) K:.Kt-4i9ipuaueHin усиления tu i-te каскадов ЗИН; Т. -постоянная однотка Воебук делил-, Т,,-пктмнная * Времени порея-козамкнутой цепи
36 Тепло -обменник ОС Лв^^-у. пТ ’W’ ns' ’Чйг*’ W(s]. М S. 11 &(0) (Т.,0*1)(ТгЗ*1} *то~ Л передаточный козерфииаент теплообменника-, Ttlrt-постолнные Времени теплообменника
37 Корректирующая КС-цепь К, a, cz’ о д • я; П ut LjdL „„ , и,(0) 7,3-) Т,-Л,С,: т1~^г Сг
Зв Корректирующая КС-цепь я* Й3 и, ЯЛ иг 0 Тс» С'Т .О awL (t,s4) (Tts*i) ’u,(01 T,7,^(1^)^ Т,-К, С, ; 7i-d,Ct
33 Мет а дин Шл\ ЭД / Ц ^кр Ъ\\]дв J.. 8^9— “п wts) - ^lsf - Wl! Ijs) s’ К 1 *" еде J- момент инерции якоря пето дина, Кн-коеффициеит яроперциональнос-ти между моментом злектродВи-еателл а током обмотки Возбуждения
58
Продолжение табл 1.3
w Соленоид я. ° Wfs 1 ж *с e *е 0,(1) Tlsl+2tcTcs^l ке- передаточный козффициент соленоида-, Te - постоянная времени соленоида; - козрмрициент с демпфирования соленоида
Поплавковый уровномер Ив h !г W(s)-№ - К-H/S) - T2s‘*2iTs^t T~hc-i-r^‘ > к Ч ’ где т-масса поплавка б-козффициен жидкостного трения-, в-диаметр поплавка к-перемещенив поплавка; h-изменение уровня жидкости; в—удельная плотность жидкости-, к6-козифицивнт жесткости прижимы
9Z Центробежный такометр ш 7*' Wfsl “ -Xj - —r- '' wlsj T’s+TtS.f V = sis № slri ~5> “з°з° к э Е Э J- . е >« ч >£ s-** *ЧЭ Ж
w г Сияыронный датчик давления жидкости й= 4 /Г] Ц| W(t). U'<S> _ *, '' Pts) Thi^KTs.l' к,-лл„ 7-/^ ; ' “с 2/^mjK кс к п- коэффициент пропорциональности между перемещением и давлением
Электродвигатель постоянного така с независимым возбуждением г§и ufi.i„ _£w_ _ хи unls> 1(Т‘г^г(Пч) Т.Г ; Мелм * **»к
*- к 2 М * «е
Гидропривод до м дввд 0 ома. _ £*“{_ —»• и... масла -ДтТ~ , XW *П1 Ws) X,(S) s(T‘s^.2iTs4) кгп-перодаточный козафициент гидрепривода; Т - постоянная времени гидропривода; % -кезффициент двмпфирввания гидропривода
"к шпщ __г—
59
Продолжение табл. 13
Пневмопривод се струйной трубкой
х
W(s)- —_____________________
а($) $(Т*5*+гЪТз*1)
к „н-передаточный коэффициент пневмопровода.;
Т- постоянная Времени пневмопривода -
^-коэффициент демпфирования пневмопривода
Гидравлический лопастной двигатель с золотниковым управлением
fi(s) К________________
XKtS) ~ S(TlS2+ZtTS*t)
к гл-лередаточный. коэффициент гидравлического лотастного двигателя-,
Т- постоянная времени гидравлического лопастного двигателя-,
5 - коэффициент демпфирования гидравлического лотастного двигателя
lEtfywJ
, К гя
Гидропривод с помпой 48 объемного регулирования
W(s)- Р11>__________________
7 a (s) sfMsi+ZZTs-.t)
?"г/у£7Гл4>«„«а/ где J-момент инерции ротора гидропривода-, V-объем рабочей жидкости в цилиндре, Е-модуль гидравлической упругости-, кГЛ-постоянная гидропривода-, к^-коэффициент ха роктеризующид умечки-, Кр коэффициент жидкостного трения-, кп-постоянная помпы
St агйагт^н*ап1^гИ
W(sl. _ K*’(Tcs.ti
t,(si scrW+ztrs+n
где йщв^-пара. метры самолета.
у B1U_____________
С «77 Д7Г/*«/,7Л7//
•т
60
П/чйолжение табл. 1. з
50 Пропорциональ -ный регулятор на пнеВмо-злементах IWrl_ W . K(Tts+l) (Tts + l) т'’ P,(S) T1S1^2^TS + 1 Т-постоянная времени, регулятора-, ^-коэ/рсрициент демпфирования регулятора; 7^ и Tf постоянные времени, задающего устройства; к - ппередаточный козффициент регулирования
Рз L li 11 & Ь —✓ 1 1 IP J Г & р
51 Корректирующий RC-контур (двойной Т- образный) и‘<‘> . ТЛгТ^Т^Т^Т,)^ Тг * Я г с1’ Tj-SjCj'-г„-я,^ Ти'Зг Cj
U Я1 1 |i?' «3 —jpu. Ю 1 Ц(1) T,TtT,a^[T,(TtJ^). __±!2i^IiiLLLL
г я’ о= -Сг “1 Тг (T^T,^T,)]al4T^T,}*Tt.Tai- + Тг)5*1 ’
5Z Баллистическая ракета Л/V аХ/л JI/S-цгол наклона л ! / вектора // / /[ скорости. У I Б^-угол поворота вХТФГ^ WeP •'V, двигателя Т^.Тг-.Т^.Т,; параметры валлистичёской
53 Корректирующая RLC -цепь сг cf Wfcl U‘,sl УУтЛ*1НЪ!Ч)зг . U,(S) T,Tt1jTt>t.T,Tl(Ti.Ttlf3 * •CT,lrt*T^r,)^TtT,]3‘-ff.5^3,1 ^Tt]s.l T,-R,C, ; Г2-К2С, ; Т.Ь-- T.h. '3 3, ' Г’ я2
«гП *>0 “> X X “г £*г Е'г
54 Я верный внере етический реактор на тепловых нейтронах. l” in j WI.I. _P,(T,»4IIT,S*I) _ llsl s{TjS*i/{TgS*fJ lie K„- X'n‘ " I* п-плотность ней-треннвго потока в активной зоне реактора-, 1-перемещение управляющих стержней р1~!Гвактивность 1*-среднее время жизни нейтронов Тз-постояняап времени реехторосутюн групп
П1
п
55 Сушильная башня вяя производство серной кислоты sot / , £ анализатор _1 Hl L_ 3<нЗ( Яд < э , Мз1-йе1- 111 WW US) (T.S*t) (Tts*l) ' х- относительная концентрация газа 30.8 смесителе-, Ta,Tg- постоянная времени сушильной башни; ъ - рремп прохождения воздуха через воздуховод; время прохождения газа через газоход и газо-подводпщую трубку
61
Продолжение табл. 1.3
S3
Электродвигатель с упругим механическим редуктором
wtsi . й'31 - >-1А*"<гз1
I,,131 IT,s^t)[l^,thtr4]
аУ, №, ;
г-расстоянив до управляющего органа ^перемещение управляющего орьана-, угловая скорость вращения вала турбины-, а-скорость
распространения гидравлического
удара;
Уо -скорость движения воды, у9-гидродинами-чоское давление-, г] - коэффициент трония;
7^ -постоянная времени, турбины
т.г . ЙЯ км к, U,is)' s(Tf‘sl.lftTrs.ll
кя1-передаточный Шффициет электродвигателя кв-передоточный коэффициент редуктора;
7J - постоянная времени механической передачи ; Ти- постоянная времени двигателя-, элентрокоэффи-ционт демпфирования механической передачи-, коэффициент демпфирования злектрдвигатеря
o,-—3-
„ Ti^t,TrT„. ' *r «и
a
Привод намоточноео устройства прокатного стана
К, кг Кос
e„(s) W<s)=-^— a
U,1s) (a,s,*a,stta,s‘.als.al
(Tts*D (T^s-U
“3'М» где квс -козффициею обратной соязи; Тг - постоянная tperiOHu зенератора-, кг -коэффициент усиления генератора по напряжению-, пеоедаточный коэффициент ряектроодигатекя-, К), Kt-козффициенты усиления ЗМУ по напряжению-, 7м - постоянная евенени электро-овиеателя-, Ки~степень демпфирования злшфеництея»-, Tf-постоянноя вренеж ни обнотяи упвавренояПФ Тч-постаяккол времени
ПриЗод барабана с Нумн. алектра-Ниеатеяяни.
0,(s)' s(Trs.1)(T^s'.^„T„s.ri
"и, • 'и,-перебатанные коэффициенты элактраббисате-hsu
(r,s.i)(T^i)
62
ънаиэйд
оннниошзои
• mHantjntbtbcoa
pnnt>ou/agadoo - а
зпнзидор aain -oifidnuiwfiead - *d
'хконапоз g
UftHaagog^d'^d 'vgwuaw goxsod -iiiuioirod ошопи чшзойоиз-л
VdosfidKbnt заяви он кпнзжоновш
ЧШЗО0ОЯЗ -
• avaujotngp озаньаиюииан —оншзной rtduauaiou
- leueaod 0U18V0U
vuModoaa - g 'eeamoangg огмш - ‘у
• nuuga онзш огончгойшнаь anHainauodau -q
odotfit6Ang 3DH3iO3U303ti~l1
И0ШО2 -ngpodujaavc gnn -agntHgteg мошоыдв пнзнзЦ b . апннавшзан - nj_ - nj^ ftavauiDtnggaituaave iiwnantinOOtox апнлошовзЗаи .
_Мвх_‘мм ' odouwfigat шизпОпЛЛеоа niwitouiogadau >d> 'ogee ndи шнапОпаЛеоз TiNxtiOwtigadau -*1» ‘oeng ovDg oaoNpoxrtg annatnoei чшао0е»з aogoean -m 'nagaumnegadtiinave апмэхшавон antnoiaegaiuh ^-n^n
€9
//чУЗг-уДГ to*
f/-»i‘3z*ls/a;» “ ton ‘
>'Л
to*l
irfi'Ziv/z
QI i/Q-DUl 911H2)KI/QQQdU
adouo poafidufi он ohtvga рохшззж pogos figatau аюннцеидэ тшэондпж
опн Dg nmauadau trap ouvg vgy
29
Zig 40
H0UU03 HNuofidnvfaadaH з agnt/uouj ыонрпж он potnotomogod чизшшпдд VI4HUI9UD0
U0UU03 HieuaUdnvUaad з
адпииош uopdaguj on ptiditHOtuogod ' ’ыашогпдд pieHhQioouadu
-ОНШЗЮ0
finaad ом ошзпа оаоаэаь'пииошаи TlhOgQU wg gogndy
Продолжен и. е та 5л. 1.3
бу
Одновальный ТРД с регулируемым соплом а
у Т—расход топлива', +е -площадь проходного сечения сопла-, Tf-Ts - постоянные времени;
к(, Kt-nepedamov-ныв козунрициеяти г- -тяга давления
д(в)
Двухдольный. ТРД с регулируемым соплом
F(s)
у -paoxoi топлива-, /с - площадь проходного сечения сопла; Tf-Tg-лостопнныв времени;
$9-коз1р1рицивнт затихания', к,, Ht -пЪродатоиныв коэффициенты r-тяеа двигателя
GT(sJ
K(T,S^HTi5^ZTi^t8*l) (TgS+fl (Т951+2Т,ЪеЧ)
б - расход топлива-, Т^Тц-поетоянные времени-, fgf fo-козффацаел-ты затухания; к -передаточный нооффициент;
г-тяга двиеа— теля
и,-управление углом поборота, соппа двигателя { к.-передаточный коеф/рииивнт устройства управлонил поворотом ооппа-, г^-ооотавлпхыхие тяги . двигателя я-, ♦ - угол рыскания-, д-угол тангажа -, ы- угол поворота сопла-, Т9-главный момент инерции МА относительно aCU 0g;
- главный момент инерции МА относительна -оси 0g.
64
Продолжение тайл. гз
К/М с двумя парами двигапклей тс ст но связанными, с керпуаом космического летательного аппарата
й- угол тангажа: </>- угол рыскания-, р- угол ярена-, и9,иг~ управления тягами
соответствующих двигателей;
к.-к{- передаточные коэффициенты устройств
управления тягой, Тя - главный момент инерции K/IA относительно оси 01}
Т.- главный момент инерции К/1А относительно оси Оу,
Тг - главный момент инерции КЛА относительно оси Ог
63 Передаточная функция программы интегрирования на управмющейЗвм, реализованная по методу трапеций r^lg~57g|"'— 1 'I 1 * хгы1 ^S^sr Т„ (3-e'ST‘)e'STl’ 1 1-е-гт° To -такт квантования
10 Передаточная Функция программы интегрирования ЗВМ,реализованная по методу Рунге-Кутта У -га порядка чи- Л/Н7 У 'i *—| g * г5Га|—' /с! %п*1 Y„(S) ' e-sli-ye'^l в 1-е T„ -такт квантования
11 Передаточная Функция программы дифференцирования на управляющей ЭМ реализованная по методу второй централь -ной разности — ХП-1 М/ ! с) YnlsC 3 1-е'15Т° 70 1*уе',т<>-е'г‘т'’ Та - такт квантования
7Z Передаточная Функция программы дифференцирования на управляющей ЭВМ, реализованная по методу третьей центральной разности у I » 1 q, гл +} — — Ч^ г И|- —РЯ~ *1 М/ fcl WnplS/~ Yn(s)' fW <-e'2sT° . “ У, -Mke T1 -ИЧе'^-З^-е'2^ То - такт квантования
3 Ю. И. Толчеев
65
Продолжение main. 1 J
Передаточная функция программы на управляющей ЭВМ реализации корректирующего устройства
Т,- постоянная Времени дифференцирования;
То - такт кбантоВания
Передаточная функция программы на управляющей ЭВМреализации корректирующего устройства
{k(Tt !>!)] [Tzs^ I
Передаточная Функция программы коррекции навигационного алгоритма, реализуемого на управляющей ЭВМ
Т, ^'Постоянные времени;
Та- такт квантования
X„*t(s) То (9M9e-iTa*Be'!sT,-'-e'!ST°)e-ST° лр (5>= УпвГ и
То - такт квантования
виде
им$, o=ir,(s, 0 + 0 =
Й у
= 7 (0 s + 1 X
. f 72(/)s2 + 7(f) [2 4- Г (Qs+ 1] )
•t [Г(/)5+1]2 f
(1.170)
Третий член ряда вычислим с помощью выражения
W^s’ ') = -Т(7)7+1-Х
, ( d[T(t)s + l] dW2 (s, t) | _
< ds dt )
kyT (t){T(t)[T (t)
—2T'2 (Q] S + [Г2 (0 + T (t) T" (/)]} [7(Z)s4-l]5
—kyT(t)[T'2 (0 + T (t) T" (01 x
v(rm T(t} T"(t)-2T'4t} c . ) I U [7'2 (t) + T (t) T" (QJ 5+1 J
[7(0 «4-if
В этом случае третье приближение будет
rni(s, Z) = r1(s, /) +
+ r2(s, /)+ lT3(s, /) =
T4s<+[2P (t)+T3 (/) (2+Г (0)] s3+ + 2 [72 (0+Г2 (Z) (24-7' (f))l s2 +
+ [Г (О (24-Г (0)4-27(0-
- T2 (0 (7 (/) T" (0 - 27'2 (0)1 s 4-_ + T2 (0 [7 (Z) T" (t) - 2T'2 (01 + 1
“ y [7 (Os 4-. I]5
(1-171)
Из выражений (1.170) и (1.171) следует, что чем меньше значения первой и второй производных Т' (t) и T"(t), тем меньше погрешность метода «замороженных» коэффициентов. С ростом значений Т' (/) и T''(t) приходится пользоваться третьим, а иногда и четвертым приближением. Таким же способом находят приближенные передаточные функции для других типов не-
66
Передаточные функции основных типовых звеньев
Таблица 1.4
Vе п]п Наименование звена Передаточная функция Wfs) Л? п/п Наименование звена Передаточная Функция Wfs)
7 Усилительное к 13 Вырожденное колебательное — Г*3х *7
2 Устойчивое апериодическое Гз*7 14 Дифференцирующие 2-го порядка ТЧг*21Ть + 1
3 Неустойчивые апериодические 7 Гз-7 15 Т*зг-2£Тз<-1
4 7 1 -Тз 16 Тгзг+2£Тз-1
5 Интегрирующ ее i-eo порядка >гдв^-1,2... s* 17 Т*е*-21Т»-1
6 Дифференцирующие 1-го порядка Тз *7 18 Вырожденное дифференцирующее ^-0 Тгз* *1
7 7-3-7 13 Вырожденное дифференцирующее ^-го порядка 8^,где >)-1,2...
8 7-7-3
S Устойчивое колебательное § <7 7 7zS/*2g7s*7 ’ 20 Чистого запаздывания е ~т*
10 Неустойчивые колебательные 1 Г»з‘-2^Теч-1 27 Трансцендентные в-/Гз
11 7 r*S«*^§7-3-7 . 22
12 ,7 Ггзг-2ёГз-7 23 1 + thlT3)
стационарных элементов (объектов) [35].
Все многообразие динамических элементов (объектов) можно представить в виде передаточных функций с постоянными или переменными параметрами. В табл. 1.3 приведены схемы и передаточные функции некоторых наиболее часто встречающихся элементов САР. Из табл. 1.3 видно, что все элементы состоят из ряда одинаковых сомножителей, каждый из которых является типовым звеном. Так как число типовых звеньев ограниченно (основные из них приведены в табл. 1.4), то, располагая их частотными характеристиками и схемой соединения (последовательное, параллельное и с обратными связями), нетрудно определить частот-
ные характеристики всего элемента любой степени сложности. Или, наоборот, по его частотной характеристике можно находить виды типовых звеньев, образующих передаточную функцию. Данная процедура осуществляется достаточно просто лишь при последовательном соединении типовых звеньев.
Дискретные и цифровые элементы
Рассмотрим применение дискретного преобразования Лапласа к ' линейным импульсным и цифровым элементам. Дискретный сигнал получается из непрерывного путем его выборок в определенные моменты времени с тактом квантования То. В этом случае применяют математический аппарат г-преобра-
з*
67
Таблица 1.5
Основные свойства «-преобразования
Наименование свойства Форма представления
во временной области г-преобразоваиие
Линейность 3 {Я1У1 (0 ± а2у2 (0) Oi/i (z) ± a2Y2 (z)
Изменение масштаба ' 5{е±аГл!/«} У[еТаГ»г]
Вычитание 3 ( Z У («То) - Z У «т° - т0)) (. i-О »-0 )
Суммирование У У (*го) } 1 (“0 ) z~lY^
Сдвиг во времен-ной области 3{у (t — кТ0)} z~KY (z)
Свертка оригиналов 3 1 У, Vi («То) Уг (к.Та — »Г0) | 1 i=0 ) У,(г) Y2 (z)
Дифференцирование изображения 3 {ку (кТ0)} dF(z) — Z j“~* dz
Определение конечного значения lim [у (/)] t->oo lim (z — 1) Y (z) z->14-0
Определение начального значения lim (У (01 t->0 lim (Г (z)] z->oo
Дифференцирование изображения по параметру a> da
зования*; тогда обозначим
z = e’r», (1.172)
откуда
s = -4-lnz. (1.173)
1 о
Подставив соотношения (1.172) и (1.173) в формулу (1.158), по
* В прил. П-1.2 приведена таблица «-преобразований простейших функций.
лучим
00
Г(^1п z) = £i/(kT0)z-k, (1.174) к=0
где У* (~ln z) = У (z).
В табл. 1.5 приведены основные свойства z-преобразования.
Передаточные функции типовых дискретных звеньев имеют форму записи, зависящую от вида приме-
68
Таблица 1.6
Таблица соответствия структурны)! схем графам
№ Наименование Структурная cxena Граф
л/л исходная приведенная исходный приведенный
Г Типовое звено Kr(s) W(s) w
2 Последовательное соединение звеньев l{Sj wt(s) X?W - w2(s) Xjfs) *ils) w,(s)w2(s) *3ls) W;fS) W2(Sl
3 Параллельное соединение звеньев Xt(S) —L Wt(s) X;(S) w,m(s) ХгИ ^(S) (x^
4 контур с жесткой обратной связью •j Ms) t(s) x,(s) was) HlVfSl x^/s) w(s) ад
5 контур с гибкой обратной связью Xr(S) — - w2(i —1 Li j—J Ws) XjW ад J w,(sj w,(s)
6 контур с переда точной функцией в цепи обратной связи ад W(s) J z(S) W 1 IH-W(S) ад Z~S 1 (ад——*yy -ад
1 Соединения звеньев в сложные М) - W2(S) ад Ws) адед i*w2{s) ад -ад w,(s)w3is)
контуры Х| S)r (S> r*v L- — X/fs) адр ад|- W|4- Xjfs) 1 X,(s) мм'® X/s) -Wz(S) MW^4(S) ©^L^)
69
Продолжение тад/i. 16
ненной вычислительной процедуры. Для интегрирующих звеньев применяют методы численного интегрирования (методы Эйлера, трапеций, Адамса — Башфорта, Рунге— Кутта и т. д.), а для звеньев дифференцирования — методы различных порядков центральной разности.
Типовые звенья
В табл. 1.4 приведены передаточные функции типовых дискретных звеньев, полученные с помощью применения различных вычислительных процедур. Вычислительные процедуры, обеспечивающие малые амплитудные и фазовые искажения, как правило, приводят к довольно громоздкому виду передаточной функции (см. табл. 1.4), а соответственно с этим и к сложной форме амплитудных и фазовых частотных характеристик.
5. СТРУКТУРНЫЕ СХЕМЫ И ГРАФЫ ЭЛЕМЕНТОВ (ОБЪЕКТОВ)
Внутреннее строение элементов (объектов) САР наиболее просто определяется с помощью структур
ных схем и графов. Последние могут составляться по дифференциальным и разностным уравнениям, записанным с использованием изображения функций или с помощью передаточных функций типовых звеньев, записанных в s-или z-формах. При этом удается оценить влияние параметров уравнений или типовых звеньев и связей между ними на динамические характеристики элементов. В результате проектировщик может упрощать структуру исследуемого элемента и находить в нем сильные и слабые связи. Исключая из структурных схем и графов слабые связи, нетрудно выполнить операции- декомпозиции.
На структурных схемах, полученных с помощью дифференциальных и разностных уравнений, динамические элементы выделяют прямоугольниками, а взаимные связи между ними — прямыми линиями (см. гл. 3). Каждая взаимная связь представляет собой переменную уравнений. При составлении структурных схем с помощью передаточных функций типовые звенья изображают на схемах также прямоугольниками, а связи — прямыми
70
S-Опя
Рис. 1.14. Граф, характеризующий пространственное движение самолета в горизонтальной плоскости
линиями. В графах переменные указывают в виде вершин, а дуги обозначают или параметры, или передаточные функции типовых звеньев. На дугах ставят стрелки, указывающие направление передачи сигнала.
Следует отметить, что между структурными схемами и графами существует однозначное соответствие, которое хорошо можно проследить с помощью таблицы соответствий структурных схем графам (табл. 1.6).
Пример 1,31. Построить граф, пользуясь системой уравнений (1.96), приведенных в примере 1.24. Для этого применим к системе дифференциальных уравнений * прямое преобразование Лапласа; тогда полу
* В системе уравнений (1.175), как и обычир, знаком тильда обозначены изображения функций для греческих строчных и латинских прописных букв, т. е.
Да = Да (s); Др = др (s); Ду = Ду (s), AV= = ДГ (s) и т. д.
чим
s Ду = а>9 Дйх — 01 ,о Дйу;
s Дф = Я2 ю Дйу;
s ДФ = а311 Дй2;
(s — а44) AV = — а45 Д0 + а47 Да;
s ДО = а54 ДУ + а57 Да;
s Д/7 = а85 ДО;
($ — O77) = 074 ДУ + о78 ДО +
4- а78 ДР 4- о7 п Д<6г — 671 Ддв;
(s — а88) ДР = 081 Ду + а84 ДУ 4-
4- а87 Да + а8э Дйх + а8 ю Дйу — 682 Ддн;
($ — O99) Д(йх “ О98 ДР +
4" 09 10 ДЙу + 692 Ддн 4" 693 Ддэ>
(s — О10 10) — О10 8 Др +
+ О10 9 Дйх + О10 11 Дйг -(-
-f-6io2 Ддн 4-дюз Ддэ;
(s — а п и)Дйг = Оц4ДК 4-
4- 0117 Да 4- 6ц 1 Ддв.
(1.175)
По системе уравнений (1.175) составим матрицу М.
71
Параметры Y ф 0 У ё н а р 1 | 0>х бг
V S 0 0 0 0 0 0 0 019 — 01 10 0
Ф 0 S 0 0 0 0 0 0 0 02 10 0
0 0 0 S 0 0 0 0 0 0 0 Оз 11
Г 0 0 0 3 — о44 — а45 0 а4т 0 0 0 0
ё 0 0 0 0s 4 S 0 O57 0 0 0 0
н 0 0 0 0 Об5 S 0 0 0 0 0
д, 0 0 0 о74 075 0 з — а77 078 0 0 а? и
р Obi 0 0 Ов4 0 0 087 3 — Овв 089 08 10 0
бх 0 0 0 0 0 0 0 098 S — Я99 ' 09 ю 0
йу 0 0 0 0 0 0 0 010 8 0)0 9 3 — О10 ю Ою 11
ё>г 0 0 0 «и 4 0 0 011 7 0 0 0 3 — Оц 11
бв 0 0 0 0 0 0 — 671 0 0 0 6ц 1
бн 0 0 0 0 0 0 0 — 6в2 6 92 610 2 0
бэ 0 0 0 0 0 0 0 0 Ъэз 6|0 3 0
С помощью матрицы М на рис. 1.14 изображен граф, характеризующий динамику движения ЛА. В этом случае в качестве опорной траектории иыбран горизонтальный полет без учета его вращения вокруг центра масс н без скольжения. Вначале разложим рассматриваемый граф на два подграфа:
для продольного движения, с вершинами ДО, ДУ, Д9, ДЯ, Да, Дшг и Дбв;
для бокового движения, с вершинами Ду, Дф, Др, Дшх, Дш^, Дбэ и Дбн- В результате получим два подграфа (рис. 1.15 и 1.16). Подграф, изображенный на рнс. 1.16, характеризующий боковое движение ЛА, можно также разделить иа два [по каналу рыскания (рис. 1.16, а) и креиа
(рис. 1.16,6)]. Для этого выделим вершины Дф,' Др, Дю», Дбн и Ду, Д<0х, Дбэ- По графам (рис. 1.15 и 1.16, а, б) можно составить три независимые системы уравнений:
для канала тангажа
. зДО = азпДйг;
(з — а44) ДУ = —а45 Д0 + а47 Да;
s Дё = а64+ аз? Да;
ДзЯ = ав6Дё; _ q 176) (s — aJ7) Да == а74 Д^ + о76 ДО +
+ о7 п Дбг — 67i Дбв;
(s — Оц п) ДЗг = он 4 ДУ +
+ ci 1 ? Да + би1 Дбв;
72
1.15. Подграф, характеризующий про-
Рнс. дольное движение самолета
для канала рыскания
S Дф 02 ю А(Вр»
(s — ass) Ар = 08 ю Айу — бег Д6н’> ’ (1.177)
(а — Дю ю) Айр = 010 s АР+ 6ю абн!. для канала крена
s Ду == дю Д<ох;
(а — 099) АсОд; b 9з Дб9.
Решить задачу
динамики движения ЛА можно и другим способом.
(1.178)
декомпозиции
Выделив для
где
характеризующий
бо-
Рис. 1.16. Подграф, ковое движение самолета: а — по каналу рыскания; б — по каналу крена
принятой траектории полета ЛА (рис. 1.14) слабые связи, обозначенные дугами, снова получим три подграфа, по которым нетрудно составить независимые системы уравнений вида (1.176) — (1.178).
Исключив из системы уравнений (1.176) переменные, характеризующие длииноперио-дические колебания, получим
s ДФ = а311 Дйг;
(s — а77) Ай = а711 Дйг — b7ii>B;
(s — ац и) Дйг — ац 7 Да + Ь\ ц Дбв.,
(1.179)*
Из систем уравнений (1.177) —(1.179) можно определить передаточные функции для короткопериодических движений, записав их через типовые звенья. С учетом знаков у коэффициентов уравнений найдем:
для канала тангажа б 4b(7.s+1)
s(^ + 2^+I)' <1Л8°)
где
Л =
03 11 (077^11 И ~Г 0Ц 767 п) . 0770Ц И — 011 707 11 ’
6ц И
7С =
0776ц и + cii j 767 и ’
i ► 1 ,
£ — ~g~ (a7? +
V ^77^11 — 7а7 П
+ Ди и) Va77au л *- 0ц 7а7 и;
для канала рыскания
в 4H(rcs+i)
В7*“ (s) “ s(7'2s2 (-2g'7,'s+ 1)”’ 1 ‘181)
где
02 10 (08в61О 2 + 088^82) П —.................. •
* 088010 10 — 010 808 10
_________610 2_____.
С 08в6ю 2 + 010 в6в2 ’
088010 10 — вю 8а8 10
— ~2~ (088 + 010 ю) V088010 10 — 010 808 10
и для канала крена
л k&3
О
(L,82)
,6a 019&9S
== —-------
V 099
1 a9s
* Система уравнений (1.179) описывает короткопериодические колебания ЛА а вертикальной плоскости.
73
« в)
Рис. 1.17. Структурные схемы последовательного соединения типовых звеньев для независимых каналов самолета: а — тангажа; б — рыскания; в — крена
замкнутый контур с отрицатель-ной обратной связью. Передаточная функция такого объекта имеет вид
На рис. 1.17 изображены структурные схемы для каналов тангажа, рыскания и крена (соответственно рнс. 1.17,а—в).
При этом видно, что каждый из каналов ЛА представляет собой последовательное соединение типовых звеньев.
Существуют динамические элементы с параллельным соединением типовых звеньев. На рис. 1.18, а показана структурная схема корректирующего устройства, состоящая из двух параллельных ветвей с результирующей передаточной функцией
<1Л83>
На рис. 1.18,6 показана структурная схема ядерного энергетического реактора на тепловых нейтронах [13], полученная путем усреднения постоянных времени. Как видно, данная схема состоит из типовых звеньев, образующих
Рнс. 1.18. Структурные схемы динамических элементов: а —с параллельным соединением; б —с соединением в виде контура, имеющего отрицательную обратную связь
-nrr-U's+l) Wnp(s) = -^----7- (1.184)
47+^ + ’)
Пример 1.32. Составить структурную схему объекта, описываемого системой линейных дифференциальных уравнений (1.65) н (1.66). Применив к этой системе уравнений прямое преобразование Лапласа, получим
зДй>1 (s)---Дй>1 (з) — (~~"7—" “зо 4“
+ Мда) Д®2 ($) — ( j—- соао +
+ Мдз) Д®3 (s) + *1 Д(031 («);
s Да>2 (s) = — (——j—— <£>зо + йгм) X
X (s) “ &2&д2 (s) — (-------- ®10 4"
\ J2
+ /гайдз ($) 4“ &2 (5);
( /2 — Ji - \
s Дш3 ($) — — изо + ^з^д1 J X
X Д<01 (s) — “10 + Мда) Д“а (s) —
— Мдз Д®з (s) + *з Д“зз (s)
(1.185)
74
и
ДшД1 (s) » йд1 Дш! (s) + ka2 Дш2 (s) +
+ йдз Д(о3 (s);
Д®д2 (s) = kai Да>1 (s) + йд2 Дш2 (s) +
+ Лдз Д(Оз ($);
Д(одз (s) = £Д1 Дй>1 (s) + /гД2 Дй>2 (s) +
+ /гдз Д(0з (s).
(1.186)
Систему уравнений (1.185) можно переписать в виде
(s + МД1) Да>। (s) = — “so +
+ Д®2 (s) — 3 j—— Иго +
+ kik^) Да>з (s) + k\ Дш31 (з);
. (s + Лгйдг) Дй>2 ($) = — ( -у^—~ ®зо +
+ k2kai) ДСО] (з) — 1 у-—- (010 +
+ *2*лз) Д(Оз (s) + k2 Д(оз2 (s);
(s + Йз^дз) Д(Оз (s) = — ( 2 -* Изо +
+ £з^д1) Д<д>1 (s) — (010 +
+ йз6Д2^ Д(о2 (s) -f- k3 Д(0зз (s).
(1.187)
Пользуясь уравнениями (1.1'86) и (1.187), составим структурную схему объекта (рис. 1.19), из которой видно, что данный объект является трехмерным.
В заключение приведем общую форму записи линейных стационарных и нестационарных элементов (объектов), имеющих высокую размерность в векторно-матричной форме. Пользуясь этими уравнениями, составим их структурные схемы [32].
Из выражения (1.155) имеем
Y(s) =
bQsm + blsm-l + b2Sm-2+ ...
• • • 4- \S 4" bm
=----------- , m~l m-------U (s).
а^+а^ *+ ... + an_!s+an
(1.188)
Принимая n — tn и формируя полином знаменателя, выражение
(1.188) можно переписать в виде
Г(5) =
Asn + 2Lsn-l + ^.sn-2+-->
а0 а0 а0
b . Ь
... + -2^-s + -*-
______________________________ TttcX
Будем считать, что ао=#О и выражение (1.189) составлено для стационарного объекта. Введем в него следующие обозначения:
а1/а0 = а1> • • • ’ ап!а0 = ап> ^о!ао = •••: bnlaQ = b'n,
• в результате получим
п
Z &/п-/
Y(s) = -^------U(s), (1.190)
Е a'n~is‘ i-i
где а'= 1.
Запишем уравнения состояния в нормальной форме без использования производных u(t), что достигается путем замены переменных
у = ц1-ЬМ;
— = v2 + kiu;
dv
-dr=-a^„-a'2vn_I- ...'
Уравнение (1.190) имеет вид
г/W -f- a[y(n-1) -f- ... + а'пу = = b'ou.™ 4- b[u{n~ *> + ... + b'nu.
(1.192)
75
Рис. 1.19. Структурная схема трехмерного объекта
Из выражений (1.191) получим
dy _________ dVj , , du
~dt~ dt dt
ИЛИ
= V2 + + k0 .
Затем, продифференцировав последнее выражение, найдем
d2y _ dv । , du । , d2u
dt2 ~ dt Rl~dT + dt2
и, учитывая уравнения (1.191), запишем
d2y . . . , du । . d2u
== t>3 "I" 4“ k\ ”77 4“ kQ .
at2 ° ’ z 1 at , J at2
Продолжая аналогичные выкладки, получим dny / / /I
—; ° = — a,v — a„v , —... — a v, + dtn In 2vn-l nt 1
it it du , , dnu
+ «пи + ftn-l -37- + • • • -Г «0 -jpr
(1.193)
В уравнение (1.193) вместо vn, un-i,...,Vi подставим выражения их
76
через производные у, полученные из уравнений (1.191), т. е.
Уравнения состояния в нормальной форме примут вид
vx = y — kt)u;
dvt , du , du , ®2~ ~dT ~ klU== ~dF ~ k<>Tt—k'U’
dv2 , d2y . d2u
V3 ~ ~di - ~~ ~dt2 Hi2 ~
-ki~ — k2U\
°n-l = -jt h d^n~^u , d^n~^u
° ~di^~ ~ R1 ~di^ ’
... — kn_2u-,
_ d(n-1^ d^n~l^u
Vn~~~dFr~ ° itn~l
(1.194)
«1
б2
(1.197)
приходим к уравнению
dny_______ Л Г d<n 1^у _
dtn ~’ °’ L dtn~l
. d{n~'}u , 1
*0 dtn-l • • • “ «n-iMj
, Г d(n"^y и d(n~^u
й2 [ dtn-2 dtn-2
• • • — — • • •
• •• + M +
+ кп_^+ ...+k0-^-. (1.195)
Сравнивая уравнения (1.192) и (1.195), получим выражения для неизвестных коэффициентов:
^0 = ^0’
2>i = axk0 + kx; kx = bx
— a,lkl + a'2kQ -f- k2, ^2~ ^2 ^1^1 ^2^0
(1.196)
и T. Д.
и выходной сигнал
y = Uj-|-^ou, (1.198)
где согласно выражениям (1.196) имеем
feo ~ ^0’
i-i (1.199)
kt = b'-^ a't_mkm.
Структурная схема стационарного элемента (объекта), описываемого уравнениями (1.197) и (1.198), построена на рис. 1.20, а.
Рассмотрим теперь нестационарную систему, описываемую уравнением вида (1.192) с переменными от времени коэффициентами
ИО-т--------------«(О- (1-200)
i-0
В этом случае также может быть использован метод приведения уравнения (1.200) к системе уравнений в нормальной форме вида (1.197). При этом коэффи-
77
i-1 i—m
S S (/) P
m=*0 fe=0
Рис. 1.20. Структурная схема динамического элемента (объекта) высокой размерности:
а — стационарного; б — нестационарного циенты а[, а'2, а'п, а также ko, kt, kn являются функциями времени. Считая, что а' = 1, имеем
M)=W;
(1.201)
Cn—i n+k — i
(rti -f- k — Z)! (n —
Структурная схема нестационарного элемента, описываемого уравнениями (1.197) и (1.198), построена на рис. 1.20,6.
78
Рис. 1.21. Структурная схема сложного одномерного динамического объекта с перекрещивающимися связями: а — исходная; б — преобразованная
6. ПРЕОБРАЗОВАНИЯ СТРУКТУРНЫХ СХЕМ И ГРАФОВ
Пользуясь табл. 1.6 соответствия структурных схем графам, можно составить более подробные таблицы преобразований структурных схем элементов (объектов) с типовыми звеньями (табл. 1.7) или графами (табл. 1.8). С помощью табл. 1.7 или 1.8 можно структурную схему (граф) сложного элемента или объекта привести к более простому виду. Это позволит в дальнейшем перейти к определению передаточных функций линейных САР (см. гл. 3).
Пример 1.33. Преобразовать структурную схему сложного линейного динамического объекта (рис. 1.21, а), имеющей несколько пересекающихся обратных связей. Последнее ие позволяет сразу же написать результирующую передаточную функцию. Поэтому воспользуемся структурными преобразованиями, указанными в табл. 1.8. В результате получим структурную схему (рис. 1.21,6), где нет перекрещивающихся обратных связей. Для каждого ее контура можно записать передаточные функции в виде
W (s) = —. (1.202) \ + W7(s)Wi0(s)Wll(s)’y ’
б)
_ (s)
l + uZj (S> IT12 (s) ri5(s) :
(1.203)
Уз (s) У4 (s) У5 ($) У» (s)
1 + У a (s) У3 (s) У4 (s) У 5 (s) У6 (s) У13 (s) ’
(1.204)
IV ' ' . , УпИ^in(s) W ’ + Уз (s) У 4 (s) У io (s)
(1.205)
У1у U)
--------yJ(S)y9(S) : (L206> 1 + yI0 (S)
w (:)_ Уу(з)У12(з)_______.
VI^ 1 + UZV(S)F12(S)F16(S)’
(1.207)
r (s) = W1 (s)Wvl (s) yH(s) V" ‘ 1+FJs) F2(s) У у, (s) yi4(s)-
(1.208)
Результирующую передаточную функцию yvn(s) определяют из соотношения (1-208), в которое должны быть последовательно подставлены передаточные функции для контуров yVi(s), Fv(s), yIV(s), Fjn(s). У„ (s) и У, (s), записанные в виде выражений (1.202) —(1.207).
Пример 1.34. Преобразовать структурную схему двухмерного линейного объекта с перекрестными связями. Исходная структурная схема с двумя замкнутыми контурами
79
Hi njn
l
J
4
5
6
7
в
9
Преобразования в структурных схемах Таблица П
линейных элементов (объектов) и систем автоматического регулирования
Наименование структурного преобразования
Исходная структурная схема
Преобразованная структурная схема
Формула для преобразованной передаточной функции или выходного сигнала
Перестановка звеньев
Объединение последовательно соединенных звеньев в одно звено
Перенос линии связи до звена
Перенос пинии связи за звено
Перемена мест пинии связи
Перестановка сравнивающих устройств
Перестройка схемы сравнивающих устройств
перенос пинии связи за сравнивающее устройство
х2
------ X,
w,(s)w2(s)
w(s}-w,(s)w2(e)
X^(S)-W(S)X,(S)
X4(S)‘X,(S)-X2(S>+X3(S)
x4(s)-x,(s)-x2(s)-x3(s)
Xj(S)-X,(S)-X3(S)
x2(s)*w,(s)x,(s) fa(VW2(S)X2(S)
x3(s)-Xi(si-x2(s)
xt(s)-x3(s)-x2(s)
*1(51
x2(s)~w(s)x,(s).
X-
~Ч *(s) I
i.
^-1
ИОД
*г ПТ7П
-Ч w(°) Х1
-Ч ИОД|-р- rLWt
Х2 ь—
Перепое пинии связи до сравнивающего устройства
л, Ъ
—1 ' н
1 wts) П
W/.'S) И Л* Hr ^s>r
80
Продолжение табл. 1.7
81
Продолжение табл. 1.7
показана на рис. 1.22, а. Для определения по ней передаточной функции первого канала ф (0 примем, что фз (0 = 0,. т. е. Ч>е(О = —Ф(0 и Uf"(s) = <pe(s)/$(s) = —1.
Введем данную передаточную функцию в исходную схему; тогда получим схему, изображенную иа рис. 1.22,6. Эту схему можно привести к двум схемам, приведенным иа рис. 1.22, в, г. Выделим на них штриховыми прямоугольниками разомкнутые передаточные функции IFi(s) и Ц7ц(з). Результирующую передаточную функцию W'o(s) найдем из условия ее линейности, а следовательно, справедливости принципа суперпозиции, т. е.
Го (s) = W, (s) + (s) = (s) +
. т (s) W3 (s) W, (s) UZ4 (s)
+ nMs)—Г+1Г6)-------------l + UMs) •
(1.209)
Пользуясь передаточной функцией (1.209), анализируют устойчивость рассматриваемого линейного объекта *.
* См. гл. 4, п. 7.
Пример 1,35. Преобразовать граф объекта (рис. 1,23, а) к более простому виду. Воспользуемся для этого схемами табл. 1.8. На рис. 1.23,6 показан первый этап преобразования графа, а на рис. 1.23, в — второй. В результате выполнения второго этапа преобразования получен граф с меньшим числом вершин и ребер, что упрощает исследование объекта и позволяет получить результирующую передаточную функцию объекта в виде -
_______________(*)
°V 1 l + [W'I(s) + W,3 (s) + Г4 (s)+ • + U76 (s) + U7e (S) + UZ7 (S)]
Применение структурных преобразований обеспечивает получение таких результирующих схем и графов, пользуясь которыми можно достаточно просто без каких-либо вспомогательных вычислений находить передаточные функции слож-
82
Таблица 1.8
Преобразования графов линейных элементов (объектов) и систел автолитического регулирования
о/л Наиненование структурного преобразования Исходная структурная схена Преобразованная структурная схена Форпула для преобразования графа
7 Последовательное соединение звеньев ^,^2^3 ^п-Ьг-^ • • "-Qy . -w,(s)w2(s)...w^a-^ (x,j —— ivfsj W(s)-W,(S)W2(3)...M^ (S)
2 Параллельное соединение звеньев 1 w,(s) wn(s)
3 Объединение двух звеньев в одно звено w’(s) -W2(sl ЛЛ w,(s)-w2(s) 'o W(s) ’ О W(s)-w,(s)-w2(s)
4 Перестройка двух звеньев в одно звено W,(s) -^ед i s-Ш (S)^. \Х^/—wVjV ^\XV -1 Xt(s)-[W,(S)-W2(S^X,(S)
5 Перестройка одного параллельно соединенного звена wt(s) -1 t X4(S)-[W,(S)-1]X,(S)
6 Объединение контура с жесткой обратной связью. 'w’<sl iv, ед w(sl. W’(SI W(' /»iv,ед
1 Перестройка схены контура сжесткой обратной связью w,(s) -1 -W2(S) X4<s)_ Wt(s) X,(s) ^Wf(s)
В Объединение контура с гибкой обратной связью в одно звено w'<s> 22^ -w2(s) W,(s) W(S) 4—' W(sl w.l!s).,. ",SI i+w,(s)w2(s)
83
Продолжение табл 1.8
ff Перестройка схены контура с гибкой обратной связью №i(S) 7 X<(s)_ W,(s) X,(S) HW,(s)W2(si
ю Объединение контура с передаточной функцией в цепи обратной связи 7 -ВД W&-
77 Перестройка контура с передаточной функцией в цепи обратной связи 7 -w,(s) l -7 Xt(S) 7 X,(S) ° 1-W(3)
12 занена одного зве- на контурон с передаточной функцией в цепи пряной связи <\ W(S) z-X W(S) _ О x//2 ^X*2j -1 XZ(S>-W(s)xt(s)
13 Занена одного эвена контурон с передаточной функцией в цепи обратной связи w<s> /T\ Qy - — 7 wiscT’ X2(S)- W(S)X,(S)
74 Соединение двух звеньев в скену занкнуто-разонкнутого (конбинирова иного) вида *l!s)*W2(S) Hj(V Wi(s> Wl(SL w^-X3(S)_^,(S)-W2(S)
V-i' w(s) V -7 W(s)-x,(3) l^7(S)
г)
Рис. 1.22. Структурная схема сложного двухмерного динамического объекта с пересекающимися связями:
д)
а — исходная: б и в — преобразованные путем введения передаточной функции равной —1; г — для передаточной функции Wj (з); д — для передаточной ФУНКЦИИ ITjj (s)
84
W4(S)* Wsis)< wf(s) ★ w7(s)]
»)
-L «4 W” *, (s) <-w<(s)*ws (s) +we(s)tw7(s)]
6)
Рис. 1.23. Преобразование графа объекта к расчетному виду: а — исходная схема; б — первый этап; а — второй этап
ных динамических элементов (объектов), используемых для построения частотных характеристик.
7. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ
Линейные типовые звенья можно разделить на два типа — непрерывные и дискретные. Частотные характеристики линейных непрерывных типовых звеньев находятся из передаточных функций после подстановки в них s = /со и выделения действительной и мнимой частей, т. е.
Wro(J®) = I/o(<o) + /VoM> (1.210) где 17о(со) и Vo(w) — соответственно действительная и мнимая частотные характеристики.
Пользуясь выражением (1.210), в декартовой системе координат строят амплитудно-фазовые частотные характеристики Wo(j<&). Для основных типов непрерывных звеньев они приведены в табл. 1.9. Если перейти к полярной системе координат, то выражение (1.210) можно переписать в виде
Wo (fo) == Н' (со) е/0“ <®>, (1.211) где Н'й (со) и 0О (со) — соответственно амплитудная и фазовая частотные характеристики.
Из выражений (1.210) и (1.211) можно найти формулы для вычисления амплитудной и фазовой ча
стотных характеристик:
(1-212)
0о(со) = arctg^gj-. (1.213)
Эти характеристики также приведены в табл. 1.9.
Частотные характеристики линейных дискретных типовых звеньев находятся путем приведения передаточных функций к комплексной переменной s—ja, которая связана с переменными s и г следующими соотношениями:
s = ^th^ (1.214)
Из соотношения (1.214) следует, что связь между переменными s и s не является взаимно однозначной из-за периодичности функции. Период ее равен 2л/7"о. Для определения соответствия переменных s и s на половине основной полосы 0 Im{s} л/Г0 воспользуемся отображением точек на плоскостях S и 5, приняв s = ст + /со и s = ст 4- /со. Сперва на плоскости S проведем линии постоянных значений л/4Г0, п12Тй, Зл/47о и л/То и нанесем на них вычисленные значения точек (рис. 1.24, а) [24].
Линии постоянных значений на плоскости S отображаются в окружности с центрами на действитель-
85
Частотные характеристики типовых звеньев
Таблица 1.9
№ п/п Переваточная функция частотная характеристика Апплитудно-фазовая
Апплитудная Фазовая
1 к Н К в JV К
0 ° У
0 (а)
2 S JV 1 (iJ-oo 1^-0
п / JT/2
U (jj 0 (а) 0 и
J TS+1 н 1 е хр хЦ 0 JV 6U-CO 1/
0 Ы°ои
и (jj (а)
4 TS-1 If 1 в л хр Y ""7 jv к (а)-0 ° й
" Cd 1/Т а>
5 1-TS н’ 1 0 си 0 1/Т JV ы-0
-Л/4 -хр (J 0 | и й>“°°
В 1 S If JV\ 1 (J ®оо
-ХЦ -яр е (а)
0. > и <11=0
0 а)
7 1 TS-1 И' 1 Нт
хЦ ш J' 0 ^*0 Ji я
0 CJ "’в
8 '1 TS-1 1/Т J4 (tjKOQ
п 1 k с 1
0 и
0 (а) в
9 1 1-TS н' 1 е хр лц JV f ^\ы=0
(а) 1/Т ы 0 1 и
Ю s2 If в Л х/2 0
ZV*oo 1 ш=0
0 и
и (а)
86
Продолжение табл. I. 9
II T2S2+1 H' 1 /Г т X Х/2 0
- Шаол * \o U
U 1)T Ы 1/Т ы
12 T2S2~1 т л Ж/2 0
1 -
* -’ й| и
o' Ы и
13 1~T2S2 H' I в
1/ hJ и ы fl 1 и
14 Т25г+2№ + 1 H’ 1 b ^2 г в X Х/2 ' U
Q (jj V ы 0 7 и
15 T2S2+2tJS-1 H' 1 0 УЛ ty^3 и* в X Х/2 0 1 '>?1>4г>Ь &>ЖОО t>1 ^2 й) . t’>ii >^2>^3 и
№ Т25г-2^1 H1 I 0 1>^1>Кг>2,3 — S Jv 1 1 w”0
Л/2 -л ^^2^3 Ш u
11 T2S2~2^TS~1 H’ 1. il Ъ Ь} в X Х/2 J* 6Moo Ы~(Г1.
<$>4.-/ 6 .f}\ и
и bj 0) b 1.243
И 1 S2 I O’ в (tJ**O 4^«o
Х/2 0)
0 и
и 0)
В 1 T2SZ+1 н‘ 1 У1\ —1\ 1 в 0 Х/2 1/т JV .
(л) о V* \^T)u
и 1/Т ы
20 1 T2s2-1 6 «“?
1 а У 1 GJ
-z 0 и
0 . (а)
21 1 1- T2S2 н' 1 0 в 0 JV йГ"ОО . 0 Ш-0 1 и
GJ (л)
.37
Продолжение табл. 1.9
22 1 T2S2*2t,TS+1 у 1 t 1>*.,>Кг>К3 ,/r I>il>i2>is JVTX>L ^*Г\ 4? ii
0 id
23 1 T2S2^2iJS-l uf *. 8 fl X/2 i2 (з й/*оо
1 1 V t дцХ- / 4 (, b is “ & и
0 (d
24 1 T2S2-28,TS+1 F -^2 8 X Л/2 jv_^ ^i^i2>i3 Iw-0
(d ЦТ Ы W*oe T 3 Г и
25 1 T2S2-22,75-1 H 1 4^. 0 Л ~ 2 -Л 7>i,>2,2>ts i, is is Jf ’>i,>i2>i3 й/еОО
~l О и
0 id
2В e~JS У 1 8 fl JV
(d
f OJ и
0 id
27 ers . If 1 8 JK_.
1) (J 0 (d 0J1 и
28 1-esr° 5 If r, \/x> e 0 Jf (tfssoa Та и
'Х^ЧЧччХч !) /ш-о
0 (d
23 (i-e-T»s)2(HTeS) W2 H 1 Q
й|жоо _ 0 Ъ и
!/" f(d*0
0 (d
30 (TlS2^jTllS^l)(l-tT«s)} H 8 0 jy (if a tn U
7$S3 (d ы-0
0 id
31 ~(i-e-sr«)e~sr° f0 У 8 0 (ш-0
’X. (d 1{^жос fl) и
и (d
88
продолжение табл. 1.9
52 1 l-.-2ST° 2Т0 eST” H1 8 Л 2 0 X “ 2 — w 0
If w (jj -i и
33 6 1-в~25Т° То l+4e~STo+e~2ST° H‘ 8 X 2 — i- JV
и 0/ Л '2 1 -i r»1 0 и
34 JBL. '0 h6-2ST0 Ы 8 ЗЯ 2 X 21 S7 jV й>*0 5 w
33 loe-sn l-e~ST’ H‘ 0 0) В 1 "2 зл ~2 (aJ 2 (u-0 : 0 и
To 3esro-e-2ST° 2 1-eST° H1 JV
36 0 (0 __' J , 0> 0 и
If \ 1 8 0 Л 2 JV 0
31 e-ST„ 2T° l-e2ST° 0 M 0) (a) ’r’l (i)- и 0
H' 1 <s q> jv 0
36 To 1+4e'ST4-t2Sr' 3 l-'isT° -o V 0> (л) y,T‘> (i)- и 0
H1 8 0 X 2 JV 0
ЗЯ To h4e^e~ST° 6 l-e~ST<> 0 (j) It) -J7’»' и ы-о
48 '8 я 0 (t) 8 8 -Л -2X (t) ( 0 w-d / U
89
Продолжение тадл. 1.3
90
Рис. 1.24. Номограммы соответствия переменных s н s на плоскостях S н 5:
а — Пл. S; б — Пл. S
ной оси с координатами —2/То и О (рис. 1.24,6). Действительная ось на плоскости S: —oo<Re{$)<0 переходит в отрезок на плоскости S: —2/То < Re{s) < 0 (рис. 1.24,6). Причем граница основной полосы левой полуплоскости [im {д} = ;
Re {д} <о] отобразится в полуин-тервал (Re {д| < — -=г-; 1т{д} = 0 .
* О J
Линии постоянных значений Re{s} (—0,28/Го; — О,69/Го; — 1,38/Го;
2,76/Tq) отобразятся на плоскости S в окружности с центрами иа действительной оси. В результате пересечения этих линий находятся' значения соответствующих точек (рис. 1.24,6). Из сравнения рис. 1.24, а, б можно установить, что полосы для непрерывного элемента при их отображении на плоскость S изменяются.
Теперь ограничимся рассмотрением полюсов в окружности |дТо]== — 1, часть которой на плоскости S выделена штриховкой (рис. 1.24,а). Соответствующее ей отображение
на плоскости S также выделено штриховкой (рис. 1.24,6). В заштрихованных областях полюсы дискретного элемента (объекта) отличаются от полюсов непрерывного примерно на 10 % вблизи окружности. Внутри окружности они различаются с меньшей погрешностью. Поэтому можно считать, что s ~ д и го ~ й (где ® называется псевдочастотой), и максимальное значение мнимой части полюса X, будет удовлетворять условию
maxim {ХД < п/Т0. (1.216)
Условием (1.216) будем пользоваться при построении частотных характеристик графоаналитическими методами. Для этого случая амплитудные, фазовые и амплитудно-фазовые частотные, характеристики некоторых типов дискретных элементов также приведены в табл. 1.9..
Если для вычисления численных значений частотных характеристик применять ЭВМ то следует пользоваться формулой (1.214). Тогда можно получить более точные значения характеристик дискретных элементов *
* См. гл. 1, п. 10.
91
црО1 0,00г нот opoeofit 0,02 0.04 цовщ иг из 0,4 це op i
Рис. 1.25. Номограмма для определения числовых значений амплитуд (в дБ)
Рис. 1.26. НомограМма для построения точных значений логарифмических частотных характеристик типовых звеньев 1-го порядка с передаточными функциями (Ts + +1)-1; (Ts- 1)~';(1 - Ts)-1;Ts+l; 1-Ts; Ts-1:
а, б-!-поправки соответственно для амплитуд и фаз
На практике часто амплитудные и фазовые частотные характеристики строят на полулогарифмической бумаге. Тогда ось <о или 6 размечают в логарифмическом масштабе, где изменение частоты в 10 раз называется декадой (дек.), амплитуду 201g Н'о —
откладывают в децибеллах (дБ) и фазу 0 в градусах. Для определения числовых значений амплитуд удобно пользоваться номограммой (рис. 1.25), где по оси ординат отложены Но, а по. оси абсцисс круговые частоты <о (с~*). Логарифмические амплитудные и фазовые характеристики для некоторых непрерывных и дискретных элементов приведены в табл. 1.10. При этом видно, что у большинства непрерывных элементов аппроксимированные логарифмические амплитудные характеристики приближенно изображаются в виде кусочно-линейных отрезков с на-
7S *7 ГППТП1ТТГИ I Illi 111II III ГГI 1ТТП 11 IT III11ГПII I 1Г11 IIII IT II11 I 11 11 1НТТ I III11II II I II'I 11)
О 5 10 15 20 25 50 55 40 45 50 55 60 65 70 75 80 85 -SO
7S-1 ш.шт ujiiiiititij I run11 tn.il 1111.1 IIIIIIIт11 III 11III itthi ittti ri птт! н nil 11 u> 1111
180 175170 165160 155150 145 140 155 150 125 120 115110105 100 35 30
1-TS IJI ГГ1ИI Г1111IIITT III11 Illi 1ГП-ПТП m-14 ПГТТТ H 1ТГГИ1 ГН ПН ITU II1П Г1III niLH 1IIIIT11
0 -5 -10 -15 -70 -25 -50 -55 -40 -45 -50 -55 -60 -65' -70 -75 SO -85 SO
s'
(Ts л)1 IT ITTI1111111111 IT II11111111111TI1111 п 111111111111114 TIT ГПТ111 Tim 1 ittti i i 1ттт i гтпт 1 т ,0 -5 -10 -15 -20 -25 -50 -55 -40 -45 -50 -55 -60 -65 -70 -75 -80 -85 -90
Ts-i)'’ 11111111111111111 i.i 1 ч|1птпнгпт111тт1 inn1! urn uh mi 11 uni in mniiuin 1 гш 11 >8'
-180 -175 -170 -165 -160 -155 -150 -145 -140 -155 -150 -125 -120 -115 -110 -105 -100 - 35 - 90
1- TS}’’ П1 ГГП'Г 11 ГТ 111111 f III Г| И111 I'll Г11111ГППТ ITTTI IIITFH H ГТПТНПТ1 Г11ТП 111 IT 1111 I 11"1! IIJ
0 5 10 15 20 25 50 55 40 45 50 55 60 65 70 75 80 85 30
92
Таблица 1Ю
Логарифмические амплитудные и фазовые частотные характеристики типовых звеньев npus-juj
NS п/п Передаточная функция Частотные характеристики
Амплитудная Фазовая
1 К 1m, дБ. к Жд 0 ui 0 01
2 S 1т,дБ 0 в Л/2 Л/А (л)
J TS + 1 1т,дБ 0 9д.Ь/дек 7/7 9 л/2 Л/А 0 1/Т <11
4 TS-1 1Л1,ДБ 0 ОдЪ/дек Т/Т ы 1 е Л Л/2 0 1 Г=вш- I 1 1 1 1/Т и
5 1-TS 1т,дБ 0 m&lssK^^ ЦТ ы е 0 -Я/А -л/2 Ш 01
6 1 S 1т,дБ 0 VT\ е 0 -я/ч -л/2 . —
1 1 TS + f 1Л1,ДБ 0 Цт в 0 -Л/А -л/2 1 ЦТ
8 1 TS-1 1т,дБ 0 ОдБ/цек в 0 -Л/2 -ЗЯ/А -л ЦТ г - 1 1
9 1 1~TS- 1т,дБ 0 ОдЪ/дек е Л/2 Я/А <й
10 S2 1т,дБ 0 ш 9 Л Л/2 0 0J
93
Продолжение табл. 1. Ю
11 t2s2<-i 1Л1ДБ 0 /ЬОдБ/дек ОдБ/дек >/Т/ « V/ \ч и л - 1/T W
12 t2s2-i 1т,дБ 0 / ОдБ/де/г/ Л ЛД fl
1/Т <о (J
13 1~T2S2 1т,дБ 0 ОдБ/декх fl X/l ЛЦ c
ЧТ 01 U)
Н T2S2+2^TS+1 |_т,дБ 0 м40ДЪ/дек fl Л Л/2 fl l/T и
15 T2S2+2^TS-1 Im,дБ 0 (j 0 Л Л/2 0 * '>4,>е2>«д
16 T2S2~2tJS+1 1т,дБ 0 1 ' 4 ^ 4 g, CD
17 TzSz-2tJS-l ЦП,дБ 0 <d fl Л 2 0 1>ki> ^2>^3 --
16 1 s2 1т,дБ 0 /X <J 0 0 -X/2 -Л
19 J J2S2+1 1Ш,ДБ 0ДБ/ О 4 0 fl -Л/2 -Л l/r 0)
94
Продолжение табл. 1. 10
20 / T2s2-1 1т,дБ 0 ОлЪ/дек в 0 д' ’I -л (i)
21 1 1-T2S2 1Л1.Д6 0 ОдЪ/дек 1/Т 8 0 Л/2
\te, ы (i)
22 1 T2S2->2t,TS-ft 1т,дБ 0 Z]\ ,>£>>5z>^j t. tz. ХхС™ 8 0 Л Л »К,>К2>1.3 in tj
23 I T2S!+2^TS~1 1П1,ДБ ? oin&l, и 8 0 •Л ‘2 -л
24 1 1т,дБ 0 1}Ь>Ъ>1} 8 Л Л/2 0 > ^2 > 1/Т ш
T2S2-21,15+1 Ы
25 1 . T2S2-2t,TS-l 1т,дБ 0 . . у. ' 0> vxX 8 0 -Л/2 -Л 1 t, «2
26 e'TS 1П?,Дб 0 ДдБ/дея (i) 8 0 -Л/2 -Л 1 — \
27 ers 1т,дБ 0 ОдБ/дек 8 Л Л/2 0 —
25 i-e-^ s 1т,дб 0 9 9
29 (l-e-Jl>s)2(l-T0S) T0S2 йп.дБ 9 — 0Дб|Д^^^д 9 9 Ы
95
Продолжение табл. t. 10
30 (Т^^Тоб^-е-7"1)3 Т20 83 Lmj6 0 '"'"\^6011.б/дек 8 Х/2
0 U)
31 4('-®’5Г(’)е’5Г‘’ 'о 1т,дБ 0 -20 0 Х/2
• и 0 ы
32 1 l-e~2S7° 2Т0 e"S7° 1т,д6 0 8 Х/2 0
й)
33 1 '~e~2ST° То i+4e'sr<’+e'2ST« 1т,д6 0 1 и 0 х/2 0
34 г» he'257" -l+34e“ST^2*n4eSTo+34e~3S7^2~e'2S7o 1т,дБ 0 8 х/2 0 —
35 Toe~ST° j-e-Sl0 1т,д5 20 0 ) 01 0 0 -Х/2 (i)
36 Is 3e~s7°-e~2s70 2 l-e17" 1т,дБ 20 0 -20 ^SSPf / 0 0 -Xl2 Ц)
33 gSTg 2T° l-e-2St° 1т,дБ 40 0 гчУ ы 0 0 -Х/2 й)
38 T„ 1+4e'ST°+eST° T 1-e-^o 1т,дб 20 0 1 8 0 -Х/2
96
продолжение табл. I. 10
39 То 1*4e~ST°l2+o's7° 6 1-e~ST° 1т,д6 20 0 7 '\ч / ы 8 0 -Л/2 (J
40 [l+^(l-e-ST°}]e-ST° 0 1т,д6 20 0 ОДб/ДЛЦ^^^Х i ы В л/2 0
41 ^k(,-e-^Je-sr0 к L IQ j 1т,дб 20 0 0дС/ДВЦ^^\/\ J ы В Л/2 0 ' \л
42 ГОТ, j-[~2STo 7 / T„ 1+4e~ST,,+ e~2ST°j 1т,дб 20 0 ОДБ/ДВ!<^^\ 7 OJ в Л/2 0 X и)
43 Jo T, i-(l-fye~sr° Ьп.Дб 0 -20 7 ОдБ/деТг^^^у <д 8 0 -л/2 1
44 To 27, T-(l-jrlfr~ST°-$ie'2Sf° 1т, дБ 0 -20 J (J 0 0 ~л -2К Т
45 To (h4e~ST°/2+eST:’)eST° 6 ,JkkJ-lL.JL}e-STo (7, 27, 87/ 24Т</ 1т,дБ 0 -20 J ОдБ/дез^. 1 W fl 0 -JC
46 К ch T0S 1т, дБ 20 0 0 дБ/дек 1 ш fl 0 и
47 Ke~T°s 7„S+I 1т,дБ 0 -20 ОдБ/ден fl 0 -Л/2 '—(J
48 *th 10S 1т,дБ 20 0 0 дБ/ ден U о л/2 0 __
48 2/CtnTpS I^Kth TaS Бт.дб 10 0 -5 Одб/дек / \ I \ П ей fl 0 -л -2Л
4 Ю. И. Топчеев
97
Рис. 1.27. Номограммы поправок для построения точных значений логарифмических амплитудных характеристик типовых звеньев 2-го порядка, имеющих передаточные функции (Г2.?2 + 2gTs + I)-1; (72s2 — — 2gTs 4- 1)' 72s2 + 2g7’.s + 1; 72,s2 -
- 2gTs + 1
частотных характеристик для сложных элементов, представляющих собой последовательное, параллельное, последовательно-параллельное соединение типовых звеньев или образующих замкнутые контуры (см. примеры 1.36—1.39).
Для некоторых часто встречающихся типовых звеньев удобно пользоваться номограммами поправок для амплитуд и фаз. Логарифмические амплитудные и фазовые частотные характеристики звеньев 1-го порядка строились по формулам, приведенным в табл. 1.10, в зависимости от ш/ш01 где о)о=1/Бо-
На рис. 1.26, а изображена номограмма поправок ALm, полученная путем нахождения разности между приближенной и точной логарифмическими амплитудными характеристиками. Для типовых звеньев
клонами 0; ±20; ±40 дБ/дек. Благодаря этому упрощается построение логарифмических амплитудных
Рис. 1.28. Номограммы для определения значений фазовых углов типовых звеньев 2-го порядка, имеющих передаточные функции (r2s2-2grs + i)"‘; (Ps2 + 2grs + i)-1;
T2s2 + 2gTs i и f2s2 — 2%Ts + 1
98
Лт.дЬ
Л I.ih ,л 6
0,t 02 03 0,4 Of Of 10If 1,6 if .10 0,0Sf 10SO v/w.
Рис. 1.29. Номограммы поправок для построения точных значений логарифмических амплитудных характеристик типовых звеньев 2-го порядка, имеющих передаточные функции (T2s2 + 2*Ts — I)-1; (7'2s2 — —Ч^Тз — I)-1; T2s2 + 2£7's~-1; T2s2-2tTs-l
с передаточными функциями (Ts4-+ 1)_|, (1 — Ts)~l и (Ts—1) ’ поправки имеют отрицательные значе-
Рис. 1.30. Номограммы для определения значений фазовых углов типовых звеньев 2-го порядка, имеющих передаточные функции (T2s2 + 2§rs — I)-1; {T2S2 — —
- 1)“'; T2s2 + 2&Zs - 1 и T2s2 - 2g7’s - 1
ния —ALin, а для звеньев Ts 4- 1, 1 — Ts и Ts — 1 — положительные значения ДЬт. На рис. 1.26,6 даны значения фазовых углов ±0° в виде номограмм для типовых звеньев (Ts 4-I)""1; (1 —Ts)-1; (Ts — - 1)-*; Ts+ 1; 1 —Ts и Ts—1. Из построенных номограмм видно, что типовые звенья с передаточными функциями (Ts 4-1)"', (Ts—I)-1, 1 — Ts являются фазозапаздывающими, а звенья (1 — Ts)-1, Ts 4~ 1, Ts — 1 — фазоопёрежаю-щими.
Составим формулы для вычисления точных значений логарифмических амплитудных и фазовых частотных характеристик типовых звеньев 2-го порядка, которые также приведены в табл. 1.10. На рис. 1.27 построены номограммы поправок для логарифмических амплитудных характеристик, а на рис. 1.28 значения фазовых углов для типовых звеньев с передаточными функциями
(T2s2 + 2^Ts4-1)-1;
(T2s2-2gTs4- l)-1;
T2s2 + 2gTs + 1; T2s2 - 2STs 4- 1 •
Для типовых звеньев с передаточными функциями (Т2$2 4-
4? о,а 0,7 о/ 45 (?4 45 0,2 0,1
О
зох^л4 •^,0^3,33 \,4,0Х '0,0 \ fj/Mo--2O,0
1,11 , 125- 0,2 \0,1
0,8' /
0.1/
W(s)-(T2s2t2^Ts-1f1 135 140 145 150 155 160 165 H(s)=T2s2*2tTs-1
no 175 180
9JLL1..U I. Ll_m -225 -220 -215 W(S)=(T2S2-2ZTs-1)'1 -210 III -205 Illi T" I -200 I I I I I ^-195 J-LLJ -190 IJ I I I I I I I 1 -185 -180 Ms)*T252-2?TS-1
g°r:i i. l i 11.1 i г i i .i—i 255 200 215 ДДДДД 210 LU—L 205 LULLU 200 _LU_LL 195 ±J_LJ 190 L-LLLL1. LLIJ 185 180
4*
99
+ 21TS-1)-'-, (T2s2 — 2ZTs — ;
T2s2 2lTs — 1; T2s2 — 2lTs — 1 на рис. 1.29 приведены номограммы поправок для логарифмических амплитудных характеристик с максимальной погрешностью А 4 дБ, а на рис. 1.30 номограммы значений фазовых углов.
Пользуясь данными табл. 1.10 и номограммами, изображенными на рис. 1.27— 1.30, можно построить приближенные логарифмические частотные характеристики динамических элементов САР.
Пример 1.36. Построить точную логарифмическую амплитудную и фазовую частотные характеристики для непрерывного динамического элемента, описываемого передаточной функцией вида ™ __________fe(T2s+l)3e-TS
° s2(r1s-l)(7’2S2 + 2g37’3s4-l)X ’
X(7-/-2g4r4s+l)
(1.217) где
k = 100 c~2; Ti = 10 c; T2 = 5 c; T3 = 0,5 c; Tt = 0,02 с; т = 0,2 с; Ь = 0,01; ^4 = 0,80.
Сравнить точное и приближенное построение логарифмических характеристик.
Подставив в выражение (1.217) s = /со и соответствующие числовые значения, получим
«%(/“) = IMUTi+'),,'4U'“
<«•(-£-/- 1)[(4 /)!+20.»1Х
(1.218)
Из формулы (1.218) найдем математические зависимости для построения логарифмических характеристик:
амплйтудной
На (со) = 20 1g 100 — 40 1g и —
- 201g д/(тг)2 + 1 +
+ 60 lg aJ(-§-)2 + 1 -
-20 1g д/[1 - (у)2]2+ 4-0,0001 (f )2-
-20 1gV[T-g)T + 4.0,64(|)2
(1.219) и фазовой
е0 (со) = -180° + 3 arctg 5<о - 180° +
+ arctg 10а» — <р 1 — ф2 — О,2со; (1.220)
Lm, дб
Рис. 1.31. Логарифмические амплитудная и фазовая частотные характеристики, построенные по передаточной функции (1.217)
( , 0,01со
= ] arctgT-0:25o2 при w<2:
V 180° + ф, при со > 2;
( , 0,032со .
ф2=J-arctgT^raw при м<50;
(—180° + <р2 при со > 50.
Для различных со — 0,005; 0,01; 0,05; 0,1; 0,2; 0,5; 1,0; 2,0; 5,0; 10,0; 20,0; 50,0; 100; 200; 500; 1000 с~‘ по формулам (1.219)— (1.220) составлены табл. 1.11 и 1.12 соответственно для амплитуд и для фаз.
По числовым данным табл. 1.11 и 1.12 на рис. 1.31 построены сплошной линией кривые точного значения логарифмической амплитудной Но (со), а штриховой линией — фазовой 0о((о) частотных характеристик динамического элемента, описываемого передаточной функцией (1.217).
Аппроксимируем полученную логарифмическую амплитудную частотную характеристику типовыми наклонами ±20п дБ/дек, п — 0, 1, 2, ... (штрихпунктирная линия на рис. 1.31). В этом случае точные и приближенные значения логарифмических амплитудных характеристик отличаются не более чем на 3 дБ, что мало влияет на правильность построения характеристик. Поэтому на практике логарифмическую амплитудную характеристику строят с помощью типовых наклонов, учитывая при этом поправ-
100
Таблица 1.11
Значения логарифмических амплитудных характеристик типовых звеньев и всего дянамнческого элемента для примера 1.36
Выражение для амплитуды типового звеиа Амплитуды Но (со), дБ
0.005 0,01 0,05 0,1 0,2 0,5 1,0
20 1g 100 40 40 40 40 40 40 40
—40 1g 10 92,04 80,0 52,04 40,0 27,96 12,04 0
- 201g 7(ш/0,1)2 + 1 -1,08-Ю-2 —4,32- 10"2 -9,69- 10"1 -3,01 . -6,99 -14,15 —20,04
60 1g V(co/0,2)2 + 1 8,14 10“3 3,25- 10“ 2 7,90-10“' 2,91 9,03 25,81 42,45
-20 1g V[1 - (co/2)2]2 + 4 • 0,0001 (ш/2)2 5,39- 10“5 2,17- 10“4 5,43 • 10"3 2,17- 10“2 8,73- 10“2 5,60- 10“‘ 2,50
—201g V [ 1 - (o/50)2]2 + 4 0,64 (0/50)2 0 —4,34- 10"7 —2,17 • 10“6 -9,55- 10“6 —3,87- 10“5 -2,43- 10“4 -9,73- 10"4
Результирующая амплитудная характеристика Ho (о) 1—4 О - 132,04 119,99 91,87 79,92 70,09 64,26 64,91
Продолжение табл. 1.11
Выражение для амплитуды типового звена Амплитуды Hq (©), дБ
2.0 5,0 10,0 20,0 50,0 | 100,0 200.0 500,0 1000,0
20 1g 100 40 40 40 40 40 40 40 40 40
—40 1g 10 — 12,04 —27,96 —40,0 —52,04 —67,96 -80,0 -92,04 -107,96 -120,0
-20 1g V(o)/O.l)2+ 1 -26,03 —33,98 -40,0 -46,02 -53,98 —60,0 —66,02 —73,98 —80,0
60 1g V(co/0,2)2 + 1 60,13 83,90 101,94 120,00 143,88 161,94 180,0 203,88 221,94
-20 1g V[ 1 - (w/2)2]2 + 4 • 0,0001 (ш/2)2 33,98 -14,40 —27,60 -39,91 -55,90 -67,96 —80,0 —95,92 -107,96
-20 1g V[1 - (0/50)2)2 -|- 4 . o,64 (o/50)2 —3,9- 10“3 —2,47 • 10“2 -1,03- 10“1 -4,74- 10"1 -4,08 — 12,84 —24,25 —40,02 —52,08
Результирующая амплитудная характеристика Но (о) 96,04 47,54 32,24 21,56 1,96 -18,86 -42,31 -74,0 —98,07
Таблица 1.12
Значении логарифмических фазовых характеристик типовых звеньев и всего динамического элемента для примера 1.36
Выражения для вычисления фаз типовых звеньев Фазы 6о («)» 0
0,005 0,01 ' 0,05 0,1 0.? 0.5 1.0 '-’.0
-180° -180 -180 -180 — 180 -180 -180 -180 -180
— 180° + arctg 10а -177,1 -174,3 -153,4 — 135,0 -И 6,5 -101,3 -95,67 -92,80
3 arctg <£>/0,2. 4,43 8.59 42,13 79,73 135,0 204,7 236,2 252,9
, 2-0,01(<о/2) arctg 1-«0/2)* —0,00286 -0,00573 —0,0286 —0,0575 -0,116 —0,306 -0,764 -90,0
_зю.+.ге1г^^ 0,0092 0,0183 0,0917 0,183 0,367 0,917 1,835 3,69
— 0,2 • 57,3а -5,73. 10~2 -0,1146 -0,573 — 1,146 —2.29 —5,73 - 11.46 -22,9
Результирующая фазовая характе-5 ристнка 60(а) S3 -352.9 —345,8 —291,8 -236,1 — 163,5 —81,69 -49,87 — 129,1
Продолжение табл. 1.12
Выражения для вычисления фаз типовых звеньев Фазы 6о (<о). °
5,0 10,0 20,0 50,0 100.0 200,0 500 0 1009,0
— 180° — 180 — 180 — 180 — 180 -180 -180 -180 — 180
— 180° + arctg 10ш -91,1 -90,53 —90,24 -90,1 -90 -90 -90 -90
3 arctg ш/0,2 263,2 266,7 268,4 269,3 269,80 270,0 270 270
. 2 • 0,01 (W/2) arctg 1 -(ш/2)» ' -179,5 -179,8 — 179,9 — 180,0 — 180 — 180 -180 -180
„ 2 • 0,8 (ш/50) -360“ + arctg 9,185 18,44 37,32 90,0 133,1 156,8 170,3 175,4
—0,2 -57,3а —57.3 — 114,6 —229,3 -573 -1146 -2293 —5730 -11460
Результирующая фазовая характеристика 0о (а) —235,4 -279,8 -373,7 —663,7 — 1194 —2316 —5742 — 11470
ки на звенья 2-го порядка (номограммы на рис. 1.27 и 1.29).
Фазовую характеристику строят по данным номограмм рис. 1.25, а, б и 1.28. Соответствующая штрих-пунктирная кривая приведена на рис. 1.31. Как видно из этого построения, точные и приближенные значения фазовых характеристик отличаются не более чем на 5°. Такую малую погрешность также можно не учитывать при приближенных способах построения логарифмических амплитудных и фазовых частотных характеристик. Поэтому, как правило, логарифмические амплитудные и фазовые частотные характеристики динамических элементов и звеньев строят приближенным способом, что значительно сокращает время на их построение.
Пример 1.37. Найти логарифмические амплитудную и фазовую частотные характеристики для непрерывного динамического элемента, описываемого передаточной функцией
ь г 1
(S) “ 2|2Г28 +7 +
+ ~ту + 2^т37+ Г ] ’ (1,221}
Перепишем соотношение (1.221) в виде Го (s) = Wt (s) [Г2 (s) + Г3 (s)]. (1.222)
Г, (8)
Примем следующие обозначения: fe
4^8-пу
1
^2(s) = --^----------------
Т 2s + 2^2Г 2s + 1
1
(s)---------------------,
+ 2§3Г38 + 1
где fe = 10 c_|; T} = 1 c; Tz — 0,1 с; Г} = = 0,05 c; £2 — 0,15; g3 = 0,05.
Соотношение (1.222) преобразуем следующим образом:
Го (8) = (8) Г2 (s)[l +
откуда
Г2(з) W3(s) । Г2 (s)
Го (s) = Г, (s) Г2(в)
Г3 (s)
(1.223)
Рис. 1.32. Логарифмические амплитудная Н (со) и фазовая 0(со) частотные характеристики
Подставив в выражение (1.223) s — /со, получим
Го (/СО) == Г, (/Ш) Г2 (/со)
Г Г2 (/со) -|~1 (/со)
, , 4^2 (/30)
L -|"гэ(/а>) J
(1.224)
Соотношение (1.222) для выполнения операции логарифмирования с помощью номограммы замыкания приведем к виду (1.224). Выражения в квадратных скобках из соотношения (1.224) можно представить в следующей форме:
<L22S’
Из теории автоматического регулирования известно [13], что можно находить логарифмические амплитудные и фазовые частотные характеристики, пользуясь выражением (1.225), т. е.
20 1g | Г (/со) | = 20lg|(1.226) arg [г (/со)] = arg -г-1. (1.227)
I 1 •“t” W J
Для соотношения (1.224) с учетом выражений (1.226) и (1.227) имеем
20 1g | Го (/со) | = 20 1g | Г, (/со) | +
+ 20 1g | Г2 (/со) 1-20 1g |
(1.228)
arg [Го (/со)] = arg [Г1 (/со)] + + arg [Г2 (/со)] - arg
(1.229)
103
Рис. 1.33. Номограмма замыкания с нанесенными на ней логарифмическими ам-плитудно - фазовыми частотными характеристиками: кривая / — для примера 1.37; кривая 2 — для примера 1.38; кривая 3 — для примера 1.39
Рис. 1.34. Логарифмические амплитудная и фазовая частотные характеристики
Н (со); 0 (со) и Н (со); 0 (со)
На рис. 1.32 сплошными кривыми показаны логарифмические амплитудные
Н (со) = 20 lg [Г, (/со) | + 20 1g |Г2 (/со)’|
и фазовые (3(со) = arg [Г, (/со) ] +arg [IP's (/со)] характеристики. Здесь же даны логарифмические амплитудные и фазовые частотные характеристики '20 lg| W(/со) | и arg[lP"(/co)]. Нанесем на номограмму замыкания (рнс. 1.33) числовые значения * этих характеристик при различных частотах со и проведем через них кривую 1. Тогда в точках их пересечения со сплошными кривыми линиями номограммы получим значения И (со), а со штриховыми 0(со). Перенесем полученные кривые на рис. 1.34 и, вычитая их из построенных характеристик Н (со) и 0 (со) (рис. 1.32), найдем результирующие амплитудную //о(со) и фазовую 0о(со) частотные характеристики рассматриваемого динамического звена. Они построены жирными линиями на рис. 1.34.
Пример 1.38. Построить логарифмические амплитудную и фазовую частотные харак
* Формулы для построения номограммы замыкания приведены в гл. 3, п. 9. Там же показано, что данная номограмма представляет собой многолистную поверхность. Поэтому для удобства ее применения в ряде задач следует пользоваться номограммой замыкания, построенной в полярной системе координат.
теристики для динамического звена, включенного в контур с отрицательной обратной связью (рис. 1.35, а). Примем 6=10 и Т = 1 с. Имея это в виду, на рис. 1.36, а построены соответствующие частотные характеристики: логарифмическая амплитудная Я(со) тонкой сплошной линией и логарифмическая фазовая 0(со) тонкой штриховой линией. Для определения результирующих характеристик данного элемента составим передаточную функцию в виде
Го (s) = Г (s)/[l + r(s)], (1.230)
где s = /со.
Пользуясь соотношением (1.230), можно числовые значения полученных характеристик перенести с рис. 1.36, а на номограмму (рис. 1.33) и, соединив их кривой 2, найти функции Н (со) и 0 (со). Нанесем их на рис. 1.36, а и, соединив точки линиями, получим результирующие характеристики //0(со) —жирная сплошная линия и 0о(со)— жирная штриховая линия.
Пример 1.39. Построить логарифмические амплитудную и фазовую частотные характеристики для динамического звена, включенного в контур с положительной обратной связью (рис. 1.35,6). В этом случае имеем
Го (s) = Г («)/[Г—Г (s)], (1.231)
где х = /со.
ВозьМем параметры динамического элемента такими же, как и в примере 1.38. Тогда /7(со) и 0(со) аналогичны соответствующим характеристикам, показанным на рис. 1.36, а. Однако для получения результирующих частотных характеристик с помощью номограммы (рис. 1.33) необходимо из формулы (1.230) определить
Г (s) = Го (s)/[ 1 - Го (s)] при s = /со.
(1.232)
Из сравнения формул (1.231) и (1.232) следует, что по своему написанию оии тождественны; только в формуле (1.231) в левой части имеем функцию замкнутого контура Го(/со), а в правой__части — функции разомкнутого контура Г(/со). В формуле (1.232), наоборот, в левой части имеем функцию разомкнутого контура Г(/со), а в правой части — функцию замкнутого контура Г0(/‘со). Поэтому можно сформулировать следующее правило построения частотных характеристик контуров с
Рис. 1.35. Структурные схемы с типовыми звеньями, включенными в замкнутый контур: а — с отрицательной обратной связью; б — с положительной обратной связью
а)
б)
105
Рис, 1.36. Логарифмические амплитудные и фазовые частотные характеристики динамического элемента в виде контура: а и б — соответственно с отрицательной и положительной обратными связями
положительной обратной связью: значения амплитуд и фаз разомкнутого контура следует брать из кривых номограммы, а значения амплитуд и фаз замкнутого контура считывать с осей их ординат и абсцисс. С учетом этого правила, на номограмме, показанной на рис. 1.33 кривой 3, нанесена логарифмическая амплитудно-фазовая частотная характеристика, построенная по функции IF (/со) — 10/(/<i> + 1), а иа рис. 1.36, б — по точкам, снятым с номограммы (значения амплитуд и фаз контура с положительной обратной связью). Соединив их жирными сплошной и штриховой линиями, получим соответственно результирующие значения логарифмической и фазовой частотных характеристик динамического звена (контур с положительной обратной связью).
Для исследования динамики сложного объекта САР следует строить логарифмическую амплитудно-фазовую частотную характеристику в полярной системе координат. В этом случае в более наглядной форме выявляется влияние слабодемпфированных элементов, представляющих собой произведение дифференцирующих звеньев 2-го рода, на колебательные при малых g и близких значениях постоянных времени. При анализе устойчивости замкнутых систем с такими объектами можно находить запасы устойчивости по амплитудам и фазам на собственных частотах колебаний слабодемпфированных элементов (см. гл. 4, п. 6).
Рассмотрим два примера построения логарифмических ампли
тудно-фазовых частотных характеристик с неминимально фазовыми звеньями и слабодемпфированными элементами. В сложных объектах таких элементов может быть несколько. Как правило, они образуют замкнутые кривые с ярко выраженными собственными частотами колебаний.
Пример 1.40. Построить логарифмическую амплитудно-фазовую частотную характеристику 20 1g Фо(/ы) в полярной системе координат для объекта, описываемого передаточной функцией
lF0(s) =
(т1? + 1) (т3з+1) (7-|з2+2|2Т6з+1)Х ___________><(т|г + 2£478з +1)__________
- 1 fl~T4s + 1) (Г- 7 5s) (ту + +2^rzs + 1) (ТУ + 2g'3T9s + 1)
(1.233)
где Г, = 999,9 с; Г6 = 0,176 с; g, = 0,0032;
Т2==499,9 с; Т7 = 0,156с; g2 = 0,61;
Т3 = 111,12 с; Т8=0,106с; g3 = 0,0016;
= 1,006 с; Т9 = 0,089 с; g4 = 0,24.
Т5 = 0,986 с.
Подставим н выражение (1.233) s = /со и вычислим числовые значения амплитудной Но (дБ) и фазовой 0S частотных характеристик. Откладывая их в полярной системе координат на плоскости W, получим логарифмическую амплитудно-фазовую частотную характеристику сложного динамического объекта 201g W(jw) (рис. 1.37). При этом видно, что объект обладает двумя замкнутыми кривыми 1 и 2. На кривой 1 указана собственная частота колебаний а>Р1 = 6,43 с-1, а на кривой 2 — <ор2 = = 11,23 с”'.
На рис. 1.38, а построены логарифмические амплитудная Н0(ы) и фазовая 00(<о) частотные характеристики в декартовой системе координат, числовые значения кото-
106
Рис. 1.37. Логарифмическая амплитудно-фазовая частотная характеристика сложного объекта с двумя слабодемпфированными элементами, построенная в полярной системе координат (пример 1.40)
рых перенесены с рис. 1 37. Из рис. 1.38, а видно, что значения нулей <ун будут: <а6 = = 1/Г6 = 5,67 с-1, «в = 1/7’в = 10,47 с-', а значения полюсов <оп равны: <о7 = 1/Г7 = = 6,41 с~!, <09=1/7’9=11,28 с-i. Пользуясь рис. 1.38, а, нетрудно найтн коэффициенты демпфирования звеньев 2-го порядка, которые входят в передаточную функцию (1.233). Они имеют следующиг значения: !•) — -—50,10 дБ; -• - 14,38 дБ, Ь = —56,27 дБ, ^4 = -12,54 дБ. Сравнивая рис. 1.37 и 1.38, а, можно установить, что логарифмическая частотная характери-
Рис. 1.38. Логарифмические амплитудная и фазовая частотные характеристики сложного объекта с двумя слабодемпфированными элементами, построенные в декартовой системе координат:
а —для примера 1.40; б —для примера 1.41
стика, построенная в полярной системе координат по амплитуде, мало зависит от принятого проектировщиком рабочего диапазона частот. Эго и позволяет на малых форматах получать логарифмические частотные характеристики в крупном масштабе. В результате построенный на рис. 1.37 годограф обеспечивает такую разрешающую способность, при которой можно достаточно точно анализировать динамические свойства исследуемого объекта. С помощью логарифмических амплитудной н фазовой частотных характеристик, построенных в декартовой системе координат (рис. 1.38, я), нетрудно найти частоты нулей и полюсов звеньев 2-го порядка и коэффициенты их демпфирования. Поэтому проектировщик строит логарифмическую амплитудно-фазовую характеристику для всего диапазона частот в полярной системе координат, 'а участки, где проявляется влияние слабодемпфироваиных элементов, он изображает в декартовой системе координат в увеличенном масштабе по частоте.
Пример 1.41. Построить логарифмическую амплитудно-фазовую частотную характеристику 20 lg lV'o(/w) в полярной системе координат для объекта, описываемого передаточной функцией
Го (s) =
(TjS + 1) (j2/ + 2^Т 4s + 1) X Х(Г*? + 2^7>-+1)(4<2 +
. .. 4 + 2ъз?'1Л + 9
(т.^- 1 )2 (ту -мУ(’
+2£27у +1) (T2s2 + 214T7s + 1) X X(r252 + 2g6T9s+l)X
X (7\os2 + 2^7 10s + 1)
(1.234)
где Ту = 25 с; Тц — 0,0988 с; =0,035;
Т2 = 2,5 с; Т7 = 0,098 с; |2 = 0,042;
107
r2 30"
Рис. 1.39. Логарифмическая амплитуднофазовая частотная характеристика сложного объекта с четырьмя слабодемпфирован-ными элементами, построенная в полярной системе координат (пример 1.41)
Т3 = 1,03 с; Т8 = 0,049 с; g3 = 0,094;
Т4 = 0,131 с; Гд = 0,046 с; g4 = 0,063;
Т5 = 0,121 с; Г.о = 0,024 с; g5 = 0,56;
Т„ =0,0205 с; g6= 0,63;
& = 0,31;
g8 = 0,53.
Логарифмическая амплитудно-фазовая характеристика построена на рис. 1.39, где кривые соответствуют слабодемпфирован-ным элементам: замкнутая 1-я кривая строится по
T2s2 + 2|,T4s + 1 передаточной функции
/ 5$ -|- 5$ “Г 1
T2s2 + 2g3T6s + 1 2-я кривая — по функции—, r27s2 + 2g4T7s + 1
ж Tls2 + 2^57’8s+ 1 3-я кривая — по функции —------------
T2s2 + 2g6r9s + 1
и 4-ая кривая* — по ~Ь Is ~Ь I функции Т*082 + 2£7Т108+1 ’
На рис. 1.39 приведены значения <о₽1 = = 8,2 с-', со = 10,3 с-1, <о_ = 26,3 с"'1 и
<ор( = 42,5с~1 —собственные частоты слабо-
* 4-ая кривая не является полностью замкнутой из-за большой разницы значений g7 и gs, а также существенного отличия постоянных времени Ti0 и Ttl.
демпфированных колебаний. Для сравнения иа рис. 1.38,6 также построены характеристики Ло(со) и 0о(со), на котором видно, что наиболее ярко выражены значения (Оп1, <1Эц | И <ОП2.
При исследовании динамических объектов со слабодемпфированными элементами, входящими в многоконтурные САР, часто строят логарифмические амплитудно-фазовые частотные характеристики в декартовой системе координат, когда по оси ординат откладывают значенйя Н0(ы) (дБ), а по оси абсцисс 0о(со). Пользуясь такими характеристиками, достаточно просто находить все запасы устойчивости по амплитудам и фазам в замкнутых САР (см. подробнее гл. 3). Для упрощения построения таких характеристик будем пользоваться обобщенной номограммой слабодемпфиро-ванных элементов, описываемых зависимостью
(¥ + 2g + 1
I со , ) ' ®иг о
Wi (8) = <--------, (1.235)
(-^—1 + 2g , + 1
I 6),. | "‘ <!) .
\ ni / п>
где <о„/ — значение собственной частоты для нулей i-ro звена; соп< — значение собственной частоты для полюса i-ro звена; gHi, gni — коэффициенты Демпфирования i-x звеньев, стоящих в числителе и знаменателе зависимости (1.235).
Запишем передаточную функцию для системы, состоящей из трех слабодемпфиро-ванных элементов:
1Гз (s) =
[s2 (1 — О[) + BjS + cof] [s2 (1 — а2) +
+ e2s + со2] [s2 (1 — а3) + е38 + со2]
[s2 (1—0, — Pj) + 8|S + со2] X
X [s2 (1 - а2 - р2) + e2s + со|] X
X [s2 (1 - а3 - р3) + e3s + со2]
(1.236)
Здесь аь а2, а3, рь Рг, Рз, еь е2, е3, соь со2, со3 зависят от конструктивных параметров слабодемпфированных элементов.
Нули и полюсы для передаточной функции (1.236) найдем при малом ес и й: « 1; р( < 1 с помощью следующих выражений [34]:
81 .СО!
SHi =------------± 1 —.
2(1—0!) V1 — Oi
82 J . <0
8н2...... " — J , — — ,
2 (1 — а2) V1 — а2
„ 8з ®з . .’
$НЗ “ — 1 ± J ' —-,
2 (1 — а3) VI — а3 j
108
е, , +
2(1 - а, -р.У* '
±/ .М|
V1 — <Х1 — р,
62 s"2-- 2(1 — а2 —р2) *
±/ .....
V1 — 02 — ₽2
о_________83 ,
пз 2(1—а3 —р3) “
±/-7=^=.
V1 — а3 — Рз
(1.237)
Коэффициенты демпфирования определим по формулам
формулам
|sHi «П1 I —
1 1
Vl — a, V1 — И1 — р, | «н2 — «п2 | —
1 1
V1 — «2 V1 — а2 — р2 I «из «пз I —
1 1
V1 — «3 V1 — «3 — Рз
(1.240)
Разложив соотношения (1.240) в ряд Тейлора и взяв его первые члены, получим
I Shi — Sni I = -Цр-L= До);;
? 61
SH1 — „ Г.-----
2 -у 1 — а, <о,
?Н2 = —7==—;
2 V1 — а2 <о2 е3
2 V1 — «з 0)3
_______81_______
2 V1 — а, — Pi <01 е2
?нз
&П1 --
?пз
2 V1 — а2 — р2 <о2
__________8з___________
2 у/1 — а3 — Рз <о3
(1.238)
Значения частот для нулей и полюсов будут
<01 «н1=-з==-;
VI — Oi
<01
V1 — а,— Pi
<ОП2
_____ <02______
V1 — а2 — р2
I 5Н2 — $П2 | — —2 — ^^2’
I «нз — «пз I = -Цр- «3 = Ло)3.
(1.241)
В соотношениях (1.241) использованы обозначения
Д<01 — <оН] <0пь*
Д<02 = <ОН2 — <0п2!
Д<о3 = <он3 — <Опз,
(1.242)
которые характеризуют близости частот нуля и полюса. Последними следует пользоваться, если собствеииая частота нуля больше собственной частоты полюса и наоборот, т. е.
Д<01 = <0п 1 — <оН1 > х
Дю2 = <оп2 — юн2; > (1.243)
Д<03 = <ОП3 — ®НЗ. '
Выражения (1.238), (1.239), (1.242) или (1.243) полностью определяют передаточную функцию (1.235).
Для составления обобщенной номограммы выражение (1.235) запишем в виде передаточной функции
(1.239)
<0НЗ
<03
V1 — а3 ’
<опз = ——.
VI — а3 — Рз
Разница в расположении нулей и полюсов для каждого из звеньев находим по
Близость частот <он< и <оп< позволяет приближенно считать равными коэффициенты демпфирования звеньев, стоящих в числителе и знаменателе.
По дайной передаточной функции невозможно построить обобщенную номограмму, так как входящие в нее значения зависят от абсолютных величин частот <вн< и шп<. Устраним этот недостаток, представив
109
передаточную функцию (1.244) в виде
Wi (s)
(1.245)
Следует отметить, что передаточные функции (1.244) и (1.245) имеют одинаковые фазочастотные характеристики и при их минимальной фазовости совпадающие с амплитудно-частными характеристиками.
Обобщенная номограмма должна описывать предельную ситуацию, когда Ди;-* О, и ini-’-O; поэтому функцию (1.235) можно представить в виде
Положим, что
Wt (s) = lim
7—(1.247)
Здесь Ci — постоянный параметр, т. е.
Доз.
с. =-г—— = const. (1.248)
i Е.о> . ' ’
Ъ1 hZ
Из выражения (1.249) найдем
(1.251)
Подставив в формулу (1.246) выражение (1.248), что справедливо для малых значений и положив s = /и, получим
(1.249)
По формулам (1.250) и (1.251) на рис. 1.40 построена обобщенная номограмма при различных значениях а. При расчетах собственные частоты со„/ и ып1- выбирались таким образом, чтобы отношение Д(0;/юИ!- было близко к нулю. На номограмме по оси ординат отложены значения амплитуд, по оси абсцисс — значения фаз. С помощью этой номограммы нетрудно построить приближенную результирующую логарифмическую амплитудно-фазовую частотную характеристику объекта со слабо-демпфированными элементами при малом е,. При этом соблюдают следующий порядок действий:
1) строят на миллиметровой бумаге логарифмическую амплитудно-фазовую частотную характеристику объекта без учета звеньев, входящих в слабодемпфированные элементы (в декартовой системе координат; амплитуда--в дБ, фаза — в градусах);
2) определяют собственные частоты колебаний слабодемпфированных элементов и наносят их на логарифмическую амплитудно-фазовую характеристику;
3) по выражениям (1.238), (1.239),
(1.242) или (1.243) и (1.248) вычисляют числовые значения шн>, Д<В; и с,-;
110
Рис. 1.40. Обобщенная номограмма для построения логарифмических амплитуднофазовых частотных характеристик слабо-демпфированных элементов
4) накладывают номограмму, вычерченную на прозрачной бумаге, на логарифмическую амплитудио-фазовую частотную характеристику таким образом, чтобы ее начало' координат каждый раз совпадало с собственными частотами колебаний мр.. и переносят замкнутые кривые номограммы с параметрами с,- на миллиметровую бумагу. В результате будет получена результирующая амплитудно-фазовая частотная характеристика объекта.
Следует отметить, что правые кривые номограммы соответствуют случаю, когда частота нуля меньше частоты полюса, а левые кривые — когда частота нуля больше частоты полюса.
Пример 1.42. Построить логарифмическую амплитудио-фазовую частотную характеристику объекта в декартовой системе координат (амплитуда — фаза) для объекта, имеющего передаточную функцию
212,+ "[Сйг)г+ + 2-0.02^-+1) ° W (40s - 1) (0,7s + 1) (0,4s + 1) X '
X (0,01s + 1)
;,[(тгп-)г+г-М05тата + 1] [(тлтУ + 2-(,02^т + |]
x [(’36.12 ) +2'°-0()4 36,12 + ']
iL < i ? d
x[(’s5Ts~) +s - о.«и-j.jfj-+ 1]
(1.252)
Нанесем сплошной линией на рис. 1.41 логарифмическую амплитудно-фазовую характеристику, пользуясь функцией, полученной из выражения (1.252), т. е.
IV'о ()<о)
_________2(2/ш+ 1)______________ (40/cu — 1) (0,7/<в + 1) X
X (0,4/<в + 1) (0,01/со + 1)
(1.253)
и разметим на ней частоты, выделив светлыми кружками собственные частоты слабодемпфированных колебаний * copi — =4,130 с”‘; со. =20,368 с ’1 и со, =80,953 с По формулам (1.242) и (1.243) вычислим Дсо, = 0,4096 с” ’; Дсо2 = 0,8576 с-1; Асоэ = = 3,9446 с-1 и по формуле (1.248) определим Ci = 4,0; с2 = 8,0; Сз — 12,0.
Наложим номограммы, как это показано на рис. 1.41, и проведем по ней три замкнутые кривые для найденных параметров С), сг и с3. Таким образом, получим приближенно построенную результирующую логарифмическую амплитудио-фазовую частотную характеристику слабодемпфироваи-ного объекта.
* Частоты заданы техническими усло-
пнями.
111
Рис. 1.41. Логарифмические амплитудио-фазовые частотные характеристики, построенные в декартовой системе координат (амплитуда — фаза) с наложенными номограммами, представленными в виде шаблонов (пример 1.42)
амплитудно-фазовой частотной характеристики на рис. 1.41 жирными точками обозначены частоты, полученные путем построения характеристики по полной передаточной функции (1.252). Из сравнения этих характеристик видно, что приближенный способ построения практически мало отличается от точного.
Пример 1.43. Рассмотрим способы построения логарифмических амплитудных и фазовых частотных характеристик динамических элементов (объектов) днскретно-ие-прерывного типа. На рис. 1.42, а показана структурная схема дискретно-непрерывного элемента, состоящая из аналого-цифрового преобразователя (АЦ) /, управляющей микроЭВМ 2, цифроаналогового преобразователя (ЦА) 3 и непрерывной части (НЧ) 4. Используя г-преобразоваиие [см. соотношение (1.172)], можно при Го = 0,2 с найти
го(г)= 0-12~'(3~^~2/1-г~1) х
Х 5 [s2 (0,1s + 1) (0,05s+1) ]' (1 '254)
Выражение, стоящее в квадратных скобках, представим в виде суммы рациональных дробей, т. е.
Го (г) = 0,1г-' (3 - г-1) X
В
s
_£_ + _£_
S+ 10 S + 20
Для определения коэффициентов А, В, С, D в выражении (1.255) коэффициенты при одинаковых степенях s можно приравнять, т. е.
400 А В
s2 (s + 10) (s + 20) — s2 + s +
С В
+-T+iy+'TW’ (L256)
откуда получим систему алгебраических уравнений
s°: 400 = 2004;
s1: 0 = 304 + 200В;
s2: 0 = 4 + ЗОВ + 20С + 10D;
s3: 0 = В + С + D.
Для проверки правильности приближенного способа построения логарифмической
Рис. 1.42. Структурные схемы САР дискретно-непрерывного типа:
а —исходная; б — приведенная с ^помощью ^-преобразования; в ~ приведенная к 5-преобра-зованию
6) 8)
112
Из решения системы уравнений находим
4 = 2; В = -0,3; С = 0,4; О = — 0,1.
В результате этого выражение (1.256) можно переписать в следующем виде:
Го(г) =
0,3 s
0,4 0,1 1
s + 10 s + 20-Г
(1.257)
Пользуясь таблицей г-преобразоваиий (см. прнл. П-1.3), выражение (1.257) представим в виде
_ . . 0,1 (3z — 1)Г 0,4г 0,3г .
(2) = — ---------- —Г+
и фазовая частотные характеристики дискретно-непрерывного элемента, построенные относительно псевдочастоты по передаточной функции (1.263)
Из выражения (1.258) получим
tr , (Зг-1) (г+1,135) (г+ 0,045) 0,0152 №б{г> г (г - I)2 (г-0,135) (г-0,0185) ‘
(1.259)
Соответствующая передаточная функция в форме (1.259) изображена на рис. Ь42, б.
Теперь воспользуемся преобразованием
(1.215), из которого найдем
г = (1+s^-)/(l-s-^), (1.260)
ИЛИ
Нтт + Ш-О
Подставив соотношение (1.260) в выра-
жение (1.259), получим
0,668 (1 - 0,006s) (0,091s + 1) X
Г (а) = X(0.2s+1)(1-0,ls)2
°'' s2 (0,1s + 1) (0,104s + 1)Х ‘
X (0,131s + 1)
(1.262)
При s = /6 из выражения (1.262) определим формулу для вычисления частотных характеристик в виде
Го (/<>)
= 0,668 (1 - 0,006/6) (0,091 /6+ 1)
= (/6)2 (0,1/6 + 1) (0,104/6 + 1) Х
(0,2/6 + 1) (1 — 0,1/6)2
24 0,131/6+1
(1.263)
Передаточная функция в форме (1.263) изображена на рис. 1.42, в.
Таким образом, из формулы (1.263) можно найти зависимости для определения: амплитуды
Яо (ш) = 20 1g 0,668 — 40 1g 6 +
+ 20 lg V0,006262 + 1 +
+ 20 lg V0,091262 + 1 + 20 lgV0,l262+ 1 —
-201gV0,104262 +1 -
- 20 lg V0,131262 + 1 +
+ 20 1g д/0,2262 + 1 (1.264)
и фазы
0O (6) = — 180° — arctg 0,0066 +
+ arctg 0,0916 — 3 arctg 0,16 —
— arctg 0,1046 — arctg 0,131 6 + arctg 0,26.
(1.265)
Характеристики //o(“) и 0o(6) построены иа рис. 1.43 относительно псевдочастоты 6. При построении логарифмических характеристик можно пользоваться приближенным способом, когда иа полулогарифмическую бумагу наносят частотные характеристики для каждого звена, входящего в передаточную функцию (1.263). Прн этом следует пользоваться значениями амплитуд и фаз из табл. 1.10, построенными также относительно 6.
Пример 1.44. Построить логарифмические амплитудную и фазовую частотные характеристики для динамического объекта, в состав которого входит управляющая ЭВМ, реализующая рабочую программу с тактом квантования То = 0,01 с. При этом передаточную функцию такого объекта в г-форме можно записать в виде
0,0 048z4 + 0,0259г3 — 0,0129г2 —
, -0,0157г- 7,4186 • 10~4
'Г° — г5 — 3,1904г4 + 4,0020г3 —
- 2,4219г2 + 0,6563г - 0,0447
(1.266)
Из соотношения (1.261) при То = 0,01 с имеем
г = (1 + 0,005s)/(l - 0,005s). (1.267)
113
Подставив соотношение (1.267) в выражение (1.266), найдем
1,6807 • 10~3s5 + 0,7441s4 — — 392,2904s3 — 390,81 • 102s2 + + 146,81 • 105s + 369,35-105
V’l — js + 246,73s4 + 187,09 • 102s3 + ' + 936,80 • 103s2 + 151,70 • 105s+ + 369,39 • 105
(1.268)
Разложив числитель и знаменатель выражения (1.268) на сомножители, получим
„ 0,0017 (s + 2,4996) (s - 200,0)
0 (S) (s + 2,9380) (s + 20.7143) X X X (s + 164,1390)
(s + 221,3930) (s - 280,9731) X
X_________X(£+701;3354J___________
24 (s2 + 58,9666s + 3699,441) u ?
Рис. 1.45. Логарифмическая амплитудно-фазовая частотная характеристика объекта, полученная экспериментальным путем (пример 1.45)
Прн s = /<й выражение (1.269) примет вид
.... 0,0017 (/й +2.4996) (/й-200,0).
ж о (/со) —-------------------------------'
(j<i> + 2,9380) (/й + 20,7143) (/й + 221,3930) (/й — 280,9731) X
X (/<0-4- 701,3354)
(/й + 164,1390) (/Й58,9666 + + 3699,441 — й2)
(1.270)
Приведем выражение (1.270) к обычной форме, т. е.
Го (/й)
(0,4/й + 1) (0,005/й - 1) X X (0,0045/й + 1)
(0,34/й + 1) (0,048/й + 1) X X (0,0061/й + 1)
(0,0036/й — 1) (0,0014/й + 1) Х [(0,0164/й)2 + 2 • 0,0164 X
(1.271)
Х0.49/Й+ 1]
Пользуясь передаточной функцией
(1.271), нетрудно определить логарифмиче-
Рис. 1.44. Логарифмические амплитудная и фазовая частотные характеристики динамического объекта, в состав которого входит управляющая ЭВМ (пример 1.44)
характеристики объекта САР с управляющей ЭВМ (рис. 1.44).
В процессе расчета САР проектировщик не всегда располагает передаточными функциями устройств управления и объектов. Иногда ему приходится иметь дело с экспериментально снятой амплитудно-фазовой характеристикой, построенной в полярной системе координат [13, 35]. Тогда для определения приближенных значений параметров передаточных функций необходимо перестроить амплитудно-фазовые характеристики в логарифмические амплитудную и фазовую в декартовой системе координат. Затем, аппроксимируя амплитудную характеристику прямыми с типовыми наклонами и пользуясь номограммами (рис. 1.25— 1.30), можно получить упрощенное выражение для искомой передаточной функции. Наличие неминимально-цифровых звеньев требует проверки соответствия логарифмической амплитудной характеристики фазовой или наоборот. Рассмотрим два примера нахождения передаточных функций и параметров объектов регулирования.
114
Пример 1.45. Определить приближенное значение передаточной функции непрерывного объекта и его параметры, если логарифмическая амплитудно-фазовая частотная характеристика имеет вид, показанный иа рис. 1.45. Перестроим годограф (рис. 1.45) в виде раздельных логарифмических амплитудной (жирная сплошная линия) и фазовой (жирная штриховая линия) частотных характеристик (рис. 1.46). Откуда видно, что при начальном наклоне логарифмической амплитудной характеристики, равном —20 дБ/дек, фазовая характеристика стремится к —270°. Это указывает на наличие неустойчивого апериодического и интегрирующего звеньев в передаточной функции объекта. Далее аппроксимируем логариф-
1т,д6
Рис. 1.46. Определение передаточной функции объекта для примера 1.45 по логарифмическим амплитудной и фазовой частотным характеристикам
мическую амплитудную характеристику прямыми тонкими сплошными линиями и по точкам их пересечения определим значения постоянных времени типовых звеньев. В результате этого получим следующее выражение:
IF I ,7,1 — —i0 (5/m + U /19791
* /со (25jco — 1) [(0,05/со)2 +' ''^
+ 2-0,02.0,05/® + И
На основании выражения (1.272) можно написать формулу для вычисления фазовой характеристики
60 = —270° + arctg + arctg ~ -
2-0,02^-
-arctg-------Tvrr- О'273)
Построим ее тонкой штриховой линией (рис. 1.46). При этом видно, что экспериментальная фазовая характеристика практически совпадает с расчетной. Таким образом, по выражению (1.272) определим
Рис. 1.47. Логарифмическая амплитудно-фазовая частотная характеристика объекта со звеном чистого запаздывания, полученная экспериментальным путем (пример 1.46)
передаточную функцию объекта k(T2s+\) и' (И5) - 7--9~9 Г»
s(T1S -l)(T^2 + 2|T3s+l)
(1.274)
где Г, = 25 с; Г2 = 5с;Т3 = 0,05 с; g = 0,02; k = 10 с-1.
Пример 1.46. Определить приближенное значение передаточной функции непрерывного объекта и его параметры, пользуясь логарифмической амплитудно-фазовой частотной характеристикой (рис. 1.47).
Перенесем эту характеристику в декар-товую систему координат. Тогда получим логарифмические амплитудную и фазовую частотные характеристики, показанные жир-
Рис. 1.48. Определение передаточной функции объекта для примера 1.46 по^логариф-мическим амплитудной и фазовой частотным характеристикам
115
иыми линиями на рис. 1.48. Аппроксимируя логарифмическую амплитудную характеристику тонкими сплошными линиями, соот-
ветствующими типовым наклонам звеньев, и пользуясь номограммой (рис. 1.27), полу-
чим
Wo (До) =
__________20 (1,25/<о + 1)_____________ /со [(5/<о)2 + 2 • 0,05 • /со + 1] X
X (0,05/со + 1)
(1.275)
На основании выражения (1.275) запишем
е0 (со) = -90° - arctg-7—+
‘-Ы
+ arctg — arctg~ (1.276)
и по этой формуле построим логарифмическую фазовую частотную характеристику (тонкая штриховая линия). Из сравнения экспериментальной н расчетной фазовых частотных характеристик видно, что они существенно различаются в области высоких частот. Это указывает на наличие звена, имеющего трапецеидальную передаточную функцию. Для ее определения на рис. 1.48 проведем жирную штриховую линию, представляющую собой разность между расчетной и экспериментальной фазовыми характеристиками. Сравнивая форму этой характеристики с кривыми табл. 1.10, пользуясь формулами табл. 1.4, можно найти искомую передаточную функцию трапецеидального звена. Для рассматриваемого примера примем, что эта функция соответствует звену чистого запаздывания, т. е.
W'(s) — e~Ts; (1.277)
фазовую характеристику звена вычислим по формуле
0' (ш) = - 57,ЗТш. (1.278)
Для нахождения числового значения Т возьмем три частоты <О] = 8 с-1, <02 = Ю с~1 и со3 = 20с-1 (рис. 1.48) и определим для них, соответственно, фазовые углы 61 (8) = = -90°, 0'(10) = -110° и 0'(20) = - 220°. Подставив значения фазовых углов и круговых частот, найдем Ti=0,196c, Г2 = = 0,192 с и Т3 =0,194 с. Значение Т в формуле (1.277) будет представлять собой среднее арифметическое, т. е.
г= 0,196 + 0,192 + 0,194 Q194 О
Таким образом, искомую передаточную функцию объекта можно записать в виде Го(з) = .-7.2/^+1>^-----------------------,
s (ту + 2lTlS + 1) (T3S + 1)
(1.279)
где k = 20 с-1, — 5 с; Т2 = 1,25 с; Г3 =
= 0,05 с; Т = 0,194 с.
Подставив в выражение (1.279) s = /со, построим логарифмические амплитудную и фазовую частотные характеристики объекта. Они нанесены иа рис. 1.48 жирными линиями (амплитудная — сплошной, фазовая — штриховой). Их близкие совпадения с экспериментальными частотными характеристиками обеспечивают достоверность выполненных расчетов.
Если соответствие между фазовыми экспериментальной и расчетной характеристиками не соблюдается как в области высоких, так и низких частот, то в передаточной функции объекта наряду с неминимальными звеньями имеется трансцендентное звено.
При экспериментальном определении частотных характеристик с помощью аналоговых или цифровых вычислительных машин проектировщик получает графическое изображение амплитудно-фазовой частотной характеристики объекта в декартовой системе координат в линейном масштабе. При этом для определения передатЬчных функций и параметров полученные характеристики необходимо пересчитать в логарифмические и получить амплитуду (в дБ) и фазу (в градусах), а затем построить их на полулогарифмической бумаге. После этого по методике, приведенной в примерах 1.45 и 1.46. находят соответствующие передаточные функции и параметры объектов.
Изложенный способ определения передаточных функций объектов по экспериментальным данным требует умения быстро анализировать логарифмические частотные характеристики и правильно подбирать последовательные наборы типовых передаточных функций звеньев [35].
8. ПРИМЕНЕНИЕ
РЕГРЕССИОННОГО АНАЛИЗА
ДЛЯ СОСТАВЛЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ
Данный метод используют в двух основных случаях:
когда после проведения экспериментов имеются кривые или таблицы с числовыми значениями, ха-
116
растеризующими изменение регистрируемых признаков (полученные таким образом массивы информации обрабатываются на универсальной ЭВМ);
когда непосредственно в ходе эксплуатации САР снимаемые с элемента (объекта) сигналы поступают с определенным тактом квантования на управляющую микро-ЭВМ, где тйкже производится их переработка.
Для обработки информации применяют метод наименьших квадратов, позволяющий построить математическую модель элемента, описываемую с высокой достоверностью его реальное поведение. В результате этого получают линейные и нелинейные регрессионные модели [13].
Линейные регрессионные модели. Допустим, что случайная величина у с последовательностью ее значений у\, у2, ..., уп зависит от некоторых физико-химических параметров, характеризуемых признаками Xi, х2, ..., хт. Для исследования зависимости у от хь х2, ..., хт регистрацию производят с помощью системы датчиков. Все признаки х регистрируются одновременно, а у — спустя некоторый интервал времени т.
В результате этого можно получить следующие уравнения регрессии:
У^щхц-^- a2xl2+ ...
• • • + amxlm +
f/2 = fliX21 + а2х22... (j 280) ... 4“ amX2m -j- t>2>
Уп>— alxnl + a2xn2 + . . .
... -|- amxnm -}-
где ai, a2, ..., am — параметры, которые необходимо определить; |i, I2, tn — случайные составляющие (помехи).
Будем считать, что число параметров не больше числа наблюдений, т. е. т п, а зависимые пе
ременные не коррелированы; тогда среднее квадратическое отклонение помехи а2(|.) = о2 = const и математическое ожидание М{|,} — 0. Из выражения (1.280) следует, что из-за ряда неучтенных факторов и случайных помех измерения у будут отличаться от линейной зависимости.
Для удобства составления вычислительных процедур * выражения (1.280) запишем в матричном виде
y = Xa + t, (1.281)
где у — вектор размерности (и X X 1); X—матрица размерности (и X т); вектор параметров а размерности (mXl); вектор помех | размерности (n X 1). Тогда в формуле (1.281) имеем
Рассмотрим три способа определения математической модели элемента (объекта) САР на основе применения метода линейной регрессии.
Первый способ. Модель линейной регрессии на основании выражения (1.281) представим в виде
у=Ха,
(1.283)
где у — оценки значения у, а — вектор оценок параметров.
Функцию ошибки представим как
F(a) = e2 + ^ + ••• +еп’ U-284)
* См. Е. 3. Демиденко. Линейная и‘нелинейная регрессия. М.: Финансы и статистика, 1981. 302 с.
117
тогда получим
п
F (а) = Z [у, — apci{ — «2.г;2 — ... j=l
... — amxim)\ (1.285)
где и—число замеров.
Из соотношения (1.285) найдем
F (а) — (у — Ха? (у — Ха). (1.286)
Для определения значений а, при которых функция F(a) будет мини
мальной, воспользуемся обычным методом минимизации функции.
В этом случае можно записать
= - 2Хту + 2ХтХа = 0.
(1.287)
При rankX = m имеем
а~(ХтХ)~1 Хту. (1.288)
Матрицу ХТХ вычисляют следующим образом:
ХТХ =
/ = 1
тг
X x[2x(i
1 = 1
п
1=1
п
п
Z, xi3xi2 1 = 1
im
(1.289)
i=i
XimXi2
i = 1
тг тг
S XimXi3 ’ ' ’ S X'im
1=1 i=l
Полученная матрица (1.289) яв- Однако в большинстве задач это
ляется симметрической. условие не обеспечивается и X\m —
Приведенные соотношения == Х(2т • :— Хит — 1 j тогда по-
(1.280) — (1.289) даны для случая, следний столбец матрицы X со-
когда в линейной регрессионной мо- стоит из единиц (1 — = 1, 1, 1)
дели отсутствует свободный член. с размерностью п. Пр и этом
п п п п
см Ц* н" Ml OJ ц Ml S XilXi3 IM
п тг тг п
... ^Xi2
ХТХ = i—i i=l 1 = I i = l (1.290)
п п _ t = l i = l n 2 S Xim%i3 i = l ... И
Погрешности линейной регрессионной модели можно определить по обычным статистическим характеристикам: среднему арифметическому значению и среднему квадратическому отклонению. Так как оценки, полученные по методу наименьших квадратов, несмещенные, то среднее арифметическое значение равно истинному значению па
раметра, а среднее квадратическое отклонение
(1.291)
Второй способ. Основан на приведении линейной регрессионной модели к средним значениям из
118
меряемых координат, при использовании которых значительно упрощаются вычисления.
При наличии в линейной регрессии свободного члена можно рекомендовать следующую процедуру:
1) вычисляют средние арифметические значения
(1.292)
2) находят новые векторы, привязанные к срединной точке координат, т. е.
х' — X,, — XT,
li и I’
y't = Уi -
(1.293)
где /=1, 2, ..., к (в ранее принятых обозначениях к — т—1), i — 1, 2, ..., п;
3) определяют а — (а}, а2, ... ..., «к)т по формуле
a=-(X/TXj~' Х'ху'. (1.294)
Как видно из выражения (1.289), нахождение вектора а сводится к обращению матрицы меньшего порядка т — 1 (х)т - 1;
4) вычисляют свободный член
ат'~и~" Г «Л- (1-295)
/ = !
После выполнения данной вычислительной процедуры получают
(1.296) /«1
Третий способ. На интервале времени (/, in) с помощью датчика с выходного объекта снимают показания yi, i/2, , уп с частотой V. Этн данные можно представить в виде
+ (1-297)
где y(at)-— истинные значения измеряемых величин; а>— параметры объекта; £,— случайные составляющие (помехи).
Как и прежде, параметры а, являются неизвестными. Для их оцен
ки будем считать — функция yi представляет собой полином 1-го порядка, что соответствует линейной регрессии, т. е.
yt = а.а + П: (tt — t0), (1.298)
где ti — время поступления i-ro замера; to — середина интервала наблюдения.
Введем обозначение
где
(1.299)
Для определения значений а0 и Ц] воспользуемся методом наименьших квадратов, по которому для измеряемой координаты минимизируем разность
п
min V (yi — у)2 —~. (1.300) °yi
Здесь ayi — среднее квадратическое значение отклонений замеров. На основании соотношения (1.300) запишем
п
V —р (yi — а0 — ауЦ)2 — 0.
да> & ayi
(1.301)
Решая систему уравнений (1.301), получим значения искомых коэффициентов, отнесенных к середине интервала наблюдения t0, т. е.
Е 12v2 Z Vz
I as 1 I» 1
a° n ’ a‘ ~~ п(пг - 1) ’
(1.302)
и их средние квадратические отклонения
119
Формулы (1.302) и (1.303) являются рекуррентными, и их можно использовать по мере поступления замеров.
Регрессионную модель объекта опишем в виде
у = ао + atr. (1.304)
В соответствии с ранее рассмотрен, ной методикой
(1.308)
Для упрощения вычислений иногда считают, что средние квадратические значения отклонений единичных замеров постоянны от замера к замеру, a v= 1; тогда °yt = д/„ (rt/_ 1) П2т- + и- — 1].
(1.305)
Из выражения (1.305) следует, что по мере возрастания числа п замеров величина <ту1- уменьшается. Подобного рода процедуру можно выполнять и для объекта регулирования, с выхода которого снимают несколько независимых переменных у, и, v, w и т. д. В этом случае можно пользоваться формулами (1.303) —(1.305).
Как уже говорилось, на практике встречаются такие задачи, когда имеется несколько различных величин, зависящих от физико-химических признаков. Например, у, и, v, w зависят от хь х2, *з, Х4, Х5, т. е.
у — OjXt -f- а2Х2 + а3х3 +
4" aix4 + О5Х5 4” SJ
и = Ь[ХГ + &2Х2 4” Ьзх3 4~
+ 6л + /.л + «;
V = С,Х1 + С2Х2 4- С3Х3 4-
4- с4х4 с5х5 + £;
w = + d2x2 4- d3x3 4-
+ d4x4 -f- d3x3 4- т].
Систему соотношений (1.306) можно переписать в виде
у= Хи 4~ и = ХЬ 4~ в;
х ~ (1-307)
v = Хс 4- w = Xd 4- Ц.
При n-замерах матрицы X, X, X и X имеют размерность (лХ5).
где
Хи Х)2 Х13 Х14 Х[5
Х21 Х22 *23 х24 Х25
-Уп— —Хп\ ХП2 Хп3 ХП4 Хп3_
Хц х12 х13 х14 х15
х2| Х22 х23 Х24 Х25
L-'-nl Хп2 Хп3 ХП4 хп3_
Ь =
; (1.309)
Хц Х12 Х13 Х14 Х]5
Х2[ х22 Х23 Х24 Х25
_Xni Хп<2 Хп3 Хп4 Хп5_
120
Имея это в виду, можно получить следующие модели регрессии:
у —Ха- и = ХЪ-, )
" ~ f (1.310)
v — Хс, w = Xd, )
где у, и, v, w— оценки значений у, и, v, w; еь е2, е3, е4 — соответствующие векторы ошибок, полученные при оценке.
Отметим основную особенность регриссионного анализа, заключающуюся в том, что независимые переменные являются детерминированными, а зависимые — случай-Таблица 1.13
Экспериментальные значении замеров
Рис. 1.49. Изменение массы выходного продукта у в реакторе в зависимости от времени и его линейная регрессионная модель у
ными. Рассмотрим несколько конкретных примеров для получения математических моделей объектов.
Пример 1.47. В химическом процессе, протекающем в реакторе, масса выходного продукта уц, измеряемого в моменты времени t, с интервалом т, будет Ви, а масса сырья хц, поступающего в реактор,—Вс. Технологический процесс должен протекать при температуре Xi2<0 °C) в присутствии катализатора Вк с массой х,3.
Результаты замеров, полученных в процессе работы реактора в различные моменты времени, приведены в табл. 1.13.
Номер замера и время отсчета Масса выходного продукта У Масса сырья XI Температура Х2 Масса катализатора хз Оценка массы выходного продукта Ошибка в оценке
и ви. кг Вс, кг е «с Вк. г У. кг <?, кг
1 140,28 252,36 96,67 8,37 136,01 4,27
2 142,00 262,54 100,07 9,07 143,42 -1,42
3 149,90 285,70 96,78 9,35 153,90 —4,00
4 147,12 277,52 101,30 9,67 147,09 0,03
5 163,20 307,95 100,35 9,45 162,83 0,79
6 173,40 322,44 104,80 10,12 172,08 1,32
7 178,86 334,88 106,17 10,35 180,41 -1,55
8 186,26 350,11 109,20 11,03 187,42 -1,16
9 183,53 346,10 104,48 10,38 182,32 1,21
10 198,76 374,91 106,88 12,15 200,87 -2,11
11 205,30 378,49 113,14 12,98 206,83 — 1,53
12 206.77 397,48 112,38 11,34 208,00 — 1,23
13 198,42 378,39 109,07 10,95 198,25 0,18
14 216,48 393,33 114,45 12,89 212,69 3,79
15 222,45 403,84 115,23 13,71 220,04 1,41
Средние значения 180,85 337,74 106,06 10,79 — 0
121
Требуется построить математическую модель реактора, в котором протекает технологический процесс получения химического продукта. На рис. 1.49 изображены штриховыми линиями отрезки, характеризующие изменение массы выходного продукта во времени y(t). По этим данным составим двумя способами модели реактора.
Первый способ. По данным табл. 1.13 запишем вектор у и матрицу X при хн — 1 в виде
Е 1~1
n E yixt2 Z = 1 "935 358,3" 289 935,3
xrr = rt = 29 782,1
E Wa i=l _ 2 712,2.
" 140,28 " "252,36 96,67 8,37 1 "
142,01 262,54 100,07 9,07 1
149,90 285,70 96,78 9,35 1
147,12 277,52 101,30 9,67 1
163,20 307,95 100,35 9,45 1
173,40 322,44 104,80 10,12 1
178,86 334,88 106,17 10,35 1
«/ = 186,26 350,11 109,20 11,03 1
183,53 346,10 104,48 10,38 1
198,76 374,91 106,88 12,15 1
205,30 378,49 113,14 12,98 1
206,77 397,48 112,38 11,34 1
198,43 378,39 109,07 10,95 1
216,48 393,44 114,45 12,89 1
_ 222,45 _ .403,84 115,23 13,71 1 _
Тогда формулу (1.290) можно представить дли четырех параметров как
ХТХ =
Располагая этими матрицами, по формуле (1.287) получим
а = (ХТХ) ‘ XrY =
0,3947 "
0,2290
3,7460
17,0830 _
В результате линейная регрессия будет у = 0,3947X1 + 0,229*2 + З,746х3 — 17,083
(1.311)
при среднем квадратическом отклонении о = 2,213.
Таким образом, выражение (1.311) представляет собой математическую модель химического реактора, в котором применяют заданный технологический процесс.
Второй способ. Приведем результаты замеров в реакторе к средним значениям, тогда получим табл. 1.14.
По данным табл. 1.14 получим
" п Е Z=1 п п ,Е i = l xilxi3 п E x = I xn
1М *i(*
п Е п xi2xil Е „2 Х/2 п Е xi2xi3 n E Xi2
Z=1 п Е 7 сИ СО */3* 1=1 п <2е *2 xi3 Z=1 n E xi3 =
1 = 1 п Е /=1 х 12 1 = 1 п Е Z = 1 xi3 Z=1 T
"1 747 425,6 541 505,3 55 592,1 5066,2" 541 505,2 169,276 17 254,3 1590,9
55 592,1 17 254,3 1 774,7 161,4
5066,2 1590,9 161,4 15,0 _
откуда
[№ =
0,0002735 - 0.001654 - 0,001926 0,1033 -
-0,00165 0,02814 - 0,05288 -1,1852
-0,001926 - 0,05288 0,2696 3,3584 ’
0,1033 -1,1852 3,3584 125,4
Х'хХ' =
п
Е ХгЗх12
1 = 1
[ 36 367,18 4132, Ц 1018,45
4132,11 534,59 126,69
1018,45 126,69 34,72
Применение второго способа привело к математической модели
у = 0,3933*! + 0,4675*2 + 3,1228*3 — 35,240)
(1.312) при о = 2,4736.
Из выражений (1.311) н (1.312) следует, что оба способа приводит практически к одной и той же математической модели химического реактора. Однако второй способ из-за меньших величин элементов матрицы Х'~Х' упрощает процесс вычислений
122
Таблица 1.14
Приведенные значения параметров реактора
Номер замера и время отсчета Масса выходного продукта У' Масса сырья Х'1 Температура /2 Масса катализатора / хз Оценка массы выходного продукта 0 Ошибка в оценке е'
*1 Ви, кг Вс, кг 0', «с вк. г у'. КГ е', кг
1 —40,57 —85,38 -9,39 —2,42 135,34 4,94
2 -38,85 -75,20 -5,99 — 1,72 143,11 — 1,01
3 -30,95 -52,04 -9,28 — 1,44 151,56 — 1,66
4 -33,73 —60,22 —4,76 — 1,12 151,45 —4,33
5 — 17,65 —29,79 -5,71 -1,34 162,29 0,91
6 —7,45 -15,30 — 1,26 —0,67 172,16 1,24
7 -1,99 —2,86 0,11 0,44 178,41 0,45
8 5,41 12,37 3,14 0,24 187,94 — 1,68
9 2,68 8,36 -1.58 0,41 182,13 1,40
10 17,91 37,17 0,82 1,36 200,11 -1,35
И 24,45 40,75 7.08 2,19 207,03 — 1,73
12 25,92 59,74 6,52 0.55 209,02 —2,25
13 17,58 40,65 3,01 0,16 198,75 -0,32
14 35,63 55,70 8,39 2,10 213,24 3,24
15 41,60 66,10 9,1,7 2,92 220,28 2,17
и позволяет получать лучшую точность определения математической модели.
Пример 1,48. На поточной линии цементного завода происходит размол сырья и по отборам проб, иа основании подсчета числа импульсов в единицу времени, снимаемых с рентгеновских эмиссионных датчиков (xSj, xai, Xfi, Xd) *, определяют состав компонент: оксида кремния SiO2, оксида алюминия А12О3, оксида железа Fe2O3 и оксида кальция СаО (рнс. 1.50). В зависимости от процентного содержания компонентов хь х2, х3, х4 изменяется технологический процесс изготовления цемента. Для выбора параметров САР необходимо получить четыре регрессионные модели, характеризующие содержание SiO2, А12О3, Fe2O3 и СаО. Экспериментальные данные, полученные с помощью рентгеновских эмиссионных датчиков, приведены в табл. 1.15.
Построим математические модели компонентов SiO2, А12О3, Fe2O3 и СаО сырья, поступающего на поточную линию для производства цемента. При этом будем считать, что линейные регрессии обладают свободным членом; тогда можно пользоваться соотношением (1.306), положив х3 = = 1. Результаты измерений приведем к средним значениям отсчетов.
Регрессионные линейные модели объекта будут:
* Здесь принято, что х, соответствует SiO2, х2 — А12О3, х3 — Fe2O3, х4 — СаО.
для оксида кремния
у = 0,030080х1 — 0,014797х2 + 0,0034275х3 — — 0,00054983х4 + 2,718 при Оу = 1,2926;
Рис. 1.50. Схема измерительной системы размолотого в мелкий порошок материала с четырьмя датчиками для определеиня SiO2, А12,О3, Fe2O3 и СаО:
У —подача сырья от транспортера; 2 — ленточный конвейер; 3 — барабан; 4 —устройство для подачи проб; 5 — канал подачи проб; 6—9 — рентгеновские эмиссионные датчики; 10 — регистрирующий прибор S1O2; // — регистрирующий прибор А120з; 12 — регистрирующий прибор Ре«Оэ; 13— регистрирующий прибор СаО; 14 — выход сырья
123
Таблица 1.15
Экспериментальные данные проб при производстве цемента
Номер пробы i SiC>2 A12O3 ИеаОз CaO
xr % X$j, нмп/с x2, % xflp имп/с x3' Хц. имп/с Х4, % *ci, имп/с
1 16,59 598,96 1,45 37,45 0,53 335,65 44,09 7185,3
2 32,13 1051,10 1,00 15,20 0,38 211,20 34,41 5739,8
3 1,88 115,50 0,19 8,68 0,18 105,50 50,54 8547,0
4 0,73 28,40 0,30 8,50 0,23 155,60 43,28 7598,5
5 28,39 910,60 6,19 183,70 1,05 738,45 32,97 5205,5
6 33,84 1102,50 6,53 205,58 1,31 999,90 30,31 4680,3
7 19,23 577,80 1,80 41,15 0,45 301,35 43,08 7317,8
8 17,36 611,50 5,11 149,85 0,95 644,85 35,97 5830,3
9 9,59 366,25 3,05 82,90 0,52 358,35 47,21 7729,5
10 15,70 605,40 3,65 96,75 0,63 472,35 41,26 6576,8
11 16,00 617,75 1,31 20,55 0,32 204,35 42,54 6965,8
12 14,17 519,20 2,28 100,02 0,68 457,45 41,42 6750,5
13 16,55 589,80 3,82 112,00 0,69 496,70 41,87 6626,0
для оксида алюминия
й = 0,00084749*1 + 0,034335х2 —
— 0,0013345хэ + 0,000046546X4 — 0,23380 при ои = 0,38376; (1.314)
для оксида железа
v = 0,000049136X1 + 0,00092204X2 + + 0,00097079хз — 0,000012890х4 + 0,18147, при аи = 0,029155; (1.315)
для оксида кальция
w = 0,0042536X1 + 0,025902х2 —
— 0,0021844Хз + 0,0071504X1 — 10,741 при 0^ = 0,69273. (1.316)
Вычисления для линейных регрессионных моделей у, й, v н ш производились с помощью программы № 1 REGR.
ПРОГРАММА №1 REGR
Программа предназначена для вычисления коэффициентов регрессионной модели.
Обращение к программе
CALL REGR (NI.NA.X, Y, AT).
Входные параметры
NI — количество проведенных экспериментов;
NA — количество аргументов регрессии;
X — матрица аргументов размерности [NI X NA];
Y—: вектор измерений размерности NL
Выходные параметры
АТ — вектор коэффициентов регрессии размерности NA.
REGR: PROC (NI, NA, X, Y, AT);
/» ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТОВ РЕГРЕССИИ »/ DCL (X (.,•), Y(»), АТ(»), XT(NA, NI), PR (NA, NA)) DEC FLOAT (12), NI, NA, XC(NA) DEC FLOAT (12); CALL TRANS (X, XT); CALL MULM (XT, X, PR); PUT DATA (PR); CALL INV (NA, PR, KS); PUT DATA (PR); IF KS=0 THEN DO; PUT EDIT (’МАТРИЦА ВЫРОЖДЕНА’) (A): GO TO FIN; END; CALL MULV (XT, Y, XC); PUT DATA (XC); CALL MULV (PR, XC, AT);
TRANS: PROC (TN, TR); /«ТРАНСПОНИРОВАНИЕ»/ DCL (TN (», »), TR(»,»)) DEC FLOAT (12); DO 1=1 TO HBOUND (TN, 1); DO J = 1 TO HBOUND (TN, 2); TR (J, I) = TN (I, J); END; END; END; , ,
MULM: PROC (GX, HX, PX); / .УМНОЖЕНИЕ МАТРИЦ»/ DCL (GX(«, »), HX (», »), PX (», »)) DEC FLOAT (12); DO 1=1 TO HBOUND (GX, 1);
124
иаидем
DO J = 1 TO HBOUND (HX, 2); PX (I, J) = SUM (GX (I, ») . HX (., J)); END; END; END;
MULV: PROC (XB, YB, AB); /» УМНОЖЕНИЕ МАТРИЦЫ НА ВЕКТОР ./ DCL (ХВ(., .), YB (.), АВ (.)) DEC FLOAT (12); DO I = 1 TO HBOUND (XB, 1); AB (I) = SUM (XB (I, .). YB (.)); END; END;
INV: PROC (N, A, KS); /.ОБРАЩЕНИЕ МАТРИЦЫ*/ DCL (A(., .), EPS, Y, W. DET, (В, C) (N)) DEC FLOAT (12), (I, J, K, R, P, Z (N)) BIN FIXED;
EPS = IE - 15; DET = 1.0; DO J = 1 TON; Z(J) = J; END; DO 1 = 1 TO N; К = Б
Y = A (I, I); R = I — 1; P = I+1; DO J = P TO N; W = A (I, J); IF ABS (W) > ABS (Y) THEN DO; К = J; Y = W;END; END; DET = Y — DET; lFKn=I THEN DET =-DET; IF ABS (Y) < EPS THEN GOTOS; Y=l/Y;
DO J=1 TO N; C (J) = A (J, K); A (J, K) = A (J, I): A (J, I) = -C(J)*Y;
В (J), A (I, J)= A (I, J) ♦ Y; END; J = Z (I); Z (I) = Z (K); Z (K) = J; A (I, I) = Y; DO К = 1 TO R, P TO N; DO J = 1 TO R, P TO N; A (K, J) = A (K, J) - В (J). С (K); END; END; END; DOR = 1TON: K = Z(R): DO J = R BY 0 WHILE (K-, =J); DO 1 = 1 TO N; W = A (J, I); A (J, I) = A (К, I); A (K, I) = W; END; I=Z(K); Z (K) = Z (J); к, Z (J) = I; END; END; KS = 1; GO TO S02; S: KS=0; S02: END;
FIN: END;
Пример 1.49. Определить дифференциальное уравнение, описывающее процесс относительного изменения содержания СаО в смесителе при производстве цемента. Обозначим через y(t) измеряемое содержание СаО в выходном потоке, а через x(t) —во входном потоке. Результаты измерений приведены на рис. 1.51 в виде кривых, снятых через равные интервалы времени т.
Дифференциальное -уравнение, связывающее переменные y(t) и x(t), можно представить в виде
= 77 {k*x ~
Решение данного уравнения при начальных условиях х((0) и у будет
У (t) = feo (1 — е т° ) х (to) + i-lo + y(to)^ Г° (L317)
Положив t — to + т, из выражения (1.317) получим следующее разностное уравнение:
У{+1 = аУ(+ bxr (.1-318)
По уравнению (1.318), описывающему ди--намику исследуемого объекта САР, определим оценку у1+1 как
$1 + 1=аУ1 + Ьхг (1.320)
Параметры а и Ь будем подбирать таким образом, чтобы ^;+i как можно меньше отличались от измеренных значений у1+1. Для этого воспользуемся методом наименьших квадратов.
Запишем функцию ошибки в виде
п
е== Е (^-^)2= i = l
п
= Z(yi-ayl-l-bxi-^ (L321> i=l
где переменные Xi и yt соответствуют моменту времени t = t0 + it, a yi+i — моменту времени t = t0 +(! + 1)т- Из сравнения выражения (1.317) с уравнением (1.318)
Рис. 1.51. Экспериментальные кривые изменения содержания СаО в смесителе цементного завода:
— входной поток; у (О — выходной поток
где п — число измерений.
Ошибки е будут иметь минимальное зна-
<?е
ченне прн следующих условиях: ~да' = ™’ де
-jj- = O. Применив эти соотношения к выражению (1.321), получим систему уравнений
П -W
Е (2у1-ау{_1~Ьх{_1)у1_1 = 0', > = 1
п
Е (2»< - ау{-1 - bxi-i) xi-i==°-
<-i у
(1.322)
125
Перепишем систему уравнений (1.322) в матричном виде
Таблица 1.16
Содержание СаО в смесителе при производстве цемента
п
Е xi-\yi~\
U Z=»l
Е Мм
n
E ¥<-,
u z=t
откуда
t, с Масса выходного продукга у^ Масса сырья х(- I Оценка массы выходного про-дукта Ошибка в оцен* ке
кг
0 60 120 180 240 300 360 420 480 446 452 466 471 475 478 469 462 455 491 501 499 501 496 460 452 449 451 446 455 462 472 476 477 470 462 454 0 -3 4 — 1 -1 1 — 1 0 1
Средние значения 464 481 — 0
табл. 1.16 на 1000 н составим табл. 1.17 для нахождения коэффициентов а и Ь.
Пользуясь выражениями (1.323) и
(1.324), определим
0,0069739
0,0097167
0,0026729
0,0097167
= 0,717723;
0,275083.
Значения оценок у найдем с помощью соотношения (1.320) и запишем их в табл. 1.16. Затем вычислим ошибки е и также внесем их в ту же таблицу. По формуле (1.291) вычислим 0= 1,903943.
Полученное значение гарантирует достаточную точность определения искомых па-
раметров: feo
0,275083
1 — 0,717723
0,974514;
Имея в виду выражения (1.318), (1.319) и (1.323), определим параметры k0 и То исходного дифференциального уравнения,
,80-92|5с-
т. е.
kt> —
Ь
1 — а ’
То = -
т
1п а
(1.324)
Имея это в виду, можно записать дифференциальное уравнение смесителя
180,9215 + у = 0,974514х. (1.325)
По приведенным экспериментальным кривым (рис. 1.51) примера 1.49 составим табл. 1.16.
Рассмотрим два способа определения дифференциального уравнения смесителя.
Первый способ. С целью упрощения вычислений разделим все цифровые данные
Рассмотрим способ определения уравнения смесителя, когда линейную регрессию выполняют с помощью приведения измеряемых координат к средним значениям
х, у, т. е.
x'i = xi ~ х> y'l = yi~y-
(1.326)
126
Таблица 1.17
Данные промежуточных вычислений параметров объекта (табл. 1.16) по первому способу
i Vi У1 — \ ViUi—l xi-l 9 yi-ixi~i У1х1-\ 2 У1-1
1 0,452 0,446 0,201592 0,491 0,241081 0,218989 0,221932 0,198916
2 0,466 0,452 0,210632 0,501 0,251001 0,226452 0,233466 0,204304
3 0,471 0,466 0,219486 0,499 0,249001 0,232534 0,235029 0,217156
4 0,475 0,471 0,223725 0,501 0,251001 0,235971 0,237975 0,221841
5 0,478 0,475 0,227050 0.496 0,246016 0,235600 0,237088 0,225625
6 0,469 0,478 0,224182 0,460 0,211600 0,219880 0,215740 0,228484
7 0,462 0,469 0,216678 0,452 0,204304 0,211988 0,208824 0,219961
8 0,455 0,462 0,210210 0,449 0,201601 0,207438 0,204295 0,213444
Вычисление п п n n n
значений для S У1У1-^ = ll_ 7 7 E yixi~i = £ y‘i-t =
определения t = l 1 = 1 1 = 1
параметров по формулам (1.323) = 1,733555 = 1,855605 = 1,788849 = 1,794349 = 1,729730
Тогда принятая модель объекта (1.318) в новых координатах будет
рг+1 = + ^xi- (1-327)
Коэффициенты а и 5 вычислим по формулам, аналогичным (1.323). Подставляя (1.326) в уравнение (1.327), получим
Si+1 = ayi + bxt + с, (1.328) где
с = у — ау — Ьх. (1.329)
Если с =£ 0, то значения х и у заменяются на х' и у', и для них имеем
&i+l =&'yt + b'xi + с'. (1.330)
Здесь
с' = у' — а'у' — Ь'х', (1.331)
Из выражений (1.328), (1.330) и (1.318) найдем
а, д йс'-^с . bl = (1.332)
с — с с — с
Располагая значениями а\ и blt определим новую оценку
£>•+1 = + Мг (1-333)
В этом случае при вычислениях приходится иметь дело с существенно меньшим числом значащих цифр при сохранении высокой точности определения и Го.
Таблица 1.18
Данные промежуточных вычислений параметров объекта (табл. 1.16) по второму способу
i *1 <1 vLi <-1 У1-1х1-1 !/№-1 , 2
1 -12 — 18 216 10 100 — 180 -120 324
2 2 — 12 —24 20 400 —240 40 144
3 7 2 14 18 324 36 126 4
4 И 7 77 20 400 140 220 49
5 14 И 154 . 15 225 165 210 121
6 5 14 70 —21 441 —294 — 105 196
7 —2 5 -10 -29 841 — 145 58 25
8 —9 —2 18 -32 1024 64 288 3
Вычисление п п п п « А
значений для ^y'ly'i-^ Е^-1 = У. У:-1х1-1 ~ Е /<<-! = Е У1-\ =
определения 1=1 1=1 i=l = 717 = 867
параметров по = 505 = 3755 = -454
формулам
(1.332)
127
Заметим, что если с уа и с <С it, то можно считать а — а и Ь = б.
Второй способ (продолжение примера 1.49). Составим табл. 1.18, пользуясь данными, приведенными в табл. 1.16.
По данным табл. 1.18 найдем
6—зда®-”'279035' ,1334>
Подставляя полученные значения в формулу (1.327), получим математическую модель объекта.
9. ИМПУЛЬСНЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ
Нестационарные объекты удобно представлять в виде импульсной переходной функции k(t, т), где т — момент времени приложения входного импульса; t — момент времени наблюдения динамического процесса. Функцию k(t, т) линейного нестационарного элемента с переменными параметрами определяют как решение уравнения
D (р, t) k (t, т) = М (р, l)b(t — т) (1.335) при нулевых начальных условиях, входном сигнале «(/) в виде 6-функции и k(t, т) = 0, если t < т.
Передаточную функцию нестационарного объекта находят с помощью преобразования Фурье [105]
t
t)= ^k(t, т)е_/а<<-х)йт
(1.336) или
00
JF0 (/®> t) — j k(t, t — x) e~lm dt. о
(1.337)
В общем случае сложный динамический объект с переменными параметрами можно описать уравнением
' dny . , dn~ly . a^dt+a^—dt+ •••
••• + =
dmu . dm~lu
=W^r + i>',mi-SrL+
• • <L338>
где n tn,
Уравнение (1.338) составлено с помощью выражения (1.200).
Если в уравнение (1.338) ввести обозначения
(1.339)
то получаем
D (р, t) у (t) = М (р, t) и (0. (1.340)
Найдем дифференциальное уравнение, которому удовлетворяет передаточная функция (1.337). Для этого применим к 'правой и левой частям выражения (1.335) преобразование Фурье по переменной т; тогда
D (р, /) Ц70 (/©, t) ela>t = М (р, t) е/и/.
(1.341)
После преобразований будем иметь дифференциальное уравнение вида
1 дпР (ja, t) dnW (ja, t) nl d dtn +
^(/1-1)1 (d/w)"-1 24
V (M 0 i । dD (ja.t)
A dtn-i +•••+ d{ja} X
X + D t) Wo (jv, t) =
= (1.342)
Введем в уравнение (1.342) обозначение
_ 1 д‘Р (ja, t) .
Ct f 9 |
nl д
4 = 0, 1, 2, .... n.
128
В этом случае имеем
+ «,(() + -
... +<-!«) +
+«,(0V.u», I) —M(j», I). (1.343)
Дифференциальные уравнения (1.342) и (1.343) описывают динамику процессов в одном и том же динамическом объекте и имеют одинаковый порядок. Однако решать уравнение в форме (1.343) удобнее, так как оно позволяет находить реакцию объекта на любое входное воздействие с помощью однократного решения. При использовании уравнения (1.338) это приходится выполнять отдельно для каждого вида воздействия.
Выше был показан способ приближенного аналитического решения уравнения с помощью метода последовательных приближений. Сущность его сводилась к применению рекуррентной формулы вида
x[«b(O^j^ +
1=1,2.......п, (1.344)
Из выражения (1.344) можно получить ряд
Wo (j®, t) = (/©, /) + Г2 (/©, /) +
+ 1Гз(/Ч о+ ... +^п(/Ч о.
(1.345)
Число членов ряда (1.345) зависит от степени нестационарности коэффициентов исходного дифференциального уравнения (1.338).
На практике [31] часто пользуются приближенным методом решения дифференциального уравне
ния (1.343). В этом случае вместо a,(f) берут постоянные коэффициенты at, равные средним значениям в рассматриваемом промежутке времени; тогда уравнение (1.343) можно представить в виде
dnIFo(/<o, t)
“°-------57я----
dn-lw0(ja>,t) , df"-1 *"
+ «1
। - dlF0 (/co, 0 । - то? /.
• • • + an-i----jt------h an^o(/®, /) =
= M (/®, /) + D' [IFo (/a>, /)], (1.346)
где
D' [l^o (/«>, /)] = [a0 — ao (/)] X
Х--УЮ) +[«i-a1(01X
dn-‘Ц70 (jo) , X dfn-‘ "l" "
• • • + L«n-i — «п-i u)J-at-----г
+ [an-an(/)]ITo(/®,/). (1.347)
Пользуясь методом последовательных приближений, найдем решение уравнения (1.347) в виде ряда (1.345), т. е.
d"r,(/<M) , а° dtn +
+ «i----------+ •••
, = dwai^t) .
+“»->—di— +
+ a„IFo (/®, 0 = М (j®, /); dnwt (ja, t) , “о dtn +
, = dn-1lFi (/<о, f) , + a,----------+ .. .
... + an_j dt +
+ anW\ (/co, t) =
(1.348)
где i = 1, 2....n.
Как показано в работах [12, 31], данный метод приводит к быстро-сходящемуся ряду лишь при от-
& Ю. И. Толчеев
129
Рис. 1.52. Импульсная переходная функция динамического объекта
носительно небольшом диапазоне изменения коэффициентов на рассматриваемом промежутке времени. Если коэффициенты значительно меняются во времени, то прн использовании метода численные результаты проверяют, прибегая к процедурам численного интегрирования исходного дифференциального уравнения на ЭВМ.
Рассмотрим несколько примеров определения передаточной функции как дифференциального уравнения линейной системы с постоянными и переменными параметрами по ее импульсной переходной функции.
Пример 1.50. На рис. 1.52 построена импульсная переходная функция стационарного динамического элемента k(t). Пользуясь рис. 1.52, определим передаточную функцию. Для этого соотношение (1.337) перепишем в виде
00
1К0 (/w) = k (О е-/ш* dt, (1.349)
О
откуда найдем действительную £7(а>) и мнимую jV(a) частотные характеристики, так как функция
где
IFo (/со) = Uo (w) + /Vo (со),
00
Uo (сй) = j k (/) cos ш (/) dt; о
00
Ко (со) = — j k (t) sin at dt. о
(1.350)
(1.351)
Рис. 1.53. Элементарная трапецеидальная импульсная переходная функция
Для вычисления выражений (1.351) разобьем характеристику на сумму элементарных трапецеидальных функций
4(') = Ё‘о,(0. (1.352)
/ж 1
где
fkQi при t < t. — t. + A. — t
*z(/)=| k0i 2^ np“
<t<ti + ^,
О при t > tt + A*..
(1.353)
Одна из элементарных' трапеций с соответствующими обозначениями изображена иа рис. 1.53.
Пользуясь соотиошеииямн (1.353) и выражениями (1.351), получим
sin at, Sin <вД
= at,/
Vz«o) = -^- +
(1.354)
cos at, sin <oA, + M at, a^T
При вычислениях по формуле (1.354) следует пользоваться таблицами функций sin х/х и cos х/х. Соответствующие числовые значения параметров функции (1.354) для шести трапеций приведены в табл. 1.19.
По данным табл. 1.19 найдем действительную и мнимую части частотной функции динамического элемента, используя
формулы
1/ (<в) -fcu, (<о); '“1
Ко (®)-Е^ (ш), i-1 '
(1.355)
и построим их шесть составляющих (рис. 1.54, а и б). Характеристики UQ и Ко приведены иа рис. 1.54, в. По формулам
130
Рис. 1.54. Определение логарифмических амплитудных и фазовых частотных характеристик динамического объекта по вещественной и мнимой характеристикам:
а—для составляющих U; б—для составляющих Vр в — суммарные частотные характеристики U и V; г — логарифмические амплитудные и фазовые частотные характеристики
(1.212) и (1.213) и кривым (рис. 1.54, в) при различных значениях <о можно вычислить функции Я0(<о) и 0о(<о). Числовые значения этих функций приведены в табл. 1.20.
По данным табл. 1.20 на рис. 1.54, г нанесены точками соответствующие значения функций Н0(в>) и е0(щ). Проведя через них жирные сплошные линии, получим значения амплитудной и фазовой характеристик (соответственно кривые . 1 и 2). Аппроксимируем логарифмическую амплитудную характеристику (штриховая кривая 3) прямыми с типовыми наклонами 0 и —20 дБ/дек. Из рнс. 1.54, г видно, что оии пересекаются при <о = 9,7 с-1 = l/TY Тогда можно предположить, что рассматриваемый динамический элемент описывается передаточной функцией
«7o(s) = (r1s+I)-1, (1.356)
характерной для типового апериодического звена.
Для проверки правильности сделанного предположения в выражение (1.356) подставим s =/<о и по формуле 0о(со) = = —arctgwT вычислим значения фаз. Нанесем их иа рис. 1.54, г и проведем через
эти точки штриховую кривую 4. Из сравнения точных и аппроксимированных частотных характеристик следует, что погрешность определения передаточной функции не превышает 8 %.
Пример. 1.51. Определить дифференциальное уравнение, описывающее динамические процессы в нестационарном объекте регу-
лироваиия, имеющем импульсную переходную функцию вида
k(t, т) = т//2, />т. (1.357)
На рис. 1.55 она построена на плоскости k(t, т)=0, где t = т; тогда на этой плоскости получим два участка: при t > т
Aft г)
4 -
t-T
Рис. 1.55. Импульсная переходная функция k(t, т) для примера 1.51
5»
131
Таблица 1.19
Значения функций Ui (и) и Vi (<о) для примера 1.50
Параметры Трапеция 1
koi “0.393 h= 0,25 A)=0,25
<0 0,2 0,5 1,0 2,0 5,0 10,0
&ti 0,0500 0,1250 0,2500 0,5000 1,2500 2,5000
0,0500 0,1250 0,2500 0,5000 1,2500 2,5000
Sin atj toti 0,9996 0,9974 0,9896 0,9589 0,7592 0,2394
sin a>Af 0,9996 0,9974 0,9896 0,9596 0,7592 0,2394
0,09817 0,09774 0,09622 0,09034 0,05663 0,00563
koi <> 1,9650 0,7860 0,3930 0,1965 0,0786 0,0393
COS <S>tj tilt I 19,975 7,9376 3,8756 1,7552 0,2523 -0,3205
Vi (<o) -0,00324 -0,00816 -0,01618 —0,03114 -0,05978 —0,04684
Продолжение табл. 1.19
Параметры Тоапеция 3
koa=O,145 «3 = 1.25 As =0,25
<0 0,2 0,5 1,0 , 2,0 5,0 10,0
<>// 0,2500 0,6250 1,2500 2,5000 6,2500 12,5000
0,1250 0,1250 0,2500 0,5000 1,3500 2,5000
sin iatj ail 0,9896 0,9362 0,7592 0,2394 —0,0053 -0,0053
sinoiA/ 0,9996 0,9974 0,9896 0,9589 0,7592 0,2394
Ut (<a) 0,17929 0,16295 0,13617 0,04161 —0,00073 —0,00023
koi (0 0,7250 0,2900 0,1450 0,0725 0,0290 0,0145
COS (Otj toti 3,8756 1,2975 0,2523 —0,3205 0,1599 0,0798
Vi (<o) -0,02283 -0,05544 —0,09975 -0,12820 -0,00700 —0,01104
Продолжение табл. 1.19
Трапеция 5
Параметры
Л05=0,08 «6=2.50 As=0.50
(О 0,2 0,5 1,0 2,0 5,0 10,0
ati 0,5000 1,2500 2,5000 5,0000 12,5000 25,0000
®Д/ 0,1000 0,2500 0,5000 1,0000 2,5000 5,0000
sin toil inti 0,9589 0,7592 0,2394 —0,1918 —0,0053 —0,0053
sin tohj <оД< 0,9983 0,9896 0,9589 0,8415 0,2394 -0,1918
(<o) 0,4000 0,1600 0,0800 0,0400 0,0160 0,0080
koi <0 0,19145 0,15026 0,04591 —0,03280 -0,00025 -0,00020
COS <otj a>ti 1,7552 0,2523 —0,3205 0,0567 0,0798 0,0396
Vi (co) —0,04956 —0,11006 —0,14147 —0,03046 -0,01218 -0,00952
132
Трапеция 2
&02 ==0,237 <а=0,75 Д2=0,25
0,2 0,5 1,0 2,0 5,0 10,0
0,1500 0,3750 0,7500 1,500 3,750 7,5000
0,0500 0,1250 0,2500 0,5000 1,2500 0,0500
0,9963 0,9767 0,9089 0,6650 —0,1524 0,1251
0,9996 0,9974 0,9896 0,9589 0,7592 0,2394
0,17702 0,17316 0,15988 0,11335 -0,02057 0,00532
1,1850 0,4740 0,2370 0,1185 0,0474 0,0237
6,5918 2,4814 0,9759 0,0472 -0,2188 0,0462
—0,01378 -0,03408 -0,06534 -0,11046 —0,07693 —0,02173
Трапеция 4
«04=0,095 «4= = 1,75 , Дч—0,25
0,2 0,5 1,0 2,0 5,0 10,0
* 0,3500 0,8750 1,7500 3,5000 8,7500 17,5000
0,0500 0,1250 0,2500 0,5000 1,2500 2,5000
0,9797 0,8772 0,5623 -0,1002 0,0714 -0,0558
0,9986 0,9974 0,9896 0,9589 0,7592 0,2394
0,4750 0,1900 0,0950 0,0475 0,0190 0,0095
0,16281 0,14546 0,09251 -0,01597 0,00901 —0,00222
2,6839 0,7326 —0,1019 —0,2676 —0,0892 0,0125
—0,4)2898 -0,06852 -0,11.176 —0,09016 —0,03026 -0,00900
Трапеция 6
«04 “ 0,05 3,50 д,- =0,50
0,2 0,5 1,0 2,0 5,0 10,0
0,7000 1,7500 3,5000 7,0000 17,5000 35,0000
0,1000 0,2500 0,5000 1,0000 2,5000 5,0000
0,9203 0,5623 -0,1002 0,0939 -0,0558 -0,0122
0,9983 0,9589 0,9589 0,8415 0,2394 -0,1918
0,2500 0,1000 0,0500 0,0250 0,0100 0,050
0,16078 0,09738 -0,01681 0,013828 —0,00234 0,00041
1,0926 -0,1019 -0,2676 0,1077 0,0125 -0,0258
-0,05912 —0,11765 -0.09405 -0,00914 . —0,00948 -0,00413
133
Таблица 1.20
Значения функций для построения логарифмических амплитудной и фазовой частотных характеристик примера 1.50
Функции — 1 й), С
0,1 0,2 0,5 0,8 1.0 2,0 5,0 8,0 . 10-°
/70 (<•>) 0,9984 0,9695 0,8333 0,6452 0,5139 0,2104 0,0418 0,0152 0,0091
Vo (®) —0,1081 -0,1775 -0,3939 -0,4907 —0,5286 -0,3996 -0,1956 -0,1131 0,1023
#о(®) 1,0042 0,9856 0,9217 0,8106 0,7372 0,4516 0,2000 0,1141 0,1027
Но (со), дБ 0,037 -0,126 —0,708 -1,824 -2,658 -6,905 -13,980 -18,859 -19,769
6о(®) -6,180 -10,375 -25,300 -37,254 -45,808 —62,232 -77,937 -82,346 -84,917
столбца иа столбец начальных условий
и t < т. На этой плоскости изобразим пространственную фигуру. Выделим иа ней штриховкой поверхность, где обеспечивается условие t > т, т. е. справедливо уравнение (1.357) [35].
Для любой нестационарной системы имеем
k (*> »)“ £ Ф( (0 Фг (*)> t > т. (1.358) i-1
В этом случае дифференциальное уравнение объекта можно записать в виде (1.340). Для определения левой части уравнения (1.340) воспользуемся определителем
D (р, t)y(t)*=
У i (0 Уг (?) ... Уп (t) У (?) yi(?) уг(?) Уп (0 у (0
... у™(?)у1п>(?)
(1.359)
Правую часть уравнения (1.340) можно представить
Ядп~11п А (т) ... " {Р' Т)И(Т)~
- Ф (Т) и (т)1 dr + о, (1.360)
J а
1=1,2......п.
В выражении (1.360) через A(t) обозначен определитель Вронского для системы функций ф1(0, <р2(1).....<р* (/):
Ч>1 (0 Ч>2 (0 ... Фп(0
Ф1 (0 фа (0 ... фп (О
Ф<"~1)(П Ф^-1)(0 ... Ф*,"-1)(0
определитель At (to) получается из предыдущего прн t = t0 путем замены »-го
У (?) = 0; у (?) = k (t0, t0) и (to);
У(0Ц«2 «(/o) +
01 1<=т = «о
+ дЦ?х) [ т / +k ый и T. Д.
Для рассматриваемого примера имеем ф| (т) = 1; ф> (t) = l/tB; ф, (t) « —2/ts.
(1.361)
Подставляя последние выражения в уравнение (1.340) н приравнивая его нулю,
получим
D (р, ?) у (/) =
&(?)
откуда
D(p, ?)у(?) = -^-у(?) + -^у(?)=О.
(1.362)
Определители будут А(1) = Ф(1); A,(t) = O.
Введем их в выражение (1.360); тогда найдем
t
$ ~ ф Юи w] dx=°-
о
(1.363)
Подставляя в соотношение (1.363)' значения ф(т) и Ф1(1), получим
t
[таЛ4 (р, т) — т] и (т) dr = 0.
о
При М(р, г) = 1/т это уравнение справедливо для любых и (г). Таким образом.
134
порядок т полинома
т
м (р, т) = У ьт_( (/) р{
следует принять циеит 60=1//.
Итак, правая имеет -вид
i—o равным нулю, а часть уравнения
М (р, t)u(t) =
Тогда из уравнения (1.362) и соотношения (1.364) получим искомое линейное нестационарное уравнение в виде
+ (1.365)
Для определения импульсной переходной функции можно пользоваться таблицами Лх-фуикций*. В этом случае применяют формулу
оо 2 Г k(t) =--------\ Vo (со) sin и/ d<o; (1.366)
Л J о
умножив и разделив ее подынтегральное выражение иа со, получим
k (t) = _ — ( [<aFo (t0)1 sin at da. (1.367) л J <o
0
Рнс. 1.56. Функция [<oVo(<o)J, представленная в виде четырех трапеций
Построив на рис. 1.56 функцию (wVo(<i>)], разобьем ее на четыре трапеции. Для каждой трапеции определим п(0), ©о; и а<и и выберем Д/Табл i-
Результаты промежуточных расчетов трапеций 1—4 сведем в табл. 1.21. По этим данным построим (тонкими линиями) иа рис.( 1.57 составляющие импульсных переходных функций ki(t). Суммируя эти кривые, получим результирующую импульсную переходную функцию (жирная сплошная линия). Штрихпунктирной линией показана точная характеристика k(t), которая перенесена с рис. 1.52. Из сравнения этих кривых видно, что погрешность построения даже по малому числу трапеций ие превышает 10 %.
Разбивая функцию [<oVo(co)] на трапецеидальные характеристики и выбирая для каждой из трапеций интервал времени Д^тавл I, определим значения Лх-фуикций (см. прил. П-П. 1). Далее вычислим истинный масштаб времени
Д<Ист/ = Чабл//“о/ И
трапеции. По выбранному х; и интервалу времени (sit, находим значения Лх<-функции, которые умножим иа высоту трапеции п(0). Затем, отложив по осн абсцисс Д<Яст, а по оси ординат соответствующие величины г. (0) и h , определим для каждой из трапеции составляющие импульсной переходной функции — кривые ki(t). В результате суммирования этих кривых получим результирующую характеристику k(t).
Пример 1.52. По мнимой частотной характеристике Vo(w) стационарного динамического элемента (рис. 1.54, в) определить импульсную переходную характеристику.
Рис. 1.57. Составляющие импульсных переходных функций и результирующая k(t)
* См. гл. 5 и прил. П-П. 1.
135
Таблица 1.21
Значения составляющих нмнульсной переходной функции для каждой из трапеций
Трапеция 1 г, = —0,78; X, =0,00; Д/ИСТ| =0,6/1,60=0.375 с
^табл 0,6 1,2 1,8 2,4 3,0 3,6 4,2 4,8 5,4 6,0 6,6
0,1890 0,3671 0,5246 0,6548 0,7546 0,8244 0,8681 0,8912 0,9006 0,9028 0,9029
^ИСТ1 0,375 0,750 1,125 1,500 1,875 2,250 2,625 3,000 3,375 3,750 4,125
Г, <0)^(0 -0,147 -0,286 -0,409 -0,511 -0,589 -0,643 -0,677 -0,703 -0,703 -0,703 -0,704
Трапеция 2 г,=-0.15; х2=0,37; Д/ИСТ1=1 ,4/4,33 =0,323 с
^табл 1,4 2,8 4,2 5,6 7 8,4 9,8 11,2 12,6 14 15,4
0,5742 0,9624 1,1060 1,0293 1,0293 1,0022 1,0005 0,9969 0,9867 0,9827 0,9900
^нст. 0,323 0,646 0,969 1,292 1,615 1,938 2,261 2,584 2,907 3,230 3,553
г 2(0) h^t) -0,086 —0,144 -0,166 -0,163 -0,154 -0,150 -0,150 -0,150 -0,148 -0,147 -0,149
Трапеция 3 гз =-0,03; х3= 0,40; 4^,= 4/11,00=0,364 с
^табя 4 8 12 16 20 24 28 32 36 40 44
4(0 0,1774 0,9976 0,9888 0,9992 1,0039 1,0017 0,9962 0,9996 1,0028 0,9992 0,9986
SCT* 0,364 0,728 1,092 1,456 1,820 2,184 2,548 2,912 3,276 3,640 4,004
г3 (0)4(0 —0,005 —0,030 -0,030 -0,030 -0,030 -0,030 -0,030 -0,030 -0,030 -0,030 -0,030
Трапеция 4 г4=0,96; х4 = 1; Д/Вст<=4/11,00=0,364 с
Оабл 4 8 12 16 20 24 28 32 36 40 44
4<о 1,1193 1,0022 0,9581 1,0317 0,9856 0,9898 1,0216 0,9831 1,0028 1,0103 0,9856
^ист» 0,364 0,728 1,092 1,456 1,820 2,184 2,548 2,912 3,276 3,640 4,004
г4 (0)4(0 1,075 0,962 0,920 0,990 0,946 0,950 0,981 0,944 0,963 0,970 0,946
10. ОБОБЩЕННАЯ ФОРМА ПРЕДСТАВЛЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ НЕПРЕРЫВНЫХ
И ДИСКРЕТНЫХ ЛИНЕЙНЫХ ЭЛЕМЕНТОВ (ОБЪЕКТОВ) НА ОСНОВЕ ПРИМЕНЕНИЯ ВЫЧИСЛИТЕЛЬНЫХ ПРОЦЕДУР, РЕАЛИЗУЕМЫХ НА ЭВМ
При проектировании непрерывных, дискретно-непрерывных и дискретных САР необходимо располагать математической моделью элемента (объекта). Все ранее рассмотренные способы построения таких моделей были основаны на системах линейных дифференциальных уравнений, записанных в формах передаточных функций, структурных схемах (графах), частотных характеристиках и импульсных переходных функциях. Несмотря на большую наглядность данных способов представления, ими удобно пользоваться лишь при относитель
Рис. 1.58. Структурные схемы стационарных и нестационарных многомерных линейных объектов, представленных в векторно-матричной форме:
а, б — типовые; в. г — с параллельным подключением внутренних контуров с матрицами
но невысоких порядках математических моделей.
При высоких порядках моделей такие процедуры требуют значительных затрат времени проектировщика и не обеспечивают необходимую точность решения задач анализа и синтеза систем. Поэтому стали пользоваться уравнениями, составленными во временнбй области и записанными в векторноматричной форме.
Рассмотрим две наиболее часто встречающиеся формы представления многоконтурных стационарных н нестационарных линейных элементов (объектов). При этом будем считать, что в линейный объект регулирования после ряда структурных преобразований входят лишь две матрицы: А и В. Тогда первую форму представления стационарного 'объекта можно записать в виде векторно-матричного уравнения
у(0 = Лу(0 + Ви(0, (1-368) где у и а—-векторы размерностей (n XI) и (т X 1); Л и В — матрицы размерностей (n X ») и (n X я»).
В соответствии с векторно-матричным уравнением (1.368) на
137
Рис. 1.59. Структурные схемы многомерных линейных нестационарных объектов, представленных в векторно-матричной форме:
а — типовые; б — с параллельным подключением элементов, описываемых матрицами D и D (О
рис. 1.58, а построена структурная схема многомерного объекта, которую в дальнейшем будем называть типовой. t
Для нестационарного объекта уравнение (1.368) перепишем в виде
y(t) = A(t)y(t) + B(t)u(t). (1.369) Здесь векторы у, и и матрицы A(t) и B(t) имеют те же размерности, как и в уравнении (1.368). Отличие уравнения (1.369) от (1.368) заключается в том, что матрицы А и В зависят от времени. Структурная схема, соответствующая уравнению (1.369), приведена на рис. 1.58,6.
Во второй форме представления в объект входит контур с отрицательной обратной связью. В этом случае для стационарного объекта имеем уравнения
у (!) = Ау (!) 4- Ви' (/); j 3
и' (!) = u(i)- Ку (i), J
где К—матрица, имеющая размерность (т X п).
Исключив из системы уравнений (1.370) u'(i), получим
у(!) = [А —BK]y(t) +Bu(i). (1.371)
Размерности векторов у, и и матриц А и В соответствуют уравнению (1.368). На рис. 1.58, в построена структурная схема по уравнениям (1.370) или (1.371). Если
разность матриц А — ВК обозначить через А, то уравнение (1.371) можно привести к виду (1.368), т. е.
у(П = Ау(0 + Вв(П-
По аналогии можно записать уравнения и для нестационарного объекта
у(0 = [А(0-В(0К(0]у(/) +
+ В (/)«(/). (1.372)
Размерности векторов и матриц в уравнении (1.372) полностью совпадают с размерностями векторов и матриц уравнения (1.371). Структурные схемы, обставленные по уравнениям (1.371) и (1.372), приведены соответственно на рис. 1.58, в и г.
Существуют и другие формы построения структурных схем элементов (объектов), отличающиеся способом введения дополнительных отрицательных и положительных обратных связей. Эти структурные схемы здесь не рассматриваются. Следует отметить, что большинство из них может быть приведено к типовым схемам, изображенным на рис. 1.58, а и б.
Если в многомерных стационарных и нестационарных объектах имеются параллельно включенные динамические устройства, задаваемые матрицами D или D(i), то структурные схемы можно изобразить, как показано на рис. 1.59, а и б. По этим структурным схемам составим системы уравнений:
для стационарных объектов y(0=yi(04-y2(0; 1
у{(!) = Ayx(i)Bu(i)‘, > (1.373) у2 (0 = Du (t); J
138
a)
Рис. 1.60. Структурные схемы многомерных линейных стационарных и нестационарных объектов, представленных в векторно-матричной форме:
а, б — типовые; в, г—с параллельным подключе-нием контура со строкой k
г)
щие уравнениям (1.375) и (1.376). При наличии внутреннего контура уравнения (1.371) и (1.372) можно переписать в виде
У (0 = U -&ЛТ] у (t) + bu(t), (1.377)
для нестационарных объектов
у (*) = У1 (0 + Уг (0; '
у, (/) = А(0У1(0+В (/)«(/); (1-374)
у2 (0 = D (t) и (0.
В уравнениях (1.373) и (1.374) матрицы D и D(t) имеют размерность (n X т).
Наиболее часто встречаются САР с одним входным и одним выходным сигналом. В таких системах векторно-матричное уравнение (1.368) для стационарного объекта примет вид
у (t) = Ay + (1.375)
где у—вектор размерности (пХ1); и — скаляр; А — матрица размерности (n X п); b — вектор размерности (n X 1); для нестационарного объекта уравнение (1.369) имеет вид
у (П = A (t)y (t) + b(1.376) Размерности векторов и матриц, входящих в уравнения (1.375) и (1.376), одинаковы.
На рис. 1.60, а и б изображены структурные схемы, соответствую-
где kT — строка размерности (IX X п),
й)=[л(о-*(о*т(оЬ(п+ + b(t)u(t). (1.378)
По уравнениям (1.377) и (1.378) на рис. 1.60, в, г построены структурные схемы объектов.
На рис. 1.61, а и б приведены соответствующие схемы объектов, полученные по уравнениям (1.378) и (1.380)
y(t) = y2 (t) + y3 (0;
У! (о = Ау1 (/) 4- Ви (/);
y2(t)~ du(t);
Уз (0 = lTVi (0
и
У(*) = У2(!) + Уз(*У> у, (t) = A(t)yi(t) + + B(t)u(t)-, y2(t) = d(t)u(f); у3а}=1чоуло,
(1.379)
(1.380)
где у2(0> Уз(0. ^(0—скалярные функции; ZT — строка размерности (1 X п), состоящая из единиц.
139
Рис. 1.61. Структурные схемр одномерных линейных стационарных и нестационарных объектов, представленных в векторно-матричной форме:
а — типовая; б — с параллельным подключением коэффициентов d и </(О
С целью использования одинаковой формы описания объектов непрерывных, дискретно-непрерывных и дискретных САР воспользуемся теорией спектрального разложения матриц, которая с помощью специально созданных алгоритмов [26] позволяет получать единые математические модели в дискретной форме, а по ним и рабочие программы, реализуемые на ЭВМ [20, 37]. К основному преимуществу такого подхода следует отнести возможность представления моделей с использованием матриц до 50—80-го порядков, без существенного понижения точности спектрального разложения матриц [26]. Кроме того, с помощью теории спектрального разложения матриц удается создавать алгоритмы для вычисления коэффициентов, полюсов и нулей передаточных функций построения частотных характеристик, корневых годографов и переходных процессов не только полного объекта, но и всей системы в целом (см. гл. 4 и 5). Можно также отметить, что по данным алгоритмам нетрудно сформировать пакет прикладных программ, пользуясь которым можно обеспечить диалоговый режим проектирования систем на ЭВМ. При этом намного упрощается процеса анализа и синтеза сложных САР (см. гл. 8 и 12).
Рассмотрим алгоритмы, с помощью которых составляются диск-
ретные модели многомерных объектов, описываемых типовым векторно-матричным уравнением (1.368). Аналитическое решение этого уравнения при начальных условиях у (to) имеет вид
у(О = ел<<-<«>уо(О4-t
+ \еА«-*>Ви(т)с1т. (1.381) to
В моменты времени t = кТ0 и / = («+' 1) То состояние объекта Ук+i связало с предыдущим состоянием ук соотношением
Ук+1=ФУк4-То
+ J ел(т)4т, ,(1.382) о
где Ф = еЛГо — переходная матрица системы уравнений (1.381). Способы вычисления переходной матрицы приведены в прил. П-1.1.
Соётавйм математические зависимости для алгоритмов дискретных моделей с тремя типами экстра-поляторов.
Самая простая дискретная модель может быть получена, если положить, что внутри интервала квантования сигнала а(т) экстраполируется по одной точке ступеньками со значениями ик, т. е. перед объектом включен экстраполятор нулевого порядка Эо. В этом случае соотношение (1.382) можно представить в виде
Ук+1 = ФУк + ^«к- (1.383)
Здесь F = (Ф — I) А-1 В — матрица коэффициентов, обеспечивающих
140
Рнс. 1.62. Структурные схемы дискретных стационарных объектов с различными типами экстраполяторов:
а и г — с экстраполятором нулевого порядка; б и д — с экстраполятором 1-го порядка; в и е — с экстраполятором 2-го порядка
передачу сигналов по входам дискретной модели.
С помощью выражения (1.19) можно построить структурную схему дискретной модели в форме z-преобразования, которая приведена на рис. 1.62, а.
При предположении о линейном изменении и(г), когда через две точки проходит прямая, т. е. в дискретную модель входит экстра-полятор 1-го порядка, обозначаемый как Э\, имеем
«K+1(t) = «K + -5^£=J-t, (1.384) 1 о
а дискретную модель записать в виде
Ук+1 = ФУк +
Го
4- J (Ик dx
О °
Полученную формулу перепишем следующим образом:
Го
Ук+1 = Фук + J w°-x>BuK dr + о
Го
+ ( е^-^В Ик~Ик-'-т^т, J la
о
откуда находим рекуррентное выражение
Ук+1=ФУк + ^«к +
+ [(o-/M_,-n№Bx
X (1.385)
* о
Обозначая матрицу [(Ф—I) Л-1— —/Г0]Л~*В через R, дискретную модель можем записать в виде
Ук+1 = фук + ^«к +
+ в Uk~tUk-^.. (1.386)
I о
На рис. 1.62,6 изображена структурная схема дискретной модели, полученная с помощью выражения
141
(1.386). Блок задержки сигнала ик на один такт на рнс. 1.62,6 имеет обозначение z~l.
Если вместо линейного закона изменения и(%) считать, что через три точки проходит кривая высокого порядка, т. е. в модель входит экстраполятор 2-го порядка Э2, тогда
Ц(т)^Нк+ +
1 о
4- цк-.2У*-2! т2. (1.387)
то
В этом случае дискретная модель объекта описывается выражением
То
ук+1 = ФУк + $ е^-^В X о
+ и-*.у-к^т + 1 о
**к ~~ 2ик-14«к-2
л J
Учитывая предыдущие обозначения матриц, получим
Ук+i = ФУк + *Х+ R +
1 о
То
+ ( ел<г»~т>В. ц^~ 2-|С^1 + ц*-а т2 dx
(1.388)
В выражении (1.388) интеграл дважды берется по частям, в результате этого рекуррентная формула (1.388) примет окончательный вид
Ук+. = ФУк + Рик + +
1 о
+ н «K.-2UK-14-UK-2 , (1 389)
где Н — {2 [(Ф - Z) А"1 - ZT0] X
X A-1 — 1То}А~1В.
Соответствующая этому случаю структурная схема изображена на рис. 1.62, в, где введены два блока задержки сигнала ик на два такта z-'-z-'.
Для объектов со структурой на рис. 1.61, а рекуррентные соотношения (1.383), (1.386) и (1.389) следует переписать в виде
Ук+1==ФУк+К; (1.390)
Ук+1 = ФУк + /«к + г “к-у~' ;
° (1.391)
Ук+1 = ФУк + fик + г ^5Як-1 4-1 о
+ Л «к- 2^ 4-«к-2 (j 392)
Здесь
/ = (O-Z)A-B; (1.393)
r = [(O-Z)A-I-ZT0]A-IB; (1.394) Л = {2 [(Ф—Z) A-’-ZTo]Л"1-Til} X
ХА->В. (1.395)
С целью упрощения математических выкладок будем рассматривать [26] скалярный входной сигнал, который постуйает на объекты систем регулирования в виде
у (0 = Ay(t) + &«(/). (1.396)
Тогда дискретную математическую модель можно представить
То
Ук+1==Ф(Го)Ук-|- $ Ф^о—т)6м(т)е/т.
(1.397)
Аппроксимируем входной сигнал ц(т) степенной функцией порядка I
“Но"
Ц1
«(т) = £ Ц/? = [1тт2. . .-?] ^2 .
/-0
_Hz_ (1.398)
Для оценки коэффициентов функции (1.398) возьмем Л^-измерений В МОМеНТЫ «к-1 «к—1—1 «к-У и проведем через них кривую /-го порядка, обеспечивающего нанлуч-шее среднее квадратическое приближение. В компактной форме
142
записи получим [26]
• «уXi — Stfxu+i).uo + i)xь (1-399)
Здесь векторы
«к-1
«к-2
UNXI =
L «к-tf J
Но MiT'o
Ц(/+1)Х1 =
а матрица
Syxtz+l) =
"1 0.............О
= 1 1.............(-1)'
.1 -(N- 1) . . [-(ЛГ-1)]1
Соотношение для оценки неизвестного вектора у, вытекающее из метода наименьших квадратов, будет иметь вид
£ = s*u, (1.400)
где s* — матрица, псевдообратная матрице измерений sxX(»+i|, а miniV = п.
Соотношение (1.400) можно переписать в виде
ц = (sTs)~1sTu. (1.401)
Подставив соотношение (1.398) в выражение (1.397), получим искомую дискретную модель
Ук+1 — Фук + [-Еоб : Еф1Тй • ...
... • ВД7'о]в*и = Фхк +
+ /о«к + Л«к-1 +<•••+ fNUK-N>
(1.402) где
Го
Ef — ^(То-т)?^,/ = 0, 1, о
Для вычисления матрицы Е/ воспользуемся соотношением
= О-403)
где
£0 = [елг° — Z] Л-1.
Определим дискретную модель UUtJCKiU ХЮ IpOpMJrVXC при*
меняя три вычислительные процедуры *. Первая — для спектрального разложения произвольных действительных матриц с помощью QR-алгоритма [37], с предварительным приведением матрицы к верхней форме Хессенберга в виде программы № 7, именуемой OWN, включающей восемь подпрограмм OWN1—OWN8, написанных на языке ПЛ/1 **.
Используется программа № 8 MFUNC и получение дискретной модели в виде (134)—программа № 9 DISCR. Действительно, во всех вычислительных процедурах и рабочих программах матрицы А для элементов объектов и Л3 для замкнутых систем будут также обозначаться как А, что позволит пользоваться единым программным обеспечением.
Процедура DISCR обеспечивает вычисление массивов Ф и F с по
* Для унификации всех вычислительных процедур, используемых в этой книге, применена одна н та же форма записи векторно-матричных уравнений:
у (t) = Ay (t) + Bg (t), нли
где А, В — матрицы, а Ь — векторы, соответствующие замкнутым или разомкнутым системам.
** Представление уравнений элементов объектов и САР в одной форме позволяет пользонаться одинаковыми вычислительными процедурами для спектрального разложения матриц (программа № 7, гл. 3), вычисления функций от матриц (программа № 8, гл. 3) и получения дискретной модели (программа № 9, гл. 3). Все эти программы приведены в гл. 3, п. 4—8, как для объектов, так и для САР.
143
мощью следующих выражений [26]:
ф(М + # JV- 1, АГ + М АГ — 1) = Ф(Т'о)! А 1/21 ••• i/aw-i
= "о"’! ~О" '""б” ;
I а I
_ |/(N, N-2)X(N.JV-2)I _
(1.404)
F(N + NN- l) = [f0:1 iO]T. (1.405)
Векторы fi, i=l, 2, ..., NN—1 и вектор f0 находятся из массивов
размерности (W X NN) в виде > [Fq : Fl: F2 •... ]=[/о ! f 1: fi: • • • : Avv-1]=
=» [£0£; EiB/T0: ... : ElB/tR X A
(1.406)
где s* = (INV (sT X «)) X sT, a sT — матрица транспонированная s; £0, £b El — матрицы, определяемые по формулам (1.403).
Пример 1.53. Составить дискретную, математическую модель непрерывного объекта с экстраполятором нулевого порядка, когда То — 0,01 с, пользуясь для этого следующими матрицами:
‘ 0,4 0 0 0 0 0 —0,4
0,06 0,05 0 0 0 0 -0,01
0,0015 0,05125 0,05 0 0 0 -0,00025
А = 0,015 0,5125 100,5 - 100 0 0 -0,0025
0 0 0 100 —100 0 0
0 0 0 0 400 -400 0
.0 0 0 0 0 2500000 0
» = [0,4 0,01 0,00025 0,0025 0 0 О]1
С помощью программ OWN, MFUNC и DISCR получим
‘ 1,0040 0,0000 0,0000 0,0000 0,0000 0,0000 о.оооо-
6,01 • Ю“4 1,0005 0,0000 0,0000 0,0000 0,0000 0,0000
1,52- 10~5 5,13 10-4 1,0005 0,0000 0,0000 0,0000 0,0000
Ф= 1,02- ю-4 0,0034 0,6355 0,3679 0,0000 0,0000 0,0000 »
4,16- ю~5 0,0014 0,2656 0,3679 0,3679 0,0000 0,0000
2,82- ю-5 9,55-10-4 0,1814 0,3351 0,4661 0,0183 0,0000
_ 0,2260 7,6777 1,47.. 103 4,51 • 10» 1,29 • 103 6,14.10» 1,0000.
1 == [5,25 • 10 “6 8,04 • 10”7 3,70.10-8 -7,27 • 10~6 7 ,82 • 10~6 -2,27 • 10-4 1,4350] т
Пример 1.54. Составить дискретную ма- То = 0,2 с, пользуясь для этого матрицами
тематическую модель непрерывного объек- А, Ь из примера 1.53. Тогда по аналогии
та с экстраполятором 1-го порядка, когда с примером 1.53 получим
" 1,4908 0,4006 0(6410 0,0028 0,0028 7,12-10”» 1,1410”» 1,10-10»
0,0691 0,9483 -1.6360 -0,0025 -0,0023 -5,65-10”» -9,04-10”» -8.76-10»
0,0076 -0,0080 0,7712 -4,22*10”» -4,22-10”» -1,05-10”» -1,69-10”» -1,63.10»
ф = 0,0081 —0,0036 0,7672 -4,33-10“» — 4,33*10”» — 1,08*10”» -1,73-10”» -1,68-10»
0,0081 -0,0041 0,7676 -4,32-10”» -4,32-10”» — 1,08*10”» —1,73*10”» —1,67*10»
0,0081 -0,0042 0,7677 -4,32*10”» -4,32-10”» — 1.08*10”» -1,73*10”» -1,67-10»
2,23-10» —7,04-10""» -5,81-10» 2,24-10» 2,24-10» 5,59* 103 0,8944 -1.02-1013
_ 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,000 1 _
f«=[—1,10.10» 8,76- 10е 1,63.10е 1,68.10» 1,67-10» 1,67-10» 1,02-1013 1,0000]т.
По данным примера 1.53 в гл. 3, п. 7 ее обобщенная математическая мо-рассмотрена замкнутая САР н приведена дель
144
Г л а в a 2
МАТЕМАТИЧЕСКИЕ МОДЕЛИ НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ
Рассмотренные в гл. 1 методы линеаризации применимы, когда нелинейность, входящая в объект или устройство САР, хотя бы один раз дифференцируема или аппроксимируется касательной с малой погрешностью в некоторой окрестности, близкой к рабочей точке. Существует целый класс нелинейностей, для которых оба эти условия ‘не выполняются. Обычно их называют существенными нелинейностями. К ним относятся: ступенчатые, кусочно-линейные и многозначные функции с точками разрыва 1-го рода, а также степенные и трансцендентные функции. Использование цифровых вычислительных устройств, обеспечивающих выполнение логико-алгебраических операций в системах, привело к новым типам нелинейностей, которые представляют через непрерывные переменные с помощью специальной логики. Для математического описания таких нелинейностей применяют эквивалентные передаточные функции, зависящие от коэффициентов линеаризаций, которые получают путем минимизации среднего квадрата ошибки воспроизведения заданного входного сигнала. Форма входных сигналов, поступающих на вход нелинейности, может быть произвольной. На практике наибольшее распространение получили гармонические и случайные виды входных сигналов, а также их взаимные комбинации. Если на вход нелинейности поступает синусоидальный сигнал, то метод линеаризации называют гармоническим. Можно отметить, что входной сигнал может быть представлен не только в виде первой гармоники, но и суммой нескольких гармоник. Если действует случайный входной сигнал, то метод линеаризации называют статистическим [12, 32, 33]. При входном сигнале, представляю
щем собой сумму гармонических и случайных сигналов, имеет место совместная гармонико-статистическая линеаризация [33, 39].
1. ОБЩИН МЕТОД ОПИСАНИЯ ЭКВИВАЛЕНТНЫХ. ПЕРЕДАТОЧНЫХ ФУНКЦИИ НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ
Весь класс существенных нелинейных элементов разделим на две группы. К первой группе относят однозначные нелинейности, у которых связь между входным х и выходным у векторными сигналами зависит только от формы статической характеристики нелинейности F, т. е.
y = F(x). (2.1)
В этом случае при определенной форме входных сигналов x(t) = = xi(t) с помощью матрицы коэффициентов линеаризации a(«i) можно найти приближенное значение выходных сигналов
y1(O = a(*i)*i. (2.2)
Из выражения (2.2) следует, что матрицы коэффициентов линеаризации однозначных нелинейностей являются действительными величинами и их эквивалентные передаточные функции J (*1) = а(*1).
Ко второй группе относят двухзначные (многозначные) нелинейности, у которых связь между входными и выходными сигналами зависит не только от формы статической характеристики, ио также определяется предысторией входного сигнала. В этом случае соотношение (2.1) следует записывать в виде
у(0=^[*(0]. (2-3)
Для учета влияния предыстории входного периодического сигнала
145
Рис. 2.1. Структурная схема определения многомерных периодических коэффициентов линеаризации в векторной форме, обеспечивающих условие минимального значения квадрата разности ошибки между точным и приближенным средними значениями выходных сигналов:
а — для однозначных нелинейностей; б —- для дву« значных нелинейностей
будем учитывать не только сам сигнал х,, но и скорость его изме-
нения X,-
При входных сигналах x(t) = = Xi(t) приближенное значение выходного сигнала будет
у,(/) = а(х,)х, + *i. (2.4)
где a(xt) и Ь (х,) — коэффициенты гармонической линеаризации двузначных нелинейностей; Т — период колебаний по первой гармонике, когда *1(0—периодическая функция.
Эквивалентная передаточная функция
Z(x1) = a(x,) + ^(x,). (2.5)
Существуют нелинейности более общего вида
jr(O = ^(*i, *1)> (2.6)
т. е.
у, (t) = a(xIt х,) х, + -Ь~2^')Г *i, (2.7)
где a(xh Xi) и б(х1( xi)—коэффициенты гармонической линеаризации.
Здесь к — номер гармоники.
Матрицы коэффициентов линеаризации являются периодическими с периодом Т. Имея это в виду, передаточную функцию для двузначной нелинейности (2.6) мо.жно представить по аналогии с передаточной функцией (2.5):
7(xi, xi) = a(xb xi) + jb(xi, xi).
(2.8)
Пользуясь выражениями (2.2), (2.4) и (2.7), определим обобщенные формулы для вычисления передаточных функций однозначных и двузначных нелинейностей.
В случае однозначной нелинейности матрицу коэффициентов линеаризации а, зависящую от параметров вектора х,(/), выберем таким образом, чтобы минимизировать среднее значение квадрата разности между точным у и приближенным y\(t) сигналами на вы
ходе, т. е.
||e(0|2=lim4r
1 —>оо
г
$|(8<Л, (2.9)* -т
где
' е(0 = Г(х1)-а(х1)х1. (2.10)
В общей4 форме для различных типов векторных входных и выходных сигналов выражение (2.9) можно записать в виде
| ё [I2 = (F - ах,)т (F - ах,) = ’
= F F - (Fox, + x,aTF) + 'хТатхь
(2.П)
* Во всех формулах гл. 2 черта сверху — символ усреднения.
146
Представим выражение (2.11) в виде суммы квадратов разностей соответствующих координат
в виде системы матриц от i=l; j = 1, 2, ..., п:
Iе I2 = Е (*i) - Е an (*i) *i/]2-tel /»1
(2.12)
Будем считать, что в выражении (2.12) X\(t) является периодической функцией хп(С; тогда структурную схему, иллюстрирующую линеаризацию в векторной форме, изобразим, как показано на рис. 2.1, а.
Для определения а1у- воспользуемся соотношением
Подставив в соотношение (2.13) выражение (2.12), найдем
— 2Р{Хц + 2хц £ а1кх1к = О, (2.14) к«=1
откуда
Е анЛЛ/ = FiXu; i, j= 1,2, ...,n. X“1
(2.15)
х12хн .. .х1пхн
Fixn
до i = n; j — 1, 2, ..., п
ап1
ап2
..апп_
Хц Х12Х1Г. . .ХщХц
х11х12 Х12 . . -х1пх12
-х11х1п х12х1п‘ • -х1п
Fnxll
РпХ12
F
(2.17)
Из выражений (2.15) можно получить систему уравнений
—2 , ,
ОцХц + 012X12X11 + ...
• • • + а1пх1пх11 = ^1Х11 ’•
О11ХЦХ12 + 012X12 -р • • •
• • • + а1пх1пх12 — F 1Х12<
allXllXln + а12х12х1п + • • • • • • + OlnXln = FiXin,
(2.16)
Onlxllxln~^~On2x}2xln~^~ • • •
. . . -f- OnnXln — Fnxlti‘
Эквивалентные передаточные функции определим из уравнений (2.16)
Перейдем к рассмотрению нескольких примеров использования общего метода нахождения коэффициентов линеаризации для однозначных нелинейностей.
Пример 2.1. Определить коэффициент линеаризации для однозначной нелинейности, когда на ее вход поступает первая гармоника синусоидального сигнала
Xi (!) = A sin a>t = A sin ф, (2.18) где со/ = ф.
Из системы матриц (2.17) имеем
. (xi)lxi
х
(2.19)
Тогда прн периоде Т, изменяющемся от О до 2л, усредненные значения функций определяют в виде
2Л
[F (х,)1Х1 ( F (A sin ф) sin ф 4ф,
2Л J
О
( 2.20)
147
Рнс. 2.2. Структурная схема определения коэффициентов линеаризации однозначных нелинейностей при нескольких периодических сигналах, обеспечивающих условие минимального значения квадрата разности ошибки между точным и приближенным средними значениями выходных сигналов: а — двух входных н одного выходного сигналов; б — Двух входных и двух выходных сигналов
а
2л
*1=-^-$ sin2^«h|> *=-у-. (2.21) о
Подставив в выражение (2.19) зависимости (2.20) и (2.21), найдем
2Л
а(Л) = —F (Л sin ф) sin ф б/ф. (2.22) ЛЯ J
о
Формула (2.22) представляет собой коэффициент линеаризации по первой гармонике для однозначной нелинейности; она определяет эквивалентную передаточную функцию /(Л).
Пример 2.2. Определить эквивалентные передаточные функции ап н а)2 для одно
значной нелинейности при двух входных' сигналах Хц и Xi2 и одном выходе [32].
Воспользовавшись системой (2.16), запишем
«11*11 + al2xl2xn = Fxn; а11х11х12 + а12х12 = Р*12-
(2.23)
Систему уравнений (2.23) можно представить с помощью рис. 2.2, а, полученного нз рис. 2.1, а. Из рнс. 2.2, а видно, как формируется среднеквадратнческая ошибка воспронзведення выходного сигнала.
Будем считать, как и в примере 2.1, что входные сигналы изменяются по синусоидальному сигналу со сдвигами фаз <р2 и ф2, т. е.
х11=Л1 sin (ф + <р1); |
Xi2 = Л2 sin (ф + <р2). J
Усредненные значения функций
И (*||, Х12)] Хн =
2Л
= “5л' § Sin + о
Л2 sin (ф + <р2)]} sin (ф + ф,) cf ф;
[F (хи, х12)] х12 =
2Л
“"ST sin <Ч> -ь Ф1).
X7i> J о
Л2 sin (ф + ф2))} sin (ф + ф2) б/ф;
2 Л1 Г Л1
*11 “ЪГ} sin2’H'i’ = —; о
Л2 г” Л?
-2 Л2 С . , . , . л2.
Х12 = ‘2}Г J зш2фг/ф = —;
О
2Л
Х.2хн = J sin (Ф + ф.) х о
X sin (ф + ф2) б/ф =
Л;Л2 ---
= —2 COS (ф1 — ф2) = ХцХ12.
Введем следующие обозначения: 2Л
h = {F [Л sin (ф+ ФО, о
Л2 sin (ф + ф2)] } sin (ф + ф1) б/ф; 2я
{г [Л. sin (ф + Ф1), о
Л2 sin (ф + ф2)]} sin (ф + ф2) б*ф
(2.25)
(2.26)
148
ц дерепишем систему уравнений виде
At , Л1Л2соз(ф1-ф2)
~2~ Oi14-------g--------Д12 =
Л142с°5(ф1-ф2) а\ --- ---2~------Л11 4—j" а‘2 ~
(2.23) в
'2.27)
Л2 , 2л 2 ’
Решая систему уравнений (2.27), получим два коэффициента линеаризаций раздельно для каждого входа:
<2ц (Ль Л2; фь ф2) =
1 rZ1 ~ z2C0S^i —Фа) xAi L sin2 (Ф1 — ф2) .
<212 (Ль Л2; фь ф2) =
1 Г/2 — /1 cos (ф! — ф2) лЛ2 L 81П*(ф1— ф2)
(2.28)
Пример 2.3. Определить коэффициенты линеаризации Дц, д!2 н Д]3 при одном выходе н трех входных сигналах
Хи == Л1 sin (ф4- Ф1); -j
Х12 = Аг sin (ф 4- фа); > ' ’ (2.29)
Х1э = Л3 sin (ф4-фз). *
Из системы уравнений (2.16) найдем а11х11 + а12х12х11 + а13Х13Х11 = f 1Х1Р 1
а 11Х11Х12 + а12х12 + а13Х13Х12 = Х12> I
а11х11х13 + а12х12х13 + а13Х13 = f 1Х13’ |
(2.30)
Запишем формулы для усредненных значений функций в виде
[Г (Хц, Х12, Х1з)КХц = 2л
= $ {Л1Л sin (* + ф,)> о
Аг sin (ф 4- Фа).
А3 sin (ф 4- Фз)]} sin (ф 4- Ф1) </ф;
[F (Хц, Х12, х13)] х12 =
2Я sin о
Аг sin (ф 4- ф2), А3 sin (ф 4-Фз)1} X
X sin (ф 4- ф2) г/ф;
(Хц, Х|2, Х1з)] Х13 = 2я
= ^5 sin <м> 4- фо. ;
0 .i
Аг sin (ф 4- ф2), А3 sin (ф 4- Фз)]} X ф X sin (ф 4- фз) </ф;
А2 г" А2
*п = 257 J sin2 ф<*ф----
о
А2 г" А2
*‘2”“йИ 5!п2фйф = —; о
А2 г* А2
X13 = lFj s,n м>^=—; о
2л
хахц = А'Аг-1 sin (ф 4-Ф1)Х £Л J
О
X Sin (Ф 4" фа) </ф =
Л|Л2 . , -----
= —— cos (ф| — ф2) = ХцХ12;
2Я
х[2Хц = А^А'- 8Ш(ф+ф1)Х
о
X sin (ф4-фз) </ф =
Д1^4з / к
= —g—cos (ф1 — фз) =ХиХ13;
2Л
Х13Х12 = sin (ф 4- фа) X
О
X sin (ф 4- Фз) <*Ф =
Л2Л3 . .
= %- COS (ф2 —фз) = Х|2Х13.
Введем следующие обозначения:
2Я
/1 = (F [Л sin (ф4- Ф1).
О
Аг sin (ф 4- ф2), А3 sin (ф 4- фз)1 }Х
X sin (Ф4- Ф1) <^Ф;
2я
1г — {F Mi sin (ф 4- Ф1). o’
A2 sin (ф 4- Фа)> 43 sin (ф 4- Фз)] }Х
X sin (ф 4- Фа) </ф!
2Я
/з = J {Г Hi sin (ф 4- Ф1). о
Аг sin (ф 4- фа). А3 sin (ф 4- <р3)] }Х
X sin (ф + фз) <<ф.
(2.31)
(2.32)
149
Перепишем систему уравнений (2.31) в виде
А? Л,Л2со5 (<р. — <р2)
~ +-----------2------а'2 +
, Л1Л3 cos (ф, — ф3) _ Л, , .
+---------j--------а'3 = 2л 1 ’
Л]Л2 СО8(Ф1 — Ф2) А22
-------2-----------Я11 + ~2~ ai2 +
, Л2Л3 cos (ф2 — ф3) _ Л2 , .
+---------2--------“13 “ ~2л /2>
Л1Л3сов(ф1 — Фз) „ ,
---------2------ 11 +
Л2Л3со8(ф2-ф3) +---------j--------а>2 +
, Аз п Аз + ~2"fll3= 2Г/з’
Из решения системы уравнений
(2.33)
получим
описания коэффициентов линеаризации однозначной нелинейности относительно трех входов в виде
flu (ЛI, Л2, Л3; фь ф2, ф3);
Д12 (Лj, Л2, Л3; фь ф2, ф3);
д1з (Ai, Л2, Л3; фь ф2, ф3).
Пример 2.4. Определить коэффициенты линеаризации вц, а12, a2i, а22 при двух сигналах Хц н х12 на входе и двух выходах. В этом случае систему уравнений (2.16) можно записать в виде
а11х11 + а12х12хп =s,^lxll>
а12х11х12 + a22^ = flx121 _2 ----- ------- (2.35)
а21х11 +а22х12х11 Х1Р
а21х11х12 + а22х12 ” ? х12
и представить с помощью рис. 2.2, б, где показано формирование ошибок воспроизведения выходного сигнала.
Пи
Л]Л2 cos (ф1 — ф2) Л1Л3 cos (ф] — ф3)
Л| AtA3 cos (ф2 - ф3) -
Л2Л3 cos (ф2 - ф3) Л^
1 «12= д-
А1
А1А2 cos (ф! — фг)
Л1Л3сов(ф1 — ф3)
Л^зсов (Ф1 — Ф3)
Л2Л3 cos (ф2 — ф3)
А2з
(2.34)
П13
А
А
Л1Л2соз(ф1-ф2)
Л,Л3 cos (ф1 — ф2)
А{А2 cos (ф[ — ф2)
Л2Л3 cos (ф2 — ф3) —/3
где
Д =
Л21
Л1Л2со8(ф1 — ф2)
Л1Л3СО8(Ф1 —ф3)
AtA2 cos (ф, — ф2) Л |Л3 cos (ф, — ф3)
Л| Л2Л3соз(ф2 ф3)
Л2Л3 cos (ф2 ф3) Л3
Раскрыв определители (2.34), найдем формулы для вычисления общих форм для
Входные сигналы задаются соотношениями (2.24), а усредненные значения фуик-
150
ций в системе уравнений (2.35) будут
[Fi (Хл, Хц)]Хи = 2л
= {f. Hi sin (ф+ <₽,),
о ;
Аг sin (ф + <р2)]} Sin (ф + <Р1) <7ф;
[fl (Хп, Х12)] Х]2 =
2Л
= {fi Mi sin (ф4-ф;), о
Аг sin (ф + <р2)1} sin (ф + <р2) d^;
[fj (Хп, Х12)] Xll =
2Л
{f» Mi sm (n>+<₽!),
ZJv J
0
At sin (ф 4- <p2)] } sin (Ф 4- Ф1) «7ф;
[f 2 (Хи, X12)] X12 =
2л
“-ЙЛ {fs Mi Sin (ф + Ф,),
*Jv J
0
At sin (ф1 + ф2)[} sin (ф + ф2) rf-ф-
Введем следующие обозначения:
2л
Л = {fl Ml sin (ф + Ф1), о
А2 sin (ф + ф2)] } sin (ф + ф,) <7ф; 2л
It = {fi М. sin (ф + фО, о
Лг sin (ф + ф2)]} sin (ф 4- ф2) </ф; 2Л
h = {Ft Mi sin (ф 4- фО, о
Ах sin (ф 4- ф2)]} sin (ф 4- фа) <*ф; 2Л
It = {fa [Л1 sin (ф 4- ф|), о
Аг sin (ф 4- ф2)] } sin (ф 4- ф8) </ф;
д2 А2
=2 _ Л1 . -2 _ Л2
*и==—. *12—2~;
----- AjAt . ,
*12*11 = —2— cos VP> ~ Ф») -
(2.36)
(2.37)
Подставив выражения (2.36) и (2.37) в систему уравнений (2.35), получим
Л? , Л1Л2соз(ф1 — ф2) __ 01, _(-------------- 012 =
Л1Л2соз(ф1-ф2) Л| -------2--------а,! ' ~2~ а>2 =
Л^ 2л '2’
Л? , Л1Л2соз(ф1 — ф2) ~2~ <hi 4-------2-------“22 =
2
Л]Л2 cos (ф( — Ф2) , Л2
~— a2i 4" ~2~ =
— 7
2л
откуда найдем
_ 1 Г 71 — /2 cos (ф] — фг)1. а” лЛ] L sin2 (ф! — ф2) J’
_ 1 Г /2 — 7i cos (ф! — ф8) ~|.
а>г лЛ2 I sin2 (ф1 — ф2) J’
_ 1 [73 — 7« cos (ф1 — ф8)1.
°13 лА> 1 81п2(ф!—ф2) .Г
1 Г 74 — 73 cos (ф1 — <ра) "I 014 лЛ2 L sin2 (ф| — ф2) J
(2.38)
(2.39)
В общей форме коэффициенты линеаризации (2.39) можно записать в виде
Оц (Ль At, фь фг)> 012 (Ль At, фь Ф2)» 01з (Ль At, фь ф2)> 014 (Ль At, фь фа).
В дальнейшем сравним формулы для определения коэффициентов линеаризации простейших нелинейностей при подаче на их вход периодических сигналов: синусоидального, треугольного, меандрового и покажем целесообразность применения получаемых эквивалентных передаточных функций в решении ряда задач, с которыми встречаются проектировщики в своей практической деятельности.
Теперь перейдем к распространению обобщенного метода описания коэффициентов линеаризации на двузначные нелинейности. В этом
151
случае, учитывая соотношение (2.8), выражение (2.10) можно записать
8(0 = ^(*i, ii) — [а(*ь *i)*i +
+ (2-40>
н формула (2.12) примет вид
I'.f - i,)-
(-1
Структурную схему, иллюстрирующую определение многомерных периодических коэффициентов гармонической «линеаризации в векторной форме для двузначных нелинейностей, составим по условию минимального значения квадрата разности между точками и приближенными средними значениями выходных сигналов и приведем ее изображение на рис. 2.1,6.
Для определения a(/(xb *i) и bi{(xlt *i) воспользуемся соотношениями daij dbu
и формулой (2.41), откуда найдем систему уравнений
О] 1*11*1» 4- 012*12*1» 4- ••• ... 4-0inxu = ^"ixln;
О»1*Ц*1» 4- О„2*12*1» 4- • • •
• • • 4" 0nnXln =
И _ .
6ц*11 4" 612*12*11 4- • • •
• • 4- btnxlnxn = (Хц; 611*11*12 4-612^2 4- •••
• • 4- blnxlnxI2 = ^’1*I2;
6ц*11*1п 4" 61пХ12*1п 4" • • • ... 4" 6щ*1» = у 1*1п>
6п1*н*1л 4- 6П2*12*1л 4~ • • •
4-Ь ?? — 2lt*
• • • 7" vnnxln — т п*1п‘
Коэффициенты линеаризации определим из уравнений (2.41) в виде системы матриц от i = 1; /= 1, 2, .. „л
Г Оц
I 012
Г 7.2
Х~ц Х12ХИ . . . Х1пХц
*п*12 *12 ... *1,1*12
LoinJ
I------------- —2
L*ll*ln *12*1» • • • *1'i
1*12
п ______ _____
22 OitcXhcXfi = к —1
п ______
bMi=^-Ptxu. к-1
(2.42)
_2 l_g~ i*i„ J_________
*11 *12*11- • •*!»*!!
Х12
Перепишем ее в следующем виде:
ОцХ11 4" 012*12*11 4" • • •
• • • 4-ain*in*ii=^’ Ли ОцХпХ12 4" 0^X12 4" • • • ... 4-ain*ln*12 = ^'l*12;
......................... 4-
2лк /я-~|.
у 1*12
ХцХ1п Xj2^1 п * • •
152
до i = n', j= 1, 2.....................п I
На интервале от 0 до 2л усредненные значения функций будут
&П1
ап2
Хц ХцХц. . .Х1пХц
ХцХ12 Хц ... ХщХ12
а.
пп-
-ХцХщХцХщ.
~2 Xln
^ПХц
пхц
~bni
Ьп2
_&~nxi
П—
2л
У (Xi) Xi = У (4 sin ф) sin ф йф;
о 2л
У (-*1) Xi = -g— j У (4 sin ф) cos ф йф; о
2л х>=-й5 8!п2фйф=4:
• о 2л 42<о2 С 2 >. j . 42<о2
_С08ф</ф =--------—.
О
72
-Ьпп_
Хц ХцХц . . . XinXn
ХцХц Хц . х1пХц
-ХцХ1п ХцХ1п . . ~^-^1
~^ц
2jt* Д- Z. ~ У ~ ПХ1п
-Т2 Xln
(2.47)
При первой гармонике входного сигнала x(/)=4sina/ по формуле (2.45) можно найти для двузначной нелинейности первые два коэффициента гармонической линеаризации а(А)ги,Ь(А) в виде
а (А) = (Х')] Х| ;
*1 •
МЛ)=Ддг<хД].х^,
*1
(2.48)
где
(2.44)
Рассмотрим несколько примеров нахождения коэффициентов линеаризации для двузначных нелинейностей при к= 1.
Пример 2.5. Определить коэффициенты линеаризации двузначной нелинейности, когда иа ее иход поступает первая гармоника синусоидального сигнала и имеется одни выход. Тогда из системы матриц (2.44) получим
а(х1)=-^'(Х|)]Х| ;
*1
„ ,---------- (2.45)
h (г \ 2Л (*1)] *1
0(Х1) Т р-------•
В данном примере входной сигнал запишем и виде
Xi (0 = 4 sin <о/ = 4 sin ф,
откуда
*1 (0 4ш cos <о< = 4а cos ф. (2.46)
2л
о
У (4 sin ф) sin ф г/ф;
(2.49)
2л
5 (4) = У (4 sin ф) cos ф йф. (2.50) о
Тогда для двузначной нелинейности общую эквивалентную передаточную функцию представим как
7(4) = а (4) + /5(4). (2.51)
В соотношении (2.51), так же как и в выражении (2.5), имеются действительная и мнимая составляющие эквивалентной передаточной функции двузначной нелинейности.
Пример 2.6. Определить коэффициенты линеаризации ан, <212, 5ц и Ьц для двузначной нелинейности при двух входных сигналах Хц(0 = 41 81п(ф -|- <₽i), xtJ(0 = = Аг sin (ф + <ра) н одном выходе.
Из системы уравнений (2.43) имеем
“11*11 + “12Х12*11 “ ^1Х11>
“11*11х12 +“12*12 = ^1*12: (252)
*11*11 + *12*12*11 °* ®&~1ХЦ.
*11*11*12 + *12*12“®^ 1*12-
153
Рис. 2.3. Структурная схема определения периодических коэффициентов линеаризации двузначных нелинейностей при нескольких периодических сигналах, обеспечивающих условие минимального значения квадрата разности ошибки между точным и приближенным' среднийи' зйачёниями* выходных сигналов
Формулу (2.39), по которой формировалась система уравнений (2.52), можно проиллюстрировать рис. 2.3. Как следует из уравнений (2.52), в них приведены зависимости для усредненных значений функций
2л
(х1Ь х12)] хи =-^{#'(/l1sin(A|)4-qp1), О
Л2<о cos (ф -|- фг)]} sin (ф + «рО с?ф;
2л
(^(Хн, *12)]Х>2—М {ЗГ[Л, SinW-Hh), хЛ J О
Л2ш cos (ф + <р2) ]} sin (ф + q>2) йф;
2л
5 Э1п(ф + ф!>, О
Л2а> cos (ф + ф2)]} cos (ф + ф,) </ф; 2л
У1(хц, xi2)xi2 = sin (ф -1-ф,),
2Л J О
Л2<о cos (ф + ф2)]} cos (ф + ф2) </ф;
Л? г" Л2
J Sin2*rf*’=“2i-: о
Л2 с" Л2
х12 = ^- $ зш2ф<*ф = -^-; ;
о |
Л2<о2 2
72
2л |
Х12*п = А^2 8т(ф+ф1)зт(ф-|-ф2)</ф= •
о ’
Л(Л2 / .
= —2—cos (<Pi — Фа);
2 2 2я Л)со с • " 2 - \ cos2 ф йф = о
2 2 2я Л2Ш С 2 ,
ХЬ = _27~ Jcos
о 2л
—г- Л|Л2<В2 f ,
Х12Х“ =—2л—J C0S
О
. . / l , \ j l Л^гШ2 . .
X cos (ф + ф2) 4ф =-------cos (ф1 — ф2).
Л2<о2 2
(2.53)
Введем в систему уравнений (2.53) следующие обозначения:
2л
7, — J {^1 [41 sin (ф + ф!). о
Л2<о cos (ф +ф2)]) sin (ф + фО йф;
2л
Л = [Л sin (ф + Ф1), oJ
Л2<о cos (ф + ф2)]} sin (ф + ф2) cfф;
2л (2-54)
Л = {F1 [^41 sin (ф + ф(), о
Л2со cos (ф + ф2)]} cos (ф + ф|) йф;
2л
Л = {^"1 [л1 sin (ф + фО, о
Л2Ш COS (Ф + ф2)]} cos (ф 4- ф2) йф
и, подставив (2.53) и (2.54) в систему уравнений (2.52), найдем
У
. 4j42 cos (Ф] — ф2)
— «11 +-----------2----------а'г = 1"
Л[Л2со5(ф| ф2) , Л2 42
---------2--------““ + ~“‘2 = 17 '2'
j, ( 41Л2соз(ф1 — ф2) Л1
— Т----------6>2= йГ7”
Л1Л2со8-(ф1 — ф2) 4| 42 7
---------2--------*и + —
(2.55)
154
Решая систему уравнений (2.55), определим составляющие эквивалентной передаточной функции
_ 1 ГЛ — /2 cos (<Р1 — фа)!. а“ nAi L sin2 (ф!—ф2) J’
= 1 Г /а —Л cos (ф, —фг) I. 012 = лЛ2 L sin2 (ф1 — ф2) J’ b = 1 Г Гз — Л cos (ф1 — фа)~|
11 лЛ! L sin2 (ф! — ф2) J’
Ь — 1 Г Л — Л cos (ф1 — ф2) 1
12 лЛ2 L sin2 (Ф1 — фа)
(2.56)
Общие формы эквивалентных передаточных функций, полученные с помощью системы соотношений (2.56), будут
/(Л1, л2; Ф1, ф2; и) =
= пи (Л 1, Л2; фь фа) + jbu (Ль Л2; фь Фа)> 7 (Ль л2; фь фа; (О) =
= aia (Ль Л2; фь фа) + /6ia (Ль Л2; Фь фа).
(2.57)
Пользуясь приведенными математическими зависимостями в примерах 2.1, 2.2, 2.4—2.6, можно найти коэффициенты гармонической линеаризации для существенных нелинейностей.
Для нелинейностей вида^х^хО с учетом соотношения (2.6) выражение (2.40) перепишем в виде
8 (0 = ST (xb xi) — [a (xj, Xi) х, +
+ >(,Ul)r *]’ <268>
откуда формула (2.41) при «=1 примет вид
i.)-1 — 1
+
+ ~bil (х"2*‘);е‘/Г])}2 • (2.59)
Для определения Xi) и
6//(хь xi) воспользуемся соотношениями
аЦ7Ц2_п. а||7||2__0
<4/ ’ Ыц
и формулой (2.42); тогда найдем систему уравнений
п _________
к=1
п
У, (Хц.
К = 1
1(2.60)
2. ГАРМОНИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ ТИПИЧНЫХ НЕЛИНЕЙНЫХ элементов
Классическая теория гармонической линеаризации типичных нелинейностей предполагает, что сигнал, снимаемый с выхода нелинейности, является периодическим и имеет основную частоту, совпадающую с частотой синусоидального входного сигнала. В' результате такого допущения при нахождении эквивалентных передаточных функций нли коэффициентов гармонической линеаризации учитывают только первую гармонику, а влиянием высших гармоник пренебрегают. Это справедливо лишь для таких САР, линейная часть которых является низкочастотной и подавляет колебания высоких частот. Однако данное положение иногда нарушается, н в входных и выходных сигналах наряду с первой гармоникой содержатся высшие гармоники. От их действия в некоторых САР возникают автоколебания, недопустимые по требованиям эксплуатации.
Рассмотрим аналитическое определение коэффициентов гармонической линеаризации по первой гармонике входного сигнала и приведем их графическую интерпретацию. Для этого примем, что на вход однозначной нелинейности поступает сигнал
Х[ (/) — A sin at. (2.61)
Выходной сигнал можно представить
y(t) = F (Л sin at). (2.62)
Приближенное значение выходного сигнала, как было показано в
155
Рис. 2.4. Геометрическая интерпретация гармонической линеаризации:
а — однозначной нелинейности; б — двузначной нелинейности
п. 1 гл. 2, имеет вид
ух (t) = Л] sin со/, (2.63)
где Ai — первая гармоника сигнала на выходе нелинейности.
Выражение (2.63) запишем через коэффициент гармонической линеаризации
yi (/) = Аа (Л) sin со/. (2.64)
Имея в виду выражения (2.61) и (2.64), получим
У1(/) = а(Л)х1(/), (2.65)
откуда
a(A) = yi(t)/xi(t). (2.66)
Подставив в выражение (2.66) выражения (2.61) и (2.63), найдем
а(Л) = Л1/Л. (2.67)
Из формул (2.66) и, (2.6.7) следует, что коэффициент гармонической линеаризации однозначной нелинейности представляет собой коэффициент усиления, определяемый отношением амплитуды 1-й гармоники выходного сигнала yi (/) К ВХОДНОМУ
Проиллюстрируем это положение с, помощью рис. 2.4, а, из которого видно, что при подаче на вход нелинейности типа насыщения синусоидальных сигналов с амплитудами Л и Л на выходе образуются сигналы только первых гармоник с
амплитудами Л1 и Л'. Тогда нелинейная функция F (xi) может быть аппроксимирована прямыми линиями 1 и 2 с коэффициентами наклона а (Л) и а (Л'). На рис. 2.4, а также показан графический способ определения коэффициентов гармонической линеаризации однозначных нелинейностей в соответствии с соотношением (2.64).'Зависимость коэффициентов гармонической линеаризации от амплитуды входного сигнала указывает иа то, что основное свойство нелинейной характеристики F(xl) полностью сохраняется.
Перейдем к аналитическому и графическому определению коэффициентов гармонической линеаризации для двузначных нелинейностей (рис. 2.4,6). В этом случае при действии ,на входе нелинейности сигнала, записанного в виде, аналогичном (2.63), на выходе имеем приближенное значение сигнала
yi (/) = С[ sin (со/ + <₽[), (2.68) где q>i — сдвиг фазы, зависящий от величины амплитуды входного сигнала. Как видно из рис. 2.4, б, с ростом амплитуды входного сигнала происходит уменьшение фазового сдвига.
Выражение (2.68) можно переписать
yi (/) = Л1 sin со/ 4- Bi cos со/, (2.69)
где _____________
С\ = Л1 -|- Bi; sin Ф1 = Ai/Ci', cos ф! = BilCi.
156
Таблица. 2.1
Вычисление коэффициентов гармонической, линеаризации типовых однозначных нечетных нелинейностей
Nt л/л
Вид нелинейности
g(t)
а. (А) =<^(А)
^rfarc sin -b-nrcsin + Я А А
2
157
Продолжение табл г.1
158
Продолжение табл. 2/
y-8stn[x-£( l*+cl-l*-cl)J
Ун
г1е
J,(A). J,(A)uJ2n(A) функции Бесселл
у =8 соз к «sjnx
IBS.,, (А)
ХА
S.,,,(A)-
-функция Лонмелл
•/fJAkstn С~ т
-2S.t1(A) COS С]; lie Jt '(A)-
- функция Бесселя ;
S.t1(A)-
- функция Лопмеля
Г с х arc sm — +—
А А
159
Продолжение табл. 2.1
160
Продолжение табл Z. 1
23
у=! 8 + £xz)sgnx
11
6 К). И. Толчеев
161
Продолжение main. 2.1
Пользуясь значениями коэффициентов гармонической линеаризации а(Л) и Ь(А), из выражения (2.69) получим
г/1 (0 = Аа (Л) sin <о/ + АЬ (Л) cos a>t,
(2.70)
где а(Л) и Ь(А)—коэффициенты гармонической линеаризации по 1-й гармонике.
Формулу для определения выходного сигнала в соответствии с (2.70) найдем
5,1(0 = а(Л)х1(0 + -^х1(0, (2.71) или
w- <2-72>
Ранее было показано (2.51), что эквивалентная передаточная функция имеет вид
/ = а(Л) + /й(Л), (2.73)
или
/ = 9(Л)е^<л>, (2.74)
где q(A) и ц(Л)—соответственно эквивалентные амплитудная и фазовая характеристики двузначной нелинейности по 1-й гармонике.
Эквивалентные амплитудная
q (Л) = Va2 (Л) + Ь2 (Л) (2.75) и фазовая
pM) = arctg-|^- (2.76) характеристики можно представить в виде рис. 2.4, б. При этом видно, что нелинейность аппрокси-
мируется прямыми линиями 1 и 2, проходящими через точки 7\ и Т2 с коэффициентами наклона q(A) и q(A'). Здесь же показаны значения фазовых углов ц(Л) и ц(Л').
Пример 2.7. Определить формулы для вычисления коэффициентов гармонической линеаризации однозначной (рис. 2.4, а) и
двузначной нелинейностей (рис. 2.4, б) и
построить шаблоны 20 1g
____1_
<7 (-4)
и -180°-
— ц (Л) иа полулогарифмической бумаге. Для однозначной нелинейности было по-
казано (см. п. 1 гл. 1), что
2л
а(Л) = -М ЛА J 0
F (Л sin ф) sin ф йф. (2.77)
Из рис. 2.4, а видно, что выходной сигнал является симметричным на интервале от 0 до л; тогда его можно описать
f A sin ф при 0 sj ф sC фь yi (/) = < В при ф1СФ<л—фь (2.78) Л sin ф при л — ф1=С ф^л.
Подставив (2.78) в (2.77), получим
Чь
9 Г
а (Л) = —-г- \ Л sin2 ф ф +
JlA j
0
n-tpi
2 С
+ -v \ В sin ф dty +
ЛА J
Чь
л
-|—( Л sin2 ф йф = лЛ J
л-Ч>1
|>i — sin 2ф1 + -^-.cos Ф1)- I2-79)
Так как
51пф1=-^- и cos ф1 — /у 1 — -jp , (2.80)
162
О 5 Who 5 10 А
6) г)
Рис. 2.5. Коэффициенты гармонической линеаризации для однозначных нечетных нелинейностей типа:
а — насыщения с i - 1, В - 1; б-ограничения сигнала в виде треугольника с ii - 4>« 1, В = Г, в— ограничения сигнала в виде трапеции с Л, = Ла = 1, В-1; г — переключения по уровням Ви —В (В = 1)
в} г)
Рис. 2.6. Коэффициенты гармонической линеаризации для однозначных нечетных нелинейностей типа:
а —насыщения с зоной нечувствительности при Ci - В — 1, Ла - Г, б — переключения с зоной нечувствительности С — В — 1; в — ограничения сигнала в виде треугольника с зоной нечувствительности при Л| — kt — 1, В — 1; г — ограничения сигнала в виде трапеции с зоной нечувствительности прн kt — Л2 = 1, В — 1
6*
163
а— синусоиды с одним периодом при В = в — синусоиды с зоной нечувствительности уровням В и —В (В « 1)
1; б — косинусоиды с одним периодом при В - 1;
С — В «= 1; г — косинусоиды с ограничениями по
6) г)
Рис. 2.8. Коэффициенты гармоническор линеаризации для однозначных нечетных нелинейностей типа:
а — синусоиды с .зоной нечувствительности ha полупериоде при 2С — 1; б — кусочно-линейной с двумя наклонами kt = I, k2 = 1,5; в — нечувствительности с С = 1, k = 1; г — переключения с постоянным наклоном к - I при ограничениях по уровням В и —В (В = 1)
6)
6)
г;
Рис. 2.9. Коэффициенты гармонической линеаризации для однозначных нечетных нелинейностей типа:
а — кусочно-линейной с зоной нечувствительности 2С, = 1 и двумя наклонами kt = 1, fe — 0,5; б — с ограничениями по уровням В и —В (В = 1), с последующей кусочно-линейной частью
5) г)
Рис. 2.10. Коэффициенты гармонической линеаризации для однозначных нечетных нелинейностей типа:
в —функции Вх + гх3, В = 1, е-1; б —параболы четвертой степени с В — 1: в —с ограничениями по уровням В н —В (В = I), с последующим участком в виде квадратической параболы; а — с ограничениями по уровням В и —В (В — 1), с последующим участком в виде кубической параболы е — 1
Рис. 2.11. Коэффициенты гармонической линеаризации для однозначных нечетных нелинейностей типа:
а—функции тангенса от -у до - -у; б—квадратической параболы, начинающейся с зоны не-чувствительности С«1; в — кубической параболы, начинающейся с зоны нечувствительности 0=1; г — функции Вх—ех2, £=1, 8=1; д—цифрового преобразования прн 2^ = С^=»1
то из выражения (2.79) можно определить формулу для вычисления коэффициента гармонической линеаризации нелинейности типа насыщения в виде
а(Я)=1(аГс51п-£+4д/1-^.).
(2.81)
В табл. 2.1 эта формула записана для случая В = С = 1.
Формулы для вычисления коэффициентов гармонической линеаризации других наиболее часто встречающихся типов однозначных нечетных нелинейностей также приведены в табл. 2.1. По этим формулам на рис. 2.5 2.11 построены кривые, характеризующие изменение коэффициентов гармонической линеаризации в зависимости от амплитуды входного сигнала. У всех типов однозначных нелинейностей Ь(А) = 0 а следовательно, а(Л) = <?(Л). Тогда по данным табл. 2.1 нетрудно получить формулы для построения шаблонов, с помощью которых находят амплитуды автоколебаний в нелинейных САР (см. гл. 7). Для нелинейности типа насыщения эта формула
будет 1 9
20 1g—Агг = —201g--Я (A) s л -201е(агсз1п4 + ~д/1-£1).
(2.82)
Шаблон показан иа рис. 2.12, а. Для других нелинейностей эти шаблоны изображены на рис. 2.12—2.18.
Для вычисления коэффициентов гармонической линеаризации двузначных нелинейностей используем формулы вида
2л
а ="лЛ J s*n s'n
о *,
2л (2.83)
b (А) = —( F (Л sin ф) соз ф </ф.
ЛЛ J о Пользуясь рис. 2.4, б, опишем выходной сигнал как
/ —В при 0<ф<фи
(0 = < В при ф1 < ф С л + ф,; (2.84)
*• —В при я + ф1 С Ф < 2л.
166
Рис. 2.12. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с однозначными нечетными иелииейиостями, с параметрами, указанными иа рис. 2.5, а—г, типа:
а — насыщения; б — ограничения сигнала в виде треугольника; в — ограничения сигнала в виде трапеции; г — переключения
Рис. 2.13. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с однозначными нечетными нелинейностями, с параметрами, указанными на рис. 2.6, а—г, типа: а — насыщения с зоной нечувствительности; б — переключения с зоной нечувствительности; в — ограничения сигнала в виде треугольника с зоной нечувствительности; а — ограничения сигнала в виде трапеции с зоной нечувствительности
167
ных системах с нечетными нелинейностями, с параметрами, указанными на рнс. 2.7, а—г.
типа:
а — синусоиды с одним периодом; б — косинусоиды с одним периодом; в — синусоиды с зоной нечувствительности; г — косинусоиды с ограничениями по уровням В и —В (В — 1)
Рис. 2.15. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетными нелинейностями, с параметрами, указанными иа рис. 2.8, а—г, типа:
а — синусоиды с зоной нечувствительности на полуперноде и ограничением по уровню В 1; б — кусочно-линейной с двумя наклонами; в — нечувствительности; г — переключения с постоянным наклоном к — 1 при ограничениях по уровням В и —В (В - I)
168
Рис. 2.16. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетными нелинейностями, с параметрами, указанными на рис. 2.9, а—г, типа:
а _ кусочио-лииейиой с зоной нечувствительности; б —с переключением по уровням В и —В (В = 1), с последующей кусочно-лииейиой частью при ki — 1, k2 = 0,5; в — квадратичной параболы; г — кубической параболы
степени; в — с ограничениями по уровням В и
—В {В = 1), с последующим участком в виде квадратической параболы; г — с ограничениями по уровням В и —В (В — О, с последующим участком в виде кубической параболы
169
Рис. 2.18. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетными нелинейностями, с параметрами, указанными на рис. 2.11, а—д, типа:
а — функция тангенса; б — квадратической параболы, начинающейся с зоны нечувствнтельностн; в — кубической параболы, начинающейся с зоны нечувствнтельностн; г — функции Вх — ех3; д — цифрового преобразователя
Подставив формулы (2.83) в (2.84), получим
1 Г Г
а (А) = -^д-1 — \ В sin ф </ф 4-L о
я+ф, 2Л
j В8шф<7ф— В sin ф г2ф Ф> л+ф,
4В = —j- cos ф(;
nA т
Ф>
В cos ф с/ф +
о
Я+ф1 2я _
+ Всовфйф — Всовфйф
Ф> Л+Ф1 J
4В . . ------j- Sin ф|.
яА т
Имея в виду соотношение (2.84), из. выражения (2.85) определим формулы для коэффициентов гармонической линеаризации в виде
а(А) =
С2
А2
Ь (А) = -
4ВС яА2
6(A)
(2.85)
при А>С; (2.86)
при А>С. (2.87)
Пусть В — С = 1; тогда по формулам (2.86) и (2.87) можно получить зависимости а (А) и 6(A), которые приведены в табл. 2.2. Кривые, характеризующие изменение коэффициентов гармонической линеаризации в зависимости от амплитуды входного сигнала, построены иа рис. 2.19— 2.26.
По выражениям (2.86) и (2.87) можно найти формулы для вычисления эквивалентных амплитудной
дя с q(A)=^£± при А>С (2.88) /1
170
Таблица 2.2
Вычисление козцнрициентов гармонической линеаризации типовых нечетных двузначных нелинейностей
№ П/П вид нелинейности у,<и а (А) в(А)
/ -с У В с У 0 — x^v, IX ЧВ i/ с1' ЯА<1 Аг А*С ЧВС ЛА 2 AiC
0 -в / 3i Ti 2 4» !v
2 -с У л тС _ У> 0 V, э-ы « , гх * F41 м |Ъ| + 2ВС f. । 1) А г-С
чпС 0 -в С X 11LJ"
3 В У 0 _ 2Я а.(А)=О А = С ЧВ ЯА А = С
-С 0 -В — С X — я я _ 2 4х
ч У В -с Г ' У 0 ГТ^гН* ХА У Аг А>^С ЧВС КАг А^С
ч J с % W-* ичя Я I •"2 <_ IV
5 У в -с / t/fi _ У 0 "™к Г fc* | |\ 7*^2Я АЪС ЯА I А) А»С
/а / X -в цр-к f Я ¥Я\ 2 \
6 У К \ 8 а*лс к -с7 W У 0 /I LL 1 4- чг-. 5£* ^(arcsin ,arcsin^+^ (В*КС)1 В-КС 4-^ ЧВС ЯА1 А^^-К
1/» I/ 7 /с д**с х к -в tgP=K Ж •ж L
171
Продолжение табл г.1
7 У В -с/ /р , У я /Г~\ /; (Хп1 ~2ji s[l' A*C ХА \ А! АЪС
/о. fc X -в tgJ3=K / Я FJT\ I 1V 1 \ /
в у в -тС-С У 0 й-“ t Jr.L n, i-ч Ffe гх К zb !J, cl 1 йГлг + + Г A1 / АЪС МО .. . ~^-т} АЪС
0 /77 С С Л -в v я v 1 2
9 У в ~С-тС п У 0 П . ZB J, m2Cz ПА Г Az A = C _ZB [ mC \ я А к А / А-С
и. тС С 'х -В чrt U г
10 У В*кС в А \-C-mC j 0 ТЬ-тС С\ X _я 8*кС 8 ~к~ У 0 /ГК A W\.\\jz*V l{ftapcs£n - УУ~т^]-ат1п-У A J A mC -arcsin ~ + A 2вС Л С\, \ Г 1л7 Vm яА \ А/' '
11 У В+кС в Л \ -С-тС ж У 0 /ТХ J\\ К Г , в*ХС . S,n>K х^Тл-^^Тл - a min У -arc sin v-f+ A A B'ltC IS’kCF S*mxl кА V №Л2 кА ,k 1±ткС)г' С.П7 ~аГа‘~ тС I m2cz] ~7~Г~Т2 J АЪ Д / к с ZBC(l-m) Я А2 , В + КС А^~
Ж тС С \ X и 8+КС ~В ~ tj/M
1Z -в У В с У 0 4-ni z 1 , а(А)=О А = С 9В А А=С
0 -в X я 2 я 2 ЯГ
172
Продолжение табл. 2 1
13 У В -С-гпС ILL У 0 _3Г Тч-V 2Л zb ,/. тгсг TiA r A1 Аг-тС 2В [ тС ) ЯА\ А / Аг тС
0 тб С X -В V Jl_ Я | | F
/4 У -с_ 0 У 0 — Ti /\ г 2Г^ К I A^C К Я АгС
/ С X Л s\ I ¥ 2
15 У -Сг-С, 0 У 0 /Я . к, .6 -(arcsLn — + 3i A c ./, сг ’] + 7 Г'Л/ АЪС, при А=Сг я. A ' 2AI A>Ct при А=Сг
1 1 / С, Сг X -fl ^\j_| zs- v
16 УЬ в -С / '/р , У 0 , в+кс А-~к~ ПА 1 А/ А- к~
/0 /с X -в ЧР-* v я \7zfiv
и фазовой
С
/, С2 v
Л/ А2
(2.89) характеристик рассматриваемой двузначной нелинейности. Эти формулы внесены в табл. 2.3. Там же приведены зависимости и для других типов двузначных нелинейностей.
Для построения шаблонов рассматриваемого примера воспользуемся следующими формулами:
“'«W — 20|e-Hr-20l|iT <290>
И
Т)(Л) = - 180°-д (А). (2.91)
На рис. 2.27, а н б изображены шаблоны, построенные по формулам (2.90) и (2.91). Для других типов двузначных нелинейностей онн построены в логарифмическом масштабе на рис. 2.27—2.34.
С помощью этих шаблонов находят амплитуды и частоты автоколебаний в нелинейных САР и строят области устойчивых и неустойчивых состояний по пара
метрам линейной нлн нелинейной частей систем (см. гл. 7).
Следует указать, что существует два типа двузначных нелинейностей — пассивные и активные. Под пассивной понимается такая двузначная нелинейность, в которой за один период входного сигнала нелинейная характеристика обходится против часовой стрелки. В этом случае в выходном сигнале наблюдается фазовое запаздывание. Если же обход нелинейной характеристики происходит по часовой стрелке, то двузначная нелинейность является активной и в выходном сигнале имеет место фазовое опережение. Формы сигналов на выходе пассивной нелинейности изображены на рис. 2.35, а, а активной — на рис. 2.35, б. Активные нелинейности применяют в устройствах коррекции САР для обеспечения их устойчивости. Реализация таких устройств может быть выполнена на электронных
173
b(A)
г)
линеаризации двузначных нечетных нелиней-
Рис. 2.19. Коэффициенты иостей при В = С и трех а и б — однопознцнонного реле соответственно для а(Л) н 6(Л); в н г — однозначного реле с неполным смещением соответственно для а(Л)
гармонической т типа:
Рис. 2.20. Коэффициенты гармонической линеаризации двузначных нечетных нелинейностей типа:
а — характеристики идеального гистерезиса; б и в — однопознцнонного реле с С — S - 1 н k— 1 соответственно для а (А) н Ь(А)
н
b(A)
174
a)
bW
Рис. 2.21. Коэффициенты гармонической линеаризации двузначных нечетных нелинейностей при С = В типа:
а и б —люфта с шириной 2С н k - 1 соответственно для а(А) н Ь(А)
в)
Рис. 2.22. Коэффициенты гармонической линеаризации двузначных нечетных нелинейностей типа:
а и б — однопознцнонного реле с гистерезисом при k— 1 соответственно для а(Л) и Ь(А); в и г — гистерезиса с С - В — 1 соответственно для а (Л) и Ь(Л)
175
Рис. 2.23.\ Коэффициенты гармонической линеаризации двузначных нечетных нелинейностей типа:
а н б — двухпозицнонного реле с зоной нечувствительности соответственно а (Л) и Ь(Л); в н г — гистерезиса с зоной нечувствительности соответственно для а (Л) н Ь(А)
элементах или в виде рабочих программ на управляющих ЭВМ.
Рассмотрим гармоническую линеаризацию нелинейностей, когда на их вход поступают сигналы типа Xi (t) = х0 + A sin ф, где Хо — постоянная составляющая входного сигнала.
Для определения формул гармонической линеаризации снова воспользуемся нелинейностями, приведенными в примере 2.7, но при наличии смещения х0 (рис. 2.36,а). При этом сигнал на выходе нелинейности
У1 (<) =
*о+ А sin ф В
Хо + A sin ф
—Хо—A sin ф — В
—Хо—A sin ф
при О Ф Ф11
при Ф1 < ф < л — фи
при л — ф1 ф л;
при л ф л + ф2;
при л+ф2<ф<2л—ф2;
при 2л — ф2 < ф < 2л.
(2.92)
bM
г)
Тогда первое приближение для выходного сигнала имеет вид
У1 (0 = Ро (хо, >1) + Аа (х0, Л) sin ф, (2.93)
где Fo(xo, Л)—функция смещения выходного сигнала (постоянная величина при заданных значениях х0 и Л).
Для нахождения коэффициентов линеаризации
2я
Fo (хо, Л) = -^-^ F (х0 + A sin ф) </ф, (2.94) о
2я
а (х0, Л) = F (х0 + A sin ф) sin ф йф
о
(2.95)
подставим в формулы (2.94) и (2.95) выражение (2.92); тогда получим
4»
Fo (*о. А) = (х0 + A sin ф) </ф +
О
л-м>, я
5 Г 1 С
+ 2л J ^^Зл J (хо + А sin фМф—
фх я-ith
176
AM)
a)
-0,2'-----------------------
г)
в)
Рис. 2.24. Коэффициенты гармонической линеаризации двузначных нечетных нелинейностей типа: о н б — двухпозицнонного реле с зоной нечувствительности при ft = 1 соответственно для а(Д) и Ь(Д); в н г —гистерезиса с зоной нечувствительности соответственно для а (А) н б (А); д — однозвенного элемента с фазовым опережением
д)
177
a)
a(A)
bM 0,6
0,4
0,2
0
b(A)
/т-0,25
т-0,5
т-0,75
2 4 6 8 A
6)
-cj^' 0 с
tgP’A
0 2 4 6 8 A
г)
-Сг-С,ВО &
LJZ
tgjw
О 2 4 6 в А
а) а (А)
У
-г 1
/0, 'С ’ -в
tgp-b
О 2 4 6 в А
Рис. 2.25. Коэффициенты гармонической линеаризации двузначных нечетных нелинейностей типа:
а и б — гистерезиса с зоной нечувствительности, с фазовым опережением соответственно а(А) и Ь(А); в н г — двухзвенного треугольного элемента с фазовым опережением С «• k — I соответственно а (Л) н Ь(А)
Рис. 2.26. Коэффициенты гармонической линеаризации двузначных нечетных нелинейностей типа:
а н б — двухзвенного трапецеидального элемента соответственно а(А) н о(А); в н г — идеального гистерезиса с фазовым опережением и k — 1 соответственно а(А) и &(А)
6)
178
таблица 2.3
Вычисление коэффициентов усиленияf фазовых углов для типовых нечетных двузначных нелинейностей
№ л/л вид нелинейности Форнулы для Вычислений
Ч(А) У (А)
с
у в
1 с X 4В С_ ЛС А при АгС -aictg ГЧГ при А >С
-с 0
-в
2 У в при А г С
-С тС ‘ X
-т С 0 а“'9\Я'ЯР при А ъС
-в
3 У , В 4В С ЛС А при А-С -30° при А-С
-С С X
0
-в
4 У |С к . / , 18В2 С2 Т +Л2С2 ' Аг ВкВ С Г С2 ЛС А V А2 при А* С 4В С^ _Qxctg ^А2 к ЛС aV а2 при А* С
-С 0 tg/5-л
5 У, -с / к /Гл . /, 2С\12 л\1[7 zcs V~T/j +
+4а('~а) + [л+2а1С5'п{'-г]х ° 9 Л 1 2С\ ^+ (ucsin |J“ H- , 2 к А /
/о /С при А»С при А
179
Продолжение табл. 2.3
У в -С -тС тт»
”’C,S V-W-’r
в 0 тС С -В при А» С при АъС
при А = С
/ тС
. \ А - axctg\ /----
\/ 1+т — V А
при А= С
180
Продолжение тадл.2.5
к . //л Г с/,-т)7 ^^atcsmp- д J С . тС12 - atcsin — - atcsin — I + A A J At*1 с 4
т-t -т
' ^СЧ С \21, v If, Al\ 1
10 ^ЫНпГаГ ULLiy —+aicsin 2 г,-«^5-
У, В-кС В к -С -тС F7 » .С . тС -atcsm atcsin —7- + А А
«Ч ’ <*ч 1 т- О < 1 Lj- е|< ; -'5> । а 1 1 1 д 1*-^» ।
тС С В-кС -в к tgP-K . С . mCl -atcsin—atcsm — А А тС ,/ т2С21 А V A2 J , в + при А = — Ag- кС
11 1 . / ,/7 . В+кС . В+ткС — \/ к2//atcsm ——+ atcsm—— л, V Ц кА кА
.С . тС -atcsin--atcsin — А А \2АВ2С2. f В+ткС X
| кА V к2А2 кА , /, (В+ткС)2 С,/, С2 тС V' к2А2 АV' А2 А Х . /, m2C2\J . В + кС ^-^^(atcsin—+ aiLig к Г . В+кС aicstn А + кА
У В-кС в к -С-тС /тг.» . В+ткС . С * aicstn—: aicsin— - А А . тС В+кС . I, (B-^kcV -atcsmT^— В+ткС, / В+ткС + кА У к2А2 "AV А2~тС V1' A2 J’ , В+кС npuA = —j^~
JLL тС С В-к С -В к tgB = K
. В+ткС . С + atcsin—- atcsin — - кА А . ткС\/В+кС . /, (В*кс1 -atcsin-— —— и /——т А Д кА V к2А2
В+ткС . / (В+ткС)2_ + кА V к?А2 С./ С2_ткС,Г т2С2}1 "А V '~А2 А V A2 JJ’ . в+кв при А=-^—
181
Продолжение табл. 2.5
12 у в X п п >1^ 90° Ь = С
-с 0 -в с 1
13 У -С -тС в X £\Д/;-Л!£) ЯС А V V А / ' А=С 11 — axct9\/ me ,+ lT A = C
1± тС С -в
И а _-со х ' " с 1 Я V 4 32,5°
.15 У в -с 'о /О * к !( кС]2 , —\/аъсяп —) + я V\ я/ , №] “XCt9 . cJcTp7
1 с -fl tgj3 = K
/6 У, -С/ * J\Z/2+aXCSinp-ff+ ++xH)+2A+2axcsin('f| , АГ Л QXCtg Я . (~2C\Z 7+axcstn^--j +
/о /с tgj3-/c
182
Рис. 2.27. Шаблоны для графического определеиия режимов автоколебаний в нелинейных системах с нечетными двузначными нелинейностями, с параметрами, указанными на рис. 2.19, а—г, типа:
а и б — однопозиционного реле; в и г — однозначного реле с неполным смещением
Рис. 2.28. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетными двузначными нелинейностями, с параметрами, указанными иа рис. 2.20, а—в, типа: а и б — характеристики идеального гистерезнса; в и г — однопозициоииого реле с наклоном
183
Рис. 2.29. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетными двузначными нелинейностями, с параметрами, указанными на рис. 2.21, а, б, типа люфта
Рис. 2.30. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетными двузначными нелинейностями, с параметрами, указанными иа рис. 2.22, а—г, типа:
а и б — однопозиционного реле с гистерезисом при k — 1; ей г — гистерезиса
184
Рис. 2.31. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетными двузначными нелинейностями, с параметрами, указанными на рис. 2.23, а—г, типа:
а и б — двухпозициоиного реле с зоной нечувствительности; в и г — гистерезиса с зоной нечувствительности
Л+фг 2Л—ф;
(х0 + A sin ф) йф — — j б/ф —
Л Л+ф2
2л
$ (ХО + 4 sin ф) dip =
2Л—ф2
= — [(Хо — С) ф; — A cos ф; + Л
+ (х0 + С) ф2 + A cos фа]. (2.96)
Заменив sin ф; = (С — х0)/Д, 5тф2 = = (С + х0)/Д, окончательно запишем
Fo (Хо, А) = ± | (С + х0) arcsin С + *0' —
— (С — х0) arcsin дХ° +
при А > С + | Хо |. (2.97)
Теперь определим коэффициент линеаризации
Ф1
а (х0, А) — —-г \ (х0 + A sin ф) sin ф dф + ТС A J
о
Л—-ф1 л
+-^д S sinфdф + ^- (х0-|-Д sin ф)Х
Ф> л-ф,
Л + 1|);
X sin ф dф—i- (xo+Дsiпф)sinфdф—
Ф2 sin ф dф —
Фг
—г \ (х0 + A sin ф) sin ф dф = nA J
2 л-ф2
= (ф‘ — А°^— с°5ф1 + Ф2 +
+ ^^-со5ф2), (2.98)
2Л-— ( nA j л+
2Л
откуда
/ 1 Г . С + Хо ,
а (х0, Д) = — I arcsin —---------1-
+ arcsin
С — х0 , С + Хо
А + А
(С + х0)2 , С — х0
А2 + А
д/1 _ <С. 1 при 4>С + | х0|.
(2.99)
185
Рис. 2.32. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетными двузначными нелинейностями, с параметрами, указанными на рис. 2.24, а—д, типа:
в и б — гистерезиса с зоной нечувствительности при k — 1; в и г — двухпозиционного реле с зоной нечувствительности при k — 1; д и е — однозвенного элемента с фазовым опережением
186
Рис. 2.33. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетными двузначными нелинейностями, с параметрами, указанными на рис. 2.25, а—г, типа:
а и б — гистерезиса с зоной нечувствительности с фазовым опережением; в и г — двухзвенного и треугольного элемента с фазовым опережением
Рис. 2.34. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетными двузначными нелинейностями, с параметрами, указанными на рис. 2.25, а—г, типа:
а и б — двухзвенного трапецеидального элемента с фазовым опережением; вне — гистерезиса с фазовым опережением прн k — 1
187
Рис. 2.35. Формы сигналов иа выходе нелинейностей: а — пассивной; б — активной
Рис. 2.36. Формы сигналов на выходе нелинейностей при наличии смещения х0: а — однозначной нечетной нелинейности; б — двузначной нечетной нелинейности
Рис. 2.37. Коэффициенты гармонической линеаризации для однозначной нечетной нелинейности типа насыщения со смещением при В = 1, k = 1:
а) Ра (Хо, 4); б) а (Ха, А)
Рис. 2.38. Коэффициенты гармонической линеаризации для однозначной нечетной нелинейности типа переключения по уровням В и —В (В = 1) со смещением:
в) Ра (xQ, Л); б) а (Ха, Л) _
188
Запишем полученные формулы в табл. 2.4. Формулы для других типов однозначных нелинейностей F0(x0,A) и а(х0,Л) также приведены в табл. 2.4. Кривые коэффициентов гармонической линеаризации со смещением построены на рис. 2.37—2.44, а шаблоны для них 20 1g ~ё~7 тг и 20 1g —7 тг показаны
ь Fa (х0, Л) Б q (х0, Л) на рис. 2.45—2.60.
Рассмотрим прохождение сигнала со смещением через двузначную нелинейность, приведенную в примере 2.7. Форма выходного сигнала yi (t) показана на рис. 2.4, б, откуда следует
f — В при 0 ф ф,;
У1(О=< в при ф|<ф<л — ф2; (2.100) I — В при л — ф2<ф<2л.
При смещении ха первое приближение для выходного сигнала будет
yi (0 = ^"о («о, Л) + Аа (х0, Л) sin ф + + АЬ (х0, Л) cos ф.
Формулы для определения &~а(ха. Л) и а(х0, Л) получим, подставив в выражения (2.94) и (2.95) соотношение (2.100); тогда
2л
&~о(ха, Л) (*о + A sin ф) йф =
0 л-ф2 2 л
В dф 4- В г!ф—В </ф
0 ф, л-ф2
= 4 + ф2): (2.Ю1)
Таблица 2 А
Вычисление коэффициентов гармонической линеаризации типовых несимметричных однозначных нелинейностей
NS П/П Вид нелине ’(// юсти fd(a) а(х0,А)
I У, В -с 0 1 у 1 U- ^(C+x0)aicsin - (C-x0)* к Г С+х0 . С~Хп —/aicsin-T—2+ aicsin —~ + Л[ А А
V 1 X JCo tg/3=K C-x0 , Г. /, (C+x0)2 xaxcsm д°+а/\/'- д2°-при А» С+/х0/ + £ + Х0 \ / т (2 А дг + С~ХО \ (F-Xq)2 1 А V A2 J при А » С + /х0/
2 -Сг 'С, \ 1 У В 0 - -в Cj 0? X *0 —/fo+x0) arcsin -(Ci“X0) * JC[ A Cj~Xq1 К? Г/ /» X x axcsm A л/ ^c’’x°^x / Cj-X0\ x faicstn -axcsLn -д~/“ х/ C2+X0 -(C,+x0)(aicsin A - _ aLCSin £ip|- T- A J Л I V A2 \ 11-(B<+XoY] K2AT l,(C2~X$_ (К^ + К2}/ С1~Хл С/ + Х(Л -Л-— (arcsm —4—5+ai.csin——у - л 1 А A j Х1[С1~Х0 , / (С|~хо]г, С; + Хв л[ А V ' А2 А Х 7'-1 А А_ V А2 ^1~Хо 1 / J f^rXpV. ^2+х0 \ /г (^2+Хд V'—7Г-+—
4Pi‘Ki V A1 J Jt / V A2 •• C2 + Xo) “QTCSID д ) при А»Сг+1х01 2В, Г. /. (С; х0)2 / (C2-x0)2t ЛА[ V А2 V А2 при A^Cz+|x„|
Продолжение табл. 2.4
3 У В 'СзЧЧ У > В / Сз~Хо Cj ~X0 — aicsin-^-^-aicsin —: JC\ A A . C3+X0 - aicsin —- “ + A . Ci<-X0'\ X,X0/ , C,"X0 +aicstn ——x +-!—1-aicsin-1—y+ A / Jt 1 A . С,+Х(Л xpf/o x ★aicsin ^/V*o)x x (aicsin ~4~ -aicsin - -(Cz+Xo)^csin ^^-aicsin при A >C, +/x0/ Kj Г t Bl"Xn Bi^Xn J axcsln-^+ausm-V-2- -Ц-5 JCl A A A ХуГ C3~Xn , C^~Xq -—laxcsin , °-axcsin . “+ XL a A . C3+x0 . c2+xo Cj-Xo * axcsin -x^-S - aicsin д ° - -^—- Ч'-^’Ч-^] при А> Cj+/Xo/
\ 1 1 > V 1X С] Cj X ад=*1 tgj32-x2
4 и в 0 2fi . x0 — aicsin-11 Л A — \/'-4 ЛА V Ai
— -в До x при А»lxDl при А »/х0/
5 У. в -с2-с, -1 1 * 1 %-, rS^—| '°7^ 'J x * * , + ® f < + ч ЛГ 1 « tp « «1 a «— 1 >— = . -L c i J- ® 3 ,* >?l Й L'->» “ Cj * О 4>- + 7 .5 in Й l F-Л ° s = °i 4 + L „ a _ £ ? F ~ 'V й гГ £Г £ | .5 F 1 <= Д 1 c 3 3 <L ®IH । , । к Г . Cz-Xn . Ci-xB - aicsin \ - aicsin -'. ? + х[ А А . - С?+Хо ^)+хо +aicsin -f, -У - aicsin -4-^ + А А Cj~Xq / - (C]~Xq)2 С?“Хл А V' Ai А * Ч’-'^^Ч'-'^ Ч'-^№^: + \/i-]при а>с2+1хо1
_У0 1 cr X 4^ tgfl-к
6 У в -с И 1 В/ . C+xB . C-x0\ — axcsin-r-^ - axcsin —^1 ^Ч-^Ч-'^
0 C X До при А»C+/х0/ при А> С +/х0/
190
Продолжение табл. 2А
в
л'[(С2’С,^агс51П 5Д 0 . С2-х0 . Cj + xD -aicsin , ° - aicsin * А А +aicsin ~^Cj-x0)x x/aicsin C* x° -atcsin -(c;+x0) (aicsin —-+x° -\ A Cj*Xq\*| к?!,- \[ . Сух* -aicsin ——/ + -’(Crxo) aicsin—-A /J JLL \ A Xf / ^2~Xq —4aicsin —--Ч -Jt t A Cl-x0 Ci + Xn - aicsin -4-2+aicsin ——2 -A A
-aicsin i/l-M A A V Az
_ C2~Xq (Cj-X^f C, + Xp .. A V' A2 A x
к2Г, . Cj-x0 . c2-x0 /aicsin -4-2- aicsin -- + Л[ A A + aicsin £4^-aicsin -22x9 _ A A
В в -Cj-C^-C]
Л£7 |С, Ci Cj X -в |*о -aicsin }-{C2+x0)x 1 . C3+Xq . С2-»Хп\| /GA x aicsin -i—s-aicstn -S-s --1- x 1 A A /J Л ^3~XQ 1/. (^3~X0P Cg-Xp v A V’’ A* " A X
xV'’^+^
#444--44’-
ЧР2 к2
~ла[^ a^' +!c^x
при A> С2+/х0/ ,,/j (^ХоУ ^ВГ / (C2-x0y
V A2 J XaLV' a’
4'-444'-4^'- при A»C3+/x0/
Atf.^ С* В -Ct-Cj-fy-Cj *-|х0| tgp2=K2 *!ог j[(c2-^ (aicsin -^#2 - - aicsin -Ц-^2 -mcsin -C-^x° + A A , ^»2*Хп\| К j * aicsin . l~— x A // Jt * pC/-Xo)(aicsin - дХ° - - aicsin ---- -(C;*xB) x A ! . Ci+Xq . Cj+XqXI x aicsin —7-2-atcsin-4-£ + \ A A /J ♦^/(Cj-Xorfoicsin С4дХ|!~ KtC . C2-xa . Ci-xB -t/aicsin-4—2- aicsin —r-2 + ЛI A A . C2+x0 . Ct+x0 Cj~xo + aicsin aicsin —-+-7— x A A A ,\ /. (Cr*o? C2-x0 / (C2-xoy &+Xp \г~аГ' a V ~aT~ a f . C+-Xo . C3-x0 x /aicsin - aicsin —- + I A A . C4+X0 . Cj*x0 C4-x0 *aicsin aicsin - -~-x x A - A A
р С2 CJ С+х А
\ /. (CA~Xp)2 Cj~Xq 1 /. (Сз~Х0}2 У’ A2 A V1 A2 +
г
191
Продолжение табл. 2.4
9 У в 'rZ/JtJofA) Sin Xg /Л l oo ~2n-l C°s x°| n~ n-l J где J0(a) u J^-rfA) - функция Бесселя -£/jrJr(A)COSX0-Л A L -2S_1>](A)Sinx0j, где Jj(а)-функция Бесселя 1-го рода -, S-^ (А)- функция Лоннеля
0 X La Г*о
10 У. -С 0 x2xo + ^{fC-x0)x K^-hr[aiCSin~A^ +
1 /\Рг id • C’Xg . . . C+Xn xaxcsin-^p+fc-xglaxcsin + talcsinCp+£^;-^
1 1 > 1 С х *о при A > С+/х0/ c+xo / (C*XOH 1 A V A2 j при А>С+/х0/
tgjl)-''; tgj32-«2
11 У -с 0 UL- «*0-^С; + Х0)х к Г • С-х0 j. к- —laicsin ——+ XL А
d-^’7 при A x C+/xqI при А > С+/х0| Г
! с х I r*0 tg/3-х
12 у в 0 Kt_ 2 В Xn XX0+-~ QXCSLn-^ л A 4В , /, xj к+Та V'-tt
-в 1 x |х_о Г^~ tgj3=«
13 У. В -с 0 K2xo~^lxo(K2-l<i)-Bjaicsin^^ при A*C+lxol г i > *2-^(хг + хг)х • С+х0 С»х0 ,(С+х0)2,С xaicsin—
! c x '8j_Xo V A2 JTaV Д2 при A^C*lxol
1 tgj»,-*» tg^2«x2
14 У. 0 f 2Bf[, A2] . x0 3 ,, /~xj] л|(Х»+Г]аШ1ПА+2ХоА\/,Л ?[Xoalcsin?+(7+w)^’^
X x "0 g-x2sgnx
192
Продолжение табл. 2.4
Рис. 2.39. Коэффициенты гармонической линеаризации для однозначной нечетной нелинейности типа насыщения с зоной нечувствительности Ci = В = 1, k = 1 со смещением:
о) Pt (х«, Л); б) а (хо, А)
Рис. 2.40. Коэффициенты гармонической линеаризации для одиозиачиой нечетной нелинейности С = В =: 1 со смещением:
a) Fa(x«, А); б) а (х«. А)
7 Ю. И. Топчеев
193
О 2.4 6 8 А
3)
Рис. 2.41. Коэффициенты гармонической линеаризации для однозначной нечетной нелинейности С — 1, k = 1 со смещением: в) Fa (х#. А); в) а (х», А)
Рис. 2.42. Коэффициенты гармонической линеаризации для однозначной нечетной нелинейности типа квадратической параболы при В = 1 со смещением:
в) Fo (х0, А); б) а (Хо, А)
а)
Рис. 2.43. Коэффициенты гармонической линеаризации для однозначной нечетной нелинейности типа кубической параболы при В =* 1 со смещением:
a) F» (хо, А); б) а.(хл. А)
194
SO 40 20
О 2 4 6 в А
О)
линеаризации для функции у = Вх — ех3
Рис. 2.44. Коэффициенты гармонической при В = 6 = 1 со смещением:
a) Fo (Хо, А}-, б) a (fco. А)
Рис. 2.45. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной однозначной нелинейностью типа насыщения при В — 1, fe — 1 со смещением: я) 2018 6)20,8
Рис. 2.49. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной однозначной нелинейностью типа ограничения сигнала, в виде треугольника при ki = kt — 1, В ь= 1 со смещением:
а)201g "г,/--»; g) »»gT7Z,'"лГ
** 0 A) Q (Хо» л)
7»
195
Рис. 2.47. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной однозначной нелинейностью типа ограничения сигнала в виде трапеции при k\ = kg = 1, В — 1 со смещением: а) 20 ig д-.1 б) 20 1g Го (Хо, A) Q (Хо, А)
Рис. 2.48. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной однозначной нелинейностью типа переключения сигнала по уровням В и. —В (В = 1):
а) 20 Ig -й-А—ТТГ б) 20 Ig — '
Б Ft, (Хо, А) Ч (Хо, А)
Рис. 2.49. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной однозначной нелинейностью типа ограничения с зоной нечувствительности при Ci = В = 1, k = 1, со смещением:
20*-5м£аг> «20”7сгЬ)
196
Рис. 2.50. Шаблоны для графического определения режимов нейиых системах с нечетной однозначной нелинейностью типа ню В и —В (8 = 1) с зоной нечувствительности С = 1:
а) 20 1g -.; ; б) 20 1g —
F<) (ж», Л) g (х<?, Л)
автоколебаний в йели-переключения по уров-
Рис. 2.51. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной однозначной нелинейностью типа ограничения сигнала, в виде треугольника, с зоной нечувствительности, при С, = В = 1, k\.= kt = 1 со смещениям:
а) 20 1g -/-J . ; б) 20 1g .1 Го (Хо» А) д (Хо» А)
Рис. 2.52. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной однозначной ' нелинейностью типа ограничения сигнала, в виде трапеции, с зоной нечувствительности при Cj = В =•), ki = #2=1, со смещением:
201«ТйЪг: « №1е-^Ьй
197
Рис. 2.53. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной однозначной нелинейностью типа синусоиды, с одним периодом при В = 1, со смещением:
л>,201« РлЬгг;
Рис. 2.54. Шаблоны для графического определения режимов нейных системах с нечетной однозначной нелинейностью в прямых, с двумя наклонами fa = 1, fa= 1,5, со смещением: л) 201g у.-; б) 20 1g - ' г-
/*о (Хо, Л) <7 (Хо, А)
автоколебаний в нели-виде кусочно-линейных
Рис. 2.55. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной однозначной нелинейностью в виде зоны нечувствительности при С = 1, k — 1, со смещением:
20’8 р J j,-; б> 20*8
Г9 (Хо, A) Q (Хо, А)
198
Рис. 2.56. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной однозначной нелинейностью типа переключения, с постоянным наклоном k = 1 при ограничениях по уровням В и —В (В = 1) со смещением:
а) 20 1g б) 20 Ig n
Г С (Хо, л) Q \Хо, А)
а) ' 0)
Рис. 2.57. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной однозначной нелинейностью типа с переключением по уровням В и —В (В = 1) с последующей кусочно-линейной частью при kt = 1, Й2 = = 0,5 со смещением:
4 201ё-р-7^~7: ; б)201г'Т7тЦг го (Хо, А) <7 (Хо, л)
Рис. 2.58. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной однозначной нелинейностью в виде квадратической параболы с В = 1 со смещением:
л) 20 1g „ .! ; б) 20 1g . -1
Ft (х0. Л) ’ q (Хо, Л)
199
Рис. 2.59. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с иечетиой однозначной нелинейностью в виде кубической параболы с В = 1 со смещением:
О) 20 1g р , ‘ Ф 20 1g , 1 -j;-® Ft (Хо. A) Я (Хо. А)
2я
а (х0, А) = —-г \ 9~ (х0 + A sin ф) sin ф4ф= ЛЛ J
о
Ф< я
—В j sin ф 4ф + В sin ф с/ф — о ф1
2Л п
SI 2В
sin ф 4ф I = (cos ф] + созфа).
Я-Фо J
(2.102) Подстарив в формулу
,2я
b (х0, 4) = У (х0 + A sin ф) cos ф Йф о
Рис. 2.60. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной однозначной нелинейностью в виде функции Вх — ех* при В »= 1, е = 1: в)20,87л£АГ;
соотношение (2.100), найдем
2Я
b (хо, 4) = У (х0 + sin ф) cos ф dф = о
Ф1 я—фо -
~—В cos ф 4ф + В созф^ф 1= о ф| J
2й
и»----j- (sin ф1 + sin фа). (2.103)
ЛЛ
Так как sin ф] = (С — х0)/4, a sin фа == ==(С + х0)/4, то из выражений (2.101) — (2.103) можно получить
SFо (х0, А) = - (arciin С д*° +
+ arcsin • А С + | х01;
, о, 2Я г . Л (С-х0)» ,
а (хо, 4) [ Д/1 -----да---- +
+ (СУ^], Л > С + | х01;
&(хо. 4) = ~4j4’ л>с + 1*о|.
Формулы для вычисления коэффициентов Уо(хо, А), а(хо, А), Ь(хо, 4) для этих и других типов двузначных нелинейностей приведены в табл. 2.5. Коэффициенты гармонической линеаризации для них приведены иа рис. 2.61—2.71. Формулы для вы-
200
Рис. 2.61. Коэффициенты гармонической линеаризации двузначной нечетной нелинейности типа однозначного реле при С я= = В = 1 со смещением:
a) (х«, А); б) а (х0, Л); в) 6 (хо, Л)
числений q(xa, Л) н ц(хо,Л) даны в табл. 2.6, а шаблоны 20 Ig .---------у-;
“ 0 А)
201g' , 1 ..
e q Л)
— 180° — g (х0, Л) построены
на рис. 2.72—-2.84.
В нелинейных САР при недостаточном уровне подавления линейной частью высших гармоник необходимо учитывать дополнительные гармонические составляющие автоколебаний. При этом эквивалентная передаточная функция зависит от двухчастотного или многочастотного входного сигнала. Использование таких эквивалентных передаточных функций в нелинейных САР >
Таблица 25
Вычисление козрнрициентов гармонической линеаризации типовых двузначных несимметричных нелинейностей
Д'* Щп Вид нелинейности Т(х,.А) а(х,.А) BfXg.A)
1 -с 5 0 it- -в fc- ..с х Arcsin Я' А А/ при Л^С+JxJ при AtC-\x,\ ЧВС ЯАг при A t С*|х,|
2 ~т 11 а|- С а ft ис| . Jc х -U» A tensing*arcsinH!^~>-.arcstnAl'-msinS^la) 'А А / при А » С* 1х,1 при A t С*/х,/ при AtC + IXgl
J -с в -0 -в / у* Т Г,(Х,,А)-0 при А = С + |ХО| а(х( при А= ,А)-0 С + IxJ ЧВ " Я А при A-C + IXgl
Ч Л 0 1, гр с X KX'-jurcsln^fl _ -arcsin и / при А» С\|Х0| к гв ЯА ‘ при X iL + и (С-Хц)1 At J » |х,| ЧВС Я А2 при At С^/Х,1
5 *: -С,/ п X в кх„ при At С С,-С при At С С,-С ЯА 1 А/ при At С С,’С
201
Пройвлжение тайл, z.s
6 qq У hz -arcstn ±^X21f|_ (c-л,) » xGrcstn-**^"*^ arcstn-I*£~*»1 L хЛ *4 J -X Гarcstn XlXX2i2 -ZX L kA - arcstn !lH^ipi,arcstn^f^^-kA kA -arcstn ХЛ<£2*дЛ _ JX. , kA J 2Я JL [arcstn /'''Af ± ZfiL kA + arcstn --* ( P+xq) t kA arcstn хо^-агс$Си^'х» кА kA . + JL (C-XalS^1~ я/ kW -lr Klc\)^t- . |/. rW(Ctxjj»i д 1' K‘AX fXA Jll t LB*k (С-кв)]г '. ’V "" - 4SC XAX . s+aC , , при л>—-+|XO| Л ct-c i
a Jp = H . |/* lB ~K (C~XO) JZ t y/- ..a.. t
*з P -^P^,2.P- _ 1/, IB-к (C-x,)l 2' I Г Л1! J при A »——-/ X,l Ct~C * L Wk (С + х„]]г'. Г кЧ1 J к fe*K(C-X0) |/, LBr-KfB-Kjg!. 2T\ kA . B-K<C-X„1 J, IB-Kfc-Xyf. кА г к‘Аг B+Ktc+x,,) L [K->x(C*x^l'‘ kA K‘Al * x B-KfCt-Xgl ^,_IB-K(ctx,)]‘ при A^ +)x,|. C,‘C "
1 Л-ntf, B К — к fC, -ci r kk0 к * ч г zx j(C, txs) arcstn J^LUL^al- -(C-Xularcsin - X [arcstn МСЙ-Хд! _ 2x\_ kA - arcstn -^~У(С7Я«)~1 -кА J (i/. Й-лГСлх»)]8 ZX у'~ - при A = ffiXx, и A.S±rJ^ к ° _x Г X ' я [ z Jsrcstn + Z kA + -!, arcstn / g~ltp)~| _ 2 kA _2Xff+CJ+2L^ ЯА ' ЯАг . B*ac , при A - — x0 и . B+KC A=" +Хд Л °
-Ji. t ’Ey S-ntC "X X Jp =« ^-x,/y?-j> XA\V K’A’ . a-x(c-x,) i/, cfl-x(c-xj]< кА У' kW t
202
Прпволжение таВл. 2 5
S в -С -тС J_L! Lf C X ~0 | _л о 2% A A £A[I A2 I A2 ^tnJ^L^tnS^) A A / f Аг 1 A* J при АъС+/Х01 Л/Ш A^G+lKgl 2BC (,-m} при AZ-C+Ixol
3 5 ~mGf U' j Uc|g 1 x #i X XD В , mC.i-x, я 1 (rnC-xJ1' 2t(arcsin A - -ansin^i.j ' при. A= C-x0 a nPu A~C-x, и 4- C, + xt A “^iX, -А. Г, CT/g*c>/ ЯА [J Л при Л» C-x, и A-C, ixs
13 a b * A. Farcsin -52-SJSzXj> + 2л Ц ЛЛ + tirtsin. * f r •&. npf^tn В + к ( C+xp) + я+ ; L kx +arcsm *x°) _ -aresU-f^-fc-x,), _ercsii, ^a.jrtsfn c±j0 -^[arcsin - _ aifatn д^.тй^ -arcrtn-^ie j+fmC^x.M ^j<c->>) - ^[nrcsin -в15^£1М - - p-L£^jt^lc.Kii) , -arcsln —-fmC-xt) n i - — «[arosin - arcstn -Z?Lg^*oJJ> - 1 .Cii-K^njC-XtH2 _ —§=- farcsln l+A- x 4Л I » лл f Д* ) ЛА 2B3 ., , -(1-m) ЯА2 Bi-AfC+IXnl) при A к --
x«. *s fi-K X StKC l—к .arcstn -^(C-tliL _ «W j-l^xfC-blJ2 + । KA U ’ каЛ* -arcsln -ShJ^LiAd - ^l-^jcix,lV t - ansi.n -А^с^Л-М, хМ'^гу.'Л; ^у-д)Г }- \ , Д*й(дс-<п1 |/,_ИчМ-/,»‘. - |Г гд^/с/х.и1 + й f да \ + Pusap^ Л - Шд(спл\ |/. [!*л1тС1Х,13х _ . г.А Г iU£_ L г «М« xfl««toC*XoJ У, .t8»x(mt4JI
i/x <C-X»)J. 14 rC-Jf,)1 KA 1' x^A‘ У A2 V' A2 1 4-Xj |/z_ (C-x,)2.. Ciftl - \lt (тС-X,)2. t!< ImCixA ?-.. '. ,A Г , А2 Г А2 /х/г-Л^хД’ -m^ix при A9..?.*K<C*W 1 . P&C-7,)»- mcixo .
npuA>l^nML
203
Продолжение main 2.5
fl . -с С _ / ^(Хд.А)-О При А -С+1х0| а (Ха,А)=0 при A^C+IXtl ХА при А-С+1ха1
-а j X
12 и в -тС, LEL -£-(arc$tn - -arcsin—™£_1Аа) А / при. А^С-Хд а А * ВЛ ^л1у Л» , |/, ImCt+Xg)2 ГА* 1 при А'С-хв и А * С,+ха В Г, л>{С*С,)1 ^Л [ A J при А - С-Хв и А • Gf + Xg
0 tnC G X
13 г ‘ х arcsin——7й^г'|'Х>) _ кА -(c-xjarcstn В~~КД~Х,^~ 2Х кА -arcsin кА J кА J~ i/, [В~К1С*Х,)]г 2Я\| кгА 'arcsin-t!^^ X[2 2 кА bJ-arcstn-8~K(lc~:,l>} [-г кА J ХА(С С’> ХАГ при А-^^-Хд и к \ X I
ХА *7 кхАг
У в 1 xfl Й/, 1Д-Х/С,лл,)]г ' +ЯЛ\Г' K^i \/, tH-Kltrfill1 L И К‘А* J _ Л / й-xffitx,) л 2Х 1 кА
~ Л 1В~к 1 г-х,>)]2Д. Г л’Л J при А--^~-Хо Л- г +х0 / Лу,_ 1Ц^12г +
в-лгс-х,) |/, гАпт-л.»* ★кА V к*Аг J при А-^£-Хв ; Л = М+Х0
целесообразно, когда требуется оценить влияние высших гармоник на появление автоколебаний. Например, в нелинейной системе на 1-й гармонике отсутствуют автоколебания, а от действия 3-й гармоники появляются автоколебания (см. гл. 7).
Пусть на вход двузначной нечетной симметричной нелинейности поступает сигнал
Xj (/) = At sin at + А3 sin (Зсо/ Д- Фз)>
где Ai и Д3 — соответственно амплитуды 1-й и 3-й гармоник; <р3 — сдвиг фазы 3-й гармоники.
Тогда : на ее выходе образуется сигнал вида
sin соЛ-^з sin (Зш/+фз)], (2.104)
или, положив, как и раньше, Ai = — А, найдем
yi (t) =* А [а (Я) sin ф + b (Я) cos ф +
+ Оз(Д)81П(Зф + фз)-|-
+ 63(Л)соз(Зф + фз)], (2.105) где а(Л), Ь(А) и а3(А), Ь3(А) — коэффициенты гармонической линеаризации соответственно по 1-й и 3-й гармоникам.
204
Рис. 2.62. Коэффициенты гармонической линеаризации двузначной нечетной нелинейно' сти типа однопозиционного реле при С = В — 1 со смещением: a) о (Хо, Я); б) а (х0, А); в) b (х0, Я)
Рис. 2.63. Коэффициент гармонической линеаризации двузначной нечетной нелинейности с характеристикой идеального гистерезиса С = В = 1 со смещением
Рис. 3-64. Коэффициенты гармонической линеаризации двузначной нечетной нелинейности типа однопозициоииого реле при С <= = В == 1 и k = 1 со смещением:
a) (Хо> А); б) а (хо, А); в) Ь (х«, Л)
а) б) б)
Рис. 2.65. Коэффициенты гармонической линеаризации двузначной нечетной нелинейности типа гистерезиса при С — В = 1 и £ = 1 со смещением:
a) & о (хо, Я); б) а (х0, Я); в) Ь (х0, Л)
205
Рис. 2.66. Коэффициенты гармонической линеаризации двузначной нечетной иелниёй-ностн типа одиопозициониого реле с гистерезисом при А = 1 со смещением:
а) (хо, Л); б) а (х0. Л); в) Ь (х«. Л)
Рис. 2.67. Коэффициенты гармонической линеаризации двузначной нечетной нелинейности типа гистерезиса с фазовым опережением при k = 1 со смещением:
а) <Р"о (хо, Л); б) а (хо, Л); в) b (Ха. Л)
Рис. 2.68. Коэффициенты гармонической линеаризации двузначной нечетной нелинейности типа двухпозициоииого реле с зоной нечувствительности со смещением при т = 0,25:
а) ^о (Хо, Л); б) а (хо, Л); в) Ъ (х0, Л)
206
la) б) в)
Рис. 2.69. Коэффициенты гармонической линеаризации двузначной нечетной нелинейности типа гистерезиса с зоной нечувствительности при т — 0,25:
4) <^"о(Хо, А); б)а(х0, А); в) &Ч*о. А)
Рис. 2.70. Коэффициенты гармонической линеаризации двузначной нечетной нелинейности типа двухпозициониого реле с зоной нечувствительности при k = 1 со смещением при т = 0,25r j
a) (Хо, А); б) а (х0, А); в) b (х0, А)
Рис. 2.71. Коэффициенты гармонической линеаризации двузначной нечетной нелинейности' Типа гистерезиса с зоной нечувствительности со смещением при т = 0,25: a) <Sro(x«, А); б) а(х0. А); в) Ь(Хо, А)
207
опре-
180е
целине со
Рис. 2.73. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной двузначной нелинейностью типа одиопозиционного реле ст значениями функции со смещением:
Рис. 2.74. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной двузначной нелинейностью, имеющей характеристику идеального гистерезиса со смещением:
а) 20 lg vj б> -ИО’-и (», А)
Ч \*<h Л)
208
Таблица Z.6
бичисление амплитудных и фазовых характеристик длк типовых вврзначных несимметричных нелинейностей
пЩ Вид, нелинейной харакагеростики
"Г -
1
-с о j ГТ
' -д| |<х»
Г| т
-г- i ,g .
2 -С +тС 1 тС я
Формулы для Вычисления
?0 (Xq, А) Ч, _
— (arcsin C*xf -Я А - arcsin - С~гл) при А * f*/xj ' £FF~ 'arcts Г Аг + + j/ при A * C*lx,l
при. A^C*lx,l
4'т=‘”-£т‘. ♦ arcsin A C-Xg - arcsin —~ ~ A mG-Xg - arcsin — Л при. A^C+lxol /etk± JntC-xt)(niC . A* x,VC^x,\ A* HXa)*4C*mt /*/n) "mt9 i, f'-d1 ~ L'~ iL-r 1 А‘ Г A‘
^(-LO^1 ’ при A* C+/xol
Г, (mC+xJ. L' A* j
. i
0 при A C+ixe) ' 46 ЯА при 4-C+IXjl X ~ z. при- A‘C<-pr0| ,
В , . с~*ч KXt~—(arcsin—-*-° Я , A -arcsin при Л»С+|х,| Г ЯА при A»C^lxol
' 66‘ > ZW /♦ + лг
при Л-С+/Хо|
при А^С
tj /«к
209
Продолжение main. ZB
В
кА J [arcstn ±^+ +arcstn kA JJ * Гяга£я £!^ . 2л L кА - arcstn kA .win kA - arcstn _ - KA J к1 A2 ^{’arcan ^y-x*> + Ш A1
+ X Bresin s~k(c+xq} * г ka
.Jarcstn^L'a^stn^ Z kA I kA C-k„ ,/. rJ-K(C-f,Uz C-iJl-KfC-K, А Г K-A1 Al K‘A! (Z - kA I kA I kA
C+x, L ^к1Сч,0‘ С/х, * А Г к2А2 А Гк’А2
-L arcstn tf&J, ctx,Sxff-xji I nA A ' K2A2
В J. [8«K{t-xj!\8 ^-KfC-x„^ кА 1 к2А2 кА 1 K2A2 C-x„ 1/. Ц-л(С-х0Рг OXjiffiffnij А 1 к2А2 АГ K2A2
,!_ Jf.[B*K(P*xJ]\ S ife-KlIW1 кА 1 к‘А2 кА I it1!1 B*K(C-X„i |Д1 [Л^хГС-Щг ~~"ZkA 1 kW P-KfC-x,,) {f-K(C-K,lil " ZKA Г k>A‘ C^Kti b-KfC^Jl2 8 it tW(C-x,)f Л K!A2 KA 1 K‘A2 s L fB-Ktc-xji2 a J (1>к(сч2 KAI K*Ae кА' кгАг
+ J l/t У1-к1с^!‘а*к1с-х,)Мн. KAI k‘Az ZkA 1 к‘Аг
в+к( С*х,} 1лВ*к(С*хУ? ZkA r k2A2
|/ IB~K (t-K,}]2 1 к2А2 B-k(C-Xi) I :I/-k(C-x,)1‘ ZkA 1 к‘Аг
е-к (c<-x„) l.y-xT^f ZkA f к2 A2 ~!SB2C2 при ^sl±^+|x„|
1/, u*K(c*x,}it ’ г ; B-к (Ci-Xtl [/ b^KfC^x,)]2 ZKA *
- R-ppq npil Ла^+/Х,| b-k(c*x,) / ZkA ' кгАг J при A , t|xt|
k(C,-C> kx0 к ♦ Z ' ZX x[(c, +x„) arcstn L v kA -<4 + arcstn ^Xl\Z кА r + arcstn * tti CJ UH _ T kA A 1 ZIC'C,) (C-C,)‘ A A1 a’"ct^ Я B-K(C,-X„I
.J, CB-k(C-k.)Jz C,KS <’ к'А* ~ A * Г^п-
Jarcsia^ML^K kA A
Ji fB-K(C,^l,IJ2r в
Л rBrcstne^hL 2Я L kA -arcstn г KA J 1' ' к‘А1 kA J . k*A2 kA J. 'С6-к(С,*К,)]с B-KlC,-/,) Л, tB~K(C~Xa)ll C,rx. ' K>A2 А У J. СВ*к1С,-Хв)]г t В ' к*Аг t кА .
J. K2_Ai _ ZkA __ J tB-Kic-x,i)2 a ll [s-Kic^ji
лЛ Jll. CB-KfC,-/,)!2 ZSt\l ’ K2A‘ s 1 СВ-к(С,-Х,112 8-к(С,*х,1 Xf K>A* ZKA / ' К2Аг KAI к‘Аг _в-к<с,-х,) Il .^iB-KlCrx^f ZkA f 1 к‘А*
_ (/.-.rs-ntf,+x„tr 1 2 1В-к(С,^к,}1‘ \ .
I КгА2 J , Bi-kC Л= к A^^+KB я ° T „Mi J + B-K(el*x,)ii. ta-K(c,*xeiil ZkA 1 kka1 при A » ^^-x, и 1 к '
. [Z(C,*CI „ (C-С,!2 ? + L A A^- J . B*kC d A ’ —J X» u A - — tK,
210
Продолжение main. г. 6
s ! 8 -С -тС л В Г £+Хд --(urw -Т-- -arcsln — *° + тС-ха (тС-ХцКтс+Хц]^ с1 -ret’ l/^F ’ / A_2 Ai_J _ A2
. j Л. !с'х‘,г Л* , 4^] ik а'*°)г гТ~~лг . 1 (С*Ха1г' Аг J +^_ <'/пС~хд)г при А*С< ' _(тС-х,]г L А1 . ' (тС*ха)г L' Аг \ (тС-х„}г . А2 и ОлС+Хд)*] w
А тС-x,,} -arcsin —- ; А • при А * с+/х0| Il (mC + xa)2 Г A1 при A^ C<-|x0|
0 тс с х 1 ~S\ х ЖЛО
3 В -Ci -тС h В , тС +Х„ ^т11П А ~ - a'rcsin ; А ' при. А ~С-хв и А-С^Хц 8 iL[,.№-*,)(тС,i-x,) _ Г,А А* - гт (.c+ci'l А ar^ ,/ (!П C, Mg)2 4! A* при А=С-хаг и АГС,^х0
Е < С X д[ при А= С-Хц и А^С^хе
211
Продолжение-табл. 2.6
ю - к ,Г . В*к(С*хР -arcsin Г . В+к(С-хЛ х aicsin । <; 19 ~ [ 'кА -atc$in~^j+(mC+x0)x Г . В+к(тС+ха) х/aicsin ! - - L кА - atcsin-^y^J-f/nC-Xo)» Г . В^к(тС~х„\ х /aicsin 4—& - 1 кА -aicsin -L[aicslnBM!!p>)+ 2Л[ кА . В + к(С~Хп) +atcsin 4—~~ КА В+к1тС+х0) -aicsin ' — - К -aicsin±^i7-КА J ха f / [в+к(с-х0]]2, 2л[У К2 А2 Г [В*к(тС~ха]]2 У к2А2 к,П1 . В*к(С-хв) —\ itaicsin 4—~ + л У 12 кА I . В+кЬпС-Хд} 1 . В*к(Ся +TQICS1П 4—- +-QICSIO 4- 2 кА 2 кА 12 кА
! . fl+xfmC+x») Г . С-х» *тагс$1 п —4—--rQtcsin L КА i А 1 . В+кбпС-х») +7 aicsin n-r1”* а» КА
1 . тС-Xg I . /пГ-Хп --aicsin —-— -aicsin —г-2 + 2 А 2 А / . В+к(С+Хд) +-aicsin —4—- + 2 кА
С-Хд./ [В->к(С-ха]]г С-ха А V к2А2 А * f , В+к/иС+Хо) I . С-Хд +jatcsin——^yaicsm—-
/. ^-х0)2 С’Х„ / ГВ’х/С’Хд)/2 V А2 А V', к!А2 1 . Ох» 1 . тС-хд --aicsin-T-i-ratcsin —гл-2 А . 2 А
С+Хд , /, (С+Xg)2 тС-ха А У А2 " А ’ 1 . тС+Хд С-Хд --ausm——-х L A А
Z [8*к(тС-х01]2 mt-KQ, ! ImC-xj, * к&А^ AV А х \ 11 ^~х0 х ХГ~ к2А2 А.
mC+Xj / /В-»х(тС+х0У2 тС+Хд * А V' к2А2 А Х / (С-Хд}2 Сххд , /, [В+К^ХдУ У' А2 + А V' KW ’
/. (тС+ха)г В / [B+KfC-Xg)]2 V1 A2 ’ xaVT к2А2 + С*Х, /, (С*Хд)2 тС-Хд „ А V А2 А
Д[B^(^xg)]2 ( xAV х2Аг / ffl-xfac-x,!!2 I7ic-xo, / (niC-xtf V' .KW а л a2 1
В -С -тС j l<) '/ [р |гаС С х fl + [Вхк(тС-х0]]2 + КАУ к2А2 t mC+Xg / _ f8*KfrnC+x0U2 A V K2A2
В / [В+к(тС-ха}]г В кАУ к2А2 +кАХ mCxxg /, (mC*XgY fl / ffl*x(C-x^2 A V A2 +XAV k2A2
I [В+к(С+хвЦ2 У , к2А2 . /. [’B^xfmCtXg)]2 S+x(C-.x0) VH" к2А2 ‘ 2кА Х В Л [В-к(Сххд)]2, кАУ K2A2
_Л, Лв+к(тСххв)]2__ V к2 А2 Л [Вхк(С-Хд)^ Вх-к(тС~Хе} У К2А2 2кА B_ / [Вх-к1тС-Хд}]2, кА V k2A2
./ [В-хк(Сх-Хд)]2 В^к(тС-»х^ V1 к2 А2 2 кА Х ,.—\jl ff^xlinC^Xiiff fl*x(C-xn\ *xAV ' к2А2 2хД ”
. /, [B+K(niC+Xg'S2 В-Хд V к2А2 2А /, [Вхк(С-Хд)]2 B+Klt>Xg} Л1' K2A2 ” 2kA X.
. 8+к(С+1хд1) при Д » I— — l^2, с+2<> 1 /т (с**^2. Г А2 2А V А2 [BxK(Cxxg1]2 8х-к(тСх-х0)_ V' x2A2 ’ 2xA X
4- тС"х» 1 /1 mC+xO , 2А У А2. 2А /, [Вхк/тСххд}}2 C-Xg x\/'- KW -+2A
лриА> B+xf^M) mc-xg 1 (mC-Xg}2 mC + Xg + 2A V1' A2 +~2A~
212
продолжение табл 2.6
If в У 0 при А =“С+/х,| М ХА при A* C+lKtl я 2 при А=С+/Хд1
-с 0 С X
1 J 'о
/г В lamin тС'**' - , пиос,) А
в -С -тС У ‘ $ |/г М-ХдН. ' А*
2X(m3in А тС-ха) - arcsin —-——I при А = С-Хд и А^С^Хд ЯА 1‘-{3 Аг _
J. Zm(C+C,}' т/г (тС-х,)1 х А ' Г L Аг .1L fmCf+Xg)1' 1 А‘ при А - С-Хд и Л- nt4o
BlmCf х
Г (Л7С,*Х,)*П L Аг JJ при А = С-х, и А = 6,1-Х,
^0
/j к(С,-С).кх,+ к Г , 2(С*С,) (С-С,)1 А ' А‘
К Л Я , в-X (С.-Х.) ~пт + arcs tn г2—с * Я| 1^2 кА
В~К( Cj+Xq) > arcsin —=— кА ^Х В-к(С,-Хд) ^arcsin J » +
v 2 гя Гх* В~я ( Bf + Х д) *a.rcsin —-- «Л , в-к(с.-х.!\
С-Хд V [В-к(С-х,)]г ~ А 1 кгАг в-х (C,<-xJ rarcsm /—*- - «А
С-к, f. ra-x(c,txj? А 1 к‘Аг . _ С~Х» CB-K(C,tXg)]ii .А 1 к’А1
в -с,/\ У кА J В Г , В-к(С,+Х,) ~ arCStn . L - 2JL кА B-K,(C-xt)1
+ А |/ M-x(C-x0)J» t + кА 1 ’ к‘А* + ± 11 СВ-к(С,-ха}11 гкА Г KW
'/.в , + В [В-к(С,гХ,)]Х _ B-K(t,-Xg) / CB-KlCf-xji
/0 ~в С X кА j . кА Г кгАг 2кА 1 ' КгАг
kAJ |/ fe-xf’fi-x.U* 2д[Г хМ* L I 1 К‘Аг J . В+kG при Л = х0 и .ца=а!-г±^'- С’^О 1Г,[В-К(С,-Хд)]\ А Г кМ‘
WK в-к(с,чв)Л [1-к(с,-х,)1А (в II [В-к(С,-Хв)]‘
r ZkA 1 к‘Аг ] ' КА 1 к‘Аг
Г2(С*С,) (С-С,)‘Лг . +1 А 1 Аг J ' В + КС при Л= —— ~*д и В-^кС, А = —^Хд В-к (С, *х,) /Л [B-k(C,+xJ
‘ ZKA I' VA* . В + кС При: А Хо U К . В*кС, „ /, = -Г“^+х» л
213
Рис. 2.76. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной двузначной нелинейностью типа люфта со смещением: а) 20lg^CT; « 2O,«-Tohr: 8) -180°-— Л)
Рис. 2.77. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной двузначной нелинейностью типа однопозиционного реле . гистерезисом при k = 1 со смещением: а) 20 le idbrб) 201е а: —ц ta, 4)
214
Рис. 2.78. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной двузначной нелинейностью типа гистерезиса со смещением:
в) - 180е—-Ц (Хо» Л)
Рис. 2.79. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной двузначной нелинейностью типа двухпознционяого реле с зоной нечувствительности со смещением:
°> 20 ‘8 -у-Л"4Г; б) 20 18 ~о<х~4Г;
су» о (Xoj Л) Я -Л)
в) -180“—Ц (Хо, А)
Рис. 2.80. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной двузначной нелинейностью типа гистерезиса с зоной нечувствительности со смещением:
а) 20 б) 20 lg
& о (Хо, Л) Q (X®, А)
в) -180е— Ц№, Л)
to
35
-100
-120
-140
-ISO
-180
1,0 10 A
Рис. 2.81. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной двузначной нелинейностью типа двухпозиционного реле с зоной нечувствительности при k = 1 со смещением:
а> 201g-=-^---—; 6) 201g
(Хо. А) <7(Хо, А)
в) — 180°—Ц(Хо, А} *
Рис. 2.82. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной, двузначной не-
линейностью типа однозвенного элемента с фазовым опережением со смещением:
a) 201g . ?—б) 180°—М*>, Л)
<7 (Хо» А)
Рис. 2.83. Шаблоны для графического определения режимов автоколебаний в нелинейных системах с нечетной двузначной нелинейностью типа гистерезиса с зоной нечувствительности с фазовым опережением со смещением:
в) 201g в) 20 1g в) !80°-
' * 9о (Хо. Л) <7 (хо. Л)
— й (Хо. Л)
линейностью . типа гистерезиса с фазовым опережением со смещением:
а)20,г-^(Ьл);б)201г7СТ; в) 18°-— И(Хо. Л)
217
Для вычисления коэффициентов гармонической линеаризации воспользуемся формулами:
2Л'
О
+ &з sin (Зф + Фз)]}
2л
Ь = f?in + О
4- d3 sin (Зф + Фз)]} cosipdij);
2л
аз(А) = ^^{А[щпф4-о
(2.106)
4~б3 sin (Зф4~Ф3)]} X
X sin (Зф + фз) d$;
2Л
МЛ) = ^^{А[8тФ + о
+ '63sin (Зф + Фз)]} X
X cos (Зф + фз) г/ф,
гДе 63 = А3/А — относительная амплитуда 3-й гармоники.
Подынтегральные функции в формуле (2.106) относятся к классу обобщенных, так как большинство из рассматриваемых нами нелинейностей являются кусочно-линейными, первые производные которых представляют собой дёльта-функции. Разложим обобщенные функции в ряд Тейлора и возьмем только первые члены разложения; тогда из формул (2.106) получим
2л а^==~^ J (А sin,i’)+ о
+ S2" ]А {sin ф + е [б3 х
X sin (Зф-f-ф3)]}] X
ХА [б3 sin (Зф+ф3)]} sin ф</ф;
2л (2.107)
${^'И.8шф) +
0
-HF[A{sin ф-]-е[63 51п(3ф+ .
+ Фз)1) 1 А [63 sin (Зф+ф3)]} X :
Хсозф^ф;
. f I
аз(А) = ~^ р^"(^8Щф)+ • О
+ &~ [A {sin ф-j- е[б3Х X sin (Зф + фз)]}] X X А [63 81п(3ф + фз)]} X
X sin (Зф 4- ф3) </ф;
${^Мзтф) + о
4- ЯГ [ A{sin Ф4-8[63 sin (Зф + +Фз)]}1 А [б3 sin (Зф4-фз)]} X X cos (Зф 4- фз) б/ф.
(2.107)
В выражениях (2.107)
& [A {sin ф 4-е [63 sin (Зф 4- ф3)]}] ==
__ДУ (Л {sin ф + е [63 sin (Зф + ф3)]}] - d (Л sin ф)
*
Параметр е удовлетворяет неравенству 0 < 8< Г, а остаточный член разложения можно записать в виде
/? =
У [A {§in ф + е [63 sin (Зф + <р3)]}] X __ X [63 sin (Зф + <рз)]2__ 2!
(2.108)
По величине остаточного члена можно оценить ошибку, которая может быть получена, если пользоваться только первым членом разложения, а не всеми последующими. Для рассматриваемых нами однозначных и двузначных кусочно-линейных нелинейностей (см. табл. 2.1, 2.2, 2.4 и 2.5) -> 0, и при приме-
нении формул (2.107) практически не вносятся погрешности вычисления коэффициентов гармонической линеаризации [30].
Для удобства использования формул (2.107) положим, что еб3 ввиду
218
его малости равно нулю; тогда из выражений (2.107) найдем
2л
а(Л}==-^£ iF (Л sin ф) sin фйф + о
2л
+ j д (4 sin ф) sin Зф Х
о
Xsin +
2л
X § & (Л sin -ф) cos Зф sin фйф; о
2я
Ъ (Л) = --т- ST (Л sin ф) cos ф«/ф + ЛЛ J
0
2я
+ бз^МРз J (Л sin ф) sin Зф X о
ХсозШ--Ц^Х
2Л
х J И sin ф) cos Зф cos ф^ф; о
2л
$^"(4Sinitsin(3$4-о
2л
+ Фз) + -?--C-^ Фз $5Г (Л sin ф)Х '
О
х Sin2 Зф</ф + 2дз sin cos фз X
2Л
X J (Л sin ф) cos Зф sin Зфг/ф 4-о
2Л
4- дз S1" ф», д- (Л sin ф) cos2 Зфг/ф;
о 2я
Ьз М) = ~ J (Л sin ф) cos (Зф 4-о
2л
4- 4- J д- (Л Sin ф)х
о
х Sin Зф cos Зфггф 4- .^‘Р.Мфз Х
2л
X J (Л sin ф) cos2 Зфг/ф — о
2Л
- ^_8^--°-фз. j д- (Д' sin ф) X •
о >
X sin2 Зфйф - **1^1 х I
2Л
X J (Л sin ф) sin Зф cos Зфйф. I о J
(2.109)
Формулы (2.109) запишем через основные и добавочные коэффициенты гармонической линеаризации в виде
а (Л) = а{ (Л) 4- Да13 (Л) 63 cos q>3 4-
4- Д'а13 (Л) 63 sin q>3;
b (Л) = bt (Л) 4- Д% (Л) 63 cos Фз —
— Дй13(Л)63зтф3;
а3 (Л) = а' (А) 4- Да33 (Л) 63 cos2 ф3 4-
4- Дх«зз (Л) 2б3 sin Фз cos фз 4-
4- Д&зз(Л)63 8Ш2 ф3;
(А)*=Ь'з (А) +дЧз И) бз соз2ф34-
4- Д633 (Л) 63 sin фз cos фз —
— Да33 (Л) 63 sin фз cos ф3 —
— Д'азз (Л) б3 sin2 фз,
(2.110) где 2л
а^Л) = -^д (Л sin ф) sin о
Да13 (Л) = j Т (A sin ф) X
о
X sin Зф sin фйф;
2л
Д'а13(Л) = -^ J (Л sin ф) X о
X cos Зф sin ф«/ф;
2я
(Л) = ( У (Л sin ф) cos ф дГф;
> Л/Ч J
о
Д'61з(Л)=^ $ЗГ(Л8тф)Х о
X sin Зф cos ф«/ф;
2л
ДМЛ) = и<Г(Лзй1ф)Х . о
X cos Зф cos ф^ф; j
219 \
2л
азМ)=^А ^Hsint)X ; о
X Sin (3^ + q>3)dij); 2л
Aa33(4) = -^- ^^(4 sin t) sin23tdt; о 2л
Д'аззМ) = ^ \&-(А sint)X* о
X cos Зф sin 3tdt;
2я
&з<л) = -£4 $ (4sint)X 0
X cos (Зф + q>3) dt;
2Л
Д6зз(Л) = ^- J^(4sint)X О ч
X cos2 Зф^ф.
(2.1Н)
В формулах (2.110) и (2.1,11) функции cti(4), bi(A) являются коэффициентами гармонической линеаризации по 1-й гармонике, a Adi3(4), A'ai3(4), Д'&1з(4) и Д513(4)—добавочные коэффициенты гармонической линеаризации, учитывающие влияние 3-й гармоники на 1-ю. Функции а3'(4), b\{ 4) являются основными коэффициентами гармонической линеаризации по 3-й гармонике, а Да33(4), Д'а33(4), Д633(4) — добавочные коэффициенты гармонической линеаризации по 3-й гармонике.
Для удобства вычисления коэффициентов гармонической линеаризации введем следующие обозначения:
а3 (4) = cos ФзОзз (4) -f- sin ф^ (4); | Ь'й (4) == cos ф36зз (4) — sin ФдС^ (4), J
(2.U2) где 2л
°зз (4) = -zt ( У (4 sin t) sin Зф dt;
JCzt J о
2Я
&зз (4) — -^д $ (4 sin t) cos Зф dt-
о
(2.113)
С помощью формул (2.110) можно найти выражения для определения эквивалентных амплитудной и фазовой характеристик двузначных нечетных симметричных нелинейностей в виде
di(4) —
= v [d! (4) + Ad13 (4) бз cos Фз +
+’Д'а13 (4) бз sin Фз]2+[61 (4)+”*
4-Д'б13 (4) 63 cos фз — '*
— Д613 (4) б3 sin фз]2; (2.114)'
И1(4) =
МА) + Д'М (A) ds cos Фз—
—~ ДМ (A) d3 SH1 ф3 /911ЕХ
С ga, (А) +Да,з (А) б3 созф3 + - (2Л 15>
+ Да и (А) д3 sin фз
В качестве первого приближения для нахождения бз и ф3 примем
б3 = Л/^(4) + ^(4);
. (А)
Фз = 180° + arctg
(2.116)*
Подставив значения б3 и ф3 из формул (2.117) в 3-ю и 4-ю формулы (2.110), найдем второе приближение для бз и фз в виде
63 = Va2(4) -f- б2 (4); ' ф3!= 180° + arctg -^1. ,
(2.118)
Определив б3 и ц3 по формулам (2.118) и подставив их в выражения (2.114) и (2.115), в окончательной
* Следует иметь в виду, что истинные значения З3 и фз зависят не только от вида нелинейности, но и определяются частотными характеристиками линейной части системы регулирования, т. е.
дз= \W(j3a>)\^/a3t(A) + b'32(A)-'
фз =» 180° + arg [IF (J3<a)] +
+ arctg
ь'з (A) а'з (A)
>(2.117)
Угол 180° во 2-й формуле (2.116) введен для возможности исследования устойчивости нелинейной системы (см. подробнее в Гл. 7).
220
форме получим эквивалентные амплитудную и фазовую характеристики для двузначной нелинейности.
Данную методику можно распространить на нелинейные системы, в которых наряду с 3-й приходится учитывать 5-ю [102] и более высокие гармоники. Одиако при практических расчетах для многих типов нелинейных САР можно ограничиться влиянием лишь 3-й гармоники (см. гл. 7).
Пользуясь найденными коэффициентами гармонической линеаризации, двузначную нечетную симметричную нелинейную характеристику можно записать в виде
(х) «<х (Л) *, (0 + i, (0 +
+£[Мл)мо+.ЦИЧ(()]
(2.119)
и заменить прямой с наклоном, равным q(A), и фазовым углом ц(А).
Формулы для однозначных нечетных симметричных нелинейностей можно получить из (2.110) и (2.111) в виде
а (4) tZj (А) + Да13 (A) d3 cos фз;
Ь' (А) = — А613 (А) б3 sin ф3;
а3 (А) = а3 (А) + Аа^ (A) б3 cos2 ф3 +
+ А633 (А) б3 sin2 ф3;
Ь3 (А) = Ь3 (А) + Д633 (А) X
X б3 sin Фз cos фз —
— Дйзз (А) б3 sin ф3 cos фз,
(2.120)
где
а'(А) = созф3а33(А); |
' 6'(А) = з^ф3а33(А). J (2Л21)
С помощью формул (2.120) можно найти выражения для определения эквивалентных амплитудных и фазовых характеристик однознач
ных нечетных симметричных нелинейностей в виде
4i (А) =
= V[at (А) + Да13 (A) б3 cos ф3]2 + *
*’vTM3(A)63sin Фз]2 ; (2.122)
Н1 (А) =
— — ягг+а А^13 (^) Дз sin <р3 ® ai (Л)+Да1з (Л) d3 cos <р3’
(2.123)
Из формулы (2.123) следует, что при учете высших гармоник на выходе однозначных нелинейностей за счет их действия образуется ёдвиг фазы, который оказывает существенное влияние на определение частот и амплитуд автоколебаний. В этом случае для нахождения бз и ф3 следует пользоваться формулами (2.] 16) — (2.118).
Однозначную нечетную симметричную нелинейность можно описать зависимостью
F(x) «а^х.^ + ^-х, (/) +
+ "б? La3 М Хз ------ЗФ~ *3 J
(2.124)
и заменить прямой с наклоном q(A) и фазовым углом ц(А).
Рассмотрим методику определения коэффициентов гармонической линеаризации для однозначной (рис. 2.4, а) и двузначной (рис. 2.4, б) нелинейностей. >
Пример 2.8. Определить основные н добавочные коэффициенты гармонической линеаризации для однозначной нечетной симметричной нелинейности типа насыщения. Сигнал на выходе нелинейности можно записать в виде (2.71). Подставив в него те основные и добавочные коэффициенты гармонической линеаризации из выражений (2.111) и (2.113), которые относятся только к однозначным нелинейностям, найдем формулы для их вычисления. Основные коэффициенты гармонической линеаризации определяют по 1-й гармонике при А^С щ (4) =. I (arcsin д/ 1 - £)
(2.125)
221
Таблица г. 7
Формулы вычисления основных и дополнительных коэффициентов гармонической линеаризации типовых однозначных нелинейностей по 3-й гармонике
Вид нелинейной ырактеристини <*33 Аа,3 Ав,3 AS я
V в -с-i / 0 С X -в при А * С при АлС D 2к ~ агсзъп—- ~ Я A JX при А * С при А^С i 1 и|5? ft ’ 1 1 $ V —* В-"Жя
' 9 в U 0Ct С3 С3Х -I цд-х, ЧА'л» ‘FJ} при А^С3 -fi АЙ при ~-[к. arcsin - *1 , А -r2(ercsw^-en:stn^- при А^С3 ЯГ]} при А^С3 г Г . с{ -=-<«. arcsin -г — • л (J А Xjfarcsin-y-amin При А^Сз >
у -с / ° С X при А * С ок e3 i/. ' c* ~я при А±С К 2К .С arcsin дл А * + ,йл’) АЛТ ,S А")А V А1 при А^С - £.’)_? , Я 1 АЧ А «RI при А»С -- — arcsin — -J л А 2к ,, Сг -зя!ЗЧВ-р + + ,г^’Ц|О1 + " аЧА 1' Ai при A s-C
а составляющую по 3-й гармонике
'•w>-ra('-j)V‘-5'(2!26)
Добавочные коэффициенты линеаризации, учитывающие влияние 3-й гармоники иа 1-ю, будут
Дай (Л) = x\J 1 — — ; (2.127)
(2.128)
Добавочные коэффициенту линеаризации, учитывающие взаимное влияние по 3-й гармонике для однопознционного реле, находим по формуле
А /ЛЧ 2 Г .С С f
Ддзз (А) = — arcsin—:-— ( 3 —
л L А ЗА \
ДЬзэ(Л)-|-[атс81п + ~ (з-4^)х
х(1“45)д/^5’- (2129б)
Формулы для основных н добавочных коэффициентов гармонической линеариза
ции однозначных нелинейностей приведены в табл. 2.7. Соответствующие коэффициенты гармонической линеаризации для однозначных нелинейностей в зависимости от амплитуды А построены в виде кривых на рис. 2.85, а, б — 2.87, а, б.
Формулы для вычисления основных и добавочных коэффициентов гармонической линеаризации двузначных нелинейностей приведены в табл. 2.8. Коэффициенты гармонической линеаризации в зависнмостн от изменения амплитуды А изображены в виде кривых на рнс. 2.88, а—г н 2.89, а—к.
Пример 2.9. Определить основные и добавочные коэффициенты гармонической линеаризации для двузначной нелинейности (рис. 2.4, б), если сигнал на выходе нелинейности можно записать в виде (2.78). Подставив последнее в выражения (2.111) и (2.113), наймем формулы для вычисления основных 'н добавочных коэффициентов гармонической линеаризации, которые определяют по 1-й гармонике:
п₽нл>с:|
ч /лч 4ВС л-^/> |
01 И)-» — при Л>С, I
(2.130)
222
Рис. 2.85. Основные и дополнительные коэффициенты гармонической линеарнзацнн однозначной нечетной нелинейности типа насыщения с учетом 3-й гармоники:
о) а„(4); б) Да,3(4), ДЬи (Л)
Лам.ДЬц
В)
Рис. 2.86. Основные н дополнительные коэффициенты гармонической линеаризации однозначной нечетной нелинейности типа ограничения в виде трапеции с учетом 3-й гармоники:
о) о» (4); б) Да13 (4), Д6» (4)
Рис. 2.87. Основные н дополнительные коэффициенты гармонической линеаризации однозначной нечетной нелинейности типа зоны нечувствительности:
а) о» (4); б) Да» (Л), ДЬц(4)
223
I
Таблица 2.8
Вычисление осноВных и дополнительных коэффициентов гармонической линеаризации дбд злачных нелинейностей по 3-й гармонике
Вид нелинейной характеристики °зз А а и A‘a„ A a 33 A'a33
У в -С/ /о /с х -в tgfl*k ВВС 1,^0 ,.С2] Ух У Г А) А ЗЛА \ А А1/ 8k/ л ( Л/ 1 NJ ‘IN 'Т1 8k f , с a с2 I — -3 +8-r-B—2 / x Я 1 A A* J '№ при А2>С \k 2k . Л 2B1V [j+Farcs,nrT/J d/(.s+6itL ЗЛ | A C2 C3 - 320 Ti +512~J -A A3 sfd-d^r- •(’-m при A
УИЯ' при А » \ n / /1 при A &C ^Jarcsm^Mn^ kA A arcstn^ -grcsln ^kC) _ х(в*ксШ f6^c)r.iy kV J 1 K2A2 3 'H^+l(e+m/c£) x
• в+кс 2k (B*kCf\ 1 (B+kC)2' Г kW* 2k\(B+kC)}\ / _ (B+kC)2' л LfrW V7 k2A2 CS\L C2' m3Cs 'а~3У''а* + A3 X i\/i mid (B+mkC)3, V k3A3 ^/._(В*ткйГ] V7 " Ш J . B*kC при A^ k 2k(/B+kClf (8+ X \ kA / ! k‘ ’A2 f Я’ kCl2t I2 ± Ml* 09 *<;, Ч г-*а>а,<*> * + Э 1—-1 + ь J Г1 + M r> £i N rs i > , ^,r-~' 1 V 1 J i . ” - * Xln “I’S ' I h*
У В _ -С -тс /jQ тС С х -В Wkcyd (B*kC)2 l k2A2 J rA^ \L_d_ zkC\L c2' V A2 ЗлАу A22 .h-A-U^ML, I A2) jjfA Л /, !S1C1 (8+m XV7 Л2 ' kh ,Г, (B^mkC)2]^ XL7 k2A2 J
ткС)2 гА2 2k (В ^/nkC)3 г k’A3 * Д/ (B + mkC)2 V7 k2A*
z_,_£L V7 k2A2 7 * Z ’ A kA x fc ^rnkG)2 fB^mkC^ll/. (B+mkC)2 'I Г6 k2A2 +’C JV k2A2 f
V k2A2 *A У1 /л2Сг 2mkC\L A2 ЗЛА У A2 \ A2 /
00
3 S
Толчеев
to
to
СП
Продолжение тадл. 2.3
вид нелинейной характеристики Ьзз Д'Ь/з ^Ь13 ^'Ьзз 46jj
у в -с/ ь X X 1—Г"1 5? 7 -тЧ »!<> Л 1 Оа , biri + X х **("$- ->ЯЯ)‘ при А &С л ( А „ С2 I С +2 —т) — » А1/ А при А Вк (г С 77 Р"16 Т + <//Г | А Г к 2к . /, 2CI1 [r-arcs>np--^ + 77Л-*4 + Зл ( А С2 С2 + 320-^~Я2—3 * Я-Я' при а ЪС
/о 'С -в tgfi=k ('-Я] при A t-C при А ъС
*_Г, 2fS<XdZl К Г . !В*кС)г. гл[' М j'M's ТР kflB^kC)2\ (B^HC)2] 4 В2A2 L ‘ кгА2 J £2 / , Р \jn2C2f, 'а2Г2^Г^-(3' ?тгСг\ (В*ткС)г , 2 А2 / К2А2 . B+kC при Z*/ <в+*с! Г л | кА К\(8->-кС)\ (В-^кС)2] 2_ ЗЛ\ кА Г* к2А2\ , сг\г..тС\-, ’Тг4р] 4~Г" , отгсг12 (в+ткс)\, -* А2 Г кА ?' ^.(arcsin +arcsin- кА А - arcsin -j - arcsin " + А КА •/&>»$ -J-SFp-x'W''* B + kC при А 7 к
у. в -С -тС ч X к * + * х W ] г^А«/'*жЛ , (В+кСРА.ИВ+ктСр.. J * nW J зл**! х х К Г» В(в*ткс)г М Кг А^ tB^mkC)'.'] 2ктгСг КАА* J ЗхА* (В^КС)г\\/, (ВАКС)2 к2А2 J V' к2А2 С / С2 П/, Qi тС 'a[1'a2H1'a2 А
//\В
/ тгСг\\! т2С2 (В-АткСК (8+ткС)А кА Г к2А2 Г Д /. . (B+mkC)z\ Г к2А2 J А-, BA-ВС при А к (В+ткС/2]2 к2 A2 J приА? к
jjo тсс •» -В tgJ3=k
Рис. 2.88. Основные и дополнительные коэффициенты гармонической линеаризации двузначной нечетной нелинейности типа гистерезиса с k = 1г
а) аи (А); б) Лаи (А). Аби (А); в) б» (А); г) Д'ац(А), Л'in (А)
составляющие по 3-й гармонике при А С
(2.131)
Добавочные коэффициенты, учитывающие влияние третьей гармоники на первую, будут прн А С
. ... 4ВС2 / . С2\
Да1з(Д) = —ф_4_);
Д'а13 (Л) «=
Aa'tf.Ab'u
3-й гармонике, запишем в виде при А С
. ... 4ВС2 /, . С2\2
Лазз(л) = -^йг l3-4^) ’
x(-‘£)V-5’
,,ч 4ВС /, лСг\ /. С2 Д6зз(Л)=» 3лД (1 4лз)/\/1 Аг-
(2.133)
У нелинейностей, выходной сигнал которых определяют с помощью выражения (2.7), имеем
2я/а>
а (А, со) — -U- SF (Л sin со/, ЗТЛ J
о
Лш cos ©Л sin art dart',
(2134Г
b (Л, ©) = £Г (Л sin со/,
о
Лео cos ©О cos art dfst.
(2.132)
Добавочные коэффициенты линеаризации, учитывающие взаимное влияние по
* Формулами (2.134) можно пользоваться при нахождении коэффициентов гармонической линеаризации симметричных нелинейностей, иа входе которых образуется сигнал
Xi (t) = Ai sin <ot + A3 sin (2<oi + <p»).
226
Рис. 2.89. Основные двузначной нечетной тельностн прн k = 1: а) Д»Ц(Л); б) Дап(Л); u) A'iM (А); к) Д'д13(А)
и дополнительные коэффициенты гармонической линеаризации нелинейности типа двухпознцноиного реле с зоной нечувстви-
в) Ai»(A); 3} AaJS(A); д) азг (А); е) Д'а„(А); ж) А'ац(А); з) Ь„ (А);
8*
227
Для более полного воспроизведения выходного сигнала наряду с 1-й гармоникой приходится учитывать и 2-ю гармонику; тогда
у{ (/) = ЯГ [(Л] sin со/, А,со cos со/) 4* + (Д2 s>n (2со/ 4- ф2),
242со2 cos (2со/ 4- Ф2))1 , (2-135)
или, положив А, — А, А2=62А, со/ = = ф и 2со/— 2"ф, получим
2л
а(4,<о)=-^Д {ЯГ [(4зтф, 4сосо8ф)4-ЭТ/i J
О
+ [д2Л sin (2ф + cp2),
262 Д(дСО5(2*ф + ф2)]1} sin фйф; (2.136)
2л
ь (Л, <о) = —^ {Т [(4 sin Ч».
О
Л<о cos ф) + [62 A sin (2ф + qp2), 2д2Дсо cos (2ф+ф2)]]} cos ф д?ф; (2.137)
2л
а2 (А, со) = ~д- {& 1(4 sin ф, о
4<о cos ф) 4- [624 sin (2-ф 4- ср2), 2624<о cos (2ф 4- <р2)] 1} sin (2-ф 4- <Рг) с^ф!
(2.138)
2л
b2 (А, со) = {&~ [(4 sin ф,
о
4<о cos ф) 4- [б24 sin (2ф 4- ср2), 2624со cos (2ф 4- ф2)] ]} cos (2ф 4- ф2) с/ф.
(2.139)
Разложив подынтегральные функции в выражениях (2.135) — (2.139) в ряд Тейлора и взяв лишь первые члены разложения, получим
2л
а (А, со) = {&- (4 sin ф,
о
4ш cos ф) 4- /F [(4 sin ф, 4со cos ф) 4-4-е (624 sin (2ф 4- Фг), 2&24<о cos (2ф 4-
4- Фг))] • [62А sin (2ф 4- ф2) 4-
4- 2б24ш cos (2-ф 4- ф2)]} sin ф с/ф;
(2.140)
2л
Ь (А, со) = —^л- {/F (4 sin ф,
Л/i J о
4<о cos ф) 4- ЯГ ](Л sin ф, 4со cos ф) 4~
4- е (d24 sin (2ф 4- Фг), 2624со X
X соэ(2ф 4-фв))] IM 81п(2ф 4-ф2)4-
4- 2d24co cos (2ф 4- Фг)!} cos ф с?ф;
(2.141) 2л
а2 (4, со) = {<F (4 (sin ф,
о
4со cos ф) 4- ЯГ [(-4 sin ф, 4со cos ф) 4-4- e(d24’sin (2ф 4- Фг),
2д24со cos (2ф 4- Ф2))] • [524 sin (2ф 4-
4- ф2) 4- 2d24co cos (2ф 4- Фг)]} X
X sin (2ф 4-Фг) с^ф; (2.142)
гл
Ь2 (4, со) = -^- (4 sin ф,
о
4со cos ф) 4- ЯГ [(4 sin ф,
4со cos ф) 4- е (624 sin (2ф 4- Фг), 2624<о cos (2ф 4- Фг))] ’ 624 sin (2ф 4*
4- фг) 4- 2624<о cos (2ф 4- Фг)1} X
X cos (2ф 4-фг) ^Ф-- (2.143)
Как и прежде, при е = 0 из выражений (2.140) — (2.143) найдем с точностью до остаточного члена формулы для вычисления коэффициентов гармонической линеаризации в виде
2л
а(4, со) =-^- Г [(4 sin ф,
О
Дсо cos гр)] sin ф йф +
2л
4- 62 c°s ф2 J зг [(4 sin ф, О
Д<о cos ф)] sin 2ф sin ф йф +
2Л
4- б2..ух j зг [(4 sin ф,
О
Лео cos ф)] cos 2ф sin ф с^ф 4-2л
4- 26^os<p2 j 0Г[(48тф, О
228
Дш cos ip)] cos 2-ф sin ip dip —
2л
_ 2б2ш Jn ф, j ^[(4sin^ о
Д® cos ip)] sin 2ip sin ip dip; (2.144)
b (Л, co) = -U- [(Д sin ip,
jt/1 J
0
4® cos ip)] cos ip dip +
2л
+ da c°s ф2 $ ST [(4 sin ip, 4<o cos ip)] X о
X sin 2ip cosip dip +
2л
+ 62 S^n-ф2 j [(Л sin ip, Дсо cosip)]X 0
X cos 2ip cos ip dip +
2л
+ 26^OS «У* j дг [(д sin ip, 0
Лео cos ip)] cos 2ip cos ip dip —
2л
_ j ^[(X sin ip,
0
4(ocosip)] sin 2ipcosipdip; (2.145)
2л
a2 (A, co) = J T [(A sin ip, о
Д® cos ip)] sin (2ip + <p2) dty +
2л
+ Й2 С^ -У2- j g~ [(Л sin ip, Д® cosip)]X о
x Sin2 2ip dip + 262 sin^ cos?2 x
2л
X $ &~[(A sin ip, Дсо cos ip)] X 0
X cos 2ip sin 2ip dip +
2л
+ Й2 ф2 ( ЯГ [(Д sin ip, Дсо cos ip)] X
\ z 2 r> 1. j 1 1 262co cos2 ЧР2 \ z
x COS2 2ip dip ч--------й—:x
2л
xj &~[(A sin ip, Дсо cos ip)] X 0
\ z r> , • n , j 1 262co sin2 q>2 . ,
X cos 2ip sin 2ip dip-----—-—— X
2л
X J [(Д sin ip, Дсо cos ip)] X
0
X sin 2ip cos 2ip dip +
, 262<b sin <p2 cos <p2 4Z
+ л X
2л
x$ &~[(Asin ip, Дсо cosip)]cps22ipdip—
0
2л
262co sin^p2 cos qp2 j [(л s.n
0
4(0 cos ip)] sin2 2ip dip; (2.146)
2л
b2 (Д, co) = J T [(Д sin ip, 0
4(0 cos ip)] cos (2ip + (p2) dip +
2Л
+ д2С0$ ф2 $ [(4 sin ip, 4(o cos ip)] X
0
, . . a . o 1 J 1 I ^2 Sin фз COS (fj \_y
X sin 2ip cos 2ip dip H---------------— X
2л
X 1И sin Ч1» cos Ч>)1 X
0
X z 2 П 1 л I 62 sin Ф2 COS ф2 к/
X cos2 2ip dip--------------------X
2л
x J [(4 sin ip, 4(o cos ip)] X
0
ч ✓ • 9 n 1 J 1 ^2 Sin2 ф2
X sin2 2ip dip--------------X
2л
x J [(Д sin ip, Ди cos ip)] X
0
, . „ _ ,. , 262<o cos2 ф2 , z
X sin 2ip cos 2ip dip H---------------X
229
2л
х $ & [(Asin г!?, шсо&ф)]со&22фс/ф— о
4d2a) sinqpacoscpa л
2л
x 5 & [(A sin if, a cos -ф)] X
0
X sin 2-ф cos 2ф t/ф +
2Л
26а(О j ST [(A sinip, о
Aa cos-ф)] sin22i|) rfip. (2.147)
Формулы (2.144) и (2.147) запишем через основные и добавочные коэффициенты гармонической линеаризации, т. е.
а (А, а) = а1(А, а) + Да12(А, а) X X f>2 cos <р2 + A/qi2 (Л,.ю) d2 sin <р2 +
+ 2Д'д12 (А, ®) d2a cos <р2 —
— 2 Да12 (А, ®) d2a sin <р2;
b (А, а) = bt (А, ®) + Д^12 (Л, ®) X X 62 cos <р2 + А^12 (А, ®) б2 sin ф2 +
+ 2Дй12 (А, ®) d2® cos ф2 —
— 2Д'Ь12 (А, и) д2а sin ф2;
а2 (А, ®) = а' (А, ®) + kd22 (А, а) X
X б2 cos2 ф2+ 2Дс22 (А, ®) д2 sin ф2 X
Xcos ф2 + Де22 (А, о) д2 sin2 ф2 +
+ 2 Дс22 (А, о) д2а cos2 ф2 —
— 2 Дс22 (А, а) д2а sin2 ф2 —
— 2 Де22 (А, а)»д2а sin ф2 cos ф2 —
— 2 Дб/22 (А, ®) д2а sin фа cos ф2;
Ь2 (А, а)=6' (А, ®)+Дс22 (А, ®) д2Х
X cos2 ф2 + Де22 (А, о) д2 sin ф2 X •
ХС03ф2—ДЙ22(А, ®)д2 5Шф2СО8ф2— |
— Дс22(А, а) д2 sin2<p2 + 2 Де22 X I
X (А, ®) д2а cos2 ф2 — 4 Дс22 X
X (Л, ®) д2а sin ф2 cos ф2 + + 2 Дй22 (А, ®) 2д2а sin2 ф2,
(2.148)
где
2л
ах (А, а) = [(A sin ф,
ЛЯ J
о
Л<оcos-ф)] sin ф^ф;
2Л
Да12 (Л, со) = $ & [(Л sin ф,
о
Л<о cos ф)] sin 2ф sin ф б/ф;
2Л
Д'а12(Л, <о) = -^- ^"[(Лзтф, о
Лш cos ф)] cos 2ф sin ф <2ф;
2л
МЛ, ®) = ^4 j S' [(Л sin ф, О
Лш cos ф)] cos ф б/ф;
2Л
Д'д12 (А, ®) = j ST [(A sin ф, о
A® cos ф)] sin 2ф cos ф йф;
2л
Дй12 (А, а) = -^- ^ ST [(A sin ф, о
A® cos ф)] cos 2ф cos ф д?ф;
2л
«2 О4’ ®) = Sil1 ’
О
Лео cos ф)] sin (2ф + Фг) ^Ф;
2л
Дс22 (А, ®) — [(A sin ф,
о
(2.149)
A® cos ф)] sin 2ф cos 2ф ^ф;
2л
Ad22 (А, а) = Т [(A sin ф, о
A® cos ф)] sin2 2ф ^ф;
2л
Ъ2 (А, а) = J Т [(A sin ф, • о *
230
A cocos-ф)] cos(2-ф + <p2)I
2Л
Де22 (Л, co) = — ^ (F [(Л sin ф, •
° I
Лсосоэф)] соз22фс/ф. f
Коэффициенты линеаризации o'(A, co) и b2(A, co) можно записать в виде
а' (А, со) = cos ф2а22 (А, со) +
+ 5Шф2622(Л, со);
Ь'2 (Л, со) = cos ф2622 (Л, со) —
— sin ф2а22(Л, со).
Здесь 2л 1
022 (Л, со) = Т [(л sin ф,
о
Лео cos i|0J sin 2*ф dfy
*22 (А со) = 9~ [(Л sin ф,
о
Лео cos ф)] cos 2ф с/ф.
(2.151)
Пользуясь формулами (2.148), определим выражения для вычисления эквивалентных амплитудной и фазовой характеристик для нелинейностей рассматриваемого типа
(Л, со) — -y/la^A, со)+б2 (cos ф2— *
* —2со sin ф2) Да12 (Л, со) + *
* + 62(sin ф2 + 2сосоэф2) X *
*'" ХДЧгМ, со)]2 Н- [А (Л, со)+‘ ’ ’ *
+ б2(созф2 — 2со sin ф2) X *
X А*12(А <о) + б2(5Шф2-|- *
* +2сосозф2) Д612(Л, со)]2; (2.152)
н.(А =
&1 (Д, со) + d2 (cosq>2 — ® sin q>2) X ХЛ612(Д, со) +d2(sin <j>2 +
_ arcfe + 2co cos ф2) А&12 (Я, co)
® at (Д, co) +d2 (cos <p2 — 2co sin <j>2) X ’
X ЛП12 (Д, co) + d2 (sin <J>2 +
-|-2cocosq>2) Aza,2 (Д, co)
(2.153)
В качестве первого приближения возьмем
б2 = V[cos ф2а22 (Л, w) +
+ sin ф2622 (Л, со)]2 +
+ [COS ф2*22 (^» —
* — sin ф2а22 (Л, со)]2 ; ф2 = л + cos q>2&22 (Д, со) — яггс„ ~ sin 111)2022 (Л’ <0)
' ь cos <р2а22 (Д, со) + + sin Фг^22 (Д, со)
Подставив значения б2 и ф2 в 3-ю 4-ю формулы (2.148), найдем вто
рое приближение для 62 и ф2 в виде
б2 = д/а^Л, со) + 62(Л, со); . . Ь2(А, со)
ф2 = л+ arctg аг(А> m)--
(2.154)
и
(2.155)
Определив бг и ф2 по формулам (2.155) и подставив их числовые значения в выражения (2.152) и (2.153), в окончательной форме получим эквивалентные амплитудную и фазовую характеристики нелинейности.
Найдем формулы для вычисления коэффициентов гармонической линеаризации и построения шаблонов, с помощью которых могут быть определены эквивалентные амплитудные и фазовые характеристики нелинейностей при действии суммы входных сигналов одной частоты. Для простоты будем считать, что на вход нелинейностей поступают двухчастотные синусоидальные сигналы
х (0 = А{ sin ф + А2 sin (ф + ф).
(2.156)
Тогда нелинейную функцию можно записать через коэффициенты линеаризации at и а2 в виде
х/(0 = Г(х) = а1(Л)х1 (0 +
-|- а2 (Л) х2 (0, (2.157)
где х1(0 = 41з1пф; x2(t) =
= А2 sin (ф + ф).
231
В этом случае коэффициенты гармонической линеаризации будут
aiG4)= 2^5д7$ JfMjsinW
0 о
+ А2 sin (ф + <р)] sin ф dty dtp; (2.158)
2Л 2Я
2^ $ 5 F [Л1 sin Ф-h
0 о
+ A2 sin (ф + ф)] sin (ф + ф) с?ф dtp.
(2.159)
Формулы (2.158) и (2.159) перепишем в виде
“'м» = ЖГ/|; <2160>
<МЛ> —<2161) где
2Л 2л
7] = J i/ф j F [Л] sin ф +
+ А2 sin (ф + ф)] sin ф dtp; (2.162)
2Л 2Л
12 = </ф F [At sin ф 4-о о
+ Aj sin (ф + ф)] sin (ф + ф) dtp.
(2.163)
Рассмотрим несколько примеров двухчастотной гармонической линеаризации для однозначных нечетных симметричных нелинейностей.
Пример 2.10. Пусть на вход нелинейности типа идеального реле с уровнями переключения В — 1 н В = — 1 действует входной сигнал (2.156). В этом случае переключения реле будут происходить при Ai sin ф + + Л2sin (ф + <₽)= 0, т. е.
F(x) =
1 при ОСФ + фСл+arcsin-ф-sinф; Л2
—1 при л + arcstn -ф- sin ф < ф + Ла
+ Ф < 2п —- arcsin -4- sin ф; Лг
А
1 при 2л —arcsin-4- з1пф<ф+ф<2л. ^2
(2.164)
Выражения (2.164) запишем для случая, когда As > Ар
Пользуясь соотношением (2.164), вычислим 2л
?! = 4 sin ф arcsin sin ф) йф ™ о
2Л
= 16 J sin ф arcsin sin ф) йф. (2.165) о
Введем в последнее выражение следующее обозначение k — Ai/A2; тогда получим
Я/2
Z, = 16
о
k cos2 ф
Vl — k* sin2 ф
йф =
Л/2
, 1 -н
A J V1 - sin2 ф
Л/2
+ л/\—Л2зШ2ф <2ф. (2.166)
Первый член в выражении (2.166) является эллиптическим интегралом 1-го рода K(k), а второй — эллиптическим интегралом 2-го рода E(k), т. е.
Л = 16-£~-К(А:) + -£-E(k). (2.167)
Подставив выражения (2.167) в (2.162), найдем первый коэффициент линеаризации “|Л|-55мт1'г<‘>+ттаг',<‘>-
(2.168)
Второй коэффициент линеаризации после подстановки в формулу (2.159) выражения (2.164) будет иметь вид
as^-szL-^ + A). (2.169)
/Л‘Л2
где
Л/2
Sk cos2 ф ,. —. йф =
V1 — k* s*n2 Ф
= К{k) + .Цс^ф
k
(2.170)
k
= 16
k
Я/2 г , „ . С k cos2 ф 73 = 16 sin ф \ —, — -.. ..... <2ф =
J Vl -k1 sin2 ф
^--Vslny- К (k) +1^12. E(k).
(2.171) подстановки выражений (2.170) | в формулу (2.169) получим
«>2 (А) — |(fe2-1) (cos ф + sin ф) К (Л)+
+ (cos ф + sin ф) Е (А)]. (2.172)
После н (2.171)
232
По формулам (2.168) н (2.172) иа рнс. 2.90, а построены зависимости коэффициентов линеаризации at от At прн различных значениях Аг, а на рис. 2.90,6 — а2 от Аг прн- различных значениях Д, и <j> = 15°, 45°.
Пример 2.11. На вход нелинейности типа насыщения действует входной сигнал (2.156). В этом случае имеем
-£• (Д1 sin ф + Аг sin (ф + q>)) прн 0 «С Ф + Ч>
[С — A, sin ф I
-------Аг-------J1
. Г С — Д, sin ф
В прн arcsin -----------д-------
ГС — Д, sin ф 1 ------------------1-
Аг
Рнс. 2.90. Коэффициенты гармонической линеаризации для нелинейности типа идеального реле с переключениями по уровням В и —В (В = 1):
a) ai (А); б) аг(А2, <р)
F(x) =
(Д1 sin ф + Аг sin (ф + ф)) прн
л + arcsin
С — At sin ф
Аг
+ arcsin
sin
, . Г С — Д| sin ф 1
+ arcsin 1----------------'•
Дг.
Подставив выражения (2.172) в формулы (2.158) н (2.159), получим
а, {-^-pi (0. Ф*. *о, k) + Л Ai <, С L
+ 4-(1 +2сО53ф*) — о
— cos ф* — 12 (0, ф*. k0, k) +
+ /3 (0, ф*. k0, *)] + -у cos ф* —
-/4(ф‘,-^-, k0, *)}. (2.174)
— В при л + arcsin
[С — Д| sin ф -------г-------
Аг
[С — Д1 sin ф 1
Аг J’
(Д1 sin ф + Аг sin (ф + <р)) прн
2л — arcsin sin ф
[С — Д1 sin ф Аг
(2.173)
где (С + А।)/Аг 1; /г0=вС/Аг', k = At/A2-
Здесь
Ф*
It (0, ф‘, k0, k) = k sin2 ф arcsin (k0 — о
— k sin ф) йф;
/2 (0, ф*, k0, k) =
Ф*
= S Vl - (feo - * sin ф)2 sin3 ф йф; о
/3 (0, ф‘, k0, k) =
Ф*
= 5 лЛ ~ (^° — ^ s*n Ф)2 sin Ф cos2 Ф ^Ф> о
Л (0, ф", k0, k) = л 2
= arcsin (fe0 — k sin ф) sin ф йф.
♦*
233
Рнс. 2.91. Графики решения трансцендентного уравнения (2.175):
а— для 1-го коэффициента; б —для 2-го коэффициента
Кроме того, ф* = ©Г, а /* - решение уравнения вида
/* — _L arcsin [£0 — k sin (to + А©) /], co
(б<ф<-у), Ф =
at, ср = Дсо/.
(2.175)
Здесь
М>‘
Z5 (0, ф", k0, k) = arcsin (k0 — k sin ф) йф; о
Ze (0, ф*, fe0, k) =
= S V1 - (*о - fe Sin ф)2 (kg — k sin ф) C/ф; о
h Т’ fe°’ л/2
= л/1 — (&о — £ 5!пф)2 sin2 ф <7 ф.
ф*
Графики зависимости решения ф* от А2 при различных значениях Л, показаны на рнс. 2.91,6 (С = В == 1).
С помощью ЭВМ вычислим коэффициенты гармонической линеаризации по формулам (2.174) и (2.176); на рис. 2.92, а построим зависимости сц от Л1 при различных значениях Л2, а на рис. 2.92, б — а2 от Л2 при различных значениях Л1 (С = В= 1).
Рассмотрим приближенный способ определения коэффициентов гармонической линеаризации для однозначных и двузначных нелинейностей, задаваемых графически [38, 39]. Для однозначной нечетной симметричной нелинейности выражение (2.77) можно переписать в виде л/2 2 С
а(А) = —j \ F (Л sin ф) sin ф dty.
Графики зависимости решения ф* от Л, при различных значениях Л2 показаны на рис. 2.91, а (С = В = 1):
9 о г д г 1
= 4 (1+2 cos’ ф*)-созф‘-
- 11 (О, ф’, fe0, k) + l3 (О, ф*, fe0, fe) +
+ |[т’1’‘2+(*о + 4) sinV-
4 4,2 __ 1
—- kok sin3 ф* Ч-------------g— sin4 ф* +
+ /6 (0, ф*. k0, k) - It (0, ф*. ka, k)] +
Г Г k
+ -4- 1- sin2 ф*+-х-(1 — sin3 ф‘) + л ц о
Рис. 2.92. Коэффициенты гармонической линеаризации для нелинейности типа насыщения:
a) ai (Ai); б) а2 (Л:)
+ Z7 (ф’, 4-. *)]} (2.176)
234
В выражении (2.177) введем новую переменную х = A sin ф и ах = A cos ф d§, где cos -ф = = ± V1 — (Х/А)2. Знак плюс в последнем соотношении берется при углах ф, находящихся в 1-м и 4-м, а знак минус — во 2-м и 3-м квадрантах. Тогда выражение (2.177) будет
<2-178>
где z = х/А, Ft (z) — F (z) z.
Интеграл (2.178) можно вычислить по формуле квадратур Стеклова, т. е.
а(Л)=4[т{'7'(1) + Г',-1) +
+ 2Г,(1) + 2Г, (_|)} +Я].
(2.179)
д (6) (е) где остаточный член R = — 6 р.
Заменяя z и F^z) на и и отбрасывая остаточный член, получим
a(X)«^-[F(X) + F(4)]- (2.180)
Так как остаточный член содержит производную 6-го порядка, то выражение (2.180) дает точные результаты для полиномов до 5-й степени включительно, а при более высоких порядках полиномов получим приближенные значения а(Д). В тех случаях, когда требуется обеспечить более точное нахождение коэффициента гармонической линеаризации, следует брать вместо выражения (2.180) формулу
oW)_^.[fH) + f(4) +
+ VS’F^d)]. (2.181)
а)
Рис. 2.93. Графический способ определения коэффициента гармонической линеаризации для однозначной нечетной нелинейности типа насыщения с двумя наклонами: а — без смещения; б и в — со смещением
Формула (2.181) позволяет получить точное решение для полиномов до 11-й степени включительно.
Пример 2.12. Найти графическим способом значения коэффициентов гармонической линеаризации для однозначной нечетной симметричной нелинейности, изображенной на рис. 2.93, а. При построении будем использовать формулу (2.180). На рис. 2.93, а показано нахождение коэффициентов а(Д) для двух амплитуд: А, = = 2,5 и А2 = 4 (жирная сплошная линия).
Данный метод построения может быть распространен на случай поступления на вход однозначной нелинейности F(x) сигнала с постоянной составляющей Хо, т. е.
235
x(t) = Хо + A sin wt; тогда получим еле дующие приближенные формулы:
Л>(Хо, Л) (хо + Л) +
+ 2F (*о + 4) +
+ 2Г (х0 - 4) + f Uo- Л)]; а (Хо, Л) — (х0 + Л) +
+ Г (х° + 4) +
+ 2F (х0-4) (Хо-Л)].
(2.182)
Пример 2.13. Найти графическим способом значения коэффициентов гармонической линеаризации для нелинейности, приведенной в примере 2.12. Необходимые построения по формулам (2.182) приведены на рис. 2.93, б, в соответственно для Fo(xn, Л) и а(хо, Л), когда х0 = Л и А = == 2,5. Здесь же жирными сплошными линиями показаны зависимости Го(хо, Л) и а(х0, Л), полученные графическим способом для ряда значений А, но при Хо = 1.
Для двузначных нечетных нелинейностей, записываемых в виде
9Г(Л) =
(Л),
3\ (Л),
если
если
Л > 0;
Л < О,
можно пользоваться следующими приближенными формулами [39]:
2
(4)-
1=1
-3-i (-4) -^-/(-Л)]; (2.183) (4)+у'(-4)-
-Ч4)-Ч-4)]- <2184> Если функция несимметричная, то
(Л)=~4 X (л)+2£Г; (4)+ Z=1
+ 2<П (~4) + ^(-Л). (2.185)
Пример 2.14. Найтн графическим способом значения коэффициентов гармонической линеаризации для двузначной нечетной симметричной нелинейности. Порядок построении показан на рис. 2.94, а, б соответственно для а(Л) и Ь(А). Здесь же жирными сплошными линиями построены зависимости а (Л) и b (Л).
Рис. 2.94. Графический способ определения коэффициента гармонической линеаризации для двузначной нечетной нелинейности типа однопозиционного реле:
а) а (4); б) Ь (А)
Этот способ можно распространить и при поступлении на вход двузначной нелинейности сигнала х (t) = Хо + A sin at. Тогда вместо формул (2.183) — (2.185) следует пользоваться
2
а (х0, Л) =1 £ 4 (х« + ») + 1=1
- 3-i [- (х0 - Л)]|; (2.186)
(2187)
2
^о(х°’ Л) = “4? X (х°+ Л) +
+23-1 + 23-i [- ( *°р--)]+
+ 3\ [- (х0 - Л)]}. (2.188)
В целом ряде практических задач по заданной кривой коэффициента
Рис. 2.95. Графический способ определения по коэффициенту гармонической линеаризации типа нелннейностн: а) а(Л); б) F(x)
236
гармонической линеаризации однозначной нелинейности необходимо найти вид нелинейной функции Г (Л). Тогда на основании формулы (2.180) можно записать [39]
^-a(X) = F(4) + F(4);
(2.189)
Просуммируем все слагаемые в выражении (2.189) и отбросим член (—1)п^(-^т); тогда получим
И)=£[(->)“^ <.(£)]. п=0
(2.190)
При использов.ании формулы (2.190) можно ограничиваться тремя-четырьмя членами.
Пример 2.15. По зависимости коэффициента гармонической линеаризации а (Л), показанной на рис. 2.95, а, определить вид нелинейной характеристики. Для этого воспользуемся формулой (2.190) и по трем ее членам найдем характеристику F(x), которая построена жирной сплошной линией на рис. 2.95, б. При этом видно, что она соответствует однозначной нечетной симметричной нелинейности типа насыщения.
Наряду с рассмотренным графическим методом нахождения коэффициентов гармонической линеаризации можно использовать другой способ [39]. В этом случае выражение (2.181) следует записать в виде
х(т)"(-г)- <2191>
В формуле (2.191) знак плюс берется в первом и четвертом квад
рантах, где d(x/A) > 0, а знак минус — во втором и третьем, где d(x/A) < 0.
Выпишем следующее соотношение: __________
,2Л92>
Подставив его в выражение (2.191), найдем
1
аИ) = т-^ -(W-
-1 (2.193)
Если ввести новую переменную интегрирования
v = V1 — (х/А)2
и обозначить F (х) через F{ при х > 0, х > 0; через F2 при х > 0, х < 0; через F3 при х < 0, х < 0 и через F4 при х < 0 и х > 0, то из выражения (2.193) получим
г 0 1
аИ) = -^4 — $ F'dv + $ F*dv +
L i о
+ J F3dv— J F4dol; (2.194) i о J
а(Л) = J (F, + F2 - F3 - F4) dv.
(2.195)
Рассмотрим три случая:
a) F(x) — нечетная функция, тог-да F3 = — Fi и Fi — — F2; при этом формула (2.195) имеет вид
1
\VA + F2)dv, (2.196) о
б) Е(х) — однозначная функция, в этом случае F\ = F2 и Ез = Е4; тогда формулу (2.195) можно записать
а(Л) = ^- \(Fi~F2)dv, (2.197) о
в) Е(х) — однозначная нечетная функция; при этом Fi = F2, и фор-
237
Таблица 2.9
Значения функции ^/] _ (Xi/A)2
i Xj//1 i х,./л
1 0,05 0,9987 6 0,55 0,8352
2 0,15 0,9886 7 0,65 0,7399
3 0,25 0,9683 8 0,75 0,6615
4 0,35 0,9368 9 0,85 0,5268
5 0,45 0,8930 10 0,95 0,3122
мула (2.196) имеет вид
1
F>dv-
о
(2.198)
Для приближенного нахождения коэффициентов гармонической линеаризации интеграл в формуле (2.194) заменим суммой; тогда формулы (2.196) — (2.198) примут вид п
1=1
XAV1-U/M)2; (2.199)
п
XAVl-(xl-M)2; (2.200) а (Л) = X F1 (Xi) А Vl-(x,M)2.
(2.201)
Составим табл. 2.9 значений функции V1—(Х/М)2 для 10-и интервалов i от 0,05 до 0,95 [39].
Для определения коэффициента гармонической линеаризации Ь(А) можно использовать формулу (2.50). Тогда по аналогии с выражением (2.194) найдем
Ж)
, 1 о
= '^4 J Fidv + 5 Fidv +
Lo 1
-1 О -J
+ j F3 dv + j Fi dv I. (2.202) о -i J
a)
i)
Рис. 2.96. Графический способ определения коэффициента гармонической линеаризации однозначной нелинейности, полученной экспериментальным путем по 10 точкам: а — вид нелинейности; б — коэффициент гармонической линеаризации а{А)
При двузначной нечетной функции (х) имеем F3 — —F{ и Ft — = —F2; в этом случае из выражения (2.202) получим
1
(2.203)
о
или
2 Д х.
Ъ (Л) = ItA £ [Л| ~ Л -Т
(2.204)
Пример 2.16. Найти графическим способом зависимости коэффициентов гармонической линеаризации для однозначной нечетной симметричной нелинейности, харак-
Таблица 2.10
Коэффициенты гармонической линеаризации однозначной нелинейности для 10-и значений i
i Л а (Л) i Л а (Л)
1 0,8 0,69 6 3,4 0,35
2 1,6 0,63 7 3,6 0,30
3 2,1 0,57 8 3,8 0,26
4 2,7 0,49 9 3,9 0,25
5 3,1 0,40 10 4 0,23
238
Рнс. 2.97. Графический способ определения коэффициентов гармонической линеаризации для двузначной нелинейности:
а—вид нелинейности; б — коэффициенты линеаризации
теристнка которой изображена на рнс. 2.96, а. Определим по ней значения функции F и составим табл. 2.10.
Для определения коэффициентов гармонической линеаризации а (Л) воспользуемся формулой (2.201) и табл. 2.10. На рнс. 2.96, б построена зависимость коэффициента гармонической линеаризации а(Л).
Пример 2.17. Определить формулы для вычисления коэффициентов гармонической линеаризации для двузначной нечетной нелинейности, изображенной иа рис. 2.97, а, при А > х. Для этого воспользуемся формулами (2.196). и (2.203). Перепишем их в виде
1 2 Г а(Л)=-^-\иГ.(х) + ЯА J 0
+ (х)1 d (V1 - (ХМ)»); (2.205)
I 2 Г
ь (Л)="ял" г~ W] d (*/Л)-о (2.206)
Подставив в формулы (2.205) и (2.206)
значения #"i (х) — -4 + ~ sgn (х — С) и
^2 (X) = -у + -у Sgn (х — тС), определен
ные по рис. 2.97, а, получим
1
°(л>=7т $ [А + т(sgn “ С) + о
+ sgn (х - тс)) ( д/1 - (тг)2);
(2.207)
!
о
— sgn (х — znC))J d (4-). (2.208)
После ряда преобразований и подстановок формулы (2.207) и (2.208) примут вид
+V1 - (4)7 <22о9>
НЛ) = --~(1~'«)- (2.210)
Формулы (2.209) и (2.210) совпадают с ранее приведенными в табл. 2.2 зависимостями для данного типа нелинейности.
Пример 2.18. Найти графическим путем зависимости коэффициентов гармонической линеаризации а (Л) и Ь (Л) для двузначной нелинейности типа петли гистерезиса якоря электромагнитного реле (рис. 2.98, а). При этом видно, что рассматриваемая нелинейность состоит из четырех участков кривых —9"Для получения коэффициентов гармонической линеаризации данной нелинейности воспользуемся формулами (2.195) и (2.202), записанными в виде
п а(Л)=^г2>1(4)+ £ = 1
+ ^2(4)]д(71- (4/л)2)-л
1=1
+ ^4(4)1д(7ГЯ4/лТ): (2.211)
п 6(Л)==-^г2>>(4)-м
п
-^2(4)]д(4/Л)--^-£Г3(4)-i = 1
-^4(4)]Д(4/Л)- (2.212)
239
Рис. 2.98. Графический способ определения гармонической линеаризации двузначной нелинейности:
а — вид нелинейности; б — коэффициенты линеаризации
Разобьем, как это показано на рис. 2.98, а, каждую из кривых i—3~4 на 10-ть участков и составим табл. 2.11, пользуясь данными которой и формулами (2.211) н (2.212) вычислим коэффициенты гармонической линеаризации а(Д) н Ь(А). На рис. 2.98, б построены кривые изменения коэффициентов гармонической линеаризации а(Д), Ь(А).
Если нелинейность описывается нелинейным дифференциальным уравнением y = f(x,x), то пользу-
Таблица 2.11
Коэффициенты гармонической линеаризации двузначной нелинейности для 10-н значений 1
£ 2 (х£) &з (*i) 3 Q •О
1 —2 6 2 -6 0,07 -0,02
2 0 7 0 —7 0,22 —0,08
3 2 8,2 —2 -8,2 0,43 —0,22
4 4 9 —4 -9 0,65 -0,31
5 6 9,8 -6 -9,8 0,82 -0,26
6 8 10,6 —8 — 10,6 0,90 -0,22
7 9,2 11 -9,2 — И 0,95 —0,21
8 10,4 11,4 -10,4 -11,4 0,97 -0,20
9 11,2 11,8 -11,2 -11,8 0,99 —0,19
10 12 12 -12 -12 1 -0,18
ются рассмотренным выше приближенным способом определения коэффициентов гармонической линеаризации. Запишем следующую зависимость:
( \ (х, х) при х > 0; 1
(х, х) I (х, х < 0. J
(2.213)
Подставляя в формулу квадратур Стеклова выражения
хЗ~ (хА, ± ш.4 У1 ~ х2), У1 — х2 X Х^(хД, ^аДУГ^х5), ^(хД± ± ш.4 У1 — х2), получим
а (Д, а)= ^_£[<ГДД, 0) +
1=1
+^(4- (-п'-'ад^)-
-^(-4- (-1),-1«>д#)-
-^(-Д, 0)]; (2.214)
^-) + #г(-4, «л^п)-
-^2 (-4- (2.215)
240
Рис. 2.99. Построение эквивалентных характеристик нелинейного дифференциального уравнения (2.223): а — при е = 4; б — при е = 8
2
°н-
+ 2^г(д, (-1)'->соД^-) +
+ 2^(- А, (-1)‘->соД^-)4-
+ 0)]. (2.216)
Пример 2.19. Допустим, что нелинейное дифференциальное уравнение имеет внд
р = х —е('. -х2)х, (2.217)
где е — некоторый параметр.
С помощью формул (2.214)—(2.216) нетрудно найти коэффициенты гармониче
ской линеаризации
а (Л, со) = 1; Ь (А, со) = — есо (1—)
/о(Да)=О. (2.218)
Для проверки правильности полученных выражений подставим соотношения х = = A sin со/, х = со A cos со/ в уравнение (2.217); тогда получим
у = A sin со/ — е (1 — A2 sin2 со/) соА cos со/ —
— A sin со/ — ecoA cos со/ + ecoA3 cos со/ — — ecoA3 cos3 со/ или
у = A sin со/ — ecoA (1 — A2) cos со/ —
— ecoA3 cos со/ + — cos Зсо/). (2.219)
Отбрасывая в уравнении (2.219) 3-ю гармонику, найдем
yt = A sin со/ — есоА (1 — у) cos со/. (2.220)
Пример 2.20. Рассмотрим решение примера 2.19 другим способом. Как известно
241
методике гармонической линеаризации [см. формулу (2.7)] принято считать, что
yi (0 = а (А со) х, (/) + х, (/); по
этому
а (А, со) = 1;
З^о (А со) == 0.
Ъ (Л, со) = — есо
(2.221)
Если x(f) — A sin art, то гармонически линеаризованное уравнение (2.217) можно записать
у = х - есо (1 --у-) * (2.222)
Из выражения (2.221) можно получить эквивалентную передаточную функцию нелинейного уравнения (2.217) в виде
7 (А /со) = ^//l + ew(l--^-y X
X exp р arctg ( — есо (1 — (2.223)
где
откуда
у = — Л3со sin2 св/ cos art = xfa
---------— (1 — cos 2art) cos art —
=--------- <cns at — cos 3art). (2.227)
Из выражения (2.227) следует, что в сигнале на выходе нелинейности содержится 3-я гармоника. Ее амплитуда сильно ослабляется линейной частью системы, представляющей собой низкочастотный фильтр. В результате этого выражение (2.227) можно переписать в виде
Аа> . А2 . oot>.
у =-------—cos art =-----(2.228)
Эквивалентное характеристическое уравнение нелинейной системы (рис. 2.100, а) можно представить в обычной форме, т. е.
еА2 .
1 + , • ч2 = 0, (2.229)
(ja>)2 — ещ> + 1
откуда
(1 - о»2) - /во» (1 + « 0. (2.230)
Из выражения (2.230) получим формулы для вычисления эквивалентных амплитуд-
Характеристики 20 Ig q(A, со) = И и ц(А со) =0 построены на рис. 2.99, а, б соответственно прн е = 4 и 8.
Пример 2.21. Найти формулы для вычисления коэффициентов гармонической линеаризации и эквивалентную передаточную функцию нелинейной системы с отрицательной обратной связью, если ее объект управления с устройствами управления и измерения описывается дифференциальным уравнением Ван-дер-Поля
у' = х + е (х2 — 1) х + х. (2.224)
Уравнение (2.224) при х, — х, х2 = х н у’ — 0 можно записать в виде
х, = х2; •)
/ох > (2.225)
х2 = — е [х[ — 1 ] х2 — Х[. J
По уравнениям (2.225) при р = по-
строим схему, показанную на рис. 2.100, а.
Для определения эквивалентной передаточной функции воспользуемся тремя способами.
Первый способ. Примем, что на вход нелинейности поступает гармонический сигнал. Тогда на выходе образуется сигнал
У = - XjXp (2.226)
Рис. 2.100. Вычисление коэффициентов гармонической линеаризации для уравнения Ван-дер-Прля:
а _ структурная схема (блоки: / — сравнения сигналов; 2 —возведения в квадрат; 3 —дифференцирования; 4 — умножения; 5 — линейная часть системы; 2—4— нелинейная часть системы); б—<Э — эквивалентные характеристики при различных е и амплитудах Л
242
ной и фазовой характеристик системы, т. е.
q (А, со) =
= arctg
(2.231)
Пользуясь выражениями (2.231), найдем эквивалентную амплитудно-фазовую характеристику нелинейной системы в виде
7 (Л, со) = д/(1 — а2)2 + е2а2 (1— X
(2.232)
Второй способ [39]. Подставим в уравнение (2.224) следующие сигналы: х = = A sin at; х = Ла cos at и х — = —Аш2 sin <о(; тогда получим
у' = (1 — a2) A sin at — еаЛ cos at +
+ еа/12 cos at — еаЛ3 cos3 at
или
у' = (1 — a2) A sin at — еаЛ (1— A1) cosat—
( 3 1
— ea/131 — cos at 4- -r cos 3at \ 4 4
В выражении (2.233) отбросим 3-ю гармонику; тогда
у' — (1 — a2) A sin at —
— еаЛ (1-----) cos at. (2.234)
Из выражения (2.234) имеем а (Л, а) = (1 — а2);
Ь (Л, а) = - еа (1 - . (2.235)
Пользуясь соотношениями (2.235), получим формулу для эквивалентной амплитудно-фазовой характеристики нелинейной системы
7 (А а) = д/(1 - а2)2 + е2а2 (1- ^Х
которая совпадает с формулой (2.232).
На рнс. 2.100, б—д построены эквивалентные амплнтудно-фазовые характеристики 7 И, а) в зависимости от а, вычисленные по формуле (2.232) для двух значений е = 1 н 10 при четырех амплитудах Л = 1; 3; 4; 5.
Пример 2.22. Найти формулы для вычисления коэффициентов гармонической линеаризации и эквивалентную передаточную функцию нелинейной системы уравнений кинетики точечной модели ядерного реактора
6
п = -^п-^С;; (2.236)
« = 1
Рх
Ct =-±-п- 'kiCt, (2.237)
где бк — изменение реактивности; [J,- — доля запаздывающих нейтронов t-й группы; 1/а,— время жизни запаздывающих нейтронов i-й группы; Ci — концентрация носителей запаздывающих нейтронов i-й группы; I* — среднее эффективное время жизни нейтронов.
Нелинейным является уравнение (2.236) из-за наличия произведения бкп. Положив 6к=Лв51ПаЛ, п = Л„ sin(at + ср„), получим
Г Ап cos ф„ ,
L
Лп sin Фп Л.а о
sin at.
(2.238)
После чего, нелинейность эффициентов найдем
а (Л, а) -
подставляя преобразованную в исходные формулы для ко-гармоннческой линеаризации,
(2.233)
4Ап cos фп лЛ6
л/2
j (sin3 ф +
о
+ sin2 ф cos ф) i/ф;
6 (Л, а) =
л/2
4Л„ sin Фп f . , , ...
————— 1 sm3 ф cos ф аф.
ГС/1. J
6 о
Точные значения данных интегралов совпадают с интегралами, вычисленными с помощью квадратур Стеклова:
. 4ЛП (2 cos ф„ + sin фп) .
а <Л- =-----------з^Т----------’
О
b(A о) (sin фп + cos фп)
' ’ ' ЗлА6
Откуда получим
q (Л, а) = д/2 + 3 cos2 фп + 3 sin 2ф„;
ЗлЛ
(2.239)
И (Л, а) = arctg Г osin cos.g»_l. (2.240) L 2 cos фп + sin фп J
Значения Ап и ф„ находятся из следующих трансцендентных уравнений:
Лп = |^,вк(>’ АгР
Фп = аг8[^„,йк(/“. А,- Фя)]>
где W . (ja, А , <р )—передаточная фуик-
X М Tlf
243
ция от бк к п гармонически линеаризованной системы 7-го порядка (2.236) н (2.237).
В нелинейных САР довольно часто действуют два сигнала в виде гармонических составляющих: низкочастотной Хо(() и высокочастотной (автоколебательной) х* (() = = A sin <j>t. Тогда на входе нелинейности образуется сигнал вида
х (t) — х0 (t) + A sin со(. (2.241)
От действия автоколебаний происходит изменение формы нелинейности для сигнала Xo(t). В результате этого приходится выполнять двойную гармоническую линеаризацию функции смещения ф(хо).
Известно, что на начальном участке функция смещения имеет вид плавной однозначной кривой около начала координат, т. е. иначе говоря, наблюдается процесс сглаживания нелинейности для низкочастотной составляющей xo(t) за счет высокочастотных колебаний х* (/). Это и позволяет производить обычный процесс линеаризации функции смещения
^о(хо, А) = 4г| х0. (2.242)
ОХ» 1хо-О
В выражение (2.242) можно ввести
-^-1 =кЙ, (2.243) ах° Ьсо=О
где кн является нелинейным коэффициентом усиления по низкочастотной составляющей.
Как известно, в общей форме коэффициенты линеаризации можно записать в виде формул
2л
^о(х0, А, со) = -^ &~(х0 + Asinip, О
Л© cos i|)) dip; (2.244)
2Л
а (х0, А, со) = j (х0 + A sin ф, О
Л© cos *ф) sin di|); (2.245)
2л
Ъ (х0, А, со) = (х0 + A sin ф,
о
Асо cos ф) cos ф с/ф. (2.246)
Из формул (2.244) — (2.246) видно, что для определения кн следует пользоваться выражением
/ дУ0 . дУ0 dA
\ дх0 ' дА dx0
. dSF~0 da \
-t" ди dxa JX^Q
(2.247)
Можно показать, что если в нелинейной САР имеется однозначная или нечетная суммарная нелинейность, то
дУ0 I
да> L=o
дУ0 дА г
Хо** >
2л
1 f дУ
2л J дх о
sin ф с/ф = 0;
1х=Л sin Ч>
тогда формула (2.247) примет вид
,2-248>
где Зго = ^"о(А, х0); А = А(х0, Ас).
Здесь Ас — амплитуда симметричных одночастотных вынужденных колебаний с малой частотой при Хо=О. Ее определяют через параметры всей системы управления (см. гл. 7).
Рассмотрим порядок определения функции смещения и коэффициентов линеаризации по низкочастотной составляющей. Тогда для однозначных нечетных нелинейностей из формулы
а(х0, А) = ас(Ас) (2.249)
можно определить следующее соотношение:
А = А(х0, Ас). (2.250) Подставив последнее в выражение Fq = Fq (xq, А), получим формулу для функции смещения
Е0 = Ф(х0) Ас), (2.251) откуда и находится соотношение (2.243).
244
А(хв,Ас)
Рис. 2.101. Определение А и функции Ф в зависимости от амплитуды симметричных колебаний Ас при различных смещениях Хо: в) А (Хо> Ас); б) Ф (Хо, Ас)
Для двузначных нечетных нелинейностей имеем
а(х0, А) = ас(Ас); 1
Ь(х0> Д) = &С(ЛС); > (2.252)
#"0 = Ф(х0) Дс) J
при кн = кн(Лс)-
На практике обычно применяют аналитический и графический способы нахождения коэффициентов кн. Рассмотрим оба эти способа на конкретных примерах.
Пример 2.23. Определить коэффициент кя для идеальной релейной характеристики. По данным табл. 2.1 и 2.4 нетрудно найти формулу (2.249) в виде
(2.253)
откуда получим уравнение
(2.254)
Из решения уравнения (2.254) найдем
(2.255)
Формула (2.255) справедлива при —Лс/2 Хо Дс/2. Перед вторым квадратным корнем берется знак плюс, так как А = Ас Только при х0 = 0.
Для удобства вычислений можно ввести следующее обозначение:
-^2-=sinP; (2.256)
Лс
Ф(хо>Ас)
тогда
А/Ас — cos р/2, откуда найдем
4 = Ас cos (у arcsin (2.257)’
Функцию смещения определим по формуле, приведенной в табл. 2.4, т. е.
Fo = — arcsin 4?-, (2.258)
Л А
где ___________
x0/4 = Vl ~(А/Ас)2 нлн
sin (у arcsin • (2.259)
Подставив соотношение (2.259) в формулу (2.258) н имея в виду соотношение (2.251), найдем
& = — arcsin-^-. (2.260)
Формула (2.259) справедлива лишь при —4с/2 iC Хо 4с/2.
График функции Д=4(х0,4с), построенный по формуле (2.257), показан иа рис. 2.101, а, а для Ф(хо, 4С), определенной по формуле (2.260), изображен на рис. 2.101, б.
Нелинейный коэффициент усиления по низкочастотной составляющей вычислим, используя формулы (2.242) и (2.243), с помощью выражений
dF
дх
2В
К" ~~ лАс '
Хо=О
В табл. 2.12 приведены формулы для вычисления нелинейных коэф-
* Для вычисления амплитуды А можно использовать формулы (2.255) или (2.257).
245
Таблица 2.12
Определение нелинейных коэффициентов усиления
фициентов кн других типов однозначных и двузначных нелинейностей.
Выполним повторную гармоническую линеаризацию для нелинейности типа реле при xo=Mosina/
Я/2
ао (х0, Лс) = Ф (Ло sin ф) X
О
X sin фг/ф =-^-Х
Я/2
X$ arcsin (-^-2-sin ф) sin ф dip, о с
(2.261) которую можно переписать в виде
Оо(х0, Лс) =
Я/2
4В f fe2 — 1 + 1 — fe2 sin2 ф n2A0k J 1 — k2 sin2 ф
(2.262)
Из выражения (2.262) получим
ao (xo> Л) = я2?1о X г я/2
I fe2 — 1 Г _____dip______.
|_ * j" V1 — k2 sin2 ф
+ V1 — k2 sin2 ф dt|)l = о J
+4-^(1’ *)]}’ (2-263) где К (-у, и -Б(-у. л) — эллиптические интегралы соответственно первого и второго рода.
По формуле (2.263) вычислим а0(х0, Лс) при |х0| <Лс/2 и построим на рис. 2.102, а, б соответствующие графики.
Для некоторых нелинейностей аналитический способ определения коэффициентов ао(хо, Лс), Ь0(х0, Лс) и 3~0 — Ф(х0) Лс) с помощью повторной гармонической линеаризации представляет определенные трудности. В этом случае можно применить графический способ. Тогда параметры нелинейностей запишем относительно переменных С/Ас и
246
Рис. 2.102. Аналитический способ определения коэффициентов гармонической линеаризации а (До, Ас):
а—в зависимости от Ас при трех значениях AQ; б—в зависимости от Ао при трех значениях Ас
а по табл. 2.1 имеем
BfAz. Для однозначных нелинейностей повторную гармоническую линеаризацию выполним также графическим способом по формуле (2.180), а для двузначных нелинейностей — по выражениям (2.252) с повторной гармонической линеаризацией по формулам (2.185) — (2.187).
Пример 2.24. Рассмотрим графический способ определения коэффициентов гармонической линеаризации на примере однозначной нелинейности типа релейной характеристики с зоной нечувствительности; тогда, по данным табл. 2.4, можно записать
«<*о, Л)=-ЭТХ
Рис. 2.103. Аналитический способ определения коэффициентов гармонической линеаризации:
а) а (х0, А); б) А/Ас в зависимости от х0/А
''''-тЙ'ЧН' <2265)
По формуле (2.264) вычислим значения а(х0, А) и построим их в виде семейства кривых на рис. 2.103, а. Затем по формуле (2.265) найдем ас(Ас) и проводим горизонтальную прямую соответственно этой величине. Тем самым обеспечим выполнение формулы (2.249). Тогда точки пересечения прямой ас(Ас) с кривыми а(х0, А), построенными при разных хо/Ас, позволяют найти на оси абсцисс значения А/Ас. Пользуясь ими, на рнс. 2.103,6 построим кривую в системе координат (х0/А,А/Ас).
Для построения графика функции Ф воспользуемся формулой
— arcsin
70] } <2266>
которую нетрудно получить по данным табл. 2.4. Подставляя значения А/Ас, снятые с рис. 2.103, а, в формулу (2.260), получим кривую Fo/B = Ф(хо/Ас)/В, которая построена на рнс. 2.104, а.
Нелинейный коэффициент кн, как следует из выражения (2.243), представляет собой значение угла наклона прямой, проведенной через начало координат. Соответствующее построение показано на рнс. 2.104, а, и к„ = 0,3. По данным табл. 2.12, коэффициент к„ = 0,27, что указывает на хо-
247
Fo. в
0,5
0,4
0,3
0,2
0,1
О 2 4 6 8 Хо 0 2 4 0
а) б)
Рис. 2.104. Повторная гармоническая линеаризация:
a) Fa!B от xQ; б) FQ (х0/В) в зависимости от Лс при двух значениях х0: в) а0 (Ло, Лс)
рошее совпадение результатов графического определения числового значения кн. В результате этого можно найти функцию
Fo (ха/В) = кнх0/В.
Графически она изображена на рис. 2.104,6.
Для повторной гармонической линеаризации воспользуемся формулой (2,180), записанной в виде
(2.267)
Соответствующее графическое построение по формуле (2.267) и методике, приведенной в примере 2.14, показано на рис. 2.104,в.
Применение методов гармонической линеаризации для исследования нелинейных САР рассмотрено в гл. 7.
3.
В САР в реальных условиях эксплуатации на вход существенных нелинейностей наряду с детерминированными поступают и случайные управляющие и возмущающие сигналы. Следует указать, что иногда детерминированный сигнал является малым, и его влиянием на САР можно пренебречь. В этом случае следует считать, что на вход нели
8 10 12 Ас о 2 4 6 8 10 12. Ао В)
нейности поступает случайный сигнал.
Существующие строгие методы анализа нелинейных САР со случайными сигналами требуют учета законов распределения случайных величин (т. е. моментов высшего порядка), что приводит к громоздким математическим выкладкам, затрудняющим процесс проектирования. Поэтому в инженерной практике принято пользоваться приближенным способом — методом статистической линеаризации [13, 30], сущность которого состоит в замене нелинейного элемента статистически линеаризованным, но позволяющим учитывать особенности нелинейного преобразования сигнала. Таким образом, однозначную нечетную нелинейную характеристику y(t) — F(x) заменяют линейной, т. е.
yn(t) = komx+kix(t), (2.268) где коэффициенты ka по математическому ожиданию шх, и центрированной случайной составляющей О
х = х — шх выбирают так, чтобы приближенный процесс на выходе нелинейного элемента yn(t) был бы практически близок к y{t) При этом считают, что на вход поступает случайный сигнал с нормальным законом распределения, который получается за счет эффекта «нормализации», создаваемого линейной частью системы.
Существует два подхода определения коэффициентов статистической линеаризации.
248
Первой подход. Коэффициенты выбирают из условий
М Ш‘)] = М [z/(0];
Л1{[ул(/)-т,л(0]2} =
= М[у (0 — ту (О]2.
Подставляя эти соотношения в выражение (2.268), получим
М (0] = м [Мх + *(iI>x°W] = komx
или
= komx (2.269)
M{[y„(t) — my «} =
= М \kQmx — k^x (t) — my]2
или
^[^р2. (2.270)
Коэффициенты статистической линеаризации, определяемые по этому методу, вычисляют по формулам
W(mx’ СТх) =
оо
= -±- ( F(x)f,(x, t)dx; (2.271) тх J
— оо стх) =
f2toMx,0dx-m£(0,
(2.272) где
(у~тх)г
, 2а2
f1(x,0 = —1=е х (2.273) сх -у 2л
— нормальная плотность вероятности.
Второй подход. Коэффициенты статистической линеаризации выбирают из условия минимума квадрата ошибки от замены y(t) на ул(0, т. е.
т1п{Л4[1/(0-гМ0]2}. (2.274)
где коэффициенты k0 и удовлетворяющие условию (2.268), находят
из уравнений
-±-{M[y(f)-komx-
-^(0]2} = О;
-^7 {М [у (0 — kQmx —
-М(0]2} = О.
Решая уравнения (2.275), определим
= W (%.®.). (2.276) а
й<2) (тх, ох) == -V J (х — т*) X °Х _то
X F (X) fi (х, 0 dx. (2.277)
Из формул (2.272) и (2.277) следует, что применение первого и второго подхода приводит к различным результатам. Для многих типов нелинейностей числовые значения коэффициентов статистической линеаризации и /г(2> одинаковы. В тех случаях, когда наблюдается некоторое отличие, используют соотношение
Нетрудно показать, что из формул (2.277) и (2.271) получим
kl\mx> О =
Г °° т
д I F (х) fi (х) dx I
= -------1. (2.279)
При вычислении коэффициентов статистической линеаризации проще использовать формулу (2.279). В первом подходе применяют обозначения Л*)0, А!<°, а во втором — k®\ #2).
Пример 2.25. Определить формулы для вычисления коэффициентов статистической линеаризации однозначной нелинейности типа идеального реле. Для этого будем применять формулы (2.271), (2.272) и (2.279). Тогда для нахождения коэффициента статистической линеаризации
249
выражение (2.271) запишем в следующем виде:
(х-тх)2 оо —
V2jx fnxax J
— оо 0 (х~тх)2
В f 2а2 -------—£------- \ е х dx +
V2ji тхох J
— оо (x-mx)2 оо —
В Г 2а2
+ -----\ е х dx. (2.280)
V2n тхах J
Выполним в выражении (2.280) замену переменных (х — тх)/ах — и\ тогда найдем
оо
= ’ ( t-^du-
тх V 2л J тх L —
тх/стх Т
---( е-“2/2 du . (2.281)
V2n j J
Если в выражение (2.281) подставить функцию Лапласа
тх1°х
Ф(тх/<Тх) = —^=- ( е-“2/2 du, (2.282)
72л J ’ л
то формула (2.282) примет вид
4’-£{[4-+7г)]-
Для коэффициента статистической линеаризации выражение (2.272) запишем в виде
М” = д/ J F2(x}fl(x,t)dx-m2(t) = — ОО
_£71_1ф.(^) (2.284) и, наконец, для коэффициента статистической линеаризации fc}2) из формулы (2.279) имеем
0 (х-тх)2
/о\ В Г 2О2
М * ----7=—Г \ (х—тх) е х dx +
V2n cr J л —оо оо (Х~тх)2
В Г ,
+ ~7=-Г \ (* — «*) е х dx.
о£ J
(2.285)
Подставляя в формулу (х — тх)!ах — и, найдем
(2.285)
В 72л ах
J ue U^2du — ~mxlax
... 2В с-^/2^ 72л ах
(2.286)
Пример 2.26. Определить формулы для вычисления коэффициентов статистической линеаризации двузначной нелинейности типа реЛе (рис. 2.4,6). Для двузначных нечетных нелинейностей статистически ли
неаризованная характеристика примет вид
Уп (О = k(^mx + + k%}°x{-,
тогда коэффициенты k^\ k ]2* и k удовлетворяющие условию
min {М [у (0 — ул (О]2}, W V?
находятся из уравнений
{-«[, (0-4'Ч-Ж;в - 0;
Ок j
4® {и [,
2
Используя приведенные зависимости и функции Лдпласа (прил. П-1.4), запишем *(>) =—{ф (с + ™х>) - ф (_ ° тх I \ ах ) \ <зх )
(2.287)
1 z С—тх \2 , гхх (С - тх) 1 I-5?-)
+----^2--- е
1 ( С+тх\2) гх±(С+/их)1 21 °х /I
ххУ .. .-il I е 4 7 11 (2.288)
а^л J )
250
Таблица 2.13
Коэффициенты статистической линеаризации нечетных однозначных нелинейностей
№ п/п Вид нелинейности по постоянной составляющей *0 По случайной составляющей
Пердый сnocoS к'(' Второй способ
1 в -С (7 У 7\\ .H.'W где т^Ир-, а=^-
I > I 7 с' -В
2 5 £ У та* ^нп,)«^^т,)Ф^ ' '7 0’ . J 2л- /А?)'- .-№р где В,Ах 2 ац Сг-т’ = Т -^*?ЖНт/ , ^[(1^(1^т,^-2]л(!^ /Ьг(1-р)г е ' 7 .^[М^-^-рл?] .Жр\г т,в,-а, +Тн$-е2у')+ т,д, +0, ”т(т?) К*т2 /2 + Ы е в’ / б*+т]-т, Г (р-т\ рр)д, Р\0,) -P&yj-k'Tril/ed.у/
\| 7 \| 7 Cj с2 -В
3 в ^г 0 У В (чип, /чип,] 1<-т, (1ип\ mJ 1-ч tf,/ /-v Ф\ 4/ -рА\ьГГчФ\~РГ 1 .4 )ВД/ -e*\7’/ +?7 ' л 1 г Г, Сг ^г;- v-~3 Р^Ш‘ У^У("гн)е-'№!1')+ + 0,(т,-р)е*&У)У (1-ч) / Г (’-Р т,д,-а, АА2) Р (1-р / т‘ л °л т,-— ; Л=— G G Ш El V i -EtjS'E v л Л it SS-Jf.!t i il«- S' It В? ©В?® "?F 1 V W F P
V 1 / с, <л -в
251
Продолжение та до. 2.13
В у X iH^)f mi 2B ~e% 12^
В ~в
в У x^)Am'-v)x _е-^),е-^) + т tyt . X ^Х i> G т'=й’ 'n>; v‘t В фп1 (l*m^(l-m,-2e)-e‘ \6J (t-v) - J fhaii? + (l-mt-2v) e °’' + lfmr^ z/mrvf/A ‘ufrOf^e A * /[f Ar)]
с, Сг' -В
в -с У _1 f ГПг т’=Т' а’-с 1 If k’m’ e, [ Вг • /гМ,-КМ/ vTTTY j
6 U (7 С -в
7 » -Q-Q-b-C, У /ТЪ АУГНГ)-ГТНГ) * ъ№И?)‘ ^гнг)у %№)-№)] „« Ш=Л Т/2я(ь-^[ /'М/. « .. J у}я (1-v,) B_hmhe' л /*>Л'+т’к ?'7г(^г/+ 'AW'tv} if L +y^[eIm^"' V ₽‘? (‘V'jy + (V-f- -зй/^ M + p№’L Ко /П, l г вг I -^)^)~ АГ)]<-IAr)Ary ^rHr)I + 1_ 7-v, _ 2(v3nm,) ₽-^!^Д v2-v, 1rv, ★ +^el^L^e^t vrvi 1-v, 1-v, J . /77» x ^x .1 0 . VIA; V3A Li G
'и/: f , С; С, £$ -в
252
Продолжение табл. 2. /5
8 С 'У т,^я1 jj Ш, , gn т^Т’ e’=T -^[Н'‘’^\; -[^Ш]
1 0 С X
9 вг в, -с , У /1 1 / -2е'*&) ]] т mt л бх wgpsH)V* ^J^1 •''l('L^('-&-
1 1 1 > 0 с ’ -Bt -Вг
10 У . / * т! Ргпч-и '* к-0 р=0,1,... /4л*2 /х 5 J V Гк Г ~Л.\2^ L^2 тх > / к’° / 75 X сгпч m? Ргп-2-к ux k-o
0 * „2л*Г у*Вх п 0,1,...
11 У / Л *7М/
0 уВ xs
12 У / х _t_ ”/ 1 +^elgT / }2пбх е J [ mj ml . ’1^+6^ + s!gi / t ml 1 J
0 !j-8i2sign>
И вг в, -сг -С, У Е1. <H!W - < Ж gU dl ex 5 ?IJ_ l.1 II -—4 *»k , ***? ji д^д
в G сг -в, -В,
253
2 В 2о; Г,т. (С — тх\ , .— е л I Ф {---------------| -р
V2п с. L \ ах )
4- Ф
(2.289)
^хх
где г„;.==------< 1.
лл стхах
В табл 2.13 приведены формулы для вычисления коэффициентов статистической линеаризации других типов нечетных однозначных нелинейностей, а в табл. 2.14 — для нечетных двузначных нелинейностей.
По формулам табл. 2.13 и 2.14 на рис. 2.105, а—в — 2.108, а—в построены графики коэффициентов статистической линеаризации, которыми будем пользоваться в гл. 7.
4. (ОВМЕС ТИЛЯ ГАРМОНИЧЕСКАЯ и - т атипическая ЛИНЕАРИЗАЦИЯ
При поступлении на вход нелинейного элемента суммы двух сигналов, представляемых в виде
О
х (t) = тх (/) + х. (t) + A sin со/, (2.290) можно считать, что коэффициенты статистической линеаризации являются периодическими функциями
времени. Тогда для однозначных нелинейностей выходной сигнал
с/= 5 [* (/)]. (2.291)
Применив к функции (2.291) совместную гармоническую и статистическую линеаризации [39], получим приближенную зависимость
у (/) « F* (Л, пгх, oQ +
+ а (Л, тх, <ух) Л sin ф +
+ ^(Л, тх, <гх)х°(/), (2.292) где
mx> ах) =
2.Т
== -^- ^ F (тх + Л sin ф, ах) с/ф;
(2.293)
а (А, тх, ах) =
2П
— -U- F (тх + A sin ф, <тх) sin ф с/ф;
JT/1 J
(2.294)
k* (А, тх, ах) =
2JX
= "ЙГ S Х sin Сх>>
(2.295)
254
Раблица 2.74
Коэффициенты статистической линеаризации нечетны/ двузначны/ нелинейностей
№ л/л вид нелинейности По постоянной составляющей Л, По случайной составляющей
Первый спасав К^ Второй спасав к,1
7 у в X Г 1 fC-fyf ifOMifn **№)] А $** 1 -0^ <1
-С 0 в с
2 У mjf ' <с~^ t/mC-mtf xe”i[ е2 ЦЛ~КГ)+ z « г» (c'trn/'ll. " )/2л Оя J * ПтС-т,\! г У ’М'[г<№-\ :И у'Тл бх J J ei^L , l(fnC~mxV !/С* /пх\211 +/А л Лр Л )J
~с тС X
пС 0 -в г.'
5 У -с/ А3 г1) \ V'-'-xx / при r,t < 1 т* \&* / при rxi=1 к ml 2вС -^1
/о /г х K~tgp
4 У, в ~G / -If ^Н^)- < Г -221 ~ е!е'[е - ~е Jr^c5-C^ ([ (Cz-rn,)1 (Сг"Л‘ J е- -,е -‘Г + й(к„тх) атя d(komx) dmx
1 \/ Г' ч / । / /GQ G -в
255
Продолжение табл. 2. 74
(Сз^х)2 (Сг-тх)г 7 + е' _е J + г г Г (с^)! <сг^1 . Г Ч~тх) IW7 &т 2в‘ ~е г \ ох / \ о, / . Г г т (с^т^2 + 1 СЛГЧк р id _ V??/ бх Г т <сз-тх}2 (Ctw$ - е"ЯГ gX Ь
5 В -С-тс 7 »э 1 + <"> + -а 41 41 Л । ~ । - ' ”, S’ls? JB S* п I I 5 >•» э *7 т> 1£ £|э „ /г (^"к? (тС-тх)2-! в //„ 2в,? ге$ / g3^[ J [нш^- +^tri . 2я [тС+тх х -jr-е в“ ~ (с-нп,)1 (C-mxf е+тх —L-m. —гл-—е 2вз +—^е гвз бх gx (тС-1п,}2~1 тС~т>. „ гц* gl -J V2fgx [Фт _ (тС-mA (тС+тЛ -0 —+ф —-JSI-у ох / у <?х / _й/.147+ Вг^ т* х \gx /J al т1 Г (С*т^г (тС^тх)2 * е^Че -е г‘х _^и!)2 (тС-тх)21 +;^-е- 2“з j
, 0 тС С -В
256
Рис. 2.106. Графики коэффициентов статистической линеаризации для ограничения сигнала по постоянному уровню при А С: а) б) 4°; в) 42>
Рцс. 2.107. Графики коэффициентов статистической линеаризации для двухпозициоиной релейной характеристики при А С: а) 6) «<2>; в) 42>
9 Ю. И. Топчеев
257
Рис. 2.108. Графики коэффициентов статистической линеаризации для однопозиционной несмещенной релейной характеристики при А С:
. J1). к S<2>. „,S<2)
a) ; б) Л| ; в)*2
При нечетной характеристике первый член зависимости (2.292) можно записать в виде
Г;(Л, тх, Ox) = k'0(A, тх, ах)тх.
(2.296)
Полученные формулы (2.293) — (2.296) показывают, что F*o и коэффициенты k*0 и k\ представляют собой усредненные за период 2л значения гармонической составляющей
функции F и статистических коэффициентов k0 и ki. Коэффициент а * — статистически усредненный за период 2л коэффициент гармонической линеаризации.
Для двузначных нелинейностей выходной сигнал
y = F[x(t), х(/)]. (2.297)
Применив к функции (2.297) совместную гармоническую и статистическую линеаризации, получим при-
258
Таблица 2.15
Коэффициенты совместной гармонической и статистической линеаризации Оля нечетно- симметричных однозначных нелинейностей
nfn Вид нелинейности а*
1 У В -С 0 /VI х П*0 Xi‘C№<Sx при тх +х0 ‘ 0 оо Чп b_\^L , б, Lu 2п * 1 Л’О *Сп(Г}'> при тх-> х0 =0
<— С в K = tgB
2 в 0 X Во (Г) при тх+хо=0 Г Со (j-) 0Х при тх + х0 *0
— -в
3 У в -с | ж -А^пвп п-0 х^С/Яб* при тх + хо=О ^г1псп(г/; п-0 x-f=C/V26x при тх+х0 =0 1
— 0 с -в
4. у -с п-0 “8Л frl] ; Х'-С/Ябх при тх+х0 *0 *Г/'7 х L бк X L-, 2п + 1 ПгО *Сп(г)} ; x.’CI^Ok при тх+хв=0
/ 0 С X k=tgfi
9*
259
Продолжение табл. 2.16
s (2п^1)! х (2п-1)!г
0 2П к ^"A^^Pi при тх+Х0 ‘О
2п
У = X ВХгпЧ к!(п-к)!(п*Ц при. тх*хо“0
6 У я ^ВА2 ч при тх+х0 =0 ^В(А2-2Рх) при тх*х0 •О
X у= Вх3
7 У 0 ВАР (у) при т^+хо'О ВбхЕ(г) при тх -i-Xo sO
*х ^«8x2sgn х
блаженное соотношение
y\t} = &-*0(A, tnx, сгж, ог,) +
+ а* (А, тх, ох, оА) A sin ф + 4-Ь*(4, тх, ах, at) A cos ф +
+ (4, тх, ах, ст±) Д (0 +
+ ^(4, тх, ах, (2.298)
О
°, /л\ dxi
где
В зависимости от (2.298) имеем
&~о (А, тх, ох, ot) =
2я
= 3~ (тх + A sin ф, 4© cos ф,
о
oXt Oi)cty, (2.299) 2я
а’(4, тх, ах, о^) = J (т,+ о
4- 4 sin ф, Аа cos ф, ах, at) sin ф ^ф, (2.300)
260
Таблица 2.16 Коэффициенты совместной гармонической и статистической линеаризации для нечетно - симметричных двузначных нелинейностей
и л/л Тип нелинейности а* ь* k*
/ в sM«C^28 . К 5) Ic-J л eL *% £ х st 1 : 1 «5 1 К to Cl «Ol’S + х С 2В°(^бУ С бхх/,[1/26x1 8- АЛ/?) MW ^xx<5jii^ 1 ^//тсбхх ,n / A -2R- 1 . ffi6xx + 1- 2B Г £м УЗБпЗм [ A oo , . _ jM 1 При Mx+Xo^O
„ . . б* б*г йХ'й'.- / А ) 1^/ у тх +х0 •0
-с 0 С X оо \ 2л •| * ]’О
8 п*Ъ при ^°х —) /пх + л ;чгб(// чЬЯця J при mx+xo-0
2 В Д fykLtf ^б*1 ^гп)Сп(х)^ 8 Аб *ВС 0 Г i* 6}i^B6}6x
У В -С -тС ,1 / V 1» *1 / А ' ’(VT^/ IIIJ * + fA f .Л 6XCM ffir6lt •o -i^n Г C(1*m)
, бхбх х 2л’(3»/х 6^ оо 2л дан при тх + х0 *0 2jv X'\c^+m 1 ]cn(fr X У-^г 'C(l+m) ~f . tf6x(2n$
0 тС С х -в 2згбхб/°
при mx+xo*0 „ I A ) ‘c"l tie,) при mx+x0‘D
3 В А г о© 2п а© г. -,2п В А 1-Bo(r)* 1 К» 1 C«4 + 1
у В 1/2ябх ^Ябх
-С тС -L С(1-т) L^J Mfr .5x6j ( А 1JC 1^бх/. при тх+х0 “0 ^+2C(1+m)» X * г / A \
-тС 0 С X 2ТГ1^6ХГМ при тх+Хо^0 X при mx+xo*O
-в о© 2n да» при mx+Xa ‘0
261
2л
b'(A, тх, ах, tfx) = ^4 (тж + о
4- A sin -ф, А<а cos ф, ах, а±) cos ф с?ф,
(2.301)
2Л
тх> °Х’ ki (j”x +
о
+ A sin ф, Лю cos ф, ах, ст*) с?ф,
(2.302)
2л
л;(Л, тх, стх, 3.) = ^ J Ь2(тх + 0
4-A sin ф, Дю cos ф, ст*, стл)йф. (2.303)
В формулах (2.299) — (2.303) коэффициенты а * и b * являются статистически усредненными за период 2л коэффициентами гармонической линеаризации а и Ь. Коэффициенты и k2 — усредненные за период 2л статистические коэффициенты Л, [по xt(0] и Л2[по х[(0].
В табл. 2.15 приведены формулы для вычисления коэффициентов совместной гармонической и статистической Линеаризации нечетных однозначных нелинейностей, а в табл. 2.16 — для нечетных двузначных нелинейностей *.
* Формулы, приведенные в табл. 2.15, заимствованы из киигн И. Е. Казакова. Статистические методы проектирования систем управления.—М.: Машиностроение, 1969.— 262 с.
Рис. 2.109. Графики функций, используемых при вычислении коэффициеитои совместной статистической и гармонической линеаризации:
о) Рп (v); б) с„ (y); «) D (у); в м
В формулах табл. 2.15 и 2.16 использованы функции В„(у), С„(у), D (y), Е(у) и Ф(у), которые вычисляют по выражениям
В„(у)= ..
. 4 (-»)ft+"[2(^ + n)]l f Y\2ft+I
(2n)t(ну(k+n)i u; :
Л-0 c„(y) =
rV2 p (—l)fe+" [2 (fe + n)]| /_y\2t (2п)1(Л!)2(Л + п)1 U) ’
v Д-0
где n = 0, 1,2,... и у = —; ax V2
£(y) =
_ Г V (—l)fe+1 (2Л)1 /уч»"1
“Л(Л1)’(2Л-1)1(Л+1)1 \ 2 J ’
¥ fe-0
E (V) = V? Y2 [1 + 2Y2 -
E(-l)ft(2fe + l)t / у k\ [(Л + 2)1]* I 2 )
Л-0
Графики для определения коэффициентов Вп(у), Сп(у) приведены на рис. 2.109, а и б, а Г>(у) и Е(у) — на рис. 2.109, в. Таблица для функции Лапласа Ф(у) приведена в прил. П-1.4.
262
5. ЛОГАРИФМИЧЕСКИЕ ЭКВИВАЛЕНТНЫЕ АМПЛИТУДНЫЕ И ФАЗОВЫЕ ХАРАКТЕРИСТИКИ СЛОЖНЫХ НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ
В п. 2 гл. 2 были приведены таблицы с формулами для вычисления логарифмических эквивалентных амплитудных и фазовых характеристик однозначных и. двузначных простейших типов нелинейных элементов q(A), q(x0, А), &"0(хй, 4) и ц(4), р,(Хо> 4). Там же изображены таблицы, построенные в полулогарифмическом масштабе для характерис-тик SOlg^. 2018-77^45-2016тйЬп,дБ) ” -|80°-нИ). —180° — .ц(хо, 4) (в град), которыми следует пользоваться при исследовании обычного типа нелинейных САР.
Для подавления автоколебаний или расширения областей устойчивых состояний в некоторых типах нелинейных систем иногда применяют сложные нелинейные элементы, представляющие собой сумму параллельных нелинейностей или последовательное соединение двух нелинейностей, разделенных между собой линейным динамическим звеном, или нелинейных и линейных элементов, образующих внутренние контуры с отрицательной и положительной обратными связями.
Рассмотрим первый тип построения сложных нелинейностей, которые состоят из суммы нескольких простых однозначных или двузначных нелинейных характеристик. Для определения коэффициентов гармонической линеаризации таких нелинейностей следует применять табл. 2.1 и 2.2 и использовать процедуры, приведенные в следующих трех примерах.
Пример 2.27. Определить формулы для вычисления коэффициентов гармонической линеаризации сложной иелииейиости, состоящей из суммы трех простых однозначных нечетных симметричных нелинейностей, структурная схема которой изображена иа рис. 2.110, а. Построить шаблон для данной иелииейиости.
Как следует из рис. 2.110, а, суммарный коэффициент линеаризации сложной иелииейиости ас определим по формуле
вс (А) = ai (А) + аг (А) + а3 (А). (2.304) f
По данным табл. 2.1 находим соотношения для коэффициентов гармонической линеаризации аь аз и аз. Подставив их в (2.304), получим
ас (А)
С, С,
arcsin —j- 4- arcsin +
Л
2(Bi- В,) v
(2.305)
Графическая зависимость для коэффициента гармонической линеаризации ас в соответствии с формулой (2.305) может
сложной иелииейиости:
а—структурная схема нелинейности; б— графики коэффициентов ои а3, а3, ас; в—шаблон 20 1g (!/Чс(Л)]
263
Рис. 2.Ш. Гармоническая линеаризация сложной нелинейности: а—структурная схема нелинейности; б—.графики коэффициентов аг а3, ас, Ьс; в—шаблон
20 1g [1/?с (4)]; а—шаблон—180°—цс (Л) .
быть найдена суммированием элементарных коэффициентов гармонической линеаризации простых нелинейностей, снятых с рис. 2.5, а, 2.6,6 и 2.8, в, как это показано иа рнс. 2.110,6. Графнк ас(Л) изображен иа рис. 2.110,6 жирной сплошной линией. Логарифмическая амплитудная характеристика 201g д) приведена в виде шаблона (рнс. 2.110, в).
Пример 2.28. Определить формулы для вычисления коэффициентов гармонической линеаризации сложной нелинейности. Построить шаблон для дайной нелинейности, показанной на рнс. 2.J 11, а.
Суммарный коэффициент гармонической линеаризации для нее определим по формулам' '(.‘Г.’ Г- Г.
«С (Л) — 1 + «1 (Л) + а, (Л); (2.806)
5С(Л) —6,(Л). (2.307)
Для вычисления коэффициентов а<, Oj И bi следует пользоваться табл. КГ и 2.2. Тогда получим 1
2 г £
Ос(Л)-«1+-jj-1 fe arcsin-j-+
+т«в+с*) д/'-Ст-)1} (2.308)
МЛ)---^-. (2.309)
Графические зависимости для коэффициентов гармонической линеаризаций ас и Ьс в соответствия с формулами (2.308) и (2.309) могут быть найдены суммированием коэффициентов гармонической линеаризации простых нелинейностей, взятых с рис. 2.5, а и 2.19, а и 6. Соответствующие кривые показаны иа рис. 2.111,6, где характеристики ас в Ьс показаны жирными лиииямй.
Для нахождения эквивалентных амплитудной и фазовой характеристик сложного нелинейного элемента (рнс. 2.111, а) воспользуемся формулами (2.308) и (2.309). При этом
(Л) — jl + [fe arcsin -j- +
+ ^да+С*>дД-(^)1]}’ +
pe(A)B*arctg<
4ЙС
1 .. г1 С
яЛ* 4-2 |ЛЧ arcsin +Л(2Д+С*)д/1-ЦУ
(2.311)
264
1k (Л) =
Логарифмические амплитудные и фазовые характеристики 201g и
— 180s —Цс(Л) приведены в виде шаблона, (рис. 2.111, в, г).
Пример 2.29. Определить формулы для вычисления коэффициентов гармонической линеаризации сложной нелинейности, состоящей из суммы двух двузначных нелинейностей, структурная схема которой изображена иа рнс. 2.112, а. Построить шаблон для данной нелинейности.
Из рис. 2.112, а видно, что суммарные коэффициенты гармонической линеаризации ас(Л) = а.(Л) + аа(А); (2-312) 6с (Л) = 6, (Л)+ 6, (Л). (2.313)
Для вычисления коэффициентов ah aj, di и bt будем пользоваться табл. 2.1 и 2.2. Графические зависимости для коэффициентов гармонической линеаризации ас и Ьс в соответствии с формулами (2.312) и (2.313) могут быть найдены суммированием коэффициентов гармонической линеаризации простых нелинейностей, снятых с рис. 2.19, а ибн 2.21, а и б. Соответствующее построение показано на рис, 2.112,6, где суммарные характеристики ас и Ьс изображены жирными линиями.
Эквивалентные амплитудные и фазовые характеристики сложного нелинейного элемента (рис. 2.112.в) будем находить с помощью формул (2.312) и (2.313);,
хд/4(-4)Г+
— arctg
(2.315)
Логарифмические амплитудная
2018 —77Г и фазовая —180° — цс (Л) ха-<7с (Л)
рактеристики показаны в виде шаблона (рис. 2.212,0, г, жирные линии).
Аналогичным образом можно находить формулы вычисления коэффициентов гармонической линеаризации и строить шаблоны для сложных нелинейностей, представляющих собой суммы нескольких элементарных нелинейностей различных типов, включая нелинейности со смещением хо-
Пример 2.30. На рис. 2.113, а показана структурная схема сложной нелинейности, образованной суммой простых нелинейностей при подаче иа вход сигнала х(1) = = х0 4-Л sin wf. На рис. 2.113,6—г изображен шаблон с характеристиками
20lg ^o(t. Л)’ 2018 Сс(х0, Л) "
— 180s —Цс(х0, Л).
265
Рассмотрим второй тип построения сложных нелинейностей, которые образованы последовательным соединением двух простых нелинейностей, разделенных между собой линейным динамическим звеном. Если линейное звено с частотной характеристикой Ч7л(/<о) обеспечивает хорошую фильтрацию сигнала, то иа выходе второй нелинейности образуется гармонический сигнал в виде 1-й гармоники. В этом случае эквивалентные амплитудные характеристики двух однозначных нелинейностей qc можно находить как произведение двух эквивалентных амплитудных характеристик элементарных нелинейностей, т. е.
<?с (Л,, со) = <7, (Л,) <?2 (Л2), (2.316) где амплитуды иа входе второго нелинейного элемента будут
А2 = Л191 (Л,) | Гл (/со). (2.317)
Если линейное звено ие обеспечивает достаточную фильтрацию, то ие выдерживается условие
| Г3 (/Зсо) |< | «7, (/со) |. (2.318)
В этом случае следует учитывать влияние высших гармоник (см. п. 2 данной главы). Наличие линейной части приводит к сдвигу фазы р.с(Л,.со). Таким образом, шаблон состоит из двух характеристик 20,g^cb^ и-18°в-Мс(»в«>).
Пример 2.31. Определить логарифмические характеристики 201g —— и
—180° — |к(Л|, со) для сложной нелинейности, состоящей из последовательно соединенных нелинейности Fi, линейного звена 117, и нелинейности F2 (рис. 2.114, а), и построить шаблон 20 lg[l/<7c(A|, со)] и —180°— — Цс(Л,,ш).
Из рис. 2.114, а видно, что при условии (2.317) амплитуда иа входе второй нели-
нейности
Лг = Л191 k' (2.319)
4 А‘ 7 VM+i
Эквивалентный коэффициент линеаризации первой нелинейности вычислим по формуле
( С, \ 2 ( . С, ,
91 bd==n(arcsin дг +
<-£- V' - (-хгУ) (2“’
Пусть параметры имеют следующие числовые значения: Ci = 1 рад; й, = 2 и Т, = 0,04 с. Подставляя их в выражения (2.319) и (2.320) при со.- = 2; 4; 6 и 10, получим зависимости А2 = f(4i,со;), которые в виде семейства кривых изображены на рис. 2.114, б.
Эквивалентные коэффициенты линеаризации для второй нелинейности вычислим по формуле
где С2= 0,5 рад.
По кривым, приведенным на рис. 2.114,6 для ряда значений Ci/Ai, найдем А2, а затем вычислим С2/А2 Подставляя в формулу (2.321) значения Сг/Ai, получим семейство кривых q2(C2/A2). На рис. 2.114, в построена зависимость 20 lg[l/gc(4,,«)] для ранее принятых значений со;. Фазовые характеристики вычислим по формуле
Нс <>) = — arctg со/Т,. (2.322)
На рис. 2.114, г построена характеристика — 180° — цс “У Таким образом, кривые иа рис. 2.114,8, г образуют
266
Рис. 2.114. Гармоническая линеаризация двух нелинейностей, разделенных линейной частью:
а—структурная схема сложной нелинейности; б — семейство функций А2 (А,, <о); в —шаблон
20 18 [1/<7с (А,, <>)]; а—шаблон —180°—цс (Ар а)
шаблон, с помощью которого можно исследовать нелинейные САР (см. гл. 7).
Пример 2.32. Определить логарифмические характеристики 20 lg [1/дс (Аь (о)] и —180° — |1С Аь со) сложной нелинейности (рис. 2.115, а). Рассмотрим два случая.
Первый случай. В передаточной функции линейной части 7’2>7’i, т. е. 'обеспечивается фильтрующее действие сигнала на входе второй нелинейности. При этом можно пользоваться методикой, приведенной в примере 2.29, т. е. находить семейство характеристик
( С, \ / 1 + Г]®2
A2 = Ai91 -i- д/——(2.323) \ А, / у 1 + 72®
Рис. 2.115. Гармоническая линеаризация двух нелинейностей, разделенных линейной частью:
а—структурная схема сложной нелинейности; б— семейство функций А2 (А(, <о); в —шаблон
20 18 [1/<7с (АР <“)]: г—шаблон —180°—|*с (Ар <о)
где эквивалентный коэффициент первой нелинейности будем вычислять по формуле
"• (^)“|4(а"=!",Т7 + +4rV'-(-x-)!)- <2-зм>
Пусть параметры имеют следующие числовые значения: Ci = 1,0 рад; Т\ = 0,04 с; 7*2 = 0,4 с. Подставляя их в выражения (2.323) и (2.324) при со = 2; 4; 6 и 10, получим зависимости Аг = /(Сь/Ai. со), которые в виде кривых изображены на рис. 2.115, б.
Эквивалентный коэффициент линеаризации для второй нелинейности вычислим по формуле
/ С2 \ 2 f С2
•Ш-Д™ Х +
« £-7'-(£)’)• <2Ж>
где С2 = 0,5 рад.
По кривым, приведенным на рнс. 2.115,6 для ряда значений С|/Аь найдем А2, а затем С2/А2. Подставляя значения С2/А2 в формулу 12.325), получим семейство кривых <72(С2/а2). На рис. 2.115,в построены
267
Рис. 2.116. Гармоническая линеаризация двух нелинейностей, разделенных нефильтрующей лниейиой частью:
а—структурная схема сложной нелинейности; б— семейство функций A2i (А,. ш): в—семейство функций б3 (А,, ш); г—функция <р3 (ш); б—шаблон 20 1g [1/<7с (А,, <в)]; е—шаблон —180’—рс (Ар ш)
зависимости 201g[l/gc(4i, ш)]. Фазовые характеристики вычислим по формуле
На рис. 2.115, г построена характеристика —180° — р.с ш). В результате полу-
чим шаблон (рис. 2.115, в, г).
Второй случай. В передаточной функции линейной части Т2 < Ti, т. е. в сложной нелинейности ие обеспечивается условие (2.318). При этом необходимо с помощью структурных преобразований исключить нуль s = —1/Ть Преобразованную исходную схему сложной иелииейиости (рнс. 2.115, а) можно привести к виду, изображенному на рис. 2.116, а, где нелинейность Fi совместно с последовательным соединением двух звеньев образует нелинейность F*, которая выделена на рис. 2.116, а штриховой линией.
На рис. 2.116,6 построены характеристики
X21-^-=L=, (2-327)
7 2 со + 1
где
^21 = Л1<71 (Ci/Ai) aJ 1 + Т, ®2. (2.328)
Семейство характеристик построено для параметров Ci — 1, Г; = 0,4 с, Т2 == 0,04 с и ранее принятых он. Для учета влияния
3-й гармоники иа нелинейность F2 запишем
выражение для ее амплитуды:
- л/1 , /1+^(За»2
V Ai у 1 + Т1 (з°>)2
(2.329)
Семейство характеристик 0з(41,ш) = — А«зМ1> где Ацз было вычислено по формуле (2.329), построено на рис. 2.116, в.
Воспользуемся следующими формулами, учитывающими влияние 3-й гармоники иа первую гармонику для нелинейности F2:
вг (А21) = q2 (A2i) + бз cos фз Д01з (^21),
(2.330)
да (^21)1=8 — дз sin <Рз Дб^з (^4ai)» (2.331)
где
. (Т|-Г2)«О
Фз — arctg j + TiTi(j)2
(7i — Та) 3<а
arctg 1 + Т’1Г2(3(о)2- ( 33
сдвиг фаз между 1-й и 3-й гармониками иа входе нелинейности Р2. График зависимости фз от е> приведен иа рис. 2.116, е. Шаблон 20lgfl/фсИь <о)], с учетом того, что фс = у а2 + Ь2> построен иа рис. 2.116, д, а шаблон—180° —цс построен иа рис. 2.116, е. Далее вычислим
268
семейство фазовых характеристик, учитывая при этом влияние 3-й гармоники:
рс = -180° - arctg —. (2.333)
аг
Шаблон для фазы по формуле (2.333) построен на рис. 2.116, е для двух значений Л|.
Рассмотрим третий тип сложных нелинейностей, структурные схемы которых представляют собой контуры с обратной связью, состоящие из линейной части и однозначной или двузначной нелинейности (рис. 2.117, а — в). Причем нелинейная и линейная части могут находиться в прямой цепи (рис. 2.117, а) или линейная часть — в прямой, а нелинейная — в обратной цепи (рис. 2.117, б), и наоборот (рис. 2.117, в). Нелинейная часть в контуре может состоять и из двух нелинейностей, разделенных между собой линейным звеном. В этом случае структурные схемы будут иметь вид, как показано на рис. 2.117, г — е.
Частотные характеристики замкнутого нелинейного контура, изображенного на рис. 2.117, а, можно записать
1 + <2-334>
Рис. 2.117. Структурные схемы замкнутых нелинейных систем:
а— замкнутая система с нелинейностью н линейной частью в прямом канале; б — замкнутая система с нелинейностью в обратной связи; в — замкнутая система с линейной частью в обратной связи; а —замкнутая система с линейной частью н нелинейностью в обратной связи; д — замкнутая система с двумя нелинейностями, разделенными линейной частью, в прямом канале; е — замкнутая система с двумя нелинейностями, разделенными линейной частью, в обратной связи
Разделив числитель и знаменатель выражения (2.334) на /(Л), получим
Фк (A, /а) == —, Гл(/М)---. (2.335)
7(лТ + ^(/<о)
Ранее было показано (гл. 1, п. 7), что для линейной системы передаточная функция замкнутого контура Ф (/©) = И70 (/©)/[! + И70 (/со)]. (2.336)
Из сравнения формул (2.335) и (2.336) следует, что если логарифмическую амплитудно-фазовую характеристику линейного замкнутого контура строим относительно центра номограммы с координатами 0 дБ и — 180° [эти координаты соответствуют формуле (2.336)], то логарифмические амплитудно-фазовые характеристики замкнутого контура с нелинейностью определим относительно центров номограммы, смещенных на величину 1//(Л), вычисленную в дБ *.
Величина смещения зависит от вида нелинейности и амплитуды сигнала А на ее входе. В результате можно получить семейства амплитудных 20 1g | Фк(4, /©) | и фазовых агд[Фк(Л, /©)] характеристик замкнутого контура.
* Для однозначных нелинейностей J(A) — q(A) н характеристики 20lg[l/<7(А)] откладывают по оси ординат номограммы замыкания. Для двузначных нелинейностей координаты амплитудно-фазовых характеристик замкнутого контура наносят в виде точек на номограммы замыкания 20 lgfl/?(A)J по оси ординат и —180° — — Н(А) по оси абсцисс. Затем эти точки соединяют сплошной линией.
269
1т,дБ
a)
Рис. 2.118. Определение частотных характеристик замкнутой системы с однозначной нелинейностью: а—графики характеристик
20 lg [1/<? (С/А)] и 20 lg «7Л (/<»), построенные в координатах номограммы замыкания; б — семейство амплитудно-фазовых логарифмических частотных характеристик замкнутой системы
270
Для удобства нахождения логарифмических амплитудных и фазовых характеристик замкнутых контуров с нелинейностями необходимо логарифмическую характеристику линейной части контура строить на прозрачной бумаге в масштабе номограммы. На оси ординат, проходящей через точку, соответствующую центру номограммы, откладывают значения характеристики 20 lg [ 1 lq (А) ]. Затем накладывают прозрачную бумагу с кривой 201g так, чтобы точка ха-
рактеристики 20 lg [Xjq(Л) ] с интересующей нас амплитудой At совпадала с началом координат номограммы. Точки пересечения характеристики 201g со
сплошными линиями номограммы соответствуют значениям амплитуд, а точки пересечения той же характеристики со штриховыми линиями номограммы — значениям фаз замкнутого контура с нелинейностью. Для другой амплитуды А2 смещают прозрачную бумагу и по новым точкам пересечения с кривыми линиями номограммы получают значения амплитуд и фаз контура. Таким же образом, изменяя значения амплитуд А3, Д4, ..., At, получают семейство искомых амплитудных и фазовых характеристик замкнутого контура.
Пример 2.33. Построить семейства логарифмических амплитудных и фазовых частотных характеристик для замкнутого контура (рис. 2.117, а) с однозначной нечетно-симметричной нелинейностью типа насыщения и линейной частью с передаточной функцией
W\(s) = 40/[s(0,ls + 1)]. (2.337)
Подставим в выражение (2.337) s = /со и построим на прозрачной бумаге характеристику 20 1g В7л(/со) (рис. 2.118, а). Здесь же на оси абсцисс точками нанесем значения 20 lg[l/?(C/4)] при С/Л = 0,2; 0,4 и 0,8. Эти значения взяты из графика, показанного на рис. 2.12, а. Наложим прозрачную бумагу на номограмму замыкания, как это изображено иа рис. 2.118, а (для С/Л = 0,2), и по точкам пересечения определим амплитуды
20 1g | Фк (Л, /со) | и фазы arg [Фк (Л, /со)].
На рис. 2.118,6 нанесены полученные таким образом точки. Соединив их сплошными линиями, построим логарифмическую амплитудную и фазовую характеристики замкнутого контура с однозначной нелинейностью. Перемещая прозрачную бумагу по номограмме, получим семейство характеристик замкнутого контура (рис. 2.118,6).
Пример 2.34. Построить семейство логарифмических амплитудных н фазовых частотных характеристик для замкнутого контура (рис. 2.117, а) с двузначной нелинейностью типа люфта при С/Л = 0,2; 0,4 и 0,8. Полученные значения 201g[l/?(CA4)] и —180°-р(С/Л) нанесены точками иа рис. 2.119, а. По ним построена кривая /; кривой 2 показана амплитудно-фазовая частотная характеристика линейной части системы, полученная с помощью передаточной функции (2.337). Накладывая прозрачную бумагу на номограмму замыкания, найдем семейство частотных характеристик замкнутого контура с двузначной нелинейностью (рис. 2.119,6).
Рассмотренная методика может быть применена к САР с двумя нелинейностями, разделенными собственной линейной частью. В этом случае структурную схему контура можно представить, как показано иа рис. 2.117,6. Тогда выражение (2.335) можно переписать в виде
фк(Д,/о) =------- --------------, (2.338)
ч 7-7---Г + «’'л (/СО)
7с (Л, /со)
где 7с (Л, со)—эквивалентная передаточная функция сложной нелинейности, зависящей от двух переменных Л и со.
Для получения семейства логарифмических амплитудных и фазовых частотных характеристик контура со сложной нелинейностью необходимо на прозрачной бумаге построить два типа кривых: для сложной нелинейности по точкам с координатами 20 lg[l/q(Л, со)], — 180° — ц(Л, со) и для линейной части характеристики 20 lg Wx(ju>). Затем следует наложить прозрачную бумагу с построенными кривыми иа номограмму, совмещая ее начало координат с точкой иа кривой функции * 20 lg[l/7c (Л,/со)], имеющей заданную амплитуду Ai и частоту со,-. Значения амплитуд 20 1g | Ф*.к) (Л, /со) | и фаз arg [Ф*к) (Л, /со)} для замкнутого нелинейного контура находятся по точке пересечения логарифмической амплитудно-фазовой характеристики с кривыми номограммами только при частоте со/ (рис. 2.119, а). Следует отметить, что при таком построении обеспечивается выполнение условия, заданного в виде формулы (2.338). Перемещая прозрачную
* В этом случае функция 7с (А °) =
. /Г-180»-|1с(А.й»]
= 9с (Л, со) е 1 с J.
271
Lm, дб
ш=то a"i
Рис. 2.119. Определение частотных характеристик замкнутой системы с двузначной нелинейностью:
а — графики характеристик 20 lg [1/<? (С/Л)1 и 20 1g Гл (/<>) в координатах номограммы замыкания; б — семейство амплнтудио-фазовых логарифмических частотных характеристик замкнутой системы
272
бумагу с кривыми 20 Ig[l/^с (Л/, со)] и 201g Жл (/со) по номограмме, получим семейства амплитудных фазовых частотных характеристик замкнутого нелинейного контура (рис. 2.119, б).
Пример 2.35. Построить семейство логарифмических частотных характеристик для замкнутого контура со сложной нелинейностью (рис. 2.117, д). Как видно из рис. 2.117, д, сложная нелинейность состоит из двух нелинейностей Ft и Fz, разделенных между собой линейным звеном Гь Структурная схема и параметры такой нелинейности приведены в примере 2.31.
По кривым 20 lg[l/<?c(4i, со)] (рис. 2.114, д) и —180° —Цс(Ль со) (рис. 2.114, е) построим на прозрачной бумаге характеристику 20 Igfl/^n,/со)] и, накладывая ее несколько раз иа номограмму, как это показано на рис. 2.120, а, получим в виде точек значения амплитуд 20 lg|®„(4b /со) | и фаз arg[<DK(4i,/ю)]. Соединив их сплошными линиями, построим иа рис. 2.120,6 семейство логарифмических амплитудных (рис. 2.120,6) и фазовых (рис. 2.120, в) частотных Характеристик для замкнутого контура со сложной нелинейностью.
Для построения семейства логарифмических амплитудных и фазовых характеристик замкнутого контура, структурная схема которого изображена на рис. 2.117,6, будем применять формулу
Фк (Д, /со)
Гл(/ю) -1
+ /м’'
(2.339)
которую можно представить в виде
20 1g | Ф<к> (Д, /со)| =
= 201g
Гл (/сэ)
+ Гл (/со)
1
/(Д)
(2.340)
Из формулы (2.340) следует, что порядок построения частотных характеристик замкнутых контуров с помощью номограммы замыкания в основном сохраняется. Различие заключается лишь в изменении масштаба разметки оси ординат для амплитудных характеристик в 1//(Д) раз. Масштаб разметки фазовых характеристик не изменяется.
Для построения семейства логарифмических частотных характерис
тик замкнутого контура (рис. 2.117, д) воспользуемся формулой
201g| ФК(Д, /<о)| =
= 201g
(2.341)
В этом случае с помощью номограммы также получим семейства логарифмических амплитудных н фазовых характеристик. Затем следует изменить значения амплитуд для каждой частоты <о; в l/У(Д, (о() раз и уменьшить фазовые углы при тех же частотах на — arg \ f (Д, (оОЬ
Построение логарифмических частотных хар!актеристик замкнутого контура (рис. 2.117, в) выполним по формуле
201g] ФК(Д, /<о)| =
НГл (/Ш) 1 1 )
— +Гл(/<0)
/(4) + лЧ ’ J )
(2.342)
Из формулы (2.342) следует, что полученные по номограмме семейства характеристик необходимо перестроить, изменяя значения амплитуд при о)< в 11/1Гл(/(щ) | раз и соответственно фаз на arg[^(/(o<)].
Рассмотрим последний вариант из числа возможных структурных схем сложного замкнутого контура (рис. 2.117, е). В этом случае для построения семейств логарифмических частотных характеристик воспользуемся формулой
20^|Фк(Д, /ш)| =
= 201g
Гл (/со) 1 _____1_____+ /с (А /®)
+ Гл(/<о) J
Zc (4. /ю)
(2.343)
Полученные по номограмме амплитудные и фазовые частотные характеристики перестроим в соответствии с сомножителем 1//с(Д, /со).
273
a)
Рис. 2.120. Определение частотных характеристик замкнутой системы с двумя нелинейностями, разделенными линейной частью:
а—изображение характеристики 20 lg [ 1/<?с (Л,, <>>)] в координатах номограммы замыкания; б — амплитудная логарифмическая характеристика замкнутой системы; в — фазовая характеристика замкнутой системы
274
6. СТАТИСТИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ СУЩЕСТВЕННЫХ ДИСКРЕТНЫХ НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ
В гл. 1 было показано, что в САР наряду с непрерывными применяют и дискретные способы преобразования сигналов. В зависимости от типа квантования сигнала системы подразделяют на импульсные (с квантованием сигнала по времени), релейные (с квантованием сигнала по уровню) и цифровые (с квантованием сигнала как по времени, так и уровню). Квантование по времени осуществляется импульсным устройством иа основе трех типов модуляции: амплитудно-импульсной (АИМ), широтно-импульсной (ШИМ) и частотно-импульсной (ЧИМ). При амплитудно-импульсной модуляции с входа быстродействующего импульсного устройства в тактовые моменты времени То снимаются импульсы в виде сигналов б-функций. При широтно-импульсной модуляции на выходе импульсного элемента образуются импульсы, ширина которых в тактовые моменты То изменяется в зависимости от амплитуды входного сигнала. При частотно-импульсной модуляции сохраняется постоянная ширина импульса малой длительности, а период квантования определяется амплитудой входного сигнала.
Быстродействующие устройства с АИМ (преобразователи аналог — код) являются линейными импульсными элементами, а устройства с ШИМ и ЧИМ — нелинейными. Устройства с квантованием по уровню для управляющих ЭВМ часто относят к нелинейным импульсным элементам. Нелинейный импульсный элемент для удобства математического описания можно представить в виде совокупности линейного и нелинейного элементов.
При проектировании САР с цифровыми устройствами и нелинейными импульсными элементами воспользуемся методами гармоничес
кой и статистической линеаризаций [38].
Сигнал на выходе двузначного нелинейного импульсного элемента в соответствии с выражением (1.123) запишем в виде
у (кТй) = [х (t)]6 (t), (2.344) где
6(0 = Z б^-кТо)- (2.345)
К»-сю
При этом будем считать, что входной сигнал является гармоническим, т. е.
х (0 = A sin (<oZ + <р), (2.346) причем
о = п/(пТ0), (2.347)
где пТ0 — полупериод гармонического колебания (n = 1, 2, ...).
Подставив формулу (2.347) в
(2.346), а затем в выражение (2.344), найдем
у (кГо) = Т [A sin + <р)] б (О-
(2.348)
При учете 1-й гармоники выходной сигнал
4/1 (л^о) = А [а (А, п, ф) sin ~~ +
+ Ь(А, п, ф)соз-^-]б(/). (2.349)
Определим условия наилучшего квадратического приближения yi (кТ0) к у(кТ0). Для этого запишем следующее соотношение:
Г»/2
II ёт ||2 = у- ( ег(/)й, (2.350) 7 О J
0
где Го/2 — полупериод функции е(/).
Подставив в соотношение (2.350) соответствующие выражения, полученные из (2.348) и (2.349), найдем
1|8т|Р = лГо
—йт j {^г[Лsl"(йh+'|^)]-О
— А |а(А, п, ф) sin -^у- +
+ b (А, п, ф) cos |2 б (0 dt.
(2.351)
275
Условия минимума средней квадратической ошибки при замене точного выходного сигнала приближенным будут
aiiemll2 дАа (Л, п, qp)
д || ёт II2 дАЬ (Д, п, ф)
(2.352)
Учитывая соотношение (2.352), из выражения (2.351) при условии (2.345) получим
л—1
Ё МлsinGr + *’’)]-к-0
— А [а (А, п, qp) sin +
+ ь (Л, п, ф)соз-^-]}х
X sin — = 0;
Ё {^р^п(^+ф)~ к-0
— Л [а (Л, п, ф) sin +
+ 6 (Л, п, ф) cos -] } X пк п
X cos — = 0. ' п
(2.353)
Из выражения (2.353) после ряда преобразований определим формулы для вычисления коэффициентов гармонической линеаризации в виде
а (Л, п, ф) =
л—1
-ж-Ё^[-”|"(^-+»)]х
к-0
к > • Л/С
Xsin---;
п
Ь (Л, п, ф) =
л-1
[л sin (-Т- + *₽)]X
к-0
V . як
X cos —. п
(2.354)
Пользуясь формулами (2.354), найдем эквивалентную передаточную функцию
/(Л, п, ф) = <7(Л, п, ф)е ' п: Л
(2.355) где
q (Л, п, ф) =
= '\/а2(А, п, ф) + ^2(Л, п, ф); (2.356)
(лк . \ , Ь (А, п, ф)
—+ <p)--arctg7lT^i.
(2.357)
По формуле (2.356) находим эквивалентную амплитудную характеристику дискретного нелинейного элемента, а по (2.357) — эквивалентную фазовую характеристику.
Для однозначного дискретного нелинейного элемента в соответствии с формулами (2.354) имеем
q(A, п, ф) = а(Л, п, ф) (2.358) и
н(^+ф)-о.
В работе [38] показано, что коэффициент гармонической линеаризации дискретного нелинейного элемента а (А, п, ф) равен сумме непрерывных коэффициентов гармонической линеаризации по всем гармоникам (1 + 2кп)-го порядка т. е.
ОО
а (А, п, ф)= £ а1+2кпИ> ф)-
(2.359)
В табл. 2.17 приведены формулы для вычисления коэффициентов гармонической линеаризации однозначных дискретных нелинейных элементов и построены соответствующие характеристики в координатах Re а (Л, п, ф) и Im а (Л, п, ф). В табл. 2.18 приведены формулы для коэффициентов гармонической линеаризации двузначных дискретных нелинейных элементов. Здесь также построены характеристики ЯГ (Л, п, ф) в той же системе координат.
При применении логарифмических характеристик для исследования дискретных или дискретно-непре-
276
Таблица 2. П
Коэффициенты гармонической линеаризации однозначных дискретных нелинейных элементов
277
Таблица 2.18
коэффициенты гармонической линеаризации двузначных дискретных нелинейных элементов
Продолжение таблицы 2.18
2 У В -тС ^+sgn^ A sin <р j- с|]х х[/+ sgn )] + + рулр Sin к+<р + + sgn (a sin {^-х+<р j + С jj х xp-jj/rcwpy/r+pjjpM -mcj+sgn^A sin [-^x + g> j- fjjx xQ+syn гм p^x + gijj + +рдл pj/л {jfx+<f j+fl/Cp + sjnpj/Tzppr + yj + C )]x х[/-$0л см^к+^jj jcor-^K a ’Л J,o o,« 0,6 o,^ 0,2 1 1 1 8 0,4 0,8 0 -0,2 -0,4 -0,6 -0,8 '
-С тС
Г 1 1 * j 5^TJ0 A -1 / / _ у (p=o
-тС 0 С X
-В
0 n = 5 10 A 2; 8=M;A»C; (f>=0; f ,fv
3 У 8 -С -тС ^гс\ +sgn ^Asin (^-к + /р [ /* ♦*?я( *?))]+ +[гулр5/л^+^ j+f)+ + sgn p sin (jpK+<p 'j-mc j] p--s^cwpEjr *^]p/n-£* ^{[ЦЧН4 +sgn pj/n ^л’+^j+w^] p+ +J?npWp^))]+ + [^лрг/л pf/r+y^ ->-c}+ + sgn ^Asin^x+p'j - wfjp- a 1,2 1,0 0,8 0,6 0,6 A i i i 8 1,2 1,0 0,8 0,6 0,6 1
0 тС С х -В
5 W A =2; В=С=Г, A^C,m-0,15 -°’ f 0 5 / 10 A tf = O
Тайлица. 2.19
280
рывных систем используют шаблоны 201g [Ifq(Л, п, <р)] и— 180° — ц(Л, п, ф). Поэтому в табл. 2.19 и 2.20 приведены формулы для вычисления амплитудных и фазовых характеристик соответственно однозначных и двузначных нелинейных элементов (там же построены и шаблоны).
Теперь перейдем к определению формул для вычисления коэффициентов статистической линеаризации однозначных дискретных нелинейных элементов из условия наилучшего средиеквадратического приближения замены тбчного выходного сигнала приближенным. В этом случае формулы (2.268) и (2.274) следует записать в виде
Ул («^о) = [*од (Чд)’ ст?‘) Чд) +
+ ^>(ЧД). <д))^(кГо)]6(П;
min {Л4[^(кТо)-^(кТо)]26(О},
к<Д>,
(2.360) где kfi и удовлетворяющие условию (2.360), находим из уравнений
Если считать, что плотность вероятности распределена по нормальному закону, т. е.
ww, (кт0)]=
[х(хГ0)-т<Д>]2
1 -----------е * ^2я а^д)
(2.364)
то с помощью формул (2.362) и (2.363) можно найти значения коэффициентов статистической линеаризации для однозначных дискретных нелинейностей.
Пример 2.36. Определить коэффициенты статистической линеаризации однозначной дискретной нелинейности типа идеального реле (см. пример 2.23) я построить кривые
^д)- - и й(д> - * - в зависимости от
Для вычисления воспользуемся формулами (2.362), (2.363); в этом случае можно записать
п
X Bs*ro)]x х к— — п
xfi к (кГо). KT0]dKT0-,
п
Мд'=-4г Е [Ч*го)-4д)]х
х к----------
X в sgn [х (кТо)] fl [х (кТо) кТо] dtiT0.
- Л<Д)х(/сТо)]2б(О) = О.
(2.361)
Из уравнений (2.361) имеем *од)(Чд)> °хд)) =
X fi [х (кТ0), (кТо)] d (кТй)-, (2.362) ^(т<л>,а<Д>) =
= -^Г £ ^(^О)-ЧД)]Х
Х К-Л
X F [х (кГ0)] f, [х (кто), (кГо)] d m.
(2.363)
Соответствующие кривые построены на рис. 2.121. Можно получить также фор-
Рис. 2.121. Графики коэффициентов статистической линеаризации и Л<д> для дискретной нелинейности типа идеального реле
281
Таблица 2.20
Амллитудно - фазовые характеристики и шаблоны для двузначных дискретных нелинейных элементов
мулы для совместной гармонической и статистической линеаризации; тогда вместо функции (2.290) применяют функцию
х(кГо)-[4Д) + *1(^о) +
+ A sin (-^+ ф)] « (0.
но при этом значительно усложняются формулы для расчетов коэффициентов k\n\
7. ВЫЧИСЛИТЕЛЬНЫЕ ПРОЦЕДУРЫ ДЛЯ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ ГАРМОНИЧЕСКОЙ И СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ НЕЛИНЕЙНЫХ ЭЛЕМЕНТОВ
Для сложных видов дискретных нелинейностей довольно трудно получать формулы, позволяющие вычислять коэффициенты гармоничес
282
кой и статистической линеаризации. В этом случае можно рекомендовать пользоваться программами, составленными на языке ПЛ/1 для различных численных процедур интегрирования.
При гармонической линеаризации непрерывных нелинейностей [см. формулы (2.147), (2.148)] вычисляют следующие коэффициенты:
2л/0)
<*(4) = ^ J ^HsiiwOX о
X sin со/ dt', (2.365)
2л/ш
= j ^HsincoOX о
X cos at dt. (2.366)
Если считать, что хк = Лк sin <а(к — последовательность значений входного синусоидального сигнала, а ук — последовательность соответ
ствующих значений на выходе нелинейности в моменты (к, то формулы (2.365) и (2.366) при вычислительной процедуре по методу трапеций можно переписать в виде
я
К-1
X Sin ( ^+2^-‘-(о)А; (2.367) я
Ь^ = ^аХ-'К±2У-~' X К-1
X cos (о) h, (2.368)
где h — шаг измерений; п = = 2л/(®/i) — число измерений выходного сигнала за один период.
По формулам (2.367) и (2.368) составлена программа численного (по методу трапеций) определения коэффициентов линеаризации (программа № 2 TRP).
ПРОГРАММА № 2 TRP
Программа предназначена для вычисления коэффициентов гармонической линеаризации произвольной неоднозначной нечетно-симметричной нелинейности методом трапеций.
Обращение к программе
TRP (N,A,AA,BB)
Входные параметры
N — число шагов интегрирования на интервале от 0 до л;
А — амплитуда входного гармонического сигнала.
Выходные параметры
АА, ВВ — коэффициенты гармонической линеаризации.
Программа использует подпрограмму UNL(Y,Y0,F), содержащую аналитическое описание нелинейности и обеспечивающую получение значения нелинейной функции при заданном значении аргумента и его производной.
Входные параметры подпрограммы
Y — значение аргумента на данном шаге интегрирования;
Y0 — значение аргумента на предыдущем шаге интегрирования;
F — значение функции на предыдущем шаге.
Выходные параметры подпрограммы
F — значение функции.
TRP: PROC (N, А, АА, ВВ); Y = A. SIN(T); CALL UNL (Y. Y0. F);
DCL (N, K) BIN FIXED (15); FK = F; SUMA = SUMA + (FK + FKM1)/
DCL (А. АА, ВВ, T, ТК, TKM1, FK, FKM1, 2 . SIN ((TK + TKMl)/2);
F, SUMA, SUMB, H, PI, Y, Y0) DEC SUMS = SUMB + (FK + FKM1)/
FLOAT (12); PI == 3.141593; H=PI/N; 2 . COS ((ТК + ТКМ1)/2); TKM1 = TK;
Y0 = 0; T=0; F=0; Y = A.SIN(T); FKM1 = FK; Y0 = Y; END;
CALL UNL (Y, Y0, F); Y0=Y; AA — 2 . SUMA/(A . N);
FKM1 = F; TKM1 = T; SUMA, SUMB = 0; BB=2 . SUMB/(A « N); END TRP;
DO K=1 TON; T = K*H; TK = T;
283
Для повышения точности численного интегрирования формул (2.365) и (2.366) пользуются методом Рунге — Кутта 4-го порядка В этом случае вместо формул (2.365) и (2.366) будем иметь
Ж) =
Л *к+1 <0
яА К-0 tK
X U — tK) + Ук] sin со/ dt =
X (/ — /к) + Ук] cos со/ dt =
м V ( Г ук+1 ~^к f sin(0< яЛк4?1-'к+1-'к “2
По формулам (2.369) и (2.370) составлены программы численного интегрирования для определения коэффициентов гармонической линеаризации (программа № 3 RQ4).
ПРОГРАММА № 3 RQ4
Программа предназначена для вычисления коэффициентов гармонической линеаризации произвольной неоднозначной нечетио-симмётричиой нелинейности методом Рунге — Кутта 4-го порядка.
Обращение к программе
RQ4 (N.A.AA.BB)
Входные параметры
N — число шагов интегрирования на интервале от 0 до л;
А — амплитуда входного гармонического сигнала.
Выходные параметры
АА, ВВ — коэффициенты гармонической линеаризации.
Программа использует подпрограмму UNL(Y,Y0,F) (см. описание программы № 2 TRP).
RQ4: PROC(N,A,AA,BB); DCL (N.K.KD) BIN FIXED (15); DCL (A.AA.BB.T, TK,TKM1„FK,FKM1,F,SUMA,SUMB,H,PI,Y,Y0) DEC FLOAT (12); PI = 3. 141593; H=PI/N; Y0 = 0; T==0; F = 0; Y = A.SIN(T); CALL UNL(Y,Y0,F); Y0= Y; FKM1 = F; TKM1 = T; SUMA, SUMB=0; DO K = 1 TO N-l; T = K«H; TK = T; Y = A. SIN(T); CALL UNL (Y,Y0,F); FK = F; TR = TK; KD = 1;
M: SUMA = SUMA + ((FK - FKM1)/H . (SIN(TR) - TR . COS(TR)) + ((FK - FKM1)/H • TKM1 - FKM1) • COS(TR)) . KD; SUMB — SUMB 4-((FK - FKM1)/H . (COS(TR) + TR . SIN(TR)) + (FKM1 -(FK~FKM1)/H«TKM1).SIN(TR)).KD; IFKD-, = 1 THEN GO TO MARK; TR — TKM1; KD = -I; GO TO M;.
MARK: TKM1 = TK; FKMl-wFK; Y0=Y; END; AA = 2 . SUMA/(PI • A); BB = 2 . SUMB/(PI • A); END RQ4;
В неоднозначных нелинейных элементах гистерезисного типа выходная переменная зависит ие только от входной переменной, но и от ее производной. Рассматривая производную входного сигнала как дополнительный аргумент передаточ-
ной функции нелинейного элемента, по аналогии с формулами (2.276) и (2.277) получим выражения для коэффициентов статистической линеаризации. При этом для простоты будем полагать, что входной нормальный случайный сигнал и его
284
производная являются некоррелированными. Статистическую характеристику непрерывного нелинейного элемента определим по формуле ^2)(mx, т*, ах, стА) = ОО оо = ~ (х, х)<а(х, x)dxdx. _ оо —оо (2.371) лы (2.371), (2.372) и (2.373) примут вид ^2)(тх> тг °х> = I л , _ 1 у Ук + ук_, h д/2лаЛтх 2 (2.375) где (хк-"»х)г 2(у2 Г «* У к. ~ е х > 0) X
Выражение для коэффициента усиления по центрированному случайному входному сигналу имеет вид (тх, тх> стх, ст*) = 00 = -^- (х—тх)ЗГ(х, х)ш(х, x)dxdx. Ж — оо (2.372) В некоторых задачах требуется определить коэффициент усиления по центрированному значению производной случайного входного сигнала X (о,5 - Ф + ST (хк, хк < 0)Х х(о,5 + Ф (£))]; Л®(тх, mi, ах, d) = = -7=^ У -Ц,-к-‘ И. (2.376) Здесь (хк-тх)г “5 ХрГ(х, X > 0) (о,5 - Ф (-^У) +
&22) (тх, тх, ах, стх) = ОО = (х—mi) (F (х, х) ю (х, х) dx dx. + Г (х, х < 0) (о,5 + ф ; ^22)(mx, mt, ах, <Si) =
(2.373) Двумерную плотность распределения вероятности определим по формуле (x~mx)i 1 20% (*-тх)г 202. Хе х (2.374) п. -2»^ Ё (2-377> Х * к Я где (*k~wx)2 т\ 2О2 2а2 zK = e х е х% Х(^(х, х<0)-^(х, х>0)). По формулам (2.375), (2.376) и (2.377) составлены программы для
С помощью вычислительной процедуры по методу трапеций форму- нахождения коэффициентов статистической линеаризации: программы Ns 4—6.
ПРОГРАММА М4 STALK0
Вычисление статистического коэффициента усиления К0 произвольной неоднозначной нелинейной функции, заданной аналитически, при фиксированных значениях вероятностных моментов входного сигнала и его производной.
Обращение к программе
S ТALK0 (MX, MDX, DXX, DDXDX, DDXX, HX, Е Р S, FI)
285
Входные параметры
MX — математическое ожидание входного сигнала;
MDX — математическое ожидание производной входного сигнала;
DXX — дисперсия входного сигнала;
DDXDX — дисперсия производной входного сигнала;
DDXX — корреляционный момент входного сигнала и его производной;
НХ — шаг интегрирования;
EPS — точность вычисления коэффициента статистической линеаризации.
Выходные параметры
FI — статистическая характеристика нелинейной функции
STALK0: PROC (MX.MDX,DXX,DDXDX,DDXX,НХ,EPS,FI);
DCL (NMX.IP.IN) BIN FIXED (15), (MX,MDX,DXX,DDXDX,DDXX,HX,EPS,FI, DR,MRP, MRN,X0P,X0N,XIP,XIN, SQRT2, PI, FNEGP, FNEGN, F0P.F0N, FIP, FIN) DEC FLOAT (12); DCL UNL ENTRY RETURNS (DEC FLOAT (12)); PI=3.141593; SQRT2=SQRT (2); FI=0; DR=(DXX * DDXDX — DDXX • DDXX)/DXX; NMX=MX/HX; X0P,X0N = MX; IP, IN = NMX; GO TO М3; Ml: IP = IP + 1; IN=IN— 1; М3: XIP=IP . HX; XIN=IN . HX; MRP=MDX + DDXX/DXX . (XIP-MX); MRN = MDX + DDXX/DXX * (XIN - MX);
IF MRP>=0 THEN FNEGP = 0.5 — ERF (MRP/SQRT(DR)/SQRT2)/2; ELSE FNEGP = 0.5+ERF (-MRP/SQRT (DR)/SQRT2)/2;
FIP = UNL (XIP,XIP + 1) • FNEGP + UNL (XIP, XIP — 1) • (1 — FNEGP);
IF IP = IN THEN DO; F0P. F0N = FIP; GO TO Ml; END;
IF MRN>=0 THEN FNEGN = 0.5 — ERF (MRN/SQRT (DR)/SQRT2)/2;
ELSE FNEGN = 0.5+ERF (-MRN/SQRT (DR)/SQRT2)/2;
FIN = UNL (XIN,XIN + 1) • FNEGN + UNL (XIN,XIN - 1) . (1 - FNEGN);
FI = FI + (EXP (- (X0P - MX) . . 2/DXX/2) . F0P
+ EXP (- (XIP - MX) . .2/DXX/2) . FIP + EXP (- (XIN - MX) . . 2/DXX/2) • FIN + EXP (- (X0N - MX) . . 2/DXX/2) . F0N)/2 . HX; X0P = XIP; X0N = XIN; F0P = FIP; F0N = FIN; IF EXP (—(XIP — MX) • • 2/DXX/2) » ABS (FIP) + EXP (—(XIN—MX) » » 2/DXX/2) » ABS (FIN)>EPS! IP»HX<1 THEN GO TO Ml; PUT SKIP DATA (XIP,XIN); FI=FI/SQRT (2 » PI» DXX); PUT SKIP LIST (’FI=’,FI); END STALK0;
UNL: PROC (X.Y) RETURNS (DEC FLOAT (12));
DCL (X,Y,F,X1,X2,X3,X4,F1,F2,F3,F4,K1,K2,K3,K4,AX,AY) DEC FLOAT (12); XI =3; X2 = 7; X3 = 3; X4=l; Fl = 1; F2 = 5; F3 = 5; F4 = 3; K1=F1/X1; K2 = (F2 - F1)/(X2 - XI); КЗ = (F3 — F4)/(X3 - X4); K4 = F4/X4; AX = X; AY = Y; MA: IF AX>=0 THEN IF AX > AY THEN IF AX < = XI THEN F=K1«AX;
ELSE IF AX > XI &AX < =X2 THEN F = Fl + K2 » (AX — XI); ELSE F = F3; ELSE IF AX < = X4 THEN F=K4*AX;
ELSE IF AX > X4 & AX < = X3 THEN F = F4 + КЗ • (AX - X4); ELSE F = F3; ELSE DO; AX = - AX; AY = —AY; GO TO MA; END; IFAX-,=X THEN F = —F; RETURN (F); END UNL;
ПРОГРАММА № 5 STALK1
Вычисление статистического коэффициента усиления К1 по центрированному случайному входному сигналу произвольной неоднозначной нелинейной функции, заданной аналитически, при фиксированных значениях вероятностных моментов входного сигнала и его производной.
Обращение к программе
STALK1 (MX, MDX,DXX, DDXDX, DDXX, HX, EPS, KX)
Входные параметры
MX — математическое ожидание входного сигнала;
MDX — математическое ожидание производной входного сигнала;
DXX — дисперсия входного сигнала;
DDXDX — дисперсия производной входного сигнала;
DDXX — корреляционный момент входного сигнала и его производной;
НХ — шаг интегрирования;
EPS — точность вычисления коэффициента статистической линеаризации.
Выходные параметры
КХ — статистический коэффициент усиления по центрированному случайному входному сигналу.
286
STALK1: PROC (MX,MDX,DXX,DDXDX,DDXX,HX,EPS,KX);
DCL (NMX.IP.IN) BIN FIXED (15), (MX,MDX,DXX,DDXDX,DDXX,HX,EPS,KX, DR,DR 1,MRP,MRN,X0P,X0N,XIP,XIN, SQRT2,PI,FNEGP, FNEGN, F0P,F0N, FIP, FIN,F210P,F21IP,F210N,F21IN) DEC FLOAT (12);
DCL UNL ENTRY RETURNS (DEC FLOAT (12)); PI = 3.141593; SQRT2 = SQRT(2); KX = 0; DR = (DXX . DDXDX - DDXX . DDXX)/DXX;
DR1=DDXX/DXX/SQRT (2 • PI • DR); NMX=MX/HX; X0P, X0N=MX; IP, IN = NMX; GO TO М3; Ml: IP = IP4-1; IN — IN-1;M3: XIP = IP • HX; XIN = IN»HX; MRP = MDX + DDXX/DXX * (XIP - MX); MRN = MDX + DDXX/DXX • (XIN - MX); IF MRP>=0THEN FNEGP =0.5 — ERF (MRP/SQRT (DR)/SQRT2)/2;
ELSE FNEGP =0.5 +ERF (—MRP/SQRT (DR)/SQRT2)/2;
FIP = UNL (XIP, XIP + 1). FNEGP + UNL (XIP, XIP — 1) • (1 — FNEGP); F21IP = (UNL (XIP, XIP + 1) - UNL (XIP, XIP - 1)) • EXP (- MRP • MRP/DR/2); IF IP = IN THEN DO; F0P.F0N = FIP; F210P, F210N = F21IP; GO TO Ml; END; IF MRN>=0 THEN FNEGN = 0.5 — ERF (MRN/SQRT (DR)/SQRT2)/2;
ELSE FNEGN = 0.5+ERF (-MRN/SQRT (DR)/SQRT2)/2;
FIN = UNL (XIN, XIN + 1). FNEGN + UNL (XIN,XIN — 1) •( 1 — FNEGN); F21IN = (UNL (XIN,XIN + 1) - UNL (XIN,XIN — 1)) • EXP (—MRN • MRN/DR/2); KX = KX + (EXP (- (X0P — MX) * . 2/DXX/2) * (((X0P - MX)/DXX) . F0P + DR1 . F210P) + EXP (- (XIP - MX) * • 2/DXX/2) . (((XIP - MX)/DXX) . FIP + DR1 . F21IP) + EXP (- (X0N - MX) » . 2/DXX/2) . (((X0N - MX)/DXX) . F0N + DR1 . F210N) + EXP (,- (XIN - MX) • . 2/DXX/2) . (((XIN - MX)/DXX) . FIN + DR1 » F21IN))/2 • HX; X0P==XIP; X0N = XIN; F0P = FIP; F0N = FIN;
F210P = F21IP; F210N = F21IN; IF EXP (—(XIP — MX) • • 2/DXX/2) • (ABS ((XIP - MX)/DXX . FIP) + DR1 . ABS (F21IP)) + EXP (- (XIN - MX) . . 2/DXX/2) • ABS ((XIN — MX)/DXX • FIN) + DR1 • ABS (F21IN)) > EPS!
IP ♦ HX<1 THEN GO TO Ml; PUT SKIP DATA (XIP,XIN); KX=KX/SQRT (2 . PbDXX); PUT SKIP LIST (’KX =’, KX); END STALK1;
UNL: PROC (X,Y) RETURNS (DEC FLOAT (12)); DCL (X,Y,F,X1,X2,X3, X4,F1,F2,F3,F4,K1,K2,K3,K4,AX,AY) DEC FLOAT (12); Xl=3; X2 = 7; X3 = 3; X4=l; Fl = 1; F2 = 5; F3 = 5; F4 = 3; K1 = F1/X1; K2 = (F2 - F1)/(X2 - XI); КЗ = (F3 - F4)/(X3 - X4); K4 = F4/X4; AX = X; AY = Y;
MA: IF AX > = 0 THEN IF AX > AY THEN IF AX < = XI THEN F=K1 • AX; ELSE IF AX > XI & AX < = X2 THEN F = Fl + K2 • (AX — XI); ELSE F = F3; ELSE IF AX < = X4 THEN F = K4*AX;ELSE IF AX > X4 & AX < = X3 THEN F = F4 + КЗ »(AX — X4); ELSEF = F3; ELSE DO; AX = - AX; AY = —AY; GO TO MA; END; IF AX-, = X THEN F = —F; RETURN (F); END UNL;
ПРОГРАММА № 6 STALK2
Вычисление статистического коэффициента усиления К2 по случайному центрированному значению производной входного сигнала произвольной неоднозначной нелинейной функции, заданной аналитически, при фиксированных значениях вероятностных моментов входного сигнала и его производной.
Обращение к программе
STALK2 (MX,MDX, DXX, DDXDX, DDXX,HX, EPS ,KDX)
Входные параметры
MX — математическое ожидание входного сигнала;
MDX — математическое ожидание производной входного сигнала;
DXX — дисперсия входного сигнала;
DDXDX — дисперсия производной входного сигнала;
DDXX — корреляционный момент входного сигнала и его производной;
НХ — шаг интегрирования;
EPS — точность вычисления коэффициента статистической лииеарнзации.
Выходные параметры
KDX — статистический коэффициент усиления по центрированному значению производной случайного входного сигнала.
STALK2: PROC (MX, MDX, DXX, DDXDX, DDXX, HX, EPS, KDX);
DCL (NMX,IP,IN) BIN FIXED (15), (MX,MDX,DXX,DDXDX,DDXX.HX.EPS,KDX,
DR, MRP, MRN, X0P, X0N.XIP, XIN, SQRT2, PI, FNEGP,
FNEGN, F210P, F21IP, F210N, F21IN) DEC FLOAT (12);
DCL UNL ENTRY RETURNS (DEC FLOAT (12)); PI = 3.141593; SQRT2 = SQRT (2);
KDX =0; DR = (DXX . DDXDX - DDXX • DDXX)/DXX; NMX = MX/HX; X0P,
287
X0N = MX; IP, IN = NMX; GOTO М3; Ml: IP = IP + 1; IN = IN-1; М3: XIP = IP.HX; XIN = IN • HX; MRP = MDX + DDXX/DXX . (XIP - MX);
MRN = MDX + DDXX/DXX . (XIN-MX); F21IP = (UNL (XIP, XIP-J-1)
-UNL (XIP, XIP — 1)) • EXP (—MRP • MRP/DR/2); IF IP = IN THEN DO; F210P, F210N=F21IP; GO TO Ml: END; F21IN = (UNL (XIN,XIN + 1) - UNL (XIN,XIN - 1)) . EXP (- MRN . MRN/DR/2); KDX = KDX
- (EXP (- (X0P - MX) » . 2/DXX/2) » F210P + EXP (- (XIP - MX) . . 2/DXX/2) . F21IP + EXP (- (X0N-MX) . . 2/DXX/2) . F210N + EXP (- (XIN - MX) • . 2/DXX/2) * F21IN)/2 • HX; X0P = XIP; X0N = XIN; F210P = F21IP; F210N = F21IN; IF EXP (- (XIP-MX) . • 2/DXX/2) < ABS (F21IP) + EXP (- (XIN - MX) . . 2/DXX/2) . ABS (F21IN) > EPS! IP » HX < 1 THEN GO TO Ml; PUT SKIP DATA (XIP, XIN); KDX = KDX/(2 . PI . SQRT (DXX . DDXDX - DDXX . DDXX));
PUT SKIP LIST (’ KDX =’, KDX); END STALK2;
UNL: PROC(X,Y) RETURNS (DEC FLOAT (12)); DCL (X,Y,F,X1 ,X2,X3,X4, Fl,F2,F3,F4,K1 ,K2,K3,K4,AX,AY) DEC FLOAT (12); XI =3; X2 = 7; X3 = 3; X4=l; Fl = 1; F2 = 5; F3 = 5; F4 = 3; K1 = F1/X1; K2 = (F2 - F1)/(X2 - XI); КЗ = (F3 - F4)/(X3 - X4); K4 = F4/X4; AX = X: AY = Y;
MA: IF AX > = 0 THEN IF AX>AY THEN IF AX < = XI THEN F=K1 * AX; ELSE IF AX.> XI & AX < = X2 THEN F = Fl + K2 . (AX-XI); ELSE F = F3; ELSE IF AX < = X4 THEN F = K4 • AX; ELSE IF AX > X4 & AX < = X3 THEN F = F4 + КЗ . (AX - X4); ELSE F = F3; ELSE DO; AX = - AX; AY = —AY; GO TO MA; END; IF AX-, — X THEN F = -F; RETURN (F); END UNL;
При фиксированной величине шага h определим отдельно число шагов интегрирования п для каждого коэффициента статистической линеаризации из условия обеспечения наперед заданной' точности вычислений.
Пример 2.37. Определить коэффициенты гармонической линеаризации для сложной двузначной нелинейности (рис. 2.122), пользуясь при интегрировании формулами для определения коэффициентов а (А) и Ь(А) методами трапеций и Рунге — Кутта 4-го порядка. На рис. 2.123, а изображены кривые изменения коэффициентов а в зависимости от А, полученные обоими методами интегрирования. При этом видно, что они полностью совпадают.
Кривая 1 показана в виде функции изменения коэффициентов Ь, полученная с помощью метода трапеций (рис. 2.123,6), а кривая 2 — по методу Рунге — Кутта 4-го порядка. Эти кривые отличаются друг
от друга лишь в области малых амплитуд входного сигнала.
Пример 2.38. Определить коэффициенты статистической линеаризации для двузначной нелинейности (рис. 2.122) по методу интегрирования трапеций в виде зависимостей <!q2) (рис. 2.124), (рис. 2.125) и fe(2) (рис. 2.126) от математического ожидания случайного входного сигнала тх при следующих статистических параметрах скорости изменения входного сигнала: а* = 1) тЛ = -2; -1; 0; 1; 2.
Пример 2.39. Определить коэффициенты гармонической и статистической линеаризации для однозначной сложной нелинейности, изображенной на рис. 2.127. Коэффициент гармонической линеаризации а(А) вычисляют с помощью интегрирования по методу трапеций (рис. 2.128). Коэффициенты статистической линеаризации (рис. 2.129) и £]2) (рис. 2.130) вычисляются тем же методом. При построении коэффициентов £|2) и fe<2) дисперсия входного сигнала составляет Dx = 1.
Рис. 2.122. Сложная двузначная нелинейная характеристика типа упругого люфта
Рнс. 2.123. Коэффициенты гармонической линеаризации двузначной нелинейности (рис. 2.122), полученные путем численного интегрирования: а —для а (Л); б—для Ь (Л)
288
k(z) Ко
г” //у'' Ч’-оу
т^-2 Л 'тг-1/ \ X л
у/.
///
• //о
-10 -1 -1 А тх
' //! //1
-5
Рис. 2.124. Коэффициент статистической линеаризации k^1 в зависимости от тх при пяти значениях математического ожидания скорости изменения входного сигнала
Рис. 2.125. Коэффициент статистической линеаризации А® по центрированному случайному входному сигналу при пяти значениях математического ожидания скорости изменения входного сигнала
Ю Ю. И. Топчеев
289
Рнс. 2.126. Коэффициент статистической линеаризации по центрированному значению производной случайного входного сиг
нала при пяти значениях математического ожидания скорости изменения входного сигнала
Рнс. 2.127. Сложная однозначная нелинейная характеристика
Рис. 2.128. Коэффициент гармонической линеаризации однозначной нелинейности (рис. 2.127), полученный путем численного интегрирования по методу трапеций
Рис. 2.129. Коэффициент статистической линеаризации в зависимости от тх
Рнс. 2,130. Коэффициент статистической линеаризации в зависимости от тх
290
Глава 3
МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Из теории автоматического регулирования известно [1, 6, 13, 14, 33], что основное назначение САР заключается в том, чтобы выходной сигнал во время нормальной эксплуатации системы с наибольшей точностью отслеживал изменение входного -сигнала, уменьшая вредное влияние возмущающих воздействий. Для этого в каждую систему, кроме объекта регулирования и устройств управления, должны входить измерительные устройства, с помощью которых производится измерение управляющих и возмущающих сигналов, позволяющих создать замкнутую динамическую систему за счет введения в нее главной обратной связи. Таким образом, большинство САР можно привести к двум типовым структурам, упрощенные схемы которых показаны на рис. 3.1, а и б. На этих схемах управляющий сигнал 2 формируется в задающем устройстве 1. Он сравнивается в устройстве 3 с выходным сигналом, который измеряется датчиком 11. В результате сравнения сигналов образуется сиг-
Рис. 3.1. Схемы САР:
а — с отработкой ошибок от сигналов управления и возмущения; б — с комбинированным управлением и компенсацией ошибок
нал разности 4, поступающий через устройства управления 5 и 6 на объект регулирования 7. При этом обеспечивается такой процесс регулирования объектом, когда на его выходе удается получить требуемую форму и параметры выходного сигнала. От действия сигнала возмущения 8, поступающего в систему через сумматор 9, происходит некоторое искажение выходного сигнала 10. Замыкание системы осуществляется ’ с помощью главной обратной связи 12. Если на схеме рис. 3.1, а исключить задающее устройство, то ее назначение сводится к парированию вредного влияния возмущающего воздействия. Подобного рода системы принято называть автоматическими системами или системами автоматической стабилизации, отрабатывающими сигнал возмущения.
Системы (рис. 3.1, а) с задающим устройством 1 в зависимости от типа сигнала управления принято относить к программным (если задан закон его изменения) или следящим системам, когда закон изменения является произвольным. Динамическая точность работы таких САР определяется статическими и динамическими характеристиками измерительных устройств, устройств управления и объекта регулирования. Система, изображенная на схеме рис. 3.1, б, отличается от системы, показанной на рис. 3.1, а, тем, что в ней для получения более высокой точности применяются три датчика 11, которые не только измеряют выходной сигнал 10, но и сигналы управления 2 и возмущения 8. Эти два сигнала после прохождения устройств 5 поступают на сумматор 13 и уменьшают влияние сигналов на ошибку САР. Обе эти схемы можно привести к структурным системам (рис. 3.2, а, б), ко-
10*
291
Рис. 3.2. Структурные схемы типовых САР: а — с управлением по ошибке (изображения: G(s) — функции управляющего воздействия; X(s) — функции выходного сигнала; F\(s), Fits) — функции возмущающих воздействий; E(s) — функции ошибки); б —с комбинированным управлением
торыми обычно пользуются проектировщики при решении задач анализа и синтеза САР. В отличие от схем, приведенных на рис. 3.1, а, б, структуры систем, показанные на рис. 3.2, а, б, содержат не одно, а два возмущающих воздействия. При наличии большего числа динамических звеньев их количество может быть существенно увеличено. Для расчетов необходимо располагать такой математической моделью, в которой кроме динамических характеристик устройств и объектов регулирования должны быть указаны не только виды сигналов управления и возмущения, но и места их приложения. Наиболее просто это обеспечивается на основе применения структурных схем или графов.
На рис. 3.2, а изображена структурная схема системы с управлением. по ошибке, а на рис. 3.2, б — с комбинированным управлением. На схемах объект регулирования обозначается передаточной функ
цией U/q(s), а устройство управления—передаточной функцией Wy(s). В комбинированной системе введены три корректирующих устройства U^ik(s), №2к($) И U73k(s). Приведенные на рис. 3.2, а, б структурные схемы изображены на рис. 3.3, а, б в виде графов. Цифрами в кружках обозначены вершины графов.
В структурных схемах и графах наряду с линейными элементами, описываемыми передаточными функциями U7;(s) (t=l, 2, ...), встречаются и нелинейные элементы с эквивалентными передаточными функциями вида //(А) или /;(А,(о) (/= 1, 2, ...). При этом путем последовательного или параллельного соединения, а также соединений с помощью обратной связи отдельных САР или их комбинаций получают более сложные системы — комплексы.
При традиционных способах проектирования математическую модель обычно представляют в виде структурной схемы или в виде графа. Различные типы соединений линейных и нелинейных элементов в виде структурных схем и графов приведены в табл. 1.7 и 1.8. При этом
Рис. 3.3. Графы типовых САР:
а — с управлением по ошибке; б — с комбинированным управлением (1—6 — вершины графов)
292
необходимо сохранять положения нелинейных элементов неизменными.
При структурных преобразованиях дискретно-непрерывных САР учитывают места включения импульсных элементов. Иногда для возможности выполнения структурных преобразований приходится вводить дополнительно фиктивные импульсные элементы.
Применяемые в последнее время автоматизированные способы проектирования систем с помощью ЭВМ. основаны на приведении непрерывной или дискретно-непрерывной математической модели к дискретной форме. Это позволяет применять аппарат спектрального разложения матриц к любым типам систем и получать единое представление в виде передаточных функций в замкнутом или разомкнутом виде.
!• СТРУКТУРНЫЕ СХЕМЫ
И ГРАФЫ САР
С помощью преобразования структурных схем и графов можно любую сложную многоконтурную САР привести к одноконтурной, имеющей вид, показанный на рис. 3.2 и 3.3, а также получить передаточные функции замкнутых систем относительно различных сигналов (по ошибке, возмущающему воздействию и т. п.).
Выходной сигнал для структурной схемы, изображенной на рис. 3.2, а, можно записать в виде
Гу(я)Г0(я)
Х 1 + Гу (s) Го (s) G (s) +
+ 1 + Гу (s) Го (s) f 1 +
1 + Wy (s) Го (s) ^2 (s)• (3.1)
Из выражения (3.1) можно найти передаточные функции замкнутой системы:
по управляющему воздействию при действии сигнала G(s)
w O(s) l + r,(.)r,(.> • 1 '
по возмущающему воздействию сигнала /ч ($)
ф /с) — % (3 3)
F,(s) - 1 + Гу(з)Г0(з) ’ ( ’ } по возмущающему воздействию сигнала
= 1 + Гу (S) Го (s) (3,4)
Введем в формулы (3.2) — (3.4) следующее обозначение:
W(s) = Wy(s)W0(s), (3.5)
где IT(s)—передаточная функция разомкнутой системы.
Имея в виду выражение (3.5), можно записать передаточные функции (3.2) — (3.5) в виде
Ф(5) = Г($)/[1 + Г(я)]; (3.6)
O1(s) = r0(s)/[1 + r(s)]; (3.7)
O2(s) = 1/[1 + IT (s)]. (3.8)
Если в выражение (3.1) подставить соотношение
X (s) = G ($) — Е ($), (3.9)
то получим
Е 1 -г Wy (s) Го (s) G — _ r0(s) „ , , _
1 + Гу (s) Г» (s) к ’
— 1 + Гу (s) Го (s) 7=2 или
E(s) = Ee(s)-EeI(s)-Ee2(s). (3.11)
Из выражений (3.6) и (3.7) найдем передаточные функции относительно сигналов ошибок в виде
ф (s\ = J-jety). =-----!------•
W g (s) 1 + Гу (s) Го (s) ’
(3.12) ф Ее. (з> ^o(s)
^el W — Fl (s) 1 _|_ ry (s) Го (S) ’
(3.13)
.ту / \__ Е'еД (s) _ 1______
^62 W— p3{s} — l + ry(s)r0(s)
(3.14)
293
После введения соотношения (3.5) в (3.12) — (3.14) имеем
Фе = 1 + F (s) ; (3.15)
ф-^’—ГТ¥%Г (3'16>
Фе2 ($) = 1 + IF (s) ’ (3-17)
Отметим, что для любых сложных САР в результате преобразований структурных схем или графов можно получить расчетные передаточные функции вида (3.5) — (3.8) и (3.15) —(3.17).
Выходной сигнал для структурной схемы (рис. 3.2, б) будет
Fy(s)F0(s)+F2K(s)Fy(s)
Х ~ 1 + Fy (s) Wo (s) “l"
, Fo (s) + F1K (s) Fy (s) Fo (s) p ( + 1 + Fy (s) Fo (s) n(s) +
, l + F3K(s)Fy(s)F0(s) c z /oio4 1 1 + Wy (s) Fo (s) • (3 •18)
Из выражения (3.18) определим передаточные функции замкнутой комбинированной системы:
по управляющему воздействию G(s)
ф (s) . =
' ’ О (s)
Fy (s) Fo (s) + F2k (s) Fy (s) )пч — 1 + Fy (s) IFO (5) ’
по возмущающему воздействию F,(s)
ф / i— *(s) — uz°<s)ll+UZ1*<s>uzy(s)J F,(s) — 1 + Fy (s) F0(s) 1
(3.20) по возмущающему воздействию
F2(s)
Ф I — *(s) _ 1 + w'3K(s)W'y(s)U70(s) — F2 (s) — 1 + IFy (s) Fo (s) •
(3.21) Вводя в формулы (3.19) — (3.21) соотношение (3.5), получим
ф(5)== 'Г(5)+^к(^у(^). (3.22)
1 + V (s)
ф М _ (s) + F)K (s) F (s) .
ЧМЗ) —-------------1 + JF(S)--------•
= (3.24)
Подставляя в выражение (3.11) соотношение X (s) = G ($) — Ё ($), найдем
E(s)
1 — F2K(s)Fy(s) ч ~ 1 + lFy (s) Fo (s) °
_ Fp (s) - F,K (s) , , _
1 + Fy(s) F0(s)
— 1 + Fy (s)KF„(s) (3l25)
или
Ё (s) = Ee (s) - Eel (s) - Ee2 (S). (3.26)
Пользуясь выражениями (3.25) и (3.26), запишем передаточные функции относительно сигналов ошибок в виде
Ф = Ёе (S) _ 1 ~ ^2К (S) Гу (S) («) — q (S) — 1 + Fy (S) IFо (s) :
(3.27)
ф (-Л : (s) Fq(s)-F,k(s) .
F,(S) 1 + IFy (s) Fo (s) ’
(3.28)
Ф fcl Eq2 (s) 1 F3K (s)
F2(S} 1 + IFy (s) IFo (s) •
(3.29)
Вводя в формулы (3.27) — (3.29) соотношение (3.5), получим
1 - F2k (s) Fy (s)
Фе(*)= T+F(s) ; (3’3°)
Фе.(*)= (i+~F^) : <3-31>
<3-32>
Для любых сложных комбинированных САР путем структурных преобразований схем или графов можно получить передаточные функции (3.15) — (3.17).
2. СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ
И НЕЛИНЕЙНЫХ СИСТЕМ
ИЛИ ИХ ГРАФОВ
Рассмотрим структурные преобразования схем на ряде конкретных примеров. При этом будем пользоваться способами, приведенными в гл. 1.
294
е)
Рис. 3.4. Структурные схемы сложных САР: а — исходная миогокоитурная без перекрещивающихся линий обратных связей; б — приведенная к форме, удобной для расчетов; в — с перекрещивающимися линиями обратных связей; г — преобразованная с исключением перекрещивающихся линий обратных связей; д — преобразованная к одноконтурной; е — приведенная к форме, удобной для расчетов
Пример 3.1. Привести исходную структурную схему САР (рис. 3.4), состоящую из линейных элементов, к расчетной. Для этого воспользуемся структурными преобразованиями, приведенными в табл. 1.7.
Из рис. 3.4, а видно, что исходная структура имеет один входной и один выходной сигнал и ие содержит перекрещивающихся связей. Поэтому путем объединения внутренних контуров в передаточные функции получим
^W-i-rTwr.(.>; <3'33)
1Fhk(s) =
^4 (S) FtK (s) IF7 (s)_________
1 + IF4 (s) IFIk (S) IF7 (s) IFs (S) Ц7. (S) ’
(3.34)
Ушк (s) =
=___________V?3 (8)В7Пк (s)F,o(s)__________.
1 + IF3 (s) WUK (S) IF1O (S) (S) IF12 (S) ’
(3.35)
UZivk (s) =
1 + UZ2 (s) W'lHK (s) w13 (S) IFie (s) X ’ X [U7u (S) + ir16 (S)J
(3.36)
IF, (s) IFIVk (s) IF 17 (s)
= (3-37)
или после введения обозначения IF (s) = = IF, (s) ITivk (s) ITi7 (s) найдем
ф (S) = IF (s)/[l + IF (s)], (3.38)
295
Рис. 3.5. Структурные схемы двухканальных САР: а — исходная; б и в — с заменой сравнивающих устройств по второму каналу: г — преобразованная из рис. 3.5,6; д — преобразованная из рнс. 3.5, в
т. е. получим расчетную схему системы (рис. 3.4,6), где IT(s)—передаточная функция разомкнутой системы, a Ф(э) — передаточная функция замкнутой системы по управляющему воздействию G(s).
Пример 3.2. Привести исходную структурную схему САР (рис. 3.4, в), состоящую из линейных элементов с перекрещивающимися связями, к расчетной. Снова воспользуемся структурными преобразованиями, приведенными в табл. 1.7, с помощью которых в исходной схеме устраним перекрещивающиеся связи. В результате получим схему, изображенную иа рис. 3.3, г. Далее, объединяя внутренние контуры, можно записать следующие передаточные функции:
W4k(s) =
____________«75(.s)«7,3(.s)_______.
1 + «72 (s) (s) U7s (s) IF7 (s) X ’ 1 '
XW!3(s)Wl5(s)
U^iik (s) =
=___________ITik (s) 1F,6 (s) 1T,9 (s)___
1 + 1T1K (s) «76 (s) «7,2 (S) W7„ (s) «7,, (s) ’
(3.40)
W^IIIK (s) =
=_________________IFiik (S)_______________.
1 + W^iik (s) IF,, (s) IF,7 (s)/U75 (s) «7,9 (S)>
(3.41)
IFivk (s) =
=___________IFniK (s) Wz ($)________
1 + IFiiik(s) (s) «7,4 (s)/»74 (s) (3.42)
rVK (S) = 1 - Wzz (s) 1F23 (s) ’ (3’43)
_________IFvk (s) «724 (s)
VlK ' ; 1 - IFVk (s) IF24 (s) «72s (S)
(3.44)
«7у11к(з)=^к(Ч); (3.45)
IFviiik (s) =
_ ____________IFivk ($) IFviik (s)________
1 + IFjvk (s) IFvhk (s) W3 (s) «7,0 (s) X ’
X «720 (s) «722 (s)/«724 (s)
(3.46)
IF' (s) = «727 (s) + (3.47)
U/24 (s)
Так как контур IX образует всю замкнутую систему, то его передаточную
296
функцию можно записать в виде
rviliK(s)r(s)ir,(s)ITa,(s)
1 + Гушк ($) Г'(s) Г, (s) X '
X Г28 GO Г18 (s)
(3.48)
Вводя в формулу (3.48) обозначение
W" (s) = ГуШк (s) V (S) Г, (S) Г28 (s).
получим
Ф (S) = UZ" (s)/[l + W" (s) Г„ (s)]. (3.49)
Формула (3.49) соответствует структурной схеме, изображенной на рис. 3.4. д После введения в нее обозначения
lF(s) = r"(s)r18(s) (3.50)
получим структурную схему (рис. 3.4, д), которую можно привести к расчетной (рис. 3.4, е).
Пример 3.3. Для исследования устойчивости многосвязной САР с линейными элементами (рис. 3.5, а) определить передаточную функцию в разомкнутом состоянии. Для этого воспользуемся способом, рассмотренным в примере 1.34, когда можно пренебречь влиянием второго управляющего сигнала G2(s).
Из рис. 3.5, а видно, что САР состоит из трех основных элементов, выделенных штрихпунктириыми прямоугольниками: 1 — измерительных устройств; 2 — объекта регулирования; 3 — регуляторов. Если G2(s) =0, то исходную схему (рис; 3.5, а) легко представить в виде двух схем, как это показано на рис. 3.5, б и в, с помощью которых нетрудно получить структурные схемы, изображенные на рис. 3.5, гид.
Пользуясь преобразованными структурными схемами, можно записать передаточные функции для двух разомкнутых подсистем в виде
Г2 (s) = ГИ1 (s) Гр2 (s) Г02 (s) -
Гн1 (s) ^pl (s) ^01 (s) ^04 (s) X
ХГи2 (s) rp2 (s)
1 + Гя2 (s) Гр, (s) Wоз (s)
(3.52)
Рассматриваемая CAP является линейной, и для нее справедлив принцип суперпозиции. Поэтому результирующая передаточная функция всей разомкнутой системы в соответствии с передаточными функциями (3.51) и (3.52) будет
W (s) = Г, (s) + Г2 (S) = Ц7И1 (S) X
X [Гр1 (s) Г04 (s) + Гр2 (s) Г02 (s)] -
- ГН1 (s) Гр1 (s) Ги2 (а) Гр2 (а) X
„ Г Го2 (а) Г03 (а)
А L 1 + ги2 (S) Гр2 (а) Го, (а)
. Гр, (а) Гр4 (а) 1
1 + Ги2(а) Гр2(а) Грз(а) J'
Пример 3.4. Привести исходную структурную схему САР (рис. 3.6, а), состоящую из одного нелинейного и пяти линейных элементов, к расчетной [128].
Структурные преобразования будем выполнять только для линейных элементов, но таким образом, чтобы место положения нелинейного элемента в исходной и преобразованной схемах оставалось неизменным (что показано далее на нелинейных элементах штрихами). На рис. 3.6,6, в даны соответственно промежуточные и расчетная схемы. С помощью последних исследуются нелинейные системы (см. гл. 7).
Пример 3.5. Привести исходную структурную схему многоконтурной САР с одной нелинейностью (рис. 3.7, а) к расчетной [38]. Структурные преобразования показаны на рис. 3.7, б, а расчетная схема — на рис. 3.7, в.
r,(s) = r„,(s) Гр1(з)Го4 (s)-Ги2 (s) Гр2 (s) Г02 (s) ГИ1 (s) Гр1 (s)
1 + Ги2 (s) Гр2 (s) Г01 (а)
(3.51)
Рис. 3.6. Структурные схемы многоконтурных САР с нелинейностью:
а — исходная; б — преобразованная к двухкои-турной; в — преобразованная к одноконтурной с гибкой обратной связью; г—преобразованная к одноконтурной с жесткой обратной связью
297
в)
Рнс. 3.7. Структурные схемы сложных САР с нелинейностью:
а — исходная; б — преобразованная к вложенным контурам; в — приведенная к форме, удобной для расчетов
Пример 3.6. Привести исходную структурную схему САР с тремя нелинейностями (рис. 3.8, а) к расчетной. Для этого необходимо объединить нелинейные элементы в одну нелинейность, т. е. /П(А) = = /1(А)+/2(А) + /зИ), как показано штрнхпунктнрнымн линиями на рис. 3.8, б. Затем с помощью структурных преобразований линейных элементов получим расчетную схему системы (рис. 3.8, в).
Пример 3.7. Привести исходную структурную схему САР со сложной нелинейностью (рис. 3.9, а) к расчетной. Нелиней
ная часть системы выделена иа схеме штрихпунктирным прямоугольником.
Сначала приведем нелинейную часть системы к виду
7п (А /со) = </п (^4. ®) <Л Ш)
и покажем это на рис. 3.9, б. Затем выполним несколько промежуточных структурных преобразований линейных элементов (рис. 3.9,в, г). После выделения двух линейных элементов 1 и 2 получим расчетную схему, показанную на рнс. 3.9, г.
3. СТРУКТУРНЫЕ СХЕМЫ ДИСКРЕТНО-НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ И НЕЛИНЕЙНЫХ СИСТЕМ
С помощью структурных преобразований дискретно-непрерывных ли
298
нейных и нелинейных систем (рис. 3.10) можно получить расчетные формулы для нахождения передаточных функций замкнутых систем относительно выходного сигнала G* (s) или сигнала ошибки E*(s). На рис. 3.10, а, б приведены две наиболее простые структурные схемы дискретно-непрерывных систем, где передаточные функции МДз), ITi(s) и U^2(s) могут состоять из нескольких последовательно или параллельно соединенных типовых непрерывных линейных звеньев.
Из рис. 3.10, а следует, что
Е‘ (s) = G* (s) - X* (s) (3.54) и
X' (s) = W* (s) E’ (s). (3.55)
Исключив из выражений (3.54) и (3.55) E*(s), получим передаточную функцию замкнутой дискретнонепрерывной системы относительно управляющего сигнала в форме дискретного преобразования Лапласа
Ф’ (s) = Г (s)/G‘(s) = W * (s)/[ 1 + W *(s)], (3.56) где W* (s) — передаточная функция разомкнутой дискретно-непрерывной системы.
Исключая из выражений (3.54) и (3.55) X*(s), найдем передаточную функцию замкнутой дискретнонепрерывной системы относительно сигнала ошибки
O;(s) = E-(s)/G-(s)=l/[l + UT(S)].
(3.57)
Как было показано в гл. 1, передаточную функцию элемента (объекта) или разомкнутой САР можно записать в форме г-преобразования, т. е.
Г (г) = з[Г (s)]. (3.58)
Для простейших передаточных функций IT(s) таблицы z-преобра-зований приведены в прил. П-1.3.
Из теории дискретно-непрерывных САР известно [13, 16, 24], что все передаточные функции со звездочками можно заменить функциями от
переменной z. В этом случае (3.56) и (3.57) будут иметь вид
Ф (z) = W (г)/[ 1 + W (г)]; (3.59)
Фе(г)=1/[1 + Г(г)]. (3.60)
Для структурной схемы, изображенной на рис. 3.10, б, имеем
Е‘ (s) = G* (s) - X* (s) (3.61) и
X[(s) = ttZ1r;(s)E,(s). (3.62)
Откуда, исключив E*(s), найдем передаточную функцию замкнутой дискретно-непрерывной системы относительно управляющего сигнала
Ф’(5) = Г(5)/0-(5) =
= Г!(з)/[1+ г1г;(з)]. (3.63)
Передаточную функцию замкнутой дискретно-непрерывной системы
5)
W, (s) (s)
1*W,(S) W2(S) W}(S)
Рис. 3.8. Структурные схемы CAP с параллельно соединенными нелинейностями:
а — исходная; б — с объединением трех нелинейностей в одну; в — приведенная к форме, удобной для расчетов
299
CL)
Рнс. 3.9. Структурные схемы САР с нелинейностями:
а — исходная с двумя нелинейностями, разделенными фазозапаздывающим динамическим звеном: б, © — преобразованные; г — приведенная к форме, удобной для расчетов
Рис. 3.10. Структурные схемы дискретнонепрерывных САР:
а — с жесткой обратной связью; б — с гибкой обратной связью
300
Таблица 3.1
Передаточные функции линейных дискретно - непрерывных систем автоматического регулирования
/Vя п/п Структурная схема В форме дискретного преобразования Лапласа В форме z-преобразования
W*(s) X(s); X*(s} W(z) X(z),[<l>(z)]
I * Т° 1 [йад] fs) w,w}(s) x(s^ ^(S^ls) X(sl hw,w2'(s) w,w2(z) '«ЖА"
1 щ(з)\ Т >о 1 Xi(s) . , , . Tq 1 ВД к—-o-"o L£LJx7s) <fs) w^siw^s) wWWs) ' ’ i*w,*(s)wf(s) w,(z)w2lz) X(Z,-[mW,(z)W2(z)]C!zI
3 | то n—1 ъ 1 |>щ| fsj w;4s)w24s) YV?, . tV,7s)G«fs) 11 i*w,4s)w;(sj W,lz)w2(z) XfZ,~[l*W,(z)W2(zjClZl
4 X,fsj| j To 1 w3(s) k—o'4»*-J w2(s) L— 1 Ix’l'S) X2(s) 1 1 Xis) w,w2w'(s) X(s)‘CW,(s)-CW,W^s)W,W3(s) p-W,W2Wf(S) WjW^lz) X(S)‘CWif!]- CW,W2(z)W,W3lz) l^W,W2W3(z)
5 Cfs) Elz) । . -kQ«<wJ w,ls) J w2(s) k-| Л To 1 ' T° LZ-J^ i [йад] X(s) wlf(s)w2w3‘(s) W^S}W2(S)C*(S) l^(s)W2W^s) w,(pw2w3lz) XM=[ wdz)W2(zl ) x'zl [hw,(z)w2w3(z)]cit
6 *(4 W,W2W*(s) cw:is)w2(s) 1 ' r>W,W2W$(s) w,w2w3(z) cw,lz)w2(z] HW,W2W3(Z)
1 ОД~E(s) r(5lr—№Sl £(S> 1 П щ (S) Lkc^okJ w2 fs) u J X7(S)T , X*(5) 1 IV/SjL-o^o 1 1 To ад WT(S)^(S}W/(S) , w,Ys)^s)cYs) lSh i*w;is]w$(s)w$(s} W,(z^(z)W3(z) W,lz)W2(z) PW,(z)W2(z)W3lz)
8 Cfs) x,(s) fH |Ш| 1 T To 1 1 1 1 Г—-1 1 |адр X(s) ^W2(s}+WjWj(s) w,w2(s)C4s) 11 hWdffls^WfWrts) mz)^(z)
301
Продолжение табл 3.1
9 X,(s) ед ИО W >^>Чади<>о^га-0 \ X3{s) &S- |ад| ед w2wt(s)+ ^*(s)w2w;( wris)w2ls)c'(s) 11 “^(s) W2W3(z}-> 11 b^w2w3(zh ^W/fzIWiWifz)]^1
10 Чад| 1 x4 (s) ад од E*(s) 1 ЭД 1 ^хед 1 W2W*(s) Xfs^WjWiGl'sh ! w2w3(s)[ew?(s)-1^W2W^S) -O^i(s}] W2W3(z) x(z)-w3w40(z)->- + W2W3(Z) _ HW2W3(Z) >[GW,(z)-CW3W4(z)]
11 ед, <(5) E*(S) г»</<>Чад]-Ч *ед|-| ед т° x^4kJ —। 1 |ад>| <(s) Ws)w4(sl ' и U^s)Wi(s)! xk}... W3(s)0(s) 11 l-W3(s)Wi(s) + wtts}w2(s) + l^W3(s]Vli(s} 1 ед i* _ li+w3(s)w4(s)J 3{H/3(s)W4(s)} и U-WjIsJWifslI хы-3/-Ж^1 ll+W3(s)W4(s)J ^(s)w2fs)l . 1 !^w3(s)w4(s)f з('—^ I 1 l^w3(s)w4(s)J
I l+W3(s)W4(s) J JWl(s)W2(s)W4(s)[- I I-W3(S)W4(S) J
12 ед, X,® ед .—. x Э Чад| 1 T°X3(s}x,(s). —1 Вдку>о*0-Ч адн Xj(s) | (s) W’ls)^ ^W,W2W^(S} x(s)-w,(s)C(s)-_w,fs)w3(s)w,w2e*(s) i+w*(s)<-w,w2w;(s] W3{z) + ^w,w2w3Sz) X(z)’=GWjfz}~ WtW3(z)W,W20{z) 1^W3(z^WtW2W}(z)
13 ад ——Чад]—। ° e(s) rw |ад xfs) Ч w2(s) |—<+>Чад |~г» | 'о X^S'x/S) I w2w;(s) »S)-^N3W4(s} + W2w3(s)[cw^(s)-1+W2W3'(s) -Wsiw3wf(s)] w2w3lz] X(z)-ow3w4(z) ; W2w3(z) 1<-W2w3(z) [Wfz)-C(z)w3W4/z)J
/4 од Чад|—I X,fs) ОД ПО ' U(S) Чад ксх'Ч адЬчэЧад Т 0 ^%/У |и£<4 X(s) W2W3W?(s) X(S)-OW3W4(S)± + W2w3(s) 1-W2w3w^(s} [ew;(s)-OIV3W4W^s)] w2w3ws(z) X(z)-CW3W4(z)-b W2W3(z) I^W2W3W3(Z) [CWt(zl-CW3W4Ws(z)]
302
Таблица 3.2
Характеристические уравнения нелинейных дискретно-непрерывных cuemen автоматического регулирования
Л'° /7//7 Структурная схема характеристическое уравнение системы в срорме дискретного преобразования Лапласа характеристическое уравнение системы в форме z- преобразования
1 ед^ £(s} £*(s) )*axo*-|jfA,f?,p)|—W(s) | x(s) 1+J (A,n,$W*(s)-0 l*3(A,n,ip) [W(z)]-0
2 ед^ То xls) IfJ (A.n,^)W,W*(s)-0 1*3(А,п,у>) [W,W2(z)]~0
Y° 'Wfj , \AL(c\ L—
3 ”^^,.,„1-1 U 1 1 w2(s) | X(s) М (A,n,ip)W,Wf(s)-0 1~J(A,n,<p) [W,W2 lz)]=0
4 F*/c) г- п 1 1 W,(s) |— W ° 1 1 W2(s) Н-°> 'о xfs) 1*3 (A,n.ip)W*(s)W2(s)-0 l*3(A,n,ip)W,(z)W2(z)-0
5 Clsl x,!s)' ед/ (sr 1 1 1 ^»<^o»|7fA,n,y)|-—| W,(s) p*-o^>*-| W2(s) |— x(s) 1*3 (A,n,ip)W*(s)W2W3(s)-0 M(Ap.ip)W,(z) [W2W3(z]=0
1 1
6 w’(s> wz® h ° X*(s) 1 1 W3(s) P*o> ’o t(s) 1*3 (AflipjW'IsjW^W^sj-O l*3(A,n,ip)W,{z) W2(z) tVj(z)-0
7 ед, x,(s) ед-f,(s)^s> 1 I T 7° 1 7-1 I 1 И^(5) P (S) -| W2(s) |- x(s) 1*3 lA,n,lf)[w,W’(s)*W,WT(s)]-0 !*3(A,n,lf) [w,w2(z) * W,Wjf4 -0
303
относительно сигнала ошибки запишем в виде
ф;(5)=е- (S)/g* ($)=
= 1/[Ц-Г,Г;(«)]. (3.64)
Из формул (3.63) и (3.64) следует, что передаточная функция всей разомкнутой системы
Г’(«) = Г1Г2(в). (3.65)
В форме z-преобразования формулы (3.63) и (3.64) имеют вид
Ф (г) = Г1(г)/[1 + W (г)] (3.66) и
Фе(г)= 1/[1 + W (г)], (3.67) где W (г) = 1^ W2 (г). (3.68)
В табл. 3.1 приведены структурные схемы и передаточные функции для некоторых типов линейных дискретно-непрерывных систем в разомкнутом и замкнутом состояниях, записанных в форме дискретного преобразования Лапласа и г-преоб-разования. Подставив в формулы z = (2/Т0 4- s)/(2/7’o — s), получим характеристики, с помощью которых при $= /й можно исследовать устойчивость дискретно-непрерывных систем, а также анализировать показатели качества и точности процессов регулирования (см. гл. 4—6).
В табл. 3.2 даны структурные схемы и характеристические уравнения для некоторых нелинейных дискретно-непрерывных систем регулирования. Пользуясь формулами, записанными в форме z-преобразования,
Рис. 3.11. Графы САР:
а —с жесткой связью; б—с гибкой связью (/, 2 — вершины графов}
в)
Рис. 3.12. Структурные схемы линейных дискретно-непрерывных САР с экстраполятором нулевого порядка:
а — исходная^ б — в форме z-преобразоваиий; в — в форме ^-преобразований
и приведя их к форме «-преобразования, получим характеристические уравнения, в которые входят наряду с передаточными функциями линейных элементов и эквивалентные передаточные функции дискретных нелинейных элементов. Для однозначных нелинейностей они совпадают с коэффициентами гармонической линеаризации (см. табл. 2.17), и проектировщик может исследовать обычно применяемыми методами устойчивость дискретно-непрерывных САР. Соответствующие примеры исследования таких систем с конкретными рекомендациями приведены в гл. 7.
Если передаточные функции линейных элементов состоят из большого числа звеньев, то традиционные методы проектирования линейных и нелинейных дискретнонепрерывных систем приводят к значительным затратам времени. Для упрощения расчетов применяют вычислительные процедуры, которые приведены в п. 2.7.
При проектировании дискретнонепрерывных систем вместо структурных схем можно пользоваться графами. На рис. 3.11, а, б показаны графы эквивалентных структурных схем соответственно с изображенными на рис. 3.10, а, б передаточными функциями. Если вместо дискретного преобразования Лапласа проектировщик будет использовать ма
304
тематический аппарат г-преобразо-вания, то на структурных схемах и графах исключаются импульсные элементы (ключи), а передаточные функции записываются в виде ^i(z), .... Wm(z) или j[UMs)b .... 3[UMs)].
Пример 3.8. Определить передаточные функции разомкнутой и замкнутой линейной дискретно-непрерывной САР по структурной схеме, изображенной на рис. 3.12, а.
Используя z-преобразование для разомкнутой передаточной функции W'(s), получим
Г (Z) = ~ * [s2 (0,1s + l)‘(0,05s + 1)]=
z- 1 Г 2 0,3 0,4 0,1 1
z 4 s2 s + s + 10 s + 20 J
0,4 , 0,4 (z-1) 0,1 (z-1) nq_
“ z- 1 + z-0,135 z-0,0185 ’
_ 0.152 (z+ 0.045) (z+ 1,135)
(z - 1) (z - 0,135) (z - 0,0185) 1 ’
В соответствии с формулой (3.69) на рис. 3.12,6 изобразим структурную схему замкнутой системы, передаточная функция которой в форме z-преобразования имеет вид
0,152 (z + 0,045) (z Ч- 1,135)
, (z - 1) (г-0,135) (г-0,0185) = 0,152 (z + 0,045) (z+ 1,135)
1 + (z - 1) (z - 0,135) (z - 0,0185)
_ 0.152 (z + 0,045) (z+ 1,135)
(z + 0,015) (z2 - l,017z + 0,350) ’ ' ‘ '
Подставив в формулы (3.69) и (3.70) соотношение z = (10 + s)/(10 — s), запишем передаточную функцию разомкнутой системы в s-форме (рис. 3.12, в):
2 (1 — 0,1s) (0,091s Ч- 1) (1—0,006s) W (S) s (0,131s + 1) (0,104s + 1)
(3.71)
По формуле (3.71) определим передаточную функцию замкнутой системы в виде
_ (1 —0,1s) (0,091s + 1)(1 —0,006s)
Ф (0,096s + 1) (0,07s2 + 0,389s +1) '
(3.72)
Пример 3.9. Определить передаточные функции разомкнутой и замкнутой нелинейной дискретио-непрерывиой САР с нелинейностью типа насыщения по структурной схеме, изображенной на рис. 3.13, а. Так как линейная часть этой системы аналогична случаю, рассмотренному в примере 3.7, то на структурной схеме (рис. 3.13,6) функцию W(z) можно записать в виде выражения (3.69). Эквивалентную передаточную функцию перепишем
из табл. 2.17, т. е.
J (А, п, ф) = / п — (k! + ki + 1) —
ТС
sin — (fc| + &2 + 1) -2/[ф+-^-(fei-fe.)J
тс sin — п
2С Sin "£r{kt+fei+l) -/[ф+^.-м]
+ А . л е | ’
sin -г— 2п
(3.73)
где Е — целая часть от числа, стоящего в фигурных скобках.
Характеристическое уравнение в s-форме (рис. 3.13,в) можно записать в виде
2 (1 — 0,1s) (0,0924s + 1) X
. , ... . X (1 — 0,006s)
1 + 7 (А, п, ф) . (01312-+ (0,i038s+1) °’
(3.74)
По уравнению (3.74) определяют периодические режимы, возникающие в нелинейной дискретно-непрерывной системе, с помощью построения годографа и кривых —1/7(А,п, ф)=—l/q(A,n, ф) при разных я= 1, 2, ... и ф или по логарифмическим характеристикам (см. гл. 7).
Пример 3.10. Привести исходную структурную схему дискретно-непрерывной САР с широтно-импульсным модулятором (рис. 3.14, а) к схеме в пространстве состояний и составить соответствующие уравиеиия. Для этого воспользуемся методикой, изложенной в п. 2.3. Тогда ис-
а)
б)
б)
Рнс. 3.13. Структурные схемы нелинейных САР с экстраполятором нулевого порядка: а — исходная; б — в форме z-преобразованнй; в — в фбрме з-преобразованнй
305
a.)
Рис. 3.14. Структурные схемы САР с ШИМ:
а — исходная; б — преобразованная к форме с изменяющимся коэффициентом Хн
ходную схему при нулевых начальных условиях можно привести в дискретной форме к виду, изображенному на рис. 3.14, б.
При действии на входе единичной ступенчатой функции воспользуемся схемой, приведенной иа рис. 3.14,6; запишем уравнения в переменных состояния.
§(кГо + О) = §(кТ());
и (кГо + 0) = g (кТ0) — х (кТ0);
У (кТй + 0) = у (кТй);
х (кТа + 0) = х (кТй)-,
У № = и (кТо) -±у (кТ0);
1 I i 1
(3.75)
х (кТ0) = у (кТ0), где Ян — переменный коэффициент усиления ШИМ, который можно для к-го периода прерывания представить в виде
Яи = [и, (/сГ0 + 0)1/[м (кТ0 + 0)]. (3.76)
Следует отметить, что переменный коэффициент усиления при исследовании нелинейных дискретно-непрерывных систем в зависимости от их структуры можно отнести к импульсному элементу типа ШИМ
или к корректирующему устройству, реализованному в виде рабочей программы на языке ассемблер иа ЭВМ, или к непрерывной части. С помощью схемы, приведенной на рис. 3.14,6, и векторно-матричных преобразований можно достроить переходный процесс х(кТ0) в системе (см. гл. 5 и 8).
4. СТРУКТУРНЫЕ СХЕМЫ ЗАМКНУТЫХ НЕПРЕРЫВНЫХ И ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ В ВЕКТОРНО-МАТРИЧНОЙ ФОРМЕ
Типовые структурные схемы линейных стационарных систем, имеющие один вход g(t) и один выход x(t), изображены на рис. 3.15, а — в. В систему кроме объекта входят по одному последовательному корректирующему и исполнительному устройству, а также датчик, формирующий сигнал ошибки е(0- Обозначим эти устройства через ш. Из рис. 3.15, а—в видно, что системы замкнуты жесткой отрицательной обратной связью. В некоторых из них в главную обратную связь может входить коэффициент, меньший 1. Структурные схемы, когда
306
связью*. В этом случае с помощью рис. 3.15, а запишем следующую систему уравнений при нулевых начальных условиях у(0) = 0:
Рис. 3.15. Структурные схемы линейных непрерывных стационарных САР, представленные в векторно-матричной форме с одним входом и одним выходом:
а — типовая; б — с параллельно включенным динамическим элементом d; в —с динамическими элементами с матрицей Лт’ находящейся во внутренней обратной связи
объект и элементы системы нестационарны, показаны на рис. 3.16, а — в.
Если системы имеют сигналы на входе и выходе в векторной форме, то типовые структурные схемы для стационарных систем примут вид, изображенный на рис. 3.17, а — в, а нестационарных — на рис. 3.18, а — в. Так как эти схемы являются многомерными, то в них входит несколько исполнительных и корректирующих устройств. Кроме того, введены измерительные датчики. Все эти устройства на рис. 3.18, а — в обозначены матрицей M(t).
Пользуясь структурными схемами (рис. 3.15, а — в — 3.18, а — в), можно привести их к форме векторно-матричных уравнений для замкнутых систем с главной отрицательной или положительной обратной
Из уравнений (3.77) имеем
У (О = (А — тЬст) у (t) + btng (/); | х(0==сту(/). 1
(3.78)
Введем в уравнения (3.78) следующие обозначения:
А — тЬс* = А3;
Ьт — Ь3,
тогда векторно-матричные уравнения для замкнутой системы будут
* См. п. 3.8.
Рис. 3.16. Структурные схемы линейных непрерывных нестационарных САР, представленные в векторно-матричной форме с одним входом и одним выходом:
а — типовая; б — с параллельно включенным динамическим элементом d(t); в— с динамическими элементами, описываемыми матрицей Ат (О» находящейся во внутренней обратной связи
307
откуда
y(t) = A3y(t) + b3g(t); |
* (t) = cT3y (t) + d3g(f), J где
(3.82)
,_____mb
3 1 + md ’
, md й'л~~ l+md'
-- -------
3 1 + md
С помощью рис. 3.15, в составим систему уравнений
Рис. 3.17. Структурные схемы линейных непрерывных стационарных многомерных САР, представленные в векторно-матричной форме:
а —типовая: б —с параллельно включенными динамическими элементами, описываемыми матрицей О: в—с динамическими элементами, описываемыми матрицей К, находящейся во внутренней обратной связи
у(t) = Ay (t) + bu'(t); ' u'(t) = m[g(t) — x(t)]+ > + kTy(t)-,
x(t) = cTy (t).
(3.83)
иметь ВИД
у (0 = А3у (г) + b3g (/); j x(t) = cTy(t). )
Для рис. 3.15, б запишем систему уравнений
y{i) = Ay (/) + &«(/);
«(/) = m[g(t) — х(/)];
г/ДО^нЦ); (3.80)
У1 (t) = с‘у (/);
х (0 = У1 (0 + у? (/)•
Из системы уравнений (3.80) найдем
’|,1=(л-тУЪ ДМ +
л (б = Тх.1 ~й' сТУ (0 + 1 у ё (0,
(3.81)
Рис. 3.18. Структурные схемы линейных непрерывных стационарных многомерных САР, представленные в векторно-матричной форме:
а — типовая; б — с параллельно включенным динамическим элементом, описываемым матрицей D (/); в — с динамическими элементами, описываемыми матрицей К (/), находящейся во внутренней обратной связи
308
Из уравнений (3.83) найдем
у(0 = (Л—mbcT+bkT)y(t)+ '
+ mbg(ty, x(t) = cTy(t),
(3.84)
а после подстановки в первое уравнение (3.84) А3 — А — mbc' + bkT и b3 = mb получим систему уравнений
у (t) = А3у (t) 4- b3g (t); 4 X{l) = CTy(t). J
В случае нестационарных CAP, структурные схемы которых изображены на рис. 3.16, получим векторно-матричные уравнения вида (3.80), (3.82) и (3.85), где матрицы и векторы зависят от времени t.
Если на входе и выходе САР имеются не скаляры, а векторы, то структурные схемы можно представить в виде, показанном на рис. 3.17, а — в и 3.18, а — в. Как и для ранее рассмотренных структурных схем, составим системы векторно-матричных уравнений в другой форме. Для рис. 3.17, а можно записать
x(t) = Cy(t).
Имея в виду систему уравнений (3.85), найдем
у (t) — (А — ВМС) у (t)Ч
+ BMg(ty, !> (3.87)
«(/)== Су (/) )
или
y(t) = A3y(t) + B3g (ty, |
x(t) — Cy(t). J
Пользуясь рис. 3.17,6, определим
у (t) = Ay (t) + Bu (t); u(t) = M[g (/) — *(/)];
Vi (t) = Du (ty,
У2 (t) = Cy (0;
x(t) = yi (0 + У2(0-
(3.89)
Откуда для замкнутой системы нетрудно получить
У (0 = А3у (t) + B3g (ty, | x(t)^C3y(t) + D3g(ty j
где
A3 = A - В (I + MD)~'MC;
B3 = B(IyMD)M,
C3 = [/ - D (I + MD)"'Л] C;
D3 = D (I + MD)lM.
Из рис. 3.17, в имеем
y(t) = Ay (0 + Ви' (t);
u'(t) = M[g(t)-x(t)] + Ky(ty, (3.91) x(t) = Cy(t),
откуда
у (t) = Ay (t) + BMg (t) - BMx (t) + + BKy(ty, x(t) — Cy (t)
или
y(t) = A3y (t) + B3(t) g (ty, x(t)~Cy(t),
где
A3 = A - BMC + BK;
B3 = BM.
Для нестационарных систем из рис. 3.18 получим зависимости типа (3.88), (3.90) и (3.92), в которые войдут матрицы А(/), B(t), C(t) и D(t).
Теперь перейдем к рассмотрению линейных дискретно-непрерывных САР с различными типами экстра-поляторов. С помощью рис. 1.62 нетрудно получить структурные схемы систем, изображенные на рис. 3.19. На рис. 3.19, а — в показаны системы с векторными сигналами, а на рис. 3.19,г — е — с одним входным и одним выходным сигналами.
Выше было показано, что векторно-матричные уравнения, описывающие динамику САР, по своему написанию ничем не отличаются от соответствующих уравнений объектов
309
Рис. 3.19. Структурные схемы линейных дискретно-непрерывных нестационарных САР, приведенные к z-форме с экстраполяторами различного порядка:
о—в — многомерные; г—е — с одним входом и одним выходом
Рис. 3.20. Структурные схемы замкнутых САР с одним входом и одним выходом, представленные в векторно-матричной форме:
а — для рнс. 3.15, а; б—для рнс. 3.15,6; в — для рнс. 3.15, в
Рис. 3.21. Структурные схемы замкнутых САР с векторным входом и выходом, представленные в векторно-матричной форме: а —для рис. 3.17, а; б —для рис. 3.17,6; в — для рис. 3.17, в
310
(устройств). Только в них входят расширенные матрицы А3, В3, С3, D3 или &3, k3, в которых учитываются уравнения датчиков, корректирующих и исполнительных устройств в виде матрицы М или скаляра т. Поэтому методика представления математических моделей непрерывных и дискретных систем основана на формулах (1.404) — (1.406).
На рис. 3.20 показаны структурные схемы замкнутых САР с одним входом и одним выходом, записанные в векторно-матричной форме. Структурные схемы для замкнутых систем с векторными входом и выходом приведены на рис. 3.21. Из рис. 3.20, а — в и 3.21, а — в нетрудно получить передаточные функции разомкнутых САР:
UZ(s) = cT[s7- А]~'Ьт; (3.93)
F(s) = {cT[s7- + (3.94)
W(s)==cT[sI - A + bkx]~'btn; (3.95)
IF (s) = C[s7 — A]-1 BAf; (3.96) IF(s) = {C[s7-Ar1B+Z)}Af; (3.97)
W (s) == C [si-A +
(3.98)
Передаточные функции разомкнутых непрерывных систем, записанные в векторно-матричной форме (3.93) — (3.95), можно представить в виде дробно-рациональной функции от оператора s. В функции IF(s) порядок числителя всегда меньше порядка знаменателя.
Для построения математических моделей САР с различными экстра-поляторами необходимо пользоваться вычислительными процедурами спектрального разложения матриц.
5. СПЕКТРАЛЬНОЕ РАЗЛОЖЕНИЕ ПРОИЗВОЛЬНЫХ ДЕЙСТВИТЕЛЬНЫХ И КОМПЛЕКСНЫХ МАТРИЦ
Рассмотрим решение системы дифференциальных уравнений (3.85), описывающей динамическую стаци
онарную САР. Будем предполагать, что эта система имеет один вход g(t), один выход x(t) ив начальный момент времени to = 0 задан вектор фазовых состояний* y(to)=yo.
В выражении (3.85) матрица А3 является действительной, размерности (п X п); &3 — вектор передачи управления размерности (п X 1); ст — вектор формирования функции выхода размерности (1 X п). В дальнейшем индекс «з» для простоты записи будем опускать; тогда можно записать
у = Ау + Bg-, (3.99)
х — сТу. (3.100)
При этом согласно формуле (1.381) решение системы (3.99) имеет вид
t
У (/) = eAty (to) + 5 еЛ {t~x)Bg (т) dr, 0 (3.101)
а выражение для выхода x(t) может быть получено путем подстановки y(t) из (3.101) в соотношение (3.100), т. е.
х (t) = сТеА<у (/0) + t
+ $стеЛ(/-ЧВ£(г)Дг. (3.102) о
Аналитическое решение (3.102) стационарной системы (3.99) — (3.100) удовлетворяет начальным условиям y(to) = yo и описывается с помощью фундаментальной матрицы eAt.
Вычисление фундаментальной (переходной) матрицы выполняют различными способами. Пусть матрица А являемся матрицей простой структуры размерности (п X п) и, следовательно, имеет различные действительные собственные значения Х2....Хп. Воспользуемся спектраль-
ным разложением матрицы А (см. прил. П-1. 1) и найдем аналитическую функцию от матрицы eAt. При
* Наличие одного входа и одного выхода не нарушает общности изложения.
311
спектральном разложении матрицы определяют все ее собственные значения и системы собственных векторов, которые используют для записи матрицы через произведение трех матриц
A = RAL", (3.103)
где R — матрица, образуемая собственными векторами матрицы А; Л — диагональная матрица, на диагонали которой стоят собственные значения; £н—матрица, образуемая собственными векторами матрицы Ат.
Поскольку считаем, что матрица А простой структуры, то и Ат будет матрицей простой структуры, и собственные значения этих матриц совпадают. В общем случае спектральное разложение действительной матрицы А (3.103) определяемся произведением матриц /?, Л, L", получаемых следующим образом. Матрица К является матрицей правых собственных векторов и удовлетворяет условию
AR = RA. (3.104)
Для получения матрицы L" заметим, что матрица R — невырожденная, и из выражения (3.104) найдем
/?1А = Л/?1; (3.105)
перепишем последнее в виде
АТ£ = £ЛН. (3.106)
Согласно выражению (3.106) матрицу £ называют матрицей левых собственных векторов, имеющей
блочную структуру:
1п], где вектор lt яв-
следующую £=[Z,U2: .
ляется собственным вектором матрицы Ат. Эти собственные векторы также образуют линейно-независи
мую систему.
Для эрмитовой матрицы А имеем
£н = R1,
и выражение (3.103) сохраняет свой вид.
Выражение (3.103) в координатной форме запишем следующим образом:
А=^МпГ{. (3.107)
»=1
Соотношение (3.107) представляет собой сумму п матриц. Система собственных векторов и собственных значений матрицы А полностью определяет любую аналитическую функцию от А; тогда в нашем случае имеем
tAt = (3.108)
1 = 1
где kt, i = 1, п — собственные числа матрицы A; r„ I— \,п—множество собственных правых векторов, определяемых условием (3.104), а ZHt, i=l, п— множество собственных левых векторов, определяемых выражением (3.106).
Подставив представление фундаментальной матрицы tAt через сумму матриц (3.106) в решение (3.102), получим
п
x(t) — cT £rzZ?e^0 +
1 = 1
+ ст$ x}Bg(r)dr.
0 i = l
Вынесем из последнего выражения за знак интеграла величины, не зависящие от т; тогда значение выходной функции
х(/) = ст г^^Уо +
nt -1
+ eKi{t~x)g(r)dr ,
1 = 1 о J
(3.109)
где ст — строка размерности (1-Х п
X «); У, TiVt — матрица размер-
ности (п X п); у0 — вектор-столбец размерности (пХ1); В — вектор-столбец размерности (пХО-
312
В произведении получим размерность (1X1) выходной функции х(/) [здесь (1 Х«) («Х») («X XI)—размерность первого слагаемого, а (1 X п) (п X п.) (п X 1) — размерность второго слагаемого].
Таким образом, для решения системы уравнений (3.85) стационарной замкнутой системы необходимо найти собственные значения и собственные правые и левые векторы матрицы А. Вычислительные алгоритмы решения полной проблемы собственных значений и собственных векторов для произвольных матриц были разработаны сравнительно недавно [36]. В основном имеется два подхода: метод Якоби, разработанный сначала для действительных симметричных матриц, и обобщенный — на случай комплексных матриц; QL и Qfl-алгоритмы (см. прил. ГТ-1.1) для любых матриц.
Рассмотрим второй подход [37]. В теоретическом плане QL и QR-ал-горитмы почти совпадают. Основное их различие состоит в том, что интерационные матрицы Ак в QL-алгоритме сходятся к блочной левой треугольной матрице и собственные значения в диагональных блоках упорядочиваются по неубыванию их модулей; в Q/f-алгоритме итерационные матрицы Ак сходятся к блочной правой треугольной матрице, диагональные элементы которой расположены в порядке невозрастания модулей.
QL-алгоритм выгоднее применять в тех случаях, когда большие элементы матрицы А сосредоточены в ее нижнем правом углу;
Qfl-алгоритм удобен, когда большие элементы матрицы находятся в ее левом верхнем углу.
При использовании Q/J-алгорит-ма предварительно матрицу А следует привести к почти треугольной форме, что позволяет существенно уменьшить объем вычислений при определении собственных значений. Матрицы, имеющие нули при всех значениях i > / + 1, называют верх
ней формой Хессенберга и обозначают через Н [37].
Для приведения матрицы А к форме И необходимо провести (/1 — 2) элементарных преобразований. Если проведено (к— 1) шагов, в результате которых сформирована матрица Ак, такая, что (к— 1) первых ее столбцов соответствуют верхней форме Хессенберга, то на к-м шаге:
1) определяют максимальный по модулю элемент |а^|, / = к+1, к + 2, ..., л; если все элементы равны 0, то нужно переходить к следующему шагу, так как к-й шаг считается законченным; если среди этих элементов будет несколько максимальных, равных между собой по модулю, то берут из них с меньшим номером /, который обозначают а!к + 1Г, к!
2) производят перестановку строк и столбцов с номерами (к 4- 1)' и (к+ 1);
3) вычисляют для каждого значения /, j — к -|-2, п величину
и по /-Й строке находят соответствующие произведения (к + 1) строки, умноженной на х/, к+i. Эти преобразования матрицы Ак можно записать в матричном виде, введя элементарные матрицы преобразований:
AK+i = N +iPk+i, (К+ j/ X
X ЛР(к+1), (k+D'Vk+1, (3.111)
где Рк+i, (к-м)' — элементарная матрица перестановок вида
Рк+1,(к+1)' =
(к+ 1)' к +1 _
1 0 0...0 0...0.. .0
0 1 0...0 0...0...0
= 0 0 0...0 0...1...0 (к+ 1)'.
0 0 0...1 0...0...0 к+ 1
0 0 0...0 0...0...1 (3.112)
313
У этой матрицы по диагонали стоят единицы, кроме (к + 1) и (к+1)' строк, единицы которых с диагонали сдвинуты соответственно на (к + 1)' и (к + 1) места. Эта матрица содержит в каждой строке и столбце только один элемент, равный 1; остальные равны нулю. При умножении слева на Рк+i, (к+1)' в матрице А переставляются строки, а справа — столбцы.
Элементарная матрица определяется элементами
«И =«/,«+!. / = к + 2, П-
«тата-к-
где на всех остальных местах 6/к — символ Кронекера.
Итерационная процедура (3.111) не более чем за (п — 2) шага приводит матрицу А к форме Хессен-берга. Если матрица А комплексная, то алгоритм (3.111) обеспечивает сходящийся процесс с
комплексными величинами. В этом случае главный элемент в столбце проще определять по величине max(Rea^+I) + Imа$+1)), а не по максимальному значению модуля комплексного числа.
Для действительных матриц общего вида рассмотрим другой способ приведения ее к типу Хессен-берга за счет унитарных преобразований. В этом случае необходимо также (п — 2) шагов. По аналогии с предыдущим будем считать, что исходная матрица приведена к Ак, у которой первые (к—1) столбцов имеют нули с номерами
а*/’, i = 1, к — 1, / > i + 1;
/= 1, п.
Следующая итерация имеет вид
Л+1 = ЛЛКРК, (3.113) где Рк — ортогональная матрица вида
к к+1 к + 2
"0 0 . . 0 0 0 0
0 0 . . 0 0 0 0
00...О 0 0 ... 0 к
00...0 (<“,.„ + о!
о о ... о «ед к «д «+о (“Й!.«)! »Й2. л к+2;
О О ... ° а^> (а1к> + о ) айайз «
Пл \ КтЬ Л К / Tin ЛТ4
(<к>)2
здесь
Вычисление матрицы Дк+1 следует производить последовательно: сначала умножить Ак слева на Рк‘, тогда получим
Ах+. = Л-^«к(»А), (3.114)
где
“к = [°> 0...0, а«1 + + СТк> а&2,К. •••> <к].
Затем полученную матрицу AK+i справа умножаем на Рк, в результате имеем
Ак+1 == -Ак+1Рк == Дк+1 "^"(^k+1Uk) Ик‘
(3.115)
За (п — 2) шагов итерационных
314
процессов (3.114) и (3.115) определим матрицу верхней формы Хес-сенберга.
Для вычисления собственных значений матрицы А воспользуемся <?/?-алгоритмом. Сначала допустим, что действительная матрица имеет действительные и все различные собственные значения. В основу этого алгоритма положено преобразование матрицы А к треугольному виду, т. е.
А = QR,
где Q — унитарная матрица; R— верхняя треугольная матрица.
Матрица RQ унитарно подобна исходной А. Поскольку матрицу Q можно определить только с помощью последовательно выполненных элементарных преобразований, строим итерационный процесс вида
А = QsRs, ^s+l == Qs^sQs>
(3.116)
который имеет своим пределом верхнюю треугольную матрицу.
Для улучшения сходимости итерации (3.116) необходимо матрицу А привести к верхней форме Хес-сенберга, используя итерационный процесс (3.113) или (3.114) — (3.115).
Запишем Q/J-алгоритм со сдвигом (см. прил. П-1.1), имеющим следующие рекуррентные формулы:
Rs = Qs(^s-<ysIY,
3^s+i — RsQs +
= H, s = 1, 2, ...
(3.117)
где Qs — ортогональная матрица; Rs — верхняя треугольная матрица; Os — сдвиг.
Для всех преобразований (3.117) матрица 3%s+l сохраняет свою структуру и согласно исходной матрице Н является верхней формой Хессен-берга.
В случае, когда собственные значения матрицы А действительны и различны, последовательность 3^s+i имеет пределом верхнюю треугольную матрицу, диагональные элементы которой представляют собой собственные значения, расположенные в порядке убывания их модулей.
Если исходная матрица А имеет кратные действительные собственные значения, то предельная матрица не будет верхней треугольной, а содержит диагональные блоки порядка кратности собственного значения. Величины <ys выбирают близкими к собственному минимальному значению матрицы 3^s; в этом случае обеспечивается быстрая сходимость итерационного процесса (3.117). Поскольку действительная матрица 3fts может содержать комплексные собственные значения, необходимо использовать комплексносопряженные значения сдвигов.
Рассмотрим два шага итерационного процесса (3.117) с двумя значениями сдвигов as и cFs+i, которые можно считать действительными или комплексно-сопряженными. Для двух итераций имеем
^s+2 = Qs+iQs^sQTsQTs+l. (3.118)
Так как Qs и Qs+i — ортогональные матрицы, то выражение (3.118) можно переписать в виде
MsQsQl+i = QTsQTs+iMs+2, (3.119) откуда
QsQs+i (Rs+iRs)=
= (^ - <rj) (^ - as+1Z). (3.120)
Из равенства (3.120) следует, что ортогональное преобразование QsQs+l приводит матрицу, являющуюся произведением — <ysI) X Х(^>- <ts+iZ), к треугольному виду. В самом деле, рассмотрим подробнее произведения входящих в это выражение матриц. Произведение
315
двух треугольных матриц Jts+iJts является треугольной матрицей (см. прил. П-1.1), а произведение двух ортогональных матриц QsQs+ — ортогональной матрицей, обладающей свойством
(QsQs+i)"1 =
= (QsQl+1)T = Qs+i<?L (3.121)
Согласно выражению (3.121) из равенства (3.120) получим соотношение
Ks+lKs = Qs+iQl - <Tj) X
X(^-ai+J). (3.122)
В любом случае, являются ли и <Ts+i действительными числами или комплексно-сопряженными, матрица (3^s — <ysI) (3%s — <rs+1/) действительная, которую всегда можно привести к треугольному виду последовательным умножением слева на элементарные эрмитовы матрицы вида
С/к =
К к+1
'1 0 0... 0 0 ... 0 0"
010... 0 0...00
00... 1 0... 0 0 к
0 0... -пк+1,к 1 ...00 к + 1.
0 0... ’ 0 ... 1 о
0 0... — пт 0 ... 0 1
Таким образом, преобразование Qs+iQs определяется произведением элементарных матриц UK. Значе
ние сдвигов <rs и (Ts+i на каждом шаге зависит от собственных значений матрицы размерности (2Х Х2), расположенной в правом нижнем углу текущей матрицы Ms, и
сле-
их можно определить, решая дующую систему уравнений:
+ °s+i = hn\ n-i +
<r,or „ ,A<S>
s s+1 * П—1, ft—1 fl, n
(3.123)
№. „ M5> . fl— I, n n, n— I
При сходимости итерационного процесса возможны два варианта: элементы или п_2 ста-
новятся достаточно малыми.
Если элемент достаточно мал, то элемент h^n можно считать собственным значением и уменьшить размер преобразующей матрицы за счет вычеркивания последней строки и последнего столбца.
Если же элемент h[^}_, л_, достаточно мал, то в качестве собственных значений матрицы 3€s следует принять пару собственных значений матрицы размерности (2X2), стоящую в нижнем правом углу матрицы Ж.. В этом случае уменьшается порядок преобразуемой матрицы до (п — 2)-го порядка вычеркиванием последних двух строк и двух столбцов.
Сходимость итерационного процесса является достаточно быстрой, если в качестве исходной матрицы в формулах (3.117) берется почти треугольная верхняя матрица.
Результирующая матрица при использовании <?/?-алгоритма не является строго треугольной и может содержать блоки размерности (2X2) на главной диагонали. Каждый такой блок соответствует действительным собственным значениям или комплексно-сопряженной паре.
Рассмотрим теперь QL-алгоритм для определения собственных значений симметричной матрицы А. Аналогично формулам (3.116) имеем рекуррентные формулы QL-алгоритма вида
A. = QSLS; 1
1 (3.124)
as+1 = qXQs. )
где Qs — унитарная матрица; Ls — нижняя треугольная матрица.
Когда собственные значения матрицы А действительны и различны, предельную матрицу процесса (3.124) можно представить в нижней треугольной форме. При этом
316
ее диагональные элементы являются собственными значениями исходной матрицы, расположенные в порядке возрастания их модулей. Сходимость итерационного процесса существенно улучшается, если вместо алгоритма (3.124) взять следующие выражения:
== QsLs Н- л
As+l = LsQs + osI-, Л, = А; 1(3.125) As+i QsAsQs. J
Матрица As унитарно подобна исходной матрице А. Элементы матрицы в процессе итераций стремятся к значению
(Ь — Os)/(^j — <rs).
Если сдвиг Os выбран близким к величине М, которая является наименьшей по модулю из собственных значений, то в пределе внедиагональные элементы первой строки будут равняться нулю. Элемент в пределе равен 1. Если в QL-алго-ритме матрица А действительная и симметричная, то все матрицы действительные и симметричные, а Qs все ортогональные и определяются последовательным перемножением матриц элементарных преобразований. Таким образом, используя соответствующие итерационные процедуры последовательных преобразований (3.125) исходной матрицы А, получим в результате все собственные значения.
Для определения собственных векторов вернемся, не нарушая общности рассуждений, к Qfl-алго-ритму, который был применен к матрице Хессенберга Ж (3.116). Обозначим предельную верхнюю треугольную матрицу через тогда
= (3.126)
где Q — произведение всех матриц преобразования, используемых в ф/?-алгоритме.
Поскольку матрица А была получена из исходной матрицы путем
конечного числа преобразований (3.114) и (3.115), в общем виде можно записать
^ = S-1AS, (3.127) где S — невырожденная матрица, являющаяся произведением всех элементарных матриц преобразования, используемых при приведении действительной матрицы А к виду Хессенберга.
Тогда выражение (3.126) примет вид
R^Q S ASQ. (3.128)
Собственные значения матрицы А расположены на главной диагонали матрицы R.
Будем считать, что диагональный элемент матрицы R. г.ц X;. является t-м собственным значением. Собственный вектор матрицы R, соответствующий действительному собственному значению Z,,, запишем в виде
x2i
Xni_
и определим его компоненты из условий
Пх{ = ^Х{, i = TT~n, (3.129) которые представим в виде системы алгебраических уравнений
О, к = i + 1, п-
(3.130)
Для решения системы (3.130) могут быть использованы стандартные программы решения систем алгебраических уравнений (например, метод Гаусса, метод итераций
317
и др.). Как только получим компоненты вектора то собственный вектор матрицы А определим в виде
P^SRXi. (3.131)
Поэтому для нахождения собственных векторов необходимо помнить все матрицы преобразования для получения матрицы SR. У комплексно-сопряженной пары собственных значений матрица содержит диагональный блок размерности (2X2). В этом случае компоненты собственных векторов можно определить с помощью следующих выражений:
(гK_lr к-! — kj) i + "Ь Gc-l, к •'•Ki ==
i = — £ /-к+1 ^*к, к— 1-^k—1, i (3.132)
+ (ГКК
i
= — 2 Гк1Хц-/ = к+1
i = 1, tv, к = 2, п.
Паре комплексно-сопряженных собственных значений соответствуют комплексно-сопряженные векторы.
В заключение приведем программу № 7 OWN спектрального разложения произвольных действительных матриц с помощью Qfl-алго-ритма.
Пример 3.11. Найдем решение полной проблемы собственных значений для дей-
ствительной матрицы вида
"3125"
. 2 13 7
A =
3 12 4
.4 1 3 2_
С помощью унитарных преобразований (3.114) и (3.115) матрицу А можно привести к верхней форме Хессенберга, а с использованием Р₽-алгорнтма определить приближенные собственные значения М = = 10,59; Х2 = —2,36; А3 = 0,19; =
= —0,42, которым соответствуют полу
ченные с помощью (3.130) векторы
" 0,85 ”
1
Г‘ = 0,78 ’
_ 0,79 _
" -0,29 "
о.и
_ -0,08
выражений (3.129),
’ 0,36 “ 1 2 = 0,09 ’
_ -0,62 _
" -0,01 ‘
1
Г 4 =
-0,24
_ -0,09 _
Собственные векторы и — rt образуют матрицу правых собственных векторов R
в выражении (3.103):
"0,85 0,36 —0,29 —0,01 '
1 1 1 1
0,78 0,09 0,11 -0,24
_ 0,79 —0,62 —0,08 —0,09 _
Согласно свойству собственных правых и левых векторов действительной матрицы А (см. прил. П-1. 1) с различными действительными собственными значениями, получим матрицу левых собственных векторов в виде
£=(«-1)Т =
"0,37 0,59 —1,64 0,68 ”
0,11 0,02 0,34 0,53
0,26 0,5 1,55 —2,34
_ 0,44 —1,1.6 —0,19 0,91 _
или, соответственно,
li = " 0,37 " 0,11 0,29 ; 1г = " 0,59" 0,02 0,5 »
_ 0,44 _ _-1,16_
"—1,64 — " 0,68 —
1з = 0,34 1,55 _—0,19 0,53 —2,34 0,91
Матрица Л имеет диагональную форму
" 10,59 0 0 0 "
А = 0 —2,36 0 0
0 0 0,19 0
0 0 0 — 0,42 _
£н =
В спектральном разложении (3.103) матрица L" имеет вид
0,37 0,11 0,29 0,44"
0,59 0,02 0,5 -1,16
-1,64 0,34 1,55 -0,19 '
0,68 0,53 -2,34 0,91 _
318
Таким образом, с помощью спектрально- также множества собственных левых Ц—Ц го разложения матрицы А получены при- и правых г,—г4 векторов.
ближенно собственные значения X, — Х4, а
ПРОГРАММА № 7 OWN (0WN1 - 0WN8)
Программа предназначен^ для спектрального разложения произвольных действительных матриц с помощью QK -алгоритма, предложенного Дж. Франсисом и В. Н. Куб-лановской, с предварительным приведением матрицы к верхней форме Хессенберга.
Обращение к программе
OWN (N,A,W,R,L,INT)
Входные параметры
N —порядок матрицы А;
А — произвольная действительная матрица.
Выходные параметры
А — матрица собственных значений в канонической форме Жордана;
W — массив с N строками и двумя столбцами, в первом из которых размещена действительная, а во втором — мнимая часть собственного значения;
R — матрица правых собственных векторов, приведенная к канонической форме Жордана;
L — матрица левых собственных векторов, приведенная к канонической форме Жордана;
INT — вектор, определяющий тип собственного значения. Его компоненты принимают значения 0, если соответствующие собственные значения действительные, и 1 — если они комплексные.
OWN: PROC (N,A,W,R,L,INT); DCL (A,W,R ,L) (*,♦) DEC (16), (N,LOW,K,I,J) FIXED BIN, (PR,LV,RV) BIT (1), INT (*); PR = ’0’B; LV,RV=’1’B; IF N < 0 THEN DO; N=—N; PR=’1’B; END; IF ADDR (A) = ADDR (R) THEN RV = ’0’B; IF ADDR (A) = ADDR (L) THEN LV = ’0’B; IF ADDR(R) = ADDR (L) THEN LV = ’0’B; BEGIN; IF PR THEN PUT LIST (’НАЧАЛО OWN’, TIME) SKIP; DCL (U.TOL, (D,D1) (N)) DEC (16); TOL = IE-12; IF RV! (iRV & -,LV) THEN DO; IF LV THEN DO 1 = 1 TON; DO J=1 TO N; L (I,J) = A (I,J); END; END; CALL OWN1 (N,A,LOW,K,D); IF PR THEN PUT EDIT (’ПРОШЛА БАЛАНСИРОВКА’,TIME,’LOW=’,LOW, ’K=’,K) (SKIP.3 A,2 (F(3),A)); CALL 0WN2 (N,LOW,K,TOL,A,D1); IF PR THEN PUT LIST (’ПРОШЛО ПРИВЕДЕНИЕ’,TIME) SKIP; IF RV THEN CALL 0WN3 (N,LOW,K,A,DI ,R); CALL 0WN4 (N, LOW, K, TOL, A, R, W, INT, RV, FAIL); IF RV THEN CALL 0WN8 (N,LOW,K,TOL,A,R,W); IF PR THEN PUT EDIT (’СОБСТВЕННЫЕ ЗНАЧЕНИЯ’, TIME, ((W (I, J) DO J = 1,2), INT (I) DO 1= 1 TO N)) (SKIP.2A, (N) (SKIP,2F (12,6), F(8))); IF RV THEN DO;
CALL OWN5 (N,LOW,K,D,R); CALL 0WN6 (N,W,R);
IF PR THEN PUT EDIT (’УПОРЯДОЧЕННЫЕ’,TIME, ((W (I, J) DO J = 1, 2), INT (I) DO 1=1 TON)) (SKIP.2A, (N) (SKIP,2F (12,6), F (8))); END; END; IF LV THEN DO; IF RV THEN DO I = 1 TO N; DO J = 1 TO N; A (I,J) = L (J,I); END; END; ELSE DO I = 1 TO N; DO J = I + 1 TO N; U = A(I,J); A (I, J) = A (J,I); A(J,I) = U; END; END; CALL OWN1 (N, A, LOW, K, D); CALL 0WN2 (N,LOW,K, TOL, A, D1);CALL 0WN3 (N,LOW,K,A,D1,L); CALL 0WN4 (N,LOW,K,TOL,A,L, W.INT, LV, FAIL); CALL 0WN8 (N, LOW, K, TOL, A, L, W);
IF PR THEN PUT EDIT (’СОБСТВЕННЫЕ ЗНАЧЕНИЯ’, TIME,((W(I,J) DO J =1,2), INT (I) DO 1 = 1 TO N)) (SKIP,2A,(N) (SKIP,2F (12,6), F (8)));
CALL 0WN5 (N,LOW,K,D,L); CALL 0WN6 (N,W,L); IF RV THEN CALL 0WN7 (N,W,A,R,L,INT); IF PR THEN PUT EDIT (’УПОРЯДОЧЕННЫЕ’, TIME, ((W (I, J) DO J =1,2), INT (I) DO 1=1 TO N)) (SKIP,2A, (N) (SKIP,2F (12,6), F (8))); END; GO TO RET; FAIL: DO 1 = 1 TO 5; DISPLAY (’БОЛЕЕ 30 ИТЕРАЦИИ’); PUT EDIT (’БОЛЕЕ 30 ИТЕРАЦИИ’) (SKIP (2),X (10),A); END;
RET: IF PR THEN DO 1= 1,2; PUT LIST (’КОНЕЦ OWN’,TIME) SKIP; END; END; IF PR THEN DO 1 = 1, 2; PUT LIST (’OWN ENDED’,TIME) SKIP; END; END OWN;
Подпрограмма 0WN1
OWN1:PROC (N,A,LOW,HI,D); DCL N,(A (»,»),D (*)) DEC (16), (LOW,HI) FIXED BIN; /* ПОНИЖЕНИЕ НОРМЫ МАТРИЦЫ A (N,N)*/ /♦ТОЧНЫМ ПРЕОБРАЗОВАНИЕМ ПОДОБИЯ*/
319
/* ИНФОРМАЦИЯ О КОТОРОМ ПРЕДСТАВЛЕНА В МАССИВЕ D (N) */ DCL (I,J,K,L), (B,B2,C,F,G,R,S) DEC (16), NOCONV BIT (1); EXC : PROC (M); DCL M; D(M) = J; IF M = J THEN RETURN; DO I = 1 TO K; F = A(I,J); A (I, J) = A (I,M); A (I,M) = F; END; DOI = 1TON; F = A(J,I); A (J,I) = A (M,I); A(M,I)=F; END; END EXC; В = 16; B2 = В * В; L = 1; К = N; D = 1;
/* ВЫДЕЛЕНИЕ НУЛЕВЫХ СТРОК И СДВИГ ИХ ВНИЗ»/
LI: DO J = K BY - 1 ТО 1; R = 0; DO I = 1 TO J - 1, J + 1 TO K; R = R + ABS (A (J,I)); END; IF R < IE - 16 THEN DO; CALL EXC (К); K = K — 1; GO TO LI; END; END;
/«ВЫДЕЛЕНИЕ НУЛЕВЫХ СТОЛБЦОВ И СДВИГ ИХ ВЛЕВО*/
L2: DO J=L ТО К; С = 0; DO I = L ТО J - 1, J + 1 ТО К; С = С + ABS (А (I, J)); END; IF С < IE - 16 THEN DO; CALL EXC (L); L = L + 1; GO TO L2; END; END;
/♦МАСШТАБИРОВАНИЕ ПОДМАТРИЦЫ, C L ДО К */ LOW = L; HI = K;
ITERATION: NOCONV=’0’B; DO I = L TO K; C,R=0; DO J = L TO I - 1, 1 + 1 TO К; С = C + ABS (A (J,I)); R = R + ABS (A (I, J)); END;G=R/B; F = 1; g _ Q |
L3: IF C < G THEN DO; F = F * В; С = С * B2; GO TO L3; END; G = R ♦ B;
L4; IF C>=G THEN DO; F=F/B; С = C/B2; GO TO L4; END; IF (C + R)/F < 0.95 * S THEN DO; G = l/F; D (I) = D (I) * F; NOCONV = ТВ; DO J = L TO N; A (I, J) = A (I, J) * G; END; DOJ=1TOK; A (J,I) = A (J,I) . F; END; END; END; IF NOCONV THE GO TO ITERATION; END 0WN1;
Подпрограмма 0WN2
0WN2: PROC (N,K,L,TOL,A,D); DCL N,K,L,(A (*,*), D (*), TOL) DEC(15), I,J,M,LA, (F,G,H) DEC(15); LA = L-1; DO M = K+1 TO LA; H = 0; DO 1 = L BY - 1 TO M; F ,D (I) = A (I,M - 1); H = H+ F » F; END; IF H < =TOL THEN DO; G = 0; GO TO SKIP; END; G = SQRT (H); IF F > = 0 THEN G = - G; H = H — F * G; D (M) = F — G; DOJ = MTON; F = 0; DO I = L BY - 1 TO M; F = F + D (I) * A (I, J); END; F = F/H; DO I = M TO L; A (I, J) = A (I, J) - F * D (I); END; END; DO I = 1 TO L; F = 0; DO J=L BY-1 TO M; F = F + D (J) * A (I, J); END; F = F/H; DO J = M TO L; A (I, J) = A (I, J) — F » D (J); END; END;
SKIP: A(M,M — 1) = G; END; END 0WN2;
Подпрограмма 0WN3
0WN3: PROC (N, LOW, UPP, H, D, V); DCL (N, LOW, UPP, I, J, К, M) FIXED BIN, (H (*,*), D (*), V (*,*), X,Y) DEC (15); DO I = 1-TO N; DO J = 1 TO N; V(I,J) = 0; END; V(I,I)=1; END; DO К = UPP - 2 BY - 1 TO LOW; M = K+1; Y = H(M,K); IF Y = 0 THEN GO TO SKIP; Y = Y * D (M); DO I = K + 2 TO UPP; D(I) = H(I,K); END; DO J = M TO UPP; X = 0; DOI = MTOUPP; X = X + D (I) * V (I, J); END; X = X/Y; DO I = M TO UPP; V (I, J)=V (I, J)+X * D (I); END; END;
SKIP: END 0WN3;
Подпрограмма 0WN4
0WN4: PROC (N, LOW, UPP, MACHEPS, H, VECS, WW, CNT, RV, FAIL); DCL (N,LOW,UPP,CNT (*), I, J, K, L, EN) FIXED BIN, ((H, VECS, WW) (*,*), MACHEPS,P,Q,R,S,T,W,X,Y,Z, RA, SA, VR, VI, NORM) DEC (16), M, NA, ITS, (NOTLAST.RV) BIT (1); DO I = 1 TO LOW - 1, UPP + 1 TO N; WR (I) = H (1,1); WI(I) = 0; CNT(I) = 0; END; EN = UPP; T = 0; NEXTW: IF EN < LOW THEN GO TO FIN; ITS = 0; NA = EN - 1;
NEXTIT: DO L = EN BY - 1 TO LOW+1; IF ABS (H (L,L - 1)) < = MACHEPS * (ABS (H(L - 1,L - 1)) + ABS (H(L,L))) THEN GO TO CONTI; END; L = LOW;
CONTI: X = H(EN,EN); IF L = EN THEN GO TO ONEW; Y=H(NA,NA); W=H (EN,NA) * H (NA.EN); IF L=NA THEN GO TO TWOW; IF ITS=30 THEN DO; CNT(EN) = 31; GO TO FAIL; END; IF ITS = 10! ITS =20 THEN DO; T = T + X; DOI = LOW TO EN; H (1,1) = H(I,I) — X; END; S=ABS(H(EN,NA)) + ABS (H (NA,EN — 2)); X,Y = 0.75 * S; W = — 0.4375 * S * S; END; ITS = ITS + 1; DO M=EN —2 BY — 1 TO L; Z=H(M,M); R = X - Z; S = Y - Z; P = (R * S — W)/H (M + 1 ,M) + H (M,M + 1); Q = H (M + 1 ,M + 1) — Z — R — S; R = H (M + 2,M + 1); S = ABS (P) + ABS (Q) + ABS (R); P = P/S; Q = Q/S; R = R/S; IF M=L THEN GO TO CONT2; IF ABS (H(M.M- 1)) * (ABS (Q) + ABS (R)) < = MACHEPS * ABS (P) ♦ (ABS (H(M - 1, M-l)) + ABS (Z) + ABS(H(M+1, M+l))) THEN GO TO CONT2; END;
320
CONT2: DO I = М + 2 TO EN; H (1,1 — 2) = 0; END; DO I=M + 3 TO EN; H (1,1 - 3) = 0; END; DO K=M TO NA; NOTLAST=K-,=NA; IF K-,=M THEN DO; P = H(K,K- 1); Q = H (K + 1 ,K — 1); IF NOTLAST THEN R =H(K + 2, К — 1); ELSER=0; X = ABS (P) + ABS (Q) + ABS (R); IF X = 0 THEN GO TO CONT3; P = P/X;Q = Q/X; R = R/X; END; S = SORT (P * P + Q * Q+R * R); IF P < 0 THEN S=—S; K-, = M THEN H (К, К - I) = - S * X;
ELSE IF L-, = M THEN H (К, К — 1) = —H (К, К — 1); P = P + S; X = P/S; Y = Q/S; Z = R/S; Q = Q/P; R = R/P; /* МОДИФИКАЦИЯ */ DO J = К TO N; P = H(K,J) +Q*H(K+ L J); IF NOTLAST THEN DO; P = P + R * H (K + 2, J); H (K + 2, J) = H (K + 2, J) — P * Z; END; H (K + 1, J) = H(K+L J) - P * Y; H(K,J) = H(K,J)-P*X; END; IF К + 3 < EN THEN J = К + 3; ELSEJ=EN; DO 1 = 1 TO J; P = X»H(I,K) + Y*H(I,K+ 1); IF NOTLAST THEN DO; p = p + Z * H (I, К + 2); H (I, К + 2) = H (I, К + 2) - P * R; END;
H(I, K+ 1) = H (I, K+ 1)- P»Q; H(I, K) = H(I, К) - P; END; IF RV THEN DO I = LOW
TO UPP; P = X* VECS (I, K) + Y* VECS (I, К + 1); IF NOTLAST THEN DO; P = P + Z * VECS (I, К + 2); VECS (I, К + 2) = VECS (I, К + 2) — P * R; END; VECS (I, К + 1) = VECS (I, К + 1) — P * Q; VECS (I, K) = VECS (I.K)-P; END;
CONT3: END; GO TO NEXTIT;
ONEW: WR(EN), H (EN,EN) = X + T; WI(EN) = 0; CNT (EN)=ITS; EN=NA; GO TO NEXTW;
TWOW: P = (Y — X)/2; Q = P • P + W; Z = SQRT (ABS (Q)>;
X,H(EN,EN) = X + T; H (NA, NA) = Y+T; CNT (EN) = - ITS; CNT(NA) = ITS; IF Q>0 THEN DO; IF P < 0 THEN Z = P - Z; ELSE Z = P + Z; WR (NA) = X + Z; WR(EN), S=X—W/Z; WI (NA), WI (EN)=0; X=H(EN, NA); R=SQRT (X * X+Z*Z); P = X/R; Q = Z/R; DO J = NA TO N; Z=H (NA, J); H (NA, J)=Q • Z+P • H (EN, J); H (EN, J) = Q * H (EN, J) — P * Z; END: DO 1=1 TOEN; Z = H(I, NA); H(I, NA) = Q»Z +P»H(I,EN); H (I, EN) = Q • H (I, EN) - P • Z; END;
IF RV THEN DO I=LOW TO UPP; Z = VECS(I, NA);
VECS (I,NA) = Q * Z + P * VECS (I,EN); VECS (I,EN) = Q » VECS (I,EN) — P * Z; END; END; ELSE DO; WR (NA), WR (EN) = X + P; WI (NA) = Z; WI (EN) = - Z; END; EN = EN — 2; GO TO NEXTW;
FIN: ; DCL FAIL LABEL, ,WR (N) DEC (16) DEF WW(1SUB, 1), WI (N) DEC (16) DEF WW(1SUB,2); END OWN4;
Подпрограмма OWNS
OWN5:PROC(N, LOW, HI, D, R); DCL (N, LOW, HI) FIXED BIN, (D(*), R (*,*)) DEC(16); /«ПРОГРАММА ФОРМИРОВАНИЯ R ИЗ СУЩ. ИЛИ ДО НИХ*/ DCL(I,J,K), S DEC (16); DO I = LOW TO HI; S=D(I), DO J =1 TON; R (I, J) = R (I,J) * S; END; END; DO I = LOW - 1 BY - 1 TO 1, HI+1 TO N; K = D(I); IF K-, = I THEN DO J=1 TO N; S = R(I,J); R (I, J) = R (K, J); R(K,J) = S; END; END OWN5;
Подпрограмма 0WN6
OWN6: PROC(N,W,T); DCL (W,T) (*,*) DEC (16), N, I, J, K, (A,U) DEC (16); DO 1= 1 TO N- 1; A = ABS (W (1,1)) + ABS (W(I,2)); K = I; DO J = 1+ 1 TO N; U = ABS (W (J, 1)) + ABS (W (J,2)); IF U = A THEN IF W(I,2)<0 THEN K = J; IF U > A THEN DO; A = U; К = J; END; END; IF К > 1 THEN DO J = 1 TO N; A=T(J,K); T(J,K) = T(J,I); T(J,I) = A; IF J < 3 THEN DO; A = W(K,J): W (K,J) = W (I,J); W (I, J) = A; END; END; END; END OWN6;
Подпрограмма 0WN7
OWN7: PROC (N,W,A,R,L,INT); DCL ((A, W,R,L) («,»), U, Ul) DEC (16), N, I, J, К, M, INT (»), (S,S1) CPLX DEC (16); A = 0; INT = 0; DO 1=1 TON; IF W (1,2) >0 THEN DO; DO J = 0,1; A (I + J, I + J) = W (I + J, 1); A (I + J, I + 1 — J) = W (I + J> 2); INT (I + J) = 1; END; U = 0; S = CPLX(U,U); DO J = 1 TO N; S = S + COMPLEX (R (J,I), R (J, I + 1))* COMPLEX (L (J,I), L (J, I + 1)); END; S = S/2; DO J=1 TO N;
COMPLEX (L (J,I), L (J,I + 1)) = CONJG (COMPLEX (L (J,I), L (J,I + 1))/S); END; 1 = 1+1; END; ELSE DO; A(1,1) = W(1,1); U = 0; DO J=1 TON; U = U + R (J,I) * L (J,I); END; DO J = 1 TO N; L (J, I)=L (J,I)/U; END; END; END; /* ТРАНСПОНИРОВАНИЕ МАТРИЦЫ L */ DO I = 1 TO N; DO J = I + 1 TO N; U = L(I,J); L (I,J) = L (J,I); L(J,I) = U; END; END; END OWN7;
11 Ю. И. Толчеев 321
Подпрограмма 0WN8
OWN8: PROC (N, LOW, UPP, MACHEPS, H, VECS, WW);
DCL (N, LOW, UPP, M, NA, ITS, I, J, K, L, EN) FIXED BIN, ((H, VECS, WW) (*,*), MACHEPS, P, Q, R, S, T, W, X, Y, Z, RA, SA, VR, VI, NORM) DEC (16); NORM = 0; K=l; DO 1=1 TO N; DO J = К TO N; NORM=NORM + ABS (H (I,J)); END; K = I; END; DO EN = N BY - 1 TO 1; P = WR (EN); Q = WI(EN); NA = EN — 1; IF Q = 0 THEN DO; M = EN; H(EN,EN)= 1; DO I=NA BY-1 TO 1; W = H(I,I)-P; R = H(I,EN); DO J = M TO NA; R = R + H (I,J) * H (J.EN); END; IF WI (I) < 0 THEN DO; Z = W; S = R; END; ELSE DO; M = I; IF WI(I) = 0 THEN IF W-, = 0 THEN H (I,EN) = — R/W;
ELSE H (I,EN) = — R/(MACHEPS * NORM); ELSE DO; X=H(I,I+1); Y=H (1+1,1);
Q = (WR (1) — P) * * 2 + WI (I) * * 2; H(I,EN), T = (X*S-Z*R)/Q;
IF ABS (X) > ABS (Z) THEN H (I + 1 ,EN) = (—R — W * T)/X;
ELSE H (I + 1,EN) = (—S — Y * T)/Z; END; END; END; END; ELSEIFQ<0 THEN DO; M = NA; IF ABS (H (EN.NA)) > ABS (H (NA.EN)) THEN DO; H (NA,NA) = — (H (EN,EN) - P)/H (EN,NA); H (NA.EN) = -Q/H (EN,NA); END; ELSE CALL CDIV (-H (NA, EN), 0, H(NA,NA)-P, Q, H(NA,NA), H(NA,EN)); H(EN,NA)=1; H(EN,EN) = 0; DO I = NA - 1 BY-1 TO 1; W = H(I,I)-P; RA = H(I,EN); SA = 0; DO J = M TO NA; RA = RA + H (I.J) * H (J.NA); SA = SA + H (I, J) * H (J, EN); END; IF WI (I) < 0 THEN DO; Z = W; R = RA; S = SA; END; ELSE DO; M = I; IF WI (I) = 0 THEN CALL CDIV (—RA, —SA, W,Q,H(I,NA), H(I,EN)); ELSE DO; X = H(I,I+1); Y = H(I+1,I);
VR = (WR (I) — P) * * 2 + WI (I) * * 2 — Q * Q; VI = (WR (I) - P) * 2 * Q;
IF VR = 0 & VI = 0 THEN VR = MACHEPS * NORM * (ABS (W) + ABS (Q) + + ABS (X) + ABS (Y) + ABS (Z)); CALL CDIV (X * R — Z * RA + Q * SA, X*S — Z*SA —Q*RA, VR, VI, H (I,NA), H (I,EN)); IF ABS (X) > ABS (Z) + +ABS (Q) THEN DO; H (I + 1, NA) = (—RA - W * H (I,NA) + Q * H (I,.EN))/X; H (I + 1,EN) = (—SA —W*H(I,EN) — Q * H (I,NA))/X; END;
ELSE CALL CDIV (—R — Y * H (I,NA), —S — Y * H (I,EN), Z, Q, H(I+1, NA), H(I+1,EN)); END; END; END; END; END; DO 1 = 1 TO LOW-l, UPP + 1 TO N; DO J = I + 1 TO N; VECS (I, J) = H (I, J); END; END; DO J = N BY - 1 TO LOW; IF J < = UPP THEN M = J; ELSE M = UPP; L = J - 1; IF WI (J) < 0 THEN DO; DO I = LOW TO UPP; Y,Z = 0; DO K=LOW TO M; Y = Y+VECS (I,K) * H (K,L); Z = Z + VECS(I,K)*H(K,J); END; VECS(I,L) = Y; VECS (I,J) = Z: END; END; ELSE IF WI(J) = 0 THEN DO I = LOW TO UPP; Z = 0; DO K = LOW DO M; Z = Z + VECS (I,K) * H (K, J); END; VECS (I,J) = Z; END; END;
DCL CDIV ENTRY (DEC (16), DEC (16), DEC (16), DEC (16),,), WR (N) DEC (16) DEF WW(1SUB,1), WI(N) DEC (16) DEF WW(ISUB,2); END OWN8;
Программа OWN может быть настроена на несколько режимов работы: решение полной проблемы собственных значений с вычислением правых и левых собственных векторов; вычисления только правых или левых собственных векторов или вычисления только собственных значений. При этом времена решения этих трех режимов будут находиться в отношении 1; 0,5; 0,1. Для выделения из общей задачи частных задач используют различные способы обращения к программе OWN.
Вычисление собственных значений и только правых собственных векторов можно задать двумя способами:
OWN(N, A, W, R, A, INT);
OWN (N, A, W, R, R, INT);
аналогично при вычислении только левых собственных векторов:
OWN (N, A, W, A, L, INT);
OWN (N, A, W, L, L, INT).
Для вычисления только собственных значений обращение к программе должно быть таким:
OWN (N, A, W, A, A, INT).
6. АЛГОРИТМЫ ВЫЧИСЛЕНИЯ ФУНКЦИЙ ОТ МАТРИЦ
В п. 5 была использована функция от матрицы вида Ф(А) = ел/, записанная в форме (3.108) через сумму легко вычисляемых матриц. Рассмотрим любые аналитические функции от матриц.
Согласно правилам умножения матриц (см. прил. П-I.l) произведение квадратной матрицы на се
322
бя можно записать как степень матрицы
А • А = А2, и, обобщая это произведение на к сомножителей, имеем
АК = А-А- ... -А;
при этом выполняются следующие правила:
АкАт = Ак+т-(АТ = Акт; А° = 1.
(3.133)
Те же правила справедливы и для отрицательных степеней, если матрица А неособенная, т. е.
(А~1)т = А~т.
Очевидно, что теперь можно записать многочлен от матрицу в виде
f (А) = а0/ -|- atA + а2^2 + • •
... +a„A"=SMi (3.134) i«=0
ИЛИ
/(А) = а„(А-М)И-V) ••• ...(А-М), (3.135)
где Xi, А-2, ..., Хл— корни многочлена f(z), удовлетворяющие уравнению
Оо + a^z -j- a2z2 -j- ... -|- anzn = 0.
Бесконечный ряд по А можно записать следующим образом:
/(А)=£а<А'. (3.136)
(«0
При этом ряд (3.136) является сходящимся [28], если сходятся соответствующие скалярные ряды f(XK), к—1, п, где Хк — собственные значения матрицы А.
Вопросы сходимости матричных рядов (3.136) здесь не приводятся ввиду их сложности. Укажем лишь
матричные ряды для элементарных функций: экспоненциальной
(3.137)
синусоидальной
. я я А3 , А5
sinA = A--5f + -5i----...
exp (/А) — exp (— /А) . 138)
косинусоидальной
cosA = T-^r + —- ... _ exp (/А) + exp (— /А) .
гиперболического синуса
Л3 Л 5
shA = A + 4r + 4r+ ...
... =ехрА-ехр(-А) . (3 Д40)
гиперболического косинуса
лл-/+4+4-+...
exp А + exp (— А)
2
Возьмем для простоты симметричную матрицу А, которую, как известно, с помощью матричного преобразования Р можно привести к диагональному виду, т. е. ее можно записать в виде
(3.142)
Нетрудно для любого
убедиться в том, что целого к справедливо
11*
323
равенство
Ai 0 ... О 1
АК = Р
О Лг ... О
Р\ (3.143)
L О О ... Л* J
Следовательно, используя выражения (3.133), (3.134), (3.142) и (3.143), имеем
(3.144)
Матрица (3.144) справедлива, когда Хь Х2, .... не являются корнями многочлена f(z). Если выбранный многочлен (3.134) является характеристическим многочленом матрицы А, то f(M) = = 0, ..., f(Xn) = O, и матрица А удовлетворяет своему собственному характеристическому уравнению А — X/ = 0.
Заметим, что при характеристических числах матрицы А, отличных от нуля, обратную матрицу можно записать в виде
Эти рассуждения обобщаются на случай, когда f(z) является аналитической функцией аргумента z; тогда матричная функция f(A) записывается ' аналогично формуле (3.144). Подобные формулы были получены для любой квадратной матрицы в работе [11].
Рассмотрим выражение (3.104). Согласно формулам (3.133), (3.143) можно записать равенство
АКЦ = РАК, (3.146)
в котором в координатной форме матрица Ак имеет следующий вид:
Ак=£л“< (3.147)
i1
Таким образом, согласно соотношениям (3.144), (3.147) многочлен от матрицы А определяется соответствующим многочленом от собственных значений. При этом слагаемые собственных правых и левых векторов не изменяются.
Используя выражение (3.144) и покоординатную запись спектрального разложения, получим
f (A) (М г til (3.148)
<=1
Выражение (3.148) используют при построении алгоритмов вычисления аналитических функций от матриц на областях, содержащих собственные значения квадратной матрицы А. Приведем некоторые матричные функции, встречающиеся при исследовании САР.
Фундаментальная матрица Ф = ел< как функция приведена в выражении (3.108), а несколько других матричных- функций представим конечными рядами вида
е"лг°= Le-^r»nZ"; (3.149) f (А) = (елг°-/) =
= £ е Л ~ (3.150)
i«l *
Т(Л)_А‘Н2ф._
п о 1 Т
= 2 rill (3.151)
л—J 1 0
<F(A)=Ath-^A-16 = n th ^i^O
= У TTf^r^bi. (3.152) fe(^9
Программу № 8 MFUNC используют для вычисления функций, приведенных в табл. 3.3.
324
Программа № 8 MFUNC
Программа MFUNC предназначена для вычисления аналитических функций от действительных матриц, спектр которых не содержит кратных собственных значений. В программе в качестве исходных данных использовано спектральное разложение исходной матрицы А, которое может быть получено с помощью программы OWN.
Прн каждом обращении к программе вычисляют пару матричных функций, используемых в теории динамических систем. Определяемые функции приведены в табл. 3.3. Они задаются прн обращении к программе по параметрам Q, С н Е>[26].
Таблица 3.3
Матричные функции
Признак Q | Вычисляемые функции | Признак Q 1 Вычисляемые функции
С D с D
1 елт° (елт°—/)А-1 3
2 А"1 А 4 -^-(Ф + ТГ^Ф-Т) J 0 -^-(Ф+7)"1^ * 0
А — матрица исходной непрерывной системы; Ф —переходная матрица; £==(ф—./) А~'.
Обращение к программе
MFUNC (N,T,Y,A,R,L,C,D,P,Q)
Входные параметры
N — порядок динамической системы;
Т — такт дискретности;
Y — информационный вектор, задающий порядок следования собственных значений в матрице;
А — действительная матрица в канонической форме Жордана, содержащая собственные значения исходной-' матрицы;
R — матрица правых собственных векторов исходной матрицы;
L — матрица Эрмитово сопряженных левых собственных векторов исходной матрицы; Q — параметр, задающий вид вычисляемых матричных функций.
Выходные параметры
C.D — вычисляемые матрицы;
Р — массив собственных значений матрицы.
MFUNC: PROC (N, Т, Y, A, R, L, С, D, Р, Q); С = 0; D = 0; Р=0; DCL (N, I, J, К, Q) FIXED BIN,Y(*), (Т, (A, R, L, С, D, Р) (*,*), X, G, Н, LAM, ОМЕ, SI, СО, REC, IMC, RED, IMD) DEC (12), (М (9), Z (9)) LABEL; IF Q>=4 THEN Q = 4; IF Q< = 1 THEN Q = 1; DO 1=1 TO N; LAM=A(I,I); H = EXP (A (1,1) • T); IF Y (I) < 0.5 THEN DO; IMC,IMD = 0.0; GO TO M(Q);
M(l): REC = Hi IF ABS (H — 1) < 10E - 10 THEN RED = T;
ELSE RED = (REC- 1.0)/LAM; GO TO OUT;
M(2): REC = 1.0/LAM; RED = LAM; GO TO OUT;
M(3): REC=2.0/T*(H-1.0)/(H+1.0); IF ABS (H—1)<10E—10 THEN RED=1; ELSE RED = REC/LAM; GO TO OUT;
M (4): RED = 2.0/T/(LAM +1.0); REC = RED * (LAM - 1.0); GO TO OUT;
OUT: ; END; ELSE DO; ОМЕ = A (I + 1,1); G = LAM * LAM + ОМЕ * OME; CO = COS (ОМЕ * T); SI = SIN (OME * T); GO TO Z (Q);
Z (1): REC = H*CO; IMC = H*SI; RED = ((H • CO—1.0) ♦ LAM + H* OME * SI)/G; IMD = (H * SI * LAM - ОМЕ * (H * CO - 1.0))/G; GO TO OUT1;
Z (2): REC=LAM/G; IMC=-OME/G; RED = LAM; IMD = OME; GO TO OUT1;
Z (3): X = (H»H+ 1.0 + 2.0» H* CO) ♦ T/2.0; REC = (H ♦ H — 1.0)/X; IMC = 2.0 * H * SI/X; RED = (REC * LAM + IMC * OME)/G;
IMD = (IMC * LAM - REC • OME)/G; GO TO OUT1;
325
Z (4): X = ((LAM + 1.0)*»2 + ОМЕ * ОМЕ) * T/2.0;
REC = (LAM* LAM - 1.0 + OME * OME)/X; IMC = 2.0 * OME/X;
RED = (LAM + 1.0)/X; IMD = —OME/X; GO TO OUT1;
OUT1: ; 1 = 1+ 1; END; DO J = 1 TO N; DO K=1 TON; H=L (I,K) * R (J.I); G=0.0; IF Y(I)>0.5 THEN DO; H = H + R (J,I - 1) * L (I - 1 ,K);
G = R (J,I) * L (I — 1 ,K) — R (J,I - 1) * L (I, K); END; C (J,K) = C (J,K) + REC * H + IMC*G; D (J,K) = D (J,K) + RED * H + IMD * G; END; END; P (1,1) = REC; P (2,1) = IMC; IF Y (I) >0.5 THEN DO; P (1,1 - 1) = REC; P (2,1 — 1) = —IMC; END; END; END MFUNC;
7. ДИСКРЕТНЫЕ МОДЕЛИ CAP
Так как в современные САР входят управляющие электронно-вычислительные машины, то необходимо для реализации вычислительных процедур строить дискретные модели. В п. 1.10 даны обобщенные формы представления математических моделей для объектов в дискретной форме, структурные схемы которых приведены на рис. 1.62. Пользуясь этими схемами и формулами п. 3.4, нетрудно получить структурные схемы САР,
как это показано на рис. 3.20 и 3.21.
Для определения дискретных моделей необходимо пользоваться последовательно реализуемыми на ЭВМ программами № 7 OWN, № 8 MFUNC и № 9 DISCR. Программа DISCR обеспечивает получение дискретной модели системы. Все формулы, с помощью которых получается дискретная модель, приведены в п. 1.10 для динамических объектов с экстраполяторами 0, 1 и 2-го порядков.
Приведем программу № 9
DISCR.
Программа № 9 DISCR
Предназначена для получения дискретной модели непрерывной системы.
Обращение к программе
DISCR (N,AA,H,TAKT,M,L,А,В)
Входные параметры
N — порядок исходной непрерывной системы;
АА — матрица исходной непрерывной системы;
Н — вектор передачи управления непрерывной системы;
ТАКТ — такт дискретности;
М — число измерений входного сигнала;
L — порядок степенной функции;
А — матрица размерности (N + M—1)X(N + M—1), в верхнем левом углу которой расположена матрица размерности (NXN); остальные элементы нулевые. Выходные параметры
А — матрица дискретной модели; В — вектор передачи управления;
DISCR: PROC (N, АА, Н, ТАКТ, М, L, А, В); DCL I, J, К, L, М, N, ((А, АА) (*,»), (В,Н)(*), D(N,N), S (M,L + 1), (ST,T) (L + I ,M), (STS,TS) (L + 1,L + 1), (C,G)(N,N), E(N,L + 1), B(N,M), ТАК, ТАКТ) DEC(12); CALL FAD(AA,N,D); C,G = 0; E = 0; KOT = L + 1; B=0; S = l; DO J=2 TOL + 1; S (1,J) = 0; DO 1 = 3 TO M; S (I,J) = (I — 1)» * (J — I); END; END; CALL MATRT (S, M, KOT, SI); CALL MATR (ST, S, KOT, M, KOT, STS); CALL FAD (STS, KOT, TS); CALL MATR (TS, ST, KOT, KOT, M, T); DO 1=1 TON; DO J =1 TON; G (I, J) = A (I, J); END; END; DO 1= I TON; G (1,1) = G (1,1) _ 1; END; CALL MATR (G, D, N, N, N, C); DO K=1 TOL + 1; DO I = 1 TO N; DO J = 1 TO N; E (I,K) = E (I,K) + С (I, J) • H (J)/TAKT **(£-!); END; END; TAK=—ТАКТ * * K; DO 1=1 TO N; DO J=1 TO N; C (I,J)=K * С (I, J); END; END; DO 1=1 TO N;' C (1,1) = C (1,1) + ТАК; END; G = C; CALL MATR (G, D, N, N, N, C); END; CALL MATR (E, T, N, KOT, M, R); B=0; DO 1=1 TON; B(I) = R(I,M); END; IF M > 1 THEN DO; B(N+l) = l; DO 1 = 1 TO N + M-l; DO J=1 TO N + M-l; IF I>N I J>N THEN A(I,J) = 0;
326
Рис. 3.22. Структурная схема САР для примера 3.12
END: END; DO I = 1 TO N; DO J = N + 1 TO N 4-M - 1; A (I, J) = R (I,N + M-J); END; END; IF M > 2 THEN DO I = N 4- 1 TONfM-2; A (14-1,1) = 1; END;END;
MATRT: PROC (A, N, M, AT); DCL ((A, AT) (*,*)) DEC (15), N, M, I, J; DO 1 = 1 TO M; DO J=1 TO N; AT (I, J) = A (J,I); END MATRT;
MATR: PROC (A, B,N, K,M, C); DCL N, M, К, I, J, КЛ, ((A,B,C) (»,*)) DEC (15); DO 1=1 TON; DOJ=1TOM; C(I,J) = 0; DO КЛ = 1 TO K: C (I,J) = С (I, J) 4-A (I.KJl) * В (КЛ ,J); END MATR;
FAD: PROC (A,N,B); DCL N, I, J, К. P DEC (15), ((A, B) (*,*), Al (N,N)) DEC (15); DO 1 = 1 TON; DO J =1 TON; Al (I, J) = A (I, J); IF I = J THEN В (I, J) = 1; ELSE B(I,J) = 0; END; END; DOK=ITON; IF К = 1 THEN GO TO Ml; CALL MATR (A,B,N,N,N,A1);
Ml: P=0; DO 1 = 1 TO N; P = P - Al (I,I); END; P = P/K; IF P=0 THEN PUT SKIP LIST (’СЛЕД = 0’); IF K<N THEN GO TO М2; DO 1 = 1 TO N; DO J=1 TO N; В (I.J) = В (I,J)/P; END; END; GO TO М3; М2: ; DO 1 = 1 TO N; DO J=1 TO N; IF I = J THEN В (I,J) = Al (I,J) - P; ELSE В (I, J) = Al (I, J); END: END;
М3: ; END FAD; END DISCR:
Пример 3.12. Определить матрицы Ф, F ме объекта регулирования входят рулевой
н ст для дискретной модели непрерывной привод н корректирующее устройство. Рас-
системы с экстраполятором 0-го порядка. ширенная матрица системы полученная до-
Структурна э схема САР с объектом, займ- бавлением к объекту элементов регулиро-
ствованным нз примера 1.6, изображена на вания, приведена в виде матрицы (3.153).
рис. 3.22. Откуда видно, что в схему кро-
0,4 0 0 0 0 0 0 0,4 0 0 0
0,06 0,05 0 0 0 0 0 0,01 0 0 0
0,0015 0.05125 0,05 0 0 0 0 0,00025 0 0 0
0,015 0,5125 100,5 - 100 0 0 0 0,0025 0 0 0
0 0 0 100 -100 0 0 0 0 0 0
А = 0 0 ' 0 0 400 -400 0 О' 0 0 0 (3.153)
0 0 0 0 0 2,5.10е 0 0 0 0 0
0 0 0 0 0 0 0 3000 -9 • 10’1 9000 9- 106
0 0 0 0 0 0 0 0 - -3000 ! о,ооз з
мв «в мв ам м • 1В •
0 0 0 0 0 0 0 0 0 Г” o’ 1 !
0 0 0 0 0 0 -0,22 0 0 ? 0 -ю
во • во •
Соответствующие векторы b и ст имеют Строки F и ст для дискретной модели
вид
JT = [0 0 0 0 0 0 0 0 0 0 0,22];
cT = [0 0 0 0 0 0 I 0 0 0 0].
В матрице А выделим жирными линиями: сплошными — подматрицу объекта, штриховыми — подматрицу коррекции, а штрнхпунктирными — подматрицу рулевого привода. Остальные невыделенные жирными линиями подматрицы учитывают взаимное влияние выделенных подматриц.
Дискретная модель разомкнутой системы регулирования, состоящая из корректирующего устройства, рулевого привода н объекта, приведена в виде матрицы (3.154).
FT = [0,0013 3,13 • 10“5 7,83 • КГ7 8,13 • 10~6 -4,04 - 10"7 1,90-10-7 7,97-Ю-4 -1,4598 2,65-10~6 9,51 • 10“7 -1,01 • 10-9];
ст = [0 0 0 0 0 0 1 0 0 0 0].
В гл. 4 по данной дискретной модели построены логарифмические амплитудно-фазовые частотные характеристики разомкнутой системы (пример 4.22), а в гл. 5 приведен переходный процесс x(f) (пример 5.21):
327
8. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ
Управляемость и наблюдаемость линейных и нелинейных замкнутых систем относится к основным понятиям теории автоматического регулирования, позволяющим оценивать правильность выполнения структурных преобразований. При этом следует иметь в виду, что управляющие сигналы g(t) должны переводить системы из любого начального состояния в установившееся за конечное время tK (управляемость) и по выходному сигналу x(t) однозначно определять ее начальное состояние (наблюдаемость). Пользуясь данными понятиями, проектировщик САР может при различных преобразованиях исходной схемы путем ввода дополнительных сигналов или их исключения без нарушения правильности ее структуры получить управляемые и наблюдаемые системы. В ряде случаев проектировщик пользуется системами, в которых обеспечивается управляемость.
Сформулируем понятия управляемости и наблюдаемости для любых систем, в которых протекают изменяемые во времени процессы x(t). Эти процессы называют управляемыми, если на каждую переменную состояния y(t) можно целенаправленно воздействовать с помощью сигнала управления g(t) в течение конечного времени.
Если переменная состояния не зависит от управления g(t), то отсутствует возможность требуемого ее изменения во времени и она является неуправляемой. Когда это касается всех переменных состояния, то система в целом является неуправляемой.
В ряде случаев требуется определить переменные состояния по результатам изменения входных и выходных сигналов, например, иногда появляется необходимость оценить по изменениям входных и выходных сигналов те переменные со-
328
Рнс. 3.23. Графы состояний:
а — не полностью управляемой системы; б — не полностью наблюдаемой системы
стояния, которые необходимы для закона управления. Здесь появляется понятие наблюдаемости.
Процесс g(t) называют наблюдаемым, если каждая переменная состояния процесса обусловливает изменение некоторых выходных переменных. На рис. 3.23, а изображена схема состояния процесса с двумя переменными yi и у2. Так как входной сигнал g(t) воздействует только на переменную yi(t), то переменная состояния y2(t) является неуправляемой, а процесс не полностью управляемым или неуправляемым. На рис. 3.23, б изображена схема, соответствующая состоянию ненаблюдаемого процесса. В самом деле, переменная состояния y2(t)< не связана с выходной переменной x(t); поэтому, если сигнал x(t) измерен, можно определить переменную y\(t), поскольку yi(t)=x(t). Однако по имеющейся информации об yi(t) нельзя определить переменную y2(t). Значит, процесс можно охарактеризовать как не полностью наблюдаемый или ненаблюдаемый.
Определение управляемости линейных непрерывных и дискретных систем совпадает, за исключением того, что во втором случае уравнениями состояния являются линейные разностные уравнения 1-го порядка.
Согласно уравнениям (1.18), (1.90), (3.83) запишем состояние
процесса в виде разностных уравнений для нестационарных систем У ('к+1) = А (/к) у (tK) + В (tK) g (tK); j * (tK) = C (tK) у (tK) + D (tK) g (tK), ]
(3.155)
где у (/K), g (tK), x (tK) — соответственно векторы размерности (n X 1). (mXl), (г XI); W, B(tK), C(tK), D(tK) — матрицы коэффициентов соответствующих размерностей (nXrt)» (nXm), (rXn), (rXm).
Определим понятия полной управляемости по состоянию и полной управляемости по выходу:
1) система, описываемая уравнениями (3.155), является полностью управляемой по состоянию, если для произвольного начального момента времени to существует последовательность управлений g(t0), g(ti), •••, g(tN-\), которая переводит каждое начальное состояние у (to) в некоторое конечное состояние у (In) за конечное tN t0',
2) система, описываемая уравнениями (3.155), является управляемой по выходу, если для произвольного начального времени t0 существует последовательность управлений g(t0), g(t\), ..., g(tN-\), таких, при которых некоторое конечное значение выходной переменной x(tN) может быть достигнуто из произвольного начального состояния за конечное время fo to-
Иногда говорят об абсолютной управляемости системы, имея в виду, что система является полностью управляемой (по состоянию или по ВЫХОДУ) ДЛЯ любых to и tN to.
Приведем условия об управляемости линейных стационарных систем. Уравнения состояния такой системы имеют вид
У (Ui) = Ay (tK) + Bg (fo); | x(tK) = Cy(tK) + Dg(tK), Р -10 >
где А, В, С, D—матрицы постоянных коэффициентов соответствующих размерностей, как в системе (3.155).
329
Линейная стационарная САР, описываемая уравнениями (3.156), полностью управляема по состоянию тогда и только тогда, если матрица размерности (nXNtn)
К = [В АВ А2В . . . AN 'B] (3.157)
имеет ранг п.
Линейная стационарная САР, описываемая уравнениями (3.156), является полностью управляемой по выходу только в том случае, если матрица
Т = [CAN~'B С AN~2B ... CAB СВ]
(3.158)
имеет ранг г.
Для линейных нестационарных систем, описываемых уравнениями вида (3.155), необходимые и достаточные условия полной управляемости по состоянию состоят в том, что матрица вида
£ = [£0 ^1 • • • Av-J размерности (nXNm) (3.159)
должна иметь ранг п, где Lt — = W(tN, ti + x) B(tj) — матрица размерности (n X tn), i = 0, N-—2;
(^V> ^i + l) = (^N-l) & (^-2) • • •
... A (//+1) — матрица размерности (n X n);
V(tN, ti+l) = I, i = N—l.
Если система (3.92) имеет только один вход т—\, матрица L имеет размерность (лХ«), и в этом случае условие полной управляемости по состоянию состоит в том, что эта матрица должна быть невырожденной.
Линейная нестационарная система, описываемая уравнениями (3.155), является полностью управляемой по выходу тогда и только тогда, если матрица вида
8 = [So, 8Ь ..., S,v] размерности
[rX^+l)™] (3.160)
имеет ранг г.
Здесь матрицы S,- определяются следующим образом:
C(tN)W(tN, ti+l)B(ti),
Si
» = 0, N — 1; D(tN), i = N.
Кроме того, для полной управляемости по выходу (m X tn)-мерная матрица Грамма
,v
ss'= £ s.s;
1=0 *
должна быть невырожденной.
Пример 3.12. Рассмотри.^ САР, описываемую следующими уравнениями:
M'K+1) = «MU +(3.161)
y2(/K+i) = ^2(Q + M(U- <3-162)
где а 0, 0, 62 =5^ 0.
С физической точки зрения состояния у> (/к) и угОк) являются несвязанными. Однако, поскольку динамика этих состояний совпадает, не представляется возможным независимо управлять ими с помощью одной входной переменной g(t).
Покажем, что эта система не является управляемой по состоянию. Составим матрицу К. ..гласно выражению (3.157)-
Г^1
К = [В АВ}=|
L «2
аЬ^ ab2
(3.163)
Очевидно, что матрица К является вырожденной, следовательно, ранг К меньше 2 и система (3.161)—(3.162) неуправляема по состоянию.
Введем определения полной и глобальной наблюдаемости.
Линейная автоматическая система, описываемая уравнениями (3.155), является полностью наблюдаемой, если для некоторого t0 состояние у (to) может быть определено по известному входу £(/к) и выходу х(/к) для tQ С (к tn, где In — конечное время. Если же система является полностью наблюдаемой для всех to и tK > to, то ее называют глобально наблюдаемой.
Рассмотрим условия наблюдаемости для стационарной системы,
330
описываемой уравнениями (3.156). Линейная стационарная система является полностью наблюдаемой тогда и только тогда, когда матрица размерности (n X Nr)
G = [Ст АТСТ (Ат)2Ст ... (АТ-’СЧ
(3.164)
имеет ранг п.
Запишем переходное уравнение состояния в виде
у(/к)=^ак, /о)у(/о)+
к —1
+ S *(tK, ti^Bdi) g(tt), (3.165) /»0
где Т (tK, to)—A (Q A (tK_j)... A (t0)— матрица размерности (n X п).
В этом случае необходимые идо-статочные условия полной наблюдаемости для нестационарных систем состоят в том, что матрица Q размерности («Х") имеет ранг п:
лг-1
Q=Z ч'Ж *о)Ст(6)Х
«“О
(3.166)
Приведем примеры для иллюстрации применения представленных методов проверки управляемости и наблюдаемости САР.
Пример 3.13. Рассмотрим систему уравнений 2-го порядка вида
У^)-АУ((К) + ВИ(^ где
А = Р ®1. В=Г 1 1.
L0 3 J’ L2 J
Составим матрицу К согласно выражению (3.157):
Очевидно, что det К = 0, следовательно, система является неуправляемой. С физической точки зрения состояния yi и у2 являются . несвязанными, т. е. состояниями нельзя управлять независимо с помощью одной входной переменной g.
Рис. 3.24. Структурная схема системы с тремя связями
Пример 3.14. Имеем линейную цифровую систему управления, описываемую разностными уравнениями:
y(/K+i) = ^(U + B,(/K);
х (<к) = Су (tK), где
ГО 1 1 Г°1
-2J= B = L1J: С = [22]-
Составим матрицу
K=[B4B] = [J _*].
Поскольку ранг К = 2, то рассматриваемая система является полностью управляемой по состоянию для переменных t/i(/K), у2(/к). Наблюдаемость системы исследуют с помощью матрицы G вида (3.164):
[о __о 1
2 -г]
Так как полученная матрица является вырожденной, то система неиаблюдаема. Следовательно, не все состояния У1(М, ytdt.) могут быть определены по известной выходной переменной x(t0) за конечный интервал времени (t0, tN). Наконец, составим матрицу Т и проверим управляемость системы по выходу.
Согласно матрице (3.158) имеем
Т = [С АВ СВ] = [-2 2].
Так как ранг этой матрицы равен единице, то система является управляемой по выходу. Таким образом, рассмотренная линейная цифровая система является управляемой по состоянию и по выходу, но ненаблюдаемой.
Пример 3.15. Дискретная модель динамики космического аппарата описывается векторно-матричным уравнением состояния
»w=wB«('K)-
где А и В — матрицы, имеющие соответственно размерности (11 X И) и (ЧХО-Запишем эти матрицы:
331
Поскольку система имеет только одни вход, исследовать ее управляемость можно с помощью вычисления определителя матрицы К размерности (11 X11) вида
К=[В АВ А2В ... А,0В);
det К = 44,6- 10".
Следовательно, система является полностью управляемой по состоянию.
В случае исключения отдельных связей и передаточных функций из структурных схем, а также изменения их параметров происходит потеря управляемости и наблюдаемости. Например, из анализа структурной схемы (рис. 3.24) можно показать, что за счет выбора ее параметров теряется управляемость и наблюдаемость. Откуда следует
U (s) — W3(s)G (s) + W[(s)G (s)—
— kisW 1 (s) W2(s)G(s) —
— k2Wl(s)W2(s)G (s) (3.167) или
W(S)=U^L =
W {) G (s)
_ IF, (s) + IF3 (s) /qtfiRl
l + (fc1S + fc2)IF,(s)IF2(s) ’
Примем, что IF1(s) = (7'Is + I)-1; UZ2(*) = №$+ I)]-’ и W3(s) = k; тогда после их подстановки в выражение (3.168) получим
t/(s) G(s)
(fe17’1s + fe+l)(r2s+1)
s(F,s+ l)(F2s+ l) + fe2(^s+ 1)
(3.169)
Если принять k\/k2 = T2, то можно записать
U(s) = —^Gts) +
s + 77
+ Tf^G<s) + 7fi7G<s)’ (ЗЛ70) где
(s + Ф1) ($ + <P2) = s2 + 77 + 4? •
(3.171)
332
В выражении (3.170) при условии (3.171) получим вычеты передаточной функции (3.168) в полюсах системы
Y1 = Res {Г (s)} | s т2
Y2 = Res{IF(s)}|s._(pi; (3-172)
Уз = Res {Г (s)}!^. J
Опишем данную систему в пространстве состояний в виде
Xi(s) = —H-j-GW;
s+n
*3(s)=ThrG(s)-
Имея в виду эти соотношения, запишем следующую систему уравнений:
*1 (0 = — 77 х, (/) + y,g (/);
-МО = — Ф1Х2(0 + Тг£(О: (3.173) А (0 = — <Р2*з (0 + (0;
и (() — Х1 (0 + х2 (0 + х3 (0- J
Условие управляемости данной
системы можно представить в виде
det К = у!у2у3 (ф( — (ф! — ф2) X
X (ф2 — —) #= о.
Так как Yi — 0, то det К = 0, что указывает на отсутствие управляемости САР.
Если изменить переменные состояния системы, приняв
то уравнения состояния и выхода будут иметь вид
*1 (О = — 77 xi (0 + g (0;
М0 = — Ф1Х2(0 -+- «г(0;
М0 = — ф2М0 + £(0;
U (0 = У 1Xj (0 + у2х2 (0 + '+ Узхз (0-
} (3.174)
Система (3.174) управляема по входу и не наблюдаема по выходу u(t), так как
det {Г} = у(у2уз (ф( — X
X (Ф1 — ф2)(ф2 — 1/Г2) = О при У! = 0.
Возможны и более сложные случаи потери управляемости и наблюдаемости, связанные с изменением нескольких параметров системы.
9. НОМОГРАММЫ И ВЫЧИСЛИТЕЛЬНЫЕ ПРОЦЕДУРЫ ДЛЯ ПОСТРОЕНИЯ
ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЗАМКНУТЫХ СИСТЕМ
При исследовании многоконтурных систем автоматического регулирования необходимо определять логарифмические амплитудную и фазовую частотные характеристики замкнутых (контуров) * или систем по частотным разомкнутым характеристикам разомкнутых систем. Для этого пользуются номограммой замыкания Никольса, которая может быть построена с помощью следующих формул:
Г (/(о) = Д'(®)е/0(“) (3.175) и
Ф(» = А (ш) е/ч>(и). (3.176)
В формулах (3.175) и (3.176) через Н' ((d) и А (со) соответственно обозначены амплитудные и фазовые частотные характеристики разомкнутой и замкнутой систем;
* См. гл. 1, п. 4.
333
-340 ~320 -ЛЮ '200 -260 '240 220 200 ИО /60 '140 120 100 -60 ~60 ~40 ~20 0 20 40 60 60 100 120 140 160 100 200 220 240 260 200 000 320 340 0°
Рис. 3.25. Номограмма Никольса в декартовой системе координат
Рис. 3.26. Номограмма Никольса в полярной системе координат:
стрелка 1 — направление положительных углов 0”; стрелка 2— отрицательных углов; в случае положительных 0° значения ф° указаны в кружках на штриховых линиях; для отрицательных значений 0° углы ф® — результат суммы с углом — 360°
0(ш) и <р((о)—соответственно фазовые характеристики разомкнутой и замкнутой систем.
Имея в виду, что частотные характеристики разомкнутых и замкнутых систем при наличии главной отрицательной обратной связи * связаны между собой соотношением
ф«“)—TTiFW- ,3177'
* Построение частотных характеристик контуров с положительной обратной связью изложено в гл. 1, п. 7.
после подстановки в (3.177) формул (3.175) и (3.176) получим
А (^ • (3-178)
' ’ 1 + Н' (ш) е70(и) v
Выделим из выражения (3.178) отдельно амплитудные и фазовые частотные характеристики; тогда найдем
А «о) = , , "4<й) ;
VН'г (<о) -|- 2Н' (со) cos 0 (<о) -|- 1
(3.179)
z \ if sin 0 (со) ) ф((0) = arctg
(3.180)
По формуле (3.179) в логарифмическом масштабе строится амплитудная частотная характеристика замкнутой системы (приведена на рис. 3.25 тонкими сплошными
335
Рис. 3.27. Номограмма Никольса, построенная в пространстве
линиями), а по формуле (3.180) в логарифмическом масштабе изображена фазовая частотная характеристика замкнутой системы (показана на рис. 3.25 тонкими штриховыми линиями).
Числовые значения Д(со) в дБ обозначены кружками, которые расположены на сплошных линиях номограммы, а <р(со) в градусах — кружками на штриховых линиях. Номограмма Никольса в декартовой системе координат приведена на рис. 3.25. На рис. 3.26 построена номограмма Никольса в полярной системе координат.
Если пользоваться номограммой Никольса в декартовой системе координат, то необходимо помнить, что по оси ординат отложены значения * И (а), а по оси абсцисс 0(<о). Кривая 201g которая
получена по точкам, соответствующим Д(со) и 0(со) при пересечении со сплошными линиями, даст 20 1g Л (со), а со штриховыми — <р(ш).
Практическое использование номограммы Никольса (рис. 3.26)
* В гл. 1 введено следующее соотношение: 201g/Г (со) = Н (w).
также требует построения кривой 20 lg W{jio), но в этом случае значения Я(со) и 0(<о) откладываются в полярной системе координат.
Как уже говорилось раньше, декартова система координат представляет собой сочетание многолистных . фазовых поверхностей, изображенных на рис. 3.25 в виде нескольких плоскостей, линией раздела которых являются прямые, проходящие вверх от начала координат (—180°,‘ 0 дБ) или (+180°, 0 дБ). Выделим эти прямые жирными сплошными линиями. Тогда при пересечении кривой 20 lg W(ja) штриховых линий номограммы (рис. 3.25) не происходит скачкообразного изменения фазы ср с 0° до 360°.
С целью доказательства этого на рис. 3.27 построена номограмма Никольса в пространстве на трех плоскостях. Откуда видно, что изменение характеристики 20 lg №(]<&) (кривые / и 2) никогда не приводит к скачкообразному изменению фазы <р(со). Данное положение подтверждается с помощью номограммы Никольса, построенной в декартовой системе координат.
Итак, при применении- номограммы Никольса в декартовой системе координат переход характеристикой 201g W(ju>) жирных прямых обеспечивает непрерывность по
336
строения фазы <р(со). Для ее получения фазовую характеристику замкнутой системы следует смещать на ±360°. Номограммами (рис. 3.25 и 3.26) следует пользоваться при графоаналитических расчетах простых типов систем автоматического регулирования.
В случае сложных систем для замыкания разомкнутых систем необходимо применять вычислительную процедуру, которая приведена в программе № 10 N0M0, предназначенной для соединения устройств и объектов регулирования в замкнутые динамические системы.
Программа № 10 NOMO
Программа предназначена для вычисления логарифмических амплитудно-фазовых характеристик замкнутых систем автоматического регулирования.
Обращение к программе
САН. NOMO (OM.LR.TETR.LZ.TETZ)
Входные параметры
— круговая частота;
I.R — значение логарифмической амплитудной характеристики разомкнутой системы; FETR — значение фазовой характеристики разомкнутой системы.
Выходные параметры
LZ — значение логарифмической амплитудной характеристики замкнутой системы;
TETZ — значение фазовой характеристики замкнутой системы.
Указанные значения характеристик вычисляются при данном значении круговой частоты
NOMO: PROC (ОМ, LR, TETR, LZ, TETZ); DCL (OM,LR,TETR,LZ,TETZ, HZ, HR, ('. V) DEC FLOAT (16); DCL (WR.WZ) CPLX DEC FLOAT (16); HR = 10.0 * * (LR/20.0); WR = HR * CPLX (COSD (TETR), SIND(TETR));
WZ = WR/(1.0 + WR); U = REAL(WZ); V = IMAG(WZ); HZ = ABS(WZ); TETZ = ATAND (V,U); LZ = 20.0* LOG10(HZ); END NOMO;
Hi. COЕДИНКНИГ CAP
В ДИНАМИЧЕСКИЕ КОМПЛЕКСЫ
зуясь этой схемой, запишем
Большинство CAP соединяются в комплексы управления с помощью следующих видов соединений: последовательного, параллельного и их взаимных комбинаций с обратными связями [32]. Каждая САР может быть описана в векторно-матричной форме с помощью уравнений вида
Д = Г^.. &0)с(2)т
L о А<2)
Г 6<‘W<2> I
6=L ь<2> J:
СТ = [С(1)Т = Д(1)С(2)т];
d =
(3.182)
У = Ay + bg\
X = с1 у + dg.
(3.181)
При параллельном соединении двух САР (рис. 3.28,6) имеем следующие соотношения:
На рис. 3.28, а изображена структурная схема двух последовательно соединенных САР*. Поль-
' Принадлежность к структурной схеме обозначают индексами: (1)—для первой схемы; (2) — для второй схемы.
Г ДО) I 0 1 4 _ .....!.....
L О [ Д<2> .
Г6<1) 1
ь=L б<2) J: СТ = [С(1)Т ; С(2)Т]. d = до) + Д(2).
(3.183)
337
Рис. 3.28. Структурные схемы соединения САР в комплексы:
а — последовательная; б — параллельная; а —с обратной связью
Если соединить рассматриваемые системы с помощью обратной связи по схеме на . рис. 3.28, в, то получим
где q = 1/(1 + Верхний
знак в этом соотношении соответствует положительной обратной связи, а нижний — отрицательной.
Процедура вычислений соответствующих матриц и векторов систем в комплексе реализована в виде программы № 11 JOINT.
ПРОГРАММА № 11 JOINT
Программа предназначена для соединения динамических систем с одномерными входами и выходами, описываемых уравнениями вида
у = Лу + bg;
х = сту + dg.
Осуществляются четыре вида соединения: последовательное, параллельное, а также этн соединения с отрицательной обратной связью. При этом рассмотрены следующие последовательности соединений: 1) вторая система является выходом; 2) первая система является выходом.
338
Обращение к программе
CALL JOINT (A1,B1,C1,D1,N1,A2,B2,C2,D2,N2,A0,B0,C0,D0,N0,P)
Входные параметры
N1 —порядок системы Si;
Al (N1,N1), Bl (NI), Cl (NI), DI—описание системы S,;
N2 — порядок системы S2;
A2(N2, N2), B2(N2), C2(N2), D2 — описание системы S2;
P — признак соединения (см. рис. 3.29).
Выходные параметры
N0 — порядок объединенной системы;
A0(N0,N0), В0 (N0), С0 (N0), D0 — описание объединенной системы.
JOINT: PROC (Al, Bl, Cl, DI, NI, A2, B2, C2, D2, N2, A0, B0, C0, D0, N0, F); DCL Al (*,*), Bl (*), Cl (*), A2 (*,*), B2 (*), C2 (*), A0(*,*), B0(*), C0(*); N0 = N1+N2; A0=0; IF P>0 THEN DO; D7=D1*D2; IF D7=-l THEN GO TOM; Q=l/(1 + D7); DO 1=1 TONI; B0 (I) = Q * Bl (I); DOJ=1TON1; A0 (I, J) = Al (I, J) — Q * D2 * Bl (I) * Cl (J); END; DO J = N1 + 1 TO N0; A0 (I,J) = —Q * Bl (I) * C2 (J — NI); END; END; DOI = N1+1 TO N0; B0 (I) = Q * Cl * B2 (I — NI); DO J = 1 TO NI; A0(I,J) = Q* B2 (I-Nl)* Cl (J); END; DO J = N1 + 1 TO N0; A0 (I, J) = A2 (I-Nl, J-Nl) - Q*D1 * B2 (I-Nl) * C2 (J-Nl); END; END; IF P > 1 THEN DO; DO 1 = 1 TONI; C0 (I) = Q * Cl (I); END; DO I = N1 + 1 TO N0; C0 (I) = —Q * DI * C2 (I — NI); END;D0 = Q*D1; END; ELSE DO: DO 1= 1 TO NI; C0 (I) = Q * D2 * Cl (I); END; DO I = NI + 1 TO N0; C0 (I) = Q * C2 (I — NI); END; D0=Q*D1*C2; END; END; ELSE DO; IF P> = 1 THEN DO; DO 1=1 TONI; B0(I) = B1(I); C0(I) = C1(I);
DO J = 1 TONI; A0(I,J) = Al (I, J); END; END; DO I = N1 + 1 TO N0; B0 (I) = B2 (I — NI); C0(I) = C2(I —NI); DO J = Nl+l TO N0; A0(I,J) = A2 (I-Nl, J-Nl); END; END; D0=D1 + D2; END; ELSE DO; DO 1=1 TO NI; B0(I) = B1(I); C0 (I) = Cl (I) * D2; DO J=1 TONI;
A0(I,J) = Al (I, J); END; END; DO I = NI + 1 TO N0; B0 (I) = B2 (I - NI) * DI; C0(I) = C2 (I — NI); DOJ=1TON1; A0(I,J) = B2 (I - NI) * Cl (J); END; DO J = N1 + 1 TO N0; A0 (I, J) = A2 (I - NI, J-Nl); ENI?; END; D0=D1*D2; END;
M: END JOINT;
Пример 3.16. Составить результирующие матрицы и векторы для четырех типов схем (рис. 3.29,а—г), если исходные уравнения имеют вид
y = A!y+6ig; у — Агу + b2g-, 1
> (3.185)
X = с\у + d,g; х = с^у + d2g. )
Примем, что матрицы и векторы систем (3.185) имеют следующие числовые значения:
Рис. 3.29. Соединения CAP $i и $г в комплексы при реализации процедуры №11 JOINT: а — при Р — —1,5; б — при Р - —0,5; в — при Р — 1,5; г — при Р — 0,5
339
Тогда при последовательном соединении, пользуясь процедурой № 11 JOINT, получим
“-1 60000“
4 -10 0 0 0 0
. 0 0 -12 3 4
.Ал =
0 0 0 -9 6 7’
2 098-34
При параллельном соединении
"—1 6 0 0 0 0
4 —10 0 0 0 0
0 0 -1 2 3 4
° ~ 0 0 0 —9 6 7
0 0 9 8 —3 4
Если комплекс образован последовательным соединением систем с отрицательной обратной связью, тогда
“—1 60000“
4 —1 —1 —2 0 0
, 0 0 -1 2 3 4
До —
0 0 0 -9 6 7’
2 0 9 8 —3 4
_ 4 0 5 5 7 —5_
а при параллельном соединении систем получим
-— 1 6 0 0 0 0“
4 —1 —1 —2 0 0
, 0 0 —1 2 3 4
До==
0 О 0 —9 6 7 ’
2 0 9 8 —3 4
_ 4 0 5 5 7 —5 _
11. ВЫЧИСЛИТЕЛЬНЫЕ ПРОЦЕДУРЫ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИИ РАЗОМКНУТЫХ И ЗАМКНУТЫХ САР
При исследовании устойчивости, качества и точности САР не в пространстве состояний (гл. 4—6) используются передаточные функции разомкнутых систем с числовыми значениями коэффициентов. Раньше было показано, что они записываются в виде дробно-рациональных функций относительно аргументов s, s и z. Числитель функции представляет собой полином, где корни являются нулями передаточной функции, а знаменатель — полюсами.
Для вычисления передаточных функций применяется программа № 12 TRFUNC, входными параметрами которой являются матрицы А, В и С. При переходе к передаточным функциям для анализа устойчивости необходимо знать полюсы и нули дробно-рациональной функции. Для этих целей используется программа № 13 BERSTOW.
340
ПРОГРАММА № 12 TRFUNC
Предназначена для вычисления передаточных функций динамических систем, заданных векторно-матричными тройками {А, В, ст}. Передаточная функция формируется в виде отношения двух полиномов
«7 „ Р1*п~‘+ Ргхп~2 + ... +РП
хл + сцх”-1 + а2хл-2 + ... 4-а„’
где х — комплексная переменная s.
Обращение к программе
TRFUNC (N,P,F,FB,C,BETA,ALPHA)
Входные параметры
N — порядок системы;
Р — массив собственных значений матрицы;
F — матрица системы;
FB — вектор передачи управления;
С — вектор формирования выхода.
Выходные параметры
ВЕТА — вектор коэффициентов числителя;
ALPHA — вектор коэффициентов знаменателя.
TRFUNC: PROCEDURE (N, Р, F, FB, C, BETA, ALPHA);
DCL N, ((P,F) (*,*), (FB, C, BETA, ALPHA) (*)) DEC (12); DCL I, J, K, (CC, (Cl, PP, Y) (N), POL (0: N + 4)) DEC (12); POL=0; BETA = 0; PP = 0; POL(2)=1; DO 1=1 TO N; C1(I) = C(I); END; DO 1=1 TO N;
IF ABS (P (2,1)) < IE-9 THEN DO J = I4-2 BY-1 TO 2;
POL (J) = POL (J—1)—POL (J) * P (1,1); END; ELSE DO;
DO J = I-|-3 BY-1 TO 2; POL (J) = POL (J) * (P (1,1) * P (1,1) + P (2,1) * P (2,1))
—' POL (J—1) * P (1,1) * 2 + POL (J — 2); END; 1 = 1+1; END; END;
DO 1=1 TON; ALPHA (I) = POL (N — I + 2); DO J= 1 TO N; PP (I) + Cl (J) * FB (J);
CC = 0.0; DOK = 1 TON; CC = CC + С (K) * F (K,J); END; Cl (J) = CC; END; DOK=1TON; C(K) = C1(K); IF К > = N - I + 1 THEN BETA (I) = BETA (I) + POL (K + 2) * PP (К + I — N); END; END; RETURN; END TRFUNC;
ПРОГРАММА № 13 BERSTOW
Предназначена для вычисления корней алгебраического уравнения порядка N.
Обращение к программе
BERSTOW (N.H.UV)
Входные параметры
N — порядок алгебраического уравнения;
Н — массив коэффициентов алгебраического уравиення.
Выходные параметры
UV—массив корней алгебраического уравнения размером (NX 2), расположенных следующим образом:
1-й корень: UV (1,1) = Re Ай UV (1,2) = Im
2-й корень: UV (2,1) = Re Л2; UV (2,2) = Im Л2;
N-й корень: UV (N, 1) = Re UV (N,2) = Im
BERSTOW: PROC (N.H.UV); 14 = -1; 12 = 14; N1=N + 1; P,Q,R = 0;
L: IF H(l)-, =0 THEN GO TO L50; N1=N1-1; V(N1), U(N1) = 0;
DO 1 = 1 TO Nl; H(I) = H(I+1); END; GO TO L; L50:IF Nl = l THEN GO TO L199; IF Nl_,=2 THEN GO TO L55; R = —H(1)/H(2); GO TO L150;
L55: IF N_,=3 THEN GO TO L60; P = H(2)/H(3); Q = H(1)/H(3); GO TO L160; L60:IF ABS (H (Nl — 1)/H (Nl))-, = ABS (H(2)/H(l)) THEN GO TO L87; I2 = -I2; M = Nl/2; DO 1=1 TOM; N2 = N1 + 1 —I; F = H(N2); H(N2) = H(I); H(I) = F; END; IF Q = 0 THEN P=0; ELSE DO; P = P/Q; Q=l/Q; END;
341
IF R-, =0 THEN R = 1/R; L87 : В (Nl), C (Nl) = H (Nl); В (Nl 4-1), C (Nl 4-1) = 0; N3 = N1 - 1; E =5.0E - 14; L100: DO J= 1 TO 100; DO II = 1 TO N3; I = N1 -II; B(I) = H(I) + R*B(I+1); C (I) = В (I) + R * С (I + 1); END;
IF C (2) = 0 THEN R = R + 1; ELSE R = R — В (1)/C (2); DOI1 = 1TON3; I = N1—II; В (I) = H (I) — P * В (I + 1) — Q * В (I 4-2); C(I) = B(I)-P* С (I + 1) — Q » С (I + 2); END; IF H (2)-, = 0 THEN GOTO L123;
IF ABS (B (2>/H (1)) > E THEN GO TO L125; GO TO L124;
L123: IF ABS (B (2)/H (2)) > E THEN GO TO L125;
L124: IF ABS (B (1)/H (1)) < = E THEN GO TO L160;
L125: Cl = C (2) — В (2); D = C (3) * * 2 — Cl * C (4); IFD = 0THENDO; P = P - 2; Q = Q * (Q + 1); END; ELSE DO; P = P + (B (2) * C (3)-B (1) * C (4))/D; Q = Q-4-(—В (2) * Cl 4-В (1) * C (3))/D; END; END; E = 10*E; GO TO L100; L150:N1=N1 - 1; V(N1) = 0; IF 12 < 0 THEN U (Nl) = 1/R; ELSEU(N1) = R; DO 1=1 TONI; H(I) = B(I + 1); END; GO TO L50; L160: Nl = Nl - 2;
IF 12 <0 THEN DO; QI = 1/Q; P1 = P/(Q*2); END; ELSE DO; Q1 = Q; Pl = P/2; END; F = Pl * * 2 - QI; IF F > = 0 THEN GO TO L176; U (Nl 4-1), U (Nl) = -Pl; V (Nl 4- 1) = SQRT(—F); V (Nl) =-V (Nl 4-1); GOTO L195; L176:
IF Pl =0 THEN U (Nl 4- 1) = - SQRT(F); ELSE U (Nl 4- 1) = -P1/ABS (Pl)* (ABS (Pl) * SQRT (F)); V (Nl), V (Nl 4-1) = 0; U (Nl) = Ql/U (Nl 4-1); L195: DO I = 1 TO Nl; H (I) = В (I 4- 2); END; GO TO L50; L199:; DCL (Pl, QI, Cl, D, E, F, R, P, Q, H (*), UV (*,*), (B.C) (N4-2)) DEC (16), U (N) DEC (16) DEF UV (1 SUB, 1), V (N) DEC (16) DEF UV(1SUB,2); END BERSTOW;
Пример 3.17. Пользуясь процедурой TRFUNC для непрерывного объекта САР (пример 1.53), определить передаточную функцию W(s). Результатом работы Процедуры TRFUNC являются массивы коэффициентов передаточной функции, которце можно представить в следующем виде:
Пример 3.18. Пользуясь процедурой BERSTOW, определить нули и полюсы передаточной функций U7(s), которая задана в виде выражения (3.186).
Результатом работы процедуры BERSTOW являются массивы нулей и полюсов, которые можно записать в виде
Степень Числитель Знаменатель
7 0 1
6 0 599,500
5 0 8.9700E 4- 04
4 0 3,955IE 4-06
3 2.5000E 4- 08 —1.996.6E4-06.
2 3.5000E 4- 09 1.7009E 4- 05
1 1.1000E 4- 10 —4.0079E 4- 03
0 10.000E 4- 09 —0,0040
Нули Полюсы
Re Im Re Im
-2,0 0 — l,0E—06 0
0,5 0
-2,0 0 0,5 0
0,4 0
— 10,0 0 -100,0 0
-100,0 0
-400,0 0
Таким образом, передаточная функция объекта САР может быть записана в виде
Нули и полюсы изображаются на плоскости Пл. S.
W(s) =
2,5 • 10’s3 4- 3,5 • 109s2 4-1,1 • 1010s 4- Ю9
“ s’ 4- 599,5s® 4- 8,97 • 104ss 4-
4-3,96-10®s44-4^2 -10®s3-b . -
4- 1,7 • 10ss — 4008s - 0,004
(3.186)
РАЗДЕЛ II
АНАЛИЗ СИСТЕМ АВТОМАТИЧЕСКОГО
РЕГУЛИРОВАНИЯ
Располагая различными способами описания САР, которые были рассмотрены в разделе I, и зная все параметры входящих в них устройств, проектировщик может анализировать поведение непрерывных, дискретных и дискретно-непрерывных систем, определять устойчивость, находить показатели качества и характеристики точности линеаризованных систем.
При анализе устойчивости таких систем применяют критерии устойчивости: Ляпунова (первый метод), Гурвица, Рауса, Льенара — Шипара, Шур — Кона и частотные характеристики, представленные в форме Михайлова — Найквиста или D-разбиения. Показатели качества определяют косвенным путем (интегральные оценки, корневые годографы) или прямым (построение переходных процессов с помощью Лх-функций). Ошибки в системах от действия управляющих и возмущающих воздействий находятся по амплитудным частотным характеристикам замкнутых систем (при регулярных сигналах в виде коэффициентов добротностей, а случайных — по средним квадратическим погрешностям). Все эти процедуры доведены до рабочих программ.
Реальная САР всегда нелинейна, и- ее представление в виде математической линеаризованной модели не всегда позволяет получить' адекватное описание: Сложность исследования нелинейной системы связана с большими трудностями, а часто с невозможностью нахо
ждения аналитического решения и анализа нелинейных дифференциальных уравнений. Можно указать, что нелинейные зависимости, которые приходится учитывать при проектировании нелинейных систем, иногда нельзя выразить в математической форме, и их задают в виде графиков.
Наличие нелинейностей в системе не позволяет пользоваться принципом суперпозиции, и действие управляющих и возмущающих воздействий и начальных условий приходится рассматривать совместно. Все это намного усложняет процесс проектирования нелинейных САР. В таких системах возникает целый ряд особенностей, нарушающих обычные представления об их поведении. Например, характер протекания переходного процесса зависит от величины сигнала управления и начальных условий. При этом могут возникать колебания, когда форма сигнала на выходе существенно отличается от гармонической. Нелинейная система может быть устойчивой при низкочастотном входном сигнале и неустойчивой при высокочастотном, или наоборот. Кроме того, в ней при определенных частотах происходят скачкообразные изменения амплитуды и фазы. Возникают в системах режимы автоколебаний, которые при больших амплитудах и малых частотах могут привести к поломке устройств уп-правления или выходу из строя объектов регулирования. Данный перечень свойств нелинейных систем является далеко не полным,
343
однако показывает, с какими большими трудностями приходится сталкиваться проектировщику не: линейных систем по сравнению с линейными.
Исследование устойчивости нелинейных систем выполняется по второму методу Ляпунова, способам гармонической и статистической линеаризаций, а также абсолютной устойчивости Попова. В результате находятся границы устойчивых состояний и автоколебаний в зависимости от параметров. Рассматриваются различные способы подавления автоколебаний, определяются амплитуды вынужденных колебаний и области захватывания. Анализ нестационарных линейных и
нелинейных САР проводится с использованием функций Ляпунова, рядов Неймана и Вольтерра 1-го рода. Показываются возможности данных методов с помощью численных расчетов.
Проектирование систем в пакетном и интерактивном режимах на ЭВМ проиллюстрировано на конкретных примерах непрерывных, дискретно-непрерывных, экстремальных и самонастраивающихся систем с эталонной моделью. Приведены примеры корректирующих устройств, реализуемых на управляющих микроЭВМ в виде рабочих программ, написанных на языке ассемблер.
Глава 4
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ И ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Понятия устойчивости стационарных и нестационарных линейных непрерывных и дискретно-непрерывных САР существенно различаются. Для случая стационарных систем необходимым и достаточным условием устойчивости следует считать такое, когда единственным положением равновесия будет начало координат,. если характеристическое уравнение не имеет полюсов ни в правой части комплексной плоскости, ни на мнимой оси при входном сигнале, равном нулю. Сразу же отметим, что для определения устойчивости систем нет необходимости вычислять корни характеристического уравнения. Необходимо только знать, как они располагаются на комплексной плоскости. Для этого существуют некоторые правила, называемые критериями устойчивости.
В нестационарных системах изменение параметров может привести к нарушению сформулирован
ного условия устойчивости стационарных систем; так, в характеристическом уравнении могут появиться полюсы как в правой полуплоскости, так и на мнимой оси. Поэтому при использовании критериев устойчивости приходится накладывать дополнительные ограничения.
1. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ ПО ПЕРВОМУ МЕТОДУ ЛЯПУНОВА
В общем случае уравнение динамики замкнутых линейных стационарных САР в соответствии с п. 3.4 будет
i(0 = A3*(04-B3<(0. (4-1)
Для этой системы при постоянном управляющем воздействииg(t) и наличии матрицы ЛГ*, обратной А3, положение равновесия находится в точке хе — Аз1В3г, где g(t) равно постоянной величине г. Ког-
344
да управляющее воздействие g(t) зависит от времени, то в общем случае не представляется возможным найти такое преобразование, которое определяло бы единственное положение равновесия. Тогда исследование устойчивости линейных систем по методу Ляпунова нельзя переносить непосредственно на системы с произвольным входным воздействием. Однако заметим, что если для некоторых уравнений вида (4.1) удается найти частное решение, то, пользуясь полученными частными решениями, можно проанализировать устойчивость таких систем. Поэтому сначала с целью более ясного изложения способа нахождения устойчивости линейных замкнутых систем по первому методу Ляпунова будем рассматривать автономные линейные стационарные замкнутые системы. Далее этот способ будет распространен на исследование устойчивости линейных нестационарных замкнутых систем [32].
Итак, линейную непрерывную автономную стационарную систему можно описать уравнением
x(t) = A3x(f). (4.2)
норов удовлетворяет
Д1 — Ри >0! Дг — ...; detP > 0.
Ри
Р21
условиям:
Р12
Р22
>0; ...
Пример 4.1. Допустим, что функция Ляпунова имеет вид
V (х) = xf + 2х{х2 + 2х| + (4.6)
тогда ее квадратичная форма
Г 1 1 °1
Р= 1 2 0 - 0 0 1 -
При этом миноры
Д, = 1 > 0; Д2 = |
1 1 0
Представим функцию Ляпунова в векторно-матричном виде
где
V (х) = х'Рх, (4.3)
Pll i Р12
• • • Pin
Pin
(4.4)
— Рп\ Рп2 * • • Рпп —
или в обычной квадратичной форме
Все они положительны, значит, квадратичная форма положительно-определенна.
Пользуясь выражением (4.4), можно установить, что матрица Р будет положительно-определенной при хтРх > 0 и отрицательно-определенной, когда хтРх < 0; знакоположительной, если хтРх > 0, и знакоотрицательной при хтРх.^0. Все остальные квадратичные формы являются знакопеременными. При положительно-определенной матрице Р неравенства хтРх > 0 справедливы для любого вектора хУ=0.
Существуют признаки, с помощью которых можно проверить, каким из указанных выше свойств обладает матрица Р. Для этого необходимо найти собственные значения А< (i=l, 2, ..., п.) как решение характеристического уравнения
det(V-P) = |U-P| = 0, (4.7) или
п п
V (*) = Е Е PijXiXj, (4.5)
где pij — постоянные коэффициенты.
Квадратичная форма (4.5) будет положительно-определенной, если каждый из ее главных угловых ми-
А —
Р21
~ Pl2 • • ~ Pin
Р22 • • • Pin
= 0.
~ Рп1 — Рп2 • • ^ — Рпп
(4.8)
Заметим, что матрица Р положительно-определенна, если собствен-
345
ные значения X, положительны; отрицательно-определенна, если к; отрицательны; знакоположительна и знакоотрицательна, если X, имеют разные знаки, и неопределенна, если X, — 0.
В заключение укажем, что для положительно-определенной матрицы Р по критерию Сильвестра необходимо и достаточно, чтобы каждый из ее главных угловых миноров Дк был бы положителен. При V(axj, ахг, axn)=aKV(X|,
х2, ..., хп) функция V(x) знакопеременна при нечетном к.
Пример 4.2. Функция (x)=(*t+*2)2+ + *2 + *3 положительно-определенна на всем пространстве переменных; функция V2 (х) = (Х[ + х2)2 + *3 знакоположительна, поскольку она обращается в нуль при Х[ = — х3 и х3 = 0; функция l'3(x)=xi + 4- х2 + *3 знакопеременна.
Пример 4.3. Функция V4(*) = = 2х1х2х3 + 8*|*3 + 4х2*з — нечетная функция 3-го порядка, т. е. оиа знакопеременна.
Пример 4.4. Функция V5(x) = *f+ + 4Xj*3 + *2 + 4*2*3 + *3>
Vs (*) = [*1*2*3] X
При этом миноры Ai = 1 > 0; Д2 = г 1 0 2 -.
10 I I
= = 1 > 0; Дз = I о 1 2 =
1 L 2 2 1 J
= —7 < 0.
Так как третий минор отрицателен, то функция Vs(x) неопределенно-положительна.
Пример 4.5. Возьмем матрицу Р из примера 4.4 и составим для нее характеристическое уравнение в виде (4.8). Тогда
X- 1 0
0 X - 1
-2 -2
-2
-2
X - 1
откуда (X — 1) (Xs — 2Х — 7) = 0.
Корни полученного характеристического уравнения
4
, 2 - -у/29 Л
Хз=-------<0,
т. е. У5(х) неопределенно-положительна, что совпадает с результатом примера 4.4.
Определим производную от функции V(x), которая была записана в виде (4.3), т. е.
V (*) = = *Рх + х'Рх =
= х1Ат3Рх + хтА3Рх =
= хт (AIP + РА3) х. (4.9)
В уравнение (4.9) введем следующее обозначение:
А3РРА3 =—Q. (4.10)
Сформулируем основное положение об асимптотической устойчивости Ляпунова.
При положительно-определенной матрице Q V (х) = — xTQx <0 и V > 0 в некоторой области х е X, включающей в себя начало координат, положение равновесия в начале координат будет асимптотически устойчиво. Данную формулировку теоремы Ляпунова можно изложить также следующим образом.
Для того чтобы нулевое решение автономной линейной замкнутой системы, записанной в виде (4.2), было асимптотически устойчиво, необходимо и достаточно, чтобы для произвольной положительно-определенной матрицы Q существовала положительно-определенная матрица Р, удовлетворяющая уравнению (4.10); тогда матрица Р симметрична, т. е. Рт = Р и
QT = -(A13P + PA3)T =
= -P A3 + A3TP = -Q. (4.11)
Из равенства (4.11) следует, что матрица Q симметрична. Справедливо также и обратное положение.
При анализе устойчивости линейных автономных систем будем использовать также способ, связанный с исследованием корней характеристического уравнения матрицы А3.
346
Обозначим корни характеристического уравнения через к; тогда
det (AJ —A3) = |AJ —А3| =
X — U[ j — «21 — «12 • X а22 . • — а1п • — «2п = 0.
— ап1 — ап2 . • «пп (4.12)
Раскрыв определитель (4,12), по-
лучим
Г + а.Г-1+а2Г~2+ ...
• •• 4* 4" ап = 0. (4.13а)
При исследовании устойчивости в ряде случаев вместо формулы (4.13а) можно использовать уравнение
а0Г + а1Г-1 + а2Г"2+ ...
• •• 4* «п-1^ 4* «п = 0. (4.136)
Если все корни характеристических уравнений (4.13а) или (4.136) имеют отрицательные вещественные части, то нулевое решение системы (4.2) асимптотически устойчиво. Если же среди корней уравнений (4.13) имеется хотя бы один корень с положительной вещественной частью, то нулевое решение системы неустойчиво. Когда уравнения (4.13) не имеют корней с положительной вещественной частью, но некоторые из них содержат нулевые вещественные части, в этом случае могут возникать явления как устойчивости (не асимптотической), так и неустойчивости. Таким образом, при нулевом решении уравнения (4.2) необходимо производить дополнительные исследования устойчивости.
Рассмотрим способы применения функции Ляпунова для анализа устойчивости стационарных и нестационарных систем. Дифференциальное характеристическое уравнение стационарной системы имеет вид
х + ах + £>х = 0, (4.14)
или
х, = х2;
х2 = — Ьх\ — ах2,
} (4.15)
где а и b — постоянные коэффициенты.
Зададимся квадратичной формой 2 2
W (xh Х2)= £ £ Wi/XiXj-, =
(4.16) и представим функцию Ляпунова в виде 2 2
V (хь Х2) = Е £ PilXiXf, ри = Pjh
(4.17) которая удовлетворяет уравнению
У(хь x2) = 2U7(x„ х2), (4.18)
где
V (х1( Х2) = 2рцХ1Х, + Pi2X!X2 + + Р1гХ1Х2 + Р21Х2Х1 +
+ Р21Х2Х1 + 2р22х2х2. (4.19)
Подставляя значения производных из системы (4.15), получим
V (хр х2) = 2рнх,х2 + Р12х2 -- fePl2Xl ~ аР12Х1Х2 - *Р21Х1 -- ар21х1х2 + р21х22 -
— 2bp22xlx2 — 2ар22х%. (4.20)
Функцию Г(хь х2) запишем в
виде
IT (хр х2) = wux* + ш12х1х2 +
+ W2lx2xt + w22x2. (4.21)
Воспользовавшись выражениями (4.19)—(4.21), приравняем в выражении (4.18) коэффициенты при одинаковых переменных:
: ~ bPi2 ~ bPn = 2wii’
Х]Х2: 2рц — api2—ap2l—2bp22=4wi2;
%2 ' Р12 4” Рц ^Рц 2^22‘
(4.22)
Из выражения (4.17) имеем Р12 = ргГ, тогда систему уравнений (4.22) можно переписать в виде
— Ьр12 — ^п>
Pii—api2 — bp22 = 2wi2; (4.23)
Р12 — ар22 — 0У22.
347
Определитель этой системы
о — ь — а
О 1 О
-Ь
— а
1
= — ab. (4.24)
А =
В качестве квадратичной формы (4.16) возьмем W (хр х2) = х2; тогда в системе (4.23)
&'11 = 0; и/12=0; и/22 = I.
Решая систему уравнений (4.23), получим
Р12 = 0; Р22=—1/а; рп = — Ь/а.
В этом случае функцию Ляпунова можно записать в виде
V (*ь х2) =
= & (Pll*l "t" %Pl2XlX2 + Р22Х2^) ~
= _a6(_Ax2_lx2) =
= b2x2 + Ьх2, (4.25)
для которой имеем
У (хь х2) = 2Ь2ххХ1 + 2bx2x2 = — 2b2xlx2 — 2&2xtx2 — 2abx2 —
= -2abx2. (4.26)
Если а е > 0 и b е > 0, где 8 — малая произвольная постоянная, то одновременно выполняются неравенства У(хь х2) > О и У(хь х2) < О в некоторой области плоскости (xi, х2), включающей в себя начало координат. Согласно первому методу Ляпунова система уравнений (4.15) является асимптотически устойчивой в начале координат. На рис. 4.1, а область устойчивого состояния системы, зависящего от параметров а и Ъ, выделена штриховыми линиями. Полученное решение тривиально, так как стационарное уравнение (4.19) 2-го порядка.
Существует несколько условий неустойчивости замкнутых стационарных САР [32]. Рассмотрим три
Рис. 4.1. Области асимптотической устойчивости нестационарной линейной системы в начале координат в зависимости от ее параметров, полученные с помощью применения 1-го метода Ляпунова:
а—для стационарной функции V (х,. х.) и 6(t)>6i: б—для стационарной функции V (хь х>) и условий а, < а (Г) < а-, б, < b Ц) < Ь2
условия неустойчивости системы по Ляпунову.
Первое условие неустойчивости. Если автономная система описывается дифференциальным уравнением (4.2), для которой существует непрерывная функция V(x), имеющая непрерывные частные производные в области Г, включающей начало координат, такие, что У.(О) = 0, а ее производная 16 определена вдоль всех траекторий системы, но при этом в любой окрестности начала координат Vi не является знакоотрицательной функцией, то начало координат неустойчиво.
348
Пример 4.6. Запишем уравнения автономной системы
Xi — х2;
х2 = —х,.
(4.27)
Составим функцию Ляпунова в виде
V (хр х2) = у (xf + х22) > 0, (4.28)
откуда
V (Х), Х2) = XjX] + Х2Х2 = Х,Х2 — х,х2 =0.
(4.29)
Из выражений (4.28) и (4.29) следует, что автономная система 'неустойчива в начале координат по первому условию Ляпунова. На справедливость этого положения указывает и то, что корни характеристического уравнения (4.27) комплексно сопряжены и Л], г = ±/.
Второе условие неустойчивости. Если для автономной системы, описываемой дифференциальным уравнением (4.2), существует функция УДх) в области Г, включающей в себя начало координат, такая, что Vi — 0 и У(х) вдоль траекторий имеет вид
У(х) = ЛУ,(х) + 1Г(х), (4.30)
где Л>0иЦ7(х)>0в той же области Г, а в произвольной окрестности начала координат функция V(x) не является знакоотрицательной, то начало координат неустойчиво.
Пример 4.7. Запишем уравнение автономной системы
Составим функцию Ляпунова в виде
V1 (xj, х2) = xf + 4xjX2 + х2 > 0, (4.32)
откуда
V] (хр х2) = 2x(xJ + 4XjX2 -J- 4xlx2+2x2x2=
= 2XjX2 + 4х2 + 4Х| + 2XjX2. (4.33)
Выражение (4.33) перепишем в форме (4.30). Тогда получим
V] (*i, х2) = Л (*? + 4х,х2 + x|)+3xf+3x|.
(4.34)
В выражении (4.34) Л = 1 > 0 и
U7 (хр х2) = Зх| 4-Зх2 > 0. (4.35)
Из выражений (4.32) и (4.35) следует, что система неустойчива в начале координат по второму условию Ляпунова. Корни характеристического уравнения (4.31) будут Xi = = L что также характеризует
неустойчивость системы.
Третье условие неустойчивости (Ляпунова — Четаева). Допустим, что функция V(x): а) имеет непрерывные частные производные в области Гь входящей в область Г с началом координат; б) Г(х) и V(x) положительно-определенны в области Гь состоящей из внутренних точек области Г; в) на границе Г1 17(х) = 0; г) начало координат принадлежит границе области Гь В случае выполнения условий а)— г) начало координат неустойчиво.
Пример 4.8. Запишем уравнение системы x^a^ + bix2, | (4
х2 = — а2х2 + Ь2х2, )
где ai >0; bi > 0; а2 > 0; Ь2 > 0 и Ьх > я,. Составим функцию Ляпунова в виде
х*
V (х„ х2) = xi - -у-, (4.37)
откуда
V (xi, х2) = Xi — х2х2 = Я1Х] + Ьix2 + + а2х2 — b2xtx2. (4.38)
Из выражений (4.37) и (4.38) следует, что при Х| >0 и х2> 2xj найдется достаточно малая е — окрестность нуля, в которой V > 0, V > 0, и выполняется третье условие неустойчивости Ляпунова—Четаева. Следовательно, система неустойчива в начале координат.
В отличие от стационарных систем автономные нестационарные системы описываются уравнениями вида
x(t) = A3(t)x(t). (4.39)
Для таких систем скалярная функция Ляпунова V(х, t) зависит от времени и является положительно-определенной в области Г, содержащей начало координат, если
У(0, 0 = 0 и Г(х, О>0(11х||), где 0 — непрерывная и возрастающая функция, для которой 0(0) — = 0.
349
Наличие нестационарности систем приводит к необходимости изменения условий устойчивости по Ляпунову. Укажем только на три из них, позволяющих оценивать устойчивость замкнутых систем, описываемых уравнениями (4.39).
Первое условие устойчивости. Если для системы (4.39) существует положительно-определенная скалярная функция V(x, t), имеющая непрерывные производные по переменным х и t в некоторой окрестности Г начала координат, а ее производная V(x, t) <0, то начало координаты устойчиво.
Второе условие устойчивости. Если к первому условию добавить неравенство
V (х, 0(11*11), (4.40)
то начало координат эквиасимптотически устойчиво.
Третье условие устойчивости. Если существует непрерывная строго возрастающая функция р, такая, что р(0) = 0, и в дополнение к первому и второму условиям устойчивости в области Г для всех t выполняется неравенство
7(х, 0<р(И*И), (4.41)
то начало координат системы равномерно асимптотически устойчиво.
Отметим, что при решении практических задач об устойчивости замкнутых нестационарных систем крайне желательно выбирать функцию V, не зависящую от времени t. Тогда для равномерной асимптотической устойчивости необходимо иметь У(х)>0, *¥=0, У(О) = 0, и функция ]/ должна удовлетворять условию (4.40). При этом существенно упрощается анализ устойчивости нестационарных систем.
Дифференциальное характеристическое. уравнение нестационарной системы запишем в виде
х + a (f) х + b (t) х = 0 (4.42) или
xI = х2; 1
х2 = — b (t) Xj — а (/) х2. ) (4.43)
Исследование замкнутой системы (4.42) состоит в том, чтобы на функции a(t) и b(t) были наложены такие ограничения, при которых обеспечивается асимптотическая устойчивость в начале координат. Для этого необходимо найти функцию Ляпунова. В работе [32] показано, что можно сформировать две функции Ляпунова: стационарную в виде (4.17), если положить Рп = Pi/2; pi2 = 1/2; р22 = р2/2,
V (xi> х2) = ’7" Х1 + х1х2 + 1Г х2
(4.44)
или нестационарную, когда
V (Х], х2, /) = х^ + ь х2 при 0 < b b (/) Ь2. (4.45)
Для стационарной функции Ляпунова при pi > 0 и р2 > 0 функция 7(Х1, х2) положительно-определенна, и для нее справедливо соотношение
V (хр х2) = plx]x2 + х2 — Ь (/) х2 — — a (t) х{х2 — b (/) p2XjX2 — a (t) р2х22,
откуда
Й(*Р х2) = -{&«)*? +
+ [& (0 Р2 + а (/) — pj х,х2 '+ + [а(/)р2 — !]*!} =
+ [а (0 Pz — 1
(6 (о рг + а (О — рО2! , 1
46 (О J 2 J
(4.46)
Если b(t)^bi>0 и коэффициент при х| положителен, то V(xi, Хг) будет отрицательно-определенной. В этом случае получим
(4.47)
После ряда преобразований неравенство (4.47) перепишем в виде
[а (0 — b (/) р2 — pj2 —
— 4b (0 [pip2 — 1 — е] < 0. (4.48)
350
и
Из выражения (4.48) следует, что
м 1 J [а (О + Ь (Z) р2 — р,]г рЛ ±b(t)
+ 1+е}>0. (4.49)
Если неравенства (4.48), (4.49) записать в виде равенств и воспользоваться условием b(t)=b\, то на плоскости (а, Ь) можно найти область, где обеспечивается асимптотическая устойчивость. Эта область на рис. 4.1, а выделена штрихами. Кривая ./ соответствует уравнению параболы
а (0 — Ь (/) р2 — pi =
= 2| y/b (VpiP2 — 1 — е)|, (4.50) прямая 2 — условию
b(t) = bi, (4.51) а кривая 3—уравнению a(t) — b (t) р2 — pi =
= — 21 y/b (y/pip2— 1 — e)|. (4.52)
P-‘ / /-r~\2 [й|
(Vb2 - Vfel )
-\fa\- ~ + e>];
(<\/1>2 + л/b i) _ 1 + e
Pl =--------- pcj -4--------~ .
,l 4 ' рг
(4.55)
Так как p2 является действительным числом, то, используя выражения (4.54) и (4.55), нетрудно показать, что
a(>(V62 ~ V6i W1+е- <4-56)
Из уравнений (4.50), (4.52) определим ординаты парабол при постоянном значении bi с учетом соотношений (4.54) и (4.55). Для этого воспользуемся уравнениями
Учитывая условия
0 < at < a (t) < a2; 0 < b{ < b (t)^.b2, (4.53)
где a>, bt, a2 и b2 — постоянные параметры, построим иа рис. 4.1,6 штриховой линией параболу 2. При этом видно, что оиа проходит через точку с координатами bi, а{. При этом нижняя ветвь параболы 2 проходит через точку с координатами 6', ар когда Ь'2^Ь2. Подставляя эти координаты в уравнения (4.50), (4.52), найдем два уравнения относительно pi и р2. Исключив р2, определим рь Затем, записав pi через р2, получим
2 Г I
$2 z i-у- --------\2 [Я] 4~
(VЬ2 ~ V6! )
+ ~ (V^2 ~ V^)2 (1 + е)];
(V61 + V*1)2 - , !+e Pl =-------4------P2 + —
(4.54)
а‘
4(V^2 + у/bi )
а
,2
(4.57)
Полученная с помощью уравнений (4.57) парабола 1 изображена на рис. 4.1,6 сплошной линией.
Поскольку а2 > а2 и а2 изменяется обратно пропорционально Ь2, то максимум этой величины достигается при меньшем значении Ь2, т. е. Ь2. Имея этд в виду, выражение (4.56) можно переписать в виде
a!>(Vfe2 — VbT) V1 4-е. (4.58)
351
Анализируя выражения (4.56) и (4.57), найдем
lima! = У&2 — V^i J е->0
lim&2 = е->0
ai (5bi 4- Ьг + л/b\bi) Ц- 4(b, 4- л/Ь1ЬгУХ.
х д/а^ - (УК - УК)2 (Уb2 — VЬ\ )2
Откуда получим необходимые условия для определения коэффициентов
а] > У&2 — У&1;
ai (561 4-б2 4-2д/б16г) + 4" 4 (bi 4- *Jbibz ) X
х д/а1 ~ (Уb2 ~ У
2 (VK’-VK')2
(4.59)
В соответствии с неравенствами (4.59) на рис. 4.1,6 штрихами выделена внутренняя область, определяемая этими параболами, в которой возможна асимптотическая устойчивость системы в начале координат. Область, изображенная на рис. 4.1, а, существенно больше области, показанной на рис. 4.1,6.
Для нестационарной функции Ляпунова по выражению (4.45) найдем
V (xi, х2, t) =
— («0)
Принимая
(b + 2ab)/b2^e> О, имеем
а>-е--у. (4.61)
Из выражения (4.60) следует, ЧТО фуНКЦИЯ V(X\, Х2, t) зиакоотри-цательна и начало координат асимптотически устойчиво, так как У(ж, t) > 0 и имеет непрерывные производные по х и t в окрестности начала координат, a V(x, t) < 0.
Рассмотрим применение первого метода Ляпунова к дискретным или дискретно-непрерывным системам, приведенным к дискретным моделям. В этом случае автономное уравнение замкнутой системы можно записать в виде
xK+i = А3хк. (4.62)
Функция Ляпунова в форме (4.4) имеет вид
V(*K) = ^P\. (4.63)
Обозначим первую разность этой функции ДУ на траектории х* следующим образом:
(4.64) или
ЖкТ [А1РЛз — Р] Жк = —
(4.65) где Q — симметричная положительно-определенная матрица вида AlPA3 — P= — Q. (4.66) Автономная дискретная система (4.62) будет устойчива, если существуют положительно-определенные симметричные матрицы Р и Q, которые удовлетворяют соотношению (4.66):
4V(<) = V«+,)-V(«:) =
----(4.67)
Из выражения (4.67) следует, что
»'«+,) = v (<)
— *к+П-1Ф*К+П~Г
(4.68)
Подставляя• первое уравнение (4.68) во - второе, а полученное в результате этого уравнение — в третье и т. д., найдем п— 1
V (<«)=V К) - S, <4 в9>
352
Если рассматриваемая система (4.62) асимптотически устойчива, то lim V (*к+п) = V’ (0) = 0; из уравне-т-»оо 4 7
ния (4.69) получим искомую функцию Ляпунова
со
(47"> т=к
Функцию V (ж*) можно также определить из выражений (4.63) и (4.69):
т=к
= х”Рх*к. (4.71)
Функция V (х‘), записанная в виде (4.71), положительно-определенна, и рядР= [Al]" КрАз-к п=к СХОДИТСЯ.
Пример 4.9. Необходимо исследовать устойчивость дискретной линейной системы по Ляпунову, описываемой уравнением вида
_ Г 0,8 —0,4 1
*к+1~ [1,2 0,2 J к‘
Выбирая Q — 1, из условия (4.66) имеем
Г1 01 Г 0,8 1,21 Г р„ р121
Lo I ] L —0,4 0,2jLp21 Р22 J Х ’
хГ0,8 - 0,4 1 Грп р121
L 1,2 0,2 J I. Р21 Р22 J
систему
Так как р12 = р2ь получим
уравнений
г —0,36 1,92 1,44 1Г Рн '
I —0,32 —1,32 0,24 I 021
L 0,16 —0,16 —0,96 1 1- ргг -
откуда найдем матрицу
Г 3,904 71
Р =
L ,057 2,223 J'
г-1
о
—г
Ее диагональные миноры Д[ = 3,904 > 0 и Д2 = 7,56 > 0, поэтому матрица Р положительно-определенна, а автономная замкнутая система, согласно выполнению условия (4.66), устойчива.
2. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ ГУРВИЦА, РАУСА, ЛЬЕНАРА—ШИПАРА И ШУР-КОНА
Алгебраические критерии устойчивости не требуют выполнения вычислительной процедуры определе
ния корней характеристического уравнения и при относительно невысоких порядках дифференциальных уравнений (до 15-го) позволяют находить условия асимптотической устойчивости автономных замкнутых систем.
Критерий Гурвица. Корни характеристического уравнения (4.13а) 15-го порядка будут иметь отрицательные действительные части, если составленный из его коэффици-
ентов at > > 0 определитель <73 я7 Яд Яц я13 Я[5 ... 0 а4 а8 а10 а12 <714 • • • 0
а1 <23
1 0 0 0 0 0 а2 ai 1 0 0 0
Я3 Я3 Я7 Яд Я2 Я4 Яб я8 Я! Я3 Я5 Я7 Яц я13 ... 0 я10 я12 . . . 0
Яд Я8 Я7 Яц • • 0 я10 . .. 0 Яд ... 0
1 0 Я2 Я4 Яб
я. Яз я5
&15= 0 0 0 1 #2 ^4 «6 я8 ... 0
0 0 0 0 Щ а3 а5 я7 ... 0
0 0 0 0 1 Яд я6 ... 0
0 0 0 0 0 Я! Оз я5 ... 0
0 0 0 0 0 1 а2 я4 ... 0
0 0 0 0 0 0 я3 ... 0
0 0 0 0 0 0 1 я2 ... 0
0 0 0 0 0 0 0 я, ... я15
(4.72)
и все его диагональные миноры
Д2 —
Ai = ai;
Д3 —
а3
а2
1 О
а, 1
а5
аЛ ;
а3
я2 ’
а3
д15 ==а15Д14 положительны.
Для удобства организаций вычислительной процедуры принято определитель Гурвица Дп-1 приводить к треугольному виду (см. прил. П-1.1). В этом случае нетрудно составить рабочую программу № 14 на языке ПЛ/1.
12 Ю. И. Топчеев
353
ПРОГРАММА № 14 GURWITZ
Предназначена для вычисления диагональных миноров определителя Гурвица ие более 15-го порядка и выдачи сообщений: «Система устойчива» или «Система неустойчива» в замкнутом состоянии.
Обращение к программе
GURWITZ (A.N)
•Выходные параметры
N — порядок характеристического уравнения;
А — коэффициенты характеристического уравнения V 4- яД'1-1 4- ... +<Jn-iA> + Яп=О в виде 1, Ль аг....ап.
Выходные параметры
1. Определитель Гурвица.
2. Сообщения «Система устойчива» или «Система неустойчива».
GURWITZ: PROC (A,N); DCL (N,I,J) BIN FIXED (15,0); PUT SKIP EDIT (’РАЗМЕРНОСТЬ СИСТЕМЫ:’,N) (A,F (5)); BEGIN; DCL (A (0; ((N/2) * 2 + 1)),
В (N — 1, N-l)) FLOAT DECIMAL (6); PUT SKIP EDIT (’КОЭФФИЦИЕНТЫ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ:’) (A);
PUT SKIP EDIT ((A (I) DO 1=0 TON))(E(12,5)); IF A(1)<0! A(N)<0 THEN GO TO M; IF (N/2) * 2=N THEN A(N4-1)=0; B=0; DO 1=1 T0(N-l)/2; DOJ = I TO(N/24-I); В (2*1-1, J) = A (2 * (J — I) 4-1); В (2 * I, J) = A (2* (J —I)); END; END; IF(N/2)*2 = N THEN DO J = (N-l)/2 4-l TO N-l; В (N - 1 ,J)=A (2 * J-N4-1); END; PUT SKIP EDIT (’СООТВЕТСТВУЮЩИЙ ОПРЕДЕЛИТЕЛЬ ГУРВИЦА:’) (A); PUT EDIT (В) (SKIP, (N — 1) (E (12,5))); DO 1 = 2 TO N— 1;
IF DET (B,I) < = 0 THEN GO TO M; END; PUT SKIP EDIT (’СИСТЕМА УСТОЙЧИВА’,) (A); GO TO E;
M: PUT SKIP EDIT (’СИСТЕМА НЕУСТОЙЧИВА.’) (A);
DET: PROC (B,N); DCL B(*,*) FLOAT DECIMAL (6), (I, J,K,N) BIN FIXED (15,0), (T, D, MAX) FLOAT DECIMAL (6); BEGIN;
DCL A(N,N) FLOAT DECIMAL (6); A=B; D = 1; DO K = 1 TO N; MAX = 0;
DO I = K TO N; T = A(I,K); IF ABS (T)>ABS (MAX) THEN DO; MAX = T; J = I; END; END; IF MAX=0 THEN DO; D=0; RETURN (D); END; IF J_,=K THEN DO; D = — D; DO I = К TO N; T = A(J,I); A (J,I) = A (K,I); A(K,1) = T; END; END; DO I=K+1 TO N; T=A (I,K)/MAX; DO J=K +1 TO N; A (I, J)=A (I, J) - T * A (K, J); END; END; D = D*A(K,K); END; RETURN (D); END DET;
E: END GURWITZ;
Пример 4.10. Характеристическое уравнение линейной замкнутой системы имеет вид
А6 + 16,4AS + 107,4 V + 364,2V + 1146,5 V 4-
-4-771,2X 4- 292,1 = 0. (4.73)
Так как коэффициенты характеристического уравнения (4.73) больше нуля, можно воспользоваться программой № 14. В результате найдем Ai = 16,4 > 0; Д2 = = 1,3972 -10э > 0; Дз = 2,1313-105 > 0; Д« = 1,4923-10» >0; Д5 = 9,7199- Ю10>0. Поскольку Л| = 16,4 > 0, то Де = 16,4Д5> > 0, и замкнутая система асимптотически устойчива.
Критерий Рауса [38]. Зная коэффициенты характеристического уравнения, составляют таблицу Рауса. Для характеристического уравнения 15-го порядка, записанного в виде (4.136.), в табл. 4.1 приведены коэффициенты Рауса. Для того чтобы замкнутая система была устойчива асимптотически, необходимо и достаточно, чтобы все коэф
354
фициенты Рауса первого столбца таблицы при at > 0 были положительны, т. е. d, 1 > 0 (t = 1, 2, ... ..., 14. ...). Для вычисления элементов табл. 4.1 можно использовать следующие рекуррентные формулы: для первой строки таблицы
- __ а1а2к— а2к+1 „ ___ 1 о
С lie 1 L , /V ’ 1 1 * « • • •
1к а, ’ ’
.... 7, ...;
для второй строки таблицы
„ ___С11а2к+1 ~ а1С1.к+1 _ 1 о
С2к----------—--------, К — 1, Z, ...
.... 7, ...;
для остальных строк ciK = ci-l, lci-2, к+1 ~ cl-2, к-1
1 = 3, 4, .... 13, ...;
к — 1, 2, ..., 6, ...
(4-74)
Пользуясь соотношениями для вычисления коэффициентов Рауса, приведенных в формуле (4.74), можно составить программу № 15 для
анализа устойчивости или неустойчивости замкнутых систем, характеристическое уравнение которых не превышает 15-й порядок.
ПРОГРАММА № 15 RAUSS
Предназначена для вычисления коэффициентов Рауса по характеристическому уравнению ие выше 15-го порядка и выдачи сообщений: «Система устойчива» или «Система неустойчива» в замкнутом состоянии.
Обращение к программе
RAUSS (A.N)
Входные параметры
N — порядок характеристического уравнения;
А — коэффициенты характеристического уравнения № + aiA/1-1 4- ... 4- + ап = 0
в виде 1, ai, а2...ап.
Выходные параметры
1. Коэффициенты таблицы Рауса.
2. Сообщения «Система устойчива» или «Система неустойчива».
RAUSS: PROC (A,N); DCL (N.M) BIN FIXED (15,0); M = N/2 4-l;
PUT SKIP EDIT (’РАЗМЕРНОСТЬ СИСТЕМЫ:’, N) (A,F(5)); BEGIN;
DCL (A (0: N + 1), C (N + 1, M + 1)) FLOAT DECIMAL (6), (I.K) BIN FIXED (15,0);
IF (N/2)*2 = N THEN A(N 4-1) = 0;
PUT SKIP EDIT (’КОЭФФИЦИЕНТЫ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ:’) (A);
PUT SKIP EDIT ((A(I) DO 1=0 TO N)) (E (12,5)); DO 1=1 TO M;
C (1,1) = A (2 * (I — 1)); C (2,1) = A (2 * I — 1); END; C(*,M4-1) = 0;
DO K = 3 TO N4- 1; DO 1= 1 TO M; C(K,I) = (C (К - 1, 1)*
С (K — 2, I 4-1) — С (K — 2,1) ♦ С (K — 1, I 4-1))/C (K — 1,1); END; END;
PUT SKIP EDIT (’КОЭФФИЦИЕНТЫ ТАБЛИЦЫ РАУССА:’) (A);
PUT EDIT (((C (K,I) DO 1 = 1 TO M) DO K=1 TO N 4- 1)) (SKIP, (M) (E (12,5)));
DO 1=1 TO N4- 1 WHILE (C(I,1)>0); END;
IF I<N4-2 THEN PUT SKIP EDIT (’СИСТЕМА НЕУСТОЙЧИВА.’) (A);
ELSE PUT SKIP EDIT (’СИСТЕМА УСТОЙЧИВА.’) (A); END; END RAUSS;
Пример 4.11. Для характеристического уравнения линейной замкнутой системы (4.73), приведенного в примере 4.10, определены коэффициенты первого столбца: щ = 16,4 > 0; сп = 85,2 > 0; с2,= 152,7> > 0; с31 = 700 > 0; с4| = 651,3 > 0; с8, = = 292,1 > 0. В соответствии с критерием Рауса это указывает на асимптотическую устойчивость замкнутой системы.
Критерий Льенара — Шипара. Запишем условия устойчивости в форме Льенара — Шипара для характеристических уравнений до 6-го порядка включительно, пользуясь определителем Гурвица (4.72). Обозначим через V</> миноры определителя Гурвица, стоящие на главных диагоналях, где индексы: i — порядок минора, а / — степень рассматриваемого характеристического уравнения. САР будет устойчива, если при ai > 0 нечетные миноры главной диагонали будут поло
жительными. Для характеристических уравнений разных степеней вида (4.13а) условия устойчивости имеют следующий вид:
ДЛЯ 1-й степени 0;
ДЛЯ 2-й степени v<2>=v<l): >0;
для 3-й степени >0;
V(3)== aia2a3 “' al >0;
для 4-й степени V«) = V<1); >0;
= ata2a3 - -ф2~аГ >0;
для 5-й степени V(5) = V(l) ; > 0;
V(5> = ар2а3 + а^ - afa -a23>Q-,
V'5) = а5 (ala^i+20^-а^а5- ;
- «М - - «I+w) > °; i
12*
355
Таблица 4.1
Коэффициенты Рауса
Номера строк Номера
1 0 3
Коэффициенты
1 02
Коэффициенты
«1 a3 «5
1 аха2 — а3 ata4 — a5 ^1^6 — a7
С ] । 01 at C“ ' «!
2 £11#3 — a j Ci 2 £| 1Д5 — Л1 £ 13 £ 11^7 O' 1 £14
£21 С} 1 £ц £23 £ 1 v
3 С21С12 — £1]£22 £2i£ i з — £ц£2з C21C14 — СцС24
£31 "" £21 , £32 £21 £21
4 „ С31С22 — С21С32 O31C23 — O21C33 C31C24 — C21C34
£41 £3! £42 “ £31 £43 — £31
5 „ ^41^32 — С31С42 O41O33 — C31C43 C41C34 — C31C44
£ы £41 cb2 " £41 £*>з e £41
6 „ _ 0sic42 — C41C52 c51c43 — C41C53 . C51C44 — C41C54
£ы — £51 £62 — £51 £ьз " £51
7 „ _ _ С61с52 — С51С62 c61c53 — C51C63 C61C54 — C51C64
£у । £б1 £6i £73 _ £si
8 _ С?1Сб2—С61С72 С?1СвЗ — C51C73 C71C64 — C61C74
£fij и £71 C82 £71 £«3 £71
9 „ С81С72 — С71С82 C81C73 — C71C83 C81C74 — C?lc84
Cei £81 “ C81
10 „ _ С91СВ2 — С81С92 C91C83 — C81C93 С10.З == 015
£iu.i “ £91 £iu.2"“ £91
11 „ _ . C10.1C92 — C91C10.2 C10.1C93 — C91C10.3 C11.3 = 0
010.1 £11.2 —1 £j 0.1
12 „ C11.1C10.2 — C10.1C11.2 C12.1 Сил C12.2 — O15 0
13 я С12.1Сц,2 — Сц.1С12.2 013.1 £12.1 0 0
14 014.1 — 015 0 0
15 0 1 0 0
356
столбцов
4 5 6 7 8 9
с четными индексами
с нечетными индексами
dj а9 011 ап 0|5 0
alas — Og 0,0,о — О|| „ _ 0)0,2 — 0,3 С)7 = С18=о 0
с‘° «1 Й1 _ 0)0,4 — 0)5
01
Сцйд — О,С,5 С| )О| 1 — О)С)5 01,0,3 — 0)0,7 С27 = 0,5 Сгз=С 0
СН С“™ Си Cjb “ Л
С21С15 — СцС25 С21С16 — СцСгв С21С17 — СцС27 С37 = 0 0 0
С21 С21 С21
_ _ _ С31С25 — С21С35 С31С26 — С21С36 С46 = 0,5 о о 0
£31 С4Ь в С31
„ ... С41С35 — С31С45 С4)Сзв — С31С46 С56 = 0 о о о
С41 ^55 „ С41
„ С51С45 — С41С55 С 65 = 0)5 0 0 0 о
^5!
„ С6|С65 — С51С65 С75 = 0 0 0 0 о
^61
С84 = О,6 0 0 0 0 0
CJ4 = 0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
1 0 0 0 0 0 0
357
для 6-й степени *
v<6)=vu)>o; :
V(i) = V(5)>0; о о
V‘56) = «Л (¥А + + а1а2аб ~
-а^-й^-а2^-
~ а5 (Ф« + а5 - Ws ~ а1аА) “ — а3аб (а1а2аз + а1а5 - а1а4 - а1) +
+ aia6 (ala2fls - а2а6 - а3а5) > 0.
(4.75)
Пример 4.12. Для характеристического уравнения линейной замкнутой системы 6-го порядка, приведенного в примере 4.10, все коэффициенты характеристического уравнения больше нуля; поэтому можно воспользоваться последними неравенствами
в соотношениях (4.75). Подставив числовые значения, получим
V<6> = 16,4 > 0; v(j6, = 2,13-105 > 0;
Vg^ = 9,7 • IO10 > 0,
что указывает на устойчивость системы..
Критерий Шур — Кона. Данный критерий позволяет анализировать устойчивость дискретных и дискретно-непрерывных систем по характеристическому уравнению замкнутой системы, записанному в форме z-преобразования. Для уравнения n-го порядка имеем
zn + alzn-1 + a2zn-2+ ...
• • • + Яп-iZ + an — 0. (4.76)
По уравнению (4.76) запишем коэффициенты в виде определителя
ап 0 0 ... 0 1 «I «2 • • • Ofe-l
an-i ап 0 ... 0 0 1 ai • • ak-2
ап—2 an-i ап ... 0 0 0 1 •• o*-3
an—k+1 an—k+2 Un-k+з ... ап 0 0 0 ... 1
1 0 0 ... 0 an-l a‘ 2 п—z •• an-k+l . (4.77)
1 0 ... 0 0 a* . n-1 •• an-*+2
<4 1 ... 0 0 0 an '• an-k+3
7 • * ле <3 ak-2 а*-з ... 1 0 0 0 ... a n
где k = = 1, 2, . ., п; а*. а' ... • . а — Шур — Кона, имеющего Дл<0 —
сопряженные значения тех же коэффициентов. Корни характеристического уравнения (4.77) будут находиться внутри единичной окружности, если коэффициенты уравнения (4.76) удовлетворяют всем определителям для нечетных k и Д* > 0 для четных k. В этом случае замкнутая система будет устойчива. Для нахождения определителей уравнения 15-го порядка составлена рабочая программа № 16 SHURCON на языке ПЛ/1.
ПРОГРАММА № 16 SHURCON
Предназначена для вычисления определителей Шур — Койа по характеристическому уравнению дискретной или дискретно-непрерывной замкнутой системы, записанной в z-форме, и выдачи сообщений: «Система устойчива» или «Система неустойчива».
Обращение к программе
SHURCON (A,N)
Входные параметры
N — порядок характеристического уравнения;
А — коэффициенты характеристического уравнения V-f- + ... + + ап =0
в виде 1, аГ а2, .... ап.
' Выходные параметры
Сообщение «Система устойчива» или «Система неустойчива».
358
SHURCON: PROC (A,N); DCL N BIN FIXED (15,0);
PUT SKIP EDIT (’РАЗМЕРНОСТЬ СИСТЕМЫ:’, N) (A.F (5)); BEGIN; DCL (A(0:N), B(2*N, 2*N)) FLOAT DECIMAL (6), (I,K) BIN FIXED (15,0); DCL DET ENTRY ((*,♦) FLOAT DECIMAL (6), BIN FIXED (15,0));
PUT SKIP EDIT (’КОЭФФИЦИЕНТЫ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ:’) (A); PUT SKIP EDIT ((A (I) DO 1 = 0 TO N)) (E (12,5)); DO К = 1 TON;B=0; DO 1= 1 TO K; DO J=1 TO I; В (I, J), B(2*K-I+ 1, 2 *K —J 4- 1)=A (N—I-f-J); END; DOJ = K+I TO 2*K; В (I, J), В (2 * К - I + 1, 2 ♦ К - J + 1) = A(J-I-K); END; END; L = K/2; IF ((L * 2 = K) & (DET (B,2 * K) < = 0))!
((L*2n =K)&(DET(B,2*K)> = 0)) THEN DO;
PUT SKIP EDIT (’СИСТЕМА НЕУСТОЙЧИВА. ’) (A); GO TO E; END; END; PUT SKIP EDIT (’СИСТЕМА УСТОЙЧИВА.’) (A);
DET: PROC(B.N); DCL B(*,«) FLOAT DECIMAL (6), (I.J.K.N) BIN FIXED (15,0), (T,D,MAX) FLOAT DECIMAL (6); BEGIN; DCL A (N.N) FLOAT DECIMAL (6); A = B; D=l; DOK = 1TON; MAX = 0; DOI = KTON; T = A(I,K); IF ABS (T) > ABS (MAX) THEN DO; MAX=T; J = I; END; END; IF MAX = 0 THEN DO; D = 0; RETURN (D); END; IF J., = К THEN DO; D = -D; DO I = K TON; T = A(J,I); A (J,I) = A (K,I); A (K,I) = T; END; EfiD; DO I = K4- 1 TO N; T = A (I,K)/MAX; DO J = K+ 1 TON; A (I,J) = A (I,J) — T » A (K,J); END; END; D = D*A(K,K); END; RETURN (D);
END DET; END;
E: END SHURCON;
Пример 4.13. С помощью программы № 16 по методу Шур — Койа исследовать устойчивость замкнутой системы, описываемой характеристическим уравнением z3 - 1,01446а2 + 0,302017г - 0,00506 = 0.
Нечетные определители
Л, = —0,999974 <0; Д3 = —0,324203 < 0.
Четные определители
Д2 = 0,911809 > 0.
Из полученных определителей следует, что дискретная система устойчива.
3. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ САР ПО МИХАЙЛОВУ—НАЙКВИСТУ
При проектировании САР малых и больших порядков часто используют частотные критерии устойчивости Михайлова— Найквиста [13] или D-разбиения. Сформулируем эти критерии.
Критерии устойчивости одноконтурных САР по Михайлову—Найквисту [13]
Замкнутая САР будет устойчива, если ее частотная характеристика в разомкнутом состоянии 1Г (/со), имеющая m полюсов в правой полуплоскости, при изменении <о от 0 до оо охватывает точку с координатами (—1,/0)тп/2 раз в положительном направлении (против часовой стрелки).
Для построения в полярной системе координат на плоскости W (Пл. W7) частотную характеристику необходимо представить в виде (3.175). Если это выражение записать в декартовой системе координат, то получим
U7(/®) = t/(®) + /V(®), (4.78) где U (а>) и У(а>)—соответственно вещественная и мнимая частотные характеристики разомкнутой системы *.
На рис. 4.2, а построена частотная характеристика Wi(ja) (годограф) разомкнутой системы при т = 0. Из рис. 4.2,а видно, что годограф не охватывает точку с координатами (—1, /0). Это указывает на устойчивость рассматриваемой системы в замкнутом состоянии.
Дадим другое определение частотного критерия устойчивости, которым удобно пользоваться на практике. Для этого сформулируем следующее правило знаков. Переход годографа W(ja) отрезка действительной оси (—оо, —1), выделенного на рис. 4.2 штриховкой, из верхней полуплоскости в нижнюю считается положительным и обозначается + 1, а из нижней полуплоскости в верхнюю — отрица-
* См. гл. 3.
359
Рис. 4.2. Годографы Михайлова — Найквиста для анализа устойчивости непрерывных линейных стационарных систем, построенные иа плоскости W:
а) F, </со); б) W, Цшу, в) W, Ца); г) Wt (/<о): в) Ws (/<»); е) w,(j<s>y, ж} WAin>y. з)
тельным и обозначается — 1. Пользуясь этим правилом знаков, сформулируем критерий устойчивости.
Замкнутая САР, имеющая в разомкнутом состоянии ш полюсов в правой полуплоскости, будет устойчивой, если разность между числом всех положительных и отрицатель
ных переходов годографом W(j&) отрезка действительной оси (—оо, — 1) равна т/2.
Применим это правило к годографу показанному на
рис. 4.2, а, из которого видно, что при т = 0 годограф не пересекает отрезок (—оо, —1). Следовательно, замкнутая система устойчива. Воспользуемся этим критерием применительно к годографу W2(j<b), изображенному на рис. 4.2, б. Как видно из последнего, годограф 1Г2(/®) при т = 0 делает один отрицательный —1 и один положи
360
тельный +1 переходы отрезка (—оо, —1), т. е. общее число переходов —1-|-1=0. Поэтому система в замкнутом состоянии устойчива. На рис. 4.2, в приведен годограф Гз(/(о), когда /п = 3. Здесь дуга радиуса R оо и дана штриховой линией. Откуда видно, что эта часть годографа совершает —1/2 отрицательного перехода. Другая часть совершает два положительных перехода отрезка. Общее число переходов равно 3/2. В соответствии с предложенным критерием система устойчива в замкнутом состоянии. На рис. 4.2, г изображен годограф (/©) при т = 2. Откуда видно, что 4*1 + 1— — 1 = 2/2, и система в замкнутом состоянии устойчива. Для годографа IP's (/<о) имеем —1/2 + 1 ss 1/2, и при т — 1 система в замкнутом состоянии устойчива (рйс. 4.2, д).
Рассмотрим три случая неустойчивых систем в замкнутом состоянии. Если в W6 (]'а) т = 2 (рис. 4.2, е), то +1 + 1 Ф 2/2, т. е. система в замкнутом состоянии неустойчива. Для при т —О
(рис. 4.2, ж) имеем —1 /2 0, и
система в замкнутом состоянии неустойчива. Если в 1^8 (/со) т = 0, то нз рис. 4.2,з видно, что +1/2 — — 1 Ф 0, т. е. система в замкнутом состоянии неустойчива.
С помощью частотных характеристик разомкнутых систем №(>), построенных в декартовой системе координат и устойчивых в замкнутом состоянии, можно определить запасы устойчивости по модулю ±Ям(со) и фазе Уф(со) > О, гарантирующие работоспособность исследуемой системы даже в случае отклонений ее параметров от номинальных, вызванных изменением режимов эксплуатации. САР, устойчивая в замкнутом состоянии, обладает запасами устойчивости по модулю, если ее модуль | W(/со) | при 9 = ±180° имеет значения, отличающиеся от единицы не менее чем на заданную техническими условиями величину в дБ, на
зываемую запасами устойчивости по модулям.
Одновременно с этим положительные фазовые углы в частотах среза ©с», отсчитываемые относительно линии ±180° не менее чем на угол Уф в градусах, устанавливаемые техническими условиями, называются запасами устойчивости по фазам.
На рис. 4.2, а — д приведены частотные характеристики IV7 (/со) и показаны запасы устойчивости по модулям ±#м и фазе 9ф. Годографы, изображенные на рис. 4.2, е — з соответствуют неустойчивым системам; поэтому для них нет необходимости находить запасы устойчивости по модулям и фазам.
При анализе устойчивости сложных САР проектировщики часто пользуются логарифмическими частотными критериями устойчивости, так как для построения логарифмических характеристик ие требуется больших затрат времени. Кроме того, логарифмические характеристики обладают большей наглядностью и с их помощью можно достаточно просто выбирать необходимые корректирующие устройства для получения в замкнутых системах требуемых показателей качества и точности процессов регулирования.
Если частотная характеристика разомкнутой системы
W (/а) = | W (jo) | е/0 <“), (4.79)* то ее логарифмическая амплитудная характеристика (в дБ)
Lm = 201g| W(ja) | = Я(со). (4.80)
Логарифмическая фазовая характеристика разомкнутой системы 9 (со) строится в градусах. Для построения логарифмических частотных характеристик Lm и 9° используют, как и ранее (см. п. 1.4), полулогарифмическую бумагу. Теперь сформулируем логарифмиче-
* См. выражение (3.175).
361
Рис. 4.3. Логарифмические амплитудные и фазовые частотные характеристики для определения запасов устойчивости по фазе и модулю непрерывных линейных- стационарных систем:
а) Я, (ш), 0, (ш); б) Я2(й>), 02(ш); в) Н, (<о), 02(о)
ский критерий устойчивости Михайлова — Найквиста.
САР будет устойчивой в замкнутом состоянии, когда разность между числом подъемов и спусков фазовой частотной характеристики разомкнутой системы при пересечении прямых 0 — —]80°, —540°, —900° равна пг/2 раз и при этом обеспечивается условие Lm > 0 дБ.
На рис. 4.3, а — в построены логарифмические амплитудные и фазовые частотные характеристики разомкнутых САР с различным числом полюсов в кривой полуплоскости. Из рис. 4.3, а видно, что если в W) пг — 0, то система в замкнутом состоянии будет устойчива, так как при Lm > 0 фазовая характеристика 0i(co) не пересекает прямую —180°. Здесь же указаны запасы устойчивости по модулю Нп, (в дБ) и фазе На
рис. 4.3, б приведены логарифмические Н2((д) и фазовые 02(со) частотные характеристики, построенные по передаточной функции lV'2(s) при пг = 0. Как видно из рис. 4.3, б, фазовая характеристика пересекает ось —180° один раз вверх +1 и один раз вниз —1, т. е. при Lm > 0 имеем +1 — 1 s 0, что указывает на устойчивость системы в замкнутом состоянии. Запасы устойчивости системы по модулю + НКг и — Ям>, а по фазе
Рассмотрим разомкнутую систему, в передаточной функции которой и^з(х) имеется один полюс в правой полуплоскости (т = 1). Ее логарифмические амплитудная и фазовая частотные характеристики построены на рис. 4.3, в. При этом видно, что фазовая характеристика при Lm > 0 пересекает ось —180° один раз в положительном и 1/2 раза в отрицательном направлениях (—1/2+ 1 355 1/2). Следовательно, данная система в замкнутом состоянии устойчива. На рис. 4.3, в указаны запасы устойчивости по модулям НМ}, — и по фазе
362
Рис. 4.4. Логарифмические амплитудная и фазовая частотные характеристики для определения запасов устойчивости по фазе и модулю для непрерывной стационарной линейной системы с четырьмя неустойчивыми звеньями
УфГ Наконец, в системе Wt (s) с т — 4 (рис. 4.4) фазовая характеристика пересекает оси —180°, —540° два раза в положительном направлении -f-l +1. При этом обеспечивается условие устойчивости, так как 2 = 4/2, т. е. система устойчива в замкнутом состоянии.
В случае дискретных и дискретно-непрерывных линейных САР на плоскости W(ja) строятся такими же способами, как и для непрерывных систем, амплитудио-фазовые (в обычном масштабе) или амплитуд
ные и фазовые (в логарифмическом масштабе) характеристики. Однако построение ведется относительно псевдочастоты й. Для исследования устойчивости дискретных и дискретно-непрерывных систем здесь также применим критерий устойчивости Михайлова — Найквиста.
На рис. 4.5, а построены логарифмические характеристики (й) и th (й) для системы, в передаточной функции которой l^i(s) имеется один полюс в правой полупло-
Рис. 4.5. Логарифмические амплитудная и фазовая частотные характеристики для исследования устойчивости дискретно-непрерывных линейных стационарных систем в замкнутом состоянии при т = 1: а — для устойчивой системы; б — для иеустой-чивой системы
S) 363
Рис. 4.6. Структурные схемы непрерывных линейных стационарных систем:
д — для примера 4.14; б —для примера 4.15;
6 — для примера 4.16; г — для примера 4.17
скости, т. е. т— 1. Из кривых видно, что при Lm > 0 результирующее число переходов фазовой ха-
рактеристикой оси —180° будет равно -|-1 — 1/2 1/2, что соот-
ветствует условию устойчивости. Следовательно, замкнутая система будет устойчива. На рис. 4.5, б построены логарифмические характеристики Я2(й) и 02(<о)- Откуда видно, что при Lm > 0 обеспечивается один положительный переход фазовой характеристикой оси —180° (т. е. 4-1 1/2). В этом
случае условие устойчивости не обеспечивается и замкнутая система неустойчива. Обратим внимание на то, что при ю-> оо и й—>0 нарушаются условия минимальной фазовости. Это является отличительной чертой логарифмических характеристик дискретных или дискретно-непрерывных систем.
Рис. 4.7. Определение устойчивости одноконтурной непрерывной линейной стационарной системы для примера 4.14 по логарифмическим частотным характеристикам при четырех значениях К или Тз: а — определение областей устойчивых и неустойчивых состояний по Уф в зависимости от К и Т3; б—области устойчивых и неустойчивых состояний по уф в зависимости от К при Т3=0.71 с; в —области устойчивых и неустойчивых состояний по +Яд и —Ufa при Т3=0,71 с в зависимости от К; а—области устойчивых и неустойчивых-состояний по Уф при К=3,17-10' в зависимости от Г3
364
Пример 4.14. Исследовать устойчивость одноконтурной САР со структурной схемой, показанной на рис. 4.6, а. Пусть она имеет следующие передаточные функции:
“’'“’-тД-П
_ ki(T4s + !)2 .
Гз (s)—(Ks+TF’
IV/ *4 (T'sS + I)2 . . _ k5
W^)- {TeS+1)2 . ^5 (s) - + 1
с параметрами
kt = 103; k2 = 2 • 102; k3 = 158,5; = 10;
fes = 0,5; 71=0,01 с; Г2 = 0,025 c;
T3 = 0,71 c; T4 = 2,88 c; Ts = 28 c;
Te = 250 c; T7 = 30 • 103 c.
Определим общий коэффициент усиления системы К = kikakikiki = 3,17-108. Размыкая главную обратную связь, запишем передаточную функцию в виде
3,17-10е (28s + I)2 (0,71s + I)2
1 ’ (30000s+l)(250s+l)2(2,88s+l)2X ‘
X (0,025s + 1) (0,01s + 1)
Подставив в полученное значение s = /о>, построим на рнс. 4.7, а логарифмические амплитудную Н2 и фазовую 02 частотные характеристики. В передаточной функции разомкнутой системы нет полюсов в правой полуплоскости (т = 0); поэтому разность между числом подъемов и спусков фазовой характеристики прямой линии —180° при Lm > 0 должна быть равна нулю.
Из рис. 4.7, а видно, что имеется один спуск —1 и один подъем 4-1 фазовой характеристики оси —180°, т. е. +1 4-1 в
s 0. Поэтому рассматриваемая система устойчива в замкнутом состоянии. Ее запасы устойчивости по модулям 4-Ям = = 74 дБ, —Ям = 23 дБ, а по фазе Уф = = 83°.
Пример 4.15. Исследовать устойчивость одноконтурной САР, имеющей структурную схему, изображенную на рис. 4.6, б. Пусть она имеет следующие передаточные функции:
r‘(s)=n7+T- r2(s)= (74s+ip~
W3 (s) = fe3j.T4S+ ° ;
/ 5S — 1
XVI 4s + 1)
S(7.6S_1)2-
с параметрами
ki = 400; fe2 = 100; fc3 = 100; fe4 = 0,25 c~‘;
74 = 0,0025 c; 74 = 0,01 c; 74 = 0,1 c;
7’4 = 0,5 с; 74 = 2,5 c; 74 = 20 c.
Определим общий коэффициент усиления системы
/C = fe1fe2fe3fe4= 1 • 106 с-1.
При этом ее передаточная функция в разомкнутом состоянии будет иметь вид
U7 1,1 = 1 • 106 (0,5s 4-I)2 (0,1s+D
' J s(20s — I)2(2,5s- 1)(0,01s + 1).2X ‘ X (0,0025s 4- 1)
Подставив в передаточную функцию s = = /<*>, построим на рнс. 4.8 логарифмические амплитудную Я и фазовую 0 частотные характеристики. В передаточной функции разомкнутой системы имеется три полюса
Рис. 4.8. Определение устойчивости одноконтурной непрерывной линейной стационарной системы с помощью логарифмических частотных характеристик для примера 4.15
365
в правой полуплоскости (т = 3). Число переходов оси —540° равно —1/2+1 а « 1/2, а осн —180°—1-1. Следовательно, общая разность числа переходов этих осей будет равна 3/2. И в соответствии с приведенным логарифмическим критерием устойчивости замкнутая система будет устойчива. Ее запасы устойчивости по модулям +ЯМ =12 дБ, — —10,5 дБ, а по фазе уф = 40°.
4. ЧАСТОТНЫЕ
КРИТЕРИИ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ САР ПО МИХАЙЛОВУ-НАЙКВИСТУ
Для анализа устойчивости многоконтурных систем воспользуемся логарифмическими частотными характеристиками. При построении частотных характеристик элементов (объектов) с внутренними отрицательными и положительными обратными связями были применены номограммы замыкания Никольса (см. гл. 1 и 3), пользуясь которыми без особых затрат времени были найдены логарифмические частотные характеристики элементов (объектов) в замкнутом виде. Поэтому при исследовании устойчивости многоконтурных систем традиционными методами также будем пользоваться номограммой Никольса. Сформулируем логарифмический критерий устойчивости для многоконтурных систем.
Многоконтурная САР с замкнутой главной обратной связью будет устойчива, когда во всех входящих в нее передаточных функциях, имеющих m полюсов в правой полуплоскости, при Lm > 0 обеспечивается разность между числом подъемов и спусков пересечений прямых с 0 = —18(Р, —54(Р,
-у90СР ... всеми фазовыми частотными характеристиками, получаемыми путем последовательного замыкания каждого из контуров обратными связями, равными т/2.
Пример 4.16. Исследовать устойчивость двухкоитуриой САР, структурная система которой показана иа рис. 4.6, в. Пусть передаточные функции разомкнутой системы
имеют следующий вид:
W'1(s) = fe1; BZ2(S) = —;
1 \S I
где
А, = 1,4; А2 = 63; k3 = 0,316 с"1; = 3,56;
Tt = 0,5 с; Т2 = 0,25 с; Т3 = 0,05 с; Г4= 0,01 с.
Частотную характеристику разомкнутой системы запишем в виде
rw-itTw' (4S"
,4<в>
,4'Ю|
В рассматриваемой системе имеется одно неустойчивое звено, т. е. один полюс в правой полуплоскости (m = 1). Логарифмические амплитудная |W'e(/<a)| и фазовая arg[ire(;<o)] частотные характеристики, описываемые выражением (4.83), построены на рис. 4.9, а. Так как m = 1, то для устойчивости внутреннего контура в замкнутом состоянии необходимо, чтобы разность числа подъемов и. спусков фазовой характеристики оси —180° была бы равна 1/2. Из рнс. 4.9, а видно, что имеется один подъем + 1 и —1/2 спуска фазовой характеристики, что обеспечивает устойчивость внутреннего контура в замкнутом состоянии. Запасы устойчивости контура по модулю +Ямк — 12,5 дБ и фазе УфК = 35°- Поэтому можно перейти к построению логарифмических частотных характеристик для замкнутого контура
<4JM>
Из сомножителя, выделенного квадратными скобками в формуле (4.84), следует, что логарифмические амплитудную На и фазовую 0в характеристики необходимо нанести на номограмму Никольса (рис. 4.9,6). В этом случае получим амплитудно-фазовую характеристику 201g Точки ее
перебечения со сплошными линиями номограммы дадут амплитудную характеристику 20 Ig | j- 4/йУд<(/т)~|’ а со штриховыми линиями — фазовую характеристику
arg^.„ J. Перенесем их с номо-
граммы на рис. 4.9, а, а затем, просумми-
366
Рис. 4.9. Определение устойчивости двух-коитурной непрерывной линейной стационарной системы с неустойчивым звеном, находящимся внутри контура I:
а—логарифмические частотные характеристики для
1+уд (/ю) ; б—иомограмма Никольса с нанесённой на -ней логарифмической амплитудио-фазовой частотной характеристикой контура I; в — логарифмические частотные характеристики для 1гк (/со) и всей разомкнутой системы V </ш>
ровав их с частотными характеристиками
20,g| arg[T7w](pHC'4'9,a)’
получим логарифмические характеристики
замкнутого контура 11ГК (/о) | и
argfHM/и)] (рис. 4.9, в).
Передаточную функцию всей разомкнутой системы запишем в виде
W (» = WK (/и) (/®) (/О). (4.85)
На рис. 4.9, в построены логарифмические амплитудная | | и фазовая
агв[У1(/а>)У«(/а>)] характеристики. Сложив их с соответствующими частотными характеристиками замкнутого контура, получим |Н7(;<1))| и агд[Н7(/ш)]. Они и являются частотными характеристиками всей разомкнутой системы. По этим кривым найдем запасы устойчивости по модулю Ям = —8 дБ и фазе Уф = 24*. Следова-
367
Рис. 4.10. Определение устойчивости контура I четырехконтурной непрерывной линейной стационарной системы:
л—логарифмические частотные характеристики для
И Г+^1а(/о>)! б-^арифми-ческие частотные характеристики для IFjj </о>) и WlK </а»
тельио, рассматриваемая замкнутая система устойчива в замкнутом состоянии.
Пример 4.17. Исследовать устойчивость четырехконтурной САР с тремя внутренними контурами, структурная схема которой приведена на рис. 4.6, г. Пусть передаточные функции элементов разомкнутой системы имеют следующий вид:
«Ms) = fe>; 1Г2 (з) = ---**
У 1$ + 1
W- ($) =_____кз W. (о) — .
{) s(TiS+\)’ Wi(s) T3S+1'
W3 (s) == fe5; ir6 (s) = fe6;
kt
r7(s)°7wriiFs~+ir
5 4* “F Zg/ -j- 1J
г'(«)=77тт; UMs) = fe8,
где k{ = 6600; 62 = 0,5; k3 = 12,6 c_|;
fe« = 5,75; *s==0,16; fe6 = 82,5; fe7=19 c"1; fee = 0,28; fe9 = 0,002; T, = 0,05 с; Тг = 0,13 c; T3 = 0,15 c; Tt = 0,0375 c; T6=0,25 c; § = 5,0.
Передаточная функция замкнутого контура I
______fe2fe3___
riK (s).—s(ri5^VK+1)—•
. , _______k3k3K4S______
(Т,з+ IXT2S+ l)(T3s + 1)
(4.86)
368
369
Рис. 4.11. Номограмма Никольса с нанесенными иа ней логарифмическими амплитудио-фазовыми частотными характеристиками: кривые 1—3 — соответственно для разомкнутых контуров I—Ш
В выражение (4.86) введены следующие обозначения:
(о) _________kiklkiS______
(r,s+ l)(f2s+ 1)(Гз«+ 1)
(4.87)
И
При s = /ш из выражений (4.86) — (4.88) получим
«'.и»—гтОо- <‘-89 * *>
Выражение (4.89) перепишем в виде ____________1___
Г1к (/«) --Г1а '-р-(М (4.90)
1 + IMW
пользуясь которым можно по номограмме Никольса построить частотные характеристики замкнутых контуров.
На рис. 4.10, а построены логарифмические амплитудная |1Г1а(/со)| и фазовая arg[irIa(/co)] частотные характеристики разомкнутого I-го контура. При этом видно, что замкнутый контур устойчив, так как имеет запасы устойчивости в “и, Угф,= 100° н в “ic, у!ф2 = 35°.
Обратные частотные характеристики
, и arg Г——rr-r| показаны
также на рис. 4.9, а. Перенеся их на номограмму Никольса (кривая 1, рис. 4.11), получим логарифмические амплитудную ll+y.'.wI"ф,”,ую аге1 частотные характеристики, которые также приведены на рнс. 4.10, а. На рис. 4.10,6 нанесены логарифмические амплитудная 1| и фазовая argflTu, (/со)'] частотные характеристики и результирующие характеристики замкнутого контура I | И71К(/м) | н arg[lT|K(/ci))]. Построение частотных характеристик замкнутого контура осуществлялось по формуле (4.90).
Передаточная функция замкнутого контура II
Гпк (S) - j + (s) И75 (s) Гб (s) • ( • )
При s = /а формулу (4.91) можно переписать в виде
<4-92>
ИЛИ
1
1ГПк (/а) = —-Па(^.....- 1Гць (/а), (4.93)
1 -I---~----
1Г Па (/<->)
где ^Па(/а) = ^1к(/а)Мв (4.94)
и
rIIft(/a)--=irlK(/a)fe5. (4.95)
Построим на рнс. 4.12, а логарифмические амплитудную |1Рпа(/ш)| и фазовую arg[lTiia(/a)] частотные характеристики. Как видно из этих кривых, контур II устойчив в замкнутом состоянии. , Запас устойчивости его в частоте среза а11с по фазе Упф, = 38°, а запас по модулю Нщл = — 48 дБ. Обратные логарифмические ча-
I 1 I стотные характеристики и
j ' ГПа (/<*>) I
erg -757--7т-г| показаны на рис. 4.12, а. По
LWziia(;a)J
ним, пользуясь номограммой Никольса (кривая 2, рис. 4.11), получим частотные
I 1 I характеристики - ----—— и
н I 1 + |
arg^ t j. Перенесем эти харак-
теристики на рис. 4.12, а. Затем, просуммировав с ними частотные характеристики I IFih>(/co) | и argtlFujG’fi))], найдем результирующие характеристики П-го замкнутого контура | ТГлк (/ю) | и arg[IFilK(/‘co)]. Они также изображены на рис. 4.12, а и построены на основе формулы (4.93).
Передаточную функцию Ш-го замкнутого контура построим по формуле
w-, + ^„Tw' <"'9S>
или при s = /со
И7Шк (/ф) = Й71иа((ф) (.ш)>
1+ ^Ша (/<>)
(4.97)
где
Й^Ша (/Ш) = 1Гцк (/Ш) X feyfes/Ci)
(4.98)
[(Г4/со)г + 2^4/ш + 1] (Т5/<в + 1)
U7nib(/a) = U’,iiK(/a)X
Х /ы[(Т4/о))2 + 2|Т4/ф+1] • (4’99)
На рнс. 4.12,6 изображены частотные характеристики | 1Fiiu(/<b) | н arg [U7IIIa(ja)], нз которых следует, что контур III устойчив в замкнутом состоянии. Там же по формуле (4.97) с помощью номограммы Никольса (кривая 3, рис. 4.11) построены частотные характеристики , , -----тт-т >
I 1 + ITinaOa) arg[ 1 + frniaW ]’ КОТОрЫе пеРенесе-ны на рис. 4.12, а, б. Частотные характеристики 11Г'111б(/со) | и arg[U7in»(/<o)[ по-
370
Рис. 4.12. Определение устойчивости контуров II и III четырехкоитурной непрерывной линейной стационарной системы: а—логарифмические частотные характеристики для а (/“)’ а (/<о) ’ 1 + ГПа(/<о) ' » (/ш)
и б—логарифмические частотные харак-
теристики для а и»), ^-1-^.
ГП1 h (lai), к (/ш) и всей разомкнутой системы W (/ш)
лучеиы по формуле (4.99) и результирующие частотные характеристики замкнутого контура III |ГШж(/й>) | и arg{IFntK(/®)] также построены на рис. 4.12, б.
Передаточная функция всей разомкнутой системы
W (s) = ITniK (s) IFi («) Г, (з). (4.100)
Подставляя в выражение (4.100) s = /<о, получим в окончательном виде логарифмические амплитудную | IF (/со) | и фазовую arg[IF(/®)] частотные характеристики, которые изображены жирными сплошной и штриховой линиями иа рис. 4.12,6. Высокочастотный участок амплитудной характеристики иа этом рисунке обозначен цифрой 3. При этом видно, что система имеет запасы устойчивости по фазе Уф == 60° и по модулю Ям=—12 дБ, что гарантирует ее работоспособность в замкнутом состоянии.
371
5. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ САР
С ТРАНСЦЕНДЕНТНЫМИ ЗВЕНЬЯМИ ПО МИХАЙЛОВУ-НАЙКВИСТУ
Существуют системы регулирования, в которых наряду с типовыми динамическими звеньями 1-го и 2-го порядка входят трансцендентные звенья с различными передаточными функциями (см. табл. 1.9 и 1.10). Наиболее часто в системах встречаются звенья чистого запаздывания с передаточными функциями
UZ3(s) = e-K2\ (4.101)
где к = 1, 2, ...; Т — постоянная времени.
Звено чистого запаздывания не изменяет амплитудную характеристику, но вносит значительные фазовые искажения в характеристику разомкнутой системы, так как
03(<о) = -57,37(0, (4.102)
что может явиться причиной нарушения устойчивости системы в замкнутом состоянии.
Когда система является достаточно сложной, то для оценки ее устойчивости в замкнутом состоянии следует пользоваться логарифмическими амплитудными и фазовыми частотными характеристиками. Рассмотрим два случая при m = 0.
Первый случай. Если логарифмическая амплитудная характеристика разомкнутой системы со звеном чистого запаздывания имеет один участок, где Lm > 0, то она будет устойчивой в замкнутом состоянии при одновременном обеспечении двух условий
201gF(/<oc) = 0 дБ; j
Уф (ис) > 180° — 0° (ис) > 0. J }
На рис. 4.13 показано положение логарифмических амплитудной и фазовой (кривая /) частотных характеристик, соответствующих условиям (4.103). Здесь у® = 60°, а на рис. 4.13 показано определение кри-
Рис. 4.13. Определение устойчивости одноконтурной непрерывной линейной стационарной системы со звеном чистого запаздывания
тического значения времени чисто-го запаздывания 7кр, при котором система в замкнутом состоянии находится на грани устойчивости, т. е. запас ее устойчивости по фазе Уф = 0 (кривая 2, рис. 4.13). Из рис. 4.13 нетрудно определить, что
7'kp = Y:p(«>c)/(57,3(dc). (4.104)
Второй случай. Если логарифмическая амплитудная характеристика разомкнутой системы со звеном чистого запаздывания имеет несколько участков, где Lm > 0, то она будет устойчивой в замкнутом состоянии, когда обеспечиваются два условия
201gUZ(j<oC2Z_,) = 0 дБ;
y*(%_.)>180°(2Z“1)-
► (4.105)
-e°(o)c2i_1)>0.
Построим на рис. 4.14, а одну логарифмическую амплитудную (кривая /) и четыре фазовые (кривые 2—5) частотные характеристики при i— 1. Из рис. 4.14,а видно, что при Т = Т[ и Lm — 0 дБ фазовая характеристика (кривая 2) в частотах среза <оС1 и соС2 обеспечивает положительные запасы устойчивости Y^(®C1) и УфК®*)- Сле’ довательно, система в замкнутом состоянии при Т\ устойчива. На рис. 4.14,6 приведена амплитуднофазовая частотная характеристика в обычном масштабе, полученная из рис. 4.14, а. Она подтверждает, что система в замкнутом состоянии устойчива, так как
372
амплитудно-фазовая характеристика не пересекает отре-
зок (—оо, 1).
Фазовая характеристика (кривая 3) при Т2 > Т\ ие удовлетворяет условию (4.105), потому что в <оС1 ?ф2 (“с.) > 0, а в <осз у<ф3> (®С!) < 0. Поэтому система при времени чистого запаздывания Т2 неустойчива в замкнутом состоянии. На рис. 4,14, в приведена амплитудно-фазовая характеристика 1^2 (/<о). Она пересекает ось (—оо, —1) один раз в отрицательном направлении. В этом случае —1=#= 0, и система неустойчива.
Фазовая характеристика (кривая 4) построена на рис. 4.14, а при Тз > Т2. Она отвечает условиям устойчивости (4.105), так как в “с, и “с, Y(^(®c.)>° и Уф! (О > °-Соответствующая этому случаю амплитудно-фазовая характеристика Г3(/<о) построена на рис. 4.14, г. Она не пересекает ось (—оо, —1),
Рис. 4.14. Определение устойчивости непрерывной линейной стационарной системы с четырьмя различными значениями .постоянной времени звена чистого запаздывания: а) логарифмические частотные характеристики; б) «Г, (/ш) при т=т,; в) W, (/<!» при Т—Т2; г) U73 (До) при Т - Т3; д) Wdi<a) при Т = Т4
что обеспечивает устойчивость системы в замкнутом состоянии.
Фазовая характеристика (кривая 5) построена на рис. 4.14, а при Л > Тз. В этом случае условия устойчивости не удовлетворяются. При частотах среза <оС1 и исз УФ!(шС1)< <0 и Уф! (®cs) < 0’ т- е- замкнутая система при Г4 неустойчива. Амплитудно-фазовая характеристика (/«), изображенная иа рис. 4.14, д, подтверждает данное положение. Из рис. 4.14, а — д видно, что с увеличением времени чистого запаздывания Т происходит чередование устойчивых и неустойчивых состояний в замкнутой системе. Такое явление наблюдается у многих типов САР с «чистым» запаздыванием.
Рассмотрим логарифмические амплитудно-фазовые характеристики, когда в передаточной функции разомкнутой системы имеются три полюса в правой полуплоскости (т = 3). Логарифмическая амплитудная частотная характеристика Н построена на рис. 4.15 сплошной линией. При Lm > 0 фазовая характеристика, изображенная на рис. 4.15 штриховой линией до частот <оС1, пересекает прямые —540° и —180° снизу вверх по одному
373
Рис. 4.15. Определение устойчивости непрерывной линейной стационарной системы с тремя неустойчивыми звеньями:
а — логарифмические частотные характеристики; б — амплитудно-фазовая частотная характеристи' ка иа Пл. W
6. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВЫХ И НЕУСТОЙЧИВЫХ СОСТОЯНИЙ И ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ СО СЛАБОДЕМПФИРОВАКНЫМИ ЭЛЕМЕНТАМИ
разу, т. е. два раза в положительном направлении, а на участке от шС1 до <оСз — один раз в отрицательном направлении при Уф(<о3) < < 0. Это показывает, что условия (4.105) не соблюдаются и система в замкнутом состоянии неустойчива.
На рис. 4.15,6 по логарифмическим характеристикам перестроена амплитудно-фазовая характеристика W(ja), из которой видно, что -|-1 + 1 — 1 й 3/2, т. е. система неустойчива.
Для систем регулирования подобного типа
т е°(%-.) 180°(2t —1)
7 к₽ 57,3ш„ “Г 57,3в>_
с2/-1 C2i-1
(4.106)
где i=l, 2, ...
Для выделения областей устойчивых и неустойчивых состояний проектировщик сначала устанавливает возможные диапазоны изменения параметров разомкнутой системы, например, общий передаточный коэффициент К или одну из постоянных времени. В примере 4.14 под такой постоянной времени было принято Уз. Затем при измененных параметрах К и Г3 строились семейства логарифмических амплитудных и фазовых частотных характеристик, а по ним находились запасы устойчивости по фазам у® и модулям Ям, — Ям.
На рис. 4.7, а построены четыре логарифмические амплитудные характеристики Hi — Н4 с различными коэффициентами Ki — Ki- Для определения областей устойчивых и неустойчивых состояний в зависимости от К строятся 10—20 лога
374
рифмических амплитудных характеристик и одна фазовая. Откладывая по оси абсцисс запасы коэффициента К, а по оси ординат запасы устойчивости по фазе у®. на рис. 4.7,6 получим кривые, разделяющие области устойчивых от неустойчивых состояний в системе. Как видно из рис. 4.7,6, имеются две области устойчивых состояний (они выделены штриховкой). Области устойчивых и неустойчивых состояний можно построить и в зависимости от Нм и —Нм- Они показаны на рис. 4.7, в. При четырех различных значениях постоянной времени Т3 на рис. 4.7, а построены участки семейства фазовых частотных характеристик 0j — 04, близкие к частоте среза <ос. Пользуясь этими характеристиками, находим запасы устойчивости по фазе у® и> откладывая по оси абсцисс значения Гз, а по оси ординат у^,, получим кривую, которая разделяет области устойчивых состояний от неустойчивых (рис. 4.7, г).
В технических требованиях на проектируемые САР задаются допустимые значения запасов устойчивости по фазам у^, и амплитуде ±Ям. Примем, что у^, = 45°, 4-Ям =16 дБ и —Ям = —12 дБ. Проведем по этим установленным значениям жирные штриховые линии (рис. 4.7,6—г). Как видно из рис. 4.7,6 — г, происходит некоторое сокращение областей устойчивости по К Ц Гз, в которых гарантируется нормальная работоспособность замкнутой системы. При меньших запасах устойчивости системы обладают показателями качества, недопустимыми по техническим требованиям *.
Перейдем к исследованию устойчивости сложных систем со слабо-демпфированными элементами. В гл. 1 на рис. 1.37 и 1.39 были построены в полярной’ системе координат логарифмические амплитуд-
♦ См. подробнее в гл. 5.
Рис. 4.16. Определение устойчивости непрерывных стационарных слабодемпфирован-ных систем управления по логарифмическим амплитудно-фазовым частотным характеристикам, построенным в полярной системе координат
но-фазовые частотные характеристики объектов со слабодемпфиро-ванными элементами. Подключим к объектам устройства управления и измерения, а затем замкнем внутренние контуры системы с помощью отрицательных обратных связей. В результате получим такие динамические САР, в которых в ряде узких диапазонов частот наблюдаются крутые подъемы и спуски амплитудных и фазовых характеристик (резонанс). Как видно из рис. 1.37 и 1.39, максимумы амплитуд близко подходят к оси 0 дБ, создавая малые запасы устойчивости по амплитуде ±ЯМ, или пересекают эту ось, что недопустимо по техническим требованиям и является причиной неустойчивости систем в замкнутых состояниях (рис. 1.38, а, б).
Для получения устойчивости таких систем необходимо вводить корректирующие устройства, обеспечивающие снижение логарифмических частотных характеристик, при которых увеличиваются запасы устойчивцсти по модулю до заданного уровня. В этом заключаются так называемые амплитудные способы стабилизации систем.
375
Резкие изменения фазовых характеристик (рис. 1.38, а, б) приводят к уменьшению запасов устойчивости по фазам или неустойчивости систем на резонансных частотах, где у(<£ < 0. В этом случае добиться устойчивости систем можно путем введения дополнительных корректирующих устройств, обеспечивающих фазовое опережение > 0) на резонансных частотах — фазовые способы стабилизации систем.
Пример 4.18. Исследовать устойчивость САР со слабодемпфированным объектом, частотная характеристика которого приведена на рис. 4.16 в полярной системе координат, где приведены запасы устойчивости по модулям + /7М =17 дБ ; — =
==—15 дБ и фазе Уф = 41°.
На резонансных частотах ы*р^ — 5 с-1 и w^ = 5,6 с-1 указаны запасы устойчивости по модулям — ~ ~9 дБ и
— W^P’*=—13 дБ. Здесь же отмечены на частотах (0(3Р) =10,5 с-1 и ш^р^=12,3 с-1 значения фаз — 52° и Уф'* = —64°, т. е. система неустойчива.
Следует обратить внимание, что выбор параметров корректирующих устройств, обеспечивающих устойчивость систем со слабодемп-фированными звеньями, представляет значительные трудности, связанные с близостью собственных частот колебаний по частоте среза <ос к резонансным частотам и(р), ш<р>. В свою очередь резонансная частота <о^Р) может быть близка к <о<р>. При этом происходит значительное падение фазовой характеристики, и получить желаемые ее подъемы до требуемого уровня с помощью обычных RC-корректи-рующих устройств не всегда удается. Поэтому для получения устойчивости системы в замкнутом состоянии вводится двухзвенный КСЬгфильтр, обеспечивающий «запирание» резонансной частоты колебаний, например по ю’р>. Тогда на этой частоте исключается воз-
( можность появления неустойчивости.
В примере 1.42 рассмотрен способ построения логарифмических амплитудно-фазовых частотных характеристик в декартовой системе координат (амплитуда — фаза) для слабодемпфированных объектов (рис. 1.41). Наличие в последних близко расположенных нулей и полюсов приводит к замкнутым контурам на плоскости 1Г. Для упрощения построения таких логарифмических амплитудно-фазовых характеристик удобно пользоваться обобщенной номограммой (рис. 1.40).
Пример 4.19. Перестроим логарифмическую амплитудио-фазовую частотную характеристику системы из полярной системы (рис. 4.16) в декартову. На рис. 4.17 амплитудная характеристика изображена жирной сплошной линией, а фазовая — штриховой. Здесь также указаны все запасы устойчивости по модулям и фазам.
В гл. 3 было показано, что по логарифмическим амплитудным и фазовым частотным характеристикам САР в разомкнутом состоянии можно получать логарифмические амплитудные и -фазовые частотные характеристики систем в замкнутом состоянии. На практике наиболее часто встречаются следующие два типа передаточных функций систем в замкнутом состоянии:
<D1(s) = r(s)/[l + IT (з)] (4.107) или
Ф2(з) = У(з)/[1 + Г(з)]. (4.108)
С помощью номограммы Никольса нетрудно получить по частотным характеристикам U7(/co) частотные характеристики Ф] (/со). Для этого по числовым значениям логарифмических амплитудной | W(j(D) | и фазовой arg [И? (/со)] частотных характеристик разомкнутой системы строим амплитудно-фазовую характеристику 20 lg W(/со). По точкам ее пересечения со сплошными линиями номограммы снимем амплитудную | Ф1 (/со) |, а по точкам пересечения со
376
Рис. 4.17. Логарифмическая амплитуднофазовая частотная характеристика, перестроенная из полярной системы координат (рнс. 4.16) в декартову
штриховыми линиями фазовую arg[i(Di(j<o)] частотные характеристики.
Для получения аналогичных характеристик по передаточной функции (4.108) ее необходимо переписать в виде
1
Ф2(я) = —^4— V(s). (4.109) 1 -I---------------
IT (s)
Подставив в выражение (4.109) s — строим обратные логарифмические амплитудную | w j и фазовую аг&[ц7 (/^)~] характеристики, числовые значения которых наносим на номограмму. В результате получим логарифмическую ам-, пл! Г 1/«7(/<0) 1
плитудно-фазовую 201g[1 + 1/ff, (.^J характеристику. По точкам ее пересечения с соответствующими кри-
выми номограммы строим логариф-мические амплитудную 11 (/(0) |
, I 1/1Г (дв) I
и фазовую argj t + 1/Ц7 (/^у | частотные характеристики. Далее, сложив их с характеристиками | V (ja) | и arg [У (/©)], соответственно получим |Ф2(/©)| и arg [Ф2 (/©)].
Существуют и такие системы, в которых результирующие передаточные функции можно представить в виде
Ф3(5)= 1 + F,(s). (4.110)
Ф4(х) = 1 + Г1(х)+1Г2(5), (4.111)
Ф5(в) = («) + W2(s), (4.112)
а также их различных комбинаций.
Рассмотрим сначала передаточную функцию Фз(«). Для этого перепишем ее в виде
После подстановки в выражение (4.113) s = jo> по логарифмическим
377
частотным характеристикам
201g [цу (fo)-] с помощью номограммы Никольса получим
1 IF, (j<o)
О)
Частотные характеристики |Фз(/®)| и arg[d>3(/(o)] строим как зеркальные отображения характеристик
Рис. 4.18. Структурные схемы систем: а—для примера 4.20; б—для примера 4.21
1 w. (j<o)
I--------—
r if. (Ю
относительно оси со.
Теперь перейдем к формулам для построения частотных характеристик по передаточной функции (4.111), которую можно представить в виде
несем 1Г1 (s) за скобки в выражении Фв(з); тогда получим
®sW=y,(S)[l+^-]
или
Ф5(3) = ^(3)
откуда
Ф4(я) =
где
1
IT, (з)
14 1
W* (з) 1 l+UMs) J’
(4.114)
(s) _
1 "-I
1Е"(з)
14 1
W" (з) _
W'(s) =
Wt (s)
1 4- IF, (s)
(4.115)
По формулам (4.115) и (4.116) при s = /со строим соответствующие частотные характеристики |Ф4(/со) I И arg[<D4(/©)J.
В заключение рассмотрим формулы, по которым можно построить частотные характеристики для передаточной функции (4.112).Вы-
1Г,(з) ~-1
!Fa (s)
. , ДМ»)
W2 (®> _
(4.117)
По аналогии с ранее рассмотренными передаточными функциями нетрудно при s = /со построить частотные характеристики системы |Ф5(/о>) I и arg[Ф5(/со)].
Пример 4.20. Построить логарифмические частотные характеристики замкнутой системы, структурная схема которой изображена иа рис. 4.18, а. Передаточные функции элементов системы имеют следующий вид:
1171 = T,s + 1 : = Tts 4- 1 :
^3(3)=^^-; ^(з) = 4-;
w5 (s) = fe5s, где
kt = 10; k2 = 103; k3 = 10“l; fe4 = 10 c-1; fes = IO-2; Ti == 0,1 c; T2 = 1 с; T3 = 10-3 c.
Передаточная функция I-го замкнутого контура
кг
^W- "’‘If;--------- «"в’
+ (7as + l)(73s 4-1)
Введем в выражение (4.118) следующие обозначения:
Wla (s) = Ыз/[(Т2з 4- 1) (Тзз 4- D1.
Wib(s) = k2/(TiS+V).
378
Рис. 4.19. Логарифмические амплитудные и фазовые частотные характеристики двухконтурной непрерывной замкнутой линейной системы интегрирующего типа (пример 4.20):
а—логарифмические частотные
характеристики
внутреннего контура lFIa(/a>),
1
б—логарифмические
частотные ха-
рактеристики прямой цепи системы Wjj(/e>)H WlKU<s>)
I 1 I частотные характеристики f-fr- (/ю) | и arg[l + wla (/«>)]• .
На рнс. 4.19,6 построены характеристики | W'n, (/со) | и arg [(Гн, (/<»)]• Сложив их с соответствующими частотными характеристиками, найдем частотные характеристики замкнутого I-го контура, т. е. |U7lK(/w) | и arg [^к (/<о)].
Передаточную функцию П-го замкнутого контура запишем в виде
Тогда при s = /со имеем
(4Л|9)
W^IIk (s) =
kikt s(T>s+ 1)
«Ms>
1+^TZT«7ik(s)'
(4.120)
На рис. 4.19, а изображены логарифмические амплитудные и фазовые частотные характеристики |lFia(/6>)| и arg[Wri0(/co)j, из которых видно, что I-й контур в замкнутом состоянии устойчив. Пользуясь характеристиками | —~(/с>)~ | и
1 1
ц7[ с помощью номограммы
Никольса (кривая 1, рис. 4.20) получим
arg Г
или при $ = /со имеем
’vW-lX'w |,Л2'1 где
^11а(/®) = ^^^1к(/®) (4.122) 1 1/С0 -f- 1
и
(4Л23>
379
Ьт.дб
По формуле (4.122) на рис, 4.21, а построены логарифмические частотные характеристики | 1Гца (/w) | И arg[lTiia ] . Из них видно, что П-й контур в замкнутом состоянии устойчив. Здесь же даны зеркально отраженные характеристики тт-у
I "ПаI и аге[ц7п (yajj' Эти характеристики нанесены на номограмму Никольса (кривая 2, рис. 4.20). В результате получим логарифмические амплитудную , , ---тг-г
I 1 + * па (/со) | и фазовую arg частот-
ные характеристики, которые также изображены на рнс. 4.21, а. На построены характеристики arg[V(/co)] по формуле (4.123). Сложив их с ранее построенными на рис. 4.21, а частотными характеристиками, получим результирующие логарифмические амплитудную |<М/ш)| и фазовую arg[<Dy(/со)] частотные характеристики.
Пример 4.21. Построить логарифмические частотные характеристики замкнутой системы, структурная схема которой показана на рис. 4.18, б. Будем считать, что на вход
>нс. 4.21,6 V(/’w)| и
Рис. 4.20. Номограмма Никольса с нанесенными на ней логарифмическими амплитудно-фазовыми частотными характеристиками:
кривая 1 — для разомкнутого контура I; кривая 2 — для разомкнутого контура II системы, рассматриваемой в примере 4.20; кривая 3 — для внутреннего разомкнутого контура системы, приведенной в примере 4.21
объекта системы поступают ненулевые начальные условия в виде Х[(0) = 0,1. Передаточные функции элементов системы
1171 (S) = (Tis 4- 1) (r2s + 1):
Г2 (*) ° т i • «Ms) = e~r‘s;
(s) = (Г6з+ l)(Tes+ 1) ’
где =20; fe2 = 0,68; fe3 = 0,042; fe< = 0,7;
Г, =0,05 с; Г2 = 8 с; Г3 = 15 с; Г4 = 0,4с;
Т6 = 24 с; Тв = 100 с.
380
Передаточную функцию замкнутой системы запишем в виде
k
ф (S) = (Tss+lHTes+J) *(0)
. . _______feifeaMue"* 1 * * * * * **8_
(T-.s+lH^s + inrss+OX
X(T6s+ l)(Tes+ 1)
(4.124)
Псдставляя в выражение (4.124) s = /<о и вводя следующие обозначения
ь
u ’ (Т./шЧ-1)(7’2/и+1)(7’3/и+1)Х
X (Ts/<o + 1) (Г6/и + 1)
(4.125) и
(4.126)
получим
,/Х)- <4127)
где ka == 6,3; fej = 4.
Рис. 4.21. Логарифмические амплитудные и фазовые частотные характеристики двухконтурной непрерывной замкнутой линейной системы интегрирующего типа для примера 4.20:
а) замкнутого контура II IFj, а (1а), —ц— и
; б) V (1а) и всей замкнутой системы
1 + **11 а
Фу (/ш)
На рис. 4.22, а построены логарифмиче-
ские амплитудная | W(ja>) | и фазовая
arg[lF(/<o)] частотные характеристики ра-
зомкнутой системы. Откуда видно, что си-
стема устойчива в замкнутом состоянии. Там же приведены зеркальные отображения характеристики разомкнутой системы Iwd И arg[wd • Пользуясь ими
и номограммой Никольса (кривая 3, рис. 4.20), получим логарифмические амплитудную и фазовую частотные характе-Ристики ITW) I ’ arg [iW) ] • Частотные характеристики | V(/а) | и
381
Рис. 4.22. Логарифмические амплитудные и фазовые частотные характеристики одноконтурной непрерывной замкнутой системы: e> н б) v н всей замкнутой системы Ф (/«>)
arg[V(/<o)] рассчитаны по формуле (4.126) и построены на рис. 4.22, б. Сложив их с ранее полученными, найдем результирующие логарифмические амплитудную |Фи(/ш)| и фазовую arg[<Dy(/<i>)] частотные характеристики замкнутой системы.
7. ВЫЧИСЛИТЕЛЬНЫЕ ПРОЦЕДУРЫ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ НЕПРЕРЫВНЫХ
И Д И С К Р Е ТИО Н Г. Л Г Е Р Ы В Н Ы X СИСТЕМ ЧАСТОТНЫМИ МЕТОДАМИ
В гл. 3 были рассмотрены способы построения непрерывных и дискретно-непрерывных систем в виде дискретных моделей; процедуры спектрального разложения матриц;
способы вычисления функций от матриц. В результате их использования удается получить формулы для вычисления частотных характеристик непрерывных и дискретных моделей разомкнутых систем. Пользуясь этими результатами, запишем для непрерывных и дискретных систем согласно работе [26]
ИЛ28)
Z-1 откуда
IF (/«>) =
_ V c\l^b th 2 v
“ 2 th TaKl
Li-i /ш_ —th-^- — J
X(1_Z^). (4.129)
382
Из выражения (4.129) имеем
^(М)= Е с/,(®) +
Z-1 1=1
(4.130)
Составляющие t/<(®) и V)(®) частотной характеристики при действительных собственных значениях X,- = а< + /р, вычисляются по формулам
стг7(;н'б
^(<о) = _Х< (4.131)
(0 At-
cFr.l^b
Vz (©) = -©-5^-. (4.132)
® + az
Для дискретной модели непрерывной системы в формулы (4.131) и (4.132) вместо X, и ® подставим
Xz^#th^n®; (4.133)
тогда получим
стг Лн’6 t/Д®)--^.-^-^; (4.134) ® ~г \-
cTr ?н)& ^(6)=-®^-^. (4.135) co -г
В формулах (4.131), (4.132),
(4.134) и (4.135), как и ранее,-приняты обозначения-л — правые собственные векторы, соответствующие значению Xz; ZzH) — левые собственные векторы, соответствующие значению Х(-; © — круговая частота; ® — псевдочастота.
При комплексных собственных значениях X,- = а< + /р( формулы (4.131), (4.132) необходимо заменить на
Ut (®) = -ст х
az (Re rl Re — Im rt Im Z(zH)) + • v + (₽<““) (Re riIm 4н)+1гпг/ ReI(zH>) X l,У й \2 I „2 X
(“ “ PJ + aZ
X»; (4.136)
V((<o) = -CTX
az (Re r{ Im ZzH) + Im r{ Re Z(zM>) — v ~(Pz--®)(RerzReZ<H>-ImrfImZ)H)) X (<o - Pi)2 + az
Xb. (4.137)
_ Для_ дискретной модели имеем Х(- — a,- + /р,. При этом формула (4.130) примет вид
^(/®) = Г7 (©) + /¥(©), (4.138)
где п th
б<“>=к2Д‘(6>
‘“1 _ 2 _
П th
~ътг
1 = 1 _ 2 _
(4.139)
Выше было показано, что для дискретных моделей вместо X,- необходимо подставлять X,-. В этом случае формулы (4.136) и (4.137) можно переписать в виде
t7z(®) = —стХ
az (Rer(. ReZzH> — Im Im z)H)) +
+ (Pz-®)(RerfImZ(zH,+ImrzReI(zH))
Z\ . 5 .9 , -2
(®-₽i) z+ az
Xb\ (4.140)
Fz(®) = -cTx
“z (Re ri ^ZH> 4" Im ri Re <H)) ~
/ - a . - 2 (®-₽z)2+ai
Xb, (4.141)
где - _ _2_____________sh (aiFo) .
“г To ch (azr0) + cos (piT0) ’ 5_____2________sin (PiTp)
P‘ ~ Г» ch (aiT0) + cos (ргТ0) ’
(4.142)
Для вычисления шага изменяемой части воспользуемся соотноше--нием
J—1
Д<о = (^)К - (4.143)
Для дискретных моделей систем по формулам (4.134), (4.135) и (4.140), (4.141) находят соответственно t7z(®), К(ш) или
383
Р/(б), а по формулам (4.130) и (4.138) — амплитудно-фазовые характеристики разомкнутых систем IF(/<o) или №(/©). При определении амплитудно-фазовых частотных характеристик применяют процедуру FREQLS, представленную в виде рабочей программы № 17.
Процедура FREQLS позволяет строить логарифмические амплитудную и фазовую частотные характеристики. При этом можно использовать последовательность частот в пределах одной декады: со = = 1; 1,20; 1,58; 1,99; 2,52; 3,16; 3,98; 5,01; 6,31; 7,94; 1.0,0.
ПРОГРАММА № 17 FREQLS
Программа предназначена для вычисления частотных характеристик динамических систем, задаваемых векторно-матричными тройками:
{ст, А, Ь) — для непрерывных моделей;
{ст, V, <р) — для дискретных моделей.
Обращение к программе
FREQLS (N,CT,R,A,LH,B,Y,W,FR)
Входные параметры
N — порядок системы; '
СТ — вектор формирования выхода;
R — матрица приведения к канонической форме Жордана;
А — матрица собственных значений в канонической форме Жордана;
LH — матрица, обратная R;
В — вектор передачи управления;
Y—информационный вектор, указывающий тип собственного значения;
W — массив, элементами которого являются:
W (1)— нижняя граница диапазона частот;
W (2) — верхняя граница диапазона частот;
W (3) число точек частотной характеристики.
Выходные параметры
FR — двумерный массив размера (W (3), 3), элементами которого являются: FR(»,1) — значения частот;
FR (»,2) — значения Re W (/<£>);
FR (*,3) — значения Im W (jo).
Входные массивы R, A, LH, Y должны быть OWN.
вычислены с помощью программы
FREQLS: PROC (N, СТ, R, A, L, В, Y, W, FR);
DCL N, K, (W0, T, (CT, B, W) (*), (A, R, L, FR) (*,*)) DEC (12), Y (*); DCL (Wl, CR, ICR, LB, ILB, IMA, U, V, RK, IK, D) DEC (12), I, J, M; W1=W(1); T=W (2); K=W (3); DO M=1 TO K; U, V=0; DO 1=1 TO N; IF Y(I)<0.5 THEN DO; CR,LB = 0.0; DO J = 1 TO N; CR = CR + CT (J) * R (J,I); LB = LB + L (I,J)*B(J); END; D = CR*LB/(W1 *W1 + A (1,1) * A (1,1)); U = U — A (1,1) » D; V = V — Wl * D; END; ELSE DO; IMA = A (1,1 + 1); CR,ICR,LB,ILB = 0.0; DOJ=1TON; CR = CR + CT (J) * R (J,I); ICR = ICR+CT (J) * R (J,1+1)! LB=LB+B (J) * L (I, J)/2; ILB = ILB - В (J) • L (I + 1, J)/2; END; RK = CR * LB - ICR * ILB;
IK = CR + ILB+ICR * LB; DO J = 1,2; D = (Wl — IMA) * (W1-IMA)+A (I,I)*A(I, I); U = U - (A (1,1) * RK + IK * (IMA - Wl))/D; V=V-(A (1,1) * IK—RK * (IMA-W1))/D; IMA =-IMA; IK = —IK; END; 1 = 1 + 1; END; END; FR(M,1) = W1; FR(M,2) = U; FR(M,3) = V; W1=W1*T; END FREQLS;
Пример 4.22. Вычислить и построить амплитудно-фазовую н соответствующие ей логарифмические амплитудную и фазовую частотные характеристики для непрерывной САР, структурная схема которой изображена на рис. 3.22, а ее расширенная матрица Ф дана в примере 3.12, По этой матри
це с помощью программы № 17 FREQLS вычислены числовые зиачеиия логарифмических частотных характеристик для дискретной модели системы. Амплитудная характеристика построена жирной сплошной линией, а фазовая — штриховой. Из рис. 4.23 видно, что запасы устойчивости
384
Рис. 4.23. Определение устойчивости линейной стационарной системы с помощью амплитудно-фазовой частотной характеристики, полученной с помощью вычислительной процедуры FREQLS, реализованной на ЭВМ (пример 4.22)
по модулю составляют НЯ1 = 17 дБ и —Я«1 = —9 дБ, а запасы по фазе Уф,= = 18°. На этом же рисунке для сравнения построены тонкими линиями характеристики для непрерывьий системы. Запасы устойчивости будут следующими: Ннг = = 18 дБ; -Ям2 =-17 дБ; =36°. Следовательно, система устойчива в замкнутом состоянии.
Пример 4.23. С помощью вычислительной процедуры FREQLS вычислить и построить логарифмическую амплитудно-фазовую частотную характеристику разомкнутой системы со слабядемпфированными звеньями, имеющей годограф объекта, приведенный на рис. 1.37 при корректирующем устройстве:
(0,8/<й + 1) (0,22 (/со)2 + + 2-0,2-0,5/а + 1) (0,12 (/о)2+
В7 +2-0,1-0,3/0+!)
Й7К (/о) - 0,8 (10.ш + (ОД552 (.ш)2 + • + 2-0,155-0,0035/о+ 1) X X (0.0882 (/о)2 + 2 • 0,088 X
X 0,002/0 + 1)
Соответствующая логарифмическая ам-плитудио-фазовая частотная характеристи
ка построена на рис. 4.24, откуда можно найти запасы устойчивости по модулям + #м = 11,3 дБ, — Ям = —11 дБ и по фазеуф = 30°иа низких частотах. На собственных частотах колебаний слабодемпфи-роваиных объектов оР< = 6,43 с-1, оРг = = 11,23 с~1 соответственно находим запасы устойчивости по модулю Hvi = 15,1 дБ,
Рис. 4.24. Определение устойчивости непрерывной линейной стационарной САР по логарифмической амплитудно-фазовой частотной характеристике, полученной с помощью вычислительной процедуры FREQLS, реализованной иа ЭВМ в интерактивном режиме работы проектировщика (пример 4.23)
13 Ю. И. Толчеев
385
Рис. 4.25. Определение устойчивости первой подсистемы IFif/'w) с помощью логарифмических амплитудной и фазовой частотных характеристик, полученных иа основе вычислительной процедуры FREQLS, реализованной иа ЭВМ в интерактивном режиме работы проектировщика (пример 4.24)
НР2 = 21,0 дБ, ЯРз = 36,0 дБ. Отсюда видно, что система устойчива в замкнутом состоянии.
Пример 4.24. Вычислить и построить логарифмические амплитудную и фазовую частотные' характеристики двухканальиой САР, структурная схема которой приведена иа рис. 3.5, а. Логарифмические частотные характеристики для первой подсистемы, построенные по формуле (3.51), приведены на рис. 4.25, для второй [формула (3.52) ] — на рис. 4.26, а их сумма [соотношение (3.53)] изображена иа рис. 4.27. Как видно из этих рисунков, обе подсистемы и вся система в целом являются устойчивыми в замкнутом состоянии.
Для вычисления частотных характеристик многомерных систем, приводимых путем структурных преобразований к нескольким одномерным, следует использовать процедуру FREQLS столько раз, какова размерность входного сигнала.
8. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВЫХ и неустойчивых состоянии с помощью 0-РАЗБИЕНИЯ
Рис. 4.26. Определение устойчивости второй подсистемы №г(/и) по логарифмическим амплитудным и фазовым частотным характеристикам, полученным с помощью вычислительной процедуры FREQLS, реализованной иа ЭВМ в интерактивном режиме работы проектировщика (пример 4.24)
ной двухкаиальной непрерывной САР с помощью логарифмических амплитудной и фазовой частотных характеристик, полученных по рис. 4.25 и 4.26 при следующих передаточных функциях:
Уи1Щ='уИ2^=1; «Ws>=_olrrr: rp2<s>= 4k+1 , 10-3 n-z —
= 0,ls + l’ r’1(S> 0,01s+1_*3 r"(s)
- looses^(s>=
4s2 + 0,4s + 1
Применение метода D-разбиения позволяет исследовать устойчивость замкнутой системы с помощью характеристического уравнения {4.13а) на плоскости, выделяя один или два параметра. В качестве таких параметров могут быть приняты передаточные коэффициенты ki или постоянные времени передаточных функций Tt G = l,2,...).
Рассмотрим сначала систему, в которой можно выделить из уравнения (4.13а) один параметр w. В этом случае характеристическое уравнение (4.13) перепишем в виде *
Q (X) + wR (X) = 0. (4.144)
Из выражения (4.144) найдем w=-Q(K)/R(K). (4.145)
Положим, что w — комплексное число, и отобразим мнимую ось
* Приведенный подход возможен, лишь когда параметр w входит линейно в характеристическое уравнение замкнутой системы.
386
плоскости корней X на плоскость w. Тогда при X —/® из уравнения (4.144) получим
“’«“-Ж (4Л46) или
w (/со) — и (со) + jv (со). (4.147)
Изменяя значения со от —оо до Н-оо, построим в плоскости w (или «, v) кривую, отображающую мнимую ось /со плоскости S на плоскость ш(/со). Получаемая в результате этого кривая является кривой D-разбиения [1, 13]. Такая кривая всегда симметрична относительно действительной оси; поэтому можно строить лишь участок, соответствующий изменению чистоты от 0 до оо, а затем дополнить его зеркальным отображением кривой Р-разбиения относительно действительной оси. В результате получим несколько областей. Однако судить о том, в какой из областей все корни характеристического уравнения имеют отрицательные действительные части, не представляется возможным. Для этого необходимо пользоваться правилом штриховки кривых /)-разбиёния. Сформулируем это правило применительно к Р-разбиению плоскости относительно одного параметра ki или Т; в следующем виде.
При перемещении вдоль кривой D-разбиения от частоты w -э--оо
до ее следует штриховать
слева, как показано на рис. 4.28 [1]. Таким образом, на плоскости получим несколько зон, отделенных одна от другой кривой О-раз-биения.
Рассмотрим рис. 4.28, а, где показаны три области / — III. Будем считать, что в зоне I каждой точке плоскости соответствует комплексное число к корней с отрицательной действительной частью. Если при переходе из зоны / в зону // происходит пересечение кривой О-раз-биения с незаштрихованной стороны на заштрихованную, то в зоне // число корней с отрицательной
действительной частью увеличивается на единицу и отметка точки к становится равной к+ 1- При переходе кривой О-разбиения из зоны / с заштрихованной стороны на незаштрихованную (зона III) число корней с отрицательной частью уменьшается на единицу, и отметка точки будет равна к — 1.
Практически интерес представляет исследование только действительных значений параметра w. Поэтому, построив кривые .О-раз-биения, находят такой отрезок действительной оси на плоскости w(j®), который принадлежит области устойчивости. Равенство числа отрицательных корней степени характеристического уравнения позволяет выделить зону, где точки плоскости с наибольшим числом соответствуют области устойчивости системы. Числовые значения на действительной оси в этой области определяют принятые параметры ki или Ti.
Из рис. 4.28, а можно установить, что в зоне // имеется самая большая отметка точки к+ 1, и если она равна п, то в зоне II обеспечивается устойчивость. Числовые значения по оси абсцисс для рассматриваемого параметра в области II гарантируют устойчивость работы системы. На рис. 4.28, б изображена кривая Р-разбиения с пятью зонами I—V. В зонах II и V обеспечивается условие к + 1 — п, и система устойчива. Кривая D-разбиения (рис. 4.28, в) выделяет две зоны. В зоне // будет точка с отметкой к + 1 = п. Она соответствует устойчивости системы. В заключение воспользуемся кривыми Р-разбиения, приведенными на рис. 4.28, г. При этом видно, что наибольшая отметка числа к в зоне /; при к = п зона / является областью устойчивости.
Для удобства вычислений можно брать w = 0 и находить корни оставшегося уравнения. При их числе, равном I с отрицательными действительными частями, имеем
13*
387
Рис. 4.28. Кривые D-разбиеиия по одному параметру иа пл. w для определения областей устойчивых и неустойчивых состояний систем:
а, в, г —с тремя областями; б — с пятью областями
к = /, а область устойчивости системы будет иметь отметку с точкой I + i (где i=l, 2, 3, ...), равной порядку характеристического уравнения п. Воспользуемся данным положением. Допустим, что кривая £>-разбиения, изображенная на рис. 4.28, в, построена по характеристическому уравнению вида
з4 + а^3 + а2з2 + «з5 + а4 = 0>
(4.148)
где щ, а2, аз, а*— постоянные коэффициенты.
Это нетрудно показать, если уравнение (4.148) можно переписать в виде
at = — (з4 + ajs3 + а2з2 + a3s).
(4.149)
Пусть s = /<о; тогда выражение (4.149) будет иметь вид
а4 = (а2со2 — со4) + / (а^3 — Озсо).
(4.150)
Задаваясь в уравнении (4.150) различными значениями ®, построим на рис. 4.28, в кривую £)-разбиения.
Теперь положим а4 = 0; тогда из уравнения (4.149) получим
—s (s3 + а^2 + a2s + а3) = 0, (4.151)
откуда «1 = 0. Из уравнения
з3 -|- ais2 + a2s + а3 = 0
определим
з2 = — а,; з3 = —аг-Н’Рг;
«4 = —«2 — /02-
Итак, устанавливаем, что один корень имеет нулевое значение, а в трех остальных действительные части отрицательны, т. е. I — 3. Так как в зоне II к + 1 = I + i, то
388
при i = 1 найдем «+1=4, так как порядок уравнения (4.150) четвертый. Следовательно, зона II соответствует устойчивой системе. При этом ее параметр ai изменяется в диапазоне действительных чисел, выделенных на рис. 4.28, в жирной стрелкой.
Перейдем теперь к рассмотрению САР, в которых можно выделить два параметра р, и v. Если эти параметры входят в характеристическое уравнение (4.13а) линейно, то его можно переписать в виде
pS(Z) + vQ(Z) + fl(X) = O. (4.152)
При X = j® из уравнения (4.152) получим
pS (/©) + vQ (j®) + 7? (/со) =
= и (и) + /и(®). (4.153)
Для построения кривой D-разбиения необходимо определить р и v при различных значениях ®, решая совместно уравнения
u(®) = 0; v (о) = 0. (4.154)
В результате из выражений (4.153) и (4.154) найдем два уравнения, в которых можно выделить р и v, т. е.
м(ш) = pSJw) + vQJco) + 7?i (©) = 0; ~) у(ш) = pS2(®) + vQ2(®) + 7?2(<о) = 0.)
(4.155)
Из уравнений
I -7?, (и) _ | — R2(co) |+(<о)
I + (<о)
(4.155) имеем
Q. (со) I
Qa (со) I Д1 .
Qi (со) I Д ’
<?2 (<0) I
ISi(co) —Ri(co)l
_____ I + (co) —Ra (co) I ____ Aa V IS, (co) Qi (co) I Д’
I $2 (co) Ql (co) I
(4.156)
Пользуясь соотношениями
(4.156) и изменяя ® от —оо до +°о, получим в системе координат pOv кривые D-разбиения.
Сформулируем правило штрихов
ки кривой D-разбиения, построенной относительно двух параметров.
При перемещении вдоль кривой D-разбиения от частоты со —оо до со->+оо ее следует штриховать слева кривой в тех точках, для которых Д > 0, и справа при А < 0. Отметим, что при изменении со кривая D-разбиения пробегает дважды от(о = 0досо = +оо и от со = 0до со =—оо, и ее следует выделять двойными штрихами. На рис. 4.29, а изображены две различные кривые D-разбиения, которые обозначены цифрами 1 и 2. Из рис. 4.29,а видно, что если переход через кривую 2 от точки к происходит с не-заштрихованной стороны на заштрихованную, то число корней с отрицательной действительной частью увеличивается на два и отметка точки к становится к + 2. При переходе кривой 1 из зоны с заштрихованной стороны на неза-штрихованную число корней с отрицательной действительной частью уменьшается на два и точка отмечается как к — 2.
При движении по кривой D-разбиения в плоскости двух параметров знак Д может изменяться только в бесконечности или при частотах со, которым соответствуют особые прямые [1]. В результате этого направление штриховки кривой D-разбиения меняется только в тех: точках, где кривая пересекается с особыми прямыми.
Рассмотрим особую прямую при и = 0 (рис. 4.29,6); тогда вблизи этой точки прямую штрихуют одинарной штриховкой, совпадающей с двойной штриховкой кривой D-разбиения. Особую прямую при со = = оо штрихуют таким же .образом, как и при со = 0 (рис. 4.29,в). Кроме особых прямых О) = 0 и (D = ОО, существуют особые прямые, соответствующие тем значениям ® =®, при которых одновременно удовлетворяются условия Д = 0, Д1 = 0. Такую особую прямую вблизи точки ® = й штрихуют двойной штриховкой, совпадающей с двойной
389
Рис. 4.29. Кривые Р-разбиения по двум параметрам v и ц на пл. w для определения областей устойчивых и неустойчивых состояний:
л — иллюстрирующие правило штриховки кривых; € — при наличии особой прямой, проходящей через точку <о = 0 в — при наличии особой прямой, проходящей через точку о = оо; а —при наличии особой прямой, проходящей через точку со - S, где Д = 0
штриховкой кривой D-разбиения (рис. 4.29, г). На рис. 4.29, а — г приведена разметка точек при пересечении кривых D-разбиения.
Сравнение различных методов анализа устойчивости САР рассмотрим на примере.
Пример 4.25. Допустим, что CAP дизеля [1] можно представить с помощью передаточной функции
V («) =---------------------------Г"’ <4-157)
(TlS + l)(T*s2 + T3s + 1)
тде Т2 = 0,45 с; Г, = 5 с; k2 = 25, а Tt и Й1 могут принимать различные значения в диапазоне
С помощью выражения (4.157) при принятых числовых значениях параметров составим характеристическое уравнение
(Tis + 1) (0,2025s2 + 5s + 1) + = 0,
(4.158) т. e.
(Tts + 1) (0,0408s + 1) (4,9592s + 1) +
+ *,25 = 0. (4.159)
Уравнение (4.159) при ^ = 0,0408 с и
Т3 = 4,9592 с запишем в общем виде d^Y + r,r3' + т2т'3) +
dx
+ (r, + T2 + T'3) + (1+ klk2)x = 0.
(4.160)
Введем в уравнение (4.160) новую пере-t менную т
d3x
+
1 , —; тогда получим
т^+т^+т^ d2x i (^т/т'т')2 dr2
Т1 + Т2 -|- To dx
- + (1 + Мг)х = 0,
УТХГ, .dt
0 < Ti < 20 с; 0 < *! < 40.
(4.161)
390
или
х (т) 4- ах (т) + Ьх (т) + сх (т) = 0. (4.162)
Здесь
Т^+Т^ + Т'^ а (Ш- ’
Тг + т'2+т'3 з/-----7—г 1
с = 1 4“ k\k2.
Перепишем уравнение (4.162) в виде следующей системы уравнений:
Х1(т) = х2(т); ]
х» (т) = — ах2 (т) 4-*з (т); >(4.163)
Х3 (т) — — CXi (т) — Ьх2 (т). )
Зададимся квадратичной формой
з
w (*1- х2- %з) = Е wiKxix,e wiK = wKi
К=1
(4.164)
и будем искать функцию Ляпунова в форме
з
V (хр х2, х3)= £ о/кх4хк; «/к = окГ
к=1
(4.165)
удовлетворяющей, с учетом системы уравнений (4.163), соотношению
V (х,. х2, xi) = 2W(xl, х2, хз). (4.166)
Соответствующая система для определения коэффициентов имеет вид
aii^i 1 4“ 4- a3i^i3 = Г.
а 12^1 1 4" (<2ц 4" а22) 012 4" 2232^13 4"
4" а21^22 4" <2з it>23 = 2tt> 12;
2213^1 1 4" а2зО|2 4" (22ц 4" 22зз) 0|з + 4" 2221O23 4" 2231O33 = 2to13;
2212^12 4“ a22V22 4” 22з2О23 — ^22»
2213^12 4" 2212^13 4" а23О22 4“
4- (а22 4- 2233) Огз 4" 2232O33 = 2 ау 2з;
221зС*13 4- a23V23 4” 2233O33 = 20зз,
(4.167)
где
2211 — 2113 = 2221 = 2I33 = 01 2112 = 2123 — U
2222 = — 2ZJ O32 == — Ь\ 213) = — С.
Определитель будет системы уравнений (4.167)
ТО ВС ЦИ V 211 «I 211 0 0 0 Заг гда Пу ех 2 = ю Д = 1 a2i Цз1 ООО 2 2211 + а22 а32 Л21 21з1 0 3 2223 221 1 4“22зз 0 Д21 ^31 И12 0 а22 а22 0 2213 2212 а22 а22 4" 22зз 0 0 2213 0 2*23 2Х33 = с (ab — с). (4.1( шшем функцию Ляпунова V = Д У=2Д1Г. (4.К сть W = х2, т. е. все w {к= 0 п i, fe, за исключением i = fe = 2 = 1. Имея это в виду, запишем фу> Ляпунова как 0 Х[ 2Х[Х2 2Х(Х3 х2 2х2х3 х 0 0 0 —с 0 0 0 0—-1—а — b 0—с 0 001 0 0 0 -с 10 1 0 —а —Ь 0 ООО 1 1 —а —Ь ООО 0010 58) 59) ри и <к- »
откуда
V (Хр х2, х3) = — с ^acxl+2cxlx2+bx2+xl)
илн
V (xi, х2, Хз) =
= -^-xi4-cXjX24--|-x| 4-уХз (4.170)
И
V (хр х2, х3) = (с — ab) х%. (4.171)
Условиями положительной определенности функции V по критерию Сильвестра являются ас > 0; c(ab — с) > 0, которые одновременно характеризуют отрицательную определенность W. Так как
Г1Г'4-Г^з 4'7’27’3 „
а - п
(4/г^'гз)2
а с — fetfe2 4-1, то неравенства можно переписать в виде
с > 0; ab - с > 0 (4.172)
нли
feife2 4” 1 > 0;
(г17’2л 4-7’1^ +Г^)(Г,4-Т’; 4-7-;)
7’17’27’3
- (kik2 - 1) > 0. (4.173)
391
Рнс. 4.30. Сравнение областей устойчивых и неустойчивых состояний по параметрам Г1 и fei, полученных на основе различных методов
Подставив в неравенство (4.173) числовые значения, найдем уравнения границы областей устойчивых и неустойчивых состояний
1 0 2
- -5Е-; = 4,9383 + 0,98777! + -^=-.
2D 1 ]
(4.174)
По формуле (4.174) определим числовые значения, характеризующие границы устойчивости по Ляпунову при различных kt и Гь
условия устойчивости Льенара — Шипара будут
V(,3) = a>0; )
„го ? (4Л75>
= с (аЬ — с) > 0. J
Из неравенств (4.175) видно, что последние аналогичны условиям устойчивости по первому методу Ляпунова. Поэтому, пользуясь этим критерием, получим полное совпадение с кривой 1, которая ранее была построена на рис. 4.30.
Исследуя устойчивость системы с помощью построения частотных характеристик, из выражения (4.157) найдем
1Г(/®) =
£125
(Tijta + 1) (0,0408/ш + 1) (4,9592/ш + 1) ‘
(4.176)
Задаваясь значениями Ti и ki, построим семейства логарифмических амплитудных и фазовых частотных характеристик. Они показаны на рис. 4.31, а прн 7\ = 0,1 с, ki = = 7,04; на рис. 4.31,6 при Г1 = 0,3 с,
= 5,9; на рис. 4.31, в прн Tt — 1 с, fei = 6,13 и на рис. 4.31,а прн 71 = 3 с, fei=7,97. Из рнс. 4.31,а — г видно, что системы в замкнутом состоянии при этих параметрах находятся на грани устойчивости, так как их запасы устойчивости по фазе Уф = 0°. По числовым значениям Г1 н £i строим на рис. 4.30 кривую 1, которая совпадает с ранее полученной. Следовательно, частотный графоаналитический метод анализа устойчивости также позволяет выделять области устойчивых и неустойчи-
Ti, с 0,05 0,1 0,2 0,3 0,450 1,0 2,0 3,0 5,0 10,0
£i 8,9877 7,0371 6,1358 5,9013 5,8272 6,1260 7,0137 7,9681 9,9168 14,8353
По этим числовым данным строим границу областей устойчивости (кривая 1, рис. 4.30). Для определения минимального значения Timin воспользуемся соотношением
= 0,9877
0,2 А
0,
откуда Timin = 0,450 с.
Кривая 1 имеет две асимптоты, определяемые уравнениями Т1 = 0 — ось ординат и £i=4,9383-|- 0,9877Ti — наклонная асимптота (прямая 2). Асимптоты показаны штриховыми линиями. Область устойчивости системы выделена иа рис. 4.30 штриховкой.
Воспользуемся для построения границ областей устойчивости критерием Льенара — Шипара. Если характеристическое уравнение (4.162) имеет 3-й порядок, то
вых состояний замкнутой системы. Данный метод рекомендуется использовать при относительно высоких порядках передаточных функций разомкнутых систем.
В заключение рассмотрим возможности метода D-разбиення при исследовании устойчивости систем. Для этого воспользуемся следующей формой представления дифференциального уравнения (4.161):
До (Г]) к3 + at (Г,) Х2+ а2 (Гi) Х + a3(£]) =0,
(4.177)
«о(Г1) = (Г2^)Г1:
«1(ЛК^з + (Г2 + гз)Г1; a2 (^i) — ^з + 72 + 71; “з(£1)г=1
392
Рис. 4.31. Логарифмические амплитудные и фазовые частотные характеристики, построенные с помощью выражения (4.176) при;
a) Ti=o,l с, fei—7,04; б) Ti=0,3 с, ft; =5,9; в) Л-1 с. Л,=6,13; г) Г,=3с, ftt=7,97
Рис. 4.32. Кривые D-разбиения для выделения областей устойчивости системы в плоскости параметров Ti, fei
Подставив в уравнение (4.177) числовые значения, получим
О.гогбТ^3 + 0.2025Л2 + 5Г]Л2 + 5Л +
+ ЛЛ +25£, + 1 =0. (4.178)
При л = /а» из уравнения (4.178) найдем и (<в) = — 5(о2Т 1 +
+ 25k i + 1 — 0,2025<о2 = 0;
v (о») = (о(1 -0,2025а»2) X f (4Л79) X Л+ 5<о=0.
Из системы уравнений (4.179) определим Si (а») = —5ш2; S2 (<о) = о» (1 — 0,2025а»2); Qi = 25; Q2 (<о) = 0; /?, = !- 0,2025а»2;
/?2 = 5(0
и вычислим следующие определители:
Д = -25<о(1 -0,2025а»2);
Д] = 125а>;
Д2 = 25а»3 + а» (1 — 0,2025а»2)2, откуда
т Д. _ 5
1 Д 1 - 0,202Е»а>2 ’
ь Дг
fe, __
— 25а>2 —(1 —0,2025а»2)2
в 25(1 — 0,2025а»2)
(4.180)
Давая о» различные значения от 0 до оо, построим по формулам (4.180) кривые D-разбиеиия (рис. 4.32). Определитель Д = = 0 при о» = 0 и о» = 2,222. Однако в
последнем случае Д1 н Д2 не обращаются в нуль. Поэтому имеются две особые прямые: а» = 0 и о» = оо.
Приравняв к нулю свободный член я3(Л1) характеристического уравнения (4.177), получим 1 + kikt = 0, где ki = —1/25 = = —0,04, т. е. уравнение первой особой прямой. Приравняв До (Г») = 0, найдем уравнение второй особой прямой Г» = 0.
Воспользуемся правилом штриховки, двигаясь по кривой D-разбиения от точки о>= = 0 к точке о» = 2,222, и нанесем двойную штриховку (рис. 4.32). Затем в соответствии с ранее сформулированными условиями выполним одинарную штриховку особых прямых (рис. 4.32).
Для параметров Г» = —0,04 с и Л» = 1 из уравнения (4.178) имеем один нулевой корень и к — 1 = I отрицательных корней. На рис. 4.32 это показано точкой Г». Затем по правилу переходов кривых D-разбиения и особых прямых найдем точки Г2 — Те, каждой из которых соответствует свое значение /=«+!—/ (/= 1, 2, 3). Наибольшую отметку имеют области с I — к = = 3. Так как порядок уравнения (4.178) равен трем, то зоны с / = 3 соответствуют областям устойчивости системы.
Кривые D-разбнения, построенные в 1-м квадранте на рис. 4.32, полностью совпадают с кривыми, разделяющими области устойчивых и неустойчивых состояний (рис. 4.30). Следовательно, все четыре рассмотренные нами метода выделения областей устойчивости системы в зависимости от изменения параметров дают одинаковые результаты.
В заключение отметим, что метод D-разбнення позволяет исследовать влияние как положительных, так и отрицательных параметров иа области устойчивых и неустойчивых состояний, что в ряде практических задач представляет определенный интерес.
Для выделения областей устойчивости в плоскости параметров можно применять ЭВМ [28]. При этом необходимо выбрать диапазон изменения параметров fcimin
^Imax И 7*imin Г, sc Ti max И принять числовые значения прира-щений А7\, AZ>i. В этом случае вычислительную процедуру можно реализовать следующим образом. Сначала выбираем Timin и Ziimin и по одному из рассмотренных в гл. 4 алгоритмов (первый метод Ляпунова, Гурвица, Рауса, Льена-ра — Шипара, Р-разбиения и т. д.) определим, устойчива или неустойчива система при этих параметрах. Затем увеличим на A6lt сохра’
394
няя остальные параметры системы неизменными, и проанализируем снова состояние устойчивости в точке k\ + Afei и т. д. до тех пор, ПОКа Не ДОЙДеМ ДО ТОЧКИ Л1тах-
На рис. 4.33 показано несколько случаев перемещения точек по прямым, параллельным осям координат, с изменением числовых значений k\ и Т\.
Первый случай. Примем за начальную точку Т11 и будем перемещать ее слева направо по горизонтали с приращением Д£ь Приходим последовательно в точки Т12, Т13 и т. д. до Т17. В рассмотренном случае все точки первой строчки не пересекают кривую выделения областей устойчивости в плоскости параметров системы и не принадлежат области устойчивости.
Второй случай. Выбрав приращение ATi, из точки Т11 переместимся в точку Т21. Продолжая движение по второй строчке, из Т21 попадаем в Т22. Такая последовательность действий будет продолжаться до тех пор, пока не достигнем Т23. В этом случае происходит пересечение кривой, разделяющей неустойчивую и устойчивую области. На рис. 4.33 показано, что точ-
Рис. 4.33. Формирование процедуры определения областей устойчивых и неустойчивых состояний с. помощью ЭВМ
ка Т22 принадлежит области неустойчивости, а Т23 — области устойчивости. На основании этих данных выдается команда на печать точки Т23. После этого происходит переход на третью строчку и т. д.
Третий случай. Проверим точку ТЗЗ на устойчивость. Если она соответствует области устойчивости, то совершаем перемещение налево, и наоборот. В случае нахождения точки в области устойчивости движение выполняется против часовой стрелки, а в случае расположения точки в области неустойчивости — по часовой стрелке (рис. 4.33).
Четвертый случай. После третьего случая перемещение производится не по развертке, а вокруг границы области устойчивости. ЭВМ автоматически прекращает обход, когда все граничные точки определены.
Для нахождения областей устойчивости можно составить алгоритм, а затем и рабочую программу на языке ПЛ/1. При этом необходимо указать, что для устойчивой системы идентификатору К1 присваивается значение 4-1, а неустойчивой — 1. При увеличении ki на Д&1 система вновь проверяется на устойчивость (идентификаторы К2 = = 1 для устойчивой системы; К2 = =—1 для неустойчивой). С помощью анализа знака произведения KI ХК2 проверяем, пересечена ли граница области устойчивости. Если эта граница пересечена, то идентификатор К1 сохраняет свое первоначальное значение, и т. д.
После того как найдена первая точка области устойчивости или неустойчивости (значения KI X ХК2<0), текущие значения параметров k\ и Т\ фиксируются, а идентификатору К1 приеваивается значение ±1 в зависимости от того, устойчива или неустойчива система. Обход границы области устойчивости осуществляем так, чтобы область устойчивости всегда была расположена справа. При этом параметр Т\ сначала увеличивается
395
от Timin до Tlmax с шагом ДТЬ а затем уменьшается от Т1тах до Timin. Это позволяет выделить замкнутые ограниченные области устойчивости или неустойчивости.
Точность вычисления границы областей устойчивости равна \k\. Ее можно повысить без существенного увеличения вычислительных затрат, задавшись величиной максимальной погрешности Е*, при помощи следующего алгоритма: при фиксированном 7\ вычисленному значению k\ дается положительное или отрицательное приращение Afei/2, смещающее точку на пло
скости параметров в сторону границы области устойчивости. Если граница пересечена, то вновь полученному значению параметра ki дается приращение А&1/4, но противоположного знака, а если нет — то знак приращения остается без изменений. Процесс продолжается т раз до тех пор, пока не будет выполняться условие A^i/2m < Е*.
Пользуясь ранее приведенной программой для метода Рауса (программа № 16 RAUSS) и указанным алгоритмом, составим программу № 18 выделения области устойчивости.
ПРОГРАММА № 18 STAB
Вычисление границы устойчивости линейной динамической системы на плоскости параметров.
Обращение к программе
STAB (N,KN,KK,DK,EPSK,QH,QK,DQ)
Входные параметры
N — порядок системы;
KN — минимальное значение параметра k, дБ;
КК — максимальное значение параметра k, дБ;
DK—шаг вычисления границы области устойчивости по параметру k, дБ;
EPSK — максимальная погрешность определения границы области устойчивости по параметру k, дБ;
QH — минимальное значение параметра Г;
QK — максимальное значение параметра Т;
DQ — шаг вычисления границы области устойчивости по параметру Т.
STAB: PROC (N,KH,KK,DK,EPSK,QH,QK,DQ);
DCL (N, I, NQ, NK, INF, SIG, KL K2, КЗ) BIN FIXED (15), (КН, KK, QH, QK, DQ, DK, EPSK, KHR, QHR, DQR, DKR,' DKR1, A(N-H), Q,K,KS) DEC FLOAT (12); NQ = FLOOR ((QK — QH)/DQ + 0.5);
NK = FLOOR ((KK-KH)/DK +0.5); BEGIN; DCL (MMQ (NQ + 1,2), MMK(NQ +1,4)) DEC FLOAT (12); INF = 1; QHR = QH; DQR = DQ; KHR = KH; DKR, DKR1 — DK; MMK = 0;
Ml: K= 10* * (KHR/20); DO 1=1 TO NQ + 1; Q = QHR+(I—1) » DQR; KS=K;
M8: CALL XAPAKT (Q,K,A); CALL RAUSS (N,A,K2);
IF I=1&K=KS THEN DO; PUT SKIP LIST (’В ТОЧКЕ T = ’,Q,’ K = ’,K);
IF K2 > 0 THEN PUT SKIP LIST (’СИСТЕМА УСТОЙЧИВА.’);
ELSE PUT SKIP LIST (’СИСТЕМА НЕУСТОЙЧИВА.’); END;
IF (K — KS) * (1.5 — INF) > 0 THEN GOTO M9; IF I>1 THEN DO;
IF K3*K2<0 THEN DKR1 = -DKR; ELSE DKR1 = DKR; GO TO MK; END; ELSE IF K = KS THEN DO; K3 = K2; GO TO MK; END;
M9: IF K3*K2<0 THEN DO; MMQ (I,INF) = Q; MMK (I,INF) = KS; MMK (1,2-f-INF) = 1; GO TO MQ; END;
MK: KS=K; К = К * 10 * * (DKR 1/20); IF К > 10* * (КК/20)!
К < 10* * (KH/20) THEN DO; К = 10* * (KHR/20); GO TO MQ; END; GO TO M8;
MQ: END; IF INF > 1 THEN GO TO М2; QHR =QK; DQR = —DQ; KHR = KK; DKR, DKR1 = - DK; INF = 2; GO TO Ml;
М2: /* УТОЧНЕНИЕ ГРАНИЦЫ*/
PUT SKIP LIST (’ГРАНИЦА УСТОЙЧИВОСТИ’); INF = 1;
М3: DO 1 = 1 TONQ + 1; SIG = 1;-4F MMK (I,2+INF)<0.S THEN GO TO M5; Q = MMQ(I,INF); К = MMK (I,INF); DKR = DK; IF INF > 1 THEN IF 20* LOG10(K/MMK(NQ+2-I,l))<= ABS (DK) THEN GOTOM5; CALL XAPAKT(Q,K,A); CALL RAUSS (N.A.Kl);
396
М4: DKR = DKR/2; DKR 1 = SIG * DKR; К = К * 10 * * (DKR1/20);
CALL XAPAKT (Q,K,A); CALL RAUSS (N.A.K2);
IF KI * K2 < 0 THEN IF ABS (DKR) < EPSK THEN DO;
PUT SKIP LIST (’T =’, Q, ’K =’,K); GO TO M5; END; ELSE DO; SIG = -1;
GO TO M4; END; ELSE DO; SIG=1; GO TO M4; END;
M5: END; /«УТОЧНЕНИЕ ВТОРОЙ ГРАНИЦЫ «/IF INF>1 THEN GO TO M6;
DK = -DK; INF = 2; GO TO М3;
M6: /* РАСЧЕТ ОКОНЧЕН */ END;
END STAB;
Примечание. Аналитическая зависимость коэффициентов характеристического уравнения системы от параметров Т и k должна быть задана в подпрограмме XAPAKT, которая для каждого примера пишется заново.
Обращение к подпрограмме
XAPAKT (Q,K,A)
Входные параметры
Q — значение параметра Т; К — значение параметра k.
Выходные параметры
А — вектор коэффициентов характеристического уравнения системы aQKn + + ... + ап_1Л + ап = 0
для заданных значений параметров Т и k.
Подпрограмма XAPAKT для примера 4.26 приведена ниже.
Пример 4.26. Построить области устойчивости и неустойчивости замкнутой динамической системы, передаточная функция которой в разомкнутом состоянии имеет вид
W (S\ = K 1^7’sS +
Л (Tjs+ l)(T2s+ l)(T3s+ 1) ’
где Л == 1 с; Т2 = 0,2 с; Т3 = 0,1 с; Г4 = = 0,01 с; Ts = 0,005 -г- 0,04 с; К = 10 4-90 дБ.
Характеристическое уравнение замкнутой системы
0,02s3 + (0,32 + 0,01 КТ5) s2 +
+ [l,3+K(T5 + 0,01)]s + K+l=0
Рис. 4.34. Определение областей устойчивых и неустойчивых состояний для системы (пример 4.26) с помощью программы № 19 STAB и критерия Рауса
записывается в подпрограмме XAPAKT в виде аналитических зависимостей коэффициентов от параметров Л и К:
XAPAKT: PROC (Q, К, А);
DCL(Q, К, А (*)) DEC FLOAT (12);
А(1)=0, 02;
А (2) = 0, 32 + 0, 01 * Q * К;
А (3) = 1,3 + (0, 01 + Q) * К;
А(4) = К + 1;
END XAPAKT
Результаты работы программы STAB приведены на рнс. 4.34, где изображены области устойчивых и неустойчивых состояний замкнутой динамической системы для примера 4.26.
9‘ V( ГОПЧМВ0СТН
Н ЕСТ АН и и н А!’ Я Ы *• J1 и И Е И Я bi X
С И СТ £ М, ОСНОВАННЫЙ
РЯДАХ ИСЙ1НАНА
И ИНТЕГЕАЛЫЬ/Х УНАВНГПИЯХ HcmutpPA ;-го года
При исследовании устойчивости нестационарных линейных систем необходимо учитывать влияние изменения параметров во времени, так как для одних значений параметров автоматическая система в замкнутом состоянии устойчива, а для других — неустойчива. Анализ
397
устойчивости таких систем может проводиться несколькими способами.
Первый способ
Нахождение передаточных функций в виде ряда в форме Заде [см. выражение (1.165)], или приведение нестационарных дифференциальных уравнений типа (1.200) к нормальной форме с коэффициентами k0(t), ..., ki(t) [см.
выражение (1.201)]. Однако оба эти способа применяют лишь к одномерным системам, в которых, кроме того, наблюдается малый диапазон изменения параметров.
Второй способ
Отыскание базисных функций в виде бесконечных полиномов при определении выходного сигнала по методу вариаций постоянных. Таким образом, находят базисные функции для уравнений Бесселя, Лягерра, Лежандра и некоторых других. Второй способ пригоден для одномерных систем. Следует также отметить, что определение базисных функций большинства нестационарных уравнений представляет значительные трудности.
Третий способ
Основан на итеративном методе интегрирования, приводящий к ма-трицианту в виде ряда Неймана [39] или к интегральному уравнению Вольтерра 1-го рода [24]. Третий способ применяют и к многомерным САР, описываемым уравнениями
y(t) = A(t)y(t) + B(t)g(t), ' у (to) = Уо;
x(t) — C(t)y(t).
(4.181)
В этом случае условие устойчивости можно записать в виде
[t -|
*(0 — Q (t, т) g(т) dx I = 0, л J
где О(/, т) = С(0Ф(Л т) В (^ — импульсная переходная матрица.
Рассмотрим применение данной методики, пользуясь уравнением dnx , dn~lx , -^г + «1(0^тт+...
•••+«„_.(/) ^ + an(t)x(t) = kg(t).
(4.182)
Перепишем уравнение (4.182) в виде системы дифференциальных уравнений 1-го порядка в виде
x(t) = A(t)x(t) + R(t), (4.183)
где
_ kg (t) _
Найдем приближенное решение уравнений (4.183), используя ма-трициант соответствующей однородной системы
x = A(t)x(t). (4.184)
Матрициант представим в виде ряда Неймана
оо t
QU^) = 7+£ j
to
T1
X j A (r2) dx2 ..
*0
TZ-1
$ A (xt) dxt, (4.185)
398
который сходится абсолютно и равномерно на отрезке |70, /] при непрерывных функциях матрицы А(0.
Решение неоднородной системы (4.183) будет
= (4.186)
где #(/)—неизвестная вектор-функция.
Подставляя выражение (4.186) в систему (4.183), получим
AQt(^)e- + Ot(A)^ =
= AQ5o (A)fr + R, откуда
*=[^о(А)]-1Я. (4.187)
Интегрируя уравнение (4.187), найдем t
«(0=5 [0t(4)]~**W dr + Cv
(4.188)
Здесь Ci — произвольная постоянная.
Подставляя выражение (4.188) в уравнение (4.186), получим
t
ж(О=«'о(Л) $[оил)]_,х
*0
XJK^dT + OU^Cj. (4.189)
При t = to имеем x(Iq) — Сг, поэтому формула (4.189) примет вид
х (о=(А) а0> +
t 1
+ j[Qt(<‘ (4.190)
to '
Откуда следует, что, зная матри-циант для однородной системы дифференциальных уравнений, можно найти решение для неоднородной системы в форме (4.190) при любом столбце R(t). Данное решение удовлетворяет начальному условию х(/о) = *о-
Пользуясь предложенной методикой, определим передаточную функ
цию для линейной нестационарной системы, описываемой дифференциальным уравнением 3-го порядка.
Пример 4.27. Нестационарную систему представим в виде дифференциального уравнения
d3x(t) , _ d2x(t) , ~ dx(t) , ~dP~ + a'~di^~+ a2~di~ +
+ a3(t — t0)3 x (i) = g (t), (4.191)
где g(t)—заданная непрерывная функция на отрезке [/0, /], x(ta), x(t0) н x(tQ)—начальные условия.
Воспользуемся заменой переменных в уравнении (4.191)
x(t) = xt(f); х (/) = х2 (/); х (0 — х3 (t); тогда получим систему трех дифференциальных уравнений 1-го порядка вида (4.183), где
[Xi (f) -I Г Xi (0 -
Ха (О I; х (О — I х2 (/) ;
х3 (О J *- х3 (О -I
(4.192)
° 1
1 .
Для определения передаточной функции рассмотрим отработку системой начальных условий
г Хо -I
х(/о) = | О I, где Xi (io) = x (<о) = Хо.
L о J
Допустим, что вектор функции R(t) = 0. В этом случае формула (4.190) может быть записана следующим образом:
x(/) = ftJo(A)x(/o). (4.193)
Внося постоянный вектор х(/0) в подынтегральное выражение в формуле для мат-рициаита (4.190), преобразуем соотношение (4.193) к виду
ОО
х (о = У, (о, 1=0
(4.194)
где х0(/) = х(/0)
и t Ti
rz(0= 5 A(Ti)dT! j A(T2)dT2... to io
to
399
Согласно выражению (4.194) для рассматриваемой системы
t
Г (0=^4 (г,) х (t0) dxi = io
О
О — а3х3ха
х — t — t0.
Используя выражение для r\(t), определим значение г2(/) по формуле
t
г2 (0 = j А (х) ti (т) dx =
to
Г ° -1
т5
= -азТ^Ха
т5
La*a3 jTs Хо J
Дальнейший расчет составляющих х,(т) удобно выполнять по рекуррентному соотношению
А (т) г. (т) dx, i = О, 1, 2, ...
(4.195)
Ограничимся вычислением семи составляющих переходного процесса. Подставляя значения xt(t)......x7(t) в соотношение
(4.194), получим решение x(t) в виде ряда Неймана
{т® т7
-gj--“yj—к
+ (“1 - аз) -jf + (2а1а2 - + а2 -
-з^2+ 4) 4 4
(4.196)*
Передаточную функцию системы вычислим, применяя прямое преобразование Лапласа к соотношению (4.196), т. е.
X (s) — -Д- — 6хоа3 --------at -g- +
+ (а1 - а2) 4" + (2а1а2 “ а1 +
+ а2-3^а2 + а?) (4.197)
* Построение переходных процессов по формулам, аналогичным (4.196), рассмотрено в гл. 5.
Для передаточной функции системы Ф(«) запишем следующее соотношение:
ф<”-(Х<”~г)тгЬг ,4IM, где
/?(«) = --^2-
После подстановки /?(s) и X(s) в выражение (4.198) получим
ф(5)=ТГ “ fl>7r + (а1“а2)4" +
+ (2flifl2 — а3 + а2 — За|а2 + а|) — + ...
(4.199)
Для исследования устойчивости нестационарной системы с помощью ряда Неймана найдем передаточную функцию разомкнутой системы
U7(s) = O(s)/[l-Ф(«)]. (4.200)
Подставляя в выражение (4.200) значение Ф(«) в виде ряда (4.199) и ограничивая число членов шестым порядком в разложении по 1/s, получим приближенное значение для передаточной функции разомкнутой системы
s3 — a.s2 + fa? — a2) s 4-W <s> « -6--TJ--------------------• • •
s° — s3 + a{s — faj — a2j s —
4- (2a,a2 — a3 + a2 — 3a2a2 a*)
— (2a,a2 — a3 + a2 — 3afa2 + af)
(4.201)
Из выражения (4.201) следует, что коэффициент аз не оказывает влияния на передаточную функцию IF(s), так как ои появляется лишь при учете членов разложения в формуле (4.199) выше 7-го порядка.
Исследуем устойчивость нестационарной системы, используя передаточную функцию (4.201). На рис. 4.35 изображены частотные характеристики разомкнутой нестационарной системы для значений коэффициентов at =—0,01; a2 = —0,1 (кривая 1) и а, = — 0,01; а2 = 0,1 (кривая 2). В обоих случаях годографы начинаются из точки (—1, /0). Это объясняется тем, что в передаточной функции, записанной в форме (4.199), Ф(«) -’-оо при s->0. Передаточная функция разомкнутой системы имеет один полюс в правой полуплоскости (mP = 1); поэтому для устойчивости замкнутой системы необходимо иметь одни положительный полупериод отрезка [—оо; —1] годографом W(ja). Это выполняется лишь для кривой 1. Таким образом, кривая 1 соответствует устойчивой нестационарной системе, а кривая 2 — неустойчивой.
400
Рис. 4.35. Частотные характеристики разомкнутой нестационарной САР (годограф), полученные с помощью рядов Неймана
Рассмотрим дифференциальное уравнение (4.182), предполагая, что ап #= 0, преобразуя его к виду
=' (4.202)
где
а . (/) -----
Ci(0 = -~-(ц , « = 1,п; Оо(0=1;
Для его решения представим функцию x(t) в виде разложения в ряд Вольтерра
х(О=22 */(*„ .... Q (4.203) i-1 \
Подставим предполагаемое решение (4.203) в исходное дифференциальное уравнение (4.202) и применим к нему многомерное преобразование Лапласа. Тогда получим
22 ($1> s2> • • •, $к) + 22 С/ (S[) X
к-1 i-1
X 22 (*2 + s3 + ... + sk/ X к-1
X^K-lfe, S3........SK) = B(Si)G(S2).
(4.204)
Приравнивая члены при одинаковых степенях переменных 5, получим рекуррентное решение в виде
Х2 (sb s2) — В (s0 G (s2);
XK(slt s2, ..., sK) = — £ Ci (sj X i=l '
X ($2 + s3 + • + SK)‘ X I
X хк_, (s2, s3.....sK), к = 3, 4, ... J
(4.205)
Для сокращения числа переменных используем оператор объединения
7?i[XK(si, s2, ..., sK)] =
==^k(S1> S2......SK-1) =
= ф XK (sb s2, • • •, sk-i — u, u) du,
(4.206)
где интегрирование будем проводить по соответствующему контуру.
Для оператора объединения переменных справедливы следующие соотношения:
XK(s1) = 7?K_1[XK(s1, s2, ..., sK)j —
= —RK-i £ 22 Ci (S[)(s2 + s3 + ...
• • • + sK)f XK_, (s2, S3, ..., sK)J = = — Ri 122 Ci (si) rk_2 [(s2 + s3 + ...
• • • + Sk)" ^k-1 (s2> 53.sk)]| =
— —Ri Г 22 C{ (si) 5гХк_1 (s2)l, Li-l J
K = 3, 4, ... (4.207)
Аналогичным образом запишем X2(si) в виде
Х2(^)==Я1[В(*1)С(*2)]. (4.208)
На основании выражения (4.207) для XK(si), к = 3, 4, ... справедливы рекуррентные соотношения %к (si) — —Ri Ct (Si) s2XK_! (s2)J .
(4.209)
401
Удобно ввести еще один оператор
Qi K(S1)] = XK(SZ+1). (4.210)
С его использованием соотношение (4.209) принимает вид
Ш—^Х
х[£с< (*!)*&> Пк-! (*!)]]. (4.211)
Li=i J
На основании выражения (4.203) для X(si) справедливо следующее представление в виде ряда
оо
Х(^)=ЕХк(Д1), (4.212)
/== 1
где Xi(si) = 0 для рассматриваемого нами случая.
В результате подстановки значений Хк($1) в форме (4.211) в выражение (4.212) и последующего суммирования получим
------рг!--------=— х
1 +*1 [Е C/(Ms2j <21
X Ri [В (Sj) G (s2)], (4.213)
где R\ и Qi — коммутирующие операторы объединения переменных.
Таким образом, выражение (4.213) представляет собой общее решение исходного уравнения с переменными коэффициентами. Оно является аналогом передаточной функции стационарных линейных систем.
Пример 4.28. Для нестационарной системы, которая в разомкнутом виде задается дифференциальным уравнением’
*Ю + С1-^ + С2-^ + Сз(04£==£(0.
(4.214)
где Ci = l, с2 = 0,1, с3 = определить эквивалентную передаточную функцию и исследовать устойчивость замкнутой системы.
Для определения передаточной функции рассмотрим решение уравнения (4.214) при g(t), являющейся единичной ступенчатой функцией.
Решение будем искать в форме, задаваемой соотношением (4.212); тогда
Xi(s.) = /?i[G(s2)] = 1/s,. (4.215)
Рис. 4.36. Частотная характеристика разомкнутой нестационарной САР (годограф), полученная на основе интегральных уравнений Вольтерра 1-го рода
Остальные составляющие определим по формуле
XK(Si) = -/?,
Г Е ^i (Sl) S2^K-l (S2) J ’
к = 2, 3, 4, ...
(4.216)
Найдем, используя выражение (4.126), в явном виде значения XK(si), к = 2, 3, ... Для %2(si) можно записать следующее соотношение:
= -^[Е ci W5’"1 (4-217>
где 9? и S’-1—соответственно' Операции прямого и обратного преобразований Лапласа. Подставив в выражение (4.217) значения d(/), i = 1, 2, 3, получим
Х2 (s.) == - {с, + c2s + 2 [/S’"1 [s2]]}.
Воспользовавшись свойством дифференцирования изображения, получим для X2(sJ следующее выражение:
( ds2)
Х2 (Si) = — 1 Ci -|- C2S -|- | —
= — Cl — (c2 + 2) s.
Аналогичным образом вычислим X3 (sO, X4(Si), ...
*3 (si) = *1 [E Ci (si) s2 (^ +
[3
Ec/ (OS-’X
i-i
X[c1s< + (c2 + 2)s<+1]] =
402
= cjsj + ci (2c2 + 5) s, + + (c2 + 6c2 + 8) sf.
После ряда преобразований найдем для X4(st) следующее соотношение:
^4 (Sl) = ~ clsl ~ С1 РС2 — 9) si ~
- с{ (Зс2 + 18с2 + 13) sf - (с2 + + 12с2 + 44с2 + 48) s’.
Ограничимся вычислением четырех составляющих переходного процесса X(si). Тогда можно записать решение уравнения (4.214) в виде
х <si)= ТГ ” С1 + (С> “ с2 ~ 2) S‘ “
— С] (с2 — 2с2 — б) s2 -|- (С2 + 6с2 + + 8 — 3cjc2 — 9с2) Sj — с, (Зс2 + + 21с2 + 33) sf - (с| + 12с% + 44с2 + 48)Х Х«?+... (4.218)
Искомую передаточную функцию 1Г(з) найдем, умножая X(st) на и полагая Si = s, т. е.
ft? (s) = 1 — CjS + (с2 — с2 — 2) з2 —
— с, (с2 — 2с2 — б) s3 + (с2 + 6с2 +
+ 8 — 3cfc2 — 9с2) з4 — С! (Зс2 +
+ 21 с2 + ЗЗ) s3 — (с2 + 12с2 +
+ 44с2 + 48) s6 + . . . (4.219)
Подставляя в выражение (4.219) s = /®, получим частотную характеристику разомкнутой системы (кривая 1, рис. 4.36). При построении W(/со) было принято с4 = 1, с2 = 0,1. Из рис. 4.36 видно, что исследуемая система будет устойчивой в замкнутом состоянии. Для сравнения на рис. 4.36 по--казан годограф (кривая 2) В7(/<о) для стационарной системы, когда Сз (/) = const.
Глава 5
ИССЛЕДОВАНИЕ КАЧЕСТВА НЕПРЕРЫВНЫХ
И ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ
ЛВТОМАТИ ЧЕСКОГО РЕГУЛ И РОВАН ИЯ
Оценку правильности .выбора структуры и параметров спроектированной линейной системы можно проводить путем сравнения вычисленных показателей качества (гл. 5) и точности (гл. 6) процессов регулирования, полученных ручными или автоматизированными методами, с аналогичными данными технических условий. Если определенные показатели качества полностью удовлетворяют заданным, то улучшение показателей качества, как правило, приводит к снижению точности системы. Поэтому при проектировании приходится прибегать к компромиссным решениям, что намного увеличивает затраты труда проектировщика при исследовании системы.
С целью сократить затраты времени следует рекомендовать прибегать к косвенным методам таких показателей (интегральные оценки, корневой годограф), позволяющим
оценивать влияние изменения параметров замкнутой системы на ее показатели качества. Однако для окончательного решения правильности выбора параметров системы приходится применять прямые методы, связанные с построением переходных процессов.
Характер протекания переходного процесса зависит не только от параметров замкнутой системы, но и от типа управляющего g(t) и возмущающего f(t) воздействий, а также ненулевых начальных условий: х(О)=хо; x(0)=Xi;
... ; х(я~1)(0) = хге-1. Имея это в виду, для регулируемой переменной x(t) с помощью преобразования Лапласа для линейной системы можно записать в общем виде зависимость
' 1 + W (s) Г W ' 1 + W(s) ' [0,lf
403
где £) (s) = 1 + IT (s) = sn + ajs"-1 + + а2$я-2 + ... + an_is 4- an — характеристическое уравнение замкнутой системы.
Введем в зависимость (5.1) следующие уравнения:
Мя ($) = XoS"-1 + Ui + OiXo) sn~2 + • • • • • + (*л-2 + «Л-з + • • • + аге-зх1 + + ап-2хо) s + + аА-г + • • •
... + an^2xi + are-i*o) — относительно ненулевых начальных условий, ИЛИ Л1н(5)=&о^т+^15'”~1 + ^2«'П“2+ • • • • • • Мв($)=СоЗГ+с1$г“14-
4- c2sr~2 + ... 4- cr_ts + cr —- относительно внешних возмущений.
Тогда из зависимости (5.1) получим
x<s)=W GM+JW-f<s)+ + (5.2)
Характеристическое уравнение D(s) имеет три типа корней: действительные (некратные корни) Alt Л2.....Zs; комплексно-сопряженные
Л/ = а<4-/Р,; A,i+1 = az—jpi', . . .;
= ^ft+1 = aft —/0*; кратные
Р/ р/
Л/'....Л/ (здесь ру — кратность
j-ro корня).
Уравнение (5.2) в зависимости от требований проектирования можно разбить на три части: при /(/) =0 и нулевых начальных условиях
J>(s)=4SrG(s); <5-3)
и \Ъ)
при g(t) = 0 и нулевых начальных условиях
x^ = -^rF^’ <5-4)
при g(/) = 0, /(0 — 0 й ненулевых начальных условиях
<5-5)
\*J
Для любой формы представления уравнений (5.3)—(5.5) можно определять показатели качества САР и оценивать спроектированную систему. Если же требуется получить переходный процесс системы
при действии g(0, f(t), ненулевых начальных условий, то это можно сделать, суммируя отдельные составляющие *1(0, Хг(0 и х3(0, так как система является линейной и для нее справедлив принцип суперпозиции.
Для построения переходных процессов в линейных стационарных системах, описываемых уравнения ми в векторно-матричной форме, используют вычислительные процедуры, основанные на определении переходной матрицы. Разработанные методы вычисления переходных матриц стационарных систем достаточно просты и изложены в гл. 3. В линейных нестационарных системах построение переходных процессов с помощью переходных матриц приводит к значительным трудностям, связанным с появлением бесконечных рядов Неймана или Вольтерра. При решении некоторых задач число членов этих рядов достаточно велико, что требует больших затрат времени на ЭВМ. Здесь же возникают вопросы сходимости и точности решений.
Существует много различных показателей качества систем. На практике же пользуются лишь основными показателями. К ним обычно относят: хт — максимальное отклонение регулируемой переменной-, от — значение максимума перерегулирования в %; t? — время протекания переходного процесса-, tm — время наступления 1-го максимума-, N — число колебаний-,
— максимальную скорость отработки регулируемой переменной.
В зависимости от структуры САР и ее параметров в ней могут возникать различные виды переходных процессов: колебательный с М-колебаниями; колебательный с одним колебанием; монотонный. Виды переходных процессов определяются расположением нулей и полюсов передаточной функции замкнутой системы на плоскости X.
404
При таком подходе целесообразно рассматривать только влияние доминирующих корней, т. е. расположенных близко к мнимой оси плоскости X.
* ИН i И'РЛЛЬНШ «НМ iiMi
наш s: i нл
Интегральные оценки качества являются обобщенными показателями, позволяющими по переходной динамической составляющей ошибки системы исследовать характер протекдния переходного процесса (степень его колебательности, коэффициент затухания, оптимальные параметры). Для их определения пользуются следующими интегральными оценками [14, 35]:
оо
70= \e2(t)df, О
(5.6)*
оо
Л = 5р(О + т?(^-)2]л; (5.7) О оо
о
+ 1(т)’]* <5-8»
оо
(5.9)
Для аналитического вычисления интегралов (5.6)—(5.9) перейдем
* Интегральная оценка качества /0 является относительной мерой оценки быстродействия переходных процессов. Вычисленное одно числовое значение /0 для системы не позволяет судить о ее быстродействии. Если же при выбранных параметрах систем будут вычислены такие значения /<>» и /<2>, при которых
то в системе, имеющей интегральную оценку переходный процесс будет протекать быстрее, нежели в системе с интегральной оценкой
от анализа во временной области к частотной. В этом случае формулы (5.6)—(5.9) следует записать в виде
оо.
/о=~ j | Е (/©) |2 cfa>; (5.10) — со
2 00
/* = /о + ^Г 5 | Е(1)(/со) |2dco; (5.11)* — оо
/2 = Л4
J | Е<2> (j®) |2 d(o; (5.12)
— co
Т2ге С
/п = /п-1 + -^ J | Е(")(/со) I2 Jco.
— оо
(5.13)
С помощью выражений (5.10) — (5.13) нетрудно показать, что вычисление интегралов сводится к определению
= 1 f dtt>;
2л J А (/<£>) А (—]<£>)
B(s) = blSn~l + b2sn-2+ \
+ • • • + bn_{s 4- bn', Л (s) = Ur>sn * 4-4-a2sn 2+ • 4'an-is+an’
(5.14)
(5.15)
Когда полином A (s) не имеет нулей на мнимой оси, то интеграл (5.14) может быть вычислен по формулам [26]
k = 1,2....п-,
(5.16) /О = 0; / = /„.
В выражении (5.16) рекурсия связана с понижением порядка полиномов (5.15). Если полиномы имеют порядок k п, то можно
* Здесь и далее будем использовать обозначение (s)=s£ Е (s)— X X *=i
Хе'*"1» (0).
405
пользоваться следующими выражениями:
Bk (s) = b^sk-1 + b^sk-2 4-
+ • • + + ь^-,
Ak (s) = a(0A)s* a\k'lsk~l + + a(/)s4_2+... +a(*21s+a(ftA>,
(5.17)
коэффициенты которых находят с помощью следующих рекуррентных соотношений:
f (5.18)
Л4_! (s) = Ak (s)—aksAk (s), )
k = n, n—1, n — 2, ..., 1,
где
Из выражений (5.18) найдем
ЛА(«) = Л(«) + Лй(«). (5.20)
В соответствии с соотношениями (5.17)—(5.20) можно записать
Л*(*) = 4 [Л (з) + (-1)* Л*(-<'
Лф)=т ИИ*) “ (- 1)*л*(~ *)!>.
(5.21)
когда все корни полинома лежат в левой полуплоскости.
При нахождении значения интеграла 1к по формуле (5.14) необходимо вычислять коэффициенты Ak(s) и B*(s). Воспользуемся для этого табл. 5.1. Каждая четная строка в табл. 5.1 а(Л> получается сдвигом элементов предшествующей строки влево с соответствующим введением нулей. Из табл. 5.1 нетрудно установить, что четные строки правой части идентичны строкам левой
Таблица 5.1
Коэффициенты Ak (в) и Bk (s) для вычисления интеграла Ik
Коэффициенты
Номер строки i
1 ... ...
2 а^Оа^Оа^ ... а’Ла^’Оа^’ ... 1 О □
3 а^-1)а(п-1)а^-1)а^-1) ...
4 а<,’-1>0а£’-,)0 ... a<1n-1)04n~1)0 ...
2л — 3 д(2)д(2) (2) “0 “1 а2 ь<№
2п — 2 а<2)0 а<2>0
2п — 1 а0 <2[ i'/'O
2п aV’0 а<‘>
2п+ 1 а*0’ “0 0
406
части. Элементы же нечетных строк получаются из двух предыдущих элементов по формулам
1 = 0, 1
где I четно, _ 4*’ а^ ~ aka<i+2> где i нечетно, k- 1;
Ш-1) =
6^,, где i четно № а(*>
4*4 - М+р где i нечетно
i = 0, 1, — 1.
(5.22)
(5.23)
Формулы (5.22) и (5.23) получены путем приравнивания коэффициентов при степенях s в разложении (5.18).
Из Теоремы Рауса об устойчивости известно, что все нули полинома тогда и только тогда лежат в правой полуплоскости, когда все коэффициенты а)*) положительны.
После нахождения значений и р* интеграл 1к определим по формуле
= ± рИ2^]-’= ±
fc-1 fe = i (5.24)
vz ГоД*и*)1-1
X 1Уао ai j .
Для вычисления интеграла до 4 = 20 по формуле (5.24) следует применять вычислительную процедуру ISQERR, реализуемую в виде программы № 19 [26].
ПРОГРАММА № 19 ISQERR
Обращение к программе
ISQERR (N,А,В,V,IERR)
Входные параметры процедуры
N — порядок полинома знаменателя передаточной функции;
A(N + 1) —массив коэффициентов знаменателя передаточной функции;
B(N) —массив коэффициентов числителя передаточной функции.
Для нумерации коэффициентов воспользуемся соотношением
В (s) В (1) яЛГ~1 Ч-В (2) ... +B(N)
A (s)~ А (1) sN + А (2) злг-‘ + ... -J- A (N + 1) ’
где А (1) >0.
Выходные параметры процедуры
V — значения интеграла (5.14);
IERR — переменная, с Помощью которой выдаются данные об устойчивости системы. При IERR = 1 все нули полинома знаменателя расположены в левой полуплоскости а. Когда IERR = 0, то А(1) на какой-то итерации является отрицательной, и система неустойчива.
Перейдем к примерам оценки качества САР иа основе вычислительной процедуры ISQERR и традиционными способами.
ISQERR; PROC (N, А,В,V, IERR); DCL N, IERR; DCL (A (*),В (*), V) FLOAT (12); DCL K,K1; IERR= 1; V = 0; IF A (1) < = 0 THEN GO TO NEWI;
NA: DO K=1 TON; IF A (K + 1) < = 0 THEN GOTO NEWI;
ALFA = A (K)/A (K + 1); BETA = В (K)/A (K + 1); V = V + BETA * * 2/ALFA; KI = К 4- 2; IF KI - N > 0 THEN GO TO TWENTY;
NB: DO I = KI TO N BY 2; A (I) = A (I) - ALFA * A (I + 1);
В (I) = В (I) - BETA * A (I + 1); END NB; TWENTY: END NA; V = V/2;
RETURN; NEWI: IERR =0; END ISQERR;
407
Пример 5.1. С помощью вычислительной процедуры ISQERR построить зависимости интегральной оценки /» от параметров К и Тг при отработке исследуемой САР единичного ступенчатого воздействия g(t) = 1[/], если ее передаточная функция в разомкнутом состоянии имеет вид
VF(s) =_______________________________,
s (7ts + I)2 (73s + 1) (74s + 1)
(5.25)
откуда можно найти оптимальные параметры Копт н Гголт, соответствующих min/о-
Пусть параметры системы имеют значения: Ti = 2,8 с; Тз — 0,025 с; 7t = 0,01 с. Выберем следующий диапазон изменения параметров: К=1 4- 40 с-1 и 7г=1 4- Юс.
Значение сигнала ошибки вычисляется с помощью передаточной функции замкнутой системы
Е«-Т+ТГЙТ- <5'28'
Подставив в выражение (5.26) передаточную функцию (5.25), получим
Е , , = bps* + bts3 + b2s2 + b3s + b4 ' a0s5 + ats* + a2s3 + a3s! + ’
+ + Ц5
(5.27) где
ao = rlr3r4 = 0,00196, as = 2Tj 7374 +
+ 7,73 + 7,74 = 0,2758;
a2 = Tf + 27^3 + 27j74 + 7374 = 8,03625;
«3 = 27, + K72 + 73 + 74= 5,635 + K72;
Щ = 1 + 2K72; a5 = K;
bp == Hol 5i = Oil b2 = <з2; b3 = 271 + 7j + + 74== 5,635; b4=l,
откуда
0,00196s4 + 0,2758s3 + 8,03625s2 + p / , + 5,635s + 1
' 1 0,00196s5 + 0,2758s4 + 8,03625s3 + '
+(5,635 + KT2) s2 + (l +2K72)X
Xs + K
(5.28)
Для нахождения линий равных значений по функционалу /0(К, Т2) по ISQERR составим табл. 5.2.
Линии равных значений 10 построены на рис. 5.1. В результате получено пять областей, вложенных одна в другую. Шестая малая по площади внутренняя область близка к точке, где обеспечивается условие min /0. Приняв за такую точку 1р == 0,0366,
Рис. 5.1. Определение оптимальных параметров К1Опт н 71опт по минимуму интегральной оценки /о для примера 5.1
найдем по рнс. 5.1 оптимальные параметры системы Kionr = 14,2 с-1 и 72оПт = 4,95с. Для примера 5.1 определим переходный процесс н построим его на рис. 5.2, а. Используя график, определим максимум перерегулирования <jm = 38 %, a fp = 0,29 с. Из рис. 5.2, а видно, что для найденных параметров переходный процесс мало отличается от оптимального по быстродействию.
Интегральная оценка (5.7) позволяет обеспечить наилучшее приближение в исследуемой системе к эксйоиенте е(£) е постоянной времени Ть Перепишем интегральную оценку (5.7) в виде
р(0+тЦ-^у]^= о
= $ [c^)+Xi'sf] dt~2X1S е(*) ^~dt = о о
оо
= J[e(I) + T, -g.]2 d/+ т,е2 (°), (5.29)
о
где е(0)—начальные условия сигнала ошибки.
Из выражения (5.29) следует, что min It будет при
Tie (I) + е (t) = 0 (5.30)
или
е(£) = е(0)е .
(5.31)
Минимальное значение интегральной оценки /1 зависит от коэффициентов уравнения, записанных о’гиосительно ошибки, и обеспечивает наилучшее приближение к экспоненте с постоянной времени Ть
408
Таблица 5.2
Вычисление линий равных значений по функционалу /0 (К, Т2)
/0 = 0,0368
К. с"1
Параметр 4 8 12 16 20 24 28 32
Л, с — 5,25 5,57 4,48 4,81 4,01 4,23 3,78 3,83 — —
/о = 0,037
Параметр К, с-1
4 8 12 16 20 24 28 32
6,23 4,89 4,22 3,78 3,51 3,37 3,41
Ti, с — 7,08 5,87 5,08 4,50 4,07 3,80 3,60
/0 = 0,04
К. с~‘
Параметр 4 8 12 16 20 24 28 32
Г2, с 7,56 12,81 4,95 8,41 4,03 6,69 3,51 5,78 3,13 5,18 2,88 4,70 2,75 4,31 2,73 4,08
/0 = 0,05
Параметр К, с"1
4 8 12 16 20 24 28 32
Ti, с 5,85 14,82 3,95 9,51 3,21 7,52 2,76 6,47 2,46 5,77 2,24 5,25 2,14 4,86 2,08 4,57
/о = 0,08
К. с"1
Параметр 4 8 12 16 20 24 28 32
Г2, С 4.23 17,01 2,67 12,13 2,23 8,64 1,85 7,44 1,92 6,59 1,56 5,97 1,51 5,50 1,50 5,20
409
Рассмотрим интегральную оценку 1п (формула 5.9), т. е.
О
+ <5-)’+ х$)>4» + О
. , de , f d2e. .
+ “n-l dt +“л-2 d/2 + ---
••+ао4?-Г+с> <5-32>
где С — постоянная, зависящая от начальных условий е2(0).
Проинтегрируем по частям (5.32) при следующих начальных условиях: е(О) = ео, ё (0 ) = ...=
= е(л-1)(0) =0, тогда получим c==an-ieo2;
<2-i “ 2«-2 = ТР
«п-2 - 2«п—1“п—3 + 2аХ-4 = 4 а'2 , — 2а' ,а' , + 2а' ,а' . — л—3 п—2 л—4 1 п— 1 л—5
— 2а'а' „ = т®; л л—о 3’
«о2 =
тп-
(5.33)
Для симметричной формы записи соотношений (5.33) введем в них коэффициент а' = 1.
Рис. 5.2. Переходные процессы в системе автоматического регулирования с различными передаточными функциями:
а—для передаточной функции примера 5Л с оптимальными параметрами опт н Г, опт, взятыми с рис. 5.1; б — для передаточной функции примера 5.2 с различными параметрами К\ и Г1 (кривые 1 и 2) н при наилучшем приближении к экспоненте с tib 0,26 с (кривая 3)
Из выражения (5.32) следует, что min 1п достигается, когда е(0 является решением уравнения
, dne । z dre-1e , , dn~2z , +“1-dFTT. +“21?Г72 + “-
...+<_14г + е(0 = °. (5.34)
Значения постоянных времени ть т2, ..., тя определим из соотношений (5.33).
Перепишем уравнение (5.34) в следующем виде:
dne . dn~le . dn~2e .
^ + a>-^r + “2-^=2-+---
••• +an-i4r + ane(0=0, (5.35)* r r
Ct । ©2
где a1 = —7-; a2 = —; . -.;
a0 °0
°n-l 1
• • •; «п-i = —an=—• «0 °0
* В операторной форме выражение (5.35) имеет вид
s* + aiSn-1 + aiSn-2 + .. .-Fan_ls+an = 0.
(5.36)
n
410
Если в процессе проектирования необходимо найти интегральную оценку качества САР относительно выходного сигнала x(t), то при имеем е(0= 1—x(t), и интегральную оценку (5.6) можно представить в виде
Zo = J [1 -x(0J2dt (5.37) о
По аналогии с уравнением (5.35) составим уравнение замкнутой системы
d"x । , d" lx j , d" 2x ,
dt" + °* dt"~l + °2 dt"~2 + ’ • ’
...+a'n_l-^ + a'nx(t) = Q. (5.38)
Теперь можно найти способ определения оптимальных переходных процессов *, основанный на минимизации функционала (5.37). Для этого в уравнение (5.38) введем новую’ переменную т = и при а'п = оз" получим
••• +а„-1-^- + х(т) = 0, (5.39) где
а\=а\!^ а2 = а'2/а2; ...;
Функционал (5.37) можно записать в виде
°2’ •••’ <5-4°)
* См. Кузовков Н. Т. Системы стабилизации летательных аппаратов. М.: Высшая школа, 1976. 304 с.
где
Q =
ап-Г ап-2 ап-4 ап-6 • • • 1 ап-1 ап-3 ап-5 • • • о 1 ап_2 ап_4 ... 0 0 а„_! ап_3 ...
ап-1 ап-3 ап-5 ап-1 • 1 £„-2 ^л-4 а„_6 • • •
0 а„-1 ап-3 ап-5 • • 0 1 ап_2 ап-4 •
Минимизируя (5.40) по всем at, находим стандартные формы * левой части уравнения (5.38). Для систем до 8-го порядка стандартные формулы, обеспечивающие минимум интегралу от квадрата ошибки, приведены ниже:
s + ®0
s2 + ®os + ®о
s3 + и0з2 + 2co2s + и3
s4 + + 3<o2s2 + 2co3s 4- и4
s5 + coos4 + 4co2s3 + 3co3s2 + 3co4s 4- co®
s6 + co0s5 + 5co2s4 + 4co3s3 + + 6co4s2 + 3co®s + co®
s7 + coos6 + 6co2s5 + 5co3s4 + lOco4^3 + 4- 6co®s2 + 4co®s + co7
s8 + coos7 + 7co2s6 + 6co3s5 + 15co4s4 + + 10«»3s3 4- 10co®s2 4- 4w7s 4- co8.
Если необходимо продолжить строчки, то числовые значения коэффициентов при прохождении строки справа налево будут
Ci = р|
П(р — t)I
(/ 4- п)/2, когда i 4- га четный член;
р ~ (i + n— 1)/2, когда
4 4- п нечетный член.
* На практике иногда прибегают к стандартной форме Баттерворта (см. гл. 8).
411
Здесь п — порядок уравнения, a i — номер члена стандартной формы при отсчете справа налево (i = О, 1, 2, ..., п).
Корни стандартных полиномов, обеспечивающих минимум интегралу от квадрата ошибки в уравнениях, можно записать в виде
Кории уравнений
п = 2* — О,5со0 ± 0,87/со0;
п = 3: —О,57со0; — О,215со0 ± 1,31/и0;
п — 4: —О,39со0 ± 0,505/со0;
—0,105(о0 ± 1 ,'57у со0;
п —5: —О,41со0; —О,235со0 ± 0,88/со0;
—0,06со0 ± 1,70/со0;
п = 6: —О,315сйо ± 0,362/coq;
—О,155сйо±1,5О/сйо; —О,03со0±1,78/и0; п — 7: —О,33ио; —О,22со0 ± О,665/со0;
—0,09со0± 1,35/и0; —0,025со0± 1,83/со0;
л = 8: —О,27ио ± О,283/со0;
—О,15ио ± 0,91/со0; —0,068со0 ±
± 1,50/«>0; —О,О13соо ± 1,86/cOq.
Пользуясь приведенными выше выражениями при нулевых условиях, можно получить характеристики переходных процессов, к которым при действии единичного ступенчатого воздействия с минимальной погрешностью будут стремиться переходные процессы исследуемых систем.
Интегральную оценку 1п можно записать в окончательном виде
Zo + X (5.42)
Г-1 где оо _
* Из первой строки стандартных формул следует, что Ti = 1/о>о и имеет место уравнение Tix(<) + x(t) = g(t); при нулевых начальных условиях и g (t) = 1 [/] по-
лучим х (t) = 1 — е г' .
Вычисление Ли производят с помощью изображений функции е(0
<?{е(П} = Е(5);
<?{-g} = SE(s)-6(0);
& №Л = з‘Е(з) -
I dt1 J
i k=i
} (5.43)
а затем используют вычислительную процедуру ISQERR с целью нахождения Л».
Для вычисления интегральных оценок Zi, /2, , In, позволяющих обеспечить приближение кривой к решениям уравнений 1, 2, ..., п-го порядков, будем использовать вычислительную процедуру ISQERR два, три и т. д. раз.
В этом случае подынтегральные выражения имеют вид
I 2
(/©)гЕ(/со) — Е (»i-fe 8*-1 (°) • k =1
Пример 5.2. Определить оптимальные значения Копт и Гюпт. обеспечивающие наилучшее приближение переходного процесса к экспоненте с постоянной времени Ti = = 0,26 с, когда передаточная функция разомкнутой системы имеет вид
. __________K(7,s+ 1)__________
s(7'2s2 + 2|7'2s+1)(T3s+ 1) ’
(5.44)
где Тг = 0.1 с; Т3 = 0,1 с; g = 0,75.
На вход системы действует единичное ступенчатое воздействие g(t) = 1[<].
При этом условии по формуле (5.26) найдем
„__________М3 + bxs2 + b2s + b3 1
's' a0s4 + fliS3 + a2«2 + o^s + a, s’ где
a0 = T2T3 = 0,001; a, = + 2gT2T3=0,025;
a2 = T3 + 2gT2 = 0,25; a3=l + KTr, a4 = K; Ь0 = аг, bl = al-, b2 = a2; &з = 1.
откуда
0,001s3 + 0,025s2 + 0,25s + 1 1
E(s)— 0,001s4 + 0,025s3 + 0,25s2 + s'
+ (1 + КТ>)8 + ^
(5.45)
412
Рис. 5.3. Определение оптимальных параметров: Ki опт, 7" 1 од? — по минимуму интегральной оценки /0; К\ опт, Т\ опт - по минимуму интегральной оценки h для примера 5.2
Рассмотрим интегральные оценки качества протекания переходных процессов в САР «ручными» методами без применения ЭВМ. Для этого воспользуемся формулой (5.10) и функцией для сигнала ошибки, записанной в общем виде,
Е (s) =
aosn + a1s'1 *+.. ,+an_1s +an
(5.49)
Если m — n—1, то в работе [14] показано, что первая интегральная оценка
----5- fН” 1
U l П П 1 /71—1 ГП—1
...+В'Аа+...+В'А0-2&Х-1ЛЬ
(5.50) где
С помощью процедуры ISQERR определим линии равных значений функционала 1о(К, Л) (штрихпунктирные кривые на рис. 5.3), а ПО НИМ Копт = 5,29, Tlonr = = 0,35 для min/o = 0,148. Далее можно записать
Л = /0 + Т2/01. (5.46)
Интеграл 70i вычислим по следующему выражению:
оо
J I /®Е (j®) - е (0) |2 d<o, (5.47) — ОО
т. е. для его нахождения можно воспользо-ваться вычислительной процедурой ISQERR. В результате из выражений (5.46) и (5.47) получим
1,(К, Т,) = 7о(К, Л) + 0,26=Z0i (К, Т,).
(5.48)
По формуле (5.48) на рис. 5.$ построены линии равных значений для Ц (сплошные кривые), с помощью которых определены К'пт = 4,25с~1 и опт = 0,33 с при условии min /1. Из рис. 5.3 видно отличие значений К'пт и Т[опт, найденных по функционалу 11 от Ком и Лопт, полученных с помощью функционала /о. Сравнивая переходные процессы (рис. 5.2,6), отметим, что переходный процесс, вычисленный по функционалу /j, обеспечивает иаилучшее приближение к экспоненте е (i) = 1 — е 0,26 (штриховая кривая).
&п—2 ^п—6 • • • 0
0 a„_i —a„-3 а„_5... 0
0 ап С1п—2 ^п — 4 • • • 0
0 0 —a„_i а„_3 ... 0
0 0.......................щ
... + 2 (—\)к b'mb'2k_m',
6о~6о(&о ao);
(5.52)
(5.51)
A* (k = 0, 1, 2, ..., tn) — определитель, получающийся в результа-
413
те замены [п — 6] -го столбца столбцом вида
[a„_i ап 0 ... 0]т.
Заметим, что при т<п—1 выражение (5.50) примет вид
h = -~Т~(Вт+Дт+1 + Вт\т + ...
... + Bk\k + ... + В^), (5.53) где
Вт,, = Ь2т; В =Ь2 . — 2bmh w+i т’ т т- 1 т т—2.’
^k+i ^k+fik-i "Ь • • •
•••+2(-DV2fe_m;
Вг = %;
(5.54)
A* (k = 1, 2......ffi+1) — определи-
тель, получающийся в результате замены [п — kJ- 1]-го столбца столбцом вида [ап_1 ап 0 ... 0]т.
Пример 5.3. Определить оптимальные значения Кот и Тюпт САР при отработке единичного ступенчатого воздействия Я(0 =![/]. соответствующие минимуму первой интегральной оценки (5.6), если
Г (5) = -^--А (5.55)
s(T is+ l)(T2s + 1)
где Т2 = 0,04с.
Определим
Е / \ _ s (/'is + 1) (T2s + 1) 1
' ’ s(T,s+ l)(T2s+ 1) + К s ~
_ TJ2s2 + J x + Tt) s + 1 _
TJ2s3 + (Tl + T2)s2 + s + К ~
______bps2 -f- b,s 4- b2 ~ a0s3 + ats2 J a2s + a3 '
(5.56)
где up = bp TJ2; и। = bx === Ti 4- T2j
a2 = &2=l; a3 = K.
Интегральную оценку качества найдем по формуле (5.50). Для выражения (5.56) имеем
/0 — 2 Л [S2 Д2 + В1 Д1 + Во До —
2а3 д
-2^Д>-^, (5.57)
где
ft - (Тх + Т2) 0
д = 0 1 -TJ2 0 -ft Тх + Ti — К (Тх + Т2 — КТхТ2); —
До = 0; Д1 = 0; (5.58)
1 - (Тх + Ti) 0
д2 = ft 1 -TJi 0 -ft т1 + Ti =:
Tt + T2-KTJi + K(Tx + Ti)2.
Подставив полученные матрицы в выражение (5.57), найдем
Г, + Т2 - ftT,T2 + K(Tt + Tj)2 _
0 2К (Тх + Т2 — КТ J2)
____1 , (Tl + Ti)2
- 2K + 2 (Л + Ti - KTJ2) ' • ’
Для определения минимального значения интегральной оценки по ?! и К воспользуемся следующими зависимостями:
1
дТ3
az0 1
2 L т, +т2-кт,т2 ft^
(т. + т2-кт ji)2 \ 0: (5,60)
dip 1 Г 1 , дК 2 [ № +
TJiJ\ + T2)2 1
J\ + Ti-KTJ2)2\
= 0. (5.61)
Из последних двух выражений получим
Т1 опт — Т2
КГ2+1 кт2- 1
= 0,04
0,04ft + 1
0,04ft - 1 ’
Т,_+ Т2________=
TJ2 + ^TJ\ Jx + Т2) __________Тх + 0,04_________ 0.04Т1 4- 0,2 д/Л (Тх + 0,04) '
(5.62)
Зависимости T10nT(ft) и ftonr(Ti) показаны на рнс. 5.4. Найдем теперь оптимальные значения Т1опт и Копт- При ft = 50 с-1 имеем Тюпт = 0,12 с. Для значения Ti = = 0,2 с получим Кот = 8,14 с-1.
Пример 5.4. Определить коэффициент в системе САР, передаточная функция которой в разомкнутом состоянии
w (s) =---7272—- I5-63)
нз условия наилучшего приближения переходной функции замкнутой системы к экспоненте с постоянной времени Тэ.
414
Рис. 5.4. Определение зависимостей Т] Опт= = Ti от (К), Копт = Копт (^i) из условий минимума интегральной оценки /о по параметрам 7\ и К
Запишем прямое преобразование Лапласа для сигнала ошибки, вводя оператор 1/з, в виде
2 [хж (0 - х (01
-уф(з)
__ 1_____________
s (T3s + 1)
1________
s (T3s + 1)
2gTs + 1
s (T2s2 + 2gTs + 1) “
(T2 - 2gTT3) s - T3 T3T2s3 + (T2 + 2gTT3)s2 + ~
+ (T3 + 2gf) s + 1
bps 4~ bj
a0s3 + O|S2 + a2s + аа ' (5.64)
Здесь хж(/)—желаемый переходный процесс, к которому должна приближаться функция x(t) с наименьшими ошибками; 5о = Г(Т-2^Тэ); 51 = -Т3; а0 = Г3Т2;
a1 = T(T + 2gT3); а2 = Т3 + 2gT;
а3 = 1 — коэффициенты.
Первую интегральную оценку, обеспечивающую желаемое качество, представим в виде
Л>ж=$ [хж(0-х(/)]2Л. (5.65)
О
* Из выражения (5.63) найдем передаточную функцию замкнутой системы относительно выходного сигнала
1 + %Ts T2S2 1 + 2jTs ~ T2s2
2g7s + 1
T’s2 + 2grs+ 1 •
- , . W (з)
Ф(®)-Т+Г(з)
В соответствии с соотношением (5.64) из выражения (5.50) найдем
Л>ж = —4— (В2 Д2-+-В, А.), (5.66)
2а$ Д
где В2 = 52 = Т2; В, = 52 = Т2 (Т - 2^Тз)2, а столбец [(Гэ + 2g Г) 1 0]т;
1 -Т(Т + 21Т3) О О
тз + 2gT — 1
Д =
1 о о
Т3 + 21Т 1 О
О - Т3Т2 T(T-)-2gT3)
Д> =
Дг =
О
— Т3Т2 Т (Т + 2g?3)
= 2g7’[T2-(-2gT7’3 + 7’2];
-T(f + 2gr3) Т3 + 2gT — 1
Т3 + 2gT 1
О
= т (Т + 2gT3).
= 1;
1 О О
значения В2, В^ Д, Дь Д2 в
Подставив
(5.66), определим
Tl(T + 2lT3) + T(T-2lT3f
4g[T2 + 2gTT, + T2] ’
Для получения минимального значения интегральной оценки по £ воспользуемся соотношением
Т [12T2T2g2 — 4ТТЭ (Т2 + Т2) X ^ож хё-(т2 + г2)2] <?g 4 [g (Т2 + 2g.TT3 + Т2)]2
= 0, (5.68) из которого найдем
1опт = (т1 + Т2)/(2ТТэ). (5.69)
По формуле (5.69) при Т3 = Т получим £опт = 1.
Ручные методы определения интегральных оценок качества не требуют больших затрат времени проектировщика при низких порядках передаточных функций систем (не выше 5—6-го). При более высоких порядках следует пользоваться вычислительной процедурой ISQERR в интерактивном режиме работы на ЭВМ.
В заключение укажем, что на основе интегральных функционалов качества решаются задачи синтеза
415
оптимальных непрерывных и дискретно-непрерывных САР, которые подробно будут изложены в гл. 11 и 12.
2 МЕТОД KOf'lH BU1 О >'ОД(Я P.V* ч
Определение полюсов нулей в передаточных функциях (5.3)— (5.5) связано с решением алгебраических уравнений высоких порядков [28, 37], что представляет значительные трудности даже при применении ЭВМ. Однако для предварительной оценки качества САР проектировщик должен знать картину перемещения полюсов и нулей замкнутой системы (корневой годограф) в зависимости от изменения ее основных параметров [6, 13]. Корневой годограф может строиться ручными графоаналитическими способами [13, 35] или в диалоговом режиме на ЭВМ с помощью вычислительной процедуры, реализованной на ЭВМ.
Для удобства выполнения графоаналитического построения корневого годографа в работе [13] приведены восемь основных правил. Прежде чем сформулировать эти правила, напомним, что корневой годограф представляет собой геометрическое место точек, для которых выполняется условие
М_ (s)
l + U7(s)=l+K-^==°;
s = fa>, (5.70)
где
Alp (/<>) Np (j®)
<o=O
1 =
(5.71)
Из выражения (5.70) следует, что характеристическое уравнение замкнутой системы
D(s)=Np(s) + KMp(s) = 0. (5.72)
Совокупность точек s,, удовлетворяющих уравнению (5.72) при
различных К, образует корневой годограф системы.
Правило 1. Из уравнения (5.72) следует, что в корневом годографе при К->0 полюсы замкнутой системы совпадают с полюсами разомкнутой и годограф начинается в полюсах разомкнутой системы.
Правило 2. Из уравнения (5.72) также следует, что в корневом годографе при К->оо полюсы замкнутой системы совпадают с нулями разомкнутой системы. Если при этом число нулей разомкнутой системы т меньше п — числа полюсов замкнутой системы, то оставшиеся п — т полюсов стремятся к бесконечности. В этом случае необходимо найти положение асимптот.
Правило 3. Число асимптот равно п — т\ их углы определим из условия
<Pv =
180° п — т
360° ------V п — т
(v = 0, 1, 2, ..п — т — 1). (5.73)
Все асимптоты пересекаются в точке оси абсцисс с координатой
’ п :п
Е - Е у/ f-1 z-l
(5.74)
где Лг = 1/Tt — полюсы передаточной функции разомкнутой системы (i=l, 2, ..., и); у, = 1/Т/ —нули передаточной функции разомкнутой системы (/==1,2,..., т).
На рис. 5.5 показано положение пяти асимптот (Aj — Л5).
Условие (5.73) следует из соотношения
М
Pv J ____a/(180o+v360°).
Np (*)
v — 0, 1, . ..
(5.75)
Для получения условия (5.74) необходимо, чтобы s->oo в уравнении
> <5-76>
416
Рис. 5.5. Построение участка корневого годографа по правилам 1—8
Уравнение для аргумента можно записать в виде
т п
S arg(s — у,)- £ arg(s —Х,) = /-1 i-1
= 180° + v360°; v = 0, 1, 2, ...
(5.77)
Последнее уравнение можно, также получить из соотношения (5.75).
Выражениям (5.71)—(5-77) удовлетворяют все точки корневого годографа, в том числе и при К->оо.
Правило 4. Участки годографа на оси абсцисс определяются только действительными нулями и полюсами, так как влияние комплексно-сопряженных полюсов равно нулю. Угол, обусловленный действительным полюсом или нулем справа от рассматриваемой точки, равен 180°, а полюсом или нулем слева от нее равен 0°. Поэтому участки годографа на оси абсцисс чередуются, как это показано штриховкой на рис. 5.5.
Правило 5. Точки отхода годографа от действительной оси определяются следующим образом: если точка отхода имеет координату (а, 0), а точка s' с координатами (а, в) принадлежит участку корневого годографа, близкому к оси
абсцисс (е->0), то сумма углов, обусловленных векторами, проведенными из полюсов в s', удовлетворяет условию
8.8.8
я — — + -т-— + -г-- — л. (5.78)
(X Дд ““ Q Дд —— (X
Расположение корней на плоскости $ построено на рис. 5.5 по формуле (5.78). Зная числовые значения Кг и Хз, можно из (5.73) найти квадратное уравнение, из которого определим два корня cq и а,2. Корень, расположенный между Xi и yi, формирует годограф Г1 на рис. 5.5. Годограф между полюсом X* и нулем yk обозначим Гг-
Правило 6. Нахождение точки пересечения годографа с мнимой осью /® можно получить путем решения системы уравнений
П(ш) = 0;|
V(®)==0. J
(5.79)*
Из системы уравнений (5.79) определяется частота со, соответствующая точке пересечения с осью ординат, и числовое значение К (рис. 5.5).
Правило 7. Углы выхода годографа из комплексных полюсов и их подходы к комплексным нулям определяются по второму соотношению (5.71) для точки, близкой к рассматриваемому нулю или к полюсу.
Правило 8. На корневом годографе (кривые Г, и Г2) размечаются значения соответствующего параметра, например, разбивка по коэффициенту К(К1, ..., Кд) показана на годографах Г1 и Ks — на годографах Г2 (рис. 5.5).
Итак, под корневым годографом понимают траектории движения корней в комплексной плоскости s, полученные с помощью уравнения замкнутой системы (5.70). Корне-
* Уравнение (5.79) получим путем подстановки в характеристическое уравнение (5.72) • з = /©. Таким образом, найдем соотношения для действительной U (ш) = 0 и мнимой V (со) = 0 частотных характеристик замкнутой системы.
14 Ю. И. Толчеев
417
Рис. 5.6. Построение корневого годографа по передаточной функции разомкнутой системы для примера 5.5:
а — участок с нанесенными полюсами X, = О, »»-!, A.s — —2 и двумя асимптотами, проведенными под углами 60° и 300°; б — ветви годографа Ti с нанесенными квадратиками зна-X fx
ченнямн К; в — расположение полюсов н $2
на Плоскости $ для определений показателей качества
вой годограф состоит из нескольких ветвей: действительной положительной и действительной отрицательной— для действительных корней и комплексных — для комплексных корней.
При нанесении на рисунки корневых годографов будем пользо
ваться следующими обозначениями: полюсы %, указывают крестиками; нули у/ — кружочками; асимптоты— штриховыми линиями; корневой годограф — жирными сплошными линиями; разметку годографов по параметрам осуществляют квадратиками, треугольниками и ромбиками. Стрелками иа годографах показывают направления возрастания параметров и соответствующие перемещения к нулям.
Пример 5.5. Построить корневой годограф в зависимости от коэффициента усиления, если передаточная функция разомкнутой системы имеет вид
2
(5-80)
418
Используя последнее выражение, определим характеристическое уравнение замкнутой системы
D (s) = s3 + 3s2 + 2s 4- 2К. (5.81)
В соответствии с правилом 1 в участок годографа, расположенный на оси абсцисс, входят три полюса: М = 0, Кг — —1 и Х3 = —2 (рис. 5.6, а). По правилам 2 и 3 можно иайти три асимптоты. Угол асимптоты 1 q>Vi = 180’/3 == 60*, а асимптоты 2 4>V1= 60° + 36^ = 300°. Точка пе-
0-1-2 ресечеиия асимптот s0 =-----5----= —1.
На рис. 5.6 асимптоты 1 и 2 построены штриховыми линиями, проходящими через точку с координатой (—1, 0). Асимптота 3 является участком оси абсцисс, проходящим дерез точку So. Имея в виду правило 4, заштрихуем два участка годографа, как это показано на рис. 5.6, а. Подставив в условие (5.78) числовые значения полюсов, получим
е е е _____________
2 + а 1 4- а <х *
2 откуда а2 + 2а 4- у = 0 и at = —0,422, а2= —1,58.
Второй корень не принадлежит участку корневого годографа на осн абсцисс, поэтому его следует исключить. И точка отхода годографа от действительной оси соответствует —0,422 (рис. 5.6,6). По правилу 6 находим
U (®) = -З®2 4- 2К = 0; •»
У(о) = /(2<о-®з) = 0. J (5'82)
Из второго уравнения (5.82) определим <о(2 — ®2) =0, т.е. ®=-у^2. Подставив это значение в первое уравнение (5.82), найдем К = 3. Откуда следует, что пре
дельное значение коэффициента Кпр«д = 3, так как годограф пересекает ось ординат в точке с частотой <в = 1,41 с-1. В рассматриваемой задаче комплексные нули и полюсы в исходной передаточной функции отсутствуют. Поэтому нет необходимости прибегать к правилу 7. Для построения корневого годографа решаем уравнение (5.81) на ЭВМ при шести значениях параметров К. Результаты расчетов сведены в табл. 5.3.
По данным табл. 5.3 на рис. 5.6, б построен корневой годограф Г», пользуясь которым можно вычислить основные показатели качества замкнутой системы. Кроме того, видно, что при ЛГ 0,45 замкнутая система имеет пару преобладающих комплексно-сопряженных полюсов. Они в основном и определяют качество переходных процессов в системе. При К — 0,45 имеем полюсы замкнутой системы
SX = - 0,35 4- 0,52/; s£ = - 0,35 - 0,52/;
Расположение полюсов на плоскости s изображено на рис. 5.6, а, пользуясь которым, можно определить:
а) коэффициент демпфирования замкнутой системы
£с =
«1
^а1 + Р1
s* = — Qi 4- /Рь (5.83)
б) время наступления 1-го максимума переходного процесса
<т = 4-[я+ Z arg(sf-s*)-
pi L i-3
— s arg (s* “ s/)l ’ <5-84) /-1 J
X 0
где S( и Sy — соответственно полюсы и нули замкнутой системы.
Таблица 5.3 *
Числовые значения полюсов при различных К Для характеристического уравнения s’ 4- 3s2 4- 2s 4- 2К = 0
Полюсы к
0,2 0,45 0,9 1,2 3 12
sx Действительные Комплексные -2,16 —0,42±0,09/ -2,30 —0,35 ±0,52/ -2,49 —0,26±0,81/ —2,59 —0,21±0,94/ -3,0 ±1,41/ -4,0 0,5±2,4/
Здесь s*, s*, ..., и s°, s°, ... — собственно полюсы и нули замкнутой системы.
14*
419
Если систему представить колебательным звеном, то вместо формулы (5.84) можно пользоваться выражением
(5.85)
в) максимальное перерегулирование
От — 20! m п -X _ „0 si sj o X
д/а2 + pf /-1 si
п оХ
хП 1-2 -X _ -X S1 si -a e ,/m.ioo%, (5.86)
Рис. 5.7. Построение приближенного переходного процесса по данным корневого годографа, изображенного иа рис. 5.6
где —ai — действительная часть 1-го полюса (а» = <о^с).
Для пары комплексно-сопряженных полюсов выражение (5.86) можно записать в более простой форме
л
" ~п1Г
ат = е V с =е ; (5.87)
г) время регулирования переходного про-
цесса
3 + In 2
ip ------------
s
• (5.88)
В случае комплексно-сопряженных полисов формулу (5.88) можно представить в более простом виде
(5.89)
По формулам (5.84) и (5.86)—(5.88) строим приближенную картину протекания переходного процесса. Для этого сначала вычислим по формуле (5.83) коэффициент демпфирования
. °-35 п чя
V0.352 4- 0,522
а затем по формуле (5.84) определим время наступления 1-го максимума
_ 3,14 + 0,26
tm-------0Д2----= 6’5 С-
Максимальное значение перерегулирования находим с помощью соотношения (5.86), т. е.
ат= 1,14е-0,35’6,5- 100% = 12%,
а время регулирования — по формуле (5.88)
. 3 4- In 1,5 3,4
tp~ 0,35 — 0,35 “9,7 с-
На рис. 5.7 по найденным значениям построена приближенная картина протекания переходного процесса в исследуемой системе.
Процесс проектирования САР обычно производят с помощью передаточных функций разомкнутых систем, в которых полюсы X,- можно заменить на 1/Т,, а нули у/ на l/Tj. Эти передаточные функции обычно записывают в виде произведений типовых звеньев. На практике наиболее часто встречаются следующие типы передаточных функций, в которых могут отсутствовать некоторые типовые звенья:
K(TiS-+ 1) ... (Tts+ 1)Х X(^s2 + 2gvTvs+l) ...
W (s} = -(frW^ + l)
U s₽ (TyS + 1) ... (T^s + 1) X "
X (Г2з2 + 2lrTrs + 1) ... ... (7>2 + 2gpTpS + 1)
После получения по данной передаточной функции характеристического уравнения замкнутой системы строят корневой годограф.
Располагая корневыми годографами, проектировщик оценивает не только влияние изменения параметров в САР на основные показатели качества, но и выбирает необходимые типы корректирующих устройств. Как будет показано в гл. 10, с помощью корневого годографа можно упростить методику проектирования систем, особенно на этапе выбора структуры коррек
420
тирующих, усилительных, измерительных и управляющих устройств. Такой подход особенно важен при проектировании дискретных и нестационарных САР, когда в процессе эксплуатации системы происходит изменение параметров объекта, ухудшающих его показатели качества. Для сохранения неизменных показателей качества приходится менять в процессе работы не только параметры, но и структуру системы. Поэтому на этапе предварительного исследования таких систем применяют метод корневого годографа.
Рассмотрим несколько конкретных параметров построения корневых годографов САР с оценкой их показателей качества.
Пример 5.6. Построить корневой годограф по передаточной функции разомкнутой системы и оценить влияние ее параметров на качество системы.
Пусть передаточные функции объекта и регулятора имеют следующий вид:
Рис. 5.8. Построение для примера 5.6
корневого годографа
Тогда результирующая передаточная функция всей разомкнутой системы
W(s) = W0 (s) Гр (з) = Л (Гр,з + 1) (Т2з + 1) = s(TP2s+l^ry-WfcjTjS+l) ’ (5,90)
421
где 71=0,5 с; ^=0,1; 72 = 0,33 с, а К = =kokp — коэффициент усиления разомкнутой системы.
Для повышения точности САР необходимо повышать коэффициент усиления, а для улучшения показателей качества — коэффициент демпфирования замкнутой системы.
Одновременно удовлетворить эти условия нельзя в силу их противоречивости. Поэтому на практике приходится прибегать к компромиссным решениям.
Из приведенных правил построения годографов следует, что асимптоты пересечения в точке недействительной оси
п т
У [полюсов W (з)] — У,[нулей IF(s)]
(5.91)
Точка пересечения асимптот в нашем
случае
0J5 Тр2)
Неравенство (5.92) записано из условия необходимости повышения показателей точности и качества за счет перемещения вертикальной асимптоты А в левую полуплоскость.
Пользуясь неравенством (5.92), нахо-• дим -=— < — — 2,6, т. е. чем больше 1Р1 1 Р2
Tpt, тем значительней сдвигаются влево вертикальные асимптоты. При 7Р1 = оо $пред = (— 0,4 — 12 + 3)/2 = — 4,7 (здесь 7Р2=1/12). Одиако при большом значении 7Р1 и значении коэффициента К -> оо предельное значение отрицательного корня слишком близко к оси /со, что недопустимо по требованиям качества. Поэтому, если принять з( пред = —2, то допустимое наименьшее значение 7Р1 = 1/2 и центр асимптот «о = —3,7.
На рис. 5.8 показано положение вертикальной А] и наклонных асимптот Аз, А3 для комплексных корней при £ = 0,28; А4, А5 при g = 0,1 *.
* Расположение наклонных асимптот Аз—А5 и близость полюсов данной замкнутой системы s2x и з3х к мнимой оси позволяют получить большое значение К при достаточио высоком коэффициенте демпфирования £с замкнутой системы.
Рис. 5.9. Построение корневых годографов для примера 5.7 при двух различных значениях параметров:
т(1) Л1). т(2) Л2)
О) ”1 , S1 » о) ”1 . si
Для построения корневого годографа по передаточной функции (5.90) составим характеристическое уравнение
D (з) = 1 + W (s) = 1 +
К(7Р1з+1)(72з+1) = о
+ s(7P2s+1)(r|s2 + 2g1r1s+l)
(5.93) откуда получим
НгР/+(г? + 2£1717Р2)з3 +
+ (ГР2 + 251Г1 + атрт2)82 +
+ (1 + ктР1 + КТ2) з + К = о. (5.94)
Подставив числовые значения в уравнение (5.94), найдем
0,0208s4 + 0,2583s3 + (0,1833 + 0,165 К) s2 +
+ (1 +0.83Л)з + К = 0.
Решая это уравнение иа ЭВМ при различных'параметрах К, получим годограф Г). Ои построен на рис. 5.8 жирными
422
сплошными линиями. Здесь же дана раз-метка квадратиками для параметров Ki = = 2 с-', Kt = 4 с-1, К3 = 10 с-1 и Кк = = 11 с-'.
Значение К, обеспечивающее максимально возможный коэффициент демпфирования £с, определяют по точкам касания лучей At и Аз годографа Гь Как видно из рис. 5.8, в точке касания имеем К = — 11 с. По мере приближения полюсов к нулям уменьшается максимум перерегулирования. '
Пример 5.7. Построить корневые годографы по передаточной функции разомкнутой системы
(5.95)
при двух различных значениях параметров 7’14 Si'* и При этом необходимо
проанализировать основные показатели точности и качества. Пусть обе системы имеют одинаковую постоянную времени
Рис. 5.10. Структурные схемы САР, используемые при построении годографов:
а — для примера 5.8; б — для примера 5.9; в — для примера 5.10
Tt = 0,333 с. Из передаточной функции (5.95) получим характеристическое уравнение в виде
D (s) = Г2®4 + + s2 + KT^s + К = 0.
(5.96)
В первом варианте системы = 0,5 с и £^ = 0,1; асимптоты А{ — А3 начинаются в точке 4» = 0,87 (рис. 5.9, а). По уравнению (5.96) при принятых Г*/* и вычислим для различных параметров К корневой годограф и построим его иа рис. 5.9, а жирными сплошными линиями в виде двух ветвей Г1 и Га. Сделаем на иих разметку по параметру К. При этом видно, что первая система устойчива лишь при малом значении К Кпред = 0,83. Для таких малых значений нельзя получить высокие показатели точности и качества системы.
Во втором варианте системы: =
= 0,167 с, Е|2,=»О,7; асимптоты Aj —А3 начинаются в точке = — 1,8, а асимптоты At и А$ — в начале координат. На рис. 5.9, б построены жирными сплошными
а)
в)
423
линиями годографы Г1 и Г2. При этом видно, что вторая система устойчива при значениях АПРед = 7,55. Это показывает, что вторая система обладает более высокими показателями точности и качества. Действительно, при росте коэффициента демпфирования £с и убывании постоянной времени 7*1 уменьшается время протекания переходного процесса /р.
Пример 5.8. Пользуясь структурной схемой САР, изображенной на рис. 5.10, а, построить корневые годографы для внутреннего и внешнего контуров системы в зависимости от параметров kt и k4.
Запишем передаточную функцию замкнутого внутреннего контура в виде
__________________fejfes (7*38 4- 1)___ т ч _ (7’1s+l)(r22s2 + 2gr2s+l)
K(S> 1 + fe2fe3fe« (7’3s + 1) (T1s+i)(T2s2 + 2gr2s + i)
(5.97) ИЛИ
m is) _ . MaCT'ss+l)____________
(Л*+1)(^2 + 2^+1)+'
+ ktk3kt (T3s + 1)
(5.98)
Передаточная функция разомкнутого контура всей системы
jpr ___________feife2fe3 (73s + 1)___ 1
(7'iS+ l)(T2s2 + 2gr2s+l)+ s'
+ k3k3kt (T3s + 1)
(5.99)
По выражению (5.99) найдем характеристическое уравнение замкнутой системы:
T1T!s4 + (T2 + 2gT2T1)s3 +
+ (7'i+ 2g7'e + kik3ktT3) s2 +
+ (1 + ksk3kt + ktk2k3T3) s + kjktks = 0.
(5.100)
Положим kiktk3 = К', тогда по уравнению (5.100) строим корневой годограф. При этом будем использовать числовые значения параметров системы, приведенные в табл. 5.4.
Таблица 5.4
Значения параметров системы примера 5.8
kl к, ki kt г. Tt Ts £
6с“0.6 «с-о
1.4 15 1 0,32 1,2 0,1 0,365 3,27 0,83
3,3 25 1 0,32 2,0 0,1 0,365 3,27 0,83
На рис. 5.11, а построены корневые годографы Г| и Г2 замкнутого виутреииего контура системы при двух значениях kt = = 2 с-1 и 1,2 с-1. Как видно из рис. 5.11, а, при fe*41) = 2c~1 корни замкнутого внутреннего контура являются действительными; оии обозначены на рисунке квадратиками. Если уменьшить kt до 1,2 с-1, то появляются комплексные корни, которые выделены на рисунке треугольничками. Для выбора наилучшего значения kt необходимо, как и в примере 5.7, компромиссное решение, т. е. для получения требуемого значения времени протекания переходного процесса /р и максимума перерегулирования ат.
Для иллюстрации данного положения на рис. 5.11,6, в построены корневые годографы замкнутого внешнего контура, полученные из уравнения (5.100). При этом видно, что для = 1,2 и k[ = 15 коэффициент демпфирования всей системы £с = 0, а это нежелательно. Если уменьшить коэффициент fei до 1,4, то £с = 0,6. Теперь увеличим до 2 и при ki = 25 получим |с = 0, а при fei = 3,3 tc = 0,6.
Итак, на основании анализа внутреннего и внешнего контуров можно сделать следующее заключение. При большом коэффициенте kt возрастает недемпфированная частота колебаний* что связано с перемещением полюсов внутреннего контура вдоль асимптоты, перпендикулярной к оси абсцисс (рис. 5.11,а). Получить высокую точность системы не удается, так как для обеспечения gc = 0,6 необходимо значительно уменьшить коэффициент kt. С целью улучшения точности стабилизации системы целесообразнее вводить в структурную схему звено вида (7Ks + l)/s, позволяющее получить в системе астатизм 1-го порядка.
На рис. 5.11, а—в показаны асимптоты и годографы для данного примера.
Пример 5.9. Пользуясь структурной схемой САР, изображенной на рис. 5.10,6 с объектом, имеющим одно неустойчивое апериодическое звено, построить корневой годограф внутреннего и внешнего контуров системы при параметрах, указанных в табл. 5.5.
Таблица 5.5
Значения параметров системы примера 5.9
А, к, к, к. Ti Тг Т. Т,
По ннжнему уровню По верхнему уровню
1,56 2,63 1 0,246 0,23 0,1 0,264 0,346 0,33
1,12 5,78 1 0,246 0,53 0,1 0,264 0,346 0,33
424
Пл-S
П л. s j w
Рис. 5.11. Построение корневых годографов для примера 5.8:
а — замкнутого внутреннего контура прн двух значениях — 1,2с-1, —2с-1; бив —
замкнутого внешнего контура прн различных параметрах системы
425
. а—замкнутого внутреннего контура; б—замкнутого внешнего контура, где Д—*(0-0,23; □—*<2)-0,53
4 4
426
Передаточную функцию замкнутого демпфирующего контура запишем в виде
_________________fe2fe3 (Г4З Ч- 1)___ П7 - (7’.^+ l)(r2s+ 1)(T3S- 1)
14 ЫзМГ4з+ 1)
‘^(T'.s+DCTas+lXTaS-l)
(5.101) или
Ц7 , Ч __________fe2fe3 (TtS + 1)____
к = (Г 1Д + 1) (T2S + 1) (T3s - 1) + •
+ fe2fe3fe4 (Т4s + 1)
(5.102)
Подставив соответствующие числовые значения из табл. 5.5 в выражение (5.102), построим на рис. 5.12, а корневой годограф замкнутого внутреннего контура прн двух значениях Л^^О.гЗ и fe^ = 0,53. Разметка годографа прн коэффициенте выполнена квадратиками, а при — треугольничками. Из рнс. 5.12, а видно, что по мере увеличения коэффициента kt полюс X], расположенный в правой полуплоскости, движется к нулю yi, лежащему в левой полуплоскости. Это улучшает качество системы. Здесь же на годографах нанесены значения полюсов замкнутой системы. Полюсы замкнутого внутреннего контура являются полюсами разомкнутого внешнего контура, так как
«7 __________feife2fe3 (7~4s + 1)__
(T,s+l)(T2s+l)(T3s-1) + Л
+ fe2fe3fe4 (Tts + 1)
X -y. (5.103)
Для построения корневого годографа всей замкнутой системы составим характеристическое уравнение внешнего контура D (з) = TiTzT^+IJiTs+TiTs - TiTt) s3 +
+ (Г3 - Г, - г2 + k2k3ktTt) s2 +
-4- (kik3k3T4 4“ fe2fe3fe4 — 1) S + fejfe2fe3 == 0;
(5.104)
Примем fejfe2fe3 = К и при заданных параметрах, приведенных в табл. 5.5, построим (рис. 5.12, б)'два корневых годографа: жирными линиями для fe^ = 0,53 (Г1—ветвь для si) и для fe(4’* = 0,23 (Г2 — ветвь для з2).
Из рис. 5,12, 6 можно также установить, что при малых коэффициентах (fe4=fe*4*) полюс в правой полуплоскости далеко отстоит от начала координат, и вся замкнутая система устойчива лишь для малого диапазона значений коэффициента усиления kt. С ростом значений k4 до k^ вся замкнутая система устойчива и при боль
шом диапазоне значений коэффициента feb Итак, если полюс правой полуплоскости слишком далеко отстоит от начала координат, то независимо от коэффициента ki вся замкнутая система неустойчива. На рнс. 5.12,6 годографы Г2 соответствуют расположению полюсов и нулей всей замкнутой системы, в которой обеспечивается наименьшее значение времени протекания переходного процесса.
Пример 5.10. По структурной схеме (рис. 5.10,в) внешнего контура самолета с управлением по ускорению [4] построить корневой годограф. В систему управления самолета входит и внутренний контур демпфирования, передаточная функция которого в замкнутом состоянии
kckpn (Tcs + 1)
(ГрЗ2 + 2^0r0s + 1) (Трпз + 1)
(T’cS + 1)
+ (TqS2 + 2^oros + 1) (Грпз + 1)
(5.105) где £o = 0,159 — коэффициент демпфирования самолета; То = 0,354 с, Тс = 0,25 с — постоянные времени самолета; Трп = = 0,1 с — постоянная времени рулевого привода; kc = 0,75 с-1 — передаточный коэффициент самолета по угловой скорости тангажа 41; fepn = 1—передаточный коэффициент рулевого привода; fe* = 0,23 — передаточный коэффициент датчика угловой скорости.
После ряда преобразований из выражения (5.105) найдем
U7 (-Л s^<s)__________kt(T4s+ 1)
ЕИ®) (t^ + V^ + Ox
Х(Г3з+ 1)
(5.106) ИЛИ
W (4- 0,64 (0,25s+D
’ (0,102s + 1) (0,3242s2 + 2 • 0,18 X '
X 0,324 s+ 1)
(5.107)
Для получения на выходе системы сигнала по ускорению аг введем в структурную схему передаточную функцию W* , на выходе которой образуется выходной сигнал flz(s) внешнего контура. Для этого можио воспользоваться следующим соот-
ношением:
где Fp®(s)
W^(S) Г*в (з) ’
(5.108)
5г(s) . бв (в)
F*B(s) =
sO (s) 6B(s)
427
Из соотношения (5.108) определим передаточную функцию
W^(s)
Ьи Tjs2-!
__ а2 (s) rgs2 -j- 2gQ7’Qs Ц- 1
~ 8*0 (s) = kc Tzs+\
72s2 + 2£0Г08 + 1
k3 (Tss + 1) (Tas — 1)
res + 1 ’ (5Л09)
где T6 — 0,129; T6 = Tc = 0,25 c; *3 = = *a/*c == 0,042;
Подставив в формулу (5.109) числовые значения, найдем
* 0,042 (0,129s + 1) (0,129s - 1)
W аг{S) ~ 0,25s + 1
(5.110)
Передаточную функцию (s) получим путем перемножения выражений (5.106) и (5.109):
= fe»fe3 (Tss+ 1) (T5s - 1) “г (r2s2 + 2^T2s + 1) (73s + 1) *
(5.111) ИЛИ
e 0,027 (0,129s + 1) (0,129s — 1) (s) = (0.102s + 1) (0,3242s2 + 2 X '
2 X 0,18-0,324s + 1)
(5.112)
Из выражения (5.112) следует, что нули передаточной функции (s) заменяются нулями передаточной функции IF" (s), а полюсы остаются постоянными.
Для построения корневого годографа воспользуемся выражением (5.112) и по
нему составим передаточные функции всей замкнутой системы в виде
ф(8)=^ЦЦ- = 4(s)
0,027*, (0,129s + 1) (0,129s — 1)
s (0,102s + 1) (0,3242s2 + 2 • 0,18 X
X 0.324s + 1)
0,027*1*4 (0,129s + 1) (0,129s — 1) ’ + s (0,102s + 1) (0,3242s2 + 2 • 0,18 X
X 0,324s+1) (5.113)
откуда при *i =2,2 и *< = 1 найдем
(0,129s + 1) (0,129s - 1) ' ’ (16,623s + 1) (0,102s + 1) X ‘
X (0,3262s2 + 2 • 0,171 • 0,326s + 1)
(5.114)
Корневой годограф построен иа рис. 5.13. Он состоит из трех ветвей, на которых указаны квадратиками зиачеиия К^ = 50; К(42)= 100; К(43) = 500; К(44)= 1000; К'45) = = 5000; К(46) = б000.
Существенным достоинством данной системы управления является повышение быстродействия при наборе высоты самолетом за счет выдерживания максимально допустимой перегрузки. При этом удается сократить время выхода самолета на заданную высоту. Кроме того, упрощается реализация закона самонаведения, так как с данной системой управления нетрудно обеспечить прямую пропорциональность между угловой скоростью линии визирования и перегрузкой.
Однако введение во внешний контур датчика перегрузок приводит к появлению нежелательных ускорений, связанных с воздействием возмущений от турбулентности атмосферы в виде шумовых помех. Следует также иметь в виду, что в системе
Рис. 5.13. Построение корневого годографа внешнего контура самолета с управлением по ускорению (пример 5.10)
428
Рис. 5.14. Построение корневого годографа с введением в контур самолета счетно-решающего устройства:
а — при семи значениях К', б—участок в начале координат
необходимо компенсировать ускорение силы тяжести при выполнении самолетом маневров на больших углах атаки. Последний недостаток может быть устранен введением средств компенсации перегрузок с помощью счетно-решающего устройства.
В результате получим корневой годограф, который изображен на рис. 5.14, а при К<‘> = 10-4, /(<’> = 10-3, К<3> = 10-», = 10-‘, К<5> = 1, /(<«> = 5 и Я<7> = = 10. Из участка корневого годографа в начале координат, выделенного иа рис. 5.14, а штриховкой и изображенного на рис. 5.14,6, видно, что по мере роста К система из неустойчивой становится устойчивой и ее показатели качества улучшаются.
3. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ВЕЩЕСТВЕННЫХ ИЛИ МНИМЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЗАМКНУТЫХ СИСТЕМ С ПОМОЩЬЮ Лх-ФУНКЦИЙ
Вычисление и построение переходных процессов в линейных САР
запасы-
/>0,
(5.115)
производят с помощью обратного преобразования Лапласа, ваемого в виде интеграла
С+/оо
* (0 = $ Х etds’
c—j<x>
где с—абсцисса абсолютной сходимости функции x(t), характеризующей искомый переходный процесс.
Функция X(s) состоит из двух слагаемых: Xp(s)— регулярной части, содержащей все полюсы функции X(s) в левой полуплоскости-, ХИ (s) — нерегулярной части, содержащей все полюсы в правой полуплоскости и на мнимой оси, т. е.
X(s) = Xp(s) + XH(s). (5.116)
Подставляя выражение (5.116) в (5.115), получим
с+/оо
$ *p(s)es<ds + с —/оо
С+/ОО
+ $ X„(s)es<ds. (5.117)
С —/оо
429
В Xp(s) все полюсы находятся в левой полуплоскости; поэтому с — = 0.
Имея в виду выражение (5.117), запишем
х (Г) = хр (о + хн (о, (5.118) где
/оо
ХР = ~ J Xp(s)estds (5.119) -/оо
И с+/оо
^н(0 = ^ S *H(s)estts. (5.120) C — i«>
Располагая полюсами нерегулярной части системы, можно найти составляющую хн (О по формулам решения дифференциальных уравнений с вычислением произвольных постоянных. С ростом порядка дифференциальных уравнений такой метод становится громоздким и обычно осуществляется с помощью вычислительных процедур иа ЭВМ.
Существуют следующие четыре графоаналитических способа нахождения переходных процессов: а) функция X(s) не содержит корней в правой полуплоскости и на мнимой оси; б) ив) соответственно в нее входят один и два полюса в начале координат; г) функция имеет два сопряженных полюса на мнимой оси. Рассмотрим эти четыре способа.
Первый способ. Функция X(s) не имеет полюсов в правой полуплоскости и. на мнимой оси. В этом случае имеется только регулярная часть Ap(s). Тогда, подставив в выражение (5.119) s =/<в, получим
ОО ,
xp(0=i $ *₽«««>• (5.121) — оо
Отделим в формуле (5.121) действительную часть функции Хр(]а>) от мнимой, т. е.
*Р (/«*) = /?Р (®) + /Sp («>). (5.122)
Подставив выражение (5.119) в соотношение (5.122) и выполнив
ряд преобразований, найдем
оо
2 С
хр (0 = — \ /?р (<в) cos atdat;
о
оо 2 Г
Хр (0 — — — \ Sp (®) sin (Htda; о
t > О’,
(5.123)
t > 0.
(5.124)
В рассматриваемом случае отсутствуют полюсы в правой полуплоскости и на мнимой оси; поэтому формулы (5.123) и (5.124) примут вид
оо
х (t) = — Rx (<в) cos at da; о
t >0;
(5.125)
ОО
х(0 = — Sx (<в) sin at da; t > 0,
о
(5.126)
где /?х(<о) и Sx((o)—соответственно вещественная и мнимая частотные характеристики системы.
Для вычислений по формулам (5.125) или (5.126) необходимо в последние два члена выражения (5.2) подставить s = /со; тогда получим
2^. = /?f(<b) + /Sv(®); (5-127)
Г(М) = /?/(ш) + /5/(<в); (5.128)
^^• = /?h(®) + /Sh(®). (5.129)
Здесь Rf (со) и Sf (со) — соответственно вещественная и мнимая частотные характеристики по сигналу возмущения; Rn(a) и Sh(<o)—соответственно вещественная и мнимая частотные характеристики от ненулевых начальных условий.
Имея в виду выражения (5.127)—(5.129), можно получить обобщенные вещественную R(a) и
430
мнимую S(<d) частотные характеристики замкнутой системы:
R (ш) = Rv (ю) Rf (ш) — S7 (<d) Sf (а) + + /?н(®); (5.130)
S (й>)==/?^ ((D) Sf (g>) 4-Sv((D)/?f (g>) + +SH(®). (5.131)
Второй способ. Функция X(S) имеет один полюс в начале координат. В этом случае вместо формулы (5.125) следует применить
х (0 = R (0) + 4 $ S (®)-^- d®;
t>0, (5.132)
а вместо формулы (5.126) найдем
оо
x(0 = U/?(®)^-d(D; />0, (5.133)
где X(s) = ^- и X0(/(D)== = /?(<») + jS (а).
Третий способ. Функция X(s) имеет два полюса в начале .координат. Тогда формулу (5.132) и (5.133) следует заменить на
x(t) = R(0)t +
. 2 f R (0) — R (со) ,, , . n
Ч \ —-----л—— cos (D/dco; t > 0;
1 л J co2 ’ ’
(5.134)
X (0 = z? (0) / d-
+ j sin'ffl/dco; t > 0, (5.135) 0
где J(s) = ^£l и X0(/(D) = = /?(©) + jS((D).
Четвертый способ. Функция X(s) имеет два сопряженных полюса на мнимой оси в точках s — ± /юа. При этом X(s) — —, и фор-s +“а мулы для определения переходных
процессов примут вид r _________ Xo (jOg) /ш i
XV>— 2/coa 6
I *0 (—/(Da) A-/®a(
"r -2/<oa e
2 2
© — (Од
I 2 М (Иа) - R (<0)
X cos (o/d(D; t > ।
X(/) = A<J“a)
V ’ 2/C0a
i Xq (—/(Da) p-/“at —2/coa e
(5.136)
ш2
процес-выпол-
___2f ©S (©а) — ©а^ (ф)
Л J о
X sin co/dco; t > 0, где X0(/(d) = /?((d)+/S((d). Построение переходных сов для четырех случаев няют по формуле (5.133). Полученную в результате расчетов или графически с помощью номограмм кривую /?(©) разбивают на несколько типовых трапецеидальных характеристик, для каждой из которых находят коэффициент х. Далее, пользуясь /ix-функциями (см. прил. П-П. 1), находят составляющие переходного процесса. Просуммировав их ординаты для выбранных моментов времени t, получим переходный процесс в исследуемой системе.
Запишем последовательность процедур для построения переходных процессов.
1.Кривую /?(а>) представляем в виде типовых трапеций (рис. 1.53), т. е.
/?(©)«£ rt (о),
гг(ш)
(5.137)
в виде ®di;
Г i (®) =
где функция г,-(а) записана
Г01 при 0 < (D <
(Doi — (D
Г0£----------- при
1 “о/ - “di
®di < <D < ©о/!
0 ПРИ (D0/ < (D.
(5.138)
431
1)
Рис. 5.15. Круговые номограммы для определении по амплитудно-фазовой частотной характеристике разомкнутой системы вещественных частотных характеристик замкнутой системы:
•а—полная номограмма R (©); б—участок, примыкающий к началу координат
2. Находим для каждой из трапеций <в4/, соог, h0l и вычисляем значения Х; =<Bdl/<Boi.
3. В зависимости от полученных X/ выбираем табличный интервал времени Д/<табл, учитывая при этом,
что для больших коэффициентов хг выбирают меньший интервал
табл-
4. По Хг И Д/(табл находим по таблице прил. П-П. 1 соответствующие значения йхг-функций.
5. Умножая Лхг на высоты трапеций г{, получаем составляющие переходных процессов х{ (t), которые откладываем последовательно по оси ординат для каждого момента Д/,табл (*=1, 2, ...).
6. Суммируя ординаты этих кривых с учетом их знака, построим ре-
432
зультирующий переходный процесс х(0-
Таблица йх-функций составлена для второго случая по формуле (5.132), т. е.
оо
(5Л39> о
Рис. 5.16. Круговые номограммы для определения по амплитудно-фазовой частотной характеристике разомкнутой системы мнимых частотных характеристик замкнутой системы:
а—полная номограмма $(©); б—участок, примыкающий к началу координат
для четвертого случая
поэтому для всех остальных случаев следует выполнять дополнительные преобразования с подынтегральной функцией, приводящие к форме (5.139), например:
для первого случая
„ 1/\__ (foa)
X(l>— 2/<оа е
I %а (—/Ц>а)
“* —2/<оа е
'2-®D
2 Г со [coS (соа) — g>aS (со)] sin со/
" J ша (в)2 _ ш2) «о ®-
(5.142)
о
(5.140)
для третьего случая
x(0 = R(0)( + |$[-^]^<to; О
(5.141)
Для получения вещественной и мнимой частичных характеристик 7? (со) и S(co) по частотным характеристикам разомкнутых систем W(jat) применяют различные номограммы. Если имеется амплитуднофазовая частотная характеристика VF(/co), построенная в линейном масштабе, то для нахождения /?(и)
433
Рис 5.17. Номограммы для определения по логарифмическим амплитудной и фазовой частотным характеристикам разомкнутой системы вещественной частотной характеристики замкнутой системы в линейном масштабе
Рис. 5.18. Номограмма для определения по логарифмическим амплитудной и фазовой частотным характеристикам разомкнутой . системы мнимой частотной характеристики замкнутой системы в линейном масштабе
LmAg, ДБ
Рис. 5.19. Номограмма для определения по логарифмическим амплитудной и фазовой частотным характеристикам разомкнутой системы частотной характеристики /?у(ш) в линейном масштабе
435
Рис. 5.20. Номограмма для определения по логарифмическим амплитудным и фазовым частотным характеристикам разомкнутой системы частотной характеристики Sv(<o) в линейно» масштабе
436
1т,дБ
Рис. 5.21. Амплитудио-фазовая частотная характеристика разомкнутой системы
используют номограммы, приведенные на рис. 5.15,-а, б, а для определения S (а) — номограммы, показанные на рис. 5.16, а, б. Если эти характеристики построены в логарифмическом масштабе, то R(a) и S(«>) вычисляют соответственно по номограммам, изображенным на рис. 5.17 и 5.18.
В тех случаях, когда при проек-, тировании приходится прибегать к логарифмическим характеристикам, полученным по формуле Фу(/а)= 1 + (/(0) тогда для нахождения Ry (а) и Sy (а) применяют соответственно номограммы, приведенные на рис. 5.19 и 5.20. На
Рис. 5.22. Амплитудно-фазовая частотная характеристика разомкнутой системы, нанесенная на участок номограммы рис. 5.15
этих номограммах введены следующие обозначения:
Л° И = | Т+У(/ю)~1 ~ амплитудная характеристика, (5.143) а
Фо(®) = arg- фазовая
характеристика. (5.144)
В случае одновременного действия на САР управляющего и возмущающего воздействий при нулевых начальных условиях формулы (5.130) и (5.131) заменяют следующими:
R (со) = Rv (со) Rf (со) — Sy (со) Sf (со) + + R(a)Rg(a) - S(o)Sg(a); (5.145)
S (со) = Rv (a) Sf (со) + Sy (о) Rf (а) +
+ R (a) Sg (а) + S (a) Re (a), (5.146)
где ® = + G(M) =
= Rg(«>)+ jSg(a).
Из формул (5.145) и (5.146) следует, что возмущающее воздействие может быть применено к любой части структурной схемы системы.
Рассмотрим несколько примеров построения переходных процессов с помощью частотных характеристик.
Рис. 5.23. Вещественная частотная характеристика замкнутой системы с разбивкой ее иа трапеции
437
Таблица 5.6
Значения составляющих переходного процесса для примера 5.11
Трапеция 1 г01=0,33; Xj = 0.15; Д*. 1 0.4 1 =4^1=0,050 с нет 8,0
0,4 0,8 1,2 1,6 2,0 2,4 2,8 3,2 3,6 4,0 4,4
Ах. 0,1459 0,2876 0,4218 0,5452 0,6553 0,7502 0,8291 0,8921 0,9399 0,9738 0,9959
0,050 0,100 0,150 0,200 0,250 0,300 0,350 0,400 0,450 0,500 0,550
г01Ах, 0,048 0,095 0,139 0,180 0,216 0,248 0,274 0,294 0,310 0,321 0,329
Трапеция 2 Го2=О,16; Х2=О,56; Д<2 =-^-= °' Л 'ист 14»4 =0,042 а
0,6 1.2 1,8 2,4 3,0 3,6 4,2 4,8 5,4 6,0 6,6
0,2939 0,5655 0,7953 0,9701 0,0849 1,1423 1,1513 1,1261 1,0820 1,0338 0,9916
0,042 0,084 0,126 0,168 0,210 0,252 0,294 0,336 0,378 0,420 0,462
'”02Ах2 0,047 0,090 0,127 0,155 0,174 0,183 0,184 0,180 0,173 0,165 0,159
Трапеция 3 Г03==е0' 04; х3=0,80; Д/3 _ 0,6 нет 18 =0,033 с
1 0,6 1,2 1,8 2,4 3,0 3,6 4,2 4,8 5,4 6,0 6,6
Л„ 0,3380 0,6441 0,8907 1,0620 1,1535 1,1736 1,1406 1,0770 1,0065 0,9491 0,9164
*’ист 0,033 0,066 0,099 0,132 0,165 0,198 0,231 0,264 0,297 0,330 0,363
f03AXj 0,014 0,026 0,036 • 0,042 0.046 0,047 0,046 0,043 0,040 0,038 0,037
Трапеция 4 г„. = 1,13; х,=0,86; At. =.JA=0,041 с 04 4 4 нет 39,4
1,6 3,2 4,8 6,4 8 9,6 11,2 12,8 14,4 16 17,6
ч 0,8375 1,1742 1,0583 0,9119 0,9583 1,0532 1,0347 0,9666 0,9701 1,0205 1,0249
^4ИСТ 0,041 0,082 0,123 0,164 0,205 0,246 0,287 0,328 0,369 0,410 0,451
г04Лх. 0,946 1,327 1,196 1,030 1,083 1,190 1,169 1,092 1,096 1,153 1,158
Трапеция 5 Г05 °- 44; х.=0,82; At. 9 О 1.8 ист 50,4 =0,036
1,8 3,6 5,4 7,2 9 10,8 12,6 14,4 16,2 18 19,8
Ах. 0,8981 1,1740 0,9993 0,9127 1,0125 1,0552 0,9852 0,9668 1,0136 1,0205 0,9890
0,036 0,072 0,108 0,144 0,180 0,216 0,252 0,288 0,324 0,360 0,396
г05Ах, -0,569 -0,517 -0,440 -0,402 -0,446 —0,464 —0,433 -0,425 -0,446 -0,449 -0,435
Трапеция 6 '06= “°- 18; х.=0,83; At. 6 >6 _ 2,0 чет 60,8 =0,033 с
2,0 4,0 6,0 8,0 10,0 12,0 14,0 16,0 18,0 20,0 22,0
Ах. 0,9673 1,1522 0,9401 0,9505 1,0552 1,0065 0,9619 1,0117 1,0199 0,9840 0,9936
0,033 0,066 0,099 0,132 0,165 0,198 0,231 0,264 0,297 0,330 0,363
Г06АХ, -0,174 -0,207 —0,169 -0,171 -0,190 -0,181 -0,173 -0,182 -0,184 -0,177 -0,179
438
Продолжение табл. 5.6
Трапеция 7 Г07“=-°- [2; ),56; Д<7 4,( ист 108 L-0.037 С
4,0 8,0 12,0 16,0 20,0 24,0 28,0 32,0 36,0 40,0 44,0
1,1527 0,9492 1,0093 1,0070 0,9905 1,0052 0,9998 0,9970 1,0030 0,9988 0,9993
^2ИСТ 0,037 0,074 0;111 0,148 0,185 0,222 0,259 0,296 0,333 0,370 0,407
г07Лх, -0,187 -0,114 -0,121 —0,121 -0,119 -0,121 -0,120 -0,120 -0,120 -0,120 —0,120
Трапеция 8 ’’ов—° 04; х8= 0.74; AG • _ 1.0 ист 27/ -=0,037
1.0 . 2,0 3,0 4,0 5,0 6,0 7,0 8,0 9,0 10,0 11,0
Аи, 0,5304 0,9345 1,1407 1,1613 1,0723 0,9693 0,9188 0,9347 0,9870 1,0320 1,0452
0,037 0,074 0,111 0,148 0,185 0,222 0,259 0,296 0,333 0,370 0,407
г08Ах. -0,021 -0,037 —0,046 -0,046 —0,043 -0,039 -0,037 —0,037 -0,039 -0,041 -0,042
Пример 5.11. По передаточной функции разомкнутвй САР
U7 ( х 0,0035s2 + 0,37s + 9,5
(S) 0,00001s4 + 0,00103s3 + 0,02715s2 + ’ + 1,1225s + 1,315
(5.147) и действию единичного управляющего сигнала g(t) = l[t] построить переходный процесс x(f).
Подставив в выражение (5.147) s = /<в, вычислим логарифмические амплитудную и фазовую частотные характеристики разомкнутой системы W(/со), которые изображены на рис. 5.21. Нанесем их в линейном масштабе в координатах U, jV на номограмму для получения /?(<о) (рис. 5.22). Тогда по
Рис. 5.24. Построение результирующего переходного процесса по отдельным составляющим (трапециям) для системы, приведенной в примере 5.11: кривые 1—8—соответственно трапециям 1—8; кривая 9—результирующий переходный процесс
точкам пересечения 1Г(/со) с кривыми номограммы найдем числовые значения Л(ы). Определенную таким образом вещественную частотную характеристику замкнутой системы построим на рис. 5.23. Разобьем ее на восемь трапеций и с помощью формулы (5.133) и приведенных шести процедур составим табл. 5.6, по которой иа рис. 5.24 для каждой из трапеций определены составляющие переходного процесса и весь результирующий переходный процесс системы.
Для оценки точности графоаналитического способа построения переходного процесса нз выражения (5.147) определим
. 0,0035s2 + 0,37s + 9,5
Л (SJ =0,00001s4 + 0,00103s3 + 0,03065s2+X + 1,4925s 4- 10,815
X у- (5.148)
и составим дифференциальное уравнение относительно x(t), решая которое, получим
х (t) = 0,878 — 0,685е-8’3* + 0,0065е-8519< —
- 0,253е~4,42< sin (38,7/ + 0,913). (5.149)
Числовые значения х(/), вычисленные по формуле (5.149), нанесены точками на рис. 5.24. Как видно, точные н приближенные значения x(t) практически совпадают, что указывает иа целесообразность графоаналитического способа определения переходного процесса, так как на его построение затрачивается мало времени.
Пример 5.12. По Ттерёдаточиой функции разомкнутой системы
(s\ _.____________s ~Ь *’47___________
' ' 0,01 Is3 4- 0,09s2 4- 0.73s 4-1,07
(5.150)
439
Рис. 5.25. Номограммы для определения характеристики /?(<о) по амплитудно-фазовой частотной характеристике W(ja>) (пример 5.12)
построить переходный процесс, если на нее действует сигнал возмущения
F (s) = (1 — e-0,15s)/s. (5.151)
Подставив в выражение (5.150) s = /со, получим амплитудно-фазовую частотную характеристику 47(/со). Нанесем ее иа номограммы для получения вещественной R (со) (рис. 5.25) и миимой S(co) (рис. 5.26) частотных характеристик. По точкам пересечения 47(/со) с кривыми но-могоамм найдем числовые значения R(to) и 8(со), а по ним иа рис. 5.27, а, б построим соответственно вещественную и мнимую частотные характеристики. Эти характеристики для сигнала возмущения J?r(<o) и Sf(co) соответственно приведены
на рнс. 5.27, в, г. Обобщенная вещественная частотная характеристика в рассматриваемом случае
R' (e>) — R (<о) Rf (<о) - S (e>) Sf (<>). (5.152)
По формуле (5.152)1 и кривым (рис. 5.27, а—г) на рис. 5.28 построена характеристика ^'(<о). Разобьем ее иа семь трапеций. Для каждой из них в табл. 5.7 приведены составляющие переходного процесса, а иа рис. 5.29 построены составляющие и результирующий переходный процесс системы.
На рис. 5.29 штриховой линией показано точное значение переходного процесса, полученное путем приведения выражения
у _________________s + 1,47__________х
w 0,01 Is8 + 0,09s* + 1,73s + 2,54
1—e~0,1St s
(5.153)
440
Таблица 5.7
Значения составляющих переходного процесса для примера 5.12
Трапеция 1 ’’о;”2- 1 2 17; х.=0.63; Д/. =-£=- 1 'ист 16,4 =0,073 с
^’табл AXi ^*ист Г01АХ, 1.2 0.5890 0.073 1,278 2.4 0.9999 0.146 2,170 3.6 1.1576 0.219 2,512 4,8 1.1180 0,292 2,426 6.0 1.0096 0.365 2.191 7,2 0.9409 0.438 2,042 8.4 0.9441 0.511 2.049 9,6 0,9859 0.584 2,139 10.8 1,0188 0.657 2.211 12,0 1,0232 0,730 2,220 13,2 1.0099 0,803 2,191
Трапеция 2 г02=-0,43; х2=0,67; At 2.0 ист 30 -=0,067 с
^2табл AXs ^2ист г02АХ2 2,0 0,9055 0.067 -0,389 4,0 1,1625 0.134 -0,500 6,0 0,9947 0.201 -0,428 8.0 0.9328 0.267 -0,401 10.0 1.0109 0,335 -0,435 12,0 1,0276 0,402 -0,442 14.0 0.9940 0,469 —0,427 16.0 0,9915 0.536 -0,426 18.0 0.9994 0,602 -0,430 20.0 1.0002 0.670 -0,430 22,0 1.0049 0,737 -0,432
Трапеция 3 г03=—0,15; х3 = 2 П 0,74; Д/3 =5777=0,050 с 3исТ 40,4
*•» а» *•» о ш w S3 в: £ н V н 91 « & 2,0 0.9345 0.050 —0,140 4,0 1,1613 0.100 -0,174 6.0 0.9693 0.150 -0,145 8.0 0.9347 0.200 0,140 10.0 1.0320 0,250 -0,155 12.0 1.0254 0.300 -0,154 14,0 0.9770 0.350 -0,147 16,0 0.9916 0.400 -0,149 18.0 1,0119 0.450 -0,152 20.0 1,0017 0.500 -0,150 22,0 0.9967 0.550 -0,150
Трапеция 4 г04 0-.12; х4= 0,78; Д14 =•^•=0.023 с ист 87,0
^4табл Ах< ^4ист '•(иЧ 2.0 0,9493 0.023 -0,114 4,0 1.1584 0,046 -0,139 6,0 0.9554 0.069 -0,115 8.0 0.9399 0.092 -0,113 10.0 1.0442 0.115 -0,125 12,0 1.0198 0.138 -0,122 14.0 0.9683 0.161 -0,116 16.0 0.9984 0.184 -0,120 18.0 1.0182 0.207 —0,122 20.0 0.9957 0.230- -0,119 22.0 0.9921 0.253 -0,119
Трапеция 5 ’’os—1.21; xs= 0,52; Д/в 51 , 0.6 1СТ 9,2 =0,065 с
o’ ел*" СЛ*“ ей ж $ н »*п * 5» х М 91 £ ь 0.6 0.2866 0,065 -0,347 1.2 0.5593 0.130 —0,678 1.8 0.7790 0.195 -0,943 2.4 0.9519 0.260 -1,152 3,0 1,0687 0,325 —1,293 3.6 1.1308 0,390 —1,368 4.2 1,1462 0.455 —1,387 4.8 1,1277 0.520 —1,365 5.4 1.0897 0,585 —1,319 6.0 1,0455 0.650 -1,265 6,6 1,0059 0.715 —1.17
Трапеция 6 roe=-o,38; xe= 0,25;. Д#й ei _ 0.4 ст 4.8 =0,083 с
^6табл Ах. ^*ист '06Ах, 0,4 0.1585 0,083 -0,060 0.8 0,3123 0,166 -0,119 1.2 0.4578 0.249 -0,174 1.6 0,5909 0.332 -0,225 2,0 0,8090 0,415 -0,269 2.4 0,8099 0.498 -0,308 2,8 0,8931 0.581 -0,339 3.2 0.9580 0.664 -0,364 3.6 1.0058 0,747 -0,382 4.0 1.0383 0,830 -0,395 4,4 1.0573 0.913 -0,402
441
Продолжение табл. 5.7
Трапеция 7
2.0 г„=0,12; х.=0,73; At, =-^-=0,032 с 07 7 'ист 63.2
2,0 4,0 6,0 8.0 10.0 12,0 14.0 16,0 18.0 20.0 22.0
тао л 0,9304 1,1618 0.9727 0,9338 1,0297 1,0270 0,9795 0,9907 1.0099 1.0022 0.9980
0,032 0,064 0,096 0.128 0.160 0,192 0.224 0,256 0,288 0,320 0.352
0,112 0.139 0.117 0,112 0.124 0,123 0.118 0.119 0.121 0,120 0.120
к линейному дифференциальному уравнению. Его решение, дает
х (t)= 0,578 + 0,046е-1,58< + 0,652е~3>32/ X
X cos (11,6/+ 165°) —
— {0,578 + 0,046е_1'58(<“°’15) + 0,652 X
X е~3,32<<-0’15) cos [11,6 (/ — 0,15) +
+ 165°]} 1 [/ - 0,15]. (5.154)
Как видно, приближенное графоаналитическое решение и точное аналитическое решение достаточно близко совпадают друг с другом.
Рнс. 5.26. Номограмма для определения характеристики S(w) по амплитудно-фазовой частотной характеристике lF(/<o) (пример 5.12)
442
Рис. 5.27. Частотные характеристики замкнутой системы и возмущений (пример 5.12):
а — вещественная собственной системы; б — мнимая собственной системы; в — вещественная составляющая для возмущения (со); г — мнимая составляющая для возмущения S? (со)
Рис. 5.28. Обобщенная вещественная частотная характеристика R'(&) с разбивкой ее на семь трапеций
443
I
Рнс. 5.29. Построение результирующего переходного процесса по отдельным составляющим (трапециям) для системы, приведенной в примере 5.12:
кривые 1—7—соответственно трапециям 1—7; кривая 8—результирующий переходный процесс
-л* -за -зп -at -zoo -ио -га -zoo -по -160 -но -по -юв -ю -о» -ы о
Рис. 5.30. Логарифмическая амплитудно-фазовая частотная характеристика разомкнутой системы (пример 5.13), нанесенная на номограмму рис. 5.17
444
Рис. 5.31. Вещественная частотная характеристика замкнутой системы (пример 5.13) с разбивкой на трапеции
реходного процесса системы по ее составляющим (трапециям):
кривые 1— 6—соответственно трапеции 1—6; кривая 7—результирующий переходный процесс
1т,дб
20
16
12
8
4
О
-6
-8
-12
-16
-28
-360 -320 -300 -280 -260 -260 -220 -200 -130 -160
-160 -120 -108 -80 -60 -60 -20 8
Рис. 5.33. Логарифмическая амплитудно-фазовая частотная характеристика разомкнутой системы, нанесенная на номограмму рис. 5.18 (пример 5.14)
445
Таблица 5.8
Значения составляющих переходного процесса для примера 5.13
Трапеция 1 го1 = -0,05; х,= 0.25; Д4] 0.6 ист 4,0 =0,150 с
0.6 1.2 1.8 2.4 3.0 3.6 4,2 4,8 5,4 6,0 6.6
Ли, 0.2361 0,4578 0.6520 0.8099 0,9278 1.0058 1.0493 1.0659 1.0645 1.0540 1.0413
0,150 0.300 0.450 0,600 0,650 0,800 0,950 1,100 1.250 1.500 1.650
r01Axt -0,012 -0,023 —0,033 -0,040 -0,046 -0,050 -0,052 -0,053 -0,053 -0,053 -0,052
Трапеция 2 гм = 1.00; х2=0 1.2 24! Л/2ист=2ЗД =0,041 с
1.2 2.4 3.6 4,8 6,0 7,2 8,4 9,6 10.8 12,0 13,2
Ах, 0.4542 0.8041 0.9997 1,0609 1,0511 1.0299 1.0238 1.0276 1.0267 1.0172 1.0047
^2ист 0.041 0.082 0.123 0,164 0,205 0.246 0,287 0,328 0.369 0,410 0.451
Г02ЛХг 0.454 0.804 1.000 1,061 1.051 0.030 1.024 1.028 1.027 1,017 1.005
Трапеция 3 гм=0.33; х,=0,62; Д*. 03 3 Зист 47,0 =0,034 с
1.6 ' 3,2 4.8 6,4 8,0 9.6 11.2 12,8 14.4 16,0 17,6
Лх3 0.7484 1.1293 1.1196 0.9756 0.9375 0.9841 0.0213 1.0146 1,0001 0,9982 0.9970
/зист 0.034 0.068 0.102 0.136 0,170 0.204 0,238 0.272 0,360 0.340 0,374
гОЗАх3 0.247 0.373 0.369 0.322 0,309 0.325 0.337 0.335 0,330 0,329 0,329
Трапеция 4 ГО4=~0.13! Х4== 0,81; Д(4 =-^п'=0‘023 с нет 69.0
^4табл 1.6 0.819*9 3.2 1.1689 4.8 1.0740 6.4 0.9217 8.0 0.9456 9.6 1.0398 11.2 1.0424 12,8 0,9814 14,4 0.9671 16.0 1,0060 17,6 1.0236
^4нст г04Ах, 0.023 -0,107 0,046 -0,152 0.069 -0,140 0.092 -0,120 0.116 —0,123 0.138 -0,135 0,161 -0,136 0,184 -0,128 0.207 -0,126 0,230 -0,131 0,253 —0,133
Трапеция 5 ros'=~°-15: 0,84; Д4, =-Snr=°.<»8 с ист 88,0
1.6 3.2 4.8 6.4 8,0 9,6 11,2 12.8 14.4 16.0 17,6
0.8307 1,1722 1.0644 0.9163 0.9528 1,0480 1.0386 0.9722 0,9679 1.0146 1,0251
0.018 0.036 0,054 0,072 0.090 0,108 0,126 0.144 0.162 0.180 0,198
r05AXs 0.125 0,176 0,160 0.137 0.143 0,157 0,156 0.146 0.145 0.152 0.154
Трапеция 6 foe==*'0.3; xg=0 2 ,65; де. =——=о,о1з с “ист 154,0
2 4 6 8 10 12 14 16 18 20 22
Ах« 0.8986 1.1618 1.0007 0.9340 1.0055 1.0258 0.9983 0,9937 0.9973 0.9981 1.0054
0.013 0.026 0.039 0.052 0.065 0.078 0.091 0,104 0.117 0.130 0.143
Г06АХ, -0,270 -0,349 -0,300 -0,280 -0,302 -0,308 -0,299 -0,298 -0,299 -0,299 -0,302
446
Таблица 5.9
Значения составляющих переходного процесса для примера 5.14
О fi rni = ~0.16; х,=*0,00; Д<, =—=«0,083 с
01 1 ‘ист 7,2
^'табл ^‘ист г01Ч 0,6 0,1890 0,083 —0,030 1.2 0,3671 0.166 -0,059 1.8 0.5246 0,249 -0,084 2,4 0.6548 0,332 -0,105 3.0 0,7546 0,415 -0,121 3,6 0,8244 0,499 -0,132 4,2 0.8681 0.581 —0,139 4.8 0.8912 0.664 -0,143 5.4 0.9006 0.729 -0,144 6,0 0.9028 0.830 —0,144 6,6 0.9029 0.891 -0,145
Трапеция 2 Г02 = —1 ,64; х2= 0,53; Д«2 =“Т-=0,074 с ист 13,6 4
1 2 3 4 5 6 7 8 9 10 11
л„. 0,4701 0,8466 1.0728 1.1475 1.1157 1.0437 0.9818 0.9571 0.9636 0.9826 0.9975
<2ИСТ 0.074 0.148 0.222 0.296 0.370 0.444 0.518 0.592 0.666 0.740 0.814
г0гЧ -0,771 -1,388 -1,759 -1,882 -1,830 -1,712 — 1,610 -1,570 -1,580 -1,611 -1,634
Трапеция 3 Г03 = -0-62: ’,з== 0,96; Д*, 3 =ТПГ=0.070 с ист 14.2
^’табл 1 0,5915 2 1,0108 3 1,1742 4 1.1297 5 0.9979 6 0.9116 7 0.9200 8 0.9906 9 1.0523 10 1.0604 11 1.0189
0.070 0.140 0,210 0.280 0.350 0.420 0.490 0.560 0.630 0.700 0,770
г0зЧ -0,367 -0,627 -0,728 -0,700 —0,619 —0,565 -0,570 -0,614 -0,652 -0,657 —0,632
Трапеция 4 гм=1,2; х4=о 1 2 ,88; Д/, =-^-=0.060 с 4ист 20
1.2 2.4 3.6 4.8 6.0 7.2 8,4 9.6 10.8 12,0 13.2
0,6691 1.0861 1.1720 1,0520 0.9266 0.9162 0.9930 1.0570 1.0468 0.9912 0.9558
Чет 0.060 0,120 0,180 0,240 0.300 0.360 0,420 0,480 0.540 0.600 0.660
ПмЧ 1.204 1.955 2,110 1.894 1.668 1.649 1.787 1.903 1.884 1.784 1.720
Трапеция 5 1 2 rnR=~0,62; хк«0,89; Affi =-^±-«0,068 с Оо О Чист 17,6
1.2 2,4 3,6 4.8 6,0 7,2 8,4 9.6 10.8 12.0 13.2
0.6745 1,0889 1.1770 1,0478 0.9249 0.9175 0.9963 1,0532 1.0453 0,9879 0.9546
0,068 0.136 0,204 0.272 0,340 0,408 0.476 0.544 0.612 0.680 0.740
г05Лх5 0.418 0.675 0,730 0.650 0.573 0.570 0.618 0,653 0.648 0,612 0.592
Пример 5.13. Построить характеристику переходного процесса в многоконтурной САР (пример 4.17) и определить основные показатели качества, если на ее вход поступает единичный управляющий сигнал. Логарифмические амплитудные, и фазовые частотные характеристики всей разомкнутой системы перенесем с рнс. 4.12,6 на номограмму рис. 5.30. В результате этого получим вещественную частотную харак
теристику (рнс. 5.31). Разобьем ее на шесть трапеций и для каждой нз них с помощью йх-функций вычислим составляющие переходного процесса. Соответствующие числовые значения для каждой нз трапеций приведены в табл. 5.8, по данным которой на рис. 5.32 построены составляющие и весь переходный процесс в целом. После этого нетрудно найти основные показатели качества: максимум
447
Рис. 5.34. Мнимая частотная характеристика замкнутой системы (пример 5.14) с разбивкой ее на трапеции
перерегулирования ст = 9 %; время протекания переходного процесса t? = 0,35 с; максимальная скорость отработки регулируемой переменной =20 условных
единиц в секунду.
Пример 5.14. Построить переходный процесс относительно сигнала ошибки в статической САР (пример 4.16) при g(t) = = 1[1]. Логарифмические амплитудные н фазовые частотные характеристики этой системы построены на рис. 4.9, в. Перенесем нх на номограмму рнс. 5.33 и по ней построим штриховой линией S (<о) (рис. 5.34). Для того чтобы пользоваться таблицами /гх-функций и вычислять составляющие переходного процесса по формуле (5.137), необходимо найти характеристику [шЗ(ш)]. Она изображена на рнс. 5.34 сплошной линией н разделена на пять трапеций. По трапециям н йх-функцням в табл. 5.9 приведены составляющие переходного процесса, а на рнс. 5.35 — переходный процесс e(t). При этом видно, что первый максимум наступает прн tm = 0,125 с; время протекания переходного процесса /Р = 1,7 с; максимальная скорость отработки сигнала 16,8 ед/с; период колебаний /0 = 0,45 с-1. Логарифмический декремент затухания находится по формуле
d. = In -^2- = In = 0,854.
8m+l 0.4
Число колебаний в системе N = 3,5.
Пример 5.15. Построить переходный процесс в следящей системе интегрирующего типа (пример 4.20). Воспользуемся для этого формулой (5.133). Нерегулярная составляющая процесса xH(t) = 90,8/. Для нахождения регулярной составляющей
Xp(f) построим вещественную частотную характеристику замкнутой системы Ду(ы). Перенесем логарифмическую амплитудную |Фи(/ш)| и фазовую arg[Op(/<o)] частотные характеристики, показанные на рнс. 4.21,6, на номограмму рис. 5.36, с помощью которой получим Яи(<о) (рнс. 5.37). Разобьем ее на четыре трапеции н составим табл. 5.10 для составляющих Хр(0- На рис. 5.38, а штриховой линией показана регулярная составляющая переходного .процесса. Нерегулярная составляющая хн(/) показана штриховой линией на рис. 5.38, б, а сплошной линией — суммарная кривая переходного, процесса х(1) = х„(/)4- х₽(0- При этом видно, что в рассматриваемой следящей системе в отличне от идеального интегратора существует ошибка интегрирования, относительная величина которой уменьшается с ростом времени t.. Так, например, при t = 1 с она составляет 1 %. Если необходимо уменьшить погрешность интегрирования, то в следящей системе следует увеличить коэффициент усиления в обратной связи k$.
Пример 5.16. Построить переходный процесс в системе (пример 4.21) по номограмме 5и(ш). Логарифмические амплитудные н фазовые частотные характеристики из рис. 4.22 перенесены на номограмму рис. 5.39 н по ней получены характеристики 5и((о) н [<оЗу(ш)], которые построены на рнс. 5.40. Разобьем характеристику
Рис. 5.35. Построение результирующего переходного процесса для системы (пример 5.14) по ее составляющим (трапециям) : кривые 1—5—соответственно трапеции 1—5; кривая б—результирующий переходный процесс
448
Рис, 5.36. Номограмма для определения характеристики (рис. 5.19) с нанесен ной на ней логарифмической амплитудно-фазовой частотной характеристикой (прн мер 5.15)
15 Ю. И, Топчеев
449
Таблица 5.10
Значения составляющих переходного процесса для примера 5.15
Трапеция 1 го1=О,О2; Х| = =0; AL *ИС =-^-=0,010 с т 20
0,2 0,4 0.6 0,8 1,0 1,2 1,4 1.6 1,8 2.0 2.2
0.0637 0.1269 0,1890 0,2502 0,3096 0,3671 0,4223 0,4748 0,5246 0,5712 0,6147
0,010 0.020 0,030 0,040 0,050 0,060 0,070 0,080 0,090 0,100 0,110
г01Лх, 0,001 0,003 0.004 0,005 0.006 0,007 0,008 0,009 0,010 0,011 0,012
Трапеция 2 го2=О, 14; х2 = 0.31; Д/2 = -^- *нст 65 =0,012 с
0,8 1,6 2,4 3,2 4,0 4,8 5,6 6,4 7,2 8,0 8,8
0,3271 0,6178 0,8443 0,9940 1,0707 1,0913 1,0784 1,0533 1,0316 1.0192 1,0156
*2нст 0,012 0,024 0,036 0,048 0,060 0,072 0,084 0,096 0,108 0,120 0,132
г02^х2 0,406 0,086 0,118 0.139 0,150 0.153 0,151 0,147 0,144 0,143 0,142
Трапеция 3 г03 = -0,87; х3 = 0,52; Д13 1,6 ист 159 =0,010 с
1.6 3,2 4.8 6.4 8,0 9.6 11,2 12,8 14,4 16,0 17,6
0,7078 1,0953 1,1277 1.0162 0,9599 0,9748 0,9974 1,0009 1,0034 0,0101 1,0076
*3 0,010 0,020 0,030 0,040 0,050 0,060 0,070 0,080 0,090 0,100 0,110
r03flx3 -0,616 —0,953 -0,981 —0,884 -0,835 -0,848 -0,868 -0,871 -0,873 —0,879 —0,877
Трапеция 4 гп.=-0,2; х.=0,61; Д*. =^-= °* ’ ' 4 4ИСТ 260 =0,008 с
^4табл 2.0 4,0 6,0 8,0 10,0 12.0 14,0 16,0 18,0 20,0 22,0
^х, 0,8815 1,1590 1,0167 0,9391 0,9946 1,0197 1,0037 0,9997 0,9962 0,9931 1,0034
^4ИСТ 0,008 0,016 0,024 0.032 0.040 0,048 0,056 0,064 0,072 0,080 0,088
—0,176 —0,232 -0,203 -0,188 -0,199 —0,204 —0,201 —0,200 —0,199 -0,199 -0,201
Таблица 5.11
Значения составляющих переходного процесса для примера 5.16
Трапеция 1 г01 0,07; х1 = о; AL XHC1 0,6 =28,57 с
0,021
0.6 1.2 1,8 2.4 3.0 3,6 4,2 4,8 5,4 6,0 6.6
ЛХ1 0,1890 0,3671 0,5246 0,6548 0,7546 0,8244 0,8681 0,8912 0,9006 0.9028 0,9029
^ист 28,6 57,7 85,7 114,3 142,9 171,4 200,0 228.6 257,1 285,7 314,3
г01Лх, -0,013 —0,026 —0,037 —0,046 -0,053 -0,058 —0,061 —0,062 -0,063 —0,063 —0,063
Трапеция 2 0 8 г02 = -0.43; Х2=В,54: Д^-^-20,51 С
0,8 1,6 2,4 3,2 4,0 48 5.6 6,4 7,2 8.0 8.8
^xs 0,3834 0,7208 0,9610 1,1028 1.1494 1.1272 1,0713 1.0101 0,9702 0,9543 0.9597
^2ИСТ 20,5 41,0 61,5 82,0 102,6 123,1 143.6 164,1 184,6 205,1 225.6
Г02^х2 -0,165 -0,310 -0,413 —0,474 -0,494 -0,485 -0.461 -0,434 -0,417 -0,410 -0,413
450
Продолжение табл. 5.11
Трапеция 3 ГОЗ=()’3 Г; х, = 0,75; Д*, 6 -’ИС 1,2 Т= 0,061 = 19,67 с
1,2 2.4 3.6 4,8 6,0 7,2 8.4 9.6 10,8 12,0 13.2
Лх3 0,6280 1,0454 1,1720 1,0915 0,9659 0,9159 0,9555 1,0211 1.0473 1,0248 0.9882
19.7 39,3 59,0 78,7 98.4 118,0 137,7 157,4 177,0 196,7 216.4
Г03^Из 0,232 0,387 0,434 0,404 0,357 0,339 0,354 0,378 0,388 0,379 0,366
Трапеция 4 rft4«0,13; х. =0,75; М. 04 4 4ИС 1,6 т 0,081 = 19,75 с
1,6 3,2 4,8 6,4 8,0 9,6 11.2 12,8 19,4 16,0 17,6
ЛХ, 0,7980 1,1600 1,0915 0.9376 0.9357 1,0211 1,0441 0.9995 ,0,9733 0,9930 1,0129
19,8 39,5 59,3 79,0 98,8 118,5 138,3 158,0 177,8 197,5 217.3
nA, 0.104 0,151 0,142 0,122 0.122 0,133 0,136 0,130 0,127 0,129 0,132
Рис. 5.37. Частотная характеристика Rv(a)
[<о5и(<о)1 на четыре трапеции н с помощью табл. 5.11 вычислим составляющие переходного процесса. По этим данным на рис. 5.41 построены составляющие и весь переходный процесс в целом, пользуясь которыми по аналогии с примером 5.14, можно найти основные показатели качества.
Рис. 5.38. Переходный процесс в системе (пример 5.15):
а—регулярная составляющая Хр (по четырем трапециям); б—суммарный процесс с учетом нерегулярной составляющей хи; кривые 1—4—соответственно трапеции 1—4; кривая 5—регулярная составляющая
15»
451
180 ZOO 220 Z40 260 280 300 320 340 ± <f,°
Рис. 5.39. Номограмма для определения характеристики Sy (со) (рис. 5.20) с нанесенной иа ней логарифмической амплитудно-фазовой частотной характеристической (пример 5.16)
452
Рис. 5.40. Мнимые частотные характеристики Sy и [wSv] с разбивкой на четыре трапеции (пример 5.16)
4. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ИМПУЛЬСНЫХ ПЕРЕХОДНЫХ ФУНКЦИИ
В случае действия на САР управляющего или возмущающего воздействия сложной формы удобно пользоваться зависимостями, связывающими значение импульсной переходной функции замкнутой системы k3(f) с вещественной R(со) и мнимой S((o) частотными характеристиками.
Передаточную функцию замкнутой системы можно записать в виде
оо
Ф (/со) = \ k3 (/) e~lat dt; (5.155) о
тогда, учитывая, что
Ф (/со) = R (со) + jS (со), (5.156) из выражений (5.150) и (5.151) получим
ОО
7? (со) = $ k3 (/) cos со/ dt\ (5.157) о
оо
S (со) = — \k3 (t) sin at dt. (5.158) • о
Для вычисления интегралов (5.157) и (5.158) функцию k3 представим в виде суммы элементарных
Рис. 5.41. Построение результирующего переходного процесса для системы по ее составляющим (трапециям) для системы, приведенной в примере 5.16:
кривые 1—4—соответственно трапеции 1—4; кривая 5— результирующий переходный процесс
трапеций ki(t), одна из которых изображена на рис. 1.53. В этом случае формулы (5.157) и (5.158) можно переписать в виде
(со) = У ^&j(0cos®^ (5.159) i-1 0
И
S(co) = — У ^kt(f)sinwtdt. (5.160) f-i oJ
Рнс. 5.42. Импульсная переходная функция сложной формы k(t), разбитая иа пять трапеций
453
-34-0 -320 -300 -280 -Z60 -240 -ZZO -ZOO -160 -160 -140 -1Z0 -100 -80 -60 -40 0°
Рис. 5.44. Номограмма для определения вещественной частотной характеристики замкнутой системы с нанесенной иа ней логарифмической амплитудно-фазовой частотной характеристикой разомкнутой системы (пример 5.17)
454
Рис. 5.45. Номограмма для определения мнимой частотной характеристики замкнутой системы с нанесенной на ней логарифмической амплитудно-фазовой частотной характеристикой разомкнутой системы (рис. 5.17)
В выражениях (5.159) и (5.160) введем следующие обозначения:
оо
Г/ (со) = ^ki (0 COS (£)t dt\ о
оо
st (со) = — kt (t) sin at dt.
о
(5.161)
Подставив в выражения (5.161) соотношение (1.353), получим r,W=feAl(^)(^); |
X k ati ) I co A; J ’
(5.162)
rnp t _ toi + tdi . * tol — tdi где t{— g , &i— g
Если выражения (5.162) подставить в формулы (5.159) и (5.160), то найдем
R«»)-Xl^l(^)(^);
/=1
(5.163)
п
5(®)=£{--^-+[млх
i=l
х(^)(^)}- <5.164)
По формулам (5.163) и (5.164) вычисляют вещественную и мнимую частотные характеристики замкнутой системы, если задана импульсная переходная функция k3(t).
Пример 5.17. Построить переходный процесс в САР, если иа ее вход поступает импульсная переходная функция сложной формы k(t) (рис. 5.42).
На рис. 5.43 изображены логарифмические амплитудная | W(ja>) | и фазовая —arg[lF(/<))] частотные характеристики рассматриваемой разомкнутой системы. Перенесем эти характеристики на номограммы рис. 5.44 и 5.45 и получим кривые R(a>) и S(co), которые соответственно изображены на рис. 5.46, а, б.
455
СП о
Таблица 5.12
Значения вещественной Rj (®) и мнимой Sj (®) частотных характеристик сложного воздействия для примера 5.17
Параметры Трапеция 1 Трапеция 2
ftoi = —9,5 /.=0,024 Д. =0,016 ^02= — 7 <2=0,082 Д2=0,018
(0 5 10 15 20 30 40 5 10 15 20 30 40
0,12 0,24 0,36 0,48 0,72 0,96 0,41 0,82 1,23 1,64 2,46 3,28
(O&i 0,08 0,16 0,24 0,32 0,48 0,64 0,09 0,18 0,27 0,36 0,54 0,72
sin ш// &ti 0,9976 0,9904 0,9785 0,9620 0,9158 0,8533 0,9722 0,8916 0,7663 0,6083 0,2561 —0,0421
sin oAf <oAi 0,9989 0,9957 0,9904 0,9830 0,9620 0,9331 0,9987 0,9946 0,9785 0,9785 0,9521 0,9158
Rfi (®) -0,2272 —0,2248 —0,22.10 —0,2156 —0,2009 -0,1815 -0,5573 —0,5090 —0,4345 -0,3417 -0,1400 0,2221
(0 -1,9 -0,95 -0,6333 -0,475 . —0,3167 -1,4 -0,7 -0,4667 -0,35 —0,2333 —0,2333 -0,175
COS (Dtj 8,2734 4,0472 2,5997 1,7479 1,0442 0,5974 2,237 0,8320 0,2717 -0,0422 —0,3157 —0,3020
Sft (<o) 0,0157 0,0312 0,0463 0,0608 0,0877 0,1104 0,1176 0,2250 0,3126 0,3737 0,4058 0,3338
Параметры Трапеция 3 Трапеция 4
feoa = = 11 «3 = 0,128 Дз = 0,018 =25 <«= 0,227 Д<= 0,040
(0 5 10 15 20 30 40 5 10 15 20 30 40
Ш<,- 0,64 1,28 1,92 2,56 3,84 5,12 1,135 2,27 3,405 4,54 6,81 9,08
<оД/ 0,09 0,18 0,27 0,36 0,54 0,72 0,2 0,4 0,6 0,8 1,2 1,6
sin wti <s>ti 0,9331 0,7485 0,4894 0,2146 -0,1674 —0,1793 0,7987 0,3372 —0,0765 -0,2170 0,0738 0,0372
sin шД/ шД/ 0,9987 0,9946 0,9879 0,9785 0,9521 0,9158 0,9933 0,9735 0,9411 0,8967 0,7767 0,6247
Rfi (го) 1,3121 1,0482 0,6807 0,2957 —0,2244 -0,2312 4,5023 1,8629 —0,4086 -1,1043 0,3253 0,1319
(0 2,2 1,1 0,7333 0,55 0,3667 0,275 5 2,5 1,6667 1,25 0,8333 0,625
COS wti <oti 1,2533 0,2240 -0,1782 —0,3264 —0,1994 0,0774 0,3719 -0,2835 —0,2836 -0,0378 0,1270 -0,1037
§ Sfi(ro) -0,4376 -0,7863 —0,9817 -0,9997 -0,6340 -0,1752 —2,9036 -4,0662 -3,1813 — 1,4424 —0,2735 —0,9926
Параметры Трапеция 5 Параметры Трапеция 5
ftos= —12,5 /s=0,327 Дз=0,031 ^05== —12,5 <5=0,327 Д5=0,031
G) 5 10 15 20 30 40 Rfi (го) —2,4850 0,1577 0,7888 -0,1486 0,1349 —0,1172
ш/j <оД/ 1,635 0,155 3,27 0,31 4,905 0,465 6,54 0,620 9,81 0,930 13,08 1,24 koi ш -2,5 — 1,25 -0,8333 —0,625 —0,4167 -0,3125
sin oti <S>ti 0,6104 -0,0392 -0,2001 0,0388 —0,0383 0,0376 COS oti (Otj -0,0392 -0,3033 0,0390 0,1479 -0,0945 0,0666
sin coAf <оД/ 0,9960 0,9841 0,9644 0,9372 0,8620 0,7627 Sfi (co) 2,6596 2,4700 0,6796 0,0584 0,0750 0,1049
Рис. 5.46. Частотные характеристики замкнутой системы (пример 5,17):
а—вещественная Я; б—мнимая S; в—вещественная для возмущения а—мнимая для возмуще-
ния Sf
458
Таблица 5.13
Значения составляющих переходного процесса для примера 5.17
Трапеция 1 г01 =23,67; х,=0 77; А/. 1 и< = -^-=0,063 с :т 15,8
1,0 2,0 3,0 4,0 5,0 6,0 7,0 8,0 9,0 10,0 11,0
Лх, 0,5391 0,9455 1.1476 1,1592 1,0628 0,9590 0,9140 0,9392 0,9962 1.0413 1,0480
^ист 0,063 0.126 0,189 0,252 0,315 0.378 0,441 0,504 0,567 0,630 0,693
'оА, 13,134 22,380 27.164 27,438 25,156 22,700 21.634 22,231 23,580 24,648 24,806
Трапеция 2 Г02 =4; х2 = =0,97; А/ =0,055 с ‘‘ист
^2табл 1.0 2,0 3,0 4,0 5,0 6,0 7,0 8,0 9,0 10.0 11.0
0,5943 1,0128 1,1735 1,1270 0.9962 0.9099 0,9213 0.9935 1,0562 1,0604 1.0154
/о ‘‘ист 0,055 0,110 0,165 0,220 0,275 0,330 0,385 0,440 0,495 0,550 0,605
Г02^Х2 2,377 4,051 4,694 4.508 3,985 3,640 3,685 3,974 4,225 4,242 4,062
Трапеция ,5; х3=0 1.6 =0,044 с
3 г03 = 12 ,72; at, =-757 °ИСТ ЗЬ
1,6 3,2 4,8 6,4 8,0 9.6 11.2 12,8 14,4 16,0 17,6
0,7870 1.1542 1,0993 0,9471 0,9331 1,0113 1,0415 1,0059 0,9791 0,9903 1,0066
^3ИСТ 0,044 0,088 0,132 0,176 0,220 0,264 0,308 0,352 0,396 0,440 0,484
гОЗЛх3 10,218 14,428 13,741 11,839 11,664 12,641 13,019 12,574 12,239 12,379 12,583
Трапеция 1.6 = 0,033 с
4 r04e2’b7i X4=U’94’ .““ТйЯ и’ * 4исТ 48,8
^табл 1.6 3,2 4,8 6,4 8,0 9,6 11,2 12,8 14,4 16,0 17,6
0,8662 1,1781 1,0317 0,9034 0,9828 1,0649 1,0126 0,9519 0,9889 1,0379 1,0092
^*ист 0,033 0,066 0,099 0,132 0.165 0,198 0,231 0,264 0,297 0,330 0,363
г04Лх, 3,282 3,146 2,755 2,412 2,624 2,843 2,704 2,542 2,640 2.771 2,695
Трапеция 16; х,=0,97; Д«к 5 5| 1.6 =0,030 с
5 '05 = 1, ICT 54
/к - 1,6 3,2 4,8 6,4 8,0 9.6 11.2 12,8 14,4 16,0 17,6
^Xs 0,8757 1.1790 1,0232 0,9032 0,9935 1,0661 1,0022 0,9504 1,0002 1.0401 0,9999
°ист 0,030 0,060 0,090 0,120 0,150 0,180 0,210 0,240 0,270 0,300 0,330
Г05ЛХ5 1,016 1.368 1,187 1.048 1,152 1,237 1,163 1,102 1,160 1,207 1,160
Трапеция 1,83; хб= 0.6
6 гов=“ =0; Afft =-=—=0,103 С бист 5,8
^®табл 0.6 1.2 1,8 2,4 3.0 3.6 4,2 4,8 5,4 6.0 6,6
^Ха 0.1890 0,3671 0,5246 0,6548 0,7546 0,8244 0,8681 0,8912 0,9006 0,9028 0,9029
^бИСТ 0.103 0,206 0,309 0,412 0,515 0,618 0,721 0.824 0,927 1,030 1.133
г06Лх. -0,346 —0,672 —0,960 -1,198 -1,381 -1,509 -1,589 -1,631 — 1,648 -1,652 -1,652
459
Продолжение табл. 5.13
Трапеция 7
г.7 = —16,83; х7=0,52; Д/7 =-Ц-=о,1О7 с
07 7 7ист 11,2
^7табл ^Х7 ^7ист г07^х7 1.2 0,5593 0,107 -9,413 2,4 0,9519 0,214 -16,020 3,6 1,1308 0,321 -19,031 4,8 1,1277 0,428 -18,979 6,0 1,0455 0,535 -17,596 7,2 0,9774 0,642 -16,450 8,4 0,9591 0,749 -16,142 9,6 0,9748 0,656 -16,406 10,8 0,9937 0,963 -16,724 12,0 1,0007 1,070 -16,841 13,2 1,0008 1,177 -16,843
Трапеция 8 Г08 = ~3 34; х8=0,95; A/g =-^-=0,070 с ист 17,2
втабл 1.2 2.4 3,6 4,8 6,0 7,2- 8,4 9.6 10,8 12,0 13,2
Лх, 0,6876 1,1055 1.1659 1.0290 0,9136 0,9258 1,0178 1,0662 1,0306 0,9697 0,9536
0,070 0.140 0,210 0,280 0,350 0,420 0,490 0,560 0.630 0,700 0,770
г08Лх, —2,297 —3,692 —3,894 -3,437 -3,051 -3,092 -3,399 -3,561 -3,442 -3,239 -3,185
Трапеция 9 Г09=~15 67; х,= 0,84; Д/9 = -^ = 0,054 с ист 22,2
^9табл 1,2 2,4 3.6 4,8 6,0 7,2 8,4 9,6 10,8 12.0 13.2
0.6563 1,0748 1,1735 1,0644 0,9372 0,9132 0,9804 1,0480 1,0512 1,0035 0.9631
^9ИСТ 0,054 0,108 0,162 0,216 0,270 0,324 0,378 0,432 0,486 0,540 0,594
Г09Лх» -10,284 -16,842 -18,389 -16,679 -14,686 -14,310 -15,363 -16,422 -16,472 -15,725 -15,092
Трапеция 10 г010 4; *io“O’9°- =-^=0,045 с ист 44.8
^*°табл 2,0 4.0 6,0 8.0 10.0 12,0 14,0 1б‘,0 18,0 20.0 22,0
^Хю 0,9911 1,1413 0,9220 0,9703 1,0631 0,9845 0,9652 1,0314 1,0082 0,9718 1,0100
^10ист 0,045 0.090 0,135 0,180 0,225 0,270 0,315 0,360 0,405 0.450 0,495
г010Лх1() —3,964 —4,565 —3,688 -3,881 -4,252 —3,938 —3,861 —4,126 -4,033 —3,887 —4,040
Трапеция 11 гои — 2,33: Х11_" 0,96; Д/,. =-^ ,1ист 51 /у = 0,039 с
2,0 4,0 6,0 8,0 10,0 12,0 14,0 16,0 18,0 20,0 22,0
АХ.| 1,0108 1,1297 0,9116 0,9906 1.0604 0,9672 0,9785 1,0395 0,9914 0,9754 1,0252
0,039 0.078 0,117 0,156 0,195 0,234 0,273 0,312 0,351 0.390 0,429
Г011ЛХ|, —2,355 —2,632 -2,124 -2,308 —2,470 -2,254 —2,280 —2,422 -2,310 —2,273 —2,389
Для вычисления характеристики от действия сложного импульсного воздействия Rf(со) и Sf(co) разобьем k(t) на пять трапеций, как это показано на рис. 5.42. Далее, пользуясь формулами (5.158) и (5.159), а также работой [31], составим табл. 5.12, по которой иа рис. 5.46, в и г построены соответственно частотные характеристики Rf(a>) и Sf(co).
Результирующую характеристику S'(co) находим по формуле
S' (со) = R (со) Sf (со) 4- S (со) Rf (со)
с помощью кривых, изображенных на рис. 5.46, а—г. Она построена на рис. 5.47 штриховой линией. С целью возможности использования Лх-фуикций построим (рис. 5.47) сплошной линией характеристику [coS'(co)]. Разобьем ее на 11 трапеций и вычислим составляющие переходного процесса, значения которых сведены в табл. 5.13. По данным последней иа рис. 5.48 построены составляющие переходного процесса и весь переходный процесс x(t). Как видно из рис. 5.48, переходный процесс является достаточно ко-
460
реходного процесса по отдельным составляющим (трапециям) для системы, приведенной в примере 5.17:
кривые 1—11—соответственно трапеции 1 — 11; кривая 12—результирующий переходный процесс
лебательным с относительно невысоки^ логарифмическим декрементом затухания.
Изложенная в п. 3 и 4 настоящей главы методика получения переходных процессов обеспечивает их графоаналитическое построение при любых сложных воздействиях и не требует больших затрат времени проектировщика.
5. ИССЛЕДОВАНИЕ КАЧЕСТВА ДИСКРЕТНЫХ И ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ
Показатели качества дискретных и дискретно-непрерывных САР определяют с помощью выражений вида (5.2) — (5.5), но записанных в формах г- или «-преобразований ( sTa 2 Z — IX
(где z = e и « =
В этом случае формулу (5.2) можно
переписать в форме z-преобразований
X(z) = ^-G(z) +
I MB(z) Е* I Мн (z) 1СЕГ\
+ ~DWF(^+-D(zr <5-165>
или в форме «-преобразований хи=-^аси+
+ ТГ>Г(»)+^- (5.166)
Рассмотрим четыре способа вычисления характеристик переходных процессов по формуле обратного z-преобразования *, т. е.
xm==~§X(z)zK-' dz. (5.167) г
Первый способ, когда интеграл (5.167) вычисляют с помощью вычетов по теореме Коши. В этом случае сумма всех вычетов внутри контура х(«Т0)= £ ResA'(z)zK-1. (5.168) по всем полюсам г1
Второй способ, основанный на разложении функции X(z}lz на простые множители, чтобы обратное z-преобразование каждого из членов, умноженного на z, находилось из таблицы обратных z-преобразо-ваний, приведенных в прил. П-1. 2.
Третий способ, позволяющий функцию X(z) разлагать в ряд по степеням z~‘ (i = 0, 1, ..., п) путем последовательного деления членов. В этом случае частное от деления даст искомую функцию в виде суммы соответствующих составляющих, каждое из которых сдвигается относительно предыдущего на последующий такт квантования То.
Четвертый способ. Представив замкнутую систему в виде дискретных уравнений состояния в форме z-преобразования, можно с помощью
* Интеграл в выражении (5.167) берется по контуру Г, охватывающему особые точки подынтегральной функции в плоскости г.
461
вычислительной процедуры, реализованной на ЭВМ, и получить переходный процесс х(кТ’о) (см. п. 7 настоящей главы).
Намного проще вычислять характеристики переходных процессов, если пользоваться формой «-преобразования. При этом существует несколько способов. Рассмотрим только два из них, которыми наиболее часто пользуются при проектировании.
Первый способ. По частотным функциям разомкнутой системы й7(/й) и номограммам (рис. 5.15— 5.18) определяют вещественную /?(<о) или мнимую S (со) характеристики замкнутой системы. В том случае, когда функцию замкнутой системы можно представить в виде
V(/ш) е ,п
'1ц? (уй) ’ по номограммам рис. 5.19 и 5.20 строят вещественные /?у(й) или мнимые Sv(<o) характеристики. Если их разделить на типовые трапеции, то по частотным характеристикам /?(й), /?v(<ij) можно найти составляющие переходного процесса по формуле п
Л(/иТ0) = ^£[г0^1Х /=1
х/ / sin тисо/То Л ( sin mbiT0 \ /Е- lfiQA
Х( ,^гН' т^Тй )• <5-169)
Если для построения переходного процесса приходится пользоваться характеристиками S(co), Sv (со), to после их разделения на типовые трапеции вычисляют составляющие переходного процесса по формуле
i = l
I г_ „ ! ( cosmaiTo \ ( sin тД/То
+ (-^7Го ) ( т^Тй
(5.170)
Результирующий переходный процесс на единичное ступенчатое воздействие находят с помощью следующего выражения:
х(кГ0)= f Л(тГ0). (5.171) m—1
Второй способ. Разомкнутую частотную характеристику дискретной или дискретно-непрерывной САР можно представить в виде
W (jti) *= ст (/со/ - 77 th -^) ‘ X
Xy-th^-A-*6(l Z о * \ * /
(5.172)
Далее, пользуясь формулой
<5Л73>
и выражением (5.172), получим
Ф(/ш) =
1 о х. * / J
(5.174)
Вместо формулы (5.172) можно пользоваться следующим выражением:
W (&) = ст [ja>I - А (ф _|_ /)-1 х х(Ф-/)]_1-^(Ф+/г1х
Х/(1-&), (5.175)
где / = (Ф — I)A~'b.
Подставив выражение (5.175) в формулу (5.173), найдем передаточную функцию замкнутой системы.
Для вычисления переходных процессов следует находить вещественные или мнимые частотные характеристики 7?(со) =Ре[Ф(/со)] и S(co) = = Im [Ф (/со)] или пользоваться ранее приведенными номограммами. Характеристики применения переходных процессов строят по формулам (5.169) — (5.171), где круговую частоту со заменяют псевдочастотой
462
й. В случае сложной формы воздействия используют формулы
R' (й) — R (й) Rf (й) — S (й) Sf (й); | S' (й) = R (й) Sf (й) + S (й) Rf (й), )
(5.176)
а затем по выражениям (5.169) — (5.171) находят х(кТ0).
Пример 5.18. Построить переходный процесс в дискретно-непрерывной САР четырьмя способами, если ее передаточная функция в разомкнутом состоянии имеет следующий вид:
По определению, имеем
Res X (г) гк-1 = Z = Zi
= lim [(г - 0,0169) X (г) гк-11 =
г->г,
0,1304гк (г + 0,05) (г + 1,065)
\->o™69 (г - 0,2005) (г - 0,6402) X
Х(г-1)
= — 0,0014 (0,0169)к.
Аналогичным образом, определяя вычеты в других особых точках и суммируя их, получим выражение для вычисления переходного процесса:
х (кТ0) = 1 — 0,9964 (0,6402)к +
+ 0,1284 (0,2005)к — 0,0014 (0,0169)к.
0,15z (г + 0,05) (г + 1,065)
П7 (z)________________________________
17 (г-1) (г-0,135) (г-0,0185) •
Для начальных тактовых моментов времени числовые значения переходного процесса приведены ниже.
К 0 1 2 3 4 5 6 7 8 9 10 11 12
х(кТ0) 0,1304 0,3878 0,5968 0,7396 0,8330 0,8932 0,9320|0,9561 0,9714 0,9812 0,9885 0,9926 0,9952
Для нахождения переходной функции замкнутой системы воспользуемся формулой
ф(г)=_У(?)_ = 17 1 + W (г)
0,1304г (г + 0,05) (г + 1,065)
~ г3 —0,8576г2 + 0,1426г —0,0025 ’
(5.177)
При действии на вход системы единичного ступенчатого воздействия имеем
„ 0,1304г (г + 0,05) (г + 1,065)
Л (Z) z3 - 0,8576г2 + 0,1426г - 0,0025 Х
(5.178)
Воспользуемся первым способом. Для этого вычислим корни знаменателя Х(г) и перепишем выражение (5.178) в виде
0,1304г (г + 0,05) (г + 1,065)
(г - 0,0169) (г — 0,2005) (г - 0,6402) X '
Х(г-1)
(5.179)
Для построения переходного процесса используем соотношение (5.168). Необходимо вычислить сумму вычетов функции X(z)zK~1 в полюсах функции X(z)t
г, = 0,0169; га = 0,2005; г3 = 0,6402;
г4 = 1,0.
Рассмотрим второй способ построения переходного процесса с использованием метода степенных рядов. С этой целью запишем числитель и знаменатель X(z) в виде отношения полиномов по степеням г-1:
. 0,15 + 0,1673г-1 + 0,0080г-2
•Л (z) —“ I <> •
1,15 -2,1363г-1 + 1,1502г -— 0,1665г-3 + 0,0025г-4
(5.180)
Разделив числитель выражения (5.180). на знаменатель, получим бесконечный ряд по степеням г-1, коэффициентами которого являются значения переходного процесса х(кГ0) в моменты времени кТ0 (к = = 0, 1, 2, ...):
х(кТ0) = 0,1304 + 0,3878г-1 + 0,5968г-2 +
+ 0,7396г-3 + 0,8330г-4 + 0,8932г-5 +
+ 0,9320г-6 + 0,9561г-7 + 0,9714г-8 + ...
Теперь рассмотрим третий способ, основанный на разложении функции X(z)/z на элементарные составляющие. Будем искать это разложение в следующем виде:
У (г) = А В
г г —0,0169 *" г - 0,2005
С Г>
+ г—0,6402 +—•
Приведем правую часть выражения (5.181) к общему знаменателю; тогда для
463
определения неопределенных множителей А, В, С, D будем иметь
А (г — 0,2005) (г — 0,6402) (z — 1) +
+ В (г — 0,0169) (z — 0,6402) (z — 1) +
+ С (z - 0,0169) (z - 0,2005) (z — 1) +
+ D (г — 0,0169) (z — 0,2005) (г — 0,6402) =
= 0,1304z (г + 0,05) (г + 1,065). (5.182)
Тождество (5.182) справедливо при любых значениях г; поэтому, полагая в нем z = 0,0169, получим выражение для определения коэффициента А:
__ 0,1304г (г + 0,05) (г + 1,065) (г — 0,2005) (г — 0,6402) X
X(z-l)
г=0,0169
откуда А = —0,0014.
Полагая в тождестве (5.182) последовательно г = 0,8005; 0,6402 и 1,0, определим коэффициенты В = 0,1284; С = = —0,9964 и D = 1,0. При этом из выражения (5.181) следует
%(Z) = -°’OO147=W69
+ °’1248'г-0*2005 ~0-"64 *
г — 0,6402
(5.183)
Используя таблицу обратных г-преобра-зований (см. прил. П-1.2), получим
х (кТд) = 1 — 0,9964 (0,6402)к +
+ 0,1284 (0,2005)к — 0,0014 (0,0169)к,
что полностью совпадает с результатом, вычисленным по первому способу.
Рассмотрим четвертый способ построения переходного процесса. Тогда представим передаточную функцию Ф(г) (5.177) в виде отношения полиномов по степеням г-1, т. е.
_ . . X(z)
Ф U (г) ~
0,1304 + 0,1455г-' + 0,0080г-2
1 — 0,8576г-' + 0,1426г-2 — 0,0025г~3 '
Этой передаточной функции соответствует разностное уравнение вида
х (кТ0) — 0,8576х (кТ0 — То) +
+ 0,1426% (кТ0 — 2Т0) — 0,0025 X
X % (кТ0 — ЗТо) = 0,1304и (кТ0) +
+ 0,1455м (кТ0 — То) + 0,0080ц (кТ0 — 2Т0).
(5.184)
Для перехода от описания в форме разностного уравнения (5.184) к описанию с помощью переменных состояния необходимо исключить в правой части слагаемое, содержащее сомножители и(кТ0). С этой целью сделаем замену переменных
у (кТ0) = х (кТ0) — 0,1304ц (кТ0). (5.185)
С учетом этой замены переменных разностное уравнение (5.184) примет вид
у (кТ0) - 0,8576г/ (кТ0 - То) +
+ 0,1426 г/ (кТ0 - 2Т0) - 0,0025 X
X У (кТ0 - ЗТо) = 0,2573ы («То - То) -
- 0,0116и (кТ0 - 2То)+0,0003ц (кТ0 - ЗТ0).
(5.186)
Введем вектор переменных состояния «/к = [У1 (кТ0), у2(кТ0), г/з(«Т0)]т, где yi (кТ0) = у (кТ0); уг (кТо) = у(кТо — ТоУ, Уз (кТ0) = у (кТ0 — 2Т0).
Используя введенные обозначения, преобразуем разностное уравнение (5.186) к виду
г- 0,8576 -0,1426 0,0025-1
Ук=| 1 0 0 |ук-1 +
L 0 1 0 J
хк = (0,2573 -0,0116 0,0003) ук + + 0,1304цк,
(5.187) где
хк = х(кТ0), цк_,=ц (кТо-То), цк= ц (кТ0).
Таблица 5.14
Параметры переходного процесса
К 0 1 2 3 4
Ик (0; 0; 0) (1; 0; 0) (1,8576; 1; 0) (2,4505; 1,8576; 1) (2,8392; 2,4505; 1,8576)
Хк 0,1304 0,3877 0,5968 0,7396 0,8330
464
Определив начальные условия ^к [ |к_о=О „ ( 0 при к — О
и входной сигнал uK_i = <
(. 1 при к > О, вычислим переходный процесс с помощью уравнений (5.187).
Результаты вычислений приведены в табл. 5.14. Расчет переходного процесса по формуле (5.187) может быть легко реализован с помощью ЭВМ.
Все рассмотренные способы дают одинаковые результаты с погрешностью, определяемой точностью вычислений.
Рис. 5.49. Переходные процессы для системы, описываемой дифференциальным уравнением (5.188)
6. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ. ПРОЦЕССОВ НЕСТАЦИОНАРНЫХ ЛИНЕЙНЫХ САР
При построении переходных процессов в нестационарных САР следует учитывать изменение параметров дифференциальных уравнений замкнутых систем. Для этого воспользуемся методикой, основанной на ряде Неймана и изложенной в п. 4.9. Тогда по формуле (4.190) можно найти решение нестационарного линейного дифференциального уравнения. Данную методику проиллюстрируем на конкретном примере.
Пример 5.19. Определить с помощью ряда Неймана переходный процесс в нестационарной системе, задаваемой следующим уравнением:
d3x d2x , dx , .
~di^ + ai(t)~di^ + a2~dr + a3X^°
(5.188)
при х(0) = хо=1 и ai(t) = t; a2 = 2,5; a3 = 2.
Запишем уравнение (5.188) в векторноматричном виде
dx
-£ = Ах, (5.189)
где Х[ (/) = х (1), х (0) = х0 = [х0, 0, 0]т.
Тогда согласно выражению для переходного процесса справедливо соотношение (4.194), где составляющие r,(/), i = 1, оо вычисляются по формуле
t xt
г{ (0 = A (т.) rfT] А (т2) dx2 ... о о
•4-1
5 A(xi)xodxi
о
(5.190)
и ro(f) = Xo.
Для рассматриваемой системы матрица А имеет вид
[0 1 О-,
0 0 1
— йз — а2 t -
Воспользовавшись формулой (5.190), найдем первую составляющую переходного процесса
t
(/) = A (Ti) Хо dxt = [00 — а3х0/]т.
о
(5.191)
Для дальнейших вычислений удобно применять рекуррентные соотношения
t
ri(t)=^A(x)ri_i(x)dx. (5.192) о
Окончательно получим следующее выражение для переходного процесса:
i V’’ fl i
х (!) = Хо I 1 + а3 2 , bi -Jj- I- (5-193) ' /=з '
Коэффициенты bh / = 3, оо в формуле (5.193) вычисляются на основе формулы (5.192). Приведем значения bjt когда i в формуле (5.193) изменяется от 1 до 7:
Ь3= — 1; £ц = 0; 65 = (а2 —2); bs = а3;
Ьт — — 8 + 6а2 — ^8 == ?аз + 11а2>
Ь2 = — 48.
На рис. 5.49 приведены кривые для х(1) при вычислении восьми составляющих переходного процесса (/ = 0,7) — кривая 1, а при 16 составляющих (i = 0,15) —кривая 4 и точное решение х(1), полученное интегрированием уравнения (5.188)—кривая 3. Для сравнения пунктиром приведен переходный процесс в стационарной системе, где аДО = 1 (кривая 2).
465
7. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В СИСТЕМАХ
С ПОМОЩЬЮ ВЫЧИСЛИТЕЛЬНОЙ ПРОЦЕДУРЫ, РЕАЛИЗОВАННОЙ НА ЭВМ
При построении переходных процессов наряду с векторно-матричными уравнениями (3.99) — (3.100) необходимо знать вид сигнала управления или возмущения. Обычно на практике пользуются типовыми воздействиями, в результате отработки которых на выходе образуется сигнал x(t) в виде скаляра или столбца
X (/) = [х, (0, Х2 (/), хт (/)]т. При этом необходимо учитывать начальные условия y(t0) — y0.
Типовые воздействия позволяют сравнивать показатели качества различных САР. Такими сигналами обычно являются
g (0 = ао, g (0 = а0 + (t — /0);
g(O = aosin[a1 (t — Zo)],
где Z^/o-
Определение переходных процессов в замкнутых системах регулирования производят на основе расширения вектора состояния и вычисле
ния переходной матрицы системы уравнений
/(0 = AV(0. (5.194)
Матрица А' и вектор начального состояния системы у[ в зависимости от типа входного воздействия имеют следующий вид:
при g(0 = а0
[A i Ь 1 Г Vo 1
oTo J’ MU (5J95>
при g (0 = ao+ «1(^ — 4))
(5.196)
при g (0 = a0 sin [a! (t — f0)]
(5.197)
Изложенная методика построения переходных процессов при типовых воздействиях, моделируемых соотношениями (5.194) — (5.197), реализована в программе № 20 TRAGRA.
ПРОГРАММА № 20 TRAGRA
Программа предназначена для расчета переходных процессов в динамических системах, описываемых следующей системой уравнений:
У (0 = Ау (0 + bg (0, y(t0) = y0, t>io,
x(t) = <?y (t) + dg{t),
где y[N X 1] — вектор состояния системы; g{t)—типовое входное воздействие; x(t)— выход системы.
В программе предусмотрен следующий набор типовых воздействий:
1) g(0 = a0;
2) g (О — ао + ai U — Л>);
3) g (0 = а0 sin’fai (t — /0)]-
Обращение к программе
TRAGRA (N, A,B,C,D,X,TC,KB,A0,A1 ,NK,NX)
Входные параметры
N — порядок динамической системы;
А, В, С, D — параметры системы;
X — вектор начального состояния;
ТС — массив, элементы которого равны;
ТС(1) —начальное время переходного процесса;
ТС (2) — конечное время переходного процесса;
466
ТС(3) —такт съема информации;
КВ — задает вид входного воздействия (принимает значения 1, 2, 3);
А0, AI — параметры входного воздействия;
NK—количество координат вектора состояния, по которым рассчитывается переходной процесс;
NX — вектор размерности NK, элементы которого равны номерам координат вектора состояния, по которым рассчитывается переходной процесс.
Результатом работы программы является выведенная на печать таблица, содержащая следующую информацию о.переходном процессе: в первом столбце время с заданным тактом, во втором — выход системы, в остальных NK столбцах указанные координаты вектора состояния.
TRAGRA: PROC (N, А, В, С, DD, X, ТС, КВ, А0, Al, NK, NX); DCL К, NK, N, NX (*), (A (*,*), (В, C, X)(*), DD, TC (*), A0, Al, NV (2), TT (4); T0, U, T) DEC FLOAT (16); ON UFL; DCL MET (4) LABEL INIT (Ml, М2, М3, M4);
Ml: FORMAT (F (9,4)); М2: FORMAT (F (9,1));
• М3: FORMAT (E (9,1)); M4: FORMAT (F (9)); NV(1) = 1; NV(2) = KB;
К = (TC (2) — TC (1))/TC (3)-f-1; TT(1) = TC(1); TT (2) = TC (3); TT(3) = A0; TT (4) = Al; KM = 0; IF NV (2) < 0 THEN DO; KM = 1; NV (2) = ABS (NV (2)); END; T0=TT(2); Nl =N; IF NV (2) = 2! NV(2) = 3 THEN N = N + 2; ELSE N = N+ 1; BEGIN; DCL P (K, NK + 2) DEC (16), YI (N); BEGIN; DCL ((D,R,L) (N,N), W(N,2), (BB,CC,XX,X1)(N)) DEC FLOAT (16), IY(N);D = 0; BB = 0; BB(N)=1; CC = 0; X1=0; DO I = t TO Nl; DO J=1 TO Nl; D (I, J)=A (I, J); END; D (I,N1 + 1)=B (I); CC (I) = С (I); X1(I) = X (I); END; X1(N) = TT(3); IF NV (2) = 2 THEN DO;
D (N,N) = —1,0E — 05; D (Nl + 1,N)= 1; XI (Nl + 1) = TT (3); X1(N) = TT(4); END; ELSE IF NV(2) = 3 THEN DO; D (Nl + 1 ,N) = TT (4); D (N.Nl+l) =-TT (4); END; CALL OWN (N,D,W,R,L,IY); YI = IY; 1 = 1;
CALL MTAN (N,D,R,L,BB,T0,YI,I); DO 1=1 TO N; IF W (1,1)>IE-10 THEN DO; PUT SKIP EDIT (’МОДЕЛИРУЕМАЯ СИСТЕМА НЕУСТОЙЧИВА (ПРИСУТСТВУЕТ’,’ПОЛЮС =’, W (1,1)) (A, A,E (12,4)); IF IY(I)>0.5 THEN DO; PUT EDIT (’ + J * ’,W (1,2)) (A,E (12,4)); 1 = 1+1; END; PUT EDIT (’ )’) (A); END; END; DO 1=1 TO NK; IF NX (I) > N THEN NX(I) = 1; END; T = TT(1); DO 1=1 TOK; U = SUM (CC * XI); IF NV (1) = 1 THEN U = U + XI (N) * DD; ELSE U = U + XI (N — 1) * DD; P(I,1) = T; P(I,2) = U; DOJ=1TONK; II = NX (J); P (I,J + 2) = XI (II); END; IF I = К THEN GO TO L01; DO II = 1 TO N; XX (II) = SUM (D (II,*)* XI); END; X1=XX; T = T + T0; END;/* I */
L01: N = N1; DO 1 = 1 TONI; X(I) = X1(I); END; TT(1) = T; END; /♦BEGIN*/ IF NV(1)=1 THEN DO;
PUT SKIP EDIT (’ВХОДНОЕ ВОЗДЕЙСТВИЕ U (T) = ’,TT (3)) (A,F (9,2)); IF NV (2) = 2 THEN PUT EDIT (’+’,TT (4), ’* (T — T0)’) (A,F (9,2), A);
IF NV(2) = 3 THEN PUT EDIT (’* SIN (’,TT (4),’* (T - T0))’) (A,F (9,2),A); PUI SKIP EDIT (’ВРЕМЯ’,’ВЫХОД’) (X (4),A); DO 1 = 1 TO NK;
IFI<12 THEN PUT EDIT (’X (’,NX (I),’)’) (X (3),A,F (3),A); END; II = NK + 2; IF II >13 THEN 11=13; PUT SKIP LIST (’ ’); DO 1 = 1 TO K; PUT SKIP EDIT (P (1,1)) (F (9,3)); DO J = 2 TO II; U = ABS (P (I, J));
IF (U > 0.001) &<U<= 99.9999) THEN L = 1;
ELSE IF (U> 99.9999) &(U<=99999.9) THEN L=2; ELSE IF U = 0 THEN L=4; ELSE IF (U<= 0.001)! (U>99999.9) THEN L=3; PUT EDIT (P (I, J)) (R (MET (L))); END; END; /* I */ END; END;
MTAN: PROC (N,A,R,L,B, T,Y,M); DCL N,I, J,K,T,Y (*), ((A,R,L) (*,*), B(*), S, ((BL.EA) (N), E, C, D, CR, CL) CPLX,Bl, B3 (N)) DEC FLOAT (12); DCL CON RETURNS (CPLX (12)); S = T; ON UFL; DOI = 1TON-1; IF Y (I) >0.5 THEN DO; BL (I) = CPLX (A (1,1), A (I + 1,1)); BL (I + 1) = CON (BL (I)); 1 = 1+1; END; ELSE LI: DO;
BL (I) = CPLX (A (1,1), 0.0); END; IF I = N-1 THEN DO; I = N; GO TO LI; END; END; DO 1 = 1 TO N; IF M<1.5 THEN EA (I) = EXP (BL(I).S); ELSE EA (I) = TANH (BL (I) * S/2) * 2/S; END; DO I = 1 TO N; Bl =0.0; DO J=1 TON; C,D = CPLX (0,0); DO К = 1 TO N - 1; IF Y (К) > 0.5 THEN DO; CALL P (I.K.J); IF M<1.5THEN DO; C=C+(CR * EA (K) * CL+CON (CR) * EA (K+l) * CON (CL))/4; D = D + (CR * (EA (К) - 1.0)/BL (K) * CL + CON (CR) * (EA (K + 1)-1.0)/BL (K+D* CON (CL))/4; END; ELSE D = D + (CR * EA (K)/BL (K) * CL + CON (CR) * EA(K+ 1)/BL(K+ 1) * CON (CL))/4; K = K+1; END; ELSEL2:DO;
E = CPLX (R (I,K) * L (K, J), 0.0); C = C + EA (К) * E; IF ABS (REAL (BL (K))) > IE-06 THEN IF M<1.5 THEN D = D+E* (EA (К) — 1.0)/BL (K); ELSE D = D + E * EA (K)/BL (K); ELSEIFM< 1.5 THEN D = D + F * S;
ELSE D = D + E; END; IF K = N— 1 THEN DO; К = N; GO TO L2; END; END; IF M< 1.5 THEN A (I, J) = REAL (C); ELSE A(I,J) = 0; Bl = BI + REAL (D)*B(J); END; B3(I) = B1; END; B = B3; IF M > 1.5 THEN DO; A (N.N) = REAL (EA (N));
467
DO 1=1 TO N-1; IF Y (I) >0.5 THEN DO; CPLX (A (1,1), A (I + 1,1)) = EA (I); 1 = 1+1; CPLX (A (1,1), A (I — 1,1)) = EA (I); END; ELSE A (1,1) = REAL (EA (I)); END; END; CON: PROC (A) RETURNS (CPLX (12)); DCL (A,B) CPLX (12); В = CPLX (REAL (A), -IMAG (A)); RETURN (B); END CON; P : PROC (I, K, J); DCL I,J,K; CR = CPLX (R(I,K) + R(I,K+1), R (I,K) - R (I,К + 1));
CL = CPLX (L (K,J) + L (K + 1,J), L (K + 1,J) — L (K,J)); END P; END MTAN; END TRAGRA;
В процессе работы данной программы используется описанная выше программа OWN.
Для изображения переходных
процессов в виде графиков на АЦПУ можно пользоваться дополнительной программой № 21
GRAPH.
ПРОГРАММА № 21 GRAPH
Программа предназначена для вывода на АЦПУ в виде графика нескольких функций одной переменной.
Обращение к программе
GRAPH (K,N,A)
К — число точек по оси абсцисс;
N — число выводимых функций;
А — матрица значений абсцисс и ординат выводимых функций, размером К X (N + 1), компойентами которой являются:
А(*, 1) — значения ординат первой функции;
А(*, N) —значения ординат N-й функции.
Выходом программы GRAPH являются графики функций, выводимых на АЦПУ. Для различения порядка вывода графиков используются символы: •,-,О,0,А и т. д.
GRAPH: PROC (K,N,A); DCL TEMP CHAR (80) VAR, A (♦,♦),
SS CHAR (80) BASED (QS); AM,AN = 0; DO 1=1 TO K; DO J=1 TO N; IF ABS (A (I, J)) > 1E+10 THEN A(I,J)=lE+5; IF AM<A(I,J) THEN AM=A (I,J); IF AN > A (I, J) THEN AN = A (I, J); END; END; IF AM = AN THEN AM = 1; DCL G (10) CHAR (1) INIT (’*’,’,’,’O’,’0’,’А’,’В’,’Ж’); DCL SC (12,80) CHAR(l); SC = ’ ’; DO 1=1 ТОК; Il = 1 + (I * 79)/K; DOJ=1TON;
JI = ((A (I, J) — AN) * 11)/(AM — AN); JI = 12 - JI; SC (JI ,11) = G (J); END; END; DO 1 = 1 TO 12; QS = ADDR (SC (1,1)); TEMP = SS; PUT SKIP EDIT (TEMP) (A); END; END GRAPH;
Пример 5.20. На рис. 5.50 построена кривая (сплошная линия) переходного процесса отработки типового сигнала
Рис. 5.50. Переходный процесс в непрерывной и дискретной САР, полученный с помощью применения лрограммы № 20 TRAGRA
(5.195) непрерывной системы. Матрица ее коэффициентов приведена в примере 3.12. Для дискретной системы примера 5.20 характеристики переходного процесса отработки того же сигнала показаны прямыми линиями с интервалом 5Т0. При этом видно, что переходные процессы для непрерывной и дискретной систем с заданным входным воздействием практически совпадают.
Пример 5.21. Построить переходные процессы в САР бокового движения самолета, описываемого уравнением
y(t) = Ay{t) + b[u{t)+g{t)], (5.198)
где u(Z)—закон управления, задаваемый в ВИД£
и (f) = - kTy {ty, (5.199)
здесь feT — матрица коэффициентов обратных связей.
Матрицы A, b, k имеют следующие числовые значения:
468
12,910 0,000 0,000 0,000 —102,459 0,000 0,000 0,000 0,0001
So О О О О О CO
о о о о о о о
о о о о о_ о сэ
о’ o' —• о о о о о
I
**ооооооо
оооооооо
I
ОООО^ОООСЧ ООООООтГ — о
** —• ю сч
оооо — оою оооосчоооо о. о~ о о Ю 00 сч о о” o' о” о“ o' со о* 7 1
оооосоооо
— ** СЧ
I
I
ч!
Рис. 5.51. Переходные процессы в канале рыскания самолета при отработке ступенчатого воздействия
о о о о"
со
Приведем примеры построения переходных процессов САР с помощью программы № 20 TRAGRA.
На рис. 5.51 построены кривые переходных процессов отработки двух входных сигналов, задаваемых соотношениями (5.195) и (5.197) для фазовых координат: *п(0—угла рыскания самолета и х21(0— перемещения штока рулевого привода, откуда видно, что при единичном ступенчатом сигнале угол рыскания изменяется по закону, близкому к апериодическому, а перемещение штока рулевого привода происходит с колебаниями.
Переходные процессы отработки синусоидального сигнала по тем же фазовым координатам *|2(0 и Х2г(1) приведены иа рис. 5.52. В этом случае процесс по Х12(/) имеет одно колебание; при этом увеличивается амплитуда колебаний по х22(£)-Так как рассматриваемая система является линейной, то принцип суперпозиции позволяет получить иа выходе результирующие сигналы
*1(/)=*11(0 + *.2(0> j (5 203) *2 (0 = *21 U) + *22 (О- J
Суммарные характеристики *1(0 и х2(/) изображены на рис. 5.53.
Рис. 5.52. Переходные процессы в канале рыскания самолета при отработке синусоидального воздействия
469
Рис. 5.53. Результирующие переходные процессы при отработке двух сигналов (ступенчатого и синусоидального)
8. СРАВНЕНИЕ ЗАПАСОВ УСТОЙЧИВОСТИ САР С ОСНОВНЫМИ ПОКАЗАТЕЛЯМИ КАЧЕСТВА
В зависимости от вида частотных характеристик разомкнутых САР, логарифмические амплитудные характеристики которых аппроксимированы типовыми наклонами О, —20, —40 дБ/дек, а также соотношениями частот ©1/©с, <оз/<»с и передаточными коэффициентами К (в дБ), определяются кривые, связывающие запасы устойчивости систем по фазам с основными показателями качества замкнутых систем. Из номограммы (рис. 5.54, а) видно, что запасы устойчивости систем по фазам Уф для рассматриваемых видов логарифмических частотных характеристик статических систем (рис. 5.54, б) однозначно определяют запасы устойчивости по модулям ±ЯМ (в дБ). На рис. 5.54,а показана часть номограммы /?(со), где жирными линиями 1 и 2 выделены участки наиболее целесообразных значений запасов устойчивости по фазам и модулям, обеспечивающих значения показателей качества, которые обычно задаются техническими условиями.
Из рис. 5.54, а следует, что если логарифмическая амплитудно-фазовая характеристика 20 lg Wfja) расположена между кривыми 1 и 2 номограммы, то запасы устойчивости систем в замкнутом состоянии по
фазам находятся в пределах 25°
Уф 45°. Если в системах в зависимости от режимов работы параметры могут изменяться более чем на ±20 % или система обладает высокой степенью нестационарности, то ее запасы устойчивости по фазам необходимо увеличивать до 50—60°, а иногда и более. Следует указать, что существуют такие системы, в которых недопустимы перерегулирования; тогда запасы устойчивости по фазам должны быть равны или немного превышать 90°.
По номограмме рис. 5.54, виг можно найти соответствие между рекомендуемыми запасами устойчивости по фазам и запасами устойчивости по модулям ±ЯМ (в дБ). При у^ = 25° имеем -|-Ям = 16 дБ и —Ям = —13 дБ, а при уф = 45° +ЯМ = 12 дБ и —Ям = —9 дБ. Если Уф 90°, то ±ЯМ стремятся к ±оо дБ. Однако на практике часто ограничиваются значениями +ЯМ < 50 дБ, —Ям —40 дБ. Тогда перерегулирование не превышает 0,25 %.
При проектировании САР с большими значениями частот среза могут быть не учтены малые постоянные времени устройств управления и объектов. Поэтому запасы устойчивости по фазам Уф и модулям ±Ям в таких системах необходимо увеличивать на 25 %.
В заключение укажем, что на рис. 5.55, а — в построены номограммы для астатических систем 1-го поряда. Более подробные номограммы выбора частотных характеристик желаемых САР для решения задач синтеза приведены в гл. 9 и 10.
По номограммам можно находить запасы устойчивости по фазе и основные показатели качества. Покажем это на двух конкретных примерах.
Пример 5.22. Определить по значениям (Ос = 8 с-1, соз/а>с'= 2, а>|/сос = 0,025 и 201g Я = 40 дБ запас по фазе Уф и основные показатели качества для стати-
470
1т,дб
1,025
- 28
- 24
-20
- 16
кт.Дб -260 -240 -220 -200 -180 -160 -140 -120 -100
12 0,925
1ЮШ11МП^ва№^§9^яП11Л»!
---------- i»9i'iM1V/'/Z0Z ^ssswiir/^ase
SKWIlf/? 7 >5*Й
1 '///,<:
ISIS
/ 0J5-
4 0,25
_ п °’55
° 0,45
~ 8 "0,85 _ , №
4 0,65
ЙШ\
________________ 1ВЙЖ/1__________1'kv^SK
ibvwk
«SilSFzMinVkVlK ^wjiiikv
-8^
—20
—24
—28
О
-/2-«
к 0Л25Г-Г
0,05
-0^25
-260 -240 -220 -200 ~180 -160 -140 ~120 ~100 О'
\0,8 |о,7 0,6 0,5 0,4 10,3 0,2
0/
0,95 0,9
Рис. 5.54. Номограммы для определения основных показателей качества по запасам устойчивости разомкнутых статических систем:
а —номограмма для построения вещественной частотной характеристики с допустимыми зонами, расположенными между кривыми 1 и 2; б—логарифмические амплитудная и фазовая частотные характеристики статической системы; в — номограмма для определения Y—, и о при <0т/<0 =2С~1
»«—1 о - « , Ф Р с/ т г 4/ с
<о3/<|>с“8 с г—номограмма для определения у , <р<ос/10 и ат при a>3/<aQ = l с~ *, <o3/<i>c-.4 с-1
Рис. 5.55. Номограммы для определения основных показателей качества по запасам устойчивости разомкнутых астатических систем:
а — логарифмические амплитудная и фазовая частотные характеристики астатической системы; б—номограмма для определения уф,
“ ат п₽и °з/шс“2 с~тз/тс—* с~®—номограмма для определения уф, t^a>cflO и ат при ш3/шс=1с~|, ш3/шс=4с-1
ческой непрерывной САР при единичном управляющем воздействии.
Пользуясь номограммой рис. 5.54, в, найдем уф = 63°, ат = 6,5 %, /р = 0,46 с.
Пример 5.23. Определить по значениям <0с = Ю-1, й>з/(Ос = 8, <01/<0с = 0,01 и К= = 60 дБ запас по фазе Уф и основные показатели качества для астатической 1-го порядка непрерывной САР при единичном управляющем воздействии.
Пользуясь номограммой рис. 5.55, г, найдем уф = 81°, от = 6,6 %, /Р = 6,1 с.
В дискретных и дискретно-непрерывных САР в зависимости от такта квантования То меняются запасы устойчивости системы у^,, что в свою очередь приводит к ухудшению показателей качества. Для иллюстра-
Таблица 5.15
Передаточные функции разомкнутой дискретно-непрерывной системы при различных тактах квантования
Г0.с W(Z) W(S)
0,1 £,011 (l,010z — 1) (10,331г + 1) 10 (10s + 1) (1 - 0,05s) (0,0016s + 1)
(2 - 1) (1,0012 - 1) (1,2212 - 1) s(100s+ 1) (0,502s + 1)
0,5 0,354 (1,0512 — 1) (1,370г + 1) 10 (10,002s + 1) (1 - 0,25s) (0,0391s + 1)
(2- 1) (1,005г+ 1) (2,718г- 1) s (100s + 1) (0,541s + 1)
1,0 2,133 (1,1052- 1) (1,853г + 1) 10 (10,008s + 1) (1 - 0,5s) (0,1494s + 1)
(2- 1) (1,010г+ 1) (7,370г- 1) s (100s + 1) (0,657s + 1)
1,5 7,739 (1,1622- 1) (2,436г + 1) 10 (10,017s + 1) (1 - 0,75s) (0,3133s + 1)
(z- 1) (l,015z + 1) (19,987г- 1) s (100s + 1) (0,829s + 1)
2,0 23,785 (l,222z — 1) (3,090г + 1) 10 (10,029s + 1) (1 — *s) (0,5115s + 1)
(г — 1) (1,020г + 1) (54,333г - 1) ^(100s+ 1) (1,0373s + 1)
472
X
Рис. 5.56. Переходные процессы в дискретио-иепрерывиой системе с передаточной функцией, заданной выражением (5.204), в зависимости от такта квантования То
ции этого положения рассмотрим разомкнутую дискретно-непрерывную САР, разомкнутая передаточная функция которой имеет следующий вид:
( 1 _e~sr°
ИР(г) = 3{-1—£-----х
10 (10s+1) 1
s (100s + 1) (0,5s + 1) J ‘
(5.204)
На рис. 5.56 приведены переходные процессы в рассмотренной дискретно-непрерывной системе, которые были получены с помощью вычислительной процедуры, реализованной на ЭВМ. Запасы устойчивости по фазе Уф разомкнутой системы и основные показатели качества приведены в табл. 5.16.
В табл. 5.15 приведены передаточные функции разомкнутых систем на пл. z и $ при различных значениях То.
Таблица 5.16
Основные показатели качества дискретно-непрерывной системы в зависимости от такта квантования 7*0 прн К = 60 дБ
го- с йс, с 1 Уф. 0 ат- « ‘р’с
0,1 0,915 57,2 14,1 7,52
0,5 0,924 46,9 26,3 7,93
1,0 0,954 35,2 43,8 9,75
1,5 1,016 25,2 61,8 10,71
2,0 1,141 17,2 85,4 20,02
Рис. 5.57. Кривая для определения запасов устойчивости в дискретио-иепрерывиой системе с передаточной функцией, заданной выражением (5.204), в зависимости от такта квантования То
473
На рис. 5.57 построены кривые запасов устойчивости по фазам в зависимости от То по данным табл. 5.16. Из рис. 5.57 видно, что при То > 3,18 с САР становится неустойчивой, так как у^, <0°. Если
воспользоваться существующей нормой по запасу устойчивости Уф = = 24°, то для рассмотренной дискретно-непрерывной САР такт квантования не должен превышать То = = 1,56 с.
Глава 6
ИССЛЕДОВАНИЕ ДИНАМИЧЕСКОЙ ТОЧНОСТИ НЕПРЕРЫВНЫХ И ДИСКРЕТНО-НЕПРЕРЫВНЫХ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Важной характеристикой САР является ее динамическая точность, которая определяется ошибками, возникающими в системе от действия управляющих и возмущающих воздействий. Все типы воздействий можно разделить на регулярные, случайные и их комбинации; поэтому определение динамической ошибки представляет достаточно сложную задачу из-за необходимости учета их взаимного влияния. Для ее упрощения обычно считают, что регулярные воздействия являются медленно меняющимися функциями от времени по сравнению с длительностью переходных процессов. Ошибки от случайного воздействия определяются не мгновенными значениями, а ее средними квадратическими отклонениями. При этом обычно принимают случайные воздействия стационарными и обладающими эргодическими свойствами с заданным видом спектральной плотности, которую можно описать аналитически. Наиболее часто спектральную плотность представляют равномерной в рабочем диапазоне частот. *
Если на вход системы поступают два воздействия — регулярное и случайное, то с помощью дополнительно введенных сумматоров в структурные схемы производят их разделение, и тогда они независимы друг от друга. В реальных САР наряду с полезными воздействиями (регулярными или случайными) возникают сигналы шумов, которые
приводят к ухудшению точности. Поэтому в процессе проектирования необходимо выбрать такие параметры системы, при которых обеспечивалось бы подавление шумов без существенного возрастания ошибок отработки полезных сигналов. Предполагается, что полезный сигнал и шум взаимно независимы, а следовательно, некоррелированы.
Предполагаемые допущения хотя и упрощают решение задач анализа динамической точности, тем не менее создание высокоточных линейных систем представляет исключительно сложную проблему, так как уменьшение ошибок отработки полезных сигналов связано с расширением полос пропускания' сигналов замкнутой системы, что приводит к увеличению ошибок от действия шумов. Однако с помощью рационального выбора корректирующих устройств и коэффициентов усиления удается получить в системах минимальное значение сумм квадратов ошибок от полезного сигнала и шума. Если шумы достаточно малы, то можно повышать точность отработки системами регулярных сигналов путем применения комбинированного управления.
1. ХАРАКТЕРИСТИКИ ТОЧНОСТИ НЕПРЕРЫВНЫХ СИСТЕМ
ПРИ ДЕЙСТВИИ регулярных СИГНАЛОВ
Точность САР при действии медленно меняющихся регулярных сигналов определяется коэффициента
ми:
ми ошибок, которые можно получить разложением передаточной функции замкнутой системы относительно ошибки в ряд Маклорена. Рассмотрим нахождение коэффициентов ошибок в статических и астатических непрерывных САР, пользуясь выражениями
E^)= 'i+-^ (s) G(s)
или
циенты:
bmlan = A; bm_l/bm = bx, bm-zlbm — b2, • •.; bjbm = bm\ an-\lan~ ax; an-i!an —
a2, •••> ajan = an_x, а^/ап== an.
Тогда, подставляя выражения (6.3) — (6.6) в соотношение (6.1) и учитывая вновь введенные коэффициенты, получим для систем:
статической
В выражении (6.1) для систем: статической
^0(8) =
К + Ь{3 + 4- • • •
...+Ьт^зт~' + Ьтзт) 4" и]S -4" .
1 4- 4- d2s2 4- • • •
E0(s) =------‘ + а<П----------------х
(1 4-К) 4-(а, 4-&1К) S 4-
4- («2 4- Ь2К) з2 4- ... 4- dnsn
XG(s)', (6.7)
астатической 1-го порядка
1 _1_ Я <• I Я п2 I
• • • + ап_1зп 1 + artsn)
(6.3)
астатической 1-го порядка
К 4- Ьхз 4- 4- ...
s (1 4- ajs 4- a2s 4- • • • • •• 4-a„_1sn~1 4-a„sn)
(6.4)
астатической 2-го порядка
1F2(s) =
К (1 4- bxs 4- b2s2 4- ...
• • • 4- 4- bmsm)
s? 4- 4” 4- . •.
an_]S 4- ans )
(6.5)
где исходная передаточная функция разомкнутых систем имеет вид
ftosm4-blSm~l 4-b2sm~2 + ...
... 4- b ,s + b
П7 (s} =_______m-1 m
aosn 4- ахза 1 4- a2sn~2 4- ...
••+an-is + an
(6.6)
В передаточной функции (6.6) n m. Введем следующие коэффи-
,n—1 t ~ „П
Ei (s) =----' n~~.——--------X
K4-(l + blK)s +
4- (at 4- b2K) s2 4- ... 4- dnsn
XsG(sY, (6.8)
астатической 2-го порядка
ln-is 4- dns
E,(s) =------=--------------------/х
К 4- bxKs 4- (1 4- b2K) s2 4- ...
... 4- ansn
Xs2G(s). (6.9)
Из выражения (6.2) найдем для систем:
статической
_ Е0(з) =
Ао [1 4- (^t 4- Si) s 4- (5131 4- 5г 4-
4" 82) s2 4- (5з 4- а3 4- 315г 4- 8284) s3 4-
4- (dt 4- dt 4- 51йз 4- d2a2 4-
4-<?38i)s44- ...]F(s)
К 4- 14- КА 4-1) с, 4-4-a,] S 4- ’
4- [ci (Kbt 4- ао 4- КЬ2 4- а? 4-
4- (К + 1) г2] s* + [(Kb3 + a3) +
4- с3 (К 4- 1) 4- с2 (Kbt 4- <h) 4-
4- (Kb2 4- а2) Cl] s3 4- [(К 4- 1) ct 4-
4- (Kbt 4- а<) 4- ci (КЬ3 4- d3) 4-
4- сг (КЬг 4- а2) 4- с3 (КЬХ 4- щ)] s4 4-...
(6.10)
475
причем
у _____dosr + d1sr~1 + ... + dr-is + dr_
cos₽ + ctsp~ 1 + . . . + Cp_ + Cp K0(l +dlS + d2s2+ ...
... + d ,sr~' + drsr)
-----------—----, Г J , (6.11)
1 + CjS + c2s2 + . . .
• •• + Cp_ls»-1 + CpSP
где
Kv dr[cp, dr—\ldr — d i, dr__ч/dr — d2) • • • j ^o/^r — dr,
Cp-l/Cp = Ci’, ср—2/ср == c2> • • • J C\lcp = Cp_i;
С^Ср = Cp, n> m> p > r;
астатической 1-го порядка
E,(s) =
Kv [s 4- (Si + di) s2 + 4- (ds 4- aid] + ds) s3 + (З3 + asdt 4-+ a1d2 + d3)s«+ ...]F(s) К + [(КЙ1 + 1) + ciK]s +l(K&2 + di) + ’ + («!+ 1) ci + Kc2]s2 + [(K&3 + a2)+ + (Kbs + Si) Cl + (Kbi + 1) cs +
+ №3] s3 + [(Kbt + a3) + (K&3 + ds) X Xci + (Kbs + Si)c2-|-
Ш + 1)сз + Кс4] s4+...
(6.12) астатической 2-го порядка
E2(s) =
Kv [s2 + (Si + d\) s3 + + (ds 4- dtdt -|- ds) s* 4- (a3 + asdt 4-_ _______+ Sid2 4- d3) s5 4- .. ] F (s)_
К 4-lOi 4- C|K] s 4- [(^СЬг 4-1)4-4- Kbtct 4- Kc2] s2 4- ККЬз + Si) 4-4- (Kbs 4* 1) ci 4* Kbtcs 4- Kc3] s3 4-
4- 1(КЬ« 4- ds) 4- (Kb3 4- Si) <4 4-4~ (Kbs 4-1) C2 4- Kbtc3 4- c4K] s4 4- • • •
(6.13)
При медленно действующих регулярных сигналах выражения (6.7) — (6.9) можно разложить в ряде Мак-
лорена; тогда получим для систем: статической
E0(s) = C0G(S) + 4i-sG(s) +
+ ^-s2G(S) + -§-s3G(S)+ ...
•• + ^7JF^1G(s)+(6-14)
астатической 1-го порядка
E1(s) = -^-sG(s)4-~|[-s2G(s) +
+ -^s3G(S)+ ...
•• +(ЙЛ)! ^-'G(S)+ ...; (6.15) астатической 2-го порядка
E2(s) = ^s2G(S) + -§-S3G(S)+ ...
•••+7^k^-‘G(S)+... (6.16)
В формулах (6.14) — (6.16) постоянные Со, Ci, С2, , Ck-i, ... являются коэффициентами ошибок.
В табл. 6.1 и 6.2 приведены значения первых коэффициентов ошибок для рассматриваемых типов систем.
Ряды (6.14)—(6.16) при медленно меняющихся сигналах G(s) являются сходящимися. Применив к этим рядам обратное преобразование Лапласа (см. прил. П-1.2), получим для первых нескольких членов выражения (6.14)
о (А—Гп/А _L С> dS I С2 d2g I Со (0 Gog(/)+ 1( 4- 2| др +
I Сз d3S I- c< d*s . (6 17)
+ 3! dt3 + 4! dt* ’
выражения (6.15)
_ Ct dg ( Cs d2g , C3 d3g_ , eiW— 1! dt "I" 2! dt2 ‘r 3! dt3
выражения (6.16)
e . Cs d2g , C3 d3g C4 d*g 82U1— 21 dt2 "I" 3! dt3 I- 4!
(6.19)
476
Таблица 6.1
Первые коэффициенты ошибок системы автоматического регулирования с передаточной функцией W (s)/(l + W («))
Тип системы Коэффициенты ошибок
со С,/1! | С2/2' С3/3! С4/41
Статическая f 1 | 11 + К) ((5,-5,)Х) 1 (l + X)2 J [(б2-52)Х , 1 (1 + К)2 51 (5, — а,) К . Ч" (14-ю3 , 5.(5,- а.) + (1 + X)3 ) f (S3 — Ьз) К I (1 4-Х)2 [2di52 — 2&1Ь2К ~Ь +/К—I) (S2&1 + 51&г)] . (1 + Х)3 , (а,-&1)(дг + х&1)2Х] (1 + X)4 J j (a< — bt) к . (bi — a,) xa3 I (14-X)2 1 (l + X)3 + , (5i — Si)X253 (Si + 5iX) (3.3 — b3) к + (14-X)3 (l+X)3 (S3 + 52X) (S3 — Ьз) к (1 + X)4 (a2+ 52X) (5i — ао X5i (1 + X)4 (52 + 52X) (bl — 31) X251 , (1 + X)4 + (3i + 51X) 12а1йз — Ь1ЬзК + । + (X — 1) (S2bi + 5i52)] y 1 (1 + X)4 Л - y K _ (5i — 5i) (5i + X51)3X 1 A (l + X)5 J
Астатическая 1-го порядка 0 1 1 | \К J f a, — bi 1 | IX X2J J 1 -L 2^‘ ~g|) J-IX3 + X2 + . аз — Ьз j bi (bi — ai) | f 1 , 3(5,-5,) , 1 X4 1 x3 'r 2 (&2 — a2 4-ajbj — b2) — (a, — b,)2
1 X 1 X J 1 ' X2 1 . (аз—Ьз)~4_Ь1 (2fc»i——&1&2“1"51й1)—йхЬ\ ) + X J
Астатическая 2-го порядка 0 0 Hi f 31 — bl 1 I X J ( аг — Ьз ,51 (51 — 51) а2 1 1 X 1 X X2 J
478
Таблица 6.2
Первые коэффициенты ошибок системы автоматического регулирования с передаточной функцией V («)/(! + IF(«))
Тип • Коэффициенты ошибок
системы Со С 1/1! С2/2| С3/3! г4/41
Статическая f Ко 1 11 + KJ < x(5i+3i) ( 1 + К - [(ci + bi)K+ +(ci +31)] х S, Ко 1 (1 + К)2/ 1 Т'Х + Т^° (rf.®. + 1 1 + Л L +82+82) I 1 к X X[ci (К&1+31)+К&2+ + 0.2 + (К + 1) с2] — —[(ci + bi) К + (с, + +S.)1 (K°^+g,)-— [(с. + bl) К + (с, + + а‘)] (I + K)2 )]} [к0 (rf a + a3+d23i+d 182) 1 1 W К^Ьз+Зз) + Сз (К + 1) + 1 + Л 4- С2 (Kbi + 5i) + (Kbz + 5г) Ci] — _ С Ко (rf. ± Дг) _ [{gi + ii} к + + (ci+3i)] (j । /Q2)^1 (Kbi+3i)+ + КЬз + а.2 + (К + 1) сг] — -т4ггКп+5.)к+(г!.+3|)1х 1 + А X (к» (rfi 31 + З2 + З2) — -TxV^' (^Ь1 + а,) + КЬг + 1 4- д 4“ 3,2 4- (К4" 0 с%] — [(ci 4~ bi) К 4" + (С1 + 3,)] (-^4-15г) + + l(ci+b!) К+^+З,)] (У^г))]} | । । к | Ко (dt + at + di83 + d2a2 + d3a3) । । I(bC + 1) c< + (Kb< + З4) + Ci (КЬз + Зз) + + ?г (Kt>2 + Зг) + C3 (Kb3 + 83)] (" 1 L-A-” \ 1 4” A - l(c, + bl) К + (Cl + 51)1 (1 *Ркр-) X X l(Kb3 + 83) + c3 (К + 1) + сг (Kbi + Si) + + (КЬг + 3z) Ci] 77— -[Кр (diSi + rf2 + 82) ~~ Ko I (О1 + 81)+КЬг + аг + (К+ l)c2]- - I(c, + bi) к + (с, + a,)] ( Kv + a-2) - - .[(Cl + bl) к + (Cl + a,)] x (1 4- i\r /J X [?i (Kbi 4- 5i) 4- Kb2 4- 5г 4- (К + 1) сг] — । д- {Ko (d3 + a3 + 8281 + 8182) [(К5з + “з) + ез (/<+1) + ?2 (Kbi + ai) + + (Kb2 + 32) + c,] - (+ - \ 1 4" A - [(3. + bl) К + (c, + 81)] (1 j-^y) x
X [ё, (Kbt 4- 2,) 4- КЬг 4- Й2 4- (* 4- 1) ё2] — 1 । к 4- 51) * 4- (С, 4- 31)] Г*о (2121 4-1 -J- Л L 4- 22 4- 2г) 1 । [с, (*5, 4- л,) 4- *51 4- Зг 4- +(*4-1)ё2]-[(ё14-5,)*+(с1+51)](^01(1‘:уа~~ + 4 1 -f- л 4- 1(ё, 4- 51) * 4- (ё1 4- 31)] ц । ) j" X X [(ё, 4- 5>) К 4- (ct 4- «>)]}]}
Астатическая 1-го порядка 3 0 Г *2.1 1 К J {-^[*0 (3,4-2,)- --^-[(*5, 4-1)4-4-ё,*]]} {•Jr [*0 (а2 4- 3,2, 4- 22) — [(*524- 3,) 4-(*5, 4-1) с, 4- 4" Кс%] -j-г ^*0 (2, 4- dt) 4- 4--^[(*5,4-1)4-?,*]) X X[(*Ь, 4- О4-ё,*]]| {*„ (5з 4- 2г2| 4- 3]22 4- 2з) — - [(*5з 4- 32) 4- (*52 4- 51) Ct 4- (Kbt 4-1) ё24- 4- *с3] -у (*о (31 4- 2>) - [(*5! 4-1)4- 4- ё,*]) [(*б2 4- 2,) 4- (Kbt 4- 1) ё, 4- *ё2] - jr Г*о (Зг 4- 3121 4- 22) — [(*52 4- 31) 4- К L Л 4- (*52 4- 1) ё, 4- *ё2] - (*0 (31 4- dt) - - ((Kbt 4-1)4- ё,*])} [(*5. 4-1)4- 4- ё,*]} [(*5. 4-1)4- ё,*] [(*5, 4-1)4- ё,*]}
Астатическая 2-го порядка 0 0 (*2.1 1 К j [*о (2, 4- а,) — --^-(5,4-*ё,)]} |-^-Г*о (32 4- 2,21 4- 22) — ( л L - [(52 4- 1)4- btct 4- *ё2] - -^-[*0 (dt 4-2,)- - (bt 4- Kct) ] (5i 4- *ё>)] }
Соответственно для выражений (6.10) — (6.13) найдем
s,(/)-c„/(O + ^-g- + ^.-g- +
, Сз_ d3f Ci_ d*f ,g 2q\ + 3! dt3 4! dt* ’ ' ’ ’
p (/)___ df I _£г_ d* 2t _i_
61 1! dt 2! dt2
£з_ d^f_ Ci_ (6 21)
3! dt3 4! dt* ' K
- (f\ & d2f , C3 d3f
2! dt2 3! dt3 , C< d*f “r 4! dt* ’
(6.22)
При определении графоаналитическими способами динамических ошибок в САР выражения (6.17) — (6.19) записывают, используя коэффициенты
Со=1/(1+А); С1/1! = 1/Ош;
С2/2! = 1/£>е; Сз/3! = 1/£>6;
С4/4! = 1/De.
В этом случае формулы (6.17) — (6.19) примут вид
t. e.
ёо (0 = 1 . = —-— /(/) + — — + 1+А Г(’ 1 п dt 1
, 1 d3f , CD 1 d
ё1(0 4 . 1 a. w- 1 -4? - J , J г о. о. “*-« CO- ~ "1" + b-to< _ 7, 3 k J D dt* ’ (6.26) d*f , dt2 1 <6-27) , 1 d*f
е2(0 ъ dt2 1 A dt3 e dt* ’
(6.28)
Пользуясь формулами (6.23) — (6.28), определяют аналитическим или графоаналитическим способами динамические ошибки при действии сигналов g(t)—glv(t) или f(t) — fIV(/) для различных типов систем.
Проиллюстрируем аналитические способы нахождения ошибок и характеристик точности на следующих примерах.
Пример 6.1. Определить числовые значения ошибок в статических и астатических САР при подаче ’ низкочастотного управляющего синусоидального сигнала
g (t) — A sin a>Qt, (6.29)
, _L 1 rf3g 1 d*g .
T" De dt2 "r Dt dt3 r D& dt* ’
(6.23)
e /А - 1 dS _l 1 d2g
W)-D ~---------------------
(0
। 1 d3g
Dt dt3
e (fl — 1 rf2g
2 V' ~ D dt2 e । 1 d*g
dt* '
(6.24)
г D dt2 е
1 d*g _
Dt dt* ’
। 1 d3g
Г Db dt3
(6.25)
где А — амплитуда колебаний; <о0— круговая частота.
По вычисленным значениям ошибок можно оценить динамическую точность рассматриваемых типов систем.
Для статической системы имеем следующую формулу для вычисления коэффициентов ошибок:
ео(О = Л [(с0 - ®о + ®о) sin +
+ — О- <00 cos <о0^, (6.30)
откуда для малых cdq нетрудно получить
I 8о | = А д/(с0 - (О* + <О02 +
Для выражений (6.20) — (6.22) имеем
Co = 1/(1 + A); CJll = 1/Dm; CV2! = = 1/De; C3/3I = 1/O4; C^^l/De,
+ (С1ЮО-----(6-30
По аналогии с формулой (6.31) найдем соответственно |е| для астатических си-
480
стем 1-го и 2-го порядков, т. е.
е,усп. ей.
Ы~’л/(-т“?+>“01+
+ (-•§-“°)2; (6,32) ы-^7(>“«)г+(-т<
(6.33)
При Л = 0,1 рад, <£>о — 0,1 с-1, коэффициентах ошибок Со = 0,1, Ct = 0,02 с, С2 = 0,0025 с2, С3 = 0,0006 с3 и С, = = 0,000024 с4 по формулам (6,31) — (6.33) получим для систем: статической |во|= 10-2 рад, астатической 1-го порядка |ej| = 1.25-10-6 рад и астатической 2-го порядка |8г|=10~8 рад. На основании этих цифровых данных получим: точность астатической системы 2-го порядка выше в 1,25-102 раз астатической 1-го порядка и в 106 £>аз статической системы.
Пример 6.2. Построить характеристики точности статической и астатических систем 1-го и 2-го порядков при действии возмущающего воздействия f(t) — ВР/Ъ, где В = 2 усл. ед.-с-3— постоянный коэффициент. По формулам (6.20) — (6.22) соответственно найдем
ёо (0 = + 5.В'2 + C2Bt +
(6.34)
zx(t) = ClBt2 + CiBt + ^-, ’ (6.35)
и
ё2(/) = С,В/ + ^-. (6.36)
Пусть коэффициенты ошибок имеют следующие значения: Со =1, Ct = 0,1 с, С2 = = 0,01 с2, С3 = 0,003 с3. Тогда, пользуясь формулами (6.34) — (6.36), найдем
2
50 (/) = у /3 + 0,2/2 + 0,02/ + 0,002, усл. ед.;
(6.37)
51 (/) = 0,2/2 + 0,02/ + 0,002, усл. ед.; (6.38) ё2 (0 = 0,02/ + 0,002, усл. ед. (6.39)
Используя выражения (6.37) — (6,39), построим на рис. 6.1 характеристики точности систем (кривые 1—3 — соответственно для статической и астатической 1-го и 2-го порядков). При этом видно, что ошибки в системах возрастают от времени: в астатической 2-го порядка — линейно, астатической 1-го порядка—пропорционально квадрату функции, а в статической — кубу функции.
Если на систему одновременно действуют управляющие и возму-
Рис. 6.1. Характеристики точности различных типов систем автоматического регулирования
щающие воздействия, то результирующие ошибки в системе определяются как результат геометрической суммы отдельных их составляющих. Естественно, что данное положение справедливо лишь для линейных САР.
В заключение укажем, что динамические ошибки в системах при действии регулярных сигналов можно определять по характеристикам переходных процессов, которые находятся с помощью методов, приведенных в гл. 5. При поступлении управляющих сигналов на вход системы ошибка вычисляется по формуле
E(s)= .r^.--G(s). (6.40)
Когда сигналы возмущения приложены к выходу системы, то ошибка находится по формуле
e<s)=t+WF{s)- (6,41)
Для сигналов возмущения, поступающих на сумматор до передаточной функции, ошибка будет
E(s) = -:^yF(s). (6.42)
16 Ю. И. Топчеев
481
ТаИлица. б.з
Формулы для вычисления козунрицентов динамической точности в статических, системах автоматическою регулирования
Передаточная Функция ca шс <4 *>i сг
W,(s)-ж К (T,s.l)(Tas<-t)(T,s*l) 1 HfO^ шсС„(1-Са) x г 1 '(t-c,)a>, . i ] Lo>, c„u’ WjJ гш«[рШ ♦ -!— ♦ ' (L C,O)‘ шлш, ЧХЧГ QC” -Г1 , »-w<*, d, [ш, СоыГ ay " ° [a>, tu’Jti-cp' Гг// t [ a^ai/L V<x>, (t-Ca)a>, . 1 \t(l-Ca) + С,ысг ш31\Сош‘с ♦Г± + и-м J1 |_w, СцШ{ O),JX XC, P-Cjj
W,(S)‘ Г К(Т,яЧ) <W(T,S+I) 1 нт4» O>C G0( 1~Cg) X X[M+1 —fr шс_-1 Гш, a>j (t-C,)wf\ J_.fr Ь*С -1 - 7_1 X TT^frfev и), a)J -2.11 (t-CgjajX Ct)f Wjj (Vtl J {ШЛ1^ Г2/?Л)К ш,’ш} [(ш, ai}l lw; щы,/ lull a),aij '‘тгШ] (,-c>)C^ \f 2 1_ _ Cg d)e | + L<4 >j (f-Cjaif/*
W,(s)- K(TaS*l) f l*tOl'lu (л)сС9(!-C0) * [if— f * )_ fr^c ~| г/-сД‘] 2йЛл л,,*л v-ca} с„-чс} <t-ca)t jl .L )f c»^f . "ai, Ш,/[ ll-Cjai,1 . fr (i)c (^“"Cg) ш,‘ {ж-гМ +_Ц_)_Г,// .L)x ш/<ц/ L 'шг 4>jl Jlt.JL. L 1 a), a>, up . tx^c (£q) x (l-Cojrf tA_)L 1 Ш,1 O)j (t)f Шз/j -^u,j [440
W,(l) -K(T,S*I)1 t ^0 {Gfl) * -1 c — ;i/ Шс Cl> [w3 u, f (t-C0)uf J 5 jf v Й-дЬ-х •i« f~ —-'| *J *'* ’ Ji э“ А «-* ^**| 3t i । । । + tL\(l A, Ц7 [Jal; <y»/la>/ a/,' . 6 ) ^/-г./Гц_с, 1*. щи,/ Ca .t^tL ЛЛ ), ct L l4 4 <•№! 'iaya-tj 14 awY4)| /1 | (tJj fr Cg)f *('-fr)C05}
482
Таблица 6.4
~ Формулы для вычисления динамическое точности в системах автоматического регулирования с астатизмом 1-го порядка
Передаточная функция “С<Л a>cC2 ШСС3
r,(s) К (T2s + 1) _±L 10 20 ®c 2<ocCi Г(1 - <ocC,) - <ocC,l L <0i <o3 J Г <0j? ( <0j? <0® <0*Ct \ 6C[ ——-2СЛ— + — — 1 + L <0[<03 X <0j <o3 <o, /
s (T.S+ 1) (T3s+ 1) <01 ®cCl ®c ( ®c ®c 7 3 2I + -V- “ — + — ) + ®c<4 <0, <ot X <ot <o3 / J
«Ms) K(T2s+l) 10 2° ^c_ (01 2©cCi Г(1 — ©cCi) —— + —-— ©cG] L ©i ©3 j Г <o® 2<oi? (©3 2®3 и*С1 \ 6C, -|- + S 2C, —+ —r---£-L) + L®g ®!®3 V®i ®3 ®i /
s (T.S+ 1) (T3s+ Ip <o2C. / m’C. 2<o2 \ <0* .1 + _^_L(^_L £. j _ c, -c-4- шзсз <0[ X <0[ <o3 / <of J
Г3(л) K(T2s+l)2 10 20 <01 2<ocCt Г(1 — V<ocCi)-^£- + —— fflcCil L <0i <o3 J Г и’ 2®3 / и’ 2o>3 \ 6Cj -| + S 2C2I—+ —-- L <o, <0j<03 \ <o3 /
"s (T1S+1)’ (T3s+1) V \ и1) \ <0j <o3 / + 4«c2C 1 aJ f + 3 £1^. + Ш3С21 V V ®2 / ®1 J
«М«) К (T2s + 1)» _4_ 10 20 <01 4m Г 171 <Oc , ®c <0cCi 1 Г <o3 <o3 4и3 / шз шз \ -f+ -г+ £ 4C,(-^ + -^-) + L <of <o3 <0j<03 x <o1 <o3 / Li / \3 / __£l / \3 + 3<oc10 20 ( —) +4<o2Ciz\/ 10 20 ( —) - \<0j / V \ / _ 4 + £1) 10~^ f-£slV + <o’cf| X <0j <o3 / V X ®1 / J
"j^+DWl)’ KOeC.pi V<0cCJ Ш1 I 2 J
Таблица 6.5
Формулы для вычисления коэффициентов динамической точности в системах с астатиэмом' 2-го порядка
Передаточная функция
©сС2
зЛ ^с^з
(s)
K(r2s+ I)2 s2 (T1S+ 1)(Т3з+ 1)
^10 2° ®1
ЗсйдС2
2 £>
®с --20
2-4-10 20
®1
3w+2f— + — -2 с 2 \ ©1 0>з
2- ГРАФОАНАЛИТИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК ТОЧНОСТИ НЕПРЕРЫВНЫХ СИСТЕМ ПРИ ДЕЙСТВИИ РЕГУЛЯРНЫХ СИГНАЛОВ
Коэффициент статизма для статических систем и коэффициенты добротностей для астатических систем 1-го и 2-го порядков можно находить по логарифмическим амплитудным частотным характеристикам разомкнутых систем с помощью формул, приведенных в табл. 6.3— 6.5. Эти формулы получены для нескольких типовых логарифмических амплитудных характеристик для статических (рис. 6.2, а — г) и астатических систем 1-го (рис. 6.3, а — г) и 2-го (рис. 6.4, а, б) порядков.
Рнс. 6.2. Логарифмические амплитудные характеристики статических систем
Пользуясь рис. 6.2, а — г, можно определить значение
д-=Ю£1/2°, (6.43)
откуда
£1 =201g/<. (6.44)
Коэффициент статизма
Со =1/(1+К). (6.45)
Подставив в (6.45) соотношение (6.43), найдем
Со= 1/(1 + Ю£,/2°). (6.46)
Теперь вычислим значение коэффициента (OcCi. Для этого воспользуемся табл. 6.1, откуда получим
©cCj =
(6.47)
Lm.flE
484
Рис. 6.3. Логарифмические амплитудные характеристики астатических систем 1-го порядка
Из соотношения Со — 1/( 1 + К) определим К = (1 — Со) /Со- Для исключения со2 из выражения (6.47) запишем следующее соотношение: ©7(02= ю£2/4°, откуда
(®2/<ос)2=10-£2/20. (6.48)
Пользуясь рис. 6.2, а, найдем (Вг/®! = 1О(£,-£г)/20. (6.49)
Подставив в выражение (6.49) соотношение (6.48), получим
©Vo! = 10£,/2° (oVfflc)2- (6-50)
Рис. 6.4. Логарифмические амплитудные характеристики астатических систем 2-го порядка
1т,дБ
Учитывая, что Со= 1/(1 +10£1/2°), из (6.50) определим
1/(02 = (1-Со) ©ЛсХ). (6.51)
Из выражений (6.47) и (6.51) найдем
сосС1 = (ос (1 — Со) Со +
+ (6.52)
о о (Оз J
Занесем формулу (6.52) в табл. 6.3. Далее по данной методике вычислим следующий параметр:
сос2С2 == 2(о2 +
+1т^г](1-Со)Со-[^+
+ + тгТ - со) d -
Со®с 3J
__Г 1 I (1 — Со) <0| I 1 *1 у С0о>2 ®з J Л
Х(1- С0)2 Со}. (6.53)
Запишем формулу (6.53) в табл. 6.3. Таким же способом находим коэффициенты cocCi, юс2С2 для других передаточных функций.
С помощью рис. 6.3, а — г определим значения
(BcCi = (6.54)
которые внесем в табл. 6.3.
485
Для передаточной функции
W = s(TlS+ 1)' ’ (6-55)
По данным табл. 6.1 вычислим коэффициент
2Г _ 2 ( ®с . ®с ®с
С 2 К \Ш1 ©3 ©2
Пользуясь формулами
®с/®2 = 10£г/2°
(6.56)
(6.57)
и
(6.58)
исключим из выражения (6.56) ®2. Перепишем формулу (6.57) в виде
®г/®с = (6.59)
причем
(<В2/®1)2 = 1О-£1/20 • 10£1/2°. (6.60)
Подставив формулу (6.59) в выражение (6.60), получим
(©V®,)2 = 1 0£,/2°ф2/®с, (6.61)
откуда
1/<в2 = (6.62)
Так как К—1/Ci, то 1/®2 = = (фсС1)/ф1; поэтому имеем
- 2®сСр (6.63)
Формулу (6.63) запишем в табл. 6.4.
Коэффициенты (ОсСо (0сС2 для других передаточных функций (см. табл. 6.4) определим таким же путем. •
Рассмотрим системы с астатизмом 2-го порядка (рис. 6.4, а). Передаточную функцию системы в разомкнутой системе запишем в виде
..<^+0^+.) <6-м»
Пользуясь рис. 6.4, а, найдем, что К = ®il0£l/2°;
тогда на основании формул, приведенных в табл. 6.1, получим
a2cC2 = ~ = ^lO~L'120, (6.65) A (df
где К = 2/С2.
Формулу (6.65) занесем в табл. 6.5. Для определения коэффициента ф3С3 по данным табл. 6.1 запишем следующее выражение:
3z> с з С2 ( 1 . 1 2 \
®сСч = 6®с -д- I------------I.
С •’ 2 к Ш1 ‘ ©з ©2 /
(6.66)
Имея в виду рис. 6.4, а, исключим из выражения (6.66) частоту со2, т. е.
®с/®2 = 10£г/2° (6.67)
или
®2/®с= 10~£г/2°. (6.68)
Далее по ранее приведенной методике найдем
(6.69)
откуда
(Фг/©!)3 = io<£l“£"J/2° = 10£l/2°®2/®c.
(6.70)
Из выражения (6.70) имеем ®2/®1 — 2/С2фс, т. е.
1/®2== 7^/(2®!). (6.71)
Подставив выражение (6.71) в формулу (6.67), получим
<^С3 = За>1с2 (Ц- 4- — —
<6-72’
Формулу (6.72) внесем в табл. 6.5.
Таким же способом получим значения коэффициентов передаточной функции W2(s). Их также внесем в табл. 6.5.
При практических расчетах можно упростить формулы (табл. 6.3— 6.5) для определения характеристик точности статических и астатических САР. В этом случае положим Dt = 0 и £>е = 0, а остальные коэф
486
фициенты (статизма и добротностей) найдем при К — большом и Тз = 1/соз малом. Имея в виду эти соотношения, рассмотрим графоаналитический способ определения коэффициентов добротности САР сначала для статических систем. Ранее было показано, что для таких систем (рис. 6.2, а — г) коэффициент статизма
Со =1/(1 +Л). (6.73)
Здесь коэффициент К. находим по логарифмическим амплитудным частотным характеристикам с помощью соотношения 201g К=Ц, дБ. Для вычисления коэффициента добротности по скорости Dw статической системы, имеющей логарифмическую амплитудно-частотную характеристику, изображенную на рис. 6.2, а, воспользуемся формулой (6.52), которую запишем в виде
= 1/C! = ©,/Со = о, (1 + ТО- (6.74)
При выводе формулы (6.74) было принято, что Со, coi/сОс» 1/®з малы, и ими можно пренебречь.
Из рис. 6.2, а найдем <щ; тогда, зная К, по формуле (6.74) вычислим добротность статической системы по скорости. Применяя графоаналитический метод определения коэффициентов добротностей системы, следует иметь в виду, что
®к/®1 = Ю£,/20 = /(. (6.75)
При больших значениях К из формулы (6.74) получим
Da = (Bl/C. (6.76)
Сравнивая выражения (6.75) с формулой (6.76), найдем
Пш = (вк. (6.77)
Для графического определения юк продолжим прямую с наклоном —20 дБ/дек до пересечения с осью частот, как это показано на рис. 6.2, а.
Выведем формулу для вычисления добротности по ускорению. Для
этого воспользуемся теми же допущениями, которые были приняты при выводе формулы (6.74); тогда из соотношения (6.54) получим
De =
=_____________1______________
~^2 0 ~ Со) С0 — ~(1 — Со) С0 ~
~ ^(* -со)2со
______________®1__________
±i-K(l-C0)C0-(l-C0)C§- ’
-(l-Co)’Co
(6.78)
Подставляя в выражение (6.78) соотношение (6.73), найдем
п, — _ <М1+*)3 _ _ «> (1 + К)2 и'е~ К(Д + К) ~ к
(6.79)
С помощью выражения (6.74) из формулы (6.79) получим
De=-^-Da. (6.80)
Если Da = ©к, то по логарифмической амплитудной характеристике (рис. 6.2, а) графоаналитическим способом можно определить
Пе=--Ц^®к. (6.81)
Для нахождения Dt используем (см. табл. 6.3) следующую формулу:
= 6<о3((1 ~ С°'* -С I ®с°>3
(6.82)
487
По аналогии с формулой (6.78) можно найти
= —--------!--------.
-LC3(1-CO)-2X
®i
(6'83)
Умножим и разделим выражение (6.83) на со^, т. е.
Ш| О]
Dt ~ ®jCg(l-C0) “ ®,К/(1 + К)4 ’
откуда
Dt = со, (1 + К)4/К = (1 + ДОС
(6.84)
Пользуясь формулами (6.77) и (6.79), определим числовое значение коэффициента Dt.
Для остальных типов статических систем (рис. 6.2,6 — г) по данным табл. 6.3 можно вывести формулы, которые связывают между собой значения коэффициентов 1/(1 + К), Da, DR и Dt.
Теперь перейдем к выводу формул для графоаналитического определения коэффициентов добротностей Da, Dz и Dt для астатической системы 1-го порядка. Логарифмическая амплитудная характеристика одной из таких систем приведена на рис. 6.3, а, а в табл. 6.4 даны соответствующие формулы для вычисления коэффициентов сосСр <й?С2, ®зС3. Тогда нетрудно показать, что формула (6.77) справедлива и в этом случае, т. е.
£>щ = <вк. (6.85)
Для вывода формулы, позволяющей вычислять De, воспользуемся (см. табл. 6.4) следующим выражением:
+ <6-86’
Откуда при принятых ранее допу-
С>с).
(6.87)
щениях получим
Г'2,,2 С1тс
®1
При малых значениях С, формула (6.87) примет вид
Рв = ®1Рш. (6.88)
Продлив штриховой линией прямую с наклоном —40 дБ/дек, найдем
со,/©, = 10£'/« (6.89)
откуда
(^/0^= Ю£>/*>, (6.90)
но сок = со110£1/2°. (6.91)
Подставив соотношение (6.91) в выражение (6.90), получим
®?==®i®K=®A' (6-92)
Из сравнения формул (6.88) и (6.92) определим
De = ffl2. (6.93)
С помощью рис. 6.3, а графическим путем найдем он, а по формуле (6.93) вычислим коэффициент добротности по ускорению De.
Для нахождения Dt воспользуемся (см. табл. 6.4) выражением
Г ®з / <Вр
а>зг = 6С. —*-----------2С. I — +
с 3 1 I (OjCOq 1 \ (О]
®с ®сСЛ, ®сС1 ®с v г I 1 2
©3 ©j / ©j ©!
/2 2 \
х(—+ —) + ®c3q]. (6.94)
\ ®1 ®3 /
Из выражения (6.94) при приня-
тых допущениях получим
(6.95)
или
Dt — —<о5<о,/<ос. (6.96)
Графоаналитическим способом, определяя числовые значения со,, со, и сос из рис. 6.3, а, можно найти по формуле (6.96) коэффициент доб
488
ротности по производной ускорения Dt для системы с астатизмом 1-го порядка.
В заключение рассмотрим графоаналитический способ определения коэффициентов добротности для САР с астатизмом 2-го порядка. Из рис. 6.4, а имеем
Яе=(<)2. (6-97)
Справедливость формулы (6.97) можно доказать, пользуясь выражением (см. табл. 6.5)
2ш?
<=4io-£/2c, (6-98)
откуда
De = ®210L./20# (6 99)
При (®')2 = ®210£|/2° из выражения (6.98) получим формулу (6.97). Для вычисления Dt воспользуемся выражением, приведенным в табл. 6.5, т. е.
®3С„ = 3<в3СоГ— + ---2 а/^-1.
(6.100)
Подставив в выражение (6.100) формулу (6.98) и выполнив ряд преобразований, найдем
Dt = D^’Dj{\-2^/'^cY (6.101)
Располагая числовым значением £>е, определенным с помощью рис. 6.4, а, по формуле (6.101) можно вычислить Dt.
Пример 6.3. Определить характеристику точности статической САР графоаналитическим методом для примера 4.16 при отработке регулярного сигнала управления g(t), заданного в условных единицах и изображенного на рис. 6.5, а кривой 1. Логарифмическая амплитудная частотная характеристика разомкнутой системы приведена на рис. 4.9, в.
Для вычисления характеристик точности системы при отработке сигнала управления воспользуемся формулой (6.23). При вычислениях ограничимся только первыми четырьмя членами ряда. При этом необходимо знать коэффициенты К, De, Dt,
сиг-
Из
а также первые три производные от dg d2g d3g нала управления и
д,д,д,д';услед.
а)
е, с0, с,, е2>е3, усл. ед.
Рис. 6.5. Сигнал управления и составляющие ошибок в непрерывной статической системе:
°) g(0. Й(0. й(0. g'W: б) характеристики точности
рис. 4.9, в видно, что коэффициент К = = 13,5 дБ (или 4,75). По формулам (6.74), (6.80) н (6.84) соответственно найдем числовые значения
£>о = ®к = 20 с-‘; £)в = -^|-20 =
=- 24,22 с-2; D* = 20 = 800 с"8.
е 4,75
Производные от сигналов управления приведены на рис. 6.5, а в виде кривых 2—4. Составляющие характеристик точности даны в условных единицах: во — по положению; 81 — по скорости; ej — по ускорению н 8j — по производной от ускорения н построены тонкими линиями на рнс. 6.5,0. Там же жирной сплошной линией показана результирующая характеристика точности 8, представляющая собой сумму составляющих ошибок. При этом видно, что в системе устанавливается статическая ошибка 8 = 1,043 усл. ед.
Пример 6.4. Определить характеристику точности астатической системы 1-го поряд-
489
t)
Рнс. 6.6. Сигналы управления и составляющие ошибок в непрерывной астатической системе 1-го порядка:
о) 5(0> 5(0. £<0: б) характеристики точности
ка для примера 4.17 при отработке сигнала da
управления рад/с (рис. 6.6, а). Логарифмическая амплитудная частотная характеристика разомкнутой системы построена на рис. 4.12,6. Продолжим прямую в области низких частот с наклоном — 20 дБ/дек до пересечения с осью частот в точке а>» — 250 с-1 (прямая 2). В этом случае коэффициент добротности системы по ускорению De можно найти, усреднив участок характеристики |W'(/<o)| прямой 2 с наклоном —40 дБ/дек. Из рис. 4.12,6 видно, что прямая 2 пересекает ос^ частот в точке он = 5 с“*. По формуле (6.93) получим De = ш2 = 25 с-2. При а>1 =0,1 с-1, ©с = 16 с-1, пользуясь формулой (6.96), найдем = — 25-0,1/ /16 = — 0,156 с-3. Производные сигнала управления (Pg/dP, рад/с2 и (PgjdP, рад/с3 показаны на рис. 6.6, а. Составляющие характеристик точности: 8i — по скорости; 82 — по ускорению и 83 — по производной от ускорения приведены иа рис. 6.6,6. В результате сложения получим результирующую характеристику е, которая изображена жирной сплошной линией. Как
видно из рис. 6.6, б, с увеличением времени ошибка уменьшается при t = 2,5 с н достигает 2-10-3 рад.
Если передаточные функции исследуемых систем отличаются от указанных в табл. 6.2—6.4, то приходится пользоваться их приведением к табличным. Рассмотрим способы получения упрощенных передаточных функций на конкретных примерах.
Пример 6.5. Приведем передаточную функцию астатической системы 1-го порядка
Г(а) =
___________К (T3s + 1) (Г4а + 1)_________ s (TjS + 1) (Tjs + 1) (T5s + 1) (Tes + 1)
(6.102)
к табличному виду. Примем Ti>l2> > Т3 > Г4 > Г5 > Те. Имея это в виду, введем в выражение (6.102)
Tt2 = '^Ti'T2', Ти-л/Т3ТЛ Tse =
тогда получим приближенную формулу
m , , _____К (Гз4$ + О2______ /с 1АО1
Г (s) = s (Tiss + I)2 (Tees + I)2 • {6J° }
Выражение (6.103) совпадает с передаточной функцией, указанной в четвертой строке табл. 6.4.
Пример 6.6. Привести передаточную функцию астатической системы 2-го порядка
' Г(а) =
___________К(Г8з+ l)(r3s+ 1)_____________
s2 (T1S + 1) (T4s + 1) (Г,з + 1) (Tes + 1)
(6.104)
к табличному виду при Л > Тз > Т3 > > Г4 > Т3 > Т6.
Если в выражение (6.104) ввести обозначения
Тез — ^Т»Т3’, Т33 = ^Т3Т3,
то получим
, -___________К (Tt3s + I)2_________
w ™ ~ з2 (Fts + 1) (Г4з + 1) (T5es + I)2 ’
(6.105)
Ввиду того, что в передаточной функции (6.105) Т56 достаточно мало, запишем
о? К (г»з« *" (R 1061
r(s)-S2(r.s+l)(f4s + T)-- (6Л06)
Тогда передаточную функцию (6.106) приближенно можно считать соответствующей функции, приведенной в первой строке табл. 6.5.
490
з. ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ НА ОСНОВЕ ПРИМЕНЕНИЯ ПРИНЦИПА КОМБИНИРОВАННОГО УПРАВЛЕНИЯ
Повысить точность САР при действии регулярных сигналов управления или/и возмущения можно путем включения дополнительных корректирующих устройств разомкнутого типа. В результате этого исходные структурные схемы систем, работающие по принципу отработки сигнала ошибки, становятся комбинированными (рис. 6.7, а — в).
Из структурной схемы системы, изображенной на рис. 6.7, а, следует, что
Е ($) = 1 ~ Гк1 G(s) (6 107) '1[S> 1 + IF, (s) IF2(s) to.iu/;
откуда видно, что E(s) = 0, если
rK1(s)=l/r2(s). (6.108)
Однако на практике обеспечить условие (6.108) не удается; поэтому выбирают такие значения передаточных функций корректирующих устройств, которые позволяют повысить лишь порядок астатизма исходной системы на один или два порядка и уменьшить ошибки при отработке регулярных сигналов.
Из структурной схемы системы (рис. 6.7, б) имеем
г (С) - [1 — (s)] wza(s) , ,
1 + IF, (s) IF2 (s) [
(6.109)
Тогда условие (6.108) следует переписать в виде
ТГк2 =1/^(5). (6.110)
При сложной форме передаточной функции (s) обеспечить условие (6.110) также не удается; поэтому находят приближенные соотношения, повышающие порядок астатизма исходной системы.
В заключение рассмотрим структурную схему (рис. 6.7, в), по которой, используя принцип суперпози-
S)
Рис. 6.7. Структурные схемы систем автоматического регулирования комбинированного типа, инвариантные относительно сигналов:
«—управления; б—возмущения; в—при одновременном их действии
ции, из выражений (6.107), (6.109) можно найти
Е /м _ 1-^к. (s) W2 (s) G ( } ~ i + if, (S) |F2 (S)
, [1 — УГка (s)r,(s)J W2 (s) F , , 1 + IF, (s) IF2 (s) r
(6.111)
Для передаточных функций статических и астатических систем (см. табл. 6.6—6.9) и некоторых типов W'ki(s) и Н7к2($), полученных с помощью формул (6.108), (6.110), нетрудно определить выражения для вычисления ошибок. Формулы при различных порядках астатизма для исходных статических систем и действии сигнала управления, а также при отработке сигнала возмущения приведены соответственно в табл. 6.6 и 6.7.
В табл. 6.8 даны формулы для ошибок в астатических системах при поступлении управляющих воздействий, а в табл. 6.9 — при отра-
491
Таблица 66
Формулы Оля вычисления ошибок
в статических системах комбинированного типа с различными типами корректирующих устройств при действии: сигнала управления
Передаточная Функция Астатизм 1-го порядка Астатизм 2~eo порядка
E(S) W,(S) E(s)'
к1 Kz (Tls*tJ(Tt3*1j(T3s^f/ ’!k2 Tf S%+(Tf T2 + Tt fy-Tj ^)S+ (т,з-м1(тгзм1(т3зт)С + K1 K2 ЦТ^Т,хЗг.Т3)х 7кТ,7г73х1х1Т;т,Т2.
L(T,s.ll(T2s.!)(T3sM)+ Ст, Т3^ТМгТ3^ 7,727,13+
x2(t;s*i) ’ + X, XillT^Sr 1)
^^)sxels)
WtW-х, х2 (7гз+1) (7,3+1)г IT,S‘I) '/k2 Tl‘73Si+(7l‘+Z7,73)s + .. Ст', т3з+(т,г73+т,гт; +
[(T,3+tl‘(T3s. II +x, x2x . + Z7,7;73)s+lT,1+Z7,T2+ ?
x(7ts+t)l ( T^S+I) 27,7^+T;T3-T3(Z7,-72 +
( 7, 3 + 1)1 ( 733+ 1) + x, кг* ^(гт,-т2т3) „ x(tIsA) SG<S> Ktms-n /Cis-П
W3(sl-_ _xix1JT^_ll__ 1/k2 73723 + Z7, 73(7, + 73)s2 + егт^гт^т;-x^Tis-D _ -TjMI] 7/ T,373’ss+(Z7; Т,г73+27‘Т,7}х l(T,s + ll'(T,s + t)‘+x,x2x tT’73‘)s‘+ (7i7,‘+47;T,T,+
(7,з+Ц*(т3з+11*+ * +(7,2 + 47,73 + 73l)s + ♦- _+(гт, *zt3-t2) KM -+xlxt(T,s+l) sEls>
(7,3+1)* (73SM)2 'х(Тгз+1/1 (T^s + l) .t;t1i*zt,‘t3 + zt,t3!)3+ : +(2T,'T,tZTK'T3.T,2+4T,T3. ^-(27,-72^/72) s2M
Wx (31-x,k2(72S+I)‘ (T,s+1/2(T3s + 1)* • T/xt 7,373гз‘,+ (2Т,373 + 373г7,,)з,+ [(3T, + 27j * 7,1- 7^7,37313't+(Z7;7373 + 7,JTJ3 +
7 7,з + 1)ЧТ3зЫ)> + к,хг -+3T; Т,‘7321з!+(27,373 + 37,l733+
(7,i+i)3(73s+i/‘+ + ( 6Т2Т3+Зф)+Т,,№+(ЗТ}+
^(72s + 7MJ(7;s-t) . * Г,' 7,3 * 37,' 7, 73 + S7,'7,73)s2+
+бт,т3)з+(37,+273-72) ^KtKi(TzS+Dl x2(Tis*l) -ZT2lSf>l +(73+СТ,гТ3+ЗТ,Т3г + ЗТ,'7,г *.
*57,' 7, Tj + 7,' 7/ - (37, + 2 73 * .
Ti-273) 7l')3 + (372+67,T3 +
+T,‘ + 3T,T, +Z7iT3-2T2(37,+
jZT3+7,'-Z72) 73)s^
492
Таблица. 6.7
Формулы для Вычисления ошибок
В статически/. система/ комбинированного типа с различными типами корректирующих устройств при действии сигнала Возмущения
Передаточная функция AcmamusM t-го порядка. Аогпатизм 2-го порядка
ЩИ 6(S> Wt(s) E(S)
Wf ($/- лул2 (т,з*1)(тгзт)(т3з*1) Цк, (T„s*i) к + к 2 L^Kt+lTtS+lHTiS+H* + Tk'TiT3 + Гл' TtT^TfTt Tj)S+
1 (Т,з<-1/ (T,s*t)(Tss.fM * *1 к2 (Т^з + Пк, ’ где Т'-Г' + Т,* т, *т3
»(T3s+l)](TJs-n) ^Т/Т^Т'кТ^Т/Т,-1Т,Т^г
~t. T!r3 ^T>hf .s‘F(3l
Wt (з)= K,Ki(Tts+l) <Tts,ll(T3s*t) t/к. . Т?Т,1ЧТ,''1Т, 73)3 < . ‘ (Т,3^1)к,кг*(Т,3*11‘\ (T„s->t) (Тк S + 1) К, где Тк-гт,-тг^ ★Т3*Т1 , т/т, Тк'зЧт/Тз + т/т^
* [Тгз<.Ц K,Ktt(T,sMI4 t2T,T.,T/)SMT,‘-HT,T3^ "(Т3ЗЧП(ТЦЧ1 * Чт,т),-гт,Тккт}т/) .. КЗг 6(3)
W,(S)- __ Kj j T2S+ t) (TMml'lTjs-n)1 Ик, . Т,гТ?33*гТ,Т3(Т,->Т3)з\ г (T,3t1)4T,S*f)** 4t,4t,t3->t/)s * . . *K,Kt(TtS-H) ^.f.?..r,^T,-T2l.SF(s) (Tt3fl/ (Tk3+1JKj * где Тк-гт^гт,-~Тг ' Т.' . . Т,‘т3гт/з3<-(Г,‘тЧ » tn,K,(T,3-> l)f(T,sn)ir +гт,!т3т'к ^гт,т,гт/)з‘*
' МТзЗ+М1] (TJSK-t) кгт,!т31т,‘т,'^ гт, т/->
+чт, т3 П < т3‘ tDsmt,1 к
Т‘>Т,Т3*1Т,т/-Т^2Т3Т’к) .
XS6(S)
Wt (Slit, Кг (Т,!*!)1 ITit'lffy'l)1 t/к, , T,,T}s‘‘f(2T,3T>f _ (TK3ft) ТТ«3+1)к, • где Тк-ЗТ, <-2Ts--2Тг , Tl т,3Т1гзЧгт/т,3Т1-^
‘ C(T,^l)>(T33M)t^ ^т,3тЧзт/т/т‘3) s3* _
' ( Т,3*1Р(Т33*11+ *ЗТ3г Т,г)з3 *(ST,lT3* *к,кг (T,s*i)' . *3TfT,*Tl,/3t*{3Tlt+T3 f .^сътлз-кзтмгтг-т,) л К 3 F(s) ’ +Я, «1 (rtSft)*J(T, 3 ft) ^(гт,3т,*зт,гт3г^т'к т,Ч г > зт/ т, т] > ет; Т, Тг)К1 +
t(T,3 W,'T31- зът^зтТЧ _
пет^ЧТ/Тз1 -б,т‘)з+
*<зт,г-> ет,т3*т^зт',т,*
^гтк'тз -2T,T,-Tt4 * ftn
493
Ta.5nu.na. 6.8
Формулы для вычисления ошибок
в астатических системах комбинированного типа с различными типами корректирующих устройств при действии сигнала управления
Передаточная. Функция Астатизм 2-го порядка Асшатизм З-ю порядка
ад) 8(S) WK<3) l(S)
w,(s)-к,кг s(T,sn)(r,S4) (/А»М 3(7,3
[(7,3*1) K,K, 1(T,3*D* *Т37„‘ )з-*(Тг*Тг*Т,'-Т,1 Kl(Ks*llZ ' где Т'-тпт^гт;--тг СТгзП1к,кгПТ,з*й*
~>:(T}S*f)Sj ( T[s *1) H‘ 6(3) ' t(T,s*t)31*
W,(s)~ к,к,(Т,з*1)* (Z/xJS т)т,т,1з3*(гт;т3т,* : s(T,s*l) Кг(Тк!+Пг ’ где ТК~2Т^Т^ + 27} -ZTz т^т}т,гз^(гт;‘т}т,^гт^
UT'S'n'K^sthS’l)1* + т,‘ TtT^T^TjT^s'niTi^
C(Tts*l)3K,K, *s(T,s*lll ^7^ T3 *T37r2) 13*(T3T3*
\(T,3^n (Т‘з~11г
з(Т,е*1)г(ТзЗ*1) " 17,3*1)1 (7„'s*l) +z t,' 7,*zt,t,* t,‘- 7[)s *
^гт^т, ^2тЛт,т,*Кт,г- _
^(T^*73 *27,-27^^
-т^т;)з*(т;т^.гт;т, <•
+гтат, + т,г*тЛт1т,*гт;т,-» *• ~т1~гтгТ^ ,30(1)
W3(sl- Kf Kj (TgS 1)1 — — 5г Т1‘т,Т133^1т/тпТ,'Т^
[(7^з->П‘ К'К^зЧТ, г->1)1 *2Ti Т, W+fjf+ZT.lT, ♦
зг(Т,з'/)(Т,з+r) кг(Тк'з*1)* ’ к(Т,з*П1 (T^s^H1 ★Zt/Tj* Т,Тг-Г,г)з*
*<zrhT}-ZTt]s
W,(s)-K,KI(Tt34)2 - - з1 + т^т.з'чг^т^гт^
Ск,К1(Тгз->1)‘^зг(т,з^1)з ’ •♦zr; 7/ T,)s3* (гт/т^гт^
(T^sn)1 ^‘т^ъ'т, *чт;т,т,}з‘*.
зг(т,з^1)(т3з~1)г •
Kt(r;s+n* чт;^2т,г^т^т,-т^гитр
t ZTtT,}3* ( ZT,'f ZTi-ZTi’T,).
* 3s 6(3)
494
Таблица в.з
Формулы для вычисления ошибок
в астатических системах комбинированного тила с различными типами корректирующих устройств при действии сигнала возмущения
Передаточная Функция A cm a mизм 2-co порядка A cm am изн 3-го порядки
WK(s) Els) W„(s) Els)
W,(s) -к,кг17гз*1) з(Т,з+г}(Тхз*Х) 3 K,t7/s*l) , 7,7,7/347,7,*7,7,'* 2 *7,7/)S*(7 *7,*l/-7,) , 4T,S*f)s) (7)3*1) 3-SlF(s) 4T„s*1) K,l7/s*l)3’ tie TK-T,*73* *Z7/-7, . 7,T37,,s‘*(27,7]7^ ~ 2 L(7is4l lt,K4(7,s-l)’< *7,7/*7,7)г)з* . i/7,s*U31(T)s*l)i *(7l713-Z7l73'tZ737,'*7^-
-IsJiLs’fis)
w,(s)~ . К,Кг(7гЗ*1)г 3(7,3*1)3l7,S*t) 3 x,ir;s*t) *<27/7,7,* Т,^ТаТ2)з^ •141)1 IF, 3*1) +(Т/7,* 27/7,* Z7,T,*T3- s(7„s*l) 444' где ТК=2ТЯ' + Т,+ ★ 2Tt-2Tz 7)‘737,4*127^7, 7,* , 2 Cf,f,(71s*l)>*S(7,s*tliK *TX‘7,‘*7'KT37‘* * F(7,S*!I] (7)S*t)l , *ТзТ37,‘)зг*(27)7,7з*1 , 4irl'*T,7,,*7;'7,ii
-7f)s*(7/*73*Z7,*Z7t) -» ,, . , ,. .... .. .. , x *S3F(S)
t *2 7^7, *2 7,'7, 7,* 7/7, -гг2 7^)3*77/73*27/7,* : * 27}7,*7‘*7/г*.7/7з*27/7[ -ptLzw:/ S3F!S)
W, IS) = — J z_ (7"% з + f)2 s1 (7,s* t)l7,s*i) — — зг з,(7)з*1)г . 737,73з4(т/‘7,*7,'73)*
2 1ХТгЗ*?)2 Kf кг +$1(Т{3 + !}х 2Т{Т}Тз)1*+(Тк+2Т1Т1*-
4 7,3*1)1 (7/3*1)‘ ZT/73*7,7,-7})s*
‘ W,(S)- _ к,кг(7,з*1)1 Sl(7,s*1)(7,s*l)1 — — sl , 71!7i!T,s'*(7T7/*27;1T,7,*
‘ 7к,к,(72з*иг*зг/7,s*l)3 4 27/ 7, 7,)S3 * 127/^7, *
if7s3*U4 (7/S*/)‘ .+ 27/ 7}* 7/г7, *7} 7, *47/7,7,),
K:(7)s*l)1
13‘*(7/‘*27,!*47/7з-
-7{*27/7,*Z7,7,)3*l27',*Z7,-
^-UcIIlL^fIs)
495
ботке возмущающих воздействий. Как видно из табл. 6.6—6.9, с усложнением типа . дополнительных корректирующих устройств происходит повышение порядка астатиз-ма.
4. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ТОЧНОСТИ СИСТЕМ ПРИ ДЕЙСТВИИ CTAU.HO Н А Р НЫX СЛ УЧ АЙН bl X СИГНАЛОВ
Наряду с регулярными управляющими и возмущающими воздействиями на САР поступают сигналы, носящие случайный характер и обладающие различными статистическими свойствами. С целью упрощения математического аппарата для исследования таких сигналов обычно пользуются условием стационарности. В этом случае статистические свойства сигналов не изменяются при сдвиге их реализаций во времени. Наряду с условием стационарности в теории случайных процессов пользуются гипотезой эргодичности, позволяющей заменять усреднение по множеству реализаций, которое трудно осуществить на практике усреднением по времени, взятым по одной реализации при периоде наблюдений большой длительности.
Следует отметить, что не все стационарные сигналы удовлетворяют условию эргодичности. Например, если их реализация является случайной, но неизменяемой во времени, то такие сигналы относят к неэргодичным. Это положение позволяет дать удобное физическое толкование гипотезы эргодичности, заключающееся в том, что ее выдерживание связано с «хорошим перемешиванием» всех реализаций случайных сигналов. Так как данный процесс изменения сигналов практически всегда обеспечивается, то при определении характеристик точности САР пользуются условиями эргодичности и стационарности случайных сигналов. Для таких сигналов по корреляционным функциям
Я(т) находят спектральные плотности S(co).
Корреляционная функция представляет собой математическое ожидание произведения значений случайной функции X(t) и X(t-}-x), т. е.
т
Я(Г)= 2Г $ +
~Т (6.112)*
где т — сдвиг по времени.
При расчетах пользуются и взаимно корреляционной функцией
т
Яхг(*)=2Г $ X (t)Y (t + х) dt.
-т
(6.113)
Спектральная плотность определяется как преобразование Фурье от корреляционной функции-, тогда из выражения (6.112) найдем
S(®)= 7? (т)е-/“т dx, (6.114)
— оо или оо
S (®) — 2 R (т) cos сотДт, (6.115) о
следовательно, из выражений (6.114) и (6.115) имеем
00
= $ S(®)e^d<o;
— 00
00
(т) — S (со) cos шт da.
— 00
(6.116)
По взаимно корреляционной функции (6.113) можно найти взаимную спектральную плотность
00
5 (<й)= J RXY(x)t~^dx (6.117) — оо
* Формула (6.112) записана для случая, когда математическое ожидание сигнала равно нулю.
496
или
00
§ (св) = 2 RXy (t) coscotdr. (6.118)
0
Из выражения (6.117) имеем
оо
RXyW = -^ 5 $ДОе,в> — 00
оо
Ялг(т) = -<^- j S (w) COS (OTtZcO. — oo
(6.119)
Рассмотрим несколько примеров аналитического определения спектральных плотностей для некоторых типовых корреляционных функций.
Пример 6.7. Пусть корреляционная функция описывается выражением
/?(т) = е~ат,
откуда
с , . 2а
S (СО) = —я-;----=-.
ш2 + а2
Пример 6.8. При = е-а’т имеем /— (О2
S(a) = a
Пример 6.9. Для случайного процесса, все реализации которого X(t) = A (sin ш0/+ + ф) стационарны, получим
уЛ 2 м л
R (т) — ~н~ cos “of или S (со) = [S (со 4-Л Z
+ <йо)+6 (со —<йо)1. где д — дельта-функция.
Наряду с аналитическими методами определения спектральных плотностей используют приближенные графоаналитические способы, основанные на применении дробно рациональных функций [31].
Допустим, что экспериментально определенная характеристика спектральной плотности представлена в виде логарифмической зависимости
Lm(a) = 201gS(<o), (6.120)
которая построена сплошной линией на полулогарифмической бумаге. Аппроксимируя ее прямыми с наклонами ±20 дБ/дек-п, где п = О,
1,2,..., как это сделано в п. 1, получим
Lm (<о/<о;) = 20 lg [1 + (a/az)2"].
(6.121)
Итак, зная сопрягающие частоты а, и наклоны логарифмических частотных характеристик, по формулам (6.120) и (6.121) определим Lm(co).
Найдем математическую зависимость для построения логарифмической характеристики спектральной плотности при заданных он — ы5 и наклонах 0 дБ/дек, —20 дБ/дек, —40 дБ/дек; 0 дБ/дек,— 60 дБ/дек и —40 дБ/дек.
В этом случае по формулам (6.120) и (6.121) найдем
Lm (а)= 101gS(a)==201g/< —
-201g[l+(a/a1)2]-201g[l + + (a/a2)2] + 201g[l + (a/a3)4]--201g[l+(a/a4)6] + + 20 lg[l + (a/a5)2],
откуда
о — к (1 + (<о/соз)4Н1 + (сй/<п5)2] d(a>) —л [1+(©/©, )21(1 + (®/©г)2]х ’
X [1 + (<й/<в4)в]
(6.122)
т. е. здесь п — ±1, ±2.
Разложим полученное выражение на простые множители. При этом необходимо вычислить корни характеристического уравнения
l-|_Vn = 0. (6.123)
Они имеют следующие значения: An = 2V~b откуда по формуле тригонометрического представления по-
лучим
kn = cos
л (1 + 2у) 2п
+- 7 sin
л (1 + 2v) 2п
Здесь v = 0, 1, 2, ..., п — 1.
Выражение для Хп графически можно представить в виде векторов, равных по модулю и сдвинутых друг относительно друга на угол л/я. В этом случае корни выражения
В2п(аМ)=1 + (<оМ)2п (6-124)
497
Рис. 6.8. Определение единичных радиусов векторов на плоскости X: а--при п четном; б —при п нечетном
можно изобразить графически в виде симметричных прямых, вписанных в окружность единичного радиуса на плоскости X (рис. 6.8). При этом необходимо помнить, что если частота сопряжения <щ отлична от единицы, то радиус окружности будет со;. При п четной одна пара корней совпадает с мнимой осью, как это показано на рис. 6.8. Нули функции (6.124) расположены отно-
Таблица 6.10
Определение Сп (/<») при п 8
п сп (Ю
1 (1 + /<й)
2 (1 + 1,4142/© —©’)
3 (1 + /®) (1 + — <а2)
4 (1 4-0,7653/© — ш2) (1-4- 1,8477/© - <в2)
5 (1 4- /©) (1 0,6180/© — ш2) X Х(1 + 1,6180/© —©2)
6 (1 4-0,5176/©—<в2) (14-1,4142 у©-©2) X X (1 — 1,9318/ш — ©2)
' 7 (1 4- /®) (1 4- 0,4449/ш — ©2) X X (1 -г 1,2465/<о - to2) X X (1 + 1,8022/© - <о2)
8 (1 4- 0,3896/to - <в2) X X (1 + 1,110/© — <в2) X X(1 + 1,6630/to - to2) x X (1 + 1,9622/© - ©2)
сительно симметричной вещественной оси; поэтому
В2п (со) = С„ (» Сп (—]&), (6.125) где функция Сга(/£о) содержит все нули в верхней полуплоскости, а Сп(—j(a) нули в нижней полуплоскости.
Для практических вычислений следует пользоваться соотношениями, приведенными в табл. 6.10, при различных значениях п. По данным табл. 6.10 и формуле (6.122) можно найти S(ю).
Пример 6.10. Пусть •/<’=48 • 10-6 рад2 • с, <01 = 1 с-1, <O'Z = 5 с-1, <о3 = 10 с-1, <о4 = = 50 с-1 и <о5 — 200 с*1 тогда найдем
S (<в) = 48 • 10~6 X
' [1 + 1,4142/ (<о/10) - (<о/10)2] X )
У __ Х{1+/(<в/200)] I
[1+/(<о/1)] [1+/(<о/5)] [1+ |А
4- / (<о/50)] [1 + / (©/50) - (<о/50)2] )
z [1 - 1,4142/ (<о/10) - (<о/10)2] X \
у I X [1 — /(<о/200)]_______
[1-/(И/1)][1-/(©/5)]Х >
Х[1-/(<»/50)Н1-/(<о/50)- I
I - (<о/50)21 )
(6.126)
Первое выражение в фигурных скобках имеет все нули и полюсы, расположенные в верхней полуплоскости, а второе — нули и полюсы в нижней полуплоскости. По формуле (6.126) на рис. 6.9 сплошной линией построено точное значение S(<o), а штриховыми линиями — аппроксимированное по формуле (6.126). Как видно из рис. 6.9, погрешность аппроксимации характеристики S(©) не превышает 2 %.
Воспользуемся функциями Лягер-ра для определения характеристики
498
Таблица 6.11
Вычисление функций спектральной плотности по коэффициентам Лягерра
(0 cv (/<и) 3(ш)
со ci С2 сз *2
2 32,43 19,68 8,35 3,12 0,431 -0,157 0,052 -0,017 7,08
10 63,25 29,24 16,3 8,72 0,129 -0,105 0,086 -0,070 2,37
20 106,69 51,13 27,06 13,12 0,067 -0,061 0,055 —0,050 1,19
30 134,34 70,25 39,28 19,08 0,046 -0,043 0,040 -0,037 0,79
40 164,79 87,76 40,65 21,37 0,034 —0,033 0,031 —0,030 0,63
50 199,21 104,42 46,91 23,15 0,028 -0,027 0,026 —0,025 0,60
60 213,58 106,02 , 54,19 27,45 0,023 —0,022 0,022 -0,021 0,47
70 215,47 109,77 55,84 27,69 0,020 -0,019 0,019 -0,018 0,42
80 226,14 115,52 58,14 28,94 0,017 -0,017 0,017 —0,016 0,32
90 226,65 115,35 59,17 29,15 0,016 -0,015 0,015 -0,015 0,30
100 236,53 123,29 71,52 29,44 0,014 —0,014 0,013 -0,013 0,25
S(q) по обработке экспериментальной кривой спектральной- плотности. Как известно [31], функцию Лягерра v 20-го порядка можно записать в виде следующего ряда:
с , 1 1
I 2V+ Т 2V- Т
1Ч (/) = е_/1 -=—7— 4-----тт; Z*-1 +
< -vl 1 (v—1)1 1
, . 2*-”+у vK-D* v
• • • -f" z xl [(v - x)l]2 A
X/V“x+...+2T<-I)V}. (6.127)
Преобразование Фурье S’vG’a) для функции Лягерра будет
(/со) =» д/2 ,
(1 + »v+
v = 0, 1, 2, ... (6.128)
При заданном графике случайной величины Хт(0 на интервале [О, 2Т] имеем
N
cv/v(0, (6.129)*
V-0
где коэффициенты ряда Лягерра находятся по таблицам функций Лягерра;.
* При условии обеспечеиия ортогональности функции Лягерра коэффициенты cv можно вычислить по формуле
2Г
о
Для определения характеристики спектральной плотности воспользуемся соотношением
N
хх (б.1зо)
т v^O
Подставив выражение (6.130) в выражение
Sx (<й) = ^|Хт(»|2, (6.131) цолучим
$Хт (а) ~ ~2Т ] У, {]<&)
Т * V-0
X IУ с^(-/<й) V-0
(6.132)
Если каждая из функций .2\,(/о)) является дробно-рациональной, то SxT — также дробно-рациональная функция. Первый сомножитель в правой части выражения (6.132) содержит все полюсы на мнимой оси
Рис. 6.9. Логарифмическая амплитудная характеристика спектральной плотности сигнала возмущения
499
Рис. 6.10. Структурная схема системы со случайными сигналами управления и возмущения
и верхней полуплоскости, а второй — в нижней полуплоскости. ,
Пример 6.11. Для кривой S(a), изображенной сплошной линией на рис. 6.9 (пример 6.10), определить Sv (<в), пользуясь табулированными функциями Лягерра. Результаты вычислений записаны в табл. 6.11.
По данным табл. 6.11 на рис. 6.9 штрихпунктирной линией построена характеристика Sv (ш). Из сравнения с экспе-лт риментальной кривой видно, что погрешность построения спектральной характеристики ие превышает 1 %.
Рассмотрим формулы для определения дисперсий ошибок САР, возникающих от действия эргодических стационарных случайных сигналов N\(t) и 7У2(О> пользуясь рис. 6.10. При этом воспользуемся обозначениями, принятыми в п. 9, гл.' 1; тогда, если сигналы Ni(t) и АМО некоррелированы между собой, то получим
Е<0=Т+ТГотЛ,'(,,+
+ |тД.>"’(<)- <6133>
По выражению (6.133) можно записать формулу для определения спектральной плоскости сигнала ошибки в виде
I 1 I2
(со) = I 1'+¥ (/ш) I ’
+1 тт^г Г (ш)’ <6134» где S,v,(tt>) и (а)— спектральные плоскости случайных сигналов соответственно по управлению и по возмущению. .
Дисперсия ошибки системы регулировки будет ‘ 00
J Se(a)da. (6.135)
Подставив в . формулу (6.135) выражение (6.134), найдем
00
$ I 1 + U7 (/©) I SWi(a)d<B + — 00
, 1 С I U7 (» I2 О , Ч J
+ 2л J I 1 + W (ja>) I S1V‘ d<0
(6.136) или 00
де2 = 1М I Фе О) I2 (<*) do +
00
+ i J I ф О) I2 ^2 (о) do. (6.137) — 00
Для того чтобы применять номограмму Никольса при нахождении частотных характеристик для первого слагаемого формулы (6.136), воспользуемся следующим соотношением:
1 + U7 (/а) = ( U7 (/а) )/(1 + w (ja) ) • (6.138)
В этом случае на номограмму Никольса наносят обратные частотные характеристики всей разомкнутой системы.
При написании формулы (6.136) было принято
(о) = S jy2tf, (о), (6.139) т. е. сигналы Ni(t) и Мг(О некоррелированы друг с другом. Если исключить это условие и считать, что сигналы коррелированы, то формулу (6.137) следует переписать в виде 00
= i $ I фе (»I2 Sat. (<») do + — 00
оо
+ з~ J | Ф (jo) |2 Sn2 (о) do + —оо
00
+ Фе(—-/'<о)Ф (/a>)Sjv1Ar2(co)d<i)4-
— 00 00
+ Ф« № Ф SniN' d(i>-
(6.140)
500
По формулам (6.137) и (6.140) определяют дисперсии сигнала ошибки графоаналитическим способом при различных видах характеристик спектральных плотностей
S/уД®), Sn2(<£>), Sjftiv2((£>) И S,v2,v, (to).
Если спектральные плотности случайных сигналов S,v, (со) и S,vs (со) являются постоянными в полосе существенных частот системы регулирования, т. е. SJVi (со) = cf, (®)= = cl, то для определения дисперсии ошибки можно использовать выражение
/оо
, 1 Г с (з) с (— з)
" 2л/ J d (s) d (— s)
—/оо
ds (6.141)*
или
___ 1 С c (/co) с ( /co) , -257 J d(/(o) d (- /о) d<a- <6-142>
— co
Формулы для вычисления интегралов (6.141) или (6.142) приведены в прил. П-П.З до Jio-
Рассмотрим несколько примеров определения дисперсий (или средних квадратических значений) ошибок в САР при действии эргодических случайных сигналов.
Пример 6.12. Определить дисперсию ошибки для САР, имеющей частотную характеристику вида
W (jw) __________250(°-62>._+ »________,
v ’ je> (10/и + 1) (0,02/й + 1) X
X (0,01 /со + 1) (0,0018/ш + 1)
(6.143)
откуда нетрудно получить передаточную функцию замкнутой системы:
. 155/©+ 250
ф(;0)) -------------—1 .
2 • 10“6 (/со)5 + 0,0023 (/со)4 + ‘ + 0,31023 (/со)3 + 10,03 (/<в)2 + 156/(0 + 250
(6.144)
* См. формулу (5.14) и вычислительную процедуру, представленную в виде программы ISQERR.
При Sy2 = 1 < 10~6 рад2 • с определим
155/(0 + 250
2-Ю-6 (/(о)5+0,0023(/(о)4+ 4-0,31023 (/со)3 4-
4-10,03 (/(о)2 4-
4- 156/со 4- 250
X SNi (со) do. (6.145)
Пользуясь данными прил. П-П. 3, найдем [с2т0 + (сз — 2с2с4) т1 4-
4- (с? — 2с, с, 4- 2спс.) тЛ
J5 =-----+---------------° 47 2J . (6.146)
2Д5
Подставив соответствующие значения коэффициентов в выражение (6.146), по формуле (6.145) вычислим дисперсию
а2 = 14,47 10-6 рад2
или после извлечения квадратного корня из Qg найдем среднее квадратическое зна-чеиие ошибки
ае = 3,8 • Ю-3 рад.
Вместо таблицы формул (см. прил. П-П.З) можно пользоваться вычислительной процедурой
ISQERR для вычисления * 1п при произвольном п.
Данный пример можно решить графоаналитическим способом, не требующим громоздких вычислений. Рассмотрим его применение (для примера 6.12), располагая спектральной плотностью Sw, (со), приведенной на рис. 6.9.
Пример 6.13. Определить 6| и в САР (рис. 6.10), на которую действуют случайные возмущающие и управляющие воздействия.
Пользуясь кривой 1 (рис. 6.11), находим |Ф(/(о)|, которая построена на рис. 6.12, а сплошной линией. Здесь же штриховой линией приведена зависимость |Ф(/а>)|2.
Покажем иа рис. 6.12, а штрихпуиктир-ной линией функцию спектральной плотности (g>). Умножив соответствующие значения |Ф(/ю)|2 на получим
кривую | Ф (/©) |2 Sjv, (<£>) (рис. 6.12, б). Определим по рис. 6.12,6 площадь под этой кривой при —оо < (О < оо и, домножив ее на коэффициент 1/2л, найдем дисперсию ошибки. После извлечения из иее квадратного корня получим 6i = 3,4X X Ю~3 рад.
* См. гл. 5, с. 407.
501
сл о to
Рис. 6.11. Номограмма Никольса с характеристиками (кривая /), (кривая 2)
Рис. 6.12. Амплитудные частотные характеристики замкнутой системы относительно возмущающего воздействия в виде случайного сигнала:
а) 1Ф(/Ш)|, |ф(/о>)|* и SjvJw); б) 1Ф (/<й) |2 Sjy, (ш)
На рис. 6.13 сплошной линией прказана функция | Фе (/<£>) |, снятая с номограммы Никольса (кривая 2, рис. 6.11), а штриховой линией — функция | Фе (/со) |2 • с2. После определения площади под этой кривой имеем
а2 = 2,4-10~3 рад.
Если необходимо найти суммарную среднюю квадратическую ошибку от действия двух сигналов, то следует использовать формулу
= л]О’? + <^2 =
= V (3,4 • 10~3)2 + (2,4 • 10-3)2 = = 4,16• 10~3 рад.
Данная методика может быть распространена и на системы, на
которые действуют взаимно коррелированные случайные сигналы.
5, ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ТОЧНОСТИ ДИСКРЕТНЫХ
И ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ ПРИ ДЕЙСТВИИ РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ
ПЕНАЛОВ
Рассмотрим способы вычисления характеристик точности дискретных и дискретно-непрерывных систем при действии регулярных и стационарных случайных сигналов. По аналогии с непрерывными системами ошибку можно представить в
Рис. 6.13. Амплитудные частотные характеристики замкнутой системы | Фе(/ш) |а относительно сигнала управления в виде случайного сигнала типа белого шума
503
зависимости от передаточных функций Фе, формы входного сигнала и его производных, значения которых известны лишь в тактовые моменты времени t = KT0. В этом случае ошибку можно представить в виде ряда
в (кТ0) = Cog (кТ0) + g (кГо) +
+ ^ё(кт;) + ^(кГо)+....
(6.147)
где Со, Сь С2, ... — коэффициенты ошибок.
Применяя к выражению (6.147) прямое преобразование Лапласа, получим
E*(s) = (Co + -^-s + -§-s2 +
+ -^-s3+ ...)g’(s), (6.148) где ряд, стоящий в скобках, представляет собой разложение передаточной функции Фе ($) сигнала ошибки по степеням s. Ряд относительно s получен по аналогии с формулами (6.1) — (6.28) и табл. 6.1— 6.2, которые были выведены для непрерывных САР. В результате такого подхода можем записать
r _ *‘<00
i = 0, 1,2, ... (6.149)
При определении характеристик точности дискретных и дискретнонепрерывных систем вместо функции Ф*(з) будем пользоваться передаточной функцией замкнутой системы, записанной в z-форме как Фе(г). Тогда коэффициенты ошибок при произвольном То вычисляются по формулам
С0 = Фе(1); . c,=W(D;
С2 = тИФв'(1) + Фе(1)];
с3=7’з[Ф'"(1)+ЗФ;'(1)+Ф'е(1)];
Здесь
ф(0(1)
__ d(f)<De(z) dzl
z~i
(6.151)
На вход САР могут поступать и дискретные значения сигналов, когда огибающая их неизвестна. В этом случае нельзя пользоваться формулами (6.147)—(6.150) и приходится выполнять разложение сигнала ошибки е(кТ'о) в ряд, но по разностям входного сигнала, т. е. дискретный аналог выражения (6.147) будет иметь вид
8 (кТ0) = CQg (кТо) + Ag m +
+ ^Л2£(кТ0) + ^Д3£(кТ0)+ ...
(6.152)
Применяя прямое z-преобразова-ние к ряду (6.152), найдем
= Ф*(О(0), s«=0
E(z) = [c0 + 4r(z“ 1) +
+ §-(z-l)2 +
+ 4 (z - I)3 + .. .1 G (z). (6.153) О! -1
В формуле (6.153) ряд, стоящий в квадратных скобках, является разложением функции Фе(г) по степеням (z—1). Коэффициенты ряда Ci по аналогии с (6.151) будут вычисляться по формуле
Ci
dzl
= ФФ(1),
i = 0, 1, 2, ..к (6.154)
Так как z = tsT°, то разложив данное выражение в ряд Тейлора и пользуясь линейными членами (что справедливо при малых То), получим
z=l — sT0, (6.155)
(6.150)
откуда s = (z — 1)/Г0.
504
Подставив соотношение (6.155) в ряд (6.148), найдем
Е (z) == Гс0 + (z — 1) +
L 111 о
+ -^(z- 1)2 + 2! Г2 '
+ -^-(z-1)3+...1g(z). (6.156) о! У о J
Из сравнения рядов (6.148) и (6.153) определим
Со = Со; Ci — CJTq', Ci — CjTo't • •• ...; Ci = Ct/Tt0.
В этом случае ряд (6.156) можно записать в виде
E(z)=[Co + ^-(z-l)+^(z-l)2 + + -§-(2-1)3+...]g(z). (6.157) В гл. 1, п. 7 было показано, что при .|s7'o| =1 и s = s ряд (6.154) можно представить в виде
E(s)=(c0 + 4p + -^-s2 +
+ 4р3+...)g(s), (6.158) где s = /й, а й — псевдочастота.
В ряде (6.158) коэффициенты ошибок находим по формуле
=ф(ег)(0)1 as ls-0
где коэффициенты ошибок Сг == Ct.
Далее можно определить коэффициенты ошибок и в случае, когда условие | sTol = 1 не выполняется. Для этого воспользуемся билинейным преобразованием
z — (1 + ш)/(1 — u>), откуда
w = (1 — z-1)/(l + £“*)•
При z-1 = е_/шГ" имеем
(6Л59)
Записывая ряд разложения передаточной функции Фе (да) по степе
ням w, получим
Е(ш) = р0 + 4гда + -^да2 +
+ -§w+ ...]g(u>). (6.160)
Здесь
Ct = =ф^(0).
dw w~a
Подставив в ряд (6.160) формулу (6.159), найдем
е (»)-[£,+4j-(/tg 49+
+4(/^),+-]ом-
(6.161)
Сравнивая ряды (6.161) и (6.158), определим значения коэффициентов ошибок при s = /й, т. е.
__р . р .
CQ— Cq, U]— ,
tg^ii в 2
(6.162)
Сз®3
Разложение в ряд (6.158) позволяет при определении коэффициентов ошибок пользоваться логарифмическими амплитудными характеристиками, построенными относительно псевдочастоты. Если условие j.sT'ol = 1 не выполняется, то необходимо построить логарифмические амплитудные характеристики относительно частоты w = tgcoTo/2 и определить ошибки в системе по формуле (6.161). При малых То соотношения (6.162) можно переписать в виде
С0 = С0; C^Cfi/To-, С2 = С2(2/Т0)2’,
С3 = Сз(2/7’о)3, ...
505
Lm Д5
сл §
ci f)
Рис. 6.14. Логарифмические амплитудные характеристики дискретно-непрерывных систем:
а—статической; б—астатической 2-го порядка; а—реализация корректирующего устройства в виде RC-цепочки
Можно построить характеристики точности систем по коэффициентам добротности. В этом случае имеем
Со =1/(1+ Г);
C2=--2/De;, C3==Q/Dt и т. д.
Коэффициенты статизма и добротностей можно определить по формулам, приведенным в табл. 6.3—6.5, или графическим путем по логарифмическим амплитудным характеристикам, пользуясь, например, значениями 201gl/K* и частотами со*, со* Рассмотрим несколько примеров для построения характеристик точности различного рода дискретно-непрерывных САР.
Пример 6.14. Определить коэффициенты статизма и добротностей и построить характеристику точности для дискретио-ие-прерывной статической САР, если
(0,4/6 + 1) (0,005/6 — 1)2Х
X (0,0036/6 — 1) X
X (0,0014/6 + 1) «7К (/6)
(Ш) “ (0;34/6 +'Т)(0,048/6+ i)X ’ (6Л63)
X (0,0146/<о + 1) х
X [(0.0164/6)2 + + 2-0,0164/6+ 1] nr /,-s о (0,032/6+1)2 где Гк(/И) = 3,16-^^^^., а непрерывные регулярные сигналы поступают на вход замкнутой системы, которые можно представить в виде, показанном на рис. 6.5, а. В этом случае из логарифмической характеристики (рис. 6.14, а), имеем
1+/С‘ = 4,16; £>’ = 128,96;
£>* = -169,8; D* = 2938.
Составляющие ошибок построены на рис. 6.15,а сплошными линиями в виде б-функций: кривые / —для ё?; 2 —для ej; 3 — для ё£ 4 — для ё*. Общая характеристика точности е*, представляет собой сумму составляющих и также построена на рис. 6.15, а.
Пример 6.15. Найти характеристики точности САР с астатизмом 2-го порядка по передаточной функции
0,668 (1 - 0,006/6) (0,091/6 + 1)Х X (0,2/6 + 1) (1 — 0,1 /6)2Х W (/6) = X (3,3/6 + 1) 0,32 u (/6)« (0,1/6 + 1) (0,104/6 + 1) х ’ X (0,131/6+1) (0,25/6+1)
(6.164)
30
Л0
О
Рис. 6.15. Характеристики точности дискретно-непрерывных систем автоматического регулирования:
а—статической; б—астатической 2-го порядка
когда на вход замкнутой системы действуют два типа регулярных сигналов: не-прерывный (рис. 6.16, а) и дискретный (рис. 6.16, б) с тактом кваитоваиия Го — = 0,2 с. По логарифмической амплитудной характеристике (рис. 6.14,6) определим £>* = 0,213; £>£= 1,177.
Реализация дискретного корректирующего устройства на RC-цепочках показана на рис. 6.14,в. Составляющие характеристик точности замкнутой системы ё£, ё* построены на рис. 6.15,6. Результирующая характеристика точности представляет собой сумму составляющих ошибок
в(«Го)=О,0469g(кГо)+0,00085gк(Г0). (6.165)
Оиа также построена иа рнс. 6.15,6.
Пример 6.16. Сравнить точность статической САР из примера 6.14 при действии
507
Рис. 6.16. Характеристики регулярных сигналов управления:
а—непрерывного типа; б—дискретного типа
непрерывного н дискретного сигналов управления. Для непрерывного сигнала (рис. 6.5, а) ошибку определим по формуле
8 («Го) = 0,24g (кГ0) + 0,008g (кГо) -
- 0,0059g («Го) + 3,4 • 10-4g («Г»). (6.166)
Если иа вход исследуемой системы поступает дискретный сигнал (рис. 6.17, а), то результирующую характеристику точности можно записать в виде ряда (6.152) через разиоети различных порядков для входного сигнала, т. е.
в (кГ0) = 0,24g (кГ0) 4-
। о ops 0 + ~ g (КТ°)] ।
Го
[g («Го + 2Го) — g (кГо + Го) — + 0,0059----~ g s (к7»)]----1
А
[g («Го 4- ЗГ0) — 2g (кГ0 + 2Г0) + + g («Го + Го) — g (кГо + 2Г0) 4-
4- 3 4 • 10~4 + ~~ В (к^о)] _
Г®
(6.167)
8 (кГо) — 0,24g (кГо) 4-
। о оо8 (к^° + S (кГо)] I Го
(«Го 4- 2Го) 2g (кГо 4- Го) 4-
4- 0,0059-----------+.g^r°.U-------------4-
7 о
[g («Г» 4- ЗГо) - 3g («Г» 4- 2Г0) + 4-3 4 • 10~4 4~ 3g («Гр 4- Го) —- g (к^°)!
Т30
(6.168)
Подставляя в формулу (6.168) значения к = 0, 1, 2, ... и Го = 0,2 с, получим составляющие ошибок в виде б-фуикций; кривые 1 — для 81(кГ0); 2 — для в2(«Го); 3 — для 8з(кГ0), сумма которых определит результирующую характеристику в. Оиа построена на рис. 6.17, б вертикальными линиями в виде б-фуикций. Из сравнения данных характеристик следует, что точ-
Рис. 6.17. Составляющие дискретных сигналов управления и характеристики точности статической дискретно-непрерывной системы:
а) й(кГо), ё (кГо), й(кТо), ’я(кТо); б) характеристики точности
508
ность дискретио-иепрерывиой системы при поступлении непрерывного и дискретного сигналов управления одинакова.
Рассмотрим анализ точности дискретных или дискретно-непрерывных систем при действии случайных воздействий Ni(t) и N2(t), представляющих белый шум. Воспользуемся ранее приведенными зависимостями (6.137) и перепишем их в z-форме:
^==-^Г $ I Фе (г) I2 5^(2)2-424-lz|—1
+ ^Т ф | Ф (2) (2)2-42.
Izl-l
(6.169)
Для того чтобы можно было пользоваться ранее рассмотренным математическим аппаратом, введем переменную /со, тогда
оо
— оо
оо
х i V фU® I2 W®) Ниd(5-
(6.170)
Пример 6.17. Определить среднюю квадратическую ошибку САР, если на ее вход действует сигнал в виде дискретного белого шума со спектральной плотностью 5лг1(2) = с2Л'о- Допустим, что
™_ 0,363 (z - 0,840). (z + 0,486) {Z> (z - 1) (z - 0,905) (z - 0,135)
при Го = 0,05 с.
Далее определим
Фе (/ш) = 1 + W (jn) cl + /й °"
_ 2,16 (/й)3 + 70,226 (/й)2 + 131,48 (/&)
1,99 (/й)4 + 58 (уй)3 + 954 (уй)2 + ‘
+ 3557 (/й) + 2661
Перепишем формулу (6.170) в виде
s|Фе(/й)|2>< — оо
---------------2-------
Xs*.
Рис. 6.18. Значения среднеквадратических ошибок системы (пример 6.17) в зависимости от с2
Приведем подынтегральное выражение в виде дробио-рациональной функции, т. е.
Сгп—2 (j<b) I ____
dn (/®) (—/®) 1л=4 —
_ Ьо иа>)6 + Ьх + bj (уй)2 + Ър ,fil7n [а0 (/й)4 + «1 (/®)3 + а2 (уй)2 + • ' ’ '
+ а3 (уй) + а4] [dn (— уй)]
Коэффициенты для выражения (6.171) имеют следующие значения: Ьо = —4,67; 6, = 4931,7; Ь2 = —17287; b3 = 0; а0 = = 1,99; at — 60; а2 — 954; а3 — 3557; at = 2661.
С помощью данных табл. П-П. 3 вычислим интеграл в виде
/ Ьо (— axat + а2а3) —
л / —а3а3Ьх + а3ахЬ2 +
_ _ \ / + (арОз — aia2) арЬ3/сц __
V То 2а0 (аоа| + a2tat - ata2a3)
= 0,4Vc2/7\. (6.172)
Используя выражение (6.172), построим значения средней квадратической ошибки от с2 при То — 0,05 с (рис. 6.18), откуда видно, что средняя квадратическая ошибка от с2 изменяется нелинейно.
6- ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ
ПРИ ДЕЙСТВИИ случайных СИГНАЛОВ ПУТЕМ ВЫБОРА ТИПА И ПАРАМЕТРОВ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
От действия случайных сигналов управления и шумов в САР возникают ошибки, которые оказывают значительное влияние на точность
509
Рис. 6.19. Логарифмические амплитудные н фазовые частотные характеристики четырех типов следящих систем
выдерживания эксплуатационных режимов. Так, например, если на вход следящих систем поступают сигналы, спектральные плотности которых обладают высокими уровнями интенсивностей, то такие системы практически неработоспособны. Поэтому при проектировании необходимо сужать полосы пропускания сигналов в системах. Для этого в них вводятся дополнительные корректирующие устройства. Проиллюстрируем данное положение на примере исследования различных типов следящих систем.
На рис. 6.19 построены четыре логарифмические амплитудные Н\— Н4 и фазовые 61—04 частотные характеристики систем, которые отличаются своими параметрами. Из амплитудных характеристик Hi (со) и Н2((й) видно, что передаточный коэффициент К2 < Кь Это приводит к уменьшению частоты среза соС2 относительно сйс,, а следовательно, и полосы пропускания сиг
налов. Так как средняя квадратическая ошибка системы пропорциональна произведению | Ф (/со) |2£лп (to), то необходимо располагать такими характеристиками IФ (/со) I2 и Sjv, (со), чтобы в рабочем диапазоне их произведение было минимальным.
Рассмотрим первые две системы. Воспользуемся номограммой замыкания Никольса и перенесем на нее характеристики Hi (со), 01 (со) и Н2(ш), 02(со), снятые с рис. 6.19. Соответствующие кривые нанесены на рис. 6.20 сплошными линиями (/ — для Нь 01 и 2 — для Н2, 02). Используем их для построения на рис. 6.21,а характеристик |Ф1(/со)|2 (кривая 2) и |Ф2(/со)|2 (кривая 5). Откуда следует, что система с характеристикой Ф2(/со) обладает меньшей полосой пропускания сигналов, нежели система с ФД/со). Здесь же на рисунке штриховыми линиями 1 показаны характеристики спектральной плотности сигнала Sat, (со).
В соответствии с полученными кривыми видно, что | Ф] (/со) |25лп(со) > > I Ф2 (/“>) I2 Sn, (со) в рабочем диапазоне частот. И система, имеющая
510
ьт.дБ
Рис. 6.20. Номограмма Никольса с нанесенными логарифмическими амплитудно-фазовыми частотными характеристиками
характеристики Hi, 01, обладает существенно большим значением средней квадратической ошибки нежели система с Н2, 02, У которой а|2. Из сравнения амплитудных характеристик Hi (©) и Н2(а) видно, что добротности по скорости Dai> > и ускорению Dei > D&,. В результате этого вторая система имеет большие значения ^динамической ошибки е, что ухудшает точность ее работы при отработке регулярных сигналов. Естественно, что при подборе корректирующих устройств и их параметров необходимо учитывать данное явление.
Суммарную точность следящей системы можно определять суммой квадратов ошибок от регулярной составляющей ст2/32, случайной составляющей ст2 , т. е. ст2 «« ст2/32+ eNt es е/
+ ст2 . Поэтому находить наилуч-Ni
ший тип и параметры дополнительных корректирующих устройств в системах следует методами минимизации квадрата ошибок. Однако такой подход представляет определенные математические трудности.
Рассмотрим остальные частотные характеристики, которые изображены на рис. 6.19. Тогда следящая система имеет логарифмическую амплитудную характеристику Нз с наклоном в области низких частот — 60 дБ/дек (для Hi и Н2 этот наклон составил —40 дБ/дек). Из рис. 6.19 видно, что добротности по
511
скорости = Da, и ускорению De, « De,. Для получения требуемых характеристик Н3 (со) и 03 (ю) в следящую систему было введено дополнительное корректирующее устройство фазозапаздывающего типа с передаточной функцией
W' ($) = 1,255 + *
10s+1
На рис. 6.19 построены логарифмические амплитудная Н3 и фазовая 0з характеристики третьей си-
Рис. 6.21. Характеристики |Ф; (/а) |2 и SNi (<о) для четырех типов следящих систем при наклонах в области низких частот: а) —40 дБ/дек; б) —60 дБ/дек; в) —80 дБ/дек
стемы, а на рис. 6.20 (кривая 3) нанесена ее логарифмическая амплитудно-фазовая характеристика, по которой на рис. 6.21,6 построена характеристика |Ф3(/о)) |2 (кривая 2). Характеристика спектральной плотности Sjv, (©) показана кривой 1 в том же диапазоне частот, что и в ранее рассмотренных системах. Тогда произведение | Ф3 (/w) |2 Sjv, (©) меньше, чем у первой и второй систем, т. е. де, < бе, < <Те„ несмотря на то, что в третьей системе <оСз несколько меньше ©С2.
С целью дальнейшего повышения точности работы следящей системы при отработке случайного сигнала возьмем дополнительное корректи
512
рующее устройство фазозапаздывающего типа в виде
^"(s)==(2s+l)2/(10s+l)2.
Тогда наклон логарифмической амплитудной характеристики Н4 в области низких частот падает до —80 дБ/дек (рис. 6.19). Амплитудно-фазовая частотная характеристика изображена на номограмме Никольса (рис. 6.20, кривая 4). По ней на рис. 6.21, в построена кривая 2 — |Ф4(/©)|2 и здесь же приведена характеристика Sjv,(®) (кривая 1). Как видно, и в этом случае значения добротностей по скорости Da,= — Dai, а по ускорению Dti D&1. Од,-
нако | Ф4(/©) |2Sjv, (©) существенно уменьшается и Отметим,
что здесь ©с, несколько меньше иСз, но это не оказывает существенного влияния на характеристику | Ф4 (/со) |2. Основное влияние на <те связано с изменением наклона амплитудной характеристики в области низких частот.
В заключение укажем, что путем выбора надлежащих типов и параметров корректирующих устройств можно обеспечить повышение точности работы следящих систем при отработке случайных сигналов с различными характеристиками спектральных плотностей.
Глава 7
И ЕЛ И Н Е И Я Ы Е СИ СТЕМ Ы
А ВТОМДТИЧГ С КО ГО Р Е ГУЛ ИРОВ АЯИ Я
Характеристики нелинейных САР существенно отличаются от линейных, так как несоблюдение принципа суперпозиции в замкнутых нелинейных системах может служить источником появления устойчивых и неустойчивых режимов, зависящих как от величин сигналов управления и возмущения, так и начальных условий или одновременного их действия. В нелинейных системах в зависимости от параметров возникают области устойчивых состояний, автоколебаний и захватывания, которые необходимо учитывать в процессе проектирования.
Автоколебания и режимы захватывания нарушают нормальный режим эксплуатации систем и являются довольно часто причиной поломки устройств управления или объектов регулирования. Наряду с этими явлениями в нелинейных системах могут появляться субгармоники, скачкообразные изменения амплитуд колебаний и некоторые другие сложные процессы, без изучения которых нельзя рекомендовать спроектированную систему к запуску в серийное производство.
Следует также указать и на то, что в нелинейных системах при действии случайных сигналов могут наблюдаться срывы автоколебаний. Например, если в процессе работы нелинейной системы происходит изменение спектрального состава случайных сигналов, это является причиной чередования областей устойчивых состояний и автоколебаний. Рассматриваемые процессы определяются приближенными способами. Поэтому для получения достоверных данных приходится использовать несколько различных методов. И только их совпадение гарантирует правильность расчетно-теоретических исследований.
1. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ ПО ВТОРОМУ МЕТОДУ ЛЯПУНОВА
Второй метод Ляпунова позволяет исследовать устойчивость замкнутых САР в малом и в большом. Будем считать, что стационарной системе, описываемой дифференциальными уравнениями n-го порядка, поставлена в соответствие
17 Ю. И. Топчеев
513
непрерывная функция 1/(х), имеющая непрерывные частные производные 1-го порядка в некоторой области Г, включающей начало координат. При этом функция V(x) в рассматриваемой области определенно положительна, а ее производная по времени вдоль траектории системы x — f(x) знакоотрицательна, т. е.
= [VI/(Х)Г х < 0, (7.1)
где VV(x)—градиент функции V является ц-мерным вектором с i-й компонентой dV/dxt; тогда V(x) — функция Ляпунова.
Однако до настоящего времени не существует общего метода определения знакоопределенности выбранной функции Ляпунова. Выполнение данного условия достаточно просто осуществляется в двух случаях [32] [см. также формулу (4.16)].
Первый случай, если
V (х) '-= X Е PijXtXj-, Рц = рц, (7.2) или
V(x) = x~Px. (7.3)
Второй случай, когда функция V (х) является однородной функцией степени к, т. е.
V (axlt ах2, . . ., ахп) =
~aKV (xlt х2, ...,хп), (7.4)
й(х)—знакопеременная при нечетном к. Сформулируем два условия устойчивости по Ляпунову для нелинейных стационарных систем*.
* Отметим, что условия устойчивости являются достаточными, так как могут существовать такие системы дифференциальных уравнений, для которых не удается подобрать функцию Ляпунова. Одиако это не означает, что замкнутая САР является неустойчивой.
1. Если в некоторой области Г, включающей начало координат, для системы
x = f(x); х(0) = 0 (7.5)
существует функция Ляпунова й(х), то начало координат устойчиво.
2. Если для системы (7.5) существует в области Г, включающей начало координат, функция Ляпунова V(x), такая, что ее производная V(x) определенно-отрицательна, то начало координат асимптоматически устойчиво. '
Существуют также три условия неустойчивости систем по Ляпунову, описываемые нелинейными стационарными дифференциальными уравнениями. Проиллюстрируем все эти условия на конкретных примерах нелинейных САР.
Пример 7.1. Воспользуемся условием 1 устойчивости по Ляпунову для системы нелинейных уравнений
х2 = —.2х2 + xi- )
Будем считать, что функция Ляпунова имеет вид
У(хр х2) = 4х>+3х2- (77)*
Из выражения (7.7) следует, что начало координат (х, = 0 и х2 = 0) устойчиво.
Пример 7.2. Воспользуемся условием 2 устойчивости по Ляпунову для системы нелинейных уравнений
xi=x2; | (78)
= — Xi -|-1 Xi | Xi — X{. J
* Если из выражения (7.7) найти произ-водную, то = 2х^Х] + 6х2х2. После подстановки в Й уравнений (7,6) имеем <- = -2х«- 12x2. at 4 х
Таким образом, функция V(xlt х2) положительно-определенна, а ее производная отрицательно-определеииа. Согласно условию 2 Ляпунова начало координат системы (7.6) асимптотически устойчиво.
514
Пусть Xi >= 0 и функция Ляпунова имеет вид
х4
V (хр х2) = 2х? - | Xi | х? + -j- + 2XjX2 -
— I xi I xix2 + Х1 > °; (7-9)
тогда
dV 9 4
= 4x1;t1 — Зх[х, + XjX| 4- 2XjX2 +
+ 2XjX2 — 2XjX2Xj — х2х2 + 2х2х2. (7.10)
Подставив в выражение (7.10) уравнение (7.8), получим
= 4Х[Х2 — Зх2х2 4- х3{х2 4- 2х2 — 2XjX24-
4- 2х1 | Xj | x2 — 2x2 — 2 | X] | x|4-*i | X] | x2—
- | Xj |2 xtx2 4-1 xj | xf - 2xf 4-
4- 2x2 J x, | — 2X]X2 = — xf (2 — I x1 I) < 0.
(7.П)
В соответствии с условием 2 устойчивости нелинейная система (7.8) при IxJ < < 2 устойчива асимптотически, а при |Х]| >2 — неустойчива. Заметим, что при [xj =2 в системе образуется автоколебательный режим.
Пример 7.3. Рассмотрим 1-е условие неустойчивости Ляпунова, пользуясь системой уравнений
х, = — Зх2 4- х?; )
з ( (7Л2)
х2 = 2х2 4- xf, )
которое формулируется следующим образом. Если для системы дифференциальных уравнений существует непрерывная функция V(x), имеющая непрерывные частные производные в области Г, включающей начало координат [ У(0) =0], а ее производная dV/dt определенно-положительна вдоль траектории, то в окрестности начала координат V(x) не является знакоотрицательной функцией.
Для системы уравнений (7.12) функцию Ляпунова возьмем в виде
V (х1,х2) = ух44-3х2. (7.13)
Из выражения (7.13) следует, что Е(0, 0) = 0, а
= 2X[Xt 4- 6х2х2. ' (7.14)
Подставляя в соотношение (7.14) уравнения (7.12), получим
-^у=2х|(-3х24-х?)4-
+ 6х2 (2х2 4- х?) = 2х® 4- 12х2 > 0. (7.15)
Таким образом, выполняется 1-е условие неустойчивости Ляпунова для системы нелинейных уравнений.
Запишем 2-е условие неустойчивости Ляпунова. Если в системе дифференциальных уравнений в окрестности Г начала координат существует функция Vi(x), такая, что и вдоль траектории обеспечивается соотношение
V. = 0; = AVt (х) 4- Г (х), (7.16)
где А>0 и И?(х) > 0 в той же области, и, кроме того, в произвольной окрестности начала координат функция 1Л(х) не является знакоотрицательной, то начало координат неустойчиво.
Пример 7.4. Рассмотрим 2-е условие неустойчивости Ляпунова для нелинейной системы, описываемой дифференциальными уравнениями
1 (7.17)
Х2 = Х2. )
Функция Ляпунова
V (Хр х2) = х2 4* 2х2. (7.18)
Откуда
dV = 2XiX] 4- 4х2х2. (7.19)
После подстановки системы уравнений
(7.17) в соотношение (7.19) получим
= 2(х?4- 2х2) 4-2х2х2. (7.20)
Из выражения (7.20) следует, что А — =₽ 2, a IF (xj, х2) =2х2х2 > 0, т. е. согласно 2-му условию имеем систему, неустойчивую в начале координат.
Сформулируем 3-е условие неустойчивости Ляпунова — Четаева. Если Г •— произвольная окрестность начала координат, а Г1—область внутри ее, то функция И(х) обладает следующими свойствами: непрерывна и дифференцируема; функции И(х) и dV/dt—-определенно-положительны в области Г1 внутри области Г; на границе области Г имеем У(х) = 0; начало координат принадлежит границе области Г [32], в этом случае начало координат неустойчиво (рис. 7.1).
Пример 7.5. Для иллюстрации справедливости 3-го условия неустойчивости по Ляпунову — Четаеву воспользуемся следующей системой нелинейных уравнений [32]:
х( = ах2 4- 6х2; х2 = — сх2 4- dx3{.
(7.21)
17*
515
Рис. 7.1. Области Г и Гь в которых начало координат 0 неустойчиво по критерию Ляпунова — Четаева
Пусть а > О, b > 0, с > О и d > 0. Сформируем функцию Ляпунова в виде
xi
V (Xi, x2) = xi-----g-; (7.22)*
тогда
dV
-гг = х\— х2х2. (7.23)
Подставляя уравнения (7.21) в выражение (7.23), имеем
Ду- = ах? + + сх2 ~~ dx,x2. (7.24)
Внутри области Г в точках, близких к началу координат, V(0) =0, а знак производной функции Ляпунова зависит от знака суммы двух слагаемых ах? + сх2, которые всегда больше нуля. Это показывает, что функция dVjdt в этой области положительно-определенна, а начало координат неустойчиво, и соблюдается 3-е условие неустойчивости Ляпунова — Четаева.
При практических расчетах можно исследовать устойчивость нелинейных систем на основе второго метода Ляпунова, пользуясь способами, предложенными Г. Сеге и Д. Шульцем [13, 41], которые можно реализовать в виде алгоритмов, удобных для составления рабочих программ.
Сущность метода Г. Сеге заключается в том, что для системы нелинейных уравнений
# = Х(х) (7.25)
находится функция Ляпунова в форме (7.2), где коэффициенты Pa(Xi, Xj) не зависят от переменной
* См. пример 4.8.
Хп- В этом случае dV{x)/dt является полиномом второй степени относительно хп и уравнение
dV/dt = 0 (7.26)
всегда разрешимо относительно хп.
Построив решение уравнения (7.26) на фазовой плоскости (рис. 7.2), получим две кривые, пересекающиеся в начале координат, которые делят всю плоскость на области 1 и 2. Причем в области 1 функция dV/dt < 0, а в области 2 dV/dt > 0. При совпадении двух кривых обеспечивается соотношение dV/dt < 0 на всей плоскости.
Ранее было показано, что если V>0, У(0)=0 и dV/d/<0, то это является достаточным условием асимптотической устойчивости САР, описываемых нелинейными дифференциальными уравнениями вида (7,25). Метод Сеге громоздок, так как требует замены dV/dt функциями ф(х), которые представляют собой полиномы второй степени относительно хп, и применяется лишь в нелинейных уравнениях не выше 3-го порядка.
Для получения условий устойчивости необходимо, чтобы сформированные уравнения ф(х)=0 должны иметь кратные корни. Отсюда следует, что по методу Сеге снача-
Рис. 7.2. Фазовая плоскость с выделенными областями устойчивых н неустойчивых состояний нелинейных систем по критерию Ляпунова
516
ла формируется функция Ляпунова, а затем находится ее производная dV/dt. К достоинству метода Сеге следует отнести большую наглядность анализа устойчивости нелинейных систем из-за возможности построения границ нескольких областей устойчивости в зависимости от фазовых координат. При использовании же метода Шульца сначала по формуле {7.1) находится dV/dt, а затем с помощью вычисления интеграла определяется скалярная функция Ляпунова V(x). Ниже будет показано, что последний способ является более простым и может использоваться для систем управления, описываемых дифференциальными уравнениями высоких порядков [41].
Сформулируем условия устойчивости нелинейных систем, описываемые уравнениями (7.25) по Шульцу. Для этого снова воспользуемся формулой (7.1), имея в виду, что существует некоторая область Г и действительный вектор W(x) с элементами VVf = -|^-, удовлетворяющими условиям dWi/dxs = = dNVj/dXi, где W(х) не обращается в нуль ни в какой точке области Г, кроме начала координат. При этом dV{x)/dt= [W(x)]Tx^
0, если хУ=0, и dV{x)/dt — Q, если же х = 0, a dV{x)ldt не является тождественным нулем в области Г, то скалярная функция
X
7(*) = J [w (х)]тс?х (7.27) о
обладает свойствами: V (х) положительно-определенна и одна из поверхностей V — k ограничивает границы области Г. Тогда нелинейная система асимптотически устойчива в области Г.
Для применения метода Шульца, как следует из выражения (7.27), необходимо определить градиент функции VV(x) и записать его в
виде системы уравнений ~wr w2 w3
W(*) =
_w„_
ацХ1+а12Х2+а13Хз-|-.. .+а1пх„ а21 Х1 + «22Х2 + а23Х3 + • • • +^2пХп «31*1 +«32*2+«33*3 + • • +«3п*п
_«п1*1 + «п2*2+«аЗ*в+ • • • +«пп*п
(7.28)
Производная от функции Ляпунова
dV ЗУ dxi dV dx2 dt dXt dt ' дхг dt
dx3 , . dV dxn
dx3 dt + ' • ' + rfXn щ
или
n
V dV dXt
Zu dxi dt ’
i-1
(7.29)
(7.30)
поэтому из выражения (7.30) можно получить формулу (7.27).
Интеграл (7.27) не зависит от траектории движения, и его можно представить в виде
/(*•)= J VF1G,, 0, 0......O)dg,+
oJ
+ $ WM*i. g2, о, .... 0)dg2 + o
+ $¥Кз(х1,х2Лз, 0....0)^з+ ...+
о
хп.
+ J V^n(*i. *2, Х3.
о
(7.31)
517
Запишем функцию Ляпунова в обычной форме, учитывая, что исходное уравнение имеет 3-й порядок, т. е.
V (х„ х2, х3) = ап (х,)х? +
4- 2а1г (xi, х2) Х|Х2 4- 2а[3 (xi) XiX3 4-
4- а22 (х2) х2 4- 2а23 (х2) x<>x3 4- а^. (7.34)*
Из выражения (7.34) после дифференцирования и подстановки уравнений (7.33) получим
dV Гп I \ । daii(xi)l
---|2а(1 (xi) 4- Xi ——---J х(х2 4-
I о Го /г г \4- г да'2 (Х|> 1 v2 д-
' |_а12 (х1> х2) i xl J х2 ।
, Г i \ 1 d<ii2 (Х|, х2) 1 ,
4- 2 а12 (хь х2) 4- х2 ——tL XlX3 +
L OX% J
+ 2 Га13 (xi) + X! *3 1 -*2*3 +
L uX\ J
"b 2 Гага (хз) + Xj —1 X2X3 4-L 0X2 J
Рис. 7.3. Структурные схемы нелинейных динамических систем:
а—с заданной нелинейностью; б—с. однозначной стационарной нелинейностью произвольной формы; в—с однозначной нестационарной нелинейностью
+[‘.W+-!^]4-
— Д13 (Xl) (x1 4- cx2)3 Xl — bai3 (xt) xtx3 — — a23 (x2) (x, 4- cx2)3 x2 — bat3 (x2) x2x3 —
- a33X3 (X1 + cx2)3 - a33bxl <7-35)
Условия устойчивости нелинейных систем по методу Шульца являются необходимыми и достаточными из-за того, что скалярную функцию V удается получить только единственным способом, пользуясь векторной функцией VV(x).
Пример 7.6. Исследовать устойчивость нелинейной САР, описываемой дифференциальным уравнением [41]
х -|- Ьх + (х 4- сх)3 = 0 (7.32)
при Ь > 0, с > 0 по методам Сеге и Шульца *.
Уравнение (7.32) перепишем в виде
xi = х2;
Х2 = х3;
х3 — — (xi + сх2)3 — Ьх3
(7.33)
и составим структурную схему, которая показана иа рис. 7.3, а.
* Условия для произведения коэффициентов Ьс будут найдены в процессе решения примера 7.6.
В формуле (7.35) второй и третий члены обозначены как да12 (х,, х2)/дх1 = а12(Хр х2) и да12(х1, х2)/дх2 = а12(х2, х2), а все остальные частные производные будем представлять как a(j (xt, Xj). Тогда выражение (7.35) можно переписать в виде
1 а и 2 г t ' / .I
2 ~dt *3 ^азз& “23 (хг)] ~
— х3 [а33 (xj 4- сх2)3 4" ^а2з (х2) х2 4-
4- &а13 (х1) Х1 ~ а22 (х2) х2 ~ а13 (Х1) Х2 “
- аГг (хь хг) х1] - а2з (хг) (Х1 + схг)3 х2 + + а1з (xi) (Х1 + схг)2 Х1 - а12 (хр хг) х2 ~
-“ (х1) xix2‘ (7.36)
Пользуясь выражением (7.36), образуем функцию ф(х), в которой все коэффициен
* В выражении (7.34) из-за того, что анализируемое уравнение 3-го порядка вида (7.32), параметр а33 является постоянным коэффициентом.
518
ты считаем переменными, т. е.
f (*) = - хз [а^ь - а23 (х2)] -
- Х3 [“ЗЗ (Х1 + сх2)3 + 6а23 (хг) х2 +
+ 6а13 (X]) X] а22 (х2) х2 а13 (х^ х2
- “12 (х1- *2) х1] “ «23 (х2) (Х1 + сХг)3 х2 +
+ “13 (х1) (Х1 + схг)3 Х1 - “12 (х1> хг) х2 -
“ll(xl)xix2- (7.37)
Представим функцию (7.37) в виде полинома 2-го порядка относительно х3
ф (х) = Ах2 + Вх3 + С, (7.38)
где
Я = а23 (х2) а^Ь;
В = а12 (хр х2) Xj 4- о[з'(Х|) х2 + + 022 (х2) х2 - bal3 (Xj) X! -- 6“23 (хг) х2 - “зз (Х1 + схг)3;
С = а[3(х1)(х14-сх)3х1-— “23 (хг) (Х1 4- сх2)3 х2 “ -“[2(xl> *2)X2-“U(X1)X1X2-
(7.39)
Для получения устойчивости необходимо, чтобы уравнение ф(х) =0 имело кратные корни. Это обеспечивается, если дискриминант уравнения В2 — ААС = 0. Данное условие будет при В = 0 и С = 0. В коэффициенте С, как это видно из формул (7.39), возникает член при х|, если а{3Х X (*i) Ф 0. Одни коэффициент может быть лроизвольиым; поэтому примем (х2) = •= 1. Тогда при С = 0 имеем
х2 (х1 + сх2)3 =• а[3 (хр х2) х2 4-
+ “л (х1) *1х2 (7.40)
яли
х3 4- Зсх2 4- 3c2XjX2 4- с3х2 —
= “12 (х1> хг) х2 + “п (xi) х1- (7.41)
Если а'п (х,) = xf, то
“12 (*1> *2) = Зсх2 + 3cXjX2 4- с3х2. (7.42)
При В = 0 найдем
3cxj + Зс2х2х2 4- с3х2х1 4- а22 (х2) х2 =
= Ьх2 4- “33*1 + 3a'3cxfx2 +
4-3a^3c2x1x| + a^3c3x2; (7.43)
откуда, приравняв коэффициенты при х(, 2 2
XjX2> xix3’ ПОЛУЧИМ
Зсх3 — а33х3;
Зс Х|Х2 ~~ З^зз^-Х । х2 с л । л. 2 —— ’'^*33^ 1 2*
(7.44)
Из оставшейся части выражения (7.43) имеем
“22 (х22) х2 ~ &х2 4" “ззС3х2‘ (7.45)
Для первого соотношения (7.44) найдем
“зз = 3с, (7.46)
а из выражения (7.45) получим
“^2 (х2) = & 4-“33с3х2. (7.47)
Подставив коэффициенты ац(х1)> “12 (х1> хг)> “1з (х1)> “22 (хг)> “23 (хг)> “зз вместо ан(х1), а1г(х1, х2), aJ3 (xj, a22 (х2), a23(x2), а33 в формулу (7.34), определим уравнение Ляпунова в виде
У (Хр х2, х3) = a[xf 4- a2x|x2 4- a3x2x| 4-+ a4X(X2 4- a5x2 + Ьх2 4- 2x2x3 4- ex2, (7.48)
где «1—as — постоянные, которые выбираем для получения функции Ляпунова в виде
У (Хр х2, х3) — Ьх2 4- 2х2х3 4- сх2 4-
4- у (*i 4- сх2)4. (7.49)
Из соотношения (7.49) следует, что функция Ляпунова У(хь х2, х3) > 0, т. е. она положительно-определенна.
Возьмем производную от функции У, т. е.
ЙУ (Хр Х2, Х3) п/, ,2 « епх
------—2 (I — &с) х3. (7.50)
Правая часть этого выражения отрицательно-определенна при Ьс < 1, что указывает на устойчивость нелинейной динамической системы, описываемой уравнением (7.32).
Воспользуемся теперь методом Шульца для исследования устойчивости системы, описываемой дифференциальным уравнением (7.32). Последнее, как и раньше, можно записать в форме (7.33). Подобрав коэффициенты а</ такими, чтобы dV(x)/dt была отрицательно-определенна или полу-определеина в некоторой области Г, и выполнив интегрирование с помощью выражения (7.31), получим функцию Ляпунова У(х). Если она положительно-определенна в области Г и в начале координат равна нулю, то прн этом обеспечивается
519
условие устойчивости нелинейной динамической системы.
Необходимым и достаточным условием того, чтобы Е(х) можно было выразить через W(x), является следующее соотношение:
^7 <"'>/- <7-5|>
где i, j = 1, п.
Последнее определяет связь между матричными коэффициентами ац(х).
Систему уравнений (7.33) при соблюдении условий (7.28) и а13 = а31 = 0 можно записать с помощью выражения (7.29) в следующем виде: dV
—£1~= (“11*1 4" “12*г) *2 + (“21*1 + Л22х2 +
+ “23*з) *3 + (“32*2 + “з3*3) X
Х[-(х1 + сх2)3-&х3]. (7.52)
Коэффициенты “//(*), входящие в выражение (7.52), находим как неполные квадратичные формы по аргументам х} и х2, т. е.
“11 = “11*1 4-0ц*2! “12 = “12*1 + 012*2!
“21 ~ «21*1 + 021*2» “22 = a22*14'022*24”V22’»
(7.53)
“23 = Угз; “32 = Уз2> “зз = Узз-Подставляя выражения (7.53) в формулу (7.52), получим
= («11*1*2 4" 011*2*1 4" “12*1*2 4" ’ 4- 012*г) 4- («21*?*з 4" 021*2*1*з 4-4- а22*1*2*з + Р22ф3 + 722X2*3 + у23*1) -V32*2*I ЗУз2*?с*2 Зу22с2*2*1 ¥32^*2 — ¥з2^*з*2 ~ ¥33*3*1 3¥зз*1*зсх2—ЗУззС2-
*3*2*1 ¥ззс3*2*з ¥зз5*|. (7.54)
Нарушение знакоопределенности или полуопределенности выражения (7.54) можно ожидать из-за наличия в нем членов с перекрестными произведениями. Полагая эти члены равными нулю, получим систему алгебраических уравнений
*1*2: an-Y32 = 0; (7.55)
Фр 011 ~ 3Y32c2 = 0; (7.56)
*1*3: “21 Y33= 0» (7.57)
*2*1*з" 021 Зс Y33 = 05 (7.58)
*1*2*3» «22 — 3CY33 — 0; (7.59)
*2*3’ 022 с3¥зз= 0; (7.60)
*2*3: Y2» — Ьуз2 = 0. (7.61)
520
С целью дальнейшего упрощения допустим, что коэффициенты в правой части выражения (7.54) при членах с х2 и х^х2 также обращаются в нуль, т. е.
*2- 012 c3Y32 = 0; (7.62)
*2*1: “12 ~ 3Уз2с ~ °’ (7.63)
Если п = 3, то соотношение (7.51), определяющее связь между матричными коэффициентами при П1з = п31 = 0, приводим к виду
z = l, j' = 2: (^2ixi + “22*2 + о2з*з) =
= (а1!х1 4- «12*2 4- О13*з);
z == 1, j = 3: (“32*2 + “зз*з) —
ОХ[
д .
— эх (аи*1 + “12*2)»
i = 2, j = 3: (“32*2 + “з*з) —
0X2
— (“21*1 + “22*2 4- “23*з) •
Подставляя выражения (7.53) для коэффициентов ац в последние соотношения, получим
-Д- (a21xf + 02i*|*i + “22*?*2 + ₽22х| +
4- Y22*2 4" ¥зз*з) = (“11*1 4"
4" 021*2*1 4" «12*1*2 4" 012*2): (7-64)
(Y32*2 4" Узз*з) ~ ‘^“(“11*1 4"
4- 011*2*1 4" “12*1*2 4" 012*1): (7-65)
(Уз2*2 4" УзЗ*з) = дх? (“21Х1
4" 021*2*1 4" «22*2*? 4~ 022*2 4” Y22*2)’ (7.6б)
Выполняя операции дифференцирования уравнения (7.64), найдем
За21Х[ + 021*2 4" 2“22*1*2 = 2011*1*2 4” + a12X[ + Зр12х2.
Последнее выражение будет справедливым, если справедливы следующие соотношения:
3a2i=ai2; 021 = 30i2; “22= 0и- (7.67)
Уравнение (7.65) является тождеством, а выражение (7.66) имеет место при условии
Y32 = Y23. (7.68)
Из соотношений (7.55)-—(7.61) н (7.68) коэффициенты ап, 0ц, агь 02i, «22, 022, Y22, Y23, 012, «12 можно выразить через у32 и Узз- В результате имеем
On = Узг1 011— Зс2узг! «21= Узз! 1
021 = Зс2Узз1 «22 = Зсузз; 1
} (/.69) 022 = с3Узз! I
Y22 = Ь Y32; Y23 == Y32- J
Соотношения (7.67) выполняются, когда
Узз = су32. (7.70)
Учитывая, что функция Ляпунрва определена с точностью до численной) множителя, коэффициент узз, через который выражаются все остальные параметры задачи, может быть выбран произвольно. Полагая узг = 2, получим
ац=2; 0ц==6с2; al2,= &c; 01г = 2с3; \ а21 = 2с; 021 = 6с3; а22 = 6с2; 022 = 2с4; >
Y22 = 2i>; узз = 2; узз = 2с. >
(771)
Подставляя коэффициенты из соотношений (7.71) в выражение (7.51), получим
^^^ = -2 (1-М х*.
Эта формула полностью совпадает с выражением (7.50). При be < 1 рассматриваемая нелинейная система будет устойчива (рис. 7.4,/;).
Таким образом, вид градиента от функции Ляпунова VV(xi,X2, х3), задаваемый формулами (7.30), (7.53), с коэффициентами (7.71) полностью определен.’ Перейдем к интегрированию системы уравнений (7.28), которая имеет вид
дУ (Xi, х2, х3)
dxt
«11*1 + Р1И14+
+ О12х?х2 + 012Х®;
= а2[хЗ -|- 02iX2Xi + • (7.72)
dV (хь хг, х3) дх2
+ a22xfx2 + 022х2 + Y22*22 + ?23*з‘>
дУ (xi, х2, х3)
-------------------У32*2 + УззХ3.
Интегрируя эти соотношения, получим
У (хр х2, х3) = anxf/4 + 0цХ?х|/2 +
+ «12*?*2/3 + ₽12*2*1 + ЧТ (х2’ *з)’> (7-73) V (хь х2, х3) = а21Х]Х2 + 021х1х2/з +
+ а^х* + 022х2/4 + Угг^г/2 + Y23*2*3 +
+ <Ра (х,,-х3); (7.74)
V (хр х2, х3) = Y32*2*3 + Тзз*з/2 +
+ <Рз (хь х2), (7.75)
Рис. 7.4. Кривые разделения на области устойчивых и неустойчивых состояний:
a — по параметрам b и с (пример 7.6); б — по виду функции F(xi) (пример 7.7)
где <Р1(х2, х3); ,<p2(xi, х3) и <рз(хь х2)—некоторые неопределенные функции.
Из1 сравнения выражений (7.73) и (7.75) следует, что
<₽1 (х2, х3) = 732*2*3 + Тзз*з/2 + <₽4 (*г)1
<P3 (хр x2) = a11xf/4 + 011xfx2/2+ (7.76)
+ а 1з*1*2/3 + Р12*2*1 + Ч>4 (*г)-
Неизвестную функцию (р4(х2) определим, сопоставляя соотношения (7.74) и (7.76). В результате найдем (х2) = у22х|/2. Таким образом,
V (Хр х2, х3) = anxf/4 + Pu*i*i/2 +
+ О12Х?Х2/3 + 012*2*1 + V32*2*3 +
+ Узз*з/2 +Y22*2/2- (7.77)
Подставляя константы из соотношений (7.71) в выражение (7.77), получим в
521
окончательном виде функцию Ляпунова V (Х[, х2, х3) = Ьх2 + 2х2х3 + сх3 +
4-1(х14-сх2)‘. (7.78)
Функция в правой части выражения (7.78) будет положительно-определенна при условии b > 0; с > 0; be < 1.
Итак, оба метода, Сеге и Шульца, при решении примера 7.6 привели к одинаковым результатам. На рис. 7.4, а построена кривая, разделяющая области устойчивых и неустойчивых состояний в зависимости от изменения параметров бис.
Пример 7.7. Запишем нелинейное дифференциальное уравнение
х + bx + сх + F (х) х = 0, (7.79)
которое можно привести к следующей системе:
xi — хг; -j
Х2 = х3; > (7.80)
Хз = — Ьх3 — ext — F (xi) Xi. J
Проанализируем влияние формы нелинейности f(xi) на устойчивость САР.
Составим структурную схему системы по уравнениям (7.80) в виде, изображенном на рис. 7.3, б. При этом видно, что нелинейность F выделена в отдельный прямоугольник, что упрощает ее исследование, например, методами гармонической линеаризации.
Воспользуемся для решения данного примера методом Шульца и найдем градиент функции Ляпунова. Тогда систему (7.28) для дифференциального уравнения 3-го порядка (7.79) можно записать в виде
[ЯцХ1 + Я12Х2 + «13X3 -1
CI21X1 + я22х2 + Я23Х3 I. (7.81) а31Х1 + а32х2 + <133X3 J
Используя уравнения (7.30), (7.80) и (7.81), запишем
Г ^a^+lau — ся31 -
— F (xi) а32] Х[Х2 + [а21 — 6я31 —
- F (*1) «зз] х1хз + [«12 - с«зг] 4 +
+ Iais + я22 6яз2 — са33] х2х3 +
4- [«23 ~ 6а33] 4 (7.82)
Для получения неравенства dVIdt < О приравняем к нулю выражение в скобках в ф°РмУле (7.82) при парных соотношениях, т. е.
Яц = ca3i + F (xi) а32; 4
я21 = 6a3i F (xi) а33; У (7.83)
«13 + я22 = 6я32 4- са33. '
Положим а[3 = a3i = 0; а33 — 2; тогда из системы уравнений (7.83) найдем я2,=25(х1); ч я11=Г(х1)я32; I (7.84) я22 = 2с 4- 6я32. '
Из анализа уравнения (7.82) следует, что при принятых условиях в него не входит 2 t-k
сомножитель х{. В этом случае уравнение зависит только от х2 и х3. Примем
я23 = я32 = 26. (7.85)
Коэффициент <Xi2 не является постоянной величиной. Его определяют из условия
При этом производные VP) и VP2 получаются из выражений (7.81) и (7.83) — (7.85) в виде rVPij Г 26F(x1)xi 4-я12х2 1
I. VV2 J = |_2Г (хо Х14-2 (624-с) х24-26х3 J‘
(7.87)
Из соотношений (7.86) и (7.87) получим
0VV, _ дх2
Я]2;
= 2F (xj 4- 2 -J-glV хь dXi v dxi
откуда
a)2==2F(xI)4-2^^1xI. (7.88) uX\
Имея в виду выражения (7.88) и (7.81), градиент
VV =
2bF (xt) х.4-[2Е (х,)+2^^ х,] х2
= 2F (Xj) X! 4- 2 (б2 4- с) х2 4- 26х3
_ 2Ьх2 + 2х$ _
(7.89}
Располагая выражениями (7.31) и (7.89), найдем
Х\
V (хь х2, Хз) = 2b F (1)1 di, + о
4- 2F (х{) х(х2 4- (б2 4- с) х2 4- 26х2х3 4- х3.
(7.90)
По выражению (7.90) определим dV orr._ v .2 , QdF (xi) v2 — _ —2 [6c - F (X!)] x2 4- 2 dXi x2.
(7.91)
Для несимметричных нелинейностей F(xi) можно ввести следующие упрощения: я12 = ся32; | (792)
Яц = ся31 4- F (хО я32. )
При Я12=я2[ имеем
я21 = 6я31 = ся32. (7.93)
522
Таким же образом находим все остальные значения а,-/, за исключением ап. В этом случае, пользуясь соотношениями (7.92) и (7.93), получим
dt ~ ь" Г (х1) аз2х1 (х1) х1хз
(26 а2з) х3" (7.94)
Из выражения (7.94) можно определить, что dV/dt отрицательно-определенна, если Ь, с, F(xt) >0 и [be — F(xi)] >0. Откуда следует, что асимптотическая устойчивость в начале координат обеспечивается для любой несимметричной однозначной нелинейности, если выдерживается условие be > F(x1), для любых F(xI). В этом примере мы получили условия устойчивости с меньшими ограничениями, по сравнению с примером 7.6 (рис. 7.4,6).
Второй метод Ляпунова применим и к нелинейным нестационарным системам, когда скалярная функция V(x, t) положительно-определенна в области Г, содержащей начало координат, если У(0, t) = 0 и V(x, t) <р(Цх||). Здесь функция Ф непрерывная, возрастающая, но такая, что ф(0) — 0. Для нелинейной нестационарной системы
x = f(x, f) (7.95)
при /(0, () = 0 для всех t имеет место выражение
|»|
+ ^r==IVV(*, 01т/ + 4г- (7.96)
Сформулируем несколько условий устойчивости нестационарных нелинейных систем.
Первое условие. Если для системы (7.95) существует V(x, t) > 0, имеющая непрерывные первые производные по переменным х и t в некоторой окрестности Г начала координат, a V(x, t) < 0, то начало координат системы устойчиво.
Второе условие. Когда существует положительно-определенная, возможно неубывающая скалярная функция 9(z) одной переменной, такая, что в дополнение к условию V(x, 0 > 0 первого условия ус
тойчивости в некоторой окрестности Г начала координат выполняется еще одно условие
К(х, /)<-0(1И|), (7.97)
то начало координат системы неравномерно асимптотически устойчиво.
Третье условие. Для непрерывной, строго возрастающей функции p(z), такой, что р(0) =0 в дополнение первого и второго условия устойчивости, необходимо в области Г для всех t иметь
V(x, О<Р(Н*11); (7.98)
тогда начало координат системы равномерно • асимптотически устойчиво. Существует еще несколько условий устойчивости нелинейных нестационарных систем [32]. При равномерной асимптотической устойчивости требуется х #= 0, V (0) — 0 и V(x, t) < 0. Если функция V остается функцией времени, она должна удовлетворять условию (7.98).
Следует указать, что условия устойчивости нелинейных нестационарных систем определяются неравенством, в которое входит интеграл (см. пример 7.8). Последнее затрудняет анализ устойчивости; поэтому в большинстве практических задач не удается вычислить интеграл аналитически и приходится пользоваться графическим способом интегрирования или процедурами, реализуемыми на ЭВМ.
Пример 7.8. Найдем условия устойчивости для нелинейной нестационарной системы, описываемой дифференциальным уравнением вида
х + Ьх + с (х, /) х = 0, (7.99)
откуда получим
Х|==Х2’ 1 (7.100)
х2 = — Ьх2 — с (хь t) Xi. J
По уравнениям (7.100) составим структурную схему системы (рис. 7.3, в).
Определим градиент функции Ляпунова, пользуясь выражением (7.28), в виде
w ==Га“Х,+а,2Х21 (7.101)
L «21X1 + а22х2 J
523
Будем считать что <z22 = 2; тогда
dV
— = [аи — Ьа21 — 2с (хь /)] ххх2 +
2 2 dV
+ [“12 - 2Ь] Х2~с (*1- 0 “2+1 + ~оГ-
(7.102)
Так как функция c(xt, t) зависит только от фазовой координаты xt, то
(Хи = 6а21 + 2с (хь/). (7.103)
Имея в виду соотношение (7.103), из матрицы (7.101) найдем
ЬацХ1 + 2с (xb /) х, + а12х2 «21*! + 2х2
(7.104)
По формуле (7.31) сформируем функцию Ляпунова
Х1
И(Хр х2) = у a2!xf+ 2 c(g, + о
+ a21XlX2 + х2’ (7.105)
откуда
4? = ~ (26 - а21) х2 - с (х,, /) а21х? +
+ 2 J с (g, t) g dlj. (7.106) о
Теперь воспользуемся следующим соотношением: а21 = 2(Ь— у); тогда
V (Xj, х2) = (6 — у) 6xf + 2 (& — у) Х[Х2 +
+ х2 + 2 J c(g, t)l,dl (7.107) о
= -2 (6 — у) с (х„ t) xf — 2ух2 +
+ 2 j 33’ 0 g rfg. (7.Ю8) о
Если интеграл в выражении (7.108) больше нуля и V больше положительноопределенной функции
(x) = l[6(6-Y)xf +
+ 2 (6 — y) XjX2 + х2], (7.109)
то для обеспечения —dV/dt необходимо в функции c(xi, t), представляемой в виде
с(Х,, <)=Со + С! (х,, /), (7.110)
иметь малый член с0, т. е.
- = 2с0 (& - Y) x2i + 2y*2 +
+ 2(6 —y)ci (xv t)x2{ —
- 2 j S rfg. (7.Ш)
0
Если неравенство
(6 —y)c1(x1, t)x2> J g dg
о
(7.112)
соблюдается для всех Xi и t, то —dVjdt больше, чем независящая от времени положительно-определенная функция
(*) = у [2со <6 — V) Х1 +
тогда dVfdt < 0. В заключение отметим, что неравенство (7.112) соблюдается лишь для определенных функций с(хь t). Например, если функция с (Хр /) = (с0 + c{t — — с/) Xj при Со > 0, Ci > 0, с2 > 0 и с > 0, то функция V(Xi,x2) положительноопределенна и ограничена по хь а dVjdt < < 0, что гарантирует асимптотическую устойчивость рассматриваемой системы в начале координат. И, наоборот, при с (хр /) = с0 + е*х2 (с0 > 0) функция V не ограничена по хь В этом случае система (рнс. 7.3, в) неустойчива.
2. ПРИМЕР! ЛИГ. М1'!ОД\ ЕЛКМОНИЧЕСКОЯ Л И Н Е )Л -J И П ДЛЯ АНАЛИЗА >С1ОЛ'1ИВОС1 И !Л.!<PLPblbiiLIX НЕЛИНЕЙНЫХ СИС.П.'Л С УЧПиМ ВЛИЯНИЯ !-П ГАРМОНЯМ!
На практике для анализа устойчивости непрерывных нелинейных САР (определения областей устойчивых и неустойчивых состояний в зависимости от параметров) широкое применение получили методы линеаризаций, основанные на частотных характеристиках для линейных частей систем, у которых обеспечивается свойство низкочас
524
тотного фильтра * на входе эквивалентных характеристик (для нелинейных частей). В этом случае можно использовать годограф Михайлова—Найквиста для построения характеристик Н'(а) и 0(со) и шаблоны** для двузначных нелинейностей 201g (1/q) и —180° — р..
Если САР описываются линейными дифференциальными уравнениями не более 15-го порядка и имеют любой степени сложности нелинейности, то при проектировании обычно применяют методы гармонической линеаризации с использованием шаблонов.
Данный метод удобен и при слабой фильтрации высших гармоник линейной частью системы, т. е. когда условия (7.113) и (7.114) приходится заменять на следующие:
| W (2/со) | < | W(Joi) | (7.115) или
| F (3» I < I F (/со) |. (7.1L6)
При этом можно учитывать любое число гармоник.
Анализируя устойчивость нелинейных систем, линейные части которых описываются уравнениями выше 15-го порядка, следует пользоваться ЭВМ.
Рассмотрим сначала методы гармонической линеаризации при учете l-й гармоники и одного сигнала, поступающего на вход нелинейности. Тогда характеристическое уравнение системы.можно записать:
для простых нелинейностей
1 + J (А) F (/со) = 0; (7.117)
для сложных нелинейностей
1 + /(А, » F (» = 0, (7.118)
* Под свойством низкочастотного фильтра понимают условие, когда
| IF (2/<о) | 11F (/со) | (7.113)
или
| W (3/®) I « I W (/со) I, (7.114)
т. е. линейная часть системы пропускает только 1-ю гармонику сигнала, которая поступает на вход нелинейности.
** См. шаблоны для нелинейностей в гл. 2.
где /(А), /(А,/со)—эквивалентные передаточные функции нелинейных элементов.
Перепишем равенства (7.117) и (7.118) в следующем виде:
(7Л19) и
- таЬт =117 <'“>• (7Л20>
Если соотношения (7.119) и (7.120) удовлетворяются, то графоаналитическим путем находят амплитуды и частоты колебаний при различных параметрах линейной и нелинейной частей и строят области устойчивых состояний и автоколебаний.
Для использования логарифмического критерия устойчивости перепишем равенство (7.117) в виде
-1 = q (А) Н' (со) e'WWI или
е-М = q (А) Н' (со) е' iHMi+e «0)1, (7.121)
где q(А) и ц(А)—соответственно эквивалентные амплитудная и фазовая характеристики нелинейностей Д'(со) и 9 (со)—соответственно амплитудная и фазовая частотные характеристики линейной части.
Из соотношения (7.121) получим условия гармонического баланса
20 lg Н' (со) = 201g 1
К V' ® q (A) I (7122) 0(со) = —-180°—• и (А). )
При сложной нелинейности /(А,/со) формулу (7.122) перепишем в виде
20 lg Н' (со) = 201g .! . ;)
Б - 6 <7 (А со) I (7.123)*
0(<о) = —180° — и (А, со). )
При одновременном удовлетворении условий (7.122) или (7.123) находят периодические режимы в системах. Если найденные по формулам (7.122) и (7.123) амплитуда и частоты колебаний в автономной системе являются постоянными и зависят только от параметров, то
* Согласно гл. 1 201g//'(со) =//(со).
525
б)
Рис. 7.5. Структурные схемы нелинейных САР с различными типами нелинейностей:
а—зона насыщения; б—зона нечувствительности; в—с люфтом; е—с нелинейностью типа насыщения в замкнутом контуре
такие колебания называют автоколебаниями. При изменении амплитуды и частоты возникают неустойчивые колебания. Как правило, в большинстве непрерывных САР периодические режимы нарушают нормальный режим эксплуатации и являются недопустимыми. Поэтому в процессе проектирования систем вводятся дополнительные последовательные или параллельные линейные и нелинейные корректирующие устройства, которые расширяют области устойчивых состояний в зависимости от параметров.
Определение амплитуд и частот колебаний с помощью логарифмических характеристик заключается в том, что точки пересечения амплитудных Я(<о) и 201g-^ (Д) [или И Фазовых характеристик 0 (со) с —180° — ц(А) [или —180° —р(А, со)] должны лежать на одной вертикали.
В САР может возникать несколько таких положений. Для определения, являются ли частоты и
амплитуды колебаний неустойчивыми или автоколебаниями, пользуются следующим приемом. Увеличивая амплитуду А на АА, определяют, какое положение будет занимать точка пересечения амплитудной характеристики относительно линии Н(а). Если с ростом амплитуды эта точка будет выходить из области ограничений линиями Я(©) и осью частот <о, то в нелинейной системе возникают автоколебания. И, наоборот, когда точка пересечения с ростом амплитуды будет входить в данную область, то в нелинейной системе появляются неустойчивые колебания.
В случае однозначных нелинейностей формулы (7.122) соответственно примут вид
201g Д'(и) = 201g—)
6 ' ' 6 Я (А) I (7.124)
е(И) = -18о° )
и
201g//'W = 20lg^; | |26)
0(®) = —180°. J
526
Рассмотрим несколько примеров определения режимов устойчивых и неустойчивых состояний и автоколебаний при учете лишь 1-й гармоники. Изменяя параметры линейной или нелинейной части системы, можно построить соответствующие области.
Пример 7.9. Определить частоты и амплитуды автоколебаний в нелинейной САР с нелинейностью типа зоны насыщения при В = 2 и С = 2. Линейная и нелинейная части в этой системе соединены последовательно (рис. 7.5, а).
Будем считать, что передаточная функция линейной части имеет вид
F(a) = tf(7’2s+l)/[s(7’1s + l)X
X (Г3з + 1) (TiS + 1)]. (7.126)
Для построения частотных характеристик положим з — jo-, параметры системы примем Л = 2 с; Т2 — 1 с; Т3 = 0,5 с; К — = 10 с-1. Здесь может изменяться в пределах 0,1—0,25 с.
На рис. 7.6, а построены логарифмические амплитудные Н(а) и фазовые 6 (со) частотные характеристики при 7\ = 0,1 с (кривая /), Tt = 0,2 с (кривая 2), Ti = = 0,25 с (кривая 3). Здесь же показаны
два положения шаблонов (рис. 2.12, а), ко-. торые проходят через точки Bt, В2. Точки £>i, £>2 лежат на прямой, параллельной оси абсцисс, с фазой, равной —180°.
Из рис. 7.6, а видно, что точки Bb D>; В2, D3 лежат на одной вертикали. С ростом амплитуды на АА точки Bt, В2 шаблона выходят из области, ограниченной линиями Я(со) и осью абсцисс со, что указывает на автоколебания с частотами со а i = 2,04 с-1, соа2 = 2,35 с-’, и амплитудами Aai = 0,3 рад, Аа2 = 0,8 рад.
Пример 7.10. Определить частоту и амплитуду автоколебаний для нелинейной САР, имеющей структурную схему (рис. 7.5,6). Система является условноустойчивой с нелинейностью в виде зоны нечувствительности. Примем параметры системы: К — 600 с-1; Ti = 2,88 с; Г2 — = 0,4 с; Г3 = 0,025 с; С = 0,001 рад. На рис. 7.6, б построены логарифмические амплитудные и фазовые частотные характеристики линейной системы. Частоты <£>' и со" соответствуют возможным режимам колебаний. Наложив в точках £>, и О2 шаблоны, установим со' = 0,53 с-1, со" = = 1,85 с-1 и Aai = 1,09-10—3 рад, Аа2 = >= 1,3-10~8 рад. С ростом амплитуды А + АА точка В2 перемещается выше логарифмической амплитудной характеристики //(со), а точка Bt— ниже. Поэтому вертикаль B2D2 соответствует автоколебаниям, a BJDi — неустойчивым колебаниям.
а—для примера 7.9; б—для примера 7.10; в—для примера 7.11
527
Рис. 7.7. Амплитуды и частоты автоколебаний н неустойчивых состояний по 1-й гармонике для примеров 7.12 и 7.13
Пример 7.11. Определить частоты н амплитуды автоколебаний для нелинейной системы с люфтом (рис. 7.5, в). Примем параметры системы: К = 40 с-1; Т = 0,1 с; С = 0,004 рад.
Построим сплошной линией логарифмическую амплитудную характеристику И(ш) на рис. 7.6,в и фазовую 0(ш)—штриховой. Шаблон (см. рис. 2.29) нанесем на прозрачную бумагу. Накладывая шаблон * и совмещая ось CjA с осью частот со, полу-
чим первое его положение, когда кривая
20,gWM)
пересечет характеристику
Я (со) в точке Bi, а кривая —180° — —ц(С/А) характеристику 0(ш) в точке £>ь Отсюда видно, что точки пересечения Bt и не лежат на одной вертикали. В этом случае условия гармонической линеаризации (7.122) не соблюдаются и в
нелинейной системе не могут возникать пе-
риодические режимы.
Далее будем перемещать шаблон слева направо вдоль оси частот до тех пор, пока точки пересечения В2 и D2 не будут находиться на одной вертикали. При условии (7.122) в нелинейной системе возникает периодический режим с частотой ш' — — 2,52 с_|, определяемой по оси со, и амплитудой А' = 0,042 рад, которую находят по числовому значению С/А. При дальнейшем перемещении шаблона (в край-
* Для повышения точности определения периодических режимов шаблоны следует накладывать обратной стороной и находить точки Bi и Di. Это вызвано тем, что наклоны характеристик 20 lg[l/g(C/A)] и —180° —ц(С/А) близки соответственно к наклонам Я'(<в) и 0(<в).
нее положение) получают точки В3 и D3, которые также находятся на одной вертикали. В этом случае (7.122) снова соблюдаются прн со" — 14 с-1, А" =
= 0,093 рад. Последующее перемещение шаблона не дает точек пересечения, лежащих на одной вертикали.
Наличие двух частот со', со" и амплитуд А', А" колебаний требует определения, какая же нз них соответствует автоколебаниям. Дадим амплитуде А приращения ДА н посмотрим, как будут перемещаться точки В2 и В3 по характеристике 20 lg[l/c/(C7A)]. Тогда В2 выходит за кривую Я(со), следовательно, в системе возникают автоколебания с со" = ша1 = 12,2 с-1 и А" = Аа1 — 0,0067 рад. В точке В2 эта характеристика располагается ниже кривой Я (со), что соответствует неустойчивым колебаниям. Неустойчивые колебания с изменением времени становятся автоколебаниями.
Пример 7.12. Определить частоты и амплитуды автоколебаний для двухконтурной системы с нелинейностью во внутреннем контуре (рис. 7.5, г). С помощью данной структурной схемы найдем условия возникновения периодических режимов по формуле
। ._______kjk2kj_______Г k3kjT[ . 2
Ф S(ris+l)(T2s + l) L ki
+ ^£s+ i]/(^_)=°_ (7.127)
Допустим, что k2 = 140 рад/(В • с), k3 — 0,5 (В • с)/рад,_ ki = 0,005, Тi = 0,005 с, Т2 = 0,4с, а коэффициенты K.—kikjti изменяются от 125 до 250 с-1.
Для удобства построения логарифмических частотных характеристик в выражение (7.127) введем следующие обозначения: Ц7, с$) ________k\ktki-----.
Н } S(T1S+I)(r2s+1)’ (7128)
ГП (s) = s2 + з + 1. «1 «с
Рис. 7.8. Границы устойчивых состояний и автоколебаний с учетом 2-го и 3-го приближений (пример 7.13)
’5S
Область автоколебании
200 -
/50
100
50
flol-цгармонике
/ С учетом влияния 3-й гармоники на f-ю
С учетом влияния !-й и Зй гармоник
0 _______11U__I______1-----I------1--------
50 Ю0 /50 200 250 000
528
Рис. 7.9. Процесс установления автоколебаний с зоной нечувствительности
Тогда уравнение (7.127) примет вид
H-FI(s)FII(s)Z(C/A) = O. (7.129)
Из соотношения (7.129) найдем уравнения гармонического баланса в виде
20 1g | F, (/ш) Fn (/ш) | = 20 Ig ; )
01 (<о) + еи (СО) = -180°. )
(7.130)
Соответствующие характеристики | U^Fnl построим сплошными линиями для К = — 125, 140 и 250 с-1. Точки £>ь £>2, D3, В}, В2, В3 соответствуют режимам автоколебаний, а точки D3, Bit В3 — неустойчивым колебаниям (рис. 7.7).
На рис. 7.8 штриховыми линиями построены прямые, отделяющие области устойчивых состояний от автоколебаний по со, в зависимости от К по 1-й гармонике. Процесс установления автоколебаний в системе с нелинейностью типа зоны насыщения показан на рис. 7.9.
3. ПРИМЕНЕНА VI '0’1 \
ГА РМОП И Ч Е CKO И «11 i:! Е XР И.ЗАЦИ И ПРИ УЧЕТЕ ВЫСШИХ
ГА Р МОН ИЧ ЕС. К а X О' ЮГА Г< Л ,’Т h 'I <i их
В предыдущем параграфе определялись периодические режимы в нелинейных системах с учетом только 1-й гармоники. В результате были получены частоты и амплитуды автоколебаний в виде первого приближения. В гл. 2 было показано, что 3-я гармоника оказывает влияние системы с однозначными и двузначными нелинейностями на 1-ю гармонику. При этом возникают дополнительные амплитудные и фазовые искажения qi(C/A) и щ (С/А). Поэтому ранее написанные условия гармонического баланса
(7.122) и (7.123) следует заменить вторым приближением:
201g//'(а) = 201g--]
6 v & (CIA) I (7.131)
0 (®) =-180°(C/A), J
где qi (С/А) и цДС/А) определяют соответственно по формулам (2.117) и (2.118).
Так как в эти формулы входят неизвестные нам значения относительной амплитуды <53 и фазового сдвига фз, то для их нахождения следует пользоваться характеристическим уравнением для 3-й гармоники, т. е.
1+-^7з(С/А)Г(3» = 0, (7.132)
где /3(С/А)—эквивалентная передаточная функция нелинейности по 3-й гармонике.
Функцию /3(С/А) можно представить в виде
73 (С/А) = < (С/А) + jb'3 (С/А). (7.133)
В выражении (7.133) а'(С/А) и Ь'3(С/А)— коэффициенты гармонической линеаризации нелинейности без учета добавочных коэффициентов взаимного влияния собственной 3-й гармоники. В гл. 2 было показано, что коэффициенты а'3 (С/А) и Ь3 (С/А) большинства нелинейных САР достаточно велики и оказывают существенное влияние на области устойчивых состояний и автоколебаний. Для этих коэффициентов в уравнения (7.132) подставим соотношение (7.133); тогда получим
63 = -Г(3/ш) [а3(С/А) +
+ /Ь'3(С/А)]. (7.134)
Основные коэффициенты гармонической линеаризации по 3-й гармонике можно записать в виде
а3 (С/А) = азз (С/А) cos ф3 +
+ Ь3з (С/А) sin ф3;
Ьз (С/А) = Ьзз (С/А) cos фз — — Озз (С/А) sin фз,
► (7 Л 35)
529
где
ай(С/Л) = 2л
= ( ST (Л sin ф) sin Зф б/ф;
Ял J
&зз(С/Д) = 2л
= -Л- ( iF (A sin ф) cos Зф с?ф. Ял J
(7.136)
Подставив выражения (7.135) в уравнение (7.134), найдем
-бз = Ц7(3/®)[взз(С/Л) +
+ /633 (С/Л)] (cos Фз — / sin Фз), (7.137) откуда
-б3е^> = 1Г(3/®)[азз (С/Л) Ч-
+ ^зз(С/Л)], (7.138)
где
Г (3/и) = Н' (Зи) е/6(3“\ (7.139)
Из выражений (7.137) — (7.139) определим
63е/(я+ф1) =
= Н' (3®) <733 (С/Л) еу [|Х (С/Л)+е (3ft))1.
(7.140)
Пользуясь соотношением (7.140), составим уравнения для определения бз и фз в виде
б3 = Н' (3®) д/4з(С/Л) + бзз(С/Л);
(7.141)
«.-----180" + «(3») + arctg .
(7.142)
Если в САР присутствуют только однозначные нелинейности, то в соответствии с формулами (2.122) и (2.123) определяются эквивалентные амплитудные и фазовые характеристики. При наличии однозначной нелинейной характеристики и влияния 3-й гармоники на 1-ю возникает дополнительный фазовый сдвиг Ц1(С/Л). Тогда для определения параметров автоколебаний следует также пользоваться формулами (7.131).
Данная методика позволяет учитывать дополнительные коэффициенты по 3-й гармонике Аа33(С/Л), А'азз(С/Л) и Абзз(С/Л). В результате получится третье приближение для определения частот и амплитуд автоколебаний. Тогда уравнения гармонического баланса (7.128) имеют вид
20lgН'(®) = 201g- )
6 v s<72(С/Л)’ I (7 14з)
е(®) = -18о°-ц2(с/л), J
где <?2(С/Л) и |л2(С/Л) определяют по формулам, аналогичным (2.122) и (2.123).
По предлагаемой методике можно учитывать влияние и последующих гармоник.
Существенным преимуществом предложенной методики учета влияния высоких гармоник являются возможности применения шаблонов ^^УДС/Л) и —180° —Н1(С/Л) или 201^7йЬл7 И -180о~ц2(С/Л),что намного упрощает процесс исследований нелинейных систем.
Рассмотрим порядок определения второго и последующих приближений для определения частот и амплитуд автоколебаний в нелинейных САР. Его сущность заключается в следующем.
1. С помощью условий гармонического баланса для первого приближения графическим путем, основанным на методе шаблонов, или на ЭВМ находят частоту ®ai и амплитуду Aai автоколебаний.
2. Вычисляют основные коэффициенты гармонической линеаризации и 3-й гармоники а33(С/А) и ^зз(С/А).
3. Определяют относительные значения амплитуды б3 и фазовый сдвиг фз, учитывающие Я'(3®) и 6(3®).
4. Находят эквивалентные амплитудную </i(C/A) и фазовую pi(C/A) характеристики для второго приближения.
530
Рис. 7.10. Графики основных и дополнительных коэффициентов гармонической линеаризации для нелинейности типа люфта: а—основные азз(с/Л), Ьз»(с/Л); б—дополнительные
’ Да» (с/Л), Д'а» (с/Л), Д&» (с/Л), Д'&п (с/Л)
5. Пользуясь условиями гармонического баланса для второго приближения, графическим путем по методу шаблонов или на ЭВМ определяют уточненные значения частоты <йа2 и амплитуды Ла2 ЭВТОКО-лебаний.
6. Если точность полученных значений <Ва2 и Лаг недостаточна, то повторяют все процедуры согласно п. 1—4, но с учетом Аазз(С/Л), Дазз(С/Л) и АЬзз(С/Л). В результате получают третье приближение для нахождения соа3 и Ла3.
Процесс вычислений заканчивается, если значения соаз. Ла3 достаточно близко совпадают с соа2 и Ла2. Если это не удается получить, то необходимо учитывать влияние гармоник более высоких порядков [30].
Рассмотрим несколько примеров определения частот и амплитуд автоколебаний и построения областей устойчивых и неустойчивых состояний с учетом влияния высших гармоник.
Пример 7.13. Для нелинейной системы с люфтом (рис. 7.5, в) определить зоны устойчивых состояний и автоколебаний в
зависимости от изменения параметров К н Т при С = 0,004 рад, Кн = 1.
В примере 7.11 в качестве первого приближения при К = 40 с-* была получена частота автоколебаний <oai = 12,2 с-1, Л,1 = 0,0067 рад. Для второго приближения приведем на рис. 7.10 графики основных и дополнительных коэффициентов гармонической линеаризации.
Из рис. 7.10, а видно, что а33(СД4) = — 0 и &33(С/4) = —0,2. Для линейной части системы вычислим
Н' (Зсоа1) =-------г-^1 . ; )
Зсоа1 -v/(3a>al7’)2 + 1 > (7.144)
0 (Зсоа1) == —90° — arctg (Зсоа!?). )
Определяя числовые значения по выражениям (7.144), а также а33(С/А) и &33(С/Л) и подставляя их в формулы (7.141) и (7.142), найдем б3 и <р3.
По графикам рис. 7.10, б определим дополнительные коэффициенты гармонической линеаризации Aai3(C/4), Д'а13(С/Л),
Д&13(С/4) и Д'&13(С/4), а затем по выражениям (2.114) и (2.115) вычислим qi(C/A) и щ(С/Л). После этого построим шаблоны 20 lg[l/ffi(C/4)] и —180°—цДС/Л). Нанеся их сплошными линиями на прозрачную бумагу, получим шаблон, показанный на рис. 7.11. Кривые 1, 2 соответствуют характеристикам 20 lg(l/^i) и —180° — (М.
Перемещая шаблон по оси частот с характеристиками Я (со) и 0(со) (рис. 7.6, в), получим более точные значения амплитуд и частот автоколебаний (<оа3 = 15 с-1; Аа3 = 0,0075 рад). Подставляя их в формулы (7.138) и (7.139), найдем новые значения 63 и <р3, а затем по ранее приведенной методике построим шаблоны
Рис. 7.11. Шаблоны для построения характеристик нелинейности типа люфта по первому, второму и третьему приближениям
531
Рнс. 7.12. Области устойчивых состояний и автоколебаний в САР (пример 7.13 при различных гармониках i = 1, 2, 3);
а) ®а£=<ла(К); б) Аа;=Да(К); в) <оа/=а>а(Т); г) АаГАа(Т)
201g[l/<72(C/A)] и —180° — ц2(С/Л) соответственно кривые 3 и 4 на рис. 7.11. Пользуясь шаблоном (кривые 5 и 6) найдем третье приближение шаз = 16,7 с~‘ и Лаз — 0,08 рад. Отсюда следует, что третье приближение сказывает меньшее влияние на частоты и амплитуды автоколебаний, чем второе.
Построим на рис. 7.12, а—г кривыми 1—3 области устойчивых состояний и автоколебаний в зависимости от параметров К и Г при различном числе гармоник. Сходящимися стрелками обозначим границы кривых для амплитуд автоколебаний, а расходящимися стрелками — границы неустойчивых состояний. При этом видно, что области устойчивых состояний в системе за счет учета влияния 3-й гармоники уменьшаются на 24 %.
Пример 7.14. Для двухконтурной нелинейной системы с зоной насыщения (рис. 7.5, а) по данной методике опреде
лить границы автоколебаний и неустойчивых состояний в зависимости от Ki и 7\ с учетом влияния второго и третьего приближений. В этом случае также определяют 63, 63 и <р3, <р3 и шаблоны 20 Ig (1/<ц(С/Л)], 20 1g [1/<7а (С/Л)], -180° -- Ц1 (С/Л), -180° - ц2 (С/Л).
Если построить границы устойчивых состояний и автоколебаний, то, пользуясь рис. 7.7, получим, что при Т1 — 0,005 с область устойчивых состояний сокращается на 35 %. С изменением Ti в примере 7.14 можно найти такое положение границ устойчивых состояний и автоколебаний, когда по первому приближению имеется область устойчивых состояний, а по второму приближению они полностью отсутствуют. Это явление имеет важное значение, так как возникающие в системах автоколебания приводят к выходу из строя регуляторов, а иногда и объектов регулирования.
532
6)
Рис. 7.13. Логарифмические амплитудная и фазовая частотные характеристики САР при подавлении автоколебаний с помощью линейных корректирующих устройств: а — последовательного типа; б — параллельного типа
533
4. СПОСОБЫ ПОДАВЛЕНИЯ АВТОКОЛЕБАНИЙ
В САР для подавления автоколебаний применяют линейные и нелинейные корректирующие устройства. Их тип и параметры выбирают таким образом, чтобы исключались возможности выполнения условий гармонического баланса. Если в САР при Lm > 0 фазовая частотная характеристика в диапазоне частот со'— ы" располагается ниже —180°, то в таких системах с однозначными нелинейностями в зависимости от их формы в частотах со' и а" возникают колебательные режимы.
На рис. 7.13, а штриховой линией 2 изображена фазовая частотная характеристика, пересекающая в точках Z)2 и £>1 прямую —180°. Проведем через эти точки вертикальные линии до пересечения с амплитудной частотной характеристикой (штриховая линия 1). В результате получим точки В2 и Bi, через которые проводим шаблоны для нелинейности типа насыщения (прямые 3 и 4). Откуда следует, что со' = = соа — частота автоколебаний, а ее амплитуду Аа находим при заданном значении С по кривой 3. Частота со" соответствует режиму неустойчивых колебаний.
Для подавления автоколебаний в такой системе необходимо выбрать тип и параметры фазоопережающего линейного корректирующего устройства последовательного типа, при включении которого в САР будет невозможно пересечение фазовой характеристикой 0(со) прямой —180°.
Воспользуемся фазоопережающими корректирующими устройствами последовательного типа с передаточными функциями
(7.145)
или
kZ (Т„ S + I)2
WK u(s)= kV K1 < . (7.146) (W+1)
Рис. 7.14. Номограммы для определения угловых значений фазовых опережений корректирующих устройств:
а —для В7к1; б—для В7к11
На рис. 7.13, а приведена желаемая фазовая характеристика 0Ж (кривая 5), исключающая ее пересечение с прямой —180°. При этом величину подъема фазы 0К можно найти с помощью выражения
Ок(®) = Ож(ш)-0с(со), (7.147)
где 0К (со)—максимальное значение подъема фазовой характеристики; ёс (со)— фазовая характеристика первоначальной системы.
Для нахождения типа и параметров последовательного корректирующего устройства на рис. 7.14, а
534
al
fl
построены номограммы по выражению (7.145), а на рис. 7.14, б—по формуле (7.146) С помощью номограммы (рис. 7 14, а) при максимальном значении 6к(ю)=40° (рис. 7,13, а) определим параметры корректирующего устройства TKl — = 0,33 с и Тк = 0,038 с. .
Результирующая логарифмическая амплитудная характеристика с корректирующим устройством данного типа показана на рис. 7.13, и (кривая 6). Из сравнения кривых 1 и 6 видно, что включение последовательного корректирующего устройства увеличивает частоту фазы в 3 раза, что намного повышает восприимчивость полученной таким образом САР к шумовым помехам.
Рассмотрим включение в систему параллельного корректирующего устройства. При этом будем считать, что логарифмические амплитудная и фазовая частотные характеристики исходной системы совпадают с рис. 7.13,6. Введем параллельное корректирующее устройство с передаточной функцией
lFK(s) =
(Лс.* -Ы) (ЛсЛ-Ь I)2*
(7.148)
Построим 0Ж(©) и имеем минимальный подъем 0к (со) =40°. Далее, пользуясь номограммой *, по-
* Типы корректирующих устройств и их амплитудные и фазовые характеристики при наиболее часто встречающихся соотношениях приведены в гл. 10.
Рнс. 7.15. Структурные схемы систем, обеспечивающих подавление автоколебаний с линейной коррекцией: а — последовательной; б — параллельной строенной по выражению (7.148), найдем параметры корректирующего устройства: Тк, — 0,16, с; Тк,— =6.1 с; TV, = 0,0001 с; kK =0,625.
В случае применения параллельного корректирующего устройства частота фазы увеличивается в 1,3 раза, что меньше оказывает влияние на действие шумовых помех.
Структурные схемы САР с нелинейностью типа насыщения, в которых возникают автоколебания, приведены на рис. 7.15. Последовательное и параллельное корректирующие устройства, подавляющие автоколебания, выделены на рис. 7.15, а и б штриховыми линиями.
Несмотря на сложность создания нелинейных корректирующих устройств, их стали чаще применять в САР для подавления автоколебаний, так как удается создать такие системы, в которых даже при значительном изменении параметров автоколебания не возникают.
На рис. 7.16, а изображена исходная структурная схема системы с нелинейностью типа люфта. Как было показано, в такой системе возникают автоколебания и при малых значениях передаточных коэффициентов К. Введем в исходную
535
схему линейное корректирующее устройство с передаточной функцией Г к (s) и эквивалентную нелинейность JK(C2/A2). Преобразованная таким образом структурная схема показана на рис. 7.16,6.
На рис. 7.17 построены логарифмические амплитудная (кривая 7) и фазовая (кривая 2) частотные характеристики линейной части системы. Здесь же показаны положения шаблонов 20 1g (1/9) и —180°—ц для нелинейности типа люфта при Ci = 0,004 рад и К = — 40 с-1 (кривые 5, 6, 7 и 8). В результате образуются точки пересечений Bi, Di и В2, D2, лежащие на вертикальных прямых, что указывает на существование периодических режимов. Частота и амплитуда автоколебаний определяются продолжением прямой B\Di до пересечения с осями частот со и Ci/A шаблона. В результате получим <0ai = 15 с-1 и Ла1 = 0,0075 рад.
Для устранения автоколебаний введем дополнительно к I17K(s) параллельное корректирующее устройство типа насыщения; тогда
Qk^CJA^ = (arcsin C2jA2 +
+ C2IA2*J\ -Cl/Al). (7.149)
В качестве параметров параллельного корректирующего устрой-
Рис. 7.16. Структурная схема системы с нелинейностями типа люфта: а—исходная; б—с нелинейной коррекцией
Рис. 7.17. Логарифмические амплитудные н фазовые характеристики нелинейной системы прн отсутствии условия возникновения гармоническгоо баланса при Т = 0,067с
ства примем: feK = 0,25 рад/с; Тк = = 0,05 с; С2 = 0,25 В; В = 200 В.
Составим характеристическое уравнение системы в виде
, ,______Г (з) У (С,/Л,)__ __ „
1 "Г 1 + W (з) Гк (з) /к (С2/Л2)
(7.150)
Из уравнения (7.150) найдем
1 , , WK(s)JK(C2/A2)
J(CilAi)W(s) J(Ci/Ai)
(7.151)
Правую часть выражения (7.151) обозначим следующим образом: 7'(Лр ju), (7.152)
откуда
1 _|___I--
Щ/ц)
1 "* г" /” Т /п 0“)
zn(A. /®) =
(7.153)
Эквивалентная амплитудная характеристика
BkK<£t2qK (С2/А2) • 154)
536
Рис. 7.18. Логарифмические амплитудная и фазовая частотные характеристики внутреннего контура с наложенным шаблоном для нелинейности типа люфта
где амплитуда
4 _ Л1/гкш2
2 д/трчг
а эквивалентная фазовая характеристика
ц" (Aj, со) = 180° — arctg (оГк —
-ptCJAJ. (7.155)
Построим характеристики системы с нелинейной коррекцией (рис. 7.18). Кривая 1 для функции pi" (Л1( со), а кривая 5для 201g/' (Ль со). На рис. 7.18 построены характеристики 20 lg,41/<Z„ (Ль со)] (кривая 2) и — р." (Лр со) (кривая 6). Перенесем полученные значения на номограмму Никольса. По номограмме найдем значения амплитуд и фаз функции
(7.156)
и нанесем их на рис. 7.18 (соответственно кривые 4 и 3).
Условия гармонического баланса будут
201ёЯ'(со)<7'(Лр со) =
(7-157)
0 (со) + 0' (Лр со) —
= -180°-ц(С1/Л1). (7.158)
В соответствии с этими формулами геометрически сложим кривые 3 и 4 (рис. 7.18) с кривыми 1 и 2 (рис. 7.17), что позволит получить характеристики 201g Я (со) / (Лр со) (кривая 3) и 0(со) + 0'(Лр /со) (кривая 4). Эти кривые показаны на рис. 7.17.
Наложим на рис. 7.17 шаблон с характеристиками
(7.159)
и будем его перемещать вдоль оси частот. Как видно из рис. 7.17, нет точек пересечения кривой / с линией 3 шаблона, лежащих на одной вертикали с точкой пересечения кривых 2 и 4, что указывает на отсутствие режимов неустойчивых колебаний и автоколебаний.
Существуют и другие схемы включения нелинейных корректирующих устройств. Например, параллельных с двумя нелинейностями и т. д.
5. ВОЗНИКНОВЕНИЕ МЕДЛЕННО МЕНЯЮЩИХСЯ КОЛЕБАНИЙ
В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ
При подаче на вход сигналов управления g(t) или возмущения f(t), медленно меняющихся по сравнению с автоколебаниями, их можно считать постоянными внутри каждого периода колебаний. Если линейная часть системы отфильтровывает высшие гармоники, то на входе нелинейности имеем
х (0 = х0 + A sin at. (7.160)
От действия постоянной составляющей при разложении нелинейной
537
функции в ряд Фурье имеем следующие коэффициенты гармонической линеаризации (2.101) — (2.103).
Тогда для двузначной нелинейности можно записать
ЯГ (х0 + A sin tot) = (Го (х0А) +
Ь (х0, A) dx* dT ’
(7.161)
+ а (%о> А) х (/) +
со
баланса и х* (/)
(7.162)
где х* (t) — A sin tot.
Условия гармонического можно представить для х0 в виде
1 + W (0) Jo (х0, А) = 0; j
l + W^J^Xo, A) = O,J
где /о(хо, А) и Л(х0, А)—эквивалентные передаточные функции нелинейной части системы для двухчастотного входного сигнала.
Решая систему (7.162), находим смещение центра колебаний хо, частоту соа и амплитуду Аа автоколебаний.
При малых интервалах изменения функции х0 можно пользоваться формулами (2.242), (2.243), т. е.
ЗГ0 = Кх0, (7.163) где ka — ka(A).
Для определения постоянной составляющей Хо в статической системе и установившейся ошибки по скорости хо в астатической системе воспользуемся гармоническим линеаризованным уравнением
хо + х’(0 + ^(р){^о(хо, Д) +
+ [а(х0, Л) + -^р]х,(0} =
= Wf(p)f(t). (7.164)
Уравнение (7.164) при принятых условиях можно записать раздельно по постоянной и колебательной составляющим:
для статической системы
ха+W(p) <Га(х0, A)=rf(O)fo;' x*(O + F(p)[a(xo,A) +
+ р]^(0 = 0;
(7.165)
Рис. 7.19. Структурные схемы нелинейных систем с идеальным реле: а—статическая; б—астатическая
для астатической системы
Хо + W (0) ЗГ0 (х0, Д) = WfL (0) f J m х‘(О+Щр)[а(хо, Д)+ I + р] х* (0 == 0. J
(7.166)
Пример 7.15. Определить величину смещения Хо. Ов и А, в системе, структурная схема которой изображена на рис. 7.19, а. Для этого воспользуемся методом логарифмических характеристик и шаблонов. На рис. 7.20 построены логарифмические амплитудная и фазовые частотные характеристики при 'К = 100 В, Т = 1 с, Тг = = 0,5 с, Т3 = 0,33 с. При этом пересечение вертикали BD с осью частот даст частоту автоколебаний соа = 3,33 с-1.
Построим шаблон для идеального реле со смещением х0, когда В — 2В и —В=—1В, соответственно в виде
20 IS —1---лГ (штриховые кривые) и
<7о (Хо. Л)
1 *
20 1g—-----— (сплошные кривые). Нало-
ге (Хо, Л)
жим шаблон на рис. 7.20 так, чтобы ось частот со совпадала с осью шаблона А, и будем его перемещать до тех пор, пока прямая, проходящая через точку С, ие совпадет с вертикалью BD. В этом случае условия
W (0) = - .-;1 ^гг и W (/со) = - .1 .т
/о (хо, А) /1 (Хо, А)
полностью удовлетворяются; тогда получим следующие параметры периодического режима: х0 = 9,3 В; соа — 3,33 с-1; А, — = 14В.
Пример 7.16. Найти зависимости х0 = = xo(go,fo) и A—A (g0, f о) для системы
* Здесь qo(xo,A), qi(x0, А) — эквивалентные амплитудные характеристики.
538
Рис. 7.20. Логарифмические амплитудная и фазовая частотные характеристики статической системы с наложенным шаблоном с
кривыми 201g---------тг- и 20 1g ——тт-
у s q0 (х0, A) s qi (x0, A)
Так как релейная характеристика является однозначной, то
а (х0, А) = а0 (Ас),
откуда получим
с нелинейностью (типа реле), структурная схема которой изображена на рис. 7.19,6. Составим характеристическое уравнение системы:
или
T’iT’ss3 + (Г, + Т2) s2 + [1 + Tik2k3a (А)] а+
+ (ki + k3) k2a (А) = 0. (7.167)
После подстановки в уравнение (7.167) s = /со имеем
(*i + k3) k2a (А) - (Г, + Т2) со2 = 0; | [1 + 7’1/г1/г3а(Л)]со-7’1Т2со3 = О. J
(7.168)
Из соотношений (7.168) найдем частоту и амплитуду симметричных автоколебаний:
____ . / + k3 . с V Т, (T2k\ - Tik3) ’
л 4Bk2T2 (T2ki — T t/гз) c « (Гi + Т2)
(7.169)
(7.171)
Введем в выражение (7.171) обозначение 2х0/Ас = sin Р; тогда получим
А 6
— = cos-H-. (7.172)
Из соотношений (7.170)—(7.172) найдем
А = Асcos [j-arcsin -^2-]. (7.173)
Далее определим зависимость смещения Хо от воздействий. Для этого запишем
539
Рис. 7.21. Изменение характеристик Хо и А от сигналов управления g0 и возмущения h = 0,1
fei = 20; k2 = 5 с-1; k3 = 3; Т} = 0,1 с; Т2 — 0,5 с; В = 0,2 В. После их подстановки в формулы (7.179) найдем
Хо = 10,4 sin л (0,9Igo — fo);
Д= 10,4 sin-J-(O,91go - А>).
(7.180)
На рис. 7.21 построены зависимости х0 и А от go, когда fo = 0,1. При этом видно, что функция смещения х0 от управляющего воздействия имеет экстремум при go = 0,7,. а амплитуда А изменяется по экспоненте.
6. <4* Klii.-Г. КОЛ'. ЬЛ НИЯ
следующее уравнение:
(Tip + 1) (Т2р + 1)рх + (Т1^зр +
+ fei + Лз) k3F (х) = ki (Т2р + 1) pg (/) —
~(Tik3p + kl + k3)f(t'). (7.174)
Так как релейная система является астатической по сигналу g(t) и статической по f(Z), то в установившемся состоянии имеем
&2 (fei + k3) Ф (хо) — [feigo — (fei + k3) fo].
(7.175)
Функцию Ф(х0) можно определить, пользуясь формулой (2.251). Тогда получим
ф(х0) = —arcsin-^-. (7.176) Я Дс
После повторной гармонической линеаризации найдем функцию смещения
х°= "Гsin [жг ( *1 +°л3 — ^°)]’(7л77)
Определив из выражения (7.177) 2х0/Д и подставив его в (7.173), найдем
',-Нж(мк-'•)]•<7178)
Подставляя в выражения (7.177) н (7.178) соотношения (7.169), окончательно получим
„ 4Bk2T2(T2ki— Тik3)
‘ »(Г, + Г,) х
х.1„Г-Л-(тЬь--гЛ1
L Bh2 \ «1 + k3 / J и (7.179)
А — (7*gfei — Т\k3)
МП+.Т,) Л
X«,[-£-( »&-
L 2DK2 \ «1 + «3
Пусть параметры системы, изображенной на рис. 7.19,6, имеют следующие значения:
Нарушение принципа суперпозиции в нелинейных системах усложняет исследование вынужденных колебаний. Определение амплитуд вынужденных колебаний проводится по методу гармонической линеаризации.
Запишем уравнение динамики систем в виде
x(t) + W(p)^(x, px) — Wf(p)f(t),
(7.181)
где x(t) —сигнал на выходе системы; W (р) и Wf(p)—уравнения динамики по сигналам управления и возмущения.
Будем считать, что внешнее воздействие
f (t) = Вв sin ©Bf, (7.182)
где Вв—амплитуда сигнала; сов— частота.
Воспользуемся условием синхронизации, когда в нелинейной системе возникают колебания на частоте внешнего воздействия. Это явление называют процессом захватывания, т. е.
х (() = Лв sin (сов( + ф). (7.183)
Решения данной задачи требуют определения Ав и сов. Для этого воспользуемся выражением
f (0 = Вв sin [(сов/ + ф) — ф] =
= — Вв sin ф cos (®в( 4~ ф) +
+ Вв sin (сов/ 4- ф) соэф. (7.184)
540
Беря производную от функции (7.183), получим
рх (0 = Лв®в cos (®Bt + ср). (7.185)
Пользуясь выражениями (7.184) и (7.185), найдем
№ = X- (cos <₽ - р)х (°-
(7.186)
Подставляя выражение (7.186) в (7.181), определим
[1 - Wf (р) (cos <р - р)] X
Xx(t)+W(p)f(x, рх) = 0.В (7.187)
Для упрощения рассматриваемой задачи положим, что
2л
5Г (Лв sin ф, Лвмв cos ф) dty = О, о
где ф = met + ф; после чего нетрудно выполнить гармоническую линеаризацию нелинейности
P'tx, рх) — а(Ав, а>в)х +
+ Ь (Аъ’ Мв) рх, (7.188)
(Ов
где а (Л в, ив), Ь(Лв, юв)—коэффициенты гармонической линеаризации.
Подставляя соотношение (7.188) в уравнение (7.187), получим
1-1Г,(р)^-(созф-^Лр) + +V (р) [а (Л„ в,) + Л =0.
L wB j
(7.189)
Уравнение (7.189) перепишем, имея в виду, что
cos ф — j sin ф = и s = /сов;
тогда
л 1 + Н7 (Мв) [а (Лв, <ов) + jb (Ав, (ов)] _
~Ввй~1<9. (7.190)
Представим уравнение (7.190) в виде
37е/Ф==
=____________Vf(>B)____________
1 + W (/®в) [а (Лв, а>в) + jb (Лв, (Ов)1 •
(7.191)
Обозначим
7 Ив, /®в) = а (Лв, ®в) + jb (Лв, ®в).
(7.192)
После подстановки (7.192) в уравнение (7.191) получим
~-е^ =
О В
_______1_________
_ & (^В» ®в) (/®в) TV7 \
=--------------j------ *f
1 + 7 (Лв, <ов) W (jaB)
(7.193)
Откуда найдем
201g-^-20Ig|Ff (J4)| =
•°в __________1_________
= 20 1g в*в) (fos) __
1 + 7 (Лв, <ов) W (;<ов)
(7.194)
фв —arg [Fj(/coB)] =
Г 1 1
_ _____ 7 Ив, ®в) w (/<ов)
— arg j .
- 1 + 7 (Лв, (ов) W (/<ов) -
(7.195)
Используя обозначения
17(ЛВ, >в)1==<7(Лв, ®в); 1
arg[7HB, >в)] = р(Лв, сов),/
(7.196) запишем
7 Ив, ®в) = q (Ав, ®в) е't1800"11 <лв' “Д
(7.197)
В выражениях (7.194) и (7.195) имеем
1
201g /Ив- «>в)1Г(/Юв) =
1 + 7 (Лв, <ов) W (j<i>B)
= 201g|<DeHB,/(oB)|; (7.198)
- 1 -
О Г ГТ ^в’ (/®в) _
аГ£ . --------------------------
L Z(Xb,(Ob)U4/<Ob) J
= arg [Фв Ив, /®в)]. (7.199)
541
Рис. 7.22. Графики для определения вынужденных колебаний в нелинейных системах:
1 1
д—кривые -------—и .—Г-, нанесенные
' (Лв- “в) V (/fflB)
на номограмму Никольса; 6, в—зависимости соответственно для Лв— f (<ав) и Лв—f (Вв); а—пороговые значения амплитуд Вв — f (а>в); б—зона областей устойчивых колебаний, захватывания и автоколебаний
Построим номограммы с харак-1 1 теристиками и на
прозрачной бумаге (рис. 7.22, а) и наложим их на номограмму Никольса, совмещая ее начало коорди-
нат с точкой на кривой:, У Ив> /“в)
имеющей амплитуду Лв; и частоту <ов«, где соблюдается условие
201g А-20151^(^)1 =
= 201gl Фе(Лв, /®в) |. (7.200)
Перемещая прозрачную бумагу с кривыми z и по
номограмме (рис. 7.22, а), получим характеристику Лв = Лв(сов), которая построена на рис. 7.22, б сплошной линией.
542
Если управляющее воздействие поступает на вход системы, то передаточная функция замкнутой нелинейной системы
ф (Вв, 7®в) = Фв Ив. /®в) X
ХШ,М (7.201)
где W (Ав, /сов) = J (Л. /®в)^(/®в)-Зная характеристики Фе(Дв, /сов) и W (Дв, /<ов), нетрудно найти семейство логарифмических амплитудных и фазовых характеристик замкнутых нелинейных систем, откуда получим кривую Дв=/(Вв) (рис. 7.22, в). Изменяя сов, получим зависимость порогового значения амплитуды Вв пор = f (©в). Соответствующая кривая построена на рис. 7.22, г. Откуда видно, что в нелинейной системе возникают одночастотные колебания сов при Вв > Вв пор в области синхронизации, а приВВпор=0 имеем <ов = сов, т. е. в системе наблюдается режим автоколебаний. На рис. 7.22, д построена кривая, выделяющая в САР области устойчивых состояний, захватывания и автоколебаний.
7. КРИТЕРИЙ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ
Критерий абсолютной устойчивости Попова используют для определения частотными методами достаточных условий асимптотической устойчивости замкнутых одноконтурных нелинейных систем. При этом нелинейность может быть однозначной, двузначнойtи обладать свойствами как стационарности, так и нестационарности. В общем случае нелинейность описывается выражением
u(/) = ST[e(/), /], (7.202)
где е(0 —сигнал на входе нелинейности.
Укажем, что для автономных систем x(t) =—e(Z).
На рис. 7.23 изображена структурная схема системы с нелиней-
Рис. 7.23. Структурная схема нелинейной системы с нелинейностью общего типа
ностью, представляемой в форме (7.202). На нелинейности наложены ограничения, но все они должны размещаться внутри заштрихованного сектора, расположенного между двумя прямыми ге и Ze. В этом случае соблюдается условие
(7.203)
Рассмотрим несколько типов нелинейных элементов, для которых удовлетворяется условие (7.203). Для однозначных нелинейностей имеем секторы, ограниченные линиями ге и 1е (рис. 7.24, а, б). При двузначных нелинейностях (рис. 7.24, в, г) секторы ограничены осью абсцисс и линиями 1е или /е — и.
Если на нелинейность (рис. 7.24, д) наложены ограничения в виде
I е (/) К ет;) 1«(0Ю„Д
(7.204)
то можно провести такую нелинейную характеристику, при которой условие (7.203) соблюдается лишь при —em^e(Z) ет.
Для стационарной многомерной линейной системы, структура которой подобна схеме, изображенной на рис. 7.23, можно записать
У (0 = Ау (0 + Ьи (/);) (7 205) — e(/) = cTy(Z). >
Переходная матрица для данной системы будет
Ф(/)=5’-'№-А)->ф(7, 0).
Так как выходной сигнал нелинейной части определяется вторым
543
Рнс. 7.24. Характеристики нелинейностей, расположенных в секторе с заданными границами:
а и б*—однозначные стационарные нелинейности; в и г—двузначные нелинейности соответственно с пассивным и активным гистерезисом; д—при выходе однозначной нелинейности из сектора, когда -е„
т т
уравнением системы (7.205), то
е (t) = — стФ (t) у (0) — t
— стФ (/— т)6«(т)с/т. (7.206) о
Выходной сигнал САР, описываемый уравнением (7.206), с помощью импульсной переходной функции можно представить в виде
t
8 (/) = 80 (/) ~ k (t — т) и (т) dx, о
(7.207) где k — импульсная переходная функция.
Из сравнения уравнений (7.206) и (7.207) найдем
-80(0 = СТф(0У(0)-
= 27~1 [ст (Is - Л)- 'у (0)] (7.208) или
й(/) = стФ(/)&=^-1[ст (Is-А)-16].
(7.209)
Уравнения (7.208) и (7.209) показывают, что для стационарной линейной системы реакция — 80(/) на произвольные начальные условия равна импульсной переходной функции k(t).
Рассмотрим теперь ограничение, накладываемое на данный класс систем в виде коэффициента затухания а. Это означает, если а > 0, то входной сигнал (при действии импульсов или начальных условий) будет стремиться к нулю быстрее, чем функция e~at.
Из условия обеспечения асимптотической устойчивости САР с коэффициентом затухания а следует, что
lira е“*8 (0 = 0, (7.210)
£->со
если нелинейный элемент систем удовлетворяет условию (7.204).
Сформулируем основное положение об абсолютно асимптотической устойчивости Попова применительно к САР, имеющей передаточный коэффициент линейной части, равный К. Замкнутая САР будет абсолютно асимптотически устойчива, если u(t)/e,(t) принадлежит отрезку [0, К] и существует такое действительное число q, что для всех со 0 выполняется условие
Re[(l + ja>q) W (/со)] + -±-> 0.
(7.211)
Неравенство (7.211) перепишем в виде
U (со) > — + a>q V (со).
544
Откуда следует, что для любой' частоты со амплитудно-фазовая характеристика должна находиться правее прямой, определяемой уравнением
= (7.212)
Полученную, таким образом, прямую называют прямой Попова [32].
Рассмотрим несколько случаев, иллюстрирующих условие абсолютной асимптотической устойчивости. Положим q — 0; тогда прямая Попова должна быть касательной и амплитудно-фазовой частотной характеристике и находиться левее
Рис. 7.25. Расположение кривых Попова относительно амплитудно-фазовой характеристики:
а—прн <7=0; б н в—прн <7эЬ0
точки с координатой—\/К- На рис. 7.25, а прямая Попова показана жирной линией, когда она пересекает ось абсцисс в точке —1/Кь При q =И= 0 в соотношении (7.212) вводят новые переменные
t/((o) = t/((o); )
1 > (7.213)
V(®) = (oV (и), J
тогда
&(©)== -± + qV (®). (7.214)
Равенство (7.214) показывает, что сама прямая Попова не зависит от частоты.
На рис. 7.25, бив показаны положения прямых Попова, которые отличаются наклонами arctg(^co) и касательны к Итак, для на-
несения прямой Попова нужно знать положение точки —1/К на оси ординат и угол наклона arctg(gco).
Из рис. 7.25, б, в видно, что проведенная через точку с координатой — \/К кривая Попова проходит левее годографа ^(/<о). В этом случае коэффициент К определяет не только максимально возможный коэффициент линейной части системы, но и наибольшее отношение F(e)/e.
Теперь сформулируем положение об асимптотической устойчивости САР. Линейная стационарная система, описываемая уравнением (7.206), при u(t) =he,(t) обладает асимптотической устойчивостью управления для всех значений 0
( произвольной однозначной нелинейностью Г(е). В этом случае САР асимптотически устойчива, так как Г(0)=0 и 0^ F(e,)/e, К, что соответствует гипотезе А йзермана [ 1 ].
Пример 7.17. Определить характер нелинейности и сектор Попова, а также наибольшее значение коэффициента К, при котором соблюдается условие абсолютной асимптотической устойчивости САР. Для этого воспользуемся структурной схемой, изображенной на рис. 7.23, где
W - К(0.33>+1)е-^
W " ’ (0,66ju> + 1) (0,5;<»> + 1) ‘ (7‘215'
18 Ю. И. Топчеев
545
Рис. 7.26. Годограф W(ja) ной функции примера 7.17 жениями кривой Пбпова q = 0,15
для передаточ-с двумя подопри <7 = 0 и
Из выражения (7.215) при К = 1 найдем вещественную
(1 + 0,055<о2) cos <в —
77,,й -«(0,83 + 0,11 <о2) sin <о
U (®) = fr-6j436-).2—_да^)- (7.216)
и мнимую
— со (0,83 + 0,11 со2) cos (о —
V (ш) - ~ (1 + °’055tt>2) sin а (7 217)
(Ш) ~ (1 + 0,436<о2) (1 + 0,25<o2) ’
частотные характеристики.
Пользуясь выражением (7.217), вычислим функции V (<о) = <oV (<о):
<о2 (0,83+ 0,11<о2) cos со-
рт — <о (1 + 0,055<о2) sin <о
и (<о) — — (1 + 0>436(в2) (1 + 0125(+)
и
U (<о) = U (®),
а затем построим годограф W (j<£>). На рис. 7.26 показан участок годографа от <о = 0 до ш = 4,95. Затем через точку £7(со) = —0,505 проведем штриховую линию, перпендикулярную к оси абсцисс. Располагая годографом 1Г(/<о) при К — 1 и полученной штриховой линией, можно построить прямые Пбпова.
При q = 0 в соответствии с уравнением (7.212) прямая Пбпова параллельна штриховой линии и касательна к годографу №(/<о) в точке <о = 1,85 с-1, т. е. (7(<о) = = —1/1,85. Из рис. 7.26 видно, что при К = 1 система устойчива, так как годо
граф не охватывает точку с координатами (—1; /0). С нелинейностями общего вида u(t) — #"[е(0> t] условие Пбпова выполняется при 0 < Ki < 1,85. Годограф 1Г(/<о) расположен правее прямой Пбпова, когда <7 = 0. Это означает, что нелинейная система абсолютно асимптотически устойчива, если все нелинейности указанного типа расположены в секторе (u/e(t)) е е [0; 1,85]. Для линейной системы с передаточным коэффициентом Kt < 1,85 система устойчива в замкнутом состоянии.
При q = 0,15 прямая Попова касательна к годографу №(/<о) в точке <о = 1,98, когда угол наклона касательной равен arctg (0,15), т. е. нелинейная система абсолютно асимптотически устойчива для любой однозначной нелниейности и = = F[e(/)], расположенной в секторе (u/e(t)) е [0; 1,98]. Линейная система устойчива в замкнутом состоянии, если К < 1,98. Оба эти случая справедливы, так как при произвольных начальных условиях выполняется соотношение lim е(/) = 0.
f->oo
Критерий Пбпова можно распространить на более широкий класс систем, имеющих полюсы и нули. В этом случае необходимо пользоваться круговым критерием устойчивости и вводить дополнительное' преобразование, связанное со сдвигом полюсов или нулей [32].
Сначала рассмотрим преобразование для сдвига полюсов, записываемое в виде
ur (Z) = u (Z) — Ге (Z). (7.218)
В этом случае сектор (u/e(Z)) е е [г,, /J исходной нелинейности F [е((), t} преобразуется к сектору (мг/е (/)) <= [и — г, Zi — Z]. Применив преобразование (7.218), получим схему (рис. 7.27, а) с передаточной функцией в замкнутом контуре
(7'219>
[g,(0+ е,0(0] =
= Т-+^Г^[г(/) + ео(/)1- (7<220)
Из выражений (7.219) и (7.220) следует, что введение преобразования (7.218) сдвигает полюсы.
В работе [32] показано, что при г < I существует q, при котором для всех со > 0 выполняются усло
546
вия обобщенного кругового критерия Попова, т. е.
-(тЙ£)*(| + «!“!)>0 <7-22»
и
-(ттгУ^ + ^х0- (7-222)
Круговой критерий, записанный в виде (7.221), справедлив только при 1/г >• 1/1, а критерий (7.222) при 1/г < 1/1. Следует указать, что на практике наиболее часто имеет место соотношение 1/г> 1/1. Приведенные два неравенства определяются так, что г и I могут принимать и отрицательные значения.
При 1/г > 1/1 из формулы (7.221) следует, что годограф И/(/<о) должен располагаться вне круга с центром — у (1/г + 1//) + l/2jqa> X Х(1/г—1/0 и при 1/г<1/1. Из формулы (7.222) заключаем, что годограф №(/<о) должен располагаться внутри окружности с тем же центром.
Если с помощью формул (7.221) и (7.222) осуществляется сдвиг полюсов, то из выражения (7.218) формируется условие Попова
(7.211), которое можно записать в виде
Re [(1 + До?)] Wr (jv) + 7^7 > °-
(7.223)
Далее при выполнении условий (7.221), (7.222) и (7.210), с учетом преобразованной частотной характеристики Wr(ja), в системе обеспечивается абсолютная асимптотическая устойчивость [см. формулы (7.211) и (7.223)] для любых начальных условий. Данное утверждение справедливо, так как соблюдаются неравенства
^u2(f)dt < оо; ^e2(t)dt<oo; о о
оо
и2 (t) dt о
(7.224)
С целью сохранения одинаковой методики построения прямых Попова воспользуемся переменными, приведенными в виде соотношений (7.213). В этом случае справедлива формула (7.214).
Пример 7.18. С помощью обобщенного кругового критерия найти тип нелинейностей и диапазон изменений коэффициента.
Рис. 7.27. Преобразование структурных схем нелинейных систем:
а—прн сдвиге полюсов; б—влияние сдвига нулей на нелинейность; в—прн сдвиге нулей
а)
647
18*
Рис. 7.28. Амплитудно-фазовые частотные характеристики САР с полосюм в правой полуплоскости с прямыми Попова при q= = 1,2 (пример 7.18)
г, при котором сохраняется условие абсолютной асимптотической устойчивости САР, а также секторы Попова для двух значений q, если передаточная функция линейной части системы имеет вид
)(т1з)(7+1)- (7‘225)
Реакция линейной части системы на начальные условия
е0 (/) = Схъ* + С2е~3< + С3е~4<, (7.226)
где Ci, Ct, С3 — начальные условия для переменных состояния.
Из выражения (7.226) видно, что и без наличия нелинейности система в замкнутом состоянии неустойчива. Для обеспечения ее устойчивости в отрицательную обратную связь вводится звено с коэффициентом г. Это равносильно сдвигу полюса, так как для замкнутого контура линейной системы (7*219) 7 27’СПРаВеДЛНВ° выРаженне
Для передаточной функции (7.225) в соответствии с соотношением (7.219) получим
“М8)-? + <>.*А + ,-12- <7'И7>
Из выражения (7.227) найдем
Uг (<о) = Re [(/fi))3 + 6 (/fi))2 + 5/ш + г _ 12]
И
Vr (®) — <0 Im + 6 (/-(й)й+5/(й+г_12]-
Пользуясь данными соотношениями, построим на рис. 7.28 годограф №,(/<о) линией /. Прн этом отметим, что линейная часть системы устойчива, если 12 < г < < 42.
Прямая Попова прн q = 0 (жирная сплошная линия 2) проходит через точку на осн абсцисс с коэффициентом —1/12 (WMf«>) = —1/12). Это указывает на то, что нелинейная система в секторе Попова [г; К = 12] будет абсолютно асимптотически устойчива прн любой нелинейной характеристике. Если г > 12, то сектор Попова не существует.
При q = 1,2 на рис. 7.28 тонкой сплошной линией 3 для г = 12 построен годограф'
Wг (» = ,.-;3 , х ?. .
(/<о)3 + 6 (/<о)2 + 5/<о
При q = 0 через точку с координатой на оси абсцисс К — —1/4,17 проведем вертикальную прямую Пбпова (жирная линия 5). Теперь через точку с частотой <о = = 2,23, находящуюся на оси абсцисс, проведем касательную к годографу под наклоном arctg(l,2) (жирная прямая 4). Ее координата на оси и ,(<£>) равна —1/30 (т. е. IF,(/®) = —1/30). Итак, в результате построения прямых 4 и 5 можно найти сектор Пбпова. В первом случае для стационарной однозначной нелинейности ua = Er(e), (ua/e(i)) s [0; 30], а во втором при общем виде нелинейности и„ = = У. [в (/), /], («а/е (!)) е [0; 4,17].
Пример 7.19. С помощью обобщенного кругового критерия определить для нелинейной САР (рис. 7.27,6,в), передаточная функция которой имеет нуль, равный 4, сектор Пбпова при С — 1. Возьмем
W (s) = (s - 4)/(s + 2) (7.228)
и
Во (0 =Cie-2<.
Подставляя в соотношение
Fc (s) = IF (s) - 1 - (7.229)
выражение (7.228), получим
Ц7С (S) = —6/(s + 2). (7.230)
Так как линейная система, записанная в форме (7.230), при 80 имеет устойчивый выход, то можно воспользоваться условием Пбпова: при 0 < К < 1/2 имеем —оо < < q < 1/2 и соответственно q = 0. В данную нелинейную систему может входить нелинейность общего вида u(t) — ==^"[е(0, /], расположенная в полуоткрытом секторе Пбпова (и/е(/)) е [0, 0,5].
548
С целью упрощения методики анализа абсолютной устойчивости нелинейных систем используют логарифмические частотные характеристики линейных разомкнутых систем, нанесенных на номограммы Никольса. Однако их применение требует преобразования сдвига полюсов с помощью
«п (0 = «(0 — -Ц-^- е(0, I > г.
(7.231)
Пользуясь преобразованием (7.231), исходную передаточную функцию U7(s) можно привести к виду
W (s) =______W _______
"() i+£+LW{s)' (7-232)
Преобразование (7.232) переводит область Попова во внутрь окружности с центром в начале координат и радиусом 2/(1— г) на плоскости Wn (]в>) • Это преобразование соответствует взаимной связи между частотными характеристиками замкнутой и разомкнутой систем в форме номограммы Никольса (см. гл. 3).
Из выражения (7.232) можно получить соотношение
W (/<о) 1 + w
2 I-г
(7.233)
Приведем его к форме, удобной для применения номограммы Ли-кольса, т. е.
-Цр- W (j&) 1+-Ц-^ТГ(»
1 + г
1 — г
(7.234)
По соотношению (7.234) построены кривые постоянных значений* [ | j^.[, т. е. для замкнутых амплитуд А. Для использования номограммы Никольса сформулируем следующее правило. Значения г и
* Выражение (7.234) соответствует критическим окружностям Пбпова [32].
Тт.дб
Рис. 7.29. Логарифмические амплитудная и фазовая частотные характеристики САР с полюсом в правой полуплоскости
I, соответствующие максимуму 201g у— г , при которых эти кри-вые касаются годографа -у— W (до), определяют границы сектора Попова *.
Пример 7.20. Определить границы секторов [г, Z] для нелинейной системы при q = = 0 с передаточной функцией
' ’ s (s - 1) (0.25s + 1) (0,01s + 1)
(7.235)
с помощью номограммы Никольса и найти области устойчивых состояний **.
На рис. 7.29 построены исходная логарифмическая амплитудная н фазовая частотные характеристики системы по передаточной функции (7-235) прн s = /со и К = 0,4 (кривая 7), откуда следует, что исходная система неустойчива в замкнутом состоянии. Для ее устойчивости введем в отрицательную обратную связь коэффициент Ki > 2,5 (8 дБ) и получим кривую 2 устойчивой системы. В этом случае можно пользоваться круговым критерием и нахо-
* Существует и другой метод анализа абсолютной устойчивости, приведенный в работе Б. Н. Наумова. Теория нелинейных автоматических систем. М.: Наука, 1972. 544 с. В этом случае строится семейство логарифмических амплитудно-фазовых частотных характеристик B7fl(/®) = (1+ + jaq) W
** В работе [32] рассмотрен случай анализа абсолютной устойчивости при a>q Ф 0, основанный на примеиеиии новых номограмм, позволяющих определять граничные кривые Попова в логарифмическом масштабе. Тогда прямые, изображенные на плоскости lF(]co) (см. рис. 7.25,6, в), строятся в виде кривых иа плоскости {arg [F (/«)], 20 1g | KW (/co) |}.
549
Рис. 7.30. Номограмма Никольса с логарифмическими амплитудно-фазовыми частотными характеристиками (пример 7.20)
дить сектор Попова с двумя границами: верхней I и нижней г.
Построим на номограмме Никольса (рис. 7.30) логарифмическую амплитудно
фазовую частотную характеристику исходной системы (кривая /), а затем годографы 201е[(Ц^)| при
= 10 (20 дБ) (кривая 2) и (г2 + /г)/2 = 40 (32 дБ) (кривая 3), перенесенные с рис. 7.29 (кривые 3 и 4).
Как известно [32], для вычисления условий кругового критерия при q = 0 не
Таблица 7.1
Определение сектора Пбпова по номограмме Никольса
i 1 1 20 1g i- 1 ll~ri 1 ri Границы сектора Пбпова
в дБ в обычном масштабе в дБ в обычном масштабе
1 20 10 9,8 3,1 6,8 13,2 [6,8; 13,2]
2 32 40 12,0 4,0 60 20 [30; 50]
550
обходимо, чтобы кривые 2 и 3 касались лишь максимальных значений сплошных
линий номограммы 201g
li~ri
(i=l- 2).
два уравнения
dp решая кото-
В результате получим li+ri _с „ ll + rl _ l-ri С<и 2 ~
рые находим значения /ь п; /2, г2, образующие секторы Пбпова (табл. 7.1).
Если провести логарифмическую амплитудную характеристику, в которой частота среза (Ос = 12 с-1, то можно получить сектор Пбпова с наибольшими значениями г и /, при ‘которых нелинейная система будет абсолютно асимптотически устойчивой.
Методика определения сектора Пбпова, основанная на логарифмических частотных характеристиках, позволяет строить и области асимптотической устойчивости выходного сигнала и управления путем перемещения исходного годографа 1Г(/(о) вдоль оси — 180° (кривая 1, рис. 7.30). В результате определим
Таблица 7.2
Типы нелинейностей
Формула Тип иелнней-ности Ограничения на параметры
<7 К
U = F[8(0] Однозначная стационарная — оо < <q< «j 0<<7 < < оо 0<К< < ОО 5<оо
u=s F [е (f), f] Однозначная нестационарная — оо < <7==о о<к< оо
«==^-[8(01 Дву-значная стационарная — оо < <<7<0 0<<7< < оо 0<К< < оо о</« оо
и — Г [8 (0, f] Двузначная нестационарная (обобщенная) q = Q 0<К< < оо
Примечание: 0 — некоторое положительное число.
(ъ-г)/г
Область неус той. чи во ст и
Область устойчивости
(1+г) /2
о
Рис. 7.31. Область асимптотической устойчивости выходного сигнала и управления в зависимости от параметров секторов Попова
допустимые границы сектора Пбпо-
I + г 1 — г ва в зависимости от —g— и —— (рис. 7.31).
В табл. 7.2 приведены наиболее часто встречающиеся типы нелинейностей, входящих в нелинейные САР, анализ устойчивости которых можно выполнить по частотному критерию Пбпова.
8. УСТОЙЧИВОСТЬ НЕЛИНЕЙНЫХ ДИСКРЕТНЫХ
И ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ
Применение управляющих ЭВМ в нелинейных системах привело к необходимости использования математического аппарата многомерного* z-преобразования [24]. В этом случае нелинейный объект с регулятором описывается в виде суммы эквивалентных передаточных функций W„, i(z); Wh, 2<Jz); ...; WH, n(zi, z2, ..., zh) . Эквивалентные дискретные передаточные функции нелинейных систем определяют с помощью выражений
Wn(Zi, z2, ..., z„) = ik«(«i7o» •
К2Т0, ..., кпГо] =2 ... 22 wn X к,—0 кп— 0
X (kiTq, К2ТО..кп^о)П2< 1'
(7.236)
551
В выражении (7.236) функция w(KiT0, к2Т0, ..., кпТ0) — многомерная дискретная импульсная переходная функция нелинейной системы. Непрерывную часть ее можно определить в виде
С„+/о°
“U*b т2.......T«)=(‘2b’)n S •••
Сп-/оо
С1 + /°о
... J Wn(Si, S2, Sn)X
Cl-jx
X П (7.237)
z=i
Для аргументов, которые снимают лишь в тактовые моменты времени, имеем
wn(KiT0, к2Т0 кпТ0) =
= гМТЬ Т2........О 1т, = к,Го •
’п“кпго
(7.238)
Передаточные функции Wn(sit s2, ..., sn) находят по структурной схеме исходной непрерывной части нелинейной системы с использованием многомерного преобразования Лапласа. Можно использовать и другие способы вычисления многомерного z-преобразования
Сп+/<»
‘U7„(zi, z2, ..., z„) = (JL)n J ...
C1+/OO
••• $ Wn(sit s2, ..., sn)X
ХП---------k^ds‘- (7.239)
i-i i-e z‘
Реакции нелинейной системы на управляющее воздействие G(z) имеют вид
Хп fa, z2.....zn) = Wn (zb z2, ...
n
..•,гя)ПС(г(). (7.240)
i-i
Входящие в выражение (7.240) многомерные эквивалентные пере
даточные функции Wn(zit z2, ... ..., zn) для замкнутых систем (корректирующее устройство,. регулятор с объектом, имеющим нелинейную характеристику) при выходном сигнале хп определяют с помощью обратного многомерного z-преобра-зования
xn(KlTo> К2^0.....кпТо) —
= 8 1 [Xn(zi, z2, ..., zn)] —
Cj+/»o
XX (Zl, z2, .... zjJJz^"1^. ,=1 (7.241)
При к1 = к2 = • • • = Kn = K имеем xn (кТ0)=хп (kJo, k2T0, ..., кпТ0 |Ki=K .
(7.242)
Пользуясь приведенными выражениями, можно определить структурную схему нелинейной дискретнонепрерывной системы (рис. 7.32, а). Многомерные эквивалентные передаточные функции
г..а(г„
<7-243) i «=1
ИЛИ
^H13(z1, Z2, Z3) =
eoZiZ2z3 + at (ziz2 + z,z3 + z2z3) +
_________+ Д2 (Zi + Za 4~ z3) + Дз______
— (zi — e~r°/ri) (z2 — е_Го/Г1) X
X (z3 - е-Го/Г1) (Z!Z2Z3 - 1)
(7.244)
Линейную часть системы (рис. 7.32, а) запишем в обычном виде
7--------------------• (7-245)
(z - е“Го/Г1) (z - 1) ' '
Пользуясь формулами (7.244) и (7.245), получим прёобразованную
552
al
Затем по выражению (7.238) при Т #= =# 272 найдем
®2 (Т1, т2) =
Рис. 7.32. Дискретно-непрерывная нелинейная система:
а—исходная; б— приведенная с помощью многомерного z-преобразовання к одномерному
С2Ч-/00 С1Ч-/00 ff с * \ 2я/ / J J + 1
С2—/оо Ci—/оо
у *2_____________________________ V
TiSj-tI 72(s, + s2) + 1
X eS1T1+S2i:2 ds, ds2 =
Ti+Ta _ Tt Ti —Ta _______, e Га _ e Ta T, T, (T, -2T2)L
k2,k2
k\k2
ТаЧ-Та Ta Ta—Ti
____________lc T, _e Гае Га
7i(7,-272)l e
(7.246)
При т, = к,70 и т2 = к2Т0 из соотношения (7.246) имеем
нелинейно-дискретную систему, (рис. 7.32, б).
Пример 7.21. Найти двумерную эквивалентную передаточную функцию 1F2(z,, z2) дискретной нелинейной части системы (рис. 7.33, а) [24]. Сначала определим эквивалентную передаточную функцию непрерывной части с помощью двумерного преобразования Лапласа
ъ. ь >
v_______£2______
Тг (s, + s2) + 1
На рис. 7.33, а штриховой линией введен фиктивный ключ с тактом квантования 70.
, k^k9
w2 (к1Т0> к2То) = г, (Г, _ 272) Х
Г -(КI+Ка) —“ Ki £-°(К1-Ка)1
XLe т' —е т' ег‘ J;
zz k,k2
w2 (kiTq> к2Го) = т’1 _ 27-j) X
[Г 0 , . а То Tq . .”]
е Г. _е Га еГ, J
(7.247)
Используя выражения (7.247), найдем сумму членов бесконечной геометрической прогрессии в виде
W2 (2ь z2)
— ^2 Г г2 v
“ 7, (7, - 272) I z2 - е-г°/г‘ Х
Z1_________________________
Zl-e-TdTt г2_е(т>-т>)тмт^)
Рис. 7.33. Структурная схема дискретной нелинейной системы:
а — исходная; б—представленная с помощью эквивалентной передаточной функции
z,z2
А _ р-Го/Гг
z, z, - е~т°1т'
z2____________1
z2 —е-Го/г‘ z,z2 — е-Го/Г2 ’
(7.248)
где
_ ^2(е-2г«/г--ег"/г2)
К~ Tt (1,-272)
X
553
Формулу (7.248) можно переписать в виде передаточной функции
Х 1 -e“r"/r'z“1 1 - е-Го/Л2-1 ’ (7'249)
В соответствии с формулой (7.249) на рис. 7.33, б приведена эквивалентная структурная схема дискретной системы.
9. ВЛИЯНИЕ СЛУЧАЙНЫХ
ПРОЦЕССОВ НА НЕЛИНЕЙНЫЕ САР
В гл. 2 было рассмотрено влияние случайных сигналов, поступающих на вход нелинейностей, и определены формулы для вычисления коэффициентов статистической линеаризации по математическому ожиданию и случайной помеховой составляющей. В зависимости от уровня сигнала помехи f(t), а также амплитуды и частоты медленно меняющегося полезного сигнала x(t) в САР могут возникать различные процессы. При относительно малых помехах система может оставаться устойчивой, если даже она неустойчива по полезному сигналу. С ростом уровня помех в неустойчивых системах наблюдается срыв автоколебаний.
Для исследования данных процессов воспользуемся уравнениями (7.181) для вынужденных колебаний, переписанных в виде
x(t)+W(p)0-(x, рх) =
= ^f(p)[fp(O + L(O]. (7-250) где /р(/) —регулярная составляющая; /сл (0 — центрированная случайная составляющая.
Если в САР отсутствуют автоколебания, то, пользуясь методом статистической линеаризации [см. формулу (2.268)], запишем
(х, рх) = kQmx + Мсл>хсл (/), где &1Сл) — коэффициент статистической линеаризации случайного центрированного сигнала.
Уравнение (7.250) можно представить в виде двух уравнений
Xp(0 + W7(p)^ = W7f (р)/р(0;
(7.251)
Хсл (0 [1 + W (р) = Wf (р) (О-
(7.252)
Из гл. 2 следует, что коэффициенты по математическому ожиданию и центрированной случайной составляющей fe0(xp, ох), feiCJI)(xp, вх) в-уравнениях (7.251) и (7.252) зависят от хр и ах.
При решении практических задач, как это показано Е. П. Поповым, возможно несколько случаев *. Однако наибольший интерес представляют лишь три из них.
Первый случай. САР является стационарной и fp, хр, Ор— постоянные величины. Тогда уравнение (7.251)—алгебраическое, и оно имеет вид
хР (0 + W (р) k0 (Хр, ах) = Wf (0) fp (/).
(7.253)
Из уравнения (7.253) найдем Хр в зависимости’от ах.
В результате получим
хр = хр (дх), (7.254)
где
55=2й-х
7 W'r (/со) 2
X \ --------------------г Sf(o)dco,
(7.255)
где Sf(co)—спектральная плотность помехи.
Представим коэффициент статистической линеаризации в виде
^1СЛ) (S’ s) = ^СЛ> Чр (s)’
(7.256)
Располагая заданной спектральной плотностью помехи и формула
* См. Е. П. Попов. Прикладная теория процессов управления в нелинейных системах. М.: Наука, 1973. 583 с.
554
ми для вычисления интегралов (см. прил. П-П.З), найдем
д£ = Ь(хр, ctJ. (7.257)
В соотношении (7.257) К — постоянный множитель, выносимый за знак интеграла (7.255).
Подставив в уравнение (7.257) соотношение (7.254), определим ах. Затем из соотношения (7.254) найдем хр. В результате получим решение уравнения (7.250) в виде
х = хр + хсл. (7.258)
Второй случай. САР является нестационарной, т. е. в ней наблюдается неустановившийся процесс. В заданной нелинейности &~(хр, ах) (см. п. 4, гл. 2) при дх(хр) исключим ах; тогда получим функцию одной переменной, т. е.
^ = Ф(хр). (7.259)
Эта функция аналогична функции смещения. Зная Ф(хР), перепишем уравнение (7.251) в следующей форме:
Xp(t) + W(p)<S>(xp)==Wf(p)fp(t).
(7.260)
Располагая функцией /р(/), из дифференциального уравнения (7.260) найдем регулярную составляющую Xp(t).
Так как функция &~(х, рх) представляет собой плавную кривую, то в некотором диапазоне изменения хр от —Хрг до xPt ее можно линеаризовать, т. е. представить в виде
&~=кяхр, ^и = (-^-)Хр-о- (7.261)
Если САР не пропускает спектр О
помех /сл(0> то
оо
5 I !>$,(«>)*».
(7.262)
, Для определения ах следует пользоваться формулами вычисления интегралов прил. П-П.З. Из выражения (7.202) следует, что дх не зависит от SF и хр.
Тогда соотношения (7.261) можно записать
/гнхр, /г„ — Vcfxp) Лхр=0’
(7.263)
В этом случае
К = ka (ах). (7.264)
Из формулы (7.262) определим ах. После подстановки kK, вычисленного из соотношения (7.263), в уравнение (7.260) получим
[1 + KW (р)] хр (t)=--Wf(p)fP(t).
(7.265)
Для его решения можно воспользоваться характеристическим уравнением
1 + kKW (р) = 0. (7.266)
Из уравнений (7.265) и (7.266) следует, что устойчивость системы по полезному сигналу хр будет зависеть не только от параметров собственно системы, но и от спектральной плотности сигнала помехи Sf(и), так как она влияет на величину kK.
Третий случай. Если в САР невозможно выполнить линеаризацию по соотношению (7.261) или (7.264), то ее устойчивость можно исследовать на основе применения гармонической линеаризации функции смещения
2л
S,) = -sH о
X dty sin г|эйг|э, (7.267)
<Г(хр)=^<сл)(А стх)хр.
В выражениях (7.267) А — амплитуда колебаний процесса хр. Для определения Аа и соа воспользуемся гармонически линеаризован-
555
Рис. 7.34. Структурная схема релейной следящей системы с сигналом помехи f(0
ным характеристическим уравнением
[1 + Мсл)И> аж)^(р)]хра)==°, (7.268)
где дх определяют по упрощенному выражению (7.255).
Так как в данном случае 5х вычисляют через Sf(a), то амплитуду и частоту автоколебаний определяют из уравнения (7.268), которое будет также зависеть от спектральной плотности сигнала помехи.
Коэффициенты k\zn} находят по формуле
2Л
/г<сл>(Л, 6*) = -^-^ Л4 [(Г (A sin ф + о
+ хсл)] sin (7.269)
В табл. 7.3 приведены формулы для вычисления коэффициентов ^сл) в зависимости от у = Д/(стж V2).
Для определения порогового значения среднего квадратического отклонения, при котором происходит срыв автоколебаний,рассмотрим пример релейной следящей системы со структурной схемой, показанной на рис. 7.34. В данной САР автоколебания возникают при любом зна
чении К и определяются следующими соотношениями:
®а=1/Г; Ая = 2КТ/л.
Пример 7.22. Найти предельные значения случайного воздействия в виде помехи Of, при которой автоколебания срываются для следящей системы (рис. 7.34). Воспользуемся уравнением (7.268) и, подставив в него соответствующие передаточные функции, получим
[s (Ts + I)2 + О(1СЛ) (Л, aj] Хр (s) == 0.
(7.270)
По данным табл. 7.3 найдем
fe<CJ,> = B0(y)M,
где у = ЛДст* У2), а функция Во (у) приведена иа рис. 2.109.
Примем дх — &t; тогда из формулы (7.262) имеем
|Г 0®)|*=1.
Составим характеристическое уравнение
T2s3 + 2Ts2 + s + Kk[eis> (Л, af) = 0. (7.271)
Подставив в уравнение (7.271) s — fa, найдем два уравнения для определения амплитуд и частот автоколебаний:
Кй(1сл) (Ла, of) - 2Та2я = 0; (7.272) w2 = r2a3 = 0.
Из второго уравнения (7.272) имеем
<оа = 1/Т, а из первого
^сл) (Ла, df) = 2/КТ
ИЛИ
Л
уг ’
*<сл) (у) =
Во (у)_ . yaf л/Г ’
(7.273)
Рис. 7.35. Определение параметров, прн которых возможны срывы автоколебаний с ростом среднего квадратического сигнала шума:
а—кривая от Аа/в}-,
Ofkz}1 в зависимости о—граница областей
автоколебаний и их срыва в зависимости от df и КГ
556
Таблица 7.3
Формулы для вычисления ^(Л, <тх)
i Типы нелинейностей *1л (Y)
1 Идеальная релейная (см. табл. 2.1, п. 4) Во (у) А . R м — V* (—1/(20! /У\2Ж ’ “ £о (» D3G + 1) G)
B V/B (V)' b, = c •
. / . "1 an\Yb °1 /="» A <sxfi n-0 * ¥
2 Однозначная релейная с зоной нечувствительности (см. табл. 2.1, п. 6) Вп (У) = _ 4 у (-l)<+n [2 (Z + n)]l / xfi+1 "V« £0(2n)! (Z!)2 (i + n)! (i'+ 1) ’
n = 0, 1, ...
3 Петлевая релейная (см. табл. 2.2, п. 8) В V 1 + m2n .2n R A L 2 B«(Y) n-0
4 Типа насыщения (см. табл. 2.1, п. 1) в А ь* A X 2n + 1 B<*
5 С зоной нечувствительности (см. табл. 2.1, п. 15) kC Л b2in k A X 2n + 1 (v) n-0
6 Квадратичная F = = kx* sgn х (см. табл. 2.1, п. 19) kA у (-l)f+1(2Z)I /y.\2/-1 VT Zu (Zl)2 (2/- 1) (Z + 1) UJ
7 Степенная нечетной степени F = kx3 (см. табл. 2.1, и. 20) Т-(л2 + ^)
3 Степенная F = kxs
9 Степенная F = kx2n+' k (2n + 1)! у 2iA2(n~l)<J2xl 2"+2 Zu /j (n — x)i (n — Z +1)1
рис. 7.35, а. Откуда видно, что
Представим Во (у) в виде ряда
(7.274)
и при у -> О Во (у) = —т=-; тогда
““’-Ч VH., Ла-о
Кривая о^(1сл) полученная по формуле (7.273), изображена на
При заданной помехе автоколебания будут, если
К > af ^я!т,
(7.275)
то условия автоколебаний определяются
неравенством
af < КТ I-fin.
557
При пороговом df > Of автоколеба-'пор '
ния срываются.
Граница срыва автоколебаний находится по формуле
af = КТ1л/2п.
'пор
На рис. 7.35, б показана граница части области срыва автоколебаний в САР при условиях Of ' >0,3 н 0,3 КТ 1,2.
'пор
Форма сигнала (синусоидальная, треугольная, меандровая и др.) оказывает определенное влияние на параметры автоколебаний, возникающих в САР. Данное явление приходится учитывать и в тех случаях, когда указанные выше типы сигналов применяются для организации
Рнс. 7.36. Линеаризация нелинейной системы с тремя типами входных сигналов: а—структурная схема; б—виды сигналов, поступающих на вход нелинейности; в—эквивалентные амплитудные характеристики 20 lg 1/?
Рнс. 7.37. Определение амплитуд и частоты автоколебаний в нелинейной системе при действии меандрового, треугольного и синусоидального сигналов
процессов захватывания в нелинейных системах. Рассмотрим влияние таких сигналов с помощью примера нелинейной системы, структурная схема которой показана на рис. 7.36, а.
Пример 7.23. Определить зависимость параметров автоколебаний от формы сигнала f(t), подаваемого иа вход нелинейности. Прн подаче меандрового сигнала, изображенного линией 1 на рнс. 7.36, б, коэффициент гармонической линеаризации будет иметь вид
ам (А) = 4В/лА, А^С. (7.276)
В случае пилообразного сигнала (рис. 7.36, б, кривая 2) коэффициент гармонической линеаризации' запишем в виде
ап (А) =
. лС , В —С
Sin-2A+~A-
пС'
C0S,2A .
А^С, (7.277)
л у л
а коэффициент гармонической линеаризации при синусоидальном сигнале (рнс. 7.36, б, кривая 3) рассчитываем по ранее приведенной в гл. 2 формуле
... 2k f , с , с Г. ТсЪ\ а{А)^- (^arcsin - + - д/! -
А>С.
(7.278)
Шаблоны 20 1g 1/<?(С/А) для этих сигналов прн В = С построены на рис. 7.36, в (кривые 1—3).
Исследуем режимы автоколебаний в системе с передаточной функцией линейной части
W 5(Т,а+1)(Г85+1)(Г4»+1)’
558
где Ti = 2 с; Ti — 1 с; Г3 = 0,5 с; 7\ = 0,25 с; = 10 с"1.
Положив s = /ш, на рис. 7.37 построим логарифмические амплитудную Н и фазовую 0 частотные характеристики. Здесь же показаны положения шаблонов, соответствующие режиму . автоколебаний с частотой (йа. При постоянном значении а>а ам
плитуда автоколебаний в зависимости от формы сигналов существенно различается: для меандрового Ла) = 4,2, пилообразного А,2 = 3,4 и синусоидального Даз = 4. Таким образом, рассмотренный метод линеаризации позволяет находить параметры автоколебаний в системах при действии негармонических входных сигналов.
Глава 8
ПРОЕКТИРОВАНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ЗАДАННОЙ СТРУКТУРОЙ
На практике часто приходится находить параметры систем при заданных полных структурах, описанных в аналитической форме, с помощью векторно-матричных уравнений или графов, составленных по передаточным функциям. При расчетах систем иногда пользуются логарифмическими частотными характеристиками, если некоторые параметры. определены неточно В дальнейшем эти параметры уточняются для обеспечения заданных техническими условиями запасов устойчивости, показателей качества и точности процессов регулирования.
При проектировании САР этими способами необходимо пользоваться теоретическими положениями, алгоритмами и рабочими программами для ЕС ЭВМ, изложенными в I и II разделах книги. Наиболее просто такие задачи решаются для непрерывных линейных систем. Если в системы входят нелинейности, то их следует учитывать с помощью методов гармонической, статистической и совместной линеаризации (см. гл. 2 и 7), что в ряде случаев представляет определенные трудности. Для дискретно-непрерывных систем, в которые входят микропроцессоры или управляющая ЭВМ, решение существенно усложняется, так как кроме параметров систем на их характеристики влияет такт квантования и длины слов. Величина такта квантования зависит от времени реализации программ на управляющей ЭВМ, часть из которых находится в процессе расчетов.
Это приводит к необходимости прибегать к компромиссным способам, что усложняет проектирование систем. Однако с наибольшими трудностями проектировщик сталкивается при расчетах экстремальных и самонастраивающихся САР, так как в них объекты регулирования являются нелинейными или нестационарными, а в законы управления всегда входят существенные нелинейности, реализуемые на управляющей ЭВМ.
В данной главе рассмотрено несколько примеров проектирования САР с заданной структурой с помощью универсальной ЭВМ, когда определяются все параметры систем, а также находятся запасы устойчивости, показатели качества и точности.
1. НЕПРЕРЫВНЫЕ ЛИНЕЙНЫЕ
И НЕЛИНЕЙНЫЕ СИСТЕМЫ
Рассмотрим частотные методы определения основных характеристик линейных и нелинейных непрерывных САР с последовательными и параллельными корректирующими устройствами. Их использование при проектировании обладает большой наглядностью и позволяет выбирать тип и параметры усилительных и корректирующих устройств, удовлетворяющие всем требованиям технических условий. Сущность данного подхода состоит в том, что проектировщик, располагая принципиальной схемой системы, составляет ее структурную схему с передаточ-
559
ними функциями, большая часть которых задана и не может изменяться при расчетах. При этом строятся логарифмические частотные характеристики разомкнутой системы: графически по номограммам и таблицам или с помощью вычислительных процедур, представленных в виде рабочих программ на ЭВМ (см. гл. 3—7). В результате проектировщик получает запасы устойчивости по фазам уф и модулям ±Ям, показатели качества om, tp, а также характеристики точности при действии регулярных е и случайных б'е сигналов в зависимости от параметров усилительных и корректирующих устройств. После построения соответствующих графиков выбирают тип и параметры устройств изменяемой части системы. В ряде случаев приходится уточнять и некоторые параметры неизменяемой части САР.
Проиллюстрируем данные методы проектирования на конкретных примерах САР (статических и астатических). При этом будем учиты-
вать лишь ограниченное число различных типов корректирующих и усилительных устройств. Более подробные данные о таких усилительных и корректирующих устройствах приведены в п. 6 и 7 гл. 9.
Пример 8.1. Исследуем влияние последовательных корректирующих устройств двух типов и их параметров на основные характеристики статической системы регулирования температуры теплообменника с па-ронагревателем (рис. 8.1). Входом в объект 1 является положение вентиля 9, регулирующего с помощью пневматического двигателя 7 подачу пара. Клапан 8 пневмодвигателя приводится в поступательное движение от соленоида 6, сигнал на вход которого поступает с усилителя 5. Температура теплой воды О (выход) измеряется термопарой 2, включаемой в схему задатчика температуры 3, состоящего из резисторов R3—Rs, Ra и двух потенциометров R6, R7. Перемещением потенциометра R7 задается температура теплой воды системы О3.
Холодная вода поступает в теплообменник без регулирования ее расхода. В случае введения регулятора расхода в данную САР она становится двухканальной и для регулирования процессами подачи пара и холодной воды целесообразно использовать управляющую ЭВМ. Выбор программ коррекции на языке ассемблер и их влияние на основные характеристики двухканальной системы приведены в гл. 10.
Рассмотрим непрерывную САР (рис. 8.1), определим ее основные характеристики в виде запасов устойчивости, показателей качества, точности при условии, что в про-
Рис. 8.1. Принципиальная схема системы статического типа для регулирования температуры на выходе' теплообменника с па-ронагревателем с последовательным корректирующим устройством:
Гп=20е; Г-10с; Г.=0,5 с; Лк=0,01 В/»С; kkk-и 11 Л И 11 I
=20 рад/В; £0=5 °С/рад
560
(TnS+lXT'S+l)
*0
а)
5)
Рис. 8.2. Структурные схемы САР: а—статического типа с последовательным корректирующим устройством; б—с астатизмом 1-го порядка и параллельным корректирующим устройством типа RC; в —с астатизмом 1-го порядка и параллельным корректирующим устройством с тахогенератором и RC-фильтром; г—с астатизмом 2-го порядка с двумя тахогенераторами, основным и дополнительным корректирующими RC-филь-трами
цессе проектирования можно изменять только тип и параметры усилителя 5 и корректирующего устройства 4, так как структура системы полностью задана. Принципиальные схемы ряда усилительных
г)
и корректирующих устройств, которыми можно пользоваться при решении аналогичных задач, приведены в табл. 9.1—9.3 и 9.7.
Выберем фазоопережающее корректирующее устройство 4 (рис. 8.1), состоящее из двух резисторов R\, Rz и конденсатора С. Структурная схема такой системы приведена на рис. 8.2, а. Изменяя значения Ткь йк и ТК2 = kKTKi, с помощью программ № 7—13 (гл. 3); 17, 18 (гл. 4); 19, 20 (гл. 5) проведем на ЕС ЭВМ соответствующие вычисления, а затем построим графики (рис. 8.3,а—е) изменения yj,—Ям, От, tp, е и о8 в зависимости от постоянной
561
Рис. 8.3. Основные характеристики статической системы регулирования температуры теплообменника с пароиагревателем в зависимости от постоянной времеии TKi последовательного фазоопережающего корректирующего устройства:
а—для v° ; в—для—Я..; в—для <J„; г—для tn;
Ф М гп Р
д—для в; в—для 3g
времени Tki при трех значениях коэффициентов усилении £У1 = 10, kyt = 50 и kyt = 100. Из рис. 8.3, а, б видно, что при больших значениях TKi наблюдается экстремальное значение у®> ио происходит уменьшение —Ни. При отработке единичного возмущающего воздействия О3[1] происходит изменение ат в зависимости от ky. При больших ky и Т«1 ат увеличивается, ’ что приводит к ухудшению качества
работы исследуемой САР. Время переходного процесса tv уменьшается с ростом Tki независимо от ky. Ошибки отработки регулярных сигналов и случайного воздействия в виде белого шума с интенсивностью с2 = 20-10~’ рада-с практически не зависят от Ткь
По заданному техническими ус-, ловиями числовому значению Уф = = 48° находим из рис. 8.3, а оптимальное значение Tki = 7 с при kK = 0,01 В/°С и ky = 50. Затем по полученному TKi из рис. 8.3, б—е
Рис. 8.4. Принципиальная схема следящей системы с астатизмом 1-го порядка и параллельным корректирующим устройством типа RC
562
vt,pad 0,003 0,002
0,001
О 0,2 0,k 0,6 0,в ТК,С е)
Рис. 8.5. Основные характеристики следящей системы с астатизмом 1-го порядка в зависимости от постоянной времени TKi параллельного корректирующего устройства типа RC:
а—для Уф! в—для в—для <Jm; г—для <р; д—для в; в—для
0,2 0,it 0,6 0,8 1,0 TKl,C 0 0,2 44 0,6 0,8 1,0 Гц.,С 0 0,2 44 0,6 0,8 1,0 Тк„с
г) В) е)
Рис. 8.6. Основные характеристики следящей системы с астатизмом 1-го порядка в зависимости от постоянной времени TKi параллельного корректирующего устройства, состоящего из тахогенератора и цепочки RC:
а—для у* ; в—для —Н.л в—для а„; в—для f_s 3—для в; в—для в» • ф М Р
563
Рис. 8.7. Принципиальная схема следящей системы с тахогенератором и корректирующим устройством (штриховыми линиями выделена дополнительная часть системы, обеспечивающая астатизм 2-го порядка):
1—сельсии-датчик; 2, 8—тахргеиераторы; 3—дополнительный усилитель; 4, 9—редукторы; 5—усилитель; 6—электромашиииый усилитель; 7—электродвигатель; 10—сельсин-приемник
Рис. 8.8. Основные характеристики следящей системы с астатизмом 2-го порядка с двумя тахогенераторами, основным и дополнительным корректирующими устройствами в зависимости от параметра Tki:
л—для в—для ± в—для ат; г—для fp;3—для е; я—для ag
564
a)
Рис. 8.9. Линейные САР с нелинейными двухканальными корректирующими устройствами: в—последовательным; б—параллельным определим основные характеристики системы: Ям, ат, tp, е, ае.
Пример 8.2. Исследовать влияние параллельных корректирующих устройств различных видов н их параметров на основные характеристики следящей системы. Упрощенная структурная схема такой системы с параллельным корректирующим устройством типа RC изображена иа рис. 8.4. При этом видно, что параллельное корректирующее устройство охватывает лишь только часть динамических элементов. В следящую систему входят сельсины-датчики 1 и сельсины-приемники 6, связанные с задающими и выходными валами редукторов (с передаточным отношением 1 :31), приводящими во вращение обмотки роторов сельсйнов. В систему также введены усилитель 2, электромашинный усилитель 3, электрический двигатель постоянного тока 4 с независимым возбужде
5)
нием и редуктор выходного вала 5, приводящий в синхронно-следящее вращение объект регулирования. Параллельное корректирующее устройство состоит из конденсатора С и двух резисторов R с постоянной времени Тк; = 2RC (штриховой прямоугольник на рис. 8.2,6).
Пусть параметры системы (рис. 8.2, б) Ас = 1600 В/рад; Аэ=2,5; Ад=5 рад/(В-с); k =-L-; Гэ1 = 0,002 с; Тэ2 = 0,005 с; н 400
Тд = 0,2 с.
На рис. 8.5, а—е построены кривые основных характеристик следящей системы с астатизмом 1-го порядка с параллельным корректирующим устройством типа RC. При этом для Уф = 40° и k = 100 получим Гк] — 0,45 с; —Ям = —11 дБ; ат = = 30%; tP = 1,5 с; е = 0,012 рад; ае = 0,0015 рад (с2 = 2-10-6 рад2 с). Для улучшения характеристик введен в следящую систему тахогенератор с аАтг = = 0,1 В-с/рад и RC-фильтр с передаточной функцией 1ГФ (s) = TKis/(TKis + 1), образующие 1ГК(«) (рис. 8.2, в).
На рис. 8.6, а—е для такой системы приведены зависимости Уф,—Ям, от, <р, в, ае.
565
Рассмотрим три основные характеристики данной следящей системы: /р, е, ае. При этом = 0,188 с; е = 0,014 рад; ае = = 0,00125 рад *, a Tki = 0,77 си ky = 2.
Исследуем возможности применения в следящей системе принципа комбинированного управления. В схему (рис. 8.7) включен тахогенератор 2. Кроме того, в прямую цепь введен дополнительный усилитель 3 с корректирующим устройством, общая передаточная функция которого имеет вид ^Дк(5) = йдкЗ/(Тдк5+1). (8.1)
При исследовании системы комбинированного типа при различных параметрах Гк1 = 0,1 -1- 1,0 с получим характеристики, приведенные на рис. 8.8, а—е. Откуда видно, что динамическая ошибка уменьшается в 10 раз. Последнее указывает на наличие в следящей системе астатизма 2-го порядка. Однако в такой системе ухудшаются показатели качества от = 55%, /Р = = 0,36 с. Поэтому в комбинированных системах необходимо вводить специальные электронные устройства, которые при больших углах рассогласования отключают дополнительные корректирующие устройства, но обеспечивают высокие показатели качества. При малых углах рассогласования автоматически подключается дополнительное корректирующее устройство, повышающее точность слежения. Данную проблему можно также решить с помощью введения дополнительного нелинейного устройства (см. гл. 12).
В заключение рассмотрим выбор параметров последовательных и па-
* Во всех остальных примерах при определении аг была принята спектральная плотность помехи в виде белого шума с уровнем с2 = 2-10-6 рад2-с.
раллельных нелинейных корректирующих устройств САР. На рис. 8.9, а показана структурная схема САР с нелинейным последовательным корректирующим устройством, состоящим из двух каналов. В канал 1 входит линейное звено с передаточной функцией Wi (s') = 1/(7'k2s+ + 1), а в канал 2— 1Г2(з) = ^-Х _ * К1
\Z 1 ___ т \ т
X Гк25 _|_ j > где ТК1 > Тк2.
Коэффициенты гармонической ли-
неаризации такого корректирующего устройства определяются обычным способом (см. гл. 2) и имеют следующий вид:
а (А, <о)
______^К2______
ЛТК1 Vl+ffl2rK2
Х[л—29 — 2(3 cos р -j- sin р +
4- cos9 sin (9 + р) +
4- sin 9 cos (9 + Р)];
b(A, со)
_______^К2_______
яГк1 V1 + 0)2 ГК2
X[(2Р-|-29—л) sin P4-cosp4-4-sinpsin29 — cos p cos 29],
(8-2)
Рис. 8.10. Эквивалентные логарифмические амплитудные q и фазовые ц характеристики с нелинейными корректирующими устройствами при различных отношениях Ткг/Т'к!
566
Рис. 8.11. Логарифмические амплитудные и фазовые частотные характеристики САР с нелинейными последовательными корректирующими устройствами (рис. 8.9, а)
где
9 = arctg <о(к1 — arctg ’ Р = — arctg (оТ^.
Зная коэффициенты гармонической линеаризации (8.2), найдем формулы для вычисления и построения эквивалентных логарифмических амплитудных и фазовых характеристик, зависящих от частоты, т. е.
q (Л, со) = и/a2 (Л, со) -f- й2 (Л, со);
р (Л, ш) = arctg
По формулам (8.3) на рис. 8.10 соответственно кривыми 1—3 построены логарифмические эквивалентные амплитудные характеристики, а кривыми 4—6 эквивалентные фазовые характеристики при значениях (Лсг/Лп) i = 0,005; (7’к2/7’к1)2 = 0,01; (7’к2/7’к1)з = 0,1.
Из рис. 8.10 видно, что данный тип корректирующего устройства обеспечивает значительные фазовые опережения при малых изменениях амплитудной характеристики, что существенно улучшает основные показатели качества системы.
Рис. 8.12. Запасы устойчивости по фазам и модулям, а также частоты среза для САР с нелинейным последовательным корректирующим устройством в зависимости от отношения TKi/TKi:
в—для б—для — Н.л в—для со_
Ф м *•
(8.3)
557
Рис. 8.13. Логарифмические амплитудные и фазовые частотные характеристики САР с нелинейными параллельными корректирующими устройствами (рнс. 8.9, б)
Пример 8.3. Исследовать влияние последовательного нелинейного корректирующего устройства и его параметров на показатели устойчивости и качества САР (рис. 8.9, а). Для этого рассмотрим на рис. 8.11 логарифмические амплитудные Н(ы) (кривая 1) и фазовые 0(ш) (кривая 2) частотные характеристики исходной САР без корректирующего устройства. Откуда видно, что САР является неустойчивой, так как у ф < 0.
Введем в систему последовательное корректирующее устройство с различными параметрами. Тогда получим кривые 3—5, соответствующие амплитудам //ДА,©), Н2(А, ш), Нз(А, ш), н кривые 6—8, соответствующие фазам ОДА, ©), 02(А,ш), 0з(А, ш)при Уф> 0. Последовательное корректирующее устройство обеспечивает устойчивость исходной САР. Из рис. 8.11 можно определить запасы устойчивости по фазам уф и модулям — Нп, а также частоты среза ©с. На рис. 8.12 построены кривые в зависимости от отношения параметров TK2ITKi. Как видно, проектируемая САР обладает наилучшими показателями устойчивости и качества при шс = 80,3 с-1 с последовательным корректирующим устройством при Ткг/Т’к! = 0,01.
На рис. 8.9, б изображена структурная схема с параллельным двухканальным корректирующим устройством. Коэффициенты гармонической линеаризации можно вычислить по формулам (8.2).
Пользуясь формулами (8.3) и (8.4), определим эквивалентные амплитудные и фа-
зовые характеристики при значениях (TK2/TKi)x = 0,005; (Тк2/Т«)2 = 0,01;
(Тк2/Тк1)з = 0,1. Выбирая (TK2/TKi)2 — 0,01, получим Уф = 60°; —Нщ = —37 дБ; шс = = 80,3 с-* 1 (рис. 8.12).
Пример 8.4. Исследовать влияние параллельного нелинейного корректирующего устройства и его параметров на показатели устойчивости и качества САР (рис. 8.9,6). Коэффициенты гармонической линеаризации вычислим по формулам:
а(А) =
-2 2
= [(-2 3^-Р-
Г*2а>2
-^- + 2) cos р — у sin Р +
1 3
+ — (sin 2р + cos 2р) — — sin 2фj 4.
3
+ sin Р cos 2р + — sin Зр +
+ у sin (2ф! + Р) — у sin (2ф2 + Р)];
В(А) =
>2
sin р — cos р cos 2ф 1 —
— -i- sin Р cos 2ф2 + у cos (Р — 2ф2) —
(8.4)
568
a) io^-Tkz/Tki 6) ty 10г,Ткг/Тк1
Рис. 8.14. Запасы устойчивости по фазам и модулям, а также частоты среза для САР с нелинейным параллельным корректирующим устройством в зависимости от отношения Ткг/ТкС.
а—для у° ; б—для -Н„; в—для Ф М с
где
Р = — arctg соТк2;
ф1 = arcsin
С д/1 + Т'кг®2 А
ф2 — — arcsin
С д/1 + Т22а>2 А
(8.5)
0 = arcsin
(T’ki ~ Тк2) со
1 + TKiTK2(H2
На рис. 8.13 построены логарифмические амплитудные Н(а) (кривая 1) и фазовые 0(со) (кривая 2) частотные характеристики без коррекции. При принятых значениях отношений постоянных времени корректирующих устройств построим характеристики разомкнутой САР: /Л (А, со), Н2(А, со), Н3(А, со) — кривые 3—5 и 01(А, со), 02(А, ш)> 0з(А, со)—кривые 6—8. Включением параллельного, корректирующего устройства в исходную систему обеспечиваются требуемые положительные запасы устойчивости по фазам и отрицательные по модулям. Кроме того, происходит уменьшение частоты среза сосс, что улучшает показатели качества исследуемой системы. При Гкг/Тк! = 0,1 САР с параллельным корректирующим устройством данного типа обладает наилучшими характеристиками Уф= 13°, —Нп = —4,5 дБ и сое = 53 с-1 (рис. 8.14).
2. ДИСКРЕТНО-НЕПРЕРЫВНЫЕ ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ СИСТЕМЫ
Предположим, что структурная схема исходной САР, как и в п. 1, гл. 8, полностью задана. В процессе проектирования необходимо най-
ти законы регулирования, которые можно реализовать в виде последовательных, параллельных и последовательно-параллельных корректирующих устройств, создаваемых различными способами. Например, с помощью дискретных фильтров в виде RC-четырехполюсников или программ на языке ассемблер, составленных для 8—16-разрядных микропроцессорных контроллеров или микроЭВМ*. В дискретно-непрерывных системах необходимо выбрать не только параметры микропроцессоров-контроллеров или микроЭВМ, но и преобразователей аналог — код (АК) и код — аналог (КА).
Значительное влияние на запасы устойчивости, показатели качества и характеристики точности в таких системах оказывают такты квантования То и ограниченность длины слова (в 8 или 16 бит). При этом усложняется процесс определения основных характеристик дискретнонепрерывных САР.' В результате приходится строить много кривых и по ним выбирать наилучшие параметры системы, на что затрачивается много времени.
Рассмотрим несколько различных структур, предназначенных для поддержания заданной угловой скорости дискретно-непрерывных систем, с последовательным и параллельным корректирующими устройствами в виде импульсных фильтров, создаваемых на основе RC-четырех-
* Число разрядов микропроцессора или микроЭВМ обычно соответствует длине слова в 8 или 16 бит.
569
полюсников, обозначенных соответственно 1Гкп($) и 1Гкпр(з). На рис. 8.15, а показана упрощенная структура САР, в которой применено последовательное корректирующее устройство с выходным сигналом, поступающим через преобразователь КА (экстраполятор нулевого порядка) в непрерывную часть системы.
САР (рис. 8.15,6) имеет параллельное корректирующее устройство. Ее неизменяемая непрерывная часть также заключена в штриховой прямоугольник. Эквивалентная замена параллельного корректирующего устройства показана на рис. 8.15, в. Рассматриваемый класс систем будем исследовать с по
мощью z- и s-преобразований; поэтому на рис. 8.15, а, & выделены дискретные передаточные функции в z-форме, соответственно последовательного 1Гкп (z) и параллельного I^Knp(z) дискретных корректирующих устройств.
На рис. 8.16, а изображена САР с микропроцессором-контроллером серии К.580 с входным e*(t) и выходным ei (/) сигналами. Входной
Рис. 8.15. Структурные схемы дискретнонепрерывных систем с корректирующими устройствами в виде импульсных фильтров с RC-четырехполюсниками: о-—последовательным (/—усилитель мощности; 2—электродвигатель постоянного тока; 3—редуктор; 4— тахогенератор с редуктором); б—параллельным; в—параллельным, преобразованным к z-форме
Рис, 8.16. Структурные схемы для регулирования угловой скорости вращения объекта с программами управления и коррекции: а —с микропроцессором серии К580 (/ — усилитель мощности; 2 —электродвигатель постоянного тока; 3 — редуктор; 4 — тахогенератор с редуктором); б —с микроЭВМ «Электроника-60»
сигнал поступает лишь в тактовые моменты времени кТо, где к = 0, 1, 2, ... В микропроцессоре реализована вычислительная процедура регулирования * в виде рабочей.программы. Схема САР с микроЭВМ «Электроника-60», позволяющей реализовать более сложные законы регулирования и коррекции, приведена на рис. 8.16, б. В ней направление потоков входной и выходной информации рассматривается относительно микроЭВМ. На ее вход подается сигнал и(кТо), где к = 0, 1, 2, ..., от преобразователя АК. Выходной сигнал «1[(«+ 1)Г0] в виде программы регулирования и коррекции через преобразователь КА поступает на неизменяемую часть системы. Работа программы осуществляется в течение такта квантования То.
После достижения границы интервала времени длительности То производится остановка программы
* См. Б. Куо. Теория и проектирование цифровых систем управления: Пер. с англ./ Под ред. П. И. Попова. М.: Машиностроение, 1986. 447 с.
и вводится следующее значение сигнала и [ (к + 1) То].
С помощью схемы (рис. 8.16,6) выполняются различные операции регулирования и коррекции по специально составленной программе для микроЭВМ. Если в системе необходимо изменить параметры устройств неизменяемой непрерывной части системы или ее основные характеристики, например, вместо колебательного переходного процесса получить апериодический, то для этого требуется только заменить рабочую программу.^ Поэтому с помощью микроЭВМ можно создавать унифицированные САР для управления любыми объектами регулирования, что выгодно отличает данный тип систем от непрерывных с аналоговыми корректирующими устройствами.
Перейдем теперь к рассмотрению более сложных структур САР с микроЭВМ. На рис. 8.17,а изображена двухконтурная схема ориентации ЛА, состоящая из двух каналов (контуров). Как видно из рис. 8.17, а, сравнение сигналов 0з(О и 0(0 выполняется на аналоговом устройстве. Затем разность этих сигналов через преобразователь АК поступает на микроЭВМ (позиция /), где реализуются законы регулирования и коррекции. В непрерывную часть САР входят: рулевой привод
571
в)
2, ЛА и ДУС. Для перевода цифрового сигнала управления в непрерывный к выходу микроЭВМ подсоединен преобразователь КА. В главную обратную связь входит датчик ориентации 7, преобразующий угол 0(0 в напряжение u(t).
Структурная схема многоконтурной системы, предназначенной для поддержания постоянства напряжения гидроэлектростанции, изображена на рис. 8.17,6. В нее входят четыре канала (контура). В отличие от схемы, изображенной на рис. 8.17, а, задающий сигнал поступает на микроЭВМ (позиция /) в виде двоичного кода. Сравнение задающего и выходного сигналов осуществляется также в двоичном коде, что позволяет в статическом режиме получать ошибку системы с
Рис. 8.17. Структурные схемы дискретно-ие-прерывных систем с управляющей микроЭВМ: '
а —двухконтурная САР ориентации ЛА (/ — ми кроЭВМ; 2—рулевой привод; 3, 4, 6—элементы динамики ЛА; 5—-динамика ЛА; 7—датчик ориентации); б—миогокоитурная САР гидроэлектростанции для поддержания постоянного напряжения при изменениях нагрузки потребителей (7 — микроЭВМ; 2—гидравлический привод; 3, 4 — корректирующие устройства соответственно № 1 и № 2; 5—клапан; 6—турбина; 7—генератор; 8—датчик напряжения; 9—возбудитель); в —система подачи стола фрезерного станка с числовым программным управлением (/, 2—микроЭВМ; 3—тиристорный усилитель мощности; 4—электродвигатель; 5—редуктор; 6 — стол фрезерного стайка; 7—тахогенератор; 8 —корректирующее устройство; 9, 10—фотоэлектрические преобразователи с выходным сигналом в виде двоичного кода)
точностью до младшего разряда. Это большое преимущество данной структуры, так как при длине слова в 16 байт установившаяся погрешность колебаний, напряжений в сети не превышает цену младшего разряда или 0,1 %.
572
Рнс. 8.18. Корректирующие устройства с импульсными фильтрами в виде RC-четы-рехполюсников W\(s):
а— последовательное; б—параллельное; в— преобразованное параллельное; а—параллельно-последовательное; д — преобразованное параллельнопоследовательное
В станках с числовым программным управлением (рис. 8.17, е) иа вход системы регулирования подачи стола поступают два сигнала в унитарном коде по положению h*(t) и двоичном по скорости Аз (0- Таким путем в данном типе следящей системы получается астатизм 2-го порядка, и она обладает высокой точностью не только по положению, но и по скорости.
Рассмотрим метод реализации дискретных устройств (коррекции и управления) в виде импульсных фильтров с RC-четырехполюсника-ми. На рис. 8.18, а—в изображены схемы последовательных и параллельных устройств с экстраполято-рами нулевого порядка. Передаточную функцию последовательного устройства можно записать в виде
Г|й(г) = ГКА1Гкп(г) =
= ^ка(з)П7Кп(з)] =
= (8.6)
где (z) — дискретная передаточная функция последовательного корректирующего устройства в z-форме (см. рис.'8.15, а). Из выражения (8.6) получим
2ИкЯ(*)1 гй7х
« 1“7“ J= T- z-i • (8'7)
При реализации импульсного фильтра в виде RC-четырехполюс-ника все полюсы irKn(s) простые и расположены слева от оси ординат Пл. S, исключая начало координат и бесконечность, а нули irKn(s) занимают произвольное положение.
Выражение в квадратных скобках функции (8.7) можно представить в виде суммы элементарных дробей
п
Т?кп ($) ао । у1 Дк
S S "I" Zj S + SK ’
к=1
(8.8)
где а0, ак — постоянные; sK — простые отрицательные действительные полюсы при к = 1,п.
Осуществляя z-преобразование от выражения (8.8), найдем
п
j _е5кГо2-1 ’
К=1
где zK z — число полюсов функции FKn(z).
Разлагая выражение (8.9) в виде суммы элементарных дробей, запишем
ап
^кп (s) 1
s J
(8.10)
573
Используя пр ил. П-1.2, определим
^кп ($) _ До । । ।
s s s + bt ' '''
Приведя выражение (8.11) к общему знаменателю, получим формулу для передаточной функции последовательного корректирующего устройства
^кп(5) =
__ feK (7Kts 4~ 1) (TKts 4~ 1).. .(TKns 4-1)
(8.12)
Передаточная функция (8.12) реализуется в виде RC-четырехпо-люсника (см. табл. 9.7). Откуда находим значения сопротивлений резисторов и емкостей конденсаторов.
Параллельное корректирующее устройство (рис. 8.18, б) можно реализовать также в виде импульсного фильтра с RC-четырехполюсником. Для этого сначала рассмотрим структурную схему параллельного корректирующего устройства (рис. 8.18,6). Ее можно привести к последовательному корректирующему устройству №кпР, как показано на рис. 8.18, в. В этом случае, пользуясь рис. 8.18,6 и в, можно записать
,Икпр(*) о I
L $
1 П-*%(*)] 1-2-1 L F<°>np(z) J
(8.13)
Затем выражение (8.13) приведем к сумме элементарных дробей вида (8.10), после чего можно получить передаточную функцию параллельного корректирующего устройства в окончательной форме
1^кпр($) =
_ <(^+1)(^+1)...(Г^+1)
(7Ki$ + 1) (7Kjs 4-1).. .(ТкпЗ 4-1)
(8.14)
Передаточная функция (8.14) реализуется в виде RC-четырехпо-люсника, постоянные времени которого также можно найти по данным , табл. 9.7. В этом случае в передаточной функции 1Гкпр(«) все полюсы произвольные, а нули должны быть простыми, действительными и расположенными левее оси ординат на Пл. §.
В некоторых САР одновременно применяют как последовательные, так и параллельные корректирующие устройства (комбинированные). Кроме того, в системы могут вводиться последовательные и параллельные корректирующие устройства, состоящие из нескольких RC-четырехполюсников, последовательно соединенных между собой с помощью катодных повторителей или электронных усилителей. По принципу действия их можно отнести к корректирующим устройствам комбинированного типа. Исходная структурная схема одного из подобных устройств изображена на рис. 8.18,г, а преобразованная схема— на рис. 8.18,6. По ним можно иайти передаточную функцию комбинированного импульсного фильтра
rrtK)(z) — W]<AWKn (g) /g 15) (Z)— 1 + U7KAU7KII(Z) •
Если U7kK)(z) имеет комплексносопряженные полюсы и нули вне единичной окружности на Пл. z или на ней, то выражение (8.15) можно записать в виде
Пк) (г) = П7’0)пр (г) ГЙ (г), (8.16)
где IFk np(z) = 1/[ 1 + IFKAWVnptz)] -передаточная функция импульсного фильтра в z-форме в обратной связи, а йИ^г)- передаточная функция последовательного импульсного фильтра.
Выделенные составляющие импульсных фильтров обладают свой
574
ством реализуемости или нереали-зуемости нулей и полюсов*-.
Г!?’р(г) =
реализуемые нули
нереализуемые полюсы ^0,пр(г)’
(8.17) ^(z) =
нереализуемые нули <п<г) ZQ 1 04
" ' /Л. ’ (®*
реализуемые полюсы (z)
При одновременном выполнении условий (8.17) и (8.18) можно создать комбинированный импульсный фильтр с RC-четырехполюсником.
Если условия (8.17) и (8.18) не выполняются, т. е. имеется неодинаковое число реализуемых и нереализуемых нулей и полюсов, необходимо вводить дополнительные неравные нули и полюсы**.
Пример 8.5. Исследовать дискретно-непрерывную САР с импульсными RC-фильт-рами последовательного или параллельного действия, с тремя тактами квантования Го = = 0,01 с; Го = 0,03 с; Го = 0,05 с.
Неизменяемая часть системы, включающая в себя усилитель, электродвигатель с редуктором и тахогенератор, описывается передаточной функцией
fe yfeдвfeтг
В7нЧ (S) = (Гу8 + 1) (Гд15 + 1) (Гд23 + 1) ’
* К реализуемым нулям и полюсам относятся такие нули и полюсы которые являются действительными некомплексными и меньшими единицы. Комплексные положительные, включая z = 0, или кратные нули и полюсы, а также расположенные на единичной окружности либо вне ее считаются нереализуемыми.
** Например, если
1^(0) ________2 ai ________.
кп₽ (z-l)(z2-&,z+1) ’
™(0) = (z + ai) (z2 — b2z+ 1)
кп Z-Ci
их можно представить в виде
тНО) = (z — Дi) (z — a) (z — 5).
"кпр (z_ 1)(z2_6lZ+ ц •
™(0) (z + аг) (z2 —&2гЦ- 1)
кп = (z — с2) (z — a) (z — Ь) ’
где 0 < а < 1; 0 < 6 < 1 и а Ь (см. подробнее в работе, указанной в ссылке иа с. 571).
где feyfeaB = 4; Гу = 0,01 с; Гд1=0,05 с; Тд2 = 0,1 с; feTr = 0.5.
Исследование дискретно-непрерывной САР с последовательным и параллельным корректирующими устройствами проведено с помощью передаточных функций разомкнутых систем, приведенных в табл. 8.1. Так как в этих системах применены преобразователи КА нулевого порядка, то передаточные функции корректирующих устройств в z-форме обозначены на рис. 8.15, а и в соответственно через ^О2) и <nP(z).
Кривые изменения основных характеристик a‘m, /*, е‘, о* системы
с последовательным корректирующим устройством, реализованным с помощью RC-фильтра (Ri = 0,25-10б Ом; /?2 = = 105 Ом; Ci = 0,5 мкФ, табл. 9.7, № 7), в зависимости от TKi приведены на рис. 8.19. Вычисление -характеристик производилось при g(KT)m — 2,5-10~2 рад; Arg(feT)m = l; Stf (z) = 1О-4/То с помощью программ № 7—10, 13, 19 и 20 на ЕС ЭВМ. Как видно из этого рисунка, уф°, — Ям,/р и имеют экстремумы, а характеристики а*т и е’ изменяются практически линейно, причем ат возрастает, а е* — убывает.
По заданному техническими условиями числовому значению уф” = 88° при Го = = 0,03 с из рис. 8.19, а найдем оптимальное значение TKi = 0,0225 с, по которому из рис. 8.19,6—е определим основные характеристики системы: — 77 м = —9,9 дБ; а^ = 3%; /р = 1,05 с; е‘ = 0,042 рад/с; д’* = 4,57 • 10-3 рад/с.
Структура и параметры параллельного корректирующего устройства подобраны таким образом, чтобы передаточные функции всей разомкнутой системы были аналогичны соответствующим функциям W(z) и Для этого в цепь отрицательной
обратной связи вводится дополнительный усилитель с коэффициентом kty.
На рис. 8.20 приведены кривые изменения характеристик уф, — Дм, ат, /р, е , о® системы с параллельным корректирующим устройством, реализованным с помощью RC-фильтра (Го = 0,01 с; Ri — 1,5-10® Ом; Ci = 0,5 мкФ, табл. 9.7, № 43), в зависимости от Гкь Из рис. 8.20 следует, что с уменьшением такта квантования все кривые смещаются влево, а характер кривых изменяется мало, значения основных параметров системы — /7М, ат, /р, е и ае, соответствующие уф = 88° при Го = 0,03 с, практически совпадают с аналогичными параметрами, полученными для последовательной коррекции.
576
В дискретно-непрерывных системах преобразователь АК переводит аналоговый сигнал в цифровой код с помощью двух операций — квантования по уровню и кодирования. В настоящее время наибольшее распространение получили преобразователи АК следующих типов: напряжение— цифра, вал —цифра, фаза — цифра и время — цифра. Квантователь по уровню оказывает влияние не только на точность систем регулирования, но и на устойчивость.
На рис. 8.21 изображена статическая характеристика идеального квантователя по уровню с шагом квантования q, т. е.
q = 2~NuB, (8.19) где N — длина слова в битах; ив— входной сигнал (для преобразователя напряжение — цифра); ивх — выходной сигнал.
Из рис. 8.21 видно, что математическое значение ошибки квантования
q/2 = 2-N~iuB, (8.20)
а среднее квадратическое отклонение при нормальном законе распределения
а$ = ?/12. (8.21)
Квантователь, как следует из рис. 8.21, является нелинейным элементом; поэтому в замкнутых системах могут возникать автоколебания.
Пример 8.6. Исследовать влияние устойчивости дискретио-непрерывиой системы в зависимости от нелинейной характеристики квантователя преобразователя АК. Пусть неизменяемая часть дискретио-иепрерывиой системы с экстраполятором нулевого порядка описывается выражением
0,136 (2 + 1,31) (z + 0,045)
} 2(2-l)(z-0,368)
(8.22) где k = 3, или
3(1 -0,25s) (1 + 0,225s) X
w _____________X (1 ~ 0,034s)
ич — s (1+0,25s) (l' +0,543s) "
(8.23)
Запишем уравнения гармонического баланса с нелинейным квантователем
20 lg Н (со) = 20 lg [1/<7 (q/A)]-, I e«o) = -i80°. J (8,24)
Таблица 8.1
Дискретно-непрерывные корректирующие устройства в S-, -г- и s-формах
Такт квантования TQ, с Передаточные функции корректирующих устройств Передаточная функция неизменяемой части системы IFHq(z)
пос ледовательного параллельного
^КП (2) np (°) W np
0,01 0 2 °’°5s + 1 2 — 0,874 4 0,506 0,018z (2-9,85) (г—1,51)
0,01s + 1 2 — 0,0368 0,0742s +1 2 — 0,874 (2 - 0,905) (2 - 0,819) (2 - 0,368)
0,03 0 2 °’05s + 1 2 — 0,81 4 0,76 0,018 (г + 0,505) (z+1,701) (z+13,7) (2 — 0,741) (z — 0,549) (г — 0,0498)
’ 0,01s + 1 2 — 0,0498 0,142s+l 2 - 0,81
0,05 0,05s-Ц 2 — 0,801 4 0,794 0,018 (г + 0,0428) (z+1,19) (z+48,3) (г-0,607) (г-0,368) (г-6,74 • 10-3)
0,01s + 1 2 — 6,74-IO-3 0,225s+ 1 2 — 0,801
576
Рис. 8.19. Основные характеристики дискретно-непрерывных систем регулирования с последовательным импульсным корректирующим устройством в виде RC-четырех-полюсннка в зависимости от параметра Ткр
а—для v*°; б—для — Я* ; в—для а* ; г—для t*; б—для в*; е—для в* Ф М т ' р 8
Передаточная функция всей разомкнутой системы
W(z)
0,018z (z — 9,85) (z — 1,51) (z - 0,874) (z — 0,905) (z - 0,819) (z - 0,368)2 1,6 (1 -4- 4,43 • 10~3/5) (1 + 0,0742/5) (1+0,1/5) (1+0.0108/5)2 X (1 — 8,1 • 10~3/5 + 3,69 • 10~5 (/5)2) X (1+0,05/5)
0,018 (z + 0,505) (z + 1,701) (z - 0,741) (z-0,549) X (z + 13,7) (z — 0,810) X (z-0,0498)2 1,6(1 — 0,013/5)(l -5,55- 10~3/5) (1+0,101/5) (1+0,051/5) Х (1 +0,0126/5) (1 +0,142/5) Х (1+0,0166/5)»
0,018 (z + 0,0428) (z + 1,19) (z - 0,607) (z - 0,368) X (z + 483) (z -0,801) (z — 6,74 • IO-3)2 1,6 (1 - 0,024/5) (1 - 2,16 • 10~3/5) (1 + 0,102/5) (1 + 0,054/5) Х (1 + 0,023/5) (1 + 0,225/5) Х (1 + 0,025/5)»
19 К). И. Толчеев
577
Рис. 8.20. Основные характеристики дискретно-непрерывных систем регулирования с параллельным импульсным корректирующим устройством в виде импульсного RC-четырехполюсника в зависимости от параметра Txi:
а—для у1?; б—для -Я* ; в—для а ; г—для t ;
'ф М т р
д—для е ; е—для ag
Обозначим ошибку квантования по уровню на к-м шаге выборки через (кТо); тогда получим
%(KT0) = y(KTQ)-y~(kTQ). (8.25)
К соотношению (8.25) добавим уравнение состояния относительно
Эквивалентная логарифмическая амплитудная характеристика 20[lg l/q(q/A)] (шаблон) показана на рис. 8.22, а. Логарифмические амплитудные и фазовые частотные характеристики нелинейной системы построены на рис. 8.22, б. Наложив на эти характеристики шаблон (как это было рассмотрено в гл. 2), получим, что при N = 4 в системе возникает режим автоколебаний с частотой (Оа = 2,1 с-1 и амплитудой Да = 6,3«10-2 рад. С увеличением разрядности квантователя до N = 8 автоколебания уменьшаются (А, = 3,9 X X 10-3 рад), а при N = 16 практически исчезают (Да = 1,5-10~5 рад).
Рассмотрим способ определения наименьшего верхнего предела ошибки квантования с помощью метода z-преобразований *. Будем считать, что квантование по уровню является эквивалентным источником ошибки с амплитудой ±q/2.
* См. сноску на с. 571.
Рис. 8.21. Статическая характеристика квантователя по уровню для преобразователя АК (штриховая прямая является идеализированной)
578
Lm, д Б
360
270'
180
90
90
-180
270
-360
ошибок от квантователей * е^Ц/сН-1)7’о] = Ле>(кГо) —(8.26) и выхода
8* (кТ0) = С£у (kTq) — Gq, (8.27) где Ъу(кТо) — вектор ошибки квантования по переменной состояния размерностью (пХ1); У(кТо) — вектор переменной состояния‘ размерностью («XI); Уд(кТ0)— вектор переменной состояния от ошибки квантования размерностью (п X XI); Я — вектор квантования шума размерностью (тХЦ; А —матрица системы размерности («Хл); R— матрица коэффициентов корреляции, учитывающая связь между Уд ((к + 1) ] и эквивалентными
источниками шумов размерностью (nXm); е*(кГо)—вектор ошибки квантования по выходу размерностью (nXl); С — матрица выхода системы размерности (гХ«); G — матрица коэффициентов корреляции, учитывающая связь между х~(кТ0) и q размерностью (rXm).
* Вектор шума в неидеальиом квантовании состоит из суммы гармоник, которые имеют случайные фазовые сдвиги, что приводит к~ необходимости пользоваться матрицами R и G.
Рис. 8.22. Определение режимов автоколебаний дискретно-непрерывной системы в зависимости от такта квантования q: а—шаблон; б—логарифмические частотные характеристики с наложенным шаблоном
Матрицы R и G имеют диагональный вид, когда сигналы квантователей являются белым шумом. Их использование намного упрощает решение данной задачи.
Уравнение (8.26) можно записать в z-форме
Ei,(z) = (zZ — A)-1e_y(0) —
-(zZ-A)’1^-^-. (8.28)
Пользуясь уравнением (8.28), приведем для i-ro элемента вектора Е, (г) зависимость
Ey<(z) = P<(zZ-A)-‘ey(0)-
Pl(zI-A)-lR1(±ql/2)
(8.29)
где Pi — i-й столбец матрицы заданных весовых коэффициентов (масштабирование).
Наименьший верхний предел ошибки квантования для i-ro
19*
579
U '(2)
Рис. 8.23. Структурная схема внутреннего контура цифровой САР с параллельным корректирующим устройством с квантователем, входящим в преобразователь вал — цифра
состояния систем запишем в виде
I lim еу (jV)|==llim(l—z ')(z)
I Л/-»оо I I z-> 1
На основании структурной схемы (рис. 8.23) и выражений (8.32) и (8.33) запишем
E;(z) =
-1 - 0,944z-1 - 0,348z~2 +
= + 0,191z~3 + 0,106z~4 j ±qz
1 - 1,473z-i + 0,256z“2+ z-1‘
L + 0,312z~3 - 0,094z~4
(8.34)
Из выражения (8.34) находим
Ijnn -^‘^(z) | =
1—0,944z-1—0,348z-2+ -I
+ 0,191z~3 + 0,106z~4 , , l-l,473z *+0,256z 2+
• + 0,312z-3 — 0,094z“4 J
lim
= 1,65g.
(8.35)
По аналогии с выражением (8.30) для выхода САР имеем
I Ит е* (Л/)| =
|.V->oo * |
(8.31)
Пользуясь приведенным способом, рассмотрим следующий пример.
Пример 8.7. Определить наименьшее значение верхнего предела ошибки, вносимой в цифровую САР параллельным корректирующим устройством с квантователем, входящим в преобразователь вал — цифра (рис. 8.23). Если корректирующее устройство реализовать в виде программы, то при округлении чисел следует учитывать такт квантования ±<7/2. Передаточную функцию цифрового внутреннего контура системы с параллельной коррекцией запишем в виде
1У/ — Х’ & —
Н'к пр (2)--,-------
Ui (z)
1 -0,944z-1-0,348z“2 + + 0,191z“3 + 0,106z~4 “““ _ ] ' ' l~l~ «
1 — l,473z 1 + 0,256z 2 +
+ 0,312z-3 - 0,094z~4
Наименьший верхний предел ошибки квантования для выходного сигнала х может быть получен с помощью сигнала разности
e;(z)«=X'(z)-X'(z). (8.33)
При использовании преобразователя вал — цифра с N = 4 бит (q = 1/16) установившаяся ошибка в системе от квантователя ех — 7/16 = 0,103, что недопустимо по требованиям эксплуатации, так как ех при отработке единичного задающего сигнала g [1] вызывает ошибку, равную 10,3 %. Если Лг = 8 бит (q — 1/256), то ъх = 7/256 = 3,9-10-3, или 0,39 %. Такая погрешность допустима для ряда САР. В высокоточные системы должны входить преобразователи АК с N — 16 бит (q = = 1/65436); в ‘них гх = 2,52 • 10-5, или 0,00252 %.
Пример 8.8. Составить программу управления регулятором (микропроцессор-контроллер) для САР (рис. 8.17, а). Преобразуем исходную схему к расчетному виду* (рис. 8.24), а затем по ней составим уравнение регулятора в непрерывной форме
[/ 1
М (0 + ki e.(t)dt , (8.36)
*0
где йд — коэффициент датчика (тахогенератора), приведенный к сигналу ошибки.
* См. сноску на с. 571.
Рис. 8.24. Схема САР с микропроцессором-контроллером, приведенная к расчетному виду:
1 — микропроцессор-контроллер; 2—неизменяемая часть системы
580
Интеграл в выражении (8.36) имеет вид
t
у (t) = J [®з - ® (т)] dx + у (/„), (8.37) to
где <Вз — заданное постоянное значение установившейся угловой скорости задающего устройства.
Для вычисления интеграла воспользуемся численным методом Эйлера. Тогда интеграл (8.37) примет вид
(к+1)Г„
~ ® (0] dt « ®3Т0 -
кГ0
— То {[® (к + 1) Тд + <в (кТо)]}. (8.38)
При определении интеграла (8.38) будем учитывать реальный масштаб времени. Для этого введем временную задержку,
равную одному периоду квантования (к+1)То.
Запишем выражение (8.36) в дискретной форме, учитывая при этом соотношения (8.37) и (8.38); тогда при нулевых начальных условиях получим
е [(к + 1) Го] =
= Лд {М т + k2y [(к + 1) То]} (8.39)
при начальном условии е(0) = о3.
Сигналы, формируемые с помощью выражения (8.39), с выхода микропроцессора-контроллера поступают в систему в моменты времени /=(к+1)То, к — 0, 1, 2, ..., а управление изменяется через каждый такт То и остается постоянным между моментами замыкания преобразователя АК. Для закона управления регулятора (8.39) составим иа языке ассемблер рабочую программу для микропроцессора-контроллера типа К580 с фикснроваииой запятой в виде
NAME EPSLN
PUBLIC EPSLN
EXTRN MEMOR
Y EQU 1 ПОРТ ДЛЯ ВВОДА Y
EPS EQU 2 ПОРТ ДЛЯ ВЫВОДА ЕПСИЛОН
CSEG
EPSLN: DI ТОЧКА ВХОДА
IN Y ВВОД Y
ORA A ДЕЛЕ-
JP PLUS НИЕ
STC НА
PLUS: RAR 2
MOV C,A РЕЗУЛЬТАТ В С
LDA MEMOR ПРЕДЫД. ЕПСИЛОН В А
MV I B,2 УМНОЖЕНИЕ
CALL MULTB НА 4
ADD C УМ-
MVI B,1 но-
CALL MULTB ЖЕ-
MOV D,A НИЕ
MVI B,2 НА
CALL MULTB 10
ADD D
STA MEMOR ; ЗАПОМ. ТЕК. ЕПСИЛОН
OUT EPS ; ВЫВОД ЕПСИЛОН
El
RET
MULTB: ORA A
JM MN
PL: ORA A УМНО-
RAL ЖЕНИЕ
DGR В положит.
JNZ PL ЧИСЛА
RET
MN: STC УМНО-
RAL ЖЕНИЕ
DCR В ОТРИЦ.
JNZ MN ЧИС-
ORI 80H ЛА
RET
END
581
Пример 8.9. Составить программу управления САР с микроЭВМ «Электроника-60», изображенной на рис. 8.17,6. будем считать, что передаточная функция программы регулятора имеет вид
w (s) = (^K1S + I) (8 40)
k(J U(s) Гк2«+1 ' ’
Преобразуем данную передаточную функцию, записанную в аналоговой форме, в цифровую. Порядок числителя передаточной функции (8.40) не больше, чем знаменателя; поэтому, введя дополнительную переменную можно составить два
дифференциальных уравнения:
для числителя
Гк1 ~ + и (/) = «2 (0, (8.41)
для знаменателя
Гкг-§- + «! (О = *к«2(0. (8.42)
Применив к уравнению (8.41) метод первой центральной разности, найдем
^-{и (кГ0) - и [(к - 1) То]} =
7 о
— иг (кТо) — и (кТо),
откуда
«2 (кГо) = (1 + ^-)«(кГо)-
- и [(К _ 1) Го]. (8.43)
7 О
Интегрирование уравнения (8.42) выполним по методу Эйлера, т. е.
«1 [(«+ 1) 7о] = «| (кГо) +
+ (8'44)
и, (КТо) +
Для вычисления Ui(«T0) по и(кТ0) из выражений (8.43) и (8.44) исключим «г(к?'о); тогда получим
И1[(«+1)Го] = (14
+ т^(' + тг)“№’-
[(к - I) Го]. (8.45)
Составим рабочую программу, реализующую закон управления (8.45) для микроЭВМ «Электроника-60» на языке ассемблера:
VALU1
РАСЧЕТ ФОРМУЛЫ:
Ш ((К + 1) Т0) = 1,01U1 (KT0) + U (KT0) - U ((К - 1) Т0) ВХОД:
U (KT0) С РЕГ. 167776 В U
U((K-1)T0) В U0
U (KT0) В UONE
ВЫХОД НА РЕГ. 167772
R1 = % 1 R2==% 2 R3 = %3 SP=>%'6 РС = %7
VALU1: MOV Rl.-(SP) ; СОХРАНЕНИЕ
MOV R2,-(SP) ; РЕГИСТРОВ
MOV R3,—(SP) ; 1,2 И 3
I W: BIT # 100,e# 167764 ; ОЖИДАНИЕ
В EQ 1Я ; ГОТОВ. ВН. УСТР-ВА
MOV <8# 167776,U ; ЧТЕНИЕ U(KT0)
MOV UONE.Rl ; U1 (KT0) В R1
CLR R2
MOV R1.R3
DIV # 100, R2 ; 0.0Ш1 (KT0) В R2
ADD R2,R1 ; 1.01U1 (KT0) В R1
ADD U,R1 ; (R1) + U(KT0) В R1
SUB U0.R1 ; (Rl) — U ((К — 1) Т0) В R1
MOV Rl.UONE
MOV U,U0
MOV Rl,«# 167772 ; U1 В ВЫХ.РЕГИСТР
BIS #100,«# 167770; ГОТОВНОСТЬ ВЫВОДА
MOV (SP),R3 ; ВОССТАНОВЛЕНИЕ
MOV (SP) + ,R0 ; РЕГИСТРОВ
MOV (SP) + ,R1 ; 1,2 И 3
RTS PC
582
UONE: .WORD 0
U: .WORD 0
U0: .WORD 0
.END
Из программы видно, что для ее выполнения требуются операции: логические (переадресации), короткие (сложение — вычитание) и длинные (умножение). Для микроЭВМ «Электроиика-60» время выполнения переадресации тп = 2,8 мкс, коротких операций тк = 4,8 мкс, длинных — тд = 35 мкс. В результате можно найти время выполнения всей программы тв Пр = = 1,5-10-3 с. Откуда следует, что
тв пр < То. (8.46)
Общий объем оперативной памяти рабочей программы при длине слова 8 бит равен 156 байт. Технические характеристики микроЭВМ «Электроиика-60» удовлетворяют требованиям по быстродействию и объему памяти.
Применение управляющих микроЭВМ * в качестве устройств, на которых реализуются законы управления и коррекции, требует составления рабочих программ. При этом используют четыре способа программирования: прямое, последовательное, параллельное и последовательно-параллельное.
* В управляющих микроЭВМ таймер формируется в ячейках оперативной памяти.
Рассмотрим первые три способа программирования. Передающую функцию регулятора можно записать в виде
wp\z>— и (2)
_ ^1г~‘ + bjZ~2 + ... + bmz~m
1 + atz~l + а3г~г + ... + bnz~n ’
(8.47)
где ао ¥= 0, &о =/= 0, тип — положительные целые числа: т п— 1.
Прямое программирование. По передаточной функции (8.47) определим разностное уравнение
т к—О
-Еак<(/-«Т0), (8.48)
к-1
Рис. 8.25. Структурные схемы программирования:
а—прямого (1—3—ячейки памяти); б—последовательного: в—параллельного
б)
583
которое можно разделить на две части
= —«;(/), (8.49)
где
т
= £ М’(^-кГо) (8-5°) .к=0
И
u'3(t) = taKu^t-KTe). (8.51) К = 1
Структурную схему прямого программирования (рис. 8.25, а) можно получить с помощью выражений (8.49) — (8.51). Как видно из рис. 8.25, а, при реализации на ми-
Таблица 8.2
Сравнение методов программирования
Метод Программирования * Объем памяти ячеек микроЭВМ (m=l; п —1) Время выполнения вычислительных операций в микроЭВМ «Электро-иика-60», мкс
Прямое Константы ш + п + -Н Данные m + п Умножение m 4-+ /»+ 1 Сложение m + п Переадресация m + + п 105 9,6 5,6 5 12
Число операций 3m + Зя — 1 Объем памяти 5m + 5я + 2
Последовательное Константы m + п Данные п Умножение m + п Сложение m + п Переадресация п 70 9,6 2,8 6 8
Число операций 3m + Зя Объем памяти 3m + 5я
Парал- лельное Константы 2я Данные я Умножение 2я Сложение 2я — 1 Переадресация я 70 4,8 2,8 7 8
Число операций 8я — 1 Объем памяти 8л
кроЭВМ программы прямого программирования необходимо выполнить т + п + 1 умножений и т + п сложений. Каждое из полученных значений должно быть переадресовано в ячейку памяти. Все эти передачи происходят с задержкой на такт квантования Т(>. Число операций и объем памяти микроЭВМ при использовании метода прямого программирования приведены в табл. 8.2.
Последовательное программирование. При последовательном программировании передаточную функцию (8.47) следует преобразовать к виду
= U (z) “ 1 + diz-1 -X
(8-52)
где —1/ек и —l/dK — соответственно нули и полюсы функции (8.52).
Передаточная функция (8.52) образует произведение передаточных функций
^((z) = Uг (z) _ 1
Ki(z) 1 + dtz~l '
F2(z) = V. (z) _ V2(z) 1 +егг~1 . 1 + d3z~l ’
1T3(z) = K2 (z) _ Уз (z) 1 +e3z~l . 1 + dsz-1 ’ (8.53)
Г„(2) = yn(z) _ 1 + enz~l
C/(z) 1 + dnz~l '
На рис. 8.25,6 показана структурная схема последовательного программирования, состоящая из передаточных функций (8.53). Пользуясь выражением (8.53) и обратным преобразованием Лапласа, получим
г® 1 1 ^1 А 1 V 1 1 4“ » 04 -4- * со _ Р ’ & *-* С’/'- сч ео чз ’хз V I I ЛЛ 1 ♦ - ♦ см ♦ «0 & & & (8.54)
«;(п=<_1(о+еХ-1Х xc-^-dXG-^o)-
584
Откуда найдем число выполняемых операций и объем памяти и за-йесем их в табл. 8.2.
Параллельное программирование. При этом методе программирования функцию (8.52) преобразуем к виду
IF (2) =_____------1_____-------к
wpW~ i + d12-i т i + dt2-i -г
I____Рз_____|_ _|____Рп
1 -|- d3z~l 1 dnz~l
(8.55)
пе-
Pt
Передаточную функцию (8.55) репишем как сумму членов
U (z) 1 + dxz~l ’
(z\ = =-----Р*----•
w2\z) и (г) l + d2z-‘ ’
it _____-KiIeL_______Рз
^з(2)— и{г) — 1+rf32-! .
(8.56)
Wn(z)
Vn(z) __ рп
и (г) 1 + dnz~n •
На рис. 8.25, в изображена структурная схема параллельного программирования, составленная из передаточных функций (8.56). Пользуясь выражениями (8.56) и обратным преобразованием Лапласа, найдем
t>J(/) = /?1«*(/) ——Го); «2 (0 = Piu\ — d2V2 (Z — То)> и;(/) = р3«; (о-^из ^~тоУ
u(0 = u;(/) + «’2(/) + + «з(0 + • • • + W„(0-
(8.57)
Из выражений (8.56) определим необходимое число выполняемых операций и объем оперативной памяти (табл. 8.2).
Каждый из рассмотренных методов программирования имеет свои особенности. Например, прямое программирование наиболее целесообразно использовать, когда в выражении (8.47) некоторые коэффи
циенты равны нулю. В этом случае реализация данного метода осуществляется с наименьшими затратами времени работы микроЭВМ. При последовательном программировании обеспечивается наименьший объем памяти микроЭВМ. Кроме того, можно при решении задач синтеза (см. гл. 10) подбирать требуемые нули и полюсы передаточной функции регулятора (неизменяемой части следящей системы). Если используют параллельное программирование, то каждый параметр регулятора должен быть связан либо с полюсом, либо с вычетом. При этом для получения желаемого закона изменения регулирования (коррекции) необходимо изменить либо параметр pi, либо dt. В некоторых случаях более выгодно применять метод последовательно-параллельного программирования (комбинированного), так как снижаются требования по быстродействию и объему памяти микроЭВМ.
3. ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
В экстремальной САР объект регулирования должен обладать статическими характеристиками, имеющими экстремум, который может меняться в процессе работы в зависимости от изменения возмущений. Экстремальные системы применяют в нагревательных колодцах, химических реакторах, реактивных двигателях и устройствах переработки сырья на обогатительных заводах, т. е. в системах с объектами, где изменения переменных регулирования топлива, давления воздуха за компрессором двигателя на первоначальном участке приводят к возрастанию выходного параметра (температуры, реактивной тяги, выхода размолотого сырья), а после прохода экстремума к их уменьшению. Для нормальной работы экстремальной системы ее регуляторы
585
\~bffiex/7> регулирования^
6)
Рис. 8.26. Структурные схемы экстремальных регуляторов: а—с поиском по чувствительности; б—с запоминанием экстремумов с помощью RC-фильтра; в—с запоминанием экстремума иа микроЭВМ
должны обеспечивать нахождение экстремума. Наибольшее распространение получили регуляторы двух типов: а) экстремум определяется по чувствительности1, в этом случае управляющий сигнал формируется по результатам измерения крутизны статической характеристики объекта; б) экстремум находится по разности между текущим и экстремальным значениями, полученными на предыдущем шаге и хранящимися в запоминающем устройстве регулятора *.
Рассмотрим структурные схемы обоих типов экстремальных регуляторов (рис. 8.26). На рис. 8.26, а показана структурная схема экстремального регулятора с поиском экстремума по чувствительности. Сигнал ui(t) с помощью задатчика 1 вырабатывается по команде управления g(t). Объект регулирования состоит из нелинейности 7, а также входной 6 и выходной 8 линей
* В качестве устройства для запоминания экстремальных регуляторов используются RC-фильтры или микроЭВМ.
ных частей. Сигнал на выходе объекта i/i(0 измеряется датчиком 2 и в виде напряжения и2(0 поступает на сравнивающее устройство, где образуется их разность
и(1) — щ (0 — и2(0- (8.58)
Разность сигналов u(t) в устройстве 3 формируется в виде поискового сигнала un(t), который подается через исполнительное устройство 4 и динамическую часть объекта 6 к его статической характеристике 7. На рис. 8.26, а экстремальный регулятор выделен штриховыми линиями, а объект регулирования — штрихпунктирными линиями.
Параметр потерь на поиск экстремального регулятора характеризуется зависимостью
Р = У3 — У, (8.59)
где у3—экстремальное значение статической характеристики; у — среднее значение за период колебаний Тз между двумя максимумами Уз при поиске, т. е. время, необходимое для измерения y\(t).
586
На рис. 8.27, а—д показаны процессы, протекающие в экстремальном регуляторе с поиском по чувствительности, когда амплитуда установившихся колебаний в экстремальной системе определяет зону поиска
At/ = — ky (Дх)2, (8.60)
где ky — постоянная величина, зависящая от формы статической характеристики [13].
Статическая характеристика объекта приведена на рис. 8.27, а, а его чувствительность изображена наклонной прямой на рис. 8.27, б. При подаче на вход статической, характеристики объекта пилообразного сигнала ABCDE (рис. 8.27, в) на выходе образуется сигнал A2B2C2D2 (рис. 8.27, г). Пользуясь характеристикой чувствительности объекта на рис. 8.27, д, найдем точку «0», в которой скорость изменения сигнала равна нулю.
Из рис. 8.27, г видно, что экстремальный регулятор совершает колебания с амплитудой Ду. Потери на поиск определим по заштрихованной зоне:
Т’рев
f Ду(0Л, (8.61) t рев J
где Грев — полное время реверса регулятора. Как известно, Тэ = 2Трев.
Рис. 8.27. Графическое представление процессов в экстремальном регуляторе: а—д—с поиском по чувствительности; е—к—с запоминанием экстремума
Подставляя соотношение (8.60) в (8.61), получим
k V
р = -^Л- \ Дх2Л. (8.62) * рев J
0
При Дх = / • х имеем
Р“—(»вз)
но Ду = — &у7’2евх2.
Тогда
р=4ду. (8.64)
Отметим, что чем меньше параметр р, тем выше качество экстремального регулятора. Из рис. 8.27, д можно найти время выхода регулятора в нормальный режим работы Трех, которое приблизительно равно 95 % от Т'вых- Эта характеристика также оказывает большое влияние на качество работы экстремального регулятора. Для уменьшения р и Треж в систему вводят дополнительно параллельное корректирующее устройство 5 (рис. 8.26,а).
На рис. 8.26, б изображена схема экстремального регулятора с запоминанием экстремума, получаемого с помощью RC-фильтра при постоянной скорости изменения входного сигнала, а на рис. 8.26, в — с запоминанием сигнала на микроЭВМ, в которой формируется также программа параллельной коррекции. При этом можно не иметь постоянную скорость изменения входного сигнала.
587
Процессы, протекающие в экстремальном регуляторе с запоминанием экстремума, изображены на рис. 8.27, е—к, где показаны зоны поиска и стабилизации сигнала управления после интегрирования (рис. 8.27, и, к). Принцип действия такого регулятора при постоянной скорости изменения входного сигнала можно пояснить с помощью рис. 8.26, б. Запоминаемый экстремальный сигнал Ду3у снимается с блока 9 и поступает на сравнивающее устройство, где формируется в виде
Ди(0 = Ду(0-А^зУ(0- (8-65)
Если разность сигналов Ду3у = = Дуэ < Ду, то регулятор изменяет входной сигнал в направлении движения к точке экстремума. При Дузу — Дуэ > Ду в регуляторе меняется направление движения. В результате этого происходит реверс исполнительного устройства 4. Отсюда следует, что экстремальный регулятор с запоминающим устройством совершает колебания около экстремума. В точке экстремума статической характеристики всегда Ду = 0. Иногда в экстремальных регуляторах с запоминанием на выходе сравнивающего устройства вводится интегратор, увеличивающий значение сигнала на выходе до Дп (рис. 8.27, к).
В таких регуляторах часто применяют импульсные нелинейные устройства с памятью. Однако все экстремальные регуляторы имеют существенный недостаток — на их входе образуются автоколебания. Поэтому последнее время стали применять экстремальные беспоис-ковые регуляторы.
В системах с поиском экстремальных параметров объекта регулирования используют микроЭВМ, в которых реализуются различные численные методы, обеспечивающие организацию процедуры оптимизации. На практике чаще используют итерационные процедуры получения оптимальных оценок у вектора уп
равления переменных, которому соответствует минимальное значение целевой функции f(y). Указанные методы применимы также к задачам максимизации. При этом целевую функцию следует заменить на НУ)-
Представим несколько методов для решения задач безусловной оптимизации, поскольку ни один из них не отличается высокой эффективностью для оптимизационных задач различных типов. В ряде случаев приходится приспосабливать вычислительные алгоритмы нескольких методов к конкретным характеристикам решаемой задачи.
Для определения экстремума скалярных функций векторного аргумента часто используют прямые методы, основанные на свойстве градиента функции. Рассмотрим задачу отыскания минимума непрерывной дифференцируемой функции f(yi, у?.....уп), определенной в фазо-
вом n-мерном пространстве. Возьмем некоторую точку У(0) = (у(10), г/20), ..., у^^.не являющуюся точкой минимума функции f(y), и будем считать ее начальным приближением к решению задачи. Известно, что существует такая окрестность точки у(0), в которой в направлении вектора градиента V/(y<0)) функция возрастает наибыстрейшим образом, а в направлении антиградиента —Vf(y(0)) она убывает таким же образом. В соответствии с этим строятся рекуррентные процедуры прямых методов, среди которых наиболее часто употребимыми являются методы градиентов, наискорейшего спуска и Гаусса — Зейделя.
Метод градиентов. В фазовом пространстве Rn через точку у(0} проведем прямую
у = у(о)_^(у(о)), (8.66)
где t — вещественный параметр.
Поскольку вдоль вектора —Vf(y(0)) в окрестности ут функция f(y) убывает, то всегда найдется достаточно малое значение
588
параметра t Z> 0, при котором выполняется условие
Hy(0)-^f(y(0))Xf(9<0>). (8.67)
Согласно неравенству (8.67) определим некоторое т > О и следующую точку в направлении убывания функции f (у), т. е.
у^ = уМ-^(уЮ). (8.68)
На этом основании строим итерационный процесс минимизации функции
y(*+i) = y(fe) — xVf(y(fc))> (8.69)
т > О— шаг метода (некоторое фиксированное значение малого параметра t), k — 0, 1,2,...
При практической реализации счета по методу градиентного спуска (8.69) итерации прекращаются на v-м шаге, если при некотором наперед заданном малом значении е > 0 выполняется неравенство
II Vf (y(v)) || < е. (8.70)
Наряду с выражением (8.70) можно использовать и другие критерии окончания итерационного процесса, как, например,
||y(v)_y(v-i)||<e; (8.71)
l/(y(v))-f(y(v-I))l<B. (8.72)
Здесь е > 0 указывает точность
решения задачи минимизации функции f(y).
При использовании метода градиентов шаг т выбирают постоянным для всего итерационного процесса, и, как правило, он оказывается очень малым; поэтому для отыскания минимума необходимо много итераций, что вызывает большие затраты машинного времени. Наиболее экономными являются методы спуска с переменным шагом, к которым относится метод наискорейшего спуска.
Метод наискорейшего спуска. По этому методу используется основная рекуррентная формула метода градиентного спуска (8.69) с той особенностью, что на каждой k-й итерации выбирается максимальный шаг тк из условия минимума функции f(y) в направлении движения, т. е.
min f (9<*>) -xVf(yW). (8.73) % > о
Реализация метода наискорейшего спуска предполагает на каждом шаге решения довольно трудоемкой вспомогательной задачи одномерной минимизации. Тем не менее, как правило, он дает выигрыш в числе машинных операций, поскольку обеспечивает движение с самым выгодным шагом.
На рис. 8.28, а показана геометрическая интерпретация метода наискорейшего спуска для функции двух переменных f(y) ~ f(y(l))— уравнение линии уровня. Здесь направление движения из точки y<fe) касается линии уровня в точке y<-k+l'>; поэтому путь определяется звеньями ломаной линии, являющимися ортогональными между собой. Следовательно, направления спуска на двух последовательных итерациях взаимно ортогональны.
Пример 8.10. Применим метод иаиско-рейшего спуска для определения минимума функции
f (У) = + 4у|«/2 + 5j/2-
589
Рис. 8.28. Графическая интерпретация вычислительных процедур поиска минимума функции: о—методом иаискорейшего спуска; б—методом Гаусса —Зейделя [f (у)-Суравнения кривых уровней функции]; в—методом Ньютона
Зададим начальное приближение у®> =
Г 101
= 11, вычислим вектор градиента функции
Щ = Г 162/1 + 4^1.
L 4yt + 10y2 J'
Результаты вычислений по рекуррентным формулам (8.69), (8.73) запишем в
табл. 8.3.
Стремление уменьшить объем вычислений, необходимых для осуществления одной итерации метода наискорейшего спуска, привело к созданию ряда других методов. Одним из них является метод покоординатного спуска (метод Гаусса — Зейделя).
Метод Гаусса — Зейделя. Задавая начальное приближение у,0 = = [у*1*, •••> УпТ’ вычислим ча*
стную производную по первой координате df/dyi и примем
= (8.74)
Таблица 8.3
Минимизирующие последовательности Для f(y)
k У? f(yW)
1 -1,2403 2,1181 24,23
2 0,1441 0,1447 0,354
3 -0,0181 0,0309 0,0052
4 0,0021 0,0021 0,0000
где е 1 = [ 1 0 ... 0]т — единичный вектор оси Ог/ь t > 0, некоторый достаточно малый шаг на направлении е\.
Следующая итерация состоит в вычислении точки у(3) по формуле
y(3) = ?(2)_Z.W^e2> (8.75)
где вг = [0 1 0 ... 0]т — единичный вектор оси Oz/г-
Итак, в методе покоординатного спуска путь определяется ломаной, состоящей из отрезков прямых, параллельных координатным осям (см. рис. 8.28,6). Спуск по всем п координатам составляет одну внешнюю итерацию. Обозначим через г номер очередной внешней итерации, а через k номер той итерации, по которой производится спуск; тогда рекуррентная формула, определяющая следующее приближение к точке минимума, имеет вид
^rn+fe+l) = y(rn+k) _ t df Wrn+k}l e 9 V Я Qyk K>
(8.76)
r = 1, 2, ..., k = 1, 2, ..., n.
После k = n счетчик числа внешних итераций г увеличивается на единицу, a k принимает значение 1.
Если шаг tn = const в формуле (8.76), то имеем покоординатный спуск с постоянным шагом. Если на каждой итерации выбирать свой шаг tk из условия
min f (yim+k> — t eft),
i>0 V дук *}'
(8.77)
то получим метод Гаусса — Зейделя.
590
Окончание счета по формулам (8.76), (8.77) определяется заданной точностью решения задачи и использованием одного из критериев (8.70) —(8.72).
Модифицированный метод Ньютона. Нетрудно заметить, что в методах наискорейшего спуска и Гаусса — Зейделя применяется наиболее рациональная локальная стратегия поиска с использованием градиента. Однако движение в направлении —Vf(y) является эффективным лишь в том случае, когда линии уровня функции близки к окружностям. Следовательно, направление, противоположное градиенту, в общем случае ,не является глобальным направлением поиска точек экстремума нелинейных функций. Для построения более полной локальной процедуры поиска привлекается информация о вторых производных функции. Используя разложение в ряд Тейлора функции в окрестности yW с учетом членов второго порядка малости, получим квадратическую аппроксимацию f(y):
f(y, y{k>)~f(yw) + vrf(y{k})^y +
+ jA’yVWW (8.78)’
На основе выражения (8.78) сформируем последовательность итераций таким образом, чтобы во вновь получаемой точке градиент аппроксимирующей функции обращался в нуль, т. е.
Vf (у, у<*>)=Vf (у<*>) + V2/ (у^) \у=0.
(8.79)
Таким образом, из равенства (8.79) получим приращение аргумента
(yW). (8.80)
Последовательное применение схемы квадратической аппроксимации (8.78) с условием (8.79) приводит к вычислительной процедуре метода Ньютона
y(UD = у(л> _ [v2f vf (yW)
(8.81)
Итерационная формула (8.81) поиска минимума функции f(y) графически показана на рис. 8.28, в; в точке yw функция f(y) аппроксимируется квадратичной функцией, а в качестве приближения y^w* принимается минимальная ордината этой аппроксимации.
Если матрица Гессе V2f(j/(ft)) определена положительно, то направление поиска по формуле (8.81) оказывается направлением спуска и итерационный процесс сходится со скоростью геометрической прогрессии независимо от начального приближения у<°\ Когда матрица Гессе в некоторой точке отрицательно определена, то указанное направление является направлением подъема, а в случае неопределенности матрицы Гессе однозначный вывод о направлении движения сделать нельзя.
Метод Ньютона (8.81) модифицируется с тем, чтобы обеспечить уменьшение целевой функции от итерации к итерации и осуществить поиск вдоль прямой, как в методе наискорейшего спуска. Вычислительная процедура модифицированного метода Ньютона для любых функций осуществляется по формулам
y(*+D = yW - h™ [V2f (у<*>)]-1 vf (i/ft));
(8.82)
ft(*>: min f (y(ft+i)). (8.83)
»>o
Выбор согласно локальной минимизации (8.83) гарантирует монотонность целевой функции, т. е.
f(yC*+>))<f(y<*)).
Пример 8.11. Рассмотрим функцию из примера 8.10, т. е.
f (У) = М + 4У1У2 + 5^> и найдем точку минимума этой функции:
Vf (у) = [16J/1 + 4«/2 10^2 +
591
Матрица Гессе положительно определена для всех итераций. Используя итерационную формулу метода Ньютона (8.81), получим
Г 101 1 Г 10 —41 Г 200 1
Lio] "144 —4 leJ’LuoJ’
т. е. = о J ’ чт0 совпадает с точный решением. Таким образом, задача минимизации заданной функции решается с помощью одной итерации метода Ньютона (сравните с методом наискорейшего спуска, см. табл. 8.3).
Метод Флетчера — Ривса. Этот метод относится к группе методов сопряженных направлений. В нем, как и в методах градиентного спуска, используется информация только о первых производных целевой функции. Однако методы сопряженных направлений выгодно отличаются от градиентных методов более высокой скоростью сходимости, которая приближается к скорости сходимости метода Ньютона. Положительно определенная квадратичная форма п переменных минимизируется методом сопряженных направлений не более чем за п шагов. Так как любая гладкая целевая функция в окрестности точки своего минимума хорошо аппроксимируется квадратичной, метод сопряженных градиентов с успехом применяют для минимизации и неквадратичных функций. В последнем случае метод становится итерационным.
Рассмотрим квадратичную функцию п переменных
f(y) = a+(y, b) + ±(y, Су), (8.84)
где а — const; Ь — заданный вектор размерности (п X 1); С — положительно определенная симметричная матрица размерности (пХ«). Для минимизации функции (8.84) возьмем следующий итерационный процесс:
^+1) = »(Й)+Мь (8-85)
где sk — направление спуска на k-м шаге; реличину шага выбираем из
условия minf(y) по X в направлении движения.
Оптимальное X* на каждой итерации вычисляем по формуле
1 ___ tyf № sfe) io ос\
Построение п взаимно сопряженных направлений «о, «ь , Sn-i — самостоятельная задача, которая решается неоднозначно.
По методу Флетчера — Ривса последовательность направлений поиска строится на основе линейной комбинации антиградиента в текущей точке и предыдущего направления спуска. При этом имеем
So = -Vf(»,o)); (8.87)
Sk = ~Vf(!fw) + ₽л-1«л-ь 6>1.
(8.88)
Величину коэффициента 0*-i будем выбирать из условия С-сопря-жеиности векторов s* и s*-i, т. е. на основании равенства (S&, Csk-i) =0 запишем
-(Wft)), <4-i) + + Pfe-i (s»-i> Csk-i) = o,
отсюда
_ (Vf („<*>). c,,.,)
• <8-89>
Последнее выражение при использовании свойства С-сопряжен-ности и формулы (8.85) приведем к виду
a HW^H2 (8 90)
Запишем последовательность шагов вычислительной процедуры минимизации квадратичной функции (8.84) методом Флетчера — Ривса:
1) сначала вычисляем градиент в точке yw и находим «о = = -W0>);
2) затем по формуле (8.86) вычисляем Хо и определяем приближение yw = ym + XoSoi
3) дальнейшие итерации для k
1 находим по формуле (8.85) с использованием выражений (8.86),
592
(8.88), (8.90) вплоть до такого значения у(у}, в котором V/ (ум) = О, причем v п. Точка уЮ будет решением поставленной задачи.
Метод Флетчера — Ривса применяют для минимизации и неквадра-тнчных функций, но при этом он не будет конечным. Кроме того, на каждой итерации Хй из решения локальной задачи выбора оптимального шага определяют
min f (y№ + Kksk).
После п итераций (где п — размерность пространства переменных) вычислительную процедуру метода циклически повторяют с заменой ут на у<п), а счет заканчивают по любому из критериев окончания счета, например, при ||Vf(y(v))|| < е, где е > 0 — заданное число.
Изложенный метод является эффективным при решении практических задач, характеризуется простотой вычислительной схемы и небольшим объемом памяти ЭВМ, необходимым для проведения поиска. Метод Флетчера — Ривса особенно выгоден при решении задач высокой размерности, в то время как, например, метод Ньютона требует на каждой итерации обращения матрицы n-го порядка.
Пример 8.12. Найти минимум квадратичной функции
f (У) = 1/1 + 21/11/2 + 21/2 + !/з + 1/4 ~~ У\ +
Размерность пространства переменных п = 4. Следовательно, ие более чем за четыре шага методом Флетчера — Ривса най-
ти решение задачи.
Зададимся начальным приближением 0<°> = [0 0 0 0]т. Согласно заданной квадратичной функции имеем
2 О
4 0
О 2
О О
2i/i + 2j/s — 1 2р 1 + 4j/2
2у3
21/4
Первый шаг
s0 = -Vf(?0)) =
Csa =
~1~ о о
_о_
1 - (WO)),so)
° (So, Cs0) ' ~2~ 2 О _0_
Хо = тр;
₽о = 1; W’) =
Второй шаг
si = - V/(у(1)) + ₽о»о‘> "0"
1 0 _0_
.______(W (у(1>). S.)
1 (Sb Cs.) ’
1~
-1 о
0_
«1 =
Следовательно, у(2> — у* — точка минимума найдена на втором шаге итерационного процесса.
Последние два метода в виде процедур, реализованных на ЭВМ, позволяют с помощью регулятора
»(2> =
593
a)
Рис. 8.29. Принципиальная схема экстремальной системы химического реактора и его характеристики: я—схема (/—редуктор с зубчатой рейкой для перемещения вентиля В,; 2—сериесный электродвигатель; Я—поляризованное реле; 4—триггер со счетным входом; 5—предварительный электронный усилитель; 6—задатчик напряжения; 7—термосо-противлеиие; 8—химический реактор; Вг — Вг—вентили ручного управления); б—характеристики выхода готового продукта в зависимости от температуры поступающего пара в °C (кривые 1—3 характеризуют выход готового продукта в зависимости от качества поступающего сырья); в—S-импульсы, счетного входа, импульсы срабатывания на входе и выходе, импульсы иа выходе; а—сигнал, снимаемый с контактов поляризованного реле 3
получить экстремум целевых функций.
Пример 8.13. Определить параметры регулятора и основные характеристики всей системы экстремального регулирования химическим реактором (рис. 8.29, а), в котором выход готового продукта зависит от температуры пара. Статические характеристики такого объекта приведены на рис. 8.29,6. Кривыми 1—3 изображены ха
рактеристики объекта в зависимости от качества поступающего сырья, активности катализатора и давления в реакторе. При этом видно, что с увеличением температуры до определенного уровня происходит увеличение выхода готового продукта, а затем его уменьшение.
В экстремальный регулятор (рис. 8.29, а) входит триггер 4 со счетным входом, на который подаются импульсы S (рис. 8.29, в). Входные и выходные импульсы и импульсы при движении к максимуму и от него показаны иа рис. 8.29, в. В результате переключения триггера образуется меандровая характеристика срабатывания реле 3 с удвоенным тактом (рис. 8.29, г). При поступлении этого сигнала на обмотки возбуждения электродвигателя постоянного тока 2 образуется синусоидальный сигнал с удвоенной частотой 2<о и амплитудой А2, со смещением
. . хо ~ ^2
по фазе на угол а = arcsin----------.
С учетом этого иа структурной схеме рис. 8.30, а изображен нелинейный эле-
594
S) мент * с эквивалентной передаточной функцией J2 (*о> ^2)- Там же показаны и другие передаточные функции W'j(s), U72(s) и 1Гз(з). Нелинейная статическая характеристика объекта обозначена Л (At).
Для удобства проектирования системы ее нелинейные элементы, разделенные линейным звеном IF3(s), выделены штриховым прямоугольником с приведенной эквивалентной передаточной функцией Jn(A2,s). Наличие синусоидального сигнала на входе нелинейности J2(A2) позволяет применить метод гармонической линеаризации.
Так как частота колебаний на входе в 2 раза меньше частоты колебаний на выходе, то
х(<) = А13тф, ф = at (8.91) и нелинейность
F (х) = - М2. (8.92)
В этом случае формулы для определения коэффициентов гармонической линеаризации имеют вид 2л
= лЯТ’ $ F sin
1 2Л <8-93)
MAt)==-^ J F (х)соз2фйф.
____________ О
* См. Сборник задач и примеров по теории автоматического управления: В. А. Олейников, Н. С. Зотов, А. М. Пришвин и др. — М.: Высшая школа, 1969. 199 с. Оптимальное, экстремальное и программное уп-равления/Под ред. А. В. Фатеева. — М.: Высшая школа, 1969. 198 с.
Рис. 8.30. Структурные схемы экстремальных систем:
а, б—регулирования химическим реактором с поиском по чувствительности; в—с запоминанием экстремума с импульсным устройством; а—с запоминанием экстремума на микроЭВМ с реализацией последовательного корректирующего устройства
Подставляя в формулы (8.93) выражения (8.91) и (8.92), найдем
ai(A,)=«
л
— —( sin2 ф sin 2ф dф = 0;
л J о
bi (А,) =
(8.94)
sin* ф cos 2ф </ф о
Вычислим эквивалентные значения амплитудной и фазовой характеристик, пользуясь формулами (8.94). Тогда при й0=1с- С/кг по формулам табл. 2.3 получим
.. . А,. )
91( 1)== 2 ’ I (8.95)
щ (At) ==90°. )
Примем следующие передаточные функции, системы:
электродвигатель с редуктором и вентилем
W4 (s) = ki/s, ki — 0,001 с"'; (8.96)
595
линейные части объекта регулирования 1
ki = 1 кг/(с • В);
(s) = ^3+ t , k3 = 1 кг • с/°С;
Wt(s)=kt, В/(кг-с);
(8.97)
напряжение, снимаемое с клемм реле Pi, иП2 — U. (8.98)
Частотная функция ^(/ш) обеспечивает хорошую фильтрацию сигнала (см. п. 5, гл. 2). Тогда амплитудная характеристика нелинейного элемента примет вид
<7П (А,©) = <?( (Л,) д2 (4 Л0, (8.99)
а его фазовая характеристика
цп (Л,ш) = 90°---- а. (8.100)
Прн дальнейших расчетах примем
Хд = 0,5 В.
Амплитуда иа входе J2 связана с амплитудой на выходе Ji зависимостью
А| А1&4 2 V4(10<o)2-FT‘
(8.101)
Как следует из выражения (8.101), на вход J\ поступает сигнал с частотой <о и амплитудой Аь Линейное звено ^3(/а>) вызывает фазовый сдвиг 03{^о) = = —arctg 20<о, в результате образуется выходной сигнал Ti(s).
Определим коэффициенты гармонической Линеаризации нелинейного элемента J2, т. е.
л+а
аг(Аг) F (0,) sin ф йф =
ЯЛ2 -л+а
4U cos а пА2
(8.102)
л+а
*2(^2)==—~7Г \ F (01) cos ф с/ф =
ЯА» J
* —л+а
= (8.103)
лЛ2
Из выражений (8.102) и (8.103) найдем эквивалентные амплитудные и фазовые характеристики для 1г в виде
<72(^)=-^7г; (8.104)
лА2
»*2 (4)—arc‘g [-^Нг]=_ а-(8Л05)
Пользуясь формулами (8.100), (8.103), получим
«/„(A,, <d)=-^-. (8.106)
лА2
Из зависимости (8.101) найдем .. . .,о arctg 20<о
рп (А1( ®) = 45°---|----Ь
1 Аа Хл + _ arcsin(8.107)
Условия гармонического баланса запишем в обычной форме, т. е.
20 lg Н, (со) Нг (со) = 20 lg —-1—-;
ЧП t'Hb
(8.108)
61 (со) + 02 (<») = - 180° - ц„ (Аъ со). (8.109)
Воспользуемся методами шаблонов и логарифмическими амплитудами и фазовыми частотными характеристиками линейной части системы. На рис. 8.31, а кривой 1 дана амплитудная характеристика Я,(со)Я2(св), которая построена при коэффициенте усиления усилителя А41 = = 10 ( в/(кг с), кривой 2 — при kf2 = = 2,25 В/(кг-с) н кривой 3 — при й43 = — 1 В/(кг-с). Кривой 4 построена логарифмическая фазовая характеристика 0i(co) + 02(<b). Здесь же на рисунке кривыми 8—10 показаны положения шаблонов 20 1g 1/^п(Ль со) и —180° —цп(Аь со) — кривыми 5—7 при трех значениях частот СО| — со3. Все перечисленные кривые в увеличенном масштабе построены на рис. 8.31,6 для диапазона частот cd 10-2—10-1 с-1. Из рнс. 8.31, а, б видно, что в экстремальной системе в зависнмостн от коэффициента k„ кривые шаблонов 20 lg 1/<yn (А, со) пересекают логарифмические амплитудные частотные характеристики 20 lg[//i (со)/72(со)] в точках Bi, В2 и В3. Соответственно характеристики —180° — Цп(А1,ш) пересекают логарифмические фазовые частотные характеристики [01 (со) + 02(со)] в точках Dt, D3 и D3. Так как все точки пересечения Bt и Di лежат на вертикальных прямых, то в экстремальной системе возникают режимы автоколебаний с частотами <ва^ и амплитудами Аа., числовые значения которых приведены в табл. 8.4. Потерн на поиск находятся по формуле
Р = Аal ,02 (4 Ла2() Н1 (ша2г) X
ХЯ2(<Ц)«,(Аа1(). (8.110)
а время выхода системы в точку экстремума
Т’реж = 4—. (8.111)
Я/
. 596
Значения частот и амплитуд автоколебаний, параметр потери на поиск и время выхода в точку экстремума в рассматриваемой САР примера 8.13 приведены в табл. 8.4.
С целью повышения основных параметров экстремального регулятора введем в него параллельное корректирующее устройство с передаточной функцией
1Гк(а)=*ду/(Тка+1), (8.112)
которая показана на рнс. 8.30, б.
Тогда линейную часть системы можно описывать выражением
W* (s) =
________________TxS + 1_____________
( TIT- s’ + ТТ— s + 11
\ «1Кду ®1«ду /
(8.113)
Рис. 8.31. Определение параметров автоколебаний экстремальной системы регулирования химическим реактором с помощью логарифмических характеристик:
а, б—без корректирующего устройства; в, г—с параллельным корректирующим устройством с пере* даточной функцией WК($)“ЛДу/Гкз4-1
На рис. 8.31, в построены логарифмические амплитудные Ял(со) (кривые 1—3) и фазовая 0Л(со) (кривая 4) частотные характеристики по передаточной функции (8.113) с различными коэффициентами усиления k^, kKf{ и постоянной времени Тк. Здесь же приведены эквивалентные амплитудные 201g 1/<7п(Л1, со) (кривые 6—8) и фазовые —180° — цп(А1, со) (кривые 7—10) характеристики. Эти кривые в увеличенном масштабе построены на рис. 8.31, г для диапазона со = 2-10-2 ч- 5-10-1 с-1, с по-
597
Таблица 8.4
Значения частот и амплитуд автоколебаний в экстремальной САР
*4 Частота и амплитуда автоколебаний р, "С Т с * реж’ с
“а;. с“‘ »а,- °C
10 0,017 3,6 11,4 1450
2,25 0,020 3,2 9,2 1256
1 0,024 2,4 6,8 1040
мощью которых найдем частоты <oaj и амплитуды Aai автоколебаний (табл. 8.5).
Из сравнения данных табл. 8.4 н 8.5 следует, что введение параллельного корректирующего устройства и дополнительного усилителя улучшает основные параметры экстремальной системы по потере на поиск в 3—4 раза, а по времени выхода системы в точку экстремума в 1,5—2 раза.
Пример 8.14. Определить параметры регулятора и основные характеристики всей системы экстремального регулирования двухконтуриого ракетно-прямоточиого двигателя (рис. 8.32, а), в котором тяга изменяется в зависимости от расхода топлива, положения диффузора и скорости потока набегающего воздуха w (в числах М) при выделении дополнительного тепла от дожигания топлива в камере 2. Статические характеристики двигателя (тяга — расход топлива) с экстремумами при раз-
Таблица 8.5
Значения частот и амплитуд автоколебаний, параметры потери иа поиск и время выхода в точку экстремума САР с параллельным корректирующим устройством и дополнительным усилителем
*4 Частота и амплитуда автоколебаний р, °C Т . с 4 реж*
“аг с-1 »аГ °C
10 0,05 2,2 4,1 995
2,25 0,07 1,9 3,7 715
1 0,1 1,4 2,8 502
личных числах М (Mi—Мз) показаны на рис. 8.32,6.
В регулятор (рис. 8.32, а) входят: триггер со счетным входом и устройством формирования импульсов с запоминанием
Рис. 8.32. Принципиальная схема двухкои-турного ракетно-прямоточного двигателя с дожиганием топлива во второй камере: а—схема (/—двигатель; 2— первая камера сгорания с форсунками; 3—датчик температуры; 4—дополнительный усилитель; 5—запоминающее устрой, ство; 6—формирователь импульсов с тактом Го для управления преобразователем КА; 7—поляризованное реле; 8—усилитель мощности; 3—соленоид; Ю-— гидравлический привод для управления вентилем подачи топлива); о—статические характеристики тяги двигателя от расхода топлива в час при трех числах Маха (М, — М3)
598
экстремума 5; поляризованное реле 7, подающее сигналы разной полярности в усилитель мощности 8. В отличие от ранее рассмотренной принципиальной схемы САР температуры в химическом реакторе (рис. 8.29, а), в рассматриваемом регуляторе управление положением вентиля В подачи топлива осуществляется от гидравлического привода 10 с силовым цилиндром.
По рис. 8.32, а на рис. 8.30, в приведена структурная схема нелинейной системы с импульсным управлением. Как видно, в нее входят два нелинейных элемента Л и J2. Наличие импульсного запоминающего устройства позволяет отнести эту систему к дискретно-непрерывной [24].
Непрерывную часть системы опишем с помощью системы уравнений
„ dx , ,
Т 1 । х • k\Xi,
at
(8.114)
Пусть в систему уравнений входят: Т| = 2 с; То — 4 с; ko = 1 кН-с/кг; k\ = — 1 кг-с/м; ki = 0,1 м/(В-с); fe3 = 1 В/кН.
Решение системы находим прн начальных условиях Хо = 2 кг/с; ую — 0.
Составим передаточную функцию линейной части системы в виде
Гл ($) == =-----—------. (8.115)
1/(5) 5(^5+!)
Сформируем закон управления в регуляторе для n-го шага:
«п (0 = k3 [sgn (yln — ylt n_i + 2С) Ип-1].
(8.116)
Закон управления записан в дискретной форме; поэтому к передаточной функции (8.115) можно применить z-преобразование. В результате получим
5)1 = 3Г——1 = Ь (Г 15+1) J
ь,ь„ (1 — е~г«/г>) z
/ -т A- (S-H7)
(z— l)(z — е TdT')
Если принять, что на систему действует единичное управляющее воздействие, то, пользуясь выражением (8.117), найдем сигнал
Х (Z) = /М2п2( 6 ^Г/Г.) • (8Л 18) (z—lr(z —е Г»/Л)
С помощью прил. П-1. 2 найдем обратное г-преобразование для выражения (8.118)
в виде
ь,Ьое_г<|'Г1
х (кТ0) = k,kt (кТо) - +
+ М.-ЛГ- <’•"’>
Соотношение (8.119) показывает, что сигнал х(кТо) формируется в реальном масштабе времени. Первая разность для входного сигнала
Г (к+1) Г, 1
AxK = M2Ll-e Tl J. (8.120)
Для нахождения фазовой траектории необходимо исключить параметр кТ0. Тогда из выражения (8.120) имеем
(8.121) ktkte-W'
откуда
л~г- <8Л22>
Первую разность (8.120) представим в виде производной Дх„ = d.y[at\ тогда из соотношения (8.119) найдем
х __ kjkjT। Г j _ dyi/dt ~|
То L &1&2 J
-----dy'ld^;1: + С. (8.123)
1 —
При начальных условиях х = ха и dyildt = (dyjdt)o из выражения (8.123) определим произвольную постоянную
п । kik2Ti | (dyildt)o |
С = х0 -)----xi- In i-------j—г--- —
1 0 I »1«2 I
Подставив выражение (8.124) в (8.123), найдем
г—г - dy^dt ~ (rfyi/rf0o
0 е-Гс/т1
kjk2T[ I (dy\ldt)o I
То "I Ma | +
+ k,^Tl In I 1 - {dy'/dht}a I. (8.125) To | j
Подставив в выражение (8.125) соответствующие числовые значения, получим два уравнения для фазовых траекторий:
х = 2 - 1,2 -
at
— In 11 — 10-^| при u„>0; (8.126) х = 2- 1,2-^ +
+ In | 1 + 10 | при ип < 0. (8.127)
599
Рис. 8.33. Фазовый портрет экстремальной САР регулирования тягой ракетного прямоточного двигателя с дожиганием и запоминанием экстремума для определения параметров амтоколебаннй
При построении фазового портрета необходимо знать уравнения линий переключения. Для этого воспользуемся вторым уравнением системы (8.114). Подставив в него значения выходных координат переменных, найдем
У\п ~ ^охп> 1
„ 2 ( (8Л28)
У1, п-1 - - kOxn-l )
и, положив ип — 0, получим
«з [2U, -1 + k0 (dy, Idt)* - С] = 0, (8.129)
от иуда
_ fe3 [2С —&0 (dy./dQg]
2fe0 dijijdt
(8.130)
Вводя числовые значения в выражение (8.129), получим
.. 0,1 - (dyxldt)2 2 (dy[dt)
(8.131)
Для нанесения отметок времени выхода на предельный цикл н определения частот и амплитуд автоколебаний из соотношения (8.120) найдем
Дх = 1-0,1 (1 — е~4) =0,0985» 0,1 кг/с.
(8.132)
Пользуясь формулами (8.126), (8.127), (8.131) н (8.132), построим на рис. 8.33 фазовый портрет экстремальной системы регулирования тягой ракетно-прямоточного двигателя с дожиганием и запоминанием экстремума. Кривые 1 и 2 соответствуют линиям переключения, а кривая 3, состоящая из 26 точек с шагом То, определяет время прихода САР к экстремальному значению Т^ж (точки нанесены на внешней
стороне линии 3). Предельный цикл (кривая 4) размечен 27-ю точками с шагом Лх на участках, параллельных оси Ох (точки нанесены внутри цикла).
Найдем нз рис. 8.33 основные параметры экстремальной системы: время прихода САР к точке экстремума Греж = 26Г0 = = 26-4 =104 с; частота автоколебаний Wa = 2л/27Т0 = 2л/108 = 0,058 с-1; амплитуда автоколебаний Аа= 12-0,1/2 = = 0,6 кг/с; потерн на поиск р = А„/3 = = 0,6/3 = 0,2 кг/с. С уменьшением зоны нечувствительности реле (—С, С) возрастает динамическая точность экстремального регулятора с запоминанием. Прн feo < 1 линии переключения 1 и 2 на фазовой плоскости стягиваются к началу координат, что приводит к повышению точности работы всей экстремальной системы. Для уменьшения амплитуды автоколебаний значения шага Дх следует брать наименьшими [см. выражение (8.120)], что можно получить путем сокращения длительности такта Та.
Если в экстремальной системе ракетного прямоточного двигателя применяется управляющая ЭВМ (рис. 8.30,г), то на ней реализуется программа поиска экстремума с помощью одной из вычислительных процедур, приведенных выше, и программы последовательной коррекции фазоопережающего типа.
4. РАСЧЕТ И ИССЛЕДОВАНИЕ САМОНАСТРАИВАЮЩЕЙСЯ СИСТЕМЫ УПРАВЛЕНИЯ С ЭТАЛОННОЙ МОДЕЛЬЮ И СИГНАЛЬНОЙ КОМПЕНСАЦИЕЙ
При управлении объектом, собственные параметры которого изменяются в процессе функционирования в широком диапазоне, не удается обеспечить заданное качество переходных процессов введением неизменяемых корректирующих устройств. Одним из возможных путей решения задачи управления такими объектами является построение беспоисковых самонастраивающихся систем (СНС) с эталонной моделью.
Теория СНС с эталонной моделью, в которых используется сигнальная или параметрическая настройка, подробно изложена в работах [34, 35[. В ее основе лежит второй метод Ляпунова.
600
Ниже рассмотрена методика расчета СНС с эталонной моделью и сигнальной настройкой. Самонастраивающиеся системы с эталонной моделью, полученные на основе достаточных условий устойчивости, имеют довольно сложную структуру. В связи с этим исследуются некоторые способы упрощения их реализации.
Структурная схема такой системы показана на рис. 8.34. Объект управления, включая исполнительные устройства, постоянные корректирующие устройства в отдельных контурах уйравления и т. п., описывается уравнением вида
y==A(t)y + B(t)g + cm, (8.133) где А(/) — матрица системы; В(/) — матрица передачи управления; с — вектор, определяющий точку подачи дополнительного управляющего сигнала т.
Закон изменения параметров объекта [элементов матриц А(/) и В(0] может быть неизвестным, но должен быть задан порядок системы линейных уравнений системы (8.133), а также диапазон изменения параметров.
Пусть динамика эталонной модели описывается уравнением
Ум = ЛмУм + BMg, (8.134)
где уы — вектор выходных координат модели; Ам и Ви — постоянные матрицы, определенные из условия
Рис. 8.34. Структурная схема беспоисковой самонастраивающейся системы с эталонной моделью: /—эталонная модель системы; 2—закон регулирования; 3—объект с системой регулирования
обеспечения желаемого качества переходных процессов в эталонной модели.
Согласно структурной схеме (рис. 8.34) в системе осуществляется сравнение векторов выходных координат Модели и объекта и формируется вектор ошибки
в = Ум — У- (8.135)
Допустим, что структуры эталонной модели и управляемого объекта одинаковы. Тогда уравнение рассогласования, описывающее динамику системы с эталонной моделью, можно записать в виде
е — Ае — ААу — ABg — Ьт, (8.136)
где ДА — А (/) — Ам; АВ=В (/) — Вм.
Теперь необходимо выбрать т таким образом, чтобы обеспечить асимптотическую устойчивость решения системы (8.136). Для этого зададим функцию Ляпунова в виде положительно определенной квадратичной формы
У = етРе. (8.137)
Тогда производная функции Ляпунова (8.137), взятая с учетом уравнения (8.136), будет иметь вид
V==-eT[ATP + PA]e-
- 2еТР [ААу + ABg + Ьт]. (8.138)
Введем обозначения:
Q = AtP + PA; (8.139)
у = е'Р [ Д Ау + Д Bg + Ьт]. (8.140)
Так как матрица Р положительно определенна, а система устойчива, то матрица Q также положительно определенна. Следовательно, для того чтобы решение (8.136) было асимптотически устойчиво, необходимо выполнение условия у
0, т. е.
етР [ДАу + ABg + Ьт] > 0. (8.141)
601
Перепишем неравенство (8.141) в координатной форме
Z Z ( Z ЬаиРы) ekyt +
п п / п \
+ Z ^buPktj ekgt +
+ Z(Zp/A)^>0. (8.142) Обозначим
Рй/ = Z baitpki, Th/ = Z ^buPki,
° = Z (Z Piibi\et = /-i \t-i /
= &Pb=^plei.
Тогда из выражения (8.142) можно найти сигнал управления
Z П*Ы (Д ™=ArVi—|IX'l^l+
+ «7«/1 §11} sgn Ст, (8.143) где nk = max {у*/, qy! =
___Vfe/ . „ ___bki
— max——, ggi — max——.
k nk SI к пк
Разрывность сигнала управления m приводит к тому, что в системе могут возникать различные типы движения и, в частности, движение по поверхности переключения в скользящем режиме. Трудность реализации связана с тем, что при выходе на гиперплоскость переключения ст управление становится бесконечным. Но именно это условие вытекает из требования асимптотической устойчивости. Так как гиперплоскость
ст = Д PjSj —0 (8.144)
стационарна, закон управления (8.143) можно упрортить. Потребуем, чтобы на гиперплоскости в силу уравнения (8.136) существовал скользящий режим. Для этого
в качестве функции Ляпунова выберем
У = |ст|. (8.145)
Это не удается сделать сразу, поскольку неизвестно выражение для ст. Тогда производную функции Ляпунова (8.145) можно записать следующим образом:
п п / п
V = Z Р А = Z Pi ( Z atkek -/~1 \Я"1
п п \
— Z ^ajkyk — £ bbikgk — bjtn) =
/ п \ / п \
— Z P/Да/J yk — Z Р/Д&/J §k —
-(Zpa)™]- (8.146)
Управление m будем искать в виде п
т=Х (UekCk + <*укУк + <*gkgk)-k "•!
(8.147)
Подставляя последнее выражение в условие (8.146), которое должно быть меньше нуля, получим соотношение для дополнительного управления
п
Z (9ек1еЛ1 + д1,к1Ук1 + fe "1
где
+ 4 g J ёк I) sgn ст, (8.148)
Чек —
п
Z piaik
qutl = max
п
Z Р/Да/Л /-1
п
ggft = max
п
Z Pl^bjk
602
Для определения функции Ляпунова в виде (8.137) и нахождения гиперплоскости переключения ст следует пользоваться матрицей приведения к действительной жордановой канонической форме Hj. Ее столбцами являются собственные векторы матрицы Ам. В этом случае функция Ляпунова определяется матрицей
Р=[(нМ]-{- (8.149)
В выражении (8.149) требуется операция обращения матрицы. Ее можно избежать, если вместо системы собственных векторов использовать собственные векторы матрицы Ат. При этом справедлива формула
P = QtQp (8.150) где Qj — матрица приведения к жордановой канонической форме матрицы Ат.
Поскольку собственные векторы матриц определяются с точностью до постоянного коэффициента, существует множество матриц Р, определенных в соответствии с формулами (8.149) или (8.150). Для определения единственной функции Ляпунова и, следовательно, гиперплоскости переключения ст будем выбирать Р из условия минимума отношения Xmax (Р) /Xmln (Р) • ЗдеСЬ ^тах (Р) и Xmin (Р) — соответственно максимальное и минимальное собственные значения матрицы Р. При таком выборе гарантируется, что время самонастройки будет меньше длительности переходного процесса модели.
Пример 8.15. Рассмотрим систему стабилизации короткопериодической составляющей продольного движения самолета, структурная схема которой изображена иа рис. 8.35. Здесь сформированы два контура управления с постоянной структурой и параметрами, предиазиачеиными для того, чтобы частично компенсировать изменение параметров самолета по режимам полета, тем самым повысить надежность системы управления в случае выхода из строя контура самонастройки. Дополнительное управление т, вырабатываемое этим контуром, подается иа вход сервопривода. Контур демпфирования угловой скорости тангажа имеет в цепи обратной связи корректирующее устройство с передаточной функцией
= <8Л51>
а контур стабилизации заданной перегрузки в прямой цепи — интегрирующее корректирующее устройство с передаточной функцией
1Г1(з)=й1/з. (8.152)
t
Согласно изложенной выше методике необходимо знать систему уравнений относительно выходных координат. Обозначим yi — пу — приращение нормальной перегрузки; у г = в — приращение угловой скорости таигажа; у$ = о,— отклонение рулей высоты; yt — перемещение штока сервопривода; у$ — промежуточная координата сервопривода (скорость перемещения штока сервопривода); ув— переменная состояния коррекции в контуре демпфирования; yi — выходной сигнал интегрирующего корректирующего устройства в прямой цепи контура стабилизации заданной перегрузки «к,-
Тогда динамика системы, показанной на рис. 8.35, может быть описана системой
Рис. 8.35. Структурная, схема основного контура системы стабилизации перегрузки: /—корректирующий элемент; 2—сервопривод; 3—бустер; 4—динамика самолета
603
Таблица 8.6
Значения коэффициентов матрицы для трех режимов полета самолета
Номер режима полета Н, км V, —-с “и а12 а21 °22 а23
1 0 170,2 -0,94 0,28 —33,66 -1,63 16,87
2 3,0 262,9 -1,16 0,54 -32,57 -2,04 33,06
3 13,5 531,0 -0,47 0,44 -71,49 -0,59 19,71
Номинальный режим полета 5,0 242,0 -1 0,57 —34,47 -1,05 14,5
дифференциальных уравнений
Уз =
05 = ~
kyT Ki
У< — о.\\У\ + ai2t/2;
Уг — й2\У\ + ацУз + а^зУз,
"Т7Уз + ~т7у*’
У< = Уб ,1 2gcn
^2~ - тг- У* - ~у* -* к2* сп * сп * сп
1 1
Уб “ 'р У% Уб*
* к2 i к2
У7 = *1(%-^)-
Параметры исполнительных устройств имеют следующие значения: Tt, — 0,1 с; Тс = 0,05 с; В = 0,4.
Для трех режимов полета значения коэффициентов матрицы Uij (i = 1, 2; /=1,3) приведены в табл. 8.6. В качестве эталонного выбран номинальный режим полета, для которого рассчитывают параметры корректирующих устройств (s) и r2(s)-
Используя традиционные методы логарифмических частотных характеристик или корневого годографа, обеспечивают в контуре демпфирования относительный коэффициент затухания порядка 0,5—0,7 (для демпфирующего комплексно-сопряженного полюса). Коэффициент прямой передачи в контуре стабилизации выбирают из условия монотонности переходного процесса по перегрузке.
Так, полюсы разомкнутого контура демпфирования с учетом того, что Тк2 = 0,01 с, соответственно равны в порядкё убывания собственной частоты:
Ai =— 100 (коррекция в обратной связи); 12,з = — 8,0 ± 18,33/ (сервопривод);
= — 10 (бустер);
Л516 = — 1,0 ± 4,43/ (самолет).
Отсюда следует, что динамика контура демпфирования определяется главным образом доминирующим полюсом Х5,6. Поло
жим Tki = 0,125. Значения действительной и мнимой частей Xs.e, а также коэффициента относительного затухания в зависимости от коэффициента приведены в табл. 8.7.
Как видно из табл. 8.7, в наибольшей степени заданным требованиям к динамике контура демпфирования отвечает значение kK = 0,25.
Динамика контура стабилизации определяется действительным полюсом, порождаемым интегрирующим корректирующим устройством U7](s) и доминирующим полюсом %5,6 контура демпфирования. Из теории корневого годографа следует (см. гл. 5), что монотонность переходного процесса в таких системах обеспечивается при равенстве действительных частей этих полюсов. Как показывают расчеты, при значении = 3,18 доминирующие полюсы замкнутого контура стабилизации перегрузки имеют следующие значения:
Х7 = - 2,20; Х5>6 = - 2,19 ± /2,75.
Реакция системы иа ступенчатое воздействие по перегрузке в номинальном режиме полета при выбранных параметрах корректирующих устройств показана на рис. 8.36. Там же показаны переходные процессы при единичном воздействии для других режимов полета (кривые 1—3). При этом видно, что реакция системы на различных режимах полета при постоянной коррекции существенно отличается как по длительности переходных процессов, так и по величине перерегулирования.
Таблица 8.7
Параметры корневого годографа контура стабилизации самолета
Re Х5,6 Im Л5 6 S
0,05 -1,44 4,48 0,32
0,1 — 1,87 4,41 0,39
0,2 -2,74 4,11 0,55
0,25 -3,14 3,85 0,63
0,30 -3,48 3,53 0,70
604
Рис. 8.38, График зависимости ^шах (JB)Amln(P) ОТ параметра k для эталонной модели 3-го порядка
Рнс. 8.36. Переходные процессы в контуре стабилизации без самонастройки для различных режимов полета (кривые /—3)
Произведем теперь расчет контура самонастройки в соответствии с изложенной выше методикой. С целью упрощения закона самонастройки рассмотрим применение эталонных моделей 3-го и 4-го по
рядков.
В структуре эталонной модели 3-го порядка (рис. 8.37) учтены лишь динамика самого самолета и коррекция в прямой цепи (доминирующие полюсы основного контура).
Уравнения эталонной модели будут иметь' вид
//iM = ai,yiM + ai2i/2M;
^2м “ H-a23*iTi +
+ (а22 — Oi3ki) у1}л + Я2зУзм]; ^М = *(%3-У1М).
(8.153)
Подставляя параметры номинального режима, перепишем систему (8.153) в векторно-матричной форме
+ <8-154)
где I'm == (У1м, У2 ’ Уз)’ Вм = (°; °; 3,18); МММ
значение. Вычислим матрицу Р в соответствии с формулой (8.149). Умножая собственный вектор Ам, соответствующий действительному собственному значению, иа коэффициент k, получим множество матриц Р. Для каждой из них вычислим Хт.х(Р)/Хт1п(Р). График зависимости этого отношения от k показан иа рис. 8.38. Минимальное отношение A.m>x(P)Amin(P) получим при k = 1. Соответствующая матрица
[ 459,25 35,21 -205,16 -х
35,21 10,88 —15,82 I
-205,16 -15,82 112,55 -1
Если вектор, определяющий место приложения дополнительного управления &т=. = (0,1,0), то гиперплоскость переключения
а = 3,521^! + 1.088В2 - 1,582е7,
а закон управления в соответствии с формулой (8.148)
т = (8,156 | et | 4- 0,5121 ег | + 3,64 | е7 | +
+ 8,688 | ух | + 1,4441 У21 + 12,931 У11) X
X sgn (3,521b, + 1,088в2 - 1,582в7). (8.155)
В законе управления (8.155) все коэффициенты = 0, так как ЛВ = 0 на всех режимах полета.
г -1
Ам = | -24,08 L -3,18
0,57
-3,27 О
° 1
10,13 О J
Матрица Ам имеет одно действительное и одно комплексно-сопряженное собственное
Рис. 8.37. Структурная схема эталонной модели 3-го порядка
Рис. 8.39. Переходные процессы в контуре стабилизации с эталонной моделью 3-го порядка для различных режимов полета, (кривые 1—3)
605
Рис. 8.40. Структурная схема эталонной модели 4-го порядка
раметров kt, k2 для эталонной модели 4-го порядка
Результаты моделирования самонастраивающейся системы стабилизации с включением в контур самонастройки эталонной модели 3-го порядка показаны на рис. 8.39. Сравнительный анализ приведенных переходных процессов с переходными процессами, представленными иа рис. 8.36, показывает, что введение контура самонастройки позволяет сблизить показатели качества переходных процессов на различных режимах полета в основном за счет уменьшения перерегулирования по перегрузке на режимах 1 и 2.
Рис. 8.42. Переходные процессы в контуре стабилизации с эталонной моделью 4-го порядка для различных режимов полета (кривые 1—3)
У/
Управляемая система
Рис. 8.43. Реализация нелинейного закона управления контура стабилизации самолета иа аналоговых элементах
Аналогичный расчет и исследования были проведены для эталонной модели 4-го порядка, где дополнительно была учтена динамика бустера (т. е. следующего по значимости доминирующего полюса). Структура эталонной модели контура стабилизации перегрузки показана на рис. 8.40.
Динамику модели можно описать системой дифференциальных уравнений
У1 = а 11У1 + 012У2»
Уг — a2tyi 4- аггУг + а23у3; (8.156) уз = — ^2а21 у— У1 — Л» (1 + Г 1°22) У 2 —
1 + кгТ1агз , 1 .
Те Уз + Т6 ^ = *(^3-^).
Матрица системы (8.156) имеет следую-
щее численное значение:
- -1 0,57 0 0 "
—34,47 -1,05 14,5 0
Ам = 10,77 -2,17 -14,53 10,0 •
-3,18 0 0 0 _
(8.157)
606
Два из ее собственных значений действительны, одно комплексно-сопряженное. Поэтому, умножая столбцы матрицы приведения к действительной канонической жорда-новой форме, порожденные двумя действительными собственными значениями Аи, соответственно на коэффициенты kx и ki, вычислим матрицу Р по формуле (8.149). В отличие от предыдущего варианта, минимум отношения Kmtx(P)IKmin(P) зависит от значений двух параметров kt и Уг2, а ие одного. Здесь й1 является множителем собственного вектора, соответствующего собственному значению, порождаемому динамикой интегрирующего корректирующего устройства, а й2 — множитель собственного вектора, соответствующего собственному значению, определяемому динамикой бустера. На рис. 8.41 в плоскости параметров kit kt построены кривые постоянного значения Xmax(P)/Xmln(P). Минимум этого отношения достигается при значениях параметров ki = 0,08 и ki = 0,8,
Матрица
" 8,58 0,87 -1,17 —0,72"
0,87 1,11 —0,28 —0,99
-1,17 -0,28 3,52 1,29 '
_—0,72 —0,99 1,29 1,31 _
Точка приложения дополнительного управления определяется в этом случае вектором
6Т = [0 0 1 0].
Следовательно, гиперплоскость переключения можно описать выражением
а = (-1,176! -0,28е2 +З,52е3 +1,29е7).
(8.158)
Обеспечивая существование скользящего режима иа гиперплоскости а — 0, закон формирования дополнительного управления для эталонной модели 4-го порядка можно представить в виде
т = (1,0921 в! | + 9,3241 ег | + 9,848 | е31 +
+ 11,6821 е71 + 0.8 | у, | + 0,105 |у2| +
+ 0,578 | уз |) sgn сг, (8.159) где а вычисляется из соотношения (8.158).
На рис. 8.42 приведены результаты моделирования системы стабилизации с контуром самонастройки, включающим эталонную модель 4-го порядка. Из сравиеиия с результатами моделирования системы стабилизации без самонастройки (рис. 8.36) и с контуром самонастройки, включающим эталонную модель 3-го порядка (рис. 8.39), видно, что использование контура самонастройки с эталонной моделью 4-го порядка существенно уменьшает степень колебательности и сокращает время протекания переходных процессов, приближая их к характеристике эталонной модели.
Реализация нелинейного закона управления системы стабилизации самолета показана на рис. 8.43, а значения параметров синтезированного контура стабилизации pi, Pei и приведены ниже.
Pl Р2 Рз Рт Pei Ре2 Рез Qei Pxt Рх2 Рхз Рхе
-1,17 -0,28 3,52 1,29 1,092 9,324 9,848 11,682 0,800 0,105 0,570 0
Предлагаемая на рис. 8.43 схема может быть реализована на управляющей ЭВМ.
РАЗДЕЛ III
СИНТЕЗ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Синтез САР состоит в выборе структуры и параметров систем регулирования объектами, которые в соответствии с заданными техническими условиями обеспечивают наиболее рациональные характеристики по запасам устойчивости, показателям качества и точности. Сложность решения данной проблемы заключается в том, что при проектировании систем необходимо учитывать множество дополнительных факторов: надежность функционирования, массу и габаритные размеры, стоимость, возможность работы при вибрации, в агрессивных средах, при значительных перепадах температуры и влажности.
Задачу синтеза можно решить двумя методами:
если известна только динамика объекта, то выбирают структуру и параметры регулятора или следящей системы;
если одновременно с объектом заданы структура регулятора (следящей системы) и динамические характеристики привода исполнительных устройств (неизменяемая часть), то в этом случае находят усилительные и корректирующие устройства системы.
На выбор регулятора или неизменяемой части систем оказывают значительное влияние типы сигналов управления и возмущения (регулярные, случайные и их взаимные комбинации). При этом приходится учитывать не только форму самих сигналов, но и диапазоны их изменения. Для упрощения решения задач синтеза стараются отделить ре
гулярную составляющую от случайной путем подачи их на различные сравнивающие и суммирующие элементы.
В непрерывных САР используют, как правило, корректирующие устройства, создаваемые на базе RC-цепочек и дополнительных усилителей. При этом применяют несколько корректирующих устройств: последовательного, параллельного и последовательно-параллельного типов. Последовательные корректирующие устройства, вводимые в САР, вызывают повышение частоты среза системы, а следовательно, увеличение влияния случайных сигналов (флюктуаций и помех), и при их использовании требуются двигатели большой мощности для управления исполнительными органами. Параллельные корректирующие устройства, наоборот, снижают частоту среза САР и делают ее малочувствительной к флюктуациям и помехам. Корректирующие устройства данного типа уменьшают влияние нелинейностей во внутренних контурах системы. Однако их включение сокращает запасы устойчивости во внутренних контурах, что ухудшает надежность функционирования всей системы в целом. Для устранения этих недостатков применяют одновременно последовательное и параллельное корректирующие устройства.
В современных дискретных и дискретно-непрерывных САР средства формирования законов регулирования или корректирующих устройств реализуются в виде рабочих про
608
грамм на управляющих ЭВМ. Это позволяет не только упростить процесс отладки систем и запуска в постоянную эксплуатацию, но и обеспечить практически постоянство характеристик выходных сигналов без снижения точности. Выбор способа программирования зависит от типа ЭВМ, времени выполнения вычислений и значений погрешностей, накапливаемых вследствие ограниченности разрядной сетки вычислительной машины.
Первый метод синтеза осуществляют на основе принципа максимума или динамического программирования, и синтезируемые законы управления являются либо существенно нелинейными либо сводятся к рекуррентным вычислительным процедурам.
Второй метод синтеза реализуют выбором желаемых частотных ха
рактеристик, которые находятся по требованиям устойчивости, качества и точности, а также заданной неизменяемой части системы.
Оба эти метода в ряде случаев могут быть реализованы аналитически. Однако для большинства систем приходится прибегать к приближенным методам, выполняемым на универсальных ЭВМ. В силу громоздкости вычислительных процедур решения задач синтеза в последнее время стали применять интерактивный режим работы на ЭВМ, позволяющий проектировщику исследовать десятки различных структур систем и находить из них наилучшую. Для проверки правильности решения задач синтеза необходимо использовать способы сквозного моделирования САР, приведенных в гл. 12.
Глава 9
СИНТЕЗ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
ПРИ РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
В гл. 8 рассмотрены методы проектирования САР с заданной структурой, когда можно изменять лишь типы усилительных и корректирующих устройств. При этом место их включения заранее определено, а расчетно-теоретическая работа проектировщика связана с выбором схем усилительных, корректирующих устройств и их параметров, с помощью которых полностью обеспечивается выполнение заданных технических условий. Такой подход к исследованию САР даже с типовыми наборами устройств приводит не только к значительным затратам времени, но и различным техническим решениям. Определение наилучшего из них требует высокой квалификации проектировщика.
С целью устранения данного недостатка применяют методы синтеза, связанные с построением желае
мых логарифмических амплитудных и фазовых частотных характеристик линейных систем по основным показателям качества и точности регулирования. Наряду с желаемыми характеристиками проектировщик должен располагать логарифмическими амплитудными и фазовыми частотными характеристиками неизменяемой части системы. В зависимости от вида структурной схемы неизменяемой части системы проектировщик выбирает наиболее простой способ включения корректирующих устройств последовательного или параллельного действия. Если при этом не удается обеспечить выполнение технических условий, то используют последовательно-параллельное корректирующее устройство.
На построение желаемых характеристик большое влияние оказы
20 Ю. И. Толчеев
609
вает вид управляющего и возмущающего воздействий. При поступлении на вход САР регулярных сигналов проектировщик находит такой тип желаемой характеристики, когда удается получить наиболее точное воспроизведение управляющего сигнала за установленное время с заданным максимумом перерегулирования, а сигнал возмущения подавляется системой и не оказывает влияния на ее точность. При поступлении на вход системы регулярного и случайного сигналов в виде помехи необходимо выбирать такую желаемую характеристику, при которой управляющий сигнал воспроизводится с заданной точностью, а сигнал помехи практически не оказывает влияния на поведение САР. В этом случае отработка управляющего сигнала также должна воспроизводиться за указанное в технических условиях время.
1. ПОСТАНОВИ А ЗАДАЧИ СИНТЕЗА СИСГ Е V. Р С ГУЛ И РОВ А Н И Я, ОСНОВАННАЯ НА ЧАСТОТНЫХ МЕТОДАХ
В настоящее время существует несколько различных постановок задач синтеза. Ниже будут рассмотрены лишь те из них, которые получили наибольшее распространение при проектировании. При действии на систему регулярных сигналов применяют графические способы синтеза.
Первый способ, когда управляющий сигнал описывается медленно меняющейся функцией времени, а сигнал возмущения отсутствует. В этом случае задачу синтеза САР выполняют в следующем порядке:
1) по техническим условиям для заданного объекта выбирают регулирующий орган с силовым приводом, усилитель мощности и датчики, а затем, соединяя все устройства линиями связей, формируют неизменяемую часть системы;
2) по статическим и динамическим характеристикам устройств со
ставляют передаточные функции отдельных элементов, в результате чего получают структурную схему, в которой проектировщик находит места включений корректирующих устройств (последовательное, параллельное, последовательно-параллельное) ;
3) по заданным требованиям на запасы устойчивости по фазам, модулям, а следовательно, показателям качества и точности строят желаемые логарифмические амплитудные и фазовые * частотные характеристики всей разомкнутой системы;
4) по построенным желаемым и логарифмическим характеристикам неизменяемой части системы определяют коэффициенты усиления дополнительно вводимых усилителей, а также тип и параметры корректирующих устройств.
В результате выполнения этих процедур составляют полную структурную схему замкнутой САР с передаточными функциями отдельных ее устройств и вычисляют основные параметры системы. Если они удовлетворяют техническим условиям, то на этом расчетно-теоретическое проектирование САР заканчивается; в противном случае необходимо изменить параметры корректирующих устройств, что позволяет обеспечивать наиболее точное воспроизведение управляющего сигнала.
Второй способ, когда на систему действует возмущение, описываемое в форме прямого преобразования Лапласа. Тогда задачу синтеза выполняют аналогично первому способу, только синтезируемые параметры должны обеспечивать наиболее полное подавление возмущения при минимальном значении ошибки в системе.
Третий способ, когда на САР действуют управляющий и возмущающий сигналы одновременно. В этом случае синтезируемая система должна наиболее точно воспроизводить
* Фазовую характеристику строят только в районе частоты среза.
610
управляющий сигнал с максимально возможным уменьшением влияния возмущения. Последовательность синтеза 1—4 не изменяется.
Последовательные корректирующие устройства достаточно просты, ио их включение всегда приводит к увеличению частоты среза, а следовательно, и полосы пропускания системы ып, т. е. когда |Ф(/<оп) | = 1. При этом приходится применять более быстродействующие приводы, потребляющие значительные мощности. Параллельные корректирующие устройства являются более сложными, но они сужают полосу пропускания. В сложных САР обычно применяют как параллельные, так и последовательные корректирующие устройства, которые рассмотрены в п. 5 данной главы.
При действии полезного сигнала управления н сигнала шума в виде помехи возможно несколько различ: ных способов постановки задач синтеза. Сформулируем задачу синтеза на основе критерия минимума интегральной ошибки при заданном времени протекания переходного процесса. Необходимо выбрать структуру и параметры системы таким образом, чтобы обеспечить минимальную среднюю квадратическую ошибку от действия сигнала помехи при заданных технических условиях коэффициентов ошибки Со, Cj, Сг, ... (или точности воспроизведения полезных сигналов) за время tp отработки единичного воздействия £[1] [13].
Наиболее просто данный метод можно реализовать с помощью импульсной переходной функции £(т) (см. п. 9, гл. 1). Тогда прн поступлении на вход системы управляющего сигнала g(t) и помехи n(t) напишем интегральное выражение для сигнала на выходе системы
*р
х (О = [g (/ — г) + п (t — г)] k (г) dx. о
(9.1)
Ее точность определяется ошибкой от регулярной
zp
ев (0 = g(0 — J g (! — *) k (г) dx (9.2) о
и случайной
*р
еп (/) = п (t — т) k (г) dx (9.3)
о
составляющих.
Разложив функцию eg(t — х) в ряд и подставив ее в формулу (9.2), найдем
*р
8g(0 = g(0- $ g(t)k(x)dx +
0
<р 2 2
+$ x^k^dx~\iSk^dx+ •••
о о
О
(9.4)
В соответствии с формулой (6.17) и выражением (9.4) запишем
fp *р
Со = 1 — (т) dx-, Ci = \)xk (т) dx;
о о
*р
С2 = — ^ x2k (х) dx; о
*р
= (— l)r+l xr k (г) dx. о
(9.5)
Значение квадрата ошибки от действия помехи получим из выражения
d; = Игл е
*р *р
( dA [n(/—T)6(t)]2dT.
Р -<р °
(9.6)
20*
611
Перепишем соотношение (9.6) в виде
*р fp
о2 = k (0 dt Rn(t — х) k (т) dx, о о
(9.7) откуда имеем [33]
Rn (/ — г) = lim -5J- X
<Р-*ОО ^‘Р
*р
X J n(X)rt(X + /-T)dX. (9.8) _/р
Найдем импульсную переходную функцию k(x), обращающую в минимум функцию и удовлетворяющую заданным условиям (9.5). Минимум выражения (9.7) определяется с помощью вариационного исчисления через функционал
J {k (/)} = а2 — 2у0Н0 — 2YiHj — • • •
••• 2упЦп, (9.9)
где щ, р.2..... pin—моменты им-
пульсной переходной функции, связанные с коэффициентами ошибок С г, уо> , Уп — неопределенные
множители Лагранжа.
Моменты Цг выражаются через функцию k(x) в виде
*р
trk (г) dx. (9.10) о
Подставляя соотношение (9.10) в (9.9), получим
(р
J [Л ® + Ыг (/)] = $ [Л(0 + о
*р
+ bk®]dt\ Rn{t-x)[k{x) + о
*р
+ АЛ (т)] dx — 2у0 [ k (t) +АЛ (/)] dt — о
*p
- 2У! J t [Л (0 + АЛ (/)] dt - ... 0
...-2Y„ J ПЛ(0 + ал(0И= о
fp fp
=/(Л)+2А £(/)d/^ Rn(t—x)k(x)dx+ о 0
*p fp
+ A2 j k (/) dt j Rn(t — x)k (x) dx — о 0
fp fp
— 2y0A j k (f) dt — 2yiA^ tk (t) dt + ...
о 0
fp
... + 2ynA J tnk (t)dt. (9.11) о
Для нахождения экстремума функционала (9.9)" приравниваем к нулю его первую производную
-^-[/(Л + АЛ)]|д_о = О. (9.12)
Тогда после подстановки выражения (9.11) в уравнение (9.12) найдем
fp r-fp
k (/) И Rn (t — т) k (т) dx — yo —
oJ Ц
— Yi^ — — YnH dt = 0, (9.13)
или
*p
Rn (t — t) k (t) dx = о
= Vo+W+-..+vZ. (9.14)
Решение уравнения (9.14) при различных значениях входных сигналов g(t), n(t) и коэффициентов ошибок позволяет по импульсной переходной функции находить формулу для вычисления частотной характеристики замкнутой системы
(9.15)
При W (ja>) — Н (ф) е/е <ш) из формулы (9.15) имеем
{[1 -/?(©)] л
rr _ j01а -S^W + S2^) . Н (ф) — 10 1g {[1 + ,
о, S (и)_______
В (ф) — arctg R (а>)1 R _ S2 •
(9.16)
612
Рис. 9.1. Номограмма для определения массы двигателей приводов САР в зависимости от номинальной мощности на их выходном валу:
—X — X---электрические; ——гидравлические;
— ----пневматические
Примеры синтеза САР при действии регулярного и случайного сигналов приведены в п. 3 и 4 настоящей главы.
2. ВЫБОР ПАРАМЕТРОВ
НЕИЗМЕНЯЕМОЙ ЧАСТИ СИСТЕМЫ
Параметры основных устройств неизменяемой части САР выбирают
на основании технических условий, в которых указываются: ошибки при отработке типовых регулярных воздействий; время протекания переходного процесса и максимум перерегулирования; момент инерции нагрузки, приведенный к выходному валу; скорость нарастания пусковой мощности; максимальное и минимальное значения скорости на выходном валу исполнительного органа. Иногда задается полоса пропускания синусоидального сигнала при максимально допустимой амплитуде. Кроме того, приводятся массогабаритные данные, надежность действия, стоимость и некоторые другие показатели.
Выбор типа двигателя для регулирующего органа. Одной из основных характеристик двигателя
Рис. 9.2. Номограмма для определения типов двигателей приводов САР в зависимости от скорости нарастания пусковой мощности и номинальной мощности иа их выходном валу:
——гидравлические;-------электрические с по-
лыми роторами; •••• — электрические с высокими значениями движущих моментов; —. электрические с дисковыми роторами; — -пнев-
матические; —X—X электрические с номинальными значениями движущих моментов
613
является зависимость его массы от номинальной мощности, снимаемой с вала. На рис. 9.1 приведена номограмма, связывающая эти значения для трех типов двигателей: электрических, гидравлических и пневматических. При этом видно, что наименьшую массу имеют гидравлические двигатели, а наибольшую — электрические, но последние самые простые в эксплуатации. Однако пневматические и гидравлические
двигатели начинают получать все более широкое распространение в САР ввиду их высокой надежности и малой массы.
Обычно во многих САР двигатели работают в реверсивном режиме. В этом случае определяющей характеристикой двигателя является скорость нарастания пусковой мощности Рк.
Если двигатель работает в стационарном режиме, то определяю-
Таблица 9J
Принципиальные схемы тиристорных и транзисторных усилителей -преобразователей для регулирования электродвигателей постоянного тока
Наименование
Принципиальная схема
Схема двойного моста с встречно -
1 параллельным соединением тиристоров
Схема с встречнопараллельным соединением тиристоров в виде трех-сразной звезды
Н- образное включение тиристоров с током циркуляции
614
Продолжение тадл 9.1
615
Продолжение табл. 9.1
7
Дифференциальная схема тиристорного преобразователя
8
Двунаправленная схема на транзисторах
Таблица 9-2
Принципиальные схемы тиристорных и транзисторных преобразователей для 'регулирования электродвигателей переменного тока
Наименование
Принципиальная схема
Схема тиристорного преобразователя с дросселями для управления асинхронным двухфазным двигателем с однофазным питанием
Li „ Lz
-------4I----------- эдв ---
Q \овг
'хк объекту регулирования
~иПг
о
2
Схема тиристорного преобразователя для управления асинхронным двухфазным двигателем с однофазным питанием
616
Продолжение табл. 91
Схема тиристорного преобразователя для управления асинхронным двухфазным двигателем с однофазным питанием
Схема тиристорного преобразователя для управления асинхронным двухфазным двигателем с трехфазным питанием
щей является номинальная мощность Поэтому на рис. 9.2 приведена номограмма, показывающая зависимость скорости нарастания пусковой мощности от номинальной мощности при различных постоянных времени двигателя ТЛ. Пользуясь рис. 9.2, можно установить, что наименьшей постоянной времени обладают электродвигатели с полыми или дисковыми роторами, но с мощностями, не превышающими 5—6 кВт. Кроме того, видно, что электродвигатели с высокими значениями крутящих моментов обладают постоянной времени в 50 раз меньшей, чем обычные электродвигатели (с номинальными значениями крутящих моментов). При больших мощностях применяются гидравлические двигатели.
Электродвигатели постоянного тока питаются от генераторов, элек-тромашинных, магнитных, тиристорных и транзисторных усилителей. Эти усилители должны обеспечивать изменение угловой скорости в широких диапазонах с возможностью реверсирования.
В табл. 9.1 приведены принципиальные схемы тиристорных и транзисторных усилителей-преобразователей для регулирования угловой скорости вала электродвигателей постоянного тока с питанием от переменного (однофазного и трехфазного) и постоянного тока.
Схемы тиристорных и транзисторных усилителей-преобразователей для регулирования угловой скорости вала электродвигателей переменного тока с питанием от пе-
617
Таблица 9.3
Принципиальные схемы тиристорных и транзисторных преобразователей для импульсного регулирования электродвигателей постоянного тока
ременного и постоянного тока даны питание электродвигателей постоян-в табл. 9.2. ного тока (табл. 9.3). В схемах с
Для уменьшения потребляемой импульсным питанием при малой мощности используют импульсное электромагнитной постоянной вре-
Таблица 9.4
Сравнительные данные устройств управления
Наименование агрегата Источник питания Относительная масса на единицу мощности или работы
Напряжение, В Рабочее давление, МПа
Тиристорно-транзисторный усилитель-пре- — 0,6—1,2 кг/кВт
образователь переменного тока Магнитный усилитель — 8—12 кг/кВт
Электромагнитный усилитель 110(220) — 40(30) кг/кВт
Генератор постоянного тока 110(220) — 50 (45) кг/кВт
Гидравлические помпы постоянной произ- — 19,6 (31,3) 18-24
воднтельностн с индивидуальным приводом Гидравлическая помпа переменной производительности с индивидуальным приводом — 19,6 (31,3) (14—16) кг/кВт 12-20 (10—16) кг/кВт 1,2 иг/кДж
Гидравлический аккумулятор цилиндрической формы объемом 10 л — 19,6
0,8 кг/кДж
Гидравлический аккумулятор сферической — 19,6
формы объемом 10 л Пневматический компрессор 27,4 28—32 кг/кВт
Пневматический аккумулятор объемом 10 л — 19,6 0,8 кг/кДж
618
Таблица 9.5
Параметры передаточной функции W (s) =———---------3-------г-
s (Лд5 + "Ь О для электрических, гидравлических н пневматических двигателей
Тип двигателя Параметры Наименование параметров
Электрический k — k* Д Ra^v "1" Гд=а/ Л V Rakv + kMke Raln + RakvTg JnRaTg (Ra^v + ^м^е) kK — моментная постоянная электродвигателя; Ra — сумма сопротивлений обмоток якоря электродвигателя, соединительных проводов и выходной цепи ЭМУ; kv — коэффициент вязкого трения; ke — постоянная противоЭДС; In — приведенный к валу электродвигателя момент инерции вращающихся частей и исполнительного механизма; Т g= LaIRa — электромагнитная постоянная якоря; Ra — омическое сопротивление якоря; Еа — индуктивность якоря
Гидравлический
Лп^гд
*?д + kwky
JnkyE +
2^/vEJ^k^ + k^y)
Пневматический
*по ** ““ *по
kn — постоянная гидравлической помпы;
йГд— постоянная двигателя;
kw — коэффициент жидкостно-» го треиия;
ky — коэффициент, характеризующий утечкн гидравлического привода;
V — объем рабочей жидкости в цилиндре прн нормальном давлении;
Е — модуль объемной упругости;
1П — приведенный к валу двигателя момент инерции всех вращающихся частей
Рю» Рго — установившееся давление в первой и второй полостях силового цилиндра;
ро — давление воздуха в резервуаре;
ра давление в окружающей среде;
лпо — величина перемещения поршня;
£—-длина силового цилиндра за вычетом толщины поршня;
619
Продолжение табл. 9.5
Тип двигателя Параметры Наименование параметров
Пневматический у _* / ^ПО (£ ^по) '! [геР10 (£—хпо) + ир20*по] ПР'0 — *по) гаР20*ПО 2 ^F„mxn0 (£ — Хпо) п —• показатель политропы; Ль Аг — постоянные привода; Fn—площадь поршня; tn — масса поршня, штока и подвижных частей исполнительного механизма; kv — постоянная скоростного трения привода
мени возникают колебания крутящего момента; поэтому приходится вводить дополнительные индуктивности и подавать большие значения напряжений питания.
Необходимо отметить, что устройства, применяемые для управления двигателями, имеют большую массу, которая может превышать массу привода. Поэтому при выборе типа привода приходится это учитывать. В табл. 9.4 приведены относительные массы на единицу мощности или единицу работы различных устройств управления.
Пример 9.1. Определить тип и основные параметры двигателя регулирующего органа САР, если номинальная мощность на выходном валу == 1 кВт, скорость нарастания пусковой мощности Ри — = 100 кВт/с, а постоянная времени Гд = = 4 мс. Масса двигателя не должна превышать 10 кг.
Из номограммы рис. 9.1 и 9.2 находим, что в этом случае следует выбирать электродвигатель с дисковым ротором.
Пример 9.2. Определить тип и основные параметры двигателя регулирующего органа САР, если номинальная мощность на выходном валу = 100 кВт, скорость нарастания пусковой мощности Рм = = 550 кВт/с, а постоянная времени Та = = 10 мс. Масса двигателя не должна превышать 30 кг.
Из номограммы рнс. 9.1 и 9.2 находим, что в этом случае следует выбирать гидравлический двигатель.
Для определения параметров передаточной функции электрических, гидравлических и пневматических двигателей можно воспользоваться табл. 9.5.
Учитывая, что £д > 1, передаточную функцию двигателей можно представить в виде
где
гр £ц.
7 Д2-----р-г.— •
5д +1
Пример 9.3. Определить передаточную функцию электродвигателя, если R, = = 0,8 Ом; k„ = 2,4-10-‘ Н-с/рад; £а = = 200 мкГн; *м = 0,11 Н/А; ke = = 0,125 В-с/рад и 7П = 0,036 Н-м-с2.
Пользуясь данными табл. 9.5 и формулой (9.17), получим
О
W (s) = s (0,1s + 1) (0,005s + 1) (9J8)
Для Гд = 0,1 сн Wh = 10 кВт из номограммы рис. 9.2 найдем, что Рм = = 50 кВт/с. Это соответствует электродвигателю постоянного тока с высокими значениями крутящих моментов.
Выбор механической передачи. Исполнительный орган часто приводится в движение через редукторы с оптимальным передаточным отношением
1ропт = V^h/Л’ (9.19)
где /н — момент инерции регулирующего органа или объекта управления; /д — момент инерции якоря электродвигателя.
620
Рис. 9.3. Синтез САР с астатизмом I-го порядка с последовательным корректирующим устройством:
а—логарифмические амплитудные и фазовые частотные характеристики разомкнутой системы с о>с1—22 с-1; б—логарифмическая амплитудная частотная характеристика корректирующего устрой
ства Як; в—реализация корректирующего устройства; а—логарифмические амплитудные и фазовые частотные характеристики разомкнутой системы с а>с»8с~Ч б—логарифмическая амплитудная частотней характеристика корректирующего устройства Як; в—реализация корректирующего устройства
621
Привод будет согласован с нагрузкой при следующих номинальных параметрах:
Л4Я = 2ет •у//н/д,
Ги = 2(отет/и, (9.20) где Ищ, ет — соответственно максимальные угловые скорость и ускорение выходного вала.
Пример 9.4. Определить оптимальное передаточное соотношение механического редуктора, если моменты инерции нагрузки /„ = 3,6104 Нм-с2 и /д= 0,036 Н-м-с2.
Из формулы (9.19) получим = 1000.
**опт
Построим логарифмическую амплитудную частотную характеристику неизменяемой части системы, обладающей астатизмом 1-го порядка, пользуясь числовыми значениями, приведенными в примере 9.3. Проведем штриховой линией через точку ш = 1 с-1 штриховую прямую (рис. 9.3, а) с наклоном —20 дБ/дек до вертикали, проходящей через ©Hi = 1/ТД1 = 10 с-1. Далее наклон амплитудной характеристики изменяется н становится равным —40 дБ/дек до вертикали, проходящей через <0н2 — 1/Тт = 80 с-1 *. От ЧаСТОТЫ (0„2 ДО (ОнЗ = 1 / Тщ = — 200 с-1 наклон этой характеристики составляет —60 дБ/дек, а на заключительном участке —80 дБ/дек.
3. ПОСТРОЕНИЕ ЖЕЛАЕМЫХ АМПЛИТУДНОЙ И ФАЗОВОЙ ЧАСТОТНЫХ ХАРАКТЕРИСТИК РАЗОМКНУТЫХ СИСТЕМ
Построение желаемых амплитудной и фазовой частотных характеристик при действии регулярных сигналов производят по коэффициентам ошибок (добротностей) и основным показателям качества линейной системы. Из гл. 6 следует, что низкочастотная часть логарифмической амплитудной характеристики обусловливает точность рабо-
* Постоянная времени Тт = 0,0125 с определяется инерционностью усилителя мощности.
ты системы при отработке медленно меняющихся сигналов управления в установившемся состоянии и определяется коэффициентами ошибок* Со=1/(1 + Л), Cx = llDa, C2 = 2/De, C3 = 6/Dt, C< = 24/Dt.
Будем считать, что низкочастотный диапазон заключен в пределах ио < и < (On. Тогда для нахождения нижней границы по частоте а»п можно воспользоваться номограммами /?((о) рнс. 5.17 н 5(<в)— рис. 5.18. Обозначая ошибку на номограммах через А, получим
11 -/?((о)|<Д; )
IQMKA. } (9'21>
Из неравенств (9.21) и номограмм рис. 5.17 и 5.18 получим границу (On на логарифмической амплитудной характеристике разомкнутой системы при погрешности вычислений А = 5 %. Для этого воспользуемся соотношением
Lm = 201g|U7(»l>
>201g4- = 26 дБ. (9.22)
На полулогарифмической бумаге построим желаемую логарифмическую амплитудную частотную характеристику Нж первой системы с астатизмом 1-го порядка при заданных значениях добротностей Дш = = 100 с-1 и = 81 с-2. Из точки (Ок = Да» расположенной на оси частот (рис. 9.3, а), проведем прямую 1 с наклоном —20 дБ/дек, а затем из точки (oz = д/Д е = 9 с'1 прямую 2 с наклоном —40 дБ/дек до пересечения с прямой 1 в точке А. Нижняя граница (оп находится по точке В пересечения прямой 3 с вертикалью 4.
Зададимся положительным запасом устойчивости по модулю **
* Коэффициенты ошибок больше не оказывают существенного влияния на точность САР, и их можно не учитывать при практических расчетах.
** Запасы устойчивости по модулям + Ям, — Ям и по фазе уф часто указываются в технических условиях.
622
0,5
0
tp,C (
5л/шс - -
4,33 Л/to, 1-
4л/ыс-'?0
-40 Зп/шс -А-
-30-
2^120
60
*/ыс'-10
0 --------I—
7,0 7,7
tn,С 6^,,% Т60
-50_____
о)
37t/wc -
Рис. 9.4. Номограммы качества Солодовникова для определения частоты среза системы по ат и tp:
а—вещественная частотная характеристика R (0); б—для астатических систем 1»го порядка; s—для статических систем
-30
2л/ш,--
с -20
Чл/шс-
-40
л/шс-_ 7,2
R
4-Нм—16 дБ (точка С на рис. 9.3, а). Проведя через точку С прямую 5 с наклоном * —20 дБ/дек, получим частоту среза wci = 22 с-1. Пусть отрицательный запас устойчивости —Нм. = —14 дБ. В этом случае вертикальная прямая 6 пересекает прямую 5 в точке F, что соответствует частоте ыт. Таким образом определен диапазон, среднечастотной характеристики, который находится в пределах оп < со < сот.
Существует и другой способ нахождения частоты среза по показателям качества om, tp с помощью обобщенных номограмм Солодовникова [13], приведенных на рис. 9.4,6 и в. При использовании этих номограмм по характеристике /?(со) ^0
* Как правило, в большинстве САР в диапазоне частот < со < сот, соответствующих запасам устойчивости по модулям, наклон желаемой логарифмической амплитудной частотной характеристики, проходящей через частоту среза, равен —20 дБ/дек (см. рис. 9.3,а и б). При наклоне —40 дБ/дек запасы устойчивости по фазе малы и не обеспечивают заданные показатели качества.
(рис. 9.4, а) определяются следующие значения параметров: х = = (0<с/(00» Xa = (Oa/tt>t>> X = (Ой/(Оо И Rm- В зависимости от этих параметров были вычислены семейства переходных процессов и найдены <jm и tp (рис. 9.4, бив).
Для определения частоты среза со с по от и tp составим эмпирическую формулу
<ос = kn)tp, (9.23) где коэффициенты k определяются по номограммам (рис. 9.4,6 и в). Номограмма на рис. 9.4, б построена для следующих параметров: х 0,8; ха 0,4 и % 0,5, а на
рис. 9.4, в при х 0,8; ха 0,4; 0,2 0,1 =^0,5.
Если От = 35 % и tp = 0,6 с, то, пользуясь номограммой (рис. 9.4,6), для системы с астатизмом 1-го порядка получим tp = 4,33 л/с0с2 или (ос2==4133 л/0,6 = 21,7 с-1. Через ©сг проведена прямая 7 с наклоном —20 дБ/дек. Как видно из рис.9.3, а, в этом случае запасы устойчивости изменяются мало и составляют Нм =15,6 дБ, —Нм = —14,6 дБ.
623
Таблица 9.6
Импульсные и передаточные функции замкнутой желаемой системы при действии ре
№ па Заданные коэффициенты ошибки Оптимальная импульсная переходная функция ft (О Оптимальная передаточная функция Ф(а)
1 Цо = 1 с, £о + W <0 1 О» о. 7 А> И 1 V -I4 1 + и 1 V 1
2 ц0= 1 С, с2 k0 + kit + kit2 + »д т" "Н А 1 ь= + п1 ик и /"‘""Ч и | — 1 с К с|-•о 1 1 1 г' г I 1 4 а X'~'Z +
3 Цо = 1 Ci ct Сз ko + kit + + kit2 + k3t3 О. "4 1 + t 1 _ -+ V ^-7 СО °* 1 1 Ъ 1 V 1 А. Ф «о Т Ч?* ’ 1 7 « а, 1 еч А CQ 1 *» Ф 1 —< | CQ ф • А. и а " ’« Ч—о. СО 4 иё - Т « а Д - 1 * 7 1 V «о 1 1 гм |« ° 60 ф сч j «о ; 1 о> «о |» J?l 03 + от « 4? «0
4 go=? 1 Ci cs С, c4 ^o+^l^+^*+ + k3t3 + ktt* + “ “* I*. «I*. f-s + ик t-" °о»| о> /—-X , ч « ~ Со] ЬЭ 1 ч 1 1 »| О’ й»| ю • ( ft 1 Со I ьэ 1 * тз 1 Н Л со I кэ f XJ w 10 1 <»! <1 + - а и к Л TJ СО S й. 1 1 | * «о* ✓—S хГ °. । Ч~ 1 Ч*- а. и к 1 v \ 1 » и1- ф 1 1 1 1 <» А .»“|Л -1 А и ♦*. 1 СО — _** тз «О *Э Ю 43 Л -о ~ 1 1 (Ь •Qb» 1 *• | *Q**W *О *• 1 0» *© 1 1 Ч—/ ХЗ 1 , I XJ "Г ч+*х
624
гулярного и случайного сигналов
Коэффициенты, входящие в выражение импульсное переходной (передаточной) функции, или уравнения для их определения
, 4 6С. Яо в ““ У" , 4 12С?! 12C?
t 1? р р 6 12С, ~р + t3 р р c2 t t2 + t3 c fP ГР rp
9/2 - 36C.t> - 30С2 t, Р 1 Р 6 " ,3 ‘р -36fp + 192С^р + 180С2 === . , <4Р 30/2-- 180C,tD- 180С2 t5 Р 9t*-72Cit3 192C2f2-60C2<2 ~ 4 + + 360CiC2fp + 180C| 1 4
feo = 4- («Р - 30С/р - 60С2/р - 35С3), *р *1 = ТТ (“2/Р + 20С4 + 45С2'р + 28С3), ‘р k2 = 77 (4t® - 45С^ - 108С2/р - 70С3), ‘р *3 = -7г (- *р + i2Ctfp + 30C2fp + 20С3) fp -^= (16t® - 240C,<5 - 480C2fp4 -— 280C3<p 4- 1200C|f4 + 6480C|/p + + 2800C3 + 5400C1C2^ + ЗЗбОС^з^ + + 8400C2C3/p):^
k0 = 4 (5iP - 6001<р - 210C2<p ~ ХР - 280C3fp - 126C4), *1 = 7Г (~5fP + ^i'p + 316C2*P + lp + 448С3Гр + 210C4), k2 » ~ (5^ - 90C^ - 378C2<2 -tp - 560C3tp - 270C4), *3 == -Чп (~5tp + ^Ci'p + 420C2f* + tp + 640C3fp + 315C4), Й4”-^(^-20С^-90С2^- *p — l4OC3tp —70C4) ^- = (25<8-60C1;2-2100C4- - 1260C4f4 + 4800C|^ + 11 240C^4 + + 179 200C3fp + 44 100C* + 39 SOOCjC^® + + 53 760CiC3eJ + 252CjC4tp + + 235 200C2C3f| + 113 400C2C4^ + + 176 400C3C4fp): fp
625
Запасы устойчивости по модулям как в первом, так и во втором случае мало отличаются друг от друга.
Наиболее простую реализацию корректирующих устройств получим, когда наклоны желаемой характеристики в области высоких частот совпадают с наклонами неизменяемой части системы. На рис. 9.3, а от точки D, соответствующей частоте юз, желаемая характеристика 9 проведена через точки G и К параллельно неизменяемой характеристике 8. Если не требовать простоты реализации корректирующего устройства, то высокочастотную часть Нж можно строить в пределах <.’ < (О < оо.
По точкам излома логарифмической амплитудной характеристики выведена формула для вычисления желаемой фазовой характеристики
0iB((O) = _9O»-arctg-^ +
+ arctg^-arctg-J-
~arct^~arct^' <9-24>
Пользуясь этой формулой, найдем числовые значения 0ж((о), по которым построена на рис. 9.3, а жирной штриховой линией 10 логарифмическая фазовая характеристика.
В результате определим истинные запасы устойчивости +77м — —Hw = —10 дБ (точка Е на рис. 9.3, а) и ?ф= 38°.
Для проверки правильности нахождения запасов устойчивости по фазам и модулям и соответствующим им основным показателям качества и точности воспользуемся номограммой, приведенной на рис. 5.55. Откуда следует, что +#м = оо; —77м = —10,5 дБ; Уф = 39°; ат = = 32 %; /р = 0,58 с; = 100 С"1. Оба метода дают хорошее совпадение основных характеристик проектируемой САР.
На рис. 9.3, г построена желаемая характеристика системы с астатизмом 1-го порядка для 7)м = 100 с-1 и De = 48 с-2. Откуда следует, что
Юк= 100 с-1, а ьц = 4,5 с-1. Частота среза (Ос находится по номограмме (рис. 9.4,6) для от = 15 % и tp == 0,98 с, (Ос = 2,5 л/0,98 = 8 с-1. Через (Ос проведена прямая с наклоном —20 дБ/дек до вертикали, проходящей через точку А, соответствующую частоте а>з- Остальная часть желаемой логарифмической амплитудной характеристики строится аналогично кривой Нж, приведенной на рис. 9.3, а.
Для нахождения запаса устойчивости по фазе и модулю запишем следующее выражение:
0Ж ((о) = -90° -2 arctg -£- + (01
+2arcts-£--arctg-^-
“arctei~arcts-£r- (9-25)
Подставив значения (о, близкие к частоте среза, построим кривую (рис. 9.3, г), по которой найдем Уф = 54° и —77м = —22 дБ.
Для построения желаемой характеристики на основе критерия минимума интегральной ошибки при действии регулярного сигнала и случайного сигнала в виде белого шума с интенсивностью с2 воспользуемся табл. 9.6 и формулами (9.15), (9.16).,
Если на САР действуют одновременно полезный сигнал и помеха в виде белого шума с. интенсивностью с2, то интегральное уравнение (9.14) можно представить в виде
с2 S (t — т) k (т) <7т = о
— Yo + Yi^ + • • • + Уп1п- (9.26)
С помощью свертки дельта-функции получим
ОО
J /(т) 6(7-т) (7т = /(/). (9.27) — оо
Имея в виду выражения (9.26), (9.27), запишем
c2k (0 = Yo + Y17 + • + yZ- (9-28)
626
Зиая закон изменения управляющего воздействия g(t), из уравнения (9.28) можно получить импульсную переходную функциюk(t), а по ней найти передаточную функцию Ф(«) замкнутой системы.
Пример 9.5. Определить желаемую амплитудную частотную характеристику разомкнутой САР при g(f) = go + git + + gtt2 (go = 2 рад; gt = 0,2 рад/с; g2 = «= 0,1 рад/с2) и сигнале помехи в виде белого шума с интенсивностью с2 = 0,6 X X Ю-6 рад2 с.
В рассматриваемом случае k(t) — ko + + kit + kit2, что соответствует п. 2, табл. 9.6. Подставив числовые значения /Р = 1 с; Ci = 0,005 с и С2 = 0,02 с2 в эту таблицу, найдем
1 г 41 44
ф (S) = — 18,22 + 22,22e-s — -
s L
(9.29)
Заменив в выражении (9.29) s на /со, определим вещественную /?(<о) и мнимую S(o>) частотные характеристики замкнутой системы. По формулам (9.16) построим Нж(<£>) и 0ж(со), показанные на рис. 9.5, а.
Как видно, в области средних и высоких частот наблюдаются колебания амплитудной и фазовой характеристик, которые будем аппроксимировать штриховыми линиями. Следует отметить, что амплитудная характеристика в области высоких частот проводится в соответствии с логарифмической частотной характеристикой п„(а>) неизменяемой части. Из рис. 9.5, а видно, что система обладает астатизмом 1-го порядка и имеет запасы устойчивости по фазе Уф = 65° и модулю = оо и —Ям = —20 дБ. Это позволяет синтезировать параллельное корректирующее устройство (см. пример 9.9).
4. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ
И ПАРАЛЛЕЛЬНЫХ
КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
Если в САР имеется последовательное корректирующее устройство, то ее желаемую передаточную функцию можно представить в следующем виде:
^ж(5)=1Гк(5)^и(Д (9.30)
откуда при s = /со имеем логарифмические амплитудную
ЯК(®) = ЯЖ(®)-ЯИ(®) (9.31) и фазовую
ек(®)=0ж(®)-0и(®) (9.32)
частотные характеристики.
Рис. 9.5. Синтез следящей системы при одновременном действии регулярного сигнала и сигнала помехи в виде белого шума: а—логарифмические частотные характеристики; б—реализация корректирующего устройства
627
Рис. 9.6. Принципиальная схема двухканальной следящей системы с последовательным корректирующим устройством
Подняв неизменяемую логарифмическую амплитудную характеристику до уровня желаемой и построив фазовую частотную характеристику 0ж(ю), определим запасы устойчивости системы по фазе и модулю. Если они соответствуют требованиям технических условий, то, пользуясь выражением (9.31), получим логарифмическую амплитудную характеристику последовательного корректирующего устройства.
Пример 9.6. Синтезировать двухканальную следящую систему, принципиальная схема которой приведена на рис. 9.6, и
подобрать последовательное корректирующее устройство. Как видно из рис. 9.6, система состоит из сельсинов грубых 1, 4 и точных 3, 6 каналов. Причем роторы сельсинов точного канала вращаются через редукторы 2, 5 с передаточным отношением 1 :31. Точный канал работает с малыми углами рассогласования е до 0,0695 рад, а грубый канал при е = = 6,284 рад при любой частоте вращения объекта регулирования. Переключение каналов осуществляется в электронном устройстве 7, на выходе которого включено последовательное корректирующее устройство 8. Через усилитель-преобразователь 9 сигнал поступает на тиристорный мост 11, питание которого осуществляется
Рис. 9.7. Структурные схемы неизменяемых частей систем:
а—с последовательной коррекцией; б» в—-с параллельной коррекцией; а—с параллельной коррекцией, преобразованной к расчетному виду
C(s)
1
1000
Xfs)
трехфазным током от блока 10. Тиристорный мост обеспечивает соответствующее изменение полярности питания якоря электродвигателя постоянного тока 13 с обмоткой возбуждения 12 при изменении направления вращения ротора сельсинов на входе системы. Объект регулирования приводится во вращение через редуктор 14, связанный механической связью с ротором сельсина грубого канала.
Для данной следящей системы на рис. 9.3, а жирной сплошной линией построена желаемая логарифмическая амплитудная характеристика Нж(а>). Неизменяемая часть системы приведена на рис. 9.7, а, где показано место включения последовательного корректирующего устройства. Поднимем характеристику Ни(ш) (тонкая сплошная линия на рис. 9.3, а) до уровня желаемой Нж(а>). На рис. 9.3,6 построена логарифмическая амплитудная характеристика корректирующего устройства Якп(о), полученная по формуле (9.31). Реализация этого корректирующего устройства в виде RC-четырехполюсника (рис. 9.3, в) взята из табл. 9.7, № 72.
На рис. 9.3, д построена логарифмическая амплитудная характеристика /fK0(a>) последовательного корректирующего устройства, полученная с помощью желаемой амплитудной характеристики другого типа (рис. 9.3,г). Реализация корректирующего устройства в этом случае показана на рис. 9.3, е, из которого видно, что схема состоит из двух RC-четырехполюсников, соединенных через катодный повторитель для исключения их взаимного влияния. Оба четырехполюсника приведены в табл. 9.7, № 49 н 72.
Рассмотрим синтез САР с параллельным корректирующим устройством. Запишем передаточную функцию системы в виде
(s) = i + }Wk (s) • (9.33)
При условии, что |IFh(/(o)X X WK (j®) | 1, из выражения (9.33)
имеем | WK | = 1/1|, или
(«О = -#»(«>), (9.34)
где //ж (со)—желаемая логарифмическая амплитудная характеристика синтезируемой системы.
Для обеспечения требуемого порядка астатизма проектируемой системы необходимо, чтобы порядок нуля передаточной функции W'k(s) был не ниже порядка полюса IFH(s) при s = 0 [13].
Рис. 9.8. Принципиальная схема двухканальной следящей системы с параллельным корректирующим устройством
Рассмотрим несколько примеров синтеза параллельных корректирующих устройств, сначала при действии регулярных, а затем случайных воздействий.
Пример 9.7. Определить параметры следящей системы с параллельным корректирующим устройством. На рис. 9.8 изображена принципиальная схема двухканальной
629
Рис. 9.9. Синтез следящей системы при действии регулярного сигнала: а—логарифмические частотные характеристики; б—реализация корректирующего устройства следящей системы с магнитным усилителем. Измерительная часть системы состоит из сельсинов-датчиков 4, 6 н сельсинов-приемников 2, 3. Так как система двухканальная, то роторы сельсинов точного канала 6, 3 вращаются в 31 раз быстрее роторов сельсинов грубого канала 4, 2. Для этого применены два редуктора 1 и 5. Сигналы с роторов сельсинов-приемников грубого и точного каналов поступают через переключающее устройство 7. Тогда на магнитный усилитель 8 поступает сигнал либо с грубого, либо с точного канала. На выходе магнитного усилителя включены две обмотки возбуждения 9 электродвигателя постоянного тока 11. Электродвигатель приводит во вращение через редуктор 12 объект регулирования и роторы сельсинов-приемииков. Для получения требуемых за
пасов устойчивости, показателей качества и точности в систему введено параллельное корректирующее устройство тахометрического типа 10. Необходимо построить желаемую характеристику системы и выбрать параметры корректирующего устройства и коэффициент усиления усилителя.
На рис. 9.9, а построена желаемая логарифмическая амплитудная частотная характеристика Нж при коэффициентах добротности Дш==<ок= 100 с-1 и Ое = 0[ = = 81 с-2. Далее по числовым значениям ст и tv находим по ранее приведенной мето-
Рис. 9.10. Структура системы стабилизации с параллельным корректирующим устройством при возмущающем воздействии f(t): а—упрощенная схема (/—измерительное устройство; 2—усилительное устройство; 3—гидравлический привод; 4—датчик обратной связи; 5—исполнительный орган; б—объект регулирования; 7—датчик напряжения; а—RC-фильтр); б—вид сигнала возмущения (/ — участок постоянного уровня; 2 — кривая снижения до уровня 0,5 при 1 = 3 с)
630
дике частоту среза Ыс = 22,5 с-1
(рис. 9.4,6). Логарифмическаи амплитуд-иаи частотнаи характеристика Н„, по-строеииаи иа основе рис. 9.7, б, показана штриховой линией иа рис. 9.9, а. Пользуясь этой характеристикой, достраиваем Яж. Фазовая частотная характеристика 0Ж (в районе частоты среза) изображена на рис. 9.9, а жирной штриховой линией. При этом видно, что Уф = 38°, —Ям = = —10 дБ. Для определении параметров корректирующего устройства и коэффициента усиления усилителя построены характеристика Як и сумма Як + Я„ при А = 1. Соответствующая ей фазовая частотная характеристика в районе частот среза внутреннего контура <осн и <0с« показана на рис. 9.9, а штриховой линией. Откуда видно, что для обеспечения запасов по фазе уфи = 95° и Уфв = 60° необходимо поднять характеристику Я» + Ян до уровня kKK = 4 при <о = 1 с-1.
Коэффициент усиления магнитного усилителя по напряжению определяется из следующего соотношения: 1700 8йму = = 100 или йму — 7,4. Передаточный коэффициент корректирующего устройства иа-
Рис. 9.11. Синтез системы автоматической стабилизации:
а—логарифмические частотные характеристики; б—логарифмическая амплитудная характеристика корректирующего устройства Як; в—реализация корректирующего устройства
ходим с помощью соотношения kKkH = kHKl. где kH = 100, knK = 4, a kK = 0,04.
Реализуем параллельное корректирующее устройство с помощью табл. 9.7 в виде RC-четырехполюсиика, состоящего из трех устройств: тахометрического моста
(табл. 9.7, № 39), усилителя с ky = 10 и фазоопережающего RC-фильтра (табл. 9.7, № 1). Принципиальная схема и параметры корректирующего устройства приведены иа рис.1 9.9,6.
Пример 9.8. Найти параметры системы автоматической стабилизации (рис. 9.10, а) и подобрать параллельное корректирующее устройство. Данная система должна отрабатывать возмущающее воздействие с малой ошибкой. На рис. 9.10, а приведены основные устройства системы, где штрих-пуиктириой линией выделен внутренний контур, состоящий из гидравлического привода, охваченного обратной связью.
631
а штриховой — корректирующее устройство с датчиком напряжения. Возмущающее воздействие при сбросе нагрузки показано иа рис. 9.10,6, где на участке 1 действует максимальная нагрузка, а на участке 2 она уменьшается по экспоненте наполовину за 2 с. Включение корректирующего устройства в систему показано иа рис. 9.7, в (штриховая линия).
При построении желаемой логарифмической амплитудной и частотной характеристик системы стабилизации, приведенной на рис. 9.11, а, примем, что установившаяся ошибка будет составлять 0,3 % от заданного значения возмущения. Низкочастотный участок логарифмической амплитудной частотной характеристики Нж с наклоном 0 дБ/дек доходит до Юц = = 0,125 с-1. Дальнейший участок Нж имеет наклон —20 дБ/дек, а его продолжение пересекает ось частот в точке = = 37,5 с~‘. Исходя из заданного времени протекания переходного процесса t9 — 1,3 с и значения ыс=25°, по номограммам определим частоту среза для Нж (рис. 9.4, в), равную Ыс — 10 с-1. Дальнейшее построение Нж выполним исходя из условия удовлетворения требуемых запасов по фазе Уф = 40е и модулю —Нм. = —12 дБ. Участок желаемой фазовой частотной характеристики в районе частоты среза 9Ж показан на рис. 9.11, а жирной штриховой линией, а логарифмическая амплитудная частотная характеристика неизменяемой части системы Ня — тонкой штриховой линией. Высокочастотный участок характеристики Нж совпадает с аналогичным участком Ня и имеет наклон —80 дБ/дек. Далее строим характеристику корректирующего устройства Як, обратную характеристике Нж в диапазоне амплитуд от +26 дБ до —26 дБ. Ее можно продолжить иа всю область частот от +оо до —оо, так как это практически не приводит к погрешности построения.
Включение корректирующего устройства с характеристикой Нк соответствует схеме, приведенной на рис. 9.7, г. Для выбора коэффициента передачи контура коррекции
строим характеристику Н'к + Нк и соответствующий участок фазовой частотной характеристики, которые обеспечивают запасы устойчивости по фазам иа иижиих Уфн = 120° и иа верхних Уфв = 50° ча-1 стотах. Приводя структурную схему к виду, показанному иа рис. 9.7, в, получим логарифмическую амплитудную частотную характеристику преобразованного корректирующего устройства, изображенную на рис. 9.11,6. Реализация схемы коррекции в виде RC-четырехполюсиика дана иа рис. 9.11, в, откуда видно, что четырехполюсник состоит из трех элементов: фазоопережающего RC-фильтра (табл. 9.7, Xs 29), катодного повторителя с ky = 0,25 и фазозапаздывающего RC-фильтра (табл. 9.7, № 47).
Пример 9.9. Определить тип и параметры параллельного корректирующего устройства для системы, желаемая амплитудная частотная характеристика которой приведена в примере 9.5. На рис. 9.11,6 построена характеристика Нк- Реализация корректирующего устройства следищей системы (рис. 9.11, в) состоит из тахометрического моста (табл. 9.7, № 39), усилителя с коэффициентом усиления ky и фазоопережающего фильтра (табл. 9.7, № 1).
5. СИНТЕЗ
ПОСЛ ЕДОВАТЕЛ ЬНО-ПАРАЛЛ ЕЛ ЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
В сложных САР часто применяют последовательно-параллельные корректирующие устройства. Одна из наиболее распространенных структурных схем изображена на рис. 9.12, а. В нее входят последовательное корректирующее устройство с передаточной функцией №Кп (s) и параллельное корректирующее устройство с передаточной функцией №Knp(s). Передаточные функции,
Рис. 9.12. Структурные схемы САР с последовательно-параллельной коррекцией: а—исходная; б—преобразованная к расчетному виду
632
/!рчвог! зкг.центриковы» /ало!
Привоз барабанов
Рис. 9.13. Принципиальная схема системы регулирования летучими ножницами стоящие в прямой цепи, за исключением №Кп(з), образуют неизменяемую часть системы
ITH(S)=TFH(S)iry(S)TFo(S), (9.35) где AJ7H(s), Wy(s)—соответственно передаточные функции измерительных и усилительных устройств системы; Wo (s)—передаточная функция объекта регулирования.
Схему, показанную на рис. 9.12, а, преобразуем к виду, приведенному на рис. 9.12, б. Откуда нетрудно найти желаемую передаточную функцию искомой системы
т (s) Гкп (s) Гу (s) Го (s)
ИГ Ж (S) —— — -
1 + Гу(5)Г0(5)Г'пр(5)
(9.36) где
Г . Гк пр («)
Wk пр (s) — Wo (s) • (9.37)
Воспользуемся сначала методикой синтеза параллельного корректи
рующего устройства, т. е.
KnP(s)=l/^»(s). (9.38)
Для построения логарифмической амплитудной частотной характеристики параллельного корректирующего устройства воспользуемся выражением (9.37). В этом случае можно записать
Нк пр (со) = Нк пр (со)- Но (®). (9.39)
При нахождении логарифмической амплитудной частотной характеристики последовательного корректирующего устройства, используя формулу (9.36), запишем
Якп И = Нж (со) — НИ (со) +
+ 201g 11 + Wy (/со) Wo (/со) Wk пр(/со) |.
(9.40)
Пример 9.10. Найти частотные характеристики САР универсальными летучими ножницами, производящими резание выходящего из прокатного стана листового металла на мерные длины ~2\ 4; 6; 8; 30 м со скоростями движения до 6 м/с [33]. В систему включены параллельные и
633
Рис. 9.14. Синтез подсистемы регулирования эксцентриковых валов летучих ножниц: а—логарифмические частотные характеристики; б—номограмма Никольса с нанесенной логарифмической амплитудно-фазовой характеристикой внутреннего разомкнутого контура; в—реализация параллельного корректирующего устройства; г—реализация последовательного корректирующего устройства
последовательные корректирующие устройства. Принципиальная схема системы показана на рис. 9.13. Она состоит из двух следящих подсистем для управления привода вращения барабанов и привода вращения эксцентриковых валов. Обе подсистемы не только синхронизируют скорости вращения выходных валов, но и обеспечивают строгое положение ножей, исключающее погрешности прн непрерывной подаче листового металла.
Лист металла поступает через подающие ролики к барабанам 1 с двумя режущими ножами. Барабаны приводятся во вращение через силовой редуктор Р\ от электродвигателя главного привода (ЭДв). Для синхронизации угловых скоростей подающих роликов и барабанов применены два встречно включенных тахогенератора ТГ\ и ТГ2. Переключение на мерные длины, начиная с 4 м, осуществляется четырехступенчатым кинематическим редуктором КР.
Рассмотрим более детально выбор параметров для подсистемы эксцентриковых валов. Барабаны установлены на эксцентриковых валах 2, которые приводятся во вращение от мощного электродвигателя 10 с независимой обмоткой возбуждения 11 через силовой редуктор 3. Якорь электродвигателя соединен с якорем генератора 12. Обмотка возбуждения 15, питается от электромашниного усилителя 16, кото-
634
Рис. 9.15. Логарифмические частотные характеристики корректирующих устройств: а— параллельного; б—последовательного
рый имеет обмотки возбуждения 17 и 18. Напряжение на эти обмоткн поступает от магнитного усилителя 9. В этой подсистеме для снихронизацин вращения эксцентриковых валов применено последовательное корректирующее устройство 14, в которое входят тахогенераторы 7Т3, ГГ4 и RC-фильтр. Синхронизация положение валов обеспечивается сельсинной схемой, состоящей из сельсина-датчика 8, дифференциального сельсина 7 и двух сельсинов-
приемников 4 и 5. Сигналы от сельсинов поступают на магнитный усилитель через мостовые выпрямители 6. Параллельное корректирующее устройство 13 включено между генератором 12 и магнитным усилителем 9. Статорные обмотки сельсинов-приемннков присоединяются к обмоткам сельсина-датчика через контакты Кз и К4,
Рис. 9.16. Логарифмические частотные характеристики для выбора параллельной коррекции:
а — для Я ; б—для внутреннего замкнутого контура
635
Типовые корректирующие устройства систем автоматического регулирования на постоянном токе
Тадлии.а 9Л
№ п/п Схема корректирующего устройства Передаточная функция (s) 1*0 г, Тг Асимптотическая логарифмическая амплитудная характеристика
Корректирующие устройства с опережением по (разе и наибольшим наклоном амплитудной характеристики 20 дв/дек
Lm,
1 С, ° 1 ° и, Я, иг wk(S)=^L = 2LL к ' Е, (s) T,s*t 0 1 EiC, — ДЬ 0 -20 2 0$ /д*. Т, — 4 т ш
Lm,
Продолжение main. 9.7
Продолжение main. 9.7
NS п/п Схема корректирующего устройства Передаточная функция W^Ts) Co ^•QO T, Tz Асимптотическая логарифмическая амплитудная характеристика
11 С, 1 11~1 * А и, Я/ 1иг ,,,, Ег{& , ris + f 1 Q? + „«ч 5S (Rz+RyiCf <м + Ст, 1 I Illi
*» 0? QC Oc 0? + ДБ 0 -20 T,
т х ne^^z* ifllUII
+ «С
+ О Я 1
fl
12 С2 Г^г~, Z./1 Ч/ *11 о — - -Х о Wtfst-^L=, T’s*' *()~£,(s) b°T2s + 1 1 1 Lt Ст, 1 1
До 0 -20 Tt rZ J*
-StJ + Jq
/♦4 1+± Li
о 1
1 fl i
15 Rt, Ct R3 R9 Г1 Rt1 I u2 t T's+I ^(S)-£,(S) L°rlS+1 «< + $C (R2+Rfy)Cf s S 0? + N + Cm, f
*- o?|o? + >?|o? **» Oc ДБ 0 -20 Tf Tz 8i
— 1
ЧС .+ + "J
0? o? fl J
Z4 Rz :Д[?Г •- do? d«? RfCt «гТо? + «< |®Г + ч_ О?|о? do? do? +• Ст, 1 1
*- Rtf Rif ~R1+~R'} ДО а -20 Tt Tz S Си
«, <,g C/ 7 “ J /rtCl^
-S’ I zO
+ 2
15 R3 г4—’"I c' Tz(TfS+1)S 0 1 R3Ez *i*z r_ R2 + R} ' Ст, I 1 1
дБ 0 -20 г< -Л J p'rA
q A11A *zU *'1гг ^0
Т,Тг^(1^Ы(1^^)\р^1 *" Aj Kf K2 J
Продолжение тайл. 9.7
16 ,.l(:}_^_(r,^zS+f)r2S 0 8, С, 8гСг
0 II i I Т 0 Ос|ос вс*| Ос" + —•••г 1 1 1
fz R, Ut J uz дБ 0 -20 Та Г К и
E,(s) ТГ 11+ — )-^— s2 + Т~“— 1 Ч- 1 г
8? b- _T 'год” '7 j
+Гг*+7-Л+* + %)1 R* s l R* ’ R2^R24 r,+r2 + r,+r2
17 - *11—I—— ** r1—h <н=Ь| n-| ° П Cz П 0, *'[J u2 т T T n w /ci- £zfs> (TtS*1) (Тго+1) * Е,Ы TT(^K- + K-1^ + Т,Тг(,\1; ,+ T <£]=£ + 4 ^|o? «с |оГ + 8,С, 8г ^г Lm, Дб 0 -20 1 _ т 2 2 7д Т2 1
i 1 1
*? 1 ,
*4ф+Г+Г +F (t+ H(,+ T )1+L I L Rj Rj -1 Rj J Lo 11П
ZlWl
18 o-L—ii—J r~° Q "'ll u, U u2 L.i О , X' о „м_£гМ (T,s+1)(T2s+l) F /cl " f £l(s) TtT2s^(T^T2)S^ Lo 1 8, 1 8г С, 1и 8i Lm, Дб 0 -20 ir —Z—. ly-L-r ..ИО' «0 ГТ ,*1
Т“"
—Ji ДС11 ?о
_ш
19 <HZZ3 lb-1— кг fl “2 f',T ы ,<>- E*(S} - T,T2S2+T,S*1 £'(S) ‘ TtT2S^T,(1^)s^ Kf Lo 1 /+А Ь 1 8, С, Li 8, Lm, ДБ 0 -20 J—л П Та —1— к / г «оо
1 1 1
е* * од®
1
20 о w>,(3}= ¥^ = kгs, v2 (S) где R2 - постоянная тахогенератора 0 оо — — Lm,
ДБ 0 -20 Т 1.0
'^102 \
>д r ° 0? т 1111
Продолжение тавл. 9.7
N2 п/п Схена корректирующего устройства Передаточная функция WK (s) Ao Ao, A, Tz Асимптотическая логарифмическая амплитудная характеристика
2! Ka‘s}_ 027s) '7,S+7 0 ^2 Lz A? — Lm,
До 0 —20 ~fo 1
8
1_
A;
'я ' ° г
22 . К 0 I II 0 и< < : иг ° ‘ '—й—0 К= Wk() E,(s)~r,s+I 0 k h. Kt — Lm, I
Дв 0 -20 1 1 ’ A Hi Z, J
о^Й LU
-^0
25 Of ♦ I > H7*fs)= ^=Л2з K d(i) £ кг kg ’ где кг-кинетический монет ротора kg-коэффициент восстановления момента 0 DO — — Lm,
ДБ 0 -20 4- Ъ-
-20 A w
24 А, О rw\- - | Q Uf Я, u2 У*‘f,fs) ~ 7,3+7 0 / Li — Lm, 7
Дв 0 -20 1 Tf L„ ttl
*
25 «2 oi T • - • о U| /«/ 4 ^21 I Cig ^'S) f,fs) 7-2s+7 0 A, T'11^ Lm, 7
Дб 0 -20 1 \Тг 0)
k1
г<!
Топчеев
£
Продолжение matin. 9.7
Продолжение табл. 9.7
NS п/п Схема корректирующего устройства Передаточная функция ^(sl Lq L«. T, T3 Асимптотическая логарифмическая амплитудная характеристика
31 ^*2 0 Г] u, U иг L,i Т,$(Тг$+1) „ L9 R-> Т,Тгог(1ч^Т,(1+-^)о^1 L1 Kf 0 1 ,+ 4 R,C, Lt в, Lm, ДБ 0 -20 — 1 1— L Tq |Тд j Loe, 1
V ^к^20дБ/дек
т ’40дБ/дек
20д£/дек
32 Сг вг 0-4 | + 0 1—II—1 л и, с, к,II иг II « л + и =? г? 2 * si S •** 0 1 R,C, вгСг — Lm, ЛБ 0 -20 — 1_ Тг Г’ 1_ 1 |^<Х 'Ьк^ОдБ/дек (Л)
•'ifL 1дБ/де к
“^ОрБ/дек
33 «. \П \П“- ^”й’= Ois + f)(Tzs + f) - Qc" 1 Wz R3C, Lm, to 0 -20 1 Tf 7 _L Та 1 i 4оо (aJ
т 1 1 •~20дЬ +тт Улек
О 1 /додБ/дек I | |
I Ki L Rf K2 -> 1 S + T b0 + i^|qr
J. "20дБ/дек
34 Ж- ш л,- £l(s> - TfT2(T3s + 1)s* "*<SJ- , . 0 1 HtC, rzc2 L, *2 Lm, ts 0 -20 Lt-Го _ — L f - 6 Ь ГТ Тг Loo Ш
1 1 . хИ | 1 ОдБ/дек-
• ~ ' L к а, рБ/дек
+ тгт3 s2+ Г D T,(T+ Ь)+Тг. s+1 /ЦОдБ/дек Г-
35 Кг ^г .Г^ . . Ег(Я T,s (r2s+1)(r3s*1) Г, ТгТ3 sW^+T^+J?^ (t+ -^9] s+1 0 1 ^(Ct+Cz) г. г2+2 г7‘3 Lt Kt Lm, ts 0 -20 L-r тг J То Та / J-r-xL—-1 7j 1 I |£ 7.00 ш
Ц, и иг О * о “Г 1 ТТ Т 1
— 1 Л аБ, /120 дБ/дек " 0 дБ/дек -|— 'дек | /л
to
36 о-Ц F-j-4l—l—o ct П c> П *гИ *'□ “г о — 1 Io -=^g- )S + ^0
T,T2s2+\r,+r2(l L f-2 s + 1
Сг С, HI-HH °-l W~ H l-"O E2(s) (Т,5+П(Тгз*1) AS-^\,rrz+^]sZ + L A/AJ J
37 Jr Г/Д. Кг (K,+^Rs)Ks-i I ' L Rf RtK J
+ т Г/+ 2 L R,RS J S*~L ^0
38 Uf ад=^ = * £,ft) ТгТ^ + rs2 ' (Tt +Л2) s +1
W = Ars= *P (7?s+7) s,
я . ^e ^5 ege k'= 7ГПГ
Продолжение табл. 9.7
Продолжение main. 9.7
NS п/п Схена корректирующего устройства Передаточная функция Wg(s)
41 с, с, o-HHt-HHr т—о WK(s)= E^s) _ TiWhs+fHbs+Ds2 £,(s) г,тгт5Тч^\т,т}Тч(1+?р)+ L Kt
*г| <0 о->— 4 С2: «'И Т "2 - L,i ..Д ... о + т, тг r3+ Т, T2 Тч + (T, T3 Тч SJ+ АЗ.
+Г^ V* %*%>тгтз f/+ )+ Тз Т^ + Т< L А/ Кз К$ Кз
+ Т, Тч\ згч Г Т, (1ч + Т5 (1ч £.) +1Л +1 J L К1 к$ J
42 R, с, O-CZ3—II Ut L, 5 и2 О-- — - i --о IV. (s)= Ez(s) = HS) £,(s) 7,4s2+7-,s+7
Асипптатическая
Co r. Tz T, логарифмическая амплитудная
характеристика
2 J_ 1 1 2_L г T Г Т Т. Т
45 R, Ut Ct: О- —о : иг -о Корректирующие устройства с запаздываю амплитудной хара .. ЕгМ ! *(S) Ef(s) T,s31 ten no разе ктеристики 1 и наидопьш do 20 дБ/д 0 им накя ’Л RiCi 7HOM
44 ° II—с=н сг R< Ut С,: О—- ! . ——о : и2 — О = * ’ £t(s) T,s+t f ,+ T- C2 0 Ci^C2 —
45 Q_^ p—, .. О ^2 Ct А tf, tfflj u2 О — - 1 c IVtfs)= ^!= Ji. * E,(s) Tts^l t Rz i+ — R, 0 Ct R^Rz —
Продолжение тобл. 9.7
Продолжение тадл. 9.7
Прадопжение табл. 9.7
647
NS n/n
Схема корректирующего устройства
Передаточная функция
Асимптотическая логарифмическая амплитудная характеристика
(r,s+f)(7is+t)(r,s+f)
Т,Гг(Г; + ^)з3Лг,Тг(1+ ^TtTz(H &]+ L л/ л/
+ Т>Гч(1+^)+ТгТ}+Т2ъ] Sl +
+ [Г,(7+^+^)+Г* + Г' + Г«] s + '
Lm, ± 11 111
Дб 1>о Та ч Ть Тг % Т5
~~ГКЦ£||| 1 -годА&гТ’Т"-— г-голе/дёГ* HI HI
ssshii
-20дБ/дек
~TTffl
NS П/п Скема корректирующего устройства Передаточная функция W^Ls) Lg
58 Кд Тч Кд йг rf=Hh rCZZHh url 1,1Я Л f f\g Kj 1
(тт Т / Т Т Т Г / ^5 + у1т2^(-р,+ йг + тР+г,ГгТ‘'\_/+й'1 +
. А/7+^+ *5)+ ^-(1 + \ . К, ( Kz Кч' Кч 1 Кг '
Ц, С3 - - I I ^2 4L + Г/+^Г/+ J)lv2r3/i (^+ J)1a L л з r\fj г\£ г\£
+ \т,Тг Р+ V + т + ¥ (,+ )1+ L f^z ^2 %2 -1
. тт кг Кч . г Г Г. Кд Кд Kz . +7;Zj^+z'^ L'w^^j+
+ ^4’^л^[/+^Лг,Л)] + Л 2 Kj L л 4 Kg КJ
+ ’?/|s2+PZ^+A^+ ~к~^+Тг^+Т^ + Ajj L А/ л/ А2
+ /i^ + s+r К3 Kif j
59 ° ТГ 1 0 и, Я, иг О" 1 о L/. Лс-) _ _ Lg *() Ef(s) TfS+f 1
Асимптотическая
Продолжение табл. 9.7
Тг T, Тч логарифмическая амплитудная
характеристика
A’zG А3С3
Lm, Д5 О
-20
Продолжение глад л. 9.7
649
Передаточная функция WK(s) Lq Сж> r,
E2(s) T,s+1 W^= f, fs) = + 7 1 f Lz *Z
"T,
е2(з) _ r,s+f Wl,ls)~ 7^) " °r2s<-f ,+T- *1 + + Lj *2
Асимптотическая логарифмическая амплитудная характеристика
Корректирующие устройства с запаздыванием по (разе и наибольшим наклоном амплитудной характеристики -40д1>/дек
62
64
“t Ct- о >—о = Ut >- о Ejls) _ f *<Sl~ E,(S) T,T2Sl+T,3 + f 7
^z u, Q: О к, - Ct- —о : u2 —о ЙЯ- f_ Г,ггз‘+ [r,(r+ s+* 1
/?, L, C2 «< G = О - —с : и2 —О k4rfs)= -г^ = — ' £,(s) r,r2s2+r,s + 7 1 ,+ T L2
Продолжение табл. 9.7
Не п/п Схема корректирующего устройства Передаточная функция ЩК) Lq L~ r, Tz А синлтотическоя логарифмическая амплитудная характеристика
65 К, Lt щ ,s)s - L° 'Л 0 R,Rz R^Rz C' Lt *2 Lm, 1 1
0*4 V— « 0 рв а -го Та Ть
l/н C.- = d -11 —г ! L
' ’ Т>Тг^+1Т1+гг-^г^1
0 ' — - i -0 -20дБ/д г<*4
- 60 дБ/дек
66 Rif R* Ry R, Rf-*-Rz+R}+Ry 0 ft? + <* Ry^z Lm, ( /
и, Сг-- O-.-— до -го J Та 4
4- 11 ' —I— 1
-гОдБ/Aet ? *ч1
| | -60дБ/дек
67 Rs Lt Rz nu, — 44s2(,. *2 . Rs). R, R, + + 4 <, K< ^s+1 Rt Rt R2+ Rj 1 0 Rz^i Lt Rt Lm, < 1 _ <
—II ДБ 0 -го Та Ть Tt
r. 71“ " Ш “1— 1 I
*'U о * о /+’^ + ‘F’ R> Rt
гОдБ/дё г т 1
- WдБ/дек л
-го дБ/дек
68 Rz о <Jz ——о -1^? + V> eel °? „ ? 4»? tf L- "l°= к-+ + I Ct Qc be v> ч ' JSj ♦m (Л цЛ| II 0^0? *- + «?| 0? 0 RtC, Rz^z Lm, f t f
ДБ 0 -го Та 4 Ti /ti
Ui Rs C2 d 1 1 ш
f T - 20.ДБ/дек тН
0———w-4 -УОдБ/дек'' гОдБ/дек
г°-г4+^
Продолжение табл. 9.7
Корректирующие устройства с опережением и отставанием по /разе
Продолжение табл. 9.7
№ П/п Схема корректирующего устройства Передаточная функция W^(s) Lg Loo T, Тг Асимптотическая логарифмическая амплитудная характеристика
73 С2 j-—ни—-[ ^2 Rf Uf Ct -- Uz *!s}=T^ = T, T2sz+ T2s + t 1 f K1 -п,7-кг 1 (К, + К2)Сг Lm, ДЬ 0 -20 iff|?o7|7rl & |ИД“ си
-20дБ/, SMI Ri г —L 1II 20дБ/дек-
7,72s2+[7,f/+^-)+r2]5 + /
74 К, 4 ’ *г Сг “г (Tts+f) (TzS+t) J «4 c*? 4- «4 йс of П/С/ {П^П3)Сг Lm, Дб 0 —20 Lo | Та р Т, | Гг 4 |Л*! |
-20д5, НН! | 1 20 дБ/дек
T, 72 (1+ \T<!'* T>+T21s + ' 1 K$) L */ J
+ 1
75 Сг <Н=3 L=J А «/ пг о — ———1-0 ,,,, (Tts+t) (Т2з+П Я г ₽ ₽ 1 Tf T2(f+ ^)sZ+ o^lS+^ Kf L Kf Kf J 1 1 4, к, с. кгс2 Lm, ДБ 0 -20 Fitnif • 72 Н^||
1 HU; -20дБ/дек 1 1 1 1 1 г —1> /ОдБ/дек I I I 11
мН! ЗИП.
76 °~I~f |Z|pJ—I—° u, R3 c3 R< U u2 f'T (T,S+1)(T;,S + 1) 1 — t^ tk: a? + к, с, (Я2+Х,)С3 Lm, ДБ 0 -20 t_ ± L
г«н — >wrl - 20дБ/дек
-?ПпС/лек
Т,Тг\1+ К (К 4 )1S*+P'<’/+ p+rz]s+/ L *1\*2~*3>1 L Л/ J ttt
77 G j-g-—ii—I 3 П ^2 ' U, иг f'T о * о ws,= ISJ= Т^[’+^п^У+1Т'+Г^' 1 0? tk: + +“ h «С * ®c t + c + *>» /?,г, (K2+K3 + /t^C2 Lm, ДБ 0 -20 До -2 ад ОдБ/дек __ j. % 20дБ/дек 1 1 1 11
L KfiK^Ky^Ktf) J L Kf J 1! Н 11111
Продолжение табл. 9.7
653
Продолжение тадл. 9. 7
NS п/п
Схема корректирующего устройства
, W ,г
82
R^fRiRtf +^2^5 * ^4^5
г t RS(R^R6) г L RZ(R4+RS+R6)
8ч Rs
R,R2(RIi4R5 + r6)
+ Т /t » т (RzRtf+RzRs+RtRs) '/('+ т-)+ h s-p + /зf *2
+ 4 Г 8s (8ч + 8б) 1 + L ^Z+*5)^«+*S + *«)J
т Rtf Rs \ 86(8ч+85 + -Ту-) f\f ' r\2 !
Г2 R,(l<4 + 85+Rt) s + / Lo
Передаточная функция h^fs)
84 85
(8г*81(8ч+8,+86)
Т,Тг1'+82(R^ps+Rt)]
Асимптотическая
Tt Т2 логарифмическая амплитудная характеристика
85
Wk(s) =
СгМ E,(s)
R,(R2+83)
Продолжение табл. 9Л
85 Сг Я, «ННг-сЬ— "г **1] С': о - “г ~£'(s)~ 0
Hi п/п Схема корректирующего устройства Передаточная функция Мд(з) Co
86 К, 9 и, о г-i >-» с,: иг —О kJ± *'' er(s) тгт35г-кт,+тг)$+1 D
87 °-ч ° Яг С, L, А и, Л, II иг Wk(s)=T^r —й— £'п T,T2S^T,(t+ ^)s + / 0
88 f?3 Cl = T^s т^т’[(,+Тг^Т^ 0
^~1 Fjar Щ h1 pZ " " □<’ Uz
89 G Г^1-! *? и, Gil G - к, - с,- -иг T,s + ! ,+ T-R3
s2+
s+l ( *-г L /v? Аг J l>3 J Lff
Lo> T, Тг TS Асимптотическая логарифмическая амплитудная характеристика
Ыг
-90 дБ/дек
Продолжение maSn. 9.7
Продолжение main. 9.7
00
HS п/п Схема корректирующего устройства Передаточная функция №*($) /•о L„ Т,
97 Сг С, °—1'—г-и—т—0 "/ I Т й* J_± в- Т,Тг(Т5г+П(Тч3^1)зг Т,ТгТ1Тчз‘,+ Т,Тг(Т^Тч)5^ 0 1 к, с,
+ Г,Г4+6+?У+£7^Л |7, f/+ S+I
98 ДннЗ т—о Сг *'П , Т иг ч j о Го (T,T2s!+T,s+1)(/3s+!) 1 1 д,с,
Т, Тг Ts з 3+ [/, (Гг + Г,}] s 2+ </+ ^)+з+1
99 кг К3 L, г*——h ъ П и, *'[| иг п о *о — (TiS + 1)(Tzs+n 1 0 8,С,
Т,Тг Т3 s’+т, |7з+Г2 /7+ ^У+[^+|+^Н]з+'
100 0 С/ о II . о tf, Я,П иг о Го **'*fS)_ Г,£зг + Г,з+7 0 0 а,с.
Продолжение табл. 9.7
Асимптотическая логарифмическая амплитудная характеристика
а дифференциальный сельсин подключается с помощью контактов К$. Контактор К? разрывает цепь якоря силового привода в случае превышения допустимых нагрузок.
В соответствии со схемами иа рис. 9.12 и 9.13 определим логарифмические желаемую и неизменяемые частотные характеристики при следующих параметрах: ат = 30%; <р = 3 с; £>и = 300 с-1; йг = 5,85 с-2. Передаточную функцию неизменяемой части запишем в виде выражения (9.35), в которое входят
FH (s) = 0,0394;
w ,,_________________190,5__________.
у ' ; (0,69s + 1) (0,0525s + 1) X ’
X (0,02s + 1) (0,002s + 1)
UZ0 (s) =__________________________
0 v ' s (0,085s + 1) (0,0068s + 1)
По этим данным на рис. 9.14, а построены желаемые Яж, 0Ж и неизменяемая Н„ частотные характеристики, из которых следует, что Уф = 60°, Ям = °°, —Ям = — —26 дБ. По ранее рассмотренной методике определим Як пр (рис. 9.15, а), а затем Як пр = я' пр + Яо. Из рисунка видно, что до частоты <о' передаточная функция параллельного корректирующего устройства будет
Гкпр (s) = 0,318s/(l,04s+ 1).
Реализация последней, выполненная в виде стабилизирующего трансформатора (табл. 9.7, № 22), приведена на
рис. 9.14, в.
Для выбора последовательного корректирующего устройства воспользуемся формулой (9.40). На рис. 9.16,а показан порядок построения Як. С помощью номо-
граммы замыкания (рис. 9.14,6) получим характеристику Явз = — 201g|l + + пр 0®) U®) Го (до) |, приведен-
ную на рис. 9.16,6. Вычитая из Яж в соответствии с формулой (9.40) характеристики Ян и Явз, найдем логарифмическую амплитудную частотную характеристику Якп последовательного корректирующего устройства, показанную на рис. 9.15,6. Аппроксимируя Якп штриховой линией, получим передаточную функцию
,„ч . 61,5 (0,012s+1)* ^кп ( ' 0,0072s + 1
Ее реализация приведена на рис. 9.14, г.
6. ТАБЛИЦЫ ПАССИВНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
Наиболее широкое применение в САР получили линейные корректирующие устройства в виде четырехполюсников с пассивными и активными элементами. Эти типы устройств выполняют операции дифференцирования (фазоопережающие), интегрирования (фазозапаздывающие) и дифференцирования-интегрирования на разных частотах с фазозапаздыванием и последующим фазоопережением. Структурные схемы, передаточные функции, их параметры и асимптотические логарифмические амплитудные характеристики корректирующих устройств приведены в табл. 9.7.
Глава 10
СИНТЕЗ ЛИНЕЙНЫХ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Постановка задачи синтеза дискретно-непрерывных САР по своей форме не отличается от синтеза линейных непрерывных систем. В процессе ее решения также необходимо найти такую структуру и параметры системы, при которых обеспечивалось бы получение заданных техническими условиями запасов устойчивости, показателей качества и характеристик точности. Однако применение в замкнутых системах микропроцессоров или микроЭВМ, где
формируются законы регулирования и коррекции в реальном масштабе времени, а сигналы управления поступают лишь в тактовые моменты, приводит к снижению запасов устойчивости и ухудшению показателей качества до недопустимых значений. Следует отметить, что решить данную проблему только путем усложнения программ коррекции, реализуемых на микропроцессорах или микроЭВМ, часто не удается из-за больших величин такта
659
обмена информацией между дискретной и непрерывной частями системы. Поэтому в САР необходимо использовать вычислительную технику сверхвысокого быстродействия.
В настоящее время наибольшее распространение получили два способа решения задач синтеза. Первый способ основан на применении билинейного преобразования и построении желаемых логарифмических амплитудных и фазовых характеристик относительно псевдочастоты с последующим нахождением программ коррекции По второму способу сначала определяют положения полюсов и нулей характеристического уравнения замкнутой САР, а уже по ним строят желаемые формы корневых годографов с последующим нахождением условий их взаимной компенсации. Кроме того, по выбранным нулям и полюсам можно вычислить типы и параметры обратных связей по состоянию системы и ее выходному сигналу в виде динамических звеньев. Теоретической основой второго способа является векторно-матричный аппарат, позволяющий решать задачу синтеза как при полном, так и неполном измерении фазовых координат. При этом необходимо выполнить проверку условий управляемости и наблюдаемости, рассмотренных в гл. 11.
Первый способ обычно применяют при синтезе последовательных и параллельных корректирующих устройств, а второй — при синтезе устройств параллельной коррекции. Возможно объединение обоих способов; тогда выбор векторно-матричного уравнения желаемой САР осуществляют с помощью билинейного преобразования с последующим выбором нулей и полюсов замкнутой системы, а программу коррекции определяют в виде обратных связей. Данную задачу можно решить достаточно просто лишь при наличии одних полюсов. Если в характеристическое уравнение входят нули, то процедура синтеза значи
тельно усложняется. Реализация корректирующих устройств осуществляется в виде рабочих программ, составляемых на языке ассемблер.
1. МЕТОДИКА СИНТЕЗА ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ НА ОСНОВЕ БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
Синтез САР, основанный на построении желаемой логарифмической амплитудной и фазовой характеристик, полученных с помощью билинейного преобразования, состоит в следующем:
а) по требованиям точности (или коэффициентам добротностей) строим низкочастотную часть желаемой логарифмической амплитудной характеристики относительно псевдочастоты <о(Яж (<й));
б) с помощью номограмм Солодовникова (рис. 9.4, б и в) по показателям качества ат и /р находим частоту среза <вс, через которую проводим логарифмическую амплитудную характеристику с наклоном —20 дБ/дек; •
в) строим во всем диапазоне псевдочастот логарифмическую характеристику неизменяемой части Ян(й>), проходящую через точку ф = 1;
г) высокочастотную часть желаемой логарифмической амплитудной характеристики //ж(<в) выбираем аналогичной /7Н(®);
д) по точкам излома Нж(й>) вычисляем желаемую логарифмическую фазовую характеристику 0ж(й), которую наносим на полулогарифмическую бумагу, и определяем запасы устойчивости по фазе yi и модулям ±#м- Если они совпадают с данными технических условий, то построение желаемой характеристики на этом заканчивается. После этого можно приступить к формированию программ коррекции, реализуемых на микропроцессорах или микроЭВМ.
Рассмотрим применение данной методики для синтеза последовательных и параллельных корректирующих устройств.
660
a)
6)
Рис. 10.1. Структурная схема, дискретно-непрерывной системы с управляющей микроЭВМ, включенной:
а—последовательно; б—параллельно
Последовательные корректирующие устройства выбираем с использованием следующего соотношения:
ЯКп(й) = Яж(й)-Ян(й). (Ю.1)
Затем по логарифмической амплитудной характеристике Якп(а>) находим IFKn(s) и, используя формулу (1.125), получим U/Kn(z). Откуда и находим разностное уравнение, позволяющее реализовать программы коррекции.
Пример 10.1. Определить параметры системы, удовлетворяющей заданным техническим требованиям, и сформировать программу для микроЭВМ типа «Электроника-60», с помощью которой реализовано последовательное корректирующее устройство. Структурная схема системы изображена на рис. 10.1, а, где Wt (s) = 1; WMS) = W'k(s). Ее основные характеристики следующие: = 40 с-1; = 7 с-2;
<тт = 30%; /р < 3,14 с.
Непрерывная неизменяемая часть системы описывается с помощью передаточной функции вида
s(r,s+1) (7М+1) (7М+1) ’ (Ю.2) где К = 40 с"1; Т, = 0,1 с; Т2 = 0,05 с; Тз = 0,01 с.
Пусть такт обмена между непрерывной и дискретной частями Тй + 0,01 с. В этом случае на основании прил. ГМ. 2 запишем
4 • 10~4 s (2,9289 - z) (4,1966 *г2 +
В- ( » _ + 1,51032 + 0,1024)
’ (2 -1) (2 - 0,948) х
X (z — 0,8187) (2 — 0,3679)
(10.3)
Подставляя в выражение (10.3)
2
2 =-------=----, (Ю.4)
1 --l°-s
2 получим
40 (1 — 0,005s) (1 — 0,0102s) X Х(1 + 0.0042s) (1 + 0,0029s)
s (0,1s + 1) (0,0502s + 1) X ‘ X (0,0108s + 1)
(10.5)
При s = /й из выражения (10.5) имеем
40 (1 — 0,005/ш) (1 - 0,0102/й) X
X (1 + 0,0042/й) (1 + 0,0029/т)
/ш (0,1/ш + 1) (0,0502/ш + 1) X ’
X (0,0108/й + 1)
(10.6)
Характеристику На(в>) =201g 11ГН (/ш) | проводим через точку о> = 1 и наносим ее на рис. 10.2, а тонкой штриховой линией. Далее строим Нж (ы) при Дш = шк = 40 и Де = й2 = 7. По номограмме Солодовникова (рис. 9.4, б) найдем
йс = 4л/3,14 == 4.
661
Рис. 10.2. Логарифмические амплитудные и фазовые характеристики дискретно-непрерывной системы с микроЭВМ «Электроника-60», на которой реализована последовательная программа коррекции:
а —всей системы и ее неизменяемой части; б—для определения последовательной программы кор* рекции
Через точку йс на рис. 10.2, а проведем прямую с наклоном —20 дБ/дек до второго излома Я„(й). Затем достроим остальную часть желаемой логарифмической амплитудной частотной характеристики эквидистантно к высокочастотной части Ни(а>).
Располагая характеристикой Нж(й>), запишем формулу для определения 0ж(й)
в виде 0}К (ш) = Л . со , . со - arctg -д- + arctg - 2 СО] СО 2
— 2 arctg СО 1(0 . со -= arctg — arctg ~— <Он2 ®нЗ (^н4
— arctg й . й . й — h arctg — k arctg ——. «Н5 ®Н6 <0Н7
(Ю.7)
По формуле (10.7) в окрестности точки йс вычислим 0ж(й) и построим ее жирной штриховой линией на рис. 10.2, а, с помощью которой находим запасы устойчивости по фазе Уф= 45° и модулю —Ям = = —14 дБ. По номограмме (рис. 5.55)
определим от = 28 % и /Р = 2,8 с. Последние соответствуют требованиям технических условий.
Пользуясь формулой (10.1), строим Якп(й) (рис. 10.2,6) и находим передаточную функцию последовательного корректирующего устройства
«7 г -1 - U('s} - (0.5s+1) (0,1s+1)
KnW U(s) (5s + 1) (0,05s + 1) '
' (Ю.8)
Подставляя 'в выражение (10.8) s = 2 1—z-1
= 77T+F^’ получим
Гкп (2)_WF
0,1930 - 0,3638г-1 + 0,1712г~2 ,
1 - 1,8162г-1 + 0,8166г-2 ‘ ° '
По формуле (10.9) найдем разностное уравнение в реальном масштабе времени, т. с. введя в числитель дополнительный сдвиг г-1. В результате этого получим
йк — 1,8162йк_1 — 0,8166йк_» +
+ 0,1930uK_i — 0,3638uK_s + 0,1712uK_9.
(10.10)
Реализуем программу коррекции на микроЭВМ «Электроника-60» на языке ассемблер.
UK10
РАСЧЕТ ФОРМУЛЫ (10.10)
UO (К) = 1.816UO (К — 1) —0.817UO (К — 2) + 0.193U (К - 1)
-0.364U (К - 2) + 0.17Ш (К - 3)
ВХОД: РЕГ. 167766
ВЫХОД: РЕГ. 167762
662
РАСПРЕДЕЛЕНИЕ ПОЛЯ U:
U (0): ПО (К — 1), U (2): UO (К - 2)
U (4): U (К - 1).U (8): U (К — 3)
МАСШТАБ ДЛЯ UO И U 1 : 1000
R0 = % 0
Rl = % 1 R2 = о/о 2 R3 = о/о 3 R4= % 4 R5 = % 5 SP = % 6 PC = % 7
UK10:: .IRPC N,01234 СОХРАНЕНИЕ
MOV R’N.-(SP) РЕГИСТРОВ
.END 0.. .4
1 Ц: BIT # 100, @# 167764 проверка
BNE 1 Я ГОТОВН. ВХОДА
MOV e# 167766, U + 4 ЧТЕНИЕ ВХ.СИГНАЛА
CLR R0 РЕГ.ДЛЯ НАКОП.СУММЫ
CLR RI ИНДЕКСНЫЙ РЕГ.
2£: MOV U(R1),R2 ЦИКЛ ПОЛУЧЕНИЯ
MOV C(R1),R4 ВЫБОР ОЧЕРЕДНОГО КОЭФФ.
MUL R4,R2 В R2,R3 ОЧЕРЕД.ТЕРМ
ADD R3,R0 В R0 ЧАСТИЧ.СУММА
TST (Rl) +
CMP # 12,RI ПРОВЕРКА
BNE 2Д КОНЦА ЦИКЛА
MOV R0,@# 167762 ВЫВОД UO (К)
BIS # 100,e# 167760 ГОТОВ. ВЫХ. У СТР-ВА
MOV U,U±2 UO (К - 1) в ио (К-2)
MOV R0,U ЦО (К) в ио (К - 1)
MOV U +6,U ± 10 и (К - 2) В и (К - 3)
MOV U + 4,U±6 и (К - 1) В и (К-2)
IRPC N, 43210 ВОССТАНОВЛЕНИЕ
MOV (SP)+,R'N РЕГИСТРОВ
.ENDM 0...4
RTS PC
U: .WORD 0,0,0,0,0
С: .WORD 1816.,—817.,193. —364. ,171.
• END
Параллельные корректирующие устройства определяются в диапазоне ±26 дБ по аналогии с непрерывными системами, т. е.
Якпр(6) = -Яж(й). (10.11)
Данная логарифмическая амплитудная характеристика справедлива для всего диапазона частот й при условии, что порядок астатизма исходной системы с выбранной коррекцией не понижается.
Пример 10.2. Сннтезнровать систему, удовлетворяющую заданным техническим требованиям, и сформировать программу для микроЭВМ типа «Электроника-60», на которой реализовано параллельное корректирующее устройство. Структурная схема системы изображена на рис. 10.1,6. Основные характеристики системы и ее неизменяемая часть соответствуют данным, приведенным в примере 10.1.
На рис. 10.3 изображены Нж(р>) и 0ж(ш). В отличие от ранее рассмотренного примера 10.1, желаемая амплитудная характеристика имеет дополнительный участок с наклоном —40 дБ/дек в диапазоне 20 < < ш < 50. Запасы устойчивости синтезированной системы имеют следующие значения: уф = 50° и —Нк = —15 дБ. Жирной сплошной линией на рис. 10.3, согласно формуле (10.11), построена характеристика Нк пр(Й).
С целью проверки запасов устойчивости внутреннего контура на рис. 10.3 тонкой штриховой линией изображена характеристика Ннк(ш) = Нв(ш) + Якпр(ш) при К — 1. По этой характеристике построена фазовая характеристика 0нк(й). Задаваясь запасом устойчивости по фазе Уфв = 50“ и поднимая Я„к(ш) до уровня К = 2,5, получим амплитудную характеристику внутреннего контура системы (штрихпунктир-ная линия). При этом видно, что Уфн =* = 100°. Полученные значения Y^bи Уф и гарантируют высокую степень устойчивости замкнутого внутреннего контура.
663
Используя характеристику Ни Пр (й), находим передаточную функцию параллельного корректирующего устройства в виде
0,0625s2 (0,05s + 1)
"Р (s) =----6JI+1--------‘ ( }
Подставляя в выражение (10.12) s =
2 1— z~‘
= ~ получим
i 0 1 ”1 *•
*кп?(г’~~1Дг) -
272 — 766,6г-1 + 588,5г-2 — 222,6г-3 ~ 1 + 1,0198г-* — 0,9604г-2 — 0,9802г-3 '
(10.13)
Рис. 10.3. Логарифмические амплитудные и фазовые характеристики дискретно-непрерывной системы с микроЭВМ «Электроника-60», на которой реализована параллельная программа коррекции
Соответствующее разностное уравнение в реальном масштабе времени имеет вид
йк = - 1,0198йк_ 1 + 0,9604йк_2 +
-|~ 0,9802ик._э 272uK_i — 766,бн^—2 "4“
+ 588,5ик-з - 222,6ик_4. (10.14)
Данное уравнение реализовано в виде программы на микроЭВМ «Электроника-60» на языке ассемблер.
UK14
РАСЧЕТ ФОРМУЛЫ (10.14)
UO (К) = -1.020UO (К - 1) + 0.960UO (К — 2) + 0.980UO (К - 3) + + 272 U (К - 1) - 767U (К — 2) + 588U (К - 3) - 223 О (К - 4)
ВХОД: РЕГ. 167766
ВЫХОД: РЕГ. 167762
РАСПРЕДЕЛЕНИЕ ПОЛЯ U:
U (0): ПО (К-Т),...,U (4): UO (К - 3)
U (6): U (К — 1),...,U (14): U (К-4)
МАСШТАБ:
ПО 1 : 1000, 0 1:1
R0 = % 0
Rl = % 1
R2= % 2
R3 = % 3
R4 = % 4
R5=%5
SP = % 6
PC= % 7
UK14:: .IRPC N,01234 ; СОХРАНЕНИЕ
MOV R'N,—(SP) ; РЕГИСТРОВ
. ENDM ;0. ..4
664
1»: BIT BNE # 100,@ # 167764 ; ПРОВЕРКА
1 И ; ГОТОВЫ.ВХОДА
MOV @ #167766, U + 6 ; ЧТЕНИЕ BX.СИГНАЛА
CLR R0 ; РЕГ.ДЛЯ НАКОП.СУММЫ
CLR R1 ; ИНДЕКСНЫЙ РЕГ.
2 Д: MOV U(R1),R2 ; ЦИКЛ ПОЛУЧЕНИЯ UO (К)
MOV C(R1), R4 ; ВЫБОР ОЧЕРЕДНОГО КОЭФФ.
MUL R4.R2 ; В R2.R3 ОЧЕРЕД.ТЕРМ
ADD TST R3.R0 ; (RD 4- В R0 ЧАСТИЧ. СУММА
CMP #16, Rl ; ПРОВЕРКА
BNE 2Д ; КОНЦА ЦИКЛА
MOV BIS R0,@# 167762 ; #100,@ #167760 ВЫВОД UO (К)
MOV U + 2.U + 4 ; ; UO (К-2) В UO(K-3)
MOV U.U + 2 ; ЦО(К-1) в UO (К-2)
MOV R0,U ; UO (К) В UO (К - 1)
MOV U+12,U+14 ; U (К — 3) В U (К — 4)
MOV U + 10,U + 12 ; ; UO (К - 2) В Ц (К - 3)
MOV U + 6.U + 10 ; ; U (К - 1) В U (К-2)
.IRPC N,43210 ; ; ВОССТАНОВЛЕНИЕ
MOV (SP)+,R'N ; РЕГИСТРОВ
. ENDM 0. . .4
U: .WORD 0,0,0,0,0,0,0
С: .WORD — 1020.,960.,980.
.WORD .END 272. .-767. ,588. -223.
2. СИНТЕЗ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПО МЕТОДУ КОРНЕВОГО ГОДОГРАФА*
Синтез САР с использованием метода корневого годографа решается на основе размещения нулей и полюсов характеристического уравнения замкнутой системы на Пл. z, при которых обеспечивается получение основных показателей качества, задаваемых техническими условиями. Сложность решения данной задачи связана с тем, что у САР, динамика которых описывается дифференциальными уравнениями выше 3-го порядка, трудно установить связь между параметрами дискретного корректирующего устройства (программы), нулями и корнями характеристического уравнения, а также тем,что при построении корневого годографа рассматривается, как правило, изменение лишь одного параметра. Поэтому этот способ синтеза обычно выполняется путем пере
* Параграфы 2—4 гл. 10 написаны по материалам книги Б. Куо. Теория и проектирование цифровых систем управления. М.: Машиностроение, 1986, 447 с.
бора параметров корректирующего устройства графоаналитическими методами или в автоматизированном режиме работ на ЭВМ (гл. 12).
Рассмотрим синтез дискретно-непрерывных САР на основе взаимной компенсации полюсов и нулей. Для этого на Пл. z проектировщик вводит дополнительные полюсы и нули, по которым формируются импульсные корректирующие устройства или рабочие программы для микроЭВМ, обеспечивающие компенсацию нежелательных полюсов и нулей, снижающих запасы устойчивости и ухудшающих показатели качества. Если нежелательные полюсы расположены близко к окружности единичного радиуса на. Пл. z, то их компенсация средствами коррекции может вызвать неустойчивость системы.
В гл. 5 были рассмотрены способы построения корневого годографа для непрерывных систем на Пл. z и показаны, каким образом оцениваются основные показатели их качества. В данной главе изложены графоаналитические процедуры построения корневого годографа по характеристическим уравнениям за-
665
Рис. 10.4. Корневые годографы при условии: а—полной компенсации полюсов z . п г*,; б — nl П1 неполной компенсации полюсов z , и z , nl nl
мкнутых дискретных (дискретно-непрерывных) систем на Пл. z и даны рекомендации по определению показателей их качества с помощью использования номограмм.
На рис. 10.4 показаны два случая взаимной компенсации нежелательных доминирующих полюсов. Пусть в разомкнутой системе на Пл. z имеются два нежелательных комплексно-сопряженных полюса гп1 и znl, близко расположенных к окружности радиуса |г| = 1, и один НУЛЬ 2н1.
Для обеспечения взаимной компенсации полюсов введем корректирующее устройство с двумя дополнительными нулями гдн j; гДн 1 и полюсами гдп ь гдп 2. В результате этого корректирующее устройство может быть описано следующей передаточной функцией:
П7 (2 ~ 2дн 1) (2 ~~ 2дн 1)
дк / (г _ 2дп [) (г _ 2дп 2)
(10.15)
Корневой годограф системы построим по характеристическому уравнению
1 I (2 ~~ 2н1) (2 ~ 2дн 1) (2 ~~ 2ДН 1)_q
(z1 — cz + d) (г — гдп i) (г — гдп2)
(10.16)
При этом из z2 — cz + d = 0 находим гп1 = а + jb; z„i— a — jb.
f)
Рассмотрим два случая. Первый случай, когда числовые значения параметров разомкнутой системы гн1 — —0,5; гп1 = 0,5 + /0,625 и z„i = — 0,5 — /0,625. Зададимся следующими параметрами корректирующего устройства: гдн1 = 0,75 + + /0,375; гдн 1 = 0,75 — /0,375; гдп! = = 1; 2дп2 = 0,25.
Подставляя в уравнение (10.16) принятые числовые значения, запишем характеристическое уравнение в виде
г4 — 2,25г3 + 2,1406г2— 1,0508г +
+ 0,1602 + К (г3 — г2 — 0,0469г +
+ 0,3516) = 0. (10.17)
Изменяя К, по формуле (10.17) на рис. 10.4, а построим корневые годографы Г1 и Г2 замкнутой системы, на которых обозначены квадратиками соответствующие параметры Ki = 0,5; /<2 = 2; К3 = 5; К4=10. Из рис. 10.4, а видно, что принятые нами значения дополнительных нулей и полюсов компенсируют влияние нежелательных полюсов znl, z„i и в замкнутой системе обеспечивается устойчивость при всех Кл.
Второй случай, когда числовые значения параметров разомкнутой системы и дополнительно введенные полюсы гДП1, гДП2 оставим прежними, а изменим только дополнительно введенные нули, т. е. гДН1 = 0,25 + + /0,875; гдн i = 0,25 — /0,875.
Построим на рис. 10.4, б годографы Г1 и Гг при различных числовых значениях К,. Откуда видно, что при
666
Ki =0,5, /<4 = 10 система устойчива в замкнутом состоянии, а при Кз = = 2, Кз = 5 она становится неустойчивой. В данном случае при выбранных дополнительных нулях не удалось компенсировать влияние полюсов гп1 и Zni при всех значениях Kt. Полученная система относится к условно устойчивой, и изменение ее параметров во время эксплуатации может привести к неустойчивому режиму работы. Итак, обеспечить условия идеальной компенсации полюсов в САР не всегда удается.
Перейдем к рассмотрению способов определения основных показателей качества по расположению доминирующих полюсов дискретной или дискретно-непрерывной системы *. В отличие от непрерывных, в системах данного класса необходимо учитывать влияние такта квантования То.
Допустим, что при учете доминирующих полюсов передаточные функции замкнутой системы могут быть представлены в виде
Ф(г) = К (z — zHl) (2 - 2п1) (2 ~ 2п1) (10.18)
или
Ф(г) = - <10Л9)
(2 2П1) (2 2П1)
где К = (Д — г„1)(1 — z„i)/(l -+- гн,), а 2ni> гп1 — комплексно-сопряженные полюсы **.
На рис. 10.5, а, б приведены положения полюсов гп1, хп1И нуля zHi на Пл. z. При действии на САР, описываемую передаточной функцией (10.18) или (10.19), единичного сту
* См. сноску на с. 665.
** Излагаемая далее методика может быть распространена на системы более высокого порядка, чем описываемые формулами (10.18) или (10.19). В этом случае в системах также должны быть два доминирующих комплексных полюса и один нуль, расположенный в любой точке на оси ординат. Остальные полюсы и нули должны находиться на Пл. z вблизи начала координат.
пенчатого воздействия имеем сигнал на выходе
X(z) =
K(z + zHi)z
(z-l)(z-znl)(z-z*nl) '
(10.20)
В выражении (10.20) знак минус соответствует формуле (10.18), и знак плюс —формуле (10.19).
Воспользуемся обратным z-преобразованием; тогда по формуле (5.167) найдем
х (к^о) — 1 Ч~ 2
К (гп[ т z„i)
(zni - О (zni - *’п1)
X
X I Znl |к cos (КТ) + 0), (10.21)
где T] = argznl; 0 = arg(znl - zHl) — — arg(znl — 1) — -j- для формулы (10.18) и 0 = arg(znl-j-zH1) — arg(znl — — 1) — для формулы (10.19).
Из рис. 10.5, а, б следует, что ± v = arg(znl =FzH1) --arg(znl-l) + ^-; (10.22) 0 = ±v —л (10.23) и
(10.24)
Подставляя соотношения (10.23) и (10.24) в (10.21), получим
х(кГ0) = 1 +|secvlX
XI znl |к cos (кг) ± v — л). (10.25)
Выражение (10.25) позволяет строить переходный процесс для дискретной или дискретно-непрерывной САР в тактовые моменты времени. Аппроксимирующую функцию x(t), представляющую собой огибающую процесса х(кТ0) в тактовые моменты t = KTo, будем проводить штриховыми линиями. Это положение полностью справедливо лишь при большой частоте квантования То, т. е. когда соблюдается условие (1.216).
667
Рнс. 10.5. Расположение нуля и комплексных полюсов на Пл. г:
а —прн гн1>0; б—при -гн1<0
Затухающий переходный процесс обеспечивается в случае, если доминирующие полюсы передаточной функции замкнутой системы гп1 и Zni расположены в первом и четвертом квадрантах Пл. г, и в межтактовые моменты времени отсутствуют колебания с возрастающей амплитудой.
Будем считать, что в передаточной функции замкнутой системы содержится сомножитель в виде звена второго порядка с постоянной времени Т\ и коэффициентом демпфирования Тогда при t=KT0 имеем
|гп1|к = |гп1Г=е22; ' n = argznl = -^-д/1 -61 •
(10.26)
х(0
Из выражения (10.25) имеем x(t) = 1 +|secv|e~s,wr,X Xcos^1^11 /±v-n). (10.27)
Используя последнее равенство, можно определить основные показатели качества дискретных (дискретно-непрерывных) САР:
а) время наступления первого
максимума
f*= — (arctg—1=== =F v + лЛ
11 I )
(10.28)
(номограмма для определения fm в зависимости от v, rj, Ль £i построена на рис. 10.6, а);
б) максимальное значение характеристики переходного процесса
Хт — 1 + дЛ ~ 6?1 sec V | х
=F v + л
(10.29)
максимум перерегулирования
(Ут = V1 — 6i I sec V I X X exp Г farctg ~ZL-=- =F
Tv + n^l (10.30)
(номограмма для нахождения <у*т в % в зависимости от £i и v построена на рис. 10.6, б);
668
г) время регулирования переход-
ного процесса
~ it ( 3 — In | cos v | \
P~ T) I £1 )
(10.31)
(номограмма для нахождения /р в зависимости от £i, т], То и v построена на рис. 10.6, в);
д) коэффициент демпфирования замкнутой системы
рывной САР и приближенный способ определения ее основных показателей качества.
Пример 10.3. Построить корневой годограф САР, имеющий прн Та = 0,5 с передаточную функцию неизменяемой части системы в разомкнутом состоянии в. виде
0,13/С (г Ч-1,31) (г Ч-0,045)
hW z(z-1) (z-0,368)
(10.33)
in | Znl I V(ln I z„i |)2 + n2
(10.32)
(кривые постоянных значений gj в первом квадранте Пл. z приведены на рис. 10.6, г).
Приведем пример построения корневого годографа дискретно-непре
Рис. 10.6. Номограммы для определения ос-новных показателей качества дискретных (дискретно-непрерывных) САР на основе корневого годографа:
а —времени наступления первого максимума
б—максимума перерегулирования о* ; в —времени пг
протекания переходного процесса t*г—коэффи-, Р
цнентов демпфирования
669
Расположение потосод и нулей корректирующих устройств на z - плоскости Таблица 10. 1
п/п Тип корректирующею устройства Ш(г) Расположение полюсоВ и нулей на г- плоскости № П/П Tun корректирующего устройства W(z) Расположение полюсоВ и нулей на г-плоскости
1 Пербого порядка с опережением по разе * z~z"' z«>lz/w| ~ч Лл.г -У 4 Второго порядка с отстибонием по разе А fZAZw)(ZAZw> п*(г-гт)(г-г„2) ZH1 < ZHZ | z#r| < zm lzM2l< znz -l(ZH1 \ ZH2 —-ч. пл.г znz Д 1 " Чу
1 zm » zHtj
A fZ-Z^,)(Z-Zw) ^(Z-Zflf)(Z-Zfl2) ZH1 > ZH2 Z01 ZH1 zm > zh2 -l[ \ ° n^ z zhz zm \ / zm znjj
4 Z'Z*> *"^77 zhi > zm -1[ Лл.г 1
\ 0 zm ZH1J
. (^иМ^г-нг) * (z'*'zni)(z',‘zn2) ZH1 > ZH2 zm >ZH1 Znz > ZH2 -1i lm у//? znz лл.г 1 0 J
A z~z"' zni > zm -г/ Лл.г \ 1
\(П1 ZH1 0 J
5 Второго поряако с опережением и отставанием по разе k ^Z~ZHl)(z+zHZy ^(г-кгПр(г-г„2) ZH1 > ZH2 ZH1 |г#гК zni -11 ZH2 Лл.г Zfiz Л1
Z пербого порядка с отставанием по разе A z ZjV/ znt<zm -ц Лл.г zm\j
у zm ° Чу
\ ° ZH1 J l (z-z-hiXz-Zhz) *(z-ZmMz’znz) ZH1 > ZH2 ZH1 > zm ZH2< ZO2 -Ц Лл.г zm znz\ 1
* z*z"' zhi <-zm -1f Лл.г \ 1 \ ° ZHZZHlj
k (Z*ZH1)(Z+ZH2) nK(Z^inj)(Z + Z/tz) ZHt > ZH2 ZH1 > zm ZHZ < znz -7 (ZH2 zm •«-4- nj,'Z \ 1
Vm ” 0 j
yzmzHi 0 J
3 Второго порядка с опережением по разе **(z+z„t)(z<-zm) ZH1 >ZH2 ZH1 >|z m\ ZH2 >lz/72| -11 гП2 1 zm Пл. г z;z \ 1 0
6 Второго порядка с отстабанием и опережением по разе fZAZ^IfZ^Z^) ZH1 >ZHZ lZKfl < zni ZHZ> znz -1 (Z nz ZH1' yf-HZ zm Лл.г \ 1 ° J
(z-z^lz-Znz) ZH1 > ZH2 ZH1 > zni ZH2 > znz -l( к 0 Лл.г znz ZHt \ 1 zmzHij
k fZ~ZHf)(Z~zHz) *{z-zni)(z-znz) ZH1 > ZHZ ZH1 < zni zHZ > znz -11 \ 0 Лл.г znz ZHl\ 1 zH2zmj
"«(ZAZ^XZAZ^) ZH1 >ZHZ zhi > zm ZH2 > ZK2 ~lFf)2ZH2 \ zm zhi лл.г \ 7 0 /
(Z-Z„,)(Z<-ZHZ) ““(z-ZmMz+Z/n) • ZH1 >lZH2 | ZH1 < zm ZM2 > Znt -1 (. Zftz 77л. Z г*7 , Д 7
V/Z2 0 ~zmj
670
Рис. 10.7. Корневой годограф СЛР для примера 10.3
когда передаточная функция последовательного корректирующего устройства имеет первый порядок с отставанием по фазе (см. табл. 10.1)
uz ,.0,25(2-0,96) .
Гк11(г)==---7^-оУд- - <10-34)
и определить переходный процесс в замкнутой системе. Реализацию корректирующего устройства выполнить на микроЭВМ «Электроника-60» на языке ассемблер.
Характеристическое уравнение замкнутой системы
24 - 2,3580г3 + 1,722г1 2 - 0,364г +
+ КО,0325 (г3 + 0,395г2 - 1,242г -
- 0,0566) = 0. (10.35)
По уравнению (10.35) на рис. 10.7 построен корневой годограф на Пл. г в за
висимости от коэффициента К (Kt — 3; К2 = 5; Кз = 10; К, = 100; К5 = 200; Кг, = 250: Ki = 300; Кд — 400). Как видно из рис. 10.7, корневой годограф состоит из двух ветвей Г, и Г2.
Для реализации программы коррекции перепишем передаточную функцию (10.34) в виде
U (г)
U (г)
0,25 — 0,24г-'
1 —0,99г-'
. (10.36)
Тогда получим соответствующее разностное уравнение в реальном масштабе времени
йк==0,99йк-1 + 0,25«к_! - 0,24ик-г. (10.37)
Реализацию уравнения (10.38) выполним на языке, ассемблер для микроЭВМ «Элек-троника-60»
; UK37
; РАСЧЕТ ФОРМУЛЫ (10.37)
; UO (К) = 0.99UO (К — 1)4-0.2511 (К - 1) — 0.24U (К — 2)
; ВХОД: РЕГ. 167766
; ВЫХОД: РЕГ. 167762
; РАСПРЕДЕЛЕНИЕ ПОЛЯ U:
; U (0): UO (К — 1)
; U (2): U (К-1),U (4): U (К-2)
; МАСШТАБ: ДЛЯ UO И U 1 :100
; R0 = % 0
UK37:: R1 = % 1 R2 = % 2 R3 = % 3 R4 = % 4 R5 = % 5 SP = %6 PC = % 7 .IRPC N, 01234 ; СОХРАНЕНИЕ
MOV R'N.-(SP) ; РЕГИСТРОВ
. ENDM 0...4
I»: BIT # 100,®# 167764 ; ПРОВЕРКА
BNE 1Я ; ГОТОВН. ВХОДА
MOV ©# 167766,11 4-2 ; ЧТЕНИЕ ВХ.СИГНАЛА
CLR R0 РЕГ.ДЛЯ СУММЫ
CLR RI ; ИНДЕКСНЫЙ РЕГ.
671
2Ц: MOV U(R1),R2 ; ЦИКЛ ВЫЧИСЛЕНИЯ UO (К)
MOV C(R1),R4 ; ВЫБОР ОЧЕРЕД.КОЭФФ.
MUL R4.R2 ; В R2.R3 ОЧЕРЕД.ТЕРМ
ADD TST R3,R0 (RD 4- ; В R0 ЧАСТИЧ.СУММА
CMP #6,R1 ; :ПРОВЕРКА
BNE 2Й ; КОНЦА ЦИКЛА
MOV BIS R0,@# 167762 # 100,@# 167760 ; ВЫВОД UO (К)
MOV R0,U ; UO (К) В UO (К - 1)
MOV U + 2,U + 4 ; U (К - 1) В U (К-2)
.IRPS N, 43210 ; ВОССТАНОВЛЕНИЕ
MOV . ENDM RTS (SP) + ,R'N PC ;РЕГИСТРОВ ; 0...4
U; .WORD 0,0,0
С: .WORD .END 99. ,25. ,-24.
Построим переходный процесс по формуле (10.27). При К = Ki = 3 на рис. 10.7 показан штриховыми линиями треугольник Zn\DK\, из которого найдем угол v = — —45°. Там же штрихпунктирной линией через точку К, = 3 проведена линия постоянного значения gi = 0,59 (см. номограмму рис. 10.6, в).
Положив в уравнении (10.35) К = 3, определим комплексно-сопряженные корни 0,6575 + /0,309 и 0,6575 — /0,309. Откуда с помощью формул (10.26) найдем собственную частоту колебаний системы ш, = = 1,09 с-1 и 71 = 1/1,09 = 0,92 с.
Подставляя значения v, с, и 7, в формулу (10.27), получим
xm(Vlw”-,-l4
По этому выражению на рис. 10.8 построен переходный процесс в замкнутой системе. Откуда видно, что от = 10%; /р= = 5,2 с; t*m = 3,8 с.
Рассмотрим графоаналитический метод синтеза САР на основе по-
Рис. 10.8. Переходный процесс в САР для примера 10.3
строения корневого годографа, пользуясь при этом передаточными функциями корректирующих устройств в г-форме (табл. 10.1).
Пример 10.4. Определить тип и параметры последовательного корректирующего устройства для дискретно-непрерывной системы, при котором g] =0,7 и /р < 1 с. Структурная схема системы приведена на рис. 10.1, а. Пусть неизменяемая часть описывается передаточной функцией вида
U7H (s) = Ws2, (10.39)
где k0 = 5.
Синтез корректирующего устройства выполнен по желаемому расположению полюсов замкнутой системы на Пл. z. При этом найден такт квантования Та.
Преобразовав выражение (10.39) с учетом экстраполятора нулевого порядка, по-
лучим
Гн (г)
Vo <г + О
2 (г — I)2 '
(10.40)
На рнс. 10.9 построим сплошной жирной линией кривую на Пл. г, соответствующую постоянному коэффициенту демпфирования gi — 0,7 (см. номограмму рис. 10.6, г). По номограмме рис. 10.6,6 определим значение ±v, при котором достигается минимальное значение от. При ^=0,7 имеет минимум о,„ -- 4,6 % в точке —v = —45°.
Передаточную функцию замкнутой системы при учете доминирующих полюсов будем искать в виде (10.18) или (10.19), где комплексно-сопряженные полюсы задаются выражением а ± jb. По формуле (10.40) найдем значение нуля —zHi = —1. Тогда из выражения (10.22) можно получить уравнение, связывающее нули и полюсы передаточной функции Ф(г), в виде
а? + b2 + ctg (т v + (1 =F Zhi) b +
+ (=FzHi - 1)а=ТгВ|. (1°Л1)
672
Рис. 10.9. Нахождение желаемого положения полюса в синтезируемой САР примера 10.4
Подставляя в выражение (10.41) значения— Zhi = —1, —v — ——, найдем уравнение, связывающее величины а и Ь, т. е.
а2 + (6-1)2 = 2. (10.42)
Дуга окружности, описываемая формулой (10.42), точки которой удовлетворяют условию |z| 1, проведена иа рис. 10.9
штриховой линией. Она совпадает с линией 51 = 0,7 на участке АВ. Таким образом, если полюс замкнутой системы Zni расположен иа кривой АВ, то система обладает минимальным перерегулированием при заданном коэффициенте демпфирования.
Выберем в качестве желаемого положения полюса Zni точку В, так как по мере приближения к точке А для обеспечения заданного времени регулирования необходимо уменьшать такт То, т. е. увеличивать быстродействие ЭВМ. Из рис. 10.9 видно, что а = 0,62; Ь = 0,28. Откуда найдем т) — arctg — = 24,3°. По номограмме
рнс. 10.6,в для —v = —45° определим величину /*т)/Т0 = 19б° или Го = О,12 с.
Синтезируем теперь последовательное корректирующее устройство, обеспечиваю-
Рис. 10.10. Переходный процесс в САР для примера 10.4
щее выбранное расположение доминирующих полюсов, в виде (см. табл. 9.1)
Укп(г)= Мг ~/Дн1) . (10.43)
В этом случае характеристическое уравнение замкнутой системы с учетом коррекции можно записать следующим образом:
(z—l)2(z — zani) +
+ К (z + 1) (z — Хдн 0 = 0, (10.44)
где K^kKkoTl/2.
Уравнение (10.44) совпадает с аналогичным уравнением для желаемой системы
(z2 — 2аг + а2 + 62) (z — z'n j) = 0. (10.45)
Вычитая уравнение (10.44) из (10.45), получим
(z2 - 2аг + а2 + b2) (г-гдп1)-“(г-1)2(г-гдп1)-
— К (г + 1) (г — гдн j) =0, (10.46)
/
где гдп — положение полюса гди j при замыкании системы.
Приравнивая коэффициенты при одинаковых степенях z к нулю, получим систему линейных уравнений относительно пе-ременных гдп 1( гдп h К:
2дп 1 гдп 1 4" = 0>76,
1.242дп1-22дп1 +
+ (гдн1-1) К = 0,5372;
- 0,4628гдп ! + гдн =0.
Для однозначного разрешения системы (10.47) зададимся значением гдН] = 0,9 в пределах единичной окружности. Тогда из уравнений (10.47) найдем К — 0,27; гдп j = 0,53; гдп j = 0,05. Коэффициент коррекции определим по формуле
, _ 2К 2-0,27 __
Tjfco 0,122-5 =
Переходный процесс в данной системе, полученной с помощью формулы (10.27), приведен иа рис. 10.10. Откуда видно, что <тт = 4,6%, а /„<1,0 с. Эти данные соответствуют требованиям технических условий.
22 К). И. Топчеев
673
3. СИНТЕЗ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПО ЗАДАННОМУ РАСПОЛОЖЕНИЮ НУЛЕЙ И ПОЛЮСОВ С ПОМОЩЬЮ ВВЕДЕНИЯ ОБРАТНОЙ СВЯЗИ по состоянию И ВЫХОДУ
В соответствии с системой уравнений (3.155) опишем дискретную (дискретно-непрерывную) систему с одномерным сигналом управления на входе микроЭВМ в виде
y(4+i) = ^(U + ^(^)> (Ю.48) где
u(tK) = -kTy(tK). (10.49)
Здесь k — вектор коэффициентов обратной связи размерности п.
Рассмотрим решение задачи синтеза при найденных желаемых значениях матрицы А и вектора Ъ. Из выражений (10.48) и (10.49) следует, что она сводится к определению матриц коэффициентов обратной связи. Если система полностью управляема (см. п. 8, гл. 3), то справедливо следующее соотношение:
д (z) = ’ (1 °-50)
в котором числитель представляет собой характеристическое уравнение матрицы А — bkT для замкнутой системы, а знаменатель — характеристическое уравнение матрицы А (для разомкнутой системы). При этомД(г)=( 1 + feT (zl — А)"1 Ь |.
Соотношение (10.50) находим с помощью равенства
zl - А + bkT =
= (zI-A)[f4-(zf-A)-l6fcT], (10.51)
где после вычисления определителей правой и левой частей получим
| zl - А + bkT | =
= I zl - А 11 I + (zl - A)-1 bkT |. (10.52)
Определитель | I 4- (zl — A)-1 bkT |можно представить в виде
I 14- 6йт (zl - А)-11 =
= | 1 +£т(г1- А)-1б|. (10.53)
В соотношении (10.53) матрица kx(zl—А)--1^ имеет размерность (1X1); поэтому
А (г) = 1 4- kT(zl- А)~1 Ь. (10.54)
Учитывая выражения (10.52)—-(10.54), определим соотношение (10.50), которое и будем~ использовать для нахождения вектора k.
Теперь покажем справедливость следующего равенства:
kT(zl - А)-1 b = [1 4- Лт (zl - А)-16] ЛТХ
Х(г1-А4-6Лт)“'б, (Ю.55)
которое можно получить, применив к равенству (10.51) операцию обращения матриц, т. е.
(zl- А 4- ЬктГ1 =
=[1 4- (zl - A)"1 6feT]-1 (zl - А)-1, (10.56) и умножив обе части последнего равенства слева на выражение feT [I + (zl - АГ1 bkr], а справа — на вектор Ь. Тогда
Р[1 4- (zl- A)~l &feT] (zl- А 4- 6=
= £т (z/—А)-1 6. (10.57)
Из равенства (10.57) следует справедливость соотношения (10.55).
На основании приведенных выражений имеем
1 +feT(zZ-A)“‘6 =
= 1 + feT b . (10.58)
1 | zl — А | '
где adj (zl — A) — присоединенная матрица к (zl — А) (см. прил. П-1.1).
В результате из выражения (10.58) получим скалярную функцию
1 +*T(zZ-A)_,6 =
— Iг/ ~ Л I + *Т [adj(zf - А)]» /j П
— |zl-А| •
Используя соотношение (10.50), можно выражение (10.59) привести к виду
JfeT[adj (zl - A)] b = \zl - А + 6feT| -— \zI — A\. (10.60)
Из выражения (10.60) находим
коэффициенты искомого вектора k.
674
Для этого представим определители следующими многочленами:
| zl — А | = г" + щгп~1 +
4~ я2гп 2 + • • + an-i2 4~ я„;
\zl — А + bkT | = гп + а1г"-1 4~
4~ a2zn 2 4- .. • + 4- яп,
(10.61)
а вектор [adj (zl — А)] Ь запишем в виде
[adj (zl — А)] 6 =
= Е г'-' Е яя_£А'^- (10.62) /-1 1-1
В результате выражение (10.60) можно представить в виде
п п
i=«i
= Ё (o„_i — a„_J z‘. (10.63) i-o
Приравнивая коэффициенты при одинаковых степенях z в обеих частях равенства (10.63), найдем
1 0 0 ... 0"
Я1 1 0 ... 0
Яг Я1 1 ... 0 X
_Яя-1 яп_2 я„_3 ... 1_
Принимая, что синтезируемая САР является полностью управляемой, согласно выражению (3.157) матрица К = [6 АЪ А2Ь... A"-1ft] имеет ранг п.
Треугольную матрицу в выражении (10.64) обозначим через М. Она также имеет ранг п.
Следовательно, умножив слева соотношение (10.64) на (AfKT)-1, получим
Лт = (МКТ)“‘ (« - а) или
F = [(AfKT)“‘ (а - а)]т. (10-65)
Вектор k имеет размерность п и зависит от коэффициентов характеристического уравнения замкнутой системы. В этом случае можно найти выражение для Лт через желаемые собственные значения замкнутой системы * Zni, Zn2, • • • > znn- Тогда
| zBiI - A 4- bV I = 0,
4 = 1, 2, ..., n.
Из выражения (10.60) имеем
Йт [adj (zntl — A)\b —— \znlI — А\,
(10.66) где
[adj (zaiI — A)]b = q (zni);
| znlI - AI = До (zai), 4 = 1,2.m.
Выражение (10.66) перепишем в виде
lrq(zal) = -^(zni) (10.67) и для. случая полюса кратности ц имеем
krq(znm+i) = — Ao(zam+/), (10.68) где
9(2Пт+/)=^-9(2)ипй,+/;
До (2п«+/) = ту До (z) L-zn т+1 ’
/=1, 2, ...,р.
(10.69)
Таким образом, для всех собственных значений найдем
F =
== — [До (2ni) До (гп2) • • • До (2nn)] Q *»
(10.70)
* Считаем, что имеем т различных полюсов, а остальные п — т — кратные.
22*
675
Рис. 10.11, Структурные схемы САР с обратными связями:
а — по состоянию; б— по состоянию с помощью динамических звеньев
где
Q = [9(znl)g(Zn2) 0(Zn„)]. (10.71)
Следовательно, выражение (10.70) так же, как и соотношение (10.65), полностью определяет вектор обратной связи, который можно записать в виде
feT = [feife2 ... fen], (10.72) где fe,- — коэффициенты, стоящие в цепях обратных связей САР по вектору состояния.
При решении практических задач синтеза дискретных (дискретно-непрерывных) САР удобно пользоваться переходной матрицей состояния
ф(Г0)==е^г. (Ю.73)*
и вектором передачи входных сигналов
Го
7(Г0) = jO(6)6d6. (10.74)* о
Пример 10.5. Синтезировать дискретио-иепрерывиую САР с обратными связями по состоянию, где
Г 1 ъ *=г 0
[о -267,19 J [244,68
Структурная схема системы изображена на рис. 10.11, а.
Воспользовавшись формулами (10.73) и (10.74), определим матрицу Ф и вектор f в виде
Г 1 0,00276 I Г 0,00205 Ч
L 0 0,263 J ' ' ~ L 0,675 J
где принято То = 0,005.
Характеристическое уравнение разомкнутой системы или матрицы Ф, следующее:
До (z) = |zZ—Ф| =
-0,00276 I z - 0,263 I
= z2 — l,263z+ 0,263 = 0.
Так как пара матриц [Ф, fl полностью управляема, то с помощью обратной связи по состоянию собственные значения матрицы Ф — fkr можно задавать произвольным образом.
Для того чтобы свободное движение в спроектированной системе имело апериодический характер, расположим оба собственных значения замкнутой системы в точке z = 0.
Желаемое характеристическое .уравнение замкнутой системы в этом случае имеет вид г2 = 0.
В соответствии с уравнением (10.58) запишем
. , . Г 0.00205z + 0,00132 1
Вектор обратной связи определим из соотношения (10.70)
*т = -[0,263 -1,263] X
0,001323 0,002051-1
—0,675 0,675 J
= [296,3
0,970].
Изложенную методику синтеза можно распространить иа системы, имеющие несколько управляющих сигналов. В этом случае уравнение (10.48) запишем в виде
У (*к+1) = А» (<к) + Ви (tK) (10.75) и
«(<к) = -Л»(М, (Ю.76)
* Подробнее см. п. 10, гл. 1 и п. 7, гл. 3.
где К — матрица коэффициентов с размерностью (rX«). а “(М — г-мерный вектор.
676
При полностью управляемой САР требуется найти такую матрицу К, чтобы в выражении (10.76) собственные значения матрицы А — ВК размещались в произвольно заданных точках z-плоскости. Как было сказано раньше, эта задача сводится к синтезу коэффициентов в обратной связи по состоянию для системы с одним входом, описываемой следующим уравнением:
»(*к+1) = Ау(М+*«0к); (Ю.77)
b = Bw, (10.78) где w— вектор размерности г.
Вектор w должен быть таким, чтобы пара матриц [А, 6] удовлетворяла условию управляемости. В этом случае, вводя обратную связь в систему, получим
« (Ас) = - &У (tK). (10.79)
Разместим собственные значения матрицы А — bkT в тех же точках Пл. z, что и собственные значения матрицы А—ВК; тогда матрица обратной связи К полностью определена и
K = wk\ (10.80) Отметим, что вектор w не является единственным. Вектор коэффициентов обратной связи можно определить подформуле (10 65).
Практический интерес рассмотренная методика представляет для сложных САР, имеющих неполные обратные связи по состоянию или обратные связи по выходу. В таких системах не представляется возможным измерять все переменные состояния (фазовые координаты).При неполной обратной связи по состоянию будем использовать уравнения (10.75) и (10.76).
Пусть обратная связь по координате yi(tK), где i может иметь одно или несколько значений, отсутствует. Тогда соответствующие столбцы матрицы К будут иметь нули и на основе ранее рассмотренной процедуры синтеза матрица обратной связи определяется по выражению (10.80).
При неполной обратной связи столбцы матрицы kT, соответствующие нулевым столбцам К, будут также нулевыми. Данный способ синтеза применим, когда обратные
связи по выходу х измеряемы. Тогда имеем систему уравнений
У &+i) = Ay + Ви (tK);
.W-CrW, (10-81)
где х (1К) — р-мерный вектор выхода.
Обратная связь в этом случае
u(Q = -Kx(tK). (10.82)
Задача синтеза состоит в том, чтобы найти такую матрицу К, при которой будут получены желаемые собственные значения замкнутой системы. Для полностью управляемой САР выражение (10.65) перепишем в виде
kxC = 1СМКТ)-1 (а- а)]т (10.83) или в форме (10.70)
kTC =
= — [Aq (zni) До (2пг) • • • До (2пп)1 Q *•
(10.84)
Эту задачу можно решить, если ранг матрицы С больше или равен рангу матрицы В.
4. РЕАЛИЗАЦИЯ ОБРАТНОЙ СВЯЗИ ИО СОСТОЯНИЮ С ПОМОЩЬЮ ДОПОЛНИТЕЛЬНО ВВЕДЕННЫХ ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
Рассмотренные в п. 3 методы синтеза САР с использованием обратных связей по состоянию и выходу применимы к системам автоматической стабилизации. При проектировании следящих систем приходится наряду с обратными связями по состоянию вводить в обратную связь по выходу дополнительные динамические звенья.
Запишем уравнения исследуемой системы
У (^К+1) = Ау + Ви № + Fg №> )
x(tK) = Cy(Q + Du(tK) + Hf(tK), J (10.85)
где g(tK)— р-мерный вектор входного воздействия; f(tK) — s-мерный вектор по возмущению.
677
Будем считать, что рассматриваемая САР асимптотически устойчива; тогда векторы приращений по состоянию и управлению можно представить в виде
F»(^+i)-y(Ul к' L x(tK) J
с размер-
ностью (n 4- р) X 1 (10.86)
v(tK) = u(tK+i)-u(tK). (10.87)
В соответствии с соотношением (10.86) найдем
/ (U i) = R (/K+f Г \(/к+ l)l • (10.88)
Систему уравнений (10.85) можно переписать в следующей форме:
У (*к+2) = Ад (/к+1) 4- Ви (/к+1) 4- ' 4-Ffif(U;
х (^к+г) = Су (^к+1) 4“ Ви Gk+1) 4-+ Hf(tK).
(10.89)
Вектор разности
A[y(tK+i) — y(Q] +
+ B[u(tK+l)-u(tK)]~
= — [»Uk+1)~ =
C[y(tK+i)_ y(/K)]4-
_ 4-D[«(fK+1)-«(Q] .
Г A-In 0 1 Г В ]
— I C 0 J1 + L D J V ’
(10.90)
где In — единичная матрица размерности (n X n).
Выражение (10.90) в приращениях аналогично следующему равенству:
Г А 0 1 ГВТ ^(4+1)—j JI (4) 4- [ р J v (4) •
(10.91)
Здесь Гр —единичная матрица размерности (р X р) •
Задача синтеза справедлива лишь при выполнении условия управляе
мости. Для доказательства этого положения в выражение (10.91) введем расширенные матрицу А и вектор В:
А с /Р
- ГВ 1
B = [DJ (10.92)
Располагая матрицами (10.92), уравнение (10.91) можно переписать в виде
t(tK+l)^Al(lK) + Bv(tK). (10.93)
Пара матриц [А, В] полностью управляема, если матрица [AZ—А | В] размерности (n4~ Р) X (« 4- Р 4- О имеет ранг п 4- р при значениях X, равных каждому из собственных значений матрицы А. Условие управляемости перепишем в следующей форме:
[AZ — А|В]~
Г Х/„ — А О В 1 =1 __С (A —1)ZP в]
(10.94)
Из условия, (10.94) находим, что матрица А имеет не менее р собственных значений X = 1. Если X = 1, то условие (10.94) принимает вид
[AZ - А |В]
Ц-А О ВТ -С О В Г
(10.95)
При X #= 1 ранг (X — 1)/р равен р, и когда матрица [XZ„ —А|В] имеет ранг п, то матрица [А, В] имеет соответственно ранг п -j- р, т. е. матрица [А, В] управляема. Иначе го-
[ А“1п ВТ й
С D J °бладает Рангом
воря, если обеспечиваются условия: [А, В —управляемая пара, а мат-
рица'
п 4- р, то пара матриц [А, В] упра
вляема.
Таким образом, условия управляемости системы в приращенйях в форме (10.93) выражены через матрицы коэффициентов системы (10.85).
678
Рис. 10.12. Дискретная система с наблюдателем, реализованным на микроЭВМ
После этого образуем обратную связь по состоянию в виде
v(tK) = -Xl(tK). (10.96)
Здесь матрица К имеет размерность г X {п + р) и содержит постоянные коэффициенты.
Из выражений (10.86) и (10.87) с учетом соотношения (10.96) получим
®(U = «(4+i)~-«(4)^=
= — К1 [у (4+1) — У (4)] — К2* (4).
(10.97)
где Ki и К2 имеют соответственно размерности гХ« и гХр-
Найдем z-преобразование для выражения (10.97). Тогда получим
U (z) - - К.У (z) - К.Х (z).
(10.98)
Из выражения (10.98) следует, что управление «(4) осуществляется в виде обратных связей по состоянию (постоянные коэффициен
ты) и выходу (динамические звенья). Сомножитель l/(z—1) представляет собой цифровую аппроксимацию операции интегрирования, реализуемую на ЭВМ с помощью численных процедур.
Пример 10.6. Составить структурную схему замкнутой дискретно-непрерывной САР при действии управляющего g и возмущающего f воздействий по уравнениям (10.86), учитывая при этом выражение (10.98).
Ошибку системы сформируем в обычном виде
е(4)=?(4)-*(4). (Ю.99)
В z-области, определяемой выражением (10.98), запишем
U (г) = - (г) - k2Y (г) - D (г),
(10.100)
где коэффициенты обратной связи й,—йа находят из характеристического уравненйя замкнутой системы |г/ — А + &й'| = 0. По формулам (10.99) н (10.100) на рис. 10.11,6 построена структурная схема замкнутой САР с обратными связями по выходу с помощью динамических звеньев.
Если некоторые переменные в САР не измеряются, то их приходится восстанавливать с помощью наблюдателя (рис. 10.12). При этом
679
необходимо добиться такого положения, чтобы вектор Уис (/к) был как можно ближе к состоянию y(tK) за минимально возможное число тактов. Рассмотрим такую дискретную (дискретно-непрерывную) систему, описываемую следующими уравнениями:
y(tK+l) = Ay(tK) + Bg(tK); (10.101)
x(tK) — Cy(tK). (10.102)
Уравнения дискретного наблюдателя составляются аналогично, т. е. УиЖ+1) = Ауис(/К) + ВуО (Ю.ЮЗ)
*Hc(4) = CyHc(U (Ю.104)
Восстанавливаемый вектор состояния Унс(^к) используется для формирования сигнала ошибки е(/к) с помощью матрицы обратной связи G размерности («Хг):
е(/к) = Су(/к)-Суяс(/к). (10.105)
Покажем, что проектирование дискретного наблюдателя состояния связано, с критерием наблюдаемости (3.164). Для доказательства этого запишем уравнение состояния замкнутого наблюдателя в виде
Уис (^к+1) ~ (A GHCC) уяс (tK) +
+ Bg (tK) + GBcx (tK). (10.106)
Подставляя в выражение (10.106) соотношение (10.102), получим
Унс (4* 1) = Ауяс (/к) + Bg (/к) +
+ <?нсС[уЮ-унс(4)]. (10.107)
Если совпадают начальные условия у(0) и унс(0), то в правой части уравнения (10.107) последнее слагаемое исчезает, и оно становится идентичным уравнению (10.103). Это указывает на то, что проектировщик должен выбирать параметры наблюдателя при различных начальных условиях. Вычитая из уравнения (10.101) уравнение (10.107), найдем однородную разностную систему
У (^к+1) Унс (^к+1) == =(А - GHCC) [у (Q - унс (Q] (10.108) с матрицей коэффициентов А — — G„cC. Матрицу GHC можно полу
чить из условия размещения собственных значений матрицы А — GBCC на z-плоскости таким образом, чтобы траектория свободного движения системы (10.108) стремилась к нулю. Так как собственные значения матриц А — GhcC и Ат — CTGBC совпадают, то они размещаются таким образом, чтобы пара [Az, С'] была полностью управляемой, что эквивалентно полной наблюдаемости пары [А, С].
Рассмотрим синтез дискретного наблюдателя с помощью сопряженной канонической формы. Преобразуем уравнение (10.106) к виду
Уис Gk+i) — (Aj J?GHCC]) унс (/к) -|-
+ Blg(tK) + RGncx(tK), (10.109)
где преобразование
Унс</к) = ^с(4) (10.110) определяется невырожденной матрицей R соответствующей размерности. В этом случае имеем матрицы
Й?НС = [*НС1 kac2...kacnr-, (10.111)
C1 = CJ?"1 = [0 0...1]; (10.112)
В1 = ЯВ; (10.113)
" 0 0 ... 0 — ап
Aj=jRAB-i =
1 0 ... 0 — art_j
0 1 ... 0 — ап_2
0 0 ... 1 —
(10.114)
Матрица Ai представляет собой сопряженную каноническую форму фазовой переменной. Используя соотношения (10.111), (10.112) и
(10.114), получим
At — BG^Ci —
"0 0 ... 0 —an — kBCi
1 0 ... 0 an_i kBZ 2
0 1 ... 0 *— а„_2 kBC з
-О 0 ... 1 — Qj — kacn _
(10.115)
680
Запишем теперь характеристическое уравнение для преобразованной системы наблюдателя (10.109):
| U -Л + «©„^1 =
= + (а1 + kac п) лл ‘ + ...
Из равенств (10.119) и (10.120) получим матрицу преобразования
• • • + (ап-1 + &нс 2) ^ +
+ (ап + Анс1) = 0. (10.116)
Представив матрицу R в виде
%2
(10.Н7)
где Rt — строка с размерностью (1 X «) > и, подставив выражение (10.117) в матрицу (10.114), найдем
— anRn
" С СА
СА2
САп~2
СА11-1
(10.121)
AjR = RA =
^?2 — an-2^in
Vi-аЛ. (10.118)
Из выражения (10.112) следует
C,jR = [O 0 ... 1]Я = Я„; (10.119)
поэтому матричное соотношение (10.118) дает
Rn—1== СА‘,
Rn—2== Н” a^GA -j- С А2;
%2 — ап-2^ + ап-зСА + • • • ... + aiCA"-3 + САп~2;
— Qn-iC + Оп-гСА + • •. ... +aiCAn~2 + CAn-1.
(10.120)
Переписывая столбец в соотношении (10.121) как строку, получим условие полной наблюдаемости системы в виде (3.164), т. е.
G = [СТАТСТ (Ат)2 Ст ... (Ат)п-1 Ст].
Здесь показатель степени п — 1 соответствует М — 1.
Реализация G производится с помощью элементов матриц А и С.
В заключение отметим, что в случае сложных САР синтез на основе корневого годографа строится по желаемым логарифмическим амплитудным и фазовым характеристикам, записанным относительно билинейного преобразования, с последующим переходом к s- и z-формам (см. пп. 3—5, гл. 3).
Гл а в а 11
СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Ниже рассматриваются задачи оп- обыкновенных дифференциальных тимального регулирования процес- уравнений. Такие задачи имеют сами, описываемыми системами многочисленные приложения в САР.
681
Эффективным средством исследования задач оптимального управления является принцип максимума Понтрягина [18], представляющий собой необходимое условие оптимальности в таких задачах. Кроме принципа максимума, рассмотрен метод динамического программирования Веллмана, который часто используют для численного решения задач оптимального управления при наличии фазовых ограничений [3]. С помощью динамического программирования решают задачи синтеза для дискретных систем, представляющих собой важный класс дискретно-непрерывных систем, в которых сигналы управления поступают в тактовые моменты времени и фазовые координаты меняются дискретно. В разделе I показано, что любая непрерывная система может быть приближенно представлена в виде дискретной. Проблема синтеза для управляемых систем заключается в построении функции, зависящей от фазовых координат и времени, иногда называемой синтезирующей функцией и (у, t) задачи и представляющей собой значение оптимального управления при условии, что в определенный момент времени t система находится в состоянии y — y(t, Умение решать проблему синтеза крайне важно в различных прикладных задачах оптимального управления. В самом деле, если известна синтезирующая функция, то техническое осуществление оптимального управления производят по схеме системы с обратной связью.
С измерительных приборов, замеряющих в каждый момент времени фазовые состояния, сигналы поступают на ЭВМ, где вычисляются значения сигналов управления u(t) = = u(t, y(t)). После этого найденные сигналы управления реализуют требуемый оптимальный процесс. В данной главе излагаются методы решения детерминированных задач синтеза.
1. ПРИНЦИП МАКСИМУМА
Пусть движение управляемого объекта описывается системой дифференциальных уравнений
где
y = f(y^, u(t), t), (11.1)
»(0 =
~Уь (0" y?(f)
— вектор фазовых координат;
_ yn(t)_
~fi (y, u, t) " /2 (y, u, t)
f(y, и, /) =
—заданная векторная функция;
Jn(y, u, t)_
'«i(0 "
«2(0
«(/)==
—вектор управлений,
_ Чщ (0 _
или просто управление, причем /о sU sUk — отрезок времени, на котором оно реализуется.
На управление’наложено условие в(/)еЩ0, /е[/0, 4], (Н.2)
где £/(/)—заданное множество в пространстве Rm, причем считается, что вектор управления является кусочно-непрерывной вектор-функцией на всем отрезке времени to t (к, т. е. имеющей конечное число точек разрыва 1-го рода. Заметим, что ограничиться непрерывным управлением оказывается невозможным, так как с его помощью трудно моделировать моменты переключения управления, такие, как, например, включение и отключение двигателей, поворот рулей, отделение ступеней ракеты и др. Покажем, что при произвольном начальном положении y(t0)^Rn и допустимом управлении* u(t) определяется траек
* Управление u(f) называют допустимым, если оно удовлетворяет ограничению (11.2).
682
тория движения управляемого объекта.
Допустим, что вектор-функция u(t) имеет скачки в точках ть тг, • • • . . . , ТГ, £о < Ti < Т2 < ... < ii <Z tK. Предположим, что задача Коши для системы (П.1) с начальным условием у (to) —ут имеет решение y(t), определенное на всем отрезке (/о,ti], причем »(т1)=/!). Далее рассмотрим задачу Коши для системы (11.1) с начальными условиями y(iz) — yw ... Если вектор-функцию y(t) можно определить указанным способом на всем отрезке времени [/о, М> т0 получим фазовую траекторию, соответствующую допустимому управлению u(t). Отметим, что y(t)—непрерывная вектор-функция, удовлетворяющая равенству
У (О = У (to) + J f(yb), ti(i), i)dx.
(11.3)
Если вектор-функция f непрерывна и удовлетворяет условию Липшица по у с некоторой постоянной М > 0, т. е. И/(у, и, t)—f(y',u, t) || < М||у — у'||; у, у' е Rn, и 6= Rm, Ie [/0, М, то при любом начальном условии у (t0) и любом кусочно-непрерывном управлении фазовая траектория y(t) существует и является единственной на всем отрезке [^0, М- Помимо ограничения на управление, могут существовать ограничения и на фазовые координаты
у (t) еО(0, /6= [/0,/к].
Краевые условия для фазовой траектории задаются следующим образом:
у (to) е= s (to)-, у (tK) 6= S' (tK), где S(t0), S'(tK)—заданные множества из пространства Rn. В случае закрепленных концов каждое множество S(t0) и S'(tK) состоит из одной точки. Если же, например, S'(tK)==Rn для всех t, то правый
конец траектории считают свободным. Цель управления состоит в минимизации функционала вида
7 (у, и, /) = J f0 (у (t), u(t), t)df+
+ Ф(У(4). tK), (11.4)
представляющего собой сумму инте-трального функционала j f0(y> и, t)dt
*0
и терминального функционала Ф(у(/К), tK) —задача Больца. Частными случаями ее являются: задача с интегральным функционалом — задача Лагранжа-, с терминальным функционалом — задача Майера.
Интегральный функционал при fo(y, и, 0 = 1 определяет задачу оптимального управления на быстродействие.
Сначала рассмотрим задачу оптимального управления с закрепленными концами и фиксированным временем, т. е. задачу поиска такого управления u(t) и соответствующей фазовой траектории y(t), которые определяют минимум функционала
/(и, У)= \ fo(t, y(t), U(t))dt, (11.5)
удовлетворяют системе дифференциальных уравнений (11.1), ограничению (Н.2) и краевым условиям
У (Ц) = У<й у (tK) — У к, to С / С /к.
(11.6)
В рассматриваемом случае моменты времени t0, tK и координаты Уо, Ук заданы. Функции управления предполагаются Кусочно-непрерывными, а функции f0(y, и, t) и fi(y, и, t) для всех i=l, п непрерывны и имеют непрерывные частные производные по всем аргументам.
Для формулировки принципа максимума введем вспомогательные
683
функции фо, фь ..., фп и определим функцию
Ж (у, и, t, ф, фо) = фо/о (У, и, 0 + -Hif 1 (»,«,/)+.•• + Ф„/„ (у, и, t)= -t^fiiy, и, t), (11.7)
1-0
называемую функцией Гамильтона — Понтрягина.
Вектор-функция
и сопряженная система (11.8) имеет вид
ф (0 = — Фо/оу (у, U, t) — Ат (!) ф (0, (11.12)
где
foy (У, и, t) =
<*1
А
' Фо (0 "
Ф(0 =
ФЛО
_Ф» (0_
удовлетворяет системе сопряженных уравнений
(11.8)
Из однородности этой системы по ф, следует, что фо(0 является постоянной.
Системы дифференциальных уравнений (11.1) и (11.8) можно переписать через функцию Гамильтона — Понтрягина
• /а ЭЯ • ;---
У<(О = -йф-; » = 1,п;
дав . (Н-9)
В частности, если система (11.1) линейна относительно функций y(t) и u(t), т. е.
y(t) = A(t)y(t) + B(t)u(t) + f(f),
(П.Ю)
то функция Гамильтона — Понтрягина может быть записана через скалярное произведение вектор-функций
Зв (у, и, t, ф, фо) = фо/о (У, и, t) +
+ (Ф, A(t)y + B(t)u + f(t)) (11.11)
Сформулируем принцип максимума Понтрягина, выражающий необходимое условие оптимальности.
Для того чтобы вектор-функция {«*(/), у* (/)}, to t tK являлась решением задачи оптимального управления, т. е. доставляла минимум функционалу (11.5) и удовлетворяла условиям (И.1), (11.2), (11.6), необходимо существование непрерывной вектор-функции ф(/),
t tK и постоянной фо, таких, что
1) Фо(О<О; |фо1 + НФ(О11^ 0,
(11.13)
2) ф(/) является решением сопряженной системы (11.8);
3) при каждом Функ-
ция Гамильтона — Понтрягина Зв(у(Г), и, t, ф, фо) переменных и — ' «11
= • достигает своего макси-
_«r J
мума на множестве U при и* (г), т. е. max5^(jf(0, «, t, ф, Фо) =
= Зв(у(Г), t, ф, Фо). (11.14)
Для определения оптимального управления u*(t) воспользуемся условием максимума (11.14), считая, что остальные переменные у, t, ф, фо являются параметрами. В результате решения задачи максимизации получим оптимальное управление и = и (у, I, ф, Фо); u*eU, (11.15) зависящее от у, t, ф, фо-
684
Если правые части системы (11.1) линейны относительно управления, то функция (11.15) может быть получена в явном виде. Например, если
fi(y, и, = 0 +
+ i = (П.16)
и множество V определяется как
U — {u = (ub «2> • • •»ur): ai^Ui^bi,
i — 1. г),
где at, bt — заданные числа, то
Зё (у, и, t, ф, ф0) = 2 ФЛ'Чу. 0 + i-0
+ Е vd"*- (11Л7)
Из выражения (11.17) видно, что максимум а^(у, и, t, ф, ф0) определяется следующим образом:
Ьк, если 2 Ф J/2? > 0;
. _ /-о ' 'к
ик ~ п ___
ак, если 2 Ф/Л2,<0, А=1,г.
(11.18)
Очевидно, что если Ьк—1’, ак — — 1, то
f^(y, О)- (И.19)
Полученная формула (11.18) дает информацию о структуре оптимального управления; k-я координата является кусочно-постоянной (ступенчатой) функцией со значениями ак или bk, причем точки переключения определяются условием
Ефж»(о. о=о. (И.20) /-0 1 'к
Если выражение (11.20) выполняется на целом отрезке, находящемся в области регулирования [fo. М, т. е. на отрезке [п, тг] е [/о, fK], то из условия (11.17) не удается найти оптимальное управление.
В этом случае оптимальное управление на отрезке [ть т2] является особым [16].
Заметим, что функция Гамильтона—Понтрягина линейна и однородна относительно вспомогательных функций фо, фь ..., фп, т. е. 3>ё (у, и, t, аф, афо) = а<?^ (у, и, t, ф, фо) при любых а ~> 0.
Кроме того, функции ф0, фь ... ..., фп определяются с точностью до положительного множителя, который можно выбирать произвольно. На практике с учетом условий (11.13) полагают
1Фо12 + 11ф(/)Н2=1. Фо<О.
В тех задачах, где удается показать, что фо < 0, полагают ф0 = — 1.
Итак, получив оптимальное управление (11.15) как функцию фазовых координат, вспомогательных функций ф(/) и времени t, подставим его в систему (11.9); в результате система из 2п дифференциальных уравнений будет иметь вид
y = t(y, U (у, t, ф, Фо), /); I
Ф = — (у, и (у, t, ф, ф0), t, ф, фо) J
(11.21)
с 2п неизвестными функциями: у{ (t), 1/2 (0..УпУ)‘> Ф1 (О. Фг(О.Ф„(0-
Используя заданные условия (11.6), получим краевую задачу для системы (11.21). Ее решение определяет фазовую траекторию, соответствующую оптимальному управлению на отрезке [/0, М. Найдем векторные функции y(t), ф(0,-подставляя которые в выражение (11.15) получим оптимальное управление как функцию времени
«’ (0 = и (у (0, t, ф (0, Фо), /j i 22) /оС'С'к-
Так как принцип максимума есть лишь необходимое условие оптимальности, то, вообще говоря, найденное решение может не оказаться решением поставленной задачи, заданной в виде (11.1), (П-2), (Н.5), (11.6).
685
Однако если из условий физической осуществимости известно, что решение поставленной задачи существует, то управление (11.22) будет оптимальным и краевая задача (11.21), (11.6) определяет однозначно соответствующую фазовую оптимальную траекторию. Заметим также, что если максимум функции Зв (у, и, t, ф, фо) достигается по управлению неоднозначно, то для получения всех оптимальных управлений следует найти все наборы (y(t), ф(0, фо) и управления u*(/), t0
tK, удовлетворяющие условиям (11.6), (11.21), (11.22). Таким образом, принцип' максимума определяет необходимые условия оптимальности для задачи (11.1), (И.2), (11.5), (11.6) и сводит ее к краевой задаче специального вида, состоящей из условия максимума функции Гамильтона — Понтрягина (11.7), системы дифференциальных уравнений (11.21), краевых условий (11.6) и условий нормировки (11.13).
Рассмотрим задачу оптимального управления более общего вида, когда критерий содержит терминальный функционал, а краевые значения для фазовых координат являются подвижными, т. е.
mini (у, и)-,
tK (11.23)
I (У, «) = J fo (У, и, t) dt + Ф (у (/к)) ^0
у (0 = 7 (у (/),«(/),/); (1124)
у (Zo) е so; у (tK) е SK; (11.25) u(t)<=U. (11.26)
Здесь So и SK — множества, определенные следующим образом *: So = {у е= Я" : hj (у) < 0; j =ТГт0;
ЛЛ(у) = 0; k = m0+ 1, s); (11.27) SK = {ys^:gj(yX0\
gfe(y) = 0; k = mk+ 1, sK}. (11.28)
* Случай So = У" означает, что левый конец свободный (аналогично и для SK = = Rn).
Будем считать, что функции fi (У, и, t), i = 1, и, Ф (у), gj (у), j — 1, sK; hj(y), /= I, з0 непрерывны и имеют непрерывные частные производные по всем аргументам. Сформулируем принцип максимума Понтрягина для задачи (11.23)— (11.26).
Пусть {у* (/), u*(/)}, t0 / sC /к— решение задачи (11.23) — (11.26). Тогда существуют непрерывная вектор-функция ф(0, to t tK и постоянная фо, такие, что
1) Фо<О; |фоI + НФ(0II0;
2) вектор-функция ф(^) является решением сопряженной системы (11.8), соответствующей системе (11-24);
3) при каждом /е ро> М функция Гамильтона — Понтрягина Зв(у(Г), и, t, ф, фо) переменных «ь ио, ..., иг достигает своего максимального значения на множестве U, т. е.
max Зв (у, и, t, ф, ф0) = ке U
= 38(y(t), u'(t), t, ф, фо), to ^к>
4) на левом и правом концах траектории y(t) выполняются усло-
вия трансверсальности, которые означают, что вектор Ф(М — — ф^Ф(у(^к)) ортогонален к множеству SK в точке у(6<)е SK, а вектор ф(/0) — фоУФ(у(/о)) ортогонален к множеству So в точке y(to)^ е So, где
" дФ/dyi дФ!ду2
7Ф(У) =
L дФ!дуп
Первый случай. Если правый конец свободен, т. е. SK = Rn, то условие ортогональности вектора ф(/к)— — фо?Ф(у(М) ко всему пространству /?" означает, что
*(4)-Фо?Ф(у(и) = О. (11.29)
686
Следовательно, в случае свободного правого конца условие трансверсальности (11.29) дает п-гранич-ных условий для системы (11.9). Если же критерий не содержит терминального функционала, т. е. имеет вид (11.5), то при свободном правом конце условия трансверсальности (11.29) имеют вид
ф(/к) = 0. (11.30)
Второй случай. Пусть правый конец подвижный, тогда множество SK определяют следующим образом: SE=(yGl?'1:g/(il) = 0; / = Т77К).
(11.31)
Кроме того, будем считать, что
Vgi (Йк)) =
dgddyi
dgildy2 _____
=/=0, i — 1, sK,
-dgt/dyn_t=^ (П.32)
тогда найдутся числа а1( а?, ..., а4-к, не все равные нулю, и такие, что
SK
Ф Ок) — Фо?Ф (if Ок)) = S fyVgf (jf(4)).
/* 1
(11.33)
Сюда же добавляются еще условия принадлежности конца фазовой траектории y(tK)&SK, а именно
Я/(У Ок)) = 0, /=1~к. (11.34)
Таким образом, равенства (11.33) и (11.34) дают всего « + $к условий, из которых sK условий применяют для определения дополнительно появившихся параметров аь а2, • • • ..., aSk, а остальные присоединяются к краевой задаче принципа максимума.
Третий случай. Рассмотрим самую общую запись конечного множества SK в виде (11.28) и потребуем выполнения условия (11.32).
Тогда условие трансверсальности означает, что существуют такие числа ait а2....aSx, не все равные
нулю, при которых выполняются
следующие равенства:
SK
4 (U — Фо¥Ф (У (4)) = £ atVgf (у (О), /»!
(11.35)
a/«f/(»O = 0, а/>0, /= 1, mk-
(11.36)
gl (y(tK)) = 0, / = mk + 1, sK.
Итак, соотношения (11.35), (11.36) дают п + «к равенств, из которых sK условий используют для определения неизвестных коэффициентов ah а2, .... asK. Заметим, что для тех j в пределах 1
тк, для которых g, (y(tK)) < 0, из соотношений (11.36) следует, что а, — 0, и остается определить лишь те а,, номера которых соответствуют ограничениям gt(y(tK)) = 0.
Четвертый случай. Напишем условия трансверсальности для закрепленного правого конца, т. е. когда имеем фазовые координаты при t = tK:
У\ (Q
У (tK) =
(11.37)
_ Уп (^к) _
Тогда условия трансверсальности означают ортогональность вектора Ф(М — ФоХ7Ф(у(М) вектору нулевой длины, в точке ук. Очевидно,' что это всегда выполняется и означает, что условие трансверсальности в случае закрепленного правого конца вырождается и не дает никакой информации. Поэтому условия (11.37) составляют необходимое число значений для граничной задачи принципа максимума.
Следовательно, из условий трансверсальности на правом конце траектории при всех случаях имеем п граничных значений для системы (11.9).
Аналогично получим п граничных условий для системы (11.9) на левом конце траектории. В самом
687
деле, в первом случае имеем свободный левый конец, т. е. So = /?", и п условий вида
Ф (t0) = 0.
(11.38)
Во втором случае множество So определяет подвижный левый конец, и его можно записать в виде
So= {jf е /?" : hj (у) = 0, / = 1, s0}-(11.39)
Если градиент всех функций ограничений (11.39) отличен от нуля в начальный момент времени t0, т. е.
VA/(»ao))#=O, / = Т?70, (Н.40)
то условия трансверсальности
So
Ф ('<>)=(у ('<>))> (11.41) /=1
где bit b2, • ., bs„ — некоторые числа, не все равные нулю.
К равенствам (1141) добавим еще условие принадлежности точки У (to) множеству So, т. е.
(У 0 = 0, j = ~sQ. (Н.42)
Равенства (11.41), (11.42) дают п + s0 необходимых условий для определения so коэффициентов Ь\, Ь2....bs , и п граничных значе-
ний на левом конце для системы (11.9). В третьем случае множество So имеет вид (11.27), или если поло-жить, что \thj(y(t0)) =Л 0, j=l, So, то условия трансверсальности будут аналогичны (11.35), (11.36), т. е.
Ф (to) = — Ё Ь/Vhi (у (to))-, (11.43)
bih/(y(to)) = O, bf>0,
/ = 1, то, (11.44)
hj (У (to)) = 0, j = то + 1, s0-
Таким образом, условия (11.43), (11.44) дают нужные n-(-So равенства для решения краевой задачи.
Наконец, в случае закрепленного левого конца сразу имеем п условий
уЦо) =
У1 (to) y*(to)
(11.45)
- Уп (to) _
определяющих значения п фазовых координат в начальный момент времени.
На практике встречается целый ряд задач оптимального управления, в которых неизвестными являются начальный to и конечный tK моменты времени. Если в поставленной задаче (11.23) — (11.26) считать неизвестными to и tK, то все необходимые условия сохраняются, а для их определения вводят дополнительные условия. В первом случае для правого конца к равенствам (11.29) добавляют
M(y(tK), u(tK), tK, ф((к), ф0) =
= ^o^(y(Q, tK). (11.46)
В третьем случае * к условиям (11.35), (11.36) добавляют условие
(У О и (Q, tK, Ф (tK), Фо) = = Фо^-(уО и-
SK
(11.47) /-1
которое используют для определения ?к.
В случае закрепленного правого конца, определяемого условием (11.37), дописывают равенство
^(j/O u(tK), tK, 4>(tK), Фо) =
= Фо-^-(уОУ. (П-48)
Аналогичные условия вводят для левого конца траектории* если ле
* Третий случай является частным случаем второго.
688
вый конец свободен, то к равенствам (11.38) добавляют выражение
^(Jf(/o). u(t0), t0, ф(/0), to) = O.
(11.49)
Или, например, если левый конец закреплен, то к равенствам (11.45) добавляют соотношение
^(jf(^o), »(^о), to, Ф(А>), %) = 0.
(11.50)
Заметим, что если в задаче (11.23) — (11.26) начальный или конечный моменты времени известны, то соответственно выписывают дополнительные условия трансверсальности на правом и левом концах.
В результате решения краевой задачи принципа максимума получим оптимальное управление как функцию времени и соответствующую ему оптимальную фазовую траекторию. Это оптимальное решение {«*(/), y*(t)} часто называют программным [32]. В процессе конструирования оптимальной системы программное движение является первым и неизбежным этапом. Следующий важнейший шаг — это синтез системы управления. Проблема синтеза для задачи (11.1), (11.2), (11.5), (11.6) заключается в построении векторной функции и = = и(у, t), называемой синтезирующей функцией этой задачи и представляющей собой значение оптимального управления, зависящее от времени и фазовых координат.
Умение решать задачу синтеза крайне важно, так как в этом случае осуществляется оптимальное управление по схеме с обратной связью: с измерительного прибора, замеряющего в каждый момент времени t фазовые координаты y^t), ..., yn(t), на ЭВМ подаются замеры и вычисляются значения управлений
= МО. • ••> f/„(0), •••
-> (t, ухЦ),..., yn(t)), (11.51)
после чего оптимальное управление u*(t,y) передается на исполнительный механизм, непосредственно реализующий в дальнейшем требуемое изменение фазовых координат.
Однако получить явное аналитическое выражение для оптимального управления (11.51) поставленной задачи удается лишь в редких случаях. Поэтому ниже будет изложен другой подход к решению проблемы синтеза.
Пример 11.1. Рассмотрим упрощенную задачу оптимального быстродействия отработки ракетой угла тангажа при отсутствии сопротивления атмосферы и гравитационных сил, Уравиеиие движения ракеты в вертикальной плоскости имеет вид
(11.52)
где Ф — угол тангажа ракеты; — постоянная ракеты; и — управление, на которое накладывается ограничение
|и(01<1. (11.53)
В некоторый момент времени t0 ракета находилась в состоянии Фо = Ф(/о), Ф(/о) = 0. Требуется за минимальное время стабилизировать ракету по углу тангажа, т. е. перевести ее в состояние ф(<к) = 0; Ф(/к) = 0. Применим к сформулированной задаче принцип максимума Понтрягина; не нарушая общности задачи, будем считать — 0. Введем фазовые переменные //1(0 и
//1=Ф/^#; Уг — Ь/kff-, тогда уравнение (11.52) можно записать в виде системы
у>=Уг’\ (Ц.54)
Уг = и. )
В этом случае получим задачу с фиксированными концами:
иа левом конце при /0 = 0 заданы yi (0) = Фо/^; У2 (0) = 0;
на правом — при tK заданы yi(tK) = 0; i/2(tK) = 0, а конечный момент времени tK ие задан.
В соответствии с обозначениями задачи оптимального управления имеем f0 = 1; ф = 0; £/=[—1,1]. Составим функцию Гамильтона — Понтрягина
Ж (У, U, t, ф, фо) = Фо + Ф102 + Ф2«. (11.55) в которой фо = const, а ф1 и ф, удовлетворяют сопряженной системе
-£L = 0;
23 Ю. И. Топчеев
689
Рис. 11.1 Оптимальные по быстродействию программное управление и фазовая траектория ракеты по углу тангажа
Определив произвольные постоянные С! и С2 из начальных условий на левом конце, получим
г/2(0 = —/;
/2 а„
у. (О =-4 + ^, 0</</н
2 Я#
(11.61)
При t > tt общее решение системы (11.54) имеет вид
У? (0 — t +
/2 Z ,
У1 (О = -2- + с;/ + с2'.
(11.62)
Произвольные постоянные С, и С2 найдем из условия склеивания решений (11.61) и (11.62) в точке /ь В результате получим фазовую траекторию
Общее решение системы (11.56) легко выписывается в явном виде
ф1(О = С1; (/) = - + С2, (11.57)
где С1 и С2— произвольные постоянные.
Найдем оптимальное управление и* (у, I, ф, фо) из решения задачи
тах^(г/, и, t, ф, ф0) =
== max (фо + Ф11/2 + фа«), (11.58) I и|<1
откуда имеем
и* (0 = sgn ф2 (/). (11.59)
Следовательно, оптимальное управление является кусочно-постоянным, принимающим значения 1 или —1, и имеет в силу линейности функции ф2(/) не более одной точки переключения. Нетрудно проверить, что управление
о << < G;
t>tl
не приводит фазовую траекторию из положения yi(0), у2(0) в начало координат, поэтому
( —1, и’(<) = { 1 , Ш-60)
<. ‘к ‘ ‘1-
В соотношении (11.60) момент переключения управления t, неизвестен и подлежит в дальнейшем определению.
Подставим оптимальное управление (11.60) в систему дифференциальных уравнений (11.54), в результате решения которой получим фазовую траекторию при О С t С
У2 (t) — — t + Cj;
t2
yi (t) =--------g- + Ctt + C2.
У\ = <
Уг^ ( t — 2/|, t>t
-4+^’ Os£'
*2 2/ / 4- -4-
Т“2^ + <‘+ fe?’
(11.63)
Из граничных условий на правом конце находим момент переключения управления и оптимальное время стабилизации /к:
6 = V^o/fe#;
/к = 2 V^0/fe#.
(11.64)
Таким образом, оптимальному программному управлению (11.60) соответствует фазовая траектория (11.63) и минимальное время стабилизации (11.64). На рис. 11.1 показана оптимальная стабилизация ракеты по углу тангажа. На этом примере видно, что минимальное время стабилизации зависит от начального состояния 4>0, Фо и характеристики ракеты fe#.
Рассмотрим теперь ту же задачу при различных значениях 1/(0). Очевидно, при
Рис. 11.2. Фазовые траектории системы (11.54):
а — при и*=- 1; б — при и* = —1
690
любых «/(О) оптимальное управление u(t)—кусочно-постоянная функция, имеющая не более одного переключения. Для отрезка времени, на котором и* = 1, в силу (11.54) имеем
yi^-f + Ct (11.65)
и аналогично при и* — —1
yl
У. = -у--|-С,. (11.66)
Семейство парабол (11.65), (11.66) изображено на рис. 11.2, а, б. Следовательно, при любом у(0) оптимальная фазовая траектория состоит из двух кусков парабол, примыкающих друг к другу. На рис. 11.3, а, б показаны оптимальные фазовые траектории при различных числовых значениях на левом конце. На рис. 11.4 изображено полное семейство фазовых оптимальных траекторий, которое позволяет решить задачу синтеза, т. е. получить оптимальное управление как функцию фазовых координат управляемого объекта. Кривую Г на рис. 11.4 называют линией переключения, уравнение которой можно записать как
Г = |(уь Уг):у1 = -у yilyil}- (И.67)
Кривая Г делит фазовую плоскость на две области: R-, где и* = —1, и R+, где и* — 1. Следовательно, R~ является множеством состояний («/], у2), находящихся справа от Г, т. е.
Я~=|(У1. Уг)-У1 > — у 11/211. (11.68)
А множество состояний R+ определяется как область, находящаяся слева от кривой Г, т. е.
R+ ={ (Уь Уг)‘У1 < — у Z/2 IZ/2 11. (11.69)
Рис. 11.4. Синтез оптимальных управлений для задачи стабилизации ракеты
Оптимальное по быстродействию управление и‘ как функция фазовых координат имеет вид
( —1 прн (yt, Уг) е= Г и Л 1 11 при (у„ |/2)еГ+иЛ+-
(11.70)
Такую функцию называют синтезирующей функцией, определение которой является решением задачи синтеза.
Спроектируем теперь систему управления с обратной связью, которая преобразует фазовые координаты у{ и у2 и формирует оптимальное управление и*. На рис. 11.5 показана структурная схема системы оптимального по быстродействию управления с обратной связью. Сигнал на выходе реле обеспечивает управление, оптимальное по быстродействию:
если (yi(t), y2(t))e=R~, то — z(/)<0; если (уi(t), y2(t))eR+, то — z(/)>0,
Рис. 11.3. Оптимальные фазовые (по тангажу) траектории при различных расположениях начальной точки
где z (0 == yi (0 4- у уг (О | Уг (0 |.
Заметим, что возникает неопределенность, когда (yi(t), y2(t)) оказываются на линии переключения Г, где z(t) — 0. Эту сложность можно устранить за счет технических средств, например, инерциоииости реле, когда переключение происходит не точно по кривой Г, а несколько позже. Кроме того, для каждого состояния (yi, у2) существует минимальное время t* = == ИУ\> Уг) перевода этого состояния в точку (0,0). Сначала вычислим время, необходимое для перевода (уь уг) иа линию переключения Г, а затем время движения от точки пересечения траектории с кри-
23*
691
Рис. 11.5. Структурная схема системы с оптимальным по быстродействию управлением н обратной связью
вой Г до начала координат. В результате получим
/•(1/1, 1/2) =
У2 + (4У1 + 2^)I/2, j/! > -у г/2| «/21;
= - У2 + (- +^У22)'12’У1 <у1/2| У21;
\У1\> У1 = — у 1/2 11/2 |.
(11.71)
Информация о минимальном времени перевода, определяемом выражением (11.71), является крайне важной для полного решения задачи синтеза.
Пример 11.2. Рассмотрим задачу об оптимальном линейном регуляторе, которая состоит в том, что необходимо удержать состояние системы вблизи нуля с минимальной затратой энергии на управление. Пусть имеется линейная система, описываемая дифференциальными уравнениями
y=*A(t)y + B(t)u (11.72) на заданном отрезке времени /о t /к, где А(0 и B(t)—матрицы соответствующей размерности («Хп), («Хи); у — вектор фазового состояния размерности (пХ1); и — вектор управления размерности (m X 1).
Задано начальное состояние системы у (t0) = уо, и на управление ограничение не наложено. Требуется найти управление, минимизирующее функционал вида
‘к
1(У, и) = у J [ут (t) Q (t) у (t) + to
+ uT (t) R (t) и (01 dt + у (tK) Sy (tK).
(11.73)
Предположим, что матрицы Q, R, S — симметрические; матрица R — положительно определенна; матрицы Q, S — положительно полуопределенны. Применим принцип максимума Понтрягина. Составим
функцию Гамильтона—Понтрягина Ж (у (t), и (/), t, ф, фо) =
= у Фо WQy + u*Ru) 4- ФУАр 4- ф]в«,
в которой фо = const. При этом вектор-функция ф1 удовлетворяет сопряженной системе уравнений
= — Q (t) у (t) — Ат (t) (t). (11.74)
Поскольку на вектор управления нет ограничения, то для определения оптимального управления воспользуемся необходимым условием максимума функции Ж т. е.
^=0, ди
откуда
R (!) и (t) 4- Вт (/) Ф1 (О = 0. (11.75)
Из выражения (11.75) получим
и* (t) = - В"1 (/) Вт (t) ф1 (Г). (11.76)
Положительная определенность матрицы R(t) гарантирует существование обратной матрицы, т. е. R~'(t). Решение сопряженной системы (11.74) будем искать в виде
Ф>(0 =P(t)y(t), (11.77)
где P(t)—симметрическая матрица размерности (пХ«).
Подставляя выражения (11.76) и (11.77) в систему (11.72), получим
у = А (/) у (t) - В (t) R1 (t) Вт (t)P(t) у (/).
(11.78)
Кроме того, из выражений (11.77) и (11.74) следует
ф, (/) = -<? (t) у (t) - Ат (t) Р (/) у (t).
(11.79)
Объединяя выражения (11.78) и (11.79) н учитывая, что
Ф1 (t) — Р (t) У (t) 4- Р (t)y(t), запишем
P(t)y(t) + P(t)A(t)y(t)~ -P(t)B(t)R-' (t) Вт (t)P(t)y =
= -Q(t)y (t) - AT (t) P (t) у (t). (11.80)
Выражение (11.80) перепишем следующим образом:
[Р (t) +P(t)A (t) 4- Ат (/) P (0 -
-r-P(f)B(f) R~l(t)BT(t)P(t) +
+ (11.81)
Равенство (11.81) выполняется для ненулевых значений вектора y(t), поэтому
692
множитель, стоящий перед y(t), должен быть равен нулю, т. е.
P(O+P(l)A(t)+WV)-
- Р (О В (t) R1 (/) Вт (О Р (/) + Q (О = 0.
(11.82)
Таким образом, матрица P(t), введенная в выражение (11.78), должна удовлетворять матричному уравнению Риккати
. Р (t) = - Р (t) А (/) - Ат (/) Р (/) + + Р (О В (/) р~1 (/) BT(t)P(f) - Q(t) (11.83)
тогда оптимальное управление, согласно формуле (11.85), определяется выражением
«*(/) =-2 [0 1]
Ри (О Р12(01 Г Pi (01
Р21 (О Р22(0 J L 1/2 (О J
= -2 [р,2 (О У1 (0 + Р22 (О У2 (01; (11.89)
при граничном условии
P(fK) = S, (11.84)
которое имеем в силу условий трансверсальности
Ф1 (^к) = Sy (^к)-
Решение матричного уравнения Риккати при граничном условии (11.84) существует и единственно. Таким образом, получим оптимальное управление, зависящее от фазового состояния на всем отрезке управления t0 t /к
«*(/) =-/Г1 (О Вт (<) Р (f) у (f). (11.85)
Если ввести обозначение К (0 = = — R-' (t) Вт (t) Р (<)> то оптимальное управление и* будет иметь вид
«•(f) = K(O»(O. (11.86)
На рис. 11.6 показана структурная схема устройства, в котором реализовано решение задачи об оптимальном регуляторе.
Пример 11.3. Проиллюстрируем полученные формулы в примере 11.2 для системы (11.54) при функционале в виде (11.73), представленного как
з
j = 4 J [2^ (0 + ^У22 (0 + (t) у2 (t) +
о
+4 “2 (о] dt + 4 [у? (3) + 2у* (3)]. (11.87)
матричное уравнение Риккати (11.83) имеет вид
Г Ри (0 Ри (0 1_
L Р21 (О Р22 (О J
= _ГР11(0 Р12(01ГО II
L Р21 (О Р22 (О -I L о О J
_Г° o-ir-pnU) Р12(0,
Ll oJLp2I(0 Р22 (О J+
Ри (О
Р21 (О
Р12 (О
Р22 (О
Согласно выражениям (11.54) имеем
X 2 [0 1] Г Р"
L Р21 (О
Р12 (0 1
Р22 (О J
Г2 11 . 1.(11.90)
|_1 4J
Граничное условие (11.84) при t = 3 будет
Рп (3) Р12 (3) j _ Г 1 01 zjigj\
P2i(3) р22(3) J~Lo 2j 1 '
После перемножения матриц в выражении (11.90) получим систему дифференциальных уравнений
pn(0 = 2pf2(0 —2;
Р12 (0 ~ — Ри (0 + 2pi2 (О Р22 (0 — 1; ►
р22 (0 = — 2р12 (0 + 2р22 (0 — 4,
(11.92)
а из матрицы (11.91) — соответствующие краевые условия
Ри(3) = 1; 1
Рп (3) = 0; [ (11.93)
Р22 (3) = 2. )
Матрица Р является симметрической; поэтому Pis(O =p2i(0- Решая краевую задачу (11.92), (11.93), получим оптимальное
На основе функционала (11.73) получим
0 < t < 3.
Представим матрицу /?(/) как матрицу размерности (2X2) с компонентами рц, т. е.
ГРп(0 Ри (0 1, 1р21 (0 Р22 (О-Г
(11.88)
Рис. 11.6. Структурная схема линейного оптимального замкнутого регулятора
693
управление u*(t) как функцию фазовых координат, согласно формуле (11.89).
Пример 11.4. Рассмотрим задачу о регуляторе выхода, когда обеспечиваются малые величины для составляющих выходного сигнала наблюдаемой системы. Если управляемая динамическая система наблюдаема, то задача о регуляторе выхода сводится к задаче о регуляторе состояния. По существу наблюдаемость системы обеспечивает единственность оптимального управления.
Пусть имеется линейная наблюдаемая система
i(t)=A(t)y(t)+B(t)u(ty, ) 4)
x(t) = C(t)y(t), )
где состоите y(t)—n-мерный вектор; управление «(/)—r-мерный вектор; выход дс(/)—/n-мерный вектор; кроме того,
п г m > О
и задан функционал вида
J(x, и) = 1 J (хт (/) Q (/) х (0 + it
4- «т (/) R (/) и (/)] dt + у хт (/к) Sx (tK).
(11.95)
Предположим, что управление u(t) не ограничено, матрица /?(/) положительно определенна, а матрицы 3 и Q положительно полуопределенны и время управления /к задано. Найдем оптимальное управление, минимизирующее функционал (11.95) и удовлетворяющее системе (11.94). Использование функционала (11.95) определяет управление, обеспечивающее близкие к нулю координаты выхода x(t) с минимальным расходом энергии. Наличие составляющей -у хт (<к) Sx (/к) в критерии гарантирует малую величину выхода в конце интервала управления. Для решения этой задачи воспользуемся результатами примера 11.2.
Подставляя выражение x(t) = C(f)y(t) в функционал (11.95), получим
/(У. «) = у J [yT(t)C4t)Q(t)C(t)y(t) + to
+ «т (/) R (t) и (01 dt +
+ 4 УТ (*к) СТ <*«) «С «к) У («• (11-96)
Из сравнения функционала (11.96) с выражением (11.73) видно, что они идентичны, с той лишь разницей, что матрицы S и Q(t) выражения (11.73) заменены матрицами C’(O)SC(/K) и &(t)Q(t)C(f). Нетрудно показать, что если матрицы S и
Рис. 11.7. Структурная схема оптимального регулятора выхода
Q(t) положительно полуопределенны и система (11.94) полностью наблюдаема, то матрицы Ст(О)SC(tK) и CT(tK)Q(t)C(t) положительно полуопределенны. В этом случае можно воспользоваться результатами примера 11.2.
Оптимальное управление существует единственно и определяется как
«* «) = - R~l (О Вт (О Р (/) у (О, (Н.97) где положительно определенная симметричная матрица P(t) размерности (лХл) является решением уравнения Риккати
Р (t) = — Р (t) A (t) — Ат (t) Р (t) +
+ Р (О В (t) R~l (t) BT(t)P(t)~
— Ст (t) Q (t) с (t)
(11.98) с краевым условием
P(tK) = CT(tK)SC(tK). (Н.99)
Оптимальные фазовые траектории системы определяются из решения задачи Коши для системы дифференциальных уравнений у (0 = [A (t) - В (/) R-1 (о Вт (/) Р (/)] У (О с начальными условиями у(/о),= Уо, полученными в результате подстановки решения (11.98) и (11.99) вг (11.97) и затем (11.97) в систему (11.94).
На рис. 11.7 приведена структурная схе-ма оптимального регулятора выхода. Заметим, что оптимальное управление является функцией фазовых координат состояния системы у(0, а не выхода x(f). Если бы система не была наблюдаемой, то вычислить состояние по выходу было бы нельзя, и поэтому оптимально управлять системой было бы невозможно.
2. СИНТЕЗ СИСТЕМ С ПОМОЩЬЮ МЕТОДА ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
Метод динамического программирования является эффективным средством решения задач оптимального управления для дискретных систем, в которых сигналы управле
694
ния поступают в дискретные моменты времени и фазовые координаты также меняются дискретно. С помощью этого метода и его обобщений получены достаточные условия оптимальности для ряда дискретных управляемых систем. Этот метод был впервые предложен Р. Веллманом [3] и сразу получил широкое применение благодаря простоте вычислительных процедур и относительно небольшому объему операций по сравнению с другими методами при решении задач синтеза.
Рассмотрим задачу оптимального управления вида (11.23), (11.24), (11.26), в которой будем считать заданными начальные условия y(t0) = = уо, время управления (t0, tK) и ограничения на фазовые координаты
y(t)e=G(t)-, (11.100)
Сформулированную задачу приведем к дискретной. Для этого разобьем отрезок времени (to, tK) на W частей точками t0 < ti < t2 < ... .,. < tbi-i < In', tN = tK и, приняв эти точки в качестве узлов, заменим интеграл в выражении (11.23) квадратурной формулой прямоугольников, уравнения (11.24) разностными уравнениями Эйлера. В результате получим дискретную задачу оптимального управления
min/0(y; [«Ло);
<v-i
«,) + Ф(»,); (11.101) I «о
У1+1 = ^1(Уь
/ = 0, ЛГ — 1; yo = y(to)^Go; (11.102)
y{<=Gt, i — 0,N, (11.103) [и/]о==(ио> и1...“jv-i);
utf=Ur, i = Q, M- 1, (11.104)
где
(У, u) = f0 (y, u, tt) (tl+i - t{)’,
i (У, u) = yi + fi (У, u, (ti+l — ti)-, Gi = G(ti)-, Ut = U(ti).
Задача (11.101) — (11.104) представляет также и самостоятельный
интерес, поскольку описывает целый класс важных прикладных задач дискретного оптимального управления. Методом динамического программирования задача (11.101)— (11.104) высокой размерности сводится к последовательности конечного числа задач минимизации функций меньшего числа переменных.
Если задать некоторое управление [и,]о — («о, «ь .... Un-\) и на чальные условия у0 е Go, то система (11.102) однозначно определяет соответствующую дискретную фазо- \ вую траекторию
[yi(V, [и;]о)]о = (Уо> Vi, Vn)-
Обозначим через Q0(y) множество управлений [а,] о, для которых выполняются условия: удовлетворяются ограничения (11.104); дискретная фазовая траектория [у<]о, соответствующая управлению [«»] о и выбранному начальному условию Уо, удовлетворяет ограничению (11.103). Тогда пара векторов (|У/]о, [«do) определяет допустимую фазовую траекторию для поставленной задачи. Очевидно, что задача (11.101) — (11.104) имеет смысл, если существует хотя бы один вектор у е Go, для которого Ло(у)=# 0.
Введем обозначение Y0 = {y:ye е Go, £2о(у)#=0} и рассмотрим следующие вспомогательные задачи:
Ш KL) =
лг-i
= Е (УР «0 + Ф (VN) "* min;
l~k (11.105)
У1+1 = ^1(У1, u{), i = k,N—l; ук = у,
(11.106)
y(^G(, i = k,N; (11.107)
[«J* — («4» «fe+b • • •» «M-l)> ut e Uit i = k, N — 1,
(11.108)
где k — целое число фиксировано и
У Gk.
При k = 0 получим задачу (11.101) — (11.104). Обозначим че
695
рез Ш(У) множество всех управлений удовлетворяющих выражениям (11.108) и таких, что соответствующая им фазовая траектория
= (Уь, Ук+1, •••> Ун)
является решением уравнений (11.106) при наличии ограничения (11.107). В соответствии с предыдущим определением пару векторных функций ([у,] k, [«/] k) также будем называть допустимой для задачи (11.105) — (11.108). Среди этих допустимых решений найдем оптимальное ( [yjft, [“i]*)> Для которого справедливо соотношение
Ш = [«dJ
(11.109)
Заметим, что если у0=#0, то S2* (У) =# 0 хотя бы для одного у е ^Gk.
Для задачи (11.101) — (11.104) введем функцию Веллмана [3]
W7A(y) = minJA(yJ«JA), (11.110)
k = Q, N-l.
Далее запишем рекуррентное уравнение Веллмана, которому удовлетворяет функция (11.110):
№ц(у) = min Г^(у, «) +
+ ^+1(^ (?>“))]> (HUD
k = 0, N-l,
№„(у) = Ф(у), ye=GN. (11.112)
Уравнение (11.111) при k = N — — 1 очевидно. Это следует из условия (11.112) и представления
JH-l (,У> [Ui]W-l) =
«) + Ф(^лг_1(У> «)),
справедливого для любого и е е= SJv-i (у),
yN =
= &н-\ (у, и) <^Gn, у g= Gn}.
Выражения (11.111) и (11.112) позволяют последовательно определять функции Веллмана Wk(y) и их области определения Yk, k = N, N— 1, ..., 1,0, а именно
«Му)^Ф(у), ye=GN^YN,
и YN и Ф(у) известны.
Пусть также будут даны Wk+i (у) и Ffc+i, k N— 1; тогда для определения Wk(y) следует решить задачу минимизации функции
min «) + Г,+| (<Г,(9, ,))].
Таким образом, при определении функции Wk(y) одновременно находят и область ее определения У*. Еще раз покажем, что
Yk = {у : у е= Gk, Qk (у) 0).
Допустим, что функции Wk(y) все найдены, а также известны функции uk (у) <=Slk(y), у<= Yk, k =0, N — 1, по которым достигается минимум в правой части функции (11.111). Тогда можно найти оптимальные решения задач (11.101) — (11.104) и (11.105)—(11.108).
Итак, оптимальное управление [a*z]0 и соответствующая ему фазовая траектория [У/]о для задачи ('ll.101) —(11.104) определяются следующим образом. Из условия
min Г0(у) = Г0(у‘) № П
находим у’ е Уо, а затем вательно определяем
«о = «о(»о)->
У1 = ^"о(^о> ио)> и1==и1(^1)>
(11.113)
последо-
(11.114)
Ун Н-\{Уы-\' UH-1)’
Формулы (11.114) представляют собой рекуррентную процедуру. Аналогично запишем оптимальное
696
управление и оптимальную фазовую траекторию для задачи (11.105) —(11.108):
Ук = У’ u'k = uk(y'k)', у'ь+^&'М’ «!)> ик+1 ~ Uk+l (?А+1)>
(11.115)
Vn &~N-l(yN-l' UN-l)'
Полученные решения (11.114) и (11.115) показывают, что найдена синтезирующая функция u*k и тем самым решена задача синтеза.
Заметим, что, поскольку аналитическое выражение для Wk (у), Uk(y) при всех у е Yk в общем случае определить не удается, то на практике приходится ограничиваться приближенным вычислением Wk(y); Uk(y) в некоторых заранее выбранных узловых точках множества Yk. Однако согласно уравнению (11.111) при вычислении Wk(y) нужно знать значение Wk+i(&~k(.y, «)) при некоторых и. При этом возможны случаи, когда точка у*+1 = = &~к(у, и) не будет принадлежать заранее выбранному множеству, узловых точек из и нужное значение Wk+i(yk+i) еще не будет известно. Поэтому для пользования недостающими значениями
lit+i (lt+i) могут потребоваться ранее вычисленные Wk+i(y), ..., WN(y) в новых дополнительных точках, и для этого приходится расширять множества узловых точек. При решении практических задач недостающее значение Wk+i(y) получают с помощью интерполяции по значениям Wk+i (у) в близлежащих узловых точках, что, безусловно, снижает точность. Однако на практике встречается целый класс задач, позволяющих получать рекуррентные конечные формулы для оптимального управления.
Пример 11.5. Применим метод динамического программирования к решению задачи синтеза оптимальных законов стабилизации объекта. Пусть движение объекта описывается системой дифференциальных
уравнений (11.94). Будем считать, что размерность вектора управления совпадает с размерностью фазового пространства, требуется найти оптимальное управление и соответствующую фазовую траекторию из условия минимума квадратичного функционала
'к
J (х, и) = J J [(i - Мху Q (X - Мх) + «о
+ «ТЛ«]Л, (11.116)
где Q н R — заданные матрицы симметрические, положительно-определенны с соответствующими размерностями (т X иг) и (n X п).
Матрица коэффициентов М задана; ее размерность (тХи). Запишем разностную аппроксимацию поставленной задачи стабилизации. Разобьем отрезок времени to t t* на W частей узловыми точками /о < Л < /2 < ••• < tn-\ <Z tu ~ tK. Заменяя уравнения (11.94) разностными уравнениями с помощью схемы Эйлера, получим
Vi + l = У, + (^yz + Bz«z) Ы.-, (11.117) xi + l = + +
где Af£=f£+1 —г = 0, N — Г, А£ = = А (f ) — матрица размерности (л X л) Bt = В (f£) — матрица размерности (и Хи); С{ = С (t£) — матрица размерности (т X и); т л — размерность вектора фазовых координат у и размерность вектора управления и.
Вектор выхода х имеет размерность («XI).
Квадратичный функционал (11.116) заменим квадратурной формулой прямоугольников. Для простоты выкладок будем считать, что матрица С не зависит от времени, т. е. Ctj = const для любых i и тогда
JV-1
J (»’ [“<]) = S ui) + (^)-
1=0
(11.118)
Слагаемые квадратичного функционала (11.118) запишем подробнее через скалярные произведения
и() = 4-[(СА£-мс)г/г + свЛ,
Q (СА( - МС) у. + <?свг«г) + (Иг, Л«г)] Af, (11.119)
Otv)=4” MxyQ(i ~ Мх)\t-tN= = -^-(MCyN, QMCyN).
697
Рис. 11.8. Схема процедуры динамического программирования
Последнее выражение перепишем в виде
Ы = у (^’ pyNV р = CWQMC.
(11.120)
Для системы разностных уравнений (11.117) заданы начальные условия
joeG0, (11.121)
а управление представим в виде
В результате получим задачу дискретного оптимального управления, аналогичную (11.101)—(11.104).
Рассмотрим дискретную управляемую систему (11.117) — (11.122), начиная исследование процесса с последнего Д'-го шага. Уравнение Веллмана (11.111) позволяет последовательно вычислять значения Wl4, Wn-i, ..., Wi'iWz0, начиная от 0 до искомой 1Уо(«/). Практическое использование метода динамического программирования требует значительного объема памяти ЭВМ. Дело в том, что при последовательном вычислении функций WK(y) с помощью уравнения (11.111) до момента получения W<s(y) неизвестны состояния y(t), образующие оптимальную траекторию, исходящую из начального состояния «/(/о)-Поэтому отыскиваются и запоминаются значения 1FK для достаточно густой сети значений фазовых координат.
Функционал (11.118) имеет аддитивную структуру; поэтому дискретная система (11.117) допускает существование элементарной операции. Будем считать, что элементарная операция определена, если паре фазовых координат y(^-i) и у(Ь) можно
поставить в соответствие управление и(1,-1), переводящее за одни такт систему из состояния y(ti-i) в состояние y(ti). Запишем подробно основные зависимости метода динамического программирования, начиная с правого конца фазовой траектории.
Обозначая шаг в пространстве (У, t) через т, построим сеть возможных состояний системы с шагом дискретизации ДК Обозначим через Гк(0 узлы сетки, где i соответствует номеру гиперповерхности 2ц
t = Zt; i = 0, .V;
к — номер узла в гиперповерхности Sj.
Схема построения вычислительного алгоритма метода динамического программирования показана на рис. 11.8. Зададим таблицу значений вектора управления ui &Uj с некоторым шагом и будем считать, что состояние у» известно. На первом шаге -вычислительного процесса найдем W^-iiyN-i). Так как последний Л’ шаг должен перевести систему в конечное состояние уц, то в качестве Ун-\ возьмем только такие состояния, из которых за один шаг можно перейти в ун- Следовательно, имея в виду функционал (11.118) и формулы (11.111), (11.117), сначала находим
= „ тЛ Fa-1(^-1- +
“А-1 е <ЧУ-1
+ ^(^-1’^-1)]’ (Н.123)
где . t
&~n-i (В 9лг-1’ ИЛ'-1) ~
~ 2~ [((C^v~ 1 ~ МС) Уц~1 +
(11.124)
Q — МС) yN_l + QCBn-iun-i) + + (ИА-Г PuN-1)1’
N (Vn-V ИА-1) ~
~ У (9А-1 "* Т Иа-19А-1 +
PyN^ + TP (AN_lyN_l + Bv_1uw_1)).
Из выражений (11.124) видно, что минимизируемая функция
^N-l ~^N-l (9N-l' +
является полиномом второй степени относительно вектора управления и^-ь
Используя необходимые условия минимума
—- => 0, (11.125)
дик,_,
698
получим
где
+ ~2 B^_i (Р + тРАа/_1) Vn-i +
+ 1в^_1Рт(!/Л,_1 + гЛЛ,_1Ул,_1) +
+ |bta,_1ctqbw_1^_1 +
+ у«тСтВ#Л-Лм +
+ BAf_1CTQCBJV_1«jV_1 + Р“л’-1 — °>
(11.126) откуда найдем условное оптимальное управление на последнем шаге
•«-1=—2 ®N-iBN-\УN-1> (II-127) где HN_' = CAn_{ - МС-,
SJV-1 = BTN-1 № + CTQC) Ba,_! + *;
Dn^ = B^_t (P + PT) (/ + XAN_{) + + (BjJ_iCTQ + QTCTB//_l') HN_t.
Таким образом, из выражения (11.127) видно, что оптимальное условное управление иа N шаге является линейной функцией фазовых координат. Подставляя оптимальное условное управление (11.127) в выражение (11.123), получим соответствующее значение функционала, зависящее от состояния (fn-i и от управлений на предшествующих шагах. На втором шаге вычислительной процедуры воспользуемся опять уравнением (11.111), которое будет в этом случае иметь вид
WN-2 O'jV—2) =
~ т2П„ 1^”лГ-2 (УЛГ-2’ UN — 2$ + ttN-2sUN-2
+ ^N-l (!,N-2'^'X^N-2!,N-2^rXBN~2UN-2)]‘
(11.128)
Подставляя выражение
УдГ-1 = Уц~2 + Х (Лу-г^-г "Ь BN-2UN-2) в правую часть формулы (11.128), получим функцию, стоящую под знаком минимума,
^N-2(yN-2< UN~2) =
= [(^ЛГ-2УЛГ-2’ **"
+ (,UN-2' BN-2CTQHN-2УN—2 +
+ CtTCTBjj_2HN_2yN_2 +
+ B’ff_2CTQCBN_2uN_2 + P«a/-2) +
+ (Ун-2 Их-г^-г BN~2^N-2) X’
ВЫ~1Уц~2 + xBN-l X
X (^-^-2 + fiJV-2UJV-2))] У’ U 1<129)
*лг-1=У^-1**лг-1 +
+ y^_1QLyv-1 + n_1*vv-1;
1+X (Ан-1 - T ;
^N-l —Hpj-l ~ У CBN-lBN-lDN-l<
Из выражения (11.129) следует, что функция ^н-2(у^-г, un-i) является полиномом второй степени относительно вектора управления uN-2.
Поступая аналогично предыдущему шагу, нз условия
^-2 _.о dUN-2
определим оптимальное условное управление на втором шаге итерационного процесса
**N~2~ ~ У BN~2BN-2yN-2> С11-130)
где
bn-2~^n-2(xBn-i + CtQC) Ву_2 + Я;
^^-2~ BN-2 (^Ar-l+^Ar-l) (^+ Т^ЛГ-2)")*
+ (BN-2CT(i + QTCTBN-2) HN-2-
Оптимальное значение функционала, которое можно достичь, если система в момент времени t = tn-i находится в состоянии ун-г, а предшествующие значения «о, «1, .... Un-з известны, определим по формуле
^^-2 = ^-3 + ^-2(^-2)’
где
117АГ-2 (yW-2) = (Ук-2> ВН-2Ум-2)’ <Ч-132>
В^—2 У —2^М —l^V—2 "Ь
+ y^-2<?bJV_2 + VXr_2«VAr-2.
Эту процедуру легко продолжить по индукции, в результате которой получим рекуррентные формулы
»JV_V = — уBN-vBN-vyN-W (Ч-133) '
v = 2, 3...N.
699
В выражение (11.133) введены следующие рекуррентные обозначения:
SN_V - + ctqc) bn_v + R;
~ ~2~ v+l^V—v “I"
+1 £TN-vQbN _v + n_v*vN_v;
^N~v ^N-v —v+1 &N —v+1) X
X (f 4- T^jv_v) + (B^_VCTQ + + (TVBN_v)HN_v-, ^N~v = ^ + T (-^jV-v ~
2 BN—v&N—vBN—v') 1
Lfii-v = Hn-v 2" ^^Al-v^AT-v^/V-v’
^N—v ~2 N-v^N-v
Рекуррентные формулы (11.131) — (11.133) позволяют найти оптимальные условные управления на всех шагах, вплоть до величины «0 и соответственно значение функционала. На последнем шаге итерационного процесса имеем
«^-у^'Ьог/о, (11.134)
где
S0 = BS(tR0 + CtQC)B0+R;
«о = у К5«1Ко + у *Мо + V0RV0;
D0 = BS(R1+RI)(/ + tA0) +
+ (втост<2 + <?тство)яо;
^0 = Z + т (А) ~ ~2 Boso ®о) ’
Ь~о — HQ — — CB0Sq1D0;
v0 = ls0-150.
Согласно выражению (11.132) получим минимальное значение Wo, т. е.
W»(VO) = (у0> (уКотВЛо +
+ | LIQLO + V0TRV0) j/).
Безусловное оптимальное управление является приближенным, и его можно вы
числить следующим образом: u0 = u0;
“1 = — у ® 1
y^yo + riA^ + BoUo); и2 — 2 ^2 ^2^2>
у2 = г/1 + т(Д1у1 + В1«‘);
(11.135)
elV-l = 2^
^-1==г/«-2‘+'
+ т (Лу-20/У-2 + BN-2uN-i)-
Таким образом, оптимальный синтез (11.135) реализуется линейной функцией фазовых координат, причем матрицы SfjLv и Dn_v вычисляются по явным формулам. Реализация машинного счета по этому алгоритму не имеет существенных трудностей даже для задач высокой размерности. В результате решения задачи синтеза получим так называемую систему переменной структуры, когда обратная связь, , осуществляемая выражением (11.135), меняется с течением времени.
Пример 11.6. Рассмотрим управляемую дискретную систему с ЭВМ
yi (0 = [1 - ю U - 1) - Уг (t - 1)] и (t);
(11.136)
Уг {t) = i/i (/ — 1) + уг (t — 1), в которой управление u(t) —скалярный параметр, принимающий значения на отрезке [0, 1] для любого t — 1, 2....N,
т. е. когда U — [0, 1] и Лг задано.
Найдем оптимальное управление и соответствующую дискретную фазовую траекторию нз условия максимума функционала
;=£ [«s(*)-yt('-i)]- (11.137) 1=1
При этом начальное состояние уо фиксировано, и на дальнейшие состояния никаких ограничений не наложено. Согласно предыдущему имеем ss 0. Далее, в силу уравнения (11.111), с учетом максимизации функционала (11.137) и выражений (11.136), имеем
WN-i (Ур У2) = и (“2 - У1) ==1 - Ур
т. е. максимум достигается прн и = 1, и поэтому u(lV) = 1 при любом состоянии yi(N — 1), y2(N— 1). Тогда
WN~2 (Ур У2) =
= max (1 — (l — 1/i— у2)и + и2— уг). ие 10, 1]
700
Так как выражение, стоящее в правой части этого равенства под знаком максимума, представляет собой квадратный трехчлен относительно управления и с положительным коэффициентом при и2, то это выражение на отрезке [0, 1] достигает максимума в одном из концов отрезка. Следовательно,
^-2^1’ = ^+1)’
причем при 1 — yi уг + 1 максимум достигается, когда и = 0, а при 1 — у> sg sg уг + 1 он достигается, когда и = 1. Для оптимального процесса имеем
и* (N — 1) =
О, 1-{/1(ДГ-2)>{/1^-2) + 1;
1, l-yl(N~2)^y2(N-2) + \.
(11.138)
Заметим, что при 1 — 0i(AA— 2) = — y2(N — 2) + 1 оба значения u(N— 1) = = 0 и и(А—1) = 1 удовлетворяют условиям оптимальности.
Аналогично вычислим Wn-3:
^) = u2foXi]{“2~^ +
+ max(l — (1 — уi — уг) и, yi + уг + 1]} = = max [max(u2 — yt + 1 — (1— yi — yt)u), uelO, 1]
«2 + 1/2+11= max (1—1/1,02 + 2).
u=[0, 1]
Здесь при 1 — 0i 02 + 2 максимум достигается, когда и* = 0, а при 1 —.01
02 + 2 он достигается, когда и* — 1. Таким образом, для оптимального управлении получим
и* (N - 2) =
_ Г °> 1 - У У W - 3) > Уг (N ~ 3) + 2; t 1, 1 - 0! (V - 3)< 02 - 3) + 2.
(11.139)
Из выражений (11.138), (11.139) видно, что, вычислив величины Wn-2, Wh-з, найти значения и* (А—1) и u*(W — 2) не удается, так как они зависят от фазовых координат 0(А— 2) и y(N — 3), которые пока неизвестны. Аналогично продолжая процесс, найдем дальнейшие значения Wt:
Wt(yi, 02) = max(l — 0i, уг + N — t — V), и
t = N — 2, .... 1, 0,
причем оптимальное управление определяется как
«(/+!) =
Заметим, что при 1 = 0 имеем
0, 0i(O) + 02(O)<-^ -2);
1, 0!(О) + 02(О)>-(У-2).
Если точка уо = (01 (0), 02(О)) удовлетворяет условию 01 (0) + 02(0) <——2), то и(1) =0, и поэтому из уравнений (11.136) получим
0i(l) = O; 02(1) = 0.(0)+ 02(0).
Но тогда в выражении (11.140) при t= 1 справедливо и (2) =0, так как
01(1)+ 02(1) =
= 01 (0) + 02 (0) < - (Л/ - 2) < - (Л/ - 3).
В силу уравнений (11.136), имеем
01(2) = 0, 02 (2) = 01(1).
Продолжая таким образом, получим оптимальное управление и соответствующие ему значения фазовых координат
и’ (1) = «• (2) = ...=«* (IV “ 1) = 0, и* (N) = 1;
0!(l) = 0i(2)=... =01 (Л/—0 = 0;
0! (Ю = 1 ~ (0! (0) + 02 (0));
02 (1) = Уг (2) = •.. = Уг (N — 1) =
= 02 (АО = 01(0)+ 02(0). (11.141)
Если же 0о = (0i(O),02(O)) удовлетворяет условию 01(0) + 02(О) >—(W— 2), то и*(1) = 1, и поэтому из уравнения (11.136) имеем
01(1)= 1 —01 (0) —02(0), 02 (1) = 01 (0) + 02 (0),
но тогда 01(1) + 0г(1) = 1, и из выражения (11.140) определим t = 1, u(2) = 1.
Таким образом, имея в виду уравнения (11.136) и условия 0i(2)= 0, 02(2) = 1, получим оптимальный процесс
«•(!) = «’ (2)=...
... =iT(w-i) = «’ (Л0 = 1;
01(1) = 1-01(0)-02(0);
01 (2) = ... =01 (tf)=0;
02 (1) = 01 (0) + 02 (0);
0,(2)=...=02(Ю = 1. ,
(11.142)
( 0, l-0i(O>02(O + iV-<-l;
I 1, 1-01(0 <1/2(0 +AZ-/-1.
(11.140)
При условии 01(0) + 02(О) = — (АГ — 2) оба процесса (11.141) и (11.142) являются оптимальными.
701
Глава 12
АВТОМАТИЗИРОВАННЫЕ МЕТОДЫ МОДЕЛИРОВАНИЯ И ПРОЕКТИРОВАНИЯ СИСТЕМ РЕГУЛИРОВАНИЯ
При проектировании систем автоматического регулирования сложными динамическими объектами приходится выполнять большой объем вычислительных работ на ЭВМ для получения САР, удовлетворяющей всем требованиям технических условий. На практике данную задачу часто решают с помощью методов моделирования путем многократного интегрирования систем дифференциальных или разностных уравнений на ЭВМ при различных параметрах, начальных условиях, возмущениях и ряда других дополнительных факторов. В процессе моделирования системы на ЭВМ проектировщик по полученной текущей информации о запасах устойчивости, показателях качества и характеристиках точности просмотренных вариантов выбирает наилучший. Такую процедуру выполнить обычными методами практически невозможно, поэтому для ее осуществления необходимо применять систему автоматизированного моделирования, обеспечивающую диалоговый режим взаимодействия нескольких проектировщиков, одновременно работающих с одной ЭВМ. Причем каждый из них может моделировать свою собственную систему независимо от другого. Сущность режима диалогового взаимодействия заключается в возможности оперативного влияния на ход вычислительного процесса в зависимости от полученных решений.
С целью уменьшения объема вычислений на ЭВМ используется математическая теория оптимального эксперимента, позволяющая найти зависимость выбранного обобщенного критерия эффективности от исследуемых параметров. В этом случае исследование САР с помощью процедуры моделирования существенно упрощается из-за наличия
вполне определенной связи между показателем целевой эффективности и выбранными параметрами регулирования. Данная методика широко используется для задач идентификации динамических объектов и применима при автоматизированном проектировании.
При решении некоторых задач проектирования САР изменяются не только параметры, начальные условия, возмущения, но и сама структура системы. Это значительно усложняет диалоговый процесс взаимодействия проектировщика с ЭВМ, так как намного возрастает количество просматриваемых вариантов и не всегда представляется возможным найти обобщенный критерий эффективности, позволяющий учитывать изменение структуры и параметров системы. Поэтому при автоматизации проектирования САР приходится пользоваться несколькими критериями эффективности, часть из которых существенно отличается друг от друга. Если структура системы и ее параметры наиболее точно удовлетворяют одному из критериев, то данное положение еще не означает, что выбранная система является найлучшей. Поэтому проектировщику приходится прибегать к компромиссным решениям.
Сложность процессов автоматизации моделирования и проектирования с помощью ЭВМ заключается в том, что применяемые в настоящее время универсальные операционные системы ЕС ЭВМ 4.1, 6.1 не предоставляют пользователю диалогового режима работы. Вследствие этого приходится создавать специализированные операционные системы, работающие под управлением универсальной операционной системы и обеспечивающие диалоговый режим работы.
702
Приведенные в этой книге программы обеспечивают автоматизированное моделирование и проектирование при наличии универсальной и специализированной операционных систем.
1. СИСТЕМЫ АВТОМАТИЗИРОВАННОГО МОДЕЛИРОВАНИЯ
И ПРОЕКТИРОВАНИЯ
САПР относится к человеко-машинным системам, в которых все процессы, связанные со сквозным (комплексным) моделированием и проектированием, выполняются в автоматическом режиме на ЭВМ, а изменение структуры и отдельных параметров производится человеком-оператором. В зависимости от уровня знаний оператора и традиций организации, где он работает, при автоматизированном проектировании могут получиться различные варианты САР, но они всегда будут удовлетворять заданным характеристикам технических условий. Существенным преимуществом САПР является возможность быстрого просмотра оператором большого числа вариантов систем, что позволяет выбрать наилучшую по всем показателям систему.
В САПР входят следующие подсистемы: техническая, методическая, алгоритмическая, информационно-программная и организационная. Все эти подсистемы выполняют операции проектирования САР, а также обеспечивают отображение результатов проектирования на алфавитно-цифровом печатающем устройстве (АЦПУ) или графическом построителе (ГП).
В настоящее время наибольшее распространение получили технические подсистемы с одним или двумя уровнями. Одноуровневая подсистема включает в себя ЭВМ, к которой подключены несколько алфавитно-цифровых и графических дисплеев, а также по одному АЦПУ и ГП. В двухуровневую подсистему входит центральная ЭВМ с высоким бы
стродействием и большим объемом оперативной памяти, к которой подключаются несколько мини- или микроЭВМ, образующие локальную сеть, а также штатный набор периферийного оборудования. Двухуровневая система обладает большими вычислительными возможностями. Во-первых, проектировщик может вести предварительное проектирование на мини- или микроЭВМ, а затем подключиться к центральной ЭВМ для решения задач математической обработки введенных данных или полученных промежуточных результатов. Во-вторых, проектировщик получает доступ к базе данных, которая хранится в памяти центральной ЭВМ. В-третьих, ему предоставляется возможность сравнивать полученные варианты систем с целью принятия окончательного решения.
Методическое обеспечение представляет собой набор документов, на основе которых ведется проектирование САР, включающий такие параметры, как запасы устойчивости, показатели качества, характеристики точности, диапазоны изменения начальных условий, сигналов управления, возмущений и т. п.
В алгоритмическое обеспечение входят наборы математических моделей объектов, устройств управления, структурных схем и алгоритмов определения наилучших структур и характеристик систем.
j Информационно-программное обеспечение содержит совокупность необходимых сведений, полученных из базы данных, универсальную и специализированные операционные системы и пакеты прикладных программ.
Организационное обеспечение обычно задается в виде документов, по которым в дальнейшем выполняется техническое проектирование САР, содержащих информацию о связях между организациями-разработчиками.
Рассмотрим более детально состав информационно-программного
703
Рис. 12.1. Функциональная схема диалоговой системы интерпретирующего типа ДИАЛ:
1 — обмен информацией между ЭВМ и дисплеями, поддерживаемый диалоговой системой PRIMUS; 2 — преобразование полученной информации к форме, необходимой для работы монитора, и обратно; 3 —прием, редактирование, сортировка и интерпретация операторов диалогового языка; 4 — расстановка операторов программы в порядке возрастания нх номеров; 5 — редактирование текстов программ; 6 — запись, считывание, распечатка программ ..на экране дисплея и АЦПУ; 7 —запись, считывание, стирание, сортировка, распечатка на АЦПУ числовых данных; 8 — библиотека программ пользователя на языке ДИАЛ; 9 —- библиотека данных пользователя; 10— библиотека обслуживающих программ ППП; 11— обработка ошибок н выдача диагностических сообщений; 12— приведение арифметического выражения в форму обратной польской записи и его интерпретация; 13 — построение таблиц внешних ссылок для массивов и простых переменных; 14 — модули прикладных программ на языке ПЛ/1, образующие в системе оверлейную структуру; 15 — формирование списка параметров и передача их фактических значений вызываемому модулю из ППП; 16 — информация о текущем составе пакета прикладных программ; 17 — рабочий набор для размещения программ, предоставляемый независимо пользователям системы ДИАЛ; 18 — рабочий набор для размещения данных, предоставляемый независимо пользователям системы ДИАЛ
обеспечения, позволяющее сформировать функциональную схему диалоговой системы. Взаимодействие проектировщика с ЭВМ. может вестись в режиме интерпретации, т. е. процесса поочередного анализа и вы
полнения предложений диалогового языка. Режим интерпретации позволяет в диалоге формировать и отлаживать рабочие программы, изменять их структуру и прерывать в случае необходимости процесс выполнения.
На рис. 12.1 изображена функциональная схема диалоговой системы интерпретирующего типа ДИАЛ *. Эта система предназначена для одновременной работы нескольких пользователей. Если применяется ЭВМ ЕС-1033, ЕС-1035, ЕС-1037, ЕС-1047, то максимальное число пользователей равно 16. В случае использования ЭВМ ЕС-1060, ЕС-1061 их число может достигать 32.
Система ДИАЛ построена по модульному принципу, обеспечивающему добавление или исключение модулей из пакета прикладных программ, а также пополнение библиотек программ, написанных на языке диалога.
* Потемкин В. Г., Кравченко В. В. Диалоговая система проектирования ДИАЛ. М.: Изд-во МИФИ, 1980. 72 с.
704
Специализированная операционная система ДИАЛ предоставляет проектировщику следующие функциональные возможности:
а) язык диалогового взаимодействия простой семантической структуры, состоящий из директив и операторов;
б) средства редактирования, отладки и хранения программ, написанных на языке диалога;
в) интерактивный режим взаимодействия проектировщика САР с ЭВМ;
г) эффективные средства вызова модулей пакета прикладных программ и модификации его состава;
д) интерактивное взаимодействие с файлами цифровой и символьной информации;
е) возможность протоколирования на АЦПУ или ГП, отображенной на экране дисплея информации.
В основу работы монитора системы ДИАЛ положен принцип «чистой» интерпретации. В соответствии с этим принципом, как указывалось выше, операционная система производит последовательно синтаксиче
ский анализ очередного предложения программной единицы и его непосредственное выполнение. В случае выполнения программ, содержащих циклы, а подобные программы являются типичными при проектировании САР, время интерпретации
Рис. 12.2. Функциональная схема диалоговой системы интерпретирующе-компилирую-щего типа ДИАКОМ:
1 — обмен информацией между ЭВМ. и дисплеями под управлением ОС ЕС; 2 — преобразование полученной информации к форме, необходимой для работы монитора, н обратно; 3 — управление вводом-выводом программ, выбором активного пользователя и организация переключения обработки областей пользователей; 4 — модули прикладных программ на языке ПЛ/1; 5 —оверлейный супервизор ОС ЕС; 6 — организация списка параметров для вызова необходимой программы ППП; 7— формирование диагностического сообщения об ошибке и выдаче запроса на вывод его на экран; 8 — установка значений управляющих переменных, проверка условий выполнения; 9— запись предложений в рабочую область, удаление предложений, считывание предложений из рабочей областй и введение таблиц размещения пред, ложеннй; 10 — рабочая область памяти прямого -доступа; 11 — подготовка передачи управления программе пакета с массивом в качестве аргумента; 12 — выполнение оттранслированных программ пользователей; 13 — запись, чтение, уничтожение и уплотнение наборов программ пользователей; 14 — библиотека диалоговых программ на языке ДИАКОМ; 15 — анализ н преобразование предложений, поступающих с экрана или при трансляции диалоговых программ
АИД
Пр огр а нн а обнена нежду ЭВМ и АИД
Управляющая подсистема
2
Программы Ввода- вывода
Монитор системы
Программы —
AJ Модули ППП
И
Оверлейный супервизор
Г
; ВЛ Обращение у- к моделям I |?| Запуск । шагов | выполнения
ZJ '
Обработка | ошибок |
g| Обнен
с рабочей областью
>0] Рабочая область памяти пряного доступа
। М] Подготовка
I информационных
I векторов
! массивов
72]
Интерпретатор
М] Связь с I библиотекой — пользователей
Ж
Библиотека программ на языке ДИАКОМ
Й]
Транслятор
705
значительно увеличивается. Это объясняется многократным синтаксическим анализом предложений, входящих в цикл. Для преодоления указанных недостатков и повышения быстродействия диалоговой системы было предложено разделить процессы синтаксического анализа и выполнения. При этом обработка символьного представления программы и ее преобразование к выбранному для последующей интерпретации виду (вплоть до кодов ЭВМ) осуществляется на этапе трансляции. Полученное представление программы позволяет на этапе выполнения избежать синтаксической обработки, что оказывает значительное влияние на производительность системы в целом. К подобного рода системам относится специализированная операционная система ДИАКОМ, функциональная схема которой изображена на рис. 12.2.
Из рис. 12.2 видно, что в систему входит транслятор, который выполняет два типа операций. Первая — синтаксический анализ исходного предложения — перерабатывает его во внутреннюю форму представления и формирует необходимые характеристики. Вторая операция осуществляет замену номеров предложений в программе значениями адресов, а также занесение арифметических констант по отведенным для них адресам. В результате введения транслятора интерпретация с предварительным преобразованием программы увеличивает быстродействие системы в 5—8 раз по сравнению с режимом «чистой» интерпретации.
2. АВТОМАТИЗАЦИЯ МОДЕЛИРОВАНИЯ СИСТЕМ РЕГУЛИРОВАНИЯ
Автоматизация процессов моделирования САР с заданной структурой основана на математической теории оптимального эксперимента. Представим всю совокупность параметров в виде следующих групп.
1. Управляемые (входные) переменные gT — [gi gi gm], значения которых изменяются в заданных пределах
Si mln Si Si max» l== 1, Ol.
2. Выходные переменные ух = = {уху2 Уп\, характеризующие состояние системы (в качестве выходной величины может выбираться обобщенный показатель эффективности системы).
3. Контролируемые (неуправляемые) переменные zT = [ziz2...zs], не поддающиеся изменениям.
4. Неконтролируемые переменные (возмущающие воздействия) /т = = [fl /2. ..А].
Задача моделирования состоит в поиске математических соотношений между различными группами контролируемых параметров, в определении зависимости обобщенного критерия эффективности от управляемых и контролируемых переменных. В зависимости от вида полученных экспериментальных данных, необходимых для нахождения математического описания системы, используют активные и пассивные эксперименты. При пассивном эксперименте рассматривают вариации управляющих переменных в диапазоне заданных ограничений в режиме нормальной работы системы без внесения каких-либо посторонних возмущений. Активный эксперимент основан на использовании искусственных возмущений, вводимых в систему по заранее спланированной программе. В этом случае все неуправляемые и неконтролируемые переменные представляются в виде эквивалентного аддитивного шума £, отнесенного к выходу системы.
Задача нахождения математической модели системы по экспериментальным данным состоит в определении вида кривой регрессии и оценки параметров, входящих в уравнение
Y = F(g, z, а) + |. (12.1)
706
Не нарушая общности исследований в уравнении регрессии (12.1), векторы g и z можно объединить в один вектор х суммарной размерности, что соответствует обозначениям п. 8, гл. 1. Относительно функции F(x, а) возможна различная степень информированности.
1. Вид функции F(x, а) известен; тогда задача поиска математической модели сводится к определению неизвестных параметров Яь Яг, • • •, я*.
2. Функция F(x, а) выбирается из совокупности функций Fi(x, я<!)), F2(x, я<2>), ..., Fr(x, а(г'>), в которых размерность векторов я*1’, ..., а(г) различна. Требуется определить,какая из перечисленных функций является искомой, и, соответственно, найти неизвестные параметры системы.
Рассмотрим случай, когда функция F{x, а) линейна относительно неизвестных параметров и имеет вид
F(x,a) = 'Ealfj(x), (12.2) где я/ — искомые коэффициенты регрессии, хт = [х 1 х2... хг] — вектор входных переменных; f;(x)—известные функции входных переменных.
В результате эксперимента можно получить N наблюдений
Yt = F(^ + l{, (12.3)
или, воспользовавшись выражением (12.2).г получим
/-О
(12.4)
Предположим, что ошибки в отдельных наблюдениях являются нормально распределенными случайными величинами с нулевым математическим ожиданием и одинаковой дисперсией о2 и некоррелированными между собой. Тогда случайные величины Уь У2, ..., Уу также имеют нормальный закон распреде
ления с математическим ожиданием
М [У J = F (*«>) (12.5)
и одинаковым значением дисперсии о2.
Для определения оценок й/ неизвестных параметров я/ воспользуемся методом наименьших квадратов. Решим задачу минимизации суммы квадратов отклонений наблюдаемых значений У,- от их математических ожиданий в виде
У г k -12
min £ У, - £ djfu (х) . (12.6)
4, (-1 L 1-0 J
Теперь найдем оценки неизвестных параметров из необходимых условий минимума квадратичной функции относительно неизвестных
Ш6 I2)
|-о.
1-0 -* )
j==O^k. (12.7)
Вычислив частные производные и перенося в правую часть члены, не содержащие оценок 6/, получим систему нормальных уравнений
S Fi(A + S fitf + • • • l — l J“1
• • • + S F iof ik^k = i-l i — \
EFJ^A+f F?A + ••• у у (12.8)
... + S FilFiiA — S JilYi, /-1
S fikfiO^O + S + ••• i-l i-l
У У
...
В векторно-матричной форме система уравнений (12.8) примет вид
фтФя = фтУ, (12.9)
707
где
Ф =
ю /и • • • / 1k
20 f 21 • ' ’ f'2k
fl f I 2
NO fNl ' ' ‘ f Nk
fN_
прямоугольная матрица размерности [A^X (k + 1)], задающая значения функций ftj при проведении /V наблюдений; причем f{ = [fiaftl . . . ••• fik\>
— вектор искомых оценок
_4_ неизвестных коэффициентов уравнения регрессии (12.1);
у2
Из выражения (12.11) следует, что ковариация двух любых оценок и dv определяется как cov [йц, aj = <т2 [(ФТФ)-1 ]gV, где [(фтф)“‘]цч, — соответствующий элемент матрицы (ФТФ)-1-
Мерой отклонения оценки регрессионной функции от истинной зависимости является дисперсия предсказанных по уравнению регрессии значений. Дисперсия, предсказанная как функция входных переменных, записывается в виде
~ k k т2
D(x)=M Ef/to^-EF/toM
L/-o /=о ' 'J
= Af
- k -12
Е Г/ (*) (й/ — «/) =
L/-o J
= Е EJ/(*) fа{) (d;—Ц/)]= = о2Г(х)(ФтФГ7(*), (12.12)
— М-мерный вектор заме-
где
fo(x)
ров характеристик объекта.
Информационная матрица Фишера фтф является квадратной, положительно-определенной и невырожденной, когда N k + 1 и хотя бы k + 1 замер проведен в различных точках пространства входных переменных. В этом случае матрица Фишера имеет обратную матрицу (ФТФ)~’ и решением системы (12.8) будет вектор оценок
а = (фтф)“1фтУ. (12.10)
Ковариационная матрица оценок неизвестных коэффициентов вычисляется следующим образом:
cov [а] = М [(а — а) (а — а)т] = = М{[(ФТФ)-1ФТУ - (ФТФ)-1 фтг]х Х[(ФТФ)“‘ ФТУ - (ФТФ)~‘ ФТР]Т} = = (ФТФ)-1 ФтЛ-1 [(У - F) (У - F)T] х
ХФ(ФтФ)'1 = о2(ФгФ)'1. (12.11)
Трудности в вычислении оценок а возникают в рассматриваемом случае, когда матрица системы нормальных уравнений (12.9) плохо обусловлена. Тогда приходится привлекать методы регуляризации, основанные на учете априорной информации.
Статистические данные, необходимые для получения оценок неизвестных параметров, набираются по определенной программе, представляющей собой экспериментальный план, удовлетворяющий некоторому критерию оптимальности. Часть пространства входных переменных, в котором возможно проведение эксперимента, называют пространством планирования. Границы пространства планирования задаются обыч-
708
но m-мерным кубом со сторонами — t = l, tn.
Широкое распространение при решении прикладных задач получили критерии ортогональности и ротата-бельности планов. Ортогональные планы — это такое расположение Af точек в пространстве планирования, которым соответствует диагональная ковариационная матрица оценок неизвестных параметров. Эти планы оптимальны с точки зрения простоты обработки информации, позволяют получить независимые оценки коэффициентов регрессии и отбрасывают сразу все незначимые коэффициенты. Критерий ротата-бельности требует равенства дисперсий предсказанных значений регрессионной функции на равных расстояниях от центра плана. Это свойство означает инвариантность плана относительно вращения координат. Однако эти критерии никак не связаны с точностью получаемой математической модели.
В последнее время при построении экспериментальных планов используются критерии оптимальности, связанные с величинами дисперсий оценок неизвестных коэффициентов. К ним относятся: Д-опти-мальный план, который минимизирует след ковариационной матрицы, что соответствует минимизации средней дисперсии оценок коэффициентов; Е-оптимальный план, минимизирующий максимальное собственное число ковариационной матрицы оценок; D-оптимальный план, минимизирующий значение определителя соответствующей ковариационной матрицы, и, наконец, G-оптимальный план, который минимизирует величину дисперсии предсказанных значений уравнения регрессии
о2Г(*)(фтф)"7(*).
На практике применяются Е-оп-тимальные планы, поскольку в ряде случаев они совпадают с G-опти
мальными планами и уменьшают влияние случайной составляющей в выходной величине на точность получаемой математической модели.
Для построения Е-оптимального плана используется процедура непрерывного планирования в виде
ФТ(У + 1)Ф(У + 1) =
= Фт^)Ф(Аг) + Г(х*)Г(х’)> Г(х’ИФт(АГ)Ф(^)]-7(**) =
— шах F (х)[фт(^)ф(^)г7(х),
х (12.13)
где Ф — информационная матрица Фишера при + 1 и N числе наблюдений является квадратной порядка (&+!)• Здесь используется то обстоятельство, что минимизация определителя ковариационной матрицы соответствует максимизации определителя информационной матрицы.
Формулы (12.13) не накладывают никаких ограничений на вид пространства планирования и вид функций ft.
Так как непрерывный Е-оптимальный план полностью характеризуется спектром и частотами проведения наблюдений в точках спектра, представляется целесообразным разбиение процедуры получения оптимального плана на два этапа: первый этап состоит в получении точек спектра непрерывного Е-оптимального плана, а второй — в определении частот проведения наблюдений в каждой точке спектра.
Нахождение точек спектра и определение частот возможно за небольшое число циклов по рекуррентным формулам (12.13). Частота повторения наблюдений в /-й точке плана определяется по формуле
N + No ’ G2-14)
где Г[ — число попаданий глобального максимума квадратичной формы Г(х<'))[ФтФ]е“7(*(')) в точку х(,) спектра плана на втором этапе; N— число циклов по процедуре непрерывного планирования (12.13) на
709
этапе определения частот; No — число точек начального плана на втором этапе.
Отклонение полученных планов от непрерывных D-оптимальных оценивается по относительной величине 6-разности максимальных значений дисперсий предсказания регрессионной функции для найденного е-пла-на и непрерывного ZJ-оптимального плана, т. е.
maxfT (х<г’) [ФтФ]е 'f d 6= —------------------------,(12.15)
где d — max f (х) [ФТФ] lf(x).
Пример 12.1. D-оптимальный план для кубической регрессии вида
з
F (х, «) = %+£ aixi +
3 3 3 3
+ Ё t anxixi + tl Ё amx2ixi + i=l /-/+! 4-1 /-» + !
3 3
+ Ё Ё antxix2i
;_i /=./+1
получается в результате применения алгоритма (12.13). План расположен во всех вершинах куба: —1 sS xi sg 1, i = 1,3 и в середине всех ребер. Число точек спектра равно 20. Частоты повторения наблюдений т1 = -^р 6 = 0,03864.
Пример 12.2. Приведем D-оптимальный план для нелинейной регрессии вида
з
F(x, a) = aQ+ У atxi + 4—1
з з
+ S fl44x4 + S aHix3i-i-1 4 = 1
План расположен во всех вершинах единичного куба и в вершинах куба со сторонами —0,445 Xi 0,445; в точках, расположенных на ребрах, иа расстоянии 0,445 от середины ребра и в точках двумерных граней с координатами 0,445.
План содержит 64 точки. Частота повторения наблюдений т) = -^-, 6 = 0.
В последнее время возрос интерес к методам идентификации динамических объектов управления. Задача оптимальной идентификации динамического объекта состоит в опреде
лении вероятностной модели динамического объекта, оптимальной в смысле заданного критерия
/ = /(«Г(0), (12.16)
характеризующего зависимость обобщенной характеристики идентифицированной модели от входного сигнала g(t) длительностью Т — to. Выбор критерия оптимальности определяется целевым назначением идентифицируемой модели. Многообразие задач управления объектами порождает множество возможных критериев. Задача оптимального оценивания неизвестных параметров регрессионных моделей динамических объектов, функциональный вид которых известен, использует критерии, определяющие статистические характеристики векторов оценок. Функциональный вид регрессионной модели динамического объекта задается в виде
Y(t) = F(g(t), а) + В(0- (12.17)
Статистические свойства вектора оценок
ат = [d1 d2 ... ak\
определяются ковариационной матрицей
С — М [(а — а) (а — а)т], элементы которой в том или ином виде всегда присутствуют в выражении критерия. Как видно из выражения (12.16), величина критерия оптимальности при заданном методе получения оценок неизвестных параметров зависит от входного сигнала g(t), времени его поступления и выбранных моментов измерения выходных координат объекта. Простейшая задача активной идентификации является независимой от статистических характеристик получаемой регрессионной модели. При этом в качестве тестирующих сигналов используются известные, легко реализуемые сигналы.
Пример 12.3. Рассмотрим предложенную методику для исследования нелинейных динамических систем. В этом случае уравне-
710
6)
Рис. 12.3. Характеристики процессов определения коэффициентов системы, методом автоматизированного моделирования:
а — переходные процессы р2(0; б — значения искомых коэффициентов системы на различных шагах итерационной процедуры
ние. (12.1) запишем в векторно-матричном виде:
а). (12.18)
Представим уравнения динамики объекта регулирования как систему дифференциальных уравнений
yi = kil ~ aj,. (у,)~ ёЬз(уз)', х yz — kzfat (У1) + «2/22 (У1) ~ gfn (У1, Уз), ?
х = Ызз(У1), '
(12.19)
где kt, ki, ki, g, I — неизменяемые коэффициенты модели; ab а2 — неизвестные коэффициенты, значения которых необходимо определить; fi< — нелинейные функции координат движения.
Алгоритм оценки неизвестных коэффициентов в= (аьа2) с использованием выражения (12.10) реализуется в виде последовательной процедуры из-за нелинейности уравнений системы (12.19). При этом на каждом шаге осуществляется автоматизированное моделирование динамических процессов в системе регулирования.
На рис. 12.3, а приведены переходные процессы в модели при определении искомых коэффициентов at и а2 для первого (кривые /), третьего (кривые 3) и пятого (кривые 5) шагов итерационной процедуры. Точками обозначены желаемые значения координат у\, уз. Соответствующие величины искомых коэффициентов по шагам итерационной процедуры при различных исходных значениях аь а2 изображены на рис. 12.3, б. Как видно из рис. 12.3, б, алгоритм моделирования является устойчивым и мало зависит от величин начальных отклонений коэффициентов.
Предлагаемый алгоритм обеспечивает целенаправленную процедуру автоматизированного моделирования при определении параметров САР.
3. ДИАЛОГОВЫЕ СИСТЕМЫ
ОПТИМИЗАЦИИ В ПРОЕКТИРОВАНИИ
В проектировании САР задачи оптимизации занимают особое место. Практическая реализация многих численных методов решения экспериментальных задач требует большого объема вычислений; поэтому решение таких задач стали проводить с помощью диалоговых процедур, дающих возможность в процессе расчетов каждой конкретной задачи использовать различные оптимизационные методы.
Для решения задач оптимального управления появилась возможность использовать методы нелинейного программирования *, вычислительные алгоритмы которых широко развиты и представлены в библиотеках программ оптимизации. Кроме того, методы нелинейного программирования позволяют решать задачи оптимального управления с
* Евтушенко Ю. Г. Методы решения экстремальных задач и их применение в системах оптимизации. М.: Наука, 1982, 437 с.
711
ограничениями на фазовые координаты, содержащие управляющие параметры с запаздыванием, разрывные правые части в системах дифференциальных уравнений, с недифференцируемыми функционалами.
Рассмотрим оптимальное управление нелинейным объектом и проведем редукцию этой задачи к нелинейному программированию.
Пусть движение управляемого объекта описывается системой нелинейных дифференциальных уравнений вида (11.1): «(О е Um, О
Т и цель управления состоит в минимизации квадратичного функционала
т
J (U, у) = J WQy + urRu) dt, (12.20) о
где Q и R — положительно-определенные матрицы размерностей (п X п) и (tn X m) соответственно.
Проведем дискретную аппроксимацию поставленной задачи оптимального управления. Для этого разобьем отрезок времени [0, Г] на I — 1 участков точками; получим
tx = 0; ti = Г;
?i < /2 < /3
(12.21)
Интервал интегрирования системы (11.1) обозначим через т,— = Z,+i — ti и положим далее
Z-l Z-1
tl=^xs^=T-, (12.22) S-l S=1
Систему уравнений (11.1) запишем в виде конечных разностей метода Эйлера
У1+\ =yi + '4if(zi), (12.23)
где zj = [pz z —1, Z;
f(z/) = f (yi, и{, t^.
В дальнейшем будем пользоваться следующей записью системы разностных уравнений (12.23): #<+i=^’(zi), g’(gf) = yz4-Tj(zf).
i-l, I (12.24)
Управление u(t) при этом превращается в конечно-мерный вектор UT = [Ui и2... Ui] размерности (тХ X /) • При подстановке . компонент вектора U в систему (12.24) последовательно получаем полный фазовый вектор размерности (п X /) состояния объекта
У1
У2
-У1-
определенный на отрезке 0 t Т.
Функционал (12.20) в соответствии с принятыми обозначениями (12.22) запишется в виде интегральной суммы
i-l
J(Y, U)=Z^iB(Zi), (12.25)
где п п
п п
/“1
Ограничения на управление выполняются вдоль всей фазовой траектории и могут быть записаны в
виде
g (Vi, t^ = 0; h(yt, Ui, ti)^Q.
(12.26)
Вектор-функции g и h имеют соответственно размерности г и s, т. е.
g (Y, U) =
gi («i)
g2 (Z2)
_£г(*г)_
~hi(zt)
(z2)
ft(K, L/) =
_ hs (zi) _
Таким образом, получили задачу дискретного оптимального управле
712
ния (12.24), (12.25), (12.26), которая заключается в отыскании полного вектора управления UJ = — [«! и2 ... ui] и соответствующего ему полного вектора фазового состояния Кт = [jh У2 • • • yi\ , таких, чтобы функционал (12.25) принимал минимальное значение и выполнялись ограничения (12.26).
Выражение (12.25) представляет собой целевую функцию двух полных векторов Y и U. Сформулированную задачу дискретного оптимального управления можно рассматривать как задачу нелинейного программирования, для решения которой можно воспользоваться различными методами, основанными на применении модифицированных функций Лагранжа, штрафных функций, проекций градиента и др.
Решение большинства таких задач осуществляется по общей схеме: задается вектор U, вычисляются значения целевой функции (12.25) и функций, задающих ограничения (12.26), затем формируется некоторая вспомогательная функция и производится отыскание ее минимума по вектору управления U ,с помощью методов безусловной минимизации. Численные методы безусловной минимизации используют, как правило, производные вспомогательной функции по компонентам вектора U.
Отметим, что структура задач дискретного оптимального типа позволяет высокую размерность заменить меньшей с помощью вспомогательных переменных. Кроме того, выбор схемы интегрирования системы дифференциальных уравнений проводится независимо от метода оптимизации. Становится возможным интегрировать систему по рекуррентным формулам высокого порядка точности, а оптимизацию проводить достаточно грубо, и, наоборот, когда схема интегрирования имеет невысокую точность, а метод оптимизации выбирается достаточно точным. При выборе соответствующих методов интегрирования систе
мы и оптимизации следует учитывать возможности ЭВМ и требования пользователя.
Однако лучшим подходом к решению задачи оптимизации является сочетание различных методов нелинейного программирования при определенной схеме интегрирования, позволяющим убыстрять процедуру определения решения, экономить память и машинное время. Все это становится реальным с использованием диалогового режима работы с ЭВМ. В этом случае каждый используемый метод оптимизации подготавливает необходимую информацию для работы последующего более тонкого метода.
Приведем формулы для вычисления производных первого порядка сложной функции /(У, U) по компонентам вектора U. Эти формулы нужны для реализации различных численных методов приближенного решения задачи нелинейного программирования. Полная производная по компоненте вектора управления ut функции /(У, U) определяется следующим образом:
dJ(Y,U) _ dB(Zf) , d^(zl) n du, >' ди, + ди, z+l’
(12.27)
где вектор Pi+\ является решением системы уравнений:
р -т дВ^ I д^Р
Pi Xi dyt + dyt ^i + 1’
i —0, Z-1; (12.28)
^Г = £^ + £^Ч (12-29) ‘ /=i ы
= (12-30>
(12.31)
yi i-i k-\
^W=1+T (12.32>
dyt * dyt ' ’
713
В формулах (12.24) считалось, что управление внутри отрезка времени [т/, т/+1] является постоянным. Рассмотрим метод внешних штрафных функций для решения задачи (12.24) — (12.26). При этом следует обратить внимание на то, что вектор zt определен по рекуррентным формулам (12.23), (12.24), и поэтому ограничения типа равенства (12.24) не рассматриваются как ограничения метода, а используются для последовательных подстановок.
Введем вспомогательную функцию
5^ (У, U, a) — J(Y, U) +
+ « [ Z g2i (У. “ («0) +
+ (*/(»’ 1/))]. (12-33)
где целевая функция 7(У, U) задается выражением (12.25); штрафная функция Т для ограничения типа неравенства может быть построена различными способами.
Для монотонно возрастающей последовательности штрафов ао < < ai < аг < ... определяется последовательность векторов J7* (ао), U*(ai), 17* (аг), ... как решения задачи на безусловный минимум вспомогательной функции (12.33):
k k k) (12.34) IT (ай) e Argmin Ж (У, U, ak).
и
Вычислительный процесс определения последовательности {t/*} зависит от выбора последовательности штрафов [ak], от метода безусловной минимизации и точности решения задачи безусловной минимизации. Здесь можно использовать метод градиентного спуска (см. гл. 8); тогда окончание итераций определяется наперед заданной точностью е для нормы вектора градиента целевой функции 3fS(Y(Uk), Uk, a*), т..е.
\\VM(Y(Uk), Uk, aj||<8. (12.35)
В результате получаем приближенное решение задачи оптимального управления: полный вектор управления U* и соответствующий ему полный фазовый вектор y(U*), согласно выражениям (12.23).
Метод штрафных функций обычно используется на первом этапе оптимизации, когда начальное приближение известно довольно грубо. Для обеспечения более высокой точности решения задачи нелинейного программирования следует перейти ко второму этапу с использованием, например, модифицированного метода Лагранжа. В случае дифференцируемости функции (У, U, по всем аргументам вектора У, можно найти приближенно множители Лагранжа (двойственные векторы) :
d^(Y(Uk).Uk,ak) k ~ dg{
d^(Y(Uk), Uk, afe) dhf
7=1, r, (12.36)
/=177
14=
которые необходимы для дальнейших вычислений с помощью метода простой итерации. Модифицированная функция Лагранжа имеет вид
А(У, U, К ц) = ЦУ, U) +
+ U) +
+ £{а3[Л/+(У, t/)F +
/-1
+ £[1 - ЩГ, U)] + [аЛДУ, U)]2 —
-[ah, (У, t/)]3}, (12.37)
если — ht 0.
Метод простой итерации состоит
в определении
Uk е Arg min L (Y (Uk), Uk, Kk, pk) и
714
при условиях
ч+1=4+«му(^)> Z=T^
н£+1 == —4[«(Ч)+]3 + и£ U -— 2ahlk + За2 (/г{)2], если —/г{^0, где /г{ = й/(У(С/А), UJ, j=—S.
Данный метод является эффективным вблизи оптимального решения.
Изложенный подход является эффективным для решения задач оптимального управления общего вида. Здесь возможны обобщения, связанные с неполностью определенными начальными условиями, с задачей на быстродействие, с учетом ограничений на фазовые координаты, с разрывными правыми частями системы дифференциальных уравнений и др.
Отметим, что качество численных методов оптимизации характеризуется многими факторами: скоростью сходимости, машинным временем выполнения одной итерации, объемом памяти, типом решаемых задач, областью сходимости решения и др. Поскольку экстремальные задачи обладают большим разнообразием, то один и тот же вычислительный алгоритм может оказаться приемлемым для решения одних задач и совершенно непригодным для другого типа задач. В связи с этим необходимо отыскивать сочетание разнообразных методов, позволяющее обеспечить наибольшую эффективность решения задачи оптимизации.
При наличии библиотеки на ЭВМ необходимо иметь программное обеспечение, позволяющее использовать последовательно различные методы для решения поставленной задачи.
Большой объем вычислений и многометодный режим решения задач явились основными предпосылками для создания диалоговых режимов оптимизации, которые составляют важную часть программного обеспечения в системах автоматизированного проектирования.
В процессе диалога пользователь, имея сведения о текущих результатах, изменяет параметры метода, корректирует текущие состояния, определяет условия очередного прерывания расчета, осуществляет быстрый переход от одного метода к другому и т. п.
Система диалоговой оптимизации представляет собой комплекс из программ оптимизационных методов и диалогового монитора, позволяющих управлять процессом вычислений в диалоговом режиме. Пользователь имеет возможность следить за ходом решения задачи и оперативно вмешиваться в процесс расчетов.
Задачи нелинейного программирования и оптимального управления системами с фазовыми ограничениями имеют, как правило, двухуровневую структуру алгоритмов. Пользователь может установить диалоговый или автоматический режим решения любой подзадачи.
В заключение укажем на основные принципы построения диалоговой системы:
1) пакет должен иметь возможность изменения программного обеспечения по расширению его и модернизации;
2) пакет обладает иерархической структурой, отдельные его программы могут строиться по модульному принципу;
3) система проектирования должна выводить на экран дисплея любые данные о текущем процессе вычислений;
4) пользователь имеет возможность осуществлять выбор методов и соответствующих параметров, просто переходить от одного алгоритма к другому.
Для решения задач оптимизации необходимы программы, реализующие методы безусловной оптимизации на первом уровне: методы покоординатного спуска, наискорейшего спуска, методы сопряженных направлений; методы случайного поиска, методы Ньютона; на втором уровне:
715
методы внешних и внутренних штрафных функций, методы параметризации целевой функции, методы Лагранжа, методы возможных направлений, методы приведенного градиента, методы простой итерации и другие.
Пример 12.4. Рассмотрим задачу о вертикальном подъеме ракеты (см. гл. 1). Будем считать, что движение ракеты в вертикальной плоскости описывается системой дифференциальных уравнений
Ух = — «;
Уг = У г,
Уг = [2и - O,O5e-o,Ii/! (уз)2] ~--g.
У\
где У1(0—масса ракеты, отнесенная к начальной массе; у2(/)—высота над Землей (км); уз(О—скорость (км/с); u(t)—расход массы в единицу времени (с—'); g = = 0,01 км/с2 — ускорение силы тяжести.
Зададим начальные условия у\(0) = 1; у2(0) = уз(О) = 0; полное время движения составляет 100 с; конечные условия У\(Т) = 0,2 и ограничения 0 sg u{t) sg: 0,04.
Задача состоит в нахождении такого управления u(t), при котором высота подъема ракеты Уг(Т) будет максимальной. В качестве функционала имеем
J (у, и) = — у2(Т).
Используем редукцию задачи оптимального управления к задаче нелинейного программирования. Систему дифференциальных уравнений заменяем системой разностных уравнений Эйлера с т = 1 с. В качестве начального управления взята постоянная функция времени
«о (0 = 0,008.
Решение задачи проводилось в диалоговом режиме с использованием последовательности методов оптимизации. Первая итерация была сделана методом штрафных функций (12.33); следующие итерации были проведены с использованием модифицированной функции Лагранжа.
Таблица 12.1
Решение задач оптимизации
Фазовые координаты Методы
штрафных функций Лагранжа Энеева
Число итераций
0 1 2 3 50
У. (D Уг(Т) 0,2 54,687 0,17 133,642 131,174 0,2 132,13 0,19967 132,34
В табл. 12.1 приведены результаты вычислений с шагом интегрирования 0,1 с.
В последнем столбце таблицы приведены результаты расчета, полученные методом Т. М. Эиеева. Оптимальный закон u‘(t) в первые 6 с равен 0,04 с-1, что означает максимальный расход массы, затем происходит резкое снижение расхода до 0,014 с-1, которое сохраняется до 42-й секунды. Далее следует резкое падение расхода до нуля, и с 45-й секунды до конца движения масса ракеты ие меняется. Из данных табл. 12.1 следует, что диалоговые методы оптимизации требуют малого числа итераций по сравнению с классическими.
4. АОТеЛ’АТИЗДЦИЙ
ПРОЕКТ Н РО В A SHIЯ С Я СТ ЕМ
РЕГУЛИРОВАНИЯ
Автоматизация проектирования САР представляет собой сложную проблему, так как проектировщик ча<?то располагает только данными о динамике объекта регулирования и основными техническими требованиями, накладываемыми на замкнутую систему. Исполнительные устройства и усилители мощности являются совершенно различными по принципу своего действия. Например, в регуляторах или следящих системах в качестве приводов могут применяться электрические, гидравлические и пневматические двигатели, работающие в непрерывном или дискретном режимах. Большое количество различных типов устройств усиления мощности, средств коррекции и измерительных датчиков усложняет процесс проектирования. Поэтому приходится исследовать очень много различных вариантов их сочетаний и принимать решение о выборе наилучшей системы. Только после этого можно приступать к этапу технического проектирования.
В гл. 9, 10 были изложены методы проектирования систем регулирования, когда заранее выбраны их неизменяемые части, состоящие из исполнительных, усилительных и измерительных устройств. При этом процесс проектирования сводился к выбору дополнительных усилителей сигналов и средств коррекции. Реа-
716
5)
в)
Рнс. 12.4. Структурные схемы следящих систем, используемые для автоматизации проектирования:
а — типовая: б — с комбинированным управлением; в — с комбинированным управлением и дополнительным нелинейным корректирующим устройством
Рис. 12.5. Основные характеристики типовой следящей системы с различными типами двигателей и устройств управления:
а—-г — с электродвигателем, имеющим большие значения пусковых моментов; д—з — с гидравлическим двигателем; и—м — с пневматическим двигателем
717
Рис. 12.6. Основные характеристики следящей системы с комбинированным управлением с различными типами двигателей и устройств управления: д—г — с электродвигателем, имеющим большие значения пусковых моментов; д—з — с гидравлическим двигателем; и—м — с пневматическим двигателем
лизация корректирующих усилительных устройств выполнялась на аналоговых элементах, микропро-цессорах или микроЭВМ.
В данном параграфе рассмотрены результаты автоматизированного проектирования следящих систем различного типа и приведена лишь часть графиков, характеризующих основные показатели качества стт, 1Р И точности е, сте. С целью сокращения числа графиков воспользуемся несколькими типами структур линейных следящих систем (рис. 12.4) с различными типами двигателей,
усилителей мощности и корректирующих устройств.
На рис. 12.4, а изображена типовая структурная схема следящей системы с передаточной функцией W'ki(s), на рис. 12.4,6 — с комбинированным управлением IV'ki(s) и 1^к2(з), а на рис. 12.4, в —с дополнительно вводимым нелинейным корректирующим устройством Wks(s), уменьшающим максимум перерегулирования в переходных процессах при отработке различных сигналов управления. Основные характеристики типовой следящей системы (рис. 12.4, а), в которой в качестве силового привода применен электродвигатель с номинальной мощностью 5 кВт при различных постоянных времени Тл1 и тиристорным усилителем, нанесены сплошными линиями на рис. 12.5, а—г; штриховыми — с электромашинным
718
усилителем; штрихпунктирными — с магнитным усилителем. На рис. 12.5, д—з построены аналогичные характеристики для гидравлических двигателей с номинальной мощностью на валу 5 кВт (сплошными линиями — с помпой переменной производительности, управляемой от электродвигателя постоянного тока с полым ротором; штриховыми— с однокаскадным гидрав-
лическим усилителем и соленоидом; штрихпунктирными — с двухкаскад-
ным гидравлическим усилителем и дифференциальным реле). На рис. 12.5, и—м приведены характеристики ат, tP, е и стс для следящей системы с силовыми пневматическими приводами той же номинальной мощности (сплошными линиями — для гидропривода роторного типа с
Рис. 12.7. Основные характеристики следящей системы с комбинированным управлением и дополнительным нелинейным корректирующим устройством с различными типами двигателей и устройств управления: а—г — с электродвигателем, имеющим большие значения пусковых моментов; д—з — с гидравлическим двигателем; и—м — с пневматическим двигателем
управлением от электродвигателя; штриховыми — с силовым цилиндром и золотниковым устройством
управления, плунжер которого перемещается от соленоида; штрихпунк-
тарными — с силовым цилиндром и управлением от пневматического двухкаскадного золотникового усилителя с реле.
На рис. 12.6 изображены характеристики следящей системы комбинированного типа (рис. 12.4, б) с различными типами силовых приводов,
719
а на рис. 12.7 — для следящей системы, имеющей структурную схему, показанную на рис. 12.4, в. Как видно из этих рисунков, наилучшими характеристиками обладают следящие системы комбинированного типа с дополнительным нелинейным корректирующим устройством. Аналогичный вид имеют характеристики ат, tp, е и при изменении передаточного коэффициента двигателя 1гз и постоянной времени Тдг, только в этом случае изменяются масштабы по оси ординат.
Автоматизированное проектирование упрощает исследование влияния на основные характеристики си
стемы и других параметров: Tyi, Ту2 — постоянных времени устройства управления; ki, k2—передаточных коэффициентов, соответственно измерительных устройств и усилителей мощности, а также люфтов в механических передачах и упругостей мест крепления силового редуктора. Пользуясь всеми этими кривыми, проектировщик выбирает окончательный вариант структуры следящей системы и ее параметры. С целью уменьшения объема работ на ЭВМ следует пользоваться вычислительными процедурами диалоговой системы оптимизации (см. гл. И и п. 3 гл. 12).
ПРИЛОЖЕНИЯ
Приложение П-1.1
ОСНОВНЫЕ СВЕДЕНИЯ ПО ВЕКТОРНО-МАТРИЧНОМУ ИСЧИСЛЕНИЮ
Системы векторов
1. Векторы х, у размерности п заданы своими координатами:
*1 + У1 х2 + у2
а сумма векторов
х + у =
-Хп + уп
произведение вектора на число
ах{ ах2
_ах„
скалярное произведение п
(X, у) = £ xtyt. i-l
Вектор-строка (транспонированный вектор-столбец)
хт = [хь х2....
= Уг, •••> Уп]‘
Для произвольных векторов евклидова пространства Rn выполне
ны следующие аксиомы:
(х, у) = (у, х);
(Хж, у) = X (х, у), X — const;
(х + у, г) = (х, z) + (у, z),
(х, х) > 0 при х Ф 0; (0, 0) — 0.
2. Система линейно-независимых векторов ci, е2, ..., еп образует базис Rn. Для произвольных векторов х, у имеют место разложения
х — + %2е2 -+- ••• + 1пеп>
У = П1в1 + П2в2 + ••• + ЧА-
Скалярное произведение записывается в виде
(х, у) = £ 1,7ц.
i-l
3. В унитарном пространстве Un (комплексное линейное пространство) имеем для любых х, у ее Un:
(«. у) = (уГ*);
(Хх, у) = X (х, р);
(х + у, z) = (х, z) + (у, z);
(х, х) > 0 при х 0; (0, 0) = 0.
Скалярное произведение через координаты векторов можно записать в Виде
(«. У) = X l/Hi-
i-i
Со скалярным произведением можно выполнять алгебраические преобразования
Z Г S \ Г S _
X wi, Е = X X «/₽/ (хь У})
для любых xt, у/, чисел а>, 0/ и любого числа г, s слагаемых.
24 Ю. И. Толчеев
721
4. Для векторов х, у справедливо неравенство | (х, у) |2 (х, х) (у, у)
(неравенство Коши — Буняковско-го) или в координатной форме
2 / п \ / п \
i **= 1
Неравенство Коши — Буняковско-го обращается в равенство тогда и только тогда, когда векторы х, у коллинеарны, т. е. либо х = ау, либо у = ах для некоторого числа а.
5. Норму вектора ||х(| вида (х, х)1/2 будем называть длиной вектора
|| Лх |1 = | X 11| х ||.
Если векторы х(1), х(2), . . ., х(,!) попарно ортогональны, то
||ж(1) + ж(2)+ . . . +x(n)||2 =
= ||ХШ||2+ ... + || ||2.
Для произвольных векторов х и у имеют место соотношения
11|х|| = 11у|||<1|х-у||<||х|| + ||у||,
Их-Z/II2 + ||х + Jfll2 = 2(||х||2 + + ||у||2), т. е. тождество параллелограмма.
6. Вектор х является нормированным, если (х, х) = 1. Ортонорми-рованная система ненулевых векторов всегда линейно независима. Если бь е2, ..., вп — ортонормирован-ная система векторов п, то для векторов х, у имеют место разложения
х = а1е1 + а2е2+ ... + а„е„;
У — ₽ 1 е1 + ₽2е2 + • • • + ₽пеп-
При этом справедливы равенства а( = (х, ej, ₽/ = (у, 6i), при любых г,
(х, у) = аД + а2р2 + .. . + а„р„;
п
(х, х) = S I at I2.
/= 1
7. Расстояние между векторами х и у удовлетворяет свойствам:
р(х, jf) = ||x — Jfll;
Р (х, У) = р (у, х);
Р (х, У) > О, х =/= у; р (х, у) = 0, если х — у;
Р(х. У)^=р(х, г)+р(х, у), т. е. неравенство треугольника.
8. Два множества векторов являются ортогональными, если каждый вектор одного множества ортогонален каждому вектору другого множества, т. е. F ± G.
Совокупность всех векторов, ортогональных множеству F, называют ортогональным дополнением множества F и обозначают F1.
9. Две системы векторов еь е2, ... ..., еп и fi, f2, ..., fm называют эквивалентными, если каждый из векторов одной системы линейно выражается через векторы другой системы.
10. Эквивалентные линейно независимые системы векторов содержат одинаковое число векторов.
11. Разложение любого вектора по любому базису единственно.
Матрицы
12. Матрицу порядка размерности (m X п) с элементами ац записывают в виде
п столбцов
аи а12 .... Щп
^21 ^22 • • • ^2«
-_
т строк
и называют прямоугольной.
Если т—п, то матрицу называют квадратной. Квадратную матрицу, у которой все элементы, кроме
диагональных, равны нулю, называют диагональной. Диагональную
квадратную матрицу с диагональны-
ми элементами, равными единице, называют единичной и обозначают
I, т. е.
0 ... О'
1 ... о
О О ... 1
13. Суммой матриц Л и В размерностей (т X п) называют матрицу
722
С размерности (т%п), если элемент матрицы С определяют как Cij = ац Ьц. Эту операцию записывают С = A (- В.
Операция сложения матриц коммутативна и ассоциативна, т. е.
А + В = В 4- А,
(А + В) + С = А + (В + С).
При этом всегда имеет место равенство А — В = А+ (— 1) В.
14. Произведением матрицы А размерности (т X п) на число а на-зывают,- матрицу С размерности (тХ«), если элементы матрицы С определяют как сц — аац. Эту операцию обозначают С — аА.
15. Произведением матрицы А размерности (tn X п) и матрицы В размерности («Хр) называют матрицу С размерности (тХр), если элементы матрицы С определяют как
п
сц — S aufiki-
Эту операцию записывают С — — АВ. Произведение матриц некоммутативно. Если операция произведения матриц выполнима, то она ассоциативна
(АВ) С = А (ВС)
и дистрибутивна
(А + В) С = АС + ВС;
В (А + В) — DA + DB.
16. Матрицу Ат размерности (пХ X т) называют транспонированной по отношению к матрице А размерности (т X /1), если
а1/~aji’ > т> ! — 1 > п-
При этом имеют место соотношения:
(аА)т —аАт; (А + В)т = Ат + Вт;
(АВ)Т = ВТАТ; (АТ)Т = А; (А_1У = (АТ)_1-
17. Матрицу А размерности (т X Хл) называют комплексно-сопря
24*
женной по отношению к матрице А размерности (тХп), если элементы матрицы А являются комплексно-сопряженными по отношению к элементам матрицы А. При этом имеют место соотношения
аА — аА; (А-|-В) •= А-|-В;
АВ = АВ; (Л) = А; (А)Т = (АТ).
18. Матрицу А* размерности (пХ X т) называют сопряженной по отношению к матрице А размерности (тХ л), если элементы матрицы А* получают следующим образом:
а*. = aijt i. — \,nv, j — 1, п.
При этом справедливы соотноше- • ния:
(aA)* = dA*; (А + В)* = А* + В*; (А“‘)*==(А*)~1; (АВ)* = В*А*;
(А*)* = А; rank А = rank А*.
19. Матрицу А называют диагональной, если все ее внедиагональные элементы равны 0. Диагональную квадратную матрицу с равными диагональными элементами называют скалярной.
20. Матрицу А с элементами ац называют правой или верхней (левой или нижней) треугольной, если
ац = 0 при i > j (i < j).
Сумма и произведение любых двух треугольных матриц одного наименования есть, треугольная матрица того же наименования.
21. Сумму диагональных элементов матрицы А называют следом и обозначают tr А.
При этом имеют место соотношения:
trA — tr Ат; tr(aA) = atr(A),
tr (А + В) = tr А + tr В;
tr (BA) = tr (AB).
22. Определителем n-го порядка, соответствующим квадратной матрице А, называют алгебраическую сумму п! членов.
723
Используют обозначения
| А | = det А =
ап
а21
Я12 ... а1п
а22 • • •
^nl ^«2 • • • &пп
меняется при
Определитель не транспонировании матрицы; определитель равен нулю тогда и только тогда, когда строки матрицы А образуют линейно зависимую систему.
Если какую-либо строку матрицы А умножить на число а, то определитель необходимо умножить на число а.
Если все элементы матрицы порядка п умножить на число а, то определитель необходимо умножить на а".
Определитель меняет знак, если любые две различные строки матрицы поменять местами. Определитель не меняется, если к какой-либо строке матрицы прибавить любую линейную комбинацию остальных строк.
23. Определитель р-го порядка, составленный из элементов матрицы А, стоящих на пересечении строк с номерами й, i2, ..., ip и столбцов с номерами /'j, /2, .... /₽, называют минором р-го порядка и обозначают
24. Наивысший порядок отличных от нуля миноров прямоугольной матрицы А называют ее рангом и обозначают rank А.
Матрица А размерности (т X л) является матрицей полного ранга, если rank А = min (m, п). Квадратная матрица размерности (пХ«), имеющая rank —п, невырожденная, |А| #=0.
25. Пусть в строках Л, ..., ** и столбцах /1, ..., /* определителя квадратной матрицы А расположен минор М порядка k. Минор N порядка п — k, расположенный в строках и столбцах матрицы, оставшихся
после вычеркивания строк ц, • • • > й и столбцов /ь ..., /*, называют дополнительным минором для минора М. Число (— 1) У, (ip + jp)N яв-р-1
ляется алгебраическим дополнением минора М. Алгебраическое дополнение элемента ац матрицы А обозначают Ац.
26. Присоединенная матрица adj А для квадратной матрицы А получается при замене каждого ее элемента а,/ алгебраическим дополнением с последующим транспонированием.
27. Для любой невырожденной матрицы А существует единственная матрица А-1, называемая обратной, для которой АА”1 — А-1А = I.
28. Обратная матрица связана с adj А соотношением А-1 = — (|А|)-’adj А; ее элементы
Ая Ani
|А| ••• |А| Ад Ani
|А| ••• |А|
Ащ Агп Апп
_|А| |А| |А|_
Всегда выполняются равенства для невырожденных матриц:
det А-1 = (det А)-1;
(АВ)-1 = B-,A_I.
29. Число X называют собственным значением матрицы А, если существует такой ненулевой вектор х, что Ах = кх.
При этом вектор х определяют с точностью до постоянного множителя и называют собственным вектором матрицы А, соответствующим собственному значению X. Совокупность всех собственных значений образует сйектр матрицы.
30. Собственные значения матрицы А являются корнями характеру
724
стического многочлена
| А — к! | =
ац Л а12 ...
a2i а22 Л • • •
ащ
°2п
^п! &п2 ^пп
Коэффициенты характеристического многочлена
| А - XZ | = (-1)" (Г + V1 + + а2Лп 2 + ... + а„) вычисляют по формулам Ц] = — tr А;
аг = — у [ai tr А + tr (А2)];
ап = — 4 [а„_! tr A-j-a„_2tr (А2)+...
••• +а, tr(A"-I) + tr(An)].
31. Если собственные значения матрицы А действительны, различны и обозначены через Ль Л2...Лп,
то соотношение п. 29 можно объединить для всех собственных векторов х<*>, х<2), ..., х(п), соответствующих этим собственным числам, в виде
АХ = ХА, где
Х<2> ... Х'")"
г(2) х(п) л2 • • • Л2
— матрица
4° 42) ••• 4П) — Я Л п ___
собственных векторов-столбцов матрицы А;
О "
О
—- диагональ-
_ 0 0 ... Л„_
ная матрица, на главной диагонали которой стоят собственные значения матрицы А.
Матрицу X называют матрицей правых собственных векторов. Линейно независимые собственные векторы образуют невырожденную матрицу X, для которой существует обратная Х~'. В этом случае, обозначив Y = Х~1, будем иметь
УА = АУ.
Матрицу Ут называют матрицей левых собственных векторов, для которой справедливы равенства , АТУТ==УТА; yT = Z.
32. Из п. 31 следует, что матрицу А можно записать следующим образом:
А = XAZT
или в координатной форме
а= Е м(> [2<‘)]т. i-l
Это выражение называют спектральным разложением матрицы А. В нем произведение векторов ха) [г(0] т определяют следующим образом:
х(0 л2
[£</>, 44
.4°
4О4° ...
W' х<2‘>у<‘> ... х<2‘>у<‘>
... 44/(0 _
33. Присоединенную матрицу * adj А можно записать через коэффициенты характеристического уравнения, т. е.
adj А = (—l)n+1 |АП-1+
+ а\Ап 2 + ... + ап_2А + a«-i4-z
34. Для любых квадратных матриц А и В матрицы АВ и ВА имеют одинаковые характеристические многочлены.
35. Любая квадратная матрица порядка п имеет п собственных значений, в общем случае комплекс
/
725
ных; при этом каждое собственное значение считается столько раз, какова его кратность как корня характеристического многочлена.
36. Для любой треугольной (нулевой, единичной, скалярной, диагональной) матрицы ее собственные значения совпадают с диагональными элементами.
Для нулевой, единичной и скалярной матриц любой ненулевой вектор является собственным. Для диагональной матрицы любой единичный вектор является собственным.
37. Пусть Хь Хг, ..., Хп — собственные значения матрицы А. При этом имеют место соотношения
trA^EXf, detA = HXp i-1 /-1
Невырожденная матрица in? имеет нулевого собственного значения.
Если матрица А невырожденная и Хь Хг, - . Х„ — ее собственные значения, то собственные значения матрицы А"1 равны Xf1, Хг"1, . .
Хп*» а соответствующие собственные векторы совпадают.
Собственные значения матриц А и Ат совпадают. Собственные значения матриц А и А* комплексно сопряжены.
38. Если матрица имеет блочно-треугольный (блочно-диагональный) вид, то характеристический многочлен матрицы равен произведению характеристических многочленов всех диагональных блоков.
Если матрица имеет блочно-треугольный (блочно-диагональный) вид, то собственные значения матрицы совпадают с множеством собственных значений всех диагональных блоков.
39. Канонической формой Жордана называют матрицу вида
" X .1 0 0 ... О О’
О X 1 0 ... О О
О 0 0 0 ... X 1
О 0 0 0 ... О X
Диагональные элементы этой матрицы равны X, элементы, расположенные рядом с диагональными справа, равны 1; все остальные равны 0.
40. Две квадратичные матрицы А и В одинаковых размеров называют подобными, если существует такая невырожденная матрица Р, чтоВ = = Р-'АР.
Подобные матрицы имеют одинаковый след и определитель. Все подобные матрицы имеют одни и те же собственные значения.
41. Матрицу А порядка п называют матрицей простой структуры, если она имеет п линейно независимых собственных векторов. Матрица имеет простую структуру тогда и только тогда, когда она подобна диагональной матрице.
42. С точностью до перестановки в форме Жордана любая матрица может быть приведена подобным преобразованием к канонической форме единственного вида. Процесс преобразования матрицы к блочнодиагональному виду называют разложением матрицы в прямую сумму матриц меньшего размера.
43. Если прямоугольная матрица А представлена в клеточном виде
А-Г* Q1
[Я Г J’
где В — квадратная невырожденная матрица порядка г, то ранг матрицы А равен г в том и только в том случае, когда Т — RB~lQ.
44. Любую квадратную матрицу А порядка т, у которой от нуля отличны ведущие миноры всех порядков от 1 до т—1, можно представить в виде произведения левой треугольной матрицы L на правую треугольную матрицу U.
Если
726
«11 И12
«22
«1т
«2т
О
_О О ... итт_
ТО
^22«22 —
л(' 2 -
. к1 2 ... mJ .
2,...m-l\’
Л к 1 2 ... т — 1 )
/1 2 ... k — 1 з \
г . 2 ... k- 1 k J.
sk ~ lkk / 1 2 ... k \ ’
All 2 ... k)
л / 1 2 ... k — 1 A \
Ki 2 ... k— I sJ
Uks — Ukk x 2 ... k\
Akl 2 ... k)
где s = k + 1, k + 2....tn, k = 1,
2, ..., tn — 1.
Это разложение на треугольные матрицы единственно, если зафиксировать диагональные элементы матриц L или U.
45. Матрицу А называют нормальной, если она перестановочна со своей сопряженной матрицей А*, т. е. АА*—А*А. Диагональная матрица является нормальной. Для того чтобы матрица была нормальной, необходимо и достаточно, чтобы она имела базисную систему ортонорми-рованных собственных векторов.
46. Если матрица А нормальная, то матрицы А и А* имеют одинаковые системы собственных векторов.
47. Если матрица А нормальная, то собственные значения матриц А и А*, соответствующие общему собственному вектору, комплексно-сопряженные.
48. Комплексную матрицу U называют унитарной, если сопряжен
ная матрица U* совпадает с обратной U~l, т. е.
UU* = U*U — I.
Унитарная матрица является нормальной среди нормальных матриц— унитарная матрица выделяется тем и только тем, что все ее собственные значения по модулю равны 1; det А = 1.
49. Комплексную матрицу называют эрмитовой или самосопряженной, если она совпадает со своей сопряженной матрицей Ж*. Эрмитова матрица является нормальной. Среди нормальных матриц эрмитова матрица выделяется тем и только тем, что все ее собственные значения действительные. Определитель эрмитовой матрицы есть действительное число.
50. Для решения полной проблемы собственных значений матрицы А используют Q/J-алгоритм. Пусть А произвольная, невырожденная матрица. Предположим, что собственные значения матрицы занумерованы в порядке неубывания их модулей. Необходимо построить последовательность унитарных матриц Qb и правых треугольных матриц Rk по следующим рекуррентным формулам:
А = ф]Л1, A1=/?1Q1,
А[ = Q2R2, А2 = Л2(?2,
Ак-1 — QkRk, &k — RkQk-
Процесс построения по матрице А последовательностей матриц Qk, Rk называют Q^-алгоритмом.
51. Если все собственные значения матрицы А различны по модулю, то последовательность матриц Ак в основном сходится по форме к правой треугольной матрице. Диагональные элементы матриц Ак сходятся к собственным значениям матрицы А.
52. Если матрица А действительная и только комплексно-сопряженные собственные значения имеют равные модули, то последовательность Ак в основном сходится к
727
блочной правой треугольной матрице с блоками 1-го и 2-го порядков на диагонали.
53. Если матрица А нормальная и все ее'собственные значения различны по модулю, то последовательность матриц сходится к диагональной матрице из собственных значений.
54. Рассмотрим любую последовательность чисел хь хг, ... Построим унитарные Q* и правые треугольные матрицы по рекуррентным формулам:
А — TiZ = Q1/?1, Ai = RiQi + iqZ;
Al — T2Z = Q2^2, A2 == R2Q2 “1“
Ak-i — xk^ = QkRki — ^kQk + xiJ'
Этот процесс построения последовательностей матриц Qk, Rk по матрице А называют (?/?-алгоритмом со сдвигами.
Q/J-алгоритм со сдвигами инвариантен правой почти треугольной форме.
55. Имеются приемы ускорения
сходимости итераций (^-алгоритма:
1) предварительное приведение матрицы А к правой почти треугольной форме (без этого Qfl-алгоритм обычно не применяют);
2) использование сдвигов для повышения скорости убывания поддиагональных элементов (особенно при наличии комплексных собственных значений);
3) замена малых и поддиагональных элементов нулями, что сокращает размер матриц в Q/J-алгорит-ме.
56. Для произвольной матрицы А построим последовательность унитарных матриц Qk и левых треугольных матриц Lk по следующим рекуррентным формулам:
A = Qi£b A] = £1Q1;
Ai = Q2L2, А2 = L2Q2,
A-k-i — QkLkt Ak — l>kQk-
Процесс построения по матрице А последовательностей матриц Q*. £* называют <?£-алгоритмом.
Приложение П-1. 2
Таблица прямых и обратных s-и z-преобразований для сигналов возмущений
№ п/п в(0 G(s) G(z) g (*Го)
1 t 1 S2 Tz (z-1)2 кТо
2 ta 2 s’ T2z (z + 1) (z-1)3 (kT0)*
3 e~at 1 s + a z z—e“a* е-акТ0
728
Продолжение прилож. П-1.2
№ п/п g(t) G(s) G (z) g (kT,)
4 te~at 1 (s + a)2 Tze_“r° v (z_e-ar«)2 /сГое-акГ°
5 sin wt I CO S2 + CO2 z sin шГ z2 — 2z cos <оГ + 1 sin a/cTo
6 cos at s S2 + Ш2 z (z — cos a>T) z2 — 2z cos <оГ + 1 cos <s>kT0
7 1 — COS <0/ Ш2 z z (z — cos шГ0) 1 — cos <okT0
s (s2 + a2) z — 1 z2 — 2z cos шГо + 1
8 sh co/ CO S2 — (O2 zsh<ar0 z2 — 2z ch шГо + 1 sh ш/сГр
9 ch a>t s S2 — (O2 z(z — ch <йГ0) z2 — 2zch a>r0 + 1 ch шкГо
10 e~“‘ - e-₽‘ P — a 2(е-аГо-е~₽г°) е-ак?о е~15кГо
((s + a) (s + P) (z_e-“r°) (z-e-₽r“)
11 <*0 + а1^ a’(s+ ai) a°z (z+^rr°_I) До "Ь
s2 (z-1)2
12 Gq-|-G1/-|-G2/2 a° _1_ a' _L 2a‘ s s2 s3 aoz , airoz , a2roz(z + D До "Ь д^Т'о 4“ + Дз (кГо)2
z-1 1 (z-1)2 1 (z-1?
729
Приложение П-I. 3
Таблица z-преобразований для передаточных функций
№ п/п W(s) T(z) № n/n r(s) V(z)
1 k k 6 k X ( _Z®. ro \ Де П _e Ъ) xz
(T.S+ l)(T2s+ 1) Ti — Tt * < z (
2 k s kz z — 1 \z — e 1 / — e 2 7
7 k (7s + I)2 _Io /гГое T z r‘
3 k s2 kTaz (z — I)2 8 k ss (Ts + 1) k 1 _ 1 TT 1 — M Ю 1 1 Д-s o 7 I П ! ° 1 Ho-
9 k s(T’1s+l)(T2s + l)
4 k Ts + 1 k z T z— e T k , N 1 « 1 1 N N Ш । 1 £ + £ 1 *• 1 N | N 1 1
10 k .Г Tz - (L+IAl._ 1 (z — l)2 z — 1 A z T2-Tt _Zo. z — e 71 7~2 z -I T\ — T2 _'£й_ 1 z-e 72 J
5 k fc\l —e 7 ) z s2(7-1s + 1)(7’2s+1)
s(Ts+ 1) (z —l)\z—e r)
730
Продолжение прилож. П-1.3
№ п/п W(s) W(z)
11 k (T,s+ 1)(Г2«+ 1)(Тз«+ 1) k Г Zj £ L (Л - Т2) (Г, - T3) _Го. 1 L ' z — e r‘ (T2 - Tt) (T2 - T3) _Io 1 z-e T2 , 'Тз z I 1 (T3 - r,) (T3 - T2) _Zo z-e Тз J
12 k Г z T? z и 1
s(T,s+ 1) (T2s+ l)(T3s+ 1) ' z-1 (T t - T2) (Г. - T3) L z — e T22 Z (^-ТаСГг-Тз) z — e Г2 T3 z Го Го
(Т'з-Г.НТ’з-Т'г) _A z — e Гз -
13 k ЬГ Tz (Г, + Г2 + Г3) z ,
s*(Tts+ l)(72s+ l)(T3s+ 1) ,vL(z-l)2 z-1 Г? z I 1 _L
1 (Tt - T2) (Г. - T3) _ro z— e T' Г? z I 2 _L
1 (r2 - T.) (T2 - T3) _ro z — e T2 Tl z
1 (Т3-Т.)(Т3-Т2) _£o z — e Ts
14 fe (Ts + 1) s k(T+ l^z-y^-j-) z — 1
15 fe(Ts+ 1) s2 fe7z(z + -^-l) (Z-1)2
731
Продолжение прилож. П-1.3
№ п/п 1F(s) V(z)
16 k(T,s+ 1) T»s+ 1 Api +G _Zl) i 2 1 X *2 / — Д2- I L z — e J
17 fe (Г,з Ч-l) s (T3s + 1) йг, z[z+ r, e ) d Ti ( _£o\ (z—l)\z —e Тг)
18 fe(r3s+ 1) (T,s+ 1)(72s+ 1) k Tt-Tt ГО-И)*. (%-)*] r0 1 _ro. - z — er* z—e r’ -
19 fe(^s+ 1) s(T,s+l)(T2s+l) ъ Г 2 а. <7’»~7’з)г , z“‘ ( -Рч L (Tj-Щг-е т') , (Ti^-T3)z 1 + ( (Tt — T3)\z—e Ti J J
20 fe(r2s+ 1) s2(r,s+ 1) Г Toz (г,-Та)(1_е r»)z (z-1)2 ( -12Л L (z—l)Vz—e Tl ) -1
21 fe(r3s + 1) s2(71S+ l)(72s+ 1) b Г Тг . (Т3-Тх-Тг)г _ (z-1)2 1 - z-1 (Г.-Гз)г / fo\ (Тг-Т3)г n (?; '4J
732
Продолжение прилож. П-1.3
№ n/n W(s) W(z)
22 k _EZo_ feze T1 sin Vl — £2 )
Tls2 + 2lTlS+ 1 Г -5^- x TiVl —I2 1 z2 — 2ze Tl т o? r° 1 Xcos0AVl -g2 ) + e T1J
23 k s(7’2s2 + 2gT1s+ 1) k z2 — ze T1 sec q> X z Xcos — £2 + ф) z — 1 c ?'o z2 — 2ze Tl X т -2E— Xcos(-^-V1-&2)+e T1 где <₽-arctg V_L_ •
24 k(T2s+ 1) Г _ETo_ т -1 z[z— e Z‘ secqpcos (y2-Vl—g2 + <pjj
T2s2 + 2^lS+l T2 z2 — 2ze T' cos (7W1 -£2) + e T' где q> — arctg V1 - |2
k(Tts+\) s(rJs2 + 2^1S+ 1)
z2 т— ze T' sec <p X
Xcos (7^-V1 — £2 ~ <₽) ! Tpl
z2 - 2ze X
/ y1 ______ч —2£
Xcos (-jr-Vl-£2) +e
где q> = arctg
11
733
Приложение П-1.4
Таблица функций
Лапласа Ф (х) = —\ е dt У2л J
X Ф(х) X Ф (X) X Ф (х)
0,00 0,0000 0,45 0,1736 0,90 0,3159 •
01 0040 46 1772 91 3186
02 0080 47 1808 92 3212
03 0120 48 1844 93 3238
04 05 0160 0199 49 1879 94 95 3264 3289
06 0239 0,50 0,1915 96 3315
07 0279 51 1950 97 3340
08 0319 52 1985 98 3365
09 0359 53 54 2019 2054 99 3389
0,10 0,0398 55 2088 1,00 0,3413
11 0438 56 2123 01 3438
12 0478 57 2157 02 3461
13 0517 58 2190 03 3485
14 15 0557 0596 59 2224 04 05 3508 3531
16 0636 0,60 0,2257 06 3554
17 0675 61 2291 07 3577
18 0714 62 2324 08 3599
19 0753 63 64 2357 2389 09 3621
0,20 0,0793 65 2422 1,10 0,3643
21 0832 66 2454 11 3665
22 0871 67 2486 12 3686
23 0910 68 2517 13 3708
24 25 0948 0987 69 2549 14 15 3729 3746
26 1026 0,70 0,2580 16 3770
27 1064 71 2611 17 3790
28 1103 72 2642 18 3810
29 1141 73 74 2673 2703 19 3830
0,30 0,1179 75 2734 1,20 0,3849
31 1217 ' 76 2764 21 3869
32 1255 77 2794 22 3888
33 1293 78 2823 23 3907
34 35 1331 1368 79 2852 24 25 3925 3944
36 1406 0,80 0,2881 26 3962
37 1443 81 2910 27 3980
38 1480 82 2939 28 3997
39 1517 83 84 2967 2995 29 4015
0,40 0,1554 85 3023 1,30 0,4032
41 1591 86 9051 31 4049
42 1628 87 3078 32 4066
43 1664 88 3106 33 4083
44 1700 89 3133 34 4099
734
X Ф(х) X Ф(х) X Ф W
1,35 0,4115 1,80 0,4641 2,50 0,4938
36 4131 81 4649 52 4941
37 4147 82 4656 54 4945
38 4162 83 4664 56 4948
39 4177 84 4671 58 4951
85 4678
1,40 0,4192 86 4686 2,60 0,4953
41 4207 87 4693 62 4956
42 4222 88 4699 64 4959
43 4236 . 89 4706 66 4961
44 4251 68 4963
45 4265 1,90 0,4713 2,70 0,4965
46 4279 91 4719 72 4967
47 4292 92 4726 74 4969
48 4306 93 4732 76 4971
49 4319 94 4738 78 4973
95 4744
1,50 0,4332 96 4750 2,80 0,4974
51 4345 97 4756 82 4976
52 4357 98 4761 84 4977
53 4370 99 4767 86 4979
54 4382 88 4980
55 4394 2,00 0,4772 2,90 0,4981
56 4406 02 4783 92 4982
57 4418 04 4793 94 4984
58 4429 06 4803 96 4985
59 4441 08 4812 98 0,4986
2,10 0,4821
1,60 0,4452 12 4830 3,00 0,49865
61 4463 14 4838 3,10 49903
62 4474 16 4846 3,20 49931
63 4484 18 4854 3,30 49952
64 4495 3,40 49965
65 4505 2,20 0,4861 3,50 49977
66 4515 22 4868 3,60 49984
67 4525 24 4875 3,70 49989
68 4535 26 4881 3,80 49993
69 4545 28 4887 3,90 49995
2,30 0,4893
1,70 0,4554 32 4898 4,00 0,499968
71 4564 34 4904 4,50 499997
72 4573 36 4909 5,00 0,49999997
73 4582 38 4913
74 4591
75 4599 2,40 0,4918
76 4608 42 4922
77 4616 44 4927
78 4625 46 4931
79 4633 48 4934
735
Приложение П-II.l
Таблица Лх (О-функцнй
X
t 0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45
0,0 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
0,2 0,0637 0,0666 0,0701 0,0731 0,0764 0,0794 0,0828 0,0858 0,0890 0,0921
0,4 0,1269 0,1332 0,1411 0,1459 0,1523 0,1585 0,1648 0,1712 0,1774 0,1834
0,6 0,1890 0,1984 0,2079 0,2172 0,2267 0,2361 0,2456 0,2553 0,2643 0,2735
0,8 0,2502 0,2627 0,2745 0,2876 0,3001 0,3123 0,3247 0,3370 0,3493 0,3614
1,0 0,3096 0,3250 0,3405 0,3559 0,3711 0,3863 0,4016 0,4165 0,4315 0,4465
1,2 0,3671 0,3857 0,4030 0,4218 0,4399 0,4578 0,4755 0,4931 0,5099 0,5280
1,4 0,4223 0,4434 0,4642 0,4851 0,5056 0,5260 0,5462 0,5663 0,5860 0,6056
1,6 0,4748 0,4985 0,5220 0,5452 0,5682 0,5909 0,6128 0,6355 0,6571 0,6786
1,8 0,5246 0,5506 0,5765 0,6019 0,6272 0,6520 0,6735 0,7002 0,7237 0,7467
2,0 0,5712 0,5997 0,6276 0,6553 0,6824 0,7090 0,7325 0,7605 0,7853 0,8095
2,2 0,6147 0,6452 0,6752 0,7047 0,7336 0,7617 0,7892 0,8159 0,8417 0,8667
2,4 0,6548 0,6872 0,7190 0,7502 0,7806 0,8099 0,8385 0,8663 0,8928 0,9181
2,6 0,6915 0,7256 .0,7591 0,7908 0,8233 0,8538 0,8832 0,9114 0,9382 0,9638
2,8 0,7250 0,7605 0,7953 0,8291 0,8618 0,8931 0,9235 0,9515 0,9783 1,0020
3,0 0,7546 0,7917 0,8278 0,8625 0,8950 0,9278 0,9579 0,9862 1,0130 1,0375
3,2 0,7810 0,8194 0,8572 0,8921 0,9260 0,9580 0,9882 1,0162 1,0420 1,0658
3,4 0,8043 0,8437 0,8817 0,9178 0,9520 0,9839 1,0137 1,0412 1,0662 1,0886
3,6 0,8244 0,8647 0,9032 0,9399 0,9741 1,0058 1,0351 1,0616 1,0853 1,1063
3,8 0,8416 0,8827 0,9217 0,9584 0,9925 1,0239 1,0520 1,0777 1,1000 1,1191
4,0 0,8561 0,8978 0,9371 0,9738 1,0076 1,0382 1,0656 1,0897 1,1102 1,1273
4,2 0,8681 0,9102 0,9497 0,9862 1,0195 1,0493 1,0756 1,0980 1,1167 1,1315
4,4 0,8777 0,9204 0,9596 0,9959 1,0285 1,0573 1,0821 1,1030 1,1196 1,1321
4,6 0,8853 0,9281 0,9675 1,0033 1,0352 1,0628 1,0861 1,1050 1,1194 1,1294
4,8 0,8912 0,9341 0,9733 1,0085 1,0395 1,0659 1,0876 1,1044 1,1166 1,1242
5,0 0,8954 0,9385 0,9773 1,0120 1,0420 1,0669 1,0868 1,1018 1,1117 1,1166
6,0 0,9028 0,9452 0,9814 1,0126 1,0366 1,0540 1,0648 ,1,0693 1,0680 1,0616
7,0 0,9036 0,9454 0,9782 1,0059 1,0239 1,0340 1,0365 1,0325 1,0229 1,0090
8,0 0,9110 0,9513 0,9831 1,0069 1,0200 1,0242 1,0206 1,0113 0,9976 0,9818
9,0 0,9248 0,9659 0,9964 1.0158 1,0247 1,0247 1,0174 1,0056 0,9917 0,9784
10,0 0,9386 0,9800 1,0085 1,0251 1,0304 1,0270 1,0175 1,0053 0,9937 0,9852
11,0 0,9471 0,9877 1,0148 1,0281 1,0302 1,0239 1,0130 1,0019 0,9934 0,9902
12,0 0,9498 0,9898 1,0145 1,0249 1,0235 1,0148 1,0036 0,9938 0,9888 0,9899
13,0 0,9500 0,9892 1,0116 1,0188 1,0146 1,0043 0,9932 0,9857 0,9843 0,9888
14,0 0,9514 0,9899 1,0102 1,0146 1,0081 0,9969 0,9871 0,9825 0,9845 0,9913
15,0 0,9555 0,9933 1,0118 1,0138 1,0057 0,9948 0,9871 0,9858 0,9906 0,9984
16,0 0,9606 0,9979 1,0146 1,0143 1,0055 0,9954 0,9903 0,9922 0,9992 1,0065
17,0 0,9645 1,0013 1,0161 1,0142 1,0046 0,9958 0,9934 0,9978 1,0055 1,0112
18,0 0,9662 1,0023 1,0152 1,0116 1,0017 0,9943 0,9943 1,0003 1,0074 1,0103
19,0 0,9664 1,0017 1,0128 1,0076 0,9976 0,9917 0,9939 1,0006 1,0059 1,0058
20,0 0,9668 1,0013 1,0107 1,0442 0,9945 0,9906 0,9943 1,0008 1,0039 1,0011
21,0 0,9684 1,0023 1,0101 1,0025 0,9935 0,9914 0,9964 1,0024 1,0033 0,9986
22,0 0,9710 1,0042 1,0105 1,0023 0,9942 0,9941 1,0001 1,0048 1,0037 0,9983
23,0 0,9733 1,0059 1,0108 1,0022 0,9952 0,9968 1,0032 1,0064 1,0036 0,9984
24,0 0,9745 1,0064 1,0100 1,0009 0,9953 0,9984 1,0045 1,0059 1,0017 0,9978
25,0 0,9747 1,0060 1,0082 0,9989 0,9945 0,9988 1,0041 1,0037 0,9988 0,9964
26,0 0,9748 1,0053 1,0063 0,9970 0,9939 0,9988 1,0031 1,0009 0,9962 0,9955
27,0 0,9755 1,0053 1,0053 0,9961 0,9943 0,9997 1,0027 0,9993 0,9953 0,9966
28,0 0,9769 1,0062 1,0049 0,9961 0,9957 1,0013 1,0030 0,9988 0,9962 0,9990
29,0 0,9785 1,0072 1,0050 0,9966 0,9975 1,0031 1,0035 0,9990 0,9979 1,0018
30,0 0,9795 1,0074 1,0044 0,9967 0,9987 1,0039 1,0029 0,9987 0,9992 1,0033
31,0 0,9797 1,0070 1,0033 0,9961 0,9990 1,0036 1,0014 0,9978 0,9996 1,0030
32,0 0,9797 1,0064 1,0018 0,9953 0,9990 1,0027 0,9996 0,9968 0,9996 1,0018
33,0 0,9801 1,0060 1,0008 0,9953 0,9994 1,0022 0,9983 0,9967 1,0002 1,0009
34,0 0,9809 1,0062 1,0006 0,9957 1,0003 1,0021 0,9981 0,9977 1,0013 1,0006
35,0 0,9820 1,0067 1,0005 0,9966 1,0015 1,0023 0,9984 0,9992 1,0023 1,0004
36,0 0,9828 1,0069 1,0004 0,9972 1,0024 1,0021 0,9985 1,0005 1,0028 1,0001
736
0,50 0,55 0,60 0,65 0,70 0,75 0,80 0,85 0,90 0,95 1,00
0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000 0,0000
0,0955 0,0985 0,1021 0,1049 0,1087 0,1114 0,1154 0,1182 0,1233 0,1271 0,1270
0,1899 0,1962 0,2027 0,2080 0,2165 0,2218 0,2280 0,2413 0,2409 0,2465 0,2524
0,2830 0,2921 0,3015 0,3030 0,3142 0,3288 0,3380 0,3472 0,3561 0,3642 0,3744
0,3752 0,3856 0,3960 0,4096 0,4214 0,4334 0,4451 0,4567 0,4683 0,4816 0,4915
0,4611 0,4760 0,4905 0,5050 0,5193 0,5344 0,5475 0,5614 0,5752 0,5896 0,6023
0,5452 0,5622 0,5789 0,5960 0,6117 0,6280 0,6441 0,6592 0,6751 0,6876 0,7054
0,6248 0,6438 0,6624 0,6808 0,7024 0,7164 0,7339 0,7506 0,7678 0,7847 0,7997
0,6997 0,7203 0,7405 0,7601 0,7798 0,7980 0,8165 0,8342 0,8512 0,8688 0,8844
0,7691 0,7909 0,8123 0,8327 0,8500 0,8720 0,8907 0,9082 0,9260 0,9437 0,9586
0,8314 0,8556 0,8776 0,8986 0,9187 0,9383 0,9566 0,9742 0,9911 1,0076 1,0220
0,8870 0,9138 0,9360 0,9570 0,9769 0,9961 1,0096 1,0308 1,0467 1,0603 1,0744
0,9402 0,9657 0,9876 1,0080 1,0276 1,0454 1,0620 1,0775 1,0915 1,1055 1,1157
0,9863 1,0107 1,0318 1,0516 1,0682 1,0858 1,1013 1,1149 1,1273 1,1371 1,1462
1,0272 1,0491 1,0694 1,0875 1,1040 1,1188 1,1318 1,1430 1,1530 1,1604 1,1664
1,0606 1,0809 1,0996 1,1161 1,1306 1,1430 1,1535 1,1621 1,1689 1,1744 1,1769
1,0837 1,1066 1,1233 1,1378 1,1499 1,1600 1,1679 1,1734 1,1767 1,1787 1,1786
1,1086 1,1259 1,1410 1,1526 . 1,1621 1,1693 1,1740 1,1768 1,1771 1,1763 1,1726
1,1242 1,1395 1,1534 1,1611 1,1678 1,1720 1,1736 1,1732 1,1703 1,1659 1,1599
1,1350 1,1475 1,1574 1,1639 1,1679 1,1691 1,1674 1,1642 1,1581 1,1520 1,1417
1,1410 1,1511 1,1579 1,1618 1,1627 1,1606 1,1563 1,1496 1,1413 1,1322 1,1193
1,1428 1,1503 1,1543 1,1551 1,1528 1,1481 1,1406 1,1311 1,1202 1,1085 1,0940
1,1407 1,1452 1,1466 1,1444 1,1393 1,1314 1,1214 1,1094 1,0960 1,0820 1,0669
1,1354 1,1373 1,1362 1,1308 1,1227 1,1124 1,1000 1,0860 1,0705 1,0563 1,0393
1,1275 1,1266 1,1222 1,1145 1,1041 1,0915 1,0770 1,0615 1,0448 1,0290 1,0122
1,1173 1,1139 1,1067 1,0966 1,0838 1,0693 1,0530 1,0363 1,0193 1,0029 0,9867
1,0508 1,0355 1,0203 1.0007 0,9838 0,9659 0,9491 0,9341 0,9220 0,9136 0,9070
0,9923 0,9745 0,9569 0,9408 0,9273 0,9170 0,9108 0,9090 0,9111 0,9174 0,9260
0,9658 0,9517 0,9407 0,9340 0,9324 0,9357 0,9438 0,9552 0,9703 0,9865 1,0022
0,9678 0,9619 0,9612 0,9665 0,9760 0,9898 1,0062 1,0231 1,0379 1,0512 1,0600
0,9819 0,9843 0,9925 1,0055 1,0202 1,0356 1,0490 1,0586 1,0631 1,0616 1,0557
0,9930 1,0014 1,0135 1,0269 1,0388 1,0465 1,0481 1,0439 1,0341 1,0212 1,0048
0,9968 1,0071 1,0178 1,0258 1,0286 1,0248 1,0149 1,0003 0,9845 0,9697 0,9581
0,9971 1,0059 1,0117 1,0118 1,0052 0,9934 0,9789 0,9646 0,9552 0,9517 0,9545
0,9992 1,0046 1,0046 0,9983 0,9869 0,9746 0,9650 0,9611 0,9652 0,9758 0,9907
1,0047 1,0061 1,0015 0,9925 0,9829 0,9772 0,9782 0,9868 1,0007 1,0176 1,0317
1,0101 1,0081 1,0012 0,9937 0,9900 0,9930 1,0026 0,0179 1,0314 1,0396 1,0385
1,0116 1,0067 0,9999 0,9964 0,9991 1,0083 1,0205 1,0297 1,0323 1,0256 1,0123
1,0076 1,0013 0,9966 0,9973 1,0043 1,0136 1,0198 1,0185 1,0082 0,9927 0,9782
1,0005 0,9945 0,9928’ 0,9969 1,0041 1,0089 1,0059 0,9948 0,9806 0,9699 0,9668
0,9950 0,9907 0,9922 0,9981 1,0025 1,0006 0,9914 0,9796 0,9718 0,9750 0,9856
0,9931 0,9920 0,9961 1,0014 1,0018 0,9956 0,9860 0,9816 0,9868 1,0008 1,0153
0,9947 0,9968 1,0023 1,0054 1,0024 0,9953 0,9915 0,9969 1,0100 1,0239 1,0288
0,9974 1,0017 1,0067 1,0066 1,0015 0,9974 1,0007 1,0110 1,0224 1,0253 1,0157
0,9991 1,0042 1,0071 1,0039 0,9991 0,9993 1,0066 1,0152 1,0158 1,0056 0,9898
0,9995 1,0039 1,0036 0,9989 0,9959 0,9996 1,0065 1,0075 0,9977 0,9836 0,9750
0,9997 1,0023 0,9992 0,9945 0,9947 0,9999 1,0022 0,9956 0,9838 0,9776 0,9835
1,0007 1,0010 0,9965 0,9939 0,9969 1,0010 0,9983 0,9893 0,9843 0,9913 1,0060
1,0025 1,0007 0,9965 0,9967 1,0013 1,0027 0,9969 0,9918 0,9970 1,0113 1,0216
1,0038 1,0007 0,9979 1,0009 1,0051 1,0031 0,9978 0,9997 1,0112 1,0211 1,0169
1,0034 0,9996 0,9992 1,0036 1,0053 1,0015 0,9990 1,0062 1,0146 1,0116 0,9974
1,0015 0,9981 0,9998 1,0036 1,0022 0,9980 0,9995 1,0065 1,0062 0,9943 0,9815
0,9990 0,9968 0,9997 1,0017 0,9980 0,9957 0,9997 1,0023 0,9935 0,9828 0,9831
0,9974 0,9971 1,0003 0,9999 0,9956 0,9965 1,0004 0,9973 0,9878 0,9873 0,9997
0,9973 0,9988 1,0014 0,9990 0,9964 0,9995 1,0014 0,9958 0,9924 1,0030 1,0155
0,9983. 1,0010 1,0023 0,9990 0,9989 1,0031 1,0021 0,9971 1,0021 1,0152 1,0166
0,9993 1,0025 1,0020 0,9993 1,0015 1,0044 1,0010 1,0002 1,0090 1,0144 1,0028
737
X
t 0,00 0,05 0,10 0,15 0,20 0,25 0 30 0,35 0.40 0,45
37,0 0,9831 1,0066 0,9997 0,9975 1,0025 1,0013 0,9983 1,0009 1,0022 0,9992
38,0 0,9831 1,0060 0,9989 0,9974 1,0021 1,0001 0,9978 1,0008 1,0009 0,9981
39,0 0,9833 1,0055 0,9981 0,9975 1,0019 0,9991 0,9977 1,0008 0,9997 0,9976
40,0 0,9837 1,0054 0,9979 0,9980 1,0020 0,9987 0,9982 1,0011 0,9992 0,9981
41,0 0,9844 1,0057 0,9980 0,9988 1,0022 0,9989 0,9993 1,0017 0,9992 0,9993
42,0 0,9851 1,0058 0,9982 0,9996 1,0023 0,9989 1,0002 1,0019 0,9992 1,0004
43,0 0,9855 1,0055 0,9980 1,0001 1,0021 0,9988 1,0007 1,0016 0,9990 1,0011
44,0 0,9855 1,0051 0,9975 1,0001 1,0014 0,9983 1,0007 1,0006 0,9986 1,0009
45,0 0,9856 1,0045 0,9971 1,0001 1,0007 0,9979 1,0007 0,9997 0,9985 1,0006
46,0 0,9859 1,0043 0,9970 1,0004 1,0004 0,9981 1,0008 0,9992 0,9989 1,0007
47,0 0,9864 1,0043 0,9973 1,0009 1,0003 0,9986 1,0012 0,9992 0,9996 1,0008
48,0 0,9869 1,0043 0,9975 1,0016 1,0002 0,9993 1,0016 0,9992 1,0006 1,0008
49,0 0,9872 1,0042 0,9976 1,0017 1,0000 0,9997 1,0015 0,9994 1,0011 1,0005
50,0 0,9873 1,0038 0,9975 1,0016 0,9995 0,9998 1,0010 0,9989 1,0009 0,9996
Примечание. Для определения промежуточных числовых значений Лх-функций с меньшими интервалами по t н х, чем указаны в табл. П-П. 1 необходимо пользоваться ннтерполяцноннымн формулами:
Лх (0 = 0,5/1 х (/к) (tK + 1) (tK + 2)-hH(tK+ 0 (tK + 2) tK + 0,5//x(/k+2) (tK + 1) tK + 1~0,5Лх X X Uk) (2/k + 3) + 2hK (/к+i) Uk +1) 0,5/zx (/к+г) (2/к + !)]/' + [0,5Лх (/к) — Лх (/к-н) +
+ 0,5йх (/к+а)Н2 на отрезке [<к, /к+11 равном 1 с интервалом Д/ = 0,2;
йх(х) = 1/(х*+2 + xjj - 2х2к+1) {hx (хк) хк+,хк+2 - 2Лх (хк+1) хкхк+2 + hy_ (хк^2) X X хЛ+1 - [Ах (хк) (Хк + 1 + хк+2) " 2Ах (Хк + 1) (хк+2 + Хк) + Ах (Хк+2) (хк + ХК4 1)1 х +
+ 1Ах(хк) — 2Ах(хк + 1) + Ах(хк+г)] *2} на отРезке [хк’ хк + 11 равном 0,05 с интервалом
Дх = 0,01.
Вычисления Лх- функций для 2-х значений х и 2-х значений t приведены в следующей таблице
t х=0,1 х—0,8 t х=0,1 х=0,8 X / = 10,0 / = 40,0 X / = 10,0 / = 40,0
лх &х лх лх Йх Лх /?х лх
10,0 1,0085 1,0490 40,0 0,9979 0,9996 0,10 1,0085 0,9979 0,75 1,0356 0,9966
10,2 1,0103 1,0514 40,2 0,9979 1,0003 0,11 1,0127 0,9976 0,76 1,0387 0,9974
10,4 1,0118 1,0525 40,4 0,9979 1,0008 0,12 1,0165 0,9974 0,77 1,0414 0,9981
10,6 1,0131 1,0523 40,6 0,9979 1,0014 0,13 1,0198 0,9974 0,78 1,0441 0,9987
10,8 1,0141 1,0509 40,8 0,9980 1,0020 0,14 1,0226 0,9976 0,79 1,0466 0,9992
11,0 1,0148 1,0481 41,0 0,9980 1,0024 0,15 1,0251 0,9980 0,80 1,0490 0,9996
Погрешность интерполяции по t и х не превышает 0,25 %.
738
Продолжение прил. П-11.1
0.50 0,55 0,60 0,65 0,70 0.75 0,8 * 0,83 0,90 0,95 1,00
0,9998 1,0025 1,0005 0,9989 1,0024 1,0025 0,9989 1,0022 1,0078 1,0019 0,9872
1,0000 1,0014 0,9986 0,9986 1,0016 0,9991 0,9970 1,0016 1,0011 0,9892 0,9839
1,0000 1,0001 0,9973 0,9991 1,0004 0,9967 0,9972 1,0004 0,9936 0,9869 0,9953
1,0007 0,9994 0,9977 1,0003 0,9996 0,9966 0,9996 0,9994 0,9925 0,9960 1.0103
1,0016 0.9993 0,9991 1,0017 0,9995 0,9989 1,0024 0,9994 0,9970 1,0088 1,0154
1,0019 0,9994 1,0007 1,0023 0,9996 1,0013 1,0035 0,9996 1,0034 1,0134 1,0064
1,0013 0,9993 1,0014 1,0014 0,9994 1,0024 1,0019 0,9993 1,0063 1,0068 0,9921
1,0000 0,9988 1,0012 0,9997 0,9990 1,0018 0,9991 0,9992 1,0035 0,9954 0,9856
0,9989 0,9988 1,0006 0,9981 0,9992 1,0002 0,9967 0,9993 0,9986 0,9891 0,9923
0,9985 0,9995 1,0002 0.9979 1,0001 0,9991 0,9973 1,0006 0,9954 0,9931 1,0057
0,9987 1;0005 0,9999 0,998.8 1,0011 0,9989 0,9994 1,0015 0,9963 1,0032 1,0134
0,9992 1,0015 0,9998 1,0003 1,0017 0,9993 1,0018 1,0015 0,9997 1,0105 1,0087
0,9998 1,0016 0,9998 1,0011 1,0012 0,9998 1,0029 1,0004 1,0030 1,0084 0,9964
0,9999 1,0009 0,9990 1,0012 0,9998 0,9999 1,0014 0,9982 1,0029 1,0004 0,9878
Приложение П-11.2
НАЗНАЧЕНИЕ И СОСТАВ ИНФОРМАЦИОННО-ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ДЛЯ АВТОМАТИЗАЦИИ ПРОЕКТИРОВАНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Программа № 1 REGR', Вычисления линейных регрессионных моделей объектов систем автоматического регулирования (с. 124—125)..
Программа № 2 TRP. Вычисления коэффициентов гармонической линеаризации по методу трапеций (с. 283).
Программа № 3 RQ4. Вычисления коэффициентов гармонической линеаризации по методу Рунге--Кутта IV порядка (с. 284).
Программа № 4 STALK0. Вычисления коэффициентов статистической линеаризации по математическому ожиданию йо (с. 285—286).
Программа № 5 STALK1. Вычисления коэффициентов статистической линеаризации цо случайной составляющей й)1' (с. 286—287).
Программа № 6 STALK2. Вычисления коэффициентов статистической линеаризации по случайной составляющей й(12) (с. 287—288).
Программа № 7 OWN. Спектрального разложения произвольных действительных матриц с помощью QR-алгоритма, приведенного к верхней
форме Хессенберга, состоящей из восьми подпрограмм: 0WN1 — 0WN8 (с. 319—322).
Программа № 8 MFUNC. Вычисления функций от матриц (с. 325— 326).
Программа № 9 DISCR. Получения дискретной модели объекта регулирования (системы) (с. 326— 327).
Программа № 10 NOMO. Соединения устройств и объектов регулирования в замкнутые динамические системы (с. 337).
Программа № И JOINT. Соединения динамических систем: последовательное; параллельное; с помощью устройств и объектов, расположенных в обратной связи (с.338—339).
Программа № 12 TRFUNC. Вычисления передаточных функций разомкнутых динамических систем (с. 341).
Программа № 13 BERSTOW. Вычисления нулей передаточных функций разомкнутых динамических систем (с. 341—342).
739
Программа № 14 CURWITZ. Анализа устойчивости непрерывных замкнутых динамических систем по критерию Гурвица до 15-го порядка (с. 354).
Программа № 15 RAUSS. Анализа устойчивости непрерывных замкнутых динамических систем по критерию Рауса до 15-го порядка (с. 355).
Программа № 16 SHURCON. Анализа устойчивости дискретных замкнутых динамических систем по критерию Шур-Кона до 15-го порядка (с. 358—359).
Программа № 17 FREQLS. Вы
числения амплитудно-фазовых частотных характеристик в линейном и логарифмическом масштабах относительно оси частот (с. 384).
Программа № 18 STAB. Выделения областей на устойчивые и неустойчивые (с. 396—397).
Программа № 19 ISQERR. Интегральных оценок качества (с. 407).
Программа № 20 TRAGRA. Вычисления переходных процессов в непрерывных и дискретных системах (с. 466—468).
Программа № 21 GRAPH. Построения графических характеристик (с. 468).
Приложение П-П.З
ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ ОТ ДРОБНО-РАЦИОНАЛЬНЫХ ФУНКЦИЙ
/оо
г_____1 ( c(s)c(— S) ,
•'"“2л/ J d(s)d(-s) ’
— i ОО
где c(s) = cn_1s'1"1 4- ... + с0;
d (s) = dnsn 4* . • • + d0’,
2dqd1 ’ cfa, + cgd2 ’2 2d0dxd2 ’
. _ 4M1 + ~ 2c0c2) dQd3 + cfc2d3
73 2d0d3 (- dod3 + djds)
c3 (- ^з+^Л) + (с2-2с1сз)^1^4+ _^+ (c? -2c0c2) dgd^+cl (-
2V4 (- dad3 - dfa, + dld2d3)
75 = i lC4m0 + (C32 - 2C2Ci) mi + 4" (C2 2CjC3 ^^0^4) ^2 + (c2 — 2cQc2) m3 4-c^,],
где
mQ = (d3tni — d{m2y, 1Щ — — d(jd3 4~ did2, m2 = — dtfl$ 4~ d\d4,
m3 = -^- ^2fn2 ~
m4 = ^- (d2m3 — d4m2);
Д5 = d0 (d{m4 — d3m3 4- ds/n2);
4 = 2X7 lc5wo + (<ч ~ 2c3cs) "4 +
4~ (C3 2C2C4 ”1“ 2ciCs) m2 “Ь
4- (c2 - 2c,c3 4- 2c0c4) m3 + 4-(cf-2coc2)m44-c2m5],
где
m0 = -^- (d4mt — d2m2 4- d0m3); d0dtd5 4- d0d2 4- d2d4 - dtd2d3;
m2 = ^0^3^5 + ^1^8
m3 = ^0^5 + ^1^3^6
m4 = -^ ^т3 — d4m2 4-
m5 = (d2m4 — d4m3 4- dsm.2);
&f, = d0 (d^ — d3m4 4- d5m3);
h = 2K7 [C^o + (*5 ~ 2с4Сб) + 4-(c24-2c3c54-2c2c6)m24-
4- (cl - 2c2c4 4- 2c,cs - 2c0c6) tn3 4-4~ (c2 2с1сз H" 2c0Ci) “1“ 4-(c?-2c0c2)/ns4-c2/n6].
740
где
m°= -J7 ~ ^зПг2 + ^1тзУ>
ml = -(dldi-dod5)2 + 4* (dgdo — dxd2) (dod7 — — dido 4" d2do — d3dd‘, m2 = (dod7 — dxdo) (— dgds + dxdd + + (^0^3 — d\d<^ (d2d7 — d3do}\
тз = — (dgd7 — dxd6)2 4-+ (dodo — dxd<d (did7 — d^d^', m< = -^ (rf2"»3 — ditiii + d6"»i)’> m5 = (d2mt — dttn3 + d6m2y, mo = -^ (d2m5 — d4/n4 — d6m3y, Д7 = d0 (dxmo — d3m3 + d3m< — d7m3). h = 257 lCTmo + (Ce “ 2c5c7) «1 + + (C5 - 2c4C6 + 2C3C7) m2 + -f- (c2 2c3c5 4" 2c2c6 2cic7) mo 4" + (C3 - 2C2C4 + 2c1C5 - 2сосб) m4 + 4- (cl - 2^3 4- 2c0c4) m3 +
+ (c? - 2c0c2) m6 4- c2m7], где
= -J7 4- d2m3 — d^nd,
mi= (dod7 4- d2d^ (— d^txd7 4-4- Ws + 2d?de) + {d3d7 - d’) X
X(dK + ^l) + 4" d1d3d8 (dad3 — dxd2) — ~ dido (dodo — didt) 4" (— d2d7 4” 4" d3d6 — dtds) (dodo 4” d?d4) — ~~ dido (dido 4" ’idododo) — did2d3 X X (dodo — dido) 4- Sdodid.tds, /П2 — (d0d3 — dxd2) X X (dody — didodo — did8d7 4- dodvdi) 4" 4" (d2d3 — dtd7) (— dtfiido 4-4“ dodo — did2d2 4” didt) —
— dodsd7 (dodo — dxdd 4”
4” d\do (dod7 — dide), m3 — — dx (dxd3 — d2d7)2 4-4- (— dodo 4- d6d7) (d^dido — — dodo 4- didido — d2dt) 4”
4~ dod7 (— dodo 4” dxd< 4” d2d3) — — 2dodid3d7do,
= (— dodo 4- dod7) (2dodxd7 —
— dododo 4” did^o ~~ d2do) 4”
4" (— d3d3 4" dtd7) (dod3d7 —
- dM 4- dide) - dod7.
mo = 4- (d^rii — ditno 4- d6m2 — d8/ni), “O'
mo = (d2mo — d4m4 4- d6m3 — d6m^,
m7 = 4~ (d2mo — dtmo 4- dofnt — d3m3), UQ
Ag = do (dxm7 — d3m6 4- d5m5 — d7m<), J9= 2K7 [c8mo + (4 ~ 2cece) mi +
4-(c| - 2c5c7 4-2c4c8) m2 +
4” (^5 2c4c6 4” 2c3c7 2c2c8) m3 4”
+ (C4-2C3C5+2C2C6-2C1C7+2COC8) mi+
+ (C| “ 2C2C4 + 2C1C5 ~ 2с0Сб) m5 +
4- (c2- 2c1c34-2c0c4)m6 4-
+ (ci - 2сосг) m7 + come]>
где
mo —4- (d7mt — doma 4- d3mo — dxmd, UQ
mx = ai (ctjCtjo — a^io 4" O3Q6 4“ ad1o 4” 4- 2a4a6 - a2 - -a|)4-
4- a2 (- a2a6 - aza7 4- aiaz+2aia1) - a3, /712=01 (азад4"О4а9— О5ав4”<1бв7— 4”
+ a2(-afy + aia6 + (^)-^a1, тз = ai (азаю 4- «Ао 4- - а%) 4-
4- а2 (- а^10 4- - а^,
mt = ах (Овйю 4" — а^о) 4"
4-а2(а7а9-а4а1о)-а7-
741
т& — ~г (d->m4 — d4m3 4- d6m2 — d3mx), «0
m6 = {d2m3 — d4m4 4- d6m3 — d8m2),
m7 = -J- (d2m6 — d4m5 + d6m4 — d8m3), ms = (d2m7 — d4m3 + d6m5 — dsm4),
^g = d0 (dxms — d3m7 + d5m6 — — d7m5 + dam4),
где
Я] — dxd2 — dQd3, я2 = dxd4 — d3d3, <23== ^3^4 d2d3, я4 = dxd§ — d9d7, Я5 = d3d3 d2d7, Яб — ^5^6 — d4d7, <2?= dxd3 — dgdg, a8 — d3d3 d2da, ag = d3d3 — d4da, я10 = d7d3 d3dg,
Ao ~ 2A10 “1“ (cs 2с7сэ) mi +
4- (c7 — 2c6c8 4- 2c5c9) "h 4-4- (cl - 2c5c7 4- 2c4c8 - 2c3c9) m3 4-4-(c|-2c4c64-2c3c7-2c2c84-2c1C9)m44-+ (C4 ~ 2сзс5 + 2CiC6 ~ 2cic7 + 4- 2c0c8) m5 4-
+ (C32 “ 2C2C4 + 2flC5 + 2сосб) m6 + 4- (c2 - 2C[C3 4- 2c0c4) m7 4-4-(cf-2c0c2)m84-c2m9],
где
тй = ~ (d,mt — d6m2 4- d4m3 — — d2m4 4- dQm5),
mx = ax [dx (— я2Ь5 4- a4b4 — я5я|0 — — OeZ>2 — 2я7я10 4- a8Og 4- о<Д) 4-4" d3 (axb5 4” O3O10 4- CZ4CI10 — <24b3 + “1“ °5^2 a7a9 a3 aePl tf) + 4" d$ (— atb4 4” <22b8 — a^Og — a^bg —
— a4ag 4- a5as — a^a7 4- 4- a^) 4-
4- d7 (Я|Я10 — Й2а9 4- <23^6 4” <2з<28 4”
4- a3bx4-2я4я64-я4Ь1-я2-я5я7-я2)] 4-
4” (h [di (сцяю 4" flgbi — Я7Я9 4- bi) 4-4* d3 (— ОцЯю — a^bi 4- Й7<х8 4~ <*761) 4“
4- d5 (a2a9 4- а3Ь{ - - a27) 4-
4“ d7 ( — CE2b4 — я3Яу 4”
4- a4a3 4- 2a4a7)] 4-
4- a4 [a7 (— d^ 4- d5a4 — 2dxbx) 4-4-a4(d3bi-d7a4)]4-d14
ffi2 = ax [dj (— a3b4 — a7b4 4- a8b3 — °iobi 4" bxb3) 4~ d3 (a3b4 4- a4b4 — d&b2 4- dgbx — bxb2) 4- do (— a3b3 — — a«b3 4” (ЦЬ2 — Clgbi + d2b2) +
4"cMaiaio ct2flg 4" с^Яб 4- <2з<28 4-йзЬ] 4"
4- 2я4я6 4- «А - я1 - я5я7 - а|)] 4-4” а2 [^i (а4Ь4 — о7Ь3) 4~
4" d3 (— aab4 4- ЯуЬг 4* Ь?) 4~
4” d3 (agb3 — а4Ь2 — a^bi) 4* d9(—ЯоЯе — — Я2Ь! — ЯзЯ7 4- я4я5 4- 2а4я7)] 4-4" а4 [bl (— d3a7 4- d3a4 — d^) — -d#4]4-d1a72bp
Шз~а1 (—asbs — a?bs— b1b44-b2&3) 4-4" ds (flsbs + я4Ьз + bjb3 — &2) 4-
4- d7 (— ЯзЬ3—я4Ь34-я5Ь2—Я6&!+a7b2) 4-4" d3 (axb4 — a2b3 4- ct3b2 4~ я3я9 4-
4- a4ag — я5я8 4- с^я7 — a7a8 — a7bx)] 4-4* °2 [d[ (я4Ь5 — bxb3) 4- d3 (— a2b3 4*
4" bxb2) 4" d7 (я2Ь3 — я4Ь2 — a7bx) 4*
4" dg (— Я2Яд — я3Ь1 4- я4я8 4-
4- я4Ь1 4* ^?)] 4- «4 [<24 {dibx — d^a-j) — — b?d3] 4* Oybidi,
/n4 = ax [dj (— a3b3 — 2bxb3 4* b2b4) 4-4" d$ (a3b3 4" a4b5 4" bib3 — b2) 4"
4-d7(—ЯзЬ4—я4Ь44-8Ь2—я9Ь1я4-Ь1г>2) 4-
4- dg (axb$ 4" сДОю 4” а4аю ct4b3 4-4” d^bi 4" Я7Я9 — <28 — я8Ь1 bi)] 4”
742
+a2[dj(aA — *i*4)+^5 (btb2 — a2b5) + -f- 6/7 (<32^4 — Я762 — bl) 4~
4* <ig (— <^2aio — asbi + o7as -J- a7b,)] 4" + fl4K(-aHfl4Al) + + bl (d7a7 — d5bi)] + dib3i,
тц = ai [d3 (— a3b5 — 2&,&5 + b2b4) +
+ d5 (a3b$ + a7b5 + Ь^Ь4 — b2b3) 4-
4* d7 (— 0564 — a7b4 + a3b3 —
— <210^1 + bib3) + d3 (a2b5 — a4b4 4-
4- a5aio4- a6^24-2a7a10 — а8«э — a$b,)] 4-4-а2[^з(а765 — bib4) 4- d3(bib3— a4b^ +
4- d7 (a4b4 — a7b3) 4"
4- dg (— а4аю — agbi 4- а7йд — 6?)] 4-4“ ^7 Jdg Ctj) 4-
4- bi (d7a7 — ds&J] 4- b\ (d3bi — d7a4), tn&==-^- (d2m3 — d4m4 + dgm3 — — d3m2 4- diomj,
m7 = (d2mb — d4m5 4- d6m4 — — dsm3 4- cfio«2), m6~-^ (d2m7 — d4m3 4- d6m3 — — d3m4 4- digm^, mg~-^ (d2mR — d4m7 4- d3m3 — — d3m5 4- </10^4), Aio = ^0 (dimg ~ d3m3 4- d5m7 — — d7m6 4- dgm5),
где
ai== did2 — dgd3, a3 = d5d6 — d4d7, b\ — d\dig, cz2 — d [d4 dgd3t ci7 - d7ds dgdg, b2 — d3dlQ, g3 = d3d4 d2d5, a8 = d3d3 d2dg,
Ьз — d3dig, 04== dyd3 dgd7, Ug = d3d3 d4dg,
b4 = d1dlg, a3 d3d3 d2d7, = d7d3 d3dg,
bg — dgdyg
СПИСОК ЛИТЕРАТУРЫ
1. Айзерман M. А. Теория автоматического регулирования. 2-е изд. М.: Наука, 1966. 452 с.
2. Алексеев К. Б., Бебенин Г. Г. Управление космическими летательными аппаратами. 2-е изд. М.: Машиностроение, 1974. 340 с.
3. Беллман Р. Динамическое программирование: Пер. с англ. М.: Изд-во Иностр, лит., 1960. 400 с.
4. Блейнрок Д. Г. Автоматическое управление самолетами и ракетами: Пер. с англ. М.: Машиностроение, 1969. 286 с.
5. Брайсон, Хо Ю-Ши. Прикладная тео рия оптимального управления: Пер. с англ. М.: Мир, 1972. 544 с.
6. Воронов А. А. Введение в динамику сложных управляемых систем. М.: Наука, 1985. 351 с.
7. Гантмахер Ф. Р. Теория матриц. М.: Наука, 1967. 575 с.
8. Годунов С. К., Рябенький В. С. Разностные схемы. Введение в теорию. М.: Наука, 1977. 439 с.
9. Грогоно П. Программирование иа языке ПАСКАЛЬ: Пер. с англ. М.: Мир, 1982. 384 с.
10. Д’Анжело Г. Линейные системы с переменными параметрами. Анализ и синтез: Пер. с англ. М.: Машиностроение, 1974. 288 с.
И. Деруссо П., Рой Р., Клоуз Ч. Пространство состояний в теории управления: Пер. с англ. М.: Наука, 1977. 477 с.
12. Заде А., Дезоер Ч. Теория линейных систем: Пер. с англ. М.: Наука, 1970. 703 с.
13. Иващенко Н. Н. Автоматическое регулирование. Теория и элементы систем. 4-е изд. М.: Машиностроение, 1978. 736 с.
14. Красовский А. А.,. Поспелов Г. С. Основы автоматики и технической кибернетики. М.—Л.: Госэнергоиздат, 1962. 600 с.
15. Ку И. X., Вольф А. А. Применение функционалов Вольтерра — Винера для анализа нелинейных систем//Техническая кибернетика за рубежом. М.: Машиностроение, 1968. С. 145—165.
16. Макаров И. М., Менский Б. М. Линейные автоматические системы (Элементы теории, методы расчета и справочный материал). М.: Машиностроение, 1977. 464 с.
17. Макаров И. М., Менский Б. М. Таблица обратных преобразований Лапласа и
743
обратных z-преобразований (Дробно-рациональные изображения). М.: Высшая школа, 1978. 247 с.
18. Математическая теория оптимальных процессов/В. С. Понтрягин, В. Г. Болтянский, Р. В. Гамкрелидзе, Е. Ф. Мищенко. М.: Наука, 1969. 384 с.
19. Медведев В. С., Лесков А. Г., Ющенко А. С. Системы управления манипуляционных роботов. М.: Наука, 1978. 416 с.
20. Мелса Д. Л., Джонс С. К. Программы в помощь изучающим теорию линейных систем управления: Пер. с аигл. М.: Машиностроение, 1981. 200 с.
21. Мнкншев Г. Н. Экспериментальные методы в динамике космических аппаратов. М.: Машиностроение, 1978. 248 с.
22. МикроЭВМ: Пер. с аигл./Под ред. А. Дирексена. М.: Энергоиздат, 1982.328 с.
23. Модяев А. Д., Рудаков П. И., Соколов В. Б. Разработка диалоговых систем для автоматизации моделирования комплексов управления. М.: Изд-во МИФИ. 1983. 60 с.
24. Нелинейные системы автоматического управления. Дискретные нелинейные систе-мы/Под ред. Ю. И. Топчеева. М.: Машиностроение, 1982. 312 с.
25. Основы проектирования следящих си-стем/Под ред. Н. А. Дакоты. М.: Машиностроение, 1978. 392 с.
26. Потемкин В. Г. Автоматизированное проектирование (Алгоритмы исследования систем управления). М.: Изд-во МИФИ, 1980. 85 с.
27. Потемкин В. Г. Машинное проектирование. (Математическое описание динамических систем в пространстве состояний). М.: Изд-во МИФИ. 1978. 79 с.
28. Проектирование следящих систем с помощью ЭВМ/Под ред. В. С. Медведева. М.: Машиностроение, 1979. 367 с.
29. Скот Р., Сондак Н. ПЛ/1 для программистов: Пер. с англ. М.: Статистика, 1977. 224 с.
30. Современные методы проектирования систем автоматического управления: Анализ и сиитез/Под ред. Б. Н. Петрова, В. В. Солодовникова, Ю. И. Топчеева. М.: Машиностроение, 1967. 704 с.
31.. Солодовников В. В. Статистическая динамика линейных систем автоматического управления. М.: Физматгиз, 1960. 656 с.
32. Сю Д., Мейер А. Современная теория автоматического управления и ее применение: Пер. с англ. М.: Машиностроение, 1972. 552 с.
33. Техническая кибернетика. Теория'автоматического регулирования/Под ред. В. В. Солодовникова. М.: Машиностроение. Кн. 1, 768 с.; кн. 2., 680 с., 1967; кн. 3, ч. 1., 608 с. и ч. 2, 368 с., 1969.
34. Толчеев Ю. И., Потемкин В. Г., Иваненко В. Г. Системы стабилизации. М.: Машиностроение, 1974. 248 с.
35. Толчеев Ю. И., Пыпляков А. И. Задачник по теории автоматического регулирования. М.: Машиностроение. 1977. 592 с.
36. Уилкинсон. Алгебраическая проблема собственных значений: Пер. с англ. М.: Наука, 1974. 248 с.
37. Уилкинсон, Райиш. Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра: Пер. с англ. М.: Машиностроение, 1976. 389 с.
38. Пыпкин Я. 3. Основы теории автоматических систем. М.: Наука, 1977. 560 с.
39. Чаки Ф. Современная теория управления. Нелинейные оптимальные н адаптивные системы: Пер. с англ. М.: Мир, 1975. 424 с.
40. Шеридан Т. Б., Феррелл У. Р. Системы человек—машина. Модели информации, управления и принятия решений человеком-оператором: Пер. с аигл. М.: Машиностроение, 1980. 400 с.
41. Schultz D. G; The Generation of Liapunov Functions. N. Y. Academic Press, 1965, pp. 64.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоколебания 155, 556
—, амплитуда 173, 556
— вынужденные 540
— , способы подавления 534, 535
— , срыв 554
— , частота 173, 556
Алгоритм QR 143, 315
— QL 316
Амплитуда 271
— вынужденных колебаний 540 Амплитудно-фазовая частотная характеристика динамических элементов и систем 85 □* в декартовой системе координат 85 □ в полярной системе координат 106 Амплитудная частотная характеристика 85 Амплитудная эквивалентная характеристика 162 □ обратная (формула) 173, 539 □ прямая 162, 536 □ сложных нелинейных элементов 263 Амплитудные искажения 529 Анализ качества систем автоматического регулирования 403 Анализ точности систем автоматического регулирования 474 Анализ устойчивости систем автоматического регулирования 344
Беллман метод динамического программирования 695
Белый шум 509, 579
Билинейное преобразование 505, 660
Вектор ошибки квантования 579 Вещественная частотная характеристика 430
Воздействие входа 42 — возмущающее 291, 437, 611 — периодическое (формула) 540 — регулярное 474, 511 — случайное 474, 512 — управляющее 291, 437 Взаимная компенсация полюсов и нулей 665
Взаимно-коррелированные случайные сигналы 503
Время первого максимума переходного процесса 668
Время переходного процесса 404, 466, 669 Вынужденные колебания 540 Вычислительная процедура определения 282, 333, 382, 466 □, анализ устойчивости систем частотными методами 382 □ аналитических функций от действительных матриц 324 □ значений логарифмических амплитудной и фазовой частотных характеристик 333— 337 □ корней алгебраических уравнений л-го
* Знак, символизирующий понятие, состоящее из трех и более слов.
порядка 341, 342
□ коэффициентов гармонической линеаризации 282
□ — по методу трапеций 283, 285
□ — по методу Рунге—Кутта 4-го порядка 284
□ —статистической линеаризации ko, kt, kt 248—250
□ матриц и векторов при соединении систем автоматического регулирования в комплексы 337—339
□ областей устойчивости 394—397, 407
□ передаточных функций 341
□ левых и правых собственных векторов 317, 318
□ переходного процесса 466
□ собственных значений 313—318
□ правых и левых собственных векторов 317, 318
Гауса закон распределения (нормальный) 248, 707
Гиперплоскость переключения 602, 603, 607
Гипотеза эргодичности 496
Годограф Михайлова—Найквиста 359, 360
— корневой 416—418
Граф элементов (объектов) 70
— типовых систем автоматического регулирования 292
Датчики 119, 123
— измерительные 586
Двигатели 613
— гидравлические 613, 614, 619
— пневматические 613, 614, 619
— электрические 613, 614, 617, 619
----с высокими значениями движущих моментов 613
----с дисковыми роторами 613, 617
----с номинальными значениями движущих моментов 613
----с полыми роторами 613, 617
Двумерная плотность распределения вероятности 285
Декада 92
Декомпозиция 46, 70
Дельта-функция 26
Диалоговые системы ДИАЛ (интерпретирующая) 704, 705
----ДИАКОМ (интерпретирующе-компе-лирующая) 705, 706
----оптимизации 711, 715
----, проектирование 711, 716, 718
Диалоговый режим проектирования 140
D-разбиение 386—390
Динамические комплексы 337
Динамическая ошибка 480
----по положению 489
---- по производной ускорения 489
---- по скорости 489
----по ускорению 489
Динамическая точность 480
Динамическое программирование 694
745
Дискретная модель объекта или системы автоматического регулирования 140, 141— 143
Дискретно-непрерывные корректирующие устройства 576, 577
Дискретные типовые звенья 85
Дискретный наблюдатель 680
Дисперсия 286, 287, 709
Добротность 487
—, метод определения 487
—,------аналитический 487
—,------графический 488
Доминирующие полюса 605
Дополнительные динамические звенья 677
□, нули и полюса 666
Допустимое управление 682
Закон регулирования 608
— измерения параметров объекта 601
— управления нелинейный 607
Замкнутая динамическая система 291
□ комбинированная 291, 292
□ по возмущению 291
□ по отклонению 291
Запас устойчивости по модулю 361
----по фазе 361
Звено типовое 85
----апериодическое 92, 115, 131
-------- неустойчивое 92, 115
-------- устойчивое 92, 115
----дискретное 68, 95—97
----дифференцирующее 98
--------1-го рода 92
--------2-го рода 98
----интегрирующее 86, 93
---- колебательное 98
---- — неустойчивое 98
-------- устойчивое 98
—• — неминимально-фазовое 88—90
— —, апроксимация логарифмических характеристик 100
----, передаточная функция 46
----, приближенный способ построения 103
•---трансцендентное 116
—-------чистого запаздывания 372
----фазозапаздывающее 99
----фазоопережающее 99
з-преобразование 16, 85
— одномерное 140, 141
— многомерное 551, 552
— прямое 68, 504, 661, 674, 728—733
— обратное 461, 464, 728—733
—, основное свойство 68
Идентификация 15, 710
Измерительные устройства 633
Импульсная переходная функция 128
Импульсное питание 618
— корректирующее устройство 578, 594
Импульсный фиктивный элемент 293
Интегральное уравнение свертки 49, 50
Интегральные оценки качества 405
Интегрирующая система 448, 451
Интерполяция 697, 738
Исполнительные устройства 608
Качество систем автоматического регулирования 403
□, косвенное 403
□ , — по корневому годографу 416—418
□ , — по импульсным переходным функциям 453—455
□ , — По интегральным оценкам 405
□ , — по переходным процессам 429—433
□ , основные показатели 404, 668, 669
□,---времени переходного процесса 404,
669
□ ,------1-го максимума 668
□ ,-максимального отклонения регули-
руемой переменной 404, 668
□ ,-максимальной скорости отработки
регулируемой переменной 404
□ ,-максимума перерегулирования 404,
668
Квантование 26
— по времени 26, 275
— по уровню 26, 275
Колебания низкочастотные (медленноме-няющиеся) 537
— — вынужденные 540
— — субгармонические 513
Комбинированное управление 291, 717, 718
Комплексы 292, 337
Корректирующие устройства систем автоматического регулирования 636 □ дискретные 576, 577
□ — с импульсными фильтрами и RC-че-тырехполюсниками 570, 573
□ — с микропроцессорами-контроллерами 570, 580
□ —с микроЭВМ 571, 572
□ линейные 636—659
□ —в виде программ для управляющей микроЭВМ 583, 661—665, 671, 672
□ — с RCL-четырехполюсниками 636—658
□ нелинейные 536, 719
□ — псевдолинейного типа 566, 567
□--------на аналоговых элементах 565
Корреляционная функция 496
----- взаимная 496
Коэффициент гармонической линеаризации 155
□ добавочный 219
□ основной 219
— демпфирования 107, 109
— добротности 487
-----по положению (статизм системы)
1 + К 480
----- по скорости DM 480
-----по ускорению De 480
----- по производной ускорения Dt 480
— ошибок 476, 480, 504—507
-----по положению Со 476, 504—507
-----по скорости С, 476, 504—507
— — по ускорению С2 476, 504—507
— — по производной ускорения С3 476
— регрессии 707
— совместной гармонической и статистической линеаризации непрерывных нелинейностей 254
— □ для двузначных нелинейностей 261
— □ для однозначных нелинейностей 259, 260
— статистический осредненный 262
— статистической линеаризации непрерывных нелинейных систем 248
746
— □ для двузначных нелинейностей 255, 256
— □ для однозначных нелинейностей 251— 253
— статистической линеаризации для дне-кретных нелинейностей 275 — □ для двузначных нелинейностей 278, 279
— □ для однозначных нелинейностей 277 — усиления 156
-----по низкочастотной составляющей 244 Критерии ортогональности планов 709 — рототабельности планов 709 — устойчивости линейных систем автоматического регулирования 344—348 ----- алгебраические 353, 358 ----- Гурвица 353 —----Рауса 354
-------Льенара—Шипара 355 -------Шур—Кона 358
— — частотные 359
--------Михайлова — Найквиста 359 --------в линейном масштабе 359— 361
----------------с трансцендентными звеньями 372
----------в логарифмическом масштабе 361—366
------------- в декартовой системе координат 376, 377
-------------Ос трансцендентными звеньями 372—374
------------- в полярной системе координат 375
-------£>-разбиения 386—390
— — нелинейных систем автоматического регулирования 343 □ Ляпунова (второй метод) 513 □ Пбпова 543
— — □ — в линейном масштабе 544—546 — — □ — круговой 546 □ — в логарифмическом масштабе 349—551
— — □--------с помощью номограммы Ни-
кольса 550
-----□ Наумова 549
— • — □, гипотеза Айзермана 545
Лагранжа множители 612
Линия переключения управления 691 Линеаризация нелинейных элементов и систем автоматического регулирования 30 □ гармоническая (по 1-й гармонике) 155, 156 □ — двузначных 146, 162 □------со смещением 176, 185, 189, 200
□ — дискретных 276, 277—279
О — дифференциальных уравнений 241— 243
□ — однозначных 145
□ со смещением 176, 185 j
□ гармоническая (с учетом влияния высших гармоник) 218
□ — двузначных 218
□ нечетных 230
□ четных 228—230
□ — однозначных 221
747
□-------нечетных 221
□-------четных 228—230
□ совместная гармоническая н статистическая 254, 258, 262
□ — двузначных 260
□ — однозначных 259
□ статистическая с нормальным законом распределения сигнала 248
□ — двузначных 255—258
□ — однозначных 251—254
Ляпунова метод 513—518, 523
---- второй 513
------ —, условия устойчивости 514, 518
--------, — нестационарных систем 523
--------, — стационарных систем 514
----первый 344
--------, условия неустойчивости 348
--------,-----нестационарных систем 350, 353
-------, — — стационарных систем 348,349 ------------ —, условия устойчивости 344, 345 -------, -----нестационарных систем 350
— — —,--------стационарных систем 346, 347
Математическая модель 21
----, описание элементов 21
----, регрессионная линейная 117
----, — нелинейная 117, 710
Математическое обеспечение управляющих ЭВМ на языке ассемблер 662, 663—665, 671, 672 ----САПР 703
--------алгоритмическое 703
--------информационно-программное 703
— — — методическое 703
--------г организационное 703
----универсальных ЭВМ на языке ПЛ/1 124, 125, 283—288, 319—322, 325—327,337— 339, 341, 342, 354, 355, 358, 359, 384, 396, 397, 407, 466—468
Матрица 722—728
— верхней формы Хессенберга 143, 313
— диагональная 44, 312
— Жордана 42
— знакоотрицательная 345
— знакопеременная 345
— знакоположительная 345
— комплексная 44
— коэффициентов линеаризации 145
— отрицательно-определенная 346
— переходная 140, 311
— положительно-определенная 346
— преобразования 45
— простой структуры 311
— собственных векторов 312
----левых 312
---- правых 312
— фундаментальная 311
— Эрмитова 312, 316, 727
Матрицнант 398
Метод гармонической линеаризации 145
□ двойной 244
— декомпозиции 46
— интегрирования 28
----Адамса — Башфорта 28
----Адамса — Мультоиа 28
----Рунге — Кутта 27
-----Эйлера 28
— линеаризации 30, 32, 33, 39
— наименьших квадратов 39
— регрессионного анализа 21
— совмещенной гармонико-статистической линеаризации 145
— статистической линеаризации 145, 248 — трапеций 283 — центральной разности первый 28 ------- второй 28
— штрафных функций 713
Методы проектирования систем автоматического регулирбвания 13—19, 610, 611, 702, 703, □ выбором их параметров с определением основных показателей точности и качества 716—720 □ диалоговой оптимизации 711—716 □ дискретных и дискретно-непрерывных по логарифмическим характеристикам, построенным относительно псевдочастоты 661, 663 □ —' — по заданному расположению нулей и полюсов 674—677 □------по корневому годографу 665—673
□------с помощью дополнительно введен-
ных динамических звеньев в обратную связь 677—681 □ — — с реализацией программ на микроЭВМ 671, 672
О □ с импульсными последовательными и параллельными корректирующими устройствами 661—663
□ □ с реализацией программ коррекции на микропроцессоре-контроллере 580—582 □ □ с реализацией программ коррекции на микроЭВМ 582, 583, 662—665, 671, 672 □ непрерывных по логарифмическим частотным характеристикам 622—627
О □ с последовательными, параллельными и последовательно-параллельными корректирующими устройствами 627—634 □ системами автоматизированного проектирования (САПР) 703—706, 716
□ □, математическим моделированием 706—711
Механическая передача 620
Моделирование 14
— математическое 19
— натурное 19
— полунатурное 19
Модуляция амплитудно-импульсная 275
— время-импульсная 26
— комбинированная 26
— частотио-импульсиая 275
— широтно-импульсная 26, 275
Наблюдаемость САР 328
— глобальная 330
— полная 330
Нелинейность существенная 145
— двузначная 153
----- активная 173
— — пассивная 173
— дискретная 282
— многозначная 145
— однозначная 145, 155, 156, 163, 282
-----несимметричная 232
-----симметричная 221
— сложная 263
Номограмма 333
— замыкания систем (Никольса) 333 ----- в декартовой системе координат 334 ----- в полярной системе координат 335 ----- в пространстве 336 — определения значений фазовых углов типовых звеньев 2-го порядка 98, 99 ----- поправок для построения точных значений логарифмических амплитудных характеристик типовых звеньев 2-го порядка 98, 99 -----массы двигателей САР в зависимости от номинальной мощности на выходном валу 613 ----- показателей качества дискретных (дискретно-иепрерывиых) систем 669 -----показателей качества непрерывных систем 471 -----□ основных 471, 472 ----- □ по Солодовникову 623 -----типов двигателей САР 613 -----угловых значений фазовых опережений корректирующих устройств 234 ----- частотной характеристики замкнутой системы 433—436 -----О вещественной 434, 445 -----□ мнимой 4341—446
-----числовых значений амплитуд в дБ 92 — построения точных значений логарифмических частотных характеристик 1-го порядка 92 Нормальный закон распределения 248 Нормы запасов устойчивости 470
Область устойчивого состояния 173 — неустойчивого состояния 173 Обобщенные координаты 21
Операционная система специализированная 13, 705 ----- универсальная 702 Оптимальное управление 681 -----метод динамического программирования Беллмаиа 694—697 ----- □ рекуррентная процедура 696, 698 ----- □ рекуррентное уравнение 696 -----.□ уравнение Беллмаиа 696, 698 ----- □ функция Веллмана 696 -----, принцип максимума Понтрягина 682 -----, □ без ограничения иа управление 683 -----, □ задача' Больца 683 -----, □ задача Лагранжа 683 -----, О задача Майера 683 -----, □ по быстродействию 683—689 -----, □ с ограничением на управление 683 -----, □ условия трансверсальности 686 -----, □ функция Гамильтона — Понтрягина 684 ,
Передаточная функция ,46 -----дискретных лииейиых звеньев (объектов) 68, 69 -----□ нестационарных 128, 129 -----□ стационарных 88, 90 -----г- желаемая 622, 627, 629, 633
748
-----замкнутой дискретной системы по возмущающему воздействию 299 -----по ошибке 299 -----по управляющему воздей- ' ствию 299
-----замкнутой непрерывной системы по возмущающему воздействию 293, 294 -----;----по ошибке 293, 294 -----по управляющему врздей-ствию 293, 294
-----изменяемой части системы 627—634
-----корректирующих устройств 636—658 ----------- дискретных 670
----------непрерывных 636—658
-----неизменяемой части системы 571, 577
-----непрерывных линейных звеньев (объектов) 48—51 -----нестационарных 51 ----- стационарных 48
-----разомкнутой системы 293
-----разомкнутой дискретной системы 299
------- нестационарной 400
------ — стационарной 301, 302, 473, 577
-----эквивалентная 145, 147, 292
-------нелинейных элементов (объектов) 304
----------дискретных элементов (объектов) 27
------- приведенная 595
Переменные состояния 21
Подграфы 72
Понтрягин принцип максимума 682
Последовательность дискретных сигналов 47
Построение логарифмических частотных характеристик систем автоматического регулирования 361 □ для анализа качества 437, 471, 472 □ для анализа точности 484, 485 □ для анализа устойчивости 361—382 □ — желаемой (для синтеза) 660 □ — изменяемой 627, 633 □ — неизменяемой 613 Построение областей 374 -----автоколебаний 525, 530 ----- захватывания 543 ----- неустойчивости 374 ----- устойчивости 374 Преобразование Лапласа 47 ----- прямое 47
-------Для интегродифференциальных уравнений 49
—------Для линейных дифференциальных
уравнений 48
-------Для уравнений в частных производных 50
----- обратное 47
-------дискретное (з-преобразование) 68
----------многомерное 552
----------одномерное 68
Преобразование матриц 722—728
-----унитарное 44, 315, 318
-----Фурье 52, 128
-----элементарное 313, 316
Преобразование структурных схем, графов
Преобразователи аналого-цифровые 112
— цифро-аналоговые 112
Преобразователь код-аналог (КА) 27
— аналог-код (АК) 26, 571
— вал-цифра (ВЦ) 26
Принцип суперпозиции 343
Псевдочастота 91, 113
Реализация обратной связи по состоянию с помощью дополнительно введенных звеньев 677—681
— программ на управляющей микроЭВМ 583
— □, комбинированное программирование 585
— □, последовательное программирование 584
— □, прямое программирование 583
Ранг матрицы 330, 331
Регрессионные модели 117, 707
Регулятор выхода 694
— состояния 694
Резонансная частота 376
Ряды 30, 397, 475
— Вольтера 401
— Маклорена 475
— Неймана 398
— Тейлора 30
Самонастраивающиеся системы автоматического регулирования 600 □ беспоисковые с эталонной моделью и сигнальной настройкой 601 □ переменной структуры 700 □ поисковые 11
Связь 70
— главная обратная 291
— перекрестная обратная 42
— сильная 70
— слабая 70
Сигнал 121
— входной 176
--- двухчастотный 201
--- меандровый 151
---многочастотный 201
---одночастотный 176
— поисковый 11
---постоянный 176
--- синусоидальный 151
---случайный 121
---треугольный 151
— выходной 294
— детерминированный 121
— дискретный 67
Система автоматического регулирования (управления) 609 □ автоматической стабилизации 291 □ астатическая 1-го порядка 477, 479, 561 □ — 2-го порядка 477, 479, 564 □ — 3-го порядка 494, 495 □ двухканальная 296 О дискретная 299 □ дискретно-непрерывная 299, 659, 660 □ — при регулярных воздействиях 571
О---------с импульсными фильтрами н
RC-четырехполюсниками 569
□---------с микропроцессором-контролле-
ром 570
749
□ —------с микроЭВМ 572
□ линейная непрерывная 610
□ при регулярных воздействиях 610,
611
□ —------— с параллельным корректи-
рующим устройством 561, 629
□ ----------с последовательным и парал-
лельным корректирующими устройствами 627, 629 □------------с последовательным коррек-
тирующим устройством 561, 577
□ при случайных воздействиях 611,
612
□ -с параллельным корректи-
рующим устройством 608
□ с последовательным коррек-
тирующим устройством 608
□ многоконтурная 293, 295, 297
□ многомерная 308, 386
□ нелинейная 565, 566
□ непрерывная 294, 297
□ нестационарная 397
□ одноконтурная 293, 295
□ оптимальная 681
□ релейная 692
□ самонастраивающаяся 600
□ с заданной структурой 559
□ следящая с управлением комбинированным 292
□ — с управлением по возмущению 292 □ — с управлением по ошибке 292 □ с программным управлением 291 □ с регулятором 586, 593, 594, 608 □ статическая 477, 478, 560 □ стационарная 12, 307, 544 □ унифицированная 571 □ условно-устойчивая 667 □ экстремальная 585, 586
Система автоматизированного проектирования 703 □ моделирования 702 □ подсистемы 703
Скачкообразное изменение амплитуды и фазы 343
Скользящий режим 602
Собственные значения матрицы 312
-----, векторы 312
-----, — правые 312
— —, — левые 312
Спектральная плотность 496 ----- взаимная 496
Спектральное разложение матрицы 140,311, 312
Способ стабилизации (устойчивости) систем со слабодемпфированными элементами 375 □ амплитудный 375 □ фазовый 376 Статическая ошибка 481, 489 -----, коэффициент статизма 484
Структурная схема системы автоматического регулирования 293 □ двухканальная 296 □ линейная 294 □ многоконтурная 295
□ — без перекрещивающихся связей 295 □ — с перекрещивающимися связями 295 □ нелинейная 294
□ одноконтурная с отрицательной обратной связью 292
□ преобразованная 296—298, 300, 306
□ — к одноконтурной (расчетной) 295
Таблица амплитудных и фазовых характеристик 93—97
— вычисления функций спектральной плотности по коэффициентам Лягерра 499
— графов линейных элементов и систем автоматического регулирования 83, 84 — двузначных нелинейностей 179—182 --------со смещением 201—214
-----дискретных 281
-----дискретных однозначных нелинейностей 280
— з-преобразований для передаточных функций 730—733
— импульсных и передаточных функций замкнутой желаемой системы 624, 625 — коэффициентов гармонической линеаризации двузначных нелинейностей 171—173 — □ дискретные 2.78, 279
— □ однозначных нелинейностей 157—162 — □ — дискретных 277
— □ — со смещением 189—193
— О со смещением 201—204
------ однозначных нелинейностей 259, 260
— - Рауса (коэффициентов) 356, 357
- — совместной гармонической и статической линеаризации двузначных нелинейностей 261
-----статистической линеаризации двузначных нелинейностей 255, 256
— логарифмических амплитудных и фазовых частотных характеристик типовых звеньев 93-97
— однозначных нелинейностей со смещением 189—192
— основных типовых звеньев 67
— параметров передаточных функций для электрических, гидравлических и пневматических двигателей 619, 620
— первых коэффициентов ошибок систем автоматического регулирования Ц7(з)/| 1 + + IT(s)] 477
— □ V(x)/[1 4- V(s)] 478, 479
— передаточных' функций дискретных систем автоматического регулирования 301— 303
— преобразования структурных схем линейных элементов (объектов) и схем автоматического регулирования 80—82
— принципиальных схем тиристорных и транзисторных преобразователей для регулирования электродвигателей постоянного тока 614—616
— □ переменного тока 616, 617
— прямых и обратных s и z-преобразова-ний 48, 68
— □ для сигналов возмущения 728, 729 — расположения полюсов и нулей корректирующих устройств на Z-пяоскости 670 — соответствия структурных схем графов 69, 70
— сравнительных данных устройств управления 618
750
— типовых линейных корректирующих устройств на RC н RCL-четырехполюсниках 636—658
— формул для вычисления коэффициентов динамической точности в статических системах автоматического регулирования 482 — □ комбинированных 492
— □ в астатических системах 1-го порядка 483
— □ 2-го порядка 484
— функций Лапласа 734, 735
— частотных характеристик типовых звеньев 86—90
Лх-функцнй 736—739
— элементов (объектов) 53—66
Такт квантования 473, 559, 580
Таймер 583
Управление двигателями 617, 618
-----гидравлическими 618
—-------от аккумулятора (гидравлическо-
го) 618
------- —-с помпой переменной производительности 618
-------- с помпой постоянной производительности 618
— — пневматическими 618
-----— от аккумулятора (пневматического) 618
—-------от компрессора 618
-----электрическими постоянного тока 617
------------от генераторов 617, 633
—-----------от магнитных усилителей 617,
629
—------— от транзисторных усилителей
615, 616
----------от тиристорных усилителей 614- 617, 628
----------от электромашннных усилителей 617, 633
Уравнение Веллмана 696
— Ван-дер-Поля 242
— Дуффннга 23
— Риккати 693
— состояния векторно-матричное 137 ----- — каноническое 42
--------разностное 25, 47, 661
Управляемость систем автоматического регулирования 328
Условие устойчивости (нелинейных систем) 514
-----гармонического баланса 525 -----Ляпунова (второй метод) 513
-----Сеге 518
-----Шульца 517, 518
Условия синхронизации 540
— трансверсальности 686'
Устройства задающее 291
— измеряющее 291
— импульсное 594, 595
— исполнительное 586
— корректирующее 627—635
— сравнивающее 291, 586
— усилительное 560
Устойчивость систем автоматического регулирования 344
□, методы анализа 344
□ ,---дискретных, дискретно-непрерыв-
ных линейных 352
□ ,-----------нестационарных 397—399,
401, 402
—-----------стационарных 352, 353
□ ,---дискретных, дискретно-непрерыв-
ных нелинейных 551—553
□ ,---непрерывных линейных 344, 359
□ ,-----------нестационарных 350—352
□ ,-----------стационарных 346—348
□ , — — непрерывных нелинейных 513, 524
□ , —---------нестационарных 523, 524
□ , —------— стационарных 516—518
Фазовая частотная характеристика 85 ----- эквивалентная характеристика 162 -----сложных нелинейных элементов 263
Фазовое пространство 21
Фазовые искажения 529
Фильтр высокочастотный 343
— запирающий 376
— низкочастотный 524, 525
Форма представления коэффициентов дифференциальных уравнений 411
О по Баттерворту 411
□ по минимуму интегральной оценки 411, 412
Формула квадратур Стеклова 235
Формулы для вычисления интегралов от дробно-рациональных функций 740—743 Функция 46, 145, 683
Функция Веллмана 696
— Бесселя 158, 159
— Гамильтона — Понтрягина 684
— Ломмеля 158, 159
— Лягерра 498, 499
— от матриц 322
— переходная импульсная 128
— синтезирующая в оптимальном управлении 682
— смещения 244
— трапецеидальная импульсная 130
— эквивалентная передаточная 145, 146
Характеристическое уравнение 525, 666
Частота автоколебаний 526, 527, 530, 537 — собственная 108
— среза 608
Частотная характеристика 85, 367
----- действительная 85
----- мнимая 85
Частотно-импульсная модуляция 275
Частотные критерии устойчивости 359, 366
Человек-оператор 703
Численные способы организации процедуры оптимизации 588
□ , метод Гаусса—Зейделя 590, 591
□, метод градиента 588, 589
□ , метод наискорейшего спуска 589, 590
□, метод Ньютона (модифицированный) 591
□, метод Флетчера—Ривса 592, 593
Шаблон для графического определения режимов автоколебаний 173, 531
751
□ двухзначных нелинейностей 183—187
□ со смещением 214—217
□-------с дискретными нелинейностями
280, 282
□' однозначных нелинейностей 167—170
□-------со смещением 195—200
Широтио-импульсиая модуляция 305
Шульца метод 516, 517
Шур—Кона критерий устойчивости 358
Экстраполятор нулевого порядка 140
— второго порядка 142
— первого порядка 141
Экстраполяция нулевого порядка 26
— второго порядка 26
— первого порядка 26
Экстремальные системы автоматического регулирования 585 □ беспоисковые 588
□ с поиском экстремума 588
□-------с запоминанием 586, 598—600
□-------по чувствительности 586
Элемент слабодемпфироваииый 106, 107
— двузначный нелинейный импульсный 275
— дискретно-непрерывный 112
— дискретный 26
— импульсный фиктивный 293
— сложный 29
— сложный нелинейный 263
— существенный дискретный нелинейный 275
Эксперимент 706
— активный 706
— оптимальный 706
— пассивный 706
Эргодичиый случайный сигнал 501
Эталонная модель 601
Эффективность 706
— обобщенный критерий 706
Ядро нитегральиого уравнения 50
Якоби матрица 30
Якоби метод 313
УЧЕБНОЕ ИЗДАНИЕ
Топчеев Юрий Иванович АТЛАС ДЛЯ ПРОЕКТИРОВАНИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Редактор Л. П. Строганов Обложка художника А. Я- Михайлова Художественный редактор | А. И. Ро | Технический редактор Т. С. Старых Корректоры Л. Е. Сонюшкина, Л. А. Ягупьева
ИБ № 4944
Сдано в набор 20.04.88. Подписано в печать 24.01.89. Т-07928. Формат 70X100'/»- Бумага кн.-журиальная-Гарнитура литературная. Печать офсетная. Усл. печ. л. 60,63. Усл. кр.-отт. 60,63. Уч.-изд- л. 63.95. Тираж 15 900 экз. Закав 1026. Цена 6 р. 70 к.
Ордена Трудового Красного Знамени издательство «Машиностроение», 107076, Москва, Стромынский пер., 4-
Ленинградская типография № 2 головное предприятие ордена Трудового Красного Знамени Ленинградского объединения «Техническая книга» им. Евгении Соколовой Государственного комитета СССР по печати.
198052, г. Ленинград, Л-52, Измайловский проспект, 29.