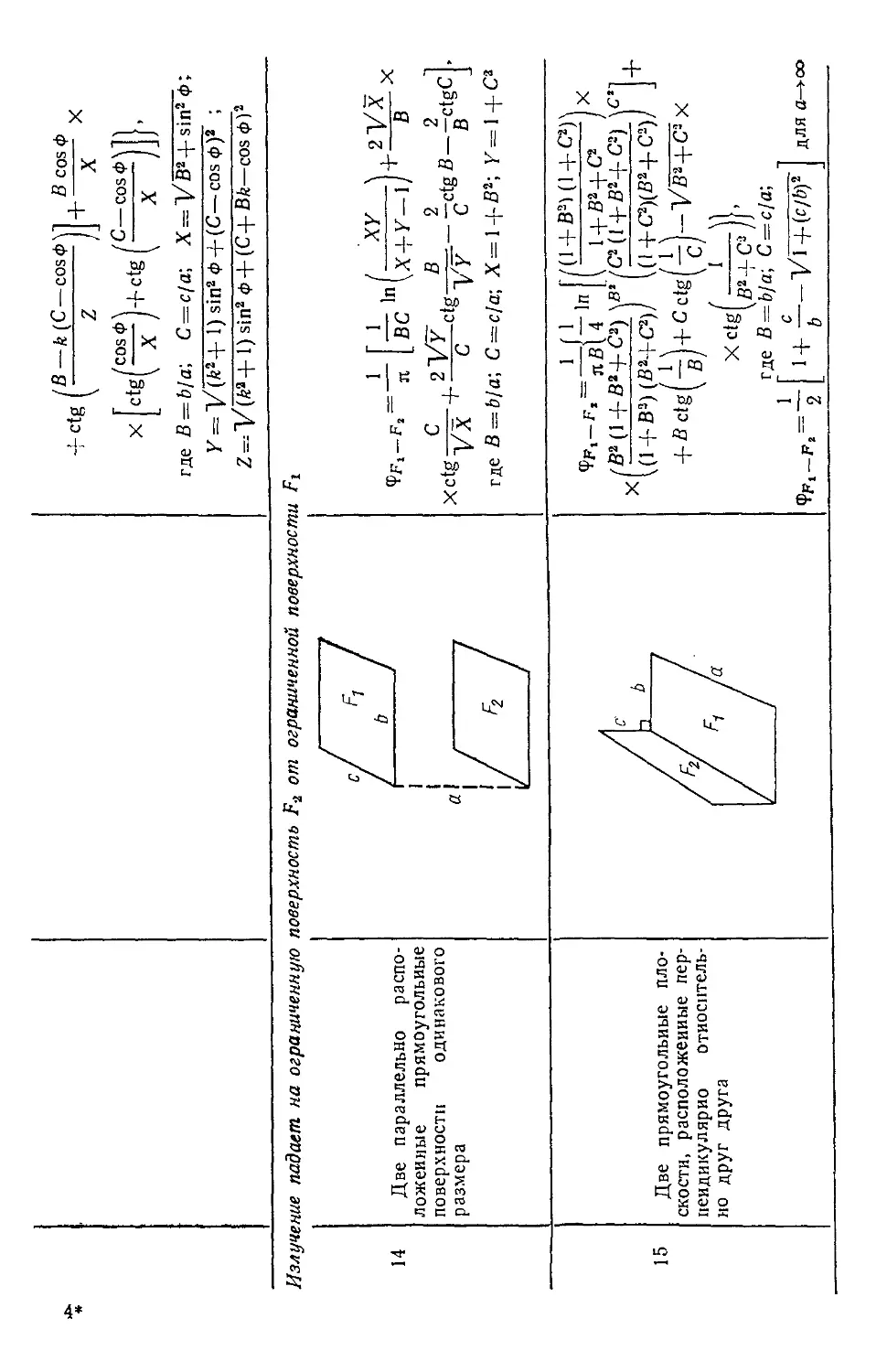
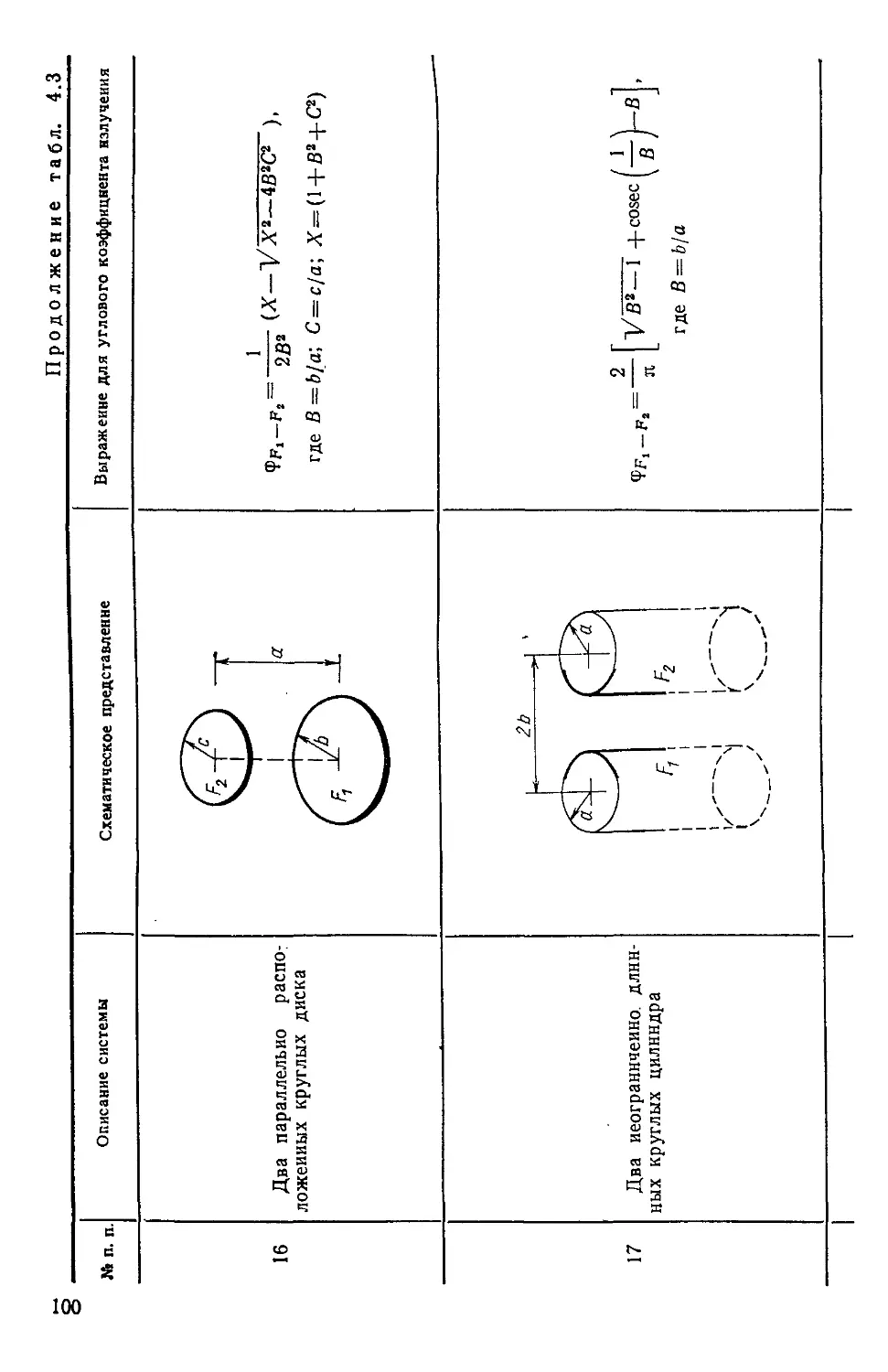
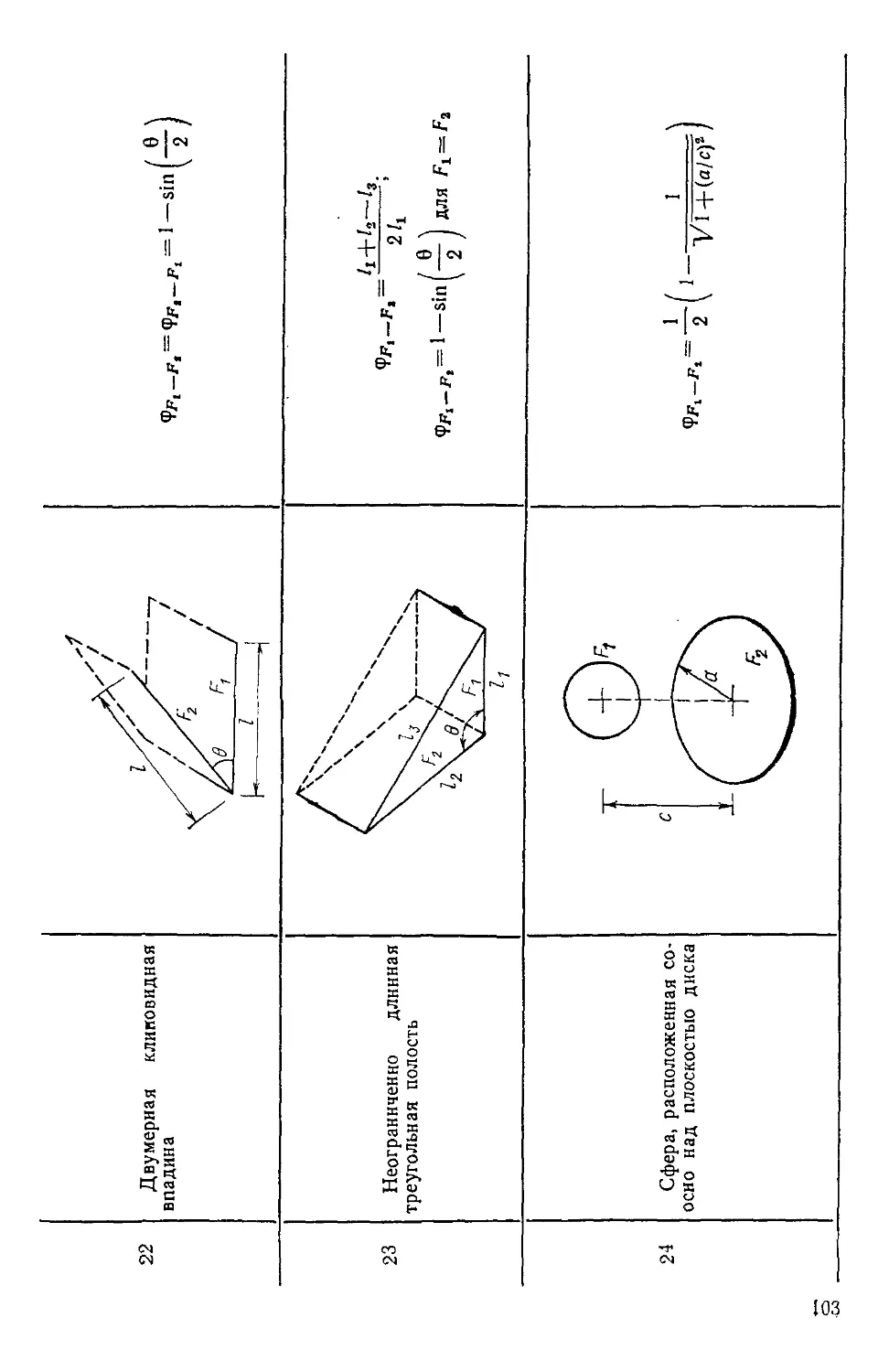
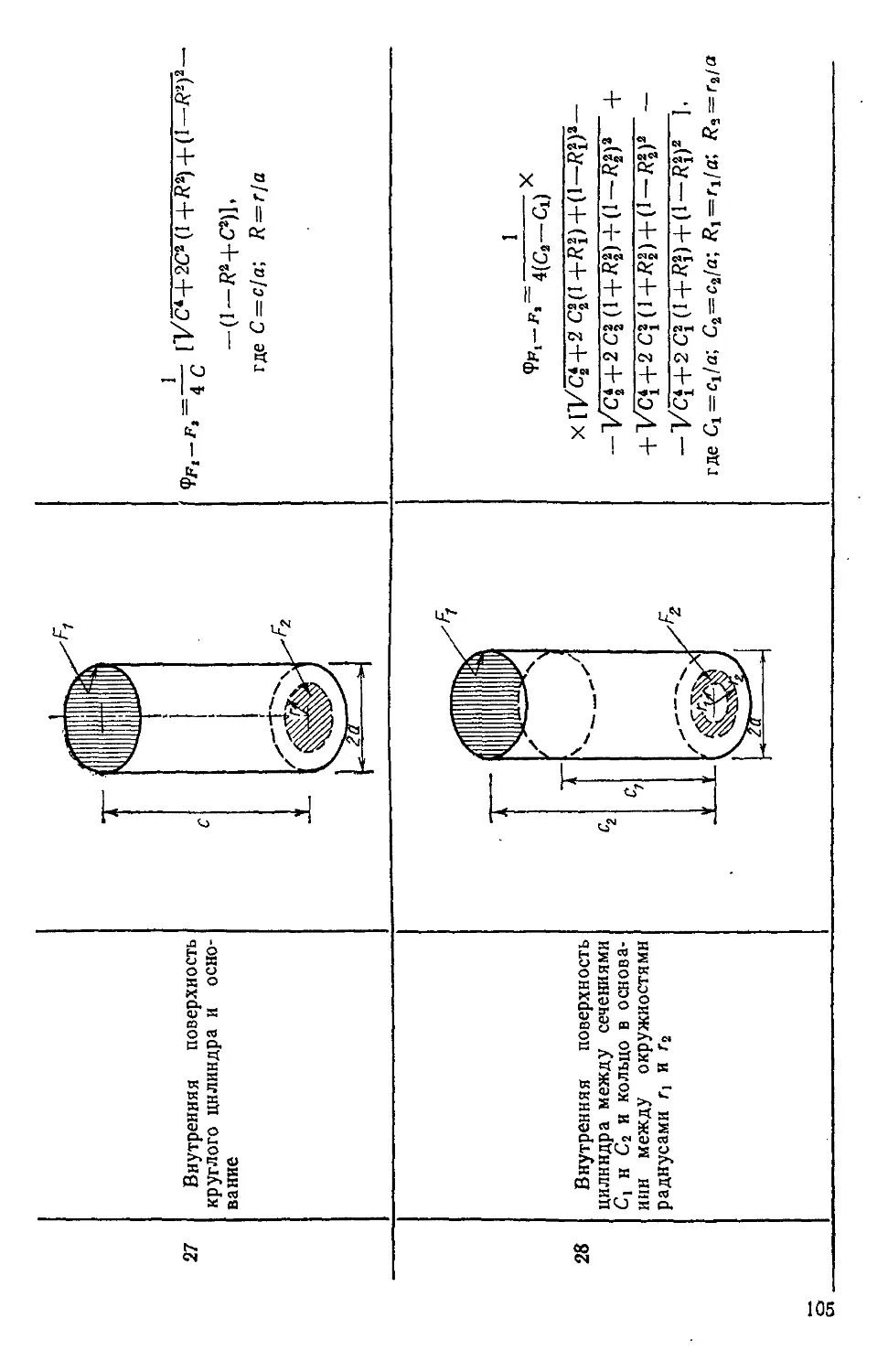
Author: Уонг Х.
Tags: физика термодинамика справочник переводная литература формулы по физике атомиздат
Year: 1979
Text
Handbook of Essential Formulae
and Data on
HEAT TRANSFER FOR
ENGINEERS
H. Y. WONG
PI PI PI
LONGMAN
LONPON AND NEW YORK
Х.Уонг
ОСНОВНЫЕ
ФОРМУЛЫ
И ДАННЫЕ
ПО ТЕПЛООБМЕНУ
ДЛЯ ИНЖЕНЕРОВ
СПРАВОЧНИК
Перевод с английского
канд. техн. наук В. В. ЯКОВЛЕВА
и канд. техн. наук В. И, КОЛ Я ДИНА
МОСКВА АТОМИЗДАТ 1979
УОНГ X. Основные формулы и данные по тепло-
теплообмену для инженеров: Пер. с англ. / Справоч-
Справочник. — М.: Атомиздат, 1979. — 216 с.
В справочнике в виде формул, таблиц н графиков при-
приведено наиболее полное количество соотношений и величин,
удобных для расчетов конкретных случаев теплопередачи.
Рассмотрены, по существу, все основные виды теплопередачи:
теплопроводность, конвективный и лучистый теплообмен, теп-
теплопередача при кипении и конденсации жидкости. Данные
могут быть использованы для оценки эффективности теплопе-
теплопередачи в активной зоне ядерных реакторов, при разработке н
выборе различных типов конструкций твэлов, охлаждаемых
однофазными, двухфазными капельными жидкостями илн га-
газовым высокотемпературным теплоносителем. Приведенные
формулы позволяют определить эффективность теплообменных
аппаратов и оценить способность к теплообмену с окружающей
средой строительных сооружений.
Справочник весьма полезен для широкого круга инжене-
инженеров, имеющих дело с теплопередачей, разрабатывающих и
эксплуатирующих различные энергетические установки (в том
числе и ядерные).
Рнс. 162. Табл. 40. Списки литературы 287 наименований.
У 3°315 Ш БЗ—42—14—1978-2303010000
034@1 )-79
© Longman Group, 1977
Данное издание книги «Основные фор-
формулы и данные по теплообмену для ин-
инженеров» публикуется с разрешения
фирмы «Лонгман Гроуп Лимитед»
© Перевод на русский язык, Атомиздат, 1979
ОГЛАВЛЕНИЕ
Перечень таблиц 7
Предисловие , 9
Глава 1. ОБЩИЕ СВЕДЕНИЯ
1.1. Виды теплопередачи 11
Теплопроводность 11
Конвективный теплообмен 12
Лучистый теплообмен 13
Сложный теплообмен 14
1.2. Температурные шкалы и реперные термометрические
точки 16
Список основной литературы 17
Глава 2, ТЕПЛОПРОВОДНОСТЬ
2.1. Введение 19
2.2. Обозначения -20
2.3. Определения 21
2.4. Параметр теплопередачи и термическое сопротивление 21
2.5. Закон теплоотдачи Ньютона 22
2.6. Теплопроводность при стационарном режиме 23
Одномерные системы 23
Двумерные системы 24
2.7. Теплопередача оребренных поверхностей 24
2.8. Нестационарные процессы теплопередачи 24
Тела с неограниченно высокой теплопроводностью ... 38
Тела с низким внешним термическим сопротивлением . 38
Тела с конечными значениями теплопроводности н кон-
конвективной теплоотдачей на поверхности 40
2.9. Уравнение Фурье — основной закон теплопроводности 41
Список литературы 49
Глава 3. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
3.1. Введение 50
3.2. Обозначения 50
3.3. Определения 52
3.4. Естественная конвекция 54
3.5. Вынужденная конвекция 55
3.6. Аналогия Рейнольдса 62
3.7. Коэффициент трения и перепад давления в каналах . . 62
3.8. Каналы и трубы 66
3.9. Теплоотдача при внешнем обтекании тел 67
3.10. Теплоотдача прн высоких скоростях 75
3.11. Конвективная теплоотдача тел вращения (дисков, ко-
конусов, цилиндров и сфер) 78
Список литературы 82
Глава 4. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
4.1. Введение 84
4.2. Обозначения 85
4.3. Определения 85
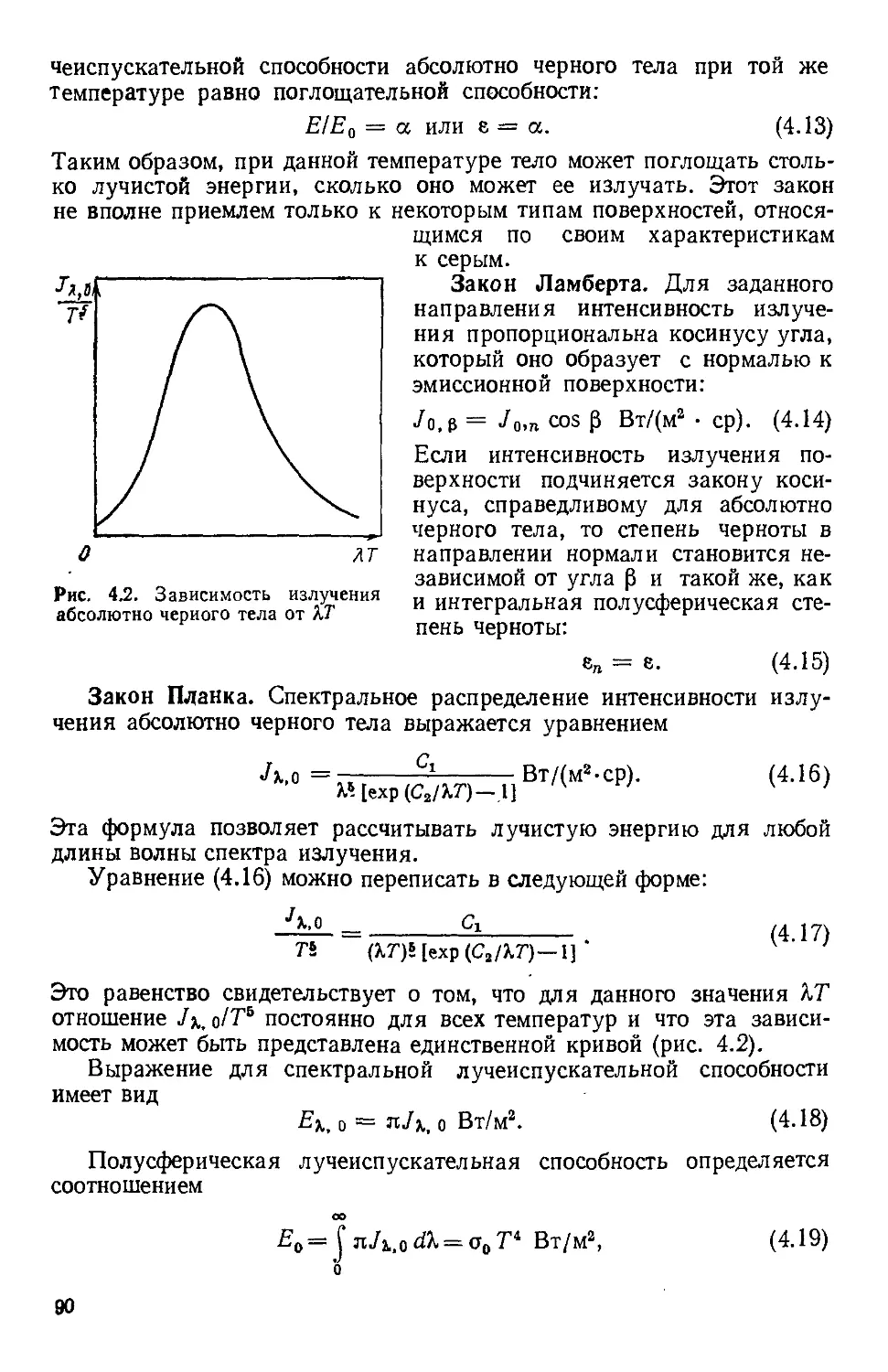
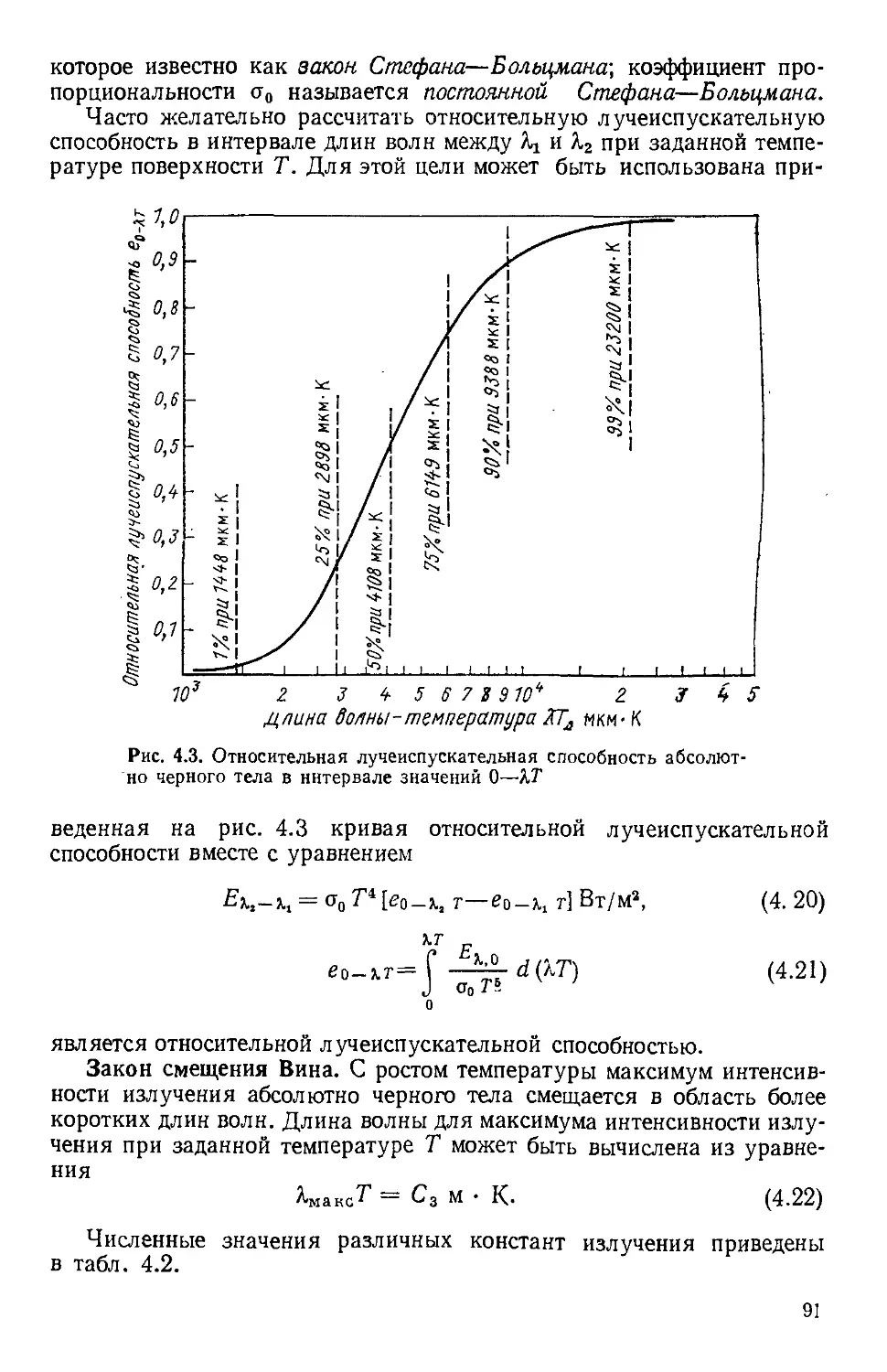
4.4. Абсолютно черное тело и основные законы излучения . 88
Закон Кирхгофа 89
Закон Ламберта 90
Закон Планка 90
Закон смещения Винл 91
4.5. Лучистый теплообмен между двумя абсолютно черными
поверхностями 92
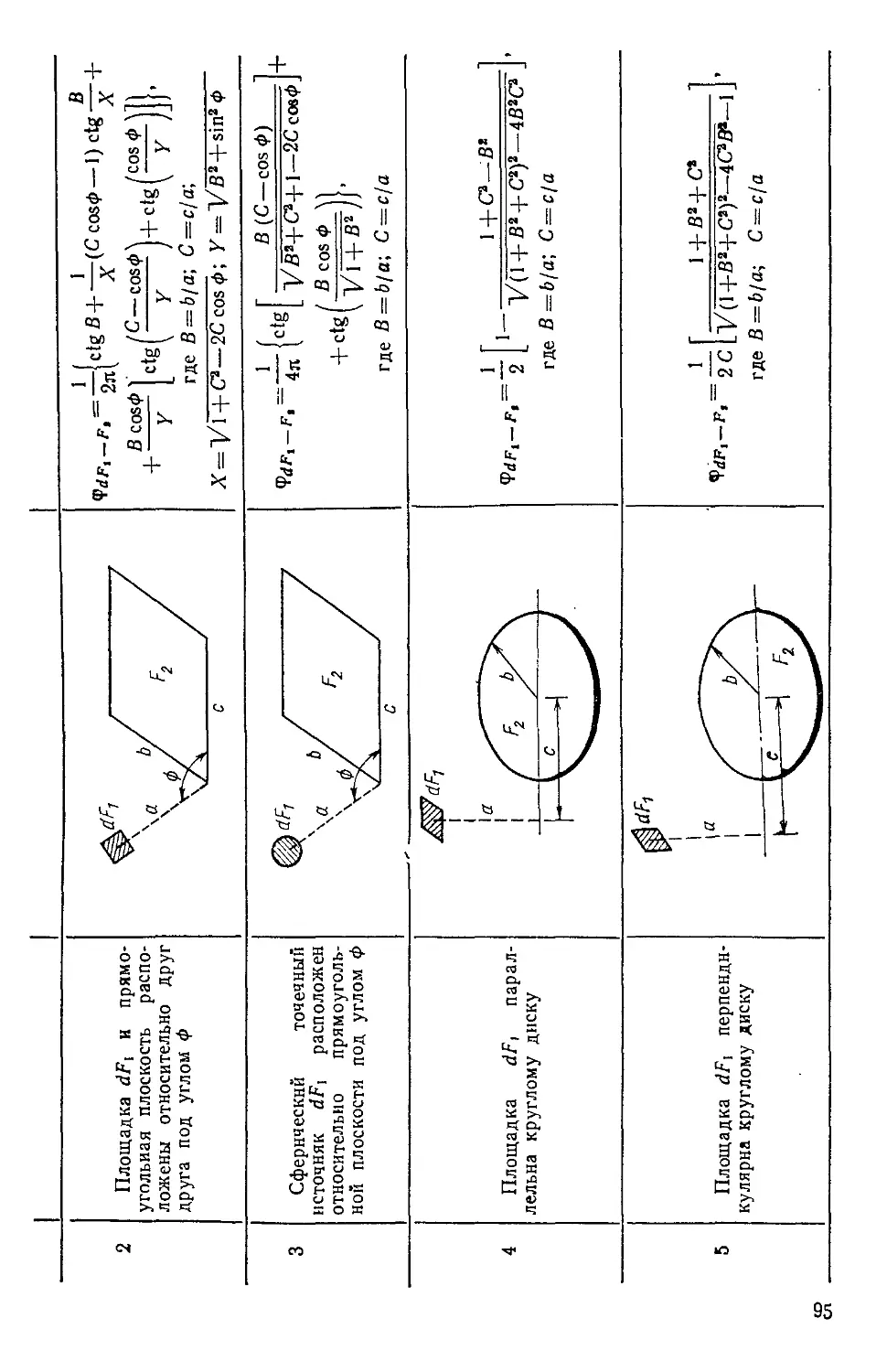
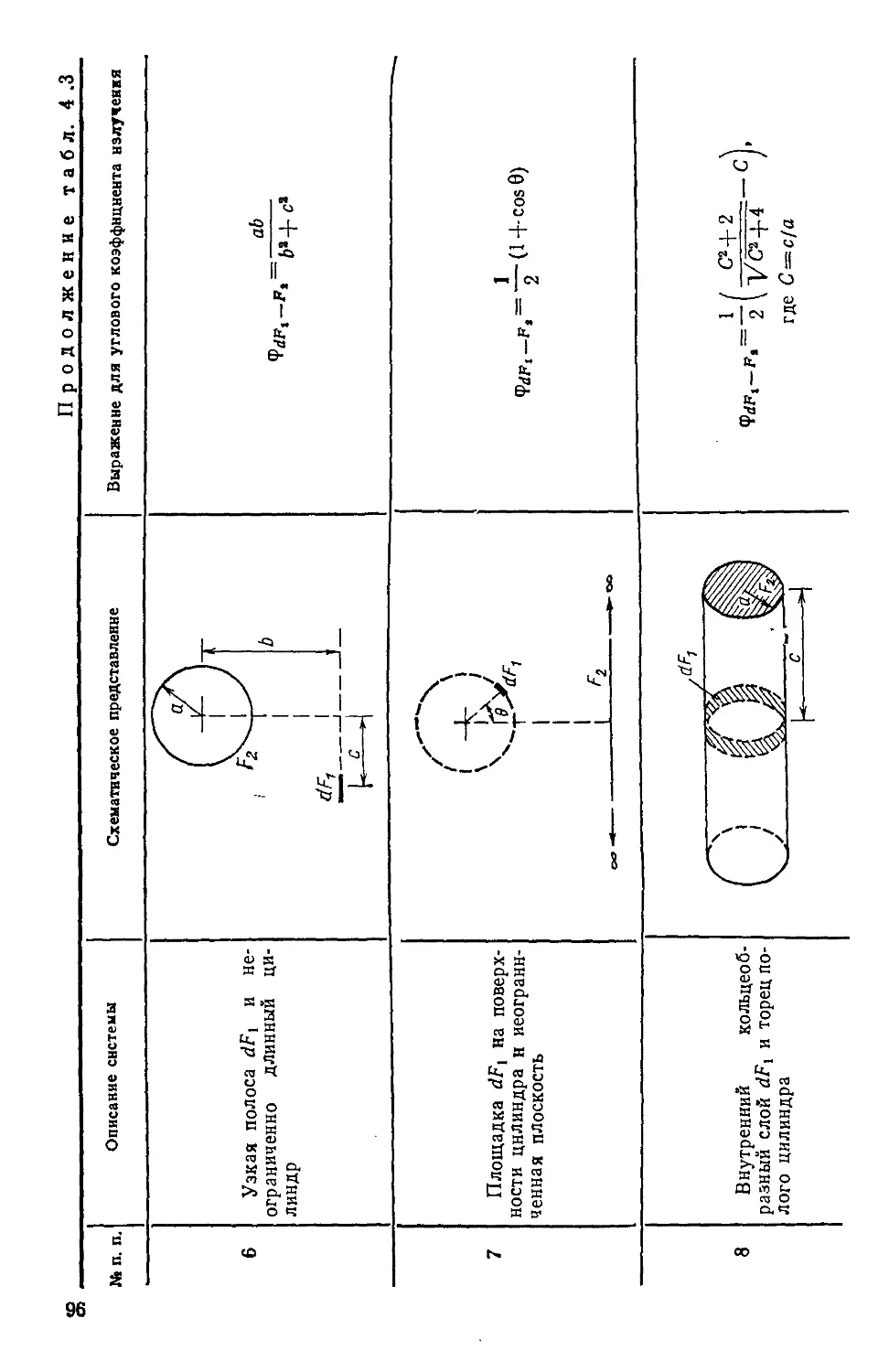
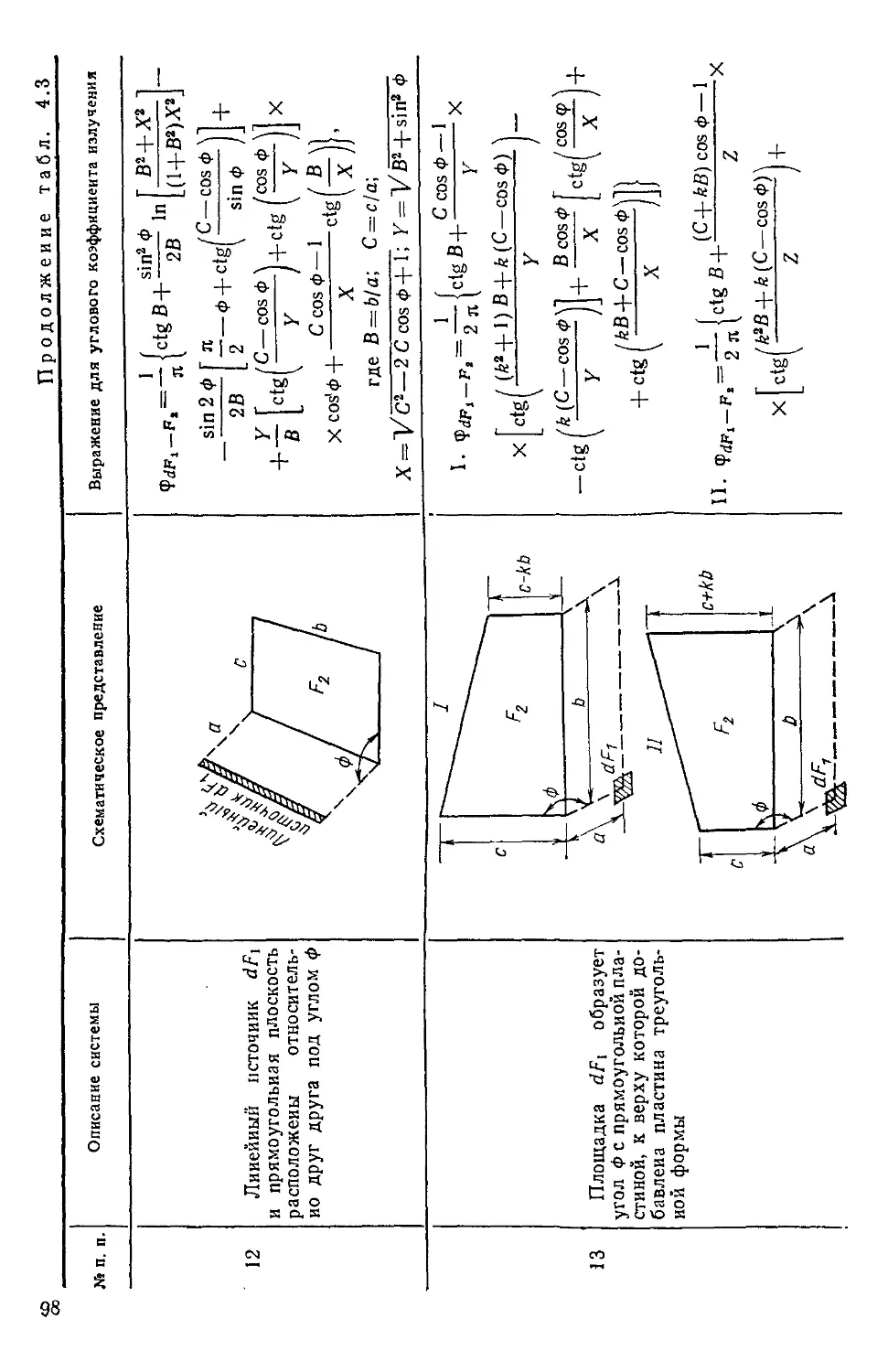
4.6. Применение алгебраического метода для определения
угловых коэффициентов излучения 93
4.7. Лучистый теплообмен между абсолютно черными поверх-
поверхностями, образующими замкнутую область 109
4.8. Лучистый теплообмен между диффузно-серымн поверх-
поверхностями 109
4.9. Защита от теплового излучения 113
Список литературы 116
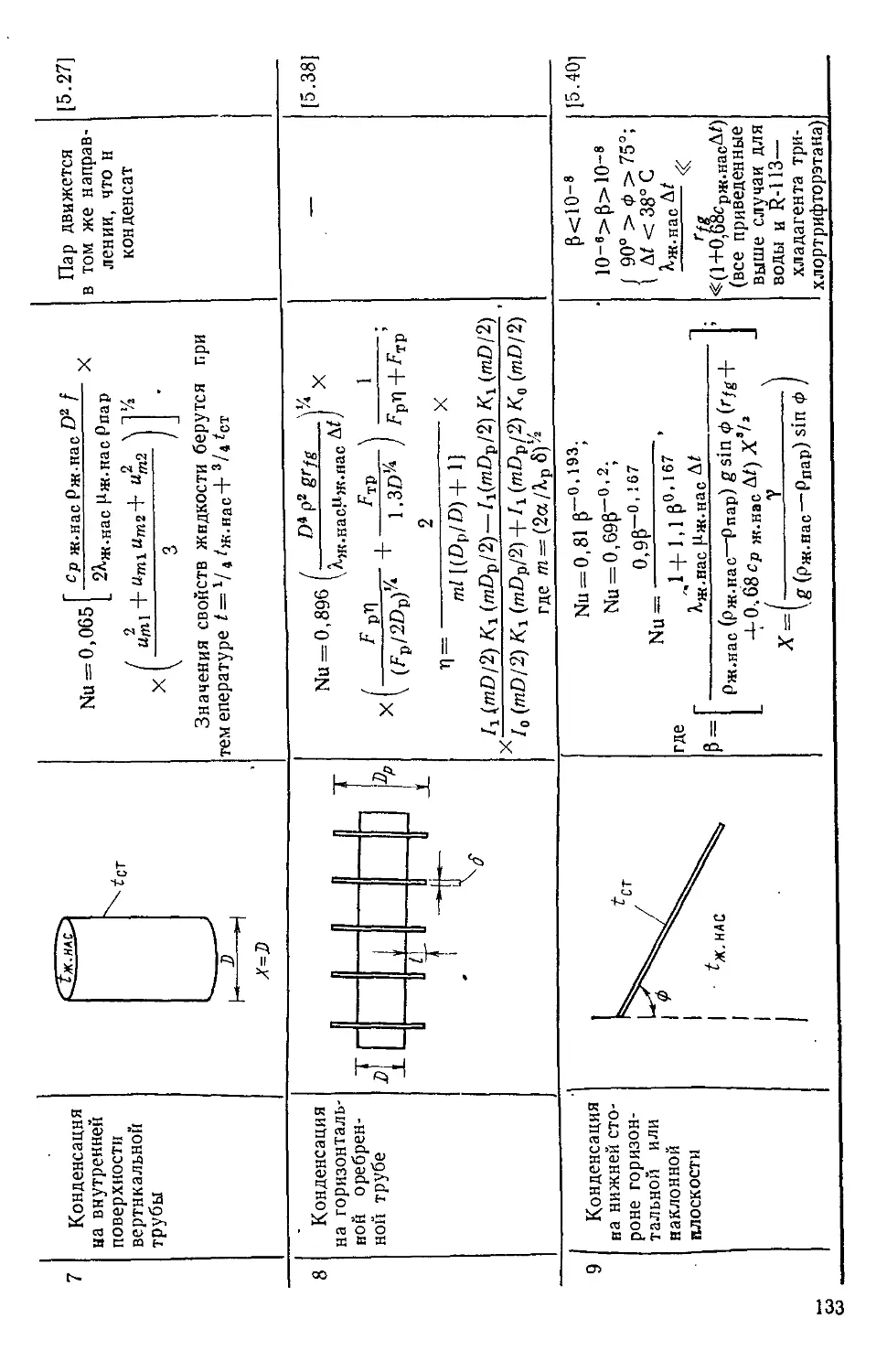
Глава 5. КИПЕНИЕ И КОНДЕНСАЦИЯ
5.1. Введение 118
5.2. Обозначения 119
5.3. Определения 120
5.4. Теплоотдача прн кипеннн 122
5.5. Теплоотдача прн конденсации 126
Список литературы , 134
Глава 6. ТЕПЛООБМЕННЫЕ АППАРАТЫ
6.1 Введение 136
6-2. Обозначения 137
6.3. Определения 138
6.4. Теплообменные аппараты с непосредственной теплопе-
теплопередачей 141
6.4.1. Расчет теплообменников 143
Метод, основанный на определении истинного значения
средней разности температуры 143
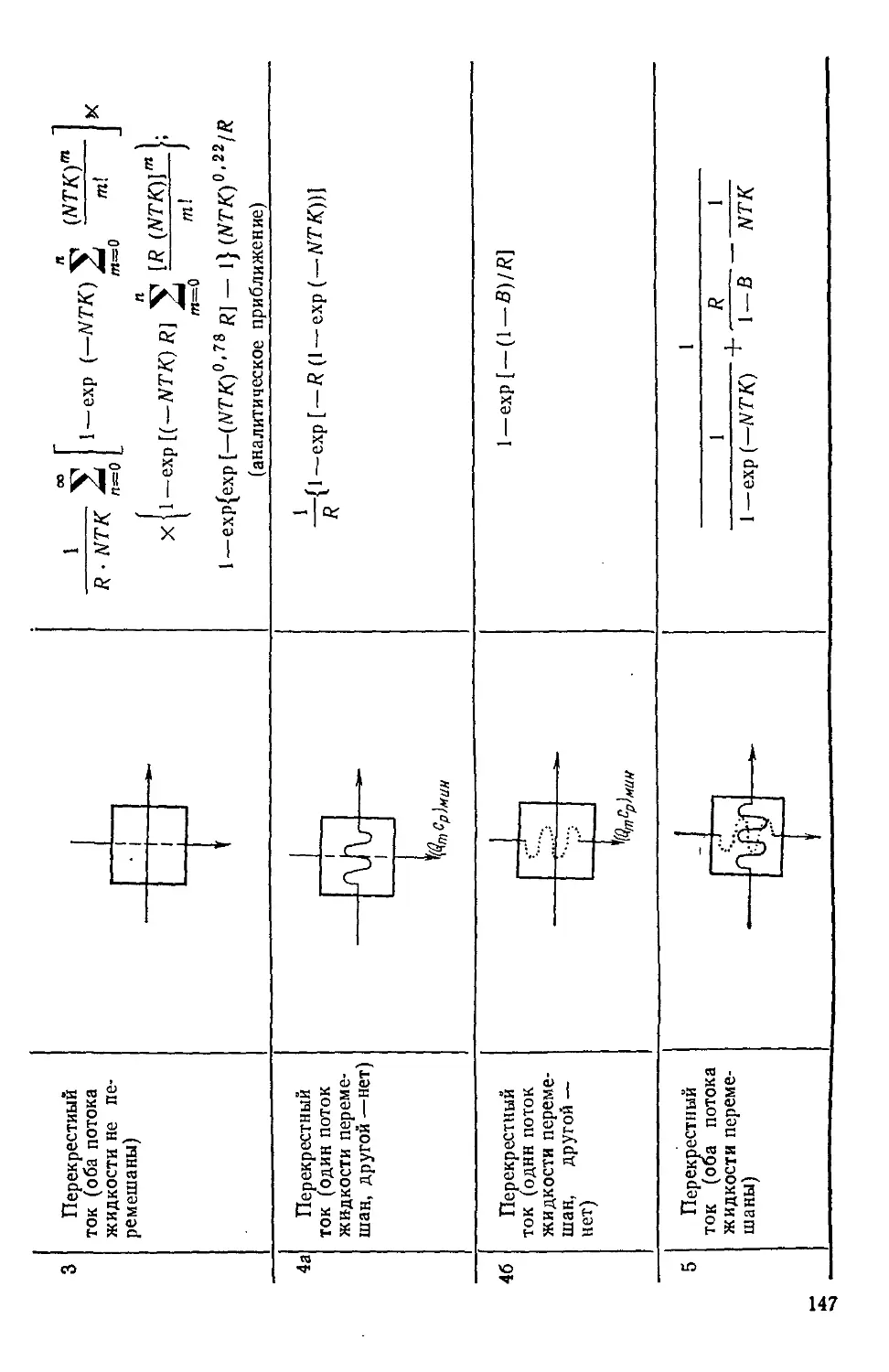
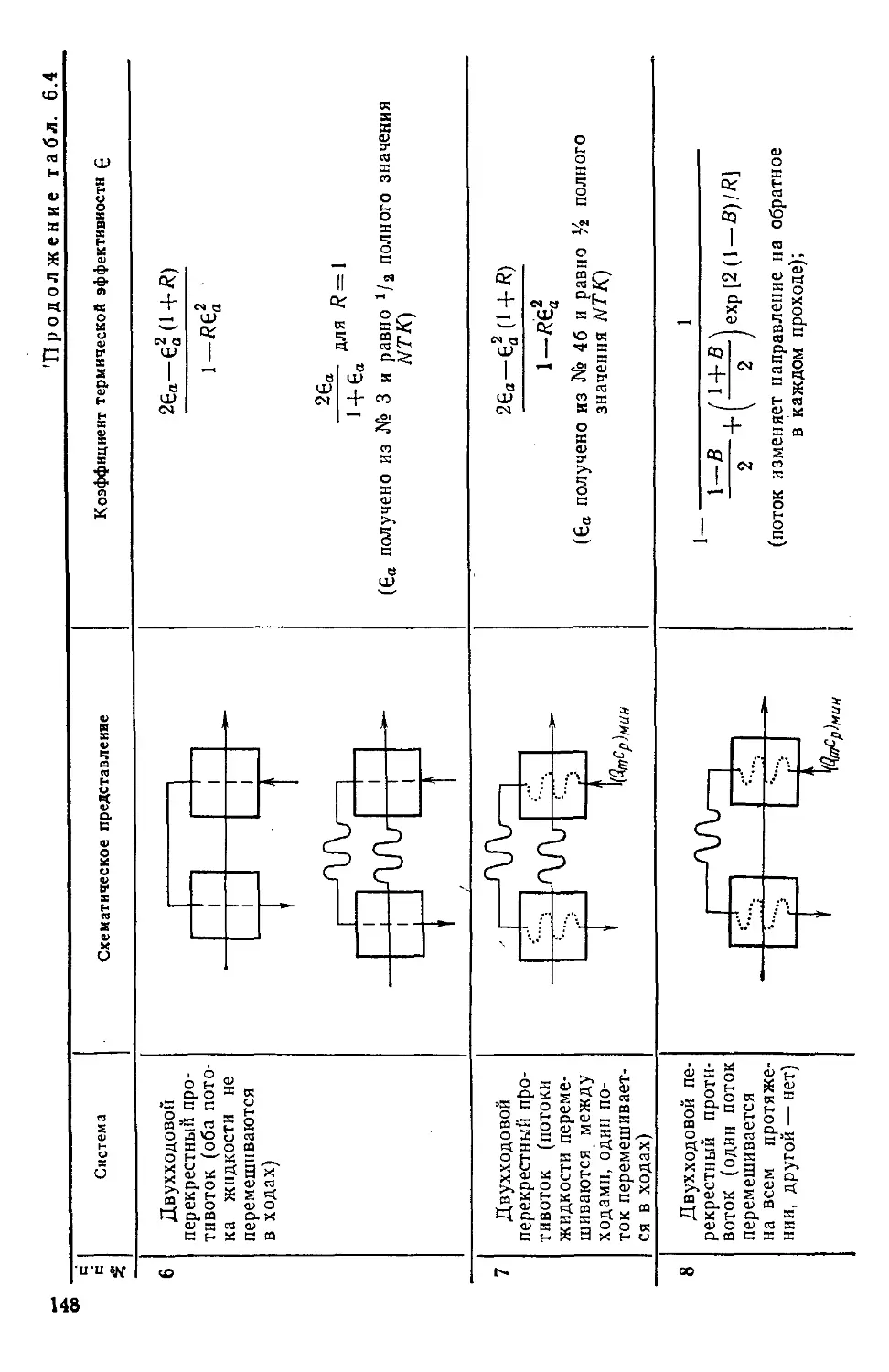
6 — Л/ГК-метод 145
6.4.2. Теплообменные аппараты пластинчатого типа . . 153
6.5. Теплообменные аппараты с косвенной теплопередачей 153
6.6. Теплообменные аппараты периодического действия . . 155
6.7. Теплообменные аппараты с непосредственным контак-
контактом теплоносителей 156
6.8. Тепловые трубы 157
6.9. Теплопередача жидких металлов 158
6 10. Средства усовершенствования характеристик теплооб-
менных аппаратов 158
Оребрепие поперхпостей 159
Турбулизаторы. 159
Список литературы 160
Глава 7. ТЕПЛОПЕРЕДАЧА СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
7.1. Введение 161
7.2. Обозначения 163
7.3. Определения 164
7.4. Теплопередача конструкций зданий 165
7.5. Теплообмен за счет утечки воздуха 169
7.6. Требования к тепловому режиму помещения 172
7.6.1. Конвективный нагрей 174
7.6.2. Нагрев излучением 177
7.7. Периодическая теплопередача 177
Список литературы 181
Приложения. Единицы и переводные коэффициенты ... 183
Теплофизнческие свойства 183
Математические функции 183
Физические свойства '83
Список литературы 207
Алфавитно-предметный указатель 209
ПЕРЕЧЕНЬ ТАБЛИЦ
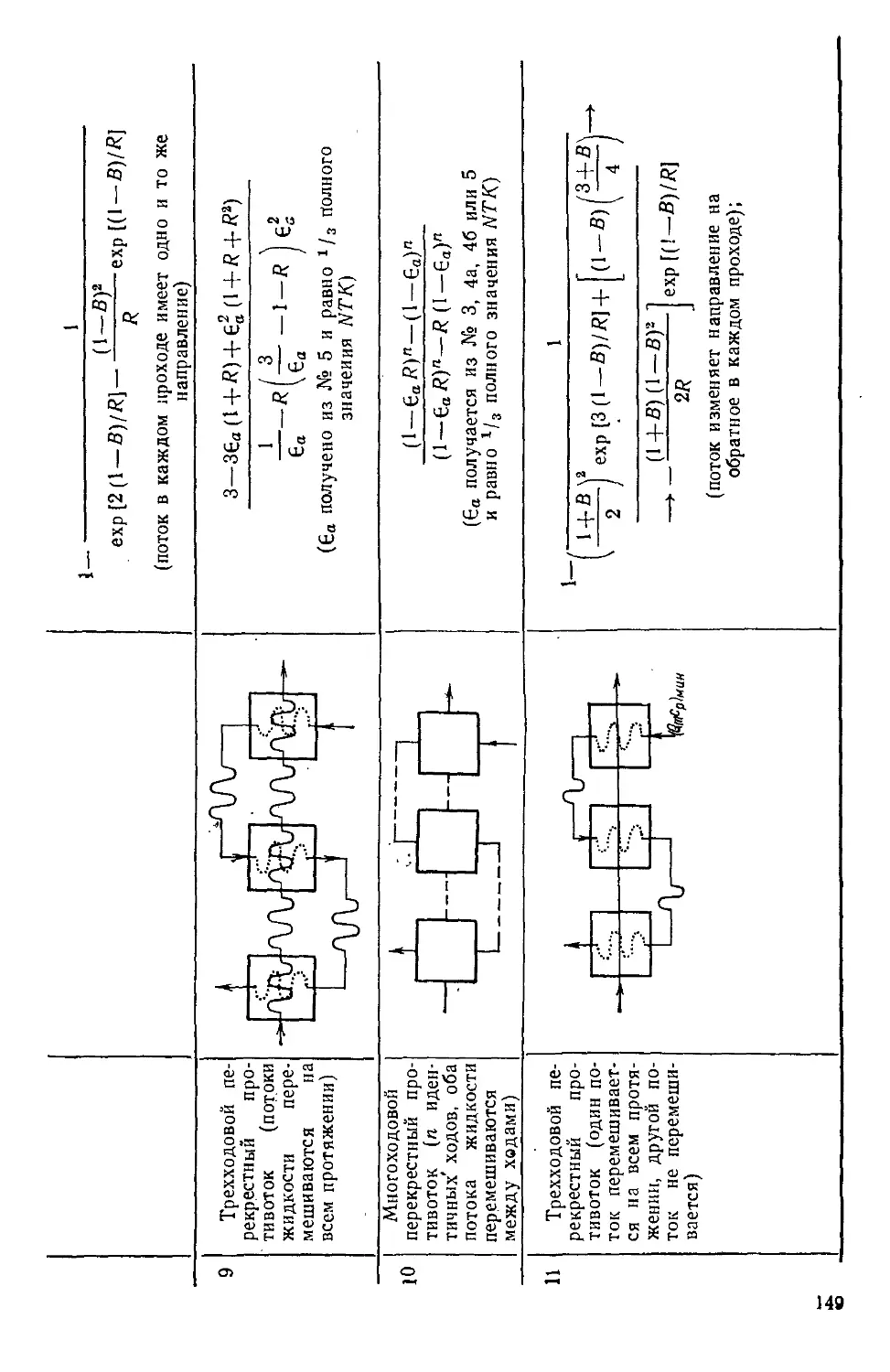
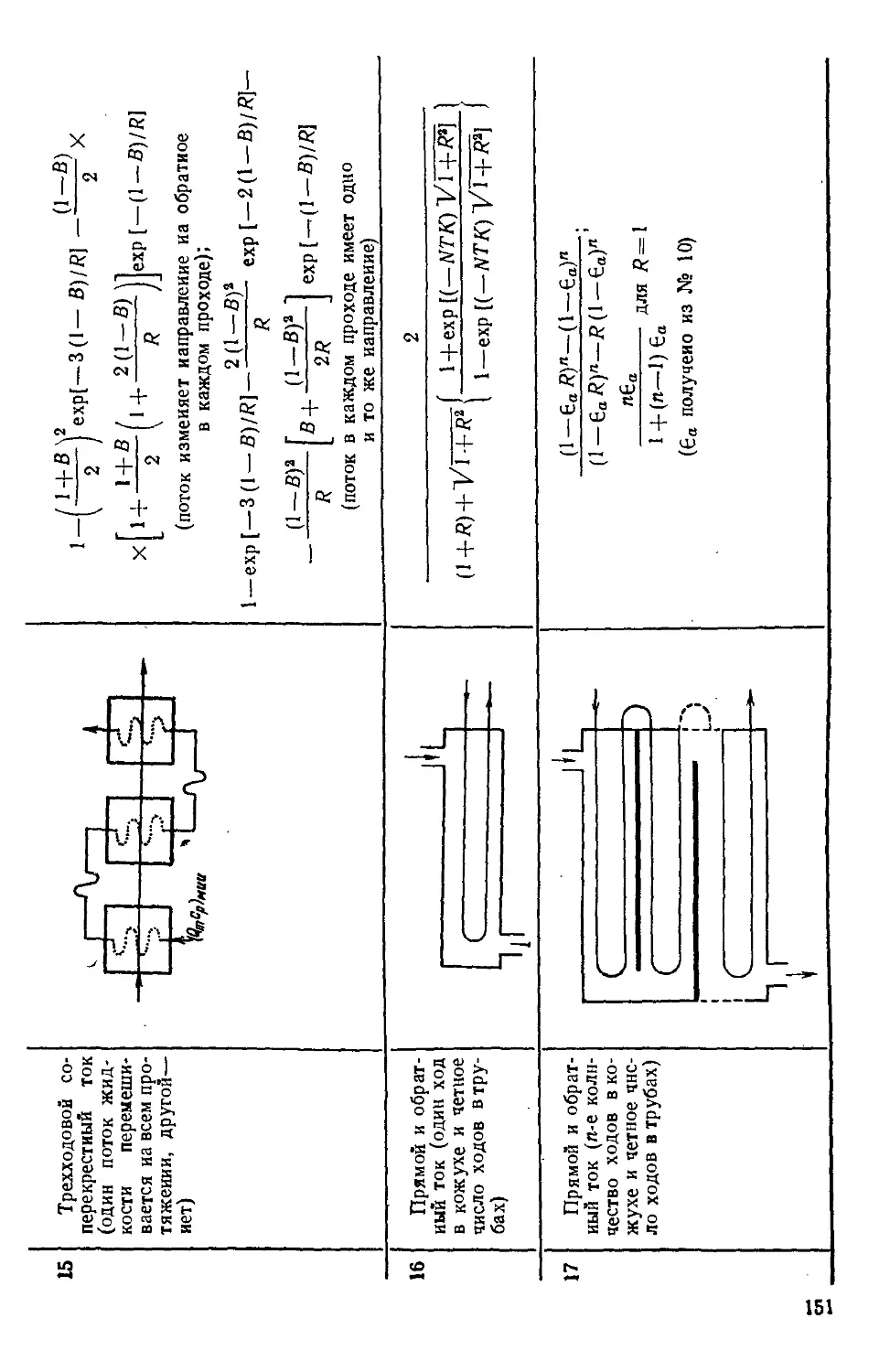
Таблица 1.1. Основные выражения для теплового потока прн
различных видах теплопередачи 15
Таблица 1.2. Основные реперные термометрические точки прн
атмосферном давлении ¦•¦ 17
Таблица 2.1. Распределение температурыТн тепловой поток в
пластине, цилиндре н полой сфере 25
Таблица 2.2. Параметр теплопередачи различных систем прн
стационарных режимах 26
Таблица 2.3. Распределение температуры и тепловой поток для
различных оребренных поверхностей 36
Таблица 2.4. Соотношения для определения распределения тем-
температур в простых телах с низким внутренним тер-
термическим сопротивлением (К -* со) 39
Таблица 2.5. Теплопередача и изменение температуры в телах
с низким внешним термическим сопротивлением
(а -* оо) 42
Таблица 2.6. Теплоотдача с поверхности и изменение темпера-
температуры в телах с ограниченными значениями внутрен-
внутреннего н внешнего термического сопротивления 44
Таблица 2.7. Основные решения некоторых распространенных
дифференциальных уравнений теплопроводности 46
Таблица 2.8. Граничные условия при теплообмене теплопровод-
теплопроводностью 48
Таблица 3.1. Сравнение параметров естественной и вынужденной
конвекции 51
Таблица 3.2. Теплоотдача прн естественной конвекции для тел
различной формы 56
Таблица 3.3. Коэффициент трепня и падение давления при вы-
вынужденном течении жидкости в трубах с различным
сечением 64
Таблица 3.4. Теплообмен прн вынужденном движении жидкости
в цилиндрических трубах с различным поперечным
сечением 68
Таблица 3.5. Решения задач конвективного теплообмена при
омыванин плоских пластин вынужденным потоком
жидкости 70
Таблица 3.6. Теплоотдача прн поперечном омываннн воздушным
потоком цилиндров с различным поперечным сечением 72
Таблица 3.7. Теплоотдача прн поперечном омываннн жидкостью
пучков труб 74
Таблица 3.8. Формулы для расчета теплоотдачи при высокой ско-
скорости потока 77
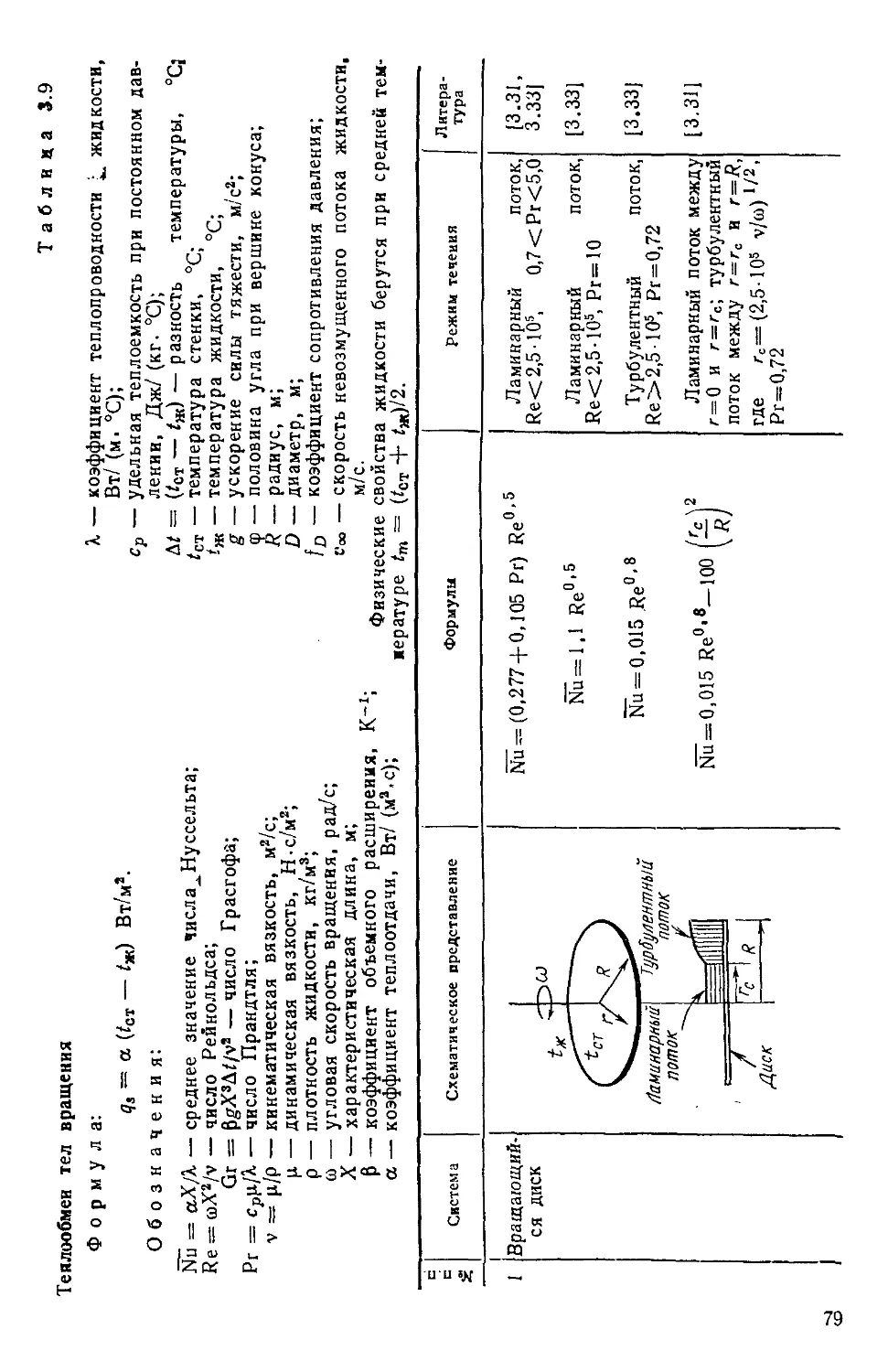
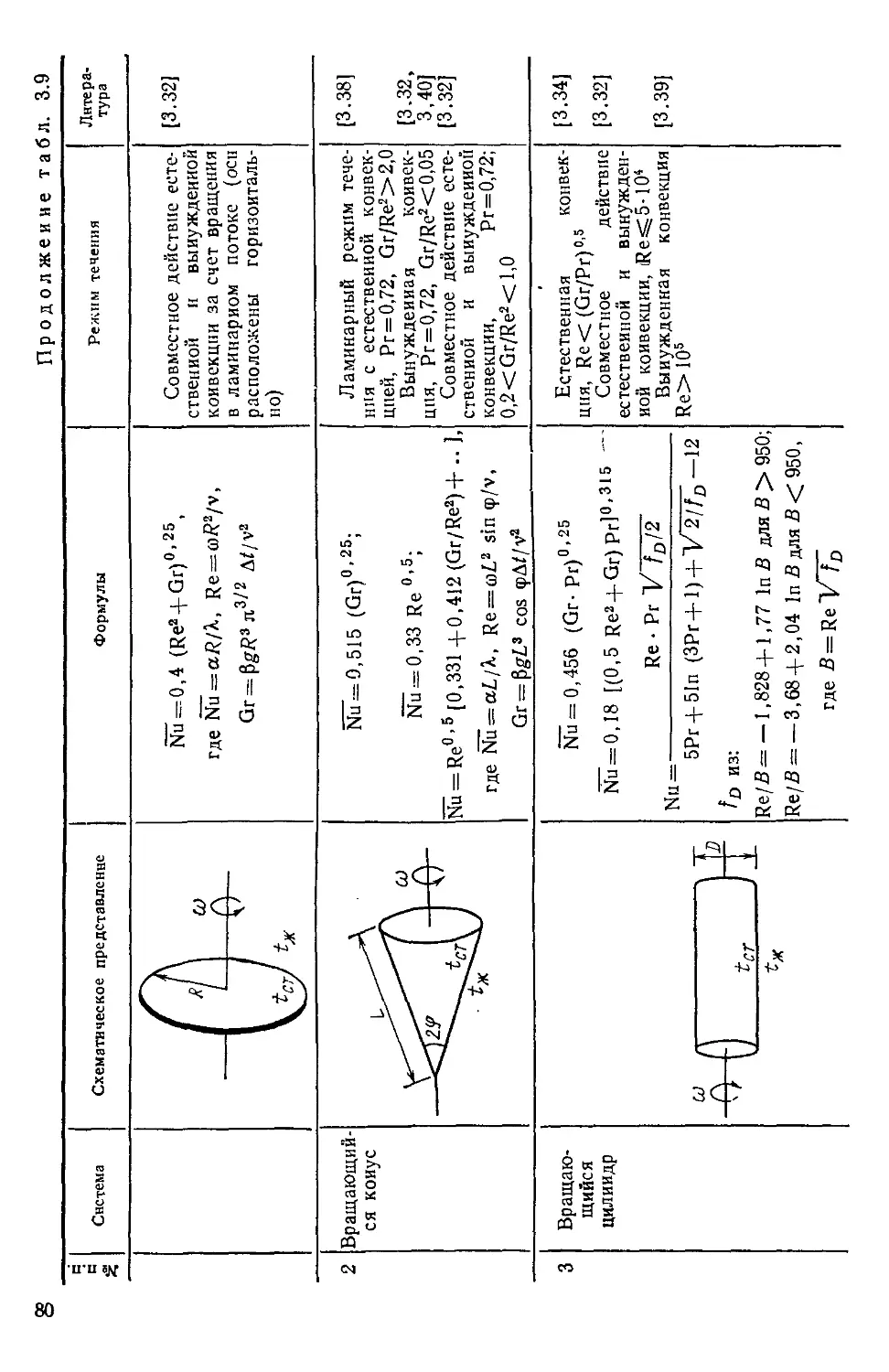
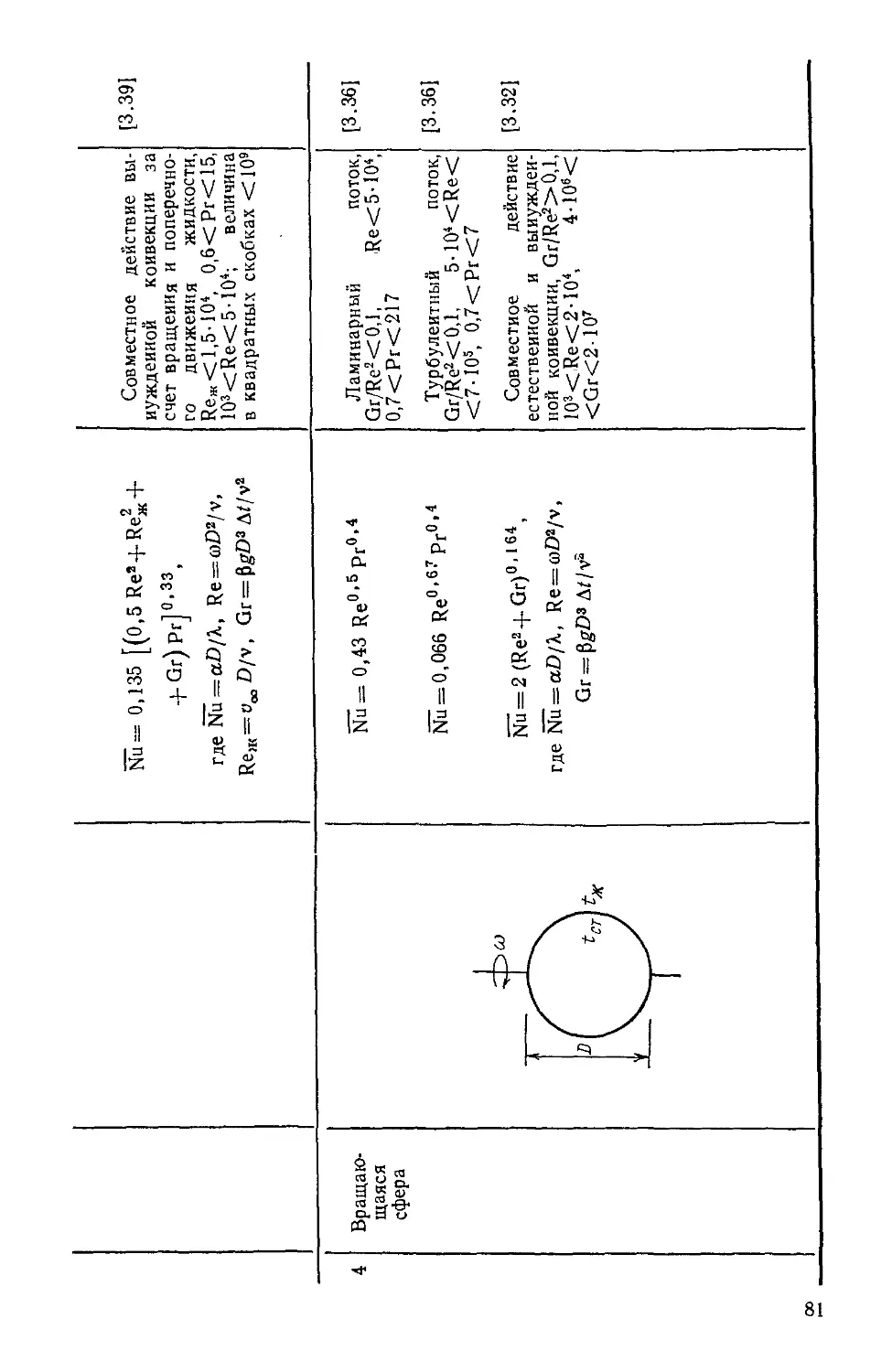
Таблица 3.9. Теплообмен тел вращения 79
Таблица 4.1. Излучательные свойства абсолютно черного тела 89
Таблица 4.2. Константы излучения в уравнениях Планка, Стефа-
Стефана—Больцмана н Вина 92
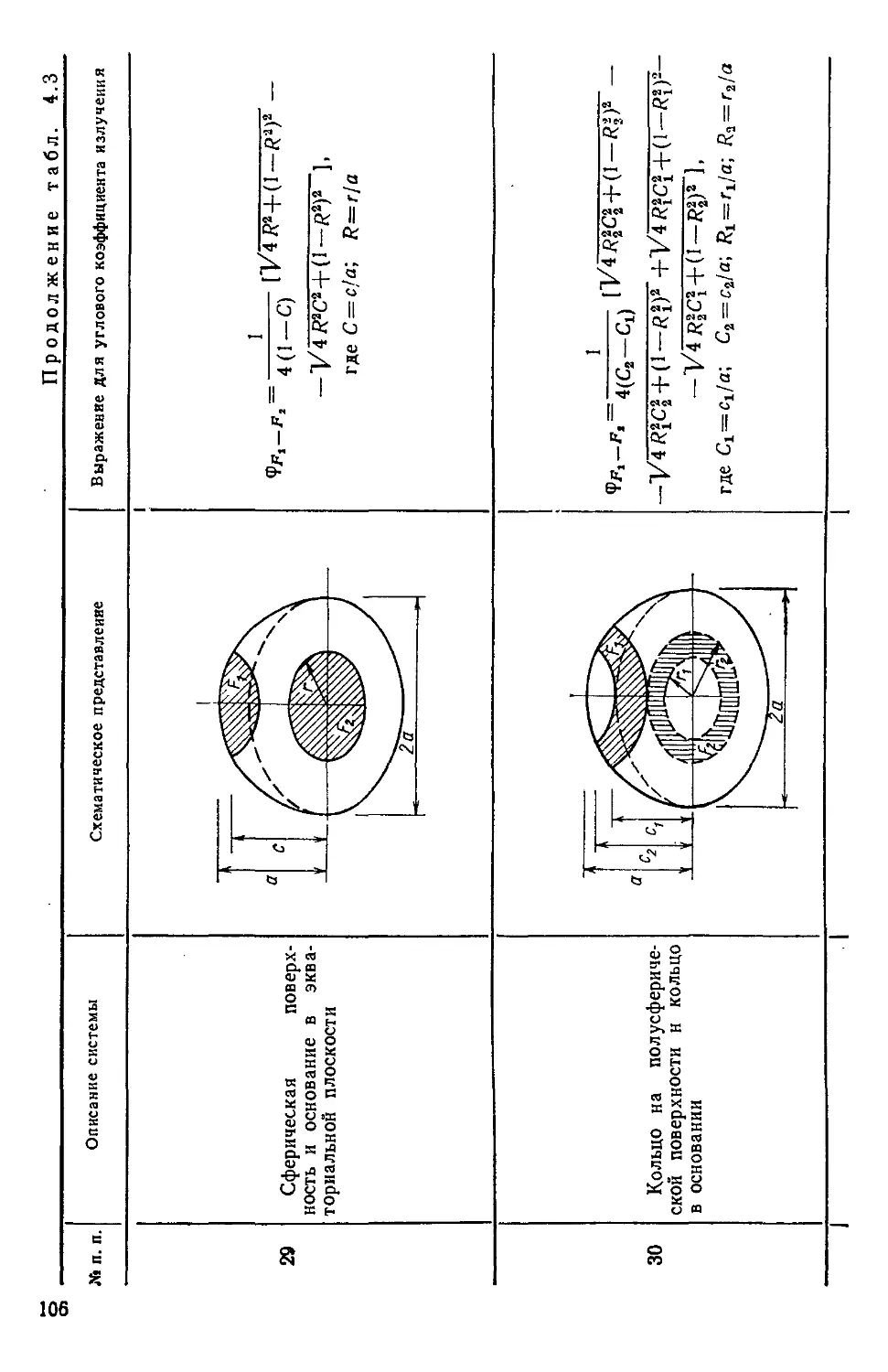
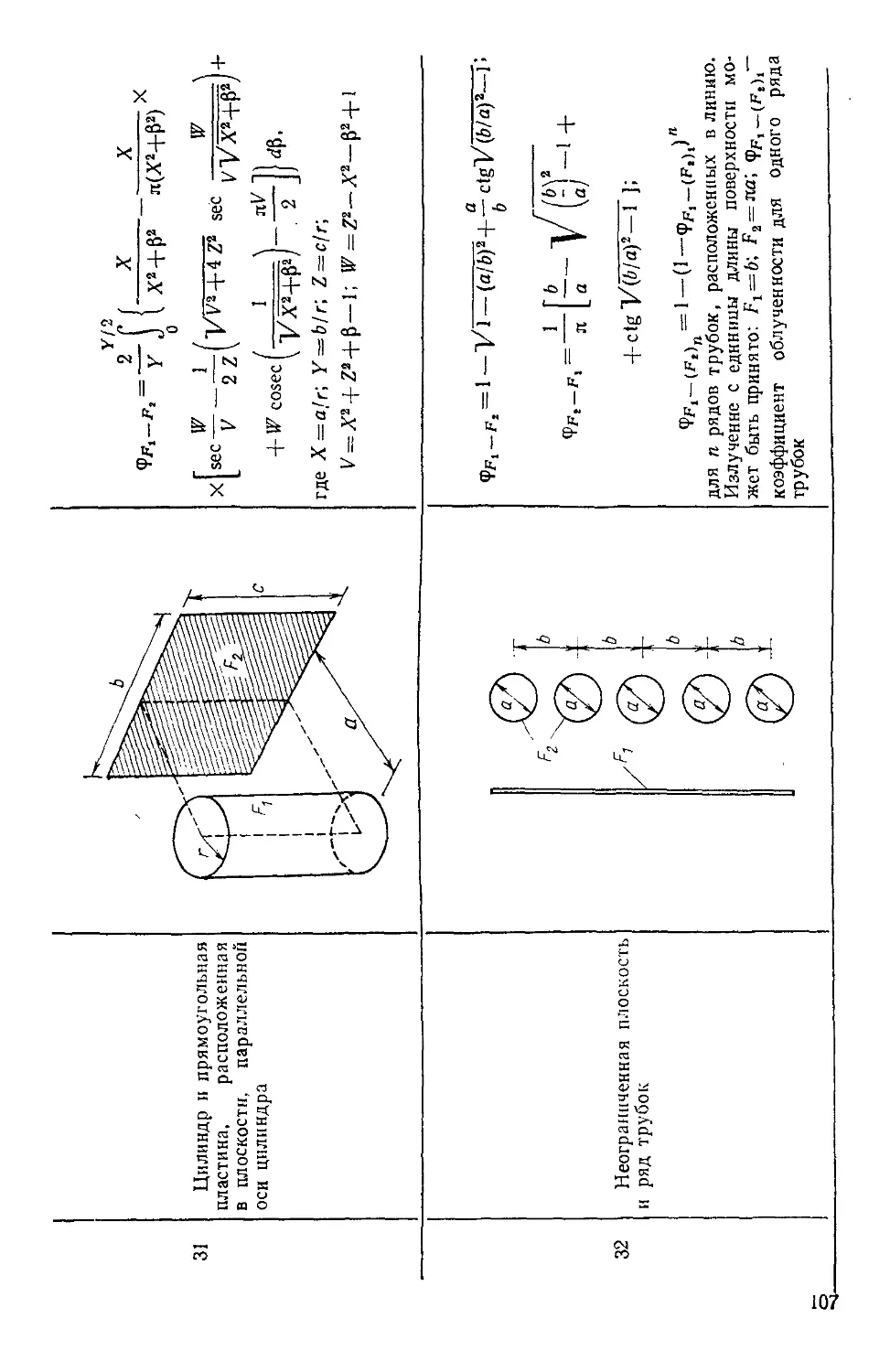
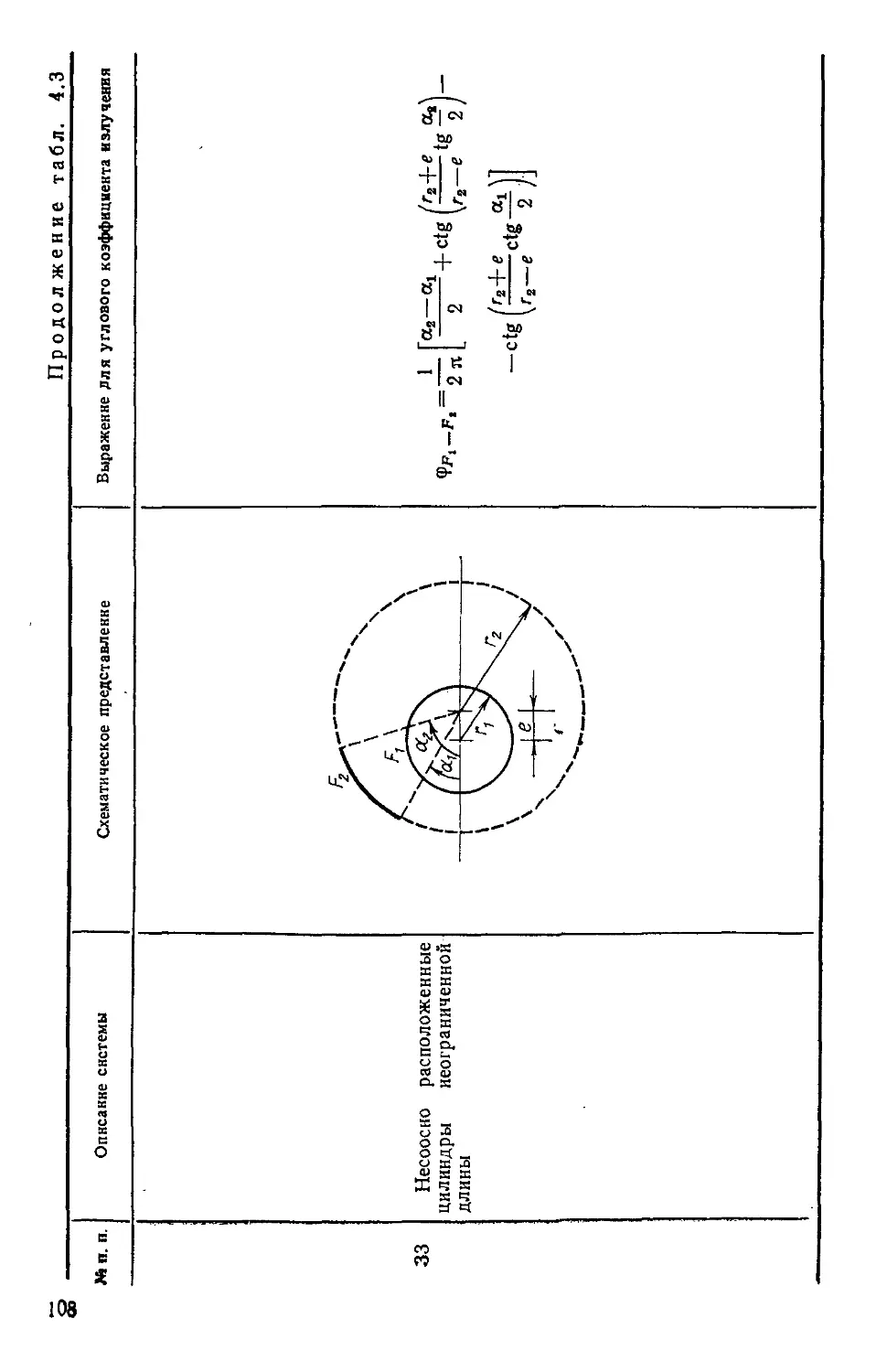
Таблица 4.3. Угловые коэффициенты излучения для двух 'днф-
фузно отражающих поверхностей 94
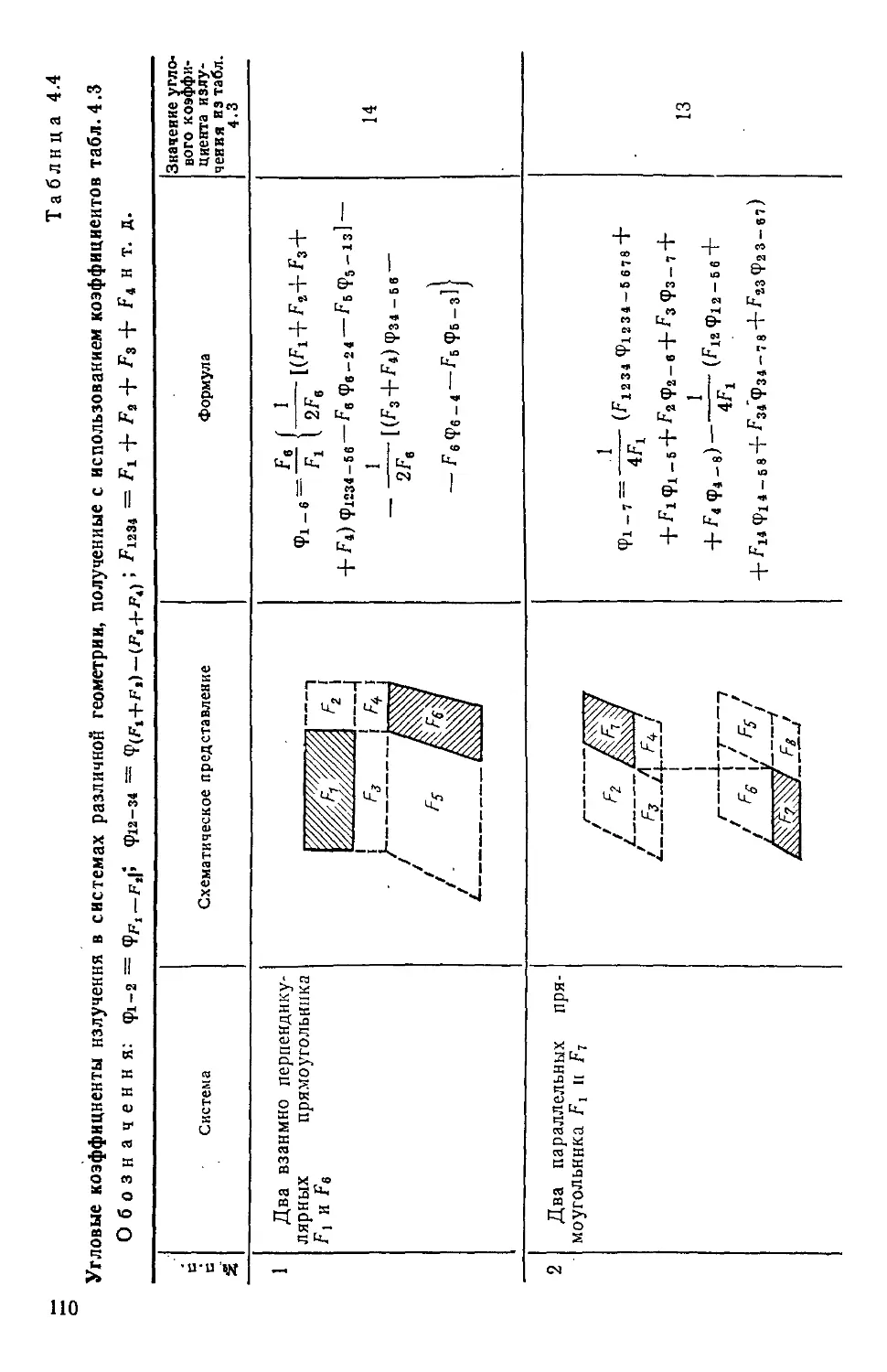
Таблица 4.4. Угловые коэффициенты излучения в системах раз-
различной геометрии! полученные с использованием
коэффициентов табл. 4.3 ПО
Таблица 4.5. Лучистый теплообмен между диффузно-серыми по-
поверхностями 114
Таблица 5.1. Сравнение эффективности теплообмена при кипении
и конденсации 119
Таблица 5.2. Формулы для определения коэффициента теплоот-
теплоотдачи при кипении 124
Таблица 5.3. Коэффициенты в уравнениях пузырчатого кипения 126
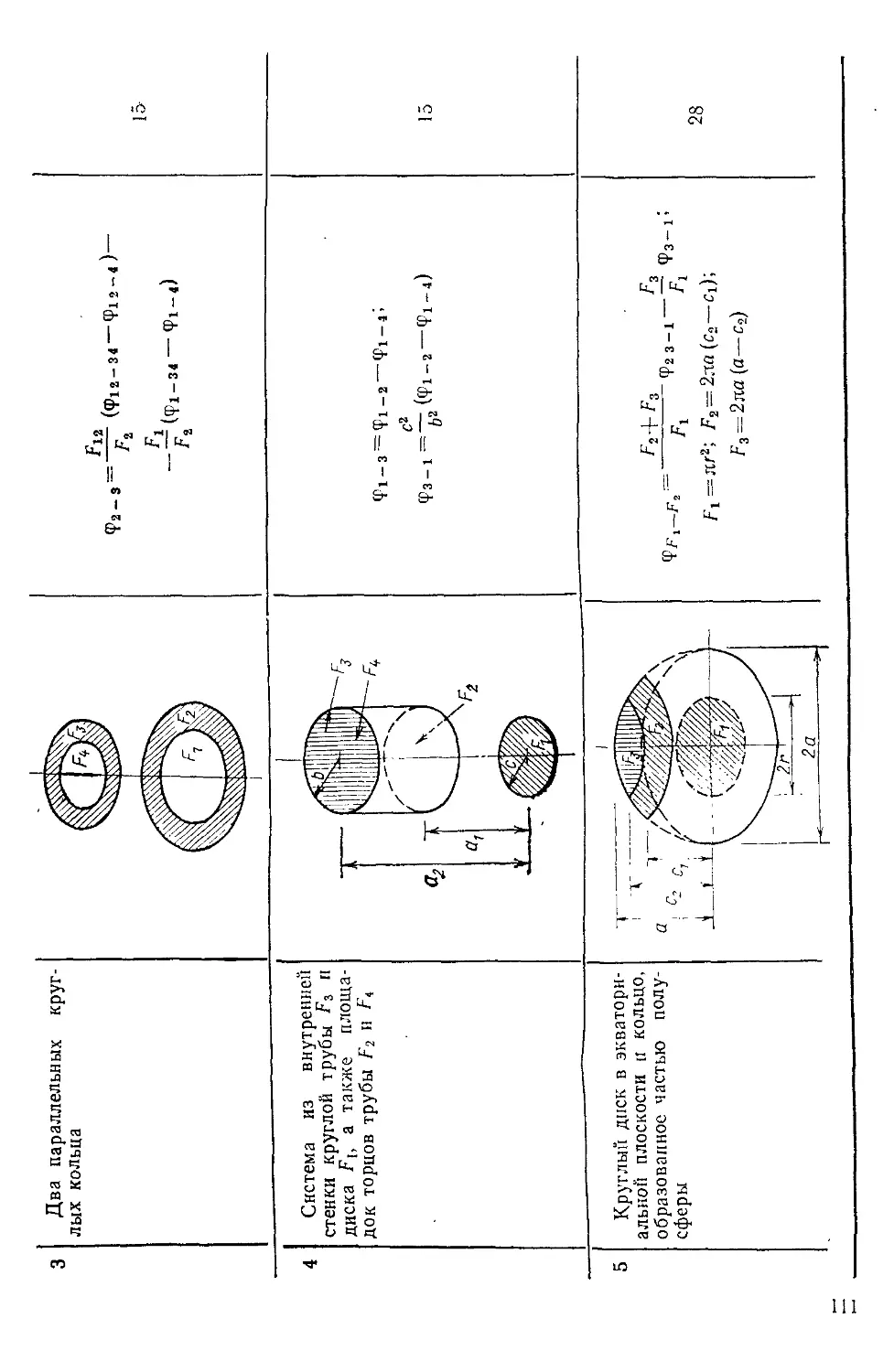
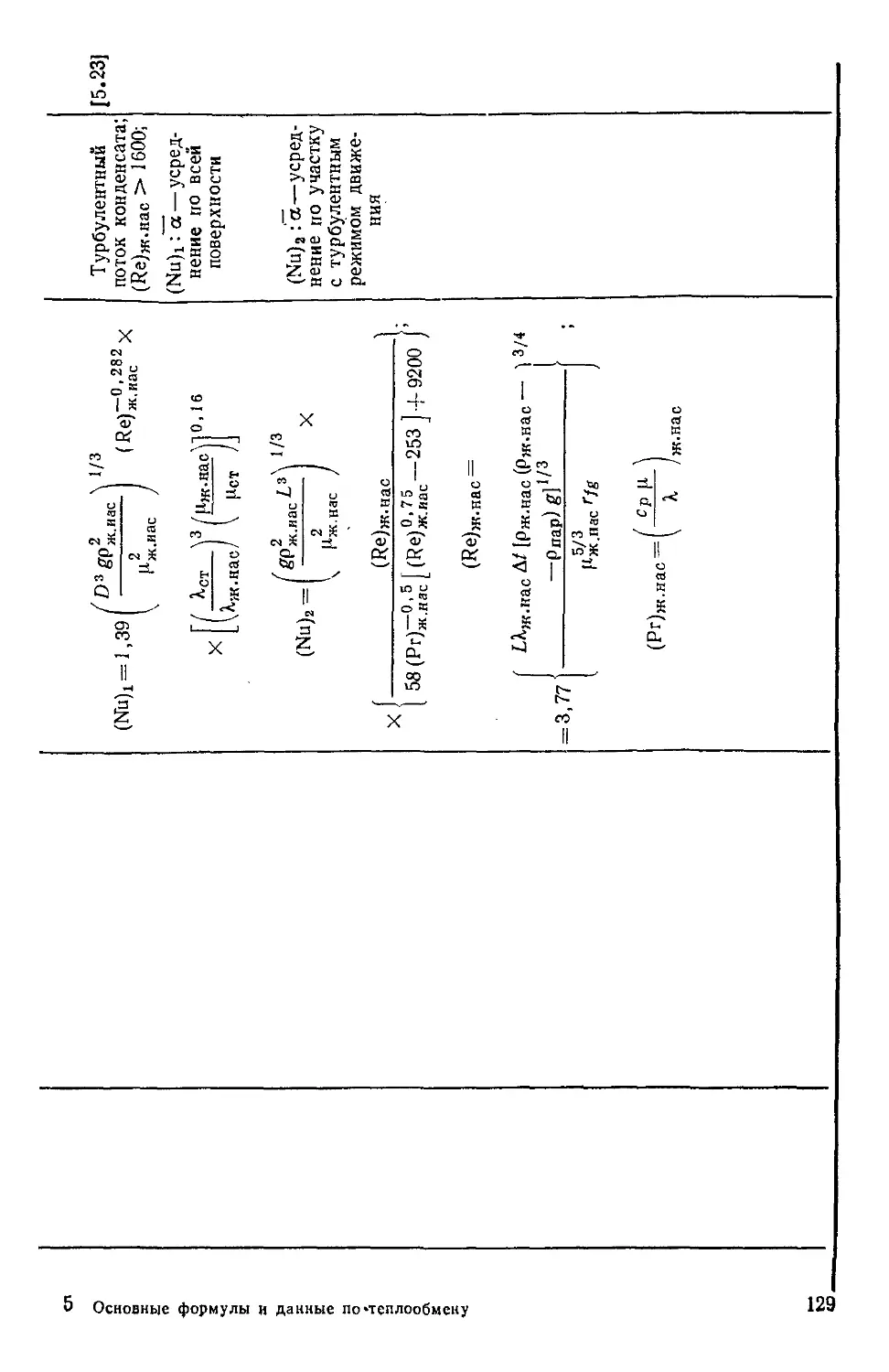
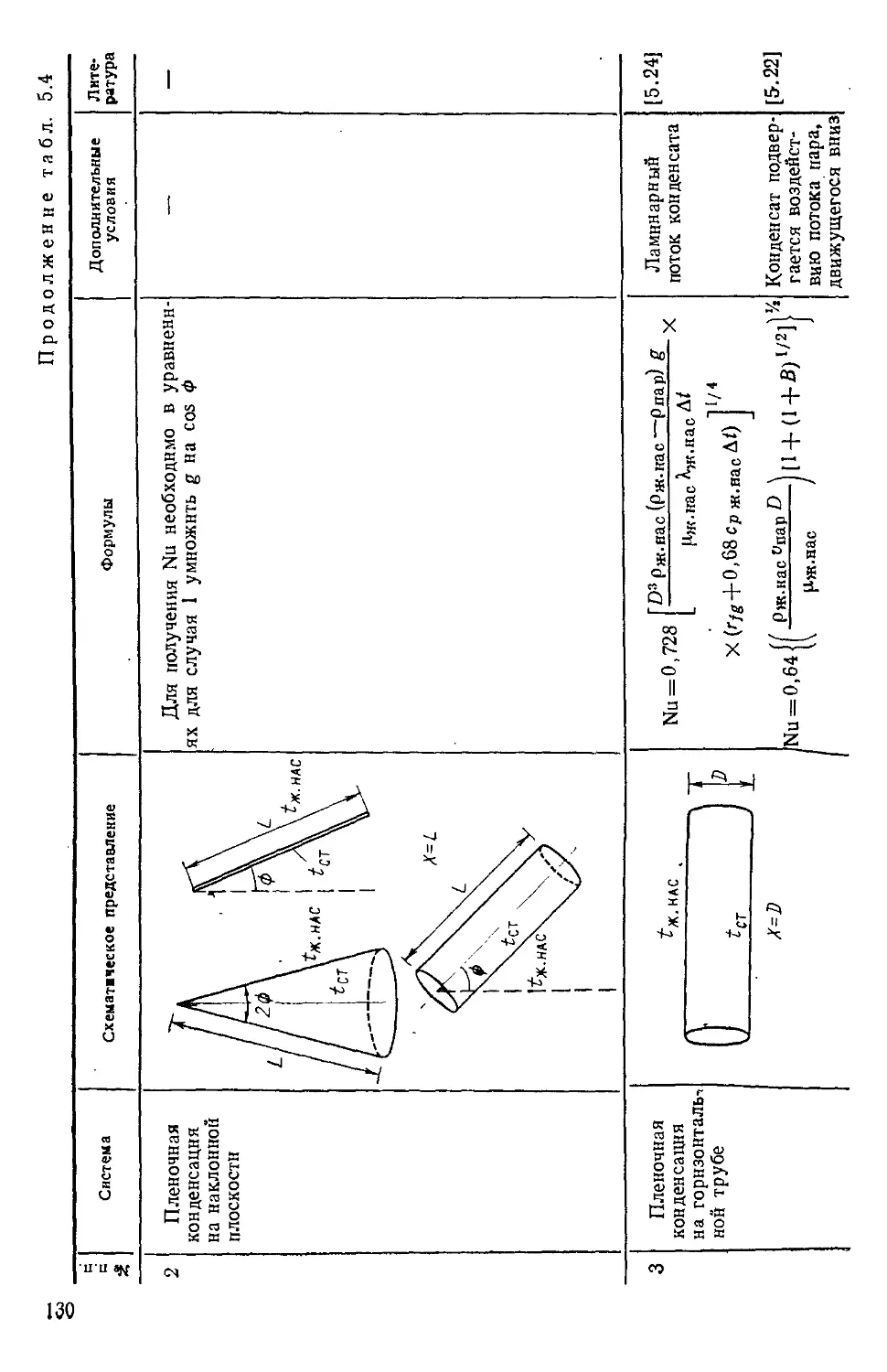
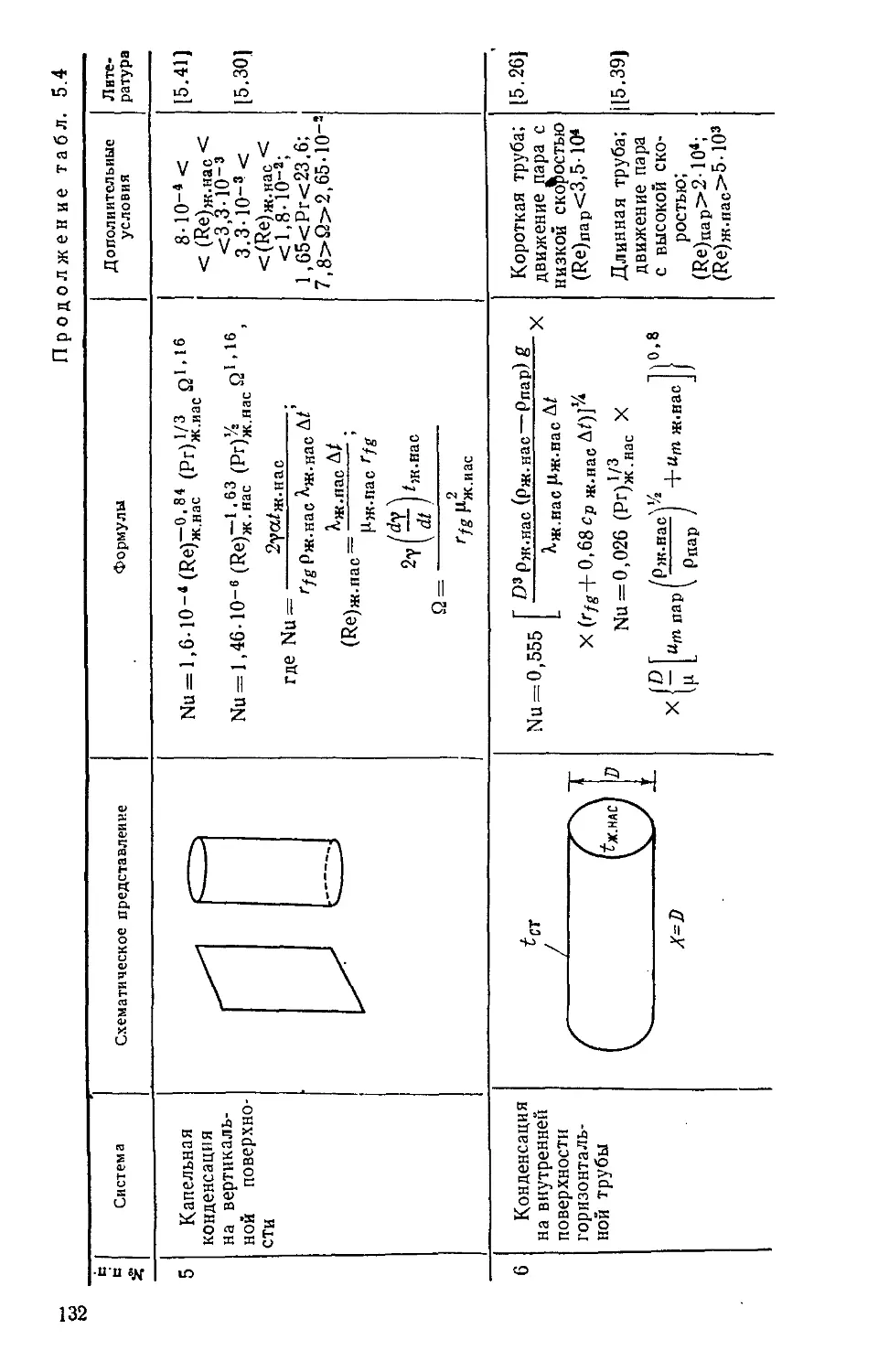
Таблица 5.4. Формулы для расчета теплоотдачи при конденсации 128
Таблица 6.1. Типы теплообменников с различными схемами дви-
движения потоков 136
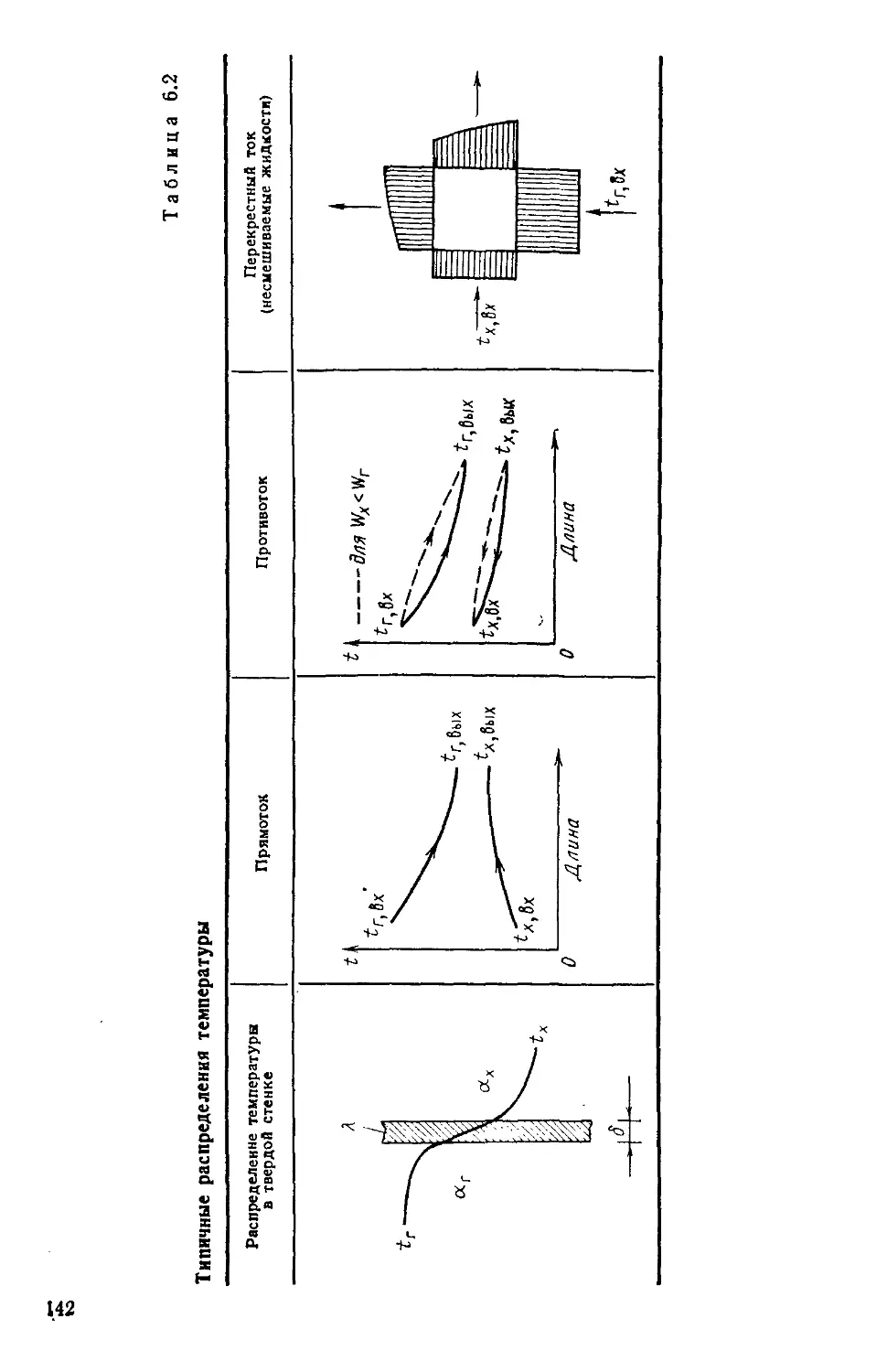
Таблица 6.2. Типичные распределения температуры 142
Таблица 6.3. Поправочные коэффициенты для расчета истинного
значения средней разности температуры 144
Таблица 6.4. Эффективность теплопередачи теплообменных ап-
аппаратов с непосредственным теплообменом 146
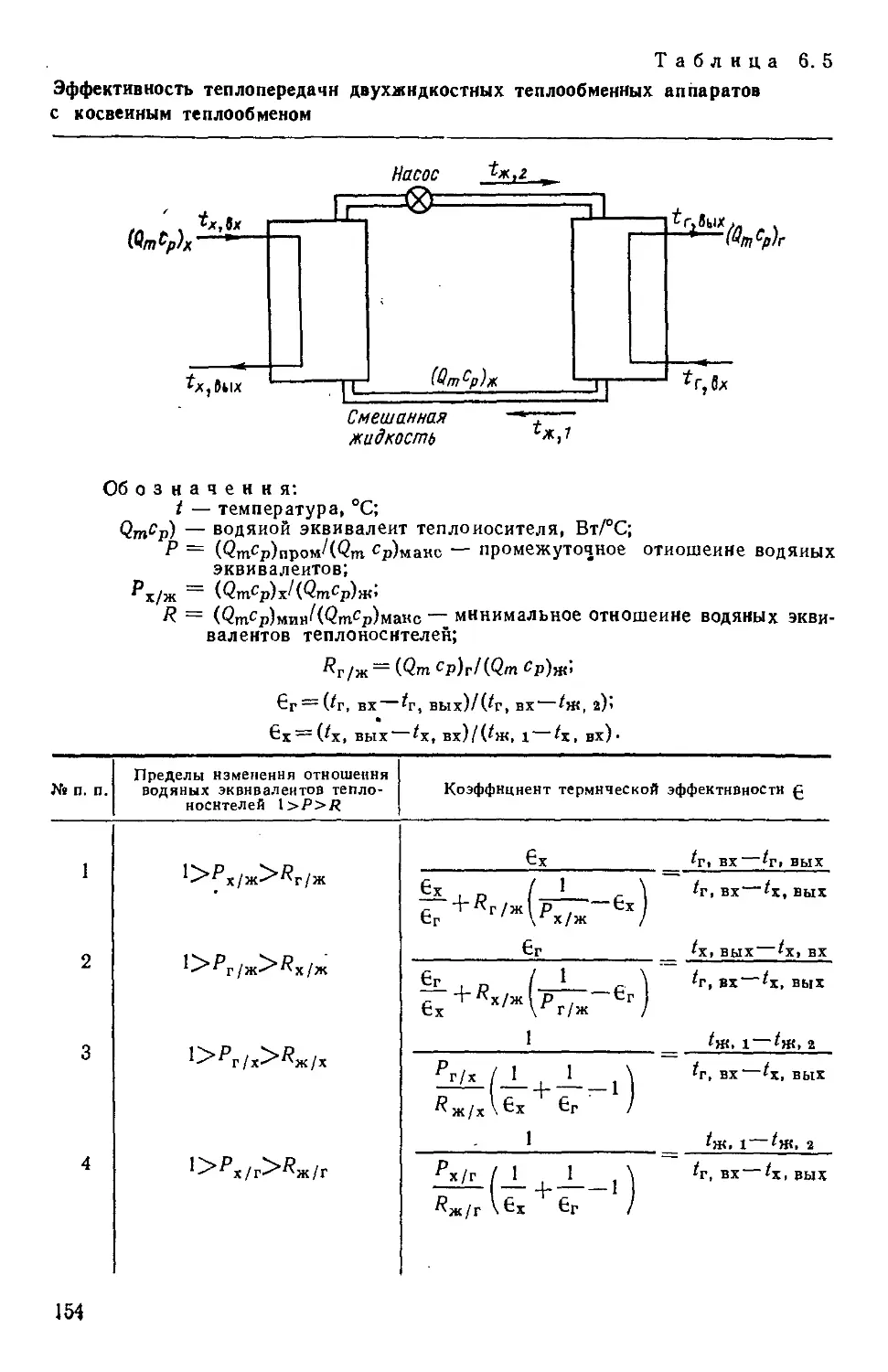
Таблица 6.5. Эффективность теплопередачи двухжидкостных
теплообменных аппаратов с косвенным теплообме-
теплообменом 154
Таблица 7.1. Формулы для характерных температур, используе-
используемых при расчетах теплообмена строительных конст-
конструкций 162
Таблица 7.2. Уравнения для расчета коэффициента теплопередачи
и потерь тепла элементами конструкций зданий 166
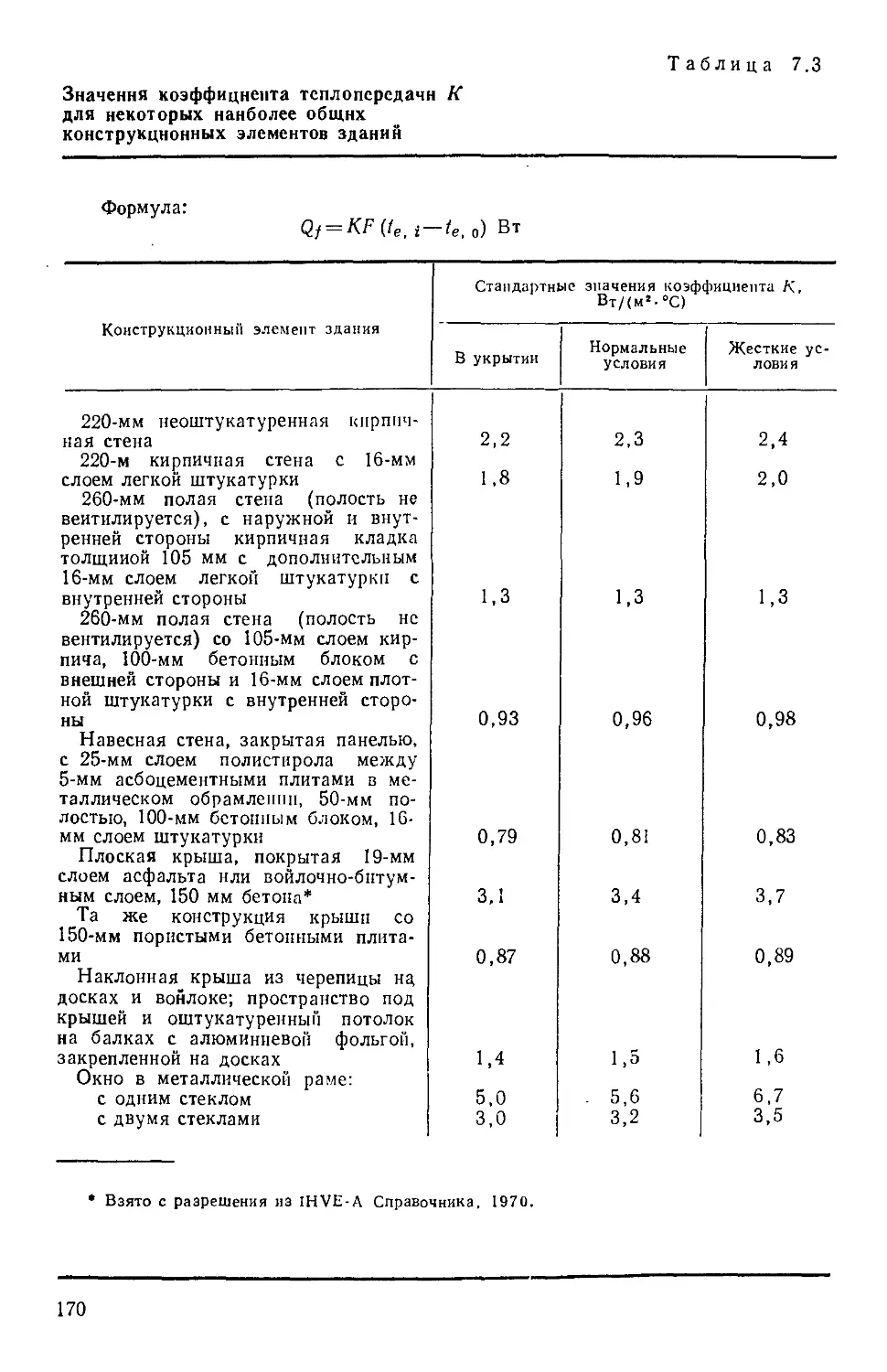
Таблица 7.3. Значения коэффициента теплопередачи К для неко-
некоторых наиболее общих конструкционных элементов
зданий 170
Таблица 7.4. Потери тепла за счет утечки воздуха 172
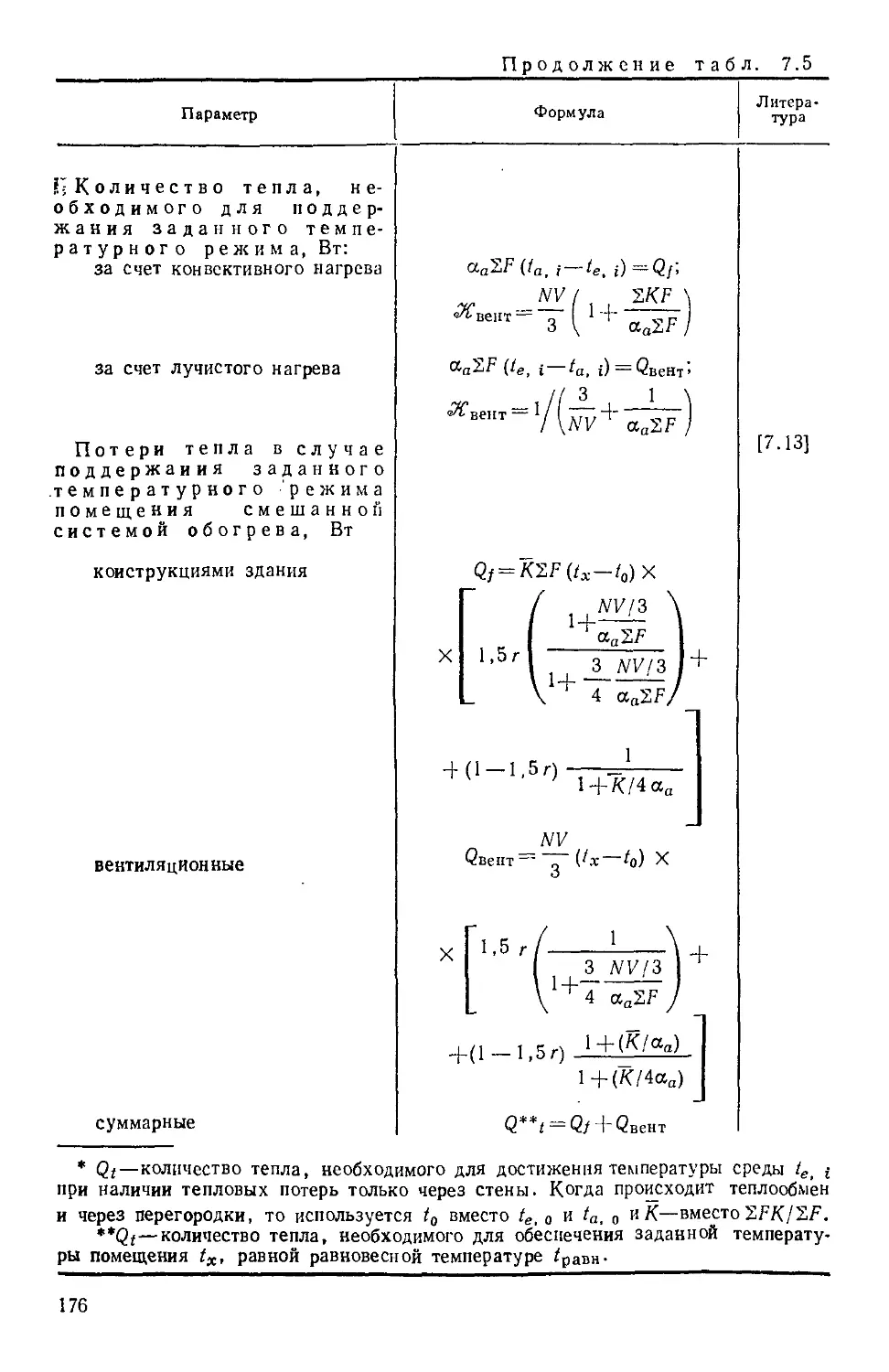
Таблица 7.5. Уравнения к расчету количества тепла для поддер-
поддержания необходимого температурного режима поме-
помещения 175
Таблица 7.6. Уравнения для определения температуры среды
внутри помещения при изменении количества под-
подводимого тепла и периодичности его подвода 179
Таблица 7.7. Некоторые типичные значения S, Sa и У 181
Таблица П.1. Переводные коэффициенты в системе единиц СИ 183
Таблица П.2. Некоторые физические константы 185
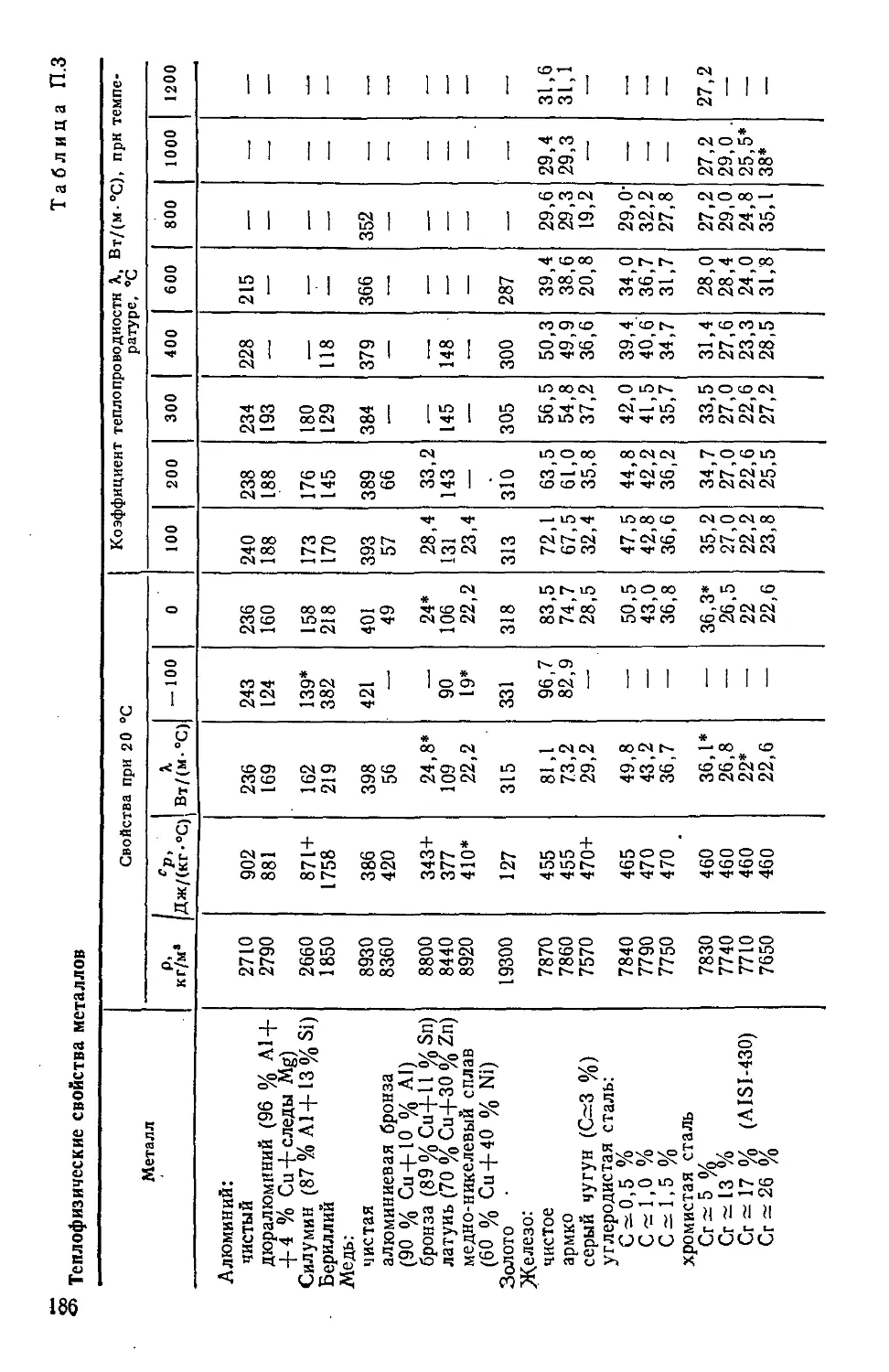
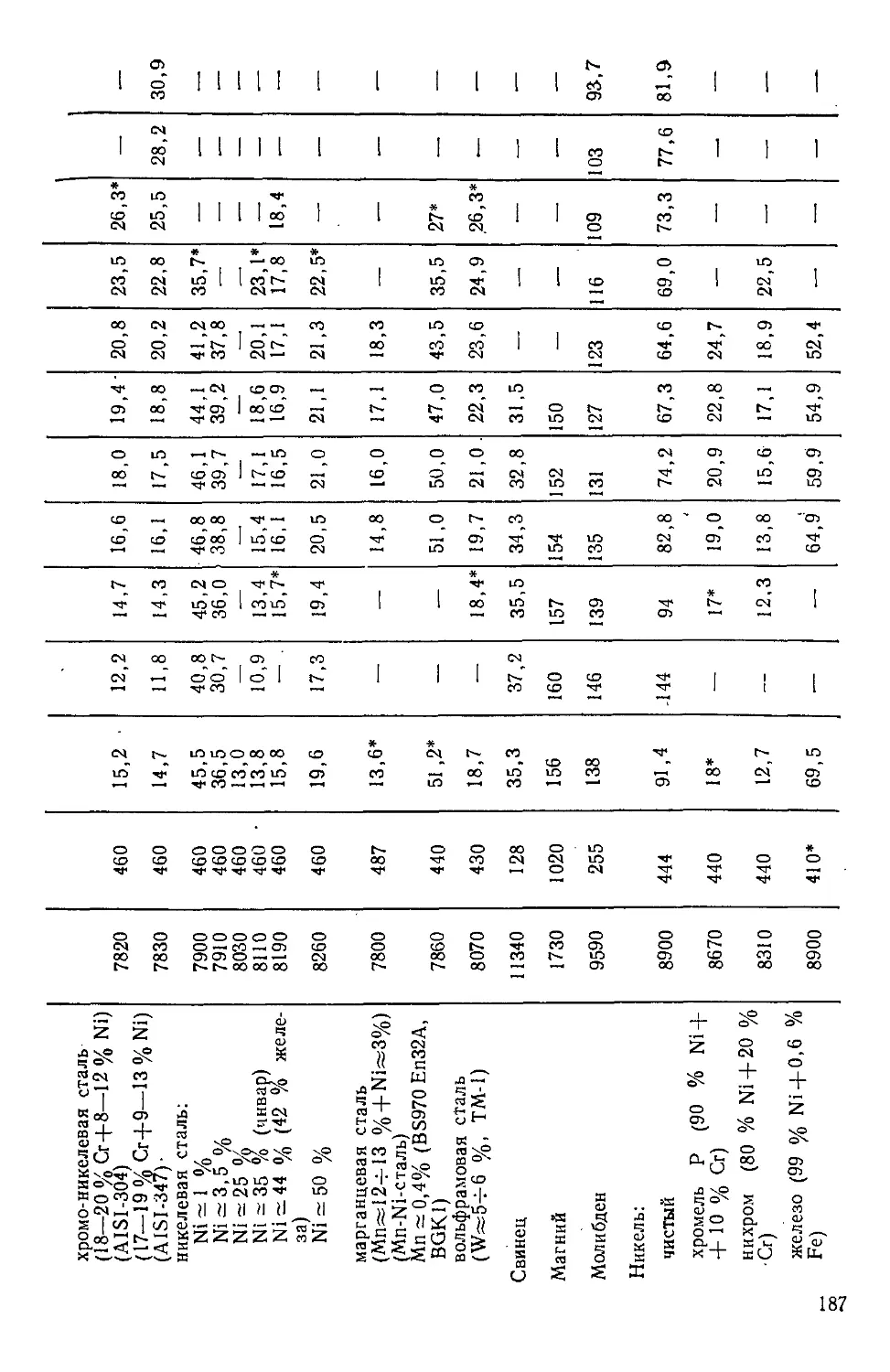
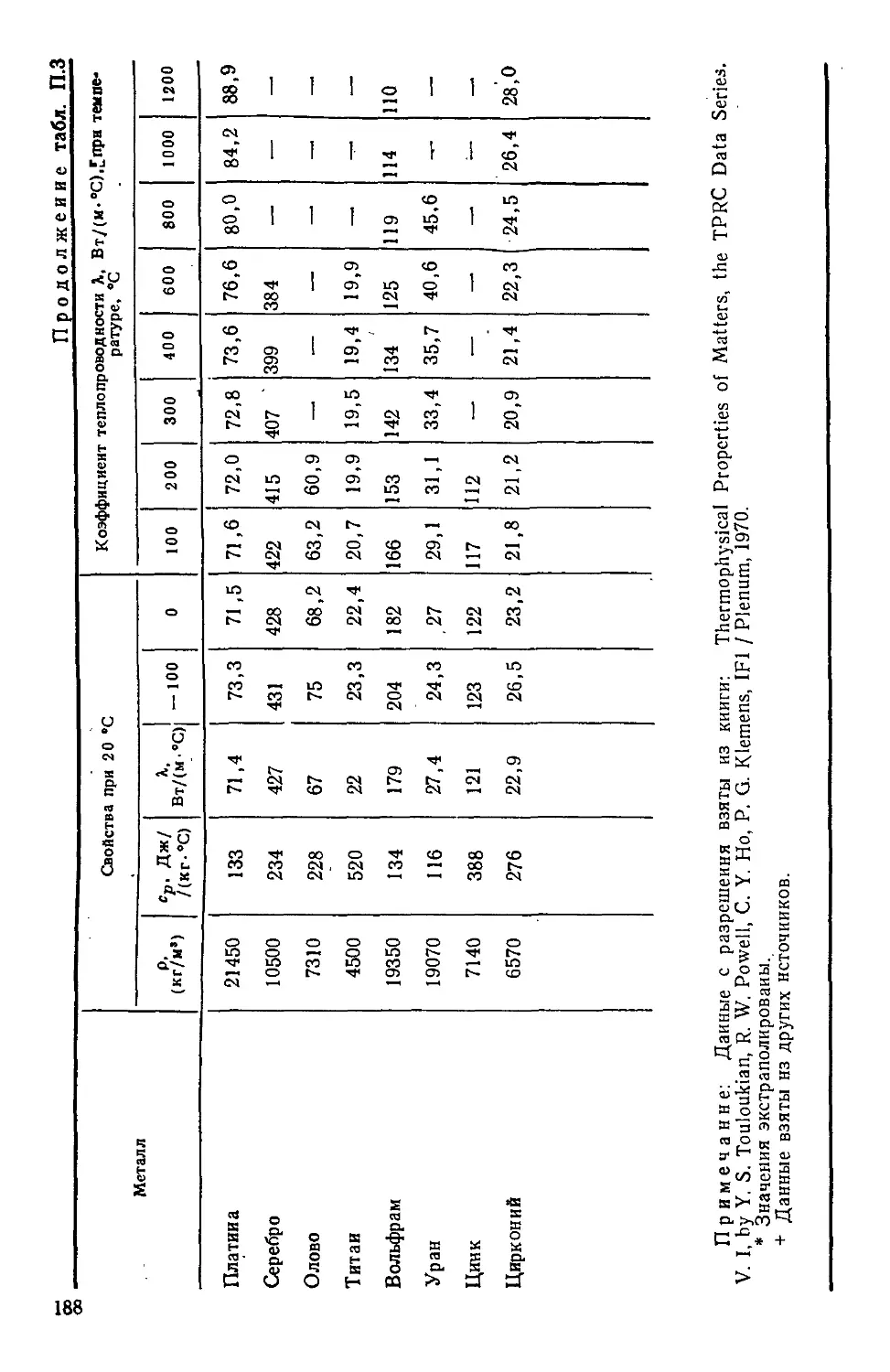
Таблица П.З. Теплофизические свойства металлов 186
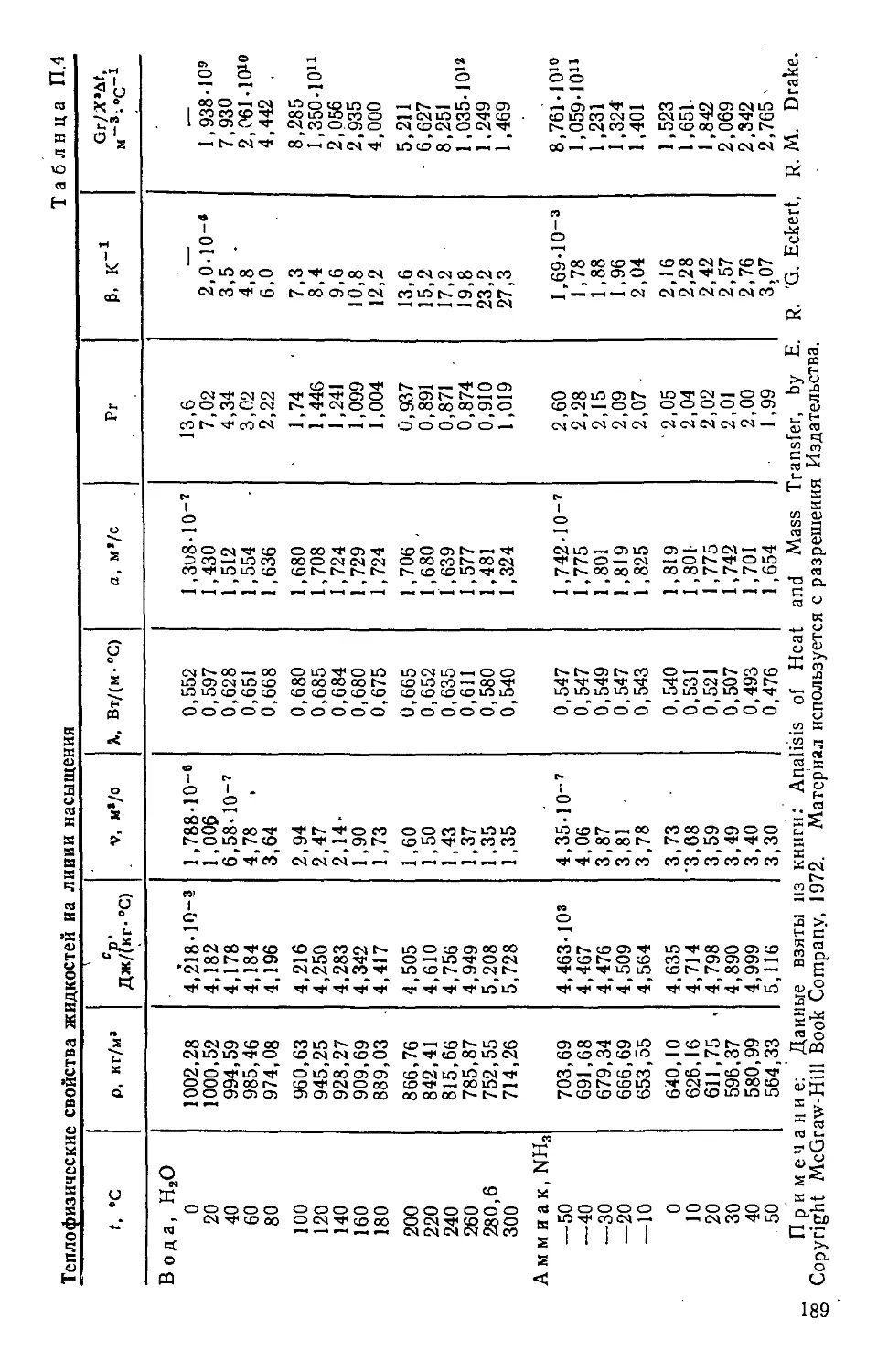
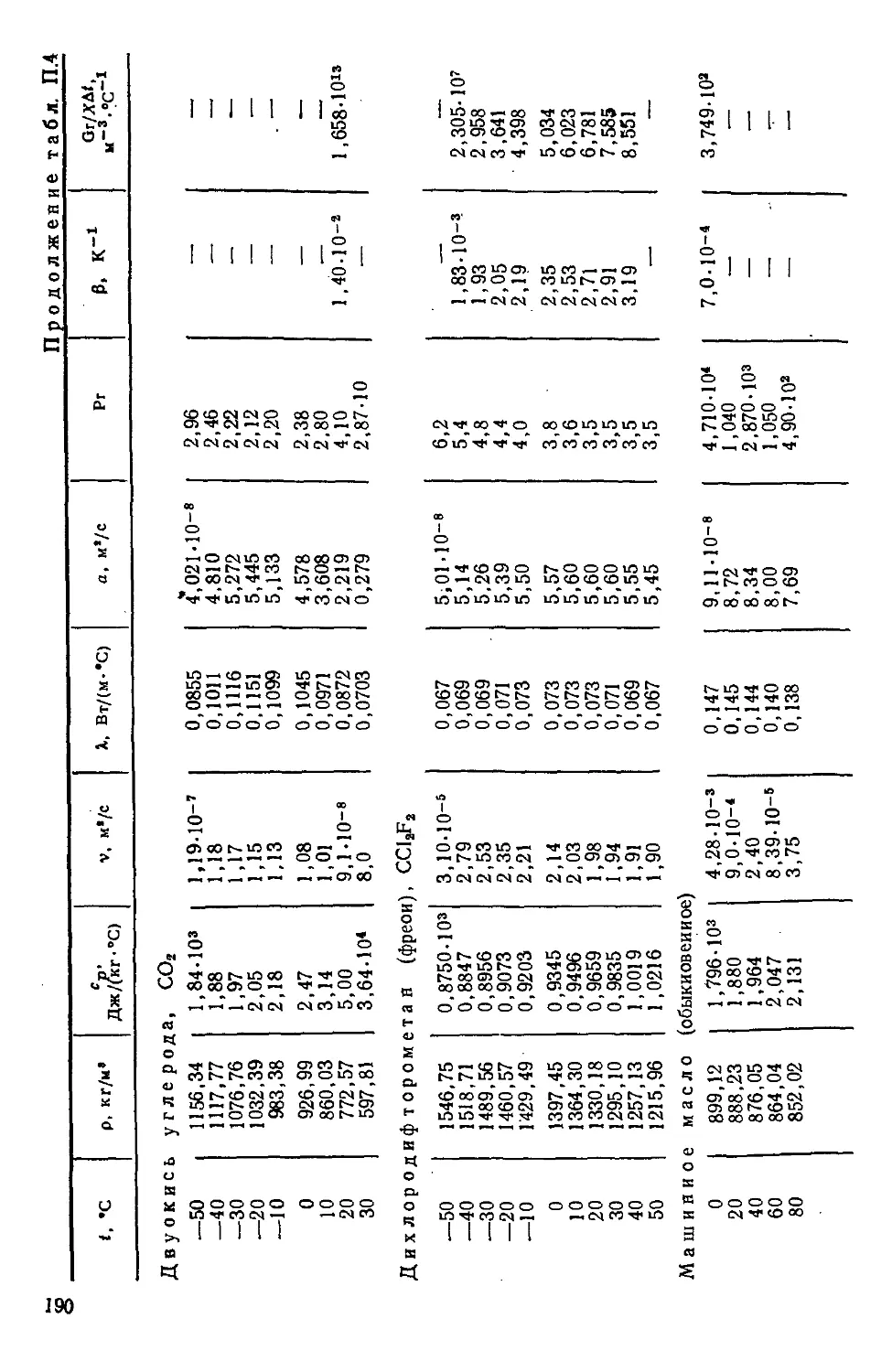
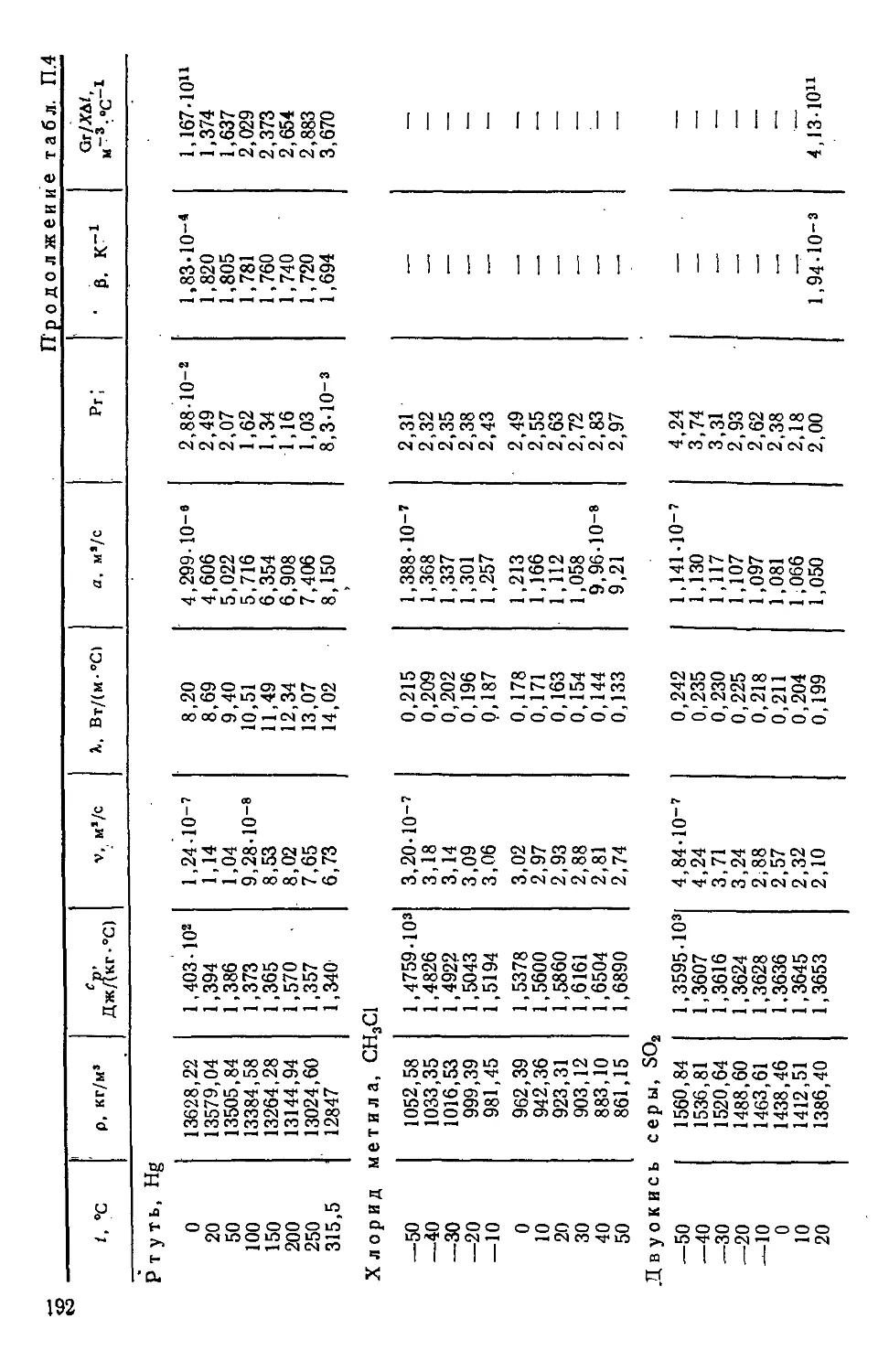
Таблица П.4. Теплофизические свойства жидкостей на линии на-
насыщения 198
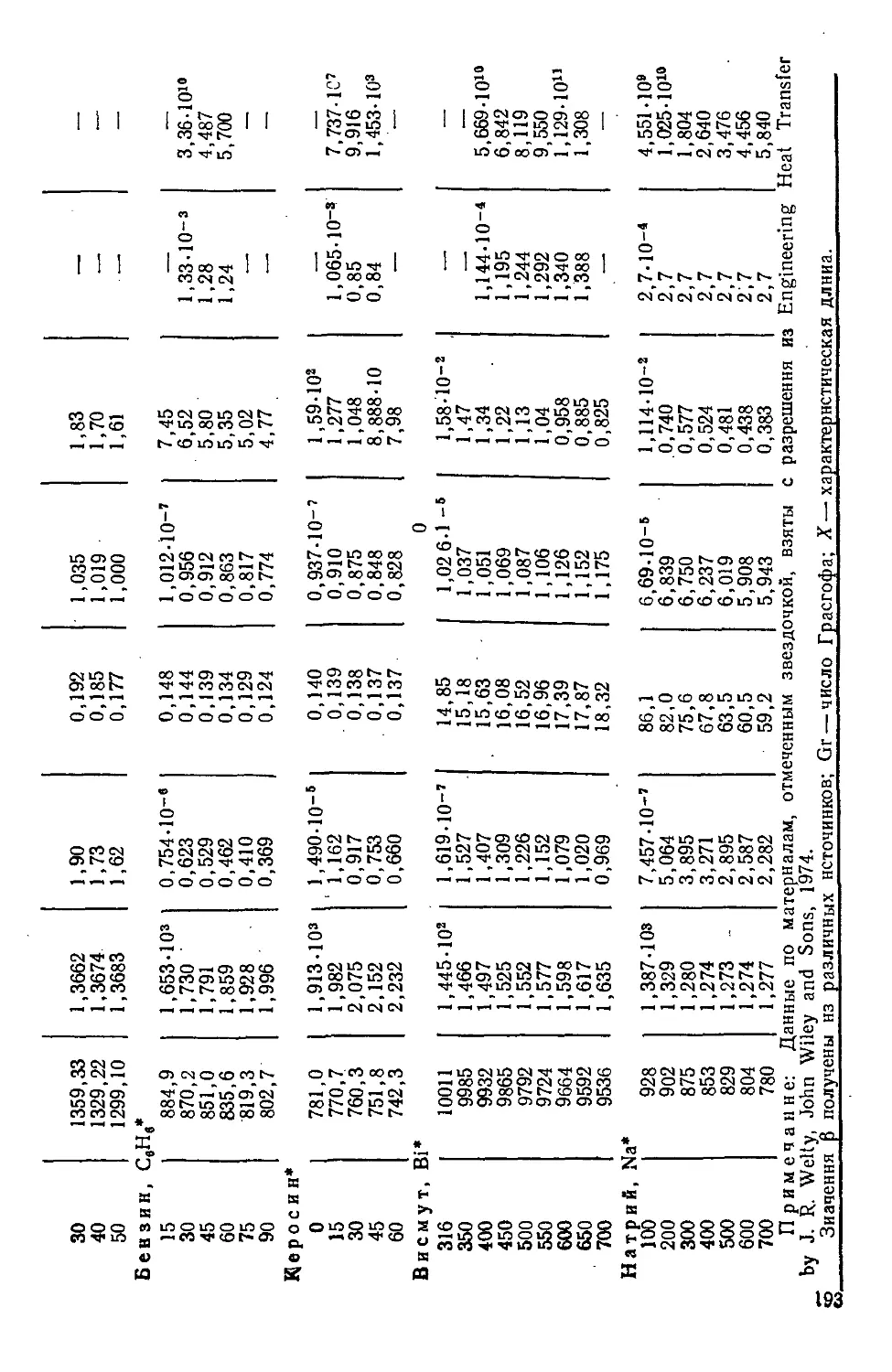
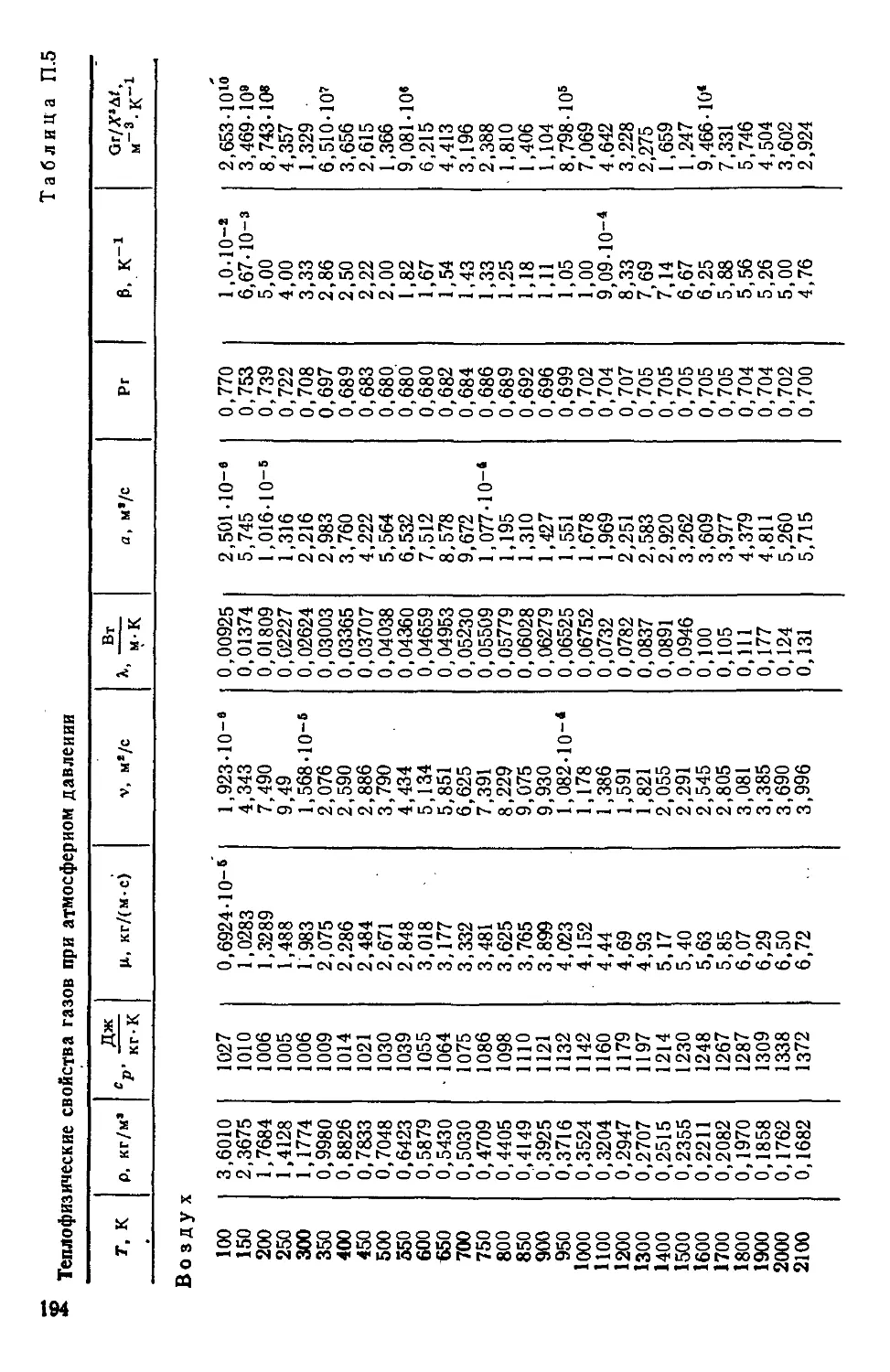
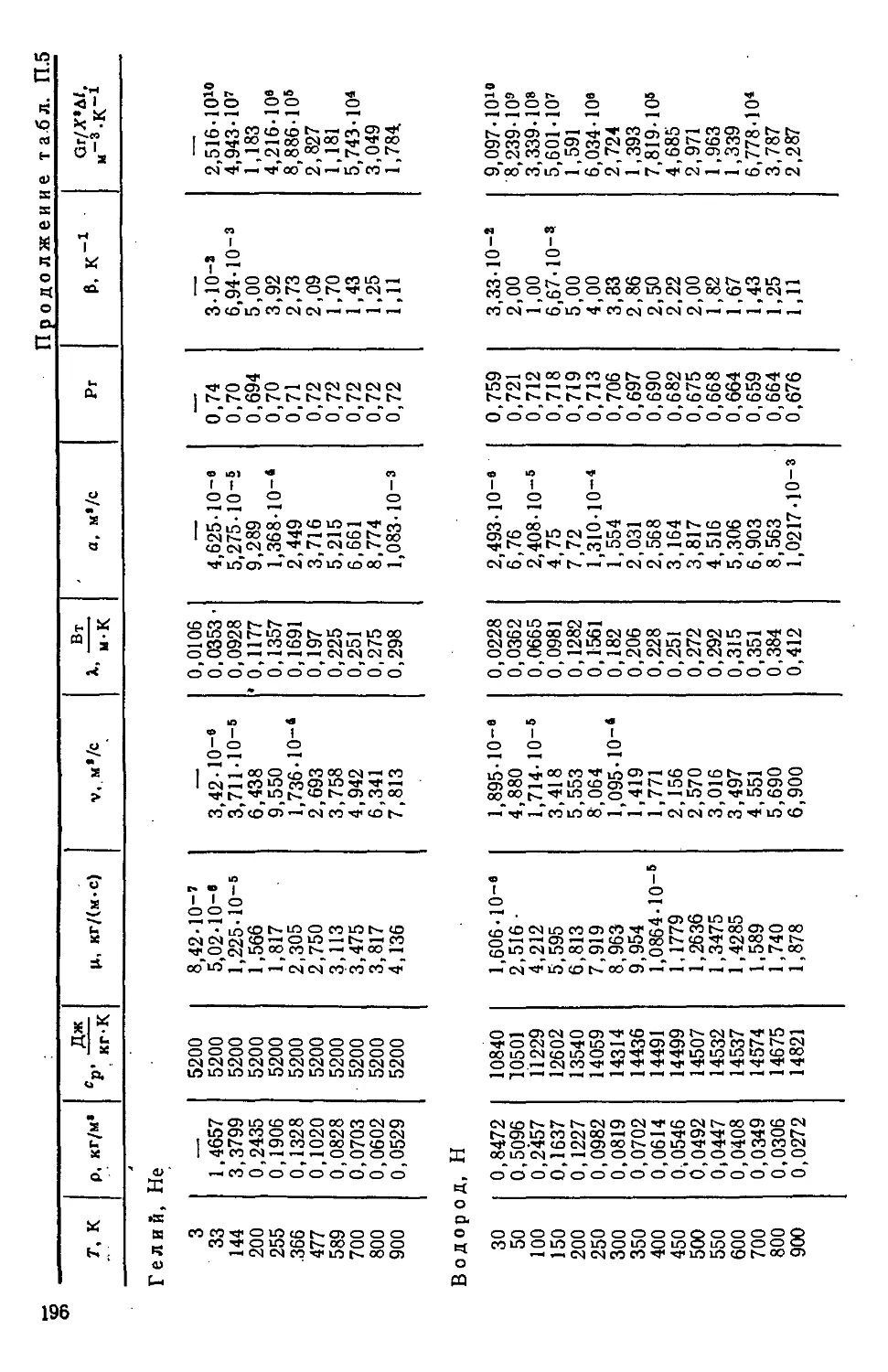
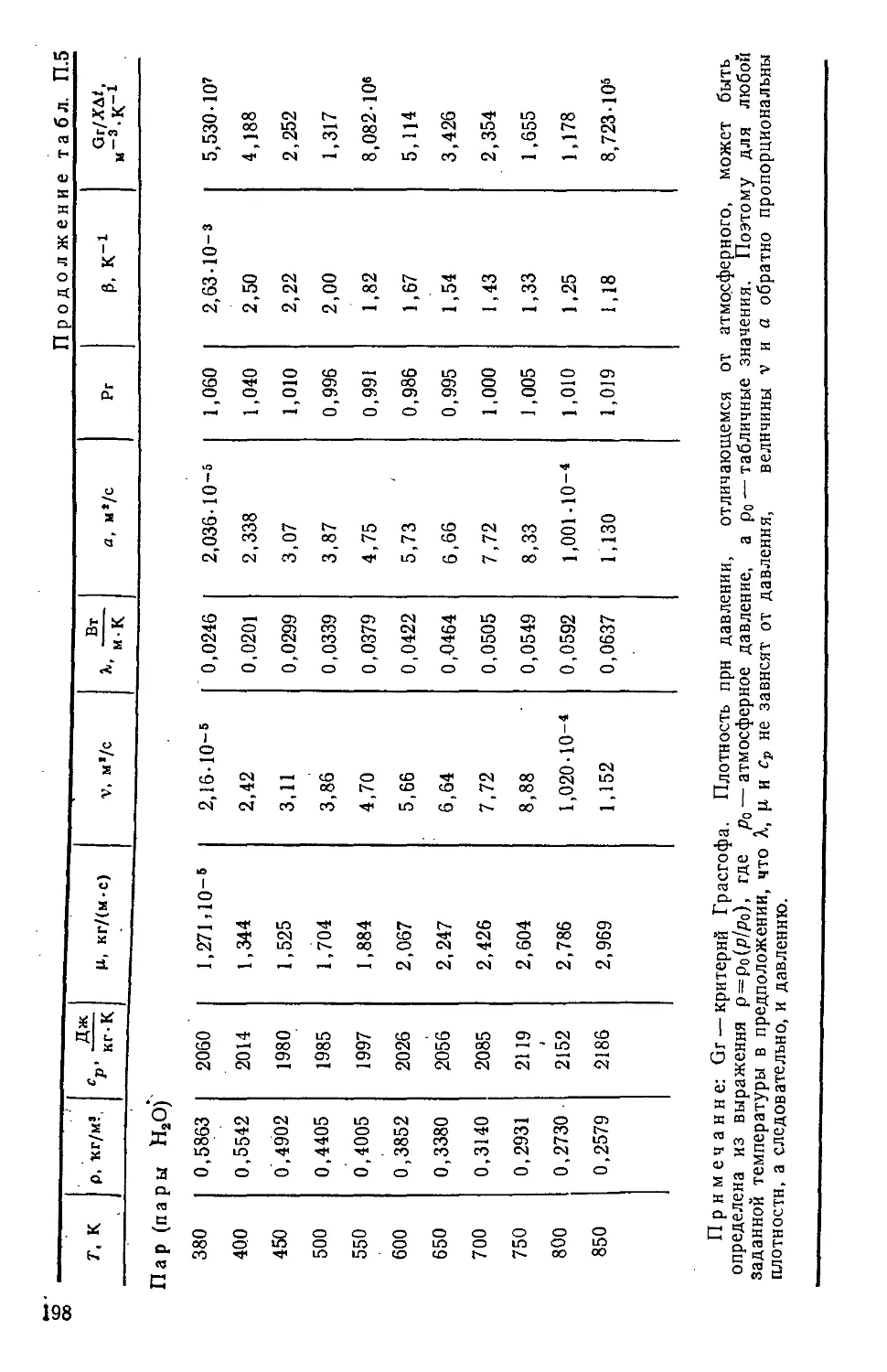
Таблица П.5. Теплофизические свойства газов при атмосферном
давлении 194
Таблица П.6. Теплопроводность некоторых широко используемых
строительных материалов 199
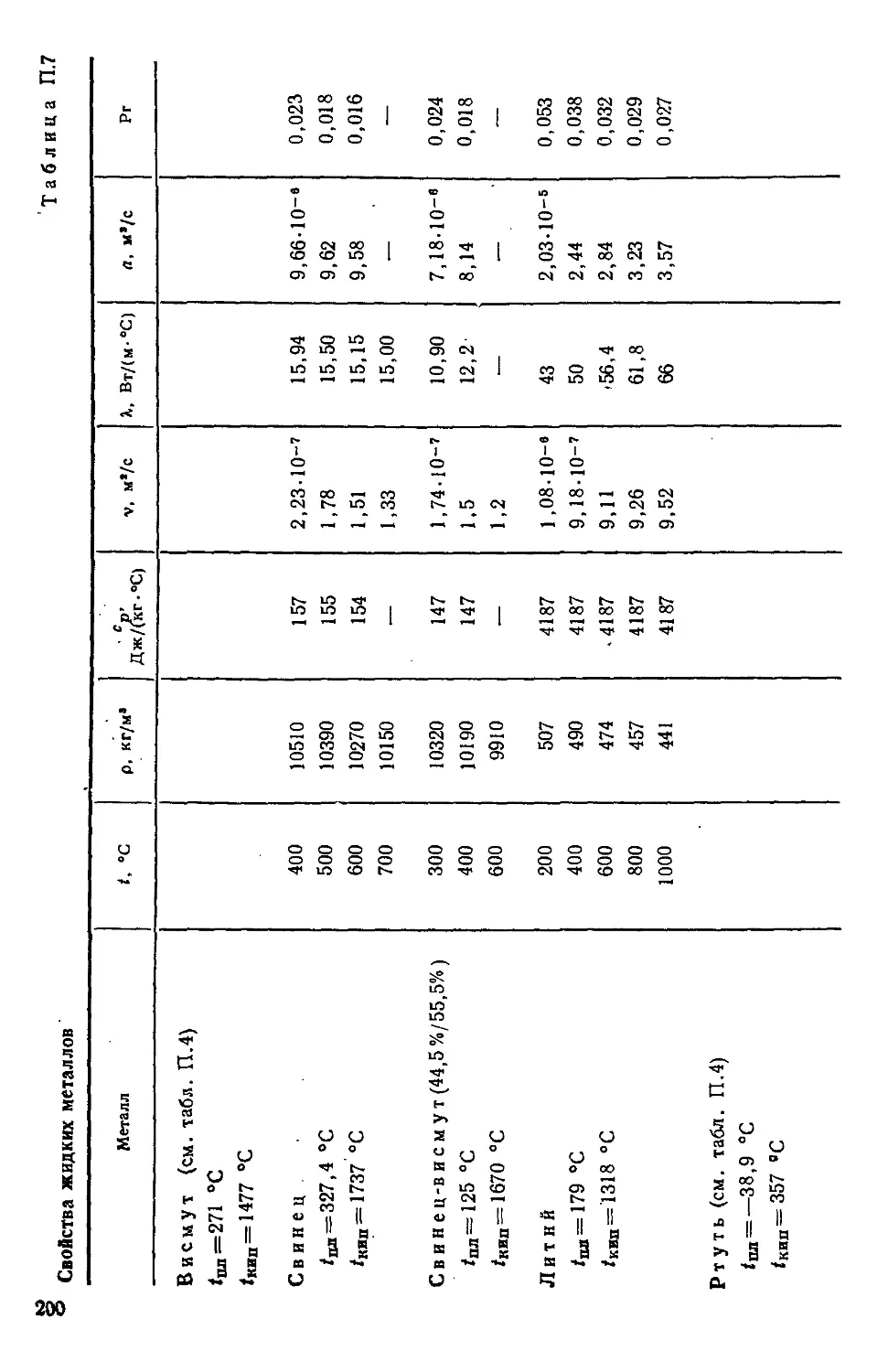
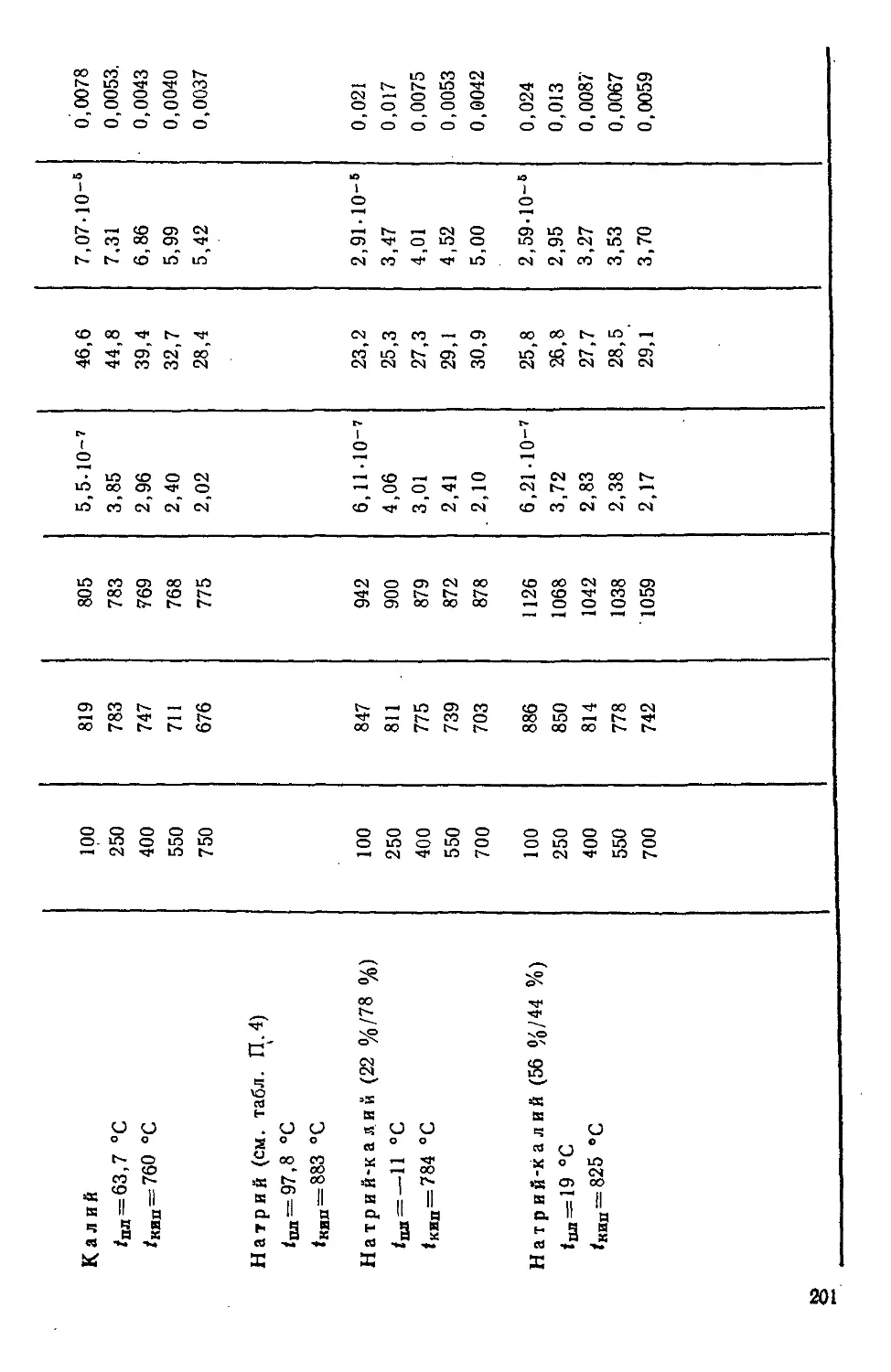
Таблица П.7. Свойства жидких металлов 200
Таблица П.8. Поверхностное натяжение жидкостей в контакте
с воздухом или собственным паром (при комнатной
и других указанных температурах) 202
Таблица П.9. Теплота парообразования жидкостей при атмосфер-
атмосферном давлении 202
Таблица П. 10. Полная нормальная излучательная способность
различных поверхностей 203
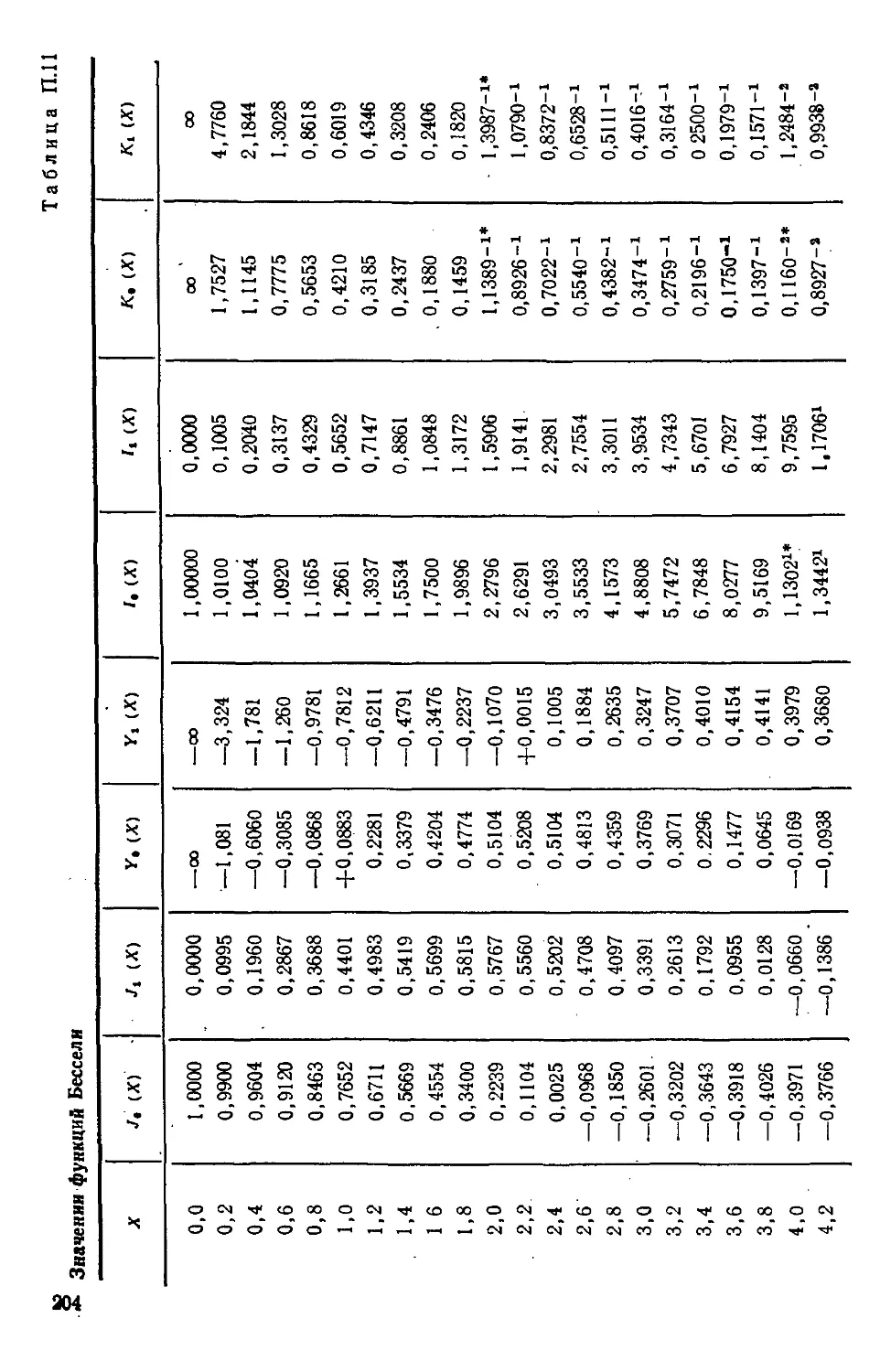
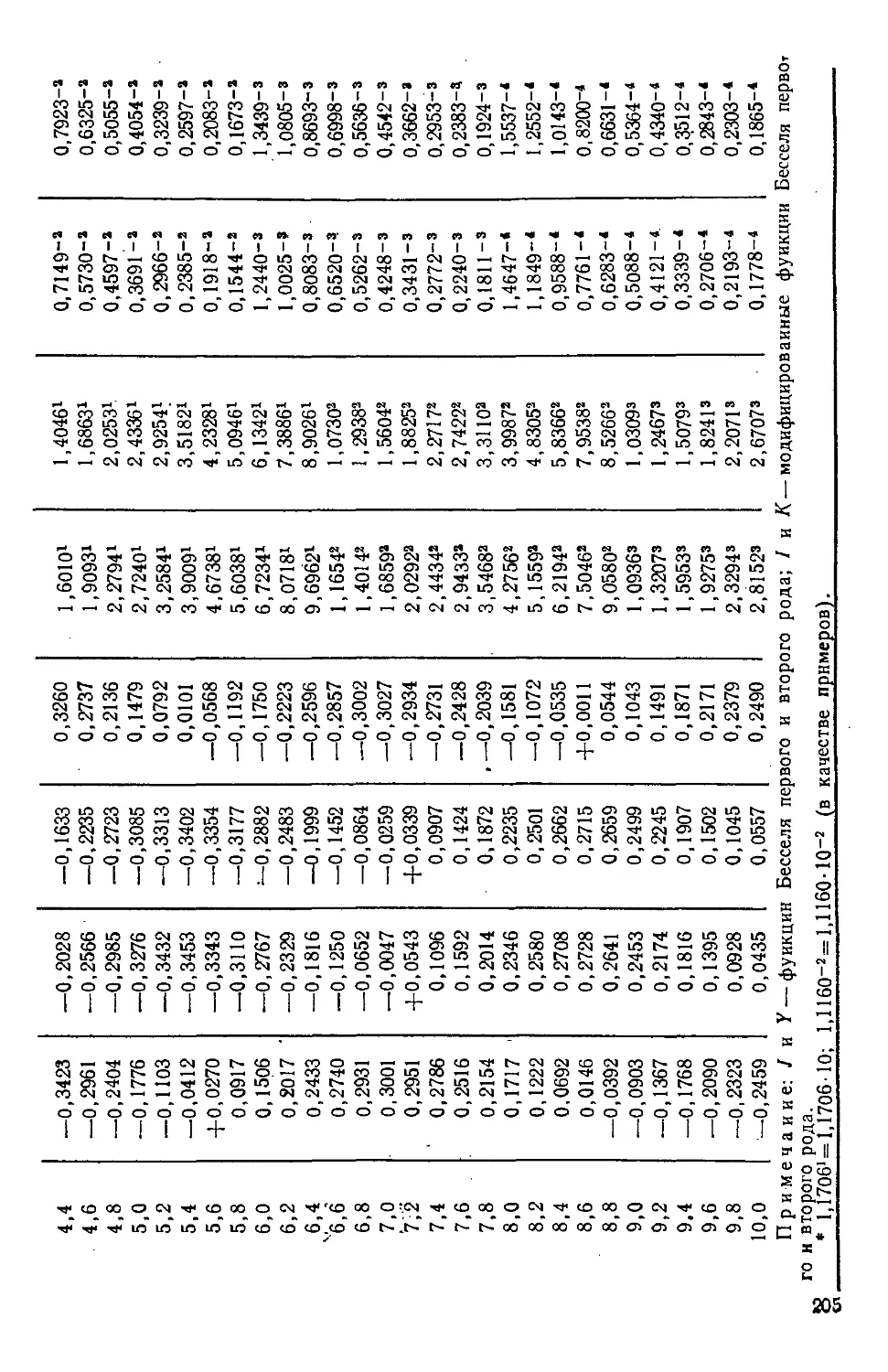
Таблица П.11. Значения функций Бесселя 204
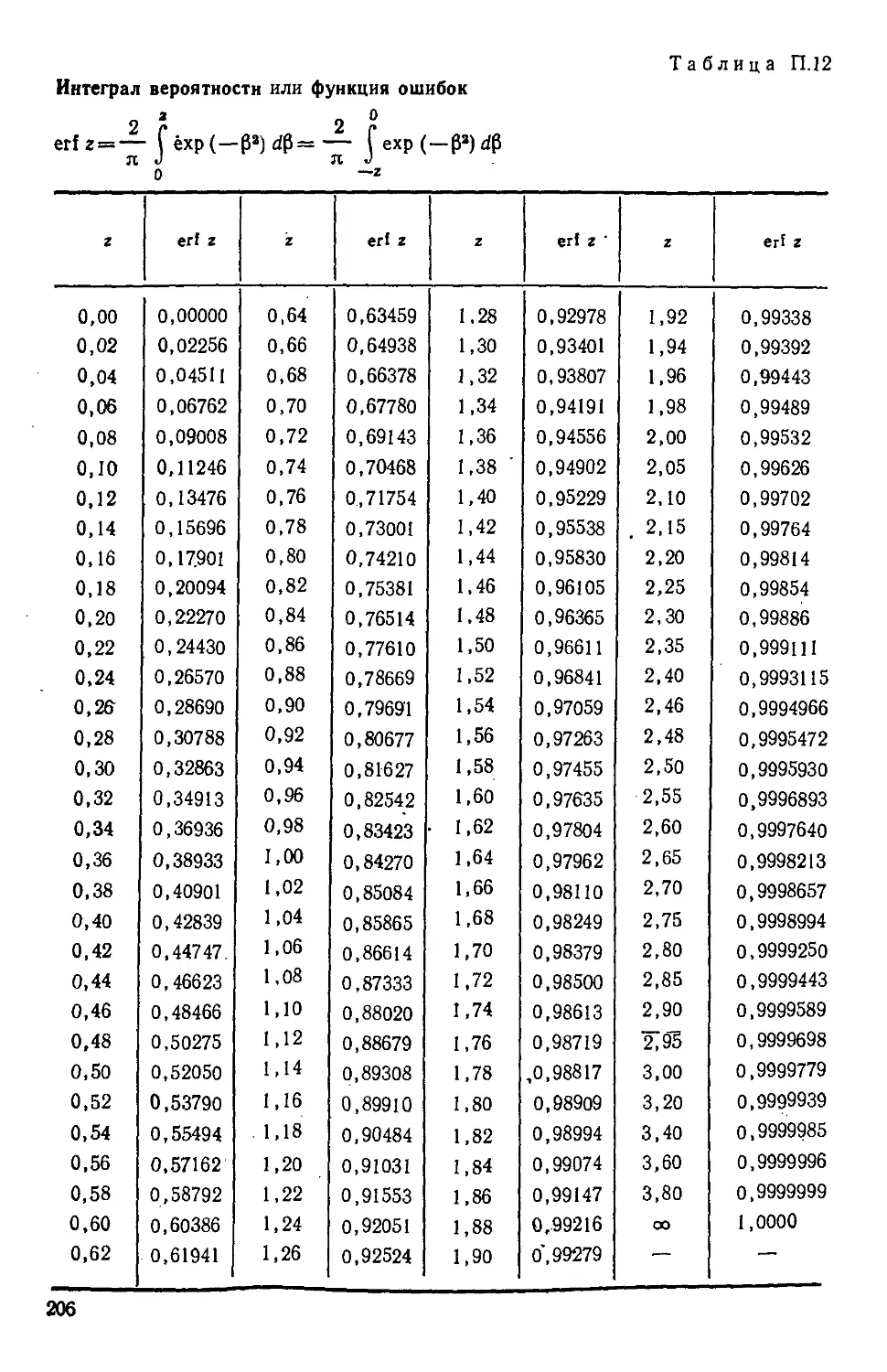
Таблица П. 12. Интеграл вероятности или функция ошибок 206
Посвящается моему брату Янгу
ПРЕДИСЛОВИЕ
В современной технике значение теплопередачи все более и более
увеличивается. Очевидность этого подтверждается возрастающим
количеством публикаций по вопросам теплопередачи. Инженеры и сту-
студенты, занимающиеся решением технических проблем теплопередачи,
часто вынуждены вести поиск требуемой информации в оригинальных
работах или в обширной научной литературе. Однако информация
в этих источниках далеко не всегда представлена в приемлемой для ис-
использования форме. Большинство же книг содержат материал, при-
пригодный только для специалистов какой-то конкретной области. Поиск
нужной литературы требует много времени и усилий и не всегда приво-
приводит к лучшему решению проблемы. Очевидно, в настоящее время
назрела необходимость в небольшом и недорогом справочнике, который
содержал бы основные формулы для расчета теплопередачи, представ-
представленные в простой и компактной форме. Написание данной книги и
было продиктовано именно этой необходимостью. Книга предназ-
предназначена в основном как справочное пособие для инженеров-практиков,
которые могут оценить полезность приведенных в ней формул для сво-
своей работы. В книге представлен весьма важный фактический материал
и изложены основные принципы теплопередачи, поэтому она может
быть использована студентами в качестве дополнительного учебного
пособия при изучении различных академических курсов. Преподава-
Преподаватели и экспериментаторы смогут найти в ней полезную информацию,
относящуюся к различным аспектам теплопередачи.
Справочник состоит из семи глав: общие сведения, теплопровод-
теплопроводность, конвективный теплообмен, тепловое излучение, кипение и кон-
конденсация, теплообменные аппараты и теплопередача строительных
конструкций. Каждая глава начинается с используемых в ней обозна-
обозначений и определений технических терминов. Обозначения объясня-
объясняются всякий раз, когда в приводимых формулах может появиться дву-
двусмысленность или путаница; В основу положена Международная
Система единиц (СИ). Для краткости опущены выводы формул. Более
подробный анализ их можно найти в учебниках, ссылки на которые при-
приведены в конце каждой главы. Включенные в справочник формулы
либо общеприняты, либо тщательно отобраны как надежные и прием-
приемлемые. Везде, где было возможно, выражения приведены, учитывая
очевидное преимущество такого представления, в безразмерной форме.
Это не сделано только для случаев, когда приводимое выражение пред-
предназначено лишь для специального применения.
Глава по строительной теплопередаче, сведения о которой редко
встречаются в обычной литературе, предназначена для читателей, ин-
тересующихся проблемами обеспечения требуемого температурного
режима зданий. Источником информации послужили в основном пуб-
публикации по строительным дисциплинам, по теплообмену и вентиля-
вентиляции, а также инструкции и справочная литература по строительным
конструкциям. В этом отношении автор особенно благодарен Лон-
Лондонскому институту инженерной теплотехники и вентиляции за раз-
разрешение использовать данные, содержащиеся в IHVE-A Справочнике
за 1970 г. В этот раздел не включены вопросы, относящиеся к влиянию
атмосферной турбулентности на теплопередачу строительных соору-
сооружений; это специальная, пока еще недостаточно разработанная тема.
Очевидно, что справочник подобного вида содержит материал, ко-
который по существу почти всецело заимствован из множества других
работ, авторам которых я глубоко обязан. И я искренне надеюсь, что
моя признательность достаточно полно отражена в ссылках на авторов
и их публикации. В тех случаях, когда должная признательность
не высказана, я приношу свои искренние извинения. Благодарю
также редакторов и лиц, давших разрешение на использование
материала для сборника.
Естественно, что, несмотря на проявленное внимание, почти невоз-
невозможно избежать ошибок. Поэтому автор будет признателен любым
предложениям читателей по уточнению и улучшению материала, ко-
которые будут учтены в последующем издании.
X. Я. У., 1976 г.
Глава 1
ОБЩИЕ СВЕДЕНИЯ
1.1. ВИДЫ ТЕПЛОПЕРЕДАЧИ
Теплопередача представляет собой процесс передачи тепла из области
с более высокой температурой в область с более низкой температурой,
который имеет место почти при каждом физическом явлении. Все те
многочисленные процессы, которые описываются передачей тепла
внутри тела или между телами и окружающей средой, являются объек-
объектами изучения на основе законов термодинамики. Разность темпера-
температуры представляет собой характерное свойство тепловой энергии,
которое и предопределяет интенсивность теплообмена. Традиционно
процесс теплопередачи подразделяют на три основных вида, а именно:
теплопроводность, конвективный и лучистый теплообмен. В большин-
большинстве случаев при решении инженерных проблем важно знать вклад
каждого из этих видов теплопередачи. При анализе задач теплообмена
зачастую приходится иметь дело с двумя или тремя видами теплопере-
теплопередачи, действующими одновременно. Поэтому необходимо уметь раз-
различать каждый из них и применять в соответствии с определяющими
их законами.
Теплопроводность. Теплопроводность — это процесс, посредством
которого тепло распространяется в твердых телах или жидкостях, на-
находящихся в состоянии покоя. Определяющие этот вид теплопередачи
законы можно представить в конкретных математических выражениях
и во многих случаях могут быть получены их аналитические решения.
Если аналитические решения получить трудно, то используются
различные графические, аналоговые и численные методы.
Основное представление о теплопроводности может быть получено
из сравнительно простого соотношения. Для бесконечно малого эле-
элемента тела плотность теплового потока пропорциональна температур-
температурному градиенту, т. е.
<7,= —Uildn Вт/м2. A.1)
Коэффициент пропорциональности к, будучи определен как коэффи-
коэффициент теплопроводности, характеризует транспортные свойства мате-
материала. В диэлектрических материалах (т. е. в материалах, не прово-
проводящих электричество) тепловая энергия передается колебаниями крис-
кристаллической решетки, в то время как в хорошо электропроводящих
материалах, таких, как металлы, вклад от механизма колебаний ре-
решетки относительно небольшой. В металлах тепловая энергия перено-
переносится главным образом за счет движения свободных электронов в ре-
решетке. Знание механизма этого переноса полезно при изучении харак-
характеристик проводимости определенного класса материалов и несу-
11
щественно для решения инженерных задач по теплопроводности.
Важно отметить, что между тепло- и электропроводностью чистых ме-
металлов существует зависимость, описываемая законом Видемана—
Франца:
Х = Lo aT Вт/(м • К), A.2)
где а —удельная электрическая проводимость, Ом -1 • м -1; T — аб-
абсолютная температура, К; Lo = 2,45 • 10~8 — число Лоренца,
Вт • Ом/К2.
Таким образом, существует возможность определения значений X
на основе данных по электропроводности. Для других материалов
выражение A.2) неприменимо и X следует определять эксперимен-
экспериментально.
Известно, что коэффициент теплопроводности зависит от темпера-
температуры. Если его изменение незначительно, то в рассматриваемом диапа-
диапазоне температур зависимость плотности теплового потока от темпе-
температурного градиента можно считать линейной. Если же коэффициент
теплопроводности заметно изменяется с температурой, то это изме-
изменение должно быть соответствующим образом учтено.
Конвективный теплообмен. Конвективный теплообмен представ-
представляет собой процесс передачи тепла теплопроводностью между нерав-
неравномерно нагретыми частями жидкости или в результате переноса
тепла при движении самой жидкости. Движение жидкости происходит
в результате внешнего воздействия или из-за различия плотности,
возникающего вследствие разности температуры в объеме жидкости.
Математический анализ проблемы конвективного теплообмена чрезвы-
чрезвычайно сложен. Для большинства случаев инженерной практики реше-
решения получают с помощью математических методов, в которых ис-
используются эмпирические зависимости.
При оценке теплообмена между поверхностью твердого тела и омы-
омывающей ее жидкостью тепловой поток удобно описывать уравнением
Q- aFAt Вт, A.3)
где а — коэффициент теплоотдачи, Вт/(м2 • °С); F — площадь поверх-
поверхности, м2; At — перепад температуры между поверхностью и жи-
жидкостью, °С.
Это уравнение, известное в основном как закон теплоотдачи Нью-
Ньютона, используется при анализе всех форм конвективного теплообме-
теплообмена. Для ламинарного течения жидкости в слое ограниченной толщины
вблизи поверхности твердого тела теплопередача может быть выра-
выражена через температурный градиент теплоносителя в непосредствен-
непосредственной близости от поверхности:
где Хт — коэффициент теплопроводности жидкости; dtjdn — темпе-
температурный градиент в направлении нормали к поверхности твердо-
твердого тела.
12
Таким образом, коэффициент теплоотдачи а, называемый также
коэффициентом теплоотдачи соприкосновением в тонком пограничном
слое, может быть определен как
Bt/(m».°C). A.5)
Коэффициент теплоотдачи сложным образом зависит от геометрии
поверхности, от характеристик потока, а также от физических свойств
теплоносителя. Он не является транспортным свойством, подобно теп-
теплопроводности. Определение этого коэффициента составляет главную
проблему конвективного теплообмена.
Лучистый теплообмен. Теплообмен излучением представляет собой
процесс передачи тепла от одного тела к другому путем испускания
электромагнитных волн. Все тела излучают и передают лучистую
энергию без участия передающей среды. Тепловое излучение несет
тепловую энергию главным образом в видимой и инфракрасной части
электромагнитного спектра.
Расчет теплового излучения основывается на законе Стефана—
Больцмана, который гласит, что энергия, излучаемая единицей пло-
площади поверхности черного тела, пропорциональна абсолютной темпе-
температуре в четвертой степени:
?0= сго74 Вт/м2. A.6)
Это уравнение определяет тепловой поток, излучаемый абсолютно
черным телом. Энергия излучения реального тела меньше, чем черного,
и может быть получена из уравнения A.6) при введении в него коэффи-
коэффициента, который называется излучательной способностью (степенью
черноты) и обозначается е. Таким образом, лучистая энергия реальной
поверхности площадью F определяется из соотношения
Q= FecioT* Вт. A.7)
Между двумя поверхностями, каждая из которых «видит» другую,
происходит непрерывный обмен энергией, при этом энергия передается
от более горячей поверхности к более холодной. Результирующий лу-
лучистый поток энергии между двумя излучающими телами зависит от
относительной интенсивности излучения и поглощения каждого из
этих тел. Если допустить, что поверхность одного тела — серая, а дру-
другого тела (или окружающей среды) — черная, то тепловой поток мож-
можно выразить в виде соотношения
Q = Рео0{Т1-П) Вт, A.8)
где 7\ и Т2 — абсолютная температура излучающего и поглощаю-
поглощающего тела соответственно. В формулу вводятся многие поправочные
коэффициенты, которые должны учитывать форму тел, углы видимо-
видимости, а также радиационные свойства поверхностей и среды, через
которую проходит тепловое излучение.
13
В некоторых случаях, основываясь на линейной зависимости теп-
теплового потока от перепада температуры, аналогично коэффициенту
теплоотдачи соприкосновением в пограничном слое ас, удобно вводить
коэффициент теплоотдачи излучением ал. Тогда выражение для расче-
расчета теплового потока может быть представлено в виде
Q^= FaJI(Tl-T2) Вт, A.9)
где
«л = есх0 G\ + Т2) (П + П) Вт/(м2 • К). A.10)
Для случая теплообмена, когда тепло передается одновременно
конвекцией и излучением, можно использовать простое уравнение,
учитывающее оба эти процесса теплопередачи:
Q= F (ас + ая) G\ - Т2) Вт. A.11)
Сложный теплообмен. Главная проблема, которая возникает при
решении инженерных задач теплопередачи, состоит в том, что прихо-
приходится рассматривать сочетание двух или трех основных видов теплооб-
теплообмена. Например, при расчетах теплового потока от зданий принимают,
что тепло, теряемое через конструкционные элементы здания, переда-
передается от внутренних поверхностей стек конвекцией и излучением. Теп-
Тепло, передаваемое через различные элементы стенной панели, проходит
воздушные прослойки посредством конвекции и излучения и затем рас-
рассеивается с внешней поверхности стены в окружающее пространство.
Расчет конвективного теплообмена довольно сложен из-за необходимо-
необходимости рассмотрения условий движения воздушного потока около поверх-
поверхности.
Очень часто, например в теплообменных аппаратах, поток горячего
теплоносителя отделен от холодного непроницаемой твердой стенкой.
Для расчета теплопередачи необходимо знать коэффициенты теплоот-
теплоотдачи с обеих сторон стенки и ее термическое сопротивление. Задача
существенно усложняется, если стенка с обеих сторон имеет ребра,
температура по длине которых неравномерна. В таких случаях удоб-
удобно использовать параметр теплопередачи Ж системы; тогда тепловой
поток можно охарактеризовать соотношением
Q= MM Вт. A.12)
Параметр теплопередачи — это величина, обратная сумме терми-
термических сопротивлений в системе, через которую распространяется
тепловой поток. Этот параметр представляет собой произведение пол-
полного коэффициента теплопередачи и соответствующей площади
поверхности, перпендикулярной направлению распространения теп-
тепла. Обобщенный параметр используется в задачах, в которых терми-
термическое сопротивление различных составных частей подчиняется зако-
закону аддитивности.
Основные уравнения для различных видов теплообмена сведены
в табл. 1.1.
14
Таблица 1.1
Основные выражения для теплового потока при различных видах теплопередачи
Система обозначений:
F — площадь поверхности, м2;
X — параметр теплопередачи, Вт/°С;
а — коэффициент теплоотдачи, Вт/(м2 • °С);
X — коэффициент теплопроводности, Вт/(м • °С);
L — линейный размер, м;
Q — тепловой поток, Вт;
R — термическое сопротивление, °С/Вт;
Т — абсолютная температура, К;
К — коэффициент теплопередачи, Вт/(м2 • °С);
t — температура, °С;
^cti *ж— температура стенки и жидкости соответственного;
8 — излучательная способность (степень черноты); "'
а0 = 5,67 • 10~8 Вт/(м2 • К4) — постоянная Стефана — Больцмана.
Вид теплопередачи
Теплопроводность
Конвективный тепло-
теплообмен
Лучистый теплообмен
Сочетание различных
видов теплообмена
Тепловой поток
dt
Q»—XF dn '
Q = aF(.tCr-tm);
Q = aF(tm-lcr)
Q = eo0FT*
Q = UJ0F(Ti-Tl)
Q=KFAt = XM =
= M/R
Примечание
• Одномерный тепловой поток
в направлении п
Тепловой поток между двумя
точками с температурами tx и
ti, расположенными на расстоя-
расстоянии L
Теплопередача от поверхно-
поверхности твердого тела к жидкости
Теплопередача от жидкости
к поверхности твердого тела
Полное количество энергии
излучаемое поверхностью пло-
площадью F при температуре Т
Результирующий тепловой
поток от серого тела с темпера-
температурой Г[ к черному телу с тем-
температурой Т2
Тепловой поток, проходящий
через систему тел с параметром
теплопередачи Ж и разностью
температуры Д/
15
1.2. ТЕМПЕРАТУРНЫЕ ШКАЛЫ
И РЕПЕРНЫЕ ТЕРМОМЕТРИЧЕСКИЕ ТОЧКИ
Температуру можно рассматривать как условие, которое определяет
теплообмен в теле. При обеспечении определенных условий конкретное
явление природы всегда происходит при одной и той же температуре.
Поэтому для описания каждого явления необходимо точно определять
точки на температурной шкале. Двумя такими фиксированными
точками являются точка таяния льда и точка кипения воды. Обычно
используют шкалы Цельсия и Фаренгейта, в которых установлены
соответственно 0° С и 32° F для точки таяния льда и 100° С и 212° F —
для точки кипения воды. Значения температуры, отличающиеся от этих
двух фиксированных точек, устанавливают с помощью термометра из-
измерением какого-либо зависящего от температуры свойства рабочего
тела. В качестве термометрического рабочего тела используют газы,
так как все они с достаточной точностью подчиняются закону иде-
идеального газа. Но при создании температурной шкалы, основанной на
свойствах рабочего тела, неизбежно допускаются определенные погреш-
погрешности. Использование теории идеального обратимого двигателя Карно
позволило Кельвину избежать этих погрешностей и ввести шкалу
абсолютной термодинамической температуры, которая не зависит от
свойств рабочего тела. Нуль градусов по шкале Кельвина на 273,15 К
ниже точки таяния льда. Начиная с 1954 г. было решено отказаться
от точки таяния льда как от реперной точки, так как ее очень трудно
воспроизводить с приемлемой точностью. Вместо нее в качестве репер-
реперной точки ввели тройную точку воды (температура фазового равнове-
равновесия между чистым льдом, водой и водяным паром), которая можетбыть
воспроизведена в лабораторных условиях с погрешностью не хуже
0,001 К и которая на 0,01 К выше точки таяния льда. Международным
соглашением тройной точке было присвоено значение 273,16 К. Дру-
Другие температуры могут быть определены с помощью газового термо-
термометра постоянного объема согласно следующему выражению:
Т _ Давление при температуре Т ,, ,п\
273,16 Давление в тройной точке воды
Температура—273,16° С, при которой давление стремится к ну-
нулевому значению, является абсолютным нулем температуры. С уста-
установлением тройной точки в качестве стандартной температуры шкала
Цельсия была видоизменена путем приведения ее нулевой точки
к значению 273,15 К. Градус Фаренгейта составляет 5/9 градуса
Цельсия. Нулевое значение шкалы Ренкина составляет — 459,67° Р
Для перевода температуры в градусы Цельсия и Кельвина исполь-
используют следующие соотношения:
ГС= Т К —273,15- 6/9 (rF —32)= 5/9 (Г R —491,67);
A.14)
Т К= ГС + 273,15= 5/9 (T°F —32) + 273,15= 5/, Т° R. A.15)
Не всегда представляется возможным выполнить градуировку
термометров; в таких случаях по-прежнему используют газовые тер-
16
мометры постоянного объема. С этой целью международным согла-
соглашением была введена Международная практическая температурная
шкала, содержащая набор значений различных фиксированных точек
при нормальном атмосферном давлении. Основные фиксированные стан-
стандартные значения этих точек приведены в табл. 1.2.
Таблица 1.2
Основные реперные термометрические точки при атмосферном давлении
Термометрическая
точка
Равновесное
состояние
Точка кипения водоро-
водорода
Точка кипения кисло-
кислорода
Тронная точка воды
Точка кипения воды
Точка плавления цин-
цинка
Точка плавления се-
серебра
Точка плавления золо-
золота
Примечание. Значения взяты
Scale of 1968. — «Metrologia», 1969, v.
Жидкость — пар
Жидкость — пар
Твердая фаза — пар—
жидкость
Жидкость — пар
Твердая фаза — жи-
жидкость
Твердая фаза — жи-
жидкость
Твердая фаза — жи-
жидкость
из The International Practical Temperature
5, № 2.
СПИСОК ОСНОВНОЙ ЛИТЕРАТУРЫ
1.1. Jacob M. Heat Transfer. V. I and II. John Wiley & Sons, 1959.
1.2. McAdams W. H. Heat Transmission. 3rd ed. McGraw-Hill, 1954.
1.3. Eckert E. R. G., Drake R. M. Heat and Mass Transfer. McGraw-Hill, 1959.
1.4. Eckert E. R. G., Drake R. M. Analysis of Heat and Mass Transfer. McGraw-
Hill, 1972.
1.5. Rohsenow W. M., Hartnett J. P., eds. Handbook of Heat Transfer. McGraw-
Hill, 1973.
1.6. Кутателадзе С. С., Боришанский В. М. Справочник по теплопередаче. Л.—
М., Госэнергоиздат, 1959.
1.7. Кутателадзе С. С. Основы теории теплообмена. Изд. 2-е, доп. и перер.
¦М.—Л., Машгиз [Ленинградское отделение], 1962.
1.8. Schack A. Industrial Heat Transfer (transl. by I. Gutman), Chapman & Hall,
1965.
1.9. Welty J. R. Engineering Heat Transfer. John Wiley & Sons, 1974.
1.10. Chapman A. J. Heat Transfer. 3rd ed. London, Macmillan, 1974.
1.11. Gebhart B. Heat Transfer. 2nd ed, McGraw-Hill, 1971.
1.12. Kreith F. Principles of Heat Transfer. 2nd ed. International Textbook Co,
1965.
1.13. Ede A. J. An Introduction to Heat Transfer. Pergamon Press, 1967.
1.14. Simonson J. R. Engineering Heat Transfer. Macmillan, 1975.
1.15. Schenck Hilbert von N. Heat Transfer Engineering. Longman, 1960.
1.16. General Electric Co. Heat Transfer and Fluid Flow Data Books. Research and
Development Centre. New York, 1976.
1.17. Bayley F. J., Owen J. M., Turner A. B. Heat Transfer. Thomas Nelson, 1972.
1.18. Heat Transfer Notes. McGraw-Hill, 1965. Auth.: L. M. K. Bpetler^.V.. H. Cher-
Cherry, H. A. Johnson, R. C. Martinelli.
17
1.19. Rohsenow W. H., Choi H. Y. Heat, Mass and Momentum Transfer Prentice-
Hall International, 1961.
1.20. Rohsenow W. H., ed. Development in Heat Transfer. Edward Arnold, 1964.
1.21. Backhurst J. R., Harker J. H., Porter J. E. Problems in Heat and Mass Trans-
Transfer. Edward Arnold, 1974.
1.22. Kern D. Q. Process Heat Transfer. McGraw-Hi.ll, 1950.
1.23. Теплопередача. [Учебник для энергет. вузов и фак.], М.—Л., «Энергия»,
1965 .Авт.: В. П. Исаченко и др.
1.24. Welty J. R., Wicks С. E., Wilson R. E. Fundamentals of Momentum, Heat and
Mass Transfer. John Wiley & Sons, 1969.
1.25. Hsu S. T. Engineering Heat Transfer. D. Van Nostrand, 1963.
1.26. Grober H., Erk S., Grigull U. Fundamentals of Heat Transfer. McGraw-Hill.
1961.
1.27. Eckert E. R. G., Goldstein R. J. Measurement Techniques in Heat Transfer.
AGARD 130, 1970.
1.28. Dusinberre G. M. Heat Transfer Calculations by Finite Differences. Interna-
International Textbook, 1961.
1.29. Adams J. A., Rogers D. F. Computer Aided Analyses Heat Transfer. McGraw-
Hill, 1973.
1.30. Holman J. P. Heat Transfer. McGraw-Hill, 1972.
1.31. Heat Transfer Heinneman Educational Books, 1971. Auth.: F. A. Holland,
R. M. Moores, F. A. Watson, J. K. Wilkinson.
1.32. Patankar S. V., Spalding D. B. Heat and Mass Transfer in Boundary Layers.
London, lntertext Books. 1970.
1.33. Advances in Heat Transfer. Academic Press, annually.
1.34. Heat Bibliography. H. M. Stationery Office, annually.
1.35. Heat Transfer, Soviet Research, Scripta Publishers, Washington, bi-monthly.
1.36. Intra-red Physics. Pergamon Press, by-monthly.
1.37. Journal of Heat Transfer, Transactions of the American Society of Mechanical
Engineers, Series C, quarterly.
1.38. Proceedings of the International Developments in Heat Transfer Conferences,
1951 (London), 1961 (Boulder and London) American Society of Mechanical
Engineers.
1.39. Proceedings of the International Heat Transfer Conferences, 1966 (Chicago),
1970 (Paris), 1974 (Tokyo), Elsevier Publishing Co., Amserdam, and Hemi-
Hemisphere Publishing Cc, USA.
1.40. Proceedings of Heat Transfer and Fluid Mechanics Institute, Stanford Uni-
University Press, California, USA.
1.41. Progress in Heat and Mass Transfer, Monograph Series, Pergamon Press,
annually.
1.42. Science Abstract A, Physics Abstracts, The Institution of Electrical Engineers.
1.43. Chemical Engineering Science, Pergamon Press, monthly.
1.44. The Chemical Engineers, Institution of Chemical Engineers, monthly.
1.45. Chemical Engineering Progress, American Institute of Chemical Engineers,
monthly.
1.46. Industrial and Engineering Chemistry, American Chemical Society, monthly.
1.47. The International Journal of Heat and Mass Transfer, Pergamon Press,
monthly.
1.48. The Journal of Mechanical Engineering Science, The Institution of Mechanical
Engineers, bi-monthly.
1.49. Heat and Fluid Flow, Institution of Mechanical Engineers, London, half
yearly.
Глава 2
ТЕПЛОПРОВОДНОСТЬ
2.1. ВВЕДЕНИЕ
Если отдельные участки твердого тела имеют различную температуру,
то тепло передается из области с более высокой температурой в область
с более низкой температурой за счет процесса теплопроводности. В этом
процессе тепловой поток пропорционален площади поперечного сече-
сечения, перпендикулярного к направлению потока, и разности температу-
температуры и обратно пропорционален расстоянию между двумя уровнями тем-
температуры. Коэффициент пропорциональности "к называется коэффици-
коэффициентом теплопроводности материала. Таким образом, тепловой поток
Q, направленный по нормали к площади поперечного сечения F, под
воздействием разности температуры At между двумя точками, разде-
разделенными расстоянием L, выражается следующим соотношением:
Q = %FMIL Вт. B.1)
Отношение изменения температуры At к расстоянию L, если L
стремится к бесконечно малому значению, приближается к предель-
предельному значению dtldL, которое представляет собой градиент температу-
температуры. Если градиент температуры изменяется от точки к точке, то выра-
выражение для теплового потока в данной точке, направленного по нор-
нормали к поверхности, записывается в виде
Q = — XF dtldL Вт. B.2
Знак минус указывает на то, что тепловой поток распространяется
в направлении убывания температуры, т. е. на отрезке dL темпера-
температура уменьшается на dt. Определение распределения температуры,
а следовательно, и градиента температуры часто является основным
требованием для решения задач по теплообмену теплопроводностью.
В случае неравномерного распределения теплового потока необходимо
уменьшить площадь поперечного сечения F, чтобы получить локальное
значение Q. Предельное значение Q, когда F стремится к бесконечно
малому значению, равное
называют плотностью теплового потока в данной точке. В действи-
действительности теплопроводность материалов зависит от температуры.
Обычно с достаточной точностью для X используется выражение
Х= %0A + Р0Вт/(м-°С), B.4)
19
где Ко — теплопроводность, отнесенная к определенной температуре;
Р — температурный коэффициент теплопроводности. Материалы
с меньшим значением E имеют более постоянную теплопроводность.
2.2. ОБОЗНАЧЕНИЯ
Л — константа;
F — площадь поверхности, м2;
с— удельная теплоемкость, Дж/(кг • °С);
Ж — параметр теплопередачи, Вт/°С;
d — толщина пластины, м;
L — линейный размер, длина, м;
U — разность потенциалов, В;
а — коэффициент теплоотдачи, Вт/(м2 • °С);
/ — ток, А;
Jn> Уп — функции Бесселя первого и второго рода n-го порядка;
Ai> Кп — модифицированные функции Бесселя первого и второго
рода л-го порядка;
Рп, Qn — функции Лежандра первого и второго рода n-го порядка;
In = loge— натуральный логарифм;
Р — периметр, м;
р — давление, Н/м2;
Qn0JIH — количество теплоты, Дж; объемная плотность источника
тепла, Дж/м3;
Q — тепловой поток, Вт;
qs — плотность теплового потока, Вт/м2;
г — радиус, радиальная координата, -м;
R — термическое сопротивление; R — \ICfC, °С/Вт;
R' — термическое сопротивление единицы площади поперечного
сечения, °С • м2/Вт;
R3 — электросопротивление, Ом;
т — время, с;
К — коэффициент теплопередачи, Вт/(м2 • °С);
V — объем, м3;
v — скорость, м/с;
х,у,г — координаты;
а=Х/рс — коэффициент температуропроводности, м2/с;
р — температурный коэффициент теплопроводности, 1/К;
Я — коэффициент теплопроводности, Вт/(м • °С);
р — плотность, кг/м3;
б — толщина слоя жидкости, пластины, м;
? — собственное значение;
Рп — корни трансцендентных уравнений;
t — температура, °С;
/— коэффициент трения;
ф, г|з — цилиндрическая и сферическая координаты соответственно.
И н д е к с'ы:
х — холодная область;
г — горячая область;
о — первоначальное состояние;
ж — жидкость;
ст — стенка;
s — поверхность.
2.3. ОПРЕДЕЛЕНИЯ
Коэффициент теплоотдачи а характеризует тепловой
поток, проходящий через единицу площади при разности температуры
между поверхностью твердого тела и омывающей его жидкостью в один
градус (его также называют коэффициентом теплоотда-
теплоотдачи соприкосновением), Вт/(м2 ¦ °С).
Плотность теплового потока qs — тепловой по-
поток через единицу площади поверхности, Вт/м2.
Коэффициент теплопередачи К — значение па-
параметра теплопередачи, отнесенное к единице площади поверхности,
Вт/(м2 • °С); он учитывает все виды процесса передачи тепла через
систему.
Удельная теплоемкость с — количество тепла, не-
необходимого для повышения температуры единицы массы материала
на один градус, Дж/(кг • °С). Она также известна как удельная
теплота.
Коэффициент теплопроводности % характери-
характеризует количество тепла, передаваемого в единицу времени через еди-
единицу площади поверхности при единичном температурном градиенте,
Вт/(м • °С).
Параметр теплопередачи Ж — тепловой поток через
тепловую систему при разности температуры Г С, Вт/°С.
Термическое сопротивление R — величина, об-
обратная параметру теплопередачи; характеризует общее сопротивление
в направлении распространения тепла, °С/Вт.
Коэффициент температуропроводности
а = Xlpc характеризует темп, с которым нестационарное распределе-
распределение температуры стремится к равновесному состоянию, м2/с.
2.4. ПАРАМЕТР ТЕПЛОПЕРЕДАЧИ
И ТЕРМИЧЕСКОЕ СОПРОТИВЛЕНИЕ
Если параметр теплопередачи равен
X = XFIL Вт/°С,
то выражение для теплового потока можно представить в виде
Q = XFJL=J*_ = X(tr-tJ Вт, B.5)
где tr и tx — температура тепловой системы соответственно горячей и
холодной зоны.
21
Если термическое сопротивление R определяется как величина,
обратная параметру теплопередачи (т. е. R =• !/<#), то выражение для
теплового потока может быть записано так:
Q= X(tv—Q~ (tr—tx)/R Вт.
B.6)
Если рассматривать (tr — tx) как разность термических потенциалов
на термическом сопротивлении R, через которое в единицу времени
проходит количество тепла Q,
то уравнение B.6) можно запи-
записать аналогично закону Ома:
tr
а. *»
Горячая
жидкость
h
h
\
г-—*__
Холодная
жидкость
а
I = U/R9,
ток, A; U -
Типичное
где / — ток, A; U — разность
электрических потенциалов на
сопротивлении R3, В.
Кроме понятия о термичес-
термическом сопротивлении по аналогии
распределение с электрическим контуром ис-
температуры пользуется представление о тер-
термическом контуре. Представле-
Представление о термическом сопротивле-
сопротивлении (или о параметре теплопе-
теплопередачи) особенно полезно для
решения задач стационарной
теплопроводности при сложной
системе тел. Так, термическое сопротивление при теплопередаче через
единицу площади поверхности многослойной стенки от одной жидкой
среды к другой может быть определено из соотношения
Рис. 2.1. Теплопередача через многослой
ную пластину
g' —I_I i_ d\ , 4г
— )°С-м»/Вт,
B.7)
где ах и a2 — коэффициенты теплоотдачи. Тепловой поток при этом
равен
Q = ( tr~ tx )f Вт, B.8)
V R' 1
где F — площадь поверхности, перпендикулярной распространению
тепла; R' — термическое сопротивление на единицу площади.
2.5. ЗАКОН ТЕПЛООТДАЧИ НЬЮТОНА
Теплообмен между поверхностью твердого тела и окружающей его
жидкостью осуществляется в основном благодаря теплопроводности,
конвекции и излучению. Установлено, что в интервале умеренных
температур (впервые открыто Ньютоном) интенсивность охлаждения
твердой поверхности приблизительно пропорциональна перепаду тем-
температуры между стенкой и жидкостью при условии, что разность тем-
температуры не слишком велика. Тогда выражение для количества тепла,
22
переданного от твердого тела к жидкости, может быть представлено
в виде
Q=aF(lor — tJBT, B.9)
где а — коэффициент теплоотдачи, Вт/(м2 • °С); tCT— температура
стенки, °С; tyK — температура жидкости, °С; F—площадь поверх-
поверхности, м2.
Хотя это выражение приближенное, оно очень полезно для оценоч-
оценочных расчетов.
Передачу тепла от поверхности твердого тела к окружающей среде
можно рассматривать как теплопроводность через прилегающий к по-
поверхности твердого тела тонкий слой жидкости, внутри которого
не существует конвекции. Тогда
6 = А, /а м,
B.10)
где Хт — коэффициент теплопроводности жидкости; <5 — эффективная
толщина слоя жидкости. Обычно коэффициент теплоотдачи определяют
экспериментально. Оценка коэффициента теплоотдачи рассмотрена
более подробно в главе, посвященной конвективному теплообмену.
2.6. ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ РЕЖИМЕ
В стационарном состоянии ни тепловой поток, ни распределение тем-
температуры в системе не изменяются во времени.
Одномерные системы. Эти системы представляют собой наиболее
простые случаи распространения теплового потока только в одном
направлении. К этой категории относятся такие очень важные прак-
практические задачи, как теплопроводность через пластину, через стенку
трубы с изоляцией и многие другие.
Уравнение Фурье [см. уравнение B.23)] в этом случае имеет вид:
in 1
—— = 0 — в декартовых координатах; B.11)
__-| — о—в цилиндрических координатах;
dr T dr B.12)
d2t , 2 dt A v '
—-Л = 0 — в сферических координатах.
dr2 r dr
Распределение температуры в теле дается решением одного из этих
уравнений. Значение теплового потока можно получить из выражения
Q= ~XF dtldx Вт B.13)
или
Q=— XFdtldr Вт, B.14)
где площадь поверхности поперечного сечения F зависит от х или г.
23
Двумерные системы. В этих случаях температура и тепловой поток
изменяются в двух направлениях. Уравнение Фурье [см. уравнение
B.23)] тогда имеет вид
дх* ду2 v
Общее решение можно представить в следующем виде:
t = (Сх sin & + С2 cos &) (СфЬ> + е-С"), B.16)
где ?— характеристические значения (собственные числа), определяе-
определяемые из решения характеристического уравнения, a Cj, C2, С3 — по-
постоянные величины, определяемые из граничных условий задачи.
Выражение B.15) представляет собой уравнение Лапласа для дву-
двумерных систем. Аналитические решения можно получить только для
относительно простых систем. Для приближенного решения более
сложных систем развиты различные аналоговые, графические и
численные методы [2.19—2.28]. Обсуждение этих методов выходит
за рамки настоящей книги. В табл. 2.2 представлены решения задач
теплопроводности при стационарном режиме для некоторых простых
систем.
2.7. ТЕПЛОПЕРЕДАЧА ОРЕБРЕННЫХ ПОВЕРХНОСТЕЙ
Для увеличения площади поверхности, с которой передается тепло
от горячей системы к окружающей среде, широко используются шипы
и ребра. Обычно их применяют для интенсификации охлаждения, од-
однако они могут быть использованы и для нагревания системы. Тепло-
Теплообмен в таких системах происходит за счет теплопроводности в твердом
теле и конвекции в примыкающем к поверхности слое теплоносителя.
При этом предполагается, что доля тепла, передаваемого излучением,
незначительна. Тогда уравнение теплового баланса принимает вид
) (n{), B.17)
dx \ dx I
где AS — площадь элементарного участка поверхности ребра (или
шипа) на малой длине ребра Ах. Периметр определяется как Р =¦
= AS/Ах.
В табл. 2.3 приведены параметры теплопередачи некоторых обще-
общеизвестных типов оребренных поверхностей.
2.8. НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ ТЕПЛОПЕРЕДАЧИ
Под нестационарными условиями понимают изменение во времени
распределения температуры тела. Особенности протекания этих про-
процессов на границах тела определяются начальными и граничными
условиями.
Для любой задачи нагрева и охлаждения тела процесс передачи
тепла от этого тела к окружающей среде зависит от внутреннего
24
Таблица 2.1
Распределение температуры и тепловой поток в пластине, цилиндре и полой сфере
Формула:
Q=—kF или
dx
dr
Вт;
= Q/(tr — tx) Вт/°С.
Обозначения: tr, tx — температура горячей и холодной поверхно-
поверхности соответственно, СС.
Проводящее тело
Схематическое представ-
представление
Распределение
температуры
Параметр теплопере-
теплопередачи ef?
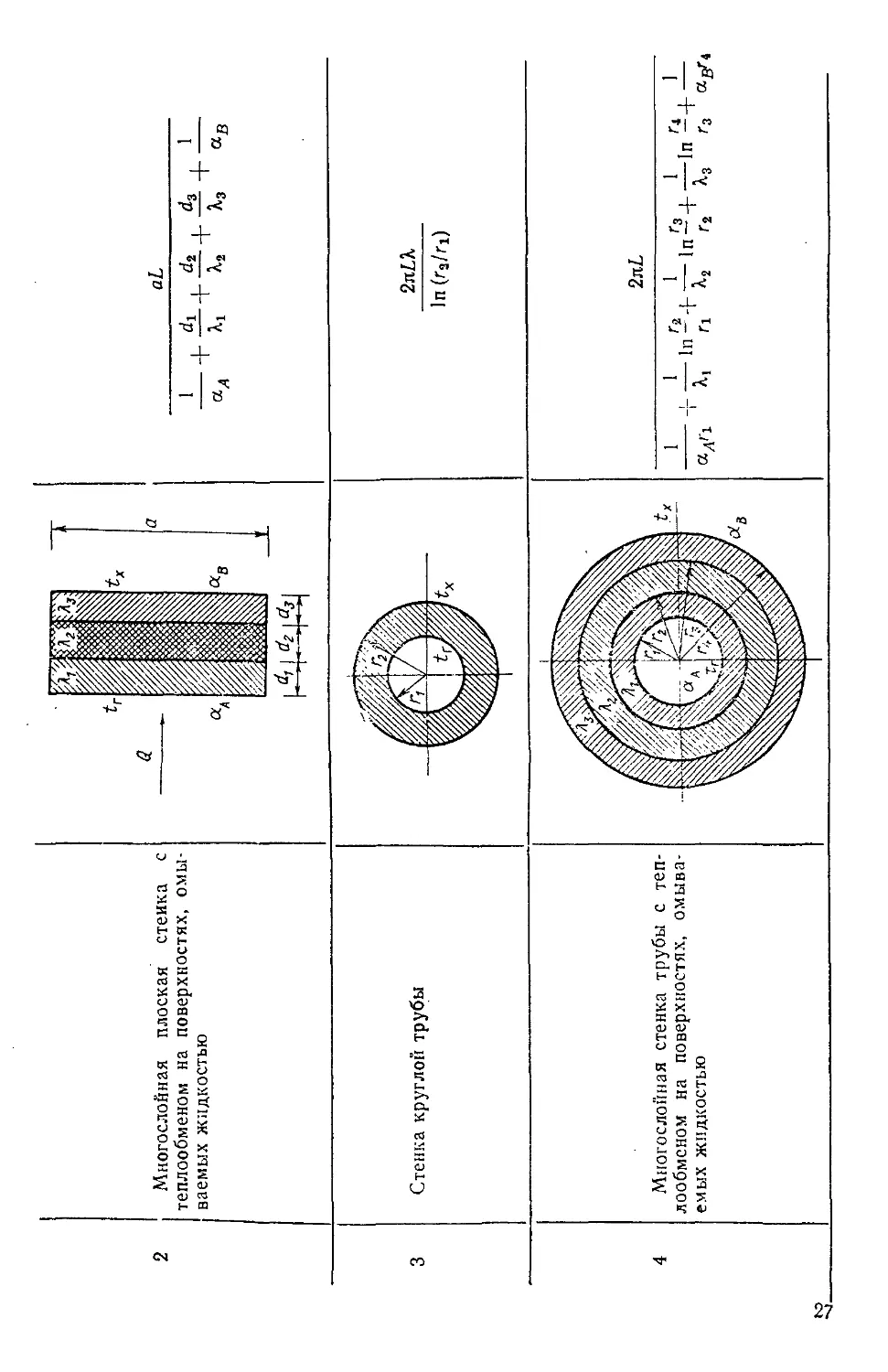
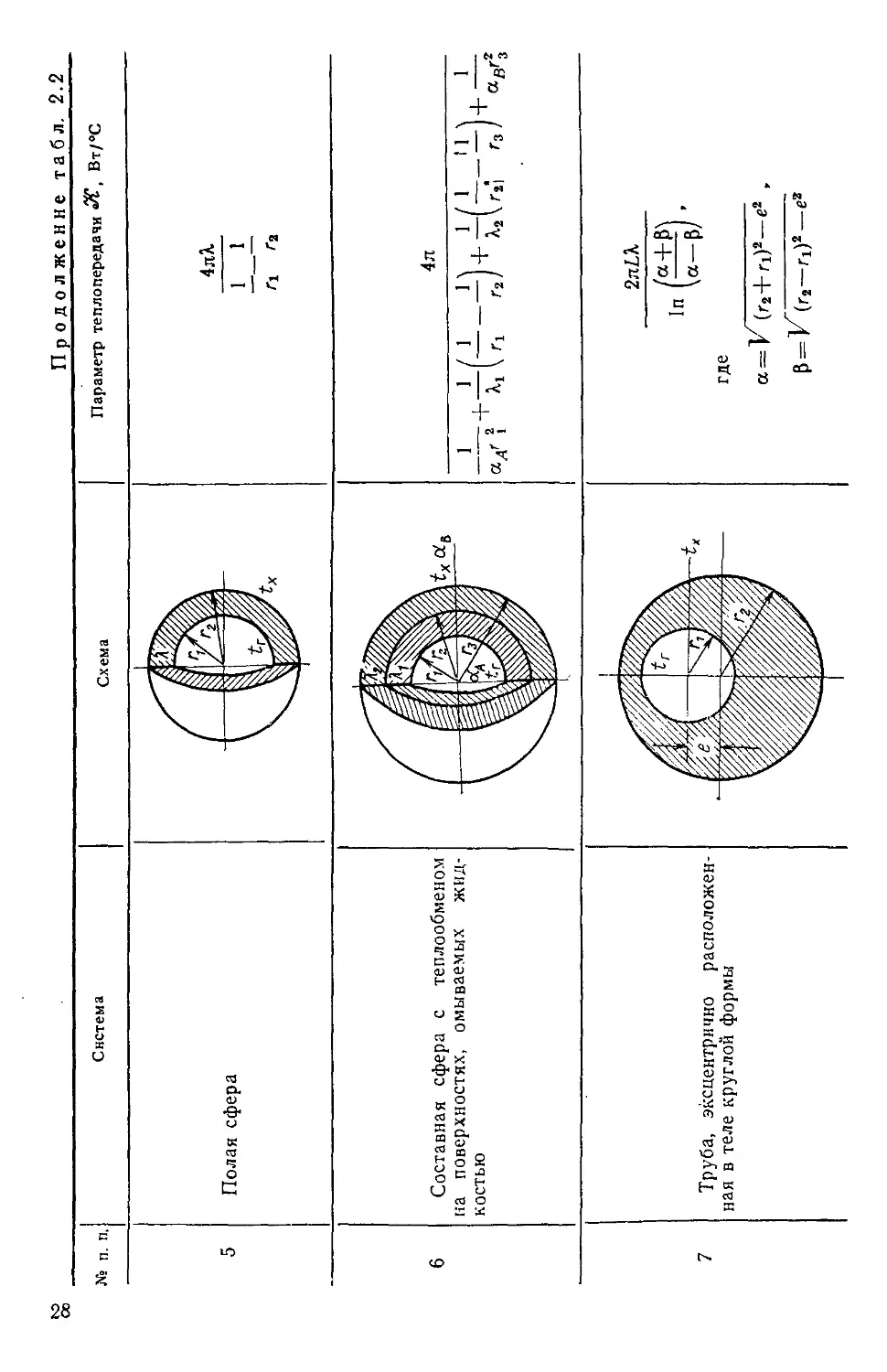
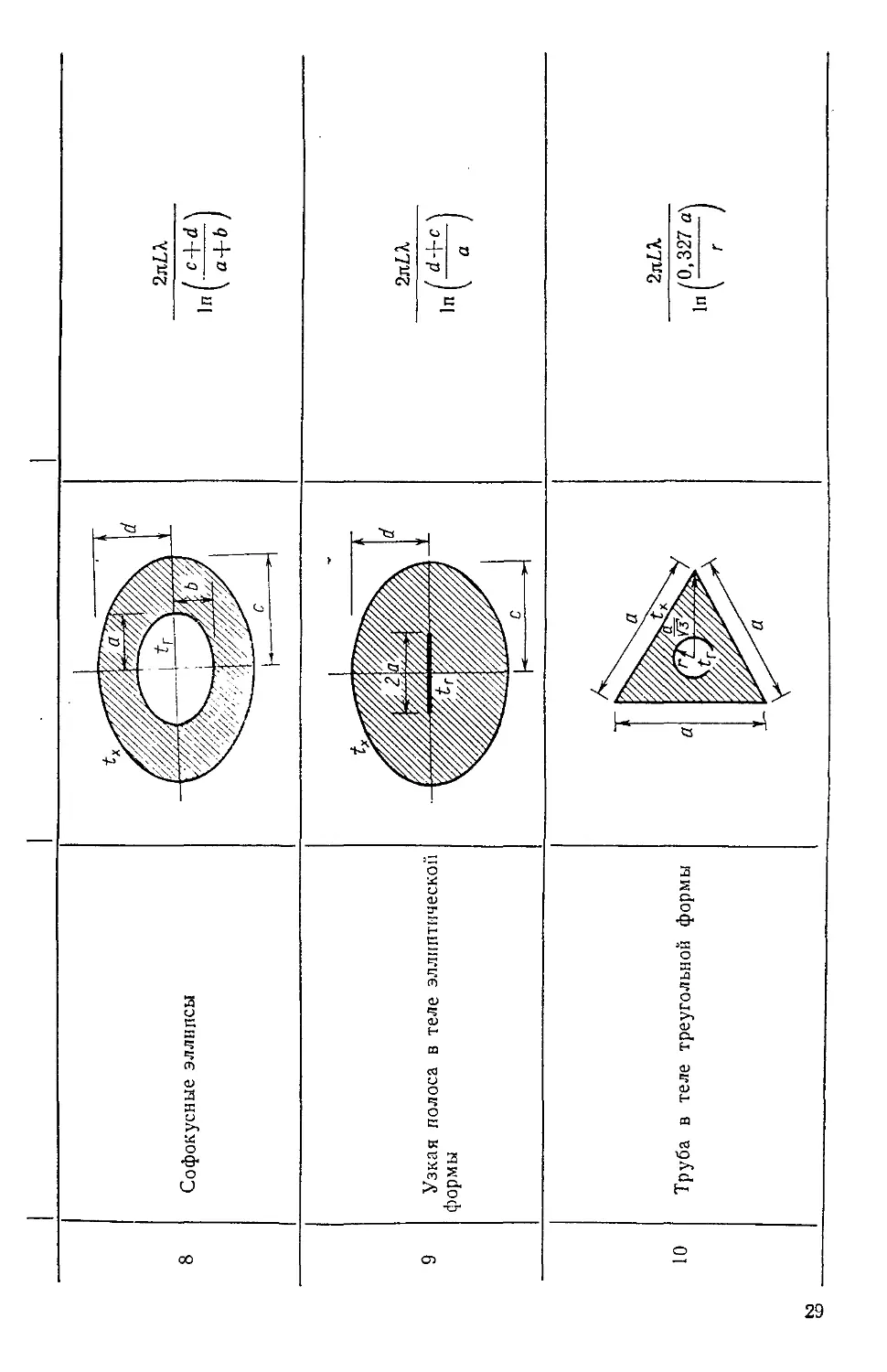
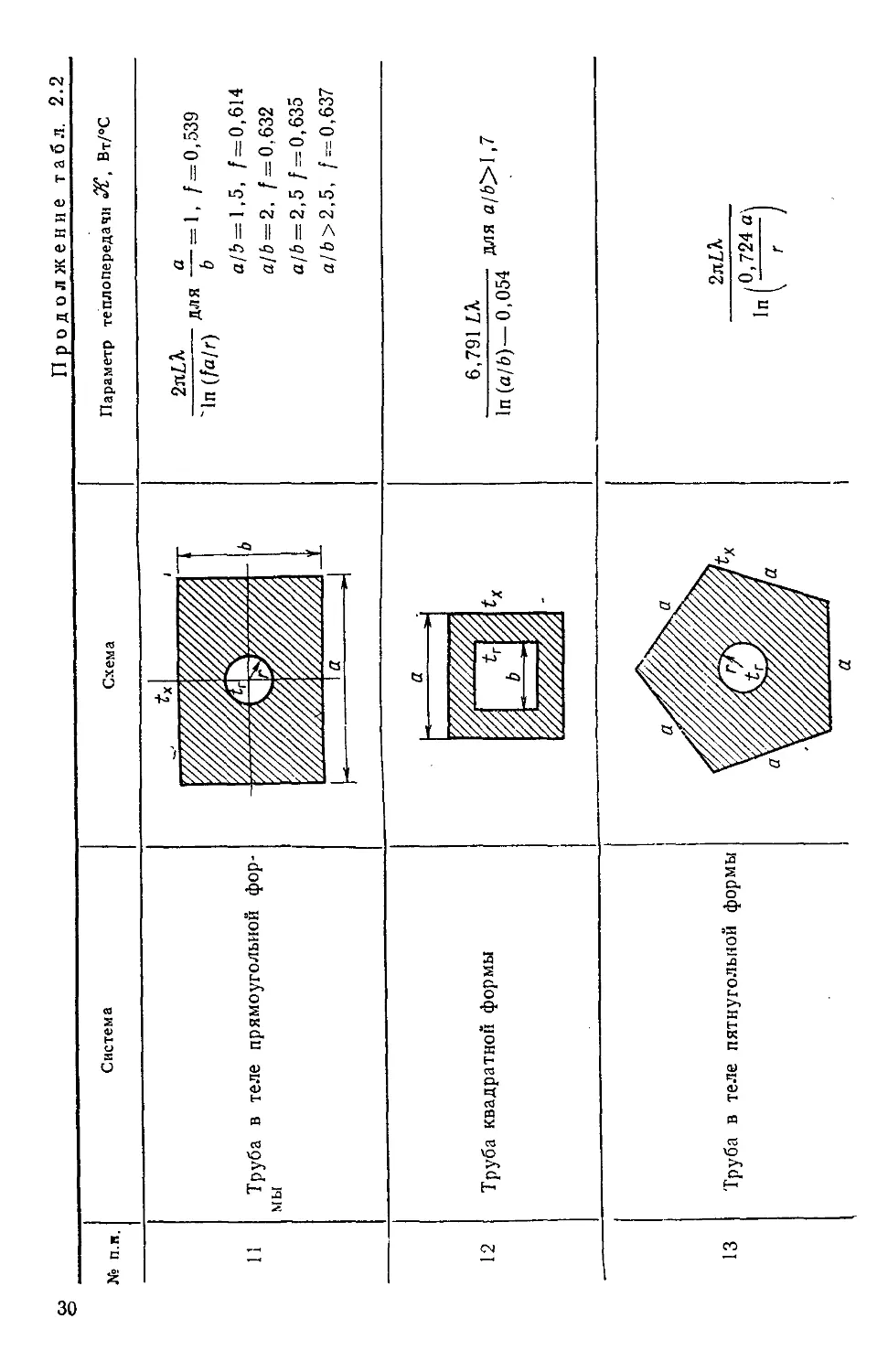
Пластина
Цилиндр
Полая сфера
*г
к d
Длина цилиндра 1
In (г—г2)
In (n — г2)
l/ri-1/r,
In
25
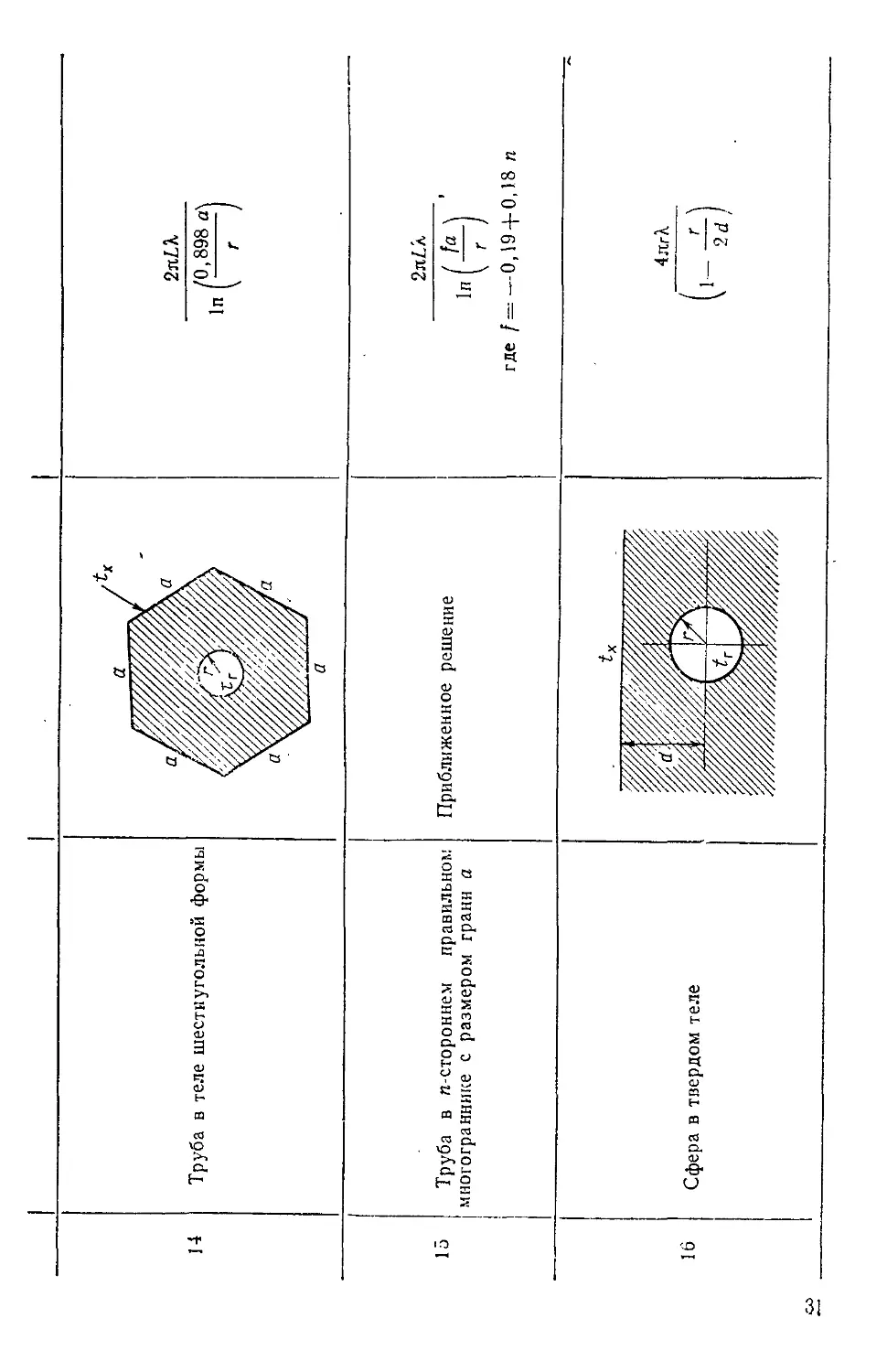
С-4
я
s
ч
\о
а
Н
t-1 U I_
с и -
CQ
ев
s
реж
X
з
X
о.
ев
ацион
В
X
Си
с
S
CJ
ИСТ
и
X
ИЧНЫ
Си
X
S1
5
с
к
X
:ен
раж
а
ю
СО
X
яется
S
S
о.
в
о
CQ
X
в1
се
S
о.
0)
с
о
ч
с
0>
1
-**
1
1
II
СП
Си се
1 8"
9 с
Си
се
С
Плоск
26
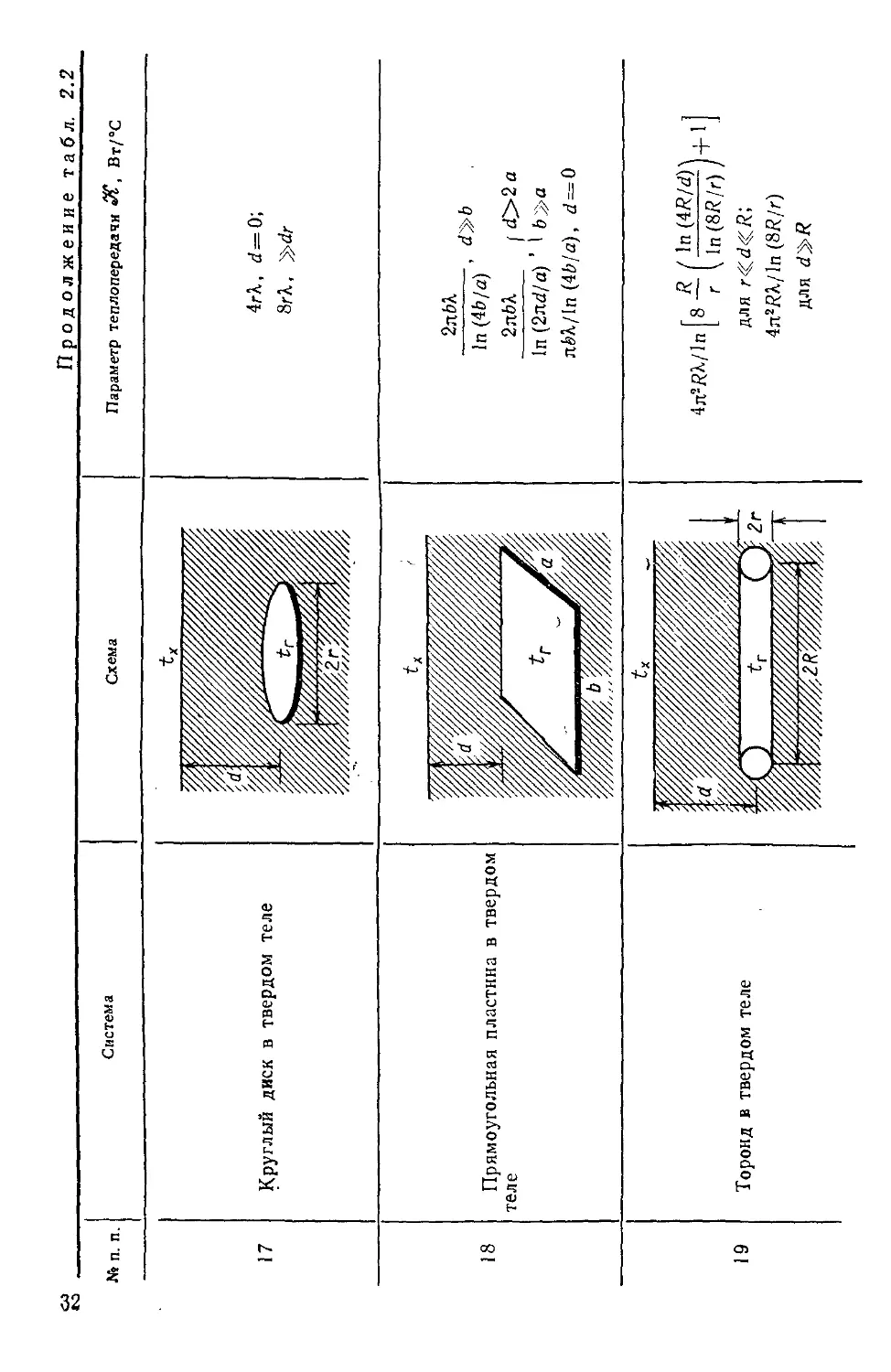
— 8
+
— 8
о
о
ч о
с с
5. с jj
3
ю
>.
о.
н
о
ч
Ст
"~ 8
3
енк;
ерх!
на
чу. g
о о 5
о я с
27
о
ч
а
s
х
о
ч
о
с(
О
о.
с
•е-
к
СО
ч
о
с
03
а
к
я
о
s
VO
о
о
с
о
о.
ф
X
3
со
со
3
г
о
х"
та ч^
о
U
(Я О
I
8
о
ч
о
с
°-з
i!
н о
52
-as-
о.
28
а
о
с
\
О
•е-
о
и
о
•е-
о.
29
с;
ч
о
ЕС
о
с
— ю со
to о со to
- го <?>
о to - о
ii т 1 л
" "а ^" а
о
I
а
I
Л
-J
to
s
о
о
1
с
о
ч
о
о
О!
а.
с
я
3
а.
о
•9-
S
а,
о
•9-
S
с
ш
аз
30
•a
о
X
JO
7.
о,
М-
«я
о
ч
о
м
хо
>,
о.
X а
Si ^
CQ rt
м о.
о. u
cs
о
sf
с «
xSe-
О. 1-
1
о.
0>
•е-
о
31
см
см'
ч
га
s-
ф
я
я
ч
о
о
а
С
о
¦я
a
-о
А
¦а
см а
Л Л
-о
К
см
'а'
с
-о
к
см
•а с
см ~-
' с<
-5 к
о
>=(
о.
к
5
ч
с
CS
я
S
о
I
ч
о
а.
о
32
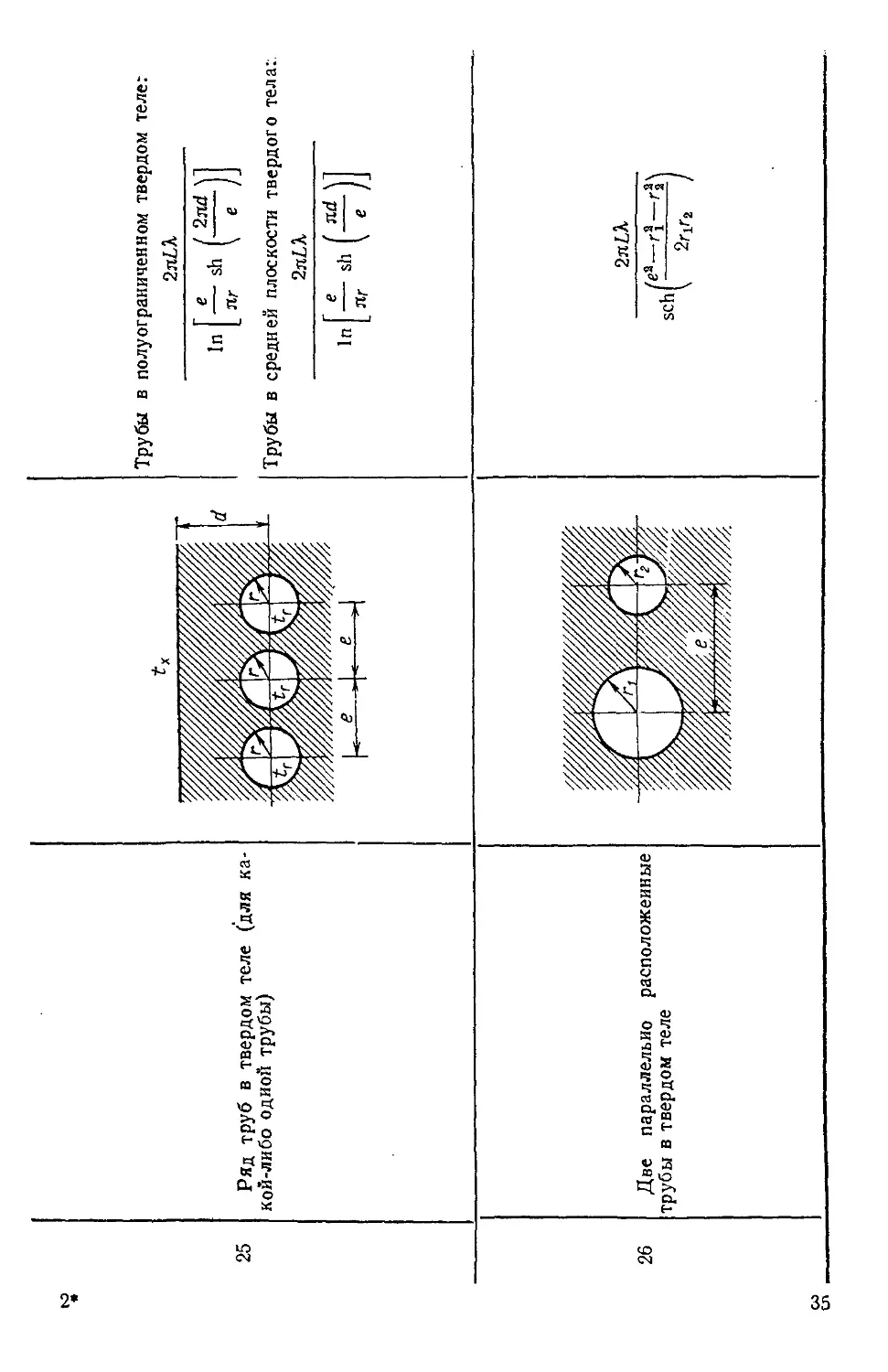
-j
ОТ
см*
п
о
3"
<<
00
см
ч
V
щ
о
01
3 н
я
II
§1
si
о§,
•е-
СМ
2 Основные формулы и данные по топлооб
мену
33
4
Ю
«
v
к
s
v
4
о
fct
о
a
С
s
t
о
i
+
in
s
s
о
ч
8-
ш
о,
3
о,
¦S
о
S
«s
S1
34
СО
СИ
8
X
о.
о.
«о
О)
о.
о
К
3
S
3*
S
Ч
О
и
о
с
1
о
3
о.
о.
1
S
S
О)
I
и
о.
о о *» •*
Н Я О) О)
и к и
s i s
я
о а ?
о|о
«88
я я я
«XX
§¦§¦§¦
So
•з.
JS
i
о
с ~ о »;
u с> (_ а
>>К О О.
.3
±1
x
о
1 I
1
%
>=(
ю
о
S
S
* S
° S-
eg
о
X
о
о,
с-в-
37
термического сопротивления Rs = L/XF и от термического сопротив-
сопротивления на поверхности Rm = 1/aF.
Предельными являются два случая: 1) нулевое внутреннее сопро-
сопротивление (при К-*- сю) и 2) нулевое сопротивление на поверхности
(при а-> со). Все другие варианты находятся между этими край-
крайними случаями и имеют конечные значения величин А. и а. Рассмот-
Рассмотрим предельные случаи отдельно.
Тела с неограниченно высокой теплопроводностью. Простейшим
примером случая нулевого внутреннего сопротивления является
процесс передачи тепла в теле с неограниченно высокой теплопровод-
теплопроводностью (т. е. с незначительным внутренним термическим сопротив-
сопротивлением), температура которого резко изменяется при контакте с теп-
теплоносителем. Обычно предполагается, что температура теплоносителя
/ж — величина постоянная. Следовательно, все полученное (или
генерированное) тепло мгновенно распространяется в материале и тем-
температура тела увеличивается равномерно по всему объему. Решения
могут быть получены с хорошим приближением, если тело, о котором
идет речь, имеет относительно своего объема большую площадь по-
поверхности. Всем этим условиям удовлетворяют такие тела, как тон-
тонкостенные трубы и сферы и тонкие пластины, выполненные из материа-
материала с высокой теплопроводностью. Определяющим уравнением явля-
является соотношение баланса тепла, т. е. количество тепла, полученного
телом, равно количеству тепла, переданного теплоносителем:
pcV — = aF(tm—t). B.18)
Если при х = 0 начальная температура небольшого тела равна
t = /0> то решение для него можно записать в виде
*~*т = ехр [—(aF/pcV) x]. B.19)
Параметр pcV/aF представляет собой постоянную времени, которая
характеризует степень реакции тела на изменение температуры.
В табл. 2.4 приведены соотношения для определения распреде-
распределения температуры в телах с низким внутренним термическим сопро-
сопротивлением.
Тела с низким внешним термическим сопротивлением. В большин-
большинстве случаев, которые могут быть отнесены к этой категории, внутрен-
внутреннее термическое сопротивление взаимодействующих тел значительно
больше внешнего. При этом можно считать,, что существует такая
неограниченно высокая интенсивность конвективного теплообмена,
что мгновенно после начала нагревания или охлаждения первоначаль-
первоначальная температура поверхности тела скачкообразно изменяется до по-
постоянно поддерживаемой температуры окружающей среды tm. Опре-
ляющее дифференциальное уравнение имеет вид
-L-^-=V2<. B.20)
а дт
38
Таблица 2.4
Соотношения для определения распределения температур
в простых телах с низким внутренним термическим сопротивлением (А,~»оо)
Обозначения:
т. — время, с;
*о — начальная температура тела при г = О, °С;
tm — постоянное значение температуры теплоносителя, °С;
t — изменяющаяся во времени температура Тела, °С;
а — коэффициент теплоотдачи, Вт/(м4 • С);
с — удельная теплоемкость материала, Дж/(кг . °С);
р — плотность материала, кг/м3;
F — площадь поверхности, ма;
а — размер стороны, м;
В — постоянная величина, °С/с;
б — толщина, м;
г — радиус, м;
V — объем материала, м3.
в
в'
1
2
3
4
5
6
7
Система
Бесконечная пластина толщиной б
Бесконечный цнлнндр радиусом г
Сфера радиусом г
Короткий цилиндр высотой, равной
удвоенному радиусу г
Неограниченный квадратный стер-
стержень со стороной квадрата а
Куб со стороной а
Тонкостенная труба с толщиной
стенкн б, к внутренней поверхности
которой подводится тепло, а темпе-
температура теплоносителя снаружи
остается постоянной и равной ta. Теп-
Теплообмен осуществляется с обеих по-
поверхностей трубы:
1 '
'-'ж
Распределение температуры
го~гж
ехр[—B<х/брс) т]
ехр [—B ajrpc) т]
ехр [—C а/rpc) т]
ехр [—C а/rpc) т]
ехр [—D а /аре) т]
ехр [— F а/арс) т]
а2 «1 .
ai+аз ai-f-«2
X ехр {—[(«!+«*)/брс] т}
39
Продолжение т л б л. 2.4
в
8
Тонкая
жидкость,
меняется
Система
пластина, погруженная
температура которой
линейно во времени, т.
¦ Вх
в
из-
е.
Распределение температуры
t — {tml)-\-Bx)—pcVBja
4-It t 4-ocVBlaF)
\ \ 0 жи 1 К / J
Xexp[—(af/pcV)T]
'о—'«,
Для одномерного теплового потока уравнение B.20) может быть
приведено к следующему виду:
1 dt d2t
= в декартовых координатах;
а дх дх2
= 1 в цилиндрических координатах;
а дх дг2 г дг
I dt д21 , 2 dt .
= 1 в сферических координатах.
а дх дг2 г дг
B.21)
Для получения аналитического решения обычно используют
принцип суперпозиции. Его реализация возможна, когда граничные
условия и определяющее дифференциальное уравнение линейны
относительно температуры и тепловые свойства X, р и с не зависят
от температуры.
В табл. 2.5 представлены соотношения для определения распреде-
распределения температуры и теплового потока на поверхности четырех систем
простой геометрии.
Тела с конечными значениями теплопроводности и конвективной
теплоотдачи на поверхности. В большинстве практических задач
нагревания и охлаждения теплопроводность материала и коэффициент
конвективной теплоотдачи имеют конечные значения, что и предопре-
предопределяет необходимость рассмотрения и анализа влияния внутреннего
и внешнего сопротивления на теплообмен. Определяющее дифферен-
дифференциальное уравнение в частных производных аналогично уравнениям
B.20), но граничное условие конвективной теплоотдачи требует, что-
чтобы
(f)±*(tni-ts) B.22)
для всех значений х > 0. Простейшими примерами этих случаев
являются системы с одномерным тепловым потоком, для которых
температура окружающей среды может быть принята постоянной.
В табл. 2.6 приведены соотношения, характеризующие теплоотдачу с
поверхности и распределение температуры для четырех различных си-
систем этого типа. Аналитические решения уравнений переходных режи-
режимов теплообмена — задача крайне трудоемкая. Явное преимущество
при решении задач этого типа дает применение техники интегральных
40
преобразований, хотя при этом могут потребоваться определенные
знания высшей математики. Большое число аналитических решений
приведено в работах [2.1—2.8J, а в [2.9—2.17] даны сведения о мате-
математических методах и таблицы с функциями. Могут быть также по-
полезны различные численные и аналоговые методы. Их описание при-
приведено в работах [2.19—2.28].
2.9. УРАВНЕНИЕ ФУРЬЕ — ОСНОВНОЙ ЗАКОН
ТЕПЛОПРОВОДНОСТИ
Уравнение теплопроводности Фурье является фундаментальным урав-
уравнением, которое отражает основные условия распространения тепла
в твердом теле. Приведем его в трех различных системах координат:
а) декартовы координаты
^ii+Jii+_iii.==J_^i B.23)
дх2 дуг дг2 а дх
где а = klpc — температуропроводность;
б) цилиндрические координаты
Z,
дЧ
дг*
.-L
г
дЧ , дЧ
дг*
дг г3 дф
через соотношения
х = г cos ф;
в) сферические координаты
дЧ , 2 dt 1 дЧ
дг* ¦ г дг
дхУ
у = г sin ф;
+ —
1 дЧ
sin
-—i—^1 = _L ^I_ B.25)
г2 tg tf дгЬ а дх
X <
через соотношения:
х = г cos ф -simp;
у — г sin ф -smif»;
z= г cos\|).
Из-за трудности получения аналитичес"
ких решений этих определяющих уравне"
ний в частных производных считается, что
большинство инженерных проблем по теп-
теплопроводности могут быть удовлетвори-
удовлетворительно решены с помощью уравнения
Фурье в предположении одномерности или
двумерности температурного поля.
Широко используемые дифференциаль-
дифференциальные уравнения с основными решениями,
представленными в общей форме, приве-
приведены в табл. 2.7. В табл. 2.8 перечислены общепринятые гранич-
граничные условия для случая передачи тепла теплопроводностью.
41
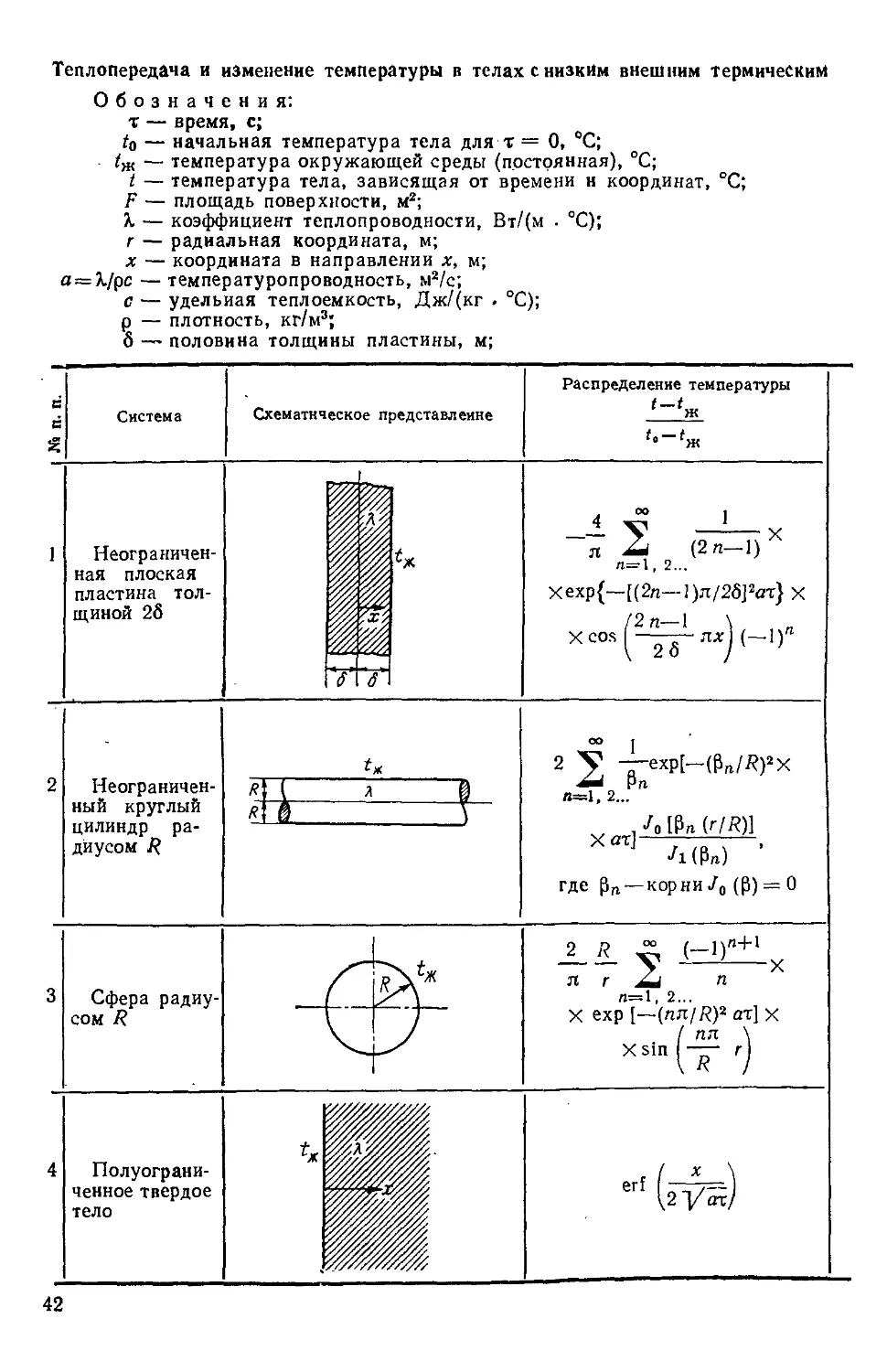
Теплопередача и изменение температуры в телах с низким внешним термическим
Обозначения:
т — время, с;
to — начальная температура тела для т = О, °С;
tm — температура окружающей среды (постоянная), °С;
t — температура тела, зависящая от времени н координат, °С;
F — площадь поверхности, м2;
X — коэффициент теплопроводности, Вт/(м . СС);
г — радиальная координата, м;
х — координата в направлении х, м;
а = Х/рс — температуропроводность, м2/с;
с — удельная теплоемкость, Дж/(кг . °С);
р — плотность, кг/м3;
б — половина толщины пластины, м;
Система
Схематическое представление
Распределение температуры
t — t...
'•-'„
Неограничен-
Неограниченная плоская
пластина тол-
толщиной 26
л
-
X
()
п=\, 2...
Хехр{~[Bя—1)л/2б]2ст} X
12 п-
Xcos
26
ЛХ (-1)"
Неограничен-
Неограниченный круглый
цилиндр ра-
радиусом i?
l, 2...
Хотг]-
где р„ — корни/0 (Р) = О
Сфера радиу-
радиусом R
п г
п=1, 2...
X ехр [—(лл/ЯJ от] X
' лл
Xsin |-— r\
К
Полуограни-
Полуограниченное твердое
тело
erf
-7=^\
42
Таблица 2.5
сопротивлением (а-> оо)
R — радиус цилиндра или сферы, м;
п — целое число A, 2, 3 ...);
Q — тепловой поток с поверхности за единицу времени, Вт;
Qijojih — полное количество тепла, переданного поверхностью за время т,
Дж;
г
erf г — функция ошибок, равная B/~1/я) f е*Р (—Р2) d$;
о
Рп — корни функции Бесселя нулевого порядка;
•Jo (Pn) = 0. например, р\ = 2,405; Р2 = 5,520;
Рз = 8,654; Р4 = 11,792-; Ps = 14,931 и т. д.
^о> А — функции Бесселя первого рода нулевого и первого порядков соот-
соответственно.
Количество тепла, переданного поверх-
поверхностью в единицу времени, <?/(*ж— 'о)
Полное количество тепла, переданного
поверхностью за время т,
2KF 2j ехр{—[Bп—
я=1. 2...
л2а Xj Bл—IJ
n=\, 2...
X
X {1—ехр[—(Bя— 1) л/25J от]}
2
л=1, 2...
на единицу длины
X{l-exp[-(pft//?)*on:]}
на единицу длины
ехР {—
п=1 2...
па
л=1,2...
43
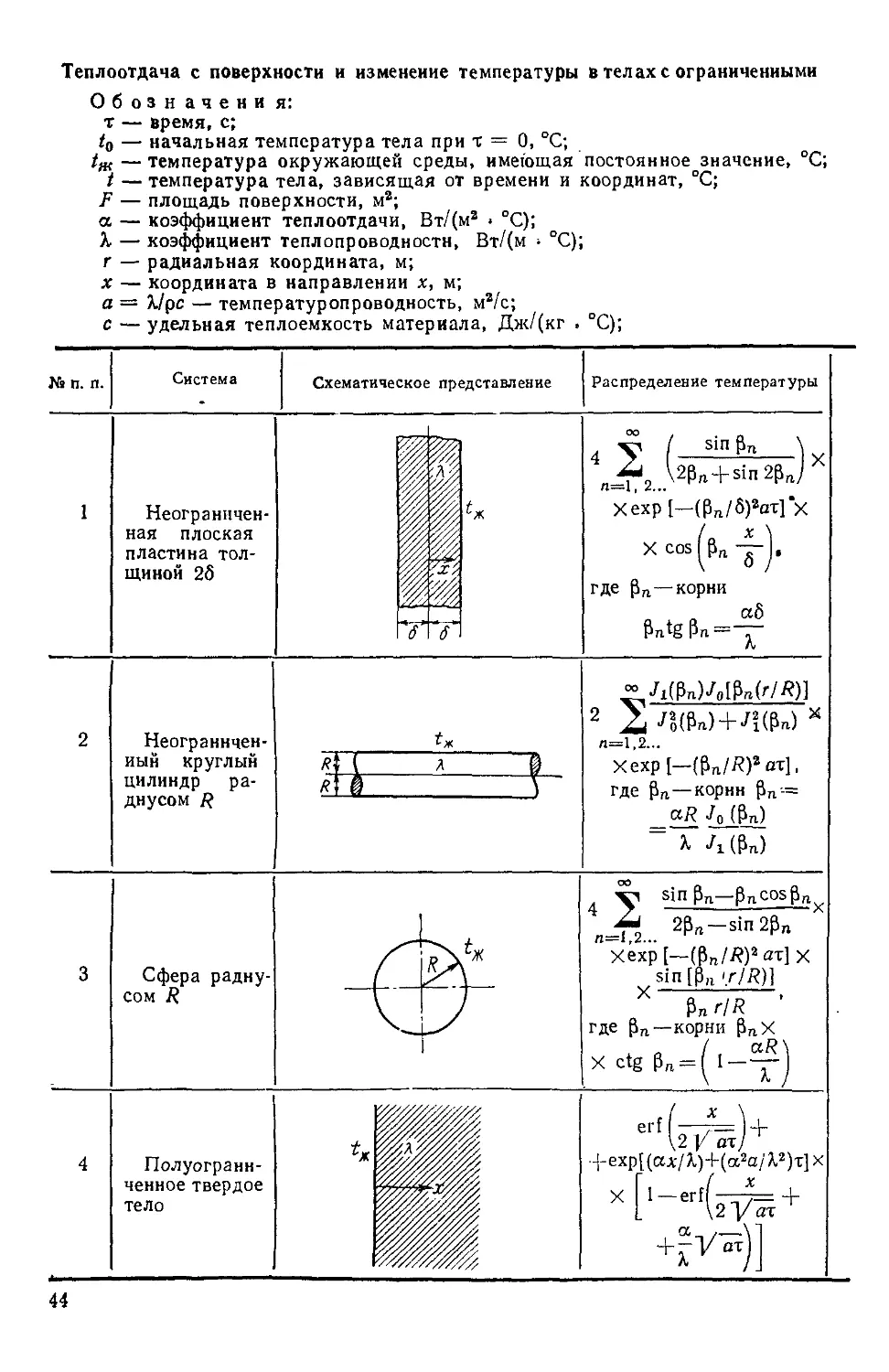
Теплоотдача с поверхности и изменение температуры в телах с ограниченными
Обозначения:
т — время, с;
<о — начальная температура тела при т = О, °С;
tm—температура окружающей среды, имеющая постоянное значение, °С;
t — температура тела, зависящая от времени и координат, °С;
F — площадь поверхности, м2;
а — коэффициент теплоотдачи, Вт/(мг • °С);
Я — коэффициент теплопроводности, Вт/(м • °С);
г — радиальная координата, м;
х — координата в направлении х, м;
а = Я/рс — температуропроводность, мг/с;
с — удельная теплоемкость материала, Дж/(кг . °С);
Система
Схематическое представление
Распределение температуры
Неограничен-
Неограниченная плоская
пластина тол-
толщиной 26
I
X
X cos IPn-g-
где Pn—корни
Ptp
Неограннчен-
ный круглый
цилиндр ра-
днусом R
Я
2i
л=1,2...
Хехр[-(Ря/Л)гат],
где рп—корнн Р„--=
Сфера радну
сом R
п^2
хёхр[-Fп/?Jат]х
sin [рд ».r//?)l
Pn rlR '
где f>n— корни р
(
Полуогранн-
ченное твердое
тело
'"(п^П
44
Таблица 2.6
значениями внутреннего и внешнего термического сопротивления
р — плотность материала, кг/м3;
б — половина толщины пластины, м;
R — радиус цилиндра или сферы, м;
п — целое число (I, 2, 3 ...);
Фполн — полное количество тепла, переданного поверхностью за время т, Дж;
2 г-
erf z — функция ошибок, равная гт= i ехр (—Р2) dp;
]/я о
Рп — корни трансцендентных уравнений;
/0, Ji — функции Бесселя первого рода нулевого и первого порядка соответ-
соответственно.
Количество тепла, переданного поверх-
поверхностью за единицу времени, Ql(t t)
Полное количество тепла, переданного
поверхностью за время х, QH^
OF v
б &
n=I,2...
sin2
? (Pa)
X
X exp [—($nIRJcn)—на единицу
длины
4л№
/? (Pn)
X
х{1 — ехр[—$п!Ю*ат]}—на еди-
единицу длины
16 nXR
(sin Pn-Pn
n=l,2...
Pn B pn—sin 2 pn)
X
1тгЬ
Xexp (-(
45
Основные решения некоторых распространенных
дифференциальных уравнений теплопроводности
Таблица 2.7
Обозначения:
t — температура, °С;
х, у, г — декартовы координаты;
г, Ф, г — цилиндрические координаты;
г> т > 'Ф — сферические координаты;
а = мер — температуропроводность, м2/с;
<7d — объемная плотность источников тепла, Вт/м3;
X — коэффициент теплопроводности, Вт/(м > °С);
с — удельная теплоемкость, Дж/(кг . °С);
р — плотность материала, кг/м3;
т — время, с;
тг = aP/XS, м-а;
Р — периметр, м;
S — площадь поперечного сечения, м2;
Jn, Уп — функции Бесселя первого и второго рода /г-го порядка;
Ль Кп — модифицированные функции Бесселя первого и второго рода /г-го
порядка;
Рп, Qn — функции Лежандра первого н второго рода /г-го порядка;
? — собственные числа.
Интегральные постоянные Си С2 н ? определяются из начальных и гранич-
граничных условий задачи.
Дифференциальное
уравнение
Общее решение
Примечание
Стационарное состояние
= 0
dH
d2t
-—m2t = i
.-?jl=o
d*t
dx*
_
dr2
dr
dr2
r
d4
dr
dt
/ = Ci sin /m + C2 cos тд;
f = Cx sh ид; + C2 ch mx
Одномерная задача,
пластина
Теплообмен между
поверхностью и окружа-
окружающей средой
То же
Одномерная задача с
внутренним источни-
источником тепла <;„
Двумерная задача,
плита
Симметричная зада-
задача в цилиндрических ко-
координатах
Задача с внутренним
источником тепла в ци-
цилиндрических коорди-
координатах
Основная одномерная
задача в цилиндриче-
цилиндрических координатах
46
П р о до л ж е н ие та б л. й.7
Дифференциальное
уравнение
Общее решение
Примечание
cPt
dt
дЧ_ 1 _dt_
дг* г дг
дЧ
дг2
~
дг2
±*+4= о
dr2 г dr
dt
dr
dr
) 1 д
П' А
dip
=0
X Pn (cos
Основная
задача в цилиндриче-
цилиндрических координатах
Двумерная симмет-
симметричная задача в цилинд-
цилиндрических координатах
Двумерная задача в
цилиндрических коор-
координатах
Одномерная задача в
сферических координа-
координатах
Основная одномер-
одномерная задача в сфериче-
сферических координатах
Двумерная задача в
сферических коорднна-
Нестационарное состояние
дх2
—
дх
d2t J_ dt_ 1_ д^
дг*+ г дг~~ а дх
ZL 2 —-- _?_
дг2 г дг~ а дт
t = i
V?)]
Одномерная
плита
задача,
Одномерная задача в
цилиндрических коор-
координатах
Одномерная задача в
сферических координа-
координатах
47
Граничные условия при теплообмене теплопроводностью
Таблица 2.8
Обозначения:
а — коэффициент теплоотдачи, Вт/(м2 • °С);
»л — лучистый коэффициент теплоотдачи, Вт/(м2 • °С);
«л = еа0 (/» + ?) (ts + /ж);
X — коэффициент теплопроводности, Вт/(м . °С);
р — давление иа границе, Н/м2;
qs — плотность теплового потока, Вт/м2;
Ф — угловой коэффициент;
и — относительная скорость, м/с;
Т — абсолютная температура, К;
е — коэффициент излучения (степень черноты поверхности);
о"о — постоянная Стефана—Больцмана;
/ — коэффициент трения.
Индексы:
к — конвекция;
ж — жидкость или окружающая среда;
s — поверхность.
№
п. п.
1
2
3
4
5
6
7
8
Граничное условие
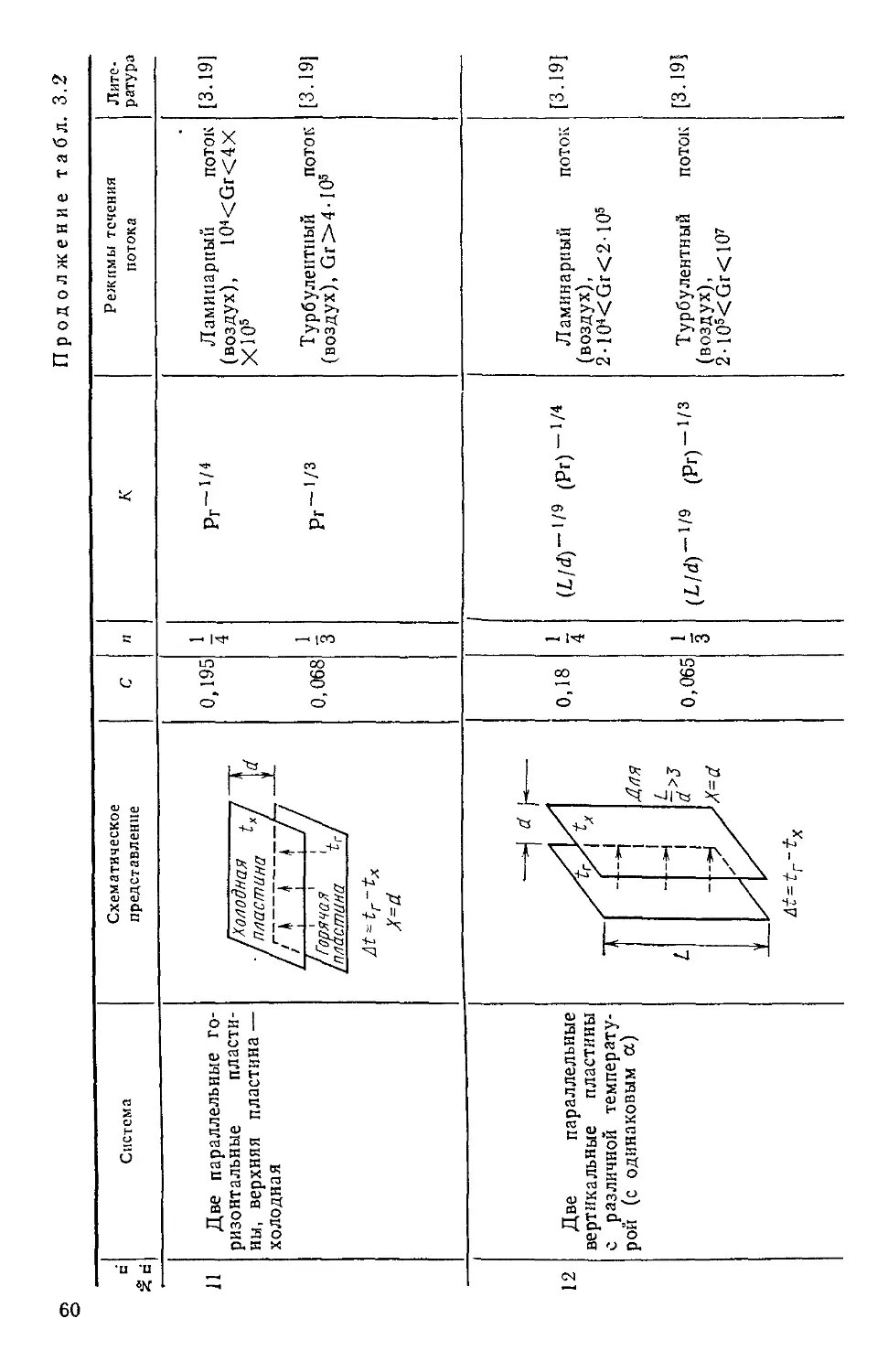
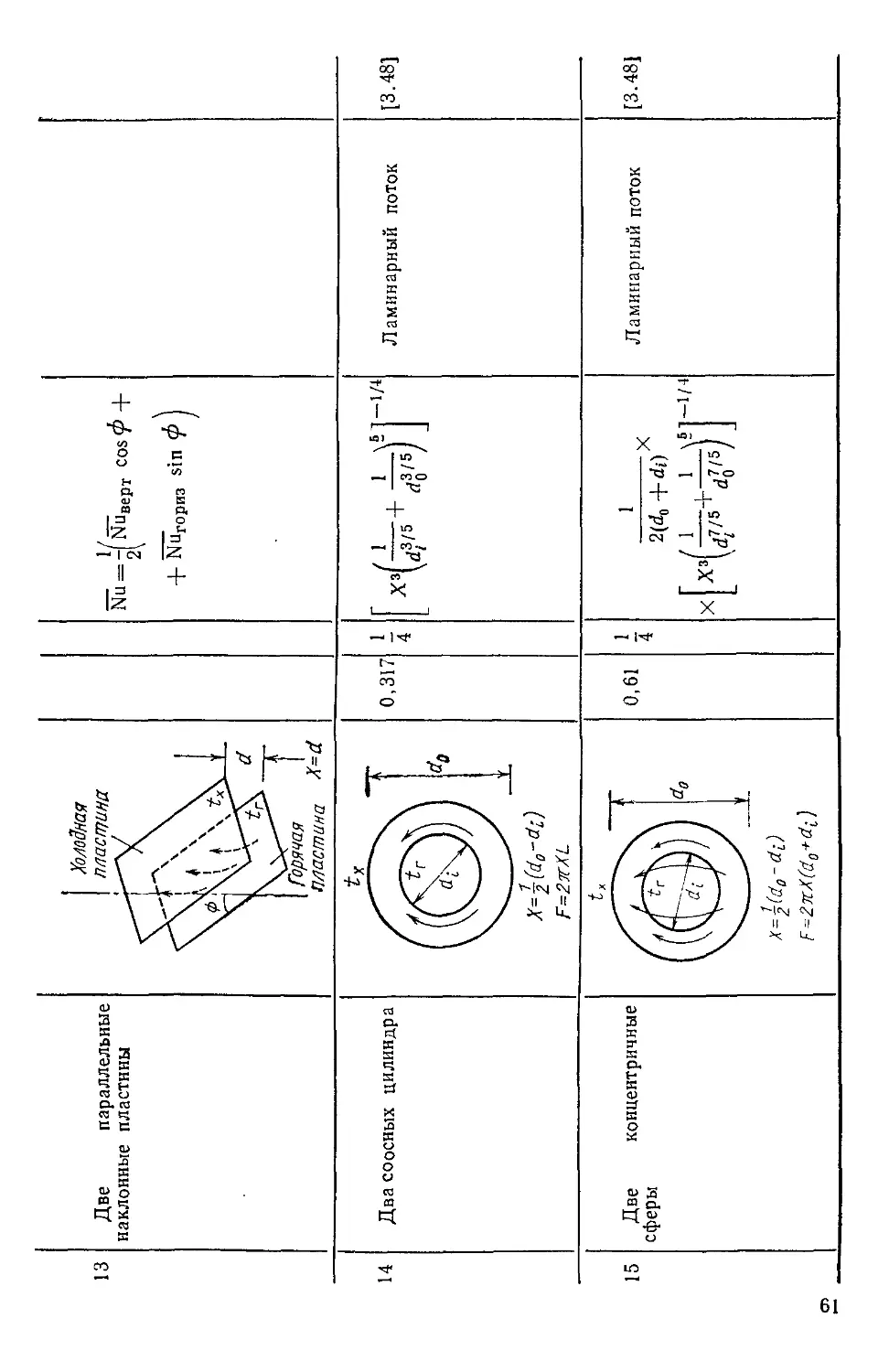
Температура на границе описывает¦•
ся выражением />к=/(т) прн низком
внешнем термическом сопротивлении
Изолированная поверхность
Постоянный тепловой поток на по-
поверхности
Границы двух тел с различной теп-
теплопроводностью прн плотном контак-
контакте и с низким контактным термиче-
термическим сопротивлением
Границы двух тел с различной теп-
теплопроводностью при скользящем кон-
контакте
Конвективный теплообмен на гра-
границе
Лучистый теплообмен на границе
Лучистый и конвективный тепло-
теплообмен на границе
Аналитическое выражение
\ дп 1,
/ dt \
V дп Is
, /дМ ( dtt\
\дп Js \ an Js
! dU \ 1 dU \
V дп Js \ дп js
I dt \
ъ{— )s = a(ts—tm) +
\dnf
+еа0 (Г|-Г^)~(ал+ас) х
Х(Гв-Гж)
48
СПИСОК ЛИТЕРАТУРЫ
2.1. Fourier J. В. J. Theorie analytiquc de la chalcur, Paris, 1822, English transl.
(Freeman). Cambridge, 1878.
2.2. Carslaw M. S., Jaeger J. С Conduction of Heat in Solids. 2nd ed. Clarendon
Press. Oxford, 1959.
2.3. Ingersoll L. R., Zobel O. J. Mathematical Theory of Heat Conduction. Boston,
Ginn and Co., 1913.
2.4. Ingersoll L. R., Zobel O. J., Ingersoll A. C. Heal Conduction. University of
Wisconsin Press, Madison, 1954.
2.5. Schneider P. J. Conduction Heat Transfer. 6th ed. Addison-Wesley, 1974.
2.6. Ozisik M. N. Boundary Value Problems of Heat Conduction. International
Textbook Co., 1968.
2.7. Arpaci V. S. Conduction Heat Transfer. Addison-Wesley, 1966.
2.8. Heat Transfer Notes. McGraw-Hiii, 1965. Auth.: L. M. K- Boelter, V. M. Cher-
Cherry, H. A. Johnson, R. С Martinelly.
2.9. Myers G. E. Analytical Methods in Conduction Heat Transfer. McGraw-Hill,
1971.
2.10. Carslaw M. S., Jaeger J. С Operational Methods in Applied Mathematics. Cla-
Clarendon Press. Oxford, 1949.
2.11. McLachlan N. W. Complex Variable Theory and Transform Calculus. Cambrid-
Cambridge University Press, 1953.
2.12. McLachlan N. W. Bessell Function for Engineers. Oxford, Clarendon Press,
1955.
2.13. Hildebrand F. B. Advanced Calculus for Engineers. Prentice-Hall, 1948.
2.14. Churchill R. V. Fourier Series and Boundary Value Problems. McGraw-Hill,
1963.
2.15. Scatt E. J. Transform Calculus. Harper, 1955.
2.16. Снеддон И. Преобразование Фурье. Пер. с англ. М., Изд-во иностр. лнт.,
1955.
2.17. Erdelyi A. Tables of Integral Transforms. McGraw-Hill, 1954.
2.18. Selby S. M. Standard Mathematical Tables. 17th ed. Cleveland, Ohio, Chemical
Rubber Co., 1969.
2.19. Boumeister K. J., Hamill T. D. Hyperbolic Heat Conduction Equation. — «J.
Heat Transfer», 1969, v. 91, № 4, p. 543—548.
2.20. Dusinberre G. N. Heat Transfer Calculations by Finite Differences. Interna-
tion Textbook, 1961.
2.21. Dusinberre G. N. Numerical Analysis of Heat Flow. McGraw-Hill, 1949.
2.22. Crandall S. H. Engineering Analysis. McGraw-Hill, 1956.
2.23. Todd J. A Survey of Numerical Analysis. McGraw-Hill, 1962.
2.24. Southwell R. V. Relaxation Methods in Engineering Science. Oxford Univer-
University Press, 1940.
2.25. Allan D. N. G. Relaxation Methods. McGraw-Hiii, 1954.
2.26. Haji-Sheikh A., Sparrow E. M. The Solution of Heat Conduction Problems by
Probability Methods. — «Heat Transfer», 1967, v. 89, № 3, p. 121—131.
2.27. Brown G. M. Monte-Carlo Methods. — In: Modern Mathematics for the En-
Engineers. Ed. by E. F. Beckenbach. McGraw-Hiii, 1956.
2.28. Liebmann G. A New Electrical Analogue Method for the Solution of Tran-
Transient Heat Conduction Problems. — «Trans. ASME», 1956, v. 78, p. 3.
2.29. Chao В. Т. Advanced Heat Transfer. Univ. of Illinois Press. Urbana, 1969.
2.30. Gardner K- A. Efficiency of Extended Surfaces. — «Trans. ASME», 1945, v. 67,
p. 621—631.
2.31. De Venbeke. Structural Dynamic Heat Conduction. International Centre for
Mechanical Sciences. Springer-Verlag, 1974.
2.32. Parrott J. E., Stuckes A. D. Thermal Conductivity of Solids. Academic Press,
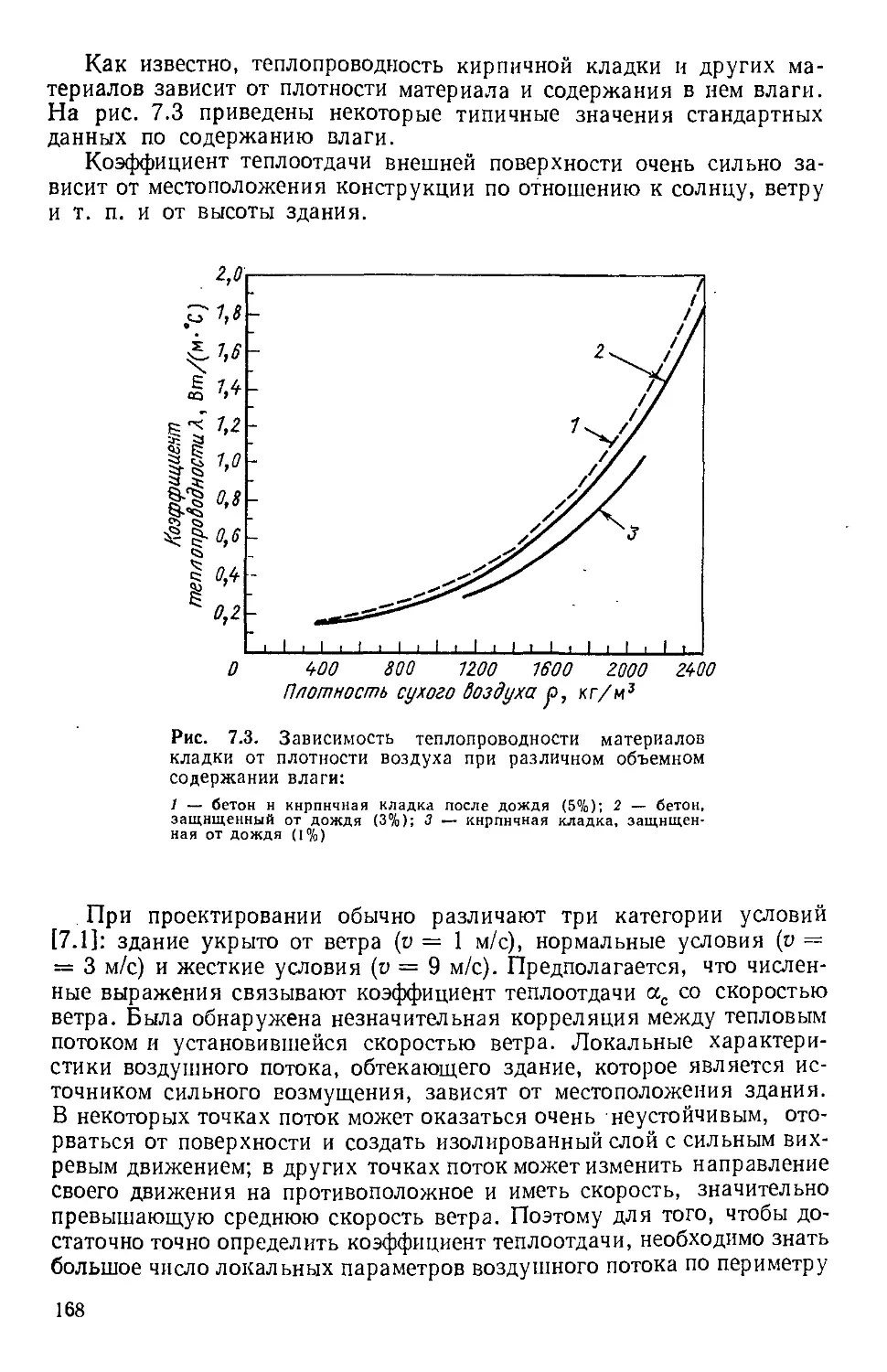
1975.
2.33. Balcerzak M. J., Raynor S. Steady State Temperature Distribution and Heat
Flow in Prismatic Bars with Isothermal Boundary Conditions. — «Intern.
Heat and Mass Transfer», 1961, v. 3, № 2, p. 113—115.
2.34. Smith J. C, Lind J. E., Lermond D. S. Shape Factors for Conductive Heat
Flow. — «J. Appl. Chem.», 1958, v. 4, p. 330.
Глава 3
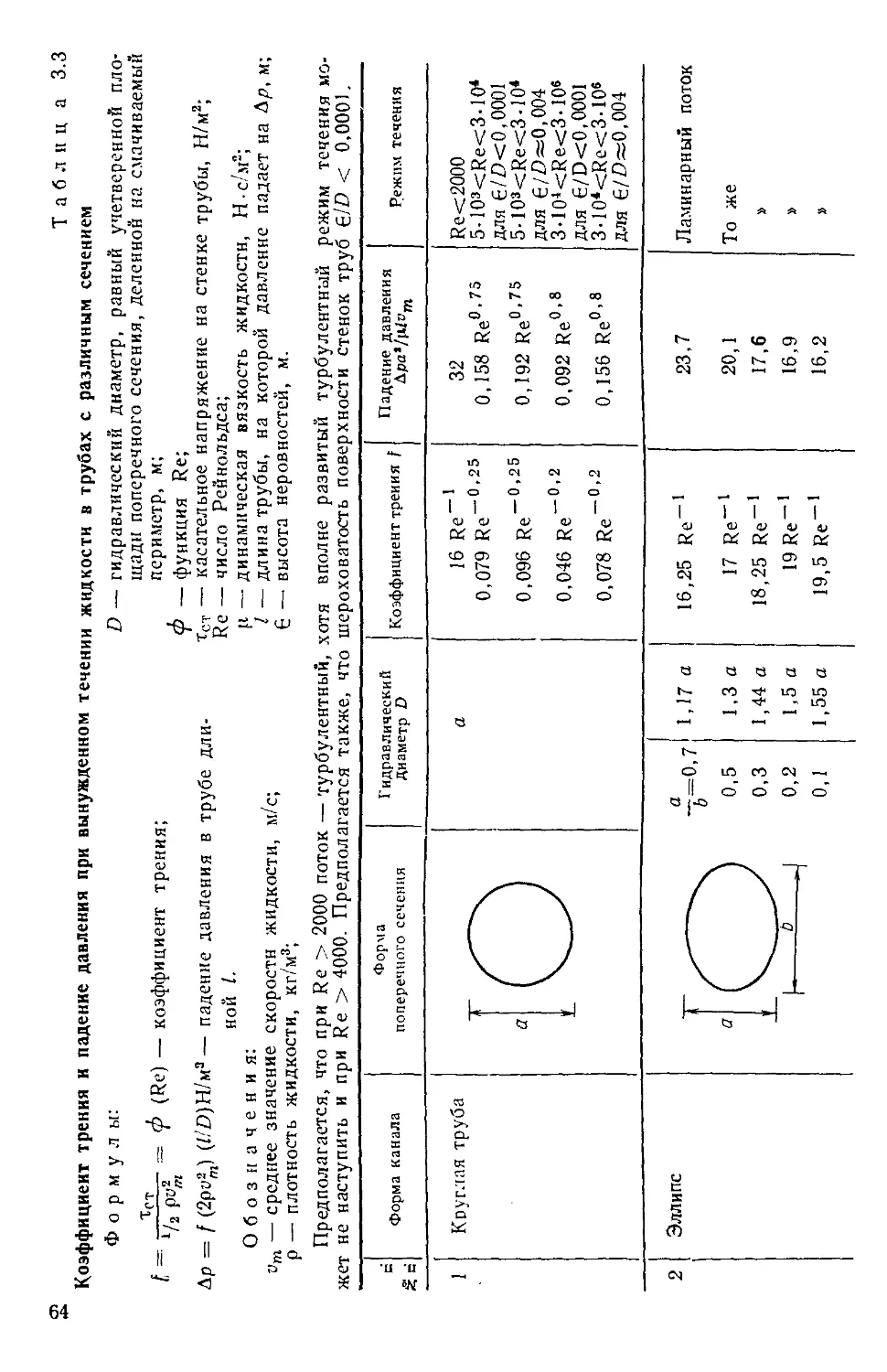
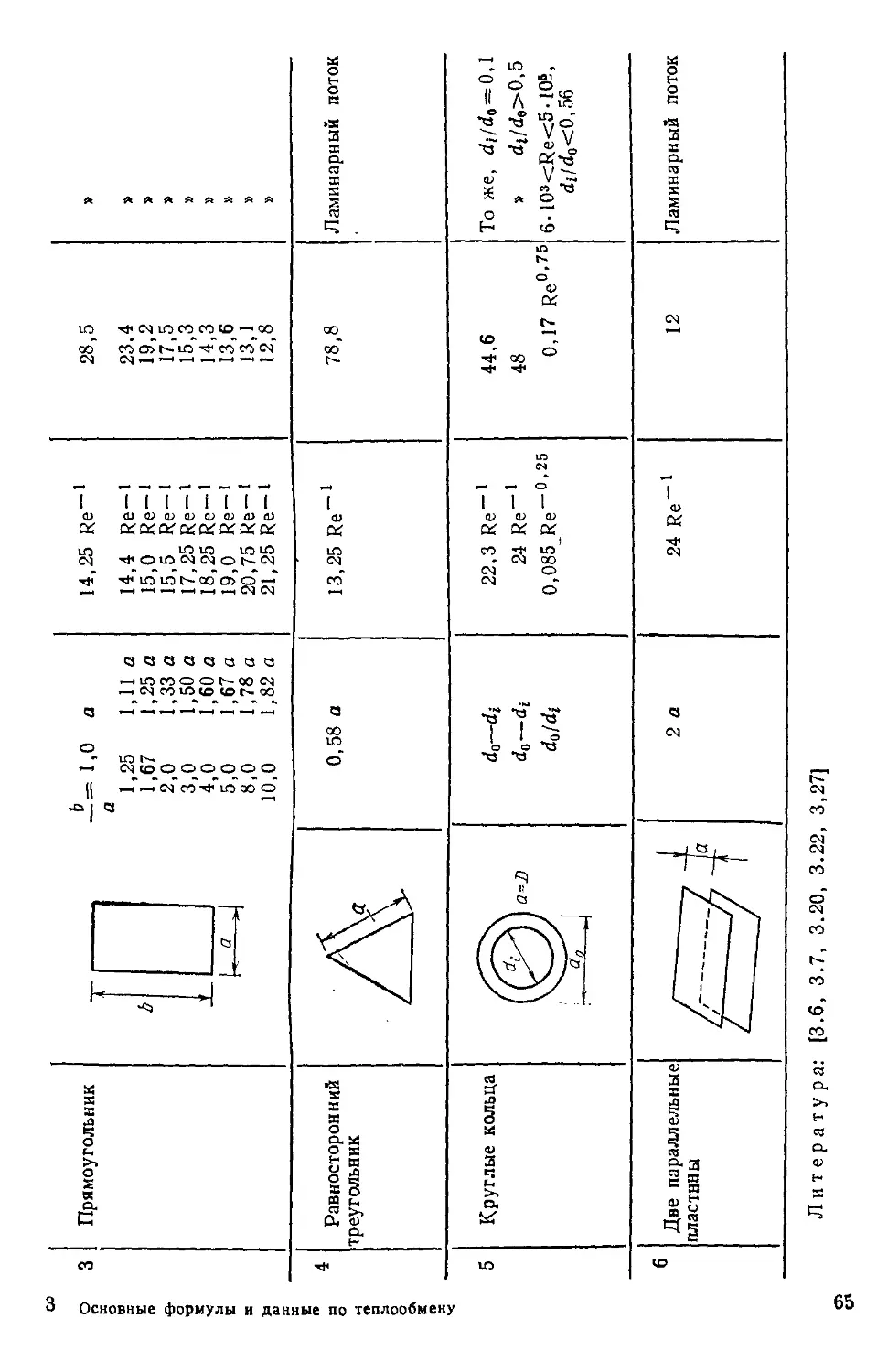
КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
3.1. ВВЕДЕНИЕ
Конвективный теплообмен или теплоотдача представляет собой про-
процесс передачи тепла между твердым телом и окружающей его средой.
В зависимости от причин движения жидкости различают теплоот-
теплоотдачу при естественной конвекции и теплоотдачу при вынужденной
конвекции. В первом случае движение жидкости происходит под дей-
действием силы тяготения и обусловлено различием плотности от-
отдельных нагретых участков жидкости; во втором случае это
движение обусловлено силами, не зависящими от разности температур
в ней и возникающими под воздействием внешней разности давления.
Конвективный теплообмен между жидкостью и граничной поверх-
поверхностью определяется с помощью выражения
Q= aF(tCT~tm) Вт, C.1)
которое известно как уравнение теплоотдачи Ньютона [см. уравнение
B.9)]. В то время как формула сама по себе очень проста, коэффициент
теплоотдачи а представляет собой очень сложную функцию потока жид-
жидкости, ее теплофизических свойств и геометрических параметров сис-
системы. Как правило, за исключением незначительного числа простей-
простейших случаев, получить точные аналитические решения этого урав-
уравнения не представляется возможным и поэтому привлекаются приб-
приближенные методы. Для большинства практических задач коэффици-
коэффициент теплоотдачи оценивают по эмпирическим уравнениям, полученным
обработкой экспериментальных результатов методом анализа размер-
размерностей. Коэффициент а обычно выражают через соотношение между
одним зависимым безразмерным комплексом — числом Нуссельта
Nu — и тремя другими независимыми безразмерными комплексами —
числами Рейнольдса Re, Грасгофа Gr и Прандтля Рг, зависящими от
вида конвекции (естественная или вынужденная). В табл. 3.1 приве-
приведены сравнительные данные по двум видам конвекции.
3.2. ОБОЗНАЧЕНИЯ
/ — характерный размер, м;
с — скорость звука, м/с;
S — площадь поперечного сечения, м2;
ср — удельная теплоемкость при постоянном давлении,
Дж/(кг • °С);
С— константа, определяемая в уравнениях C.3) и C.4);
/ — коэффициент трения;
50
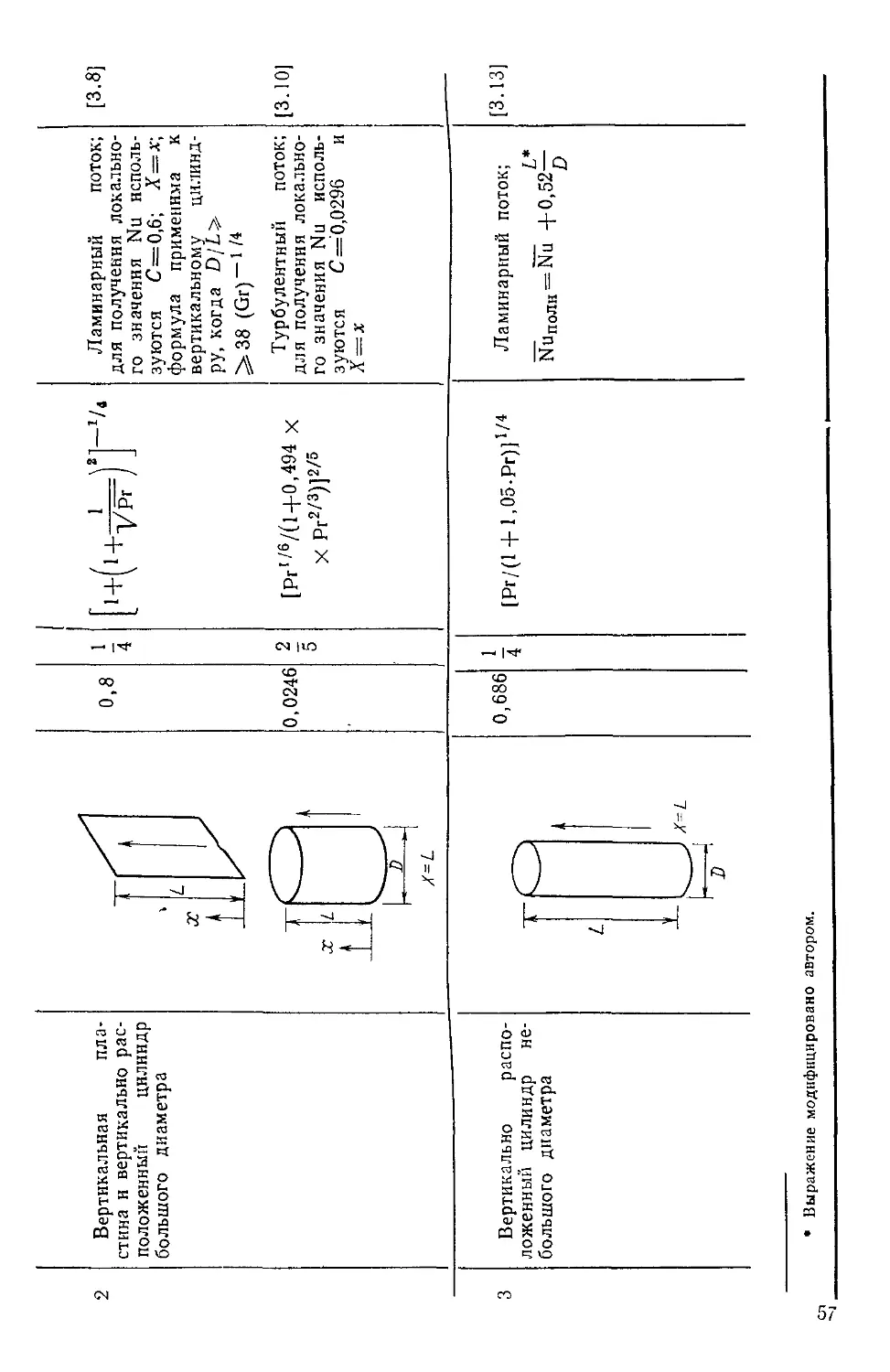
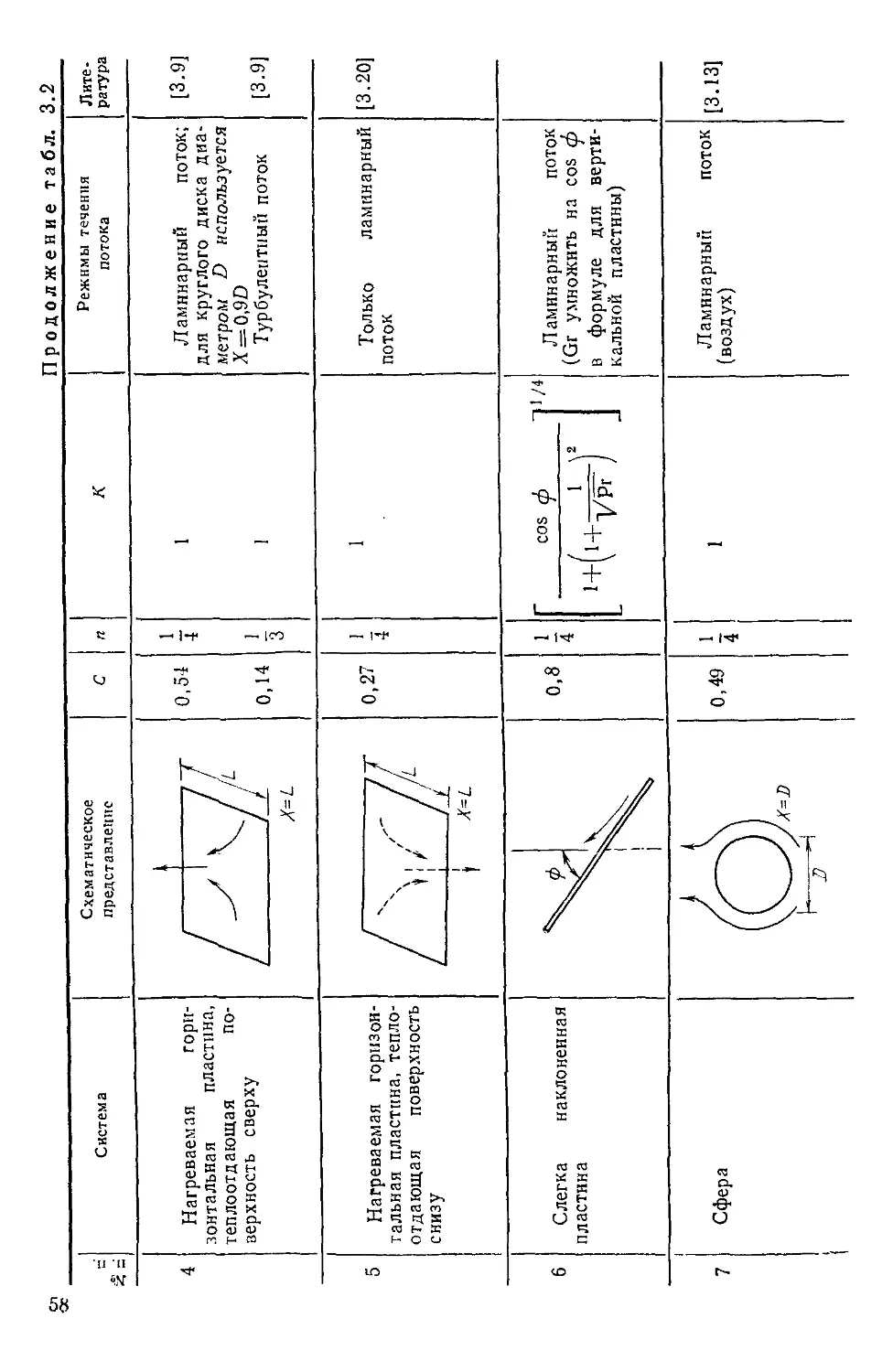
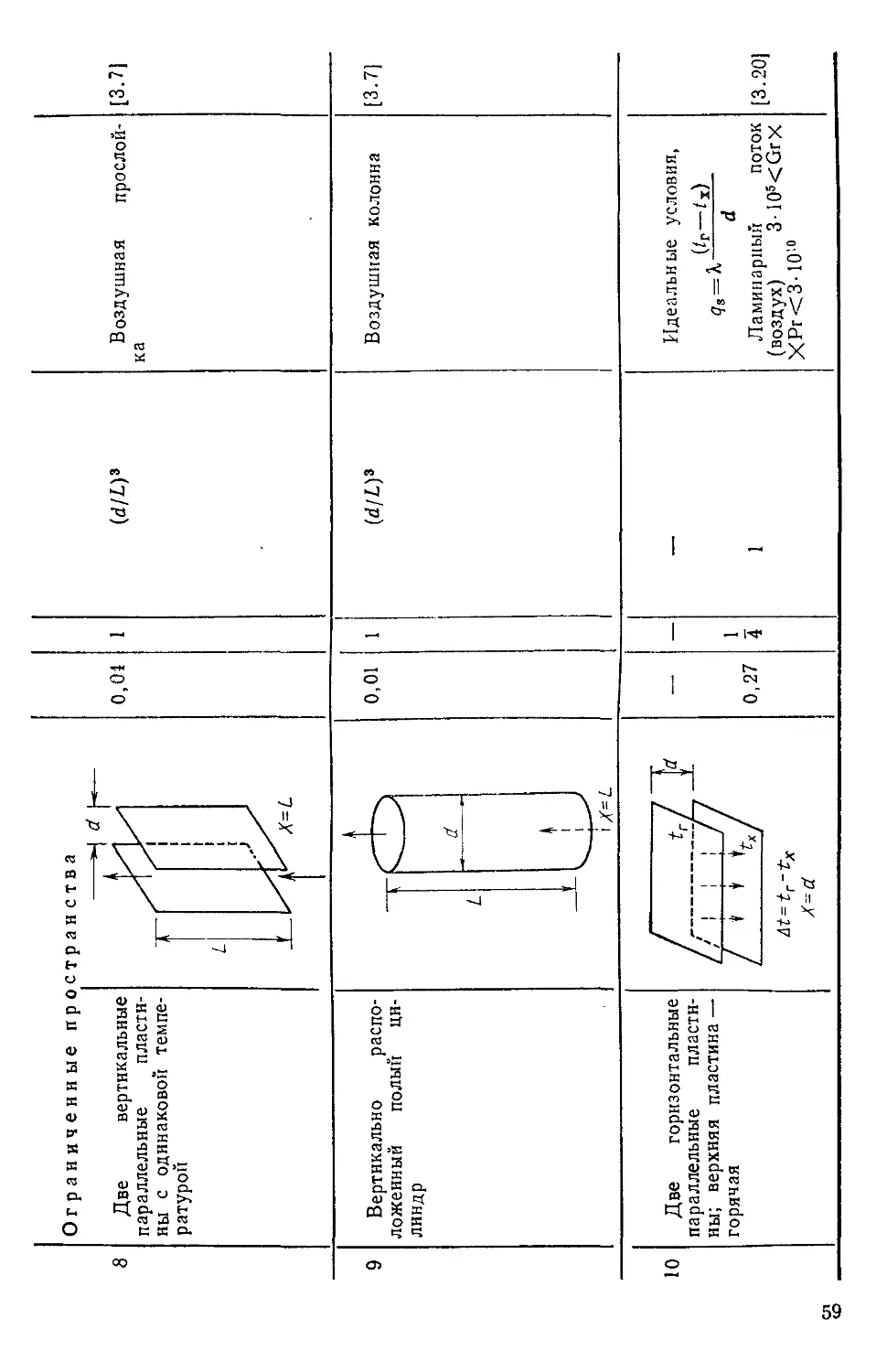
Таблица 3.1
Сравнение параметров естественной и вынужденной конвекции
1 1 л #4*1 Ч йтП
I idpaMcTp
Причина движения
ЖИДКОСТИ
Соотношение между
определяющими без-
безразмерными параметра-
параметрами
Критерий, определя-
определяющий переход ламинар-
ламинарного потока в турбулент-
турбулентный
ищи
Превалирующий па-
параметр теплопередачи
Источник энергии
Естественная
конвекция
Внутренние силы (гра-
(гравитационная сила)
Nil = / (Gr, Pr)
Gr>10s_
Nu-Gr1/4,
ламинарный;
Nu-Gr1/3,
турбулентный
Потенциальная энер-
энергия (обусловлена раз-
различием плотности при
нагреве)
Вынужденная
конвекция
Внешние силы (давле-
(давление жидкости)
Nu = / (Re, Pr)
Re>103
Nu~Re'/j
ламинарный;
Nu~Re4/6
турбулентный
Механическая энергия
(подводится от внешних
источников)
/с — коэффициент поверхностного трепня;
d — диаметр трубы, м;
D — гидравлический диаметр, м; диаметр, м;
h, к — расстояния между трубами, м;
g — ускорение силы тяжести, 9,81 м/с2;
um—QmlS— массовая скорость, кг/(м2 • с);
а — коэффициент теплоотдачи, Вт/(м2 • °С);
Я — коэффициент теплопроводности, Вт/(м • СС);
К — поправочная функция, определяемая из уравнений C.3)
и C.5);
In = loge — натуральный логарифм;
т, п — индексы энергии, определяемые в уравнениях C.3) и
C.5);
Qm — массовый расход, кг/с;
М — число Маха (vjcx)\
N — число поперечных рядов труб;
Ар — перепад давления, Н/м2;
Q — тепловой поток, Вт;
F — площадь поверхности, м2;
Т — абсолютная температура, К;
v — скорость движения жидкости, м/с;
X — характерный размер системы, м;
R — радиус, м;
Р — температурный коэффициент объемного расширения, К;
t — температура, °С;
А^ — разность температуры, °С;
51
^;к — температура смешения жидкости, °С;
Atlm — среднелогарифмическая разность температуры, °С;
р — плотность, кг/м3;
|j- — динамическая вязкость, Н • с/м2;
v — кинематическая вязкость ((х/р), м2/с;
у — отношение удельных значений теплоемкости (cp/cv);
х — касательное напряжение, Н/м2.
Индексы:
ж — жидкость;
ст — стенка;
вх — вход;
вых — выход;
т — среднее значение;
г — восстановление;
оо — свободный поток.
Безразмерные величины:
Gr= Р?B3р число Грасгофа;
Re = P— — число Рейнольдса;
Pr = Щ^- — число Прандтля;
Nu = -г- число Нуссельта;
Gz=^Re-Pr)=^E — число Гретца;
St = (Nu / Re-Pr] = — число Стантона;
Ra = (Gr-Pr) — число Рэлея;
Ре = (RePr) — число Пекле.
3.3. ОПРЕДЕЛЕНИЯ
Температурой смешения жидкости называют
среднюю температуру жидкости в данном поперечном сечении трубы
при условии, что объем жидкости находится в равновесном состоянии
без какого-либо притока или потерь тепла в окружающую среду.
Полностью стабилизированный поток —
поток, в пограничном слое которого распределение скорости уже не из-
изменяется по длине канала. При анализе турбулентного или ламинарно-
ламинарного потоков обычно предполагается, что они полностью стабилизиро-
стабилизированы.
С р с 0 и е л о г а р и ф м и ч с с к и я разнос т ь т с м п с-
р а т у р ы Atim — логарифмическое значение разности температуры
на входе и выходе, которое часто используется для расчета теплопе-
теплопередачи при движении потоков жидкости в трубах.
Ламинарный режим движения жидкости —
упорядоченный режим течения вязкой жидкости, в которой частицы
52
движутся вдоль линии тока и не перемешиваются с соседними слоями.
Его иногда называют слоист ы м потоке м.
Турбулентный режим движения ж ид кос т и—
форма течения жидкости, при которой ее поток имеет нерегулярный не-
нестационарный характер с развитым вихревым движением и активным
перемешиванием жидкости, обеспечивающим увеличение интенсив-
интенсивности теплоотдачи.
Пограничный слой — тонкий слой жидкости в непосредст-
непосредственной близости от твердой поверхности, в котором скорость течения
изменяется от нуля около поверхности до скорости невозмущенного
потока на некотором расстоянии от нее. В жидкости, протекающей
в трубе, толщина пограничного слоя может простираться от стенки
до центра трубы.
Число Грасгофа Gr = ?Рр2Х3Д//|х2 — безразмерная ве-
величина, представленная отношением подъемной силы к силе вязкости.
Оно характеризует действие гидростатической подъемной силы и силы
вязкости жидкости при естественной конвекции.
Число Нусссльта Nu = aXIK — безразмерная величи-
величина, представленная отношением конвективного теплообмена к передаче
тепла теплопроводностью в жидкости.
Число П р а и д т л я Рг = \\,ср1Х — безразмерная величина,
представленная отношением скорости диффузии (jx/p) к температуро-
температуропроводности (Х/рср). Этот критерий устанавливает связь теплопереда-
теплопередачи с движением жидкости.
Число Рейнольдса Re= puX/jx —• безразмерная величи-
величина, характеризующая течение вязкой жидкости и представленная отно-
отношением инерционных сил (ри2) к силам вязкости (|хи/Х).
Число Рейнольдса характеризует поведение потока при вынужден-
вынужденной конвекции и служит критерием стабильности ламинарного тече-
течения.
Анализ размерностей — метод, основанный на прин-
принципе однородности размерностей физических уравнений, т. е. числен-
численные представления обеих частей уравнения должны иметь одну и ту
же размерность. Благодаря этому методу уравнение можно представить
в форме, связывающей численные значения физических величин толь-
только на основе анализа размерности этих величин. Применение этого
метода должно удовлетворять требованиям геометрического подобия,
т. е. чтобы любая зависимость экспериментальных данных могла быть
представлена в единой геометрической системе.
Гидравлический диаметр D = 4S/P, м, — отноше-
отношение учетверенной площади поперечного сечения потока к смачивае-
смачиваемому периметру. Эта размерная величина используется в безразмер-
безразмерных параметрах для решения задач, связанных с движением по-
потока жидкости в трубах. Несмотря па то что требованию анализа
размерностей удовлетворяет в принципе любой характерный для
проходного сечения жидкости размер, если он является определяю-
определяющим, при рассмотрении теплообмена при движении жидкости в тру-
трубах с различной формой поперечного сечения обычно используют
гидравлический диаметр.
53
Массовый расход Qm, кг/с, характеризует количество жид-
жидкости, протекающей в единицу времени. Для решения задач теплооб-
теплообмена при движении жидкости важную роль играет параметр Gz =
= [(nD/4/) Re • Рг]. Зависимость Gz от Qm может быть выражена
в явном виде, если Gz переписать в форме Gz = QmcpIXl.
Массовая скорость, или массовый поток (um=
= QmIS = ри), кг/(м2 • с) характеризует количество жидкости, про-
протекающей в единицу времени через единицу площади поверхности,
расположенной по нормали к направлению движения потока. Сред-
Среднее значение скорости жидкости в трубах может быть получено
из выражения vm — ит/р, а важный безразмерный параметр Re
можно записать в виде Re = umX/[i.
Динамическая вязкость jx, H • с/м2. При движении
жидкости по твердой поверхности между нею и поверхностью возника-
возникает сила трения. Она пропорциональна градиенту скорости и перпен-
перпендикулярна направлению потока. Коэффициент пропорциональности \и,
(динамическая вязкость) может быть определен из выражения т =
= (л (dvldy). Динамическая вязкость является свойством жидкости и
действует как сопротивление течению жидкости. Отношение v = jx/p
называется коэффициентом кинематической вяз-
вязкости, м2/с.
Температурный коэффициент объемного
расширения р определяется в соответствии с уравнением рх=
= рг A + рД^). где рх — плотность холодной жидкости; рг—плот-
рг—плотность нагретой жидкости; At — разность температуры между двумя
областями жидкости. Его вклад в подъемную силу при теплообмене
с естественной конвекцией может быть оценен из уравнения
(Рх — Рг) ё = Pr
из которого произведение РгР и появляется в критерии Грасгофа (Gr).
3.4. ЕСТЕСТВЕННАЯ КОНВЕКЦИЯ
Движение жидкости, полностью обусловленное силой тяготения, обыч-
обычно называют свободным движением. Свободное движение жидкости
в неограниченном пространстве классифицируют как естественную
конвекцию. Однако между ними не делают никакого различия. Поэто-
Поэтому для естественной конвекции общепринято, что движение жидкости
происходит под воздействием подъемных сил, возникающих в резуль-
результате изменения плотности вследствие разности температуры между
жидкостью и находящейся с ней в контакте поверхностью. На тепло-
теплообмен при естественной конвекции, особенно во вращающихся систе-
системах, оказывают влияние и другие силы.
Интенсивность теплообмена между твердой поверхностью и окру-
окружающей ее жидкостью помимо других факторов зависит от того, явля-
является ли поток ламинарным или турбулентным, а тепловой поток может
быть определен из уравнения C.1). Коэффициент теплоотдачи а вхо-
входит в критерий Нуссельта Nu = aXIX, связь которого с критериями
54
Грасгофа Gr n Прандтля Рг устанавливается методом анализа раз-
размерностей:
Nu = С (Gr • Рг)«. C.2)
В большинстве случаев константы Сип определяют обработкой экспе-
экспериментальных данных, полученных для геометрически подобных тел.
Это простое уравнение является ограниченным и не дает полного
описания настоящей физической проблемы, поэтому для расширения
области его применения вводят поправочный коэффициент К- Тогда
уравнение C.2) можно записать так:
Nu= C(Gr • Pr)"/C. C.3)
Результаты экспериментальных исследований теплоотдачи при ес-
естественной конвекции для различных геометрических систем, обра-
обработанные в такой критериальной форме, представлены в табл. 3.2.
При расчете Gr значения свойств р и jx обычно берут при средней
температуре tm— (tCT + tm)l2, а температурный коэффициент объем-
объемного расширения для газов определяют как р= \l{tm + 273° С).
Значения р (при t = 20° С) для некоторых общеизвестных жидкостей
приведены ниже:
Уксусная кислота (СН3СООН)
Ацетон (СН8СОСН8)
Бензин (С6Нв)
Карболовая кислота (С6И5ОН)
Четыреххлористый углерод (ССЦ)
Глицерин (СН2ОН • СНОН • СН2ОН)
Ртуть (Hg)
Метиловый спирт (СН3ОН)
Пентан (С6Н12)
Серная кислота (H2SO4)
Вода (Н2О)
В основном с повышением температуры значения температурного
коэффициента объемного расширения растут.
3.5. ВЫНУЖДЕННАЯ КОНВЕКЦИЯ
Конвективный теплообмен происходит благодаря контакту движу-
движущейся жидкости и твердой поверхности, имеющих различную темпе-
температуру. При вынужденной конвекции движение вызвано не нагревом
жидкости, как это наблюдается при естественной конвекции, а воздей-
воздействием некоторой внешней силы. Энергия, поступающая извне, необ-
необходима для поддержания движения жидкости; при этом действуют две
силы—давление жидкости, зависящее от скорости потока (*/г Р^2).
и сила трения, обусловленная вязкостью жидкости (ц (dvldy)). Влия-
Влияние этих сил на теплоотдачу жидкости характеризуется безразмерным
параметром — критерием Рейнольдса Re = puX/jx. Этот параметр
характеризует также режим течения в пограничном слое, который са-
самым непосредственным образом определяет теплоотдачу жидкости.
55
р.
107
143
122
79 •
132-
47 •
18 •
119
155
56 •
20 •
к-1
• ю-5
• ю-5
• ю-5
ю-5
ю-5
10
ю-5
• ю-5
• ю-6
10
ю-6
со
s
и
VA
.. о
s
a)
CO
a.
>.
- со
Э °-
О QJ
и С
2 й
OJ
.. в
в
о
оо
Е
к
о го
g SsS g
К 5 g
S я s
Q.
CO.
сад
« 5
х Я
н я
о х
ч в
с ч
о.
О
>•»•>,
° %
v в к
I I I I I I I I
5 гаю1
о
5
a rR
сад
2
o.
о
•е-
о
s
T
a
o.
s
s
ж
ai
ffl
X
о
ж
СО
а
е-
•е-
Я
v
о
и
о
«
ft
в
а В
Е о
о в
gg
о.
а
S
^ о
gra2
III
I О О .
, к к га
твеиис
1-
S
о.
с
се
се
лоот;
S
а.
о
и.
2.
и
I =¦
12
)Вт.
-^
I
1
и
18
11
О"
к
в
в
ш
в-
го
в
со
о
о
число
1
1
><
18
II
1 3
га га
.. о. а.
S S
- ч
E В-
la <ух,<<
Лнте-
ратург
Режимы течения
потока
с
со
Схематическое
представление
Система
•u -u sj\f
СО
а>
СО
Ламинарный поток
Турбулентный поток
—i I-* —i ICO
0,47
0,1
верхности
'с»
—*¦ II
1
Омываемые по
Горизонтально рас-
расположенный цилиндр
56
оо
со
SSg" rafS
С га u">s ^ s
ё и * *
is R Z о" Е >,-J
?ч1щ
о
со*
иол
о к ч
с га
Л
о
ми
пол
нач
тся
§i§
ам
Ла
для
>,go -
дл
го
о
ую
фор
вер
ру,
•«.S&A
so
о
- 3o"
л RZ'||
я s** II
<l> 0- 5
oogis
X
<J5
a
X
oo
о
4
ч « Э
13:
ra
льная
ик
а
рт
й
нка
и 3
О) в О л
ffl я g ч
иСю
1 II
s
S
II
а
(О
00
(О
ч
о <и
с я
°-о.га
ct a.
?§
§Р
g з S
^ я §
"P
а
3
ИЗ
57
CN
CO
•If
таб
CD
Продол жен и
ig.
«a
те
я
Режимы те»
потока
<U с
о ^
у я;
тнче
<и о;
и о.
U в
я
Систем;
•» и
ее
со
в5!. §
Си2 S
Is с
Ламинарный
для круглого д
метром D исп
X = 0,9D
Турбулентный
— |-f —|со
ю —<_
о о
/
[_
\
\
\
11
ч
kik
о s
ь- н
о
с X
аемая
ая
ающая
ь свер
Нагрев
нтальн,
плоотд
рхност!
О <У CU
n S В
.20]
со
>к
3
нарн
Только ла
поток
— 1"^
О
\
Ч
/¦¦**
/
/
i 1 J3
Я О н
О Ч о
т С О
гори
на, те
>верхн
шемая
пласти
я пс
Harpei
льная
дающа
изу
го н ж
(-0 0
О (Л О-
С8 S
S Л
Ламинарный
(Gr умножить 1
в формуле дл
кальной пластн
1/4
1
-е-
и
О
о
1
^—
i
4-
_Р
1
"Г
— |тС
СО
О
/ //
/J/
У /у
—г# —
го
клоне!
го
X
Слегка
[астнна
с
.13]
о
пот
Ламинарный
(воздух)
~*
Оэ
О
<=|
11
ч
"YY1
_. V I
Сфера
г-
__
г—
co'
>s
о
4
о
о
O-
c
К
ГО
X
В
>->
CO
о
m го
со
IIP)
-
о
о"
J_
га -I V4 \\
= 1Л NT
s
со с x
CU ~4
f
О
» g g ь
3 * _
s g 'o
и &<» §
0) Six
a §S,S
г р а
Две
ралл
[ С С
туро
_ - со д со
О с и си
00
[3.
га
X
в:
о
ко.
<л
га
3
>->
П
о
m
со
-1
-
о
о"
V
-01
CJ
го
о
льн
га
ЕЕ
Верп
¦Я"
У -
У
й
8-
о
с
'К
3
1*
S X
о и
ч ч
I
/
«~
S
CD
о
si
gx
So
cv
ю
о
3 ^
в: «<
Й II
деа
3 о
5- 2
s^V
JH « ¦-
t^ ой
—X
1_
+-»
--.
—
з ?
Я о ГО
таль
пла
стин
в: со
о ч
я , с
g-is
ЛИ
Ч X
CU d.
Две
ралл
i; ве
го 3
С S
CN
о"
, ч
Vis
II X"
и -"я
W
та
э*
w
о.
о
и
о
59
ем
со'
а)
s
я
•*¦
ч
о
=t
о
п
ig
til
.1 тсче!
тока
1 g
«и tu
о s
К и
матичес
дставле:
X О.
U п
CJ
н
a
и
II II
ш
О5
СО
• зх
gy
о
V
«о
з —
а
га ..
S >•
с? о —
wX
-1/4
1
СХ
lO
О5
О
I 1
II
19]
со
о
о
¦ыый
г>4-
нО
>>*
?•=(
>> со
Н о
ш
-1/3
1—
СХ
— |СО
00
8
о"
>\
аллельные го-
ые пласти-
я пластина —
о, к к
га л S №
с ч х 5
энта
вер
одн;
гад - ч
я я о
U
"Я
II ^
I
5Г
[3.
о
!-
О
С
2
я <^
а v
га - *-.
,2 go
-1/4
(Рг)-
от
€;
00
о
\ i
к-
параллельные
ые пластины
эй температу-
наковым а)
5 з= §
Ч к О
о S Ч у
а* о
ю о о.
О5
СО
О
Н
О
с
я V
>»пО
Ho-
Horn •
со
1
(Рг)"
1
—Мсо
ю
(О
О
о
А II
-Jits Ч
\
1 ' \
1
и
и
—— ^
60
•©.
p.
о
s
с
a
—. !¦*
О
3
s
|
та ч
I
к
§
3
5
о
о
0J
3
в:
я*
s
S
о
«и 3
61
Теплоотдача при вынужденной конвекции жидкости в трубах, попе-
поперечном обтекании труб и вдоль плоских поверхностей достаточно
полно и систематически исследована. Результаты этих эксперимен-
экспериментальных исследований обычно интерполируются уравнением Нуссельта
Nu = CRe • Pr", C.4)
где С, т \\п — константы для данного типа потока и геометрии системы.
Однако существуют и другие факторы, которые могут сложным обра-
образом влиять на теплоотдачу и которые должным образом не представ-
представляются этим отношением. Для получения более полного обобщения
в уравнение Нуссельта вводят коррекционную функцию /С, и тогда
уравнение C.4) можно переписать так:
Nu= СЯет • Рг"/С. C.5)
Если число Грасгофа велико, то влияние естественной конвекции
на вынужденную конвекцию должно быть специально исследовано.
Для большинства случаев это влияние обычно рассматривается как
второстепенное.
3.6. АНАЛОГИЯ РЕЙНОЛЬДСА
Аналогия основана на предположении, что соотношения, описывающие
теплообмен и перенос количества движения поперек потока жидкости
(касательное напряжение между слоями жидкости локально равно
изменению ее количества движения), подобны для потоков жидкости
с одинаковыми граничными условиями. Хотя это предположение
справедливо только для ламинарного режима течения вдоль плоской
пластины при отсутствии градиента давления с Рг = 1, оно достаточно
общее и может применяться к турбулентному режиму течения и к те-
телам другой геометрии. В этом предположении при Рг = 1 распределе-
распределения скорости и температуры в пограничном слое идентичны. Тогда
между теплоотдачей и гидравлическим сопротивлением жидкости мо-
может быть установлена простая зависимость:
аналогия Рейнольдса:
St = Nu/Re • Pr= //2 (для Pr = 1); C.6)
аналогия Рейнольдса, модифицированная Кольбарном:
St = (//2) Рг-2/3 (для Рг ф 1). C.7)
Эти уравнения позволяют сравнительно просто получить коэффи-
коэффициент теплоотдачи а через коэффициент трения /.
3.7. КОЭФФИЦИЕНТ ТРЕНИЯ И ПЕРЕПАД ДАВЛЕНИЯ В КАНАЛАХ
Возникающее при обтекании тела жидкостью сопротивление (извест-
(известное как торможение) замедляет движение потока вблизи поверхности.
Это вызвано не только действием касательного напряжения (поверх-
(поверхностного трения), возникающего из-за вязкостных свойств жидкости,
но и существованием при определенных условиях разности давления
(сопротивления давления пограничного слоя) на поверхности тела.
Для тел затупленной формы, таких, как сфера и цилиндр, при обте-
62
кании которых поток в некоторых точках может отрываться от по-
поверхности, действие сопротивления давления является преобладающим,
в то время как для плоской пластины, расположенной параллельно
потоку, и для цилиндрических труб, внутри которых движется поток,
более важную роль играет торможение за счет трения.
Теплоотдача связана только с вязкостным торможением на по-
поверхности. Касательное напряжение (сила трения на единицу поверх-
поверхности) на поверхности определяется как
Тех = (//2) pi&, C.8)
где /— коэффициент трения и vm — средняя скорость потока.
Для плоской поверхности или для поверхностей хорошо обтекаемых
тел
/ = 0,664 Re~ 1/2 — при ламинарном движении потока; C.9)
f = 0,059 Re~ 1/s — при турбулентном движении потока, C.10)
где характерная длина X в критерия Re берется от переднего края
пластины.
Значения коэффициента трения в зависимости от Re для течения
в трубах цилиндрической формы с различным поперечным сечением
приведены в табл. 3.3.
Вследствие трения давление жидкости по длине трубы падает.
Если пренебречь влиянием условий входа и выхода, шероховатостью
поверхности и сжимаемостью жидкости, то соотношение между коэф-
коэффициентом трения и падением давления Ар может быть выражено в сле-
следующем виде:
()?=2>т"Ь (ЗЛ1)
где / — длина, на которой давление падает на Ар, аО — эквивалент-
эквивалентный гидравлический диаметр трубы.
Падение давления по длине канала для вязкой жидкости, омываю-
омывающей пучок труб, может быть определено с помощью уравнения
14 = ^е.2-^^(-^.H'14Н/м^, C.12)
Р V Ист /
где 1>Макс — максимальная скорость потока, м/с; ит макс = римакс =
— Qm/SMm — максимальная массовая скорость, кг/(м2 -с); N —
число поперечных рядов труб.
Эмпирические значения коэффициента трения fe для чисел Рейнольд-
са в интервале значений 102— 5 • 104 могут быть получены из сле-
следующих формул:
для коридорного расположения труб
/e= 0,33Re7l/5; C.13)
для труб, расположенных в шахматном порядке,
U = 0,75Re7I/5> C.14)
где Red= pvuayxd!\x,\ d — диаметр трубы; viiai{c=* vml2/(lz~ d).
63
со
со
о
ч
с
о
а
i>
?
га
m
к
а-
3 <•
s
х
I
Е
X
3"
S
ч
m
л
X
Л
о.
a
о
x
a
3
в
s
a.
с
к
s
s
4
в
Л
i
1
s
S
S О.
О)
о
: га
га
о ч
W as
о
су
ВЛШ
та
<Ц
О.
CJ
ПОП)
Ж
Re;
«
s
а
га
u
в
a
<u
*
«гага
о. и w
С ef ai
га л
... Р га
hOZ
га ч га
о о a
s s
о- а
>>га
з
ffl
S
о.
н
иент
у
ж
&
СП
о
О.
н
ffl
к
X
S
су
давл
су
X
су
Е^
га
с
S
в
о
n g о
о4
S
о
II
5°
Со
is
3 s
ю
О. X
JS °
га с
о-л
н
су У
is
о
В! О.
е су
> о
3 °"
в «
н tu
га
о -
о
о &
or
о1-
сч .
А§
су -^
?<=¦
Л
К S
о
н л
ч >•
is
О. су
С а
н
су
с
S*
О)
н
Ре>
S
Is
га-з
ение
СС
га
а
**-
а.
ЕС
си
я
я
я
•е-
о
11
с. s
ЧЕС
Я
U
к
X
GJ
У
GJ
га и
" о
Си (-
о с
е =
О1
с
о
я
га
t;
га
Я
га
ь:
га
s
О.
и и
щ
4
~8
со°.
Vo
4» V
о V~^
1С
t^
о
ОС
О
сч
— о
1 1
су су
а а;
to го
о
о
о
f
1
1
1
I
\
v
та
мэ
>,
а.
о
и:
-
О
Re<
\/
V
<я
О
Ю
«л
г^
о
192
о'
ю
сч
о
1
(У
ОС
,096
о
.
,0U4
3-10
II tu
5К
--- V
w,v
ЧСО
00
о
<и
а
IN
8
О*
сч
о
1
си
а
046
о
\
\
1
J
/
у
о \/о
Vi«
QKQ
" V -~.
К2 «
чсо «=t
00
о
tu
IX
156
о
сч
о
1
V
IX
078
о
§
1
рный
03
МИН
га
!¦-
СО
CN
|
су
IX
ч
to"
в
—
о
II
в -о
/
/
/
1
1
I
1
\
\
\
\
1
г*
и
с
S
ч
ч
СП
CN
tu
о
ь
—.
20,
7
CU
IX
СО
ю
о
^—*
*- -
fit
(О
1
(У
а
ю
сч
00
в
-Г
со
о
\
\
\
1
;
/
у
fit
го
tr
1
tv
IX
го
в
ю
CN
о
Сч
to
1
V
IX
ю
го
«
ю
ю
—"
—.
о"
64
s
iiiQi
ix ix as ix ix ix sx ix
л I в
i
>s
я
а.
а
ж
s
S
га
а
a
S
о
•к
S
X
§
в §
в ?
« >>
Л -гй
•в f,o
B
ОС
,-. _. о
s
Ю
CO
О
§
I
>,
3
s
05
S
4
a
Ц
CO
s
CO
@
C5
Я
о.
>.
н
га
о.
3 Основные формулы и данные по теплообмену
65
Рис. 3.1. Коридорное распо-
расположение труб
Рис. 3.2. Расположение труб
в шахматном порядке
I,
Некоторые данные по Ар для труб с различным поперечным сече-
сечением приведены в табл. 3.3.
Для обеспечения движения жидкости по трубе должна подво-
подводиться внешняя энергия. При этом часть подводимой от внешнего ис-
источника энергии, которая составляет ApvmS Вт, компенсирует поте-
потерю давления.
3.8. КАНАЛЫ И ТРУБЫ
Знание закономерностей нагрева и охлаждения при протекании жид-
жидкости через трубы имеет большое значение для инженеров. Если для
заданной геометрии системы и для определенных условий движения
потока коэффициент теплоотдачи известен, то тепловой поток может
быть определен из уравнения
= aF(tCT—tm), Вт,
C.15)
где tn, — температура смешения жидкости.
Для внешних задач в качестве температуры свободного потока
может быть использована температура смешения. В каналах и трубах
эту температуру можно определить только при условии, если извест-
известно распределение температуры. К сожалению, определение распре-
распределения температуры сопряжено с большими трудностями. Поэтому
используют среднюю логарифмическую разность температур, которая
определяется только на основании известной температуры жидкости
на входе и выходе и является гораздо более удобным и подходящим
параметром.
Среднелогарифмнческая разность температуры определяется урав-
уравнением
М1т =
Чт-
In
C.16)
Таким образом, тепловой поток можно рассчитать по формуле
Q= aFAtlm Вт, C.17)
где а — среднее значение коэффициента теплоотдачи.
66
Это же уравнение дает возможность найти необходимую поверх-
поверхность трубы при определенном значении плотности теплового потока
и при заданном температурном перепаде.
Если известно значение температуры /н;11 для одного из попереч-
поперечных сечений трубопровода, то значение температуры tm,z в другом
сечении, расположенном на расстоянии / от первого, можно опреде-
определить из следующего уравнения:
t _ a.Pl{2tCT — t)K,
aPl+2umcr S
где Р н S — периметр и площадь поперечного сечения трубы соответ-
соответственно; ит — массовая скорость; а — среднее значение коэффициента
теплоотдачи на длине /. Массовая скорость ит может быть оценена как
um = Qm/S = pv, где v— средняя скорость потока.
В табл. 3.4 перечислены соответствующие зависимости Nu, по ко-
которым может быть рассчитано среднее значение коэффициента теплоот-
теплоотдачи а для движущегося потока жидкости в трубах с различной гео-
геометрией сечения.
3.9. ТЕПЛООТДАЧА ПРИ ВНЕШНЕМ ОБТЕКАНИИ ТЕЛ
Этот раздел посвящен теплообмену при омывании вынужденным пото-
потоком жидкости плоских поверхностей (т. е. плоских пластин) и труб,
расположенных перпендикулярно к направлению движения потока.
Плоская пластина для анализа представляет собой простейшую гео-
геометрическую фигуру, поэтому она тщательно изучена. Результаты та-
такого анализа весьма полезны также и потому, что многие из получен-
полученных выводов могут быть распространены на хорошо обтекаемые тела,
начальные участки труб, клинья, конические тела и на любые поверх-
поверхности плоского типа. Используя модифицированную Кольбарном ана-
аналогию Рейнольдса, можно получить классические результаты. Обоб-
Обобщенные результаты значительного количества экспериментальных ис-
исследований приведены в табл. 3.5.
Ввиду сложного характера движения жидкости при обтекании тел,
имеющих сферическое или цилиндрическое сечение, получение ана-
аналитического решения связано с очень большими трудностями. Для
этого приходится прибегать к эксперименту и к методу анализа
размерностей. Коэффициент теплоотдачи при обтекании сфер воздуш-
воздушным потоком рекомендуется определять по следующей формуле [3.201:
Nu= 0,37 (ReH-6 для 17 < Re < 7 • 10\
где диаметр сферы принят за характерный размер.
В табл. 3.6 и 3.7 представлены некоторые данные по конвектив-
конвективному теплообмену при обтекании вынужденным потоком жидкости
цилиндров с различным сечением и пучков труб.
3* 67
i
Q
CO »
3 o.
«о <и
8.1-Ё
glz
3
X
я"
х
л
о
«2
U
is
с
s
ч
s
ortu
4 s a>
CUE
**2
ея a>
Э a.
РЭ
г
s
s
I
в
s
=
X
X
3
Ш
s
a.
с
s
н
к г* ... о
2
о
J5 о.
e
о о)
S
О f-1 «
IIS
is!
О '
со
4
o и
У « g
I О О) X
1S
¦* со
о о"
00
о
00
о"
о о
со to
00 СО
—| СО
со t^
S 8
H OO COC
ooo ooc
о о
о о
ся ся с5 о5 с5 cn cn
«vvvvvvv
CN СО СО «"¦* Ю Г-
а а а а а а
^ со оо
II —?&} СО ¦* 00
68
о
о
i. л
lisp
га -
И
«Н
-< |оо
00
8
ли разрез или
ie пластины
п
о §
?|
с
со
ф
Of
\
о
1-
\
^—
<о
CN
С
—-,
О
*—— i -^*
о
о
ю
г-
<о
см
~\
г-
арный пот
Re<2000,
„ 0,58 а
Щ &
а
О0
о
'
—i|CO
—. ICO
о
со
„
88
о
тре-
I г^
Равн
ГОЛЬН!
V
0,58 а
а
*— i **
—
о
о
г-
CN
а
О0
ю
о
2
арный по
мин
СЯ
—
О
о
СО
О0
<О
ельиые
паралл
2
¦и !В . ¦ >
с
ю
i
!
1
i
1
ю
CN
СО
со
СЯ
о.
СЯ
о.
G9
ю
со
га
cf
s
ч
i
о.
га
о.
о
с
ч
X
CJ
О
х
О
О
С
2
х
S
5
с
х
X
I
S
X
1
X
о.
с
я
X
I
g
а
X
ь
в-
я
к
X
X
<и
<и
а.
о. 55
^1,
S .
ii.iis
о
з
a .- о о и v
»U га о к
И° -2. а.? с я
IrlHIl
III!!
V Я
1+
si.
о.
c 11
Э s
к
со -.
¦я ч
о s
s о
33 4
<D U
ей о
33 U
со о
в1
s
33
w g
X
X
CQ
к
CO
CJ
о
* 5
аз ч
H 4
O.G
с га
ч
«с
а.га
и о.
га «
о cj
ч «
s га d
и
о
в. о
S^ со
о || о
18
ення
о-
S
I
!
a
о.
1
с:
о
X
ё
ч
с
ости вдоль
рхностн
&ш
я|
к с
О1
О1
S
ч
в
с
о
о
с
>к
3
нарн
к
Е
га
ие)
X
е значе
о
|
1
о
со
0.
V
Of
со
о
II
II
я
3
S
X
V
режим те
>s
3
X
X
д
>,
г
ГО
ш
V
н
V
о
10
о
ю
V
Of
начение
(среднее з
со
а.
О)
-Ч
V
Of
ч<
со
со
о
II
II
к
3
Z
+?
отек,
с
гный
улен'
чэ
Тур
значен
(локальное
а
in
Of
a
о
о
п
II
К
3
2
к
1
t
|
V
н
V
о
&
-ti
Л
ачение)
среднее зн
со
CU
*ч
CJ
Of
о
о
II
II
н
1 3
Iz
^ —1
s:
1-
Ч 1
70
о
о
с
•к
3
нарн
s
га
V
V
&
ю
V
|
с
•я
35
аз
^,
аз
о
ч
чэ
а.
V
V
ч-'
to
О
л
Of
i
В1
га
35
Э01
О.
Си
О)
-«г
Pi
о"
II
к
значени
ере,
0.
ю
О
S
о"
II
н
3
я
33
аз
о
3
га
лок
in
2
о
II
Iz
"о
значени
а)
<и
ef
ере,
S
X
s
аз
х
га
<и
о
аз
в1
s
н
т
71
Таблица 3.6
Теплоотдача при поперечном омываиии воздушным потоком
цилиндров с различной формой сечения
Формулы:
Nu = CRem — для цилиндра круглого сечения;
Nu = 0,43 + С Rem — для цилиндров с другими формами сечения;
Nu = 0,43 + CRemPr0-31 — при омывании жидкостью;
Q = Nu %F (fCT - tm)IX.
Обозначения:
NU = аХ/%\
Re = pvXi'n;
Pr = СрцА,;
p — плотность жидкости, кг/м3;
ц — динамическая вязкость жидкости, Н • с/м2;
ср — удельная теплоемкость, Дж/(кг ¦ °С);
а — среднее значение коэффициента теплоотдачи, Вт/(м2 i °C);
X — коэффициент теплопроводности, Вт/(м i °C);
F — площадь поверхности, м2;
'ст — температура стенки, °С;
tm — температура смешения жидкости, °С.
Предполагается, что поверхности стенок ровные. Значения свойств взяты
при средней температуре пограничного слоя жидкости tm = (tCT + tm)/2.
Форма сечения
[ Интервал значений Re
Характерный
раамер X
0,437
0,565
0,800
0,795
0,583
0,148
0,0208 0
0,0895
0,136
0,280
0,384
0,471
0,633
,814
Ю-4—4-Ю-3
4.10-3—9- 10-а
9.10-2—1
1—35
35—5-103
5.103—5 • 104
5 • 10*—5-Ю5
d
d
d
d
d
d
d
0,178
0,102
0,699
0,675
2,5.103—8-103
5.103—Ю5
4a
n
i?
0,290
0,246
0,624
0,588
2,5.Ю3—7,5-103
5.103—Ю5
4a
к
4a_
n
0,160
0,039
0,638
0,782
5-103—1,95-104
1.95.104—10s
n
6a
л
72
Продолжение табл. 3.6
Форма сечения
Интервал значений Re
Характерный
размер X
0,153
0,638
5.10я— 105
<Т
0,293i
2а
0,660
3.Ю»—2-Ю4
6а
л
¦с*
0,248
0,61:
2,5-103—1,5-10*
0,094
0,804
3-10»—1,5-10*
V
0,276
0,610
3.103—2-10*
1,09а
0,227
0,731
4-Ю3—1,5-10*
2а
Литература: [1.3, 3.1, 3.18, 3.22, 3.25, 3.26, 3.30].
73
Таблица 3.7
Теплоотдача при поперечном омывайии жидкостью пучков труб
Формула:
Nu = CRe°.ePr0-3 (ц/цстH.1*.
Обозначения:
Nu = аШ;
Re = pvd/\i;
Рг = цСр/%;
а — среднее значение коэффициента теплоотдачи, Вт/(м2 . °С);
р — плотность жидкости, кг/м3;
|х — динамическая вязкость жидкости, Н • с/м2;
Нет — динамическая вязкость жидкости при tCT, Н « с/м2;
с-р — удельная теплоемкость при постоянном давлении, Дж/(кг » °С);
Л, — коэффициент теплопроводности жидкости, Вт/(м . °С);
v — скорость невозмущенного потока, м/с;
d — диаметр трубы, м.
Значения параметра С, приведенные ниже, взяты из работы [3.9J. Они при-
применимы для значений 2000 < Re < 4 • 104.
Значения величин взяты при средней температуре пограничного слоя
жидкости tm — (tCT + tm)/2.
Рис. 3.3. Коридорное рас-
расположение труб
Значения параметра С
v-
тоооо
)OOO
oo о о
o.ooo
1,
d
1,25
2
3
4
1.25
0,888
0,613
0,427
0,356
1
2
0,890
0,613
0,427
0,356
./<*
0
0
0
0
3
,880
,638
,500
,421
0
0
0
0
4
,835
,632
,504
,421
Рис. 3.4. Расположение
труб в шахматном по-
порядке
Значения параметра С
V-
d
1,25
2
3
4
Uld
1,25
0,953
0,686
0,559
0,489
2
0,937
0,669
0,544
0,488
3
0,875
0,638
0,506
0,466
4
0,812
0,611
0,500
0,442
74
3.10. ТЕПЛООТДАЧА ПРИ ВЫСОКИХ СКОРОСТЯХ
При достаточно высоких скоростях движения потока жидкости нали-
наличие сил трения является причиной значительного повышения темпе-
температуры пограничного слоя. Для очень больших скоростей потока
изменения температуры по сечению пограничного слоя могут быть
весьма значительными. Это явление аэродинамического нагрева
особенно проявляется в авиации и ракетной технике при сверхзвуко-
сверхзвуковых скоростях движения. В этих условиях тепло от нагревающегося
пограничного слоя передается непосредственно твердой поверхности.
Для представления температуры пограничного слоя принято ис-
использовать характерную температуру Тг, называемую температурой
восстановления (или температурой адиабатной стенки). Достижение
стенкой температуры восстановления свидетельствует о том, что
отсутствует какой-либо теплообмен, обусловленный конвективной
теплоотдачей. В этом случае плотность теплового потока может быть
рассчитана по формуле
q.= a(Tr—TCT) Вт/ма C.19)
и температура восстановления — по формуле;
A, C.20)
где и.» — скорость невозмущенного потока.
Коэффициент восстановления температуры г является мерой эф-
эффективности процесса нагревания пограничного слоя и в значительной
степени зависит от числа Прандтля в соответствии с тем или иным
сформировавшимся режимом течения. Для плоской пластины (давление
вдоль поверхности постоянно) коэффициент восстановления темпе-
температуры может быть определен из следующего выражения:
при ламинарном режиме г= Рг'/2;
при турбулентном режиме г= Рг'/3. C.21)
Если г= 1, то температура восстановления становится равной
температуре торможения. Для потока, движущегося с низкой ско-
скоростью (т. е. при и»/2СрГоо <^ 1), Тг практически равна температуре
невозмущенного потока Г„, а при больших скоростях — температуре
адиабатной стенки Гст. В стационарных условиях температура стенки
определяется из теплового баланса между теплом, поступающим
к пограничному слою благодаря конвекции и падающему излучению,
и теплом, рассеянным за счет поверхностной теплопроводности, излу-
излучения и других совместно действующих процессов охлаждения.
Известно, что свойства жидкости изменяются с температурой и
давлением. При умеренно высоких скоростях потока могут быть полу-
получены приближенные результаты путем отнесения ^значений Этаких
75
свойств, как р, |х, Я, и ср, к определяющей температуре Г*. Соответ-
Соответствующее выражение, предложенное Эккертом [3.41], имеет вид
Т* = Гео + 0,5 (Гст- Гто) + 0,22 GV— Т«,) =
= 0,5 (Гто + Гст) + 0,22 -1=±М2ГТОК. C.22)
При этом удельную теплоемкость можно считать постоянной. Значение
динамической вязкости можно определить с помощью соотношения
Сазерленда:
И _f Т*\О.Ъ( 1+218/Г0
1+218/Г*
), C.23)
где [л0 — известное значение динамической вязкости при температуре
Го-
Коэффициент теплоотдачи часто выражают через число Стантона,
которое связано с коэффициентом поверхностного трения fс. При
омывании пластины ламинарным или турбулентным потоком это соот-
соотношение имеет вид
St=:Apr-2/3i C.24)
При очень высоких скоростях движения потока в пограничном слое
возникает значительный перепад температуры, и предположение о по-
постоянстве удельной теплоемкости неверно. Поэтому в формуле для рас-
расчета теплоотдачи температура не может служить определяющим
параметром. Вместо температуры в таком случае используют энталь-
энтальпию газа, т. е. i — ^cpdT. Значения свойств при этом следует опре-
опреотнесенной к соответств
, предложенное Эккертом,
U) +0,22 (ir—U) = 0,5 (ie
делять для температуры, отнесенной к соответствующему значению
энтальпии i*. Выражение, предложенное Эккертом, имеет вид
г. C.25)
При таком подходе плотность теплового потока определяется как
qs = a; (ir - »„) Вт/м2, C.26)
где а; = а (Тг — Tcr)l(ir — iCT), и энтальпия восстановления ir
,•, = »» +г, ^|-Дж/кг. C.27)
Перечень формул для расчета коэффициентов теплоотдачи через чис-
числа Стантона и Нуссельта приведен в табл. 3.8.
76
Таблица 3.8
Формулы для расчета теплоотдачи
при высокой скорости потока
Обозначения:
а — коэффициент теплоотдачи, отнесенный к характеристической темпера-
температуре, Вт/(м2 . °С);
а; — коэффициент теплоотдачи, отнесенный к характеристической энтальпии,
кг/Чм2 . с);
/с = TcT'0>5pf«—коэффициент поверхностного трения (определяется анало-
аналогично коэффициенту трения /);
Ср — удельная теплоемкость при постоянном давлении, Дж/(кг . °С);
М = Voo/coo — число Маха;
х — расстояние, отмеренное от передней кромки, м;
хКр — критическое расстояние перехода ламинарного потока в турбулентный;
г — коэффициент восстановления температуры;
г = G> — Tcr)/(vlo/2cp) — выражен через температуру;
г = (ir — icr)Kvxl2) — выражен через энтальпию;
R — универсальная газовая постоянная [для воздуха R = 287 Дж/(кг ¦ К)]1,
р — плотность жидкости, кг/м3;
ц — вязкость жидкости, Н • с/м2;
Л — коэффициент теплопроводности жидкости, Вт/(м-°С);
* = J CpdT — удельная энтальпия, Дж/кг;
Voo — скорость невозмущенного потока, м/с;
Сх, = ~\/yRTa, — скорость звука в невозмущенном потоке, м/с;
Т — абсолютная температура, К;
у = Ср/Сц — отношение удельных теплоемкостен;
St* = alp*cpvoo = ai/p*Voo — число Стантона;
Рг* = с*|гД* — число Прандтля (значения при высоких температу-
температурах могут быть заимствованы из работы [3.46] или
[3.47]);
Re* = p*i'oo*/)i* — число Рейнольдса;
Nu* = ах/Х* — число Нуссельта.
Индексы:
( — энтальпия;
оо — невозмущенный поток;
г — восстановление;
ст — стенка.
Верхний индекс (*) указывает на то, что значения свойств рассчитаны либо
при характеристической температуре Г*, либо при температуре, соответствую-
соответствующей характеристической энтальпии i*.
Характеристика
Плотность теплового
потока, Вт/м2
Характеристическая
температура, К, или
характеристическая
энтальпия, Дж/кг
Температура восста-
восстановления, К, нли
энтальпия восстановле-
восстановления, Дж/кг
ДЛЯ ПОСТОЯННОЙ Ср
qs = a(Tr-Tcr)
— r.J + 0,22 (Tr—TJ
1 f === 1 ег. ~т~ lU J AL p
Для переменной Ср
qs — ai (lV — (ct)
+ 0,22 (h—i^)
77
Продолжен и е табл. 3.8
Характеристика
Для постоянной
Для переменной ср
Коэффициент вос-
Коэффициент восстановления температу-
температуры
То же — энтальпии
Число Стантона
St* = ^-(Pr*)~2/3
г = (Рг*I/2—ламинар-
(Рг*I/2—ламинарный поток
г=(Рг*I/3—турбу-
г=(Рг*I/3—турбулентный поток
; =(Рг*)'^2—ламинарный
поток
г; = (РгI''3 — турбулент-
турбулентный поток
Формулы для плоской пластины
Локальное значение
коэффициента поверх-
поверхностного трения
Среднее значение ко-
коэффициента поверхно-
поверхностного треиия
Число Нуссельта
Nu = St-Re-Pr)
Среднее значение а от
=0 до х>х1!р
fc— 0,664 (Re*)"'2 (Польгаузен), ламинарный
поток, Re < 5-Ю5
/¦c = 0,0592(Re*)-0-11 (Блазиус), турбулентный поток,
5-105 < Re < 107
/с= 0,288 (log10Re*)~2'45 (Прандтль—Шлихтинг),
турбулентный поток, 5-105<Re<109
/с= 1,328 (Re*)~I/2 (Польгаузен), ламинарный по-
поток, Re<5-105
/с = 0,074 (Re*)~0>2 (Блазнус), турбулентный поток,
5-10'<Re< 107
7с= 0,455 (logi0Re*)~2>58 (Прандтль—Шлихтинг),
турбулентный поток, 5-105<Re< 109
Nu* = 0,332 (Re*I/2 (Рг*I/3 (Польгаузен), лами-
ламинарный поток, Re<5-lO5
Nu* = 0,029 (Re*H'8 (PrI/3 (Блазиус), турбулент-
турбулентный поток, 5-105<Re<107
Nu* = 0,144 Re* (Pr*I/3/(Iogl0 Re*J'45 (Прандтль—
Шлихтннг), турбулентный поток, 5-105<;Re<; 10е
ламинарный поток при * = 0 до х=хкр;
турбулентный поток при *>*np (Блазиус)
3.11. КОНВЕКТИВНАЯ ТЕПЛООТДАЧА ТЕЛ ВРАЩЕНИЯ
(дисков, конусов, цилиндров и сфер)
Конвективный теплообмен между вращающимся телом и окружающей
его средой играет важную роль в инженерной практике. Механизм
теплоотдачи вращающихся систем тесно связан с характеристиками
подвижного пограничного слоя потока, которые сложным образом
проявляются через центробежную и кориолисову силы. Когда скорость
78
я
*» S
U
В
о
W
Я
ч
о
со
Н
I
...i
Й
о
a
g
ш
о
н
н
s
о
я
X
G_. | „ „ О
eg eg
О. О.
S
X
си
ч
m
к с
s
х о
CU ?
ч о
m х
Я х
ё |
(J СО
о
S
а
а.
о f-1
eg •<
3*
X . о. a S eg
Я О f, В о и
о в ж-о- о. . о-
ч ^ я in о о ss
о я я о «--~ о
Q.8
CU
S3 >•
о
го
о. w
а> а
Ё&
к
я
В1
V
иулы
Фор]
о
S
сое представлен
мати1
К
О
Я)
у
о
•u-u i>{
2,co"-
«Я.
ою
sv
V
0,7
1
нна
,5-1
Зсм
га \/
Ч V
CU
ю
о
со
<Х
8
о
t
"Г
fc
<^
Т
3
п
•S3
к
1м
га к
Is
о. u
pa
—
33]
со
«"
о
н
о
а
о
"ii*
я°1
X ю
О-О
ина
,5-1
SScm
eV
^ CU
л
о
CU
-
1!
II
¦ —1
Iz
fee
со
о
н
о
с
,72
о
II
'Я и
|&"
ч-Г
'g.CN
Of
со
о
&
,015
о
II
. 3
Iz
/II
со
со"
>.«
Э 3
S а
<и н
я S
о о.
С! >•
•Я
з -а-
О, 11
s"
§ s
та
11
^
8
Т
со
о
CU
Ю
О
О
II
1 3
Iz
/lill
/ '
а;
II
к.
я
II
к.
>¦
CD
S
о
Н
о
J
-
—
S
2,5
II
So.
1С
4
79
l&
те
W
a1
г
X
UJ
p-
2
Форм}
[енне
со
s
ч
<Ы
о.
с
<Ы
о
чес
ати
z
о;
<3
2
Сне
ITU SJSf
32]
[3.
:твие есте-
V
:СТНО
а
ю
О)
о
Ui
а
о
li
1 13
1г
..—¦
с
яужденнои
вращения
1токе (осп
ризоиталь-
а S с 2
- м S 2
*" П д д
I H1 §
С щ 2 о
я, ffl Cd С
ffl К К О *—-
и § ш 2. я
з 5.
« -.
of ?1
СО
8 оо.
И !1
,1 »
1г о
где
эс
¦^ +п
^ У
ш^т^—
38]
[3.
жим тече-
о.
"а
яарн
cd
ю
О)
о
t_f
¦v_
\Г.
о
!1
-1
з:
cd
1И конвек-
§(
1
стес
01
к
S
'-I
\
\
\
иус
о
Is
РЭ
со§
CO
?2, со со
=- i g i "g <N
A § \ / ^ ^ ^
JJ ijj^ SJ ^ L.
""' a °S § °.
N" c3 . "* 7/
^ Я (N <u s V
11? i - й
CO. S S ьйО
s| -§gSV
5 5 о ^s o"
•
Ui ^
o" <N 3 t>
щ Г* I!
CO ° <S °
со -г* "
o" z; c< "Й
|| CO ~t- O2.
1 з о 8 II
lz Г II о
и S
зс
^—1
z
\ ^ /
\ «j/
\ 4° /
\ /^
\ /"^
w/
\ vi/
Vv
>-
34]
CO
32]
[3.
конвек-
D,5
действие
зынужден-
твен]
Ест
Ю
о
Ui
Ом
Ui
¦¦»_
456
о
II
II
S
«
_i С
X X
-'до
^ S ffl
i
Ю
CO
о
"S
о
ОС
ю
o_
¦^
O0
о"
il
о 5
1-^
л
о.
03
со
31
о
со
со
к
к;
. к
s га
S S
§ >¦?
Sffl '
§ с
CN
~Q
Ui
a.
а>
ОС
i
t:
CN
+
+
a.
CO
c:
ю
+
с
¦
*-•
3
О
ю
O5
Л
cq
cq
с
ZZ'I
+
ОО
см
ОО
—
1
S "
s cq
-'s
V-
- ¦¦—-^
I
1
о
Ю
V
cq
w
cq
с
,04 1
CN
+
s
CO
1
1
II
cq
Re/
1 c»
<u
Of
и
II
«5
V
ч
80
to to ол
со со со
со со со
3 т
05
о к
к s
о ES
н «
о о
»Х Ш
a) S
t=J о
Совместно
иуждеииой
1КР
1*Г1
CD О
S " " '
К К
<и <и *¦
Эй
¦*• L
О.И-
о •- м
- ^ о
1 X
<J u. К •—<
ОЙ
'з .!^
Оо"
V
5V
usu< •
«OS OCN
S ffl octf\/
§5 аи
5:
о
3 '4
со U
о" +
ш
со
о"
Iz
ш
из
Iz
°
81
вращения незначительна или когда различие между температурой
поверхности и среднеобъемной температурой жидкости достигает
значительной величины, основную роль может играть естественная
конвекция. С другой стороны, когда скорость вращения достаточно
велика, вклад от естественной конвекции становится относительно
небольшим и теплоотдача осуществляется преимущественно за счет
вынужденной конвекции. Критерием установления того или иного вида
конвективной теплоотдачи служит численное значение безразмерного
параметра (Gr/Re2). В промежуточной области значений данного
параметра в расчетах теплоотдачи необходимо учитывать совместное
действие естественной и вынужденной конвекции.
В табл. 3.9 приведены формулы для определения теплоотдачи при
вращении тел различной геометрии (дисков, конусов, цилиндров и
сфер).
СПИСОК ЛИТЕРАТУРЫ
3.1. Nusselt W. Die Abhangigkeit der Warmeiibergangszabl von der Rohrlage. —
«Zeitscher VDI», 1910, Bd 54, S. 154.
3.2. Pohlhausen E. Der Warmeaustausch zwischen festen Korpern und Fliis-
sigkeiten mit kleiner Reibung und kleiner Warmeleitung. — «ZAMM», 1921,
Bd 1, S. 115.
3.3. Prandtl L. Eine Beziehung zwischen Warmeaustausch und Stromungswieder-
stand der Flussigkeiten. — «Phys. Z.», 1910, Bd 11, S. 1072.
3.4. Reynolds O. On the Extent and Action of the Heating Surface for Steam
Boilers. — «Proc. Manchester Lit. Phil. Soc», 1874, 8.
3.5. Karman von T. The Analogy between Fluid Friction and Heat Transfer. —
«Trans. ASME», 1939, v. 61, p. 705—711.
3.6. Kays W. M. Convective Heat and Mass Transfer. McGraw-Hill, 1966.
3.7. Ede A. J. Advances in Free Convection. — In: Advances in Heat Transfer.
V. 4. Academic Press, 1967.
3.8. Ostrach S. An Analysis of Laminar Free-Convective Flow and Heat Transfer
about a Flat Plate Parallel to the Direction of the Generating Body Force. —
«NACS» TN, 1952, v. 2, p. 635.
3.9. Eishenden M., Saunders O. A. An Introduction to Heat Transfer. Oxford Uni-
University Press, 1950.
3.10. Eckert E., Jackson T. Analysis of Turbulent Free Convection Boundary Layers
on Flat Plate. — «NACA» TN, 1950, 2207.
3.11. Bromham R. J., Mayhew Y. R. Free Convection from a Sphere in Air. — «In-
«Intern. J. Heat Mass Tiansfer>, 1962, v. 5, p. 83.
3.12. Sparrow E. M., Gregg J. L. Laminar Free Convection from a Vertical Plate
with a Uniform Surface Heat Flux. — «Trans. ASME», 1956, v. 78, p. 435.
3.13. LeFevre E. J., Ede A. J. Laminar Free Convection from the Outer Surface of
a Vertical Circular Cylinder. Proc. 9th Congress, App. Mech., Brussels, paper
1167, 1956.
3.14. Ostrach S. Natural Convection in Enclosures. — In: Advances in Heat Trans-
Transfer. V. 8. Academic Press, 1972.
3.15. Gebhart B. Natural Convection Flows and Stability. — In: Advances in Heat
Transfer. V. 9. Academic Press, 1973.
3.16. Knudsen J. C, Katz D. L. Fluid Dynamics and Heat Transfer. McGraw-Hill,
3.17. Cohburn A. P. A Method of Correlating Forced Convection Heat Transfer
Data and Comparison with Fluid Friction. — «Trans. AIChE>, 1933, v. 29,
p. 174—210.
3 18. Hiibert R. Warmeabgabe von geheizten Drahten und Rohren. — «Forsch. Geb.
Ingeineurwesens>, 1933, Bd 4, S. 215—224.
3.19. Якоб М. Вопросы теплопередачи. Пер. с англ. М., Изд-во иностр. лит., 1960.
3.20. McAdams W. H. Heat Transmission. McGraw-Hill, 1954.
82
3.21. Sieder E. N., Tate С. Е. Heat Transfer and Pressure Drops of Liquids in Tu-
Tubes. — «Industr. and Engng Chem.», 1936, v. 28, p. 1428.
3.22. Кутателадзе С. С, Боришанский В. М. Справочник по трллщщреддче.
Л.—М., Госэнергоиздат, 1959.
3.23. Kay J. M., Nedderman R. M. Fluid Mechanics and Heat Transfer. Cambridge
University Press, 1974.
3.24. Grimson J. Advanced Fluid Dynamics and Heat Transfer. McGraw-Hill, 1972.
3.25. Engineering Science Data 67016, Forced Convection Heat Transfer in Circu-
Circular Tubes, ESDU Ltd., London.
3.26. Eckert E. R. G., Drake R. M. Heat and Mass Transfer. McGraw-Hill, 1959.
3.27. Rohsenow W. M., Harlnelt J. P. (eds). Handbook of the Heat Transfer.
McGraw-Hill, 1973.
3.28. Van der Does de Bye, Schenk J. Heat Transfer in Laminar Flow between Pa-
Parallel Plates. — «Appl. Sci. Res.», 1952, v. A3, p. 308.
3.29. Sellars J. R., Tribus M., Klein J. S. Heat Transfer to Laminar Plow in a Round
Tube or Flat Conduit. The Graetz Problem Extended. — «Trans. ASME»,
1956, v. 78, p. 441.
3.30. Morgan V. T. The Overall Convective Heat Transfer from Smooth Circular
Cylinders. — In: Advances in Hear Transfer. V. 11. Academic Press, 1975.
3.31. Kreith F. Heat Transfer. International Textbook Co., 1965.
3.32. Kreilh F. Convective Heat Transfer in Rotating Systems. — In: Advances in
Heat Transfer. V. 5. Academic Press, 1968.
3 33. Cobb E. C, Saunders O. A. Heat Transfer from a Rotating Disc. — «Proc.
Roy. Sow, 1956, v. 236A, p. 343—351.
3.34. Anderson J. Т., Saunders O. A. Convection from an Isolated Heated Horizon-
Horizontal Cylinder Rotating about its Axis. — «Proc. Roy. Soc.», 1953, p. 217A,
p. 555-562.
3.35. Dorfman L. A. Hydrodynamic Resistance and the Heat Loss of Rotating So-
Solids (trans. N. Kemmer). Edinburgh, Oliver and Boyd, 1963.
3.36. Convection Heat Transfer ;ind Flow Phenomena of Rotating Spheres. — «In-
«Intern. J. Heat Mass Transfer», 1963, v. 6, p. 881—895. Auth.: F. Kreith, L. R. Ro-
Roberts, J. A. Sullivan, S. N. Sinha.
3.37. Hering R. G., Grosh R. J. Laminar Combined Convection from a Rotating
Cone. — «J. Heat Transfer», 1963, v. 85, p. 29—34.
3.38. Hering R. G., Grosh R. J. Free laminar convection from a nonisothermal co-
cone. — «Intern. J. Heat Mass Transfer», 1962, v. 5, p. 1059.
3 39. Kays W. M., Bjorklund I. S. Heat Transfer from a Rotating Cylinder with
and without Cross Flow. — «Trans. ASME», 1958, v. 80, p. 70—78.
3.40. Tien C. L., Campbell D. T. Heat and Mass Transfer from Rotating Cones. —
«J. Fluid Mechanics», 1963, v. 17, p. 105—112.
3.41. Eckert E. R. G. Survey on Heat Transfer at High Speeds. — «Aeronautical
Research Laboratory 189», Dec. 1961. Wright-Patterson Air Force Base.
3.42. Monaghan R. J. Formulae and Approximations for Aerodynamic Heating Ra-
Rates in High Speed Flight ARC, CP360, 1957.
3.43. Crocco L. The Laminar Boundary Layer in Gases (Lo Strato Limite Laminare
nei Gas). — «Monogr. Sci. di Aeronautics», 1946, 3. Roma, RAE Translation.
3.44. Young G. B. W., Janssen E. The Compressible Boundary Layer. — «J. Aero-
Aeronaut. Sci.», 1952, v. 19, p. 229—236.
3.45. Van Driest E. R. Convective Heat Transfer in Gases. — In: Turbulent Flow
and Heat Transfer. Ed. by С. С. Lin. High Speed Aerodynamics and Jet Pro-
Propulsion. V. 5. Oxford University Press, 1959.
3.46. Keenan J. H., Kaye J. Gas Tables. John Wiley, 1945.
3.47. Hilsenrath J. e. a. The NBS—NASA Tables of Thermal Properties of Gases.
National Bureau of Standards, 1955.
3.48. Raithby G. D., Hollands K- G. T. A General Method of Obtaining Appro-
Approximate Solutions to Laminar and Turbulent Free Convection Problems. — In:
Advances in Heat Transfer. V. 11. Academic Press, 1975.
3.49. Spalding D. В., Pun W. M. A Review of Methods for Predicting Heat Trans-
Transfer Coefficients for Laminar Uniform Property Boundary Layers- Flows. —
«Intern. J. Heat Mass Transfer», 1962, v. 5, p. 239—239.
3.50. Streeter V. L. (ed.) Handbook of Fluid Mechanics. McGraw-Hill, 1961.
83
Глава 4
ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
4.1. ВВЕДЕНИЕ
Все тела с температурой выше абсолютного нуля (О К) постоянно ис-
испускают энергию в виде излучения.
Считается, что лучистая энергия переносится электромагнитными
волнами в соответствии с классической электромагнитной волновой
теорией или фотонами (переносчиками энергии) — в соответствии
с квантовомеханической теорией. В большинстве случаев уравнения,
полученные на основе обеих этих теорий, подобны. Однако для объяс-
объяснения радиационных явлений чаще используется волновая теория,
несмотря на некоторые ее недостатки.
Природа всех видов излучения тождественна. Для переноса энер-
энергии они не требуют проводящей среды и распространяются с одинако-
одинаковой скоростью, равной скорости света (т. е. с.= 3 • 1010 см/с). Виды
излучения различаются только частотой и длиной волны, которые
связаны следующим соотношением:
с (скорость света)•= % (длина волны) X f (частота). D.1)
Тепловое излучение, которое относится к большой группе излу-
излучений с протяженностью спектра от космического излучения до ра-
радиоволн, имеет длины волн в интервале от 0,3 мкм (I мкм>= 10~6 м)
до 50 мкм, включая видимую и инфракрасную области.
При взаимодействии падающего излучения с поверхностью часть
энергии отражается, часть поглощается, а часть, если тело прозрач-
прозрачное, проходит сквозь него. Из принципа сохранения энергии сумма
должна быть равна энергии падающего излучения, т. е.
отражение + поглощение + прохождение = падающее излучение
или
р + сс + т= 1, D.2)
где р, а и х — коэффициенты отражения, поглощения и пропускания,
характеризующие отражательную.^поглощательную и пропускатель-
ную способность тела.
Поглощенная энергия превращается в тепловую энергию, и нагре-
нагретое тело испускает лучистую энергию в соответствии со своей темпе-
температурой и условиями на поверхности. Количество излучаемой энергии
составляет
Q = ?o0T*F Вт, D.3)
где е — коэффициент излучения (степень черноты тела).
Для изучения характеристик теплового излучения и удобства вы-
вычислений введено понятие абсолютно черного тела, хотя реальные
84
поверхности чаще всего диффузные и серые. Для большинства задач
теплового излучения существенное значение имеет определение ра-
радиационных свойств и обмена лучистой энергией между поверхностями.
4.2. ОБОЗНАЧЕНИЯ
F — площадь поверхности, м2;
СъСгС3Сц — константы излучения (см. табл. 4.2);
Е — лучеиспускательная способность, Вт/м2;
е — относительная лучеиспускательная способность;
Ф — угловой коэффициент излучения;
Н — плотность потока излучения, падающего на поверхность,
Вт/м2;
J — интенсивность излучения, Вт/(м2 • ср);
In = loge — натуральный логарифм;
Ф — эффективное излучение, Вт/м2;
N — число излучающих поверхностей;
Q — поток излучения, Вт;
qa — плотность потока излучения, Вт/м2;
г — расстояние между двумя поверхностями; радиус, м;
h — глубина проникновения излучения, м;
Т — абсолютная температура, К;
а — коэффициент поглощения (поглощательная способность);
р — угол между направлением излучения и нормалью к по-
поверхности; коэффициент ослабления;
е — степень черноты (коэффициент излучения);
у — коэффициент рассеяния;
X — длина волны;
Я,макс — длина волны для максимума интенсивности излучения;
р — коэффициент отражения (отражательная способность);
ст0 — постоянная Стефана—Больцмана;
со — телесный угол.
Индексы:
0 — черное тело; начальное состояние;
п — нормаль;
1 — г'-я поверхность;
э — экран от излучения;
р — направленное излучение;
X — спектральное излучение.
4.3. ОПРЕДЕЛЕНИЯ
Коэффициент поглощения а — отношение поглощен-
поглощенной энергии ко всему количеству лучистой энергии, падающей на тело.
Коэффициент рассеяния у — см. коэффициент ослаб-
ослабления.
Угловой коэффициент излучения q>Ft—F.
(также называется угловым коэффициентом, геометрическим коэффи-
коэффициентом, коэффициентом формы или коэффициентом облученности)
85
представляет собой безразмерную величину, характеризующую долю
лучистой энергии, которая покидает поверхность /•",- и достигает по-
поверхности Fj.
Диффузно отражающая поверхность — по-
поверхность, лучеиспускательная способность которой подчиняется за-
закону Ламберта, причем падающее излучение при рассеянии от диффуз-
диффузно отражающей поверхности распределяется равномерно по всем
направлениям.
Излучение в определенном направлении —
излучение в заданном направлении по отношению к нормали к по-
поверхности.
Лучеиспускательная способность Е — энер-
энергия, излучаемая с единицы площади поверхности в единицу времени.
Интегральная полусферическая лучеиспускательная способность чер-
черного тела в я раз больше интенсивности излучения:
Ео = nJ0 = о0Т* Вт/м2. D.4)
Она представляет собой излучаемую в пространство полусферы энер-
энергию в диапазоне всех длин волн на единицу поверхности в единицу
времени.
Степень черноты в — фундаментальное свойство поверх-
поверхности; представляет собой отношение лучеиспускательной способности
поверхности реального тела к лучеиспускательной способности абсо-
абсолютно черного тела при той же температуре, т. е.
8 = ?/?„. D.5)
Если интенсивность излучения поверхности подчиняется закону
Ламберта, то относительная излучательная способность в определен-
определенном направлении определяется как
ер = J/J 0 D.6)
аналогично полусферической интегральной степени черноты е.
Полусферическая лучеиспускательная способность поверхности
реального тела представляется соотношением
Е = е?0 = га0Т* Вт/м2. D.7)
Замкнутая область —это понятие, используемое для рас-
расчета излучения, падающего со всех направлений окружающего прост-
пространства. В замкнутой области полная сумма количества тепла, переда-
передаваемого поверхностям, равна нулю (SQ = 0); при этом полная сумма
угловых коэффициентов излучения данных поверхностей равна еди-
единице Bф = 1).
Коэффициент ослабления р. Многие вещества,
в частности такие газы, как двуокись углерода и водяные пары, по от-
отношению к тепловому излучению не являются полностью прозрачны-
прозрачными. Они поглощают и рассеивают^определенное количество падающего
излучения, пропуская лишь часть* его. В результате интенсивность из-
излучения уменьшается с глубиной материала, через который оно про-
проникает.
86
Доля поглощенной энергии представляется уравнением
J = Jo exp (—а/г) Вт/(м2 • ср), D.8)
где Уо — начальная интенсивность излучения; h — глубина проникно-
проникновения; а — коэффициент поглощения.
Доля рассеянной энергии определяется уравнением
J = Jo exp (—yh) Вт/(ма • ср), D.9)
где у — коэффициент рассеяния.
Совмещение обоих процессов (поглощения и рассеяния) выражает-
выражается уравнением
J = Уо exp [—(a + y) Л1 = Jo ехр (—рА) Вт/(м2-ср), D.10)
где р = а + у — коэффициент ослабления; ехр (—p/i) характеризует
проницаемость материала, a h—эффективная длина (или среднее зна-
значение проникновения лучистого потока), рассчитываемая с учетом
всех возможных траекторий излучения, которые зависят от формы
газового объема. Эффективная длина может быть приближенно приня-
принята равной 3,4 VIF, где V — объем газа, a F — площадь ограничиваю-
ограничивающей поверхности. Если среду (обычно газ) рассматривать как серый газ,
то испускаемый газом поток излучения выражается соотношением
qs = [1 — ехр (—рА)] <то74 Вт/м2. D.11)
Серое тело — это идеальное тело, интенсивность излучения
которого принята для всех длин волн с точностью до постоянного
коэффициента пропорциональной интенсивности излучения абсолютно
черного тела. Спектральная степень черноты е^ серого тела для всех
длин волн является постоянной величиной, а его излучательные
свойства подчиняются закону Ламберта. Таким образом, с учетом этих
предположений г — г\ = а = а%, где а и о», — коэффициенты пол-
полной и спектральной поглощательных способностей.
Некоторые материалы, используемые в инженерной практике, по
своим излучательным свойствам могут быть с определенным прибли-
приближением отнесены к серым телам.
Модель абсолютно черного тела — это малое
отверстие в полой сфере, обладающее свойствами, приближающимися
к свойствам абсолютно черного тела.
Полусферическое излучение — поток излучения
в полусферическое пространство.
Падающее излучение — лучистая энергия, приходя-
приходящаяся на единицу площади за единицу времени.
Инфракрасное излучение — часть электромагнит-
электромагнитного спектра излучения, которая лежит в диапазоне длин волн 0,75—
300 мкм. Тела, которые поглощают падающее излучение с такими
длинами волн, нагреваются.
Монохроматическое излучение — этот термин
относится к излучению с одинаковыми длинами волн.
Эффективное излучение Ф — удельная лучистая
энергия, покидающая поверхность и отнесенная к единице площади,
87
Вт/ма, Эта энергия представляет собой суммарное излучение тела,
т. е. собственное и отраженное излучение.
Интенсивность излучения J — удельная лучистая
энергия, испускаемая с единицы площади поверхности за единицу
времени в единичный телесный угол, Вт/(м2 • ср). Спектральная интен-
интенсивность J% характеризует излучение в небольшом интервале длин
волн вблизи длины волны X; интегральная интенсивность относится
к полному излучению для всех длин волн.
Коэффициент отражения р—отношение отражен-
отраженного излучения к падающему на тело излучению.
Телесный угол а> — это отношение площади поверхности
участка сферы, вырезанного телесным углом, к квадрату радиуса
сферы, т. е. da> = dF/r2. Используемой единицей измерения является
стерадиан. Телесный угол полусферы равен 2л.
Спектральное излучение относится к очень узкому
участку длин волн вблизи данной длины волны X.
Зеркальная поверхность — это поверхность, для ко-
которой выполняется закон геометрической оптики: угол отражения равен
углу падения лучей на эту поверхность, т. е. она отражает лучи, по-
подобно зеркалу. Следовательно, в этих случаях необходимо учитывать
направление траекторий отраженных лучей.
Суммарное излучение — это совокупность излучений
для всех длин волн.
Коэффициент пропускания х — отношение излу-
излучения, прошедшего сквозь тело, к излучению, падающему на тело.
4.4. АБСОЛЮТНО ЧЕРНОЕ ТЕЛО
И ОСНОВНЫЕ ЗАКОНЫ ИЗЛУЧЕНИЯ
Абсолютно черное тело является идеальным телом, которое способно
полностью поглощать падающее на него излучение. Это положение
справедливо для излучения в диапазоне всех длин волн и при всех уг-
углах падения. Абсолютно черное тело считается абсолютным поглотите-
поглотителем падающего излучения и также абсолютным излучателем. Поэтому
его используют в качестве эталона сравнения для поглощения и излу-
излучения реальных тел.
Полное количество лучистой энергии, излучаемой абсолютно чер-
черным телом, описывается законом Стефана—Больцмана, а распреде-
распределение интенсивности излучения по отдельным направлениям — за-
законом Ламберта. Распределение спектральной интенсивности излу-
излучения по длинам волн устанавливается законом Планка, а связь
длины волны с максимумом спектральной интенсивности излучения
выражается законом смещения Вина.
Тепловое излучение с поверхности черного тела представляет со-
собой диффузное излучение, которое распределяется равномерно во всем
пространстве полусферы (рис. 4.1).
Приближенной моделью абсолютно черного тела может служить
малое отверстие в оболочке полого тела. Это отверстие, попадая в ко-
которое лучистый поток почти полностью поглощается вследствие много-
88
кратного отражения полостью, обладает наивысшей способ-
способностью поглощать лучистую энергию при данной температуре.
F
Потери тепла с площади F поверхности
с равномерной температурой 7\ в окру-
окружающее пространство (предполагаемое
также черным) с постоянной температурой
Т2 выражаются уравнением
Q = Fa0 (Ti ~ П) Вт. D.12)
Полусферическая лучеиспускательная
способность абсолютно черного тела
в л раз больше лучеиспускательной спо-
способности в направлении нормали к поверх-
поверхности, равной интенсивности излучения.
В табл. 4.1 представлены основные теп-
тепловые свойства абсолютно черного тела.
Излучательные свойства абсолютно черного тела
р
абсолютно черного тела
Нормаль
Рис. 4.1.
чение
Диффузное излу-
Таблица 4.1
Излучательное свойство
Спектральная интенсив-
интенсивность излучения в направле-
направлении нормали
Полная интенсивность
излучения в направлении
нормали
Полная интенсивность из-
излучения по всем направле-
направлениям
Спектральная лучеиспу-
лучеиспускательная способность по
всем направлениям
Полная лучеиспуска-
лучеиспускательная способность по всем
направлениям
Полусферическая спект-
спектральная лучеиспускатель-
лучеиспускательная способность
Полусферическая полная
лучеиспускательная спо-
способность
Максимум интенсивно-
интенсивности излучения
Формула
с,
х- ° Is [ехр (С2/ХТ)— 1]
= JK о,р
0
Jn а = ^п „COS (J = COS (J
л
E\, о, & = ^K о cos P
En a = Jn n COS (J=: COS (J
EX, 0 = пЕХ, 0, nc='nJK 0
00
0
умакс п тЬ
J}., 0 ="W'
Основной вакон
Закон Планка
Закон Лам-
Ламберта
Закон Лам-
Ламберта
Закон Лам-
Ламберта
Закон Стефа-
Стефана—Больцмана
Закон Вина
Закон Кирхгофа. Для тела, находящегося в состоянии теплового
равновесия, отношение его лучеиспускательной способности к лу-
89
чеиспускательной способности абсолютно черного тела при той же
температуре равно поглощательной способности:
Е1Ей = а или е = а. D.13)
Таким образом, при данной температуре тело может поглощать столь-
столько лучистой энергии, сколько оно может ее излучать. Этот закон
не вполне приемлем только к некоторым типам поверхностей, относя-
относящимся по своим характеристикам
к серым.
Закон Ламберта. Для заданного
направления интенсивность излуче-
излучения пропорциональна косинусу угла,
который оно образует с нормалью к
эмиссионной поверхности:
/о.р = /о,» cos p Вт/(м2 • ср). D.14)
Если интенсивность излучения по-
поверхности подчиняется закону коси-
косинуса, справедливому для абсолютно
черного тела, то степень черноты в
направлении нормали становится не-
независимой от угла р и такой же, как
и интегральная полусферическая сте-
степень черноты:
гп = е. D.15)
Закон Щанка. Спектральное распределение интенсивности излу-
излучения абсолютно черного тела выражается уравнением
Рис. 42. Зависимость излучения
абсолютно черного тела от XT
Вт/(ма-ср).
D.16)
Эта формула позволяет рассчитывать лучистую энергию для любой
длины волны спектра излучения.
Уравнение D.16) можно переписать в следующей форме:
D.17)
Это равенство свидетельствует о том, что для данного значения ЯГ
отношение J%, о1Ть постоянно для всех температур и что эта зависи-
зависимость может быть представлена единственной кривой (рис. 4.2).
Выражение для спектральной лучеиспускательной способности
имеет вид
Вт/м2. D.18)
Полусферическая лучеиспускательная способность определяется
соотношением
Вт/м2,
D.19)
90
которое известно как закон Стефана—Больцмана; коэффициент про-
пропорциональности а0 называется постоянной Стефана—Больцмана.
Часто желательно рассчитать относительную лучеиспускательную
способность в интервале длин волн между Хг и Х2 при заданной темпе-
температуре поверхности Т. Для этой цели может быть использована при-
к 7 П
J
1 0.7
1
0,9
0,8
0,6
0,5
0,2-
0,1 '
-
-
-
- 1
'. I
1
i
«41
§¦
/
"l 1 1
/
/
/
1
1
1 1^° 1
/
/ 1
v
к
/
/*¦
/ i
X
!
* 1
¦Ss [
cs? 1
§~i
S51
I I 1 1 Г r I ! t 1 1
2 3 4- 5 6 7 3 9 70* 2
длина волны-температура ХГЛ
мкм- К
Рис. 4.3. Относительная лучеиспускательная способность абсолют-
абсолютно черного тела в интервале значений 0—XT
веденная на рис. 4.3 кривая относительной лучеиспускательной
способности вместе с уравнением
о-х, г—ео-л, г] Вт/м2,
D. 20)
D.21)
является относительной лучеиспускательной способностью.
Закон смещения Вина. С ростом температуры максимум интенсив-
интенсивности излучения абсолютно черного тела смещается в область более
коротких длин волн. Длина волны для максимума интенсивности излу-
излучения при заданной температуре Т может быть вычислена из уравне-
уравнения
^ = С3 М • К. D.22)
Численные значения различных констант излучения приведены
в табл. 4.2.
91
Таблица 4.2
Коистаиты излучении в уравнениях Планка, Стефана—Больцмаиа и Вина
Константа
с2
с3
с*
Определение
Первая константа в
уравнении Планка для оп-
определения спектрального
распределения энергии
Вторая константа в урав-
уравнении Планка для опреде-
определения спектрального рас-
распределения энергии
Константа в уравнении
Вина
Константа в формуле для
определения максимума
интенсивности излучения
Постоянная Стефана —
Больцмана
Значение
1,191-Ю-16 Вт-мг/ср
1,438-Ю м-К
0,289-Ю-2 м-К
4,095-10-' Вт/(м3-К6)
5,669-10-8 Вт/(м2-К4)
4.5. ЛУЧИСТЫЙ ТЕПЛООБМЕН
МЕЖДУ ДВУМЯ АБСОЛЮТНО ЧЕРНЫМИ ПОВЕРХНОСТЯМИ
Между поверхностями, расположенными так, что они «видят» друг
друга, происходит лучистый теплообмен, причем каждая из поверхно-
поверхностей излучает энергию на другую и поглощает энергию, излученную
этой поверхностью. Для двух абсолютно черных поверхностей, нахо-
находящихся при различных температурах и расположенных в непогло-
щающей среде, результирующий обмен энергией выражается так:
где
Ju 1 V d
1 С С cos Bi с
t dF2;
D.23)
D.24)
Ф/?,_^, (аналогичное определение и для ф^-^,) представляет собой уг-
угловой коэффициент излучения поверхности 1 по отношению к поверх-
поверхности 2. Он показывает, какая доля энергии, излучаемой поверх-
поверхностью Flt попадает на поверхность F2- Полная энергия, излучаемая
в единицу времени с поверхности 1 на поверхность 2 и наоборот, опре-
определяется выражениями
й-з^оПЛФ^-^Вт D.26)
92
Рав енство
D.27)
D.28)
представляет собой соотношение взаимного лучистого обмена между
поверхностями.
Рис. 4.4. Лучистый теплообмен между дву-
двумя поверхностями
Значения углового коэффициента излучения для двух гео-
геометрических конфигураций представлены в табл. 4.3.
4.6. ПРИМЕНЕНИЕ АЛГЕБРАИЧЕСКОГО МЕТОДА ДЛЯ ОПРЕДЕЛЕНИЯ
УГЛОВЫХ КОЭФФИЦИЕНТОВ ИЗЛУЧЕНИЯ
Выражения для угловых коэффициентов излучения систем из двух
черных поверхностей, приведенные в табл. 4.3, можно с помощью
алгебраического метода использо-
использовать для многих других геометри-
геометрических систем. Этот метод основан
на принципе сохранения энергии и
соотношений взаимного обмена
для диффузных поверхностей.
Таким образом, неизвестный
угловой коэффициент излучения
можно определить, прибавляя или
вычитая известные коэффициенты
для тел сравнимых конфигураций.
Один из примеров приведен на
рис. 4.5. В табл. 4.4 перечислены
определенные таким образом уг-
угловые коэффициенты излучения
для некоторых геометрических
систем излучения.
% F=
— V
Рис. 4.5. Пример, иллюстрирующий
применение алгебраического метода
для определения углового коэффици-
коэффициента излучения
93
га
=г
as
ч
-luT су
о.
к
о.
о
е
к
I
г
о.
I
X
к
I
t
X
S
3"
о
ч
с
^ о
Ч ч
га с
_ о
sii
I
га ?
>=t О
9 к
о о.
ч с
а.
I
I
4-
_|«
•а
е-
+¦
ч
IO
о о >>
SCO.
tt, S s о
Миич
о о и
я ч в >>
а в ь
cf О t(
га ts °
Э « а с
и о
и ? о й
в* о t- о
О) с; >,i;
в; о о и.
о
l
; a.
s
га >>
U ° s-s
оно
SOB
95
со
¦*
Ч
VO
<d
t*
<U
s
я
<u
5?
ч
о
о
о.
с
К
Н
ш
<и
Г
л
S
н
0)
X
в
*
о
ы
Q
(-
1
к
к
5:
?
I
3
о.
3
а
S
«
ё
с
s
атич
3
а
3
S
S
писас
О
с
в
/С
Лч
V_
4
ev
CJ
«
1
tt.
-^ !«
- SH
Я1
та ч
и
о
11
|||
о ч
СО
(Л
О
и
—f—
\^
и
1!
т
|
1
( + /
1
il Я
а. и
на пове
[ иеогра
- с
§ к м
Я V
1
1
С4!
О
•ф
>о
-|« 5
II т
оГ
I
1
tj
' J
ю 6
9. е
кольце
и торец
•ta га
•S о.
енни
слой
ЛИНД
а. я
В нут
азный
ого ц;
D.4
со
96
a.
1
I
sr
<
II
"я
о а
го
го
Площ
О
о
элли
а4 о
«Из
гчо
;ча
J* го о
Основные формулы н данные по теплообмену
97
я
я
а
S
m
X
S
I ^ Г"
•« 8 3 |
В" —
о
н к
о га
~ л
а 2
•s s
^&g«
га о
s о. я
га _
ti
ll
о
с 2
«I
с §35*
98
X
N1
4*
*
•if
VO
Я
(-
s
ж
4
о
П род
к
a
s
g
[ЗЛ
ш
S
a:
§
о
§
4
О
s
us
2.
3
m
авленн
1
о.
с
s
i
[ати
о
3
S
S
О
О
о
а
X
<в
о
а
о
с
с
I
d t
CQ +
j О
J II
^ a
'- И
|
1 cj
fcf
—т )
6
С
О ™
2."
X Й
ч ч
га ь^
o.
ra X
с 3
X
га S
РЭ ^
to
f—"¦¦¦¦"I
03
I
о
+ s-
7 "
J щ
03 «я.
<n| t:
II
iC
l
&•
TV ^ ^У
и
«я
¦ ex
О) S
s|
и я
CO
¦ S5
о.
CO ^
n
100
ft.
I
_ CQ
ft.
I
ft.
I
i:
ft.
I
ft.
I
"• J.
щ
a.
Э-
s
X
3
a
о
о
8
101
оэ
I
о
о
X
X
о
о.
С
G
+
•о
к
4-
а
3
W
ь. в.
i i
i"
ft7
I
«С
е-
!
uT
i !
JJ-
4
в о
я в „
к 3
II!
lll
ts га В в
м га в S.
m И Я и
>> о
???
о
<N
102
ft.
I
о
с
Я
Ч
и
а
X
S
I
5 °
я «
«в
§1
о О
о.
га Ч
is
II
о
103
О)
S
X
о
о
о.
С
о.
3
ю
g
р.
о
я
о.
си
¦е-
о
я
о.
ш
¦е-
о
104
ч
уо
га
Ь
ш
Я
Я
ч
о
«
о
о.
С
>>
S
н
иен
а
я
S
OJOI
о
>.
к
&
о.
3
W
&
¦*
о:
5
о
^
«с»
Of
U
о
«ГЦ
+
OS
' О1
OS .«
о
с
а5
а) о
!§
с;
О S
С5
о со
о
со
106
S
S
ч
о
О
а.
С
О
Я о
a a
a a
СО
П
108
Если поверхностное распределение температуры неравномерно,
можно, разбив поверхность на небольшие изотермические участки и
применив алгебраический метод к угловым коэффициентам излучения,
определить полный лучистый теплообмен между неизотермическими
поверхностями.
4.7. ЛУЧИСТЫЙ ТЕПЛООБМЕН МЕЖДУ АБСОЛЮТНО ЧЕРНЫМИ
ПОВЕРХНОСТЯМИ, ОБРАЗУЮЩИМИ ЗАМКНУТУЮ ОБЛАСТЬ
Для точного определения теряемой поверхностью лучистой энергии
необходимо учитывать полное излучение от всего пространства полу-
полусферы. Таким образом, все задачи теплообмена излучением могут быть
представлены как задачи по лучистому обмену между N поверхностями
с эквивалентными условиями, образующими замкнутую область.
Например, задний план большого бокса или жилой комнаты для не-
небольшого предмета можно считать поверхностью, эквивалентной чер-
черной поверхности.
Для анализа замкнутой области чрезвычайно полезно восполь-
воспользоваться тем, что полная сумма обмениваемой энергии для N поверх-
поверхностей равна нулю, т. е.
2<2* = 0, D-29)
i= i
в то время как сумма угловых коэффициентов излучения для данной
поверхности Ft равна единице, т. е.
2cpF._F. = l. D.30)
С учетом этих предположений энергия, теряемая поверхностью i
в окружающее пространство, сформированное из N абсолютно черных
поверхностей, определяется выражением
Qi^Ft | о0(Tf-Tj) cpF._F. = Ft a0Tf- ? ao(FjTf «р^-^Вт, D.3Ц
где cpF._i7.— угловой коэффициент излучения от поверхности Ft
к поверхности Fj\ j = 1, 2, 3 N.
4.8. ЛУЧИСТЫЙ ТЕПЛООБМЕН МЕЖДУ ДИФФУЗНО-СЕРЫМИ
ПОВЕРХНОСТЯМИ
Результирующий поток теплового излучения, теряемого поверхностью,
представляет собой разность между потоком излучаемой энергии и
потоком поглощаемой энергии и может быть выражен уравнением
Яй = еа0Т4 — аН Вт/м2, D.32)
где е и а — коэффициенты излучательной и поглощательной способ-
способности поверхности соответственно; Т — температура поверхности;
109
ч
VO
га
ш
о
н
1
1 +
+
и и
3
X
S
о
Ё
'В
2
s
s
о
я
S
s
о п
* о
3 ю
g О
I
S
!. е-
tef С
II
<и о
о. >,
<У О
ю
I
n
е-
te?
S е- _
э-
+
R
О.
га
о. а
га
с
га
ю
1=(
S
голь
oyi
S
110
Ill
Н — плотность потока излучения, падающего на поверхность. Если
падающее излучение есть излучение черного тела, то уравнение
можно переписать в виде
qs = ео0Г4 — аа0ТЬ Вт/м2, D.33)
где То — температура абсолютно черного тела.
Лучистый обмен энергией между различными излучающими поверх-
поверхностями зависит как от нзлучательных и поглощающих свойств, так
и от отражающих характеристик поверхностей. Результирующая лу-
лучистая энергия, теряемая данной поверхностью, должна определяться
с учетом полных излучательных характеристик обменивающихся лу-
лучистой энергией поверхностей, для которых должны быть определены
угловые коэффициенты излучения.
Полный расчет, выполненный с достаточно высокой точностью, в ко-
котором учтено, что обмен энергией излучения происходит в условиях
многократного поглощения и отражения, получить очень трудно.
Поэтому в инженерной практике для упрощения расчета лучистого
теплообмена реальные поверхности почти всегда условно считают диф-
фузно-серыми поверхностями.
Для серой поверхности лучеиспускательная способность равна по-
глощательной способности, т. е. е = а. Тогда уравнение D.33) можно
переписать так:
q$ = 8сг0 (Г{ — 71) Вт/м2. D.34)
Это уравнение представляет результирующий поток энергии, теряемой
поверхностью с температурой 7\ в окружающую абсолютно черную
среду с температурой Г2.
Для серой диффузно отражающей поверхности отраженное излуче-
излучение имеет такое же равномерное распределение, как и испускаемое
излучение. Поэтому отражаемое излучение и покидающее поверхность
испускаемое излучение могут быть представлены единой величиной,
которая выражается уравнением
ф = е0г0г4 + рЯ Вт/м2, D.35)
где р — коэффициент отражения (отражательная способность); Я —
плотность потока излучения, падающего на поверхность. Ф пред-
представляет собой эффективное излучение с поверхности, которое состоит
частично из испускаемой и частично из отражаемой энергии. Для непро-
непрозрачной серой поверхности р = 1 — е. Комбинация уравнений D,32)
и D.35) позволяет получить следующее соотношение:
?3-8ст0Г4-аЯ=-^-(ст0Г4-Ф) Вт/м2. D.36)
1 — 8
Для диффузно-серых поверхностей полусферическая интегральная
степень черноты является только излучательным свойством, которое
должно рассчитываться. Могут быть также использованы угловые ко-
коэффициенты излучения, полученные для абсолютно черных поверх-
поверхностей.
112
Таким образом, для системы из N днффузно-серых поверхностей,
образующих замкнутую область, плотность потока излучения, теряе-
теряемого г'-й поверхностью, определяется уравнением
(о0Т«-Ф,) Вт/м2
D.37)
/=
n-._F. Вт/м2,
D.38)
где (fp р.— угловой коэффициент излучения от поверхности
Fi к поверхности Fjt a
N
Выражение D.38) состоит из N уравнений для определения Фъ Ф2, ...,
..., Ф#. По найденным таким образом значениям эффективного излу-
излучения плотность теплового потока, теряемого N поверхностями (т. е.
Qsi> <7»2i •••» Qsn), можно рассчитать с помощью уравнения D.37). Ре-
Результаты такого расчета для некоторых простых систем, составленных
из двух серых поверхностей, приведены в табл. 4.5.
Экраны
4.9. ЗАЩИТА ОТ ТЕПЛОВОГО ИЗЛУЧЕНИЯ
Теплообмен излучением можно существенно уменьшить с помощью
экранов. Экран обычно представляет собой поверхность, непрозрач-
непрозрачную для излучения и имеющую высокую теплопроводность и низкое
значение степени черноты. Эффективность экрани-
экранирования увеличивается, если экран расположен
между взаимно излучающими поверхностями или
между поверхностью нагрева и нагревателем.
Поток излучения между двумя неограниченно
большими параллельными поверхностями со сте-
степенью черноты Е] ие2 и температурой 7\ и Г2,
между которыми помещено п экранов, можно рас-
рассчитать с помощью формулы
а. 1
¦ + ¦
1
Вт,
D.39)
Рис. 4.6. Схема эк-
экранирования
где Ё! ; и e2j — степень черноты поверхности г'-го экрана. Если по-
поверхности имеют одинаковую степень черноты е, то уравнение D.39)
приобретает такой вид:
(п+1) B/8-1)
Вт.
D.40)
ИЗ
— ь
СУ
2
¦<¦ 5
ее О
о. к
ВО 0
овер
та
о
и
и
к
к
к
<и
в1
я
g
о
с
о
к
к
о
ДСТ31
о
о.
с
о
ЕР
К
н
1
о
Система
п-п w
1
1
1
1
о
ь
со
11^
СУ
lNV \
А
ч
^*
^^
и!"
чГ
/ / ^
г /
/
га
й 5
Серая поверх
кружении черной
о
ГО
•е-
-&
п
CTIt
О 0).
epxi
ЮЩ1
CQ ГЗ
с Я
Обе
о отр
э-
1
ьГ
о
О
со
II
п
СУ
/Л
U 1 \
\^
О
а
О)
3
X
Две пронзволь
грхности
со
<N
5 о
§§
и
о-в-
или
— о:
К О то
И л 3
|5§
О) ^
ГО О,
ьГ
с
—
1 c?
CO*
, 1
СУ
1
L
¦*-
-*-
-*-
—^ 41
л о
t^ ^
О <->
\о о
о в
я
Две неограничен
ие параллельные
и
as
is
я ся
Ч се
я 3
о 9
сп га
зга
узно
:ть
•&S
•Э-Я
Я X
е( О.
1 о
1 в
диф-
верх-
э или
тая по]
я о
в га
га
о.
н
^1
:ально ;
[НОСТЬ
О. О.
0J 0)
x га
te, 5,0.0.
¦&m о
¦cEsg
ш о
о
Со
•§•8.
о
о 3-6-5
g 5j ш
о. о. <
О) S- сч
I о
Jo2 ^O Сч>
¦&xS -в-х о.
И.о. со о
а©.
в я
С о
2 а;
CJ " ^
о jjj *
с- га га
«в b
со О О
сч
4-
3
о.
•в-
Э1 О1
1
О) « ";
о со ^
н о ^
СО - сх
О CU
115
В тепловых системах цилиндрической
Экран / \ геометрии используются экраны соот-
- ' '" ^ ^ ветственно цилиндрической формы. По-
Поток излучения между двумя длинными
соосными цилиндрическими поверхно-
поверхностями с расположенным между ними
цилиндрическим экраном определяется
выражением
**И1х
21
Рис. 4.7. Экран цилиндриче- _1_ TjJ 1 A Cl(JL-l__L Л
СК0Й Ф°РМЫ е, + г, I г2 ~1ГгАгп + е3Г )
Xo0Gf-7$) Вт, D.41)
где esl и 8s2 — степень черноты поверхностей экрана; / — длина ци-
цилиндров.
Если поверхности цилиндров и экрана имеют одинаковую степень
черноты е, то уравнение D.41) упрощается:
21 »(Tf- П) ВТ> DА2)
Га V е
где / — общая длина цилиндров.
СПИСОК ЛИТЕРАТУРЫ
4.1. Planck Max. Distribution of Energy in the Spectrum. — «Ann. Physik», 1901,
Bd 4, N 3, S. 553—563.
4.2. Якоб М. Вопросы теплопередачи. Пер. с англ. М., Изд-во иностр. лит.,
1960.
4.3. Katzoff S. (ed.). Symposium on Thermal Radiation of Solids. NASA SP-55.
1958.
4.4. Siegel R., Howell J. R. Thermal Radiation Heat Transfer. V. I and II. NASA
SP-164, 1968.
4.5. Sparrow E. M., Cess R. D. Radiation Heat Transfer. Brooks/Cole Publ. Co.,
1966.
4.6. Hottel H. C, Sarofim. Radiative Transfer. McGraw-Hill, 1967.
4.7. Ozisik M. N. Radiative Transfer. Wiley-Interscience Publication, 1973.
4.8. Kreith F. Radiation Heat Transfer. International Textbook, 1962.
4.9. Wiebelt J. A. Engineering Radiation Heat Transfer. Holt, Rinehart & Winston,
1966.
4.10. Siegel R., Howell J. R. Thermal Radiation Heat Transfer. McGraw-Hill, 1972.
4.11. Sparrow E. M. Radiation Heat Transfer between Surfaces. — In: Advances in
Heat Transfer. V. 2. Academic Press, 1965.
4.12. Svet D. Y. Thermal Radiation. Plenum Press, 1965..
4.13. Chandrasekhar S. Radiative'Transfer. Dover Publication, 1960.
4.14. Hottel H. С Radiant Heat Transmission. — In: McAdarns W. H. Heat Trans-
Transmission. McGraw-Hill, 1954.
4.15. Gray W. A., Miiller R. Engineering Calculations in Radiative Heat Transfer.
Pergamon Press, 1974.
4.16. Dunkle R. V. Thermal Radiation Characteristics of Surfaces. — In: Theory
and Fundamental Research in Heat Transfer, Ed. by J, A. Clark. Pergamon
Press, 1965-
116
4.17. Feingold A. Radiation Interchange Configuration Factors between Various
Selected Plane Surfaces. — «Proc. Roy. Soc. A», 1966, v. 292, N 1428,
p. 51—60.
4.18. Sparrow E. M. A Now and Simpler Formulation for Radiation Angle Fac-
Factors. — «J. Heat Transfer», 1963, v. 85, N 2, p. 81—88.
4.19. Sparrow E. M. On the Calculation of Radiant Interchange between Surfaces.—
In: Modern Developments in Heat Transfer. Ed. by W. Ibelc. Academic Press,
1963.
4.20. Howell J. R. Application of Monte Carlo to Heat Transfer Problems. — In:
Advances in Heat Transfer. V. 5. Academic Press, 1968.
4.21. Hamilton D. C, Morgan W. R. Radiant-Interchange Configuration Factors,
NASA TN 2836, 1952.
4.22. Leuenberger H., Pearson R. A. Compilation of Radiation Shape Factors for
Cylindrical Assemblies. ASME 56-A-144, Nov. 1965.
4.23. Feingold A., Gupta K. G. New Analytical Approach to the Evaluation of Con-
Configuration Factors in Radiation from Spheres and Infinitely Long Cylinders.—
«J. Heat Transfer», 1970, v. 92C, p. 69—76.
4.24. Eckert E. R. G., Sparrow E. M. Radiative Heat Exchange between Surfaces
with Specular Reflection. — «Intern. J. Heat Mass Transfer», 1961, v. 3,
p. 42—54.
4.25. Chupp R. E., Viskanta R. Radiant Heat Transfer between Concentric Spheres
and Coaxial Cylinders. — «J. Heat Transfer», 1966, v. 88C, p. 326—327.
4.26. Bevans J. Т., Dunkle R. V. Radiation Interchange within an Enclosure. —
«J. Heat Transfer», 1960, v. 82C.
4.27. Buschman A. J., Pittman С. М. Configuration Factors for Exchange of Ra-
Radiant Energy between Axisymmetrical Sections of Cylinders. Cones and Hemi-
Hemispheres and Their Bases. NASA TN D-944, 1961.
4.28. Hsu С J. Shape Factor Equations for Radiant Heat Transfer between Two
Arbitrary Sizes of Rectangular Planes. — «Canad. J. Chem. Engng», 1967,
v. 45, N 1, p. 58—60.
4.29. Richmond J. С (ed.) Measurement of Thermal Radiation Properties of Solids,
NASA SP-31, 1963.
4.30. Dunkle R. V. Thermal Radiation Tables and Applications. — «Trans. ASME»,
1954, v. 69, p. 549—552.
4.31. Smith R. A., Jones F. E., Chasmer P. E. The Detection and Measurement of
Infra-Red Radiation. Oxford, Clarendon Press. 1968.
Глава 5
КИПЕНИЕ И КОНДЕНСАЦИЯ
5.1. ВВЕДЕНИЕ
На границе раздела двух фаз жидкость—пар имеет место равновес-
равновесное протекание процессов испарения и конденсации. Испарение пред-
представляет собой процесс превращения жидкости в пар со скоростью, пре-
превышающей скорость обратного явления — конденсации. В обоих
случаях происходит теплообмен, связанный с поглощением или выделе-
выделением теплоты фазового перехода при изменении агрегатного состояния
вещества: при испарении тепло поглощается, а при конденсации — вы-
высвобождается.
Кипение — это процесс образования пара при нагревании поверх-
поверхности, погруженной в жидкость. При этом образуются пузырьки пара,
возникающие только в определенных точках нагреваемой поверхнос-
поверхности—в центрах парообразования. Интенсивность образования пузырьков
пара возрастает с повышением тепловой нагрузки в режиме пузырча-
пузырчатого кипения. При достижении высокоразвитого процесса парообра-
парообразования поверхность нагрева покрывается паровой пленкой, изо-
изолирующее действие которой приводит к снижению отводимого жидко-
жидкостью теплового потока, хотя температура поверхности нагрева продол-
продолжает расти. Максимальный тепловой поток является критическим для
проектируемой конструкции паровых котлов, выше которого на-
наблюдаются кризис кипения и последующее перегорание нагреватель-
нагревательных элементов.
Конденсация (переход вещества из газовой фазы в жидкую или твер-
твердую) инициируется центрами конденсации в паровом объеме или
на охлаждающей поверхности. Различают два вида конденсации: пле-
пленочную и капельную. В пленочной конденсации жидкий конден-
конденсат смачивает поверхность и образует на ней непрерывную пленку,
которая оказывает значительное сопротивление тепловому потоку.
В случае капельной конденсации пары конденсируются на охлажда-
охлаждаемой поверхности в центрах конденсации в виде капель. Они не сма-
смачивают полностью всю поверхность и растут только за счет конденса-
конденсации в них пара и слияния их с другими, рядом расположенными кап-
каплями.
Теплообмен возрастает при капельной конденсации и с уменьше-
шением толщины жидкой пленки в случае пленочной конденсации.
Присутствие даже небольшого количества неконденсирующихся газов
может привести к значительному ухудшению теплообмена.
В табл. 5.1 сравниваются эффективности теплоотдачи при кипении
и конденсации.
118
Т л б л и ц л 5.1
Сравнение эффективности теплообмена при кипении и конденсации
Показатель
Кипение
Конденсация
Тип теплообмена
Фазовый переход
Наилучшее условие
теплообмена
Соотношение между
безразмерными крите-
критериями
Температурный пе-
перегрев
Условие по поддержа-
поддержанию процесса
Другие воздействую-
воздействующие факторы
Кипение п большом объ-
объеме:
спободпая конпекиня
пузырчатое кипение
пленочное кппешге
Кипение при движении
жидкости:
кипение при вынужден-
вынужденной конвекции
С поглощением тепла
Пузырчатое кипение
'ст — 'нас
Перегрев жидкости
Поверхностные условия
Гравитация
Растворенные газы
Пленочная
Капельная
С выделением тепла
Капельная
Со--С (Re)-
mi а с 'с т
Переохлаждение кон-
конденсирующей поверх-
поверхности
Скорость движения
пара
Неконденсирующиеся
газы
Г>.2. ОБОЗНАЧЕНИЯ
F — площадь поверхности, м2;
В — безразмерный параметр;
с„ — удельная теплоемкость при постоянном давлении,
Дж/(кг- °С);
Cs fi Ch — коэффициенты в формулах для пузырчатого кипения;
D — диаметр трубы, диаметр сферы, м;
f—коэффициент трения (см. гл. 3);
g — ускорение силы тяжести, м/с2;
uml =QmilFi — массовая скорость на входе трубы, кг/(ма-с);
"т2 = Qm.ilРч — массовая скорость на выходе из трубы, кг/(м2-с);
а — коэффициент теплоотдачи конвекцией, Вт/(м2-с);
осл = о08(Гст+Гиас)(Г?т + TiUc)—коэффициент теплоотдачи
излучением, Вт/(м2 • К);
а, — полный коэффициент теплоотдачи для пленочного ки-
кипения, Вт/(м2-°С);
Г/ <в — скрытая теплота парообразования или конденсации,
Дж/кг;
119
L — длина, м;
Т — абсолютная температура, К;
vH. — скорость потока жидкости, м/с;
vmi>'— скорость потока пара, м/с;
X — характеристическая длина, м;
Во —- Qs/rf,gPnapv~критерий кипения;
Со = а [ц>/Р(р— pnap)g] ^3/Х—критерий конденсации;
Nu = аХ/К—критерий Нуссельта;
Gr = Cg Д^ Х3р2/ц.2— критерий Грасгофа;
Рг — срц1к ¦— критерий Прандтля;
Re -= pvX/ц — критерий Рейнольдса;
Sr = cpAt/rjg—отношение, характеризующее степень перегрева;
() — температурный коэффициент объемного расширения,
К;
/ — температура, °С;
^нас -~ температура насыщения, °С;
4Т ¦— температура поверхности нагреваемой или охлаждае-
охлаждаемой стенки, °С;
А^ — перепад температуры, °С;
At = tCJ—tHac — для кипения;
^ = ^нас—^ст ~~ Для конденсации;
К— коэффициент теплопроводности, Вт/(м- °С);
р-— динамическая вязкость, Н-с/м2;
р — плотность, кг/м3;
т) — тепловая эффективность оребрения;
у — поверхностное натяжение, Н/м;
а0 ¦— постоянная Стефана—Больцмана.
Индексы:
пуз—пузырек (пара);
пл — пленка;
нас — насыщенная жидкость в случае кипения; конденсат в случае
конденсации;
пар — пар;
ст. — стенка.
5.3. ОПРЕДЕЛЕНИЯ
Кипение— переход жидкости в пар, характеризующийся непре-
непрерывным образованием и ростом пузырьков насыщенного пара, внутрь
которых происходит испарение жидкости.
Пленочное кипение — режим кипения в условиях, когда
температура поверхности нагрева намного превышает температуру на-
насыщения жидкости и в то же время интенсивность образования пузырь-
пузырьков пара настолько велика, что нагреваемая поверхность полностью
120
покрывается их слоем. В условиях изолирующего действия паровой
пленки интенсивность теплообмена относительно невысока.
Возникновение пара на границе раздела жидкость—пар происходит
за счет тепла, поступающего от поверхности нагрева через паровую про-
прослойку посредством теплопроводности и излучения.
Кипение при вынужденном движении жид-
жидкости происходит на нагреваемых поверхностях, таких, как
стенки труб, через которые осуществляется вынужденное движение
потока жидкости со значительном скоростью.
Пузырчатое кипе и и с — это кипение, при котором на
границе раздела жидкость—пар постоянно образуются, растут и отры-
отрываются пузырьки пара. Для формирования и последующего роста пу-
пузырьков требуется, чтобы жидкость была перегрета относительно
поверхности. Достигнув определенного размера, пузырьки отрывают-
отрываются от поверхности нагрева, перемешивают жидкость в пристеночной
области и таким образом способствуют существенному увеличению ин-
интенсивности теплоотдачи. Это явление названо пузырчатым кипением
потому, что механизм кипения связан с наличием взвешенных частиц,
микронеровностей поверхности, растворенных газов или других видов
центров парообразования, на которых образуются пузырьки. Без гра-
гравитационных сил пузырьковое кипение не существует.
Кипение в большом объеме имеет место, когда по-
поверхность нагрева погружена в открытый объем с непроточной жид-
жидкостью.
Кипение насыщенной жидкости — это кипение
жидкости при температуре насыщения.
Кипение недогретой жидкости — это кипение,
при котором пары конденсируются вблизи поверхности нагрева. Тем-
Температура жидкости в этой области ниже соответствующей температуры
насыщения для данного давления.
Конденсаци я—процесс перехода паровой фазы в жидкую.
Пленочная конденсация происходит на поверх-
поверхности конденсатной пленки жидкости, которая образовалась в резуль-
результате конденсации пара на полностью смачиваемой твердой поверхности;
при этом последующая конденсация пара происходит только на грани-
границе раздела жидкость—пар.
Капельная конденсация — процесс выпадения кон-
конденсата в жидкой фазе на несмачиваемую поверхность в виде отдель-
отдельных капель; под воздействием гравитационных или иных сил капли
стекают с поверхности, укрупняясь при своем движении. Сухие и мок-
мокрые участки на поверхности чередуются, и она приобретает пятнистый
вид. При капельной конденсации наблюдается самая высокая интен-
интенсивность теплоотдачи.
Температура насыщения — максимально возмож-
возможная температура жидкости при данном давлении. Это также точка ки-
кипения жидкости в условиях, когда максимальное давление пара рав-
равно внешнему давлению.
Недогрев—когда температура жидкости ниже температуры
насыщения.
121
Перегрев — когда жидкость нагрета до температуры более
высокой, чем температура насыщения. Превышение температуры харак-
характеризует степень перегрева. При перегреве образующийся пар поки-
покидает жидкость. При этом его температура может быть выше темпера-
температуры насыщения. Такой пар после предварительного охлаждения до
температуры насыщения конденсируется на холодной поверхности.
5.4. ТЕПЛООТДАЧА ПРИ КИПЕНИИ
Теплоотдача при кипении представляет собой конвективный процесс
с фазовым переходом жидкости в пар. Механизм такого процесса су-
существенно сложнее чисто конвективного теплообмена. Существует
два вида кипения: кипение в большом объеме и кипение при вынужден-
вынужденном течении жидкости (также называемое кипением при кон-
конвекции).
Испарение при ^Пузырча- i Пденочное кипение
естественной ' тое ! __
естественной
конвекции
тое
[кипение
j Точка крити-
критического тепдо-
/вого потока
Точка пере-
перегорания
\
Рис. 5.1. Типичная кривая изменения теплоотдачи прн
кипении жидкости в большом объеме
При кипении в большом объеме теплоотдача происходит от поверх-
поверхности нагрева к непроточной жидкости, в то время как в случае кипе-
кипения при конвекции теплоотдача осуществляется между горячей
стенкой и движущейся жидкостью, смешанной с паром (двухфазный
поток).
При кипении в большом объеме (рис. 5.1) различают три режима:
испарение прн естественной конвекции, пузырчатое кипение и пленоч-
пленочное кипение.
Характеристики теплоотдачи сильно изменяются при переходе от
одного режима к другому. Если тепловая нагрузка незначительна, то
в режиме естественной конвекции температура поверхности нагрева
всего на несколько градусов превышает температуру насыщения жид-
жидкости. Тепло с помощью естественной конвекции передается слоям
жидкости, непосредственно прилегающим к поверхности нагрева, и
паровая фаза образуется па свободной поверхности жидкости. Для
недогретой жидкости парообразование может происходить локально
122
на поверхности нагрева, по конденсация пара в жидкости может све-
свести на нет увеличение паровой фазы.
Благодаря высокой интенсивности теплоотдачи пузырчатое кипе-
кипение имеет очень большое практическое значение. По мере роста темпе-
температуры поверхности нагрева процесс парообразования продолжает раз-
развиваться, и с определенного момента на центрах парообразования по-
поверхности нагрева начинают зарождаться пузырьки пара. Если жид-
жидкость недогрета, то они могут уменьшаться в размерах и разрушаться.
Если же жидкость перегрета, они могут расти и перемещаться к сво-
свободной поверхности. По мере того как пузырьков становится все боль-
больше и больше, они отрываются, попадают в соседние слои жидкости и
сильно их перемешивают, что приводит к увеличению интенсивности
теплоотдачи. Но тепловой поток, отводимый жидкостью, не может уве-
увеличиваться беспредельно. Так как с нагреванием избыточная темпе-
температура повышается и дальше, то образование пузырьков происхо-
происходит все более и более интенсивно н поверхность нагрева покрывается
сплошным слоем пузырьков, отделяющим ее от жидкости. В результате
создается опасная ситуация перегрева поверхности и ее «пережога»
(так называемый кризис кипения). Максимальный тепловой поток для
этой точки пузырчатого кипения называется критическим тепловым
потоком. Если в условиях роста температуры не наступает «пережога»,
то имеет место переходный режим, который характеризуется тем, что
поверхность нагрева поочередно покрывается то пленкой пара, то
слоем жидкости. Однако такие условия теплообмена крайне неста-
нестабильны.
В условиях пленочного кипения жидкость непосредственно не
соприкасается с поверхностью нагрева — тепло передается ей через
паровую прослойку (пленку) посредством конвекции и излучения.
В этом режиме кипения пленка пара очень стабильна, поэтому тепло-
теплоотдача в значительной степени обусловлена этой пленкой, которая имеет
относительно низкую по сравнению с жидкостью теплопроводность.
Умеренный прирост отводимого жидкостью теплового потока можно
получить, только существенно увеличив температуру поверхности на-
нагрева, которая быстро приближается к точке плавления материала.
Кипение при вынужденном течении жидкости происходит главным
образом при течении жидкости в трубах, между пластинами, через
пучки труб или стержней. Пузырьки пара, постоянно отрывае-
отрываемые течением жидкости со стенок канала, смешиваются с иен, образуя
двухфазный поток. При незначительной интенсивности теплоотдачи
энергия передается за счет теплопроводности через жидкую прослойку,
примыкающую к стенке, п процесс парообразования происходит на
границе раздела жидкость1—пар. При более высокой теплоотдаче обра-
образование пузырьков газа происходит на центрах парообразования сте-
стенок капала под пленкой. Отделение жидкой пленки от стенкн в ре-
результате высокой интенсивности парообразования может стать причи-
причиной осушения стенки, что приводит к быстрому росту ее температуры.
Это условие характеризует критическое состояние и определяется как
кризис кипения при вынужденной конвекции. Механизм этого явления
чрезвычайно сложен, и его рассмотрение выходит за рамки этой книги.
123
Та б л и ц а 5.2
Формулы для определения коэффициента теплоотдачи при кипении
Формулы:
<7.з = « Сет — 'нас) Вт/м2;
Nu =
Обозначения:
, нас-
CSf — коэффициент и формуле, теплоотдачи при пузырчатом кипении (Сд —
— 1/С|,; значения см. в табл. 5.3);
а — среднее значение коэффициента конвективном теплоотдачи; с учетом
составляющей лучистого теплообмена используется полный коэффици-
коэффициент теплоотдачи а;, Вт/(м2 • °С);
«л = 0оф {T\r + 7^ас) (Тст + Т„ас) — коэффициент теплоотдачи излуче-
излучением, Вт/(м2 • К);
Ф ~ 1/(е~1 + у.-1 — 1) — угловой коэффициент излучения;
к — степень черноты поверхности нагрева;
у, — поглощательная способность жидкости;
qs ¦— плотность теплового потока, Вт/м2;
Ы = (tcr — tHac) — разность температуры, СС.
Другие обозначения приведены в разд. 5.2.
Значения свойств берутся при температуре насыщения жидкости.
'Д
1
2
3
Теплоотдача
при кипении
Парообразо-
ствениой кон-
конвекции на вер-
вертикальной по-
поверхности
Пузырчатое
кипение
Пленочное
кипение на го-
горизонтальной
поверхности
Формулы
Nu = 0,56 (Gr • Pr))|/4Hac , ламинарный поток,
10«<Gr • Pr < 10";
•
Nu = 0,13(Gr • Pr)^/3Hac , турбулентный поток,
Gr • Pr> 10»;
X равна высоте поверхности нагрева
1 „ „7 „ 7
a c Иж-нас^ Г (Ср)ж.нас I3 \ ^ь.
Vy/g (Рж.нас-Рпар) [rfg (PrI '7Д^2 J 'ЦТые
1 ВЬ1Ра"
(Sr)jK>nac=^Cs/ (Re) ' (Pr) » ' жеиия
(K )ж-МС">*.НасГ,в>(P>)-Hac-l X ]ж.иас'
Y_ "I / Y
' ?(Рж. нас— Рпар)
Nu = 0,425 X
Г X3 рПар (Рж.нас—Рпар) g, ,пл „Л4*
X j ~ — (г/^ + 0,4српарД/) ;
Мпар ^5
V 1 ' Y
' g (Рж.нас—Рпар)
Лите-
Литература
[5.13]
[5.6]
[5.16]
124
с
с
4
5
6
7
8
9
Теплоотдача
при кипении
Пленочное
кипение иа вер-
вертикальной по-
поверхности
Пленочное.
кнпеиу!е на
внешней сто-
стороне горизон-
горизонтальной трубы
Пленочное
кипение иа сфе-
сферической по-
поверхности
Коивектнв-
иая теплоотда-
теплоотдача при вынуж-
вынужденном движе-
движении потока в
трубе
Конвектив-
Конвективная теплоотда-
теплоотдача при вынуж-
вынужденном движе-
движении потока
(вверх) в вер-
вертикальной тру-
трубе
Критическое
значение плот-
плотности теплово-
теплового потока при
пузырчатом
кипении
Продолжение табл.
Формулы
* „г Г*3 Рпар (Рж.нас—Рпар) 8е Р пар] '/3
гми — и,^ч 1 ,
L llnap лпар J
X равна высоте поверхности нагрева
»i г. Рл Г^3 Рпар (Рж.нас — Рпар) 8 .,
3
4
*т л i а Г'5*-3 Рпар (Рж.нас — Рпар) § . ,
11/3_
г» о 1 ^Рпар ^ж»нас / г» 1 '
3 _,
X = D; аг=а-т-— ал для и,к,нас < У gD".
4
7
8
Nu = 0,028 Re°l8Pr0'4;
X = D; 6,5 • 104< Re<3-105
qs = 0,18 rfg[yg (Рж.нас — Рпар)]'/4 X
.. / Рж.нас Рпар \'/2
л 1 1
\ Рж.нас—Рпар /
5.2
Лите-
Литература
[5.33]
5.17]
[5.34]
[5.18]
[5.19]
E.14]
125
Продолжение табл. 5.2
Теплоотдача
при кипении
Формулы
Лите-
Литература
10
Минималь-
Минимальное значение
плотности теп-
теплового потока
для переходно-
переходного режима от
пузырчатого
кипения к пле-
пленочному
= 0,09 рпар гfg
Г Vg(Pm.nac — Pimp) I '
[5.15]
L (PiK.iiac-l-РпарJ J
—для горизонтальных плоских поверхностей;
j>nap fjg рУ (Рж-нас—Pnap)g 1"
X
\1/2Г
(Рж.и
fl +
арJ
X
I-1/4
с—pnap)J
[5.35]
з — Рпар/ L gO2 (Рж.иас Pnap)J
— для горизонтальных цилиндров
Таблица 5.3
Коэффициенты в уравнениях пузырчатого кипения
Граница раздела
Вода —¦ нержавеющая сталь
Вода — никель и нержавеющая сталь
Вода — платина
Вода — медь
Вода — никель
Вода — латунь
п-Пентан — хром
Четыреххлорнстый углерод — медь
Бензин —¦ хром
гс-Бутиловый спирт — медь
Этиловый спирт — хром
Изопропиловый спирт — медь
35%-нын карбонат калня—-медь
50%-ный кпрбонат калня —медь
Csf
0,014
0,013
0,013
0,013
0,006
0,006
0,015
0,013
0,010
0,003
0,0027
0,0025
0,0054
0,0027
Сд/.О.
0,364
0,455
0,455
0,455
4,630
4,630
0,296
0,455
1,000
37,04
50,08
64,00
6,35
50,08
Литература
[5.10]
[5.9]
[5.7]
[5.7]
[5.6]
[5.8[
[5.12]
[5.11]
[5.12]
[5.11]
[5.12]
[5.11]
[5.И]
15.11]
В табл. 5.2 представлены некоторые полезные формулы для опре-
определения коэффициентов теплоотдачи при кипении.
5.5. ТЕПЛООТДАЧА ПРИ КОНДЕНСАЦИИ
Конденсация происходит при соприкосновении насыщенного пара с по-
поверхностью, температура которой ниже температуры насыщения. Если
температура поверхности превышает температуру насыщения, то ника-
никакой конденсации не происходит, даже несмотря на перегрев пара. Обыч-
Обычно конденсат смачивает поверхность и образует на ней жидкую пленку,
126
которая называется пленкой конденсата. Таким образом, образовав-
образовавшийся конденсат вследствие теплоотдачи с поверхности может быть
до некоторой степени переохлажденным и инициировать дополнитель-
дополнительную конденсацию пара на границе раздела конденсат—пар. Гкщблия-
нием гравитационных сил конденсат стекает вниз. Вначале пототчла-
мниарнын, и скрытая теплота конденсата передается охлаждающей
поверхности теплопроводностью через пленку. Теплоотдача в значи-
значительной степени определяется толщиной пленки, которая, в свою оче-
очередь, зависит от интенсивности конденсации пара и от скорости отвода
конденсата. Поэтому при идентичных условиях теплоотдача верти-
вертикальной поверхности более высокая, чем наклонной. При дви-
движении мощного потока пара в том же направлении, что и движение по-
потока конденсата, наблюдается уменьшение толщины пленки и тепло-
теплоотдача возрастает.
Когда толщина пленки достигает определенного критического
значения, ламинарный поток переходит в турбулентный. В тур-
турбулентном потоке тепло распространяется не только посредством
теплопроводности, но и за счет вихре-диффузионных процессов, ко-
которые способствуют лучшему перемешиванию жидкого конденсата
и увеличивают коэффициент теплоотдачи.
Турбулентный режим течения редко возникает на горизонтальных
трубах, но может устанавливаться на нижних участках вертикаль-
вертикальных поверхностей.
При капельной конденсации конденсат не смачивает всю поверх-
поверхность. Капельки формируются на центрах конденсации. Они увеличи-
увеличиваются до тех пор, пока под действием гравитационных или других
сил не оторвутся от поверхности и не стекут по ней. Благодаря тому
обстоятельству, что значительная часть поверхности не покрывается
изолирующей пленкой, может быть достигнута очень высокая теплоот-
теплоотдача.
Практически пока не существует материала, обладающего благо-
благоприятным сочетанием механических, химических и физических свойств,
которые способствовали бы возникновению капельной конденсации.
Поэтому необходимо специально обрабатывать поверхность охлажде-
охлаждения тонким слоем вещества для инициирования формирования капе-
капелек. Это вещество, которое должно иметь чрезвычайно низкую смачи-
смачиваемость жидкостью и высокую смачиваемость с твердым телом, назы-
называют каплеобразователем (промотор каплеобразования).
Если бы можно было использовать капельную конденсацию в те-
течение продолжительного времени, то это позволило бы значительно
сэкономить в массе конструкционных узлов холодильных установок
» теплообменных аппаратов. Поэтому в последние годы изучению про-
процесса капельной конденсации уделяется огромное внимание. Предло-
Предложены различные теории для объяснения механизма этого явления, од-
однако все они еще далеки от совершенства и не могут быть использова-
использованы для определения коэффициента теплоотдачи. Изложение этих во-
вопросов приведено в работах [5.28, 5.29].
В табл. 5.4 представлены только хорошо проверенные формулы
для расчета пленочной конденсации.
127
та
3
4
и
s
о
a:
a.
с
is
ь
3
I
§¦
S.2S:
я
|&
? я
" а
V
a
«о
eg
|*
О
t~f
м.
3
|
е
«и
к
я
5
<в
?*
о
S
а,
п
V
S
н
Я
<у
н
Сис
\г>
юток
минарньп
конденса
Рг>0
се
X
E0
1*.
а
с
1
о
(Рж.на
.нас
?
Q.
«
<
<-<
о
«
1
"^
ст>
о"
II
3
Л
1 1
\/
1
Г"
V
\
к к ч
га ? га
а § Й
К СП ?
9 u E
Плен
конден!
на вес
-
о
V
<
о
к
Й
с
г-
^ j
-—1
<
U
ев
X
?
в.
оо
со
о
Р
X
ч
\
\
хно-
>вер
ных л
стях
2
га
CQ -к*
|«
°о
р г
§-"
ЭИ
8.
S b
U сЗ
•S о.
О ф
о с
° S
«8
нач*
п
ГО
i
i
\
\
(—-1
(N
in
ш
нденсат
ется воз,
Ю ПОТОКЕ
о га к
X <- в
X
1/2
-"¦ '^
а
s
•нас
S
о.
нас
ё
а.
Iro 1
II
\
1
/
II
ч
\
\
\
\
\
п О,
s a
X Q
к 2
CJ л
ижущего1
скорост!
+
1
+
4-
+
X
Ъо
.ft
ж.нас'
а.
со
а
<
¦ж. нас
<-<
«И
1
128
Основные формулы и данные по «теплообмену
129
ч
вз
S3
о;
ч
о
ЕС
О
о.
4 a
вз
О)
вз
В S3
О Са
з 2
к
§3
1Л
л а
Illl
X
too
+
i
a.
и
00
X
3
Z
II
Ь5
га
S3
Плене
к
н'п
нденса
о
и:
о
S3
S3
накло
S3
S3
ОСКОСТ
ч
с
1|Ё
щ
С 5 й.вз
ото
« в: аз
с<5
130
V
X
X
X
в
i
а.
я. о
3 +
X
X
3
Z
ill
5»
131
ч
о
О
о.
ll
<У
Я
s
л
t- К
3 s
ТОЛИИТ
услов
о
3
a.
a
о
к
§
л
H
и
ct
V
a
V
о
X
и
V
s
ss
тема
Сие
11 11 Ы
.41]
.30]
V с8 1
ъ ~&
*"¦ и.
а &,
СО 1
"* Ют
-0.8
«.нас
'ж. и:
о? с.
Г в°
"if 1"
Z Z
Л
f
¦ i
\ /
\
, 6
j 5
к к ч «
льна
:аци
тика
юве{
С S 4)
rt Pi ffl
О га о
•
о«* та" 1
* V§
о
о
м
Л
Л
о
.
8^
U
и
?
.нас
S
о.
II
Z
0)
ct
U
сти
о
«
i
о
л
ё
а.
1
О
л
S
с
;\
/
I 1
i /
1/
V
\
15
\
\
\
«
в
й
р-
<м
и
S
а.
1
1
а
.26}
HI
•- о 2
алою
ороткая
ижение
ЗКОЙ CKI
*Sg
X
-Рпар]
i
U
л
и
?
с
нас (
с
Q
1
в
й
а.
о
я
в
й
1
ю
о"
п
II
3
и " "*"
III
gic
ca с
я с
СО
я
a
"a?
я
S
S
о.
GO
to
С5
X
f
А
.39)
ю
о.
нная
Щ
X
и
со
S
|
О
чс
з:
W
_—-
нтал
убы
)НЗО
1 r0F
1 Н01
п
а. о ^,
So — io
а) >я Q w Л
s о л Л "
* о В Р. в
«о ^?
СО
о
m ж.пас |
а
+
^
О
S
I
о.
—-^
а
Рпа
"-— *
пар |
, 1,
Q
X
II
)
132
m
Й й g 5
« л в я
IIIs
| К
2 ЛО.
2 Д*»Г
V Л Л\/
-те
аз.
о •
853.1
II
i
S Я
а. я
н?
« а.1
3-е-
§|
та о.
ч о
х ч
X
X -
X
i
00
Q
Q
x
к'
00
о*
аз.
I
ю <]
• с:
о «
аз. Я
- i
ь
f =6
3
Z
+
г
а
К
36
о.
а- о
;ч-
X
HI
5^Л
-II.
Я S
о 5
О D->.
rt О о» cu
Я С ш (-
та о о
я ш я
3 н
Я о
о я о
я о «
OJ JJ Ч U
я ч « о
о га та ч
;|Р5
i я
133
СПИСОК ЛИТЕРАТУРЫ
5.1. Rohsenow W. M. Condensation and Boiling. Handbook of Heat Transfer. Sec-
Section 12, part A, and section 13. McGraw-Hill, 1973.
5.2. Griffith P. Dropwise Condensation. Handbook of Heat Trasfer. Section 12,
part B. McGraw-Hill, 1973.
5.3. Tong L. S. Boiling Heat Transfer and Two-Phase Flow. John Wiley and Sons,
Inc., 1965.
5.4. Rohsenow W. M. Heat Transfer with Boiling. — In: Modern Developments in
Heat Transfer. Ed by W. Ibele. Academic Press, 1963, p. 85—158.
5.5. Jakob M. Heat Transfer. V. 1. John Wiley and Sons, Inc., 1959.
5.6. Rohsenow W. M., Clark J. A. Heat Transfer and Pressure Drop Data for High
Heat Flux Densities to Water at High Sub-critical Pressures. — In: Heat
Transfer and Fluid Mechanics Inst. Stanford University Press, 1951, p. 193—
207.
5.7. Addoms J. N. Heat Transfer at High Rates to Water Boiling outside Cylin-
Cylinder. Doctorial thesis. MIT, 1949.
5.8. Crydcr D. S., Finalborgo A. C. Heat Transmission from Metal Surfaces to
Boiling Liquids: Effect of Temperature of the Liquid on Film Coefficient. —
«Amer. Inst. Chem. Engng»,, 1937, v. 33, p. 346.
5.9. Roberts H. A. A Review of Net Boiling Heat Transfer and Pressure Drop
from the Literature. 1955, UK Rept., AERO-ED/M-22.
5.10. Kreith F., Foust A. S. Remarks on Mechanism and Stability at Surface Boiling
Heat Transfer. 1954. ASME, paper 54-A-146.
5.11. Piret E. L., Isbir H. S. Two Phase Heat Transfer in Natural Circulation Eva-
¦ poration. — «Chem. Engng Progr.», 1954, v. 5D, p. 305.
5.12. Cichelli M. Т., Bonilla С F. Heat Transfer to Liquids Boiling under Pressure.—
«Trans. AIChE», 1945, v. 14, p. 755.
5.13. King W. J. «Refrig. Engng», 1933, v. 25, p. 83.
5.14 Zuber N. Stability of Boiling Heat Transfer. — «Trans. ASME», 1958, v. 80,
p. 711—720.
5.15. Zuber N., Tribus M. Further Remarks on the Stability of Boiling Heat Trans-
Transfer.—«Univ. Calif.», 1958, 58.
5.16. Berenson P. Transition Boiling Heat Transfer from a Horizontal Surface.
ASME—AICHE Heat Transfer Conference, Buffalo, I960.
5.17. Bromley L. A. Heat Transfer in Stable Film Boiling. — «Chem. Engng Progr.»,
1950, v. 46, p. 221.
5.18. Bromley L. A., Le Roy N.. Roberts J. A. Heat Transfer in Forced Convection
Film Boiling. — «Industr. and Engng Chem.», 1953, v. 45, p. 2639—2646.
5.19. Boarts R. M., Badger W. L., Meisenburg S. L. — «Industr. and Engng
Chem.», 1937, v. 29, p. 912.
5.20. Emerson W. H. Heat Transfer in Condensing System. — «Nat!. Engr», Lab.
Rept, 1971, p. 483.
5.21. Rohsenow W. M. Heat Transfer and Temperature Distribution in Laminar Film
Condensation. — «Trans. ASME», 1956, v. 78, p. 1645.
5.22. Shekriladze I. G., Gomelauri V. I. Theoretical Study of Laminar Film Conden-
Condensation of Flowing Vapour. — «Intern. J. Heat Mass Transfer», 1966, v. 9,
N 6, p. 581. V
5.23. Лабунцов Д. А. Теплоотдача при пленочной конденсации чистого пара на
вертикальных поверхностях и горизонтальных трубах. — «Теплоэнергетика»,
1957, т. 4, № 7, с. 72; также NLL CTS, 1958, р. 454.
5 24 Sparrow E. M., Gregg J. L. Laminar Condensation Heat Transfer in a Hori-
Horizontal Cylinder. — «Trans. ASME, J. Heat Transfer», 1959, v. 81C, N 4,
p. 291.
5.25. Chen M. M. Analytical Study of Laminar Film Condensation. — «Trans.
ASME, J. Heat Transfer», 1961', v. 83C, p. 46.
5.26. Chato J. С — «J. Amer. Soc. Heating Refrig, Aircond. Engng», 1962, Feb-
February.
5.27. Carpenter E. F., Colburn A. P. The Effect of Vapour Velocity on Condensa-
Condensation-Inside Tubes Proc. Gen. Dis. on Heat Transfer IME/ASME, 1951,
p. 20-26.
134
i.28. Westwater J. W., Chapter I. Proc. 4th Annual Southeastern Seminar on Ther-
Thermal Sciences. Univ. Tennessee Space Inst., 1968.
>.29. Herman Merte. Condensation Heat Transfer. — In: Advances in Heat Trans-
Transfer. V. 9. Academic Press, 1973.
1.30. Jordan D. P. Film and Transition Boiling. — In: Advances in Heat Transfer.
V. 5. Academic Press, 1968.
5.31. Leppert G., Pitts С. С. Boiling. In: Advances in Heat Transfer. V. 1. Acade-
Academic Press, 1964.
5.32. Kalinin E., Berlin I. I., Kostyuk V. V. Film-Boiling Heat Transfer. In: Advan-
Advances in Heat Transfer. V. 11, Academic Press, 1975.
5.33. Лабуицов Д. А. Расчет теплоотдачи при пленочном кипении жидкости на
вертикальной поверхности нагрева. — «Теплоэнергетика», 1963, № 10, р. 60.
5.34. Frederking Т. N. К-, Clark J. A. Natural Convection Film Boiling on a Sphe-
Sphere. — «Advances Cryog. Engng», 1963, v. 8, p. 501.
5.35. Lienhard D. J., Wong T. Y. The Dominant Unstable Wavelength and Mini-
Minimum Heat Flux during Film on a Horizontal Cylinder. — «J. Heat Trans-
Transfer», 1964, v. 86, p. 261.
5.36. Peterson A. C, Westwater J. W. Dropwise Condensation of Ethylene Clycol.—
«Chem. Engng Progr.», Sympl., 1966, Ser. 62, p. 135.
5.37. Collier J. G. Convective Boiling and Condensation. McGraw-Hill, 1972.
5.38. Beatty K. O., Katz D. L. Condensation of Vapours in Outside of Finned Tu-
Tubes. — «Chem. Engng Prog.», 1948, v. 44, p. 55.
5 39. Akers W. W., Crosser О. К-, Deans H. A. Proc. 2nd Natl. Heat Transfer Conf.,
ASME/AIChE, August 1958.
5.40. Gerstmann J., Griffith P. Effect of Surface Instability on Laminar Film Con-
Condensation. — «J. Heat Mass Transfer», 1967, v. 10, p, 567.
5.41. Исаченко В. П. — «Теплоэнергетика», 1963, № 9, с. 81—85.
5.42. Heat Transfer in Dropwise Condensation. Part I and II. — «Intern. J. Heat
Mass Transfer», 1965, v. 8, p. 419—435. Auth.: D. W. Tanner, C. J. Potter,
D. Pope, D. West.
Глава 6
ТЕПЛООБМЕННЫЕ АППАРАТЫ
6.1. ВВЕДЕНИЕ
Теплообменник представляет собой устройство, в котором тепло пере-
передается от одного теплоносителя к другому обычно путем теплопровод-
теплопроводности и конвекцией. При этом конвекция играет основную роль в пере-
передаче тепла в теплообменных аппаратах в условиях вынужденного тур-
турбулентного потока теплоносителя. Естественная конвекция происходит
только в некоторых простых теплообменниках большей частью с га-
газовым теплоносителем при очень высокой температуре. В некоторых
случаях одновременно с теплопередачей наблюдается и массообмен.
Разрабатываемые и изготовляемые промышленностью теплообмен-
ные аппараты в зависимости от назначения часто имеют различные
наименования: паровые котлы, испарители, конденсаторы, нагревате-
нагреватели, охлаждающие устройства, парогенераторы, автомобильные радиа-
радиаторы, рекуператоры, регенераторы и т. п. Но все они в большей или
меньшей степени основаны на использовании общих принципов тепло-
теплопередачи. По существу их можно разделить на четыре основных типа
в зависимости от направления потока теплоносителя (табл. 6.1).
Таблица 6.1
Типы теплообменников с различными схемами движения потоков
Тип теплообменника
Схема движения теплоносителя
С
чей
непосредственной теплопереда-
С косвенной теплопередачей
С циклической теплопередачей
С непосредственным контактом
Прямоток
Противоток
Перекрестный ток
Сочетание прямотока
тока
и противо-
Сложные схемы движения
Тепловую мощность теплообменника обычно определяют из урав-
уравнения
Q= KFAtm Вт, F.1)
где К—полный коэффициент теплопередачи; F—площадь поверх-
поверхности теплообмена; Atm — истинная разность средних значений темпе-
температуры теплоносителей.
При проектировании тегаюобменного аппарата определенного типа
необходимо учитывать соотношение между первоначальной стоимо-
136
стью теплообменника и расходами на его эксплуатацию, обеспечиваю-
обеспечивающими требуемую мощность. Наиболее важным этапом проектирования
является выбор габаритных размеров и рабочих характеристик теплооб-
теплообменника. При этом соотношение величин должно удовлетворять урав-
уравнению F.1), которое является определяющим критерием правильности
выбора указанных параметров.
6.2. ОБОЗНАЧЕНИЯ
F — площадь поверхности теплообмена; площадь всей
оребренной поверхности трубы, м2;
В= exp[—(NTK)R] — параметр;
b — толщина ребра, м;
W — водяной эквивалент теплоносителя (Qm cp), Дж/(с-°С);
ср — удельная теплоемкость при постоянном давлении,
Дж/(кг- °С); т
D — гидравлический диаметр, м;
F — поправочный коэффициент средней разности темпе-
температуры;
/ — коэффициент трения;
ит — массовая скорость, кг/(м2<с);
g = 9,81 —ускорение силы тяЯйсти, м/с2;
а — коэффициент теплоотдачи, Вт/(м2-°С);
rig — удельная теплота парообразования или конденса-
конденсации, Дж/кг;
v. — коэффициент пропускания;
./ — высота ребра, м;
L — эффективная длина трубы, м;
т — масса, кг;
Qm — массовый расход, кг/с;
N = yrfgp/ii — коэффициент переноса жидкости, Вт/м2;
п — число одинаковых переносов;
Р — отношение коэффициентов оперативной производи-
производительности;
Q — тепловой поток, Вт;
R= (*ЭтСр)МИя/(<ЭтСр)макс—отношение водяных эквивален-
тов теплоносителей;
г — радиус капилляра фитиля, м;
5 — площадь поперечного сечения фитиля, м2;
s — шаг оребрения, м;
т. — время, с;
К — полный коэффициент теплопередачи, Вт/(м2- °С);
pn — критерий Рейнольдса;
Рг = цСр/А, — критерий Прандтля;
Nu = a?)/A, — критерий Нуссельта;
8 — угол смачиваемости капилляра;
Р — угол ориентации трубы;
у — поверхностное натяжение, Н/м;
X— коэффициент теплопроводности, Вт/(м-°С);
137
6 — коэффициент термической эффективности;
г\ — эффективность полной поверхности;
tjp — эффективность ребра;
р — плотность, кг/м3;
t — температура, °С;
А^ — разность температуры, °С;
б — толщина теплопередающей поверхности, м;
экв — эквивалентная толщина стенки матрицы регенерато-
регенератора, м;
ц. — динамическая вязкость, Н-с/м2.
Индексы:
а — отдельная единица измерения;
р — ребро;
г — горячий;
х — холодный;
вх — вход;
вых — выход;
О — начальные условия;
ж — жидкость;
т — средний;
1т — средняя логарифмическая;
мин — минимум;
макс — максимум;
ст — стенка.
6.3. ОПРЕДЕЛЕНИЯ
Противоток относится к такому движению, при котором
оба теплоносителя в теплообменнике движутся в противоположных на-
направлениях. Такая схема движения обеспечивает сравнительно малое
изменение перепада температуры и, следовательно, сравнительно оДи-
наковый тепловой поток по длине теплообменника. При этом конечная
температура холодной жидкости может достигнуть более высокого зна-
значения, чем конечная температура горячей жидкости. Как правило, пол-
полное значение коэффициента теплопередачи при противоточной схеме
движения теплоносителя больше, чем при прямоточной.
Перекрестный ток относится к такому движению, при
котором оба теплоносителя движутся во взаимно перпендикулярных на-
направлениях. Значение переданного теплового потока между двумя
теплоносителями зависит от степени перемешивания каждого из теп-
теплоносителей, движущихся по своим направлениям течения. В тепло-
обменных аппаратах с перекрестным током используются многочислен-
многочисленные комбинации перемешивающихся и неперемешивающихся тепло-
теплоносителей.
Коэффициент термической эффективности ? (тер-
(термическая эффективность теплообменника) — отношение действительно-
действительного теплового потока Q= WT {tT_ BX—tT. вых) или Q= Wx (tXi вых—/x. вх) к
максимально возможному тепловому потоку, определенному на основе
138
второго закона термодинамики QMaKC = WMms (tT_ вх — /х, вх) в
отсутствие тепловых потерь. Следовательно, ? = Q/QMaKot a WMBB
представляет собой наименьшее значение водяного эквивалента из зна-
значений для двух теплоносителей и является характеристикой теплообмен-
ного аппарата. Зная ? , тепловой поток N5o>kho получить из соотноше-
соотношения Q = 6 Wmiih (^г. вх — tX. вх)-
Эффективность ребра т)р. Для увеличения теплопере-
дающей поверхности, а следовательно, и теплового потока в теплооб-
менных аппаратах используют оребренные поверхности. Но развитие
теплопередающей поверхности однозначно не приводит к пропорцио-
пропорциональному увеличению теплового потока, так как добавление ребер
снижает среднее значение температуры и, следовательно, уменьшает
разность температуры. Эффективность ребра определяется как отно-
отношение действительно передаваемого ребром теплового потока к теп-
тепловому потоку, передаваемому ребром, температура всей поверхности
которого равна температуре основания ребра /баа, т. е.
Эффективность полной поверхности ц учи-
учитывает влияние на интенсивность теплообмена с окружающей средой
(с учетом ребер) теплопередающей поверхности. Представляет собой
отношение действительно передаваемого всей оребренной поверхностью
теплового потока к тепловому потоку, который был бы передан, если
бы температура всей поверхности была равна базовой температуре, т. е.
Т1= l-(l-Tlp)W
где F — полная площадь поверхности.
Накипь — этот термин относится к отложениям и их накоплению
на внешней стороне теплопередающей поверхности в результате ра-
работы теплообменного аппарата в течение определенного периода вре-
времени. Образование накипи приводит к снижению интенсивности теп-
теплообмена. Для точного определения полного термического сопротив-
сопротивления теплообменника в процессе его работы целесообразно учитывать
составляющую термического сопротивления за счет образования на-
накипи.
Коэффициент трения f определяется как отношение
силы трения к единице площади теплопередающей поверхности
(см. гл. 3).
Водяной эквивалент теплоносителя W,
Дж/(с- °С) — произведение массового расхода на удельную теплоем-
теплоемкость жидкости, т. е. Qmcp— важный параметр в расчетах теплооб-
менных аппаратов. Он характеризует энергию, запасенную жидко-
жидкостью в единицу времени.
Отношение водяных эквивалентов тепло-
носителейК представляет собой отношение водяных эквивален-
эквивалентов теплоносителей двух потоков жидкости (наименьшее значение —
числитель). Таким образом, если (Qmcp)x < (QmCp)r> то
R = (QmcP)x/(Qmcp)r.
139
Коэффициент теплоотдачи а, Вт/(м2-°С) — это ко-
коэффициент, характеризующий интенсивность конвективного теплооб-
теплообмена между поверхностью твердого тела и окружающей его жидкостью.
Зная физические свойства жидкости, ее расход и конфигурацию тепло-
обменной системы, можно рассчитать а по уравнению, приведенному
в гл. 3.
Площадь поверхности теплообмена F, м2 —
эффективная поверхность, через которую тепло передается от одного
потока теплоносителя к другому. Увеличение поверхности теплопе-
теплопередачи — один из путей увеличения интенсивности теплообмена. В
расчетах в качестве F используют полную площадь поверхности, омы-
омываемой горячим или холодным теплоносителем.
Гидравлический диаметр D, м. Гидравлический диа-
диаметр используется для представления геометрии проходного сече-
сечения потока в расчетах безразмерных критериев Re, Nu и др. (см.
гл. 3).
Перемешанная жидкость. Жидкость считается пере-
перемешанной, если ее температура постоянна по всему поперечному се-
сечению потока, взятому в плоскости, нормальной к направлению дви-
движения. И наоборот, температура нсперемешанного потока распределе-
распределена в поперечном сечении неравномерно.
Число единиц переноса тепла NTK опреде-
определяется как параметр теплопередачи, отнесенный к наименьшему из
двух значений водяных эквивалентов теплоносителей, т. е. NTK =
= KF/WMiill. Это безразмерный параметр, который служит критерием
оценки теплопередающих свойств теплообменного аппарата. Для теп-
теплообменников с небольшим значением NTR эффективность их работы
также низкая, и, наоборот, при больших значениях NTK эффектив-
эффективность теплообменников может возрастать и достигать постоянного
уровня, являющегося верхним пределом.
Параметр теплопередачиЗС= K.F, Вт/°С, есть произ-
произведение полного коэффициента теплопередачи на площадь теплопере-
дающей поверхности. Обычно считают, что полный коэффициент
теплопередачи имеет постоянное значение для всей теплопередающей
поверхности. Величина KF существенным образом зависит от кон-
конструкции теплообменного аппарата. Обратная величина характеризует
полное термическое сопротивление.
Прямоток — это такая схема движения, при которой два
потока теплоносителя движутся через теплообменник в одном направ-
направлении. На входном участке теплообменника, где различие в темпера-
температуре двух потоков жидкости достигает максимального значения, на-
наблюдается наибольшая степень теплопередачи. По мере продвижения
потоков жидкости через теплообменник разность температур, а сле-
следовательно, и тепловой поток становятся существенно меньше.
Рекуператор — это теплообменный аппарат с непосредст-
непосредственной теплопередачей, в котором имеются потоки горячей и холодной
жидкостей и тепло передается через разделяющую их твердую стенку.
Большинство аппаратов, используемых в промышленности, именно это-
этого типа.
140
Регенератор — это теплообменный аппарат с периодиче-
периодическим теплообменом, в котором два потока жидкости движутся попере-
попеременно в насадке, аккумулирующей тепло при протекании горячей жид-
жидкости и затем отдающей его холодной жидкости. Преимущество ап-
ларата данного типа заключается в высокой тепловой эффективности
на единицу массы и объема, так как нет необходимости передавать теп-
тепло через стационарную твердую стенку, разделяющую потоки.
К о ж у х о-т р у б н ы й теплообменник является ос-
основным типом теплообменного аппарата; он состоит из пучков труб,
размещенных в цилиндрическом корпусе. Компоновку труб внутри
ограничивающего кожуха аппарата организуют таким образом, чтобы
в соответствии с проектной схемой движения потока осуществлялось
многоходовое прохождение жидкости. Трубопроводы можно распола-
располагать вдоль и поперек направления движения теплоносителя. При про-
продольном расположении труб коэффициент теплопередачи и перепад
давления ниже, чем в случае поперечного обтекания, так как поток теп-
теплоносителя протекает как бы в каналах, образованных в межтрубном
пространстве. Поперечное расположение труб обеспечивает лучшее
перемешивание потока теплоносителя в теплообменнике, однако в нем
выше перепад давления.
6.4. ТЕПЛООБМЕННЫЕ АППАРАТЫ С НЕПОСРЕДСТВЕННОЙ
ТЕПЛОПЕРЕДАЧЕЙ
Эти аппараты представляют собой основной тип теплообменных аппа-
аппаратов, в которых оба потока жидкости непрерывно движутся по
своим каналам, разделенным твердой стенкой. Такие теплообменники
называют рекуператорами. В большинстве случаев это кожухотруб-
ные теплообменные аппараты с пучком труб в одном кожухе. В них
возможна также организация многоходовых комбинированных схем
движения потока. Обычно в основу расчета теплообменника кладут
уравнение F.1), в котором полный коэффициент ^теплопередачи К
при условии равенства теплопередающих Площадей Fr, Fx, FCT опре-
определяется из выражения
АСТ
F.2)
Если это условие не соблюдается, то удобнее пользоваться параметром
теплопередачи Ж, для которого не требуется подсчета эффективного
значения F. Тогда
dV+rV+^V °С/Вт- F-3>
Члены уравнения F.3) представляют собой различные термические
сопротивления на пути распространения теплового потока. При не-
необходимости увеличение сопротивления за счет отложения накипи
может быть учтено дополнительным слагаемым в правой части урав-
уравнения.
Ш
<N
to
CO
Я
я
«о
CO
н
"к
ы
t ТОК
3 *
Е з
а
о.
R
о.
с
U
S
а
S
а
С
га
II
IS
X О
S <
II
5s
v
I
I
I
I
I
142
В расчетах теплопередачи предполагается, что параметр теплопе-
теплопередачи постоянен. Значения коэффициента теплопередачи для различ-
различных схем движения потоков могут быть заимствованы из гл. 3. Особое
внимание следует уделять расчету средних значений перепада темпера-
температуры Ыт. Типичные распределения температуры в сечении и вдоль
теплопередающих поверхностей приведены в табл. 6.2.
6.4.1. Расчет теплообменников
Общеприняты два метода расчета теплообменников: метод, основан-
основанный на определении истинного значения средней разности температу-
температуры, и 6 — МГ/С-метод.
Метод, основанный на, определении истин-
истинного значения средней разности температу-
р ы. Разность температуры между теплоносителями изменяется от
сечения к сечению, поэтому истинное значение средней разности тем-
температуры Atm следует определять на всей длине теплообменного ап-
аппарата. Для схемы теплообменника с противотоком истинное значение
средней разности температуры называется среднелогарифмической раз-
разностью температуры, значение которой определяется выражением
•im = г. ; ; '— <-• F-4)
In
Для теплообменного аппарата с прямоточной схемой движения теп-
теплоносителя среднелогарифмическая разность температуры принима-
принимается также в качестве истинного значения средней разности температу-
температуры, но она численно существенно меньше, чем для теплообменника с
противотоком. Для других схем движения потоков можно использо-
использовать величину Atim, определенную для противотока, вводя поправоч-
поправочный коэффициент F. В этом случае &tm можно определить как
Мт = М1тР °С. F.5)
Выражения для расчета поправочного коэффициента наиболее рас-
- пространенных типов кожухотрубных теплообменных аппаратов при-
приведены в табл. 6.3.
Поправочные коэффициенты для теплообменных аппаратов с более
сложными схемами организации движения потоков обычно представ-
представляются графически. Значения их приведены в работах [6.1, 6.7, 6.8].
Таким образом, расчет теплообменника можно выполнить на ос-
основе следующей системы уравнений:
F.6)
Для непосредственного расчета Д^т, а следовательно, и Q не-
необходимо знать конечную температуру теплоносителя. Если температу-
температура теплоносителя на входе и выходе из теплообменника неизвестна,
143
Таблица 6.3
Поправочные коэффициенты для расчета истинного значения средней
разности температуры
Формулы: _
Д/т = Д/,т7,
где Д/;т — среднелогарифмическая разность температуры для противотока, °С;
x, вых
вх
е =
^Г, ВХ 'X, ВХ
^г, вх—^г. вых
t если
D __
'г, вх-
'г, вх — 'г1вых
^х, вых—tx. вх
вх
, если (Qm cp)r < (Qm cp)x;
^р)Х
(Q
, если (Qmcp)x< (Qmcp)r;
п 'х, вых'—'х, вх (Qm Ср)г /л \ /л ч
R= : =—~—tLr~ . если (Qmcp)r< (Qmcp)x,
г, вх ^г, вых
(Q
где / — температура, °С;
индексы г, х, вх, вых соответственно означают «горячая», «холодная»,
«вход», «выход»; а — параметр отдельного теплообменника.
Схема организации движе-
движения теплоносителя
в теплообменнике
Поправочный коэффициент F
2а
Противоток
Одноходовон кожу-
хотрубный теплообмен-
теплообменник с четным числом
труб
Как н в № 2, для Я=1
Двухходовой кожу-
хотрубнын теплообмен-
теплообменник с четным числом
труб
N одинаковых тепло-
теплообменников с единым
последовательно дви-
движущимся горячим пото-
потоком теплоносителя и па-
параллельными холодны-
холодными потоками теплоноси-
теплоносителя; R=NRa; e=[l—
R)N]IRN
Я —1
1п
1-е
1п
R2+l)
У2 е
A-е) in
2-е B-У 2)
2-е
— In
--аг) in
?—i) in [(я-
144
Продолжен ие табл. 6.3
Схема организации движе-
движения теплоносителя
в теплообменнике
Поправочный коэффициент F
4а
5а
Как и d № 4, для
N одинаковых тепло-
теплообменников с единым по-
последовательно движу-
движущимся ХОЛОДНЫМ ПОТО-
ПОТОКОМ теплоносителя и па-
параллельными горячими
потоками;
R^RalN; 6=1—A—
-€.)*
Как и
в № 5, для
N
_
[1— A— ?N)llN]{N— 1)
\-NR\ In [(l —6)/(l—€/?)!
для получения решения прибегают к помощи итерационного метода.
Расчет, основанный на определении коэффициентов термической эффек-
эффективности е и МГ/С-параметров, Аозволяет исключить эту трудную про-
процедуру. Поэтому метод е — NT К чаще используется в расчетах тепло-
обменных аппаратов. Следует отметить, что поправочный коэффициент
F очень чувствителен к небольшим изменениям величины е> которые
могут быть причиной больших погрешностей расчета.
е—NTK-м е т о д. Идея Л^Г/С-метода была выдвинута Нуссель-
том и впоследствии развита Кэйсом и Лондоном [6.2]. Соотношения
между коэффициентом термической эффективности'g и числом еди-
единиц переноса тепла NTK для различных систем теплообменных аппа-
аппаратов представлены в табл. 6.4. Определения этих величин, а также
отношения водяных эквивалентов теплоносителей R приведены в на-
начале этой главы. Преимущество ? — Л'77(-метода заключается в том,
что е может быть выражен в явном виде функциональной зависимостью
от NT К и R, которые'не зависят от конечных значений температуры.
Таким образом, громоздкие' расчеты значительно упрощаются.
По известному значению ? могут быть определены тепловой поток
и температура на выходе. В этом случае расчет теплообменника можно
выполнить с помощью системы следующих уравнений:
F.7)
ВТ.
Система уравнений позволяет также через параметр NTK, найти
теплопередающую площадь, необходимую для установления теплово-
теплового потока, если можно определить полный коэффициент теплопередачи
145
я
s
as
ч
га
Н
о
S
о
о
О
и
о
п.
с
с
В
2
ев
?
Ч
5
о
X
о
ч
с
га
о.
..«яр
"И
о
о
X
V
ё
о
о
ч
V
а
е-
я s «г
low
о
s
s
ч
0J
и
о
s
о
ч
с
0J
е-
OJ
s
s
и
о. <l> ЕС а>
О 0J X О X
Ч В.ч Ч Ч «
¦ с <" ч
. 0J О. 0J
о1 е- и н и е-
о-
X
о
0J
о
S
r a
ag..
м в в =¦ ч •-
d O.0J О О И
о о и, и п
2
¦е-
I- И И
к
о
s
(Я
о.
с
о
S
щ
S
о.
с
¦u-u »лг
146
Q
ЕС
я
Q.
С
О
а
Е-,
t
|
с
X
О)
1
1
о.
'И!
o.
X
X
go
& 1
2 й S
IRO.I
Is 1
и?
С м a S
J
lift
>S О S
2 Н О
peg
S о о
о.—'S'?'
<" S3
egg
н * я
147
СО
Ч
чэ
rt
*•
V
S
а:
>лже
'Про
НВН(
н
¦е-
¦е-
а
ермнческо
н
нент
Коэффнц
V
тавленн
1
с
о
ческ
матн
V
X
О
я
Е
<У
н
У
и
iru W
+
1.
a
;
a
<м а
-010U
-odu
и
га'5 "
о 3 \о
с? X О
of—
К СО
»шо
О) X
с н
ченк
га
«
о
IH01
II -?
t
е
дли
! и равнс
NTK)
-г "
учено из
о
с
в
г
1 , v .
—
11
= к
о
j га
3 2
= |1
QJ О
О.Х
га а»
а с ш
(О
+
т
а
Г
ц
4 ч
с?
S
1
о
и.
О
в
с
авно
«а _fc;
1
f-
i~
г-
t_
:-
о я
«Со
§•
о
с[
о
ухх
Ч
3 с
п ~—
а. о
а> о
а> s
с н
1 № 46 и
ачення Л
о
s
:„ получе
-ii
—^~
е ме-
между
по-
вает-
О- ш а- х
S ?¦ о S га
сост
1ЮТС
мн,
iepe
ход
HN TO jrt 1—,
jj д О о К
ОС
—-
со
[2A-
сх
X
с
,
аз
+
——
ся
+
<N
г
1
ц
С*
зэ
^1
g 5 О
О о к
о э ^ я
щ о> ^ S
о> о о>
аю с
n
ITHI
о.
xo
о
ие на
эде);
5й
направл
ждом npi
н «
S-M
s m
а>
со
s
§
о
с
*
t
р-
с».
—*^-
гяже-
- нет)
и
С О
и,
IS
m .
s
га х
в в
00
148
51
sr
о.
x
<u
о
1
II
?Г is
о
I
Of
Of
о
s
е
e
о з о
! О. и О.
I
О1
о
ш -
§1
Эх н а о
О ь * и га о-
s a. g g s с
?•&§ 5g s
" * й S ^ ^
Ф S •!< щ U
Q.H Ж S СЗ
е
с я
г
J
о
§§i
53 о х о S й
D.B D* Н О,*
«1 s s о «Г«
с н н с с S
— 5 й
с ч о,
X ОС
О> та
о о-
О) О О
с о. с
о, н н и
149
чэ
со
S
а.
S
¦е-
¦е-
5:
о.
х
аз
s
X
ч
а
о,
а
а
I «
о;
оГ
s-
о
е-
О
X
о
X
о
о.
а
о
СО
и:
as
о
о
Ui
О
га
о.
s
ю
s
s
3 в-
eg
в п
S
S
1
о
X
о
о.
с
3
f
i I
w О.
X
о; «
с
а
о.
с
га
%
т
s
л: g
— о
?:
^2- х
о.
х
a
j
о;
со а
•Ч"
to"
со *~»
3 s
а х
о _
til
х о о
[ га га
г о
а х
О о
о е-
"о
и*
si
ОН
а. ¦
6 о «=*
о р s
I—Г Л* та
ш о
га
S о
о" <и S &
с— S m >=t
тп
х ш а
O.V3 о S
<ц о о еа
150
X
X
4-
ST
в
о;
к
5
в
О)
а
о)
+
^О "с Ш m
s a s 5
о м
S о
а*-
с*
CO
га ч
is"
151
из
к
СО
V
Я
Я
<а
К
О
о
о-
С
юсти
п
i
•&
iH
о
ее:
X
терм
н
V
X
•§•
о
ение
а
i
и
V
0*
К
н
«
X
4)
К
и
я
Систем;
•iru W
4
и
и
и
о?
^.
0Q*
о.
X
ц
1
\
Нагрев
j охлаждение
i-
т
1 11 II 11 fl I
II 1 II A1
гме-
ость
по
ера-
ДКОСТН (П
шанная жи
с постоянн
сечению те
турой)
, ^
|
Как
18а
н
-*
•А
ден-
денно:
Нагрев v
О
1
<
>
а,
X
ром
186
7
о
7
II
,
о;
1
1
т
X
<и
0?
* *—
7
о.
X
OI
If
,11
•сое.
тг
* я *
Перемеша
жидкость,
лирующая
по'
fjl
п
S
теплообменн
противотоке
с»
152
/С. Коэффициент теплопередачи К зависит от температуры потока теп-
теплоносителя, поэтому для его оценки приходится использовать метод
проб и ошибок. В таких случаях конечные значения температуры
должны определяться по аналогии с первым примером.
6.4.2. Теплообменные аппараты пластинчатого типа
Теплообменные аппараты с непосредственной теплопередачей, имею-
имеющие плоские теплопередающие поверхности, в основном относятся
к классу пластинчатых теплообменников. Они состоят из определенно-
определенного числа тонких пластин с прокладками между ними, которые служат
и для предотвращения утечки жидкости н для направления потоков
жидкости по соответствующим направлениям. Обычно используются
гофрированные пластины, которые турбулизируют поток и обеспечи-
обеспечивают достаточную жесткость стенок, воспринимающих давление. Дви-
Движение потоков жидкости организуется таким образом, чтобы между
чередующимися пластинами имел место противоток. Теплообменные
аппараты этого типа благодаря высоким теплопередающим возможно-
возможностям, доступности для очистки и контроля за состоянием поверхности,
возможности изменения габаритов и удобству в эксплуатации нашли
широкое применение в химической промышленности.
Разнообразие и сложность конструкций теплообменных аппаратов
этого типа не позволяют сколько-нибудь точно определить их параме-
параметры. Поэтому тепловые расчеты выполняют на основе установленной
достаточно определенной зависимости теплового потока от формы обра-
образуемого" пластинами канала. Для формы канала в виде желоба может
быть использовано соотношение
Nu ~ Re°-65-Pr°.4 (ц/и.Ст)°-14. F.8)
При изготовлении теплообменников пластинчатых типов, к кото-
которым относятся оребренно-пластинчатые теплообменные аппараты,
обычно применяют пайку твердым припоем. Их преимущества заклю-
заключаются в незначительной массе и низкой стоимости при сравнительно
большой поверхности теплообмена. Благодаря этим обстоятельствам
они идеальны для криогенной техники.
6.5. ТЕПЛООБМЕННЫЕ АППАРАТЫ С КОСВЕННОЙ ТЕПЛОПЕРЕДАЧЕЙ
В этом типе теплообменных аппаратов жидкая среда обычно циркули-
циркулирует через два независимых теплообменника с непосредственным теп-
теплообменом, один из которых отдает тепло этому потоку теплоносителя,
а другой отбирает тепло от этого же потока. Такую систему можно реа-
реализовать относительно просто, например, в охлаждающей системе ав-
автомобильного двигателя. Теория двухжидкостного теплообменного
аппарата с косвенной теплопередачей была разработана Кэйсом и
Лондоном [6.2]. Данные по эффективности теплопередачи для тепло-
теплообменников данного типа приведены в табл. 6.5.
153
Таблица 6.5
Эффективность теплопередачи двухжндкостных теплообмениых аппаратов
с косвенным теплообменом
Насос
Смешанная
жидкость
Об о з и а ч е н н я:
/ — температура, °С;
Qmcp) — водяной эквивалент теплоносителя, Вт/°С;
Р — (Qmcp)npoM/(Qm ср)макс — промежуточное отношение водяных
эквивалентов;
/
Рх/ж =
х/ж
рр
— (Qmcp)MHH^(QmCp)MaKC — минимальное отношение водяных экви-
эквивалентов теплоносителей;
Яг/ж = (Qm cp)r/(Qm
i BX —
вых
г, вх—^ж, г)'<
ж, 1 — tx, вх) •
N» п. п.
1
2
3
4
Пределы изменения отношения
водяных эквивалентов тепло-
теплоносителей 1>P>R
'>^х/ж>Яг/ж
^Рг/жЖх/ж
l>Pr/x>Rx/x
^^х/г^^ж/г
Коэффициент термической эффективности ?
Сх ^Г, ВХ ^Г| ВЫХ
6х . D / ' \ tr, вх—(х, вых
ег +^г/ж1^х/ж бх/
6г ^Xi ВЫХ ^Х, ВХ
6г . п / 1 г \ *г. вх — ^х, вых
с +'чх/ж Р , fer
6х \^г/ж /
' ^Ш, 1 — ^Ш, 2
°г/х /1 1 \ 'г. вх—^х, вых
^ж/х\6х ?г /
' tm. 1 — tw, 2
P-x.It /1 1 \ 'г, вх — ^х, вых
154
Продолжение табл. 6.5
№ п. п.
5
6
7
8
9
Пределы изменения отношения
водяных эквивалентов тепло-
теплоносителя \>P>R
'>Рж/х>Яг/х
»Рж/г>Ях/г
х/г -^ Лж/г
Коэффициент
1
1 Rv/x 1
€г "ж/х \
1
1 «х/г /
ехЧ/Л
1 1
1 1
ех + ег ~
1
1 1
т~+ -
tx tr
термической эффективности
1
?*
1
6г
-1
р
А/ /
'г.
" /г
-1
(г.
h, вх 'г.
\ /г, вх-/х.
'Xi ВЫХ '
\ 'г, пх—^х,
_ (>К, 1 —'ж, 2
'г, вх 'х, вых
'х, вых 'х, вх
'г, вх — ^х, вых
вх 'г, вых
вх 'х, вых
'Х> ВЫХ 'X, ВХ
'Г, ВХ 'X, ВЫХ
вх — 'г, вых
е
вых
вых
X, ВХ
вых
(г, вх — tx, вых
По известным значениям 6 при незначительных потерях тепла полное ко-
количество переданного тепла можно определить с помощью выражения
Q = 6 (Qmc р)мии ('г, вх— 'х, вх) Вт.
6.6. ТЕПЛООБМЕННЫЕ АППАРАТЫ ПЕРИОДИЧЕСКОГО ДЕЙСТВИЯ
К этому типу теплообменных аппаратов относится регенератор. Он
имеет насадку из пористого материала, через которую попеременно про-
протекают потоки холодной и горячей жидкости. При этом тепло, запасае-
запасаемое в насадке от горячего теплоносителя, за короткий период времени
передается холодной жидкости при ее проходе через насадку.
В таком аккумулирующего типа теплообменнике передача тепла между
матрицей и жидкостями происходит в условиях переходного режима.
Для осуществления непрерывного процесса необходимо иметь два реге-
регенератора, оснащенных клапанами, которые обеспечивают циркуляцию
холодного и горячего теплоносителей между ними через определенные
интервалы времени. Используется также конструкция теплообменника
с вращающейся насадкой, выполненной в форме цилиндра. В процес-
процессе теплопередачи каждый элемент ротора периодически контактирует
с горячим и холодным потоками жидкости, что обеспечивает непрерыв-
непрерывность теплообмена.
155
Проведение точного анализа конструкции и параметров регенера-
регенераторов представляет чрезвычайно трудную задачу, поэтому вводят ряд
упрощающих предположений. Тепловой поток от горячего теплоноси-
теплоносителя к холодному в условиях противотока можно определить с помощью
следующего выражения:
™ Вт, F.9)
м 8 л
тг xx/ 6A, J
(tr+Tx)
где Atlm = ' г' вх—*' вых^—f г. вых х. вх/_ среднелогарифмическая раз-
1п Г1 вх~ <х; вых
v'r> вых— 'х. вх'
ность температуры, ° С; аг, ах — коэффициенты теплоотдачи между
жидкостью и стенкой в процессе нагрева и охлаждения соответственно,
Вт/(м2-°С); тг, тх — продолжительность периодов нагрева и охлажде-
охлаждения соответственно, с; F — полная площадь поверхности тела, омы-
омываемой жидкостью, м2; X— коэффициент теплопроводности материала
насадки, Вт/(м-°С); бэКВ — эквивалентная толщина стенки, м.
К регенераторам может быть применен ? —Л^Г/С-метод, если взять
за основу следующие определения из работы [6.2]:
для отношения водяных эквивалентов теплоносителей
для числа единиц переноса тепла
Г 1-
L l/(af)r+
для коэффициента термической эффективности
р __ (Qm ср)г (^г.вх — ^г.вых) и и (Qm ср)х (^х.вых —<х,вх)
(Qmcp)MHH (^г,вх —''х.вх) (Qm ср)мин Сг.вх — ^х,вх)
Для регенераторов с вращающейся насадкой
| 1-ехр[-^Г/СA-/?I in 1 | <09
11—/?ехр[—Л^Г/СA/?)]/ I 9[(<3Cp)/(QcP)]i93 / >с"^ •'
где (Qmcp)r = (Qmcp) „асадки. умноженному на число оборотов в се-
секунду.
Соотношения е = NTK> в графической форме приведены в работе
[6.2]. Основными преимуществами регенератора являются его высокие
параметры. Это обстоятельство позволяет успешно использовать теп-
теплообменники данного типа в качестве газогенераторов для нагрева
и конверсии жидкости.
6.7. ТЕПЛООБМЕННЫЕ АППАРАТЫ
С НЕПОСРЕДСТВЕННЫМ КОНТАКТОМ ТЕПЛОНОСИТЕЛЕЙ
В теплообменниках обычного типа с двумя потоками теплоносителя,
разделенными твердой стенкой, предотвращающей их смешение, во
время эксплуатации часто образуется накипь. В теплообменных аппа-
156
ратах с непосредственным контактом теплоносителей отсутствует теп-
лопередающая поверхность н обе несмешивающиеся жидкости при-
приходят в непосредственное соприкосновение; тем самым исключается
термическое сопротивление, вносимое разделяющей стенкой. Если
жидкая среда хорошо испаряется, то при распылении достигается тес-
тесный контакт ее с другой жидкостью и очень высокая интенсивность
теплопередачи. Охлаждающая колонна является именно таким уст-
устройством, в котором два потока жидкости обмениваются теплом по
схеме противотока. Подробно этот тип теплообменного аппарата опи-
описан в работах [6.21, 6.22].
Термин охлаждающая колонна обычно используют при описании
процесса охлаждения воздушным потоком водяного конденсата паро-
производящей установки. При смешении двух потоков часть воды испа-
испаряется, и в результате большое количество скрытой теплоты парообра-
парообразования усваивается воздухом. Этот процесс носит постоянный харак-
характер. При этом одновременно с теплообменом происходит массообмен.
6.8. ТЕПЛОВЫЕ ТРУБЫ
Тепловая труба представляет собой разновидность теплообменного ап-
аппарата, передающего тепло на значительное расстояние под воздейст-
воздействием относительно небольшой разности температуры. Она представ-
представляет собой полую трубку с запаянными торцами. Трубка частично
заполнена жидкостью, которая испаряется при достижении определен-
определенной температуры. При кипении жидкость у горячего торца трубы ис-
испаряется, в результате создается область повышенного давления. Под
действием этого давления испарившаяся жидкость движется к холод-
холодному торцу, где и конденсируется, отдавая именно то определенное ко-
количество тепла (при условии отсутствия потерь тепла на пути движе-
движения), которое она запасла при кипении. Конденсат затем стекает по
стенкам капилляра обратно в испарительную зону. Благодаря высоко-
высокому значению скрытой теплоты парообразования (и конденсации) при
капиллярном действии «фитиля» большое количество тепла может не-
непрерывно переноситься от одного торца трубы к другому без участия
механического насоса. Если предположить, что фитиль состоит из ма-
материала с круглыми капиллярами радиусом г, интенсивность тепло-
теплообмена с единицы площади между двумя торцами трубы можно полу-
получить из выражения
qs = — N \~ (cos ф.+ cos фс)_ -?Р?- cos pi Вт/м2, F.10)
а также
где N = (yrftg р/]х)—коэффициент переноса жидкости, Вт/м2; ^.макс
максимальная плотность теплового потока, Вт/м2; г — радиус трубки,
м; rUg — удельная скрытая теплота парообразования или конден-
конденсации, Дж/кг; у — поверхностное натяжение на границе раздела фаз,
Н/м; р — плотность жидкости, кг/м3; (л — динамическая вязкость жид-
жидкости, Н-с/м2; 5 — площадь поперечного сечения фитиля, м2; k —
157
коэффициент проницаемости фитиля; g = 9,81 — ускорение силы тя-
тяжести, м/с2; L — эффективная длина трубы, м; (ре— угол смачивае-
смачиваемости капилляра парообразующего торца; срс—угол смачиваемости
капилляра конденсирующего торца; C — угол ориентации трубы от-
относительно гравитационного вектора (положителен, когда парообра-
парообразующий торец размещен выше, чем конденсирующий).
Для положительного теплового баланса .выражение (cos <pe —
— cos(pc) должно быть величиной положительной.
Высокий удельный тепловой поток обеспечивается жидкостью,
обладающей большим коэффициентом переноса. Поэтому при расчете
и конструировании тепловой трубы большое значение имеет выбор оп-
оптимального типа жидкости и материала капилляров. Можно исполь-
использовать такие жидкости, ка-к спирт, аммиак, азот, вода и жидкие ме-
металлы, а для изготовления капилляров можно применять широкий
круг материалов, вплоть до ткани.
6.9. ТЕПЛОПЕРЕДАЧА ЖИДКИХ МЕТАЛЛОВ
Отличительной особенностью жидких металлов является высокая теп-
теплопроводность.
В отличие от жидкостей, в которых тепло передается преимущест-
преимущественно конвекцией, основной механизм теплообмена жидких метал-
металлов — процесс теплопроводности. Теплопередача жидких металлов
незначительно зависит от режима течения жидкости (т. е. от того, тур-
турбулентный он или ламинарный). Они также обладают незначительной
кинематической вязкостью и низким парциальным давлением. Бла-
Благодаря этим свойствам жидкие металлы нашли широкое применение
в качестве теплоносителей теплообменных аппаратов ядерных реакто-
реакторов, от которых необходимо отводить большое количество тепловой
энергии. Хорошо известными уравнениями для определения теплооб-
теплообмена в трубах являются уравнение Лайона
Nu = 7 + 0,025 (Re-Pr)°.« F.11)
для условия, когда на теплопередающей поверхности поддерживает-
поддерживается постоянная плотность теплового потока, и уравнение Зебана—
Шимазаки
Nu = 4,8 + 0,025 (Re-PrH-8 F.12)
для условия, когда на теплопередающей поверхности поддерживается
постоянная температура.
Для параллельных пластин и кольцеобразного слоя с DJDi < 1,4
при условии постоянной плотности теплового потока в работе [6.25)
приводится следующее уравнение:
Nu = 5,8 + 0,02 (Re-Pr)°.8. F.13)
6.10. СРЕДСТВА УСОВЕРШЕНСТВОВАНИЯ ХАРАКТЕРИСТИК
ТЕПЛООБМЕННЫХ АППАРАТОВ
При проектировании теплообменных аппаратов такие вопросы, как
назначение, размеры, масса, стоимость, удобство регулирования, за-
заслуживают самого тщательного внимания. Конструктор должен стре-
158
миться к тому, чтобы теплообменник обеспечивал по возможности
наиболее высокие параметры теплообмена. Этого можно достичь раз-
различными средствами, например, увеличив скорости потоков жидко-
жидкостей, развив площадь теплопередающей поверхности или турбулиза-
цию потоков теплоносителей. В основу разработки высококачествен-
высококачественных компактных теплообменных аппаратов могут быть положены
различные решения. Для заданной разности температуры между пото-
потоками жидкостей высокая интенсивность теплопередачи достигается
за счет высокого параметра теплопередачи СК.
Применительно в основном к кожухотрубным теплообменным ап-
аппаратам для этой цели используются два способа: оребрение труб и
турбулизация потоков.
Оребрение поверхностей. В практике общепринято развивать по-
поверхности обычно с помощью ребер и шипов, которые повышают ин-
интенсивность теплопередачи теплообменного аппарата.
Так как температура поверхности по высоте ребра не может под-
поддерживаться равной базовой температуре, то действительная эффек-
эффективность ребра ниже, чем та, которая была бы, если бы температурный
гр'адиент вдоль ребра отсутствовал. Эффективность ребра входит в мо-
модифицированные соотношения значений местных коэффициентов тепло-
теплоотдачи, используя которые основное выражение для параметра тепло-
теплопередачи теплообменных аппаратов с непосредственной теплопереда-
теплопередачей можно записать так:
161 ,С|.,
F.14)
где ц — 1 — {F-qIF) A — rip); tip = W/aFv; Ж — параметр теплопе-
теплопередачи, Вт/° С (см. табл. 2.3 для поверхности с ребрами различной кон-
конфигурации); F — полная площадь поверхности, м2; Fv — площадь по-
поверхности ребра, м2; /гст—площадь поверхности стенки без учета
ребер, м2; б — толщина стенки, м.
Соотношение для оребренных труб, расположенных в шахматном
порядке, было получено Бригсом и Янгом. Значение коэффициента
теплоотдачи а может быть получено из уравнения
Nu = 0,134 (ReH'68' (PrH-33 (s//)°- 2 {sibH' tt3 , F.15)
где Nu = Doa/A, — критерий Нуссельта; Re = D0«m/|i— критерий Рей-
нольдса; Рг = срц/А,— критерий Прандтля; Do — внешний диаметр
трубы, м; ит — массовая скорость, рассчитанная для минимальной
теплопередающей поверхности без учета ребер, кг/(м2-с); FMnH =
= Qm/^мин; s— шаг оребрения, м; / — высота ребра, ьл;"Ь — тол-
толщина ребра, м. Значения физических свойств ср, ц, К берутся при тем-
температуре смешения жидкости tm.
Турбулизаторы. Турбулизаторы обычно устанавливают в каналах
кожуха для организации механического перемешивания жидкости
и удлинения пути прохождения потока внутри корпуса. Увеличение
степени турбулизации и скорости потока жидкости через-смесители
ведет к повышению коэффициента теплопередачи кожуха теплообмен-
159
ника. Приближенное выражение для определения коэффициента теп-
теплопередачи кожуха имеет вид [6.5]
N"u = 0,36 (ReH^ (Рг)о-зз (ц/ц,.,)"." , F.16)
где Nu = aD/X— критерий Нуссельта; Re = Duml\i — критерий
Рейнольдса; Pr = cp\i/X — критерий Прандтля; D — гидравлический
диаметр, м; ит — массовая скорость, кг/(м2-с), рассчитанная на ми-
минимальную теплопередающую поверхность без учета ребер. Значения
физических свойств ср, |я, X берутся при температуре смешения жид-
жидкости tm.
СПИСОК ЛИТЕРАТУРЫ
6.1. Якоб М. Вопросы теплопередачи. Пер. с англ. М, Изд-во иностр. лит., 1960.
6.2. Kays W. М., London A. L. Compact Heat Exchangers. McGraw-Hill, 1964.
6.3. Фраас А., Оцисик М. Расчет и конструктнрованис теплообменников. Пер.
с англ. М., Атомиздат, 1971.
6.4. Institute of Mechanical Engineers. Recent Developments in Compact High
Duty Heat Exchangers. Conf., Thermodynamics and Fluid Mechanics, Oct. 1972.
6.5. Kern D. G. Process Heat Transfer. McGraw-Hill, 1950.
6.6. Afgan N., Schlunder E. U. Heat Exchangers; Design and Theory Sourcebook.
McGraw-Hill, 1974.
6.7. Bowman R. A., Mueller A. C, Nagle W. M. Mean Temperature Difference in
Heat Exchanger Design. — «Trans. ASME», 1940, v. 62, p. 283.
6.8. Standards of Tubular Exchanger Manufacturers Association, Inc., N. Y., 1959.
6.9. Briggs D. E., Young E. H. Convection Heat Transfer and Pressure Drop of
Air Flowing across Triangular Pitch Banks of Finned Tubes. — «Chem.
Engng Progr. Sympl.», 1963, Series 41, p. 59.
6.10. Feldman К- Т., Whiting G. H. The Heat Pipe. — «Mech. Engng», 1967, Feb.
6.11. Hryniszak W. Heat Exchangers. Loud., Butterworths, 1958.
6.12. London A. L., Kays W. M. The Liquid-Coupled Indirect Transfer Regenerator
for Gas Turbine Plants. — «Trans. ASME», 1951, v. 73, p. 529.
6.13. Coppage J. E., London A. L. The Periodic-flow Regencrator-A Summary of
Design Theory. — «Trans. ASME», 1953, v. 75, p. 779.
6.14. Winter E. R. F., Barsch W. O. The Heat Pipe. — In: Advances of Heat Trans-
Transfer. V. 7. Academic Press, 1971.
6.15. Cotter T. P. Theory of Heat Pipe. Los Alamos Science Lab. Rep. LA-3246-MS.
Los Alamos, NM, 1965.
6.16. Gardner H. S., Siller I. Shell Side Coefficients of Heat Transfer in a Baffled
Heat Exchanger. — «Trans. ASME», 1947, v. 69, p. 687.
6.17. Morton D. S. Thermal Design of Heat Exchangers. — «Industr. Engng Chem.»,
1960, v. 52, p. 474.
6.18. Stevens R. A., Fernandez J., Woolf J. R. Mean Temperature Difference in One,
Two, and Three-Pass Crossflow Heat Exchangers. — «Trans. ASME», 1957,
v. 79, p. 287—297.
6.19. Kays W. M., London A. L. Heat Transfer and Flow Friction Characteristics
of Some Compact Heat Exchanger Surfaces. — «Trans. ASMF.», 1950, y. 72.
6.20. Kays W. M. The Basic Heat Transfer and Flow Friction Characteristics of
Six Compact High-Performance Heat Transfer Surfaces. — «J. Engng for
Power, Trans. ASME», 1960, v. 82, p. 27.
6.21. Nance G. R. Fundamental Relationships in the Design of Cooling Towers. —
«Trans. ASME», 1939, v. 61, p. 721.
6.22. Berman L. D. Evaporative Cooling Circulating Water. Pergamon Press, 1961.
6.23. Stein R. P. Liquid Metals Heat Transfer. — In: Advances in Heat Transfer.
V. 3. Academic Press, 1966.
6.24. Seban R. A., Shinazaki T. T. «-Trans. ASME», 1951, v. 73, p. 803.
6.25. Seban R. A. «Trans. ASME», 1950, y. 72, p. 789.
6.26. Norman W. S. Absorption, Distillation and Cooling Towers. Longmans, 1961,
6.27. Jackson J. Cooling Towers. Lond., Butterworths, 1951.
Глава 7
ТЕПЛОПЕРЕДАЧА СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
7.1. ВВЕДЕНИЕ
Теплообмен между зданием и окружающей его средой в большой сте-
степени зависит от суммарной теплопроводности стен и перегородок вну-
внутри здания, от погодных условий и от разности температуры внутри
и вне помещения. В свою очередь, эти факторы находятся в тесной свя-
связи с видом строительных материалов и их способностью поглощать
влагу, с типом конструкций, качеством исполнения и месторасположе-
месторасположением строения. Очевидно, что определяющие условия могут изменяться
в широких пределах. Следовательно, любые оценки теплообмена могут
носить только приближенный характер. В целях облегчения расчетов
нагрева и вентиляции были выпущены различные пособия [7.1—7.3]
с достаточным количеством фактического материала, так что инжене-
инженеры имеют возможность получить необходимую информацию. Эти по-
пособия общедоступны и обеспечивают должную широту охвата и до-
достоверность данных. Знание баланса тепла и зависимости теплообмена
здания от внешних условий важно не только для контроля за тепло-
тепловым комфортом, но и для обеспечения стабильности температурного
режима внутри здания.
Обычно теплообмен здания с окружающей средой разделяют на
три категории.
1. Теплообмен через конструкции здания.
Тепловые потери за счет конвекции от воздушной среды помещения
к внутренним поверхностям панелей, теплопроводностью через тол-
толщину стены панелей здания к внешней поверхности, а затем конвек-
конвекцией и излучением в окружающую среду. Тепловые потери в виде лу-
лучистой энергии от стен помещения на внутреннюю поверхность наруж-
наружных панелей за счет теплопроводности через толщу стены панелей к ее
наружной поверхности, а затем конвекцией и излучением в окружаю-
окружающую среду.
2. Теплообмен за счет вентиляции. Тепловые
потери за счет утечки теплого воздуха или притока холодного возду-
воздуха в здание.
3. Периодический теплообмен. Тепловой поток, на-
направленный внутрь или из здания вследствие колебаний температуры.
Вычисление параметров для первых двух категорий традиционно
основано на стационарном методе, который играет значительную роль
в расчетах теплообмена. Наиболее трудно определить параметр для тре-
третьей категории теплообмена в зданиях при нестационарных условиях
подвода тепла, обусловленных периодическим поступлением солнеч-
солнечной энергии или тепла от источников внутри строения, а также из-
изменениями температуры внешней среды.
6 Основные формулы н данные по теплообмену 161
Обычно здания из тяжелых конструкций в меньшей степени под-
подвержены воздействиям колебаний температуры внешней среды.
Тепловой баланс при стационарных условиях требует, чтобы сум-
суммарные потери тепла восполнялись от источников тепла, что позволяет
поддерживать необходимый тепловой комфорт внутри здания. Поэтому
температуру внутри здания принимают постоянной [7.4] и тепловой
расчет проводят для различных значений температуры окружающей
среды. Для четкого представления механизма передачи тепла возник-
возникла необходимость во введении целой группы характерных темпера-
температур (табл. 7.1)
Таблица 7.1
Формулы для характерных температур,
используемых прн расчетах теплообмена строительных конструкций
Температура
Температура возду-
воздуха внутри помещения
Температура возду-
воздуха вне помещения
Средняя температу-
температура излучения в помеще-
помещении
Равновесная темпе-
температура
Температура среды
внутри помещения
Солнечно-воздушная
температура
То же, без учета сол-
солнечного излучения
Температура внут-
внутренней поверхности
Температура внешней
поверхности:
с учетом солнечной
радиации
без учета солнечной
радиации
Заданный темпера-
температурный перепад в панели
Обозначение
ta.i
^а, о
tn.i
^равн
te.i
te, о
te.o
ts.i
ts.O
ts.o
At
Формула
t . Qf ,
e, i 4- —;— (конвективный нагрев)
ts, o — QfQs, o/F
2 (Ft,, i)/ZF*
у('л, i + ta,i)*
2 /л. i . ta t*
3 '" 3
ta.. + Qfl...lf
jx — t0
* Только приближенные значения.
162
7.2. ОБОЗНАЧЕНИЯ
F — площадь поверхности помещения; площадь коридо-
коридора, м2;
2F — суммарная площадь поверхности помещения, м2;
ср — удельная теплоемкость воздуха, Дж/(кг-°С);
/d — коэффициент сопротивления давления;
•^вент — составляющая параметра теплопередачи за счет вен-
вентиляции, Вт/° С;
е — коэффициент излучения поверхности с учетом угло-
угловых коэффициентов излучения;
h — высота, м;
aa = aj(l — ас Qs;) ~ 1,6ас — гипотетический коэффициент теп-
теплоотдачи между воздухом и окружающей средой,
Вт/(м2-°С);
ас — коэффициент теплоотдачи конвекцией между возду-
воздухом и панелью, Вт/(м2-°С);
а„ ж 4a0Ts — коэффициент теплоотдачи излучением абсолютно
черного тела, Вт/(м2-К);
о0 = 5,67-Ю"8-постояннаяСтефана-Больцмана,Вт/(м2-К4);
J — плотность потока солнечного излучения, Вт/м2;
К—коэффициент теплопроводности, Вт/(м-°С);
/ — расстояние по вертикали между входом и выходом
воздуха, м;
N — кратность воздухообмена, ч—1;
Ар — перепад давления, Н/м2;
Qj — тепловой поток от конструкции здания, Вт;
QueHT — тепловой поток за счет вентиляции, Вт;
Qt — суммарный тепловой поток, Вт;
Qs — приток солнечного тепла, Вт;
Qo — объемный расход воздуха, м3/с;
R — термическое сопротивление (величина, обратная пара-
параметру теплопередачи), °С/Вт;
Q = FR — удельное термическое сопротивление, м2-°С/Вт;
г — коэффициент нагрева излучением;
S — коэффициент солнечной составляющей энергии;
Т — абсолютная температура, К;
К — полный коэффициент теплопередачи, Вт/(м2-°С);
Cf — интегральное значение параметра теплопередачи стен
здания, Вт/0 С;
К = SKF&t/ %F (tx — /0) — средневзвешенное по площади и
температуре значение коэффициента теплопередачи К,
Вт/(м2- °С);
V — объем помещения, м3;
v — скорость ветра, м/с;
vm — метеорологическая скорость ветра на высоте h, м/с;
Y — тепловая инерционность, Вт/(м2-°С);
т] — коэффициент поглощения излучения; показатель сте-
степени в законе распределения энергии ветра;
163
р — плотность воздуха, кг/м3;
б — толщина элементов конструкции здания, м;
tn — средняя температура воздуха, °С;
tf[ i — температура среды внутри помещения, °С;
U. о — солнечно-воздушная температура, °С;
t0 — заданная температура вне помещения, °С;
tn i — средняя температура излучения в помещении, °С;
/л — средняя температура излучения наружной стены, °С;
/равн — равновесная температура, °С;
ts — температура поверхности, °С;
tx — заданная температура внутри помещения, °С;
At — заданная разность температуры внутри и вне помеще-
помещения, °С.
Индексы:
i — внутри помещения;
О — вне помещения или внешняя поверхность;
s — поверхность;
/ — конструкция здания;
w — окно.
7.3. ОПРЕДЕЛЕНИЯ
Тепловая инерционность Y — мера тепловой инер-
инерционности элементов здания, которая снижает эффект периодического
воздействия притока тепла на температуру внутри помещения. Обыч-
Обычно тяжеловесные конструкции имеют более высокую тепловую инер-
инерционность.
Температура среды внутри помещения
tei — эквивалентная температура внутри помещения, применяемая,
в частности, для расчетов теплообмена в случае стационарного состоя-
состояния и при колебаниях суточной температуры. Использование темпе-
температуры среды позволяет также обеспечить лучший контроль за тепло-
тепловым комфортом в помещении.
Тепловое шунтирование характерно для метал-
металлических или других высокотеплопроводных конструкционных эле-
элементов здания, увеличивающих потери тепла. Интегральное значение
параметра теплопередачи — это сумма параметров шунтированных
элементов конструкции здания, образующих параллельную схему
термических сопротивлений, каждое из которых рассчитывается от-
отдельно для каждого элемента конструкции.
Утечка воздуха — неконтролируемый поток воздуха из
здания. Утечка воздуха происходит главным образом через трещины
в местах заделки окон и дверей и через щели и проемы, неизбежно
имеющиеся в здании.
Естественная вентиляция — поток воздуха из зда-
здания через регулируемые проходки, такие, как окна и двери, вентиля-
вентиляционные короба и т. п. Суммарное количество воздуха, входящего
и выходящего из здания, включает в себя также составляющую неконт-
неконтролируемой утечки воздуха. Предполагается, что если все регулируе-
164
мые отверстия закрыты, то естественная вентиляция сводится к не-
неконтролируемым утечкам воздуха.
Разновесная температура /„ami ~ температура,
характеризующая тепловой режим помещения. Она равна половине
суммы, составленной из значений средней температуры излучения в по-
помещении и температуры воздуха.
Солнечно-воздушная температура te0 — эк-
эквивалентная температура окружающей среды, равная такой темпера-
температуре воздуха вне здания, при которой должен обеспечиваться такой же
тепловой поток через строение, какой был бы при действительной тем-
температуре воздуха с учетом солнечного излучения.
Коэффициент солнечной составляющей
энергии S характеризует интенсивность притока солнечной энер-
энергии на единицу площади поверхности здания с учетом поглощающих
и передаточных характеристик элементов конструкций.
Эффект вытяжной трубы — один из двух основных
факторов, влияющих на утечку воздуха, возникающий при наличии
разности температуры внутри и вне помещения. Эта разность темпе-
температуры, влияя на плотность воздуха, становится причиной появления
перепадов давления на случайных отверстиях. В нагретом здании
воздух поступает в его нижнюю часть, а уходит через более высокую
часть. Если же воздух внутри здания холоднее, чем снаружи, то
происходит обратный процесс. Эффективное расстояние по вертикали
между входом и выходом воздуха из здания называется эффективной
высотой трубы
7.4. ТЕПЛОПЕРЕДАЧА КОНСТРУКЦИЙ ЗДАНИЙ
Тепловой поток через конструкции здания определяется из выражения
Q, = KF{teJ~te>a) Вт, G.1)
где К—полный коэффициент теплопередачи. Значения К опреде-
определяются экспериментально или расчетом термических сопротивлений
элементов конструкий здания, через которые распространяется тепло.
Обычно конструкционные элементы зданий представляются выпол-
выполненными таким образом, что тепловые потоки по ним распространяются
преимущественно в параллельных направлениях; К определяется
в этом случае как величина, обратная сумме термических сопротив-
сопротивлений, т. е.
K - i~ Bt/(m«.»Q, G.2)
где Qt — полное удельное термическое сопротивление.
На внутреннюю поверхность тепло передается излучением от ок-
окружающих помещение поверхностей и конвекцией воздуха, и тепло-
теплообмен определяется термическим сопротивлением Й5_г; с внешней по-
поверхности тепло снимается за счет конвекции воздушного потока,
а также за счет излучения в окружающую среду; теплообмен в этом слу-
случае определяется сопротивлением Qs_ 0. Два процесса — конвекцию
*"В Основные формулы и данные по теплообмену 165
и излучение — удобно описывать единым простым выражением путем
введения коэффициента теплоотдачи излучением ал. Величина пп
представляет собой полное удельное термическое сопротивление эле-
элементов конструкции (внутренние и внешние слои кирпичной кладки,
листы изоляционных материалов, воздушная прослойка и пр.). Оче-
Очевидно, что величина К зависит от таких факторов, как теплопровод-
теплопроводность, толщина конструкционных материалов, излучательная способ-
способность поверхностей здания, коэффициенты теплоотдачи обеих сторон
здания и скорость ветра. Уравнения для расчета К простых стен и
кровли приведены в табл. 7.2.
Таблица 7.2
Уравнения для расчета коэффициента теплопередачи
и потерь тепла элементами конструкций зданий
Формулы:
Qt = KF (<e, j - 4, о) Вт
Обозначения:
F — площадь наружной поверхности стен, м2;
8 — коэффициент излучения;
е = 0,9 для обычных строительных материалов*;
е = 0,2 для сильноокисленного алюминия*;
8 = 0,05 для полированного алюминия*;
ас — коэффициент теплоотдачи конвекцией, Вт/(м2 • °С).
Внутри помещения*:
<Хс = 1,5 для полов;
ас = 3,0 для стен;
ас = 4,5 для потолка.
Вне помещения*:
ас= 5,8+4,1 v;
ад — 4ао/Т| — коэффициент теплоотдачи излучением абсолютно черного тела,
Вт/(м2 . К):
при ts = 20° С ал = 5,7;
при 4 = 10° С ал = 5,14;
при /s = 0°С ал = 4,61;
при ts =— 10° С ал = 4,12;
% — коэффициент теплопроводности, Вт/(м • °С);
Ts — абсолютная температура поверхности, К;
v — скорость ветра, м/с;
QSt i — термическое сопротивление на внутренней поверхности, м2 ¦ °С/Вт;
Qs[ 0 — термическое сопротивление на внешней поверхности, м2 • °С/Вт;
Qn — термическое сопротивление различных структурных компонент,
м2 • °С/Вт;
Qa — термическое сопротивление воздушной прослойки, м2 • °С/Вт;
для полой стены с толщиной воздушной прослойки > 2 см* Qa = 0,18;
для конструкции, образованной наклонной крышей и плоским потолком*,
Qa = 0,11 -Н 0,14;
ta — температура воздуха, °С;
te% i — температура среды внутри помещения, °С;
•Значения рекомендованы IHVE-A Справочником 1970.
166
Продолжение табл. 7.2
< о — температура окружающей среды вне помещения; 4, о ~ 4, о при не-
незначительном солнечном излучении, СС;
/., — температура поверхности, °С;
б — толщина плиты, м.
Термическое сопротивление
1
"Sl г 1,2еехл 4-а
1
S. 0
„ б
- (см
с
(см.
. рис
рис.
С/Вт
.7.1)
7.2)
Потери тепла конструкцией здания, Вт
Q F(tl
Q -F(ts
Qf-FUs
, l — ts
"S, I
o)
o)
Температура поверхности, °С
.e. J =
. o) /,. ( + «8. tta. o)]
Рис. 7.1. Термическое сопротивление
на внутренней поверхности Й», .¦ при
средней температуре поверхности
6В*
1 2 3 't 5 S 7 S Э 10 11 12
Скорость ветра, м/с
Рис. 7.2. Термическое сопротивление на
внешней поверхности Q3,n при средней
температуре поверхности 0° С
167
Как известно, теплопроводность кирпичной кладки и других ма-
материалов зависит от плотности материала и содержания в нем влаги.
На рис. 7.3 приведены некоторые типичные значения стандартных
данных по содержанию влаги.
Коэффициент теплоотдачи внешней поверхности очень сильно за-
зависит от местоположения конструкции по отношению к солнцу, ветру
и т. п. и от высоты здания.
2,0
Е
со
, 1,1,1.1,1
_
" , 1 , 1 , 1 , 1 , 1 ,
/.
/У
/у
у/
,1,1,1,
D Ш 800 1200 1600 2000 2400
Плотность сухого Воздуха о, кг/м3
Рис. 7.3. Зависимость теплопроводности материалов
кладки от плотности воздуха при различном объемном
содержании влаги:
/ — бетон н кирпичная кладка после дождя E%); 2 — бетон,
защищенный от дождя C%); 3 — кирпичная кладка, защищен-
защищенная от дождя A%)
При проектировании обычно различают три категории условий
[7.1]: здание укрыто от ветра (и = 1 м/с), нормальные условия (и =
= 3 м/с) и жесткие условия (и = 9 м/с). Предполагается, что числен-
численные выражения связывают коэффициент теплоотдачи ас со скоростью
ветра. Была обнаружена незначительная корреляция между тепловым
потоком и установившейся скоростью ветра. Локальные характери-
характеристики воздушного потока, обтекающего здание, которое является ис-
источником сильного Еозмущения, зависят от местоположения здания.
В некоторых точках поток может оказаться очень неустойчивым, ото-
оторваться от поверхности и создать изолированный слой с сильным вих-
вихревым движением; в других точках поток может изменить направление
своего движения на противоположное и иметь скорость, значительно
превышающую среднюю скорость ветра. Поэтому для того, чтобы до-
достаточно точно определить коэффициент теплоотдачи, необходимо знать
большое число локальных параметров воздушного потока по периметру
168
здания. При проектировании это, конечно, вызывает определенные
трудности. Для расчета кривых, представленных на рис. 7.2, удобно
использовать простое уравнение ас = 5,8 + 4,1у [7.1].
За скорость ветра обычно принимают метеорологическую скорость
ветра. В Англии метеорологическую скорость ветра измеряют на вы-
высоте 10 м на открытой местности. Обычно усредненный профиль ветра
представляется рядом эмпирических выражений. Например, установ-
установлено, что логарифмический закон изменения профиля скорости [7.5]
справедлив для нижних частей пограничного слоя воздушного потока.
Гораздо проще использовать закон распределения энергии [7.6].
Тогда распределение скорости определяется как
v = vm (A/AJ* м/с, G.3)
где v и vm — среднее значение скорости ветра на высоте h и hm со-
соответственно и х — параметр, характеризующий степень неровности
местности. Если известна метеорологическая скорость ветра на высоте
hm (т. е. на высоте 10 м), то для высоты h скорость можно рассчитать
по уравнению G.3), используя при этом следующие значения,
v. = 0,15 — для ровной открытой местности; х = 0,29 — для неболь-
небольшого города и окрестностей большого города; х = 0,45 — для за-
застроек центра города.
Можно считать, что вертикальные стены способны воспринимать
силу ветра, скорость которого превышает скорость ветра на крыше
в два-три раза.
Значения К для различных конструкций зданий приведены в ра-
работе [7.7], однако предпочтительнее пользоваться расчетными значе-
значениями К, так как они обычно отражают типичные для данной мест-
местности усредненные условия. Значения К, приведенные в работе [7.1],
рассчитаны с учетом сопротивлений элементов конструкций зданий с
привлечением стандартных данных по содержанию влаги в материа-
материалах, тепловых потоков на поверхностях элементов конструкций за
, счет излучения и конвекции, а также с учетом вентилируемых воздуш-
воздушных объемов. Значения коэффициентов теплопередачи К, приведенные
в табл. 7.3, взяты из IHVE-A Справочника, 1970.
7.5. ТЕПЛООБМЕН ЗА СЧЕТ УТЕЧКИ ВОЗДУХА
Утечка воздуха из здания через трещины и отверстия — это неконт-
неконтролируемый процесс, в то время как естественная вентиляция — это
движение воздуха через специальные отверстия, например окна, две-
двери и вентиляционные отверстия, обычно контролируемые обитателями
здания. Когда все эти каналы доступа воздуха закрыты, естественная
вентиляция сводится к неконтролируемой утечке воздуха. Интенсив-
Интенсивность утечки зависит от размера и гидравлических характеристик тре-
трещин и от перепада давления. Если перепад давления устанавливается
под напором ветра, то воздух проникает в здание через трещины с на-
наветренной стороны и покидает его через трещины с подветренной сто-
169
Таблица 7.3
Значения коэффициента теплопередачи К
для некоторых наиболее общих
конструкционных элементов здании
Формула:
f = KF(te,t-te,0) Вт
Конструкционный элемент здания
Стандартные значения коэффициента К,
Вт/(н2-°С)
В укрытии
Нормальные
условия
Жесткие ус-
220-мм неоштукатуренная кирпич-
кирпичная стена
220-м кирпичная стена с 16-мм
слоем легкой штукатурки
260-мм полая стена (полость не
вентилируется), с наружной и внут-
внутренней стороны кирпичная кладка
толщиной 105 мм с дополнительным
16-мм слоем легкой штукатурки с
внутренней стороны
260-мм полая стена (полость не
вентилируется) со 105-мм слоем кир-
кирпича, 100-мм бетонным блоком с
внешней стороны и 16-мм слоем плот-
плотной штукатурки с внутренней сторо-
стороны
Навесная стена, закрытая панелью,
с 25-мм слоем полистирола между
5-мм асбоцементными плитами в ме-
металлическом обрамле , 50-мм по-
полостью, 100-мм бетонным блоком, 16-
мм слоем штукатурки
Плоская крыша, покрытая 19-мм
слоем асфальта нли войлочно-бнтум-
ным слоем, 150 мм бетона*
Та же конструкция крыши со
150-мм пористыми бетонными плита-
плитами
Наклонная крыша из черепицы на,
досках и войлоке; пространство под
крышей и оштукатуренным потолок
на балках с алюминиевой фольгой,
закрепленной на досках
Окно в металлической раме:
с одним стеклом
с двумя стеклами
2,2
1,8
1,3
0,93
0,79
3,1
0,87
1,4
5,0
3,0
2,3
1,9
1,3
0,96
0,81
3,4
0,88
1,5
5,6
3,2
2,4
2,0
1,3
0,98
0,83
3,7
0,89
1,6
6,7
3,5
• Взято с разрешения из IHVE-A Справочника, 1970.
170
роны, так как давление ветра на наветренной стене выше, чем на под-
подветренной, где оно сравнимо со статическим давлением покоящейся
массы воздуха. Если же перепад давления вызван разностью темпе-
температуры внутри и вне помещения, то имеет место так называемый
эффект трубы, когда движение воздуха в нагретом здании направле-
направлено от входа на самой нижней отметке к выходу на самом высоком уров-
уровне. Эффективное расстояние между входной и выходной точками назы-
называют эффективной высотой трубы. Направление циркуляции воздуха
может быть и обратным (когда температура воздуха внутри помещения
ниже температуры окружающей здание среды).
Существуют два метода количественной оценки утечки воздуха
из здания: 1) метод трубы, основанный на регистрации утечки через
элементы конструкции вблизи окон и дверей в соответствии с перепа-
перепадом давления на каждом из них; 2) метод воздухообмена, основанный
на предположении о постоянстве обмена между помещением и окру-
окружающей средой определенного количества воздуха за один час для
каждого помещения отдельно.
Метод трубы хотя и более точен, но очень трудоемок, так как тре-
требует знания характеристик утечек в зависимости от разновидностей
трещин элементов конструкций и перепада давления на каждой из
них. Расчетом установлено, что утечка воздуха через трещины по сво-
своей физической сущности аналогична движению жидкости через от-
отверстие с коэффициентом пропускания С = 0,65. Таким образом, с хо-
хорошим приближением объемный расход воздуха можно получить из
выражения
Qv = CFV2ApJp = 0,827F]/"K~p м3/с. G.4)
По вполне понятным причинам метод воздухообмена нашел широкое
применение. Обычно оценка эффективности воздухообмена основыва-
основывается на экспериментальных данных и здравом смысле. Эмпирические
значения N изменяются в интервале 0,25—2 в час для обогреваемых
и вентилируемых зданий различных типов. Таким образом, если объем
помещения V известен, то утечку воздуха можно получить из выраже-
выражения
Qo = NV/3Q00 м3/с. G.5)
Кратность воздухообмена N также можно выразить через вентиля-
вентиляционную составляющую, которая равна Л73. По известному значению
объемного расхода воздуха потери тепла за счет утечки воздуха можно
определить так:
QBeW = QBCPPA* Вт. G.6)
В табл. 7.4 сведены расчетные данные по потере тепла за счет утеч-
утечки воздуха.
171
Таблица 7.4
Потери тепла за счет утечки воздуха
Формула:
<2вент =
Вт.
Обозначения:
Qv — объемный расход воздуха, м3/с;
р — плотность воздуха, кг/м3;
ср — удельная теплоемкость воздуха, Дж/(кг • °С);
At = ta i — ta о — разность температуры воздуха внутри и вне помеще-
помещения, °С; '
v — скорость ветра, м/с;
F — площадь отверстия, м2;
Лр — перепад давления на отверстии, Н/м2;
f$ — коэффициент сопротивления давления; среднее значение его для квад-
квадратного или прямоугольного здания равно ~0,7 с наветренной
стороны и ~0,4 с подветренной стороны [7.3];
С — коэффициент пропускания потока (принят равным 0,65);
/ — расстояние по вертикали между входной и выходной точками; эффек-
эффективная высота трубы, м;
JV — кратность воздухообмена, ч~х;
V — объем помещения, м3;
То, Ti — абсолютная температура воздуха вне и внутри помещения, К-
Параметр
Перепад давления Лр
Объемный расход воздуха
Qv
Тепловой поток Свент
Mei
Объемный расход воздуха Qv
Тепловой поток QBeBT
Ветровой
Метод т р
1
0,827 2
1200
од воздух
эффект
у б ы
QvM
о о б м е
н а
1
3
Эффект трубы
\ ' о ' i 1
0,827 2(?ДрУг)
1200 QVM
NV/3600
- NV (ta, i-ta, o)
7.6. ТРЕБОВАНИЯ К ТЕПЛОВОМУ РЕЖИМУ ПОМЕЩЕНИЯ
Тепловой комфорт в помещении зависит от температуры воздуха в нем
и температуры окружающих поверхностей. В качестве показателя теп-
теплового режима используется равновесная температура tpaBH. Темпе-
Температура среды внутри помещения te< t также дает достаточно хорошее
172
представление о тепловом комфорте, хотя и не считается определяющей.
Поэтому представляется целесообразным формулировать требуемые
условия по обеспечению теплового режима помещения на основе рав-
равновесной температуры или температуры среды внутри помещения.
Зная точное значение температуры /равн или tci, можно вычислить
требуемое количество тепла, необходимое для обеспечения заданной
температуры независимо от погодных условий и температуры вне по-
помещения.
Обычно при таком расчете исходят из условия стационарного со-
состояния, предполагая, что на внутренних поверхностях панелей зда-
здания (стена, окно, крыша или навес) теплообмен осуществляется конвек-
конвекцией воздуха в помещении, а также излучением от других поверхностей.
Уравнение теплового потока на внутренней поверхности имеет
вид
Qf = F [еал (/л> г- -4,j) + ac (tut t — tSi *)] =
= (F/Q,. t) (te, t - tti i) Вт. G.7)
В расчетах температуры какого-либо помещения необходимо учи-
учитывать также вклад от теплопередачи соседних помещений, если они
имеют несколько отличную температуру. Полные тепловые потери зда-
здания при этом можно представить в виде алгебраической суммы Qf
от всех стенных панелей, участвующих в теплообмене. Но значение
tSt i зависит как от полного коэффициента теплопередачи К, так и от
температуры внешней поверхности t0. Расчет Q} выполняется по фор-
формуле G.1).
Часть тепловых потерь здания, а именно потери за счет вентиляции,
также должна быть учтена в суммарном количестве тепла, необхо-
необходимого для поддержания теплового комфорта в помещении.
Потери тепла за счет вентиляции определяются на основе метода
воздухообмена:
Qf =.(NV/3) (ta, t - ta- 0) = #BeHT (te, t - ta§ 0) Вт. G.8)
В режиме динамического равновесия потери тепла элементами кон-
конструкции здания восполняются за счет конвективной теплоотдачи от
воздуха помещения к внутренним поверхностям здания, тогда как по-
потери тепла вентиляцией компенсируются подводом тепла от поверх-
поверхностей помещения за счет конвекции. При рассмотрении теплового ба-
баланса необходимо иметь в виду, что теплообмен внутри помещения
в значительной мере зависит от используемой системы нагрева. Мож-
Можно рассматривать конвективный нагрев, который обеспечивается за
счет нагревания воздуха, и нагрев излучением от отопительных эле-
элементов, встроенных в панели. Другие виды нагрева по своей эффек-
эффективности находятся между этими двумя основными видами. С приме-
применением этих видов нагрева представляется возможным обеспечивать
теплообмен внутри помещения, который осуществляется главным об-
образом только между поверхностями и между поверхностями и возду-
воздухом. Для удобства расчета вводится гипотетический коэффициент теп-
теплоотдачи аа. Тогда:
173
конвективный нагрев
Qf = SFae (ta, i - tCi,) Вт; G.9)
нагрев излучением
QBeHT = ZFaa(te,i-ta.i) Вт. G.10)
Значение aa можно получить из выражения
аа = ac/(l — аеЙм) ~ 1,6ае Вт/(м2-°С). G.11)
В рамках этих предположений, если принять, что теплообмен про-
происходит гипотетически между поверхностью с заданной температурой
(подразумевается te- t) и воздушной средой с температурой ta>,-, рас-
расчет потерь можно предельно упростить. _
Уточненный способ расчета значения К, предложенный Гарри-
соном специально для случая, когда необходимо учитывать теплообмен
перегородок помещения, основан на использовании взвешенных по
температурным зонам значений:
где Л? — заданная разность температуры на элементе панели, т. е.
tx— ta0 для стен п tx— ta— для перегородок, разделяющих поме-
помещение на внутренние секции и имеющих температуру tn.
IHVE-A Справочник, 1970 г., содержит средневзвешенные дан-
данные К, т. е. К = 2/C/72F.
Метод расчета значения К изложен в разд. 7.4. В табл. 7.5 приве-
приведены формулы для расчета тепловых потерь помещения.
Формулы табл. 7.5 дают возможность определять различные тем-
температуры и суммарные утечки тепла. Например, для расчета темпера-
температуры среды внутри помещения, являющейся определяющей темпера-
температурой помещения, и требуемого для обеспечения этой температуры ко-
количества тепла может быть использована следующая схема.
7.6.1. Конвективный нагрев
а) задаются проектное значение te> 0 и проектное значение темпе-
температуры вне помещения;
б) находится значение К (см. разд. 7.4);
в) рассчитывается Qf = 2/CF (te t — te% 0).
В отсутствие солнечного излучения вместо te, о используется ta 0;
для случаев, когда тепло теряется через внутренние перегородки, ис-
используется tn вместо te 0;
г) рассчитывается 2F для помещения в целом;
д) определяется (/„_, — te_,-) = QfjaaI.F;
е) находится ta, t из (д);
ж) рассчитывается QBeHT из (NV/3) (ta i — ta 0) или из Л'вент D, >—
-ta. о), где ^вент = (NV/3) (I + 2KFlaa2F);
з) определяется Qt = Qf + <2вент-
174
Таблица 7.5
Уравнения к расчету количества тепла для поддержания
необходимого температурного режима помещения
Обозначения:
F — площадь поверхности элемента, м2;
2f — полная площадь поверхности помещения, м2;
•^-"вент — составляющая параметра теплопередачи за счет вентиляции, Вт/°С;
аа— 1,6 ас — гипотетический коэффициент теплоотдачи между воздухом и
средой внутри помещения, имеющей заданную температуру, Вт/(м2-°С);
ал с^ 4сто7'| — коэффициент теплоотдачи излучением абсолютно черного
тела, Вт/(м2 > К);
ас — коэффициент теплоотдачи конвекцией от воздуха к панели, Вт/(м2 • °С);
N — кратность воздухообмена, ч-1;
Qj — тепловой поток от конструкций здания, Вт;
<2вент — тепловой поток за счет вентиляции, Вт;
г — коэффициент, учитывающий количество тепла, поступающего вслед-
вследствие лучистого теплообмена от нагревательного элемента.
В работе [7.13] получены следующие значения г:
Система нагрева
Панели с встроенными в них
нагревательными элементами
Одиночные батареи на пане-
панели
Двойная панель н двух-
стержневой секционный кол-
коллектор
г
2/3
1/2
1/3
Система нагрева
Четырехстержневой секци-
секционным коллектор
Шестистержневой секцион-
секционный коллектор
Воздушный нагреватель
г
1/Ь
7/40
0
К — полный коэффициент теплопередачи, Вт/(м2 • °С);-
2К77 — значение параметра теплопередачи всех стен, Вт/°С;
К = XKFAt/ZF (tx — t0) Вт/(м2 • °С);
V — объем помещения, м3;
te, i —¦ температура среды внутри помещения, СС;
ta> i — средняя температура воздуха внутри помещения, °С;
'а о — средняя температура воздуха вне помещения, СС;
ie, о —¦ солнечно-воздушная температура; температура окружающей среды
вне помещения, °С;
'л, i — средняя температура излучения в помещении, °С;
ta — заданная температура соседних помещений, °С;
tx — заданная температура помещения, °С;
t0 — заданная температура вне помещения; для перегородок t0 =s ta, °C;
At — заданная разность температуры внутри и вне помещения, °С.
Параметр
Формула
Литера-
Литература
Потери тепла, Вт:
через стены здания
за счет вентиляции или неконт-
неконтролируемых утечек воздуха
суммарные
[7.1]
NV_
= «лГвент('е , i ''а, о)
_NV_ _
Увент= п На, i 'а. о) —
175
Продолжение табл. 7.5
Параметр
Формула
Литера-
Литература
П Количество тепла, не-
необходимого для поддер-
поддержания заданного темпе-
температурного режима, Вт:
за счет конвективного нагрева
за счет лучистого нагрева
Потери тепла в случае
поддержания заданного
температурного режима
помещения смешанной
системой обогрева, Вт
конструкциями здания
a. i-te. i)=Qf,
VI 1KF
[ +
i-ta, i) =
[7.13]
X
f = K2F(tx-t0)X
NV/3
1+-
1,5л1
A-1,50
3 NV/3
4 aa2
1
1 +K/4 aa
вентиляционные
X
1,5
X
3 jVV/3
l+(K/4aa)
суммарные
* <2*—количество тепла, необходимого для достижения температуры среды te> г-
при наличии тепловых потерь только через стены. Когда происходит теплообмен
и через перегородки, то используется t0 вместо te, 0 и ta< 0 и К—вместо 2F/C/2F.
**Q?—количество тепла, необходимого для обеспечения заданной температу-
температуры помещения tx, равной равновесной температуре ?равн-
176
7.6.2. Нагрев излучением
(а) — (г) — аналогично соответствующим пунктам для конвектив-
конвективного нагрева;
д) рассчитывается QDeHT = СКъйт (tc t — ta0), где ^"вент =
= l/C/NV+ l/aa SF);
е) определяется {te> t — ta< t) = QWHT/aJlF;
ж) находится tui t из (е);
з) определяется Qt = Qf + QbeHT.
7.7. ПЕРИОДИЧЕСКАЯ ТЕПЛОПЕРЕДАЧА
Для определения количества тепла, необходимого для поддержания
требуемого температурного режима внутри здания в течение продол-
продолжительного зимнего периода, обычно используют метод стационарного
режима. Условия становятся нестационарными в тех случаях, когда
здание периодически получает тепло от таких источников, как сол-
солнечное излучение, искусственное освещение, электрические нагрева-
нагревательные приборы, или когда изменяется температура внешней среды.
Все эти причины вызывают колебания температуры внутри помеще-
помещения около среднесуточного значения. Наинизшие и наивысшие значе-
значения температур могут быть использованы как исходные для определе-
определения количества тепла при нагреве и охлаждении здания. Если эти зна-
значения становятся чрезмерными, как, например, в случае летней жары,
то предпринимаются меры для обеспечения необходимого уровня есте-
естественной вентиляции или при определенных обстоятельствах — кон-
кондиционирования воздуха.
Основной метод расчета, предложенный Лоундоном и Дантером
[7.14, 7.15], позволяет определять температуру внутри естественно вен-
вентилируемого здания с учетом притока тепла за счет солнечной энер-
энергии и тепловой инерционности здания.
Из всех разнообразных причин, вызывающих изменение теплово-
теплового режима здания, излучение Солнца играет наиболее важную роль.
Поэтому наличие окон становится превалирующим фактором. Когда
солнечное излучение попадает на оконное стекло или на жалюзи окон-
оконного проема, тепло частично отражается, частично передается и частич-
частично поглощается. Поглощенное тепло затем частично отдается внутрь
помещения и частично наружу. Полное количество тепла, подводимого
к зданию, — это соответственно усредненная часть солнечной энер-
энергии, проникающей в здание за определенный период времени (напри-
(например, за 24 ч). Вводимый коэффициент солнечной нагрузки позволяет
рассчитывать поглощающие, передающие и ретрансляционные харак-
характеристики окон, так что количество тепла, эквивалентное подводимой
солнечной энергии, легко может быть получено из соотношения
Qs = S7f№. G.13)
Доля солнечного тепла, падающего на стены и проникающего затем
в помещение, обычно незначительна по сравнению с теплом, попадаю-
177
щим через окна. Для получения суммарного количества подводимого
тепла Q; кроме солнечной составляющей необходимо учесть тепло от
других случайных источников. Степень влияния ~Qt на температуру
внутри помещения зависит от значения параметра теплопередачи си-
системы Ж = ЪКР и параметра теплопередачи за счет вентиляции Ж"вепт.
Изменения интенсивности солнечного излучения и других истоь-
ников тепла могут стать причинами колебания температуры внутри
помещения около ее среднего значения. Приток тепла во времени мо-
может быть представлен синусоидой за период времени 24 ч с амплитудой
Q= Q-Q Вт, _ G.14)
где Q — максимальный приток тепла, a Q — среднее значение. Пе-
Переменные составляющие притока тепла Q определяются отдельно для
различных источников тепла и затем складываются для получения
суммарного колебания тепловой нагрузки Qt.
Под воздействием циклических изменений поступления тепловой
энергии происходят колебания температуры внутри помещения, при-
причем тепло поступает в здание или отдается им в окружающую среду
с некоторым запаздыванием. Колебания температуры внутри помеще-
помещения более плавные для здания, сооруженного из массивных конструк-
конструкций, обладающих большей теплоемкостью по сравнению с легкими
кострукциями. Реакция строительного сооружения на изменение при-
притока тепла характеризуется тепловой инерционностью Y [7.15], кото-
которая без учета времени запаздывания может быть использована в рас-
расчетах по аналогии с полным коэффициентом теплопередачи /("• Это
обстоятельство дает возможность получить простое уравнение, свя-
связывающее колебания температуры внутри помещения tej с цикличе-
циклическими изменениями подводимого тепла Qt, т. е.
&=B/Y + .»-BeBT)?.f Вт. G.15)
Из этого уравнения видно, что вентиляционная составляющая входит
в него в качестве самостоятельного слагаемого, характеризующего
переменную часть теплоподвода.
В табл. 7.6 приведены уравнения для определения значений и коле-
колебаний температуры внутри помещения под воздействием циклических
изменений подводимого тепла. Установлено, что изменение темпера-
температуры массивных конструкций здания при переменном теплоподводе
происходит спустя час после изменения температурных условий.
Чтобы учесть это обстоятельство, необходимо, как предлагается в ра-
работе [7.1], учитывать начало воздействия лучистой энергии со сдвигом
на час раньше.
Таблица 7.6
Уравнения для определения температуры среды
внутри помещения при изменении количества подводимого тепла
и периодичности его подвода
Обозначения:
Ff — площадь поверхности конструкции, м2;
Fw — застекленная площадь поверхности окна, м2;
178
П р о д о л ж е и и е т а б л. 7.6
2F — полная площадь поверхности помещения, м2;
^вент = 1/C/Л/V + l/ao2F) — составляющая параметра теплопередачи за счет
вентиляции, Вт/сС,
f — коэффициент затухания, зависящий от толщины стены; / = 0,32 -=- 0,15
для толщины от 20 до 30 см соответственно (более детально см. [7.1]);
J — плотность потока солнечного излучения, Вт/м2;
¦е i — температура среды внутри помещения, °С;
(е. о — солнечно-воздушная температура, °С;
tut о — температура воздуха вне помещения, °С;
S — коэффициент солнечной нагрузки;
Sa — переменная составляющая коэффициента солнечной нагрузки;
У — тепловая инерционность, Вт/(м2 • °С);
2/-Y — суммарная площадь всех поверхностей помещения, умноженных
на соответствующие значения У, Вт/°С.
Индексы:
a—изменение температуры воздуха;
с—нерегулярная составляющая подводимого тепла;
/—здание:
s—Солнце:
t— полный.
Символами—, ~, Л обозначены средние, переменные и максимальные зна-
значения, соответственно.
Подводимое к зданию тепло:
эквивалентное солнечному излучению,
подаваемому в помещение через осве-
освещенные окна
от осветительных приборов, оборудова-
оборудования и т. п. (нерегулярное поступле-
поступление)
от солнечного излучения и других ис-
источников (полное эквивалентное коли-
количество тепла)
Средняя температура среды
внутри помещения
Циклический режим подво-
подвода тепла:
энергии солнечного излучения через
окна
к конструкции здания
за счет нерегулярной составляющей
за счет изменения температуры возду-
воздуха внутри помещения
полное эквивалентное количество теп-
тепла, подводимого к зданию
колебания (среднего значения по отно-
отношению к максимальному) температуры
среды внутри помещения
-|-JBC11I) D,г-/
Qa= B/Cu> Fш + ^веит) ^a, 0
е, t-Qt
179
Максимальное значение тем-
температуры среды внутри поме-
помещения
Продолжение табл. 7.6
В условиях нестационарного подвода тепла за счет лучистой энер-
энергии панели здания обладают определенным полным термическим со-
С
\— J, усредненная
за сутки
Ю
макс
Рис. 7.4. Максимальная интенсивность Солнца в полдень на вер-
вертикальных поверхностях при ясной погоде на территории Велико-
Великобритании.
(Кривые на рисунке построены с разрешения по результатам,
приведенным в IHVE-A Справочнике, 1970)
противлением, в то время как в условиях стационарного режима ра-
радиационного теплоподвода это сопротивление становится неопределен-
неопределенным. Чтобы связать обе составляющие лучистого теплоподвода, вводит-
вводится коэффициент Sa, учитывающий непостоянство солнечной нагрузки.
Принимаются во внимание также различия элементов панелей по-
посредством классификации зданий на тяжелые и легкие. Некоторые
типичные значения S, Sa и Y, взятые из работы [7.14], приведены
в табл. 7.7. Максимальная интенсивность Солнца на территории Вели-
Великобритании в полдень на поверхности вертикальных стен (в августе
и январе) при ясной погоде приведена на рис. 7.4.
180
Таблица 7.7
Некоторые типичные значения S, Sa и Y
Система
Одинарное стекло
Двойное стекло
Жалюзи:
за одним стеклом
между двумя стеклами
s
0,77
0,67
0,46
0,28
Sa (лег-
кне конст^
рукцни)
0,54
0,49
0,46
0,25
Элементы здания
Окно с одним стеклом
Окно с двумя стеклами
7,5 см стены
с р=1750 кг/м3
Деревянные полы
Оштукатуренный пото-
потолок
у.
Вт/(м".°С)
5,6
3,2
5,0
2,0
3,0
Примечание. Значения взяты нз работы [7.14].
СПИСОК ЛИТЕРАТУРЫ
7.1. IHVE Guide Book A. Institution of Heating and Ventilation Engineers, 1970.
7.2. ASHRAE Handbook of Fundamentals. American Society of Heating Refrigera-
Refrigerating and Air-conditioning1 Engineers, 1967.
7.3. a) DIN 4701, Regeln ftir die Berechnung des Warme-bedarfs von Gebauden,
German Standards; b) Association des Ingeniers en Chauffage et Ventilation
de France; c) NEN 1068, Thermal Insulation of Dwellings, Netherland;
d) Dansk Forening for Varme-Venti!ation-og Sanitetsteknik.
7.4. Humphreys M. A. Environmental Temperature and Thermal Comfort. —
«Build. Services Engineers», 1974, v. 2, p. 77—81.
7.5. Simiu E. Logarithmic Profile and Design Wind Speeds. — «J. Engng Mcch.
Div.», 1973, October.
7.6. Davenport A. G. Tlie Dependence of Wind Loads on Meteorological Parame-
Parameters, Proc. Symp. Wind Effects on Buildings and Structures. V. 1. Ottowa
1967.
7.7. Loundon A. G. U-va!ues in the 1970 Guide. — «J. IHVE», 1968, September.
7.8. Jackman P. J. A Study of the Natural Ventilation of Tall Office Buildings. —
«J. IHVE», 1970, v. 38, p. 103—118.
7.9. Jackman P. J. Heat Loss in Buildings as a Result of Infiltration. — «Build.
Services Engineers», 1974, v. 42, p. 6—14.
7.10. Danter E. Heat Exchanges in a Room and the Definition of Room Tempera-
Temperature. — «Build. Services Engineers», 1974, N 41, p. 231—243.
7.11. Bull L. C. The Practical Approach of Heat Loss Calculations. — «Build. Ser-
Services Engineers», 1974, v. 41, p. 261—267.
7.12. Harrison E. Environmental Temperature and the Calculation of Heat Los-
Losses. — «Build. Services Engineers», 1974, v. 41, p. 261—267.
7.13. Harrison E. The Calculation of the Heat Requirements of Rooms. — «Build.
Services Engineers», 1975, v. 43, p. 19—23.
7.14. Loundon A. G. Summertime Temperatures in Buildings without Air-Condi-
Air-Conditioning. — «J. IHVE», 1970, v. 37, p. 280—290.
181
7.15. Loundon A. G., Danter E. Investigations of Summer Overheating. — «Build.
Science», 1965, v. 1, p. 89—94.
7.16. Milbank P. L., Marrington-Lynn J. Thermal Response and Admittance Proce-
Procedure. — «Build. Service Engineers», 1974, v. 42, p. 38—51.
7.17. Billington N. S. Thermal Insulation and Thermal Capacity of Buildings. —
«Build. Service Engineers», 1976, v. 43, p. 226—233.
7.18. Down P. G. Heating and Cooling Load Calculations. Pergamon Press, 1969.
7.19. Laue E. G., Drummond A. J. Solar Constants. — «Science», 1968, v. 161,
p. 888.
7.20. Thermal Insulation of Buildings. Dept. of Environment. HMSO, 1971.
П РИЛОЖЕН ИЯ
Единицы и переводные коэффициенты
Теплофизические свойства
Математические функции
Физические свойства
Список литературы
Переводные коэффициенты в системе единиц СИ
Таблица П.1
Длина /
Дюйм (in) =2,54-Ю-2 м
Фут (ft) =3,048-10-: м
Миля (mile) = 1,609-103 м
Объем V
Кубический дюйм (in3) = 1,639 • 10~5 м3
Кубический фут (ft3) =2,832-10-2 мз
Галлон американский (gal US) =
=3,785-Ю-3 м3
Галлон английский (ga! Imp.) (импер-
(имперский) = 4,546- Ю-3 м3
Масса т
Фунт-масса (lbm) =4,536-1Q-' кг
Слаг (slug) = 1,459-10 кг
Плотность р
Фунт-масса на метр кубический
(lbm/m3) =2,768-104 кг/м3
Фунт-масса на фут кубический
(lbm/U3) = 1,602 -10 кг/м3
Слаг на фут кубический (slug/ft3) =
= 5,154-102 кг/м3
Давление р, напряжение а, т
Бар (bar) = I05 Н/м2
Килограмм-сила на сантиметр кубиче-
кубический (kgf/cm3) =9,807-104 Н/м2
Фуит-сила на дюйм квадратный
(Ibf/in2) =6,894- Ю3 Н/м2
Атмосфера физическая (atm) =
= 1,013-105 Н/м2
мм рт. ст. A mm Hg) = 1,333-102 Н/м2
Дюйм водяного столба A in Н2О) =
=2,491-102 Н/м2
Площадь F
Квадратный дюйм
Квадратный фут (ft2) =
Квадратный ярд (yd2)
(in2)=6,45-10-4M3
= 9,29-10~2
= 8,36-10-'
м/с
Скорость v
Фут в секунду (ft/s) =3,048-10"'
Морская миля в час (mile/h) =
=4,47-10-' м/с
Морской узел или узел (knot) =
=5,144-10-' м/с
Километр в час (km/h) =
= 2,778-10-' м/с
Массовый расход Qm
Фуит-масса в секунду (lbm/s) =
= 4,536-10-' кг/с
Фунт-масса в минуту (lbm/min) =
=7,56-Ю-3 кг/с
Сила F
Фунт-сила (lbf) =4,448 Н
Тонна длинная-сила (ton) =
=9,964-103 Н
Килограмм-сила (kgf)=9,807H
Энергия Я, количество теп-
тепла Q
Килокалория (kcal) =4,187-103 Дж
Британская тепловая единица (Btu) =
= 1,055-103 Дж
1 Therm=100 000 Btu = 1,055• 108 Дж
Стоградусная тепловая единица
(Chu) = l,9-103 Дж
Киловатт-час (kWh) =3,6-106 Дж
Фунт-сила-фут (ft-lbf) = 1,356 Дж
183
Продолжение табл. П.1
Динамическая вязкость ц
Фуит-снла-час на фут квадратный
(Ibf-h/ft2) = 1,723-105 И-с/м2
Фуит-масса иа фут-час (lbm/(ft-h)) =
=4,134-10-4 Н-с/м2
Слаг на фут-секунда (slug/(ft-s)) =
=4,788-10 Н-с/м2
Пуаз (poise) = 10-' Н-с/м2
Тепловой поток Q
Британская тепловая единица в час
(Btu/h) =2,93-10-' Вт
Калория в секунду (cal/s) =4,187 Вт
Удельная теплота фазового
перехода rjg
Фунт-сила-фут иа фуит-масса
(ft-lbf/lbm) =3,0 Дж/кг
Британская тепловая единица иа фуит-
масса (Btu/lbm) =2,326-103 Дж/кг
Килокалория иа килограмм (kcal/kg) =
=4,187-Ю3 Дж/кг
Коэффициент теплоотдачи а
Калория иа сантиметр квадратиый-се-
куида-градус Цельсия (cal/(cm2-s-
•°С)) =418710« Вт/(м2-°С)
на метр квадратиый-час-
(kl/(m2h-°C)) =
ру
)) 4,187-
Килокалория р
градус Цельсия (kcal/(m2-
= 1,163 Вт/(м2°С)
Британская тепловая единица иа
квадратиый-час-градус Фаренгейта
(Btu/(ft2-h-°F)) =5,678 Вт/(м2-°С)
фут
Мощность N
Килограмм-сила-метр в секунду
(kgf-m/s) =9,807 Вт
Фунт-сила-фут в секунду (ft-lbf/s) =
= 1,356 Вт
Лошадиная сила британская (hp) =
= 745,7 Вт
Плотность теплового пото-
потока?.
Британская тепловая единица иа фут
квадратиый-час (Btu/(ft2-h)) =
= 3,157 Вт/м2
Килокалория иа метр квадратиын-час
(kcal/(m2h)) = 1,163 Вт/м2
Удельная теплоемкость с
Фуит-сила-фут иа градус Фаренгейта
(ft-lbi/°F)=5,38 Дж/(кг-°С)
Британская тепловая единица иа
фуит-масса-градус Реомюра
(Btu/(lbm-°R)) =4,187- Ю3 Дж/(кг-°С)
Килокалория иа килограмм-градус
Кельвина (kcal/(kg-°K)) =
=4,187-103 Дж/(кг-°С)
Коэффициент теплопровод-
теплопроводности К
Калория на саитиметр-секунда-градус
Цельсия (cal/(cm-s-°C)) =
=4,187-102Вт/(м-°С)
Килокалория иа метр-час-градус
Цельсия (kcal/(mh-°C) =
= 1,163 Вт/(м-°С))
Британская тепловая единица на фут-
час-градус Фаренгейта
(Btu/(ft-h-°F)) = l,731 Вт/(м-°С)
Примечание. В системе СИ
зуются следующие основные единицы:
длина —метр (м);
масса —килограмм (кг);
время —секунда (с);
температура —градус Кельвина (К).
Из них дополнительно получаются следующие единицы:
сила (ньютон) Н=кг-м/с2;
давление (паскаль)Па = Н/м2;
энергия (джоуль) Дж=Н-м;
мощность (ватт) Вт=Дж/с.
применительно к теплопередаче исполь-
184
Таблица П.2
Некоторые физические коистаиты
Ускорение силы тяжести g
Скорость света в вакууме с
Скорость звука в воздухе при 20° С а
Стандартная температура То
Стандартное давление ра
Число Авогадро N а
Удельный объем идеального газа при
нормальных условиях Vo
Универсальная газовая постоянная i?o=
— poVo/To
Солнечная постоянная S (средняя вели-
величина)
Удельная газовая постоянная R=Ro/M
Удельная газовая постоянная водяного
пара R=R0/M
Давление водяного пара при температу-
температуре 20° С
Молекулярная масса воздуха М
Молекулярная масса воды М
Отношение удельных теплоемкостей для
воздуха y=cp/cv
9,8066 м/с2
2,9979-106 м/с
3,43-102 м/с
273,15 К
1,0133-10s Н/м2
6,022-1023 моль-1
22,414-Ю-3 м3/моль
8,314 Дж/(моль-К)
1,325-103 Вт/м2
2,87-102 Дж/(кг-К)
4,61-102 Дж/(кг-К)
2,337-103 Н/м2
28,96
18,015
1,4
7 Основные формулы и данные по теплообмену
185
со
С
S
ч
га
Н
о
емп
X
а.
с
Щ
о pj
tt 03
g й
о
с
о
тепл
;нт
X
и
о
сч
гва при
Свойс
О
О
сч
о
о
о
о
(О
о
о
со
о
о
о
о
1
и
-=?
Щ
о
р.
кг/м
1-
•Я
АЛЮМИН!
1 1
I 1
1 1
1 1
1 1
1 1
Ю 1
я '
00 I
а '
^t" СО
СО О)
(N —
00 00
СО 00
(М —
О 00
Tf 00
coo
S52
со те
те (м
(М —
СО О)
со со
(N —
СМ—<
О 00
О) 00
о о
(N (N
+
СО g
•я 5
Ш
1
11
11
1
11
| 00
О О)
00 (N
СО Ю
t-- те
соо
00 00
Oi (N
CO 00
—¦ CO
<M O)
CD —
— 00
00 Г--
о о
CD Ю
CD 00
Si)
M + l
(87 %
Силумин
s
;
h
i
i
i
OJ
1/5
CO
CO
CD
CO
O)
co-
384
\
1
1
1
1
1
1
1
1
1
O)CD
00 CD
CO
CO f^
CO
о
rn
j
00 CD
О) ю
CO
CO
О
00 (N
CO ¦*
О О
CO CD
O) CO
00 00
К
C3
&
бронз:
яиевая
1
1
1
1
I
1
1
1
! °0
1 4f
145
(N
CO CO
CO Tf
00 —< CO
NMN
CM
Tf CD (N
(N О (N
1 О OI
o> —
00 (N
^J4 O) C4)
(N O(N
+ *
CO CO Tf
О О О
00 00 00
'ЁГсГ
oON
ЧРчО»
1
1
[^,
00
(N
О
305
о
со
SIS
00
со
я
315
(N
»—<
О
•С4
2 о g те
ц
т
coco
ТГ СО |
О) О) 1
смсм
CDCOCM
О) О5 О)
смсм —
¦Ч- СО 00
О) 00 О
СО СО (N
СО О) СО
О С5 СО
1Л ^J" СО
Ю 00 (N
CD ^t" t^-
Ю1ЛИ
Ю О 00
со — ю
CD СО СО
— юте
INNIN
t-- COCO
юью
СО Ч> 00
00 t— (N
t-O)
CD(N 1
ОH0
— (N (N
—. CO OJ
шю о
ю ю t^
""
о о о
t-, CD t--
00 00 Ш
CO
чугун
Железо:
чистое
армко
серый
1
i
1 I
1 i
i
l
О (N 00
OJ(N t--
мпм
ONS
Tf CO-
COCO CO CO
Tf'cO t--
0H Tf
CO ^t" CO
О Ю t--
(N — Ю
Tf rf CO
00 (N (N
TfNCO
^f ^f CO
Ю 00 CD
^ CM CD
Tf Tf CO
ЮО 00
О CO CD
юте со
]
1
00MS
OJCO CD
Tf rf CO
1ПОО
CD t-~ t~-
7840
7790
7750
сталь
к
>,
CM
- 1 1 1
sill
(N
(МОЮ
SOJIOOO
CM (N CN) CO
(NO 00 —
S OJ 4f Ю
(N(N(NCO
О Tf О 00
00 00 4f —
Tf CD CO Ю
—¦ sco со
CO (N (N (N
lOOION
MSNS
CO (N (N (N
ьоюю
4f S (N Ю
CO CM CM CM
МОМЮ
CO CM CM (N
* Ю CD
-CD (N (N
CD(N CM(M
CO
MM
*
— 00 CD
CD CD (N(N
CO(N(N (N
•
CD CD CD CD
oooo
00 t-- t— CD
t~- t-- t— t—
О
CO
Tf
f- о О
X
186
t-~ eft
со" -Г
O) 00
1
26,3*
Ю
CO
CN
00
о
CN
CN
00
CN
25,5
00
CN
CN
CN
О
CM
1 1
1
*
Й1
CN 00
— t—
Tf CO
1 1 1
18,4
* *
—'00 1П
CN—¦ CN
— —_ CO_
о с— —.
CN— CN
1
1
1
CO
00
1
27*
Ш
CO
Ш
CO
1
.26,3*
o>
24
CD
103
109
116
123
CD
73,3
о
69,
CD
Tf
CD
1
CM
1
1
Ю
22
00
1
!
1
s
-4}* 00 — <N CO СЪ — — О СО Ю CO 00
O) 00 ^tf* O^ I 00 CD •*¦* t^» I**» C4) •*-1 СЭ t**- I— W
,—i —i rj* CO -— — C^ —¦ Tt'C^COlOCN CD <N
о
18,
CD
CD
CD
*—' t^-
CD CD
¦Ч1 CO
00 00
CD 00
— in
1 ?2
¦*-
I in CD
О
21
in
о
CM
о
CD
00
о
о
о
s
о
CN
00
CO
CO
co
152
154
131
135
oo -
00
a>
о
о
CD
00
CO
a>
ю
CD
Tf Ю CO
00 Ю I— O5 rr t— Oi
™i CO LC CO O} ™• —i
ОЙ 00 00 t4- O^ CO CN
СЧ «-¦ О О О I I** I I It— О
•*- »*^ CO CO
C^ ^- Ю Ю О 00 00 CD
- to ou
CO —i ОО Ю Ю CO •—«
-^ —. CD
CD
CO
CN
00
CO
in
CO
s
00
CO
Ю ^ ЮсОПСОЮ О) СО —i 00 Ю Ю СО ^ 00 С4)
о о _____
CD CD cD CD CD CD CD
о
CD
Tf
00
о
О
CO
Tf
00
CN
t—i
О
CN
О
in
in
CN
^э сэ с? _э _э ^э _э сэ
С4) СО С? •*¦* СО •—I O^ CD
00 00 О) С) О —« — W
ь- ь- ь-ь-оо оо оо оо
о
о
00
о
CD
00
о
о
00
о
те
со
о
со
о
in
о
о
00
о
со
00
о
о
о
О)
00
со см 2: о со
II ? ? о
g ы л_- =S T +
я+ fe Sg о ^ Z
о ^^,^ ° -^ ^ ^
КСОЙ^-Я^Р „^О°
ся е>чп в ] !^ о О -^ а>
^S-COCNCO^- in ^<N.V^. я.|. в Л^ j. o
CU J >_ f-
пая» """ , 5 .jL_-^S-r в „я Sp^ ?
атяТкSiliiJlilil-sriL _«?«2Й ^ <Q M '4 I So I
Oco«ti- «ZZZZZ SZ йССЙ^'1 u 5 ^ Й о о- x
g._ < — <; s
s cu
_ .8
g gs^ssge -s | I i s s-+ >u s_
U 5. < Ж
187
с
н
<и
вз
се
ч
о
о
о
С
к
1
tg
Р ¦
н
PQ
„
3ОВОДНОСТИ %
ратуре, "С
с
о
§
о
н
я
о
ГС
Ef
Я
?
' в
О
сч
»а при
н
и
о
о
1201
о
100
о
о
00
о
о
(О
400
1
о
о
со
о
о
сч
о
о
о
о
1
и
о
н
Щ
д °.
. и
и
.а
(КГ
5
S
?
88,!
84,
о
S
со
со"
73,6
00
(N
t--
О
г--
со
71,5
со
со
71,
со
со
450
?3
тииа
Пла
1
1
1
384
399
t--
о
415
428
431
427
ТГ
СО
500
о
о
о.
Л)
Сер(
1
1
1
1
I
1
°1
о
со
сч
со
со
68,2
со
00
310
о
Оло
1
1
1
СП
оГ
19,4
in
СП
*"*
СП
2
о
22,4
со
я
я
о
500
IS
т
Тит;
о
114
119
125
134
153
со
со
182
204
179
со
350
—
я
та
Вол
1
\
со
in
со
о
35,7
со
со
«__
со
СП
(N
СО
.S
^1
27,.
со
070
—1
s
Ура
1
.1
1
1
I '
1
112
122
123
121
00
00
со
140
I
"Я
26,
ш
24,
со
а
21,4
СП
о
S
00
23,2
ю
CD
22,!
со
570
CD
в
КОНИ
i
00
га
л
Q
U
О,
а.
о
а,
*СЧ О
•S.E"
О 3
Е с
go
to
id
П —Г
о о 3 ,
О, s
Ctf g &
С c m
га га я
i
188
я
Я"
S
ч
ю
я
к
о
1
и
о
@
1
я
¦е-
00 Ю Ю СО О »—|
NMO.OIO (N
ОО-чСМСМЧ" incDOO —
о о
г-ГО — *— СО —<
ШЮСОИО О) 1Л "
t-0<NC04< mcD
— —. 00-
I
о
I
о
• O50000CD4< CD 00 О) t-- CD t—
ОЮСОО CO4«CD00(N CDCNCMOOCNCO Jq t--00 О) О -М^ЮЬО ,
^^J^^^ (NO) <N (NO) CO '
S»010N
W ra
coO)t— t~—-4— о 001Л os ^2--22
0H000000H CD СЧ — О О ОООООО)
CO t-- Ч1 COIN
3 *-ч СЧ <М О*
О* <М <N O4 С^ —
со —юсо ооосмемем ooocot—оос^
^ ЛП 1Л Щ CD^^^^ ^CDCDl^TfCO
I
О
1—.О)Ш Ol-ЮМ-чЧ*
Ь-t^ 00 00 00 00 00 t*~ t4- t*~ CD
a
(Nt--OO — 00
л сймюо
toiflcoco*
oooooot
CDCDCDCDCD
О — — t*- CO CD
OOO OO
о I
1 «-
2 о -
• r—l
coco. •
00O 00 00 ¦Ч"
NOlOSCO
I
о
.00 C0 00 05 05OO
Ч'Ч'СОСОСО COCOCOCOCOCO
I
- - CDC^-b-OOOl —
s
«CM
n
3 >.
OiCDOO
COlOOCO
CDtNCNCDO
О)
о _. . _
О О О) О) О)
*Ю* О Ю 00
СЛ 00Г> CD Ч? CN
О) CDCNIO
, _._00 СО Tf —|0Лг
0HHH0 OOOOOOt— t— t—
^j. CO — О CD CO OcD-COOTf —
Ь* О О О tO tD tD(O 1Л 1Л Ю мч
О О О О
1Л ^ СО С^ *-«
ОООООО'
>
а.
о
U
189'
11.4
ч"
н
а>
S
к
к
к
о
о
а
С
«И
1?
*
1
са
и
Ё
Щ
II! I 1т |
in оо ~* оо "чт со —' 1Л —
0 1П"*0> СОСЧООООЮ
C005CDCO О О t— ЙЮ
in со со t--" со
I
о
О5
t--
СО
I
О
о
о oo о
00 <?! 1Л Ш 1Г> Ю
со" со со сгГ со" со"
I
о
—¦O(Nir>CC 00 00 CD CD
(N ~ t— ¦* CO t--o™t—
I
о
*ию toooir>m
О ^н (N СО Ю 1Л СО СО СО гЛ ^*"
I
о
^-4 С^ "* О О
™ sno со
C0WO
0H0 00 00 t—
о ~< со со со со *^ a t4-
ооооо оооооо
2
I
о
о
s-OI
28-
Ос
1
О
зо о
Ю
1
о
.001Ш
Tf O5CM 00 СО
Й дао*s-
? О500СОЧ-СО
S ^L 00050 —
"*
«• Й^ЙЙЙ ggfeS
со t— coc>j
й—• t—со
—« i—t О О С
COO (N f-
(N CO t—O5
O5 00
-< — 00 CO (N O5 С
Ш 1П -4- •ч» .<*
о
IS
о
Ш
)OO OO OOpO
о
о.
о
ч
X
CS
о
s
ts
s
3
a
190
о
I со
I I ! I I MINI
Sinn-1 CM —i
CD CM • -4* K,
00ПШООЯ
СО1Пс<ЭСМ — cm"
I 1 I
I
О
OIOO-N
те "СЮЮ Ю ю"
—' О
ЮЧ- • О -Ч* ¦"*"
—'O CO —' CM CM
со см ел in со см
CM ООСЛ —i CD О СО СО О CO CO
— ons со со •ч* cd ю со —¦
COIN—Г 00 in" CO CM— —'—'—<"
t^ О Ю 00 Ю CO
Tf —i CM CO -4> CO
00 CO —t Ю CM —
ooo coco
со—i ooсо
t—t--ioco
Tf CT> O5 CM —¦ 00
со со со со см о
О) СЛ СЛ СЛ СГ) СЛ
I
о
_ _ -- _ СМ СО Ч"СЛ ЮОО
„ COOCOCDO CO CO CD —< Tf CD
— —СМСМСМСО СО СО СО Ч" ч>-Ч"
и
I
о
СО Ю t^ СГ) Tf СО
00 СО 4t" СМ -~ СГ)
Oi СЛ CD СЛ CD 00
t^ ш со см
со со со со
CM CDCOO ™ СО
ст>
см
(МЮОО-нСОЮ
t^ 00 CD —i СМ СО
CM •Ч* CD CD CD t^
oo oooooo oo oo
CM СЧ CM CM CM CM
о
1
О
со те Т
о см о со
см—• coin
СЛ t-- ЮСО
™ OCD 00
СМ СО СО •Ч'
Ю
1 »
О 1
™ О
со оо "Г1
1П — СТ! Ш 00 СО
t^ СЛ CD t^O) О
ш —• оо те см см
(О
о
(Я •Ч'СМ Ч> СМ О СМ
СГ СЛ 00 t--СО Ш Ч>
Ж CMC0 Ч" ЮСО t—
л
ч
га
пз
с(
S
о.
о
ч
X
о
см смем смечем
— CO 4> CD
00HH0
О 00 CO 1П
Tf CM ™O
00 00 00 00
о ooo
OCM -4" CO
I
о
I
о
I
о
I
о
CO CD'^ О СО CD Ю CM t^ CM 1П
CD 4t" t^ *~ СЛ CO CO t^ CM СЛ CO
cocm™—<<o tccocmcm—•—•
• CO —<
0ОЮ—•OOCO 0OCO0O4"CD0O
ococooo™ cocdoo—¦ со со
COCOCDCDt^ t^t^t^OOOOOO
CM CM —' CM CM CMCMCMCMCMCM
@(ОЮ«0 CD —' —« CD CO ^^
t^ cd —i ю ь- 04t"COCDm
о
—iO 00 •
CO О—•ОСМЮ
оосо™ю см—¦
—.CD СОЮСМ CO
CD -~ 00 *4* —' 00
CM CO COTf Ю Ю
CM CM CM CM CM CM
CO — CM CD—• CO
О — О О OO)
OlfOnO CDD tCM
—i — —« о О Cf)OH000t^t^
C0C0C0C0CO CM <N <N (N <N CM
Дн CD О ^f 00 С^ ^
« ь-г-со ю ю ^
О CS С^ CS CS CS CS
191
с
ч
о
I I
I [
I I
о
со
rt ™ rt с»Г см" cn с»Г co
i
о
I
о
от™о о <:
> мо оо со •ч'С
H0 00t- t- t- t
I CD
.со
I
о
1
о
00 О) t-~ CN •4* CO CO •
«¦»oton«on
CN CN CN —. ™"™ ^ 00
•нМЮООМ О5 Ш C
со со со со -ч* «3*inc
ms cod со со 2; §
CNCNCNCNCN (N (N (N (N (N (N
I
О
Si
5 Csl CO ^ 00 CO О
I
О
I
о
I
о
00 00Sf-"S CO CO C4! 00 CD <—'
00 CD CO О 1Л r-HOrilOOW
ooeoeoeooj c^*-i*-i
s
— ОТ'Ч*!—(N
п^поо
inCOCNCOt— 00 ™ CO •Ч* •Ч* CO
ooooo- oooooo
I
о
I
о
—•—•—"Ojoooot—со
I
о
I
о
n scooo ^
ommoooos
COCOCOcOCO
"и
Ш (M (N •4>O5 t—
t— 00O5 О ™ CO
•4* 4f "Ч* 1Л 1П Ю
«lOO-VO
^ -JCOC0005
>0^(N(NCO4lrt
з to со со со со со со
CO CO CO CO CO CO CO
00
о»
CO CO CO CO CO CO
т
ооооооот
™^н CNCN СО
gjcoj-cNOin с/5 -ч<„ -ч-о — со — о
СО СО СО *~ *^ *~ ^ 00 00 СО СО СО *Ч* 1Л -Ч*
(NCOcOCTi^^ (NCNCOCOCO*^
\ЛСО^^О^00 CD-4*CNOOOCO
^3 ^3 ^Э О) О) О) О) О) О) 00 00
си
S
CS
а.
о
ч
3
о.
си
о
о
ее
> CD О 00 СО 00CNCO
JCOCN00COCO — 00
ООООООО Оо<__
™ —СМСО'ЧЧЛ ^.Ш'Ч'СОСМ™ —' CN
192
I 1 I
I to ooo
со -vF
it— CO CO
I I СЛ CN оэ о СЛ 00 I ¦ ™ I
со oo™ й — со юс
i
о
со oo •ч1
CO CN CN
i 1Л
; com -4}*
о oo oo
I
о
CO
I
о
С
.'5c
CN CN CN CN CN CN CN С
w
oo t—со
I
о
' • oo 1Л1
00 t— Tl< (N CO •Ч* Si 0O
in^COcNOOJOO
I
о
ЮС1О
РЗрчО
OOO
I
О
CN CO CN CO t— •Ч1
»—< Ю »—i CD <¦¦• t—
О СЛСЛ 00 00 t—
™ oo о oo
™™ —i 00 t—
I
о
somoooo
CO ^ t^ *4* (N
O5O5 00 00 00
•OOO
Sjf t— CN 00 CO 00 cu
" ~ " t* ^* CO CL
3
m
. CT)O l4^ O^ 00 CO
л со m со —' о -Ч*
OONNOOI
о oo oo
CD CO COCO CO Ю Ю
(Mint-. 00 •Ч* О) •ч* С75 •Ч* OOlooSN
СПООК •Ч» •Ч» СО СО (N (N -Ч-СОСОСОСО |Л 00 СО 00 (М со О5 t-- (N
™—<.™. "_™~™.'-™. ™™"™.™."™. ¦»™_С0 0^1Л05 (Л 00 СО
ооо" оооооо ооооо ^Ш1Лсо*со"со"(-Г(~Гоо us tNint-ГсоосгГ
^ *"* ^* '^ '^ —« ^^ 00 00 t^ CD СО СО 1Л
СЛ t^ CO
I
о
MClNOOl
cNCNCO—СО
CO 1Л-Ч*-Ч* СО
0 CN t*~ СО
01 CD '^ IO
ч о^ t^
I
о
I
о
oiSsmcOMCDOoi
-NOONIBMNID
(OntcoN —oooi
incoo5t--o>oooo4 .2
со с
со с
3™<35 00
1О11Л
CO t- t-- 00
СО CNin (NCN
™ cot—ш со
<Л СЛ О *^ CN
t— Ю CO CO CN CN CN
о
OOO
OOCNOO^^t—^ *Ora
COCOCNCNCNCNCN %> С
а со
в >. я
ЙЙ2
C75 CM О СО СО t--
СЛ О) СЛ
ИМСП
CO CO CN
oosmco^d
00 00 00 00 00 00
1 CN •Ч1 ^CN <
ЗО5 CN !
OOttcDinL_
О) О) 0) O) O) O)
OOCNin C0O5 •Ч'О
момпмою
O5 О) 00 00 00 00 t—
4
¦ffl
•s"
OOO ПЮОЮОЮО оОЮОЮО !(OOgO(
Й'Ч'Ю д -< CO ТГ CO t~ СЛ 2, "" СО-Ч-СО о^Й^т?!
i> с es
W Ж в
O.QOC
) О О
)COt^
J3
193
1О
С
га
ts
s
ч
о
га
Н
иом давлении
•&
и
о
я
S
&
ю
о
ические свойства газ
Теплофиз
<
и
с
г
¦ i
со
Ч
S
н
аа
и
"as
а"
&
S-
и
N
S
"о1
i
с
U
О,
ъ
а
к."
(о
О
—.Ю—.SOO—1 — 0500—
lOCOCOCOOtN^COOO
Г со" го (N —
I
о
О) 00 (--"(-. СО СО Ю Ю Ю 1Г> •Ч*
О СО О) CN 00 t^ О) (
t— Ю ГО (М О О) (
:ооооооооооооооа>а>а><
5СОСОСОСОСОСОСОС" "~ —
I
о
—|Щ@<0(ОП01М*1М1МС0
о -ч1 — — ™оосое-> <о го — -
inSOMNOMNn " *
I
о
)^ЮОЬ«СОО)^(
lONOSOl-OlO
3COOtt*CD —
-.soNWocoowaimocoii
O^COOOCslCOOCOb-OCOCpO)C^u
^^ ^^ ^^ ^1 ^^ PQ PQ СО ^^*
ооооооооо
it--(Nf-(Nin(N(Nt-- — CO
It— OMIOS ГО 00 "
000500 —t— (МГО
оо — — — — — •—
I
о
05 _ .
* -Ч* Ю О Ю
o**- ю —
O5roC<3ir>(Na5
t 4* COO
ooo** ю — оюомк
O500O5roC<3ir>(Na5(Nt— COOOt—
lOOOt— 4*— COCOniNOOlO —
I
о
0>1ЛО(М00С0 — — Ю — Ю1Л—1ЛОСО
-' ^ —05(NlO05*4*O00000505
05(NlO054O00000505
Ю00О1МЮ00ОГОС005
— 4<t—O5—
"(М(М(М(МГОГОГОГО
о
^< ГОО5
(МООООООГОЮСОЧ' — OOOOt—(N — 1— — _. ,
osc^c^oooosoooos^*»—«sroooc^coOscyio^osrosoroior^osoc4!
о — — — — (М(М(М(М(мгогогогогогос0'Ч>ч<*'Ч<ч<ч<1Г>ю1Г>юсосососо
. . _._._..-4<O00t-t-0500(N
«OOOOf—iC^rocOlOCOSOOOSf—iNM^tOSOJ-^W^COCOOOr-
ioooooo. —
35 С
ocop^sSopc6pyco^ot^^*'^d>siowd)SipMiNob)o6s<o
1 — — — OOOO<
X
t^ ^э ^э ^^ c2 ^5 ^? ^5 ^Э ^? ^^ ^^ ^^ ^? ^^ ^^ ^э ^? ^э ^э ^э <_ _ _
И О 1С О Ю Q LO О >-О О Ю О 1Л OlOOlflQOOOOOOQOOOi
194
сч ™ — —
о
CN —I, t~- <N_ —_ t^ — «O_ 00
— CN —' *~CN — с
ЮГО — CDCOCN — 00 СО
та
Q
S
oi
I
о
,OM!OOCNO«S
3ОГОООЮСМОООСО
О
ONONN
ЮСМОООСО
•Ч< •Ч* ГО CN (N (N (N ¦
ш
d
т о оо t— t— ¦*
O5O5 00 t~
3 00 00»
i
о
I
о
I
о
< — (МГО ГО'Ч*
a O5 — ю
го *ч* со t*~
_^ о о t- ^ t
—.(меч «со 5;
о о о о о о
-S
« я
со о;
га
I
о
I
о
I 1
OO
fflOO Ю
(N -4* *Ч* ГО
niooi*
Г—Г—(МО) ГО
—<Ni2roo5COto
3 00 « _ -Ч- f 1 ЮО
"T •—*•— —"(N <N ГО*
oo~—Г-Г in (мгого-ч< ю
.2 к
I О
о —
I
о
I
о
О) <N •Ч* 00
00 t— 00
"ччпю
CO 1Л Tf CO
О OO О
о з oo
OO OO
<N ГО'Ч'Ю
. - _. i го ю со
t--O5 — ™ — —• _J_ — — — CN CN CN CN H —*-* — С
О °
u _
ra
"t-t'iS1010 ы «•ч'-оооммо "^ row cnm оою-^сроо
O5 t*- t^ ГО *-* O5 ^ OOONO^CO —fN О -ч*-ч* *Ч* *Ч*-Ч* Ю CD t^ 00
SSSSSS О t- 0000050505000 q. О О О О О О О О О
О, щ
<" Ч
Ч с,
^°!^22!2 "- со t—го cn ¦* оо cn о со >. _
n NNMOinO >,ГО1Л(— CDCN — ГОГОГО ГО —' <
ОООООО "° О) CN — — — — — ОО ° —О—С
* я ,„,
га « о
^ огогогогого ° ооооооооо ° oooooooot
S О) t-- CN t--. (N t— >, СЧЮОЮОЮОЮО Я <N 1Л О 1П О Ю О Ю С
g CNCNroro^* n tNNnn Wininm o
s
m a.
5 s.
о
CO
CO ™
195
in
С
ч
s
s
о
о оо о
о
о
о
С
8
I
о
I
о
СО" (N ™ ю"ш Ч" СО (N (N (N (N
™™(N(NCOCO4<ir3lO00 —
I
о
I
о
^*rf ^"cO Ю 00 ^^^ *^
I
О
I
О
(С0
— -Ф00 —
™ (N (N СО-СО СО~ТС
ж
а
5 (N— —О <
-oo a> ю in
IS
196
4"tn coco —
_ оГсо ¦* ¦*
1Л ^*" 1Л «О* N ^ Ю ^ П s О
(N* СО* 00* (N *^ СО" СО (N ^ 00* (О
I
о
Ol ON
I I
о о
I
о
о о
~ О5 00 Ь- Ь-
> СО Ю СО СО
-> ™ coco
00^0500
t~- t~-t~- coco <
о
о
815
о
со
СО
773
о
о
ш
745
о
о
о
725
о
со
со
со
709
о
со
00
(N
702
о
о
(N
695
О
СМ
(N
694
о
о
о
(N
СО
о
см
00
700
о'
со
¦ '
о
о
t-~CO 4" 4" CO
O5IN00O5 —
oet---* coo
CO 1П t^ 00
I
о
I
о
I
о
^ 2Й
00 ?0
со со
(N
ЮЯМЧ'ЯООМ-чЬСОЮОО
О500СОСОО51П—ituOVM'H
o —(N«c04>mincococot--
ooooo
О
0090
о
о
0137
о
0182
о
*^
о
о
(N
0268
о
0307
о
со
0346
о
те
0383
о
1П
0417
о
со
0452
о
(--
0483
о
I
о
I
о
I
о
I
о
I
о
00 O5 ™"™ ™
(rjt^cOirjCOoooosTfmm
¦KooOeijioOOO — OecOO™
ojcomZmoco — ooincM
г—i 4J" ^^ ,—i i-x CM CM CO CO ^ 1П
I I
о о
I I
о о
со со in 00 ^
J. ( O*
. tv. CO CO
t-- О CO
t-- ™ t-~ <M
t-- CD ™ CO
00 in coin 00
COCO CO t^ CO
O5 *~ CO Ю CO
^J" 1П 1П 1П 1П
ЮП1П01Ч1
4> (NO 00 00
(N(N
O5
947
*~*
00
917
_
913
tv.
915
CM
CO
920
(N
^^
929
CM
о
942
CM
tv.
996
CM
CM
CM
O5
CO
_
886
CO
^.
1 1004
00 C0« 00 «I
OONnNC
«MnCO
(N (N(N
О о 00 о
. . • CO (N00 *^
) CO t^O5 — ОШ
" ч*чсО
о 2
о о о о о
ООС5ОС0 — ООООООООООО
о ™ ся со со u ™ см со ¦* in со t--оо О5 о ™
о
a.
о
ч
ООООООООООО
ОЮО1ПОЮОЮО1ПО
»"^ •¦¦^ ^1 ^^ С^ СО ^J* *^ Ifo \^$ СО
197
о?
я
а.
о
S
о"
га
«
S
<
и
S
? ¦
а
а,
U
d
сч
оо
о
о
Ю ОО го
to — (J4,
— — оо"
о
о
еч
оо
ГО
ГО
о о
to ^t*
о о
о
о
to
о
о
о
о
Ю О
о о
о
о — — — —
I
о
00
со с~
СО О
еч (N со
ОО
ГО
со
из
I
о
§
§
оо — —
со — ст>
¦^ о ел
сч сч сч
о о о
СО
СО
о
сч
сч
о
о
*$* ю ст>
to о ¦*
¦ф т т
Q о о
о
о
СО
to
о
I
о
I
о
to
сч
¦*•
сч
¦"*
СО
to
ОО
СО
о
с~
¦>*•
to
1Л
¦^<
to
to
сч
с~
ОО
ОО
ОО
о ~
I
о
о
сч
сч
сч"
сч
to
сч
с-
сч"
О5
сч"
O
to
О
С
4»J*Ol0r^t?)-
»— ОО ОО СТ) СЧ
ОСТ)СТ)СТ)О
СЧ—.—.—.СЧ
СЧСЧСЧО)
а
а.
га
о.
та
С
о
Ю
Ю
о
О
to
о
to
Sri
¦§. .s.
о. ко
2 га <ч
И Ч Н
5 « о
•е-
О A)
[fll
го
to
00
о
сч
ю
ю
о
сч
о
о
ю
о
о
ю
о
о
о
сч
ОО
. СО
о
о
ОО
СО
СО
о
о
СО
о
СО
сч
о
о
СО
сч
о
сч
о
^ 3 gi
SIN
Д ffl Я rf
s1 s E и
I
198
Теплопроводность некоторых широко используемых
строительных материалов
Таблица П.6
Материал
Алюминиевый сплав
Асбоцемент листовой
Асбоцемент войлочный
Асбестовый изолирующий картон
Асфальтовое покрытие для крыши
Пробковый картон
Пробковое покрытие для полов
Рубероидный картон
Войлок подстилочный
Фибровый изолирующий картон
Стеклянный лист для окон
Стекловата
Стекловолокно, пропитанное эпоксидной смолой
Твердый картон
Линолеум (PVC)
Материалы кладки стен (см. рис. 7.3.):
Уложенная между конструкциями минеральная вата
Полистирол, раскатанный на доске
Полистирол — пенопласт
Полистирол листовой
Губчатый полиуретан
Поливинилхлорид (PVC):
Твердый пенопласт
твердый лист
Прессованная бумажная плита
Изолирующий порошок кремнезема
Углеродистая сталь
Карбамидный формальдегид (в виде насыпных гра-
гранул)
Известняковый камень
Песчаник (камень)
Сланцевый камень
Черепица глиняная
Черепица бетонная
Черепица из PVC-асбеста
Балки сосновые
Фанера деревянная
Балки еловые
Балки дубовые
Вермикулит (в виде насыпных гранул)
Прессованная деревянная стружка
Строительные плиты из тонкой древесной стружки
Плотность
р, кг/м"
2800
1600
144
720—900
1920
145
540
960
120
240—400 '
2500
25
1500
600—900
1600
50
15—25
16—40
1050
30
25—80
1350
600
90—130
7800
8—16
2180
2000
2700
1900
2100
2000
660
530
415
770
100
800
600
Коэффициент
теплопровод-
теплопроводности Я.,
Вт/(м-°С)
160
0,40
0,078
0,11—0,21
0,58
0,042
0,085
0,19
0,045
0,053—0,063
1,05
0,04
0,23
0,08—0,13
0,22
0,039
0,036
0,031
0,17
0,026
0,035—0,041
0,16
0,07
0,02—0,024
50
0,03-0,036
1,5
1,3
1,9
0,85
1,10
0,85
0,14
0,14
0,105
0 29
0,065
0,15
0,11
1970.
Примечание. Данные взиты с разрешения из IHVE-A Справочника,
199
се
и
в
ч
>о
я
н
е
I
u
(X
u
X
s
«
u
s
..?
я
- s
*
и
1
¦Ч1
с
4
«4
'СМ. ТЕ
исм
03
о
о
о t-~
II "и
J J
,023
о
0
|
О
•99
О5
О5
с-
1
О
СО
см
(N
157
о
m
о
о
о
я
<и
вин
и
,018
о
8
О5
8
-
ОО
155 1
о
О5
СО
о
о
о
и
о
= 327,
и
,016
о
00
О5
1П
-
154 1
?
сч
о
о
о
со
О
о
= 173
и
в
1
1
8
1П
со
со
1
я
о
о
024
о
te
1
О
00
t--
О
О5
О
1
О
¦Ч1
147
о
§
о
о
со
5%)
1П
in
г?
ш
31.
исму
ец-в
вин
и
018
о
г
00
см
см
1П
147 1
о
СП
о
8
О
О
= 125
II
J
1
1
1
1
О
8
о
о
со
О
о
О
= 167
а
В
к
•**
053
о
ю
1
О
•so
СМ
со
¦ч>
о
1
О
00
о
™
187
о
m
о
о
<м
*
н
в
ч
038
о
¦ч*
см
о
1П
—
1
о
00
О5
187 1
о
ТС
о
о
¦Ч"
О
о
= 179
и
J
032
о
¦Ч1
00
см
¦Ч1
О)
187 1
-
ТС
о
о
со
о
о
on
= 131
1
-к»
029
о
S3
со
00
S
СО
см
О5
187 1
Й
•ч1
8
00
о
о
й
со
8
О)
ш
О5
2.81
8
о
С
табл
s
а,
Эо 6'
= —38
II
о
о
= 357
0
в
200
0078
о
ю
1
О
•zo
со
со
1
о
.
ш
ш
О5
00
О
О
es
ч
я
&
0053.
о
со
GO
¦ч>
¦Ч1
1П
00
СО
со
00
со
00
8
(J
63,7 °
II
J
0043
о
$
со
О5
со
СО
О5
СМ
О5
О
О
О
О
О
||
с
в
X
•**
0040
о
О5
О5
S3
СМ
ОО
со
о
in
0037
о
in
•ч*
00
О)
о
in
*""
со
со
S
С
абл
н
«go о
* t- о°
es ,i II
О, II д
« 3 й
021
о
с
-01
•16
<N
СО
1
о
,^
со
О5
00
о
о
00
-^
IS
s
ч'
й-ка
es
атр
X
017
о
!?
со
со
in
<м
S
о
о
00
о
ш
см
о
о
7
II
с1
0075
0053
о о
— CN
о in
те тк
СО "*^
t— O5
CM (N
о п<
СО (N
О5 (N
00 00
Ш О5
о in
¦Ч1 1П
о
= 784 °
'кип
0042
о
о
о
m
О5
о
со
о
,—>
(N
00
00
со
о
о
о
024
о
1
о
59-
см
00
ш
1
о
см
СО
ю
112
00
о
о
es
К5
fi-к а
es
013
о
1П
О5
СМ
00
8
со
00
106
я
ОО
о
1П
о
о
О5
о. II
X
008/'
о
со
г-
см
со
00
(N
см
104
¦ч-
ОО
о
С!
те
0067
о
со
со
in
00
00
со
см
00
103
00
а
о
825 °
'кип
0059
о
о
со
29
см
1059
см
о
о
201
Поверхностное натяжение жидкостей в контакте с воздухом
или собственным паром
(при комнатной н других указанных температурах)
Таблица П.8
Жидкость
Уксусная кислота, С2Н4О2
Ацетон, (СНзЬСО
Этиловый спирт, СгНбО
Метиловый спирт, СН4О
Аммиак A1°С), NH3
Анилии, C6H7N
Бензин, С6Н6
Бром, Вгг
Четыреххлористый углерод,
; cci4 -
Этиловый эфир, С4НюО
Глицерин, СзН5(ОНK
Нефть
Фенол, С6Н6О
а. Н/м
2,78-10-2
2,37
2,27
2,26
2,34
4.29
2,89
4,15
2,70
1,71
6,34
2,58
4,09
Жидкость
Тетрахлорэтилен С2СЦ
Толуол C7Hs
Скипидар
Вода 0° С
Вода 20° С
Вода 40° С
Вода 60° С
Вода 80° С
Вода 100° С
Соляной раствор
(NaCl-5%)
Соляной раствор
(NaCl 10%)
Соляной раствор
(NaCl 15%)
Соляной раствор
(NaCl 20%)
а. Н/м
3,17-10-2
2,85
2,70
7,56
7,28
6,96
6,63
6,26
5,89
7,43
7,59
7,77
7,97
Теплота парообразования жидкостей при атмосферном давлении
Таблица П.9
Жидкость
Аммиак, ЫНз
Бутан, С4Н|0
Двуокись углерода (при
20 атм, —20°С), СО2
Дисульфид углерода, CS2
Четыреххлористый углерод
• (при 0,4 атм, 48,3° С),
ecu
Этиловый эфир, С4НюО
Фреон-12, CC12F2
Ртуть, Hg
Пропан, СзНв
Двуокись серы, SO2
Вода, Н2О
Точка кипе-
кипения, "С
—33,3
—0,5
—78,5
46,3
76,5
34,5
—29,8
356,6
—42,1
—10,0
100
Плотность
в жидком
состоянии
Рж, кг/м'
683
601
1001
1260 B0°С)
1590 B0 °С)
714 B0° С)
1480
12,75-103
582
1461
958
Плотность
пара иа линии
насыщения
рпар.нас,
кг/м5
0,89
2,76
51,16
2,99
2,10
3,31
6,24
4,06
2,41
3,10
0,598
rjg, Дж/кг
1,370-10»
0,384
0,278
0,355
0,205
0,378
0,167
0,284
0,425
0,388
2,256
202
Таблица П.10
Полная нормальная излучательная способность различных поверхностей
Поверхность
е. %
Поверхность
(, «С
Алюминий
тщательно полированный
98,3%-ной чистоты
шлифованный
грубошлифованный
коммерческий листовой
сильноокисленный
кровельный
Латунь:
тщательно полированная
G3,2% Cu+26,7% Zn)
прокат обычный
тусклая пластина
Хром:
шлифованный
Медь:
тщательно полированная
шлифованная
сильноокисленная
Золото
тщательно полированное
Железо и ста пу.
железо шлифованное
железо грубошлифованное
чугуи шлифованный
кованое железо шлифо-
шлифованное
листовое железо снльно-
окислеиное
сталь шлифованная
227
577
100
100
100
93
504
38
247
357
22
350
38
1093
80
100
25
226
427
100
200
100
25
100
3,9
5,7
9,5
18,0
9,0
20,0
31,0
22,0
2,8
3,1
6,0
22,0
8,0
36,0
1,8
5,2
78,0
1,8
14,0
17,0
21,0
28,0
69,0
6,6
Металлы
никелевая сталь AISI-304
A8% Ni+8% Cr)
Сталь:
никелевая AISI 321*
A8% Сг+9,3% Щ
обработанная на стан
ке
листовая
шероховатая листовая
Свинец
чистый неокислениый
окисленный
Ртуть
Никель:
шлифованный
окисленный при 900*С*
нихром (провод, окис-
окисленный)
Платина (нить)
Серебро шлифованное
Тантал (иить)
Олово блестящее
Вольфрам (иить)
Неметаллы
1288
23
0—90
1000
ОтЮ50
до 1430
50-400
34
22
400
33,5
96
93
75
53
94
94
94
90
Магнезитовый
ный кирпич
Краска черная
огнеупор-
Окись алюминия средней
зернистости
Асбестовый картон
Кирпич красный грубый
Кирпич из огнеупорной гли-
глины
Угольный электрод лампы
накаливания
Ламповая сажа +
Шероховатый бетон
Гладкое стекло
Стекло пирекс
Примечания: Данные взяты из книги: «Heat Transmission» W. H. McAdams,
McGraw-Hill Book Company, 1954. Материал используется с разрешения Издательства.
* Интегральная полусферическая степень черноты [П. 30. П. 31].
+ Интегральная полусферическая степень черноты [П. 33]. Для блестящих металлов ее
значения могут быть приняты выше на 20% по сравнению с полной нормальной излучатель-
ной способностью, в то время как для других блестящих поверхностей она ниже на 2—5%.
Отражающая краска
Алюминиевая краска
Вода
Дуб (обработанная
ска)
Ель (обработанная
ска)
до-
до-
100
215
490
200
400
800
1000
21
350
127
227
24
0
100
100
700
800
900
49
500
27
1227
38
371
1326
3000
50
27
1500
3300
1000
28
93
100
100
100
90
34
.203
я
•
я
(X)
•¦>
(X) •
8
8
0000
о
1,00000
8
8
0000
о
0000
о
о
,7760
,7527
1005
о
1,0100
324
1
081
т
0995
о
9900
о
<м
о
,1844
1145
о
о
1,0404
781
7
to
7
1960
о
9604
о
о
3028
7775
о
3137
о
1,0920
260
1
3085
7
2867
о
9120
о
to
о
8618
5653
о
4329
о
to
9781
о
8980
7
3688
о
8463
о
00
о
,6019
4210
о
5652
о
1,2661
7812
о
0883
о
4401
о
7652
о
о
4346
3185
о
7147
о
1,3937
6211
о
2281
о
4983
о
6711
о
<м
3208
°
2437
о
8861
о
1,5534
4791
о
3379
о
5419
о
6999
о
2406
°
1880
о
0848
о
о
3476
о
1
4204
о
5699
о
4554
о
to
1820
о
1459
о
3172
1,9896
2237
7
4774
о
5815
о
3400
о
00
*
1
*
1389-
9063
2,2796
1070
о
5104
о
5767
о
2239
о
о
(М
1
-9368
о
9141
2,6291
0015
о
5208
о
5560
о
1104
о
<м
<м
1
о
7022-
о
2981
3,0493
1005
о
5104
о
5202
о
0025
о
<м
1
о
5540-1
о
7554
<м
3,5533
1884
о
4813
о
4708
о
0968
о
to
<м
1
о
4382-
о
ЗОН
со
4,1573
2635
о
4359
о
4097
о
1850
о
00
<м
1'
to
о
о
3474-
о
9534
со
4,8808
3247
о
3769
о
3391
о
2601
о
о
со
1
to
со
о
2759-
о
со
со
5,7472
3707
о
3071
о
2613
о
3202
о
сч
со
1
о
2196-
о
6701
ю
6,7848
4010
о
2296
о
1792
о
3643
с
э
"«<
со
1
О)
о
1750-
о
7927
to
8,0277
4154
о
1477
о
0955
о
3918
7
to
со
1
1
°
1397-
о
1404
со
9,5169
4141
о
0645
о
0128
о
4026
о
00
со
1
¦¦««
00
*
-0911
о
7595
§
3979
о
0169
о
I
о
о
3971
о
о
1
9
о
8927-s
о
СО
3680
о
0938
о
1386
7
3766
о
<м
304
СО Ю Ю <*«
с^ с^ ю ю
d СЧ СЧ СО СО CO СО €0 СО СШ СО
I I I I I I I I I I I
?-сосоо>юсоооиэсчсчсо
OlODNCOOOlGn^ftOlO
I I
I I I I I
О О) СО СО Ю
О
О)
с~
о
о
1
о
со
ю
о
о
1
о
о
1
^—
со
о
о
1
СО
СЧ
о
о
1
ю
сч
о
о
1
00
о
о
1
о
1 1
о ю
^J4 ?ч)
"^f О
сч о
о
1
го
оо
п
00
о
о
1
о
гч
in
СО
о
°
1
гч
ю
in
о
о
1
го
о
о
1
со
со
о
о
1
О|
г^.
о
о
1
о
о
о
1
СП
о
1
СП
1
0Г)
1
00
00
1П
О)
о
о
1
^^
СО
о
о
1
со
Of)
гм
СО
о
о
1
00
Of)
о
in
о
о
1
,~4
сч
о
о
1
ОЭ
со
со
о
о
1
СО
CJ
о
о
1
со
о
о
1
00
~^
о
¦* Ш О * ОIО N
¦*Mob«)iMioa)Ooo2iONC(oN
IO00C4-*^C0INC0C0OW-.CN^h00
N-nO)M00ONO>lO00STf —
.. _ JrttDOCOS^SO
_ STf~0innraC4n*OC4ON
00<МС^.С0О>0000О>ЮО<М1Л00СЧС0
--1М1М1МП<|ЮШЬОЗ-
— — CNWmcO^inNOO- — — —1<МСЧ
о
to
t
S
1
a
s
to
о
о.
s
•е-
§
о
s
OnfO*O>»Mif00
^^ C7s O^ *3* 00 О CO CO CO ^^ '
О1 О
^^¦^co^^^^^^o^o
^^ ^J4 ^J4 C7s r^ r^ r^ C7s
о о о о о о
ooooooo
oooooooooooooooo
I I! I 1 I ! I +
COiftCOlfiCOOJtNNCOOKN^O)©
COCOOJCO-OlCNCQCOOlOtOlflCO
ooooooooooooooooooooooooooooo
¦ ¦¦¦¦¦¦¦¦в !¦¦¦•
11
OOOOOOOOOl
I I .1 I I I I ] +
СО(рЮ@01СОСОО^О{00(М^СО@01'^'Ю OOOOO— СО^ОЮОО
^S) ^O 00 t4*1™ CO l-O ^tf* ^"^ CO ^^ ^^^ 1Л l^ '^d^ ^t* O^ •OS ^'^ ^t' 00 *,,д ^S) ^it* l^D t*^ ^* OS ^S)
<M<M<MCOCOCOCOCO<M(M— — OOO— — <M<M<M<M ""
<M <M — —
т
ooooooooooooooooooooooooooo
оо
I +
о
о а
о s
а к
о а
? 8
О Я4
ffl га
а к
ш о
СО
к —¦
(**• О ^^ С^ ^^ О. •—•
— — О О О — OJ
ПЧ'ПОЮ0б-Ю-'МС1)^О>ОШШО11МЮ
CICNCNniMC4IMCN-'-OOOO--IMIMCN
ooooooooooooooooooooooooooooo
I I I I I I + I I I I I I .1
§
a- all
" oib
SIS
¦#'(?! ОО
СО .СО СО
X
205
Таблица П.12
Интеграл вероятности или функция ошибок
2 ? 2 г
erf г = — ёхр(—PVP=— ехр(—pa)
я J я J
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
о,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
0,
г
,00
,02
,04
,06
,08
,10
.12
,14
,16
,18
,20
22
,24
26
28
30
32
34
36
38
40
42
44
46
48
50
52
54
56
58
60
62
0
0
0
0
0
0
0
0
0
0
0
0
0
0
о
0
о
0
0
0
0
0,
о,
0,
0,
0,
о,
о,
о,
0,
о.
0,
0,
erf г
,00000
,02256
,04511
,06762
,09008
,11246
,13476
,15696
17901
20094
22270
24430
26570
28690
30788
32863
34913
36936
38933
40901
42839
44747.
46623
48466
50275
52050
53790
55494
57162
58792
60386
61941
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
I,
1,
1
1,
1,
1,
1,
1,
1,
1,
1,
1,
1,
1,
Z
,64
,66
,68
,70
,72
,74
76
78
,80
82
84
86
88
90
92
94
96
98
00
02
04
06
08
10
12
14
16
18
20
22
24
26
—Z
erf г
0,63459
0,64938
0,66378
0,67780
0,69143
0,70468
0,71754
0,73001
0,74210
0,75381
0,76514
0,77610
0,78669
0,79691
0,80677
0,81627
0,82542
0,83423
0,84270
0,85084
0,85865
0,86614
0,87333
0,88020
0,88679
0,89308
0,89910
0,90484
0,91031
0,91553
0,92051
0,92524
Z
1,28
1,30
1,32
1,34
1,36
1,38 "
1,40
1,42
1,44
1,46
1.48
1,50
1,52
1,54
1,56
1,58
1,60
1,62
1,64
1,66
1,68
1,70
1,72
1,74
1,76
1,78
1,80
1,82
1,84
1,86
1,88
1,90
erf г '
0,92978
0,93401
0,93807
0,94191
0,94556
0,94902
0,95229
0,95538
0,95830
0,96105
0,96365
0,96611
0,96841
0,97059
0,97263
0,97455
0,97635
0,97804
0,97962
0,98110
0,98249
0,98379
0,98500
0,98613
0,98719
,0,98817
0,98909
0,98994
0,99074
0,99147
0,99216
0", 99279
z
1,92
1,94
1,96
1,98
2,00
2,05
2,10
. 2,15
2,20
2,25
2,30
2,35
2,40
2,46
2,48
2,50
2,55
2,60
2,65
2,70
2,75
2,80
2,85
2,90
т,%
3,00
3,20
3,40
3,60
3,80
00
—
erfz
0,99338
0,99392
0,99443
0,99489
0,99532
0,99626
0,99702
0,99764
0,99814
0,99854
0,99886
0,999111
0,9993115
0,9994966
0,9995472
0,9995930
0,9996893
0,9997640
0,9998213
0,9998657
0,9998994
0,9999250
0,9999443
0,9999589
0,9999698
0,9999779
0,9999939
0,9999985
0,9999996
0,9999999
1,0000
.
206
СПИСОК ЛИТЕРАТУРЫ
П. 1. Touloukian Y. S., Но С. Y. (ed.) Therraophysical Properties of Matters.
V. I—XIII, IFI/Plenum, 1970.
П. 2. Thermodynamic and Transport Properties of Gases, Liquids and Solids. Symp.
in Thermal Properties, ASME, 1959.
П. 3. Engineering Science Data Units. ESDU Ltd., London.
П. 4. Thermophysical Properties Research Centre. Purdue University, West Lafayet-
Lafayette, Indiana, U.S.A.
П. 5. Туе R» R. Thermal Conductivity. V. I, II. Academic Press, 1969.
П. 6. Mantell С L. (ed). Engineering Materials Handbook. McGraw-Hill, 1958.
П.7. Perry R. H., Chilton С. Н. Chemical Engineers Handbook. McGraw-Hill,
1973.
П. 8. Handbook of Chemistry and Physics. 56th ed, Chemical Rubber Co., 1975.
П. 9. Baumeister Т., Marks L. S. Mechanical Engineers Handbook. McGraw-Hill,
1958.
П. 10. McAdams W. H. Heat Transmission. 3rd ed. McGraw-Hill, 1954.
П. 11. Eckert E. R. G., Drake R. M. Analysis of Heat and Mass Transfer. McGraw-
Hill, 1972.
П. 12. Lyon R. N. Liquid Metals Handbook. US Government Printing Office, 1952.
П. 13 Knudsen J. G., Katz D. L. Fluid Dynamics and Heat Transfer. McGraw-Hill,
1958.
П 14. IHVE Guide Book A. The Institution of Heating and Ventilating' Engineers,
Lond., 1970.
П. 15. ASHRAE Handbook of Fundamentals. American Society of Heating, Refri-
Refrigerating and .Air-conditioning Engineers.
П. 16. UK Steam Tables in SI Units. Edward Arnold, 1970.
П. 17. Reid R. C, Sherwood Т. К- The Properties of Gases and Liquids. McGraw-
Hill, 1958.
П. 18. Lee J. S., Babitt P. J. Transport Properties at High Temperatures of CO2,
N2, O2 and Ar Gas Mixtures for Planetary Entry Applications. NASA TN
D5476, 1969.
П. 19. Touloukian Y. S. (ed.). Thermophysical Properties Research Literature Ret-
Retrieval Guide. McDonald Co., Ltd., 1968.
П. 20. Jamieson D. Т., Tudhope J. S. The Thermal Conductivity of Liquids, Rep. 137.
National Engineering Laboratory, Scotland.
П. 21. Rothman A. J., Bromley L. A. High Temperature Thermal Conductivity of
Gases. — «Industr. and Engng Chem.», 1955, v. 47, p. 899.
П. 22. Kennan J. H., Kaye J. Gas Tables, John Wiley, 1945.
П. 23. Tables of Thermal Properties of Gases, Circ. 564, National Bureau of Stan-
Standards, US 1955. Auth.: J. Hilsenrath e. a.
П. 24. Hilsenrath J., Beckett C. W. Tables of Thermodynamic Properties of Argon-
free-air to 15,000 K. National Bureau of Standards, MIPR-AEDC-1, 1956.
П. 25. Tables of Thermodynamic and Transport Properties of Air, Argon, Carbon
Dioxide, Carbon Monoxide, Hydrogen, Nitrogen, Oxygen and Steam, Per-
gamon Press, 1960. Auth.: J. Hilsenrath e. a.
П.26. US Standard Atmosphere, NASA, 1962.
П. 27. Richmond J. С (ed.), Measurement of Thermal Radiation Properties of So-
Solids. NASA CP—31, 1963.
П. 28. Seban R. A. Thermal Radiation Properties of Materials. WADD-TR-60-370.
Pt. Ill, Cal. Univ., 1963.
П. 29. Wood W. D., Deem H. W., Lucks С F. Thermal Radiation Properties. Ple-
Plenum Press, 1964.
207
П. 30. Wong H. Y., Aggarwal S. R. Total Hemispherical Emittance of Stainless
Steel, AISI 321. — «J. Iron Steel Inst.», Aug.. 1971.
П. 31. Wong H. Y. Oxidized Nickel as a Heating Element in Vacuum. — «Brit. J.
App. Phys.», 1966, v. 17, p. 1329.
П.32. Slngham J. R. Tables of Emissivity of Surfaces. — «Intern. J. Heat Mass
Trans.», 1962, v. 5, p. 67.
П. 33. Dunkle R. V. Thermal Radiation Characteristics of Surfaces. In: Theory and
Fundamental Research in Heat Transfer. By J. A. Clark, Pergamon Press, -
1963.
П.34. Rohsenow W. M., Hartnett J. P. (eds). Handbook of Heat Transfer. McGraw-
Hill, 1973.
АЛФАВИТНО-ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютная температура 16
Абсолютно черное тело 87
Анализ размерностей 53
Аналогия Рейнольдса 62
Аэродинамический нагрев 75
•Безразмерные критерии 52
Взаимный обмен (см. Излучение) 93
Вентиляция (см. Строительная теп-
теплопередача) 164
Виды теплопередачи 11
Вода:
— давление пара 16
— испарение 120
— свойства 189
Вынужденная конвекция 55
Вязкость газов 194
— жидких металлов 200
— жидкостей 189
— зависимость от температуры 19
Газовый термометр 16
Гидравлический диаметр 51
Граничные условия при теплообмене
теплопроводностью 48
Данные по поверхностному натяже-
нню 202"
Двухфазный поток 122
Динамическая вязкость (см. Вяз-
Вязкость) 54
Диффузное излучение 86
Диффузио отражающая поверхность
86
Единицы перевода в систему СИ 182
Естественная конвекция:
коэффициент конвективной тепло-
теплоотдачи (см. Конвекция) 13
Жидкие металлы
свойства 186
формулы теплопередачи 158
Жидкости, свойства 189
Жидкость перемешанная 52
Закон Вндемана — Франца 12
— Кирхгофа 89
— Ламберта 90
— Планка 90
— смещения Вина 91
— теплоотдачи Ньютона 22
Замкнутая область 86
Зеркальная поверхность 88
Значение параметра К (см. Полный
коэффициент теплопередачи) 26
Излучение (см. Падающее излуче-
излучение) 87
Изоляционные материалы (см. Стро-
Строительные материалы) 170
Интенсивность излучения 88
Инфракрасное излучение 87
Капельная конденсация (см. Конден-
Конденсация) 121
Касательное напряжение 62
Кинематическая вязкость:
газов 194
жидких металлов 200
жидкостей 189
Кипение:
— в большом объеме 121
— при вынужденной конвекции 121
— кризис 123
— критический тепловой поток 123
— пузырчатое 121
— точка пережога 122
— характеристическая кривая 121
— пленочное 120
Конденсация капельная 121
— пленочная 121
— формулы теплопередачи 124
Критерий конденсации 120
Кон&екция вынужденная 55
движение с высокой скоростью 75
движение по трубам н каналам 64
естественная 54
обтекание пучков труб 74
омывание внешних поверхностей 65
тела вращения 78
формулы теплообм.ена 70
Критерий Грасгофа 53
209
— Гретца 52
— кипения 120
Критерий Нуссельта:
в теплообменниках с турбулизато-
рами 160
при вынужденной конвекции 62
при естествеииой конвекции 55
— конденсации пара 128
— обтекании плоских поверхностей
65
пучков труб 74
цилиндрических тел 72
— Пекле 52
— Прандтля 53
газов 194
жидкостей 189
— Рейиольдса 53
— Стантона 52
Кольцевой зазор 67
Коэффициент восстановления темпе-
температуры 75
— конвективной теплоотдачи 13
при движении потока с вы-
высокой скоростью 77
(см. Конвекция, см. также Крите-
Критерий Нуссельта)
через трубы и. каналы 66
естественной конвекции 56
вертикальные цилиндры 57
вертикальные поверхности 59
горизонтальные цилиндры 56
горизонтальные поверхности
59
ограниченные пространства
59
сферы 58
при кипении (см. Кипение)
124
. конденсации (см. Конден-
Конденсация) 128
обтекании пучков труб 74
омываиии цилиндров 72
Коэффициент восстановления темпе-
температуры при омывании плоских по-
поверхностей 77
сфер 78
Коэффициент излучения 84
алгебраический метод 93
формулы 94
— объемного термического расшире-
расширения 54
— ослабления 86
— поглощения 85
— поглощения солнечного излуче-
излучения 165
— пропускания 88
— рассеяния 85
— температуропроводности 21
— теплоотдачи (см. Конвективный
коэффициент) 21
— теплопередачи 21
210
— теплоотдачи излучением 14
— теплопроводности 21
газов 194
жидких металлов 200
жидкости 189
—— металлов 186
строительных материалов 199
кирпичной кладки 168
— трения (см. также Коэффициент
трения) 62
при течении в трубах 66
при обтекании пучков (см. так-
также Поверхностное трение) 63
Ламинарное течение 52
Лучеиспускательная . способность 86
Лучистый теплообмен в замкнутой
области. 109
Массовый расход 54
Массовая скорость 54
Металлы, коэффициент теплопровод-
теплопроводности 186
Метод воздухообмена (см. Строи-
Строительная теплопередача) 171
Модель абсолютно черного тела 87
Модифицированная аналогия Рей-
нольдса 62
Многоходовой перекрестный тепло-
обмениый аппарат 149
Монохроматическое излучение 87
Нагрев излучением (см. Строитель-
Строительная теплопередача)
— конвекцией
Накипь 139
Направленное излучение 86
Непосредственная теплопередача (см.
Теплообменные аппараты) 141
Нестационарная теплопроводность
(см. Теплопроводность) 24
Обтекание внешних поверхностей
— с высокой скоростью 77
— плоской пластины 70
— коэффициент восстановления тем-
температуры 75
— коэффициент поверхностного тре-
трения 77
— критерий Стантоиа 76
— температура отнесения 77
— энтальпия отнесения 77
Одномерная теплопроводность 23
Оребренная . поверхность (см. Разви-
Развитые поверхности) 24
Отражательная способность 88
Отношение водяных* эквивалентов
теплоносителей 139
Падающее излучение 87
Падение давления:
иа пучках труб 63
на трубах 66
Парообразование
— при кипении (см. Скрытая тепло-
теплота парообразования) 120
Перегрев» 121
Перекрестный ток 138
Переменная составляющая теплового
потока
Переохлаждение 127
Пластинчатые теплообменные аппа-
аппараты (см. Теплообменные аппара-
аппараты) 153
Пленочная конденсация (см. Конден-
Конденсация) 121
Плоская пластина:
обтекание с высокой скоростью 78
теплообмен 77
Плотность теплового потока (опре-
(определение) 21
Площадь теплопередающей поверх-
поверхности 140
Поверхностное треиие 55
Подъемная сила 54
Полностью стабилизированный поток
52
Поправочный коэффициент для рас-
расчета теплообменных аппаратов 143
Постоянная Лоренца 12
Противоток 138
Прямоток 140
Пузырчатое кипение 121
Развитые поверхности 36
Распределение скорости ветра 169
—' температуры:
в пластинах 25
в полуограниченных твердых телах
42
в сферах 25
в цилиндрах (ребрах) 25
Регенератор 141
Рекуператор 140
Свойства:
газов 194
жидких металлов 200
жидкостей 189
металлов 186
строительных материалов 199
Сверхзвуковой поток 75
Серое тело 87
Скорость ветра 168
Скорость звука в воздухе 184
Скрытая теплота парообразования
119
Сложный теплообмен 14
Солнечная постоянная 184
Солнечное излучение 177
Сопротивление давления 62
— трения 63
Сочетание естественной и вынужден-
вынужденной конвекции 78
Спектральное излучение 88
Средиелогарифмическая разность тем-
температуры 64
Стефана — Больцмана закон 88
— постоянная 92
Строительная теплопередача:
вентиляция 161
значения параметра 175
расчет 176
температура среды внутри помеще-
помещения 164
теплопередача конструкций здания
165
теплопередача при переменных ус-
условиях теплообмена 177
теплообмен за счет утечки возду-
воздуха:
метод воздухообмена 171
метод трубы 171
требования к обеспечению тепло-
теплового режима 172
Строительные материалы 170
Суммарное излучение 88
Тела вращения 78
Телесный угол 88
Температура абсолютная 16
— адиабатической стенки 75
— восстановления 75
— излучения 89
-• насыщения 121
— окружающей среды 162
— - равновесная 164
-— смешения 52
— солнечно-воздушная (см. Темпе-
Температура) 162
— среднелогарифмическая 64
— торможения 75
— шкала 16
Температурная шкала Кельвина 16
Температуропроводность
— газов 194
— жидких металлов 200
— жидкостей 189
Тепловая инерционность строитель-
строительных сооружений 164
Тепловое излучение (см. Излучение)
84
Тепловые потери конструкций (см.
Строительные теплопотери) 172.
Теплообмен при переходных режи-
режимах (см. Теплопроводности при не-
нестационарном режиме) 24
труба 157
Тепловой шунт 164
Теплообменники периодического дей-
действия (см. Теплообмеиные аппара-
аппараты) 155
Теплообменные аппараты:
двухжндкостные с косвенной теп-
теплопередачей 154
кожухотрубные 141
прямоточные 141
211
с косвенной теплопередачей 153
с непосредственным теплообменом
141
с теплообменом периодического ти-
типа 155 :
с оребрениой поверхностью 159
турбулизаторы: 159
перекрестный ток.
поправочные коэффициенты 144
метод истинного значении средней
разности температуры 143
расчеты конструкций 143
эффективность 139
Теплоотдача жидких металлов (см.
Коэффициенты) 158
— плоской пластины 70
— при высоких скоростях 75
— при непосредственном контакте
теплоносителей 156
(см. Теплообменные аппараты)
— тел вращения-78
Теплопроводность:
основное уравнение 11
коэффициент теплопроводности 19
при стационарном режиме (см.
Теплопроводность) 23
Теплопроводность, тепло:
граничные условия при теплообме-
теплообмене теплопроводностью 48
дифференциальные уравнения 41
стационарный режим:
развитая поверхность 24
одномерная система 23
для различных систем 26
уравнение Фурье 41
нестационарный режим 24
тела с ограниченно высокой тепло-
теплопроводностью 38
тела с конечной теплопроводностью
н конвективной теплоотдачей на
поверхности 40
тела с низким термическим сопро-
сопротивлением на поверхности 38
Термическан цепь 22
Термическое сопротивление:
в расчете строительной теплопере-
теплопередачи 165
в теплопроводности 21
репериые точки 17
Теплофизические свойства воздуха
194
газов 194
Течение в трубах 62
Толщина пограничного слоя жидко-
жидкости 53
Точка образования пара 16
— таяння льда 16
Тройная точка воды 16
Требования по обеспечению теплово-
теплового режима помещения (см. Строи-
Строительная теплопередача) 172
Трубы н каналы:
коэффициент трения 62
перепад давления 62
теплопередача 66
Турбулентный поток 53
Турбулизаторы 159
Угловой коэффициент излучения (см.
Коэффициент облученности) 85
Удельная теплоемкость:
газов 194
жидких металлов 200
жидкостей 189
металлов 186
Универсальная газовая постоянная
184
Уравнение Польгаузена 78
— Прандтля — Шлнхтннга 78
— Сюзерланда 76
— теплопроводности Фурье 41
Число Маха 51
— Релея 52
Эквивалентный диаметр (см. Гидрав-
Гидравлический диаметр) 53
Энтальпия восстановления 76
Эффективность оребрення теплооб-
менных аппаратов 139
Эффективное излучение 87
ИБ № 895
Харри Уонг
ОСНОВНЫЕ
ФОРМУЛЫ
И ДАННЫЕ
ПО ТЕПЛООБМЕНУ
ДЛЯ ИНЖЕНЕРОВ
Справочник
Редактор 3. Д. Андреенко
Художественный редактор А. Т. Кирьянов
Переплет художника С. Н. Голубева
Технический редактор Л. Ф. Шкилевич
Корректор Л. С. Тимохова
Сдано в набор 27.06.78 Подписано к печати 7.02.79.
Формат 60Х90'/и. Бумага тип. № 2. Гарнитура литературная. Печать высокая.
Усл. печ. л. 13,5 Уч.-изд. л. 14,64. Тираж 7820 экз. - Зак. изд. 77541
Зак. тип. 469 Цена 1 р.
Атомнздат, 103031, Москва, К-31, ул. Жданова, 5
Московская типография № 4 Союзполиграфпрома
при Государственном комитете СССР
по делам издательств, полиграфии и книжной торговли
Москва, 129041, Б. Переяславская ул., д. 46