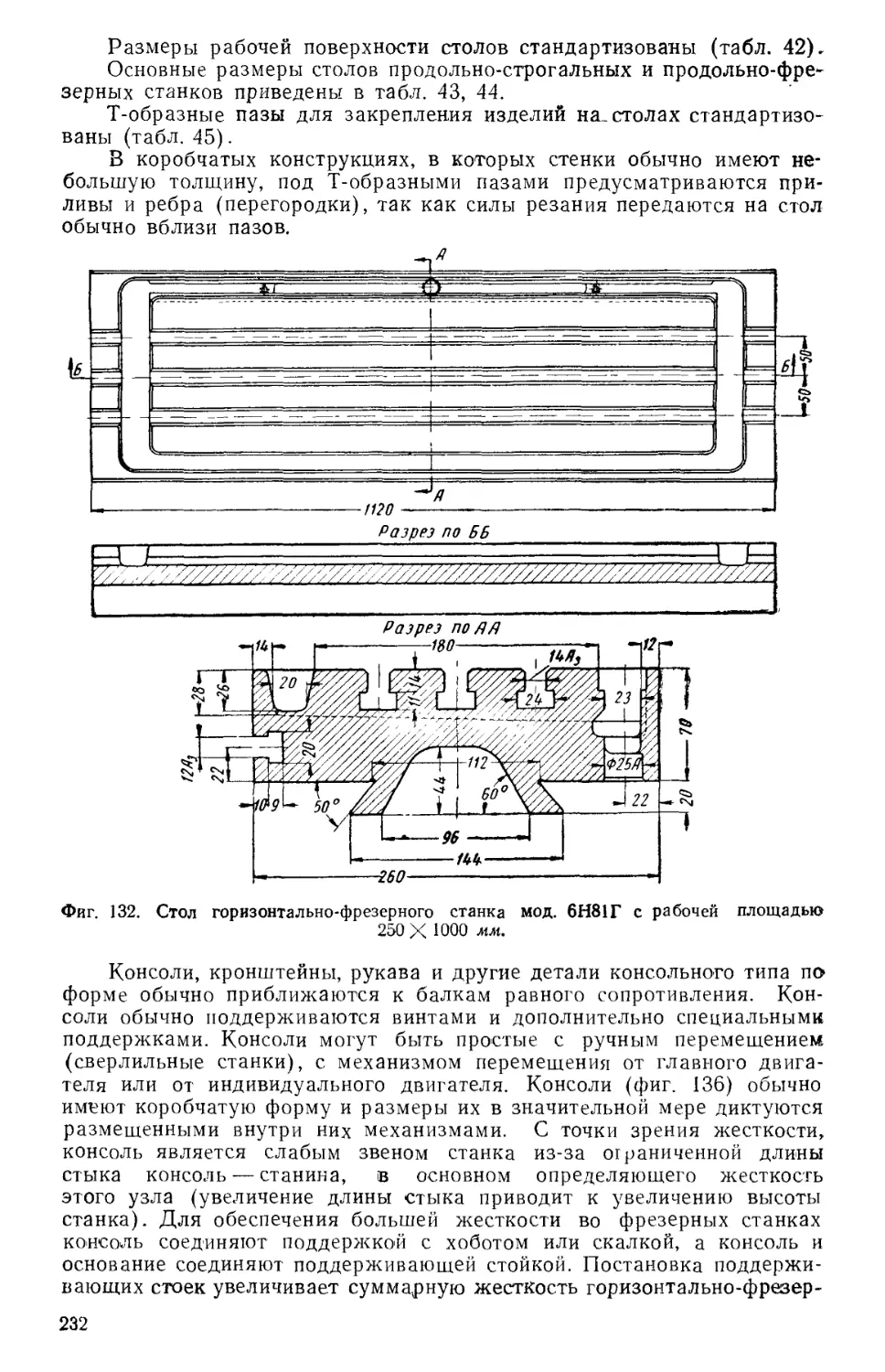
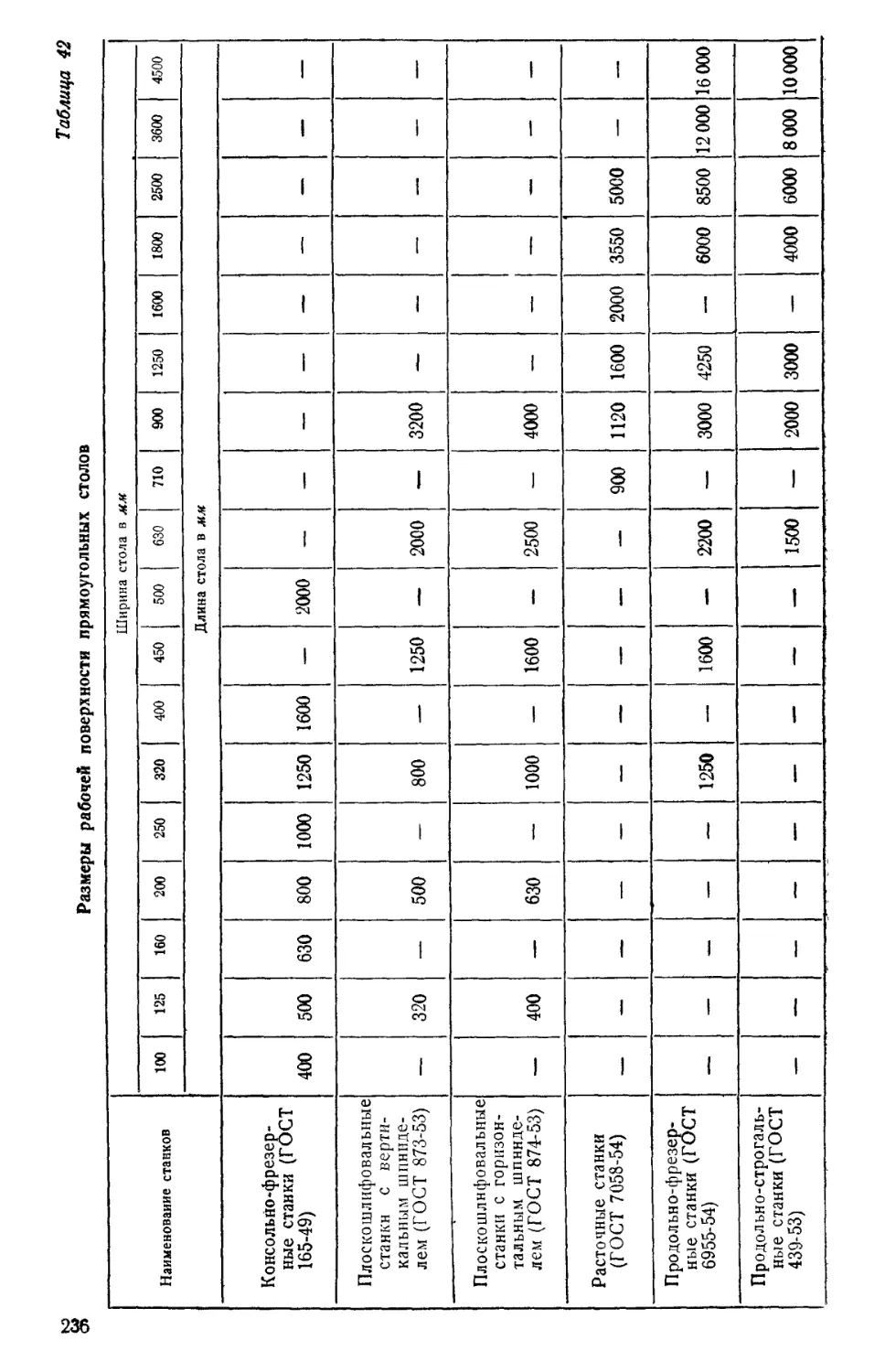
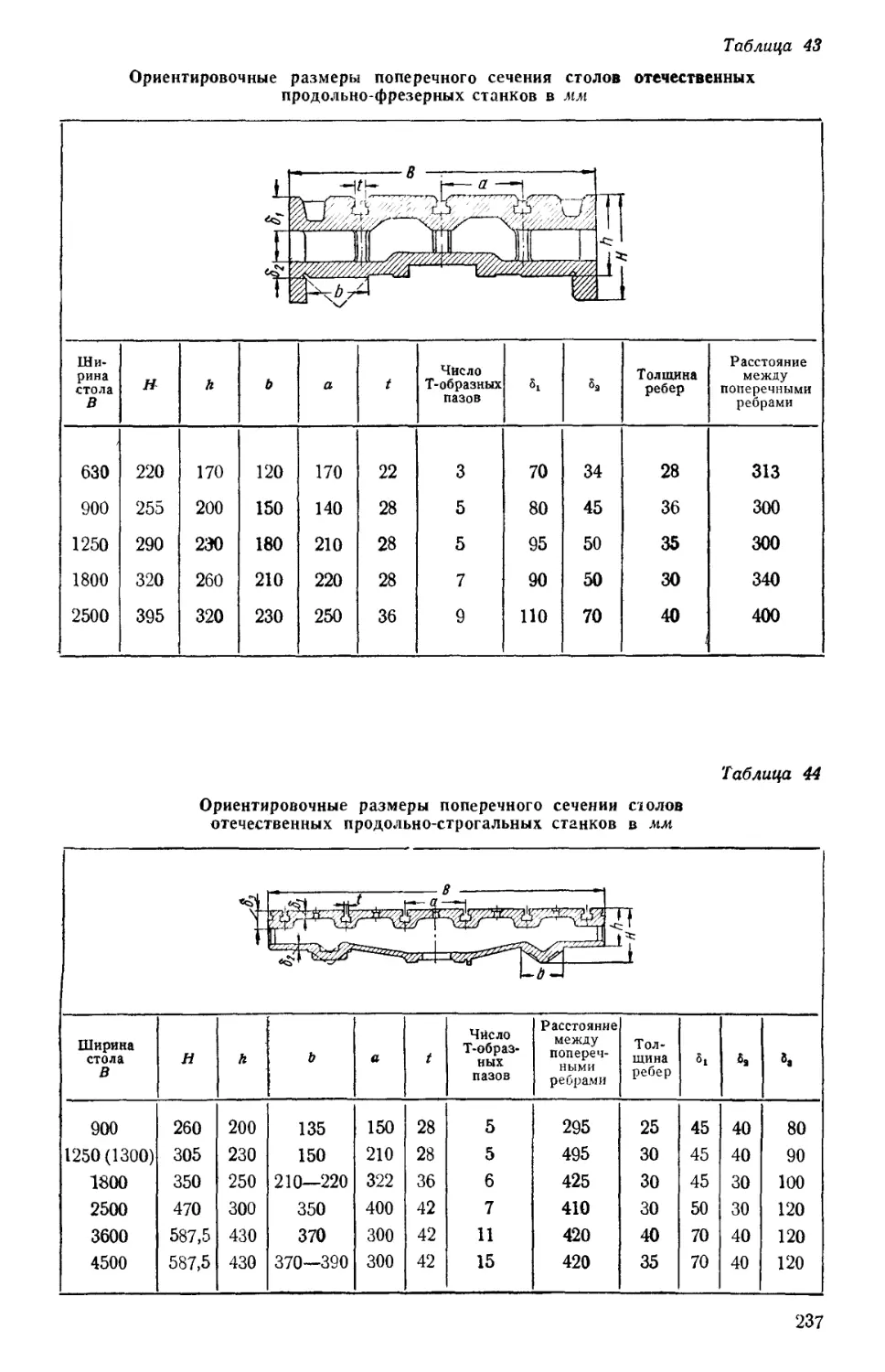
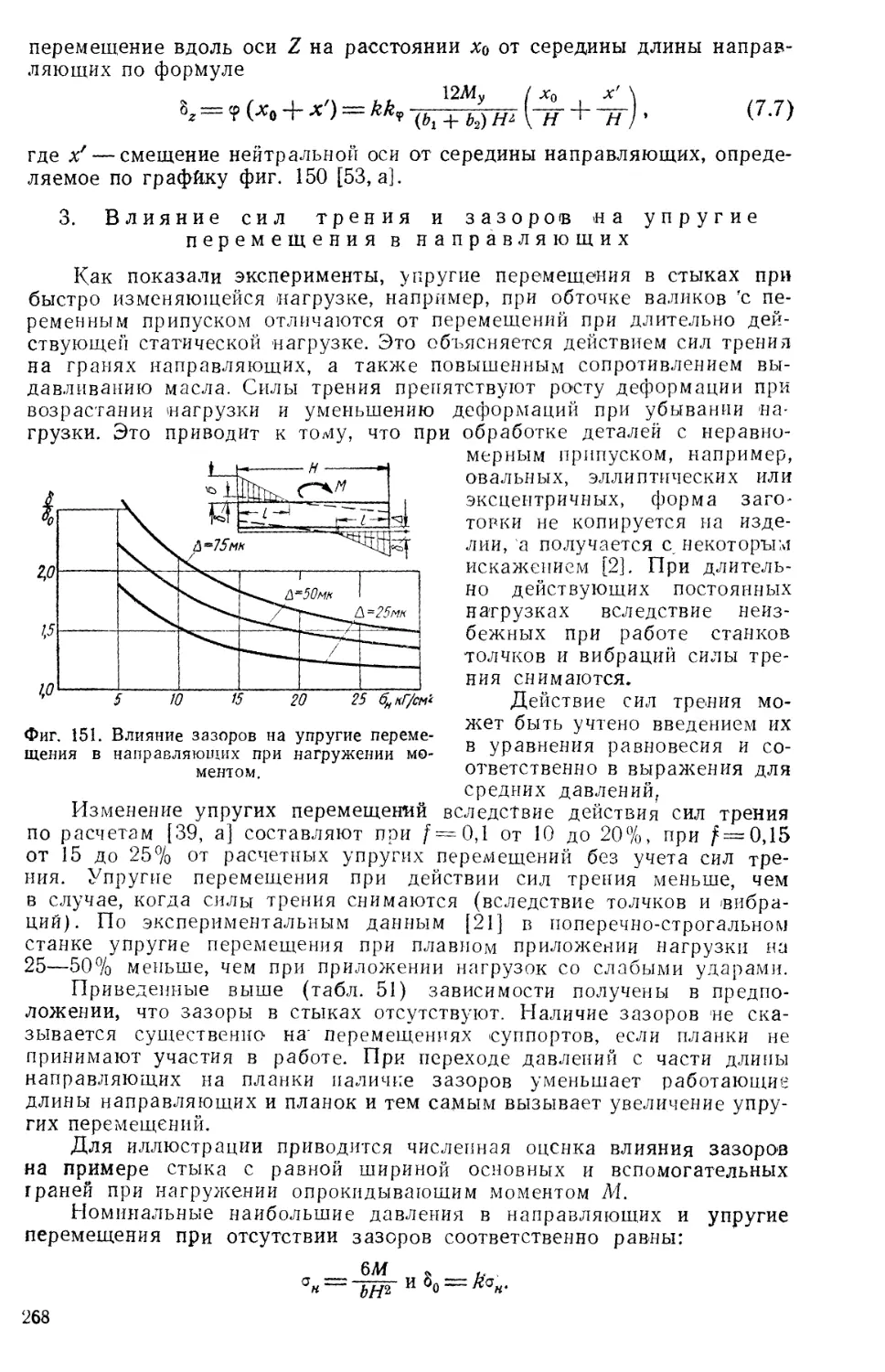
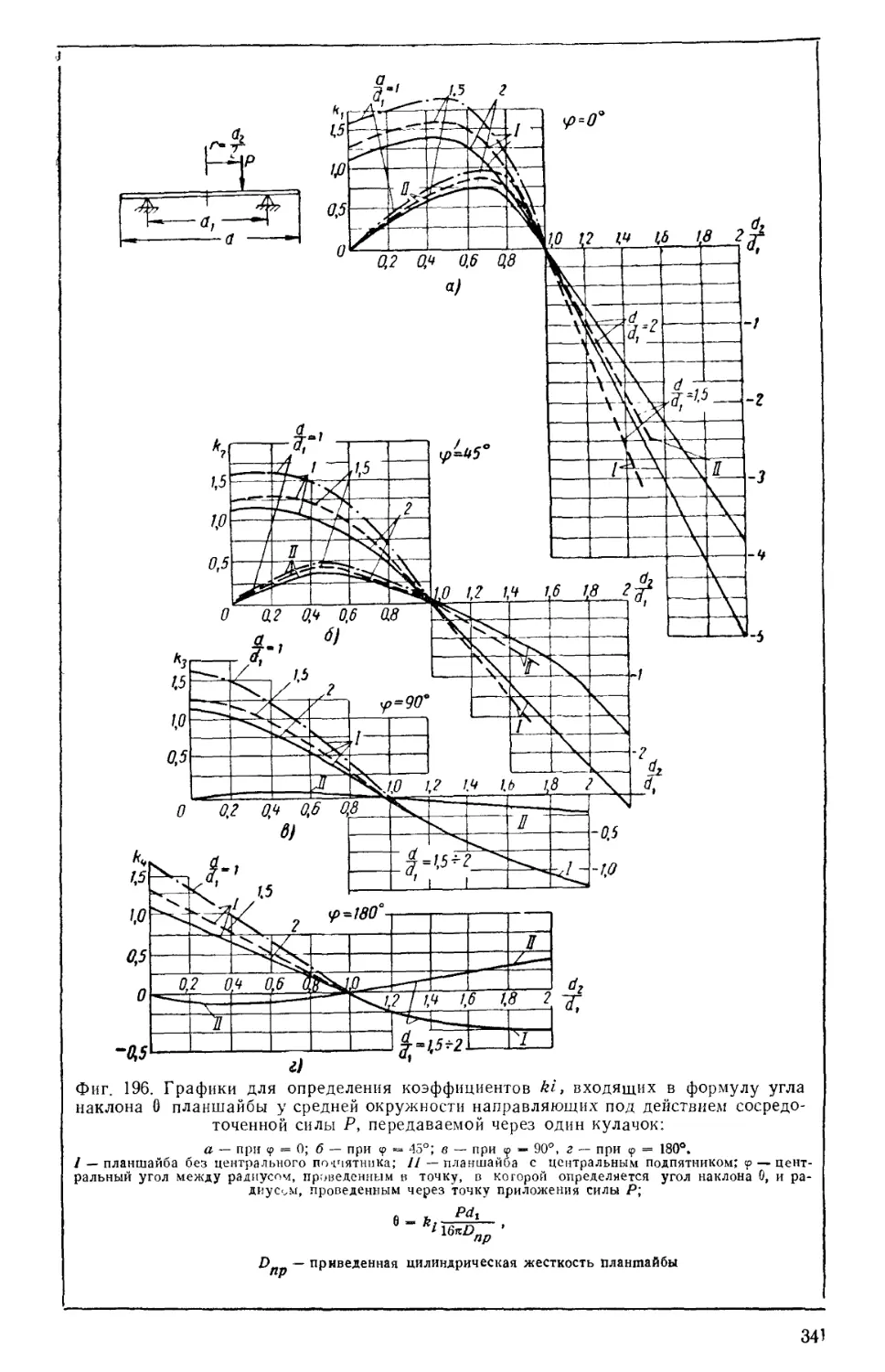
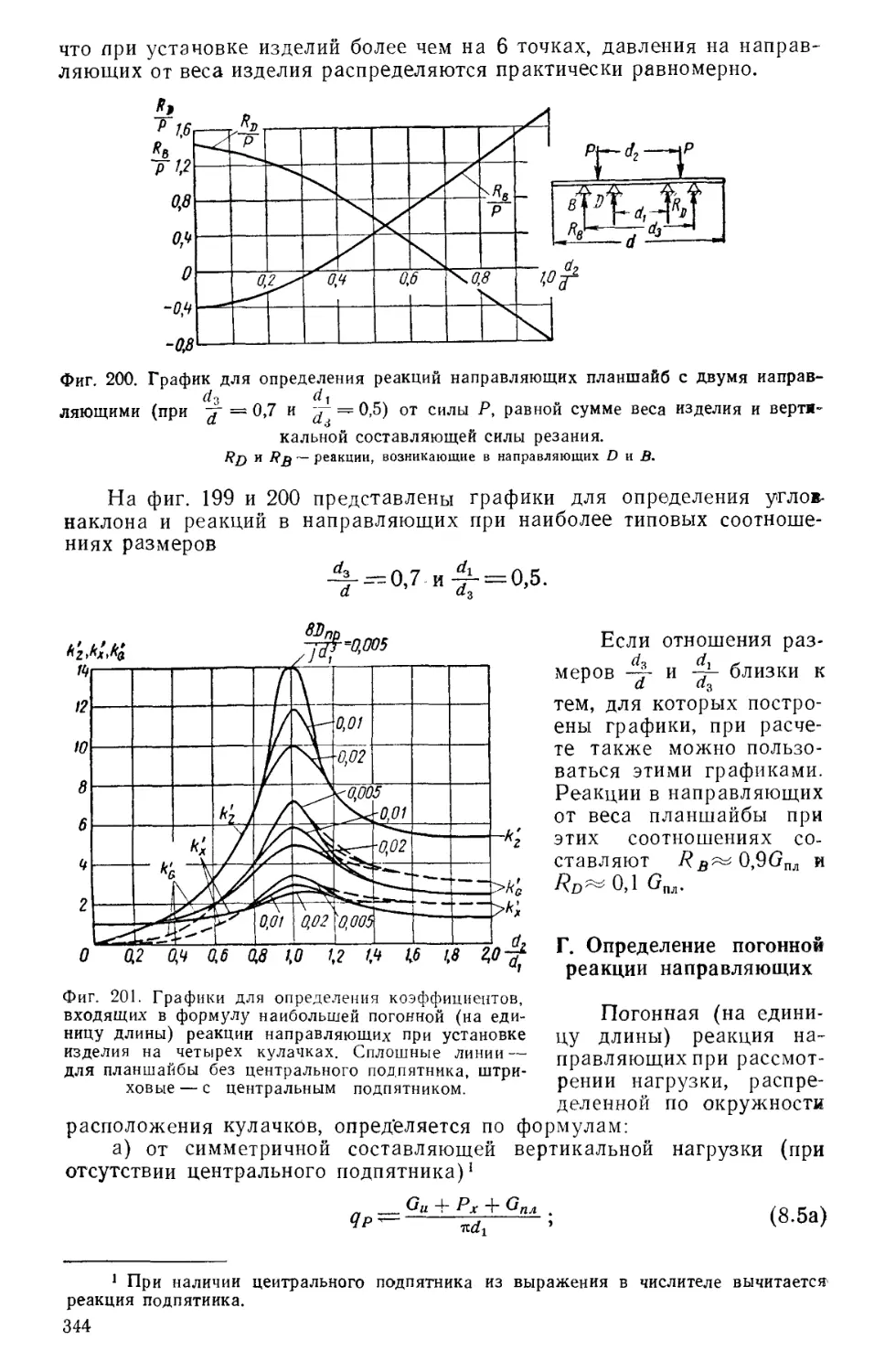
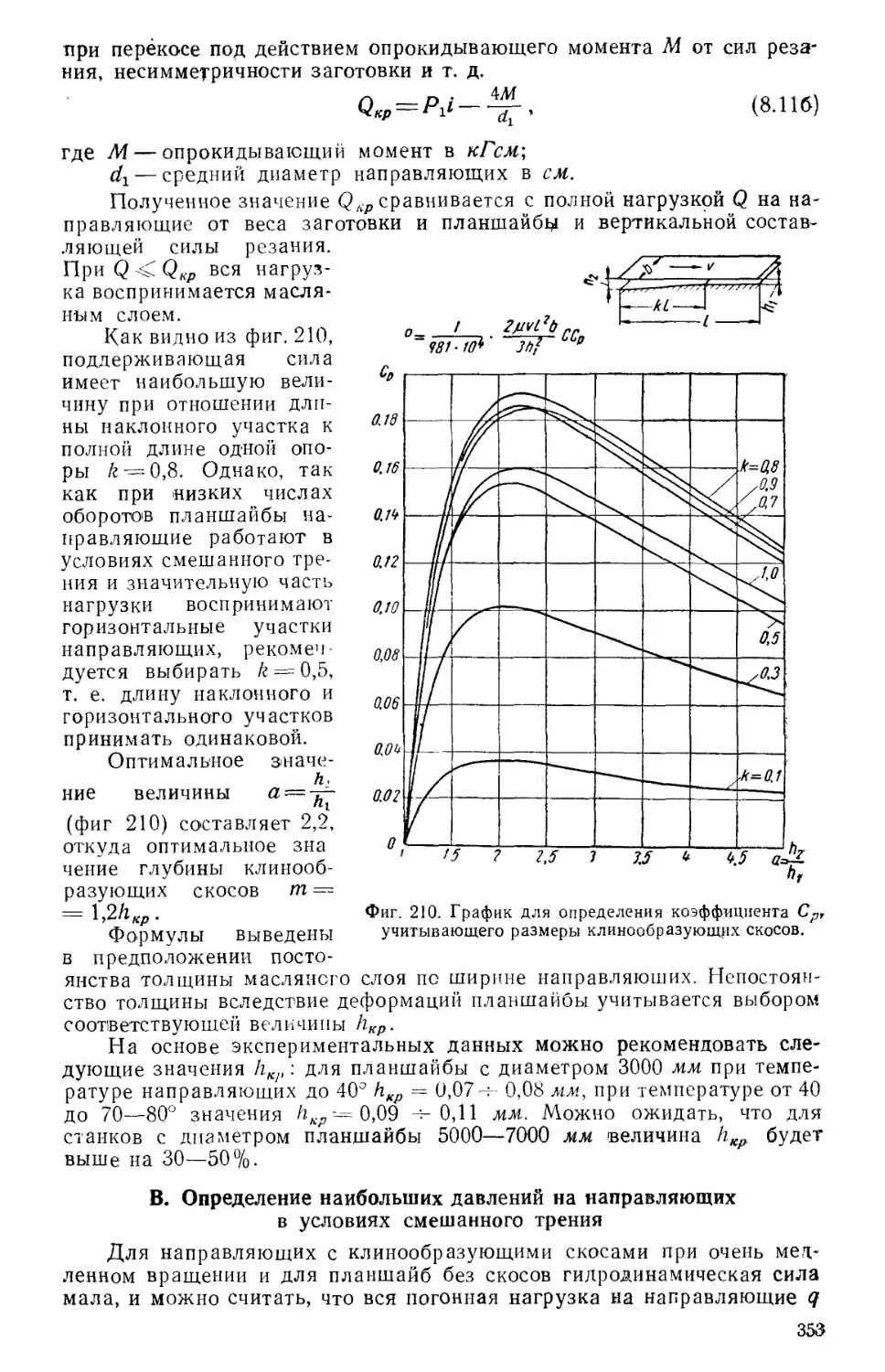
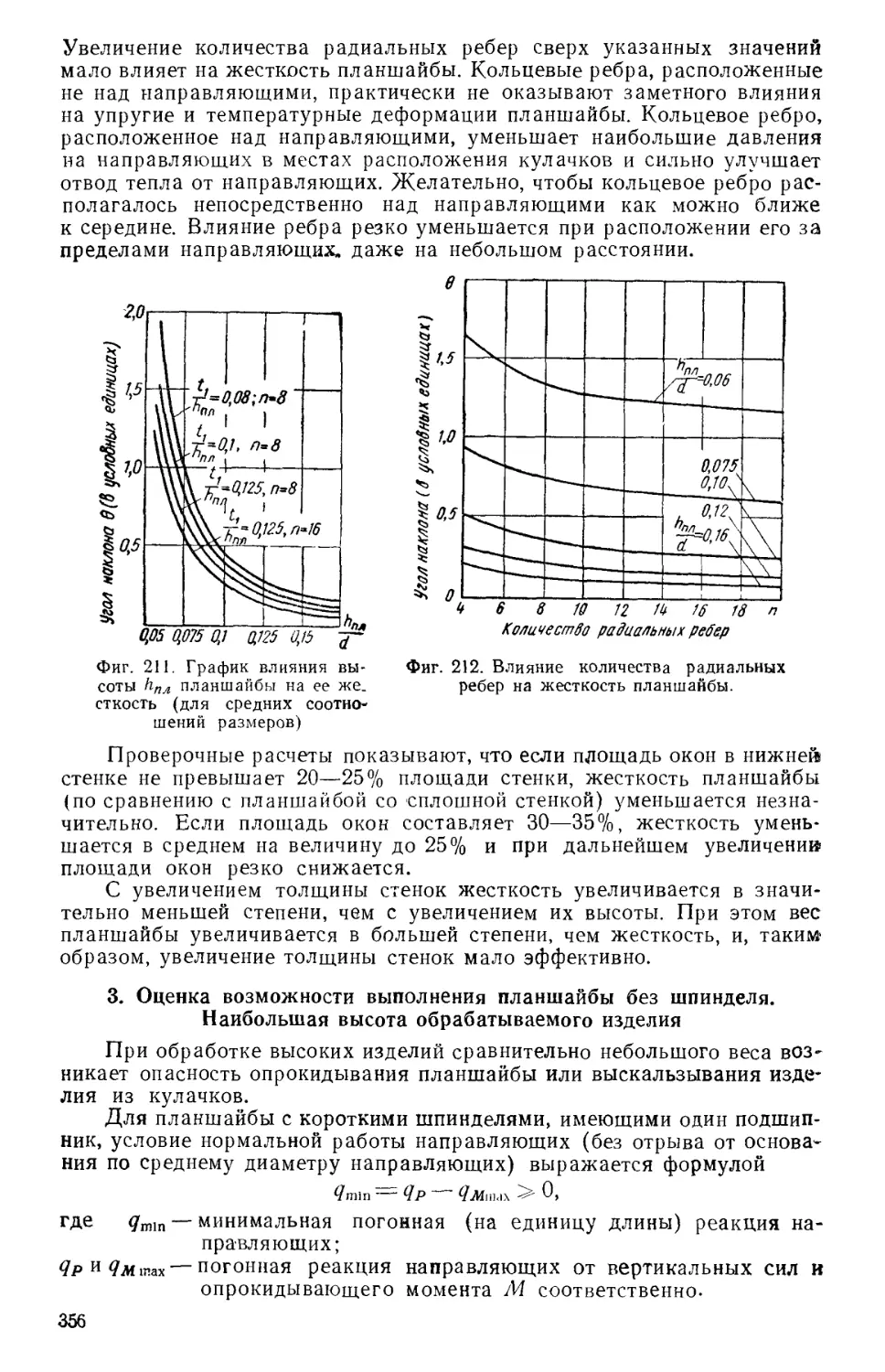
Author: Решетов Д.Н. Каминская В.В. Левина З.М.
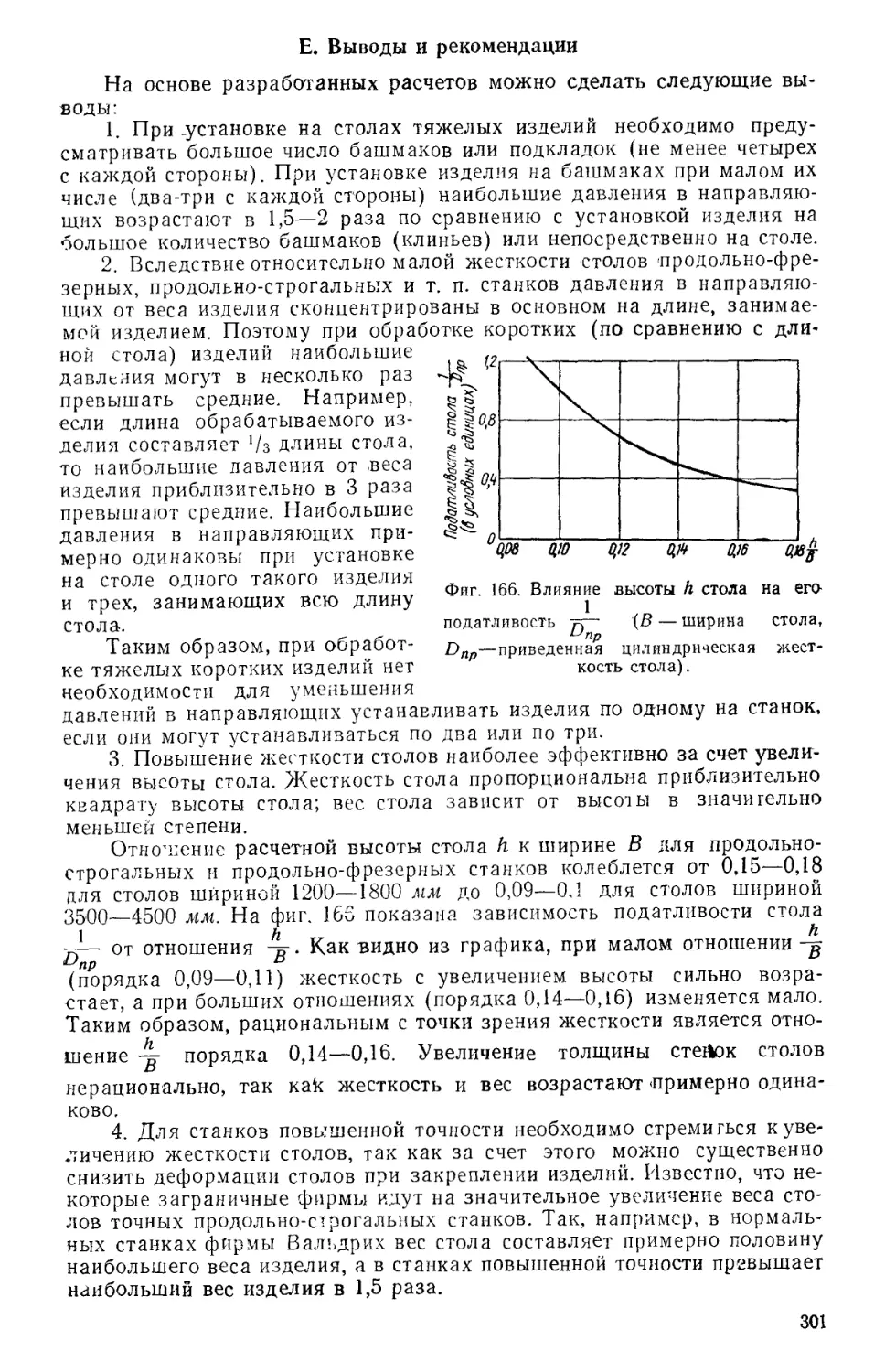
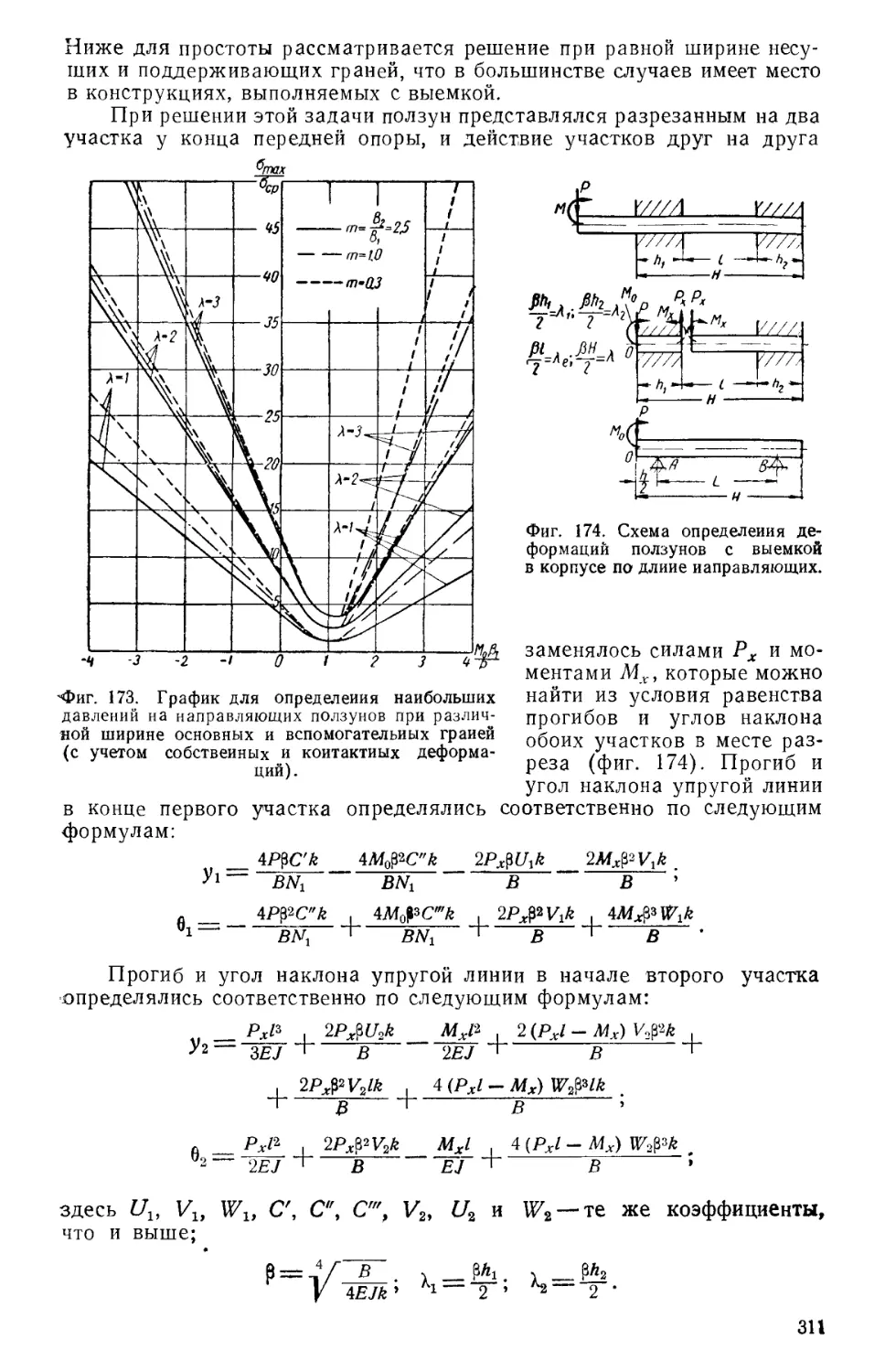
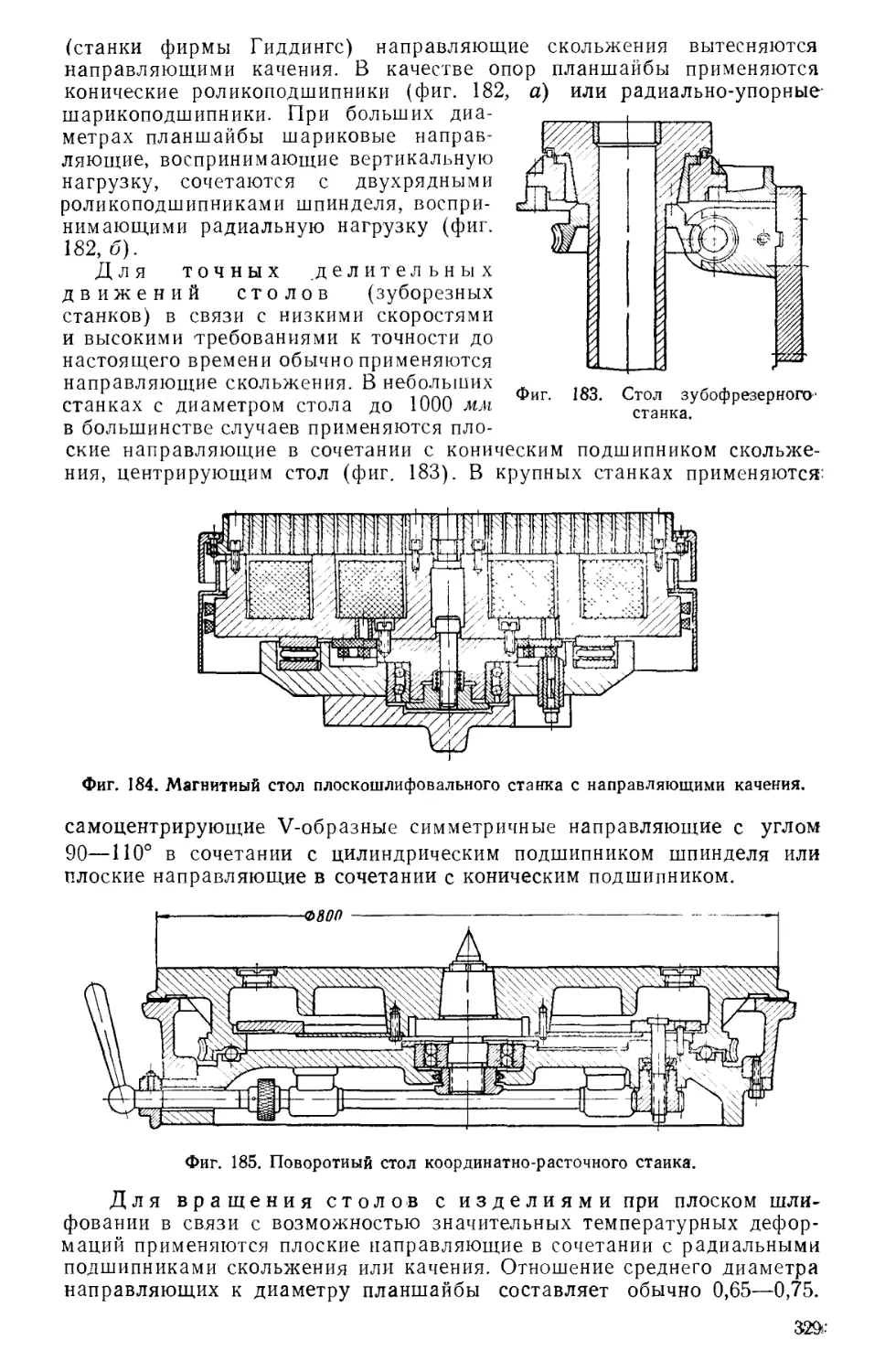
Tags: машиностроение металлорежущие станки металлургия конструирование станкостроение машгиз
Year: 1960
Text
ЭКСПЕРИМЕНТАЛЬНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ
ИНСТИТУТ МЕТАЛЛОРЕЖУЩИХ СТАНКОВ
ЭНИМС
В. В. КАМИНСКАЯ, 3. М. ЛЕВИНА, Д. Н. РЕШЕТОВ
СТАНИНЫ
И КОРПУСНЫЕ ДЕТАЛИ
МЕТАЛЛОРЕЖУЩИХ СТАНКОВ
(РАСЧЕТ И КОНСТРУИРОВАНИЕ)
Под редакцией
д-ра техн. наук проф. Д. Н. РЕШЕТОВА
ГОСУДАРСТВЕННОЕ НАУЧНО-ТЕХНИЧЕСКОЕ ИЗДАТЕЛЬСТВО
МАШИНОСТРОИТЕЛЬНОЙ ЛИТЕРАТУРЫ
Мое ква 1960
В книге изложены расчеты станин и корпусных
деталей станков, а также общие сведения по
конструированию этих элементов, связанные с расчетами.
В качестве основного критерия принят расчет на^
жесткость, при котором рассматриваются как
собственные деформации деталей, так и контактные деформации
в сопряжениях. Излагаются общие положения и допу-
' щения, на основе которых разработаны расчеты,
основные положения вывода расчетных формул и методика
технического расчета. Приведены результаты
экспериментов на моделях и на натурных станках,
подтверждающие приемлемость предлагаемых методов расчета.
В области конструирования освещены систематика
конструкций и выбор оптимальных Чрорад на основе
расчетов по важнейшим критериям работоспособности.
Книга предназначена для инженеров-конструкторов
станкостроителей, работников расчетных групп
конструкторских бюро и может быть полезной также для
конструкторов, работающих в других отраслях
машиностроения.
Редакция литературы по металлообработке и станкостроению
Зав. редакцией инж. В, Я. МИТЙН
ВВЕДЕНИЕ
Среди деталей станков удобно выделять две важнейшие группы,,
охватывающие подавляющее большинство основных деталей; 1) детали
привода — передачи, валы, подшипники; 2) детали несущей системы —
станины, корпусные детали !.
Эти группы резко различаются между собой: по форме (детали
привода преимущественно имеют осесимметричную форму, детали
несущей системы — коробчатую); по критериям работоспособности (у
деталей привода основной критерий — долговечность, у деталей несущей
системы— жесткость); по материалам (детали привода преимущественна
изготовляются из термически обрабатываемых сталей и цветных
сплавов, детали несущей системы — из чугуна и мягкой, легко свариваемой
стали).
Станины и корпусные детали по весу составляют 80—85% от веса
станка. Таким образом, экономия металла в станкостроении наиболее
эффективна в направлении снижения веса этих деталей.
Станины и корпусные детали в большой степени определяют
работоспособность станков*по важнейшим критериям — жесткости и
виброустойчивости.
Станины и корпусные детали являются значительно более
специфичными для станков, чем детали привода. Вместе с тем они гооаздо
менее исследованы и освещены в литературе, чем детали привода.
Если даже мелкие детали привода — небольшие зубчатые колеса,
валы — всегда выбираются по расчету, то размеры больших станин и
коробок до сих пор преимущественно выбираются на основе аналогии
с хорошо зарекомендовавшими себя в работе конструкциями.
Поэтому освещение вопросов расчета и конструирования станин
и корпусных деталей является первоочередной задачей.
Книга в основном посвящена расчетам. Конструирование
освещается в части-систематики конструкций и вопросов, непосредственно
связанных с расчетами, — выбора оптимальных соотношений размеров,
оптимальных форм и т. д.
Изложенные материалы разработаны в лаборатории динамики
и прочности станков отдела общих вопросов станковедения ЭНИМС 2.
1 Термин «корпусные детали» здесь применяется в его широком понимании для
обозначения деталей, составленных из отдельных стенок (преимущественно деталей
коробчатого сечения) и, следовательно, охватывает коробки, консоли, кронштейны^
•столы, суппорты и т. д.
2 В проведении экспериментов и расчетов принимали участие техники П. В.
Чиркова и В. А. Исаева.
ГЛАВА I
ОБЩИЕ СВЕДЕНИЯ ПО КОНСТРУИРОВАНИЮ И РАСЧЕТАМ
§ 1. СИСТЕМАТИКА КОНСТРУКЦИЙ
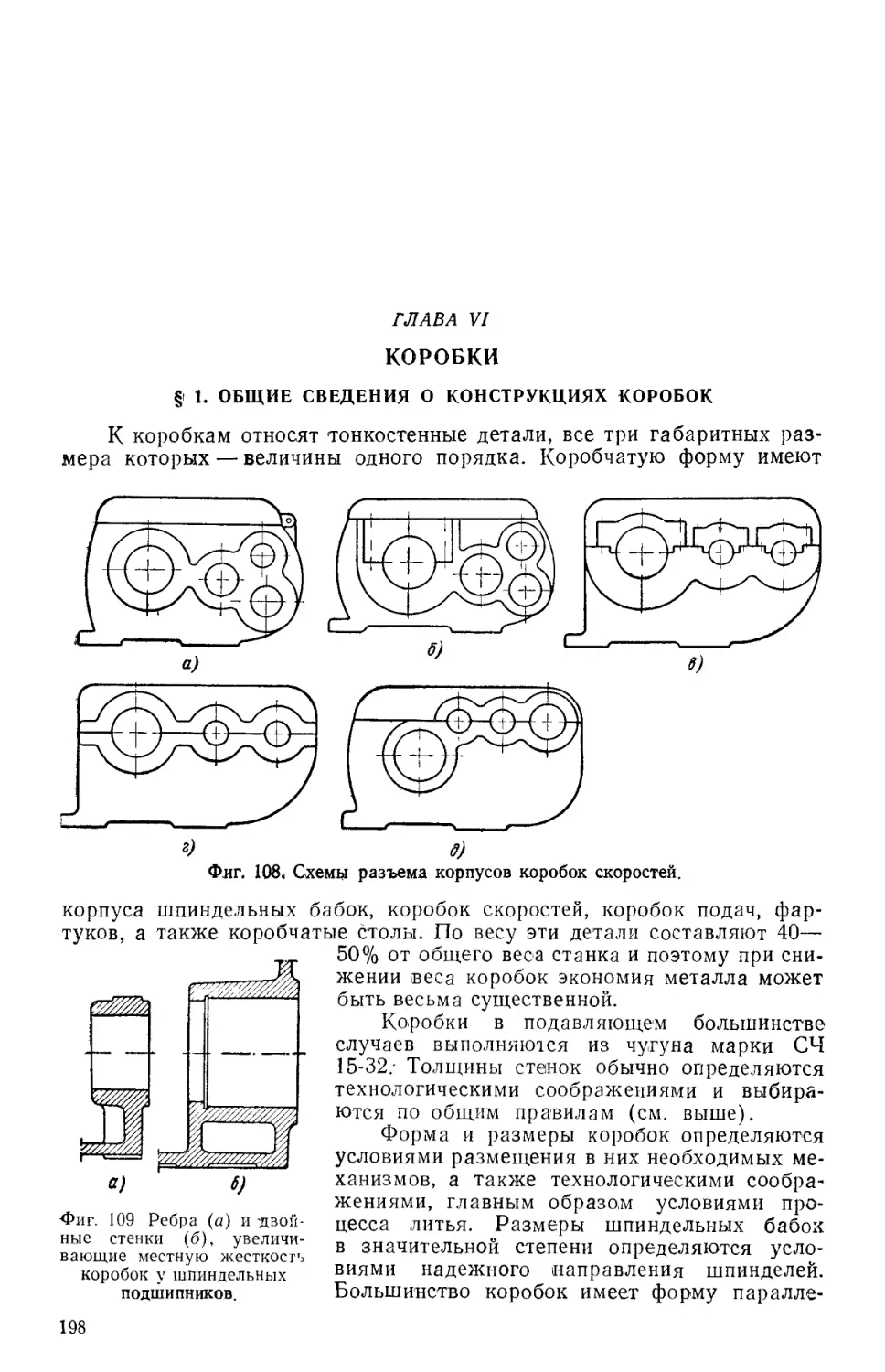
Рассматриваемые детали могут быть укрупненно разделены на
следующие группы:
1. Станины и основания.
2. Коробки.
3. Детали узлов для поддерживания и перемещения инструмента
и изделия.
Несущие системы станков удобно классифицировать (табл. 1) по
расположению оси станка — на горизонтальные и на вертикальные, по
схеме работы — на незамкнутые (балочного типа) и рамные и, наконец,
по количеству направляющих — -с одной системой направляющих,
с двумя и более системами направляющих. Элементы 'первой группы
удобно разделять (табл. 2) на основания, простые станины и
комбинированные станины.
Элементы второй группы — по назначению могут разделяться
(табл. 3) на коробки передач, на шпиндельные бабки (неподвижные и
подвижные) и на комбинированные шпиндельные бабки с коробками
передач. По конструкции они могут разделяться на закрытые и открытые,
а по форме — на имеющие форму параллелепипедов и цилиндрические.
Узлы для поддерживания и перемещения изделий и инструментов
могут быть систематизированы (табл. 4) по типу перемещений: с одним,
двумя или тремя поступательными перемещениями, с одним
вращательным перемещением без поступательных перемещений, с одним
вращательным и одним или двумя поступательными перемещениями.
Необходимые рабочие и установочные относительные перемещения
изделия и инструмента в большинстве станков производятся путем
перемещений как столов с изделиями, так и суппортов или ползунов с
инструментами. Чем тяжелее изделия, для которых предназначены станки,
тем больше перемещений отводится на долю инструмента.
Детали узлов для поддерживания и перемещения изделий могут
быть разделены: на столы (прямоугольные, круглые и коробчатые),
детали, поддерживающие столы (салазки, консоли), детали,
закрепляющие и поддерживающие заготовки в форме тел вращения (патроны,
задние бабки, люнеты).
Детали узлов для поддерживания и перемещения инструмента могут
быть разделены на инструментодержатели (простые и револьверные),
суппорты, несущие инструментодержатели, детали, поддерживающие и
5
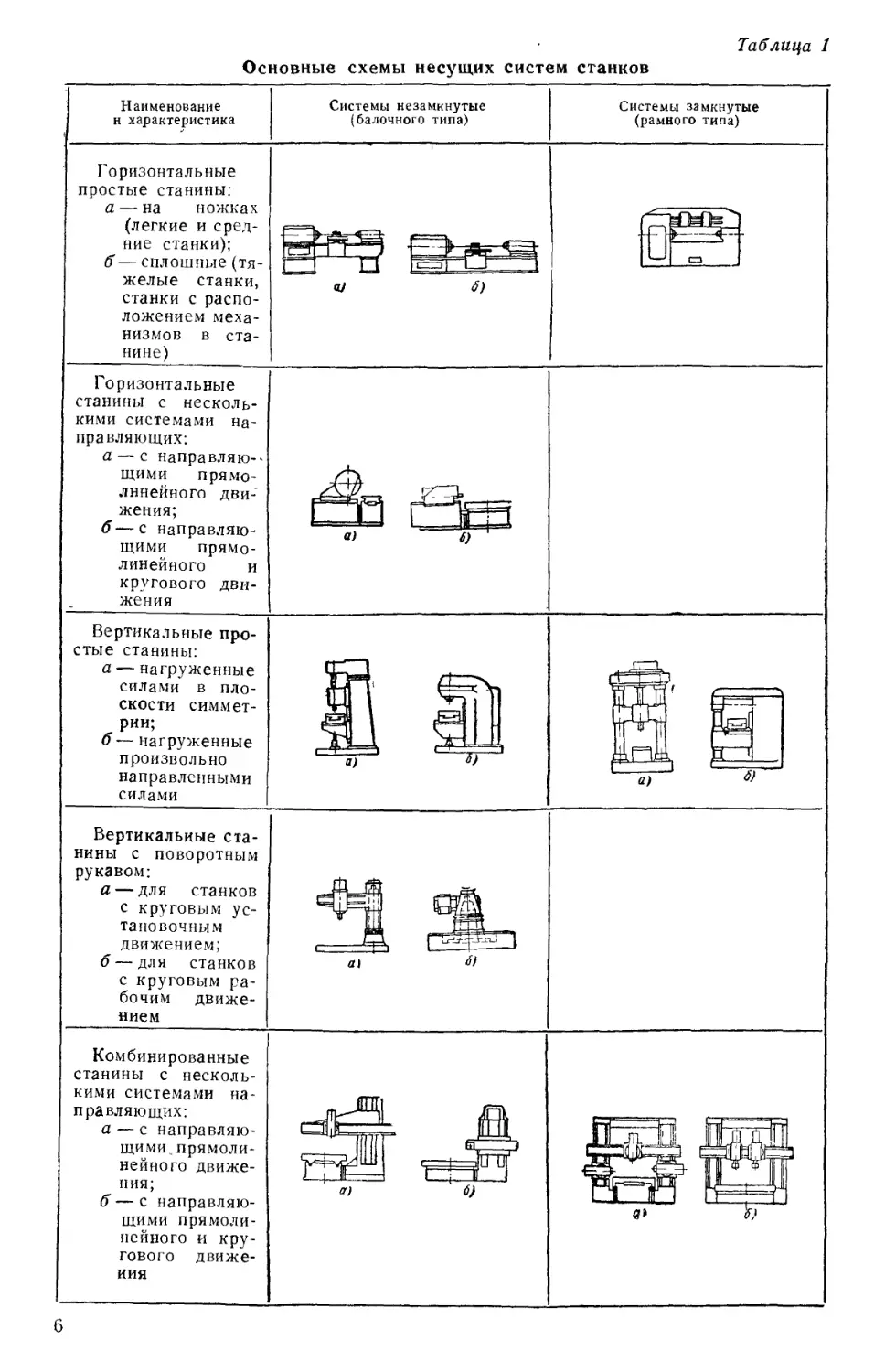
Основные схемы несущих систем станков
Таблица 1
Наименование
н характеристика
Горизонтальные
простые станины:
а — на ножках
(легкие и
средние станки);
б— сплошные
(тяжелые станки,
станки с
расположением
механизмов в
станине)
Горизонтальные
станины с
несколькими системами
направляющих:
а — с направляю—
щими
прямолинейного
движения;
б—с
направляющими
прямолинейного и
кругового
движения
Вертикальные
простые станины:
а — нагруженные
силами в
плоскости
симметрии;
б — нагруженные
произвольно
направленными
силами
Вертикальные
станины с поворотным
рукавом:
а — для станков
с круговым
установочным
движением;
б — для станков
с круговым
рабочим
движением
Системы незамкнутые
(балочного типа)
б)
Системы замкнутые
(рамного типа)
с^~~\
\ \
Й]еОС
> «=-
сз _ ;
~~5Г
Комбинированные
станины с
несколькими системами
направляющих:
а — с
направляющими^
прямолинейного
движения;
б— с
направляющими
прямолинейного и
кругового
движения
д^Ш1 г—г^7&"пГ
а) 6)
Таблица 2
Станины и основания
Наименование
и характеристика
Эскизы
Плиты
Тумбы (а)
Сплошные
основания (б)
ш
а)
6)
Горизонтальные
станины
^
Простые станины
Стойки, колонны
Станины-основания с
направляющими
кругового движения
И
Комбинированные станины
Станины с двумя
системами
направляющих:
а — с
направляющими
прямолинейного
движения;
б—с
направляющими
прямолинейного и
кругового
движения
Плиты и основания
Коробки и шпиндельные бабки
Таблица 3
Наименование
и характеристика
Закрытые
Открытые
Коробки передач
Ы Л
1н
г^
1 ц
Простые
шпиндельные бабки одношпин-
дельных станков
И
Шпиндельные бабки
с коробками скоростей
Простые подвижные
шпиндельные бабки од-
ношпиндельных станков
Уг^Ц
Подвижные
.шпиндельные бабки с
коробками скоростей
а
Ьё^
Шпиндельные бабки
многошпиндельных
станков
Г
1]
17=+^
. п 1Г-ЯР-Я-
3 __
Таблица 4
Узлы для поддерживания и перемещения изделия и инструмента
Виды перемещений
узлов
Узлы для поддерживания
и перемещения изделия
Узлы для поддерживания
и перемещения инструмент
Одно
поступательное
Два
поступательных
ГУТТ ^
ЕГТ
ет/Л
Три
поступательных
I
п ЖЕ
I ^
|И
Одно
вращательное
Одно
вращательное н одно
поступательное
*^
Одно
вращательное и два
поступательных
у
31
^ТШ
Примечание. Наклонные стрелки означают, чго движение может происходить
перпендикулярно плоскости чертежа.
9
направляющие суппорты (салазки, рукава, поперечины, ползуны) и,
наконец, кронштейны (поддерживающие сверлильные шпиндели,
фрезерные оправки и 'Т. д.) 1.
Все корпусные детали по форме можно разделить на:
1) детали, у которых одно измерение значительно больше, чем два
других (станины длинных станков, поперечины, ползуны);
2) детали, у которых два измерения значительно больше, чем
третье (плиты, шшские столы, суппорты);
3) детали, у которых все три габаритных измерения имеют
одинаковый порядок величин (коробки, консоли, короткие станины).
По условиям работы корпусные детали можно разделить на
неподвижные и подвижные.
§ 2. КРИТЕРИИ РАБОТОСПОСОБНОСТИ И РАСЧЕТА
Несущие системы станков должны обеспечивать и сохранять в
течение требуемого срока службы правильное расположение и возможность
точных и плавных взаимных .перемещений инструмента и изделий
вхолостую и при резании.
Для обеспечения этих требований конструирование станин и
корпусных деталей в настоящее время подчиняется критериям жесткости
деталей и износостойкости направляющих, а также условиям
технологичности. Как правило, условия прочности для этих деталей при выборе их
размеров и материала по указанным критериям удовлетворяются
автоматически. Расчеты и конструирование несущих систем по критерию
виброустойчивости до настоящего времени не разработаны.
Жесткость. Потребная жесткость станин и корпусных деталей
определяется следующими факторами:
1) работоспособностью станков, как технологических машин сточки
зрения точности обработки и устойчивости процесса резания;
2) работоспособностью механизмов станка;
3) условиями производительной обработки рассматриваемых
деталей и легкостью выверки станков при установке.
В балансе точности обработки упругие перемещения в
технологической системе играют решающую роль.
Упругие перемещения и отжатия, как известно, сказываются на
точности изделий следующим образом;ч
а) на поверхности изделия копируется форма заготовки;
б) происходит искажение формы изделий в местах входа и выхода
инструмента вследствие переменных сил резания;
в) на форме изделия сказываются деформации от центробежных
сил, вызванных неуравновешенностью и другими динамическими
нагрузками;
г) форма изделий искажается вследствие переменной жесткости
системы;
д) упругие деформации понижают точность установки инструмента
на размер.
В балансе упругих, приведенных к инструменту, перемещений стан-
'ков с вращательным главным движением со шпинделями, несущими
поперечную нагрузку, доля станин и корпусных деталей вместе с
направляющими прямолинейного движения достигает 50%, а в станках с
поступательным главным движением, в которых шпиндель отсутствует, —-
90% и более.
1 Подробнее этот вопрос изложен в гл. VII, § 1.
10
Жесткость системы и ее элементов, в первую очередь элементов,
обладающих значительной массой, таких как станины, существенно
влияет на устойчивость процесса резания {30], [53, б], [60].
Уменьшением упругих деформаций системы и повышением частоты
собственных колебаний можно существенно повысить
виброустойчивость. Наибольшее влияние на виброустойчивость имеет жесткость в
направлении, перпендикулярно*^ к поверхности обработки (т. е. в
направлении действия основных возбудителей колебаний), а также направление
осей жесткости или соотношение жесткостей по координатным осям.
Влияние жесткости станин и корпусных деталей на работу
механизмов станка определяется перераспределением давлений в
сопряжениях и нарушением условий правильного контакта в результате
упругих деформаций элементов системы.
- Упругие деформации суппортов и планшайб часто вызывают резкую
концентрацию давлений на направляющих, что служит причиной
повышенного неравномерного износа и заеданий. Имели место случаи, когда
из-за недостаточной жесткости станин и фундаментов оказывалось
невозможным перемещение порталов по направляющим в тяжелых
станках. Известны примеры сильного деформирования стенок коробок
скоростей при затяжке радиально-упорных подшипников валов коробок.
Станки с податливыми станинами быстрее разверяются в эксплуатации
при установке без подливки цементным раствором, чем станки с
жесткими станинами.
При обработке корпусных деталей с тонкими стенками,
недостаточно подкрепленными перегородками или ребрами, приходится
снижать режимы резания.
Жесткость несущих систем станков определяется:
а) собственной жесткостью деталей, рассматриваемых как балки,
пластинки ил(и оболочки, и б) жесткостью поверхностных слоев
сопряжений (контактной жесткостью). Вместе с контактными деформациями
условно рассматриваются местные деформации отгиба направляющих,
фланцев и т. д.
Жесткость несущих систем станков с точки зрения точности
обработки характеризуется упругим перемещением инструмента по нормали
к обрабатываемой поверхности под действием заданных сил.
Износостойкость направляющих, посадочных мест под подшипники,
резьбовых отверстий. Направляющие прямолинейного движения подачи
работают со значительным износом. Это связано с неполной защитой
направляющих от попадания стружки, песка и абразива и малыми
скоростями перемещений, которые не позволяют обеспечить образование
масляных клиньев. Направляющие главного движения в основном
выходят из строя из-за заеданий.
На посадочных поверхностях под кольца подшипников,
подвергающихся повторным сборке и разборке, происходит обмятие и износ
микровыступов и ослабление .посадок.
Долговечность направляющих станин и корпусных деталей,
точность которых сравнительно легко восстанавливается при ремонте,
например, незакаленных направляющих, а для крупных заводов,
имеющих продольно-шлифовальные станки, также и закаленных
направляющих, должна быть больше или равна межремонтным периодам.
Долговечность направляющих, точность или размеры которых трудно
восстанавливаются, например, посадочных поверхностей под подшипники,
закаленных направляющих станков, используемых на небольших
заводах, не имеющих оборудования для шлифовки направляющих,
и т. д., должна по возможности соответствовать долговечности
станка.
11
Следует считгть принципиально правильным применение накладных
направляющих или поверхностное упрочнение направляющих,
выполненных за одно целое со станинами.
Требование длительного сохранения точности по износу определяет
форму, а в некоторых станках, например в портальных, и расположение
направляющих.
Расчеты станин и корпусных деталей в настоящее время проводятся
на жесткость, а также на темлературные деформации с точки зрения
точности. Как уже указывалось, технические расчеты на жесткость
с точки зрения устойчивости процесса резания до настоящего времени
не разработаны.
Расчеты направляющих проводятся по наибольшим или средним
давлениям, а также на жесткость. Направляющие главного движения
рассчитываются из условия образования жидкостного трения.
Все эти расчеты освещаются в настоящей книге. Основное внимание
уделяется расчетам по доминирующему критерию работоспособности —
жесткости.
§ 3. СОСТОЯНИЕ ИССЛЕДОВАНИЯ ЖЕСТКОСТИ СТАНКОВ
И НОРМИРОВАНИЕ ЖЕСТКОСТИ
Теоретические исследования жесткости несущих систем станкон
ранее почти не проводились. Однако к настоящему времени проведено
значительное количество экспериментальных исследований суммарной
жесткости, баланса упругих перемещений, а также жесткости
отдельных элементов несущей системы непосредственно в станках и на
моделях.
Первое комплексное исследование собственной жесткости
несущей системы токарного станка и установление баланса
упругих перемещений было выполнено Кикебушем [66], [75]. Исследование
было проведено при нагружении токарного станка внутренней силой,
имитирующей силу резания. Упругие перемещения элементов
измерялись индикаторами с увеличителями перемещений, установленными на
специальных жестких стойках.
Первое фундаментальное исследование контактной
жесткости станков было проведено К. В. Вотиновым [10], который
показал роль контактных деформаций в балансе упругих перемещений
станков и разработал методику исследований контактной жесткости.
В дальнейшем вопросы контактной жесткости станков были развиты
в работах проф. А. П. Соколовского [59], [63], ЭНИМС [53, а] и др.
За последние десятилетия довольно широко исследовались вопросы
жесткости и баланса упругих перемещений в станках разных типов —
токарных [45], [22], карусельных [25, г], сверлильных [70],
горизонтально-расточных [22], [63], фрезерных [6], [19,6], [33], строгальных
[22], зуборезных [65], шлифовальных [20], [56].
Жесткое ть элементов несущих систем
непосредственно в станках исследовалась главным образом
с целью выяснения влияния перегородок разного типа на жесткость
станин токарных станков [44], [78]. Проводились также сравнительные
испытания сварных и литых станин [67].
Первые исследования жесткости элементов на моделях
были проведены в ЭНИМСе на моделях станин токарных станков с целью
выбора оптимальной системы перегородок [19]. Исследование
жесткости моделей стоек расточных станков в целях предотвращения
искажения контура сечения проведено на станкостроительном заводе
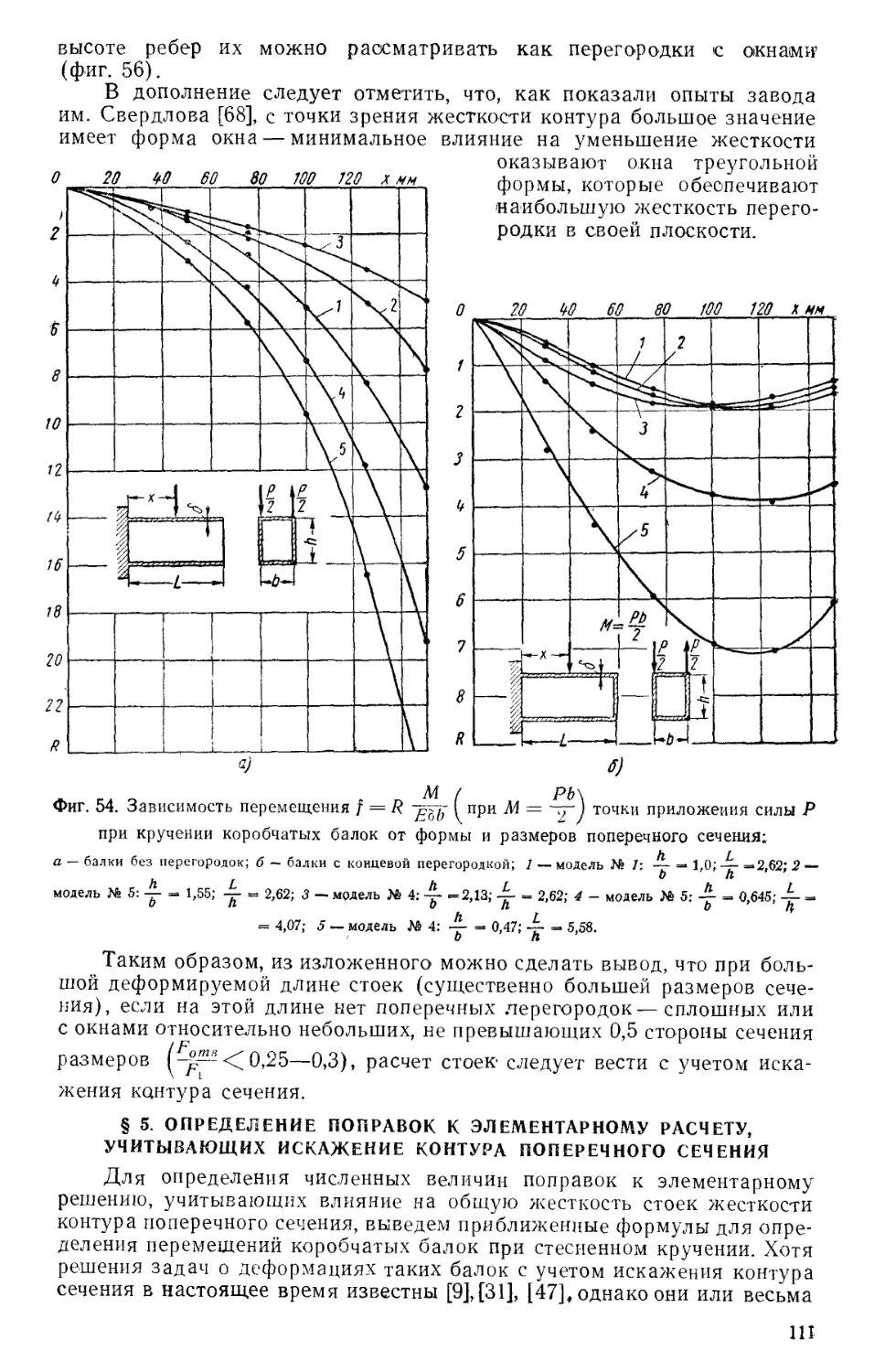
им. Свердлова [68].
12
За последнее десятилетие в ФРГ выполнено значительное
количество экспериментальных работ по жесткости сварных моделей
коробчатого сечения с окнами, различными системами ребер и лерегородок,
а также моделей станин, стоек, консолей и плит [71], [76].
Экспериментальное исследование контактной жеюткостн
с помощью моделирования проводилось на малых моделях плоских
стыков [59] и на моделях направляющих [45]. Проводились также
некоторые теоретические исследования вопросов контактной жесткости
простейших моделей с заданной микро- и макрогеометрией поверхности
[5], [16].
В области динамических исследований несущих систем
станков проводились работы по определению форм и частот колебаний
[23], [60], а также рассеяния энергии (главным образом в целях
сопоставления литых и сварных сганин) [72], [74].
Суммарная жесткость станков в настоящее время
нормируется. Нормируются упругие перемещения и отжатия по нормали
к поверхности обработки, как непосредственно влияющие на точность
обработки при заданных силах резания. При измерении жесткости
нагружение осуществляется статической силой в направлении
равнодействующей силы резания для наиболее характерного вида обработки
на станке. При выборе величины и направления силы соблюдаются
следующие условия:
а) величина силы должна быть достаточной для выборки зазоров
и для создания в сопряжениях характерных для станков давлений;
б) угол наклона силы к/направляющим должен быть больше угла
трения;
в) направление силы не должно совпадать с направлением, при
котором перемещения по нормали к обрабатываемой поверхности
равны нулю или малы (такая система названа К. В. Вотиновым
системой «бесконечной жесткости»),
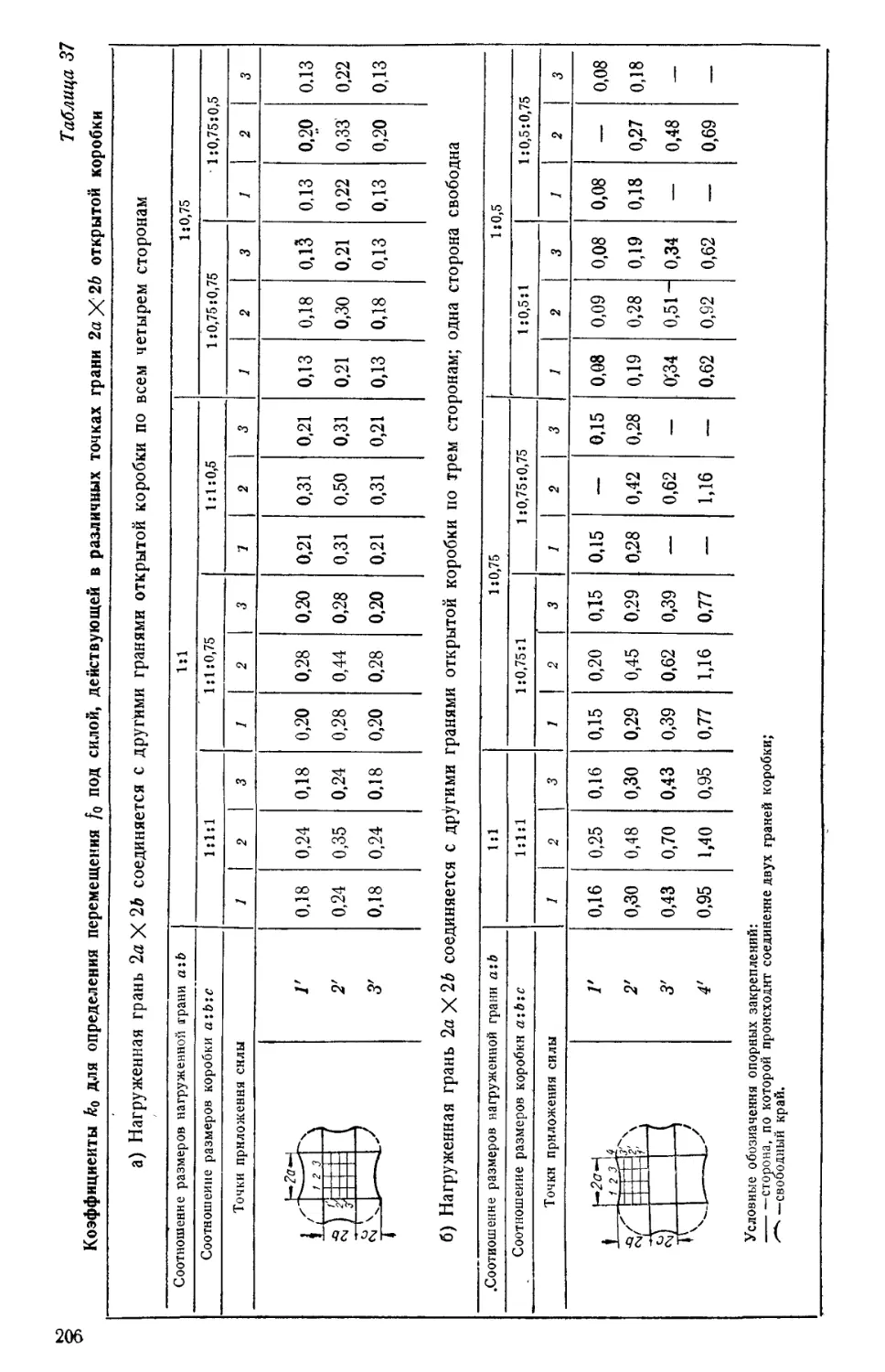
В табл. 5 .приведены сводные нормы суммарной жесткости станков.
Экспериментальные данные по балансу
упругих перемещений в станках приведены в табл. 6. Знание
баланса упругих перемещений особенно важно для создания
рациональных конструкций станков, т. е. предотвращения появления конструкций
с пониженной жесткостью системы за счет слабых элементов и с
заведомо повышенными жесткостью и массой других элементов.
Большинство указанных выше экспериментальных исследований
жесткости станков подчинено задаче общей оценки жесткости или
сравнительной оценке жесткости разных конструкций и ле содержит
никаких расчетных обобщений.
Опубликованные материалы по исследованиям с помощью
моделирования, как правило, не содержат исходных расчетных параметров
ъгоделей.
Поэтому при разработке методов расчета несущих систем станков
указанные исследования могли быть использованы в относительно
небольшой степени, главным образом в части качественной оценки
характера полученных расчетных зависимостей и влияния того или иного
фактора, а также установления усредненных коэффициентов контактной
податливости.
§ 4. ОСОБЕННОСТИ РАСЧЕТА СТАНИН И КОРПУСНЫХ ДЕТАЛЕЙ
Как уже указывалось, жесткость упругой системы станка
определяется собственйыми деформациями элементов несущей системы — станин
и корпусных деталей и контактными деформациями в сопряжениях.
Так как корпусные детали имеют весьма сложную конструктивную
форму и находятся под действием пространственной нагрузки, произве-
13
Таблица 5
Нормы суммарной жесткости станков [7], [8], [15]
I Типы станков; I Условия испытания I I I
номер государст- " 1 ; [ Суммарная жесткость
венного стандарта „ ^ „ Л „ Л ^ (условная) / - — кГ/мм Примечания
на нормы Схема нагружения Схема измерения Расположение узлов станка Нагрузка Р в кГ у* ' ' Ь '*»
жесткости |
Универсаль- Сила создаемся: Измеряются пере- Расстояние от торца Р — 0 075П1,5 * ^ л3/"— ® ~~ наиболь- |
ные токарные а) между суппор- мещения Ьп \\ д3 оп- шпинделя до торца кор- ' Зп = "§~" =? 1 ВО у О шид диаметр I
станки, том и оправкой, равки относительно пуса задней бабки равно обрабатывае-
ГОСТ 7895-56 установленной в резцедержателя по го- 0,75—0,85 наибольшего р мого изделия
шпинделе;. ризонтали в плоско- расстояния между цент- /3 «= -г— —140 у^й в мм
б) между суппортом сти действия силы: рами 3
и оправкой, уста- Ьп — перемещения
новленной в пииоли оправки, установ-
задней бабки. ленной в шпин-
Сила действует в пло- деле;
скости, перпендику- бз — перемещения
лярной к оси шпин- оправки, установи
] деля, и направлена ленной в пиноли
под углом 60° к го- задней бабки
ризонтали
Карусельные Сила создается между Измеряется переме- Расстояние от рабо- Я=6Д00,8 /=115г^5" ^ — наиболь-
станкн, планшайбой и оправкой, щение 6 оправки от- чей поверхности план- ший диаметр
ГОСТ 44-56 установленной в резце- носительно план- шайбы до точки прило- обрабатывае-
держателе верхнего суп- шайбы по горизонтали жения силы равно мого изделия
порта. Сила действует в в плоскости портала 0,4#шах; расстояние от в мм
плоскости, проходящей нижней кромки корпуса
через ось планшайбы и суппорта до точки при-
образующей угол 30° с ложения силы равно
вертикальной плоско- 7з# шах.
стыо, перпендикулярной Ятах — наибольшая
к плоскости портала, и высота обрабатываем
I направлена под углом 30° мого изделия
1 к горизонтали
14
Продолжение табл. 5
I Типы станков; I Условия испытания ^^^^ I I I
номер государст- ; [ 1 Суммарная жесткость
венного стандарта (условная) /= кПмм Примечания I
на нормы Схема иагружения Схема измерения Расположение узлов станка Нагрузка Р в кГ \ к* 5 1
жесткости | 1,1 ]
Автоматы Сила создается между Измеряется пере- Суппорт устанавли- Р =15^ /«-=875x^2 г* — наиболь-
токарные мно- суппортом и оправкой, мещение 6 оправки вается примерно в сред- шнй диаметр
гошпиндель- установленной в шпин- относительно суппор- нем положении подлине обрабатывае-
ные прутко- деле. Сила дейстзует в та в направлений по- направляющих попереч- мого прутка
вые горизон- плоскости, перпендику- перечной подачи нон подачи в мм
тальные лярной к оси шпинделя,
под углом 60° к направ- I
лению поперечной подачи I
суппорта I
~ ~ \ тя п Р & — наиболь-
Радиально- Сила создается между Измеряется верти- Рукав устанавливается Р = Я// / =» ший условный
сверлильные плитой (или столом) и кальное перемещение в среднем положении по ' 1>5г диаметр сверла
станки, оправкой, установленной б сверлильной голов- высоте колонны; свер- в млг
ГОСТ 98-59 в шпинделе, и действует кн относительно лильная головка распо- наиб'очь-
по оси шпинделя плиты (или стола) лагается на расстоянии шее расстоя
от колонны, равном 7з ние между ося-
нанбольшего ми колонны
и шпинделя
| | | [ | в м
Горизонталь- Сила создается между Измеряются пере- Расстояние от торца р = 0,75^1,5 /= 10й й — диаметр
но-расточные столом (или плптей) и ыещения- 61 н бг передней опоры шпин- Меньшее из двух выдвижного
станки оправкой, установленной шпинделя относитель- деля до точки приложе- значений жесткости шпинделя
в шпинделе. Сила дей- но стола (или плиты) ния силы равно половине должно быть не в мм
ствует на шпиндель в в плоскости действия наибольшего вылета меньше 2/3
плоскости, перпендику- силы, в радиальном шпинделя; расстояние от от большего
лярной к его оси: а) по направлении под уг- рабочей поверхности сто-
горизонтали. «отрывая» лом 60° к направле- ла до точки приложения
шпиндельную бабку; нию действия силы силы равно половине I
б) по вертикали — сверху наибольшего перемеще-
вьиз ния шпиндельной бабки
15*
; ^ Продолжение табл. 5
I Типы станков; I Условия испытания | | |
номер государст- ' 1 1 1 — Суммарная жесткость
{венного стандарта (условная^ /—_- кГ1мм Примечания
на нормы Схема аагружения Схема измерения Расположение узлов станка Нагрузка Р в кГ \ К1 ' ' Ь '
жесткости I I | || 1
Консольно- Сила создается между Измеряется переме- Стол устанавливается Р=0Д125В2 ; ^ 25 У~ЁР В — ширина
фрезерные столом и оправкой, уста- щение б оправки от- ^п0 ВЬ1СОТе сТОйки) для рабочий
станки, новленной в шпинделе, носительно стола ^горизонтально - фрезер- поверхности
ГОСТ 13-54 Сила действует в верти- направлении попереч- ных станков на расстоя- стола в мм
кальной плоскости, рас- ной подачи нпи от оси шпинделя до
положенной под углом рабочей поверхности сто-
40° к плоскости, прохо- ла> равном 0,4 наиболь-
дящей через продольную шего, для вертикально-
ось -стола, и направлена Фрезерных — на расстоя-
под углом 30° к горизон- нии от торца шпинделя
тали до рабочей поверхности
стола, равном 0,5 наи-
I I ! I большего расстояния ' I 1
Долбежные ст^^ Измеряется пере-1 Расстояние отрабо-| р = Ш 1=жУИ |#~наиболь-
станки, Ткп^Нпй РГ ппД^ мещение 6 оправки по чеи поверхности стола до У УП шая длина
ГОСТ 26-56 новленной в долбяке. гориз0нтали в плос- точки приложения силы хода долбяка
Сила действует в плос- Л, дейс" я "„„„ равно 0,35-0,65 наиболь- в мм
кости симметрии станка К0сти Действия силы 1., длины хода долб! в**
и направлена под углом (меньшие значения для
1 60° к горизонтали I I больших станков) 1 1_ I
Продольно- Сила создается между Измеряются пере- Стол устанавливается Р = 3,35В , _ Р 3Ак~ ^ ~ ширина
строгальные столом и оправкой, уста- мещения бв и Ьг в среднем положении, /в— &в =* 4\Ю у В рабочей по-
станки новленной в резцедержа- оправки относительно вылет ползуна прини- верхности
теле суппорта. Сила дей- стола по вертикали и мается наименьший. . р за— стола в мм
ствует в вертикальной горизонтали в плос- Расстояние от рабочей 1г=1~Ъ—— 150 V В
плоскости, расположен- кости портала поверхности стола до *
ной под углом 30° к точки приложения силы
плоскости, проходящей равно 0,4 наибольшего,
через продольную ось суппорт располагается
стола, и направлена под посередине поперечины
углом 30° к
горизонтали - I
16
Таблица в
Экспериментальные данные по укрупненному балансу приведенных к инструменту упругих перемещений в стайках
(без деформаций изделий) при значительных статических нагрузках [6]; [8]; [19]; [20]; [21]; [25, г]; [25, е]; [33]; [45]; [75]
I I Составляющие полного перемещения инструмента относительно изделия, определяемые I .
I деформациями отдельных элементов, в % \
Типы станков Суппорт, стол (у консольных Шпиндельная бабка со шпин- Примечания (условна составления баланса)
Станина» стойка станков вместе с салазками делем, задняя бабка с пино-
и консолью), рукав лыо (во фрезерных станках
шпиндель, хобот, оправка)
Токарные станки Станина (на нож- Суппорт: Шпиндельная бабка со Нагружение силой в плоскости, перпендикуляр-
общего назначе- ках) до 15% при точении у перед- шпинделем: при точении ной к оси шпинделя, под углом 60° к горизонтали.
ния ней бабки — около посередине изделия— Суммарное перемещение измеряется по горн-
50%; около 15%; у передней зонтали в плоскости действия силы
посередине изделия— бабки — около 50%. Зад-
около 50%; няя бабка с пинолыо:
у задней бабки— при точении посередине
около 30% изделия — около 30%;
у задней бабки—около
70%
I Двустоечные В плоскости порта- Суппорт с ползуном: — Нагружение силой, направленной под углом 30°
карусельные ла: портал—60— в плоскости порта- к горизонтали в плоскости, расположенной под
станки 80%, поперечина — до ла —20—40%; углом 30° к вертикальной плоскости, перпенди-
10%. В плоскости, в плоскости, перпеи- I кулярнон к плоскости портала. Суммарные
переперпендикулярной к дикулярной к плос- мещения измеряются по горизонтали. Вылет
плоскости портала: кости портала,— ползуна равен 'Д, а расстояние от планшайбы до
портал до 10%, по- 50—70% I точки приложения силы — 1/2 наибольшей высоты
перечина — 25—40% обрабатываемой детали
I Вертикально- Стойка —10—15% Стол н кронштейн— — Нагружение силой, действующей по оси шпин-
сверлильные 85—90% деля; суммарное перемещение измеряется в на-
станки I правлении действия силы
17
Продолжение табл. б
I ] Составляющие полного перемещения инструмента относительно изделия, определяемые
| деформациями отдельных элементов, в % 1
Твцы станков Суппорт, стол (у консольных Шпиндельная бабка со шпин-1 Примечание (условна составления баланса)
Станниа, стойка станков вместе с салазками делем, задняя бабка с пино-
и консолью), рукав лью (во Фрезерных станках
I г; шпиндель, хобот, оправка)
Радиально- Плита и колонна— Рукав—20—30% Шпиндельная бабка— Нагружение силой, действующей по оси шпнн-
сверлильные 60—75% до 10% деля; суммарное перемещение измеряется в на-
станки ] правлении действия силы. Головка располагается
на расстоянии, равном 2/з наибольшего расстоя-
| I | 1 ния от колонны
Горизонтально- Станина и стойка 7- Стол—10—20% Шпиндельная бабка со Нагружение силами, действующими в плоскости,
расточные станки 15—20% (шпинделем — 60—70% перпендикулярной к оси шпинделя. Вылет шпинч
1 деля равен половине наибольшего
Консольные Стойка — 2—3% Стол (в горизонталь- Оправка со шпинделем
I горизонтально- * ной плоскости перпенди- и хоботом (в горизон-
фрезерные кулярно к зеркалу ста- гальнон плоскости пер*
станки вины)— до 90% пендикулярно к зеркалу
о л \ Нагружение силой, направленной под углом 30°
в оалансе вертикаль- горизонтали в плоскости, расположенной под
мешенияеМеЩеННИ "'И Углом 40° к вертикальной плоскости, проходя-
„. оправки и « через продольную ось стола. Стол устанав-
шпинделя составляют по- ЛйваетсРя (п0Р высотеУ стойки) для горизонтально-
д ВЛЯКШГУЮ часть фрезерных станков — на расстоянии от оси
! _—, Л шпинделя до рабочей поверхности стола, равном
/ 0,4 наибольшего; для вертикально-фрезерных -
Консольные Стойка —до 10% Стол (в горизонталь. Шпиндель — 15—30% станков —на расстоянии от торца шпинделя до
вертикально- ной плоскости перпенди- рабочей поверхности стола, равном 0,5 наиболь-
фрезерные кулярно к зеркалу ста- шего
станки нины)—70—85%.
В балансе
вертикальных перемещений
перемещения стола с салаз- [
ками и консолью
составляют подавляющую часть
18
Продолжение табл. 6
1 ) Составляющие полного перемещения инструмента относительно изделия, определяемые I
деформациями отдельных элементов, в %
Типы станков | Суппорт, стол (у консольных Шпиндельная бабка со шпин- Примечания (условия составления баланса)
Станина, стойка [ станков вместе с салазками- делем, задняя бабка с пино-
и консолью), рукав лью (во фрезерных станках
шпиндель, хобот, оправка)
Двустоечные Портал—15—20% Стол —до 10% -— Нагружение силой, направленной под углом 30°
продольно- Суппорт (вместе с по- к горизонтали в плоскости, расположенной под
строгальные перечиной)—до 75% углом 30° к вертикальной плоскости, проходящей
станки через продольную ось стола. Суммарные
перемещения измеряются по вертикали и горизонтали
в плоскости портала. Вылет ползуна —
наименьший. Расстояние от рабочей поверхности стола до
поперечины равно 0,4 наибольшего. Суппорт рас-
I I полагается посередине поперечины
Долбежные Станина и колон- Стол и салазкн — 5— — Нагружение силой в плоскости симметрии
станки на — 25—50% 15%, долбяк — 30—60% станка под углом 60° к горизонтали. Суммарное
перемещение измеряется по горизонтали в
плоскости действия силы. Расстояние от рабочей
поверхности стола до точки приложения силы
равно 0,35—0,65 наибольшей длины хода долбяка
Круглошлифо- — Стол — до 3% Шлифовальная бабка —
вальные станки со шпинделем—до 50%.
Бабка изделия со I
шпинделем и задняя
бабка с пинолью — до
55%
Плоскошлифо- | Колонна — до 15% — Шлифовальная бабка —
вальные станки со шпинделем — около
*■*" ■« и ||.п — I. п | ,,...,,, I , ..,,., -. , , , , ■ - , ■ .1 .1 . I, I .1 11 .. . I
19
сти точный расчет этих деталей не представляется возможным. Поэтому
предлагаются приближенные расчеты.
В этих расчетах силовые факторы, действующие на корпусные
детали, рассматриваются как сосредоточенные, приложенные в одном
сечении. Деформации корпусных деталей определяются в зависимости
от их формы, как для брусьев, пластин или коробок, состоящих из
пластин, некоторой постоянной приведенной жесткости.
Детали, у которых один из габаритных размеров значительно
больше двух других, рассматриваются как брусья.
Детали, у которых два габаритных размера значительно больше
третьего, рассматриваются как пластины.
Детали, у которых все три габаритных размера одного порядка,
рассматриваются как коробки.
Приведенная жесткость элементов определяется по следующей
схеме:
а) Сложная пространственная система загоняется ей подобной,
состоящей из элементов правильных геометрических форм (например,
стенки и перегородки станин токарных станков полагаются имеющими
правильное прямоугольное сечение).
б) Такая упрощенная пространственная система рассчитывается
при некоторых частных видах нагружения, близких к реальным
(например, при определении жесткости кручения станина токарного станка
рассматривается под действием двух равных по величине и
противоположных по знаку моментов по концам).
Так как проведение точного расчета даже такой упрощенной
системы представляет существенные трудности, проводится
приближенный расчет при помощи вариационных методов решения задач
строительной механики.
в) .Точность разработанных расчетов для упрощенных систем
проверяется сравнением результатов расчетов и экспериментов на моделях
правильных геометрических форм, соответствующих рассмотренной
упрощенной системе.
При экспериментах нагружение и закрепление моделей
принимаются по возможности более точно соответствующими принятым при
расчетах.
г) Результаты разработанного и проверенного на моделях расчета
упрощенных систем распространяются на реальные конструкции —
принимается, что элементы правильной формы, образующие упрощенную
систему, имеют те же геометрические характеристики сечений, что и
соответствующие элементы реальных систем (например, что сечения
стенок элемента правильной формы имеют те же моменты инерции и
площади, что и сечения стенок станины реального станка). Возможность
такого распространения проверяется сравнением результатов расчетов и
экспериментов над реальными конструкциями при схемах нагружения,
по возможности более точно соответствующих принятым при
расчете.
д) Приведенная жесткость данного элемента определяется из
условия равенства перемещений элемента, рассматриваемого как брус или
пластина и как пространственная система, при выбранном частном виде
нагружения.
Конечная точность приближенных расчетов по выбранной схеме
оценивается сравнением результатов расчетов и экспериментов на
реальных станках при статическом нагружении, соответствующем нагруже-
нию их при резании.
Детали, перемещаемые по направляющим (суппорты, ползуны,
столы и т. п.), рассматриваются как балки или плиты на упругом осно-
20
вании (или упругих опорах), которым являются поверхностные слои
направляющих.
При расчетах принимается допущение о линейной зависимости
между давлениями и сжатиями поверхностных слоев, причем
коэффициенты пропорциональности, называемые коэффициентами контактной
податливости, определяются путем обработки экспериментальных
данных по перемещениям в сопряжениях станочных деталей.
С точки зрения расчета все сопряжения корпусных деталей можно
разделить на две группы:
1. Сопряжение деталей осуществляется на участках од*носительно
небольшой протяженности (соизмеримых с размерами поперечных
сечений контактирующих деталей), или собственная жесткость обеих
деталей существенно больше жесткости поверхностных слоев; для этих
сопряжений собственными деформациями деталей можно пренебречь
и рассматривать их взаимное смещение как смещение жестких тел
в результате контактных деформаций.
2. Сопряжение осуществляется на относительно большой длине,
и жесткость контактирующих деталей сопоставима с жесткостью
поверхностных слоев; для этих сопряжений упругие перемещения и
давления в сопряжении определяются из совместного рассмотрения
деформаций корпусов и поверхностных слоев.
Следует отметить, что в некоторых случаях в сопряжениях деталей
возникают значительные местные деформации (отгиб направляющих,
фланцев и т. п.). Однако, так как разделение местных и контактных
деформаций представляет значительные трудности, в первом
приближении эти деформации рассматриваются совместно, а наличие местных
деформаций учитывается повышенными значениями коэффициентов
контактной ^податливости.
Собственная жесткость элементов, рассматриваемых как брусья,
характеризуется приведенной жесткостью на изгиб в двух плоскостях
и кручение; жесткость элементов, рассматриваемых как пластины, и
жесткость стенок коробки — приведенной цилиндрической жесткостью.
Жесткость сопряжений можно характеризовать относительными
перемещениями в стыке (угловыми или линейными). Однако эти величины,
отдельно взятые, не могут характеризовать влияние жесткости
элементов на суммарную жесткость станка. Поэтому при расчетах станин и
корпусных деталей их суммарную жесткость предлагается
характеризовать величиной перемещения инструмента относительно изделия
в результате деформаций данного элемента (или узла) при заданной
силе.
Анализируя влияние отдельных параметров на приведенную
к инструменту податливость упругой системы станка при
существующих схемах компоновки, можно установить оптимальные с точки
зрения жесткости и веса формы и соотношения размеров элементов.
До установления норм жесткости на отдельные элементы станков
разработанные расчеты эффективно применять как сравнительные.
Для того чтобы по вычисленной величине перемещения
инструмента относительно изделия в результате деформаций данного элемента
судить о его жесткости, следует сравнить эту величину с
перемещениями, вычисленными аналогичным образом для других станков,
хорошо показавших себя в эксплуатации. Результаты проверочных
расчетов элементов несущих систем ряда современных отечественных
станков приводятся в настоящей книге.
Допустимую величину приведенных к инструменту упругих
перемещений элемента можно также оценивать по требуемой точности
обработки и балансу упругих перемещений.
21
Работоспособность направляющих в значительной мере
определяется возникающими в них давлениями. Как уже'указывалось, при их
расчете детали, перемещаемые по направляющим, — суппорты, столы,
ползуны — рассматриваются как балки или плиты на упругом
основании. Это позволяет установить распределение давлений по длине
направляющих и определить величины наибольших давлений. Расчет по
наибольшим давлениям позволяет оценить истинные условия работы
направляющих, влияние жесткости перемещающихся деталей и вида их на-
гружения (зависящего от формы, размеров и способа закрепления
устанавливаемых на столах изделий и т. п.). Допустимые давления
установлены на основе опыта эксплуатации станков.
Для направляющих главного движения, работающих с большими
скоростями, производится проверка несущей способности масляного
слоя в соответствии с гидродинамической теорией смазки.
При определении температурных деформаций критерием расчета
является точность обработки или правильность работы механизмов.
Станины и корпусные детали рассматриваются как брусья или коробки,
состоящие из тонких стенок. Определение установившихся температур
станин и корпусных деталей производится путем рассмотрения
теплового баланса при работе механизмов станка и в процессе резания.
В книге излагаются общие положения и допущения, на основе
которых разработаны расчеты, основные положения вывода расчетных
формул и методика технического расчета. Формулы, необходимые для
технического расчета, пронумерованы.
§ 5 МАТЕРИАЛЫ
Выбор материала станин и корпусных деталей определяется
основным критерием их работоспособности — жесткостью, а также
технологическими требованиями; деталей, несущих направляющие, —
дополнительно критерием износостойкости [18].
Станины и корпусные детали изготовляются из материалов со
значительным модулем упругости, допускающих изготовление деталей
совершенных форм, — чугуна и мягких, легко свариваемых и термически не
обрабатываемых сталей (термическая обработка не повышает модуль
упругости).
Станины и корпусные детали преимущественно выполняются
чугунными литыми вследствие:
а) широких возможностей получения требуемых (иногда весьма
сложных), геометрических форм, красивого внешнего вида, удобства
обтирки и т. д.;
б) относительно невысокой стоимости при серийном изготовлении,
в котором стоимость модельного комплекта раскладывается на
значительное количество отливок;
в) значительного внутреннего трения чугуна.
Стальные сварные станины преимущественно применяются при
относительно простых формах (во избежание повышенной трудоемкости
вырезных, гибочных и сварочных работ), в индивидуальном и
мелкосерийном производстве, а также при очень больших, и особенно ударных,
нагрузках. Применение сварных конструкций особенно эффективно для
деталей, размеры которых в значительной степени определяются
допустимыми прогибами от собственного веса, например, для поперечин
тяжелых продольных станков.
К достоинствам сварных станин по сравнению с литыми чугунными
относятся: а) меньший (до 2 раз) вес вследствие большего модуля
упругости стали, чем чугуна, и возможности применения более совер-
22
шенных с точки зрения жесткости форм; б) меньшая трудоемкость
механической обработки; в) возможность исправления дефектов
конструкций (вырезания окон, приварки ребер); г) ускорение процесса
производства [72].
Сварные станины, имеющие одинаковые с литыми габариты
сечений, при меньшем, чем у литых, весе могут быть выполнены более
высокой жесткости. Демпфирующая способность стальных сварных станин
близка к демпфирующей способности чугунных вследствие повышенного
рассеяния энергии в местах контакта сваренных элементов [74].
Необходимая износостойкость направляющих сварных станин
может быть обеспечена применением привертных или приваренных
направляющих, термически обрабатываемых до высокой твердости.
В качестве материалов для литых станин и корпусных деталей
основное применение имеют:
а) для станин станков средних размеров с направляющими,
выполненными за одно целое, — чугун I класса марки СЧ 21-40 перлитной
структуры или модифицированные чугуны марок СЧ ч 35-56 или
СЧ 38-60 сорбитно-перлитной структуры;
б) для станин сложной конфигурации и станин тяжелых станков во
избежание возникновения высоких остаточных налряжений и
образования трещин при остывании, станин прецизионных станков во избежание
потери точности от остаточных напряжений и станин с привертными
направляющими— чугун II класса марки СЧ 15-32 перлитно-ферритной
(феррита до 20%) структуры;
в) для корпусов коробок скоростей, подач, в связи с отсутствием
поверхностей, систематически работающих на износ, — преимущественно
чугун марки СЧ 15-32;
г) для консолей, салазок, столов, планшайб выбор марки чугуна
обычно определяется условиями работы направляющих. Наиболее
распространенный материал — чугун марки СЧ 15-32.
Для сварных станин и корпусных деталей преимущественно
применяется сталь марок Ст. 3 или Ст. 4.
Выбор материала направляющих приведен на стр. 249.
При конструировании литых деталей, как известно, должны
обеспечиваться следующие технологические условия: а) простота
изготовления моделей и стержней и простота формовки; б) получение здоровой
отливки без литейных пороков и высоких остаточных напряжений;
в) удобство очистки литья.
Толщины стенок чугунных отливок, рекомендуемые из
технологических соображений, 'можно выбирать по табл. 7 в зависимости от
приведенного габарита отливки. Приведенный габарит, т. е. размер короб-
Таблица 7
Рекомендуемые толщины стеиок чугунных отливок
I Приведенный
1 габарит в м
0,75
1,0
1.5
1.8
2Д
Толшина
наружных
стенок в мм
8
10
12
14
16
Толщина
внутренних
стенок в мм
в
10
12
12
Приведенный
габарит в м
2,5
3
3,5
4,5
Толщина
наружных
стенок в мм
18
20
22
25
Толщина
внутренних
стенок в мм
14
16
1 20
1 Примечание. Эти толщины стенок соответствуют настоящему уровню технологии и
| в дальнейшем будут уменьшаться.
23
Таблица 8
Рекомендуемые толщины стенок н сопряжения в чугунных отливках
станин стаиков в мм
I Стенки наружные
Тип I Тип П
Наружная сторона
Внутренняя \гг*^В ну тренья
сторона
I
от-до»
Н
В
Стеики наружные
вертикальные
*1
Стеики внутренние
вертикальные
Ах
Направляющие
и горизонтальные
стенки
Л*
*1
600-
1000-
1500-
2250-
3000-
4000-
5000-
6500-
8000-
-1000
-1500
-2250
-3000
-4000
-5000
-6500
-8000
-100001
300
400
500
500
600
600
700
700
800
<400
>400
<700
>700
<1000
>1000
<1200
>1200
<1400
>1400
<1б00
>1600
<180()
>1800
<2000
>2000
<2000
>2000
10
12
12
14
14
16
16
18
18
20
20
22
22
24
24
2Ь
26
28
10
10
10
10
15
15
10
12
12
15
15
20
20
20
20
30
35
35
40
40
45
45
55
55
25
30
35
40
40
45
45
50
50
10
10
12
12
14
14
16
16
18
18
20
20
22
22
24
24
26
12
12
14
14
16
16
20
20
20
14
16
18
20
22
24
26
28
30
8
8
10
10
12
12
15
15
18
20
25
25
30
30
35
35
40
25
30
35
40
45
45
50
55
60
14
16
16
18
18
20
22
24
26
10
10
10
15
15
15
15
15
20'
Примечания: 1. Размеры уклонов в мм: для стеиок стании наименьшего размера с =6; Н = 50;
с1 = 4;,Л4 *=» 35; для стенок станин остальных размеров с = 8; Н = 70; сх= 6; Н1 = 50; для стенок
станин первых трех размеров с2 = 8; йа = 70; для остальных <?2 = 10; И.2 «= 60.
2. Припуски на обработку выбираются по ГОСТу 1855-55; прн составлении данной таблицы они
не учитывались.
24
чатой отливки кубической формы, эквивалентной рассматриваемой
отливке в отношении достижимых толщин стенок, рекомендуется
определять по формуле
™ ~~ 4
где Ь, В, Н — соответственно длина, ширина и высота отливки в ж.
Толщины внутренних стенок (ребер и перегородок) в связи с
худшими условиями остывания выбираются равными бколо 0,8 от толщин
стенок. Высота ребер должна быть не больше их 5-кратной толщины.
Рекомендуемые толщины стенок и сопряжения для чугунных отливок
станин станков (по данным специального конструкторского бюро па
станкостроению) приведены в табл. 8.
Толщины стенок сварных конструкций в отличие от литых
определяются, как правило, условиями жесткости, причем технологические
соображения на выборе толщины сказываются значительно меньше, чем
в литых конструкциях. В тонкостенных конструкциях необходимая
жесткость достигается путем применения замкнутых сечений, а также
перегородок, ребер, раскосов. Это позволяет применять толщины стенок для-
деталей средних станков порядка 3—6 мм.
В обычных толстостенных сварных конструкциях,
трудоемкость изготовления которых значительно меньше, сечения близки к
сечениям литых, а толщины стенок деталей средних станков обычно
назначаются около 10 мм.
Для станков крупносерийного выпуска целесообразно применение
направляющих из профильного проката.
Перспективны конструкции с применением штампованных
элементов, так называемые штампованно-сварные конструкции, а также свар-
но-литые конструкции, расширяющие области применения сварных
деталей станков.
Важнейшей задачей при конструировании и изготовлении сварных
станин и корпусных деталей является уменьшение сварочных
деформаций. Для этого следует применять в конструкциях с симметричными
сечениями симметричное расположение швов, а в общем случае по
возможности обеспечивать условие, чтобы сумма моментов объемов
наплавленного металла относительно оси, проходящей через центры тяжести
сечений, была бы близкой или равной нулю. Уменьшение сварочных
деформаций может быть достигнуто также общим повышением
жесткости конструкции.
* Эта формула методически более правильна, чем широко распространенная*
21 + В + И
3
ГЛАВА II
ГОРИЗОНТАЛЬНЫЕ СТАНИНЫ
§ 1. ОБЩИЕ СВЕДЕНИЯ О КОНСТРУКЦИЯХ
Большая- часть станков выполняется с горизонтальными станинами.
Распространенность горизонтальной компоновки определяется
следующими обстоятельствами:
1) удобством наблюдения за зоной резания при обработке
поверхности изделий значительной длины;
2) простотой и жесткостью установки тяжелых и длшщых изделий
на столах горизонтальных станин;
3) облегчением условий работы станин в результате совместной
работы с фундаментами;
4) невозможностью выполнения станков для длинных деталей
вертикальными из-за габаритов цеха.
С горизонтальными станинами выполняется подавляющее
большинство станков для цилиндрических изделий: токарной группы, включая
тскарно-сверлильные, кругло- и резьбо-фрезерных, кругло- и внутришли-
фовальных. Исключение составляют станки карусельного типа для
обработки цилиндрических изделий значительного диаметра и малой длины
и некоторые специальные. К горизонтальным станинам следует также
отнести станины портальных и одностоечных (бесконсольных) станков
с поступательно перемещающимися столами.
Горизонтальные станины несут на себе: а) основные неподвижные
узлы — коробки скоростей и подач, .иеперемещаемые шпиндельные баб-
ки, электродвигатели (за исключением тяжелых) и б) подвижные узлы
(суппорты, столы, каретки, перемещаемые шпиндельные бабки и т. д.).
Перемещение подвижных узлов осуществляется по направляющим.
Станины широко используются для размещения резервуаров
охлаждающей жидкости и смазки.
Горизонтальные станины выполняются: а) на ножках;
б) сплошными й в) рамными1.
Сталины на ножках применяются в станках для обработки
длинных изделий при относительно небольших силах резания. Практически
на ножках выполняются станины токарных станков с диаметром
обработки до 600 мм включительно, а также частично револьверных и
некоторых других станков.
Сплошные станины применяются при значительных усилиях и
диаметрах обработки, а также при необходимости размещения в станине
1 Рамные станины здесь рассматриваются условно и только в применении к стан-
псам токарной группы. Это связано с тем, что по схеме расчета эти стаиины близки
к обычным горизонтальным станинам, так как жесткость вертикальных элементов
станины достаточно велика и их деформации можно не рассматривать.
36
механизмов станков. Сплошными выполняются станины крупных
станков токарной группы, станины шлифовальных сталков и стаиины
портальных и бесконсольных станков 'всех размеров.
Рамные станины применяются для высокопроизводительных
станков, так как при верхнем расположении суппортов облегчается отвод
большого количества стружки.
Форма сечения станины определяется условиями жесткости,
расположением направляющих, условиями удаления стружки и
охлаждающей жидкости, условиями размещения в станинах, резервуаров для
охлаждающей жидкости и смазки. Основные тшщ сечений
горизонтальных станин приведены в табл. 9,
Таблица 9
Основные типы сечений горизонтальных станин
Сечения
Области применения и характеристика
Применяется при необходимости отвода вниз
стружки и охлаждающей жидкости. Обладает по
ниженной жесткостью по сравнению с замкну
тыми. Применяемые формы перегородок
приведены в табл. 10
1г^4=^Т
^
Применяется при отсутствии необходимости в
отводе стружки вниз. В случае возможности
попадания стружки между направляющими
предусматриваются наклонные люки
Применяется при необходимости
использования станины как резервуара для масла,
необходимости значительного места для расположения
механизма привода и при невозможности
попадания стружки на станину между
направляющими
Применяется в тяжелых, в частности, в
многосуппортных станках. Число направляющих
определяется числом суппортов и размерами и
доходит до четырех—пяти. Станины особо
тяжелых станков выполняются с двойными стенками
у каждой направляющей. В случае попадания
стружки между направляющими
предусматриваются наклонные люки для отвода стружки
Высота сечений станин на ножках определяется
условиями необходимой жесткости, а сплошных станин — дополнительно
условием размещения обрабатываемого изделия на наиболее удобном
для наблюдения уровне. Поэтому у более крупных станков высоту
сечения станин часто приходится делать даже меньшей? чем у более
легких, а необходимую жесткость станины обеспечивать за счет
фундамента. Только уникальные станки проектируют так, чтобы
рабочий наблюдал за обработкой со специального помоста или
лестницы.
Ширин'а сечений станин определяется размерами
обрабатываемых изделий, условиями жесткости и условиями хорошего
направления суппортов или столов:
27
Конструктивные формы присоединения направляющих к стенкам
станины могут существенно влиять на баланс упругих перемещений
станка, а также на собственные напряжения в отливках в связи с
неравномерным охлаждением стенок станины и направляющих.
Фиг, 1. Сопряжения направляющих и стенок станин.
Конструктивно- переход от основной части станины к
"направляющим может быть оформлен в виде одной или двух вертикальных
стенок или вертикальной и наклонной стенок (фиг. 1, а—е). Направляющие
с одной стенкой иногда подкрепляются поперечными ребрами
(фиг. 1, б).
Фиг, 2. Соединения частей составных станин.
Конструктивные особенности станин, определяемые условиями
отвода стружки и размещения резервуаров для охлаждающей жидкости
и смазки, специфичны для станков разных групп и рассматриваются
ниже.
Станины большой длины делают составными. Для обеспечения
необходимой жесткости соединения минимальное давление в стыке не
должно быть меньше 15—20 кГ/см2. Точное положение соединяемых
частей фиксируется штифтами или призонными болтами (фиг. 2, а). При
больших сдвигающих силах ставятся призматические шпонки (фиг. 2, б).
Стягивающие болты обычно размещаются в карманах (фиг. 2, в).
28
В особенно тяжелых станках во избежание местных отгибов стенок,
стягиваемых болтами, предусматривают специальные коробчатые фланцы,
обладающие повышенной жесткостью, но требующие болтов
значительной длины (фиг. 2, а).
Для обеспечения возможности удобной транспортировки станин
обычно предусматривают крюки, скобы или отверстия. Следует иметь
в виду, что в станинах точных станков расположение этих элементов
должно быть таким, чтобы при подъеме не возникали напряжения выше
100 кГ/см2, так как большие напряжения, складываясь с остаточными
напряжениями, приводят к местным остаточным деформациям,
влияющим «на точность.
Установка станин на фундаменте в значительной степени определяет
точность работы и виброустойчивость станка [4], [13].
Легкие и средние ст а н к и небольшой длины, как правило,
устанавливаются на общей бетонной плите цеха и подливаются.
Станины этих станков обычно конструируются так, чтобы
достаточная жесткость станка была обеспечена без существенного участия
фундамента.
К точности установки особенно чувствительны горизонтальные
станки на ножках: например, если задняя ножка станины токарного
станка с высотой центров 200 мм при установке встанет на кромку, то
смещение направляющих по высоте" может оказаться порядка 0,3—
0,6 мм.
Тяжелые станки устанавливаются на индивидуальные
фундаменты и станины их конструируются из условия совместной работы
с фундаментами. Это обусловливается требованиями экономии металла,
условием размещения 30|Ны обработки на удобном для рабочего уровне
от пола. Поэтому станины тяжелых станков не могут быть высокими.
В этом случае жесткость системы станина — фундамент в основном
определяется жесткостью фундамента, и станины работают в условиях,
близких к условиям работы плит-
Тяжелые станки, у которых размеры основания одного порядка,
притягиваются после выверки фундаментными болтами и подливаются
цементным раствором. Длинные станки обычно подливаются и
притягиваются болтами под приводом, тяжелым порталом и т. д., а в
остальной части станины, во избежание больших температурных деформаций
и деформаций от проседания фундамента, устанавливаются на
регулируемых башмаках и притягиваются болтами без подливки.
Прецизионные длинные станки, например для
шлифовки направляющих, устанавливаются на регулируемых башмаках (в
целях возможности компенсации температурных деформаций и
деформаций от проседания фундамента).
Прецизионные станки небольшого р,а з м е р а с
жесткими станинами, имеющими размеры площади основания одного
порядка, например коюрдинатио-расточные станки, устанавливаются на
трех точках.
Особо прецизионные станки в целях изоляции от
вибраций, передаваемых извне, устанавливаются на виброизоляционных фуп
даментах или прокладках. Эти фундаменты закладываются на слой
с большим внутренним трением: шлак или песок и упругие элементы
в виде стальных пружин или специальных упругих башмаков.
Упругие элементы должны подбираться из условия, чтобы частота
собственных колебаний станка с фундаментом >на упругих элементах
была в 2,5—5 раз меньше частоты возмущающих сил.
В качестве виброизоляционных средств между станком и обычным
фундаментом или плитой цеха применяются прокладки в форме шшт,
29
цилиндрических элементов или специальных башмаков- Подбор
упругих элементов под станки производится обычно опытным путем.
При установке станков на междуэтажные перекрытия, на суда и
автомашины следует по возможности обеспечивать трехточечное
статически определимое опирание, чтобы упругое деформирование основания
не вызывало расстройки точности установленных станков.
Для размещения фундаментных болтов и снижения
давления еа фундамент до допустимых значений станины выполняются
с фланцами (фиг. 3, а).
й
Й
Щ &В
777Л
<з==г
ч)
\^
ни
ш
ШИ2
хш
Ш
б)
Если в целях уменьшения
габаритов опорная
поверхность станин развивается
внутрь и болты размещаются
не снаружи, а внутри ста-
нин, то в местах установки
болтов делаются карманы
(фиг. 3, б). Иногда для
болтов предусматривают лапы
(фиг. 3, в). Тяжелые станки
с большой шириной стани-
ны притягивают к
фундаменту не только по
периметру, но и в средней
части.
В токарных станках
станины нагружаются сложной
►пространственной
нагрузкой, вызывающей кручение
станины и изгиб в
горизонтальной и вертикальной
плоскостях. Конструкция
станин в значительной степени
определяется
необходимостью отвода большого
количества стружки, попадаю-
щей между
направляющими.
Станины легких и
средних токарных станков,
устанавливаемые на ножках, как
правило, выполняют из двух
стенок с перегородками (фиг. 4). Обычно стенки имеют Т-образное,
а перегородки Т- или П-образное сечение. В нижней части стенок,
а также на уровне верхнего конца перегородок имеются отбортовки,
которые существенно повышают жесткость стенок. Основные типы
перегородок 'станин с двумя стенками приведены в табл. 10. Расстояние
между перегородками выбирается примерно равным ширине станины.
В настоящее время в высокопроизводительных станках встречаются
станины, в которых стенки выполнены двойными, что позволяет
обеспечить требуемую жесткость при большем расстоянии между
перегородками [771; при этом облегчается отвод стружки (фиг. 5, а).
В высокопроизводительных станках станины часто выполняют
с отводом стружки на заднюю сторону станка (фиг. 5, б). Для этого
станина дополнительно снабжается наклонной стенкой, а в задней
стенке делают окна. В таких станинах обычно применяются П-образные
перегородки. С отводом стружки на заднюю сторону станка часто вы-
Фиг. 3. Фланцы станин и карманы под
фундаментные болты.
30
Таблица 10
Форма и расположение перегородок в станинах, состоящих из двух стенок
Конструкции
Области применения
и характеристика
[
ш-
а
7±Ь
С^
ч
=*
щ
%
ш
Имеет малую жесткость; ввиду
легкости изготовления приме-
няется в станках, в которых
жесткость станины не играет
существенной роли (в легких станках
для.легкой работы)
У
п
над
Я
Я
Имеет среднюю жесткость.
Благодаря относительной легкости
изготовления является наиболее
распространенной конструкцией
главным образом в коротких
станках токарного типа общего
назначения
ж
01К=Н=МЗ^
*
Имеет повышенную жесткость,
но сложнее в изготовлении, чем
предыдущие конструкции. Приме
няется при высоких требованиях
к жесткости — в многорезцовых и
других станках
Имеет повышенную жесткость;
может быть рекомендована для
применения в длинных станках,
В изготовлении сложнее, чем
станины с перегородками,
перпендикулярными к стенкам
31*
полняются и станины сплошные по высоте. На участках станины под
передней бабкой и под задней бабкой в ее крайнем положении, где
Разрез по ДЯ
2370 -
Фиг. 4. Станина токарно-винторезного станка мод. 1К62.
стружка не попадает между направляющими, станина снабжается
верхней стенкой, что существенно повышает ее жесткость.
а) 6) 6)
Фиг. 5. Сечения станин высокопроизводительных станков:
а — с двойными стенками; б — с наклонной стенкой и окнами в задней стенке; в — с замкнутым контуром
В станках средних размеров применяют также станины замкнутого
сечения с наклонной верхней стенкрй и расположением направляющих
на разном уровне (фиг. 5, в). Станины этого типа обладают высокой
жесткостью, особенно на кручение, и обеспечивают хороший отвод
стружки. Однако в этом случае конструкции суппортов получаются
более сложными и они имеют худшее направление. Рамные конструк-
■32
ции применяют главным образом для многорезцовых и
копировальных станков (фиг- 6).
В станинах токарных станков в связи с большими поперечными
нагрузками особенно большую роль в общем балансе упругих
перемещений играет отгиб направляющих. Поэтому в токарных станках
следует уделять особое внимание жесткости соединения направляющих
со стенками.
Станины тяжелых токарных станков (фиш 7) выполняют
сплошными по высоте, с тремя или четырьмя направляющими для передних
и задних суппортов. Каждая направляющая, как правило,
подкрепляется двумя стенками- Иногда дополнительная стенка,
поддерживающая направляющую, делается неполной высоты. Стружка обычно
отводится через специальные полости в фундаментах.
Длинные станины обычно изготовляют составными.
Станины токарных станков можно выполнять сварными из
тонкого (3—4 мм) или толстого листового 'материала. Формы
толстостенных сварных станин принципиально тождественны формам литых.
Тонкостенные сварные станины выполняют коробчатого типа с
замкнутым контуром поперечного сечения (фиг. 8).
Станины продольно-фрезерных и продольно-строгальных станков
представляют собой коробчатые отливки с направляющими для
перемещения столок и фланцами для крепления стоек (фиг. 9). Длина
станин выбирается обычно несколько превышающей двойную длину стола.
Станины выполняют с двумя или несколькими продольными
стенками и, как правило, с верхней стенкой. В небольших станках с^двумя
направляющими станины имеют две продольные стенки, в тяжелых
станках — три и более (до 6) стенок. При этом каждая направляющая
поддерживается обычно двумя стенками. В зоне крепления стоек
боковые стенки обычно усиливают ребрами и перегородками. Станины
разделяются поперечными перегородками на отсеки, которые
используют для расположения механизмов привода, © качестве резервуаров
для охлаждающей жидкости и масла и т. п. В особо тяжелых станках
станины для повышения жесткости снабжают диагональными
перегородками. В связи с необходимостью 'размещения механизмов привода
на части длины станины верхняя стенка отсутствует или несколько
опущена.
Станины вертикальных бесконсольно-фрезерных * станков
аналогичны станинам продольно-фрезерных. Столы вертикальных
бесконсольно-фрезерных станков имеют возможность перемещаться по двум
взаимно-перпендикулярным направлениям, а потому станины этих
станков имеют несколько меньшую высоту, чем продольно-фрезерных-
Верхнюю стенку, обычно глубоко вогнутую для размещения механизма,
привода стола, на некоторых участках делают наклоненной для стока
эмульсии и схода стружки, попавшей между направляющими.
Горизонтально-расточные станки с диаметром шпинделя до 100—
125 мм, предназначенные для обработки относительно легких и
средних деталей, выполняют со станиной, общей для стола, передней и
задней стоек.
Станки с диаметром шпинделя от 100 до 200 мм, предназначенные
для обработки средних и крупных изделий, обычно выполняют со
станиной, состоящей из двух частей: из станины передней стойки (фиг. 10)
и станины стола, или .из трех частей — с дополнительной станиной для
задней стойки.
В тяжелых станках, предназначенных для обработки особо
крупных изделий, станина состоит из двух частей — собственно станины, по
которой перемещается стойка, и плиты, на которой устанавливается
неподвижная обрабатываемая деталь.
33
34
Фиг. 6. Станина токарно-копировального полуавтомата мод. 1722,
Фиг. 7. Секция станины тяжелого токарного станка иод. 1680.
35
Фиг. 3. Сварная станина токарновинторезного станка фирмы Густлов-Верке мод. А5 (см. табл. 15)
36
Станины обычно
выполняют из нескольких продольных
стенок с жесткой системой
ребер и широкими
направляющими. Несмотря на большие
нагрузки, действующие на
станины, особенно на станины, по
которым перемещаются стойки,
высота станин делается
сравнительно небольшой, так как на
расточных станках, как
правило, обрабатывают изделия
значительной высоты.
Необходимая жесткость станин
обеспечивается за счет совместной
работы станин с фундаментами.
Координатно - расточные
станки выпускают одностоеч*
ными и портального типа.
Станины одностоечных сталков,
как правило, ниже, чем
станины портальных станков, у
которых стол перемещается в одном
направлении, и имеют меньшую
жесткость
В связи с особенно
высокими требованиями к точности
координатно-расточных
станков их желательно
устанавливать на три точки. Благодаря
этому уменьшаются
температурные деформации станин и
деформации станин от
проседания фундамента. Однако при
этом фундамент не работает
совместно со станиной и к
жесткости станин предъявляются
повышенные требования.
Обычно станины
координатно-расточных станков
выполняются из нескольких
стенок с жесткой системой
перегородок, связывающих опорные
точки. Необходимая жесткость
станин обеспечивается за счет
выполнения станин
максимально возможной высоты и
достаточно широкими.
Шлифовальные станки
характерны относительно
малыми нагрузками, и собственные
упругие деформации станин
невелики. Конструкция станин
подчиняется требованиям
уменьшения температурных
деформаций и деформаций от
остаточных нал ряжений.
ЗС^^^П^
37
Фкг. 10. Станина передней стойки горизонтально-расточного станка мод. 2652.
38
Из условий размещения механизмов, резервуаров для
охлаждающей жидкости и масла, а также из условий виброустойчивости станины
делаются сплошными по высоте с перпендикулярными перегородками
и обычно с нижней стенкой в части отсеков.
§ 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ РАСЧЕТА НА ЖЕСТКОСТЬ
Основным критерием работоспособности станин является
жесткость, которую можно характеризовать величиной перемещения
инструмента относительно изделия в результате деформаций станин при
заданной силе-
Специфика расчета горизонтальных станин обусловливается
конструкцией станин, как правило, состоящих из продольных стенок с
перегородками, заставляющими стенки работать совместно, а также
совместной работой станин с фундаментами.
При расчетах на жесткость станины следовало бы рассматривать
как тонкостенные системы под действием распределенной по
некоторому закону пространственной нагрузки от взаимодействия с
сопряженными деталями. Закон распределения нагрузки и величины деформаций
могут быть определены лишь после решения задачи о деформациях
всей несущей системы станка как единого целого с учетом контактных
деформаций в стыках и собственных деформаций. Совершенно очевидно,
что получить точное решение такой задачи в настоящее время не
предоставляется возможным.
Поскольку действительный закон распределения давлений от
взаимодействия станины с другими деталями и с фундаментами остается
неопределенным, необходимо принять некоторые допущения относи:
тельно этого закона. Целесообразно принять и упрощенную схему
расчета. Наиболее простое решение можно получить, если рассматривать
станины как ^однородные брусья постоянной жесткости, получающие
такие же максимальные упругие перемещения, как рамные станины
при одинаковых частных видах нагрузки, близких к реальным.
Рассчитав станину при каком-то частном виде нагружения как
статически неопределимую тонкостенную систему и приравняв максимальные
упругие перемещения станины — рамы и бруса постоянного
поперечного сечения, можно определить приведенную жесткость станины, а
затем— деформации станины при нагружении, соответствующем нагру-
жению ее в работающем, станке. По такой схеме и построен технический
расчет станин 1.
Так как нагрузка на станины обычно передается на участках,
длима которых, как правило, больше расстояния между перегородками,
местные деформации стенок на этих участках существенного влияния
на общую картину деформации не оказывают. Приемлемость расчетов
по предлагаемой схеме и предпосылок, .на которых основан расчет
станин как рам (см- «иже), подтверждается сравнением результатов
расчетов и экспериментов.
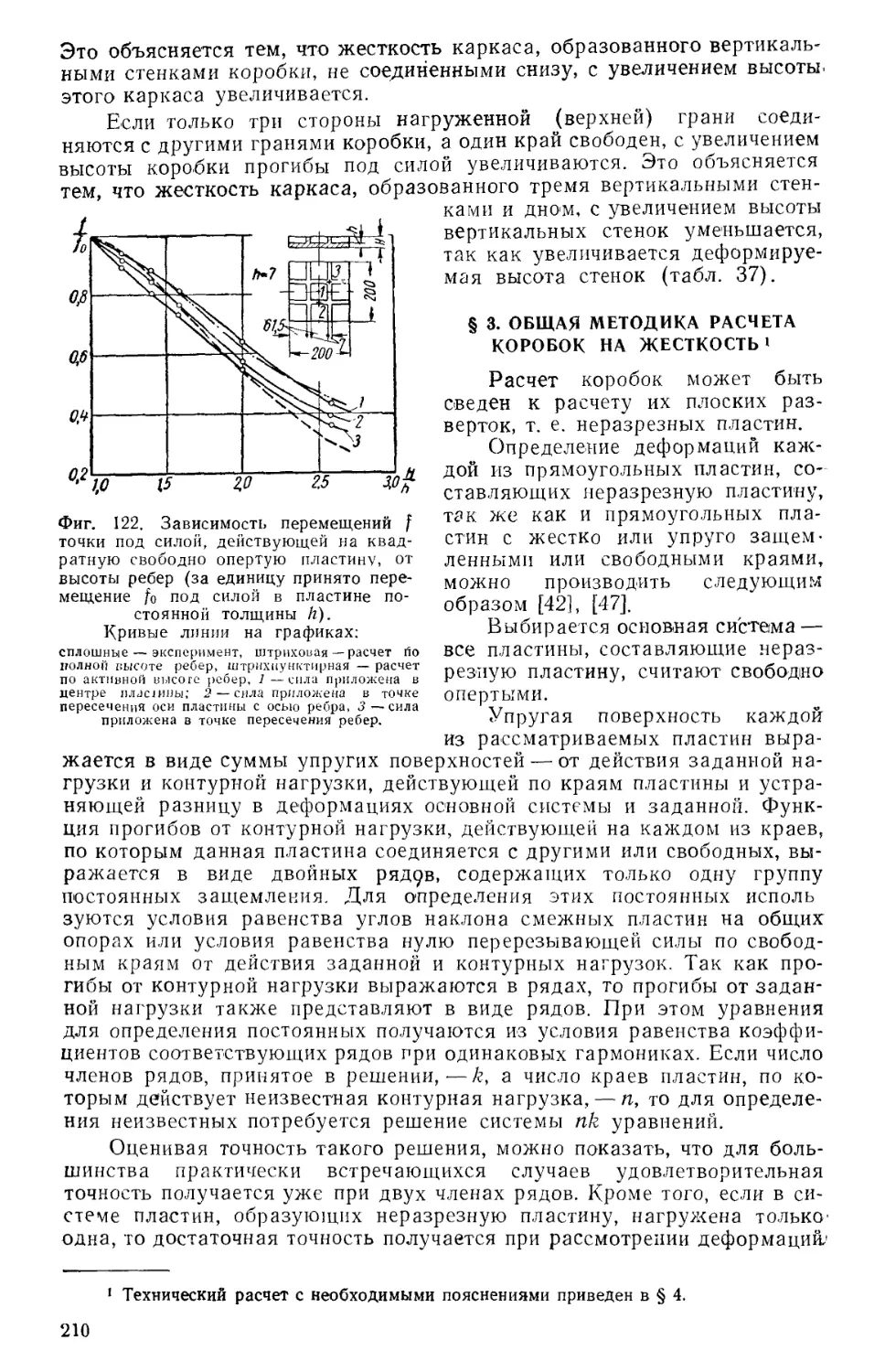
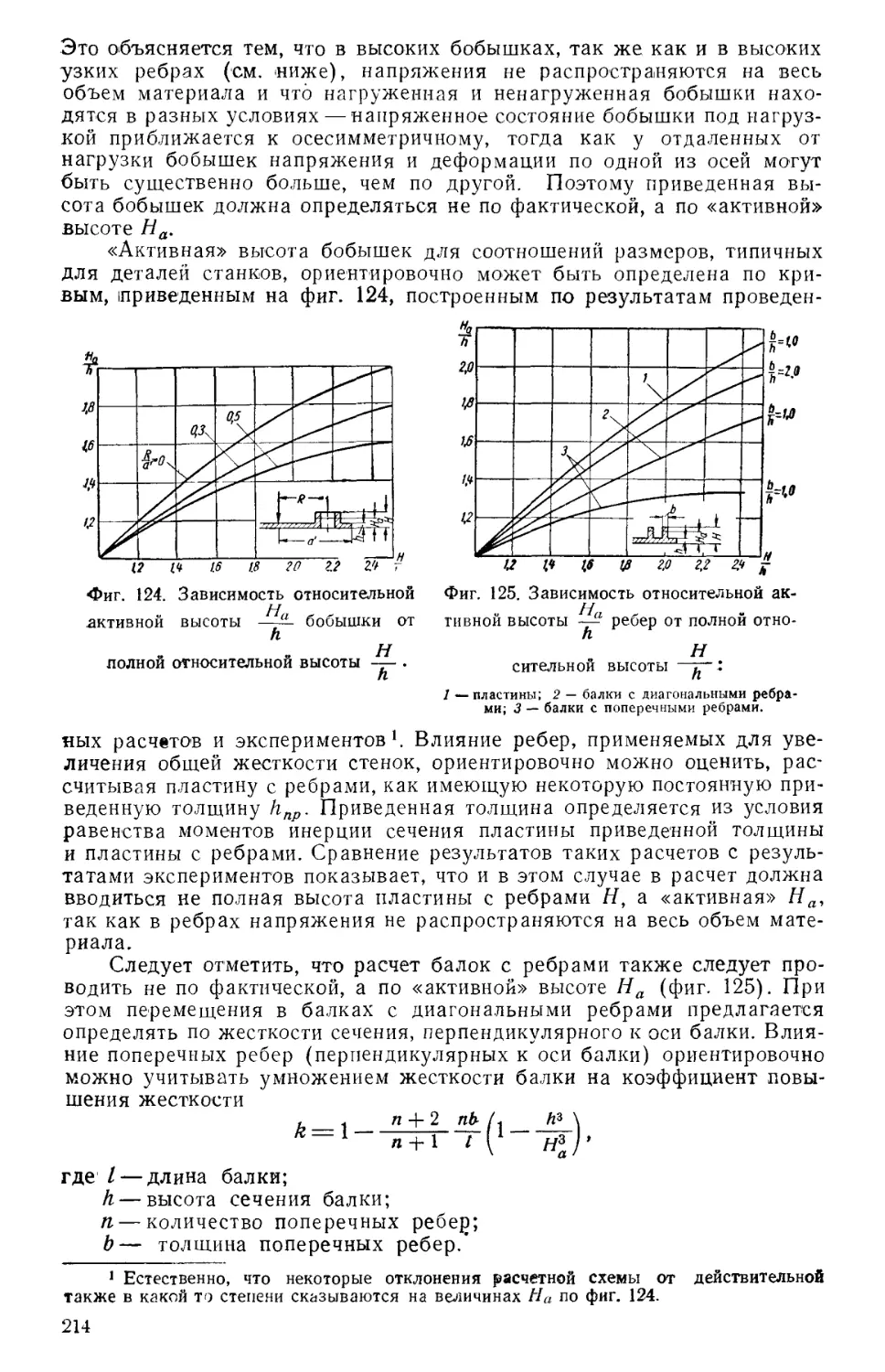
§ 3 ОПРЕДЕЛЕНИЕ ПРИВЕДЕННОЙ ЖЕСТКОСТИ СТАНИН
А. Постановка задачи
В общем случае станины испытывают изгиб в двух плоскостях
(горизонтальной и вертикальной) и кручение. Опыты показывают, что
жесткость стайин на изгиб в вертикальной плоскости определяется
моментом инерции сечения относительно горизонтальной оси, проходя-
1 Технический расчет станин с необходимыми пояснениями см. ниже, в § 5.
39
крутящий моменгЬ м^Рв
а)
щей через центр тяжести сечения; вертикальные перегородки как
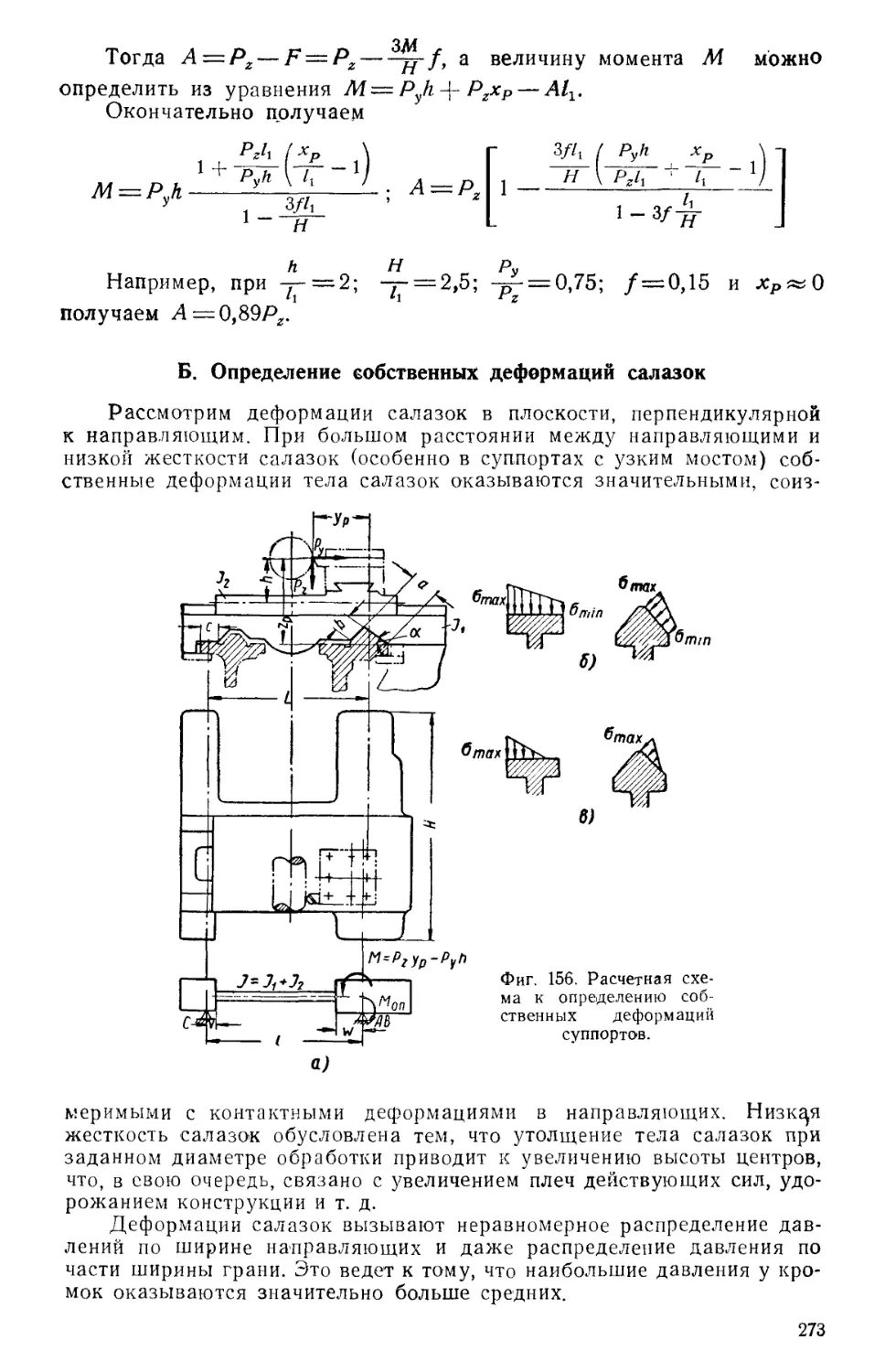
перпендикулярные, так и диагональные (см. табл. 10), практически
жесткость на изгиб в вертикальной плоскости не увеличивают.
При определении деформаций от изгиба 1в горизонтальной
плоскости и кручения станины следует рассматривать как рамы, в которых
перегородки, связывающие стенки, заставляют последние работать
совместно. Так как конструктивные формы элементов станин довольно
сложны, а расчет рам типа станин представляет известные трудности, для
упрощения расчета приходится идти на некоторую схематизацию
конструкции. В частности, жесткость обеих стенок принимают одинаковой;
также принимают одинаковыми жесткости перегородок и расстояния
между перегородками.
Если станина на каких-
то участках
соединяется с элементами,
существенно
увеличивающими ее жесткость, то
жесткость этих
участков полагается
бесконечно большой. Так,
например, бесконечно
большой полагается
жесткость: в станинах
токарных станков —
участков над ножками
(двух концевых
перегородок), в станинах
одностоечных и.
портальных станков — участка
под стойкой (одной
перегородки) . Сечения
всех элементов станины
(стенок, перегородок)
заменяются
прямоугольными, имеющими
те же основные
расчетные характеристики
(моменты инерции,
площади сечения и т. п.).
При расчете полагается, что для элементов станин применимы
формулы и выводы сопротивления материалов, т. е. принимается, что
нормальные напряжения по высоте стенок и перегородок
распределяются по линейному закону, что материал станин— чугун — следует
закону Гука (при напряжениях, не превышающих 100—150 кГ/см2, имею-
ющих место в станинах, такое предположение вполне допустимо)
и т. п.
В настоящей главе приняты следующие обозначения основных
встречающихся \в расчетах величин:
п — число перегородок;
^пу — момент инерции на изгиб в вертикальной плоскости (т. е.
в плоскости большей жесткости) сечений боковой стенки
и перегородки, соответственно, в смА;
Л-*— угловое сопротивление закручиванию сечений боковой
стенки и перегородки, соответственно, в см}\
]ти — момент инерции на изгиб в плоскости меньшей жесткости
сечений стенки и перегородки, соответственно, в см*;
крутящий мйменгп М=Р8+гп
8)
Фиг. 11. Основная система при расчете на кручение
станин из двух стенок и силовые факторы, действующие
в местах разреза:
а — станины с перпендикулярными перегородками (принято, что
жесткость стенок на кручение пренебрежимо мала); 6 — станины с
диагональными перегородками (принято, что жесткость стенок и
перегородок на кручение пренебрежимо мала)
40
Рст; Рп— площадь поперечного сечения стенки и 'перегородки,
соответственно, в см2\
Р'ст— приведенная площадь сечения стенки, т. е. площадь
поперечного сечения вертикальных участков сечения стенки,
в смг;
/^ — приведенная площадь сечения перегородки, т. е.
площадь поперечного сечения вертикальных участков
сечения, в см2;
Ь\ В — длина и ширина деформируемой части станины,
соответственно, в СМ;
I — длина отсека (расстояние между осями смежных
перегородок в станинах с перпендикулярными перегородками
или расстояние между узлами, измеренное в плоскости
стенок в станинах с диагональными перегородками), в см
(фиг. 11);
а — длина диагональной перегородки в см (см. фиг. 26 на стр. 81);
Ъп\ ^гр—ширина и высота перегородки, соответственно, в см;
Ьет\ Кт—ширина направляющих и расчетная высота стенку
станины (без направляющих), соответственно, в см;
Ь; Ьп — толщина боковых стенок станины и толщина элементов
перегородки, соответственно, в см;
*— половина угла между диагональными перегородками;
Р—площадь сечения, описанного осевыми линиями стенок
наружного контура в см2;
П —периметр наружного (замкнутого) контура в см;
Еу О — модули упругости материала станины в кГ/см2.
Б. Определение жесткости на кручение
Определение жесткости на кручение основывается ца следующих
предпосылках:
1. Жесткость станины на крушение определяется из рассмотрения
деформаций стани.ны при нагружении ее двумя равными по величине
и противоположными по знаку крутящими моментами по торцам из
условия равенства суммарного угла закручивания станины и бруса
постоянного поперечного сечения той же длины при той же схеме на-
гружения.
2. Принимается, что жесткость стенок, а в станинах с
диагональными перегородками также и жесткость перегородок, на изгиб в
плоскости, перпендикулярной к плоскости стенок, и на кручение
пренебрежимо мала1, т. е., что переменностью нормальных и касательных
напряжений по толщине стенок можно пренебречь.
3. Кручение полагается происходящим относительно оси,
проходящей через центры тяжести поперечных сечений станины.
Расчет станин из двух параллельных стенок с перегородками
проводится по следующей схеме2.
Выбирается статически определимая основная система: станина
разрезается на отсеки сечениями, перпендикулярными к оси (фиг. 11) (в
станинах с перпендикулярными перегородками—ло осям перегородок).
1 В станинах с диагональными перегородками последние обычно имеют
Т-образное сечение, а в станинах с перпендикулярными перегородками — П-образное.
Жесткость на кручение П-образных перегородок на порядок выше, чем Т-образных. Для
станин с двойными стенками (П-образного сечения) собственная жесткость стенок на
кручение учитывается приближенно (см ниже).
2 Аналогичные расчеты применительно к самолетостроению см. [28], [29], [51], [73].
41
Так как в станине отсеки соединены, то/чтобы устранить разницу
искажений соответствующих сечений в станине и в 'выбранной
основной системе, в местах разреза необходимо считать действующими
некоторые силовые факторы, вызывающие по высоте стенок нормальные
напряжения. Эти напряжения из условий равновесия можно привести
к двум равным по величине и взаимно противоположным по
направлению парам Мг. Таким образом, действие отброшенных частей
станины выразится действием крутящего момента М и неизвестных
изгибающих моментов М/.
Все внутренние силы при помощи условий статики выражаются
через внешнюю нагрузку и лишние неизвестные. Суммированием
потенциальной энергии от всех действующих сил по всем элементам
отсека составляется выражение потенциальной энергии V внутренних сил
деформированного отсека.
Величины перемещений в направлении удаленных связей
определяются по формуле В = —щ-— и приравниваются нулю.
Из системы уравнений, составленных для перемещений в
направлении каждого из неизвестных силовых факторов, значения этих
неизвестных определяются как некоторые функции нагрузки.
При сделанных допущениях (относительно малой жесткости
стенок на изгиб в плоскости меньшей жесткости и на кручение, а
следовательно, малости силовых факторов, вызывающих эти деформации) для
определения лишних неизвестных требуется решение системы
уравнений с п неизвестными (п — число перегородок). Каждое из уравнений,
составляемых при расчете станин с перпендикулярными
перегородками, содержит три неизвестных, а станин с диагональными
перегородками — пять неизвестных.
После определения неизвестных изгибающих моментов М* полный
угол закручивания станины определяется как сумма углов
закручивания отдельных отсеков.
1. Станины с перпендикулярными перегородками
Проиллюстрируем ход решения на простейшем примере—
определим угол закручивания станины в виде двух стенок с
перпендикулярными перегородками.
Разрежем станину на отсеки по осям перегородок и рассмотрим на-
гружение /-того промежуточного отсека под действием крутящего
момента'Ж и изгибающих (неизвестных) моментов Мь_х и Ми
заменяющих действие отброшенных I—1-го и /-(-1-го отсеков на /-тый
отсек. Так как было принято, что жесткость стенок на кручение
пренебрежимо мала, то крутящий момент (фиг. 12, а) может действо-
М1
вать на стенки лишь в виде пары сил М = РВ. Пара сил Р1= —^~
уравновешивается на стенке двумя равными (так как жесткость пе-
ч М1
регородок одинакова) моментами -^-, возникающими в результате
сопротивления перегородок скручиванию. Моменты Мь_х (фиг. 12, б)
делятся между перегородкой и стенкой в отношении г г^~\—; момент
М1_1Г1_1 вызывает изгиб стенки, а момент (1 — Г1_1)М1_1 — кручение
^перегородки. Аналогичным образом в отношении 1 2 . •
распределяются моменты М^ Из условия равновесия стенок момент г^М^
должен быть равен моменту Г|-1^/-1-
42
Запишем выражение потенциальной энергии внутренних сил отсека
в виде
I
"<=2[
Кзгах
2ЕЗ.
•2х
сту
О'сде*
20РСт
ЩРгВ
М\
крЬ-А
В
2Шп
2СУЛ.,
где Мизг\ 0.сЬе — изгибающий момент и сдвигающая сила,
действующие на стенки отсека;
М
кр 1">
м
кР1-х — крутящие моменты, действующие на /-тую и /—1-ую
перегородки;
*—коэффициент распределения сдвига. Все остальные
обозначения прежние.
Составляющую неизвестных изгибающих моментов т^=г/Ж1==
= 0-1^-1 определим из условия —^- = 0, выразив II 1 через силовые
факторы, действующие на отсек, М, Мь и М^г.
Перемещение 9/ сечения /-того отсека в месте действия момента Мц
по направлению действия этого момента определится из уравнения 6г. =
~~ дМ1 '
(Г-г-)М,
Фиг. 12. Схема нагружения при кручении элементов промежуточного отсека
сганииы в виде двух параллельных стенок с перпендикулярными перегородками
(жесткость стенок на кручение принята пренебрежимо малой):
а — действие крутящего момента М; # — действие изгибающих моментов М.^* и М.
Аналогичным образом, записав выражения для силовых факторов,
действующих на элементы /-(-1-го отсека, можно определить
перемещение сечеиия *'+1-го отсека в месте действия момента М[ из урав^
нения
_ дЦ1+1
^+1 ~ дм1 •
Так как в ^станине все отсеки соединены, то относительное
перемещение /-того и /-(-1-го отсеков в месте их соединения равно нулю,
и поэтому должно быть справедливо равенство
дЩ + Цщ)
дМ1
= 0.
Отсюда и получаются уравнения, связывающие неизвестные моменты
любых двух соседних промежуточных отсеков. Если жесткость
концевой перегородки значительно превышает жесткость промежуточных
перегородок, то в крайнем отсеке пара сил Р/ = -^-, действующая На
М1
стенку, уравновешивается двумя неравными моментами -^- 5 в месте
М1 ,, .
соединения стенки с прогмежуточнои перегородкой и -д- (1—5) в
месте соединения стенки с концевой перегородкой. Коэффициент 5
распределения момента Р1 определяется из условия минимума
потенциальной энергии крайнего отсека.
43
В результате, из условия отсутствия относительного смещения
отсеков в местах их соединения для определения неизвестных моментов М/
получим систему п уравнений © виде:
1) Мга~\-М2Ь = Мс;
2) Ж1& + 2Ж2й + Ж3& = 0;
3) М2й + 2ЛГ3й + М4й = 0;
гь) Мп_гЬ + Мпа= — Мс.
Значения вспомогательных коэффициентов приведены в табл. 11.
После определения моментов М, угол закручивания каждого
отсека может быть определен как производная потенциальной энергии
отсека III по крутящему моменту М.
Для определения угла закручивания отсеков получим формулы:
для первого отсека
для промежуточного отсека
для последнего отсека
Полный угол закручивания станины определяем как сумму углов
закручивания отдельных отсеков
т=2^« = т^[2/ч-(»-1)г+л(« + 0т+ *ямМ1 *]•
Следует отметить, что после раскрытия статической
неопределимости, т. е. определения 'моментов М/ , величины напряжений,
возникающих в элементах станины, могут быть определены как сумма
напряжений от каждого силового фактора, действующего на данный
элемент в отдельности.
Аналогичным образом решаются задачи о. деформациях станин из
двух стенок с перегородками и дополнительной верхней (или нижней)
или наклонной 1 стенкой.
Значения коэффициентов, входящих з полученные зависимости,
для станин указанных типов приведены в табл. 1,1.
Следует отметить, что при решении задач о деформациях станин
с дополнительной стенкой, кроме указанных выше допущений, было
принято, что дополнительная стенка соединяется с
перпендикулярными перегородками только на небольших участках около стенок. При
таком допущении перпендикулярные перегородки, как и в
предыдущем случае, будут испытывать только кручение. Приближенную оценку
погрешности, вносимой этим допущением, можно получить, если
сравнить деформации перегородки, рассматриваемой как пластина под
1 В станинах с наклонной стенкой стружка обычно отводится через окна в задней
стенке. Так как эти окна располагаются Ьллл нейтральной о~и стенки и очень
незначительно уменьшают момент инерции ее на изгиб (5—10% для реальных соотношений
размеров), для упрощения расчета было принято, что и в этом случае жесткость обеих
стенок одинакова.
44
Таблица 11
Вспомогательные коэффициенты для расчета станин с перпендикулярными перегородками
45
Станины из двух параллельных вертикальных
и наклонной стенок
Станины из двух параллельных вертикальных
и горизонтальной стенок
Коэф- Станины из двух параллель-
фици- нь!х вертикальных
ент I стенок
действием некоторой распределенной нагрузки, действующей по линии
контакта перегородки со стенками, и как брус под действием двух
крутящих моментов по концам. Можно показать, что при реальных
соотношениях размеров эта погрешность не превышает 5%.
Из изложенного выше следует, что для решения задачи о
деформациях станин с перпендикулярными перегородками необходимо
решить систему трехчленных уравнений вида ^/И^ + 2^Ж/+ &/И/+1 =0,
которые представляют собой линейные разностные уравнения второго
порядка с постоянными коэффициентами. Как известно, общее
решение таких уравнений имеет вид Мь = С\рх1 + С2/?2~Л где С^ и С2 —
постоянные, определяемые из граничных условий, а р\ и р2— корми
уравнения 1 + 2 г-р + р2 = 0 (й и Ъ — коэффициенты рассматриваемых
уравнений). Подставляя общее решение в первое и последнее
уравнения системы, определяем постоянные С\ и С2 и получаем формулу для
непосредственного определения неизвестного изгибающего
момента Мь:
М — Мг [р (а + Ьр) + рП {а + Ьр "1)] Р~1 ~ [Р~Х {а + Ь?~1) + Р~" {а + Ьр)] рЬ
где по-прежнему р = гГ+У ~^2"~*1» Л — число перегородок, а
коэффициенты а, &, с, й — определяются по формулам табл. 11 в
зависимости от типа станин.
Так как в формулу для полного угла закручивания станины
входит разность моментов — последнего и первого, то при определении
приведенной жесткости станины можно, не находя промежуточных
моментов М-ь, непосредственно определить ф, подставив
Мп — Мг — — 2Мс— !
пП-1 _ «2
Окончательно получаем
М1
<Р =
^сту
2/ + (л-1)г + Л(л + 1)т-.
2с*$
аЛ-Ъ
Р'
И-1 _ л2
Рп
Полученная формула для определения угла закручивания станины
выведена на основе ряда упрощающих допущений, важнейшим из
которых является допущение о пренебрежимо' малой жесткости стенок:
на кручение-
При обычных конструктивных формах (стенки средних станков
обычно Т-образного сечения) и соотношениях размеров элементов
станин ошибка от того, что не учитывается кручение стенок, »не превышает
*5%. Однако в некоторых станках токарного типа, например,
многорезцовых, стенки выполняют не Т, а П-образного сечения. Жесткость
кручения таких стенок существенно выше, чем жесткость Т-образных
стенок, и величина погрешности расчета, особенно для станин с
перпендикулярными перегородками, возрастает.
В этом случае жесткость кручения станины в первом приближении
может быть определена как сумма жесткости станины, вычисленной
без учета кручения стенок, и жесткости кручения стенок. Формулу для
определения приведенной жесткости кручения элементов П-образнога
сечения см. ниже, стр. 53.
46
2. Сталины с диагональными перегородками
Рассмотрим основную систему из последовательного ряда отсеков,
полученную путем разрезания станины в узлах сечениями,
перпендикулярными ее оси (см. фиг. 11, б). При принятых, допущениях в местах
разреза можно считать действующими:
1) изгибающие моменты Л1/, действующие в плоскости стенвк;
2) крутящий момент т1у действующий в месте соединения стенки,
с перегородкой (-в плоскости, перпендикулярной к оси станины);
3) силы Р> действующие в плоскости стенок. Все остальные
силовые факторы при принятых допущениях обращаются ъ нуль.
Эта система силовых факторов должна быть эквивалентна
внешней нагрузке, т. е. крутящему моменту, из чего следует равенство
РВ + т^М.
Рассмотрев нагружение элементов отсеков под действием
указанных силовых факторов и составив выражение потенциальной энергии
внутренних сил системы так же, как в предыдущих случаях, можно
получить уравнения, связывающие неизвестные соседних отсеков и угол
закручивания станины. Однако, если при решении задачи о
деформациях станины с перпендикулярными перегородками требуется решение
системы уравнений каждое с тремя неизвестными, то в данном случае
уравнения содержат по пять неизвестных. Поскольку необходимость
решения системы пятичленных уравнений не дает возможности в
общем виде получить конечную формулу для угла закручивания, для
решения задачи о деформациях станин с диагональными
перегородками принимается дополнительное допущение о линейной зависимости
между моментами Л1/, т. е- принимается М,- —/г, А119 где /г,—
некоторый коэффициент пропорциональности, а М\— момент, действующий
в месте соединения крайнего и соседнего с ним отсеков и
определяемый из условия минимума потенциальной энергии. При этом
допущении получаем следующую формулу для определения угла
закручивания станины ].
ПВ^ЕЗсту
(б71 - за, - 1)2
2 + ^+бп
а _!. ча 1 _!_ * _!_ (2я- 1)(/1- 1)[/1(ЬТ1 +2^+бта- 1) - (6Т. + 3^ - 1)]
&Т1 + <»1 - 1 + <** + (2л _ 1) (л _ 1) + л (6Т1 + 25х +ЬТ2— 1) — (Ьь + 35х — 1)
где
аъЕ1Сту Е$сту а^^сту
№пу |А 1ЮРст " 1ЮРп
Можно показать, что при реальных соотношениях размеров
разница в величинах полного угла закручивания, определенного при более
точном расчете, требующем решения системы уравнений, и при
упрощенном расчете практически ничтожна.
1 Формула выведена для стайии с нечетным числом перегородок (п = 21 -+- 1),
однако с достаточной степенью точности ею можно пользоваться и при расчете стани»
с четным числом перегородок.
47*
3. Станины с замкнутым контуром
поперечного сечения
Станины с замкнутым контуром поперечного сечения обычно
имеют несколько перегородок, а литые, кроме того, — небольшие окна
для закрепления стержней. Поскольку жесткость тонкостенной
конструкции, имеющей замкнутый контур поперечного сечения,
значительно выше, чем разомкнутой, то приближенно, полагая, что контур
сечения благодаря наличию перегороди; не искажается, жесткость
кручения можно определять как для полых труб при свободном
кручении. Влияние на жесткость перегородок и окон при реальных
соотношениях размеров можно не учитывать. Ошибка в результате
отсутствия учета этих факторов не превышает 10,%'.
4. Сравнение результатов расчетного
и экспериментального определения углов
закручивания станин
Для проверки приемлемости допущений, на основании которых
были получены формулы для определения углов закручивания станин,
были использованы результаты измерения углов закручивания
чугунных моделей станин, имеющих сечения стенок и перегородок
правильной прямоугольной формы с разными типами перегородок. При
испытаниях модели одним концом крепились в кронштейне
приспособления, а к другому концу прикладывался крутящий момент [19, а].
Эскизы моделей, а также экспериментальные и расчетные кривые
изменения углов закручивания по длине моделей станин приведены на
фиг. 13. Как видно из графика, расхождение экспериментальных и
теоретических кривых не превышает 10%.
Для оценки возможности применения предлагаемых методов рас-
чета^ к расчету реальных станин были проведены измерения углов
закручивания станин токарных станков моделей 1Д62М, 1П62 и 1П63
[24].
При измерениях станки устанавливались на двух опорных винтах
или клиньях под каждой ножкой. В центрах станка зажималась
оправка длиной, равной наибольшему расстоянию между центрами. На
станине на направляющих суппорта примерно посередине расстояния
'между центрами устанавливался специальный нагрузочный мостик
Между оправкой и мостиком при помощи винтового домкрата
создавалось усилие, имитирующее силу резания. Так как ширина мостика
была относительно невелика (~100 мм), то нагрузку, закручивающую
станину, можно было считать эквивалентной сосредоточенному
крутящему моменту, приложенному в сечении действия силы. Схема
испытаний приведена на фиг. 14. Углы закручивания станины измерялись
при помощи уровней с ценой деления 0,025 мм/м, устанавливаемых
на специальные мостики. Мостики базировались по направляющим
станины. Опоры мостиков размещались так, чтобы по возможности
исключить влияние отгиба направляющих. Мостик для измерения
углов закручивания станины станка 1Д62М приведен на фиг. 15. Для
измерения углов закручивания по длине станины мостик с уровнем
переставлялся с одного участка станины на другой. Угол
закручивания на данном участке определялся как разность показаний уровня
при нагружении силой заданной величины и без нагрузки.
Относительная погрешность измерений не превышала 1,5—2%. На фиг. 16
приведены экспериментальные и расчетные кривые изменения углов
закручивания по длине станин. Как можно видеть, расхождение результатов
48
Разрез ло дя
30 I см
Фиг, 13. Изменение углов закручивания ср по длине моделей
станин. Крутящий момент М = 5000 кГсм. Кривые линии на
графике: сплошные — расчетные, штриховые — опытные.
5 6 2
I Ч
П"И1,_,^ 1__
*/>/////////777777^//;'Л'/777.
77777/77777777//^ »//////щ///Г/7777777/777777У//////у/7.
/'7777/7777 Ч777У77Т/-?7777'//77777
Фиг. 14. Схема испытаний стании токарных станков на жесткость:
1 - оправка; 2 — нагрузочный мостик; 3 — измерительный мостик; 4—уровень; 5—домкрат; 0—динамометр.
49
не превышает 10—15%. Таким образом, можно считать, что сравнение
результатов расчетов и экспериментов подтверждает приемлемость
предлагаемого метода расчета и принятых предпосылок для
технических расчетов станин на кручение.
^~ж
ш>
п
Л-./
^
*1_
б,— ф-{-^
4^-:-$
Разрез по ДЯ ББ-ВВ
Ту
Шщ
-&И
Фиг. 15. Мостик для измерения углов закручивания станин
токарных станков.
5. Расчетные формулы для определения
жесткости станин на кручение
На основании разработанных расчетов из условия равенства угла
закручивания станины, определяемого по приведенным выше форлп/лаад,
углу закручивания бруса постоянного, поперечного сечения Ф^т?/'
можно получить следующие формулы для определения жесткости на
кручение станин из двух параллельных стенок при жестких концевых
перегородках (типа станин токарных, револьверных и других станков):
Ь Станины с перпендикулярными перегородками1
^Лр =
В*ЕЛ
осгкЬ2 + а2"
ЕЗ,
стпу
ОР„
а) из двух параллельных стенок:
а1 = 1Г> «2 = 2;
(2.1>
б) из двух параллельных и наклонной стенок:
ч +2
12(2б1 + 1)
«♦> —
3(5^4- 16е^+ 14ел + 4)
5(2^+ 1)2
1 Так как формулы, по которым определяются ел и аг, для станин с
дополнительной (наклонной илн горизонтальной) стенкой выведены без учета влияния
направляющих на жесткость стенок, то расчет этих станин дает несколько большую погрешность^
чем расчет станин других типов.
50
в) из двух параллельных и горизонтальной стенок:
8 + 6
12 (2е + 3)
а2 =
__ 3(ЗвЗ + 16е2 + 42б + 36)
5 (2в + 3)2
Коэффициенты:
ЮЗп
у= {п + 1)ВЫсту
/1 I Я3 Б
*2
у радиан
1
Ш
0
#470
г*
-*
/ 10
у> радиол
Г*~
150 300 Ш
х^>
ч^
/
600 ДЫМ
у/?
6)
1
630
о
0,510
-4
; ю
у> радиан
"*~ 600 750
\ ^ I
"" ]\\
..х ,
900
1050 1200 1350 1500 м
""^ т*~ "*"
^-^^
^
^ ММ
6)
Фиг. 16. Изменение углов закручивания <р по длине х станин*
а — станка мод. 1Д62М (станина с П-образными перегородками) при крутя-
б •— станка моя. 1П62 (станина с замкнутым
29 500 к Гсм\
в — стайка мод. ШбЗ (станина с замкнутым контуром поперечного сечения)
при крутящем моменте М = 152500 кГсм. Кривые линии на графиках:
щем моменте М { = 27 500 кГсм
контуром поперечного сечения) при крутящем моменте М
моменте М„п = 152500 кГсм.
сплошные —расчетные; штриховые — опытные.
0.9
О.в
\п=1
^2:
^5
<„р
/
^
=2=-.-
2К
ь=-
=^=
• ^^1^^
О А01 402 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,1 1
а) 1$
0,9
0,6
0,7
Г^^С
\п=2
5^
^:
^^=
г^
77Г
""^
Р
2^
\ . 1
5^4^
' 0 0,01 0,02 0,03 ОМ ОМ 0,06 0,07 0,08 00 0,1 1
б) р
\л=и
^<^
^т^^
**..->.
ЕГ1
N
^
'** -*>^1«
*-=/.
Г
:л
\
Р
-- —
^;:
--_
-^^—
^.-1
,
' 0 0,01 0,02 0,03 0,0*1 0,05 0,06 0301 0,08 0,09 0,1 А
в) Р
0,9
0,8
0,7
0,6
' 0 0,01 0,02 0,03 0,0и 0,05 0,06 0,01 0,08 0,09 0,Г^С
г) Р
0,9
0,8
0,1
0,6
%5
ОЛ - - - - .
О 0,01 0,02 0,03 0,014. 0,05 0,06 0,07 0,08 0,09 0,1 1
д) Р
^
\п=5
$^^
^
^
Ч. * V
Г "''V
^ч. ^
\
^
\
\
\
^Ч
■аЗ
-•-^
^?
---
«~_ ,
■^
^-
Фиг. 17.
Коэффициент к,
характеризующий
зависимость жесткости
на кручение
станин с
перпендикулярными
перегородками от числа
перегородок п:
а — при ч = 1; б — при
п « 2; в — при п ~ 3;
г ~ при п -4} д — при
П »5.
Для станин без перегородок коэффициент й=1; при л> 1
коэффициент к определяется по графикам фиг. 17, а—д в зависимости от
-д-, #1 или е и числа перегородок п 1.
2. Станины с диагональными перегородками:
^сту ць
клЗ КР — кхЕЗсту -ту-. (2.2)
Коэффициенты:
^ = тЫ2+'351 + 6Тг
(6Т1 - 35, - 1)а [(2н - 1) (я - 1) + п (6Ь + 6Ь -+ 25д - 1) - (6Ь + 361 - 1)]
п(2п-\){п—\)(6^1+Ьъ+2Ь1+2)+{Ьъ+ЗЬ1-1+Зп)[п(6^1+6^+2Ь1—1)~(6Ь+ЗЬ1-\)]
^ п^ФЕ^сту ^ п?Е]сту _ аг$ЕЗсту
3. Станины с замкнутым контуром поперечного сечения
О/хр = 0^. (2.3)
Обозначения всех встречающихся величин см. выше стр. 40.
Величины моментов инерции, а также площади сечения элементов и все
линейные размеры определяются по чертежам. Угловое
сопротивление закручиванию перегородок (Л.*) Т-образного сечения
определяется как для свободного кручения. Для перегородок П-образного
сечения2
0,2П„Л*
В\гп +^Г + К + 16е2"+42в~+ 36
12^(2ея+3) 8^(2.л + 3)'
где
Для станин со стенками П-образного сечения жесткость
кручения определяется как сумма жесткости станины, вычисленной по
формулам (2.1) или (2.2) и собственной жесткости кручения стенок. В этом
случае угловое сопротивление закручиванию стенок /^.^определяется
по формуле, аналогичной формуле для определения /„.* перегородок
П-образного сечения.
Формулы выведены для станин из двух стенок с перегородками,
однако в первом приближении они могут быть использованы и для
1 Если иеличина ~а~ окажется больше»0,1—0,12 (для станин с широкими П-образ-
ными перегородками), коэффициент к следует определять по формулам:
прил = 1 кш= 2(2-Н) ; ПРИЛ:=2 6==9(2 + И(4 + р)*
2 Формула для определения углового сопротивления закручиванию П-образной пере-
городки получена из условия равенства углов закручивания перегородки и бруса
постоянного поперечного сечения той же длины при нагружении крутящими моментами по
концам. При определении угла закручивания перегородки принималось, что крутящий
момент, действующий на перегородку, воспринимается только системой касательных
напряжений, распределенных по сечению вертикальных стенок. Переменность
касательных напряжений по толщине стенок не учитывалась.
53
расчета стаиин из трех стенок. Влияние средней стенки относительно
невелико и может не учитываться.
Жесткость станин с одной жесткой перегородкой (типа станин
расточных, долбежных и других станков) можно определять по этим
же формулам. При этом для станин с перпендикулярными
перегородками в формулу для определения жесткости следует подставлять
расчетную длину ЬР = 2ЬУ где ^ — длина деформируемой части станины —
расстояние от жесткой до концевой деформируемой перегородки.
В. Определение жесткости на изгиб в горизонтальной плоскости
Определение жесткости на изгиб в горизонтальной плоскости
основывается на следующих предпосылках:
1. Жесткость станины на изгиб в горизонтальной плоскости
определяется при рассмотрении деформаций станины, установленной на
двух опорах и нагруженной
сосредоточенной силой в середине
расстояния между опорами (фиг. 18),
из условия равенства
максимального перемещения станины и
балки постоянного поперечного
сечения той же длины при той же
схеме нагружения.
2. Действующие силы
полагаются приложенными к станине
в узлах (в местах соединения
стенок и перегородок).
3. Станины рассчитываются
на изгиб как плоские рамы
(станины с перпендикулярными
перегородками) или фермы (станины
с диагональными перегородками)
052].
которых основаны расчеты,
подтверждается сравнением результатов расчетов и результатов
экспериментов над моделями станин1 [19, а].
Станины в виде двух стенок с перпендикулярными перегородками
рассматриваются как плоские статически неопределимые рамы,
имеющие две оси симметрии. Расчет рам удобно проводить по методу сил
с использованием ряда искусственных приемов, построенных на
свойствах симметричных конструкций.,
Для определения максимальных упругих перемещений станины
целесообразно разложить нагрузку на симметричную и кососимметрич-
ную составляющие относительно горизонтальной оси (фиг. 19). Так
как принято, что силы действуют на станину в узлах, то симметричная
составляющая нагрузки вызывает главным образом продольные
деформации стоек-перегородок. Можно показать, что при узловой
нагрузке влиянием на перемещения симметричной составляющей нагрузки
можно пренебречь. Также можно не учитывать влияния
перерезывающих сил и определять перемещения в рамах только от изгибающих
моментов при действии кососимметричной составляющей. В табл. 12
приведены суммарные эпюры изгибающих моментов и величины пере-
1 Расчетная жесткость несколько превышает действительную вследствие менее
активного, чем по расчету, участия в работе направляющих.
а/
*р
Фиг. 18. Расчетная схема для определения
жесткости на изгиб в горизонтальной
плоскости станин с перпендикулярными (а) и
диагональными (б) перегородками.
Допустимость предпосылок, на
54
мещении точек приложения силы для рам с одной, тремя и пятью
промежуточными перегородками при весьма высокой (бесконечной)
жесткости концевых перегородок.
а)
Ы
Фиг. 19, Разложение нагрузки на симметричную (а); и кососимметрич-
ную (б) составляющие относительно горизонтальной оси.
Таблица 12
Эпюры изгибающих моментов н перемещения точек приложения силы
для рам с одной, тремя и пятью промежуточными перегородками
от действия кососимметричной составляющей нагрузки
ВЛ
(перегородки над опорами приняты абсолютно жесткими) к = —у-г
Суммарная эпюра изгибающих моментов
Ординаты эпюры
Перемещение точки
приложения силы
Станины в виде двух стенок с диагональными перегородками
рассматриваются как плоские фермы с параллельными поясами и
треугольной решеткой. Соединение стенок и перегородок полагается шарнирным,
допускающим свободное поворачивание концов элементов при
деформациях станины. Можно показать, что при реальном соотношении
размеров влияние'жесткости узлов на перемещения не превышает 3—5%.
Рассмотрим станину с диагональными перегородками под
действием сосредоточенной силы Р в одном из узлов (фиг. 18, б) и опре-
56
делим перемещение точки приложения силы (узлы нумеруются
в строго определенном порядке — слева направо).
Опорные реакции
Л= п~к-Р; С-— Р
п ' п
(п—число перегородок; к— номер узла, к которому приложена сила;
на фиг. 18, б п = 4, к = 2).
Действующие силы в перегородках:
С05 а ЛС05 а
С кР
С05 а Л С05 а
Действующие силы в элементах стенок:
ы _ А1 _ (п-к)1 п м _ С [я - (Л»+ 1)] / _ **[»-(* + !)] „
Л/ _ Л-2/ _ (л~*)2/ р. а/ - С И - (* + 2)] ' - Ы 1*-(Ь + 2)] о.
Ю - .Ж - (п-к)к1 р. д, _ С[д-(я-1)1< _ ^/[п —(п- 1)] р
уу* ~~ В ~~ яВ ^> ^я-1 ~ В ~~ лВ ^
Стержни а и & при такой решетке не работают; жесткость крайних
стоек-перегородок для станин токарных станков может быть принята
равной бесконечности.
Перемещение / любого узла &* определится по формуле
- V N,N111
где Ыру N1—нормальные силы, возникающие в элементах станины
при действии силы Р в узле к и единичной силы в узле
кь соответственно;
1ь р1 — длина и площадь поперечного сечения элемента,
соответственно.
Подставив в формулу для перемещения входящие в нее величины*
получаем перемещение узла кь от нагрузки в узле к
* — 2Р1 \ рст у
Тт— п*ЕРст ( рп Л
X
]ЕРст | ?п
(Л — к) (п — 6/)6тщ + (я — &тах) (2Йщах - &тт) &т1п
ЗШ 2а СРЗ а
*т1п л~(*тах+1)
/-1,2.. /-1,2,3...
к
"тах
+ ЬтЫ (« — Ьтшж) .2 Цп — 1)
здесь #т1п—минимальное, &тах — максимальное из значений к, и А^.
56
Перемещение точки приложения силы (& — &/)
Л
2Р1
кк~
п*ЕРс.
^ 551П 9/7. Г ПС я ' О
л-*—1
(/г-А)2 ^ /2 + *а 2 '
/-1,2...
/-1,2 .
При действии силы в середине пролета «а средний узел в станине*
с четным числом перегородок (& —~<г) перемещение точки приложения
силы получаем равным
/*=•
ЧР1
п*ЕРс>
п*
4 зт 2а соз а
*ё2*
дз(Д2 + 2)
48
На основании полученных расчетных зависимостей из условия
равенства перемещения под силой в станине, определяемого по
приведенным выше формулам, и перемещению в балки постоянного поперечного
сечения, определяемому по формуле /= ^ёГЁУ' можно получить следую-
щие формулы для определения жесткости станин на изгиб в
горизонтальной плоскости:
а) станин в виде двух стенок с перпендикулярными
перегородками
^изг — ^1^стг> (2.4)
б) станин в виде двух стенок с диагональными перегородками
Е^эг^82Е^Рст: (2.5)
Значения коэффициентов 51 и 52 приведены в табл. 13.
Вспомогательные коэффициенты для определения
жесткости станин на изгиб в горизонтальной плоскости г
Таблица 13
Станины с перпендикулярными перегородками
Станины с диагональными перегородками
Схема станины
$!
Схема станины
3 + 4
&/,,
32
ип
14^4^1
1/\/\/\>
51П а • С052 а
12
+• 51П?а
§1П а . С052 а
12
Рп
+ 3 5И13 а
81П а • С052 а
12
[Рп +
+ 6,а$1п»а
г
72«
1 1 ^стг
ЬЛАЛЛ
8Ш а . С053 а
12
+ 11 5шз а I
1 + 9
ЯЛ;
ип
1/УУУУ\1
10
81П а ' С082 а
12
/>«
+ 17б1п з а
1 Если число перегородок станины п отличается от приведенных в таблице, то для этого случая
коэффициенты $1 и 5а определяются как средние из значений 5 для соседних большего и меньшего числа
перегородок.
57
Жесткость станин из трех стежок с перегородками можно
определять по этим же формулам, учитывая влияние средней стенки
коэффициентом 1,1 —1,2 (большие значения при относительно более
высокой жесткости перегородок). Хотя формулы выведены для станин,
у которых жесткость обеих концевых перегородок значительно выше
жесткости промежуточных, однако в первом (приближении ими можно
пользоваться и для расчета станин с одной жесткой перегородкой
(одностоечных и портальных станков).
Для станин из двух вертикальных и горизонтальных или наклонной
стенок и станин с замкнутым контуром поперечного сечения жесткосггь
на изгиб в горизонтальной плоскости определяется по моменту
инерции сечения станины относительно вертикальной оси, проходящей через
центр тяжести сечения.
§ 4. СОВМЕСТНАЯ РАБОТА СТАНИН С ФУНДАМЕНТАМИ
А. Основные положения
Влияние фундамента на деформации станины определяется
способом установки станка.
При установке станков на трех точках деформации фундамента
на деформации станины влияния не оказывают.
При установке станков ма ножках фундамент оказывает
сопротивление смещению и повороту ножек, которые можно рассматривать
как упруго защемленные. Влияние упругого защемления .ножек
оказывается наибольшим для станков, закрепленных на индивидуальных
фундаментах или на общем бетонном полотне, и оценивается величинами
порядка 10—20%. В первом приближении влияние защемления ножек
может не учитываться.
В станках со сплошными станинами, опирающимися на фундамент
по всей длине, жесткость фундамента и опорных элементов станины
в значительной степени определяет величину деформаций станины.
Влияние фундамента на деформации оплошных станин
оценивается при следующих допущениях:
1. При расчетах на изгиб в вертикальной плоскости и на
кручение станина на фундаменте и фундамент на грунте рассматриваются
как балки на сплошном упругом основании.
2- При определении деформаций станин и фундаментов как балок
на упругом основании в качестве основной расчетной гипотезы
принимается гипотеза о прямой пропорциональности меаду перемещениями
и реакцией грунта.
3. Полагается справедливым предположение о сохранении связи
между фундаментом и грунтом и между станиной и фундаментом и
при отрицательных прогибах (вверх), так как наблюдения и расчеты
показывают, что деформации станин под действием сил резания
значительно меньше деформаций грунта или фундамента от действия веса
станка.
4. Сопротивление сдвигу по подошве станины и фундамента не
учитывается К Также не учитывается сопротивление по боковым
граням фундамента.
1 Для станков, ие закрепленных на фундаменте, сопротивлением сдвигу,
обусловливаемым силами трения по подошве станины, можно пренебречь ввиду неизбежного
дрожаиня стайка при работе.
Для станков, закрепленных на фундаменте, следует считать, что смещения станины
относительно фундамента ие происходит н они деформируются как одно целое. Однако,
если жесткость фундамента значительно превышает жесткость станииы, то общая
жесткость системы определяется главным образом жесткостью фундамента. При этом
влияние касательных сил, действующих в месте соединения станины и фундамента, на
деформации системы невелико, и его можио не учитывать.
58
5. Станина и фундамент рассматриваются как однороднее балки
постоянной приведенной жесткости. Жесткость станин определяется по
формулам, приведенным выше. Жесткость фундамента на изгиб
определяется по моментам инерции сечения. Для армированных
фундаментов предполагается, что нейтральная ось располагается там, где
она была бы при изгибе однородной балки. Жесткость на кручение
фундамента при сложной форме поперечного сечения приближенно
может определяться по формуле [43а]
°«Л>. кр — °Ф ^ЩТ^ТТ^у) » (2'6)
где 3ф*> ^фу' Рф—моменты инерции и площадь поперечного сечения
фундамента;
Оф—модуль упругости фундамента.
При оценке (влияния фундамента на деформации станины
следует рассматривать отдельно деформации от сил резания и от веса
перемещающихся узлов станка. Деформации станины от собственного
веса и от веса неподвижных узлов можно не рассматривать, так как
лри установке станок выверяется.
Б. Деформации станин с фундаментами
1. Деформации станин с фундаментами
от сил резания
Так как силы резания замыкаются внутри станка, то система
силовых факторов, действующих на станину и фундамент, является уравг
повешенной, т. е. статически эквивалентной нулю. По опорным
площадям станины и фундамента действует также
взаимно-уравновешенная нагрузка, препятствующая деформациям.
Рассмотрим деформации станины и фундамента как балок на
упругом основании.
Полагая, что действие фундамента на станину пропорционально
разности прогибов станины (уст) и фундамента {Уф),
дифференциальное уравнение изгиба станины можно записать в виде
где д — внешняя нагрузка на станину;
Кст~СгЬ — коэффициент жесткости стыка между станиной и
фундаментом при упругом равномерном сжатии, отнесенный
к единице длины опорной поверхности станины (Сг —
коэффициент упругого равномерного сжатия см. ниже
стр. 67; Ь — ширина опорной поверхности);
ЕЗ— расчетная жесткость станины на изгиб.
Для фундамента можно записать
Ф ФУ их* =^ст {Уст Уф) КфУф*
здесь Кст (уст—уф) — нагрузка, действующая между станиной и
фундаментом и рассматриваемая для
фундамента как внешняя;
Кф — коэффициент жесткости основания фундамента
при упругом равномерном сжатии, отнесенный
к единице длины опорной поверхности
фундамента (определяется аналогично Кст)\
Еф]ф—расчетная жесткость фундамента на изгиб.
59
Для определения деформаций станины и фундамента
воспользуемся не точными решениями этих дифференциальных уравнений, а
приближенными [50]. Запишем решения дифференциальных уравнений
в виде
Уш = сг *Уф^аъ
где % — некоторая функция, удовлетворяющая части граничных
условий; а и с — постоянные коэффициенты, определяемые из условий
минимума полной потенциальной энергии системы станина —
фундамент 1.
Выражения для полной потенциальной энергии станины и
фундамента можно записать в виде
Эст=-^-^(у"спГс1х + Др]' (уст -
Эл=
-Уф)УстаХ-$<1УстаХ'>
)(Уст-УФ)Уфс1х-
Кет
Подставляя уф — ах и уст — сх, получим полную потенциальную
энергию системы в виде
+ [^г(с- ау + %- а»] | ХЧх - с | пОх.
Из уравнений -у-= 0 и -^—= 0, обозначая
64 [чЫх г г
5 — - И Ьст— ^ у Кф— ,
где Ь--длина станины и фундамента, получим
а-.
К
1 + ^ + & + ^>+ Ф*.«* ЕЗ \ (Г)Чх
1 Можно показать (см. ниже), что при уравновешенной нагрузке предположение
о подобии упругих линий балок при разных значениях коэффициентов жесткости
(вытекающее из того, что функция % принята для станины и фундамента одинаковой) для
технических расчетов является вполне приемлемым.
60
При Кст = Ъ, т. е. если сопротивления деформациям станины
I
со стороны фундамента нет, с = ^ н упругая линия ста-
г|(х"):
вз (ГУ ах
нины уст= ^
ЕЗ Ш")*йх
№
Рассмотрим некоторые частные случаи.
1. Стык между станиной и фундаментом обладает весьма высокой
жесткостью (например, в случае, если станок подлит цементным
раствором и закреплен на фундаменте); Кст-+
со \ ^ст —* ^°»
- — Х 1 1™**
Уст-уф-. {1 + Кт ^ ■ Е^ + Еф^фу • м. х.
К>:
2(1х
где
ст, ф'
V-
ЕЗ + Еф]фу
Кф
В этом случае станину и фундамент можно рассчитывать как балку,
имеющую жесткость, равную сумме жесткостей станины и фундамента
и лежащую на упругом основании — грунте. Нагрузку, действующую на
такую балку, следует определять приведением силовых факторов к оси
станины.
2. Жесткость станины весьма мала по сравнению с жесткостью
фундамента (наиболее распространенный случай для тяжелых станков).
Полагая Е^фу->
Уст-
-со и \ф-^ 0,
1
~ 1+й„*
получим
1
§ЯХ<*х
ез \(гуах
Полагая Е] -> 0 и \т -» со, получим
У ст
"V - 1
~'* 1+45
}ЯХ<1х
1
В этом случае деформации станины можно определять как сумму
деформаций фундамента и деформаций станины относительно
фундамента, вычисляемых независимо. Так как в этом случае %ст^>\, то
деформации станины относительно фундамента оказываются значительно
меньше деформаций фундамента. Поэтому в первом приближении можно
считать, что деформации системы станина—фундамент определяются
только деформациями фундамента.
Функция %, определяющая упругую линию балки при изгибе, при
точном решении зависит от вида нагрузки. Однако для технических
расчетов можно не рассматривать все разнообразие нагрузок, действующих
61
на станины, а определить функции %с и %к для симметричной и кососим-
метричной составляющих любой нагрузки.
Запишем упругую линию балки в виде полинома 5-й степени^
у = а0-\-а^ + а^х2-\-а2х*-\-аАхъ. Составляющая прогибов от
симметричной нагрузки ус~(НХс<> гДе Хс — ~1Г + х* + "7Г х*> и от кососимме-
тричной ук = а$хк> где хЛ=-^--^ + ^8 + -^г*5 (начало координат при-
нято посередине балки). Как уже указывалось, постоянные в этих
выражениях должны быть подобраны так, чтобы удовлетворялась
часть граничных условий для балки.
При симметричной нагрузке одна из постоянных
определится из условия равенства нулю равнодействующей давления
основания на балку, т. е. из условия I %&х = 0, вторая — из условия равен-
] 1%4х = 0,
ства нулю моментов по концам балки. В результате получим
^ = х2-^т-^Щ~ и 5=0,123.
При кососимметричной нагрузке одйа из постоянных
определится из условия равенства нулю момента от давления основания
на балку, т. е. из условия I х%(1х — 0, вторая — из условия равенства
нулю моментов по концам балки. В результате получим
о б*5 3№х ЛЛ1,
Х« = * ~5Р~~280~ И 5==0>015'
Так как при типичных видах нагружения станин кососимметричнан
составляющая перемещений значительно меньше чем симметричная
(как правило -у- не больше 0,1—0,2), в первом приближении
перемещения станины и фундамента можно определять по значению 5 = 0,123
для симметричной составляющей нагрузки.
Аналогичным образом можно рассмотреть кручение станины и
фундамента. Дифференциальное уравнение кручения станины можно
записать в виде
где т — внешняя нагрузка, закручивающая станину;
Кст—С^г — коэффициент жесткости стыка между станиной и
фундаментом при упругом неравномерном сжатии, отнесенный к
единице длины опорной поверхности станины;
С9—коэффициент упругого неравномерного сжатия; С9 = 2Сг [3], [4] ;УХ —
момент инерции площади участка единичной длины
опорной поверхности станины (если станина опирается по двум
стенкам при ширине опорной поверхности под каждой
стенкой Ъ1 и расстоянии от оси поворота сечений станины до
середины опорных поверхностей Г/, то ^^ = ^^2^ Ь^ при
сплошной опорной поверхности шириной В момент инер-
ЦИИ Ух — -^ ;
ОУ^ — расчетная жесткость станины на кручение.
62
Для фундамента можно записать соответственно
где К'ф — коэффициент жесткости основания фундамента при упругое
неравномерном сжатии, отнесенный к единице длины опорной,
поверхности фундамента (определяется аналогично К'ст\;
Оф1ф.Кр — расчетная жесткость фундамента на кручение.
Полагая углы закручивания станины Уст = скх и Ф#—акЪ где т: —
некоторая функция, а ск и ак — постоянные коэффициенты, выражение
полной потенциальной энергии системы станина — фундамент можно^
записать в виде
I I
+1лг <с« - а«)2+Ч- а«] 1хЧх -с Лтхс1х-
Из уравнений -~^ —О и -у-^ = 0, обозначая
ь
С ±-
V и Кт* к — г г г ; V«— •
6ф ^ф. кр
V
получим соответственно
хст. к** [тхйх
Ь
При определении функции кручения т раздельное рассмотрение
симметричной и кососимметричнои составляющих нагрузки, вызывающей
кручение станины, нецелесообразно, так как не дает упрощения решения.
Если силовые факторы, вызывающие кручение станины,
рассматривать как сосредоточенные, то можно считать, что от сил резания станины
могут быть нагружены двумя (станины долбежных, расточных и т. п.
станков) или тремя (станины токарных, револьверных и т. п. станков)
крутящими моментами.
Рассмотрим нагружение станины тремя крутящими моментами в
сечениях с координатами хи х2 и х3 (фиг. 20, а) при условии, что М =
= М2 + М1 (как это имеет место в токарных станках).
Выберем функцию т так, чтобы она точно соответствовала кривой
изменения углов закручивания по длине балки с жесткими заделками
Так как было принято, что кривые углов закручивания балки на
жестких опорах и на упругом оснавании подобны, то, как уже указывалось,.
должно быть справедливо равенство Г хйх = 0. Из этого условия можно
определить начало отсчета (положение неповорачивающихся сечений)
63«
для кривой углов закручивания. При этом для балки, представленной на
фиг. 20, а, полагая угол закручивания в любом сечении ф=^у-т, можно
'кр
записать
для участка 0 < х < хг
11 = Хг — Х-1 -
для участка хг < х < х2
*2 ~~ *!
21
Тл Хл X '
для участка хг<х<х$
1-(х _х *»~*аУ
^ — — 2Х
.для участка дг3 < * < ^
Т. — -
То Х7 Т1~ I Хп X
Мг \ 3 21
Х\ "* -*1 , ЛГ^ *3 ~~ **2
21
Л^ 2/:
0
Фиг. 20. Расчетные схемы для оценки влияния фундамента
на жесткость кручения сплошных станин.
Подставляя приведенные значения т, в выражение $« = х
и интегрируя по участкам, получим
с а2 ~ Ч \*ъ + 2^ («2 + ЧУ Щ Дз~аа /„ I „ л V/
М? а2 - «1
V / 1 _ аз + ч \ Л- -^ (*з - аз)2 Г«э +
2 («3 - а2)2 Га3 + 2а2 (а3 + аз)2
)•
где
«1=-
■^2
"Г
-«3
лз — Т"
Отсюда, полагая М2 = 0, можно получить формулу для §к и для
случая нагружения станины двумя моментами.
Оценивая точность приведенных решений, можно показать, что
величины перемещений, вычисленные по полученным приближенным и
точным формулам, достаточно близки. Так, например, для балок на жест-
1 По этим формулам для балки иа жестких опорах, полагая ф = ^лТ, получим
с
| тъс1х ^1
с* = 1
шкр1(^уах
- о/,
кр
64
ких опорах и на упругом основании, нагруженных двумя равными
изгибающими моментами по концам, относительные перемещения,
вычисленные по точным и приближенным формулам, для X от 0,5 до 2
отличаются не более, чем на 5%. Величины относительных углов
закручивания для балок,
нагруженных двумя или
тремя сосредоточенными
моментами, вычисленных по
точным и приближенным
формулам, для кк от 0,8
до 3 практически
совпадают.
Как для изгиба, так
и для кручения с
увеличением к и КК расхождение
результатов точного и
приближенного решения
увеличивается, однако
применение лриближен-
ных расчетов все же
остается возможным, так как
с увеличением А, и ХК
резко уменьшается
абсолютная величина
деформаций.
Следует отметить, что
по приближенным
формулам изгиба балок с
достаточной точностью
определяются только
величины перемещений.
Значения производных %' и х"»
пропорциональных наклону упругой линии и изгибающему моменту,
определенные по трчным и приближенным формулам, совпадают
значительно хуже.
Влияние фундамента на деформации станин в данном сечении
удобно оценивать величинами коэффициентов повышения жесткости Ни
(при изгибе) и %К (при кручении), которые можно определить как
отношения деформаций в этом сечении от данной нагрузки балки на жестких
опорах и балки на упругом основании. Если воспользоваться не точным
решением задачи о деформациях балок на упругом основании, а
изложенным выше приближенным, то величина коэффициента повышения
жесткости для данной нагрузки будет постоянной для любого сечения
балки,1 в частности при изгибе Ни= 1 +0,123А4.
Точность такого приближенного определения коэффициента
повышения жесткости для технических расчетов оказывается вполне
достаточной (фиг. 21). Принимая величину коэффициента повышения жест-
1 Это вытекает из принятого допущения о подобии упругих линий балок на
жестких опорах и на упругом основании, которое справедливо только при таком
расположении опор, при котором обеспечивается равенство нулю равнодействующей силы и
момента от реакции основания,, пропорциональной перемещениям. Однако, так как при
уравновешенной нагрузке кривизна упругой линии и кривой углов закручивания не
зависит от расположения опор, которое определяет только ориентацию балки в
пространстве, относительные перемещения сечений станин можно определять с использование?^
полученных значений коэффициента повышения жесткости при любом расположений
опор.
Фиг. 21. Коэффициент повышения жесткости при
изгибе—приближенные значения {На = 1 + 0,123А,4)
и точные, вычисленные для разных видов нагруже-
ния.
65
кости постоянной, относительные перемещения сплошных станин,
которые следовало бы рассчитывать как балки на упругом оснований,
можно определять как для балок на соответствующим образом
расположенных жестких опорах, учитывая влияние фундамента и
упругого основания введением в расчет коэффициента повышения
жесткости (о расположении опор при определении деформаций станин
(см. § 5).
2. Деформации станин с фундаментами от веса
перемещающихся- узлов
Вес перемещающихся узлов, действующих на станину,
уравновешивается по подошве станины и фундамента распределенной по некоторому
закону нагрузкой. Характер изменения этой нагрузки зависит от
жесткости станины и податливости основания. При Е1 -+ со и К-+ 0, т. е. при
X -► 0, закон распределения близок к линейному.
Рассмотрим деформации балки под действием некоторой
неуравновешенной нагрузки и уравновешивающей ее нагрузки, распределенной
по линейному закону, который примерно соответствует закону
распределения реакции упругого основания при /(->0. Деформации такой
балки будут больше деформаций балки на упругом основании при
КфО под действием этой же неуравновешенной нагрузки.
Как уже указывалось, отношение перемещений балок при К = 0 (на
жестких опорах) и КФО (на упругом основании) можно рассматривать
как коэффициент ловышения жесткости. Тогда относительные
перемещения станин от заданной неуравновешенной нагрузки можно
определять, уравновешивая заданную нагрузку некоторой дополнительной,
заменяющей реакцию упругого основания, распределенной по длине
станины по линейному закону. При этом относительные перемещения
станины определяются как для балки на жестких опорах под действием
заданной и дополнительной нагрузок, а влияние истинного закона
распределения реакции упругого основания учитывается умножением
расчетной жесткости на коэффициенты повышения жесткости На или
Цк (см. выше).
Точность расчета на изгиб по приведенной схеме иллюстрируют
кривые — и /?й= 1 -|- 0,123Х4, приведенные на фиг. 21.
Значения -у- (у\ — перемещения в балке на упругом основании под
действием заданной нагрузки, у2 — перемещения в балке на жестких
опорах под действием заданной и уравновешивающей ее
дополнительной нагрузок) отличаются от значений коэффициента повышения
жесткости На не более чем на 3—4%.
Деформации кручения станин под действием веса узлов,
перемещающихся перпендикулярно оси станины, могут быть определены
аналогичным образом..
В этом случае закручивающая станину неуравновешенная нагрузка,
которая может быть представлена в виде сосредоточенного крутящего
момента, уравновешивается моментом, равномерно распределенным по
длине станины (фиг. 20, б). Функция кручения т и величина з,{,
входящая в формулу для перемещений (см. выше), определяются так же, как
в предыдущих случаях. Относительные углы закручивания балки на
упругом основании под действием сосредоточенного крутящего момента,
вычисленные по изложенной схеме и г!о точным формулам, различаются
на величины порядка 3—5%.
66
В. Расчетная жесткость упругого основания при разных
способах установки станков
Жесткость основания фундамента определяется коэффициентом
упругого равномерного сжатия грунта.
Для станков, подлитых и закрепленных на фундаменте, жесткость
основания станин определяется коэффициентом упругого равномерного
сжатия материала фундамента. Величины коэффициентов упругого
равномерного сжатия С/ для разных материалов приведены в табл. 14.
Таблица 14
Значения коэффициента С г упругого равномерного сжатия для разных материалов
132)
Категория грунта
Грунт средней
плотности
Грунт плотный
Грунт весьма
плотный
I рунт твердый
Грунт скалистый
Искусственное
основание
Строительные
материалы
Наименование материала
Песок слежавшийся; гравий насыпной, глина
влажная
Песок плотнослежавшийся; гравий плотно-
слежавшийся; щебень; глина малой влажности
Песчаник глинистый, искусственно
уплотненный; глина твердая
Мягкая трещиноватая скала; известняк;
песчаник
Твердая скала
Свайное основание
. Кирпич
! Бутовая кладка
; Бетон, железобетон
в кГ/см9
0.5—5
5—10
10-20
20—100
1 100-1500
5-15 1
400— 500
[ 500— то
800—1500 !
Для станков, не подлитых цементным раствором, жесткость
основания станин определяется жесткостью опорных элементов станка на
фундаменте.
Коэффициент С,, характеризующий приведенную жесткость
упругого основания при установке станка на упругих опорных элементах,
определяется из условия равенства перемещений сечений балки на
сплошном улругом основании и перемещений в опорах станка, по
формуле Сг = р. , где ко — коэффициент податливости опоры в см/кГ; Р—
площадь опорной поверхности; п — число опор на площади Р.
Податливость опоры ко вычисляется как сумма податливостей
отдельных стыков.
Податливость стыка с точечным или линейным контактом
определяется как отношение приращения перемещения, вычисляемого по
формулам Герца, к приращению нагрузки.
Податливость стыка при контакте по поверхности зависит от
коэффициента контактной податливости к (см. ниже) и площади контакта Р
и определяется по формуле к0 — -р-.
Коэффициент контактной податливости к в см3/кГ для случая
контакта металлических поверхностей может приниматься равным
(0,5-М,0) • 10""4 см3/кГ. Для стыка чугун—бетон (по результатам
экспериментов), если опоргный элемент подлит, &^0,7-10"4 см31кГ, и, если
не подлит, к= (15-:-30) • 10"4 смъ\кГ. Нижние значения следует
принимать для меньших, а верхние для больших площадей контакта.
* Как известно, величины коэффициента Сг не являются постоянными к зависят
не только от упругих свойств материала, но и от размеров фундамента, формы опорной
поверхности и т. д. Однако для технических расчетов использование приведенных
постоянных значений коэффициента можно считать допустимым.
67
При передаче давления от станины к фундаменту через элемент
с резьбой податливость в резьбе определяется по формуле
к - —
где кг — коэффициент контактной податливости в резьбе, определяемый
по кривой, приведенной на фиг. 22, в зависимости от номинального дав-
Р
ления в резьбе в^^рг;?' — площадь контакта одного витка резьбы;
2—число работающих (номинально) витков.
Податливость в результате соб-
а' ~ ственных деформаций сжатия или
растяжения элементов опоры
(винтов) следует учитывать только в том
случае, если деформируемая длина
/ этих элементов достаточно велика.
При этом ко = -^рпч где ЕР" —
жесткость элемента на растяжение—
сжатие.
Г. Расчетные формулы
для определения коэффициентов
повышения жесткости /?и и ЯК,
учитывающих влияние фундамента
на деформации станин
При установке станков на трех
точках или на ножках коэффициенты
повышения жесткости Яи ц #№
принимаются равными 1,0.
При расчете сплошных станин,
если жесткость станины и
фундамента одного порядка,
коэффициенты повышения жесткости
определяются по следующим формулам:
фиг. 22. Зависимость коэффициента к'
контактной податливости в резьбе от
номинального давления.
1. При расчете на кручение
Яж=1 +
(2.7)
(Нкри Оф^ф.кр — расчетная жесткость станины и фундамента на
кручение в кГсм2;
Ь—длина стайины и фундамента в см;
К'ст, Кф~~ коэффициенты жесткости при упругом неравномерном
кГ
сжатии основания станины и фундамента в
(см. стр. 62).
Коэффициенты зк определяются:
68
радиан
а) для случая нагружения станины двумя равными по величине и
противоположными по знаку крутящими моментами
— <„ п \ Г "2 + 2*1 («2 4 *1)21
{ — («8 - «1) [ 3 4 ] >
где
Ч — '1\ а2 —Х;
*1 их2— расстояния от края станины до нагруженных сечений станины;
б) для случая нагружения станины одним сосредоточенным
крутящим моментом и уравновешивающим его моментом, равномерно
распределенным по всей длине станины (см, стр. 66),
5 =1^._' 15а2(1-а)*
"к~—х 15 [1 -За(1 -а)] >
где * — ^-\
х — расстояние от края станины-до сечения, в котором действует
момент.
В случае нагружения станины тремя сосредоточенными моментами,
например при обработке в центрах на токарном станке, при
соотношениях размеров элементов, типичных для реальных станков, величина
коэффициента з,с получается порядка 0,01—0,025 и влияние
сопротивления упругого основания деформациям кручения станины может не
учитываться.
2. При расчете на изгиб в вертикальной плоскости
1+0,123X1
/?«..= ! + ; х* ' ■-■ » <2-8>
1 V ,. -а/
ОЛ^Кт Кт *****
где
Х^~ 4 Г—гПТ- ' V
{1
2
\П%' ^Ч
ф^фу
ЕЗХ ЕфЗфу — расчетная жесткость станины и фундамента на изгиб
в вертикальной плоскости в кГсм2;
Кст> Кф — коэффициенты жесткости при упругом равномерном
сжатии основания станины и фундамента в кГ/см? (см.
стр. 59).
3. При расчете на изгиб в горизонтальной плоскости !:
а) для станин, не закрепленных на фундаменте, коэффициент
повышения жесткости Яи принимается равным 1;
б) для станин, закрепленных на фундаменте,
Я»=1+-%?*-. (2-9)
где Е]азг, Еф]фг — расчетная жесткость ^станины и фундамента на изгиб
в горизонтальной плоскости.
1 Для станин, закрепленных на фундаменте, уменьшение деформаций за счет
сопротивления основания фундамента сдвигу и сопротивления по боковым граням
фундамента, а для незакрепленных станин уменьшение деформаций за счет сил трения
о фундамент не учитывается.
6&
В том случае, если станок подлит цементным раствором и притянут
фундаментными болтами (стык между станиной и фундаментом
обладает весьма высокой жесткостью), деформации станины при кручении
и изгибе в вертикальной плоскости можно определять, рассматривая
станину и фундамент как балку, имеющую жесткость, равную сумме
жесткостей станины и фундамента (см. стр. 61). При этом коэффициенты
повышения жесткости такой балки, учитывающие влияние отпора грунта
деформациям системы, определяются по формулам:
#«=1+*А2т.*.«; (2.7а)
/?«.. = 1+0,123^, (2.8а)
где
^ст. ф.к — /"7П—л. г I ' ""• Ф '
/~<укр+оуф.кр' ст-ф у;
Е^ ~\- ЕфЗфу
Для тяжелых станков, у которых жесткость станины мала по
сравнению с жесткостью фундамента, деформации системы
станина—фундамент определяются только деформациями фундамента (см. стр. 61).
В этом случае коэффициенты повышения жесткости, учитывающие
влияние отпора грунта деформациям фундамента, определяются по формулам:
Я*=1+^.ж; (2Л0)
/?«.• = 1+0,123^. (2.11)
Для иллюстрации количественного влияния фундаментов на
жесткость сплошных станин можно привести следующие примеры:
1. Для станины станка, установленного на клиньях, при Е1 =
= 40 • 1010 кГсм1, Еф]фу = 250 • 1010 кГсм\ коэффициенте упругого
равномерного сжатия основания фундамента С0 = 4 кГ\см?,
коэффициенте упругого равномерного сжатия приведенного основания
станины С^=10 кГ/сму> (при коэффициенте податливости опоры к0 =
= 0,15 • Ю-4 см\кГ), ширине опорной поверхности фундамента Ьф —
= 100 см, ширине опорной поверхности станины Ьст = Эд см, длине
станины 1^ = 800 см, длине фундамента 1^=1000 см, будем иметь
Е]
\ф—\,253 \ст=\,5, -рг-у— = 0,16 и коэффициент повышения жесткости
станины при изгибе
1 + 0.123*1
0Л23Х* +\**т/ + Ё^фу
ст
Расчетная жесткость системы (Е1) ~ 1,58 -40-1010 = 63- 1010 кГсм2.
2. Для того же станка, подлитого и закрепленного на фундаменте,
полагая коэффициент упругого равномерного сжатия основания станины
С* —800 кГ\смъ, получим Хст = 6. Так каклгт>)^ и жесткость
фундамента значительно превышает жесткость станины, можно считать, что
в этом случае деформации системы станина—фундамент определяются
только деформациями фундамента. При этом расчетная жесткость
(ЕТ) = (1 + 0у12314ф)ЕфУфу. При %ф = 1,25 получим {ЕЗ) = 325 -1010 кГсм2.
Если бы при значении %ст = 6 подсчитать величину коэффициента
повышения жесткости станины /?«. ,ь та можно получить Ни. в= 8,6 и
расчетную жесткость системы (Е1) = 8,6 -40- 1010 = 340 • 1010 кГсм2. Как
можно видеть, полученные результаты достаточно близки между собой.
70
§ 5. ТЕХНИЧЕСКИЙ РАСЧЕТ СТАНИН
А. Основные положения и расчетные зависимости
Жесткость станин, как уже указывалось, предлагается
характеризовать величиной перемещения (при заданной силе) инструмента
относительно изделия в результате деформаций станины при достаточно
типичном случае обработки.
Для того чтобы по вычисленным перемещениям судить о жесткости
станины рассматриваемого станка, следует сравнить эти перемещения
с (величинами допустимых погрешностей обработки или с
соответствующими перемещения-ми, вычисленными для других станков, хорошо
показавших себя в эксплуатации.
Расчетные формулы для определения перемещений инструмента
относительно изделия в результате деформаций станин выводятся на
основе следующих предпосылок:
1. Станины рассматриваются как балки постоянной жесткости,
определяемой по формулам, приведенным выше.
г
П
1 1
1
77ГГЛУ77777У7//»////*
Опорные лючки
7777У/Л77}
^---*
V
а)
7777Л
7$7У/7/,
-®Г\
Станина
Фундамент
Ък
^/У/У/У^У////УУ/У/^/УУУУУУУ^/А
б)
Фиг. 23. Расчетные схемы горизонтальных станин.
2. Расчетная схема станины определяется способом установки станка:
а) станины, устанавливаемые на три точки (станины 'прецизионных
станков), рассматриваются как шарнирно опертые двухолорные балки
при расчетах на изгиб и как заделанные в том сечении станины, в
котором размещаются две опорные точки, — при расчетах на кручение.' В этом
случае деформации фундамента не влияют на деформации станины
(фиг. 23, а);
б) станины, устанавливаемые на ножках, рассматриваются как
шарнирно опертые двухопорные балки (фиг. 23, б); влияние упругого
защемления ножек от сопротивления фундамента их наклону" и
смещению даже для станков, закрепленных на фундаменте, не превышает
10—20% и в первом приближении не учитывается;
в) сплошные станины, закрепленные и не закрепленные на
фундаменте, рассматриваются как балки на упругом основании (фиг. 23, в).
3. При определении перемещений инструмента относительно
'изделия рассматриваются деформации станины на длине между сечениями,
в которых на станину передается нагрузка от узлов, несущих
инструмент и изделие (см. ниже п. 5).
Если требуется определить относительное смещение концевых
сечений рассматриваемого участка, то одно из сечений условно принимается
заделанным; если требуется определить смещение промежуточного
сечения относительно прямой, соединяющей концевые сечения рассматривае-
71
мого участка (например, при обработке в центрах на токарном станке),,
этот участок рассматривается как опертый по концам. При расчетах по
такой схеме сплошных станин влияние фундамента учитывается
введением в расчет коэффициента повышения жесткости, определяемого по
формулам, приведенным выше, а нагрузка от веса перемещающихся
узлов уравновешивается некоторой дополнительной нагрузкой,
распределенной по линейному закону.
4. Расчетными усилиями для станин являются силы резания и веса
перемещающихся узлов:
а) для станин станков, у которых нагрузка от резания, являющаяся
для станка внутренней, замыкается в том же сечении станины, в котором
приложена (бесконсольные одностоечные, продольно-строгальные,
продольно-фрезерные и т. п. станки), а также для станков, у которых силы
резания относительно невелики по сравнению с весами перемещающихся
узлов (координатно-расточные станки), основной расчетной нагрузкой
являются веса перемещающихся узлов;
б) для станин станков, у которых нагрузка от резания приложена
в одном сечении, а замыкается в другом (токарные, револьверные,
долбежные и т. п. станки), расчетной нагрузкой являются силы резания,
а в тяжелых станках дополнительно вес изделия и перемещающихся
узлов. В станинах средних станков веса изделий и перемещающихся
узлов станка невелики оо сравнению с силами резания, и деформации
от них не рассматриваются. Исключение составляют прецизионные
станки [27].
5. Нагрузка на станины от сил резания полагается приложенной
в одном сечении: при малой жесткости узла, передающего нагрузку на
станину (например, суппорта), — непосредственно в сечении действия
силы; при высокой жесткости узла — в сечении, расположенном в
плоскости, совпадающей с осью этого узла. Нагрузка от веса
перемещающихся узлов при большой (относительно длины станины)
протяженности узла рассматривается как равномерно распределенная, при
небольшой — как сосредоточенная. Расчетная нагрузка на станину
определяется приведением силовых факторов, действующих по
направляющим, к оси, проходящей через центры тяжести сечений станины.
Технический расчет станин проиллюстрируем на примере расчета
станин на ножках токарных станков средних размеров для случая
обработки в центрах1. Следует отметить, что по сравнению с другими
горизонтальными станинами станины токарных станков находятся в
условиях наиболее сложного нагружения.
Жесткость станин токарных станков целесообразно характеризовать
перемещением инструмента относительно изделия в направлении оси
резца, т. е. в направлении, влияющем на точность станка под нагрузкой.
Выбор величины такого перемещения в качестве характеристики
жесткости является достаточно целесообразным также и с точки зрения
виброустойчивости. В частности условие обеспечения более высокой
точности под нагрузкой непосредственно совпадает с условием ограничения
весьма мощного вторичного возбуждения колебаний, связанного с
волнами на поверхности обработки от предыдущего прохода. Кроме того,
увеличение основных параметров станин, определяющее уменьшение
перемещения по нормали к обрабатываемой поверхности, приводит
к уменьшению составляющих полного перемещения и по другим
направлениям.
Поскольку при расчете на жесткость определяются деформации
станины, влияющие на точность обработки, основными деформациями,
1 Так как длина деформируемого участка станины при обработке изделия в
патроне весьма невелика, расчетное определение деформаций станины, влияющих на
точность обработки, для этого случая представляется мало актуальным.
72
на которые производится расчет, являются изгиб в горизонтальной
плоскости и кручение.
Деформации станины рассматриваются на длине, равной длине
изделия. В сечениях под передним и задним центрами при расчетах на
изгиб принимаются шарнирные опоры1, а при расчетах на кручение*
жесткие заделки.
Нагружение станины токарного станка показано на ф#г. 24;
расчетная схема — на фиг. 25.
Для определения погрешности \ур на изделии, упругие перемещения'
станины должны быть приведены к резцу.
Тогда
где/—упругие перемещения станины в сечении под резцом от изгиба
в горизонтальной плоскости;
<р — угол закручивания станины в сечении под резцом;
Н—расстояние от оси станины, проходящей через центры тяжести
сечений, до линии центров станка:
г_Рх'>(1а-хУ Мх(1и-х)(2х- 1и) __ Мх (1и - х)
Подставляя выражения силовых факторов, действующих на
станину, и выражения для угла закручивания ср и перемещения / в
формулу для }уР> окончательно выражение для определения упругого
перемещения резца в результате деформаций станины запишем в следующем
виде:
-Рхф<2*-иЩ^; (2.12)-
здесь и дальше Рх> Ру, Рг — составляющие силы резания в кГ; можна^
принимать
Ях:Ру:Рг = 0,3:0,5:1;
йи, 1и — диаметр и длина обрабатываемого изделия1
В СМ]
х— расстояние от левого конца изделия до-
расчетного положения вершины резца,
в см;
Н1 — высота центров станка в см;
И2 — расстояние от плоскости направляющих
станины до оси, проходящей через центры
тяжести сечений станины, в см;
^^кр, ЕЗиэг — расчетная жесткость станины на кручение-
и на изгиб в горизонтальной плоскости
в к Гея2;
/?ц; Нн — коэффициенты повышения жесткости
станины за счет влияния фундамента;
V—эффективный объем металла в смг
(см. стр. 80).
Остальные обозначения те же, что и ранее.
1 Такое рассмотрение возможно в связи с тем, что при обработке изделия в
центрах моменты, изгибающие станину в горизонтальной плоскости, в сечениях под
центрами равны нулю.
73-
СГ=Г1«
Фиг. 24. Нагружение станины токарного станка
при обработке изделия в центрах:
а — силовые факторы, вызывающие кручение станины.
(р Л-1р А\Н;
"V у *и 1и * 2 )
М2
з 2 2 ' У'
4 — силовые факторы, вызывающие изгиб станины в горизон-
М, - - /\ ~~- - РуН;
дне из!
тальиой плоскости:
\ и и /
Разрез по А А
а.
^~
_4*
и-5 —I
^
Фиг. 25. Расчетные схемы для определения упругих перемещений станины,
влияющих иа точность обработки:
( аи \
а — при расчете на кручение I М = Р2 ——- + Р Н I ; б — прн расчете на изгиб в
горизонтальной плоскости I Р «=• Ру; Л1 -» Р^ -«г*-).
74
В приведенных формулах первый член представляет собой
составляющую перемещения [ур в результате кручения станины, а второй —
в результате изгиба станины в горизонтальной плоскости. При обычных
конструкциях станин на долю кручения приходится от 60 до 90% полной
величины упругого перемещения резца в результате деформаций
станины.
Станины других станков токарной группы — многорезцовых,
револьверных, а также станины долбежных, расточных, резьбофрезерных
и т. п. станков — можно рассчитывать, по методике, аналогичной
приведенной выше.
Для многорезцовых станков характерной является работа
с большими силами резания при относительно малых длинах
обрабатываемых изделий. Станины выполняются либо с замкнутым .контуром
сечения либо с двойными стенками, В этом случае при определении
жесткости станины на кручение следует учитывать жесткость кручения
стенок. В станинах многорезцовых станков рамного типа верхнюю
и нижнюю часть станины в первом приближении можно рассматривать
отдельно: нижнюю часть — как сплошную станину на фундаменте,
верхнюю— как станину на ножках. Влияние фундамента на деформации
нижней части станины следует учитывать коэффициентом повышения
жесткости.
Для токарно-револьверных станков характерна
работа с большими осевыми силами от сверл. В случае работы
поперечным суппортом нагружения станин токарных и револьверных станков
аналогичны. В случае работы револьверной головкой или при
одновременной работе суппорта и револьверной головки нагружение
станины токарно-револьверного станка существенно отличается от
нагружения станины токарного станка. В отличие от обычных токарных
станков деформации станин токарно-револьверных станков в вертикальной
плоскости влияют на точность обработки.
В долбежных и расточных станках нагрузки от сил
резания передаются на станину не на трех участках по длине, как в
токарных станках при обработке в центрах, а на двух участках. При
несимметричном относительно оси станины положении стола дополнительно
следует учитывать кручение станины от веса стола. Нагрузку от веса
стола в первом приближении можно рассматривать как
сосредоточенную. Влияние фундамента на деформации станины следует учитывать
коэффициентом повышения жесткости.
Станины станков для обработки
плоскостей—продольно-строгальных, продольно-фрезерных, бесконсольно-фрезерных —
следует рассчитывать на изгиб в вертикальной плоскости под действием
веса стола и изделия, который можно рассматривать как
распределенную нагрузку. Влияние фундамента на деформации станины
учитывается коэффициентом повышения жесткости. Деформации станин
могут приводить к некоторой вогнутости изделий, тем большей, чем больше
длина и жесткость изделия. Обрабатываемая поверхность деталей малой
жесткости, упруго облегающих стол, при деформациях станины не
искажается, так как после снятия со станка детали восстанавливают
правильную форму. Для этих станков расчет станин с точки зрения
влияния их жесткости на точность обработки менее актуален, чем для
других станков.
Б. Порядок технического расчета
Предлагается следующий порядок технического расчета:
1. Выбирается расчетная схема (§ 5А).
2. Определяется расчетная жесткость станин на изгиб в плоскостях,
75
перемещения в которых влияют на точность обработки, и жесткость на
кручение, если станина подвергается кручению.
Жесткость на изгиб в вертикальной плоскости определяется по
соответствующему моменту инерции сечения. Жесткость на изгиб*
в горизонтальной плоскости станин в виде параллельных стенок с
перегородками определяется по формулам (2.4) и (2.5) на стр. 57; станин
с замкнутым контуром сечения или с дополнительной стенкой — по
соответствующему моменту инерции сечения. Жесткость на кручение
определяется по формулам (2.1), (2.2) и (2 3) на стр. 50—53.
3. Для сплошных станин определяется расчетная жесткость
фундамента на изгиб в плоскостях, перемещения в которых влияют на
точность обработки и жесткость на кручение, если фундамент подвергается
кручению.
Жесткость на изгиб определяется по соответствующим моментам
инерции сечений, жесткость на кручение — по формуле (2.6) на стр. 59.
4. Для сплошных станин определяются коэффициенты повышения
жесткости #и п Нк, учитывающие влияние фундамента на деформации
станин.
Коэффициент повышения жесткости на кручение определяется по<
формулам (2.7), (2.7а) или (2.10), коэффициент повышения жесткости
на изгиб в вертикальной плоскости — по формулам (2.8), (2.8а) или
(2.11) и коэффициент повышения жесткости на изгиб в горизонтальной
плоскости для станин, закрепленных на фундаменте—по формуле (2-9)
(см. стр. 68—70).
5. Определяются перемещения ]ур инструмента относительно
изделия в результате деформаций станин (при определении деформаций
сплошных станин под действием веса перемещающихся узлов
определяются деформации как от веса узлов, так и от дополнительной
нагрузки, уравновешивающей вес узлов и заменяющей реакцию упругого
основания, см. § 4Б). Для токарных станков перемещение }ур
определяется по формуле (2.12) на стр. 73.
Перемещения инструмента относительно изделия для станин
станков других типов определяются по аналогичным формулам, получаемым
в соответствии с указаниями, приведенными в § 5А.
Пример расчета станины. Определим наибольшую погрешность
обработки в результате деформаций станины. Изделие диаметром 130 мм
и длиной 700 мм обтачивается в центрах на станке мод. 1К62.
Основные паспортные данные станка: высота центров над станиной
#1 = 215 мм; максимальное расстояние между центрами Ь\ — 1000 мм.
Эскиз поперечного сечения и параметры станины приведены-
в табл. 15.
Определение жесткости на крушение
Жесткость на кручение определяем по формуле (2.1) стр. 50. В рас-
сматриваемом случае
Д=Ы0в кГ/см*; Лту = 1,2-104 смА\ В = й7,8 см;
1 = 123,5 см\ Р'ст~ЬА,7 см2\ ^ — -^-\ а8 = 2.
По графикам фиг. 17 в зависимости от
7о
Таблица /5
Эскизы, расчетные параметры и результаты расчетов станин некоторых токарных станков
(Расчетную схему см. фнг. 25) __
[Модель станка; I
\в. и. [п о вмм'А Эскизы и.* Перемещения / в мм
!'м*'с№ (размерил,) Расчетные параметры ** вершины ре'зца
77
Продолжение табл. 15
(Модель станка;! | I
в. ц. (Я1) вмм;\ _ е \
р. м. ц (10 Эскизы Расчетные параметры ** Пер1мпе1?,ения { в жл
в мм\ сила вершины резца
I I 1сту I 1»3 • Ю4 I а I 39,5 I
Перегородки диагональные; /7=5 У 828 а 39°
1, = 10оо I :иШ_111_11 1 иу ^ 31.6 у„р 1,1 • ю* _и,04У
Г> = /0° I и «,—Л- -гаги | ^ | ^ | ур | 3)26^|
I л л с/7. I ^стч I 1>9 -10* I а I 40,6 |
Перегородки диагональные .>" 517) ету > „ ополс
Ш63 'I «> К лу 0,4 • 10 а 39 48
^=======3====. 4Л4ъ рст 121,8 / 3,8 10» ^. _
я;=55о Л III 1111, / !м_ л, 5б м* 2 101 =0-049
1 ' г^ -пер I—г 1^1 47 1 у 15'89-1041
I Перегоровки перпендикулярные; п~3 т , I усоту I 4,2-10* I /=•, I 268 I
163 I ■ \ I |^_^ | ^ |~!^Ут У"-* 1,2 - 104 / 8,4-10* ру
^ = 1350 > и и ^ И"1 ^ 1Ш'5 ^ 5'2-104 =°,05°
1 1 то -! ' ~* | Р„ \ 144 | V 6,23 - 10* |
1П63 | , ., II V , , ^ 500 /15-10*
«1 = 315 I 1^ИЦ Р 1610 Ушг 19-10* /ур = 22 -^ =
^ = |500 | I "ГТ~| ,—' я 169 Л, 14-Ю* =0,038
Яу_175° Г— 1750 I | 5 2,2 ^ 8,75-10* |
* / — момент инерции станины иа изгиб в вертикальной плоскости.
** Линейные, размеры приведены в см% Р в см?, V в смя, У в ?/{*,
78
определим коэффициент к
л.«=-
ДД(»я + 6) Зе3„ + 164 + 42«я + 36 ' " Лл •
,2 ^ . ^ +
Подставляя
получим
12*„(2.я + 3) 8е„(2ел + 3)2
*ж=14,0; Ая = 23,2; «, = 1,6,
*„ = -Щ| = 0,6 и ■/„.„ = 2280 ел4.
^ 1
Подставляя значения 7, Ву /„.„, Зстт -^- = 2,5 и я = 2, получим у =
= 0,113 и коэффициент & = 0,71. При этих данных получим жесткость
станины на кручение
Ш*Р— 0.71.123.58 2,5-1 2-10* — *4Ш Ш *'** •
■ + 2-
64,7
Определение жесткости на изгиб
в горизонтальной плоскости
Жесткость на изгиб в горизонтальной плоскости определяем по
формуле (2.4) стр. 57.
При В = 27,8 см, Ь = 123,5 см, ^пг =0,4 • 104 см\ ]стг = 569 ел*4, по
табл. 13 для п = 3 получим 5т = 28,5. Для я= 1 коэффициент 51 = 8.
Принимая для п = 2 51 я^ 18,2, получим
^7^= 10400 • 10е кГсм*.
Определение наибольшей погрешности изделия
в результате деформаций станины
Наибольшая погрешность изделия при настройке на размер у
задней бабки будет в среднем сечении изделия, т. е. при х ~~тг . Для этого
случая по формуле (2.12) получим
/ — [ Р**" \ Р (И 1 /П1 /«(//1 + //а)Ч. ИУ1«
1ур — [ 2 +^у("1 + "з)| АШкрЯк +48ЕГмЛя-
Подставляя
Р2 = 2Ру; аи—Ш мм; /«='700 лш; //1 = 21,5 с^, Я, = 11,2 еж;
07^ = 0,34 ■ 10"; Я7«„=1,04 • 10"
и принимая для станины на ножках /?я =?/?*=! (см. § 4, Г), получим
погрешность на радиус
/ -р ГП I 91 Ч I 11 01 7°(21'5 ^ П'2> I ^^ - °'84Ру г*
^УР — ^У 113-^1,0-^ 11,^] 4-0,34-10^ »" 48-1,04-10^ "~ 10& СМ"
При расчетном значении силы резания Ру = 700 кГ, получим
/ур=№™см = 0,059 *лс.
Результаты расчетов станин некоторых современных.токарных
станков средних размеров приведены э табл. 15.
79
§ 6 АНАЛИЗ ФОРМ И СООТНОШЕНИЙ РАЗМЕРОВ
ЭЛЕМЕНТОВ СТАНИН
Анализ наиболее распространенных конструкций станин с точки
зрения их жесткости 'позволяет выявить такие формы и соотношения
размеров элементов станин, которые являются оптимальными, т. е.
обеспечивают получение заданной жесткости при минимальном весе.
В качестве критерия, по которому можно производить сравнение
и анализ форм станин, должна быть выбрана величина перемещения/^,
соответствующая такому случаю обработки, который был бы достаточно
типичным и при котором роль станины в общем балансе упругих
перемещений была бы достаточно большой.
В качестве примера проведем такой анализ для станин, токарных
станков.
В качестве расчетных параметров можно принять диаметр изделия
2 2 /
4и^=-^Ни длину изделия /ц = у2^ й координату вершины резца х =-$ ,
где #1 — высота центров, а Ь\ — наибольшее расстояние между'
центрами. При этих параметрах, полагая Р2^2РУ, формулу упругого
перемещения резца в результате деформаций станины окончательно
полупим в виде
Лр=—шйР—(-т^1 + ^) +
У1и
ШЛ
Так как под оптимальными понимаются такие формы и
соотношения размеров элементов, которые обеспечивают заданную жесткость при
минимальной затрате металла, то в качестве основного критерия
экономичности конструкции принимается величина эффективного веса
станины (веса деформируемой части станины), отнесенного к жесткости,
или пропорциональная ей величина 1урУ—произведение перемещения
/Ур на эффективный объем V металла.
Эффективный объем металла, т. е. объем металла деформируемой
части станины, ориентировочно может быть подсчитан по формуле
V = Р\Ь + пРпа, где Р\ — площадь 'поперечного сечения станины (для
станины из двух стенок Р\ ^=2Рст)1 Рп—площадь поперечного сечения
перегородки; остальные обозначения прежние.
Для того чтобы оценить влияние параметров стенок станины, типа
и параметров перегородок, количества перегородок и т. п, величины Я2,
]изг и Укр, а также Р\ и Рп должны быть выражены через основные
параметры станины ((ширину В, длину 1ит. т.) и через параметры стенок
и перегородок.
Для анализа вместо относительно сложных конструктивных форм
сечений стенок и перегородок рассмотрим схематизированные, наиболее
близко соответствующие реальным; примем, что стенки и диагональные
перегородки имеют правильное Т-образное сечение, а перпендикулярные
перегородки П-образное сечение.
Выразив через параметры схематизированных сечений стенок и
перегородок (фиг, 26) величины Н2^ ^изг, У^, Р\, Рп> можно записать
Р Р V1
где У?! и /?2 — безразмерные коэффициенты1, зависящие от: а)
параметров станка (-тМ' б) соотношений основных размеров станины -^ ,
1 Безразмерные коэффициенты такого типа используются также в других разделах
книги для сравнительной оценки конструкций и их параметров.
50
Ъ>ст
Н
Б
)■
количества
-тт- (В, Ну Ь — ширина, высота и длина деформируемой части станины);
в) параметров боковых стенок станины /-
(А Ъ \
п, ~, -~) в станинах с перегородками
или угла наклона верхней стенки в станинах с замкнутым контуром
сечения.
Кривые, приведенные на фиг. 27, иллюстрируют, как изменение
указанных параметров в диапазоне, типичном для станин токарных станков
Разрез по Йй
ца . А
С7П
—1А
II
«)
п
■з:
?ш
-И&
тг
Разрез по ЙЙ
1
5г
п
г^л-уЬг-Д
I Г
I |.
I I;
Разрез по йй
б)
Фиг. 26. Схематизированные сечения, рассматриваемые прн анализе:
а — сечение стенок; б — сечения перегородок.
средних размеров с перпендикулярными и диагональными
перегородками, влияет на изменение величин }ур и $урУ. Анализируя эти кривые,
а также аналогичные кривые для станин с замкнутым контуром
поперечного сечения, можно видеть, что получение станины заданной
жесткости лри минимальном весе можно обеспечить главным образом за счет
рационального выбора основных размеров станины В и Я; при этом
толщина стенок и перегородок должна приниматься минимально
допустимой из технологических соображений. Длину станины Ь при
заданном расстоянии между центрами Ьг следует считать заданной.
Анализируя более подробно влияние на жесткость величин В, Н и п,
можно сделать следующие выводы:
1. Из основных размеров станины наибольшее влияние на жесткость
оказывает ширина станины. Так, например, для реальных соотношений
размеров станин с П-образными перегородками увеличение ширины
станины на 10% вызовет увеличение ее жесткости на 25—30%. Поэтому
ширина станины должна выбираться достаточно большой, допустимой
конструктивными соображениями.
2. Высоту станины Н следует выбирать примерно равной ширине
станины В.
3. Количество перегородок п на жесткость станины влияет
незначительно. При заданном весе максимальная жесткость может быть
получена при некотором оптимальном количестве 'перегородок. Так, напри-
81
0,1-^0,2 для станин с диагональными перегородками еле*
6-5-8, для станин с перпендикулярными перего-
-0,4 для станин с диагональными
-8,
В
В
мер, при -]-
дует принимать п
родками п ~ 4 -*- 5; при -^ — 0,3 -
перегородками следует принимать п = Зч-5; для станин с
перпендикулярными перегородками п = 2-^-3. Ориентировочно можно считать, что
количество перегородок следует выбирать так, чтобы в станинах с
диагональными перегородками угол между ними находился в пределах от
60 до 100°, а в станинах с перпендикулярными перегородками
расстояние между перегородками было примерно равно ширине станины.
Л;
3103*
2-Ю3
1-70*
0
к2
15
20
15
10
5
и
\н ^
ш
\ '
\
,3^
>
п--5\
.'Л
т=*\
ч^ч |
Л,
5-Ю',
зю3\
210
\4
-
—
1^
«=
*&ст
^
"1
015
1,0
1 ?$&
0,05
0,1
о;1
0,2
0?1
Ж
0А
7Х
.1
\р
чк
чл^
\Д
^-~
п^12
/И
/Й
^чП
№5
090
Л2.
25
20
15 \
0,75
1,0
0,1
1,25Н
~д,зт
В 10
N
\ЬГ^
ч^
-^
\!
,_ГЗ:
"ст
И
ь-
I
■■ I—
5
4=
г
*1.
4 70*
3-10зХ
2Ю-
№Гш Ыр 0,3
(& дйаг $16
~~0$5!!ст
25
20,
15 !
>
^
I
^
^^э
Г^
=^=*
"Г^а
0А
$18
06
ОТ
0,5
0,20} В
\\
\ *""—
1 \
1
^<
у
Л
Ь4
/
/
чг
^^1
& 0,05 0,1 0,15ЬСт Кобр 0,3
0,4
0,5 А
Я 4^
«4
а;
а^
*;
090
0,5 диаг 0,16
^5^ '
0,18
$6
*/
~ж
ом
Фш\ 27. Зависимость перемещения вершины резца /у л = /?А —е-/ и веса, отнесенного
к единице жесткости, /урУ — #2—ё7" от параметров станин при у- ~ 0,2. Влияние
каждого параметра представлено при средних значениях остальных.
Кривые линии на графиках: сплошные — для станин с перпендикулярными П-образ-
ными перегородками; штриховые — для станин с диагональными перегородками:
а—влияние количества перегородок и соотношений основных размеров; б — влияние параметров боковых,
стенок; в — влияние параметроз перегородок.
Параметры боковых стенок станины, параметры перегородок, а
также наклон верхней стенки оказывают существенное влияние на
жесткость. В станинах с П-образными перегородками из параметров
перегородок наибольшее влияние на жесткость оказывает относительная
ширина перегородок (-^) , так как при кручении, являющемся
основным видом деформаций станины, перегородки работают на кручение.
В станинах с диагональными перегородками из параметров перегородок
наибольшее влияние на жесткость оказывает относительная высота
перегородок {-&) > так как при кручении станины диагональные
перегородки работают главным образом на изгиб.
Несмотря на то, что параметры стенок и перегородок оказывают
существенное влияние на жесткость, возможности изменения их кон-
82
структивных форм ограничены необходимостью обеспечения свободного
схода стружки и беспрепятственного перемещения суппорта и задней
бабки.
К 5
10
0,5
\ \ 1 \
1 \ \ *
уЛ
\\
1-1
\ \
\\Ч\
^^^
^
^228
Фиг. 28. Сравнение разных типов станин токарных станков
при одинаковых габаритах по величинам перемещений ин-
струмента относительно изделия /ур = /<1 сг (а) и веса
РуЬ*
отнесенного к единице жесткости, /ур1/=/?3 —-р— (б).
Кривые линии на графиках:
1 — для станин с П-образнымн перпендикулярными перегородками; 2 —
для станин с диагональными перегородками; 3 — для станин с
замкнутым контуром поперечного сечения.
Как уже указывалось, разработанные расчеты могут быть
использованы для сравнения разных типов станин. На фиг. 28 представлена
зависимость величин }ур и 1УрУ от параметра-^ 3 наиболее сильно
влияющего на жесткость, для станин с П-образными и диагональными пере-
83
городками и станин с замкнутым контуром поперечного сечения при
соотношениях размеров, типичных для станин средних станков.
Из рассмотрения кривых можно сделать следующие выводы,
подтверждающие полученные ранее путем экспериментального
исследования станин [44], [78] и др.
1. При одинаковых габаритах жесткость станин с замкнутым
контуром поперечного сечения выше, а вес меньше, чем у станин других
типов.
2. В станках с большим расстоянием между центрами, т. е. при
относительно большой длине, из станин в виде двух стенок с перегородками
большую жесткость и меньший вес имеют станины с диагональными
перегородками.
3. В станках с малым расстоянием между центрами, т. е. .при
относительно небольшой длине, станины с диагональными и с П-образными
перпендикулярными перегородками примерно равноценны.
Полученные выводы можно подтвердить расчетами реальных
конструкций станин наиболее распространенных отечественных станков.
Как уже указывалось наибольшую жесткость имеют станины с
замкнутым контуром поперечного сечения. Так, например, из станин станков
моделей 1Д63, 163 и 1П63 с высотой центров 300 мм и р. м. ц. 1500 мм
жесткость станины станка мод. 1П63 выше, чем станины станка мод.
1Д63, примерно в 4 раза, а станины станка мод. 163 в 1,7 раза (см.
табл. 15).
Как уже указывалось, при большой длине станин большую
жесткость имеют станины с диагональными перегородками. Так, например,
станины с диагональными перегородками станка мод. 1Д62 с р. м. ц.
1500 мм имеют жесткость примерно на 60% выше, чем станины с
П-образными перегородками станков мод. 1Д62М с тем же расстоянием
между центрами.
Как уже указывалось, с увеличением ширины станины жесткость
ее существенно увеличивается. Так, например, если бы ширина станины
токарно-револьверного станка мод. 1А36 была на 20% больше, т. е. не
187 мм, а 224 мм, то суммарная жесткость" ее была бы выше на 60—
70%. За счет увеличения ширины станины и уменьшения толщины
стенок можно существенно уменьшить ее вес. Так, например, если бы
в станке мод. 1А36 ширина станины была 224 мм, а толщина стенок не
27 мм, а 20 мм, и толщина перегородок не 20 мм, а 15 мм, то жесткость
станины была бы примерно той же, что и при ширине 187 мм, а вес
меньше на 20—25%
§ 7. ТЕМПЕРАТУРНЫЕ ПОЛЯ И ТЕМПЕРАТУРНЫЕ ДЕФОРМАЦИИ
СТАНИН ! [58]
Изменения температуры станин металлорежущих станков
вызываются следующими причинами:
а) тепловыделением в механизмах и агрегатах, размещенных на
станине или внутри нее;
б) теплообразованием в направляющих;
в) теплообменом с охлаждающей жидкостью, стекающей на
станину;
г) радиацией близко стоящих высоконагретых агрегатов;
д) колебанием температуры окружающей среды.
Изменения температуры станин вызывают температурные
деформации последних, приводящие к взаимному перемещению узлов станка,
влияющему на точность обработки (фиг. 29).
1 Раздел написан канд. техн. наук Ю. Н. Соколовым.
84
Температурные деформации станин могут быть приближенно
рассчитаны, если принять, что деформации пропорциональны средней
температуре.
Тогда линейные деформации А/, иа длине Ь определятся
выражением
где е_—коэффициент линейного расширения, для чугуна е = (1-И,1)Х
ХЮ"5 в 1/град; %с — средняя температура станины в град.
Искривление нейтральной оси
станины (стрела прогиба), вызванное
неравномерным распределением температур по
объему станины, может быть определена,
если принять линейное распределение
средних температур по высоте сечения
станины и рассматривать станину как
балку. Тогда стрела прогиба у иа длине
Ь и угол относительно поворота двух
В
^
^
ъ
эд*
г
ив у
~&г
л
V
Д
«У
Фнг. 29. Влияние температурных
деформаций станин шлифовальных
станков на точность обработки
(0. — потоки тепла в станину).
• I.
б)
Фиг. 30. Расчетные схемы для
определения температурных деформаций
станин.
сечений на расстоянии Ь друг от Друга (фиг. 30, а) определяются по
следующим формулам:
еД&12
№
9^
еДМ,
Н
где Н •
- высота сечения станины;
■разность средних температур верхней и нижней поверхностей
станины.
Наиболее общим расчетным случаем является случай нагрева
станины от расположенного на ней узла, температура которого на
поверхности контакта со станиной может быть принята постоянной. Для
упрощения расчета принято, что температура точек станины на участке под
источником тепла изменяется только в направлении, перпендикулярном
плоскости контакта. Части станины, расположенные по сторонам от
контактирующей детали, рассматриваются как ребра бесконечной длины
с тепловым потоком вдоль оси X и с теплоотдачей в окружающую среду
(фиг. 30, б).
Температура участков верхней поверхности станины приближенно
может определяться по формулам:
а) для участка /0
д. <*стР$ .
85
б) для точек с координатами х1 (от конца участка /0, см. фиг. 30, б)
I
где
/2а
ж-
Температура участков нижней поверхности станины приближенно
может определяться по формулам:
а) для участка /о
где
т
= ^Г + Т-('У#
б) для точек с координатами х-г
* 0 сЬтг1
Средняя избыточная температура по длине верхней и нижней
поверхностей станины
я - *<**« + *«'* + • • • + »А + ... + V*
где ^ — избыточная температура на участке 1Ь.
В приведенных формулах:
аст — коэффициент теплопроводности стыков в ккал\м?яас град;
для шлифованных поверхностей без смазки аст = 1500, со
смазкой а^и —2300; для шабренных поверхностей без смазки
ат = 2200, со смазкой ас/п = 3700; для одной шабренной и
одной шлифованной поверхности без смазки ссст = 1800, со
смазкой ссг/7г = 5200;
Р— площадь контакта со станиной узла,* передающего тепло
в станину, в м*\
& — температура на поверхности контакта со станиной узла,
передающего тепло в станину, в град;
а — коэффициент теплоотдачи стенок станины в ккал/м2час град
(см. стр. 225);
^ — коэффициент теплопроводности материала станины
в ккал\мяас град; для чугуна Х = 41 ч- 54, для стали* Х = 39;
Рр, II—площадь поперечного сечения в м? и периметр стенки,
отводящей тепло от контактирующих поверхностей, в м;
Ь,ВУН—длина, ширина и высота станины, соответственно, в м\
8 — толщина стенок в м\
I—расчетная длина свободных участко& станин в ж, 1 = 1 —
/0 — длина участка, на котором тепло поступает в станину, в м.
Величина п, входящая в формулу для определения т в случае,
когда источник тепла расположен у одного из концов станины,
принимается равной 1; при расположении источника тепла посередине
станины п = 2.
86
При расчете температурных деформаций станин в связи с
изменением температуры окружающей среды можно рассматривать станину
с фундаментом как балку постоянного сечения, составленную из двух
частей, обладающих различными коэффициентами линейного
расширения [57].
При равномерном изменении температуры станины и фундамента,
либо одного из них, разность температурных удлинений на единицу
длины станины выражается формулой
д=«^ (»•-•«)-*(•;-»;).
где есш еф — коэффициенты линейного расширения материала станины
и фундамента, соответственно, в 1/град.;
Кт> ^ф — расчетные температуры станины и фундамента в град.;
Кт> ^"ф — температуры станины и фундамента при установке станка
в град.
Деформации станины могут быть вычислены по следующим
зависимостям:
угол поворота концевых сечений
прбгиб посередине пролета
где Ь — длина станины;
/—момент инерции всего сечения (станины и фундамента)
относительно общего центра тяжести;
5 — статический момент нижней части сечения (фундамента)
относительно общего центра тяжести.
Расчеты, проведенные для станин тяжелых токарных, расточных
я продольно-строгальных станков показали, что прогибы станин могут
.достигать 0,3—<0,4 мм, а для очень длинных станин — 0,8 мм.
ГЛАВА III
СТОЙКИ (ВЕРТИКАЛЬНЫЕ СТАНИНЫ)
§ 1. ОБЩИЕ СВЕДЕНИЯ О КОНСТРУКЦИЯХ
Стойки, как элементы несущей системы, обычно применяются в
станках, в которых необходимы вертикальные относительные перемещения
инструмента и изделия. Основное .применение стойки имеют в
вертикальных станках, т. е. в станках с вертикальными шпинделями или
вертикальным ходом ползунов, а также в горизонтально-расточных станках.
Вертикальные станки имеют меньшие габариты в плане и представляют
значительные преимущества с точки зрения удобства обработки для
большой группы деталей, в которых по технологическому процессу ось
шпинделя или ход ползуна должны быть перпендикулярны к основной
базовой поверхности детали.
Стойки могут выполняться:
а) несущими узлы инструмента (шпиндель, головки, суппорты)
и узлы обрабатываемых деталей (консоли, кронштейны, столы) — в
консольных станках (фиг. 31, а);
б) несущими только узлы инструмента — в бесконсольных
станках (фиг. 31, б).
Бесконсольные конструкции как более жесткие удобны для
обработки тяжелых деталей и для работы в крупносерийном и массовом
производствах. Для обработки легких и средних деталей в
индивидуальном и серийных производствах применяются консольные конструкции.
Стойки консольных станков обычно устанавливаются на плиты и
притягиваются к ним винтами. Стойки бесконсольных станков крепятся
к станинам. Стойки небольших станков, требующих небольшой опорной
поверхности, иногда (главным образом за границей) делаются за одно
целое с плитами. В станках для обработки особенно тяжелых изделий
и в некоторых зуборезных станках стойки перемещаются по
направляющим.
Стойки одностоечных станков по условиям нагружения разделяются
на следующие:
а) нагружаемые силами в плоскости симметрии (стойки станков
типа сверлильных);
б) нагружаемые пространственной нагрузкой (стойки фрезерных,
расточных и других станков).
Стойки, нагружаемые в плоскости симметрии, выполняются
коробчатыми с сечениями, вытянутыми в плоскости нагрузки, и имеют
повышенную жесткость на изгиб в этой плоскости (фиг. 32, а).
Стойки, подвергающиеся сложному нагружению, выполняются
коробчатыми с контуром, близким к квадрату, и имеют повышенную
жесткость на кручение (фиг. 32, б).
88
При небольших нагрузках, а также в тех случаях, когда Должна?
быть обеспечена возможность поворота относительно оси стойки
элементов, расположенных на стойке, применяются круглые кольцевые колонны
(фиг. 32, в).
Обычно стойки делаются расширяющимися книзу, хотя бы в одной
плоскости. Такое изменение сечения стоек по высоте обусловлено харак-
Фиг. 31. Консольный (а) и
бесконсольный (б) станки.
Фиг. 32. Сечения стоек одностоечных
станков.
тером изменения изгибающих моментов, которые в большинстве станков
увеличиваются к основанию стоек, а также условиями повышения
устойчивости и архитектурными соображениями (фиг. 33, а, б).
Стенки стоек с внутренней стороны
подкрепляются ребрами — поперечными
(перпендикулярными к оси стойки) и продольными. Поверхности
стенок между ребрами не должны превосходить
400 Х400 мм во избежание колебаний стенок к#к
диафрагм.
а) б)
Фиг. 33. Стойки переменного сечения.
Фнг. 34. Стойка с
поперечными и продольными
ребрами.
В стойках, несущих тяжелые подвижные узлы, должно быть
предусмотрено место для размещения грузов, уравновешивающих вес
подвижных узлов. Для направления грузов продольные ребра делают большей
высоты, чем поперечные (фиг. 34).
Стойки значительной высоты, подверженные действию больших
поперечных скручивающих сил, должны по возможности снабжаться
перегородками во избежание искажения контура поперечного сечения и су-
щественного понижения жесткости (см. ниже). При этом иногда
оказывается необходимым размещение противовесов снаружи станка.
Для монтажа электродвигателей, электроаппаратуры и отдельных
механизмов станка стойки приходится делать с окнами (см. фиг. 33, а).
Ширина окон по возможности не должна превышать 0,7В, а длина
(измеряемая вдоль оси стойки) — (1,0—1,2)5, где 5 — ширина
соответствующей стенки стойки. По возможности окна следует закрывать доста-
точно жесткими"крышками, притягиваемыми винтами, или заменять
нишами.
Так как в балансе упругих перемещений станков значительную роль
играют отгибы направляющих, то жесткости соединения направляющих
с основным контуром сечения стоек следует уделять особое внимание.
Ширина направляющих часто принимается меньшей, чем ширина
сечения стойки, и направляющие соединяются с основным контуром сечения
переходными стенками— наклонными или перпендикулярными к
плоскости направляющих (фиг. 35, а — в); местные деформации направляющих
тем меньше, чем больше расстояние между этими переходными
стенками. Во избежание местного
деформирования стенка с
направляющими подкрепляется
специальными ребрами (фиг.
35, в).
Стойки обычно делаются
целыми.-Однако, если в части
стойки размещаются
какие-либо механизмы и необходимы
сложные расточки, то стойки из технологических соображений
приходится делать разъемными. Конструкции присоединений стоек к плитам
и соединение частей стоек между собой показаны на фиг. 36, а—е.
Сверлильные станки настольного типа выполняются, как
правило, с круглой колонной. Стойки сверлильных станков средних раз-
Фиг. 35. Сопряжения направляющих и стенок.
Фиг. 36. Крепления стоек.
меров, предназначенных для использования б серийном производстве,
выполняются коробчатыми. Стойки станков, предназначенных для
ремонтных работ, выполняются составными—-коробчатыми в верхней
части и в виде круглой колонны в нижней, что позволяет при
необходимости быстро отводить стол и сверлить отверстия в крупных деталях,
устанавливаемых непосредственно на плите.
Для наиболее тяжелых сверлильных ра^от применяются станки
портального типа.
Стойки агрегатных сверлильных и расточных станков
нормализованы. Эти стойки (фиг. 37) обычно имеют коробчатую форму с выемкой
между направляющими для размещения цилиндра подачи. Кроме того,
в агрегатных станках применяются стойки специального исполнения,
например, с наклонными направляющими для сверления и расточки
отверстий в блоках цилиндров У-образных двигателей, стойки с широкими
окнами для прохода горизонтальной головки и т. д.
Стойки радиально-сверлильных станков
выполняются круглыми и охватываются гильзами, которые поворачиваются
вместе с рукавами и служат направляющими для вертикального
перемещения рукавов. Такая конструкция обеспечивает необходимую жесткость
системы и постоянство углов наклона от упругих деформаций системы
-90
при любом положении рукава по высоте. Конструкции, в которых гильза
выполняется за одно целое с рукавом и перемещается в вертикальном
направлении по открытой колонне, имеют значительно меньшее
распространение (распространены, главным образом, в Англии). В этих
конструкциях деформации колонн при сверлении отверстий в высоких
изделиях больше, чем в низких. Кроме того, в таких станках реакции в опо-
Разрез по АД
Фиг. 37. Стойка агрегатного станка.
рах гильзы и, следовательно, деформации в опорах и их влияние на
точность обработки больше, чем в станках, выполненных по наиболее
распространенной схеме.
Стойки консольных горизонтально-фрезерных
станков (фиг. 38) характерны тем, что в них встроены шпиндели,
а также, как правило, коробки скоростей и электродвигатели. Для
поддержания конца фрезерной оправки служат хобот или цилиндрические
скалки, и действующие силы передаются на стойку через опоры
шпинделя, направляющие хобота и направляющие консоли. При тяжелых
работах консоль связывается с хоботом с помощью поддержек. Стойки
выполняются коробчатого сечения с вертикальной перегородкой, в кото-
91
рой размещаются опоры валов коробки скоростей. Верхняя часть стойки,
в которой монтируется коробка скоростей, обычно отделяется от нижней
части горизонтальной перегородкой, имеющей корытообразную форму и
служащей дном резервуара для масла. В верхней части стойки имеются
окна для монтажа коробки скоростей, в нижней —для
электрооборудования. Стойки горизонтально-фрезерных станков обычно расширяются
книзу в плоскости, перпендикулярной к оси шпинделя.
Разрез поЯД-6Б-88-ГГ-дд
Фиг. 38. Стойка консольного горизонтально-фрезерного станка мод. 6Н83.
Стойки консольных вертикально-фрезерных
станков (фиг. 39) аналогичны стойкам горизонтальных станков. Они
выполняются Г-образными или —при необходимости поворота оси
шпинделя—с прямой осью и направляющими для установки фрезерной головки.
Стойки широко универсальных станков выполняются с горизонтальными
направляющими для универсальных головок.
Стойки бесконсольных фрезерных станкоз имеют
простую форму и одну систему направляющих. Сечения стоек
незначительно расширяются книзу. Стойки станков с горизонтальным шпинделем
крепятся к станине боковой поверхностью; стойки станков с
вертикальным шпинделем обычно устанавливаются на станине и крепятся по
торцу.
Стойки горизонтально-расточных станков,
предназначенных для обработки легких и средних деталей, делаются
неподвижными, а для обработки тяжелых деталей— перемещаемыми по
направляющим. При отсутствии достаточно жестких перегородок контур
сечения стоек под действием сил резания искажается. При этом роль
92
„ г—Ида*?—-^
^ГГТ 11
л а, со
* А ^
« 5 *
О со са
е§8
93
упругих перемещений стоек в общем балансе упругих перемещений
станка оказывается весьма существенной. Стойки современных
расточных станков делаются с жесткими перегородками или поперечными
ребрами.
Стойки вертикально-протяжных станков (фиг. 40)
выполняются с сечением, близким к квадратному, обычно постоянным па
всей высоте станины. Вследствие простой конфигурации большое рас-
Разрез по Дй
-570-
ЪЪ 25
1»
Ъ*«*х
-800 •
Разрез по 66
Фиг. 40. Стойка вертикально-протяжного станка мод. МА-1,
пространение получили сварные конструкции стоек. Внутри стоек
обычно размещается гидрооборудование, между направляющими —
кронштейн для крепления цилиндра.
§ 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ РАСЧЕТА НА ЖЕСТКОСТЬ
Основным критерием работоспособности стоек, как и других
базовых деталей, является жесткость, которую можно характеризовать
величиной перемещения инструмента относительно изделия в результате
деформаций стоек при заданной силе.
К жесткости стоек предъявляются особенно высокие требования, так
как стойки обычно находятся в условиях сложного нагружения с
большими крутящими и изгибающими моментами и работают как консоли без
поддержки по длине со стороны фундамента. Так как деформируемая
длина стоек относительно невелика, то на деформации стоек
существенное влияние оказывают касательные напряжения. Помимо повышенной
роли касательных напряжений особенности работы стоек с точки зрения
94
сопротивления материалов обусловливаются искажением контура
сечения, наличием поперечных и продольных ребер, лерегородок,
направляющих и т. п. конструктивных элементов.
При расчетах на жесткость стойки металлорежущих станков можно»
рассматривать как консольные балки с замкнутым тонкостенным
контуром поперечного сечения, обычно по форме близким к
прямоугольному.
Силовые факторы, действующие по направляющим стойки от сил
резания, вызывают местные деформации стенок под направляющими и
общие деформации стойки. Для оценки общих деформаций силовые
факторы следует рассматривать действующими в плоскости стенок. От этих
силовых факторов стойки испытывают изгиб и кручение (для балок
симметричных сечений можно считать, что деформации кручения
вызываются кососимметричной составляющей нагрузки). Так как сечения стоек
у основания, а также сечения, в которых имеются перегородки, не могут
Фиг. 41. Схемы нагружения и деформаций элемента тонкостенной
балки при стесненном кручении.
свободно депланировать (т. е. точки сечения не могут свободно выходить
из своей плоскости), то кручение стоек является стесненным. Известно,
что при стесненном кручении элементов замкнутого сечения имеет места
искажение контура сечения.
Для того чтобы выяснить причины, вызывающие искажение формы
сечения при стесненном круч.ении замкнутых профилей, рассмотрим
равновесие элементарной рамки, толщиной с1х, вырезанной из тонкостенной
балки прямоугольного сечения двумя плоскостями, перпендикулярными
к оси (фиг. 41, а). Если при свободном кручении касательные
напряжения в сечениях хих + й равны, то при стесненном кручении они отли-
чаются на величину^. Из условии равновесия элемента
равнодействующие касательных напряжений, действующих на обе вертикальные или
на обе горизонтальные стенки, должны быть равны по величине, и
должно быть справедливо равенство
4?А + ^^=° или Я^ + Я2ь=оу
где <21 и <32 — силы, приходящиеся на единицу длины балки и
деформирующие контур. Таким образом, при стесненном кручении стенки
элементарной рамки оказываются нагруженными системой сил, представленной
на фиг. 41, б. Под действием этой нагрузки в рамке возникает
изгибающий момент (эпюра изгибающего момента приведена на фиг. 41, в) и
рамка деформируется (фиг. 41, г). Таким же образом искажается
и сечение тонкостенного профиля при стесненном кручении.
Влияние искажения контура на общую жесткость стоек в
зависимости от характера приложения нагрузки и конструктивного оформления
95
-стоек может быть различным и для стоек большинства станков
(сверлильных, консольных и бесконсольных фрезерных, агрегатных и т. п.)
относительно невелико. Поэтому при техническом расчете 1 стойки
предлагается рассчитывать как брусья постоянной приведенной жесткости.
Специфика работы тонкостенных конструкций в тех случаях,"когда она
оказывает значительное влияние на величины упругих перемещений стоек
(например, для стоек расточных станков), учитывается введением
соответствующих поправок, полученных из непосредственного рассмотрения
деформаций стоек как тонкостенных элементов.
§ 3. ОПРЕДЕЛЕНИЕ ПРИВЕДЕННОЙ ЖЕСТКОСТИ СТОЕК
А. Основные допущения
Расчетная жесткость стоек на изгиб и кручение принимается
равной жесткости тонкостенных брусьев соответствующего поперечного
сечения, находящихся в условиях чистого изгиба и кручения. Влияние
конструктивных факторов — ребер, окон, перегородок, а также влияние
искажения контура поперечного сечения, влияние напряжений сдвига на
перемещения при изгибе и т. п. учитывается соответствующими
поправками. Как уже указывалось, величина этих поправок определяется из
расчета стоек как тонкостенных систем. При этом принимаются
следующие допущения:
1. Собственная жесткость стенок на кручение и изгиб в плоскости
меньшей жесткости пренебрежимо мала. Нормальные и касательные
напряжения в продольных и поперечных сечениях по толщине стенок
распределяются равномерно.
2. Касательные напряжения вдоль стенок распределяются
равномерно; на свободных торцах отдельных стенок равнодействующие
касательных напряжений равны нулю.
3. Нормальные напряжения по высоте сечения стенок
распределяются по линейному закону, а касательные напряжения от изгиба — по
параболическому.
Применимость решений, полученных на /основе указанных
предпосылок для расчета стоек металлорежущих станков, подтверждается
сравнением результатов расчетов с результатами экспериментов и расчетов
по более точным формулам.
Б. Определение жесткости на изгиб
Жесткость стоек на изгиб определяется по моменту инерции
расчетного сечения, т. е. сечения, наиболее точно отражающего
конструктивные особенности рассматриваемой стойки. При изменении сечений по
высоте стойки за расчетное выбирается сечение, удаленное от наибольшего
на расстояние, равное 7з длины участка переменной жесткости. 2
Как показывают эксперименты, влияние поперечных
(перпендикулярных к оси стойки) ребер и перегородок на жесткость изгиба отно-
1 Технический расчет с необходимыми пояснениями см. ниже, в § 6.
2 Положение расчетного сечения по высоте выбирается из условия, чтобы
перемещения балки переменной жесткости были равны соответствующим перемещениям
балки постоянной приведенной жесткости. Естественно, что при разных законах
изменения сечений по высоте стоек и при разных видах нагрузок положение расчетного
сечения будет неодинаковым. Однако для наиболее распространенных случаев изменения
сечений по высоте и нагружения стоек с достаточной степенью точности можно
пользоваться указанными рекомендациями. Исключение составляет определение угла наклона
от сосредоточенного изгибающего момента, в этом случае за расчетное следует
принимать среднее по высоте сечение.
96
сительно невелико и в первом приближении может не учитываться.
Влияние окон, отбортовок, продольных и диагональных ребер учитывается
при вычислении момента инерции сечения. При наличии надежно лри-
тянутых крышек, закрывающих окна, влияние окон можно не учитывать.
Для уточнения влияния касательных напряжений на прогибы балок
с замкнутым тонкостенным контуром поперечного сечения рассмотрим
деформации коробчатой балки правильного прямоугольного сечения
с толщиной стенок 6 при изгибе ее силой Р, т. е. при действии сил Р\ =
Р'
= -у- в плоскости вертикальных стенок балки (фиг. 42). Разрежем балку
в углах и рассмотрим равновесие
каждой стенки. При принятых
допущениях в месте соединения
вертикальных и горизонтальных стенок на
длине / следует считать действующей
равномерно распределенную нагрузку ц,
величину которой можно определить
из рассмотрения равновесия
элементов вертикальной и горизонтальной
стенок длиной их.
Напряжения в стенках на участке
длиной / запишутся следующим
образом:
в вертикальной стенке с высотой к
и толщиной 6
Фиг. 42. Схема нагружения
элементов коробчатой балки при изгибе.
12(Л
в горизонтальной стенке с высотой Ъ и толщиной б
2<рс2 (
2д
т — -~ ?
Уравнения для определения д:
Их
г^
д<з2
дх
ЗР1
г&=-
л, откуда д= н^ц.
где I
А.
ь
Подставив значение ц в выражение для а и х и записав выражение
для потенциальной энергии внутренних сил системы в виде
и~~
2Е .)
+4
Ч
2 ^ ^+-*-*?) <& + 2 ^ (<,*+-*-т!)<Ь
их:
дЦ
из уравнения /— ~^р- определим величину перемещения точки
приложения силы
*~~~ЕЪ[к* ' 3 + * *~ к
3 (2# + Ш2 -I Ш + 5) 1 _ ^Р_
2^(3+О2
- Е»^'-
Полученное выражение для / можно представить в форме
соответствующего перемещения консольной балки. Для балки полого
прямоугольного сечения момент инерции сечения ^ = -57" (3 + О И площадь
97
сечения Р = 266(1 +0- Преобразуем формулу для / к виду
/=
Р/з
т^
Р1
ОР'
При этом коэффициент распределения сдвига *
_ 3 (* + 1) (2/з + 10^2 + щ + 5)
* ~ 5^ (* + 3)з
(ЗЛ>
Расхождение результатов расчетов, проведенных по предлагаемой
формуле, и экспериментов на моделях коробчатых балок (описание
эксперимента см. § 4 «Влияние
жесткости контура 'поперечного сечения на
жесткость стоек») не превышает 10—
/20 л мм
Фиг 43. Сравнение результатов расчетного
и экспериментального определения переме-
Р
щення / = Я' "с^" точки приложения силы
при изгибе коробчатых балок. Кривые
линии на графике: сплошные —
экспериментальные; штриховые — расчетные.
I—1
1 Р(%г) Т
\ ~
\
\
*р
Чх,)
и
\.^<?
1
/
/
Т?
1
1
1 1
1
0,5 0,75 /,0 /,25 1,5
175 Л
о
Фиг. 44. График для определения
коэффициентов х распределения
сдвига для полых прямоугольных сечений:
хх —- для случая действия силы Р параллельно
стороне Л; *2 — для случая действия силы Р*
параллельно стороне Ь.
12% (фиг. 43), что для технических расчетов можно считать
удовлетворительным.
Следует отметить, что при относительно большей ширине Ъ сечения
балок (см. фиг. 43) можно ожидать несколько худшего совпадения
результатов расчетов и экспериментов, так как в этом случае в работе будет
1 Коэффициент распределения сдвига, вычисляемый по предлагаемой формуле,-
получается больше, чем определяемый по общеизвестной зависимости
Р
$2 ._ 3(*+1) (2** + Ю*2 + 15*)
-'I
ш*
ар =
ЪР (I + 3)2
(5 — статический момент части сечения относительно нейтральной оси, Ь — ширина
поперечного сечения балки).
Расхождение значений коэффициента распределения сдвига, объясняемое главным;
образом учетом участия в работе горизонтальных стенок балки, при малых значениях
Н к
I = ~^~ достигает довольно значительных величин (при -у = 0,75; % = 3; у! = 2,4).
принимать участие не полная высота Ъ ненагруженной стенки, а только
«активная» часть ее, что в предлагаемом расчете не учитывается. Однако
при реально встречающихся соотношениях размеров стоек влияние этого
явления незначительно. Таким образом, при расчете стоек с сечением,
близким к прямоугольному, коэффициент распределения сдвига %
следует определять по указанной формуле или по кривым, приведенным
на фиг. 44. За величину I = —г- можно принимать отношение габаритных
размеров сечения.
В. Определение жесткости на кручение
Жесткость на кручение стоек с замкнутым контуром поперечного»
сечения э первом приближении может определяться по формуле
4/72 (3.2)
<м**=о
^ о/
где Р—площадь сечения, описанного осевыми линиями стенок
замкнутого1 контура расчетного сечения, в см2;
// — длина участков замкнутого контура расчетного сечения в смг
имеющих постоянную толщину о/ см.
При постоянной толщине 8 стенок контура
Ы п
Фиг. 45. Расчетная схема коробчатой балки
с окном при кручении.
где П — периметр сечения в см.
За расчетное выбирается то
же сечение, что и для
определения жесткости на изгиб.
Влияние на жесткость
элементов, расположенных вне
основного потока касательных
напряжений, например, продольных
ребер, направляющих,
соединяющихся с основным контуром
сечения одной стенкой и т. п.,
определяемое собственной
жесткостью этих элементов при свободном кручении, как правило, невелико
я может не учитываться.
Как показали эксперименты, влияние поперечных ребер и
перегородок на жесткость кручения при отсутствии искажения контура невелико
и в первом приближении может не учитываться.
Весьма существенное влияние на жесткость кручения оказывают
окна в стенках.
Для оценки влияния окон рассмотрим задачу о кручении
коробчатой балки правильного прямоугольного сечения с абсолютно жесткими
перегородками по концам и окном размерами Ьо X /о, расположенным
симметрично по длине и ширине одной из стенок (фиг. 45). Примем,
что по концам балки действуют равные по величине и противоположные
по знаку крутящие моменты.
Разрежем балку посередине и рассмотрим равновесие каждой
стенки. Так как система симметрична, в месте разреза действует только
1 Обычно в стойках замкнутым является контур, образованный наружными
стенками стойки. В некоторых случаях (например, в стойках горизонтально-фрезерных
станков, см. ниже, табл. 21) контур, образованный наружными стенками, разомкнут, и поток,
касательных напряжений замыкается по одной из внутренних стенок.
7*
99>
крутящий момент М^ который при принятых допущениях (см. выше)
можно представить в виде двух пар сил
М = Р1к+Р2Ь,
где
*м „ р _в-*)м
и /я — т •
Л
к
Коэффициент к распределения крутящего момента между
вертикальными и горизонтальными стенками определится из условия
дк и'
где II— потенциальная энергия внутренних сцл системы.
Фиг. 46. Нагружение стеиок участков балкн с окном (а) н без окиа (б) при крученнн.
Нагружение отдельных стенок участка балки с окном представлено
на фиг. 46, а. При этом напряжения в стенках запишутся следующим
образом:
1. В стенках 1 иЗ:
_ Пу „\М(\-к) АЯ2-гЯ1)Ь) -г- Яг-42
а'—~Шх["^ь "'"" "' у""1 + -л±т^х:
Т = _Л./] _У*\\М{1-Ь) {Щ-дО/П-г Ях-д* Я1 + Я2
ЬП \ 4
/12
(—для стенки /, +для стенки-3).
2. В стенке 2:
'ЪЬ*
X
Мк „ /Л
3, В стенках 4 и 5:
12у
Мк д2Ьх] (72
2й
2
М ^\ Г Мк __ д2М
~ 2 \- ЬЬх
{—для стенки 4, + для стенки 5).
1С0
±^-
25
Величины равномерно распределенных нагрузок Ц\ и #2,
действующих в местах соединения стенок, определятся из рассмотрения
равновесия элементов стенок длиной их из уравнений
где
Их
да2
дх
да,
у=_ Ё. дх
У 9
(Ь5
дх
ьх г
Ях=-
т
т
ЛйрД
(Ро! +ксг); ?2 = -щ^ (р2а* + ксг\у
а1 = $+2^ ^ —-4"(^+2р2 + 4р^-4Р^ —4Р^);
а2 = 1+3*; -*2 = --±- (2Р2 + 8р2* — 2* —%Р)\
^Д = 4* + Зр + 6** + 6#;
* = -
Остальные обозначения см. фиг. 46.
На участках балки без окна, помимо крутящего момента, действую-
щего на горизонтальные и вертикальные стенки ё виде сил Р\ = н
и Р2 =—-г—* действует система нормальных напряжений со стороны
элементов участка с окном, определяемая из условий равновесия этих
элементов.
Л*
№*)
Фиг, 47. Распределение силовых факторов от нормальных
напряжений, действующих со стороны участка с окном, между етенками
участка без окна.
Нормальные напряжения, действующие по вертикальным стенкам,
могут быть приведены к изгибающим моментам, которые можно
представить в виде сил #1 и сил растяжения — сжатия А'; напряжения,
действующие по горизонтальным стенкам, могут быть приведены к
изгибающим моментам, представленным в виде сил М2 и М3 (фиг. 47, а).
Эти силовые факторы некоторым образом перераспределяются между
стенками участка без окна. В частности распределение сил Ы, Nи Ы2 и Л^3
можно представить так, как это изображено на фиг. 47, б. Составляя
выражения для внутренней потенциальной энергии системы как функции
неизвестных коэффициентов распределения т), ч? 5 и § (см. фиг. 47),
определим эти коэффициенты из уравнений
дИ дЦ
дц
д$
= 0.
101
Окончательно нагружение стенок участка без окна получим в виде,
^представленном на фиг. 46, б. Напряжения в стенках запишутся
следующим образом:
1. В стенках 1 и 3:
в=т\м<1г*>х.
6 Г 1 у*]Ш(1-к) Л Чт
2. В стенке 2 тл 4:
12у Шк . , Мк, . ,Т
6/1 у2\ Шк .-] а
В этом случае
^Ж-ТгЬг^1-^1-^-
Из уравнения ^= О получим коэффициент" распределения
крутящего момента
к = -§*
о. 12
а 1*
ЗД3 + утг; 5^ н- -^
(1 - а)2
10
10
аз 1
С Я / .О 1
°бР + (1 _ а)3 ^
Г ^ 1
->еРз+(1 _ а)3 «^
Полный угол закручивания балки с окном получим из уравнения
ди
9 = ш в виде
гп_ 2М 1(1-*) (с . а <. _^ I* (!-»)» Г- аз 1
Г . а Ь* (1 -а)8
10
10
(1
-^-5II2
а /> (1 — а)2
аЗ 1
<ЭД3+(1 -а)з^
Здесь
51 = 4-^(а1 + Ра1)+^а1аа + ^ра2(р + ^) +
бд
г (2+ 30;
5, = 4р+^Р(1-*) + ^(2р»-0-|(С1+^) +
+ ^1(2 + Ы) + ^ (Р + *) + д <Р*Л + ***);
Д2
Д*
53-:4р3 + 2^+^ + ^РЧ1-0 + ^(2ра-0 +
6с?
12с;
^-(2 + 30+^(Р+0+^&Р:
5*— ТТ7(1+3Ь^+3(1-а)2};
102
6^ + 4^+1 о _ 7<»+3* + 2 _ 9^2 + 6^ + 9
Л?— 5*(1 + *) ' *>8~~' 5^(1+0 ' 9~~ 5/<1 -Ь0
[2
+ # «+ю]-.
5.,=и[-4Р+1(('-1) + Й-(2'-1>-т(',>+',») +
+ Ш (4Г т" <*) + -Д2Г ^Р + ^ да дТ] '
-^ + ^-(' + Р) + 4<« + 3)];
а— л , г:— ^ , Р — 2^г */
Ьо> А>—ширина и длина окна; Ь— полная длина балки (см. фиг. 45).
При наличии двух одинаковых окон в противоположных стенках
угол закручивания может быть определен по той же формуле. В этом
случае коэффициенты 5 следует определять по формулам;
51в = т[2-^Р+-^-(3*+4Р)];'
5и=4[-4Р -^з + ^(2*-1) +^-(» + 4Р)];
5 -1
«Э12—10
4р' + -^(2;-1)+! + _|г(,3^ + #)]
Коэффициенты 54н-59 определяются по формулам, приведенным
выше.
В этом случае А1 ==3р + 21\ с3= I — 2|$2; остальные обозначения
прежние.
Для оценки точности выведенных формул были проведены
эксперименты. Модель балки из органического стекла длиной 150 мм с
толщиной стенок 6 = 3,5 мм и соотношением размеров —г =0,645' и
-^- = 4,07 одним торцом закреплялась на угольнике, а на другом была
нагружена крутящим моментом М*.
* Крутящий момент был приложен в виде сосредоточенной силы Р, действующей
Ь
«а концевую перегородку на расстоянии от оси коробки, равном ^-; при этом коробка
РЬ
Испытывала изгиб под действием силы Р и кручение под действием момента М = -у-.
103
Толщина концевых перегородок модели значительно превышала
толщину стенок. На одной из широких стенок имелось окно, размеры
которого изменялись. Угол закручивания определялся по измеренным
величинам перемещений /1 и /2 параллельных стенок по формуле ср-
= 21^~~/2) (подробное описание моделей и общий вид установки
приведены в § 4 «Влияние жесткости контура поперечного сечения на
жесткость стоек»). тт„0„0 т.о
На фиг 48 приведены расчетные и экспериментальные кривые
изменения угла закручивания балки при изменении размеров окна. 1^ак
* ^ можно видеть, расхождение
результатов расчетов и
экспериментов не превышает 15—
17% в сечениях, близких к
концевым. На большей части
длины расхождение результатов
значительно меньше. Следует
отметить, что в значительной
степени расхождение
объясняется тем, что при расчетах
концевые перегородки
полагались абсолютно жесткими.
Влияние окон на
жесткость кручения стоек при
технических расчетах
предлагается учитывать умножением
расчетной жесткости на некоторый
коэффициент -понижения
жесткости ко. Величину этого
коэффициента можно определить
как отношение максимальных
углов закручивания стоек без
окон и с окнами при
некоторой частной схеме нагружения.
На фиг. 49 приведены
кривые для определения коэффи-
диента понижения жесткости
в зависимости от соотношений
размеров окон и стоек,
построенные на основе выведенных
формул.
Хотя формулы были получены для случая симметричного
расположения окна посередине балки, по кривым, приведенным на фиг. 49, можно*
определять значения к0 при любом положении окна. При этом
погрешность не будет превышать 5—10% (влияние окон, расположенных у
торцов, несколько больше, чем расположенных в середине).
При наличии нескольких окон коэффициент к0 следует определять
в зависимости от размеров окна, оказывающего наибольшее влияние
на жесткость, т. е. обычно наибольшего. При этом следует иметь в виду,
что при равных размерах окна в широких стенках оказывают
существенно меньшее влияние, чем в узких, и что из размеров окна наибольшее
влияние на жесткость оказывает его ширина (Ь0).
Влияние окон, имеющих размеры, существенно меньшие, чем
основное окно, по которому определяется коэффициент к0у в первом
приближении можно не учитывать [71]. При наличии двух примерно равных
окон в противоположных стенках коэффициент понижения жесткости
125 X мм
Фиг 48. Изменение углов закручивания ф —
= ,2р5~~ Я по длине коробчатых балок
замкнутого сечения с окнами разных
размеров ( у =* 0,646; -7- « 4,07; 6 =~ 3,5 мм).
Линии на графике:
-сплошные — экспериментальные; штриховые —
расчетные.
104
Фиг. 49. Коэффициент к0 понижения жесткости стоек на кручение при разных соотношениях размеров окон и стоек:
а — при — — 2: б — при — = 3; в — при — — 4. Кривые линии иа графике: штриховые — при -г- = 0,5; сплошные — при •—- = 1,0; штрихпунктирные — при — = 2,0.
определяется как произведение коэффициентов к0 и к0'. Коэффициент
къ учитывает дополнительное понижение жесткости за счет второго
окна. При реальных соотношениях размеров к<> = 0,7 -:- 0,95; большие
значения следует принимать при расположении окон в широких
стенках, ширине окон &о^О,5& и значительной длине (~х~^ 0,3-^0,5) ;
меньшие — при расположении окон в уз^йх стенках, &0^'0,56 и
небольшой длине.
Ослабление станин окнами может быть компенсировано. Для этого
■окна закрываются достаточно жесткими крышками, которые
притягиваются винтами. Можно считать, что влияние окна будет устранено в том
случае, если погонные силы трения, распределенные по контуру окна
и зависящие от затяжки винтов, будут больше погонных сил,
возникающих при свободном кручении. Из этого условия силу затяжки одного
винта, необходимую для устранения влияния окна, можно определить по
формуле
крутящий момент, закручивающий стойку, в кГсм\
размеры окна, в см;
площадь сечения, описанного осевыми линиями стенок
замкнутого контура расчетного сечения, в см2;
коэффициент трения;
число винтов, крепящих крышку,
§ 4. ВЛИЯНИЕ ЖЕСТКОСТИ КОНТУРА ПОПЕРЕЧНОГО
СЕЧЕНИЯ НА ЖЕСТКОСТЬ СТОЕК
Вопросами искажения контура поперечного сечения в применении
к стойкам расточных станков с 1936—1937 гг. занимается группа
работников завода им. Свердлова под руководством главного конструктора
М. Е. Эльясберга. На заводе была проведена большая работа по
исследованию жесткости стоек расточных станков, непосредственно в станках
и на сварных моделях. Эта работа показала, что в расточных станках
искажение контура поперечного сечения стойки зависит от характера
приложения нагрузки и в значительной степени определяет жесткость
всей несущей системы станка. Путем исследования сварных моделей
стоек было установлено, что радикальным средством, устраняющим
искажение контура, является введение поперечных перегородок. В
процессе исследования была выявлена оптимальная форма окон в
перегородках, обеспечивающая наибольшую жесткость при минимальном весе,
ориентировочно оценено влияние ребер, крестообразных и диагональных
перегородок и других конструктивных факторов. На основании
результатов этой работы была спроектирована стойка
горизонтально-расточного станка мод. 2620, вес которой оказался меньше, а жесткость выше,
чем стоек станков того же размера других моделей (см. ниже, табл. 22^.
Для того чтобы иметь возможность обобщить результаты работы,
проведенной заводом, уточнить влияние отдельных конструктивных
факторов, выявить расчетные случаи, в которых необходимо введение
поправок к элементарному расчету, а также оценить точность
разработанной методики приближенного расчетного определения перемещений
с учетом искажения контура сечения, были проделаны эксперименты.
Эксперименты проводились на моделях из органического стекла,
представляющих собой коробчатые балки правильной прямоугольной
формы с толстым фланцем, имитирующим заделку. Соотношение
размеров моделей примерно соответствовало типичным соотношениям разме-
где М —
#о> 'о
Р —
п-
106
ров стоек реальных станков. Основные параметры моделей приведены
в табл. 16*. Общий вид установки для исследования деформаций
моделей стоек приведен на фиг. 50.
В качестве основного вида нагружения было принято нагружение
сосредоточенной силой в плоскости одной из стенок. Так как на
перемещения инструмента относительно изделия в результате деформаций
стоек влияют главным образом перемещения в том же сечении, в
котором приложена нагрузка, то, как правило, измерялись именно эти
перемещения. Непосредственное измерение перемещений в данном сечении
относительно заделки обеспечивалось
закреплением приборов на фланцах
балок, что исключало влияние
деформаций в месте соединения балок
с угольником. Перемещения при
изгибе (от симметричной составляющей
нагрузки) вычислялись как
полусумма, а перемещения при кручении (от
кососимметричной составляющей) —
как полуразность измеренных
перемещений параллельных стенок.
Жесткость контура сечения
характеризовалась величиной 62~ вг (см. фиг. 51)
искажения прямого угла между
стенками.
Результаты измерений в форме
безразмерных коэффициентов (т. е.
перемещений, пересчитанных к
модулю упругости Е = 1, толщине стенок
6=1 и силе Р = 1), приведены на
фиг. 52—56.
Анализ результатов измерений
позволяет сделать следующие
основные выводы:
1. Как известно, при стесненном
кручении тонкостенных балок с
замкнутым контуром поперечного сечения,
сопровождающемся искажением
контура поперечного сечения, деформации зависят от характера
приложения крутящего момента, в частности:
а) при действии сосредоточенной силы на стенку, если в сечении под
силой нет перегородки, прямой угол между осями сечений стенок
искажается тем больше, чем больше расстояние от нагруженного сечения до
заделки или перегородки (фиг. 51, а);
б) при действии силы в плоскости перегородки нагруженное сечение
не искажается и перемещения в этом сечении примерно равны
перемещениям при свободном кручении (фиг. 51, б);
в) при действии сосредоточенной силы на консоль, соединенную с
основным контуром по стенкам (примерно аналогично тому, что имеет
место в станках, когда сила действует на консоль, стол или другие узлы,
соединяющиеся со стойкой по направляющим), в том случае, когда
расстояние с от линии действия силы до стенки (фиг. 52) равно половине
•ширины Ь сечения, деформации балки будут аналогичны деформациям
Фиг. 50. Общий вид установки для
исследования деформаций моделей
стоек:
/ — молоть ' '-пики; 2 —домкрат, 3 — динамо-
меф, 4—индикаторы для измерения
перемещений стенок, 5 ~ опорный угольник.
* Половинки каждой модели фрезеровались из целого куска и склеивались по
продольной оси. Опыты показали, что такие склеенные модели практически ведут себч
как цельные.
107
Таблица 1&
Основные параметры исследованных моделей стоек
(величины с, / и —г- вычислены по расстояниям между серединами стенок)
Эскиз
: о о
; во о<
: н о
Габариты
в мм
3 Г
/Ы
60
60
150
3,6
2.62
0,064
г/»л
"1
-1
60
60
150
3,5
2,62
0,062
1
^
*±
ОСИ
| 1
3 3^
к—^ —Ц
г°^
~1
<: 1
Г |
§0
60
150
3,5
2.62
0,062
-с:
_!
1 "^
и!
60
30
30
60
150
150
3,4
3,4
2,62
5,58
2,13
0,47
0,060
0,128
60
40
40
60
150
150
3,5
3.5
2,62
4,07
1,55
0,645
0,062
0,096
г—т-^
[ 1 ^
и •
60
40
40
во
150
150
3,5
3,5
2,62
4,07
1,55
0,645
0.062
0,096
108
при свободном кручении (фиг, 51, в, 52). Это объясняется тем, что в этом
случае нагрузка, вызывающая кручение балки, представляет собой силы,
действующие по всем стенкам сечения, причем величина этих сил такова,
что касательные напряжения по всему контуру одинаковы. При с ^-о-
искажения контура сечения тем больше, чем больше отношение -у
отличается от 72 (см. фиг. 52).
±
^ X
/г-98м, / =~/2мн
Фиг. 51. Искажение контура нагруженного поперечного
сечения модели № 5 при разном расстоянии сечения от заделки
и при разных видах нагрузки:
а—балка без персюроаок. п.л рузка — сосредоточенная сила, б — балка
с одной периорольои па конце, нл рузка — сосредоточенная сила, в—балка
без перегородок, н.п оузка — сосрслоюченнан сила, расстояние ог
нагруженного сечения до заделки д: = 0,64А, г — балка без перегородок; нагрузка —со-
средоточенный момент; расстояние от нафуженного сечения до заделки
х - 0,64*..
Примечание. Искаженная форма сечения (показана жирными линиями)
построена по перемещениям угловых точек контура сечения.
2. Максимальное искажение контура и максимальные перемещения
стенок имеют место в балках без перегородок (фиг. 53). При нагружении
таких балок на значительном расстоянии от заделки перемещения
оказываются в несколько (до 10 и более) раз больше, чем в том случае,
если бы контур сечения не искажался. При приближении к заделке эта
разница, естественно, несколько меньше, однако тоже весьма
значительна (до 2 раз). В балках без перегородок перемещения тем меньше,
109
чем больше высота к нагруженной стенки (при.тех же размерах сечения
деформации балки с -^- = 1,55 существенно меньше, чем балки
с — = 1/1,55, фиг. 54, а). Увеличение ширины сечения Ь при той же
высоте к также приводит к уменьшению деформаций, однако в несколько
меньшей степени.
Фиг. 52. Зависимость перемещения сте-
Р
нок / = Я ^ (в плоскости действия
силы) при кручении балки без
перегородок от плеча действия силы Р.
Линии на графике:
сплошные—для измеренных перемещений;.штрих-
пунктирные — для перемещении, вычисленных без
учета искажения контура, при свободном
кручении; штриховые—для перемещении, вычисленных
с учетом искажения контура.
3. Введение хотя бы одной
перегородки на Конце балки
существенно снижает величины
перемещений. В этом случае при
действии силы на перегородку
перемещения в ненагруженных
сечениях >в результате искажения
контура могут оказаться даже
больше, чем в нагруженном. Так
же, как в балках без
перегородок, 'перемещения тем меньше, чем больше высота нагруженной стенки
балки (фиг. 54, б).
4. Введение нескольких промежуточных перегородок значительна
повышает жесткость (фиг. 55). При этом уменьшаются деформации не
только в том сечении, в котором введена перегородка, но и между
перегородками, так как при увеличении количества перегородок расстояние
между ними уменьшается. При действии нагрузки на перегородку
влияние остальных, ненагруженных перегородок относительно невелико.
5. Окна в перегородках, площадь Т7^,,которых меньше 0,1—0,2
площади р1 перегородки, практически не влияют на величины перемещений.
Даже при относительно больших размерах окон наличие перегородок
значительно повышает жесткость.
Так, введение перегородки -с окном площадью примерно равной
0,5—0,6 площади перегородки, повышает жесткость на 40—50%.
Влияние поперечных ребер аналогично влиянию перегородок — при большой
110
М
Фиг 53. Перемещения / = #-^гт в
направлении действия силы при кручении короб-
/ РЬ \
чатых балок 1 при М = "у ) •
Кривые линии на графике:
сплошные —- при приложенши силы на конце балки*
{хр — /,); штриховые — при приложении силы на
расстоянии х = 0,51 от заделки.
высоте ребер их можно рассматривать как перегородки с окнами7
(фиг. 56).
В дополнение следует отметить, что, как показали опыты завода
им. Свердлова [68], с точки зрения жесткости контура большое значение
имеет форма окна — минимальное влияние на уменьшение жесткости
„Л /л сп л <лл #лл оказывают окна треугольной
о_Ж_Н_ 60 ВО 100 120 хмм формы, которые обеспечивают
'наибольшую жесткость
перегородки в своей плоскости.
*) 6)
М ( РЬ\
Фиг. 54. Зависимость перемещения / = # -^ у при М = ~т^) точки приложения силы Р
при кручении коробчатых балок от формы и размеров поперечного сечения;
а — балки без перегородок; б - балки с концевой перегородкой; 1 — модель Л* /• — - 1 0; — «2 62* 2 —
Ь г ь Ь ' й ' '
модель №5:-- 1,55; — = 2,62; 3 - модель № 4: ~ -2,13» ± - 2,62; 4 - модель № 5: -А - 0,645; А _
« 4,07; 5 — модель № 4: А - 0,47; 4- - 5,58.
^ Таким образом, из изложенного можно сделать вывод, что при
большой деформируемой длине стоек (существенно большей размеров
сечения), если на этой длине нет поперечных лерегородок— сплошных или
с окнами относительно небольших, не превышающих 0,5 стороны сечения
размеров у-р~~К 0,25—0,3), расчет стоек следует вести с учетом
искажения контура сечения.
§ 5. ОПРЕДЕЛЕНИЕ ПОПРАВОК К ЭЛЕМЕНТАРНОМУ РАСЧЕТУ,
УЧИТЫВАЮЩИХ ИСКАЖЕНИЕ КОНТУРА ПОПЕРЕЧНОГО СЕЧЕНИЯ
Для определения численных величин поправок к элементарному
решению, учитывающих влияние на общую жесткость стоек жесткости
контура поперечного сечения, выведем приближенные формулы для
определения перемещений коробчатых балок при стесненном кручении. Хотя
решения задач о деформациях таких балок с учетом искажения контура
сечения в настоящее время известны [9], [31], [47], однако они или весьма
Ш
сложны для использования при технических расчетах, или рассматривают
только частные случаи, например, действие сил на перегородки [47].
Рассмотрим балку правильного прямоугольного сечения с
перегородкой на конце под действием кососимметричной составляющей
нагрузки (фиг. 57.) Разрежем балку в местах соединения стенок и рас-
о _ го м /го во т .Шлмм СМ0ТРИМ равновесие каждой
стенки. При 'принятых
допущениях действие силы Рх может
уравновешиваться в месте
соединения вертикальной и
горизонтальной стенок: на длине /—
равномерно распределенной
нагрузкой ц, на длине Ь —
/—равномерно распределенной нагрузкой
Ц\ и в месте соединения с
концевой перпендикулярной
перегородкой— силой 5ь На
горизонтальную стенку, помимо д и #ь
действует сила 5 со стороны
перегородки.
Условие равновесия
перегородки можно записать в виде
5^ — 5й, откуда 5Г *= 5/, где
I — -у (обозначения, см, на фиг.
57). Из рассмотрения равновесия
элемента длиной их на участке
О < х < I получаем
Ч— Л(*+1)
и на утастке / < л; < I
_ я,+ $*(*- 1)
-Фиг. 55. Зависимость перемещении /я»
= ° ЕЪЪ \ ~Т) точки приложения
■силы при кручении коробчатых балок от
количества перегородок.
Подставив значения ц и Ц\
в выражения для а и т, можно получить выражение для внутренней
потенциальной энергии системы как функции основных параметров балки:
действущей силы Р\ и неизвестного силового фактора 5.
Из уравнения -^=0 определим значение
5 = -
ЛО-1М1-
ПА + 2,5
«•4- 1) Ь
]'
1 ди
а из уравнения /г = т~др величину перемещения точки приложения
силы
<1-«М*Я0
Л=
гьЕы
*?-
2 \А 4- 2,5
1+'
Здесь
-отношение толщины стенок к толщине перегородки.
Остальные обозначения приведены в табл. 17. При ^-, близком к 1,
2,5(^4-1) о Л 01
—- -^- значительно меньше Л, и поэтому при сплош-
6 0-1
величина
112
ных перегородках влияние их жесткости можно не учитывать. Для
балок без перегородок 61 = 0, 5 = 0 и
5Ре(1 - а)(1 + *)
Л
16Е5/
/??.
М ( РЬ\
Фиг. 56. Зависимость перемещения / = # -^ ( Л1 =^-^~ ) точки приложения силы
при кручении коробчатых балок от количества перегородок при разных размерах окон:
а - при -у - 1,0: 7 — балка с перегородками (без окон): 2 — Нх * 0,256; —^-- = 0,25; ^ — Аа * 0,26
отв
■■ 0,36; 4 - Л* ~ 0,156;
^1
«^0,49; 5-Л! * 0,16;
^1
^1
= 0,64; 6 — балка без
перегородок; б — при —- «*■ 1,55: / - балка с перегородками (без окон); 2 — Ах * 0,36; •
^1
- 0,29; 3 — Лх
* 0,256, %тв - 0,38,4 — Нх
0,26;
^1
■ 0,45; 5 - /Ч « 0,156;
^1
» 0,58; б — балка без- перегоро-
к; в - при -г~ — 0,645: 7 — балка с перегородками (без окон); 2 — Нх * 0,ЗЛ; -^тв - 0,29; 5- ЛХ « 0,25Л;
г4
^
= 0,38; 4 - Л! * 0,2Л; -
■ 0,4&; 5 - Лд ~ 0,15Л;
: 0,58; 6 — балка без перегородок.
Кривые линии иа графиках: сплошные — для коробчатых балок с тремя перегородками на расстояниях
-у друг от друга; штриховые — для коробчатых балок с одной перегородкой иа конце коробки; Г в —
площадь отверстия; Гх — плоиАадь перегородки.
Примечание. Перегородки с большими окнами [-—$ > 0,4 — 0,5) следует рассматривать как
поперечные ребра»
Для оценки влияния окна в перегородке на жесткость балок в
формулы для определения перемещений будем подставлять не истинную бь
а приведенную толщину перегородки б/, которую определим из условия
равенства полных углов сдвига сплошной перегородки, имеющей
толщину б/, и перегородки с окном, имеющей толщину бь
113
'Я—?■
Расчетные формулы для определения перемещений в нагру
Эскиз нагружения
Перемещение нагруженной стенки
Угол наклона нагруженной
стенки
, 5Ре(1-а)(1Ч-0 в
ЗРе2^(1 — я)2„
#5
5Рь(1-а)*(1 + *)
3/УЧ»(1 -а)2
ЗА*«»*(1 _д)2
•^в ЕПА(1 + 0 ^5
бМе*(1 — д)
Л =
ЗМе2^(1 — а)2
ЕоЛ(1 +0
V- Е8й»(1+/)
Дв
114
Таблица 1'
женном сечении коробчатых балок при разных видах кососимметричной нагрузки^
Перемещение ненагружеиной
стенки
Угол поворота сечення
наклона ненагружеиной стенки
Обозначения
/у"
5Ре(1— а) (1+0
16ЕЬ
/*=-
5Ре(1—а)(1+*)
16Ео
•* =
' ЕЬН (1 + 0
0„~=-
Е&Л(1 + *) ^
Л—
ЗА*е*0(1—ц)*
ЕоЛ (1 + О
'у*-
6Ме#(1~а)
ЕШ (1 + О
/*-~ Е»А(1 + 0 Лб1
ШФ{\ — а)
Е5Л* (1 + О
§ — толщина стенок
Е — модуль упругости
К==Т' '^т; «т;
#о
1,6
0+0* '
Для балок без перегородок вместо
#1— /?6 подставляются соответственно:!
«1 = [4А2 (1 - а)2 + З*2 + 2*+ 0,5] Д0;
Д1==[4г2>2(1-а)2+3 + 2; +
+ 0,50] д0.
Для балок с одной сплошной
перегородкой на конце вместо #4 — #
подставляются соответственно:
*?=/?;■
2Л
(1-а)Л,Л2
V
к2 — Л2 — 2^4
2(1+а)Л3
л0;
Л3Л = 1
*?-*;.
«5-1-
(1 - а>Л22
2л ^0;
2(1+»)^
(1 + «)'Л
лг-1 л .
А = 32еэ*з + 9Р + 6* + 9;
Л! = ЫР (2 - а - а2) + 7^2 + 3* + 2;
А2 = 8е2^2(2 - а - а2) + 7 + Ы + 2**
Л3 = 24е2^(1 _а2)
115-
При наличии окна расчетное определение деформаций перегородки
представляет существенные трудности. Известны частные решения для
квадратной пластины, полученные при помощи метода сеток и
показавшие хорошие совпадения с результатами экспериментов [48]. В качестве
Р
Кб
Фнг. 57. Схема нагружения стенок (а) и перегородки (б)
коробчатой балки с концевой перегородкой при
кручении.
приближенного предлагается решение, в котором деформации пластины
с окном определяются как для рамы, размерами 21\У^212 (фиг. 58, я).
При этом достаточно рассмотреть половину стороны рамы как защемлен-
п
^
1?
Г
>«е
^
^г~-»~
т
<<
/77--
ГЛ,
сеч
6 |«?
6}
■I,
О)
Фиг. 58. Расчетная схема для определения деформаций
перегородки с окном.
ную балку, нагруженную по схеме, представленной на фиг. 58, б. При
такой нагрузке перемещение конца балки определится по формуле
/о =
'ЗЕ^
ш
^(1,2-0,1^),
где Р и / — площадь и момент инерции сечения рассматриваемой
балки.
Полное смещение одного угла рамы относительно другого будет равно
2/о- Полагая, что полный угол сдвига рамы т = Т1 + Т2> гДе Ъ и Ъ—углы
наклона горизонтальной и вертикальной стенок, и выражая *[ через /о,
получим
где
*=^
2ЩГ
1 А У
— 26,48^+5,38(^+1);
остальные обозначения прежние.
116
Как можно видеть из фиг. 59, точность расчета по выведенным
формулам для практических целей вполне достаточна.
На фиг. 60 приведена кривая, характеризующая влияние отверстия
разных размеров на жесткость квадратной пластины при нагружении
касательной нагрузкой по контуру. Характер кривой показывает, что при
размерах отверстия до 0,1—0,15 от размера пластины наличие отверстия
практически не сказывается на жесткости. .
Из условия равенства углов сдвига сплошной перегородки [ т = -^)
., . 5,2 <Ь* ~ , ^ ° '
и перегородки с отверстием получим ог — 01 —^—. Эта формула
выведена для случая, когда отверстие
в 'перегородке таково, что
расстояние от края отверстия до края
перегородки (т.-е. высота ребра) по всему
контуру одинаково. В первом
приближении ей можно пользоваться и
при другой форме отверстия,
предварительно определяя ч|? в
зависимости от отношения площади отвер-
Р Шй
стия к площади перегородки Е=-#—.
1__
кпл
0,8
0,6
№
/г
0.2
#Л
м
7пк
о,г
ш
1
1
1
1
1
1 |_ 1
д
йреч\ га?у
1 -
-—ь—н
|
и
♦ |
11
г
1
0,2
№
0,6
Ь-2Ь
&
Фиг. 59. Отношение жесткостей,
вычисленных по приближенным формулам
Опо) и по методу сеток (/), для
квадратных пластин с отверстиями разных
размеров.
В этом случае
Фиг. 60. Изменение жесткости / квадратной
пластины, нагруженной равномерной
касательной нагрузкой по внешнему контуру
в зависимости от размеров отверстия (за
единицу принята жесткость \спл сплошной
пластины) [48].
+
^(1-5) ^ У **(1_б)2 'О-*)
Перемещения и углы наклона нагруженной (вертикальной) и нена-
груженной стенок в сечении под нагрузкой для балок без перегородок и
с одной сплошной концевой перегородкой приведены в табл. 17.
В табл. 18 приведены формулы для определения перемещений стенок
коробчатых балок при действии на стенки в сечении х — 1 сосредоточен-
Р М
ных сил ±~ и моментов ^-к-.
На основе принятых допущений по аналогичной методике были
получены формулы, по которым можно определять перемещения и в более
сложных случаях, например, при нагружении кососимметричной
нагрузкой консольной балки с одной концевой и одной промежуточной
перегородкой при х = ~2~ (фиг. 61, а).
Для этого случая перемещение точки приложения силы определяется
по формулам:
а) при действий нагрузки на участке между концевой и
промежуточной перегородками (о<С^<-9-)
Р1 {(1~а)[8в^2(1-а)8 + 6^ + 4^+1]-
/
Рг-
1ЕЬМ(1+ 1)
2В1В2А1 (1 - Я) - (1 - *?В\Аг - ЧВ\А
2\А\-2АгАг]
■У-
117
Таблица 18
Перемещения стенок коробчатых балок в своей плоскости
Р М
при нагружении сосредоточенными силами ± -к- или моментами ± -о"
х Ь к I
х* =: "Г ' е ^ ~/Г ' * ^ ~]Г' а==Т"' толщина стенок, Б — модуль упругости.
I. Коробчатые балки без перегородок
Участок
Направление
перемещения
От действия сил -=
М
От действия моментов —^
V
Ч
V
о
Пооси^
Л
По оси У\
Рг(\ -а)
Х (2 + «к- Злг') + 3*з 4- 2г 4- 0,5]
_ ЗМ^2
Л= Е»А(1 + 0 (1~а)Х
Х(2 + « ~ Здг') + 0,5(^— * + !)]
А "" " ВЬ/1 (1 + 0 0 ~ а) X
X (1 + « - 2х')
V
V
По оси 2/
Л(1 -а)
X (2 4- л-' - За) '4 ЗР + 2* + 0,5]
ЗЛШ
Л~" Е5А(1 +0 " ~**')2
По оси К]
Ре (1-о)
/у = ~ 2ЕЦ/4 {)[^2(1-*')Х
Х(2 + *'-За) + 0,5(/»-/ + 1)]'
Л;
ЗЛ1<2Е2
Е8Л (1 + О
(1 - *У
II. Коробчатые балки с одной концевой перегородкой
Участок
Направление
перемещения
От действия сил -т
По оси 7.
Л I
Л =
2Ш(1 + ]) {2е^2 0 - а> <2 + а - 3*'> + Згз + 2г 4- 0,5 —
V
V
о
(1— х') [8в^(2—*—«2)+7*2+3/+2] [8/2Е2(2-^—[лг/]2)-^7^+3^42]У
2 [32е^2 4 9Р + 6/ -1- 9] )
По оси У\
А - - 2Еь\г + \) (2^2(1-*) (2 + а - 3*') + 0,5(г* -* Г + 1) -
(1—-О [8г^(2-а—а2)+7^2+Зг+2] [8^(2 ~х/-г[дг>]а)Ч-2^+3^+7Ц
2 [32г^2 4. 9^ + б* + 9]
V
V
По оси 2,
Л = 2ЕЦ(1 +0 {^ ° ~ ХГ) (2 + *' "~ За) + 3^ + * + °'5~
(1—а) [8/2.2 (2—д—а2)4-7^43г4'2] [8*2е2 (2—л-;—[^]8)+7<а'+3^+21
2 [32е2^2 4- 9^ + Ьг + 9]
По оси У\
/у
/у — "*" 2Я*(г+1)
(1_а) [8^2(2-а^а2)4-7^43^+2] [В^в^ (2—дгг—{дг,]2)4-2^4-3/4-7])|
Ь^2 (1 _ *') (2 4- х' - За) + 0,5 (** - г + 1) —
2] [8^(2—*'—[*']2)+2г2-(-3;+7])
2 [32г2^ 4- 9г^ 4 6г + 9] /!
118
б) при действии нагрузки на участке между промежуточной
перегородкой и заделкой \-^-<^1<Ь)
/рг —
Здесь
2ЕЬШ
«> как и ранее,
УЩПГ {<1_й) [8е2*2(1-а)2 + 6*2 + 4* + 1] _
(1 - а)а [2В3В,Л1 - В\Аг - 2Л3В|]
2\А\-2А^АЪ\
Ах = 20е»^ + 9Р + 6* + .9;
Л2 = 8г^ + 9г2 + 6г; + 9; '
Л3 = 32е«^ + 9^2 + 6^ + 9;
Вх = 2гЧп- (5 — 6а) + 7Р + 3^ + 2;
В2 = \ШЦ2 — а — а2) + 14^ + 6^ + 4;
53 = 8е2^2 (1 + а —2а2) + 14^2 + 6^+4
в = т; * =
1_
I— расстояние от конца балки (От концевой перегородки) до точки
приложения силы.
Фиг. 61. Расчетные схемы консольных коробчатых балок:
а — с промежуточной и концевой перегородками; б — со стенками разной толщины.
Для консольной балки с концевой перегородкой при толщине одной
из стенок, отличной от толщины остальных (фиг. 61, б), перемещения
угловой точки А нагруженного сечения определятся по формулам:
а) от действия силы Р по направлению действия этой силы
б) от действия силы Р по направлению действия сил Р\ или от
действия сил Р] по направлению действия силы Р
РЬ Г ЛИЛ.
?Р1Р~'ЗЕЪПС
в) от действия сил Р\ по направлению действия сил Р\
Г - Р>1 \а АЦ
119
Здесь
9б*М(бР + Р*+0 | 1РШ | , , ОЧ ,
ж 0/2(24—12/—6/2+3/з)+р;2(3/з+40;з+Ш—96)+Р2(54-9/+18/з--4^)--рз;(9+12/+4/2) .
+^ (Зр + 2(И + 2/ ^ /2)2 >
. _ 24/Мр (3 + 0 (2 -За + а»)
*Р(3 + /)(2-За + а») , ЗВ/1 а)[в{
Зр + 2р/ + 2/ + /2М(Ц1 — а)[ЬГ
р2/ (9 + 12/ + 4*8) + р (4/* + 8*3 — 4/з — 24^ — 18) + * (12 4- 14^ — 8^— 8/з - **)]
(Зр 4- 2р/ -I- 2/ -г /2)2 ^
Л — 24*М-(2-3* + аР)(бр + р* + 0 __ л/п _ .
Л*~ Зр + 2р/ + 2* + /2 И ;Л
Г21р + 11р*4- Ш + 5/з , 6/з(1 - р)з ___
Х [ ЗР + 2р/ + 2/ 4- /2 ""Г (Зр + 2р/ + 2/ + *2)з
/ (1-**)[(*+Зр)* 4-р(/ + Э)«]
(Зр + 2р/ + 2/ -} /*)*
-]'
4 _24^2(1_а)з(3(/4 2)[*+2 + р(2* + ЗЦ- ■
^з — (Зр + 2р/ + 2/ Аг /2)2 "Г
. ом чаГс* . о 12 + 18^ — 4^2— 13/* - 4/* - р/(2/ +3)2 1
+ 3(1-а)Р|б*+р (3р + 2р/ + а + ^ ];
. _ 24^(1 _а)8(3 + *) г (3 + /) (/2 + 1)
л* — (зр + 2р/ + 2/ }- /*) °Р^ ^ а' [ Зр + 2р/ + 2/ + /2 Т
р (3 - 3/ - 6/2 _ 2/») + (/3 - /2 - 12/ - 12) -[ л
+ (Зр + 2р/ + 2/ + /2)з ] '
Л - 24»*/«(1-«)3(вр + Р*+*) , о/ап Г 2(18р+9р/ + 9/ + 4/2) ,
5~~ Зр + 2р/ + 2/ + /2 ~Г°6 \А «^ ЗР + 2р/ + 2/ + /2 "Г
. ^(12 +-6/ + 2/2 + /») + /2р(15/ + 12*» + /з - 6) 4- рЗ/а(9/ ^ 12) 1
■+" (Зр + 2р/ + 2/ + /2)з ] 5
Р = 5" ; 2 — толщина стенок основного контура;
&! — толщина стенки, на которую действует сила Р;
а = 2Г> I—расстояние от конца балки до точки приложения силы;
Ь — полная длина балки.
Остальные обозначения прежние.
В изложенном решении предполагается, что жесткость стенок на
изгиб в плоскостях меньшей жесткости пренебрежимо мала, и вся
энергия идет на деформирование стенок в своей плоскости. Это
предположение, дающее незначительную погрешность при относительно небольшой
толщине стенок, для балок с толстыми стенками, как показали
эксперименты, оказывается неприемлемым. При этом, так как балки с концевой
перегородкой имеют значительно более высокую жесткость, чем балки
без перегородок, указанное решение для балок с перегородками дает
удовлетворительные результаты в значительно большем диапазоне
толщин стенок, чем для балок без перегородок. Для того чтобы доказать
приемлемость полученного упрощенного решения при соотношениях
размеров и толщинах стенок, типичных для стоек металлорежущих станков,,
решим задачу о деформациях балок без перегородок, не пользуясь
допущением о равномерном распределении нормальных напряжений по
толщине стенок в продольных сечениях. Для решения этой задачи восполь-
120
зуемся решением задачи о стесненном кручении тонкостенных стержней
замкнутого профиля, полученным К. Ф. Ковалевым [31].
Рассмотрим сечение и отдельные стенки балки, заделанной одним
концом и нагруженной парой сил РЬ в сечении х = хр (фиг. 62). Если
Ьг —угол поворота вертикальной стенки, а 62—угол поворота
горизонтальной стенки, то можно записать перемещение угловой точки сечения
по вертикали в виде 02 = у, и по горизонтали в виде Ь\ = Ьх^-
(обозначения см. фиг, 62). В поперечных сечениях стенок действуют
касательные напряжения т, приводящиеся к поперечным силам Р\ и Яг, и*
п
Н
V X
\
1— ь -—'
г
\
Фиг 62. Схема нагружения отдельных
стенок консольной коробчатой балки.
нормальные напряжения ах. На продольных гранях стенок действуют4
касательные напряжения, образующие поток ^о — <7о(*), и нормальные
напряжения аг% связанные с искажением контура сечения.
Если считать в первом приближении, что сдвиг в стенке
то нз выражения
3±.
" аь
получим перемещения в направлении оси X для горизонтальной
стенки
Яъ* д Л*
и.
л с&
и для вертикальной стенки
<=%-*>
Ьг
2 *
Из условия равенства перемещений и/ и и<{ в угловой точке
контура определим поток д0 и затем величины:
дх
)»*>
Так как сдвиг в стенках4 определяется не только касательными
напряжениями от потока <7о, но и касательными напряжениями, возникающими
от действия нормальных напряжений вх, то в виде следующего
приближения можно записать ? = -4т-•
12Г
Тогда
г г
о о
Подставляя значения т/ и тг' в выражения для и\ и «2, 'получим
окончательные значения <7о, Щ, щу %\ и тг, которые и примем в качестве
расчетных.
Выражения для поперечных изгибающих моментов, обусловленных
деформациями стенок из своей плоскости, получим из рассмотрения
деформаций рамки шириной их под действием сил 0,\ и (^2, приходящихся
на единицу длины балки (см. фиг. 41):
На основе приведенных зависимостей было получено [31]
дифференциальное уравнение для определения 0! и 02, которое представляет собой
линейное уравнение 6-го порядка с постоянными коэффициентами.
Определим 0) и % вариационным методом, не составляя дифференциального
уравнения. Введем вспомогательные функции.
„ Щ — лбг . бх + е2
х— н + ь и *~ТТъ-
Тогда можно записать
01 = ^ —*; а1х=^у х;
02 = ИХ + х; о^ = — ^-| х;
г1 = |.[А6(6 + 2А)-12А2*]х + 0|66;
** = -1- [А* (А + 2&.) - 12&22] х + 0^5;
Зададим функции х и $ в виде полиномов
х = Аг + Яхлг-Ь С^2 +^1Л:3; Е = Л2 + #2л:.
Часть неизвестных коэффициентов определим из граничных условий,
я остальные — из условия минимума потенциальной энергии деформаций
системы.
Так как конец балки заделан, то при х = 6 должно
удовлетворяться условие 0Х — 02 =0 или ^ = х = 0. Если бы заделка была
идеальной, то при х = 0, кроме условия равенства нулю углов поворота
в,должно было бы соблюдаться условие отсутствия продольных перемещений
точек сечения, т. е. условие и = 0. Однако, так как в реальных
конструкциях заделка не может считаться идеальной, примем, что в заделке дол-
122
жно быть справедливо равенство $^ — 0 при 2 = 0, что приводит к
условию
24
х = __~ х'
-о-НЬ + Щ
Кроме этого, обеспечим равенство крутящего момента заданному.
Это условие может быть составлено для любого сечения. Для простоты
примем, что Мкр = Р\Н-\- Р2Ь в сечении заделки, тг е. при х —0, что
приводит к условию
ь - н ...
к.
24
Подбирая коэффициенты в выражениях для к и § так, чтобы эти
условия удовлетворялись, будем иметь
х — С^ + оАх
,з 1*41 + 2*)
4(7
4
ь
Г Мкр +»(1-0пу
1. Яй*Р5 4 ]'
Неизвестные С, и ^1 определим из уравнений
Щ- = ° И ЙОГ = 0'
где Э = ^7—/? — полная потенциальная энергия системы; V—потей-
циальная энергия внутренних сил; Я — работа внешних сил.
В рассматриваемом случае 7? = Рй02(аг >, где Ь2{х >—значение 62 ПРИ
х=хп. р р
и
-2Ё)
+ 4
2 |(°?, + -Й)^+2 $(+и+%$(Ь
+
2Е^
<** +
I
2 ^
2 | М\Ог + 2 I М2Чг
их,
53
где /=?9 момент инерции сечения рамки единичной ширины.
Подставляя значения 8, а, т и М, выраженные через | и х, в формулы для
/?, V и'Э и дифференцируя, получим
А = -
ш*
"С, = т?
ЕМ»
где
48е2(2
Л2
[0,57е^* — 0,5е^2 (3 + 2* + *2) +
(1 -\ О2
+ 0,52(1+2?) (2+ *2У+0,13(1-*)2]}.
123
А3 = (±
А _(1 + *)**« Г* { 48^2 52 е^]
Л*~ 12 1/^ (1 -М)3 Л2 5 ]'
1, = «4
3
е^2 ^_0,6254е(1+*+**) — 0,3125(1-^2) -
<1-
(1 +
Здесь по-прежнему
^е^^[1,041(3 + 2^+^)-2е^)|
г— ^ ; г— л
2 — толщина стенок;
/,—полная длина балки;
хР — расстояние от заделки до точки приложения силы.
Подставив выражения для % и $ в формулы для 0! и 82, можно
определить перемещения /г и /у.
Перемещение в горизонтальном направлении (по оси V)
, _ Р ф (&с , х2 _2,5_-у .
Ту — ^1 — — ^5~2"(А 6Г I2 *2 I •"
+ ^[«2<в1Г-0-625т(2 + ')]Ь
А
в вертикальном направлении (по оси 2)
Р г( Г&с & 2,5 х А
А Л
здесь х — расстояние от заделки до сечения, перемещения в котором-
определяются. Остальные обозначения прежние.
Если сравнить результаты расчета коробок без перегородок по этим
формулам и по упрощенным формулам, полученным ранее, то можно»
показать, что при отношении -т- порядка 0,01 и меньше эти результаты*
очень близки. При увеличении -^-расхождение результатов
увеличите ' а
веется. В реальных конструкциях стоек величина -^- редко превышает
0,03. При -й-= 0,03 наибольшее расхождение результатов расчета по*
уточненным и упрощенным формулам обычно не превышает
допустимого. Исходя из этого можно считать, что для технических расчетов»
можно пользоваться упрощенными формулами.
Этот вывод подтверждается также сравнением результатов
расчетов 1 и экспериментов (фиг. 63 и 64). Несколько худшее совпадение дл5г
1 Расчетные кривые, приведенные на фиг. 63 для балок с перегородками,
получены по упрощенным формулам, а для балок без перегородок — по уточненным, так как
5
при относительной толщине ~^~ = 0,06 расчет моделей без перегородок по упрощенным-
формулам дает значительную погрешность.
124
перемещений в направлении, перпендикулярном к линии действия силы,
объясняется меньшей точностью измерения перемещений в этом
направлении.
Формулы для определения перемещений коробчатых балок с учетом
искажения контура были выведены для балок, имеющих правильную
<1
Фиг. 63. Сравнение результатов расчетного и экспериментального определения
перемещения точки приложения силы при кручении коробчатых балок:
/4 ш. /?4 - :-- —» перемещения в направлении лиаии действия силы; /2 = /?, -ргт — перемещения в направ
лении, перпендикулярном линии действия силы (^ М — —к~) \
Кривые линии иа графиках: сплошные — экспериментальные; штриховые — расчетные.
а — балки без перегородок: 1 — модель № 1; -г- = 1,0; -г- — 2,62; 2 — модель №5;у- 1,55; -г- — 2,62;
3 — модель № 5; — — 0,645; —- = 4,07; б—балки с концевой перегородкой: 1—модель № 2 с дополнительной
промежуточной перегородкой при х — 75 мм\ -г- — 1,0; -г- «= 2,62; 2 — модель №. 5; -г- = 1,55, — = 2,62;
3 - модель №5;| = 0,645; ~
Ь п
■ 4.07.
прямоугольную форму сечения. Возможность применения этих формул
для технического расчета стоек реальных конструктивных форм
подтверждается сравнением результатов расчетов и экспериментов завода
им. Свердлова над сварными моделями стоек, выполненными с
направляющими, продольными ребрами, с окнами в перегородках и т. п.
Расхождение результатов этих расчетов и экспериментов не превышало
]5—20%. Следует отметить, что в этих расчетах учитывалось влияние
продольных ребер и направляющих, которое при кручении с
искажением контура может быть весьма существенным. Для этого расчет
проводился не по фактической, а по приведенной толщине стенок, опреде-
125
200 х мм
ленной из условия равенства площади сечения стенки с ребрами (или
направляющими) и стенки приведенной толщины. Как показали
эксперименты, аналогично может учитываться влияние диагональных ребер
на стенках, причем в этом случае приведенную толщину следует
определять по сечению стенки и
нормальному сечению ребра.
Таким образом, из изложенного
следует, что приведенные расчетные
формулы могут быть использованы
для технических расчетов стоек. Как
уже указывалось, влияние искажения
контура поперечного сечения
предлагается учитывать поправками к
элементарному решению. Однако картина
деформаций коробчатых балок при
искажении контура настолько сложна,
что в ряде случаев перемещения
стенок балки, которые при этом имеют
место, не могут быть выражены через
составляющие перемещений при эле^
ментарных кручении и изгибе.
Например, при действии в плоскости одной
из стенок коробчатой балки
сосредоточенного момента сечение балки не
только смещается и наклоняется, как
это происходит при элементарном
изгибе, но сечения отдельных стенок
балки поворачиваются и
искривляются, а стенки изгибаются каждая в
своей плоскости (см. фиг. 51, г).
Подобных примеров можно было бы
привести много- Поэтому поправки к
элементарному решению предлагаются
не в форме коэффициентов понижения
жесткости балки на кручение или
изгиб, я в форме поправочных
множителей к перемещениям инструмента
относительно изделия, характеризующим
суммарную жесткость стоек при
типичных для стоек ©идах нагружения.
При технических расчетах (см.
ниже) стойка рассматривается как
консольная балка, защемленная одним
концом. В первом приближении
силовые факторы, действующие на стойку, можно рассматривать как
приложенные в одном расчетном сечении1 (см. ниже § 6А). Также можно
считать, что положение узла, передающего нагрузку на стойку,
определяется перемещениями стенки, к которой непосредственно приложена
нагрузка, в том же сечении.
В общем случае положение точки приложения силы резания,
перемещения которой в результате деформаций стойки характеризуют
жесткость стойки, определяется тремя координатами —
хр = с + *ст* У*—а + Уст и хР (фиг. 65).
Фиг. 64. Сравнение результатов
расчетного и экспериментальною
определения перемещения стенок сварной
коробчатой балки при кручении:
М ( РЬ\
у =1,0; -у = 1,92; т= 0,02:
— балка с одной концевой перегородкой:
2 — балка без перегородок.
Кривые линии на Iрафиках сплошные — для
измеренных перемещений, шгрихпунктирные—
для перемещений, вычисленных без учета
деформирования стенок в своей плоскости;
штриховые — для перемещений, вычисленных
с учетом деформирования стенок в своей
плоскости.
1 Это сечение не следует смешивать с расчетным сечением, по которому
определяется жесткость стоек переменного сечения.
126
Здесь хст и уСт—расстояния от оси стойки до стенки, ближайшей
к точке приложения силы, и до направляющих, соответственно.
Принято, что направляющие расположены на стенке, параллельной оси X
(см. фиг. 65).
Определим перемещения точки приложения силы от 'составляющих
силы по осям координат.
1. Действие составляющей силы Рх (фиг. 65, а).
Запишем выражения для перемещений точки приложения силы
через перемещения стенки с направляющими в расчетном сечении1:
здесь }х и Ьхг—смещение в направлении оси X и угол наклона в
плоскости ХЪ рассматриваемой стенки; 6уАГ — угол поворота в плоскости
Фиг. 65. Схема общего^ случая нагружения стойки.
УХ узла, передающего нагрузку на гтойку, в результате деформаций
стойки. Положение этого узла определяется перемещениями
направляющих, поэтому в первом приближении можно считать, что угол 6ух
определяется смещением в направлении оси У точек А и В расчетного
сечения (см. фиг. 65). Так как нагрузка передается на стойку через
направляющие, то можно считать, что сила Рх, приложенная в точке с
координатами Хр, ур, гр, будет действовать на стенку стойки в виде
сосредоточенных силы Рх и момента Рхгрл приложенных в плоскости направля-
ющих, и пары сил Р х~ь~ > приложенных в плоскости стенок,
перпендикулярных к направляющим (фиг. 65, а). При этой нагрузке величины $х
и ®хг будут определяться перемещениями от действия симметричных
составляющих силы Рх и момента Рхгр, которые могут быть вычислены
по элементарным формулам, и перемещениями от кососимметричных со-
1 При выводе расчетных формул для определения перемещений точки приложения
силы с учетом искажения контура сечення н прн определении нагрузки на стойку от
узлов, несущих инструмент или деталь, было принято простейшее допущение о том,
что жесткость элементов, передающих нагрузку на стойку, весьма высока. Аналогичным
образом можно было бы получить решение для случая, когда жесткость этих
элементов невысока и онн деформируются так, что их сечення следуют за деформациями
стойки. Структура конечных формул при этом осталась бы неизменной, но формулы
для определения поправочных коэффициентов, учитывающих влияние искажения
контура (см. ниже), несколько усложнились бы.
127
ста,вляющих силы Рх и момента Р^р> а также перемещениями от сил
РхАг, которые могут быть вычислены «о формулам, приведенным
в табл. 17. Величина 8ул- определится перемещениями точек А и В в
направлении оси V от кососимметричных составляющих силы Рхи момента
.Рх^р, а также от сил Рх -у, которые также могут быть вычислены по
формулам табл. 17. Записав выражения для всех этих перемещений,
подставив их в формулы для/^р,/Ур,/г и преобразовав к виду, который
имеет формула, полученная элементарным путем, как для консольной
--балки, будем иметь:
* -РА ■ ^л | РЛ д д, , РА1Р м , рЛ1Р Л,.
Р /2 Р х I
(3.3)
-здесь N — поправки к элементарному решению (см. ниже).
Аналогичным образом можно получить формулы для определения
перемещений от составляющих Ру и А,.
2. Действие составляющей Ру (фиг. 65, б):
/ ~РУ1Р I %1РУ1Р_\ Р^Р1Р 1 РУ*Р1Р , РуУр дг .
'Ур~аЕ/х~Г' ОР "< я/* "Г ^Уд. "Г оу^ ^б>
'#р
ЯЛ . . />*»/Л
Лр—2Й^--^Ур- (3-4)
3. Действие составляющей Рг (фиг. 65, е):
Р**п* Р х I2
2
Здесь
/ ^УР^ ^ . м| РгУР^ дт . /о с\
/*р = -б7ГУр + -*/Г*рЛ'2-
^з== М-у, + ^. . (3.6)
Ур
в^1 „ „ 1гр 1>6
Ур \^Уст
л:?, г (г + 3)
Л 28
129
Фиг/60. Графики для определения коэффициентов Я^; #2°; ЛЛ при расчете стоек без
перегородок. Кривые линии на графиках:
сплошные — при -т~ = 0,5; штрихпунктирные — при — = 1,0; штриховые — при — - 2 О
Для стоек со сплошными (перегородками или с перегородками, окна-
в которых имеют близкую к треугольной форму или относительно
небольшие, не превышающие 0,5 стороны сечения размеры Г-~^ < 0,25-ь
-ь0,3), поправочные коэффициенты N следует лринимать равными 1.
Для стоек без перегородок и ребер при вычислении коэффициентов
N (обозначаемых №) коэффициенты ^ь #2 и 7?4 (обозначаемые /?!°, /?2°,
#4°) определяются по кривым, приведенным на фиг. 66, а—в, или по
формулам табл. 17. Коэффициенты #3, #5 и 7?6 принимаются равными 1.
Для стоек с ребрами коэффициенты N (обозначаемые №)
определяются в зависимости от соответствующих коэффициентов для стоек
без ребер (№) ■—по формулам Ыр = № (\—5) 4-5, где 5 —
коэффициент, учитывающий влияние ребер и определяемый по табл. 19,
составленной по результатам экспериментов.
Таблица 19"
Коэффициент 5, учитывающий влияние ребер на деформации стоек
при искажении контура поперечного сечения
| Н Высота ребра
1 8~ Толщина стенки
5
1
0,3-0,5
1,5
0,55-0,7
2
0*,7—0,85
3-4
0.8*-0,95 !
Примечание. Верхние значения следует применять лля стоек с отношением сторон
сечения-г— Ф 1 при действии нагрузки у верхнего конца стойки; нижние — для стоек с сечением, блнз-
1 ким к квадратному, при действии нагрузки в средних по высоте сечениях. Принято, что толщина
ребра б = 6, 1
Для стоек с одной концевой перегородкой коэффициенты N
(обозначаемые АГ/г) можно вычислять по значениям коэффициентов /?
(обозначаемых Кп), определяемым по формулам табл. 17.
Приведенные формулы для определения поправок N к
элементарному решению были получены из рассмотрения деформаций балок
правильного прямоугольного поперечного сечения. Однако, как показали
дополнительные расчеты, в первом приближении они могут быть
использованы и для расчета стоек реальных конструктивных форм. В этом*
случае $~-и отношение габаритных размеров сечения {к—размер -
в направлении оси У, Ь — в направлении оси X, см. фиг. 65).
§ 6. ТЕХНИЧЕСКИЙ РАСЧЕТ СТОЕК
А. Основные положения и расчетные зависимости
Как уже указывалось, жесткость стоек предлагается
характеризовать величиной перемещения (при заданной силе) инструмента
относительно изделия в результате деформаций стоек при достаточно типичном,
случае обработки.
Основным критерием предлагается считать перемещение в
направлении, влияющем на точность обработки. Однако, так как с точки
зрения виброустойчивости существенное значение может иметь не только1
жесткость системы в направлении, влияющем на точность обработки, но>
и направления осей жесткости, приводятся расчетные формулы для
определения всех трех составляющих полного перемещения инструментам
относительно изделия.
130
Для того чтобы то вычисленным перемещениям судить о жесткости*
стойки рассматриваемого станка, следует сравнить эти перемещения-
с величинами допустимых погрешностей обработки или с
соответствующими перемещениями, вычисленными для других станков, хорошо
показавших себя в эксплуатации.
Расчетные формулы для определения перемещений инструмента от*
носительно изделия в результате деформаций стоек выводятся на основе
следующих предпосылок:
1. Стойки полагаются защемленными у основания или в плоскости
оси элемента, несущего обрабатываемую деталь1, и рассматриваются
как балки с прямой или ломаной осью (Г-образные). Оси элементов
балки полагаются совпадающими с осями, проходящими через центры,
тяжести сечений элементов.
Ось
кронштейт
Ось
ц
гс
ц
стола
Ч-
А
"тН
ГА^—1\ось-Шки
а)
ш
-
щ
Ось
консоли
л
^
Л
Ш
1
Ц
б)
Фиг. 67. Расчетные схемы стоек:
/—/ — плоскости расчетных сечений стоек.
Ось
поперечины
станины
2. Жесткость стоек принимается постоянной по длине и
определяется по формулам, приведенным выше.
3. Расчетными силами для стоек средних станков являются силы<
резания. Действие веса узлов, размещенных на стойке, не
рассматривается, так как в станках средних размеров веса перемещающихся узлов;
относительно невелики, и станки при установке выверяются.
4. Нагрузка на стойки передается через направляющие узла,
несущего инструмент, и определяется из условия равновесия этого узла.
Силовые воздействия на стойку полагаются приложенными в одном
расчетном сечении (фиг. 67). Расчетная нагрузка на стойку определяете»
приведением силовых факторов, действующих в расчетном сечении,
к оси стойки; деформации элементов, передающих нагрузку на стойки,
не рассматриваются.
1 Так как сеченне, в котором передается нагрузка на стойку со стороны узла^
несущего деталь; близко к основанию стойки, то депланация его невелика и выбор
такой схемы можно считать допустимым.
131
5. Расчетное сечение полагается расположенным в плоскости,
совпадающей с осью элемента, передающего нагрузку на стойку.
6. Перемещения инструмента относительно изделия определяются
перемещениями стоек в расчетных сечениях. При определении этих
перемещений следует рассматривать деформации стойки на участке от
расчетного сечения до заделки, а именно:
а) в консольных станках — деформации стойки на длине, равной
расстоянию между расчетным сечением, в котором на стойку передается
нагрузка от инструмента, и плоскостью оси элемента, несущего деталь
(фиг. 67, а);
б) в бесконсольных станках — деформации стойки на длине, равной
расстоянию от сечения, в котором на стойку передается нагрузка ог
инструмента, до основания стойки, если стык стойки со станиной
горизонтальный (фиг. 67, б), или до плоскости оси станины, если стык
станины и стойки вертикальный (фиг. 67, г);
в) в стойках с ломаной осью (Г-образных) —деформации
горизонтального участка стойки на длине 1р{ от нагруженного сечения до
ближайшей стенки вертикального участка стойки (с направляющими) и
деформации вертикального участка стойки на длине 1Р от оси
горизонтального участка до плоскости оси станины, до основания стойки или до
плоскости оси элемента, несущего деталь (фиг. 67, в).
В первом приближении деформации горизонтального участка не
учитываются.
Как уже указывалось, в предлагаемых расчетах влияние
деформаций стоек на погрешность обработки характеризуется деформациями
стоек на некоторой расчетной длине. При этом влияние на деформации
стойки жесткости узлов, расположенных на стойке, не учитывается.
Более точно взаимные перемещения инструмента и изделия в результате
деформаций стоек следовало бы определять, рассматривая деформации
стоек и узлов, несущих инструмент и деталь, совместно, с учетам
собственных деформаций элементов и контактных деформаций в соединениях.
Решение такой задачи представляет существенные трудности.
Для того чтобы оценить, хотя бы ориентировочно, в какой степени
перемещения, определенные при расчетах по выбранной схеме,
соответствуют действительным перемещениям в результате деформаций стоек
с ломаной осью, были проделаны эксперименты. Для плоских П-образ-
ных рам разных размеров при нагружении их двумя сосредоточенными
силами по концам были измерены перемещения точек приложения сил.
Результаты измерений сравнивались с расчетом, в котором полагалось,
что горизонтальные участки деформируются на длине / (от точки
приложения силы до вертикального участка), а вертикальный участок—
на длине 1р = Ь — 2Л/> (фиг. 68). Зависимость расчетной длины
вертикального участка рамы от соотношения размеров элементов, полученная
из условия равенства измеренных и вычисленных величин перемещений,
приведена на фиг, 68. Как можно видеть, при симметричном сечении
горизонтальных элементов для наиболее распространенных соотношений
размеров элементов Д/>^0,1#. Так как элементы, передающие нагрузку
на стойку (столы, консоли, станина), обычно имеют горизонтальные
направляющие и центр тяжести сечений этих элементов смещен от
середины площади контакта стойки с 'рассматриваемым узлом, то в этом
случае можно считать, что расчетное сечение стойки лежит в одной
плоскости с осью данного элемента. При симметричном сечении элементов
с горизонтальной осью положения расчетного сечения можно определять
1 в соответствии с результатами проведенных экспериментов.
Измерения проводились для рам с разной формой наружного
контура. Из кривой, приведенной на фиг. 69, можно видеть, что как и сле-
132
довало ожидать, части рамы, находящиеся вне силового (нагруженного)
контура, практически не оказывают влияния на жесткость рамы;
влияние закругления острых углов наружного контура также практически
ничтожно. Из этого следует, что расчет стоек, имеющих форму кривого
бруса (вертикально-фрезерных станков), с достаточной степенью
точности также можно проводить по выбранной схеме (см. фиг. 67).
Следует отметить, что расчет ллоских рам, подобных исследованным, по
методике расчета кривого бруса, если считать, что радиус закругления
Ф
0,2
0,1
О
-0,1
'0.7
1
0,2
^Г
0,
'/
Ц
0,6
г
\р
Г 1 '
1 * ^1^
н-/—~
А *
1 ^
1 I *1^
Г *
•^
^ ,
4
1
■ Тт
V
П
41
Фиг. 68. Зависимость расчетной длины 1Р стойки от
соотношения размеров элементов ; 1р= Ь—2Д/,;
№ = <ф#ч
наружного контура равен высоте сечения элементов Н, дает результаты,
достаточно хорошо совпадающие с экспериментами.
В качестве примеров приведем методики расчета стоек вертикально-
сверлильных, консольных горизонтально-фрезерных и универсальных
горивонталыно-'расточных станков.
* ' ' ПО/—' В50Г7*
Форма наружного контура
Фиг. 69< Влияние формы наружного контура плоской
рамы на перемещение точек приложения силы / = К %§
(6 — толщина элементов)»
В предлагаемых ниже расчетных формулах используются
следующие обозначения встречающихся величин:
РХУ Рг Рх— составляющие силы резания по осям координат
в #7" (направление осей см. фиг. 65);
Р—осевая сила на сверле (сила подачи) в кГ;
1р — деформируемая длина стойки в см;
уР — а-\-уст;хР = с~+-хст; хР — координаты точки приложения силы
в см;
^у хет — расстояния в направлении оси X от точки
приложения силы и от оси стойки, соответственно, до
ближайщей стенки перпендикулярной к оси X, в см;
Ш
а, уст — расстояния от точки приложения силы и от оси
стойки, соответственно, до плоскости
направляющих в см;
р—площадь поперечного сечения стойки в ёя^\
Е/у; Е]х—расчетная жесткость стойки на изгиб в плоскостях
Х2, и К2, соответственно, в ёяк\
0]кр — расчетная жесткость стойки на кручение в ёяк\
хь х2 — коэффициенты распределения сдвига для сечения
стойки при изгибе в плоскостях У2 и Х2<,
соответственно;
Жг^ Ы6 — поправочные коэффициенты, учитывающие
искажение контура поперечного сечения;
Е, О — модули упругости I и П рода, соответственно,
в кГ/ём2;
}хру /уру /*р — составляющие по осям координат перемещения
инструмента относительно изделия в результате
деформаций стойки, в ёя\
У=Р1Р — эффективный объем металла в смъ.
1, Расчет стоек вертикально- ев ерлильных
станков
Рабочей нагрузкой стоек сверлильных станков являются осевая
сила подачи и крутящий момент на шпинделе. Основное значение с точки
зрения точности обработки имеет нагру-
жение силой подачи, так как по
сравнению -с деформациями от силы подачи
деформациями от крутящего момента
можно пренебречь.
Погрешность обработки на
сверлильных станках определяется величиной
взаимного угла наклона инструмента и
изделия, которая регламентирована ГОСТ
370-41.
По ГОСТ 370-41 для станков на
круглой колонне-стойке при силе подачи
Ря^0,8Ршах взаимный угол наклона не
должен превышать 2,5/1000. Для
станков на коробчатой стойке по проекту
нового ГОСТа и по нормам точности,
принятым на заводах зарубежных фирм,
предельный взаимный угол наклона
принимается равным 1,0/1000.
При достаточно хорошем качестве
изготовления стыков между
кронштейном ,и стойкой и между столом и стойкой
ориентировочно можно считать, что на
долю собственных деформаций базовых
деталей приходится до 30°/о полной ве-
чины взаимного наклона инструмента и изделия, а на долю одной
стойки — около 10—15%.
Нагружение стойки вертикально-сверлильного станка и расчетная
схема приведены на фиг. 70.
Взаимный- угол наклона в результате деформаций стойки может
быть определен по формуле
--РУр1' (3.7)
М=РУр
и- л —I
Фйг. 70. Расчетная схема стойки
вертикально-сверлильного станка.
Ых
134
Следует отметить, что в целях некоторого уточнения расчета осевую
-линию кронштейна, .положение которой определяет расчетную длину
-стойки 1Р, целесообразно сместить вниз от середины направляющих на
величину 0,Ш„, где Нк—длина направляющих кронштейна.
2. Расчет стоек консольных
горизонтально-фрезерных станков
При расчете стоек горизонтально-фрезерных станков нагружеиие
стоек принимается соответствующим наиболее типичному случаю
обработки— фрезерованию цилиндрической фрезой. В первом приближении
влияние диаметра фрезы на величину упругих перемещений можно не
рассматривать и считать, что
^составляющая Ру силы
резания действует по оси оправки.
Нагружение стойки
горизонтально-фрезерного станка и
расчетная схема приведены на
фиг. 71. Жесткость стойки
будет характеризоваться
смещением точки О оправки
относительно соответствующей точки
изделия в результате
деформаций стойки. Перемещение
точки О, вызываемое
деформациями стойки, определяется
перемещением опорных точек
оправки А и Аг относительно
консоли. Смещение точки А
относительно оси шпинделя в
результате деформаций стойки
определяется деформациями
верхней части стойки (над
шпинделем). Так как
нагрузка, деформирующая верхнюю
часть стойки, составляет только
часть полной нагрузки и так
как длила этого участка стойки относительно невелика, перемещения
серьги в результате деформации верхней части стойки можно не
рассматривать и считать, что перемещения точки О в результате
деформаций стойки определяются только перемещением оси шпинделя
относительно консоли.
Хотя стойки фрезерных станков и не имеют внутренних перегородок,
но деформируемая длина их относительно невелика (1р^ А-ь- 1,5/г), и
потому искажение контура поперечного сечения можно не учитывать.
Тогда, 2ассматРивая деформации стойки на расчетной длине 1Р от оси
шпинделя до оси консоли, формулы для определения перемещений
инструмента и изделия в результате деформаций стойки можно записать
в следующем виде [полагая в формулах (3.3) — (3.5) гр = 0;* ^р = 0
ж N = 1)]:
Фиг.
71. Расчетная схема стойки консольного
горизонтально-фрезерного станка.
(3.8)
135
Влияние искажения контура поперечного сечения может быть
учтено введением в выражение для }хр соответствующего поправочного
коэффициента /У3. В этом случае
Лр^^^щГ + ^^ + оТ^^3/-
При соотношениях параметров, типичных для фрезерных станков
средних размеров, Л^3 ^ 1,2.
Соотношение составляющих силы резания можно принимать
Рх :Ру:Рг = 1:0,375:0,5, что примерно соответствует случаю
фрезерования против подачи.
При обычных конструкциях стоек перемещения по оси X,
определяемые главным образом деформациями вручения (около 80%),
значительно превышают перемещения в направлении осей 2 и У.
3. Расчет стоек универсальных
горизонтально-расточных станков
При расчете стоек расточных станков нагружение принимается
соответствующим случаю расточки отверстий при правом вращении
шпинделя. В первом приближении влияние диаметра обрабатываемого
отверстия на величину упругих перемещений можно не учитывать и
считать, что сила резания проходит через ось шпинделя. При
вращающемся резце направление равнодействующей силы резания в
пространстве непрерывно меняется. Формулы для определения составляющих
перемещения инструмента относительно изделия получены из
рассмотрения деформаций стоек при одном положении резца. Для определения
перемещений при других положениях резца в этих формулах должны
быть изменены соотношения составляющих силы резания и знаки,
определяемые величиной и направлением составляющих силы в данном
положении резца.
Нагружение стойки универсально-расточного станка и расчетная
схема при правом горизонтальном положении резца (положении 1)
приведены на фиг. 72. Если принять, что ось шпинделя расположена при*-
мерно в одной плоскости с осью бабки, т. е. что гр ^ 0, то
перемещения инструмента относительно изделия в результате деформаций стойки
можно определить по следующим формулам (см. § 5 «Определение
поправок к элементарному расчету, учитывающих искажение контура
поперечного сечения»):
Р V ? 1 И3*9'
4-— • Ур р N \ •
^ Ру 2ЯУ*6/'
Как уже указывалось, при других положениях резца знаки должны
быть изменены в соответствии с направлением составляющих силы
* В этом случае коэффициент М3 определяется по формуле, несколько отличной'
от приведенной выше8 так как нагрузка передается на стойку не через направляющие^
а непосредственно на стенки — через шпиндель.
136
и~ь
фиг. 72. Расчетная схема стойки универсального горизонтально-
расточного станка.
Как показали эксперименты, проведенные на заводе им. Свердлова,
наличие крестообразных перегородок-перемычек практически не
увеличивает жесткости контура.
Приемлемость расчетов по предлагаемым формулам стоек
реальных станков подтверждается хорошим совпадением результатов
расчетов и экспериментов. Так, например, вычисленные и измеренные
деформации стоек расточных станков 262Г и 2620 для случая нагружения
силой Ру при вылете шпинделя 350 мм и расстояния от рабочей
.поверхности стола до оси шпинделя 750 мм отличались на величину
порядка 15%.
Б. Порядок технического расчета стоек
Предлагается следующий порядок технического расчета:
1. Выбирается расчетная схема (§ 6, А).
2. Выбирается расчетное сечение (§ 3, Б) и определяются:
жесткость стойки на изгиб (Е1) по моментам инерции сечения (/);
жесткость стойки на изгиб (Е1) по моментам инерции сечения (/);
коэффициент к0, учитывающий влияние окон на жесткость
кручения стоек, по фиг. 49;
коэффициент х распределения сдвига по формуле (3.1) стр. 98 ил»
по графику (фиг. 44).
* Обозначения составляющих силы резания соответствуют выбранным осям
координат (фиг 72) и отличаются от общепринятого.
137
резания. При горизонтальном положении резца можно принимать
Я* :Яу :Я^= 1 :0,5:0,3; при вертикальном положении резца Рг'Ру -Рх ^
- 0,5 :1 : 0,3 *.
Так как стойки существующих расточных станков в большинстве
случаев выполняются без перегородок, то величины коэффициентов Мг
учитывающих искажение контура поперечного сечения, как правило,
оказываются весьма значительными. Так, при средних соотношениях
размеров стоек без перегородок и ребер (I = 1; е = 3; ^- = 0,5; -|- = 0,25;
-^- = 0,75) Ых = 2; #2 = 3; АГ8 = 1,6; #4 = -0,6; #5 = 5,8; М6 = 9,5.
Таблица 20
Эскизы, геометрические характеристики сечений и результаты расчета
стоек некоторых вертикально-сверлильных станков
(Расчетную схему см. на фиг. 70)
Модель
станка;
наибольший
диаметр
сверления в мм;
сила подачи
в кГ
Эскиз сечения.стойки
(размеры в мм)
Расчетные
параметры1
Угол наклона сверла
в радианах
2А125
^=25
Р = 75§
а
'х
Р
V
70
25
3,29-104
197
$ - 0,091 -% =
-0.068-КГ8
2А135
яГ^35
Р=1200
а
*х
Р
V
75
30
5.86-10*
238
1,78-10*
I = 0,065 -^ =
= 0,077-10
-з
2А150
дГ-50
Р - 2000
>Р
а
^x
р
V
80
35
8,68 -10*
258
2,0640*
*-0,054^ =
*= 0,108-ИГ3
2170
^=75
Р = 3750
1Р
а
/*
Р
V
85
40
18,010*
394
3,35-10^
= 0.031 -^- =
= 0,118. Ю-3
: Линейные размеры приведены в см, Р в см*, / в см*, V в см8.
138
Таблица 21
Эскизы, геометрические характеристики сечений и результаты расчета стоек
некоторых консольных горизонтально-фрезерных станков
(Расчетную схему см. иа фиг. 71)
Модель станка
рабочая
площадь стола
в мм X мм;
сила резания
в кГ
6П80
200 X 800
Рх - 700
Эскиз сечения
(размеры в мм)
Расчетные
параметры*
58
72
27
316
'у
** Кр
7.5-104
6,4.10*
4,0-10*
2,3-10*
Перемещения
инструмента / в мм
/хР = 108 -§- - 0.075)
/ур-33 ^--0.01
ЛР=26^- = 0,01
6Н81
250 X Ю00
Рх = 1000
\
\*~Ь2в-\
~Ь2(1-
X
$Л
—2№+».
65
80
28
272
'у
Зкр
V
8,3.10*
7.2.10*
7,0-104
2,2.10*
/^=90^ = 0,09
/ур-«-#- = 0.015
Е
Е
6р = 31% = 0.015
6Н82
320 X 1250
Р*г=1500
68
83,5
35
715
V
37,2-104
19.4.10*
13,5-10*
6*0-10*
/*,-75^--0,11
/^13-^-= 0.01
Л/>-12§--0,01
6Н83
400 X 1600
Рх = 2000
70
89
45
687
?Кр
V
43,4-10*
24-104
18.7.10*
6,1-Ю*
Ар=80^г = 0,16
/у/,= 14-^ = 0,01
Д,= 15^-= 0,015
1 Линейные размеры приведены в см, Р в см*, У в см4, %в см9. Величины Зк вычислены с
учетом влияния окон.
139
Таблица 22
Эскизы, геометрические характеристики сечеиий и результаты расчета стоек некоторых универсальных горизонтально-расточных станков
(Расчетную схему см. на фиг. 72)
Модель станка, дна- Эскиз сечения _ , гт » „ *
I метр шпинделя вм; [ (размеры в см) Расчетные параметры1 Перемещения-2 вершины резца/ в мм
I сила резання в кГ \ \
I 11111 Р
у \ 1р 88 /г 63,5-10* /ур1 = — 24 ~^г = — 0.015
2б2Г I 1л1(Цх р
± ауДУ^У а 18 Уу 56-10* /^ = — 24 -^ ~ —0,015
РЛ = 1300 ГТЗ I * I *Р 50'5'104 ^=+32-^-0,021
10 \ Г 960 ^ 18,6-10* ЛР4= + 29-^ = 0.019
I г 11111 I
2620 ГТПГ!^] я
К . 1П]ТУ « 25 уу 55,5 10* /2 = _15-тг=-0.010
Рл = 1300 Шк.к/1 « '58 ]к" 4°'104 /,^=+37-^ = 0.024
|| 1*?/»4 1111 ! I
I—«-3 /=• 670 К 14.7-КХ /»«- +19 -^ = 0,012
■ ■■ [^ /„ 128 У* 113-КИ /у^ = -2*1-|-=-0.021
2б30 I |ГТ^П Р
_ ^ЛЦэЩЩи а 25 У, 117-10* /2р1) - - 30 -^- = - 0.03
Р,1 = 2000 ^|Ц8!Д « 79 ->«Р 15*-">* /у/й =+28-|-= 0,023
I-— 97 —Н ^ 990 К 29,2-КН ///>4 = + 40 -^- = 0,04
140
Продолжение табл. 22
I Модель станка, диа- Эскиз сечения
метр шпинделя вжж; (размеьы в см) Расчетные параметры1 Перемещения3 вершины резца в / мм
I сила резания в кГ
I 1* 1111 I Р
ГП^пЙРп^ 1р 258 ^ 960-10* /у^-—24-^г = -0,048
2660 ! || и р
5 Щ >Н—О X а 37,5 ^V 715-10* //д2- - 19-б-- —0,038
Рг1 = 4000 1 II 1.ЦЗ ] с 102 ^р 760-10* /у/?3= + 28-^- = 0,056
I щ 13Л Р 3390 V 16040* /0р4 = + 28 -^ - 0,056
2670 I В О ПГ Р
* к- I У у а 48 Л 1750-10* /*.»:= —24-тг »—0.06
р^1 = 500О II ||| ГЪ[ с \ т \ '"Р \ ™Ж'№ /уРз= + 35-^г-0,087
[^"ТГГ^-^Г /? 3890 V 240-104 /^ - + 31 -тг«= 0,077
I I ^**г""1' 176 "<и 'I ■ ^ | ! ! I I ^ I
|| 1(1 |П| ^ 410 /х 2140-10* /у^ = — 37 -^ =^ — 0.11
2680 - В I У 1 ГГ I Р
I ^ |-^^^™Хк 1 * 30 /у 2420-10* Л5ра = —29-^- = — 0.087
Ргг-6000 |1 |[1 | р| с 158 /,, 2090-10* /у/,з = + 44 ^ = 0,13
I РГ^Н У 4250 V 310-10* Д»4 =+ 40-/Г = 0.12
и— где «_4
I * Линейные размеры приведены в си; Р в см1; V в гл*8; / в см4.
I 9. Р — радиальная составляющая силы резания.
141
3. Для высоких стоек (если высота Ь > (2-н 3)Л, где к — сторона
сечения) без поперечных перегородок — сплошных или с окнами относи*
тельно .небольших размеров (со стороной, не превышающей 0,5/г)
—вычисляются поправочные коэффициенты Ы, учитывающие искажение
контура поперечного сечения, по формулам (3.6) стр. 128.
4. Определяются перемещения }Хр> /Ур /г или 6 инструмента
относительно изделия в результате деформаций стоек:
для вертикально-сверлильных станков — по формуле (3.7) г
стр. 134.
для консольных горизонтально-фрезерных станков — по формулам
(3.8), стр. 135;
для горизонтально-расточных станков^ по формулам (3.9),
стр. 136.
Расчетные формулы для станков других типов могут быть получены
из формул (3.3); (3.4); (3.5) для общего случая нагружения стоек (§ 5,
стр. 128).
В табл. 20—22 приведены эскизы, геометрические характеристика
сечений и результаты расчета стоек некоторых
вертикально-сверлильных, горизонтально-фрезерных и горизонтально-расточных станков. При
расчетах силы резания были приняты равными максимальным.
Положение узлов сверлильных и фрезерных станков было принято
соответствующим случаю обработки изделия высотой, примерно равной 2/н
наибольшей, в расточных станках расстояние от оси шпинделя до стола,
или плиты принималась примерно равным 2/3 величины хода
шпиндельной бабки. Расстояние а от точки приложения силы до направляющих
стойки в горизонтально-фрезерных станках принималось равным
расстоянию от направляющих до оси шпинделя в вертикально-фрезерных
станках соответствующ'их размеров. В горизонтально-расточных стайках
расстояние с определялось вылетом шпинделя, принимаемым примерно»
равным Уз наибольшего. Для расточных станков приведены
перемещения инструмента относительно изделия в направлении, влияющем на
точность обработки, для четырех угловых положений резца (индексы
при величинах /у и/ соответствуют обозначению угловых положений
резца на фиг. 72).
§ 7. АНАЛИЗ ФОРМ И СООТНОШЕНИЙ РАЗМЕРОВ ЭЛЕМЕНТОВ СТОЕК
Проанализировав полученные расчетные зависимости и результаты
экспериментов и расчетов, можно оценить влияние отдельных
конструктивных факторов на жесткость стоек1, а также наметить пути
получения оптимальных конструкций, т. е. таких конструкций, которые при
заданной жесткости имеют .минимальный вес.
1. В.лияние толщины стенок и размеров
поперечного сечения
Как известно, с увеличением толщины стенок элемента жесткость
и вес его -увеличиваются примерно в одной и той же степени —
пропорционально увеличению толщины стенок. Между тем, влияние на
жесткость габаритных размеров сечений значительно больше. Оптимальными
с точки зрения жесткости следует считать конструкции, имеющие мини-
1 Несмотря на то, что влияние, некоторых конструктивных факторов изучалось
главным образом на моделях стоек, ввиду идентичности явлений полученные
результаты могут быть перенесены на реальные конструкции, тем более что при исследовании
стоек реальных форм разделить влияние различных факторов чаще всего не
представляется возможным.
142
мально допустимую из технологических соображений толщину стенок^
оптимальную форму поперечного сечения и размеры сечения (которые
можно характеризовать периметром наружного контура), определяемые
требуемой жесткостью. Если уменьшить толщину стенок в к раз, то
при той же форме поперечного сечения, подобно увеличив размеры, ту
же жесткость элемента можно обеспечить при меньшей в|/ к? раз
затрате металла. Так как при увеличении размеров сечения жесткость
растет быстрее, чем вес, сечения больших размеров оказываются более
экономичными.
В большинстве случаев наиболее рациональными оказываются
сечения с одинаковой толщиной стенок контура, В тех случаях, когда необ-
Фиг. 73. Влияние разной толщины стенок на величины пе^
ремещений коробчатых балок при кручении с искажением
контура сечения. Перемещения в направленна действия
сйлы/ = #^- (сплошные линии),; величины, лропорцио-
нальные весу, отнесенному к жесткости* }У =■ /?' —1Г"
(штриховые линии).
Кривые построены при -г- — 1; -г- = 3; — = 0;5
ходимо обеспечить высокую жесткость на: изгиб только относительно
одной оси, как, например, в стойках вертикально-сверлильных станков,,
при одинаковых габаритах более рациональными оказываются сечения,
у которых толщина стенок, перпендикулярных плоскости изгиба, больше^
чем остальных.
При действии силы в плоскости одной из* стенок, если поперечное
сечение стойки может искажаться, оказывается выгодным увеличивать-
толщину нагруженной стенки (фиг. 73).
2. Влияние формы доп;еречкого сечения
Влияние формы сечения на жесткость при изгибе и кручении
иллюстрирует табл. 23, в которой приведены значения моментов инерции эле.
ментов при постоянном весе. Как известно, наибольшей жесткостью на
изгиб обладают такие сечения, у которых большая площадь отнесена
от оси на большее расстояние.. Наибольшей, жесткостью на кручение при
№&
Таблица 23
Моменты инерции тонкостенных элементов разной формы поперечного сечения
(при постоянном периметре 2р и толщине стенок 6)
Зх = к$р*\ ^у *= к2ЪрЪ; 31
кр •
■ кгЪр*
Эскиз сечения
Н\Ь
ЫЪ^
Значения коэффициентов к в формулах
момента инерции
на изгиб
относительно
момента инерции
на изгиб
относительно
оси У-У (У )
кг
углового
сопротивления
кручению (/К„)
х-
7
т
1
Ы
1.0
0,0833
0,0833
0,125
>* X
-Ь Ч
Ь2
1,33
0,0433
0.124
0.0987
У
Ь —!
Ъ>>>>>^* тг-гт
>} >> \> V *ТТ
Ь4
1,60
0,0172
ОД 50
0.0512
1.0
1,27
0,101
0.101
0,202
144.
отсутствии искажения контура сечения обладают элементы, по форме
контура приближающиеся к окружности, а из элементов
прямоугольного сечения — к квадрату.
Влияние формы поперечного сечения (при постоянном весе) на
перемещения при кручении с искажением контура поперечного сечения
иллюстрируют кривые, приведенные на фиг. 74, построенные для
соотношений параметров, типичных для стоек. Можно видеть, что и в этом
случае оптимальными являются
сечения, близкие к квадратному, т. е.
имеющие -у ^ 0,7 -*-1,2.
Так как стойки обычно находятся в
условиях сложного нагружения, то
оптимальную с точки зрения жесткости
форму сечения для стойки данного
станка можно выявить лишь из
рассмотрения деформаций стойки при на-
гружении, соответствующем нагруже-
нию ее в станке.
На фиг. 75—77 приведены кривые,
характеризующие влияние формы
поперечного сечения стоек вертикально-
сверлильных,
горизонтально-фрезерных и горизонтально-расточных
станков на перемещения инструмента
относительно изделия в результате
деформаций стоек. При построении этих
кривых сечения реальных форм были
заменены правильными
прямоугольными сечениями тех же габаритов, а
соотношения расчетных параметров
принимались средними в диапазоне,
типичном для станков данной группы.
Из приведенных на фиг. 75
кривых можно видеть, что форма
поперечного сечения стоек
вертикально-сверлильных станков оказывает
существенное влияние на жесткость до у = 2-^-3. При дальнейшем
увеличении -у перемещения инструмента в результате деформаций стойки
уменьшаются незначительно. Из этого следует, что форма стоек
выпускаемых вертикально-сверлильных станков достаточно близка к
оптимальной.
В горизонтально-фрезерных станках форма поперечного сечения
стоек^ наибольшее влияние оказывает на перемещения инструмента по
оси X (см. фиг. 71). С целью уменьшения величины этого перемещения
рациональнее было бы выполнять стойки несколько более развитыми
в направлении оси X, т. е. с у, близким к 1; при этом перемещение по
оси У, хотя и возросло бы, но на относительно небольшую величину.
В горизонтально-расточных станках форма 'поперечного сечения
в реальном диапазоне ее изменения оказывает незначительное влияние
на жесткость стоек. Оптимальными можно считать сечения с -т- ,
примерно равным 1, т. е. такие, как у большинства выпускаемых станков.
Валка с концевой
перегородкой
Фиг. 74. Влияние формы поперечного
сечения при постоянном весе на
величины перемещений б коробчатых
балок при кручении с искажением кон-
М
тура сечения; 6 = ^!-щ^" —угол
поворота стенки, перпендикулярной
силе.
145
Фиг. 75. Влияние формы\тЛ поперечно- Фиг. 76. Влияние формы у-^) поперечного
го сечения стоек
вертикально-сверлильных станков на величину угла на-
Р
клона б = Я -^- в результате
деформаций стоек при постоянном весе (1р —
расчетная высота стойки, см. фиг. 70).
сечения стоек консольных горизонтально
фрезерных станков на перемещения Ьг =
Р* ру рх
зультате деформации стоек при постоянном
весе \ъ л- Ь = ^^' ^ ""* полиаЯ Расчетиая
высота стойки, см. фиг,
.„).
^Ц75; 1,0; №
0
о
о) 6)
Фиг. 77. Искажение^/«= #~]г) формы отверстий, обрабатываемых иа расточных
станках, в результате деформаций стоек прн разной форме (у) их поперечного-
сечения:
а — стойки с поперечными ребрами высотой Н » (1,5 ~ 2) 6;
б— стойки с высокими поперечными ребрами (Л » 56) или со сплошными перегородками.
146
3. Влияние переменности сечений по длине
Изменение сечений по длине элемента преследует цель создать
конструкции, в которых напряжения были бы распределены более
равномерно, так как при этом в большинстве случаев обеспечивается
получение заданной жесткости при экономии в весе. В табл. 24 приведены
соотношения весов и габаритов стоек равной жесткости постоянного и
переменного поперечного сечения при разных элементарных видах нагру-
жения. За критерий сопоставления элементов по жесткости
принимались перемещения в нагруженном сечении. Соотношения размеров
принимались средними, типичными для стоек реальных станков.
Из табл. 24 можно видеть, что применение элементов переменного
сечения оказывается наиболее целесообразным в том случае, если
характер изменения сечений соответствует характеру изменения эпюры
моментов и в качестве критерия жесткости принимается величина
линейного перемещения. В большинстве случаев при изгибе оптимальными
оказываются такие формы, в которых сечения изменяются по длине
наиболее резко. С точки зрения обеспечения минимального влияния на
точность обработки при заданном весе для стоек вертикально-сверлильных
станков, у которых за критерий жесткости принят угол наклона,
оптимальной является форма стоек постоянного сечения по длине.
С точки зрения влияния на деформации при кручении изменение
формы сечения по длине оказывается целесообразным в том случае,
если с удалением от основания стойки форма сечений .приближается
к оптимальной, т. е. квадратной.
4. Влияние перегородок
Влияние перегородок на жесткость стоек: при изгибе, а при
отсутствии искажения контура и 'при кручении, весьма н.езнач'ительно.
#;,#у, для балки без перегородки
/?2>Яу2 для балки с концевой перегородкой
Фнг. 78. Отношение величин перемещений / = # ~вч под силой
при кручении с искажением контура сечения и величин У =
=/^/,26, пропорциональных весу, для коробчатых балок без
перегородок и с одной концевой перегородкой при разной
Н
длине Ь (при -т- = 1,0).
При искажении контура поперечного сечения введение перегородок
устраняет это явление и тем самым многократно (до 10 раз) повышает
жесткость.
Оптимальное количество перегородок зависит от деформируемой
длины стойки.' Из кривых, приведенных на фиг. 78, можно видеть, что
когда длина балки примерно равна стороне сечения, введение
перегородки на конце почти не сказывается на жесткости. Аналогично по акс-
147
Сравнительные характеристики1 жесткости и веса
Стойки с разным
законом изменения
сечен ни по высоте
Обозначение
характеристик
Критерии
Перемещения верхнего
/ = к
ЯЯ8
ЕЬП*
н
ЛЧ 1
Отношение габаритных
0,5
1,0
0,5
1,0
0,5
1,0
-м<
р
Ь2=сопл1
к
0,80 ] 0,50 | 2,29 I 0,50
1.0
1.0
1,20 | 0,75
1,0
1,0
ьг=оа5ьи+%)
А
Ло
У0
0,93
1,05
0,97
0,54
1,03
0,96
2.39
1.02
0,93
0,52
1,01
0,95
1,53
1.08
1,00
0,93
1.08
1,01
Ь^0%5Ь(п-^)
У0
0,89
1,03
0.86
0,70
1,12
0,98
2.58
1,04
0.87
0,56
1,04
0,91
2,18
1,22
1,02
1,22
1.18
КОЗ
0,5Н
Ьг=0.5ЬЪ7Ц
А
Ко
1,09
1,П
0,95
0,76
1,15
1,02
2,85
1,08
0,92
0,54
1,03
0,92
1,83
1,15
0,97
1,13
1,15
1,02
хк—коэффициент, характеризующий податливость стоек с разным изменением сечений по
кх — коэффициент, характеризующий вес стоек с разным изменением сечений по высоте;
-.. отношение ббльшнх размеров нижних сечений стоек переменного (Л) н постоянного (Лл) се-
По
-^ отношение объемов (весов) стоек переменного (V) и постоянного (У0) сечения при равной
'О
48
Таблица 24
стоек постоянного и переменного поперечного сечення
жесткости
сечения
к ЕЬЬ?
М
1 г
—-
'_/"
■>ОГ1
П^д |
размеров нижнего сечен
0,5
! 3,43
1
1
3,71
1,03
0,94
4,06
1,06
0,88
3,95
1,05
( 0,89
высоте;
чения при р
жесткости.
1,0
0,75
0
0
0,80
1,02
0,96
0.87
1,05
0,92
0,85
1,04
0,93
авной жестк
Угол иаклоиа верхнего сечения
0 = к
ТТ—-^ ^6-4
л*-
ь
0,5
2,40
1,0 1
1,50
мн
ЕШ*
N
ПИ
1
, [^У
/V
0,5 1
6,85
1,0
1.50
1,0
1,0
3,38
1.12
1,03
5,45
1,31
1,09
5,09
1,28
1,09
2,07
1,12
1.04
3,25
1,29
1ДЗ 1
2,99
1,26
1,12
Ости.
7,72
Ш
0,96
8,95
1,10
0,91
8,68
1,08
0,92
1,66
1,04
0,97
1,88
1,08
0,94
1,83
1,07
0,95
1 Угол поворота
верхнего сечения
Кг- *>
1т-1
г
0,5
3,0
1,0
1,0
1.0
1,0
' 3,36
1,07
0,99
4,77
Ыб
0,97
1 4,52
1,15
0,98
1,24
1;08 !
1.01
1,69
1,19
1,04
1,59
1Д7
1,04
Эффективный объем
металла
V - ЪХЬНН
Ь
Н
0,5
1,0
0,5
1,0
0,5
1,0
0,5
1,0
*1
3,0
4,0
2,75
3.75
2,5
3,5
2,56
3,56
149
аериментальным кривым для балок с промежуточными перегородками
(фиг. 79) при расстоянии между перегородками, равном 1,31 и 0,865
высоты сечения, перемещения под силой, действующей в сечении между
перегородками, примерно одинаковы. Таким образом, оптимальным
можно считать такое количество перегородок, при котором
расстояние между перегородками примерно равно высоте нагруженной стенки.
При увеличении количества перегородок и дальнейшем уменьшении
расстояния между перегородками вес стойки будет расти быстрее, чем
жесткость.
В реальных стойках минимальное количество перегородок,
практически обеспечивающее отсутствие искажения контура, такое, при
котором расстояние между перегородками примерно равно 2/3 длины
контакта стойки и элемента,
передающего нагрузку на стойку.
/ Ч Щ
л ^ I I I . 1 I I
П 0Л № 0,608Готв
Фиг. 80. Влияние размеров окна в кон^
цевой перегородке на перемещения / =*
=-г^гЯ коробчатых балок при кручений
с искажением контура сечения и на
величины V — Ку1<2б, пропорциональные
к I х
весу балок (при у«1, ~^ = <*; 1 —
= 0,5), Р0тв — площадь окна, Л —
площадь перегородки.
С точки зрения жесткости контура поперечного сечения влияние
диагональных связей аналогично влиянию перегородок.
Окна в перегородках, площадь которых меньше 0,2—0,3 площади
перегородки, весьма незначительно уменьшают влияние перегородки на
жесткость (фиг. 80). С точки зрения жесткости большое значение имеет
ферма окна. Минимальное влияние на уменьшение жесткости
оказывают окна треугольной формы, которые обеспечивают наибольшую
жесткость перегородки в своей плоскости.
Перегородки с большими окнами следует рассматривать как тюпе-
речные ребра.
5. Влияние ребер
Влияние продольных ребер на перемещения при изгибе оценивается
при определении моментов инерции сечений и при реальных
соотношениях размеров не (превышает 10—20%. Влияние продольных ребер на
перемещения от кручения весьма незначительно. При искажении
контура поперечного сечения влияние ребер примерно пропорционально
150
I—расстояние между .
перегородками /уя/'т1
,АЙГ
№1
Модепа
N4
№$
Фиг. 79. Перемещения /=в?Л ^ при
кручении с искажением контура сечения
коробчатых балок без перегородок, с одной
концевой, двумя и тремя перегородками при
действии силы в сечении при # = 0,83^ —
между перегородками (результаты
экспериментов), и величины !У — Яу ~]Г~ >
пропорциональные весу, отнесенному к жест-
Н Ь
кости (при -у-=1, ^- = 2,62).
увеличению общей площади сечения стенок за счет ребер. С точки
зрения общей жесткости увеличение толщины стенок обычно несколько
более рационально, чем введение продольных ребер (на величину
около 10%).
Поперечные ребра, идущие по всему периметру сечения стоек, на
жесткость при изгибе, а при отсутствии искажения контура и при
кручении практически не влияют. При кручении с искажением контура
сечения поперечные ребра оказывают существенное влияние на жесткость.
Даже при относительно небольшой высоте ребер (^^0,05-^-0,1 или
^Р-^0,8 ^-0,6) наличие перпендикулярных ребер повышает жест-
кость контура поперечного сечения на величину порядка 30—40%. Так
как с увеличением высоты ребер жесткость контура растет быстрее, чем
вес стойки (см., например, фиг. 80; концевую перегородку при больших
размерах окна в ней можно рассматривать как ребро), рациональным
является применение высоких ребер. Увеличение количества ребер, так
же как и количества перегородок, рационально до определенного
предела.
6. Влияние окон в стенках
Влияние окон на жесткость стоек при изгибе и кручении зависит
от расположения и размеров окна. Как известно, на жесткость при
изгибе наибольшее влияние оказывают окна,
расположенные в стенках, перпендикулярных
плоскости изгиба и максимально удаленных от ней-
4>иг. 81. Зависимость жесткости стоек при кручении* (при ~т » 1)) от размеров окна
в стенке:
а—влияние ширины окна Ь0; # — влияние длины окна 10; 9о — Уг°л закручивания стойки без окна;
ср — угол закручивания стойки с окном размерами Ь0 X /0.
тральной оси сечения. Количественно влияние окон оценивается при
определении момента инерции сечения и, естественно, оказывается тем
больше, чем больше размеры окна.
При кручении окно в широкой стенке оказывает значительно
меньшее влияние на жесткость, чем окно таких же размеров в узкой
стенке. Так, например, в стойке с размерами сечения а\ 2а и длиной 6а
окно размерами Ьо\10 = 0,8аX 1>2а, расположенное в стенке шириной
151
= аг
2а, снижает жесткость всего на 11%, по сравнению со стойкой без окон,
а окно, расположенное в стенке шириной а, — в 2 раза. Из этого
следует, что окна по возможности следует размещать в широких стенках.
С увеличением размеров окна жесткость стоек, как правило, резко
уменьшается (фиг. 81). При малой длине окна (размер вдоль оси
стойки) жесткость снижается существенно, если ширина окна
больше (0,6—0,7)6 (Ь—ширина
стенки с окном). При большой
длине окон их влияние
значительно при любой ширине. При
больших размерах окон
всякое, даже незначительное
уменьшение их размеров,
особенно ширины, с точки зрения
жесткости оказывается весьма-
благоприятным и дает
ощутимые результаты. При наличии
одного большого окна другие
окна, меньших размеров,
расположенные рядом или в
противоположных стенках не
вызывают существенного
дополнительного снижения
жесткости {7\}. Даже при наличии:
двух окон, примерно равных па
размерам, в противоположных
стенках дополнительное
снижение жесткости от второго
окна оказывается значительно*
меньше, чем от первого (фиг.
82). Влияние второго окна
максимально (до 30—40%) при
расположении окон в широких
стенках, ширине окон Ь0 « 0,56,.
большой длине /о> (0,3-ь0,5) Ь.
Влияние окон (при -Ц*-. = сопз!) в относительно более высоких стойг
ках больше, чем в низких.
Как показывают эксперименты [71], влияние отбортозок у окон на
жесткость кручения относительно невелико.
Влияние окон может быть в значительной степени компенсировано-
при помощи крышек достаточной жесткости, надежно притянутых к
стойке винтами.
В заключение необходимо подчеркнуть, что при* проектировании
стоек прежде всего следует по возможности обеспечить отсутствие
искажения контура поперечного сечения стоек.
Температурные деформации стоек [58] определяются по методике,.
аналогичной методике определения температурных деформаций
горизонтальных станин (см. выше, стр. 84).
Фиг. 82. Зависимость жесткости стоек при кру-
ченни (при -^ = 1; -^-= 3) от размеров и
количества окон в стенках; <ро — угол
закручивания стойки без окна; <р —угол закручивания
стойки с окнами размерами 6оХ4)»
ГЛАВА IV
СТАНИНЫ ПОРТАЛЬНОГО ТИПА1
§ 1. ОБЩИЕ СВЕДЕНИЯ О КОНСТРУКЦИЯХ
Рамные или портальные станины, обладающие повышенной
жесткостью по сравнению с простыми станинами одностоечных и
горизонтальных станков, применяются:
а) в высокопроизводительных станках токарной группы
(многорезцовых, копировальных), в которых верхнее расположение суппортов
обеспечивает удобный отвод стружки;
б) в высокопроизводительных сверлильных станках (так
называемых сверлильных прессах), у которых рамная конструкция в условиях
симметричного нагружения исключает перекос сверла в результате
упругих деформаций системы;
в) в станках для тяжелых изделий — карусельных, строгальных^
фрезерных, — в которых изделие получает одно простое движение,-
а остальные движения формообразования осуществляются суппортами,
перемещающимися по взаимно-перпендикулярным направляющим.
Кроме того, в консольно-фрезерных, зубофрезерных и других
станках несущая система станка иногда замыкается с помощью
дополнительных поддержек или тяг и приближается к портальной.
В настоящей главе рассматриваются портальные станины станков"
для крупных и тяжелых изделий — карусельных, продольно-строгальных
и продольно-фрезерных.
Несущие системы этих станков состоят из основания или
горизонтальной станины, двух стоек, перекладины и поперечины, соединенных
между собой и образующих рамную систему. Портальные станки обычно-
выполняются с неподвижным порталом, но для особо тяжелых и
длинных изделий могут выполняться с подвижным порталом. В частности
подвижные порталы применяются в портально-сгрогальных и портально-
фрезерных станках, станках для обработки листов паровозных рам и т. п.
В уникальных карусельных станках путем отодвигания портала
увеличивают наибольший диаметр обработки.
Основания карусельных станков обычно представляют собой"
цилиндрические тонкостенные отливки с фланцами для крепления стоек
и перегородками — кольцевыми и радиальными. В перегородках
делаются окна для облегчения формовки. В результате большого
тепловыделения в направляющих существенными оказываются
температурные деформации оснований, для уменьшения которых следует
предусматривать специальные кольцевые ребра, улучшающие отвод тепла от
1 В настоящей главе рассматриваются также поперечины, составляющие вместе
с порталами единую несущую систему.
153*
направляющих к наружным стенкам. Как правило, жесткость основания
весьма высока, и роль деформаций основания в общем балансе упругих
перемещений ничтожна.
Горизонтальные станины продольно-строгальных и
продольно-фрезерных станков рассматриваются в главе «Горизонтальные
станины».
Стойки портальных станин имеют коробчатую форму
прямоугольного сечения, удлиненного в направлении, перпендикулярном к
плоскости портала, так как на деформации в этом направлении влияние
перекладины относительно невелико (фиг. 83, а, б). Отношение сторон
сечения стоек у карусельных станков колеблется в пределах от 1 : 3,5 до 1 :7,
у продольно-строгальных от 1 : 3,5 до 1:5, а продольно-фрезерных от
1 : 1,8 до 1 : 3,5. Несколько более удлиненная форма сечения стоек
карусельных и строгальных станков объясняется тем, что в направлении оси
большей жесткости стоек действует главная составляющая силы
резания. Как показали
эксперименты [25, г] влияние на
общую жесткость несущей
системы деформаций стоек в
направлении оси их большей
жесткости весьма незначи-
а) 6) тельно, тогда как
деформации в направлении оси
Фиг. 83. Сечения стоек станков портального типа. меньшей жесткости в
значительной степени определяют
жесткость системы в целом (например, в карусельных станках
перемещения инструмента относительно изделия в результате деформаций
портала в плоскости меньшей жесткости стоек сотавляют от 60 до 90%
полной величины перемещения в результате упругих деформаций всей
системы). Для повышения жесткости в направлении оси меньшей
жесткости (параллельной плоскости направляющих) стойки карусельных
и строгальных станков выполняются с контуром в виде двух
прямоугольников (фиг. 83, б), с так называемым контрфорсом. Однако более
рациональными следует считать сечения стоек фрезерных станков, не
имеющих контрфорса, но несколько больше развитых в ширину
(см. ниже табл. 30).
Сечения стоек обычно несколько изменяются по высоте по
линейному или, в старых станках, по параболическому закону.
Для повышения жесткости соединения поперечины со стойками
в ряде станков на внутренней боковой стенке стоек имеется
дополнительная направляющая, по которой осуществляется зажим поперечины
(фиг. 83,6).
Форма передней части стоек определяется размещением винта
механизма подъема поперечины (фиг. 84).
Стойки снабжаются поперечными, а при сильно вытянутой форме
сечения (в карусельных и продольно-строгальных станках) и
продольными перегородками (см. фиг. 83). Стойки продольно-фрезерных
станков, как правило, продольных перегородок не имеют. В перегородках
для облегчения формовки и для возможности размещения груза,
уравновешивающего вес поперечины, делаются окна. Окна в наружных
стенках, как правило, небольшие, глазным образом для закрепления
стержней.
Поперечные перегородки оказывают существенное влияние на
жесткость стоек, устраняя искажение контура поперечного сечения. Введение
продольных перегородок оказывает сравнительно небольшое влияние
на жесткость и вызывается главным образом необходимостью увеличе-
154
ния местной жесткости стенок в зоне приложения сил зажатия
поперечины и требованиями литейного производства. При отсутствии
продольных перегородок внутренние стенки стоек обычно подкрепляются
продольными ребрами.
Направляющие стоек соединяются с основным контуром сечения
стоек посредством одной или двух переходных стенок (фиг. 84, бив).
Более жестким является соединение двумя стенками; при соединении
одной стенкой направляющие обычно подкрепляются высокими
поперечными ребрами (фиг. 84, в).
В общем балансе упругих перемещений в станках портального типа
существенную роль играют деформации соединений стоек с основанием
и станиной (до 15—20%
при малой жесткости
стыка [25, г]. Жесткость
этого соединения
определяется конструктивным
оформлением стыка
(формой и размерами
площади контакта и
размещением крепежных винтов)
и местными деформациями стоек и основания. Наиболее жесткими
оказываются соединения, в которых крепежные винты размещаются по
всему периметру стыка (в нижней части проходя через тело стоек) и
поверхность стыка максимально развита.
Влияние жесткости соединения стоек с основанием на жесткость
системы особенно большое значение приобретает в там случае, когда
УШШ
а) 6) в)
Фиг. 84. Формы передней части стоек.
Фиг. 85. Сечения
поперечин станков портального
типа.
Фиг. 86. Поперечины с переменным (а) и
постоянным (б) сечением по длине на
участке между стойками.
для станков разных размеров применяются унифицированные порталы,
а между стойкой и основанием в станках легкого исполнения
вставляется дополнительная промежуточная деталь. При этом необходимую
жесткость порталов можно обеспечить только в том случае, если стыки
оформлены достаточно жесткими.
Поперечины, как правило, имеют коробчатую форму с
сечением в виде одного или двух прямоугольников (фиг. 85, а, б). Как
.показали эксперименты [25, г], жесткость несущей системы в направлении,
перпендикулярном к плоскости портала, в значительной степени
определяется жесткостью поперечины (например; в карусельных станках
в общем балансе упругих перемещений на долю поперечины
приходится до 40%). Из деформаций поперечины решающее значение имеет
кручение (около 60%). Поэтому оптимальными следует считать сечения,
имеющие простую прямоугольную форму, аналогичные сечениям попе*
речин продольно-фрезерных станков (см. табл. 30). В тяжелых
карусельных станках встречаются составные поперечины.
Характер изменения сечений поперечины по длине определяется
конструкцией механизма зажима. В поперечинах с зажимом по основ-
155
ным направляющим стоек сечения поперечины существенно изменяются
по длине (фиг. 86, а).
В поперечинах с зажимом по дополнительным направляющим стоек
сечения поперечины на участке между стойками не изменяются или
изменяются незначительно (фиг. 86, б).
Как правило, поперечины снабжаются перегородками —
поперечными или диагональными, а также продольными, поперечными или,
реже, диагональными ребрами. Для облегчения отливки в перегородках
и наружных стенках делаются небольшие окна.
Так же как и в стойках, направляющие соединяются с основным
контуром сечения посредством одной (обычно в строгальных станках)
или двух (в карусельных и фрезерных станках) переходных стенок,,
причем при соединении одной стенкой направляющие подкрепляются
поперечными ребрами.
Для обеспечения прямолинейности перемещения суппортов по
поперечине, т. е. компенсации прогиба поперечины от собственного веса и
веса суппортов, в некоторых
случаях применяется
предварительное искривление направляющих
в процессе обработки, что может
быть достигнуто, в частности,
соответствующим расположением
а) 0} §) опор при обработке, а также
начальным деформированием попе-
Фш\ 87. Способы соединения стоек с пере- речины на станке с помощью
кладиной. винтов или стяжек.
Перекладины. Форма
сечения перекладин зависит от конструктивного оформления соединения
стоек с перекладиной. Встречаются три варианта соединения стоек
с перекладинами — по торцам стоек, с верхним расположением
перекладины, по торцам перекладины при установке ее враспор и
комбинированное (фиг. 87, а—в). По жесткости эти варианты компоновки
порталов отличаются мало; поэтому при выборе того или иного
варианта решающими являются технологические соображения/
Перекладины, соединяющиеся со стойками по торцам стоек, обычно
имеют поперечные сечения, развитые в горизонтальном направлении;
перекладины, устанавливаемые враспор, вытянуты в вертикальном
направлении. Во фрезерных станках перекладины, устанавливаемые
враспор, имеют развитую верхнюю стенку, что следует считать весьма
рациональным, так как обеспечивает надежную связь передних частей
стоек. При комбинированном соединении перекладины обычно имеют
форму в виде двух прямоугольников и в тяжелых станках выполняются
составными.
Для повышения жесткости перекладины снабжаются внутренними
ребрами и перегородками.
Перекладины часто выполняются сварными. Встречаются также
сварные конструкции стоек и поперечин.
Конструктивные формы порталов карусельных и особенно
фрезерных и строгальных станков близки между собой. Некоторые отличия
между станками разных групп и размеров объясняются не столько
спецификой условий работы, сколько традициями конструирования.
Возможность использования порталов продольно-строгальных станков для
работ типичных для продольно-фрезерных станков подтверждается
практикой эксплуатации тяжелых строгально-фрезерных станков, т. е<
строгальных станков, снабженных суппортами с фрезерными головками.
В настоящее время на некоторых заводах, выпускающих продольно-
156
Фиг. 88. Элементы системы портал—поперечина продольно-строгального
станка модели 7256:
а — стойка; б — перекладина (накладка и распорка); в —поперечина.
158
Фиг. 89. Элементы системы портал—поперечина продольно фрезерного станка
модели 6672:
а — стойка; б — перекладина; в — поперечина.
строгальные и продольно-фрезерные станки, их порталы для станков
общих размеров унифицированы.
Возможна унификация элементов порталов и станков разных
размеров. Например, на Коломенском ЗТС разработана трехступенчатая
система унификации внутри ряда карусельных станков. Станок с одним
и тем же наибольшим диаметром обработки предложено выпускать
в трех исполнениях — легком, нормальном и тяжелом — с разной
наибольшей высотой обрабатываемого изделия. В станках трех смежных
размеров разного исполнения предполагается использовать одни и те
же стойки, а поперечины и перекладины хотя и разной длины, но однога
и того же поперечного сечения. При этом отливать такие поперечины
можно по унифицированным составным моделям. В станках
нормального и легкого исполнения также предполагается использовать
одинаковые основания с введением между стойками и основанием
дополнительных промежуточных деталей — проставок. При использовании
одинаковых оснований в станках нормального и тяжелого исполнений про-
ставки отливаются за одно целое с основанием или стойками по
составным моделям. Элементы систем портал—поперечина
продольно-строгального станка модели 7256 и продольно-фрезерного станка модели
6672 приведены на фиг. 88 и 89.
§ 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ РАСЧЕТА НА ЖЕСТКОСТЬ
В станках портального типа жесткость портала и поперечины
влияет на суммарную жесткость станка в значительно большей степени, чем
жесткость станины в станках других типов. Эксперименты [25, г]
показали, что в карусельных станках на долю перемещений системы
портал—поперечина приходится от 30 до 80% полного перемещения резца
относительно изделия (большие значения характеризуют влияние
портала и поперечины на перемещения инструмента в плоскости портала,
меньшие — в плоскости, перпендикулярной к плоскости портала). Вес
портала и поперечины составляет около 40% общего веса станка.
Поэтому проведение расчетов порталов и поперечин, позволяющих
получить заданную жесткость при минимальной затрате металла, еще более
актуально, чем для станин других станков.
В настоящее время разработаны две методики расчета портальных
станин:
1. Методика уточненного общего расчета для анализа искажения
формы изделия в результате деформаций системы портал—поперечина,
решения специальных вопросов и т. п.
2. Методика технического расчета для сравнительного анализа
конструкций, оценки правильности выбора параметров и т. п.
В этих расчетах жесткость системы портал—поперечина
предлагается характеризовать перемещениями инструмента, установленного на
верхнем суппорте, относительно изделия вследствие деформаций портала
и поперечины.
Перемещения инструмента определяются как сумма перемещений
поперечины относительно ее опор и перемещений от смещения опор
вследствие деформаций портала.
Методики расчета разработаны на основе следующих предпосылок:
1. Портал рассматривается как рама с жестким соединением'
в узлах и жестким защемлением в местах соединения стоек с
фундаментом.
2. Расчетные размеры портала определяются положением осей,
проходящих через центры тяжести поперечных сечений соответствующих
элементов. Оси стоек и перекладины полагаются пересекающимися»
159-
3. Жесткость стоек и (поперечин принимается неизменной по длине
и равной жесткости, подсчитанной по геометрическим характеристикам
расчетного сечекия; жесткость обеих стоек полагается одинаковой. При
определении жесткости элементы рассматриваются как тонкостенные
стержни с замкнутым контуром поперечного сечения. (Указания по
выбору расчетного сечения и по определению расчетной жесткости
элементов с замкнутым контуром поперечного сечения см. главу III
«Стойки»).
4. Силовые факторы, действующие от сил резания, рассматриваются
как сосредоточенные, т. е. полагается, что они передаются на поперечину
непосредственно в плоскости их действия. Для обычно имеющего место
случая, когда жесткость суппортов мала по сравнению с жесткостью
поперечины, такое допущение можно считать приемлемым. Силовые
факторы, действующие от весов суппортов, также рассматриваются как
сосредоточенные.
5. Силовые факторы, действующие на стойки от поперечины,
полагаются приложенными в одном сечении, лежащем в той же плоскости,
что и ось поперечины. Перемещения поперечины в пространстве
вследствие смещения ее опор определяются перемещениями стоек в
нагруженных сечениях.
6. Влияние на жесткость портала и поперечины жесткости контура
поперечного сечения элементов, а также упругие перемещения
растяжения-сжатия и перемещения от касательных напряжений при изгибе не
учитываются 1.
7. Местные деформации в зоне приложения нагрузки не
рассматриваются.
8. При определении контактных деформаций принимается, что
жесткость элементов портала весьма велика по сравнению с жесткостью
поверхностных слоев в стыках и давления по длине направляющих
распределяются по линейному закону.
Упругие перемещения в стыках полагаются прямо
пропорциональными контактным напряжениям.
Возможность использования этих предпосылок для разработки
расчетов портальных станин подтверждается удовлетворительным
совпадением результатов расчетов и экспериментов, а также результатов
уточненных расчетов.
При общем расчете определяются перемещения инструмента,
установленного на верхнем суппорте, относительно изделия при
произвольном положении суппортов на поперечине, а также при одновременной
работе двух суппортов.
Поперечина рассматривается как балка упруго защемленная на
стойках. Деформации поперечины определяются как для свободно
опертой балки, дополнительно нагруженной моментами упругого
защемления в местах соединения ее со стойками. Величины моментов
определяются из условия равенства углов наклона упругой линии поперечины
суммам углов наклона упругой линии стоек портала и углов взаимного
поворота поперечины и стоек вследствие контактных деформаций в
местах их соединения.
Портал рассматривается как шесть раз статически неопределимая
рама. Перемещения стоек портала в местах соединения с поперечиной,
от которых зависят как величины неизвестных моментов защемления,
так и перемещения поперечины в пространстве вследствие смещения ее
1 При соотношениях размеров, типичных для элементов порталов, и при наличии
значительного количества перегородок по длине элементов влияние этих факторов
относительно невелико.
а бо
Деформации портала в плоскости У2*
Таблица 25
Г
±
гХт
/?1 = (2 + Я) (8ф2 + к + 6А/) - 12ф2;
#2 = 0,5а {3 (8ф2 + А + 6*/) - 4ф2 (3 - а) [а (? + 2) - 3$};
#3 = 2а [2ф2# (3 - а) (2 - а) + (8ф2 + к + Ьк/) - 2ф2а (5 - 2а)];
#4 = 2а<||[3-(3-а)(2 + ?)];
/?5 = 2а [8ф2 + к + 6Л/ - Зф2 (2 - а) (2а - 2д + ад)];
/гв = 6афр-1(2 + *)(2-а)];
#7 = баб/ (2 + ?);
*«
7Г
к
1/г
1Б/
Ж С/71
ял
л*р
?- яал
Л/?. Л*0
/«
ЯБ/
* ж/?
10/,
Кр. С/71
Составляющие
нагрузки
Эскиз
Деформации в точке приложения нагрузки
Перемещение
Угол наклона
Угол закручивания
(Симметричная
%
*Ля
I/
Ф>
//> =
Р№
РН*
ЗЕ1Х ст
2В ^х ст
2ЬУ^ ст
МП
ЫХ1
м ^
ф ф
МЛ
ш.
кр. ст
■х
X
I.1 2/+1]
Косо-
симметричная
V
/=
Р№
35/,
■х
РА2
25/,
X
Р№
* = ~Щ
X
[-*]
X
[-*]
Л/?. С/71
■X
X
(-3)
V
м
Л/
Л№
2-е/,
X
МИ.
Е1Х
X
X
[-*]
X
[-1]
/=■
Л№
07;
л:/;, Лл
X
X
(-*)
МИ
01
кр. ст
х
мн
о/,
X
л/;, ст
■х
ЛГЛ
С?/
кр. ст
х
X
[-3]
* Обозначения величин, входящих в формулы для $?, а, к, д и / см, стр. 165.
161
Деформации портала в плоскости Х2 *
Таблица 26
(?! = 0,5а [5 (а - З)2 + 2 (а* - За + 3)]; а = 7Г ;
и,
<?2 = а [8 (2 - а) (3 — *) + 2а2 —5а + 4]; 5 = •
(?3 = 0,5а [35 (2 - а)2 + 2 (За2 _ ба + 4)].
у ст
ЯУ
упер
Составляющие
нагрузки
Эскиз
Деформации в точке приложения нагрузки
Перемещение
Угол наклона
Симметричная
/ =
РН*
ЗЯУ
у ст
-.[--&]
РЬ?
2&Л
у ст
[>--&]
^л? ,»^
1
/ =
2Е^
у ст
[-&]
МЛ
ЕУ,
у ст
[-Т&]
ПИШИ
/=
дН№{\ -а) 8
ЧАЕЗу еж (1+25)
>9ЯГ 575
?#Л (2 - За) 5
24ЯУуГт(1 + 25)
Косо-
симмет-
ричная
ЧФ?* 9Я&
Ф" Ф
^7& ^Я
/ =
№
ЗЯУ
у ст
[!~2 (0 + 5)]
0 =
№
2ЕУ
у ст
!-^1
/ =
Л№
2ЯУ
у ст
[-^1
Л*Л
ЕУ
у ст
■['-чтт]
* Обозначения величин, входящих в формулы для а и 5, см. стр. 165.
162
опор, определяются от симметричной и кососимметричной составляющих
нагрузки отдельно по формулам, приведенным в табл. 25 и 26.
Методика общего расчета [25, д] ввиду ее громоздкости не
приводится. На фиг. 90 приведены вычисленные по этой методике
перемещения инструмента относительно изделия в зависимости от положения
суппорта на поперечине и поперечины на стойках для карусельного
станка мод. 1565. По этим данным величина погрешности обработки
в некотором сечении х вследствие деформаций системй может быть
Положения суппорта но поперечине
Услобные обозначения перемещений
\Ш\-Подрезка торца ^^-Обточка ^^-Расточма
Фиг. 90. Перемещения инструмента относительно изделия в зависимости от положения
Iх\ I к \
суппорта на поперечине \~~[~) н положения поперечины на стоиках I 77/ для каРУ'
сельного станка мод. 1565. Перемещения подсчитаны при действии максимальной силы
резания Ру = 6500 кГ на максимально допустимом для этой силы вылете ползуна
600 мм. При определении перемещений полагалось, что второй суппорт размещен у стойки,
определена как разность перемещений, вычисленных при положении
инструмента в сечении хив том сечении, где производилась установка
на размер.
§ 3. ТЕХНИЧЕСКИЙ РАСЧЕТ ПОРТАЛЬНЫХ СТАНИН
А, Расчетные зависимости
Для сравнительной оценки конструкций, накопления конструктор-
ского опыта и оценки правильности выбора размеров целесообразно
применять упрощенные расчеты при одном частном простейшем виде
нагружения. В качестве такового выбирается нагружение верхнего
суппорта в среднем положении, при котором вершина инструмента
находится на оси стола или планшайбы (для карусельных станков это
примерно соответствует случаю обработки весьма малых диаметров).
Так как из двух суппортов, расположенных на поперечине, правый
суппорт (в карусельных станках, работающий на прижатие)
используется чаще, ч.ем левый, то в качестве основного расчетного
целесообразно принять случай работы правого верхнего суппорта.
В отличие от общего расчета при техническом расчете поперечина
рассматривается не как упруго защемленная балка, а как жестко за-
щемленная балка при расчетах на кручение и как шарнирно опертая
балка при расчетах на изгиб. Проведенные эксперименты [25, г]
показали, что измеренные и вычисленные при рассмотрении поперечины как
жестко защемленной балки величины углов закручивания достаточно
хорошо совпадают. Экспериментальные и расчетные величины
перемещений от изгиба поперечины отличаются в несколько большей степени.
Однако, так как в общей величине перемещений резца доля
перемещений в результате изгиба поперечины относительно невелика (например,
в карусельных станках не более 10%), а учет защемления поперечины
на стойках существенно осложняет расчеты, то для технических
сравнительных расчетов принятое упрощение расчетной схемы можно считать
допустимым.
Ось
поперечины
Фнг. 91. Расчетная схема нагруження станин портального типа.
При этом, пренебрегая величинами второго порядка малости,
перемещения вершины инструмента в направлении осей X, У и 2 (фиг. 91)
под действием сил резания (характеризующие жесткость системы)
можно определить по формулам1:
(4.1)
1 В этих формулах за положительное направление силовых факторов принято
направление, соответствующее случаю работы правого суппорта. Для случая работы
левого суппорта знаки силовых факторов должны быть соответствующим образом
изменены.
164
Здесь и дальше (см. фиг. 91):
РХУРу>.Рх— составляющие силы резания по осям координат1
в кГ; для карусельных и строгальных станков
ориентировочно можно принимать Рх = Рг = 09ЪР \ для
фрезерных Ру ■= Рг = 0,4РХ\
Ь, Н—расстояние между осями стоек и высота портала
(от основания стоек до оси перекладины) в см;
к — расстояние от основания стоек до оси
поперечины в см;
^; у! — координаты центра тяжести сечения поперечины
в системе осей у, и 2г в см;
I — вылет инструмента в см;
Уст — расстояние от оси стойки до плоскости
направляющих СТОЙКИ В СМ;
а, 8 — расстояния от точки приложения силы до плоскостей
направляющих поперечины и стоек,
соответственно, в см;
^у\ )г; У^-т-моменты инерции площади сечения поперечины на
изгиб в вертикальной {XI,) и горизонтальной (УХ)
плоскостях и на кручение, соответственно, в см*;
Зуст>^*т>3я&ст — моменты инерции площади сечения стойки на изгиб
относительно оси У (в плоскости Х2,), отХ(ъ
плоскости У2) и на кручение, соответственно, в см};
Лл<?/>> ^гпер — моменты инерции площади сечения перекладины
на изгиб в вертикальной (Х2) и горизонтальной
(УХ) плоскостях, соответственно, в смА;
Е, О — модули упругости в кГ(!см2 (Е^2,5(3);
V—эффективный объем металла в см? (см. стр. 169).
Вылет инструмента (/) и расстояние от основания стоек до оси по-
неречины (К), зависящее от высоты обрабатываемой детали и от
вылета инструмента, для данного станка являются величинами
переменными.
В приведенных формулах первый член представляет собой
составляющую перемещений \ вследствие деформаций поперечины, а второй
член — вследствие деформаций портала.
Как уже указывалось, в станках портального типа величина
перемещения вершины инструмента определяется деформациями базовых
деталей не только от действия сил резания, но и от собственного веса
поперечины и веса суппортов.
Для цоперечины, рассматриваемой как шарнирно опертая балка
(фиг. 92), перемещение вершины инструмента в результате деформаций
от собственного веса может быть определено по формуле
где # — интенсивность равномерно распределенной нагрузки от веса
поперечины в кГ/см;
М — момент на /шоре от веса консольных частей поперечины и
механизмов на консолях \М = —~ + Ол/2, см. фиг. 92, а) вкГсм;
х — расстояние от левой опоры поперечины до сечения, в
котором, определяется прогиб, в см.
1 Обозначение составляющих силы резаиия соответствует выбранным осям
координат и отличается от общепринятого.
165
Перемещения вершины инструмента в результате изгиба и кручения
-поперечины от действия веса суппорта ориентировочно могут быть
вычислены по формулам:
К&Г
:> 5
^Л^1"^
10/,
кр
■*р,
(4.3)
7 у<? —
где Осу„— вес суппорта в кГ\
Уо—Ух+Ос — расстояние от центра тяжести суппорта до плоскости
направляющих поперечины в см (фиг. 92, б);
.х —расстояние от левой опоры поперечины до сечения,
в котором расположена вершина инструмента, в см.
Остальные обозначения
прежние.
ап Перемещения вершины
инструмента от собственного
веса поперечины и веса
'суппорта, вычисленные по
приведенным формулам, до
некоторой степени могут
характеризовать
параллельность направления
перемещения верхнего суппорта по
гюперечине рабочей
поверхности стола или планшайбы.
Однако следует иметь в
виду, что непараллельность
перемещения суппорта
определи от собственного веса и веса механизмов на консолях; б — ЛЯеТСЯ Не ТОЛЬКО ДвфОрма-
от веса суппорта ЦИЯМИ ЭЛемеНТОВ СИСТеМЫ
при перемещении суппорта,
яо и непрямолинейностью направляющих поперечины. В станках
меньших размеров обычно большую роль играет непрямолинейность
направляющих, в станках больших размеров — деформации системы. В
станках больших размеров перемещения от собственного веса элементов
обычно компенсируются К Поэтому, а также потому, что при расчете
по предлагаемым формулам защемление поперечины на стойках не
учитывается, фактические и допускаемые по ГОСТу величины
непараллельности могут быть меньше вычисленных величин /гд-\-/гО
в 1,5—2 раза.
Перемещения вследствие деформаций портала от действия веса
суппортов и поперечины относительно невелики и их можно не
рассматривать. Кроме того, превалирующие по величине постоянные
составляющие этих перемещений могут быть компенсированы при
установке стоек.
Для того чтобы по величинам перемещений инструмента
относительно изделия судить о качестве порталов и поперечин, целесообразно
полученные в результате расчета величины перемещений сравнивать
с допусками на точность обработки и с аналогичными перемещениями
для станков, хорошо зарекомендовавших себя в эксплуатации.
б)
Фиг. 92. Расчетная схема для определения
деформаций поперечины:
1 Следует отметить, что полностью компенсировать непараллельность
перемещения суппорта рабочей поверхности стола в результате деформаций от собственного
веса поперечины и веса суппорта можно только для случая работы одного суппорта.
Поэтому точные работы производятся одним суппортом.
166
Как уже указывалось, при расчетах портал рассматривался как
рама с жестким «соединением в узлах и жестким защемлением в местах
соединения стоек с фундаментом. Для того чтобы иметь возможность
оценить влияние жесткости соединений на общую жесткость системы,
перемещения инструмента относительно изделия вследствие деформаций
портала следует определять, полагая защемление стоек и соединение
стоек с перекладиной упругим.
Исследование баланса упругих перемещений в портальных станках
{25, г] показало, что жесткость портала оказывает существенное
влияние только на перемещение инструмента по горизонтали в плоскости,
параллельной плоскости портала, т. е. в направлении оси X,
Величина этого перемещения определяется перемещением стоек
(в направлении оси X) в месте их соединения с поперечиной. Для
простоты можно определять не полную величину этого перемещения, а
величину перемещения только в результате изгиба портала в плоскости
Х2, которая составляет около 80% полной величины.
При жестком соединении стоек с перекладиной и жестком
защемлении стоек эта величина определится по формуле (см. табл. 26)
1*—6Е^ст [1 2(6 + 5)] *
При упругом соединении стоек с перекладиной и основанием в
первом приближении можно записать1 следующую формулу:
/ — х-
-' х б^Уу ст
окЕЗу ст
9а
[) + ***-* 2 ( о,5_4-)[
а^конт
6Е^у стк± 24Е/у стк
?М)"
ч
здесь ]конт, Зконт\— моменты инерции площади стыка стойка —
основание и стойка — перекладина, соответственно;
к{—коэффициенты контактной податливости в
стыках стойка — основание и стойка — перекладина,
соответственно (см. стр. 251—255);
1\ — расстояние от оси стойки до плоскости /-того стыка
стойки с основанием (см. фиг. 91).
Остальные обозначения прежние.
Можно показать [26], что при реальных соотношениях размеров
элементов портала влияние на жесткость системы податливости
соединения стоек с основанием (при достаточно жестком оформлении стыка)
и стоек с перекладиной не превышает величин 10—15%. В том случае,ч
если жесткость стыка стоек с основанием невелика, влияние
податливости этого стыка может оказаться весьма существенным (до 30%),
Б. Порядок технического расчета
Предлагается следующий порядок технического расчета:
1. Выбирается расчетная схема (см. § 2, § 3, А).
2. Выбираются расчетные сечения стоек, поперечины и перекладины
(см. гл. Ш,§3, Б).
1 При выводе этой формулы влияние закрепления стоек иа фундаменте не
учитывалось. Как показали эксперименты, оно оказывается существенным только в том
.случае, если стойки подлиты и закреплены достаточным количеством болтов.
167
3. Определяется жесткость элементов на изгиб (Е7) по моментам
инерции сечений (/).
4. Определяется жесткость элементов на кручение {01):
а) для элементов с замкнутым контуром поперечного сечения по
формуле (3.2), стр. 99;
б) для элементов с разомкнутым контуром поперечного сечения
(перекладины некоторых станков) —по формуле (2,1) стр. 50.
5. Определяются перемещения 1хр,/ур, /гр инструмента относительна
изделия в результате деформаций системы портал — поперечина по
формулам (4.1), стр. 164.
6. Для станков с расстоянием между осями стоек Ь, большим 4—
5 м, определяются перемещения от собственного веса поперечины ]хд
по формуле (4.2), стр. 165 и перемещения $г0 и 1у0 от веса суппортов по
формулам (4.3), стр. 166.
В табл. 27—30 приведены эскизы, геометрические характеристики
сечений и результаты расчета порталов и поперечин некоторых станков
портального типа.
§ 4. АНАЛИЗ ФОРМ И СООТНОШЕНИЙ РАЗМЕРОВ
ЭЛЕМЕНТОВ ПОРТАЛЬНЫХ СТАНИН
А, Анализ портальных станин карусельных станков
В качестве критерия, по которому можно производить сравнение и
анализ порталов и поперечин, должны быть выбраны величины
перемещений />, соответствующие такому случаю обработки, который был бы
достаточно типичным и обеспечивал достаточное нагружение каждого^
из элементов системы портал — поперечина.
Для портальных станков переменными являются положение
суппорта на поперечине, положение поперечины по высоте и вылет ползуна.
Как уже указывалось, с целью упрощения расчетов, а также для
ориентировочной оценки наибольшего влияния жесткости системы на точность
обработки для технических расчетов в качестве расчетного было
принято такое положение суппорта, при котором сила резания проходит
через ось планшайбы (при этом деформации системы
портал—поперечина максимальны).
При выборе расчетных значений вылета ползуна / и расстояния от
оси поперечины до-основания стоек к можно руководствоваться
следующими соображениями:
По ГОСТу 600-52 наибольшая длина /щах хода ползуна
вертикального суппорта должна составлять не менее 0,6#тах наибольшей высоты
обрабатываемой детали. Можно считать, что наиболее типичным
является случай работы с вылетом, равным примерно половине
наибольшего. Кроме того, следует иметь в виду, что при работе на больших
вылетах /> (0,3 н- 0,5)/тах, допустимая сила резания обычно снижается.
Исходя из этого, в качестве расчетного» вылета _ можно принять
/« 0,3#тах.
Расстояние от основания стоек до оси поперечины определяется
высотой основания и планшайбы, высотой обрабатываемой детали,
вылетом ползуна и расстоянием от нижнего торца суппорта до оси
поперечины. Если принять высоту планшайбы и основания Н\ я^ (0,45-^0,6)#тах,
высоту обрабатываемой детали Л2 = 0,4Ятах, вылет ползуна /^0,3#тах
и расстояние от торца суппорта до оси поперечины /*з^ (0,2 н- 0,3)Яшах,
получим к ^ Н\ + к2 4- из 4- I ^ (1,35-н 1,6) #тах.
Полагая расчетную высоту портала Я= (1,9 -^2,4)#тах в качестве
расчетной величины ориентировочно можно принять /гя^0,7#«
168
Таким образом, в качестве расчетного принимается такой случай,
когда деталь высотой 0,4#тах обрабатывается на весьма малом диаметре
при вылете ползуна /^0,3#тах.
Проведенный анализ показывает, что выводы, полученные при
расчетных значениях переменных параметров, справедливы и при других
значениях этих параметров.
Так как под оптимальными понимаются такие формы и
соотношения размеров элементов, которые обеспечивают заданную жесткость
при минимальной затрате металла, то в качестве основного критерия
экономичности конструкции принимается величина эффективного веса
системы, т. е. веса деформируемой части портала и поперечины,
отнесенного к жесткости, или величины />У, пропорциональные
произведению расчетных перемещений /> на эффективный объем V
металла.
Эффективный объем металла, ориентировочно может быть
подсчитан по формуле
У^(Р + РП0р)1+2РстН,
где Р, Рпер1 Рст — площади поперечного сечения поперечины,
перекладины и стойки, соответственно;
Ь, И—расчетные размеры портала.
Из параметров, определяющих величины перемещений $р и
эффективного объема металла V, можно выделить общие параметры системы,
которые для данного станка следует считать заданными, и параметры,
определяемые формой и размерами элементов портала и поперечины,
которые могут варьироваться.
При анализе значения общих параметров можно принять средними
в диапазоне, типичном для станков данного типоразмера.
Ниже рассматривается влияние формы и размеров базовых деталей
на жесткость и вес, отнесенный к жесткости, и приводятся некоторые
соображения относительно влияния изменения сечений элементов по
длине.
1. Влияние формы и размеров поперечного сечения
отдельных элементов
Анализ встречающихся форм поперечных сечений поперечины и
стоек показывает, что наиболее употребительны сечения, которые можно
привести к двум схемам — к простейшему сечению с прямоугольным
контуром (поперечины станков фирм Кинг, Цинциннати, Беттс и др.;
стойки станков завода им. Седина, Коломенского ЗТС, фирмы Шисс
и др.) и к сечению с контуром в виде двух прямоугольников разных
размеров (поперечины станков Коломенского ЗТС, фирм Шисс, Кревен
и др.; стойки станков фирмы Вальдрих, тяжелых станков Коломенского
ЗТС и др.).
В табл. 31 и 32 приведены соотношения моментов инерции
поперечин и стоек разной формы поперечного сечения при типичных для
карусельных станков соотношениях размеров и при одинаковом весе (за
единицу приняты моменты инерции сечения поперечины и стойки с
соотношениями размеров, аналогичными имеющим место в карусельном
станке мод. 1532).
Из этих таблиц следует, что как для сечений поперечин, так и для
сечений стоек наличие дополнительного (верхнего или бокового)
прямоугольника с точки зрения жесткости не является необходимым.
169
Эскизы поперечного сечения элементов, расчетные параметры и результаты
менского ЗТС (Рх: Ру * Рг «. 0.511»0,5;
я Я Я я: «
л «о н § о «
25 ^ о 3 «
Эскизы поперечных сеченнй элементов (размеры в мм)
Поперечины
Стойки
Перекладины
1540
I Алах = 4000
1#шах - 2000
Яу»5000
то-
СВарнс»
-то-
1550
|Ошах-80001
Штах ~ 2500
\
Ру = 6250
С$арная
1563
Ртах = 6300
|#иш = 3200
Ру - 8000
Сварная
* Линейные размеры приведены в см, Р в с^, ^ в см
** В графах Аоо,) приведены величины перемещений / , /у| /г при Р
.У
1000 кГ, Р = 500 кГ,
р =500 /еГ, в верхней строке приведены суммарные перемещения, в средней —перемещения в резуль
тате деформаций портала, в нижней — в результате деформаций поперечины.
170
Таблица 28
расчета систем портал — поперечина карусельных станков новой гаммы Коло-
эскиз нагружения см. табл. 27)
б . а
СО со 2
1 ша^
к н и ^
« а> «и
О у Я я
Расчетные параметры по элементам *
Поперечины
Стойки
Перекладины
3 ч
н 3 !
СО о с
Перемещения вершины
резца / в мм
Нагрузка
кГ; кГ/см
**
470
458
330
70,0
50,0
27,5
'у
Р
Ух
*1
64,8-104
135,3-104
90-10*
906,6
32,4
54,3
°у ст
'кр. ст1
Уст
хст
730-10*
117,5-104
148-10*
1322
70
° г пер
*у пер
'кр. пер,
* пер
Упер
2пер
90,2-10*,
34,5-10*
105,7-10*
381,5
1,82
моею
Ррез
Я
(-*суп =
-3500
0,020|
0,017
о,ооз|
0,10
0,075|
0,003
0,072
0,37
0,0015
0,0025
—0,001
0,0075
А008
570
560
390|
85]
58,0]
32,0
*г\
У,
>кр
Р
*1 I
162-10*
283,5-104
195-10*
1271
39
67
**у ст
'кр. ст\
Рст
Уст
Хст
1347-104
178-104
537-10*
1774
90
^2 пер
*у пер
'кр. пер\
^пер
Упер
гпер
157-10*
42,6-10*1
150-10*
458
3,0
мооо
Ррез
Ч
&суп —
^=6500
0,021
0,019
0,002
0,13
0,059]
0,003
0,056]
0,37
—0,003
0,0025
—0,0055
—0,018
0,013
700
686
480:
105
66,5:
36,5
1*
'у
Р
Уг
*1
270-10*
|523,3.104
428-10*
1635
47,2
77,8
Зх ст
*у ст
*кр. ст\
**ст
Уст
хст
2398-104
358-10*
910-10*
2436
105
° 2 пер
*у пер
*кр. пер\
^пер
Упер
%пер
170,7-104
79,9-10*
234-10*
501
4,84
1 1000
^рез
Я
^суп ==
= 9000
0,020
0,017
0,003]
0,16
0,055]
0,0021
0,053
0,44
—0,0003
0,0025
-0,0028
—0,0024
0,616
171
Эскизы поперечного сечения элементов, расчетные параметры и результаты
некоторых продольно-строгальных станков (Рх' Ру '• Рг ■»
Модель станка,
размеры
обрабатываемого
изделия в мм;
сила резания
в кГ
Эскизы поперечных сечений элементов (размеры в мм)
Поперечины
Стойки
Перекладины
7231
вгаах =Ю00
Ятах =1000
Р„ =«= 2000
$
^
Г—Я?5—, *г
х 1±
НВЧг
~|ус/л
*
к»
\
1_
Г— 850-
|7
}У"Н
г
|-ь>
Ц
гпер
7256
Дпах - 2000
Ягаах =1500
Л, - 7500
ГГн=|з
1*
■!У/
Уст
*
%
1=
—гаев-—1
■ |7,
СТ1
ЙГ
Упер г~
^
Т
7278
Апах = 3000
Яшах =2500
Р^ = 10 000|
7289
Д„ах=,5000
«шах = 4000
Ру « 20 000
-2зио
ПС
3
+Уст~
-Р600-
[р"У/7Р/>*|
^
§гр-н
* Линейные размеры приведены в см, Г в см2, ^ в см*-.
** В графам Р1(юо приведены величины перемещений /х, / , /г при Р = 1000 л\Г, Рх = 500 «Г,
/^ «■ 500 кГ: в верхней строке приведены суммарные перемещения, в средней — перемещения в
результате деформации портала, в нижней — в результате деформаций поперечины.
172
Таблица 29
расчета систем портал — поперечина
0,5:1:0,5)
V 2 зе
2 е « :
г: а) <
О» а :
Расчетные параметры по элементам *
Поперечины
Стойки
Перекладины
со н
н «и05
?^
\СЪ о аз
Перемещения вершины
резца / в мм
Нагрузка
кГ, кГ/'см
*ж
138
256
180
7
52
40
КР\
Р
Ух
*Х
5,5 104
7-Ю4
5,1-10*
360
18
18.5
^ у ст
'кр. ст
Уст
92-Ю4
11.5-104
26,5-10*
690
52
17,2
™ г пер
-* у пер
кр. пер\
'пер
Упер
%пер
45-10^
12-10*
10-104
490
38
34
0,47
^1000
Ррез
Ч
@суп =
= 400
0,032
0,0281
0.004]
0,064
0.018
0,01
0,008
0,037
0,019
0,012
0,007
0,038
-0,001
—0,017
270
353
250
15
75
53
кр\
Р
Ух
2,
53,7-10*
56,4-10*
35-10*
1090
30.3
33,5
Зх ст
** у ст
'кр. ст
Рст
Уст
566-10*
74-104
127-Ю*
1847
75
26,3
° г пер
**у пер
'кр. пер
1 пер
Упер
*пер
75,4-10*
1Ы0*
2.5*104
700
44
2,1
1.78
Пооо
Ррез
Я
ОсуП —
= 950
0,018
0.016
0,002'
ОДЗ
0,013
0,004
0,009
0,097
0,0001
0,006
0,005
0.001
0,046
—0,007
-0,027
382
498
350
20
94
62
*Кр
р
Ух
*1
193-104
187,5-104
123-10*
1360
45
50
Зх ст
*у ст
'кр. ст
Р ст
Уст
1057-10*
179-10*
286-1О4
2380
98
37
°г пер
**у пер
'кр. пер\
Р пер
Упер
*пер
151,5-10*
273-Ю*
7,8-10*
920
50
3,8
3,24
1000
Гр€3
Я
&суп =
= 1700
0,019
10,0181
0,001
0,19
0,013
0,005
0,008
0,14
0,0002]
0,006
0,006
0,00011
0,065
0,002
—0,035
659
734
575
ЗЗ1
;34,5|
84,5
у,
'Кр\
р
Ух
*х
640-10*
769-10*
420-10*
2686
87,5
71
°у ст
'кр. ст
Уст
4577-10*
711-10*
1170-10*
4309
145
54
иг пер
** у пер
'кр. пер\
Рпер
Упер
гпер
1090-10*
154-10*
51,2-10*
1855
132
5,6
9,31
1000
рев
0,015
0,013
0,002|
0,30
л суп
4900
0.015
0,004
0,011
0,30
0,0006
0.006
0.004
0.002
0.12
-0.020
-0,080
Эскизы поперечного сечення элементов, расчетные параметры н результаты
некоторых продольно-фрезерных станков {рХ1ру\Рг =
Модель станка,
размеры
обрабатываемого
изделия в мм;
сила резания
в кГ
Эскизы поперечных сечений элементов (размеры в мм)
Поперечины
Стойки
Перекладины
6642
Яшах = 910
Ятах = 900
Рх = 2200
\
о
«^
*
Ы-1Ю0-
К*Гт~
X
Усгг
1 5
1 н
*\
6652
Д их =1260
#гаах=1250
Рх - 2500
«Г
Уу
6662
#шах = 1810т*
//„ах =1800
рх в 3700
1
Сь
\
~~1550 -
I* .
у
3 ст
Р§
^ .
Г
6672
ЯШах = 2510
^тах = 2500
Рх = 5100
6682
Ятах = 3610
Яшах-3600
Рх = 5100
!
!г1
1?
г-70ЯН
а
^ У-,
1810
г
|тт-дЫ[
и Ю80Л
* Линейные размеры приведены в см; Г ъ'см'*; ^ в см*
** В графах Рюоо приведены величины перемещений ^^ /у, /г
при Я - 1000 кГ, Р = 400 лГ;
р «= 400 /сГ: в верхней строке приведены суммарные перемещения, в средней — перемещения в
результате деформаций портала, в нижней — в результате деформаций поперечины.
Таблица 30
расчета систем портал — поперечина
1: 0,4 : 0,4)
О У 2 2
Расчетные параметры по элементам *
Поперечины
Стойки
Перекладины
1-5* 1
2ч
Д СО
ш н
Н 0»м
н 2 ам
« - СМ
0)2
•&2о
•Он г° т-н
Ф о ш
0,62
Перемещения вершины
резца / в мм
Нагрузка
кГ, кГ/см
181
248
175
10
61,5
41,5
7-104
22,8-104
10-Ю4
550
16,5
30
**хст
^у ст
^ кр. ст
Гст
Уст
127,6-Ю4
43,3-104
71,3-104
880
50
30
•*г пер
^у пер
'кр. пер\
^пер
Упер
%пер
14,5-104
15,4-104
18,8-Ю4
440
23,6
29,2
^1000
Ррез
Ч
О Суп в
-2800
0,025]
0,017
0,008
0,0561
0,007
0,003
0,004
0,015
0,0005]
0,012
0,005
0,007
0,027
-0,002
-0,091
239
333
167
12
74
56,5
1г
Уу
1цр
Р
У\
28-104
79-104
32,3-104
932
24,4
47,9
° у ст
Гкр. ст
*ст
Уст
хст
383-10*
НЗ-Ю*
223-104
1580
63,7
36,9
*г пер
**у пер
'кр. пер
* пер
Упер
%пер
66,3-104
27,3-104
31,9-104
740,5
40,3
32,5
1,45
1000
рез
(-*суп —
= 3700
0,019|
0,013
0,006
0,05
0,004
0,002
0,002
0,009 |
0,000б'
0,008
0,003
0,005
0,019
-0,002
-0,085
291
390
275
15
77
54,4
>кр
Р
У1
*1
33-104
91,5-104
53,5-Ю4
990
26,1
48
Зх ст
Зу ст
у к р. ст
^ст
Уст
хст
542-10*
178-104
310-104
1870
70
40,9
**г пер
^у пер
*кр. пер\
**пер
Упёр
%пер
109-Ю^
36,6-104
51-104
910
47,3
30
1000
1,9
^рез
ч
= 4000
&суп —
0,022
0.016
0,006
0,08
0,007
0,002
0,005
0,027
0,0005|
0,007
0,003
0,004
0,027
-0,003
-0,086
401
501
350
20
97
70
1яр\
Р
Ух
*1
76-10*
189-104
85-104
1500
34,5
58,5
^ у ст
'кр. ст
Гст
Уст
хст
966-104
334-104
537-104
2176
83,2
50,5
«Лг пер
^ у пер
3кр. пер\
^пер
Упер
%пер 1
182-104
60,6-104
80-104
1050
54,3
36
3,2
1000
рез
^суп —
= 6350
0,024
0,018
0,006|
0,12
0,006
0,002
0,004
0,032
0,0011
0,010
0,004
0,006
0,05
-0,015
-0,195
1
И
н
1
г
а
505
711
500
25
100,5
68,5
А
л
^Кр\
р\
Уг\
*1
267-Ю4
631-104
405-104
2500
50
70
*А* ст
^у ст
^кр. ст
Гст
Уст
хст
2970-104
550-104
1180-Ю4
2950
140
54,5
°г пер
/у пер
ч<р. пер\
^пер
Упер
%пер
292-1О4
232-104
230-Ю4
1570
68
61
6,3
мооо
Ррез
Я
О суп =
= 6350
0,030,
0,027
0,003
0,15
0,007
0,003
0,004
0,032
0,0004
0,005
0,003
0,002
0,028
—0,02
—0,08
§,=',**
Соотношение жесткостей и перемещений вершины
при разной форме их поперечного
Эскиз
Геометрические
характеристики
(в усл. ед.)
Перемещения
вершины резца (в усл. ед.
>гр
'УР
Эскиз
а2 Уу
%
иКР.
1*р
. *кр I действ
1,0
1.0
1,0
2,78
1.0
?-*
Щ-
1,0
аг
-0,6
&
Л
Ц±1
К* ко.
>кр
кр I действ
0,85
1,48
1,25
1,92
0,63
0,70
Й1-
1лЛ
ь
о г
0,7
0,3
*кр
< <?кр /действ
0,70
2,37
1,55
1.26
0,26
0,47
С точки зрения жесткости для поперечин более целесообразным,
<чем введение дополнительного прямоугольника, оказывается
увеличение общих высоты и ширины поперечины1, а для стоек—увеличение
ширины а\ за счет соответствующего сокращения высоты
сечения Ь.
Исходя из этого, дальнейший анализ проводился для систем, у
которых контур сечения стоек поперечины и перекладины имеет
простейшую форму — форму прямоугольника.
Для сечений в виде полого прямоугольника параметры, зависящие
от формы и размеров поперечного сечения, можно выразить как функции
1 Следует иметь в виду, что в том случае, если перекладина станка
устанавливается враспор, увеличение общей высоты поперечины потребует смещения
перекладины назад—от направляющих к оси стоек. Однако если перекладина выполнена
прямоугольного сечения с развитой вперед горизонтальной стенкой (как у продольно-
фрезерных станков, см. табл. 30), то при такой форме, обеспечивающей повышенную
жесткость перекладины на нзгнб относительно вертикальной оси, смещение
перекладины назад не вызовет снижения жесткости портала.
176
резца в результате упругих деформаций поперечин
сечения и одинаковом весе
Таблица 31
Геометрические
характеристики
.{в усл. ед.)
Перемещения
вершины
резца (в усл. ед.)
УгР УуР
Эскиз
Геометрические
характеристики
(в усл. ед.)
Перемещения
зершины резца
(в усл. ед.)
/*Р
/уР
Кр
иПр),
действ
1,0
0,97
из
2,47
0,87
0,95
I**'
•>кр
Лгр /действ
1,03
1,89
1,97
1,45
0,32
0,49
Ъ
>кр
Л:
кр /действ
0,87
1,42
1,36
1,79
0,55
0,69
7^>
%
*Кр
кр /действ
0,90
2,63
2,40
1,05
0,10
0,34
*кр
^к
0,69
2,30
1,60
1,21
0,23
кр /действ
0,46
ь
•/*
**кр
-Р-)
^кр /действ
0,73
3,76
2,78
0,73
-0,0
0,26
отношения сторон прямоугольников у и полупериметра сечения р =
= й + &. Тогда оказывается возможным записать
^уР~Иъ^у; ?хр~~М^х> ?*Р~~Еъ^**
где 8 — приведенная расчетная толщина стенок элементов,
принимаемая для всех элементов одинаковой;
Т — удельный вес материала поперечины;
/? — некоторые безразмерные коэффициенты, зависящие от:
н
к
Т7;
75;
5 а
Т' Т
а) общих параметров системы , р
б) параметров поперечины (-^ , —~ь
в) параметров стоек (А« . **« + *™|.
г) параметров перекладины Г-т^-; я ^ *]; обозначения прежние.
177
Таблица 32
Соотношение жесткостей стоек разной формы поперечного сечения
при одинаковом весе
ш
-Ь
Ъ
^А
-ь.
\ №/////у,
Т777ГЩр2^.
'~ Г"
} /■ / ; ; ; /г) ; ; /,
тгт
Т7Г ?>1П
^1,25 § = 1,75
2222222222222
ГГГГ1
Ч>1 ?>>>>>>> 1 >> ГТТ
.1
Моменты
инерцши
Моменты
инерции
Эскизы
Эскизы
Зх \ -?у \ Ъ*
1,0
1,0
&>
1,0
ОЕ
ом
1^6
0,78
2
ЕГ
уй Ц "1
Ь
ш
т
1,22
т
IX
3
ял
/,57
ЛЯ*
■ 4=«
"ТТ^Г
_к
/,<?
/;/?/
/,5/
4 = 5
&Я
^7
4^
2>
ад
7,М
1,15
0,95
2М
1,98
у г
И п1 7> а2 '
:□
Щ2
тт
1,Щ
&-П1 Ь.
"Г \Ъ*0,*'«>°~г
I
0,80\
0}96
0,76
а, '
У
2^-, 2^-#
Э^Э-
№7/
Ш
0,7/
ЕЭ
0;75
/,2/
йЭД
^^^э
0,5*
/,*/'
0,ДО
«Г" ,^' ^
^
^
*=5
3
Ч-и Й-/
0,67
/Л
0;5#
/,07
/,//
&«/•& = /
Е
ДО*
Ш]
/,0
Р5
0,46
\2М
Ь21
Примечание Мопенты инериии даны 8 условных единицах
178
Как уже указывалось, общие параметры системы можно считать
заданными. Из параметров поперечины, стоек и. перекладины
оптимальными следовало бы считать такие, при которых величины /рУ
минимальны. Так как /> и 1РУ являются функциями многих переменных, то
определить минимум этих функций технически весьма сложно. Поэтому
при анализе оценивалась зависимость этих величин от каждого из пара-
Фиг. 93. Влияние формы поперечного сечения поперечины 1-^) на перемещения вер-
1 Рх Ру РА
шины инструмента от действия сил резания ихР ~ Кх~ё§~ »/»р = &у ~е5" * ?гР в 2 ЕЬ/ *
веса
суппорта I/ 0 = Р0 с» I и собственного веса поперечины \/гд = Рд % ).
Кривые линии на графике:
сплошные — перемещения вершины инструмента в результате деформаций системы портал ^-поперечина»
штриховые — перемещения вершины инструмента в результате деформаций поперечины'.
метров при средних значениях остальных, а затем определялись
оптимальные значения только тех параметров, которые оказывают
наибольшее влияние на жесткость и вес конструкции. Зависимость величин /> от
параметров, характеризующих форму и размеры поперечного сечения
элементов, иллюстрируют кривые, приведенные на фиг. 93, 94 и 95. Из
рассмотрения кривых, приведенных на фиг. 93—95, можно сделать
следующие выводы:
1, Форма {-А и размеры (—^—] поперечного сечения поперечины
оказывают существенное влияние на перемещения по оси 2* (1{г\ /?0;
17&
Н^ и по оси У(ЯУ). На перемещение по оси X влияние формы и
размеров поперечины незначительно,
2. С увеличением высоты сечения поперечины к и уменьшением
ширины Ъ (при постоянном весе) перемещения по оси У, естественно,
возрастают. Перемещения по оси 2, величина которых определяется как
разность перемещений от изгиба поперечины в вертикальной плоскости
и кручения, вычисленные без учета действия веса суппорта, вначале
уменьшаются, доходят до нуля, а затем меняют знак и начинают
возрастать по абсолютной величине. Перемещения по оси 2, вычисленные
15
10
#х.Яу
20
15
и
о
\Х
^Г^
<^
Ч
л
X
\
/^
\
>
Уу т^Э-^ ^
1
~ЬШ Н
«фЦ>
3 Ь 5 6 /1ст
1 1 1 ^ )
;
^7
Чч^<^
^
аз
05
а 75
10
X,
т..
РхКу
60
м\
20
О
44 Ь*Ь
\]
к,
\
Л/Лу
\§Л
*гйу
К2Ву
75
50
15
п
Х^лЛ' |
^*
_^^7 Ку
0.3 ОЛ
а)
I
аи о.б
5)
Фиг. 94. Влияние формы попе-
речного сечения стоек I ~/Г~ )
и перекладины (-т- I на пере-
ПРх
мещения /хР = Кх -^ , /у/> =
Р Р /
= Яу Ж • Лр = ** Ж веРши- {?хРУ = Я*ЯУ
ны инструмента от действия
сил резания:
/ -пт влияние формы сечения
перекладины; 2 — влияние формы сечения
Фиг. 95. Влияние размеров поперечного сечения
элементов на перемещения вершины инструмента
от действия сил резания 1/хР = Ях -%%* ?уР ^
Р Р \
= ЯУ Ж ' ^Р = Л* "Б8/ и . иа величииы»
пропорциональные весу, отиесенному к жесткооти
-V
/уР'
а — влияние размеров поперечного сечения поперечины; б —
влияние размеров поперечного сечения стоек.
с учетом действия веса суппорта, минимальны при у = 1 -*- 2. Как и сле-
довалр ожидать, при увеличении —рг1 (в станках больших размеров)
к н
оптимум отношения -у смещается в сторону больших-у л так как доля
перемещений в результате изгиба поперечины в вертикальной плоскости
возрастает.
3. Как и следовало ожидать, форма (^-) и размеры ( ст 1 ст )
поперечного сечения стоек оказывают наибольшее влияние на
перемещение в том направлении, в котором жесткость стоек минимальна, т. е.
по оси Хч Несколько меньшее влияние размеры поперечного сечения
стоек оказывают на перемещение по оси 2. На перемещение по оси У
форма и размеры поперечного сечения стоек влияют незначительно. С
увеличением размеров поперечного сечения стоек, а также с уменьшением
высоты сечения стоек Нст и увеличением ширины ЬСт при постоянном
весе перемещения [хр, естественно, уменьшаются.
180
4. Форма (-^) поперечного сечения перекладины на жесткость
влияет мало и потому может выбираться из конструктивных
соображений.
2. Влияние
соотношении размеров
сечения элементов
поперечного
Для того чтобы установить оптимальное соотношение размеров
стоек и поперечины следует проанализировать влияние этого
соотношения на величину
/^поскольку на перемещения по оси
1 влияют как размеры
поперечины, так и размеры
стоек. На фиг. 96, а
приведена зависимость величин
Я_. и ПДу от Л-^- и * + *
при соотношении размеров
н л
поперечины -г = 2 и
соотношения размеров стоек -т—-=
= 5. Из кривых,
приведенных на фиг. 96, а, видно, что
к + Ь
при всех значениях —~— в
исследованном диапазоне
(для станков с диаметром
обработки от 2,5 до 7 м)
наиболее рациональными
оказываются конструкции, у
которых размеры поперечин
на 15—25% меньше разме-
ров стоек (тр-^гт—=0,75-*-
-0,85).
На фиг. 96, б
представлена зависимость величины
/хР от соотношений размеров
перекладины и стоек. Из
приведенных кривых
следует, что размеры
перекладины оказывают
незначительное влияние на
жесткость. Оптимальными
сточки зрения использования
материала являются
конструкции, у которых
размеры перекладины в 1,5—
2,5 раза меньше размеров
стоек.
20
15
ю А
40
5 А 20
Йг
'~ Сечение I
перекладины
-Ц
МН
ко
*)
у
ьп+ьп
Фиг. 96. Влияние соотношений размеров
элементов на перемещения вершины инструмента от
действия сил резания (/^ = К*^;/хР = Кх]%)
и на величины, пропорциональные весу, отнесен-
кому к жесткости
(/^ =
«**у-
*Аг
-)■■
>-. /хрУ =
а — влияние соотношений размеров поперечины и стоек; б -
влияние соотношений размеров перекладины и стоек.
3. Влияние изменения сечений по длине
Как показали эксперименты и как можно видеть из фиг. 93—95,
перемещения вершины инструмента (в результате деформаций базовых
деталей) по осям У к 2 определяются главным образом деформациями
181
поперечины, а по оси X — деформациями стоек. Влияние изменения
сечений поперечины по длине на перемещения 1уР и /гр иллюстрирует табл. 33,
а влияние изменения сечений стоек по высоте на перемещение 1хр —
табл. 34. Из данных, приведенных в табл. 33 и 34, следует, что
изменение сечений как стоек, так и поперечин является рациональным. Для
стоек наибольший эффект дает значительное изменение сечений — от к
до 0,5/г (строка 3 табл. 34); при том же весе жесткость стойки
переменного поперечного сечения оказывается примерно на 30% выше, чем
стойки постоянного сечения. Для поперечин влияние переменности
сечений несколько меньше.
Таблица 33
Сравнительные характеристики 1 жесткости и веса поперечин карусельных станков
к
с разным изменением сечений по длине (при —г = 1,0)
Эскизы поперечины
Обозначение
характеристик
Критерий жесткости — перемещения
вершины инструмента
от
собственного веса
поперечины
от сил резания
/уР=
Р I8
( У
1 ЕШ
^
_ со о
Си О
к
к
/о
0,0781
1,0
—0,117
1,0
0,135
1,0
4,0
1.0
к
Л
/о
0.0814
0,80
-0,167
0.97
0,172
0,88
3,5
1,14
к
/
/о
0,0773
0,76
-0,168
0,98
0.173
0,87
3,5
1,14
1 к — коэффициент, характеризующий перемещения вершины инструмента в результате
деформаций поперечины с разным изменением сечений по длине;
-т- ~ отношение перемещений в результате деформаций поперечины переменного (/) и
постоянно
ного (/о) сечения при постоянном весе;
кх —коэффициент, характеризующий вес поперечин с разиым изменением сечений по длине.
182
Таблица 34
Сравнительные характеристики * жесткости и веса стоек карусельных станков
постоянного и переменного поперечного сечения
Эскизы стоек
4-ОД6
н й) а «
о =г а- гр
° 2 « :-
*зй о,
я
З^ и
5 О^
кх
«0,30
Л |
: ю о д
! а>с О,
> К ее Н
« 1=:
«а
из*
СО о^
*1
31,0
гз
1,0
ьо
8,35
2,6
1.0
1,0
Жк Ьг=*[0,75+0,25%]
* мЛ 1
36,7
2,05
0,77
1.12»
9,04
2,35
0,80
1,11
^ ил ±
39,9
1.8
0,56
1.28
10,1
2.1
0,64
1.24
38,6
1,85
0,59
1,24
9,83
2,16
0,68
1,20
1 к—коэффициент, характеризующий перемещения инструмента в результате деформаций
стоек с разным изменением сечений по высоте;
Ъг — коэффициент, характеризующий вес стоек с разным изменением сечений по высоте;
~ отношение перемещений в результате деформаций стоек переменного {() и постоянного (/<>)
/о
сечения при постоянном весе;
--. отношение больших размеров нижних сечений стоек переменного (Л) и постоянного (Ло) сече-
«о
иия при постоянном весе.
4. Общие рекомендации по выбору оптимальных
форм порталов и поперечин карусельных станков
(с диаметром обработки от 2,5 до 7 м)
Проведанный анализ позволяет установить оптимальные формы и
соотношения размеров элементов, имеющих сечение в виде полого
прямоугольника. В действительности форма поперечных сечений элементов не-
183
сколько отличаются от прямоугольной, из-за наличия направляющих,,
ребер и т. п. Для реальных станков оптимальными можно считать такие
конструктивные формы и соотношения размеров элементов, при которых
величины перемещений инструмента будут примерно такими же, как
и в системах с сечениями элементов в виде правильных
прямоугольников при оптимальных соотношениях размеров.
Исходя из изложенного, можно предложить следующие
рекомендации для конструирования:
1. Поперечные сечения поперечин и стоек целесообразно выполнять
максимально приближающимися к форме правильного
прямоугольника (т. е. без дополнительных верхнего или бокового
прямоугольников).
2. При оптимальной форме сечения поперечины (приближающейся
к форме правильного прямоугольника) соотношение габаритных
размеров сечения целесообразно выбирать так, чтобы отношение высоты
сечения поперечины к к ширине Ъ находилось в пределах от 2,2 до 1,5
(большие значения — для станков больших размеров, у которых -тр* = 3^-4);
в том случае, если перемещения от действия собственного веса
поперечины и веса суппорта компенсируются, соотношение габаритных
размеров следует выбирать ближе к нижнему пределу.
3. При оптимальной форме сечения стоек (без контрфорса)
соотношение габаритных размеров сечения целесообразно выбирать так, чтобы
отношение высоты сечения стоек к к ширине Ь находилось в пределах
от 3 до 4.
4. При оптимальной форме поперечного сечения элементов
оптимальными следует считать такие соотношения размеров элементов, при
которых площадь поперечного сечения перекладины в 1,5—2,5 раза,
а площадь поперечного сечения поперечины на 15—25% меньще, чем'
площадь поперечного сечения стоек.
5. Изменение поперечных сечений поперечин по длине и стоек по
высоте следует считать рациональным. Для стоек оптимальными
оказываются такие формы, при которых поперечные сечения изменяются
значительно. Для поперечин несколько более целесообразным следует
считать изменение ширины сечения (размера в направлении
оси У).
Следует отметить, что рекомендуемые формы сечений элементов
рациональны и с точки зрения получения более высокой жесткости
контура сечения, так как известно, что наибольшей жесткостью контура
при прочих равных условиях обладают сечения с соотношением сторон,
близким к 1. С точки зрения обеспечения отсутствия искажения
контура сечения рациональным является выполнение стоек и поперечин
с перегородками или высокими поперечными ребрами.
Если проанализировать конструкции современных станков разных
размеров, то можно видеть, что основные соотношения параметров
в станках разных размеров различны. Станки меньших размеров (#тах —
= 2500 — 3000 мм) имеют относительно узкие вытянутые стойки и
поперечины, сечения которых больше развиты в высоту, чем в ширину.
В станках больших размеров (Отах = 6000-^-7000 мм) стойки обычно
относительно короче и шире, а сечения поперечин приближаются
к квадратным.
Соотношения параметров в больших станках примерно
соответствуют рекомендованным как оптимальные. Различие соотношений
параметров в станках больших и меньших размеров может объясняться
разницей в условиях нагружения их элементов и главным образом
относительно большим Бесом суппорта в тяжелых станках (в станках с диа-
134
метром обработки 2—3 м -0%^* 1-^-2, а в станках с диаметром обра-
ботки 6—7 ж %а = 4).
Проделанный анализ показал, что оптимальная форма поперечного-
сечения стоек от веса суппорта практически не зависит и что при
больших значениях —§^ оеченйе поперечины должно быть больше развито
в высоту, чем при меньших (см. фиг. 93).
Таким образом, серьезного обоснования имеющегося различия
конструкций порталов и поперечин станков разных размеров нет.
На основании изложенного можно считать, что в диапазоне
диаметров обработки от 2,5 до 7 ж конструкции порталов и поперечин станков
должны быть аналогичны, причем соотношения параметров должны
приближаться к имеющимся у станков больших размеров.
Изложенные рекомендации были использованы на Коломенском
ЗТС при проектировании новой гаммы карусельных станков.
Результаты расчета порталов и поперечин базовых станков этой гаммы
приведены в табл. 28. Сравнивая результаты расчета систем
портал—поперечина старых станков Коломенского ЗТС (см. табл. 27) и новых,
соответствующих размеров, можно видеть, что у станков новой гаммы по
сравнению со старыми станками жесткость системы портал—поперечина
выше в 1,5—2 раза, а эффективный объем металла, отнесенный к
суммарной жесткости, меньше в 1,5—3 раза.
При испытаниях в работе новые станины также показали хорошие
результаты.
Б. Анализ портальных станин продольно-строгальных и продольно-
фрезерных станков
Проведя (при соответствующим образом выбранных переменных
параметрах — / ^0,1#тах и к «=* 0,7#гаах) анализ форм и размеров
элементов продольно-строгальных и продольно-фрезерных станков, можно
показать, что основные выводы, полученные для карусельных станков,
справедливы и в этих случаях. В частности, так же как и для элементов
карусельных станков, более рациональными оказываются сечения стоек
и поперечин с контуром, приближающимся к правильному
прямоугольнику; форма и размеры стоек оказывают влияние главным образом на
перемещение по оси X, а форма и размеры поперечины— на
перемещения по осям У и 2; форма поперечного сечения перекладины на
жесткость влияет мало и т. п.
Эта общность выводов объясняется тем, что некоторое сравнительно
незначительное различие параметров станков разных групп не меняет
характера влияния этих параметров на жесткость системы.
Поскольку размерные ряды продольно-строгальных и продольно-
фрезерных станков близки между собой, целесообразно с позиций
расчетов оценить возможности унификации порталов строгальных и
фрезерных станков. Для решения вопроса о возможной унификации
порталов сопоставлены основные параметры продольно-строгальных и
продольно-фрезерных станков близких размеров (табл. 35). На основании
данных, приведенных в табл. 35, сопоставляя условия работы станков,-
можно сделать следующие выводы:
1. Для фрезерных и строгальных станков близких размеров
составляющая Рх* млксимальной силы резания, имеющая наибольшее значе-
* Здесь, как и ранее, обозначение составляющих соответствует выбранным осям
координат, см. фиг. 91.
185-
ние с точки Зрения работы портала, примерно одинакова. В
строгальных станках составляющая Ру примерно в 5 раз, а составляющая Рг
в 2,5 раза больше, чем во фрезерных.
Таблица 35
Отношения параметров продольно-строгальных станков к соответствующим параметрам
продольно-фрезерных станков близких размеров (обозначения см. стр. 165)
1 Сравниваемые
| модели
1 станков
7256 и 6662
7278 и 6672
Сравниваемые параметры
Наибольшие размеры
обрабатываемого
изделия
-"шах
1Д1
1,2
"тах
0,83
1,0
Расчетные размеры
Ь
0,93
0,95
н
0,91
1,0
а
0,97
0.89
^
0,97
0.97
Силы резання и вес
суппорта
рх
1,01
0.98
ЯУ
5,0
5,0
р*
2,5
2,5
°суп |
0.24
0,27
Продолжение табл. 35
1 Сравниваемые
1 модели
] станков
7256 и 6662
7278 и 6672
Сравниваемые параметры
Геометрические характеристики
сечения поперечины
Р
1,10
0,91
'у
у ||.
0,62
0,99
'*
1,64
2,54
'*
0,66
1,45
Геометрические характеристики
сечения стоек
ст
•0,99
1,10
уст
0,42
0,54
*хст
1,04
1.10
*кр. ст
0.41
0,53
Однако при чистовой обработке, которая играет решающую роль
с точки зрения точности изделия, различие между силами резания
фрезерных и строгальных станков несколько меньше. Учитывая, что в
балансе перемещений во фрезерных станках существенную роль играют
деформации фрезерной оправки и шпинделя и формообразование
производится инструментом, имеющим большую ширину, а также учитывая
пульсирующий характер нагрузки при фрезеровании, можно считать,
что допустимые деформации порталов фрезерных станков должны быть
несколько меньше, чем строгальных. Поэтому, несмотря на меньшие
максимальные силы резания во фрезерных станках, требования к
жесткости порталов строгальных и фрезерных станков можно считать
примерно одинаковыми.
2. Существующие продольно-фрезерные и продольно-строгальные
станки близких размеров имеют примерно одинаковые площади сечения
базовых деталей.
3. При примерно одинаковых площади поперечного сечения стоек
фрезерных и строгальных станков близких размеров и жесткости на
изгиб в плоскости У2(1хст) жесткость стоек на кручение и на изгиб
в плоскости XI у фрезерных станков в 2—2,5 раза выше, чем у
строгальных. Это объясняется тем, что форма сечения стоек фрезерных станков
выбрана более рационально и подтверждает сделанный ранее вывод
о нецелесообразности выполнения сечений стоек с боковыми
прямоугольниками (контрфорсами).
4. При примерно одинаковой площади сечения поперечин жесткость
на изгиб в горизонтальной плоскости поперечин строгальных станков
в 1,5—2,5 раза выше, чем фрезерных. Так как составляющая сила Ру
,186
в строгальных станках значительно больше, чем во фрезерных, то такую
разницу в величинах жесткостей можно считать рациональной.
Действительно, по кривым, приведенным на фиг. 97, можно видеть, что при
том же весе минимальная величина перемещения инструмента по
вертикали ]гр в строгальных станках обеспечивается при — — 1, а во
фрезерных станках при -^ я^ 1,5. Однако при соотношениях размеров сече-
ния -^ от 1 до 2 значения перемещений для фрезерных станков достаточно
Фиг. 97. Влияние
формы (^-у)
поперечного
сечения поперечин продольно-строгальных и
продольно-фрезерных станков на перемещения
вершины инструмента от действия сил резания
Лр — Кг'
хР
ВЬ
<?ур = ку Ж/ и веса С>ГПП°Р-
та [Г
*суп
гО'
Ю ЕЬ
)■■
сплошные кривые — для продольно-фрезерных станков;
штриховые — для продольно-строгальных.
близки к минимальным. Кроме того, при -г = 1 перемещения в
направлении оси У(1ур) меньше, чем при у = 1,5ч-2, Из этого следует, что как
для строгальных, так и для фрезерных станков оптимальными следует
считать сечения, близкие к квадратным, примерно такие, как у
существующих строгальных станков. Это положение подтверждается и
сравнением параметров поперечин станков мод. 7278 и 6672—при одном и
том же весе поперечин и одной и той же жесткости на изгиб в
вертикальной плоскости (Лд,), жесткость на кручение и на изгиб в
горизонтальной плоскости поперечины строгального станка в 1,5—2,5 раза выше,
чем фрезерного.
Из изложенного следует, что формы и соотношения размеров
базовых деталей строгальных и фрезерных станков должны быть едиными
и поэтому они могут быть унифицированы. При этом стойки следует вы-
187
полнять с соотношением габаритных размеров сечения в пределах от 2
до 3 (примерно таким, как у фрезерных станков), а поперечины —
с соотношением габаритных размеров около 1 (примерно таким, как
у строгальных станков). Сечения стоек и поперечин целесообразно
выполнять простейшей формы без дополнительных (верхнего или
бокового) прямоугольников.
По данным результатов расчетов систем портал—поперечина
существующих продольно-строгальных и продольно-фрезерных станков
(см. табл. 29, 30) можно видеть, что при таких соотношениях размеров
базовых деталей станки будут иметь жесткость системы в направлении
оси X примерно в 1,5 раза выше, чем существующие строгальные,
а в направлении осей У и 1 в 1,3—1,5 раза.выше, чем существующие
фрезерные при том же весе.
В заключение следует подчеркнуть, что так как жесткость
соединения стоек с основанием или станиной может оказывать существенное
влияние на жесткость всей системы, конструктивному оформлению
соединения следует уделять серьезное внимание (см. выше).
ГЛАВА V
ПЛИТЫ МЕТАЛЛОРЕЖУЩИХ СТАНКОВ
§4. ОБЩИЕ СВЕДЕНИЯ О КОНСТРУКЦИЯХ ПЛИТ
Плиты в станках служат:
а) для повышения устойчивости и надежности установки станков
с вертикальными стойками;
б) для установки неподвижных узлов станков (если станки не
имеют общей станины, например, лоботокарные станки);
в) для установки изделий в станках с неподвижным изделием.
а) д) в)
Фиг. 98. Типовое расположение ребер в плитах:
а — консольно-фрезерных, вертикально-сверлильных, расточных станков; 6 — радиально-сверлильных
станков; в — лоботокарных станков.
Плиты имеют одно измерение (высоту), значительно меньшее, чем
два других. В отличие от станин плиты не имеют направляющих.
Плиты конструктивно выполняют:
а) в виде пластины с системой стенок и ребер;
б) в виде двух пластин, скрепленных стенками и ребрами (с окнами
в нижней пластине для установки стержней).
Первый вид плит более прост для литья, второй-—обеспечивает
более высокую жесткость.
Контуры плиты определяются устанавливаемыми на них узлами
станков. По форме контура плиты выполняют прямоугольными
(большинство плит), комбинированными из прямоугольника и полукруга
(плиты радиально-сверлильных станков), сложного очертания —
комбинированными из нескольких прямоугольников, (плитц лоботокарных
и других станков).
Основные системы ребер, применяемых в плитах, приведены на
фиг. 98. Большинство плит снабжают системой
взаимно-перпендикулярных ребер, параллельных сторонам плиты (плиты расточных,
вертикально-сверлильных, консольно-фрезерных и других станков). Некоторые
189
плиты имеют кроме взаимно-перпендикулярных еще и диагональные
ребра. Круглые части плит радиально-сверлильных станков снабжаются
радиальными и кольцевыми ребрами. Для уменьшения остаточных
напряжений применяют системы сотовых ребер.
Плиты воспринимают нагрузки от сил резания и веса. По условиям
нагружения плиты можно разделить на плиты, нагружаемые
симметрично относительно плоскости симметрии, и плиты, подвергаемые
сложному нагружению. Схемы нагружения типовых плит приведены
в табл. 36.
Таблица 36
Основные схемы нагружения плит металлорежущих станков
Схема нагружения
Нагрузки на плиту
Тяжелые
расточные станки
Радиально-
сверлильные
станки
Ои + Ру
М = Рхк-Рх
у~р
Ои + Р
*1= Тх
Ост + Отр + Ос
М = Рхх — Осх2 — Отр • хг
Консольно-фре-
зерные,
кально-сверлильные станки
Для незажатой консоли
О = ру + ои + оК
М = Р 1 + РхН- С}хРхЬ
Для зажатой консоли
л — Ост + 6к+0д
Г2
<? » О, М = Ру1 - РХН
Лоботокарные
станки
м
41
?2
Ос
~ Р%
о3
- л
Ру1г —
Рг1
Условные обозначения: О.^,, 0-п, С„, С„, Ои, С- — вес стойки, траверсы, суппорта, изделия, кон-
стп тпр с и к з
соли, задней бабки; Рх% Р , Р„ — составляющие сийы резаиия; <Р% — площадь контакта изделия с пли-|
1той; Р>> Г3, р± — площадь, очерченная контуром стыка плиты со стойкой» суппортом, задней бабкой»
соответственно.
190
' Зотв
Разрез по Л Л
Плиты выполняются цельными и сборными. Цельными выполняют
большинство плит средних станков. Сборными изготовляют плиты
тяжелых станков. Плиты тяжелых
расточных станков выполняют из трех,
четырех и шести частей. Отдельные части
скрепляют винтами по торцам. Число
винтов обычно 8—12 (фиг. 99).
Плиты устанавливаются на
фундамент:
а) на регулируемых башмаках
(плиты прецизионных и тяжелых
станков) ;
б) на клиньях с последующей
заливкой цементным раствором.
Башмаки обычно располагают:
а) несколькими рядами (в
тяжелых широких плитах, фиг. 100, а);
б) по контуру (в узких и
фигурных плитах, фиг. 100, б). Клинья
обычно располагаются по периметру
опорной плиты, причем часть клиньев
регулирует положение плиты в
продольной плоскости, а часть — в
поперечной. Закрепление плит на
фундаменте производят с помощью
фундаментных болтов. Для плит,
устанавливаемых на башмаках, болты
размещаются рядом с башмаками (фиг.
101, а) или пропускаются через специальные отверстия в корпусе
башмака (фиг. 101, б). В последнем случае исключается деформирование-
Фиг. 99. Пример соединения Гяжелыэс
составных плит.
Г
р
р
к»
г-%
/■■>
сз
СЗ
п
и
:з
сз
п
п
г>
п
СЗ
г 2
о
V*
-
-
-
Г"»
° ]
С2
сз
п
[Г!
к> ч.
П
гт
Г 1
Г 1
1.1 1^
*;
б)
Фиг. 100. Типовое расположение башмаков:
а — несколькими рядами (в тяжелых горизонтально-расточных и других станках);
6" — по контуру (в лаботокарных н других станках).
Фиг. 101. Крепление плит к фундаменту:
а — фундаментные болты расположены около башмаков; 6 — фундаментные болты проходят через
башмаки.
плиты в результате несоосности сил на станину от башмаков и болтов.
Для заливки башмаков и колодцев в плитах предусматривают специаль-
191
ные окна. После выверки производят предварительную затяжку и
заливку плиты цементным раствором. Окончательную затяжку болтов
производят плавно и равномерно после окончательного затвердевания
цементного раствора. Для крепления плит на фундаментах иногда
употребляют фундаментные гайки.
9-$+&2
Стойко Изде/ше^
~1«
- , . - .3*ТГ
§ 2. РАСЧЕТ ПЛИТ
1. Определение деформаций плит
Основным критерием работоспособности плит является жесткость.
Обеспечение достаточной жесткости необходимо:
а) для получения требуемой точности обработки устанавливаемых
на плитах изделий;
б) для облегчения точного изготовления и установки плит.
Напряжения в плитах, как правило, сравнительно невелики и
расчета плит на прочность не требуется.
В общем виде плиты рассматриваются как пластины на
сплошном упругом основании. Для плит, устанавливаемых на фундамент или
общее полотно цеха, эта
расчетная схема непосредственно
соответствует действительности. Для
плит, устанавливаемых на
башмаках, определяется приведенная
(к сплошному) податливость
основания из условия равенства
перемещения плиты, установленной
на приведенном сплошном
основании (подробно см. ниже), и
плиты, установленной на
башмаках.
Определение деформаций
плит, представляющих собой
сложные системы из двух стенок
и взаимно-пересекающихся (в
большинстве случаев взаимно-
перпендикулярных) ребер (перегородок) на упругом основании при
сложных видах нагрузок, какие имеют место, представляет очень
большие трудности [14]. Решение такой задачи не может быть доведено до
формы, удобной при технических расчетах.
Поэтому приближенно плиты станков рассматриваются как
сплошные пластины некоторой приведенной жесткости. Приведенная
жесткость плиты определяется из рассмотрения деформаций плиты как
сложней системы при одном простейшем виде опирания и нагружения.
Предполагается, что и при других видах нагружения и опирания величины
деформаций плиты будут близки деформациям такой приведенной
сплошной пластины. Определение приведенной жесткости плиты
см. ниже.
В большинстве металлорежущих станков типа радиально- л
вертикально-сверлильных и т. п. ширина стоек, установленных на плиты, и
крупных изделий близка к ширине плиты, и приближенно можно
принять, что нагрузки от веса стоек, изделий и сил резания приложены по
всей ширине плиты. В этом случае для определения деформаций плит
оказываются применимыми формулы для расчета балок на упругом
основании. В общем виде схема нагружения такой плиты силами реза-
192
Фиг. 102. Простейшая расчетная схема плит
с нагрузкой, распределенной по ширине.
ния и весом представлена на фиг. 102. За критерий жесткости Плиты
принимается относительный угол б поворота сечений плиты под стойкой
и изделием, который характеризует перекос инструмента относительно
изделия, вызванный деформациями плиты:
где
6 и 6 —углы поворота плиты у стойки и изделия под действием
равномерно-распределенных нагрузок цх и д2,
передаваемых на плиты через стойки и изделия соответственно
(табл. 36);
0^ — угол поворота плиты у стойки и изделия под действием
момента М от сил резания и веса;
К — коэффициент жесткости упругого основания в нГ1см2
(см. ниже);
Ь — ширина плиты в см;
т — коэффициент жесткости плиты в \\см\
-V
т— К
^к^пр
Е — модуль упругости материала ллиты в кГ}сяг\
]пр — приведенный момент инерции поперечного сечения
плиты в см*\ ^пр^-ф"* ^—момент инерции
поперечного сечения;
4> — коэффициент снижения жесткости плиты в результате
влияния касательных напряжений в ребрах,
определяемый по графику фиг. 103. Коэффициент ф определен
из рассмотрения напряженного состояния сложной
пластины по методу, предложенному П. Ф. Папковичем
[46]. Так как в нижней стенке плиты имеются окна, то
под толщиной нижней стенки и следует понимать
условную толщину стенки, которая имела бы место при
отсутствии окна и той же площади поперечного сечения
стенки, что и в действительности;
^чху ^я*> ^м"""" безразмерные коэффициенты, определяемые по
графикам фиг. 104 в зависимости от расстояния между
сечениями, в которых определяется угол, и размеров
опорных площадей стоек и изделий. Графики фиг. 104
построены по формулам для 'балок на упругом
основании [32].
Представляет интерес определение деформаций плиты от сил
затяжки болтов. Обычно болты располагаются поперечными рядами.
Наибольший угол наклона плиты под действием суммарной силы Р
затяжки болтов одного ряда может быть определен по формуле
где КР — коэффициент, определяемый по графику фиг. 105.
Если наибольший угол наклона плиты от болтов одного ряда 6, =
= ~^-Л'Я), а другого е2 = —д^ЛТРа, то относительный угол наклона
двух сеченцй плиты 6 = 61-|-62.
193
Фиг. 103. График для определения коэффициента снижения жесткости
плиты, учитывающего действие касательных напряжений в ребрах.
\^Ь
II
Ь/
г
гм
11
ИГ
Ц7
и?
и2 —Н
ТП
-н
Ы'
2.
ЫМ-*,) „ <5
Фиг. 104. Графики для определения коэффициентов Кдъ Кдъ, Км,
входящих в формулу относительного угла наклона 0 стойки и изделия в
результате деформаций плиты.
194
Как видно из графика фиг. 105, наибольшие углы наклона
получаются от болтов, расположенных у краев плиты (а = ат[П). Таким
2,0
15
Ю
0,5
/
т(.=1/^
т1=1>5 и
\ _ I
Шее
и^ ,
уу/////;//;//;//;/;//,
\+ 21 ^
^тах— х '
Р
0,2
ОЛ
0,6 0,8
1,0
1,2 а=ат
Фиг. 105. График для определения коэффициента, входящего в формулу наибольшего
угла наклона плиты под действием сосредоточенной силы: а и I — в см, т—*в 1/рм.
образом, наибольший относительный угол наклона концов плиты (пр»
симметричном расположении крайних болтов)
2РгФ
К
•Кп.
2. Определение коэффициента жесткости упругого основания
Для плит, установленных на клиньях, подлитых цементным
раствором, коэффициент жесткости упругого основания может быть принят
в соответствии с литературными данными К = Сгй, где Сг —
коэффициент упругого равномерного сжатия; для бетона и железобетона Сг =*
= 800ч- 1500 кГ/см* [32].
Для плит, установленных на
башмаках, упругие перемещения в опоре
складываются из перемещений 61 в стыке
между башмаком и плитой,
перемещений 62 в стыке между верхней и нижней
частью башмака и перемещений бз
между башмаком и фундаментом
3 = 81 + 82 + 83>
где
81 = К
\ — Ь>ч-р-
х = к
3^Г
• 6, =350
Фиг. 106. Типовая конструкция*
башмака к плитам горизонталь*
ио-расточных станков.
Р —сила, приходящаяся на один башмак, в кГ\
&и &2, ^з— коэффициенты контактной податливости отдельных
стыков в см*\кГ\
Ри Р2> Рь — площади соответствующих стыков в см?.
Коэффициенты к\ и кг приближенно могут быть приняты равными
(0,5н- 1,0) 10~4 см3/кГ. Коэффициент к3 по результатам испытания
жесткости стыков чугун-—бетон площадью 100—500 см2 составляет в
среднем: а) если башмак поллит цементным раствором 0,7-10~4 смУкГ;
б) если башмак не подлит (15-^30) • 10~4 см3/кГ (нижние значения для
меньших площадей, верхние для больших). Коэффициент жесткости
упругого основания, приведенного к сплошному,
К--
пЬ
&1 р. + ^2 р 4" ^3 р
кГ/см2,
где к — число башмаков;
Р — плрщадь плиты.
195
Например, для башмака, изображенного на фиг. 106, Р\ = 264 см2,
^2= 150 еж2, /^ = 718 еж2, Р = 256000 еж2, /г = 30. Принимаем
#1 = 0,5-10~4 смг/кГ (ввиду хорошей приработалности стыка); &2 =
= 1 • 10~4 см3/кГ\ к3 = 0,7 • 10~4 смъ/кГ. Тогда приведенный коэффициент
жесткости упругого основания К— 125• 6 кГ/см2.
3. Пример расчета плиты
Определить относительный угол наклона стойки и изделия радиаль-
но-сверлильного станка в результате деформаций плиты, схематически
изображенной на фиг. 107.
Расчетные данные: д} = 0,4 кГ/см2; д2 == 0,2 кГ/см2, М =
= 300 000 кГсм; Ь = 177,5 еж, а - 490 еж, Я = 45 еж, &! = 170 еж, Ь2 =
= 120 еж, «1 =430 еж, а2 = 405 еж, Е = 1 .10° /сГ/еж2, / - 190 000 еж4,
* = 1,65 (по фиг. 103).
-то-
-1775-
§
<*
ЩтЙг—~Ж--(^3 гйт Г?1 Йг-гйз й
о=
—Ы-.—/50/7—1
#50
М^ЗОООООкГсм
д,=0Акг/см2
-I*
К0—
Р77777
/7^1
600\-
-а=й900
(?7=О02кг/см*
Фиг. 107. Расчетная схема плиты.
Коэффициент упругого равномерного сжатия принимаем Сг =
= 1000 кГ/см3. Приведенный момент инерции и коэффициент жесткости
плиты
'«р = ^=П5О0с*' ^Уж^^0'025 11см-
Относительный угол наклоца сечений плиты от сил резания и веса
определяется по формуле
А Ч\гпЬ ьг ^_ ч*тЬ
К хл
/с
Коэффициенты КЯх9 Кда, КдМ определяем цо графику фиг. 104. От
нагрузок дч и #2 получаем у1=.а1т = 10,8, р1 = &1/и = 4,25, /С =0,3 и
Ф2=я2лг=10,1, р2 = 62/7г = 3, АГ^ =0,12; от момента М получаем <р =
= ^/11=10,8, р1 = 61/л = 4,25, /Сд4 = 1,0.
После подстановки численных значений получаем 6 == 0,027/1000 рад.
Кроме этого, оценим возможный наибольший относительный угол
наклона плиты от сил затяжки болтов,
Болты, крепящие плиту к фундаменту, расположены тремя
рядами—два ряда на расстоянии 240 мм от концов плиты и один ряд
296
в среднем сечении плиты на расстоянии от левого края 1740 мм. В
каждом ряду расположено по два болта, каждым болтом может быть
развита сила в 4000 кГ.
Таким образом, в каждом ряду сила Р = 8000 кГ. Коэффициент Кр
определяем по графику фиг. 105.
Вычисляем вспомогательный коэффициент
Х = т1=: о,о25 • 245 = 6,15,
откуда для крайних бштов а = ат = 24 • 0,025 = 0,6 и Кр — 0,57,
для средних болтов а> 1,5 и /Ср= 0,32.
Наибольшие углы цаклона плиты, вызываемые крайними болтами,
составляют
й г, Рт* 0,016
Так как концы плиты наклоняются в разные стороны, суммарный
0,032
относительный угол составляет щтг- рад.
Для плит, выверенных при установке, следует учитывать только
действие веса изделия и силы резания.
ГЛАВА VI
КОРОБКИ
§ 1. ОБЩИЕ СВЕДЕНИЯ О КОНСТРУКЦИЯХ КОРОБОК
К коробкам относят тонкостенные детали, все три габаритных
размера которых — величины одного порядка. Коробчатую форму имеют
г) б)
Фиг. 108, Схему разъема корпусов коробок скоростей.
корпуса шпиндельных бабок, коробок скоростей, коробок подач,
фартуков, а также коробчатые столы. По весу эти детали составляют 40—
50% от общего веса станка и поэтому при
снижении веса коробок экономия металла может
быть весьма существенной.
Коробки в подавляющем большинстве
случаев выполняклся из чугуна марки СЧ
15-32; Толщины стенок обычно определяются
технологическими соображениями и
выбираются по общим правилам (см. выше).
Форма и размеры коробок определяются
условиями размещения в них необходимых
механизмов, а также технологическими
соображениями, главным образом условиями про-
4>иг. 109 Ребра (а) и двои- цесса литья. Размеры шпиндельных бабок
в^ГГстнй' жГс" в значительной степени определяются уело-
коробок у шпиндельных виями надежного направления шпинделей,
подшипников. Большинство коробок имеет форму паралле-
198
лепипедов, значительно реже применяются коробки цилиндрической
формы (шпиндельные бабки шшгошпиндельных токарных автоматов).
Фиг. НО. Варианты расположения коробок.
Коробки снабжаются перегородками для концевых опор коротких
валов и для промежуточных опор длинных валов.
Коробки выполняются
неразъемными и разъемными по осям всех или части
валов. Расположение валов в одной
плоскости обычно вызывает некоторое
увеличение габаритов коробки.
Неразъемные коробки (фиг. 108, а),
имеющие широкое применение в легких
и средних станках, требуют осевого
монтажа валов и шпинделей. Для
облегчения монтажа, где это возможно,
предусматриваются расточки, обеспечивающие
возможность узловой сборки отдельных
валов.
При наличии разъема (фиг. 108,
*б—(Э, ИЗ) облегчается монтаж валов
с комплектом сидящих на них деталей.
Из технологических соображений
диаметры соосных отверстий в коробках
станков, изготовляемых при
индивидуальном и мелкосерийном производствах, §)
по возможности выбираются
одинаковыми. В коробках станков,
изготовляемых при крупносерийном производстве,
диаметры отверстий в одной стенке
выполняются большими, чем диаметры
соосных отверстий в другой стенке, для
того чтобы иметь возможность завести
инструмент при одновременной расточке
отверстий на агрегатио-расточных
станках и в кондукторах.
Для повышения жесткости в
направлении, перпендикулярном к стенкам,
применяются специальные ребра, двои- Фиг, III. Схемы крепления корпу-
ные стенки под передним подшипником сов коробок скоростей.
шпинделя (фиг. 109) и т. д.
Бобышке для подшипников валов обычно размещаются внутри
коробки; наружу выводят только небольшую часть высоты бобышек,
позволяющую обработать торды. Если отверстия расположены близко друг
\[п*п) (яЫ
199
Фиг. 112. Корпу<
шпиндельной баб
ки токарно-винто
резного станка мо
дели 1К62.
200
Фиг. 113. Корпус шпиндельной бабки тяжелого токарного станка цодели 1680.
20*
Фиг. 114. Корпус
коробки подач токарно-винто
резного станка модели
1А62.
202
к другу и бобышки занимают большую часть площади стенки, стенка
выполняется утолщенной и обрабатывается фрезерованием или
дополнительно шлифованием.
Крышки коробок, как правило, выполняются привинчивающимися.
В легких и средних станках горизонтальные крышки коробок,
которые часто приходится открывать для регулировки механизмов, например
муфт, выполняются откидными на петлях. Тогда изоляция коробки от
попадания пыли извне и предотвращение вытекания масла
обеспечиваются пришабровкой крышки и наличием канавки для стока масла.
Жесткость таких коробок меньше, чем коробок с привинчивающимися
крышками.
Большинство коробок неподвижно крепятся к станине. Эти коробки
можно разделить на: а) коробки внешнего расположения, крепящиеся
к станине по плоскости, совпадающей с одной из стенок коробки
(фиг. ПО, а); б) коробки, утопленные в станину (фиг. ПО, б и в), причем
плоскость фланца может быть параллельна или перпендикулярна осям
валов.
Применяются коробки, перемещающиеся )по направляющим.
Коробки крепятся к станине обычно по одной плоскости,
фиксируются коническими штифтами и притягиваются винтами.
Шпиндельные бабки, требующие, как известно, очень точного углового положения
по отношению к направляющим станины, устанавливаются как на одной
плоскости, так и с дополнительным направлением по боковой грани или
призме, или с регулировкой положения винтами (фиг. 111, а—д).
Крепежные винты должны обеспечивать равномерное распределение
давления по поверхности стыка, которое не должно быть ниже 10-5-
-*-20 кГ[см2. Для размещения винтов коробки снабжаются карманами
или фланцами. Крепление коробок изнутри неудобно и связано с
вытеканием смазки.
Примеры конструктивного выполнения коробок приведены на
фиг. 112—114.
§ 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ РАСЧЕТА НА ЖЕСТКОСТЬ И РЕЗУЛЬТАТЫ
ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ ЖЕСТКОСТИ
Основным критерием работоспособности коробок в стйнках является
жесткость, поскольку жесткость коробок необходима для правильной
работы механизмов, влияем на точность обработки и на виброусто,й-
чивость системы.
Известны случаи, когда при регулировке радиально-упорных
подшипников валов возникали недопустимо большие деформации стенок
коробки, нарушавшие правильную работу подшипников, недостаточная
жесткость стенки шпиндельной бабки, несущей упорный подшипник
способствовала возникновению колебаний при резании.
В бабках тяжелых станков-наблюдалось деформирование контура,
перекосы осей шпинделей и валов и искажение плоскостности
направляющих при изменении положения бабки (например, при монтаже
шпиндельной бабки расточного станка на стойке).
Недостаточная жесткость коробок часто вызывает необходимость
снижения режимов резания при их обработке и ведет к понижению
точности обработки.
Здесь рассматриваются коробки основного типа с плоскими
стенками. Как правило, в таких коробках внутренние перегородки не могут
обеспечить одинаковый порядок упругих перемещений граней,
непосредственно воспринимающих нагрузку и ненагруженных.
203
Нагружения коробок можно разделить на два основных вида:
а) силовыми факторами, действующими в плоскости стенок;
б) силовыми факторами, действующими в плоскости,
перпендикулярной к плоскости стенок.
Нагрузки,, действующие в плоскости стенок (например,
радиальные реакции в подшипниках), вызывают деформации наружного
контура.
Нагрузки, действующие перпендикулярно плоскости стенки,
вызывают прогибы нагруженной стенки, значительно превышающие
перемещения в результате деформаций наружного контура.
Поэтому при исследовании вопроса жесткости коробок
деформациями наружного контура в первом приближении можно пренебречь.
Так как все силовые факторы, действующие на коробки, как
правило, распределены по небольшой площади контакта стенок коробки
с другими деталями, то их можно рассматривать как сосредоточенные
силы и моменты. Момент на стенке коробки возникает только в том
случае, если опоры вынесены из плоскости стенок или если они
оказывают на шпиндель (вал) некоторое защемляющее действие, например,
если шпиндель устанавливается в корпусе на длинных подшипниках
скольжения или если в одной опоре устанавливается по два подшипника
качения. Однако величины моментов относительно невелики. Поэтому
для всех деталей типа коробок жесткость можно характеризовать
перемещением точки приложения нагрузки при действии только
сосредоточенной силы. Такая характеристика жесткости может быть
использована для сравнительного анализа конструкций и ориентировочной
оценки правильности выбора размеров. По прогибу под силой, задаваясь
формой упругой линии стенки, можно приближенно оценить угол
наклона оси подшипника и сравнить его с допустимым.
Так как теоретические расчеты коробок, особенно таких, в которых
имеются отверстия, бобышки и ребра, очень сложны, технические
расчеты коробок приходится базировать на данных экспериментов.
Эксперименты проводились на квадратных пластинках со стороной
200 мм, круглых пластинах с диаметром 200 мм и на оварпых открытых
(без одной грани) коробках с соотношениями размеров 1:1:1;
1:1: 0,75; 1:1: 0,5; 1 : 0,75 : 0,75 и 1 : 0,75 : 0,5, с большей стороной
250 мм. Влияние ребер дополнительно исследовалось на балках длиной
200 мм.
При испытаниях установка пластин и балок производилась
так, чтобы практически осуществлялось свободное опирание;
коробки испытывались при установке на четырех опорах (под углами
коробки).
В качестве основного вида нагружения было принято нагружение
сосредоточенной силой (точнее, по окружности весьма малого радиуса)
Измерялись перемещения точки приложения силы. Так как в реальных
коробках нагрузка передается на стенки через подшипники, то в случае
нагружения пластины по периметру отверстия нагрузка передавалась на
пластину через специальную переходную деталь.
Установка для исследования жесткости коробок и устройство для
измерения перемещений точки приложения силы представлены на
фиг. 115.
Погрешность принятого метода измерений, в значительной степени
определяемая наличием хотя и небольших (менее 0,05 мм при проверке
щупом) зазоров на опорах, контактными деформациями в местах
приложения нагрузки и на опорах и т.п., оценивалась величинами порядка
4—6%. Так как все результаты измерений представлены в
относительных величинах—в долях от соответствующих перемещений пластины
204
или балки постоянной жесткости (измеренных аналогичным образом), то
влияние некоторых погрешностей сведено к минимуму.
Исследовалось влияние на величину перемещения точки приложения
силы следующих факторов: -
а) соотношения размеров коробок;
б) опирания сторон пластин;
в) размеров и расположения отверстий без бобышек и с бобышками
при нагружении по центру пластины и по отверстию;
д) размеров и расположения
ребер в пластинах и балках при
нагружении по центру пластины
и по ребру.
Фиг. 115. Установка для исследования жесткости коробок (а) и устройство для
измерения перемещений точки приложения силы (б):
/ — модель коробки; 2 — динамометр; 3 —индикатор, измеряющий перемещение.
Результаты измерений на коробках и пластинах с тремя и двумя
опертыми сторонами, представленные в виде коэффициентов ко к
формуле, применяемой для расчетного определения перемещения под силой
У о — «е Екъ
где к — толщина; а — половина большего размера нагруженной
грани, — приведены в табл. 37, 38; результаты измерений на балках и
пластинах с отверстиями, бобышками и ребрами приведены на
фиг. 116—122.
Анализ результатов измерений позволяет сделать следующие
основные выводы:
1. В пластинах с несколькими отверстиями в определенных
пределах существует практическая независимость влияния одного отверстия
от влияния других. Это положение вытекает из примерно линейного
характера кривых на фиг. 117, а также из сравнения величин
перемещений в пластинах с различным расположением отверстий, измеренных
непосредственно и вычисленных, исходя из относительной независимости
влияния отверстий—расхождение результатов не превышает 3—4%.
2. В исследованных пределах соотношений размеров,
соответствующих реально встречающимся, существует прямая пропорциональность
между площадыр, занятой отверстием ( или несколькими отверстиями,
расположенными на одном расстоянии от центра), и приращениями
прогиба в результате влияния отверстия. Коэффициент пропорциональ-
205
Таблица 37
Коэффициенты к0 для определения перемещения /о под силой, действующей в различных точках грани 2а X 26 открытой коробки
а) Нагруженная грань 2а X 2Ь соединяется с другими гранями открытой коробки по всем четырем сторонам
Соотношение размеров нагруженной грани а:Ь 1:1 1:0,75 I
Соотношение размеров коробки а:Ь:с 1:1:1 I 1:1:0,75 I 1:1:0,5 1:0,75:0,75 I 1:0,75:0,5
Точки приложения силы 1 2 \ 3 \ 1 2 \ 3 \ 1 2 \ 3 \ 1 2 \ 3 \ 1 2 3
. ^4с!?Гк V 0,18 0,24 0,18 0,20 0,28 0,20 0,21 0,31 0,21 0,13 0,18 ОДЗ 0.13 0,20 0.13
^)1^Ш( 2' а24 °'35 °*24 0,2В ом °'28 °'31 0,5° 0,Э1 °'21 0,3° °'21 0>22 0,за °'22
^ Ч,и~^У 3' 0,18 0,24 0,18 0,20 0,28 0,20 0,21 0,31 0,21 ОДЗ 0,18 ОДЗ ОДЗ 0,20 ОДЗ
б) Нагруженная грань 2а X 2Ь соединяется с другими гранями открытой коробки по трем сторонам; одна сторона свободна
.Соотношение размеров нагруженной грани а\Ъ 1:1 1:0,75 [ 1:0,5
Соотношение размеров коробкн а\Ь\с 1:1:1 1:0,75:1 I 1:0,75:0,75 1:0,5:1 I 1:0,5:0,75
Точки приложения силы |/ 2 \ 3 \ 1 \ 2 | 3 | / \ 2 \ 3 \ 1 2 3 1 2 I 3
ъ-2а-\ V 0,16 0,25 0,16 0,15 0,20 0,15 0Д5 — 0Д5 0,08 0,09 0,08 0,08 — 0,08
у^|:ч^ 2' 0/3° °'48 °'30 °'29 °'45 °'29 °'28 °'42 °'28 °'19 °'28 °'19 °'18 °>27 °>18
3) 1 _П 3' 0,43 0,70 0,43 0,39 0,62 0,39 — 0,62 - (У,34 0,51 Н 0,34 - 0,48 -
VI—Х.^ 4' 0,95 1,40 0,95 0,77 1,16 0,77 — 1,16 — 0,62 0,92 0,62 — 0,69 —
Условные обозначения опорных закреплений:
сторона, по которой происходит соединение двух граней коробки;
^^ —свободный край.
206
Таблица 38
Коэффициенты ко для определения перемещения /0 под силой, действующей
в различных точках квадратной пластины при различных способах опорных закреплений
Опорное
репление
Пластина оперта по
всем четырем сторонам
/ 2 У 4 5
Точки
приложения
силы
и^
-2
)
1
1
с?-—
\
о
■^
\
Пластина оперта по трем
сторонам
> 2 3 4 5
-2а-
ч
7
\
-^
Пластина оперта по двум
противоположным сторонам
12 3*5
и
2а—\
2
0,68
1,20
0,68
3
0,54
0,92
0,54
4
0,68
1,20
0,68 ]
2>
3'
4'
0,27
0,37
0,27
0,37
0,56
0,37
0,27
0,37
0,27
0,29
0,38
0,29
0,47
0,73
0,47
0,61
1,09
0,61
1,34
2,34
1,34
1,36
2,44
1,36
Условные обозначения опорных закреплений:
—- —шарнирно опертая сторона;
"""^ —свободный край.
1,36
2,44
1,36
ности зависит от расстояния центра отверстия до точки приложения
силы (см. фиг. 116, а, 117).
3. При нагружении по отверстию (при действии равномерно
распределенной по краям отверстия нагрузки) влияние увеличения диаметра
отверстия определяют два фактора — ослабление пластины большим
отверстием, увеличивающее прогибы, и распределение нагрузки по
контуру большего диаметра (т. е. приближение нагрузки к опорам),
уменьшающее прогибы. При малых диаметрах отверстий преобладает
влияние ослабления пластины, при больших — преобладает влияние^
приближения нагрузки к опорам (фиг. 116,6).
4. Увеличение высоты и диаметра бобышек с точки зрения влияния*
На жесткость целесообразно до определенного предела, так как с
увеличением этих параметров относительное влияние их приращения на
прогиб уменьшается. Влияние диаметров отверстия (й) существенно до
величин -7 порядка 1,4—1,6. При больших величинах -р- (при м!а-
лых й) отверстия в бобышках на величину перемещений практически
не влияют (фиг. 118 и 119).
5. Влияние ребер на местную жесткость стенок относительно
невелико и при реальных соотношениях размеров не превышает 20—30%*
С точки зрения влияния на жесткость увеличение высоты ребер
целесообразно до определенного предеда, зависящего от ширины и типа
ребер (фиг. 120, 122).
6. В балках влияние диагональных ребер, как и следовало ожидать*
существенно больше влияния поперечных ребер (фиг. 120).
Наибольшее влияние ребра оказывают в том случае, если они размещаются
в наиболее нагруженных участках балки. Местное повышение жесткости
в малонагружениых участках оказывается нецелесообразным (фиг, 121),
7. При действии сосредоточенной силы на верхнюю грань коробки,
если все четыре стороны нагруженной грани соединяются с другими
гранями, прогибы под силой с увеличением высоты коробки уменьшаются.
20?
О 0,01 ОМ 003 1М 0.05\ афГппас>п] )
а) щПГ\Ь~
Фиг. 116. Зависимость перемещения / точки под силой, действующей иа пластину
постоянной толщины, от размера и расположения отверстий:
а — нагружение по центру пластины (за единицу принято перемещение /0 в пластине без отверстия);
б — нагружение по отверстию (за единицу принято перемещение /0 точки, соответствующей центру
отверстия, в пластине без отверстия), ^отй — площадь отверстия; ^пласт— площадь пластины.
N4
:Ы \г=ЬОим
г^\ 9=80мм
ь №3
№2
N01
/ 2 3^56
Число отверстий на пластинах №1и №2
Цисло пар отверстий на пластинах №3 и N4
Фиг. 117. Влияние отверстий, расположенных равномерно по окружности, на
перемещение / точки под силой, действующей в центре пластины (за единицу
принято перемещение /о в пластине без отверстий) ;ги/? — радиусы расположения
отверстий.
Примечание. Отверстия диаметром 25 мм сверлились последовательно в порядке,
указанном цифрами на эскизах, перемещения измерялись после сверления каждого отверстия (или
пары отверстий).
"•"о т т о.об о,о8 аю~ оп лр\
Фиг. 118. Зависимость перемещения /
точки под силой, действующей в
центре квадратной свободно опертой
пластины, от высоты бобышек (за
единицу принято перемещение /0
точки под силой в пластине постоянной
толщины к). Кривые линии на
графике:
сплошные — эксперимент; штриховые —
расчет по полной высоте бобышек; штрихпунктир-
ные —расчет по акшвпой высоте бобышек
см . ниже).
0,06 0,08
б)
0,10 0,12 ~1Г
га 2а
Фиг. 119. Зависимость перемещения / точки
под силой, действующей на квадратную
свободно опертую пластину, от размеров и
расположения отверстий, подкрепленных
бобышками (за единицу принято
перемещение /о под силой в пластине постоянной
толщины к):
а — нагружение по отверстию; б — иагружение в
центре квадратной пластины. Кривые линии на графиках
сплошные — эксперимент, штрихпунктирные — расчет
по активной высоте бобышек. '
0.95
09€
0.85
0,80
| = 0,035,
-2=г^1
1^-МН
4^ 41 *
и—1 = 200—~^ .
1 !
0,1
02
0,3
Фиг. 120. Зависимость перемещения / точки
под силой, действующей в середине
свободно опертой балки, от высоты поперечных и
диагональных ребер (за единицу принято
перемещение /0 под силой в балке
постоянной жесткости высотой к). Кривые линии
на графике:
сплошные — эксперимент, штриховые — расчет по
полной высоте ребер,. штрихпунктирная — расчет по
активной высоте ребер (см. ниже).
*
Фиг. 121. Зависимость перемещения
/ точки под силой, действующей в
середине свободно опертой балки, от
расположения поперечных ребер (за
единицу принято перемещение /о под
силой в балке постоянной жесткости
высотой к).
209
Это объясняется тем, что жесткость каркаса, образованного
вертикальными стенками коробки, не соединенными снизу, с увеличением высотьь
этого каркаса увеличивается.
Если только три стороны нагруженной (верхней) грани
соединяются с другими гранями коробки, а один край свободен, с увеличением
высоты коробки прогибы под силой увеличиваются. Это объясняется
тем, что жесткость каркаса, образованного тремя вертикальными
стенками и дном, с увеличением высоты
вертикальных стенок уменьшается,
так как увеличивается
деформируемая высота стенок (табл. 37).
§ 3. ОБЩАЯ МЕТОДИКА РАСЧЕТА
КОРОБОК НА ЖЕСТКОСТЬ *
Расчет коробок может быть
сведен к расчету их плоских
разверток, т. е. неразрезных пластин.
Определение деформаций
каждой из прямоугольных пластин,
составляющих неразрезную пластину,
так же как и прямоугольных
пластин с жестко или упруго
защемленными или свободными краями,
можно производить следующим
образом [42], [47].
Выбирается основная система —
все пластины, составляющие
неразрезную пластину, считают свободно
опертыми.
Упругая поверхность каждой
из рассматриваемых пластин
выражается в виде суммы упругих поверхностей — от действия заданной
нагрузки ^и контурной нагрузки, действующей по краям пластины и
устраняющей разницу в деформациях основной системы и заданной.
Функция прогибов от контурной нагрузки, действующей на каждом из краев,
по которым данная пластина соединяется с другими или свободных,
выражается в виде двойных ряддв, содержащих только одну группу
постоянных защемления. Для определения этих постоянных исполь
зуются условия равенства углов наклона смежных пластин на общих:
опорах или условия равенства нулю перерезывающей силы по
свободным краям от действия заданной и контурных нагрузок. Так как
прогибы от контурной нагрузки выражаются в рядах, то прогибы от
заданной нагрузки также представляют в виде рядов. При этом уравнения
для определения постоянных получаются из условия равенства
коэффициентов соответствующих рядов при одинаковых гармониках. Если число
членов рядов, принятое в решении,—&, а число краев пластин, по
которым действует неизвестная контурная нагрузка, — п, то для
определения неизвестных потребуется решение системы пк уравнений.
Оценивая точность такого решения, можно показать, что для
большинства практически встречающихся случаев удовлетворительная
точность получается уже при двух членах рядов. Кроме того, если в
системе пластин, образующих неразрезную пластину, нагружена только-
одна, то достаточная точность получается при рассмотрении деформаций;
1 Технический расчет с необходимыми пояснениями приведен в § 4.
210
°'21,0 15 10 2,5 Л0%
Фиг. 122. Зависимость перемещений ^
точки под силой, действующей на
квадратную свободно опертую пластину, от
высоты ребер (за единицу принято
перемещение /о под силой в пластине
постоянной толщины К).
Кривые линии на графиках:
сплошные — эксперимент, штриховая— расчет по
полной высоте ребер, штрихнунктирная — расчет
по активной высоте ребер, 1 —сила приложена в
центре пллоины; 2— сила приложена в точке
пересечения оси пластины с осью ребра, 3—сила
приложена в точке пересечения ребер.
только нагруженной пластины и с ней смежных. При этих упрощениях
максимальное количество неизвестных, которое потребуется определить,
будет равно восьми. Некоторое дополнительное упрощение решения
можно получить, если в симметричной системе действие симметричной
и кососимметричной составляющих нагрузки рассматривать отдельно.
Поскольку за основную систему выбирается пластина, свободно
опертая по всем четырем краям, указанное решение может быть
использовано лишь для тех комбинаций пластин, решения для которых при
условии свободного опирания их краев известны. Для пластин с
ребрами, произвольным образом расположенными отверстиями, бобышкам»
в настоящее время таких теоретических решений нет.
Ориентировочно влияние отверстий, подкрепленных бобышками,
можно оценить, рассмотрев задачу о деформациях пластины с
прямоугольными участками, жесткость которых выше жесткости остальной
части пластины. Приближенный расчет пластин с такими
«квадратными» бобышками можно производить, используя решения задач о
деформациях свободно опертой пластины под нагрузкой, действующей на
узком участке, параллельном одной из сторон [11], [61]. В таких задачах
уравнение, выражающее упругую поверхность нагруженного участка
пластины, представляется в виде суммы гю = гю1^гю2, где т&)\ — частное
решение дифференциального уравнения для нагруженного участка
пластины; 102 — общее решение соответствующего однородного уравнения.
Если интенсивность нагрузки не изменяется по ширине (т. е. по-
оси У, фиг. 123, а) нагруженного участка, то этот участок можно
рассматривать как свободно опертую полоску — балку. В этом случае прогибы
Ш\ можно рассматривать как прогибы двухопорной балки и выразить
их в тригонометрической форме:
2пп (а -4- х)
а*81п—Чг^'
При этом упругая поверхность нагруженного^участка
2Л . пк (а + х)
Таким образом, выражения для упругой поверхности нагружен-
ного участка при разной нагрузке (не изменяющейся по ширине
участка) отличаются только коэффициентами ап.
Если на нагруженном участке имеется «квадратная» бобышка
шириной, равной ширине участка, то этот участок можно рассматривать
как балку переменной жесткости. Выразим прогибы такой балки в
тригонометрической форме и определим коэффициенты ап. Для этого
вместо балки с бобышкой рассмотрим эквивалентную ей, т. е. получающую
такие же деформации, балку без бобышек. Деформации этих балок
будут одинаковыми в том случае, если балка без бобышек
дополнительно будет нагружена некоторой нагрузкой, которая подбирается
так, чтобы для обеих рассматриваемых балок было обеспечено
тождество приведенных (к одной жесткости) эпюр изгибающих моментов.
211
г
г*1
ЧЬШ
Г
сГ X
КГ
1^2№2|
<Г X
Влияние бобышек на жесткость оценим для двух случаев — для
случая действия нагрузки непосредственно на бобышку и на
некотором расстоянии г от бобышки. Для простоты примем, что нагруженный
участок пластины с бобышкой расположен симметрично относительно
оси X (фиг. 123, а). Так как в коробках осевая сила, действующая на
бобышку через подшипник, распределена по окружности, то для оценки
влияния нагруженной бо-
у\ бышки рассмотрим
действие на бобышку
равномерно распределенной
нагрузки цу = щ^г ДЛя
оценки влияния ненагру-
женной бобышки
рассмотрим действие нагрузки
Р
Я — птг > распределенной
вдоль оси У по ширине
участка с бобышкой.
На фиг. 123, б
приведены схемы \нагруже-
ния участка пластины
с бобышкой,
рассматриваемого как балка
переменной жесткости, на
фиг. 123, в — эпюры
изгибающих моментов,
приведенных к жесткости
основной части балки, на
фиг. 123, а — схемы на-
гружения эквивалентных
балок постоянной
жесткости. Силовые факторы,
обеспечивающие
тождество эпюр изгибающих
моментов, равны:
Р
д' = кг- , распределенной вдоль
«*тМИ^
I р р
Нагрузка д"-ЩЩ
распределена по
площади бобышки
Р
Нагрузка ?'в^у*
распределена вдоль оси У по
полоске длиной 2Ь}
Фиг, 123. Расчетная схема для оценки влияния
бобышки на жесткость пластины.
для Случая действия нагрузки
оси У
для случая действия равномерно распределенной нагрузки ц' = 2Ь2Ь
на бобышку
(1 + т): ".-4(>-*)('-^ *--№
Л = 4(ь
/*з
мг = .
■(>
я*
1 + -
г~ Ь2);
М-
.-4(»-ж)(»-т)С"+'-».)-
Выразив прогибы балки постоянной жесткости в форме
тригонометрического ряда как сумму прогибов от каждого силового фактора
(Рь Р2, М\ и т. д.) в отдельности (выражения для прогибов балок
212
в тригонометрической форме при элементарных видах нагружения см.г
например, [62]), получим коэффициенты ап:
для случая действия нагрузки ц' = ^, распределенной вдоль оси У
16А*3 1 [ . тс Г пп(а-г). гпсЬ2 ,
_|81п^^а^со8 \а '51П-5Г +
71+Е1
О
, ПТС Л Г \ . Я71 (а — Г) . Л1Г^3
+ ~Т(1-Т)5Ш 2а 81П^~
П*Чс05П*(*~Г)С05^
Р
для случая действия равномерно распределенной нагрузки ^ = ^-^
на бобышку
16Ряз 1 Л1г(л —г) ( 2а . п%Ь2 ^ Г 2а яяб,
тс гЬ2 ппЬ2 , тс (а — г) ,
-ТГ-г-с08Т._с1в Б— +
+-т('-±~г)-^Ч|:
здесь
Я/0 = 261Л; Д = 12 (1 _ |х2) ' а=1 —• т/Г •
Подставив эти выражения для ап в общую формулу для ш,
получим приближенную1 формулу для определения упругих перемещений
пластины на нагруженном участке с учетом влияния «квадратных»
бобышек.
Для того чтобы учесть влияние формы бобышки — круглой с
отверстием, в расчет следует вводить не фактическую (Я), а приведенную
(И\) толщину пластины с бобышкой. Принимая сторону «квадратной»
бобышки, равной диаметру круглой бобышки с отверстием диаметра йу
приведенную толщину Нх можно определять, полагая, что на площади
В2У занятой квадратной бобышкой, влияние на жесткость участков
разной высоты пропорционально площади этих участков и высоте в
третьей степени- Тогда величина а, входящая в выражения для ал,
определится по формуле
0*2 \ №
->-&)'
0,785|(1 -ж ж-1
0,215 + 0,785
Однако, как показывает сравнение результатов расчетов и
экспериментов, если при определении приведенной высоты Н\ бобышки
учитывать ее полную фактическую высоту Я, то влияние бобышек на
жесткость, определенное расчетом, окажется значительно большим, чем это
имеет место на самом деле. Расхождение результатов оказывается тем
бблышш, чем дальше бобышка отстоит от зоны приложения нагрузки.
1 В приведенном решении не учитывается, что наличие бобышки изменяет упругую
поверхность пластины не только в направлении оси X, но и в направлении оси У,
Поэтому перемещения, определяемые по указанным формулам, будут несколько больше
фактических.
213
Это объясняется тем, что в высоких бобышках, так же как и в высоких
узких ребрах (см. «иже), напряжения не распространяются на весь
объем материала и что нагруженная и ненагруженная бобышки
находятся в разных условиях — напряженное состояние бобышки под
нагрузкой приближается к осесимметричному, тогда как у отдаленных от
нагрузки бобышек напряжения и деформации по одной из осей могут
быть существенно больше, чем по другой. Поэтому приведенная
высота бобышек должна определяться не по фактической, а по «активной»
высоте На.
«Активная» высота бобышек для соотношений размеров, типичных
для деталей станков, ориентировочно может быть определена по
кривым, (приведенным на фиг. 124, построенным по результатам проведен-
Фиг. 125. Зависимость относительной ак-
тивнои высоты —- ребер от полной
относительной высоты —г~:
/ — пластины; 2 — балки с диагональными
ребрами; 3 — балки с поперечными ребрами.
яых расчетов и экспериментов1. Влияние ребер, применяемых для
увеличения общей жесткости стенок, ориентировочно можно оценить,
рассчитывая пластину с ребрами, как имеющую некоторую постоянную
приведенную толщину кпр. Приведенная толщина определяется из условия
равенства моментов инерции сечения пластины приведенной толщины
и пластины с ребрами. Сравнение результатов таких расчетов с
результатами экспериментов показывает, что и в этом случае в расчет должна
вводиться не полная высота пластины с ребрами Я, а «активная» ЯЛ,
так как в ребрах напряжения не распространяются на весь объем
материала.
Следует отметить, что расчет балок с ребрами также следует
проводить не по фактической, а по «активной» высоте На (фиг. 125). При
этом перемещения в балках с диагональными ребрами предлагается
определять по жесткости сечения, перпендикулярного к оси балки.
Влияние поперечных ребер (перпендикулярных к оси балки) ориентировочно
можно учитывать умножением жесткости балки на коэффициент
повышения жесткости
А=1—я+г-тО-^-).
где / — длина балки;
к— высота сечения балки;
п — количество поперечных ребер;
Ь— толщина поперечных ребер/
1 Естественно, что некоторые отклонения расчетной схемы от действительной
также в какой то степени сказываются на величинах На по фиг. 124.
214
*
щ
{6
■До
№
\л
#л\
^
<г
«*ч
^
V
Г* гтттг^Ш1
■?72}/?К77ГЛ {
Зг
^т
12 14 16 18 20 12 2'/
активной высоты
Фиг. 124. Зависимость относительной
тт
—— бобышки от
к
полной относительной высоты —— .
/г
Изложенная общая методика расчета коробок на жесткость ввиду
своей громоздкости и технических трудностей, возникающих при
расчете, непригодна для технического расчета. Для того чтобы иметь
возможность обобщить результаты экспериментов и оценить влияние
жесткости отдельных граней, защемления сторон, влияния бобышек и т. п.,
по общей методике были решены некоторые частные задачи о
деформациях коробок и пластин с разным закреплением сторон. Результаты
этих расчетов, представленные в виде коэффициентов &0 к формуле
перемещения ПОД СИЛОЙ /о~А • ^Ет^ ' пРивеАеНЬ1 В табл- 39'
Анализ результатов расчетов позволяет сделать следующие
основные выводы:
1. Оценивая влияние отдельных факторов — закрепления сторон
нагруженной грани, ребер и бобышек на прогиб под силой, можно видеть,
-что в определенных пределах существует практическая независимость
влияния на прогиб одного фактора от влияния других. Так, например,
в табл. 39 можно видеть, что соотношения между величинами
перемещений под силой в пластинах постоянной жесткости, с абсолютно
жестким ребром и бобышкой при разных видах закрепления сторон
нагруженной грани примерно одинаковы — расхождение не превышает
-2-3%.
2. Прогиб 1Под силой в основном определяется жесткостью
нагруженной грани коробки и с ней смежных, влияние остальных граней
-весьма незначительно. Так, например, сравнивая величины
перемещений под силой, действующей на грань куба и на соответствующую
'Неразрезную пластину, которую можно рассматривать как неполную
развертку куба (включающую нагруженную и смежные с ней грани),
можно видеть, что расхождение результатов не превышает 3—4%.
3. Наибольшее относительное влияние на прогиб оказывает
увеличение жесткости в месте приложения нагрузки. Так, например,
перемещение под силой, действующей на квадратную пластину со стороной
"2а, с абсолютно жесткой квадратной бобышкой со стороной 26 = 0,4а,
на 45% меньше, чем перемещение под силой в (пластине без бобышки.
Перемещение под силой в пластине с абсолютно жестким ребром
меньше, чем перемещение в пластине с бобышкой, всего на 6%.
Увеличение жесткости грани, смежной с нагруженной, оказывает на прогиб
-относительно меньшее влияние (порядка 10—30%—большие значения
при действии силы вблизи грани бесконечно большой жесткости).
4. Ребра, подкрепляющие бобышку, дают больший эффект с точки
зрения'увеличения жесткости в том случае, если они располагаются
перпендикулярно к двум наиболее жестким граням коробки. Так,
например, при наличии свободного края при одинаковой жесткости стенок
коробки и одинаковом расстоянии от точки приложения силы до
взаимно-перпендикулярных опертых сторон нагруженной грани
целесообразно располагать ребро параллельно свободному краю.
Сравнение результатов расчетов и экспериментов для пластин,
опертых по трем сторонам (см. табл. 38 и 39), показывает, что во всех
случаях, кроме случая нагружения пластины у свободного края,
расхождение результатов не превышает 3—4%.
Для случая нагружения у свободного края, как и следовало
ожидать, расхождение результатов больше и составляет около 10%. Это
объясняется тем, что при нагружении у свободного края форма
упругой поверхности хуже апроксимируется выбранными рядами, а
результаты расчетов получены при двух членах рядов.
Сравнение результатов расчетов и результатов экспериментов для
коробок (см. табл. 37 и 39) показывает, что для всех случаев, кроме
215
Коэффициенты к0 для определения перемещения
Схема
нагружения
Схема пластины
Квадратные пластины
□
ШШ
шцщ
□
1. Нагруженная грань имеет постоянную толщину к (коэффициенты
±
№
0,517
0,234
0,267
0,302
0,298
0,319
0,324
0,417
0,387
±
1Щ-
0,352
0,139
0,249
0,141
0,250
0,260
0,283
0,928
0,318
±
маТ~
0,352
0,139
0,141
0,797
0,250
0,829
0Д54
0,156
ОД 68
0,352
0,139
0,149
0,154
0,157
0,160
0,283
0,352
0,291
0>5а
0,352
0,139
0,149
0,154
0,157
0,160
0,154
0,165
0,291
2. Нагруженная грань толщиной Л имеет участки, жесткость которых принимается
±
0,283
0,125
0Д44
0,164
0,161
0,174
ОД 76
0,229
0,211
±
0,252
0,109
0,125
ОД 87
0,252
0,092
0Д43
0*221
0,109
0,130
-шарнирное закрепление; наклонная штриховка — же-
Условные обозначения опорных закреплений:-
сткое закрепление; '—"• свободный край. В коробках и неразрезных пластинах нагруженная грань
заштрихована. Грань, принятая абсолютно жесткой, обозначена двойными линиями.
Примечание. Некоторое незначительное несоответствие в величинах к0 объясняется тем, чтв
они подсчитаны при двух членах разложения, а сходимость рядов для разных схем неодинакова.
216
/о под силой Р, действующей на квадратную пластину.
Таблица 39
или коробкн
□
п
□
Куб с гранями
одинаковой жесткости
вв
®
Куб, у которого
жесткость одной
грани принята
бесконечно большой
Ш%{\
ш&
ш
Керазрезные пластины
пм .
С1Р СЖЗ
1 1И1 г
и
вычислены на основе общих методов расчета)
0,461
0,369
0,178
0.288
0,941
0,553
1,089
0,182
0,371
0,371
0,756
0,395
1,223
0,469
0,469
0,457
0,230
0,939
0,270
0,270
0,324
0,218
0,218
0,218
0,218
0,329
0,222
0,222
0,222
0,222
0,422
0,159
0,957
0,257
0,257
0,296
0,248
0,151
0,207
0,207
0,458
0,231
0,982
0,272
0,272
0,426
0,158
0,980
0,260
0,260
0,333
0,223
0,223
0,223
0,223 1
| 0,280
0,220
0,152
0,211
0,2 П
бесконечно большой (коэффициенты вычислены на основе приближенных методов расчета))
0,254
0,339
0,146
0,305
0,291
—
0,419
0,372
0,546
0,251
0,222
0,352
0,176
0,155
0.155
0,178
0,158
0,158
0,232
0,204
—
0,160
0,141
0Д21
0,252
0,222
0,368
0,234
0,206
—
0,181
0,160
0,160
0,162
0,143
0,122
217
случая нагружения у свободного края, расхождение результатов не
превышает 8—10%.
Для пластин с бобышками (см. фиг. 118 и 119) сравнение
результатов экспериментов и расчетов по «активной» высоте бобышек
показывает, что расхождение результатов не превышает 3—6%.
Расхождение результатов расчетов по «активной» высоте и экспериментов для
балок и пластин с ребрами (см. фиг. 120 и 122) оказывается равным
3-5%
1
§ 4, ТЕХНИЧЕСКИЙ РАСЧЕТ КОРОБОК
Предлагается следующий порядок расчета, проводимого как
проверочный в форме определения перемещения под силой:
1. Выделяется нагруженная грань коробки и для этой грани»
полагая ее имеющей постоянную толщину Л, вычисляется перемещение точки
приложения силы /0-
2. Влияние отверстия и бобышки под силой учитывается
введением в расчет коэффициента кх.
Влияние на перемещение под силой остальных- отверстий и
бобышек нагруженной грани учитывается коэффициентом &2, влияние ребер—
коэффициентом &3.
3. Определяется искомая величина перемещения / под силой
1. Определение перемещения /о нагруженной стенки постоянной
толщины к
Величина перемещения под силой зависит от координаты точки
лриложения силы и соотношения размеров коробки — размеров
нагруженной грани 2а (больший размер) и 26 и третьего размера 2с. При
'Определении перемещений в коробках предлагается пользоваться
результатами экспериментов, приведенными в табл. 37.
Для определения перемещения точки приложения силы следует:
а) определить соотношение размеров коробки (при наличии
в коробке внутренних жестких перегородок можно рассматривать
только часть коробки, ограниченную ближайшей к нагруженной грани
перегородкой); координату точки приложения силы выразить в долях
от а и Ь\
б) по табл. 37 для рассматриваемой коробки определить
коэффициент ко для заданной точки нагруженной грани;
в) определить перемещение в рассматриваемой точке коробки по
формуле
1 —Ь Ра*У -<*>
у о — Ко 2?#$ >
где к — расчетная толщина пластины;
а — половина большего размера нагруженной грани;
Е и |х — упругие постоянные материала коробки.
В том случае, если рассматриваемая схема близка к тем,
результаты расчета которых приведены в табл. 39, для определения
коэффициента к0 можно пользоваться указанной таблицей.
1 «Активная» высота определялась из сопоставления результатов расчетов и
экспериментов, что и обусловливает их хорошее совпадение. Однако расхождение резульи
татов расчетов и экспериментов объясняется не только тем, что при большой высоте
.ребер работает неполная их высота, но также тем, что ребра находятся в условиях
более сложного напряженного состояния, чем это принимается при таком расчете.
В некоторых случаях расчет по «активной» высоте может дать несколько большую
(до 10—15%) погрешность.
218
2. Определение коэффициентов к\, к2у кг
Коэффициент ки учитывающий влияние отверстия и бобышки под
силой, определяется по кривым, приведенным на фиг. 126; коэффициент
№Ш
0,01
0,02
0,03
б)
№
0,05
006
Ж.
2а2Ь
«Фиг. \2% Коэффициент ки учитывающий влияние отверстия с бобышкой на величину
упругого перемещения под силой при действии силы на бобышку:
а — для —-- — 1,2; б — для —г
й а
1,6.
к2, учитывающий влияние нечагруженных отверстий и бобышек,
определяется при помощи кривых, приведенных на фиг. 127. Кривые»
приведенные на графиках фиг. 126 и 127, построены для двух средних
значений ^= 1,2 и -^ =1,6.
219
Для соотношений размеров, при которых влияние подкрепления*
бобышкой превалирует над ослаблением пластины отверстием, кривые
V?
Щ 0,2
V
10
0,9
0,8
0,7\
0У5\
"2222222.
й
ш
-а'Ы-А
77
- 2а(2Ь) -
шдля~
'0,3
для а> =^5
для
а'
-а?
0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,0д 0,09 0,1 ^^
а2
№-ШТ
2*1,64
И
Ь4
п
2о(2Ь) —-
-длй-%-0,3
для ^0,5
для-#=0,7
0,0! 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,1-^Ш
|_- I I »., I, 1 а2
0,01 0,02 0,03 Ф^'Шь
*)
Фиг. 127. Коэффициент &2, учитывающий влияние отверстий и бобышек,
расположенных на расстоянии /? от точки приложения силы Р, на величину упругого перемещение
под силой: / — перемещение точки приложения силы в пластине без отверстия; Д/ —
приращение перемещения в результате влияния отверстия и бобышки;
0 1 О К 0
а — для —г- — 1,2; б — для —г- =
а а
1,6
построены на основе расчетов по общей методике. Кривые,
позволяющие оценивать влияние отверстий без бобышек и с бобышками, не
компенсирующими ослабление пластин отверстиями, построены по
результатам экспериментов.
220
Из кривых, приведенных на фиг. 126, видно, что влияние
координаты расположения нагруженного отверстия с бобыщкой (—\ весьма
незначительно. Кривые, приведенные на фиг. 127, построены для случая
приложения силы в центре пластины, и коэффициент к2 является функ-
п
цией отношения расстояния от точки приложения сшШ, т. е. от
центра до центра отверстия к половине стороны пластины. Отдельные
опыты показали возможность использования этих графиков и для тех
«лучаев, когда сила приложена не в центре, но в центральной области
нластины (погрешность не превышает 5-^6%). В этих случаях вместо ~
следует вычислять — , где # — по-прежнему расстояние от точки
приложения силы (при нагружении по отверстию— от центра нагруженного
отверстия) до центра рассматриваемого отверстия, а аг—расстояние от
точки приложения силы до опертой стороны пластины, ближней к
рассматриваемому отверстию.
Для определения коэффициентов к\ и к2 следует:
1. Вычислить соотношения размеров элементов: для отверстий
с бобышками ^а -2Ь ' ~2Г' ~7Г й ИГ или ~~а и для ОтвеРстий без бо*
2. Определить «активную» относительную высоту На бобышек по
кривым, приведенным на фиг. 124.
3. Определить к\ по кривым, приведенным на фиг. 126.
4. По кривым, приведенным на фиг. 127, определить величину от-
Д/
иосительного приращения перемещения точки приложения силы у
в результате влияния ненагруженных отверстий и бобышек и
определить #2 по формуле
Если на нагруженной грани пластины, кроме нагруженного,
расположено только одно отверстие, величину к2 можно определи 1Ь
непосредственно по графикам, приведенным на фиг. 127, пользуясь
шкалой &2.
Следует отметить, что ненагруженные отверстия и бобышки,
расположенные у свободного, не опертого, края нагруженной грани, из
рассмотрения следует исключить.
Поскольку влияние ненагруженных граней коробки на перемещение
под силой относительно невелико, влияние отверстий и бобышек в
ненагруженных гранях полагается малым и не учитывается.
Если площадь, занятая бобышками, весьма велика и они
подливаются друг к другу, целесообразно влияние отдельных бобышек не
рассматривать, а расчет вести по приведенной толщине стенки.
Приведенную толщину Нпр целесообразно определять, принимая, что влияние
на жесткость участков разной толщины пропорционально их площади
и кубу высоты, по формуле
где к — толщина стенки;
Н—толщина стенки с бобышкой;
Рбоб — площадь, занятая бобышками, за вычетом площади отверстий;
г — площадь пластины.
221
Для коэффициента к3, учитывающего влияние ребер, прилитых
к стенкам, можно принимать следующие значения:
1. Для ребер под бобышками, через которые передается основная
нагрузка, в том случае, если ребро подлито к соседней стенке, имеющей
толщину того же порядка, что и нагруженная, ориентировочно можно
принимать к3 = 0.8-:-0,9.
2. Для ребер, предназначенных увеличивать общую жесткость
стенок, можно принимать й3 = 0,75^-0,85 (меньшие значения для системы
пересекающихся ребер, большие —для не связанных между собой
ребер).
В первом приближении влияние ребер можно учитывать, «производя-
расчет по (приведенной толщине стенки, определяя последнюю из
условия равенства моментов инерции стенки приведенной толщины и стенки
с ребрами. При этом в расчет должна вводиться не полная высота
стенки с ребрами Я, а активная На> определяемая при помощи кривых,
приведенных на фиг. 125, в зависимости от -^-. Расчеты реальных
конструкций коробок станков, проделанные по предлагаемой методике,
показали хорошее совпадение с экспериментами.
Так, например, для корпуса передней бабки станка 1К62 при нагру-
жении осевой силой Р = 510 кГ по оси шпинделя измеренное
перемещение под силой / = 0,085 мм, вычисленное / = 0,1 мм;
3. Пример расчета корпуса коробки скоростей
Определим перемещение под силой для коробки скоростей
токарного станка. Размеры коробки 2а : 2Ь : 2с = 550 : 360 : 560.
Нагруженная передняя стенка коробки с размерами элементов представлена на
1
Разрез по ДД-55 Разрез по 68
Фйг. 128. Передняя стенка коробки.
фиг. 128. Действующая сила Р —300 кГл Нагружение осуществляется
по шпиндельному отверстию Л
1. Определение перемещения /о под силой
х _- />д»(1-е«)
/о — «о 2Ш »
55
Р = 300 кГ, а = -у- = 27,5 см; А= 1 см; Е= 1,0 • 106 кГ\см*; [*=0Д
Соотношение размеров коробки 2а : 26 :2с = 1 :0,6:1.
Соотношение размеров нагруженной грани 2а: 26» 1 :0,6*
222
Координаты точки приложения силы
л; = 0,5я; у = 1,16.
По табл. 37 коэффициент ко для случая приложения нагрузки
в точке с координатами х = 0,5а; у= 1,16 для коробки с соотношением
размероз 1:0,75.1 равен 0,31, для коробки с соотношением размеров*
1 : 0,5 : 1 равен 0,22.
Отсюда, для заданных соотношений размеров можно принять
к0 = 0,26 и
г А п^ 300 • 27,52 . 0,91 Л Лс-, Л сА
/о = 0,26 1 о . {да ; 1— ^ °'05^ см — °>54 мм-
2. Определение коэффициентов к1у къ к%.
Отверстие /:
А-.-Ю-0. _^_~99. °2 - 195 -ОЮ-
Л ~~ 10 ~*' А ~^> 2а -2Ь " 550-360 ~и'1У'
а ~ 160 ~ !'А а "" 275 ~~ иДУ' *1 —Ц40.
Отверстие //:
Л-.40-4- А _Ж_ 0 48- -22—17-
Л ~ 10 ~ *> а' "" 415 ~~ и/*°' Л ~ х'' >
Р2 _ 1202 __ПЛТО. Д _ 120 _ - А/ _ П1-
2а . 26 " 550 • 360 " и>и/С>> "7 ~ Ж" ~~ 1,°' "7" ~ '
Отверстие ///:
и 40 А. Я _ 200 п ,„ и* ~ 1 т.
Д2 __ НО2 п000. Я_140_. <. А/ _ о1Я
2а. 26 ~ 550 . 360 ™ У>иУУ> 1Г ~ ~95~ ~ 1>*6* ~/~ ~~ ~ '
Отверстие /V:
^ — 15 -^ 1 е. Я __ 145 __ п 73- ^ _1 ос.
Л ~ 10 "~ 1)0' ^ ~ 200 — и''*' ~~ 1>*°>
& _ ВО2 ^._80__123' -М- + 002
2а . 26 ~~ 550 • 360 ~ и,ША <* — 65 ~~ 1'^' / ~ + и'^
Отверстие V и V/:
<*2 _ 522 _ПП10- Л 360_ПЯ7. Д/_0П1
"2^Т^- 550-360— °'0135' ^ = 115-0>87> ^-°'01'
Влияние отверстия VII не учитывается, так как отверстие,
расположено у свободного края:
*а = 1 + 2-^ = 1 —0,15 — 0,18+0,02+2*0,01=0,71.
Коэффициент к3, учитывающий влияние ребер, подкрепляющих
бобышку шпиндельного отверстия, примем равным 0,9 (нагруженная
грань имеет свободный край).
3. Определение полной величины перемещения
под силой
/=/0 . кг . к2 . /г3 = 0,54 • 0,45 • 0,71 • 0,9 = 0,15 мм.
22$
§;5. ТЕМПЕРАТУРНЫЕ ПОЛЯ И ТЕМПЕРАТУРНЫЕ ДЕФОРМАЦИИ
КОРОБОК1 [58]
В результате теплообразования в работающих механизмах коробок
передач происходит нагрев коробок и возникают температурные
деформации, приводящие к перемещению осей шпинделей. При
проектировании станков, особенно прецизионных, желательно заранее определять
величину ч направление возможных температурных деформаций
коробок. Величина и направление температурных деформаций, влияющих на
точность, в основном определяются температурой стенок на участках,
размеры- которых входят в размерную цепь станок — изделие —
инструмент (например, на участке от оси шпинделя до плоскости
направляющих). Обычно такими стенками являются стенки, несущие опоры
шпинделей. Для технических расчетов принимают, что температурное
удлинение А пропорционально средневзвешенной температуре^
рассматриваемого участка
Д = еА&ц, мм,
где е — коэффициент линейного расширения в 1/град;
к — расчетный размер коробки (например, расстояние от оси
шпинделя по плоскости направляющих — высота центров).
При определении средневзвешенной температуры Ъср следует
различать два случая:
1. Тепловыделение происходит в основном в механизмах,
заключенных внутри коробки, и стенки нагреваются примерно равномерно.
Ё этом случае Ьср определяется как средняя температура коробки $к.
2. Тепловыделение происходит в основном в подшипниках, которые
можно рассматривать как сосредоточенные источники тепла, и стенки
нагреваются неравномерно. В этом случае ФГ/, определяется как
средневзвешенная температура на рассматриваемом участке (размеры
которого входят в размерную цепь станок—изделие — инструмент).
При тепловыделении, равномерно
распределенном по всему объему коробки, средняя избыточная температура^
может быть определена по формуле (при этом влияние теплового
сопротивления стыка на отвод тепла в сопряженные детали не учитывается)
где С} — общее количество* тепла, выделяющееся в единицу времени
в ккал/час;
<хл и <хс—коэффициент теплоотдачи наружных поверхностей коробки
и сопрягаемой детали, соответственно, в ккал\мгчас град;
X — коэффициент теплопроводности материала, сопрягаемой
детали; для чугуна Х = 41^-54, для стали X —39
в кал\м час град;
Зк — площадь теплоотдающей поверхности коробки в М?;
Рс — площадь контакта сопряженных деталей в м2;
Цс — периметр площади контакта сопряженных деталей в м.
Количество выделяемого тепла (Э определяется по формуле
^ 2*
где N1 — подводимая мощность в кет;
1 Раздел написан канд. техн. наук Ю. Н. Соколовым.
224
щ — коэффициент полезного действия;
т/ — длительность времени использования мощности Л^- в сек.
При наличии часто включаемых муфт или тормозов дополнительно
следует учесть теплообразование в этих элементах.
Коэффициент теплоотдачи коробки можно определять как
средневзвешенное коэффициентов теплоотдачи отдельных поверхностей
коробки по формуле
_ а181 + а25д + ... + Д/5/ + ... + ап$п
где ^ и 5,- — коэффициент теплоотдачи в ккал/час м2град и площадь
отдельной стенки в м2, соответственно.
Коэффициенты теплоотдачи отдельных поверхностей а, могут
приниматься в следующих пределах: для поверхностей при естественной
циркуляции воздуха — Зн-6; для поверхностей, примыкающих к хорошо
обдуваемым поверхностям или имеющих выходящие гладкие валы,
вращающиеся с числом оборотов не более 100 в минуту,—12-:-15; для
поверхностей, имеющих воздушные потоки от валов, вращающихся
с п = 300 -М000 об/мин, — 25-ьЗО; для поверхностей, хорошо
обдуваемых вращающимися патронами, кругами, шкивами при п = 1000ч-
2000 об/мин,—60-^80, при п = 2000-ьЗООО об/мин — 80-ь 100;
При сосредоточенных источниках тепла точки,
лежащие около подшипника, нагреты интенсивнее, чем точки,
удаленные от подшипника. Средневзвешенную температуру ®ср на участке,
размер Н которого входит в размерную цепь станок —
изделие—инструмент, можно определить, если участок Н представить в виде суммы
участков Л/ по средней температуре $, этих участков
ь* = —ь— •
Средняя температура О/ участка Л; может характеризоваться
температурой точки, лежащей посередине этого участка. Величина #г
определяется по формуле
о _ а Л (тп) Кх (тг02) + Л (гпг02) Ко (/иг,-)
1 У0 («Ли) Кг (тг02) + Л (тгт) Ко (тг01) ГРаД"
где
Ьх — температура подшипника, масляного слоя или колец в град.;
г01 — радиус расточки под подшипник в м;
Л)2 — радиус окружности, описанной вокруг стенки из центра
подшипника в м;
г{ — расчетный радиус — расстояние от центра подшипника до
середины /-того участка в м;
а{ — коэффициент теплоотдачи стенки в ккал/м2 час град.;
X—коэффициент теплопроводности в ккал/м час град.;
Ь — толщина стенки в м;
^^{x),^1{x),Ко{x), ^(х)— Бесселевы функции мнимого аргумента.
225
Когда основное тепловыделение происходит в шпиндельном
подшипнике, тепловыделения остальных подшипников можно не
учитывать. Если тепловыделение в подшипниках соизмеримо или они
находятся на участке, входящем в размерную цепь, температурное поле под-
считывается указанным путем для каждого из источников тепла с
учетом теплового потока соседних подшипников.
Влияние температурных деформаций на точность станков может
быть снижено:
а) уменьшением теплообразования и увеличением теплоотдачи
(выполнением жалюзи на крышках, оребрением поверхностей коробок,
увеличением площади контакта с базовыми деталями, созданием
воздушных потоков, омывающих наружные стенки, охлаждением масла);
б) направлением температурных деформаций так, чтобы они не
влияли на точность;
в) введением температурных ком пенс аторов,
ГЛАВА VII
ДЕТАЛИ УЗЛОВ ДЛЯ ПОДДЕРЖКИ И ПОСТУПАТЕЛЬНЫХ
ПЕРЕМЕЩЕНИЙ ИНСТРУМЕНТА И ОБРАБАТЫВАЕМЫХ
ИЗДЕЛИЙ (САЛАЗКИ, СУППОРТЫ, ПРЯМОУГОЛЬНЫЕ СТОЛЫг
ПОЛЗУНЫ), НАПРАВЛЯЮЩИЕ ПРЯМОЛИНЕЙНОГО
ДВИЖЕНИЯ1
§ 1. ОБЩИЕ СВЕДЕНИЯ О КОНСТРУКЦИЯХ
Детали, перемещаемые по направляющим. Систематика
рассматриваемых деталей приводится в табл. 40 и 41. По форме можно различать
три группы деталей, у которых:
а) все три измерения одного порядка (консоли); б) одно
измерение значительно меньше двух других (столы, планшайбы); в) одно
измерение значительно больше двух других (ползуны).
Таблица 40
Схемы деталей узлов для поддержки и перемещения изделия
Столы плоские
прямоугольные
перемещаемые
поступательно
Столы плоские
круговые
поворотные
1 Ниже детали, перемещаемые по направляющим, рассматриваются вместе с
направляющими. Это связано с тем, что конструкции деталей рассматриваемого типа
особенно салазок, в значительной степени подчиняются условию работоспособности
направляющих, и расчет таких деталей должен производиться совместно с
направляющими
Здесь в основном рассматриваются расчеты направляющих как задачи
строительной механики машин (расчеты по контактным напряжениям, расчеты на жесткость),
непосредственно связанные с расчетом корпусных деталей Остальные вопросы расчета
и конструирования направляюших даются в виде краткого обзора. ЭНИМСом
проведены большие работы по повышению несущей способности направляющих путем
подбора оптимальных материалов, оптимальной защиты, смазки и т. д Эти вопросы будут
освещены в особой монографии.
227
Продолжение табл. 40
Столы
коробчатые
га
Салазкн
ь- и
Консоли
Задние бабки
№*
Таблица 41
Схемы деталей узлов для поддержки и перемещений инструмента
Инструменто-
держатели
с щ—I
-№
Суппорты
а
Салазки:
а—плоские
о"—коробчатые
228
Продолжение табл. 41
Рукава
Поперечины
в
■)Г ''~~'Г У>НГ "><-
т»е^?к—^ч^п-^--?-1! А г-*—г^-^-^я. '1_'1л-|' л-.
Ползуны
Ч...ХХ«
■>г--
_л^__^
Кронштейны
Хоботы
й
гс )'•_
—и и—'
__Л Л_
ГЧ
Разрез по Б В'В В
Разрез пой Я
Фиг. 129. Каретка с узким мостом токарного станка мод. 1620 с высотой центров 200 ллс
229
При расчете первые должны рассматриваться как коробки,
вторые— как пластины и третьи — как балки.
Конструирование салазок (кареток) в значительной степени
подчиняется условию получения минимальных габаритов по высоте.
Разрез по йй
Фиг. 130. Каретка тяжелого токарного станка мод. 1660А с высотой центров 650 лш.
Салазки средних станков выполняются обычно сплошными
(фиг, 129), салазки тяжелых станков вследствие больших нагрузок
и менее жестких ограничений по высоте выполняются коробчатыми
(фиг. 130). Салазки токарных станков в целях повышения жесткости
имеют на участке между направляющими увеличенную высоту или
снабжаются специальными ребрами. Салазки средних токарных станков
выполняются с узким мостом (фиг. 129) для подвода к передней и зад-
230
ней бабкам, салазки тяжелых станков в целях обеспечения
максимальной жесткости имеют в плане прямоугольную форму (фиг, 130).
Салазки (фиг. 131, б) большинства станков в целях уменьшения высоты
выполняются хотя бы с одной системой направляющих по форме
профиля «ласточкин хвост». Поворотные части суппортов (фиг. 131, а)
имеют цилиндрическую направляющую и крепятся к салазкам,
снабженным кольцевыми Т-образными пазами, с помощью болтов.
Конструкции прямоугольных столов показаны на фиг, 132—135.
Столы небольшой ширины (консольно-фрезерных, плоско-шлифоваль-
Разрез по ДА
Фиг. 131. Поворотная часть (а) и салазки (б) вертикального суппорта
продольно-строгального станка мод. 7256.
ных, малых продольно-фрезерных станков) выполняются сплошными
(фиг. 132), широкие столы (продольно-строгальных,
продольно-фрезерных, расточных станков) —коробчатой формы (фиг. 133, 134).
Столы шириной до 4—4,5 м выполняются с двумя
направляющими (фиг. 133), широкие столы обычно выполняются с тремя
направляющими (фиг. 135). Столы большой длины (более 8 м) изготовляются
составными (фиг. 133) из участков длиной 4—6 м. Соединение частей
осуществляется винтами, располагаемыми в 'специальных
карманах.
Столы коробчатой формы снабжаются большим числом поперечных
ребер (фиг. 133—134). Расстояние между поперечными ребрами
составляет обычно -300—400 мм. Столы станков, работающих с охлаждающей
жидкостью, по периферии снабжены канавками или лотками для стока
жидкости.
231
Размеры рабочей поверхности столов стандартизованы (табл. 42).
Основные размеры столов продольно-строгальных и
продольно-фрезерных станков приведены в табл. 43, 44.
Т-образные пазы для закрепления изделий на_столах
стандартизованы (табл. 45).
В коробчатых конструкциях, в которых стенки обычно имеют
небольшую толщину, под Т-образными пазами предусматриваются
приливы и ребра (перегородки), так как силы резания передаются на стол
обычно вблизи пазов.
Фиг. 132. Стол горизонтально-фрезерного станка мод. 6Н81Г с рабочей площадью
250 X Ю00 мм.
Консоли, кронштейны, рукава и другие детали консольного типа по
форме обычно приближаются к балкам равного сопротивления.
Консоли обычно поддерживаются винтами и дополнительно специальными
поддержками. Консоли могут быть простые с ручным перемещением
(сверлильные станки), с механизмом перемещения от главного
двигателя или от индивидуального двигателя. Консоли (фиг. 136) обычно
имвют коробчатую форму и размеры их в значительной мере диктуются
размещенными внутри них механизмами. С точки зрения жесткости,
консоль является слабым звеном станка из-за ограниченной длины
стыка консоль — станина, в основном определяющего жесткость
этого узла (увеличение длины стыка приводит к увеличению высоты
станка). Для обеспечения большей жесткости во фрезерных станках
консоль соединяют поддержкой с хоботом или скалкой, а консоль и
основание соединяют поддерживающей стойкой. Постановка
поддерживающих стоек увеличивает суммарную жесткость горизонтально-фрезер-
232
233
Фиг. 133. Составной стол продольно-строгального станка мод 7256Б,
Фиг. 134. Стол продольно-фрезерного станка с рабочей площадью 650X2200 мм.
234
и
Фиг. 135. Поперечный разрез стола продольно-строгального станка с тремя направляющими, мод. 7А288 с рабочей площадью
3600X12 000 мм.
235
Таблица 42
Размеры рабочей поверхности прямоугольных столов
Ширина стола в мм
! Наименование станков 10° 125 160 200 250 з20 4°° 450 500 630 71° 9°° 1250 1600 1800 2500 3600 4500
| Длина стола в мм
Консольйо-фрезер- I ( I I I
ные станки (ГОСТ
165-49) 4(Ю5М6308(Ю1000 1250Ш-Ш^
Плоскошлифовальные
станки с
вертикальным
шпинделем (ГОСТ 873-53) — 320 — 500 - 800 — 1250 — 2000 — 3200 —— — — — —
Плоскошлнфовальные I I I I I I I I I I I I I I I I I I
станки с
горизонтальным шпннде- I I
лем (ГОСТ 874-53) — 400 — 630 — Ю00 - 1600 — 2500 — 4000 — — - ~ |— —
Расточные станки
(ГОСТ 7058-54) __________доо 1120 1600 2000 3550 5000 — —
Продольно-фрезер- I I I
ные станки (ГОСТ | I
6955-54) _ _ _ _ _ 1250 — 1600 — 2200 — 3000 4250 — 6000 8500 12 000 16 000
I .——I 1 ! 1 1 1 . . ! . Л ^|
Продольно-строгаль- I I I I I I
ные станки (ГОСТ | I I (
439-53) _________ 1500 — 2000 3000 - 4000 6000 8000 10000
236
Таблица 43
Ориентировочные размеры поперечного сечения столов отечественных
продольно-фрезерных станков в мм
~1'}- Г~ а "~~1
Ширина
стола
Число
Т-образных]
пазов
Толщина
ребер
Расстояние
между
поперечными
ребрами
630
900
1250
1800
2500
220
255
290
320
395
170
200
230
260
320
120
150
180
210
230
170
140
210
220
250
22
28
28
28
36
70
80
95
90
ПО
34
45
50
50
70
28
36
35
30
40
313
300
300
340
400
Ориентировочные размеры поперечного сечении столов
отечественных продольно-строгальных станков в мм
Таблица 44
Ширина
стола
В
И
Число
Т-образных
пазов
Расстояние
между
поперечными
ребрами
Толщина
ребер
900
|1250(1300)
1800
2500
3600
4500
260
305
350
470
587,5
587,5
200
230
250
300
430
430
135
150
210—220
350
370
370—390
150
210
322
400
300
300
28
28
36
42
42
42
5
5
6
7
11
15
295
495
425
410
420
420
25
30
30
30
40
35
45
45
45
50
70
70
40
40
30
30
40
40
80
90
100
120
120
120
237
Таблица 4&
Размеры в мм станочных пазов по ГОСТу 1574-42
а
Ь
с
к
а
Ь
с
Н
\ _
10
1б+1,5
у+0,5
6—13
(24)
40+2
18+1
17—30
12
20+1»5
д + 0,5
8—15
28
46+3
20+2
21—36
щ
//Л
(-0-1
1
1?
\ш/у/////м
14
24+1.5
ц+0,5
10—18
(32)
52+8
22+2
' 24—42
(16)
27+2
12+1
11—20
36
60+3
25+2
27—46
18
30+2
1 14+1
13—23
42
70+3
29+2
32—54
(20)
33+3
15+1
14-25
48
80+3
34+2
36—60
22
36+3
16+1
16-28
54
90+3
1 38+2
1
42—70
ных станков в вертикальном направлении на величину около 20%,
причем зажим стоек на опорах существенного влияния на жесткость не
оказывает. По данным исследований, выполненных в Чехословакии,
установка между консолью и хоботом жестких поддержек («ножниц»)
существенно расширяет зону безвибрационных режимов резания, однака
при этом усложняется обслуживание станка.
Конструкции поперечин определяются в основном собственной
жесткостью. В связи с этим расчет и конструирование их
рассматривается вместе с расчетом и констр>ированием несущей системы
(см. главу IV). Основные формы поперечного сечения ползунов
приведены ниже.
Направляющие. В станках 'применяются направляющие скольжения:
и качения. Наибольшее распространение до настоящего временя имеют
направляющие скольжения. В станкостроении наиболее часто
применяются направляющие скольжения следующих типов: прямоугольные,
треугольные, трапециевидные (типа профиля «ласточкин хвост») и
круглые в комбинациях, указанных в табл. 46. Наиболее распространенные
формы направляющих станков отдельных типов приведены на фиг. 137—
139. При стесненных габаритах применяют' по одной направляющей
с замкнутым контуром: круглой, как наиболее легкой для изготовления
(пиноли, гильзы, колонны, фиг. 140,- а); с плоскими гранями — в случае
необходимости предотвращения проворачивания под действием больших
моментов (ползуны карусельных и других станков, фиг. 140, б*—г).
238
Фиг. 136. Консоль горизон
талыю-фрезерного станка
с рабочей площадью стол.
400 X Ю00 мм.
СГ «^ — гЯ 3 л «3 м (- I
Таблица 46
Основные типы направляющих скольжения прямолинейного движения
| I Условия работы I
напоа^ляюышх Большие скорости I Применение, характеристика
направляющих перемещении, Малые СКОростн
хорошие условия перемещений
смазки 1
Применяются при необходимости повышенной точности, достигаемой вследствие
гч >я гч >л /0ч ^Ь некоторого саморегулирования (меньшего, чем у других форм направляющих, влия-
у)%Д " Ю$ Щг ^%\ ния регулировки планок), а также меньшего влияния износа на точность обработки.
^ I Направляющие а хорошо сохраняют смазку и являются основной формой для сто- I
\ с) \ б) \ лов продольно-строгальных станков. Направляющие б обеспечивают хорошее удале-
I ние стружки, применяются в точных токарных и токарно-рсвольверных станках
Применяются в условиях, аналогичных условиям применения треугольных направ-
I ляющих, сохраняют значительную часть преимуществ последних, но более просты
I |%%§ &^1 ^^^ ^2 в изготовлении. Осуществляют принцип узкого направления.
Комбиниро- | \А I Выполняются преимущественно с симметричной формой треугольных направляю-
ванные а.) б) \ щИх, а в токарных станках также часто с несимметричной; а —основная форма для
I [ столов шлифовальных станков, применяются также в столах продольно-строгальных
1 станков, б — наиболее распространенная форма в токарных станках
Применяются при нормальных требованиях к точности. Наиболее просты в изго-
^^ товлении при любых размерах, но относительно сложны в регулировке, особенно при
п Й%ЗЭ ■ 6^9 ^|Р §^2 большой длине, так как требуют трех планок или клиньев. Смазка удерживается
Прямоуголь- И . -ч? хорошо; вследствие возможности задержки стружки защитные устройства должны-
йые &) б) \ удовлетворять повышенным требованиям; а—имеет ограниченное применение, б —
основная форма, применяемая в станинах тяжелых токарных, протяжных, агрегатных,
I продольно-фрезерных станков, в вертикальных станинах (стойках) и консолях кон-
сольно-фрезерных станков
240
Продолжение табл. 46
Условия работы
няппяплатлтиу Большие скорости Применение, характеристика
направляющих перемещении, Малые СКОр0сти
хорошие условия перемещений
смазки
I <?7! гтъ \ Применяются при малых габаритах по высоте; характерны простотой регулировки,
| По форме \л%ггт^—~%$1 'У?7?л77?7у/777Л производимой одним клином или планкой. Плохо работают на отрыв при действии
профиля у^777%777%77у^а больших опрокидывающих моментов. Имеют повышенные потери на трение, а потому
.ласточкин \ а) \ $) \ практически не применяются при больших скоростях перемещений, а — основная форма
хвост" направляющих столов консольно-фрезерных станков, б — то же поперечных суппортов I
токарных станков (
ванные—прямоугольные ргр I Применяются при действии больших односторонних опрокидывающих моментов,
и половина ъ%2%7яя%?% Ц7$>7777?/$ причем необходимо обеспечение высокой жесткости планок или клиньев со стороны,
по форме \ V, \ подверженной отрыву; широко применяются для боковых суппортов (в многорезцовых,
профиля карусельных, радиальн о-сверлильных станках и т. д.).
„ласточкин
хвост" I
^к /к Применяются при осевом симметричном по отношению к направляющим нагруже-
Цилиндрн- К^^^#?^Э I 'ф- "ф- нии (пресса, протяжные, хонинговальные станки), а также в целях облегчения изготов-
ческие ления. Позволяют достигнуть повышенной износоустойчивости благодаря применению
благоприятной фрикционной пары закаленная сталь — чугуи
I I I
к Ж Применяется преимущественно при необходимости получения различных движений
Комонниро- §~ ^ (например, для продольной, поперечной, конусной и фасонной обточки, когда иаправ-
ванные ляющая выполняется в виде копирной линейки)
241
Фиг. 137. Основные формы направляющих токарных станков;
л, б, в, г — направляющие перемещения каретки; д, е, ж — направляющие верхнего продольного
н поперечного суппортов
штж.
о)
шщ
()
в)
г~—■—
*щШт
1
^
уЩШ \
_
1
<С 1
1 \—1^
1
■
Фиг. 138. Основные формы направляющих консольно-фрезерных станков:
а, б, в — направляющие станины, г, <), <?, луг, з — направляющие консоли; я, к» л — направляющие
стола.
242
При больших нагрузках и габаритах станков в ряде случаев
применяются тройные направляющие (столы тяжелых продольно-строгальных
и продольно-фрезерных станков, фиг. 141, а и б, фиг. 139, в).
Фиг. 139. Основные формы направляющих столов продольно-строгальных станков:
а — У-образные; б, в — комбинированные.
Основные виды направляющих скольжения нормализованы
(нормаль ЭНИМС Н20-10). Высоту направляющих Н (фиг. 142) следует
брать из следующего ряда: 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40;,
а) б) 6) г)
Фиг. 140. Основные формы направляющих с- замкнутым контуром.
50, 65, 80, 100, 125, 160, 200, 250, 320 мм. Для прямоугольных
направляющих в нормали рекомендуются размеры Н в пределах от 8 да
100 мм, треугольных от 6 до 320 мм, по форме профиля «ласточки»
а) 6)
фиг. 141. Основные формы тройных направляющих.
хвост» от 4 до 80 мм. Соотношения размеров направляющих в
соответствии с нормалью Н2Ь 10 приведены на фиг. 142 и табл. 47.
Рабочие грани направляющих, а также точку приложения тягового
усилия следует располагать на станине так, чтобы реакции и
перекашивающие моменты были минимальными.
243
В процессе обработки изделия давление должно восприниматься
одними и теми же гранями направляющих во избежание повышенного
влияния зазоров на точность изделий и чистоту поверхности.
Отношение длины столов и кареток к ширине направляющих в ответственных
сопряжениях должно быть не менее 1,5 при «узком» направлении и не
менее 2 при «широком». Так называемое «узкое» направление
способствует повышению точности, облегчая точное изготовление и
измерение ширины направляющих.
\РядВ
Фиг. 142. Основные соотношения размеров направляющих (по нормали станкостроения
Н20-10).
Зазоры в направляющих, как правило, регулируются.
Регулирование зазоров производится:
а) путем шлифования или шабрения планок;
б) перемещением планок с помощью винтов в направлении,
перпендикулярном к рабочим поверхностям планок;
в) осевым перемещением клиньев.
Планки и клинья по возможности располагаются с менее
нагруженной стороны. Применяемые способы регулирования и формы клиньев
и планок по нормали ЭНИМС Н20-10 приведены на фиг. 143.
Шлифование или шабрение планок применяется для регулирования
направляющих в плоскостях, в которых зазоры мало влияют на
точность обработки, а также при высоко износостойких материалах
направляющих. На поверхностях, подлежащих шабрению* часто делают
выемки для уменьшения площади шабрения.
Регулирование планок винтами применяется при малых и средних
нагрузках и необходимости тонкого регулирования Планки
выполняются с жестким закреплением после регулирования и без
закрепления. Планки с жестким закреплением обеспечивают большую жесткость
к их применение в ответственных случаях предпочтительнее. Планки
244
Таблица 47
Рекомендуемая ширина направляющих А ъ мм
(по нормали станкостроения Н20-10)
тЧёГ'И? ЧИН «Чйй
I Высота направляющей Л в жж
I Тип направляющих | } ] \ Г" | ""1 » | | | \ I Г \ ' ! | | *] |
4 ; 5 б 8 10 12 16 20 25 32 40 50 65 80 100 125 160 200 250 320
_ _ 50 55 70 90 110 140 180 225 280 360 450 560 630 710 800 900 1000 1100
_ _ 55 60 80 100 125 160 200 250 320 400 500 630 710 800 900 1000 1100 1250
_ — 60 70 90 110 140 180 225 280 360 450 560 710 800 900 1000 1100 1250 1400
— — 70 80 100 125 160 200 250 320 400 500 630 800 900 1001) 1100 1250 1400 1600
— - 80 90 110 140 180 225 280 360 450 560 710 900 ЮОО 1100 1250 1400 1600 1800
Треугольные
— — 90 100 125 160 200 250 320 400 500 630 800 1000 1100 1250 1400 1600 1800 2000
I — I — 100 110 140 180 225 280 360 450 560 710 900 1100 1250 1400 1600 1800 2000 2250
— I — ПО 125 160 200 250 320 400 500 630 800 1000 1250 1400 1600 1800 2000 2250 2500
_ I _ 125 140 180 225 280 360 450 560 | 710 900 1100 — — -_ — _--_ —
__ _ _ 160 200 250 320 400 500 630 800 1000 — — — — — — — —
245
Продолжение табл. 47
I Высота направляющей Н в мм
Тнп направляющих ; | ] •— 5 « 1 I 1 I I ; ", 1 I [ ; I I
4 1 б 6 8 10 12 16 20 25 32 40 50 65 80 100 125 160 200 250 320
_ ! _ 50 55 70 80 100 140 180 225 280 360 450 560 710 — — — I _ _
I — — 55 60 80 90 ПО 160 200 250 320 400 500 630 800 — — — — —
_ _ ■ 60 70 90 100 125 180 225 280 360 450 560 710 900 — — — — —
- — ■ 70 \ 80 100 ПО 140 200 250 320 400 500 630 800 1000 — — — — —
| _ '■ _ I 80 90 ПО 125 160 225 280 360 450 560 710 900 1100 — — _ — --
Прямоугольные — , — | 90 | 100 125 140 180 250 320 400 500 630 800 1000 1250 —-* — -- —
| _ ( _ Ю0 [ 110 140 160 200 280 360 450 560 710 900 1100 1400 — — - — —
I — I — I 110 125 160 180 225 320 400 500 630 800 1000 1250 1600 — — — — —
I — I — 125 140 180 200 250 360 450 560 710 900 1100 1400 1800 -___.__-
— — — 160 200 225 280 400 500 630 800 1000 1250 1600 2000 — — — — -
______ 250 320 -- — — _—__ — _-_ — --
20 25 32 40 50 60 80 100 125 160 200 250 320 400 — — — — — —
22 28 36 45 55 65 90 ПО 140 180 225 280 360 450 — — — — — —
I Остроугольные по 1
*Л Л ™Л*т,па 25 32 40 50 60 70 100 125 160 200 250 320 400 500 - — — - - —
форме профиля
«ласточкин хвост» 28 36 45 60 65 80 110 140 180 225 280 360 450 560 I — — — — — -
32 40 50 65 | 70 90 125 160 200 250 320 400 500 630 — — — — — —
246
без жесткого закрепления значительно более компактны, но они
требуют применения винтов с контргайками.
Регулирование клиньями применяется в ответственных случаях при
больших нагрузках и необходимости тонкого регулирования, а также
для обеспечения высокой жесткости и при малых габаритах. Уклон
клиньев обычно равен 1 : 50. Применение клиньев усложняет
изготовление и сборку. Во избежание самозатягивания необходимо хорошее
крепление клиньев.
Фиг. 143, Основные способы регулирования зазоров в направляющих (по нормали стан*
построения Н20-10):
а — с помощью планок; б — с помощью клиньев.
Ширины клиньев трапецеидального сечення (в верхнем ряду) могут выбираться несколько меньшими
(от 10—15% для малых размеров до 40% при больших размерах)
Направляющие качения применяются в станках в следующих
случаях:
а) для повышения точности перемещений или осуществления
равномерных медленных перемещений (в координатно-расточных,
шлифовальных, копировальных станках, станках с программным
управлением);
б) для повышения допустимых скоростей и обеспечения требуемой
долговечности (в карусельных и других станках);
в) для облегчения ручных перемещений (в заточных станках).
Области применения направляющих качения непрерывно
расширяются.
Основные типы направляющих качения приведены в табл. 48.
Применяются тела качения в виде шариков (при малых нагрузках),
роликов (при существенных нагрузках) или игл (при стесненных
габаритах).
Представляет большой интерес специальная роликовая цепь,
применяемая в угловых направляющих (табл. 48, столбцы 2 и 3). Ролики
этой цепи имеют диаметр немного больше, чем высота, и ставятся через
один с расположением под прямым углом. Таким образом, направляющая
247
Таблица 48
Направляющие качения
| I Направление воспринимаемых нагрузок I I
Тип направляющих Одноосное (не замкнутые В пределах некоторого угла Произвольное (замкнутые Область применения
направляющие) (не замкнутые направляющие) направляющие)
Шариковые ^лг -т*т% '4( \ -V/ Щк^Ш ^^^^у^^//^^^^^к Малые нагрузки 1
Роликовые ^— г°Е%? 5^ч ЛЕ* > \/ ' \/ '~\/ 1 ч/~1
[ I I Повышенные
$Ш $Ъ$ 11 ^^1 нагрузки
Игольчатые и и и п . \\\ ы \\\ ^$^$^* ^^х^\ч\\\> уч ,\\^х
\//&"///''/'''Мг'щгм/!В*$& '"Щ^^^Ш^^ЧШс Малые и средние
Роликовые на осях ЙЬч 77 'щ#*^$ ^ЙГЭД- ЩЩЩ^^А^ Ж^кк — I
248
Таблица 49
Материалы направляющих станины н сопряженных узлов (36], [37)
Материал и термическая обработка х Характеристика направляющих по износостойкости Применение и рекомендации
Чугун марки СЧ 15-32 без тер- Направляющие движения подачи при несовер- До последнего времени имели наибольшее при»
мической обработки—чугун марки шенных защитных устройствах и отсутствии при- менение. Возможно сохранение для направляю-
СЧ 21-40 без термической обработки нудительной смазки характеризуются боль- щих подачи и главного движения только при
I шим износом Направляющие главного движения легких режимах работы, хорошей изоляции от
запри значительных скоростях и давлениях пока- грязнений и хорошей смазке
зывают недостаточное сопротивление заеданию.
Допускаемые скорости скольжения ие более
3—3,5 м/сек
Чугун марки СЧ 15-32 — модифи- Небольшое повышение износостойкости в срав- В современных напряженных условиях работы
цированный чугун без термической нении с парой чугун марки СЧ 15-32 — чугун станков возможность применения ограничена
обработки марки СЧ 21-40
Чугун марки СЧ 15-32 — модифи- Повышенная износостойкость (в условиях абра- Применяются для направляющих, выполненных
цированный чугун термообработан- зивиого изнашивания) и многократно увеличенная за одно целое со станиной, обеспечивая необхо-
ный (поверхностная закалка НКС 50) сопротивляемость заеданию, увеличенная стой- димую долговечность направляющих I
кость против случайных повреждений (забоин).
Чугун марки СЧ 15-32 — сталь тер- То же. Стальными выполняются накладные или при- |
мообработанная- Недостатки в сравнении с ненакладными на- варенные (в сварных станинах) направляющие. [
а) конструкционная углеродистая правляющими из модифицированного чугуна: Применение наиболее* целесообразно в тех слу- |
(Н&С 50—52); большая трудоемкость изготовления и меньшая чаях, когда трудно использовать закаленные чу-
б) конструкционная углеродистая жесткость из-за наличия дополнительных стыков гунные направляющие
цементуемая типа 15, 20 (НКС 55—
60);
в) хромистая типа шарикоподшип- |
никовой (НКС 58—62).
249
Продолжение табл. 49
Материал и термическая обработка 1 Характеристика направляющих по износостойкости Применение и рекомендации
Чугун марки СЧ 15-32 — сталь аза- Более высокая износостойкость, чем у направ- Направляющие станины выполняются с наклад-
тированная ляющих станины из термообработанного модифи- ками из азотированной стали. Применение огра-
цированного чугуна и стальных, рассмотренных ничивается высокой стоимостью и сравнительно
выше малой глубиной азотированного слоя
Текстолит—чугун без термической Значительное повышение долговечности направ- За последнее время получили широкое рас-
обработки ляющих по сравнению с парой чугун—чугун пространение, особенно в тяжелых станках. На-
(без термообработки). Заедания не наблюдаются. кладные пластмассовые направляющие устанав-
I Чугунные направляющие в паре с текстолитовыми пиваются на закрытых направляющих перемещае-
изнашиваются обычно значительно меньше, чем мых узлов и выполняются приклеиваемыми или
в паре с чугунными. Суммарный темп износа привертными.
трущейся пары чугун — текстолит также ниже, Рекомендуются: а) для направляющих подачи
чем пары чугун — чугун. тяжелых станков; б) для направляющих главного
движения карусельных и строгальных станков
I 1 I |
Полиамиды (кордный капрон) — Большая износостойкость при абразивном из- Находятся в стадии экспериментов. Могут по-
чугун нашивании, чем у пары текстолит — чугун, мень- лучить применение для направляющих подачи
шая податливость слоя (при малой толщине). станков средних размеров в тех случаях, когда
Заеданий не наблюдается. Меньшая теплостой- не могут быть применены закаленные направляю-
кость и больший коэффициент линейного расти- щие. Накладные пластмассовые направляющие
рения, чем у текстолита выполняются в виде приклеиваемых пластин
Цветные сплавы—чугун СЧ 21-40 Повышенное сопротивление заеданию. Преиму- Рекомендуется в первую очередь для
направили СЧ 15-32. Цветные сплавы: щество по сравнению с парой текстолит — чугун пяющих главного движения и для направляющих
а) цинковый сплав марки ЦАМ- для направляющих главного движения — лучшие подач тяжелых станков. Цветные сплавы нано-
10-5; условия для создания жидкостного трения. ЦАМ сятся на направляющие перемещаемых узлов:
б) бронза; 10-5 и баббит недостаточно износостойки при аб- а) в виде привертных накладок; б) путем на-
в) баббит разивном изнашивании (загрязненной смазке). плавки (особенно целесообразно для конических
круговых направляющих) Сплав марки ЦАМ 10-5
в несколько раз дешевле, чем бронза и тем более
I 1 баббит
| * Первый из указываемых ниже материалов — для перемещаемого узла (салазок, стола), второй — для станины. |
250
работает как две плоских, воспринимающих нагрузки в двух взаимно-
перпендикулярных плоскостях и имеющих удвоенный шаг роликов.
Сепарирование тел качения осуществляется следующим образом:
а) при малых ходах применяются простейшие сепараторы в форме
планок с гнездами для тел качения. Для игольчатых направляющих
за границей выпускаются секции игл. разных размеров с сепараторами
в виде планок, которые соединяются между собой с помощью замка по
форме профиля «ласточкин хвост» (столбец 1, табл. 48);
б) при больших ходах — между рабочими телами качения
прокладываются сепарирующие тела качения несколько меньшего диаметра
(последние иногда подвергаются воронению).
Важнейшим средством повышения долговечности направляющих
является защита от загрязнения: на плохо защищенных направляющих
даже при малых давлениях наблюдаются большой износ и задиры.
Основные типы защитных устройств можно разделить на:
а) защищающие поверхности направляющих, находящиеся в
контакте (уплотнения из маслостойкой резины и тонкошерстного войлока
с поджимом пружинками, латунные скребки в сочетании с войлоком и
др.); в основном применяются при незначительных скоростях
перемещений и невозможности поставить щитки;
б) комбинированные, защищающие поверхности, находящиеся
в контакте, и закрывающие часть свободной поверхности направляющих
(щитки в сочетании с уплотнениями); преимущественно применяются
при незначительных скоростях перемещений, рекомендуются в качестве
основного типа для токарных станков;
в) закрывающие свободные поверхности направляющих, обычно
бесконтактного типа (щитки, ленты и др.); преимущественно
применяются при значительных скоростях перемещений.
Указания по выбору материалов направляющих приведены
© табл. 49. Основным условием работоспособности направляющих
является точность работы под нагрузкой в течение требуемого срока
службы станка. Начальная точность направляющих обеспечивается
выбором надлежащей технологии изготовления. Сохранение точности после
приложения нагрузки обеспечивается достаточной контактной и
собственной жесткостью направляющих. Сохранение точности в течение
всего требуемого срока службы обеспечивается при надлежащей
износостойкости направляющих, надлежащей смазке и защите.
§ 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ РАСЧЕТА НАПРАВЛЯЮЩИХ
Я ПЕРЕМЕЩАЕМЫХ ПО НИМ ДЕТАЛЕЙ (СУППОРТОВ, ПОЛЗУНОВ и др.)
Физические условия работы суппортов и ползунов очень сложны,
так как эти детали обычно представляют собой весьма податливые
системы, и их деформации существенно сказываются на распределении
давлений в направляющих.
Основным критерием работоспособности столоь, салазок, суппортов
является жесткость, определяющая правильность контакта и
перемещения по направляющим, а также точность обработки и
виброустойчивость системы.
Основным критерием работоспособности направляющих является
износостойкость в части сопротивления схватыванию и абразивному
изнашиванию, в значительной степени характеризуемая истинными
давлениями в направляющих. Расчет суппортов, ползунов и столов
производится на жесткость и по давлениям в направляющих.
Жесткость суппортов, ползунов и столов с точки зрения ее влияния
на точность обработки и виброустойчивость характеризуется упругими
251
перемещениями, приведенными к режущей кромке инструмента.
Жесткость суппортов, ползунов, столов (в комплексе с направляющими
базовых деталей) определяется собственной жесткостью при
рассмотрении их как пластин или брусьев и контактной жесткостью.
Общие упругие перемещения суппортов и ползунов в балансе
упругих перемещений станков составляют довольно существенную часть.
Так, в карусельных двухстоечных станках упругие смещения ползунов
в горизонтальном направлении составляют до 50—70% общих
смещений, приведенных к резцу [25, г]; в токарных станках упругие смещения
суппортов составляют 25—50%.
В свою очередь, смещения вследствие контактных деформаций в
направляющих составляют значительную часть общих упругих смещений
ползунов и суппортов. Так, например, в суппортах токарных станков
приведенные к резцу контактные деформации в направляющих
составляют до 80—90% общих перемещений суппорта, а у ползунов
поперечно-строгальных, долбежных, карусельных станков приведенные к резцу
деформации на длине направляющих составляют 40—70% общих
упругих смещений ползунов у резца.
В общем виде ползуны, суппорты, столы и другие перемещающиеся
детали станков могут рассматриваться как балки ияи пластины на
упругом основании, которым являются поверхностные слои направляющих.
Упругие перемещения и давления в направляющих могут быть
определены только при совместном рассмотрении деформирования корпусов
и поверхностных слоев. Определение давлений и контактных
деформаций в направляющих без учета собственных деформаций корпусов
приводит в ряде случаев к занижению их в несколько раз и не дает
правильной картины распределения давлений на длине направляющих.
Поэтому ниже определение давлений в направляющих рассматривается
совместно с расчетом корпусов на жесткость.
Контактные деформации при больших площадях контакта,
характерных для направляющих, определяются деформированием
микровыступов поверхности и распрямлением макронеровностей. Определение
контактной жесткости принципиально возможно путем
непосредственных экспериментов и путем расчетов на основе измерения или задания
микро- и макрогеометрии поверхностей и физико-механических свойств^
поверхностных слоев. Однако расчетное определение контактной
жесткости для реальных поверхностей чрезвычайно трудно и выполнено-
только для относительно простых моделей [51, [16]. Применение
указанных и других аналогичных решений для моделей к расчетам машин
в настоящее время преждевременно, так как эти решения основываются
на ряде допущений и на экспериментальных данных, получить которые
более сложно, чем провести непосредственно испытания на жесткость.
Технический расчет на жесткость суппортов, ползунов и столов
основывается на прямых экспериментах по контактной жесткости на
моделях и узлах машин. При расчете принимается допущение о том,
что нормальные сжатия поверхностных слоев 6 пропорциональны
нормальным давлениям а
где к — коэффициент пропорциональности, именуемый ниже
коэффициентом контактной податливости.
Поверхностные слои металла можно рассматривать как тонкие
упругие прокладки между сопрягаемыми деталями, так как
деформации поверхностных слоев многократно выше, чем деформации
^материала на некотором расстоянии от стыка. Поэтому гипотеза о
зависимости давления от сближения только в данном сечении (гипотеза Вин-
252
жлера [35] в линейном или обобщенном виде) для стыков деталей
станков достаточно хорршо отражает сущность их работы.
Линейная зависимость между 6 и 0 принята на основе следующих
соображений:
а) нелинейные зависимости между напряжениями и деформациями
в стыках наблюдаются на малых образцах, а в реальных станках при
повторных нагружениях выражены не так резко. Кривые контактных
сближений в узлах станков и на больших образцах [2], [21], [45] близки
к прямым и жесткость близка к постоянной;
б) резко выраженные
нелинейные зависимости
между давлениями и
деформациями были получены на
малых образцах в основном
при центральном нагруже-
нии [59]. Если
распространить степенную зависимость
,0 = Л6Х, полученную при
центральном нагружении
стыка, на более общий вид
нагружения плоского стыка
моментом М и некоторой
центральной силой ф, то
в довольно широких
пределах 'зависимость между
углом наклона в стыке а и
моментом М получается
прямолинейной (фиг. 144). При
этом имеет место следующее
соотношение коэффициентов
контактной податливости:
— « X -^ / Л1х + 1
*а ' Здесь 6 - у —р—.
где кг~ — — коэффициент контактной податливости при нагружении
центральной силой С;
ка= -ду — коэффициент контактной податливости при нагружении
стыка моментом М и той же центральной силой (2;
/—момент инерции площади стыка.
Для большинства материалов а — 2-^3;
в) принятое допущение с точки зрения техники расчета является
наиболее простым и, по-видимому, единственным, при котором
возможен технический расчет направляющих. Увеличение жесткости стыков
с увеличением центральной нагрузки <3 может быть учтено введением
поправок на коэффициент контактной податливости.
Для большинства технических расчетов дополнительно принимаются
^ще два допущения:
1. Жесткость поверхностных слоев на разных гранях
направляющих одинакова.
2. Давления и, следовательно, деформации по ширине граней
распределяются равномерно.
Первое допущение вполне естественно, так как отдельные грани
направляющие, как правило, обрабатываются в одинаковых условиях
и имеют близкую макро- и микрогеометрию. После накопления
необходимого экспериментального материала при необходимости данный расчет
Фиг 144. Зависимость угла наклона а (в
условных единицах а • !•) в плоском стыке от момента
на основе степенной зависимости между
сближением: б в стыке и давлением а.
253
легко может быть распространен на случай разной жесткости
поверхностных слоев отдельных граней.
Второе допущение возможно ввиду относительно малой ширины
граней. Распределение давлений по ширине граней в случае малой
жесткости суппорта рассматривается специально в разделе Б § 3.
Коэффициент контактной податливости к определяется путем
обработки экспериментальных данных. Подтверждением правильности
принятых допущений является близость коэффициентов к для разных форм-
и размеров направляющих и при разных видах нагружений.
Следует отметить, что так как значения коэффициента к
определяются путем обработки результатов экспериментов по той же
методике, что и предлагаемый расчет, то этим в значительной степени
компенсируются некоторые различия между расчетной моделью и
действительным процессом деформирования в направляющих.
В некоторых случаях (например, в направляющих станин токарных
станков) возникает значительный отгиб направляющих. Разделение
местных и контактных деформаций представляет значительные
трудности и поэтому в первом приближении эти деформации рассматриваются
совместно, а наличие местных деформаций учитывается повышенными
значениями коэффициента контактной податливости.
Большое количество обработанных экспериментов (выполненных
авторами и взятых из литературы) позволяет дать рекомендации по
выбору величины коэффициента к в зависимости от размеров и
условий работы направляющих.
Расчетные значения коэффициентов контактной податливбсти
приведены в разделе А § 3 и разделе Г § 6. Значения коэффициента
контактной податливости существенно меняются с изменением
фактической площади контакта. Коэффициент к зависит от: а) качества
поверхностей— микронеровностей, макронеровностей и волнистости; б)
размеров стыка — с увеличением размеров стыка отношение фактической
площади контакта к номинальной уменьшается; в) материала деталей
и механических свойств поверхностных слоев; г) среднего давления —
с увеличением среднего давления фактическая площадь контакта
увеличивается.
Испытания, выполненные в ЭНИМСе на лабораторных образцах,
показали следующее:
1. Коэффициенты контактной податливости для стыков с
шлифованными и шабренными поверхностями мало отличаются друг от друга.
Однако этот результат, полученный на малых образцах площадью
100 см2, нельзя полностью распространять на натурные стыки большой
площади из-зй влияния макрогеометфии.
2. Наличие и количество смазки в стыках при статическом
эксцентричном деформировании не сказывается существенно на величину
коэффициентов контактной податливости, так как масло может
свободно перетекать из более нагруженной области в менее нагруженную.
Впервые этот результат был получен К. В. Вотиновым [10]. При
центральном нагружений наличие смазки повышает жесткость стыков.-
с шлифованными и шабренными поверхностями на величину до 20%,
так как масло заполняет замкнутые объемы, образуемые микройеровно-
стями. Такой же результат получен И. Т. Гусевым [16].
3. Жесткость несмазанных стыков при колебаниях и статическом
деформировании одинакова и не зависит от частоты колебаний.
4. Жесткость смазанных стыков при колебаниях выше, чем при^
статическом деформировании, до 1,5—2 раз и возрастает с увеличением
количества и вязкости смазки в стыках и с уменьшением начального
давления.
254
5. Коэффициенты контактной податливости стыков чугун — чугунг
сталь — сталь и чугун — цветной сплав (бронза ОЦС 6-6-3, ЦАМ 10-5)
близки между собой.
6. Коэффициенты контактной податливости стыков большинства
неметаллических материалов и чугуна выше, чем стыков чугун — чугун.
Разница в коэффициентах контактной податливости зависит от
вида нагружения. Наибольшая разница в коэффициентах контактной
податливости — при центральном нагружении, и с увеличением
эксцентрицитета эта разница уменьшается.
С точки зрения расчета все сопряжения корпусных деталей станков
можно разделить на две группы:
1. Сопряжения, в которых собственная жесткость деталей на
порядок выше жесткости поверхностных слоев. Для этой группы
сопряжений собственными деформациями деталей можно пренебречь и
рассматривать относительный поворот и смещение деталей как твердых тел за
счет деформаций поверхностных слоев. При этом принимается, что
давления и, следовательно, деформации по длине направляющих
распределяются по линейному закону. Сюда относятся суппорты токарных,
карусельных, долбежных и других станков, консоли и шпиндельные головки
фрезерных станков, короткие столы и т. п.х. Расчет их рассмотрен в § 3.
2. Сопряжения, в которых собственная жесткость одной из
сопрягаемых деталей соизмерима с жесткостью поверхностных слоев. При
этом, как правило, жесткость одной из сопрягаемых деталей на порядок
выше другой и при расчете можно пользоваться теорией балок и плит
на упругом основании. Сюда относятся ползуны карусельных,
поперечно-строгальных и долбежных станков, суппорты и длинные столы
продольно-строгальных станков и т. д. Расчет их рассмотрен в § 5 и 6.
§ 3, РАСЧЕТ СУППОРТОВ И СТОЛОВ БОЛЬШОЙ ЖЕСТКОСТИ
И ИХ НАПРАВЛЯЮЩИХ
А. Определение давлений и контактных деформаций в направляющих
Для упрощения расчетов упругое деформирование стыков
последовательно рассматривается в двух взаимно-перпендикулярных
плоскостях: а) в поперечной плоскости направляющих (рассматриваются
средние давления на гранях и вызываемые ими упругие смещения
в направляющих); б) в продольной плоскости (рассматриваются
наибольшие давления у концов направляющих и относительные упругие
повороты, связанные с неравномерным распределением давлений па
длине).
Принимается следующее направление осей координат: ось X — в
направлении движения суппорта или стола, ось У—в основной
плоскости направляющих перпендикулярно направлению движения, ось 2 —
перпендикулярно основной плоскости направляющих. Ниже
принимаются следующие основные обозначения:
Рх, Ру, Рх — составляющие силы резания по осям координат в кГ\
01у 02, 03 — вес суппортов, столов, изделий и т. п. в кГ\
Мх, Ж,, Мг — моменты, воспринимаемые направляющими (от
внешних сил и тягового усилия), в гсГсм;
Л, В, С, О—реакции основных граней направляющих в кГ\
А\ В', С— реакции планок в кГ\
О., ^г> ^у — тяговое усилие него составляющие по осям коорди-.
нат в кГ\ для привода винтом (2у = (^ —0, для
привода зубчатым колесом
^г=^^(а«±р), <гУ=<?*ет;
1 В ряде случаев высокая жесткость обеспечивается за счет присоединения
деталей (например, фартуков токарных станков).
р — угол трения на зубьях, равный 5—8°;
Т — угол подъема зуба (для косозубого зубчатого колеса);
хР, уР> гР, хвУ у0, г0—координаты сил резания и веса в см;
а, Ьу с — ширины рабочих поверхностей направляющих, на которые
действуют силы А, Ву С, в см;
л'> Ь\ с' — ширины соответствующих планок в см;
И—длина контакта направляющих в см;
а> Р — углы наклона отдельных граней направляющих;
/—коэффициент трения на направляющих.
Порядок технического расчета изложен на стр. 275,
1. О преде л ен ие средних давлений на
направляющих и упругих перемещений при
повороте салазок в поперечной плоскости
В табл. 50 для основных типов направляющих приведены
расчетные формулы для определения тягового усилия, реакций
направляющих, средних давлений и упругих перемещений, приведенных к резцу.
Тяговое усилие, реакции направляющих и реактивные моменты
направляющих определяются из уравнений статики и в некоторых случаях из
дополнительных условий
деформаций. Дополнительные условия
деформаций приходится применять
для определения реакций
направляющих, если одновременно
работает более трех граней, а также для
выяснения распределения моментов
между отдельными
направляющими. Средние давления определяются
делением реакции данной грани на
ее площадь. Определение упругих
перемещений за счет контактных
деформаций в направляющих
производится, исходя из предположения
о повороте салазок, как жесткого
тела.
При определении давлений на
направляющих веса деталей учитываются наравне с силами резания.
На точность обработки упругие перемещения от веса столов и изделий
влияют только в том случае если в процессе обработки существенно
меняется положение центров тяжести перемещающихся узлов
относительно направляющих (например, в расточных и консольно-фрезерных
станках). В этих случаях вес узла также учитывается наравне с силами
резания. В остальных случаях моменты от сил веса постоянны и веса
учитываются только при выяснении распределения нагрузок между
основными гранями и планками. После этого при вычислении упругих
перемещений учитываются только силы резания.
Рассмотрим общую схему расчета упругих перемещений с помощью
определения центра поворота на примере прямоугольных
направляющих. Условие поворота салазок как жесткого тела (фиг. 145):
Фиг. 145. Расчетная схема к
определению центра поворота суппорта с
прямоугольными направляющими.
"А "В
коЛ
каш
У~У€
?~УС
'256
где %а* ^в» $с— нормальные сжатия поверхностных слоев;
°л« °Д' °с — средние давления на, гранях;
у, г — координаты центра поворота,
откуда координаты центра поворота
У = Ус . х ^ Ус
°А-°С ' аЛ~аС
Перемещение вдоль оси У в точке приложения силы Ру и Ргт
Ъу = 9{г + гР)=[*в+^±^г^к. (7.1)
На фиг. 145 и в табл. 50 штриховкой показаны области возможного
положения центра поворота для основных видов направляющих. Как
видно на фиг. 145, в прямоугольных направляющих токарных станков
при обычном конструктивном исполнении центр поворота всегда
располагается ниже горизонтали, проходящей через резец, и,
следовательно, за счет деформаций в этих направляющих резец всегда
перемещается в одну сторону (от изделия). В других случаях, например, в
направляющих верхней части суппорта токарных станков, как показано
далее, центр поворота может располагаться как выше, так и ниже
резца, что будет соответственно, вызывать перемещения от изделия или
на изделие (так называемое «клевание»).
Рассмотренный способ определения упругих перемещений особенно
для направляющих с наклонными гранями является относительно
сложным, так как в каждом конкретном случае требуется определить
координаты центра поворота.
Оказывается возможно определять упругие перемещения по упро-
щенным схемам, для чего применяются следующие приемы:
1. Все направляющие, имеющие наклонные грани, приводятся
к условным прямоугольным, с шириной граней, определяемой из
условия равенства жесткости действительной и условной грани.
2. Смещение суппортов и столов рассматривается как сумма
смещений от поворота относительно начала координат и поступательного
перемещения вместе с ним.
Например, для комбинированных направляющих токарных станков
(табл. 51)
8,=Чр+^=* (°^+ч7с"ас^)' <7-2>
соответственно условные давления на
горизонтальных и вертикальных приведенных гранях:
°йгор — йгН ; *йверт ~ ^Н '
горизонтальная и вертикальная реакции
приведенных граней;
приведенные ширины граней I см\ под
приведенной шириной наклонной грани понимается ширина
грани, нормальной к действующей силе, при
которой имеет место такое же упругое смещение в
направлении действия силы, что и при наклонной грани
с1г = Ьз1п2$; 4ё — асо52а -}- Ь со$2 р;
горизонтальное перемещение точки О салазок
(начала координат), 8д^= коВг0р.
257
где ай , ов
*-^гору ^верт
игор
Определение перемещений инструмента или изделия в направлении, перпеи
Момент, воспринимаемый
Расчетная схема. Тип направляющих направляющими
(относительно начала координат)
Вспомогательные направляющие для токарных станков:
а — направляющие верхнего суппорта (прн положении Основные направляющие для токарных станков: а — прямоугольные;
оси направляющих параллельно оси изделия) б—комбинированные
258
Таблица 51
дикуляриом поверхности обработки, в результате контактных деформаций
Реакции иа гранях
Средние
давления на гранях
Перемещения, отнесенные
к инструменту
25У
Расчетная схема» Тип направляющих
Момент, воспринимаемый
направляющими
(относительно начала координат)
260
Направляющие радиально-сверлильных станков: а - для "рХ^ьГ-сверлил'ькых" "аТов: Вспомогательные направляющие
перемещения суппорта; б - для перемещения рукава ^ поямоугольные- б - по Фооме для Т0КаРных станков: б - направля-
(кольцевые) | п^ял /1асточки„ ХВОст» Н | ющие для поперечного перемещения
Продолжение табл. 51
Реакции на гранях
—
—
А-РуСХ%а— С
„ мх
—
Средние
давления на гранях
—
-
А
°А^ аН
С
мх
0Ь(Н-2Ь+Щ
Перемещения, отнесенные
к инструменту, и углы
поворота в направляющих 1
где к - коэффициент,
зависящий от величины
смещения нейтральной
оси, находится по
графику фиг. 148
ЬМУ
к находится по
графику фиг. 148
- 2ашах
2кМх
261
Расчетная схема. Тип направляющих
Момент, воспринимаемый
направляющими
(относительно начала координат)
Рг> Р*,* &* — составляющие сил резаиия по осям координат в кГ;
х, у, х — координаты точек приложения "сил в см;
а, Ь, с — ширина рабочих поверхностей направляющих в см;
а'у Ь\ с' —ширина планок или вспомогательных граней в см;
Н —• длина контакта направляющих в см;
а> Р — углы наклона направляющих к осям координат;
ку — коэффициент изменения угла <р поворота в стыке, зависящий от смещения нейтральной оси;
к — коэффициент пропорциональности между давлениями и деформациями в стыках.
Примечание. Полное относительное перемещение инструмента и изделия в результате
деформаций в стыках находится суммированием значений <р или б для отдельных стыков.
262
Направляющие вертикально- и горизонтально-фрезерных станков: а — для продольного перемещения;
б — для вертикального перемещения; в — для поперечного перемещения
Продолжение табл. 51
Реакции на гранях
Средние
давления на гранях
Углы поворота
в направляющих
при
Л~ у л
Вг=Ру
Вв + Св=А- Р2
А- Р2>РУ с1й «
ал=т
Н
ср = к
°*с.
+ «д
'ВС,
Ул
верт 2#в//
где Ьв' = Ь'СО&2а
Уа + Уо +
Р*Уо
Уа^Уо
Вг = Ру; О = Рг - А + Ру с1§ а
при О>0
"А
О
г
СВ
Ьг'~-
А-
- ън
Вг
Ь'гН
В
~ЬН
= Ь' з1п2а
= к
Уа + Уо
к9 находится по
графику фиг. 148.
263
Для обычных соотношений размеров направляющих, принятых
в станках, относительная погрешность при таком упрощении не
превышает 7—10%.
Приближенные формулы для определения относительных
перемещений инструмента и изделия в результате контактных деформаций
в направляющих основных типов станков приведены в табл. 51.
В случае разных коэффициентов контактной податливости на
разных гранях направляющих перемещения определяются по следующим
формулам:
для прямоугольных направляющих токарных станков
\=Ьв*в+ ААус ССгР;
для комбинированных направляющих токарных станков
Ъу = к0о0 + °°^т _2
У и игор 1 у 2р.
Здесь кЛу кВу кс> к0— коэффициенты контактной податливости
отдельных граней. Для других форм направляющих перемещения
определяются аналогичным образом.
2. О пре дел ение наибольших давлений
в направляющих ч упругих перемещений
при повороте салазок в продольной плоскости ХЪ
Для выяснения распределения момента Му (или Мг) между
передней и задней направляющими используется уравнение деформаций —
условие равенства друг другу относительных углов наклона в обеих
направляющих, т. е. равенства друг другу углов наклона прямых,
очерчивающих эпюры давлений.
При значительной жесткости салазок моменты МЛу (Мйу) и МСу>
воспринимаемые соответственно передней и задней направляющими,
определяются с помощью графика фиг. 146-; при этом сплошные линии
соответствуют случаю, когда планки отрегулированы без зазора и
принимают участие в работе, штриховые линии — когда планки
отрегулированы с большим зазором.
Если салазки имеют малую жесткость на кручение относительно
оси К, а нагрузка действует на одну из направляющих (салазки
токарных станков с узким мостом), то можно считать, что момент Му
полностью воспринимается этой направляющей.
Для треугольной направляющей, если определены -{по фиг. 145)
моменты, воспринимаемые передней направляющей М0у и М0,, то из
уравнений статики легко определить мрменты, воспринимаемые
отдельными гранями А и В:
Мл==МОу$\п$ — М02со$$ и Мв~М0усо$$+М02$т$. (7.3)
Для комбинированных направляющих (из плоской и треугольной)
М])г — М„ для двух треугольных направляющих МВг определяется
с помощью графика фиг. 146 аналогично МВу.
Наибольшее давление атах на отдельных гранях направляющих
определяется с помощью графика фиг. 147, на котором приведены
отношения в зависимости от -ггтг, где М^ и Рь — момент и реак-
23*
Прямоугольные направляющие
Комбинированные направляющие
с н* ч>
4? ^Ч^а д~~с~
Приведенная ширина
треугольной направляющей
"у
г>5сн
Фиг. 146. График для определения распределения момента Му между гранями А (О)
и С. Кривые линии на графике: сплошные — соответствуют случаю, когда планки
участвуют в работе; штриховые — когда планки не участвуют в работе. Момент,
воспринимаемый передней гранью А(й), определяется по формуле
М
Ау
~м,{1-^)™ »» = му{*-%гУ
С — реакция задней грани.
Фиг. 147. График для определения наибольших давлений на направляющих под
действием момента Му.ц силы Я/. Кривые линии на графике: сплошные-—соответствуют
давлению на основных гранях направляющих; штрихпупктирная — соответствует дай*
лению на вспомогательных гранях направляющих; штриховая—давления на основных
гранях, когда планки отрегулированы с зазором.
265
дия, воспринимаемые отдельной гранью направляющей1. Под оср
понимаются средние давления ка гранях, определенные по формулам
табл. 50.
Ч
м
Фиг. 148. График для определения коэффициента к^.
Угол поворота в стыке при равной ширине обеих основных
граней Ъ определяется по формуле
(7.4)
где к9 — коэффициент, определяемый по графикам фиг. 148;
значения к9 получены при подстановке значений давлений в
направляющих [53, а] в общие выражения для относительного угла поворота
(фиг. 149).
I Графики фиг. 146 и 147 построены на основе уравнений статики и условия
равенства друг другу относительных углов наклона кареткн и станины у передней и задней
направляющей [53, а],
266
В общем виде при разной приведенной ширине основных граней Ь\
и Ь2 угол поворота в стыке определяется по формуле
у — ккп
(7.5)
Эта формула получена при предположении, что момент Му
распределяется между направляющими пропорционально приведенным
ширинам.
1к
"*(&
6гдг
ШШ1ШЩшш^\е
Фиг. 149. Распределение перемещений и давлений по длине направляющих под
действием момента Му и силы Рг:
а — давление распределяется по всей длине основных граней; б — давление распределяется не по всей
длине основных граней; в — давление распределяется между основными гранями и планками (или
вспомогательными гранями).
Фиг. 150 График для определения относительного смешения нейтральной оси
в направляющих.
Перемещения вдоль оси X в любой точке на высоте г0 от
направляющих находим по формуле
12Му20
Ъх = <?г* = кк9 № + ад№; (7.6)
267
перемещение вдоль оси 1 на расстоянии Хо от середины длины
направляющих по формуле
8, = <р(хв+ *') = **
12МУ
х0 х
<р (Ьх + ь2) № \ТГ + "77
(7.7)
где л/ — смещение нейтральной оси от середины направляющих,
определяемое по графику фиг. 150 [53, а].
3. Влияние сил трения и зазоро© «а упругие
перемещения в направляющих
Как показали эксперименты, упругие перемещения в стыках при
быстро изменяющейся нагрузке, например, при обточке валиков 'с
переменным припуском отличаются от перемещений при длительно
действующей статической нагрузке. Это объясняется действием сил трения
на гранях направляющих, а также повышенным сопротивлением
выдавливанию масла. Силы трения препятствуют росту деформации при
возрастании ^нагрузки и уменьшению деформаций при убывании
-нагрузки. Это приводит к тому, что при обработке деталей с
неравномерным припуском, например,
овальных, эллиптических или
эксцентричных, форма
заготовки не копируется на
изделии, а получается с некоторым
искажением [2]. При
длительно действующих постоянных
нагрузках вследствие
неизбежных при работе станков
толчков и вибраций силы
трения снимаются.
Действие сил трения
может быть учтено введением их
в уравнения равновесия и
соответственно в выражения для
средних давлений.
Изменение упругих перемещений вследствие действия сил трения
по расчетам [39, а] составляют при / = 0,1 от 10 до 20%, при / = 0,15
от 15 до 25% от расчетных упругих перемещений без учета сил
трения. Упругие перемещения при действии сил трения меньше, чем
в случае, когда силы трения снимаются (вследствие толчков и
-вибраций). По экспериментальным данным [21] в поперечно-строгальном
станке упругие перемещения при плавном приложении нагрузки на
25—50% меньше, чем при приложении нагрузок со слабыми ударами.
Приведенные выше (табл. 51) зависимости получены в
предположении, что зазоры в стыках отсутствуют. Наличие зазоров 1не
сказывается существенно на" перемещениях суппортов, если планки не
принимают участия в работе. При переходе давлений с части длины
направляющих на планки наличке зазоров уменьшает работающие
длины направляющих и планок и тем самым вызывает увеличение
упругих перемещений.
Для иллюстрации приводится численная оценка влияния зазоров
на примере стыка с равной шириной основных и вспомогательных
граней при нагружении опрокидывающим моментом Л1.
Номинальные наибольшие давления в направляющих и упругие
перемещения при отсутствии зазоров соответственно равны:
25 б„кГ/см'<
Фиг, 151. Влияние зазоров на упругие
перемещения в направляющих при нагружении
моментом.
_ 6М
°н~ Ь№ И
:%Он.
268
При наличии зазоров зависимость между наибольшим упругим
перемещением 6 и наибольшим давлением а может быть получена из
совместного решения уравнений равновесия и деформаций в стыке:
где Я и Ъ — длина и ширина стыка всм\ А —* зазор в направляющих
в еж.
После совместного решения получаем
ая— (2Ъ + А)к [[ 3(2& + Д) ]'
На графике фиг. 151 построены отношения 6/б0 перемещений при
наличии зазоров и без зазоров для случая к = 1 • Ю-4 смг/кГ. Влияние
зазоров возрастает с уменьшением номинального давления он. В
действительности влияние зазоров несколько меньше вследствие
деформирования суппортов и неравномерности зазоров по длине
направляющих.
4. Значения допускаемых давлений
и коэффициентов контактной податливости
Допускаемые наибольшее давления [53, а! на чугунных
направляющих универсальных станков средних размеров при скоростях движения
подач составляют 25—30 кГ/см2, тяжелых станков—10—15 кГ/см2,
При подсчете по средним давлениям допускаемые значения примерно
в 2 раза ниже. Для специальных станков, работающих с постоянными
режимами, допускаемые давления следует брать на 30% ниже.
Для определения коэффициентов контактной податливости было
обработано большое количество (более 100) экспериментов ряда
авторов по жесткости станков различных типов с различной формой
направляющих и больших моделей направляющих. Охвачены все основные
виды направляющих, ширины направляющих составляли от 20 до
400 мм, средние давления от 0,5 до 10 кГ/см2, наибольшие до 30 кГ/см2.
Величина коэффициента контактной податливости зависит в
значительной степени от размеров стыков и их расположения; при прочих
равных условиях коэффициент к для вертикальных стыков несколько
больше, чем для горизонтальных. Это объясняется б основном влиянием
постоянного давления в горизонтальных направляющих от веса. Кроме
того, в вертикальных стыках имеет место уменьшение фактической
площади контакта, связанное с деформированием элементов под действием
собственного вес#.
На фиг. 152 показана зависимость коэффициента контактной
податливости от среднего давления по результатам обработки 25
испытаний больших моделей направляющих (площадью 300—400 см2)
с шабреными поверхностями. Влияние среднего давления на
величину к на больших моделях выражено слабее, чем на малых
лабораторных образцах, а в реальных станках еще слабее, чем на больших
моделях. В общем при средних давлениях от 3 и до 10 кГ/см* коэффициент к
меняется мало.
Значения коэффициента к по результатам испытания жесткости
станков в зависимости от ширины граней направляющих нанесены на
графике фиг. 153. Коэффициенты контактной податливости стыков сильно
зависят от макро- и микрогеометрии поверхностей и качества пригонки
сопрягаемых деталей и поэтому имеют большой разброс. Для
269
расчетов можно рекомендовать следующие средние значения
коэффициента контактной податливости: для горизонтальных
направлю <смг/кГ
• -По опытам ЗНИМС
По опытам А А Анненкова
]
Среднее
дадление
нГ/см*
Фиг. 152. Зависимость коэффициента контактной податливости от среднего давления
(по результатам испытаний на больших моделях).
ляющих при средних давлениях до 3 кГ/см2 и при ширине
граней до 50 мм — (1,0 ч- 1,5) • 10~4 сж3/кГ; 100 мм — 1,8-10"* см*/кГ\.
мк-см2/кГ_
I
\
I
I
I
$
100 200 300
Ширимо основных граней
Фиг. 153. Зависимость коэффициента контактной податливости от размера
направляющих:
/—для средних давлений до 2 кг/см2; 2— лля средних давлений, больших 3—4 кг/см2. Цифры около точек:'
соответствуют среднему давлению на направляющих. Условные обозначения:
0 — по испытаниям больших моделей направляющих; О — по испытаниям и нормам жесткости К. В. Воти-
нова; Н по испытаниям суппортов токарных станков мод. 1Д62; V—по испытаниям горизоитальио-фрезер-
ного станка; (Ъ — по испытаниям горизонтально-фрезерных станков моделей 682 и 683; О — по испытаниям
долбежного станка мод. 745; >)<; — по испытаниям суппорта тяжелого токарного станка мод. 1660; X — по
испытаниям суппортов карусельных станков (вертикальные стыки)
200 мм — 2,5-10~4 смъ/кГ\ 300 мм — 3,2 • 10"4 см*/кГ; 400 мм —
4*10~4 см^/кГ; для средних давлений выше 3—4 кГ/см2 к на 40—50%
ниже. В тех случаях, когда можно ожидать больших местных отгибов
270
направляющих из-за большого вылета (например, в станинах токарных
станков), значения к следует повышать на 40—50%. Для вертикальных
стыков (по результатам испытания суппортов карусельных станков) при
прочих равных условиях значения к
можно принимать на 30—40% выше.
Все испытания, результаты которых
приведены выше, проводились при
хорошо отрегулированных клиньях и
планках. При плохо отрегулированных
клиньях и планках вследствие зазоров
в стыках действительные перемещения
могут быть значительно больше
расчетных. Наилучшее прилегание по граням
получается на направляющих по типу
«ласточкин хвост», в которых
регулирование наиболее удобное.
Коэффициенты контактной
податливости затянутых стыков ниже, чем для
незатянутых, и зависят от давления
затяжки. Соотношения коэффициентов
контактной податливости для затянутых и
незатянутых стыков по данным
лабораторных испытаний на малых моделях
приведены в табл. 52. Следует отметить, что для стыков станков
влияние затяжки несколько меньше.
Таблица 52
Соотношения коэффициентов контактной податливости
в затянутых и незатянутых стыках
Форма стыка
Кольцевой ....
Прямоугольный .
Постоянное давление в кГ/см2
8
1,0
15
0,5
0,65
20
0,4
0,55
30
0,3
0,4
40
0,2
0,35
Примечание. Разные значения коэффициентов для кольцевых и прямоугольных стыков
определяются формой стыков. Их соотношение также может быть оценено теоретически.
Значения коэффициентов контактной податливости для стыков
текстолит— чугун (фиг. 154), полученные при испытании лабораторных
образцов, выше, чем для стыков чугун—чугун, примерно в 2—2,5 раза.
Учитывая лучшую приработку текстолита, следует ожидать в
станках, несколько меньшей разницы в коэффициентах контактной
податливости.
5. Особенно с;т и расчета направляющих перемещения
консоли одностоечных станков
Консоли консольно-фрезерных станков, столы сверлильных станков
и т. п. с точки зрения расчета являются статически неопределимыми
системами: нагрузки от сил резания и веса воспринимаются
направляющими и винтом подъема консоли. Для определения нагрузок на
направляющие необходимо определить силу Л, действующую на винт
(фиг. 155). При этом могут быть два расчетных случая: а) консоль
зажата; б) консоль не заката.
мксмфс?
12 3 4 5 6 7бкГ/см>
Среднее дабление
Фиг. 154. Зависимость
коэффициента контактной податливости от
среднего давления для разных
сочетаний материалов. Обработка
стыков — шабрение, 5—7 пятен иа
кв. дюйм. Ширина стыков 300 мм,
площадь около 700 см2:
1 — чугун — чугун, 2 — текстолит
ПТ—чугун
271
Консоль зажата на направляющих (фиг. 155>а). Предполагается, что
сила зажатия достаточно велика.
Для определения нагрузки, воспринимаемой винтом, кроме
уравнений равновесия Рг =А-\-В и М = Рук-\-Ргхр —А1и используем
уравнение деформаций, т. е. условие равенства перемещений в направлении
оси винта от деформаций в механизме подъема и от деформаций в стыке
консоль — станина (собственные деформации консоли не учитываются)
*л = <Р*1 = Л **;
здесь ср—угол наклона консоли, определяемый по формуле (7.4);
е — суммарная податливость механизма подъема, определяемая
смятием в резьбе винта, сжатием винта, деформациями
опорных подшипников и втулок и т. д.
После совместного ре-
ры шения уравнений получаем
4 1
'т77777777777777/,
о)
6)
Фнг. 155. Схема нагруження консолн:
а — консоль зажата; б — консоль не зажата.
еЬН*
И
В = Рг-А,
где #—коэффициент
контактной
податливости стыка;
Н — длина
направляющих консоли;
Ь — ширина
направляющих.
Наибольшее значение силы В имеет место при приближении зоны
резания к стойке (т. е. при хр^ 0 и В -> А,).
Проверочные расчеты показывают, что вследствие большой
податливости механизма подъема сила А мала по сравнению с силами
резания и приближенно можно считать
М = Рук-\-Ргхр и В = Рг.
Погрешность такого приближения не превышает 10%.
Консоль не зажата на направляющих. Упругие перемещения консоли
вдоль направляющих ограничиваются жесткостью механизма подъема
консоли. Обычно при работе станка в результате толчков и вибраций,
силы трения в направляющих выбираются. Тогда соответственно из
условий равновесия получаем
М
-^[ч-та-^-О]' А=р-
При безвибрационной работе можно считать, что на консоль со
стороны направляющих действует сила трения. Если предположить, что
нагрузка на направляющие от момента М распределяется по
треугольному закону (фиг. 155,6), то сила трения
/?=2Я/=
ш/
где Р-
/-
и >
-равнодействующая давлений для половины длины консоли;
■коэффициент трения на направляющих.
272
ЗА!
Тогда А = Рг— р = Рг ^-/, а величину момента М можно
определить из уравнения М=Ру/г-\- РгхР— А1г.
Окончательно получаем
М = Рук-
Рук \ ^'Ч л_п\л И \ Рг1х + /, V
, Рг1,
1
3//,
Л = Р,
3/^г
Например, при у-=2; -у-= 2,5; -^- = 0,75; / = 0,15 и лгр^0
получаем Л = 0,89Р^
Б. Определение собственных деформаций салазок
Рассмотрим деформации салазок в плоскости, перпендикулярной
к направляющим. При большом расстоянии между направляющими и
низкой жесткости салазок (особенно в суппортах с узким мостом)
собственные деформации тела салазок оказываются значительными, соиз-
^ «г
6)
Фиг. 156. Расчетная
схема к определению
собственных деформаций
суппортов.
меримыми с контактными деформациями в направляющих. Низкая
жесткость салазок обусловлена тем, что утолщение тела салазок при
заданном диаметре обработки приводит к увеличению высоты центров,
что, в свою очередь, связано с увеличением плеч действующих сил,
удорожанием конструкции и т. д.
Деформации салазок вызывают неравномерное распределение
давлений по ширине направляющих и даже распределение давления по
части ширины грани. Это ведет к тому, что наибольшие давления у
кромок оказываются значительно больше средних.
273
В ряде случаев, в частности в токарных станках, собственные
деформации тела салазок могут быть ориентировочно определены путем1
рассмотрения салазок как балки или пластины с упругим защемлением
в направляющих. Салазки и поперечный суппорт соединяются при
помощи ласточкина хвоста и смещаться в вертикальном направлении
относительно друг друга не могут. Поэтому их следует рассматривать
как двухслойную балку, оба слоя которой изгибаются совместно, но
могут сдвигаться один по отношению к другому. Если корпус
поперечного суппорта занимает всю или почти всю длину моста, то салазки и
поперечный суппорт можно рассматривать как балку постоянной
жесткости. Жесткость такой составной балки Е1 равна -сумме жесткостей
Е1\ + Е12 составляющих балок. Для кареток с узким мостом ввиду
большой жесткости «крыльев» можно рассматривать деформации только
моста, т. е. участки на длине крепления поворотной части и «крыльев»
считать абсолютно жесткими (фиг. 156, а). При этом нагрузку удобней
приводить к сосредоточенному моменту М и вертикальной силе над
передней опорой. Ниже учитывается влияние защемления только в перед-
ней опоре, в задней опоре оно на порядок меньше.
1. .Оп р ед е л е н ие собственных деформаций
Момент упругого защемления Моп в месте соединения салазок с ре-
редней направляющей определяется из условий равенства углов наклона.
Угол наклона салазок в передней опоре из рассмотрения их каьс
балки (фиг. 156, а)
(М - Моп) [(/, - дг)з „ рз]
Угол наклона в передней направляющей из рассмотрения
контактных деформаций
\2МАк \2Мпк
где МА и Мв — доли опорного момента Моп, воспринимаемые гранями
А и Ву М0П = МЛ + МВ.
Отсюда имеем уж = (д3 + 6Э)я '
Приравнивая <р и <рЛ, получаем выражения для опорного момента/
Моп и угла наклона ср салазок в передней опоре:
м = м • — 9м
где
0П ~ 126 ЖЛ* ' т — (^ + Ь6) Щм >
1 + (Ф + Ь*) и ' [(I - ту - г/з] 1 + у2Ш
го _ М К* - КО3 ~ «3] пял
9М — зЕТГа ' ^7'8^
Перемещение 6у вершины резца в результате деформаций салазок и
поперечного суппорта
8у = <рЛ, (7.9)
где к — расстояние от оси резца до нейтральной оси нижнего суппорта.
Угол наклона упругой линии салазок у задней направляющей С
(М - Моп) (Ь - т -р. у) [Ь (Ь 4- т + у) - 2 (ш2 -+ ^ +. V*)] п л т
Если корпус поперечного суппорта имеет небольшую длину и
расположен над передней направляющей, то салазки и поперечный суппорт
274
следует рассматривать как балку переменной жесткости. На участке
поперечного суппорта жесткость принимается равной сумме жесткостей
салазок и поперечного суппорта, на остальной части — равной
жесткости салазок. В остальном решение не отличается от предыдущего.
2. Распределение давлений по ширине
направляющих
Давления на направляющих могут быть распределены по закону
трапеции (в работе участвует полная ширина грани, фиг. 156,6) или по
закону треугольника (в работе участвует неполная ширина грани)
(фиг. 156, в).
Наибольшие давления на гранях:
2Ао\
а) когда в работе участвует полная ширина грани (ср
^ с )
<?шах = а + -|^; (7.11, а)
б) когда в работе участвует неполная ширина грани (<р > -~-\ >
с=ТЛ^; (7Л1,б)
здесь о — средние давления на грани в кГ/см2; с — ширина грани в см\
ф—относительный угол наклона в стыке у рассматриваемой грани.
Ширина грани, принимающая участие в работе:
ср:
/2а6
ус
Расчеты показывают, что в суппортах токарных станков с узким
мостом в ряде случаев участвует только часть ширины (70—80%)
граней а и с (фиг. 156) и наибольшие давления у кромки превышают
средние в два и более раза.
В. Порядок технического расчета
Технический расчет суппортов, салазок, консолей и столов большой
жесткости и их направляющих производится следующим образом:
1. Определяются реакции граней направляющих и средние давления
(табл. 50).
2. Определяются моменты, воспринимаемые отдельными
направляющими, и наибольшие давления на гранях по формулам (7.3) и
графикам фиг. 146 и 147.
3. Определяются упругие перемещения, отнесенные к инструменту
в результате контактных деформаций в направляющих по формулам^
(7.1), (7.2), (7.4) — (7.7) и формулам, приведенным в табл. 51.
Коэффициенты контактной податливости к выбираются в соответствии с
рекомендациями, приведенными на стр. 270.
Г. Расчеты, связанные с износостойкостью направляющих
Расчеты направляющих на долговечность по износу пока не нашлю
практического применения, так как износ в очень большой степени
определяется попаданием на направляющие абразивных частиц, окалиныг
стружки, что трудно учитывается расчетом.
Практический интерес представляют основанные на
экспериментальных данных расчеты, позволяющие выявить условия, при которых
обеспечивается минимальное влияние износа на точность обработки-,
275
Таблица 53
Примеры определения формы изношенной поверхности направляющих станины и [49]
Кривая распреде
ления
перемещении
суппорта (р(х)
Зпюра
удельных
даблений 6^
<рорми
изношенной
направляющей
участка ^ Г( ' '
Примечание,*!
■ коэффициент износа материала, представляющий величину
линейного износа в мк даииой пары ма1ериалов на пути треиия 1 км при давлении 1 кг [см? и в даииых
условиях изнашивания; 5 (км)\ — общий путь треьия; I (см) — длина хода; 10 (см) — длина суппорта*
<х1 (кГсм*) ~- давление в сечении направляющие с координатой I; <р (а-— I) - выражение кривой
распределения перемещений суппорта, отнесенной к точке направляющих суппорта с координатой I; <р (х) —
выражение кривой распределения, отнесенной к левой точке направляющих суппорта.
Эпюра и имеет 3 учлежа — крайние I и Ш, где каждое сечение станины изнашивается частью
длины суппорта, и средний II, где каждое сечение станины изнашивается всей длиной суппорта. Пределы
интегрирования 1$ и /3 Для каждого из участков и для каждого расчетного случая разные.
276
в частности установление оптимальных углов й соотношении ширин'
граней.
В связи с тем, что на работоспособность трущейся пары в основном
влияет неравномерный износ, представляет определенный интерес
расчетное исследование формы износа направляющих по длине. В табл. 53*
приведены примеры определения формы изношенной поверхности
направляющих станины при разных эпюрах давлений и законах
распределения перемещений суппорта по длине направляющих. Зависимости
в табл. 53 получены при следующих предположениях:
1. Величина износа направляющих пропорциональна пути трения
и давлению, что является приемлемым для абразивного износа,
характерного для направляющих.
Фнг. 157. Схема одределения погрешности изделия, вызванной нзиосом нарравляющих
токариого станка.
2. Эпюра давления сохраняется неизменной при изнашивании
направляющих. Из табл. 53 видно, что если длина хода Ь больше длины
направляющих суппорта /о (токарные, расточные и т. п. станки), то
основное влияние на форму изношенной поверхности оказывает закон
распределения перемещений ф(#)> а эпюра давлений влияет
незначительно. Чем меньше отношени Ь/1о, тем больше форма кривой износа
приближается к форме эпюры давлений.
Смещение лезвия режущего инструмента в результате износа
определяется аналогично смещению в результате упругих деформаций (см.
раздел А). Например, для комбинированных направляющих токарного
станка (фиг. 157, а) смещение вершины резца равно [37]
5 := ив соз а — иА $1п а ■
(иА С08 а + ив з!п а — ис),
Ус
где иА, ав и ис — соответственно износ граней А, В, С на данном
участке станины в мк.
Для прямоугольных направляющих (фиг. 157, б)
Ь = ив + -г(иА — и€).
Ус
Для двух треугольных направляющих (фиг, 157, в)
1 = 2/2> ^2А + ^^в _ Пс) + (2А ~~ Ус) ^А — ^'
где и0 — соответственно износ грани О.
Для получения правильной формы изделия необходимо, чтобы
смещение вершины резца В в результате износа было равно нулю или
отрицательно (для компенсации упругих смещений).
277
Кривые на фиг. 158 представляют соотношения между износом
отдельных граней, при которых отсутствует искажение формы
изделия ($ = 0). Для прямоугольных направляющих обычно иА^> ис
избежать искажения формы изделия при износе невозможно. Для боль-
иА
шинства станков с комбинированными направляющими -— = 0,8 -г- 1,5
ав
иА
т. —^ = 2-^4,5. Наименьшее влияние износа на точность при комои-
ил а*0° сх=25 д=23°
«
• -тг=0,65
Ус
*Р 2 1,5
^1\
\35\
^л
I 2 3 15 6 7 8 9 !0пт
6)
Фиг. 158. Соотношение между величинами износа граней направляющих токарных
станков, при которых отсутствует искажение формы изделия.
а — для комбинированных направляющих; б — для треугольных направляющих.
нированных направляющих имеет место при <х = р=45° (фиг. 158, а).
иА
Для станков с двумя треугольными направляющими -^— = 0,8 -г- 1,5,
«,
—=2,5-^9, — = 1 -^3,5. Искажение формы изделия отсутствует
при равном износе граней —- = —
ав с
-^-=1 (фиг. 158,6). Для сохра-
нения точности обработки следует, главным образом, уменьшать
— с тем, чтобы 1<—— < 2, что может быть достигнуто умень-
ис ис
шением износа передней направляющей.
Д. Анализ работы направляющих и выбор оптимальных форм
и конструктивных соотношений размеров
1.Выбор оптимальных форм и соотношений
размеров направляющих
При выборе форм направляющих должны учитываться условия
обеспечения наибольшей жесткости, условия минимального влияния
износа на точность обработки, а также технологические требования.
С точки зрения износостойкости наивыгоднейшими являются такие
конструктивные формы направляющих, при которых износ
направляющих в меньшей мере сказывается на точность обработки и давления на
наиболее нагруженных гранях минимальны. Как правило, при этом
получаются и наименьшие приведенные к инструменту смещения
суппортов за счет контактных деформаций, т. е. в большинстве случаев
оптимальные формы направляющих с точки зрения жесткости являются
оптимальными и с точки зрения износостойкости. Ниже при сравнении
жесткости различных применяемых форм направляющих принимается
одинаковый коэффициент контактной податливости к для разных форм
278
направляющих. ЭтоЛ в некоторой мере условно, так как площадь
действительного контакта и местные деформации при разных формах
направляющих несколько различны.
Анализ форм и соотношений размеров
направляющих токарных станков
За основной критерий принимаются перемещения резца по нормали
к обрабатываемой поверхности при обточке.
Эксплуатационные наблюдения [37] показывают, что из наиболее
употребимых форм направляющих станин токарных станков
наименьшее влияние износа на точность получается при применении двух
симметричных треугольных направляющих и комбинированных из
симметричной треугольной (а =(3 = 45°) и прямоугольной. В станках с
несимметричной передней направляющей (а = 15-:- 30°) наблюдается менее
благоприятное распределение износа между гранями.
В табл. 54 приведено сравнение давлений на наиболее нагруженной
грани направляющих и перемещений, приведенных к резцу, в
результате контактных деформаций в стыке каретка—станина.
Как видно из табл. 54, наименьшие давления и деформации имеют
место при симметричной треугольной направляющей, наибольшие — при
прямоугольной. При симметричной треугольной направляющей давления
на грани В и упругие перемещения ниже, чем при несимметричной
(а = 25°, (3 = 65°), на 20—25% в случае равной ширины направляющей
и на величину до 15—20% при равной высоте. Эти выводы
подтверждаются экспериментально [45]. Давления и упругие перемещения при
применении увеличенной (на 20%) ширины грани В (графа 4) ниже на
15—30%, чем при равной ширине граней А и В.
Следует отметить, что при симметричной направляющей возникает
опасность «взбирания» суппорта по передней направляющей. Если
суммарная сила, воспринимаемая передней гранью, наклонена к вертикали
на угол у, равный или близкий к углу (3 наклона крутой грани, то при
малейших толчках и вибрациях суппорт будет «взбираться» по
направляющей.
Условия отсутствия «взбирания»: 7 <С Р-
Величина угла у может быть определена по формуле1
где уо — расстояние от оси шпинделя до середины передней
направляющей; й — диаметр обработки; /? — высота центров.
Опасность «взбирания» имеет место при малых диаметрах
обработки й и больших отношениях Ру/Рг.
При сравнении жесткости разных форм направляющих поперечного
и верхнего суппортов за постоянные параметры принята равная ширина
стыка В, равная ширина основных граней а и равная минимальная
ширина корпуса / (табл. 55).
Для поперечного суппорта рассматривается поворот в продольной
плоскости направляющих, для верхнего суппорта — в поперечной
плоскости.
Как видно из табл. 55, в обоих случаях наибольшая жесткость
обеспечивается при направляющих прямоугольного типа, наименьшая
жесткость имеет место при направляющих по форме профиля «ласточкин
хвост» с углом 55°. Следует отметить, что в преобладающем большин-
1 В формуле не учтен вес суппорта, что допустимо для станков средних размеров.
При учете веса суппорта запас против «взбирания» несколько повышается.
27$
Таблица 54
Сравнение жесткости и наибольших давлений при различных формах направляющих кареток токарных станков
Давление на грани В в условных Перемещение у кромки резца I г
единицах в условных единицах Соотношение жесткостеи
Форма вв'НГД "^) в'*(ГДе*-Тя7) 77^17
| направляющих ■ 1 1 . -
^» I -^-0,5 ^-0,8 ^-0,3 -^--0,5 ^-0,8 ^-0,3 I -^ = 0,5 -^-0,8
1 ^ГГ К 4 4 4 1,85 2,65 3,85 1 1 *
I I I I I I I I I I
2 еО=1 1,65 2 2.7 1,65 2.2 3,1 М2 1.19 1.25
! При равной 1 : 1 } : 1 1 г— 1
| ширине
направляющей 5уОч /го
3 Щ*^Б 1,3 1,5 1,8 1,35 1,65 2,05 1.37 1,62 1.85
' II | | I I I I I г I I
280
Продолжение табл. 54
I Давление на грани В в условных I Перемещение у кромки резца I Соотношение жегткостей I
единицах в условных единицах ьоотношение жесткостеи
Форма ,а.«(«,5--^_) 6.ф(гдеф = -^) ±-^
направляющих . , 1 —
-^=0,3 I ^ = 0,5 I ^--0,8 ^ = 0,3 -^ = 0,5 ^-0,8 ^ = 0,3 -^ = 0,5 1^-0,8
1 р У П 0,65 0,8 1,05 0,65^ 0,85^ 1.2 -^ 1 1 *
При равной
высоте на- 1 1 ^ > 1 1 1 1 » 1
правляющей I I I ! I I I I
2 вЗ^^ 0,65 0,75 0,9 0,65^ 0,8 ~ \ 0,9 \ 0,95 1,05 1,3
1А62 ШМ/^Ч - - - 0,4 0,55 0,75 1 11
Для моделей ! ! ! ! !
1К62и 1А62 | ^22ь21~- III
1К62 ^ ^^\1В "~ ~ ~~ 0,ЗЭ °'4 °'5 !'2 1,Э5 *'5
Примечания:
1. ~ принято равным 0,65, что является средним применяемым соотношением.
2. Реакция задней грани С ввиду ее малости при обработке деталей средних диаметров (70—130 мм при высоте центров 200 мм)
принята равной нулю. |
281
Таблица 65
Сравнение жесткости разных типов направляющих поперечного и верхнего суппортов токарных станко*
I Направляющие продольного перемещения Направляющие иопереч юго перемещения
Перемещение у кромки резца* в условных Перемещение у кромки резца в условных единицах
. I единицах | ..„ , 1 {
Форма / ИИ \ > . / I аИ \
Ь . 5 (где * - -4^-1 в • ф (где ф = Примечание
направляющих ^ кРг ) \ отгря у
\ Р„ \ Р„ \ Р^ \ М \ М \ М \ М \
р В ■ Н Приняты следующие
*-|/ Iм* а'——1 *1 „ * соотношения размеров:
1 1Ш| -П.4 +3,7 +7,6 1,0 1,07 1,20 1,28 , \ Р
I ра-Ъг П -^- = 0,22; -д-= 0,7; (
I \\\\\\\\ьа1\
\—\ ! ! ! ! ! ! ! — = о,б; — = о,28
Для направляющих
[^ ° "М поперечного переме-
2 ^/[г1*— 4-ЩАчп9 -^»5 —4,5 +3,0 1,0 1,05 1,14 1,20 щения, кроме того,
' Указанные соотно- г
I _1 | | ! I I I шения размеров явля-
I | 1111111 ются сРеДними приме-
Н В —| няемыми соотиошеиия-
3 Ц/р^е=д^ —16,7 -8,5 +1,8 1,0 1,04 1,12 1,18
* Большие перемещения верхнего продольного суппорта в. направлении, противоположном перемещению других элементов суппорта, I
вызывают уменьшение суммарных перемещений резца.
М
** Обычно в станках -5-7^ < 0,21ч- 0,25.
282
стве случаев у направляющих поперечного суппорта вспомогательные
грани не принимают участия в работе и поэтому разница в расчетной
жесткости направляющих разных форм (при равной ширине основных
граней) невелика (не превышает 5—7%).
Расстояние между направляющими желательно выполнять
наибольшим, возможным из конструктивных соображений (см. формулы на
стр. 257 и стр. 277). Желательно также максимально возможное
смещение оси шпинделя от рабочего. При этом достигается увеличение
нагрузки на малонагруженную заднюю направляющую и уменьшение на
переднюю. Оптимальным, как с точки зрения влияния износа на
точность, так и с точки зрения жесткости, является такое положение оси
шпинделя, при котором в большинстве возможных случаев обработки
работает не задняя планка, а задняя направляющая.
Условие работы задней направляющей (С>0), (см. формулы
табл, 50):
Уо Ру 0,5а
к > Рг + н >
где (I—диаметр обработки; у0 — расстояние от оси шпинделя до
передней направляющей; к — высота центров (принято Яр^к).
Если принять, что в большинстве случаев
и
то
-^ < 0,5,
х>1,1.
Формулу для перемещений на резце за счет контактных деформаций
в стыке каретка—станина можно согласно формуле (7.2) и табл. 51
развернуто записать следующим образом:
Обозначения см. стр. 256—257.
Как видно из формулы, с увеличением -~ и -^- деформации
уменьшаются. Следует отметить, что в тех узких пределах увеличения этих
соотношений, какие возможны из конструктивных соображений,
жесткость меняется несущественно.
Из изложенного можно сделать следующие выводы.
Уменьшение влияния износа на точность обработки и уменьшение
приведенных к резцу контактных деформаций в стыке каретка—станина
токарного станка может быть достигнуто в результате:
1) целесообразного выбора углов наклона граней
направляющих (45°);
2) целесообразного выбора ширины граней (Ь> а):
3) смещения оси шпинделя назад от рабочего;
4) увеличения расстояния между передней и задней направляющими
при заданной высоте центров.
Анализ форм направляющих консольно-фрезер-
лых станков. За основной критерий жесткости принимается угол
283
поворота в стыках вследствие контактных деформаций, как
непосредственно влияющий на точность обработки. Сравниваются два основных
вида направляющих, применяемых во фрезерных станках, —
прямоугольные и по форме профиля «ласточкин хвост». Все рассуждения
проводятся по отношению к стыку консоль — станина, однако они
распространяются и на другие стыки этой группы станков.
При сравнении для обоих видов направляющих ширина
направляющих Ь, высота к и проекция вспомогательных граней Ъ' приняты
одинаковыми (табл. 56).
Угол поворота в продольной плоскости направляющих
(относительно оси У) определяется по формуле (7.4).
Для прямоугольных направляющих коэффициент к9 (см. фиг. 148),
а следовательно, и угол поворота на 15—25% меньше, чем для
направляющих по форме профиля «ласточкин хвост», вследствие большей вели-
Ь'
чины отношения т (для прямоугольных направляющих т = ~^-^0,35-н
4-0,55, для направляющих по форме профиля «ласточкин хвост»
Ьг СО$а Л __. л ог\
т = —т— « 0,25 -*- 0,35).
9а
°в ^с
УА\А 2 С05 а
Ульн
Угол поворота в поперечной плоскости (относительно оси X, см,
табл. 56) для направляющих по форме профиля «ласточкин хвост»
\а + (А9:,р*)Ь].
Угол поворота в прямоугольных направляющих
^ = 2^К + ^с) = 2^ш[Л + V ]'
Результаты численного сравнения жесткости обеих форм
направляющих для отдельных видов нагружения приведены в табл. 56.
Таблица 56
Сравнение жесткости направляющих по форме профиля «ласточкин хвост»
и прямоугольных для фрезерные станков
И Цы I
л
с'
Соотношение сил резания
н реакций
Соотношение углов поворота
в результате контактных
деформаций Ул/1?
Примечание
Ру^ЪЬРг
л = о
1,56
Предельные
соотношения для торцового
фрезерования
Ру = 0,5Р*
1,67
Средние соотношения
Р* = 0
1,70
Соответствует
фрезерованию канавок дисковой
фрезой
284
Угол поворота в боковой плоскости (относительно оси 2):
для прямоугольных направляющих
для направляющих по форме профиля «ласточкин хвост»
_ 12Мг
откуда
Таким образом, расчетная жесткость стыка с прямоугольными
направляющими выше, чем с направляющими по форме профиля
«ласточкин хвост», при повороте в продольной плоскости на 15—25%,
поперечной— на 50—70%, боковой — на 30%. В действительности разница
в жесткости этих двух видов направляющих несколько меньше, чем по
расчету, вследствие неодинаковых коэффициентов контактной
податливости. Как показала обработка экспериментальных данных,
коэффициент контактной податливости у направляющих по форме профиля
«ласточкин хвост» ниже, чем у прямоугольных, вследствие лучшего
прилегания по граням.
По результатам экспериментов, проведенных в ЭНИМСе, жесткость
стыков с прямоугольными направляющими выше, чем с направляющими
по форме профиля «ласточкин хвост», при повороте в продольной
плоскости на 15%, в поперечной — на 35—44%, при одновременном повороте
в обеих плоскостях — на 35—50% [45].
2. Уменьшение упругих перемещений суппорта
путем поворота осей жесткости. Влияние диаметра
обработки на упругие перемещения суппорта
токарного станка
В связи с тем, что направление действия сил резания и направление
упругих перемещений суппортов б,, влияющих на точность обработки
(по нормали к обрабатываемой поверхности), не совпадают, можно
значительно уменьшить эти перемещения путем оптимального поворота
главных осей жесткости суппорта К
В частности, можно спроектировать суппорт, у которого в
определенных условиях обработки упругие перемещения по нормали к
поверхности обработки будут равны нулю (так называемый суппорт
«бесконечной жесткости» по терминологии К. В. Вотиноза). В простейшем
случае эти перемещения будут равны нулю, например, тогда, когда
отжатие инструмента г«од действием радиальной составляющей силы
резания равно врезанию инструмента под действием вертикальной
составляющей силы резания.
Поворот осей жес! кости суппортов происходит при изменении
вылета резцов, при изменении диаметра обработки, при изменении
расположения или типа направляющих и т. д.
Рассмотрим изменение упругих перемещений суппортов при
изменении диаметра обработки. Перемещения инструмента складываются
из приведенных к вершине резца контактных деформаций в направляю-
1 Под главными осями жесткости суппортов ниже понимаются оси, в направлении
одной из которых жесткость максимальна, а в направлении другой — минимальна.
Жесткость определяется по перемещениям инструмента.
285
щих каретки в/с, поперечного суппорта б„.г, верхнего суппорта бй. с>
собственных деформаций каретки 6^, с и деформаций в передаче винт—гайка
поперечного суппорта 6в. Упругие перемещения 6К и Ьк.с зависят от
диаметра обработки й, а 6л.г,^.сио8 не зависят. Упругие перемещения
каретки, определяемые по формулам (7.2) и (7.9), развернуто можн©*
записать следующим образом:
где
А = Р*к*р Л 4- *Ь РгН [{1 ~ ^)3 ~ ^
ЧйН [усу V +*' / + (да + И [^ - т)ъ „ у*] И ;
^[^о+$*-(»-н,+^ш-
ЗЕЛа +" ш
Обозначения см. в табл. 51.
Очевидно, что можно определить диаметр обработки, при котором
суммарное упругое перемещение вершины резца равно нулю:
я0 — д •
Аналогичным образом может быть оценено влияние наклона силы
резания, т. е. соотношения составгЯяющих РК и Р..
В качестве примера для суппорта токарного станка мод. 1А62
определим диаметр, при котором упругие перемещения по нормали к
поверхности обработки равны нулю. Проведем расчет для значения Ру\Рх =
= 0,35 и вылета резца 20 мм.
После подстановки численных значений размеров в формулы
табл. 51 получаем
8, + 8*.с= (-13,45+ 1,<Ш)Ю-7Я, см; *л.с=1,42 • Ю~7Рг см;
&,.,= —20,5 • Ю-7/^ см.
Коэффициенты контактной податливости в соответствии с
результатами испытаний приняты для направляющих каретки 1 • 10" /} смг/кГ, для
направляющих поперечного и верхнего суппортов 0,7*10 ' см^/кГ.
Перемещения, определяемые деформациями в винтовой паре
поперечного суппорта, по результатам испытаний [45] составляют
&в=*19,6-10-7Яг см.
Окончательно диаметр, при котором суммарные перемещения
суппорта равны нулю, йо = 12 см. Таким образом, в рассматриваемом слуг
чае при диаметре обработки меньше 120 мм суппорт будет «клевать»,
т. е. вершина резца будет перемещаться по направлению к оси
Р
изделия. При отношении составляющих сил резания ~р- = 0,37
получаем с/а = 75 мм. Эти результаты подтверждаются
экспериментами [21].
Следует отметить, что полученные расчетом значения йъ
ориентировочны, так как определены по усредненным значениям коэффициентов
контактной податливости.
286
3. Определение упругих деформаций под действием
веса перемещающихся узлов и деталей
(на примере консольно-фрезерных станков)
Перемещения узлов, имеющих большие массы или нагруженных
тяжелыми изделиями, могут вызвать значительные упругие деформации
в стыках ', в результате которых в станке возникают существенные
перекосы (например, при перемещении столов координатно-расточных, кон-
сольно-фрезерных станков и т. п.). В частности большие перекосы
в стыках возникают в крайних положениях столов при свешивании или
при наличии нескольких подвижных стыков в узле.
В качестве примера определим угол наклона стола горизонтально-
фрезерного станка мод. 6Н82 при перемещении его в крайнее положение.
Вес стола О = 225 /сГ, ход стола (от среднего положения) хс —350 мм.
Опрокидывающий момент в крайнем положении М = Оха==7900 кГсм
Направляющие стола и консоли выполнены по форме профиля «ласточ*-
кин хвост», направляющие салазок — прямоугольного типа.
Вычисляем углы поворота в стыках.
1) Стык консоль—станина (см. табл. 51). Расчетные данные: # =
= 44 см; V == 4,9 см; а = 55°; Ь9Р= 6'зт255° = 3,3 см; к = 0,3 • 10~4 см3/кГ
(стык затянут).
Угол поворта в стыке
2) Стык салазки—консоль. Расчетные данные: И = 44,5 см; а =
= 11 см; с/ == 2 см; ус' = 32,5 см; уР = 21 см; к = 1,8 • 10~4 см3/кГ.
Напряжения на гранях: <?* —0,755 нГ(см2\ *^ = 1,63 мГ/см2.
Угол поворота в стыке
к (с. -1- о'Л
т = \ *; с> — и мк/м.
Ус
3) Стык стол—салазки. Расчетные данные: Н = 67,5 см; Ь = 6,3 смлг
Ь' = 3,3 см; а = 55°; к? = 1,8 (по фиг. 148).
Ввиду большого влияния зазоров принимаем й —2«10~ смъ/кГ.
Угол поворота в стыке
6МЬк
?__
Ь№
? = —^- = 8мк1м.
Суммарный угол наклона стола в результате упругих контактных
деформаций ф = 27 мк/м.
§ 4. РАСЧЕТ НАПРАВЛЯЮЩИХ КАЧЕНИЯ
Определение погонных нагрузок и распределение нагрузок между
направляющими, а также определение деформаций суппортов и столов^
на направляющих качения можно приближенно производить так же,
как и при расчете этих узлов на направляющих скольжения. Это
вытекает из следующих соображений:
1. Число тел качения на длине направляющих, как правило,
достаточно велико, вследствие чего с требуемой степенью точности
перемещающуюся деталь (суппорт, стол) можно рассматривать как балку на
сплошном основании.
1 Одновременно возникают и деформации деталей станка — станины, основания,
консолн, которые здесь не рассматриваются.
287
2. Между телами качения и направляющими обычно имеется
начальное давление от веса или дополнительно искусственный
предварительный натяг, вследствие этого зависимость между упругими сжатиями
и нагрузкой от сил резания в определенной зоне давлений можно с
некоторым приближением принять линейной. Вместо коэффициента
контактной податливости к в расчетные формулы следует подставлять значение
приведенного коэффициента кпр (см. ниже).
Нагрузка на наиболее нагруженное тело качения (в предположении
идеально точных размеров тел качения) определяется по формуле
Лпах = ?пих ' а, (7.12)
где а — расстояние между телами качения (шаг) в см;
Ятах—наибольшая погонная нагрузка на направляющих
(вычисляемая по тем же зависимостям, что и давления на направляющих
скольжения !) в кГ\см.
Для шариковых направляющих с У-образными канавками,
аналогичных треугольным или У-образным направляющим скольжения, расчет
ведется по наибольшей погонной нагрузке, действующей на наиболее
нагруженную грань.
Наибольшие контактные напряжения между телами качения и
направляющими определяются по формулам [1];
для шариковых направляющих
«та* = Сш У^Р кГ\см\ (7.13)
для роликовых направляющих
,-с,У-
где й — диаметр шарика или ролика в см;
Ь — ширина ролика в см;
€Ш9 Ср — коэффициенты: для стальных направляющих Сш= 10000,
Ср = 850, Для чугунных направляющих Сш = 7600, Ср = 687.
Приведенный коэффициент контактной податливости кпо для
роликовых направляющих может быть определен по формуле [55] (в
предположении, что в направляющих имеется предварительный натяг от веса
узла или специального натяжного устройства):
кпр = Аа(В-\&5) смЧкГ. (7.14)
к
Для шариковых направляющих вместо величины -у в формулы для
направляющих скольжения следует подставлять
Са
Здесь А и В — коэффициенты, зависящие от диаметров тел качения,
толщин 1\ и и направляющих и модуля упругости материала
направляющих (табл. 57); для стальных направляющих С = 1,27 • 10~4, для
чугунных направляющих С= 1,57-10~4; Р0 — средняя нагрузка на одно
тело качения от веса перемещающегося узла, предварительного натяга
и сил резания <в кг.
Проверочные расчеты [55] показывают, что жесткость роликовых
направляющих в предположении участия в работе всех тел качения выше
1 <7тах — (Ттах Ь, где атах — наибольшие давления по формулам § 3, Ь — ширина
направляющей скольжения.
(7.15)
288
жесткости направляющих скольжения, а жесткость шариковых
направляющих примерно того же порядка или несколько ниже-
Таблица 57
Значения коэффициентов Л и В для определения податливости направляющих качении
I *1-/а в ^Ю2
! 10
25
1 40
Модуль упругости материала направляющих Е в кГ/см2
1,0-10&
А
2.10е
В
6,9
7,2
7,3
1,5.10е
А
1,55-106
в
6,2
7,25
7,35
2,1 -10* 1
А
1,23-106
в
7,05
7,25
7,35
В особо точных станках целесообразно применять тела качения
меньшего диаметра и за счет этого увеличивать число тел качения. При
одинаковом заполнении канавок несущая способность тел качения
с уменьшением их диаметра практически не меняется, в то же время
увеличивается жесткость направляющих и улучшается направление,
В настоящее время в отечественном станкостроении еще не накоплен
опыт выбора допускаемых контактных напряжений для направляющих
качения. Поэтому пока можно пользоваться общими правилами выбора
допускаемых контактных напряжений. Подавляющее большинство
направляющих качения является направляющими движения подачи или
других медленных перемещений. Для них основным условием
работоспособности является условие отсутствия остаточных деформаций, и
расчет должен производиться аналогично расчету подшипников качения на
статическую нагрузку.
Для направляющих, работающих при высоких скоростях, которые
имеют в настоящее время ограниченное применение, условием
работоспособности является отсутствие выкрашивания. В связи с этим расчет
следует вести по выносливости поверхностных слоев.
Наибольшие допустимые давления из условия отсутствия
остаточных деформаций составляют: при стальных закаленных шариковых
направляющих— 15 000 кГ/см2, роликовых—10 000 кГ/см2у при чугунных
незакаленных шариковых направляющих — 6000 кГ/см2, роликовых1 —
4000 кГ/см2. Шариковые направляющие обычно оказывается
необходимым выполнять стальными закаленными в связи с недостаточной
грузоподъемностью при работе шариков по чугуну. Роликовые чугунные
направляющие в конструкциях без предварительного натяга обычно
обеспечивают достаточную грузоподъемность. В конструкциях,
требующих предварительного натяга, и при больших скоростях движения
применяются стальные закаленные роликовые направляющие.
Меньшие значения допустимых давлений в направляющих качения
по сравнению с 'подшипниками качения2 объясняются:
а) меньшей надежностью расчета направляющих,
б) меньшей точностью изготовления направляющих по сравнению
с подшипниками.
Проверочные расчеты показывают, что действительные давления
в направляющих качения при равномерной (по длине) нагрузке за счет
разброса диаметро,в тел качения в пределах допуска на 25—40% выше
средних расчетных (нижние значения при больших нагрузках, верхние
при меньших).
Практически давления в роликовых направляющих прецизионных станков
(шлифовальных, координатно-расточных) без предварительного натяга составляют
1000—1500 кГ[-см*.
2 Допустимые давления в подшипниках качения при статических нагрузках
принимаются 26 000 кГ/см2 для роликовых и 40 000 кГ/см2 для шариковых.
289
§ 5. РАСЧЕТ СТОЛОВ ПРЯМОУГОЛЬНОЙ ФОРМЫ И ИХ НАПРАВЛЯЮЩИХ
А. Основные положения
По своей конфигурации столы можно разбить на две группы:
1. Столы станков типа сверлильных, поперечно-строгальных и т. д.,
т. е. столы, в которых высота стола соизмерима с остальными
размерами и жесткость поверхностных слоев направляющих ниже собственной
жесткости стола.
2. Столы станков продольного типа (продольно-строгальных,
продольно-фрезерных, плоскошлифовальных, а также
горизонтально-расточных), в которых высота стола мала по сравнению с остальными
размерами и, соответственно, жесткость поверхностных слоев в
направляющих много выше собственной жесткости стола.
Столы первой группы с достаточной степенью точности можно
рассматривать как жесткие тела, совершающие в результате контактных
деформаций в направляющих поворот относительно некоторой оси.
Фиг. 159. Общая схема нагружения стола станка.
Расчет их направляющих рассмотрен в § 3.
Упругие перемещения столов второй группы соизмеримы с
контактными деформациями в направляющих. Эти столы следует рассматривать
как пластины на упругих опорах. Однако для технических расчетов
приближенно столы можно рассматривать по двум упрощенным схемам:
при оценке распределения давлений по длине направляющих, т. е. в
плоскости XI (фиг. 159) —как балки на упругом основании, а при оценке
распределения давлений по ширине направляющих (в плоскости У2) —
как пластины на жестких опорах.
Порядок технического расчета изложен на стр. 300
Столы станков подвергаются нагрузкам от собственного веса Ост
веса изделия Ои и силы резания. В тяжелых станках силы резания
относительно невелики по сравнению с весом стола и изделия, и основной
нагрузкой является нагрузка от веса. Для случая установки изделия
непосредственно на стол обработанной поверхностью, а также в случае
установки изделия на подкладках (башмаках), если число их больше
четырех-пяти над каждой направляющей, вес изделия принимается
равномерно распределенным по длине изделия, а для случая установки
изделия на подкладках, если число их не более трех над каждой
направляющей, вес изделия предполагается передающимся на стол в виде
сосредоточенных сил в местах расположения подкладок.
Стол представляет собой сложную пластину, состоящую из двух
стенок и системы взаимно-перпендикулярных ребер. Определение
упругих перемещений таких пластин при общем виде нагружения очень
сложно вследствие большого влияния касательных напряжений в ребрах;
поэтому ниже определяется условная приведенная жесткость при
наиболее характерном виде нагружения (равномерно распределенная
нагрузка по всей поверхности) и распространяется на остальные виды-
нагружения.
290
Упругие перемещения сложной пластины, опертой по двум сторо*
нам и нагруженной равномерно распределенной нагрузкой, могут быть
приближенно определены, если в расчетные формулы вместо цилиндри*
ческой жесткости Э подставить значение приведенной цилиндрической
жесткости Опр:
А*=ТТ*- <7Л6>
где ^ — коэффициент, учитывающий влияние сдвигающих напряжений'
в ребрах.
Для столов станков удобнее рассматривать сечение стола в продоль*
ной плоскости 1 Х2, тогда
где /ж — момент инерции сечения стола относительно продольной
оси X' в см* (фиг. 159);
Р—суммарная площадь сечения ребер (по всему сечению стола)
в см2;
В и Ь — соответственно ширина и длина стола в см;
Е—модуль упругости в кГ/см2;
\ь—'Коэффициент Пуассона; для чугуна |х^0,25.
Величина коэффициента я)>, учитывающего влияние касательных
напряжений в ребрах, колеблется в некоторых пределах в зависимости
от вида нагружения, сечения, в котором определяются упругие
перемещения, и различна для прогибов и углов наклона. В качестве основного
расчетного выбрано значение ^ для угла наклона на опоре пластины
(балки), нагруженной равномерно распределенной нагрузкой. Такой вид
нагрузки наиболее характерен для столов (действие веса изделия). Угол
наклона на опоре в наибольшей степени влияет на работоспособность
направляющих.
Б. Определение нагрузок на направляющие
Моменты сил, относительно осей координат, воспринимаемые
направляющими (фиг. 159), равны
Мх = РгуР — Ругр + Оиуа — <22ур;
Му^Р^р + Р^р-
гд$ РХ9 Ру9 Р2 — составляющие силы резания по осям координат в кГ\
Ост и @и—вес стола и изделия, соответственно, в кГ\
С}2—вертикальная составляющая тягового усилия в кГ
[53, а].
Моментом от горизонтальной составляющей тягового усилия можно*
пренебречь.
Вертикальные составляющие реакций отдельных граней
А = ±(Ост + Рв) + ^
I иих0 У^о» )
С — ~2 ^ ст^~ ^*' ~В~ *
(7.18)
где Рв — вертикальная нагрузка на стол, Ре = С?м + Рг—(}г.
Горизонтальные силы, действующие на направляющие:
где у — угол наклона зубьев рейки.
1 Принято, что влияние сдвигающих напряжений в обеих плоскостях симметрии'
приблизительно одинакова.
291
Доли момента Му9 приходящиеся на отдельные грани в
предположении, что момент распределяется пропорционально приведенным
ширинам (под приведенными ширинами наклонных направляющих
понимаются ширины горизонтальных направляющих той же жесткости),
определяются следующим образом:
где Ъх и Ьп —приведенные ширины граней Л и С, равные произведению
ширины грани на соз2 а, где а—- угол наклона соответствующей грани
направляющих относительно горизонтали.
В. Определение средних давлений на направляющих
Средние давления на направляющих определяются делением
вертикальных реакций на горизонтальную проекцию площади направляющей:
где Ь — длина стола в см;
ЬА и Ьс — соответственно горизонтальные проекции ширин отдельных
граней в см.
Часто упрощенно среднее давледие определяют следующим обра-
о
Ост + Ов + Р*
ср-
(7.21)
где Р— суммарная горизонтальная проекция площади всех граней в см2.
Средние давления на чугунных направляющих столов продольно-
фрезерных, продольно-строгальные и т. п. станков составляют обычно
около 2 кГ/см2.
Расчет по средним давлениям не позволяет оценить влияния разных
факторов, в частности жесткости стола, размеров и формы изделия,
способа установки изделия и т. д.
Ниже приводится определение наибольших давлений с учетом
неравномерного распределения давлений по длине и ширине
направляющих.
Г. Определение наибольших давлений на направляющих
В результате деформаций столов давления на направляющих
распределяются неравномерно как по длине направляющих, так и по
ширине, причем наибольшие давления могут превышать средние в 2—Зраза
и более.
Жесткость столов в продольной плоскости вследствие их
значительной длины невелика по сравнению с жесткостью поверхностных слоев
направляющих, и давления от веса изделия и сил резания в основном
распределяются на длине, равной длине изделия. Кроме того, при
обработке узких или нежестких изделий столы деформируются и в
поперечной плоскости, и поэтому давления по ширине направляющих
распределяются неравномерно, достигая максимума на внутренней кромке
направляющих. При обработке широких жестких изделий в результате
закрепления изделия на столе жесткость стола значительно повышается,
и деформации в поперечной плоскости направляющих оказываются не-
1 При упрощенном определении средних давлений действие вертикальной
составляющей тягового усилия обычно не учитывается.
292
значительными. При неправильной выверке жестких изделий и
притягивании их болтами к столу, а также при зажатии изделий кулачками на
направляющих могут возникнуть значительные концентрации давлений,
связанные с деформированием стола.
1. Распределение давлений по длине направляющих
В продольной плоскости стол с закрепленным на нем изделием
следует рассматривать как балку переменной жесткости на упругом
основании, причем жесткость такой балки на длине изделия равна
суммарной жесткости стола и изделия. Такое решение является весьма
трудоемким и требует знания размеров и формы изделия, которые для
универсальных станков колеблются в весьма широких пределах. Поэтому
ниже приводятся решения для двух расчетных моделей,
соответствующих двум крайним случаям:
1. Стол рассматривается как балка постоянной жесткости, вес
изделия и силы резания передаются на стол в виде распределенной нагрузки
на длине изделия. Эта модель соответствует случаю, когда жесткость
изделия много ниже жесткости стола.
2. Стол рассматривается как балка с абсолютно жестким
участком на длине изделия. Эта модель соответствует случаю, когда
жесткость изделия много выше жесткости стола.
Действительные значения давлений и упругих перемещений в
направляющих находятся между значениями, полученными для этих
расчетных моделей.
Практически для столов продольных (продольно-строгальных,
продольно-фрезерных, плоскошлифовальных станков) применимы формулы
для бесконечно длинных балок на упругом основании [62].
Для первой модели давления на направляющих определяются по
формулам *:
от веса стола на длине стола
от веса изделия и вертикальЬой составляющей силы резания
2Ы
2-е созр(у— *) — е со8рЬр+*)
где Ь и / — длина стола и изделия, соответственно, в см;
х— текущая координата, отсчитываемая соответственно от
середины стола или изделия, в см\
Ь — приведенная (к горизонтальной) суммарная ширина
направляющих, # = 2^;С052а; в см;
Ь1 — ширина /-той грани направляющих, наклоненной к
горизонтали под углом «/;
~~Ь 1
>=у
40прВЬ см у
Опр—приведенная цилиндрическая жесткость стола в кГсм (см.
выше);
В — ширина стола в см;
к — коэффициент контактной податливости направляющих
3 смъ\кГ (см. стр. 270).
* Действие момента Му пока не рассматривается. Учет момента Му произведен
в окончательных формулах (см. ииже|.
293
При наличии чисто жидкостного трения (столы с клинообразую-
щими скосами на направляющих при больших скоростях) вместо
отношения у в формулу для р следует подставлять значение —^-, где /л* —
жесткость масляного слоя
й-\ ^—. 11*]" . - в кГ/см; Ь — длина стола
в см. Жесткость масляного
слоя существенно зависит
от скорости и вязкости
масла.
Когда жесткость
изделия велика, давления на
направляющих по длине
изделия постоянны и
определяются по формуле [32]
+ (аа + остТ + р2)№,
где
(1 + № ь
5П 0 (/, - /) - $Ш р (I - /)
~~ сН р (Ь - I) + соз р (/. - /) - 2 #
Как видно из графиков
фиг. 160, для обеих
расчетных моделей за пределами
изделия давления от веса
изделия быстро затухают К
давления2,
Наибольшие
определенные для обеих
расчетных моделей,
отличаются не намного (в данном
случае на 10—12%). При
относительно малой длине
изделия разница может по-
Фиг. 160. Распределение давлении по длине
направляющих стола продольно-строгального станка
мод. 7242А (длина стола I = 6000 мм) при
различных схемах расчета:
7 — изделие абсолютно податливое (с учетом податливости
стола); 2 — изделие абсолютно жесткое (с учетом
податливости стола); 3 — стол абсолютно жесткий; а — при ОСт =
~7000кГ, Ов- 10 000 «Г, / - -| I; б — при Оет = 7000 кГ; ЛуЧИТЬСЯ НеСКОЛЬКО боЛЫИе,
ой- юооо кг, г «ч. о,5Л; в-при от-7ооо *г, • аи- однако этот случай не ха-
-5ооо кг, ^--|"/" рактерен. Графики фиг. 160
посгроены в
предположении смешанного трения и наличия контакта между
направляющими стола и станины. В случае чисто жидкостного трения жесткость
масляного слоя ниже контактной жесткости стыка, однако это мало
сказывается на величине наибольших расчетных давлений.
Давления на направляющие от веса изделия на длине изделия
близки к средним давлениям, вычисленным из предположения, что они
передаются на направляющие только на длине изделия. Аналогичная
картина имеет место и для давлений от момента Му. Закон распределе-
1 За пределами изделия давления на направляющих уменьшаются до нуля уже на
длине, составляющей 5—10% длины стола.
2 В действительности у краев изделия и стола на направляющих имеют место
резкие всплески давлений, быстро затухающие по длине. Однако принятая за основу
расчета гипотеза о пропорциональности давлений и перемещений в стыках не позволяет
их оценить*
294
•ния давлений на длине изделия близок к линейному и давления на
расстояние х от середины определяются по формуле
6Му
2х
Т
щ>
I
-ш-
*и
и^-
Таким образом, применявшийся до последнего времени расчет
давлений из предположения об абсолютной жесткости стола, в котором
соответственно нагрузки от веса изделия и силы резания
предполагаются распределенными по всей длине направляющих (штрихпунктир-
ные линии на фиг. 160), может
привести к занижению расчетных
давлений до 2—3 раз.
В случае установки изделия на
башмаках или подкладках, если их
число не превышает трех над
каждой направляющей, а также при
обработке деталей на ножках (типа
станин токарных станков) вес
изделия и усилия резания передаются
на стол в виде сосредоточенных сил.
Ввиду статической неопределимости
системы для определения нагрузки
от веса изделия на отдельные
башмаки, можно представить изделие
состоящим из отдельных
независимых частей, вес каждой из которых
воспринимается одним башмаком.
При этом сосредоточенные
нагрузки, передаваемые на стол ьтым
ж.
\~-Д/шна изделия—*
Длина стола
Фиг. 161. Эпюры давлений на
направляющих продольно-строгального станка
от веса изделия при разных способах
установки изделия (длина изделия равна
половине длине стола):
/ __ установка изделия непосредственно на стол
(изделие жесткое), 2 — установка изделия на
башмаках (по два башмака над каждой
направляюще); з — установка изделия па башмаках (по три
башмака над каждой направляющей); 4 — средние
давления.
башмаком, могут быть определены по следующей формуле:
Рг-
Си + Рг МуХ1
~~ Л*! -ж—« О
(7.22)
где п — число башмаков;
х. — координаты отдельных башмаков, отсчитываемые от
середины изделия.
При установке изделия на башмаках наибольшее давление (под
наиболее нагруженным башмаком) определяется по формуле
(7.23)
Ост [ Рм&\ \
Ы
где г шах ■
2 *
-нагрузка на наиболее нагруженный башмак;
-показатель жесткости стола;
-приведенная ширина направляющей, над которой
расположен башмак.
В формуле не учитываются давления от соседних башмаков, что
допустимо, если расстояние между башмаками больше /-^-н--^-|1.
Следует отметить, что в случае установки изделия на башмаках,
если число их мало, на направляющих возникают весьма высокие
давления (фиг. 161).
Таким образом, с достаточной для технических расчетов степенью
точности давления в направляющих при установке изделий на башма-
295
ках при большом их количестве или непосредственно на столе с
прилеганием по всей длине определяются по следующим формулам:
на грани А (фиг. 159)
на грани С
Ост
°А~2Ь^Г
жуА
2ЬА1
°С
Ос
Рш
ВгЬА1
Мх
РЬЛ
6М
2х
7 ;
2ЬС1
2ЬС1
*Л'
1ЧГ
2х
I '
(7.24а)
(7.246)
где ЬА и Ьс—горизонтальные проекции ширины соответствующих
направляющих;
/ — длина изделия в см;
Ь — длина стола в см.
Наибольшие давления имеют место у конца изделия, т. е. при
В формулах (7.24а) и (7.246) давления от горизонтальных сил не
учитывались. Обычно они на порядок меньше, чем от вертикальных сил.
Ввиду большой жесткости стола в горизонтальном направлении,
давления от горизонтальных сил распределяются по длине направляющих
р равномерно или <по ли-
(д | нейному закону'И при
необходимости легко
могут быть учтены.
Обычно
наибольшие давления в
направляющих (Продольно-
строгальных,
продольно-фрезерных и т. п.
станков составляют
6—7 кГ/см2.
2. Особенности
расчета столов
с тремя
направляющими
Доли общей на-
грузки,
воспринимаемые отдельными
направляющими зависят
от жесткости стола.
Проверочные расчеты
показывают, что соб-
проДольно-строгальных, продольно-фре-
• Фнг. 162. Зависимость реакций отдельных
направляющих от размеров изделий для столов с тремя
направляющими под действием веса изделия Ои и
вертикальной составляющей силы резания Рх\ Рь~ Ои+ Рг-
а — установка изделия на двух точках в поперечной плоскости;
б — установка изделия на трех точках в поперечной плоскости,
в — установка нескольких изделий по ширине стола (нагрузка
принята равномерно распределенной).
ственная жесткость столов
зерных, расточных станков в поперечной плоскости на порядок ниже
контактной жесткости * направляющих, в связи с этим упругие переме-
И пк
1 Коэффициент 7 ^^Тв^' хаРактеризующий отношение жесткости стола н
контактной жесткости направляющих, близок нулю (здесь к— коэффициент контактной
податливости направляющих в см3/кГ; Впр — приведенная цилиндрическая жесткость
стола, рассматриваемого как пластина, в кГсм\ Ь — ширина одной направляющей в см;
#з — расстояние между соседними направляющими в см).
Если т ~* 1> то столы в поперечной плоскости надо рассматривать как пластины на
упругих опорах.
296
щения и реакции направляющих таких столов в поперечной плоскости»
можно определять с достаточной степенью точности, как для упругих
пластин на жестких опорах.
На фиг. 162 представлены кривые суммарных реакций отдельных
направляющих от веса изделия и вертикальной составляющей силы
резания для разных случаев установки изделия на столе. Принято, что
изделия устанавливаются на отдельных точках (подкладках,
башмаках), деформации изделий не учитываются.
Основным расчетным случаем следует считать установку изделия
в поперечной плоскости на трех точках (сплошные кривые).
Таким образом, если ширина изделия В2 составляет половину
расстояния между крайними направляющими В\ (В^В^ = 0,5), то на
среднюю направляющую приходится 0,8 всей нагрузки, при В2/В1 = 0,75
приходится 0,6 всей нагрузки, при В21В\ = 1 — всего 0,33 всей нагрузки*
Реакции направляющих от момента Мх\
Л1 = -Аг = ^> С = 0.
Реакции направляющих от веса стола при расстоянии между сере*
динами крайних направляющих, равном 0,8 ширины стола, что обычно
имеет место: С = 0,46 Ост, А\ = Л2 = 0,27 Ост. Доли момента Му3
воспринимаемые отдельными направляющими:
где &!, Ьп — приведенные ширины направляющих Л, С.
Принято, что ширина крайних направляющих одинакова.
Наибольшие давления в направляющих:
а) в средней направляющей
сс
0,460м, , (С_\ ^_ , ^С
' ЬЬС ^\Рв) 1ЬС "Г" Ьс1*
б) в крайней направляющей
_0,270^ , (А\Рв ^ Мх тул ,
А С
Отношения -р~ и у- определяются по графикам фиг. 162.
3. Опреде л ен и е наибольших давлений
на направляющих с учетом деформаций столов
в поперечной плоскости
При обработке узких изделий, ширина которых меньше расстояния*
между направляющими, а также при обработке нежестких изделий на
крайх направляющих возникают высокие кромочные давления,
обусловленные деформациями столов в поперечной плоскости.
При пренебрежимо малой гидродинамической поддерживающей
силе масляных клиньев (при малых скоростях движения) давления на
направляющих определяются по следующим зависимостям:
если давления распределяются по всей ширине направляющих (при.
2к
297
о
если давления распределяются не по всей ширине направляющих
прие>2*), _
к '
(7.27)
где о — давления по средней линии направляющих, определяемые по
формулам (7.23) и (7.24) в кГ/см2;
Ь — горизонтальная проекция ширины направляющих в ся\
6— угол наклона стола у направляющих (см. ниже).
При обработке узких изделий эти давления могут превышать
давления по средней линии направляющих до 1,5 раз.
'7ц)/
гс<
'/ф;
■в,-
шш
ту 2
•Г+ГЗ&
°)
и 5)
Фнг. 163. Схема нагружения стола:
а — от собственного веса; б — от веса изделия.
п/в,
Фнг. 164. Зависимость коэффициента
к\ входящего в формулу для
определения деформации столов в
поперечной плоскости от размеров изделий.
Угол наклона 0, а также наибольший прогиб стола могут быть
определены при рассмотрении стола как плиты, опертой по двум
сторонам.
1. Действие собственного веса. Деформации стола в любом сечении,
перпендикулярном к направляющим, идентичны деформациям двухопор-
<ной балки с двумя консолями (фиг. 163, а).
Прогиб хм стола в центре и угол наклона 0 у направляющих
определяются следующим образом:
ю-.
а Р4
О тВ
2. Действие веса изделия. Деформации стола, если длина изделия
меньше длины стола, можно определить, рассматривая стол как
пластину, опертую по двум сторонам и нагруженную на участке аЬсй
(фиг. 163, б). Изделие принимается симметрично расположенным
относительно центра стола. Изогнутую поверхность можно представить
в виде ряда:
для незагруженного участка стола
со
/ V / л1 1 тпх I л' и тпх I /^' т^х и тг'х I
да = 1 (Ат СЬ -ВТ + Вт 8Ь ~ВГ + С- ~ВГ 8Ь ~К +
/71-1
, ~, ткх , ткх\ . тку
+ °т-вГсЬ-вг)*™-ъ
298
я Для загруженного участка
ео
VI / ■ л *.< тих , 0 < тих . ^ тих , ткх ,
, г. тих 1 тих\ . тиу
Эти выражения удовлетворяют дифференциальным уравнениям и
граничным условиям при у = 0 и у = Ви Постоянные Ат, Вт , ..., Ц/
определяются из условия непрерывности на границе между
нагруженным и ненагруженным участками и из граничных условий при х = гЬ-к-:
Л(В = аЯ1(8Ь2т —сЬ2т)(1+т); А'т = ат($Ь2^ -сп2Г);
Ст = ^(сЬ2Т-8Ь2т); Ст = -ат$Ь2Г,
Вт = 0; 5т = ат(ТсЬ2г —8Ь2г);
А» = 0; Я;, = ^$п2т.
Здесь ^ = т^-. Принято (как обычно имеет место в столах)
|->3, тогда *Ь*5^«1 и—^д-даО.
сН"Щ~
Прогиб в центре стола Гаг = 0, У —у):
™ = 2ая,[1+(8Н2т-сЬ2Т)(1 + т)](-1) 2 •
1, 3, 5
Угол наклона на направляющих в среднем сечении стола (л; = 0,
со
в=2ай,[Ц-(зЬ2т-сЬ2Т)(1+т)]^1.
1
Коэффициент ат зависящий от закона распределения нагрузки,
для случая нагружения равномерно распределенной нагрузкой на
некотором участке (фиг. 163, б) определяются по формуле
т-Л
Для этого случая наибольший прогиб и угол наклона стола на
направляющих (у = 0) определяется по формулам
аВ\ ип&\
*> = к'±±, * = *'-&—' (7.29)
где &'— коэффициент, определяемый по графикам фиг. 164.
4. Определение деформаций столов при з, а ж а т и и
изделий
При зажатии изделий возможно значительное искажение формы
стола. Зажатие изделий на столах может осуществляться вертикальными
силами (с помощью прихватов) и горизонтальными (с помощью кулач-
299
ков). При зажатии вертикальными силами (фиг. 165, а) на стол в месте
зажима действуют три взаимно уравновешивающиеся силы,
вызывающие местные деформации столов. Оценка таких деформаций'расчетным
путем затруднительна. При зажатии горизонтальными силами
ш ^ (фиг. 165, б) столы нагру-
$[Ш\^? ^шш! жаются сосредоточенными
—4т» м^—| изгибающими моментами и
Р р
1 I их деформации могут быть
77777777777777777777777777777777. оценены расчетом.
^1 Относительный угол
наклона сечений стола в про-
\р
агм.» •'тала — *^ ^ч.лч.д^хп ^*^1и ^ иу^
РГГ ^ "П5^ дольной плоскости под кон-
~\нейтро/1ьна* цами изделия от действия
Тплоскость
\ ПЛОСПии по -
'777////////////////////////////// сил зажатия может быть
б) определен по формуле 1
Фиг. 165. Схемы нагружения стола силами от за- д пхРзажк ^ .
жима изделия. "х ~2Г> 8В~ ' (/.оО/
здесь А» — приведенная цилиндрическая жесткость стола в кГсм%
В — ширина стола в см;
^заж
— сила зажатия, приходящаяся на один кулачок, в кГ\
А —расстояние от линии приложения сил зажатия до
нейтральной плоскости стола в см;
Я! —число кулачков с одной стороны, перпендикулярной
к продольной оси стола;
р—показатель жесткости стола в \\см (см. стр. 293).
Угол наклона стола над направляющими в поперечной плоскости
стола 2
*• = ^Й#- (7-31)
2 ''л/>*
где дополнительно В2 — ширина изделия в см;
п2— число кулачков с одной стороны, параллельной продольной оси
стола.
Д. Порядок технического расчета столов с направляющими
Технический расчет столов может быть выполнен двояко:
а) по упрощенной методике —в форме определения средних
давлении на направляющих по формулам (7.20) и (7.21);
б) по уточненной методике (с учетом деформаций'столов) в форме
определения наибольших давлений.
Порядок уточненного расчета:
*• Определяются нагрузки на направляющие по формулам (7.17) —
2- Определяются наибольшие давления на гранях по формулам
(/.26) и (7.24) без учета деформаций столов в поперечной плоскости.
3. Для случаев обработки узких или нежестких изделий
определяются дополнительно наибольшие давления, связанные с
деформированием столов в поперечной плоскости по формулам (7.27) — (7.29). При
этом приведенная цилиндрическая жесткость стола Опо вычисляется по
формуле (7.16).
1 Формула получена при рассмотрении стола как балки на упругом основании
под действием сосредоточенных моментов.
2 Формула получена при предположении о равномерном распределения сил зажа*
тия по длине стола.
300
Е. Выводы и рекомендации
На основе разработанных расчетов можно сделать следующие
выводы:
1. При „установке на столах тяжелых изделий необходимо
предусматривать большое число башмаков или подкладок (не менее четырех
с каждой стороны). При установке изделия на башмаках при малом их
числе (два-три с каждой стороны) наибольшие давления в
направляющих возрастают в 1,5—2 раза по сравнению с установкой изделия на
большое количество башмаков (клиньев) или непосредственно на столе.
2. Вследствие относительно малой жесткости столов
продольно-фрезерных, продольно-строгальных и т. п. станков давления в
направляющих от веса изделия сконцентрированы в основном на длине,
занимаемой изделием. Поэтому при обработке коротких (по сравнению с дли^
ной стола) изделий наибольшие
давления могут в несколько раз
превышать средние. Например,
•если длина обрабатываемого
изделия составляет 7з длины стола,
то наибольшие давления от веса
изделия приблизительно в 3 раза
превышают средние. Наибольшие
давления в направляющих
примерно одинаковы при установке
на столе одного такого изделия
и трех, занимающих всю длину
стола.
Таким образом, при
обработке тяжелых коротких изделий нет
необходимости для уменьшения
давлений в направляющих устанавливать изделия по одному на станок,
если они могут устанавливаться по два или по три.
3. Повышение жесткости столов наиболее эффективно за счет
увеличения высоты стола. Жесткость стола пропорциональна приблизительно
квадрату высоты стола; вес стола зависит от высоты в значительно
меньшей степени.
Отношение расчетной высоты стола к к ширине В для продольно-
строгальных и продольно-фрезерных станков колеблется от 0,15—0,18
для столов шириной 1200—1800 мм до 0,09—0,1 для столов шириной
3500—4500 мм. На фиг. 165 показана зависимость податливости стола
Фиг. 166. Влияние высоты к стола на его
податливость тТ~ № — ширина стола,
О
пр
Е>пр—приведенная цилиндрическая
жесткость стола).
пр
от отношения -д . Как видно из графика, при малом отношении -^
(порядка 0,09—0,11) жесткость с увеличением высоты сильно
возрастает, а при больших отношениях (порядка 0,14—0,16) изменяется мало.
Таким образом, рациональным с точки зрения жесткости является
отношение -^ порядка 0,14—0,16. Увеличение толщины стейок столов
нерационально, так как жесткость и вес возрастают «примерно
одинаково,
4. Для станков повышенной точности необходимо стремиться к
увеличению жесткости столов, так как за счет этого можно существенно
снизить деформации столов при закреплении изделий. Известно, что
некоторые заграничные фирмы идут на значительное увеличение веса
столов точных продольно-строгальных станков. Так, например, в
нормальных станках фирмы Вальдрих вес стола составляет примерно половину
наибольшего веса изделия, а в станках повышенной точности превышает
наибольший вес изделия в 1,5 раза.
301
§ 6. РАСЧЕТ ПОЛЗУНОВ
А. Основные положения
До последнего времени деформации ползунов определялись как
деформации балки на свободной длине в предположении идеальной
заделки в направляющих, т. е. без учета контактных деформаций в на-
Мод 1532
Вылет 1500мм
<5>
3
г
<,5
/
0,5
45%
г.!11!!
Мод /532
Вылет 600мм
Ра=Ь000кГ
б,
ь7о
Г/о
Уод /53?
[вылет 600м,
.' г~гА?0°/о 0,1
<0
мод 1556
уме/пМ"* тдгт00
50дО«Г
Вылет ьООмн
Р„ =?500кГ
7%
азот изгиба ползуна на длине опоры \\\\\\\\\\\ - От изгиба ползуна на свободной длине
От закручивания яолзцна на длине опоры^щ^ - От кручения ползуна на свободной длине
1
фиг. 167. Диаграммы баланса перемещений ползунов карусельных станков (по
экспериментальным данным ЭНИМСа, СКЬ-4 и Коломенского ЗТС);
3 — перемещения точки приложения силы в горизонтальном направлении, перпендикулярном к плоскости-
портала; 5. — перемещения точки приложения силы в горизонтальном направлении, параллельном плоскости
портала (по оси X); аив — нагружсние составляющими силами; б и г — нагруженне наклонной силой
Ра с составляющими Р - 0,775 />а> Рх -> Рг ~ 0,446Ра#
правляющих. Между тем, приведенные к резцу смещения вследствие
деформаций на длине напраьляющих составляют значительную часть
общих деформаций ползунов. Даже при больших вылетах ползунов
перемещения на резце, обусловленные контактными деформациями,
вполне соизмеримы с
деформациями на свободной длине
и для ползунов карусельных,
поперечно-строгальных,
долбежных и других станков
составляют до 70% общих
перемещений (фиг. 167).
Следовательно,
рассмотрение ползунов в
предположении идеальной заделки у
кромки направляющих, как
это принималось ранее,
не дает представлений о
действительных величинах
перемещений пбд
нагрузкой.
Существенный интерес
представляет уточненное
определение давлений в
направляющих ползунов, так как
эти давления оказываются
Ы05
т Длима нопроЗлятш Н-
фиг. 168. Эпюры давлений и упругих перемещений
в направляющих ползуна поперечно-строгального
станка мод. 737:
/, //, III, — разные положения -ползуна.
весьма высокими и в ряде случаев ведут к появлению задиров и
повышенному износу. Как .показали приведенные ниже расчеты, наибольшие
302
давления в направляющих ползунов достигают 100—130 кГ/см2, в то
время как наибольшие номинальные давления в направляющих
суппортов и столов составляют 25—30 кГ/см2 (на планках в отдельных редких-
случаях несколько выше).
До последнего времени наибольшие давления в направляющих
ползунов определялись при рассмотрении ползунов как абсолютно жестких
тел. На фиг. 168 представлены эпюры давлений в направляющих
ползуна поперечно-строгального станка. Тонкими прямыми линиями
нанесены эпюры давлений, получающиеся при рассмотрении ползунов как
абсолютно жестких тел. Как видно на фиг. 168, предположение об
абсолютной жесткости ползунов приводит к занижению наибольших
давлений в 2—3 раза и не дает правильной картины распределения давлений
по длине направляющих.
На опертом участке ползуны рассматриваются как балки
постоянного поперечного сечения на упругом основании. Пр.и определении
деформаций ползуна
рассматриваются два отдельных его участка — , у
консольная часть и часть,
лежащая на упругом основании (на
направляющих). В большинстве
случаев нагрузку на V ползун в
каждой из главных плоскостей из- * ^ » 7>
гиба ползуна можно представить
в виде сосредоточенной силы Р и
изгибающего момента М на
конце (фиг. 169). Кроме того,
вследствие несовпадения вершины
резца с осью 'ползуна на ползун дей- мкР - р* ' а.
ствует крутящий момент Мкр.
Перемещения и углы наклона ползуна в любом сечении х его
консольной части можно определить, рассматривая его как брус или балку,
имеющую у кромки направляющих начальный прогиб уо, угол наклона
упругой линии 60 и угол закручивания фо.
Перемещения, угол наклона упругой линии и угол закручивания
у вершины резца определяются соответственно по следующим формулам:
А А,
е
У/////////////////Л
о
У////////////ШЛ
Фиг. 169. Схема нагружения ползуна:
Л-0; Л10--/у:;
в плоскости ХУ:Р = Р ; М = Рха; М0
в плоскости Х2.\
V;
У = Уо+ве^
РЦ>
М1%
Р№
М1
2Е/
+ ср0а-
Мкр1а
ад
кр
2Е^
Е]
? — ?о-
Мкр1
о^^
кр
(7.32)
где Е — модуль упругости материала ползуна I рода в нГ/см2;
0 — модуль упругости материала ползуна II рода в кГ/см?;
/—момент инерции площади поперечного сечения ползуна
относительно рассматриваемой главной оси инерции сечения в см*\
Кр — угловое сопротивление закручиванию ползуна в см^\
1 — вылет ползуна (расстояние от вершины резца до начала
направляющих) в см\
а—расстояние по оси у от вершины резца до оси ползуна в см..
Знаки перед слагаемыми соответствуют изображенному на фиг. 169-
направлению сил и моментов.
Специфическим для ползунов как балок на упругом основании
является участие в работе вспомогательных граней (или планок),
ширина которых в общем виде не равна ширине основных граней. Ниже
для расчета вводится понятие несущих и поддерживающих граней.
Несущими именуются грани, в направлении которых действует основная
303
сила, а поддерживающими — грани, от которых сила отжимает
ползун.
Порядок технического расчета изложен на стр. 318.
Б. Определение деформаций и давлений в направляющих
ползунов в результате изгиба
1. Ползуны с несущими и поддерживающими
гранями направляющих одинаковой ширины.
Прогиб у0 и угол наклона 60 у кромки направляющих в соответствии
с теорией балок на упругом основании [32] определяются по формулам:
Уо:
= ЯЬ[Р1Г-М$У\; 80 = ^[Я1/-2М0рИ7].
В
Здесь М0 — момент относительно кромки направляющих в кГсм\
Н — длина направляющих в см; В— приведенная ширина
направляющих в см\ к — коэффиидент контактной податливости в см3/кГ\
*=у
В
1
АЕЛг см '
Р"
Ц, V, Ц7—коэффициенты, зависящие от показателя Х:=^-^-(табл, 58).
Таблица 58
Значения коэффициентов V, V7, УР для расчета балок на упругом основании
X
0,8
1,32
1,43
1,31
0,9
1,22
1,25
1,16
1,0
1,14
1,13
1,08
1,2
1,05
1,03
1,02
1,4
1,01
1,003
1,004
1,6 и более
1,000
1,000
1,000
Для большинства ползунов Х> 1,6 и С/« V» и^ж1.
В этом случае
(7.33)
Под приведенной шириной направляющих В понимается ширина
упругого основания, контактные деформации которого равны
контактным деформациям направляющих, принимающих участие в работе:
Я = 5>/Соз2аь
(7.34)
где Ь1 — ширина г-той грани направляющих;
&1 — угол наклона /-той грани к нейтральной оси.
Суммирование распространяется на грани, принимающие участие
в работе при рассматриваемом нагружении (табл. 59).
Нормальные давления на гранях направляющих в соответствии
с принятой гипотезой определяются цо формулам:
.304
Таблица 59
Формулы для определения приведенной ширины й углового сопротивления кручению ползунов
Ползуны карусельных станков Ползуны поперечно-строгальных
3 ^ и долбежных станков
Приведенная
ширина несущих Бх = 26 соз^ а Вх — 2Ь В1^=2Ь1 В1 = 2Ь1 Вг = 2ЬХ Вх = 2ЬХ
Изгиб в граней
плоско- ! ^ ! ! ! и
сти УХ \ I I I | I I
Приведенная
ширина поддержи- В2» 2Ь соз2а В2 « 2Ь В3 =^2Ь2 В2 = 2Ь% В2 = 2Ьг соз2а В2 ■= 262
вающих граней
Изгиб в пРиведенная ши- I II I
сти ^л I граней 1 | | | | I
4 4/73 Р—средняя арифметическая площадей, очер-
I Угловое сопротивление , — о 108 * 0 1//4 / = 0 141а4 —0,2163+0,33с^3— у^_ _-_ ченных наружным и внутренним конту-
закручиванию /-высота попе *-0,№ — 0,105^ + \т Р™и;
\и вышдд 1шпе ' 44*1 5,—длина участка толщиной 5*.
речного сечения &з „
Примечание. Предполагается, что сила в начале нанравляющих прижимает ползун к граням В±.
При обратном действии силы ширина несущих граней равна В2, а поддерживающих В1ш
305
Переход деяний на I участке с
основных граней на вспомогательные
-т=0,3 0,6 1,5 2,5 -
На Iучастке работают
вспомогательные грани
Фиг. 170. Графики для определения сил Рхк моментов Мх в сечении ползуна
по нейтральной линии стыка (линии перехода давлений с основных граней
направляющих на вспомогательные).
306
Как показывают расчеты, наибольшие давления в направляющих
в большинстве случаев имеют место на кромке направляющих со
стороны консоли. При этом
'тах^^СОЗСЬ (7.35)
и только при значениях 0,5 <-^--< 1,5 наибольшие давления имеют
место в некоторых сечениях по длине направляющих. Однако в этом
случае абсолютные величины давлений невелики.
2. Ползуны с несущими и поддерживающими
гранями направляющих разной ширины.
В работе, как правило, принимают участие как несущие, так и
поддерживающие грани. Податливости упругого основания, определяемые
коэффициентами |3, различны для частей ползуна, опирающихся на
несущие и поддерживающие грани. При решении задачи о деформациях
такого ползуна последний предполагался разрезанным на две части [38]
в месте перехода давлений с несущих граней на поддерживающие, к
действие обеих частей друг на друга заменялось неизвестными
изгибающими моментами Мх и силами Рх (фиг. 170). Неизвестные силовые
факторы Мх и Рх и положение нейтрального сечения (граница двух
участков) определялись из условия равенства между собой углов наклона »
прогибов обеих балок в сечении разреза и из условия равенства нулю
прогибов балок в этом сечении. Прогиб и угол наклона на конце первой
балки определялись соответственно по следующим формулам:
Прогиб и угол наклона в начале второй балки определялись
соответственно по следующим формулам:
307
Условия равенства нулю прогибов балок в месте сопряжения
(у1==:0 и У2 = 0) дают выражения для Рх и Мх\
Р, = -
С - 1С"
^2
2Я ^ _ С - 1С" 2Е78Р
где
Сюда входят неизвестные — длина первого участка Н\ (в
коэффициенты с индексом 1) и длина второго участка Л2 (в коэффициенты с
индексом 2).
%?[1тт^
1М
Фиг. 171. Графики для определения координаты нейтральной линии стыка.
Равенство углов наклона обеих балок в месте сопряжения (01 = &2)
дает услдвие для определения Нх и Н2:
(С — %С)
(Уг _ а*У2) + "^ « (^ 4- аЩ)
&2
._ С" + 6С" = 0.
Уравнение — трансцендентное и непосредственно относительно /ь
я А2 не решается. Решение уравнения производилось подбором. Прогиб
и угол наклона в начале координат (фиг. 170) определяются из
рассмотрения первого участка как балки на упругом основании под действием
силовых факторов Р, М0, Мх, Рх\
Уо = -%Г [^Р - ^оР! V, - ЯМА -$■ ~ 2Я, ^-] ;
2№к Г С'" С]
в; = 4- [ УгР - 2Ж0р! Г1 - 2УИА ж - 2Р, ^] .
308
Результаты решения представлены в виде графиков. Значения
—~ и —ф- приведены на фиг. 170, значения (З^ — на фиг. 171:
?1 = УЛ"
Вг
4Е№ '
Под р1 и В\ понимается соответственно показатель жесткости и
приведенная ширина несущих граней. Ширина поддерживающих граней
обозначается В2, а показатель жесткости (32.
Для технических расчетов были просчитаны значения
коэффициентов ку и кв, представляющих отношение деформаций ползунов с
разной шириной несущих и поддерживающих граней к соответствующим
деформациям ползунов при предположении, что ширина
поддерживающих граней равна ширине несущих граней (фиг. 172, а, б). С
использованием этих коэффициентов прогиб и угол наклона в начале
направляющих могут быть определены по следующим формулам (при А,3> 1,4-5-
-1,5):
28 к 2В2&
У° = -Ж- (Р~М^ кг 9о = -§Г С-2ЛШ К (7.36)
Для отношения гп = ~- > 1 коэффициенты ку и кь меньше единицы,
р>
для т = -~- <1 — больше единицы.
На практике для ползунов поперечно-строгальных станков, у
которых сила резания прижимает ползун к наклонным граням
направляющих с профилем «ласточкин хвост» (или планкам прямоугольных на-
правляющих), значения т=~~ обычно составляют 2,25-4-2,75; для
суппортов и ползунов остальных станков (долбежных,
продольно-строгальных, карусельных станков при работе суппорта на прижим и т. д.)
т = 0,25-^0,35.
Из графиков на фиг. 172 видно, что три 1> = ~-р1- , изменяющемся от
оодо +1, значения коэффициентов ку и к0 близки к единице. Это
объясняется тем, что сечение перехода давлений с несущих граней на
поддерживающие находится далеко от начала направляющих (фиг. 171),
и этот переход мало сказывается на величине деформаций в начале
направляющих. Излом кривой при %=1 объясняется условностью
значений коэффициентов ку и кь для |> 1, так как в действительности на
первом участке ползуна в этом случае работают не несущие грани, как
предполагается, а поддерживающие.
Наибольшие давления на гранях при |<1 и при |^>1,5, как
и в случае равной ширины несущих и поддерживающих граней, имеют
место в начале направляющих и определяются по формуле (7.35).
Значения ашах- приведены на фиг. 173. Под средними давлениями здесь
Сср р
понимается величина аср ~ ^-^соза/. Как видно из графика,
наибольшие давления могут превышать средние в 30—40 раз.
3, Ползуны с выемкой всреднейчасти корпус а.
Корпуса ползунов некоторых станков, в частности тяжелых карусельных
станков, выполняются ке сплошными, а с выемкой посередине. Таким
образом, ползун опирается на два отдельных участка основания. При
малой длине участков такие ползуны с достаточной степенью точности
можно считать как балки на упругих опорах, при большой длине как
балки на сплошном упругом основании. Однако в ряде случаев длина
этих участков такова, что не соответствует ни той, ни другой схеме.
309
Фиг. 172. Графики для определения значений коэффициентов ку и к$,
входящих в формулы деформаций ползунов с разной шириной несущих и
поддерживающих граней направляющих.
310
Ниже для простоты рассматривается решение при равной ширине
несущих и поддерживающих граней, что в большинстве случаев имеет место
в конструкциях, выполняемых с выемкой.
При решении этой задачи ползун представлялся разрезанным на два
участка у конца передней опоры, и действие участков друг на друга
„<!__
Х///Л
У///Л
У7Щ у/7Л
к Л, -Л— ( —I—Л?-|
*^&»др-
Шё
ША
"°Ф-
8^
Фиг. 174. Схема определения
деформаций ползунов с выемкой
в корпусе по длине направляющих.
заменялось силами Рх и
моментами Мх, которые можно
найти из условия равенства
прогибов и углов наклона
обоих участков в месте
разреза (фиг. 174). Прогиб и
угол наклона упругой линии
в конце первого участка определялись соответственно по следующим
формулам:
\Р$С'к Ш$*С"к _ 2Рх^к 2МхрУхк #
-Фиг. 173. График для определения наибольших
давлений на направляющих ползунов при
различной ширине основных и вспомогательных граней
{с учетом собственных и контактных
деформаций).
У1 =
ВМХ
4Р^С"к
ВМХ
выг
Ш0рС"'к
в
в
2РхфУ1к ■ Шхр^к
В ^ в
Прогиб и угол наклона упругой линии в начале второго участка
•определялись соответственно по следующим формулам:
у2
_ Рх1* , 2Рх$Ц3к МХУ , 2(Рх1-Мх)УфЧ
зя/ ~ в
2РлрУ21к
+
Рх&
2ЕУ
2ЕЗ 1 В
4 (Рх1 - Мх) \Г$Чк
+
в ~ в
2Рх^У2к Мх1 . 4 (Рх1 - Мх) ЧГ2рк
В
Е^
в
здесь Ци 1/ь Щ9 С, С", С% 1/2, Ц% и №2 —те же коэффициенты,
что и выше;
•V-
1 = _У В
ЬЕМ
311
Приравниваем У\=У2 и 61 = 62 и для удобства рассматриваем
отдельно действие силы Р и момента УИо- При действии силы Р имеем
Рх =
с ч- с%
М [*/, + -§*/+2 у^1 +2 ^]
(*Л + 2,66X3 _,. 21/]Х; + 4Г,Х2) С*
м,=-
2 (Г, + Х|)
+ ко
]
#! [^ + -| Х» + 2^Х< + 2 Г1Х/]
а;
к;
2,0
V
V
}>2\
Г %9
Г
к$ор)с>
7/?
^Х-9
л=з
\
0}2 0,4
а)
0,6 0,6 Фя^О
У0р=1<р(Уор)с/!/1
А=3
/*
1
А~2
0,2 0}Ч 0,6 0,8 1,0 Ь 0 0}2
6)
0,6 0,8 1,0%
Фиг. 175. Зависимость коэффициентов кр, км> кр, км, входящих в формулы для
определения деформаций ползунов, от размеров выемки в корпусе по длине направляющих.
При действии момента Мо имеем
п С" + С"\1
мх=
(#1 + 2,66X3 + ЪУ^ + Ш^) С» 1
2(^1 + ^) + С"Ч
рл»0;
м1\и1 + ^\* + 2у1к + ш1к21\
Мь\
здесь ^ = -^-.
Прогибы и углы наклона упругой линии в начале направляющих
(сечение О на фиг. 174) записываем аналогично предыдущему:
при действии силы Р имеем
2Р$к/гт Рх 2С
"ор:
Б
2Ррк
В
мл
(к,
р
2С«
2С"
Р
Мх$ 2С
\Ст\
312
'1С
N1
С
N1
,м*
1 М0
1С"
N1
С''
""ЯГ.
при действии момента М0 имеем
Уом- д— (У1+~Щ
«еж — В"(^1+1ад
Расчеты [38] показывают, что при относительной длине выреза
~^9 меньшей 0,4, ползуны с выемкой в корпусе можно рассчитывать как
балки на сплошном упругом основании, при-^-> 0,8—как балки на
точечных упругих опорах. При этом погрешности расчета не превышают
5—7%. При 0,4 <т7 < 0'^ ползуны следует рассматривать как балки
на прерывистом упругом основании.
При техническом расчете прогибы и углы наклона вначале
направляющих могут быть определены по следующим формулам:
К^Щ-(Рк'Р~2М^км), (7.37)
где к'р, кру к'м> к*м — поправочное коэффициенты, учитывающие
наличие выемки в корпусе (фиг. 175, а — г).
В. Определение деформаций и давлений в направляющих ползунов
в результате кручения
Принимается, что давления по ширине граней направляющих
ползунов распределяются по линейному закону.
Условия равновесия внешних и внутренних сил в поперечном
сечении ползуна выражаются формулой
йМКр
=!2>,й+4).
ах
где ср—угол закручивания ползуна;
Мкр — крутящий момент в кГсм\
6/ —ширина /-той грани в см;
гь — расстояние от центра тяжести поперечного сечения до
нормали, проходящей через середину /-той грани, в см;
л: —координата вдоль длины направляющей.
Суммирование распространяется на все грани, принимающие
участие в работе.
Подставляя это выражение в дифференциальное уравнение
кручения бруса на упругом основании [34], от действия сосредоточенного
крутящего момента Мкр9 приложенного вне длины направляющих,
получаем угол закручивания в начале направляющих
_ Мкр
где
2
Ч^ + тЬ
313
Угол закручивания ползуна в сечении, проходящем через вершину
,резца,
* = Ш1+?^Ьн)- (7-39>
Первый член учитывает закручивание ползуна на консольном
участке, второй —на участке направляющих.
В большинстве случаев р„//>2,5 и ИпфкНж \.
Как уже говорилось, суммирование в выражении для $к
распространяется на грани, принимающие участие в работе. Приближенно
можно считать, что контактные деформации от изгиба, как эго обычно
имеет место, больше, чем от кручения, и суммирование следует
распространять на грани, воспринимающие изгибающие нагрузки. Это
положение подтверждено экспериментально при испытании на жесткость
ползунов карусельных станков.
При разной ширине несущих и поддерживающиих граней
приближенно можно производить расчет на кручение, предполагая, что в
работе принимают участие те грани, которые воспринимают изгибающие
нагрузки в передней части направляющих, т. е. при —^- < 1 —
несущие грани, а при -^г~> 1 — поддерживающие. Это не вызовет
больших погрешностей, так как деформации кручения весьма быстро
затухают 'по длине направляющих. Таким образом, ,в первом случае
В = 1,Ь1 — суммарная ширина несущих граней, во
втором—поддерживающих.
Угловое сопротивление закручиванию ]\ для большинства
поперечных сечений может быть определено только приближенно. Для
толстостенных сечений без входящих углов с отверстием приближенно I к
определяется как разность углового сопротивления сплошного сечения и
полярного момента инерции круга диаметром, равным диаметру отверстия.
Испытания ползунов карусельных станков подтвердили приемлемость
такого приближения. Для тонкостенных поперечных сечений У' к
определяется по известной формуле Бредта. Формулы для 1к для типовых
поперечных сечений 'ползунов приведены в табл. 59.
Наибольшие давления на г-той грани направляющих в результате
кручения определяются по формуле
атах— к уЧ Г 2)'
Г. Значения коэффициента контактной податливости
Коэффициенты контактной податливости определяются в результате
измерения жесткости ползунов. Измерения жесткости [39, б]
производились на трех станках с ползунами восьмигранной формы и одном
станке с ползуном полого таврового сечения. Ползуны подвергались
изгибу в двух взаимно-перпендикулярных плоскостях и кручению,
причем измерялись деформации ползунов на свободной длине и контактные
деформации в стыке ползун — корпус.
Величины жесткости ползунов при изгибе Е/ и при кручении С1к,
входящие в выражения, по которым подсчитывались коэффициенты
контактной податливости к (по измеренным перемещениям), определялись
по деформациям ползунов на консольной длине. Результаты обработки
экспериментальных данных представлены ,в табл. 60.
314
Таблица 66
Результаты испытания жесткости ползунов карусельных станков моделей 1532, 1556, 2Щ-300 и 1553
I I Модель станка .
Условия нагружения Г ^ I 2ИК-300 I 1553 (табл. 59, графа 3)
| и измеренные деформации .„_ , _ _Л . ,. I ^ !____
I I (табл. 69, графа 1) Прижим Отрыв
Вид нагружения (см. примечание 2) и вели- \Ру= Рг= Р^уН Л> = П-^Н"""^ I ^= ^а== ^а= ^^ ^а= ~\ Р*~
чина силы в кГ «4000=4000=3000=2500=2500=2500=4000=4000 «3000 =-2500 =3000 «1500
Вылет ползуна I в мм 600 ' 600 600 1500 1500 1500 600 500 400 400 325 325
Расстояние от точки приложения силы до осн 230 230 230 230 230 230 230 230 230 230 180 180
ползуна а в мм
в плоскости УХ 0,8 — 0.60 1,34 — 1,32 0,60 0,51 0,29 0,18 0,13 0,14
Углы поворота в плоскости IX ~ °'99 ~ — *'18 "" ~~ °'20 °'085 "" °'12 °'085
в начале стыка 0жг10а
в плоскости 1У I 1,0 — I 0,46 0,39 - 0,43 0,93 1,04 0,97 0,275 0,035 0,225
от нзгнба в плоскости УХ 103 — 77 103 — 107 74 74 54 71 63 20
Наибольшие дав- 111111111111
I ления в стыке ■ ! г 1 ; ; ; ; ; т 1 ! р
I о в 1сПсм? I I I I } I I I I I ! I I I
от изгиба в плоскости XI — 62 — — 125 — I — 26 21 — 19 7
315
Продолжение табл. 60
Модель станка
яиз^~ыНеТф~циИ I 1556 | 2ИК-300 I 1553 (таол. 59, графа зТ
1532 (табл. 69, графа 1) ~Г1—^ ^ 1ч — 1 Г
1 г у (табл. 59, графа 1) Прижим Отрыв
от кручении 28,5 — 34,0 27,5 — I 25,5 36 32 41 47 — —
Наибольшие
давления в стыке ■ ——■— -~ 1 : ; 1
с в кГ\см* 111111111111
суммарное 131,5 62 [ 111 130 125 132,5 ПО 132 126 118 82 27
1 в плоскости УХ 0,78 — 0,78 1,46 — 1,41 0,77 0,70 0,50 0,18 0Д1 1.13
при I I | [ I I | | [ I I I I
Коэффициент изгибе ! I I I I I I ! I I I
поХливостЙи в плоскости XI - 2.7 - - | 1,02 - -0.90 0,42 - 0,86 2.8
Л-10* смЦкГ I I I I
при кручении 1,5 — 0,57 0,6 — 0,72 1,1 1,38 2,1 0,25 — —
4/-г в. плоскости УХ 0,094 — 0,094 0,11 — 0,109 0,094 0,0913 0,084 0,065 0,057 0,103
У* в плоскости XI — 0,129 — — 0,101 — — 0,0974 0,081 — 0,096 0,13
Примечания:
1. Принято С1едующее направление осей: X — вертикальная; 2. — горизонтальная, параллельная плоскости портала: У - горизонтальная, перпендикулярная к плоскости
портала.
2. Индекс означает направление силы. Ра соответствует нагружению наклонной силой с составляющими Рх = Рг = 0,445 Ра , Ру - 0,775Ра. I
3. Большой разброс значений к объясняется тем, что к примерно пропорционально четвертой степени измеренных углов поворота в стыке и, следовательно, все
неточности измерения здесь влияют весьма* резко. Для оценки совпадения результатов при разных видах иагружений приведены значения уГь » примерно пропорциональные I
измеренным углам |
316
Коэффициенты контактной податливости определялись только по
«измеренным углам наклона в стыке, так как точность измерения
линейных перемещений в ряде случаев оказалась недостаточной. Наибольшие
давления в стыке определялись расчетом по измеренным перемещениям
в стыке и полученным из эксперимента значениям коэффициентов
контактной податливости.
Кроме того, были измерены деформации ползуна тяжелого
карусельного станка с диаметром стола 9000 мм. Коэффициент контактной
податливости в среднем составил 1,4-10~4 см^/кГ при Приведенной
ширине граней 130—160 мм.
На основании результатов экспериментов можно сделать
следующие выводы:
1. Деформации в стыке ползун — корпус примерно
пропорциональны нагрузке и, следовательно, коэффициент контактной податливости не
зависит от нагрузки.
2. Коэффициент контактной податливости для направляющих с
приведенной шириной 80—120 мм в среднем составляет (0,8-^1,2) X'
X Ю-4 см3/кГ, для направляющих крупных ползунов с шириной граней
более 130—150 мм коэффициент к несколько выше и достигает 1,4-Х
X Ю-*4 смЧкГ.
3. Для расчета ползунов в среднем коэффициент контактной
податливости может выбираться равным ! • 10~4 см3/кГ.
4. Значения коэффициента контактной податливости направляющих
ползунов хорошо согласуются с полученными ранее значениями
коэффициентов контактной податливости на суппортах и столах при той же
ширине граней. Это подтверждает правильность выбора расчетной схемы
Ползунов как балок на упругом основании.
Д. Особенности расчета хоботов горизонтально-фрезерных станков
Хобот, как и ползун, можно рассматривать как консольную балку,
опирающуюся на упругое основание. Нагрузка на хобот определяется
из рассмотрения упругой системы оправка — серьга — хобот.
Силы резания, действующие на фрезе,
частично передаются на хобот через серьгу,
а частично на стойку через шпиндель. В
первом приближении оправку можно
рассматривать как балку, жестко заделанную
в шпинделе и опертую в месте соединения
с серьгой \ нагруженную в вертикальной
плоскости силой Р = Р7 и моментом М —
'жт
= р
йфр
, а в горизонтальной плоскости си-
Фиг. 176. Схема определения
нагрузки н? хобот
горизонтально-фрезерного станка.
лой Р = Рх (фиг. 176).
Сила А, возникающая в месте
соединения оправки и серьги и нагружающая
хобот, определяется как реакция в опоре такой балки (принято, что хобот
существенно более жесткий, чем оправка):
реакция от силы Р
реакция от момента М
л — _ ш (2± _^Л
ЛМ— 21 [ I &)'
1 Уточненное решение с учетом упругости опор и экспериментальная проверка
показывают применимость для технического расчета такого допущения.
317
По этим формулам можно определить, какая часть силы Р
передается на хобот через серьгу: при -у = 0,25, реакция Лр = 0,09Р;
X X
при -у = 0,5 реакция Лр = 0,31Я и при —=0,75 реакция Лр = 0,63Р.
Таким образом, хобот следует рассчитывать по тем же формулам,
что и ползуны, предполагая, что он нагружен на конце силами А =
= АР — АМ.
Силовые факторы, действующие в начале стыка хобот — стойка:
в плоскости 2Х
р — ^(*^ — ^\-*^(2*.— *.). М—-Р1
^~ 2 [° /2 р ) 2/ \ I Р )•' УК1о~ ™»
в плоскости XV
Коэффициент контактной податливости для хобота (при хорошей
затяжке стыка) следует брать на 30—40% ниже, чем для незатянутых
стыков ползунов.
Е. Порядок технического расчета ползунов
Технический расчет производится следующим образом:
1. Выбирается схема нагружения ползуна и расчетные нагрузки
(см. фиг. 169).
2. Определяются жесткость ползунов при изгибе Е1, при
кручении 01к и приведенная ширина граней 5! и В2 (табл. 59),
3. Определяются перемещения (прогиб, угол наклона и угол пово-
рота) в направляющих от кручения по формуле (7,38) и от изгиба:
а) для ползунов с одинаковой шириной основных и вспомогательных
граней по формулам (7.33); б) для ползунов с разной шириной — тю фор-
мулам (7.36); в) для ползунов с выемкой в средней части корпуса —
по формулам (7.37). Рекомендуемые значения коэффициентов
контактной податливости приведены на стр. 317.
4. Определяются перемещения, приведенные к инструменту, в
результате деформаций ползунов по формуле (7.32).
5. Определяются наибольшие давления в направляющих — по
формулам (7.35) или графику фиг. 173.
Пример расчета ползуна. Определить упругие перемещения ползуна
поперечно-строгального станка мод. 737 (табл. 61).
Исходные данные для расчетов: Я = 120 см; Ь\ = 9,8 см; г\ = 15 см;
Ь2 = 7,5 см; г2 = 14,5 см; У = 1,35- 104 см*; к = 1 • 10 ~4 см?/кГ; 5 - 0,8 X
X 10е кГ/см2 (материал —чугун); СУЛ=560-10в кГсм2; ВХг=2Ъ1Х
X соз* а -6,5 см; р1 = -{/Г-А- = 0,035; Х = 1^ = 2,1.
Принимаем -^ = 0,5; -^^0,3; рЛ = ]/-^^ =0,28 (при
работе наклонных граней); рл = у -^~|-= 0,237 (при работе
горизонтальных граней). Результаты расчетов приведены в табл. 62.
318
Таблица &Г
Определение перемещений резца в результате упругих деформаций ползуна
|-Ч,=Ш-
-365
1. Определение прогибов и углов наклона в начальном сечении ползуна
в результате изгиба
в см
М0 = Рг.с- Ру1
Ч
по фиг. 172
Деформации в начальном сеченин
в см
2^к
{Р-2ММ къ в рад,
80
40
10
-20Рг
0
+ 15Р*
0,97
0,99
1
0,97
0,99
1
1,2б.10-6Яг
0,54-10-6Рг
0
6,95.10-8Р2
1,86-10-8Р2
-1,88. Ю-8/**
2. Определение вертикальных перемещений у кромки резца
в см
За счет деформаций
свободной части ползуна
РуЬ* РгсК
За счет деформаций
I направляющих ползуна
У - Уо + ео^ в СМ
Суммарные
перемещения
в см
Суммарные
перемещения
при силе резания
Рг - 1000 кГ
в мм
80
40
10
-0,49-Ю-6/^
—0,077-КГ6Я*
6,8-НГ"/^
—0,19-10-6Рг
8,75 Л О"6/^
0,79.10-6Яг
-0,267-Ю"6/^
0,087
0,008
- 0,0026
3. Определение перемещений у кромки резца в результате кручения
I
в см
Крутящий
момент
Мкр
в кгсм
Грани,
работающие иа
переднем
конце
ползуна
1
в —-
см
Угол наклона резца
(закручивания ползуна)
в рад.
Перемещения
кромки резца
в направлении
оси X
5 = у-с в см
Перемещения
кромки резца
при силе
Р„ - 1000 кГ
80
40
10
6Л
Наклонные
Наклонные
Горизонтальные
0,28
0,28
0,237
90-10-8Рг
46,6-Ю-8Рг
\Ь2Л(Г*РХ
1,8-НГ5/^
0,93-Ю"5/^
0,305-10"5Р2
0,18
0,09
0,03
319
Таблица 62
Сравнение жесткости различных форм ползунов карусельных станков
Форма ползуна
Вылет
ползуна
Упругие перемещения
вершины резца (в условных
единицах)
в направлении
оси У
Вес при равной
жесткости (в ус
ловных един.)
2
со
со
а: К
СИ О
«-0.935&
а=0,95Ь
1*=гь
Ь « 7,ЬЬ
0,83
0,87
0,89
0,83
0,87
0,89
1,04
1,03
1,01
1,09
1,07
1,03
1,04
1,03
1,01
1,09
1.07
1,03
0,8
0,85
0,83
0,82
0,97
0,96
0,95
1,05
1,04
1,02
0,86
0,89
0,90
0,90
0,93
0,92
0,80
0,84
0,84
0,87
0,90
0,91
1 = 36
Ь « 7>ЬЬ
1,38
0,65
0,62
0,65
0,62
0,39
0,49
0,57
0,61
0,90
0,86
0,79
0,84
I - 7.5Й
0,97
0,97
0,95
1,13
1,16
0,64
0,80
0.99
1,15
0,94
0,92
0,96
1,11
I =^7,56
0,56
1,28
1,32
1,72
1,80
0,97
1,27
1,50
1,76
0,72
0,74
0,84
0,99
Ь = 7,5&
2,1
0,63
0,61
0,58
0,58
0,46
0,57
0,55
0,57
1,32
1,28
1,16
1,20
Продолжение табл. 62
Форма ползуяа
Вылет
ползуна
шых
о
% «*
СО а)
1,65
Упругие перемещения
вершины резца (в условных
X
ас
направл
и X
о
ю о
0,66
0,63
единицах)
в направлении
оси У
изгиба
**
о ]
0,60
0,59
4)
о,
ь ас
о ас
0,48
0,60
Он
СО
>»э
у К
0,57
0,59
Вес при
равной
жесткости (в
условных
ас
ас
направл
и X
ей о
1,09
1,04
един.)
X
X
ас
ей
СО
та
X К
ой о
0,94
0,98
I
— а
^Р
1
/аГ 1 7/
'Ш/Л
а?—*
~ГТ
1
^
\
I = 7,561
Примечание. Приняты следующие типовые соотношения размеров* й = 0,7Ь; йх = 0,7а,
^2 =* 0.85&, */., = 0,6&, с = 0,5&, «! — 1,1^, ^ = 0,17&, е — 0.37&, а2 =- 0,7«!. Вылет резца от оси ползуна
принят равным 1.056.
Ж. Анализ влияния формы поперечного сечения ползунов на жесткость
С помощью предлагаемого метода расчета может быть проведено
сравнение различных вариантов конструкций ползунов с целью
выявления оптимальных конструктивных форм. В табл. 62 представлены
результаты сравнения упругих перемещений ползунов (наиболее
распространенных форм) карусельных двухстоечных станков. Сравнение
производится при равной высоте Ь поперечного сечения, характеризующей
вылет оси ползуна от направляющих поперечины. В двух последних
графах таблицы даны значения веса ползунов при равной жесткости. Эта
величина характеризует эффективность использования материала. Чем
меньше вес ползуна при равной жесткости, тем, следовательно,
рациональнее распределен материал. Кроме того, эта величина является
некоторой характеристикой ползунов с точки зрения виброустойчивости,
так как чем меньше вес при равной жесткости, тем выше частота
собственных колебаний ползуна.
Расчет производился при вылете ползуна, близком к наибольшему
Хтах = 7,56 и при Ь = ЗЬ *. Второе значение примерно соответствует
наибольшему вылету, при котором работа идет с наибольшей силой
резания.
Расстояние от вершины резца до оси ползуна принято а = 1,056
(в соответствии с размерами употребляемых резцедержавок). При
расчете ползунов различных форм принимались типовые соотношения
между отдельными размерами. Ползуны предполагались
изготовленными из одного материала — стали, модуль упругости при растяжении
принимался Е = 2 • 10° кГ/см2. Коэффициент контактной податливости к
принимался одинаковым для всех конструкций ползунов и равным
1 . 10~4 смУкГ.
На основании данных табл. 62 можно сделать следующие выводы:
1. Наиболее распространенная конструкция ползуна в виде
правильного восьмигранника не является оптимальной с точки зрения жесткости.
* Эти значения получены из следующих соображений- в среднем для карусельных
станков Ь = 0,06 й0бр, ^тах = 0,45 й0бр> I* = 0,18 й0ору тле^0бр — наибольший диаметр
обработки.
321
2. При равной высоте ползуны квадратного и таврового сечения
имеют меньшие упругие перемещения, чем восьмигранные, на 35—40%.
Вес их при этом несколько выше— на величину около 40% для
квадратного и 65% для таврового сечения.
3. При равной высоте ползуны с сечением в виде неправильного
восьмиугольника обладают большей жесткостью кручения, чем ползун
с сечением в виде правильного восьмиугольника (на 15—20%), в
основном вследствие большей жесткости направляющих (при близкой
жесткости изгиба и меньшем на 10—17% весе).
4. С точки зрения использования материала (две последних графы
в табл. 62) оптимальными являются ползуны с сечением в виде
восьмиугольника с удлиненными фланцами по типу применяемых в станке
мод. 1570 (табл. 62, графа 5) и в несколько меньшей степени —
ползуны с квадратным сечением и с сечением в виде неправильного
восьмиугольника. При равной высоте ползуны по типу применяемых
в станках мод. 1570 имеют большие упругие перемещения, чем
восьмигранные, но при этом вес их в 1,8 раза ниже. При увеличении высоты
ползунов по типу ползуна станка мод. 1570 на 30% по сравнению с
восьмигранными при равном весе жесткость их оказывается вдвое более
высокой.
ГЛАВА VIII
ПЛАНШАЙБЫ (КРУГЛЫЕ СТОЛЫ) И НАПРАВЛЯЮЩИЕ
КРУГОВОГО ДВИЖЕНИЯ
§ 1. ОБЩИЕ СВЕДЕНИЯ ПО КОНСТРУКЦИЯМ
Планшайбы, Планшайбы с горизонтальной осью (токарных»
лоботокарных станков), в том числе планшайбы больших диаметров —
до 4 м, выполняются с^з направляющих и поддерживаются только
шпинделями. При больших диаметрах планшайб шпиндели должны выпол^
няться существенно повышенных размеров.
Фиг. 177. Стол карусельного станка мод. 1553:
1 — планшайба; 2 — шпиндель.
Круглые столы и планшайбы с вертикальной осью (карусельных,
зуборезных, плоскошлифовальных и других станков), как правило,
выполняются с направляющймл. Пля^шайбы с направляющими обычна
работают в сочетании со шпинделями или неподвижными шипами.
У станков, предназначенных для обработки высоких деталей, у которых
силы резания приложены на большом расстоянии от плоскости
планшайбы, применяются длинные шпиндели (фиг. 177). У станков,
предназначенных для обработки низких деталей, а также у крупных станков*
применяю ся короткие шпиндели или неподвижные шипы {фиг. 178).
Круглые поворотные столы с установочным вращательным движением
выполняются без шпинделя.
323
Планшайбы небольших
диаметров (до 1000 мм) и
поворотные столы с
установочным вращательным
движением обычно
выполняются сплошными по высоте,
с ребрами. Планшайбы
более крупных станков
выполняются коробчатыми и
снабжаются ребрами (фиг. 179).
Оребрение планшайб
имеет большое значение.
Планшайбы выполняются
с радиальными ребрами, и,
как правило, с кольцевым
ребром над направляющей.
Большие планшайбы с
двумя направляющими имеют
два кольцевых ребра (фиг.
180). Планшайбы без
кольцевого ребра обладают
пониженной жесткостью в
зоне направляющих.
Планшайбы диаметром
до 5—7 м выполняются
цельными (фиг. 179), при
больших диаметрах —
составными (фиг. 180) из двух
или четырех частей. В
станках (в основном
карусельных) для обработки деталей
больших диаметров — более
9 м — применяются по две
планшайбы, из которых
наружная — кольцевая.
Средние соотношения
основных размеров
планшайб следующие: для
планшайб диаметром до 3 д
■^ = 0,12, -^ =0,012, %=*
= 0,12; для планшайб
диаметром от 3 до 7^-^ = 0,10,
^-=о,оо9, 4-=°>08; для
планшайб диаметром свыше
8 м 4=°>08> ^- = 0,006,
4 = 0,05,
где к — высота планшайбы
(без направляющих);
О — наружный диаметр;
I -— толщина стенок
(средняя);
й — диаметр отверстия
шпинделя.
324
Фиг. 180. Составная планшайба крупного карусельного станка,
Фиг. 179, Планшайба карусельного станка среднего размера.
По мере совершенствования литейной технологии толщину стенок
целесообразно несколько уменьшать.
Диаметры круглых столов (планшайб) стандартизованы. Для
планшайб карусельных станков применяют ряд диаметров по ГОСТу 600-52:
710, 900, 1120, 1400, 1800 2250, 2800, 3600, 4500, 5600, 7500, 8750,
11200, 14 000, 18000 мм. Для столов долбежных станков применяют
ряд диаметров по ГОСТу 1141-54: 360, 500, 630, 800, 1000, 1250,
1600 мм.
В планшайбах карусельных станков Т-образные пазы для
закрепления изделий располагаются радиальными рядами (фиг. 179, 180) обычно
под углом 45° друг к другу, причем в каждом ряду имеется
от 2 до 6 пазов (в зависимости от размера стола). Планшайбы
токарных станков средних размеров обычно имеют четыре радиальных
паза под углом 90°.
В столах долбежных станков Т-образные пазы обычно расположены
взаимно-перпендикулярно, причем в одном направлении обычно
выполняется несколько пазов (от одного до пяти в зависимости
от размера стола), а в другом один диаметральный. Круглые
•столы шлифовальных станков в большинстве случаев выполняются
магнитными.
В станках имеют применение круговые направляющие:
а) скольжения — плоские, конические и \^-образные; б)
качения — шариковые и роликовые.
Схемы направляющих кругового движения приведены в табл. 63.
До настоящего времени большее применение имеют круговые
направляющие скольжения.
Обычно планшайбы диаметром более 7—8 м выполняются с двумя
направляющими.
У столов с медленным вращением (долбежных,
универсально-фрезерных, зуборезных станков) диаметр направляющих скольжения
выбирается близким к диаметру стола. У столов, имеющих большую скорость
вращения, отношение среднего диаметра направляющих к диаметру
стола составляет обычно 0,5—0,75.
Основная причина выхода круговых направляющих скольжения из
строя — контактное схватывание рабочих поверхностей с последующим
образованием задиров. Абразивный износ круговых направляющих (при
нормальной эксплуатации и отсутствии задиров) весьма мал, что
объясняется хорошей защитой их от стружки и грязи. Для направляющих
кругового движения применяются материалы чугун — чугун,
текстолит— чугун, цветные сплавы — чугун (см. табл. 49).
Направляющие качения в оснсзном получают применение
при больших скоростях вращения столов (карусельные станки) и при
необходимости осуществления точного установочного вращательного
движения (поворотные столы координатно-расточных станков). Критерием
работоспособности этих направляющих является долговечность по
усталости (при больших скоростях вращения) и отсутствие
остаточных деформаций на направляющих, а также стойкость
сепаратора.
Для главного движения (в карусельных станках)
применяются направляющие скольжения и качения. Из направляющих
скольжения в связи с совершенствованием шпиндельных подшипников качения
основное применение получают плоские направляющие. Отношение
среднего диаметра направляющих к диаметру стола составляет обычно
0,45—0,7; отношение ширины направляющих к среднему диаметру обычно
0,11—0,17, наиболее часто 0,13—0,14. В станках небольших размероь
направляющие часто выполняются привертными.
326
Таблица 63
Основные типы направляющих кругового движения
Схема
Характеристика и область применения
Плоские направляющие
Основная конструкция, рекомендуемая для
направляющих широкого круга станков, в
частности для направляющих, работающих при
значительных скоростях и нагрузках
(карусельных станков). Применяется обычно в
сочетании с радиальными регулируемыми
подшипниками качения; обеспечивает высокую
точность работы, проста в изготовлении,
допускает удобное применение накладок из
листового материала.
В столах с малой скоростью вращения и без
шпинделя (например, при необходимости
поперечных перемещений стола) плоские
направляющие применяются в сочетании с
конической радиальной опорой, выполняемой за одно
целое с направляющими
Конические направляющие
Конструкция, применяющаяся в
американском станкостроении; относительно проста в
изготовлении (по сравнению с У-образными).
Недостатком является трудность обеспечения
соосности конической поверхности
направляющих н опор шпинделя Применяется в
сочетании с мощным шпинделем, вращающимся в
нерегулируемом подшипнике. Угол наклона обра
зующей принимается обычно 30°
V- образные конические
на правляющие
<*)
б)
I
в)
Конструкции, широко применявшиеся в
первой половине двадцатого века (в
отечественном и европейском станкостроении);
сохраняют применение для кольцевых планшайб.
Конструкции сложны в изготовлении. Между
крутыми направляющими в конструкции а,
как правило? предусматривается зазор для
компенсации температурных деформаций.
Подвод масла к направляющим осуществляется
обычно по круговому каналу между гранями.
Применяются со шпинделями, вращающимися
в регулируемых и реже нерегулируемых
подшипниках скольжения. В конструкции б
лучшие условия смазки рабочей пологой
направляющей, так как масло под действием
центробежных сил отбрасывается к ней, и меньшая
опасность заклинивания в результате
температурных деформаций, чем в конструкции а.
Углы наклона граней обычно 20 и 70°.
Конструкция в остается основной для тяжелых
зуборезных станков. Угол между гранями
составляет 120—140°
327
Продолжение табл. 6$
Схема
# 1 т
Характеристика н область применения
Направляющие, применяемые при больших
скоростях и при необходимости осуществления
точного установочного вращательного
движения. Достоинства направляющих качения —
малые силы трения, отсутствие заедания,
возможность работы при повышенных скоростях,
отсутствие всплывания, характерного для
быстроходных направляющих скольжения,
простая система смазки. В качестве опор
планшайбы применяются подшипники качения
большого размера (радиально-упорные или
упорные в сочетании с радиальными)
Наличие подпятника шпинделя в значительной мере улучшает
условия работы круговых направляющих. Рекомендуется устанавливать
постоянную величину центральной
Разрез по А Я
Сечение по В В
Схема
разгрузки [12]: при диаметре
планшайбы до 1000 мм — 0,02 -н0,03 мм,
свыше 1000 до 2000 мм — 0,03 ч-
0,04 мм, свыше 2000 до 3500 мм —
0,05-т-0,06 мм, свыше 3500 да
5000 мм — 0,07 -=- 0,08 мм.
Для повышения несущей
способности масляного слоя при больших
скоростях на рабочих поверхностях
направляющих основания
выполняются клинообразующие скосы
(фиг. 181), способствующие
возрастанию гидродинамической
подъемной силы. При реверсивном приводе
станка скосы выполняются по обе
стороны каждой смазочной
канавки, при отсутствии реверса —
только с одной стороны — по
направлению вращения планшайбы. Скосы
выполняются ступенчатым
шабрением, причем глубина каждой ступени около 0,01 мм при паре чугун —
чугун или чугун — цветной сплав и около 0,015 мм при паре чугун —
текстолит [41].
Длина шабрения
Направление штрихов
Фиг. 181. Клинообразующие скосы на
направляющих карусельных станков.
<*|«ч.
Фиг. 182. Планшайбы карусельных станков с направляющими качения.
В настоящее время в новых моделях станков с наибольшим
диаметром обработки до 2500—3000 мм, а в отдельных случаях до 5000 мм
328
(станки фирмы Гиддингс) направляющие скольжения вытесняются
направляющими качения. В качестве опор планшайбы применяются
конические роликоподшипники (фиг. 182, а) или радиально-упорные
шарикоподшипники. При больших
диаметрах планшайбы шариковые
направляющие, воспринимающие вертикальную
нагрузку, сочетаются с двухрядными
роликоподшипниками шпинделя,
воспринимающими радиальную нагрузку (фиг.
182, б).
Для точных делительных
движений столов (зуборезных
станков) в связи с низкими скоростями
и высокими требованиями к точности до
настоящего времени обычно применяются
направляющие скольжения. В небольших
станках с диаметром стола до 1000 мм
в большинстве случаев применяются
плоские направляющие в сочетании с коническим подшипником
скольжения, центрирующим стол (фиг. 183). В крупных станках применяются:
Фиг. 183.
Стол зубофрезерного*
станка.
Фиг. 184. Магнитный стол плоскошлифовального станка с направляющими качения,
самоцентрирующие У-образные симметричные направляющие с углом
90—110° в сочетании с цилиндрическим подшипником шпинделя или
плоские направляющие в сочетании с коническим подшипником.
Фиг. 185. Поворотный стол координатно-расточного стайка.
Для вращения столов с изделиями при плоском
шлифовании в связи с возможностью значительных температурных
деформаций применяются плоские направляющие в сочетании с радиальными
подшипниками скольжения или качения. Отношение среднего диаметра
направляющих к диаметру планшайбы составляет обычно 0,65—0,75.
32&
В некоторых последних конструкциях получают применение шариковые
направляющие качения, свободные от явления всплывания планшайб
от масляных клиньев в направляющих (фиг. 184).
В поворотных столах координатно-расточных
станков применяются плоские направляющие скольжения и
шариковые направляющие (в связи с высокими требованиями к точности
поворота, фиг. 185).
§ 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ РАСЧЕТА
Работоспособность планшайб в основном определяется
работоспособностью направляющих. Направляющие планшайб при высоких
скоростях должны работать в условиях жидкостного трения. При средних
и низких скоростях направляющие работают в условиях смешанного
трения.
Вследствие температурных и упругих деформаций планшайб в
направляющих возникают относительные смещения планшайбы и
основания (главным образом взаимный перекос). Это ведет к
перераспределению давлений, возникновению высоких кромочных давлений и
изменению толщины масляного слоя по ширине направляющих.
До последнего времени проводился только условный расчет
направляющих по среднему давлению. Ниже в дополнение к расчету по
среднему давлению предлагается уточненный расчет с учетом упругих и
температурных деформаций планшайбы и основания. Для направляющих,
работающих в условиях значительных скоростей, расчет ведется по
несущей способности масляного слоя при заданных условиях работы
направляющих (скорости, температуре, наименьшей толщине масляного слоя
и т. д.). Наименьшая толщина масляного слоя может быть определена
с учетом угла наклона планшайбы у направляющих. Для направляющих,
работающих при малых скоростях скольжения и, следовательно, в
условиях смешанного трения, расчет ведется по наибольшим давлениям.
Наибольшие давления обычно имеют место у кромки направляющих в
радиальном сечении, проходящем через наиболее нагруженный кулачок.
Неравномерность распределения давлений, по площади направляющих
обусловливается:
а) осесимметричным деформированием планшайб вследствие
неравномерного нагрева и нагружения равномерно распределенной нагрузкой;
в результате этого возникают высокие кромочные давления;
б) деформированием планшайб вследствие нагружения кососим-
метричной нагрузкой от сил резания и установки изделия на небольшом
числе кулачков (планшайба нагружается силами, близкими к
сосредоточенным). Это вызывает перераспределение давлений по длине
направляющих.
Для оценки наибольших давлений определяется погонная реакция
(на единицу длины направляющих) и угол наклона планшайбы и
основания в среднем сечении направляющих.
Расчет собственно планшайб производится на жесткость, которую
можно характеризовать углом наклона планшайбы в среднем сечении
направляющих. Для планшайб без направляющих основными
критериями работоспособности являются жесткость с точки зрения влияния
на точность обработки и виброустойчивость станка, а также прочность.
Из планшайб станков отдельных групп в принципиально более
тяжелых условиях, чем другие, работают планшайбы карусельных станков.
Они подвергаются большим нагрузкам,, работают при больших скоростях
скольжения, в их направляющих часто имеют место заедания.
Планшайбы зуборезных и шлифовальных станков работают при значительно
меньших нагрузках и скоростях и, как правило, безотказно. Поэтому
330
основные расчеты разработаны в применении к планшайбам карусельных
станков. Однако при необходимости эти расчеты вполне могут быть
распространены на планшайбы других станков.
Порядок проведения технического расчета изложен на стр. 355.
Ъ}>>>)>>>>^7
^1 О
\№»Ш»>»»»»»»»/7Ъ
Сечение по аа
§ 3. ОПРЕДЕЛЕНИЕ УПРУГИХ ДЕФОРМАЦИЙ ПЛАНШАЙБ
И РЕАКЦИЙ В НАПРАВЛЯЮЩИХ
А. Определение приведенной жесткости планшайб
Планшайба представляет собой круглую сложную пластину,
состоящую из двух горизонтальных стенок, соединенных системой
радиальных и кольцевых ребер, и опирающуюся по кольцевой поверхности.
Она имеет обычно переменную высоту (большую— в зоне
направляющих и меньшую —по краям). Однако при расчетах планшайбу
приходится рассматривать как пластину постоянной высоты, равной высоте
средней части (фиг. 186).
Экспериментальное исследование (см. ниже) показало, что форма
упругой поверхности такой сложной пластины при разных видах нагру-
жений соответствует форме
упругой поверхности сплош- | ^ ^
ной пластины (за исключе- \к»>>>>>»»>>>*»>>>>>>>,%\ \&гшгт
нием небольшой зоны
вокруг точки приложения
нагрузки). Следовательно, к
расчету планшайб
применимы формулы для сплошных
пластин, если в них вместо
цилиндрической жесткости
сплошной пластины В =
= 12(1-^2) (рДе « — высота
пластины, Е и \1— модуль упругости и коэффициент Пуассона
материала пластины) подставлять некоторую приведенную жесткость Впр.
Значение приведенной жесткости В„р может быть получено из
рассмотрения деформаций сложной пластины, снабженной только радиальными
ребрами, основные ее стенки испытывают изгиб и двухосное растяжение-
сжатие, радиальные ребра — изгиб и сдвиг. Точное решение такой
задачи даже при частной нагрузке представтяет большие трудности;
поэтому ниже приводится приближенное решение с помощью
потенциальной энергии деформации. Рассматривается простейший случай — нагру-
жение пластины, опертой по краю, центральной силой Р.
Предполагается, что прогиб пластины изменяется по радиусу, следуя закону
косинуса (фиг. 187):
71?
у = асо8-г^-,
а)
пг
<9
Фиг. 186. Схема к определению приведенной
жесткости планшайбы:
а — действительная форма планшайбы; б — условная форма
планшайбы.
причем в ребрах часть этих перемещений у1 = а1 саз-—- происходит за
счет изгиба, а часть у2 = а2со$^г за счет сдвига, где а
—перемещение в центре пластины, а = а1-|-а2.
Упругие перемещения растяжения-сжатия стенок щ и и2 связаны
с перемещениями ребер через угол наклона поперечных сечений
следующим образом:
* к ~ 2г 81п 2г '
331
Внутренняя потенциальная энергия планшайбы:
2тс г
1Г
-Я-
Ы ( ^1 \2 \ 0Р ( дУ
2
др2
+
1*+П
-1 оо
\( диЛ*
2{\-^)
д? } + Р2 +
2тс г
] О О
*М2 + -^- +
здесь /** и / — соответственно площадь и момент инерции площади
поперечного сечения радиального ребра;
Е и О — модули упругости первого и второго рода;
п — число радиальных ребер*
яр
\ 2г
Фиг. 187. Схема деформирования круглой плиты с радиальными ребрами.
Первое слагаемое представляет энергию изгиба и сдвига ребер,
второе и третье — энергию растяжения-сжатия верхней и нижней стенки.
Энергией изгиба стенок ввиду ее малости пренебрегаем. После
подстановки значений уи у2, ии и2 [47] получаем окончательную формулу
внутренней потенциальной энергии планшайбы:
и
ъЮРа\'
1Ьг~
4?2
где О =
Е№
(х(2
цилиндрическая жесткость пластины, состоя-
щей из двух жестко связанных стенок толщиной 1\ и /2, расположенных
на расстоянии /г. Принято предположение, что в сложной пластине
нейтральная поверхность проходит через центр тяжести сечений. Полная
энергия сложной пластины 3= V — Р(а\ ~\-а2). Составляющие полного
перемещения <Х\ и а^ находятся из условия минимума потенциальной
дЭ Л дЭ гч ~ ~
энергии системы -^-=0; -^7 = 0. Отбрасывая слагаемые второго
порядка малости, получим
да2
а.
2РГ2
тсз/>(1,2 + {х)
1 +
4*Р(1,2 + Е)
ОРпг
Выражение перед скобкой представляет собой прогиб в центре
сложной пластины, состоящей из двух стенок, при предположении, чта
332
стенки работают как единая система, в соответствии с гипотезой плоских
нормалей, а член в квадратных скобках учитывает влияние сдвигающих
напряжений в радиальных %ц
ребрах.
Отсюда приведенная ,
жесткость пластины
И
пр— 1 +ф
К1 СЛ€9
ом
он
где О — цилиндрическая
жесткость пластины, состоя- оя
щей из двух жестко
связанных стенок:
Д = • —— кГсм;(8Л) фиг- 18& Зависимость коэффициента 5/, учиты-
1 —. р2 ^ + 12 ваюшего влияние окон в нижней стенке, от
размеров окон.
ф — коэффициент,
учитывающий влияние сдвигающих напряжений в ребрах;
4*Р(1.2 + 10
' — ОРпг
Фиг. 189. Форма исследованных пластин:
а, б% 6 — с разным количеством кольцевых ребер и сплошными горизонтальными стенками; а — с
утолщенными сплошными горизонтальными стенками; д, е — с окнами в нижней стенке.
Для планшайб с окнами в нижней стенке принципиально решение
остается тем же, только меняются пределы интегрирования при
определении потенциальной энергии стенки.
333
Окончательно формула для Впр остается прежней, только вместо
толщины 12 нижней стенки подставляется приведенная толщина 1ъпр*
Величина ипр определена из условия равенства внутренней
потенциальной энергии стенки с окнами и сплошной стенки приведенной толщины
/- 1
где т — число рядов окон;
а/ — суммарный центральный угол в радианах, занимаемый г-тьш
рядом окон;
^— коэффициент, определяемый по графику фиг. 188 в
зависимости от размеров окон.
Фиг. 190. Сравнение экспериментальных и расчетных величин упругих перемещений
моделей планшайб при симметричном нагружении. Точками нанесены экспериментальные
данные, линиями — результаты расчетов:
1 — для модели с утолщенными стеиками (ф; 2 — для модели с тонкими стенками (О — с одним кольцевым*
ребром, Ч с двумя кольцевыми ребрами, ф — без кольцевых ребер); 3 — для модели с окнами в
нижней стенке (X). Все модели с восемью радиальными ребрами.
Коэффициент |/ получен из рассмотрения потенциальной энергии
стенки с окнами. Суммирование распространяется на число рядов окон
по радиусу планшайб. Обычно число рядов окон т = 1-ь-З.
Влияние кольцевых ребер сводится к тому, что углы наклона и
радиальные перемещения в местах сопряжения кольцевых ребер со
стенками не могут быть больше, чем соответствующие угловые и радиальные
перемещения этих ребер. Действие кольцевых ребер на пластину
приближенно можно представить в виде моментов, величина которых
определяется из условия равенства углов наклона пластины и ребра в местах
сопряжения. Кольцевые ребра при йаличии радиальных ребер очень
мало изменяют упругую линию сложной пластины и поэтому в
техническом расчете влияние кольцевых ребер не учитывается. Это положение
334
оценено теоретически и подтверждено экспериментально (см. ниже).
Исключение представляет кольцевое ребро, расположенное над
направляющими. Как показывают расчеты, при приложении нагрузки
непосредственно над направляющими наличие такого ребра понижает
давление на направляющие на величину до 15—20%.
Полученные зависимости были проверены экспериментально на
моделях и реальном станке с диаметром планшайбы 3000 мм (мод. 1532).
Фиг. 191. Сравнение экспериментальных и расчетных величин упругих перемещений?
моделей планшайб при эксцентричном нагружении. Точками нанесены
экспериментальные данные, сплошными линиями — результаты расчетов, штрихпунктирными
линиями — местные деформации в зоне нагружения;
/ — для модели с утолщенными стенками ((Ъ); -2 — для модели с тонкими стенками (+ с двумя кольцевым»
ребрами, ф — без кольцевых ребер); 3 — для модели с окнами в инжией стенке (х). Все модели с восемью-
радиальными ребрами.
Расхождение между расчетными и экспериментальными данными в обоих
случаях не превышало 10—15%. Модели были выполнены из
органического стекла, нижняя стенка приклеивалась. При моделировании были
выдержаны типовые соотношения размеров планшайб. Модели
выполнялись с разным количеством радиальных и кольцевых ребер и разной
толщиной горизонтальных стенок (фиг. 189). Нагружение
осуществлялось сосредоточенной вертикальной силой в центре, распределенной па
кольцевой поверхности нагрузкой и сосредоточенной эксцентрично
приложенной вертикальной силой.
Сравнение экспериментальных и расчетных величин
перемещений для некоторых видов нагружения приведено на фиг. 190, а—г
и 191, а, б.
Эксперименты показали, что форма упругой поверхности планшайбы
при всех видах нагружения соответствует форме, полученной расчетом
для сложной планшайбы, за исключением очень небольшой зоны нагру-
335
женной стенки вокруг точки приложения сосредоточенной силы.
Местные деформации нагруженной стенки в ючке приложения силы при на-
гружении между ребрами превышают общие расчетные для сложной
пластины на величину до 60—70%.
Приведенная жесткость планшайбы станка мод. 1532 по расчету
А ~
X \0*кГсм.
пр — 9,5-10* кГсму по экспериментальным данным Впр = (9-М1)Х
Б. Определение нагрузок, действующих на планшайбы
Планшайбы воспринимают силы от веса изделий, от резания,
зажима кулачков и приводного зубчатого колеса. Нагрузку на планшайбу
можно представить в виде суммы четырех нагрузок (сил и
изгибающих моментов,
приложенных по окружности
расположения кулачков,
фиг. 192):
а) симметричной,
вызванной действием
вертикальных сил,
Фиг. 192. Схема нагружения планшайбы.
в) равномерно распределенной ■
(стцла)
Р=Ои + Рх кГ; (8.2а)
б) симметричной,
вызванной действием
момента Мк от силы зажатия
кулачков,
Х{К + К)кГсм; (8.26)
■от собственного веса планшайбы
кФ
кГ/см2;
(8.2в)
ЯИЯ,
г) кососимметричной, вызванной действием момента М от сил реза-
м=У^бРА т руну -+- (Я,я)2;
(8.2г)
знак минус —для случая наружного точения, плюс — для растачивания.
Здесь Ои и Опл — вес изделия и планшайбы, соответственно, в кГ;
РХ) Руу Рг — осевая, радиальная и тангенциальная составляющие
силы резания (в применении к обработке
цилиндрической поверхности) в кГ\
Рзаж" сила зажатия на одном кулачке в кГ\
2— число кулачков;
(I и й0 — диаметр планшайбы и диаметр обработки,
соответственно, в см\
Н—расстояние от точки приложения силы резания до
нейтральной плоскости планшайбы в см;
к* И" Ля —расстояние от рабочей поверхности планшайбы до
середины зажимной поверхности кулачков и
нейтральной плоскости ллдншайбы, соответственно, в см.
336
Положение нейтральной плоскости планшайбы приближенно может
быть оценено следующим образом (фиг. 186):
где кн — расстояние от нейтральной плоскости до зеркала планшайбы;,
Нх — расстояние от центра тяжести верхней стенки до рабочей
поверхности планшайбы.
Моменты, изгибающие планшайбу, от сшГна приводном зубчатом
колесе на порядок меньше сил на кулачках и в технических расчетах.
могут не учитываться.
Вследствие
относительно малой опорной
поверхности кулачков
нагрузки на
планшайбы, передаваемые
через кулачки, могут
рассматриваться как
сосредоточенные силы.
Ниже
рассматриваются два расчетных
случая.
1. Нагрузка на
планшайбу
принимается в виде
сосредоточенных сил под
кулачками (фиг. 193 и табл.
64) — расчетный
случай для средних
станков. С точки зрения
давлений в
направляющих и деформаций
планшайб этот случай
является наиболее
неблагоприятным. В
основном
рассматривается установка изделия на четырех кулачках.
2. Нагрузка принимается распределенной по всей окружности
расположения кулачков — расчетный случай для планшайб тяжелых
станков, так как для них характерна установка изделия на большом числе
кулачков и подставок. Этот случай может использоваться также для при-
кидочных расчетов планшайб средних станков.
Вес жесткого изделия при установке на четырех нерегулируемых
кулачках, вследствие неодинаковой высоты кулачков, распределяется
поровну между двумя противоположными кулачками, при установке на
трех кулачках — между всеми тремя кулачками.
При установке изделия на четырех кулачках за расчетное
принимается положение планшайбы, при котором резец находится над
кулачком, не воспринимающим вес изделия, например, над кулачком 4, на
фиг. 193, если вес воспринимается кулачками / и 3. Наиболее нагружен
при этом кулачок /, который воспринимает вес изделия и в направлении
которого действует сила Рг. Наиболее опасным с точки зрения
выскальзывания изделий из кулачков (при обработке высоких изделий) является
положение планшайбы, при котором резец расположен между
кулачками, причем сила Рх направлена на один из кулачков, воспринимающий
вес изделия. Наименьшее усилие имеет место на кулачке 4'.
&
Фиг.
и нагрузки на
установки изделии
кулачки:
а — установка на четырех кулачках; б — установка на трех кулачках.
Заштрихованными прямоугольниками и цифрами /, 2, 3, 4
обозначены кулачки в положении, когда резец находится над одним из
кулачков. Незаштрихованиымн прямоугольниками и цифрами Г, 2Г, 3',
4' обозначены кулачки в положении, когда резец находится между
кулачками.
33?
Таблица 64
Формулы для определения сил, передаваемых на планшайбу кулачками
| Способ уста-
1 новки изделия
] На
четырех
кулачках
\
А На трех
I кулачках
»1 случай — резец находится над
I одним из кулачков
Рх Н
Л ~ 4 + Рг ^
Рх И
Р _ Щх . *кЛ Р Л_
\И*" 4 I1 т <ь ) - ру а2
О ГГ ГГ
1
II случай — резец находится между
кулачками
Р2 = ^(Р*+РУ) +
У"2 Я
2 Я „ Я
-Т^-^ + ЫбР^
2 Я . . ,Я
В. Определение упругих деформаций планшайб
Ввиду того что определение деформаций пластин на кольцевой опоре
конечной ширины представляет большие трудности, опора принимается
линейной (т. е. бесконечно малой ширины), расположенной по среднему
диаметру направляющих. Это не вносит серьезных погрешностей в
расчет, так как ширина направляющих обычно на порядок меньше диаметра
планшайбы.
Основным критерием, характеризующим жесткость планшайбы,
предлагается считать угол наклона планшайбы по средней окружности
направляющих, как непосредственно влияющий на работоспособность
направляющих.
.338
Наибольший угол наклона планшайбы по средней окружности
направляющих при рассмотрении нагрузки, распределенной по окружности
расположения кулачков, определяется по формуле
рахкр
Мккк
Мк
м
1бпО
пр
4гсД
'ПР
4гсД
'*Р
(8.3)
тде
.Ар, кК
&х — средний диаметр направляющих в см;
км— коэффициенты, определяемые по графикам фиг. 194,
в зависимости от диаметра окружности, расположения
кулачков й<1 и размеров планшайбы. Остальные обозначения
были указаны выше.
Фиг. 194. Графики для определения коэффициентов кр, км, кК, входящих в формулу угла
жаклоиа 6 планшайб у средней окружности направляющих (в предположении, что на«
грузка распределена по окружности кулачков):
а — планшайба без центрального подпятника; б — планшайба с центральным подпятником.
Наибольший угол наклона планшайбы по средней окружности
направляющих при рассмотрении нагрузки, передающейся на планшайбу
через четыре кулачка1:
16тсД
пр
РАх + Ока + Рг-^-к^
МКк'К
4пО„„
(8.4)
где кЖ9 кСп кг, к
коэффициенты, определяемые по графикам на
фиг. 195.
Значения коэффициентов кР и кк вычислены по общеизвестным
формулам для круглых плит под действием распределенной нагрузки.
Значения коэффициентов кХУ ка, кг, кк' получены из рассмотрения деформаций
круглых пластин, опертых по окружности произвольного диаметра, под
действием эксцентрично приложенных силовых факторов. Решения
выполнены в рядах. Количество членов ряда выбиралось из условия
получения погрешности не более 5% и обычно составляло 8 членов
[39, д]. Коэффициент км для кососимметричной .распределенной
нагрузки определен с помощью первого члена этих же рядов.
1 Наибольший угол наклона имеет место, как правило, в радиальном сечении,
проходящем через наиболее нагруженный кулачок.
339
При наличии центральной гидравлической разгрузки силой Рг из
определенных по приведенным выше формулам с помощью* фиг. 194 и*
Р (I к
195 значений 6тах следует вычесть значения 6г — ^ ^ г
•>пр
' к
^ 4>
V. •
'УУ
-^о
■^^
ДО"4
Л
^
Г/
Г V
1 й
X ~" *-*
I *1
. л=
ч«
(
•7 -
«9
К]
V
^
«к
*»
1 ^
.
А
Л
^\
\\
V
^
2
/
</
/1
X
\ *
1
Л
\
\
\
ч
\
Л
/
ч
'^Л
\
\
N 1
Л
1— --л
5)
Фиг. 195. Графики для определения коэффициентов кх,к0, кг, к/, входящих в формулу
наибольшего угла наклона 0 планшайб у средней окружности направляющих (в
предположении, что нагрузка на планшайбу передается через четыре кулачка):
а — планшайба без центрального подпятника; б — планшайба с центральным подпятником.
Значения коэффициента кг приведены в табл .65.
Значения коэффициентов кг и кпл
Таблица 65
кпл
а
кг
Планшайба с
Планшайба
центральным
под-
без центрального
1
! 1,55
0,31
1.6 !
1,2
1,41
0,135
0,82
1,4
1,30
—0,08
0,245
1.6
1,23
—0,28
—0,4
1,8
1,18
—0,5
-0,9
2,0
1,15
-0,68
-1,3
Угол наклона планшайбы по средней окружности направляющие
под действием собственного веса Опл определяется по формуле
в 6пл&\кпл
32*Д
"Р
Значения коэффициента кпл приведены в табл. 65.
При установке изделия с зажимом другим числом кулачков или при.
необходимости определения углов наклона планшайбы в любых точках,
направляющих используются графики фиг. 196.
340
Фиг. 196. Графики^для определения коэффициентов Ы, входящих в формулу угла
наклона 6 планшайбы у средней окружности направляющих под действием
сосредоточенной силы Р, передаваемой через один кулачок:
а ~~ при 9 = 0; б ~ при ? "* 45°; в — при (р - 90°, г — при <р = 180°.
/ — планшайба без центрального подпятника; // — планшайба с центральным подпятником; <р —
центральный угол между радиусом, проведенным в точку, в которой определяется угол наклона 0, и
радиусам, проведенным через точку приложения силы Р;
1- к
рах
&пр — приведенная цилиндрическая жесткость планшайбы
341
Угол наклона планшайбы в любом сечении направляющих под
действием сил резания и веса, передаваемых через кулачки, может быть
определен по формуле
\6кО
'пр
^Л,
/-1
где Я/ — сила, передаваемая на планшайбу через /-тый кулачок
(табл. 64);
кь— коэффициент, зависящий от радиуса расположения кулачков
и центрального угла ср/ между радиальной плоскостью, в
которой определяется угол наклона, и плоскостью
расположения /-того кулачка (фиг. 197);
г—число кулачков.
На графиках фиг. 196 приведены значения коэффициентов кп
построенных для углов ф/= 0°; ф/ = 45°; 90° и 180°. Значения й/ для
других углов определяются интерполированием.
Например, если изделие установлено на четырех кулачках (фиг. 197)
и нагрузки на каждый кулачок соответственно Р\, Р2, Рг и Р4, то угол
наклона планшайбы в точке а
направляющих можно определить по
формуле
« - - * -(РА+ РгК + Р3к< + Л*,);
р,
Р'ГП
\р, 1а \р>
16тгО
ТЯГ
1 очна,6 которой
определяется
угол наклоне
пр
в точке Ъ
-(Р2к1+Р1к, + Ргк3 + Р4кА).
Окружность
нопрабляющия
Окружность
кцлочкаЬ
Фиг. 197. Расчетная схема для^
определения угла наклона планшайбы в
произвольном сеченин
направляющих.
На фиг. 198 приведены примеры
эпюр углов наклона планшайб в
направляющих от сил резания и веса при
обработке изделий различных
размеров. Из графиков видно, что
наибольшие углы наклона 6шах планшайб в
направляющих под наиболее
нагруженным кулачком превышают средние
углы 0ср до 1,5—2 раз. При установке
изделия на трех кулачках углы
наклона планшайб за счет более
равномерного распределения веса изделия уменьшаются по сравнению с углами
при установке на четырех кулачках на .величину до 25—30%.
Нагрузку на планшайбы крупных станков, имеющие две круговые
направляющие, с достаточной степенью точности можно считать
распределенной равномерно по окружности кулачков. Это допустимо по
следующим причинам:
1. Вес обрабатываемых на таких станках изделий значительно
превышает силы резания. Для станков с диаметром планшайбы 8—12 м
наибольший вес изделий превышает наибольшее суммарное усилие
резания в 4—5 раз. При этом угол наклона планшайбы и реакции в
направляющих от момента, создаваемого силами резания, обычно составляют
не более 10—15% полного угла наклона и суммарной реакции в
направляющих.
2. Изделия на таких планшайбах обычно устанавливаются на
сравнительно большом числе кулачков и подкладок. Расчеты показывают,.
342
о 0^?</, а0=аг> н~\а, ?газб
втал^ибвср
у & та л = **вср
V йг<1; йоа№: ***\бч ?гО,2С
Фиг. 198. Эпюры распределения углов наклона 6 планшайб (в полярных координатах)
у средней окружности направляющих при обработке изделий, установленных на четырех
кулачках:
а — планшайба без центрального подпятника; б — планшайба с центральным подпятником (/, 2, 3, 4 —
плоскости установки кулачков). Принято, что вес изделия воспринимается кулачками / и 3; — —1,5; Р~—
их х
- Ру - 0,5РГ
Фиг. 199. График для определения углов наклона 0у средних окружностей направляю-
щих планшайб с двумя направляющими при -^ = 0,7; ^~ = 0,5; 6^ — угол наклона
у направляющей й\ $$— угол наклона у направляющей Б.
Сплошными линиями показаны кривые для случая деформирования планшайбы от силы Р, распределенной
по окружности кулачков, штриховыми — от суммарного момента М , равномерно распределенного между
отдельными кулачками.
343
что яри установке изделий более чем на 6 точках, давления на
направляющих от веса изделия распределяются практически равномерно.
«1
р /А
оА
4
-о,ч\
Р
4
1^
' ОуЧ
0,6
р
\0,8
-
#
"р*—;'
/Ь^-1 А1—*
ил—^ ^ ^
Фиг, 200. График для определения реакций направляющих планшайб с двумя иаправ-
ляющими (при -д = 0,7 и ^- = 0,5) от силы Р, равной сумме веса изделия и
вертикальной составляющей силы резания.
&0 и &В ~~ Реакдии, возникающие в направляющих Я и В.
На фиг. 199 и 200 представлены графики для определения углов-
наклона и реакций в направляющих при наиболее типовых
соотношениях размеров
4— 0,7и|- = 0,5.
Если отношения
размеров
й*
и
*1
близки к
0>Ч 0,6 ад 1,0 1,2 1,4 КО 1,8 2,0-^
Фиг. 201. Графики для определения коэффициентов,
входящих в формулу наибольшей погонной (на
единицу длины) реакции направляющих при установке
изделия на четырех кулачках. Сплошные линии —
для планшайбы без центрального подпятника»
штриховые—с центральным подпятником.
тем, для которых
построены графики, при
расчете также можно
пользоваться этими графиками.
Реакции в направляющих
от веса планшайбы при
этих соотношениях
составляют Яв^0,9Опл и
^0,1СПЛ.
Г. Определение погонной
реакции направляющих
Погонная (на
единицу длины) реакция
направляющих при
рассмотрении нагрузки,
распределенной по окружности
расположения кулачков, определяется по формулам:
а) от симметричной составляющей вертикальной нагрузки (при
отсутствии центрального подпятника)1
Яр-*—
Ых
(8.5а)
1 При наличии центрального подпятника из выражения в числителе вычитается*
реакция подпятника.
344
б) от кососимметричной нагрузки, вызванной действием момента М
от силы резания 1 (при с12 < й\)>,
^=^-[о'885"о'и51-о'и5(,~1)(,~^)
где ф — угол между плоскостью действия момента М и радиальной
плоскостью, в которой определяется реакция направляющей. При -/- > 0,4
а
и -у-= 1,5-^2, что обычно имеет место в преобладающем большинстве
случаев,
Ям-
(3,5-^4) АГ со $ у
(8.56)
Ц2 ф Об о\н^\{Г1г % 1/> 1,8 2$
0,5
0
"г
€^
/
—
у*ц
-^
-1
0'~у 1
у>=180°
~^г
"
Л
^'
^1^"
А
ъ
""Я
0,2 ф 0,6 0,8 1,0 \2 ф 1,6
18 г
\у*9(Г
Фиг. 202. Графики для определения погонной реакции направляющих под Действием
сосредоточенной силы Р, передаваемой через один кулачок (для ~т = 1,3^-2):
<р — центральный угол между радиусом, проведенным в точку, в которой определяется реакция, и радиу-
сом, проведенным в точку приложения силы Я; ц — средняя погонная реакция, Яг„ = —=■ , Я — горизон-
тальная проекция площади направляющих.
Сплошные линии —для планшайбы без центрального подпятника» штриховые—для планшайбы с
центральным подпятником: а) <р = 0 и <р = 45°, б) у = УФ? н <р=180°.
Наибольшая погонная реакция (при ср
Ятах — 9.Р + ЯМ таз
о)
Наибольшая величина погонной реакции направляющих (под
наиболее нагруженным кулачком) при рассмотрении нагрузки, передающейся
на планшайбу через четыре кулачка, определяется по формуле
1^1 ["
РЖ + ОЛ' +Р,
н
к'
(8.6)
где к'х, Ы0> к'г—коэффициенты, определяемые по графикам, фиг. 201.
Если диаметр расположения кулачков близок к среднему диаметру
направляющих, то погонная реакция направляющих зависит от
соотношения жесткости планшайбы йпр и жесткости направляющих / (опреде-
1 Формула получена при рассмотрении реакции опоры круглой пластины,
нагруженной кососимметричной нагрузкой или сосредоточенными силами в местах
расположения кулачков, Для случая нагр ужения сосредоточенными силами решения выполнены
в рядах [39, д].
345
ляемой как жесткостью поверхностных слоев направляющих и
масляного слоя, так и местной жесткостью самих направляющих) *.
Графики на фиг. 201 построены для среднего отношения жесткости
кольцевого ребра Е1, расположенного в зоне направляющих, к
жесткому,
= 0,01-^-0,025 и для нескольких соотношений
сти йпр планшайбы
А«А
Фиг. 203. Эпюры распределения давлений а по
средней окружности направляющих планшайбы,
при обработке изделия, установленного на че-
й
тырех кулачках (Р*-= Ру=^ 0,5/^; —д—= 1,5):
1, 2, 3, 4 — плоскости установки кулачков (принято, что'
вес изделия воспринимается кулачками / и 3); а
среднее давление в направляющих
-0,36 О
и'
И
V
б) й.
в) а2 - 1,5^,
- 0,130,,
ср
о,7а,
жесткости планшайбы и
направляющих:
8А,
'пр
№
: 0,005; 0,01; 0,02.
Жесткость направляющих
приближенно оценивается по
формуле
#С05а г-., «
У = ——кГ/см*,
где & — ширина проекции
направляющей на
горизонтальную плоскость
в см;
а — угол между
направляющей и горизонтальной
плоскостью:
к — коэффициент
пропорциональности между
упругими сжатиями
поверхностных слоев
направляющих и
давлениями в данной точке
направляющих (см.
ниже) в см%\кГ.
Погонная реакция з
любом сечении направляющих
при установке изделия на
любом числе кулачков
определяется по формуле
/«г
*-1
*<*!
ЛЯср)'
где Я/ — сила, передаваемая на планшайбу через /-тый кулачок;
—^-— соотношение действительной и средней погонной нагрузки
ЧсР
в среднем сечении направляющих з точке, расположенной
под углом <р от плоскости расположения *-того кулачка
(фиг. 202).
Графики для определения погонной реакции направляющих
планшайб с двумя направляющими приведены на фиг. 200.
На фиг. 203 показаны примеры эпюр распределения давлений а =
= -~- по средней окружности направляющих (где д — погонная реакция,
1 Следует отметить, что. при выводе расчетный зависимостей ширина
направляющих предполагалась бесконечно малой. При этом наибольшие расчетные погонные реак-
дии и соответственно давления при ~^~ -+■ 1 получаются несколько завышенными.
ЗШ
Ь — ширина направляющих). Как видно из фиг. 203, давления по
средней окружности направляющих в результате неравномерности
распределения погонной реакции превышают средние в несколько раз.
§ 4. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ НАПРАВЛЯЮЩИХ И ТЕМПЕРАТУРНЫХ
ДЕФОРМАЦИЙ ПЛАНШАЙБ И ОСНОВАНИЙ <
Теплообразование в направляющих, работающих с большими
скоростями (в частности, карусельных станков), вызывает понижение
несущей способности масляного слоя из-за снижения вязкости масла,
температурные деформации планшайбы и основания, и, как следствие,
ограничивает режимы резания и веса обрабатываемых на станке изделий.
Температурные деформации планшайбы и основания ведут к
резкому перераспределению давлений на направляющих — возникновению
высоких кромочных давлений на внутренней окружности направляющих
(фиг. 204).
Фиг. 204. Схема температурных деформаций планшайбы карусельного станка,
вызванных теплообразованием в направляющих.
Относительный угол наклона направляющих планшайбы и
основания в результате температурных деформаций в отдельных случаях
достигает 0,5—0,6 мм/м. Большие температурные деформации могут явиться
причиной появления задиров на трущихся поверхностях
направляющих.
Избыточная температура масляного слоя, определяемая из
уравнения теплового баланса при рассмотрении направляющих как
прямоугольных пластин, а поддерживающих их стенок как прямоугольных
ребер охлаждения бесконечной длины, выражается формулой
» - От + «ТУ»о гпая ,Я7.
"*— ьп + к0 + С1У гРад*' (8-7>
где $* и $0 —избыточная температура масляного слоя и масла,
подаваемого в направляющие, соответственно, в град.;
(}т — тепло, выделяемое в направляющих, в ккал\час\
(?т = 3600
427
где о — давление на направляющих в кГ\см2\
5^—площадь рабочей поверхности направляющих в см2;
г/ —средняя скорость скольжения рабочих поверхностей в м\сек\
/—коэффициент трения (фиг. 205);
с — теплоемкость масла, составляющая 0,4—0,5 ккал\кГград\
у — удельный вес масла; при 50° С для индустриальных масел
у = 0,87-н 0,89 кГ/л;
1 Раздел написан канд. техн. наук Ю. Н. Соколовым.
347
1
Фиг. 205. График для определения
коэффициента трения / в круговых
направляющих (график построен на
основании экспериментальных данных,
полученных для материалов
направляющих чугун — чугун и ЦАМ 10-5—
чугун, при обильной смазке
индустриальным маслом марки 45 и
установившейся температуре направляющих.
При неразогретом станке значения
коэффициента / могут быть в 1,5—2 раза
выше; для материалов текстолит —
чугун значения коэффициента / выше
указанных на графике на 20—30%
(меньшие значения для высоких
скоростей);
р — средняя удельная нагрузка.
Фиг. 206. Значения коэффициента теплоотдачи от
масляного слоя направляющим карусельных станков в
зависимости от окружной скорости направляющих.
4 5 I/ м/сек
348
V—объем масла, прокачиваемого между рабочими поверхностями
направляющих в л/час; для У-образных направляющих
учитывается только масло, прокачиваемое между пологими
направляющими;
кппк0 — коэффициенты, учитывающие теплоотвод планшайбой и
основанием, соответственно, в шал/час • град;
± = ^ + 1
где 5! и52 — площади теплоотдающей поверхности направляющих
планшайбы и основания в м2;
ам — коэффициент теплоотдачи масляного слоя
в ккал/м2 • час • град,; определяется по табл. 66 и
фиг. 206 в зависимости от температуры и сорта масла.
При выборе ям задаются предварительно ожидаемой
температурой &л (впоследствии значение &л при
необходимости корректируется);
Таблица 66
Значения коэффициента #1 для масел при различных температурах
Марка масла
Температура масла в с
30
1,25
1.19
1,16
1,10
1,07
40
1,35
1,28
1,25
1,19
1,15
50
1,44
1,36
1,33
1,26
1,22
С, отсчитываемая от нуля шкалы
60
1,5
1,43
1,40
1,32
1,28
70
1,57
1,49
1,45
1.38
1,34
80
1,62
1,54
1,50
1,43
1,39
ЬО
1,67
1,59
1,55
1,44
1,43
а1 и а2—средние коэффициенты теплоотдачи планшайбы и
основания в ккал/м2 • час • град; для основания можно
принять а2 = 3 ккал/м2 • час • град; для планшайбы
коэффициент теплоотдачи определяется по формуле ^ =
= 0,5 (а + а'), где оси а'— коэффициенты теплоотдачи
внутренней и наружной поверхностей планшайбы. Если
принять линейный закон распределения температур по
радиусу, то о! определяется как среднее
арифметическое коэффициентов теплоотдачи при ^ —0 и ъ = ътах.
Ввиду плохого теплоотвода внутри планшайбы можно
принять а —3 ккал/м2 • час • град;
\г и Х2 — коэффициенты теплопроводности материала планшайбы
и основания, соответственно; для чугуна
л = 40-^55 ккал/м • час • град;
Рг и р2— площадь поперечного сечения стенки или ребра,
примыкающего к направляющей, в месте примыкания,
соответственно для планшайбы и основания в м1;
иг и (/2 — периметр площади поперечного сечения стенки или
ребра, примыкающего к направляющей, в месте
примыкания, соответственно для планшайбы и основания в м.
Знак 21 указывает, что если от направляющей отходит несколько
стенок-ребер (включая кольцевые и радиальные ребра), то суммируется
тепло, отводимое каждым ребром. Для У-образных направляющих кару-
349
сельных станков при малых и средних числах оборотов планшайбы,
последними слагаемыми в формуле для ®м, учитывающими теплоотвод
в масло, можно пренебречь, так как основная часть масла
перекачивается через зазор между крутыми гранями и кольцевую канавку.
Избыточная температура масляного слоя направляющих
карусельных станков доходит при высоких скоростях до 70—80°. Сравнение
результатов расчетов температуры масляного слоя с
экспериментальными данными показало удовлетворительное совпадение.
Температурное поле план-
ктл/м^час град
^ 0 60 120 №0 2Чб 300 360 420 Чд0ум/мин
Окружная скорость
Фиг. 207. График для определения
коэффициента теплоотдачи а от теплоотдающих
поверхностей в окружающую среду.
шайбы и основания может быть
определено, если допустить, что
стенки планшайбы и основания
являются прямыми ребрами
конечной длины, отводящими тепло
от направляющих.
Температуры отдельных
точек планшайбы и основания
могут быть определены по формуле
д (ч сН т (I — х)
где
т
=у-
сЬ т1
2аср
§н — средняя температура направляющей в град.; в случае
отсутствия неметаллических накладок на направляющих &„ — *«;
/ — длина теплоотводящей стенки в м\ для нижней стенки
планшайбы и верхней стенки основания принимается равной
расстоянию от направляющей до центра планшайбы или
основания; для верхней стенки планшайбы-—суммарной длине
верхней, боковой наружной стенки и части нижней стенки
от направляющей до наружной боковой стенки;
х—координата точки, отсчитываемая по теплоотводящей стенке
от направляющей к центру планшайбы или основания, в* м;
X — коэффициент теплопроводности (см, стр. 349);
$ — толщина стенки планшайбы или основания в месте
примыкания к направляющей в м;
ьср — средний коэффициент теплоотдачи стенок в ккал/м2-час-град.
Для определения аср теплоотводящие стенки планшайбы или
основания разбиваются на равные участки длиной 200—ЗСО мм и для
каждого участка определяются коэффициенты теплоотдачи ал; тогда
*сР— п >
где ап— коэффициент теплоотдачи отдельных участков внутренней и
наружной поверхностей направляющих, определяемый по
фиг. 207.
Угол наклона планшайбы или основания в среднем сечений
направляющих
6 = 277 ' РаДиан> <8-8)
где Оср — средний диаметр направляющих в мм;
Я— высота основания или планшайбы в мм;
г — коэффициент линейнЪго расширения в град.; для чугуна
е=(1-5-1,1) • 10б 1/град;
350
Ов и &н — средние температуры верхней и нижней стенок планшайбы
или основания в град.;
^л и ^п — средние температуры отдельных участков верхней и
нижней стенок в град.
Суммарный относительный угол наклона 6 направляющих равен,
сумме углов наклона планшайбы и основания.
§ 5. РАСЧЕТ НАПРАВЛЯЮЩИХ КРУГОВОГО ДВИЖЕНИЯ
А. Технический расчет направляющих по номинальному давлению
Для выбора размеров направляющих в основном применяется
условный расчет по номинальному давлению, определяемому делением
вертикальной нагрузки на горизонтальную проекцию площади
направляющих:
л_ ОаА-Рх + Опл
%йхЬ
(8.9)
где Ои и Опл — вес изделия и планшайбы в кГ\
Рх — вертикальная составляющая силы резания в кГ\
йх и Ь — средний диаметр и ширина направляющих в см,
В станках с двумя направляющими вертикальная нагрузка на
каждую направляющую ориентировочно определяется в предположении, что
изделие и планшайба как бы разрезаны посередине между
направляющими и каждая направляющая нагружена весом соответствующей
части. По данным практики допустимые средние давления на чугунных
направляющих при больших скоростях скольжения (карусельные
станки):
при диаметре планшайбы до 3000 мм— 4 кГ/см2;
при диаметре планшайбы свыше 3000 мм и одной направляющей—
3 кГ/см2;
при диаметре планшайбы свыше 3000 мм и двух направляющих—
2 кГ/см2, для больших кольцевых планшайб— 1,5 кГ/см2.
Б. Гидродинамический расчет направляющих [40]*
Как уже указывалось, для повышения гидродинамической несущей
способности масляного слоя на направляющих основания выполняют
(вышабривают) пологие скосы.
Расчет сводится к определению максимальной гидродинамической
поддерживающей силы при заданной скорости вращения. Эта сила
возникает в условиях, когда наименьшая толщина масляного слоя Нх равна
критической величине Нкру при которой еще нет непосредственного
соприкасания трущихся поверхностей. При Н\ > Нко вся нагрузка
воспринимается гидродинамическим давлением, развиваемым в масляном слое,
при Н\<кКр масляный слой в состоянии воспринять только часть <Зкр,
общей нагрузки <2, соответствующую толщине масляного слоя Нк
остальная часть воспринимается непосредственно соприкасающимися
поверхностями основания и планшайбы.
Планшайбу со скосами (фиг. 208, а) можно представить
опирающейся на ряд комбинированных опор, каждая из которых состоит из
* Расчет разработан канд. техн. наук Г. А. Левитом.
351
наклонного участка // (заштрихован на фиг. 208, б) и горизонтального
участка Л Половина пологих скосов, имеющих обратное направление,
при данном направлении вращения не работает.
Приводимые ниже формулы получены в результате решения
дифференциального уравнения Рейнольдса и учитывают несущую
способность обоих участков комбинированной опоры — наклонного и
горизонтального.
Сечение по а а
Участок П
Участок I
еонпмшзоб
"20 30
80 СС
Фиг. 208. Расчетная схема опор
планшайбы для определения
гидродинамической подъемной силы.
Фиг. 209. Зависимость вязкости \х от
температуры / для различных масел:
/ — масло индустриальное марки 20 (веретенное 3);
2 — масло индустриальное марки 30 (машинное Л);
3 — масло индустриальное марки 45 (машинное С).
Гидродинамическая поддерживающая сила, действующая в одной
комбинированной опоре [40], выражается формулой
1 2^14
/V
981 . 10*
ЪН
(8.10)
кр
где у< — вязкость масла в сантипуазах (фиг. 209), зависящая от сорта
масла и температуры масляного слоя (см. стр. 347);
V — скорость скольжения в м\сек\
с — коэффициент, учитывающий боковое истечение,
с = -
*(тГ
Ы, /, Ь — размеры направляющих в мм (фиг. 208);
ср — коэффициент, учитывающий совместную работу наклонного
и горизонтального участков (фиг. 210).
Общая поддерживающая сила всех I опор равна:
при равномерном распределении нагрузки между всеми опорами
0*р = 1Рг\ (8Л1а)
352
♦ /я —~у /л
при перекосе под действием опрокидывающего момента М от сил
резания, несимметричности заготовки и т. д.
0кр = Р11-^, (8.116)
где М — опрокидывающий момент в кГсм\
йх — средний диаметр направляющих в см.
Полученное значение <2ЛР сравнивается с полной нагрузкой <3 на
направляющие от веса заготовки и планшайбьд и вертикальной
составляющей силы резания.
При <2 < <)кр вся нагруз- ^ |//^ А
ка воспринимается
масляным слоем.
Как видно из фиг. 210,
поддерживающая сила
имеет наибольшую
величину при отношении
длины наклонного участка к
полной длине одной
опоры й-=0,8. Однако, так
как при мизких числах
оборотов планшайбы
направляющие работают в
условиях смешанного
трения и значительную часть
нагрузки воспринимают
горизонтальные участки
направляющих,
рекомендуется выбирать /г = 0,5,
т. е. длину наклонного и
горизонтального участков
принимать одинаковой.
Оптимальное значе-
иие величины
а гд
0,16
0.1 Ь
а п
0,10
0,08
ОМ
ОМ
а-
лГ №
1
г
I
V
II
/
/
М
1
^^
-^~*^.
^
^
^
^
^
^
•^
^
^
^
Л9\
Й
ом
лз\
|
.ыоА
15
2,5
15
Ь.5
Ьг
Фиг. 210. График для определения коэффициента Срт
учитывающего размеры клинообразующих скосов.
(фиг 210) составляет 2,2,
откуда оптимальное зна
чение глубины
клинообразующих скосов гп =
= 1,2йжр.
Фо»рмулы выведены
в предположении
постоянства толщины масляного слоя по ширине направляющих.
Непостоянство толщины вследствие деформаций планшайбы учитывается выбором
соответствующей величины Нкр.
На основе экспериментальных данных можно рекомендовать
следующие значения Нкр: для планшайбы с диаметром 3000 мм при
температуре направляющих до 40° Нкр = 0,07^- 0,08 мм, при температуре от 40
д0 70—80° значения /*«,,--= 0,09 н-0,П мм. Можно ожидать, что для
станков с диаметром планщайбы 5000—7000 мм величина Н^ будет
выше на 30—50%.
В. Определение наибольших давлений на направляющих
в условиях смешанного трения
Для направляющих с клинообразующими скосами при очень
медленном вращении и для планшайб без скосов гидродинамическая сила
мала, и можно считать, что вся погонная нагрузка на направляющие Я
353
воспринимается непосредственно соприкасающимися поверхностями
направляющих. При наличии клинообразующих скосов при средних
скоростях скольжения приближенно можно принять, что непосредственно
соприкасающимися поверхностями направляющих воспринимается часть
Окр . г
полной погонной нагрузки ц—^~ (где й\—средний диаметр
направляющих).
Наибольшие давления на краях направляющих при смешанном
трении приближенно определяются по формулам:
а) если давление распределяется по всей ширине направляющих,
/ Окр \ 1 М.
°™*= [Чш**— -^)~Ъ + "2* ; <8Л2а>
б) если давление распределяется не по всей ширине направляющих,
т. е. при е>2(^ах--^)^
бшах— 1/ Л у (8.126)
где ^х—наибольшая погонная реакция направляющих в кГ/см,
определяемая по формулам, приведенным в разделе
„Определение погонной реакций направляющих" (стр. 344—346);
Ь — проекция ширины направляющих на горизонтальную
плоскость в см;
б — наибольший суммарный угол наклона в рад. (вследствие
упругих и температурных деформаций), определяемый по
формулам, приведенным в § 3 (стр. 339—342) и §4;
к — коэффициент контактной податливости направляющих
в см?\кГ.
Измерение коэффициентов к на реальных планшайбах представляет
большие трудности из-за малых величин перемещений и
невозможности выделить в чистом виде контактные деформации.
Для направляющих кругового движения из-за малой жесткости
планшайб и относительно большой длины направляющих можно
ожидать более высоких значений коэффициентов контактной податливости,
чем в направляющих суппортов. Ориентировочно для расчетов при
материале направляющих чугун—чугун можно рекомендовать при ширине
направляющих 200—300 мм принимать значения к порядка
(4-н5) 10~* см?1кГ, при ширине 300—450 мм — порядка (5^6) \0~г'см3/кГ.
Для пары направляющих текстолит—чугун значения к в 2—2,5 раза
выше, а для пары ЦАМ—чугун на 30—40% выше, чем для пары чугун—
чугун.
Расчетами были определены давления для нагрузок, при которых на-
наблюдалось резкое возрастание момента трения на направляющих,
ведущее к заеданиям (по экспериментам на карусельном станке и
станке-стенде Коломенского ЗТС с диаметром планшайбы 3000 мм).
Наибольшие давления для этих случаев составляли 20—25 кГ/см2. В
соответствии с этим допустимым можно считать наибольшие давления
порядка 15 кГ/см2. Эти значения несколько выше допустимых давлений
для направляющих суппортов тяжелых станков, так как для планшайб
дополнительно учитывалась неравномерность распределения давлений
по ширине направляющих.
354
§ 6. ПОРЯДОК ТЕХНИЧЕСКОГО РАСЧЕТА ПЛАНШАЙБЫ
1. Определяются нагрузки на планшайбу по формуле (8.2).
2. Определяются средние давления на направляющих по
формуле (8.9).
3. Вычисляется приведенная цилиндрическая жесткость планшайбы
по формуле (8Л).
4. Определяется угол наклона в направляющих в результате
упругого деформирования по формулам (8.3), (8.4) и графикам фиг. 199 и
тепловыделения в направляющих по формуле (8.8).
5. Для направляющих, работающих в условиях жидкостного
трения, производится гидродинамический расчет по формулам (8.10)
и (8.11).
6. Для направляющих, работающих в условиях смешанного трения,
определяются наибольшие давления на направляющих по формуле
(8.12). Погонная реакция направляющих ц определяется по формулам
(8.5) или (8.6).
§ 7. РЕКОМЕНДАЦИИ ПО СООТНОШЕНИЯМ РАЗМЕРОВ ПЛАНШАЙБ
1. Расположение направляющих планшайб
Отношение диаметра планшайбы к среднему диаметру
направляющих в карусельных станках колеблется в пределах 1,4—2,2.
При уменьшении диаметра направляющих уменьшаются скорости
на направляющих при заданных числах оборотов, но увеличиваются
средние удельные давления и деформации направляющих при
обработке изделий больших диаметров.
При оценке влияния положения направляющих на жесткость
планшайбы было принято [55, б], что оптимальным является такое
расположение, при котором углы наклона планшайб в направляющих (в
радиальном сечении) одинаковы при действии: 1) наибольшей нагрузки
внутри опорного контура, 2) наибольшей нагрузки на наибольшем
диаметре планшайбы. Нагрузка от веса изделия и сил резания принималась
равномерно распределенной по окружности расположения кулачков.
В результате расчетов получены следующие величины оптималь-
а
-«ого отношения ~г:
1. Для планшайб без центрального подпятника в среднем,
^ «11опт
■=1,4-г- 1,45,где й — диаметр планшайбы, й\ — средний диаметр
направляющих.
2. Для планшайб с центральным подпятником в среднем [-гЛ =
\ * /опт
— 1,2-2-1,25.
2. Высота планшайбы, толщина стенок, количество
и расположение ребер
На фиг. 211—212 представлено влияние на жесткость высоты
планшайбы и количества радиальных ребер при некоторых средних
соотношениях размеров. Как видно из графиков, с увеличением высоты
планшайбы упругие деформации сначала резко уменьшаются, а при
отношении полной высоты планшайбы НП1 (без направляющих) к диаметру
более 0,12—0,1 б изменение высоты сказывается мало. Отношение -41 =
а
= 0,12-^-0,16 и является птимальным. Аналогично оптимальное
количество радиальных ребер (фиг. 212) составляет: для станков с диамет-
ром планшайбы 2000—4000 мм (среднее отношение -~ ^0,12) —10-*-12,
с диаметром планшайбы 5000—8000 мм (Ц* =0,08^-0,09] — 12-:-16.
355
Увеличение количества радиальных ребер сверх указанных значений
мало влияет на жесткость планшайбы. Кольцевые ребра, расположенные
не над направляющими, практически не оказывают заметного влияния
на упругие и температурные деформации планшайбы. Кольцевое ребро,
расположенное над направляющими, уменьшает наибольшие давления
на направляющих в местах расположения кулачков и сильно улучшает
отвод тепла от направляющих. Желательно, чтобы кольцевое ребро
располагалось непосредственно над направляющими как можно ближе
к середине. Влияние ребра резко уменьшается при расположении его за
пределами направляющих, даже на небольшом расстоянии.
Фиг. 211. График влияния вы- Фиг. 212. Влияние количества радиальных
соты Ь,пл планшайбы на ее же. ребер на жесткость планшайбы.
сткость (для средних
соотношений размеров)
Проверочные расчеты показывают, что если площадь окон в нижней
стенке не превышает 20—25% площади стенки, жесткость планшайбы
(по сравнению с планшайбой со сплошной стенкой) уменьшается
незначительно. Если площадь окон составляет 30—35%, жесткость
уменьшается в среднем на величину до 25% и при дальнейшем увеличений
площади окон резко снижается.
С увеличением толщины стенок жесткость увеличивается в
значительно меньшей степени, чем с увеличением их высоты. При этом вес
планшайбы увеличивается в большей степени, чем жесткость, и, таким
образом, увеличение толщины стенок мало эффективно.
3. Оценка возможности выполнения планшайбы без шпинделя.
Наибольшая высота обрабатываемого изделия
При обработке высоких изделий сравнительно небольшого веса
возникает опасность опрокидывания планшайбы или выскальзывания
изделия из кулачков.
Для планшайбы с короткими шпинделями, имеющими один
подшипник, условие нормальной работы направляющих (без отрыва от
основания по среднему диаметру направляющих) выражается формулой
?тш = Яр — ЯМпых > 0>
где <7т1п—-минимальная погонная (на единицу длины) реакция
направляющих;
Яр^Ямтах — погонная реакция направляющих от вертикальных сил и
опрокидывающего момента М соответственно.
356
Подставляя значения ^р и <7ж™х по формулам (8.5 а и б), получаелг
Ж<
(О и
0ПЛ^ <*1
Испытания на станке—стенде Коломенского ЗТС показали, что при
суммарном весе изделия и планшайбы 10,5 т отрыв планшайбы от
основания начался при опрокидывающем моменте М = 5,8-:~ 6,2 т, по
расчетным данным этот момент составил 6 т. Таким образом, расчет
хорошо согласуется с экспериментальными данными.
Пользуясь данной формулой, можно оценить предельную высоту
обработки при данном весе или предельную силу резания, а также
определить, для каких размеров карусельных станков возможно выполнение
планшайб без шпинделя.
Ям
В табл. 67 приведены средние значения ах для карусельных
Яр
станков при наиболее неблагоприятных условиях обработки. Из таблицы
видно, что, начиная с диаметра примерно 3000—3500 мм, планшайбы
можно выполнять без длинного двухопорного шпинделя. Расчет
выполнен с некоторым запасом, так как обычно вес изделий больше, кроме
того, раскрытие стыка в одной точке не определяет начало
опрокидывания.
Таблица 67
г> ^ ЯМтах
Средние значения —-— для направляющих карусельных станков
Яр
Наибольший диаметр
обработки в мм
2000
2500
3000—3200
4000—4500
Среднее отношение наибольшей
высоты обработки к диаметру
планшайбы ——
а
0,87
0,75
0,62
0,57
^Мтах
"Р
2,4
1,9
1,0
0,75
Примечание. При составлении таблицы приняты средние соотношения: —г- —1,6 нР„«
1 \
— 0,5Р~. Принято также, что наименьшее значение веса нзделня для планшайб диаметром 2000—4000 мм
\ 1
составляет 1000 кГ и наибольшее значение Р при обработке высоких изделий не превышает ——
1
суммарного наибольшего уснлня по паспорту станка (рассчитанного на одновременную работу двумя
суппортами) и диаметр обработки мал по сравнению с высотой.
Наибольшая высота обрабатываемого изделия из условия
надежного зажатия может быть определена из следующей зависимости:
где Рзаж —сила зажатия на кулачке;
Апш — максимальная отрицательная реакция кулачка;
/— коэффициент сцепления между кулачком и изделием.
Реакция Рт1П при установке изделия на четырех кулачках (см*
табл. 64) может быть определена по формуле
Ршп = 0,707 (Ру +Р,)-%- - 0,6ЯЖ.
Отсюда получаем условие надежного зажатия изделия:
(8.13>
0,707 (Я. - Ру) '
Полученное таким образом значение высоты обработки Н является
предельно допустимым из условия надежного зажатия.
ЛИТЕРАТУРА
1. А черкан Н. С, Расчет и конструирование металлорежущих станков, Маш-
тиз, 1949.
2. Бакст А. С, Исследование влияния неравномерности припуска на точность
обработки, диссертация, 1949.
3. Б а р к а н Д. Д., Динамика оснований и фундаментов, Стройвоенмориздат,
1948.
4. Безухов К. И., Фундаменты металлорежущих станков, Машгиз, 1947.
5. Б о б р и к П. И.: а) Зависимость жесткости плоских стыков от качества
обработки поверхностей, Труды МАТИ, вып. 5, 1949; б) Деформации плоских эксцентрично
загруженных стыков, Труды МАТИ, вып. 9, 1949.
6. Васильева 3. Н., Статическая жесткость консольно-фрезерных станков
мод. 6Н82Г и 6Н12, ЦБТИ, МС и ИП, 1955.
7. В е д е н с к и й В. А., Нормы/ жесткости на токарные станки средних
размеров, ЭНИМС, 1954.
8. В е д е н с к и й В. А., Б р о у и ш т е и н С. ЯУ А б р а м о в Я- Е.: а) Нормы
жесткости токарно-карусельных, консольно-фрезерных и долбежных станков, ЭНИМС,
1957; б) Нормирование жесткости станков — проект норм жесткости раднально-свер-
лильных станков, ЭНИМС, 1958; в) То же многошпиндельных прутковых автоматов,
ЭНИМС, 1958; г) То же продольно-строгальных станков, ЭНИМС, 1958; д) То же
горизонтально-расточных станков, ЭНИМС, 1959.
9. Власов В. 3., Строительная механика тонкостенных пространственных
систем, Стройиздат, 1949.
10. ВотиновК В, Жесткость станков, ЛОНИТОМАШ, 1940
11. Галер кнн Б. Г., Упругие тонкие плнты, Госстройиздат, 1953.
12. Гладков Б. А., Грачев Л. Н., Левит Г. А., Л а п и д у с А. С. и др.,
Модернизация токарно-карусельных станков, Машгиз, 1958.
13. Г лик Г. В., Проектирование фундаментов под станки, «Бюллетень
строительной техники» № 5, 1946.
14. Горбунов-Посадов М. И., Балки и плиты на упругом основании, Маш-
стройиздат 1949.
15. ГОСТ 7895-56, ГОСТ 44-56, ГОСТ 98-58, ТОСТ 26-56, ГОСТ 13-54.
16. Г у с е, в И. Т., Деформации стыков при многократном их нагруженнн. Сб.
^Новые исследования в области обработки резанием металлов и пластмасс», Машгиз,
1952.
17. Джанелидзе Г. Ю., Па но в ко Я. Г., Статика упругих тонкостенных
стержней, ОГИЗ, 1948.
18. Д и к у ш и н В. И., Выбор материала для станков, в книге «Труды Всесоюзной
конференции по станкостроению», вып. 2, Машгиз, 1943
19. Ени к е е в X. М.: а) Методы повышения жесткости станин токарных станков,
труды ЭНИМС. вып. 1. ЦБТИ МС, 1948. б) Отчет о результате изучения жесткости
фрезерных станков ГЗФС, ЭНИМС, 1941.
20. Е н н к е е в X. М., Ьроунштейн С. Я ., Исследование жесткости станков
шлифовальной группы, ЭНИМС, 1949.
21. Жесткость металлорежущих станков, ЛОНИТОМАЩ, кн. 26, Машгиз, 1952.
22. Жесткость, точность и внбрацни прн механической обработке. Сб. под ред.
В. А. Скрагана, Машгиз, 1956.
23. Исследование колебаний металлорежущих станков при резании металлов, под
ред. В. И. Дикушнна и Д. Н. Решетова, Машгиз, 1958.
24. Каминская В. В., Расчет и исследование жесткости станин токарных
станков, диссертация, 1952.
25. Каминская В. В., Решетов Д. Н.: а) Расчет и сравнительный анализ
жесткости станин токарных станков, «Станки и инструмент» № 2, 1957; б)
Исследование и приближенные расчеты жесткости коробчатых деталей станков, «Станки и инстру-
Л58
мент» № 2, 1956; в) Расчет и анализ жесткости порталов и поперечин станков
портального типа, «Станки и инструмент» № 9, 1957; г) Исследование жесткости карусельных
<гганков, «Станки и инструмент» № 4, 1956; д) Расчет корпусных деталей, ЭНИМСГ
1953; е) Экспериментальное исследование статической жесткости станков, ЦБТИ,
М'С, 1957
26. К а м и н с к а я В. В., Пратусевич Р. М, Некоторые вопросы компоновки
порталов карусельных, продольно-строгальных и продольно-фрезерных станков, «Станки
и инструмент» № б, 1957.
27. Каминская В. В.. Французов Ф. А., Влияние способов установки
одностоечных координатно-расточных станков на их жесткость, «Станки и
инструмент», № 5, 1960.
28. Кан С. Н., Па но в ко Я. Г., Элементы строительной механики
тонкостенных конструкций, Оборонгиз, 1949.
29. Кан С. Н., Свердлов И. А., Расчет самолета иа прочность, Оборонгиз,
1940.
30. К а ш и р и н А. И ; Исследование вибраций при резании металлов, Изд-во
АН СССР, 1944.
31. Ко валов К. Ф., Изучение стесненного кручения тонкостенных стержней
замкнутого профиля, диссертация, 1955.
32. Кор н ев и ц Э. Ф., ЭндерХ<.В., Формулы для расчета балок на упругом
основании, Госстройиздат, 1932.
33. К о п ы л е н к о В. П., К вопросу о жесткости фрезерных станков,
Исследования в области металлорежущих станков, Машгиз, 1952.
34. Кречмер В. В., Расчет железобетонных оснований и фундаментов, ОНТИ,
1937.
35. Крылов А. Н., О расчете балок, лежащих на упругом основании, изд. АН
СССР, 1931.
36. Л а п и д у с А. С.: а) Накладные направляющие из пластмасс для станков,
«Станки и инструмент» № И, 12, 1955; б) Оценка жесткости пластмассовых
направляющих станков, ЭНИМС, 1960.
37. Л а п и д у с А. С, Р е ш е т о в Д. Н., Выбор материала и конструкции
направляющих, методы повышения их долговечности, «Станки и инструмент» № 11, 12,
1953.
38. Л е в и н а 3. М, Исследование и расчет суппортов, ползунов и столов
металлорежущих станков в совместной работе с направляющими, диссертация, 1955.
39 Левина 3, М., Решетов Д. Н.: а) Расчет станков на контактную
жесткость, «Станки и инструмент» № 1, 1951; б) Расчет ползунов металлорежущих
станков, «Станки и инструмент» № 12, 1956; в) Расчет планшайб (круглых столов)
металлорежущих станков на жесткость, «Станки и инструмент» № 8, 1958; г) Расчет и
экспериментальное исследование изгиба круглых сложных пластин, снабженных
радиальными и кольцевыми ребрами, «Вестннк машиностроения» № 2, 1959; д) Изгиб круглых
пластин, свободно опертых по произвольной окружности при несимметричном нагру-
жении, «Научные доклады высшей школы» № 4, 1958.
40. Л е в и т Г. А., Гидродинамический расчет направляющих прямолинейного и
кругового движения, «Станки и инструмент» № 9, 1958.
41. Левит Г А., Лапидус А С, Цирлии М. М., Материалы,
конструкции и системы смазки ипор планшайб тяжелых карусельных станков, «Станки и
инструмент» № 5, 1958.
42. Л и х а р е в К. К., Расчет систем, составленных из жесткосоединенных
прямоугольных плит, Труды кафедры «Сопротивление материалов», МВТУ, 1947.
43. «Машиностроение». Энциклопедический справочник: а) т. 1, ч. 2, б) т. IX,
Машгиз, 1947—49 гг.
44. О г р и н ч у к А. Н., Е н и к е е в X. М., Сравнительные испытания станка
ДИП-200 со станинами с прямыми и диагональными ребрами жесткости, ЭНИМС, 1945.
45. Огринчук А. Н, Броунштей-н С. Я., Исследование жесткости
станков токарного типа, ЭНИМС, 1947.
46. Папкович П. Ф., Строительная механика корабля, ч II, Оборонгиз, 1948.
47. П о н о м а р е в С, Д., Б и д е р м а н В. Л. и др., Расчеты на прочность
в машиностроении, т. 1, Машгиз, 1956.
48. П о п о в а Т. А., Некоторые вопросы статической работы пластины с
квадратным отверстием в своей плоскости. Сб. «Исследование прочности, жесткости и
устойчивости крупнопанельных конструкций», Стройиздат, 1954.
49 Проников А. С, Износ и долговечность станков, Машгиз, 1957.
50. П р а т у с е в и ч Я. А., Вариационные методы в строительной механике, Гос-
техиздат, 1948.
51. Прочность и устойчивость тонкостенных конструкций в самолетостроении,
ЦАГИ, 1937. Н
52. Раб и н о в и ч И. М., Курс строительной механики стержневых систем, ч. I,
Госстройиздат, Г938; ч/ТТ, Госстройиздат, 1940.
359
53. Р е ш е т о в Д. Н.: а) Расчет деталей станков, Машгиз, 1945; б) Метойы
снижения интенсивности колебаний в металлорежущих станках, ЦБТИ, МС, 1950.
54. Р е ш е т о в Д. Н , Каминская В В., Л е в и- н а 3. М., Руководящие
материалы*по расчету и конструированию станин, ЭНИМС, 1948.
55. Р н в и н Е. И.: а) Некоторые вопросы расчета направляющих. Сб.
«Исследования в области металлорежущих станков», Машгиз, 1955; б) Расчет на жесткость узла
планшайба — основание карусельных станков, «Станки и инструмент» № 6, 1955.
56. С и н д е е в В. А., Исследование жесткости универсального круглошлифо-
вального станка, Труды Станкина, т. VII, 1940.
57. С м и р н о в В. Э. и Р е ш е т о в Д. Н., Влияние тепловых деформаций иа
точность металлорежущих станков, «Станки и инструмент» № 1 1952.
58. Соколов Ю., Н., Расчет температурных полей и температурных
деформаций металлорежущих станков, ЦБТИ, 1958.
59. С ок о л о в с к и й А. П-, Жесткость в технологии машиностроения, Машгиз,
1946.
60. Т л у с т ы и И., Автоколебания в металлорежущих станках, Машгиз, 1956.
61. Тимошенко С. П., Пластинки и оболочки, ОГИЗ, 1948.
62 Тимошенко С. П., Сопротивление материалов, ч. I, ГТТИ, 1932; ч. Нг
Госстройиздат, 1946.
63. Точность механической обработки и пути ее повышения, под ред. А. П.
Соколовского, Машгиз, 1951.
64. У м а н с к и й А. А., Изгиб и кручение тонкостенных авиаконструкций, Обо-
ронгиз, 1939.
65. Филатов В. П., Веденский, .В. А., Нормы жесткости на
зубофрезерные станки, ЭНИМС, 1957.
66. Ш л е з и н г е р Г. Металлорежущие Станки, Машгиз, 1938.
67. Ш т е р н Л. Т., Сварные конструкции в станкостроении, Машгиз, 194$.
68. Экспериментальное определение жесткости конструкции стойки универсального-
расточного станка типа 2620 методом моделирования, краткий отчет (№ 131) ЛИС-ОГК
завода им. Свердлова, Ленинград, 1956.
69. Экспресс-информация, С7С, вып. 14^ № 53—56, апрель, 1958.
70. Я к о б с о н М. О., О жесткости легких сверлильных станков, «Станки и
инструмент» № 4, 1937.
71. В1еЛе!е1с1 I., МойеИуегзиспе ап \Уегк2еи§тазсптепе1етеп1:еп, а) 1пс1из1:г1е-
Апге1§ег, №™8, 1956; № 63, № 80, 1957. Реферат в журн. „Машиностроение",
сборник переводов и обзоров иностранной периодической литературы, № 4, 1957;
б) Зс1ше1ззеп ипс! ЗсппеЫеп, Н. 10, Ок1оЬег 1959.
72. В о Ь е к К., Н е I Й А., 3 с п т \ с* I Рг., З^аЫЫсЫЬаи уоп МазсЫпеп, Вег-
Нп, 1955.
73. ЕЬпег П., 01е Веапзргислип^ <ЗйппшапсН#ег Ка$1еп{га§ег аи! ^т^\\ипц^
2еИзспгШ !йг Р1и§1есптк ипс! МоЮгзсп., Вс1. 24, № 23-24, 1933.
74. Не ИЗ А., ЗсИичп^ип^зуегпаИеп уоп ШегИгеидтазсптепдезгёИеп, V^^—Рог-
зспип^зпеП, № 429, 1949/50.
75. К 1е кеЬ и зсЬ Н., Б1е \Уегкгеидтазсп1пе ихиег Ьа$1, V^I — Рогвспип^зпе!*,.
М360, 1935.
76. Ьо е V/ е п ?е 1 с! К-, Оез1аЙз1:с1геип{ег8испип§еп ап Кспзо1еп ипс! 51апс1егп;
В1е ОезШНз^е^е уоп Каз*еп; Уегпрр1е В1есЪр1аМеп ипс! Оорре1\уапс1р1аиеп, ОгШеп
Рогзспип^з- ипс! Копз1гикиоп^ко11<Х[Шигп А^егкгеидтазсЫпеп ипё Ве{г1еЬ&лу1з-
зепзспаП, Мйпснеп, Ок*оЬег, 1957.
77. МогЛиз \У., Конструктивные варианты станины универсального
центрового токарного станка, 1пс1и5гпе-^пге1§ег., № 78, 1956. Реферат в журн. „Машинострое-
ние", сборник переводов н ибзоров иностранной периодической литературы, № 4, 1957.
78. Ре(егз Е., Ыеие \гегЫе1!ип§зЬаиаг( гиг ^егкгеи^тазсптепЬеиеп, \Уегк-
$*а1Ыесптк, И. 16, 1920.
79. Т п и т А., Р е I г 1 О., 31еШдкеИ ипс* Vег1о^гаипд уоп Ка5^еп^иег5спп^иеп^
V^^Рог5спип25ЬеI^, № 409, 1941.
Введение 3
Глава I. Общие сведения по конструированию и расчетам ...... 5
§ 1. Систематика конструкций . . . . 5
§ 2. Критерии работоспособности и расчета 10
§ 3. Состояние исследования жесткости станков и нормирование жесткости 12
§ 4. Особенности расчета станин и корпусных деталей 13
§ 5. Материалы 22
Глава II. Горизонтальные станины 26
§ 1. Общие сведения о конструкциях 26
§ 2. Исходные положения расчета на жесткость 39
§ 3. Определение приведенной жесткости станин 39
А. Постановка задачи 39
Б. Определение жесткости на кручение 41
В. Определение жесткости на изгиб в горизонтальной плоскости . . 54
§ 4, Совместная работа станин с фундаментами 58
А. Основные положения 58
Б. Деформации станин с фундаментами 59
В. Расчетная жесткость упругого основания при разных способах
установки станков 67
Г. Расчетные формулы для определения коэффициентов повышения
жесткости Ru и Rk, учитывающих влияние фундамента на
деформации станины 68
§ 5. Технический расчет станин 71
А. Основные положения и расчетные зависимости 71
Б. Порядок технического расчета 75
§ 6. Анализ форм и соотношений размеров элементов станин 80
§ 7. Температурные поля и температурные деформации станин .... 84
Глава III. Стойки (вертикальные станины) 88
§ 1. Общие сведения о конструкциях 88
§ 2, Исходные положения расчета на жесткость 94
§ 3. Определение приведенной жесткости стоек 96
А. Основные допущения 96
Б. Определение жесткости на изгиб . 96
В. Определение жесткости на кручение 99
§ 4. Влияние жесткости контура поперечного сечения на жесткость стоек 106
§ 5. Определение поправок к элементарному расчету, учитывающих
искажение контура поперечного сечения 111
§ 6. Технический расчет стоек 130
А. Основные положения и расчетные зависимости 130
Б. Порядок технического расчета стоек 137
§ 7. Анализ форм и соотношений размеров элементов стоек 142
Глава IV. Станины портального типа 153
§ 1. Общие сведения о конструкциях 153
§ 2. Исходные положения расчета на жесткость 155
§ 3. Технический расчет портальных станин 163
А. Расчетные зависимости 163
Б. Порядок технического расчета 167
§ 4. Анализ форм и соотношений размеров элементов портальных станин 168
А. Анализ портальных станин карусельных станков 168
Б. Анализ портальных станин продольно-строгальных к
продольно-фрезерных станков 185
Глава V. Плиты металлорежущих станков 189
§ 1. Общие сведения о конструкциях плит 189
§ 2. Расчет плит 192
Глава VI. Коробки 198
§ 1. Общие сведения о конструкциях коробок 198
§ 2. Исходные положения расчета на жесткость и результаты
экспериментального исследования жесткости 203
§ 3. Общая методика расчета коробок на жесткость 210
§ 4. Технический расчет коробок 218
§ 5. Температурные поля и температурные деформации коробок 224
Глава VII. Детали узлов для поддержки и поступательных перемещений
инструмента и обрабатываемых изделий (салазки, суппорты, прямоугольные столы,
ползуны), направляющие прямолинейного движения 227
§ 1. Общие сведения о конструкциях 227
§ 2. Исходные положения расчета направляющих и перемещаемых по ним
деталей (суппортов, ползунов и др.) 251
§ 3. Расчет суппортов и столов большой жесткости и их направляющих 255
А. Определение давлений и контактных деформаций в направляющих 255
Б. Определение собственных деформаций салазок 273
В. Порядок технического расчета 275
Г. Расчеты, связанные с износостойкостью направляющих .... 275
Д. Анализ работы направляющих и выбор оптимальных форм и
конструктивных соотношений размеров 278
§ 4. Расчет направляющих качения 287
§ 5. Расчет столов прямоугольной формы и их направляющих 290
А. Основные положения 290
Б. Определение нагрузок на направляющие 291
В. Определение средних давлений на направляющих 292
Г. Определение наибольших давлений на направляющих 292
Д. Порядок технического расчета столов с направляющими 300
Е. Выводы и рекомендации 301
§ 6. Расчет ползунов 302
А. Основные положения 302
Б. Определение деформаций и давлений в направляющих ползунов
в результате изгиба 304
В. Определение деформаций и давлений в направляющих ползунов
в результате кручения 313
Г. Значения коэффициента контактной податливости 314
Д. Особенности расчета хоботов горизонтально-фрезерных станков 317
Е. Порядок технического расчета ползунов 318
Ж. Анализ влияния формы поперечного сечения ползунов на жесткость 321
Глава VIII. Планшайбы (круглые столы) и направляющие кругового движения 323
§ 1. Общие сведения по конструкциям 323
§ 2. Исходные положения расчета 330
§ 3. Определение упругих деформаций планшайб и реакций в направляющих 331
А. Определение приведенной жесткости планшайб 331
Б. Определение нагрузок, действующих на планшайбы 336
В. Определение упругих деформаций планшайб 338
Г. Определение погонной реакции направляющих 344
§ 4. Определение температуры направляющих и температурных
деформаций планшайб и оснований 347
§ 5. Расчет направляющих кругового движения 351
А. Технический расчет направляющих по номинальному давлению 351
Б. Гидродинамический расчет направляющих 351
В. Определение наибольших давлений на направляющих в условиях
смешанного трения 353
§ 6. Порядок технического расчета планшайбы 355
§ 7. Рекомендации по соотношениям размеров планшайб 355
Литература 358
Табл ица 27
Эскизы поперечного сечения элементов, расчетные параметры и результаты расчета систем портал-поперечина
некоторых карусельных станков (Рх: Ру: Рг = 0,5:1:0.5)
и
И
л
а
г*г
У77777777777777777*
Модель станка,
размеры
обрабатываемого
изделия в мм, сила
резания в кГ
1553
Амж = 23<Ю
#1щи = 130О
Ру - 3000
1556
Дпах = 2750
Ятах = 1600
Ру = 3250
1557
Дпах = 3150
«пах - 1600
Ру = 3250
2Ж—300
(Шисс)
Апах = 3200
Ятах - 1600
Ру = 3125
1532
Отах « 3400
Ятах=2000
Ру = 3250
1565
ЭШах - 5000
Ушм «3000
Ру = 5250
1570
0«:;ах = 6500
Чпаж—4000
Ру = 10 000
57
Отах = 7000
Ятах = 4000
ру = 8000
Эскизы поперечных сеченнй элементов (размеры в мм)
Поперечины
Стойки
-1500^*3
-2000-
Перекладины
Основные
расчетные
параметры
системы
в см
Расчетные параметры по элементам*
Поперечины
ь
н
н
1
5
а
Ь
Н
Н
1
5
а
265,5
370
259
39.8
47,5
24 1
311
357
250
46,7
46
235 1
/у
$кр
р
Ух
*1
23,8-104
50,3-10*
24,2* 10*
837
23.8
36,3
Л
икр
Р
Ух
1 1375^
и25\
■^у,
375
388
272
56.2
47
23,5
/у
Р
Ух
23-104
79-10*
31-10*
773,5
23,9
49.7
Стойки
<*уст
*кр. ст\
Уст
иуст
'кр. ст\
Рст
Уст
252,6-104|
40,2-10*
82-10*
1000
57,3
27.7
Перекладины
игпер
Зупер
^кр. пер
Рпер
Упер
&пер
488,8* 104|
46-10*
86,6-10*
1210
87.2
16,2
''гпер
^упер
*кр. пер
Рпер
Упер
°пер
167.6-10^
10,4-104
11,8-10*
600
12,6
81
7,9-10*
12,9-10*
14,9-10*
216
23
32
34-104
96-10*
46.5-10*
1029
24,8
50
иуст
?кр. ст
^ст
Уст
260-10*
51-10*
102-104
1036
58
30
'гпер
''упер
*кр. пер
Гпер
Упер
спер
97-104
8,14-10*
0.03-10*
492
68,8
12,3
Эффективный
объем
металла
в 10а см3\
Перемещения вершины резца / в мм
Нагрузка
кГ, кГ/см
1.06
1.14
1000
рез
-1900
*1000 \
Ррез
Я
@суп =
= 3600
1.31
525Л
1
с
1 ]
-/475-
Я
1
н
н
Л
.5
а
360
362
254
54
46
23,5
и
1у
^нр
Р
Ух
%х
23-10*
79-10*
28.10*
730
23,9
49,7
^уст
*кр. ст
^ст
Уст
хст
552-10*
40-10*
88-10*
1288
89,3
16,4
пришив
Й *
-2800-
&
\—Устг
и^зоД
385
394
276
58
46
23.5
1*
->кр
Р
Ух
590
566
396
88,5
64
31,5
770
844
590
115,5
100
52
820
793
555
123
98
50
/у
Зкр
р
Ух
*х
%/кр
р
У\
*кр
р
Ух
24,8-10*
78,9-10*
27,3-Ю*
788
23,9
46,6
°уст
кр. ст\
Рст
Уст
■Хст
888-10*
33,8-10*
96-Ю*
1456
111
23
^гпер
Зупер
«кр. пер
Рпер
Упер
2 пер
''гпер
Зупер
*кр. п4р
Рпер
Упер
^пер
1,9-10*
7,4-10*
4,8-10*
141,5
13.5
31,5
25-10*
55,2*10*
51,8*10*
572
26,5
44,5
1,08
1.67
мооо
Ррез
Я
0Суп ~
-1400
0,039
0.036
0,003
0,12
0,05
0,006
0,044
0,16
0,0003
0,032
0,029
0,003
0,10
0,039
0,036
0.003
0,14
1000
"рез
Я
^суп
0,047
0,043
0.004
0,15
0,073
0,002
0,071
0.24
0,0007
0,081
0,005
0,076
0,26
0,0003
0,111
0,002
0,109
0.35
1000
~рез
^сУп —
= 3600
9Ы0*
262-Ю4
104-10*
1336
30,9
65
«уст
'кр. ст\
1 ст
Уст
2010-10*
154-104
360-10*
2380
115
37,2
^гпер
''упер
* кр. пер
*" пер
Упер
^пер
42-10*
149-Ю4
94-10*
874
26.5
59
3,99
1000
рез
Я
т
7000
@суп —
0.041
0.037
0,004
0,13
0.124
0,002
10,122
0.40
0.001 | —0.102
0.027
0.024
0.003
0,14
2520-10*
2580-10*
1530-10*
4770
112
101
730-10*
1100-10*
595 -10*
2600
76
86,5
''уст
'кр. ст\
Уст
''уст
'кр. ст\
Рст
Уст
4053-10*
777-10*
1100-10*
3623
140
28
3560-10*
580-10*
1060-10*
4030
135
36
''гпер
''упер
*кр. пер
гпер
Упер
2 пер
''гпер
''упер
^кр. пер
Рпер
Упер
спер
575-10*
333-Ю*
124-10*
2000
74
59,3
890-10*
500-10*
710-10*
2140
83,7
60,7
11.3
10,3
**
*1000
*рез
Я
Осуп —
— 22000
0,019
0,018
0,001
0,19
0,112
0,002
0,11
0,61
0,0015
0,016
0.003
0.013
0.16
0,0018
Р100О 1
1
Ррез
Я
Осуп =*
-15 000
0.019
0.017
0,002
0,16
—
—
0.045
0,003
0,042
0,36
0.0028
***рЛиНеЙНЫе разм еры "РивеДенЬ1 в см, Р в см*, У в см*.
В графах Р100о приведены величины пеоемешений г„. Г.., Г- пои Р .-1000 кГ. Р„-500 кГ я Р,-500 кГ\ в веохней стопке ппиирггрны стммаоные пеоемещення.
» средней—перемещения в результате деформаций портала, в нижней—
Таблица 5
Определение нагрузок, средних давлений н упругих перемещений, отнесенных к инструменту (прн повороте в поперечной плоскости направляющих) для направляющих основных типов
I напоавля- I Ряеиетня* схема Расчетный момент, воспринимаемый направляющими, « Углы поворота и пере-
ющих Расчетная схема и тяговое усилие Реакции и средние давления иа гранях направляющих Уравнение деформаций и координаты центра поворота мощения, отнесенные
* __ . к инстпументу
Примечания: 1. Составляющие моментов М и реакций от веса суппортов и изделий, заключенные в приведенных формулах в скобки, учитываются только при определении давлений. При определении упругих перемещений в процессе обработки их следует отбрасывать.
2. Штриховкой выделены области возможного положения центра поворота. Разное направление штриховки соответствует разным расчетным случаям.
3. В трех последних столбцах при Мх < О вместо ус подставляется у^, __________ .^^.^^-^--^.^^-„-—ш^*^*-^—-^--—-——-^---——----—
по форме профиля «ласточкин хвост» ""* окаРных станков, <Г-для фрезерных станков 1 а - для токарных станков; б - для и продольно-строгальных
г I 1 продольно-строгальных станков станков