Международный институт "ИНФО-Рутения"
В.Г. Зубков, ВЛ. Ляховский,
А.И. Мартыненко, В.Б. Миносцев
Курс высшей математики
Учебное пособие
для студентов заочной
(дистанционной) формы
обучения
ТОМ!
Рекомендовано Министерством образования Российской Федерации
в качестве учебного пособия для студентов
высших учебных заведений
Москва 2007

К 93
Курс высшей математики: Учебное пособие для студентов заочной (дистанционной)
mUhpSTJ- 'м/В,Г:,3убк0В' 8А Л*™™»*> А.И Мартыненко, В Б Миносцев. - М,
МИИР, 2007, - 440 с., Ил 162, библиогр. список 25 наим.
„u,fiJ4e6HOe П0С°-бИе "° КУРСУ ВЬ'СШей мате"*™ки предназначено для студентов высших
учебных заведении, изучающих предмет с использованием дистанционных технологий
ооучсния.
Учебное пособие написано в соответствии с образовательным стандартом высшего
профессионального образования и может быть использовано при изучении курса высшей
математики для различных специальностей и специализаций. Количество изучаемого
материала возможно изменять за счет отдельных тем, набранных мелким шрифтом
Пособие содержит как необходимый теоретический материал для изучения курса так и
подробно разобранный практический материал, для его закрепления. Проверить свои
возможности обучаемый сможет, решая задачи и примеры самостоятельной работы
Авторами.разработан простой и удобный алгоритм освоения материала, который в
сжатые сроки и с хорошим качеством позволяет приобрести основные математические навыки
Первый том учебного пособия содержит 36 лекций и 36 практических занятий по
следующим разделам: множества, системы координат, функция одной переменной, теория
пределов, числовые ряды, дифференциальное исчисление функции одной переменной, элементы
линейной и векторной алгебры, аналитическая геометрия.
Рецензент: У.Г. Пирумов, чл.-корр. РАН, проф.
Подготовлено и издается по заказу
Международного института "ИНФО-Рутения"
Редактор: Л.В. Мормыло
Подписано в печать 19.12.2007. Сдано в производство 19.12.2007.
Формат бумаги 60 х 90/16 Бум. множ. Гарнитура Times.
Усл.печ.л. 27,75 Уч.изд.л. 27,5 Тем. план 2007 г.
Тираж200 Заказ №2203
ООП МИИР, 109280, Москва, ул. Автозаводская, д. 16^
© В.Г. Зубков, В.А. Ляховский,
А.И. Мартыненко, В.Б, Миносцев, 2000
© Институт ИНФО, 2000
ПРЕДИСЛОВИЕ
3
ПРЕДИСЛОВИЕ
Данное учебное пособие предназначено для студентов высших
учебных заведений системы дистанционного обучения. Основное отличие
таких студентов от студентов очной формы обучения в том, что они не
слушают лекции и не занимаются на семинарах непосредственно под
руководством преподавателей, которые специально подбирают и дозируют
материал, приучая студентов к регулярным занятиям.
Авторы поставили своей целью создать такое учебное пособие,
которое бы помогало студенту-заочнику изучать материал подобно тому, как
это делает студент очной системы обучения. Первый том пособия
предназначен для изучения в первом семестре. Теоретический материал этого
тома разделен на 36 лекций, объем каждой из которых охватывает
материал, который может быть изложен лектором за два академических часа.
Кроме лекций в него включены 36 практических занятий (семинаров). Как
правило, за каждой лекцией следует одно практическое занятие. Но
иногда методически оказывается удобным проводить практические занятия
после двух лекций.
При изучении материала данного пособия и выполнении
индивидуальных типовых расчетов, которые включены в отдельную книгу, студент
должен следовать рабочей программе, определяющей порядок работы над
предметом. Таким образом, обучающийся имеет возможность
самостоятельно осваивать дисциплину теми же частями и в том же порядке, что
и студент очного отделения. Рекомендуется за одно занятие изучить
материал одной-двух лекции или проработать одно-два практических
занятия с выполнением задаваемых для самостоятельного решения
примеров из части типового расчета, относящегося к изучаемому материалу. В
неделю следует прорабатывать две лекции и два практических занятия.
Помните,что только при регулярных занятиях можно приобрести
прочные математические знания, которые сохраняются надолго.
Авторы понимают все трудности самостоятельного изучения
вузовского курса математики и то, каких усилий и самоограничений это требует.
Поэтому в рамках университетской программы бакалаврской подготовки
мы постарались, по возможности, облегчить обучающимся выполнение
этой задачи. Курсивом в пособии выделены определения и теоремы,
формулировки которых после осознания следует выучить наизусть.
Материал, набранный мелким шрифтом при первом чтении можно
опустить.
На практических занятиях вначале разбирается ряд примеров по
пройденному лекционному материалу, а затем даются примеры для
самостоятельного решения, к которым в конце книги приведены ответы.

4
Л А ТИНСКИЙ И ГРЕЧЕСКИЙ АЛФАВИТЫ
На практических занятиях вначале разбирается ряд примеров по
пройденному лекционному материалу, а затем даются примеры для
самостоятельного решения, к которым в конце книги приведены ответы.
Авторы выражают благодарность за помощь в создании
компьютерного набора первой и второгй частей студентам МГИУ Бельчихину В.А.,
Платонову Д.О., Трофимову М.В., Уткину С.Н. и Черняеву М.С.
ЛАТИНСКИЙ АЛФАВИТ
Строчные латинские буквы.
а
9
тп
S
У
Ь
h
п
t
Z
с
г
о
и
d
3
Р
V
е
к
Я
w
f
1
г
X
Прописные латинские буквы.
А
G
М
S
Y
В
Н
N
Т
Z
с
I
о
и
D
J
Р
V
Е
К
Q
W
F
L
R
X
ГРЕЧЕСКИЙ АЛФАВИТ
Строчные греческие буквы.
а
У
€
С
в
г
е
i
А
V
о
W
д
Е
Q
Я
V
Ч>
Ф
Прописные
Ф
О
р
S
с
V
д
греческие буквы.
А
Л
К
V
е
7Г
Р
п
т
а
т
ф
X
ш
Ф
7 ЛЕКЦИЯ - МНОЖЕСТВА. СИМВОЛИКА И ТЕРМИНОЛОГИЯ
5
ГЛАВА
Введение
1. ЛЕКЦИЯ - МНОЖЕСТВА. СИМВОЛИКА И
ТЕРМИНОЛОГИЯ
Предмет математики. Множества. Операции над множествами.
Кванторы общности и существования. Необходимое и достаточное
условия. Числовые множества.
1.1. Предмет математики. Математика — это точная абстрактная наука,
оперирующая своими специальными понятиями, структурами и символами. Основными
методами в математических исследованиях являются строгие логические
рассуждения, а объектами изучения — математические модели. Но абстрактность математики
н€ означает ее отрыв от реальной жизни. Реальные задачи описываются в
математических терминах, как правило в безразмерном виде. Это есть так называемая
математическая модель явления. При решении уже поставленной математической задачи
используются абстрактные математические методы.
Одна и та же математическая модель может описывать свойства различных
реальных явлений. Само реальное явление рассматривается вновь после решения
математической задачи и ее анализа, на основании которого могут быть сделаны выводы
не только о состоянии явления, но и о его развитии. В этом смысле без математики нет
науки. Еще великий Леонардо да Винчи писал: " Никакой достоверности нет в науках

6 1 ЛЕКЦИЯ - МНОЖЕСТВА. СИМВОЛИКА И ТЕРМИНОЛОГИЯ
там, где нельзя применить ни одну из математических наук, ив том, что не имеет
связи с математикой." И еще: " Ни одно человеческое исследование не может называться
истинной наукой, если оно не прошло через математические доказательства."
Математические методы играют огромную роль в образовании современного
высококвалифицированного специалиста в технических областях, предоставляя ему
аппарат исследования, дисциплинируя, приучая к строгим логическим рассуждениям.
Поскольку язык и методы математики широко используются при современном
преподавании всех естественно-научных и технических дисциплин, математика изучается с
первого семестра в любом высшем техническом учебном заведении, и на нее выделяется
значительная часть бюджета времени студента.
Перейдем теперь к рассмотрению некоторой математической символики и
терминологии.
1.2. Множества.Основные понятия. Под множеством понимается
совокупность каких-либо объектов, называемых элементами этого
множества. Например, можно говорить о множестве студентов данного
вуза, множестве учебников по математике, множестве треугольников,
множестве действительных чисел и т.д. Множества, содержащие конечное
число элементов, называются конечными (множество студентов,
множество учебников). Множества с бесконечным числом элементов называются
бесконечными (множество треугольников, множество действительных
чисел).
Множество обычно обозначается заглавными латинскими буквами
Л, В, С, ..., а их элементы — малыми а, Ь, с,
Утверждение "элемент х принадлежит множеству А" записывается
так : "ж € А ", а противоположное утверждение " элемент х не
принадлежит множеству А" записывается так : "я £ А ".
Определение 1.1. Если все элементы множества А принадлежат
также множеству В, то говорят, что " А содержится в В" или: " А
является подмножеством В", и записывают так: А С В.
Определение 1.2. Два множества называются равными
(совпадающими), если они состоят из одних и тех же элементов: А — В.
ПРИМЕР 1.1. Сформулируйте словами утверждение:
Л = В <=$> АсВиВсАи докажите его.
Конечное множество можно задать перечислением его элементов. Так,
запись А = {1;2;3} означает, что множество А состоит из трех чисел
1,2,3. При этом порядок перечисления элементов не играет роли: {1;2;3}
- {3;2;1}.
Бесконечное множество можно задать, написав условие, которое
выполняется для всех элементов данного множества и не выполняется для
других. Запись
В = {х | К х < 2}
1 ЛЕКЦИЯ - МНОЖЕСТВА. СИМВОЛИКА И ТЕРМИНОЛОГИЯ J
означает множество всех чисел, больших одного, но меньших двух, т.е.
интервал (1;2). ^
Множество удобно схематически изображать в виде 'диаграмм
Эйлера" — геометрических фигур на плоскости, взаимное расположение
которых отражает отношение между множествами. Так, например, если
Ас В т В С С, то А изображается частью Б, а Б частью С (рис. 1). С
помощью диаграммы Эйлера на рис. 1 наглядно видно свойство
транзитивности операции включения множеств: Ас В СС => А С С.
Рис. 1. Диаграмма Эйлера
Определение 1.3. Множество называется пустым, если оно не
содержит ни одного элемента. Пустое множество обозначается
символом 0.
Так, например, множество отрицательных натуральных чисел пусто.
1.3. Операции над множествами.
Определение 1.4. Пересечением множестве А и В называется
множество С, состоящее из всех элементов, одновременно входящих и в А,
и в В. Это записывается следующим образом: АПВ = С.
Иллюстрация пересечения двух множеств с помощью диаграмм
Эйлера приведена на рис. 2, где множество С заштриховано.
Рис. 2. Пересечение множеств А и В

8
1 ЛЕКЦИЯ - МНОЖЕСТВА. СИМВОЛИКА И ТЕРМИНОЛОГИЯ
Пример 1.2. Если множество А есть интервал (1;5) а множество
В есть интервал (2;7), то пересечение множеств А и В есть интервал
(2;Я
Свойства операции пересечения множеств приведем без доказательств:
1. А П В = В П Л (коммутативность).
2. АП{ВГ\С) = (АГ\В)Г)С = АПВП С(ассоциативность).
3. АсВ=> АГ)В = А.
4. АПА = Л.
5. А П 0 = 0
Определение 1.5. Объединением множеств А и В называется
множество С, состоящее из всех элементов, каждый из которых
принадлежит хотя бы одному из данных множеств или А, или В, или А и В
одновременно. Это обозначается следующим образом : A U В = С.
Рис. 3. Объединение множеств А и В
Иллюстрация объединения с использованием диаграмм Эйлера
приведена на рис. 3, где множество С заштриховано.
Пример 1.3. Если множество А есть отрезок [1;3]> множество В
есть отрезок [2;5], то AU В есть отрезок В=[1;5].
Свойства операции объединения множеств приведем без доказательств:
1) AUB=BUA (коммутативность).
2) AU(BUC)=(AUB)UC=AUBUC (ассоциативность).
3) АП(ВиС)=(АПВ)и(АПС) (дистрибутивность).
4) АсВ=*АиВ=В.
5) АиА=А.
6) AU0=A.
Определение 1.6. Разностью множеств А и В называется множест
во С, состоящее из всех элементов, принадлежащих множесву А, но
не принадлежащих В. Разность А и В обозначается А\В и изображена
штриховкой на рис. 4-
Операция вычитания множеств не коммутативна : А\В^В\А.
Пример 1.4. Если А = (1; 10), В = (3; 20), тоА\В=(1;3], В\А=[10;20).
1 ЛЕКЦИЯ - МНОЖЕСТВА. СИМВОЛИКА И ТЕРМИНОЛОГИЯ 9
Рис. 4. Разность множеств А и В
1.4. Кванторы общности и существования. При изложении
материала мы будем использовать знак V, называемый квантором общности,
и знак 3, называемый квантором существования. Символ Vx означает:
"для любого х", "для всех х", "для каждого х", "какое бы ни было х".
Запись Vx > 0 означает: "для всех положительных х" ЗаписьУх G М
читается: "для всех х, принадлежащих множеству М".
Обозначение Зх означает: "существует такое х, что ...", "по крайней
мере для одного х...", запись Зх > 0 читается: "существует такое
положительное число х, что...", запись 3xi,x2 € М означает: "существуют такие
#ь ^2 — элементы множества М, что ...".
Нам также неоднократно придется использовать символы =» и <==>.
Запись логического следования А ==> В означает, что если верно
утверждение А, то верно и утверждение В, то-есть из А следует В.
Запись логической равносильности <=> означает, что из А следует В
и наоборот, из В следует А.
Так, например, запись: Ve > 0 3N Vx > N =*=► |/(х) - b\ < е читается
следующим образом: "для любого е больше 0 существует N такое, что для
любых х, больших Ny будет выполняться неравенство |/(х) — Ь\ < £."
1.5. Необходимое и достаточное условие. Любая теорема может
быть сформулирована в виде: если выполняется условие А, то верно
утверждение В. Будем называть это прямой теоремой и схематически запишем
в виде:
Теорема 1.1.
А=>В.
В качестве примера приведем теорему, называемую достаточным
условием экстремума непрерывной функции, изучаемую в курсе математики
средней школы.
Теорема 1.2. Если функция f непрерывна в точке а и производная
/' меняет знак при переходе через эту точку, то а является точкой
экстремума функции /.

Ы 1 ЛЕКЦИЯ - МНОЖЕСТВА. СИМВОЛИКА И ТЕРМИНОЛОГИЯ
Условие А стоит после слова "если", утверждение В написано после
слова "то".
Определение 1.7. А называется достаточным условием для
выполнения В. В свою очередь, В является необходимым условием для
выполнения А.
Применительно к теореме 1.2 это выглядит следующим образом.
Достаточным условием для существования экстремума непрерывной
функции / в точке а является изменение знака ее производной при переходе
через эту точку.
Для лучшего усвоения введенных понятий рассмотрим очевидно справедливое
утверждение не из области математики.
Теорема 1.3. Если человек здоров, то у него есть голова.
Здесь здоровье является достаточным условием наличия у человека головы.
Наоборот, наличие головы является необходимым условием здоровья. Подумайте, будет
ли это условие достаточным для того, чтобы человек был здоров? Реально ли вообще
сформулировать достаточное условие того, что человек здоров?
Обозначим А утверждение, заключающееся в отрицании утверждения А(читается
"не А"). Если справедлива прямая теорема 1.1, то методом "от противного" легко
можно доказать справедливость следующего утверждения, которое называется
"противоположная к обратной теорема":
Теорема 1.4. В => А.
Доказательство. Имеем A =з- В, нужно доказать, что В ==> А Предположим
противное: В => Л, но в соответствии с теоремой 1.1 А => В. Полученное противоречие
(В => В) доказывает теорему.
Аналогично можно доказать, что если справедлива теорема 1.4, то верна
теорема 1.1, т.е. эти утверждения равносильны.
Для теоремы 1.2 противоположной к обратной будет теорема: "Если точка а не
является точкой экстремума функции /', непрерывной в этой точке, то производная Г
не меняет знак при переходе через эту точку".
Для теоремы 1.3 противоположным к обратному будет утверждение: "Если у
человека нет головы, то он не здоров".
Проведите доказательство этого утверждения самостоятельно методом "от
противного".
Наряду с прямой теоремой 1.1 можно рассмотреть утверждение, называемое
"обратной теоремой" :
Теорема 1.5.
В=> А.
Однако обратная теорема не всегда справедлива, если верна прямая. Так,
например, для теоремы 1,3 обратное утверждение: "Если у человека есть голова, то он
здоров", очевидно, не верно.
Если все же теорема 1.5 справедлива, то методом "от противного" исходя из нее
доказывается справедливость утверждения, называемого "противоположная теорема":
1 ЛЕКЦИЯ - МНОЖЕСТВА. СИМВОЛИКА И ТЕРМИНОЛОГИЯ
и
Теорема 1.6. А => В
Наоборот, из теоремы 1.6 вытекает справедливость теоремы 1.5, т.е. эти
утверждения равносильны. Заметим, что из прямой теоремы 1.1 не обязательно следует
справедливость противоположной теоремы 1.6.
Приведенные связи удобно запоминать, представляя себе следующий "логический
квадрат" (рис. 5):
■ В Прямая теорема
В =Ф> А Обратная
теорема
В => А
Противоположная к обратной теорема
А => В
Противоположная теорема
Рис. 5. Логический квадрат
Если наряду с прямой теоремой выполняется также обратная теорема,
то А является "необходимым и достаточным" условием для В. То же
самое можно сказать про В по отношению к А.
Так, например, то, что треугольник прямоугольный, является
необходимым и достаточным условием того, что квадрат одной из сторон равен
сумме квадратов двух других.
1.6. Множество N натуральных чисел.
Определение 1.8. Числа 1,2,3,... называются натуральными.
Сумма и произведение натуральных чисел будет числом натуральным,
а разность и частное - не всегда. При вычитании натуральных чисел
может получится отрицательное число, а при делении - не целое. Например,
при делении | получится целая часть 2 и 1 в остатке, что записывается
следующим равенством: f =2+|.
Приводя к общему знаменателю, получим равенство: 7 = 2-3+1. В этих
равенствах 7 называется делимым, 3 — делителем, 2 — целой частью и 1 — остатком
(остаток всегда меньше делителя). Если остаток равен нулю, то говорят, что делимое
делится на делитель, как, например, б делится на 3. Если натуральное число, большее
единицы, делится только на 1 и на себя (что всегда справедливо), то оно называется
простым. Простыми числами являются числа 2,3,5,7,11,13,17,19,23 и т.д. Любое
натуральное число может быть представлено в виде произведения простых сомножителей.
Например : 12 = 1 • 2 • 2 • 3, 18 = 1 • 2 • 3 - 3, 7 = 1 • 7 и т.д.
ОПРЕДЕЛЕНИЕ 1.9. Наименьшим общим кратным двух данных натуральных чисел
называется наименьшее из чисел, которые делятся на каждое из них.
Для любых двух натуральных чисел всегда найдется наименьшее общее кратное,
поскольку их произведение всегда делится на каждое из двух данных.

12 1 ЛЕКЦИЯ- МНОЖЕСТВА. СИМВОЛИКА И ТЕРМИНОЛОГИЯ
Наименьшее общее кратное 12 и 18 равно 36. Для того чтобы найти наименьшее
общее кратное двух чисел, нужно первое число домножить на простые множители,
входящие в разложение второго числа и не входящие в разложение первого: 12 • 3 = 36.
ОПРЕДЕЛЕНИЕ 1.10. Наибольшим общим делителем двух данных натуральных
чисел называется наибольшее из чисел, на которые делится каждое из них.
Для любых двух натуральных чисел всегда найдется наибольший общий делитель,
поскольку любые два числа всегда делятся на единицу. Если у двух натуральных
чисел нет других общих делителей кроме единицы, они называются взаимно простыми.
Наибольший общий делитель 12 и 18 равен 6. Для того, чтобы найти наибольший
общий делитель двух чисел, нужно перемножить общие простые множители, входящие
в разложение и одного, и другого числа: 1*2*3 = 6.
1.7. Множество Z целых чисел.
Определение 1.11. Натуральные, отрицательные натуральные
числа и ноль образуют множество целых чисел (множество Ъ).
Сумма, произведение и разность целых чисел является целым числом,
а частное — не всегда. Иногда множество отрицательных целых чисел
обозначается Ъ~.
Множество натуральных чисел является подмножеством множества
целых чисел: NcZ.
1.8. Множество Q рациональных чисел.
Определение 1.12. Рациональными числами называются числа вида
~, где т - целое (т 6 Ъ), п — натуральное (п € N), тип взаимно
простые. Множество рациональных чисел обозначается Q.
Множество целых чисел является подмножеством множества
рациональных чисел, т.к. любое целое число m можно рассматривать как
рациональное, представив в виде у. Сумма, произведение, разность, частное
рациональных чисел ( при ненулевом знаменателе) является числом
рациональным, однако корень из рационального числа — не всегда, как,
например, л/2,\/3 и т.д.
Всякое рациональное число — можно представить в виде десятичной
дроби, конечной или периодической. И наоборот, любая конечная или
периодическая десятичная дробь может быть записана в виде простой дроби.
Пример 1.5. \=0,5; 1=0,8 ; 1=0,666... =0,(6) ; Щ=7,31(06).
Две последние десятичные дроби бесконечные периодические.
Повторяющиеся цифры называются периодом дроби и пишутся в скобках,
количество этих цифр называется длиной периода. Для обратного
преобразования конечной десятичной дроби ее нужно представить в виде простой
1 ЛЕКЦИЯ - МНОЖЕСТВА. СИМВОЛИКА И ТЕРМИНОЛОГИЯ 13
и сократить: 0,8=~=§. На самом деле разница между конечной дробью
и периодической непринципиальная. Так, 0,5=0,4(9).
Перевод периодический десятичной дроби в простую объясним на
примере.
Пример 1.6. Записать в виде простой дроби 0,(6). *
Решение: Периодическую дробь 0*(6) обозначим за х\ 0,(6)=?х,
тогда, т.к.10 • х = 10 • 0,666... = 6,666..., легко заметить, что 10 • х = 6 + х.
Решая это уравнение, получаем: 9 • х = 6 <=> х= § = §.
Определение 1.13. Целой частью числа называется наибольшее
целое число, не превосходящее данное. Целая часть числа х обозначается
[4
Примеры. [3,56]=3; [0,12]=0; [-0,12]=-1; [-^]=-4;
[5]=5; [0]=0.
Определение 1.14. Дробной частью числа называется разность меж
ду самим числом и его целой частью. Дробная часть числа обозначается
{х}. Она строго меньше единицы и находится в пределах : 0 < {х} < 1.
Примеры. {3,56}=0,56; {0,12}=0,12; {-0,12}=0,88;
{-? }=!; {5}=о; {о}=о.
1.9. Множество J иррациональных чисел.
Определение 1.15. Иррациональным числом называется
бесконечная непериодическая десятичная дробь.
Примерами иррациональных чисел являются s/2, n/3, ^П, тг, е, и т.д.
Заметим, что JflQ = 0 Иррациональное число нельзя представить в виде
простой дроби, его также невозможно "выписать до конца" (представить
в виде конечной десятичной дроби), поэтому запись >/2 = 1,41 ошибочна,
следует писать у/2 « 1,41.
Заданное бесконечной непериодической дробью иррациональное
число определяет две последовательности конечных (рациональных)
десятичных дробей, называемых десятичными приближениями по недостатку и
по избытку. Например, для \[2 можно написать:
1<ч/2<2,
1,4<У2<1,5,
1,41< ч/2<1,42.
В инженерных расчетах при замене иррациональных чисел их
рациональными приближениями достаточно во всех вычислениях брать на один
^нак больше, чем требуется в результате, и затем округлить результат.

U i ЛЕКЦИЯ - МНОЖЕСТВА. СИМВОЛИКА И ТЕРМИНОЛОГИЯ
Для иррациональных чисел можно также определить целую и дробную
части, причем для х G J => {х} G J.
1.10. Множество К действительных чисел.
Определение 1.16. Все рациональные и иррациональные числа обра-
зуют множество действительных (вещественных) чисел: R = Q U Jf.
В множестве действительных чисел всегда выполнимы сложение,
вычитание, умножение, деление (не на ноль), возведение в любую
действительную степень положительного числа, извлечение корня нечетной степени
из отрицательного числа.
В множестве действительных чисел невозможно извлечение корня
четной степени из отрицательного числа.
1.11. Числовая ось. Множеству действительных чисел можно дать
простую геометрическую интерпретацию. Выберем на прямой
положительное направление (указывается стрелкой), начало отсчета и единицу
масштаба. Такая прямая называется числовой осью. Каждой ее точке
можно поставить в соответствие единственное действительное число
следующим образом: положительное число х изображается точкой,
расположенной на оси на расстоянии х в направлении стрелки (на рис. 6 справа от
О), отрицательное с другой стороны (на рис. 6 слева от О) на расстоянии
х от О.
Число х называется координатой соответствующей точки на числовой
оси. Из двух чисел больше будет то, которое расположено на числовой оси
дальше в направлении стрелки (на рис. 6 - правее).
]Л ъ/г У*
Н 1 -Н —I—Н—г—I—Н—1 ^
-2 -1 О 1 2 3
Рис. 6. Числовая ось
Например, -1 > -2.
1.12. Числовые промежутки. Если известны два действительных
числа а и b, a < 6, то можно определить следующие множества
действительных чисел, находящихся между двумя данными - числовые
промежутки.
Отрезок (сегмент) [а; &]= {х \ а ^ х ^ &},
Интервал (а; Ь)= {х \ а < х < о}.
В частности, можно рассматривать бесконечные интервалы:
1 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - МНОЖЕСТВА
15
(-oo;-hoo)={x€R}, (а;+оо)={х|х>а}, (-oo;b)={x|x<b}.
Полуинтервал. [a;b)={x|a^x<b}, (a;b]={x|a<x^b}.
В частности, можно рассматривать бесконечные полуинтервалы:
[а;+оо)={х|х^а}, (-oo;b]={x|x^b}.
Числовые промежутки изображают на числовой оси, причем если
граничная точка принадлежит промежутку - она закрашена, если нет -
изображается светлым кружком ("выкалывается"). На рис 7 изображен
полуинтервал (2;5].
О 2 5
Рис. 7. Полуинтервал (2;5]
Числовые промежутки будем выделять штриховкой или утолщенной
линией.
1. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - МНОЖЕСТВА
При решении примеров данного практического занятия используется
материал средней школы и материал лекции 1. Применение метода
интервалов для решения неравенств иллюстрируется примерами 1.2-1.5
Пример 1.1. Пусть А = (-3;5],£ = (-5;7),С = [1;2]. Найдите мно-
жество: А0 = (AC) B)U(BC)C).
Решение: Для нахождения результата операций над числовыми
промежутками их удобно изображать на числовых осях, расположенных
одна под другой с согласованным началом и одинаковым масштабом.
Если исходные промежутки А и В заштриховать, то их пересечением будет
множество точек, заштрихованных на каждой из осей (рис. 8), а их
объединением - множество точек, заштрихованных хотя бы на одной из осей
(рис. 9).
Пользуясь этим правилом, последовательно получим А П В, В Г\С и,
наконец, (А П В) U (В П С) (рис. 8, 10, 11).
Ответ: А0 = [-3;5].
Пример 1.2. Найдите элементы множества:
Ао = {х | (2 - Зх){х +4)(х - 2) > 0}.
Решение: Неравенство (2 - Ъх){х + Щх- 2) > 0 решим методом
интервалов, для чего нанесем на числовую ось значения х, при которых

16
1 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - МНОЖЕСТВА
-5
-3 5
н+н-
+И+Н
нш
-3
/////hlllilk
А
-в
АПВ
РиСс 8. Нахождение пересечения [—3;5] П (-5; 7)
ит
\IIIIIVIIII
|/////|///Ш////Г ' в
тнг
AUB
Рис. 9. Нахождение объединения [-3; 5] U (-5; 7)
-5 7
W////J/////J/////'
mm
ниц
1
в
— с
— вас
Рис. 10. Нахождение пересечения (-5; 7) П [1; 2]
левая часть неравенства обращается в ноль: х\ = §,х2 = -4,х3 = 2. (рис.
12)
Сами эти значения не удовлетворяют неравенству, поэтому
соответствующие точки "выколоты".
Знаки выражения в левой части неравенства определим, подставляя в
него по одному значению из каждого интервала, на которые все
множество R разбилось точками х\,Х2, #з- Отметим штриховкой те интервалы, на
которых выражение в левой части неравенства положительно. Это
множество является искомым.
Ответ:Л0 = (-со; -4) U (|; 2).
1 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - МНОЖЕСТВА
11
-3 5
Ullll\HIIII\llllll\ -Апв
»
/////(/////
mi
♦3
впс
(АПВ)и(ШС)
Рис. 11. Решение примера 1.1
/////////-
-4
+
4llllllh
У:
з
Рис. 12. Решение примера 1.2
ПРИМЕР 1.3. .Задайте характеристическим свойством множество:
Aq— множество всех натуральных чисел, меньших 5 или больших 10.
Решение: В условии требуется,чтобы натуральные числа были
меньше 5 или больше 10, т.е. искомое множество есть объединение двух
подмножеств: множества натуральных чисел, меньших 5 и больших 10.
Ответ:Л0 = {х\х < 5, х € N} U {х\х > 10, х € N}.
ПРИМЕР 1.4. Решите систему неравенств:
{
(х-3)(а: + 2)<0,
(5-2х)(х + 1) >0.
Решение: Решение системы неравенств есть пересечение множеств
решений каждого из входящих в систему неравенств. Аналогично тому,
как это делалось при решении примера 1.2, решим каждое из неравенств
системы методом интервалов и найдем их пересечение (рис 13).
Ответ: х Е (-1;2,5).
Пример 1.5. Решите совокупность систем неравенств:
х3 -5х2 + 6х > 0,
(х2-1)(х2 + 7)<0,
1 < 0,
i3-i2 + a;'
-ha;-2 < 0.

18
1 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - МНОЖЕСТВА
illfll //////////
НШ
ит
2,5
2,5
(х-3)(х+2)<0
-*- (5-2х)(х+1)>0
{
(х-3)(х+2)<0
(5-2хХх+1)>0
Рис. 13. Решение примера 1.4
Решение: Решение совокупности систем неравенств есть
объединение решений каждой системы, входящей в совокупность. Для решения
разложим каждый многочлен в произведение с помощью корней:
х3 - 5х2 4- 6х > О,
(х2-1)(х2 + 7)<0,
х3 - х2 4- х - 1 < О,
х2 + х - 2 < 0.
х(х-2)(х-3) > 0,
(х + 1)(х-1)(х2 + 7)<0,
(х - 1)(х2 + 1) < 0,
(х + 2)(х-1) <0.
Решение совокупности систем методом интервалов представлено на
рис. 14
+
-1
0
ли I
11ll I
0
J! f 11
ill It
If 11 i
1 ill1
\\\\\k
lit I Г
1!! 1 i
lltll
+
1
1
|2 2j
r/ / /*
1.1 Г
ттттф
+ -2
/////////]' *
2/////////i'
mm
mm
m+m1
■нтМ-
mm1
fx(x-2)(x-3)X)
l(x+l)(x-l)(*+7)<0
{(x-l)(x**l)<0
<x*2)(x-l)<0
Рис. 14. Решение примера 1.5
Ответ: х € (-2; 1)
Пример 1.6.
множества:
Ах = А П В П С,
л2 = л и в и с
л3 = (4ив|пс.
Л4 = (ЛПВ)и С.
Самостоятельная работа
Пусть А = [-3;5],В = (-5; 7),С = [1;2). Найдите
1 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - МНОЖЕСТВА
19
Аъ = Аи{ВГ\С).
Лб = АП(ВиС).
А7 = В\А.
Пример 1.7. Найдите элементы следующих множеств:
Ах = {х|5х - 6 - х2 = 0}, В3 = {у|6у.+ у2 ^ 0},
А2 = {а|5 - а2 = 0}, В4 = {х\{х - 1)(2х + 1)х < 0},
Лз = {у|6у + у2 = 0}, В5 = {х|х2 +1 > 0},
А4 = {х\{х - 1)(2х + 1)х = 0}, С = {х\ - 1, К х < 5,х € ЛГ},
Л5 = {х\х2 + 1=0}, Z> = {х|х = (-1)п,п € JV},
Bj = {х|5х - б - х2 < 0}, Я = {х|х = 1 + (-1)" • 3, п 6 JV}.
Б2 = {а|5 - а2 > 0},
5,
Пример 1.8. Задайте характеристическим свойством множества:
Ах — множество всех действительных чисел, больших 2 и меньших
А2 — множество всех действительных чисел, не больших 5,
А$ — множество всех отрицательных рациональнных чисел,
At — множество всех неотрицательных действительных чисел,
Аь — множество всех отрицательных целых чисел,
А6 — множество всех цифр, га.е.{0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.
Решите системы неравенств, приведенные в примерах 1.9 - 1.13.
t n f х2 - 6х + 15 > 0,
Пример 1.9. (Х2_4х + з>0.
11Л fi2-4i-8>0,
Пример 1.10. (х2_8<а
1 it Г (х-3)(2-х)5*0,
Пример 1.11. (i^ + J^ + A^o.
f 8 - х2 ^ О,
\ х + 2> 8-х2.
{х + 5 ^ О,
1 - х > 0,
х + 5<(1-х)2.
Решите совокупности систем неравенств, приведенные в примерах
1.14-1.18.
Пример 1.12.
Пример 1.13.

20
1 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - МНОЖЕСТВА
Пример 1.14.
Пример 1.15.
Пример 1.16.
Пример 1.17.
Пример 1.18.
-х2 + Ъх - 5 > (8 - 2я)2,
8 - 2х ^ О,
1 ^ х < 5,
8 - 2я < О.
х2>1,
2 + х<х2,
2 + я>0,
О < х2 < 1,
х2 < 2 + х.
х - 3 ^ О,
а?2-5х+6 ^ ^>
X - 3 < О,
3—X ^ су
7 - X ^ О,
5х -f 1 ^ (7 - х)2,
5х + 1 ^ О,
7 - х < О.
х > 1,
5(1-х) ^ Х>
0<Х<1,
Пример 1.19. Разложите па простые множители числа:
а)%; 6)120; e)4S; 8,154.
Пример 1.20. Найдите наименьшее общее кратное и наибольший
общий делитель чисел:
а)90 и 120; 6/48 и 54.
ПРИМЕР 1.21. Найдите целую часть и остаток от деления чисел:
ПРИМЕР 1.22. Представьте в виде десятичной дроби-
Пример 1.23. Представьте в виде обыкновенной дроби:
аД 04; ^-3,12; вД(3); гД,2(3).
Пример 1.24. Вычислите без помощи калькулятора'
«А (2)+ 0,(3),
2 ЛЕКЦИЯ - СИСТЕМЫ КООРДИНАТ
21
6)0, (2)-0, (37),
e/0,12(3)-f 0,0925 Т1^ U'^'
Предварительно переведите периодические дроби в простые и не
забывайте порядок операций: сначала вычисляется выражение в скобках,
потом операции возведения в степень (извлечение корня), умножение и
деление, затем сложение и вычитание.
2. ЛЕКЦИЯ - СИСТЕМЫ КООРДИНАТ
Абсолютная величина действительного числа. Положение точки на
прямой, на плоскости, в пространстве. Расстояние между двумя
точками. Преобразование координат. Полярные координаты.
2.1. Абсолютная величина действительного числа.
Определение 2.1. Абсолютной величиной или модулем
действительного числа х называется само это число, если х ^ 0 и число —х, если
х < 0:
/о i\ \~\ / х> если х ^ °>
(2Л) |*| = | ^
если х < 0.
Например: |2| = 2,т.к.2 > 0, | - 3| = -(-3) = 3,т.к. - 3 < 0,
\х2 + 4| = х2 + 4, т.к. х2 + 4 > 0 при всех х € Я, |0| = 0.
, 0, f х-3, если х - 3 ^ 0,
|л - 3| = <
"♦"-{'^Ч.
-(я - 3), если х - 3 < 0;
если а + 5 ^ 0,
если л 4- 5 < 0.
Модуль дейтвительного числа х равен расстоянию на числовой оси от
точки х до начала координат.
Расстояние между двумя точками на оси с координатами х\ и я2
выражается формулой:
(2.2) d=\x2-x1\.
Докажем эту формулу для случая, когда х2 ^ Х\ ^ 0 (рис. 15)
В этом случае
ОМ\ = zb ОЛ/2 = х2 и d = M\Mi = OM2 - OMi = з2 - an = |s2 -^ll-
Если xi > x2 > 0 (рис. 15), то d = MiM2 = OM2 - О Mi = x\ - x2 =
-(x2 - a?i) = |ar2 — a:i|, т.к. x2 - x\ < 0.

22
2 ЛЕКЦИЯ - СИСТЕМЫ КООРДИНА Т
х\ *2 *2 х\
Н 1 и- -н 1 1_^
О Mj М2 О Mj М2
Рис. 15. Растояние между точками на оси
Для остальных случаев расположения Мх и М2 формула доказывается
аналогично.
Пример 2.1. Для данных a u R > О отметить на числовой оси
множество М - {х\\х - а\ < R}.
Решение: В соответствии с формулой 2.2 множество М есть
множество точек числовой оси, расстояние от которых до данной точки
меньше Я, т.е. интервал с центром в а и длиной 2R:
М = {х\\х - а\ < R} = {х\х € (а - R; а + R)} =
= {х\а - R < х <а + R].
Ответ: см. рис. 16.
V//////////////> ^
a-R a a+R
РИС. 16. {x\\x~a\<R}
Приведем свойства модуля действительного числа, которые вытекают
из определения модуля и свойств арифметических операций.
1)
2)
3)
4)
1*1^0, 5)|*| = |-4
\х ' У\ = W • \У\, 6) |*| ^ а <& -а $ х ^ а для Va > 0,
-й 7)|* + у|<|*| + М,
И = |*|« если 3*°, 8) |* - у| £ М - Ы-
Заметим, что из свойств модуля и того факта, что арифметический
корень квадратный неотрицателен, следует, что корень квадратный из
полного квадрата некоторого выражения а равен модулю этого
выражения:
(2.3) V?=|4
Так, например, л/Р=5; у/(-3)2 = 3(а не - 3);
\/(х + Ь)*=\х + 5\.
Аналогичное замечание справедливо при любом сокращениии
показателя корня и степени подкоренного выражения на четное число:
2 ЛЕКЦИЯ - СИСТЕМЫ КООРДИНА Т
23
(2.4) 2У^=</№ Vfc,n€iV.
Например: f/(x - З)6 = у/\х - 3|3,
2.2. Положение точки на прямой.
Определение 2.2. Координатой точки М на числовой оси
называется действительное число х, которое соответствует этой точке
(см. п. 1.11 лекции 2).
2.3. Положение точки на плоскости. В декартовой системе
координат положение точки на плоскости определяется уже двумя
числами. Зададим на плоскости две взаимно перпендикулярные числовые оси
Ох и Оу, имеющие общее начало О (совпадающее с точкой пересечения).
Плоскость в которой, расположены оси, назовем координатной плоскостью
Оху. Произвольная точка М плоскости имеет две координаты, одна из
которых — ее проекция * на ось Ох, а другая ее проекция у на ось Оу
(рис. 17).
У
<
У
0
1
М
X
Рис. 17. Координатная плоскость Оху
Определение 2.3. Координатах называется абсциссой точки М', а
координата у — ординатой точки М. Упорядоченная пара чисел (х; у)
называется прямоугольными или декартовыми координатами точки М
на плоскости Оху. Каждой точке М координатной плоскости
соответствует единственная упорядоченная пара чисел (х;у) и, наоборот,
каждая такая пара чисел определяет единственную точку М
плоскости, расположенную на пересечении перпендикуляров к осям в точках х
и у соответственно. Ось Ох называется осью абсцисс, ось Оу — осью
ординат, точка О — началом координат.

24
2 ЛЕКЦИЯ - СИСТЕМЫ КООРДИНАТ
Заметим, что обычно горизонтальную ось называют осью абсцисс и
устанавливают положительное направление направо, а вертикальную ось
называют осью ординат и устанавливают положительное направление
вверх, как на рис. 17. Оси Ох и Оу делят координатную плоскость на
четыре четверти (на четыре квадранта): в 1-й х > О, у > О, во П-й
х < О, у > О, в Ш-й х < О, у < О, в IV-й х > О, г/ < 0. Запись М(1;2)
будет означать, что точка М имеет абсциссу 1 и ординату 2.
2.4. Положение точки в пространстве. В декартовой системе
координат положение точки в пространстве определяется тремя числами.
Зададим в пространстве три взаимно перпендикулярные числовые оси
Ох, Оу, Oz, имеющее общее начало О (совпадающее с точкой их
пересечения). Оси назовем координатными осями: Ох — ось абцисс, Оу —
ось ординат, Oz — ось аппликат. Координатное пространство обозначим
Oxyz.
Произвольная точка М пространства Oxyz имеет три координаты —
ее проекция х на ось Ох (пересечение плоскости, проходящей через точку
М перпендикулярно оси Ох, с этой осью), ее проекция у на ось Оу и
ее проекция z на ось Oz (рис. 18). Упорядоченная тройка чисел (х; у; z)
называется прямоугольными или декартовыми координатами точки М в
пространстве.
Очевидно, между точками в пространстве Oxyz и упорядоченными
тройками чисел существует взаимно-однозначное соответствие.
Координаты х, у, z называются аналогично осям — абсцисса, ордината и
аппликата соответственно. Кроме координатных осей можно рассмотреть
также три взаимно перпендикулярные координатные плоскости Оху, Oyz,
Ozx, проходящие через оси приведенные в обозначении. Мы будем
стараться располагать координатные оси как показано на рис. 18.
Координатные плоскости делят пространство на 8 октантов: в 1-м х > 0, у >
0, z > 0, во Н-м х < 0, у > 0, z > 0, в Ш-м х < 0, у < 0, z > 0, в IV-m
х > О, у < 0, z > 0, в V-м х > 0, у > 0, z < 0, в VI-м х < О, у > 0, z < 0,
в VII-м х < 0, у < 0, z < 0, в VHI-m х > 0, у < О, z < 0. Запись
М(-1; —2; —3) будет означать, что точка М имеет абсциссу -1, ординату
-2, аппликату -3 и расположена, следовательно, в VII октанте.
2.5. Расстояние между двумя точками. Найдем расстояние d
между точками Мх(хх;ух; zx) и M2(x<i\Уг\ zt) в пространстве. Построив
прямоугольный параллелепипед, диагональю которого является отрезок МХМ2
2 ЛЕКЦИЯ - СИСТЕМЫ КООРДИНАТ
25
Z '
Z
9
\
ц
S
/
f
у
Рис. 18. Координатное пространство Oxyz
и с гранями, параллельными координатным плоскостям (рис. 19), на
основании известной теоремы курса стереометрии средней школы получим:
МХМ\ = MXN2 + МХР2 + MXQ2.
Спроектировав концы ребер MXN, МХР, MXQ на оси Ох, Оу, Oz,
получим на этих осях отрезки M[N', M"P', M["Q' и в соответствии с
формулой ( 2.2): MXN = M[N' = \х2 - хх[, МХР = М'{Р' = \у2 - ух\; MXQ =
Подставив эти выражения в предыдущую формулу, получим:
МХМ\ = \х2 - хх\2 + \у2 - </i|2 + |*2 - zx\2,
или:
(2.5)
d = у/(х* - хху + (2/2 - Ух)2 + {z2 - *!)*.
Данная формула остается, безусловно, справедливой, если отрезок
ЫхМг параллелен каким-либо координатным плоскостям (рассмотрите
эти случаи самостоятельно). Если точки М\(хХ',ух) и М2{х2;у2) лежат в
плоскости Оху, то формула для расстояния между этими точками
принимает вид:

26
2 ЛЕКЦИЯ - СИСТЕМЫ КООРДИНАТ
1
/'
/
£ 1 *
1 /
•
У
1 * 1
; tfjZl
\/
z
Q'
Кг
/'''■
ц; i
1 '
•
у/
ад"
7
1 ~/
*
*
м,
•
>
•
р'
ад'
X
Рис. 19. Расстояние между двумя точками в пространстве
(2.6) d = >/(*2 - *i)2 + (ft - 2/i)2.
ПРИМЕР 2.2. Найти расстояние d\ между точками Mi(—1; —2; —3;)
« Мг(0; —2; 5), расстояние d2 между точками Мз(2; 3) и М4(—1; 0) и
расстояние d$ между началом координат О и точкой М*> (—2; 1; 3).
Решение: По формуле ( 2.5):
di = д/(0 -(-I))2 + (-2 - (-2))* + (5 - (-3))2 = n/12+02 + 82 = V65.
По формуле ( 2.6):
* = V(-l ~ 2)2 + (0 - З)2 = ч/З^Тз2" = Зл/2-
По формуле ( 2.5):
dz = v/(~2-0)2-F(l-0)2 + (3-0)2 = v/22 + l2 + 32 = \/14.
2об. Параллельный перенос осей координат. В некоторых
случаях приходится одновременно рассматривать две системы координат на
плоскости и решать следующую задачу: зная координаты точки в одной
2 ЛЕКЦИЯ - СИСТЕМЫ КООРДИНА Т
21
системе координат, найти ее координаты в другой системе. Эти формулы
называются формулами преобразования координат.
Мы будем предполагать, что обе системы — декартовы
(прямоугольные), причем одноименные оси этих систем параллельны и одинаково
направлены, и на каждой из осей выбрана одна и та же масштабная единица.
На рис. 20 изображены две такие системы Оху и 0\XY'. Система 0\XY
может быть получена параллельным переносом осей Ох и Оу.
Рис. 20. Параллельный перенос осей координат
Условимся называть координаты точек в системе Оху старыми, а в
системе 0\XY — новыми. Пусть хо, Уо — координаты нового начала
0\ в старой системе. Предположим, что произвольно выбранная точка М
на плоскости имеет старые координаты х и у и новые координаты X и
Y. Выведем формулы, выражающие старые координаты точки М через
новые. Проектируя новое начало 0\ и точку М на ось Ох, а также точку
М на ось 0\Х, получим соответственно точки А, Р и N. Очевидно,
OiN = АР. Но OxN = |*|, АР = \х - х0|,так что
т.е. новая абсцисса X и разность х-хо равны по модулю. Нетрудно
заметить, что и знаки этих величин одинаковы. В самом деле, если N лежит
правее 0\, то Р расположена правее Л, и обе величины X и (х — хо)
положительны. Если же N находится левее Oi, то Р - левее А и,
следовательно, X и (х — х0) отрицательны. В обоих случаях X = х — х^,

28
2 ЛЕКЦИЯ - СИСТЕМЫ КООРДИНАТ
откуда х = X Н- xQ. Аналогично получается формула для старой
ординаты г/. Таким образом, мы получили следующие формулы преобразования
координат (параллельного переноса осей):
(2.7) х = X + х0, у = Y + у0.
Пример 2.3. Дана точка М(2; —1) в системе Оху. Найти ее новые
координаты X uY при параллельном переносе осей, если новое начало
в старой системе имеет координаты — 1 и 3.
Решение: По формулам ( 2.7) получим 2 = X — 1, — 1 = У + 3,
откуда X = 3, Y — -4
2.7. Полярные координаты. Наряду с декартовыми координатами
на плоскости употребляются полярные координаты, в которых положение
точки М на плоскости задается (рис. 21) полярным углом <р и полярным
радиусом г, называемыми полярными координатами точки М : М(ф]г).
Пусть на плоскости задана числовая ось I. Назовем ее полярной осью, а
ее начало — точку О — полюсом. Проведем через точку М и полюс ось /i,
начало которой совпадает с О (см. рис. 21), а положительное направление
от О к М. Полярный угол (р - это угол между полярной осью / и осью /i,
отсчитываемый со знаком "+" против часовой стрелки и со знаком "—" по
часовой стрелке. Полярный радиус г - это расстояние от О до точки М
по оси li(r ^ 0). Если значение полярного угла </? ограничить
промежутком 0 ^ (^ < 27г, то между точками плоскости и упорядоченными парами
полярных координат (<р; г) будет существовать взаимно-одназначное
соответствие.
0^"Ф1 1
v*Z- _I 1 >_
Рис. 21. Полярные координаты
Пример 2.4. Построить в полярной системе координат точки
Jfi(f;3); M2(|;2); Мз(тг;4); Л/4(0;3).
Решение: Точки Мь Мг, М3, М4, отмечены на рис. 22
2 ЛЕКЦИЯ - СИСТЕМЫ КООРДИНАТ
У
29
Рис. 22. Решение примера 2.4
Выведем формулы, связывающие декартовы и полярные координаты
точ!и нГпло?коРсти, для чего расположим полярную ось / совпадающую
с осью Ох, а полюс О — с началом координат О (рис. 2.6)
х М
Рис. 23. Связь декартовых и полярных координат
Из Д ОММ' находим: cos <р = «, sin 9 = ?, г2 = х2 + у2, откуда :
Г х■ = г cos </?,
(2-8) \2/ = rsin<£.
(2.9)
Легко понять,что формулы ( 2.8), ( 2.9) будут справедливы при любом
расположении точки М на плоскости. Формулы ( 2.8) дают зависимость

30
2 ЛЕКЦИЯ - СИСТЕМЫ КООРДИНА Т
декартовых координат (х\у) от полярных (г;<р), а формулы ( 2.9) -
наоборот. В последней формуле ( 2.9) из двух значений угла <р,
соответствующих найденной величине tg</?, выбирается то (0 ^ <р < 27г), при котором
удовлетворяются условия ( 2.8).
ПРИМЕР 2.5. Найти полярные коодинаты точки М с декартовыми
координатами х = 2, у = -2.
Решение: По формулам ( 2.9) находим : г = у/22 + (-2)2 =
2v% tgip — —1 Найдем угол <р : tg(p = —1 => у? = arctg(—1) -f П7Г, га €
Z «=^ <р = - J + П7г, п € Z Условию 0 ^ <р < 2п, удовлетворяют два
значения: (рг = ~, и у?2 = х> °Днако равенства ( 2.8):
2 = 2\/2cosy?,
-2 = 2\/2sin^ '
удовлетворяются только при (р = ~. Ответ: М(2\/2; *р)-
2.8, Поворот осей координат. Пусть на плоскости заданы две
системы координат, имеющие общее начало О: система Оху (старая) и
система OXY (новая), которая получена поворотом старой системы на угол
а.Это значит,что угол (Ох; ОХ) = а (рис. 24) и, следовательно, угол
(Оу; OY) = а. Найдем формулы, выражающие старые координаты х п у
произвольной точки М плоскости через ее новые координаты X иУ.
1 '
(
О' N
Рис. 24. Поворот осей координат
Введем полярные координаты: старые - с полярной осью, совпадающей
с осью Ох, и новые - с полярной осью ОХ. Пусть точка М в новой
Я ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - СИСТЕМЫ КОР ДИН AT
31
полярной системе имеет полярный угол ip и полярный радиус г.В старой
полярной системе полярный угол точки М равен а+ф, а полярный радиус
такой же, как и в новой системе. Поэтому по формулам ( 2.8) имеем:
х — г cos(a -f </?), у = г sin(a -f лр).
Используя тригонометрические тождества для косинуса и синуса суммы
двух углов, получим:
х = r(cos a cos у> — sin a sin ф) = (г cos <p) cos a — (г sin </?) sin a;
у = r (sin a cos ip -f cos a sin <p) = (r cos ip) sin a + (r sin (p) cos a.
Ho r cos <p = X и г sin v? = У, поэтому
(2.10) x = Xcosa - Y sin a, у = X sin a 4- Y cos a.
Формулы ( 2.10) называются формулами поворота осей. Выразив отсюда
X и Y, получим
(2.11) X = х cos a 4- у sin a, У = — xsina -f г/cos a.
Пример 2.6. Выразить старые координаты точки х и у через ее
новые координаты X uY при повороте осей на угол а = 7г/4.
Решение: Так как cos(7r/4) = \/2/2, то по формулам ( 2.10)
получим:
>/2 J2 s/2 уД
2 2 * 2 2
или
x=^(X-Y),y=^(X + Y).
2. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - СИСТЕМЫ КОРДИНАТ
В этом практическом занятии на основании материала лекций 1 и 2
решите примеры с модулями, а также — на преобразование координат.
Пример 2.1. Запишите с помощью знака модуля неравенство —3 <
х < 3.
Решение: Неравенство — 3 < х < 3 на основании свойства б
модуля действительного числа (лекция 2) равносильно неравенству \х\ <
3. Ответ: -3 < х < 3 <Ф |г| < 3. , :
Пример 2.2. Решите неравенство \х — 1| < 5.

32
2 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - СИСТЕМЫ КОР ДИН А Т
Решение: Неравенство можно решить с помощью свойства б
модуля действительного числа (2), однако здесь целесообразно использовать
определение модуля:
; - 1, если х — 1 ^ О,
, если х — 1 < 0.
, -, Г х - 1, есл:
Исходное неравенство равносильно совокупности двух систем:
|г-1|<5
{?"
Г*^1
Lz<6,
х<1
Г {а
Решение последней совокупности представлено на рис. 25. Следует
помнить, что решение системы неравенств получается как пересечение
множеств решений каждого, а решение совокупности систем (неравенств)
получается как объединение множеств решений каждой.
1 6
wm
,4f//////y|//////f6
Рис. 25. Решение примера 2.2
Для решения этого примера можно также воспользоваться решением
примера 1.1 лекции 2.
Ответ: х G (—4; 6).
Самостоятельная работа
Пример 2.3. Запишите с помощью знака модуля следующие
неравенства:
а)-~4 < х < 4;
б)-7 < х^7;
в)-4 < х + 1 < 4;
г)-Ь < х < 3;
д)-3 < х ^ 5;
е)-% ^ х - 1 < 4.
2 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - СИСТЕМЫ КОР ДИН AT 33
Пример 2.4. Решите неравенства:
а)\х + 3\>2; 6)\х\<х+1;
в)\х2 - 5| > 2; г)\х2 - 2х - 3| > х2 - 2х - 3;
<?)|х2 - 12х| > х2 - 12а; е)\х + 2| + |яг + 4| < 10;
Пример 2.5. Решите уравнения:
а)\2х + 3| = х2,
в^|х2 - 5х -f б| = ж2 - Ъх + б;
г)| sin2x| = \;
<ty|cosx| = \.
Решите эти примеры, заменяя уравнения совокупностью систем
уравнения и неравенства в соответствии с определением модуля.
Выполнение неравенства в системе удобнее проверить подстановкой в него корней
уравнения. Заметим, что уравнение вида 0=0 справедливо при всех
значениях х.
Пример 2.6. Найдите новые координаты X, Y точки М(х,у) при
параллельном переносе осей с последующим поворотом на угол а, если
новое начало в старой системе имеет координаты хо, уо-
а) х = 0, у = 0, хо = 1, 2/о = 2, а = £;
б) х = 1, у = 1, хо = -1, 2/о = 1, а = -f;
в) х = 1, у = 1, х0 = -1, уо = -1, а = f.
/7ри решении этого примера последовательно используйте формулы
( 2.7), ( 2.11) лекции 2.
Пример 2.7. Найдите полярные координаты точки Р с декартовы-
ми координатами х, у:
а) х= 1 у= 1;
б; х = -3 у = 3;
в) х == -2 у = -2.
Пример 2.8. Найдите декартовые координаты точки М с
полярными координатами г, tp:
а) г = 2 р==; ^r = 3 у> = -§;
б^ г = 4 р=—|; г)г = 1 <p — ir.

34
3 ЛЕКЦИЯ - ФУНКЦИЯ
I ГЛАВА
Функция одной переменной
3. ЛЕКЦИЯ - ФУНКЦИЯ
Понятие числовой функции. Способы задания. Четные, нечетные,
периодические функции. Обратные функции.
3.1. Понятие числовой функции.
Определение 3.1. Пусть даны два множества действительных
чисел X и У. Числовой функцией у = f(x) называемся правило, кото-
рое каждому числу х € X ставит в соответствие единственное число
у € Y. Переменную х называют независимой переменной или
аргументом, переменную у — зависимой переменной или функцией, множество
X называется областью определения D(f), множество Y называется
областью изменения или множеством значений функции E(f).
Наряду с обозначениями функции у = f(x) используются и другие,
в частности у = у(х). Значение функции для фиксированного значения
аргумента х0 будем обозначать у0 = f(xQ) или у0 = у(х0). Сама
функция, ее аргумент и значение могут быть обозначены и другими буквами,
например: V = F(u).
3 ЛЕКЦИЯ - ФУНКЦИЯ
35
Если переменные х и у рассматривать как декартовы координаты
точек на плоскости, то графиком числовой функции у = f(x) называется
множество точек координатной плоскости Оху с координатами (x;f{x)).
Основными способами задания функции являются аналитический,
графический и табличный.
При аналитическом способе функция задается посредством формул.
При этом она может быть задана в декартовых и полярных
координатах в явном и неявном виде, в параметрическом виде.
Если в уравнении, определяющем функцию, значение функции у
выражено в явном виде (изолировано в левой части уравнения), то говорят,
что функция задана в явном виде:
V = /(*>•
Пример 3.1. у = 2х + 1.
Данная функция, заданная в явном виде, каждому действительному
числу х € R ставит в соответствие единственное действительное число
г/, для получения которого необходимо значение х умножить на 2 и к
результату прибавить 1.
Область определения данной функции £>(/) = (-оо;+оо), область
изменения E(f) = (-oo;+oo).
Если в уравнении, определяющем функцию, значение функции у не
выражено в явном виде (не изолировано в левой части уравнения), то
говорят, что функция задана в неявном виде уравнением вида:
F(x,y) = 0.
Заметим, что при этом остается требование, чтобы каждому числу
х из области определения соответствовало единственное значение у из
множества значений. Так, например, уравнение х2 + у2 = R2 определяет
две функции: у = \/R2 - х2 и у = -\AR2 -я2- К этому примеру мы еще
вернемся.
Пример 3.2. ху = 1.
Функция задана уравнением в неявном виде. Для каждого
действительного значения х ф 0 существует единственное значение у,
удовлетворяющее этому уравнению. Область определения этой функции D(f) =
(-оо; 0) U (0; +оо), область изменения E{f) = (~оо; 0) U (0; +оо).
При графическом способе функция задается с помощью графика.
Например, по графику функции, изображенному на рис. 26, можно
установить, что значению х = 0 соответствует единственное значение
у = 1, значению х — 1 соответствует единственное значение у = 2и т.д.

36
3 ЛЕКЦИЯ - ФУНКЦИЯ
Рис. 26. Графическое задание функции
При параметрическом задании функции в декартовых координатах
значение функции у и ее аргумента х задаются как функции от
третьей переменной величины, так называемого параметра t из множества Т:
(3.1)
x(t),
y(t).
Если эти функции вычислить при одном и том же значении параметра
t, мы получим координаты точки на плоскости М(х; у); когда
переменная t пробегает все значения из множества Т, точка М(х, у) описывает
некоторую линию в плоскости Оху.
Уравнения ( 3.1) называются параметрическими уравнениями этой
линии. Иногда, исключив параметр t из системы ( 3.1), можно получить
явное или неявное уравнение функции.
Пример 3.3.
(3.2)
Rcost,
Rsint.
Если эти уравнения почленно возвести в квадрат и сложить, то в силу
тождества sin2* -f- cos2£ = 1 получится уравнение х2 + у2 = R2. Этому
уравнению удовлетворяют координаты точек окружности с центром в
начале координат и радиусом Я, так как в силу формулы ( 2.6) для точек
М(х; у), координаты которых удовлетворяют этому уравнению,
расстояние до начала координат О(0; 0) постоянно и равно R.
Если из уравнения х2 + у2 = R2 выразить у в явном виде, получим
две элементарные функции: у — \/R2 — х2 ту-— \JR2 - х2. Каждая из
этих функций задается параметрически одними и теми же уравнениями,
но области изменения параметра для этих функций различны: для первой
3 ЛЕКЦИЯ - ФУНКЦИЯ
31
из них 0 ^ t ^ 7г (графиком служит верхняя полуокружность), для второй
7г ^ t ^ 27Г графиком является нижняя полуокружность).
Пример 3.4.
(3.3)
Г х = a(t - si
\у = а(1-с(
sin£)i
cos*)-
Эти уравнения называются параметрическими уравнениями
циклоиды. Можно показать, что линия, описываемая этими уравнениями
(циклоида), получается как траектория фиксированной точки М окружности
радиусом а, касавшейся в начальный момент оси абсцисс в начале
координат, которая катится без скольжения по оси абсцисс (рис. 27). При этом
в начальный момент точка М совпадает с началом координат.
Рис. 27. Циклоида
При изменении параметра t от 0 до 2тг окружность совершит один
полный оборот. Точка М при этом опишет одну арку циклоиды.
При задании функции в явном виде в полярных координатах полярный
радиус г выражается через полярный угол ip:
(3.4)
г = г(^).
При этом каждому значению ц> из области определения соответствует
единственное значение г. Это, однако, не гарантирует, что при переходе
к декартовым координатам каждому значению х будет соответствовать
единственное значение у.
Пример 3.5. г = а(1 + cosy?).
Кривая, описываемая этим уравнением в полярных координатах,
называется кардиоидой (рис. 28).
Составив таблицу для некоторых значений полярного угла у> и
соответствующих им значений г, построим получившуюся кривую

38
3 ЛЕКЦИЯ - ФУНКЦИЯ
При
ч>
г
0
2а
тг/4
«ф.
тг/2
' 9 ■
Зтг/4
7Г
Q
5тг/4
1*
Зтг/2
а
7тг/4
•'Ф
2тг
2а
табличном способе функция задается посредством таблицы. На-
пример, следующая таблица устанавливает закон, который каждому из
перечисленных в этой таблице значений аргумента х ставит в
соответствие единственное значение у.
X
[У_
-2
-3
-1
-1
-0,5
0
0
1
1
3
Рис. 28. Кардиоида
Пример 3.6. Найти область определения и область изменения
функции у = \/2х - 1.
Решение: Так как операция извлечения квадратного корня
определена только для неотрицательных величин, то данная функция
определена только для значений аргумента х, удовлетворяющих неравенству:
2х-1 ^ 0. Решая это неравенство, получаем: D(f) = [0,5; -f oo).
Поскольку арифметический корень не может быть отрицательным, заключаем,
что область изменения E(f) — [0; -f oo).
Ответ: ОД = [0,5;-boo), E(f) = [0;+оо).
Пример 3.7. Найти область определения и область изменения
функции
У = fogjfr2 - Зх + 2).
Решение: Поскольку областью определения логарифмической
функции является бесконечный интервал (0; -f oo), заключаем, что область
определения D(f) = {х\х2 - Зх -f 2 > 0}. Решим это неравенство, для чего
определим корни уравнения:
х2 - Зх + 2 = 0 ==> xi = 1, х2 = 2. Следовательно, решением
неравенства я2 - Зх + 2 > 0 является (— оо; 1) U (2; +оо).
3 ЛЕКЦИЯ - ФУНКЦИЯ 39
Областью значений логарифмической функции является множество Я,
поэтому E(f) = {у\у е Я}.
Ответ: D(f) = (-оо; 1) U (2; +оо) E(f) = (-оо; +оо).
Пример 3.8. Найти область определения функции у = (ТиК7=2)-
Решение: Недопустимыми значениями аргумента х являются
решения уравнения (х + 1)(х - 2) = 0. Решениями данного уравнения
являются х\ ~ — 1, Х2 = 2, следовательно
ОД Н-оо;-1) U (-1; 2) U (2;+оо).
Ответ: D(f) = (-оо; -1) U (-1; 2) U (2; + оо).
Пример 3.9. Найти область определения функции у = ^^а.
Решение: Допустимые значения аргумента х удовлетворяют
неравенству 1 — х2 > 0. Решая это неравенство, находим, что D(f) =
Ответ: ОД = (-1;+1).
3.2. Операции над функциями. Пусть даны две функции: у = /(х)
и у = £(х) с областью определения D(f) и D(#) соответственно. Тогда
можно определить новую функцию у = /(х) 4- <?(х), значения которой при
каждом х из области определения вычисляются как сумма значений /(х)
и д(х). Область определения функции у = /(х) + д(х) есть D(/) П D(^).
Аналогично определяются функции у = f(x)g(x), у = /(х) - <?(х) и
у = £М причем область определения функции у = ^ есть множество
одпадп{хЫх)^о}.
Пример 3.10. Найти область определения функции у = %/х - 1 + 7^1*
Р е ш е н и е: Представим нашу функцию в виде у = /(х) + #(х), где
/(х) = \/х - 1, д(х) = ^~• Найдем область определения каждой функции.
ОД:х-1^0Ф=>ОД==[1;+оо),
£>(</) : х - 1 ф 0 <=» 1%) = (-оо; 1) U (1; + оо).
Область определения исходной функции есть пересечение этих
множеств.
Ответ: (1; 4-со).
3.3. Сложная функция. Пусть и = /(х) - числовая функция с
областью определения D(f) и областью изменения E(f), at/ = д(и) -
числовая функция с областью определения D(g), E(f) С D{g) и областью
изменения Е(д).

40
3 ЛЕКЦИЯ - ФУНКЦИЯ
Тогда каждому х € D(f) соответствует единственное значение у е
Е(д): каждому х 6 D(f) функция и = f(x) ставит в соответствие
единственное значение и € E{f), которому функция у = д(и) ставит в
соответствие единственное значение у € Е(д). Полученная функция
называется сложной функцией (или суперпозицией двух функций) и обозначается
У = 9(f(x))- Функция и = f(x) называется внутренней функцией, функция
у — д(и) — внешней.
Например, если и = х2 - Зх 4- 2, и у = log2 и, то можно определить
сложную функцию у = log2(a;2 — Зх -f 2).
Пример 3.11. Записать сложную функцию, являющуюся
суперпозицией двух функций ; « = 1 - х2 и у = 4j.
Решение: В данном примере f(x) = 1 - ж2 => #(/) = Я, #(/) =
(-оо; 1), 0(и) = ^ =* £>Ы = (0;+оо), £(#) = (0;+оо). Как видим,
E(f)<j£. D(g). Однако, если определить внутреннюю функцию на
множестве {х\1 - х2 > 0} = (-1; 1), это требование будет выполнено.
Ответ: у — ~?™f при х € (—1; 1).
3.4. Четные и нечетные функции.
Определение 3.2. Множество X с R называется симметричным
относительно начала координат, если —х € X для любого х € X. На
числовой оси симметричное множество X расположено симметрично
относительно точки О.
Определение 3.3. Числовая функция у — f(x) называется четной,
если область ее определения симметрична относительно начала
координат и f(—x) = f(x) для всех х € D(f).
График четной функции симметричен относительно оси ординат, т.к.
точки (х;/(а;)) и (~x;f(-x)) для четной функции симметричны
относительно оси Оу, поскольку f(—x) = f{x). Например, функция у = х2 + 1
является четной, поскольку D(f) = (—оо;+оо) симметрична
относительно начала координат и /(-х) = {-х)г + 1 = х2 + 1 = f(x).
График функции у = #2+1 симметричен относительно оси Оу (рис. 29).
Сумма, разность, произведение и частное двух четных функций есть
четная функция.
Попробуйте доказать это самостоятельно
Определение 3.4. Числовая функция у = f(x) называется нечет-
ной, если область ее определения симметрична относительно начала
координат и f(-x) ~ -f(x) для всех х £ D{f).
3 ЛЕКЦИЯ - ФУНКЦИЯ
4*
у=х>1
Рис. 29. График функции у = х2 + 1
У*
- *.з
Рис. 30. График функции у = х
График нечетной функции симметричен относительно начала
координат (точки О), т.к. точки (я;/(г)) и (—х; f(—x)) для нечетной функции
симметричны относительно точки О, поскольку f{-x) = — f(x).
Например, функция у = хг является нечетной, поскольку ее область
определения D(f) = (-оо; + оо) симметрична относительно начала координат и
/(-*) = (-Х)3 = -X* = -/(«).
График функции у = х3 симметричен относительно точки О ( рис. 30).
Сумма и разность нечетных функций есть нечетная функция.
Произведение и частное нечетных функций есть четная функция.

42
3 ЛЕКЦИЯ - ФУНКЦИЯ
Доказательство этих утверждений проводится аналогично тому, как
это было сделано для четных функций: сначала устанавливается
симметричность области определения, затем проверяется справедливость
требуемого равенства. Докажите их самостоятельно.
Наряду с четными и нечетными существуют функции, не являющиеся
ни теми, ни другими, т.е. не обладающие свойством четности-нечетности.
Например, функции у = х3 + 1, у = ^/х, у = 2*, у = Igx не являются ни
четными, ни нечетными.
Заметим, что любую функцию у = <р(х) с областью определения £>(/),
симметричной относительно начала координат, можно представить в
виде суммы четной и нечетной функции: <р(х) =? f(x) + д(х), где f(x) =
f{x)*f~x) есть функция четная (докажите), а д(х) = ?<«)-*{-«) есть
функция нечетная. Например, функция у = х3 + 1 представима в виде суммы
четной функции f(x) = 1 и нечетной функции д(х) = х3.
Пример 3.12. Функция у = у/х не является ни четной, ни нечетной,
т.к. ее область определения D(f) = [0; -boo) не является симметричной
относительно О.
Пример 3.13. Является ли функция у = ^- четной или нечетной
?
Решение: Область определения этой функции D(f) = (-оо; 0) U
(0; + оо) симметрична относительно О. Проверим выполнение одного из
равенств:
/(-*) = /(*) ют/(-*) =-/(*),
/(-*) = ^ = *=**/(*),
Ответ: t/ = ^-^ не является ни четной ни нечетной функцией.
Пример 3.14. Является ли функция у = ^гт четной или нечетной ?
Решение: Область определения этой функции
D(f) - (-оо; -1) U (-1; 1) U (1; -foo) симметрична относительно О.
Проверим выполнение одного из равенств:
"/(-*)=/(*) ИЛИ /(-*) = -/(*)•
Ответ: у = ^зг четная функция.
3.5. Периодичность функции. Функция у = /(х) называется пё^
риодической с периодом Т ф 0, если х-Гих + Т принадлежат области
определения, f(x) = f(x±T) для любого х € D(/). Обычно под периодом
функции понимают наименьший из всех положительных периодов, если
3 ЛЕКЦИЯ - ФУНКЦИЯ
43
такой период существует. В этом случае все периоды Т кратны
наименьшему периоду То : Т = п • Т0, где п € Z. Из определения следует, что
Г0 > 0.
ПРИМЕР 3.15. Функция у = sinx гмееет период Tq = 27г; т.к. я -f 2?r €
£>(/), х - 2тг € D(f) и sin(x ± 2тг) = sinх.
ПРИМЕР 3.16. Функция у = {х} гшеет период Т0 = 1, т.к. х + 1 €
D(/),s-l€-2>(/)tt{* + l} = {*}«
Сумма, разность, произведение и частное периодических функций с
периодом Т является периодической функцией с периодом Т.
Например, у = {х} + 1 является периодической функцией с периодом
Т = 1, т.к. г/ = {х} и у = 1 периодические функции с тем же периодом.
Если и = /(х) есть периодическая функция с периодом Т, то сложная
функция у = g(f(x)) тоже периодическая (возможно с другим периодом),
если выполняется первое требование в определении периодической
функции.
Например, у = sin2x является периодической функцией с периодом
7о = 7Г.
В пункте 5.2 лекции 5 будет показана справедливость следующего
утверждения:
Теорема 3.1. Если функция у = /(х) периодическая с периодом Т,
то функция у = Kf(kx + Ь) -Ь а будет также периодической с периодом
Т\ = щ, А: € R.
Пример 3.17. Найти период функции у = 2sin(3x + 2).
Решение: у = sin х имеет период Т = 27г, А; = 3. Поэтому период
Ti функции у = 2sin(3x + 2) будет равен 7\ = 2—.
Ответ: 7i = ^.
Пример 3.18. Является ли функция у = \/я периодической ?
Решение: Эта функция не является периодической, т.к., например,
для х = 0 и Т > О х — Т не принадлежит области определения. При Т <0
х 4* Т при х = 0 не принадлежит области определения. Таким образом, не
выполняется первое требование определения периодической функции.
Пример ЗЛ9. Является ли функция у = х периодической ?
Решение: D(f) = (-оо; +оо), поэтому х+Т € £>(/) и х-Т € £>(/),
если х € £>(/). Найдем период Т0 из условия: /(х + Т0) = /(х), т.е.
х + То = г. Отсюда Т0 = 0.
Ответ: у = х не является периодической функцией.

и
3 ЛЕКЦИЯ - ФУНКЦИЯ
3.6. Ограниченные функции.
ОПРЕДЕЛЕНИЕ 3.5. Функция у = f(x) называется ограниченной сверху,
если существует такое число М, что для всех х 6 D(f) выполняется
неравенство: f(x) < М. Функция у = f(x) называется ограниченной
снизу, если существует такое число т, что для всех х € D(f)
выполняется неравенство: f(x) ^ т. Функция, ограниченная сверху и снизу,
называется просто ограниченной.
Например, у = х2 ограничена снизу, например, числом т = -2 и
не ограничена сверху. Функция у == -х4 ограничена сверху, например,
числом М = 1 и не ограничена снизу. Функция j/ == sin х ограничена: -1 <
sin а: < Ь Функции у = ж, у = ^(х), у = tg(ar), # = £ не ограничены.
3.7. Возрастание и убывание функций.
Определение 3.6. Функция у = /(я) называется возрастающей на
множестве X С D(f), если для любых Х\ € X и х2 € X из
неравенства х\ > х2 следует f{x{) > f(x2) (т.е. "чем больше х, тем больше у"),
функция у = f(x) называется убывающей на множестве X С D(f), если
для любых х\ € X UX2 6 X из неравенства х\ > х2 следует f(xx) < f(x2)
(п.с- "ч^к больше х, тем меньше у"). Функция у = f(x) называется
неубывающей на множестве X С D(f), если для любых х\ € X и х2 € X из
неравенства х\ > х2 следует f(x\) ^ f(x2). Функция у = f(x)
называется невозрастающей на множестве X С D(f), если для любых Х\ € X
их2 € X из неравенства Х\ > х2 следует f(xi) ^ f(x2). Функции
только возрастающие или только убывающие, называются монотонными, а
соответствующие множества X — областями монотонности.
Например, функция у = х2 на (-оо;0] убывает, а на [0; 4-оо)
возрастает.
ПРИМЕР 3.20. Доказать возрастание функции у — у/х.
Решение: D(f) — [0; -Ьоо). Возьмем х\ > х2 > 0 два значения
аргумента из области определения. Необходимо доказать, что f(x\) > /(a^)-
рассмотрим разность f(x\) - f(x2) = \fx[ — >/х2. Умножим и разделим
на сумму корней:
у/Х\ у/Х2 ~ V^T+V^ v^T+v^2*
Т.К. Х\ > Х2&ХХ -Х2 >0«* Д*+^ > 0<Ф у^Г- V5* >0
& }(х\) - /(#2) > 0 <=> f(x\) > f{x2). Утверждение доказано.
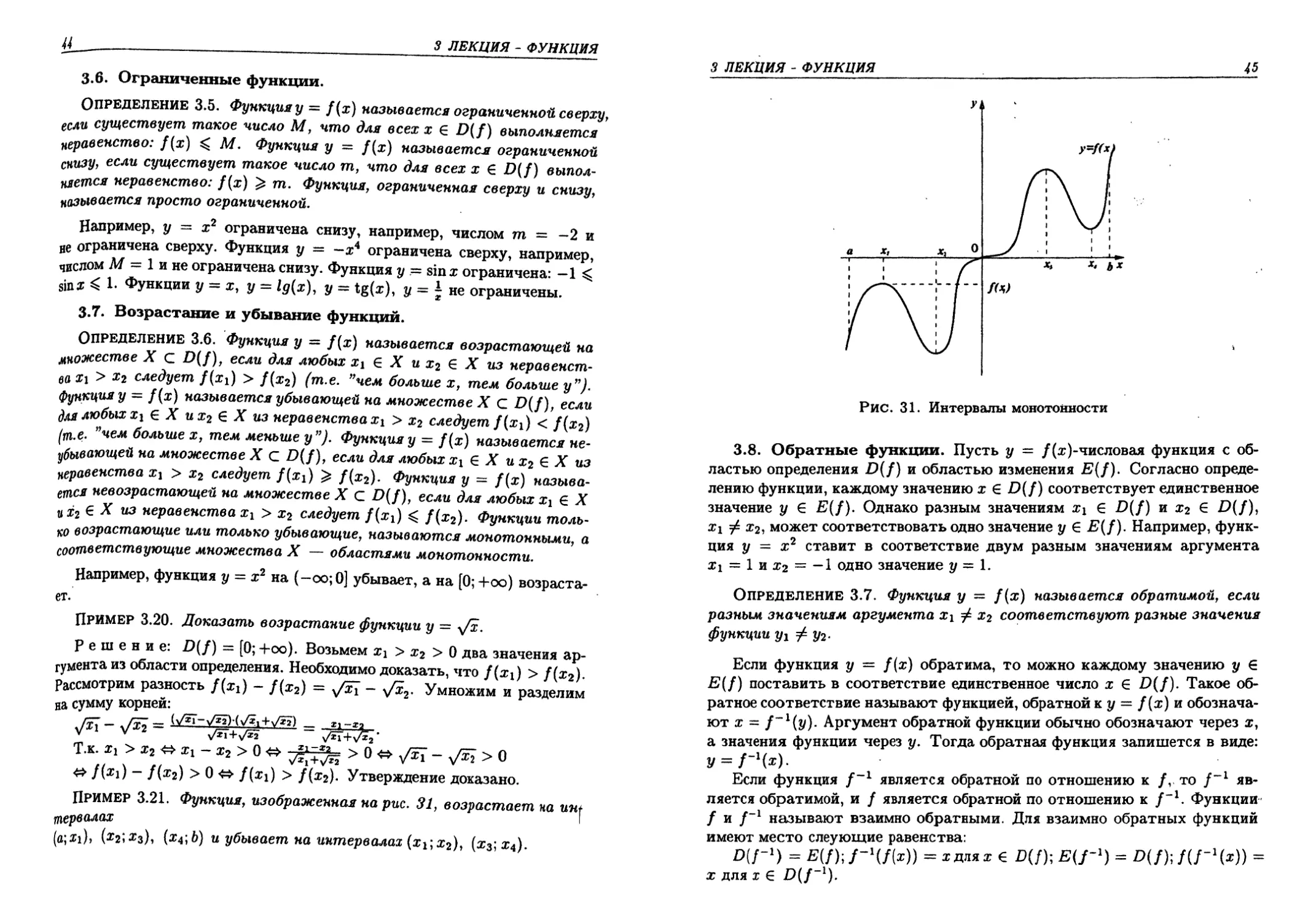
ПРИМЕР 3.21. Функция, изображенная на рис. 31, возрастает па unf
сервалах
(a;#i)> (#2;#з)> {ха\Ь) и убывает на интервалах (х\\х2), [х^х^).
3 ЛЕКЦИЯ - ФУНКЦИЯ
45
УЬ
У=/(х>
Х4 Ь*
fa)
Рис. 31. Интервалы монотонности
3.8. Обратные функции. Пусть у = /(х)-числовая функция с
областью определения D(f) и областью изменения E(f). Согласно
определению функции, каждому значению х € D(f) соответствует единственное
значение у € E(f). Однако разным значениям хх € D(f) и х2 € £>(/),
Х\ ф гг2, может соответствовать одно значение у G E(f). Например,
функция у = х2 ставит в соответствие двум разным значениям аргумента
Х\ = 1 и Х2 = — 1 одно значение у = 1.
Определение 3.7. Функция у = /(а?) называется обратимой, если
разным значениям аргумента Х\ Ф х2 соответствуют разные значения
функции у\фу2.
Если функция у = f(x) обратима, то можно каждому значению у €
E(f) поставить в соответствие единственное число х € D(f). Такое
обратное соответствие называют функцией, обратной к у = f(x) и
обозначают х = /~х{у)- Аргумент обратной функции обычно обозначают через ж,
а значения функции через у. Тогда обратная функция запишется в виде:
У = Г1(х).
Если функция / 1 является обратной по отношению к /, то / 1
является обратимой, и / является обратной по отношению к /-1. Функции
/ и f~l называют взаимно обратными. Для взаимно обратных функций
имеют место слеующие равенства:
D(f~l) = E{f)J~\f{x)) = хдлях € D(f); £?(/">) = Z>(/);/(/-»(*)) =
ж для х € £>(/ *).

46
3 ЛЕКЦИЯ - ФУНКЦИЯ
Функция является обратимой тогда и только тогда, когда каждое свое
значение она принимает только один раз. В частности, периодические и
четные функции не являются обратимыми.
Графики взаимно обратных функций симметричны относительно
прямой у = х ( рис. 32), что является следствием замены х на у и у на х.
Примем без доказательства следующую теорему.
Теорема 3.2. Если у = f(x) возрастающая (убывающая)
непрерывная функция, то она имеет обратную, которая тоже является
возрастающей (убывающей).
Функция, обратная нечетной, также нечетная.
Пример 3.22. Найти обратную функцию к функции у = 2х — 1.
Построить графики обеих функций.
Решение: Выразим значение х через у : у — 2х — 1 <=> х = *^.
Заменим х на у, а у на х. Уравнение обратной функции примет вид:
У — ^f^- Графики этих функций изображены на рис. 33.
Рис. 32. График прямой и обратной функций
Функция у = х2, как отмечалось, необратима, однако если ее
рассматривать только при х 6 [0; f оо), то она будет монотонной и, следовательно,
обратимой. График обратной функции у = у/х изображен на рисунке 34
4- ЛЕКЦИЯ - ФУНКЦИЯ
47
У
1
7
1 у=2х-1
/ !
X
Рис. 33. График функции у = 2х - 1 и обратной к ней
♦у
y=x^x>0)j
Рис. 34. Графики функции у = х2 и у = у/х
4. ЛЕКЦИЯ - ФУНКЦИЯ
Элементарные функции. Свойства основных элементарных функций.
4.1. Основные понятия.
Определение 4.1. Основными элементарными функциями
являются: постоянная функция (у — с), степенная (у = хп,п € jR),
показательная (у = а*), логарифмическая (у = logaz);
тригонометрические (у = sin я, у = cos ж, j/ = tgx,*/ = ctgx) м обратные к ним (у =
arcsinx, у = arccosx, у = arctg:r, у = arcctgx).
Определение 4.2. Элементарными функциями называются те
функции, которые можно задать в явном виде одним аналитическим

48
4. ЛЕКЦИЯ - ФУНКЦИЯ
выражением из основных элементарных функций с помощью
арифметических операций и нахождения функции от функций, примененных
конечное число раз.
Примерами элементарных функций являются многочлены,
дробно-рациональная функция (отношение двух многочленов), иррациональные
(корень из элементарной функции) и т.д. Не являются элементарными,
например, функции:
Г 1,щ
У = < 0, щ
1-1,
при х > О,
при х = О,
при х < О,
при х € Q,
при х € /,
{х2 + 2х + 3, при х < О,
3, при 0 ^ х < 5,
^/х, при х > 5.
и т.д.
Рассмотрим свойства некоторых элементарных функций.
4.2. Линейная функция. Прямая на плоскости.
ОПРЕДЕЛЕНИЕ 4.3. Линейной функцией называется функция вида:
(4.1) у = кх + 6.
£>(/) = (_оо;+оо); при А; ф 0 £7(/) = (-оо;+оо), функция неограни-
чена, непериодическая. При 6 = 0 функция нечетная; при к > 0 функция
возрастает, при к < 0 — убывает, при к = 0 — постоянна. (Докажите
все эти свойства самостоятельно).
Точки пересечения с осями координат (0; 6) и (—|; 0); Графиком
функции у — kx + b является прямая с угловым коэффициентом (тангенс угла
с осью Ох) А: = tg<p (рис. 35, 36) при к ф 0. Обратная функция у = £=й
также является линейной.
Условием параллельности двух невертикальных прямых на плоскости
у = к\Х 4- &i и у = &2Х + &2 является:
(4.2) *,=■**, ,
т.к. tpi = у?2 <=> tg<Pi = tgy>2 «=» &i = fc2-
Угол между двумя прямыми на плоскости определяется с помощью
известной тригонометрической формулы: tg(<p2 - <р\) = i+tgVrtg^ = 1+^-
^. ЛЕКЦИЯ - ФУНКЦИЯ
49
(4.3)
¥>2 - <^i = arctg
&2 - Ari
' 1 + fci • fc2
Используя формулу ( 4.3), получим условие перпендикулярности двух
невертикальных прямых. В этом случае <р2 - <рх = 90° =» tg(<p2 - ¥>i) =
00 ===> 1+*i "*2 = 0. Окончательно получаем условие перпендикулярности
двух прямых на плоскости:
(4-4) *i-Jb2 = -l.
Как известно, две точки определяют прямую на плоскости. Покажем,
что уравнение прямой на плоскости, проходящей через две точки (хх\уЛ
и {Х2\У2), имеет вид:
(4.5)
У -2/1
X!
2/2-2/1 х2 - хх
Действительно, выразив у из уравнения (4.5), получим уравнение вида
I *л; при л _ £-*- и 6 = ^ - и-JQ.. ал; кроме того, координаты данных
двух точек удовлетворяют уравнению ( 4.5), т.е. эта прямая проходит
через данные две точки.
y=kx+b, k>0
Рис. 35. Линейная функция у = кх+ Ь щт к > 0
Из изложенного следует, что уравнение ( 4.5) описывает любую
прямую на плоскости, кроме вертикальной. Действительно, если две точки

50
I ЛЕКЦИЯ - ФУНКЦИЯ
,к<0
y=kx+b, k<0
Рис. 36. Линейная функция у — кх + 6 при к < О
лежат на вертикальной прямой, то Х\ — х2 и в уравнении (4.5) к = *?_£
не существует (угол у? = 90° ==> А: = tgy? = oo). Заметим также, что
если две точки лежат на горизонтальной прямой, то у\ — у2 => к = 0
и уравнение прямой ( 4.5) приобретает вид у = 6. Данная точка прямой
(я0; Уо) и угловой коэффициент к также определяют прямую. Легко
показать (сделайте это самостоятельно по аналогии с предыдущим), что ее
уравнение имеет вид:
(4.6) у - уо = к(х - х0).
Определение 4.4. Пучком прямых, проходящих через данную точку
{хо;уо), называется множество всех прямых на плоскости, проходящих
через данную точку.
Из сказанного следует, что однопараметрическое уравнение всех
прямых пучка, кроме вертикальной, имеет вид (4.6). Уравнение конкретной
прямой пучка получается из ( 4.6) при фиксированном к.
Наряду с уравнением ( 4.1) прямая на плоскости может быть задана
так называемым общим уравнением прямой: ^
(4.7) Ах + By + С = 0,
где коэффициенты Л и Вне равны нулю одновременно.
Действительно, уравнение ( 4.1) легко записать в виде ( 4.7), перенеся
все члены в левую часть. Наоборот, если В ф 0 в уравнении ( 4.7), то
выражая г/, получаем уравнение у — -^ж - ~
-|х - § вида ( 4.1) При В = О,
4. ЛЕКЦИЯ - ФУНКЦИЯ
51
А ф 0 из уравнения (4.7) можно выразить х = - ~ и получается уравнение
вертикальной прямой. Таким образом, уравнение ( 4.7) является более
общим уравнением прямой, чем ( 4.1), что объясняет его название.
4.3. Обратная пропорциональная зависимость.
Определение 4.5. Обратной пропорциональной зависимостью
называется функция вида: у = \; D(f) = (-oo; 0) U (0; +оо); E(f) = (-oo; 0) U
(0;+оо).
Функция неограниченная, непериодическая. Функция нечетная т.к. D(f)
симметрична относительно точки О и /(-х) = •— = —£ = -/(#)•
Функция убывает на(-оо; 0) и на (0; -f оо).
Докажем последнее утверждение. Возьмем х\ > X2 > 0 и рассмотрим
/On) - f(x2) = £ - £ = а=а. хх > х2 > 0 4=* х2 - хг < 0, хг • я2 > 0 «=>
^ < 0 <=» /(*х) - /(*2) < 0 *=* /(хО < /(*2).
Точек пересечения с осями координат нет. Графиком функции у — j
является гипербола (рис. 37). Функция обратимая, обратная функция у =
I
Неправильно говорить, что у = - убывает на (—оо;0) U (0; +оо), т.к.,
например, для zi = 1, х2 = —1, Xi > х2, /(#i) > /(х2). Нельзя так
же утверждать, что функция на объединении интервалов возрастает, т.к.,
например, /(2) < /(1).
4.4. Квадратичная зависимость у = х2. D(f) = (-oo; -f oo); E(f) =
[0; -f-оо) Функция ограничена снизу: у ^ 0; не периодическая. Функция
четная, т.к. D(f) симметрична относительно О и /(—я) = (-х)2 — х2 = /(я).
Функция убывает на (-оо;0) и возрастает на (0;+оо). Докажем
возрастание на (0;+оо).Возьмем хх > х2 > 0 и рассмотрим /(xi) - /(х2) =
х\ - х\ = (х\ — х2)(хх +х2),хх > х2 > 0 <==> Х\ - х2 > 0, xi + х2 > 0 <=»
(zi - x2)(a:! + x2) > 0 <!=> /(хх) - f(x2) > 0 <=» /(xj) > f(x2). Точка
пересечения с осью Оу (0; 0). Графиком функции у = х2 является
парабола (рис. 38).Функция необратимая, но если рассмотреть одну ее ветвь на
[0;+оо) (или на (-оо;0]), то существует обратная функция у = у/х (или
у=-у/х).
4.5. Степенная функция у = хп. Рассмотренные функции у = х,
у — х2,у—\ являются частными случаями этой функции при п = 1,2, -1
соответственно. Рассмотрим другие случаи, у = х3; /}(/) = (-оо;+оо),
-£(/) ~ (—оо;-Ьоо) Функция неограниченная, непериодическая. Функция
яечетная. Функция монотонно возрастает. Точка пересечения с осями (0;0).
Графиком функции у == х3 является кубическая парабола (рис. 39).
Функция имеет обратную функцию у = tfx. Функции у = х5, у = х7, у = х9 и

52
I ЛЕКЦИЯ - ФУНКЦИЯ
т.д. обладают аналогичными свойствами и имеют приблизительно такие
же графики. Функции у = х*,у — хв,у = я8 и т.д. обладают свойствами,
аналогичными свойствам функции у = х2 и имеют похожий график.
Рис. 37. График гиперболы у = ~
У-
1
\ 1
/
у=х^/
/ •
0 1 х
Рис. 38. График параболы у = х2
4.6. Показательная функция у = ах,а > 0, а ф 1. D(/) =
= (-оо; +оо), E(f) = (0; + оо) Функция ограничена снизу: у > 0;
непериодическая. Функция ни четная, ни нечетная. Функция при а > 1 возрастает,
при а < 1 убывает. Точка пересечения с осью Оу : (0; 1). График функции
приведен на рис. 40. Функция обратимая, обратная функция у = log0 х.
4.7. Логарифмическая функция у = 1о^х,а > 0, а ^ 1-
Поскольку функция у = loga а: является обратной к функции у — ах, она обладает
следующими свойствами: £>(/) = (0;-foo), E{f) = (-оо;4~оо). Функция
неограниченная, непериодическая. Функция ни четная, ни нечетная.
Функция при a > 1 возрастает, при о < 1 убывает. Точка пересечения с осью
4. ЛЕКЦИЯ - ФУНКЦИЯ
53
Рис. 39. График параболы у — х3
У=ах, 0<а<1 Ау
у=а* а>1
log#, а>1
y=log^t, 0<а<1
Рис. 40. График показательной и логарифмической функций
Ох : (1;0). График функции приведен на рис. 40. Функция обратимая,
обратная функция у = а*.
4.8. Тригонометрические функции.
у = sin ж.
Щ/) — (-оо;-hoc), E(f) = [—1;1]. Функция ограничена: ~1 ^ sinx ^
1. Функция нечетная, т.к. D(f) симметрична относительно О и f(—x) =

54
4. ЛЕКЦИЯ - ФУНКЦИЯ
sin(-:r) = -sinz = ~/(х). Функция периодическая с периодом Т = 2я\
Функция не монотонная: возрастает на (-| + 2тгп; \ +27гп), n € Z; убывает
на (f+27гп; у+2тгп), где п е Z. Точки пересечения с осью Ох : (тгп; 0), п €
Z, с осью Оу : (0;0). Графиком функции является синусоида ( рис. 41).
Функция необратимая, но если рассмотреть ее на [-|; |], то существует
обратная функция у = arcsinrr.
у = cos х.
D(f) — (-оо;+оо), E(f) = [-1;1] Функция ограничена -1 ^ cosx ^
1. Функция четная, т.к. £)(/) симметрична относительно О и f(-x) =
cos(-x) = cos я = f(x). Функция периодическая с периодом Т = 2п,
Функция не монотонная: убывает на (27гп;7Г + 2тгп) и возрастает на
(я- + 27гп; 2тг + 2тгп), п € Z.
Точки пересечения с осью Ох: (| + тгп;0); n € Z точка пересечения с
осью Оу: (0;1).
График функции у = cos а: изображен на рис. 42.
Функция необратимая, но если рассмотреть ее на [0; 7г], то существует
обратная функция у = arccos x.
Рис. 41. График
функции у — sin х
Рис. 42. График
функции у = cos х
y = tgx.
D(f) = {х| х€ К,хф - + тгп,где n G Z}; £(/) = (-оо;+оо).
Функция неограниченная.
Функция нечетная, т.к. D(f) симметрична относительно О и /(—ж)
tg(-z) = - tga;■= -/(я).
Функция периодическая с периодом Т — п.
4. ЛЕКЦИЯ - ФУНКЦИЯ
55
Функция не монотонная; возрастает на (—§ + тгп; | + 7гп), п 6 Z.
Точки пересечения с осью Ох: (7гп; 0); n € Z, точка пересечения с осью
Оу: (0;0).
График функции у = tg x изображен на рис. 43
Функция необратимая, но если рассмотреть ее на (-§; |), то
существует обратная функция у = arctg x.
у = ctg х.
D{f) = {х\ х е R, х ф тгп, где п € Z}; £(/) = (-оо; +оо).
Функция неограниченная.
Функция нечетная, т.к. D(f) симметрична относительно О и f(-x) =
ctg(-:r) = - ctgs = -f{x).
Функция периодическая с периодом Т = 7г.
Функция не монотонная; убывает на (7гп; яг + 7гп), п € Z.
Точки пересечения с осью Ох: (~ + 7гп; 0) п € Z.
График функции у = ctg s изображен на рис. 44.
Функция необратимая, но если рассмотреть ее на (0; 7г), то существует
обратная функция у = arcctg x.
Рис. 43. График
функции у — tg х
Рис. 44. График
функции у — ctg х
4.9. Обратные тригонометрические функции. Свойства этих
функций получаются из свойств тригонометрических функций на
основании п. 3.8
у = arcsm x.

56
4. ЛЕКЦИЯ - ФУНКЦИЯ
D(/) = [-l;l];E(/)=[-J;Jj.
Функция ограничена: — | ^ arcsin а: < |.
Функция нечетная: arcsin(-x) = - arcsin х.
Функция непериодическая.
Функция возрастает на области определения.
Точка пересечения с осями: (0;0).
График функции изображен на рис. 45.
у = arccos х.
£>(/) = [-1;1]; E(f) = [Q;n].
Функция ограничена: 0 ^ arccosx ^ п. Можно показать, что
arccos(-a;) = 7г — arccosx.
Функция убывает на области определения.
Точка пересечения с осью Ох: (1;0); с осью Оу: (0; §•).
График функции изображен на рис. 46.
л/2
-7t/2t
Рис. 45. График
функции у = arcsin x
Рис. 46. График
функции у = arccos x
у = arctg я.
Я(/) = (-оо;+оо); Е{}) ^ {-\,\)
Функция ограничена: -| < arctg x < |.
Функция нечетная: arctg( —х) = — arctg x
Функция непериодическая.
3 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИЯ
51
Функция возрастает на области определения.
Точка пересечения с осями: (0;0).
График функции изображен на рис. 47.
у = arcctg х.
£>(/) = (-оо;+оо); £?(/)=(-|;|).
Функция ограничена: 0 < arcctg х < 7г.
Можно показать, что arcctg(-a:) == 7Г - arcctg x.
Функция убывает на области оределения.
Точка пересечения с осью Оу: (0; |).
График функции изображен на рис. 48.
УА
J я/2
О
__</
X
-я/2
Рис. 47. График Рис. 48. График
функции у - arctg х функции у = arcctg x
3. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИЯ
На этом занятии мы на практике познакомимся с основными
свойствами функций.
ПРИМЕР 3.1. Найдите область определения функции:у = л/^х+-^=ш.

58
3 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИЯ
( х^О
\ х > -:
Решение: Область определения данной функции есть пересечение
областей определения функций у = у/^х т.е.-ж ^ 0 и у = ~m^i T-e-:
Г 2 + 00
\ 2 + я^0
Таким образом, область определения искомой функции есть решение
системы неравенств:
2 + х^0 <^
2 + х/О
Ответ: (-2;0].
Пример 3.2. Найдите область определения функции у = arcsin(x -f
i)3.
Решение: Область определения данной функции есть множество
решений системы неравенств:
/ (х + 1)3^1
\ (х + I)3 > -1
Решая данную систему, получаем:
/ 1+Ц1 f i<0
\ z+l>-l \0-2
Ответ:Д(/) = [-2;0]
ПРИМЕР 3.3. Исследуйте функцию на четность и нечетность:
Решение: Область определения данной функции D(f) — (—00; +00)
симметрична относительно начала координат. Проверим выполнение
второго условия: f(-x) = е~*+е* = /(ж), т.е. функция четная.
Ответ: четная.
ПРИМЕР 3.4. Исследуйте функцию у = х2 — Ъх + 6 на четность и
нечетность.
Решение: Область определение этой функции есть (-оо;+оо),
симметрична относительно 0. Проверим выполнение второго условия:
/(-ж) = (-х)2 - 5(-ж) + 6 = я2+ 5*+ 67^ ±f{x)
Следовательно, данная функция свойствами четности, нечетности не
обладает. Заметим, что ее можно представить в виде суммы четной (у —
х2 + 6) и нечетной (у = -Ъх) функций.
Ответ: четностью, нечетностью не обладает.
ПРИМЕР 3.5. Для приведенной функции найдите наименьший
положительный период Т, если она периодическая: у = 5 sin За;.
3 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИЯ
59
Решение: Период функции у = sin x равен 2п. В соответствии с
теоремой п.3.5 наименьший положительный период функции у = 5sin3x
будет равен ^.
Ответ: Ц.
Пример 3.6. Найдите наименьший положительный период функции
у — 3 sin Ъх 4- 4 cos 7x.
Решение: В соответствии с теоремой 3.1 функция у = 3 sin Ъх будет
периодической с периодом 7\ = ^р функция j/ = 4cos7x — периодической
с периодом Т2 = у. Таким образом значения первой функции будут
повторяться через 2£, ^, ~,..., второй — через ^, у1, Очевидно, что
наименьший общий положительный период этих двух функций равен 2п;
это и будет наименьшим положительным периодом их суммы.
Ответ: Т = 2яг
Самостоятельная работа
Найдите область определения функции:
Пример 3.7. у = у/ТТх.
Пример 3.8. у = \/1 + х.
Пример 3.9. у = ^~2.
Пример 3.10. у = \/9 - я2.
Пример 3.11. у - \/2 + а:- я2.
Пример 3.12. з/ = ^2.
Пример 3.13. p = ln(f±f).
Пример 3.14. у = arccos(~^).
Пример 3.15. у = lg(*';y2).
Пример 3.16. г/= arcsin(lg(^))
Исследуйте функцию на четность и нечетность:
Пример 3.17. г/= 21^11.
Пример 3.18. у = v^9 - я2.
Пример 3.19. 2/ = ч/ГТТТх2 - v/1 ~ x + а:2.

60
4 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИЯ
Пример 3.20. у = i/(x + l)2 + {/{х - I)2.
Пример 3.21. y = lg(£f).
Пример 3.22. у = х2 - х + 1.
Для приведенной функции найдите наименьший положительный период
Т, если она периодическая.
Пример 3.23. у = 2 sin Зх + 7 cos 5х.
Пример 3.24. у = >/tgx.
Пример 3.25. у = sin2x.
Пример 3.26. у = sin х/я-
4. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИЯ
Пример 4.1. Для данной функции определите область, в которой
она будет обратимой, и найдите обратную функцию: у — 2х + 3.
Решение: Данная линейная функция монотонно возрастает при
х 6 Я, поэтому обратима. Для нахождения обратной функции выразим х
через у и затем обозначим х через у а у через х: у = 2х + 3<=*х = f ~" § **
» = !-!• (
Ответ: Множество, на котором функция обратима: R. Обратная
функция у = f - §.
Пример 4.2. Пусть f{x) = \/1 + х2; найдите 2/(х) - /2(х).
Решение: Подставим в искомую функцию у = 2^х* - /2(х) вместо
f(x) данное выражение: f(x) = л/1 + х2. Получим:у = 2^1+х2-(л/1 + х2)2
или: у = 2v/IT?r - 1 - х2.
Ответ: 2><*> - /2(х) = 2^+**-1-х2.
Пример 4.3. Найдите уравнение прямой, удовлетворяющей
следующим условиям: прямая проходит через точку М(1; 1) под углом 135° к
оси Ох.
Решение: В уравнении прямой (4.6) у — уо = k(x - xq) угловой
коэффициент равен тангенсу угла прямой с осью Ох : А: = tg(<p). Для
данной прямой к = tgl35° = -1. Подставив в уравнение прямой (4.6)
координаты точки М, получим у — 1 = -(х — 1).
Ответ: у = -х -f 2.
Л ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИЯ 0/
Пример 4.4. Вычислите углы треугольника, стороны которого
даны уравнениями: li : 18x+6y-17 = 0,/2 : 14х-7у+15 = 0,/з = 5х+10у-9 =
0.
Решение: Обозначим -4-точку пересечения прямых 1Х и l2, В-
прямых /2 и /3l С-прямых /i и /3. Найдем угол А А Л£?С по формуле:
tg /LA = ^~^ , где fci, &2-угловые коэффициенты прямых 1\ и /г- Выразим
у из уравнений /i и l2: h : 18х + бу — 17 = 0 <=» у = -Зх 4- ^; Ь :
14х - 7у 4- 15 = 0 <==> у = 2х + у; осюда fej = -3, k2 = 2. Получаем:
tgZi4 = ~тт = +1 ^^ ^ = 45°. Остальные углы ААВС найдите
самостоятельно.
Пример 4.5. Найдите координаты вершины А в ААВС, стороны
которого даны уравнениями: АВ : у = х, АС : у = —х + 4, ВС : у = 5х — 4.
Решение: Найдем координаты вершины А как решение системы
уравнений:
{;=!,+4 ~{j=2 ^л(2;2)- °твет:л(2-2)-
Пример 4.6. Функция f(x)-линейная. Найдите эту функцию если
/(-l) = 2ti/(2) = -3;
Решение: Линейная функция имеет вид /(х) = А;х 4- Ь. Подставив
данные значения аргумента и функции, получаем систему уравнений для
нахождения неизвестных параметров к и Ь:
f-l.* + 6 = 2, _J*=-f>
\ 22fc + &=-3; ^\ 6= |,
Ответ: /(х) = -§х + |.
Пример 4.7. Напишите условия, задающие множество точек ААВС,
если Л(1;1), В(2;3), С(3;0).
Решение: Напишем уравнение сторон ААВС, используя уравнение
прямой, проходящей через две точки.
АВ: |5г=|5г^У = 2х-1
ВС: 5Е§ = fEf «*у = -Зх + 9
^^ • 0-1 3-1 ^ * 2^2
Прямая >IjB делит плоскость Оху на две полуплоскости: у ^ 2х — 1 и
у ^ 2х - 1. ААВС расположен в той из них, в которой находится
вершина С. Поскольку координаты точки С(3;0) удовлетворяют второму из
приведенных неравенств, заключаем, что ААВС лежит в полуплоскости,
удовлетворяющей неравенству у $ 2х - 1.

62
4 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИЯ
Аналогично определяем, что координаты точек ААВС удовлетворяют
неравенствам у < -Зх + 9 и i/ ^ ~"f "*** §• Окончательно заключаем,
что ААВС определяется пересечением этих полуплоскостей, т.е. системой
неравенств:
{У ^ 2х - 1
у ^ -Зх + 9
»>-! + §
Самостоятельная работа
Для данной функции определите область, в которой она будет
обратимой и найдите обратную функцию.
Пример 4.8. у = х2 - 1.
Пример 4.9. у = v^l - х3.
Пример 4.10. г/ = 1п(|).
Пример 4.11. у = arctg(3x).
Пусть </?(£/) = arcsin(/,/(&) = lg(x); найдите:
Пример 4.12. у?(/(х)).
Пример 4.13. ^(/(0,1)).
Пример 4.14. <р(/(10));
Пример 4.15. у>(/(1));
Пример 4.16. f(ip(x));
Пусть f(x) = >/1 + х2; найдите:
Пример 4.17. f(-l).
Пример 4.18. f(-z).
Пример 4.19. /(£).
Пример 4.20. у^у.
Найдите уравнения прямых, удовлетворяющих следующим условиям:
Пример 4.21. Прямая проходит через точку М(2; 1) под углом 60° к
оси Ох.
Пример 4.22. Прямая проходит через точки Mi(-2; 1) и М2(0;3).
5 ЛЕКЦИЯ - ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ 68
Пример 4.23. Прямая проходит через точку М(1; 2) параллельно
прямой у = Зх 4- 7.
Пример 4.24. Прямая проходит через точку М( —2;3)
перпендикулярно прямой у = 2х - 8.
Пример 4.25. Прямая проходит через начало координат и образует
угол 45° с прямой у — 2х 4- 5.
Функция /(х) — линейная. Найдите эту функцию если:
Пример 4.26. /(0) = 0 к /(2) = 5.
Пример 4.27. /(-1) = 2 и /(2) = 3.
Пример 4.28. /(2) = 3 и /(4) = 3.
5. ЛЕКЦИЯ - ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ
ГРАФИКОВ
Параллельный перенос, сжатие и растяжение графиков. Построение
графиков с модулями.
Графики многих функций можно получить из ранее рассмотренных с
помощью элементарных геометрических преобразований: параллельного
переноса, сжатия, растяжения, симметричного отображения. Рассмотрим
некоторые из этих преобразований. Для каждого из элементарных
преобразований предлагается два способа построения графика: с помощью
преобразования графика и с помощью преобразования системы координат.
Обучающийся должен выбрать тот, который кажется ему проще и
овладеть им. В каждом случае считается известным график функции у = /(х).
5.1. Параллельный перенос графиков. График функции
У ~ /М + Ь получается из графика функции у = /(х) с помощью его
переноса на вектор b — (0;Ь). Действительно, в этом случае ко всем
ординатам графика у — f(x) прибавляется величина 6, что означает сдвиг
графика вдоль оси Оу. Если b > 0, то график функции у = /(х)
переносится вверх параллельно оси Оу на 6, если b < 0, то график функции
у = f(x) переносится вниз параллельно оси Оу на |6| (рис. 49). Заметим,
что вместо переноса графика, можно перенести в противоположном
направлении ось Ох (если 6 > 0 - вниз, если b < 0 - вверх), прибавив ко всем
значениям по оси Оу величину 6.

64 5 ЛЕКЦИЯ - ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ
Рис. 49. Построение графика функции у = f(x) + Ь
Пример 5.1. График функции у = х2 - 1 (рис. 50) смещен на 1 вниз
параллельно оси Оу относительно графика функции у = х2.
Рис. 50. Построение графика функции у = дг - 1
График функции у = /(аг+а) получается с помощью переноса графика
функции у = /(ж) на вектор а = (-а;0). Действительно, перейдя к новым
координатам X = я + a, Y = у параллельным переносом вдоль оси Ох
на -о, заметим, что относительно новых координат получится исходный
график функции Y = f(X). Если а > О, то старые координаты
получаются из новых сдвигом направо вдоль оси Ох на а, т.к. х = X — а. Если же
сдвигать график, а не систему координат, то его нужно двигать в
противоположном направлении — налево. Итак, если а > 0, то график функции
у =s f(x) переносится налево параллельно оси Ох на а, если а < 0, то
график функции у = f(x) переносится направо вдоль оси Ох на \а\ (рис. 51).
Вместо переноса графика можно перенести в противоположном
направлении ось Оу (если а > 0 - вправо, если а < 0 - влево), отняв от всех
значений по оси Ох величину а.
Пример 5.2. График функции у = (я — 2)2 смещен на 2 ед. вправо
параллельно оси Ох относительно графика функции у — х2. (рис. 52).
5 ЛЕКЦИЯ - ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ 65
y=f(x+a)
y=ft»
Рис. 51. Построение графика функции у = f(x -f a)
У=(х-2)2
Z. х
о| Г
Рис. 52. Построение графика функции у = (я - 2)2
5.2. Сжатие и растяжение графиков. График функции у = kf(x),
где k € R, получается с помощью "растяжения" графика функции у =
f(x) в А: раз в направлении от оси Ох. "Растяжение" здесь понимается
как умножение на к ординат всех точек графика у ='/(ж). При к > 1 это
будет действительно растяжение в к раз от оси Ох вдоль оси Оу. При
0 < fc < 1 это будет сжатие в £ раз к оси Ох вдоль оси Оу. При к ^ -1 это
будет растяжение в \к\ раз с последующим симметричным отображением
относительно оси Ох (перевернуть сверху вниз); при -1 ^ к < 0 это будет
сжатие в щ раз и симметрия относительно оси Ох ( рис. 53). В
частности, график функции у = -/(х) получается симметричным отображением
относительно оси Ох графика функции у = f(x).
Вместо преобразования графика при к > 0 можно исправить значения
по оси Оу, умножив их на *. При Л < 0 в этом случае пришлось бы менять
направление оси, что неудобно; лучше перевернуть график сверху вниз.
График функции у = f(kx), где к € Я, получается с помощью
"сжатия" графика у = f(x) в к раз в направлении к оси Оу. "Сжатие" здесь
понимается как деление на к абсцисс всех точек графика у = f(x).
Действительно, если, например, /(1) = 0, то, сделав замену X = кх> У = у,
У

66
5 ЛЕКЦИЯ - ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ
=-3sin х
Рис. 53. Построение графика функции у = —3sin x
получим, что функция у = f(kx) обращается в нуль при кх = 1, т.е. при
х = 1
х к-
При к > 1 график функции у = f(x) сжимается в к раз к оси Оу
вдоль оси Ох; при 0 < к < 1 график функции у = /(х) растягивается в
£ раз от оси Оу вдоль оси Ох; при А; ^ -1 исходньй график сжимается в
|fc| раз и симметрично отражается относительно оси Оу (слева направо);
при — 1 < к < 0 исходный график растягивается в щ раз с последующей
симметрией относительно оси Оу,
В частности, график функции у = /(-х) получается из графика
функции у = /(—х) симметрией относительно оси Оу.
Вместо преобразования графика при к > 0 можно исправить значения
по оси Ох, поделив их на А;. При к < О в этом случае следует
предварительно перевернуть график слева направо.
Пример 5.3. График функции у = cos 2x получается из графика у =
cos х сжатием в 2 раза к оси Оу; график функции у = 1п(—х) получается
из графика у — In х смлиеетрией относительно оси Оу ( рис. 54)-
Рис. 54. Построение трафика функции у = 1п(—х)
5 ЛЕКЦИЯ - ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ
67
Пользуясь изложенными методами, приведем последовательность
преобразований при построении графика функции у = f(kx + 6), если дан
график функции у = /(х):
с нарисовать график функции у — f{x);
о получить график функции j/ = /(x-f-6), сдвинув исходный на вектор
6 = (-6; 0), как описано в п. 5.1;
о получить график функции у = /(А:х 4- 6), "сжав" предыдущий в к
раз к оси Ог/, как описано выше.
Пример 5.4. Написать последовательность преобразований и
построить график функции у = у/А — 5х. Решение:
о нарисуем график функции у = у/х;
о получим график функции у = у/х + 4, сдвинув исходный на 4
единицы влево вдоль оси Ох;
о получим график функции у = у/—Ьх 4- 4, сжав предыдущий в 5 раз
к оси Оу и затем отобразив симметрично относительно оси Оу.
Построение графика показано на рис. 55
Замечание. Теперь понятно, что если функция у = /(х) периодическая
с периодом Т, то функция у = К • f(kx + 6) + а тоже периодическая с
периодом Т\ — щ. (п. 3.5 лекции 3). Действительно, график последней
функции получается из исходного сдвигом вдоль оси Ох, что не меняет
период, последующим "сжатием" вдоль оси Ох, что "уменьшает" период
в |А;| раз (период Т делится на |А:|), и окончательным умножением всех
ординат на К с последующим прибавлением а, что также не изменяет
получившийся период 7\ = щ.
5.3. Построение графиков с модулями. График функции
у = |/(х)| получается из графика функции у = /(х) следующим
образом (рис. 56)
в все части графика функции у = /(х), лежащие ниже оси Ох, следует
отобразить вверх симметрично относительно этой оси;
в оставшиеся внизу части исходного графика следует стереть.
Действительно, по определению модуля действительного числа имеем:
(5.1)
1/(
если /(х) ^ 0,
если /(х) < 0.
Таким образом, те участки исходного графика, которые лежат не ниже
оси Ох (/(х) ^ 0), менять не нужно, а для тех участков, которые лежат
ниже оси Ох, нужно построить функцию у = —/(х). В соответствии с
п. 5.2 это получается симметричным отображением исходного графика

68 5 ЛЕКЦИЯ - ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ
относительно оси Ох. Заметим, что полученный график лежит не ниже
оси Ох, что естественно, т.к. \f{x)\ ^ 0 для Vx € D(f).
х .4
4/5 х
Рис. 55. Построение графика функции у = у/4 - 5я
Рис. 56. Построение графика функции у = |/(я)1
Пример 5.5. Построение графика функции у = |х2 — 1| показано на
рис. 57.
График функции у = /(|я|) получается из графика функции у = f(x)
следующим образом (рис. 58):
© все части графика функции у = /(х), лежащие слева от оси Оу,
следует стереть;
о оставшуюся часть графика следует отобразить налево симметрично
относительно оси Оу.
Действительно, по определению модуля действительного числа имеем:
(5.2)
f г, если х > О,
\х\ = \
\ ~х, если х < 0.
5 ЛЕКЦИЯ - ЭЛЕМЕНТАРНЫЕ ПРЕОБРА ЗОВАНИЯ ГРА ФИКОВ 69 <.
Рис. 57. Построение графика функции у = \х2 — 1|
Таким образом, не нужно изменять те участки исходного графика, для
которых х ^ 0, а для х<0 (слева от оси Оу) следует построить график
функции у = /(-х). В соответствии с п. 5.2 это получается
симметричным отображением исходного графика относительно оси Оу. Заметим,
что полученный график симметричен относительно оси Оу, что
естественно, т.к. функция у = /(|х|) четная (докажите самостоятельно).
Рис. 58. Построение графика функции у = f(\x\)
Пример 5.6. Построение графика функции у = (\х\
рис. 59
- 2)2 показано на
Элементарными методами можно строить эскизы графиков более
сложных функций.
Пример 5.7. Построить эскиз графика у — \/sinx
Решение: Построение графика показано на рис. 60. Заметим,
что график отсутствует таму где sinx < 0, так как D(x) = {x\ sin ж ^
0}.

70
5 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПОСТРОЕНИЕ ГРАФИКОВ
Рис. 59. Построение графика функции у = (|х| - 2)2
Кроме того, так как у/и > и при О < и < 1, то график у = vsinx
(сплошная линия) будет лежать не ниже графика у = sin х (пунктирная
линия), если их нарисовать в одних осях.
Рис. 60. Построение графика функции у = \Jsmx
5. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПОСТРОЕНИЕ
ГРАФИКОВ ФУНКЦИЙ
Пример 5.1. С помощью элементарных преобразований постройте
график функции: у ~ х2 — х - 2.
Решение: Выделим полный квадрат из правой части уравнения
функции: у
■х-2
y = *a-x+i-S«=»y = (s-!)2-f. Граф]
этой функции получается следующей последовательностью элементарных
преобразований (рис. 61):
1)У = х2-
5 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПОСТРОЕНИЕ ГРАФИКОВ
71
2) у = {х - |)2. Сдвиг вправо вдоль Ох на \.
i) у — {х - \)2 - |. Сдвиг вниз вдоль Оу на |.
Рис. 61. Построение графика функции у = х2 — х — 2
Пример 5.2. Используя сложение, деление функций, постройте
график функции: у = х + К
Решение: В одних осях координат нарисуем графики следующих
функций (рис. 62):
1)у = х,
2)у = J,
3)у = х + 1.
^ у=х+1/х
Рис. 62. Построение графика функции у = а: 4- j
Пример 5.3. Постройте график сложной функции у = sin2 x.
Решение: В одних осях координат нарисуем графики функций:
1)?/ = sinx,

п
5 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПОСТРОЕНИЕ ГРАФИКОВ
2)у = sin2 х.
Учитывая, что квадрат числа меньшего единицы, меньше исходного
числа, получим график (рис. 63).
ч/\/\
y=sinx
Рис. 63. Построение графика функции у — sin2 х
Пример 5.4. Постройте график функции в полярной системе
координат: г = -Д- (прямая линия).
sin у?
Решение: Вычислим значения г для некоторых значений (р 6 (0; 7г)
■ см. таблицу.
yi
г
Го
00
7Г
fi
2
7Г
4
у/2
Я"
2
7Г I
2
СО
I
0
У
А
/Ъ
I
I
X
3
Рис. 64. График функции г = ;Д-
Соединив плавной линией найденные точки, получим линию вдоль оси
Ох, проходящую через точку (0;1). Докажем что эта линия - прямая (рис.
64). Действительно: из АОЛВ => cosy? = ^| = J ==> г = ~-.
Пример 5.5. Постройте линию, описываемую уравнением, у — ыгг
Решение: Сначала построим график функции у = ^±1 (рис. 65).
Затем, пользуясь определением \х\ (2.1), строим график (рис. 66) функции
jxi+i = / ёт при О0,х^1,
Iх1"1 1 гй при х < 0.
Наконец, строим линию описываемую уравнением у — if!rf (рис. 67):
5 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПОСТРОЕНИЕ ГРАФИКОВ
73
Ч
Рис. 65. График функции у = f^j
Рис. 66. График функции у = J-j^f
Рис. 67. График функции у = jfjrr

74
5 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПОСТРОЕНИЕ ГРАФИКОВ
|l£l±i|_/ (^приу^О,
||1М' I -Ц}^приу<0.
Пример 5.6. Постройте линию, описываемую уравнением у = щ^-
Решение: Для построения графика данного примера сначала
постройте график функции у = •—, Затем, в соответствии с определением
\х\, сотрите ту часть графика, которая расположена слева от оси Оу, а
оставшуюся справа часть, отразите симметрично оси Оу.
Ответ: рис. 68.
щ
j T i х
Рис. 68. График функции у = ^зрл
Пример 5.7. Постройте линию, описываемую уравнением у = \х2 —
х-2|.
Решение: Для построения графика данного примера сначала
постройте график функции у = х2 — х - 2. Затем отразите симметрично оси
Ох ту часть графика, которая осталась снизу от оси Ох. Затем сотрите
ту часть графика, котарая расположена в нижней полуплоскости.
Ответ: рис. 69.
5 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПОСТРОЕНИЕ ГРАФИКОВ
75
Рис. 69. График функции у = \х2 - х — 2\
Самостоятельная работа
Постройте графики функций:
Пример 5.8. у = 2 - х2;
Пример 5.9. у = (х - I)3 + 2;
Пример 5.10. у = 2=2;
Пример 5.11. у = ^;
Пример 5.12. у = v^r.
Пример 5.13. j/ = ln(l - ж).
Пример 5.14. у = cos2x.
Пример 5.15. у = 5sin(2a; - |).
Используя сложение, деление функций, постройте графики функций:
Пример 5.16. у = 4,.
Пример 5.17. у = я + £.
Пример 5.18. у = ^.
Пример 5.19. у = :^у- Локон Аньези.
Пример 5.20. у = ^у. Серпентин Ньютона1.
Пример 5.21. у = я;2 + £. Трезубец Ньютона.
1И.Ньютон( 1643-1727) — великий английский математик, механик, физик и

76
5 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПОСТРОЕНИЕ ГРАФИКОВ
Постройте графики сложных функций:
Пример 5.22. у = tg2x.
Пример 5.23. у = \/sin х.
Пример 5.24. у = -4-.
* sin я
Пример 5.25. у = xsinx.
Пример 5.26. у = j~.
Пример 5.27. y = lg(cosx).
Пример 5.28. у = 2~хsinx.
Постройте графики функций в полярной системе координат:
Пример 5.29. г = <р. Спираль Архимеда2.
Пример 5.30. г = е*\ Логарифмическая спираль.
ПРИМЕР 5.31. г = ~. Гиперболическая спираль.
Пример 5.32. г = 2cos</?. Окружность.
Пример 5.33. г = 1. Окружность.
Пример 5.34. г = 3 cos 4<^?. Четырехлепестковая роза.
Постройте линии, описываемые уравнениями:
Пример 5.35. у = |lg|x||.
Пример 5.36. у = 2К
Пример 5.37. у = х • |х|.
2Архнмед(Ш в до н. э.) — великий греческий математик и механик.
в ЛЕКЦИЯ - КРИВЫЕ ВТОРОГО ПОРЯДКА
77
6. ЛЕКЦИЯ - КРИВЫЕ ВТОРОГО ПОРЯДКА
Уравнение линии. Кривые второго порядка. Окружность. Эллипс.
Гипербола. Парабола. Приведение к каноническому виду.
6.1. Уравнение линии в декартовых и полярных координатах.
В лекции 3 было введено понятие неявной функции, задаваемой
уравнением вида F(x, у) = 0.
Определение 6.1. Множество точек плоскости, координаты
которых удовлетворяют некоторому уравнению
(6.1) F(x;y)=0
называется линией (плоской кривой).
Не всякое уравнение определяет линию. Например, уравнение x2-f у2 =
-1 не определяет никакой линии. Кроме того, линия может состоять из
отдельных точек. Так, например, уравнению х2 ■+■ у2 — 0 удовлетворяет
только начало координат.
Линия не обязательно является графиком функции. Так, например,
уравнение х2 -I- у2 = 1 определяет окружность с центром в начале
координат и радиуса 1 (т.к. d = yjx2 4- у2 = 1, расстояние от начала координат
равно 1). Однако это не будет графиком функции у от х, т.к. каждому х,
|х| ^ 1, соответствует два значения у: у — ±\/1 — х2, т.е. линия задается
двумя функциями у = у/\ — х2 (верхняя полуокружность) и у = — v/Г—х2
(нижняя полуокружность).
Уравнение произвольной окружности с центром в точке М(а;6) и
радиусом R будет иметь вид:
(6.2) (х - а)2 + (у - Ь)2 = Л2,
т.к. окружность радиусом R есть геометрическое место точек
плоскости, находящихся на расстоянии R от центра, т.е. в соответствии с
формулой ( 6.2) d = у/(х - а)2 + (у - Ь)2 = Л.
В частности, окружность с центром в начале координат, радиусом Я,
описывается уравнением
х2 + у2 = Д2.
Пример 6.1. Какую линию описывает уравнение х2 + у2 = Ях?

78
6 ЛЕКЦИЯ - КРИВЫЕ ВТОРОГО ПОРЯДКА
Решение: Перенося Rx в левую часть и выделяя полный квадрат,
получаем:
х2 + у2 = Rx <=Ф х2 - Rx + у2 = 0 <=> х2 - Да: + Щ- + у2 = ~ <==^
(*-f)+3/2 = £.
Ответ: данное уравнение описывает окружность с центром в точке
М(|;0) и радиусом f.
Линия может определяться на плоскости уравнением как в декартовых,
так и в полярных координатах: F((p; г) = 0. Если при этом зависимость
г от (р обладает тем свойством, что каждому значению у? из области
определения соответствует единственное значение г, то данная линия будет
графиком функции г от <р : г = /(у>).
Пример 6.2. Построить график функции, заданной в полярных ко-
ординатах уравнением г = 2 sin3y?, у? € (—оо; со).
Решение: Составим таблицу некоторых значений этой функции:
\<р\
г
0
0
7Г
18
1
IT
9
у/г
б
2
2w
9
v/3
5тг
18
1
7Г
3
0
7Г
2
-2
А1
>тз 1 Утиз о
1ц
г
/ 7С/3\ /27С/3
v
Рис. 70. График функции г = 2 sin 3<р в декартовых координатах
Далее, пользуясь тем, что из вида графика функции г = 2 sin 3y>,
приведенного в декартовых координатах на рис. 70, следует, что
неотрицательные значения г повторяются на промежутках tp € [0;|], у> €
l2^'71"]' Ч> € [-^м"~з1 и т*д" Отсюда заключаем, что если в
полярных координатах построить график в секторе ip Е [0; |], то в секторах
у? 6 (у; 7г], у? б [—у; -§] и т.д. вид графика будет аналогичный, а в
секторах (р € (|;у), Ч> € (~§;0) и т.д. графика не будет, т.к. там г < 0.
Соединяя плавной линией точки с координатами, приведенными в
таблице, получаем график рис. 71.
6 ЛЕКЦИЯ - КРИВЫЕ ВТОРОГО ПОРЯДКА
19
Рис. 71. График функции г = 2 sin Зу> в полярных координатах
Такой график называют называют "трехлепестковая роза".
6.2. Кривые второго порядка.
Определение 6.2. Кривой второго порядка называется линия,
определяемая в декартовых координатах уравнением:
(б.З) Ах2 + 2Вху + Су2 + 2Dx + 2Еу + F = 0.
Здесь коэффициенты - действительные числа и, по крайней мере,
одно из чисел А,В или С не равно нулю. Удобство таких обозначений для
коэффициентов (2£, 2D, 2Е) станет ясно позже.
Всего существует три "реальных" кривых второго порядка: эллипс,
(окружность — частный случаи эллипса) гипербола и парабола, не
считая такие линии, как "пара пересекающихся прямых" (ху = 0), "пара
параллельных прямых" ((х - у)2 = 4), "точка" ((х - 5)2 + (у - I)2 = 0),
"прямая" (х - I)2 = 0) и "мнимые кривые" (х2 4- у2 + 5 = 0), которым не
соответствует ни одна точка.
6.3. Окружность. Ранее было получено уравнение ( 6.2)
окружности с центром в точке М(а;Ь), радиусом Я. Это уравнение вида ( 6.3),
т.е. окружность есть кривая второго порядка — можно показать, что
уравнение ( 6.3), в котором Л = СиЯ = 0с помощью дополнения до
полного квадрата каждой группы членов Ах2 -f 2Dx и By2 + 2Ey
приводится к виду ( 6.2), определяющему окружность радиуса Я, или к виду:
(х - а)2 •+ (у - Ь)2 = -Я2, не определяющему линию при R ф 0. Покажем
это на примере.
Пример 6.3. Показать, что уравнение 2х2 4- 2у2 — Ах + 8г/ — 13 = 0
определяет окружность.

so
6 ЛЕКЦИЯ - КРИВЫЕ ВТОРОГО ПОРЯДКА
Решение: Поделив обе части на 2, получим уравнение в виде:
х2 + у2 - 2х + 4у - б, 5 = 0 или, выделяя полный квадрат: (х2 - 2х + 1) +
(у2 + 4у + 4) = 11,5 ^ (х - I)2 + (у + 2)2 = И, 5. Мы получим уравнение
окружности с центром М(1; -2) и радиусом Л = \/1\, 5.
Пример 6.4. Показать, что уравнение х2 + у2 + 6х - 6у + 22 = 0 ме
определяет никакой линии.
Решение: Аналогично предыдущему, выделяя полный квадрат,
получаем: х2 + у2 + 6х-6у + 22 = О Ф» (х2+6х + 9) + (у2 -6y-f 9) = -4 «»
(* + 3)2 + (у-3)2 = -4.
6.4. Эллипс.
Определение 6.3. Эллипсом называется множество всех точек плос
кости, сумма расстояний каждой из которых от двух данных точек
этой плоскости, называемых фокусами, равна постоянной величине.
Обозначим фокусы Fx и F^, расстояние между ними 2с, а сумму
расстояний до них от точек эллипса через 2а (2а > 2с). Выберем декартову
систему координат как показано на рис. 72. По определению эллипса:
MF\ + MF2 = 2а. Пользуясь формулой (2.6) получаем:
у/{х + с)2 + у2 + у/(х - с)2 + у2 = 2о & у/(х + с)2 + г/2 =
= 2a~v/(*-c)2 + 2/2=* (х+с)2+у2 = 4a2+(x-c)2+t/2-4a v/(s - с)2 + у2 «*
4» а2 - сх = а^-с)2^^2 => fl2 ~ 2cxa2 + с2х2 = а2((х - с)2 + у2) «»
^(а2-с2)х2 +aV = a2{a*-<?)
F,(-c;0)
'У
^М(х;у)
° f2(c;°) x
Рис. 72. Фокусы эллипса и гиперболы
6 ЛЕКЦИЯ - КРИВЫЕ ВТОРОГО ПОРЯДКА
81
Обозначив Ь2 = а2 - с2 > 0, получаем: 62х2 4- а2у2 = а2Ъ2 или:
(6.4) ~ + fr = 1.
а2 + Ь2
Уравнение ( 6.4) называется каноническим уравнением эллипса, аиб-1-
полуосями, а — большая полуось, Ь — малая, т.к. Ь = у/а2 — с2 < а.
Поскольку х и у входят в уравнение только в четных степенях, эллипс
симметричен относительно осей Ох и Оу. Выразив у из уравнения ( 6.4),
получаем: у = ±-у/а2 - х2, |х| ^ а, что означает, что эллипс
состоит из двух симметричных половин, верхней у
у = -%у/а2 - х2. При х = а, у
= -\/а2 - х2 и нижней
а-
с2. При х = а, у = 0, при убывании х от а до 0, у
возрастает от 0 до Ь. С учетом симметрии получаем линию, изображенную
на рис. 73. Точки пересечения эллипса с осями координат называются
вершинами Ai(-a;0), A2{a;0), Bi(0;-ft), В2(0;Ь). Отношением = J
называется эксцентриситетом эллипса.
Рис. 73. Эллипс
Так как 2а > 2с, то е < 1. Эксцентриситет определяет форму эллипса:
чем меньше £, тем меньше его малая полуось Ь отличается от большой
полуоси а (£| = —^ = 1 — ^ =• 1 - е2), т.е. тем меньше эллипс вытянут
вдоль фокальной оси Ох. В пределе, при е -» 0, a ■= b и получается
окружность х2 + у2 = а2 радиусом а При этом с = у/а2 — Ь2 — 0, т.е. F\ — F2 = 0.
Если эллипс расположен тах, что центр его симметрии находится в точке
Р(хо',Уо), а полуоси параллельны осям координат, то, перейдя к новым
координатам X = х — хо, У = У — Уо, начало которых совпадает с
точкой Р, а оси параллельны исходным (см. п. 2.8), получим, что в новых
v-2 у2
координатах эллипс описывается каноническим уравнением ^ + р"
Уравнение такого эллипса в старых координатах будет:
уг __
= 1.

82
6 ЛЕКЦИЯ - КРИВЫЕ ВТОРОГО ПОРЯДКА
(лч\ (д-агр)2 (у-уо)2
(6.5) ___ + ___ = 1
6.5. Гипербола.
Определение 6.4. Гиперболой называется множество всех точек
плоскости, модуль разности расстояний каждой из которых от двух
данных точек этой плоскости, называемых фокусами, равен постоянной
величине.
Обозначим фокусы F\ и F2, расстояние между ними 2с, а модуль
разности расстояний до них от точек гиперболы через 2а (2с > 2а > 0).
Выберем декартову систему координат, как показано на рис. 72. По
определению гиперболы: MF\ - MF2 = ±2а. Пользуясь формулой (2.6),
аналогично тому, как это было сделано для эллипса, получаем:
у/{х + с)2 + у2 - у/(х-с)2 + у2 = ±2а =* (а2 - с2)х2 + а2у2 = а2(а2 - с2).
Обозначив Ь2 =г с2 — а2 > 0 (сравните с выводом формулы (6.4) для
эллипса), получаем: —Ъ2х2 + a2j/2 = —b2a2, или:
<м> £-£ = 1
Уравнение ( 6.6) называется каноническим уравнением гиперболы, а и 6
— полуосями, a - действительной полуосью, b - мнимой. Так как х и у
входят в уравнение только в четных степенях, гипербола симметрична
относительно осей Ох и Оу. Выразив у из уравнения ( 6.6)^ получаем:
у = ±^у/х2 — а2, |я| ^ а, что означает, что гипербола состоит из двух
симметричных половин, верхней у — \\/х2 — о? и нижней t/ = — \\/х2 — а2.
При я = а у = 0, при возрастании я от 0 до -Ьоо, у для верхней части
возрастает от 0 до -f 00. С учетом симметрии, получаем линию,
изображенную на рис. 74
Точки пересечения гиперболы с осью Ох (фокальной осью)
называются ее вершинами Лг(а;0), A\(—a\G). С осью ординат гипербола не
пересекается, поэтому фокальная ось называется действительной осью (а
— действительная полуось), а перпендикулярная ей ось — мнимой осью
{Ь — мнимая полуось). Можно показать, что при неограниченном
возрастании абсциссы точка гиперболы неограниченно приближается к
прямой у = £г (изображена на рис. 74 пунктиром). Такая прямая, к которой
неограниченно приближаете л некоторая линия, называется асимптотой.
Из соображений симметрии вытекает, что у гиперболы две асимптоты:
у = £# и у = --я, изображенные на рис. 74 пунктиром. Прямоугольник, с
6 ЛЕКЦИЯ - КРИВЫЕ ВТОРОГО ПОРЯДКА
83
F^
ч
-с
i
*х
У
ь
••Чч
'" Ц
С
^
X
Рис. 74. Гипербола
центром в начале координат, со сторонами 2а и 26, параллельными осям,
называется основным. Асимптоты являются его диагоналями.
Отношение е — J называется эксцентриситетом гиперболы. Т.к. 2а <
2с, то е > 1. Эксцентриситет определяет форму гиперболы: чем меньше
£, тем более вытянут в направлении фокальной оси ее основной
прямоугольник (£* = с ~" = jjj — l=e2 — 1). Если a = 6, гипербола
называется равносторонней (равнобочной). Для нее х2 — у2 = а2, асимптоты:
у = х, у — —х, е — у ota = -\/2. Если центр гиперболы (центр ее
симметрии) находится в точке Р(#о;2/о)> а оси параллельны осям координат,
то, применяя параллельный перенос координат (п. 2.8), аналогично тому,
как это было сделано для эллипса, получим уравнение гиперболы:
(6 7ч (* ~ *о)2 (у - Уо)2
= 1
а2 Ь2
Уравнение асимптот такой гиперболы будет: у — уо
6.6. Парабола.
±£(х-*о)
Определение 6.5. Параболой называется множество всех точек
плоскости, равноудаленных от данной точки F, называемой фокусом,
и данной прямой d, называемой директрисой (F £ d).
Обозначим расстояние от фокуса до директрисы р. Эта величина
называется параметром параболы. Выберем декартову систему координат
как показано на рис. 75.
По определению параболы MF-MN. Из рис. 75. ясно, что:

84
6 ЛЕКЦИЯ - КРИВЫЕ ВТОРОГО ПОРЯДКА
N
Р
"2
d
1
и
О
X "Р )
2
Рис. 75. Фокус и директриса параболы
MN = х + |; MF = J(x - |)2 + у2.
Приравнивая, получаем:
* + f = V(s-~!)2 + y2=**2 +рх + £ = *2 ~ рх + £ + у2 **у2 = 2рх
(6.8) у2 = 2рх
Уравнение ( 6.8) называется каноническим уравнением параболы. Т.к. у
входит в уравнение в четной степени, парабола симметрична
относительно оси Ох. Выразив у из уравнения, получаем: у = ±у/2рх, х ^ 0. При
х — 0 у = 0, при возрастании я от 0 до +оо г/ для верхней части
возрастает от 0 до +оо. С учетом симметрии получаем линию, изображенную
на рис. 76.
Ось симметрии параболы называется фокальной осью (ось Ох на рис.
76), точка пересечения пораболы с ней называется вершиной пораболы
(точка О на рис. 76). Если вершина параболы находится в точке Р(х0\ у0),
фокальная ось параллельна и одинаково направлена с осью Ох и
расстояние от директрисы до фокуса равно Р, то с помощью параллельного
переноса осей координат нетрудно получить уравнение такой параболы:
(6.9) (у-2/о)2 = 2р(я-х0)
ПРИМЕР 6.5. Найти фокус, директрису, фокальную ось для параболы
у — 4я2.
6 ЛЕКЦИЯ - КРИВЫЕ ВТОРОГО ПОРЯДКА
85
1
Р:
2б °1
d:
1Y -
V °р *х
\2
Рис. 76. Парабола
Решение: Как известно, осью симметрии параболы у = х2 является
ось Оу> а вершиной - точка О, поэтому фокальной осью будет ось Оу>
вершиной — начало координат.
Для определения фокуса и директрисы запишем уравнение данной
параболы в виде: х2 '"'= \у, откуда 2р = |, р = |. Поэтому фокус имеет
координаты F(0; ^), а директриса - уравнение у = -™ (см. рис. 77).
Рис. 77. График параболы у = 4х
= 4т2
6.7. Понятие о приведении общего уравнения второго
порядка к каноническому виду. Если в общем уравнении кривой второго
порядка (6.3)
Ах2 + 2Вху + Су2 + 2Dx + 2Еу + F = О

86,
6 ЛЕКЦИЯ - КРИВЫЕ ВТОРОГО ПОРЯДКА
коэффициент 2J5 Ф 0, то методами, которые будут изложены позже
(лекция 34) это уравнение преобразуется к виду, в котором отсутствует член
с произведением координат (т.е. 2В = 0).
Для приведения к каноническому виду уравнения ( 6.3), в котором
2Б = 0, необходимо дополнить члены, содержащие х и у, до полных
квадратов.
Если при этом {В = 0) А = С, то получится окружность (пример 6.3),
точка или мнимая окружность (пример 6.4).
Если при этом (В = 0) А ф С и АС > 0, то получится эллипс (пример
6.8) или мнимый эллипс.
Если при этом (В = 0) А ф С и А • С < 0, то получится гипербола
(пример 6.6).
Если при этом (В = 0) А • С = 0 (т.е. А = 0 или С = 0), то получится
парабола (пример 6.7)
Пример 6.6. Привести к каноническому виду уравнение кривой х2 -
2у2 4- 2х 4- 12г/ - 33 = 0, определить и построить ее.
Решение: Для членов, содержащих х, и членов, содержащих у,
выполним следующие преобразования с выделением полного квадрата:
х2 + 2х = х2 + 2х + 1 - 1 = (х + I)2 - 1;
~2у2 + 12г/ = -2(у2 - 6у) = -2(t/2 - 6у + 9 - 9) = -2(у - З)2 + 18.
Данное уравнение теперь можно переписать так:
(х4- I)2 - 2(у - З)2 - 1 + 18 - 33 = 0,
откуда
(х -Ь I)2 - 2(у - З)2 = 16
или г^п« г.,-а*'_
16 8
Выполним преобразование параллельного переноса осей с новым
началом Oi(-l; 3): X = х + 1; У = у - 3. Тогда уравнение кривой примет
вид:
16 8
Это уравнение гиперболы с полуосями а = 4 и 6 = 2v2. На рис. 78 эта
кривая построена в системе координат 0\XY. Но можно отнести ее и
к исходной системе координат Оху, которая также имеется на рис. 78.
В соответствии с изложенным в п. 6.5, уравнение асимптот в исходной
системе координат будет: у-3 = ±^(х4-1). После упрощения получаем:
6 ЛЕКЦИЯ - КРИВЫЕ ВТОРОГО ПОРЯДКА
81
vi
*%
X
V\
^v »»
^s. ч»^
*ч>?>
yf
..-'
*-'
s «•'
Х-'
„*'
.'* yS
t» ^r
3
s*.
** V^
V
k
Ч >v
^ \
То *%*„\.
v*
„"'
"
ч
"Ч
X
Рис. 78. Гипербола Щ±£ - ^t = i
Пример 6.7. Приведите к каноническому виду уравнение и
определите вид кривой: х2 - 6х - 4у 4- 29 = 0.
Решение: Выделим полный квадрат: х2 - 6х - 4у + 29 = 0
х2 - 6х 4- 9 = \у - 20 <±=> (х - З)2 = 4(г/ - 5). Сделав замену координат
Х=х-3,К = у-5 мы получим каноническое уравнение параболы X2 =
4Y с осью OY и параметром р = 2. Таким образом исходная парабола
имела вершину Л(3; 5) и ось х = 3 параллельную оси Оу (рис. 79).
Пример 6.8. Приведите к каноническому виду уравнение и
определите вид кривой: х2 4- 4у2 4- 2х — 24у 4- 21 = 0.
Решение: Выделив полный квадрат, получим уравнение: (х +1)2 4-
4(у - З)2 = 16. Сделав замену координат: Л" = х 4-1, У = у - 3, получим
каноническое уравнение эллипса: X2 4- 4У2 ^ ^ + ^ = 1 с параметрами
а = 4, 6 = 2. Таким образом, исходный эллипс имел центр Л( —1;3) и
полуоси а = 4, 6 = 2 (рис. 80).

88
6 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - КРИВЫЕ ВТОРОГО ПОРЯДКА
Рис. 79. Решение примера 6.7
3.
-5 -l: I 3
Рис. 80. Решение примера 6.8
6. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - КРИВЫЕ ВТОРОГО
ПОРЯДКА
ПРИМЕР 6.1. Составьте уравнение окружности, имеющей центр
0(2; -5) и радиус R = 4.
Решение: В соответствии с формулой (6.2) искомое уравнение
имеет вид: (х - 2)2 -f (у Н- 5)2 = 16.
Ответ: (х - 2)2 + (у + 5)2 = 16.
Пример 6.2. Составьте уравнение эллипса, зная, что сумма
полуосей равна 8 и расстояние между фокусами равно 8.
Решение: Из условия имеем: а + Ь - 8, 2с = 8. С учетом того,
что Ь2 = о2 — с2, находим с = 4, а = 5, b — 3. Искомое уравнение эллипса
будет: g + £=l.
Ответ: §| + £ = 1.
Пример 6.3. Составьте уравнение гиперболы, зная, что фокусы
Fi(10;0) и F2(-10; 0) и что гипербола проходит через точку М(12;3\/5)
6 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - КРИВЫЕ ВТОРОГО ПОРЯДКА 89
Решение: Из условия имеем: с = 10, \MF\ - MF2\ = 2а & 2а =
1^/(2 - 10)2 + (3n/5 - О)2 - д/(12 + 10)* +.(3>/5 - 0)2| ф* а = 8. С учетом
того, что б2 = с2 — а2, находим а = 8, с = 10,6 = 6. Искомое уравнение
гиперболы будет: ^ - ^ = 1.
Ответ: g - g = 1.
Пример 6.4. Составьте уравнение параболы, зная, что фокус
имеет координаты (5;0), а ось ординат является директрисой.
Решение: Поскольку расстояние от директрисы параболы до ее
полюса равно параметру р, а вершина находится на середине, из условия
следует, что р = 5 и вершина расположена в точке Л(2,5;0). Таким
образом, в новых координатах X = х — 2,5; У = у каноническое уравнение
параболы будет: У2 = 10Х, а в старых координатах: у2 = 10(а; -2,5).
Ответ: у2 = 10х - 25.
ПРИМЕР 6.5. Приведите к каноническому виду уравнение х2 + у2 —
2х + 6у — 5 = 07 определите вид кривой и ее параметры.
Решение: Выделим полный квадрат: х2 — 2х Н- у2 + 6у — 5 = 0 <=>
х2 - 2х + 1 + у2 + 6у + 9 - 1 - 9 - 5 == 0 <* (х - I)2 + (у + З)2 =' 15
В соответствии с формулой (6.2) это есть уравнение окружности с
центром в точке Л(1; -3), радиусом у/Ъ.
Ответ: (х - I)2 + (у + З)2 = 15.
Пример 6.6. Приведите к каноническому виду уравнение х2 + 4у2 +
4я — 16у — 8 = 0, определите вид кривой и ее параметры:
Решение: Выделим полный квадрат: х2 +Ах + 4у2 - 16у - 8 = 0 <=>
а:2+4х + 4 + 4^2--16у4-16~4--16~8 = 0^(а:4-2)2 + 4(у2--42/ + 4)--28^
(х + 2)2 + 4(у - 2)2 = 28 <* ^Ц^ + &=р~ = L Сделав замену координат:
X = # 4- 2, У = у — 2, в новых координатах получим уравнение эллипса
28 + у = 1 с полуосями о = \/28 и Ь = \/7. Таким образом, в старых
координатах эллипс имеет центр Л(-2; 2) и полуоси а = 2\/7 и 6 = \/7-
Ответ: ^ + « = 1
Пример 6.7. Приведите к каноническому виду уравнение х2 4- 2у2 4*
8х - 4 = 0, определите вид кривой и ее параметры.
Решение: Выделим полный квадрат:
гЧ2у2+8а:-4 = 0 Ф» я2 4-8*4-164-2i/2-16-4 = 0 *► (х4-4)24-2y2-20 =
U ^ 20 ^ 10 А
Сделав замену координат X = а: 4- 4, У = #, убеждаемся, что эта
кривая — эллипс, с полуосями а = 2у/Ъ и 6 = \/10 и центром Л(-4;0).

90
6 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - КРИВЫЕ^ТОРОГО ПОРЯДКА
Ответ: ^ + £ = 1.
Самостоятельная работа
Пример 6.8. Составьте уравнение окружности, имеющей центр
0(—3;4) и проходящей через начало координат.
ПРИМЕР 6.9. Составьте уравнение окружности, проходящей через
точки
М1(0;2),М2(1;1),М3(2;-2).
ПРИМЕР 6.10. На оси абсцисс найдите центр окружности,
проходящей через точки Л (2; 3) и В(5; 2) и напишите уравнение этой окружное-
ти.
Пример 6.11. Составьте уравнение эллипса, зная что полуоси
равны 4 и 2.
ПРИМЕР 6.12. Составьте уравнение эллипса, зная что расстояние
между фокусами равно 6 и большая полуось равна 5.
Пример 6.13. Составьте уравнение эллипса, зная что большая
полуось равна 10 и эксцентриситет е = 0,8.
Пример 6.14. Составьте уравнение эллипса, зная что малая полу-
ось равна 3 и эксцентриситет £ = ^.
ПРИМЕР 6.15. Найдите длину полуосей, координаты фокусов и
эксцентриситет эллипса: 25ж2 4- 169у2 = 4225.
Пример 6.16. Составьте уравнение гиперболы, зная что
вещественная полуось равна 5 и вершины делят расстояние между центром
и фокусами пополам.
Пример 6.17. Составьте уравнение гиперболы, зная что
вещественная полуось равна 6 и гипербола проходит через точку (9;~4)-
Пример 6.18. Составьте каноническое уравнение гиперболы, зная что
гипербола проходит через точки Мх(-5;2) и М2(2\/2; \/2).
Пример 6.19. Составьте уравнение гиперболы, зная что фокусы
Fi(10;0) и F2(-10;0) и гипербола проходит через точку М (12; 3\/Е).
Пример 6.20. Найдите координаты фокусов, эксцентриситегпу урав-
2 2
нение асимптот гиперболы ~— ^ = 1.
Пример 6.21. Составьте уравнение параболы, зная что парабола
симметрична оси Ох, проходит через начало координат и через точку М(1; -4)
6 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - КРИВЫЕ ВТОРОГО ПОРЯДКА 91
Пример 6.22. Составьте уравнение параболы, зная что парабола
симметрична оси Оу, фокус помещается в точке F(0;2) и вершина
совпадает с началом координат.
Пример 6.23. Составьте уравнение параболы, зная что парабола
симметрична оси Оу, проходит через начало координат и через точку М(6; —2).
Пример 6.24. Определить координаты вершины А, величину
параметра р, и направление оси параболы у2 4- 8х — 16 = 0.
Приведите к каноническому виду уравнения, и определите вид кривых
и их параметры:
Пример 6.25. 9х2 - 2Ьу2 - 18х - Шу - 291 = 0.
Пример 6.26. Ъх2 - 6г/2 + Юх - \2у - 31 = 0.
Пример 6.27. х2 - 4у2 + 6х + 5 = 0.
Пример 6.28. Зх2 - у2 4- 12ж - 4у - 4 = 0
Пример 6.29. у2 - 10* - 2у ~ 19 = 0.
Пример 6.30. у2 - 6х 4- Ыу н- 49 = 0

92
7 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
III ГЛАВА
Теория пределов и
числовые ряды
7. ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
Числовые последовательности, предел последовательности,
прогрессии, предел функции, односторонние пределы, ограниченные
функции.
7-1- Числовые последовательности.
Определение 7.1. Функция у — f(n), областью определения
которой является множество натуральных чисел N, называется функцией
натурального аргумента, или числовой последовательностью.
Члены числовой последовательности располагаются в порядке
возрастания аргумента:
Я = /(1), Уг = /(2), Уз = /(3),... , уп = f(n),... .
2/i~/(l) — первый член последовательности, у2 = /(2) — второй, уп =
/(п) — n-й член последовательности, или общий член
последовательности» Последовательности кратко обозначают {уп}- Примеры числовых
последовательностей :
7 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ *?
Пример 7.1. 1,1/2,1/3,... ,1/п,... или {1/п}.
Пример 7.2. -1,1,-1,1,...,(-1)п,.., шш{(-1)п}.
Пример 7.3. 1,3,5,...,2п - 1,.., или{2п-1}.
Пример 7.4. 0,1/2,2/3,..., (п - 1)/п,... или {(п - 1)/п}.
Характер изменения членов последовательности различен. Из
представленных примеров видно, что последовательность может быть
возрастающей уп < уп+1 (примеры 7.3 и 7.4), убывающей уп > г/„+1 (пример
7.1), ограниченной снизу (пример 7.1), ограниченной сверху (пример 7.4),
неограниченной (пример 7.3). Понятия возрастающей, убывающей, огра-
ниченой функции были даны ранее в лекции 3.
7.2. Предел числовой последовательности. Очевидно, что
элементы возрастающей или убывающей, но ограниченной
последовательности неограниченно приближаются (сходятся) к некоторым ограниченным
числовым значениям Ь, т.е. имеют предел.
Определение 7.2. Число Ь называется пределом числовой
последовательности {уп}, если для любого положительного сколь угодно
малого числа е найдется такое натуральное число N, что для всех п > N
выполняется неравенство \уп — Ь\ < е.
Символическая запись предела последовательности
(7.1) lim Уп = Ь:
п-+оо
V(e > 0) 3 N V(n > N) => \уп -Ь\<е.
en
Поскольку неравенство \уп - Ь\ < е равносильно Ь - е < уп < о + е, то
геометрический смысл предела последовательности можно представить
следующим образом: если последовательность имеет пределом число 6, то
каково бы ни было е > 0, найдется такое N, что все точки,
изображающие члены последовательности с номерами n > JV, попадут в полосу,
ограниченную прямыми у = b- e,y = b + e (рис. 81).
7.3. Прогрессии. Частным случаем последовательности являются
прогрессии. Общий член арифметической прогрессии: ап — ах 4- d(n - 1).
Характеристическое свойство арифметической прогрессии: ап+х — ^(ап +■
ап+2). Сумма ^-членов арифметической прогрессии S* = ai+a2H f-a* =
|(ax + ofc)fc = |(2ai + rf(fe —
Геометрическая прогрессия — числовая последовательность, первый
член которой отличен от нуля, а каждый член, начиная со второго, равен
предшествующему члену, умноженному на одно и то же не равное нулю

94
7 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
к
[ь+е
(
у//////////////
у////////////^^
Щ
Ь-е
Щх,
i
>
у///Л
ууу/Л
о
/уу
///
У/,
»
///
W,
у/У//
УУУуУ,
W///y
уШуу,
//л
УХ,
ж
0 12 3 4 ...п-2 п-1 л п+1 п+2 X
Рис. 81. Геометрический смысл предела последовательности
число q, называемое знаменателем геометрической прогрессии =» Ьх =
b{b^0);bn+1 = bnq(q^Q).
Общий член геометрической прогрессии: bn = b\- qn~l.
Характеристическое свойство геометрической прогрессии:
|&n+l| = \Ai ' Ьп+2-
Формула суммы к членов геометрической прогрессии: S* = б1^Г* К
Для бесконечно убывающей геометрической прогрессии \q\ < 1 и сумма
* ~ 1-я'
7.4. Предел функции. Выше мы рассмотрели предел
последовательности уп% но уц = f(n) есть функция натурального аргумента, значит мы
фактически имеем дело с пределом функции натурального аргумента.
Теперь введем понятие предела функции от непрерывного аргумента. В
отличие от предела последовательности определение предела функции
зависит от условий стремления аргумента функции (х —> со, ж -> —оо, а; —» хо
и т.д.). Рассмотрим некоторые из них.
7.4.1. Предел функции при х -> -foo. Проследим характер изменения
функции у = f(x) = 2 - £ при возрастании значения аргумента х:
X
У
1
1
2
1.5
10
1.9
100
1.99
1000
1.999
и построим ее график (рис. 82).
7 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
95
2Н-
d / ,х
Рис. 82. График функции у = 2 - \
Пусть М(х,у) — текущая точка графика, функции у = 2 - К Тогда
расстояние MN от этой точки до прямой у = 2 можно определить как
<* = |у-2| = |/(*)-2| = |(2-±)-2
Совершенно очевидно,что с ростом значения аргумента х расстояние d
уменьшается. Если х > \, то \f(x) - 2| = ^ < £, следовательно, функция
неограниченно приближается к числу 2, или при бесконечно
возрастающем х (х —> оо) имеет пределом число 2.
Определение 7.3. ^«сло 6 называется пределом функции у = /(я)
при ж —> оо, если каково бы ни было положительное число е, можно
найти такое число N, что для всех х > N выполняется неравенство
\№ ~Ь\<е.
Символическая запись предела функции при х -* оо:
(7.2) lim f(x) = 6
I-ЮО
V(e > 0) 3 N V(* > W) =» |/(яг) - Ь| < е.
Замечание 7.1. Сравнив определение предела последовательности
и предела функции при х —> оо, можно сделать вывод о том, что они
подобны. При этом предел последовательности является частным
случаем предела функции при х —> оо. Следовательно, все сформулированные
ниже теоремы о пределах функции при п —> оо переносятся на пределы
последовательности при гс —►.
С учетом того, что неравенство \f(x) - b\ < e эквивалентно двойному
неравенству b — е < f(x) < b -f e, геометрический смысл предела функции
при х -> оо можно проиллюстрировать (рис. 83).
—х
Ы

96
7 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
к
V//^///////////
ЩШяш
шШшш
рШЗШШ
У/////////////
шжж
ШшУ////
{ШШу,
»».
О N
Рис. 83. Геометрический смысл предела функции при х -» оо
Аналогично пределу функции при х —> оо можно ввести понятие
предела функции при х —» -оо.
7.4.2. Предел функции при х -> х0.
Определение 7.4. Число Ь является пределом функции у == f(x) при
х —> Хо, если каково бы ни было е,можно найти такие числа N и М (N <
Хо < М)учто для всех х, лежащих в интервале (N; М) (за исключением,
быть может, точки xq), выполняется неравенство
|/(*)-Ь|<£.
Символическая запись предела функции при х —> Хо'-
(7.3) lim fix) - b.
Геометрический смысл этого предела легко понять из графика на рис. 84.
Определение предела функции можно дать в несколько ином виде.
Определение 7.5. Число Ь является пределом функции у = f(x) при
х —> xq> если для любого е > О существует S — 6(e) > 0, такое, что
\f(x) - Ь\ < е при 0 < \х - х0\ < S.
Число S определяет собой некоторую S — окрестность точки хо —
интервал (х - 6,х + 5), содержащий точку хо. Оба определения предела
функции при х -> xq (7.4 и 7.5) равносильны.
7.5. Односторонние пределы. Рассмотрим сперва случай, когда
независимая переменная х приближается к х0 слева.
7 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
97
ON x„ M
Рис. 84. Геометрический смысл предела функции при х -> хо
Определение 7.6. Число b называется пределом функции у = f(x)
при х —► х0 слева, если каково бы ни было положительное число е,
найдется такое число N (меньше х0), что для всех х, лежащих между N и
х0 (N < х < х0), выполняется неравенство \f(x) — b\ < ё.
Предел функции при х —> х0 слева обозначают так: lim f(x) = b.
Х-+Хо— О
Символ х —► х0 — 0 означает, что х стремится к х0 слева.
Геометрический смысл предела функции при х —> х0 — 0 заключается в
следующем: каково бы ни было е > 0, найдется такое число N(N < х0),что
для всех х, заключенных между N и х0, график функции лежит в полосе,
ограниченной прямыми у = 6-еиу = 6+£ (рис. 85).
Аналогично пределу функции при х -> х0 слева вводится понятие
предела при х -» х0 справа.
Определение 7.7. Число b называется пределом функции у — /(х)
при х —> х0 справа, если каково бы ни было положительное число е,
найдется такое число М (большее х0), что для всех х, лежащих между
х0 и М (х0 < х < М), выполняется неравенство |/(х) — 6| < е.
Предел функции при х —> х0 справа обозначают так: lim /(х) == Ь.
X-+Zo+0
Если функция у = f(x) при х '-> х0 справа имеет пределом число 6, то
геометрически это означает, что график функции лежит в полосе,
ограниченной прямыми у = Ь — е и у = Ь + е для всех х, заключенных между
х0 и М (рис. 86).

98
7 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
О N х. х
Рис. 85. Геометрический смысл предела функции при х-> xq - О
Ь+е
b
b-e
О х. М *
Рис. 86. Геометрический смысл предела функции при х-» xq + О
1
\/////////
шй
/
'тттт.
'шттт.
Пределы функции при х -» х0 слева (х —>• х0 - 0) и при х ~> х0 справа
(х -* х0 4- 0) называют односторонними пределами.
Бели оба односторонних предела существуют и равны между собой, то
говорят, что функция /(х) имеет двухсторонний предел при х -> х0, или
просто имеет предел при х ~> х0.
Замечание 7.2. Можно доказать, что если функция имеет предел,
то он единственный.
7.6. Теоремы об ограниченных функциях. Следующие две
теоремы устанавливают связь между понятиями ограниченной функции и
функции, имеющей предел. Для определенности рассмотрим случай
предела функции при х —> оо.
7 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ 99
Теорема 7.1. Если функция у — /(х) имеет предел при х -*• оо, то
она ограничена на некотором бесконечном интервале (ЛГ,оо).
Дано: lim /(х) = Ь, т.е. функция имеет предел.
х-»оо
Доказать, что |/(х)| ^ С, т.е. /(х) функция ограниченная.
Доказательство.Так как lim f(x) = 6, то |/(х) - 6| < е при х -» оо
«-►ОО
(по определению предела функции). По свойству абсолютных величин
|/(х) - 6| > |/(х)| - |6|, а следовательно,
|/(*) - *| > 1/(*)1 - 1*1 < е или |/(х)| < |Ь| + е = С.
Это и означает, что функция у = /(х) ограничена на исследуемом
интервале.
Теорема 7.2. Ясли функция у = /(х) гшеет предел, отличный от
нуля (при х —► оо^, то функция у = ущ ограничена на некотором
бесконечном интервале (TV, оо).
Дано: lim f(x) = Ь и Ь ф О, т.е. функция имеет предел.
аг-юо
Доказать, что yjhX ^ С» т.е. функция ^ограничена.
Доказательство.Так как lim f(x) = 6 и b ф О, то на основании определе-
х—юо
ния предела и с учетом свойств абсолютных величин будем иметь:
|/(«) - Ь\ = \Ь - /(х)| > Н - |/(х)| < е или
|/(*)|>|6|-£^0или |7ij| = -Lf<|^ = C.
Таким образом, теорема доказана.
Теорема 7.3. Всякая возрастающая (убывающая) ограниченная
функция (последовательность)имеет предел.
Теорема приводится без доказательства.
В качестве примера на применение этой теоремы рассмотрим
последовательность, общий член которой уп = (l -f £) . Покажем,что
последовательность возрастает и ограничена.
Воспользуемся формулой бинома Ньютона(см. лекцию 20):
(«+6)" = a" W''^^f^""^" '(" 7 'I '(Г2) а"-ЧЗ+- -**•■
Полагая а = 1,6= К получим
fc.(.+i)-.
1 n-(n- 1) 1
n-(n-l)-(n-2) J_ п-(п-1)-(п-2) 2-1 1
+ 1-2-3 "n3 + " 1-2-3-----П ' n-

100 7 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
Замечая, что
п • (та - 1) 1 та • (та - 1) • (та - 2) та - 1 71-2 _ Л ЛЛ _ 2^
п2 та' та3 та та \ та/ \ та/
та • (та - 1) - (та - 2) • (та -- 3) 2 -1 _ п - 1 та - 2 та - 3 та - (та - 1) _
пп та та та та
= И)И)И) (-Ч1).
получим
Hl+i)"-1+'+iVH)*nb-NK"-S)+-"
-+i.2.»1--.-('-;)-(1-;) i1'^)
С увеличением номера та дроби £, £, | и т.д. уменьшаются, а
разности 1-£,1-|,1-|и т.д. увеличиваются. Следовательно, yn+i > уп и
последовательность #п = (l + ~)п — последовательность возрастающая.
Если в разложении уп отбросить в скобках дроби £,~,~ и т.д., то
каждое слагаемое, начиная с третьего, увеличится, и мы получим сумму,
большую первоначальной:
Но
1 11 1 1 1 1 1
2-3<2-2~22,2-3-4<2.2.2~23''"'2-3-4--та< г""1"
Поэтому
-N)"<'+N+*+-+£)-
Сумму l-f|+^Н Н^т найдем по формуле суммы членов бесконечно
убывающей геометрической прогрессии (п -> оо) :
, 1 1 11 1
Откуда t/n = (l -f £) < 1 -f 2 = 3, а, следовательно, данная
последовательность ограничена.
На основании теоремы 7.3 делаем вывод,что данная возрастающая и
ограниченная последовательность имеет предел. Его называют числом е.
7 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ Ш
Итак,
(7.4) lim (l + M =e.
п-+оо \ П/
Иногда данный предел называют вторым замечательным пределом.
Число е иррациональное. Его приблизительное значение с точностью
до 10~8 : е = 2,71828182. Аналогично, предел функции lim(l + Мх = е.
Обозначив \ = t, этот же предел можно записать в виде
(7.5) lim(l + *)*=e.
Предел 7.4 играет большую роль в математике. Показательная
функция с основанием е, т.е. у = ех, называется экспоненциальной, или экспо-
нентой. Логарифмы с основанием е называются натуральными
логарифмами, причем вместо logex принято писать In ж.
7. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
Для закрепления пройденного теоретического материала рассмотрим
подробно процесс решения следующих примеров.
ПРИМЕР 7.1. Для приведенных ниже последовательностей записать
формулу общего члена последовательности.
Рекомендация. После анализа первых членов последовательности
необходимо установить закономерность получения каждого члена
последовательности в зависимости от номера члена последовательности п, где
п=1, 2, 3, 4, ....
о 1,2,3,4,... . Здесь члены последовательности совпадают с номером
члена последовательности. Ответ: уп = п.
° 2' !' f»5»" " ' Числитель последовательности соответствует
номеру члена последовательности, а знаменатель на единицу больше.
Ответу = ^г__
в \/2, V 2\/2, у 2у/2\/2. Перепишем члены последовательности в
виде показательной функции с основанием 2: 25,2*,2»,2*6. Нетрудно
заметить, что знаменатель показателя степени изменяется как
геометрическая прогрессия со знаменателем q=2, т.е. 2П, а числитель
на единицу меньше знаменателя, т.е 2П — 1. Ответ: уп = 2~**~.

102
7 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
ПРИМЕР 7.2. Последовательность уп задана формулой общего члена
последовательностиуп = 2s±I. Найти ую,Уп-иУп+1-
Решение: Для вычисления соответствующего члена
последовательности необходимо в формулу общего члена последовательности
подставить соответствующий номер.
Улп = 2*10±1 21 2(п-1)+1 _ 2п^1 _ 2(п+1)+1 _ 2п±3
^0 10+3 13>У"-1 (п-1)+3 "" п+2'У«+1~ (п+1)+3 "~ ТГМ '
Пример 7.3. Найти предел последовательности
0,2; 0,23; 0,233; 0,2333;....
Решение: Общий член заданной последовательности можно
записать в виде:
уп = 0,2 + [0,03 + 0,003 + 0,0003 + ...] = 0,2 + S.
Выражение в квадратной скобке образует бесконечно убывающую
геометрическую прогрессию со знаменателем q = 0,1 и первым членом
последовательности bi = 0,03. Сумма первых п ее членов (n-я частичная сумма)
Sn = iZq " Сумма бесконечно убывающей геометрической прогрессии
есть предел Sn и вычисляется по формуле 5 = ~^-. Предел
последовательности в таком случае будет равен
lim{yn} = Вт [0,2 + Sn] - (о,2 + -М = (о,2 + -^Л = ^
п-+оо п-*оо \ 1-9/ \ 1-0,1/ ЗС
30
Пример 7.4. Найти предел последовательности
г /1 2 3 п-1\
hm (_ + _ + _ + ...+ —— ) .
п-+оо \ГГ Я* П2 П2 )
Решение: Числители дробей образуют арифметическую
прогрессию: 1 + 2 + 3 + ...4-п- 1. Сумма первых п членов арифметической
прогрессии
Поэтому
ах + ап 1 + (п - 1) п2
5„ = -у--п = п=-.
"5, (* + * + » + • • • + ^) - к»1+2+3^-'
7 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
103
Пример 7.5. Найти предел последовательности
n-чоо \2 4 8 2П/
Решение: Слагаемые |, J, J ... —- образуют бесконечно убывающую
геометрическую прогрессию, n-я частичная сумма которой равна Sn =
М1"?"). Следовательно:
1-д
г /1 1 1 Mr mi-о г К1 - (1)п)" 1
n-*oo \2 4 8 2n/ n-+oo 1 - q n->oo 1 - i
Пример 7.6. Найти предел последовательности
2n"H i з»-и
lim — -—.
n->oo 2n + 3n
Решение: Разделим числитель и знаменатель на наибольшее
выражение при п —> со —► 3n+1 :
,. 2"+' + 3"-" ,. Щ£^
\1т — _ = 11т Д — =
n-юо 2П + 3П п-4оо ^3_
?2±1 + 1 2П+1 , j n 1
(т. к. показательная функция с основанием § при п —>» оо стремится к
нулю.)
Пример 7.7. Найти односторонние пределы:
1) lim 5^Ь; 2) lim 5^.
' ar-->3-0 Х-+3+0
Решение:
1)Если х->3-0, тох-3-»-0и~з-> -оо как частное от деления
ограниченной величины на бесконечно малую отрицательную,
следовательно
lim 5^* = 5-°° = —- = — = 0.
*-*3-0 5°° ОО
2)Если Z-+3 + 0, то х - 3 -» +0 и ^чоо, следовательно,
lim 5^5 = 500 = оо.
z-*3-M)

щ
7 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
Самостоятельная работа
Для приведенных ниже последовательностей записать формулу общего
члена последовательности.
Пример 7.8. l,j,£,£,•••.
Пример 7.9. 2, |, |, |, |, ..."
Пример 7.10. 1,4,9,16,25,•••.
Пример 7.11. f ,!,§,&,....
Пример 7.12. 1,-1,1,-1,....
Пример 7.13. Последовательность уп задана формулой общего
члена последовательности {уп} = ~ Найти Уг,уь,уп+\-
Найти пределы последовательностей
Пример 7.14.
1,6; 1,86; 1,666; 1,6666;...
Пример 7.15.
Пример 7.16.
Пример 7.17.
Пример 7.18.
Пример 7.19.
lim
П-+00
["1+3 + 5 + 7+... + (2n- 1)1
L n2 I'
lim
n-юо 1
i.i+i.i + ... + (ziril
3 9 27 3n~l
9n + 8n
ИГО 7ГТ\ Г-Т7-
n-+oo 9n+1 + 8n+1
n/2, у[Л, y\/v^,....
lim
n sin n\
n->oo П2 + 1
Найти односторонние пределы:
Пример 7.20. lim 2^».
n->4-0
Пример 7.21. lim 2^*.
n-*4+0
8 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
105
8. ЛЕКЦИЯ - ТЕОРИЙ ПРЕДЕЛОВ
Бесконечно малые функции, бесконечно большие функции, связь
бесконечно больших и бесконечно малых функций,основные теоремы о
шределах. >>..•
8.1. Бесконечно малые функции.
Определение 8.1. Функция у = f(x) называется бесконечно малой
при х —> а(х —» оо,х —> —оо и т.д.), если ее предел при х -> а равен
нулю.
На основании понятия предела имеем для бесконечно малых функций
lim f{x) = 0 или \f(x) - 6| = |/(х) - 0| = |/(х)| < е.
Определение 8.2. Функция у = f(x) называется бесконечно малой
при х —у а (х —> оо, х —> —оо и т.д ) если каково бы ни было е > 0, можно
найти такое число N, что при всех х > N выполняется неравенство
(8.1) \f(x)\<e.
Пример 8.1. Показать, что функция у = р является бесконечно
малой при х —> 0.
Решение: Чтобы функция была бесконечно малой при х -> со,
необходимо выполнение условия | р \ < е. Это возможно при р < е или при
х > 4* = N. При х —► оо это условие выполняется.
Замечание 8.1. Можно показать, что функция р (где а — любое
положительное число) есть бескрнечно малая при х —у оо.
Пример 8.2. Показать7 что функция у = х5 является бесконечно
малой при х -> 0.
Решение: Чтобы функция была бесконечно малой при я —► 0,
необходимо выполнение условия |х5| < е. Это возможно при всех значениях
|аг| < \/е или -^е < х < f/e. При х —► 0 это условие выполняется.
Замечание 8.2. Можно показать, что функция у = хт (где т > 0)
бесконечно малая функция при х —> 0.
Пример 8.3. Функция у = 2 - - we является бесконечно малой при
х —> оо, так как lim (2 — -) = 2 ^ 0.
Z-ЮО Х *9 Г
Рассмотрим теперь несколько теорем о бесконечно малых функциях.
Для определенности проведем доказательства теорем при х —> оо.

106
8 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
Теорема 8.1. Если функции ip(x) иф(х) являются бесконечно
малыми функциями (при х ч> +оо),то и их сумма ip(x)+ip(x) также является
бесконечно малой функцией (при х —¥ +оо/
Дан0 : |$х)| < t при х > Nl 'те- ^Х) И ^Х) бесконечно малые
функции при х -» оо. Доказать, что f(x) = tp(x) + ф(х) бесконечно малая
функция при х -> оо, т.е. |/(х)| < е при х > N, где N наибольшее из N\
и N2.
Доказательство.
|/(х)| = \ф) + ф(х)\ < \ф)\ + №(z)'| < | + | = е,
что и требовалось доказать.
Эта теорема может быть легко обобщена на любое конечное число
бесконечно малых функций'. Кратко ее читают так: сумма нескольких
бесконечно малых функций есть функция бесконечно малая.
ПРИМЕР 8.4. Функция у = ^ + -^ 4- ^ является бесконечно малой
функцией при х -> +00, так как каждое слагаемое 4^ ^ и -р есть
бесконечно малая функция при х -> +оо.
Пример 8.5. Функция у — х + х3 + х5 есть бесконечно малая функция
при х -» 0, так как функции у = ж, у = х3 и у = х5 бесконечно малые
при х —► 0.
Теорема 8.2. Произведение бесконечно малой функции (при х -> оо,/
ка функциЮу ограниченную (при х -+ +оо^ является функцией
бесконечно малой.
Дано: |у?(х)| < С при х -> оо — ограниченная функция;
\ф(х)\ < § при х -> оо - бесконечно малая функция.
Доказать, что /(х) = <£>(х) -?/>(х) бесконечно малая функция при х -> оо,
т.е. |/(х)| < е.
Доказательство.
|/(l)| = И*) • ф(х)\ = \ф)\ ■ \Ф(Х)\ <С ^ = £,
что и требовалось доказать.
Пример 8.6. Функция у = ^г является бесконечно малой при х ->
+00, так как она является произведением ограниченной функции cos x
на бесконечно малую (при х -> +00,/ функцию у = ^.
5 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
107
Пример 8.7. Функция у == х(1 + sinx) является бесконечно малой
при х —>• 0, так как ома является произведением ограниченной функции
1 + sinx на функцию х, бесконечно малую при х -* 0.
Следствие. 1. Так как всякая бесконечно малая функция ограничена,
то из только что доказаной теоремы вытекает, что произведение двух
бесконечно малых функций есть функция бесконечно малая.
Следствие.2. Произведение бесконечно малой функции на число есть
функция бесконечно малая.
Теорема 8.3. Частное от деления функции /(х), бесконечно малой
при х -¥ +00, на функцию (р(х), предел которой (при х —► +оо^ отличен
от нуля, является функцией бесконечно малой.
Доказательство.Функция Ц& может быть представлена в виде
произведения бесконечно малой функции /(х) на ограниченную функцию -fe.
Но тогда из теоремы 8.2 вытекает, что частное 4§j = /(x) • -~г является
бесконечно малой функцией.
8.2. Бесконечно большие функции.
Определение 8.3. Функция у = /(х) называется бесконечно боль-
той при х —> +оо, если для любого положительного числа L можно
подобрать такое число N, что для всех значений х > N выполняется
неравенство |/(х)| > L.
Так, например, функция у = х2 является бесконечно большой при
х —»- +оо. Какое бы положительное число L мы ни взяли, эта
функция может быть сделана больше, чем L (для всех значений х > N = y/Z).
Символически бесконечно большая положительная функция записывается
в виде:
lim /(x) = оо.
«-►оо
Если бесконечно большая функция отрицательна, то говорят, что она
стремится к — оо и пишут:
lim /(x) = -оо.
х-юо
8.3. Связь бесконечно больших и бесконечно малых функций.
Между бесконечно большими и бесконечно малыми функциями
существует тесная связь, которая устанавливается в следующих теоремах.
Теорема 8.4. Если функция /(х) является бесконечно большой при
х -> +оо, то функция ущ— бесконечно малая при х —»> +оо.

108
8 ЛЕКЦИЯ-
Доказательство.Возьмем произвольное е > 0. Покажем, что для
достаточно больших х выполняется неравенство |тщ| < е, а. это и означает,
что jhfi — бесконечно малая функция. Так как по условию /(х) —
бесконечно большая функция, то существует такое число ЛГ, что |/(х)| > ^ при
х > N. Но тогда \jh\\ < £ для тех же х. Тем самым теорема доказана.
ПРИМЕР 8.8. Функции у = х2 бесконечно большая при х -> 4-оо.
Следовательно , функция Д* является бесконечно малой при х -> +оо.
Теорема 8.5. Если функция /(х) не обращающаяся в нуль, есть
бесконечно малая при х -> -Мх>, то ущ— бесконечно большая функция при
х -> +00.
Теорема приводится без доказательства.
8.4. Основные теоремы о пределах. Ниже приводятся основные
теоремы о пределах, которые позволяют облегчить определение
пределов. При этом формулировки и доказательства теорем для случаев х —►
оо, х -> -оо, х —> хо, х -> хо - 0, х -* Хо -f 0 совершенно аналогичны.
Поэтому здесь они предлагаются для общего случая х -» а.
Теорема 8.6. Если функция у = /(х) имеет предел (при х —> aj,
равный 6, то ее .можно представить в виде суммы числа Ъ и бесконечно
малой функции а{х) при х -> а:
(8.2) /(*) = Ы-а(х).
Дано: lirii a(x) = 0 — бесконечно малая, Нт /(х) =6 — функция имеет
х-ю х-*в
предел.
Доказать, что при этом /(х) = 6 + а(х).
Доказательство.lim/(х) .= 6 => |/(х) - 6| < е, а это значит, что
lim(/(x) — b) = 0, т.е. /(х) - 6 = а(х) — бесконечно малая функция,
следовательно, /(х) = 6 + а(х).
Теорема 8.7. (обратная, без доказательства). Если функцию у =
/(х) можно представить как сумму числа Ь и некоторой бесконечно
малой функции (при х -> а), то число b является пределом функции /(х)
(при х -> aj.
Теорема 8.8. Предел суммы (разности) двух функций равен сумме
(разности) их пределов.
8 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
109
Если limip(x) = Ь и Игп^(х) = с, то функции /(х) = у?(х) 4- ^(^) и
«-►а х-ю
/(х) = <р(х) - ^(х) тоже имеют пределы при х -► а.
х—►а а-4о х-4о
Дано: lim <р(х) = 6, lim ф(х) = с.
х-ю х-+а
Доказать, что ШпЫх) 4- Ф(х)] = lim <р(х) 4- lim гр(х).
х-ю х-ю х-+а
Доказательство.
lim v?(x) = 6, ) ( у(х\ = ^ + а/д.\
lrni°^(x) = c; f на основании теоремы 8.6 =*( ^) = c + /jW. >
х-ю у
где а(х) и /?(х) — бесконечно малые при х —>■ а.
Тогда
/(х) = у?(х) + ф(х) = [Ь + а(х)] + [с + /?'(х)] = (6 + с) + [а(х) + /3(x)j,
lim /(х) = НтЫх) + ^М] = lim {(6 + с) + [а(х) 4- /3(х)]} = 6 4- с.
х-ю х-ю х-ю
Последнее равенство вытекает из теоремы 8.7.
Следовательно:
lim/(x) = lim[y?(x) 4-^(х)1 = \irrnp(x) 4- lim^(x).
х-ю х-ю х-ю х-ю
Аналогично доказывается, что
limta(x) - ф(х)] = Нту>(х) - 1ши/>(я).
х-ю х-ю х—ю
Теорема 8.9. Предел произведения двух функций равен
произведению их пределов.
Если Итгир(х) = 6 и Нт^(х) = с, то функция /(х) = </?(х) • ф(х) также
х—►а х-ю
имеет предел при х -> а, причем
НтЫх) • ^(х)1 = Нт у>(х) • Нт ^(ж)-
х—ю х-ю х—ю
Дано: Нт </?(х) = 6, Нт <ф(х) = с.
х-ю х—ю
Доказать, что Нт[</?(х) • ф(х)] = lim <р(х) • lim ip(x).
х—ю г—ю х-ю
Доказательство.
Um*(*) = c; f на основании теоремы 8.6 => ( ^(г) = с + /3(х). -
где a(x) и /3(х) — бесконечно малые при х —> а.
/(х) = у(х).^(д;)= [&+а(х)]-[с+/?(х)] = (Ь-с) + [с-а(а;)+6-/?(а:)+а(ж)./?(х)].
lim /(x) = lim[^(r) • ip{x)] = lim{(6 -c) + {c- a(x) 4-6 -/3(х) 4-а(х) • /?(х)]} =

110
8 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
6 • с + \\т[с • а{х) + Ь • /3{х) + а(х) .• /3(х)] = 6 • с = lim </>(я) • lim ф(х).
х-ю х~+а х~*а
Здесь limlc • а(х) + Ь ■ /?(х) + а{х) • /3(х)] = 0, т.к. все слагаемые бесконечно
х-ю
малые функции.
Следствие 1. Постоянный множитель можно выносить за знак предела,
т.е.
limffc • (р{х)} = к • lim у?(х).
х-ю x-fa
Следствие 2. Из теоремы 8.9 вытекает, что предел степени равен
степени предела:
lim[/(x)]" = (lim/(*)]".
ТЕОРЕМА 8.10. (без доказательства). Предел дроби равен
отношению предела числителя и знаменателяf если последний не равен нулю.
Если lim ф(х) = Ь, lim ф(х) = с и с Ф 0, то
х~+а х-*а
ИтШх)Шх)} = lim^(x)/lim*/>(x).
х—»а х—»а х-ю
Пример 8.9. Найти lim(x2 + 2х - 1).
х->2
Решение: Воспользуемся теоремами о пределах функции.
© По теореме о пределе суммы
lim(x2 + 2х- 1) =
х->2
• Так как предел степени, равен степени предела, то
limx2 = [limx]2=22=4.
х~>2 Lx->2 J
• Постоянный сомножитель можно выносить за знак предела
lim2x = 21imx = 2-2 = 4.
х-»2 х-*2
« Предел постоянной равен самой постоянной
Окончательно получим:
lim(x2 + 2х - 1) = linr
х-*2 *-+:
Пример 8.10. Найти lim-^tffia4
lim(x2 + 2х - 1) = lim x2 + lim 2x - lim 1.
х->2 а?-+2 х->2 х-*2
iim 1 = 1.
г-»2
lim(z2 + 2х - 1) = lim х2 + lim 2х - lim 1 = 4 + 4 - 1 = 7.
х-+2 х-*2 х->2 x-*2
8 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
111
Решение: На основании навыков, приобретенных при решении
предыдущего примера находим:
предел числителя lim(x4 + 3x2 + 4) = lim х4 + lim Зх2 + lim 4 = 1 + 3 + 4 = 8,
х-»1 х-*1 х-*1 *'-*J'
предел знаменателя lim(x2-2x+3) = lim х2 - lim 2х + lim 3 = 1-2 + 3 = 2.
х-*\ x-fl х-*1 х-И
Применяя теорему о пределе дроби, получим
lim *4 + 3*2 + 4 = ga(g4 + 3ag2 + 4) = 8 =
«-♦1 х2 - 2х + 3 lim(x2 - 2х + 3) 2 ~
Теорема 8.11. (о промежуточной функции). Пусть даны три
функции удовлетворяющие неравенствам (р(х) ^ /(х) ^ д(х) для
достаточно больших значений х. Если функции ip(x) и д(х) имеют один и тот же
предел при х -> оо, то и функция f(x), заключенная между ними, имеет
предел, равный пределу функций у?(х) и д(х).
В качестве доказательства приведем простую геометрическую
интерпретацию условий теоремы (рис. 87):
Рис. 87. Геометрическая интерпретация условий теоремы о
промежуточной функции
Теорема 8.12. Если функция у = /(х) ^ 0 для всех достаточно
больших значений х при х -> со имеет предел, то этот предел не
может быть отрицательным, т.е. lim /(х) ^ 0 (без доказательства).
х-юо
Пример 8.11. Найти lim^.
х-Ю х
Решение: Рассмотрим окружность единичного радиуса.
Предположим, что 0 < х < |. Дуга АС численно равна центральному углу
х, выраженному в радианах, а отрезок АВ численно равен sinx. Так
как 0 < АВ < АС, то 0 < sinx < x. По теореме о пределе
промежуточной функции 8.11 при х -» 0 sinx должен стремиться к нулю, т. е.

112
8 ЛЕКЦИЯ-
lim sinx = 0. Можно также показать, что lim cos х = 1
х-»0
х->0
lim cosx = lim(l - 2sin2 -) = 1 - 2 lim(sin2 -) = 1 - 2 ■ 0 = 1.
О cosx в С
Рис. 88. Иллюстрация к определению lim
х-+0
Как следует из представленного рисунка 88:
S&OAB < SceKTOAC < S&odc-
Так как
S&OAB =
О В • В A cos х sin x
5сект о ас — «Я х ~ о 21
ОС • CD _ ltgx _ tgx
S&odc — « "- 9 2 '
то подставив выражения для площадей в неравенство, получим:
cos х sin x x tgx
2 <2< 2 "
Разделим все члены неравенств на \ sinx и проведем сокращения:
или
COSX <
1
- >
X
sinx
sinx
1
cosx
> cosx.
cosx
8 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
113
Эти неравенства справедливы, как при х > 0, так и при х < 0. Как
показано выше, при х -► 0 => lim cosx = 1. Применив к частному ^^
теорему о пределе дроби, получим
г 1 * 1 V
hm = - = т = 1.
*-*о cos х hm cos x 1
Поскольку обе крайние функции последнего неравенства при х -> 0 имеют
одинаковый предел, равный единице, по теореме о пределе промежуточной
функции (основные теоремы о пределах) функция 2~~ имеет тот же предел
при х '-* 0, т. е.
,. sinx
hm = 1.
Х-40 X
Данный предел lim 2~£ = 1 иногда носит название первого замечатель-
ного предела.
Пример 8.12. Найти lim^~.
*-к> х
Решение: Числитель и знаменатель дроби при х -> 0
одновременно стремятся к нулю. Теорема о пределе дроби здесь неприменима. Для
нахождения предела преобразуем, данную дробь:
S1I1X Г 111
• hmcosx = 11 = 1.
х *-*о
х->0 X яг-+0 у X COSX/ *-*0
Пример 8.13. Найти Km ** .
Решение: При подстановке х = 0 имеем дело с неопределенностью
вида §. Обозначим arcsin Зх = у, тогда sin у = Зх и х = ~*. При х -> 0 и
2/ -> 0. Следовательно:
5х .. 5 ^ 5V sin у 5 , 5
hm —-- = hm — = - hm —- = - • 1 = -.
x-*o arcsin Зх v->o у Зу-*о у 3 3
8. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
Теория пределов составляет фундамент математического анализа.
Именно поэтому обучающемуся небходимо хорошо владеть приемами
нахождения пределов функции. Естественно при этом использовать
рассмотренный выше в лекциях теоретический материал. В теории пределов
существенное значение имеют теоремы о пределах, применение которых в

щ
8 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
практических приложениях способствует нахождению пределов
различных функций.
Для приобретения практических навыков нахождения пределов
рассмотрим несколько примеров. При этом при раскрытии
неопределенностей будем использовать замечательные пределы:
lim = 1 и lim (1 -f- - ] = lim (1 -f у)* = е.
х-»0 X х-»оо \ X/ У~*0
Пример 8.1. Найти lim ^.
х-+0 х
Решение: Вид заданного примера очень похож на первый
замечательный предел, однако не равен ему. Для приведения данного предела к
замечательному можно использовать два следующих приема:
1)Умножить числитель и знаменатель выражения на 5:
.. sin5x .. sin 5а:-5 „ _. sin5ar '„
\1т — iim »— = 5 hm —— = 5-1=5.
а?~>0 X х—>-0 X • 5 ж-40 ОХ
2)Обозначить 5х=у. Тогда х — |. При х -> 0 и у —► 0 :
,. sin5x ,. sin у „,. sin u „
hm = lim —77— = 5 lim = 5.
*->o x y-*o * у-^о у
Пример 8.2. Найти limsm
Решение: Опять решаем пример, который на первый взгляд очень
похож на первый замечательный предел. Однако следует обратить
внимание на предельное значение аргумента. Здесь х -> 2, а не к бесконечности,
как в случае с первым замечательным пределом. При подстановке х = 2
под знак предела получаем:
, sin^f5 sin2?2 sin37r 0 Л
hm 2_ = ——*- = —-— = - = 0.
х->2 х 2 2 2
Пример 8.3. Найти lim ^.
Решение: Вспомнив замечания, сделанные в предыдущем примере,
мы приходим к выводу, что и этот пример не связан с замечательным
пределом lim ^ = 1. При х -* оо знаменатель выражения есть бесконечно
большая величина (lim х — оо), а числитель - ограниченная (| sinx| < I),
8 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
115
и отношение ограниченной величины к бесконечно большой есть
бесконечно малая величина. Следовательно,
sin а:
hm = 0.
ж-юо х
Пример 8.4. Найти lim -%-.
Решение: При х —► 0 имеем дело с неопределенностью типа §.
Совершим элементарные преобразования
_*_ .. _£__,. совЪх ^COs5x
Известно, что lim cos Ъх = 1, а в примере 8.1 показано, что lim ^^ = 5,
х-+0 х-*0 *
следовательно,
lim —— = -.
«-►о tg 5x 5
При решении примеров, связанных с нахождением пределов от
тригонометрических функций, в некоторых случаях рекомендуется воспользо-
ватся тригонометрическими тождествами, чтобы затем либо вычислить
предел непосредственной подстановкой предельного значения аргумента,
либо привести полученный предел к первому замечательному пределу
lim***.
х-+0 х
Пример 8.5. Найти lim l~c<f5x.
*->0 х
Решение: При х -> 0 имеет место неопределенность вида §,
так как limfl - cos5x) = lim 1 - lim cos 5x =1-1=0. Воспользуемся
тригонометрическим тождеством 1-cos Ъх = 2 sin2 у и перепишем пример
в виде:
,. l-cos5x ,. 2sin2^
hm г = hm т—*-.
Выполним необходимые преобразования для того, чтобы привести
полученный предел к виду первого замечательного предела. Обозначим
у = г/, откуда х = ^. Очевидно, что при х->0и.у->0:
2sin2f 2 sin2 j/ ,. 2sin2.y '"" 25,. sin2y
hm r-^- = hm yo ч2 = hm , . = — hm —;— =
x->0 X2 y->0 /2цу y-40 ^y2 2 y->0 y2
:=^lim/!^)2=25.1 = aE.
2 y-*o V 2/ / 2 2

116
8 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
Пример 8.6. Найти lim i-^-I,
1Г—Х
Решение: При подстановке х = тг под знак предела получим
,. 1 - sin f 1 - sin f 1-1 О
x->it 7Г — X 7Г — 7Г 7Г — 7Г U
т.е. неопределенность. Для раскрытия неопределенности обозначим
х — тг = г/, а значит х = у 4- тт. При х —> 7г, х — яг -* 0 и, следовательно,
У -> 0.
sin - = sm —-— = sin ( - + — ) = cos -,
2 2 V2 2/ 2
,. 1 - sin f 1 - cos |
*-** 7Г — X JJ-+0 —у
Неопределенность § сохранилась, но теперь мы сможем воспользоваться
формулой 1 - cos ^ = 2sin2 J.
1-cos* 2sin2£
lim - = lim -.
y-yO —у y->0 —у
Обозначим * = z, откуда у = 4г. При у —► 0, z —> 0 :
t. 2 sin2 J . 2sin2z L. sin2z
hm = lim — = — - lim =
у-Ю — у z-»0 —4,2 2 «-+0 2;
1 ,. sinz .. . 1 . Л
= --hm • hmsinz = —-.1.0 = 0.
2 г-+0 z *-+0 2
Следовательно, lim -~гт* = 0.
х-иг *~x
Пример 8.7. Найти lim(cos(mx) - cos(nx))/x2.
Решение: При подстановке х=0 под знак предела получаем
неопределенность ^р = §. Применим тригонометрическое тождество
cos(mx) - cos(rcx) = -2sin {m^Rx) • sin (mjIix):
,. cos(mx) - cos(nx) t. -2 sin (^s) • sin l^x)
hm —-——z = hm ——-— ——- =
a->0 X£ ar->0 Xz
Л1. sin(^x) sin(^x)
= -2 hm —^—L • lim L-2-—1 =
x-*0 X x-+0 X
m-fn
Sin (^x) . 22=S . Sin (ffipj)
= -2lim ——m,„ 2—- lim m „
ft wifn f. sin(2fHx) m-n ,. sin(^px)
_2 hm m\'— hm mv/—-
2 x-*0 2»±П . x 2 x-»0 22^2 . ^
g ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ 117
«■-(т»-п»)-1-Г>>"т2.
41
Пример 8.8. tfatimii lim (l + 2)*
ar-+oo v *'
Решение: По внешнему виду данный пример напоминает второй
замечательный предел. Введем переменную t = 5, отсюда х = ?. При
x-»oo*=2->0.
X
j*a(i+!)"=^
Пример 8.9. Найти lim (^4)х
Решение: Воспользуемся свойством предела функции и совершим
следующие элементарные преобразования, разделив числитель и
знаменатель на х:
ta(£fiy_ta(£^V-SJii^-c;-.-
-~Л* + 1/ '->»\*(1 + ЯУ lim(l + l)*~ t ~ '
Пример 8.10. Найти lim (%Щ)Х
*-юо v2«-l/
Решение: Обозначим 2х - 1 = у, откуда х = «±1, 2х + 3 = у + 4.
При х -> оо и у -> со.
Пример 8.11. Найти lim (ln(2x -f 1) - ln(ar + 2)).
Решение: При х -+ оо имеем дело с неопределенностью вида оо - оо.
Воспользуемся свойством логарифмической функции 1п(2х + 1) - 1п(х +

118
9 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
2) = ln~*jr. Числитель и знаменатель подлогарифмического выражения
разделим на х => In 2г±1 = In j^f и подставим в исходный пример:
lim (ln(2x -I-1) - ln(:r + 2)) = lim (In ^-f | = In 2,
х-юо x-*oo V 1 -|- - /
так как при х —у со £ и | равны нулю.
Самостоятельная работа
Найти пределы функций.
Пример 8.12. lim2^. Пример 8.18. lim-^.
х->0 x x-»f *~2x
Пример 8.13. Hingg. Пример 8.19. limsin*~sinQ.
х-»и х_>0 х а
Пример 8.14. lim *u. Пример 8.20. lim (-ihT-
Пример 8.15. lim $*. Пример 8.21. lim (f±*)*.
Пример 8.16. lim =Ji. Пример 8.22. lim (^f^)** •
Пример 8.17. lim &^а-. ПримЕр g 23 Um ь^
Пример 8.24. lim х (1п(х + 1) - \пх).
х-»оо
9. ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
Сравнение бесконечно малых функций. Эквивалентность бесконечно
малых функций. Приемы раскрытия неопределенностей.
9.1. Сравнение бесконечно малых функций.
Определение 9.1. Функции <р(х) и гр(х) называются бесконечно
малыми одного порядка малости при х -» а, если lim ®£\ = 6 ф 0 и ^ оо.
х-ю \у\х)J
Определение 9.2. Функция <р(х) называется бесконечно малой
более высокого порядка малости, чем функция ф(х) при х —» а, если
9 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ 119
Определение 9.3. Функция <р(х) называется бесконечно малой бо-
лее низкого порядка малости, чем функция ф(х) при х -> а, если
Определение 9.4. Функции <р(х) и ф{х) называются несравнимыми
бесконечно малыми при х -» а, если lim ||Й|н не существует и
не равен оо. х~*а
Пример 9.1. Сравнить бесконечно малые функции
у = х2 и у = Зх при х -> 0.
Решение:
*-*о Зх *-ю 3 3
Следовательно, функция у = х2 бесконечно малая при х —► 0 более
высокого порядка малости, чем функция у = Зх.
Пример 9.2. Сравнить бесконечно малые функции
у = х2 + х — 6 иу — 4 — х2 при х —► 2.
Решение:
.. х2+х-6 _. (я - 2)(я + 3) ,. х + 3 5 /л
hm — г— = um *~7 ^г; 7Х = ~ Ьт = -- ^ 0.
z_>2 4-a:2 *-+2-(a;-2)(:r-f 2) *->2 я + 2 4^
Следовательно, указанные функции являются бесконечно малыми одного
порядка малости при х —> 2.
Пример 9.3. Сравнить бесконечно малые функции
cos ж 1
у = иу= - при я —>- оо.
х х
Решение:
COSX
lim —f— = lim cos a;.
x-»oo - x-»oo
X
Так как cos а; не имеет предела при х —» оо, указанные функции являются
несравнимыми бесконечно малыми при х -> оо.
Определение 9.5. Функции ц>(х) и ip(x), бесконечно малые при х —►
а, называются эквивалентными (равносильными), если предел их
отношения lim |S{fy| = 1-
Тогда для значений я, близких к а: = о, имеет место приближенное
равенство lim fjf} ~ 1, или <р(х) « ^(я)> точность которого возрастает
с приближением ж к а.Если (р(х) и гр(х)—эквивалентные бесконечно малые
при х -* а, то пишут ^>(a:) ~ ^(я).

120
9 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
9.2. Эквивалентность бесконечно малых функций.
Теорема 9.1. Предел отношения двух бесконечно малых функций
равен пределу отношения эквивалентных им функций, т. е. если у? ~ <ръ а
ф <*» ф\ при х —► а, то
„„fEWl.tafsai.
Дано: ip ~ ^ь а ф ~ ф\ при х
Доказательство.:
lim
х-+а
ф)
[ф(х)\
= lim
х—¥а
(р(х) v>i(i)
[■ф(х) <pi(x)
Пример 9.4. Найти lim &§*.
ж—► О
Решение: Так как lim^ = 1, bm^ = 1, то sin5s ~ 5s,
sin 3s ~ 3s при x -* 0, и
sin 5s .. 5s 5
lim . 0 = hm — = -.
x->o sin 3s *->o 3s 6
Теорема 9.2. Бесконечно малые функции ф) и ф(х)
эквивалентны, если их разность [ф) - Ф(х)} есть бесконечно малая функция более
высокого порядка малости, чем ф) и ф(х).
Дано: Мтф) = Мтф(х) = 0 — функции ф) и ф(х) бесконечно
х—*а х-+а
малые при s -» а и /3(х) = ф) - V4*)'
Доказать, что ф) ~ ^г(х) т. е. lim gj = lim ^ = 0.
Доказательство.
ф{х)
lim ~-т = lim /Г = hm
*~>а ф) *-+а ^(s) *"+а
1-
Ф)
1
hm—r-r
= 1-1 = 0.
Следовательно, /J(z) есть бесконечно малая функция более высокого
порядка малости, чем ф). Аналогично можно доказать, что lim ^ = 0.
9 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
121
Теорема 9.3. Сумма конечного числа бесконечно малых функций раз-
личных порядков эквивалентна слагаемому низшего порядка.
Дано: lim/(x) = lim^(s) = \[тф1х) = 0 —функции /(х),ф),ф(х)
х-*а х-*а х-+а
бесконечно малые при х —> а. Пусть для определенности /(s)—бесконечно
малая функция низшего порядка малости по сравнения с остальными
слагаемыми, т.е. lim 44 = lim 4f4 = 0.
Доказать, что lim /W+ffiH^W = i т.е. сумма бесконечно малых функ-
ций при х -> а эквивалентна в данном случае /(х).
Доказательство.
цт/(«) + у(») + »(«) = Вт1 + Ит^ + ЦшШ,1+0+о-1.
*-+<* f(x) х->а х-+а }(х) *-+<* f(X)
Пример 9.5. Найти Нт ^±£d.
х->0 sm2x
Решение: Так как при х —► 0 Ъх •+• 6s2 ~ 5s (по теореме 9.3) и
sin 2s ~ 2х (по теореме 9.1), то lim У,*2 = lim |f = i•
9.3. Приемы раскрытия неопределенностей. При рассмотрении
арифметических операций над пределами предполагается, что обе
переменные величины имеют предел, а в случае предела частного
оговаривается, что знаменатель не равен нулю.
Существуют случаи, когда эти условия не выполняются. Например,
переменные, стоящие в числителе и знаменателе, стремятся
одновременно к нулю или бесконечности. В этом случае говорят, что имеет место
неопределенность соответствующего типа: § или ~.
Если сумма бесконечно больших величин одного знака есть величина
бесконечно большая, то о пределе разности таких величин заранее ничего
сказать нельзя — неопределенность типа оо — оо.
При умножении бесконечно малой величины на бесконечно большую
возникает неопределенность типа 0 • оо.
Раскрыть неопределенность - это значит определить поведение
выражения, приводящего к данной неопределенности, и найти его предел.
Рассмотрим несколько приемов раскрытия неопределенностей
различного типа.
Пример 9.6. Найти lim |sj|.
Решение: В данном примере числитель и знаменатель —
бесконечно большие величины, т.е. имеет место неопределенность типа ~. Чтобы

122
9 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
раскрыть эту неопределенность, разделим числитель и знаменатель на х.
Получим
t. 3x4 5 ,. 3 4 5/х 3
x-+oo2x + 7 *-юо2 4-7/х 2
так как при x -> oo каждая из дробей | и ^ стремится к нулю.
На основании рассмотренного примера можно сделать определенный
вывод относительно предела дробно-рациональной функции, записанной
в общем виде, при х—> со:
,. Qm{x) v omxm + am_1a:m-1 + ...-fao
hm ■ , . = hm —; : — :
*->oo Pn(X) *-юо bnXn 4 bn-.iXn-1 + ... 4 b0
в если степень числителя меньше степени знаменателя (га < п), то
предел равен нулю;
о если степень числителя больше степени знаменателя (т > п), то
предел равен бесконечности;
в если степени числителя и знаменателя равны (т = п), то предел
равен конечному числу.
Чтобы определить предел дробно-рациональной функции в случае,
когда при х ->' Хо числитель и знаменатель имеют пределы, равные нулю
(неопределенность jj), надо числитель и знаменатель дроби разделить на
(х - Хо) и перейти к вычислению предела. Если же и после этого
числитель и знаменатель новой дроби имеют пределы, равные нулю при х —> хо,
то надо произвести повторное деление на (х - х0) и т.д., до тех пор,
пока не будет получен окончательный результат. В некоторых случаях эту
неопределенность можно легко раскрыть, разложив предварительно
числитель и знаменатель на сомножители и сократив на (х - хо).
Пример 9.7. Найти lim Ф^.
Решение: При подстановке предельного значения аргумента х = 3
числитель и знаменатель дроби стремятся к нулю. Имеет место
неопределенность §. Разложим выражение в числителе и знаменателе и произведем
сокращение на (х - 3):
.. х2-9 .. (х-3)(х4 3) .. х4 3
hm -г—— = hm , ' ч— = hm = 2.
х-*з х1 - Зх *->з х(х — 3) *-+з х
При вычислении пределов, содержащих иррациональные выражения,
часто используют следующие приемы:
о введение переменной для получения рационального выражения;
9 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
123
о перевод иррациональности из знаменателя в числитель и наоборот,
при этом используются формулы тождественных преобразований
алгебраических выражений:
(V* + у/у) • (y/i- у/у) = {у/х~)2 - {у/У? = х-у (х > О,у > 0),
(v^±v^)4^Ti^F^+{/^) = (^)3±(^)3 = x±2/ (x^ 0,у^0).
Пример 9.8. Найти lim(>/x2- 1 -х).
х-юо
Решение: Здесь неопределенность типа оо - оо. Умножим и разде-
лим выражение под пределом на сопряженное ему выражение у/х2 — 1 -I- х.
Ш(У^1-Х)= lim (у^Л-х)(У^Т+х) =
*-юо аг-*оо у/х2 — 1 4 X
г х2~1-х2 ,. -1
= hm . о = hm , п = 0.
х-*оо у/х2 — 1 4 X х-+°° у/х2 — 1 -f X
Пример 9.9. Найти lim v'x + l - у/х-
Х->00
Решение: Опять мы имеем дело с неопределенностью типа оо -
оо. Устранить эту неопределенность можно, если умножить и разделить
исходное выражение на неполный квадрат суммы двух выражений. После
этого можно применить формулу разности кубов двух выражений.
lim ^П - Ух =
х-+оо
r (#F+T- ^£)(У(х +1)2+ VxTiyx'+ Ух2)
— iim ... -—: =
У(х 4 l)2 -h tfT+iyi' 4 yfx2
= lim (^^l)3-(^)3
*-<*> {/(^+1)2 + \/(х + 1)х -f V^
х4-1 - х
= lim
*•+«> ^(x4l)24-v/FTlr4 ^х2
= lim —, . nt -== = 0.
»-►«> ^/(x4l)2 + ^^Пг 4 n/x2
Замечание 9.1. При нахождении пределов вида
\\т[р{х))ф{ж) = С
х—ьа
следует иметь в виду, что:

Щ
9 ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ
е если существуют конечные пределы А — \iimp(x) и В = lim^(j),
х—va х-+а
тоС = Ав;
© если \innp(x) = А ф 1 и lim^(x) = ±оо, то вопрос о нахожде-
х-¥а х-+а
нии предела решается непосредственно подстановкой предельного
значения аргумента;
в если lim ip{x) = А — 1 и lim ф{х) = оо, то полагают </?(х) = 1+ a(x),
х-*а х-+а
где а(х) -> 0 при х -* а и, следовательно, С = lim [у>(я)1 =
х-+а
Шп{[1 + в(*)]=Цв«*<*> = eJ^o(*w*> = ви->(-)-Ч*(-)| так как в
х—*а
Лхнкол* случае при х '—► а lim[l + а(ж)]«<^ = е.
Пример 9.10. Яайлш lim(^)
4x\l+ar
х-+0
Решение: Здесь lim —^ =2и lim (а: -f 1) = 1. Следовательно,
х->0 lz х-*0
,. /sin4s\1+* . Л
lim —— ) = 21 = 2.
*-*o \ 2x /
Пример 9.11. Найти lim (^^)
Решение: Здесь lim £$k = lim (т-?-) = i, lim (я -f 3) = оо,
z-юо *x ' * x->oo \q~^/ * x-»oo
этому
Пример 9.12. Явйт« lim (?Ц)*.
Решение: Здесь lim fjf = lim —f- = 1, lim x - оо, т.е. имеет
X-400 X->00 * ж Ж—ЮО
место неопределенность 1°°. Произведя указанные выше преобразования
(у?(х) = 1 + а(ж)), получим
ш. f£i|V . ,im f, + (• + • - ЛГ . ,im f, + (JL.)}' .
*->oo \x - 2/ x-*oo [ \x - 2 /J x->oo [ \:r-2/J
c-+oo M 2 — ZJ
10
• -2*
цт<Ц + _Г^| \ =c,«SDrf = e10.
P. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
В данном случае, не прибегая к общему приему, можно найти предел
проще:
„(flfV.-jlljE. Ы<1 + »'Г
г-*оо\,Х~2У x->oo(l-l)* ,._ [Л , f_21v-f
е8
Ы(1+<*»Ч
~2 ~ е-2
= е*
В дальнейшем полезно помнить, что lim (l + zY = «*, или в более
общем виде
s-юо V xm/ г-н» IV дг^у у
00, п > га; а& > О
= ^ 0, п > га; аб < 0е°6, га = т;
1, п < т.
9. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
Пример 9.1. Сравнить бесконечно малые величины а = t • sin2 ^ и
0 = 2£ • sin £ при £ —> 0.
Решение: Найдем отношение бесконечно малых функций
.. а *-sin2t 1Г . . 1 п п
lim -г = lim :— = - lim sin t = - • 0 = 0,
t-ю /? t-»o 2* • sin t 2 <->o 2
т.е. а есть бесконечно малая более высокого порядка чем /?.
Пример 9.2. Найти lim(5± + 2).
Решение: В простейших случаях нахождение предела сводится к
подстановке в выражение предельного значения аргумента. Так как при
х -> 4 —^ 5x4-2=22, то в результате
lim(5a: + 2) = 22.
х-*4
При отыскании предела отношения двух целых многочленов
относительно х (gff)) ПРИ х "^ °°» т,е' когДа имеет место неопределенность
вида ~, оба члена отношения рекомендуется предварительно разделить
на жп, где п — наивысшая степень этих многочленов.

126
9. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
Пример 9.3. Найти lim |^.
Решение: При х -> оо числитель и знаменатель исследуемой
дроби неограниченно возрастают.В этом случае говорят, что имеет
место неопределенность вида ~. Разделив на х одновременно числитель и
знаменатель дроби, получим:
Ъх -4 ,. Цг4 .. 6-4 5
lim -~ = lim -£г* — Иш
*-+<х> 4х + 2 х-юо 2£Х£ х_>оо 4 + £ 4
так как при х —> оо каждая из дробей | и | стремится к нулю.
Пример 9.4. Найти lim ^f+ffi1.
Решение: При х —► оо мы имеем дело с неопределенностью типа ~.
Разделим на х2 одновременно числитель и знаменатель дроби, получим
r Зх2 + 2х + 1 r ^ф^ _. 3+f + £ 3
Ьт ——г—-— = lim . * = lim —/ / = -,
х-юо 2X2 + 3 *-юо 2x2+3 моо 2 + Л 2
х2 **
так как при х -4 оо каждая из дробей |, хт, ^т ~> 0.
Пример 9.5. Найти lim Ф^¥.
Решение: Поскольку при х —> -оо опять имеем дело с
неопределенностью ~£ при исследовании предела отношения двух многочленов
воспользуемся предложенной выше рекомендацией. Старшая степень
рассматриваемых многочленов равна 2, поэтому разделим числитель и
знаменатель дроби на х2.
х2 _ 2х ^=г^ 1 - - 1
lim -~ — = lim * 7 = lim -~ f- = —- = -co.
«-♦-оо 6х + 7 х-+~оо fi£fi х-ч-оо а + Jf -0
Пример'9.6. Найти lim ^'г^4.
>/4х4+5~
Решение: В данном случае имеем неопределенность ~. В
соответствии с рекомендацией разделим числитель и знаменатель на хп,где а -
старшая степень многочленов. Учитывая, что в знаменателе х4 стоит под
квадратным корнем, делим все на х2.
.. 5х2-Зх + 4 5*2;f+4 5~| + £ 5-0 + 0 5
lim —. л = lim . ж. = lim —, * х = —. = -.
з-*оо уЧх4 + 5 *-+ое V 4x45 х-кх> Л _5_ V 4 + О 2
Я ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
127
Предел lim ^(4, где Р(х) и <?(х) целые многочлены и хотя бы один из
них в точке а ф 0 находится непосредственной подстановкой в функцию
предельного значения аргумента х = а. Если же Р(а) = Q(a) = 0 и имеет
место неопределенность jj, то дробь ЩА рекомендуется сократить один
или несколько раз на разность (х — а).
Пример 9.7. Найти lim 4jf.
г_+_1 яг2+1
^J зШ е Н_И е: ПрИ подстановке ж = -1 в числитель имеем х3 +
12-~^ + 1 = -1 + 1=0. При подстановке х = -1 в знаменатель —
х 4-1 — —1 +1 = 1 + 1 = 2. Следовательно,
lim -=—- = - = 0.
*->-ix2 + l 2
Пример 9.8. Найти lim /V*
Решение: При подстановке х = 2 имеем неопределенность вида
~. Разложим числитель и знаменатель на сомножители и произведем
необходимые сокращения. В результате получим:
х2-4 ,. (х~2)(х + 2) .. х + 2 А
11т -_—_ = jim 1 ^1 -L — iim _ — 4.
х-*2а;2~Зх + 2 х-*2 (X ~ 2)(Х ~ 1) X-+2I-1
Выражения, содержащие иррациональность, приводятся к
рациональному виду во многих случаях путем введения новой переменной.
Пример 9.9. Найти lim ^ЗЦ-.
Решение: При подстановке х = 0 имеем неопределенность вида
§. Обозначим 1+х=у6 для того, чтобы при извлечении квадратного и
кубического корней получить целые степени. Учитывая, что при х-»0,
у—>1, имеем:
г vTTx"-l _. у/у*-1 .. у3-1
lim _. = lim -~== = lim ~—-.
*->o v^l +x - 1 y-n -j/j/в _ j у-*1 У - 1
Прием нахождения последнего предела аналогичен тому, который мы
использовали при решении примера 9.8. Для раскрытия неопределенности §
(при у=1) разложим на множители числитель и знаменатель, произведем
необходимые сокращения и в результате получим
2/->i2/2-l v->i (y-l)(2/ + l) !/->i 2/+1 1 + 1 2

128
9. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
Другим приемом нахождения предела от иррационального выражения
является перевод ирациональности из числителя в знаменатель или,
наоборот, из знаменателя в числитель. При этом используются формулы
тождественных преобразований алгебраических выражений:
(х/хЧ у/у)№- у/у) = (уД)2 - Ш2 = Х~У (х>0,у>0)
(Vi±y/y)(\/^T ?fiy+ V?) = (W ± (^3 = * ±У (* > 0,2/ > 0).
Пример 9.10. Найти lim (>/х2 -5х + 6 - х).
Х-ЮО
Решение: При х-» оо мы имеем неопределенность вида оо-оо.
Умножим и разделим выражение, стоящее под пределом, на выражение
ему сопряженное (на сумму таких же слагаемых). В данном случае на
{у/х2 - Ъх + б + х). После элементарных преобразований получим:
lim (ч/я2 -5х + 6 - х) = lim
(ч/ж2 - 5х + 6 - х)(л/х2 - 5х + 6 + х)
у/х2 - Ъх + б + а:
,. х2~5х + 6-х2 г 6-5х
= lim -====== = lim
*-♦<» v^x2 - 5х + б + х *-+°° л/х2 - 5х + б + х
Очевидно, что при х-> оо последний предел приводится к
неопределенности вида —. Разделим числитель и знаменатель одновременно на хп, где
00
п - старшая степень многочленов. В данном случае на х.
б - Ъх ^^ й ~ 5
lim -7==== = iim ,h * ... ■ = lim x -
*-+<*> y/x2 - 5x + 6 + x «-+00 ^2ИН1±£ *->«> ./l - 4 + 4 + l
0-5 -5 -5 5
Пример 9.11. tfaumu lim (x - ^x3-f 8x2).
X->00
Решение: В данном случае при х -> оо имеем неопределенность
вида оо-оо. Умножим и разделим выражение, стоящее под знаком
предела, на неполный квадрат суммы слагаемых, чтобы в итоге получить в
числителе формулу разности кубов двух чисел:
9. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
129
lim (х - у/х* + 8х2) =
(х - ffx3 + 8х2)(х2 +■ х^ТШ + Щх^ТЩ2)
*-><*> х2 + х v"x3 + 8х2 + ^/(х3 + 8х2)2
х3 - (^х3 + 8х2)3
= lim . =========== =
*-*оо Х2 + д.^.3 + 8Д.2 + ^/(х3 + 8x2)2
X3 - (Х3 + 8Х2)
= lim — '
*-+оо ^2 + Х^Ч8^2 + ^/(а;3 + ЗХ2)2
-8х2
= lim . .
*-<*> х2 + х^х3 + 8х2 4- s/(x3 + 8х2)2
= -8 lim
*2(i + ^T+I+^(i+ *)»)■
i
^-i + yiTf + ^i + f)2 'i+i + i з"
= -8 iim , 1 , = -8 • * 8
Пример 9.12. Найти lim f1*^-
Решение: При х = 4 имеем дело с неопределенностью вида §.
Раскроем эту неопределенность следущим образом: числитель умножим
и разделим на выражение, сопряженное числителю -» (3 + у/Ъ И- х), а
знаменатель — на выражение, сопряженное знаменателю -> (1 + у/Ъ — х).
_з-^Tg _,_(3- VFF»).Eg
= lim (3 ~ \/5Ti)(3+ У5+~х)(1 + уТ^ _
*™ (1 - уТ^"*)(1 + v/5"=~x)(3 + v/STx) ~
= lim (9 ~ (У5+7)2)(1 + у^¥) = (9-(5+х))(1 + >/Г^) =
*-< (1 - (ч/5^*)2)(3 + у/ЕП) *'" (1 - (5 - *))(3 + у/Ъ + х)
lim (9 ~ 5 ~ »))(! + У/5Г^) = lim (4-x))(l + y/5^i) =
«-♦« (1 - 5 + х))(3 + vT+lr) *™(-4 + x))(3+>/5PFz)
= lim
, .. 1+n/5^ 1+1 1 1
= -1 • hm . = -1 • = -1 • - = —
«-ИЗ+ vCfi 3+3 3 3

130
9. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ
При нахождении пределов от разности двух дробей, когда имеет
место неопределенность вида оо-оо, рекомендуется предварительно привести
дроби к общему знаменателю.
Пример 9.13. Найти lim (•£$ - ;£§).
Решение: При х = 3 имеем дело с неопределенностью вида оо-оо.
Воспользуемся рекомендацией и приведем дробь к общему знаменателю.
После элементарных преобразований получим:
/ 1 6 \ ,. * + 3-6 _
^3^7=3-?39;""S5(x-3)(x + 3)
-1^(х-з)(х + з) «** + з з + з 6*
Самостоятельная работа
Сравнить бесконечно малые величины:
Пример 9.14. а = t2 tg t и (3 = t2 sin2 tnput-* 0.
Пример 9.15. а = Ы2 + 2*5 t» /9 = З*2 + 2*3 njni t -> 0.
Найти пределы функций.
Пример 9.16. liin 4±i
«А-1**+*"
Пример 9.17. Ит^Й*5.
х-*1 * +1
Пример 9.18. lim ^.
Пример 9.19. lim 4±fr-
Пример 9.20. lim^fp
х-»1 х 1
Пример 9.21. Umg£g*§.
Пример 9.22. lim ^'л+У"1'
х-»оо А ^
Пример 9.23. lim^^.
х-»3
Пример 9.24. lim^fs+iS-
i0. ЛЕКЦИЯ - НЕПРЕРЫВНОСТЬ ФУНКЦИИ
131
Пример 9.25. Нт-ЙЦ.
х-И v*-l
Пример 9.26. lim V*1***8-1.
х-»0 ж
Пример 9.27. Ит Ш*=±л
х-+0 х
Пример 9.28. lim ^P"i.
Пример 9.29. lim д* _.
Пример 9.30. lim j£±I=j£=I.
Пример 9.31. lim \fx~TT- ^i".
х-юо
Пример 9.32. lim (-1^ - -L,).
10. ЛЕКЦИЯ - НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Непрерывные функции, точки разрыва и их классификация,
действия над непрерывными функциями, свойства функций,
непрерывных на сегменте.
10.1. Непрерывные функции.
Определение 10.1. Функция у = f(x) называется непрерывной в
точке хоу если:
© функция определена в точке хо и в некоторой ее окрестности,
содержащей эту точку;
© функция имеет предел при i -4 хо;
в предел функции при х —» xq равен значению функции в точке Xq:
(10.1) lim /(*) = /.(«в).
X —►ХО
Если в точке хо функция непрерывна, то точка Хо называется точкой
непрерывности функции.
Пример 10.1. Исследовать на непрерывность функцию у = ех в точке
х = 1.

132
10. ЛЕКЦИЯ - НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Решение: Чтобы доказать, что функция у = ех непрерывна в
точке х = 1, необходимо проверить выполнение трех следующих условий
(определение непрерывности):
в функция у = ех определена в точке х = 1=»/(1) = е;
о существует lim/(x) = lime* = e;
© этот предел равен значению функции в точке х = 1 :
lim/(z) = /(l) = e.
Таким образом, доказано, что функция у - ех непрерывна в точке х = 1.
ЗАМЕЧАНИЕ 10.1. Формулу (10.1) можно записать в виде
(10.2) lim /(x) = /(lim х),
X-*Xq X-*Xq
так как lim x = х0. Это значит, что при нахождении предела непре-
х~-*хо
рывной функции можно переходить к пределу под знаком функции.
Введем понятие непрерывности функции в точке х0 справа и слева.
Если, существует lim fix) = /(х0), то функция называется непрерыв-
ной в точке Xq слева. Аналогично определяется непрерывность функции
справа.
Так как Ах = х^-х0, a Av = /(я)-/(х0), то условие (10.1) равносильно
следующему:
lim /(х) ^ /(х0) =» lim [/(х) - /(х0)] = 0 =* lim Ay = 0.
ОПРЕДЕЛЕНИЕ 10.2. Функция у = /(х) называется непрерывной в
точке Хо, если бесконечно малому приращению аргумента
соответствует бесконечно малое приращение функции
(10.3) lim Ди = 0.
ПРИМЕР 10.2. Показать, что функция у = х3 непрерывна для любого
значения аргумента х.
Решение: Найдем приращение функции Ду.
Ду = (х+Ах)3~х3 = х3+ Зх2Дх+ ЗхДх2+Дх3-х3 = Зх2Дх+ЗхДх2+Дх3.
Используя теоремы о пределе суммы и произведения функции, получим
lim Ay = lim (Зх2Дх + ЗхДх2 + Дх3) = 0.
Дж-»0 Дх->0
Следовательно, функция у = х3 непрерывна при — оо < х < оо.
10. ЛЕКЦИЯ - НЕПРЕРЫВНОСТЬ ФУНКЦИИ
133
10.2. Точки разрыва функции и их классификация.
Определение 10.3. Точка хо называется точкой разрыва функции
У ^ f(x)y если она принадлежит области определения функции или ее
границе и не является точкой непрерывности.
Так, например, функция у = <х*х\а (рис. 89) терпит разрыв при х =
1. Эта функция не определена в точке х = 1, и не существует предела
функции в этой точке.
Рис. 89. График функции у = frrjp
Определение 10.4. Точка разрыва хо функции у = /(х)
называется точкой устранимого разрыва, если существуют оба односторонних
предела в точке х0 и они равны, т. е. lim f(x) = lim fix) = A.
X-+XO—0 a?-fa?o-f0
Пример 10.3. Исследовать на непрерывность функцию
1+х3
■У =
1 + х
Решение: В точке х = -1 функция не определена, так как,
выполнив подстановку, получаем неопределенность §. В других точках
дробь можно сократить на (1 + х), так как в них 1 + х ф 0. Легко видеть,
что односторонние пределы слева и справа в точке х = -1 равны между
собой и их можно вычислить:
,. 1 + х3
у = hm лу ■■
lim
♦ -1+0*
lim
x->-l-fO 1+Х
1 + х 1-х+х2) .. • 2ч t , ,
hm - - = hm (1 - x + x2) = 1 + 1 + 1
->-l+0 1+X ar->-l+<T
3.

щ
10. ЛЕКЦИЯ - НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Таким образом, при х = -1 данная функция имеет устранимый разрыв.
Он будет устранен, если положить, что при х = -1 => У - 1+х - 3-
Определение 10.5. Если в точке х0 односторонние пределы слева и
справа существуют, но не равны, точка х0 называется точкой разрыва
I рода.
ПРИМЕР 10.4. Исследовать на непрерывность функцию
1
у = arctg
х-4
(рис. 90).
Рис. 90. График функции у = arctg ^34
Решение: Вычислим односторонние пределы функции в точке ее
разрыва х = 4. w
Предел слева — ^lim^arctg ^) = arctg(-oo) - -3.
Предел справа — ^lim^arctg ^) = arctg(H-oo) = f.
Пределы слева и справа существуют, но не равны, следовательно
точка х = 4 для данной функции - точка разрыва I рода (точка скачка).
Определение 10.6. Точки разрыва, не являющиеся точками
разрыва I рода, назыаются точками разрыва II рода.
В точках разрыва II рода не существует хотя бы один из
односторонних пределов. Функция у = ^, представленная на рис. 89, не имеет ни
левого, ни правого конечного предела в точке х = 1. Следовательно, для
данной функции х = 1 является точкой разрыва II рода.
10. ЛЕКЦИЯ - НЕПРЕРЫВНОСТЬ ФУНКЦИИ
135
10.3. Действия над непрерывными функциями.
Теорема 10.1. (Непрерывность суммы, произведения и частного
непрерывных функций.) Если функции <р(х) и ф{х) непрерывны в точке Хо,
то их сумма и произведение также непрерывны в точке xq. Если, кроме
того, знаменатель в рассматриваемой точке не равен нулю, то
частное непрерывных функций есть функция непрерывная.
Докажем непрерывность произведения.
Дано: непрерывность функций в точке xq:
lim (p(x) = (р(х0) и lim ф(х) = ф(хо).
х-ч-хо х-+х<>
Доказать, что f(x) = у>(х) • ф(х) есть функция непрерывная в точке xq,
т. е. lim f(x) = /(х0).
X—¥XQ
Доказательство.
lim f(x) = lim [<p(x) - ф(х)) = lim (p(x) • lim ip{x) =
X—KPO X-+XQ X—►XO X-+XO
= <p(xo) • Ф(х0) = /(x0).
Можно строго доказать, что все основные элементарные функции
непрерывны при всех значениях х, для которых они определены.
Например, степенная у = хп, показательная у = ах,
тригонометрические у — sin х и у = cos х функции непрерывны на всей числовой оси (х £
Л), логарифмическая функция у = \о^ х непрерывна при х > 0, а
тригонометрическая у = tg х непрерывна в каждом из интервалов (-|-Ь&тг; §+А:7г)
и терпит разрыв II рода в точках Xk = (2A; + 1)| (А: = 0; ±1; ±2;...).
ТЕОРЕМА 10.2. (Непрерывность сложной функции.) Если функция и =
tp(x) непрерывна в точке хо, а функция у — f(u) непрерывна в точке
щ = <р(хо), то сложная функция у = / [</?(х)] непрерывна в точке Xq.
Без доказательства.
В заключение этого раздела рассмотрим два предела, которые нам
понадобятся в дальнейшем.
Пример 10.5. Вычислить lim logg(1"fa?).
ае-И> х
Решение: Заметим, что при х -> 0 числитель и знаменатель
одновременно стремятся к нулю, т.е. имеет место неопределенность вида
§. Выполним преобразование
lim 1о^(1 + ж) = lim I - 1о&(1 + х)
limf-l
limlogJl -f х)«

136
10. ЛЕКЦИЯ - НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Так как данная логарифмическая функция непрерывна в окрестности
точки х = 0, то можно перейти к пределу под знаком функции (lim f(x) =
х-*х0
/(lim*)).
ar-»at0
limloga(l + x)- = 1о& [lim(l + x)*| ,
но lim(l + x)« = e — второй замечательный предел.
Следовательно,
(10.4) liml0go(l + s)
В частности, при а — е
(10.5) ' НтМ1±£)=1пе=1.
Таким образом, j/ = ln(l-fx) иу = х — эквивалентные бесконечно малые
функци при х —у 0.
ПРИМЕР 10.6. Вычислить lim fi-zl.
Решение: Здесь мы имеем дело с неопределенностью вида §.
Для нахождения предела сделаем замену переменной, положив ах — 1 = t.
Тогда х = loga(£ -f 1). При я -> 0 также и t -> 0.
lim — iim. —^ = ijm
Так как на основании результата, полученного в предыдущем примере^
UmSbfiltt^iogae, то
(10.6) iim^-^ = г^- = lna.
В частности, если a = е, имеем
е* - 1
цт = lne = 1,
х-+0 X
т.е. у — ех — I и у = х — эквивалентные бесконечно малые функции при
а;->0.
10.4. Свойства функций, непрерывных на сегменте.
Определение 10.7. Функция у = f(x) непрерывна на сегменте [о, 6],
если она непрерывна во всех внутренних точках этого сегмента, а на
концах сегмента (в точках a ub) непрерывна соответственно справа и
слева.
10. ЛЕКЦИЯ - НЕПРЕРЫВНОСТЬ ФУНКЦИИ
137 ,
ТЕОРЕМА 10.3. Если функция у = f(x) непрерывна на сегменте [a, ft],
то она достигает на этом сегменте своего наибольшего и(или)
наименьшего значения.
Простым доказательством этой теоремы, является геометрическая
иллюстрация функции у = f(x) на рисунке 91. Непрерывная на сегменте
[а, ft] функция достигает наименьшего своего значения в точке х = х\ = а,
а наибольшего значения в точке х2-
у
5*- х
..
Рис. 91. Геометрическая иллюстрация условий теоремы 10.3
Следствие. Если функция у = f(x) непрерывна на сегменте [a, ft], то
она ограничена на этом сегменте.
Действительно, если по теореме 10.3 функция достигает на сегменте
наибольшего М и наименьшего т значений, то имеет место неравенство
тп ^ f(x) ^ M для всех значений функции на рассматриваемом сегменте.
Т. е. |/(х)| ^ М и, следовательно, функция у - f(x) ограничена на
сегменте [a, ft].
ТЕОРЕМА 10.4. (Теорема Больцано-Коши.) Если функция у = f(x)
непрерывна на сегменте [a, ft] и на ее концах принимает значения
разных знаков, то внутри этого сегмента найдется, по крайней мере, одна
точка С, в которой функция равна нулю.
Геометрический смысл теоремы заключается в следующем: если
точки графика функции у = /(я), соответствующие концам сегмента [a, ft],
лежат по разные стороны от оси ОХ, то этот график хотя бы в одной
точке сегмента пересекает ось ОХ. На данном рисунке 92 это три точки
xiyx2,zz-
y = f(x)

138
10. ЛЕКЦИЯ - НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Рис. 92. Геометрическая иллюстрация условий теоремы 10.4
Теорема 10.5. (О промежуточных значениях функции.) Если
функция у = f(x) непрерывна на сегменте [а, Ь] и /(а) = А и f(b) — В, то для
любого числа С, заключенного между А и В, найдется внутри этого
сегмента такая точка с, что f(c) — С.
Из графика на рисунке 93 видно, что непрерывная функция, переходя
от одного значения к другому, обязательно проходит через все
промежуточные значения.
У
i
У = С /
f(a)\ '
а с
y=f(b) у
1
f(b)
ь
Рис. 93. Геометрическая иллюстрация условий теоремы 10.5
Теорема 10.6. (О непрерывности обратной функции.) Если функция
у = f(x) непрерывна на сегменте \а,Ь] и возрастает (убывает) па этом
сегменте, то обратная функциях = j~l{y) на соответствующем
сегменте оси OY существует и является также непрерывной
возрастающей (убывающей) функцией.
Эту теорему мы принимаем без доказательства.
10 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - НЕПРЕРЫВНОСТЬ ФУНКЦИИ
139
10. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - НЕПРЕРЫВНОСТЬ
ФУНКЦИИ
Пример 10.1. Показать, что функция у = 4х2 непрерывна в точке
х = 2.
Решение: Для этого необходимо показать, что в точке х = 2
выполняется все три условия непрерывности функции:
1) функция у = 4а;2 определена в точке х = 2 =$> /(2) = 16;
2) существует \imf(x) = Mm Ах2 = 16;
z-42 ' v ' s->2
3) этот предел равен значению функции в точке х = 2
lim/(а;) ===/(2)^16.
Пример 10.2. Показать, что функция у = sinx непрерывна для
любого значения аргумента х.
Решение: Найдем приращение функции Ду, используя формулы
тригонометрических тождеств
а • / . а ч • Л • дя ( ДаЛ
Ay = sm(x -f Ax) - sin x = 2 sin —- cos I x H I =
n . Да: / Ax\ Az sin^ / ДаЛ А
= 2sin — coe{*+— J — e_^.«*(* + — у Ax.
2
SID i
Так как lim ^j^- = 1, a |cos (x + —*) | < 1, то при любом х имеем
.. Л .. fsin^ ( Ах\ л \
hm Ay = lim j * cos ( x + —- } • Ax =
д*-+о * д*-»о I £& \ 2 / у
':. sin ^ 1# / Ax\
= lim —Т-Г- • hm cos I x -h —- 1 • lim Да; = 1 • cos x • 0 = 0.
(•♦*)
Дх-»0 ^ Д*-+0 у 2 / Дх-^0
Следовательно, функция у = sin а; непрерывна при -оо < х < со.
Пример 10.3. Исследовать на непрерывность функцию
— 1, еслиО ^ х ^ 3,
= Гх-1,
\з-ж,
° ~ если 3 < а; ^ 4.
Решение:

ЦО 10 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - НЕПРЕРЫВНОСТЬ ФУНКЦИИ
4 х
Рис. 94. График функции примера 10.3
Эта функция (рис. 94) определена во всех точках сегмента [0,4] и ее
значение при х = 3 =>■ у = 2. Функция терпит разрыв, так как она не
имеет предела при х —> 3 :
lim /(*) = 2,
Х-+3-0
lim fix) = 0.
Следовательно, точка х = 3, точка разрыва первого рода. При этом в
граничных точках исследуемого сегмента [0,4], функция /(х) непрерывна
справа (х = 0) и непрерывна слева (х = 4).
Пример 10.4. Исследовать на непрерывность функцию у = xxZl5 -
Решение: В точке х — 5 функция не определена, т.к., выполнив
подстановку, получаем неопределенность вида 0/0. Легко доказать, что
lim у = lim у = 10.
Х-+5-0 х-*5+0
Следовательно, точка х — 5 точка устранимого разрыва.
Пример 10.5. Исследовать на непрерывность функцию у = р.
Решение: В точке х = 0 функция (рис. 95) терпит разрыв, так
как она не определена в этой точке. Пределы функции слева и справа от
точки х = 0 равны оо. Следовательно, точка х = 0 для данной функции
является точкой разрыва второго
ПРИМЕР 10.6. Исследовать на непрерывность функцию у = *тт^
Решение: В точке х = 0 функция терпит разрыв 1-го рода, так
как односторонние пределы существуют в этой точке, но не равны:
lim *Й* = lim ^ = _!,
предел слева
предел справа
lim sin(x)
х-»0+0
->0-0
lim ■-£&
z->0+0 x
1.
10 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - НЕПРЕРЫВНОСТЬ ФУНКЦИИ
Щ
Рис. 95. График функции у = р
Пример 10.7. Исследовать на непрерывность функцию у = sin £.
Решение: Функция у = sin £ определена для всех значений х, кроме
х = 0. В этой точке она имеет разрыв. Точка х = 0 есть точка разрыва II
рода, так как при х ~> 0 как справа, так и слева, функция sin ^, колеблясь
между -1 и 1, не приближается ни к какому числовому значению. График
ее приведен на рис. 96.
Рис. 96. График функции у = sin \
ПРИМЕР 10.8. Исследовать на непрерывность функцию у = aj£.
Решение: Функция ^ не определена в точке х = 0. Точка х = 0
является точкой разрыва I рода, так как при х -» 0 существуют пределы
справа и слева:
sinx „ .. sinx '
lim = 1, lim = 1.
x-+0+0 X x-*0-0 X
Если доопределить функцию ™£ в точке х = 0, полагая /(0) = 1, то
получим уже непрерывную функцию, определенную так:
sin х
/(х) = , если х ^ 0; /(0) = 1.
х
Доопределив функцию в точке х = 0, мы устранили разрыв.

Ц2
11. ЛЕКЦИЯ ** ЧИСЛОВЫЕ РЯДЫ
Самостоятельная работа
Пример 10.9. Показать, что функция у=1пх непрерывна в точке
х=е.
ПРИМЕР 10.10. Показать, что функция у = cosx непрерывна для
любого значения аргумента х.
Пример 10.11. Исследовать на непрерывность функцию У = о-
Пример 10.12. Исследовать на непрерывность функцию у = /^4.1a)7x12_4j ♦
Пример 10.13. Исследовать на непрерывность функцию у = tg \.
ПРИМЕР 10.14. Исследовать на непрерывность функцию у = х "ffiL&g^"6
Пример 10.15. Исследовать на непрерывность функцию у = ^.Д.^.
ПРИМЕР 10.16. Вычислить limlntgx.
11. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
Основные определения, простейшие свойства числовых рядов,
необходимый признак сходимости ряда.
11.1. Основные определения.
Определение 11.1. Числовым рядом называется сумма членов
бесконечной числовой последовательности:
оо
(11.1) Ui +и2 + Щ + ' •• + Un -f ... = У\п.
п=1
Числа ui, 1*2, из,..., un,... называются членами ряда. Ряд считается
заданным, если известен общий член ряда ип как функция его номера п:
ип = /(п).
Приведем несколько примеров рядов:
П. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
US
1) } + l + i + - + i + -
3 •♦"•••+ я "*■■•'••■» ^п =
1.
2) 2 + 6+18+.-.+ 2-Зп-1 + ..., 1*п = 2 - 3я-1;
3) 1-1 + 1-1 + ... + (-l)»-i + ..., un = (-1)»-1;
4) cos f + cos f +cos | + ... + cos I + ..., un = cos .£.
Определение 11.2. Сумма Sn первых п членов ряда называется п-й
частичной суммой ряда:
п
(И-2) 5W = щ + ц2 + ц3 + • • + ип = У^ Ц&.
Иногда, исследуя частичную сумму ряда, можно сделать вывод о
характере поведения самого ряда.
Пример 11.1. Исследовать частичную сумму ряда:
12 2-3 3.4 + ""+п(п + 1)+"';
Решение: Составим последовательность частичных сумм Sn
этого ряда. Для этого прежде всего заметим, что общий член ряда можно
записать следующим образом:
1 1 1
п(п +1) п п + 1'
Поэтому
S - l -1-, *•
51-Г^-2-1_2'
2 I-2+2-3 1 2 2 3
s - * + l + * iiiii
3 l-2 + 2-3 3-4 1 2+2 3 + 3
Подобным же образом найдем, что
с -J_ + J_ + ..l 1
" 1-2 + 2-ЗЧ-41 '(n-Dn'n
1 1+1 1+1 Ч + * * *
122334 п—1 n ' n я
1
3'
-н-
1
(п + 1)
тт-
1
4'
1
п + 1
Отсюда следует, что предел последовательности частичных сумм этого
ряда равен единице:
Urn Sn = lim [ 1 L-Л = i - um —L- = i.
n-+oo n-*oo у 7Z 4- 1 у n-+oo n + 1

ш
11. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
ПРИМЕР 11.2. Исследовать частичную сумму ряда:
2 + 6 + 18 + •.- + 2 • Зп-1 + ....
Решение: Найдем последовательность его частичных сумм:
5i = 2,52 = 2 + 6 = 8,
53 = 2 + б +18 = 26,...,
Sn = 2 + 6+18 + --- + 2-.3n-1.
Эти частичные суммы можно переписать следующим образом:
51 = 2 = 3-l,S2 = 8 = 32-l,S3 = 26 = 33--l,...,S„ = 3n-l.
Отсюда следует, что
lim Sn = lim (3n - 1) = оо.
n-*oo n-+oo
Пример 11.3. Исследовать частичную сумму ряда:
1-1 + 1-1 + --- + (-1)в"1 + ....
Решение: Последовательность частичных сумм имеет вид
S1 = l,52=0,53 = l,54 = 0,....
В этом примере последовательность частичных сумм не стремится ни к
какому пределу.
Таким образом, для некоторых рядов последовательность частичных
сумм стремится к определенному пределу, для других же рядов такой
предел не существует.
Определение 11.3. Ряд называется сходящимся, если существует
конечный предел S последовательности его частичных сумм Sn при
неограниченном возрастании номера п, т.е.
(11.3) lim Sn = S.
n-юо
Определение 11.4. Предел S последовательности частичных сумм
сходящегося ряда называется суммой ряда.
Если S является суммой сходящегося ряда щ + и2 + щ + • • • + ип 4-...,
то пишут:
с»
(11.4) S =-tii + u2 + -u3 + -"+ ип + ... = У^Цп-
Если последовательность частичных сумм ряда не имеет предела, то
ряд называется расходящимся. Расходящийся ряд суммы не имеет.
11. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
Ц5
Одним из простейших, но очень часто встречающихся рядов, является
геометрическая прогрессия (лекция 7):
(11.5) &i+M + M2+ • + *>i<7n~1 +."..;
&i называется первым членом прогрессии, а множитель q — знаменателем
прогрессии.
Сумма п первых членов (n-я частичная сумма) прогрессии, как
известно, может быть вычислена при q ф 1 по формуле
1-д
1) Если \а\ < 1, то qn -» 0 при п -* оо и
lim Sn = lim — — = lim ^—1 lim л -•■= .
n->oo n-чоо 1 — q n-*oo 1 — q П-+О0 1 — q 1 — q
Таким образом, при \q\ < 1 геометрическая прогрессия является
сходящимся рядом, сумма которого S = ^-. '
2) Если \q\ > 1, то qn -> оо при п -> оо и
г с г fci - ЬхЯп
lim 5Я = lim —— = оо.
л-юо rt-*oc 1 — <j
Следовательно, в этом случае ряд расходится.
3) Если q = 1, то ряд (11.5) принимает вид
bi + bi + fti + • • • + 6i + .,..
Для него 5n = nbi и при &i ф О lim Sn = оо, т.е. ряд расходится.
П-+0О
4) Если q — — 1, то ряд (11.5) принимает вид
fti - bi + fci - bi +.... •
В этом случае Sn = 0 при п четном и 5П = Ьх при п нечетном.
Следовательно, при &i ф О lim 5n не существует и ряд расходится. Итак,
п-+оо
геометрическая прогрессия является сходящимся рядом при \q\ < 1 и
расходящимся при \q\ ^ 1.
11.2. Простейшие свойства числовых рядов. Рассмотрим
несколько свойств числовых радов, которые нам понадобятся в дальнейшем.
Теорема 11 Л. Если ряд
(П.6) Ux +U2+tt3 +...+М„ + ...
сходится и имеет сумму 5, то ряд
(11.7) ащ ■+- аи2 + <шз Н 1- aun + • • •,
где а — заданное число, также сходится и его сумма равна aS.

Ц6
11. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
Доказательство.Пусть 5П есть n-я частичная сумма ряда (11.6), а ап
есть n-я частичная сумма ряда (11.7). Тогда
ап = ащ 4- аи2 4- ащ 4 h <ш„ = а{щ + и2 + щЛ \-ип) = aSn.
Отсюда
lim an = lim aS„ = a lim 5„ = aS.
П—ЮО П—ЮО П—ЮО
Таким образом, ряд (11.7) сходится и имеет сумму aS.
Теорема 11.2. Если ряды
(11.8) 111 + И2 + «3 + • • ' + Un + • • • 1
(11.9) wi 4- ti2 4- v3 4- • • • + vn + ...
сходятся и имеют соответственно сумму S и S, то ряд
(11.10) (t*i + Vi) + {U2 + V2) + (l*3 + *>з) + ' • • + («n + Vn) + • • • ,
получающийся почлекньш сложением данных рядов, также сходится и
имеет сумму S -У S.
Доказательство.Обозначим n-е частичные суммы рядов (11.8), (11.9)
и (11.10) соответственно через 5„, 5П и оп. Имеем:
<гп = (Щ + vi) + (и2 4- v2) 4- (u3 4- vz) 4- h (wn + v„) = 5„ 4- 5n.
Переходя к пределу, получаем
lim on = lim (5n + 5n) = lim 5n + lim 5n = 5 + 5.
п-юо n—юо п-юо n—юо
Итак, ряд (11.10) сходится. Ряд (11.10) называется суммой рядов (11.8) и
(11.9).
Замечание 11.1. Аналогично можно доказать, что сходится ряд
(11.11) {щ - v\) -У (и2 - v2) -У (щ - v3) 4- Ь (и„ - vn) 4- ...
и его сумма равна S - S. Ряд (11.11) называется разностью рядов (11,8)
и (11.9).
Рассмотрим два ряда
(11.12) их 4- и2 + и3 4- ••• + Ufc-i + ufc -f ixfc+i + * •■ + wn-i -f un + ...
и
(1 1.13) lifc+i "f • • • + Un_! -f ti„ + . . . .
Теорема 11.3. Если сходится данный ряд (11.12), то сходится и ряд
(11.13), полученный из ряда (11.12) отбрасыванием конечного числа к
его первых членов. Обратно, если сходится ряд (11.13), то сходится и
данный ряд (11.12).
11. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
Ц7
Доказательство.Обозначим через 5„ сумму п первых членов ряда (11.12),
через Sk — сумму к отброшенных членов (к < п) и через <тп_* — сумму
п — к первых членов ряда (11.13):
Sn = Щ + и2 -У щ 4 У ик 4- Щ+i Н h un,
Sk = ux 4- u2 4- u3 4- • • • + ик, оп-к = uk+i 4~ ufe+2 -f • • • 4- ttn.
Следовательно,
(11-14) 5п = 5* + <7п_ь
причем 5^ — некоторое число, не зависящее от п.
1. Пусть ряд (11.12) сходится и имеет сумму 5, т.е. lim 5n = 5.Тогда
п—юо
из равенства (11.14) следует:
lim оп-к = lim (5n - Sk) = lim 5n - lim Sk == 5 - 5*.
п-юо п—юо п—юо п-юо
Итак, частичные суммы ап~к ряда (11.13) при п -> оо имеют предел, т.е.
ряд (11.13) сходится.
2. Пусть ряд (11.13) сходится и имеет сумму о, т.е. lim ап_* = о. Из
п-юо
( 11.14) следует:
lim 5n = lim (Sk 4- <тп_*) = Sk 4- lim <тп_* = Sk 4- a,
n—юо п-юо n—юо
т.е. ряд (11.12) сходится.
Теорему 11.3 можно сформулировать также следующим образом.
На сходимость ряда не влияет отбрасывание любого конечного числа
его первых членов.
11.3. Необходимый признак сходимости ряда. Приведем
необходимое условие сходимости ряда.
Теорема 11.4. Если ряд щ 4- и2 4- щ 4- • • • 4- ип 4-... сходится, то
его общий член ип стремится к нулю при неограниченном возрастании
номера п.
Доказательсгво.Пусть дан сходящийся ряд
Щ 4- Щ 4- щ Н У ип 4- ...,
имеющий сумму 5. Рассмотрим его частичные суммы
Sn = v>i 4- и2 4- u3 4 У un~i -У ип
и
Sn-i = Щ 4- fc2 4- из 4 1- un_i.
Отсюда ип — 5„ — 5n_i. Следовательно,
lim кп = 1ш (5n - 5n_i) = lim Sn - lim Sn-\-

Ц8
11. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
lim Sn = S и lim Sn-\ = 5, так как при п->ооип-1->оо. Поэтому
lim wn = S - 5 = 0. Итак,
П-40С
lim
(11.15) lim un = 0.
n-*oo
ОПРЕДЕЛЕНИЕ 11.5. (достаточный признак расходимости ряда).
Если общий член ряда не стремится к нулю при неограниченном
возрастании его номера п, то ряд расходится.
Действительно, если бы ряд сходился, то по предыдущей теореме его
общий член обязан был бы стремиться к нулю, что противоречит условию.
ПРИМЕР 11.4. Исследовать на сходимость ряд.
12 3 п
Решение: Ряд расходится, так как его общий член ип — ~~ не
стремится к нулю при п —► оо:
lim ип = lim = lim ■ ■ , = 1.
п-юо п-*ос п ■+■ 1 п-»оо 1 + \/П
Условие lim un = 0 является необходимым для сходимости ряда, но
П-+0О
не достаточным. Это означает, что существуют расходящиеся ряды, для
которых lim un = 0.
п-юо
Примером может служить ряд
(11Л6) 7г + 71 + ^ + -+^ + --
lim u„ = lim 4- = 0. Однако легко показать, что ряд расходится. Для
п-юо п—юо vn
этого рассмотрим частичную сумму ряда
Sn~ v/l + V2 + ч/3 + '" + у/п'
Так как ^ > fa ^ > fa ^ > fa ..., то очевидно, что
sjn ф, yjn у/П
Sn > п - fa т.е. Sn > у/п. Отсюда непосредственно следует, что lim Sn -
оо, и, следовательно, ряд расходится.
11. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ
Ц9
11. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ
Числовые ряды являются одним из важнейших разделов
математического анализа. Приступая к практическому изучению рядов, прежде всего
следует усвоить понятия сходящегося и расходящегося числового ряда, а
затем перейти к изучению признаков (условий) сходимости рядов.
Следует понимать и правильно применять необходимые и достаточные условия
сходимости. Равенство lim ип = 0, где ип - общий член ряда, является
п-юо
лишь необходимым условием для сходимости ряда. Если это условие не
выполняется, то исследуемый ряд расходится, а если это условие
выполняется, то окончательно ответить на вопрос о сходимости числового ряда
можно только после исследования его с помощью одного из достаточных
признаков сходимости.
Пример 11.1. Дан общий член ряда ип = ~j-. Записать первые
четыре члена ряда.
Решение: В числителе записан общий член геометрической
прогрессии, знаменатель которой q=2. В знаменателе мы имеем дело с
факториалом п! произвольного целого числа п^О, который определяется
формулами: 0!=1, 1!=1, 2!=1-2, 3!=1-2-3, п!=Ь2-3-...-п. Следовательно, ряд
можно записать в виде:
12 4 8 2"-1
1! 2! 3! 4! п!
Пример 11.2. Найти общий член ряда
, 1 1 1
1+3+5 + 7 + -*--
Решение: Как и в случае с общим членом последовательности, здесь
необходимо установить закономерность изменения каждого члена ряда от
его номера п. В данном случае изменяются только знаменатели, которые
образуют арифметическую прогрессию 1, 3, 5, 7,... Известно, что n-й член
арифметической прогрессии можно найти по формуле ап — а\ + d(n - 1).
Здесь ах = l,rf = 2, поэтому ап = 1 + 2(п - 1) = 2п — 1. Следовательно,
общий член ряда ип = j^l-
Пример 11.3. Найти общий член ряда
1-4 1-4-9 1 • 4 - 9 • 16
+ 1-4 + 1.4-7 + 1-4-7-10+'""

150
11. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ
Решение: В числителе сомножители образуют последовательность
с общим членом п2. В знаменателе каждый член ряда представляет
собой произведение нескольких первых членов арифметической прогрессии
{а\ — 1, d = 3). В соответствии с формулой общего члена арифметической
прогрессии (см. предыдущий пример) ап = Зп — 2. Следовательно, общий
член ряда ип = ^i^i^Uy
Пример 11.4. Найти сумму ряда
111 1
+
1-12 12-23 23-34 (11п-10)-(11п+1)'
Решение: Разложим общий член ряда на сумму двух дробей по
методу неопределенных коэффициентов:
х A\un+i в\пп-м ^ A(iln + I) + щПп _ щ
(lln-10)-(lln + l) lln-10 lln + 1 (lln-10)-(lln+1)
Две дроби равны, если равны их числители и знаменатели, следовательно:
1 = Л(11п + 1) + В(11п-10).
Полагая п=0, имеем f А — 10В = 1.
Полагая п=1, имеем \ 12Л + В = 1.
Решив полученную систему уравнений относительно неизвестных А и
В, найдем Л = i, В = -^. Общий член ряда можно переписать в виде:
1 _ 1 / 1 i\
U" (lln-10)-(lln + 1) И \lln-10 lln + 1/'
Запишим несколько первых членов ряда:
Следовательно:
Sn = ТТ у ~ 12 j + П \12 " 23 ) + П \23 " 34 J + "
I / *. _ 1 \ =
II Vlln-10 .lln + 1/
11 у 12+ 12 23 + 23 34+" lln-10 lln+1/
= ±Л _2_\
11 V lln + 1/
Ответ: S=~.
Итак, S = lim S„ = lim £ (l - п£п)<
ii. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ
151
Пример 11.5. Исследовать сходимость ряда и вычислить сумму
ряда, если он сходится.
2 1111
- + - + - Н 1 1 .
33612 24
Решение: Ряд составлен из членов бесконечно убывающей
геометрической прогрессии &i = |,g = |, и поэтому сходится. Найдем сумму
ряда:
3:_, * _ I _*
l-q 1-i 3-
Пример 11.6. Исследовать сходимость ряда.
5п+1
4п - 1
Решение: Проверим необходимый признак сходимости:
,. 5п+1 5 /Л
n-foo n-юо 471 — 1 4
Ответ: Данный ряд расходится, т.к. невыполняется необходимый
признак сходимости.
Самостоятельная работа
Пример 11.7. Найти общий член ряда
, l l l
Пример 11.8. Найти общий член ряда
Пример 11.9. Найти сумму ряда
111 1
1-3 3-5 5-7 (2п-1)(2п+1)
Пример 11.10. Найти сумму ряда
111 1
■ +
3-4-5 n(n+l)(n + 2)
Пример 11.11. Исследовать сходимость ряда и вычислить сумму
ряда, если он сходится
, l I 1
1+2+4+8+""

152
12. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
Пример 11.12. Исследовать сходимость ряда
п
12. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
Достаточные признаки сходимости знакоположительных рядов
Как мы уже знаем, суммой ряда называется предел
последовательности его частичных сумм: 5 = lim 5„. Однако нахождение этого предела во
п-юо
многих случаях связано с большими трудностями. В таких случаях сумму
ряда находят приближенно, заменяя ее частичной суммой 5„ с
достаточно большим номером п. Но для этого надо быть уверенным, что данный
ряд сходится. Сходимость или расходимость ряда во многих случаях
удается установить с помощью так называемых достаточных признаков. В
этом пункте мы рассмотрим достаточные признаки сходимости и
расходимости для рядов с положительными членами. Такие ряды называются
знакоположительными.
Замечание 12.1. Вес полученные ниже выводы будут справедливы
и для рядов с отрицательными членами, т.е. для знакоотрицателъных
рядов.
Прежде всего заметим следующее. Так как в знакоположительном
ряде все члены положительны,то его частичные суммы Si = uy.S^ = Щ +
u2, S3 = Щ + и2 + u3,..., 5„ = щ + и2 + щ Н Ь ип возрастают с
увеличением номера суммы п. Таким образом, частичные суммы ряда образуют
возрастающую числовую последовательность
5i < S2 < 53 < • • • < 5П < ....
Здесь возможны два случая.
1. Последовательность частичных сумм неограничена. В этом случае
iim 5„ = оо и, следовательно, ряд расходится.
2. Последовательность частичных сумм ограничена, т.е. Sn < С при
любом п. В этом случае последовательность частичных сумм имеет
предел и, следовательно, ряд сходится.
Таким образом, при доказательстве того, что тот или иной
знакоположительный ряд сходится, достаточно установить только ограниченность
последовательности его частичных сумм.
Теорема 12.1. (Первый признак сравнения.) Даны два
знакоположительных ряда:
щ + и2 + щ ~\ h ип + ..., (U)
12. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
153
Vi + V2 + t/3-+--- + tfn + .... '■' '''- - (V)
Пусть члены первого ряда не превосходят соответствующих членов
второго ряда:
U2-1) «1 ^ t/i,tl2 < Ь2,Щ < 1/3, ...,Wn <1>n,".,
и второй ряд сходится. В таком случае первый ряд также сходится,
и его сумма не превосходит суммы второго ряда (заключение теоремы
остается в силе, если некоторые члены ряда (U) равны нулю).
Доказательство.Обозначим через Sn и ап соответственно n-е
частичные суммы первого и второго рядов:
Sn = ui + и2 + щ Н -fw„, <тп = vi + v2 + v3 + • • • + vn.
Из неравенств (12.1) следует, что Sn< <?n- Так как ряд (V) сходится, то
существует lim an = о. При этом, поскольку члены ряда положительны,
п—>оо
очевидно, что оп < <т, а, следовательно, и Sn < а. Таким образом,
частичные суммы ряда (U) ограничены и, следовательно, ряд (U) сходится,
причем его сумма не превосходит суммы ряда (V), как это следует из
неравенства Sn < о.
Теорема 12.2. (Второй признак сравнения.) Даны два
знакоположительных ряда
«1 + 1*2 + Из + • • • + «я + ■ • • , (U)
vi + v2 + vz + • • • + vn + •... (V)
Пусть члены первого ряда не меньше соответствующих членов второго
ряда
(12-2) «1 ^ vi, и2 ^ г/2,Щ ^ v3,.. • ,ип ^ г/„,...,
и второй ряд расходится. В таком случае первый ряд также
расходится.
Доказательство.Обозначим снова через 5„ и ап соответственно
частичные суммы первого и второго рядов:
Sn = щ + щ + щ + • • • + ип, ап = vi + v2 -f v3 + • • • + vn.
Из неравенств (12.2) следует, что Sn ^ ап. Так как ряд (V) расходится
и его частичные суммы возрастают, то lim an = оо. В таком случае и
lim Sn = оо и, следовательно, ряд (U) расходится.
При исследовании рядов необходимо иметь для сравнения ряды,
относительно которых достоверно известно, сходятся они или расходятся.
Геометрическая прогрессия представляет собой ряд, сходящийся при
\q\ < 1 и расходящийся при |g| ^ 1.

154
12. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
Ниже во втором семестре в разделе интегральных исчислений будет
показано, чтр ряд
(12.3) т- + ;г + ;г + --- + — + • •
v ' IP 2р Зр пР
сходится при р > 1 и расходится при 0 < р ^ 1.
ряд
111 1
(12.4) _ + . + ..+ ... + _ + ...,
•
При р = 1 получается
который называется гармоническим. Ряд (12.3) называется обобщенным
гармоническим рядом.
Геометрическая прогрессия, гармонический и обобщенный
гармонический ряды очень часто используются при исследовании рядов с
помощью признаков сравнения в качестве эталонных рядов.
Пример 12.1. Исследовать на сходимость ряд
Решение: Рассмотрим вспомогательный ряд
(12.6)' J- + J- + J- + ... + _!_ + ....
Ряд (12.6) представляет собой геометрическую прогрессию со
знаменателем q = 1/2 < 1 и, следовательно, сходится. Так как члены ряда (12.5) не
превосходят соответствующих членов ряда (12.6), то по первому признаку
сравнения ряд (12.5) также сходится.
ПРИМЕР 12.2. Исследовать на сходимость ряд
111 1
(12.7) -т= + -г= +" "т= + - • • + —г~, :+ • • • -
v ' %/Ь2 л/пТз у/Ш у/\п(п + 1)
Решение: Рассмотрим вспомогательный ряд
(12.8) -= + -= + -= + ..-+ , , -f . • ■,
1 ; уД уД у/А v^+T
который расходится. Так как каждый член ряда (12.7) больше
соответствующего члена ряда (12.8):
Inn < n, Vlnn < \/п, ■■ . > -т=>
V In n Vn
то в силу второго признака сравнения ряд (12.7) также расходится.
Замечание 12.2. Признак сравнения иногда удобно представить в
иной форме.
12. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
155
Теорема 12.3. (Третий признак сравнения.Без доказательства.)
Если существует конечный и отличный от нуля предел lim ¥?• = k, то оба
п-юо Уп
исследуемых ряда одновременно сходятся или одновременно расходятся.
ПРИМЕР 12.3. Исследовать на сходимость ряд:
(12.9) 1+] + J + ... + _LT + ....
Решение: Рассмотрим вспомогательный ряд vn = ~, о котором
известно, что он расходится.
lim ^ - lim Щ± = i ф 0.
п П
На основании третьего признака сравнения оба ряда ведут себя одинаково
и, следовательно, в данном случае расходятся, т.е. ряд (12.9) расходится.
Применение признаков сравнения при исследований рядов часто
бывает затруднительно из-за необходимости составлять вспомогательный ряд.
Поэтому часто применяются другие достаточные признаки.
Теорема 12.4. (Признак Даламбера z). Если для
знакоположительного ряда
(12.10) ui + и2 + щ + • • • + ип + ...
существует предел отношения последующего члена к предыдущему при
неограниченном возрастании номера члена п, т.е.
(12.11) lim^±i=p,
n-юо ип
то при р < 1 ряд сходится, а при р > 1 ряд расходится.
Доказательство, а) Пусть р < 1. Покажем, что ряд сходится. Действительно,
так как lim ****■ = р, то на основании определения предела последовательности для
любого € > 0 можно подобрать такое натуральное число N, зависящее от £, что для
всех членов ряда, номер которых n ^ JV, выполняется неравенство \~!г " Р < е-
Отсюда следует, что
-е < ^^ - р < + £, или р - € < ^2±! < р + е.
Полагая р + € = q, получим ^J^ < q. Так как р по предположению меньше единицы,
а € произвольно мало, то е можно выбрать настолько малым, чтобы q = р + € < 1.
Таким образом, для п ^ N имеем:
< Я> < Я, < Я, • •.,
UN Uflf+i Ujv + 2
3ЖДаламбер(1717-1783) — французский математик.

156
12. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
uN+i < uNq,uN+2 <uN+lq <UNq2,uN+s < uN+2q < uNq3,
Рассмотрим два ряда:
(12.12) UJV + Utf+l + «JV+2 + ИЛГ+З + • • • »
(12.13) un + uNq + unq2 + uxq3 +
Ряд (12.13) сходится как геометрическая прогрессия со знаменателем \q\ < 1. Так
как члены ряда (12.12) не превосходят соответствующих членов ряда ( 12.13), то на
основании первого признака сравнения ряд (12.12) также сходится.
Но ряд (12.12) получается из данного ряда (12.10) отбрасыванием конечного числа
членов ui+U2+«3+—Htttf-i. Следовательно, по теореме 3 ряд (12.10) также сходится.
б) Пусть теперь р > 1. Покажем, что ряд расходится. Действительно, в этом случае
lim ^^ = р > 1. Отсюда следует, что начиная с достаточно больших значений
n-too Un
п ^ N выполняется неравенство —^ > 1, или un+i > un. Таким образом, члены
ряда возрастают с увеличением номера члена п. Поэтому lim un ф 0, т.е. выполнен
достаточный признак расходимости ряда и, следовательно, ряд расходится.
Замечание 12.3. Если lim ^^ = оо, то ряд также расходится,
п-юс Un
так как и в этом случае ^^ > 1 для достаточно больших п и,
следовательно, lim ип ф 0.
п-+оо
Замечание 12.4. Подчеркнем еще раз, что, если расходимость ряда
установлена с помощью признака Даламбера, то общий член ряда не
стремится к нулю.
Замечание 12.5. При р = 1 признак Даламбера на вопрос о том,
сходится или расходится ряд, ответа не дает. Как показывают
примеры, в этом случае может иметь место как сходимость, так и
расходимость.
Рассмотрим примеры исследования рядов на сходимость с помощью
признака Даламбера.
ПРИМЕР 12.4. Исследовать на сходимость ряд
13 5 7
3 З2 З3 З4
Решение: Находим
г2(п + 1) - 1
v un+l ,. р
о = Jim = lim -
n-юо Un n->ooL
3n+l
2n-l
2n- li
3n J ~
+ ...
lim
n—tooo
lin, *±i£ Л
3n(2n +
3n+1(2n -
1)
-1)
1 ,. 2n + l 1,
= - lim - = - lim t .
3 n~>oc 2n - 1 3 n->oo 2 - 1/n 3
Итак, р=1/3<1и, следовательно, данный ряд сходится.
12. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
157
Пример 12.5. Исследовать на сходимость ряд
2 4 8 2П
Решение: Находим
p = lim = lim -. — : — = lim -t щхл „ =
n~>oo Un n->ool(n+ l)4 n4J n-tooo (n -f l)4 ' 2n
П4 1
= 2 lim 7 -^ = 2 lim —rr = 2.
n-*oo (n + l)4 n->oo (1 + 1/n)4
Так как р = 2 > 1, то данный ряд расходится.
Пример 12.6. Исследовать на сходимость ряд с общим членом ряда
ип = $(а>1,к>1).
Решение: Применим признак Даламбера:
lim H=±I = lira
n-юо Un n-юс
Г a"*1 an]
[(n + 1)* ! nk\
an+1 • n*
= lim
n-^ooan • (n + 1)*
Так как по условию а > 1, можно сделать вывод о том, что ряд ип = |£
расходится, т.е. показательная функция возрастает быстрее степенной с
ростом аргумента.
Рассмотрим теперь два примера рядов, для которых р = 1, и покажем,
что один из этих рядов сходится, а другой расходится.
Пример 12.7. Исследовать на сходимость ряд
111 1
лЛ л/2 v3 v/n
Решение: Находим по признаку Даламбера
р= lira ^±i= lira (1 : 4=) = li» -Д= = 1.
На основании признака Даламбера сделать заключение о сходимости или
расходимости ряда мы не можем. Однако, как было указано ранее,
обобщенный гармонический ряд (р = | < 1) расходится.
Пример 12.8. Исследовать на сходимость ряд
— — -L 1
1-2+2-3 + 3.4 + "'* п{п + 1) + ""

158
12. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ
Решение: Находим по признаку Даламбера
,. ип+\ ,. Г l l 1 Г п(п + 1)
р = hm = hm — — : —; — = lim — rr = 1.
n-^oo Un n-*ooL(n + l)(rH-2) n(n+l)J n-wo(n+l)(n + 2)
Выше в (пример 11.1) непосредственным нахождением суммы этого ряда
было показано, что он сходится.
В тех случаях, когда признак Даламбера не позволяет сделать вывода
о сходимости или расходимости ряда, наряду с признаками сравнения
часто применяется следующий достаточный признак сходимости ряда.
Теорема 12.5. (Радикальный признак Коши *.) Если для ряда
щ 4- и2 + Щ И Ь ип + ...
существует lim л^ = q, то этот ряд сходится при q < 1 и расходит-
п-+оо
ся при q > 1. В случае, когда q = 1, вопрос о сходимости ряда остается
открытым.
Пример 12.9. Исследовать на сходимость ряд
Решение: Применим признак Коши.
lim фГп = lim Г/i- • (\ + i J = lim | £ ■ ( 1 + - ) 1 = J < 1-
Следовательно, по признаку Коши данный ряд сходится.
Следует отметить, что для исследования сходимости
знакоположительных рядов существует еще один достаточный признак сходимости
— интегральный признак Коши. Однако к его использованию мы сможем
приступить только после изучения интегралов.
12. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ
Пример 12.1. Исследовать сходимость ряда
In 2 1пЗ Inn
- + — + ... + + ... .
2.3 п
Решение: В качестве достаточного признака сходимости
используем признак сравнения. Для сравнения используем гармонический ряд
vn = -. Каждый член ряда и больше соответствующего члена ряда v
(— > -). При п -> оо ряд v расходится, следовательно, расходится и ряд
и.
4О.Коши(1789-1857) — французский математик.
12. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ
159
Пример 12.2. Исследовать сходимость ряда
1
ип =
4.2»-3*
Решение: Сравним этот ряд с рядом vn = ~, который, как
известно сходится. Используя вторую формулировку признака сравнения
вычислим (третий признак сравнения):
lim ^ = lim ±ф* = lim А Т „ = lim —~ = ].
п-юо vn п-юо ф п-юо 4 • 2П — 3 п-юо 4 — ~ 4
Так как предел конечен и отличен от нуля и ряд ~ сходится, то и ряд
ип = 4.2п..з также сходится.
Пример 12.3. Исследовать сходимость ряда
_ 1
Un~2n>-3n
Решение: Сравним этот ряд с рядом vn == ^, который, как известно
сходится. Используя третий признак сравнения, будем иметь
lim 2== Вт^фЕ = 1^о.
п-юо Vn п-юо -±2 2
Так как предел конечен и отличен от нуля, а ряд vn = ^ сходится, то
сходится и ряд ип = 2пь_Лп.
Пример 12.4. Исследовать сходимость ряда
. 1
ип = sin—.
п
Решение: Для сравнения выбираем расходящийся ряд vn = £.
Опять используем третий признак сравнения.
ип sin£ sinm , . л
lim — = hm —у-2- = hm = 1^0.
п-юо yn п-юо i n-f 0 m
Следовательно, на основании условий третьего признака сравнения
данный ряд ип = sin £ расходится.
Пример 12.5. Исследовать сходимость ряда
_ 2 • 5 • 8 ... (Зп - 1)
Un~ l-5-9...(4n-3)*

160
12. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ
Решение: Для исследования сходимости используем признак Да-
ламбера. Запишем п + 1 член ряда
2 • 5 • 8... (Зп - 1)(3(п + 1) - 1) 2 • 5 ■ 8... (Зп - 1) • (Зп2) .
*п+1
1 • 5 • 9... (4п - 3) (4(п + 1) - 3) 1 • 5 • 9... (4п - 3) • (4п + 1)"
Вычислим lim ~±L = т~~ = | < 1. Следовательно, по признаку
Даламбера данный ряд сходится.
Пример 12.6. Исследовать сходимость ряда
п\
еп
Решение: Исследуем ряд по признаку Даламбера
,. ^n+i ,. (п + l)!/en+1 .. (n + l)!-en .. n + 1
hm -^ == lim r~ = hm -—;——— = hm = oo > 1.
n~f<x> un n-+oQ n\/en n->oo n! • en+I n-к» e
Следовательно, на основание признака Даламбера данный ряд
расходится.
Пример 12.7. Исследовать сходимость ряда
Решение: Здесь удобно применить признак Коши.
I— г nlf'n + l\n г п + 1 1 л
hm уи^ = hm Г/ = hm —-—- = - < 1.
n-чоо n-foo у у2п — 1/ п->оо 2п — 1 2
Следовательно, по признаку Коши данный ряд сходится.
Самостоятельная работа
Пример 12.8. Исследовать сходимость ряда (признак сравнения)
1
ип = .
Inn
ПРИМЕР 12.9. Исследовать сходимость ряда (признак сравнения)
2п
Пример 12.10. Исследовать сходимость ряда (признак сравнения)
1
13. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
161
Пример 12.11. Исследовать сходимость ряда (признак сравнения)
1
un = tg-.
п
Пример 12.12. Исследовать сходимость ряда (признак Даламбера)
ип =
10п
п
Пример 12.13. Исследовать сходимость ряда (признак Даламбера)
_ п
Wn~3^
Пример 12.14. Исследовать сходимость ряда (признак Коши)
13. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
Знакопеременные ряды, признак Лейбница, достаточный признак
сходимости знакопеременных рядов, абсолютная и условная
сходимость, остаток ряда и его оценка.
13.1. Знакопеременные ряды.
До сих пор мы изучали только ряды, все члены которых были
положительными. Теперь мы перейдем к рассмотрению рядов, содержащих
как положительные, так и отрицательные члены. Такие ряды называются
знакопеременными.
В качестве примера знакопеременного ряда приведем ряд
12 22 З2 42+52 б2 72*82 + 92 "* + ( ' п2+
Изучение знакопеременных рядов мы начнем с частного случая — так
называемых знакочередующихся рядов, т. е. рядов, в которых за каждым
положительным членом следует отрицательный, а за каждым
отрицательным— положительный.
Обозначая через щу щ,..., ип,... абсолютные величины членов ряда и
считая, что первый член положителен, запишем знакочередующийся ряд
следующим образом:
щ - и2 + щ - щ + • - • + (-1)п~1ип +

162
13. ЛЕКЦИЯ -г ЧИСЛОВЫЕ РЯДЫ
Для знакочередующихся рядов имеет место достаточный признак
сходимости Лейбница5.
13.2. Признак Лейбница.
Теорема 13.1. Если в знакочередующемся ряде абсолютные
величины членов убывают:
щ > и2 > щ > • - > ип > ...
и общий член ряда стремится к нулю: lim un = 0, то ряд сходится,
п->оо
причем его сумма положительна и не превосходит первого члена ряда.
Доказательство. Рассмотрим частичную сумму четного числа членов
ряда
Сгруппируем члены попарно:
S2m = («1 - Щ) + (U3 - 1А4) + ' • ' + («2m-1 - 1*2m)-
Так как по условию абсолютные величины членов ряда убывают, то все
разности в скобках положительны и, следовательно, сумма 5гт
положительна и возрастает при увеличении т.
Запишем теперь 5гт, группируя члены иным образом:
Щ - [(м2 - щ) + (щ - us) + • • • 4- (гг2т-2 - ti2m-i) + и2т]-
Сумма в квадратной скобке также является положительной. Поэтому
S^m < Щ для любого значения т. Таким образом, последовательность
четных частичных сумм S2m возрастает с увеличением т, оставаясь при
этом ограниченной. Следовательно, 52ш имеет положительный
предел lim 52m = S. При этом, так как 52т < щ, то ясно, что 0 < 5 ^ щ.
т—юо
Рассмотрим теперь сумму нечетного числа членов:
При т -¥ оо имеем:
lim S2m+i = lini (52т + «2т+1) = Ит S2m + lim u2m+i = 5,
m—юо m-юо m—>oo m—юо
так как по условию lim un — О и, следовательно, lim и2т+\ = 0.
п—Юо m-юо
Таким образом, частичные суммы как четного, так и нечетного числа
членов ряда имеют общий предел S. Это означает, что вообще lim Sn —
Г п-ю©
S, т.е. ряд сходится. При этом, как видно из доказательства, сумма ряда
5 не превосходит первого члена ряда.
5Г.Лейбниц(1б46-171б) — немецкий философ, математик, физик, языковед.
13. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
163
Пример 13.1. Исследовать на сходимость ряд
1-2» 2-3* 3-4* v ' n(n + l)2 ""
Решение: Этот ряд удовлетворяет условиям признака Лейбница:
п 1 1 1 1
'l-2* > 2-32 >3-42 > "> п(п + 1)* > "''
2) lira |u„| = lim ^то = 0.
n-юо n-юо nln+1J
Следовательно, ряд сходится.
13,3. Достаточный признак сходимости знакопеременных
рядов.
Перейдем теперь к рассмотрению общего случая знакопеременного ряда.
Предположим, что в ряде
щ + и2 + щ Н h и,» + ... .
числа t*i, W2, щ,..., ип,... могут быть как положительными, так и
отрицательными.
Для таких рядов имеет место следующий признак сходимости.
Теорема 13.2. (достаточный признак сходимости
знакопеременного ряда). Если для знакопеременного ряда
(13.1) щ 4- и2 + щ Н h ип + ...
сходится ряд
(13.2) Ы + М + |и3| + --- + Ы + ...,
составленный из абсолютных величин его членов, то данный
знакопеременный ряд также сходится.
Доказательство.Рассмотрим вспомогательный ряд, составленный из
членов рядов (13.1) и (13.2):
(13.3) «l + lttll ( М2 + |Ц2| ( ) Ця + Ы (
Имеем:
прИи„>0: Ы = ипии-^ = Ь^М = Ы;
Таким образом, члены ряда (13.3), либо равны членам сходящегося ряда
(13.2), либо меньше их. Поэтому ряд (13.3) сходится на основании первого
признака сравнения.

164
13. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
Умножив все члены ряда сходящегося ряда (13.2) на |, получим
сходящийся ряд
(13.4) М + Ы + ... + Ы + ....
Рассмотрим теперь ряд, являющийся разностью сходящихся рядов (13.3)
и (13.4):
{щ + \щ\ |«i|\ , (иг + \и2\ Ы\ , , (и„ + \ип\ \ип\\
[—2 -Т) + {—2 Т)+-+{— 2-)+-
Этот ряд также сходится.
Но ряд (13.1) получается из последнего ряда умножением всех его
членов на 2:
2-
v+w wi _2 —
2 2 J 2
Следовательно, на основании свойств числовых рядов исходный ряд (13.1)
также сходится.
Пример 13.2. Исследовать на сходимость знакопеременный ряд:
1_1-1 1 1-1-
(13-5) 12 22 32 + 42 + 52 б2 ""'
Решение: Рассмотрим ряд, составленный из абсолютных величин
членов данного ряда:
1111
j 1 1 L
I2 22 З2 42
Этот ряд сходится, как обобщенный гармонический ряд с показателем
р = 2 > 1. Следовательно, на основании доказанного признака сходится и
данный знакопеременный ряд.
13.4» Абсолютная и условная сходимость.
Признак сходимости знакопеременного ряда является достаточным, но не
необходимым. Это значит, что существуют знакопеременные ряды,
которые сходятся, в то время как ряды, составленные из абсолютных величин
их членов, расходятся.
Действительно, рассмотрим ряд
(13.6) 1_!+!_j+...+(-iri.i+...,
который, очевидно, сходится по признаку Лейбница. Между тем, ряд,
1111
13. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
16В
составленный из абсолютных величин членов данного ряда (13.6),
является гармоническим и, следовательно, расходится.
Хотя оба рассмотренных выше ряда (13.5) и (13.6) сходятся, однако
характер их сходимости различен.
Ряд (13.5) сходится одновременно с рядом, составленным из
абсолютных величин его членов, тогда как ряд, составленный из абсолютных
величин членов сходящегося ряда (13.6), расходится.
В связи с этим введем следующие определения.
Определение 13.1. Знакопеременный ряд и\ + и2 + щ-\ V ип +...
называется абсолютно сходящимся, если сходится ряд \и\\ + \щ\ -f \и$\ +
Н Ып\ + ..., составленный из абсолютных величин его членов.
На основании достаточного признака сходимости знакопеременного
ряда всякий абсолютно сходящийся ряд является сходящимся.
Определение 13.2. Знакопеременный ряд щ ■+• иг + щ Н Ь ип 4-...
называется условно сходящимся, если он сходится, а ряд \щ\ -f ji^i +
\щ\-\ h \un\ -f ..., составленный из абсолютных величин его членов,
расходится.
Возвращаясь к рассмотренным выше примерам, можем сказать, что
ряд (13.5) является абсолютно сходящимся, а ряд (13.6) — неабсолютно
сходящимся, или условно сходящимся.
Среди знакопеременных рядов абсолютно сходящиеся ряды занимают
особое место. Это объясняется тем, что на такие ряды переносятся
основные свойства конечных сумм. Особое значение имеет свойство
переместительности, которым обладают только абсолютно сходящиеся ряды.
Это свойство, которое мы приводим без доказательства,
формулируется следующим образом.
Сумма абсолютно сходящегося ряда не меняется от любой
перестановки его членов.
Наоборот, в неабсолютно сходящемся ряде нельзя переставлять члены,
так как в случае их перестановки может изменяться сумма ряда и даже
получиться расходящийся ряд.
Говоря о перестановке членов, мы подразумеваем, что меняем местами
бесконечное множество членов, так как, переставляя два, три, четыре или
любое конечное число членов, мы, очевидно, не изменим суммы ряда.
Рассмотрим в качестве примера неабсолютно сходящийся ряд (13.6)
1-1 l-l l-l i-I i_
2 + 3 4 + 5 б + 7 8 + 9 '",
сумму которого обозначим через 5.

166
13. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
Переставим члены этого ряда, поместив после каждого
положительного члена два отрицательных. Получим ряд
Обозначим частичные суммы ряда (13.6) через 5„, а ряда (13.7) — через
ап. Тогда
с _1 1_1 о _, 11 1 7
52-1-2-"2'54-1~2 + 3~4 = 12'
9-1 Ч1 Ч1 1 37 •
. 111 ,111117
азв1"2"4г=4'(7в = 1"2"4 + з"в"8 = 24'
-L 11 1 _ 37
'9~24 + 5 10 12 "" 120'
Следовательно, <т3 = 0,55г,0б ~ 0,554,0о = 0,55в,... и вообще, как
можно показать, <r3m = 0,552т- Так как lim 52т = 5, то lim a3m =
т-кх> m-+oo
0,5 lim 52m = 0> 55. Таким образом, последовательность частичных сумм
т-+оо
ряда (13.7) с номерами, кратными трем, имеет своим пределом 0,55.
Далее, находим
lim <r3m+i = lim f aZm + J = 0,55
m-»oo m-Юо \ 2m +1/
И
lim (73m+2 = Hm [a3m + - — ) = 0,55.
m~>oo m-+oo у 2m +1 Am + 2/
Итак, мы показали, что lim <rn существует при любом законе стрем-
п-*оо
ления п к бесконечности. Это и означает, что ряд (13.7) сходится. При
этом его сумма составляет половину суммы ряда (13.6), из которого он
получен перестановкой членов.
13.5. Остаток ряда и его оценка.
Рассмотрим сходящийся ряд
(13.8) щ -f и2 + и3 Н Н ип + u„+i + ип+2 + ....
Как известно, его сумма 5 является пределом последовательности
частичных сумм 5П = Ui-f-«2+u3-H • •+ип при п -» оо, т.е. 5 = lim 5n- Поэтому
п—юо
для достаточно больших п имеем приближенное равенство
(13.9) S*Sn,
точность которого возрастает с увеличением п. Для оценки точности
приближенного равенства (13.9) введем понятие остатка сходящегося ряда.
13. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
161
Определение 13.3. Разность между суммой ряда 5 и его п-й
частичной суммой 5„ называется п-м остатком сходящегося ряда (13.8).
Остаток ряда обозначается через гп:
(13.10) rn = S-Sn.
Как видно из равенства (13.10), остаток ряда представляет собой
сумму сходящегося ряда, полученного из данного ряда отбрасыванием п его
первых членов:
Гп = tt„+i + Un+2 + h ttn+fc + . . . .
Из определения остатка ряда ясно, что
lim rn = 0.
n-*oo
Действительно,
lim rn = lim (5 - Sn) = S - lim 5„ = 5 - 5 = 0.
n-*oo n-*oo n—►oo
Абсолютная погрешность при замене суммы ряда 5 его частичной
суммой 5П, очевидно, равна модулю остатка ряда:
As = |S-5n| = |rn|.
Таким образом, если требуется найти сумму ряда с точностью до € > 0, то
надо взять сумму такого числа п первых членов ряда, чтобы выполнялось
неравенство \гп\ < е. Однако в большинстве случаев находить остаток г„
точно мы не умеем. Поэтому выясним, как найти номер остатка п, чтобы
его модуль не превосходил заданного числа е.
Теорема 13.3. (об оценке остатка знакоположительного ряда). Ее-
ли все члены сходящегося знакоположительного ряда
(13.11) щ + и2 + щ + -- + ип + ...
не превосходят соответствующих членов другого сходящегося
знакоположительного ряда
(13.12) vi + v2 + vs + • • • + t>n + • • • *
то п-й остаток ряда (13.11) не превосходит п-го остатка ряда (13.12).
Доказательство.Обозначим n-е остатки рядов (13.11) и (13.12) через
гп и гп:
гп = ия+1 + un+2 + ...;
Г» = Vn+i + Vn+2 +
Каждый из этих остатков является суммой сходящегося
знакоположительного ряда.

168
13. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
Так как по условию un+i ^ vn+i,un+2 ^ Vn+2,----> т0 на основании
первого признака сравнения сумма первого ряда не превосходит суммы
второго ряда, т. е. rn ^ г'п.
Если даны два сходящихся ряда:
(13.13) щ + и2 + щ + • • • + ип +...,
(13.14) vi + v2 + v3 + • • • + vn + ...,
причем члены ряда (13.14) больше соответствующих членов ряда (13.13),
то ряд (13.14) называется мажорирующим рядом по отношению к ряду
(13.13).
Из предыдущей теоремы следует, что остаток мажорирующего ряда
всегда больше или равен остатку основного ряда.
Обычно в качестве мажорирующего ряда берут ряд, остаток которого
г'п можно легко вычислить (например, геометрическую прогрессию).
Тогда, по только что доказанной теореме, мы легко оценим остаток гп
данного ряда.
Пример 13.3. Оценить третий остаток ряда
1 1 1 1
2 • 5 + 3 • 52 + 4 • 5s + '"" + (п + 1)5" + " *'
Решение: Каждый член этого ряда меньше соответствующего
члена геометрической прогрессии
111 1
со знаменателем (7 = 1/5. Следовательно, третий остаток г3 данного ряда
меньше третьего остатка г3 этой прогрессии:
111 1 1/54 1
Таким образом, сумма данного ряда отличается от суммы его трех первых
членов меньше, чем на —>.
Теорема 13.4. (об оценке остатка знакопеременного ряда). Пусть
дан абсолютно сходящийся знакопеременный ряд
(13.15) щ + и2 + щ + • • • + ип + ... .
Тогда абсолютная величина его п-го остатка не превосходит п-го остат
ка ряда, составленного из абсолютных величин членов данного ряда.
18. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
169
Доказательство.Пусть знакопеременный ряд (13.15) сходится
абсолютно. Это значит, что сходится и ряд
(13.16) н + M + KI + --- + М+„■... .
Рассмотрим n-е остатки рядов (13.15) и (13.16):,
Гп = Un+l + Un+2 + 1*п+3-+ • • • ; *n = lwn+l| + |tW*l "MUn+sl
При любом р имеем:
К+1 + и„+2 + • • • + un+p| ^ |г/п+1| + |un+2| + • • • + |un+P|.
Переходя в этом неравенстве к пределу при р —> оо, получим
lim \ип+1 + ип+2 + • • • + гг„+р| < lim \ип+х\ + |wn+2| + ••'• + |и„+р|,
р-»оо р-*оо
или |rn| < rJJ, что и требовалось доказать.
Пример 13.4. Оценить третий остаток г3 рлтЛг
sinl sin 2
~ +~2*~
sin3
+
smn
23 . '. ' 2п
Решение: Данный ряд — знакопеременный, так как, например,
sin 1 > 0,sin2 > 0,sin3 > 0,sin4 < 0,sin5 < 0,sin6 < 0, sin 7 > 0,
Рассмотрим ряд
sinl
2
+
sin 2
22
+
sin3
23
+ ••• +
sinn
2" |
.+ .
Так как | ~5г | ^ ~, то его члены не превосходят соответствующих членов
геометрической прогрессии
2 + 22 + 23 + '
1
Поэтому данный ряд сходится абсолютно.
Обозначим остатки данного ряда, составленного из абсолютных
величин, и геометрической прогрессии соответственно через гз,г3,г3', где
1гз| < г3 < гз- Таким образом, находим оценку третьего остатка данного
ряда:
1
1
Ы <г$ = я + ;*г + ;зг + '-- + ;е: + -'- =
24 25 26
2п
1/24
1-1/2
Теорема 13.5. (об оценке остатка знакочередующегося ряда,
сходящегося по признаку Лейбница). Если знакочередующийся ряд сходит-
ся по признаку Лейбница, то его остаток по абсолютной величине не
превосходит модуля первого из отброшенных членов ряда.

170 IS. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ
Доказательство. Пусть ряд
щ - и2 + щ - щ + • • • + (-l)n"1un + ...
сходится по признаку Лейбница. Тогда n-й остаток ряда
rn = ±(ttn+i - ип+2 + txn+3 ~ • • •)
сам является суммой знакочередующегося ряда. На основании признака
Лейбница остаток гп по абсолютной величине должен быть не больше
модуля первого члена этого ряда, т. е.
\Гп\ ^ tin+1.
Пример 13.5. Вычислить с точностью до 0,01 сумму ряда
1_1 + 1_...+(_1Г1_1_+ .
1! 3! 5! К ' (2п-1)!
Решение: Данный ряд сходится по признаку Лейбница, поэтому
As = |S-S„| = |rn| <«„+,.
Так как сумма ряда должна быть вычислена с точностью до 0,01, то
достаточно, чтобы выполнялось неравенство |г„| < ип+\ < 0,01, или
(2^Т)!<0'01-
Это неравенство выполняется, начиная с п=3. Таким образом, S «
Sa = i-^« 1-0,17 = 0,83.
13. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ
111
13. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ
Пример 13.1. Исследовать сходимость знакопеременного ряда
2 22 + 23 24 25 + *''
Решение: Составим ряд из абсолютных величин членов данного
ряда
, 11.1 11
-i + 5 + ? + ? + ? + ? + —
Полученный ряд - бесконечно убывающая геометрическая прогрессия
с основанием q = \ < 1 и, следовательно, ряд сходится. По признаку
сходимости знакопеременных рядов, если сходится ряд из модулей членов
данного ряда, то сходится и сам знакопременныи ряд, причем сходится
абсолютно.
Пример 13.2. Исследовать сходимость знакочередующегося ряда
Е-
5п + 6
п=1
Решение: Знакочередующиеся ряды исследуются на сходимость
по признаку Лейбница, который для сходимости ряда требует выполнения
двух условий:
о 1) lim \un\ =0 для данного ряда lim т-~ = 0,
п-юо n-юо оп"г°
о 2)\ип\ ^ |un+1| для данного ряда £ > ^ > ^ > • • •
Следовательно, условия признака Лейбница выполняются и ряд
сходится. С учетом, того,что ряд, составленный из модулей членов исходного
знакочередующегося ряда ип = ~~ расходится, знакочередующийся ряд
{-i)n+1
ип = v 5w' 6 сходится условно.
Пример 13.3. Исследовать сходимость знакочередующегося ряда
(~1)п-1-п
Е-
10п + 9
п=1
Решение: Для данного ряда не выполняется первое условие
признака Лейбница lim |мп| = 0. Действительно lim 10"4.9 = ^ ф 0. Следо-
П-*О0
вательно, ряд расходится.
Пример 13.4. Исследовать сходимость знакочередующегося ряда
Е
П=1
= , ,п+13-5-7...(2п + 1)
V ' 2-5-8...(3n-l)'

172
13. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ
Решение: Исследуем по признаку Даламбера ряд, составленный
из модулей членов данного знакочередующегося ряда.
U, 1 3.5-7...(2п+1Н2п+3)
n->oo u„ n->oo 3.5-7...<2n+l) п_юо Зп + 2 3
1 ' 2-5-8...(Зп-1)
По признаку Даламбера ряд из модулей сходится. Значит сходится
абсолютно данный знакочередующийся ряд.
Пример 13.5. Исследовать сходимость знакопеременного ряда
Е°° _ sin па
, - (In 10)"'
Решение: При любых значениях п функция sin па - функция
ограниченная |sinna| ^ 1, поэтому члены данного ряда будут меньше
соответствующих членов ряда vn = (1п|0)те, который сходится по признаку
Коши: _____
Urn ?/v^ — lim Г /t „ „ч = lim ;—~г = :—rr < 1.
n->oo V П n->oo у (In 10)n n->oo In 10 In 10
Следовательно, по признаку сходимости знакопеременных рядов сходится
исследуемый ряд, причем сходится абсолютно.
Пример 13.6. Сколько членов ряда ]_ = ^~£— необходимо взять,
чтобы вычислить его сумму с точностью до 0,001?
Решение: По признаку Лейбница данный знакочередующийся ряд
сходится, поэтому по теореме об оценке остатка сходящегося
знакочередующегося ряда:
Д5 = \S - Sn\ = |гп| ^ |tin+i| ^ 0,001 или
K+il = —ГТ < 0,001 = —— =^ п + 1 ^ 1000 =» п > 999.
п + 1 1UU0
Ответ: п=999.
Самостоятельная работа
Пример 13.7* Исследовать сходимость знакопеременного ряда
1 24 З4 ^ 44 5* б4 ^
Пример 13.8. Исследовать сходимость знакочередующегося ряда
ИГ1
ln(n-H) '
£-* 1п(п-
п=1
13. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ
113
Пример 13.9. Исследовать сходимость знакочередующегося ряда
Пример 13.10. Исследовать сходимость знакочередующегося ряда
п=1
Пример 13.11. Исследовать сходимость знакочередующегося ряда
Е°° — ( л\п 1-4-7...(Зп-2)
~ V х/ 7 9Л1...(2п+5)'
п=1
Пример 13.12. Исследовать сходимость знакочередующегося ряда
г»=1
Пример 13.13. Исследовать сходимость знакочередующегося ряда
у* _!___
2L-* 2* •
п=1
оо
Пример 13.14. Сколько членов ряда У^ = (2n+i)-sn нужно взять, что-
п=1
5ы вычислишь его сумму с точностью до 0,01?
оо
Пример 13.15. Оценить второй остаток r2 /wrAi-^ — f^ff.

щ
Ц. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
IV ГЛАВА
Дифференциальное исчисление
функций одной переменной
14. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
Задачи, приводящие к понятию производной. Определение
производной. Производные некоторых основных элементарных функций.
14.1. Задачи, приводящие к понятию производной.
Задача о касательной. Пусть функция у — f(x) определена и
непрерывна в точке М0(хо, Уо) и в некоторой окрестности этой точки. Требуется
провести в точке Мо(хо>2/о) касательную к графику функции в
предположении, что касательная существует. Понятие касательной интуитивно
понятно, однако до сих пор с ее определением мы не встречались.
Поступим следующим образом. Возьмем на графике функции (рис. 97) еще одну
точку М(х, у) и проведем через точки Mq и М секущую. Устремим затем
точку М к точке М0, то есть положим, что х - х0 = Ах -> 0. Так как
точка Mq неподвижна, то секущая будет поворачиваться вокруг точки М0
и в пределе займет положение МТ.
Ц. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
175.
Определение 14.1. Касательной к графику функции y=f(x) в точке
Мо(хо>уо) называется предельное положение секущей М0М при условии,
что точка М(х,у) стремится к М0(я<ь2/о)-
Очевидно, что угловой коэффициент секущей М0М к = ^^ = *6^'в
пределе станет равным угловому коэффициенту касательной.
Ау
(ИЛ)
кт = tg a = lim A .
Дх-*о Ах
Зная этот угловой коэффициент и точку Мо(х0,уо), можно провести
касательную. Уравнение касательной к графику функции у = f{x) в точке
Af0(x(h2fo) мы получим в лекции 16.
1
У
N
'МЛх^уЛЧА
/9
О
)AS \
х0
Т
|*М(х,У)
.Р
1 X
X
Рис. 97. К задаче о касательной
Задача о скорости. Пусть по прямой линии в одном направлении
движется материальная точка по закону s = s(t). Ко времени t точка
пройдет путь s(t)> а ко времени 14- At - путь s(t + At). Следовательно, за
время At точка пройдет путь As = s(t + At) - s(t).
Средняя скорость прямолинейного движения vcp за промежуток
времени At определяется отношением
(14.2)
vcp =
As
At
пройденного пути ко времени.

176
11 ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
Если считать начальный момент времени t фиксированным, а
промежуток At* - переменным, то средняя скорость будет переменной
величиной, зависящей от At.
Определение 14.2. Скоростью v в данный момент времени t
называется предел средней скорости vcp при At —► 0, т.е.
(14.3) v=.lim^.
д*->о At
Рассмотренные задачи, несмотря на их разное физическое
содержание, привели нас к нахождению предела одного и того же вида - пределу
отношения приращения функции к приращению аргумента при условии,
что последнее стремится к нулю. К нахождению таких пределов приводят
многие задачи в разных областях науки и техники. Поэтому рассмотрим
этот алгоритм, отвлекаясь от физической сущности задачи.
14.2. Определение производной. Пусть дана непрерывная в
интервале (а; Ь) функция у = /(х).
Зафиксируем какое-то значение аргумента х € (а; 6). Ему
соответствует значение функции у = /(х). Теперь изменим аргумент х на величину
Дх (дадим ему приращение Дх.) Тогда величина у получит приращение
Ау. Согласно определению непрерывной функции Ау -> 0 при Дх -» 0.
Таким образом, отношение %£ при Дх -> 0 является неопределенностью
типа jj.
Пусть lim £* существует.
Определение 14.3. Производной функции у = /(х) в точке х
называется предел отношения приращения функции Ау в этой точке к
вызвавшему его приращению аргумента Ах при условии, что Ах —> 0.
Производная функции у = /(х) в данной точке х обозначается
символом f(x).
Итак,
(14.4) /•(») = lim %L - lim /(* + *«>-/(»).
д*-ю Дх д* -»о Дх
Наряду с обозначением /'(х) используются и другие обозначения:
* л* |. *£>■
Соответственно, в фиксированной точке хо производная обозначается:
(14.5) у'\яят9 = </(х<>) = ГЫ = £|,.ао = ^.
^. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
177 :
Иногда оказывается целесообразным указывать переменную, по
которой берется производная в виде индекса. Например; для функции у = у(х)
производная у\х) обозначается yz, а для функции х = х(у) производная
х'{у) обозначается х'у.
Возвращаясь к рассмотренным ранее задачам, можем отметить
геометрический и физический смысл производной:
1.Угловой коэффициент касательной к графику функции в точке с
абсциссой х0 равен значению производной этой функции в данной точке х<>
(см. (14.1)).
2.Скорость прямолинейного движения материальной точки в момент
времени t есть значение производной в этой точке от пути s по времени t
(см. (14.3)).
Пример 14.1. Найти производную у = х2.
Решение: Находим приращение функции Ду:
Ау = (х + Дх)2 - х2 = 2хДх + Дх2.
Разделив приращение на Дх, и переходя к пределу при Дх -* 0, найдем
. . Дv 2хДх 4- Дх2
fix) = lim =± = lim л = 2х.
д*->о Дх Д*-ю Дх
В общем случае производная является функцией, в конкретной же точке
она равна числу. Так, производная функции у = х2 в точке х = 0,5 равна
единице.
В определении 14.3 подразумевалось, что lim %£ существует и не за-
Дх-+0 **Х
висит от способа стремления Дх к нулю и, в частности, в фиксированной
точке хо производная
ги ч ,. &У ,. У~Уо
/ (х0) = lim -т-2- = lim .
Дх-Ю Дх Дх-»0 X — Хо
Однако можно подходить к точке Хо слева или справа. Такие способы
стремления к х0 обозначаются соответственно х-*х0-Оих-»хоЧ-0
(см. лекцию 7).
Определение 14.4. Правосторонней производной (производной
справа) функции у = /(х) в точке Хо называется величина
/'(х0 + 0)= lim ^.
V ' аг^хо+0 Дх
Левосторонней производной (производной слева) функции у = /(х) в
точке Хо называется величина
/'(*о-0)= lim ^.
х->хо-0 Дх

118
Ц. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
В соответствии с определением 14.3 производная /'(х) существует в
точке хо, если левосторонняя и правосторонняя производные существуют
в этой точке и равны, т.е.:
lim -— = hm -r-2-.
i^xo-0 Дх а?-»жо+0 Дх
Бели хотя бы один из этих пределов не существует или оба они
существуют, но не равны, производная /'(х) в точке х0 терпит разрыв первого
или второго рода.
Если пределы равны -Ьоо или -оо,принято говорить, что функция в
точке xq имеет бесконечную производную, т.е. соответствующая
производная равна -foo или — оо.
Определение 14.5. Если функция у = f(x) имеет в некоторой
точке производную, то она называется дифференцируемой в этой точке.
Определение 14.6. Функция у = f(x) называется
дифференцируемой в интервале (а; 6), если она дифференцируема в каждой точке этого
интервала. Если существуют односторонние производные /'(а-ЬО) и /'(6—
0), то функцию называют дифференцируемой на отрезке [а; Ь].
Установим теперь связь между дифференцируемостью и
непрерывностью функции.
Теорема 14.1. Если функция у = f(x) дифференцируема в некоторой
точке, то она в этой точке непрерывна.
Доказательство. Пусть в точке х приращение Дх ф 0. Тогда
приращение функции в этой точке можно представить в виде
Ди = т^Ах.
У Дх
Переходя к пределу, получим
Ди
lim Ay = lim -^ lim Дх = fix) 0 = 0,
откуда следует непрерывность функции. Обратная теорема неверна:
существуют непрерывные функции, которые в некоторых точках недиффе-
ренцируемы. Таким образом, непрерывность функции является
необходимым, но не достаточным условием ее дифференцируемости
1.Непрерывная на (-оо;+оо) функция у = |х| не имеет производной в
точке х = 0, так как хотя в этой точке левосторонняя и правосторонняя
производные существуют, но они не равны:
/'(-0)=-1, /'(+0) = 1.
Ц. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
179
2.Непрерывная на (—оо;+оо) функция у = tfx не имеет производной
в точке х = 0, так как в этой точке производная у' = —h^s обращается в
бесконечность при любом стремлении Дх к нулю. Поэтому не существует
производной ни справа, ни слева.
14.3. Производные некоторых основных элементарных
функций.
Производная постоянной у = С. Так как функция у = С сохраняет
постоянное значение на всей числовой оси, то в любой точке приращение
функции равно нулю. Поэтому
(14.6) (С)' = lim ^ = lim -?- = 0.
v Д*-*0 Дх Ах->0 Дх
Производная степенной функции у = хп. Имеет место формула,
вывод которой будет дан в лекции 16.
(14.7) {хп)' = п-хп-1.
Рекомендуется кроме общей формулы (14.7) запомнить два часто
встречающихся частных случая:
(14.8) п=ф (V5)' = (IV2r = I/2.a;-V2 = _L.
(14.9)
»-l: (i)'«(.-К «--I-
Производная показательной функции у = а*. Найдем
приращение функции
Ау = ах+Ах - а* = ах(а*х - 1).
Тогда на основании рассмотренного в лекции 10 предела
hm = In a,
sc-+0 X
получим
(14.10) (а*)' = lim ^ = lim а*(а** " *} - а* 1п а.
д*-+оДх д*-+о Дх
В частности, при о = е получим
(14.11) (е*)' = е*.

180
Ц. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
Производная логарифмической функции у = log,, х. Найдем
приращение функции
Ау = logjx + Дх) - lo^x = log,, Х+ = log,, (1 + — ) .
Ж \ X )
Следовательно,
Дх-»0 Дх
Сделаем следующее тождественное преобразование:
tofcP + g) = Ио&,(1 + ^) = 1
Лт -Г й* ~
'log,,
(^):
Устремив Да: -> 0, на основании рассмотренного в лекции 10 предела
г logjl + х) . 1
hm —22 - = logfl е = ;—,
*-+о х Ьа \па
найдем
(14-12) (Iog.*)'= l-
xlna
В частности, при а — е получим
(14.13) (1пх)'=Д
х
Производная функций у = sinx и у = cosx. Найдем приращение
функции
Дх / Ах \
Ду = sin(x + Дх) - sin х = 2 sin — • cos ( х + — J .
Следовательно,
, . v .. 2sin^cos(x + ^)
(sinx) = hm 2—-—^ *-4
Д*-И) Дх
Записав этот предел в виде
Ах
sm±f / Дх\
hm —тг~~ hm cos ( х + — J ,
дж-»0 QZ Д*->0
2
получим
(14Л4) (sin z)' = cosx,
15. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
181
так как первый сомножитель на основании теоремы о первом
замечательном пределе равен единице.
Аналогично можно доказать, что
(14.15) (cosx)' = -sinx.
15. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
Основные правила дифференцирования - производные суммы,
произведения, частного. Производная сложной и обратной функции.
Таблица производных.Производная элементарной функции.
Основные правила дифференцирования. Находить производные
проще не исходя из определения 14.3, а на основании некоторых правил,
к рассмотрению которых мы переходим.
15.1. Производная суммы.
ТЕОРЕМА 15.1. Если функции и(х) и v(x) дифференцируемы в
некоторой точке, то в этой точке производная их суммы существует и
равна сумме производных слагаемых.
(15.1) (ti + v)' = ti' + v\
Доказательство. Дадим аргументу х функции у(х) = и(х) 4- г/(х)
приращение Дх. Тогда
Ау = {и(х + Дх) - и(х)) + (v(x + Дх) — v(x)) = Аи + Av.
Следовательно,
. ,. Ау ,. Au + Av ,. Аи • Av , ,
у = hm -— = hm : = hm h hm -— = и + v .
Дх-+0 Дх Ах->0 Ах Д*->0 Ах Д*-»0 Дх
Теорема доказана. Ее легко обобщить для любого конечного числа
слагаемых.
15.2. Производная произведения.
Теорема 15.2. Если функциии(х) uv(x) дифференцируемые
некоторой точке, то в этой точке производная их произведения существует
и находится по формуле
(15.2) (u-v)' = u' v + v -и.

182
15, ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
Доказательство. Дадим аргументу х функции у(х) = и(х) • v(x)
приращение Дх. Тогда
Дг/ - (и + Дгг) • (v + Дv) -и v.
Открыв скобки и приведя подобные члены, получим
Дг/ = v - Аи + и т Av.+ Дгг • Дv.
Следовательно,
, х/ v v •.Аи + гг • Дг; 4- Аи • Av
(u-v) — hm .
Да?-»0 Ax''
Разделив числитель на знаменатель, представим последний предел в
виде суммы трех слагаемых:
lim I -г— • v ) = и ♦ v,
ь*->о\Дх- у
lim -г— • и ] = г/ • и,
1x^0 \Дх )
im [ -г^ • Av ) = и' • 0 = 0.
*-ю \Дх у
lim
Дх-+0
В третьем слагаемом
lim Дг; = О,
Даг-Ю
так как из дифференцируемости функции v следует ее непрерывность.
Сложив три слагаемые, получим искомую формулу (15.2).Теорема
доказана.
СЛЕДСТВИЕ: 15.1. Постоянный множитель можно выносить за
символ производной.
Действительно, по формуле (15.2) и учитывая (14.6), имеем
(15.3) (с • и(х))1 = с'и(х) + с • и\х) = с • и'{х).
На основании этого следствия:
(и - v)' = и' - г/, так как (-г;)' = -v'.
Теорема о производной произведения обобщается на большее (но
конечное) число сомножителей, например:
(и • v - w)' = и' • v • w -f- и • г/ • w -Ь гг ♦ v • и/.
75. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
183
15.3. Производная частного.
ТЕОРЕМА 15.3. £?слифункциии{х) uv(x) дифференцируемые
некоторой точке я, причем v(x) ф 0, то в этой точке производная их частного
существует и находится по формуле
u'v — v'u
(1,4, (=)'-^
Доказательство. Дадим аргументу х функции у(х) = *щ приращение
Ах. Тогда
и(х -f Ах) и(х)
* v{x + Ax) v(x)
Очевидно,
и(х + Ах) = гх + Дгх; г;(я 4- Ах) = v + Дг;;
Поэтому
_ и + Ди w _ уАи —■ «Дг;
v 4- Дг; г; г;(г; И- Дг;)
Разделив обе части этого равенства на Да;, и учитывая, что при
Ах -» 0
,. Аи , ,. Av ,
hm -г— = г/, hm -r— ^ v ,
д*-*о Ах Д*-»о Дя
lim Дг; = 0 (из дифференцируемости функции v следует ее непрерыв-
Дх-И)
ность), получим искомую формулу (15.4). Теорема доказана.
Учитывая, что постоянный множитель можно выносить за символ
производной, отметим два частных случая:
\v) ~ v2 ' \с) ~ С
Производная функций у = tgx и у = ctgx.. Воспользовавшись
формулами производных синуса (14.14), косинуса (14.15) и частного
(15.4),получим
'cosx — (cos x)' sin a: 1
\ cos х /
3SZX COS^X
Аналогично можно доказать, что
(15.6) (ctgx)'=--L-.
sin х
Иногда, как отмечалось в лекции 3, удобно обозначение функции у =
у(х), что мы и используем при доказательстве следующих двух теорем.

184
15. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
15.4. Производная обратной функции. Определение обратной
функции и условия ее существования даны в лекции 3. Пусть функция
х = х(у) монотонна в некотором интервале (а; 6) и имеет в некоторой
точке у этого интервала производную х'(у), не равную нулю. Покажем, что в
соответствующей точке х обратная функция у = у(х) имеет производную
у'(х), причем
(157) y'{x) = W)™y'* = k
Так как функция х = х(у) монотонна и дифференцируема (а
следовательно, и непрерывна), то функция у = у(х) существует, монотонна
и непрерывна. Дадим аргументу х приращение Ах ф 0. Тогда функция
у = у(х) получит приращение Ау ф 0. Вследствие же непрерывности
lim Ay = 0.
Тогда
у (х) = \\тл
д*->оДх lim %* х'(у)
Производные функций arcsinx и arctg х. Функция х = siny (у €
[-7г/2;7г/2]) обратна функции у = arcsinx. Она монотонна в интервале
(~7г/2; 7г/2). Ее производная
х1 = cos у ^ 0 на этом интервале.
Следовательно, по (15.7):
, 1 1 1
*у cost/ y/l-sin2!/'
Но так как sin у = х, то
(15.8) (arcsinx)'= . 1 .
Vl - ж2
Аналогично находится производная функции arctg x
= cos2 у =
(15.9) У'х = 1 = 1 : -J_ = cos2 = 1" = _1_
ж!. cos2j/ y H-tg2j/ 1 + r2'
"у
Производные функций arccos x и arcctg х. Известны формулы,
связывающие в общей области определения обратные тригонометрические
функции
arcsin х -f arccos x = -,
2
arctg x + arcctg x = -.
i5. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
185
Дифференцируя эти равенства с учетом того, что (7г/2)' = 0, найдем
1
(15.10) (arccos x)' =-
у/Г=^'
(15.11) ■(arCctg*)'«-I-l?.
15.5. Производная сложной функции. Пусть у — у(и) и и = и(х).
Тогда у есть сложная функция переменной х, а переменная и -
промежуточный аргумент: у = j/(w) = у(и(х)).
Как найти ее производную? Ответ на этот вопрос дает следующая
теорема.
Теорема 15.4. Если функция и = и(х) имеет производную и'х в
точке х, а функция у = у (и) имеет производную у'п в соответствующей
точке и, то сложная функция у = у(и(х)) в данной точке х имеет
производную ух, которая находится по формуле
(15.12) ух =у'ии'х.
Доказательство. Дадим х приращение Дх. Тогда и и у получат
соответственно приращения Аи и Ау. Предположим, что при Ах —► 0
приращение Аи не принимает значений, равных нулю.
Тогда
Ау _ Ау Аи
Ах ~" Аи Ах'
Так как функция и = м(х) дифференцируема, а следовательно, и
непрерывна, то при Да: -*> 0 также и Аи -> 0.
Поэтому
,. Ду .. Ду ,. Д^
hm -— = lim -т— • hm -г—,
д*-»о Да: Ди-чо Ди Дх-»о Да:
откуда следует искомая формула (15.12). Теорема доказана.
Можно доказать справедливость формулы (15.12) и в случае, когда
приращение Аи при Да: -4 0 принимает значения, равные нулю.
Пример 15.1. Продифференцируйте функцию у = sin3x.
Решение:
у = u3, u = sin х, у' = (и3Уи • (sin х)'х = Зи2 • cos х = 3 sin2 х • cos x.
Пример 15.2. Продифференцируйте функцию у = sinx3.

186 15. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
Решение:
у = sin г/, и = х3, у1 — (sin и)'и • (х3)^. = cos u • Зх2 = Зх2 cos a:3.
Последние две функции - результат суперпозиции (объединения) двух
функций. В общем случае сложная функция может быть составлена не из
двух функций (звеньев), а из большего их числа. Так, например,
функция у = sin5 у/х состоит из трех функций. Для нахождения у по данному
значению х, необходимо соверщить три действия:
о найти квадратный корень из х;
о найти значение sin у/х;
• найденное значение sin у/х возвести в пятую степень.
В аналогичных случаях необходимо ту величину, над которой
производится последнее действие, принять за промежуточный аргумент и. В
данном примере — это возведение в пятую степень. Поэтому и = sin у/х
и у = у5. Ее производная по формуле (15.12):
У* = (и5Уи • (sm vG); = 5 sin4 yfc • (sin V*)L.
Но функция sin у/х также является сложной и последнее действие в ней
- нахождение синуса аргумента х. Применяя опять формулу (15.12) для
функции у = sin w, и = v^> найдем
(sin v5)J. = cosu • —F = cos y^ • г-т=.
2yx z^/x
Окончательно получим
(sin5 y/x)'x — 5 sin4 y/x • cos \/x • т—т=.
2^х
При достаточном навыке буква и для промежуточного аргумента
опускается. Вот как находятся производные функций, рассмотренных выше
(sin3 х)1 — 3 sin2 x(sin x)' = 3 sin2 x cos х,
(sin л:3)' = cos x* • (ж3)' = За:2 cos х3.
Вот решения еще нескольких примеров (без тождественных
преобразований):
ний)
15. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
187
(arcsin 5х)' = , = • 5,
V ' v/1 - (5х)2
1 -1
(v/arcctg Зх)' = —7====== *:;—т^т? * 3,
vv ь ' 24/arctg3x l + (3x)2
/ IV .1 -1
cos- ) = -sin r-,
\ X/ XX2
№*•)' = 2*»ь* • In2 • * -,
' cos2 In xx
(ctg3>/2^^)' = 3ctg2v/2^^ • ^ • * (2 - 2*).
sin (2x — xz) 2v2x — xz
При наличии еще больших навыков в дифференцировании и
промежуточные выкладки опускаются.
15.6. Таблица производных. Сведем теперь все выведенные
формулы дифференцирования основных элементарных функций в таблицу. В
ней для общности положим аргумент, равным дифференцируемой
функции и = и(х).
1. (С)' = О,
3. (ou)' = ou In о • и'. (еи)' = е" • и',
4. (log. «)'=-£-, (lnU)' = £,
и In a u
5. (sinu)' = cosu u\
6. (cos и)' = — sin и и',
и'
7.(tgt*)' =
cos'w
«'
8. (ctgu)'=—^-j-,
siiru
9. (arcsin u)' =
10. (arccosu)' = -
11. (arctgu)' =
и'
1+u2'

188
Ц ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВОДНАЯ ФУНКЦИИ
12.(arcctgi*)' = -
1 + и2
15.7. Производная элементарной функции. Напомним, что
элементарной называется функция у - /(х), которую можно задать одним
аналитическим выражением, составленным из основных элементарных
функций с помощью четырех арифметических действий (сложения,
вычитания, умножения и деления) и операций взятия функции от функции
(сложная функция), последовательно примененных конечное число раз.
На основании знания таблицы производных основных элементарных
функций и правил дифференцирования можно взять производную от
любой элементарной функции, какой бы сложной она не была. И эта
производная также будет элементарной функцией.
Пример 15.3. Найти производную функции
In (х + 3)
Решение:
у' = 2si°2 *3 In 2 • 2 sin x3 • cos x3 • Зх2 • arctg Jx~ + 2si"2 *3 fa ^+
"1 ln4(x+3) "~
= 2si*2*3 (Зх21п2 • sin2x3 • arctg V* + vfe) +
■ 1 / ln(x+3) _ 2tgjM
b3(x+3) V 3^2 cos2 #x* x+3 J
14. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВОДНАЯ
ФУНКЦИИ
Вспомните определение производной 14.3.
Исходя из него, найдем производные двух функций:
Пример 14.1. у = л:3.
Решение:
в /(х 4- Дх) = (х + Дх)3,
Ц ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВОДНАЯ ФУНКЦИИ 189
вДу = /(х 4- Ах) - /(х) = (х 4- Дх)3 - х3 = Зх2Дх 4- ЗхДх2 4- Дх3,
• |* = Зх2 + ЗхДх + Дх2,
о у' = lim £* = цт (Зх2 + ЗхДх + Дх2) =? Зх2
Пример 14.2. у = у/х.
Решение:
в /(х 4- Дх) = у/х +" Дх,
в Ду = /(х 4- Дх) - /(х) = \/х 4- Дх - у/х,
&2L — >/а?+Дх-л/х _ Vx-f Дх->/х # л/хННДжН-л/ж _
Дх ~" Дх ~~ Дх >Jz+&z+y/x
— 1
n/x+Ax+v/*'
* Дх-+0 Az Дх-*0 ч/х+Дх+л/* 2v/x
Находить так производные — долго и сложно. Поэтому при
практическом дифференцировании будем пользоваться формулами, полученными в
лекциях. Решим так несколько примеров, на основе формулы (14.7)
дифференцирования степени.
Пример 14.3. у = х5.
Решение: у' = (х5)' = 5х5~* = 5х4.
Пример 14.4. у = у/х*.
Решение: у1 = (#?)' = (х3'7)' - 3/7Х3/7"1 = jfe.
Пример 14.5. у = js-
Решение: ^ = (£)' = (*~2)' = -2х"3 = -£.
Пример 14.6. у = ^^.
Решение: у' = (^^)' = (*-1 - 2х~3/2)' = -х~2 + Зх"5/2 =
1 j 3
~х^ + хЧ^'

iHL Ч ПРАКТИЧЕСКОЕ ЗАНЯТИЕ- ПРОИЗВОДНАЯ ФУНКЦИИ
Пример 14.7. у = ах~ъ.
Решение: у' = (ах-5)' = а(Х-5)' = -5ааГ6 = ||.
Пример 14.8. у = </х.
Решение: у' = (уЪ)' = (хУпу = ^Mi/n-i _ _i__
Пример 14.9. у = у^х.
Решение: у' = (v/^x)' = (я1/6)' = 1/6х~5/6 = -1
Пример 14.10. у = х3^х.
Решение: у1 = (х3^х)' = (х16/5)' = 16/5Х11/* = "^fri
А теперь продифференцируем функции, содержащие
тригонометрические и обратные тригонометрические функции.
Пример 14.11. у = sinx + cosx.
Решение: у' = (sinx + cosx)' = (sinx)' + (cosx)' = cosx - sinx.
Пример 14.12. у = &*■.
Решение:
. х—sin x-cosx
X COS2 X
Пример 14.13. у = ctgx • arccosx.
Решение:
У1 = (ctgx • arccosx)' == (ctgx)'arccosx + (arccosx)'ctgx =
— arccosx ctgx v ' ь
sin^x
Найдем производные функций, содержащих показательные и
логарифмические функции:
Пример 14.14. у = log2х-2*.
Решение:^- (log2 х)'2* + (2*)'log2 х = ^ + 2* • In 2 • log2x.
Пример 14.15. г/ = А
* ШХ
/5 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВОДНАЯ ФУНКЦИИ
191
Самостоятельная работа.
Найдите производные, исходя из определения 14.3:
Пример 14.16. у = К
Пример 14.17. у = cosx.
Найдите производные функций с помощью формул табличного диф-
ференцированил:
Пример 14.18. у = #г.
Пример 14.19. у = х(1 - х2).
Пример 14.20. у = sinx + 3cosx.
Пример 14.21. */ = xarctgx.
Пример 14.22. у = ^^.
Пример 14.23. у = ^.
Пример 14.24. г/ = arcsinx -f arccosx.
Пример 14.25. у = arcctgx + xlnx - ^.
15. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВОДНАЯ
ФУНКЦИИ
Перед этим занятием вспомните правило дифференцирования сложной
функции (15.12).
В первых двух примерах подробнее, чем обычно запишем процесс
дифференцирования сложной функции. Подробно об этом процессе рассказано
в лекции 15.
Пример 15.1. y = cos3x.
Решение: у' = gcos2ж, (-sinx) =
производная от степени производная от косинуса
- 3 sinx cos2 x.
Пример 15.2. у = y/Xgx.
1 1
Решение: у1 —
1
2cos*x/tgx*
2v^tgx ^cos^x,
производная от корня производная от тангенса

15 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ -ПРОИЗВОДНАЯ
Пример 15.3. у = ^arctgz - (arcsinz)3.
Р е Ш е Н И е: У' = Й^ТЬ ~ 3(arcsins)2 - -fa.
Пример 15.4. у = lgsinar.
Решение: у' = ^Л-. . cos x.
Пример 15.5. у = arcctg(lm) + In(arctgx).
Решение: у' = -—i ! + _!_
"l+ln2aj ar "*" arctgxl+x2"
Пример 15.6. у = (еЬх - ctg 4х)5.
Решение: у1 = 5(е5* - ctg4z)4 • (5е5х + -4—)
'V sin45 4at /
Пример 15.7. у = cose3*.
Решение: г/' = -sine3* • е3х • 3 = -Зе3х sin е3*.
Пример 15.8. у = arctg yf^x.
Решение: у' ~ Л- . -* . (_п i.
Пример 15.9. y = inj|=fjJ.
Р е ш е н и е: у'= (lng=fjj)' = (51ш> - 2) - 31ш> + 1))' = £- - ^.
Пример 15.10. у = г*"*1»3* + (1 - arccos Зя)2.
Решение: т/' = (г*"8**3* + (1 -arccosЗх)2)' = 2arcsin3*In2 г ♦ 3 +
2(1 - arccos За?) /t * . • 3
Самостоятельная работа
Найдите производные:
Пример 15.11. у = х5 - 4г3 + 2а: - 3.
Пример 15.12. у = х2\/х*.
Пример 15.13. у = Л2*+3.
у аг2 -5х+5
Пример 15.14. у = -т4%
Пример 15.15. i/ = xctgx.
Пример 15.16. у = (1+»а)^8»-«>
Пример 15.17. ?/ = х31п:г - ad.
iff. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
193
Пример 15.18. у = (я2 - 2а: 4- 2)ех,
Пример 15.19. у = Me* — 5sinx - 4arcsinx).
Пример 15.20. у = -~cos(5:r2) - \cosх2. <
Пример 15.21. у = arctg In x.
Пример 15,22. у = lnarcsinx -h |In2a: 4- arcsinlnx.
16. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
Логарифмическая производная. Производная функции, заданной
параметрически. Производная неявной функции. Геометрические
приложения производной. Уравнения касательной и нормали к графику
функции. Угол между двумя кривыми. Приложение понятия произ-
Iводной к задачам физики. ■■'•' |
В этой лекции мы прежде всего рассмотрим некоторые дополнения к
дифференцированию функций, а затем приложения понятия производной
к геометрическим и физическим задачам.
16.1. Логарифмическая производная. Пусть дана некоторая
дифференцируемая функция у = f(x). Прологарифмируем обе части этого
выражения:
1пу=ш/(х).
А теперь продифференцируем его по х, помня, что у = f(x):
(toy); = (\nf(x)Yx =>^У' = 0»/(*))'„ откуда
(16.1) у' = y(ln/(*))'= /(*)(ln /(*))'.
Определение 16.1. Операция, состоящая в последовательном при-
менении к равенству у = f(x) сначала логарифмирования, а затем
дифференцирования, называется логарифмическим дифференцированием, а
производная, определяемая по формуле (16.1) — логарифмической про-
изводной.
С помощью логарифмического дифференцирования мы легко можем
вывести формулу (14.7), которая ранее была дана без вывода:
In
у = хп ==»- In t/ = гатя ==» -у' = — => у' = (хп)' = пхп~1.

196
16. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
Из полученного уравнения находим:
, y2-xsiny
У ~
x(xcosy - 2у\пх)
16.4. Геометрические приложения производной. Они основаны
на ее геометрическом смысле, установленном нами в лекции 14.
Получим на основании этого уравнение касательной Т к кривой у =
f(x) в точке М0(х0;2/о) (рис. 97).
Уравнение любой прямой L, проходящей через данную точку М0(х0; Уо)
с заданным коэффициентом к получено в лекции 3: у — уо = к(х — Хо).
Для касательной к графику функции у = /(я) в точке Мо(хо;уо)> как мы
установили в лекции 14, угловой коэффициент кт = t/'(x0) = f'(xo). Тогда
У ~ /(#о) = /'(яо)(я - х0) и уравнение искомой касательной Т будет:
(16.3) У = /(*о) + Л*о)(*-*о).
Как известно, если прямые L\ и L2 перпендикулярны, то их угловые
коэффициенты связаны соотношением к\ • к2 = — 1. Тогда если угловой
коэффициент нормали N в точке Мо(хо;уо) к графику функции у = /(я)
обозначить &лг, то он будет равен к^ = — jp = ""Т7^)' следовательно,
уравнение нормали JV в точке Мо(хо;г/о) к графику функции у = /(я)
примет вид:
/Ч*о)
Определим теперь угол в между двумя кривыми Ai и Л2 в точке их
пересечения (рис. 98). Очевидно, что этот угол равен углу между
касательными 7\ и Тг к кривым Ai и Лэ, проведенным в точке их пересечения
Afo(x0;t/0). '
Очевидно, что 0 == а2--c*i. Откуда
tgfl = tg(a2-aij =
Следовательно,
(16.5) в = arctg
tga2-tgoi 2/2 — 2/i
l + tga2-tgai 1 + yi -и
Й-Й
Mo
1+2/1-2/2
Пример 16.5. Найти уравнения касательной и нормали к параболе
у = х2 в точке Мо(2;4).
16. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
197
Рис. 98. Угол между двумя кривыми
Решение: х0 = 2, у0 =/Ы ■ = 4. По (16.3) и (16.4) имеем уравнение
искомой касательной Т:
У = /Ы + /Ч*о)(* - хо) => у = 4х— 4
и нормали JV:
у:=/(хо)"?ы(а:"1о)
i 9
У = ~4 + 2-
ПРИМЕР 16.6. Найти угол 0, под которым пересекаются параболы
Ai : у = (х - 2)2 и А2 : у = -4 + 6х - х2.
Решение: Найдем точки пересечения кривых Ai и А2. Для этого
решим систему:
(
У = (х - 2)2,
у = -4 + 6х - х2 ==> xi = 1, х2 = 4.
Таким образом, параболы пересекаются в двух точках: Mi(l;l) и
М2(4;4) (рис. 99)
По формуле (16.5) находим углы.
В точкеМПИ 1) : в = arctg ^Г+^Л) = ~ arct6 § = -40°36''
В точкеМ2(4; 4) : в = arctg ^^gfe?,) = arctg f = 40°36'.
В первом случае угол получился отрицательным, так как кривая Ai
при х > 1 расположена выше А2, а при выводе формулы (16.5), да и в

*JL. iff. ЛЕКЦИЯ -ПРОИЗВОДНАЯ ФУНКЦИИ
Производная показательно-степенной функции. Пусть и = и{х)
и v = v(x) — дифференцируемые функции. Тогда функция у = u(x)v{x)
называется показательно-степенной. Ее производная может быть найдена
также с помощью логарифмического дифференцирования:
у = u(x)v{x) ==> In у = vlnu =»
^' = г/ In и + у ==» у' = (uv)' = u» (*/ In и + у).
Пример 16.1. Найти производную функции у = (sin:r)cosx.
Решение:
у' = (вшх«**)' = sinscos* ( S^l - sinжlnsinx) m
\ smx у
Логарифмическое дифференцирование также удобно использовать,
когда функция задается в виде произведения и частного нескольких
степенных выражений.
Пример 16.2. Найти производную функции у = sinaT*fr^,
2'в * >/arcsin х3 "
Решение:
In у = In ZXT^ = ln sin i«4
+ In v^lnx - 1п2*х - In ^arcsins3 =
cosslnsinx + §ln2 + |lnlnx~tgxln2~ \lnarcsinr* ==>
У = lEf ~ sinarlnsinr + W 4 3*?, , =»
V*7 smar 3xlnx cos2 x 4arcsinx3>/l-x6
*/ = smxc°"ffiTx^
fe - sinstnsinx + -f- - Ja^' **2, \
\ smx 3xlnx cos2x 4arcsinx3\/l-x6/
Вычислить производную заданной функции, непосредственно как
частного, оказалось бы значительно сложнее.
16.2. Производная функции, заданной параметрически.
Параметрическое задание функции и примеры такого задания приводились
нами в лекции 3. Напомним, что функция задается параметрически, если
16. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ
195
она определяется через параметр t по закону:
| У = УМ,
|х = ж(£).
Будем считать х = x(t) и у = y(t) дифференцируемыми функциями
параметра t и, следовательно, непрерывными. Отсюда следует, что если
Ах -> 0, той Д* -+ 0.
Найдем
r Ay Ay/At .. Ay I Ax y\
у' = hm -г2- = hm А ' = hm -г7 / hm тг = -7.
*х Дх-*0 Дж Д*-*0 Ax/At Д*-*0 Д£ / Д*-*0 Д* irj
Таким образом, производная функции, заданной параметрически,
определяется формулой:
(16'2) у»"^-?(0-
Пример 16.3. Найти производную функции
\ х = a(t'— sin*),
j у = а(1 — cos£),
график которой называется циклоидой (рис. 27).
Решение: По формуле (16.2):
, _ а(1 - cos*)' _ sini _ 2sin f cos § _ £
fc~ a(t-sint)'"~ 1-cos* ~ 2sin2| ""Cg2'
I;
16.3. Производная неявной функции. Определение неявной
функции было дано в лекции 3.
Напомним, что функция называется неявной, неявно-заданной, если
она определяется выражением F(x,y) = 0. В каждом конкретном
случае, продифференцировав такое выражение по я, считая у функцией х,
получим линейное уравнение для производной у' = у'х, из которого ее и
определим.
Пример 16.4. Найти производную у* функции, заданной неявно
х sin у - у2 In х = 0.
Решение:
и
(xsiny — у2\пх)х = sini/4- xcosy у' - 2yy'lnx - — =0.
t
X

198
16 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВОДНАЯ ФУНКЦИИ
Рис. 99. К примеру 16.6
нашем примере в другой точке пересечения при х > 4, Лг расположена
выше Ль
16.5. Приложение понятия производной к физическим
задачам. Эти приложения основаны на физическом смысле производной как
скорости изменения какой-нибудь физической величины. В лекции 14 мы
рассмотрели простейший случай — производную от пути по времени как
скорость прямолинейного движения точки.
Пример 16.7. Точка движется прямолинейно со скоростью,
определяемой законом s = \Д. Показать, что движение замедленное.
Решение: Если s = \Д, то скорость v = jfc = А| с ростом времени
уменьшается, это означает, что движение замедленно.
Пример 16.8. Зависимость количества вещества, полученного в
химической реакции, от времени определяется формулой Q = а(1 + be"kt).
Определить скорость реакции.
Решение: Скорость реакции ^ = — abke~kt. Можно эту скорость
выразить через.Q. Действительно, из формулы Q = a(l + be~kt) имеем
abe~kt = Q - а. Следовательно, ^Я. = k(a - Q).
16. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВОДНАЯ
ФУНКЦИИ
Решим два примера на логарифмическое дифференцирование. Как
говорилось в лекции 16, этот прием целесообразно применять при
нахождении производных показательно-степенных функций, а также функций,
содержащих достаточно большое число сомножителей.
16 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВОДНАЯ ФУНКЦИИ
199
Пример 16.1. г/ = (sins)"***."
Решение: In у = ln(sia ж)8"*8* ==> In у = arctg х • In sin x.
Дифференцируем обе части последнего равенства:
\ •lf, = !?Sf+ arctg*-ctgx.
Отсюда, умножив обе части последнего равенства на у = (sin ж)*"***,
найдем:
у' = (ипх)1"*»* (feggf + arctgx •-ctgu) .
ПРИМЕР 16.2. у= *&$£*. ^
Решение:
1пу:= 21пх + 31п(ж - 1) +.| 1п(2х + 3) - 2.1п(3ж - 4) -\ 1п(3х + 2) =»
Пл «V — !?/' — 2 4- -3— 4- 2 JLl 3— ^^
Vluy;ar — уУ — g ^ z-1 ^ 2(2*+3) Зх-4 4{Зх+2) ^^
,/_ *2(*-1)3>/2Т+з/г . з | 1 6 з Л
У "~ (Зх-4)* ^3x4-2 \ж «-1 2х+3 Зя?~4 4(3*+2)./ '
А теперь вспомним, как дифференцируются функции, заданные неявно
(см. пункт 16.3).
Пример 16.3. y2cosx = a2sin3x.
Решение: Дифференцируем обе части, считая у функцией х:
, о . Л <> , 3a2 cos За: + у2 sin а:
2у • у cos а: - у smx = 3a cos За: => w = г- .
2ycosa:
Пример 16.4. ж3 + у3 - Заа:у = 0.
Решение: Дифференцируем обе части, считая у функцией х:
2
З*2 + ЗуУ - За(у + xj/') = 0 =» j/' = ^—^|.
ах — у .
Найдем производную функции, заданной параметрически.
Пример 16.5.
{х = cos2 £,
y = sin2£.
Решение: Пользуемся формулой (16.2):
{sin2^
у' (cos2 о; ,
А теперь решим несколько задач на геометрические и физические
приложения производной.

200
16 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВОДНАЯ ФУНКЦИИ
Пример 16.6. Составьте уравнения касательной и нормали к кри-
вой f(x) = у = х3 - 2х2 + 3 б точке с абсциссой xq = 1.
Решение: В точке ж0 = 1 находим значения функции и ее
производной:
/Ы=Уо = /(!) = 2,
f'(x) = Зх2 - 4х, 1ф0) = Уо = /'(1) = -1.
Подставим теперь хо = 1, |/о = 2 и i/J = -1 в уравнения касательной
(16.3) и нормали (16.4):
уравнение касательной:
У = /(*о) + /'Ы(* -х0)^У==2-(х--1)==>х + у--3 = 0,
уравнение нормали:
у = /(я0) - 7^(x ~ *о) =* У = 2 + (я - 1) = О =* я - у + 1 = 0.
Пример 16.7. Составьте уравнения касательной и нормали к
кривой, заданной параметрическими уравнениями
/у = *3,
\x = t2
в точке со значением параметра to = 2.
Решение: В точке, где to = 2 находим значения х, у и производной:
яо = х(*о) = 4,
Уо = y(to) = 8,
»iW = S = ^ = i«==>l4(*o) = 3.
Следовательно, уравнения искомых кривых будут:
уравнение касательной:
У = /Ы + Л*о)(ж - х0) => у = 8 + 3(х - 4) =» За: - у ~ 4 = О,
уравнение нормали:
У = /Ы - 7^)(х - х0) => У = 8 - |(х - 4) = О
=>х-ьЗу-28 = 0.
Пример 16.8. Найти угол пересечения кривых у = sin я; и у = cos я
не отрезке [0; тг/2].
Решение: Находим точку пересечения кривых:
sin х = cos x => tg x = 1 =» х = 7г/4.
По формуле 16.5:
fl— arctg (sms)'-(cossy I - arrtg (cos^sinx I
P - arctg !+(.!,!«)'.(«».)'|жав1г/4 - аГС16 l-smx.cosa;|:c=ir/4
= arctg ^~ = arctg 2\/2.
10 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВОДНАЯ ФУНКЦИИ
201
Пример 16.9. Две точки движутся по одной прямой s no законам
si = 100 + Ы и s2 = ^2/2. С какой скоростью они будут удаляться друг
от друга в момент встречи? Размерности времени и пути — секунды
и метры.
Решение: В момент встречи:
Sl = s2 ==> 100 + bt = t2/2 => t2 - I0t - 200 = 0.
Квадратное уравнение имеет один положительный корень t = 20. Находим
скорости точек в момент встречи:
Vl(t) = ^ = 5 ii/c,t*(t) = ^г = ь => v*№) = 20 м/с-
ас ас
Следовательно, скорость расхождения v2 - v\ = 15 м/с.
Пример 16.10. Количество электричества (в кулонах),
протекающее через проводник, определяется законом Q = 2t2 + 3t 4- 1. Найдите
силу тока в конце 3 секунды.
Решение: Сила тока J = ^ = 4* + 3. При t = 3 J = 15
кулонов/с=15 ампер.
Самостоятельная работа
Пример 16.11. Найти производную функции, у = xsm*:.
Пример 16.12. Найти производную функции: у = ^.^°t*g
Пример 16.13. Найдите ух из уравнениях* + ту - х2еу = 0.
Пример 16.14. Найдите у'х из уравнения х2 4- у2 = 1.
Пример 16.15. Найдите ух функции
{х- -22*-
Пример 16.16. Составьте уравнения касательной Т и нормали N к
кривой х2 4- 2ху2 4- Зу4 = б б точке М(1; —1).
Пример 16.17. В какой точке касательная к кривой у = у — у — 4х
имеет угловой коэффициент, равный 2?
Пример 16.18. Найдите углы между кривыми у = х2«я4-у = 2в
точках их пересечения.

202
17; ЛЕКЦИЯ - ДИФФЕРЕНЦИАЛ ФУНКЦИИ
ПРИМЕР 16.19. Точка движется по прямой так, что ее расстояние
s от начального пункта через t с равно s — \tA — 423 -4- Ш2, Определите,
в какое время t — to точка еще раз пройдет через начальный пункт и
при каком t — tu ее скорость равна нулю?
Пример 16.20. Тело массой Зг движется прямолинейно по закону
s = 1 +1 -f £2, где s —• пройденный путь в см, t — время в с. Определите
кинетическую энергию mv2/2 тела через 5 с после начала движения.
17. ЛЕКЦИЯ - ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Дифференциал функции. Геометрический смысл и свойства
дифференциала. Инвариантность формы первого дифференциала.
Приложение дифференциала к приближенным вычислениям. Повторное
дифференцирование
17.1. Дифференциал функции. Пусть функция у = /(х)
дифференцируема в некотором интервале (а; 6), т.е. имеет в каждой точке этого
интервала производную
/'(*) - lim %L.
' Дх-*оДх
Но тогда на основании теоремы о связи между функцией, ее пределом и
бесконечно малой функцией
^ = f'(x) + a(Ax),
где а(Дх) — бесконечно малая величина при Дх -> 0. Поэтому
приращение функции
(17.1) Ay = /'(х)Дх + а(Дх)Дх
может быть представлено в виде суммы двух слагаемых, первое из
которых пропорционально приращению аргумента Дх с коэффициентом
пропорциональности, равным /'(х) и зависящим, следовательно, от х, а
второе является бесконечно малой более высокого порядка, чем Дх.
Только для линейной функции у = кх -f 6 приращение функции Ау =
к • Ах и второе слагаемое равно нулю, а первое пропорционально Дх с
коэффициентом, не зависящим от х.
Справедливо и обратное: если для данного значения х приращение
функции
(17.2) Ау=аАх + а,
17. ЛЕКЦИЯ - ДИФФЕРЕНЦИАЛ ФУНКЦИИ
203
где а — бесконечно-малая более высокого порядка, чем Дх, то функция
У ^ f(x) в точке х имеет производную /'(х) = а. Действительно, из (17.2)
следует, что
lim -г— = а + lim -—,
Дх->0 Дх Дх-+0 Дх
где в силу сказанного lim #- = 0 и, следовательно, а = /'(х).
Определение 17.1. Дифференциалом функции у = /(х) в точке х
называется главная часть приращения функции, линейная
относительно приращения независимой переменной. Дифференциал функции у = /(х)
обозначается dy или df (х).
(17.3) dy = df(x) = f'(x) • Ах.
Пример 17.1. Найти приращение и дифференциал функции у = х2.
Решение:
Ау = (х + Дх)2 - х2 = 2хДх + (Дх)2 =► dy = 2хДх, так как
(Дх)2
lim А = lim Дх «= 0.
д*-*о Дх Дх-+о
После введения определения дифференциала функции доказанные
выше положения для приращения функции можно сформулировать в виде
теоремы.
Теорема 17.1. Для того, чтобы функция у = /(х) имела бы в
некоторой точке х дифференциал, необходимо и достаточно, чтобы в этой
точке существовала производная.
Пример 17.2. Найти дифференциалы функций:
у = х3. Решение: dy — d(xz) = (х3)'Дх = Зх2 • Дх.
у = х. Решение: dy = dx = (х)'Дх = 1 • Дх.
Так как из последнего примера следует, что
(17.4) Дх = е*х,
то формулу для дифференциала функции записывают так:
(17.5) dy = y'dx = f'{x)dx.
В фиксированной точке х0 дифференциал функции у — /(х)равен:
(17.6) dy = f'(x0)dx.
Определение 17.2. Дифференциал функции у = /(х) в точке х равен
произведению производной на дифференциал независимой переменной.

204
17. ЛЕКЦИЯ - ДИФФЕРЕНЦИАЛ ФУНКЦИИ
Пример 17.3. Найти дифференциал функции у = \/sinx при х = к/4.
Решение:
l . .. I- COS X
dy = dvsinx = (Vsinx)'cfx = —== • dx.
2 vsin x
При x — 7г/4 дифференциал dy = -A^dx.
Из формулы (17.5) следует, что
(17.7)
У
dy^
dx'
т.е. что производная функции у = f(x) в точке х равна отношению
дифференциала функции в этой точке к дифференциалу независимой
переменной. Правую часть формулы (17.7) мы ввели ранее, как символическое
обозначение производной.
17.2. Геометрический смысл дифференциала. Пусть х -
абсцисса точки М на графике некоторой функции у = f(x) (рис. 100). Дадим
х приращение Ах. Точке с абсциссой х + Ах соответствует точка N.
Проведем через точку М касательную MP. Очевидно, что Ах = dx —
МК, Ay = NK, у* = tgZPMK. Тогда из треугольника МРК имеем:
МК • tg АРМ К = y'dx = PK = dy.
Определение 17.3. Дифференциал функции в данной точке равен при
ращению ординаты касательной к графику функции, проведенной в
данной точке при переходе от точки с абсциссой х к точке с абсциссой
х + Дх.
МК=АХ
PK=dy
NK=Ay
Х+Дх X
Рис. 100. Геометрический смысл дифференциала
17. ЛЕКЦИЯ - ДИФФЕРЕНЦИАЛ ФУНКЦИИ
205
17.3. Свойства дифференциала. Свойства дифференциала
вытекают из его определения и свойств производной:
l.dC = 0;
2.d(u + v) =du + dv\
3.d(uv) = v du -f- и • dv;
A.d(cu) = cdu\
Предполагается, что и и v - дифференцируемые функции х.
Докажем, например, 3 свойство:
d(uv) = (uvYdx = (u'v -f v'u)dx = v • u'dx + и • v'dx = v • du + u • dv.
17.4. Инвариантность формы первого дифференциала.
Теорема 17.2. Формула для дифференциала dy = y'dx сохраняет вид
как в случае, когда х является независимой переменной, так и в случае,
когда х зависит еще от одной переменной, например, и.
Доказательство. Если х - независимая переменная, то
(17.8) dy = y'dx.
Пусть теперь имеется сложная функция
(17.9) У = у{х), х = х(и).
Ее дифференциал равен
(17.10) dy = y'udu = y'x- (х'и • du) = у'х • dx.
Равенство соотношений (17.8) и (17.10) и доказывает теорему.
Это свойство дифференциала называется инвариантностью
(неизменностью) .
17.5. Приложение дифференциала к приближенным
вычислениям. Из определения приращения и дифференциала функции следует,
что они отличаются друг от друга на величину, являющуюся бесконечно
малой более высокого порядка, чем Ах.
Поэтому при малых Ах имеет место приближенная формула
(17.11) Ay^dy.

206
14. ЛЕКЦИЯ - ДИФФЕРЕНЦИАЛ ФУНКЦИИ
А на основании формулы (17.5) можно записать:
(17.12) /(ж + Дж) « rfy + /(ж) « f{x) 4-yVfc.
Формула (17.12) может применяться к приближенным вычислениям
значений функций в точках, близких к тем, в которых оно уже известно.
Пример 17.4. Пользуясь формулой (17.12), найти sin 29°.
Решение: Будем рассматривать sin 29° как частное значение
функции у = fix) = sin ж. За начальное значение аргумента, при
котором значение функции известно без таблиц и калькуляторов, примем
х = 30° = 7г/6. За значение х + Дж примем 29°, выраженное в радианах.
Следовательно,
Формула (17.12) в нашем случае примет вид:
sin(x 4- Да) « sin ж 4- (sin ж)'Дж, или sin(a: 4- Дж) « sin ж 4- Да: cos ж.
Подставляя сюда численные значения ж = 7г/6 =■ 0,52359,
Дя = -0,01745, получим
sin 29° « sin 30° - cos 30° • 0,01745 « 0,4849.
Пример 17.5. Пользуясь формулой (17.12), найти ^/8,05.
Решение: Будем считать ^8,05 как частное значение функции
t/ = #г при ж 4- Дж = 8,05. Тогда ж = 8, Дж = 0,05.
Формула (17.12) в этом примере примет вид:
\/х 4- Дж « ^+ (^х)# • Дж, или^ж4-Дж я jfc + —р= • Дж.
Подставив сюда численные значения ж и Дж, зная, что у8 = 2,
получим
0,05
^/8705 «2 4- ~-т « 2,0041.
'о • 4
17.6. Повторное дифференцирование. Производная некоторой
дифференцируемой функции у = /(ж) в общем случае также может быть
дифференцируемой функцией.
Определение 17.4. Производная от производной называется
второй производной (производной второго порядка) и обозначается у" или
Пх):
(17.13) /"(*) = (/'(ж))'.
11. ЛЕКЦИЯ - ДИФФЕРЕНЦИАЛ ФУНКЦИИ 201
Пример 17.6. Найти вторую производную функции у = ж5.
Решение: у' = (ж5)' = 5ж4, у" = (5ж4)' = 20ж3.
Определение 17.5. N-й производной (производной п-го порядка)
называется производная от производной порядка п — 1.'
(17.14) уМ = /<»>(х) = (/^(ж))'.
Пример 17.7. Найти п-ю производную функции у = sin ж.
Решение: у1 = совж, у" = -sinж, г/3) = -совж,... ,г/*п) =
sin(s 4- *£).
Производные порядка выше первого называются производными
высшего порядка. В названии "производная первого порядка" или "первая
производная" слова "первого порядка" и "первая" обычно опускаются, что
мы и делали ранее.
Определение 17.6. Вторым дифференциалом ( дифференциалом
второго порядка) называется дифференциал от дифференциала функции,
d2y = d2 fix) = d{dy) = diy'dx) = iy'dxY = y"dxdx = y"dx2.
При вычислении производной iy'dx)' надо помнить, что dx от ж не
зависит. Произведение dx на dx принято обозначать dx2.
Определение 17.7. П'М дифференциалом ( дифференциалом п-го
порядка) называется дифференциал дифференциала порядка п — 1.
(17.15) dTy = a™ fix) = didr-ly) = y™dxn.
Пример 17.8. Найти три первых дифференциала функции у = sin3x.
Решение:
dy = у* dx = 3 cos Зж • dx,
d2y = у" • <*ж2 = -9 sin3x • dx2,
d3y = yW . <fo3 = _27 cos Зж • (fa3.
Дифференциалы порядка выше первого не обладают свойством
инвариантности. Из равенства (17.7) следуют еще и такие обозначения высших
производных:
(17.16) 2/(п) = —•
' у dxn

208 17 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ДИФФЕРЕНЦИАЛ ФУНКЦИИ
И если первая производная равна отношению дифференциалов, то для
производных высших порядков такие обозначения носят условный
характер.
У второй производной есть ясный физический смысл. Если
материальная точка движется по прямой по закону s = s(£), то ускорение этого
движения первой производной от скорости движения v, а так как скорость,
в свою очередь, есть производная от пути s, то ускорение равно второй
производной от пути по времени:
(17.17) • = ' = '" = £■
17. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ДИФФЕРЕНЦИАЛ
ФУНКЦИИ
Вспомним сначала определение 17.1 дифференциала, формулу (17.5)
для его нахождения и найдем дифференциалы функций:
Пример 17.1. у = Ух1.
Решение: dy = <*(#?) = (#?)'<fc = Цк
Пример 17.2. у = |J.
Решение: <fr = d(g) = (£)'& = 3'<ln3^-3*23*ds =
= 3*(*ln3-3)ds
ж4
Пример 17.3. ?/ = х2 cos Зх.
Решение: dy — d(x2cosЗх) — (х2cos3x)'dx = (2а:cosЗх-Зх2sin3x)dx
Найдем несколько производных и дифференциалов высших порядков.
Пример 17.4. Найти вторую производную функции у = хе3*.
Решение:
у' = e3r -f Зхе3* = е3*(1 + За:), у" = Зе3ж(1 + Зх) + е3х3 = 3(2 + Зх)е3ж.
Пример 17.5. Найти первые четыре производные функцииу = sin Зх.
11 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ДИФФЕРЕНЦИАЛ ФУНКЦИИ
209
Решение:
y' = 3cos3x, y" = -9sin3x, y(s) = -27cos3x, y{4) = 81sin3x.
Пример 17.6. Найти все производные функции у = хп(п € N).
Решение:
у' = пхп~\ У = п • (п - 1)хп~2 • • -y(n) = n!, t/(fc) =0 при * > п.
Пример 17.7. Найти три первых дифференциала функции у = я шаг.
Решение:
dx dx
dy = 2/'</х = (lnx + l)dx, d2y = y"dx2 = , dzy = y{z)dx3 = r.
a: xz
Пример 17.8. Найдите все дифференциалы функции у = 4х.
Решение:
dy = 4х ln4dx, d2y = 4x(ln4)2dx2, • • • , <ft/ = (ln4)n4xdxn.
А теперь вспомним приложение дифференциала к приближенным
вычислениям (пункт 17.5), формулу (17.12) и решим на эту тему два
примера.
Пример 17.9. Пользуясь формулой (17.12), найти tg46°.
Решение: Будем рассматривать tg 46° как частное значение
функции у = f(x) = tg x. За начальное значение аргумента, при котором
значение функции известно без таблиц и калькуляторов, примем х = 45° = 7г/4.
За значение х + Да: примем 46°. Следовательно,
А 467Г А 7Г л л--,.,
Х + А1=180=^ЛХ=ШЙ:0'01745-
Формула (17.12) в нашем случае примет вид:
Дх
tg(x + Да:) я» tg х + (tg х)'Дх, или tg(x + Да:) « tg х +
tU3" О/
Подставляя сюда численные значения х = 7г/4 = 0,78538, Дх = 0,01745,
получим
tg46° « tg45° + °,°1^5 « 1 + 2 • 0,01745 « 1,0349.
cos2 45°
Значение tg46° с точностью до четырех знаков 1,0355.
Пример 17.10. Пользуясь формулой (17.12), найти ^70-

*Е }7 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ДИФФЕРЕНЦИАЛ
Решение: Будем считать ^ как частное значение функции
у = ф; при х + Ах = 70. Тогда х = 64, Дх = 6.
Формула (17.12) в этом примере примет вид:
у/хЛ- Ьх ъ #х+ (№)'-Ьх, или ^х + As«#J + -4=. Дх
3^X2
Подставив сюда численные значения х и Дх, зная, что ^64 = 4
получим '
^70 » 4 + -iL » 4,125.
о ♦ 10
Отметим, что v/70 с точностью до 10~3 равен 4,121.
Самостоятельная работа
Найдите дифференциалы функций:
Пример 17.11. у = х2у/х.
Пример 17.12. y = xarctgx.
Пример 17.13. у = ^.
Пример 17.14. Найдите вторую производную функции
у = (1 +x2)arctgx.
Пример 17.15. Найдите производную порядка п функции у = -*-.
Пример 17.16. Удовлетворяет ли функция у = ^f- соотношению
У" - 2у' + у = ех?
Пример 17.17. г/ = x2e"z, найти d3y.
Пример 17.18. у = ^, кайт« dV
Вычислите приближенно, заменяя приращение дифференциалом:
Пример 17.19. In 1,02.
Пример 17.20. ^35.
Пример 17.21. arctgl,05.
18. ЛЕКЦИЯ - ТЕОРЕМЫ О ФУНКЦИЯХ
211
18. ЛЕКЦИЯ - ТЕОРЕМЫ О ФУНКЦИЯХ
Некоторые теоремы о дифференцируемых функциях - Ферма, Рол-
ля, Лагранжа,Коши, Лопиталя. Примеры раскрытия
неопределенностей с помощью правила Лопиталя.
Теоремы, которые мы рассмотрим в этой лекции являются
фундаментом для применения дифференциального исчисления к исследованию
функций и построению графиков.
18.1. Теорема Ферма. 6
Теорема 18.1. Пусть функция у = f(x) :
о определена в интервале (а; Ь);
о принимает в некоторой точке £ € (а; 6) этого интервала
наибольшее или наименьшее значение.
В таком случае, если в точке £ существует производная, то она
равна нулю.
Доказательство. По определению производной:
Положим для определенности, что /(£) = М - наибольшее значение
функции в интервале (а; 6).
Поэтому при любом знаке Ах:
и выражение в числителе (18.1) неположительно. Следовательно:
(18.2) если Ах > О, то/(* + Af) ~ т ^ 0 =» /'(£) < 0;
£ЛХ
(18.3) если Дх < 0, то/(* + ААЖ) ~ f® > 0 =* /'(О > 0.
/ах
Так как производная в точке £ существует, она не должна зависеть
от знака Ах. Производная будет удовлетворять условиям (18.2) и (18.3)
только в случае /'(£) = 0. Теорема доказана.
6П.Ферма( 1601-1665) — французский математик.

212
18. ЛЕКЦИЯ - ТЕОРЕМЫ О ФУНКЦИЯХ
18.2. Теорема Ролля. 7
Теорема 18.2. Пусть функция у = f(x) :
• непрерывна но отрезке [а;Ь\;
© дифференцируема в интервале (а;Ь);
о принимает на концах отрезка значения, равные нулю, т.е. f(a) =
/(b) = 0.
В таком случае в интервале (а;Ь) найдется хотя бы одна точка £,
в которой производная функции равна нулю, т.е. /'(£) = 0.
Доказательство.
Так как функция непрерывна на отрезке, то она достигает на нем
своего наибольшего М и наименьшего т значений.
Если М = т, то функция на отрезке постоянна и ее производная равна
нулю в любой точке отрезка.
Пусть теперь М ф т. Тогда одно из этих чисел, например, М, ф 0.
Тогда это значение принимается в какой-то внутренней точке £, так как
на концах отрезка функция равна нулю. На основании теоремы Ферма
/'(£) = 0. Теорема доказана.
Касательная в точке £ параллельна оси ОХ. Очевидно, теорема
справедлива и при f(a) = /(ft) ^ 0.
18.3. Теорема Лагранжа. 8
Теорема 18.3. Пусть функция у = f(x):
о непрерывна на отрезке [о; ft];
• дифференцируема в интервале (a;ft).
Тогда внутри этого отрезка найдется хотя бы одна точка £, в
которой выполняется равенство
(18.4) f(b)-f(a) = f'(0(b-a).
Доказательство. Запишем уравнение хорды А В (рис. 101):
У. - /(«) /W ~ /(«) тпя
= _ ? откуда :
х — а о — а
ь./(.)+/!^М(1..,.
о — а
7М.Ролль(1652-1719) — французский математик.
8Ж.Лагранж(1736-1813) — французский математик и механик.
18. ЛЕКЦИЯ - ТЕОРЕМЫ О ФУНКЦИЯХ
213
Разность между у = f{x) и ух обозначим F{x).
(18.5) F(x) = у - у. = /(х) - № - ПЬ)Ь Z [(а) (х - а).
Легко проверить, что полученная функция F(x) удовлетворяет на
отрезке [a; ft] всем условиям теоремы Ролля.
Действительно F(x) :
© непрерывна на отрезке [о; ft];
в дифференцируема в интервале (о;ft). Ее производная
,18.6) Г(1).Г(,)_М^И
существует в интервале (a; ft), так как в нем существует Г(х)\
© F(a)=F(b)=0.
Поэтому на основании теоремы Ролля внутри отрезка [a; ft] найдется
хотя бы одна точка £, в которой F'(0 = 0. На основании равенства (18.6)
находим
(18.7)
*•<« = /'(«>-4^=0.
откуда и следует равенство (18.4). Теорема доказана.
♦ У
(18.8)
ас ь
Рис.101. Геометрический смысл теоремы Лагранжа
Из равенства (18.4) вытекает соотношение
f(b) - f(a)
ЯО
Ь — а
= 0.
Левая его часть равна угловому коэффициенту касательной к графику
у = f(x) в точке с. Правая- угловому коэффициенту секущей АВ.

2Ц
18. ЛЕКЦИЯ- ТЕОРЕМЫ О ФУНКЦИЯХ
Поэтому геометрический смысл теоремы Лагранжа следующий (рис.
101): в интервале (а; Ь) найдется хотя бы одна точка, в которой
касательная параллельна хорде, соединяющей концы дуги.
Из формулы (18.4) следует еще одно название теоремы Лагранжа. Она
называется также теоремой о конечных приращениях и может быть
сформулирована так:
Приращение дифференцируемой функции на отрезке [а; Ь] равно
длине этого отрезка, умноженной на значение производной от этой
функции в некоторой внутренней точке этого отрезка. А формула 18.4
соответственно называется формулой Лагранжа или формулой конечных
приращений.
18.4. Теорема Коши.
ТЕОРЕМА 18.4. Если функции f(x) и tp(x) удовлетворяют на [а;Ь]
условиям теоремы Лагранжа, причем <р*(х) Ф 0, то в интервале (а; 6)
найдется такая точка £, в которой
nan /'(fl^/W-flo)
Доказательство этой теоремы проводится аналогично доказательству
теоремы Лагранжа с помощью вспомогательной функции
Мы его проводить не будем.
18.5. Теорема (правило) Лопиталя. 9
Знакомство с понятием производной позволяет нам ввести новое
правило раскрытия неопределенностей вида % и g.
Теорема 18.5. Пусть f(x) и ip(x)-функции, дифференцируемые в
некоторой окрестности точки xq, за исключением, быть может, самой
этой точки. Пусть при х —> Хо обе функции одновременно стремятся
к нулю или к бесконечности. Тогда предел их отношения при х —> xq
равен пределу отношения их производных, если последний существует.
Следовательно,
(18.10) lim Щ = lim Щ.
X-+ZQ (р(Х) х-+хо (р'\Х)
Доказательство этой теоремы проводится на основании теоремы
Коши. В нашей лекции мы его опустим.
9Г.Лопиталь(16б1-1704) — французский математик.
18. ЛЕКЦИЯ - ТЕОРЕМЫ О ФУНКЦИЯХ
215
18.6. Примеры на нахождение пределов.
Неопределенность вида §•
Пример 18.1. Найти предел
,. sin За;
lim .
х-+0 X
Решение:
,. sin За: ,. (sin За;)' .. 3 cos За; n
hm = lim = lim — = 3.
x-*0 X x->0 X x->0 1
Пример 18.2. Найти предел
1 — cos a;
hm -—.
x-*0 X2
Решение:
,. 1 —cosa; ,. (1-cosrr)' .. sina;
lim - = hm r-rr; = hm —-—.
x->o xz *-*o \x ) x"*° 2a;
Хотя этот предел, как и предел в примере 18.1, можно найти с
помощью теоремы о первом замечательном пределе, мы применим правило
Лопиталя еще раз:
,. sin a; ,. (sin а;)' ,. cos а; 1,. 1
hm -—— = hm ' ч, = hm ■ = - hm cos x = -.
x-+o 2x x->o (2xy «-+o 2 2 *->o 2
Неопределенность вида g. В следующем примере правило
Лопиталя применяется трижды.
Пример 18.3. Найти предел
х3
lim —.
х->+оо ех
Решение:
г х* v Sx* v 6x v б о
hm — = hm = hm — = hm — = 0.
x-++oo ex x-»+oo e* z-»+oo ex x-++oo ex
Ясно, что предел также равнялся бы нулю, если бы степень многочлена
была не 3, а выше.
Следствие: 18.1. Многочлен любой степени при х —> оо растет
медленнее показательной функции.

216 18. ЛЕКЦИЯ - ТЕОРЕМЫ О
Пример 18.4. Найти предел
х + sin х
lim .
ar-++oo X
Решение:
x + sinx ,. (x-fsinx)' t. 1 + cosx
X-4+0O X X-+ + 00 X X-> + 00 1
При решении этого примера нельзя применять правило Лопиталя,
поскольку предел отношения производных не существует, так как не
существует
lim cosx.
х-*+оо
Как же тогда найти этот предел? Разделив числитель и знаменатель
на х, найдем, что он равен единице.
Неопределенность вида оо - со. Этот случай после
тождественных преобразований, сводится к рассмотренным выше неопределенностям
Пример 18.5. Найти
lim [ tg x J .
x->+ir/2 \COSX /
Решение: Так как оба слагаемые при х —> -f тг/2 неограниченно
возрастают, то - это неопределенность вида оо - оо.
Выполним следующие тождественные преобразования:
1 1 sin х 1 - sin x
tgx = = .
cosx cosx cosx cosx
При x —* 4-7г/2 числитель и знаменатель последней дроби стремятся
к нулю. Следовательно, от неопределенности вида оо — оо мы пришли к
неопределенности вида §. Применяем правило Лопиталя:
1-sinx lt -cosx
lim = lim —: = 0.
X-++1T/2 COSX x-++ir/2 SinX
Неопределенность вида 0 - оо. Этот случай также после
тождественных преобразований, сводится к рассмотренным выше
неопределенностям § или —.
Пример 18.6. Найти предел
lim xlnx.
18. ЛЕКЦИЯ -ТЕОРЕМЫ О ФУНКЦИЯХ
217
Решение:
lnx
lim xlnx = lim -7— = lim —V = - Hm x = 0.
x->+0
x-++0
x-++0 — -
x-4+0
При нахождении следующих неопределенностей необходимо искать
предел логарифма исходного выражения и, найдя его, вернуться к заданному
пределу.
Неопределенность вида 1°°.
Пример 18.7. Найти предел
lim(l+axm)b/xW, m>0, n > 0.
Решение:
2/ = (l + axm)6/*n =>1пг/ =
61n(l + axm)
В последнем выражении числитель и знаменатель одновременно
стремятся к нулю при х —> 0. Получилась неопределенность вида §. Поэтому
,. , ,. (Mn(l + axm))' 1# abmxm~l abm,.
lim In у = lim -7—Г,—— = Ьш т; -г——г = hmxm n =
*-ю *-»о (хпу х-+о (1 + axm)nxn~1 п х-*о
= <
0, т > п,
аб, ш = п,
оо, m < п.
Откуда
Ге° = 1, т > п,
lim(l + ахт)6/хП = <
г->0
еа6, т = п,
В частности, при a = 6 = 1иш = п мы получаем второй
замечательный предел
(18.11)
lim(l+x)1/x = e.

218
18. ЛЕКЦИЯ - ТЕОРЕМЫ О ФУНКЦИЯХ
Неопределенность вида 0°.
Пример 18.8. Найти предел
lim хх.
Решение: Обозначим у = хх. Логарифм этого выражения In у =
lnx* = xlnx> Из примера 18.6 следует, что величина In у стремится к
нулю, следовательно,
lim у = lim xx = 1.
Неопределенность вида оо°.
Пример 18.9. Найти предел
lim (tgx)cosx.
аг-»7г/2
Решение: Обозначим у = (tgx)cosx. Логарифм этого выражения
In г/ = cosxlntgx = bsing-incos^ jj числитель In sin x - lncosx, и знамена-
сое ж
тель —^ стремятся к бесконечности при х —> 7г/2.
Применяем правило Лопиталя:
(Insinx - lncosx)' ,. /cosx sinx\ cos2x
lim - ——, = hm -— + • - = 0.
х-иг/2 f —i—Л x-Hr/2VSinX COSX/ Sin X
Vcosx/ v '
Так как In у стремится к нулю, то
lim t/= lim (tgx)cos* = 1.
x-tn/2 x-+n/2
Заметим, что если <р(х) —> 0, a ^(x) —► oo при x -» x0, то
lim <p{xfW = 0
и, следовательно, 0°° не является неопределенностью.
Действительно, в этом случае
In у — ф{х) In <р(х) —> -оо, а у —> 0.
i* ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРЕМЫ О ФУНКЦИЯХ
219
18. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРЕМЫ О
ФУНКЦИЯХ
Пример 18.1. Проверьте справедливость теоремы Ролля для
функции у = /(х) = х3 + 4х2 — 7х - 10 на отрезке [-1; 2].
Решение:
« Функция является многочленом и непрерывна на любом множестве,
в том числе и на [—1;2]..
о Многочлен дифференцируем на любом множестве,
о Находим значение функции на концах отрезка: f(-l)=0, f(2)=0.
Все условия теоремы Ролля выполнены — теорема справедлива для
данной функции.
Пример 18.2. Покажите, что уравнение х3 — Зх 4- с = 0 не может
иметь два различных корня на отрезке [0; 1].
Решение: Функция у = х3 — Зх + с является многочленом и на
отрезке [0; 1] удовлетворяет условиям теоремы Лагранжа. Предположим,
имеются два корня а, Ь € (0; 1) =» /(а) -/(&) = 0. Тогда в интервале (а; 6)
должна быть хотя бы одна точка, в которой производная равна нулю. Но
/(а) = /(0) = с, f(b) = /(1) = с - 2, mbZfa{a) = -2 ^ 0. Следовательно, из
теоремы Лагранжа следует, что исходное уравнение не может иметь двух
различных корней на отрезке [0; 1].
Далее решим примеры на теорему (правило) Лопиталя (см. 18.5). При
вычислении пределов мы также будем использовать различные
преобразования и полученные ранее замечательные пределы.
Пример 18.3. Вычислить
lim [ неопределенность типа — ) .
*->octgx V оо/
Решение:
lnx ,. (lnxV ,. sin2x
lim = hm г- = - hm .
*-*octgx *-+o(ctgx)' *->o x
Получили неопределенность типа jj, однако применять правило Лопиталя
нет надобности, так как
sin2x ,. sinx ч л
lim = . hm sm x = 1 • 0 = 0.
х-+0 X x-f0 X
Таким образом, окончательно находим:
lnx
hm = 0.
*->0 Ctg X

220
18 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРЕМЫ О ФУНКЦИЯХ
Пример 18.4. Вычислить
lim ( —s г) (неопределенность типа оо — оо).
*->o\Sin2x x2J
Решение: Приведя дроби к общему знаменателю, получим:
г / 1 1 \ .. fx2-sm2x\ ( 0\
hm I —« « = 1ш —-—«— I неопределенность типа - .
x-M>\snrx х1) х->о\ x2surx / \ О/
Прежде чем применять правило Лопиталя, заменим знаменатель
последней дроби эквивалентной ему бесконечно-малой х4 х2 sin2 x ~ х4. Получим:
1 / 1 1 \ .. /x^-sin^xX / 0\
hm I —о о I = bm I г-г— } I неопределенность типа - .
*->o\sin2x x2J *->о\ хА ) \ О J
По правилу Лопиталя
lim [ -7-5 г I = lim
«-►о у sura: х2/ *->о
2х - sin 2х .. 1 - cos 2x
= hm
lim
4х3 *-»о бх2
2 sin2 х 1
х-*о бх2 3'
Пример 18.5. Вычислить
lim(cos2x)3/z (неопределенность типа 1°°).
х->0
Решение: Логарифмируя и применяя правило Лопиталя, получим:
lim ln(c
Следовательно,
rw * \3/х2 г 31ncos2x tg2x
hm lnfcos 2x r/x = hm = -6hm —— = -6.
- - v ' - ^ ~2 x->o 2x
lim(cos2x)3/3r2-e-6.
Пример 18.6. Вычислить
limxx (неопределенность типа 0°).
x->0
Решение: Имеем
хх = у; In у — х In x;
1/» _|
limlny = lim ft* = lim -^ = 0
limy — 1 ==► limxx = 1.
x-»0 x->0
IS ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРЕМЫ О ФУНКЦИЯХ
221
Пример 18.7. Вычислить
limctgxsmx (неопределенность типа оо°).
х->0
Решение: Имеем
ctg xs,nx = у; In у = sin x In ctg x;
lim In у = lim ^^ = lim ~V ft *•*/*»'» = q ^
x_>0 * x-fO Vera» *-><) -l/sin^sr-cosx
limy = 1 => limctgxsinx = 1.
x-+0 x->0 °
Самостоятельная работа
Пример 18.8. Проверьте справедливость теоремы Ролля для
функции у — f(x) = х3 - 5х2 4- бх на отрезке [2; 3].
Пример 18.9. Проверьте справедливость теоремы Ролля для функ-
ции у — 4sinx на отрезке [0; 7г].
Пример 18.10. Составьте формулу Лагранжа для функции у = х(1 —
lnx) на отрезке [а; 6].
Найдите пределы:
Пример 18.11. Мтх\2х2-*+\
х-+1 **-'*+6
Пример 18.12. lim ***"*"*.
Пример 18.13. limxsin*.
х-+0
Пример 18.14. limlnxln(x - 1).
Пример 18.15. lim x1/x.
X—>+00
Пример 18.16. lim(l-x)tg^.
X—>1 £

222 19. ЛЕКЦИЯ - ФУНКЦИОНАЛЬНЫЕ РЯДЫ
19. ЛЕКЦИЯ - ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Область сходимости функционального ряда. Правильно сходящиеся
ряды и их свойства. Степенные ряды.
19.1. Область сходимости функционального ряда. Ранее мы
познакомились с рядами, членами которых являются числа. Рассмотрим
теперь ряд
оо
(19.1) щ(х) + и2(х) + ... + ип(х) + ... = ]Г ип(х).
71=1
Определение 19.1. Ряд (19.1), членами которого являются
функции, определенные в некоторой области изменения аргумента х,
называется функциональным рядом.
Если в функциональный ряд вместо х подставить некоторое значение
xq из области определения всех его функций, то получится числовой ряд.
Определение 19.2. Точка х = х0, при подстановке которой в (19.1)
получится сходящийся числовой ряду называется точкой сходимости
функционального ряда (19.1).
Определение 19.3. Множество всех точек сходимости функциональ
ного ряда называется его областью сходимости.
Частичная сумма функционального ряда, т.е. сумма первых п его
членов
п
(19.2) Snix) = Y2 **(*) = иЛх) + «ate) + ... + unix)
является функцией переменой я, определенной в области сходимости ряда.
Действительно, из определения области сходимости функционального
ряда следует, что для любой точки х этой области существует предел
Snix) при п —^ оо.
В точках же, не принадлежащих области сходимости, 5п(х) не имеет
предела. Если функциональный ряд сходится и имеет сумму 5(ж), то
разность Six) - Snix), как и для числового ряда, называется га-м остатком
00
ряда и обозначается гп = ]П и*.
Очевидно, что если ряд сходится, то должен быть выполнен
необходимый признак сходимости, т.е.
(19.3) lim и^х) = О
п—юо
19. ЛЕКЦИЯ - ФУНКЦИОНАЛЬНЫЕ РЯДЫ 223
во всех точках сходимости ряда, где также
(19.4) lim гп(х) = 0.
п-*оо
Для определения области сходимости функционального ряда обычно
сначала используют признак Даламбера, применяемый к ряду,
составленному из абсолютных величин ряда (19.1).
(19.6) Km|*#|<l.
n-fool Un(X) I
Все точки х, удовлетворяющие (19.5), входят в область сходимости ряда.
Из признака Даламбера следует, что в случае, если предел
последующего члена ряда к предыдущему равен единице, ряд может сходиться или
расходиться. Поэтому в граничных точках промежутка, точки которого
удовлетворяют (19.5), ряд также может сходиться, так как в них
(19.6) Hm|^±iMUl.
n-+oo| Un\X) I
Вопрос о сходимости ряда в точках удовлетворяющих (19.6), решается
непосредственной подстановкой их значений в ряд (19.1).
Пример 19.1. Определить область сходимости функционального ряг
да
1
у—-—.
^-f nix + 3)"
Решение:
Un — n(z+3)"' Un+l ~~ {n+l)(z+3)n+l '
lim |h=±i| = lim 1, "1Д,+|| = lim г£*
Следовательно, \х + 3| > 1 =» x > -2 и х < -4.
Проверим сходимость ряда в точках j = -2hi = -4:
оо оо
о х = -2 : ^2 (x]z)n = YL —гармонический ряд, расходится;
оо оо
о i = -4 : 5Z п(Д3)л = J2 я(Л)ц—знакочередующийся ряд, сходится
п—1 п=1
по признаку Лейбница, но сходится условно, так как ряд,
составленный из абсолютных величин данного ряда,
оо ..
п—1
является расходящимся.

19. ЛЕКЦИЯ - ФУНКЦИОНАЛЬНЫЕ РЯДЫ
оо
Таким образом, область сходимости ряда £ ,Д3)П состоит из всех точек
х€ (-оо,-4] U (-2,оо).
Пример 19.2. Определить область сходимости ряда £) п\/со$пх.
п=1
Р е.ш е н и е: ип = n^cosnx, un+1 = (п + l)^co8n+1s;
lim Ы = lim l<nnfc°rixl - lim \У*Ш\.
П-400 J U« I П-+ОО I П \/COSn X I „-Ю0 I V »
Этот предел меньше единицы при всех х, кроме ж* = for, А: = 0, ±1,....
При целых значениях к получатся ряды:
00
• при четном А;: £ ntycosnXk = 1 + 2 + 3 + ...,
с»
в при нечетном к: £ ntycosnXk = -1 -b 2 - 3 + ... 4- (-l)nn-f ....
Оба ряда расходятся, т.к. не выполняется необходимый признак сходимос-
оо
ти, следовательно, областью сходимости ряда £) ntycosnx является вся
п=1
числовая ось, кроме точек ж* = for, А; = 0, ±1,....
19.2. Правильно сходящиеся функциональные ряды и их
свойства. Известно, что сумма конечного числа непрерывных функций есть
функция непрерывная, и производная суммы конечного числа функций
равна сумме производных этих функций. Функциональные же ряды
содержат бесконечное число слагаемых и указанные свойства не всегда
справедливы и для них.
Определение 19.4. Функциональный ряд (19.1) называется
правильно сходящимся в области D, принадлежащей области его сходимости,
если в любой точке этой области все члены ряда не превосходят по
абсолютной величине соответствующих членов сходящегося
знакоположительного ряда.
В некоторых учебниках правильно сходящийся ряд называется
мажорируемым, а соответствующий числовой ряд, с которым он
сравнивается, мажорирующим. В более подробных курсах вводят определение
равномерной сходимости, на котором в наших лекциях мы останавливаться
не будем. Приведем без доказательства три теоремы для правильно
сходящихся функциональных рядов, определяющих их свойства, о которых
говорилось в начале этого пункта.
ТЕОРЕМА 19.1. Всякий функциональный ряд, правильно сходящийся в
области D, сходится абсолютно в любой точке этой области.
19. ЛЕКЦИЯ - ФУНКЦИОНАЛЬНЫЕ РЯДЫ
225
Пример 19.3. Доказать, что ряд £) ^^ абсолютно сходится при
п=1
любом х € (-оо,оо).
Решение: Действительно, |~р| ^ ^ при любых х, а
следовательно, члены данного ряда не превышают по модулю соответствующие
оо оо
члены сходящегося ряда £ Л, тогда по теореме 19.1 ряд £ a?F£ сходит-
п=1 п=1
ся правильно и абсолютно при любых х.
Теорема 19.2. Если ряд из непрерывных функций правильно
сходится в области D, то его сумма есть функция непрерывная в этой
области.
Теорема 19.3. Если ряд (19.1), составленный из функций, имеющих
непрерывные производные, сходится в области D и его сумма равна S(x),
а ряд из производных его членов сходится в этой области правильно,
то производная суммы ряда S'(x) равна сумме ряда, составленного из
производных его членов. Это значит, что такой ряд можно почленно
дифференцировать в области D.
Из функциональных рядов мы рассмотрим лишь степенные ряды, а в
дальнейшем (в третьем семестре) — тригонометрические ряды.
19.3. Степенные ряды.
Определение 19.5. Степенным рядом называется функциональный
ряд
оо
(19.7) У^а>п(х - х0)п = а0 + ах(х - х0) 4-... 4- ап{х - х0)п + ...,
п-0
членами которого являются произведения постоянных ао, а\, ... , ап,...
на разность (х-xq) в соответствующих целых степенях п. Постоянные
oi, ... , ап,... называются коэффициентами степенного ряда.
Если х0 = 0, степенной ряд (19.7) примет вид
оо
(19.8) ]Ра„хп = а04- а\Х + ...4- апхп+ ...,
п-0
который мы прежде всего и рассмотрим.
Определим область сходимости этого ряда. Для этого рассмотрим
знакоположительный ряд, составленный из абсолютных величин членов ряда

1 — область, где ряд расходится;
2 — область, где ряд сходится;
3 — область, где ряд расходится.
Рис. 102. Область сходимости степенного ряда
(19.8) и применим к нему достаточный признак сходимости Даламбера
(19.5).
lim
п-юо
г*п+1
= lim
П-+О0
an+ix
,л+1|
апхп
| lim
п—►оо
Яп+1
< 1.
Откуда
(19.9)
\х\ < lim
an+i
= Я.
Определение 19.6. Число R = lim l-2*-! называется радиусом схо-
п-юо,вп+1'
димости степенного ряда (19.8), при всех \х\ < R ряд абсолютно
сходится, при \х\ > R — расходится. Интервал (—R,R) называется
интервалом сходимости ряда (19.8).
В точках х = ±Я сходимость или расходимость ряда устанавливается
проверкой сходимости числовых рядов, полученных после подстановки в
(19.8) х = -Я и х = R. Областью сходимости степенного ряда (19.8)
является интервал (-Я;Я), к которому, в зависимости от конкретных
случаев, могут быть добавлены один или оба конца отрезка [—Я; Я] (рис.
102). В каждой точке интервала (—R;R) ряд (19.8) сходится абсолютно.
Очевидно, любой степенной ряд вида (19.8) сходится при х = 0. Если
других точек сходимости нет, радиус сходимости Я = 0. Если же ряд
сходится при любых х € (-оо; оо), то будем считать, что радиус сходимости
Я = оо.
Пример 19.4. Определить радиус, интервал и область сходимости
оо
степенного ряда ]Г ^=.
п=1
Решение: itn = ^ un+i
Д= lim 1тН= Ит ^ = 1.
Интервал сходимости (—1; 1).
хл+1 1 1
- 7^и; °n ~ 7»' an+1 *"" \/^ьГ;
/Р. ЛЕКЦИЯ - ФУНКЦИОНАЛЬНЫЕ РЯДЫ
221
Проверяем граничные точки:
оо оо оо
• х = 1: J2 ^ = Y1 Г7Е — обобщенный гармонический ряд £ ^,
п=1 ж п=1
при а ^ 1 — расходится;
дится.
n=l
знакочередующийся ряд условно схо-
Следовательно, область сходимости ряда [—1; 1).
оо
Пример 19.5. Найти область сходимости ряда ^2 *£.
п=1
Решение: ап = ±; an+1 = т^; Я = lim ^ = lim ^^ =
lim(n + 1) = оо.
п-+оо
Следовательно, область сходимости ряда а: € (-оо; оо).
При определение радиуса сходимости в этом примере использовано
соотношение (п + 1)! = п!(п + 1).
Для степенных рядов может быть доказана теорема.
Теорема 19.4. Пусть степенной ряд (19.8) имеет интервал
сходимости (—Я; Я), а г < Я произвольное положительное число. Тогда ряд
(19.8) является правильно сходящимся на отрезке [-г; г]. По свойству
правильно сходящихся рядов:
о Степенной ряд (19.8) абсолютно сходится в любой точке
интервала сходимости и, следовательно, степенные ряды можно
почленно складывать и умножать (как многочлены). При этом
интервалом сходимости полученного степенного ряда будет
множество всех точек, в которых сходятся складываемые или
перемножаемые ряды.
о Сумма степенного ряда (19.8) является непрерывной функцией в
каждой точке его интервала сходимости.
о Степенной ряд (19.8) можно почленно дифференцировать в любой
точке его интервала сходимости.
Естественно, что радиус сходимости степенного ряда (19.7) также
равен
Я:
lim
п—>оо
йп-Ы
однако интервал сходимости будет
(19-Ю) (*в-Д;*о + Я),
т.к. применив к ряду (19.7) признак Даламбера, получим

228 19 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ ~ ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Я= lim
п-юо
un+i
= lim
П-ЮО
fln+ifo -a?d)'
n+1
^(я - x0)n
= \х — х0| lim
fln+l
< 1
и, следовательно, ряд (19.7) сходится в интервале
I°п+1I
(19Л1)
\х - хо| < Нт
= Я.
В точках ж = хо-Яих = х0Ч-Я сходимость устанавливается так же,
как и для ряда (19.8) в точках х = -Я и х = Я.
оо
Пример 19.6. Найти область сходимости ряда £ ^ •
Решение: ап = £, an+i = ^^т; R = jimj^-|
Интервал сходимости |х - 3| < 4 или х € (-1; 7).
Рассмотрим граничные точки х = 7их = — 1 :
п=0
= lim ££■ = 4.
п=0 п=1
15=21 eg 1=^*1 = !_i + i_i.
* = -1: Z%
Оба ряда расходятся, т.к. предел ип не равен нулю. Область
сходимости совпадает с интервалом сходимости хб(-1;7).
19. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИОНАЛЬНЫЕ
РЯДЫ
Рассмотрим пример, в котором требуется определить, является ли
данная точка точкой сходимости функционального ряда.
Пример 19.1. Исследовать сходимость функционального ряда
(19.1)
^ Зп + 2 \Sx - 3/ 2 \8* - ЗУ 5 V** -3/ 8 \8х - 3/
6 точках х=0 и х-1.
Решение:
• В точке х=0 функциональный ряд
19 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИОНАЛЬНЫЕ РЯДЫ
229
превращается в числовой ряд
f» (-1)"
п-й член которого по абсолютной величине
(!)"•■
как
Тз(1) =°°'
не стремится к нулю, так как
lim
n-юо Зп *
что является достаточным признаком расходимости ряда. Следова-
оо
тельно, ряд £ зп+2 (Из Г расходится.
п=0
в В точке х=1 ряд (19.1) превращается в числовой ряд
(19.2) £—(-)"•
п=0
В этом случае
lim un = lim —
п—юо n=oo 3fl
ыэ'-
и необходимый признак сходимости ряда выполнен.
Применим теперь достаточный признак сходимости Даламбера
к ряду (19.2):
Un = Зп+2 \ъ) ' ttn+l = змЗ (б)
J™ ^ = £™ SS ' Н I < 1 =► Р« (19-2) сходится.
Рассмотрим теперь тот же функциональный ряд, но определим всю
область сходимости.
Пример 19.2. Определить облость сходимости ряда (19.1).
Решение: В область сходимости функционального ряда входят
точки в которых выполняется неравенство (19.3).
(19.3) Ит
n-foo
«n+l(s)
un(x)
< 1.

230
19 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИОНАЛЬНЫЕ РЯДЫ
В нашем случае
Un\X) ~ 3^+2 \bx^s) ' Un+1 ~~ 3^+5 \*х-з)
lim |**}Ф| = lim fgjg 1^1 < 1.
Так как
,. 3n + 2 ,
lim -—— = 1,
n-+oo 3n -f 5
то область сходимости определяется неравенством
5-х
|8х —3
Решаем систему:
>-1
5 — х
< 1 или системой - 1 < < 1.
ОХ — о
8х-3
5~» < 1
8х-3 ^ Х*
fe + i>o,
^ё^-к0-
22±2 > О
9x^8 > q
k8x-3 * и*
Методом интервалов определяем, что этой системе удовлетворяют точки
х € (-оо, -|) (J (§, оо). Исследуем дополнительно сходимость ряда (19.1)
в точках, где предел отношения последуюшего члена ряда к предыдущему
равен единице:
оо
о х = | =» $3 зТиЗ* Сравнив этот ряд с гармоническим, получим,
что он расходится;
о х = —|
сходится по признаку Лейбница. Ясно, что
ряда (19.1)
^ Зп+2
п=0
в этой точке ряд сходится условно.
Итак, окончательно область сходимости
«е (-оо,-?]U(|,оо).
Перейдем теперь к примерам, в которых рассматриваются степенные
ряды (19.8)и требуется определить радиус сходимости и область
сходимости указанных рядов.
Пример 19.3. Исследовать сходимость степенного ряда
^Г:гп = 1 + х4- я2 +
• + хп.
п=0
Решение:
ап =an+i, R = lim
п-юо
Проверим точки х=1
0>п
Оп+1
и х=
-1:
интервал сходимостия 6 ( — 1,1).
19 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ-ФУНКЦИОНАЛЬНЫЕ РЯДЫ
231
© При х=1: 53 жп = 1 + Ц Ь 1 + ... — ряд расходится.
п=0
оо
в Прих=-1: 53 хп = 1-1 + 1-И + (-1)п + ... — ряд расходится.
Следовательно, область сходимости данного ряда равна его интервалу
сходимости х € (-1,1).
Пример 19.4. Исследовать сходимость степенного ряда
Е°° хп _ х х2 хг хп
, n-2"~2 + 2-22 + 3-23+"'+n-2"+"*'
n=l
Решение:
л — -JL. п — 1
"П — „.2п, «П+1 — (п+1).2п+1 1
П-+0О П"2
Следовательно, интервал сходимости х € (—2,2).
Проверим точки х=2 и х=-2:
оо оо
в При х=2: 53 ^г =EJ — гармонический ряд расходится.
оо п оо
• При х=-2: 53 ;TF = 53 ^Г Рад знакочередующийся сходит-
п=1 п=1
ся по признаку Лейбница, так как lim ^-£- = 0, но так как ряд,
п—юо п
составленный из абсолютных величин членов ряда, будет
гармоническим, при х=-2 данный ряд сходится условно.
Область сходимости включает интервал сходимости и левую
границу х € [-2,2).
Пример 19.5. Исследовать сходимость степенного ряда
х2 х'1
п=1
Решение:
ап — зг5 Gn+i —
пн, "П+1 — (п+1)п+-1»
Д= limi2±^= Ит(а±1)п(п + 1) =
п-»оо " п-4оо х п '
Ит (1 -I- ~)п • lim (п + 1) = е • оо = оо.
п-*оо и/ п-юо
Следовательно, ряд сходится при любых х е ( —оо, оо).
Пример 19.6. Исследовать сходимость степенного ряда
оо
У^ п! - хп = х + 2! • д2 + • • - + п! ■ хп + ....
п=1

232 19 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИОНАЛЬНЫЕ РЯДЫ
Решение:
а„ = п!, ап+г = (n + 1)!,
Область сходимости состоит из одной точки я = 0.
Рассмотрим теперь соответствующие примеры для степенных рядов
по степеням разности х - xQ (19.7).
оо
Пример 19.7. Исследовать сходимость ряда 52(х—2)п, то естьх0 =
Решение: Так же, как в примере (19.3), радиус сходимости R=l, a
область сходимости будет, согласно формуле (19.10) лекции 19 ж € (1,3).
Пример 19.8. Найти область сходимости ряда £ ^21 ,
то есть xq = 3.
Решение: Так же, как в примере (19.4), радиус сходимости R = 2,
а область сходимости, согласно формуле (19.10) лекции 19 х € [1,5).
оо
Пример 19.9. Найти область сходимости ряда ]£ '**?" ♦
Решение: Так же, как в примере (19.4), радиус сходимости R = оо
и, следовательно, область сходимости также х 6 (-оо, оо).
оо
Пример 19.10. Найти область сходимости ряда £ п\ • (я + 5)п.
п=1
Решение: Так же, как в примере (19.6) радиус сходимости R=0,
следовательно, область сходимости данного ряда состоит из одной точки
х = -5.
Самостоятельная работа
Пример 19.11. Исследовать сходимость функционального ряда
f_L_(±z£.y
^2n-l \7x-¥2)
П=1 x
в точках х=0 и х=1.
Пример 19.12. Определить область сходимости ряда
20. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА
233
Определить радиус, интервал сходимости и область сходимости
следующих степенных рядов
Пример 19.13. £(n:r)n.
71=1
ПРИМЕР 19.14. £ ТГ&Гу
п=1
Пример 19.15. £ i^1.
Пример 19.16. У) ^.
п=1
20. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА
Многочлен Тейлора.Формула Тейлора. Ряд Тейлора.
Формула и ряд Тейлора10 относятся к числу важнейших понятий
математического анализа. Они широко используются в математике. В
частности, в этом семестре мы будем использовать их при исследовании функций,
приближенном вычислении значений функций, численном решении
уравнений и оценке возникающих при этом ошибок.
20.1. Многочлен Тейлора. Пусть функция у — f(x) n раз
дифференцируема в некотором интервале, содержащем точку xq. Построим
многочлен степени т < п
Рт(х) = Со + d{x - х0) -f С2(х - хо)2 + • • • + Ст(х - хоГ
т
(20.1) = £Ct(s-*0)\
'Б.Тейлор( 1685-1731) — английский математик.

234
20. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА
коэффициенты которого определим из условия совпадения значений этого
многочлена и его m производных с соответствующими значениями
функции у = f(x) и ее производных в точке хо.
{ Рт(х0) = Со = /(х0),
Fm(x0) = Сг = /'(*о),
р;Ы = 2.ьс2 = Г(1„),
(20.2)
Р™Ы = 3-2-1С3 = /'"Ы,
р£]Ы = к(к-1)...2 • 1 • ск = /<*>Ы,
Р^\х0) = т(т- 1)...2 • 1 • Ст = /<т>(*о).
Члены в производных от многочлена (20.1), содержащие множитель (х -
Хо) в точке Хо равны нулю. Производные порядка выше т от многочлена
тп-й степени также равны нулю. Из (20.2) имеем
(20.3)
^к — —_-—? л = 0,1,..., т.
В (20.3) положено 0! = 1,/(0)(х0) = /(х0).
Следовательно, искомый многочлен (20.1) с коэффициентами Си,
определяемыми по формуле (20.3), будет
/(т)ы,
(20.4)
Рт(х) = /Ы + /'(*0)(* - «о) + ' ' • +
т!
-(ж - х0)т =
*=о
fc!
Определение 20.1. Многочлен (20.4) называется т-м многочленом
Тейлора функции f(x) по степеням (х — хо).
Бели функция f(x) сама по себе является многочленом степени га, то
запись ее в виде (20.4) всегда возможна и означает лишь представление
данного многочлена по степеням разности (х — хо).
Пример 20.1. Представить функцию f(x) = х2 в виде многочлена
Тейлора по степеням (х - 3).
Решение: Имеем /(3) = 9, /'(3) = б, /"(3) = 2. Все производные
выше второго порядка от f(x) = х2 равны нулю. Следовательно,
многочлен Тейлора при Хо = 3 для f(x) = х2 имеет вид
Р2(х)=9 + 6(х-3)т-(ж-3)2.
Раскрыв скобки и приведя подобные члены, очевидно получим данную
функцию f(x) = х2.
20. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА
235
рт(*нЕ((а+;; w-(«+«г,
Пример 20.2. Пусть /(х) = (а + х)т и х0 = 0.
Тогда по (20.4)
" ((fl + xniS0Jh
где
((а 4- x)m)(Af) = m(m - 1)... (m - fc + l)(o + х)£Г0* =
m(m - 1)... (m - fc -fl) am~*
есть fc-я производная от (а + x)m в точке х = 0. Положив теперь х = 6,
получим формулу бинома Ньютона:
~ , т(т- 1).._. (т - fc + 1) ^m_fcj> __ л.т А _m-U
(20.5)
го 1<т Л\ (чт — h Л. 1 I
. am~kbk + • • • + mabm-1 + 6m,
/ ,ш v^4 ro(m ~ 1) • • • (wi — A; + 1) m_i.,i. m , m-iL ,
(a + b)m = 2^ —- ^—jj am kbr = am + mom *6 +
m(m - 1)... (m - fc 4- 1) _то-^ , , _^m-i , ^m
fc!
которую мы использовали в лекции 7 при выводе предела
lim(l + i)n = e.
20.2. Формула Тейлора. Если функция /(х) не является
многочленом, ее всегда можно представить в виде
(20.6) Дх) = Рт(х) + JU*) = £ ^ТГ^ <* " х^ + ^m(x).
Определение 20.2. Формула (20.6) называется формулой Тейлора
для функции f{x)y a Rm(x) называется т-м остаточным членом форму-
лы Тейлора и определяет отличие f(x) от многочлена Тейлора (20.4)-
(20.7)
Будем искать остаточный член в виде, подобном т + 1-му члену
(m + 1)!
где функция Q(x) неизвестна. Выразим ее через /<т+1Цх).
Поскольку многочлен Рт(х) определен на основании (20.2), то из (20.6) получаем
Ят(*о) = R'm(*o) = ••• = R{™4*o) = 0,*Lm+,)(*) = /(т+1,(*)-
т.к. Рт* (г) = 0. Обозначим <р(х) = (х - а?о)т+1- Очевидно, что
Фо) = <р'(*о) = •••= Ч>{т)Ы = 0,^ш+1^(х) = (ш + 1)!.

236
20. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА
Функции Rm(x) и <р(х) на отрезке [хо,х] удовлетворяют всем условиям теоремы Коши,
приведенной в лекции 18. Следовательно, на основании этой теоремы и указанных
выше свойств функций Rm(x) и <р(х),
¥>(*) V>(*)-¥>(*o) V»'(*l) '
где xi 6 (x0,x). Применяя теперь теорему Коши к R'm{xi) и y?'(ai) и последующим их
производным, получим
~ V<~>(*m) " V><m)(«m)-Vm>(*0) ¥><т + 1>(*т+1Г
где Xfc+i 6 (хо,xjb),fc = 1,2,...,т. Следовательно,
*m(«) - HJT + Vm+l) - /(m + n(»m + l)
где последнее соотношение получено на основании расмотренных выше свойств
функций Rm(x) И у?(х).
Обозначив xm+i = {, имеем
Следовательно, искомая функция Q(x) = /<m+1)({).
(20.8) ^(a:) = :£Tlf(x_:Eo)m+1'
где £ € (x0, x) и вся неопределенность остаточного члена, т. е. отличие
нашей функции f(x) от многочлена Рт(х), заключена в неизвестном
значении £. Положив для удобства т+1 = п, формулу (20.6) можно записать
в виде
fe=0
Определение 20.3. Формула (20.9) называется формулой Тейлора
для функции f(x) с остаточным членом в форме Лагранжа
(20.10) Rn-X(x) = ^Р (ж - *о)п,
в которой точка £ € (х0, ж) не определена и зависит от я и п. Формула
(20.9) при хо = 0 является представлением функции f(x) в виде
многочлена в окрестности начала координат и часто называется формулой
20. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА
237
Маклорена11.
п-1
(2o.il) fM^iimj + rii-,,-
/(*)(0) k /<»>(в*)
где положено £ = 6х, 0 < 6 < 1.
При х близком к хо, остаточный член является, очевидно, неизвестной
бесконечно малой величиной порядка п при х -> х0 и формула (20.9) может
быть записана в виде
(20.12) Дх) = £ ^^ (х - х0)* + 0((х - хо)*),
*=о *'
где 0(ап) есть обозначение бесконечно малой величины порядка п при
а -+ 0. Выведенные выше формулы (20.9) и (20.12) позволяют
сформулировать важную теорему.
Теорема 20.1. Если функция /(х) имеет в точке х0 и ее некоторой
окрестности непрерывные п производных, то она может быть
представлена в виде (20.9) или при х -» х0 по формуле (20.12).
20.3. Ряд Тейлора. Докажем еще одну важную теорему.
Теорема 20.2. Если функция /(х) имеет в точке х0 и ее некоторой
6-окрестности, т. е. для всех х € (|х — хо| ^ 6) непрерывные
производные любого порядка, ограниченные одним и тем оке числом М, то она
разлагается в этой окрестности точки Хо в сходящийся к /(х)
степенной ряд.
(20.13) /(х) = ^^о)(1_Хо).
11=0
Доказательство. По условиям теоремы \f^n)(x)\ ^ М, п — 0,1,2, Тогда
из (20.10):
А/
(20.14) \Rn-i{x)\ ^ — |х - хо|п -► 0 при п -► оо.
п!
Приведенная оценка (20.14) получена на основании того, что lim ~ = 0
для любого а. Следовательно, формула (20.9) переходит в ряд (20.13), что
и доказывает теорему (20.2).
Определение 20.4. Ряд (20.13), к которому по теореме (20.2)
сходится функция f (х), называется рядом Тейлора.
пК.Маклорен(1б98-174б) — шотландский математик.

238
21. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА
Для х0 = 0 соответствующий ряд (20.13) часто называют рядом Мак-
лорена .
оо
/<»>(0)
(20.15) /(x)==y;i-^x".
п=0
Покажем, что выведенная в лекции 18 формула Лагранжа (18.4), или
формула конечных приращений, является частным случаем формулы
Тейлора (20.9) при п = 1.
Действительно, из (20.9) при п = 1 следует
(20.16) /(*) = /Ы + ЯО(*-*о).
Положив х0 = а и а: = 6, получим f(b) - /(а) = /'(£)(& - а),где £ е (а,Ь).
Это и есть формула конечных приращений Лагранжа.
21. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА
Формулы и ряды Тейлора для некоторых элементарных функций
и использование их для вычисления пределов и в приближенных
вычислениях.
Рассмотрим представление по формуле Тейлора (20.9) (чаще всего это
будет формула Маклорена (20.11) ) и разложение в ряд Тейлора (20.13)
или Маклорена (20.15) некоторых элементарных функций и определим их
области сходимости.
21.1. Показательная функция f(x) = e*, х0 = 0. Так как х0 =
0, /<*>(*) = е*, /<*>(0) = 1, к = 0,1,..., /<">(0 = е*, то по формуле (20.11):
(21Л) e*=£fr
п~1 хк е** „
Дг=0
где 0 < в < 1.
Поскольку для функции f(x) = ех при любом х — N € (-оо, оо)
производные любого порядка /М(х) — eN ограничены одним и тем же числом
М = eN, то по теореме (20.2) предыдущей лекции формула (21.1)
переходит в соответствующий ряд Маклорена:
(21.2) e* = V4-
который сходится к ех на (-оо,оо).
Пример 21.1. Вычислим е"1 = 1/е с точностью до 10~4.
21. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА __ £М
Решение: По (21.2) при х = —1,
i/e = e-> = i-i + i-i + ---+^+ ••• = ?; Ц^-
п=0
Это знакочередующийся ряд и по теореме Лейбница остаток ряда не
превышает своего первого члена. Следовательно, ошибка при вычислении
величины е-1 не больше первого из отброшенных членов ряда ее
представляющего
е <- |Ь^|,п! > 1/е - Ю4, откуда п = 8, т. к. 8! = 40320 > 104.
Итак, 1/е = 1/2 - 1/6 4-1/24 - 1/120 + 1/720 - 1/5040 =■ 0,3679.
Первый из неучитываемых членов 5^320 < 0,25 • 10" •
Пример 21.2. Вычислить число е с точностью до 10~"4.
Решение: Ряд Маклорена (21.2) при х = 1 будет
знакоположительным и для оценки ошибки вычисления числа е надо воспользоваться
формулой (21.1). Оценим величину остаточного члена ^f хп при х = 1 ■:
е = ее/п\ < е/п\ < З/n!, п! > ^,
т.е. также п = 8. Следовательно, с заданной точностью
е = 1 + 1 + 1/2 + 1/6 + 1/24 + 1/120 + 1/720 + 1/5040 - 2,7183.
21.2. Функция /(х) = sinx, x0 = 0. Как показано в лекции 17
/<*>(х) = sin(x + irk/2), /(fe)(0) = sin(7rA:/2). Так как |sin(x + irfc/2)| ^ 1
и, следовательно, все производные f(x) не превышают единицу, по
теореме (20.2) предыдущей лекции sinx разлагается в сходящийся к ней на
(-оо,оо) ряд Маклорена.
х3 (-1)"х2л+1 ^(-1)кх2М
(21.3) апх = *-¥ + -+ (2п + 1)! +---=^123ГГ1)Г'
21.3. Функция /(х) = cos х, х0 = 0. Продифференцировав обе части
(21.3), получим
(21.4) ™ = 1-й + -+ (^ + --- = S"15^"
В качестве примера рассмотрим применение разложений (21.3) и (21.4) к
нахождению предела.
Пример 21.3. Показать, что
7?
i*m cosmj—cosrez

240
21. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА
Решение: Из (21.4) имеем
cosx = l- ^ + 0(х4)
2>«2
и, следовательно,
—з—-—2 3—а
= Я!^+ 2^,^ + 0^)^^
21.4. Функция f(x) = (1 + x)m, x0 = 0. Здесь
/<*>(*) = т(т - 1) •... • (га - к + 1)(1 + x)m"fc,
/<*>(0) = m(m - 1) •... • (m - fc + 1).
Запишем формально ряд Маклорена для этой функции
(21.5) (1 + .)- = 1 + ± m(m-l)--..-(m-fc + l)(l + ,)-*xfc|
где m — любое действительное число. Определим радиус сходимости
этого ряда:
R _ Ит |m(m-l),.,(m-n+l) [п+Ц! I
Л п"^| n! m(m-l)....-(m-n+l)(m-fi)|
= lim |f^| = l.-
Следовательно, правая часть формулы (21.5) есть сходящийся при \х\ <
1 ряд и, как показывается, он сходится к функции (1 + х)т. Сходимость
при |х| = 1 необходимо рассматривать отдельно, что мы делать не будем.
Определение 21.1. Ряд (21.5) для (1 + х)т называется
биномиальным рядом.
Используем (21.5) для вычисления предела.
тт л. л ,т 1. у/1 + Х - у/\- X
Пример 21.4. Найти hm .
х-»0 х
Решение: Из (21.5) имеем при т — - :
у/Т+х = (1 + ж)« = 1 + - + 0(х2),
ч/ГГ^ = (1 - x)i = 1 - | + 0(х2).
.. >/\+Х-у/\-Х .. X + 0(x2) u
Следовательно, hm = hm = hm(l+0(x)J = 1.
2i. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА
241
Рассмотрим еще пример приложения биномиального ряда к
приближенному вычислению корней у/а. Прежде всего надо найти число 6,
близкое к а, из которого корень m-й степени извлекается элементарно, и такое,
чтобы их разность была бы, по крайней мере, меньше Ь.
Тогда ^5= VbTx'= V6t/iT|= V&(l + ^)™.
Затем (l -f f) ™ необходимо разложить в биномиальный ряд и взять
необходимое для нужной точности число членов.
Пример 21.5. Вычислить \/5 с точностью до 10~3.
Решение:
л/5 = у/аП = л/4(1 + 0.25) = 2(l + J) * =
-•O+H-tfGf*...).
Полученный ряд является знакочередующимся и для того, чтобы
вычислить у/Ъ с нужной точностью, необходимо учитывать лишь те члены,
которые по модулю больше 10""3.
Поэтому у/ъ = 2 + 0,25 - 0,0156 + 0,0020 = 2.236.
21.5. Функция f(x) = ln(l + х), х0 = 0. Для этой функции
fW(x) = (-У^*;1)'; /Ю(0) = (-1)^(* - 1)!.
(1 + х)к
Соответствующий ряд Маклорена примет вид
(21.6) in(i+x) = f;(-ir+i-.
Он сходится к функции 1п(1 + х) на множестве (-1 < х ^ 1)
Полученный ряд (21.6) можно также использовать для вычисления
пределов.
гт о, * 1- *{1+х) -ln(l-f-x)
Пример 21.6. hm — -—г—^ - =
r-vO X2
,. х + х2-х+^ + 0(х3) 3
hm г-^ = -.
х-+о х2 2
Займемся теперь вычислением логарифмов. По формуле (21.6)
вычислить логарифмы можно лишь для чисел от 0 до 2. Получим теперь
формулу, позволяющую вычислить логарифмы любых положительных чисел.
Заменим в формуле (21.6) х на —х:

242
21. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА
(21.7) .in(i-Х) «-££-•
Вычтем теперь из равенства (21.6) соотношение (21.7):
1+Т JSL Х2п+1
(21.8) ы-~ = 1п(1 + х)-1п(1-х)=25;5Г?1.
п=0
1 + х а-1
Положив = а, получим ж = -.
1 — х а + 1
Формулу (21.8) можно использовать для вычисления логарифмов
любых положительных чисел.
Ошибки при вычислении логарифмов с помощью конечного числа
членов ряда (21.8) можно оценить следующим образом. По а определим х,
затем берем несколько членов в формуле (21.8):
/ х3 x2n+1 \
(21.9) ,пв = 2(х + _ + ... + __)+г„.
Остаток ряда тп и есть ошибка. Учитывая, что
1111
< -, < и т. д., получим
2n + 5 2n + 3' 2n + 7 2п + 3
г2п+3 т2п+5 ч , г2п-}-3 д;2п+5
(21.10) гп = 2(- - + - *+•••) <2(^"
v ' \2n-f3 2п + 5 / \2п
+
2п + 3 ' 2п + 5 ' '"'-/ "~V2n + 3 2n + 3
ч ~2n+3 T2n+3 1
2п + 3 "/ 2n + 3v ""' 2/1 + 31-х2'
Так как |х| < 1 то 1 4- х2 + х4 -f ... есть бесконечно убывающая
геометрическая последовательность с q — х2, ее сумма равна j
Пример 21.7. Вычислить 1пЗ, с точностью 10~4.
3 — 1 1
Решение: В формуле (21.8) положим а — 3, а х = -—- = -. Тогда
От 1 ^
по (21.10) должно быть (2w + 3) ,3 .22п+з = з(2п + 3)-4" < "^ ^
неравенство выполняется при п = 5 следовательно, In 3 = 2 ( - + 3 4-
1 1 1 11 \ _ JL_ _J_ 1 1 1 =
5-25"f7-27"f9-29 + 3-211J "~ +3 • 4 + 5 • 1б + 7 • 64 + 9 • 256 11-1024
1.0986..
Хотя в данной сумме шестое слагаемое и меньше 10~4, его нельзя
отбрасывать, так как тогда ошибка будет больше 10~4. Напомним, что
20 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФОРМУЛА И РЯД ТЕЙЛОРА 243
только для знакочередующегося ряда ошибка не превышает первого из не
учитываемых членов, а в случае знакоположительных рядов ошибку
чаще всего оценивают сравнивая остаток ряда с геометрической убывающей
прогрессией, что мы и сдели в нашем примере.
20. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФОРМУЛА И РЯД
ТЕЙЛОРА
В лекциях 20 и 21 получены формулы, дающие представление
некоторых функций по формуле Тейлора и рядом Тейлора. На практическом
занятии проделаем подобные операции для некоторых других функций, а
также воспользуемся разложениями (21.2) - (21.9).
Пример 20.1. Разложить в ряд Маклорена (20.11) функцию /(х) =
3*.
Решение: Найдем значение функции f(x) — 3х и ее производных в
точке х=0:
/(0) = 3*|х=0 = 1,
/7(0)=3*.ln3|««o = ln3,
/7/(0) = 3*-ln23|x=0 = ln23,
/("-^(О) = 3* • In"-13|х=0 = ш"-13,
/<n>(0x) = 3'*1пп3.
Подставим полученые выражения в формулу (20.11):
ох , , о х2\п23 xn~l\nn-l3 3^1nn3 п
Г = 1 + X • 1П 3 + —— + • ■ • + — -гт— + j Хп.
2! (п - 1)! п\
Покажем, что
hm Rn-i(x) = lim
П-+0О Л-ЮО fl\
при любом фиксированном х=С равен нулю. Действительно,
3'clnn3^n oCl. (CMn3)n oC ,. ап
hm - Сп < 3е hm - —^- = 3е hm —,
п-*оо п\ п-+оо П\ n-юо П!
так как при любом конечном a lim ^ = 0. Следовательно, по теореме
n-юо п-
(20.2) функция f(x) — 3х представима своим рядом Тейлора(Маклорена)

244 20 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФОРМУЛА И РЯД ТЕЙЛОРА
при любых х:
i2ln23 xnlnn3 ^zn-lnn3
3* = l + x-ln3 + =-^f^ + --- + ~ 7 ~ + ... = Y±-^
п=0
Это представление можно было бы получить и просто заменой х на xln3
в формуле (21.2) и не проделывать все вышеприведенные выкладки.
ПРИМЕР 20.2. Представить рядом Маклорена функцию f(x) = cos2 x
Решение: Найдем значения функции /(х) = cos2 ж и ее производных
в точке х=0:
. /(0) = cos2x|x=0 = l,
/7(0) = -2cosxsinx|x=0 = ~sin2x|a.=o = 0,
/"(0) = -22cos2xU=o = -2sin(2x + §)!*=<> = -2,
/ш(0) = 22 sin2x|x=0 = -22 sin {2x + 2 • |)|,e0 = 0,
//v(0) = 23cos2xU=0 = -23sin(2x + 3 • |)U=0 = 23,
/<»-D(0) = -2n"2 sin (2x + §(n - 2))U=0,
/<»)(ftc) = -2n-1sin(2^x-hf(n- 1)).
При любом фиксированном х=С остаточный член в формуле Маклорена
для функции /(х) = cos2 х стремится к нулю при п —► оо. Действительно,
lim |#n_i(x)| = lim
2n*1sin(2^C + f(n~l))
п\
on—1
^ lim —г- = 0.
n-*oo n!
Таким образом, функция /(х) = cos2 x разлагается в ряд Маклорена,
сходящийся к ней при любом х:
cos2x = l-!x2 + £x4-fx6 + ...
Можно было бы не проделывать все эти вычисления, а воспользоваться
формулой cos2x = \(\ + cos2x) и разложением (21.4), заменив в нем х на
2х:
cos2x = 1-1й£ + 1*р-1й£1 + ..., тогдасо82х = |(1 + cos2x) =
20 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФОРМУЛА И РЯД ТЕЙЛОРА 245
В приведенных примерах, мы видим,что если удается воспользоваться
известными разложениями (21.1) - (21.6) предварительно преобразовав
функцию /(х),то результат может быть получен значительно быстрее.
Пример 20.3. Разложить в ряд Маклорена функцию /(х) = е~* .
Решение: Заменив в формуле (21.2) х на х2, получим
2 X4 X6
е х =1-а:2 + _-— + ..., (-со < х < оо).
Пример 20.4. Разложить в ряд Маклорена функцию /(х) = sin (x -f |)
Решение:
sin (x -f |) = sin x • cos (|) + cos x • sin (|) =
= ^(an* + coe*) = ^(l + «-£-*f + ^ + £-$-*f + ...).
Мы здесь воспользовались разложениями функций sinx hcosx в ряд
Маклорена. Так как они справедливы при любых х,то и полученное нами
разложение sin (х + |) в ряд Маклорена справедливо при любых х.
Пример 20.5. Разложить & ряд Маклорена функцию /(х) = Л ±.
Решение: Вынесем 4 из-под корня в знаменателе, затем заменим
в формуле для биномиального ряда (21.5) х на ~ и, положив т == — |,
получим
— 1 (л _ *1 л. ЬЗх4 _ 1-3-5-а* I A _
~" 2 \ 2-4 ^ 22.2I42 23-3!-43 Т" . . . у —
= J (i + £ ьнь^аьт,^.
Так как биномиальный ряд (21.5) сходится при |х| < 1, в нашем случае
~- < 1, то есть, -2 < х < 2.
Пример 20.6. Разложить в ряд Тейлора по степеням х — 1 функцию
/(х) = 1пх.

246 20 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФОРМУЛА И РЯД ТЕЙЛОРА
Решение: Подставив в формулу (21.6) х — 1 вместо х, получим:
lnz = ln(l + (х-1)) =
= (* -1) - fe^fi + fe^e _ c«ii + ..- = £ i=ac±i<- - D--
Так как ряд Маклорена для функции f(x) = 1п(1 + х) сходится при
-1 < х ^ 1, полученный ряд сходится при 0 < х < 2.
Пример 20.7. Разложить в ряд Маклорена функцию f(x) = е~х sin x.
Решение: Поскольку степенные ряды можно почленно
перемножать, ряд для e~xsinx можно получить почленным перемножением ряда
Маклорена для е"х на ряд для sin ж:
e-'sins = (!-§ + £-¥ + •••)(*-£ + £-£ + .-•) =
= X - X + 3S "" 40Х + ЗбО^ + * ' *
Полученный ряд сходится к данной функции на всей числовой оси,
поскольку ряды (21.2) для е~х и (21.3) для sin а: сходятся также на всей
числовой оси.
Самостоятельная работа
Пример 20.8. Разложить в ряд Маклорена функцию f(x) = 2х.
Пример 20.9. Разложить в ряд Маклорена функцию f(x) = sin2 ж.
Пример 20.10. Разложить в ряд Маклорена функцию f(x) = е2х.
Пример 20.11. Разложить в ряд Маклорена функцию
f(x) = cos (х - |).
Пример 20.12. Представить рядом Маклорена функцию
}(х) = у/9^1^.
Пример 20.13. Разложить в ряд Тейлора по степенямx-f 1 функцию
f(x) = \n(2 + x).
Пример 20.14. Разложить в ряд Маклорена функцию f(x) = т~щг •
21 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФОРМУЛА И РЯД ТЕЙЛОРА 247
21. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФОРМУЛА И РЯД
ТЕЙЛОРА
Рассмотрим применение формулы и рядов Тейлора к нахождению
пределов и приближенному вычислению значений функций.
Как было отмечено в лекции 20, при вычислении некоторых пределов
удобно использовать формулу Тейлора в иде (20.12). Рассмотрим
несколько примеров.
Пример 21.1. Найти linv
2е*-2-2ж-ж2
*->0
Х—81ПХ
Решение: Непосредственная подстановка х = 0 показывает, что
данный предел является пределом типа jj. Заменив ех и sin я их
представлениями по формуле Маклорена (21.2) и (21.3) с точностью до величин
0(xz), получим
Ит 2е«-2-2«-«» = Ит 2<1+«+£ + £+0(««))-2-2«-«» =
= Ит4±^ = Ит#£Ц> =2.
Здесь использовано, что
9<^1 = 0(х) и 9^1 = о(х2), а ИтО(гг) - limO(:r2) = 0.
Х3 X3 х-+0 *-*0 V '
Пример 21.2. Найти lim ъ{*+*)-*{*+*Г a
Х-40 Х
Решение: В этом примере также мы имеем неопределенность типа
jj. Подставляя вместо (1 + х)т и 1п(1 + х) их представления по формуле
Маклорена (21.5) и (21.6), получим:
lim lnQ+*)-*(l+*)m _ i:m x-£+0{x3)-*(l+mx+0(x2)) _
x-»0 x x->0 *
= lim -ih+m)*l+o{x>) = x __m + 0{x)) = _ 1
Рассмотрим теперь применение, полученных нами в лекции 20 формул
и рядов Тейлора (Маклорена) к приближенному вычислению функций и
оценке ошибки таких вычислений.
Пример 21.3. Вычислить приближенное значение у/е, взяв три
члена представления функции f(x) = ех по формуле Маклорена, и оценить
ошибку вычисления.

248
21 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФОРМУЛА И РЯД ТЕЙЛОРА
Решение: Подставив х = | в формулу (21.2), получим
■ ,/- i,lll 11 11
С учетом трех членов
о 18
Ошибка такого вычисления равна остатку ряда
162 ГГТ 324 ^ 1и '
При вычислении Rz(x) мы использовали то, что \ • | < 1; ^2 < ^ и
т.д., и формулу для суммы бесконечно убывающей прогрессии S = —^
при ai = 1 и g = 1.
Пример 21.4. Вычггслглшь приближенное значение -А=, взяв mpti
члена разложения функции f(x) = е* в ряд Маклорена.
Решение: Подставив ж = -| в формулу (21.2), получим
#е " 6 * " 3 + 2! ' З2 3! ' З3 + *' *
Полученный ряд является знакочередующимся и ошибка 6 при замене
его суммой первых трех членов не превышает по абсолютной
величине четвертого члена, т.е. S < ^ ~ 0,00617 < 10~2. Следовательно,
-^=0,722 •••«0,72
В этом примере оценка проводится значительно проще, чем в предыду-
щем,так как можно использовать признак Лейбница для
знакочередующегося ряда, а не проводить оценку остаточного члена в формуле Тейлора.
Пример 21.5. Вычислить sin 18° с точностью до 10~4.
Решение: Подставим 18° = ~ = 0,314159 вместо х в ряд (21.3):
1Пв •. JT 7Г I / Ж \3 I / 7Г \5 7Г I / 7Г \3 л лллл
18 =smio = Io-3!(io) + *Ы +-eio-e(io) й0'Ш
Этот результат получен с точностью до 10~4, так как первый из
неучтенных членов ~ (~) < 104.
Пример 21.6. Вычислите v^70 с точностью до 10~"4.
sin
21 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФОРМУЛА И РЯД ТЕЙЛОРА
249
Решение: Ближайшее к 70 целое число в кубе равно 64, тогда
^=^§4 + 6 = 4«1 + ^.
Используя выражение для биномиального ряда (21.5) при т = | и х = ^,
получим:
^70 = 4(1 + ^)3 =
А (л _i_ 1 А. __ 1-2-32 , 125-33 _ 1-2-5-834 , \ ^
* V 3 * 32 32(32)2 "^ 33(32)3 3«-(32)« Т - - - ) ~
~МХ^32 322 ^ 323/ *'Х1°*
Здесь также первый из неучтенных членов 4'232458 < 10"3.
Пример 21.7. Вычислить In 5 с точностью до 10~3.
Решение: Для вычисления In 5 воспользуемся разложением (21.8),
положив в нем ^ = 5, откуда х = | :
ln5 = 2(l+-Jgr + ^ + ...) =
_ 4 Л , 22 . 2* , , 22" , \
— 3 \/ "^ 3 З2 "*" 5 З4 ^ ^ (2п+1)32п ^ * * * ) '
Если мы не будем учитывать члены ряда, начиная с ^n+m2»,. то остаток
ряда . » • ,
4 ( 22" | 22<"+*> . 22<"+2> . \
3 \^(2п+1)32" "•" (гп+ЗР2*"*1) "*" (2п+5)32<Л+2) '" J
_ 4-22" Л , (2n+l)22 (2n+l)2< \ " '
~~ 3(2п+1)32» \/ ^ (2п+3)32 ^ (2п+5)34 ^ ' ' * J ^
<3^S-(i + (I)2 + (i)4+--) =
_ 4-22rt 22w+2
3(2»+l)3*»(l-J) ~" 5(2f»+l)32""1
должен быть меньше 10~3. При оценке остатка ряда учитывалось, что
IS+з < 1' 2^+5 < 1 и Т-Д- и,чго сумма членов бесконечно убывающей
геометрической прогрессии с ai = 1 и g = | равна |.

250
22. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
Итак, задача будет решена, если взять sfcn^m»»-1 < Ю~3- Это
соотношение выполняется при п = 7. Следовательно, с нужной нам точностью
Самостоятельная работа
Пример 21.8. Найти lim^^.
Пример 21.9. Найти lim ШВ=Ш*.
х-*0 х
Пример 21.10. Вычислить приближенно 4= с точностью до 10""4.
Пример 21.11. Вычислить cosl° с точностью до 10~3.
Пример 21.12. Вычислить v^250 с точностью до 10~3.
Пример 21.13. вычислить In 6 с точностью Л> 10"4.
22. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
Необходимое и достаточное условие монотонности функций.
Локальный и глобальный экстремумы функций.
22.1. Необходимое и достаточное условия возрастания и
убывания функции. Напомним, что функция у = /(х), определенная на
отрезке (или интервале) называется возрастающей (или убывающей) на
этом отрезке (интервале), если из неравенства х2 > хи где х\ и х2 —
любые две точки, принадлежащие сегменту (или интервалу), следует
неравенство f{x2) > f(xi) (или f(x2) < f{xi)).
Обозначив Х2 - х\ = Ах и /(х2) - f(xi) = Aj/, получаем, что при
х2 — Х\ = Дх > 0 для возрастающей функции f(x2) - /(ях) = At/ > 0 и
Ду At/
— > 0, а для убывающей функции f(x2) — f{x\) = Ay < 0 и — < 0.
L*X 1тЛХ
Теорема 22.1. Необходимое условие возрастания (убывания)
функции: Если дифференцируемая в интервале (а; Ь) функция у = f(x)
возрастает, то ее производная не может быть отрицательной
(положительной) ни в одной точке данного интервала, то есть f'{x) ^ 0 (f*{x) ^ 0)
для а < х <Ь.
22. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
251
Доказательство. Проведем его для возрастающей в интервале (а; 6)
функции у = /(х). Пусть точки х и х -f Ах принадлежат (а; 6), Ах > 0.
Тогда, как было указано выше,
Дг/ /(х + Ах).- /(х)
> 0. Откуда
Ах Ах
lim ^ ^ 0, так как предел положительной функции не может быть
отрицательным, и, следовательно, так как у — f(x) дифференцируема,
/'(х) = lim Xй ^ 0. Аналогично проводится доказательство теоремы для
Дх-^О
убывающей функции.
Дадим геометрическую иллюстрацию этой теоремы. График
возрастающей функции при перемещении вправо по оси абсцисс поднимается
вверх. В таком случае, касательные к графику образуют острые углы а с
положительным направлением оси х или, быть может, в некоторых
точках (например, в точке xi рис. 103) параллельны ей. Так как тангенсы
острых углов положительны, а в точках, подобных хь равны нулю и по
геометрическому смыслу производной tg a = /'(х), то для возрастающей
функции /'(х) ^ 0.
Рис. 103. Угловой коэффициент касательной возрастающей функции
Аналогично, если функция убывает, то касательные к графику
функции образуют тупые углы а с осью х или в некоторых точках ей
параллельны, например, в точке х2 на рисунке 104. Так как тангенсы тупых
углов отрицательны, а в точках, подобных х2 равны 0, то для убывающей
функции f'(x) ^ 0.
ТЕОРЕМА 22.2. Достаточное условие возрастания (убывания)
функции: Если непрерывная на [а; Ь] функция у = f(x) имеет в каждой
внутренней точке этого отрезка положительную (отрицательную)
производную, то эта функция возрастает (убывает) на отрезке [а;Ь].

252
22. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
Рис. 104. Угловой коэффициент касательной убывающей функции
Доказательство. Проведем доказательство для /'(я) > 0. Пусть х\ и
Х2 две произвольные точки из [а; 6], причем хг > ж. Применим формулу
Лагранжа (18.4) к отрезку [ж^жг]:
/(ж2) - f{xx) = (ж2 - *i)/'(0i хх < £ < ж2.
Так как во всех точках [а; 6] производная /'(ж) > 0, то и /'(£) > 0.
Кроме того, и ж2 - Х\ > 0. Следовательно, и (ж2 - Ж1 )/'(£) > 0 и
/(ж2) - f{xi) > 0. Откуда /(ж2) > /(жх), то есть функция /(ж) возрастает
на [а; 6].
Аналогично доказывается теорема и для /'(ж) < 0 на [а; 6].
Напомним, что функция только возрастающая или только убывающая
в каком-либо интервале называется монотонно возрастающей или
монотонно убывающей в этом интервале.
22.2. Локальный и глобальный экстремумы функций.
Опрбдблбниб 22.1. Экстремумом функции у = /(ж) называется ее
наибольшее или наименьшее значения на некотором множестве
значений аргумента ж. Наибольшее значение принято также называть мак-
симумомг а наименьшее— минимумом.
Экстремумы (максимумы и минимумы) бывают локальными и
глобальными. Локальные максимумы достигаются в точках ж*, к = 1;3
(рис. 105), для которых существует такая окрестность (она может быть
сколь угодно малой), что для всех точек из этой окрестности /(ж) ^ /(ж*).
Локальные минимумы достигаются в точках хк (к = 2; 4 (рис. 105),
для которых существует такая окрестность (она может быть сколь угодно
малой), что для всех точек из этой окрестности f(x) > /(ж*).
22. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
253
a Xj х2 хз х4 Ь
Рис. 105. Экстремумы функции
Глобальные экстремумы на [а; 6] могут достигаться в точках
локальных экстремумов или на границах отрезка.
В дальнейшем мы часто локальные экстремумы (максимумы или
минимумы) будем называть просто экстремумами (максимумами или
минимумами), а глобальные экстремумы — наибольшим и наименьшим
значением функции на отрезке [а; Ь]. На рисунке 105 экстремумы достигаются
в точках Ж1,жг,ж3 и х^ наименьшее значение в точке о, наибольшее — в
точке ж3.
Перейдем к рассмотрению необходимых и достаточных условий
существования локальных экстремумов.
Теорема 22.3. Необходимый признак существования экстремума
функции: Если дифференцируемая в точке ж = х0 функция у = f(x)
имеет в этой точке максимум или минимум, то ее производная в этой
точке обращается в нуль, то есть /'(ж) = 0.
Доказательство. По определению (22.1) максимумом и минимумом
называются соответственно наибольшее и наименьшее значения функции и,
поскольку, по условию теоремы производная /'(ж) в точке жо
существует, то по теореме Ферма 18.1 она равна 0, /'(ж0) = 0. Теорема доказана.
Однако производная в точках экстремума может и не существовать.
Например, в точке х4 на (рис. 105). График функции в этой точке имеет
излом и производные слева и справа не равны между собой (разрыв на
конечную величину).

254
22. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
У функции /(х) = 1 - v^x2" производная /'(х) = — jfe т°чке х = 0 не
существует (бесконечный разрыв), несмотря на это функция имеет в этой
точке максимум (рис. 106).
1
~"~^1
^■"^-^ х
о г—'
Рис. 106. График функции у = 1 — Ух*
Определение 22.2. Точки, в которых производная равна нулю,
называются стационарными точками данной функции. Стационарные
точки и точки, в которых производная не существует, называются
критическими.
Поэтому можно обобщить необходимый признак существования
экстремума, сформулированный в теореме 22.3:
Если непрерывная функция у = /(х) имеет в точке хо экстремум,
то точка х<> является критической точкой функции.
Однако не во всякой критической точке существует экстремум. То,
что точка х0 критическая, является лишь необходимым, а не достаточным
условием. Например, точка х = 0 является критической для у = х3, но
экстремума в точке х = 0 у этой функции очевидно нет.
Для нахождения экстремума прежде всего надо найти критические
точки, а затем проверить, выполняется ли в них так называемые
достаточные условия, к рассмотрению которых мы и переходим.
Теорема 22.4. Достаточный признак существования экстремума
функции. Если точка х = Хо является критической точкой функции
у ч= f{x), и в некоторой 6-окрестности этой точки производная /'(х)
слева от этой точки, т.е. при х € (хо — S;x^) и справа, т.е. при х G
Яо;$о + <$) существует, но имеет разные знаки, то f(x) в точке хо
имеет экстремум. Причем, если /'(х) > 0 при х € (хо — S;xq) и /'(х) < 0 при
х € (х0;х0-<5) — максимум, если f'{x) < 0 прих € (х0-5;х0) и /'(х) > 0
при х € (х0; Xq — S) — минимум.
22. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
255
Доказательство. Пусть Хо — критическая точка и для определенности
/'(х) > 0 при х е (х0-£;х0), /'(х) < 0 при х G (х0;х0 + £). Следовательно,
функция у = /(х) возрастает в интервале (хо - 6; xq) и убывает в
интервале (хо; Хо + £). Тогда значение функции в точке хо больше значения этой
функции в любой точке интервала (х0 - 6; х0 + 5), а это и означает, что в
точке хо функция у = /(х) имеет локальный максимум. Теорема доказана.
Аналогично доказывается теорема и для случая минимума.
График функции в окрестности точек минимума или максимума в
случае стационарной точки (точки Xi и х2 на рис. 107) имеет вид бугорка
или ямки с плавно меняющимся контуром (см. рис. 107), или контура с
изломом для точки, в которой производная не существует (на рис. 107
производные слева и справа в точках хз и х\ не равны, а в точках х$ и Хб
не существуют).
хг 8 xj xj+ 8 xj 5 х3 xjt- 8 Х5 8 х5 х + 8
х2 8 х2 х£ 8 Х4 8 х4 xf- 8 х^ 8 х6 х^ 8
Рис. 107. Виды экстремумов функции
Пример 22.1. Исследовать на экстремум функцию у = /(х) = х3 —
4х + 2 и определить ее интервалы монотонности.
Решение: Эта функция определена и дифференцируема на всей
числовой оси.
в Находим производную f'(x) = Зх2 — 4.
о Приравниваем производную к нулю и находим стационарные точки.
Зх2 - 4 = 0; X! = -^, х2 = ^.
Эти числа разбивают всю область определения данной функции
на три интервала -оо < х < - 4=; -4- < х < 4-; 4j < х < оо.
в В каждом из этих интервалов производная сохраняет свой знак, так
как они не содержат более критических точек, а производная
может изменять знак только при переходе через критическую точку.
Поэтому для исследования знака в каждом интервале можно взять
любую точку, а не обязательно вблизи критической точки.

256
22. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
В интервале (-4; со J f'(x) = Zx2 - 4 > 0, так как при достаточно
больших х первый член Zx2 больше 4. • '
Аналогично и для интервала (-оо; --7| Ь /'(х)> О, так как х входит
в/'(я) только как х2 . .Л
В интервале --4 < х < -4» удобнее всего положить х = 0, тогда
/'(0) = -4 < 0, поэтому /'(ж) во всем интервале ( —-7§; ^) отрицательна.
На основании сказанного функция в точке х = — \ имеет максимум
2/ГОО1 = у(-^) = (-^)3-4(-^)+2«5.0792,
а в точке х = -4» — минимум.
**=»(*) = Ш3 - 4Ш+2 * -10792-
Полученные результаты целесообразно занести в таблицу.
X
У'
У
(-со;-2-Л/5)
+
/
-2/V5
0
max
5.08
(-2/n/3;2/v^)
-
\
2/%/3 I (2/V3; +оо)
0
mm
-1.08
+
f
График функции изображен на рис. 108. Точки £ь &> £з пересечения с осью
ОХ определены в лекции 25 и на практическом занятии 25.
Рис. 108. График функции у = я3 - Ах + 2
Рассмотрим еще один пример, в котором наряду со стационарной
точкой будет и точка, в которой производная не существует.
Пример 22.2. Исследовать на экстремум и определить интервалы
монотонности функции у = f(x) = у/х2 — ж3 = у/х2(1 - х).
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
Решение: Эта функция определена при всех х € (-оо; оо), но как
мы сейчас покажем не при всех х дифференцируема.
© Находим производную f'(x) = л ь2*~**2 t2 = пт=
гух{\~х)2
Функция имеет одну стационарную точку х = |, в которой f'(x) = О,
и две точки 1 = 0иа: = 1, в которых производная обращается в
бесконечность. Эти точки разбивают всю область определения функции
на четыре интервала -оо < х < О, 0 < х < §,§ < х < 1, 1 < х < оо,
в каждом из которых функция является монотонной.
© Исследуем знак производной в каждом из этих интервалов. В ин-
' - Л " Л^т? < 0, в чем
тервале —оо < х < О производная f'(x) =
зу х{1-х)~
можно убедиться, непосредственно подставив в fix) любое число
х < 0. Функция убывает в этом интервале, производная f'(x) > 0,
так как при любом х из этого интервала числитель отрицателен,
а знаменатель положителен для всех х > 0. Функция возрастает.
Аналогично рассуждая, получаем, что в интервалах | < х < 1 и
1 < х < оо производная f'(x) < 0. Функция убывает.
Следовательно, в точке х = 0 функция име$т- минимум г/„иП = 0, в точке х = | -
максимум 2/тах = (|) = у (|)2 (1 ~ |) = ЗВ. « 0; 53. В точке я = 1
экстремума нет, у(0) = 0.
о Результаты заносим в таблицу
-оо <х < О
<0
\
ТОО
0
"о<*<1
>0
г
0.53
I <г < 1
<0
\
О
1 < х < оо
<0
\
^ . . « _JL__ I — 1 I I I
© Строим график функции. Он изображен на рисунке 109. Роль
представленной на рисунке прямой у = -х + | будет объяснена в лекции
24.
22. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ
ФУНКЦИЙ
Определение интервалов монотонности и экстремумов функций.
Напомним, что для определения интервалов монотонности (интервалы
возрастания и убывания) и экстремумов функции прежде всего надо найти
критические точки, т.е. точки, в которых производная функции равна
нулю или не существует, а затем по знаку производной в интервалах между
критическими точками определить интервалы монотонности и выделить

258 22 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
у=;-х+1/3
Рис. 109. График функции у = \/х2 - х3
те критические точки, которые на основании достаточного признака
существования экстремума являются точками экстремума функции.
В следующих примерах необходимо определить критические точки,
интервалы монотонности и экстремумы функций у = f(x).
Пример 22.1.
у = х2 - х3
: х2 • (1 - х).
Решение: Функция определена на всей числовой оси.
о Находим производную у' = f'(x) = 2х - Зх2 = х • (2 - Зх), которая
существует при всех х € (—оо,оо);
9 Приравниваем производную к нулю и находим корни производной:
/'(х) = х(2 - Зх) = 0
xi = 0, х2 = -.
Таким образом, функция у = х2 - х3 имеет две стационарные
критические точки, которые разбивают область определения на три
интервала монотонности: (-оо < х < 0), (0; |), (§; +оо).
9 Исследуем знаки производной у' в каждом из этих интервалов, взяв
для определения знака любую точку соответствующего интервала.
В интервале -оо < х < 0 производная у' < 0, т.к., например,
y'(-l) = -1 • (2+ 3) = -5 < 0, функция в этом интервале убывает.
В интервале 0 < х < § производная у' > 0, т.к., например,
у'Ф = | • (2 - 3 • ~) = I > О, функция в этом интервале возрастает.
В интервале | < х < оо производная у' < 0, т.к., например,
у'(1) = 1 • (2 - 3) = -1 < 0, функция в этом интервале убывает.
22 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
259
с Так как при переходе критической точки х = 0 производная меняет
знак с минуса на плюс, в этой точке достигается минимум г/т1П =
»(0) = 0.
При переходе критической точки х = | производная меняет знак
с плюса на минус, эта точка есть точка максимума утах = у (|) =
1 j.
3 27*
Полученные результаты занесем в таблицу.
X
\у'
У
-оо;0
<0
\
0
0
0
min
"5TF
>о
/"
2
3
0
4
27
max
i*oo !
<0
^ 1
Пример 22.2. у = х(1 + tfx).
Решение: Функция определена при всех х G [0; оо).
• Находим производную у' = /'(х) = 1 + \\fx~.
о Производная /'(х) = 1 + |^х существует при всех х ^ 0 и нигде в
нуль не обращается. Критических точек функция не имеет.
• Очевидно, что /(х ^ 0) = (1 + |^х)|х^о > 0, функция у = х(1 + tfx)
монотонно возрастает при х ^ 0.
в Экстремумов нет.
Пример 22.3. у = 1 +-#х.
Решение: Функция определена при х ^ 0.
о Находим производную у' = /'(х) = ~й==.
4 vz3
• Производная /'(х) в точке х = 0 не существует. Следовательно,
функция у = 1 + ^х имеет одну критическую точку х = 0, которая
является граничной точкой ее области существования. Производная
определена в интервале 0 < х < оо.
© Очевидно, что /'(х > 0) = ry=f U>o > 0, поэтому функция
монотонно возрастает в интервале 0 < х < оо.
9 Экстремумов нет.
Пример 22.4. у = 2х - Зу'х2.
Решение: Функция определена на всей числовой оси.
© Находим производную у' = f'(x) = 2
в Приравниваем производную нулю:
2 _ 2^-2
/'(*) = 0,
= 0, v/x=l, х = 1.

260
22 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИИ
Следовательно, х = 1 является стационарной критической точкой.
Кроме того, в точке х = О производная не существует, значит и
точка х = 0 является критической точкой.Эти две критические точки
разбивают область существования на три интервала:
~оо < х < 0; 0< х < 1; 1 < х < оо.
о Исследуем знаки производной в каждом из этих интервалов:
В интервале -оо < х < О производная у1 = 2ty^2 > 0, т.к.,
например, у'(-\) = 2("Д"1? = 4 > 0. Функция в этом интервале
возрастает.
В интервале 0 < х < 1 производная ?/' = ^ < 0, т.к.
числитель в любой точке этого интервала < 0, а знаменатель > 0.
Функция в этом интервале убывает.
В интервале 1 < х < оо производная у1 = 2у^2 > 0, т.к. в любой
точке интервала и числитель и знаменатель > 0. Функция в этом
интервале возрастает.
о Так как при переходе критической точки х = 0 производная меняет
знак с плюса на минус, в ней достигается максимум утах = t/(0) = 0.
При переходе критической точки х = 1 производная меняет знак
с минуса на плюс, следовательно, точка х = 1 есть точка минимума
l/bu. = y(l) = 2.1-3tfT=-l
Полученные данные занесем в таблицу.
X
Т
\~У~
-оо;0
>0
•у
0
±00
0
max
ГоГГ
<0
\
1
0
-1
min
1;оо I
>о1
/
Пример 22.5. у = х3еж.
Решение: Функция определена при всех х € (-оо; оо).
• Находим производную у' = /'(*) = Зх2ех + хгех = xV{3 + х),
которая существует при всех х € (-оо; оо).
• Приравниваем производную к нулю и находим корни производной:
/'(*)= О, xV(3 + x)=0, е*^0, х=0, х=-3.
Таким образом функция у = х3ея имеет две стационарные
критические точки i = 0 и а; = -3, которые разбивают область
существования на три интервала :
~оо < х < -3; -3 < х < 0; 0 < х < оо.
Я8 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
261
• Исследуем знаки производной в каждом из этих интервалов:
В интервале -оо < х < -3 производная у' = х2ех(3 + х) < 0, т.к.
х2 > 0; ех > 0; 3 + х < 0, при х < —3. Функция убывает в этом
интервале.
В интервале -3 < х < О производная у' = х2е*(3 + х) > 0, т.к.
х2 > 0; ех > 0; 3 + х > 0, при — 3 < х < 0. Функция возрастает в
этом интервале.
В интервале 0 < х < оо производная у* = х2е*(3 4-х) > 0, т.к.
х2 > 0; ех > 0; 3 + х > 0, при х > 0. Функция возрастает в этом
интервале,
о Так как при переходе критической точки х = -3 производная
меняет знак с минуса на плюс, в этой точке функция имеет минимум
tfcb = y(-3)=-(-3)»e-*=-g.
При переходе второй критической точки х = О производная не
меняет знак. В этой точке экстремума нет.
Занесем все полученные данные в таблицу.
X
'У'
У
-оо;-3
<0
\
-3
0
27
min
-3;0
>0
/*
0
0
экстремума
нет
0;оо
>0
/*
Самостоятельная работа
Пример 22.6. у = х3 - Зх2.
Пример 22.7. у = х(1 + у/х)
Пример 22.8. у = 1 + у/х.
Пример 22.9. у - \fx* - х.
Пример 22.10. у = е» - х.

262
23. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
23. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИИ
Достаточный признак существования экстремума функции по
высшим производным. Наибольшее и наименьшее значение функции на
отрезке (глобальный экстремум). Выпуклость и вогнутость кривой.
Точки перегиба.
23.1. Достаточный признак существования экстремума
функции по высшим производным. В теореме 22.4 предыдущей лекции
достаточный признак существования экстремума в критической точке
основывался на определении знака производной слева и справа от этой точки.
Рассмотрим теперь еще одно достаточное условие, в котором
участвует производная только в самой критической точке. Критическая точка
может быть только стационарной.
ТЕОРЕМА 23.1. Достаточный признак существования экстремума
по высшим производным: Пусть в стационарной критической точке Xq
функции f(x) наряду с первой могут обращаться в ноль и последующие
производные. Тогда, если первая не обращающаяся в ноль, производная
является четной (п = 2к, к = 1.2-••) и непрерывной, то в точке
х = хо функция f(x) имеет экстремум. Причем если эта производная
/^(^о) > 0, в точке х = х0 функция f(x) имеет минимум, если же
/*2**(яо) < 0 - максимум. Если же первая не обращающаяся в ноль,
производная является нечетной (n = 2fc + l,fc = 1,2, • • •) и непрерывной,
причем /<2*+1)Ы > 0, то функция /(*) в окрестности точки хо
является возрастающей, если же /*2*+I*(so) < О — убывающей.
Доказательство. Пусть для определенности /*2**(хо) > 0. Покажем, что в точке
хо функция /(х) имеет минимум. Согласно формуле Тейлора (20.9) при п = 2к ъ
окрестности точки хо при /'(хо) — • • • = /*2*-1*(жо) = 0 имеем :
(23.1) /(*)=/Ы + ^^(*-*о)2\
причем (х - хо)2* > 0 при любых х. Поскольку /^2кЦхо) > 0, в силу непрерывности
всегда найдется такая окрестность точки хо, что для точки £, принадлежащей этой
окрестности /(2кЦ0 > 0 и, следовательно, в этой окрестности (2к)Р (х ~ х°) > ^
Таким образом доказано, что всегда существует некоторая окрестность точки хо, в
которой на основании (23.1) f(x) > /(хо)- Следовательно, функция /(х) в точке хо
имеет минимум. Аналогично доказывается, что если /^2кЦхо) < 0, то функция /(х) в
точке хо имеет максимум.
Пусть теперь f^2k+l^(xo) > 0, Покажем, что в окрестности точки хо функция /(х)
является возрастающей.
23. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
263
Согласно формуле Тейлора (20.9) при п = 2к + 1 в окрестности точки хо при
/'(хо) = -.. = /<2*>(хо) = 0имеем:
(23.2) /(х) = /(хо) + f^^j (х - хо)2**1. ;;
В силу непрерывности всегда найдется такая окрестность точки хо, в которой для
любой ее точки f будет выполняться условие /*2fc+1*(0 > 0, а (х - xo)2fc+1 будет иметь
разные знаки при х > хо и х < хо- Следовательно, при х > xq :
72гщг( о) >0,
а при х < хо :
(2* + 1)! {Х Хо) <0'
Таким образом доказано, что всегда существует некоторая окрестность точки хо, в
которой на основании (23.2) /(х) < /(х0) при х < х0 и /(х) > /(х0) при х > х0. И,
следовательно, в этой окрестности функция /(х) возрастает.
Аналогично доказывается, что если /*2fc+1,(xo) < 0, то существует некоторая
окрестность точки хо, в которой функция /(х) убывает.
Пример 23.1. Существует ли экстремум у функции f(x) == хА ?
Решение: Вычисляем первую производную f'(x) = 4х3. Она
обращается в ноль при х = 0. Следовательно, х = 0 является стационарной
критической точкой.
При х — 0 обращаются в ноль также /"(0) = 12я2|*=о = 0,/"'(0) =
24ж|ж=г0 = 0, но четвертая производная /*4)(0) = 24 > 0. Следовательно,
функция f(x) = хА в точке х = 0 имеет экстремум, а именно минимум.
Пример 23.2. Существует ли экстремум у функции f(x) ==■ хь ?
Решение: По аналогии с предыдущим примером имеем /'(0) =
/"(0) = /"'(0) = /(4)(0) = 0, а /<5>(0) = 120 > 0. Следовательно,
экстремума нет, а функция f(x) = х5 является монотонно возрастающей при всех
х.
Очевидно, что любая парабола четной степени у = х2к имеет минимум
в точке х = 0, а любая парабола нечетной степени у = х2к+1 является на
интервале (—оо; сю) возрастающей функцией.
Наиболее часто встречается случай, когда первая не обращающаяся в
ноль в стационарной точке производная является второй. Тогда теорема
(23.1) для этого частного случая может быть сформулирована так:
Теорема 23.2. Пусть х$ стационарная точка функции /(х), и в
точке ж0 существует непрерывная вторая производная f"(x) ф 0.
Тогда если fn(xo) < 0, 77К? Xq есть точка максимума функции f(x), если
/"(хо) > 0, то Xq есть точка минимума.

264
23. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
Применим этот критерий к примерам, рассмотренным ранее.
Пример 23.3. Найти экстремум функции у = f(x) = я3 - 4х + 2,
используя теорему (23.2).
Решение: Обе критические точки этой функции хг = -4и
х* = 7з являются стационарными точками. Вторая производная f"(x) =
6х в первой из них /" (-^) = ~щ < 0. Следовательно, точка Х\ = -4-
является точкой максимума, во второй точке /" (75) = ~§ > 0 и, таким
образом, точка яг = -те является точкой минимума.
Пример 23.4. #а осиоважщ теоремы (23.2) исследовать
критические точки функции f(x) = \/х2 - хг.
Решение: Из трех критических точек этой функции лишь одна
х = | является стационарной, и лишь к ней применима теорема (23.2) .
f"™ = ~9V*4-*)6 = ^9^(|)4(1)Б <'° И> СЛеД°ВаТеЛЬНО' Т0ЧКа Х = I
для функции f(x) = Ух2 - х3 является точкой максимума.
23.2. Наибольшее и наименьшее значение функции на
отрезке, (Глобальный экстремум). Как уже говорилось в пункте (22.2)
предыдущей лекции, глобальный экстремум на отрезке [а; Ь] может
достигаться или в критических точках интервала (а; 6), или в граничных х — а
И1 = б.Таким образом, чтобы найти наибольшее или наименьшее
значение функции на отрезке [а; Ь] необходимо :
© найти все критические точки я* в интервале (а; Ь) и значения
функции /(я) в этих точках /(х*),
е найти значения функции f(x) на концах отрезка /(а) и /(b),
* выбрать наибольшее значение М и наименьшее значение m из всех
/(*») и f(a) и /(b).
Очевидно, что для этой задачи нет необходимости даже знать,
являются ли точки Xk точками экстремума функции.
Пример 23.5. Найти Мит функции f(x) = х3 — 4x4- 2 на отрезках
[0;i],[-i;i],(-2;2].
Решение: Из примера 22.1 предыдущей лекции определяем, что
в интервале (0; 1) критических точек у данной функции нет, определяем
значения функции f(x) на границах отрезка /(0) = 2,/(1) = —1.
Следовательно, М = /(0) = 2,т = /(1) = -1 достигается на границах отрезка
[0;1].
23. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
265
В интервале (-1; 1) критических точек также нет, и так как /(-1) =
5,/(1) = -1, тоМ = /(-1) = 5,ш = /(1) = -1. Рассмотрим теперь
отрезок [-2; 2]. В интервале (—2; 2) имеются две критические точки хг =
-^* и х2 ~ ^j, значение функции в которых (-71) « 5.0792 и (АА %
-1.0792. Сравнивая эти значения со значениями функции на границах
отрезка /(-2) = 2 и /(2) = 2 имеем, что наибольшее значение М =
/ ("-*7з) и наименьшее значение т = / (^) достигается во внутренних
точках отрезка [-2; 2].
23.3. Выпуклость и вогнутость кривой. Точки перегиба.
Введем понятие выпуклости и вогнутости кривой.
Определение 23.1. Кривая, являющаяся графиком
дифференцируемой функции у = f(x), называется выпуклой в интервале (а; Ь), если она
расположена ниже касательной, проведенной к ней в любой точке xq
этого интервала (рис. ПО). .
=f(x)
Рис. 110. График выпуклой функции
Определение 23 2. Кривая, являющаяся графиком
дифференцируемой функции у = /{Х), называется вогнутой в интервале (а,Ь)> еслиона
расположена выше касательной, проведенной к ней в любой точке хп
этогоинтервала(рие.Щ). Зд(! 1о
Определение 23.3. Тачка х0 называется точкой перегиба кривой
если существует такая ее окрестность (х0 -5;х0 + S), в которой с
одной стороны от точки х0 кривая выпуклая, а с другой вогнутая

266
23. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
Рис. 111. График вогнутой функции
Так, изображенная на рис. 112 кривая у = f(x) вогнутая в интервале
(a; so) и выпуклая в интервале (ж0; 6), а точка х0 является точкой перегиба
кривой.
a Xq Xj x2 b
Рис. 112. Точка перегиба функции
Теорема 23.3. Пусть функция у = f(x) имеет вторую производную
f"(x) во всех точках интервала (а; 6). Если во всех точках этого
интервала f"{x) < 0, то график функции в этом интервале выпуклый,
если f'(x) > 0 — вогнутый.
Доказательство. Возьмем на графике функции произвольную точку Mq
с абсциссой xq € (а; Ь) и проведем через точку М0 касательную Т к кривой
у = f{x) (см. рис. ПО и 111). Уравнение касательной к кривой у = /(ж) в
точке М<>:
(23.3) 2/т = /Ы + /Ч*о)(* - *о).
3& ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
267
Представим теперь функцию у = f(x) в окрестности точки х0 по формуле
Тейлора (20.9)) при п = 2 :
(23.4) у = /(х) = /Ы + /'(*«)(* - хо) + ^/"(0(* - *о)2.
Из сравнения формул (23.3) и (23.4) видно, что
(23.5) У = Ут+1Г(0(х-Хо)2.
Из формулы (23.5) следует доказательство теоремы.
Действительно, если в точке х € (а; 6) вторая производная f"(x) < 0, то
поскольку £ заключено между х и яо, то по условию теоремы и /"(f) < 0,
а, следовательно, из (23.5) следует, что у < г/т-, Это означает что, график
функции у == f(x) в интервале (а; 6) расположен ниже касательной Т и,
следовательно, является выпуклым в этом интервале (см. рис. ПО).
Аналогично доказывается, что, если f"(x) > 0 в интервале (а; 6),
кривая у == /(я) располагается выше касательной Г, проведенной в любой
точке Mq с абсциссой дго € (а; 6), и является вогнутой (см. рис. 111).
Пример 23.6. Определить интервалы выпуклости и вогнутости
графика функции у — x2k.f
Решен и е: Вторая производная у" = 2А:(2А: - l)xl2k~2) > 0 при
х € (—оо;оо). Следовательно, параболы четной степени вогнуты при
всех х € (-оо;оо).
ПРИМЕР 23.7. Определить интервалы выпуклости и вогнутости
графика функции у = дЛ2*""1)-.
Решение: Вторая производная у" = 2(к - 1)(2к ~~ 2)х^2к~3) < 0
при х<0иу">0 при х > 0. Следовательно, парабола нечетной степени
выпукла при г<0и вогнута при х > 0.
Пример 23.8. Определить интервалы выпуклости и вогнутости
графика функции у = х3 — Ах -f 2.
Решение: Вторая производная у" = 6х < 0 при я < 0 и г/" = 6х > 0
при а: > 0. Следовательно, график этой функции является выпуклым при
я < 0 и вогнутым при х > 0 (см. рис. 108).
Пример 23.9. Определить интервалы выпуклости и вогнутости
графика функции у = Ух2 — я:3.
Решение: Вторая производная f"(x) = — , 2 меняет знак
9 у/х*{1—х)ь
при переходе через точку х = 1, именно f"(x) < 0 при х < 1 и /"(а:) > 0
при х > 1. Следовательно, график этой функции является выпуклым при
х<1и вогнутым при х > 1 (см. рис. 109).

268
23. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
Теорема 23.4. Необходимое условие существования точки перегиба
графика дифференцируемой функции: Если xq есть точка перегиба
кривой у = /(х) и /"(х0) существует, то /"(хо) = 0.
Доказательство этой теоремы очевидно следует из теоремы 23.3.
Естественно, что точкой перегиба может также являться точка, в
которой вторая производная не существует.
Точки, в которых /"(х) = 0 или не существует, являются
критическими точками по второй производной. И если точки перегиба существуют,
их надо искать среди этих точек.
Сформулируем теперь достаточные условия существования точки
перегиба.
Теорема 23.5. Если в точке ха вторая производная функции у =
/(х) равна нулю или не существует и существует такая окрестность
этой точки (хо — б\хо ■+- 6), в которой с одной стороны от точки хо
вторая производная /"(х) > 0, о с другой /"(х) < 0, то это есть точка
перегиба.
Доказательство. Пусть для х € (х0 - 6; х0) вторая производная /"(х) >
0, а для х € (х0;х0 4- 6) вторая производная / (х) < 0. Это означает,
что слева от хо кривая у = /(х) вогнутая, а справа выпуклая. А это есть
определение точки перегиба кривой.
ТЕОРЕМА 23.6. Достаточное условие существования точки
перегиба дифференцируемых функций: Пусть в точке xq вторая производная
j"(x) = 0, а также последующие производные могут обращаться в ноль,
и пусть первая не обращающаяся в ноль производная нечетная и
непрерывная, тогда точка хо есть точка перегиба.
Теорема доказывается аналогично теореме (23.1).
Рассмотрим примеры (23.6) - (23.9). Очевидно из примера (23.6)
следует, что парабола четной степени у = х2к не имеет точек перегиба, из
примера (23.7) - парабола нечетной степени у = х(2*+1) имеет
единственную точку перегиба х = 0. Эта же точка х = 0 является точкой перегиба
кривой у = х3 - 4х + 2 из примера (23.8).
Как видно из примера (23.9), кривая у = \/х2 - х3 также имеет
единственную точку перегиба, в которой вторая производная не существует, это
точка х = 1, у кривой еще существует одна точка, в которой /"(х) не
существует, это х = 0. Однако она не является точкой перегиба кривой,
т.к. /"(х) слева и справа от нее имеют один знак.
Найденные интервалы выпуклости, вогнутости и точки перегиба
функций у = х3 — 4х + 2 и у = \/х2 - х3 записаны в таблицы.
23 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
269
Таблица для функции у — х
X
у"
график
У = /(*)
-оо;0
<0
выпуклый
3
0
0
точка
перегиба
Таблица для функции у = \/
X
у"
график
У = f(x)
1 -оо;0
<0
1 выпуклый
0
-00
0;1
<0
выпуклый
- 4х + 2.
0;оо
>0
вогнутый
X2 - X3.
1
^foo
точка
перегиба
1;оо
>0
вогнутый
23. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ- ИССЛЕДОВАНИЕ
ФУНКЦИЙ
Применим теперь достаточный признак существования экстремума по
высшим производным к исследованию функций в стационарных
критических точках, а также определим области выпуклости и вогнутости и точки
перегиба функций из примеров, рассмотренных на предыдущем
практическом занятии.
/'(*) = 2х - Зх2, у" = /"(х) =
Пример 23.1. у = х2 - х3.
Р е ш е н и е:
© Найдем вторую производную у1
2-бх.
в Функция имеет две стационарные критические точки х = 0 и х = |.
Определим знаки второй производной в этих точках.
/"(0) = 2 > 0. Точка х = 0 является точкбй минимума.
/" (!) = 2 - 6 ■ § = -2 < 0. Точка х = | является точкой
максимума.
© Определим корни второй производной /"(х) = 0, 2 — бх = 0, х —
\. Точка х = | разбивает область определения функции на два
интервала :
1 1
-оо <х<-~, -<х<оо.
3 3
© исследуем знаки второй производной в этих интервалах.
В интервале -со < х < |, /"(х) > 0, как мы видели, /"(0) = 2 >
О— функция вогнута в этом интервале.
В интервале \ < х < оо, /"(х) < 0, в частности, как было
показано, /"(§) < 0— функция выпуклая в этом интервале.

270 23 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
о Так как при переходе точки х = | вторая производная меняет знак,
точка х = \ является точкой перегиба.
Составим таблицу
X
у"
график
-оо;±
>0
вогнутый
1
я
0
точка перегиба
y=h
v°°
<0
выпуклый
Пример 23.2. у = х(х + v^).
Решение:
© Найдем вторую производную у" = /"(я) = 16to*
© В этом случае критических точек нет.
о Вторая производная нигде в ноль не обращается, в точке х = О,
находящейся на границе области определения, она не существует.
© В области определения (при х > 0) вторая производная больше нуля,
график функции вогнутый,
в Точек перегиба нет.
Составлять таблицу в данном примере излишне.
Пример 23.3. у = 1 + tfx.
Решение:
© Найдем вторую производную у" = f"(x) = - 1Qbp-
© Имеется одна критическая тока х = 0, производная в которой не
существует.
© Вторая производная нигде нулю не равна. В точке х = 0,
находящейся на границе области определения функции, она не существует.
© В области определения (при х > 0) вторая производная меньше
нуля, график функции выпуклый.
© Точек перегиба нет.
Составлять таблицу в примере излишне.
Пример 23.4. у = 2х - 3#г*.
Решение:
© Найдем вторую производную
_2__ 2(#£-1)
• = /'(*) = 2-
/=/"(*) =
т5 #х
о Имеется одна стационарная критическая точка х - 1. В этой точке
вторая производная /"(1) = jS^\xss\ = | > 0. Следовательно, в
точке х = 1 функция имеет минимум. Во второй критической точке
х = 0 функция не дифференцируема.
23 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
211
© Вторая производная нигде нулю не равна. В точке х = 0 вторая
производная не существует, эта точка разбивает область определения
функции на два интервала:
-оо < я < 0, и 0 < х < оо.
© В интервале -оо < х,< 0 вторая производная /"(х) == -Д== > 0 —
график функции вогнутый.
В интервале 0 < х < оо также /"(х) > 0 и график функции
вогнутый.
о Поскольку при переходе точки х = 0 вторая производная не меняет
знак, точка х. = 0 не является точкой перегиба.
Составим таблицу
X
\ У"
! график
У = /(ж)
-оо;0
>о
вогнутый
0
оо
точки перегиба
нет
0;оо
>0
вогнутый
Пример 23.5. у = xV.
Решение:
© Найдем вторую производную
У' = /'(*)=Л*(3 + *), $/" = (х3 + 6х2 + 6х)е*.
о Функция имеет две стационарные критические точки х = -3 и х =
0. Определим знаки второй производной в этих точках.
/"(-3) = (-27 + 54 - 18)е~3 = *- > 0.
е3
Функция в этой точке имеет минимум.
/"(0) = 0. Необходимо определить знак следующей производной
в этой точке:
/'"(0) = (х3 + 9х2 + 18* + 6)е*|х=0 = б■ > 0.
Так как первая, не равная нулю производная в точке х = 0 оказалась
нечетной, экстремум в этой точке не существует, так как /'"(0) > 0,
функция в окрестности этой точки монотонно возрастает.
© Определим корни второй производной:
Г(х) = 0, (х3 + 6х2 + 6х)е* = 0, ех ф 0, х(х2 + 6х + 6) = 0, хг = 0,
и х2 + 6х -ь б = 0, х2,3 = -3 ± ч/9^б = -3 ± уД.

272 23 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
Указанные три точки разбивают область на четыре интервала:
-оо < х < -3 - \/3; -3 - уД < х < -3 + уД;
-3 + \/3<х<0;0<х<оо.
о Найдем знаки второй производной в этих интервалах:
В интервале -оо < х < -3 — \/3 вторая производная f"(x) =
(х3 + бх2 + 6х)ех < 0, т.к. ех > О, а многочлен (х3 + бх2 + бх) < О
при х << 0. Следовательно, график функции в этом интервале
выпуклый.
В интервале -3 - >/3 < х < -3 + \/3 вторая производная f"(x) =
(х3 + бх2 + бх)ех > 0, т.к., например, /"(-3) = £ > 0, график
функции вогнутый.
В интервале -3 + \/3 < х < 0 вторая производная /"(я) = (х3 +
бх2 + 6х)е* < 0, т.к., например, /"(-1) = (-1 + 6 - 6)е~г = -\ < 0,
график функции выпуклый.
В интервале 0 < х < оо вторая производная /"(х) = (х3 + бх2 -f
6х)е* > 0, т.к., например, /"(1) = (1 + б + б)е = 13е > 0, график
функции вогнутый,
о Поскольку при переходе точек х = -3- у/3 « -4,732; х = -3-Ь\/3 «
— 1,268 и х = 0 вторая производная меняет знак, эти точки являются
точками перегиба.
Составим таблицу:
X
у"
график
У = fix)
-оо;-3- >Д
<0
выпуклый
-3-\/3
0
точка перегиба
у « 0,93
-3 - >/3; -3 + л/5
>о 1
вогнутый
X
у"
график
2/ = /(ж)
-3 + V5
0
точка перегиба
у «-0,57
-3+ л/3;0
<0
выпуклый
0
0
точка перегиба
0;оо
>0
вогнутый
Аналогичным образом теперь решите самостоятельно следующие
примеры из предыдущего практического занятия
Пример 23.6. у = х3 - Зх2.
Пример 23.7. у = х(1 4- у/х)
Пример 23.8. у = 1 + >/з.
Пример 23.9. у = n/x2 - х.
&? ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
273
Пример 23.10. у = е* - х.
Займемся теперь примерами на определение наибольших М и
наименьших т значений функций на отрезке (глобальный экстремум)ч у
Найти Мит функции у = х3е* на [а; 6], которая имеет'один минимум
в точке х = -3.
Пример 23.11. а = -2; 6 = 2.
Решение:
© На интервале (-2;2) экстремумов у /(х) нет.
© Находим значения функции на концах отрезка:
/(-2) = (-2)V2 = -4; /(2) = 2V = 8е2.
© Поскольку экстремумов в интервале (-2;2) нет, наибольшее М и
наименьшее т значения функции достигается при х = —2их = 2:
М = /(2)=8е2, то = /(-2) = -1
Пример 23.12. 6 = -4; 6 = 2.
Решение:
© На интервале (-4;2) есть минимум функции в точке х = -3, у^п =
• /(-4) = (-4)3е-4 = -J}, /(2) = 8е2.
© Выбираем наибольшее и наименьшее значения из
/(-4) = -", f(-3) = ~^y(2)=8e2.
Очевидно, что m = /(-3) = —1| й М = /(2) = 8е2.
Очевидно,что при всех а < -4и6> 2 наименьшее значение
т = /(-3), аМ = /(6).
Самостоятельная работа
Найдите наибольшее М и наименьшее m значения функции у = х3 —
Зх2 на отрезке [а;Ь].
Пример 23.13. а = -1; 6= 1.
Пример 23.14. а = -2; 6=4.

274
21 ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИИ
24. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
Ассимптоты графика функции. Общая схема исследования функции
и построения ее графика. Применение теории экстремума к решению
задач.
24.1. Асимптоты графика функции. При исследовании функций
особый интерес представляет вид графика этой функции при
неограниченном удалении его текущей точки от начала координат, или, как
говорят, при удалении ее в бесконечность. Если при этом график функции
неограниченно приближается к некоторой прямой линии L, то эта
линия называется асимптотой графика функции. Различают вертикальные
и наклонные асимптоты.
Определение 24.1. Прямая х = о является вертикальной
асимптотой графика функции у = /(х), если хотя бы один из пределов lim f(x)
s-ю+О
или lim f(x) равен оо.
Пример 24.1. Исследовать поведение функции у = —^ и у = . jL* в
окрестности точки xq = 2.
Решение:
hm - = -оо, lim = +оо, lim 7 ^ = +о°-
х-*2-0 X — 2 Х-+2+0 X - 2 ж-+2±0 (х — 2)2
Следовательно, прямая ж = 2 является асимптотой как первой, так и
второй функции. Но графики у = /(х) в окрестности точки х0 = 2 имеют
различный вид (рис. 113 и 114).
Очевидно, что графики гипербол нечетной степени у = , Л^ в
окрестности точки х0 = 2 похожи на рис. 113, а гиперболы четной степени
У= (^2рг —на рис. 114.
Определение 24.2. Прямая у = fcx + b называется наклонной
асимптотой графика функции у = f(x) при х ->- +оо /или х —у —оо), если
(24.1) /(х) = fcx + b-}-a(x),
где а(х) есть бесконечно малая величина при х —> -+-оо (х -> —оо), т.е.
lim a(x) = 0 или
lim a(x) = 0.
&f. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
275
Рис. 113. Поведение функции у = ~2 в окрестности точки х = 2
Рис. 114. Поведение функции у = ^i^ B окрестности точки
Если к - 0, асимптота у - Ъ называется горизонтальной.
Теорема 24.1. Для того чтобы график функции у = f(x) при х ->
+оо (пли х -+ -оо; имел наклонную асимптоту у = кх + 6, необходимо
и достаточно, чтобы существовали два конечных предела

276
24. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
(24.2)
lim № = к,
х-»+оо х
lim (/(*)
аг-++оо
кх) = Ь или при х -> -оо.
Доказательство.
Рассмотрим пределы при х -* -Нею (аналогично рассматриваются
пределы при х -> -оо).
Необходимость. Пусть /(х) имеет наклонную асиптоту при х -> +оо.
Тогда по определению (24.2) функция f(x) = fcx + 6 + a(x), где
lim а(х) = 0.
Х-++00
Рис. 115. Взаимное расположение графиков и их наклонных асимптот
Следовательно,
lim flsU lim (fc+i + 2^)=*t
-♦+00 * «-4+00 V X * J
z-*+oo
lim (/(x)-fcx) = lim (6 + a(x))=6.
Достаточность. Если пределы (24.2) существуют, тогда по
определению предела /(*) - fex - Ь = а(х), где а(х) -> 0 при х -+ +оо, то есть
/(х) = Ь + b + а(х). И, следовательно, ?/ = fcx + 6 есть асимптота кривой
» = /(*).
Если пределы (24.2) прих, стремящемся как к -оо, так и к +со, равны,
то наклонная асимптота одна, если разные — то две. В первом случае при
вычислении пределов можно записывать, что х -* оо.
Если хотя бы один из пределов (24.2) не существует, то наклонной
асимптоты у кривой нет. Асимптотическое поведение функции у = /(х)
при х -» -foo И14 -00 может быть совершенно различным, кривая у =
24. ЛЕКЦИЯ -ИССЛЕДОВАНИЕ ФУНКЦИЙ
277
f(x) может подходить к асимптоте с одной стороны при х —> -f 00 и х —>
-оо (рис. 115,а), с разных сторон (рис. 115,Ь), может иметь асимптоту
только при х —> -foo, а при х —► -оо не иметь (рис. 115,с) или иметь
разные асимптоты при х —> -foo и х -» — оо (рис. 115,d).
ПРИМЕР 24.2. Определить, при каких значениях тип имеются наклонные
асимптоты у графика дробно-рациональной функции
_ Qm{x) _ ЬтХт + frm-iS"1-1 + • • • + М1 + 60
У Р„(х) a„xn + an^ixn-1 + ••• + <цх1 + о0 '•
Решение: Используя правила нахождения пределов отношения многочленов
(лекция 9), имеем:
»-юо x ♦ F„(ar) *-*<» (anxn H f-ai^1 + ao)z I a"
6= Um(4=W-Jb) =
Ч-ЬЬ1гЧЬо-Ья»п-|-'-<!оп_1»я ka0x _
если m < n -f 1,
если m = n + l,
если m > n + 1.
a„ a?n+an _ 1 *" - *+ •••-f «и х *+a0
^ 0, m < n, т.к. при этом m<n + l-+fc = 0,
-, rn = n + I.t.k. k — ^m-.
On
( OO, 771 > П + 1
Таким образом, график функции у ~ р(У имеет асимптоты
у = 0, при т < п,
(24.3) 2/= !£♦ прит = п
*«... . ft"»-1
2/ = -*-х + —**—, при т = п + 1.
Наклонная асимптота не существует при т > п + 1.
Пример 24.3. Найти наклонную асимптоту кривой у — 2х2~*+*.
Решение: Так как в нашем примере m = 2, п = 1, т — п + 1, то
согласно (24.3) наклонная асимптота существует и ее уравнение у = 2х + 1, поскольку
а„ = 1, 6m = 2,6m_i = -1, an_i = -1.
Наклонные асимптоты графика дробно-рациональных функций можно
находить, разделив числитель на знаменатель (например, уголком).
Так,
2х2 - х + 1 Л , 2
= 2х + 1 -f
х- 1

278
21 ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
По определению (24.2) прямая у = 2х + 1 является наклонной
асимптотой кривой
2х2 - х + 1
2/ =
гг-1
так как а(:г) = ^т ~* 0 при х —► оо. Отметим, что эта кривая имеет
также и вертикальную асимптоту ж = 1.
В предыдущих лекциях мы занимались исследованием функций у =
Зх2 — 4х + 2 и у = v^x2 — х3, графики которых были приведены на рис. 108
и 109. Очевидно, что первая функция асимптот не имеет.
ПРИМЕР 24.4. Имеет ли асимптоту кривая у — \/х2 — х3?
Решение: По (24.2):
k= iim iSEH= ит з/1-1 = -1,
х-»±оо х a?-f±oo V х
6= lim (v^x2 - x3 -t-x) = lim
Асимптота у = -x 4- | и изображена на рис. 109. Асимптоту кривой
у = \/х2 - х3 можно было также найти с помощью биномиального ряда
(21.5):
г/ = (х2_хз)1/з = _1(1_1)1/з = _:с(1 + 1(_1)+оШ) = _х+1 +
o(i).
По определению (24.2) прямая у = —х -f | и есть искомая асимптота,
что совпадает с результатом, полученным выше.
24.2. Общая схема исследования функции и построения ее
графика. На основании всего изложенного в лекциях 22-24 можно
рекомендовать следующий план исследования функции и построения ее графика.
1. Найти область определения функции. Установить, является ли
функция четной, нечетной или общего вида. Если функция
периодическая, найти период. Определить интервалы непрерывности и точки
разрыва. Построить вертикальные асимптоты.
2. Найти и нанести на график точки пересечения с осями.
3. Найти и нанести на график наклонные асимптоты.
4. Найти критические точки, точки максимума и минимума,
интервалы монотонности.
5. Найти точки, в которых /"(х) = 0 или не существует. Определить
точки перегиба и интервалы выпуклости и вогнутости.
6. Построить график.
24- ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
219
Замечание 24.1. Чтобы выполнить п.2 необходимо решить
уравнение f(x) = 0, что часто возможно лишь численными методами. Этому
вопросу будет посвящена следующая лекция.
В наших лекциях мы подробно исследовали две функции у = х3 — 4х 4- 2 и
у — \/х2 — х3, хотя и не в том порядке, как рекомендуем теперь. Это было
связано с последовательностью введения новых понятий. На основе
проведенных исследований по пунктам 1-5 целесообразно построить таблицы,
аналогичные тем, что были построенны для функции у = х3 — 4х + 2 и
функции у — \/х2 — х3 в лекциях 22 и 23.
Пример 24.5. Проведем еще полное исследование по предложенной
схеме и построим график функции у = 2х ~^1, асимптоту которой мы
нашли в примере 24-3.
Решение:
© Функция определена и непрерывна при х € (—oo,l)U(l,oo), функция
общего вида, не периодическая, точка разрыва х = 1, вертикальная
асимптота х = 1, у(1 — 0) = —оо, у(\ + 0) = +оо.
о Точки пересечения с осями: у(0) = — 1, с осью х пересечения нет,
т.к. 2х2 - х + 1 ф 0.
© Наклонная асимптота у — 2х ■+• 1.
. Находим у' = <-1М*-1Н*»--»И = *£=*1.
г/(0) = 0, у'(2) = 0, г/'(1) = -оо. Следовательно, критические точки
х = 0, х = 1, х = 2 На интервале (-оо,0) производная функции
у' > 0 — функция возрастает, на интервале (0; 1) у' < 0 — убывает.
Следовательно, у(0) = — 1 — max. На интервале (1;2) производная
функции у' < 0 — функция убывает, на интервале (2;оо) у' > 0 —
возрастает. Следовательно, у(2) — 7 — min.
• y,f = 2^-1>2-2(^:^2-2g)2(^1) = —Lp. На интервале (-оо; 1) вторая
производная функции у" < 0 — кривая выпуклая, у" > 0 на
интервале (1, со) — кривая вогнутая. Точек перегиба нет. Для данной
функции целесообразнее составлять одну общую таблицу.
X
у'
У
у"
график
y=«W
-оо;0
>0
асимптота
у = 2х + 1
<0
выпуклый
0
0
-1
<0
У=-1
max
0;1
<0
\
<0
выпуклый
1
—оо
асимптота
х = 1
ТОО ..
ТОО.
1;2
<0
\
> Q
вогнутый
2"
0
7
>0
У=7
min
2;оо
>0
г
>0
вогнутый
График функции приведен на рис. 116. В заключение рассмотрим
применение дифференциального исчисления к решению текстовых задач.

280
21 ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
Рис. 116. График функции у = 2*2~*?1
24.3. Применение теории экстремума к решению текстовых
задач. Изложенную в лекциях 22 и 23 теорию экстремума можно
применить к решению некоторых геометрических, физических и технических
задач. Как правило, в таких задачах нужно найти наибольшее и
наименьшее значения искомой величины в зависимости от другой величины,
изменяющейся в определенных пределах. Следовательно, эти задачи подобны
задаче о нахождении наибольшего и наименьшего значения функции на
отрезке. Рассмотрим два примера.
Пример 24.6. Вписать в эллипс ^ + р = 1 прямоугольник
наибольшей площади со сторонами, параллельными осям эллипса (рис, 117).
21 ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
281
♦ У
1(х;у)
Рис. 117. К примеру 24.6
,«,,.?(
у/а2 — х2 —
Решение: Искомая площадь прямоугольника S = 4жг/, х и у не не-
зависимы, а связаны уравнением эллипса.Выразим из него у — £>/а2 — х2
и подставим в 5. Тогда S будет функцией одного переменного х.
S(x) = f xyja2 - х2, 0 ^ ж < а.
Найдем производную
х2 \ _АЬ(а2-2х2)
у/а2 - х2 ) ау/а2 - х2
Производная равна нулю в точке х = -3- и не существует в точке х — а.
Так как 5(0) = S(a) = 0, то наибольшее значение достигается при х = ~%=
Искомая площадь 5 = 4-#?j = 2ab.
ПРИМЕР 24.7. Выбрать место для постройки моста через реку,
чтобы длина дороги между двумя пунктами А и В, расположенныхми на
разных берегах реки, была бы наименьшей. Реку считать постоянной
ширины h, расстояние от А до реки а, от В до реки — Ь, расстояние
от А до В по прямой — d.
Решение: На схеме (рис. 118) АА\ ~ а, ВВ\ = b, CD = Л, А В — d.
Очевидно, что О В есть также величина постоянная, обозначим ее буквой
с = y/d2 - (a-f /i-f-b)2. Длина дороги L = АС + CD + DB зависит от
расположения точки с. Введем переменную х = А\С, 0 < д: ^ с, тогда
L — у/а2 + х2 + Л 4- yfb2 + (с- х)2. Следовательно, L = L(x).
Определим
*Х' Va*+x* ^/ь* + (х-с)2 ч/(а2+х2)(б2+(1-с)2) *

282 24 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
Рис. 118. К примеру 24.7
V = О когда ху/Ь2 + (х - с)2 + (х - с)\/о2 + х2 = 0. Перенесем одно из
слагаемых на другую сторону и обе части возведем в квадрат— х2(Ь2 +
(х-с)2) = (х-с)2(а2+х2). Откуда62х2 = а2(х-с)2. Решив это квадратное
уравнение получим xi = —^ и Хг = ~ц. Первое значение х\ не подходит,
т.к. при а > 6, xi > с и при а < 6, Xi < 0. Точка Хг расположена между
i4i и Е, т.к. £ц < 1. Очевидно, что путь ACDB короче АО В и ЛЕВ,
поэтому длина дороги между пунктами А и В будет наименьшей, если
построить мост, где расстояние А\С = '—%.
24. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ
ФУНКЦИЙ
Прежде всего на этом практическом занятии определим, имеют ли
асимптоты графики функций примеров из двух предыдущих
практических занятий. Тем самым, если мы найдем еще пересечение графика
функции у = f(x) с осями координат, и, если это будет необходимо, значение
у = /(х) и у' = /'(х) в некоторых точках, мы полностью завершим
исследование этих функций и можем построить их графики.
Пример 24.1. у = х2 - х3 = х2(1 - х)
Решение:
в Очевидно, что эта функция не содержит линейной части и поэтому
не имеет наклонных асимптот,также нет и вертикальных асимптот.
в Определим пересечение графика функции у = х2 — х3 с осями
координат:
2/(0) - 2,(1) = 0.
24 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ 283
© Для более точного построения графика вычислим:
у (-1) = Тт у ("I) - f; у (I) = -5? и у'(1) =
© Построим график функции у = х2 - х3 (рис. 119).
-1.
♦У
Рис. 119. График функции у = хг - х
Пример 24.2. у = х(1 + у/х)
Решение:
© Очевидно, что график этой функции также не имеет асимптот.
© Точки пересечения с осями у(0) — 0.
© Вычислим дополнительно:
у(1) = 2; у(2)«4,38иу'(0) = 1.
© Построим график функции у = х(1 + у/х) (рис. 120).
Пример 24.3. у = 1 + ^х
Решение:
© Очевидно, что график этой функции также не имеет асимптот,
о у(0) = 1, с осью х пересечений нет.
© Вычислим дополнительно
уЧ+0) = оо; у(1) = 2; г/(2) % 2,19; у(3) « 2,32; (0,5) « 1,89
© Построим график функции у = 1 -Ь у/х (рис. 121).
Пример 24.4. у = 2х - 3#ё*.
Решение:
© Очевидно, что график этой функции также не имеет асимптот.

24 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
Рис. 120. График функции у = х(1 + #х)
Рис. 121. График функции у = 1 + tfx
• Пересеченние с осями. Запишем в виде у = \fj?{2tfx - 3). Откуда
получаем
у(0) = 0, 2^ - 3 = 0, & = |, х = У|.
"• у'(то) = 2Ugpa = ±00> У'(?) = |, у(_1} = _5.
• Построим график функции у = 2х - 3v^ (рис. 122).
Пример 24.5. у = sV.
Решение:
в Вертикальных асимптот нет. Ищем наклонные асимптоты:
24 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
285
Рис. 122. График функции у = 2х - Z\fx*
к = lim ^ = lim х2ех = оо — асимптоты при я
4-оо нет.
А: = lim £& = lim x2ez
lim 4=0,
e-»+oo в
b = lim (/(ж) - kx) = lim xV = - lim l-t = 0.
Таким образом, при ж —> -оо имеется горизонтальная асимптота
У = 0.
ф Пересечение с осями у(0) = 0.
0 2/(0,5) й 0,206;у(1).= е;у(-1) = |;у(-2) = -£;у(-4) « -1,17;
у(-5)«-0,84у(-8)«-0,17
в Построим график функции у = х3ех (рис. 123).
В качестве примера полного исследования функций по схеме лекции 24
рассмотрим
фик.
ПРИМЕР 24.6. Исследовать функцию у = -^^ и построить ее гра~
Решение:
о Область определения функции D(y) = (—оо; —2) l_J(—2; 2) |J(2; oo).
® Функция нечетная, т.к. f(—x) = —f{x). Непереодическая.
в Точка пересечения с осями я = 0, у = 0.

286
24 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
Рис. 123. График функции у = х3ех
« Точки разрыва : х = -2 и х = 2, прямые х = -2 и х = 2
являются вертикальными асимптотами. При этом lim -£- = ±оо и
,. ^3 *-+2±0* ~4 '
х-»-2±0х *
^Наклонные асимптоты. Если поделить х3 на ж2 - 4, получим
у ~ х ~ ^4* Тк- J™> х^Ц = °» прямая, определяемая уравнением
3/ = х, является наклонной асимптотой.
* Найдем производную
V = Пх) = r_£l_V = (Д^2 ~ 4)3s2 - s32x х4 - 12х2 х2(х2 - 12)
• Критические точки функции: х = 0, х = ±2у^, x = ±2. Они
разбивают область определения на интервалы :
(~оо < х < -2V5); (-2у/3 < х < -2); (-2 < х < О)-
(0<х<2); (2 < х < 2N/3); (2^3 < х < оо).
На интервале -оо < х < -2n/3 производная больше нуля —
функция возрастает.
На интервале -2^5 < х < -2 производная меньше нуля —
функция убывает.
На интервале -2 < х < 0 производная меньше нуля - функция
убывает.
При определении интервалов монотонности при х > 0
воспользуемся нечетностью функции. На интевалах (0;2) и (2;2\/3) функция
24 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ 287
убывает, на (2\/3; оо) — возрастает. Поведение функции в
окрестности точек х ± 2 исследовано ранее.
При переходе точки х = 0 производная /'(х) = х^х ~^' знак не
меняет, следовательно, эта точка не является точкой экстремума.
При переходе точки х = 2\/3, знак производной меняется с
минуса на плюс, следовательно, эта точка является точкой минимума.
В силу нечетности функции точка х = — 2\/3 является точкой
максимума.
Найдем вторую производную:
,,« _ t»<r\ - /»2(«а-И)у _ (х2-4)2(4хэ-24х)-(*4-12х2)2(х2-4)2х _
У — J К*) — \ (г2_4)2) ~ (х2-4)4 ""
— 4х5 -24х3- 16х3+96х-4х5+48х3 __ 8х(х2+12)
~~ (х2-4)3 """ (х2-4)3 '
f"(x) обращается в нуль в точке х = 0 и не существует в точках
х = ±2.
На интервалах (-оо;-2) и (0;2) вторая производная /"(х) < О
— график функции выпуклый.
На интервалах (—2;0) и (2; оо) вторая производная f"(x) > О —
график функции вогнутый.
При переходе точки х = 0 вторая призводная меняет знак,
следовательно, х = 0 является точкой перегиба
На основании проведенных исследований построим таблицы и
график функции (рис. 124.
| X
К
У
-оо;-2д/5
>0
/*
-2%/3
0
-3V3
max
-2%/3; -2 1
<0
\
-2
-оо
точка
разрыва
-2;б
<0
\
0
о
экстремума
нет
0;2
<0
\
2
-с»
точка
разрыва
2;2\/3
<0
\
2v/3
0
3\/3
| min
2\/3;оо
>0
f
X
У"
график
y=f(*)
-оо;-2
<0
выпук.
-2
qFoo
точка
разрыва
-2;0
>0
вогн.
0
0
точка
перегиба
0;2
<0
выпук.
2
=Foo
точка
разрыва
2;оо
>0
вогн.
В заключение данного практического занятия рассмотрим один
пример на решение экстремальной задачи с физическим содержанием.

288 24 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ
х
II
X
Рис. 124. График функции у = х3/(х2 - 4)
Пример 24.7. Пункт В находится на расстоянии 60 км от
железной дороги. Расстояние по железной дороге от пункта А до ближайшей
к пункту В точки С составляет 285 км. На каком расстоянии от
точки С надо построить станцию, чтобы затрачивать наименьшее время
на передвижение между пунктами А и В, если скорость движения по
железной дороге равна 52 км/ч, а скорость движения по дороге равна
20 км/ч.
Решение: Построим схему (рис. 125). АС ± С В
Рис. 125. К примеру 24.7
АС = 285км,СВ == 60км, DC = x;AD = 285- х\
#ж.д. = 52км; #ш = 20км/ч
24 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ ФУНКЦИЙ 289
4. _ АР _ 285-х. + __ DB _ s/DC*+CB* _ x/*2+6Q2
Д'~^^~~12~' *ш~.*ш~ *ш 20
Общее время t = *ж.д. + *ш = ^^ + ^У03 должно быть
минимальным, необходимым условием этого является равенство нулю производной
Ф)
fUlzi х = -5yfo2 + 6Q2 4--13* ^Q
dx ~ 52 + 20V*2 4- 602 ~ 260ч/*2 + б2
5VW602 = 13я; 25х2 + 52 • 602 = 1б9х2; 144я2 = 52 • 602; х = 25
Ответ: DC = 25 км.
Самостоятельная работа
Исследуйте функции и постройте их графики.
Пример 24.8. у = х3 - Зх2.
Пример 24.9. у = х(1 + ^/я)-
Пример 24.10. у = 14-v/i.
Пример 24.11. у = \/х* - х.
1
Пример 24.12. у = е* - я. '
Пример 24.13. £р.
Пример 24.14. Гонцу нужно добраться из пункта А, находяшемся
на одном берегу реки, в пункт В, находящемся на другом. Зная, что
скорость движения на берегу в к раз больше скорости движения по
воде, определить, под каким углом гонец должен пересечь реку для того,
чтобы достичь пункта В в кратчайшее время. Ширина реки— h,
расстояние между А и В (вдоль берега) — d.

290
25 ЛЕКЦИЯ - РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
25. ЛЕКЦИЯ - РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Отделение корня. Оценка приближенного значения корня. Методы
уточнения корня. Метод половинного деления. Метод Ньютона.
25.1. Корень уравнения.
Определение 25.1. Корнем уравнения
(25.1) 7(*)* О
называется число £, которое будучи подставлено вместо х в уравнение
обращает его в тождество.
Найти корни уравнения (25.1) в аналитическом виде представляется
возможным лишь в исключительных случаях. Общими методами
нахождения корней (25.1) являются численные методы последовательных
приближений, которые распадаются на два этапа, первый — отделение
корня и второй — уточнение значения корня. В дальнейшем будем считать,
что функция f(x) непрерывна на интервале, где ищется корень уравнения
(25.1) и имеет первую, а иногда, это будет оговорено, и вторую
производные.
25.2. Отделение корня. Если мы построим график функции у =
/(я), то корнями уравнения (25.1) будут точки пересечения этой
функции с осью абсцисс, и таким образом, мы можем найти приближенные
значения корней уравнения, т.е. найти интервалы, на которых
находится по одному корню. Так, на рис. 108 изображен график функции у =
ж3 - 4х + 2, ясно, что х3 - Ах + 2 = 0 в точках 6,£ь£з- Грубо отделим
корни 6 € (-3; -2);£а <Е (0; 1);& € (1; 2).
Графическое решение уравнения (25.1) может быть произведено еще и
следующим образом: представим уравнение (25.1) в эквиваленитном виде
(25.2) ф)=ф(х).
тогда корнями (25.1) будут точки пересечения функций у = <р(х) иу =
ф(х), (рис. 126).
Пример 25.1. Найти графически корни уравнения xz - 4ж + 2 = 0.
25 ЛЕКЦИЯ - РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
291
У=Ч<х)
4i
i
———
0
' У
,
>
у=чх
! х
^2 *3
Рис. 126. Корни уравнения (р{х) = гр(х)
Рис. 127. Корня уравцения хъ = Ах - 2
Решение: Запишем уравнение я3 -4а? + 2 = 0 в эквивалентном виде
х3 = 4ж - 2, обозначим у = ч?(х) - хъ и у = ф(х) = 4я - 2. Таким образом,

292
25 ЛЕКЦИЯ - РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
корнями уравнения х3 - Ах + 2 = 0 являются точки пересечения параболы
у = х и прямой у == 4а:-2. Из рис. 127 имеем & б (-3; -2);& G (0; 1); & €
(1; 2), что, естественно, соответствует результатам, полученным на
основании рис. 108.
Рассмотрим еще один пример.
я2 = 0
Пример 25.2. Найти графически корни уравнений 2х - х2 = 0 и 2х +
У^(х)=27
у=у(х)=
У=Ф(х)=2Х
Рис. 128. Корни уравнения х2 = 2х
Решение: Запишем первое уравнение 2х - я2 = 0 в эквивалентном
виде 2х = х2 и положим у = у(х) = 2гиу = 0(х) = х2. Таким образом,
корни уравнения 2х - х2 = 0 являются точками пересечения графика
показательной функции у = 2х и параболы а/ = х2. Из рис. 128 видно, что
имеются три точки пересечения & е (-1;0);& = 2;& = 4. Очевидно, что
при х > А пересечений кривых больше нет, т.к. при больших х
показательная функция растет быстрее, чем степенная.
25 ЛЕКЦИЯ - РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИИ
293
Уравнение 2х + х2 = 0, очевидно, не имеет корней, т.к графики функций
у — 2х и у = -х2 (пунктир на рис. 128) не пересекаются.
Перейдем теперь к анализу результатов графического отделения
корней. Из приведенных выше рисунков очевидно, что, если на интервале
(а, Ь) производная f'(x) не меняет знака, а на границах при х = а и х = b
функция f(x) принимает значения разных знаков, то на этом интервале
имеется один корень. Это и есть правило отделения корней.
Следовательно, мы можем определить, сколько и на каких интервалах
имеется корней у уравнения f(x) = 0, не прибегая к построению графиков.
Достаточно определить интервалы монотонности функции и ее значения
в некоторых избранных точках. Рассмотрим уравнение х3 - Ах + 2 = 0.
Пример 25.3. Определить аналитически число корней уравнениях3 —
Ах + 2 = 0 и отделить их.
Интервалы монотонности и эктремумы функции у = х3 - Ах + 2
приведены в соответствующей таблице лекции 22, откуда, учитывая, что
у —* —со при х —> —оо и у —> со при х -» оо, делаем вывод, что
уравнение х3 - Ах + 2 = 0 имеет три корня: £i € (-оо; -^з);£г € (-4р -Tj) и
£з € (-^; оо). В дальнейшем мы можем уменьшить эти интервалы,
выбирая точки на каждом из них, знак функции в которых разный. Например,
для первого интевала /(—3) = -13 < 0, /(—2) = 2 > 0, для второго
/(0) = 2 > 0,/(1) = -1 < 0, для третьего /(1) = -1 < 0, /(2) = 2 > 0.
Следовательно, & е (-3; -2); & € (0; 1); & € (1; 2).
25.3. Оценка приближенного значения корня. Пусть корень
уравнения (25.1) отделен и находится в интервале (а; Ь). Положим, что его
приближенное значение разно х € (о; 6). Пусть точное значение этого корня
равно £ € (а; 6), тогда, применяя формулу Лагранжа 18.4 к отрезку [£; я],
имеем
1/(0-/(*)1 = 1/'К)1К-*1,
где £ 6 (£, х). £- точный корень уравнения, следовательно, /(£) = 0, и
\т\ = 1/Ч01К - «I-
Пусть mi есть наименьшее значение модуля производной f'{x) на [а; 6],
тогда |/(я)| ^ 7rii|^ - а:| и, следовательно,
(25.3) £ - £| < М.
mi
Формула (25.3) и дает оценку отличия значения корня х от точного £.
Пример 25.4. Оценить ошибку приближенного значения корня х =
0,5 уравнения х3 - Ах + 2 = 0

294
25 ЛЕКЦИЯ - РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Решение: х € (0; 1), на котором, как мы определили ранее,
например, в предыдущем примере 25.3, имеется корень £2- Определим
f(x) = /(0,5) = 0,125,
производная f'(x) = Зя2 - 4 принимает значения /'(0) = —4, /'(1) = -1,
mi = наим.знач|/'(х)| на [0;1] = 1. Подставляя полученные величины в
(25.3), получим |£ - 0,5| < 0,125. Следовательно, приближенное значение
корня х = 0,5 отличается от точного £ не более, чем на 0,125, а это значит
0,375^^0,625
25.4. Методы уточнения корня. Все методы, решающие эту
задачу, являются методами последовательных приближений или, как их иначе
называют, итерационными методами. В принципе эти методы, при
некоторых условиях, специфичных для каждого метода, позволяют найти
решение уравнения (25.1) с любой заданной наперед точностью.
Поэтому их часто называют точными методами определения корней уравнения
(25.1). Мы остановимся на двух методах: первый - это метод половинного
деления, второй — метод Ньютона (или метод касательных).
Метод половинного деления. Метод относится к числу простых и
абсолютно надежных методов. Пусть корень уравнения (25.1) отделен и
находится в интервале (а; Ь). Положим для определенности /(а) < 0, f(b) >
0. Разделим отрезок [а; Ь] пополам и вычислим /(а + ~=&). Если это
значение равно нулю, то £ = а + —*, если f(a + ^) > 0, то f € (а; а 4- Цр);
если /(а + &=£) < 0, то £ € (а + ~&; Ь). Выбираем соответствующий
отрезок, где находится корень, и повторяем процедуру. И так до тех пор, пока
не достигнем заданой точности. Поскольку в каждой итерации (в каждом
последовательном приближении) отрезок, содержащий корень делится
пополам, точность метода может быть оценена по формуле
(25.4) k„_£|<J^i,
где п— номер итерации, ахп — значения корня в n-ной итерации.
Из формулы (25.4) следует: чтобы ошибка в значении приближенного
корня уменьшалась в 10 раз необходимо произвести четыре итерации, т.к
23 = 8 и лишь 24 = 16 > 10.
Пример 25.5. Применить метод половинного деления для уточнения
корня уравнения х3 — Ах + 2 = 0, находящегося в интервале (0; 1).
Решение: Этот корень мы обозначили ранее £г>/(0) = 2 >
О, /(1) = — 1 < 0, положим приближенное значение корня х\ = 0,5,
/(0,5) = 0,125 > 0 => & € (0,5; 1,0). Следующее приближенное значение
25 ЛЕКЦИЯ - РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
295
корня положим х2 = 0,75, /(0,75) = 0,753 - 3 + 2 < 0 => £2 € (0,5; 0,75).
Отметим, что в промежуточных действиях нам не обязательно точно
вычислять f(xn), достаточно определить знак. Далее я3 = 0,625; /(0,625) =
0,6253 - 2,5 + 2 < 0 => & € (0,5; 0,625). Определим х4 = 0,5625 и т.д.
Ошибка в определении £ по х4 согласно (25.4) не превышает ~ =
0,0625.
Метод половинного деления абсолютно надежен, но очень медленно
сходится, т.е. ошибка \хп — £| уменьшается медленно.
Метод Ньютона (или метод касательных). Этот метод
относится к наиболее быстро сходящимся методам. Однако условия его
сходимости более жесткие. Будем считать, что корень уравнения (25.1) отделен и
находится на интервале (а; 6) и на этом интервале f'(x) и f"(x) сохраняют
знаки. Представим функцию у = f(x) в окрестности точки £ по формуле
Тейлора (20.6), положив h = f - х„, где хп - n-ное приближение корня
(25.5) /(О = f(xn) + f'(xn)h + 0(h2) = 0,
это выражение равно нулю, т.к. £- точный корень уравнения (25.1)
Отбросим в (25.5) величину 0(h2), заменив h на hn = a;n+i - х„,где x„+i
следующее приближение к корню £ :
f{xn) + f'(xn)hn = fUn) + /'(*»)(*«+! - хп) = 0.
Откуда
(25.6) xn+1=xn~-^4,n = 0,l,2,...
Это и есть формула метода Ньютона.
Рассмотрим рис. 129. Проведем из точки (хп;уп) касательную Т к
кривой у = /(х):
Ут = f(xn) + f'{xn)(x - хп).
Ее пересечение с осью абсцисс и даст значение следующего приближения
arn+i, т.к. ут(хп-н) — 0. Поэтому метод Ньютона еще и называют методом
касательных. Мы подходим к корню £ заменяя кривую у = f(x)
касательной к ней в точке (хп; уп)
ТЕОРЕМА 25.1. Достаточное условие сходимости метода Ньютона.
Если j"{x) на [а; Ь] сохраняет знак и в точке приближенного значения
корня хп имеет тот dice знак, что f(xn), то следующее приближение
хп+\, определяемое по (25.6) будет ближе к точному корню £.
Дадим геометрическое доказательство этой теоремы. В точке хп
значение функции f(xn) > 0, а для вогнутой функции, как на рис. (129),
f"(x) > 0 и, как видно, хп+х ближе к корню £. Если бы мы взяли за

296
25 ЛЕКЦИЯ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
*П+1
РИС. 129. К методу Ньютона (касательных)
приближение корня точку хп, в которой f(xn) < О, то касательная к
кривой, проведенной ку = /(х)в точке гп может пересечь ось абсцисс в точке
яп+ь расположенной дальше от точки £, чем х„, а там кривая может быть
такой, что следующее приближение хп.п будет еще дальше и итерации,
как говорят., разойдутся.
Оценим ошибку приближенного решения уравнения /(#) = 0 по методу
Ньютона.
Пусть х = rrn+i в формуле (128)
Fn+i -£К — •
Запишем формулу Тейлора (20.2) для точки ж„+1 при п = 2
где С € (sn>Sn+i) Подчеркнутое выражение равно нулю, согласно (25.6).
Тогда
где М2 равно наибольшему значению |/"(г)| на [а;6], и следовательно,
(25.7)
2rn i
25 ЛЕКЦИЯ - РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
т
Формула (25.7) показывает, что отличие приближенного значения от
точного в методе Ньютона уменьшается пропорционально квадрату разности
двух последовательных приближений.
ПРИМЕР 25.6» Уточнить корень уравнения хг — Ах -f- 2 = 0,
находящийся в интервале (0; 1) по методу Ньютона.
Решение: Запишем формулу (25.6) для f(x) = ж3 - Ах -+• 2
(25.8) *„+! = *я - Xn~tXnf2i n = 0,1,2,..,
/'(а;) = За;2 - 4; И*) - 6z
/(0)-2; ПО)-в; /(1) --1; /"(!)-«
С точки х — 1 начинать итерации не рекомендуется, т.к. это
противоречило бы теореме 25.1 и процесс итерации мог бы не сойтись. Поэтому в
качестве начального приближения возьмем точку хо = 0, тогда по (25.8)
гг, - тЛ - go-^O*2 — ft _ °-°+2 - ft Ч
Xl - Х° 3zg-4 - U 0-4 - U> °'
«. _ «. s?-4a?i+2 п с 0,125-2+2 __ п соос
Х2 = #1 - 'to|l4 = 0, 5 !0|75-4 °' 5385'
«. — «. а;2-4аг2+2 п с 0,53858-4 0,5385+2 п сопоо
Ж3 = «2 ~ 23а?2-4 = °>5 - 3.0,538502-4 = 0,53923.
Проведем оценку отличия х$ от точного значения £г- На отрезке [0,1], как
мы уже определили в примере (25.4), гщ — 1, a /"(#) = б, следовательно,
М2 = б, тогда по (25.7):
|яг2 - 6 К о (°'5392 ~ °>5385)2 w 10""6*
Таким образом все пять знаков в ж3 = 0,53923 являются точными.
На практическом занятии, которое следует после этой лекции, будут
найдены и другие корни £i, £з уравнения я3 — Ах 4- 2 = 0.
Применим теперь метод Ньютона к решению уравнения f(x) = хт —
а = 0, т.е.к вычислению корней х = у/а. Формула (25.6) в этом случае
примет вид:
(25.9) хп+1 = хп- ^-=^ = ~((т - 1)хп + -^), п = 0,1,2,...
Для вычисления квадратных корней х — у/а, га = 2
(25.10) хп+1 = -(*„ + —), п = 0,1,2,...
£i Xji
Пример 25.7. Найти у/В по методу Ньютона с точностью до 10~4.

298 25 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Решение: В этом случае а = 5 и по (25.10), положив х0 = 2 имеем
*i = *(*o + £) = i(2 + f) = 2,25,
*2 - §(*, + £) = |(2,25 + 5$j) = 2,23611,
хз = |(х2 + А) = 1(2,23611 + j^jj) - 2,23607.
Следовательно, ж3 = 2,2361 дает решение нашей задачи. Оценка ошибки
по (25.7) дает величину меньше 10~4.
25. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - РЕШЕНИЕ
НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Для проведения этого практического занятья, посвященного
определению корней нелинейных уравнений f(x) = 0, достаточно иметь
калькулятор, позволяющий вычислять простейшие элементарные функции.
Пример 25.1. Найти по методу Ньютона с точностью 10"*3 корни
уравнения хг — Ах 4 2 = 0, принадлежащие интервалам (—3; — 2) и (1; 2).
Решение: Найдем сначала корень & £ (-3; ~2).
f{x) - хг - Ах 4 % f'{x) = Зж2 - 4, /"(ж) - 6я.
Определим значения /(ж), /'(ж) и /"(#) в точках х = -3 и х = -2 :
/(-3) = -13, /'(-3) - 23, /"(-3) - -18,
/(-2) - -2, /'(~2) = -12, Г(-2) = 8.
Согласно теореме 25.1 за начальное приближение возьмем Хо — —3, тогда
по формуле (25.6) последовательно определяем:
*t = ™3-| = -2,4348,
х2 = -2,4348- «-ЭДгаУ1 - -2,2415,
хз = -2,2415- '-'ДУ - -2,2151.
Оценку точности проведем по формуле (25.7):
18
|*з - 61 ^ ^7s(2,2415 - 2,2151)2 < ИГ».
Следовательно, с точностью до 10"3 корень £i = —2,215.
Аналогично найдем корень £3 € (1; 2) :
/(1) = -1, /'(1) = -1, /"(1)= 6,
/(2) = 2, /'(2) = 8, /"(2) = 12.
25 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 299
Возьмем хо — 2. Тогда:
^ = 2-§ = 1,75,
х2 = 1,75 -iqfc$gl = 1,6811,
*з - 1,6811 - 1J%*;g^ = 1,675.
Поскольку первая производная на отрезке (1; 2) меняет знак, для
оценки корня по формуле (25.7) возьмем отрезок [1,5; 2]. На этом отрезке:
М2 - /"(2) = 12, тг = /'(1,5) - 2,75.
Итак,
,ХЗ " €| * 22"Т75(1'б81 ~ *' 675)2 < 10~3-
Следовательно, с точностью до 10~3 корень £3 = 1,675.
В доследующих двух примерах следует графически определить имеют
ли корни данные уравнения. Если имеют, найти их с помощью метода
половинного деления и метода Ньютона с точностью до 10"4.
Пример 25.2. /(*) = 2х - х = о.
Решение: Запишем нате уравнение в виде 2х = жи изобразим на
рис. 130 две кривые у = Т и у - х>
РИС- 130- К примерам 25-2 и 25-3
Очевидно, что эти кривые не пересекаются и, следовательно,
уравнение 2х - х — 0 решений не имеет.

300 25 ПРАКТИЧЕСКОЕ ЗАНЯТЫЕ - РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Пример 25.3. /(ж) - Т \ х = 0.
Решение:
ф Запишем это уравнение в виде 2* = -ж и изобразим на том же
рисунке 130 еще и кривую у - -ж, которая, очевидно, пересекается с
кривой 2/ = 2* в точке, находящейся в интервале (-1;0).
Следовательно, уравнение 2х f х — 0 имеет один корень £ G (—1; 0). Таким
образом решена задача отделения корня.
9 Займемся уточнением корня £ по методу половинного деления. В
нашем случае а = — 1, Ь =* 0.
Число итераций(приближений), необходимых для того, чтобы
достичь точности S = 10~4, определяется на основании (25.4);
\xn-t\<^-~<W~\T>lQ\n>l3.
Вычислим /(-1) = 2"1 - 1 « -| < 0 и /(0) = 2° + 0 = 1>0.
Положим Ж1 = —0,5.
Далее /(-0,5) = 2~* - £ = ^ - 0,5 = 0,207 > 0, следовательно,
£ е (-1; -0,5). Положим ж2 — -0,75.
Вычислим /(-0,75) - 2"? - 0,75 = -^ - 0,75 = -0,1554 < 0,
следовательно, £ € (-0,75; -0,5). Положим хг = 0,625.
Вычислим (-0,625) = 2 t - 0,625 = -gfc- - 0,625 - 0,0234 > 0,
следовательно, £ е (-0,625; -0,75) и ж4 = -0,6875 и т.д. до х\$.
© Проведем уточнение корня по методу Ньютона;
f(x) = 2х +*,/'(*) - 2* In 2 + 1,/"(*) - 2*1п22 > 0.
Поэтому, согласно достаточному условию сходимости метода, в
качестве начального приближения возьмем жо ~ 0. Для оценки
точности приближений определим ть— наименьшее значение |/'(ж)| —
2х In2+ 1 на [-1;0] и М2 — наибольшее значение |/"(а?)1 = 2" In2 2
на [-1;0]. Очевидно, что mi = In 2 4 1, М2 = In2 2. Таким образом,
формула (25.4) в нашем случае будет |жп+1 - £| ^ цш+х)^*1 "х^)1'
Для нашего случая формула метода Ньютона (25.6) будет
2й* 1» 2+1'
тогда*! = **- JSfc -°" ЭТ^х - -d+i « "0,5906 и
1*1 - el ^ 55Й&рг « 0,05,
*2 = *i - ^т - "0,5906 - PS~^f - -0,6441,
l^-fl^5Sfe(0»0B35)ae4-10''4'
*• = »i - ЙТ^Т - -0,0441 - ^Щ^МШ = "0,6602,
£5 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ №
1Ж* -Ж ЩКЩуО). 0061)* я 0, 5 • Ю-5 < Ю-4.
Следовательно, жз = -0,0502 с точностью до 10~4 является
корнем уравнения. Для решения поставленной задачи понадобилось
всего три приближения, а не 13, что надо было бы сделать, если
пользоваться методом половинного деления.
В качестве еще одного примера применения метода Ньютона
рассмотрим вычисление корня m-й степени из числа <х.
Пример 25.4. Найти tfb с точностью до 10~4.
Решение: В нашем случае надо положить а=5 и т—3 в формуле
(25.9):
* ^ /*>«, i a \ ~ _ л 1 л
^п+1 й- « 1*хм -Г —2 У, " = и, 1, л, . . .
В качестве ж0, очевидно, надо взять число несколько меньшее 2, например,
ж0 = 1,7. Тогда хг = |(3,4 + jfa) = 1,7100.
Для определения точности приближений по (25.7) поступим
следующим образом:
/(ж) = ж3, /'(ж) = Зж2, /"(х) = 6ж. Положим лц = /'(2) = 12; М2 -
/"(2) = 12. Тогда
kn+i - £1 < |(^n+i - ж„), п = 0,1,2,...
и |a?i —^| = 1.0,012 < 10~4. Следовательно, уже #i = 1,71 с нужной
точностью решает поставленную задачу.
Самостоятельная работа
Пример 25.5. Определите графическщ имеет ли корень уравнение
cos ж — х = 0, и если да, найдите его с точностью до 10~4 по
методу половинного деления и по методу Ньютона.
Пример 25.6. Найдите \/Ъ с точностью до 10~4.

302
26. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Элементы векторной и
линейной алгебры
260 ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Матрицы, действия над матрицами, определители второго порядка
и их свойства, определители высших порядков.
26.1. Матрицы.
Определение 26.1. Прямоугольная таблица
( «и <М2 ••♦ а>ы \
(26.1) А = (ау) =
a2i а22
д>2п
\ Gmi am2
/
составленная изтхп чисел а#, называется матрицей размером тхп.
Числа aij, входящие в матрицу, называются элементами матрицы.
Горизонтальный ряд чисел называется строкой, а вертикальный — столбцом
матрицы. Первый индекс г — номер строки (г = 1,2,...,?п), второй j —
номер столбца (j — 1,2, ...,п). Матрицу принято обозначать заглавными
буквами, например Д В и т.д.
26. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
303
Приведем основную терминологию матриц, которую будем
использовать в дальнейшем.
© Матрица, в которой число строк не равно числу столбцов (т ф га),
называется прямоугольной.
в Матрица; в которой число строк равно числу столбцов (т = го),
называется квадратной. Причем число ее строк или столбцов
называется порядком матрицы.
Например, матрица
А » ( Vbl1 "1Z j — является квадратной матрицей 2-го порядка.
_. ( an ai2
\ а21 ^22
• Последовательность элементов квадратной матрицы с
одинаковыми индексами (г = j) называется главной диагональю матрицы
(aU7a22,... yann).
о Если в квадратной; матрице все недиагональные элементы равны
нулю (a{j = 0 при i ф j), то матрица называется диагональной
/ аи О О .
О а22 0 .
О 0 азз ,
V О О О
О »
О
а„п /
© Квадратная диагональная матрица, у которой элементы главной
диагонали равны единице, называется единичной матрицей Е.
Е-
/ 1 0 0 ... О \
О 1 0 ... О *
О 0 1 ,,. О
\ 0 0 0 ... 1 /
б Матрица, все элементы которой равны нулю, называется
нуль-матрицей.
в Матрица, состоящая только из одной строки, называется матрицей-
строкой
А~(ап,а12,... ,а1п)

804
26. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
9 Матрица, состоящая только из одного столбца, называется матрицей-
столбцом.
/ flu
I a21
А =
\ ат\
о Матрица В называется транспонированной по отношению к
матрице А, если она получена из матрицы А заменой строк этой матрицы
ее столбцами, и, наоборот, столбцов строками. Транспонированная
матрица обозначается АТ.
Например, по отношению к матрице
/ а а а \ / «и «21 \
А = ( и 19' 13 ) транспонированной будет Ат = | а12 а22 I
V«2i а22 а23у - ^ aMJ
26,2. Действия над матрицами.
Определение 26.2. (Равенство матриц.) Две матрицы А и В
называются равными (А = В), если они имеют одинаковое число строк
и одинаковое число столбцов и их соответствующие элементы равны,
aij -Ъ^.
Определение 26.3. (Сложение матриц.) Суммой двух матриц А и
В одинакового размера (т х п) называется матрица С того же размераf
элементы которой равны сумме соответствующих элементов матриц
А и В;
(26.2) А + В = С, Cij = aij + fry.
( 1 2 3 \ /241\
Пример 26.1. Сложить матрицы A — I . „ J uB ~ I „ q 5 I
Решение:
/123\/24 1\/Зв4\
\2 4 5J + \3 0 5J 1^5 4 loj'
Сложение матриц подчиняется переместительному и сочетательному
законам:
А + В = В + А, (А Л-В) ч- С « A + (В + С).
Нуль-матрица при сложении матриц выполняет роль обычного нуля при
сложении чисел:
/If 0 = А.
26. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
305
Определение 26.4. Произведением матрицы А на число а
называется матрица В:
(26.3) B = A-a*BCt-A-(a- atj).
/1 2
Пример 26.2. Умножить матрицу А = [ 3 1 ) на число 3.
Решение:
(И)
(ii)
При умножении матрицы на нуль получается нуль-матрица.
Определение 26.5. Произведением матрицы А = (а^) на матрицу
В = (Ь^) называется матрица С = (су) = А В, каждый элемент
которой определяется выражением
п
Cij = anbij + a,'2&2j H 1" flin&2n = 2J a**&*i-
Jfc=l
Как видно из определения произведения двух матриц, перемножить
можно лишь матрицы, у которых число столбцов первой матрицы
сомножителя А равно числу строк второй матрицы сомножителя В.
/ \ f °ll &12 \
Например, если А = ( u 12 13 ] и В — ( 621 &гг I ,то
\ап а22 а23 J { ^ ^ )
С = АВ = Г апЬп + ai2^21 + ai3^31 ai1^12 + fl12fe22 + «13^32 "\
\ «21^11 + «22^21 + «23^31 «21^12 + ^22^22 + ^23^32 /
В результате перемножения двух матриц получается матрица,
содержащая столько строк, сколько их имеет матрица-множимое, и столько
столбцов, сколько их имеет матрица множитель.
Рассмотрим еще примеры умножения матриц.
Пример 26.3.
/3 -1 \ / 1 1 \ _ / 31-1-3 3-1-1-1 \ /0 2 \
Л*-{-1 2 У^3 1у"\-1-1 + 2-3-1-1 + 2-iy"V51/
/1 1W 3 -1\ /1.3 + 1.(-1) 1-(-1) + 1-2\
^Л~^3 1 Д-1 2 ) " ^ 3-3 + 1 •(-!) 3-(-1) + 1-2у~

306
26. ЛЕКЦИЯ ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
-(!-'.)
Эти примеры показывают, что произведение двух матриц, вообще
говоря, не подчиняется переместительному закону:
АВ ф В А.
Определение 26.6. Матрицы А и В, для которых АВ = В А,
называются коммутативными.
Можно проверить, что умножение матриц подчиняется
сочетательному закону
А{ВС) = (АС)В
и распределительному закону
(А + В)С^АС + ВС.
ЗАМЕЧАНИЕ 26.1. Как известно, произведение двух отличных от
нуля чисел не равно нулю. Для матриц подобное обстоятельство может
и не иметь место, т. е. произведение двух не нулевых матриц может
оказаться равным нуль-матрице.
Пример 26.4. Умножить матрицу А = ( 1 - ) на матрицу
-(л -О
Решение:
«-(НМЛ лих х)
26.3. Определители второго порядка и их: свойства.
Рассмотрим матрицу
__ ( «и «12 \
\ «21 «22 /
Определение 26.7. Определителем (или детерминантом) второго
порядка, соответствующим данной матрице, называется число «п«22 ~
«2i«i2« Определитель обозначают символом
(26.4) Ш =
«11 «12
«21 «22
26. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
307
Таким образом, определитель второго порядка можно вычислить
(раскрыть) по формуле:
(26,5)
L4h
~ ^llfl22 — «21«12
«11 «12
«21 л22
Числа «il, «127 «2ь «22 называются элементами определителя.
Пример 26.5. Вычислить определитель матрицы
Решение:
(з-<)
2 5
3 -4
= 2 • (-4) - 5 • 3 = -23.
Приведем свойства определителя второго порядка.
• Определитель не изменится, если его строки поменять местами с
соответствующими столбцами, т. е.
«И «12
«21 Л22
«11 л21
Д12 «22
в При перестановке двух строк (или столбцов) определитель изменит
знак на противоположный, сохраняя абсолютную величину, т. е.
an «12
«21 «22
«21 а22
«11 «12
• Определитель с двумя одинаковыми строками (или столбцами)
равен нулю.
л Общий множитель всех элементов строки (или столбца) можно
вынести за знак определителя:
£«12
«и
«21 fcd22
**k
«И
«21
«12
«22
в Если все элементы какой-либо строки (ил% столбца) равны нулю,
то определитель равен нулю.
о Если к элементам какой-либо строки (или столбца) определителя
прибавить соответствующие элементы другой строки (или
столбца), умноженные на одно и то же число, то определитель не изменит
своей величины, т. е.
ац -+- Л«12 «12 _ «11 «12
«21 + А«22 «22 I «21 а22
Все перечисленные свойства доказываются непосредственно раскрытием
определителя.

308
26. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
26.4. Определители высших пороков.
Рассмотрим квадратную матрицу
(26.6)
Л-
ап
«21
«12
«22
а2п
«nl «п2
/
Определение 26.8. Определителем (или детерминантом) высшего
порядка, соответствующим данной квадратной матрице, называют
число, получаемое из элементов матрицы А по определенному закону —
закону раскрытия определителя.
Это число обозначается
(26.7)
И|
«п
«21
ani
«12 ••
«22 '
««2 ' '
ttin
' «2п
«?т
Прежде, чем формулировать закон раскрытия определителей высшего
порядка, введем понятие минора и алгебраического дополнения.
Определение 26.0. Минором, соответствующим данному
элементу определителя п го порядка, называется определитель (п — 1)-го
порядка, полученный из данного вычеркиванием строки и столбца, на
пересечении которых стоит данный элемент.
Миноры будем обозначать заглавными буквами Мц с двумя
индексами. Так, например, минор Mis, соответствующий элементу л12 определи-
а2\ «23 ' " * «2л
теля (26.7), есть определитель М12 =
«31 «33
«Зп
. Он получает-
«nl «пЗ ' ' апп
ся, если вычеркнуть в определителе /г-го дорядка первую строку и второй
столбец.
Определение 26.10. Алгебраическим дополнением элемента
определителя называется его минор, взятый со знаком плюс, если сумма
номеров строки и столбца, в которых стоит, -мслент, четна, и со знаком
минус, если эта сумма нечетна.
Алгебраическое дополнение элемента ai3 обозначается через Л^. Здесь
г означает номер строки, a j - номер столбца, на пересечении которых
находится данный элемент.
26. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОМ АЛГЕБРЫ
309
Связь между алгебраическим дополнением элемента и его минором
выражается следующим равенством:
(26.8) ^ = (-1)'>'М„.
Например: Ап = (-1)1+1Мц - АГп; А12 = (~1)1+2А/12 - -М12.
В этом случае закон раскрытия определителей можно записать
следующим образом:
л
(26-9) |i4| = ^\cLijAij для любых г
i=i
или
(26.10)
\А\ — ^2 aijAij Дл* любых j.
Приведенная выше для раскрытия определителей второго порядка
формула (26.5) является частным случаем указанных формул (26.9) и (26.10).
Этот результат можно сформулировать следующим образом.
Определитель п - о порядка равен сумме попарных произведений
элементов какой-либо его строки (или столбца) на их алгебраические до-
полнения.
Так как согласно определениям 26.9 и 26.10 алгебраическое дополнение
любого элемента определителя п - о порядка является определителем п — 1
- о порядка, из формул (26.9) и (26.10) следует, что любой определитель
п - о порядка сводится к сумме п определителей п — 1 - о порядка.
В качестве примера использования формул (26.9) и (26.10) приведем
формулы разложения определителя третьего порядка
(26.11)
И| =
ап
(221
«31
«12 «13
«22 «23
«32 «33
по элементам первой строки |Л| = оцЛц + а^Аи + «i3^i35 и элементам
второго столбца |Л| = auAi2 4- ^22^22 4- 032^32-
Пример 26.6. Вычислить определитель третьего порядка
I -1 -2 -10
(26.12) \А\ = 1 9 10
j 1 2 0
Решение: Воспользуемся формулой (26.9) и раскроем определитель
(26.12), например, по элементам третьей строки (i = 3) :
(26.13) \А\ = a3ii43i -f «32^32 4 ^зз^зз-

310
26. ЛЕКЦИЯ ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Предварительно вычислим алгебраические дополнения, входящие в
формулу (26.13)
An = (-1)3+1Мз1 - 1
Л32 = (~1)3+2М32 - -1
Лзз = (-1)3+3Мзз = 1
-2 -10
9 10
-1 -10
1 10
= (-2)10 - 9(-10) = -20 4- 90 = 70;
Ч(-1)10-1(-10)] = 0;
-1 -2
1 9
= (-1)9-1(-2) = -9 + 2 = -7.
Подставим полученные числовые значения алгебраических дополнений в
формулу
(26Л3) и вычислим определитель
|А| = 1-70 + 2.0 + 0-7 = 70.
Замечание 26.2. Рекомендуется раскрывать определители по
элементам той строки или того столбца, которые содержат нулевые эле-
менты, т.к. это значительно сокращает процесс вычислений.
Укажем еще одно важное свойство определителя высшего порядка.
Сумма произведений элементов какой-либо строки (или столбца)
определителя на алгебраические дополнения соответствующих элементов
другой строки (или столбца) равна кулю. Так, для определителя третьего
порядка можно записать
«11^21 + «12^22 + «13^23 = 0;
«12-^11 + «22^21 + «32^31 = 0.
Проверим, например, первое равенство. Используя связь между
алгебраическими дополнениями и минорами и определение минора элемента
определителя, можем написать:
«п^21 + «12^22 + «13^23 = «n(-M2i) + о19М22 + а13(-М23) =
-«11 •
а>п «13
азг «зз
+ «12 '
«11 «13
«31 «33
-«13
«11 «12
«31 «32
- -aii(ai2a33 - а1з«зг) +«1г(«п«зз - «i3«3i) - «1з(«и«32 — «i2«3i) =
= -~«Па12азз + «11<&13«32 + «12«И«33 — «12«13«31 ~ «13«11«32 + «13«12«31 = б.
Все свойства, перечисленные выше для определителей второго
порядка, остаются справедливыми и для определителей высших порядков и
могут быть использованы для того, чтобы в какой-либо строке ( или столбце
) все элементы, кроме одного, сделать равными нулю.
26. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 311
Покажем это на примере вычисления определителя (26.12):
I -1 -2 -10 I
\А\ = 1 9 10 из примера 26.6. Решение: Прибавим к эле-
I 1 2 О J
ментам первой строки элементы третьей строки и вычтем из элементов
второй строки элементы третьей строки
I 0 0 —10
|Л| = 0 7 Ю
J 1 2 0
Теперь раскроем полученный определитель по элементам первого столбца
и запишем результат, известный из решения примера 266-
0 -10
\А\ = апАп + a2i-A2l + апА31 = 1
10
= 70.
Таким образом мы можем сформулировать общее правило, согласно
которому любой определитель п - о порядка может быть сведен к
одному определителю п — 1 - о порядка. Вычисление определителей часто
удобнее и быстрее проводить^ пользуясь этим правилом,
26. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ
ЛИНЕЙНОЙ АЛГЕБРЫ
Пример 26.1. Найти сумму матриц;
/ 1 5 3\
А~\ 2 -10 и В =
V-l 2 2/
Решение: Для того чтобы найти сумму матриц, необходимо
сложить элементы этих матриц с одинаковыми индексами; су = оу + by.
/ 1+3 5+2 3+4\ / 4 7 7 \
С = А + В=\ 2 + 2 -1 + 3 0-2 = 4 2 -2 .
\-1+4 2+0 2+2} \3 2 4 /
Пример 26.2. Найти матрицу D=2A +SB, если
"-(Si).-(i-'O-
Решение; Имеем С — а • А => с^ = &■ а^.
«-' -(:;)=(2 ?)■«=•• 0-30U-\5o)

312 26. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Пример 26.3. Найти произведение матриц А- В и В • А.
Решение; Как показано выше в лекции, элемент матрицы-
произведения, стоящий в г-й строке и j-u столбце, равен сумме
произведений соответственных элементов г-й строки первой матрицы-сомножителя
и элементов j»ro столбца второй матрицы-сомножителя.
(~1)+0-2 20 + 4-2 + 01 \
1)А-В=\ 2-2 + 0 1+4-3 2-1+0 (1) + 4-2 2-Q + 0-2 + 4-1 1 =
(-1)4-3.2 10 + 2-2 + 3-1 /
2-0 + 1-4 + 0-3
2)В.А= | 1.2 + (-1).2+2-1 1 4+(-1)-С+ 2-2 I 0 + (-1) < 4 + 2 .
3-0 + 2-4 + 1.3
)■
/634
= 282
\ 11 14 11
В результате мы еще раз убедились, что произведение матриц не
подчиняется переместите л ьному закону, т.е. А В ^ В А,
ПРИМЕР 26.4. Найти произведение матриц
(
л / 2 -1 3 5 \ _
А=\А О 1 2)>В =
-2 1
-1 5
4 0
3 1
0
-2
1
-1
Решение: Напомним, что о произведении двух прямоугольных
матриц можно говорить только в случае, когда число столбцов первой
матрицы, стоящей в произведении, равно числу строк второй матрицы.
В данном примере это условие выполняется: число столбцов матрицы А
равно 4, число строк матрицы В также 4. Выполним умножение матриц:
А Я^ ( 2-(-2) + Ь(-1) + 3 4+5-3 2-1 + (-1) - 5 4-3 • 0 + 5 ■ 1
\ 4-(-2)+0-(-1) + 1 4+ -2-3 4-1 + 0-5 + Ь0 + 2.1
26. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 313
2-0+(-1)-(-2) + 3 <1 + 5'(-1) \ _ / 24 2 0 \
4-04-0-(-2) + Ы + 2.(-1) / \2 6 -i )
Как мы видим, число строк матрицы-произведения равно числу строк
матрицы-множимого, а число столбцов матрицы-произведения равно
числу столбцов матрицы-множителя. Легко убедиться в том, что найти
произведение В А в данном случае невозможно.
Пример 26.5. Найти миноры М13, М%2 и алгебраические дополнения
Л\3у Ам> матрицы
(2-10
-12 3
4 1 3
Решение: Минор с соответствующим номером ij является
определителем, получающимся из данной матрицы путем вычеркивания г-й
строки и j-vo столбца. Алгебраическое дополнение Ац — (~1)1+«*Му.
Mi
13
-1
4
-Ы -4-2 = -1-8 = -9.
^13 = (-1)1+3М13 = (-1)4-(-9) = -9.
М32 =
2 0
-1 3
= 2-3-(-1)-0 = 6.
АЪ2 = (-1)3+2М32 - (-1)5 • 6 = -6.
ПРИМЕР 26.6, Вычислить определитель третьего порядка
5
0
7
6
1
4
3
0
5
Решение: Целесообразно раскрывать данный определитель по
элементам второй строки, т.е.
\А\ = 021^21 + 022^22 + «23-^23 = —«21^21 + «22^22 _ «23^23 =
= 0-
6 3
4 5
5 3
7 5
+ 1
5 3
7 5
5 6
7 4
-0-
= 5-5-3-7 = 25-21 = 4.

ЗЦ 26. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Пример 26.7. Вычислить определитель четвертого порядка
4 2 14
1 -2 О 3
-2-3 2 1
3 2 0 1
Решение: Данный определитель целесообразно раскрыть по
элементам третьего столбца, т.е.
\А\ = аггАп + аззАзз + ^зз^зз 4- а^А^г = 1 • Аи 4- 0 • Лз + 2 • Л33 + 0 - Л43 «
= Ли 4- 2Л33 = М13 4- 2М35.
Вычислим миноры М\% и Мзз раскрывая определители по элементам
первой строки;
М13 =
1 -2 3
-2 -3 1
3 2 1
= 1-
-3 1
2 1
- (-2) ■
-2 1
3 1
4-3-
-2 -3
3 2
= 1(-3 -1-2.1)+- 2(~2 1-3-1)4- 3(-2 • 2 - 3 • (-3)) = -5 - 10 + 15 = 0.
М33 =
4
1
3
2 4
-2 3
2 1
= 4-
-2 -3
2 1
1 3
3 1
44-
1 -2
3 2
= 4(-2 • 1 - 2 - 3) - 2(1 -1 - 3 • 3) + 4(1 • 2 - 3 • (-2)) = -32 + 16 + 32 = 16
В итоге \А\ = Mis + 2М33 = 0 + 2 • 16 = 32.
Вычислим теперь данный определитель по правилу,
сформулированным в конце лекции.
© Прибавим к элементам третьей строки соответствующие элементы
первой строки, умноженные на —2 :
\А\:
4 2 14
1-203
-10 -7 0 -7
3 2 0 1
© Раскроем этот определитель по элементам третьего столбца:
И| = 1 • (-1)
1+3
1 -2
-10 -7
3 2
i -2 3
-10 -7 ~7
3 2 1
20, ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 315
В полученном определителе прибавим к элементам второго и
третьего столбцов элементы первого столбца, умноженные
соответственно на 2 н —3 :
\А\
1 0 0
-10 -27 23
3 8-8
• Раскроем полученный определитель по элементам первой строки:
W = i-(-i)1+l
-27 23
8 -8
= 8
Пример 26.8. Решить уравнение
0-15
3 4 7
х х 8
-27 23
1 -1
12.
8(27 - 23) = 32.
Решение: Разложим определитель по элементам первой
строки и получим уравнение первого порядка относительно х,'решая которое
можно найти неизвестное х.
0
4 7
х 8
(-!)■
3 7
х 8
+ 5
=> 24 - 12х = 12
3 4
х х
12 => 24 - 7х + 5(3* - Ах) » 12
Самостоятельная работа
Пример 26.9. Найти сумму матриц:
*-(л;)'л=0!)-
/5 8 4\
Пример 26.10. Дана матрица А = I 3 2 5 A*ukj/jo матрицу В
\ 7 б 0 /
нужно прибавить к матрице А, чтобы получить единичную матрицу
третьего порядка?
Пример 26.11. Найти матрицу D = ЪА + ЬЕ, если Е - единичная
I 1 1 а\
мат/года третьего порлдка7 А ~ I 0 1 4 | .
1-12 3/

316
27. ЛЕКЦИЯ ~ ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
( 1 1 2 \
Пример 26.12. Найти А2, если Л = ( 1 3 1 I .
Пример 26.13. Найти произведение матриц А В.
/1 3 2\ /2\
А - 2 0 4 , В = 1 .
V1 2 О/ VS/
Пример 26.14. Найти миноры Мц, М22 и алгебраические дополнения
Ац, Ац матрицы
I 1 3 1\
Л= -2 -1 2 .
V О 1 8 У
Пример 26.15. Вычислить определитель третьего порядка
и =
1 О 4
-2 2 3
1 О 5
Пример 26.16. Вычислить определитель четвертого порядка
И1 =
3 2 12
О 2 3 0
-2-3 2 1
4 12 4
Пример 26.17. Решить уравнение
1 1 О
4 ж 6
Ъх 1 4
= 2.
27. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Ранг матрицы, элементарные преобразования матриц, обратная
матрица.
27. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
317
27.1. Ранг матрицы. Рассмотрим прямоугольную матрицу
/ «и аи • • • он» ... oi„ \
a2i
(27.1)
Ol2
ац а«
\ ttml flm2
«21:
Ott
GmJb
«2n
имеющую m строк и п столбцов. Выделим в этой матрице произвольные А;
строк и к столбцов. Элементы, стоящие на пересечении выделенных строк
и столбцов, образуют квадратную матрицу порядка к.
Напомним, что минором fc-ro порядка матрицы А называется
определитель квадратной матрицы, получающийся из данной матрицы
выделением произвольных А; строк и к столбцов.
Например, для матрицы
А =
2 3 4 5
0-231
0 2 2 4
ка является определитель
, полученный выделением первой,
имеющей три строки и четыре столбца, одним из миноров третьего поряд-
'2 3 4"
0 -2 3
0 2 2
второй и третьей строк и первого, второго и третьего столбцов матрицы
А. Минором второго порядка является, например, определитель ^ о
Сами элементы матрицы можно рассматривать как миноры первого
порядка. Некоторые из миноров матрицы могут быть равны нулю, другие
— отличны от нуля.
Определение 27.1. Рангом матрицы называется наибольший из
порядков отличных от нуля ее миноров.
Если ранг матрицы А равен г, то это означает, что в матрице А
имеется хотя бы один отличный от нуля минор порядка г, но всякий минор
порядка, большего чем г, равен нулю. Ранг матрицы А будем обозначать
символом г (А).
Рассмотрим матрицу
Л =
1
0
0
0
2
1
0
-1
5 3 \
7 4
0 0
00/

318
27. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Единственный минор четвертого лорядка
1
0
0
0
2
1
0
-1
5
7
0
0
3
4
0
0
= 0
как определитель, все элементы одной та строк которого равны нулю.
Один из миноров третьего порядка отличен от нуля, например
1 2 5,
7^0. Следовательно, ранг данной матрицы равен 3,
Ми =
0 1
0 -1
т.е. г(А) = 3.
27.2. Элементарные преобразования матриц. При определении
ранга матрицы, как правило, приходится вычислять большое число
определителей. Чтобы облегчить этот процесс, применяют специальные
приемы. Прежде чем излагать эти приемы, введем понятие об элементарных
преобразованиях матрицы.
Элементарными называются следующие преобразования;
• умножение всех элементов какой-либо строки (столбца) матрицы на
одно и тоже число, отличное от нуля;
о прибавление к элементам какой-либо строки (столбца) матрицы
соответствующих элементов другой строки (столбца), умноженных на
одно и тоже число;
о перемена местами строк (столбцов) матрицы;
• отбрасывание строк (столбцов) матрицы, все элементы которых
равны нулю.
Матрицы, получающиеся одна из другой при элементарных
преобразованиях, называются эквивалентными. Эквивалентные матрицы, вообще
говоря, не равны друг другу, но, как можно доказать, ранги
эквивалентных матриц равны. Этим обстоятельством пользуются при вычислении
ранга матрицы.
Пример 27.1. Вычислить ранг матрицы
/2 3 5-3-2
Л= 3 4 3-1-3
V 5 6 -1 3 -5
27. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
319
Решение: Разделив элементы первой строки на 2, получим
эквивалентную матрицу
/ 1 Z/2 5/2 -3/2 -1 \
Ах = 3 4 3 -1 -3 .
\5 6-1 3 -5 /
Вычитая из второй и третьей строк матрицы А\ первую строку,
умноженную соответственно на 3 и 5, получим матрицу
/ 1 3/2 5/2 -3/2 -1 \
Л2= 0 -1/2 -9/2 7/2 0 I .
\ 0 -3/2 -27/2 21/2 0 /
Вычитая из третьей строки матрицы А2 вторую строку, умноженную на
3, получим матрицу
/ 1 3/2 5/2 -3/2 -1 \
Л3 - 0 -1/2 -9/2 7/2 0 1 .
\0 0 0 0 0/
Отбрасывая в матрице А% строку, состоящую из нулей, получаем матрицу
А _ / 1 3/2 5/2 -3/2 -1 \
Ла ~ \ 0 -1/2 -9/2 7/2 0 J
ранг которой равен, очевидно, двум. Следовательно, ранг данной матрицы
А также равен двум, т.е. г (а) = 2.
27.3. Обратная матрица. Рассмотрим так называемую обратную
матрицу, понятие которой вводится только для квадратной матрицы.
Определение 27.2. Если А — квадратная матрица, то обратной
для нее матрицей называется матрица, обозначаемая А~~х и
удовлетворяющая условию
(27.2) АА~* = Е.
Можно доказать, что матрицы А и А"1 являются коммутативными*.
А-1 А = Е.
Приведем теперь следующую основную теорему.
ТЕОРЕМА 27.1. (об обратной матрице). Для того чтобы квадрат-
пая матрица А имела обратную, необходимо и достаточно, чтобы
матрица А была невырожденной, т.е. чтобы ее определитель был отличен
от нуля.

320
27. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Доказательство. Необходимость. Предположим, что для матрицы А
существует обратная матрица Л~\ Покажем, что в этом случае матрица
А должна быть невырожденной, т.е. ее определитель \А\ ф 0.
Действительно, если бы \А\ = 0, то определитель произведения
\АА'
Ицл-^о.
Но это невозможно в силу того, что |ЛЛ_1| = \Е\ = 1.
Достаточность. Для простоты проведем доказательство для случая
матрицы третьего порядка. Пусть
А =
невырожденная матрица, т.е. ее определитель
И1
«И «12 ft13
^21 ^22 ^23
ft31 «32 «33
7^0.
Покажем, что в этом случае существует обратная матрица.
В самом деле, пусть Ац — алгебраическое дополнение элемента ау.
Матрица Л"1, обратная матрице Л, получается следующим образом.
• Составим матрицу В, заменяя в матрице А каждый ее элемент ац
его алгебраическим дополнением Ац, деленным на определитель \А\
матрицы А:
В =
Лп/\А\
А21/\А\
АЛ1/\А\
А12/\А\
А22/\А\
Ап/\А\
Ли/\А\
Ак/\А\
Аы/\А\
Образуем матрицу
к матрице В. Имеем
В7
транспонированную по отношению
в1
(Ап
= I An
\Аа,
1\А\
1\А\
1\А\
Ап1\А\
Ап!\А\
Ani\A\
Ап/\А\
4и/И|
Л33/\А\
Покажем, что матрица Вт,
го составим произведение
•т __
является обрг-гной матрице Л. Для это-
АВЛ =
Ап/\Л\
Лх2/\А\
Аи/\А\
Лп/\А\
А22/\Л\
Ап/\А\
A*if\A\ \
Аы!\А\ =
Аю/\А\ I
21. ЛЕКЦИЙ ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
821
\А\
ааМиЧчиаДт-ЬадяДи
ш
а).\Ау1+9'.}?Лп+а1лЛ'л% ttl I Аяг +а\цАл*+Ал я Алл
3
yAii +ь-кАгг +a*sA™ аъ\ A&i +амАм+амАяя
- Й
«ai Mi -ьдаа^22+ааз^88 «m^ai+032^32+033^33
1 0 0
■ 10 1 0|=15,
0 0 1
т.к. числители элементов на главной диагонали равны \А\
(раскрытие определителя по элементам строки), а числители всех
остальных элементов равны нулю (сумма произведений элементов одной
строки (столбца) на алгебраические дополнения другой строки
(столбца) равна нулю).
Таким образом, АВТ = £, откуда Вт = Л*"1. Итак,
\А\ \А\ Ш
ft Р Р
А\з Ml £21
\А\ W \А\
Следовательно, обратная матрица существует.
(3 2 2\
1 3 1 ) - Найти обратную
5 3 а)
матрицу.
Решение: Вычислим определитель матрицы Л
3 2 2
\А\ = I 1 3 1
5 3 4
= 27 + 2 - 24 = 5.
Находим алгебраические дополнения элементов этого определителя по
формулам Aij = (-l)'+i • Miji
I о о I I о о I
= -4,
= -1,
= 7.
An =
3
3
4l2 = -
^13 =
1
4
1 l
5 4
1 3
5 3
= 9, Л2, = -
= 1, A22 =
= -12,i4» =
Следовательно,
A~* =
2
3
2
4
3 2
5 4
~"
=
-2, Лз1 -
= 2, Л32 = -
3 2
5 3
= 1, Лзз =
/9 -.2-4\
I 1 Л \
l -Si I f
\
5
5
5 /
2 2
3 1
3 2
1 1
1 3 2
1 l 3

322 27. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
27. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ
ЛИНЕЙНОЙ АЛГЕБРЫ
ПРИМЕР 27.1. Определишь ранг матрицы
/12 3 4 \
А= 2 4 6 8 .
\ 3 б 9 12 )
Решение: Все миноры второго и третьего порядка данной матрицы
равны нулю, так как элементы строк этих миноров пропорциональны.
Миноры же первого порядка (сами элементы матрицы) отличны от нуля.
Следовательно, ранг матрицы равен г (А) = 1.
Пример 27.2. Определить раиг матрицы
/3 5 7\
П. = j JL ь О | .
V1 з ь)
Решение: Совершим элементарные преобразования матрицы.
Элементарные преобразования матрицы не меняют ее ранга, но существенно
сокращают объем вычислений. Цель использования элементарных
преобразований — получить строку (столбец) матрицы, целиком состоящую
из нулей. Для дальнейших исследований такую строку (столбец) можно
вычеркнуть.
в» Сложим соответствующие элементы 1-й и 3-й строк, поместив
результат в первую строку:
(3 5 7 \ /3 + 15 + 37 + 5\ /4 8 12\
1231-1 2 3=1231.
135/ \ 1 3 5/ \ 1 3 5 /
е Разделим на 4 (умножим на ~) элементы 1-й строки
(3 5 7\ /12 3
12 3 - 12 3
13 5/ \ 1 3 5
• Из элементов 1-й строки вычтем соответствующие элементы 2-й
строки и результат поместим в первой строке:
27. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 323
© Вычеркнем первую строку, содержащую элементы, все равные нулю
/357
12 3
V 1 3 5
j - (Л!)-
Ранг последней матрицы равен 2, так как, например, минор
1 2 I
^=3-2 = 1^0. Следовательно, и ранг исходной матрицы
равен 2.
Пример 27,3. Найти ранг матрицы
2-431
1-2 1-4
0 1-13
4-7 4-4
А~
Решение: Совершим элементарные преобразования матрицы.
е Переставим первую и вторую строки матрицы местами!
2-4 3 1 0 \ /1-21-42
1-21-42 2-43 10
0 1-13 1 ~ 0 1-13 1
4-74-45/ \ 4 -7 4 -4 5
В левом верхнем углу матрицы теперь стоит единица. С ее помощью
легко обратить в нуль все элементы первого столбца ниже главной
диагонали. Для этого, прибавим последовательно, ко 2-й строке 1-ю,
умноженную на (-2), к четвертой первую, умноженную на, (-4). В
результате получим
Переставим вторую я третью строки последней матрицы местами
А~
<? Проделаем с последней матрицей элементарные преобразования,
аналогичные второму пункту, чтобы образовать нули во втором
столбце ниже главной диагонали. Для этого из четвертой строки этой

824 27. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
матрицы вычтем вторую.
/1-2 1 4 -2 \
А 10 1-13 1
А ~ 0 0 19-4
\ 0 0 19-4/
• Из четвертой строки вычитаем третью и вычеркиваем четвертую
нулевую строку
1-214-2
0 1 =1 Я 1
А~
( 1 -2 1 4 -2 \
0 0 О О О I \° ° ' 9 "4/
• Ранг последней матрицы равен 3, т.к. больше трех он быть не
может, а отличный от нуля минор 3-то порядка существует, например,
минор, составленный из трех первых столбцов:
-2 1
М =
1
0 1
О О
-1
1
= 1
-1
1
= 1^0.
Следовательно, ранг исходной матрицы также будет равен 3.
Пример 27.4. Найти матрицу, обратную матрице
Решение: Определитель этой матрицы |Л| =
1 2
3 2
0 1
= -9.
Так как \А\ ф 0, то матрица А-невырожденная, и, следовательно,
существует обратная ей матрица.
Вычисляем алгебраические дополнения:
l+i
Аи - (-1)
Ап = (~1)2+1
2 1
1 2
= 3, .
Лз = (-1)ИЗ
2 0
1 2
42
3 2
0 1
= -4,
(-1)1+2
= 3.
А22 = (-1)2+2
3 1
0 2
1 0
0 2
= 2,
27. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ №
А23 = (-1)5+3
1 2
О 1
-1.
2 0
2 1
An = (~l)3+l
ЛМ = (-1)3+3
Составляем матрицу
= 2, Л32 = (-1)3+г
-4.
1 0
3 1
-1,
1 2
3 2
(-3/9 6/9 -3/9
4/9 -2/9 1/9
-2/9 1/9 4/9
Меняем местами строки и столбцы в этой матрице, получим матрицу
/ -1/3 4/9 -2/9 \
Л"1 - 2/3 -2/9 1/9 .
V -1/3 1/9 4/9 /
Самостоятельная работа
Пример 27.5. Определить ранг матрицы
(10 0 0 5 \
0 0 0 0 0 .
2 0 0 0 11 /
ПРИМЕР 27.6- Определить ранг матрицы
/ 4 3 2 2 \
А= 0 2 1 1 I .
\0 0 3 3 /
ПРИМЕР 27.7. Определить ранг матрицы
( 1 2 3 6 \
А= 2 3 1 6 I .
\ 3 1 2 6 /
ПРИМЕР 27.8. Определить ранг матрицы
/ 0 2 0 0 \
А= 1 0 0 4 .
\ 0 0 3 0 /
Пример 27.9. Найти матрицу, обратную данной
( 10 20 -30 \
А = 0 10 20 .
\ 0 0 10 /

326
28. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
ПРИМЕР 27.10. Найти матрицу, обратную данной
/1 2 2 \
А = 2 1 -2
\2 -2 1 )
28. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
I Система линейных уравнений, теорема Кронекера-Капелли,
решение системы уравнений матричным способом, формулы Крамера,
метод Гаусса. |
28.1. Система линейных уравнений.
Рассмотрим систему т линейных алгебраических уравнений с п
неизвестными Хх,Х2,--">хп:
( ацх\ 4- аих2 + • • • + аъкхк Ч h o>inxn = С\
a2iXi -У апХч Л У a>2kXk Н У о>2пХп — Ъ
ацХ\ -У ацХг Л Ь OikXk Н У <*inXn = с%
\ ат\Хх -У ат2Х2 Н У dmkXk Н У о,тпхп ~ ст
Здесь первый индекс в обозначении коэффициента а^ означает номер
уравнения, а второй номер неизвестного. Каждая неизвестная обозначена
одной буквой х с индексом, означающим ее номер.
Система линейных уравнений называется совместной, если она имеет
решение, и несовместной, если она не имеет решений.
Совместная система линейных уравнений называется определенной,
если она имеет единственное решение, и неопределенной, если она имеет
бесчисленное множество решений.
Две совместные системы уравнений называются равносильными, если
каждое решение первой системы является решением второй и, обратно,
каждое решение второй системы является решением первой.
Можно доказать, что следующие преобразования переводят систему
уравнений в равносильную ей:
• перемена местами двух любых уравнений;
в умножение обеих частей любого из уравнений на произвольное
число, отличное от нуля;
• прибавление к обеим частям одного из уравнений системы соотвест-
вующих частей другого уравнения, умноженных на любое
действительное число.
28. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
327
Эти преобразования, по аналогии с элементарными преобразованими
матрид, будем называть элементарными.
Возможно, что после нескольких таких преобразований в системе
появится уравнение, все коэффициенты которого и свободный член равны
нулю. Поскольку такому уравнению удовлетворяют любые значения
неизвестных, оно может быть отброшено. В этом случае мы получим
систему, равносильную данной и содержащую на одно уравнение меньше, чем
данная система.
Если в результате применения элементарных преобразований в
системе появится уравнение, в котором все коэффициенты левой части равны
нулю, а свободный член отличен от нуля, то это указывает на то, что
уравнение не удовлетворяет никаким значениям неизвестных и,
следовательно, полученная система несовместна. Поэтому несовместной является
и первоначальная система.
Если обозначить через А матрицу, составленную из коэффициентов
при неизвестных (28.1);
(28,2)
4-
ап аи ... аш
an ait ... atn
amlam2 • • • amn
Через X-матрицу-столбец, составленную из неивестных
(28.3)
Х =
( хх
I х2
\ Хп
Через С-матрицу-столбец, составленную из свободных членов
(23-4)
С-
Cl
^2
\ С„
Произведение А • X есть матрица -столбец

28. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
(28.5)
ЛХ =
/ anxi + ai2x2 + Ь аыхп \
а21Жх 4- аг2Ж2 Н h а2пжя
а^Да 4- a»2^2 -I Ь a>inXn
\ flml^l +• ttm2^2 H h flmn^n /
Тогда система линейных уравнений может быть записана в матричном
виде
(28.6)
АХ-С.
28.2. Теорема Кронекера-Капелли. (Теорема существования
решения системы линейных уравнений).
Часто бывает важно дать ответ на вопрос о совместности или
несовместности системы линейных алгебраических уравнений, не находя самих
решений. Ответ на этот вопрос дает следующая теорема.
ТЕОРЕМА 28-1. (Теорема Кронекера-Капелли)
Дам того чтобы система линейных уравнений была совместной,
необходимо и достаточно чтобы ранг матрицы системы
(28.7)
j4 =
/ Gil ^12 ... й\п \
«21 а22
- «2n j
\ • • • (Ътп )
\ a<m\°>m2 •
был равен рангу ее расширенной матрицы
(28.8)
£ =
/ «11 dU
#21 а22
* 0>2п С2
\ 0>т\0чп2 • • • атпст /
т.е. г(А) = г(В).
Расширенная матрица получается из матрицы системы добавлением
столбца, состоящего из свободных членов уравнений системы.
При этом, если ранги матриц А и В равны числу неизвестных, т.е.
г(А) ~ г(В) = п система уравнений имеет единственное решение.
Если же ранги матрицы равны между собой и меньше числа
неизвестных, т.е. г (А) — г (В) < п, то система уравнений имеет бесконечное
множество решений. Теорема приводится без доказательства.
28. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
329
28.3. Решение системы линейных уравнений матричным
методом.
Если число неизвестных системы равно числу уравнений и матрица А
системы невырожденная, т.е. \А\ ф 0, то уравнение А • X — С решается
следующим образом:
а Умножаем обе части уравнения на матрицу А~1, обратную матрице
А:
А"1 - (А - X) - Л"1 - С.
9 Используя сочетательный закон умножения матриц, можно
записать:
о Так как А~1»А — Е, а ЕХ — X, то решение матричного уравнения
получится в виде:
(28.9) X = А"1 - С.
Пример 28.1. Решить матричным способом систему уравнений
i
За?! 4- 2х2 4- 2хъ = 5,
Xi 4- Зж2 4- х3 ss О,
шшется в Bi
Решение: В матричной форме эта система запишется в виде
/ 3 2 2 \ ( хх
АХ = С. Здесь Л » I 1 3 1 ] Х=ж2| С =
\5 3 4/ \х3
Матрица Л*"1 найдена нами в примере 28.2.
/ 9/5 - 2/5
А'1 - 1/5 2/5
\ -12/5 1/5
Решение системы записываем в виде
/ 9/5 - 2/5 •
X = ( 1/5 2/5 ■
\ -12/5 1/5
Отсюда на основании определения равенства матриц следует, что х\ =
1, X2 = —1,^3 = 2. Непосредственной проверкой убеждаемся, что эти
значения неизвестных удовлетворяют данной системе.

330
28. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
28.4. Формулы Крамера.
Рассмотрим еще раз систему п уравнений с а неизвестными А*Х = С,
для которой \А\ ф 0. Запишем матричное равенство (28.9) в следующем
виде:
X ^А~1Х.
Или
(рр-р\
\ frfa-fr J
с\ \ I AnA2i...Ani \
С2 I - JL ^12-^22 • - - Ап2
\л\\
\ AinA2n • • • Ann )
х2
V Хп
/ And + А21С2 + - • • + А
Anci + A22C2 И h Л^п J
\ Alnci 4- A2nC2 4- I- Anncn J
Вспомним, что две матрицы равны, если равны их соответствующие
элементы, т.е.
(28.10)
х* = Щ (AnCl + ^2lC2 + •'•+ Атсп)
Х2 = щ(^1^1 + А22С2 + • • • + ^«2СП)
хп = щМьЛ + Л2|гс2 + h -Anncn)
Обратим внимание на то, что выражения в круглых скобках равенств
(28.10) представляют собой определители, полученные из определителя
системы \А\ заменой соответствующего номеру неизвестного столбца столб
цом свободных членов данной системы уравнений (28.1). Обозначим их
следующим образом:
Ах\ = АцСх 4- A2ic2 H Ь Anicn =
Ciai2 ... aln
C2Q.22 • • • «2п
Сп^п2 • • • ^пп
Ах2 = Auci + Л22С2 + 1- An2cn =
auCi-.-ain
Я21С2• • • a2n
0"fil^n • • • ^nn
И Т.Д.
С учетом этих обозначений формулы (29.10) можно переписать в виде:
28. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
:ш
(28.11)
XI
Ахх __ Аж3 _ Ахп
Формулы (28.11) называются формулами Крамера 12.
Пример 28.2. Решить систему уравнений методом Крамера,
Зхх + 2я2 + 2я3 = 5,
«1 4- Зж2 + я?з = 0,
5xi + Зх2 + 4х3 = 10.
Решение: Ранее определитель системы
I 3 2 2
|v4[ = 1 3 1
I 5 3 4
уже был вычислен: |Л.|=5. Вычислим определители неизвестных:
Д*1 =
ДХ2 =
Д*з =
5 2 2
0 3 1
J 10 3 4
3 5 2 1
1 0 1
5 10 4 1
3 2 5
1 3 0
5 3 10
= 5,
= -5,
= 10.
1ы Крамера, найдемгх] = ~^-
ю _ 9
5 " Z*
_ ft -
— 5 ~
= 1;х2 -
- 4*z —
"" \А\ ~
б Li х3~ |Л|
28.5. Метод Гаусса решения и исследования систем линейных
уравнений (метод последовательного исключения).
Метод Гаусса- метод решения систем линейных уравнений, в которых
число неизвестных может быть либо равно числу уравнений (т ~ га), либо
отлично от него.
Метод Гаусса заключается в следующем. Допустим, что в системе
(28.1) коэффициент при первом неизвестном au -ф 0.
Если an = 0, то всегда можно перенумеровать неизвестные так, чтобы
коэффициент при первом неизвестном стал отличен от нуля.
12G.Крамер (1704-1752) — швейцарский математик.

332 28. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Исключим сначала неизвестное xi из всех уравнений системы, кроме
первого. Для этого прежде всего разделим ибе части первого уравнения на
коэффицент оц Ф 0; тогда получим новую систему, равносильную данной:
(28.12)
*1 + ^*2 +
■ + 2Е** + -
a2xxx + a22#2 + V а2кХк + '
ацХ\ 4 ai2x2 H h aikXk 4-
4 ^^n = ~^S
4- o2„a;„ = c2,
' 4~ 0>inXn — Cii
amiXi 4 am2^2 4 +• <*>mk%k H 1" flmn^n = C„
Умножим теперь первое уравнение системы (28.12) на а2\ и вычтем из
второго уравнения. Затем умножим первое уравнение на аг\ и вычтем из
третьего уравнения и т.д. В результате получим новую систему, также
равносильную данной:
( х\ + а!12х2 -г • ■ • + о!1кхк + - - - + а'1пжп = с\,
а22х2 4 f agft^fc "^ ^ а2
2плп
v2)
1
1
Здесь введены
aik =
a'i2x2 4 • • • 4- %жЛ 4-
а'т2х* 4- •• - 4 а'ткхк 4- ••
обозначения;
а1Л , ttu.
—, aife — a^ ал;
an <Mi
- + a'inxn = c£,
, + л' Г j= C1
t = 2,3,...
,n;
all лп
?,3,...,m.
Разделим теперь второе уравнение системы (28.13) на коэффициент
а22? предполагая, что он отличен от нуля; затем умножим второе
уравнение полученной системы последовательно на а^2,..., а^> • • •»а'т2 и вычтем
поочередно из соответствующих уравнений системы, кроме первого и
второго.
Если, продолжая этот процесс, мы придем к системе, содержащей
уравнение, в котором все коэффициенты левой части равны нулю, а свободный
член отличен от нуля, то эта система несовместна. В том случае, когда
системе совместна, мы придем либо к системе
| хг -г Ьих2 4 • - - 4- Ьхкхк 4 f ЬщХп = Ви
Х2 4 - " 4 &2*Л Н Ь &2л£л = #2,
(28.14)
хр-\- -
Г ирпхп — &р-
28. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
333
(причем р < п), либо к системе
#i 4 ЪыХг ^ h frifez* 4- • • • 4- binXn = 2?i,
(28.15)
я* 4-'
■ 4- teas* 4- ■
x*4--
' 4" fanXn = #2»
' 4" 6jtn^n = Дк,
*n = Bn,
Система вида (28.14) называется ступенчатой, а система вида (28.15)-
треугольной.
В случае треугольной системы из последнего уравнения находим хп =
Вп; затем подставляя значения хп в предыдущее уравнение, находим хп-\
и т.д.
Таким образом, если данная система уравнений (28.1) после
выполнения ряда элементарных преобразований приводит к треугольной системе
(28.15), то это означает, что система (28.1) является совместной и
определенной.
Если же данная система (28.1) после элементарных преобразований
приводится к ступенчатой системе (28.14), то система (28.1) совместна и
неопределенна.
В самом деле, перенося в каждом из уравнений системы (28.14) члены
с неизвестными Яр+ь • • • > хп в правую часть, получим систему вида
xi 4 Ъ\2х2 Л- V bipXp = В\ — &1,р+1
х2-\ ь Ь2рхр = В2 - b2iP+i
binxn
b2nXn
Д, - Ъ
hp+i
-К
Придавая неизвестным Жр+i, ..., ж„, которые называются свободными,
произвольные значения a^+i, atp+2,..., a„, получим треугольную систему,
из которой последовательно найдем все остальные неизвестные
ггр,Хр+х,...,хп. Так как числа Ofp+i,arp+2,• • -,^п могут иметь различные
значения, то исходная система (29.1) имеет бесчисленное множество
решений.
Пример 28.3. Решить систему уравнений методом Гаусса:
{Зхг 4 2х2 + 2ж3 = 5,
х% 4- Зх2 4- яз = 0,
Ьхг 4- Зж2 4- 4ж3 = 10.
Решение: Совершим элементарные преобразования, которые
каждый раз будут приводить нас к равносильной исходной системе уравнений.
© Переставим местами первое и второе уравнения системы для
удобства дальнейших преобразований:

334
28. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
{
XI + Зхй + 23 = О,
За*+ 2*2+ 2*з=* 5,
5xi + Зх2 + 4х3 = Ю-
* Умножим первое уравнение на 3 и вычтем из второго, умножим
первое уравнение на 5 и вычтем из третьего уравнения;
!xi + Зж2 + ж3 = 0,
-12ж2 - ж3 = Ю.
в Разделим второе уравнение последней системы на -7.
!xi + Зх2 + хл = 0,
Х2 + |ж3 = -у1
-12x2 -ж? = 10.
о Умножим второе уравнение этой системы уравнений на 12 и сложим
с третьим уравнением.
Х\ + 3X2 + Х3 = 07
Х2 + 7^3 — -р
7Ж3 — 7 *
Полученная треугольная система является совместной, определенной
и равносильной исходной. Из этой системы последовательно находим:
{
х3 - 2;
1 5 2 5_ 1в
*2 = -7*з-7 = -7~7- *'
Ж1 = -Зх2 - хз = (-3)(-1) -2 = 3-2 = 1.
Прежде, чем перейти к решению других примеров по методу Гаусса,
заметим, что нет неоходимости каждый раз переписывать системы
уравнений. Все преобразования можно проводить над расширенной матрицей
системы (29.8).
Пример 28.4. Решить систему уравнений методом Гаусса
xi + 5х2 + 4х3 + Зх4 = 1,
2xi - х2 + 2х3 - а4 = 0'
5xi +3х2+8х3 + х4 = 1.
28. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
335
Решение; Составим расширенную матрицу системы и выполним
над ней элементарные преобразования, указанные в методе Гаусса
/ 1 5 4 3 1 \
2 Ч 2 -1 О U
\5 3 8 11/
/ 1 5 4 3 1 \ / 1 5 4 3 1 \
-0 11 672-0 11 672-
\ 0 11 6 7 2 / V 0 0000/
1
0
0
5
-11
-22
4
-6
-12
3
-7
-14
1
-2
-4
( 1 5 4 3 1 \
^ \ 0 И 6 7 2 j
Отсюда ранг матрицы Системы равен рангу расширенной матрицы,
т.е. г(А) = г(В) = 2, а количество неизвестных равно 4. Следовательно,
система уравнений имеет бесчисленное множество решений. Последняя
матрица в преобразованиях есть расширенная матрица системы.
{#i + бжз + 4ж3 + Зж4 = 1,
11х2 + 6хз + 7х4 = 2.
Если в качестве базисных неизвестных выбрать, например, хг и ж2?
тогда Свободными неизвестными будут х§ и х\ и систему уравнений МОЖНО
преобразовать к виду
{Xi + 5ж2 = 1 - 4ж$ — Зж4?
2xi - хч — —2хз + Х4.
Применим к решению системы уравнений метод Гаусса. Исключим из
второго уравнения неизвестное х\ (из второго уравнения системы вычтем
первое, умноженное на 2) и получим
{xi + &х2 = 1 — 4х3 - Зх4?
-11ж2 « -2 + бж3 + 7ж4.
откуда после элементарных преобразований следует
Xl = ТТ ~" Лх* "^ ТТ^4»
{
I *! = П ~ П^З - fa*>
Полагая, например, х3 ~ 1,Ж4 ~ 1, получим xi = -1,Х2 ~ —1, т.е.
некоторое частное решение системы уравнений.

336
28. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ -
ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Пример 28.5. Решить систему уравнений методом Гаусса
2xi + *2 4- £з - ^4 = 8,
Зя?1 + 2хъ + 5х4 = 12,
8^1 4- ж2 4- 5#з 4- 3x4 = Ю.
Решение: Составляем расширенную матрицу и выполняем над ее
строками элементарные преобразования:
8\ /1
Полученной матрице соответствует система уравнений
Г>1
+ |ж2 +
\хг
Х2 - *^3
0 • хх 4 0 - ж2 + 0 • ж3 4- 0
- f хл = 0,
-6ж4 = 0,
• Ж4 ~ —««•
Так как последнее уравнение этой системы противоречиво, то она
является несовместной. Следовательно, несовместна и равносильная ей исходная
система уравнений, т.е. она не имеет решения.
28.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ
ЛИНЕЙНОЙ АЛГЕБРЫ
ПРИМЕР 28.1. Решить матричным способом систему уравнений
{х 4- 2у 4 z -- 0,
х 4 Zy + я = 0.
2В. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГКЫГЫ
.V.V7
Решение: Для данной системы
/ 1 2 1\ /0
Л= 2 1 1 ,Я =
Обратная матрица вычисляется по соответствующему правилу,
рассмотренному в предыдущем разделе.
/-2
-1
5
А-г =
Тогда
Х = А~
-1 -3
Ответ: х = 1, у = 0, z =
ПРИМЕР 28.2. Решить систему уравнений методом Крамера.
2х 4- Зу = 7,
4д? - 5?у =5 2.
Решение: Здесь
2 3
4 -5
14 =
= -22,Ал =
7 3
2 -5
= -41, Ая
2 7
4 2
-24.
Так как определитель системы | А\ ф 0, то система имеет единственное
решение, определяемое по формулам:
А,
41
24
\А\ 2ГУ \Л\ 22
12
11'
Пример 28.3. Решить систему уравнений методом Крамера.
2х + Ъу = 3,
4ж 4- Юг/ = 6.
Решение: Здесь
\А\
2 5
4 10
0,Д,
3 5
6 10
= 0,АУ
2 3
4 6
0.
Второе уравнение получается из первого умножением обеих частей
первого уравнения на Л — 2. Поэтому система равносильна одному
уравнению 2х + Ъу = 3 и имеет бесчисленное множество решений. Придавая

338 28. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
3- 5у грак^ например^
произвольные значения неизвестному ?/, найдем х — 2
если у = О, то ж = 3/2; если ?/ - 1? то х — -1, и т. д,
Пример 28.4. Решить систему уравнений методом Крамера.
Ъх + Зу = 7,
10* f 6у - 2.
Решение: Здесь
|А| =
5 3
10 6
= 0,Д* =
7 3
2 6
= 36^0,ДУ =
5 7
10 2
= -60 # 0.
Следовательно, данная система несовместна, т. е. не имеет решений.
В этом убеждаемся и непосредственно. Умножая почленно обе части
первого уравнения на -2 и складывая со вторым уравнением, приходим к
противоречивому равенству 0 = -12.
ПРИМЕР 28.5. Решить систему уравнений методом Крамера,
И1 =
Решение: Здесь
|Л| =
1 2
2 -3
3 1
Ду =
1 2 -1
2 2 2
3 8 1
х 4 2у - z = 2,
2х - Зу 4 2г = 2,
Зж + у + z = 8.
= -8, А,
= -16, А
По <*юпмуяам Крамера находим;
-8
2 -
-3
1
2 2
-3 2
1 8
= -8.
= -24.
— -2
-24
Пример 28.6. Решить систему уравнений методом Гаусса.
{2х\ 4 х2 - *з - 1,
Zxi 4 2*2 - 2ж3 = 1,
xi - *2 + 2х3 = 5.
28. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 339
Решение: Разделив все члены первого уравнения на коэффициент
оц = 2, получаем систему
{xi 4- 0,5^2 - 0,5*з = 0,5,
Зжц + 2ж2 - 2я3 = 1,
*i - *2 + 2*3 - 5.
Сначала умножим все члены первого уравнения полученной системы
на 3 и вычтем из второго уравнения; затем из третьего уравнения вычтем
первое;
{xi + 0,5*2 ~ 0,5х3 = 0,5,
0,5ж2 - 0,5ж3 = -0,5,
-1,5*2+ 2,5а*=4,5.
Разделим все члены второго уравнения на af22 = 0,5:
{rj + 0,5х2 - 0,5х3 = 0,5,
х2 - хг « -1}
-1,5x2 + 2,5x3-4,5.
Умножим второе уравнение на —1,5 и вычтем из третьего. Тогда
получим систему
Xi 4- 0,5*2 - 0,5я?з = 0,5,
^2 - *з ~ -1,
х3 = 3,
из которой последовательно находим
{
х3 = 3, х2 = -1 + 3 = 2, xi = 0,5 - 0,5*2 + 0,5*з = 0,5 - 1 + 1,5 = 1.
Итак, решение треугольной системы, а, следовательно, и равносильной
ей первоначальной, таково: xi = 1; хг - 2; *з — 3. Данная система
является совместной и определенной.
ПРИМЕР 28.7. Решить систему уравнений методом Гаусса.
( хг 4- 2х2 + 4ж3 - ж4 - ЗжБ = 77
^ 2*i 4- *з 4 *5 = 4,
^ *2 + 2*4 - *Л ~ 6.
Решение! Составим расширенную матрицу и выполним над ней
элементарные преобразования, указанные в методе Гаусса!
(1 2 4 -1 -3 7 \ /1 2 4 ~1 -3 7 \
2 0 1 0 14-0-4-7 2 7 -10 I ~
010 2-10/ V 0 1 0 2-1 б/

840 28. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
1 2 4-1-3 7\
0 1 0 2-1 6 1.
0 0-7 10 3 14 /
Здесь мы последовательно провели следующие преобразования:
ф умножили первую строку на 2 и вычли из второй;
• переставили вторую и третью строку;
о к третьей строке прибавили вторую, умноженную на 4.
Последней матрице соответствует ступенчатая система уравнений;
{Xi + 2х2 + 4а:3 ~ х\ ~ %ХЬ = 7;
х2 + 2ж4 — Хъ — 6,
-7x3 + Юх4 + Зх5 = 14,
равносильная данной. Перепишем полученную систему следующим
образом:
!х\ 4- 2x2 + 4хз = 7 -h x4 4- 3 t5l
я2 = 6 - 2ж4 + ж*,
-7х3 — 14 - 10^4 - За?5.
Мы видим, что неизвестные хь х2 и х3 можно выразить через ж4 и ж&:
Жз — — 2 4" у&4 + у #5»
Х2 = 0 — 2X4 4 ^5i
ХХ = 3 - |Ж4 - f#5-
Придавая ж4 и ж5 произвольные значения, получим соответствующие
значения Хи х% и х3. Неизвестные х4 и х5 в этом случае являются
свободными неизвестными, а хь х2 и хъ - базисными.
Таким образом, данная система -- совместная и неопределенная. Ее
решениями, например, служат х5 ~ 0, х4 ■= 07 х$ = -2, я2 = 6, жх = 3 или
х5 = 7, х4 = 7, х3 = 11, х2 = -1, жх = -7 и т. д..
Самостоятельная работа
ПРИМЕР 28.8, Решить матричным способом систему уравнений.
{2х | Зу Н- 2z = 9,
х + 2у - 3js = 14,
Зж f % 4- г - 16.
29. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА W
Пример 28.9. Решить систему уравнений методом Крамера.
{х 4- у 4- z - -2,
* - !/ + 2* = -7,
2*4-Зу-* = 1.
Пример 28.10. Решить систему уравнений методом Крамера.
i
ж — у — js = 5,
2ж 4- у 4- Зхз == 3,
х - 4у - 6л = 7.
ПРИМЕР 28.11. Решить систему уравнений методом Гаусса.
i
2х\ 4- #2 — #з ~ 5,
xi — 2x2 4- 2хз = —5,
7^i 4- *2 - *з = Ю.
Пример 28.12. Решить систему уравнений методом Гаусса.
2х\ 4- д?2 4- #з — хе* ^ ®»
3^! 4- 2хз 4- 5х4 = 12,
Zi - ^2 4- *з = 4,
8^! 4- ^2 4- 5х3 4- За* = 10.
29. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
Векторы, основные определения, линейные операции, проекция и
составляющая вектора по оси.
29.1. Основные определения. При изучении физики, химии и
технических наук встречаются величины, которые полностью определяются
заданием их численных значений — действительных чисел. Такие
величины называются скалярными. Скалярными величинами являются длина,
площадь, объем, масса, температура, валентность и др.
Наряду со скалярными, встречаются величины, для определения
которых необходимо знать их направление в пространстве, например, сила,
скорость, ускорение и т.д. Такие величины называются векторными, они
описываются с помощью векторов.
Определение 29.1. Вектором называется направленный отрезок.

342
29. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
А
Рис. 131. Вектор а
Вектор характеризуется длиной и направлением. Одна из
ограничивающих его точек принимается за начало, вторая — • за конец, который на
рисунке показывается стрелкой (рис. 131).
Если даны начало вектора (точка А) и его конец (точка В), то вектор
обозначается АВ. Будем также обозначать векторы малыми латинскими
буквами с черточкой наверху: а, или жирным шрифтом: а.
Определение 29,2. Модулем вектора а называется его длина.
Модуль вектора обозначается |а|.
Определение 29.3. Нуль-вектором называется вектор, у которого
конец совпадает с началом, он обозначается: 0 или 0.
Очевидно, что |0| = 0. Направление нуль-вектора не определено.
Можно считать, что нуль-вектор имеет любое желаемое в данный момент
направление.
Определение 29.4. Векторы "а иЬ называютсяколлипеарными, если
они расположены на параллельных прямых или на одной прямой. Будем
записывать в этом случае а \\ Ь.
ОПРЕДЕЛЕНИЕ 29.5. Векторы а и b называются сонаправленными,
если они коллинеарны и направлены в одну сторону. Будем обозначать
зто так: a |f b.
Определение 29.6. Векторы а иЬ называются
противонаправленными, если они коллинеарны и направлены в разные стороны. Будем
обозначать зто так: a f 4, b.
Определение 29.7. Векторы а и b называются равными, если они
сонаправлены и имеют одинаковую длину. Будем записывать зто так:
а = 6.
Из последнего определения следует, что вектор можно переносить
параллельно в любую точку пространства, и он от этого не изменится.
Пример 29.1. Для прямоугольника, изображенного на рис. 132, ВС =
AD, ~АВ П CD.
29. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
«ф/
A ~^D
РИС. 132. Коллинеарные векторы
29.2. Линейные операщш; над векторами. Линейными
называются операции сложения, вычитания векторов и умножение вектора на
число.
Определение 29.8. Суммой двух векторов а+Ъ называется вектор,
полученный по правилу "треугольника"; второй вектор b откладывает»
ея так, чтобы его начало совпадало с концом первого вектора а (рис.
133).
Рис. 133. Сумма векторов
Суммой будет являться "замыкающий7' вектор а + 6, начало
которого совпадает с началом первого вектора й, а конец — с концом второго
вектора Ь.
Ту же самую сумму можно получить но правилу "параллелограмма";
второй вектор b откладывается из начала первого вектора а, на этих
векторах строится параллелограмм ( рис. 133) и суммой а -\- 5 в этом случае
является диагональ этого параллелограмма.
Докажите самостоятельно, что сумма двух данных векторов а и 6,
полученная по правилу треугольника, совпадает с суммой, полученной по
правилу параллелограмма.
29.3, Свойства сложения векторов. 1. Коммутативный закон
сложения; а + 6 — 6 + а.
2. Ассоциативный закон сложения: (а + Ь) + с = а + (Ь + с).
3. a + 0 = а.

щ
29. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
Доказательство 1-го свойства следует из рис. 133, а 2-го — из рис. 134.
В силу того, что три вектора можно складывать в любом порядке, эту
сумму записывают без скобок: a+6-f с. Суммой нескольких векторов будет
являться "замыкающий" вектор: если слагаемые векторы расположить
один за другим (конец одного является началом следующего), то суммой
будет вектор с началом в начале первого слагаемого и с концом — в конце?
последнего (рис. 134). Третье свойство докажите самостоятельно.
РИС. 134. Ассоциативный 'закон сложения векторов
ОПРЕДЕЛЕНИЕ 29.9. Противоположным к вектору а называется та-
кой вектор у что его сумма с а равна пуль-вектору
Противоположный к а вектор обозначается —а; а 4- (—а) = 0. Одним
из векторов —а будет, например, такой, что его начало совпадает с концом
вектора а, а конец — с началом а.
Определение 29.10. Разностью двух векторов а—Ъ называется
сумма векторов а и противоположного к Ь: а — Ь — а 4 (—&)•
Очевидно, что (5—6)4-6 — а, т.к. (о—6)4-6 = 54-(—6)4-6 = а+((—6)4-6) =
а + О^а.
Таким образом, если с = а - 6, то а ~ Ь 4 с.
Из определения вытекает правило построения разности векторов а — 6:
строим противоположный к 6 вектор, "переворачивая" его в
противоположную сторону (изменяя его направление на противоположное) и,
откладывая его от конца вектора о, строим сумму векторов и и (-6) (рис. 135).
Если на векторах 5 и 6. отложенных из общей точки О? построить
параллелограмм О АС В ( рис. 136), то вектор ОС, совпадающий с одной
диагональю, равен сумме а 4*_&, а вектор В А, совпадающий с другой
диагональю, равен разности a — 6.
ОПРЕДЕЛЕНИЕ 29.11. Произведением вектора а на действительное
число X называется вектор с, коллипеарпый вектору Ъ, имеющий длину
\с\ ~ |А| • |а| и сонаправленный с а? вели А > 0, и противонаправленный с
а, если А < 0.
29. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
Щ
Рис. 135. Вычитание векторов
А__ С
Рис. 136. Сумма и разность векторов
Пример 29.2. 2а есть вектор, сонаправленный с а и имеющий длину
в два раза больше, чем а, —-а есть вектор, противонаправленный с а
и имеющий длину вдвое меньшую, чем а.
Противоположный вектор —а можно рассматривать как результат
умножения вектора а на число А = — 1: -а — (—1)а.
29.4. Свойства умножения вектора на число. 1.
Коммутативный закон: Аа = а~А.
2. Ассоциативный закон; Xxfaa) = (AiA2)a.
3. Дистрибутивный закон: А(а 4 Ь) = Аа 4 ХЬ.
Доказательства, очевидно, вытекают из определения операций.
Попробуйте провести их самостоятельно.
Теорема 29.1. Два вектора aub коллинеарны тогда и только
тогда, когда b = Ха или а — ХЬ.
Доказательство. Если Ь — Ха или а — А6, то b || а по определению
умножения вектора на число.
Если 5 || а и сгф 0, то b = Ха (по тому же определению). Даже в случае
6 = 0, получаем 0 = 0 • а. Если а = 0, то можно записать, что а = 0 = 0 • Ъ.

846
29. ЛЕКЦИЯ ВЕКТОРНАЯ АЛГЕБРА
ОПРЕДЕЛЕНИЕ 29.12. Единичным называется вектор, длина
которого равна единице*
Пусть дан вектор а. Обозначим через еа единичный вектор, сонаправ-
ленный с а. Из определения умножения вектора на число следует, что:
а — \a\e~a, или
а
(29.1) «« =
3
Заметим, что для каждой числовой оси I определен единичной вектор
ё| с началом в точке О и концом в точке с координатой 1 ( рис. 138).
Определение 29.13. Углом между двумя векторами а иЪ
называется наименьший угол <р, на который нужно повернуть один из них до
совпадения с другим, если эти векторы отложены из одной точки ( рис.
137).
Ъ
Рис. 137. Угол между векторами
Из определения ясно, что угол <р между векторами находится в
пределах: 0 < ф < 7Г.
Определение 29.14. Углом между вектором а и осью I называется
угол между вектором а и единичным вектором оси ех ( рис. 138).
I
Рис. 138. Угол вектора с осью
29. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА 3j7
Определение 29.15. Проекцией точки А на ось I называется точка
пересечения плоскости ос7 проходящей через точку А перпендикулярно I
с осью I ( рис. 139). Проекцией вектора АВ на ось I называется число,
равное разности координат проекций конца и начала:
*\
а ^
*i
Ag
-J*
*2
Рис. 139. Проекция и составляющая вектора по оси
(29.2) ЩАВ = x2-xi.
Заметим, что если угол ip между вектором АВ и осью / острый, как на
рис. 139, то $2 > xi и ILpjAB положительна. Если угол кр тупой, то UptAB
отрицательна. Если АВ ± I (<р = 90°), то UptAB — 0.
ОПРЕДЕЛЕНИЕ 29.16. Составляющей вектора АВ по оси I
называется произведение проекции вектора АВ на ось I на единичный вектор
этой ocue*i.
Составляющая вектора А В по оси I есть вектор, соединяющий
проекцию начала и проекцию конца вектора ( рис. 139)!
(29.3) Сост, Aff = Пр,3# е, = 1^Щ.
29.5. Свойства проекции вектора на ось. 1. Проекция вектора
а на ось I равна модулю вектора л7 умноженному на косинус угла между
вектором и осью;
(29.4) Пр,а = |a|cossP.
Доказательство.
Проекция вектора а на ось / не изменится при любом его параллельном
переносе, поэтому рассмострим случай, когда вектор а отложен от точки
О (рис. 140).
В соответствии с формулой (29.2) Пр,а = x-Q = х* Из прямоугольного
&OBBi i cos^ = iff, откуда ж — |a| cos tp, т.е. Пр/й = |а| cos<p.

348
29. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
РИС. 140. Проекция вектора на <
2. Проекция суммы равна сумме проекций:
(29.5) пР|(а + 5) в ПР^ + Пр'5'1
Доказательство. -=-?*
Пусть -ЖС = 'АВ + Ш( рис. 141). Тогда Пр,АВ = х2 - хи Пр,В6
х3 -х2 ПрДС = а* -а*. Запишем последнюю^роекцию в виде: Пр,ЛС
хз - *i = (*« - *i) + (% " *») = ПР'-4В'+ П*ВС-
Теорема верна для любого числа слагаемых.
РИС. 141. Проекция суммы равна сумме проекций
3. Если вектор умножить на число, то проекция умножается на то же
число, т.е. постоянный множитель можно выносить за знак проекции:
(29.6)
Пр,(Аа) = АПрга.
Доказательство.
Заметим, что если А > 0 и вектор я составляет с осью I угол у, то
вектор Ха также составляет с осью I угол <р. Если же А < 0, то вектор Аа
составит с осью / угол ir — (р.
Для первого случая (Л > 0) получаем; Ир,(Ао) = | Аа| cos tp - |Л||а| cos tp =
ЛПр^а.
Для второго случая (Л < 0) получаем!
SO. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
349
ПрДЛа) — \\a\cos(ir-ip) = |Л||г|сбз(7г-у>) = -A|a|(-cosy?) = A|a|cos<p -
АПрД
4, Проекция разности равна разности проекций.
Действительно: ПрДа-6) = ПрДа-{-(-1)6) « Пр,5-ьПр,(-1)<5 «* Пр^-f
(-1)Прг5=Пр,а-Пр,5.
30. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
Разложение вектора на составляющие, координаты вектора.
Деление отрезка в заданном отношении. Направляющие косинусы
вектора. Условие коллинеарности векторов. Скалярное произведение
векторов.
30.1. Разложение вектора на составляющие по осям
координат. Рассмотрим прямоугольную систему координат в пространстве Oxyz
(рис. 142). На каждой из осей выберем единичный вектор с началом в
точке О и концом в точке с координатой 1. Обозначим г — единичный вектор
по оси Ox, j — по оси Оу, А; — по оси Oz.
РИС. 142. Разложение вектора на составляющие по осям координат
l?l = UI = щ = 1.
Эти три единичных вектора называются ортами, они образуют
декартов ортогональный базис. Рассмотрим вектор а в пространстве. Отложим
его из начала координат О (рис. 142). Через его конец проведем
плоскости, параллельные координатным плоскостям. Получим прямоугольный
параллелепипед, диагональю которого является вектор а.
Из рис. 142 ясно, что:
о = UM = СУР + ТЫ = UP 4-ОМз = (ОМГ+ ОЩ) + Шз.

350
Ж ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
Векторы О Ми ОМъ, ОМз являются составляющими вектора а но осям
координат. В соответствии с формулой (29-3) имеем: ОМ\ — Ир0ха • г,
ОМч = Пр0уа • j, ОМ$ ■= Пр0(га • А;. Обозначив Пр0а.а ~ ах, Пр0уа = %,
Пр0га = az, получаем:
(30.1) а = аж - г + ау • j -+- az - к.
Формула (ЗОЛ) называется разложением вектора на составляющие по
осям координат, ах, ау, az называются прямоугольными декартовыми
координатами вектора а. Координаты вектора будем также записывать в
виде; a ~ (ax;ay'jaz).
ОПРЕДЕЛЕНИЕ 30.1. Радиус-вектором Тм точки М(a,i; а2] а3)
называется вектор ОМс началом в начале координат и концом в данной
точке.
В соответствии с формулой ЗОЛ координаты радиус-вектора
совпадают с координатами точки г~м = ОМ = (аг; а2; аз)-
Рассмотрим теперь вектор АВ, начало которого имеет координаты
А{х\\ У\\ 2i)> & конец — В(х2; уч\ ^2)• Из определения проекции вектора на
ось следует, что Нр0хАВ — х2-хи Пр0уА£? — у2- у и Пр02 ~АВ = z2-z^
Поэтому координаты вектора АВ равны: ах — х2 — а?ь ау — у2 — у и аг =
z2 — z\j а разложение на составляющие по осям координат принимает вид:
(30.2) ~Ш = {х2 - xi) • 1 + (2/2 - Ы • J + (22 - *i) • *.
Заметим,что любой вектор Л2? выражается через радиус-векторы его
начала и конца по формуле :
(30.3) ~АВ = гЪ - fl.
Действительно, на основании определения операции вычитания ( рис.
136) следует: ЛБ = ~ОВ - ОЛ = F£ - fj.
Если известны координаты вектора, то линейные операции над
векторами можно заменить соответствующими арифметическими действиями
над координатами. Вывод этих формул (30.4) вытекает из разложения
(ЗОЛ) и свойств операций над векторами (коммутативность,
ассоциативность и т.д.). Проведите доказательство самостоятельно.
(30.4) Ха = Хах - % -f \ау • j + Xaz • k.
a±b = (ах± bx)i + (ay ± by)j + (a- ± 62)fc.
Если a = 5, то aa. = bx, ay = byi az — bz и наоборот.
m ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
351
Зная координаты вектора а можно вычислить модуль вектора. Из рис.
142 в соответствии с теоремой о длине диагонали прямоугольного
параллелепипеда, получаем: |ОМ|2 = \ОМх\2 + \ОМ2\2 + |0М3|2, |OMi|2 - o|,
|ОМ2|2 - oj, |ОМ3|2 = а», поэтому: \а\2 = oj 4- a* + aj или:
(30.5) |а| = у^
+ «; + «;
Пример ЗОЛ. Ламы векторы a = (1;2;3), Ь - (2;-1;0). Найти ш
модули и координаты вектора а — 26.
Решение: |а| = VV + 2* + 3*_= ^/П, |Е| =у2> + (-1)2 + О2 = V5,
В - 25 = (1 - 2 • 2)7 + (2 - 2(-l))j + (3 - 2 - 0)fc - -3? + 4j+ 3fc.
Замечание. Если вектор УШ определен координатами начала
-A(*i; Уг, *\) и конца В(жг; 2/2; z2)} то его модуль в соответствии с
формулами (30.2) и (30.5) равен:
(30.6) \АВ\ = \гв- ?7| = л/(*а " *i)2 + (V2 - 2/i)2 + (^ - <*i)2-
Это выражение совпадает с формулой (2.5) для расстояния между
двумя точками А и Б.
30-2. Деление отрезка в данном отношении. Пусть отрезок
М\Мъ определен своими конпами Mi(a?x;yr,Zi), Мъ(хг\углхг) и задано
положительное число А. Поставим задачу найти такую точку М отрезка
MiM2, чтобы Щ = А ( рис. 143).
*1
Рис. 143. Деление отрезка в заданном отношении
Обозначим х, у, х — искомые координаты точки М. Так как $щ =
Igg, то ЩВ = Аи, следовательно: М^М = ШЩ или (ж - хг)1 + (у-
У\)1 + (г - *i)f = А((лв» - в)? + (у2 - у)] + (л» - z)k).
Из равепства векторов следует равенство их координат: х—Х\ — Л(ж2 -
*)i !/-Ji = ЦУ2 -у), z-zt= А(гг - г), откуда находим х,у и z:
(30.7) *- ,»- ,* 1 + А

352
30. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
ПРИМЕР 30.2. Даны точки Мх(1; 2; 3) • М2(2; 1; 1). Найти
координаты точки М — середины отрезка M\Mi.
Решение; Для середины отрезка MiM2: А = $$- = 17 поэтому:
* = If* = 1,5; у = 2^ = 1,5; *«***« 2.
Ответ: Af(l,5;l,5;2).
30.3. Направляющие косинусы вектора. Как говорилось в
начале лекции 29, вектор характеризуется длиной и направлением. Длина
вектора (его модуль) вычисляется по формуле (30.5). Направление же
вектора в пространстве можно задать углами а, (3 и 7, которые составляет
вектор с осями координат (рис. 144). Косинусы этих углов cosa, cos/? и
cos 7 называются направляющими косинусами вектора.
Рис. 144. Направляющие тсосинусы вектора
Пусть дан вектор а — ах • г; +• ау • jЧ- а2 • Х\ Тогда: с*х = Пр0а.а = |а| • cos a;
ау = Пр0уа = \а\ - cos/?; ай = Пр0гй = |л| cos7, откуда:
(30.8)
Да. а^ аА
cosa — rrr;cos/7 = rrr;cQS7 ~ т=т*
|а| \а\ \а\
Подставляя в формулы (30.8) выражение (30.5) для |й|, получим:
(30.9)
cos a =
=;cos/? =
-;coS7--^
y/al + al + a*'
y/al + al + a? r sf^A °^~^
Возводя каждое из выражений (30.9) в квадрат и складывая, получим:
(30.10) cos2 a 4- cos2 fi + cos2 7 = 1.
Таким образом, среди трех углов а, (3, 7 независимыми являются
только два, а третий определяется из соотношения (30.10).
30. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
353
Замечание. Легко видеть, что координаты любого единичного вектора
ёа равны его направляющим косинусам, и значит его разложение по осям
имеет вид:
(30.11) еа - cos а • г 4- cos р • j + cos 7 * Л.
Такие же направляющие косинусы имеет вектор а, связанный с
единичным вектором соотношением (29-1).
Вектор в трехмерном пространстве задается тремя скалярными
величинами. Это могут быть три координаты или два угла и модуль (длина)
вектора и т.д.. Аналогично атому вектор в двумерном пространстве
определяется двумя скалярными величинами: двумя координатами или углом
и модулем и т.д.
ПРИМЕР 30.3- Найти направляющие косинусы вектора ABt если
А(1;2;-2),£(2;-1;0).
Р е ш е н и е: Найдем координаты единичного вектора, сонаправ-
ленного с ~АВ. АВ = (2 - 1)? + (-1 -_2)J + (0 - (-2))Z? - г - 3j + 2k.
Ответ; cosa = ^j; cos/? = -^; cos7 = fa
30.4. Условие коллинеарности векторов. Пусть векторы а = ахг+
ayj±azk и& = b*i+byj+b2k коллинеарны. В соответствии с теоремой 29.1
Ь — \а или a = АЬ, что означает для координат выполнение следующих
соотношений: Ьх ~ \ах, Ьу = Хау, bz = Aa2 или ae =в А6в, ау = АЬ^, аг = \bs.
Выразив А из этих равенств и приравняв, получим:
(30.12) ^ = ^ = ^ «£ = ^ = ?£.
ах ау а& bx by Ьг
Таким образом, для того, чтобы два вектора а и b были коллинеарны,
необходимо и достаточно, чтобы их координаты были пропорциональны.
ПРИМЕР 30.4. Установить, коллинеарны ли векторы а = (1; 3; 5) и
6 = (2;б;0).
Решение: 5 = § т^ §• Последнее неравенство следует понимать
так, что равенство 5 = А • 0 не выполняется при А = \.
Ответ: а и Ъ не коллинеарны.
Пример 30.5. Установить, коллинеарны ли векторы а = (1;3;0) и
6 = (2;6;0).

354 30. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
Решение: ^ = | = §. Последнее неравенство верно, т.к. О — Л • О
при любом Л.
Ответ: а \\ Ь.
30.5. Скалярное произведение. Выше было определено
произведение вектора на число. Далее мы определим несколько операций умножения
вектора на вектор.
ОПРЕДЕЛЕНИЕ 30.2. Скалярным произведением векторов a ub
называется число, равное произведению их модулей на косинус угла между
ними:
(30.13) а •&- |а|-|6| -cos^.
В соответствии с формулой (29.4) Пр-6 — \b\ cos y?? поэтому подставив
это выражение в формулу (3013), получим: а-Ъ=\а\- Пр^б, откуда:
(30.14) Пра5=1др
30.6. Свойства скалярного произведения. 1. a b = 5 а
(коммутативный закон)
Действительно: а - Ъ = \а\ - \Ь\ • cos ^ = |Ь| • |а| • cos <р — b-a.
2. А(а • Ъ) — (Ха) • Ъ = а • (ХЬ) (ассоциативный закон).
Действительно, например, при Л > 0: Л(а • Ь) — Х\а\ • |6| • cos у? ==
\Ха\ • |6| • cos ip — (Ла) • 6. Остальные случаи рассматриваются аналогично.
3. а(Ъ + с) = а - Ъ 4- а - с (дистрибутивный закон).
Действительно, используя формулу (30.14) ж свойства проекций,
получаем: а(Ь + с) = \а\ • Пр^(6 + с) = |а|(Пр^6 + Прдс) = \а\ • Пр^ + \а\ • Пр-с ==
а-Ъ + а-с.
4. Для того чтобы два вектора были перпендикулярны, необходимо и
достаточно, чтобы их скалярное произведение равнялось нулю.
(30.15) 516^5-6 = 0.
Действительно, если а _1 Ьу то ip = 90° =Ф> cos у? = Оий-6 = |а| •
|6| • coscp — 0. Наоборот, если a b = 0, то |а| • |&| • cos</> = 0 =» один
из сомножителей равен нулю. Если cosy> = 0, то <р — 90°_и а JL \ если
|а| = 0, то а — 0 и его направление - любое, например, _L b. Если |6| = О,
то b = 0 — аналогичный случай.
50. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА
355
Заметим, что из формулы (30.13) следует, что: а - b > 0 ч=^ (а; 6) —
острый, а • 5 < 0 «=* (а; &) — тупой.
5. Скалярный квадрат вектора равен квадрату его модуля:
(30.16) а2 - |of.
Действительно: а2 = а а = \а\ • |а| • cos0° = |a|2. Из формулы (30.16)
следует, что
(30.17) V?=|e|.
Это справедливо и для действительных чисел: %/я^ — \х\.
ПРИМЕР 30.6. Найти (а - 2Ь)2, если \а\ = 1, \Ц ~ 2, (S; 6) « 60°.
Решение: (а- 26)2 = й2 -4а-5-ь4Ь2 =* |а|2 -4|д| |Б| сов60о + 4|Б|2 =
1-4 1 2-1+4-4 = 13.
Ответ: (й - 2Ь)2 = 13.
Для получения выражения для скалярного произведения двух векторов
через их координаты, заметим, что: ^=J2 = ifc2~l,z-J = z<fc=J'A;-0.
Если а = ах • г + % • j; + а, * &, 6 = 6Х • г + Ьу • 7 + t>z • к, тоа«6 =
(ох • г: + ау • j• + аг. *) (6Х . i + 6у • J 4- ЬЛ - fc) = а* Ъ9 • г2 + ау by J2 + ая - 6,
* + Лж • К *' i + — + ау bz j ■ k = а* - Ья 4- % * fry -I- а2 • 62. Окончательно;
(30.18) г • 5 = a«. • Ьш + 0|, • bv + af • ЬЛ.
ПРИМЕР 30.7. Установить острый или тупой угол между
векторами а = (1; 0; 2) ti S » (-2; 1; 3).
Решение: a-5 = 1. (-2)+0-1 + 2-3 = 4 > 0 ^=^ угол (л;Б) острый.
Учитывая формулу (30.18) и свойство 4 скалярного произведения,
получаем, что для перпендикулярности двух векторов необходимо и
достаточно, чтобы выполнялось равенство;
(30.19) aXi - Ъх | ау ■ Ьу + я, • Ья = 0.
Пример 30.8. При каком значении т вектор а — (l;-~3; rn) будет
перпендикулярен вектору b = (2; 1; 4) ?
Решение: а^бФ^о-ЬО =^ 1-2 + (-3)-1 + 4ш = 0 =^ т = £.
Ответ: а ± 5 при m = \.

356
29 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЛИНЕЙНЫЕ ОПЕРАЦИИ
Для получения выражения для косинуса угла между двумя векторами
подставим выражения (30.18) и (30.5) в формулу (30.13). Получим:
/лл ЛЧ а - Ъ ахЬя 4- афу 4 а2Ь
(30.20) cos <р = —-=- = - —
\а\ • |5| Va2 + 4 + a*' V5^^**
Заметим, что знак cos<^ зависит только от знака числителя дроби
(30.20), т.е., как уже отмечалось, перпендикулярность векторов, острый
или тупой угол между векторами — все это определяется знаком
скалярного произведения.
ПРИМЕР 30.9. Найти угол между векторами а = (1; 2; 3) и
Ь=(-2;-1;-1).
Решение: В соответствии с формулой (30.20):
Принципиально задача решена, т.к. угол между векторами однозначно
определяется значением cossp(0 < ч> < тг). В данном случае угол тупой,
т.к. cos ip < 0.
При необходимости найти приближенное значение ц> с помощью
калькулятора, производим приближенные вычисления:
cos<p~ -£7Й ~ ~0,7б4==^ р« 2,44.
Ответ; cos<£> = — ^Ж*
29. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЛИНЕЙНЫЕ ОПЕРАЦИИ
Пример 29.1. В параллелограме ABCD точка О — пересечение
диагоналей ~АВ - a, JiD = Ь. (рис. 145) Выразите, через эти векторы
следующие: CD, ~СВ, СО, Ш).
Р е ш е н_и_е; <52Ь= -а, тл^ \CD\ - \АВ\ = \a\mJCD П й; 55 = -5
аналогично; СО = \СА = \{-АС) ^ --^-Ь^т.к^С ^г + Мточка О
— середина диагоналей и СЛ = -ЛС; J5i3 = BC+CD - AD+CD - 6-a.
Рис. 145. Пример 29.1
30 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЛИНЕЙНЫЕ ОПЕРАЦИИ
357
Пример 29.2. В Д Л2?С mwica О — переге^иие ^<9«ан, АВ ~ а,
АС = Ь (рис. Ц6). Выразите через эти векторы следующие: ВС, ANt
КО.
Решение: ~ВС = ~ВА + АС = -а + 6 = Ь - S. АЛГ = ЛВ + ВЛГ «
а4-|ВС = о 4- f (6-а) = а+£&—£а = ~a+\Ь = *(л-|-Ь). Этот же результат
можно получить достроив Д АВС до параллелограмма ЛВЛ'С, в котором
AN — |ДЛ' = \(а + 6). Для нахождения А*0 напомним, что медианы в
точке пересечения делятся в отношении 2:1, считая от вершины. Поэтому
КО = $\КВ\. КО = $КВ - \(КА + ЛВ) = 1(-1ЖУ +д) e J(-i5 + a) .
S»-
Самостоятельно найдите векторы CW, ВО, СО, ОМ.
ъ-ъ
Ответ: ОЛГ = ^, ВО = ^, СО = 2jsf ОМ -
26-
ь к
Рис. 146. Пример 29.2
Пример 29.3. В правильном шестиугольнике точка О —
пересечение диагоналей, АВ = a, AF = Ь. (рис. Ц7) Самостоятельно выразите
через эти векторы следующие: DE, ОВ, ОС, AD, ВС, CF. Учтите
при этом, что все треугольники на рис. Ц1 — правильные.
Ответ: DE = -а,ОВ = -Ь, ОС = a, ID = 2(a -f b), ~BC ^а + Ъ,
CF = -25.
Пример 29.4. В д АВС С А = а, СВ = 6, точки_М и N делят
сторону АВ на три равные части. Найдите вектор СМ (рис. Ц8).
Решение: ЛВ = 6 - а, ТШ = f ЛВ = | (Ь - а), ОМ = lJA + AM =
2+I(5_5)==ffl£
Пример 29.5. В д ЛВС AM ~ биссектриса (рис. Ц9), АВ = Ь,
АС = с. Найдите вектор AM.

358
29 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ ЛИНЕЙНЫЕ ОПЕРАЦИИ
Рис. 147. Пример 29.3
В
Рис. 148. Пример 29.4
Решение: Вспомним из курса средней школы, что биссектриса
угла в треугольнике делит противоположную сторону в отношении
прилежащих сторон:
\Ь\
\Ш\ _ \Щ _ \Ц \вм\
|МС|" \ШГ И ^ \ВС\ "|Ь| + |сГ
т.к. \ВС\ = \ВМ\ + \МС\< С учетом того, что J5C = с - 6, получаем:
ВМ = -г
14
1*1 + |с
(с -5)
_ |Ь| , -ч |6|-с+|с|-6
AM = ЛВ + БМ - 6 + ^гЦ-г с - Ь) = ^г--Н— -
Рис. 149. Пример 29.5
20 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЛИНЕЙНЫЕ ОПЕРАЦИИ
35$
Пример 29.6. Даны радиус-векторы вершин Д ABC — п, r£, rg.
Найти радиус-вектор г точки М — пересечений медиан ( рис. 150, где
точка О — начало координат).
Решение; ~BC - гз - г2, BD = ^В{? = *(г3 - г2) как середина
ВС, АВ = F2 - fif ТВ = 1Ш + Aff = и^а + г2 - гг = ^3 + ^-2^),
ЛМ = §уШ = |(г3+^2-2п) =* г = ОМ = Fi+ЛМ = п + ^гз+гг-Йп) =
Рис. 150. Пример 29.6
Пример 29.7. Найдите длину и направляющие косинусы вектора а —
3i + ij 4- bk.
Решение: В соответствии с формулами (29.5), (29.10) получаем:
\а\ = \/32 + 42 + 52 = V50 = 5\^2,
3 3\/2 „ 4n/2 5\/2
ПРИМЕР 29-8. Докажите, что ABCD — трапеция, если вершины
имеют координаты: Л(3; 2; -2), 5(4; 4; 1), С(-1; 2; 0), Р(-3; -2; 6).
Решение; Сделайте эту задачу самостоятельно, проверив
коллинеарность одной из пар векторов на противоположных сторонах.
Используйте условие коллинеарности векторов (30.12).
Пример 29.9. Найдите единичный вектор, противонаправленный
вектору а ~ г -f 3j; — k.

360 30 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
Решение: \а\ = ^12 + 32 + (-1)2 = л/ТГ. В соответствии с
формулой (30.9) единичный вектор того же направления (сонаправленный) с
вектором а имеет координаты:
_ _ й _ 1 , 3 ^ 1 -
ea~N~7ff+ 7if ~7п
Искомый единичный вектор противонаправленный вектору а, равен
1 3_-, _ 1 j
Самостоятельная работа
Пример 29.10. В Л ABC точка М делит сторону ВС в отношении
1:5, АВ = a, 7lC = с. Найдите вект,ор AM.
ПРИМЕР 29.11. Даны радиус-векторы вершин A ABC: rx = t+2j+3k,
г2 = Зг 4- 2j + fc; F3 = г + 4J + fc f рис, 29.6). Докажите, что Д ABC —
Пример 29.12. Даны координаты точки Ail; -Б; 3). Найдите
координаты точки В, если вектор АВ — i -- j + bk.
Пример 29.13. Найти проекции и составляющие по осям координат
вектора 2а — 36, если а = — i + 2&7 Ь = 2?! 4- 7 ~~ 2&.
ПРИМЕР 29.14. Найдите направляющие косинусы и координаты
единичных векторову параллельных вектору АВ, ссль,А(2; -3; 1), 2?(Г, — 1; —1)
ПРИМЕР 29.15. Докажите, что если О — точка пересечения медиан
A ABC, moW + BO + CO-=Q,
30. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - СКАЛЯРНОЕ
ПРОИЗВЕДЕНИЕ
Пример 30.1. Найдите скалярное произведение а Ъ? если а =^ 2г —
3j + fc,b=-» + J+3fc.
Решение: По формуле (30.18) получаем:
a . Ь = 2 • (-1) 4 (-3) • l-hl-З = -2.
Т.к. а • b < 0, угол между векторами а и 6 тупой.
30 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ 361
ПРИМЕР 30.2. Найдите проекцию разности а—Ъ на ось 1} если \а\ = 2,
\b\~lf углы векторов а иЬ с осью I равны тг/3 и тг/4 соответственно.
Решение: Пр,а » |з| coe(ir/3) = 2 - (1/2) *= 1, Пр,5 « |5| • cos(?r/4) =
\/2/2, Пр/(а - 6) = Пр,а - Пр,6 = 1 - уД/2.
Пример 30.3. При каком значении параметра т векторы а(2; 3; 5) и
fr(—2; 1; т) перпендикулярны?
Решение: Условие перпендикулярности двух векторов дается
формулой (30.19):
а - Ь = 0 =* 2 - (-2) + 31 + 5-m = 0=>m=i.
Пример 30.4. Найдите (3a-26)-(2a+36), если |а| = 1, \Ь\ = 2 t/a X 5.
Решение; al5=>u-ft = 0,a2 = |а|2 = 1,6 s |S|2 = 4, поэтому:
(За - 2Ь)(2а + 36) = ба2 - 6§2 + 9аЬ - 4а5 = б • 1 - б - 4 в -18.
ПРИМЕР 30.5. Найдите угол вежду векторами а =в (~1;0;3) и 6 =
(2;1;0).
Решение: В соответствии с формулой (30.20 ):
аЬ -1.2 4-0 + 0 2 1
COS tp :
N1*1 ^(-1)2 + 32л/2г4Т2" V40 ч/То"
1_
vTo
V? = arccos I —т= I = * ~~ arccos -7= (угол тупой)
Пример 30.6. Найдите угол между векторами а и Ь, если: \а\ = 2,
|5| = Зи(2а-5)±(а + 2Ь).
Решение: В соответствии с формулой (30.15) имеем:
0 = (2а - Ь)(а + 26) = 2а2 - 2&2 + Заб = 2|а|2 - 2|6|2 + 3|а|. |6| • cosy? =>,
5 5
=>2-4 — 2-9 + 3-2-3-cos<^ = 0=> cos <p = - =*► tp = arccos -.
ПРИМЕР 30.7. Найдите проекцию llpm+jja, если а = (1; 2; 3),
Б=(-2;1;0).

362 SO ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
Реше ние: 2а + Ь^ (2 • 1 - 2)7 + (2 • 2 + 1)7 + (2*34 0)fc = Ц + 6fc:
12а + 6| = V52 + 62 = \/61- В соответствии с формулой (30,14), получаем:
g(2g + 3i) _ -2 - 0 4- 1 • 5 4 0 • 6 _ 5
ПРаМ* " |2а + Ь| ~ VSI " V°T
Пример 30.8. Найдите внутренний угол А Л ABC, если А(1;1;1),
В = (1;2;3),С = (-1;2;1).
Решение: Внутренний угол А Д ABC равен углу между
векторами АВ и ЛС. Найдем их координаты, вычитал из коордиват конца
координаты начала вектора: А2?(0; 1; 2), АС (—2; 1; 0).
АВ-ЗС 0 1-1 + 0 1 /А 1
cos Л = — = , , = •- -г => LA — arccos -.
ПРИМЕР 30.9. Векторы р uq образуют угол 45° 7 |р| = 2, \q\ = 3,
найдите длину вектора 2р — q.
Решение: В соответствии с формулой (30.17):
|2р - 5| = V(2p-?)2 = \/4р-4р5 + ^ = /4|р|2 - 4|р| • |5l соврд + \q\2 =
- W4-4-4-2-3 — + 9 = V^5" 12^-
Самостоятельная работа
Пример 30.10. Найдите проекцию вектора 2а — 36, на ось /, ec^w a
ub — единичные векторы, образующие с осью I углы 27г/3 и 37г/4
соответственно.
Пример 30.11. Найдите проекцию Пщ(Ъа - 26), если a = 2г 4- jf - ЗА;,
5 — J — fc. Используйте свойства проекций и формулу (30. Ц)-
Пример 30.12. Определите — острый или тупой угол составляют
векторы~АВ и CD, если А(1;2; 1), В(-2;0;2), C(-3;l;2), D(2;5;0).
Пример 30.13. Найдите Пр^+Ъ{2а - 36), если а = (1;-2;-3), Ъ =
(-3;2;1).
ПРИМЕР 30.14. При каком значении параметра, s вектор (2а - 6) J_
(a + b), если а = (0,5; 2; 5), 6= (s;2;-l).
51 ЛЕКЦИЯ - ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ
$е$
Пример 30.15. Найдите угол между векторами АС и BDf для дан-
пых в примере 29.12 точек А, В, С, D.
Пример 30.16. Найдите внутренний угол В А АВС для данных в
примере 30.8 точек А, В, С.
31. ЛЕКЦИЯ - ВЕКТОРНОЕ И СМЕШАННОЕ
ПРОИЗВЕДЕНИЯ
Векторное, смешанное произведение векторов, двойное векторное
произведение
31.1. Векторное произведение. Перейдем теперь к определению
второго вида произведения векторов.
Определение 31.1. Векторным произведением вектораа на вектор
b называется вектор с, такой, что;
1) вектор с перпендикулярен перемножаемым векторам.' с ± а, с _1_ Ъ;
£) направление вектора с определяется по правилу "буравчика", т.е.
если ручку правого буравчика вращать от первого из перемножаемых
векторов (а) ко второму (Ь) по кратчайшему пути, тб движение самого
буравчика указывает направление вектора с;
3) модуль вектора с определяется формулой:
(31.1) |z| = |a|-|b|-ein(ff;b).
Векторное произведение будем обозначать а х ft.
Если нарис. 151 вектор а направлен направо, а вектор b — вверх, tq
вектор a xb перпендикулярен плоскости листа и направлен к читателю.
Стрелкой показано направление вращения ручки "буравчика".
ча'Ь
Рис. 151. Векторное произведение

$(Ц 31 ЛЕКЦИЯ - ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ
31.2. Свойства векторного произведения. 1. а х b = — b x а
(антикоммутативность).
Действительно, из определения следует, что векторы axb и Ьха имеют
одинаковую длину: |а| * |Б| • sin (а; Б) = |Б| - |а| - sin (Б; а) и противоположные
направления.
2. Л(а х 6) = (Ла) х 5 (ассоциативность).
Докажем это свойство для Л > 0: вектор А (а х Б) имеет то же
направление, что и вектор а х Б. Вектор (Ла) х Б при А > 0 имеет то же
направление. Длины этих векторов также совпадают: \Х(а х Б)| = |А| • |а х Ъ\ =
А • |а| • \Ь\ • sin (а; Б), |(Ла) х Ъ\ = |Ао| • |Б| - sin (а; Б) = А|а| -|Б| • sin (а; Б).
Аналогично проводится доказательство для случая А < 0.
3. ax(b-\-c) = axb + axc (дистрибутивность).
Это свойство оставим без доказательства.
4. Условие коллинеарности векторов.
Для того чтобы два вектора были коллинеариы, необходимо и
достаточно, чтобы их векторное произведение равнялось нулю:
(31.2) а || Б <=> ахЬб.
Действительно, если а || Б, то ip = 0° =$■ simp = 0 и а х 6 = 0-
Наоборот, если а х Б — 0, то \а\ • \b\ • sin (a; 5) =с^ один из сомножителей
равен нулю. Если sin (о; Ь) = 0, то (а; Б) = 0 или (а; Б) = тг и а || Ь, если
|а| ~ 0, то а — 0 и eix> направление — любое, например, || 6. Если |Ь| = 0,
то Б = 0 — аналогичный случай.
5. Векторный квадрат равен нулю: аха -- 0.
Это свойство является следствием свойства 4
6. Геометрический смысл векторного произведения:
Модуль векторного произведения ^авея площади параллелограмма,
построенного на перемножаемых векторам ( рис. 152).
Рис. 152. Геометрический смысл векторного произведения
Действительно, |3 х Б| ~- |а| - |Б| sin (а; Б), что совпадает с формулой
площади параллелограмма, известной из курса средней школы.
31 ЛЕКЦИЯ - ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ
S6S
Пример 31.1. Упростить выражение; (2г + j - fc) х j - t х (j — 2к).
Решение: Пользуясь свойствами векторного произведения,
получим^ (HfJ - k)x J_-ix(J-2l) = 27xJ-fJxJ-fcx7-«xj4-27xfc^
ii X j + 2г х к + j x к.
Для нахождения г х j заметим, что \ъ х J| = |?| - |J| • sin 90° = 1, а
направление совпадает с вектором к ( рис. 153), т.е. г х J = fc. Аналогично
убедитесь, что г х kj= — j, j X fc_= i, поэтому окончательно! i x J -f 2i x
/
J -
РИС. 153. Векторное произведение координатных ортов
Ответ; i — 2j + /;,
Для получения выражения для векторного произведения двух векторов
через их координаты, найдем все парные векторные произведения
единичных векторов г, jy j так, как это было сделано в предыдущем примере:
гХг =7 xj = ~к хк = О
гх]^к,
7 х к = 7,
fc х i = j,
7 х г = -fc,
* х 7 = -i,
1 х к = —7»
Аналогично тому, как это делалось при решении примера 31.1, найдем
произведение:
а х Б = (ах • г + «^ • 7 + а* • *) х (&* *» 4- Ъу • 7 + 6* • fc) =
= axby -ixj4 а^б* • г х к + ау6х • j х г + ауЬг -jxH azbx • А: х г +
Н~ аг6у • к х j = axby • А: — ax6z • j — aybx • A; 4- ayb2 • г + azftx • j — аг6у • i =
= (ау6г - a2by)i - (ax6z - azbx)j + (axby - aybx)k.

300 31 ЛЕКЦИЯ - ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ
Разности, стоящие в скобках, равны определителям второго порядка:
(31.3)
охб
Qy
Ьу
az
bz
■ i —
От
bx
at
bz
■3 +
ax
CLy
Полученное выражение есть разложение определителя третьего
порядка по элементам первой строки;
(31.4)
а х Ь —
г
ах
Ьх
J
ау
by
к
0>z
b2
Формулы для координат векторного произведения (31.3) удобнее
запоминать в виде символического определителя (31.4;, раскладывая его по
первой строке.
Нужно отметить, что ранее определитель вводился как число,
вычисляемое по некоторому правилу исходя из его элементов.
Здесь мы используем это правило для получения разложения (31.3)
вектора а х 6 на составляющие. Таким образом, (31.4) не является
определителем, но такая запись облегчает запоминание формулы (31.3).
ПРИМЕР 31.2. Найти векторное произведение векторов а — (1;2;3)
ub = (2;0;-l).
Решение: а х b
г j k
1 2 3
2 О -1
2 3
О -1
J +
fc = (—2 — 0)г - (-1 - 6)j + (0 - 4)к - -2» 4- lj - 4*.
1 2
2 О
Ответ: 3x6= ~~2г 4- 7j — 4/с.
31.3. Смешанное произведение.
ОПРЕДЕЛЕНИЕ 31.2. Смешанным^ произведением трех векторов а, Ъ
и с называется число, равное (охб)- с, т.е. скалярному произведению
векторного произведения первых двух па третий вектор.
Найдем выражение для смешанного произведения трех векторов через
их координаты, для чего запишем скалярное произведение вектора (31.3)
на вектор с - сх • г 4- су • j 4- cz • k:
31 ЛЕКЦИЯ - ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ
301
(a xb) с —
by bs
Сх ~
а,. ай
bx bz
,су +
Otm Qtai
С* =
ax
Ь.
Сх
by Ья
Таким образом, смешанное произведение равно определителю третьего
порядка7в строках которого стоят координаты перемножаемых векторов.
Пользуясь свойствами определителя, докажем, что: (a xb)-c — a- (bx с).
Действительно, аналогично выводу предыдущей формулы, получаем:
6хс =
Ьх by bz
Сх Су Cz
=
by bz
Су Cg
•г —
С% Сх
•7+
К ьу
Сх Су
а • {Ь х с) —
! by bz
Су Cz
•dx ~
bx bz
cx Cz
•au +
bx by
as =
bx by bz
Мы получили тот же определитель, что и в формуле для ((ах Ь) >с).
Таким образом доказано, что знаки скалярного ш векторного
произведения "•" и "ж" в смешанном произведении можно переставлять. Поэтому
смешанное произведение принято обозначать (a be).
(31.5)
(abc)
ах ау а%
bx by bz
Пример 31.3. Найти смешанное произведение (аЬс)1 если а(1;2;3),
Б-(-2;1;0),В=(1;-1;2).
Решение: Раскладывая определитель по последнему столбцу,
получаем:
{abc)
2 3
1 0
-1 2
= 3-
-2 1
1 -1
4-2-
1 2
-2 1
= 3(2-1)+2(1+4)=13.
Ответ; 13.

368 31 ЛЕКЦИЯ ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ
31.4. Свойства смешанного произведения.
1. (a be) — (cab) = (be a) *= -(5 ас) — -(а с Ь) — --(с Ъ а).
Доказательство этих соотношений проводится аналогично выводу
формулы (31.4). Чтобы их запомнить заметим, что при "циклической
перестановке" векторов (вектор передвигается на следующее место, а
последний — на первое) знак не меняется, а при перестановке двух соседних
векторов знак меняется.
2. Геометрический смысл смешанного произведения.
Модуль смешанного произведения равен объему параллелепипеда,
построенного на этих векторах, как на ребрах ( рис. 154).
Рис. 154. Геометрический смысл смешанного произведения
Для доказательства этого построим вектор d = а х 6, длина которого в
соответствии с геометрическим смыслом векторного произведения, равна
площади параллелограмма, построенного на векторах а а 6, т.е.
площади основания параллелепипеда; \а х 6| — 5. Из определения смешанного
произведения (a b с) = (а х Ь) • с — |а х 6| • \с\ • cos уэ, где tp — угол между
векторами d и с. На рис. 154 изображен случай ср < |. Для этого
случая получим, что высота параллелепипеда h = |е| cos (p. Окончательно:
(о b с) = |а х 6| • \с\ • cos ср = S - h = V — объему параллелепипеда,
изображенного на рис. 154. В случае ц> > | получим /i — — |с| • cosy> (т.к.
cos<p < 0) и а • b • с — -V. Окончательно получаем: V = \(ab с)\.
Пример 31.4. Вычислить объем пирамиды с вершинами А(2\ —1; —1)7
В(5;-1;2),С(3;0;3) и/?(6;0;-1).
Решение: Рассмотрим векторы DA — (-4; -1\ 0), JDS' = (-1; -1; 3),
DC = (-3; 0; -2). Из школьного курса геометрии известно, что объем
пирамиды, построенной на ребрах DA, DB1 DC в шесть раз меньше объема
параллелепипеда, построенного на этих ребрах:
31 ЛЕКЦИЯ - ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ
309
Vimp =
-Н-4
Ответ:
= \\{DA
•2 + 1(2
Чгар =
DS
+ 9)1 =
1
2'
DC)\--
-1.3-
-k\
. 1
" Я*
-4
-1
-3
-1
-1
0
0
3
-2
3. Условие компланарности векторов.
Определение 31.3. Векторы, параллельные одной плоскости,
называются компланарными. Очевидно, что два вектора всегда
компланарны.
Для того, чтобы три вектора были компланарны, необходимо и
достаточно, чтобы их смешанное произведение равнялось нулю.
Доказательство.
Если три вектора компланарны, можно считать, что они лежат в одной
плоскости и тогда, конечно, объем параллелепипеда, построенного на этих
векторах, равен нулю, т.е. смешанное произведение равно нулю.
Если наоборот, смешанное произведение равно нулю, то объем
параллелепипеда равен нулю и, значит, все векторы параллельны одной
плоскости (компланарны) или хотя бы один из них равен нулю, что тоже
означает компланарность всех трех векторов.
Другими словами, необходимым и достаточным условием
компланарности трех векторов является равенство нулю определителя,
составленного из координат этих векторов:
(31.6)
ах ау
Ьх Ьу
Cm С«
Пример 31-5. Устаповить1 будут ли компланарны векторы АВ, ВС
и CD7 если даны координаты точек: А(1;2;-1), 5(0; 1; 5), С(—1; 2; 1),
Я(2;1;3).
Решение: Найдем координаты векторов, вычитая из
координат конца координаты начала: А В = (-1; -1; 6), ВС = (—1; 1; —4), CD =
(3; —1; 2). Вычислим значение определителя и проверим выполнение
условия (31.6)
-1-1 б t
-1(2 - 4) + 1(-2 +12) + 6(1 - 3) = 2 + 10 - 12 = 0.
-1
о
1 -4
-1 2
Ответ: векторы компланарны.

370 31 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
31о5о Двойное векторное произведение. Наряду со смешанным
произведением, для трех векторов а, 5, с можно найти так называемое
двойное векторное произведение: (а х Ь) к с, которое будет вектором.
Легко видеть, что: (йхБ)хб = ах(Ьхс) ~ axbxc,axbxc — cxaxb — бхсХа,
axbxc~—bxaxc=z—cxbxa~~axcxb~ (докажите это
самостоятельно)
Вычислим, например, г х ] х к. Учитывая, что i х j — к (см. пример
31.1), получаем: i x j x fc = 0. Аналогичным образом можно определить
тройное векторное произведение; а х b x с х d, которое будет вектором и
т.д.
В дальнейших лекциях рассматриваются приложения векторной
алгебры к аналитической геометрии в пространстве.
31. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВЕДЕНИЯ
ВЕКТОРОВ
Пример 31.1- Найдите векторное произведение a xb для векторов
а = 2г~-37+ к, Ь= -4-}-J + 3fc.
Решение: В соответствии с формулой (31.4):
-3 1
1 3
-J
2 1
-1 3
4-Х'
2 -3
-1 1
- ?(-9 - 1) - j(6 + 1) + Jfc(2 - 3) = -НИ - Ij - к.
Пример 31.2. Упростите выражение (вычислите):
J х г 4- 3j х к - Ьк х г 4 (3* +* 5J - к) х (г - 6] + Бк).
Решение: На основании определения и свойств векторного
произведения (п. п. 31.1, 31.2) получаем: г х j = А;, г х к — —j, j х к = i, поэтому
искомое выражение равно:
~ix7+3jxfc+5*x*4-3fxi-18txjT-16ixfc+5jx*--307xJ-|-25jxfc--fcx?4-
+6fc-J-5*-k = -fc+3t-5jH-3-S-18fc- 15j-5fc-30-6+25*+J-6*-5-O =
= 22t - 19j - 24k.
Пример 31.3. Вычислите площадь треугольника A ABC, если A(l; 1;1),
Я(1;2;3),С(-1;2;1).
ахЬ =
г
2
-1
i
-3
1
А:
1
3
31 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
371
Решение: Площадь д ABC равна половине площади
параллелограмма, построенного на векторах АВ и АС, которая в соответствии с п.
31.2 равиа модулю векторного произведения этих векторов:
Slabs ~\Щ*Щ-
Найдем координаты векторов АВ и АС и их векторное произведение:
АВ(0;1;2), ЖУ(-2;1;0),
АВхАС-
0
-2
1 2
1 О
= г
1 2
1 0
0 2
-2 О
+*
0 1
-2 1
= -2i-4j+2A;.
Вычисляем модуль этого вектора по формуле (30.6):
| AS х Щ = д/(-2)2 + (-4)* + 2* - V^4 = 2vfr
Окончательно: S&abc = f • 2\/б = \/б-
Пример 31.4. Вычислите площадь параллелограмма, построенного
на векторах p — q и 2рН~д, еслир «5 — единичные векторы, образующие
угол 60° -
Решение: Найдем сначала векторное произведение:
(р-</)х(2р4-<?) =2pxp+px$-2?xp-5x7e2'54-JJxg+2pXg-0 = 3px?.
Используя геометрический смысл и определение векторного произведения,
получаем;
S = \3pxg\= т ■ 1^1 -sin60° в 3 • 1 -1 - ^ = Т-
ПРИМЕР 31.5. Найдите высоту CD A ABC из примера 31.3.
Решение: Высоту CD = /i на сторону АВ найдем используя
формулу для площади треугольника; Saabc = зИ^1 *» которую мы
нашли через векторное произведение в примере 31,3: Saabc = у/6. Зная
координаты вектора АВ = (0;1;2), найденные ранее, определим длину
основания треугольника;
\АВ\ - VI2 -г 22 «* А
из уравнения л/б — \Vbh находим:

372
31 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
Пример 3L6. Найти единичный вектор, перпендикулярный векто*
рам а = (2; -1; 5) и b = (-2; 3; 0).
Р е_ш е н и е: В качестве вектора, перпендикулярного как вектору а,
так и 6, выберем их векторное произведение:
5X6 =
i 3 k
2 -15
-2 3 0
= i
-1 5
3 0
-J
2 5
-2 0
+ fc
2 -1
-2 3
= -15i-10j" + 4*.
Теперь найдем вектор, сонаправлениый этому и единичной длины:
ах 6 -15i-10j"4-4fc
15
10
t'J +
4 А
\axb\ V152 + 10* + 42 л/ЗЗГ v/341e/ ' л/§41
Заметим, что наряду с вектором ё, искомым вектором может быть также
вектор — ё.
ПРИМЕР 31.7, Найдите смешанное произведение векторов а = (1; — 1; 2)
6=(0;1;2),с = (2;0;1).
Решение: В соответствии с формулой (31.5) находим:
(abc) =
1 -1 2
0 1 2
2 0 1
= 1-
1 2
0 1
+ 1-
0 2
2 1
+ 2-
0 1 1
2 0
= 1-4-4=-7.
Ответ: -7.
Пример 31.8. Найдите объем треугольной пирамиды с вершинами
4(2; 2; 2), 5(4; 3;3), С(4;5;4), £>(5;5;6).
Решени е: Нетрудно показать, что объем треугольной пирамиды
У пир с вершиной в точке А в б раз меньше объема параллелепипеда У пар,
построенного на векторах АВ} AC, AD. Действительно: Vnup = \SnupH~>
Упар ~ SnapH, где Snup, Snap, # — соответственно площадь
основания пирамиды, параллелепипеда и их общая высота. Если учесть, что
Snup = 2^naP (плошаДь треугольника равна половине от площади
параллелограмма), то получим: У пир = \Упар- Вычислим координаты
перечисленных векторов: ~АВ = (2;1;1), АС - (2:3; 2), ~AD = (3; 3, 4).
Найдем смешанное произведение:
2
(ABACAD) =
1 1
3 2
3 4
= 2-
3 2
3 4
-!•
2 2
3 4
+ !•
2 3
3 3
У! ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
373
= 2.6-1-2-1-3«7.
Окончательно: Vnup « |V^op = $|ЛВ ACCI>| = j.
ПРИМЕР 31.9. Найдите высоту треугольной пирамиды из примера
31*8, опущенную из вершины А.
Решение: Так как высота пирамиды равна высоте
параллелепипеда найдем Н из формулы УПар — SnapH* Для нахождения Snap
площади основания параллелепипеда вычислим векторное произведение
ВС х BD. Вычитая из координат конца координаты начала, получим
ВС? - (0; 2; 1), В7У - (1; 2; 3),
BCxBD =
г j k
0 2 1
12 3
= i -
2 1
2 3
-з
0 1
1 3
+ *■
0 2 1
1 2
Snap = \BC X BD\ = s/& +12 + (-2)
7
75Г
получаем Я = -jL
= 4i4-j-2*.
2 = V5T- Из уравнения: 7 = \/21#
Пример^ 31.10. Проверьте компланарность векторов а = 2i-f5j4-7fc,
6 = г 4- J - k, с а= г ■+■ 2j -f 2A;
Решение: Найдем смешанное произведение
2 5 7
оЬс=| 1 1 -1 I =2-
12 2
1 -1
2 2
1 -1
1 2
4-7-
1 1
1 2
= 8-15+7 = 0.
Пример 31.11. Проверьте) лежат ли четыре точки -4(1; 1; 3)
J3(-l;-l;-l), С(2;0;3), jD(0;1;2) в одной плоскости?
Решение; Данные четыре точки будут лежать в одной плоскос-
ти, очевидно, тогда и только тогда, когда векторы АВЛ AC, AD будут
компланарны. Проверим это: АВ = (-2; -2; -4), АС = (1; —1;0), AD —
(-1;0;-1).
{ABACAD).
-2 -2 -4
1 -1 О
-1 0 -1
= -2-
-1 0
0 -1
+ 2-
1 0
-1 -1
-4-
1 -1
-1 0
= -2 4- 2 (-1)4- 4 = 0.
Так как смешанное произведение равно нулю, векторы компланарны
и точки лежат в одной плоскости.
Самостоятельная работа

Щ $й ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Пример 31.12. Найдите векторное произведение a xb7 для векторов
а = -Аъ -\-6j -2k ub = i~j-3k
ПРИМЕР 31.13- Вычислите ((р + 25) х (2р - q)f, если \р\ = I, \q\ = 2,
(Й) = 120°.
ПРИМЕР 31.14. Вычислите высоты параллелограмма, построенного
па векторах а = г — j ~\- к и Ь = i + 2j.
Пример 31.15. Найдите два вектора, перпендикулярные векторам
IBuCD, если Л(1;2;3), £(2; 1; 4), C(2;l;3), D(3;3;3).
Пример 31.16. Найдите высоты & ABC, если Л(1; -1;2), #(0;-1;-3),
С(2;1;-2).
Пример 31.17. Найдите смешанное произведение (abc), если
а = (1; -2; 1), 5 = (0; -2; 3), с = (-3; 1; 2).
Пример 31.18. Найдите смешанное произведение (Ъас) для векторов
из примера 31.17.
Пример 31.19. Найдите объем параллелепипеда, построенного на
векторах а = —Зг — Aj, b = 3j ~ k,c — —2j — bk.
Пример 31.20. Проверьте компланарность векторов а = (2; -6; -4), Ъ —
(-2; б; 8), с = (б; -24; -12).
Пример 31.21. Лежатли в од.ьой плоскости точки Л(1; 0; 1), J5(2; 1; 1),
C(-l-,-4;-l), D(0;0;2)?
ПРИМЕР 31.22. Найдите объем треугольной пирамиды с вершинами
в точках
Л(-2;1;1), (-5;1;-2), <7(-3;0;3), D(-6;0;l).
Пример 31.23. Найдите высоту пирамиды с вершинами в точках
А(-2; -3; -1), В{-А\ -1; 2), С(-~6; -3; -7), D(5; 4; -8), опущенную из вер-
шины D.
32. ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В
ПРОСТРАНСТВЕ
Плоскость, нормальный вектор. Связка плоскостей. Условие
параллельности и перпендикулярности плоскостей. Угол между
плоскостями. Расстояние от точки до плоскости.
32 ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 375
Аналитическая геометрия в пространстве изучает взаимное
расположение и свойства линий и поверхностей, позволяет решать методами
алгебры геометрические задачи. Применим методы векторной алгебры для
решения задач аналитической геометрии.
32.1. Уравнение плоскости. Положение плоскости в
пространстве можно задать точкой М0(х0; уо\ zq) принадлежащей этой плоскости и
вектором ЛГ = (Л; В; С), перпендикулярным этой плоскости ( рис. 155).
Рис. 155. Нормальный вектор плоскости
Вектор N, перпендикулярный плоскости, называется нормальным
вектором этой плоскости.
Выведем уравнение плоскости, задаваемой нормальным вектором N и
проходящей через данную точку М0. Рассмотрим произвольную точку
М(х\у;z), принадлежащую плоскости. Вектор MQM _L iV, поэтому MqM-
N = 0. Найдя координаты вектора MqM — {х- Xq)i + (у - yQ)j + (z - z0)k,
приравняем нулю скалярное произведение. Обозначив 7 ~ ОМ и Щ =
ОМа радиус-векторы точек МиМ0 соответственно, по формуле (30.3)
получим; MqM = ¥ — rfi и далее, на основании условия (30.4) приравняв
нулю скалярное произведение, получим векторное уравнение плоскости:
(32.1) (F - F5) • Jf - 0-
Записав это уравнение в координатной форме, получаем уравнение
плоскости, проходящей через данную точку с заданным нормальным
вектором:
(32.2) А(х - хл) + В{у - ш) + C{z - zQ) *- 0.
Координаты любой точки М плоскости удовлетворяют уравнению
(32,2), а точки, не принадлежащие плоскости, не удовлетворяют, т.к. в
этом случае MQM JL N.
Пример 32.1. Написать уравнение плоскости, проходящей через
точку М0(1; 2; 3) перпендикулярно вектору N = (2; —1; 1).

376 32 ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Решение: Здесь А — 2, В — -1, С — 1. На основании формулы
(32.2) получаем:
2{х ~ 1) - \{у - 2) + 1(я - 3) = 0 или 2х - у + z - 3 - О
Ответ. 2х — у + z — 3 = 0.
Если в уравнении (32.1) раскрыть скобки, получится векторное
уравнение плоскости в виде:
(32.3) г.ЛГ + 1> = 0,
где D s= -щ - Ж
Записав далее это уравнение с помощью формулы (30.18) в
координатах, получим следующее уравнение:
(32.4) Ах + By 4 Gz 4 D = 0.
Легко показать, что всякое уравнение первой степени вида (32.4)
является уравнением некоторой плоскости, если хоть один из коэффициентов
А, В, С не равен нулю. Действительно, если, например, А ф 0, то
уравнение (32.4) можно записать в виде (32.2);
А (Х + f) + В{"У ~ ^ Л~ С^ " ^ = °'
Т.е» уравнение (32.4) есть уравнение плоскости с нормальным вектором
N =■ (А; В; С), проходящей через точку М0 (- ^; 0: 0).
Определение 32,1. Уравнение (32.4) называется общим уравнением
плоскости, уравнение (32.2) уравнением плоскости, проходящей через
данную точку, уравнения (32.1) и (32,3) - соответствующими
уравнениями в векторной форме.
Выведем уравнение плоскости, проходящей через три точки, не
лежащие на одной прямой: М\{х\\ уг, z\), М2(х2: уч\ z2), М3(я3; уг; zz) ( рис. 156).
Обозначим ?7, rj, rj, r - радиус-векторы этих точек и текущей точки
плоскости М(х] у] z) соответственное
В качестве нормального вектора плоскости выберем вектор N = Ъ^1М2 х
MiM$, очевидно перпендикулярный плоскости. В соответствии с (32.1)
получаем векторное уравнение:
(г - гГ)((г2 - г\) * (гз - ПГ)) = 0.
Поскольку в соответствии с определением 31.2 левая часть этого
уравнения есть смешанное произведение, векторное уравнение плоскости через
три точки принимает вид:
32 ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 377
РИС. 156. Плоскость через три точки
(32.5) ((f - гГ)(г* - П)(Щ - ц)) - 0.
Записав это уравнение с помощью формулы (31.5) в координатах,
получим уравнение плоскости через три точки в координатной форме:
(32.6)
x-xi у-Ух z- zi
%2 -31 У2 - У\ *2 - Zi
яз - х\ Уз - 2/1 *з - «i
= 0.
Определение 32.2. Совокупность плоскостей, проходящих через
данную точку, называется связкой плоскостей.
Уравнение (32.2), в котором коэффициенты А, Вт С могут принимать
любые значения, является уравнением связки плоскостей.
32.2. Особые случаи расположения плоскости. Если
коэффициент D — 0, то плоскость проходит через начало координат, т.к.
координаты точки О(0; 0;0) удовлетворяют уравнению
Ах 4- By + Cz = 0.
Если коэффициент А = 0, то нормальный вектор плоскости
перпендикулярен оси Ох (проверьте самостоятельно перпендикулярность
векторов N = (0;В;С;) и г = (1;0;0)) и, следовательно, данная плоскость
By 4- Сг 4- -D = 0 параллельна оси Ож.
Если коэффициенты А = 0 и J9 = 0, то плоскость J5«/ 4 Cz = 0
проходит через ось Ох, т.к. она параллельна оси Ох и проходит через начало
координат.
Если коэффициенты А = 0 и В = 0, то нормальный вектор плоскости
параллелен оси 0.г (проверьте самостоятельно коллинеарность векторов

378
32 ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ 8 ПРОСТРАНСТВЕ
N = (0; 0; С) и к = (0; 0; 1) и, следовательно, дан над плоскость Cz -f- D = 0
параллельна плоскости Оху и перпендикулярна оси Oz.
Если коэффициенты А = В = D = 0, то данная плоскость
z = 0 является координатной плоскостью Ож?/ (параллельна плоскости
Оху и проходит через начало координат).
32.3. Угол между плоскостями. Двугранный угол между двумя
плоскостями равен углу между их нормальными векторами ( рис. 157).
Рис. 157. Угол между плоскостями
Если даны две плоскости
ах : А\х 4- В\у + C\z + A = 0,
а2 : А2х 4 В2у + С2г + D2 = 0,
то угол между ними вычисляется как угол между их нормальными
векторами Tfi = (Аг; Bi; Ci) и ЛГ2 = (Л2; Я2; С2);
(32.7)
АгА2 + BiB2 + СхСз
(32.8) cosu? = , ,—, , = — , ,
|^i|-|^a| л/^i + B\+Cl • v^2 + J3| + C?
Пример 32.2. Определить угол между плоскостями 2x + y — z + \
и х — у -t- 3z = 0.
Решение: По формуле (32.7) получаем:
= -^в =* * = * ~ arccosW ~ Х'82'
COStf = 2-1-Ц(-1)-13
^ ^22+12+(-1)2у12+(~1)2+32
Ответ: cos<£> = ~~7Ж°
32.4. Параллельность и перпендикулярность плоскостей. Две
плоскости будут параллельны тогда и только тогда, когда их
нормальные векторы параллельны и плоскости не совпадают. Т.е. необходимым
и достаточным условием параллельности двух плоскостей (32.7) является
условие (32.9):
32 ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 379
(32.0)
h = Si = £l
А2 o2 С/2
при условии, что плоскости не совпадают. Последнее условие легко
проверяется приравниванием левых частей уравнений (32.7).
Аналогично, две плоскости перпендикулярны тогда и только тогда,
когда их нормальные векторы перпендикулярны. Т.е. необходимым и
достаточным условием перпендикулярности двух плоскостей (32.7) является
условие (32.10):
(32,10) Аг - А2 -г Вг В2 Ч~ d • С2 = 0.
Пример 32.3. При каком значении т две плоскости 2х — Зу 4- 5
и тх •]- 1у — б = 0 будут параллельны?
Р е ш е к и е: Проверим выполнение условия (32.9); ^ = ^ = jj.
Решаем первое уравнение
2 „ -3
m ~~ 7
m = — ^. При этом плоскости
2# - Зу Н- 5 = 0 и -у£ т 7у - б = 0, очевидно, различны, т.к. равенство
2х - Зу + 5 — — у я -f 7t/ - 6 не является тождеством.
Ответ: m — — у.
32.5. Расстояние от точки до плоскости. Пусть даны точка
М0(х0., #0; *о) и плоскость а : Ах 4- ffy 4- Cz 4- Г> = 0. Докажем, что
расстояние d от точки Мб до плоскости or, т.е. длина перпендикуляра МбМ\
на плоскость а ( рис. 158), вычисляется по формуле:
(32.11)
<*»
мп
m,
Рис. 158. Расстояние от точки до плоскости
Решение: Обозначим N — нормальный вектор плоскости а: N =
(А; В] С), координаты точки M\(xi\ yi\ z{). d « |MiM0|, где вектор М\М0

380 32. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПЛОСКОСТЬ
имеет координаты; Mi Mo = (xo-xi)i+(yQ-yi)j+(zQ-Zi)k. Поскольку N ||
MiMo (<р - 0 или ip = я*), имеем по определению скалярного произведения:
(32.12) 77 - ЖЩ = |77| • \ЖШ\ • cos у = ± |JV| • J~ЩЩ\.
С другой стороны, в соответствии с формулой (30.18):
(32.13) N . МХМ0 = А(ж0 - дгО 4- В{уо - уг) + C(z0 - z\).
Но точка Мг €jx, поэтому Ахл +• Bi/i 4- Czi + D = 0 ==*► —Лж2 -
Вух - C*i = JD и TV - MiMo - Лж0 4-Jfyo + С^о - Axi - Ву\ - Czx =■.
Axq + ByQ + CzQ + D Учитывая, что IN] - VA2 + В* + С2, ^Мд) = d,
из формул (32.12), (32.13) получаем:
±VA* + В2 + С2 - d - AxQ + i?2/0 + Cso 4- A
откуда
и9 т.к. d > 0, получаем формулу (32.15). В векторной форме формула
расстояния от точки до плоскости получается с учетом (32.3) в виде:
(3214) d=lJL^ *
Замечанпва Аналогично можно доказать, что расстояние от точки
Мо(хо', у&) до прямой Ах -f- By 4- С --■ 0 на плоскости Оху определяется
по формуле (32.15):
(32.15) d=]A*+^* + Cj
32. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПЛОСКОСТЬ
Пример 32.1. Проверьте, проходит ли плоскость а : 2х — Зу 4-z — 1 ==
0 через точст Mi(l,0, -1) и М2(1,1,1)?
Решение: Подставив координаты точки М\ в уравнение плоскости,
получим: 2 - 1 — 1 — 0, т.е. точка М\ 6 а. Для точки М2 аналогично
получаем; 2-3 + 1-1^0, т.е. М2 $ а
Пример 32.2. Найдите расстояние от. точки М2 до плоскости a v
примере 32.1.
32* ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПЛОСКОСТЬ
381
Решение: По формуле (32.10) получаем;
|2-3+1-1| 1
d~
V2* + (-3)2 + I2 y/U
ПРИМЕР 32.3. Найдите уравнение плоскости, проходящей через
точку М(2; 1; 1) параллельно плоскости 2х — 2у + 2z + 1 ss 0.
Решение: Используем уравнение (32,2) плоскости, проходящей
через заданную точку М. В качест»е_нормйльного вектора возьмем
нормальный вектор заданной плоскости N — (2, -2,2), т.к. они параллельны.
Получим:
2(х - 2) - 2(» - 2) + 2(* - 1) = 0.
или после упрощения; я — у + * — 2 = 0.
Пример 32.4. Найдите уравнение плоскости, проходящей через тон-
ку М(2; 0; 3) перпендикулярно вектору N — (2; 2; —2).
Решение; Используя формулу (32.2), получаем 2(х - 2) + 2(у -
0) - 2(z - 3) = 0. Упрощая, получим: я + г/-2 + 1=0.
Пример 32.5. Найдите уравнение плоскостщ проходящей через три
точки: О(0; 0;0), Afi(-4;2;-l), М2(-2;-4;3).
Решение: Используя формулу (32.6), получаем:
= 0<*
= 0<*
«* дг(б - 4) - 2/(-12 - 2) + ^(16 + 4) = 0 Ф* х + 7у + 10* - 0.
Пример 32.6. Найдите уравнение плоскости, проходящей через
точки Мх(2; 0; — 1), М2(1; — 1; 3) перпендикулярно плоскости Ъх+2у—х—Ь — 0.
Решение: Используем формулу (32.2) уравнения плоскости,
проходящей через данную точку. В качестве нормального вектора искомой
плоскости возьмем вектор N, перпендикулярный вектору МХМ2 и
нормальному вектору заданной плоскости N\ = (3; 2; —1), например, их векторное
произведение MiM2 x N\ Найдем координаты вектора МХМ2 = (—1, -1,4)
и нормальный вектор:
* 1 &
-1 -1 4
3 3-1
\ х- 0
у-о
z-Q
-4-0 2-0 -1-0
-2-0 -4-0 3-0
<& х -
2 -1
-4 3
-у
= 0«*
4 -1 1
2 3
X
У *
-4 2 -1
| -2 -4 3
+ Z
-4 2
-2 -4
N^MiM2xNi =
= г •
-1 4
2 -1
-j-
-1 -4
3 -1
+ *•
-1 -1
3 2

382
32. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПЛОСКОСТЬ
= —7г Ч- llj-h Л: ^0.
Искомое уравнение плоскости, проходящей через точку Мх с
нормальным вектором N будет иметь вид:
-7(х - 2) + il(i/ - 0) 4- 1(г 4-1) = 0 или - 1х Н- Ну 4- z 4-15 = 0.
Пример 32.7о Найдите угол между плоскостями ctx : ж-2/+2£—3 = 0
иа2- 2ж 4- 2/ — 0.
Решение; Зная JVi — (1, —1,2), JV2 = (2,1,0) нормальные векторы
данных плоскостей, по формуле (32.8) получаем:
NXN2
cos у? — — —
1-24- (-1) - 1 4 2 0
1
\Ni\\N2\ у/1*+ (-!)* + 22 • ^22 4-12 + О2 VS5'
г j А;
1 1 1
1 1 -1
= г •
1 1
1 -1
- J '
1 1
1 -1
4-Ь
1 1
1 1
Пример 32о8. Найдите уравнение плоскости, проходящей через
точку М(0,2,1) параллельно векторам а = г 4- J 4- & u 6 = г 4- j; — к
Решение: В качестве нормального вектора искомой плоскости
выберем векторное произведение данных векторов:
N = axb~
= -2z4-2j
В соответствии с формулой (32.2) получаем уравнение плоскости:
-2(з - 0) 4- 2(у - 2) = 0 или х - у 4- 2 = 0.
ПРИМЕР 32.9. Найдите уравнение плоскости, проходящей через
середину отрезка АВ перпендикулярно к этому отрезку, если концы отрезка
имеют координаты А(—7; 2; —2), £(3;4; 10).
Решение: Координаты точки М0 — середины отрезка АВ
вычисляются по формулам (30.7): х0 = :zl^ = -2, </0 = ^ = 3, z0 = :::2^ = 4.
В качестве норамльного вектора возьмем АВ = (10, 2,12). Искомое
уравнение будет: 10(ж 4- 2) 4- 2{у - 3) 4-12(* - 4) или Ъх 4- у 4- 6z — 17 = 0.
ПРИМЕР 32.10. Найдите расстояние между параллельными
плоскостями: ах : 2ж + у-24-3 — Ог/аг: — 2х -у4г -5 = 0.
Решение: Выберем точку М на плоскости а\ и найдем расстояние
от этой точки до плоскости аг- Задавая две координаты точки М: х0 — 0,
ЯЯ ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 383
ус ~ 0, найдем г0 = 3, т.е. М(070,3). Искомое расстояние находим по
формуле (32.11):
tf 13 —SI ^_
^(-2)2 + (-1)2 +1* "ч/б"
Самостоятельная работа
Пример 32.11. Найдите расстояние от точки М, делящей отрезок
АВ в отношении 1 ; 2 до плоскости х — 3^ + £ — 6 = 0, если Л(2,0?1),
£(-1,3,1).
Пример 32.12. Через точку А отрезка АВ проведите плоскость,
перпендикулярную этому отрезку, если Л(—1,2, —3), 2?(Q, 2,4).
Пример 32.13. Найдите уравнение плоскостщ проходящей через
точки Mi (2, — 57 0), М2(6,07 2) перпендикулярно плоскости #4-5jt/4-2z~ 10 = 0.
33. ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В
ПРОСТРАНСТВЕ
Общие, векторные, параметрические, канонические уравнения
прямой в пространстве. Угол между прямыми. Пучок плоскостей.
Пересечение прямой и плоскости.
33.1. Прямая в пространстве. Прямую в пространстве зададим
пересечением двух плоскостей (рис. 159), т.е. системой (33.1) в векторной
форме или системой (33.2) в координатной:
(331) \W2~r + D2~Q.
m 9г Г i4xaj 4- Дх» 4 Cl2 + А = 0,
16,5'^ \ Л2ж + Ау 4- Ciz 4- А> = 0.
Если эти плоскости не параллельны, т.е. их нормальные векторы не
коллинеарны: Nx = {Ai\Bi\&),N2 = {A^B^C^.Nx Jf i\T27 то системы
(33.1), (33.2) определяет единственную прямую.
ОПРЕДЕЛЕНИЕ 33-1- Уравнения (33 Л), (33.2) называются общими
уравнениями прямой.

3$4 33 ЛЕКЦИЯ ■ АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Рис. 159. Прямая как линия пересечения плоскостей
Наряду с рассмотренным способом прямую в пространстве можно
задать, определив принадлежащую ей точку Мо(хо,?/о;^о) а вектор s ~
(га; щр)> параллельный этой прямой. Вектор .5 называется направляющим
вектором прямой.
ДЛЯ ПРОИЗВОЛЬНОЙ ТОЧКИ М(х;у].?;) Прямой I (рмС. 150) Имеем:
ОМ = ОМо + МоМ. Вектор WqM || з =* Л^М = 5' • *, где параметр
t б (—оо;+оо). Обозначая радиус-векторы точек Мс и М соответственно
г0 =5 0МО и гх = ОМ, получаем:
(33.3)
г = f0 f /< • «.
Рис. 160. Направляющий вектор прямой
Уравнение (33-3) называется векторным уравнением прямой. Здесь
каждому значению параметра t соответствует радиус-вектор F точки
Me L
Для получения параметрических ур&ваешш прямой представим
уравнение (33.3) в координатной форме:
f = ОМ = хг + ю 4- **, го - ОМц - .K0i' + Vvj -Ь ^ofc, *S = tm? ■}■ in] -f- tpfc.
33 ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 385
Получим:
(33.4)
{х sas xq 4- im,
2/ = 2/о 4- Ьщ
Z = 20 4- J/7.
Определение 33.2. Уравнения (33.4) называются
параметрическими уравнениями прямой. Они также определяют прямую заданием
точки М0 и направляющего вектора s. При изменении параметра t
изменяются координаты ж; у] z и точка М(х\ у\ z) перемещается по прямой.
Выразим параметр t из каждого уравнения системы (33.4) и
приравняем правые части полученных уравнений;
т п р
Получим уравнения:
(33.5) izfii.lL^.iz*,
т п р
задающие прямую.
Определение 33.3. Уравнения (33.5) называются каноническими
уравнениями прямой.
Заметим, что уравнения (33.5) равносильны системе двух уравнений
первой степени:
Г *-»! — У~У1
(33.6) { ^ = «^1*
Третье уравнение *^ = L=S1 является следствием этих двух.
Таким образом, канонические уравнения (33.5) задают прямую
пересечением двух плоскостей. Плоскости, задаваемые уравнениями (33.6) обладают
особенностями; первая из них параллельна оси Oz, вторая - оси Ох (см.
п. 32.2 лекции 32).
Замечание. Договоримся писать уравнения (33.5) в виде:
х-xi _ у- 2/1 _ z-zi
0 п р '
если вектор s имеет координаты s = (0;n;p). В этом случае s ± Ох и
х = х\. Аналогично прямая
х-xi _ а/-2/1 = z- zi
0 0 р
параллельна оси Oz, т.к. в этом случае s ± Ох и s J_ Оу (х = a?i, 2/ = yi)-

386 33 ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЙ В ПРОСТРАНСТВЕ
Пример 33.1. Привести общие уравнения прямой
<-) {Г--ЛГЛВ=0'
к каноническому виду.
Решение: Для получения канонических уравнений необходимо
найти точку М0 и направляющий вектор s прямой.
Для нахождения точки М0 дадим одной из координат какое-нибудь
значение, например, z = 0, и найдем две другие координаты из системы:
/оооч J 4х-г/+12 = 0, Г я?о = —f,
<33'8) \ г,-2 = 0, ^ \ 1/0-2.
Таким образом точка М0(-§; 2; 0) €• / найдена.
Для нахождения направляющего вектора $ заметим, что векторное
произведение нормальных векторов N\ — (4;—1;—1) и N2 = (0; 1; — 1)
данных двух плоскостей можно принять в качестве направляющего
вектора прямой их пересечения, т.к. вектор $ параллелен / ( рис. 150): s =
\ г j k
Поэтому * = 4 -1 -1 | ===== г(1 4-1) - j( ~4) + к(4) = 2? 4- 4] 4- 4*.
I 0 1 -1
Окончательно, канонические уравнения прямой имеют вид:
5
~ 4'
* + ! t/-2 _ г
*+2 -_ I/-2 _ £
Пример 33.2. Записать уравнения прямой —^ = *^р = | в
параметрическом виде.
Решение: Обозначим общее значение данных в условии выражений
через t: Ц* = ^ = f = *, откуда:
X
=
2/
-1 + 2*,
= 2 + 4*,
z = 4*.
2±i = t
4 *'
4 C'
ПРИМЕР 33.3. Записать общие уравнения прямой, заданной в
параметрическом виде:
(х^ -§4-2*,
у = 2 + 4*,
z = 4*.
55 ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ $$У
Решение: Выражая параметр t из каждого уравнения и
приравнивая правые части, получим канонические уравнения прямой:
? п Г: I * ~ ~' х+й
(33.9)
I * = *.
цгопг уравж
\ 0-2 «*. ^*\ у- г -2 = 0.
Г 2аг
\ 2/
{д; = — £ -1-2*
»-* + £ «-►< «-«^ *=*¥-*?-5
Выбирая два из последних уравнений, получаем;
- 7 4 '
й^2 = £
4 4*
Ответ;
г - 2 » 0.
Заметим, что полученные общие уравнения (33.9) отличаются от уравнений (33.7),
которыми эта прямая была задана в примере 33-1. Однако и те и другие задают одну и
ту же прямую. Чтобы убедиться В этом, проверьте, например, ЧТО ТОЧКИ Л4в(—§;2;Q)
и Afi(-1;5;3) удовлетворяют уравнениям (33.7) и (33.9). Другими словами, уравнения
(33.7) и (33.9) задают одну прямую MqM\.
Для получения канонических уравнений прямой, проходящей через две
точки МоОад */о; *о) и Mi(a?i;yi;*i), заметим, что в качестве
направляющего вектора в этом случае можно выбрать
s = MaMi = (*i - *о№ + {yi - Vo)j + (zi - zo)k, Тогда канонические
уравнения прямой, проходящей через две точки, примут вид
(ЗЗ.Ю) ±^*- = MzH. = JLJ0L.
Х1-ХйУ1-У0*1- *0
Пример 33.4. Написать канонические и общие уравнения прямой,
проходящей через точки Af0(—§;2;0) и Mi(—1;5;3).
Решение: в соответствии с формулами (33.10) получаем
канонические уравнения;
* + § _у-2 z , , у + § у-2 z
-1 + 1 5-2 3 " " \ 3 3*
Для получения общих уравнений выберем два из последних трех
уравнений:
^ = ^, ^ | 2* + Б = »-2, <__>/2Ж-г/+-7 = 0,
к 3 ~" 3' V
Мы получили уравнения (33-9)
{

388 33 ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
h
h
■ яа—xi
mi
1712
— У-У1 _
ill
— У~Я2 _.
Р\ '
P2
33.2. Угол между прямыми. Пусть в пространстве даны две
прямые:
(33.11)
Угол между ними вычисляется как угол между их направляющими
векторами sx = (m^n^pi) И52 = (т2;п2]р2) :
/оо 10\ ^г ' *2 mim2 + щп2 + pip2
(oo.lz) cos<£> — ~
N ■ Ш s/7n\ 4- п\ +j$yfal 4-nf +й'
Условием параллельности двух прямых (33.11) является условие
коллинеарности их направляющих векторов:
(33.13) ^ = * = Ь.
тч ii2 vi
при условии, что эти прямые не совпадают. Последнее условие легко
проверяется подстановкой пары точек одном из этих прямых в уравнТзнйе
другой.
Условием перпендикулярности двух прямых является условие
перпендикулярности их направляющих векторов:
(33.14) тх • т2 + пх • п2 4 pi * pi --- 0.
33.3. Пересечение прямой ж плоскостм. Пусть в пространстве
даны прямая / и плоскость а:
(33.15) /:£^°^Ш* = 1^±.
т п р
(33.16) <*:Ax + By+Cz + D = 0.
Найдем координаты точки Р(х\; у\ \ z\) пересечения прямой I н
плоскости а, для чего запишем уравнения прямой в параметрической форме (33.4)
и, подставив значения х, у, z в левую часть уравнения (33Л6), найдем
значение параметра £ь при котором одновременно выполняются уравнения
(33.15) и (ЗЗЛв):
А(х0 4- mt) 4- B(y0 -i nt) -i C{zD I pi) 4- Z> - 0. =>
.?£ ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ 389
(33.17) *> - >т»тСатР
Подставив затем эти значения в формулы (33.4), получим координаты
точки пересечения;
(ЗЗЛ8) х\ = яо 4- iim, 2/1 = у0 4- £in, л = 20 + Jip.
Заметим, что формулы (33.15)7(ЗЗЛ6) являются координатной формой
записи соответствующих векторных уравнений прямой и плоскости:
_• То 4-1 • s,
■AT 4- D = 0.
Выразив г из первого уравнения системы и подставив во второе,
получим для 11 формулу:
х~ 77-5
33.4. Угол между прямой и плоскостью. Угол tp между прямой
(ЗЗЛ5) и плоскостью (ЗЗЛ7) легко определяется (рис, 161) через угол
между направляющим вектором $ прямой и нормальным вектором N
плоскости:
cos(JV;s) = cos(90° - (р) = sin v?.
С другой стороны, по формуле (30.20) получаем:
/Т7 -v Ат-\-Вп + Ср
cos(JV; s) =
у/А2 4- £2 + CVrn2 + n2 + Р2
Окончательно:
> v . Лт + Вп + Ср
8Ш(Р ~ у/А2 4- В2 + CV™2 + п2 +р2'
Условием параллельности прямой (ЗЗЛ5) и плоскости (ЗЗЛб) является,
очевидно, условие перп^эвдикулярности направляющего вектора s прямой
и нормального вектора N плоскости
(33.20) Am 4- Вп 4- Cm = 0
при условии что прямая не принадлежит плоскости. Последнее условие
легко проверить подстановкой в уравнение плоскости двух точек прямой.

390 33 ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
Рис. 161. Угол между прямой и плоскостью
Условием перпендикулярности прямой и плоскости является условие
коллинеарности направляющего вектора s и нормального вектора N
плоскости:
/™Л„ч т п р
(33.21) - = - - §.
33.5. Пучок плоскостей.
Определение 33.4. Совокупность всех плоскостей, проходящих
через данную прямую Z, называется пучком плоскостей, а прямая I- осью
пучка (сравните с определением связки плоскостей в лекции 32).
Пусть ось пучка задана общими уравнениями прямой:
/«-> 09л / Агх + Вгу f Ciz + L>i = О,
^"^j { А2х + В2у + С722 + D2 = 0.
Докажем, что уравнение пучка плоскостей, проходящих через прямую
(33.22) имеет вид:
(33.23) (Агх + Вгу + Cxz + Dx) + А(Л2ж 4- В2у 4- C2z 4- £>2) = 0.
где параметр А принимает любые действительные значения от -оо до
Ч-оо.
Доказательство. Уравнение (33.23) при любом конкретном значении А определяет
некоторую плоскость, т.к. является уравнением вида (32.4), где А = А\ 4- АЛ.2» В — В\ +
АВг,(7 == С\ -f- \C2,D = D\ 4 AD2. Эта плоскость проходит через прямую (33.22), т.к.
значения ж; у; z удовлетворяющие системе (33.22) обращают в тождество и уравнение
(3323) (выражения в скобках равны нулю).
33 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРЯМАЯ В ПРОСТРАНСТВЕ
391
Наоборот, покажем, что всякая плоскость пучка (кроме плоскости аг: Ачх + В%у +
Ciz-i- Di = 0) может быть представлена в виде (33.23). Выберем произвольную точку
Mo{xQ,yQ]20) f <*2, т.е. Л2Я0 + ВгУо + Сг*о + Dt #0- Найдем значение А0 ИЗ УСЛОВИЯ,
чтобы координаты ТОЧКИ Мо удовлетворяли уравнению (33.23):
АХХ0 + ВгУо 4 CiZo + D\ 4- Afl(^2*0 + #22/0 + ^2*0 + В2) = 0 =*=*
_ ^1Д?о + £i3fo + С\Ч + Ui
g "" A2xQ 4 В2уо 4 C2z0 4 D2
Подставив в уравиение (33.23) А = А0 можно быть уверенным, что это будет
уравнением плоскости, проходящей через прямую (33.22) (см. первую часть доказательства) и
точку Мл (значение Aq выбиралось из ЭТОГО условия). Т.к. прямая (33.22) и точка М0,
не принадлежащая этой прямой (М0 ^ Oft)» однозначно определяют плоскость пучка,
вторая часть доказательства закончена.
33. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРЯМАЯ В
ПРОСТРАНСТВЕ
Пример 33.1. Проверьте, проходит ли прямая I
х — 1 _ у _ z
2 "" Zi "" 0
через точки Mi(3; —1;0), М2(—1; 1; 1)?
Решение! Подставляя координаты точки Mi в канонические
уравнения прямой, получаем 2=1 = fj = J. В соответствии с изложенным
в лекции 29 считаем, что эти равенства верны,включая последнее, т.е.
М\ € / (см. пример 30.4 лекции 29).
Для точки Mi\ :=^ = гх = о' т-е- &f2 $ I
ПРИМЕР 33.2. Напишите общее уравнение прямой I из примера 33*1.
Решение: Выберем два равенства из канонических уравнений
прямой /:
1-1 - -*- < ~ '-2»-1=0,
Заметим, что уравнение z = 0 второй плоскости (?яу можно было
получить сразу из канонических уравнений, т.к. последняя дробь не имеет
смысла при z ф 0.
Пример 33.3. Проверьте, проходит ли прямая I через точки
М0(0; —1;2), Mi(l; 1; 1) и запишите канонические уравнения прямой:
. ( х 4- у - я + 3 --= О,
* \ 2* - у - 1 = 0.

Щ 33 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРЯМАЯ В ПРОСТРАНСТВЕ
Решение: Подставляя координаты точки М0 в уравнение прямой,
получаем
Г -1-2 + 3-0 жж ,
| г _ х = 0 , т.е. М0 е I.
Делая то же самое с координатами точки Ми получаем
Г -1-1 + 3^0,
1-1 = 0,
т.е. Мх £ L
Для нахождения канонических уравнений нужно знать точку прямой и
направляющий вектор. Для нахождения точки возьмем х0 — 0 и из системы
найдем у о — — 1, zq — 2 (получили точку М0). В качестве направляю-
щего вектора в соответствии с изложенным в лекции 32 возьмем вектор
s = Nt х JV2, где Nt = (1,1,-1) и N2 = (2,-1,0) нормальные векторы
данных плоскостей:
s = JV2 х N2 ■-=
i j к
1 1 -1
2-10
1 - 1
-1 0
-i - 2] - 3*.
-.?
1 -1
2 0
+ к
1 1 1
2 -1
Окончательно канонические уравнения прямой имеют вид:
х
У + 1
-2
z-2
~з~
или
t/ -f I z - 2
Пример 33,4с Напишите параметрические уравнения прямой из
примера 33,3.
Решение: Обозначим общее значение дробей в канонических
уравнениях прямой через t:
х __ г/4 1 _ г_--_2
I ~ 2 ~~ "з ~L
Отсюда
? = *,
а+1 - *
2 — ''
2=2 - /.
з — 1>
ч
1
X --• А.
у«-1 + 2*
а - 2 + 3*.
ПРИМЕР 33.5. Найдите угол между прямыми /j м /2;
; х у -hi г - 1
*2 ' "З " ~~Т~ ^ "~0_ *
/ £ - У-1 _ * + 2
1 " 2 ~ 3 ~ 2 '
55 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРЯМАЯ В ПРОСТРАНСТВЕ
393
Решение; Выпишем координаты направляющих векторов прямых;
Щ = (2,3,2), Ц = (-3,1,0) и по формуле (33.12) получим;
~§1'Щ 2 ■ (-3) + 31 + 2-0 3
\Ж\\Щ V22 + 32 + 22 • уЧ-З)2 + I2 л/170*
ПРИМЕР 33.6. Найдите угол между прямой I и плоскостью а:
х t/+1 z -1 . ft
J; - = *_.__; а; 3* - » + 2* - 1 - 0.
Решение: Выписав координаты направляющего вектора прямой 3 =
(2,3,1) и нормального вектора плоскости N = (3, — 1,2), в соответствии с
формулой (33.19) имеем:
• _ У'АГ = 2-3 + 3-(-1) + 1-2' _ 5
81П^ \s\\N\ ~ >/22 + 32 + 12 • ^3* +(-1)2 + 2* 14'
ip = arcsin(^).
Пример 33.7. Найдите точку пересечения прямой I и плоскости а
us задачи 33.6.
Решение; Запишем уравнения прямой I из примера 33.6 в
параметрическом виде:
Подставим эти выражения в уравнение плоскости и найдем значение
параметра t, удовлетворяющее уравнению плоскости:
3 • 2t - (-1 + 3*) + 2(1 + 0 - 1 = 0 => t■ = -§.
5
Из параметрических уравнений прямой находим:
f » = 2(-|) = -|,
b-i+H) = i-
Итак, точка с этими координатами принадлежит одновременно прямой и
плоскости, т.е. является точкой их пересечения.
Ответ: М(-4;-^;|).
Пример 33.8. Найдите уравнение плоскости, проходящей через
прямую | = *~ = f и точку М(1,1,2).

Щ 33 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРЯМАЯ В ПРОСТРАНСТВЕ
Решение: Проще всего решить эту задачу выбрав две точки
Мо и М\ прямой и написав уравнение плоскости, проходящей через три
точки М, М0, Mi. В качестве точки М0 удобно взять точку, задаваемую
каноническими уравнениями прямой: М0(0,1,0). Для нахождения другой
точки М\ запишем уравнение прямой в параметрическом виде:
х
2
Подставляя какое-нибудь значение t $ 0, например, t = 1, получаем
координаты точки Мх: Xi ~ 2, у\ = 4, z\ = 1, т.е. Мх(2,4,1). Наконец,
уравнение плоскости через три точки М, Mi, M2 имеет вид (32.6):
х-1 у-1
0-1 1-1
2-1 4-1
z-2,
0-2,
1-2,
= 0<£>
ж-1
-1
1
У-1
о
3
z-2,
-2,
-1.
0^>
/ -v I 0 —2
^(я-1) з -1
-(y--i)ir1
-2
-1
+ (z-2)
-1
1
-0
4=>2х-у--£ + 1 = 0-
Пример 33.9. Найдите уравнение и длину медианы треугольника
ABC, выходящей из вершины А, если Л(1; 2; -1), 5(1; -2; -2), С(3; 4; 0).
Решение: Найдем координаты другого конца медианы из вершины
А, т.е. середину отрезка ВС:
__ /1 + 3 -2 + 4 -2 + 0\
М (_.__. __j f T.e. M(2;l;l).
Уравнение медианы AM получается как уравнение прямой через две
точки (33.10):
ж - 1 у - 2 z-\-l ж - 1 у ~ 2 _ z + 1
2-1 ^ 1-2 = -1 + 1 ^ ~Т~ =" ~^Г " ~~0~'
Длина медианы определяется по формуле (30.5):
d = /(У^Т (1 - 2)2 + (-1 + 1)2 = у/2.
Пример 33.10, Найдите уравнение плоскости, проходящей через
пересечение плоскости ct\ : х 4- у + 5г — 1 = 0, а2 : 2ж + Зу — z + 2 = 0 г*
через точку М(3,2,1).
55 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРЯМАЯ В ПРОСТРАНСТВЕ
395
Решение: Проверив, что М <£ а^ напишем уравнение (33.23) пучка
плоскостей, задаваемого плоскостями ftj и л2:
(х + у + bz - 1) + А(2ж + Зу - z + 2) = 0.
Подставив в это уравнение координаты точки М, найдем А ; 3 + 2 + 5 -
1 + А(6 + 6 — 1 + 2) =0^А = —^ т.е. уравнение искомой плоскости
пучка:
(х + у + bz - 1) - — (2я? + Зу - г + 2) = 0
или 5аг + 14у - 74я + 31 = 0.
ПРИМЕР 33.11. Найдите уравнение плоскостщ проходящей через
пересечение плоскостей а\ : д: + Зу + 5г — 4 — Q и ai: х — у — 2^+ 7 = 0 ад
параллельной оси Оу.
Решение: В соответствии с изложенным в пункте 32.2, если
плоскость параллельна оси Оу, то коэффициент В в общем уравнении
плоскости равен 0. Напишем уравнение пучка плоскостей, задаваемого
c*i ж ач\
(ж+Зу+52-4)+А(ж-у-2я+7) = 0 <* (1+А)ж+(3-А)у+(5~2А)г+(7А-4) = 0.
Приравнивая нулю коэффициент при у, находим А ; 3 — А — 0 =^ А = 3.
Подставляя найденные значения А в уравнении пучка, получаем уравнение
плоскости: Ах — z + 17 = 0.
Самостоятельная: работа
ПРИМЕР 33.12. Напишите уравнения прямой, проходящей через
точку М( 1,-1,1) параллельно плоскостям ая : 2х - у + z — 1 = 0 и
а2 : ж - я =s 0.
Пример 33.13. Напишите уравнения прямой, проходящей через
М(0; 1; 2) перпендикулярно векторам а = (1; 2; —3), Ь = (—3; -2; 1).
Пример 33.14. Определите направляющие косинусы прямой.
* + 0 + * + 1 = О,
ж-у-2-1 = 0.
Пример 33.15. Найдите координаты проекции точки М(2,1,3) на
плоскость да + 2у -£ + 5 = 0.
Пример 33.16. Найдите уравнение плоскости, проходящей через
прямую I : —^ =5 ^ a= *#- перпендикулярно плоскостщ а ; у + 4у — 3z +
1=0.

396 34 ЛЕКЦИЯ - ПОНЯТИЕ N- МЕРНОГО ВЕКТОРНОГО ПРОСТРАНСТВА
34. ЛЕКЦИЯ - ПОНЯТИЕ п - МЕРНОГО ВЕКТОРНОГО
ПРОСТРАНСТВА
Понятие гс-мерного вектора. Линейное отображение. Преобразование координат.
Приведение квадратичной формы к каноническому виду.
34.1. Понятие n-мерного вектора. Как отмечалось в лекции 29, вектор в
пространстве определяется тройкой чисел — его координатами: а -: (ai^t^^). Если вектор
лежит на плоскости, то он определяется парой чисел: а — (aj7a2). Для дальнейшего
удобно координаты обозначать xi, хг, х$. Вектор а. — (xi,x2) называется двумерным, а
вектор а — (хг\Х2',хз)- трехмерным. Понятие n-мерного вектора вводится аналогично.
Определение 34.1. Система п действительных чисел Х\,Х2,^,,хп, заданных в
определенном порядке, называется n-мерным вектором. Будем записывать п-мерный
вектор следующим образом: а = (#15 Жг5 •••? Жет). Числа SPj, Х2,..., хп называются
координатами вектора.
Вектор, у которого все координаты равны нулю, называется нуль-вектором, или
просто нулем: О = (0; 0;...; 0).
Вектор (—a?i; — Xi\..", — хп) называют противоположным вектору
а — (х\;Х2\-.'',Хп) и обозначают-а.
Пример 34.1. Рассмотрим систему линейных уравнений:
( а\\Х\ Ч- «12^2 +" ••• + й>1пХп — &1»
J а21а:1 + Л22ж2 + ■•• "Ь ^2пЖ« = Ь±,
•тпХп ~ От
Пусть набор значений х\ = cq;^ = a2l —;яп = ап является решением данной
системы. Это решение молено рассматривать как п-мерныи вектор % — (at; ct<i\...; ап)
Набор значений свободных членов bi,b2,,..;Ьт можно рассматривать как т-мерный
вектор b- (fci;b2;.»;&m).
Определение 34.2. Два вектора а » (xi\X2\»*\xm) ч Ь — (у\\уг;.»',Ут)
называются равными: а = Ъ, если равны их соответствуюгцие координаты, т.е. Xi — yi(i '■-
l,2,...,n).
Как известно, линейные операции над векторами на плоскости и в пространстве
можно заменить соответствующими арифметическими действиями над их
координатами. По аналогии введем линейные операции над n-мерными векторами.
Определение 34.3. Суммой двух векторов а = (xi\x2;..^xn) иЪ~ (у\\У2'ч—\Уп)
называют новый вектор
(34.1) с = a + Ь = (х\ + у\; ж2 + у3; -; *п + уп),
a UX разностью — вектор
(34.2) d = a - b = (ai - зл; х2 - у2\ ...; хи - уп).
Произведением вектора а = (a?i; a?i;...; я™) на число Л называют вектор
(34.3) Ла= {\хц\хх.-.]\хп}.
Линейные операции над n-мерными векторами обладают свойствами, установленными
для линейных операций над векторами на плоскости и в пространстве.
84 ЛЕКЦИЯ - ПОНЯТИЕ N- МЕРНОГО ВЕКТОРНОГО ПРОСТРАНСТВА 391
Определение 34.4. Множество всех п-мерных векторов, для которых
установлены операции сложения и умножения на число, называется арифметическим
векторным пространством и обозначается Rn.
Векторы ^^fx^jx^V.^x^J^^Cx^^x^.-.i^^...^^
/ (к) (к) (к)л
(х\ 1,х\ ';.-;хп ) называются линейно зависимыми, если существуют такие числа
Ai; Аг;...; А*, не все равные нулю, для которых имеет место равенство
(34.4) AioT + А2«? +... + AjboT = 0.
Равенство ( 34.4) равносильно аналогичным равенствам для координат вектора:
(34.5) ХгхФ + \24*} + ... + Хн4к) - °.
Здесь нижний индекс означает координаты, а верхний-номер вектора, (г = 1,2,3,..., п)
ПРИМЕР 34.2. Четырехмерные векторы of = (2; 3;4; 5), О? = (1; —2; 2; -1) U Щ =
(6; 2; 12; 8) линейно зависимы, так как имеет место равенство 2щ + 2щ -а^кО.
Действительно, для соответствующих координат имеют место аналогичные
равенства. Например, для первых координат: 2 • 2 -f 2 • 1 + (—1) • 6 = 0; для вторых
координат: 2 • 3 + 2(-2) + (-1) • 2 = 0 и т.д.
Определение 34.5. Максимальное число линейно независимых векторов
называется размерностью векторного пространства.
Можно показать, что в пространстве Rn существует п линейно независимых
векторов, а любые п -f 1 векторов линейно независимы.
Таким образом, пространство Rn имеет размерность п. Поэтому оно называется
арифметическим n-мерным пространством. В частности, совокупность векторов
плоскости образует арифметическое двумерное пространство Ri, а совокупность векторов
пространства — арифметическое трехмерное пространство #3-
Определение 34.6. Базисом векторного n-мерного пространства называют
любую совокупность, состоящую из п линейно независимых векторов этого
пространства.
Таким образом, число векторов базиса совпадает с его размерностью. Одним из
базисов пространства Rn являются векторы
ёТ = {1; 0; 0;...; 0},Щ « {0; 1; 0;...; 0},..., е^ = {0; 0; 0;...; 1}.
Заметим, что кроме указанного базиса в /i-мерном векторном пространстве существует
бесчисленное множество других базисов.
Как и в случае 3-мерного векторного пространства имеет место следующее
утверждение, которое примем без доказательства.
Теорема 34.1. Всякий вектор n-мерного пространства единственным образом
может быть представлен в виде линейной комбинации векторов его базиса.
Определение 34.7. Числа Аь Аг,..., А„ называются координатами вектора в
данном базисе, а равенство (34-6) называется разложением вектора а по базису
(34.6) а = AioT-f-А202~+... + Апа^ = Q.

398 34 ЛЕКЦИЯ - ПОНЯТИЕ N- МЕРНОГО ВЕКТОРНОГО ПРОСТРАНСТВА
Определим координаты Ai,A2,...,An вектора в базисе ё7(1;0;0;...;0),
ё^(0;1;0;...;0),...,ё^(0;0; ...;0; 1). В этом случае по формуле ( 34.6) имеем: а = Aia7 +
Ага^Ч* — + А^а^, или в координатах:
{ xi = Ах • 1 + А2 0 + ... + А2 • О,
J i2 = Ai-0 + Aa-H-... + A2-0,
[ хп = Ai • 0 + А2 • 0 4-... + А2 • 1.
Следовательно: Ai = Si,A2 = ж2,...,АЛ = хп. Итак, в пространстве Rn для п-
мерного вектора а = (хцх2]...]хп) числа х\]Х2]-~',хп являются его координатами в
базисе ёГ,ё^, ...,ё^.
Следует отметить, что n-мерное векторное пространство является частным
случаем так называемого "линейного векторного пространства", в котором векторы будут
иметь свойства, аналогичные изложенным в лекциях 28, 29.
Для n-мерных векторов можно ввести операцию скалярного произведения и
понятие угла между векторами аналогично тому, как это сделаго в лекции 29.Если даны
двавектораа = (xi\X2\..-;Xn) и5= (у\\У2]—\Уп), тоа4= (х\ + у\\хъ + у2\...\хп + уп).
Скалярное произведение будет обладать свойствами, аналогичными изложенным в
лекции 29 для трехмерных векторов.
34.2. Линейные отображения. Пусть в плоскости Q задана прямоугольная
система координат. Для упрощения записи и удобства преобразований координаты точек
будем обозначать не х и у, а через х\ и ж2 или у\ и з/2 и т.д., а основные орты вместо
г и j — через е\ и eV
Рассмотрим уравнения, связывающие переменные х\ и а,2 с переменными у\ и уч'.
/34 rjx Г У\ - ацхг 4- ai2x2,
\ ' ' \ у2 = a2ixi+а22Х2.
где ац,а12,а21,а22-постоянные.
Каждой точке М плоскости Q с координатами х\ и х2 соответствует в этой же
плоскости единственная точка JV, координаты которой у\ и у2 определяются
соотношениями (34.7).
Определение 34.8. Точка N называется образом точки М. Если точка М
описывает в плоскости Q некоторую линию L, то ее образ описывает, вообще говоря,
также некоторую линию А. Как говорят, с помощью уравнений (34-7)
устанавливается отображение или преобразование плоскости Q в себя.
В связи с тем, что правые части уравнений (34.7) имеют первую степень
относительно х\ и #2, это отображение называется линейным. В заданной системе координат
Ох\х2 линейное отображение вполне характеризуется квадратной матрицей
А=( аиаи V
\ ^21 G22 /
составленной из коэффициентов линейного отображения (34.7).
Если ввести матрицы-столбцы X — ( l I , Y — I ,то систему уравнений
(34.7) можно записать в следующей матричной форме:
(34.8) Y = АХ.
34 ЛЕКЦИЯ - ПОНЯТИЕ N- МЕРНОГО ВЕКТОРНОГО ПРОСТРАНСТВА 399
ОПРЕДЕЛЕНИЕ 34.9. Матрица А называется матрицей линейного отображения,
а ее определитель \А\ = " ait - определителем линейного отображения. Линей-
кое отображение называется невырожденным (или аффинным), ССЛП его матрица
невырожденное, т.е. если \А\ ф 0. Если же \А\ = Q, то отображение НООЫваетСД
вырожденным.
При аффинном отображении система (34.7) однозначно разрешима относительно
#1 И #2- По формулам Крамера (28.11) имеем:
X! =:
х2 =
2/1 «12 1
1 2/2 «22 |
«11 «12
«21 «22
flu 2/i I
«21 Уг |
«11 «12 1
«21 «22
Итак,
а22 ai2
а2\ аи
(34.0)
1 *2--ffi¥l-
+ р^
Уравнения (34.9) показывают, что, обратно, каждой точке N(yx\y2) соответствует
единственная точка M(a?i;s2), а именно та точка А/, образом которой является точка
N. Таким образом, аффинное отображение определяет взаимно однозначное
отображение плоскости Q в себя. Из равенств (34.9) следует, что обратное отображение также
аффинно, а его матрица есть матрица, обратная матрице А:
-1-( а22/ \Л\ ~а12/\А\
-а21/\А\ +ап/\А\
)
К формулам (34.9) можно также прийти, если умножить обе части матричного
уравнения (34.8) на матрицу А'1:
A~lY - A~lAX.
Так как А~1А = (Ц) = Е и ЕХ « ЛГ, то A~lY = X. Итак,
(34.10) X = A-lY.
Очевидно, тождественному отображению
(34.11) / 2/1 =хь
\ 2/2 = *2
соответствует единичная матрица Е = ( ft 1 ).
Пример 34,3. Линейное отображение
(34.12) / W ='
\ 2/2 =<
: 2я?1 + За?2,
! Зя?1 f 5я?2

400 34 ЛЕКЦИЯ - ПОНЯТИЕ N- МЕРНОГО ВЕКТОРНОГО ПРОСТРАНСТВА
( 2 3 \
является аффинным, так как матрица А = ][ „ _ ) имеет определитель \А\ —
л к =1» ОЯШЮКЫЯ от нуля. Обратное отображение получим, разрешая систему(34» 12)
J О О J
относительно х\ их2:
[™-Ы) \ Х2 = -3J/! + 2|Ь.
Это отображение имеет матрицу А~1 — f « о )'
Образ точки М(1;2) есть топка JV с координатами у\ — 2 • 1 + 3 • 2 =z 8, #2 =
3 • 1 4- 5 - 2 = 13. Образом прямой L : %\ 4- 2x2 — 2 = 0 служит прямая Л, уравнение
которой получится, если в уравнение х\+ 2х2 — 2 = 0 подставим выражения х\ и %ъ
через ух и у2 по формулам (34-13):
(52/i - 3j/2) + 2(-3t/i 4- 2y2) -2 = 0, или — г/i h 2/2 — 2 = 0.
Можно доказать, что в общем случае при аффинном отображении образом прямой
является прямая.
Пример 34.4. Линейное отображение
(34.14) \Ш^lXlllX2,
v ' ( уч = 4xi + "ж2
вырожденное: его матрица
имеет определитель
"(50
w= П
равный нулю. Это отображение не имеет, обратного и не устанавливает
взаимно однозначного отображения плоскости в себя. Действительно, из соотношений
(31Л) легко видеть, что любая точка М прямой 2xj 4- Ъх<> » 0 имеет своим образом
начало координат, так как у\ = 2xi 4- Зх2 и у2 ~ 4хх -f 6x,j = 2(2хх 4- Зжг) =20 = 0.
Пример 34.5. Линейное отображение
{
у\ — хь
У2 = -х2
с матрицей А = I п 1 ) невырожденное. При этом образом каждой точки М(хi;X2)
является точка N, симметричная относительно оси Оя\ (зеркальное
отображение). Так, например, образ точки Af(l;2) есть точка Лг(1; —2).
Пусть ОМ-радиус-вектор точки M(xi\X2): ОМ — Х\в\ Ч-Жзег. Отображение (34.7)
ставит ему в соответствие радиус-вектор ON точки N} яшзюгпейся образом точки
Af : ON — 2/161 + У2£ъ Проекции х\,х% и щ,у2 этих векторов связаны формулами
(34.7).
34 ЛЕКЦИЯ - ПОНЯТИЕ N- МЕРНОГО ВЕКТОРНОГО ПРОСТРАНСТВА Щ
В заключение отметим, что в случае пространства Оххх2х^ введя матрицы столб-
цы и матрицу отображение:
"•(:)■'■(
)•
2/i \ / Ли л12 а13
J/2 I у A as I U21 ^22 а33
2/3 / \ <*31 «32 «33
для невырожденного отображения (\А\ ф Q) получим уравнения аналогичные (34.8),
(34.10):
У = АХ, Х = А-1УВ
При аффинном отображении пространства, как можно показать, образом плоскости
является ПЛОСКОСТЬ, а Образом прямой-прямая.
34.3» Преобразование координат» Рассмотрим в плоскости Q прямоугольную
систему координат Oxjxg с ортами ei и ёг. Наряду с системой координат Oxi&2i
которую будем называть старой, рассмотрим НОВУЮ СИСТвму координат Ох[х2 С Ортами
ei и е^. Начала координат старой и новой систем совпадают (рис 162).
Рис. 162. Преобразование координат
Возьмем в плоскости Q произвольную точку М. Пусть Х\, х2-ее координаты в
старой системе, а х[7 х2 — в новой. Найдем связь между старыми и новыми координатами.
Для этого разложим радиус-вектор ОМ точки М на состовляющие по ортогональным
базисам е\, ё2 и ё\, ё'2:
ОМ = rtiei 4- х2ё2, ОМ = х'хё\ + х2ё'2.
Таким образом,
(34.15) х\ё\ 4- х2ё2 — х[ ё'г 4- х'2ё2.
Обозначим скалярные произведения ортов:
ац = ё{ё\\ an = ё\Ъ'2, tx2\ - ё2ё\\ с&22 = е~2&2.

402 34 ЛЕКЦИЯ - ПОНЯТИЕ N- МЕРНОГО ВЕКТОРНОГО ПРОСТРАНСТВА
Можно показать, что из векторного равенства ( 34.15) следует равенство для
координат:
(34.16) ( *i-*»*i+fl»*i>
Формулы ( 34 Л б) называются формулами преобразования координат на плоскости, а
матрица
(34.17) L=( aua" )
К * \ CL21 G22 /
- матрицей преобразования.
Рассмотрим матрицы-столбцы X = ( г 1 и X' = I ,l J . Тогда пресбразование
координат ( 34.16) в матричной форме запишется в виде
X^LX'.
Матрица L обладает рядом интересных свойств: сумма квадратов элементов
строки (или столбца) равна единице, сумма парных произведений элементов строки
(столбца) равна нулю. Матрица, обладающая этими свойствами, называется ортогональной.
Рассмотрим транспонированную матрицу Ьт - \ 1 I , которая получается
\ 0-12 &22 /
из матрицы L заменой строк столбцами. Составим произведение матриц ЬтЬ.
Учитывая вышеперечисленные свойства матрицы L, получим
LTL=( aua21 Va"ai2 ^
\ а12 «22 ) \ «21 «22 /
(34 18) = ( а" Ч"а^ ttnai21 а21°?2 ^ = ( 1 ° "\ = Е.
К ' ' V а12«11 + «22«21 «i2+rt22 / \01 /
Таким образом, матрица Ьт является обратной по отношению к матрице L, т.е.
LT =L"1.
Замечание. Если новая система координат получена из старой системы поворотом
осей на угол а, то легко видеть, что формулы ( 34.16) аналогичны формулам поворота
осей координат, рассмотренным в лекции 2.
Пусть теперь в старой системе координат Ох\Хг задано линейное отображение
( 34.8) плоскости Q в себя: Y — АХ, которое точку М(ху,Х2) переводит в точку
ЩУ1\У2)-
Если обозначить X' и У'-матрицы столбцы координат этих точек в новой системе
координат (X = ЬХ'), то можно показать, что эти координаты связаны формулой :
(34.19) Y' = L~lALX'.
Другими словами, если в новой системе координат точка М(х'1\х'2) переходит в точку
N(y\\у2)у то это отображение и в новой системе координат будет линейным отображе-
ним с матрицей А' = ( }1 }2 1 : У = А'Х1 и матрица этого отображения связана
\ «21 «22 /
со старой матрицей соотношением: А' = L~lAL.
Все, сказанное для плоскости легко переносится на случай трехмерного
пространства.
34 ЛЕКЦИЯ - ПОНЯТИЕ N- МЕРНОГО ВЕКТОРНОГО ПРОСТРАНСТВА 403
34.4. Приведение квадратичной формы к каноническому виду.
Квадратичной формой двух переменных хг и х2 называется многочлен второй степени:
(34.20) F(#i,#2) = awx\ 4- 2aX2Xix2 + a22x\.
Заметим, что слагаемые второго порядка, стоящие 8 начале Общего уравнения КРИВОЙ
второго порядка, образуют квадратичную форму. Наша цель сейчас: подобрать такое
преобразование координат £i,X2, чтобы в квадратичной форме исчез член С
произведением координат.
Прежде всего, запишем квадратичную форму в матричном виде. Полагая ojg — a21)
перепишем ( 34.20):
F\X\SX2) » (ftn^i + Cbi2X2)Xi + (a>2lxl +«22x2)x2-
Матрица A = I ll l2 I называется матрицей квадратичной формы. Введя мат-
рицу-СТОлбец X ss I и транспонированную ей матрицу-строку Xf — (%\',%ъ),
ИЗ последнего равенства видим, что квадратичную форму (34.20) можно записать в
матричном виде:
(34.21) F(xlfx2)**XTAX.
Проверьте это самостоятельно, проведя требуемые операции над матрицами.
Будем трактовать переменные Х\ и х2 как координаты точек в прямоугольной
системе координат Ох\Х2. Рассмотрим новую систему координат Ох\х2. Пусть коорди-
наты точек в старой и новой системах связаны между собой формулами преобразования
( 34.16):
Г Х\ =011^ +О120?2,
\ х2 ~аг\х\ +«22*2-
С ортогональной матрицей преобразования L — [ J . Формулы преобразования
V а12 «22 У
( 34.16) можно записать в следующей матричной форме:
(34.22) X = LX'.
3-ьА-=(*:),Х<=(*>).
ЕСЛИ ВМеСТО Xi И Х2 В Квадратичную форму ( 34.20) подставить их выражения 34.16
через х\ и ж2, то получим квадратичную форму переменных х\ и х'г-. F(xi,x£).
Поставим перед собой задачу: выбрать новую систему координат Ох\хг так, чтобы
В квадратичной форме F{x\, Я2) Отсутствовал член С произведением координат, иными
словами, чтобы она приняла следующий вид:
(34.23) ^(*i,*i) = Ai*;4Waa.
который называется каноническим.
Для сокращения записи преобразования будем проводить в матричной форме.
Рассмотрим прежде всего матрИЦу-СТрОКу X' ~ (х[ Xf2). Легко убедиться, что имеет место
следующее равенство:
(34.24) ХТ = Х'ТЬ~1.

Щ 34 ЛЕКЦИЯ - ПОНЯТИЕ N- МЕРНОГО ВЕКТОРНОГО ПРОСТРАНСТВА
Подставим в правую часть равенства ( 34.21) выражения X? и X из равенств
( 34.24) и ( 34.22):
F(xfvx2) = Х'Т{Ь~1АЬ)Х\
Выберем теперь новую систему координат Ох\х\ так, чтобы матрица А приняла
следующую форму:
В этом случае говорят, что матрица приведена к диагональному виду. При этом
квадратичная форма F(xtlix'2) запишется в виде (34.23).
Итак, новую систему координат надо выбрать таким образом, чтобы матрица L
преобразования удовлетворяла соотношению
Умножим обе части этого равенства слева на матрицу L:
1 ( о* л° ) = LL~lAL = EAL = AL-
Итак, матрица L преобразования удовлетворяет условию
'(о\!)—
Так, как
( Л1 ° \ _ / ап «12 \ / Ai 0 \ _ / ацМ Л12Л2 \
\ О А2 ) ~ \ Q21 Л22 / V О А2 ) \ ft2iAi Л22А2 /
и
AL~ ( аИ а12 ^ Г аП а12 ^ - ( апап +ai2Q21 а11а12+а12а22 \
V «21 «22 / V а21 а22 / V a12°il + а2йа21 а21«12 + а22а22 / '
ТО
( GL\\X\ OC12A2 \ _/ *ЦЛН +«120121 flllfl(l2 + ftl2«2'2 \
\ a2iAi Л22А2 / \ fti2Aii + о>21<*-п апап + «220:22 / '
Отсюда, на основании определения матриц, получаем
«21^1 = "12all + «22«21
«хгАг = «uO:i2 4«liO:?*.
Q22A2 = A2jO;i2 + ^22^22*
или
(34 251 / Qll(ftll — Ai) + ^21 «12 = 05
\ ощап -Ь а-ц(а22 ~ Ах) - 0;
И
(34.26) / ai2(au ~ Л*) + Л22«12 - О,
I «i№i f 0:22(022 - Ai) ^ 0.
34 ЛЕКЦИЯ - ПОНЯТИЕ N- МЕРНОГО ВЕКТОРНОГО ПРОСТРАНСТВА 405
Таким образом, неизвестные коэффициенты преобразования <Лц, «ц, «ii,
a22 находятся из систем уравнений ( 34.25) и ( 34.26). Каждая из этих систем
является однородной. Для того чтобы они имели отличные от нуля решения, необходимо
и достаточно, чтобы определитель каждой из этих систем был равен нулю:
«21 U22 — Ai
= 0?
«П - Л2 tti2
«21 «22 — А2
= 0.
Таким образом, числа Х\ и А2 являются корнями квадратного уравнения
(34.27)
Ли — А Л|2
а21 <*22 ~ *
= 0,
или
(34.28) А2 - (an + «22)Л + (йцАзз - ai2«2i) « 0.
Дискриминант D этого квадратного уравнения всегда неотрицателен. Действительно,
D - («11 + Л22)2 - 4(ail022 - «I2tt2l) =
= a?! + а\г - 2оца22 + 4ai202i = («и - O22)2 + 4aJ2,
так как ai2 = 021. Итак, уравнение ( 34.27) всегда имеет действительные корни. Оно
называется характеристическим уравнением матрицы А,
Определение 34Л0. Корни Aj и А2 этого уравнения называются собственными
значениями матрицы А.
Подставлял найденные из уравнения (34^7) значения Aj и А2 в системы ( 34-25) и
( 34-26) и решая их, найдем коэффициенты преобразования координат ац,сиг, «21, «22 •
Пример 34.6. Привести к каноническому виду квадратичную форму
F(x\,X2) = Ьх\ + ix\X2 + 2ж2.
Решение: Здесь ац = 5, aj2 = «21 = 2, «22 = 2. Матрица квадратичной формы
иммет вид А - I 2 ~ J .
5-А 2
2 2-А
= 07илиА2-7А+б =
Составим характеристическое уравнение ( 34.27):
0, откуда Ai = lt A2 = 6. Таким образом, заданная квадратичная форма приводится к
каноническому виду F(x\yX2) = x\ -f бж'2 .
Замечание. Квадратичная форма трех переменных Ж1,а?2,а?з имеет вид
(34.29) F(xux2,X3) = ацх\ + аггх\ + азз^з + 2а12Я1Л?2 + 2апх\х^ -f 2й23аг2.т3
Матрицей этой квадратичной формы называется матрица третьего порядка
(он Л12 013 \
«2i л22 а2з I , в которой ai2 = «2Ьа13 = <*зъа23 = «32- Матрица А в этом
аз1 аз2 «зз /
случае называется симмметрической.
Квадратичную форму трех переменных можно привести к виду
„/2 , ч ^/2 , ^ „, 2
(34.30)
F(x,lix,2>x'3) == Ai^i + А2ж2 4-А3#з

406 84 ЛЕКЦИЯ - ПРЕОБРАЗОВАНИЕ КООРДИНАТ
где числа Ai,A2 и Л3 всегда действительны и удовлетворяют характеристическому
уравнению
лц - А а\2 ^13
ft3i Лз?. «зз — А
Если за новую систему координат выбрать ту, в которой квадратичная форма
F(x\)x2) — Ai#i2 + А2#22, то в этой системе координат, как было показано выше,
матрица А' имеет вид ( * 1 , и формулы линейного преобразования (34.7) в системе
координат Ох\х2 запишутся следующим образом:
Г у\ =А1х'1 + 0.*'2?
1 yi=0-«i + A2x'2.
или
Рассмотрим в новой системе координат Ох\х2 точки Afi('l; 0), М2(0; 1). Очевидно,
что ОМ\ — ё\ и ОМъ — ё2. В силу формул (34.31) образами точек М\ и М2 служат
соответственно точки Qi(Ai;Q) и (?2(0;А2). Вектор OQi = Х\ё\ есть образ вектора
OMi = ё'1э а вектор OQ2 = А2с2 образ вектора ОМг = ё'2.
Итак, при линейном отображении ( 34.31) векторы ё\ и е'2 преобразуются в
соответственно коллинеарные векторы Aie'i и А2ё2-
Определение 34.11. Если при некотором линейном отображении существует
не равный нулю вектор г, образом которого является коллинеарный ему вектор Airr
то вектор г называется собственным вектором зтого линейного отображения, а
число А — собственным значением отображения.
Таким образом, векторы ё\ и с2 являются собственными векторами линейного
отображения ( 34.31).
34. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРЕОБРАЗОВАНИЕ КООРДИНАТ.
КВАДРАТИЧНАЯ ФОРМА
Пример 34.1. Напишите формулы, выражающие новые переменные 2/1,1/2 через
старые х\,Х2 для данной матрицы А линейного преобразования. В какую точку N(yi\y2)
перейдет при этом преобразовании данная точка М(ж};х2) ?
( 11 12 \
V 21 22 ) '
М(1;2).
Решение: Запишем систему уравнений (34.7), связывающую новые переменные
со старыми (У = АХ):
{1/1 = onaji -М12Ж2,
Vi — 0,21X1 -f а22Ж2.
Для данной матрицы А получаем:
Г у! - Пхх +12ж2,
\ уз = 21^1 + 22ж2.
Поставим сюда координаты точки М(1;2), получаем у\ — 35, у2 = 65.
Ответ: ЛГ(35;65).
34 ЛЕКЦИЯ - ПРЕОБРАЗОВАНИЕ КООРДИНАТ
407
{
Пример 34.2. Для данной в примере 3$А матрицы линейного преобразования А
напишите формулы7 выражающие старые переменные х\,Х2 через новые У\7у2- Какая
точка M(xi;x2) перешла при атом преобразовании в данную точку N(yi'4y2) =f
iV(58;108)?
Решение: Запишем систему уравнений (34.9),связывающую старые переменные
с новыми (А' = Л-1 У):
** - -latin + ЩУ2-
Для данной матрицы А получаем:
|Л| « И-22-12-21 »-10.
f *i = ^цРг - =hv*> ^ { *i - -2,2У1 + 1,2у2т
I *2 - -ГШУ1 + ibv2\ \ *2 = 2,1У1 - 1,1У2.
Подставляя сюда координаты точки N(58,108), получаем: х\ — 2;
х2 = 3.
Ответ: М(2;3).
ПРИМЕР 34.3. Дана точка М(х; у) в системе Оху. Найдите ее новые координаты
X и У при параллельном переносе осей, если новое начало О' в старой системе имеет
координаты Оу(х,'у):
Щ2;3), 0'(1;Я).
Решение см. пример 2.3.
ПРИМЕР 34.4. Найдите старые координаты я и у точки Мг Зная ее новые
координаты X и У при повороте осей на угол &:
*^1,У = 2,а=|.
Решение: По формулам (2.10) получим:
х = A'cosa- У sin a « lcos J - 2sin J = ^ - 1 « ^^i
у = Xsina + Уcosa = Ism J + 2cos J = \ + <Л = Щ&.
Ответ:я?-^,з/-^|^.
В этом занятии на основании изложенного в лекции 34 мы найдем преобразование
координат,приводящее квадратичную форму к каноническому виду. В результате, как
указанно в лекции, может получиться одна из следующих линий: эллипс (в частности
окружность), гипербола, парабола, пара пересекающихся прямых, пара параллельных
прямых, одна прямая, точка, мнимый эллипс, мнимые параллельные прямые.
Пример 34.5. Приведите к каноническому виду данное уравнение кривой второго
парадна, определите вид кривой и ее параметры, ж2 + бху + у2 f бж + 2у - 1 — 0
Решение: В соответствии с изложенным в лекции 34, составим
характеристическое уравнение (34.27).
а.21 ftg2 ~~ А
Для данной кривой Лц ~ 1, ац «в ац =* 3, д22 = 1. Характеристическое уравнение
имеет вид:
1 -А 3
:0.
3 1-
= 0. *+ (1 - А)2 - D = 0 =* Ai - -2, Л2 - 4.
Подставляя найденные значения в системы (34.25) и (34.26), получаем:

408
34 ЛЕКЦИЯ - ПРЕОБРАЗОВАНИЕ КООРДИНАТ
\ аг1(1 - (-2)) + a2i 3 = О, Г ап(1 - 4) + а22 • 3 = О,
\ On • 3 + a2i(l - (-2)) = 0; \ а12 • 3 + а22(1 - 4) - 0.
решая которые получаем: Qn — -«гь «22 = «i2> например: а21 = 1, ац ~ -1,
а12 = 1 = а22, Матрица преобразования координат L имеет вид:
L — [ .. 1 , а формулы преобразования координат (34.16)
Г ж = -а?' -I- у',
\ 3/ = s' + y'.
Подставляя эти выражения в уравнение кривой, получаем: (у' - х')2 + 6(у' - xf ) -f
(х' + г/')2 + 6?/' - ж') + 2(а' + у') - 1 = 0 «* -4я?/2 + 8]/'2 - 4а/ + V - 1 = 0. Заметим,
что полученное линейное преобразование уничтожившее слагаемое с произведением
ху, есть не что иное, как поворот системы координат (см. лекцию 2). Для получения
канонического уравнения кривой, выделим полный квадрат, как это делалось в примере
указанной лекции.
-4а'2 + Ъу'2 - 4а?' + Ьу' - 1 = 0 & -Цх'2 + *'+£) + Цу'2 + у' + J) = 2 <*
-2(*' + |)2 + 4(1/' + ±)2 = 1 * <^ - <^ = 1.
Сделав замену координат: X = ж' + i, Г = у' + |, в новых координатах Х,У
получим каноническое уравнение гиперболы: ^- - 4- ~ 1- Заметим, что последняя
4 2
замена координат есть параллельный перенос системы координат. Резюмируя
вышесказанное, мы получили каноническое уравнение кривой второго порядка, расположив
нужным образом систему координат.
Ответ: гипербола ^— тг = 1.
4 2
Пример 34.6. Приведите к каноническому виду данное уравнение второго
порядка, определите вид линии, которое оно определяет,, и ее параметры: ху — 2х — $у+б '-
Решение: Для данного уравнения аи = 0, й\2 ~ «21 — %, а±2 ~ 0,
характеристическое уравнение имеет вид:
7 1
: 0 <=> О2 - \ = 0 =*■ Л1 == |, Л-2 = ~\
• 2
Подставляя найденные значения в системы (34.25) и (34.26), получаем:
/ -iau + Jaai - 0, { 5«i2 + |«22 = 0,
1 |лц - |a2i - 0; I |«и - |«22 - 0, '
решая которые найдем: Qn — o^i» 0:22 — —fti2»
Например: Лц - Л21 — Ctn — 1» «22 = -!■ Матрица преобразования имеет вид:
L = ( ), а формулы (34.16) преобразования координат:
Г х - х' -f </
\ у = я' - 2/'
Подставляя эти выражения в уравнение линии, получаем: (х1 -\-у')(х - У) — 2(я? +
у') - Цх* - у') + 6 - 0 ФФ ж'2 - </2 - 5я?' +• у' + 0 = 0.
Полученное линейное преобразование, уничтожившие член с произведением ху,
есть поворот системы координат. Для получения канонического уравнения выделим
полный квадрат: (х'2 ~ 5х' + f) - (г/2 -1/ -f \) = 0 <* (.г' - |)3 - (?/ - J)2 - 0 Сделав
34 ЛЕКЦИЯ - ПРЕОБРАЗОВАНИЕ КООРДИНА Т
409
замену координат: X «* ж' - §< .У = у* - \, ь новых координатах X и У получим
каноническое уравнение пары прямых: X1 - У* =г 0 <£> {-£ - У)(ЛГ + У) = 0 ИЛИ, В болев
привычной форме: Y — X uY = ~Х, Последняя замена координат есть параллельный
перенос системы координат.
Ответ: пересекающиеся прямые У * Jt и Г = -I.
Самостоятельная работа
Решите пример 34.1 для следующих данных:
Пример 34.7. А - ( "* ^ \ ,М(--1;1).
Пример 34.8, А= ( * "М ,М(0;0).
Пример 34.9. ^- ( q 3 ) >М(-1;1).
Пример 34.10- А=(Ц ) ,М(-1;-2).
Решите пример 34.2 для следующих данных:
Пример 34.11. АГ(7-.8).
Пример 34.12. N(7,9).
Пример 3413. А^(10;12).
Пример 34.14. iV(9;ll).
Решите пример 34.3 для следующих данных:
Пример 34.15. М(0;0), 07(3;-2).
Пример 34.16. М(-3;-1), О'(0;4).
Пример 34.17. М(4;0), 07(~7;2).
Решите пример 34.4 для следующих данных:
Пример 34.18. X = 1,У = 1,а = ^ь.
Пример 34.19. А' » 2, У = 1,а = f.
Пример 34.20. X = 4, У = 3,а = 7г.
Решите пример 34.5 для следующих данных:
Пример 34.21. За?2 - 2ху + Ъу2 + Ах + Ау - 4 = 0.
Пример 34.22. х2 - Аху + Ау2 + 2х - 2у - 1 = 0.
Пример 34.23. х2 ~ ху - у2 - я - у - 0.
Пример 34.24. 2у2 + 8ж + 12у - 3 = 0.
Пример 34.25. х2 + у2 - Ах - 6у = 0.
Решите пример 34.6 для следующих данных:

ш
34 ЛЕКЦИЯ - ПРЕОБРАЗОВАНИЕ КООРДИНАТ
Пример 34.26. 9х2 - Ъху + у2 - 6х + 2у = 0.
Пример 34.27. 4а?2 - 4а?» + з/2 + 4* - 2у + 1 = 0.
Пример 34.28. у2 + Ъху - 14ж2 = 0.
Пример 34.29. х1 - 4ху + З*/2 + 2х » 2у = 0.
Пример 34.30. ж2 - 2жу + 5а? = 0.
Пример 34.31. х2 - 4ху + 4t/2 = 0.
Пример 34.32. 4а?2 - Х2а?з/ + 9у2 - 25 = 0.
Пример 34.33. 4х2 - 12ху + 9уа + 12ж - 18у +13 = 0.
Пример 34.34. а?2 - 4а? + 4*/2 -4- 12у +13 = 0.
ОТВЕТЫ
4U
ОТВЕТЫ
1.6 А, = [1; 2), А2 = (-5; 7), А3 - [1; 2), Л4 = [-3; б], Аъ - [-3; б], Л6 -
[-3;5], А7 - (-5;-3)U(5;7). 1.7 Л - {2;3}, Л2 - {-л/5; л/5}, Л3 -
{-6;0}, Л4 = {-3;-|;1>, Л5 - 0, А = (-оо;2) U (3;+oo), А =
(-V5; ч/б), А = [-6;0], А = (-оо;-3)и(~|;1)? А « (-005+00), С =
{2; 3; 4}, D - {-1; 1; -1; 1,....}, Я = {-2; 4; -2; 4,,.. .} 1.8 4i = {х|2 <
х < б}, Л2 - {ж|ж ^ 5}, i43 « {х\х е Q7 1? < 0}7 Л4 « {ж|ж ^ 0}, Л5 «
{ж|,ж < 0, я? € Z}, Л6 = {ж|ж € Z, 0 ^ ж ^ 9}. 1.9 (-оо;1) U (3;+оо).
1.10 (-2V^;2V5). 1-11 [2;3J. 1.12 (2;2\/2). 1.13 [-5;-1). 1.14 (-oo;l,5]U
(2;3). 1-15 (-2;-l)u(-l;0)u(0;l)u(2;+oo). 1.16 [§;2). 1.17 [3;+оо).
1.18 (0; g). 1.19 90 = 2 З2 5, 120 = 23 3 5, 48 = 24 - 3, 64 »
2-3*. 1.20 а) НОК(90;120) = 360, НОД(90; 120) « 30; б) НОК(48;54) -
432, НОД(48;54) = 6. 1.21 а) целая часть 5, остаток 2; б) делая часть 4,
остаток 2; в) целая часть 37 остаток 0; г) целая часть 0, остаток 2. 1.22
а) -0,16; б) 0,(2); в) -1,0625; г) 2,(36). 1.23 а)§; б) - |§; в)£; r)g. 1.24
а)§; 6)^5 в)7.
2.3 а) |*| < 4; б) \х\ ^ 7; ъ)\х + 1| < 4; г) \х + 1| < 4; д) \х - 1| ^
4; е) |ж + 1| ^ 6. 2.4 а) ж е (-оо; -5] U [-1; +оо); б) ж е (-|; +оо); в) ж G
(-со; -ч/7) U (-ч/З; \/§) и (v^5+<»); г) х е (-1;3); д) л е (0; 12); е)х е
[-8; 2]; ж) ж е (-1; 0). 2.5 а) ж е {-1; 3}; б) ж € (-оо; -1)U[1; +00); в) ж е
(-оо; 2] U [3; +оо); г) х = ±§ + ^, п € Z; д) х - ±§ + тггс, га € Z. 2.6
а) X = -^ - 1, Г = | -> V3; 6) X = V5, У = \/2; в)Х - 2, Y = 2. 2.7
а) г = </2, ^ - J; б) г = 3%/2, ц> = %/§тг4; в) г - 2>/2, V? = т- 2-8 а) ж =
V5, У = \/2; б) х = ^1, у = -|; в) х = 0, у = -4; д) х = -1, у = 0-
3.1 (-2;0]. 3.3 Четная. 3.5 ^. 3.7[-1;+оо) 3.8 [-оо;+оо). 3.9 (-oo;-2)U
(-2; 2)и(2; +во). ЗЛО [-3;3[. 3.11 [-1;2]. 3.12 [-i/2;0)u(0; ^5]. 3.13 (-2;2).
3.14 [-|;1]. 3.15 (-1;1). 3.16 [1;100]. 3.17 Нечетная. 3.18 Четная. 3.19
Нечетная. 3.20 Четная. 3.21 Нечетная. 3.22 Четностью или нечетностью
не обладает. 3-23 27г. 3.24 7г. 3.25 7г. 3.26 Неперирдическая.
4.8 [0;+оо);2/ = у/хТТ. 4.9 Щу = а/Г^з. 4.10 (0;+оо);;у » 2е*. 4.11
д;у ^ !вМ. 4.12 arcsinlg(ir). 4.13 -|. 4.14 |. 4.15 Q. 4.16 lg(arcsin(^)).

412
ОТВЕТЫ
4.17 ч/2. 4.18 vTTa^ 4.19 i/l + Л- 4.20 -7=^=5. 4.21 у = V^ +1 - 2 л/3.
4.22s/ = x+3. 4.23 у = Зх-1. 4.24 у = ^я + 4. 4.25 # = -Зж или у = -±ж.
4.26 /(*) = f х. 4.27 /(*) = \х + |. 4.28 /(ж) » 3.
5.8 рис. 163. 5.9 рис. 164. 5.10 рис. 165. 5.11 рис. 166. 5.12 рис. 167.
5.13 рис. 168. 5.14 рис. 169. 5.15 рис. 170. 5.16 рис. 171. 5.17 рис. 172.
5.18 рис. 173. 5.19 рис. 174. 5.20 рис. 175. 5.21 рис. 176. 5.22 рис. 177.
5.23 рис. 178. 5.24 рис. 179. 5.25 рис. 180. 5.26 рис. 181. 5.27 рис. 182.
5.28 рис. 183. 5.29 рис. 184. 5.30 рис. 185. 5.31 рис. 186. 5.32 рис. 187.
5.33 рис. 188. 5.34 рис. 189. 5.35 рис. 190. 5.36 рис. 191. 5.37 рис. 192.
6.8 (*+3)2 + (</-4)2 = 25. 6.9 (ж+3)2 + (£/+2)2 = 25. 6.10 {x-\fW = f.
6.11 £ + £ = 1. 6.12 £ + fi = 1. 6.13 JL + g = 1. 6.14 f| + $ = 1.
6.15 a = 13; 6 = 5; FU2 (±12;0);e = }§. 6.16 a! - £ = 1. 6.17 §£ - |£ = .1
6.18 g - £ = 1. 6.19 g - £ = 1. 6.20 Fi,2(±5;0);e = §;y = ±f*- 6.21
у2 = 16ж. 6.22 x1 = 8y. 6.23 x2 = -18t/. 6.24 А(2;0),я = -4;ось - Ox.
6.25 Гипербола ^- - ^ = 1. 6.26 Гипербола &%£ ~ Ц^ = 1. 6.27
Эллипс ls&£ + £ = 1. 6.28 Гипербола ^- - ^-}- - 1. 6.29 Парабола
(у - l)2 = 10(ж + 2). 6.30 Парабола (у + 7)2 = 6ж.
7.8 gir. 7.9 *±i. 7.10 п2. 7.11 ^-. 7.12 blpl. 7.13 £,£,*&.
7.14 §, 7.15 1. 7.16 J. 7.17 ±. 7.18 2. 7.19 0. 7.20 0. 7.21 оо.
8.12 4, 8.13 §. 8.14 2i|l. 8.15 1. 8.16 |. 8.17 1. 8.18 1. 8.19 cosa.
8.20 е*"1. 8.21 1. 8.22 0. 8.23 -3. 8.24 1.
9.14 lim£ = 00. 9.15 lim§ = |. 9.16 0. 9.17 4. 9.18 \. 9.19 со. 9.20 3.
9.21 1. 9.22 0. 9.23 \. 9.24 §. 9.25 \. 9,26 §. 9.27 §. 9.28 *&. 9.29 3.
9.30 1. 9.31 0. 9.32 -1.
10.9 Нт1пж = 1. 10.10 Непрерывна. 10.11 х ~ 0 — точка разрыва
первого рода. 10.12 х = —2, 2, -1 — точки разрыва второго рода. 10.13
х — 0 и х = ,0 ?п , где п = 0,17 2 10.14 х = 1, 2 - точки устранимого
I £Пт1 )7Г
разрыва. 10.15 Непрерывна при х € R. 10.16 1.
11.7 un - biTli. ц.8 Wn = (jlLL)». ц.9 I. НЛО ±. 11.11 Ряд
сходится, 5 — 2. 11.12 Ряд расходится.
ОТВЕТЫ
Ш
12.8 Ряд расходится. 12.9 Ряд сходится. 12.10 Ряд сходится. 12.11 Ряд
расходится. 12.12 Ряд сходится. 12.13 Ряд расходится. 12.14 Ряд
расходится.
13.7 Ряд сходится абсолютно. 13.8 Ряд сходится условно. 13.9 Ряд
сходится абсолютно. 13.10 Ряд расходится. 13.11 Ряд расходится. 13.12 Ряд
расходится. 13.13 Ряд сходится абсолютно. 13.14 2. 13.15 \r2\ ^ 0,01.
14.16 -4г. 14.17 -sins. 14.18 jfe*. 14.19 1 - Зж2. 14.20 cos ж - 3sinz.
14.21 ^4-arctgs. 14.22 '""'^Г**'-14'23 *§?^1- *4-24 0. 14.25
-тЬ + ins +1 + *;;™г™2ах.
15.11 5*4 - 12*2 + 2. 15.12 |х5/3. 15.13 TJggffi- 1514 $Г&- 1515
ct«* " А- 1516 zarctga; - 1. 15.17 За?*1паг. 15.18 a;V. 15.19
(e^;pT2Sb-15-20 §(sin<5*2) +sin<*2))-15-21 ^fe-15-22
arcsin arv'i—ж* *
16.11 у1 = xsinxcosslnz + sina;a;sin:i!*-1.
16.15 ^~~i. 16.16 Г : ж - 4у - 5 = 0, /\Г : 4ж + г/ - 3 = 0. 16.17
Ж1 = -2, ж2 = 3. 16.18 вх = - arctgO, 6; 02 = arctg3. 16.19 *0 = 8с, tx =
Ос, t2 = 4с, i3 = 8с. 16.20 181,5 эрг.
17.11 Ix^/xdx. 17.12 (arctgo; + ф;) dx. 17.13 xco*xJsinxdx. 17.14 2arctgaj-f
i^f- 17«15 Й5эт- 17.16 Да. 17.17 -e-'^-ex + e)*^. 17.18 j&pdx4.
17.19 0,02. 17.20 2,0375. 17.21 « 0,81.
18.8 Теорема справедлива. 18.9 Теорема справедлива. 18.10 а(1 -Inа) -
Ь(1 - In Ь) = (Ь~а) 1п^, где а < £ < Ь. 18.11 0,5. 18.12 3. 18.13 1. 18.14
0. 18.15 1. 18.16 2/тг.
19.11 В точке х = 0 — рассходится, в точке х = 1 — сходится. 19.12 а; €
(-оо;-lj U (1/4;+оо). 19.13 R-0, х=0. 19.14/2=1, |ж| < 1, -1 ^ х < 1.
19.15 /2 = 1, |яг - 5| < 1, 4 ^ х < 6. 19.16 Д = 1, \х\ < 1, -1 < а: < 1.
20.8 2* = 1 + х1п2+^Й + '-'+г:1^ + ---, ж € (~оо;+оо). 20.9
.О О о оЗ л /_ 1\п22п+1_2(п+1)
sm2x = fa;2- ^ + • • ■ + t-lL^__^ + ..., х е (-oqj+oo). 20.10

ш
ОТВЕТЫ
е2х = 1 + 2х + ^х2 + • • • + ^хп + - - • , же (-оо; +оо). 20.11 cos (ж - |) =
f (l + \/Зж - ^ - &хъ + •••), ж е (-оо; +оо). 20.12 vlT-^? =
° I 2 9 222! ^ 9 У 233! \ 9 / 244! \9 ) J >
х (Е (~3;3). 20.13 1п(2 + ж) = ж + 1 - &^£ + ^- + • • • 4- (-l)"*1*^ 4
•■•, ж€(-2;0].20.141^ = -3 + 7ж--11ж2 + -'- + (-1)п-1(1-4п)жл-Ч
•••, *€(-1;1).
21.8 1. 21.9 i - i. 21.10 0,7788. 21.11 1,000. 21.12 3,017. 21.13 1,7918.
22.6 Критические точки х = 0, ж = 2, ушах = у(0) = 0, t/min = у(2) = -4.
Функция возрастает в (—оо;0) и (2;+оо), убывает в (0;2). 22.7
Критических точек нет. Функция определена и монотонно возрастает при
ж > 0. 22.8 Функция определена при ж > 0, критическая точка ж =
О, функция монотонно возрастает при ж > 0. 22.9 Критические точки
х = 0, ж = ^г, з/тах = у{§}) = £, 2/min = у(0) = 0. Функция убывает в
(—оо;0) и (^; Н-оо), возрастает в (0; ~). 22.10 Критическая точка ж = О,
экстремумов нет. Функция убывает в (—оо; 0) |J(0; -Ноо).
23.6 у"(0) = -6 < 0 - max, у"(2) > 0 - min, ?/"(1) = 0 - точка перегиба,
график у = /(ж) выпуклый при ж € (—оо, 1) и вогнутый при ж £ (1,оо).
23.7 у"(х > 0) > 0— кривая вогнутая. 23.8 у"(х > 0) < 0— кривая
выпуклая. 23.9 у" < 0 при ж 6 (—оо;0) U (0;+оо), график у = /(ж) выпуклый,
точек перегиба нет. 23.10 х — —\— точка перегиба, график у = /(ж)
выпуклый при ж < — |, вогнутый при ж > — |, t/"(0) не существует. 23.13
т = /(-1) = -4, М = /(0) = 0. 23.14 m = /(-2) = -20, М = /(4) = 16.
24.8 Асимптот нет. График на рис. (193). 24.9 Асимптот нет. График
на рис. (194). 24.10 Асимптот нет. График на рис. (195). 24.11
Асимптот нет. График на рис. (196). 24.12 Асимптоты ж = 0иж + г/ = 1.
График на рис. (197). 24.13 D(y) — (—oo;0)|J(0;oo), функция общего
вида, асимптоты ж — 0 и у = ж. Возрастает на (—со;0) (J(2; оо) убывает
на (0;2), y^n = у{2) — 3. Кривая вогнута на (-оо;0) |J(0;oo). Точек
перегиба нет. График на рис. ?? 24.14 Угол равен наибольшему из чисел
arccos^ и arctg|.
25.5 £ = 0,7391. 25.6 1,4954.
ОТВЕТЫ
415
/ 4 -8 -4 \ /836
26.9 ( " Z !• 26.10 -3 -1 -5 . 26Д1 0 8 12
V -7 -6 1/ V -3 6 14
0 0-
/ 10 6 5 \ / 11 \
5.12 8 11 6 . 26.13 16
\ 9 8 10 / \ 4 )
М13 - -6
26.12 18 116 1. 26.13 I 16 I . 26.14 ^я = f 26.15 2. 26.16
Аит 6
An - 3.
27. 26.17 1.
/ 1/10 -1/5 7/10 \
27.5 2. 27.6 3. 27.7 3. 27.8 3. 27.9 0 1/10 -1/5 . 27.10
V 0 0 1/10 /
28.8 х = 2, у - 3, г = -2. 28.9 z = -3, у = 2, г = -1. 28.10
Решения нет. 28.11 Si = 1, х2 = 5, ж3 = 2. 28.12 Система несовместна —
решений нет.
29.10 ~Ш = Sja. 29.12 5(2;-6; 8). 29.13 2а - ЪЬ = -8i - 3j + 10fc.
29.14 5j^2 = ±(-§?+ §j - §1), cosa= -\, cos/9 = |, cos7 = -3.
30.10 *&*. 30.11 4л/2- 30.12 Тупой. 30.13 -л/2. 30.14 ±\/53-
30.15 со8(Ж?;ВО) = -j^j. 30.16 cosS - ^.
31.12 20* + 14j + 2*. 31.13 25\/3- 31.14 {Л0 = ^f, h = ^}. 31.15
{±(-2? + J+ 31)}. 31.16 {Л.-1; ftb-^, Л, = ^}. 31.17 5. 31.18
-5. 31.19 51. 31.20 Некомпланарны. 31.21 Лежат. 31.22 *. 31.23 11.
32.11 ^-. 32.12 x + 7z + 22 = 0. 32.13 2y-5z + LQ = 0-
33.12 «=i = «±i = *=i. 33.12 ^ = «=i = s=2. 33.13 jl = «^1 » »^». 33.14
л - 90«,/3 - 45',7 = 135». 33.15 Af'(1; -1; 4). 33.16 11ж - Пу- IQb +10 -
0.
34.3 x = 1, у = 1. 34.7 ЛГ(3; 0). 34.8 ЛГ(0; 0). 34.9 ЛГ(2; 6). 34.10 АГ(-7; -5).
34.11 А/(3,5). 34.12 М(2,-1). 34.13 М(5,б). 34.14 М(3,2). 34.15 х =
-3,2/ = 2. 34.16 ж = -ity - -5. 34.17 ж = 11,у = -2. 34.18 х =

416
ОТВЕТЫ
ШлУ = &. 34.19 х = -1,г/ = 2. 34.20 ж = -4,# = -3. 34.21 Эллипс:
^ + Г2 = 1. 34.22 Парабола: У2 = ^Л\ 34,23 Гипербола. 34.24
Парабола. 34.25 Окружность: X2 + Y2 = 13 34.26 Параллельные прямые. 34.27
Прямая. 34.28 Пересекающиеся прямые. 34.29 Пересекающиеся прямые.
34.30 Прямая. 34.31 Прямая. 34=32 Параллельные прямые. 34.33
Мнимые параллельные прямые. 34.34 Точка.
РИСУНКИ К ОТВЕТАМ
417
РИСУНКИ К ОТВЕТАМ
ГУ
Рис. 163. График функции у = 2 - х2
Рис. 164. График функции у = (х — I)3 + 2

РИСУНКИ К ОТВЕТАМ
Рис. 165. График функции у = |~|
Рис. 166. График функции у = j~
♦У
Рис. 167. График функции у — у/—х
РИСУНКИ К ОТВЕТАМ
РИС. 168- График функции у — 1п(1 — х)
-1С \
л
-i.
Y;
-i
.i
0 \
-1
?
/ Л
/-? х
Рис. 169. График функции у «в соэ2ж
I t Y
Рис. 170. График функции у ~ 5sin(2aj - тг/3)

РИСУНКИ К ОТВЕТАМ
-1 01
Рис. 171. График функции у = -V
S
Рис. 172. График функции у — х+\
РИС. 173. График функции у == Д2
РИСУНКИ К ОТВЕТАМ
Рис. 174. График функции у — —
ж"+1
Рис. 175. График функции у = ^j
Рис. 176. График функции у = от 4-
-^2,1

422
РИСУНКИ К ОТВЕТАМ
Рис. 177. График функции у = tg2 x
vt
-2л -fcv
О п\ / X
Рис. 178. График функции у = Vsin а;
-4 X-
-2я -if.
2t\
3* X
Рис. 179. График функции у = ^
РИСУНКИ К ОТВЕТАМ
4&?
Рис. 180. График функции у = ж sin ж
Рис. 181. График функции 3/ ~ j~
У
-5я/2 -ЗЯ/2-Я/2 t
! •'"% ! i Л1
?' - \! !/ о
1
II
Я/2 ЗЛ/2 5л>2
\! " { х
If
!
Рис. 182. График функции у = lg(cos#)

''424
РИСУНКИ К ОТВЕТАМ
1
п
/
1У
! у* ?y
л\-'
---
V* /
\^ )
Рис. 183. График функции у — 2 *8тж
Рис. 184. График функции г ~ ц>
Рис. 185. График функции г -- с*
Рис. 186. График функции
РИСУНКИ К ОТВЕТАМ
Рис. 187. График функции г — cos tp
Рис. 188. График функции г = 1
Рис. 189. График функции г = 3cos4<p

РИСУНКИ К ОТВЕТАМ
РИС. 190. График функции у = | lg \x\
Рис. 191. График функции у = 2'ж'
РИСУНКИ К ОТВЕТАМ
427
РИС. 192. График функции у = х • |х|
Рис. 193. График функции у - х% - Зх2
У
РИС. 194. График функции у = х(1 -f V^)

428
РИСУНКИ К ОТВЕТАМ
О
РИС. 195. График функции у = 1 + \/х
°1 8/27 0,5
РИС. 196. График функции у — ух2 — х
Рис. 197. График функция у =- е* — х
ЛИТЕРАТУРА
№
ЛИТЕРАТУРА
1. Беклемишев Д. В. Курс аналитической геометрии и линейной
алгебры. - М. : Наука, 1984.
2. Беклемишева Л. А. , Петрович А. Ю. , Чубаров И. А. Сборник
задач по аналитической геометрии и линейной алгебре. - М, : Наука, 1987.
3. Берман Г. Н. Сборник задач по курсу математического анализа. -
М. ; Наука, 1985.
4. Боревич 3. И. Определители и матрицы. - М. : Наука, 1988.
5. Бугров Я, С- , Никольский С. М. Элементы линейной алгебры и
аналитической геометрии. - М. : Наука, 1980; 1984; 1988.
6. Бугров Я. С. , Никольский С. М. Дифференциальное и
интегральное исчисление. - М. : Наука, 1980; 1988.
7. Бугров Я. С. , Никольский С. М. Высшая математика: Задачник.
- М. : Наука, 1982.
8. Головина Л.И. Линейная алгебра и некоторые ее приложения. - М.
: Наука, 1985.
9. Данко П. Е. , Попов А. Г. , Кожевникова Т. Я. Высшая
математика в упражнениях и задачах: В 2 ч. - М. : Высш. шк. , 1986. - Ч. 1,
2.
10. Ильин В. А. , Поздняк Э. Г. Аналитическая геометрия. - М. :
Наука, 1981.
11. Ильин В. А. , Поздняк Э. Г. Линейная алгебра. - М. : Наука,
1983.
12. Ильин В. А. , Поздняк Э. Г. Основы математического анализа. -
М. : Наука, 1980. - Ч. 1; 1982. - Ч. 2.
13. Под ред.Демидовича Б.П. Задачи и упражнения по
математическому анализу для ВТУЗОВ. - М. : Наука, 1996.
14. Клетеник Д. В. Сборник задач по аналитической геометрии. - М.
: Наука, 1986.
15. Кудрявцев Л. Д. Курс математического анализа. - М. : Высш.
шк., 1981. - Т. 1, 2.
16. Кудрявцев Л. Д. Курс математического анализа. - М. : Высш.
шк., 1988. - Т. 1 - 3.
17. Кудрявцев Л. Д. Краткий курс математического анализа. - М. :
Наука, 1989.
18. Кудрявцев Л. Д. , Кутасов А. Д. , Чехлов В. И. , Шабунин М.
И. Сборник задач по математическому анализу: Предел. Непрерывность.
Дифференцируемость. - М. : Наука, 1984.

430
ЛИТЕРАТУРА
19. Кудрявцев Л. Д. , Кутасов А. Д. , Чехлов В. И. , Шабунин М.
И. Сборник задач по математическому анализу: Интегралы. Ряды. - М. :
Наука, 1986.
20. Кузнецов Л. А. Сборник задач по высшей математике /типовые
расчеты/. - М. : Высш. шк. , 1983.
21. Мантуров О. В. , Матвеев Н. М. Курс высшей математики. - М.
: Высш. шк., 1986.
22. Минорский В. П. Сборник задач по высшей математике. - М. :
Наука, 1987.
23. Никольский С. Мс Курс математического анализа. - М. : Наука,
1983. - Т. 1, 2.
24. Щипачев В. С. Высшая математика. - М. ; Высш. шк. , 1985.
25. Шнейдер В. Е. , Слуцкий А. И. , Шумов А. С. Краткий курс
высшей математики: Учебное пособие для втузов. - М. : Высш. шк. ,
1972.
Предметный указатель
Абсолютно сходящийся ряд, 165
Алгебраическое дополнение, 308
Алгебраического форма комплексного
числа, 412
Асимптота графика функции, 274
Бесконечно большая функция, 107
Бесконечно малая функция, 105
Биномиальный ряд, 240
Вектор, 341
Вектор N-мерный, 396
Векторное произведение двух векторов,
363
Векторное уравнение плоскости, 375
Векторное уравнение пространственной
прямой, 384
Вертикальная асимптота, 274
Вогнутая функция, 265
Второй призанак сравнения рядов, 153
Выпуклая функция. 265
Гармонический ряд, 154
Геометрическая прогрессия, 153
Геометрический смысл дифференциала,
204
Гипербола, 82
Двойное векторное произведение, 370
Деление отрезка в данном отношении,
351
Диаграммы Эйлера, 7
Дифференциал функции, 203
Дифференциалы высших ПОРЯДКОВ, 207
Дифференцируемость функции, 178
Достаточное условие возрастания
(убывания) функции, 251
Достаточное условие выпуклости
(вогнутости), 266
Достаточные условия точки перегиба,
268
Достаточный признак расходимости
ряда, 148
Достаточный признак СХОДИМОСТИ
Знакопеременного ряда, 163
Достаточный признак существования
экстремума по первой производной, 254
Достаточный признак существования
экстремума по высшим производным,
262
Инвариантность формы первого
дифференциала, 205
Канонические уравнения
пространственной прямой, 385
Касательная к графику функции, 175
Кванторы общности и существования,
9
Коллинеарные векторы, 342
Компланарные векторы, 369
Координаты точки на плоскости, 22
Координаты ТОЧКИ В пространстве, 22
Координаты вектора, 350
Корень уравнения, 290
Кривые второго порядка, 79
Критическая точка, 254
Левосторонний предел, 97
Логарифмическая производная, 193
Матрица, 302
Метод половинного деления, 294
Метод Ньютона, 295
Минор, 308
431

432
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Мнимая часть комплексного числа, 411
Многочлен Тейлора, 234
Множество, 6
Множество J иррациональных чисел, 13
Множество N натуральных чисел, 11
Множество Q рациональных чисел, 12
Множество R действительных чисел, 14
Множество Ъ целых чисел, 12
Модуль действительного числа, 19
Модуль вектора, 342
Наклонная асимптота, 274
Напраг ляющие косинусы вектора, 352
Направляющий вектор прямой, 384
Необходимое и достаточное условия, 9
Необхо, щмое условие точки перегиба, 268
Необхо, щмое условие возрастания
монотонности функции,250
Необходимый признак сходимости
ряда 147
Необходимый признак экстремума, 253
Непрерывность функции, 131
Непрер леность сложной функции, 135
Нормальный вектор плоскости, 375
Область сходимости функционального
ряда, 222
Обобщенный гармонический ряд, 154
Обратная матрица, 319
Общая схема исследования функции и
построения ее графика, 278
Общие уравнения пространственной
прямой, 383
Объединение множеств, 8
Односторонние производные, 177
Операпли над множествами, 7
Определитель, 306, 308
Основное правила дифференцирования,
181
Остаточный член формулы Тейлора, 235
Остато шый член формулы Тейлора в
форме Лагранжа, 236
Отделение корня, 290
Парабола, 83
Параллельный перенос осей координат,
25
Параметрические уравнения пространст
венной прямой, 335
Пересечение множеств, 7
Первый признак сравнения рядов, 152
Плоскость, 375
Полярные координаты, 26
Понятие числовой функции, 34
Последовательность, 92
Поворот осей координат, 28
Правило Лопиталя, 214
Правильно сходящийся ряд, 224
Правосторонний предел, 97
Предел функции, 96
Предел функции при х -» оо, 95
Предел последовательности, 93
Признак Даламбера, 155
Признак Коши, 158
Признак Лейбница, 162
Производная функции, 176
Производные высших порядков, 206
Пучок плоскостей, 390
Радиус-вектор, 350
Ранг матрицы, 317
Расстояние между двумя точками, 23
Расстояние от точки до плоскости, 379
Размерность векторного пространства,
397
Разность множеств, 8
Ргзность векторов, 344
Решение линейных систем методом
Гаусса, 331
Ряд Маклорена, 238
Ряд Тейлора, 237
Сходящийся ряд, 144
Система линейных уравнений, 326
Скалярное произведение двух векторов,
354
Сложение матриц, 304
Сложная функция, 39
Смешанное произведение трех векторов,
366
Собственные значения матрицы, 405
Составляющая вектора по оси, 347
Сравнение бесконечно малых функций,
US
Стал попарная точка, 254
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
438
Степенной ряд, 225
Сумма ряда, 144
Сумма векторов> 343
Свойства проекции вектора На ОСЬ, 347
Свойства числовых рядов, 145
Связка плоскостей, 377
Связь между дифференнируемостыо к
непрерывностью функции, 178
Таблица производных, 187
Теорема о промежуточной функции, 111
Теорема о пределе монотонной
ограниченной функции, 99
Теорема о существовании обратной
функции, 46
Теорема о существовании обратной
матрицы, 319
Теорема о связи между производной и
дифференциалом, 203
Теорема Больцано-Коши, 137
Теорема Ферма, 211
Теорема Коши, 214
Теорема Кронекера-Капелли, 328
Теорема Лагранжа, 212
Теорема Ролля, 212
Теоремы о бесконечно малых
функциях, 105
Теоремы о функции, пределе и
бесконечно малой, 108
Теоремы о пределах, 108
Теоремы о связи между бесконечно
малыми и бесконечно большими
функциями, 107
Точка перегиба, 265
Точки разрыва функции, 133
Третий признак сравнения рядов, 155
Тригонометрическая форма
комплексного числа, 414
Угол между плоскостями, 378
Угол между прямыми, 388
Угол между векторами, 346
Умножение матриц, 305
Уравнение плоскости, 375, 376
Уравнение плоскости, проходящей
через три точки, 377
Условно сходящийся ряд, 165
Формула Тейлора, 235
Формулы Крамера, 330
Функциональный ряд, 222
Частичная сумма ряда, 143
Числовая ось, 18
Числовой ряд, 142
Числовые промежутки, 19
Экстремум функции, 252
Элементарные преобразования матриц,
318
Эллипс, 80

Щ ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
ОГЛАВЛЕНИЕ
4SS
ОГЛАВЛЕНИЕ
ПРЕДИСЛОВИЕ 3
I. ГЛАВА — ВВЕДЕНИЕ 5
1. ЛЕКЦИЯ - МНОЖЕСТВА.
СИМВОЛИКА И ТЕРМИНОЛОГИЯ 5
1. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - МНОЖЕСТВА 15
2. ЛЕКЦИЯ - СИСТЕМЫ КООРДИНАТ 21
2. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - СИСТЕМЫ КОРДИНАТ 31
II. ГЛАВА — ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ 34
3. ЛЕКЦИЯ - ФУНКЦИЯ 34
4. ЛЕКЦИЯ - ФУНКЦИЯ 47
3. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИЯ 57
4. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФУНКЦИЯ 60
5. ЛЕКЦИЯ - ЭЛЕМЕНТАРНЫЕ ПРЕОБРАЗОВАНИЯ
ГРАФИКОВ 63
5. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПОСТРОЕНИЕ ГРАФИКОВ
ФУНКЦИЙ 70
©. ЛЕКЦИЯ КРИВЫЕ ВТОРОГО ПОРЯДКА 77
6. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - КРИВЫЕ ВТОРОГО
ПОРЯДКА 88
III. ГЛАВА — ТЕОРИЯ ПРЕДЕЛОВ И ЧИСЛОВЫЕ РЯДЫ 92
Т. ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ 02
7. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ 101
8. ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ 105
8. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ ИЗ
9. ЛЕКЦИЯ - ТЕОРИЯ ПРЕДЕЛОВ 118
9. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРИЯ ПРЕДЕЛОВ 125
10- ЛЕКЦИЯ - НЕПРЕРЫВНОСТЬ ФУНКЦИИ 131
10. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - НЕПРЕРЫВНОСТЬ
ФУНКЦИИ 139
11. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ 142
11. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ 149
12. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ 152
12. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ 158

436
ОГЛАВЛЕНИЕ
13. ЛЕКЦИЯ - ЧИСЛОВЫЕ РЯДЫ 161
13. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЧИСЛОВЫЕ РЯДЫ 171
IV. ГЛАВА — ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ 174
14. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ 174
15. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ 181
14. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВОДНАЯ ФУНКЦИИ 188
15. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВОДНАЯ ФУНКЦИИ 191
16. ЛЕКЦИЯ - ПРОИЗВОДНАЯ ФУНКЦИИ 193
16. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВОДНАЯ ФУНКЦИИ 198
17. ЛЕКЦИЯ - ДИФФЕРЕНЦИАЛ ФУНКЦИИ 202
17. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ДИФФЕРЕНЦИАЛ
ФУНКЦИИ 208
18. ЛЕКЦИЯ - ТЕОРЕМЫ О ФУНКЦИЯХ 211
18. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ТЕОРЕМЫ О ФУНКЦИЯХ 219
19. ЛЕКЦИЯ - ФУНКЦИОНАЛЬНЫЕ РЯДЫ 222
19. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ ~ ФУНКЦИОНАЛЬНЫЕ
РЯДЫ 228
20. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА 233
21. ЛЕКЦИЯ - ФОРМУЛА И РЯД ТЕЙЛОРА 238
20. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФОРМУЛА И РЯД ТЕЙЛОРА 243
21. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ФОРМУЛА И РЯД ТЕЙЛОРА 247
22. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ 250
22. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ
ФУНКЦИЙ 257
23. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ 262
23. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ
ФУНКЦИЙ 269
24. ЛЕКЦИЯ - ИССЛЕДОВАНИЕ ФУНКЦИЙ 274
24. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ИССЛЕДОВАНИЕ
ФУНКЦИЙ 282
25. ЛЕКЦИЯ - РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ 290
25. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - РЕШЕНИЕ НЕЛИНЕЙНЫХ
УРАВНЕНИЙ 298
V. ГЛАВА — ЭЛЕМЕНТЫ ВЕКТОРНОЙ И ЛИНЕЙНОЙ
АЛГЕБРЫ 302
26. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 302
26. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ
АЛГЕБРЫ 311
27. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 316
ОГЛАВЛЕНИЕ
4S7
27. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ
АЛГЕБРЫ 322
28. ЛЕКЦИЯ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ 326
28. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЭЛЕМЕНТЫ ЛИНЕЙНОЙ
АЛГЕБРЫ 336
29. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА 341
30. ЛЕКЦИЯ - ВЕКТОРНАЯ АЛГЕБРА 349
29. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ЛИНЕЙНЫЕ ОПЕРАЦИИ 356
30. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - СКАЛЯРНОЕ
ПРОИЗВЕДЕНИЕ 360
31. ЛЕКЦИЯ - ВЕКТОРНОЕ И СМЕШАННОЕ ПРОИЗВЕДЕНИЯ 363
31. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРОИЗВЕДЕНИЯ
ВЕКТОРОВ 370
32. ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В
ПРОСТРАНСТВЕ 374
32. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПЛОСКОСТЬ 380
33. ЛЕКЦИЯ - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В
ПРОСТРАНСТВЕ 383
33. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРЯМАЯ В ПРОСТРАНСТВЕ
391
34. ЛЕКЦИЯ - ПОНЯТИЕ п - МЕРНОГО ВЕКТОРНОГО
ПРОСТРАНСТВА 396
34. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ - ПРЕОБРАЗОВАНИЕ
КООРДИНАТ. КВАДРАТИЧНАЯ ФОРМА 406
ОТВЕТЫ 411
РИСУНКИ К ОТВЕТАМ 417
ЛИТЕРАТУРА 429
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 431
ОГЛАВЛЕНИЕ 435