ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ
УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра теоретических основ радиоэлектроники (ТОР)
Н.А. Каратаева
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ
Дискретная обработка сигналов
и цифровая фильтрация
Методические указания
по выполнению курсовой работы
2002
Рецензент:
Заведующий кафедрой ТОР ТУСУР, д.т.н., профессор Пуговкин А.В.
Корректор: Красовская Е.Н.
Каратаева Н.А.
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ Дискретная обработка сигна-
лов и цифровая фильтрация: Методические указания по выполнению курсо-
вой работы. - Томск: Томский межвузовский центр дистанционного образо-
вания, 2002 - 93 с.
Изложены цель, содержание, исходные данные, варианты заданий и примеры расчета
для выполнения курсовой работы по теме «Дискретная обработка сигналов и цифровая
фильтрация» Работа предназначена для студентов всех форм обучения, изучающих дис-
циплину «Радиотехнические цепи и сигналы»
Разработчик электронной версии: Круглов Р.С.
© Каратаева НА.,	2002
© Томский межвузовский центр
дистанционного образования 2002
3
СОДЕРЖАНИЕ
1	Введение.................................................... 5
2	Задание к курсовой работе................................... 5
2.1	Дискретная обработка аналогового сигнала. Задание к первой
части курсовой работы....................................... 5
2.2	Цифровая фильтрация. Задание ко второй части курсовой работы
(вариант 1). Синтез цифрового фильтра (ЦФ по известному
аналоговому фильтру-прототипу).............................. 6
2.3	Цифровая фильтрация. Задание ко второй части курсовой работы
(вариант 2). Синтез ЦФ Баттерворта или Чебышева по заданной
амплитудно-частотной характеристике (АЧХ) цифрового фильтра 7
3	Основные определения и комментарии к дискретной обработке
сигналов....................................................... 7
3.1	Дискретизация сигналов.................................. 7
3.2	Дискретизация сит налов по частоте...................... 8
3.3	Дискретизация сигналов но времени...................... 10
3.4	Ряд и теорема Котельникова.............................. 15
3.5	Дискретное преобразование Фурье (ДПФ).................. 16
3.6	Прямое и обратное /-преобразования......................20
4	Основные определения и комментарии к рекомендуемым методам
анализа и синтеза цифровых фильтров (ЦФ)....................... 25
4.1	Описание алгоритмов работы трансверсальных (ТЦФ)
и рекурсивных (РЦФ) цифровых фильтров.................... 25
4.2	Определение системных функций и построение структурных
схем ТЦФ и РЦФ.............................................. 26
4.3	Синтез ЦФ методом билинейного /-преобразования
передаточной функции известного аналогового
фильтра-прототипа........................................ 29
4.4	Синтез ЦФ по импульсной характеристике известного
аналогового фильтра-прототипа............................... 30
4.5	Синтез ЦФ методом билинейного /-преобразования по
заданной АЧХ цифрового фильтра.............................. 33
4.5.1 Определение параметров АЧХ аналогового
фильтра-прототипа................................... 33
4.5.2 АЧХ фильтра Баттерворта............................ 36
4.5.3 АЧХ фильтра Чебышева............................... 36
4.6	Расчет системной функции, анализ устойчивости, реализация ЦФ. 37
4.7	Расчет АЧХ цифрового фильтра............................ 40
4.8	Расчет импульсной характеристики ЦФ..................... 42
4.9	Расчет дискретной последовательности на выходе ЦФ....... 43
5	Указания к выполнению курсовой работы....................... 44
6	Список рекомендуемой литературы............................. 45
4
7	Приложение А. Шифры и исходные данные к курсовой работе...... 47
8	Приложение В. Примеры выполнения отдельных пунктов задания к
курсовой работе................................................. 52
ВЛ Пример дискретной обработки аналогового сигнала.............. 52
B.	I Л Расчет спектральной плотности аналогового сигнала.... 52
ВЛ .2 Дискретизация аналогового сигнала по времени........... 54
ВЛ .3 Расчет спектральной плотности дискретизированного сигнала... 55
В.	1.4 Расчет коэффициентов Ск с помощью ДПФ................ 57
В.	1.5 Восстановление исходного сигнала по ДПФ.............. 59
В.	1.6 Z-преобразование дискретной последовательности....... 60
В.	1.7 Восстановление аналогового сигнала с использованием ряда
Котельникова................................................ 62
В.2	Пример анализа аналогового фильтра-прототипа............... 63
В.2.1	Расчет передаточной функции цепи...................... 63
В.2.2	Расчет и построение частотных характеристик........... 63
В.2.3	Расчет и построение временных характеристик........... 65
В.З	Пример синтеза ЦФ методом инвариантности импульсных
характеристик................................................... 67
В.З	Л Дискретизация импульсной характеристики аналогового
фильтра-прототипа........................................... 67
В.З.2	Расчет системной функции трансверсального и рекурсивного
ЦФ..............................*........................... 68
В.3.3	Расчет АЧХ трансверсального и рекурсивного ЦФ......... 70
В 4 Пример синтеза ЦФ методом билинейного /-преобразования...... 72
В.4.1	Расчет системной функции ЦФ........................... 72
В.4.2	Расчет АЧХ ЦФ канонического вида...................... 74
В.4.3	Расчет импульсной характеристики ЦФ................... 75
В.4.4	Обсуждение полученных результатов..................... 76
В.4.5	Прохождение дискретного сигнала через ЦФ.............. 76
В.5 Пример синтеза по заданной АЧХ.............................. 79
В.5.1	Определение параметров АЧХ цифрового ФНЧ.............. 79
В.5.2	Определение параметров АЧХ аналогового фильтра-прототипа. 80
В.5.3	Анализ аналогового фильтра Баттерворта................ 80
В.5.4	Синтез цифрового фильтра Баттерворта.................. 84
В.5.5	Анализ аналогового фильтра Чебышева................... 87
В.5.6	Синтез цифрового фильтра Чебышева.................... 91
1	ВВЕДЕНИЕ
Одним из новых и перспективных направлений современной обработки
радиосигналов является цифровая фильтрация. В ее основе лежит преобразо-
вание аналоговых сигналов в последовательность чисел и обработка этой по-
следовательности в цифровом вычислительном устройстве, роль которого
может играть как универсальная ЭВМ, так и специализированный цифровой
процессор.
Применение в радиоэлектронике цифровой фильтрации открывает до-
полнительные возможности при обработке сигналов. В частности, могут быть
реализованы сложные алгоритмы фильтрации, которые аналоговыми метода-
ми в ряде случаев вообще не удается осуществить. С другой стороны, возмо-
жен синтез в цифровой форме аналогов известных радиотехнических уст-
ройств различного функционального назначения, а именно: фильтров, преоб-
разователей частоты, детекторов и т.п.
Настоящая курсовая работа ставит своей целью привить студентам
практические навыки в области дискретной и цифровой обработки сигналов
на примере решения конкретной задачи, включающей в себя элементы как
синтеза, так и анализа цифрового фильтра (ЦФ).
Задание к курсовой работе состоит из двух частей. Первая часть вклю-
чает подготовку аналогового сигнала к цифровой обработке и называется
дискретной обработкой аналогового сигнала. Вторая часть посвящена цифро-
вой фильтрации и содержит синтез ЦФ, анализ частотных и временных ха-
рактеристик ЦФ и расчет отклика ЦФ в виде выходной дискретной последо-
вательности. Сокращенно вторая часть курсовой работы называется цифро-
вой фильтрацией. Предусмотрено два варианта задания по цифровой фильт-
рации. Исходные данные к курсовой работе рассмотрены в приложении А
Шифры студентов представлены в таблице А 1
2	ЗАДАНИЕ К КУРСОВОЙ РАБОТЕ
2.1	Дискретная обработка аналогового сигнала. Задание к
первой части курсовой работы
2.1.I Дискретизировать заданный шифром сигнал (таблица А.2) и вос-
становить аналоговый сигнал, используя ряд Котельникова. При определении
верхней частоты спектра сигнала использовать пороговый критерий (для
а» со(- амплитуды спектральных составляющих не превышают уровня 0,1 от
максимальной).
2.1.2 Рассчитать спектр дискретной последовательности, определенной
в пункте 2.1. Построить график.
6
2.1.3 Найти Z-преобразование найденной в пункте 2.1.1 дискретной по-
следовательност и.
2.1.4 Определить дискретное преобразование Фурье (ДПФ) той же дис-
кретной последовательности. Построить график комплексных коэффициентов
. Восстановить аналоговый сигнал, используя тригонометрический ряд
Фурье.
2.1.5 По результатам пункта 2.1.4 найти исходную дискретную после-
довательность, применяя обратное дискретное преобразование Фурье к Ск.
Построить график.
2.1.6 Произвести сравнение результатов вычислений:
1)	сравнить форму спектра дискретизированной последовательности со
спектром исходного аналогового сигнала;
2)	установить связь между:
а)	результатом Z-преобразования и спектральной плотностью дискрет-
ной последовательности;
б)	спектром исходного периодического аналогового сигнала и дискрет-
ными отсчетами его спектральной плотности.
2.2	Цифровая фильтрация. Задание ко второй части
курсовой работы (вариант 1). Синтез ЦФ по
известному аналоговому фильтру-прототипу
2.2.1 Для заданной аналоговой электрической цепи (таблица А.З) найти
операторное выражение передаточной функции К(р) и импульсную характе-
ристику g(t).
2.2.2 Осуществить синтез цифровой цепи методом билинейного
/-преобразования по найденной в пункте 2.2.1 К(р). Построить схему алго-
ритма цифрового фильтра (ЦФ).
2.2.3 Рассчитать и построить амплитудно-частотную (АЧХ), фазоча-
стотную (ФЧХ) и импульсную характеристики ЦФ.
2.2.4 Произвести синтез ЦФ с помощью метода инвариантности им-
пульсной характеристики по найденной в пункте 2.2.1 g(t). Построить схему
алгоритма 1ДФ.
2.2.5 Найти отклик одного из рекурсивных ЦФ в виде выходной дис-
кретной последовательности на входную дискретную последовательность,
полученную в первой части курсовой работы.
2.2.6 Сделать выводы о сравнении методов синтеза по трудоемкости,
сложности конечного результата, о физической достоверности полученной
формы отклика в реальных условиях прохождения дискретного сигнала через
синтезированную цепь.
7
2.3	Задание ко второй части курсовой работы (вариант 2).
Синтез ЦФ Баттерворта или Чебышева по заданной АЧХ
цифрового фильтра
2.3.1 Методом билинейного Z-преобразования синтезировать цифровой
фильтр нижних частот (ФНЧ) с частотой среза/,с, равной ширине основного
лепестка (в области положительных частот) спектра входного сигнала s(t),
При этом в зависимости от варианта задания в качестве аналогового прототи-
па необходимо использовать фильтр одного из двух типов:
а)	ФНЧ с максимально плоской АЧХ (фильтр Батгерворта), обеспечи-
вающий на удвоенной частоте среза аналогового фильтра й)А2 - 2го^| затуха-
ние не меньше а, дБ.
б)	ФНЧ с равноволновой в полосе пропускания АЧХ (фильтр Чебыше-
ва) с неравномерностью р, дБ, позволяющий, как и в первом случае на часто-
те соЛ2	получить затухание не меньше а, дБ. Неравномерность АЧХ
цифрового ФНЧ в пределах полосы пропускания задана в таблице А.4. Зату-
хание АЧХ в полосе задерживания представлено в таблице А.5.
2.3.2 Рассчитать АЧХ, ФЧХ и импульсную характеристику синтезиро-
ванного цифрового фильтра.
2.3.3 Определить вид дискретного сигнала на выходе фильтра при воз-
действии на его вход последовательности отсчетов, рассчитанных в первой
части курсовой работы.
3	ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И КОММЕНТАРИИ
К ДИСКРЕТНОЙ ОБРАБОТКЕ СИГНАЛОВ
3.1	Дискретизация сигналов
В первой части курса «Радиотехнические цепи и сигналы» [9] рассмат-
ривались сигналы, моделью которых являлась функция времени s(t), значения
которой заданы для непрерывной совокупности всех точек по оси времени
(рисунок 3.1,а). Такие сигналы называются непрерывными или аналоговыми.
Сигнал s(t) может быть задан спектральной плотностью S{a>), посколь-
ку s(t) и S(<w) связаны парой преобразований Фурье:
+оо
S(ty)= \s{t)e~jta,dt,	(3.1)
s(/)= — fs(a))eJMda).	(3.2)
2л J
8
Как и s(t), спектральная плотность также является аналоговой
функцией частоты (рисунок 3.1,6).
Рисунок 3.1 - Временное (а) и частотное (б) представления аналогового непе-
риодического си! нала
В радиотехнике часто встречаются задачи, в которых значения сигнала
могут быть определены лишь в счетном множестве точек по оси времени
(..., /о, 6, *2, •••)• Обычно моменты времени t„ следуют через равные промежут-
ки Та, которые называются шагом (интервалом) дискретизации. В этом случае
моделью сигнала являются отсчетные значения (..., s(0), s(T„), s(2Ta), ...,
s(nT0), ...) в точках (..., О, Гй, 2Тд,пТд). Такие сигналы называются дискрет-
ными (от лат. слова discretis — раздельный, прерывистый).
Спектральная плотность сигнала также может быть задана своими от-
счетными значениями (..., 5 (гл/), 5(2^), 5'(3ол). ...). Шаг дискретизации по
оси частот обозначен
Ясно, что, чем меньше шаг дискретизации То (или <»]), тем точнее сиг-
нал s(l) (или S(a>)) может' быть восстановлен по своим отсчшным значениям.
Однако с уменьшением шага дискретизации увеличивается число отсчетных
значений, поэтому задача о выборе шага дискретизации требует специального
исследования.
3.2	Дискретизация сигналов по частоте
Рассмотрим для определенности аналоговый непериодический сигнал
лгТДрисунок 3 1,а), длительность которого равна г, а спектральная плотность
описывается функцией £(ту). Преобразуем непериодический сигнал s(t) в пе-
риодическую последовательность сигналов s-rft) с периодом Тс> т(рисунок 3.2.а).
М') =	(3.3)

где m~ ±0, ±1, ±2, ...
a
Рисунок 3.2 Временное (а) и спектральное (б) представления аналого-
вого периодического сигнала
Периодическую последовательность sr(t) представим рядом Фурье:
зт (0 = Е^keJkea}t = Q + £ 2|Q I cos(by + argQ ), - oo < / < oo.
k=\
Здесь коэффициенты Q вычисляются по формуле:
Гс
2
‘с к
~ ‘ 2
(3.4)
(3-5)
Сравнение выражений (3.1) и (3.5) позволяет утверждать, что S(kn>.) -
отсчетные значения (отсчеты) спектральной плотности с шагом дискретиза-
ции (рисунок 3.2.6), с точностью до постоянного множителя Тс совпадают
с комплексными коэффициентами Q:
s(o)=rc-co, s(^)=7’c-c1, ..., s(k(o}^Tcck. (3.6)
Исходный непериодический сигнал s(i) совпадает с периодической по-
следовательностью Sr(t) на интервале 0 < t < Т и вычисляется по дискретным
отсчетам S(kco.) спектральной плотности, взятым с шагом дискретизации
=2/4 •
/ 1 с
10
Формула (3.4) с учетом (3.6) имеет вид:
1с к -ос
5(0)
Тс
— cos(a^|Z
+ argS^i))
0< 1<ТС.
(3.7)
Для увеличения шага дискретизации необходимо уменьшать период Тс.
Но формула (3.4) справедлива при условии Тс > т. Следоват ельно, наиболь-
ший шаг дискретизации - по оси частот (при Тс - г).
Заметим, что ширина спектральной плотности реально ограничена, т. е.
существуют верхние частоты +сов. На частотах j со | > сов спектральную
плотность можно считать равной нулю (рисунок 3.2 б). Это означает, что
число слагаемых, учитываемых при вычислении ряда (3.4) или (3.7), конечно.
Для оценки числа учитываемых слагаемых N достаточно поделить ширину
спектральной плотности 2сов на шаг дискретизации Щу	(рисунок
3.2,6):
= 2fe-Tc.
(3-8)
Итак, используя (3.7), можно восстановить непрерывный сигнал s(t) по
дискретным отсчетам S(kco}) спектральной плотности, взятыми с шагом cot.
Число слагаемых Д', учитываемых в (3.7), оценивается формулой (3.8).
3.3	Дискретизация сигналов во времени
Сравнение моделей сигналов, изображенных на рисунках 3.1 и 3.2 и
описанных в предыдущих параграфах, позволяет сформулировать следующие
обобщения.
1.	Аналоговому непериодическому сигналу s(t) соответствует аналого-
вая непериодическая функция частоты, называемая спектральной плотностью
5(«).
2.	Дискретизация аналоговой спектральной плотности с шагом при-
водит к преобразованию непериодического сигнала s(t) конечной длительно-
сти г в периодическую последовательность S/(t) с периодом повторе-
ния cot =	- г •
/ ' г
11
3.	Уместно предположить (и нетрудно показать, учитывая взаимообра-
гимость преобразований Фурье), что дискретизация аналогового непериоди-
ческого сигнала s(t) с шагом Т<> приведет к преобразованию спектральной
плотности, реальная ширина которой равна 2со„. в периодическую последова-
тельность с периодом повторения с>(} = ^-п/т , причем должна быть
/ 1 d
больше или равна 2г»« (рисунок 3.3,а и б).
а)	б)
Рисунок 3.3 - Временное (а) и частотное (б) представления дискретизи-
рованного по времени сигнала
Модель дискретного сигнала, показанного на рисунке 3.3,а, задается
отсчетами s(nT0) непрерывного сигнала s(t), взятыми в дискретные мо-
менты времени t = пТ,>, где Та- шаг дискретизации, п = ±0, ±1, ±2, ...
Для фиксации моментов времени пТ.у воспользуемся периодической
последовательностью ^-функций:
ОС
70=
п=-оо
(3 9)
Математической моделью дискретного сигнала, заданного в фиксиро-
ванные моменты времени, является
*<>0=50 70= 50 ±3(t-пТд).
п--«>
(3.10)
Так как 3(t-nTt) существует лишь в момент t - пТ(), то из формулы
(3.10) можно получить второй вариант математической модели дискретного
сигнала:
12
\>0= Е^^ХО-^)-
(З.Н)
Периодическую последовательность ^функций с периодом Тд можно
выразить рядом Фурье (см. (3.4)):
И-- СО
1 Л
=г
(3-12)
так как для 5 -функции Сп = ft .
Подстановка (3.12) в (3.10)
дискретного сигнала:
дает третий вид математической модели
1
"т‘
'д п-~^>
(3.13)
Для вычисления спектральной плотности дискретною сигнала
воспользуемся прямым преобразованием Фурье (3.2):
У(®)=
(3.14)
Подстановка в (3.14) сигнала.?^ в виде (3.13) дает
. 00	00	/п2л-.- f
\>М=ур(')2> т" -е 'мЛ	(3.15)
д - оо М=-СО
Изменяя порядок интегрирования и суммирования, получаем
1 со *	--г |г
^0)=— Е	й dt- <3-16)
М И=-оо_оо
Интеграл

(3.17)
т
1 о
13
является спектральной плотностью непрерывного сигнала s(t), перемещенной
по оси частот на величину яТаким образом,
/ *д
(3-18)
Формула (3.18) устанавливает связь спектральной плотности дискрет-
ного сигнала S6(a>) со спектральной плотностью непрерывного сигнала
S(co). Из формулы (3.18) следует, что дискретизированному по времени сиг-
налу s^t) (рисунок 3.3,а) соответствует периодическая последовательность
спектральных плотностей с периодом п  ^п/т по оси частот (рисунок 3.3,6).
Замечание
Следует обратить внимание на тот факт, что размерность спектральной
плотности аналогового сигнала 5(л>) равна произведению размерности сиг-
нала s(t) и времени (например, Вольт-секунда). Размерность спектральной
плотности дискретного сигнала Sd(co) совпадает с размерностью .отсчета
s(nTd).
Спектральную плотность дискретного сигнала Sd(co) можно вычислить
непосредственно по отсчетам сигнала s(nTe>). Для этого воспользуемся выра-
жением (3.14), подставив в него вместо sd(t) математическую модель (3.11):
ОС 00
У(<а)= J ^пГМ-”г<>)е^“а-	а1<”
Изменяя порядок интегрирования и суммирования и используя фильтрующее
свойство ^функции, получаем
У(®)=
(3 20)
Определим модуль и аргумент комплексной спекзральной плотности
дискретного сигнала по формулам:
if °0	V Г °°
cos^T^w) + s(nTd )sin(s?7^ct>)
J \n=-00	,
<3.21)
14
ТАпТд )sin(nTda))
argSd(ft)) = -arctg n=~K-------—
Ел'(/77й)со^^)
Формулы (3.21) и (3.22) позволяют рассчитать амплитудно-частотную
(АЧХ) и фазочастотную (ФЧХ) характеристики спектральной плотности дис-
кретного сигнала.
Спектральную плотность аналогового сигнала S(tw) можно выразить
через спектральную плотность дискретизированного сигнала на ин-
тервале частот -сов< ах а)в:
S(a))=TdSd(a>), |со|<юв.
(3.23)
Подставляя в (3.23) спектральную плотность дискретного сигнала в ви-
де (3.20), получим

Н<СОе.
(3.24)
Формула (3 24) справедлива, если 2а)в <
/ * д
откуда следует требова-
ние к шагу дискретизации Тд\
(3.25)
Если 7> выбрать из условия Г д - IZ f , то
£(*0 = 77 ^(пТд\е J 2fe, H<we.
п =-00
(3.26)
Формула (3.26) позволяет восстановить спектральную плотность анало-
гового сигнала s(t) по его дискретным отсчетам, взятым с интервалом
т — \/
д' Л/е'
Заметим, что при заданной длительности сигнала Тс число слагаемых А,
учитываемых при вычислении ряда (3.26), конечно и оценивается отношени-
15
ем длительности Т, к шагу дискретизации Тд~
N^/T ~2feTc.
/ Jd
(3.27)
Полученный результат для оценки числа требуемых отсчетов сигнала
совпадает с оценкой числа требуемых отсчетов спектральной плотности
(формула (3.8)).
3.4	Ряд и теорема Котельникова
Получим выражение, связывающее аналоговый сигнал s(t) с его дис-
кретными отсчетами s(nr6). Для этого найдем s(t) по его спектральной
плотности S(<w), используя (3.2) и (3.26):
« (ов Г |	00
- (ur L J в п—<х>

(3.28)
Изменяя порядок интегрирования и суммирования и учитывая, что
а>„ =	, Тд = у2^, получаем
1 со	сон	1
„=-00	_^в	2сОе
00
__ 1
<*>e(t-nTd)
eja>e (t ~ »тд) _	)
2j
jeoit-nra)
ejx -e~JX
Так как ---------= sinх, то окончательно имеем
27
у(/) =

(3.29)
Полученное выражение называется рядом Котельникова.
Из (3.29) следует, что непрерывный сигнал s(t). ширина спектральной
плотности которого офаничена верхней частотой гу„. может быть полностью
16
восстановлен по его дискретным отсчетам, взятым с интервалом дискретиза-
ции y-у . Это положение доказано В. А. Котельниковым в 1933 голу и на-
зывается теоремой Котельникова.
Ряд (3.29) представляет собой разложение непрерывного сигнала s(l) в
ряд по элементарным сигналам вида
WsinLz (/- л/7 Л]	,
•	(з.зо)
Сигналы (3.30) называются функциями отсчетов (или функциями Ко-
тельникова), которые показаны на рисунке 3.4
Рисунок 3.4 - Функции отсчетов, сдвинутые друг относительно друга на ин-
тервал времени пТд
Коэффициентами ряда (3.29) являются отсчеты s(nTd) сигнала s(t) в мо-
менты времени I - пТ(„ Функции Котельникова sincn(t) равны единице в мо-
мент времени t - пТд и равны нулю в других отсчетных точках t = kT0, к* п.
Следовательно, ряд (3.29) всегда принимает отсчетное значение s(nT(>) в точ-
ках t = пТа. Последнее свойство позволяет использовать ряд (3.29) для при-
ближенного нахождения s(t) по его дискретным отсчетам s(nTa) в тех случаях,
когда частота <ов является приближенной оценкой ширины спектральной
плотности
3.5 Дискретное преобразование Фурье (ДПФ)
Аналоговые преобразования Фурье (3.1) и (3.2) связывают между собой
два текущих параметра: время t и частоту Дискретные преобразования Фу-
рье (ДПФ) связывают меж чу собой два дискретных параметра: дискретное
время пТс и дискретную частоту ка>\. При дискретизации по частоте и по вре-
мени выполняются два условия:
I) функция, описывающая сигнал во временной области, будет перио-
дической (с периодом Тс =
) и дискретизированной с шагом пТ0’,
2) функция, описывающая сигнал в частотной области, будет периоди-
ческой (с периодом сод = 2cje
- 2^7 ) и дискретизированной с шагом kcoh
/ ‘ д
Модели периодических и дискретизированных сигналов показаны на
рисунке 3.5.
Рисунок 3.5 - Временное (а) и частотное (б) представления сигнала,
дискретизированного по времени пТ6 и по частоте ксо}
Вернемся к выражениям (3.7) и (3.26). Эти выражения позволяют по N
дискретным отсчетам сигнала или его спектральной плотности получить не-
прерывные значения s(t) или 5(гу) для всех значений I или со. Конечно, эти
выражения можно использовать и для нахождения дискретных отсчетов
s(nTn) и S(kcox \ Формула (3.7) при вычислении s(t) справедлива для 0 < t < Тс
(рисунок 3.5,а, сплошная линия). Если - со < / < ос, то формула (3.7) дает пе-
риодическую функцию времени sr(t) с периодом Тс (рисунок 3.5,а, пунктир-
ная линия). Очевидно, что отсчетные значения s(nT0), полученные по форму-
Т /
ле (3.7) для моментов времени t = пТ0, где Тд - у^, периодически повторя-
ются с периодом N, т.е. sfnTj = s[(n+N)T()].
Формула (3.26) при вычислении справедлива для |<у| <сов (рису-
нок 3.7,6, сплошная линия). Если - ос < сю < со , то формула (3.26) дает перио-
дическую функцию частоты Sc,(fc>) с периодом щд = 2гу6 (рисунок 3.5,6,
пунктирная линия).
18
Отсчетные значения S(Ar®,), полученные по формуле (3.26) для
а> = к(О\, где (О\, периодически повторяются с периодом N, т.е.
) - *$[(& + Л' ].
Как указывалось, в формулах (3.7) и (3.26) необходимо учитывать N
членов ряда. Так как отсчетные значения s(nT0) и	полученный по
формулам (3.7) и (3.26), периодически повторяются с периодом N, то сумми-
рование в этих формулах можно начинать с любого номера Для определен-
ности примем, что суммирование в формулах (3.7) и (3.26) проводится в пре-
делах от 0 до /V- 1.
Таким образом, если в формуле (3.7) и (3.26) положить t = пТа, = к(О\,
Та= ад =	, то они записываются следующим
д /2fe 1 /тс /Тд /а\
образом:
1 Уд^  ч 1пк?-я'
Tck=Q
S(ka}})-Td^ s(nTd)s nk 'N.
n=0
(3.31)
(3.32)
Обычно вводится обозначение, связывающее обсчеты спектральной
плотности S(ka>}) и коэффициенты комплексного ряда Фурье Q:
' с
Отсчеты спектральной плотности нормируются, чтобы размерность от-
счетов сигнала и нормированных отсчетов спектральной плотности была
одинаковой Окончательно формулы (3.31) и (3.32) преобразуются к виду:
1 УД - тк^л
Л п=0
АО
(3.33)
(3.34)
Здесь использовано сокращенное обозначение отсчетов sfnTj = sn. По-
луденные выражения называются дискретным преобразованием Фурье
(ДНФ). Из них выражение (3.33) является прямым преобразованием и позво-
19
ляет по У дискретным отсчетам сигнала получить N дискретных нормиро-
ванных отсчетов спектральной плотности Ск. Обратное преобразование
(3.34) позволяет найти N отсчетов сигнала s., по N нормированным отсчетам
спектральной плотности Ск.
Для дискретных преобразований Фурье (3.33) и (3.34) справедливы
многие теоремы, доказанные для пары стандартных преобразований Фурье
(3.1) и (3.2), такие как теорема о линейности преобразования, теорема о за-
паздывании и др.
Принципиально новым свойством преобразований (3.33) и (3.34) явля-
ется их периодичность с периодом N, г. е.
Sn~Sn N >	С к ~ ^k+N •	(З.э5)
Следовательно, в формулах (3.33) и (3.34) суммирование можно начинать с
любого значения кип, однако общее число слагаемых при этом должно оста-
ваться равным N.
Если отсчеты сигнала s(nT()) представляют действительные величины,
то комплексные коэффициенты Ск обладают свойством
Ск=С'_к.	(3.36)
Учет периодичности (3.35) позволяет преобразовать (3.36) к виду
Поэтому коэффициенты Ск на интервале от 0 до N-I образуют ком-
плексно-сопряженные пары (при любом к, за исключением к - 0 и к =
при N - четном):
с2=с; 2,.... q=c;-_*.	(з.з?>
Коэффициент Со является действительной величиной при любом значе-
нии N. Коэффициент Cv 2 равен действительной величине, если N - число
четное.
Для восстановления аналогового сигнала s(i), дискретизация которого
дала N отсчетов, можно использовать ряд Фурье (3.7), представляющий ко-
нечную сумму двух видов:
20
4/)=с0
(3.38)
если N - нечетное число;
Л ?’1
s(r) = C0+ £ 2|Q|cos(foiy + argCk)+CN
k=\
(3.39)
если N — четное число.
Следует особо подчеркнуть, что восстановление непрерывного сигнала
по формулам (3.38) и (3.39) есть не приближенная, а точная операция, полно-
стью эквивалентная получению текущих значений сигнала с ограниченным
спектром по его выборкам, образующим ряд Котельникова. Однако процеду-
ра, использующая дискретное преобразование Фурье, в ряде случаев пред-
почтительна, поскольку она приводит к конечным суммам гармоник, в то
время как ряд Котельникова для периодического сигнала принципиально
должен содержать бесконечное число членов.
3.6 Прямое и обратное Z-преобразования
Рассмотрим дискретный сигнал, заданный моделью (3.11):
00
^(0=
П-- 00
Спектральная плотность такого сигнала, равная
п -00
может быть записана в виде
00	/	\ и
П=~<Х>
(3.40)
Формула (3.40) показывает, что спектральная плотность дискретного
сигнала выражается через трансцендентную периодическую функцию часто-
jT.ro
ты eJ ° .
21
Естественно, появляется желание ввести новую комплексную перемен-
ную
v = ey7<jW,	(3.41)
в результате чего приходим к Z-преобразованию.
Определение. Пусть задана последовательность отсчетов (числовая по-
следовательность) {s(nTj}. Тогда прямым Z-преобразованием последова-
тельности {s(nTd)} называется сумма
«(-)=
«--00
где z - комплексная переменная.
(3.42)
Функцию S(z) называют Z-образом дискретного сигнала. Функция S(z)
определена лишь для тех значений z, при которых ряд (3.42) сходится. Это
означает, что в теории Z-преобразования комплексная переменная z рассмат-
ривается для большей области значений, чем дается формулой (3.41).
Выясним, как по Z-преобразованию S(z) можно найти последователь-
ность {s(nTa)}.
Умножим обе части (3.42) на г"2-1 и вычислим от обеих частей контур-
ный интеграл в Z-плоскости по любому замкнутому контуру в области схо-
димости S(z), охватывающему начало координат:
00
И=-СО
(3.43)
Из теории функций комплексного переменною известно, что
2nj, и = —1,
(3.44)
Таким образом, контурные интегралы от всех слагаемых в правой части
(3.44) обращаются в нуль, кроме случая т = п. Следовательно, обратное
Z-преобраювание определяется выражением
s(nTd)=^S(:):"-'dz.
2л/ J
(3.45)
22
Полученный интеграл вычислим с помощью теоремы о вычетах:
£ Res,5U)>	(3.46)
Res,5(.-) - Jim ™	- z, )* z"~' ].	(3.47)
где к - кратность полюса.
Рассмотрим основные свойства /-преобразования.
Линейность
Если X(z) и Y(z) являются Z-преобразованиями последовательностей
{х(пТд)} и {у(пТд)}, то последовательности {а-х(пТд) + by(nTJ } соответствует
Z-преобразование aX(z) + bY(z).
Теорема о задержке
Если последовательность {х(пТд)} имеет /-преобразование X(z), то по-
следовательности	соответствует/-преобразование z~mX(z).
Теорема о свертке
Если X(z) и Y(z) являются /-преобразованиями последовательностей
{х(пТ))} и {yfnTj}, то дискретной свертке
со	СО
X Л[(п-т)Тд ]Г[»>Г()]=	%[«?<>]	(3.48)
m=-oo	т -ое
соответсз вует /-преобразование X(z) Y(z).
Перечисленные свойства доказываются непосредственным вычислени-
ем /-преобразования.
В таблице 3.1 в комплексной форме представлены, с одной стороны,
односторонние сигналы и изображения по Лапласу, а с другой стороны одно-
сторонние дискретные сигналы и их /-образы. В таблицу 3.2 помещены наи-
более распространенные модели аналоговых и дискретных сигналов, а также
/-образы дискретных последовательностей.
23
Таблица 3.1 - Преобразование Лапласа аналоговых сигналов
и Z-преобразование дискретных сигналов
№	Преобразование Лапласа		/-преобразование		
	Оригиналы s(t)	Изображения S(p)	Дискретные сигналы s(nTo)	Z-образы S(z)	
1	^s(t]e~ptdt 0	s(p)	ЕРЪР” n=0	S(z)	
2	40	C+Joo — \S(p)eptdp C-pn	4nTo)	-	
					[S(z>"
				Z/4/	
3	asi(t)+bs2{t)	aS1(p)+6S2(p)	asi(nTd)+bs2(n7'(})	aS,(	z) + iS2(z)
4		s(pYpt	s[(w-Afo]		?(-k’A
5		S(p + a)	sinTt^aT^	Si	z.C^)
6	'40	-~s(p) dp	ns[nTd)	-	^S(z) az
7	0	S\(p}sz(p)	ЕлК«-аК]-52(^) к -0	5	(-’fe(--)
8	lim hit) t-*0+	lim pH{p) p—>«>	lim A(/77\) n-+0	lim H(z)	
9	lim h(t) Z->00	lim pH(p) t->Q	lim h(nTd) n—±(X>	lim( z >1	
10	L [$(/>)]=£/ hm		t Pk)	fef]		
11 i	Z"p(-)]=f z ' .. lim		1 6е 1 i 'N. ч 7 ~ £ i	j	z-1)	
2^
Таблица 3.2 - Связь между дискретными сигналами и Z-образами
1 - № 1	Односторонние аналоговые сигналы s(t) ' [а 7= о. [о, t*0.	Односторонние дискретные сигналы s(n Tj fx, /7 = 0, 0, n / 0.	Z-образы Sfr I
2		(т(п)=1, n = 0,1,2,...	z z-1
з	t	пГд	1 1
4	f		7a-z(z+l) (z-lf
' 5 Н 6	t1		rj-c(z2+4z + l) a-1)4
	e°l		z z-e~aT°
7	tea'	nT^e-^f	
! 8 ।	a		z-a1()
9	ta'		Tpa1*:
16	sin cot	sin(ftw7'<))		 zsin(coTd) z^ ~2zc,ns{coTf))+1
1 1 12	cos cot sin cot	cosfswTa) sin(/mTd)	s(z-cos(o;7'J) z2 -2zcos(/»T())+l ze^aT° sin^T^)
			z2 -2ze aT° cos{coTd)+e~al(i
13	e-£rt cos cot	'a7”° J cos(conTd ) 	i	z(z - e"aT(y cos(coTd ))
			z2 - 2ze~aTd cos(affd )+e'aTti
25
4 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И КОММЕНТАРИИ К РЕКОМЕН-
ДУЕМЫМ МЕТОДАМ АНАЛИЗА И СИНТЕЗА ЦИФРОВЫХ
ФИЛЬТРОВ
4.1 Описание алгоритмов работы трансверсальных (ТЦФ)
и рекурсивных (РЦФ) фильтров
В цифровом фильтре над элементами последовательности осуществ-
ляются операции сложения, вычитания, умножения и задержки во времени
согласно заданному алгоритму обработки, в результате чего на выходе
фильтра формируется новый дискретный сигнал.
Отличительной особенностью цифровой обработки является квантова-
ние сигнала по уровню, необходимое для перевода его значений в числовую
последовательность и преобразования ее в вычислительном усгройстве
цифровом фильтре. В основе анализа цифровых и дискретных устройств ле-
жит один и тот же математический аппарат теория линейных дискретных
схем. Учет эффектов квантования представляет собой самостоятельную и
весьма сложную задачу.
Будем понимать под цифровым фильтром устройство, на вход которого
поступает поток отсчетов х„, а на выходе образуется поток у„. Причем после-
довательность уп представляет собой линейную комбинацию, состоящую из
(М+1) равноотстоящих входных отсчетов хп к (некоторого входного сигнала),
а также вычисленных ранее (N) выходных отсчетов уп_*.
Если учесть односторонность воздействия, то алгоритм работы ЦФ
можно представить в виде двух взвешенных сумм:
Л/	А'
Уп ~	' хп-к + Уп-k 	(4-1)
Г=0	А-=1
Обработка входной последовательности (первая сумма в выражении
(4.1)) начинается с нулевого входного отсчета (А = 0). Обработка выходной
последовательности (вторая сумма в выражении (4.1)) начинается после
предварительного вычисления и запоминания выходного отсчета, т.е. А = 1.
Выражение (4.1) называется разностным уравнением цифрового
фильтра, т.к. оно связывает между собой разности соседних значений вход-
ного х(кТ) ~Хк и выходного у(пTt)) =уп дискретных сигналов.
Различают цифровые фильтры трансверсальные (ТЦФ) и рекурсивные
(РЦФ).
Отсчеты сигналана выходе ТЦФ зависят только от отсчетов входно-
го сигнала и описываются разностным уравнением:
26
л/
Уп = ’хп—к ~ а0 хп+а\ ’хп-Ч+а2 хп 2+—
Л=0
(4.2)
Отсчеты сигнала у„ на выходе РЦФ зависят не только от входных л„, но
и от выходных>>„, отсчетов и описываются разностным уравнением:
Ун ~ хп + ^^к ‘ Уп-к •
*=1
(4-3)
В общем случае цифровой фильтр, содержащий трансверсальную и ре-
курсивную части, называется фильтром канонического типа и описывается
разностным уравнением (4.1).
4.2 Определение системных функций и построение
структурных схем ТЦФ и РЦФ
Системная функция K(z) цифрового фильтра определяется как отноше-
ние Z-преобразований его выходного и входного сигналов:
Применяя прямое Z-преобразование к уравнению (4.1), получим
( М	\	f N	А
№)+	г(г).
U=o	J	U-i	J
(4-4)
Уравнение (4.4) связывает между собой Z-образы входной X(z) и вы-
ходной Y(z) последовательностей. Разрешая (4.4) относительно Y(z), найдем
м
^Lak- к
Г(г)=Л(.-)^-
i-pv*
(4.5)
Разделив правую и левую части выражения (4.5) на X(z), выведем фор-
мулы для расчета системных функций трансверсального фильтра (Kruv(z)\
рекурсивного фильтра (Кр11Ф(г)} и цифровою фильтра канонического вида
(Ккцф(~))-
W
-ТЦф(2)~	к =
А'=0
?v
1-1^
А = 1
" А( )
А / _Ч к=0__________________ Л(~)
ККЦФ^)- х _/'1-ВС-)‘
/с=1
(4.6)
(4.7)
(4.8)
Из формул (4.6), (4.7) и (4.8) видно, что для реализации фильтров необ-
ходимы устройства, выполняющие три операции: задержку (запоминание) от-
счетов сигналов, сложение и умножение и соединяющие эти устройства ли-
нии передачи сигналов.
На рисунках 4.1, 4.2 и 4.3 изображены структурные схемы, реализую-
щие алгоритмы работы ТЦФ, PI (Ф и цифрового фильтра канонического вида
а)
Рисунок 4.1 Обобщенное представление (а) и структурная схема (б)
трансверсального цифрового фильтра (ТЦФ)
8
Рисунок 4.2 - Обобщенное представление (а) и структурная схема (б)
рекурсивного цифрового фильтра (РЦФ)
Рисунок 4.3 - Обобщенное представление (а) и структурная схема (б)
цифрового фильтра канонического типа
29
4.3 Синтез ЦФ методом билинейного Z-преобразования
передаточной функции известного аналогового фильтра-
прототипа
Среди различных методов синтеза цифровых фильтров особое место
занимают такие, которые основаны на применении опыта, накопленного ра-
диоспециалистами при разработке аналоговых устройств соответствующего
назначения. Использование аналогового фильтра-прототипа дает возмож-
ность синтезировать цифровой фильтр либо исходя из требуемой импульсной
характеристики, либо обеспечивая заданную частотную характеристику.
Чаще всего применяется метод билинейного Z-преобразования, суть ко-
торого требует следующих комментариев.
Допустим, что известен вид коэффициента передачи К(р) в операторной
форме, который имеет необходимый аналоговый фильтр-прототип. Чтобы
преобразоваз ь коэффициент передачи К(р) в системную функцию цифрового
фильтра K(z), необходимо выполнить замены вида:
z = epT<>,	\nz=pT^,	p = \x\z/Ta.	(4.9)
Очевидно, подстановкой /?=1пг/ГЛ вытекающей из определения
Z-преобразования, легко получить системную функцию K(z) цифрового
фильтра, который будет иметь частотную характеристику, в точности совпа-
дающую с исходной характеристикой аналогового фильтра-прототипа. Однако
данная системная функция окажется нереализуемой, так как при дробно-
рациональном характере К(р) она будет содержать трансцендентные выраже-
ния. Чтобы добиться физической реализуемости системной функции и одно-
временно не исказить существенно частотную характеристику фильтра-
прототипа, используют разложение зависимости р = \nz/T<t в ряд по степеням
отношения двух линейных функций (г - !)/(- -+ 1).
При сохранении только первого члена ряда получают следующее били-
нейное соотношение Ц-6]:
В этом случае при подстановке комплексной переменной р в форме
(4.10) в выражение для операторного коэффициента передачи фильтра-
прототипа удается получить дробно-рациональную системную функцию K(z).
Однако вследствие принятых приближений происходит трансформация час-
тотной оси при переходе от аналогового фильтра-прототипа к цифровому ва-
рианту, а именно: точки частотной характеристики аналогового фильгра, со-
ответствующие текущему значению частоты соА, будут расположены на час-
тотной характеристике цифрового фильтра на частоте	Связь между
30
(4.11)
данными частотами устанавливается из соотношения (4.10), если положить в
нем p=ja)A, а - = eJM^Ta. Она носит нелинейный характер и имеет вид
2 t а>ц-Тд
7 a z
Это означает, что при использовании метода билинейного Z-
преобразования прежде всего необходимо привести в соответствие частотные
характеристики синтезируемого цифрового фильтра и аналогового фильгра-
прототина. Следует также отметить, что приближенный характер рас-
сматриваемого метода синтеза, даже при учете трансформации частотной оси,
позволяет реализовать частотную характеристику прототипа с некоторой по-
грешностью, исчезающей лишь в том случае, когда исходная частотная ха-
рактеристика имеет вид ступенчатой функции.
Как и в случае аналоговых цепей, существует одно тачная связь между
сис темной функцией цифрового фильтра К(з) и его частотной характеристи-
кой Ка{а>). Переход от системной функции K(z) к частотному коэффициенту
передачи осуществляется заменой комплексной переменной г на комплекс-
ную функцию eja}l(>:
Кц(Ы)=Кц^е1е,Т<'\	(4.12)
4.4 Синтез ЦФ по импульсной характеристике известного
аналогового фильтра-прототипа
Импульсной характеристикой линейной аналоговой электрической це-
пи с нулевыми начальными условиями называется отклик цепи на воздейст-
вие дельта-функции с>(/).
Импульсной характеристикой цифрового фильтра с нулевыми начальны-
ми условиями называется реакция ЦФ на воздействие единичною отсчета £(«).
Рисунок 4.4 11редставлеиие дельта-функции £(/) и единичного отсче-
та применяемых для испытания аналоговых (а) и цифровых (б) цепей
31
Дельта-функцию <50 можно представить пределом импульса прямо-
угольной формы, длительность которого совпадает с шагом дискретизации
Т(>, а амплитуда равна ут (площадь 8 -функции равна I):
/ ' д t
(ос, при I - 0.
<50 = Нт ОХОМ	(4 13)
V То^ v ” [О, при /*0,
Цифровую дельта-функцию <5(/?)можно получить путем умножения
аналоговой дельта-функции <50 на интервал дискретизации:
/ч /з Р- " = 0>
<$(„)= т„ <?(') = „ . .	(4.14)
10, Л7^0.
Можно предположить, что синтезируемый ЦФ должен обладать им-
пульсной характеристикой, представляющей собой последовательность чисел
go, gt, g?,..., g„. Эта последовательность может быть получена путем дискре-
тизации импульсной характеристики аналоговою фильтра-прототипа и по-
следующей нормировки путем умножения на интервал дискретизации:
g(n)=Tdg(t = nTd).	(4.15)
Для определения системной функции ЦФ и последующего построения
структурной схемы необходимо применить прямое /-преобразование к по-
следовательности g(n).
Системная функция трансверсального фильтра имеет вид
V
М-)= £>(")	0.16)
и=0
Следует обратить внимание на конечность импульсной характеристики
((Л/+1)-отсчст) ТЦФ.
Системная функция рекурсивного цифрового фильтра определяется с
помощью сворачивания бесконечной геометрической прогрессии (4.16).
В общем виде импульсная характеристика g(t) аналоговой цепи (с пере-
даточной функцией К(р)) представляв! обратное преобразование Лапласа от
передаточной функции К(р).
g{t)=B-8(t)+YA>er,t.	(4.17)
z-0
где В = lim К(р);
m порядок аналогового фильтра-прототипа.
32
Первое слагаемое в выражении (4,17), содержащее <5-функцию, при-
сутствует в том случае, если lim К(р)^0.
Второе слагаемое в выражении (4.17) представляет взвешенную сумму
экспоненциальных функций, количество которых зависит от порядка m ана-
логового фильтра-про готипа.
Дискретизация импульсной характеристики выполняется по тем же
правилам, что и дискретизация сигнала по времени, рассмотренная в п.З.
В результате дискретизации и последующей нормировки с учетом
(4.14) получается последовательность g(n):
В, при n = Q,
т
g(n) =
при и = 1,2,3...,
(4.18)
где а, = ег,Т° .
Применение Z-преобразования и последующее сворачивание геометри-
ческой прогрессии дает системную функцию РЦФ
т	со
(4|9>
/=1	П=1
КрцФ(г)=В + Х А,Тд-^-
/=1	\-a,z
(4-20)
Если импульсная характеристика аналогового фильтра-прототипа не
содержит 8-функции, то
т
gn = YAlT^al>" "Р« « = 0,1.2...,	(4.21)
/=1
/и оо	т	1
= Т.Л,Тд £(«,)" Г" = XAiTo--------------И-22)
/=1	и=0	/=|	1
Порядок РЦФ будет совпадать с порядком аналогового фильтра-
прототипа. Импульсная характеристика РЦФ - бесконечная затухающая по-
следовательность.
33
4.5 Синтез ЦФ методом билинейного Z-преобразования
по заданной АЧХ цифрового фильтра
4.5.1 Определение параметров АЧХ аналогового фильтра-
прототипа
Амплитудно-частотная характеристика цифрового филыра
является периодической функцией и повторяется через интервал, кратный
частоте дискретизации, т.е.
соТд ^(пад)Тд =п-2л.
АЧХ идеальных цифровых фильтров нижних частот, полосовых, верхних
частот, заграждающих и всепропускакмцих представлены в таблице 4.1.
Таблица 4.1 - АЧХ цифровых фильтров
Наименование
фильтра
АЧХ цифровых фильтров
Фильтр нижних
частот
Полосовой фильтр
-<оо
Фильтр верхних
частот

34
Заграждающий
фильтр
Проектируемый цифровой ФНЧ должен удовлетворять следующим ус-
ловиям:
1.	Частота среза Ыц\ по уровню 3 дБ должна быть много меньше, чем
частота дискретизации а)(>, т.е.
<
2.	Затухание в полосе задерживания не менее а, дБ.
3.	Неравномерность АЧХ в полосе пропускания (0 < со не более
Д дБ.
Переведем цифровые критерии в аналоговый эквивалент по формуле
аАтд 1Р(),ЧТ^
2 Х 2
Пусть заданы три частоты цифрового фильтра (Oll2 - 2&vn;
соцз = 0,940/л.
Полагая сощ = 0.2 пересчитаем в аналоговые частоты а>А1; а>А2, соА3.
тА\ = ~ig—~— = -^u[fg\---------------- =1,156^|,
/d 2 л- I (оцх 5 I
2	5
03.42 tg----------------:
I д 2 л
5 (оц1 л j Л п
= -(ОцМ\------ = 4,9<»
7Г	1^! 5J

35
2	в>ц\то	5
L3	|/g
тд 2	л	I
ыц\
- 1,01б9//|.
Сравним между собой соотношения цифровых и аналоговых частот
°>Ц2 = 2.	С0А2 =	= д 24,
(»ц\	'	а>А[ 1,156т9//|
^=0,9;	= '01й,Ц| = 0,873.
^Л1	1,156й>£/[
Итак, билинейное Z-преобразование приводит к сжатию аналоговых
_	69л /
частот. Причем сжатие тем меньше, чем больше отношение /соц\ '
ЕСЛИ ПОЛОЖИТЬ (Оц ( =0,169d, то
10 69Л1	— 69щ/£ л	°>ц\	л 10;	= 1,03469//],
10 69л2	-—CO^tg		л 10>	= 2,31 Зб9//|
10 69 43 ~ OJu\tg л		л 10	= 0,92469//]
Соотношение аналоговых частот при этом будет равно
ЫА2_ = 2313 = 2,237,
69 ц 1,034
=2^21 = 0,894.
69 Л1	1,034
Замечание
Максимальное значение частоты среза й)ц\ цифрового фильтра не
должно достигать четверти частоты дискретизации:
69/д < 0,25б9^ .
36
4.5.2 АЧХ фильтра Баттерворта
Максимально плоская АЧХ аналогового фильтра Баттерворта описыва-
ется таким выражением:
(4.23)
где a>At - частота среза аналогового фильтра, на которой АЧХ падает до уров-
ня 0,707 от своего максимального значения;
п - 1,2,3,... - порядок фильтра.
Индекс при обозначении текущего значения частоты подчеркивает, что
речь идет об аналоговом фильтре. Для полного описания данной АЧХ необ-
ходимо установить две величины: частоту среза a)At и порядок филыра п.
Первая из них рассчитывается в соответствии с соотношением (4.11), в кото-
рое должны войти найденный в 4.2 тактовый интервал Та и значение необхо-
димого затухания а его АЧХ на удвоенной частоте среза <0А2~ 2(oAh Это ус-
ловие записывается таким образом1.
20'1g

(4-24)
Приведенное неравенство позволяет определить наименьшее значение п.
4.5.3 АЧХ фильтра Чебышева
Равноволновая в полосе пропускания АЧХ фильтра Чебышева имеет
следующий вил:
\КЧ (44 Л = ~1 ' ---- -------у >
"И
V \	*<41 )
(4.25)
где с- параметр, характеризующий неравномерность АЧХ в полосе пропус-
кания;
Т/х) - полином Чебышева перво! о рода порядка п.
37
Полиномы высших степеней таковы
Tj(x)=x, Т,(х)=2х2-\,	Т3(х)=4х-Зх,
(4-26)
Т4(х)~ 8х4-8а?+ 1,	ВД=16?-20х3+5х
Соотношение (4.15) содержит три параметра, подлежащие определе-
нию, а именно: £, соА1 и п.
Частота среза аналогового фильтра а>А1 находится так же, как и в 4.5.2.
Величина £ вычисляется по заданной неравномерности р ЛЧХ в полосе про-
пускания фильтра. При этом следует исходить из выражения
l/G/l птах
20-1в Т-
(4.27)
где |/Gjmax и 'Кч|min - наибольшее и наименьшее значения ЛЧХ фильтра
Чебышева в полосе пропускания, причем необходимо заметить, что они не
зависят от порядка фильтра.
Порядок фильтра определяется, как и в 4.5.2, приведенной в задании
величиной затухания АЧХа, но несколько более сложным образом. Для этого
следует решить неравенство
20 1g
| Klf | max
I ^/(*<41)1
(4.28)
|/C/|max имеет тот же смысл, что и в соотношении (4.27), а |Ki{(соАi)
определяется известной уже величиной £ и значением полинома Чебышева
порядка я при х=2, т.е. 7„(2). Следовательно, установив из неравенства (4.28)
требования к значению Тп (2), необходимо, пользуясь формулами (4.26), по-
добрать подходящую величину п, которая и будет являться порядком фильт-
ра.
4.6 Расчет системной функции, анализ устойчивости,
реализация цифрового фильтра
При синтезе цифрового фильтра методом билинейного / преобразования
его системную функцию K(Z) определяют исходя из передаточной
функции аналогового фильтра-прототипа К(р).
38
Фильтр Баттерворта нижних частот порядка п имеет следующее выра-
жение для коэффициента передачи:
Р />(ря ) —--------------;--------------— 7-------г—7--------г, (4.29)
pH + «л 1  РН + + рН +\ (рн~ Р\ )-(Рн - Рп)
где ptrp/МдГ,
а], а2, .... а,,./ - вещественные коэффициенты;
Pi, р2, р„ - полюса функции К, (р„).
Для фильтров Баттерворта некоторых порядков вид знаменателя опера-
торного коэффициента передачи приведен в таблице 4.2 [6,7].
Аналогично для фильтра Чебышева
------7
\Рн -Р\)Арн - Рп)
_________________Ьр________________
РН +	1 ' Р’н 1 + — + ’ Рн + ^0
(4.30)
Особенность выражения (4.30) по сравнению с (4.29) заключается в от-
личии от 1 свободного члена знаменателя, вследствие чего коэффициент А
появляется и в числителе, обеспечивая необходимую нормировку функции
Кч (рн)-
В таблице 4.3 для различных значений неравномерностей Д ЛЧХ
фильтров Чебышева некоторых порядков приведены полюса операторного
коэффициента передачи [7].
После того как установлен вид коэффициента передачи аналогового
фильтра-прототипа в операторной форме К(рн) указанной подстановкой, на-
ходится системная функция K(z) соответствующего цифрового фильтра, т.е.
K(z)=K
(4.31)
Таблица 4.2 - Исходные данные к передаточным функциям фильтров Баттерворта
п Знаменатель функции К^рн) фильтров Баттерворта
"__________________________Рн ь 1,414/-?/z +1_________________________
3	_______ (ря+Р//+ *дР//4 О________________________~__________
4____	(ря +0J65p/y + ljp^ 41,848/?^ + 1J_______
 (ря 4	1 *Рн 4 ^н + U618/>^ + \\ри +1) __________
39
4 3 - Значение неравномерностей /3 АЧХ и полюса передаточных функций
фильтров Чебышева ______
Р,ДБ	п			
	2	3	4	5
0,5	-0,713^1,004	-0.626 -0,313±/1,022	-0,175±/1,016 -0,423 ±/0,421	-0,362 -0,112+71,012 -0,293370,625
1	-O,549±jO,895	-0,494 -0,247+J0,966	-0,14+70,983 -0,377370,407	-0,289 -0,089+70,99 -0,234370,612
1,5	-0,461 ±70,844	-0,42 -0,21 ±70,939	-0,119+70,968 -0,288370,4	-0,248 -0,077+70,98 -0,2370,606
2	-0,402±/0,813	-0,369 -0,184±70,923	-0,105±j0,958 -0,253+70,397	-0,218 -0,067±/0,973 -0,177±/0.602
2,5	-0,358±/0,792	-0,33 -0,165370,912	-0,094±/0,951 -0,2273/0,394	-0,196 -0,06370,969 -0,158±/0,599
3	-0,322370,777	-0,299 -0,149370,904	-0,085370,946 -0,206370,392	-0,178 -0,055±/0,966 -0,144+/0,597
В качестве примера приведем выражение для цифрового фильтра чет-
вертого порядка в желаемой форме:
(4-32)
где d\^-ds вещественные коэффициенты.
При выполнении алгебраических преобразований полезно иметь в виду
следующее:
-	знаменатель исходного выражения для К(рц), описываемого форму-
лой (4.30), удобно представить в форме, аналогичной представленной в
таблице 4.3;
-	окончательное соотношение для системной функции следует выра-
зить через отрицательные степени аргумента г, а его знаменатель получить в
виде произведения сомножителей не выше второй степени.
Получив соотношение для К(~) в виде, подобном выражению (4.32), не-
обходимо установить, соответствует ли оно устойчивому цифровому фильт-
40
ру. При этом следует руководствоваться таким правилом: если полюса сис-
темной функции K(z) лежап внутри окружности единичного радиуса на плос-
кости комплексной переменной го рассматриваемый цифровой фильтр ус-
тойчив. Далее естественно получить разностное уравнение, описывающее
реализуемый цифровой фильтр. Это можно сделать, если учесть, что соотно-
шения для системных функций (4.6), (4.7) и (4.8) К(~)=Y(z)!X(z) цифровых
фильтров ле!ко выводятся из разностных уравнений (4.1), (4.2) и (4.3) в ре-
зультате применения Z-преобразования к обеим его частям. В данном случае
используется свойство линейности данного преобразования, а также тот факт,
что запаздывание дискретного сигнала на один элемент соответствует умно-
жению его Z-преобразования наг1.
Следуя методике построения структурных схем цифрового фильтра, из-
ложенной в [1-5], требуется реализовать полученную системную функцию в
прямой и канонической формах.
4.7	Расчет АЧХ цифрового фильтра
Известная системная функция цифрового фильтра позволяет, как видно
из выражения (4.12), определить его частотную характеристику; при этом со-
отношение для АЧХ будет выглядеть следующим образом:

(4 33)
где обозначение частоты с индексом введено, чтобы избежать путаницы при
трансформации частотной оси в методе билинейного Z-нреобразования.
Приведенное выражение может быть использовано для расчета АЧХ
цифрового фильтра, однако данный путь не является самым простым в рас-
сматриваемом случае. При заданной АЧХ аналогового фильтра-прототипа
Ки АЧХ цифрового фильтра	может быть приближенно вы-
числена, если учесть трансформацию частотной оси (рисунок 4.5) в соответ-
ствии с формулой (4.11) [4].
Необходимое соотношение имеет вид
|А'// ) -
-tg-
{Т 2
(4.34)
41
Рисунок 4.5 - Графическое представление соотношения (4.34)
Таким образом, если аналоговыми фильтрами-прототипами служат
схемы Чебышева и Баттерворта и-го порядка, то для АЧХ цифровых фильт-
ров могут быть записаны следующие формулы;
(4.35)
где соц\ - частота среза цифрового фильтра.
Приведенные соотношения (4.34), (4.35) рекомендуется использовать
для расчета АЧХ цифровых фильтров. Следует отметить, что в силу перио-
дичности рассмазриваемых функций расчет нужно проводить лишь для
. Кроме того, при посгроении АЧХ чебышевского типа полезно
предварительно выяснить расположение нулей и максимумов функций Т„{х}
О —
_ ‘ д.
42
при |лг|< 1 [8], что позволяет грамотно выбирать шаг по частоте и не пройти
мимо характерных точек АЧХ в полосе пропускания цифрового фильтра.
4.8	Расчет импульсной характеристики ЦФ
Импульсной характеристикой g(kT) цифровою фильтра называется по-
следовательность отсчетных значений, формирующаяся на его выходе при
воздействии на вход единичного дискретного сигнала ё(кТ), имеющего вид
Л(*Т)=
1, А = О,
О, Л*0.
(4.36)
Импульсная характеристика связана с системной функцией K(z) цифро-
вого фильтра /-преобразованием [1 -5J. Поскольку выражение K(z) уже полу-
чено в п. 4.6, можно воспользоваться формулой обратного /-преобразования
11.21. Однако ее применение вызывает определенные трудности и необходимо
в тех случаях, когда нельзя использовать более простые методы.
Положив m = п и переходя к положительным показателям степенной
переменной z, получим общее выражение (4.8) для системной функции K(z)
цифрового филыра:
*(-)=
4 <7|'+ —+ <?„
И А п 1	L
z -b\z
(4.37)
С целью отыскания импульсной характеристики g(kT) данного фильтра
необходимо выполнить некоторые преобразования:
М-)-с0 +
(4.38)
где Со,С|,..., с„ вещественные коэффициен гы.
Значения коэффициентов с„ легко устанавливаются, если учесть, что
выражения (4.37), (4.38) тождественно равны. Из неправильной дроби (4.37)
выделяется целая час гь Со-
Второе слагаемое в формуле (4.38) является правильной дробно-
рациональной функцией и, следовательно, может быть разложено на сумму
простейших дробей, причем, как известно из математики, вещественному
43
корню -г и паре комплексно-сопряженных корней ~(и знаменателя еди-
ничной кратности соответствует следующее выражение:
A В~лР
(4.39)
где А, В, D - вещественные коэффициенты.
(6]:
Обратное Z-преобразование можно определить с помощью вычетов
(4.40)
где к - кратность корня.
Импульсная характеристика равна сумме вычетов:
I
g(^d) =	‘
i=]
(4.40)
4.9	Расчет дискретной последовательности на выходе
цифрового фильтра
Выполнение курсовой работы завершается решением задачи анализа
синтезированного филыра во временной области. Постановка ее проста и со-
стоит в следующем. Имеется цифровой фильтр с импульсной характеристи-
кой g(nT)=g„, вычисленной в п. 4.8. На его вход поступает последователь-
ность отсчетов, полученная в п. 3.3 в результате дискретизации непрерывного
сигнала x(t). Требуется установить вид сигнала уп на выходе цифрового
филыра.	*
Можно решить данную задачу методом дискретной свертки 19], описы-
ваемой соотношением
Уп = ^gkxn-k 
Л=0
(4 42)
44
Либо рассчитать отклик, используя алгоритм работы цифрового фильт-
ра (4.1):
V/	л'
Уп ~ 52	' хц-к + 52 ' Уп-к 	(4-43)
А=0	А=0
Процедура вычисления дискретной свертки является досгаточно тру-
доемкой. Ее можно осуществить двумя путями, а именно: следуя непосредст-
венно выражению (4.43) или применяя метод косвенного вычисления, осно-
ванный на использовании дискретного преобразования Фурье [2]. В обоих
случаях расчеты целесообразно выполнять на ЭВМ.
Рассчитать сигнал на выходе цифрового фильтра можно применяя раз-
ностное уравнение вида (4.43).
5 УКАЗАНИЯ ПО ОФОРМЛЕНИЮ КУРСОВОЙ РАБОТЫ
В пояснительную записку должен войти следующий материал:
I)	задание к курсовой работе;
2)	разделы, содержащие дискретное представление и анализ сигнала во
временной и частотной области, подробный расчет цифрового фильтра в со-
ответствии с настоящими методическими указаниями. В пояснитель-
ную записку необходимо включить ряд иллюстраций:
•	график амплитудного спектра входного непрерывного сигна-
ла. построенного согласно требованиям п. 2.1;
•	графическое изображение последовательности отсчетов х(пТ,) вход-
ного сигнала;
•	изображение спектральной плотности дискретизированного сигнала;
•	схемы реализации синтезируемых фильтров (прямую и кано-
ническую);
•	построенные в общих координатных осях графики ЛЧХ цифровых
фильтров и скорректированной, как указано в и. 4.7, АЧХ аналого-
вого фильтра-прототипа;
•	графические изображения импульсной характеристики g(nTt,) циф-
рового фильтра и последовательности отсчетов у(пТ,) на его выхо-
де;
3) список используемых источников.
45
6	СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1.	Гоноровский И.С. Радиотехнические цени и сигналы. - 4-е изд., перераб. и
доп. - М.: Радио и связь, 1986. - 512 с.
2.	Баскаков С. И. Радиотехнические цени и сигналы. - 2-е изд., перераб. и
доп. М.: Высш, шк, 1988. -448 с.
3.	Хемминг Р.В. Цифровые фильтры. Пер.с ажл./Под ред. А. М. Грахтмана. -
М.: Сов. Радио, 1980. - 224 с.
4.	Цифровая обработка сигналов. Справочник/ Л.М. Гольденберг, Б.Д. Ма-
тюшкин, Ml 1. Поляк - М: Радио и связь, 1985. - 312 с.
5.	Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов.
- М.: Мир, 1978.- 848 с.
6.	Лэм Г. Аналоговые и цифровые фильтры. Расчет и реализация. Пер. с
англ. В. Л. Левина, М. Н. Микшиса и И. И. Теплюка /Под ред. И. Н. Теп-
люка. - М.: Мир, 1982. - 592 с.
7.	Карни Ш. Теория цепей. Анализ и синтез. - М.: Связь, 1973.
8.	Янке Е., Эмде Ф., Леш Ф. Специальные функции. - М.: Наука, 1977.
9.	Каратаева Н.А. Радиотехнические цепи и сигналы: Учебное пособие. -
Томск: Томский межвузовский центр дистанционного образования 2002.
Ч. 1: Теория сигналов и линейные цепи. - 260с.
46
7	ПРИЛОЖЕНИЕ А. ШИФРЫ И ИСХОДНЫЕ ДАННЫЕ
К КУРСОВОЙ РАБОТЕ
Шифр (Таблица A.I) состоит из четырех цифр N|N2, N3N4 и одной из
букв А, Б или Ч.
Шифр определяется вариантом студента (первый столбец) и номером
группы или годом набора (четвертый, пятый или шестой столбец). Например,
первому варианту из первой группы соответствует шифр 11 11 А, а второму
варианту из второй группы соответствует шифр 21 21 Ч.
Первые две цифры -N|N2 - определяют сигнал (таблица А.2). Причем
первая цифра Nj модель сигнала, а вторая цифра N2 - вариант сигнала за-
данной формы.
Вторые две цифры - N3N4 - определяют либо вид аналогового фильтра-
проготипа (таблица А.З), либо требования к АЧХ проектируемого цифрового
ФНЧ.
В последнем случае цифра N3 задает затухание (а) в полосе задержива-
ния цифрового ФНЧ на частоте сощ, в два раза превышающей частоту среза
(О]ц (таблица А.4). Цифра N4 определяет неравномерность (fi) АЧХ цифрового
ФНЧ в пределах полосы пропускания (таблица А.4).
Буквы А, Б или Ч соответствуют типу фильтра-прототипа:
А - аналоговый фильтр-прототип, электрическая схема которого пред-
ставлена в таблице А.З;
Б - фильтр Баттерворта, аппроксимация АЧХ которого рассмотрена в п.
4.5.2, а параметры АЧХ цифрового ФНЧ заданы в таблице А.4;
Ч — филыгр Чебышева, аппроксимация АЧХ которого рассмотрена в п.
4.5,3, а параметры АЧХ цифрового ФНЧ заданы в таблице А.4.
Примечание
1. С разрешения преподавателя можно выбрать ту модель цепи, которая
использовалась при выполнении самостоятельной работы в предыдущем се-
местре.
2. По согласованию с преподавателем можно использовать сигнал
сложной формы и индивидуальные параметры АЧХ цифрового фильтра.
47
Таблица А. 1 — Шифры для 30 вариантов и трех групп (или годов набора)
Вариант №	Шифр сиг- нала	Шифр це- пи N3N4	Шифр типа фильтра (А, Б. Ч)		
			1 группа	2 группа	3 группа
I	И	11	А	Ь	Ч
2	21	21	Б	Ч	А
3	31	31	Ч	А	Б
4	41	41	А	Б	Ч
5	51	51	Б	Ч	А
6	61	61	Ч	А	Б
7	71	12	А	Б	Ч
8	81	22	Б	Ч	А
9	91	32	Ч	А	Б
10	12	42	А	Б	Ч
11	22	52	Б	Ч	А
12	32	62	Ч	А	Б
13	42	13	А	Б	Ч
14	52	23	Б	Ч	А
15	62	33	Ч	А	Б
16	72	43	А	Б	Ч
17	82	53	Б	Ч	А
18	92	63	Ч	А	Б
19	13	14	А	Б	Ч
20	23	24	Ь	Ч	А
21	33	34	Ч	А	Б
22	43	44	А	Б	Ч
23	53	54	Б	Ч	А
24	63	64	Ч	А	Б
25	73 *	15	А	Б	Ч
26	83	1	25	Б	Ч	А
27	93	35	Ч	А	Б
28	14	45	А	Б	Ч
29	24	Г 55	Б	Ч	А
30	34	65	Ч	А	Б
48
49
Таблица А 3 - Модели линейных электрических цепей (аналоговых
фильтров-про готипов). Шифр Nt N4
50
Таблица Л.З (продолжение)
Примечание
Все электрические цепи составлены из сопротивлений R, индуктивно-
стей L, емкостей С.
51
Таблица А.4 - Параметры АЧХ цифровых ФНЧ Чебышева или Баттер-
ворта
Шифр N,	Затухание (а) АЧХ в полосе задерживания (децибеллах) на частоте	Шифр N,	1 (сравномерность (fi) АЧХ в пределах полосы пропуска- ния 0 < ы< сощ (для фильтра Че- бышева) 0 < со< 0,869/д (для фильтра Баттерворта)
1	а = 20 дБ	1	>3=0,5 дБ
2	« 22 дБ	2	/?- 1 дБ
3	« - 24 дБ	3	1,5 дБ
4	а = 26 дБ	4	/3-=2 дБ
5	а- 28 дБ	5	0= 2,5 дБ
6	а ~ 30 дБ	6	>3=3 дБ
Примечание
Частота среза цифрового ФНЧ по уровню 3 дБ обозначена <оих.
52
8 ПРИЛОЖЕНИЕ В. ПРИМЕРЫ ВЫПОЛНЕНИЯ ОТДЕЛЬНЫХ
ПУНКТОВ ЗАДАНИЯ К КУРСОВОЙ РАБОТЕ
В.1	Пример дискретной обработки аналогового сигнала
В качестве примера рассмотрим прямоугольный импульс, изображен-
ный на рисунке В.)
Рисунок В. I - Исходный аналоговый сигнал
Поинтервальное описание сигнала выглядит следующим образом:
Е, при 0<t <т;
О, при 0 > t > г.
Для составления математической модели можно использовать функции
Хевисайда:
s(/)= Eo(t) Ecr(t- г).
В.1.1	Расчет спектральной плотности аналогового сигнала
Спектральная плотность прямоугольного импульса, изображенного на
рисунке В.1, равна
S(co)=Et-
сот
2
-}
е
Ы1
2
Фазовый множитель е ' 2 свидетельствует о сдвиге сигнала во временной
области на -
53
Для построения частотных характеристик спектральную плотность по-
лезно нормировать относительно интервала описания сигнала Тс-2т.
s(o>) Е яп(й>г2) -у«г2
Гс ~ 2
На рисунке В.2 представлен график модуля спектральной плотности сигнала.
На рисунке В.З представлен график фазы спектральной плотности сигнала.
Рисунок В.2 - График модуля спектральной плотности
б)
Рисунок В.З - Г рафики аргумента комплексной спектральной плотности: не-
нормированный (а) и нормированный (б) относительно 2m
54
Анализируя рисунки В.2, В.З, можно сказать, что сдвиг сигнала во вре-
менной области не изменяет значения модуля спектральной плотности, а при-
водит к изменению фазовой характеристики.
В.1.2	Дискретизация аналогового сигнала по времени
Руководствуясь теоремой Котельникова, частоту дискретизации а>д
выбираем так, чтобы = 2сив. Для определения верхней частоты ыв спек-
тра chi нала воспользуемся пороговым критерием: для частот выше «верхней»
модуль спектральной плотности не превышает уровня 0,1 от максимального
значения:
0 1	= &/
0,1 /2 /2
sin 2
/у Г
« 2
Полагая sin (ов = 1, получим сов ®	~	. Таким образом частота
дискретизации и интервал дискретизации Т() будут равны
Л>, _	_ 127г/ -г -2л/ — л/ — ‘с/
Строго говоря, все реальные сигналы имеют конечную длительность и,
следовательно, бесконечно протяженный спектр. Однако начиная с некоторо-
го значения частоты спектральные составляющие становятся настолько малы,
что ими можно пренебречь.
Сигнал может быть приближенно описан конечным числом выбороч-
ных значений. Число выборочных значений, которыми полностью описыва-
ется сигнал, называют числом степеней свободы сигнала.
Число степеней свободы W будет равно
Т
А = —=12.
тд
На рисунке В.4 приведены огсчегы прямоугольного импульса.
55
Рисунок В.4 - Отсчеты исходною аналогового сигнала
Таким образом, сигнал задается последовательностью отсчетов вида
Е{ 1,1,1,1,1,1,0,0,0,0.0,0}.
Запишем математическую модель дискретного сигнала sd(t) с помо-
щью дискретных функций Хевисайда:
sd (/) = Ебт(и) - Е&(п - б).
В.1.3	Расчет спектральной плотности дискретизированного
сигнала
Для нахождения спектральной плотности дискретизированного сигна-
ла применим прямое преобразование Фурье (3.19). Выполняя нормировку от-
носительно числа степеней свободы N, найдем
Г
= £ Д<5(0+4, - Т„ )+... + S(l - 5Гд	.
Используя фильтрующее свойство «5-функции, получим
_ _£ Z -jOwT’rt + е~ /7 N N 5 Т Г 3 Т Е -J~<oTo =—е 2 е 2 ч 12 5 г Г 2Е =	е z со	°Т<> +е J2mTd	+е	+e-J^)^ = 1 т	I т	.3	.5 „ 1 - е 2 +е 2	+ е 2 +е 2	= С 5 А	<3 A	fl V s —соТл +cos —ыТа +cos —о>Та .
12	L U J Sd(co) 2Е и ' —е 2	со /V 12	V2 )	\2 | ыТд ]l2 cos^T,)) +1 ].
56
Проанализируем полученное выражение. Для этого на рисунке В.5 изо-
\)(«)
оразим множители выражения —, отвечающие за модуль спектральной
плотности
2 cos(26?rf)) I 1
cos —соТл
12
Рисунок В.5 - Представление множителей, входящих в выражение
На рисунке В.6 изображен модуль спектральной плотности дискретного
непериодического сигнала .
Рисунок В.6 Модули спектральных плотностей исходного аналогового
(пунктирная линия) и дискретизированного (сплошная линия) сигналов
Анализируя рисунок В.6, можно сделать очень важный вывод: при дис-
крешзации сигнала во временной области спектральная плотность становится
периодической функцией частоты с периодом, равным а>„. В то время как
континуальный сигнал имеет апериодический спектр.
57
В.1.4	Расчет коэффициентов Ск с помощью дискретного
преобразования Фурье
В тех случаях, когда последовательность отсчетов периодична, можно
установить однозначную связь между временными отсчетами сигнала и от-
счетами его спектральной плотности с помощью прямого дискретного преоб-
разования Фурье (ПД! 1Ф):
, Л-1
G=— Е * 
Л и=0
Расчет комплексных коэффициентов ряда Фурье С\ с использованием
ЭВМ не составляет труда. Однако необходимо представлять себе, каким об-
разом происходит векторное суммирование компонент в выражении ПДГ1Ф.
На рисунках В.7 - В.9 изображены векторные диаграммы, отражающие
расчет комплексных коэффициентов ряда Фурье.
Рисунку В.7 соответствует математическое выражение
2л
1+/7'~2
Ап 6п ,8л Юл
+ е 12 +е 12 +е 12 +е 12 + 0+ 0 + 0+ 0+0+0
= £(0,083-70,311}
Рисунок В.7 - Векторная диаграмма определения коэффициента С|
58
Рисунку В.8 соответствует математическое выражение
£
12
+ 0 + 0 + 0 + 0 + 0 + О
= 0.
4л
12 +е
8л 12л	16л	20л
12 +/7Т2 +eJ 12 +е'7 12
Рисунок В.8 Векторная диаграмма определения коэффициента С2
Рисунку В.9 соответствует математическое выражение
30л
' '2 +040 + 0 + 0 + 0 + 0
12
,6л	12л	_ 18л	_ ,24л
112	12 +е 12 +е 12
= £(0,083 — >0,083)
Рисунок В.9 - Векторная диаграмма определения коэффициент а С3
59
В таблице В. I приведены все коэффициенты ряда Фурье.
Таблица В.1 - Комплексные коэффициенты ряда Фурье СА
	0,5 £	с сб	0
	£(0,083-/0,311)	Q	^Е(0,083+/0,022)
С’2	0	' С8”	0
	£(0,083-/0,083)	С9	£(0,083+70,083)
	0	Qo	0
	£(0,083-j0,022)	Qi	£(0.083+70,311)
На рисунке В. 10 представлены графически модули комплексных коэф-
фициентов Фурье
Рисунок В. 10 Отсчеты спектральной плотности, полученные по ДПФ
Дискретный периодический сигнал обладает дискретным периодиче-
ским спектром. Отсчеты во временной и частотной областях связаны парой
ДПФ. При этом число степеней свободы, как в области времен, так и в облас-
ти частот, имеет одно и то же значение N:
«>в
2л-
В.1.5	Восстановление исходного сигнала по ДПФ
Если на основании совокупности отсчетов sn, st, s?. некоторого
сигнала найдены коэффициенты ДПФ Ct),Cто по ним всегда мож-
но восстановить исходный сигнал s(t) с ограниченным спектром, который
был подвергнут дискретизации. Ряд Фурье такого сигнала (для четного числа
N) принимает вид конечной суммы
60
s(j ) — С о + 2|с
[ 4тг	|
COS ----1+<Р1 +...+
\	/
COS —— 1 + <Рк
где (р, = argC, - фа ювый угол коэффициента ДПФ.
Следует подчеркнуть, чго восстановление непрерывного сигнала по
данной формуле есть не приближенная, а точная операция, полностью экви-
валентная получению текущих значений сигнала с oi раниченным спектром
по его отсчсчам.
На рисунке В. 11 представлен результат восстановления сигнала по от-
Восстановленный сигнал является периодической функцией времени.
Он точно проходит по отсчетам выборки на первом периоде. Очевидно, что
при большем значении N восстановление будет точнее.
В.1.6	Z-преобразование дискретной последовательности
Прямое Z-преобразование последовательности sinT^) определяется
формулой
4--)=
и-О
Функцию S(-) называютZ-обраюм последовательности
Рассматриваемый дискретный сигнал представляет собой сумму двух
дискретизированных функций Хевисайда, одна из которых сдвинута относи-
тельно другой на 6 отсчетов.
Найдем Z-образ дискретной функции Хевисайда сг(и):
61
z[a(„)]=CT(z),
CT(z) = l+z 1 +z 2+z 3+... + z "...
zlCT(z) = z^1 + z~2 + z~3 +z'4 + ... + z	-
(i-z'l)O'(z) = l*z_("4’)
Если |z| < 1, to lim z <"+l> = О, откуда
П->оо
CT(Z)=T^H-
Сдвиг дискретной последовательности приводит к умножению Z-образа
на оператор сдвига z 6:
Z[cr(n —6)]= (T(z)z-6.
Таким образом, Z-образ дискретизированного прямоугольного импуль-
са равен
S(z) = £^T(z) - CT(z)z"6]= Е .
Преобразуем Z-образ к виду, удобному для получения спектральной
плотности дискретного сигнала:
_3_,-3	_5
50=	2.
~ 2 _ - 2
Для того чтобы на основании Z-образа последовательности отсчетов
было возможно получить спектральную плотность, необходимо сделать заме-
ну вида
z = eja,T*
В результате подстановки получим
j(,(0,)=£Zi^7k) ,е
sinl со n I
62
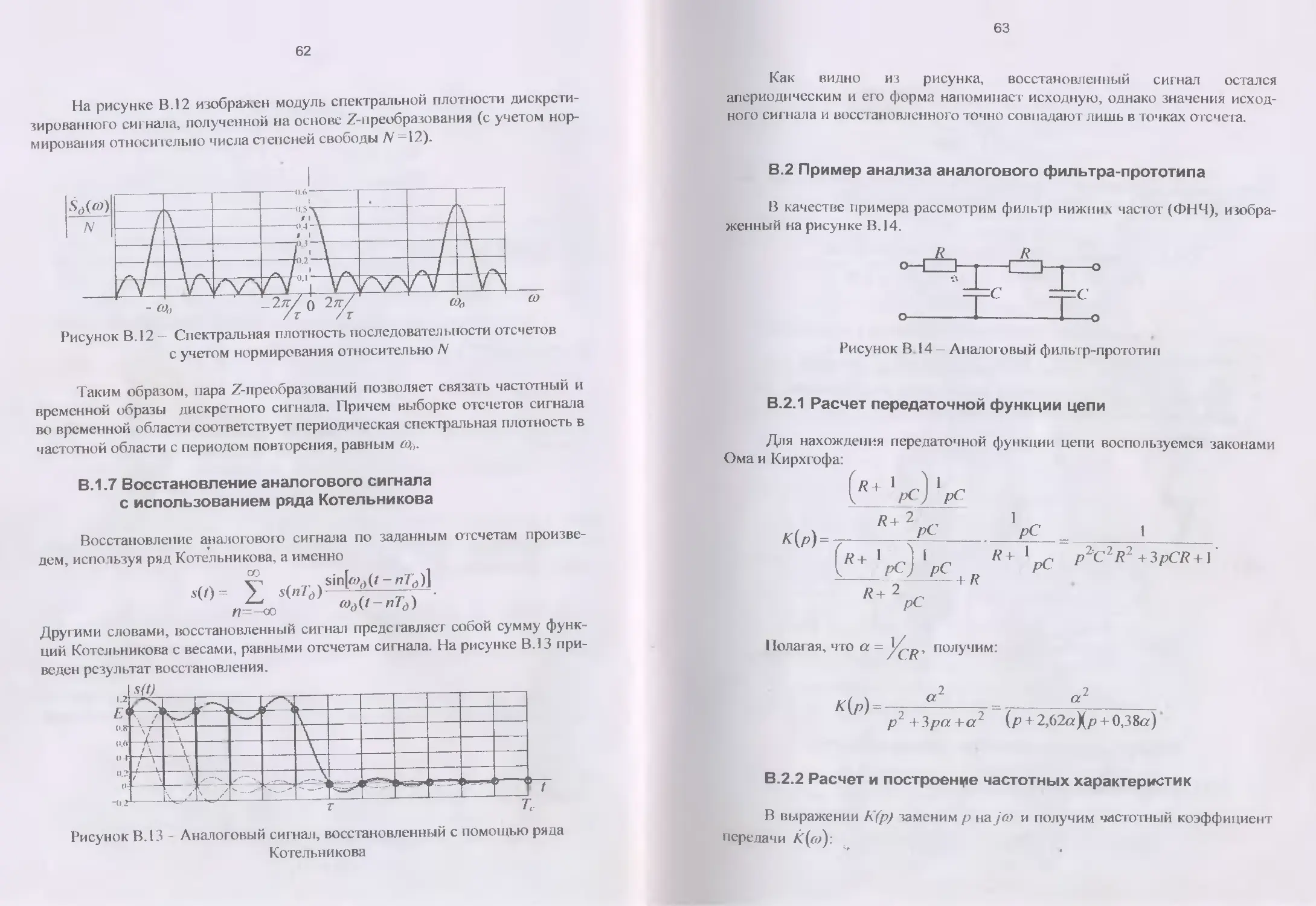
На рисунке В. 12 изображен модуль спектральной плотности дискрети-
зированного сигнала, полученной на основе Z-преобразования (с учетом нор-
мирования относительно числа степеней свободы /V=12).
Таким образом, пара Z-преобразований позволяет связать частотный и
временной образы дискретного сигнала. Причем выборке отсчетов сигнала
во временной области соответствует периодическая спектральная плотность в
частотной области с периодом повторения, равным со,}.
В. 1.7 Восстановление аналогового сигнала
с использованием ряда Котельникова
Восстановление аналогового сигнала по заданным отсчетам произве-
дем, испозьзуя ряд Котельникова, а именно
s(z)= f
л	cod(t-nTd)
Другими словами, восстановленный сигнал представляет собой сумму функ-
ций Котельникова с весами, равными отсчетам сигнала. На рисунке В.13 при-
веден результат восстановления.
Рисунок В.13 - Аналоговый сигнал, восстановленный с помощью ряда
Котельникова
63
Как видно из рисунка, восстановленный сигнал остался
апериодическим и его форма напоминает исходную, однако значения исход-
ного сигнала и восстановленного точно совпадают лишь в точках отсчета.
В.2	Пример анализа аналогового фильтра-прототипа
В качестве примера рассмотрим фильтр нижних частот (ФНЧ), изобра-
женный на рисунке В. 14.
Рисунок В 14 — Аналоговый фильтр-прототип
В.2.1	Расчет передаточной функции цепи
Для нахождения передаточной функции цепи воспользуемся законами
Ома и Кирхгофа:
I________
p^C2R2 +3pCR+\
Полагая, что а = получим:
к( ) =	« =  ____________«__________
р1 + 3>ра+сг (р+ 2,62«Хр + 0,38«)
В.2.2	Расчет и построение частотных характеристик
В выражении К(р) заменим р на jco и получим частотный коэффициент
передачи Af(w).
64
a2
=	----2'
(jcoj + 3ja>a+a
Возьмем модуль от полученного выражения, в результате чего получим ам-
плитудно-частотную характеристику (ЛЧХ) фильтра-прототипа:
Ш = г, V -- = Г,	’
+ (3e*zJ2	+(зюаУ
На рисунке В. 15 приведен график АЧХ фильтра-прототипа с параметрами:
•	частота среза а>А] по уровню 0,707 составляет - 0,374а;
•	верхняя частота, определенная по уровню 0,1, равна а>и - 2,655а;
•	на частоте соА2, равной удвоенной частоте среза 2л^ь коэффициент пе-
редачи аналогового фильтра-прототипа равен	= 0,437, т.е. по-
давление составляет 7,2 дБ.
ФЧХ цепи определим следующим образом:
65
Фазочастотная характеристика АФП приведена на рисунке В. 16.
Рисунок В.16 - ФЧХ аналогового фильтра-прототипа
В.2.3 Расчет и построение временных характеристик
Расчет переходной характеристики h(t) выполним по формуле

Л(г)= Г
_Р\Р + 3ра + а
р(р-Р\\р~ Рг)
'к(р)'
р=°[ р J р=А|_ р
Р=Р1\_ Р
-2,62 си -0,38at
h(t)= 1 + -----Г = 1 + 0,17с~2’62“ - 1,17е~°-38от, при t > 0.
2,62 V5 0,38 <5
При построении (рафика переходной характеристики (рисунок В. 17)
целесообразно нормировать временную ось через al.
Рисунок В.17 - Переходная характеристика фильтр-прототипа
Расчет импульсной характеристики g(t) выполним по формуле
к(р)],
g(0=
а1
\р~ + 3ра+а2}
~К{р)
(р- p\ip-pi)
Res
Р йк Р _
р=рА. Р J
у(/) = -дР°-38 И-e-2^], ПРИ <> 0.
На рисунке В 18 приведена нормированная импульсная характеристика
филь гра-прототипа
Рисунок В. 18 - Импульсная характеристика фильтра-прототипа
Для проверки полученных результатов можно воспользоваться пре-
дельными соотношениями, связывающими передаточную функцию и пере-
ходную характеристику цепи.
lim К(р)= lim A(f) = O,
р—><х>	р->0
Нт К(р)- Нт Л(/)=1.
£-»()
АЧХ анализируемого ФНЧ быстро затухает, следовательно, интегри-
рующие свойства цепи довольно высоки.
Необходимо обратить внимание на то, что ФЧХ цепи изменяется от 0°
до -180°. Этот факт скажется на виде АЧХ синтезируемого цифрового фильт-
ра методом инвариантности импульсных характеристик.
67
В.З	Пример синтеза цифрового фильтра методом
инвариантности импульсных характеристик
Необходимо ясно представлять себе, что получение цифрового филыра
с точной копией АЧХ аналогового фильтра-прототипа невозможно. Дело в
юм, что частотная характеристика синтезируемого цифрового фильтра явля-
ется периодической функцией частоты с периодом, определяемым шагом
дискретизации. Поэтому существует несколько методов синтеза ЦФ по за-
данному аналоговому фильтру-прототипу.
Метод инвариантности импульсных характеристик базируется на пред-
положении о подобии импульсных характеристик фильтра-прототипа и циф-
рового фильтра, т.е. импульсная характеристика ЦФ представляет собой вы-
борку из импульсной характеристики соответствующего аналогового фильт-
ра-прототипа.
Наиболее простым является тот случай, когда число отсчетов дискрети-
зированной импульсной характеристики конечно. При этом реализуется
трансверсальный ЦФ (фильтр типа КИХ, т.е. фильтр с конечной импульсной
характеристикой). При рассмотрении бесконечного числа отсчетов импульс-
ной характеристики получается рекурсивный ЦФ (фильтр типа БИХ, т.е.
фильтр с бесконечной импульсной характеристикой).
В.3.1	Дискретизация импульсной характеристики аналогово-
го фильтра-прототипа
Для дискретизации импульсной характеристики g(i) необходимо непре-
рывный аргумент / заменить на дискретный - пТа. Затем пронормировать по-
лученное выражение относительно 7’(:
= g(«ra)-7„ =	f	)’]
Параметр 7L определим по формуле (3 25)
где «6. частота, на которой коэффициент передачи аналогового фильтра-
прототипа (рисунок В.15) достигает уровня 0.1 от своего макси-
мального значения (в примере - безразмерная величина, т.к.
частотная ось проградуирована в долях сД
Таким образом, Тд ~
° 2,655сг /а
На рисунке В. 17 представлена дискретизированная импульсная харак-
Рисунок В. 17 - Дискретизированная импульсная характеристика
В.3.2	Расчет системных функций трансверсального
и рекурсивного ЦФ
Системная функция трансверсального ЦФ представляет собой сумму
следующего вида:
где an=g(nTd)-Td.
м
К(г)^ап-Г\
п=0
Трансверсальный ЦФ имеет конечную импульсную характеристику
(КИХ-фильтр).
Для реализации КИХ-фильтра необходимо взять конечное число М
нормированных отсчетов импульсной характеристики. Для определения по-
рядка фильтра воспользуемся пороговым критерием. Коэффициенты ап соот-
ветствуют значениям отсчетов импульсной характеристики, т.е. и при-
ведены в таблице В. 1.
69
Таблица В I - Коэффициенты а„ трансверсального ЦФ пятого порядка
а»
О
_ #/	__ |________________С1з	|_____Clj______.
0,314	0,214 I 0,137 j 0,088	0.056
Максимальное значение ап равно 0,314. С ростом п значения коэффици-
ентов уменьшаются. Начиная с п- 6 значения коэффициентов не превышают
уровня 0,1 от максимального. Поэтому порядок М трансверсального фильтра
равен 5
Структура КИХ-фильтра приведена на рисунке В. 18.
Рисунок В.18 - Структурная схема трансверсального цифрового фильтра
Работа трансверсального ЦФ пятого порядка описывается алгоритмом
уп =0,314х;7_! + 0,214х„ 2 + 0,137х„_3 + 0.088хп_4 + 0,056хп 5.
Цифровой фильтр с бесконечной импульсной характеристикой (БИХ-
фильтр) реализуется при учете в дискретной импульсной характеристике бес-
конечного числа слагаемых. При этом мы имеем бесконечно убывающую
геометрическую прогрессию, сворачивая которую, получим системную
функцию ЦФ канонического вида:
0,314-z 4________
l -[o.683 -z-1 -0,029 г-2]
Трасверсальная часть ЦФ описывается числителем системной функции,
а рекурсивная - знамена!елем. Коэффициенты ап и Ь„ цифрового фильтра
приведены в таблице В.2
Таблица В.2 - Коэффициенты а„ и Ьп рекурсивного ЦФ
а, в/_______________________________в?
0,314	0,683	I - 0,029
Структура БИХ-фильтра приведена на рисунке В. 19
Рисунок В. 19 - Структурная схема рекурсивного цифрового фильтра
Работа рекурсивного БИХ-фильтра описываемся алгоритмом
У„ = 0,314х„ , +0,683y„_j -0,029ул_2.
В.3.3	Расчет АЧХ трансверсального и рекурсивного ЦФ
Чтобы от системной функции цифрового фильтра перейти к его ампли-
тудно-частотной характеристике, достаточно в К(:) сделать замену следую-
щего вида:
z = eJa,r“.
На рисунке В.20 приведена АЧХ трансверсального цифрового фильтра пятого
порядка с параметрами:
сод - 5,31а; <Мц[ = 0,556а;
ад/ = 96
/
71
Рисунок В.20 - АЧХ трансверсального цифрового фильтра
На рисунке В 21 приведена АЧХ рекурсивного цифрового фильтра с
параметрами:
Рисунок В.21 - АЧХ рекурсивного цифрового фильтра
На рисунках В.20 и В.21 пунктиром изображены АЧХ аналогового
фильтра-протогипа, частота среза которого по уровню 3 дБ составляет
гу 41 - 0.374а .
72
Периодичность АЧХ ЦФ стала результатом дискретизации импульсной .
характеристики аналогового фильтра-прототипа и представляет собой нало-
женный вариант частотной характеристики аналогового фильтра Если шаг
дискретизации достаточно мал, то эффект наложения минимален. На рисун-
ках В.20 и В.21 в точке со,, описанный выше эффект проявляется в двукратном
увеличении коэффициента передачи относительно исходного. В точках
п где п- 0,1,2... эффект наложения также присутствует. Однако в ре-
зультате того, что комплексные коэффициенты передачи, складываемые в
этих точках, находятся в разных четвертях комплексной плоскости, эффект
проявляется в уменьшении коэффициента передачи относительно исходного.
Пульсации АЧХ трансверсального фильтра объясняются ограничением
импульсной характеристики во времени (конечным числом отсчетов g„).
АЧХ рекурсивного фильтра, полученного методом инвариантности им-
пульсных характеристик, более точно повторяет частотную характеристику
аналогового филыра-протэтипа. Однако рекурсивный фильтр необходимо
проверять на устойчивость.
В.4	Пример синтеза ЦФ методом билинейного
Z-n реобразования
В.4.1	Расчет системной функции ЦФ
Данный метод позволяет с помощью билинейной замены (4.10) устано-
вить однозначное непрерывное отображение из ^-плоскости в z-плоскость.
Эта связь имеет следующий вид:
При такой подстановке изменится масштаб АЧХ ЦФ В облас'и малых
частот АЧХ ЦФ и аналогового фильтра-прототипа практически совпадают.
При й) -> происходит сжатие АЧХ аналогового фильтра-прототипа по за-
кону (4.10):
2
®А
1 д
ь)Ц?д
2
73
Используя билинейную замену, преобразуем передаточную функцию
аналогового фильтра-прототипа следующим образом:
(^о)?	, ,_____(«L,)2 г-1 ,	(ц7'<>)2 г-2
4 + ЬаТ+ (аТ & )	4 + БаТ & + (аТ$ )	4 + ЬаТ+ {ctT$ )2
п	+ 4-to7-d +(«/>7 ..-2
4 + 6аТд+(аТд)2 '	4 + 6аГд+(аТд)2
Параметр аТ() определим точно так же, как в п. В.3.2:
77
аТд - а—,
где а)в частота, на которой коэффициент передачи аналогового фильтра-
прототипа достигает уровня 0,1 от своего максимального значе-
ния.
Таким образом, аТд -------= 1,18.
2,655
В результате подстановки значения аТд в системную функцию ЦФ по-
лучим
/ ч 0,112+ 0,224-z'1 + 0,112-z~2
l-jo,416-z-1 +0,136-z"2]-
Трасверсальная часть ЦФ описывается числителем .системной функции,
а рекурсивная - знаменателем.
Таблица В .3 - Коэффициенты ап и Ь„ рекурсивного ЦФ канонического вида
L	ai	«2	в/	в?
0,112	0,224	0,112	0,416	0,136	1
Структура цифрового фильтра приведена на рисунке В.22.
74
Рисунок В.22 Структурная схема ЦФ
Работа рекурсивного БИХ-фильтра описывается алгоритмом
уп = 0,112х„ + 0,244xw4 +0,112х„_2 + 0,416^-! + 0,136у„_2.
В.4.2	Расчет АЧХ ЦФ канонического вида
Чтобы от системной функции цифрового фильтра перейти к его ампли-
тудно-частотной характеристике, достаточно сделать замену следующего вида:
z = е^Г<> .
На рисунке В.23 приведена АЧХ цифрового фильтра с параметрами:
Фд =5,31а; (Оцх =	°)д//О)цх =14,4.
Рисунок В.23 - АЧХ цифрового филыра
75
В.4.3	Расчет импульсной характеристики ЦФ
Для получения импульсной характеристики цифрового фильтра необ-
ходимо произвести обратное Z-преобразование системной функции ЦФ
g„=z“k(.-)]=z
0,112 •(- ч-1)2
-0,416 -z- 0,136
0,112-(z + l)
2)
- ReS| + Res2.
Здесь 3] - 0,631, z2 = -0,215 - корни полинома знаменателя системной функ-
ции ЦФ.
ReS[ = lim
0,112 (z + 1)2
(z-Z]Xz-z2)
0,112 (0,63 l + l)2
(0,631+0,215)
(0.63 If1

= 0,352 • (0,631)"-1, при и>1.
Res-> = lim
z- >z2
0,112-(z + l)2
(z-Zj Xz-z2)
(z-z2)z-’
0,112-(-0,215+ 1)2
(-0,251-0,631)
0,251)" 1 =
= -0,081 •(- 0,215)" ', при и>1.
g„ =0.352-(0.631)" 1 -0.081 •(-0.215)"4, при л> 1.
Значение нулевого отсчета импульсной характеристики go равно ао. Это
значение мы определим непосредственно из схемы фильтра (см. рисунок
В.22)
Дискретная импульсная характеристика ЦФ приведена на рисунке В 24
Рисунок В.24 Отсчеты импульсной характеристики ЦФ (пунктиром показа-
на импульсная характеристика аналогового фильтра-прототипа)
76
В подтверждение правильности проведенного расчета определим от-
счеты импульсной характеристики ЦФ с помощью алгоритма его работы:
J’„ =0,112*,, + 0,244хп_( + 0,112*„_2 + 0,416j„_! + 0,136j„_2
Массив входных данных для определения отсчетов импульсной харак-
теристики имеет вид
{1,0, 0,0,
go = j0 =0,112*0 =0,112,
g] = jj =0,112*! +0,244*0 +0,416jo =0,217,
g2 = J2 =	’2*2 +0,244*! + 0,112*o +0,416j] +O,136jo =
= 0,112 + 0,416 • 0,271 + 0,136  0,112 = 0,24
Полученные результаты полностью совпадает со значениями отсчетов,
вычисленных методом обратного Z-преобразования.
В.4.4	Обсуждение полученных результатов
Метод билинейной замены позволяет избежать эффекта наложения
АЧХ. При этом в области малых частот, где Z-преобразование почти линейно,
АЧХ ЦФ точно повторяет АЧХ аналогового фильтра-прототипа. Сжатие АЧХ
аналогового фильтра-прототипа в области высоких частот привело к искаже-
ниям дискретной импульсной характеристики в области малых времен. От-
счеты импульсной характеристики ЦФ при большом п точно повторяют ис-
ходную импульсную характеристику аналогового фильтра-прототипа.
На частоте сов АЧХ обращается в ноль, тем самым обеспечивая затуха-
ние много больше исходного. Это связано с тем, что вся бесконечная ось час-
тот, соответствующая аналоговому фильтру-прототипу, преобразуется интер-
вал частот ЦФ, равный со...
В.4.5	Прохождение дискретного сигнала через ЦФ
Проводя параллель между цифровыми и аналоговыми цепями, отклик
на выходе ЦФ можно получить двумя способами: перемножив Z-образ сигна-
ла на входе фильтра с системной функцией цепи, получить Z-образ выходно-
го сигнала. Затем с помощью обратного Z-преобразования перейти к выход-
ной дискретной последовательности.
Либо воспользоваться аналогом временной свертки, т.е. дискретной
сверткой, получив при этом значения отсчетов выходного сигнала. Рассмот-
рим подробно второй способ для расчета на выходе ЦФ, полученных разными
способами.
Дискретная свертка задается следующим соотношением:
п	п
У„ = Y.xkg„_t = Т.ёкх„-к .
k=Q	к=0
Значения отсчетов входного сигнала были вычислены в примере В.1
Отсчеты импульсной характеристики для каждого из видов ЦФ различны и
также были рассчитаны в соответствующих примерах.
На рисунках В.25 - В.27 приведены отсчеты сигнала на выходе различ-
ных ЦФ.
Рисунок В.25 Результат прохождения прямоугольного импульса через
трансверсальный ЦФ (КИХ-фильтр)
Рисунок В.26 - Результат прохождения прямоугольного импульса через ре-
курсивный ЦФ (БИХ-фильтр)
78
Рисунок В.27 - Результат прохождения прямоугольного импульса через ЦФ.
полученный методом билинейной замены
Отклики ЦФ оказываются довольно предсказуемыми:
КИХ-фильтр имеет лишь трансверсальную часть, поэтому отклик этого
фильтра обладает конечной длительностью.
БИХ-фильтр имеет как трансверсальную, так и рекурсивную части, по-
этому отклик этого фильтра к нулю стремится лишь асимптотически, имея
бесконечную длительность.
Следует обратить внимание на точность совпадения переходных про-
цессов в моменты переключения с аналоговым фильтром-прототипом (t =5 О,
Z = 67b).
В целом для фильтров, построенным по методу ИИХ, характерно уве-
личение коэффициента передачи в окрестности точки сов в сравнении с
фильтром-прототипом (эффект наложения АЧХ). Поэтому при сравнении от-
кликов фильтра-прототипа и ЦФ можно отметить незначительное ухудшение
интегрирующих свойств ЦФ. Проявление данного эффекта можно умень-
шить, если увеличить сод.
Для ЦФ, синтезированного по методу ИЧХ, характерно искажение им-
пульсной характеристики в области малых времен, что приводит к заметному
искажению переднего фронта прошедшего импульса.
„	_	Тс л
В процессе расчета мы предполагали, что Г дс = Тдцф, т.е. — =--,
12 2,655а
поэтому отклик ЦФ схож с откликом фильтра-прототипа при аТс 14.
79
В.5	Пример синтеза ЦФ по заданной АЧХ
В.5.1 Определение параметров АЧХ цифрового ФНЧ
Если требуется монотонно спадающая АЧХ, то необходимо рассчиты-
вать фильтр Баттерворта. Если требуется равноволновое приближение к АЧХ
идеального ФНЧ, то выбирают фильтр Чебышева.
Согласно заданию, цифровой ФНЧ с частотой среза Ющ должен удовле-
творять двум условиям:
1)	неравномерность АЧХ в полосе пропускания не более /3 дБ, напри-
мер, Р= 1 дБ для 0 < й>< где а>ц3 - 0,8й^(;
2)	затухание АЧХ в полосе задерживания не менее а дБ, например,
а = 20 дБ на частоте (Ощ = 2й^ь
При выборе частоты среза ЦФ необходимо предусмотреть, чтобы в по-
лосу прозрачности фильтра помещалась основная часть энергии заданного
сигнала (заданным сигналом считаем прямоугольный импульс с длительно-
стью г).
Если опенивагь полосу частот сигнала по половине ширины главного
лепестка спектра, то частота среза ЦФ определится по формуле
2л
Кроме того, чтобы в дальнейшем при синтезе ЦФ Z-преобразование в
области малых частот было практически линейным, рекомендуется выбирать
<4) »а>цХ.
Наконец, скорость обработки сигнала должна совпадать со скоростью
работы ЦФ, т.е. частота дискретизации сигнала и период АЧХ цифрового
фильтра должны быть одинаковыми. Например, для рассматриваемого в п.
ВЛ сигнала
Щ =12л/ = 2я/ .
д /тд
80
В.5.2 Определение параметров АЧХ аналогового фильтра-
прототипа
Произведем пересчет частот, соответствующих ЦФ а>ц\, (Оцз, в час-
тоты аналогового фильтра. Для этого воспользуемся следующим соотноше-
нием:
й>д
12zr
_____г
2л-.
г
= Ьыц\ 
<*>А =

л"
г   ------——
<6
соД} = 1,103®щ = 1,1032^/ = 6,93/,
<од1 = 3,308иц1 = 3,3082л/ = 20,78/,
®лз = 0,85^=0,85 2л/ = 5,34/
Значения частот аналогового фильтра, нормированные относительно
часто гы среза, равны
^12=3,	^ = 0,77
«41	О)А{
В.5.3 Анализ аналогового фильтра Баттерворта
1.	Определение порядка фильтра Баттерворта.
Условие определения порядка фильтра Баттерворта сводится к условию
выполнения необходимого затухания на удвоенной частоте среза и выглядит
следующим образом:
81
20-Ig
f(o)
A. (^7
Следовательно, необходимо рассчитать коэффициент передачи
да) для фильтров разных порядков и выбрать фильтр удовлетворяющий
данному условию.
АЧХ аналогового ФНЧ Баттерворта описывается таким выражением:
На рисунке В.28 приведены АЧХ фильтров Баттерворта разного порядка.
Чтобы обеспечить затухание а = 20дБ, необходимо выбрать фильтр по-
рядка п - 3.
а = 20-
1g
Л-(0)
х(з)
= 28,64 > 20 дБ.
Проверим также величину неравномерности АЧХ в полосе пропускания
/* = 20 1g
к(о)
/<(0,77)
= 0,82 дБ.
82
Таким образом, фильтр Баттерворта третьего порядка полностью удов-
летворяет вышеуказанным требованиям.
АЧХ анализируемого филыра Баттерворта выглядит следующим обра-
зом:
I 1	6
! 1+(”- I
V k^/ii)
2.	Определение передаточной функции аналогового фильтра Баттерворта.
Фильтр Баттерворта нижних частот порядка п имеет следующее выра-
жение передаточной функции цепи:
Рн + ап—\' Рн 1 + — + а\ ’ Рн +1	~ Р]У-(Рн Рп )
где рн=р/(£>АС\
а/, а?, .... а,,./ - вещественные коэффициенты;
pt, Р2, —,рп- полюса функции К(рн}.
Для рассматриваемого фильтра третьего порядка знаменатель функции
K’Cpfy) выглядит следующим образом:
{рн + Рн + 1рРн + О-
Поэтому
(рн + Рн +]\рн +
3.	Расчет и построение временных характеристик аналогового фильтра
Баттерворта.
Для расчета временных характеристик необходимо перейти от рн к р,
для этого необходимо воспользоваться подстановкой ри=р/а>А\.
83
«JI
(p - Pl® 41 Xp - P2®JI Xp - Pt«JI )'
'Mp)1 l
_ p
K(p)
A(/)= Г
- Res
p=o[ P
p(p - Pi® л Xp - Ргюл Xp - Рз® л)
*(p)
P=Pl^AlL P J P=P2tt’.4lL P
Res
Res
k(p)
Res
p=ps ®xiL P

Л0=1-е-<алг' + /0,577е^0’5+-,0’87^л|'/ -у0,577е^0’5-у0’87^л|7 =
= 1	- 1,1 Se^41 '2 sin(0,87r??yf| •/).
При построении графика переходной характеристики целесообразно
нормировать временную ось через соау 4.
Рисунок В.29 - Переходная характеристика фильтра
g(0=z.-[K(P)]=z.-
_____________"Л1______________
(р - Pl^Al Хр - P2^Al Хр - РЗ&Л1)
=	/?es[A(/?)]l Лел-^^)].
Р=РР(,}А\	Р=-Р1-ЮА\ Р=РЗ^А\
+[-O,5-j0,289]e^°'5+yO'87^‘'/ +
+ [- 0,5 + уо,289]е^ О'5“-/О’87^-'1' }=
= <нм1е 1 + 0,58е W >] 2 sin(0,87л>Л| t)-e 2 cos(0,87ft?• t)
84
На рисунке В.30 приведена нормированная импульсная характеристика
фильтра.
Рисунок В.ЗО - Импульсная характеристика фильтра
В.5.4 Синтез цифрового фильтра Баттерворта
1.	Расчет системной функции ЦФ
При синтезе цифрового фильтра методом билинейного Z-преобразования
его системную функцию K(z) определяют исходя из коэффициента
передачи К(р) аналогового фильтра-прототипа. При этом производится заме-
на следующего вида:
= _2 l-z-1	1-z4 1?32 l-z~'
Г<>®41 1 + Z-1	1 + Z-1	’	1+.Z-1’
которая приводит к изменению масштаба частоты
Л-С-) = 7-----------------------^4^-------------------------—71
((1,732 - Р1)-(1,732 + р,	)..((!,732- р})-(1,732 + р3 )=~‘ )
15,67-15,12с-' +9,12с 2-1,66с 3’
Из структуры системной функции видно, что полученный ЦФ является
фильтром третьего порядка С технической точки зрения, реализация сумма-
тора как элемента ЦФ проще, чем реализация линии задержки, поэтому целе-
сообразно представить ЦФ в виде каскадного соединения двух фильтров пер-
вого и второго порядков:
/ф)=-!--------—г 1+2-г.'+^2 --п.
15,67 1 _ 0,268с- 1 - [0,698с 1 - 0,398с 2 ]
85
Таблица В.4 - Коэффициенты а„ и Ь„ цифрового фильтра
15,67
0,268
2
1	0,698	-0,398
_____1____________' __
С груктура ЦФ приведена на рисунке В.31.
Рисунок В.З I - Структурная схема цифрового фильтра Баттерворта
2.	Получение АЧХ цифрового фильтра Баттерворта.
Чтобы от системной функции цифрового фильтра перейти к его ампли-
тудно-частотной харак геристике, достаточно сделать замену следующего ви-
да:
i ,2л а>
Z^eJ0)Tf' =	6
На рисунке В.32 приведена АЧХ цифрового фильтра Баттерворта.
Рисунок В.32 - АЧХ цифрового фильтра
86
3.	Расчет импульсной характеристики ЦФ Баттерворта.
Для получения импульсной харак i еристики цифрового фильтра необ-
ходимо произвести обратное Z-преобразование системной функции ЦФ:
g„ = /[*+)[ =
=Z-Lj о--)3
15,67 z3 -0,965z2 + 0,582z' -0,106 '
8n
1
15,67
(l+z,)3z,"-' . (l + z2)3zr' , (l+z3)M4 * *
(21 ~Z2XZ1 -£з) (z2 ~Z1XZ2 ~гз) (z3 ~Z1XZ3 ~z2)
где Z|, z2, z2 - корни полинома знаменателя системной функции ЦФ.
gn = 0,064^7,253-(0,268)”' +(-1,643 + у’5,209)(0,349-J0,524)'7'1 +
+ (-1,643 - j’5,209)  (0,349 + /0,524)"~1 ] , при п > 1.
Хотя в данном выражении и присутствуют комплексные величины не
трудно проверить то, что значения всех отсчетов импульсной характеристики
будут действительными числами.
Значение нулевого отсчета импульсной характеристики равно av, кото-
рое мы определим непосредственно из схемы фильтра (рисунок В.31)
Дискретная импульсная характеристика ЦФ приведена на рисунке В.ЗЗ.
Рисунок В.ЗЗ - Отсчеты импульсной характеристики ЦФ
4. Прохождение дискретного сигнала через ЦФ Баттерворта.
Сигнал на выходе фильтра определим воспользовавшись дискретной
сверткой:
87
к	к
Ук = Z xngk_„ = £g„xk_n
п~0	м-О
На вход фильтра подадим прямоугольный импульс, который рассмат-
ривался выше.
На рисунке В.34 приведены отсчеты сигнала на выходе ЦФ Баттерворта
В.5.5 Анализ аналогового фильтра Чебышева
1.	Определение порядка фильтра Чебышева.
Порядок фильтра Чебышева зависит лишь от величины необходимого
затухания на удвоенной частоте среза. Данное условие представляется в виде
неравенства
20- lg у™*
а.
Следовательно, необходимо рассчитать коэффициент передачи )
для фильтров разных порядков и выбрать фильтр, удовлетворяющий данному
условию.
АЧХ аналогового ФНЧ Чебышева описывается следующим выражением.
1

(О лл
У \ V Л1 ) )
где е - параметр, характеризующий неравномерность АЧХ в полосе пропус-
кания;
Т„(х) - полином Чебышева первого рода порядка п.
88
Как видно из формулы, необходимо задать параметр £, характеризующий
величину флуктуаций АЧХ в полосе пропускания:
-V100J/? -1
Я] max
где /3 - величина неравномерности в дБ, р - 20 • 1g|—j-.
I Я'| min
Пусть 1дБ. тогда £- 0,259. На рисунке В.35 приведены АЧХ фильт-
ров Чебышева разного порядка.
Рисунок В.35 - АЧХ фильтра Чебышева
Чтобы обеспечить затухание ci ~ 20дБ, надо выбрать фильтр порядка
п = 3:
20
lAmaxL 34 >20,
Таким образом, АЧХ анализируемого фильтра Чебышева выглядит сле-
дующим образом:
>2
л
1 + 0,067 4] А
V°A\)
^4
-3 ---
1^/11 J
89
2.	Определение передаточной функции аналогового фильтра Чебышева.
Фильтр Чебышева нижних частот порядка п имеет следующее выраже-
ние передаточной функции цепи:
) = _______Л0 =______________________Jo_______________
(Рн ~ Р\ )—(Рн ~ Рп) р” + Л/7_|  p^~i +... + Л]  Рн +&о
где ри=р/(чАС\
bo, Ь/, Ьп./ - вещественные коэффициенты;
р/,р?, ..../л, - полюса функции K(pf{).
Для рассматриваемого фильтра третьего порядка полюса операторного
коэффициента передачи имеют следующие значения:
pt = -0,494,
Р2, рз= -0,247±/0,966.
Поэтому
А—	°’49
к\Рн) - ~г--------ч------------------
РН + 0,988/^+1,238/7// +0,49
3.	Расчет и построение временных характеристик аналогового фильтра
Чебышева.
Для расчета временных характеристик необходимо перейти от рн к р,
для этого необходимо воспользоваться подстановкой рн р/шЛ\.
0,49^,
(Р - Р\^а\ Хр - Р2^Л1 Хр ~ Рз"/1)
/?(/)=£“
L р
_______________0.49ш,1|	_________
р(р - Р1 «л 1 Xp - Р^АI Хр - РЗ^Л! )
= 0,49-
~^(р)
Res
Р = Р\^А\{. Р
к(р)
Res
Р=Рг<»а\\_ Р
>(р)'
Res
P=Pif’}Al\_ P
Р _
90
Л(/)= 0,998 - о,988е~0’494"41'4 /0.255е( 0,247+>0,966)^, •/ _
— JO25^e^ 0,247-/0.966)б£>4|7 _
= 0,998 -0,988е°'4;4и,/"7 -0,5k"°’274ft?4r/ sin(0,966^. t).
При построении графика переходной характеристики целесообразно
нормировать временную ось через o)M t.
Рисунок В.36 - Переходная характеристика фильтра Чебышева

0,4969^
(р - Р\^А\ \Р - Р103 А1Хл - РЗ“>А\ )
= 0,49] Res[Л(р)] ь /?es[K(p)}4 А<лл[А.(р)] '•
Р=Р1®4)	Р=Р1^Л1 Р=РУ™А\ .
g(/) = ®41 |э,493е~0’494®л’7 +[-0,246-J0,063]е^°’247 ^А966)^7 +
4 [- 0,246 4 J0,063]e( °’247->°-966>>!i 7 }=
= «л[|з,493е’0’494юл17 4 0,126е~°’247бУя'78ш(0,966«л1 •/)-
0,492е”0-247й?л‘7 cos(0,966©xl ч)}
На рисунке В.37 приведена нормированная импульсная характеристика
фильтра.
Рисунок В.37 - Импульсная характеристика фильтра
91
В.5.6 Синтез цифрового фильтра Чебышева
1. Расчет системной функции ЦФ.
При синтезе цифрового фильтра методом билинейного Z-преобразования
его системную функцию /\(z) определяют исходя из коэффициента
передачи К(р) аналогового фильтра-прототипа. При этом производится замена
следующего вида:
2	l-z-1	l-z 1 . рз2 l-z'1
1 + гЧ л'шлС 1 + z-1	’	1 + z-1
которая приводит к изменению масштаба частоты:
к(л_________________________О.49-(1 + г~'У __________________
((1,732-Pl)-(1,732 + р{>-1)..((1,732-р3)-(1,732 + р3)z ’)
_	0,49(l+ z ’У______________
10,795-14,933z ' 4-11,952г-2 -3,885г-3 *
Из структуры системной функции видно, что полученный ЦФ является
фильтром третьего порядка. С технической точки зрения, реализация сумма-
тора как элемента ЦФ проще, чем реализация линии задержки, поэтому целе-
сообразно представить ЦФ в виде каскадного соединения двух фильтров пер-
вого и второго порядков:
tf(z) = 0,045——-г —Г ,	----
1 - 0,556г- 1 - l0,827z - 0,647z
Таблица В.5 Коэффициенты а„ и Ьп цифрового фильтра
ао	1	в'		'У а2	в?	О «2
0,045	1	0,556	2		1	0,827	-0,647
Структура ЦФ приведена на рисунке В.38.
92
Рисунок В.38 — Структурная схема цифрового фильтра Баттерворта
2. Получение АЧХ цифрового фильтра Чебышева.
Чгобы от системной функции цифрового фильгра перейти к его ампли-
тудно-частотной характеристике, достаточно сделать замену следующего вида:
I ,2л-	|
Z = eJO>Ta = У
На рисунке В.39 приведена АЧХ цифрового фильтра Чебышева.
Для получения импульсной характеристики цифрового фильтра необ-
ходимо произвести обратное Z-преобразование системной функции ЦФ:
Sn=Z~{K{z)] =
__ ___0,045(1 + z)3_____
Z3 -l,383z2 + 1,107г1 -0,36
где z\, z2, z2 - корни полинома знаменателя системной функции ЦФ.