ББК 30.12ІЯ73 П 34
УДК 539 3/ 6(075 8)
Рецензенти д р тези наук проф / А Цурпад (Український держав ннй аграрний університет) д р техн наук проф А С Дехтяр (Українська академія мистецтв)
Редакція літератури з машинобудування і будівництва
Редактор А. С Мнишенко
Дикіролетрсосьі'МІ
Інститут Ікжеч» з
валізиичного
транспорту
БІБЛІОТЕКА
ПисаренйЬ Г С та Ін
П34 Опір матеріалів Підручник / Г. С Писаренко О Л Квіт ка, Е С Уманський За ред Г С Писаренка — К Вища шк , 1993,- 655 с . іл.
І8В.М 5 11 004083 4
Висвітлено основні питання опору матерів тіа, то відбивають с>чагннй рівень науки і техніки Викладено загальні методи визначення переміщень і метод сил. питання пружних коливань, розрахунки при повторно змінних та ударних навантаженнях Наведено елементи теорії тонкостінних оболонок основи механіки руйнування подано багато детатьпо протимізованих ари кладів
Дія студентів машинобудівних спеціальностей вищих иавіатьннх за кладів
2004030000—043
"-----ІТГ-ІЗ----83-83
ББК ЗО І21я73
15ВN 5 11 904083 4
© Писаренко Г. С. Клітка О Л, Уманський Є С 1993
ЗМІСТ
Передмове ......................... .	.	7
Глава І Вступ .......	.	В
6 І Наука про опір матеріалів Об екти вивчення ...	...	8
§ 2 Види деформацій стержня Поняття про деформований стан матеріалу	II
§ 3. Основні гіпотези науки про опір матеріалів	.	14
Глава 2 Геометричні характеристики плоских перерізів	15
§ 4	Статичні моменти площі. Центр вагн перерізу .	15
§ 5	Моменти інерції плоских фігур .	,я
§ 6	Моменти інерції складних перерізів
§ 7	Моменти іперціі відносно паралельних осей
| 8 Залежність між моментами інерції при повороті координатних осей
§ 9 Визначення напрям) головних осей інерції Головні моменти інерції
§ 10 Графічне зображування моментів інерції'
| 11 Поняття про радіус і еліпс інерції
§ 12 Порядок розрахунки
Глава 3 Зовнішні й внутрішні сили Метид перерізів Епюри внутрішніх сил
§ 13 Класифікація зовнішніх сил
| 14 Внутрішні сили Метод перерізів Епюри
§ 15 Епюри поздовжніх сил
116	Епюри крутнях моментів
17	Балки і їхні опорн
18	Визначення реакцій
19	Поперечні снти і моменти в перерізах балкн
20	Побудоха епюр і М у балках .	.
21	Диференціальні залежності при згинанні Деякі особливості епюр С) і М
§ 22	Побудова епюр внутрішніх зусиль для рам
$ 23	Побудова епюр внутрішніх зусиль для криволінійних стержнів
§ 24	Диференціальні залежності при згинанні птоских криволінійних стерж нів . .	...
$ 25	Побудова епюр внутрішніх зусиль для просторових рам
§ 26	Напруження в перерізі
Е888Л38В В 338 8288ЙЙЇЙ488 8 ‘ввв&якїї:
Глава 4 Розтягання 1 стискання Механічні характеристики матеріалів
Ж27 Напруження і деформації при~розтягаЇ!ій"й стисканні‘Розрахунок ніГ>
І ___ МІЦНІСТЬ І ЖОПСТКІСТЬ	~	*---------”* ~
Л 28~~ “Умови мТцностціжорсткості Види розрахунків
29 Випробування мітеріатіа па розтяг ний
ЗО Деякі піші види механічних аипрдбуВйКГа
§ Зі Поняття про’мекЯИІЗкІ утворення деформацій
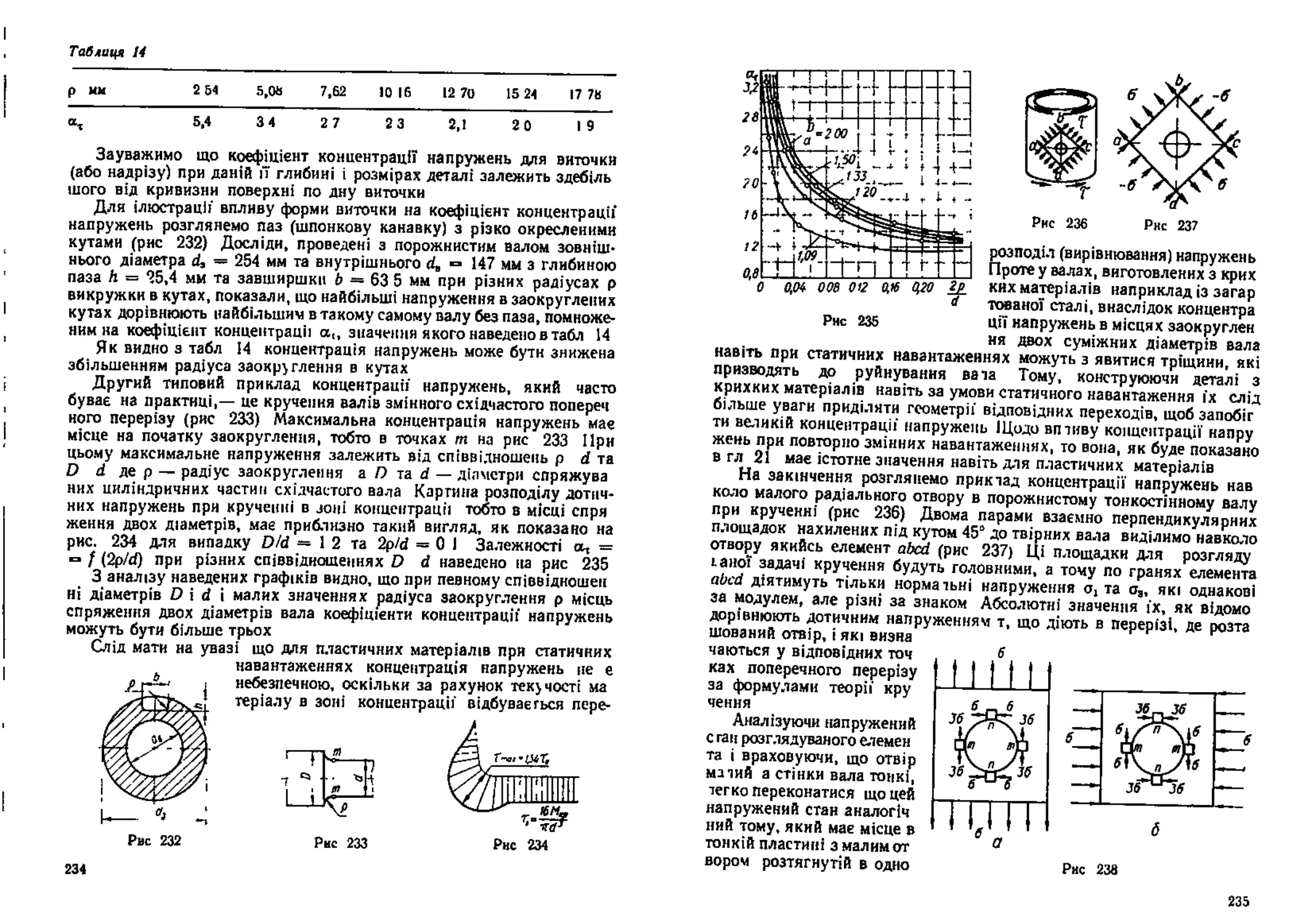
§ 32 Поняття про концентрацію напружень
§ 4.1 Вплив різних факторів на механічні властивості матеріалів (Ь ,'М.Иапустимі напруження*"* .	.......... •
Глава 5 Розрахував ва міцність і жорсткість при розтяганні А стискана! 115
§ 35	Приклади розрахунків при дії зосереджених сил	115
§ 36	Урахування власної ваги і сил інерції	123
§ 37	Статично невизначувані конструкції	130
$ 38 Розрахунок гнучких ниток	140
Глава 6 Основи теорП напруженого І деформованого стану	152
§ 39	Напруженая в точці .	  152
§ 40	Закон парності дотичних напружень Головні	площадки	і	головні на
Жуження	154
пійннй напружений стан	156
§ 42	Плоский напружений стан ......	158
143	Пряма задача в плоскому напруженому стані	Круг	напружень	162
44	Зворотна задача в плоскому напруженому стані .	165
45	Об’ємний напружений стан Напруження на довільній площадці . 168
46	Деформації при об’ємному напруженому стані Узагальнений закон Гука 174
47	Потенціальна енергія деформації	І77
Глава 7 Кратері! міцності	180
§ 48	Завдання теорій міцності	180
§ 49	Класичні критерії міцності (теорії міцності)	182
§ 50	Поняття про нові теорії міцності	186
Глава 8 Зсув	.	•	193
§ 51	Зсув Розрахунок на зріз	І93
§ 52	Чистий зсув	194
Глава 9 Кручення	.	............. 206
§ 53	Напруження і деформації при крученні Умови міцності й жорсткості 206 §54 Аналіз напруженого стану і руйнування при крученні	211
155 Розрахунок ва ів на міцність і жорсткість при крученні	212
56 Кручення стержнів некруглого перерізу	216
57	Кручення тонкостінних стержнів	222
58	Розрахунок гвинтових циліндричних	пружин	227
59	Концентрація напружень при крученні	.	233
Глава 10 Згивааяи	236
§ 60	Нормальні напруження при плоскому згинанні прямого стержня	236
§ 61	Дотичні напруження при згинанні .	243
| 62 Розрахунок па міцність при згинанні . .	249
§ 63	Про раціональну форму перерізу балки	.	257
§64	Повний розрахунок балок на міцність	.	258
§ 65	Концентрація напружень при згинанні	261
§ 66	Диференціальне рівняння зігнутої осі балки .	В65"
§ 67	Приктадн визначення переміщень інтегруванням диференціального рів 4 яяння зігнутої осі балки ...	.	263
§ 68	Визначення переміщень у балках за методом початкових параметрів 276 § 69 Розрахунок балок змінного перерізу на міцність і жорсткість	290
§ 70	Розрахунок на дію сял інерції при згинанні	302
Глава П Додаткові питання теорії згинання .	.	335
§ 71	Про розрахунок складених балок	. ,	.	.	305
§ 72	Дотичні напруження при згинанні балок тонкостінного профілю Центр
згинання .	...	.	308
§ 73	Розрахунок балок на пружній основі .	. •	314
§74	Зі ііцпіпія балок матеріал яких не відповідає закону Гука	. . 319
Глава 12 Складний опір ..................................................
§ 75	Складне ) косе згинання ..........................................
| 76 Згинання з розтяганням (стисканням).................................
§ 77	Згинання з крученням .	............ ...................
Глава 13. Загальні теореми про пружні системи Загальні методи визначення переміщень ...	.	........
ь 78 Узагальнені сили і переміщення .....................................
§ 79	Робота зовнішніх сил ................. ...........................
§ ЗО	Робота внутрішніх сил.............................................
§ 81	Застосування лрнндмпу початку можливих вереміщень до пружних систем.......................................................... •
§ 82	Теореми про взаємність робіт і переміщень .	....
§ 83	Загальна формула для визначення переміщень Метод Мора .....
§ 84	Переміщення, спричинені дією температури	.	.
§ 85	Обчислення інтегралів Мора способом Верещагіиа .	...
§ 86	Застосування способу Верешагіна до стержнів змінного поперечного перерізу .	....	....	....	•
6 87 Потенціальна енергія деформації ...	....	.
186 Теорема Кастільяио Теорема Лагранжа .	.	.	....
§ 89 Теорема про мінімум потенціальної енергії ...
Глава 14 Статично невизначувані системи .	. .	...
§ 90 Основні поняття та визначення Етапи розрахунку статично невизначу ваної системи	........
191 Розрахунок простих статечно невнзначуваних балок 92 Канонічні рівняння методу сил .	...
93 Багагопрольотні нерозрізні балки Рівняння трьох моментів 94 Вплив неточного розміщення опор по висоті .	....
95 Розрахунок статечно иевизиачуваннх криволінійних стержнів 95 Визначення переміщень у статечно невнзначуваних системах 97 Контроль правильності розв’язання статечно невизначуваної системи 98 Про розрахунок просторових рамних систем
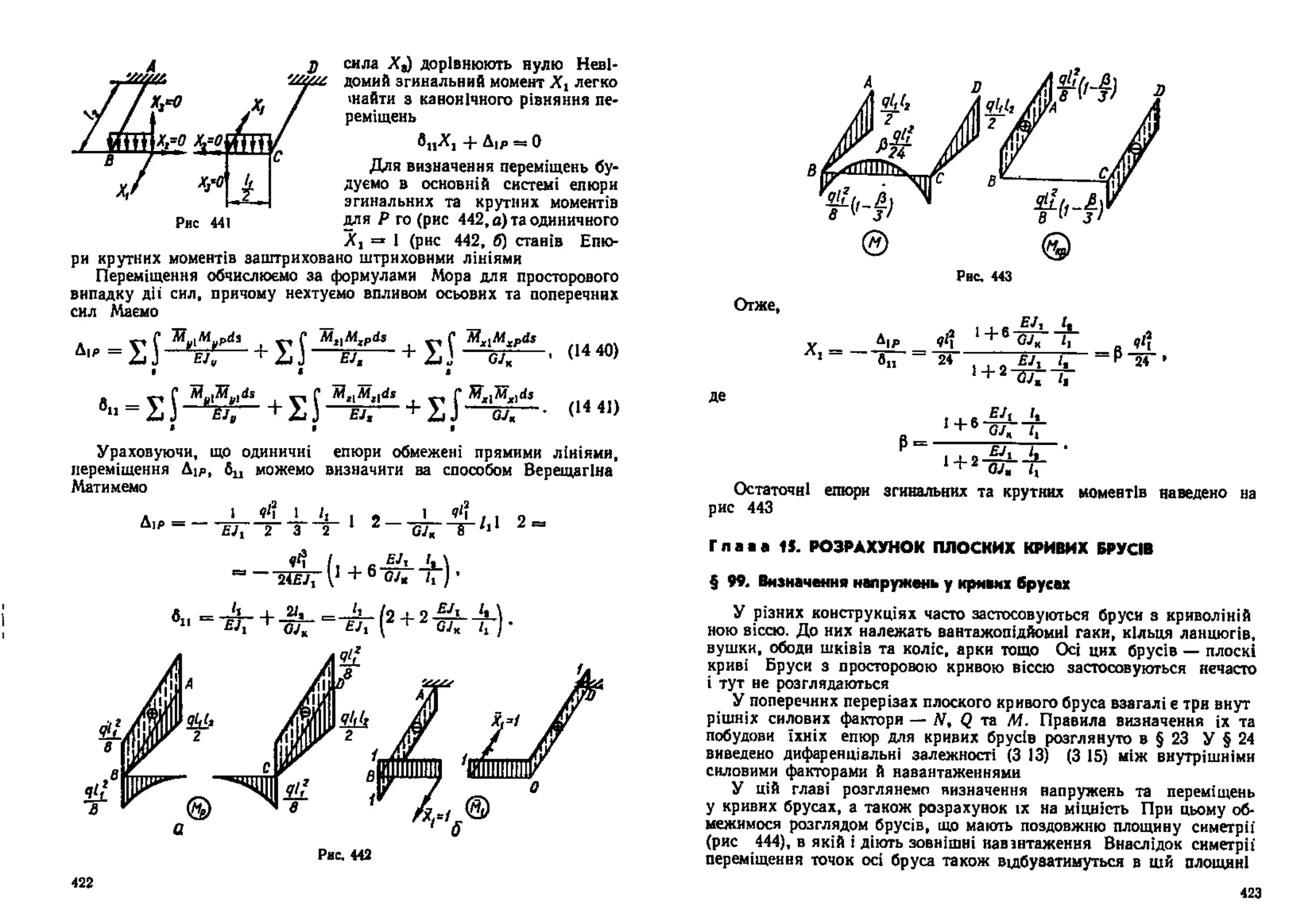
Глава 15 Розрахунок плоских аривнх брусів........................
§ 99. Визначення напружень у кривих брусах...........................
б 100 Розрахунок на міцність кривих брусів ...	....
§ 101 Визначення переміщень у кривих стержнях .	...
Глава 16 Розрахунок товстостінних циліндрів і обертових дисків .
1102 Товстостінний циліндр, що зазнає дії внутрішнього і зовнішнього тисків 103 Розрахунок складених циліндрів ......................................
104 Температурні напруження в товстостінних циліндрах...............
106 Приклади розрахунку товстостінних циліндрів	...........
106 Розрахунок обертових дисків ...	....................
Глава 17. Елементи теорії тонкостінних оболонок..................і
ІІ07. Вступ .	...	............ .	.	...........
108 Напруження в осасиматрнчній оболонці .	.	...............
109 Розпірні кільця в оболонках ....................................
ПО Крайова задача для тонкостінної циліндричної оболонки ....
111	Приклади врахування згннатьннх напружень в оболонках . . .
Глава 18 Розрахунок вонструкцій ве граничними станами .	....
§112	Основні відомості про граничний стан	....	 478
§	113 Розрахунки при розтяганні й стисканні...........................481

§	114 Розрахунки при крученні
|	115 Розрахунки при згинанні
Глава 19. Стійкість стиснутих стержнів
§ 116	Стійка та нестійка пружна рівновага	........
§ 117	Формула Ейлера для визначення критичної сили стиснутого стержня
| 118 Вплив умов закріплення кінціа стержня на значення критичної свій
§ 119	Поняття про втрату стійкості при напруженнях, шо перевищують гра кицю пропорційності ...
§ 120	Розрахунки на стійкість за допомогою коефіцієнтів зменшення основ його допустимого напруження
$ 121 Про добір матеріалу і раціональних форм поперечних перерізів для стиснутих стержнів	. .
$ 122 Поздовжньо*поперечяе згинання
Глава 20 Пружні колившвя
$ 123 Вступ. Класифікація иеханічннх коливань
$ 124 Власні гармонійні коливання пружної системи з одним ступенем оіль ності ....
1)25 Вимушені коливання пружних систем з одним ступенем вільності
126	Власні коливання з в язвим демпфуваниям
127	Вимушені коливання механічної системи з в язкнм демпфувянням
128	Критична швидкість обертання вала
129	Власні коливання системи з двома або кількома ступенями ві шості 130 Крутильні коливання валів і систем передач
§	131 Поперечні коливання стержнів із зосередженими масами
$	132 Коливання пружних тіл з розподіленими масами
$	133 Поперечні коливання призматичних стержнів
Глава 21 Опір матеріалів дії повторно-змінних напружень
§ 134	Явище втоміеності матеріалів ...	...
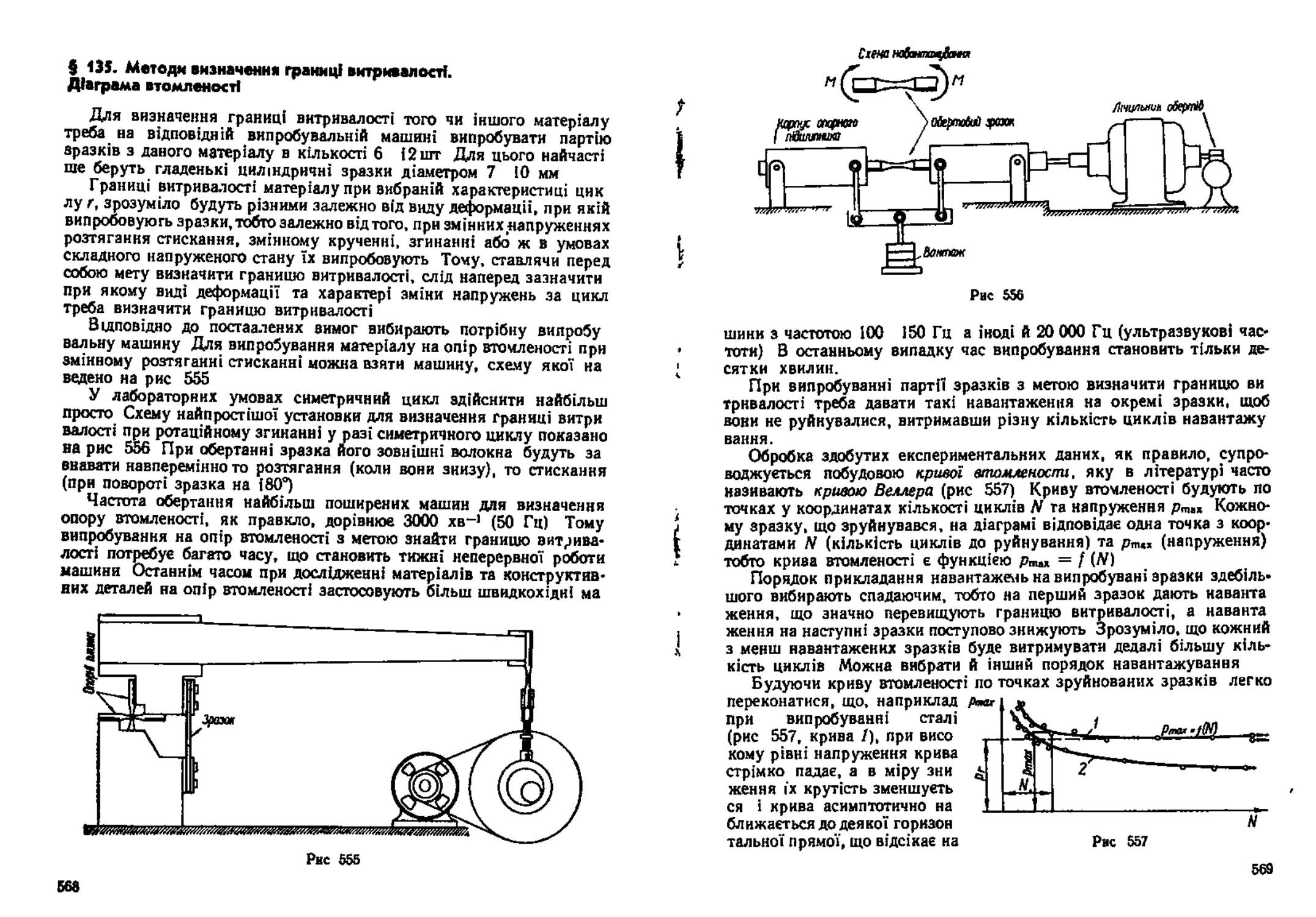
в 135 Методи визначення границі витривалості Діаграма втомленості
§ 136	Вплив конструктивно технологічних факторів на границю оіітрпвттості § 137 Розрахунок на міцність при повторно змінних навантаженнях
Глава 22 Розрахунки ари ударних навантаженнях
§ 138	Розрахунок при осьовій дії ударного навантаження
б ІЙ Напруження при ркручувальному ударі
§ 140	Напруження І деформації при згинальному ударі
§ 141	Механічні властивості матеріалів при уларі	*
Глава 23 Коитахтві напруження
§ 142	Основні поняття .	. .
§ 143	Формули для визначення контантннх напружень
§ 144	Перевірка міцності при контактних напруженнях
Глава 24 Освовн механіки руйнування
1145 Загальні поняття
146	Крихке руйнування. Теорія Гріффітса
147	Ситові критерії руйнування
148	Оцінка розмірів пластичної зони вадовж тріщини .
149	Методика експериментального визначення трішнпосіійкості консгрук Рійних матеріатів
Податки
Список рекомендованої літератури ...	.	.
§ = § 858» 8 =§§ § =8§§ §	8 8ШШ85В § §	§ і ® 88
ПЕРЕДМОВА
Сучасний етап науково технічного розвитку потребує швидкого поліпшення якості продукції, що випускається, впровадження нових технологій, інтенсифікації виробничих процесів, а стосовно до такої важливої галузі промисловості, як машинобудування,—підвищення надійності й довговічності машин —головних показників їхньої якості
Зараз у світі кожні п ять-сім років створюються нові покоління ба гатьох тилів машин Незалежній Україні необхідно прагнути різкого підвищення якості машин, які випускаються, щоб вони стали конкурентоспроможними на світовому ринку У виконанні цього завдання важлива роль належить розвиткові наукової бази для вирішення пи тань міцності машинобудівних конструкцій, забезпечення надійності й довговічності машин Основною наукою, яка навчає методам розра хунку на міцність та надійність конструкцій, саме йєопір матеріалів
Цей підручник розрахований на студентів машинобудівних спеціальностей вищих навчальних закладів України, написаний відповідно до діючих програм і містить у собі основні розділи сучасного курсу опору матеріалів Водночас ним можуть користуватися студенти й інших спеціальностей, оскільки матеріали, передбачені будь якою програмою, стисло викладено у відповідних главах та параграфах
Для якнайкращого засвоєння студентами складного матеріалу увагу приділено однаковості виведення основних розрахункових формул, наведено багато докладно проаналізованих прикладів Розглянуто розрахунки на міцність та жорсткість не тільки стержнів, а й стержньових систем (ферм, рам) Порівняно з іншими курсами, що були видані в Україні останнім часом, з урахуванням зрослих вимог щодо міцності машин та конструкцій у підручнику докладніше розглянуто основні питання розрахунку на міцність та жорсткість при динамічному навантаженні
При підготовці цієї книги було використано матеріали В А Ага-рьова та В Г Полкова, які брали участь у написанні підручника «Со-противленне материалов»1.
1 Совротиалеііне материалов / Г. С. Писаренко, В. А Агарев А. Л Квитка, В Г. Попков, З С Уманскнй — К Гостехнздат УССР, 1963 — 791 с.
Глава 1. ВСТУП
§ 1 Наука лр<? «іір матеріалів.
Об’єкти ВИВЧАННЯ
Опором маґпер^лів називають науку про інженерні методи розрахунків на міцніапь. жорсткість і стійкість елементів машин та споруд
У процесі експлуатації машин та споруд їхні елементи (стержні, балки, пластини, болти, заклепки тощо) так чи інакше беруть участь У роботі конструкції й зазнають дії різних сил — навантажень Для забезпечення нормальної роботи конструкція повинна задовольняти необхідні умови міцності, жорсткості та стійкості
Під міцністю розуміють здатність конструкції, її частин та деталей втримувати певне навантаження не руйнуючись
Жорсткістю ~ ие здатність конструкції та н елементів протистояти Деформуванню (змінюванню форми і розмірів) під дією зовнішніх на-ваггажень При заданих навантаженнях деформації не повинні перевищувати певного значення, встановленого відповідно до вимог, що ставляться вР конструкції
Стійкістю називають здатність конструкції або її елементів зберігати певну початкову форму пружної рівноваги
Для того Щ06 конструкція цілком відповідала вимогам міцності, жорсткості тз стійкості, а отже, була надійною в експлуатації, треба надати її елементам найбільш раціональної форми і, знаючи властивості матеріалів, з яких вони виготовлятимуться, визначити відповідні роз міри залежно від навантаження та його характеру
На перший погляд може здатися, що для надійного опору елементів ховструкції зовнішньому навантаженню досить збільшити їхні розміри Дійсно іноді не приводить до бажаних результатів Однак тоді, коли власна вага становить значну частину навантажень, що діють на конструкцію збільшення розмірів її елементів а отже, і ваги, не підвищує мідності Збільшення розмірів рухомих деталей механізмів і машин спричинює зростання сил інерції, підвищує навантаження, а це небажано оскільки також може призвести до руйнування Збільшення розмірів^ яке необумовлене вимогами надійності роботи конструкції призводить до зайвої витрати матеріалів і підвищення її вартості Машини і споруди треба будувати міцними і надійними в експлуатації, але водночас легкими й дешевими
Опір матеріалів розв язуе зазначені задачі міцності, грунтуючись як на теоретичних, так і на дослідних даних, що мають у цій науці однаково важливе значення У теоретичній частині ця наука базується
а б	6	г
Рис і
на теоретичній механіці й математиці а в експериментальній — на фі зиці та матеріалознавстві
Опір матеріалів е конче важливою інженерною наукою, необхідною для формування інженерів будь якого фаху Без фундаментальних знань у цій галузі не можна створити такі конструкції, як різноманітні машини і механізми, цивільні Й промислові споруди, мости, лінії електропередач та антени ангари, кораблі, літаки й вертольоти, тур бомашини й реактивна техніка та ін
Отже, опір матеріалів — це найбільш загальна наука про міцність машин і споруд Однак вона не вичерпує всіх питань механіки дефор мівннх тіл Цими питаннями займаються й інші суміжні дисципліни будівельна механіка стержньовнх систем теорія пружності й теорія пластичності Між цими дисциплінами немає чіткої межі Основна ж роль у вирішенні задач міцності належить опору матеріалів
Усю різноманітність видів конструктивних елементів, що застосо вуються в спорудах і машинах, можна звести до порівняно невеликої кількості основних форм Тіла, які мають ці основні форми, і є об’єкта ми розрахунку нз міцність, жорсткість і стійкість До них належать стержні, оболонки, пластинки й масивні тіла
Стержнем або брусом називається тіло, в якого один розмір (дов жина) значно перевищує даа інших (поперечних) розміри
У машинах та спорудах застосовуються стержні як прямолінійні (рис 1, а), так і криволінійні (рис і, б), як призматичні (рис 1, а), так і змінного перерізу (рис і а) Прикладами прямих стержнів е вали, осі, балки прикладами кривих—вантажопідйомні гаки кільця лан цюгів тощо
Стержні, товщина стінки яких значно менша від габаритних розмі рів поперечного перерізу, називають тонкостінними (рис 1, е) Зараз вони широко застосовуються в будівельних конструкціях, судно- і особливо авіабудуванні
Оболонка — це тіло, обмежене криволінійними поверхнями, які розташовані на близькій відстані одна від одної
Поверхня, рівковіддалена від твердих поверхонь оболонки, назн ваеться серединною За формою серединної поверхні розрізняють обо-
а	б б г д
Рис 2
лонки циліндричні (рис 2, а), конічні (рис 2, б), сферичні (рис 2, в) таін Дооболонок належать неплоскі стінки тонкостінних резервуарів, котлів, куполи будинків обшивки фюзеляжу, крила та інших частин літальних апаратів, корпуси підводних човнів тощо
Якщо серединна поверхня є площиною, то розрахунковий об єкт називають пластинкою (рнс 2, г) Пластинки бувають круглі (рис 2, д), прямокутні (рнс 2, а) й інших обрисів Пластинками можна вважа ти плоскі диища й кришки резервуарів перекриття інженерних споруд, диски турбомашин
Тіла, в яких усі три розміри одного порядку, називають масивними тілами До них належать фундаменти споруд, підпірні стінки тощо
В опорі матеріалів задачі, як правило, розв язуються простими ма тематичними методами за допомогою спрощувальних гіпотез та з використанням експериментальних даних, розв’язки при цьому доводять до розрахункових формул, придатних до застосування в інженерній прак тиці
Виникнення науки про опір матеріалів пов'язують з ім'ям видатного італійського вченого Галілео Галілея (1564—і642), який провадив досліди щодо вивчення міцності, хоча джерела цієї науки мн бачимо ьже в творіннях великого Леонардо да Вінчі
У і678 р англійський вчений Роберт Гук (1635—І703) установив закон деформування пружних тіл, за яким деформація пружного тіла пропорційна діючому на нього зусиллю Цей закон е основним у теорії опору матеріалів
Швидкий розвиток науки про опір матеріалів почався в кінці XVI і і ст. у зв'язку з бурхливим розвитком промисловості та транспор ту Проблемами міцності займались академік Петербурзької академії наук Леонард Ейлер, видатні вчені М О Белелюбськкй. М Г Бубнов, А М Воропаєв, А В Гадолін, X С Головін, Д 1 Журавський, Ф С. Ясннський та ін
У XX ст Значну роль у розвитку механіки й поширенні наукових знань у галузі опору матеріалів відіграли підручники видатних учених В Л Кирпичова С П Тимошенка, М М Бєляєва О О Уманського, В І Феодосьєва, О А ільюшина, 1 А Біргера та ін
$ 2 Види деформацій стержня.
Поняття про деформований стан матеріалу
Реальні тіла можуть деформуватися, тобто змінювати свою форму й розміри Деформації тіл відбуваються внаслідок навантажування їх зовнішніми силами або зміни температури При деформуванні тіла його точки а також мислено проведені лінії або перерізи переміщуються в площині або в просторі відносно свого вихідного положення
При навантажуванні твердого тіла в ньому виникають внутрішні сили взаємодії між частинками, що протидіють зовнішнім силам і нама гаються повернути частинки тіла в положення, яке вони займали до деформації
Деформації бувають пружні, тобто такі, що зникають після припи нення дії сил. які спричинили їх, та пластичні або залишкові,—ті, що не зникають
із збільшенням зовнішніх сил внутрішні сили також збільшуються, але до певної межі, яка залежить від властивостей матеріалу Настає момент коли тіло вже не здатне опиратися дальшому збільшенню зов нішніхснл Тоді воно руйнується Найчастіше для деформацій елемен тів конструкції встановлюють певні обмеження
Основним об’єктом, що розглядається в опорі матеріалів, є стержень з прямолінійною віссю
В опорі матеріалів вивчають такі основні види деформацій стержня розтягання, стискання, зсув (зріз), кручення та згинання
Розглядають також більш складні деформації що утворюються внаслідок сполучення кількох основних
Розтягання або стискання виникає, наприклад, тоді, коли до стерж ня вздовж осі прикладені протилежно спрямовані сили (рис 3) При цьому відбувається переміщення перерізів уздовж осі стержня, який при розтяганні подовжується а при стисканні вкорочується Зміну Ді початкової довжини І стержня називають абсолютним подовженням при розтяганні або абсолютним укороченням при стисканні Відношення абсолютного подовження (укорочення) Д/ до початкової довжини І стрежня називають середнім відносним подовженням на довжині І і, як правило, позначають еср
Єср = Д//І.
На розтягання або стис кання працюють багато елементів конструкцій стержні ферм, колони, штоки парозих машин та поршневих насосів стяжні гвинти тощо
Зсув або зріз виникає тоді коли зовнішні сили зміщують два паралель
Рис. 4
них плоских перерізи стержня один відносно одного при незмінній відстані між ними (рис 4) Зміщення Д$ називається абсолютним зсувом. Відношення абсолютного зсуву до відстані а між площинами, що зміщуються (тангенс кута у), називають відносним зсувом Унаслідок малості кута у при пружних деформаціях його тангенс вважають таким, що дорівнює куту перекосу розглядуваного елемента Отже, відносний зсув
у » Дз/а
Відносний зсув е кутовою деформацією, яка характеризує перекіс елемента На зсув або зріз працюють, наприклад, заклепки й болти, що скріплюють елементи, котрі зовнішні сили намагаються зсунути один відносно одного
Кручення виникає при дії на стержень зовнішніх сил, які утворюють момент відносно осі стержня (рис 5) Деформація кручення супроводжується поворотом поперечних перерізів стержня один відносно одного навколо його осі Кут повороту одного перерізу стержня відносно іншого, що перебуває на відстані і, називають кутом закручування на довжині І Відношення кута закручування ф до довжини і називають відносним кутом закручуваннях
На кручення працюють вали, шпинделі токарних і свердлильних верстатів, а також багато інших деталей
Деформація згинання (рис 6) полягає у викривленні осі прямого стержня або в зміні кривизни кривого стержня Переміщення будь якої точки осі стержня, що відбувається при цьому, виражається вектором, початок якого суміщено з початковим положенням точки, а кінець — з положенням тієї самої точки у деформованому стержні У прямих р стержнях переміщення точок які спрямовані перпендикулярно до початкового положення осі. назива
Риє. 6	Рис 6
Рис 7
Рис 8
ють прогинами й позначають літерою ш При згинанні відбувається також поворот перерізів стержня навколо осей, що лежать у площинах перерізів Кути повороту перерізів відносно їхніх початкових поло жень позначають літерою 0 На згинання працюють, наприклад, осі залізничних вагонів, листові ресори, зуб'я шестерен, спиш коліс, балки міжповерхових перекриттів, важелі та багато інших деталей
Унаслідок одночасної дії на тіло сил, що спричинюють різні види зазначених основних деформацій, виникає більш складна деформація Так часто елементи машин і конструкцій зазнають дії сил що одно часно спричинюють згинання і кручення, згинання і розтягання або сти екання тощо
Описані деформації стержня дають уявлення про зміну його форми й розмірів у цілому, але нічого не кажуть про ступінь та характер де» формованого стану матеріалу Досліди показують, що деформований стан тіла взагалі нерівномірний і змінюється від точки до точки
Для визначення деформації в якій небудь точці А (рис 7) проведе' мо в недеформованому тілі відрізок прямої АВ, що виходить із цієї точки в довільному напрямі й має довжину з Після деформації точки А та В перемістяться й займуть положення Л, та В, відповідно, а від* стань $ між ними зміниться на Д$. Відношення Дз/х » вср називається середньою відносною лінійною деформацією відрізка АВ Наближуючи точку В до точки А, тобто зменшуючи довжину відрізка а, дістанемо граничне значення
і- Дї
•нп —. = елв
Величина вдв є відносною лінійною деформацією в точці Лу напря мі АВ Якщо відомо, що відстань між точками А і В збільшується, то називають відносним подовженням, при зменшенні цієї відстані — відносним укороченням
У одній і тій самій точці А відносні лінійні деформації в різних напрямках можуть бути різними Як правило, основними вважають напрями, паралельні осям вибраної прямокутної системи координат Тоді відносні лінійні деформації в точці позначають відповідно еа, е.
Для повної характеристики деформації в точці вводять ще й кутові деформації. Якщо до деформації тіла з точки А (рис 8) провести два відрізки АВ і АС, що утворюють прямий кут, то після переміщення точок унаслідок деформації тіла відрізки займуть положення А^В, та А,Си а кут між ними зміниться на величину 2. ВАС— ^.В^Сі Наближуючи точки В і С до точки А, матимемо граничну зміну початкового прямого кута на величину
Іші ВАС — В^С^ = уалс
1-М)
1*-»О
Ця зміна прямого кута, виражена в радіанах називається відносною кутовою деформацією в точці А у площині, де лежать відрізки АВ та АС У тій самій точці А відносні кутові деформації в різних площинах різні Як правило, відносні кутові десрормації визначають у трьох взаємно перпендикулярних площинах Тоді їх позначають відповідно
Деформований стан у точці тіла повністю визначається шістьма компонентами деформації — трьома відносними лінійними деформаціями вх еу, е( та трьома відносними кутовими лінійними деформаціями Ух», ї«, У»Х
$ 3. Основні гіпотези науки про опір матеріалів
Для побудови теорії опору матеріалів вводять деякі гіпотези щодо структури й властивостей матеріалів а також про характер деформацій Це такі гіпотези
1	Гіпотеза про суцільність матеріалу Припускається, що ма теріал суцільно заповнює форму тіла Атомістична теорія дискретної будови речовини до уваги не береться
2	Гіпотеза про однорідність та ізотропність Матеріал вва жається однорідним та ізотропним, тобто в будь якому об ємі та в будь-якому напрямі властивості матеріалу вважаються однаковими Хоч кристали, з яких складаються метали, анізотропні проте хаотичне розташування їх дає змогу вважати макрооб'ємн металів ізотроп ними
інколи припущення про ізотропію неприйнятне Наприклад, до анізотропних матеріалів належать деревина, властивості якої вздовж та впоперек волокон істотно різняться, армовані матеріали тощо
З Гіпотеза про малість деформацій Припускається, що деформа ції малі порівняно з розмірами тіла Це дає змогу здебільшого нехтувати змінами в розташуванні зовнішніх сил відносно окремих частин тіла й складати рівняння статики для недеформованого тіла Інколи від цього принципу доводиться відступати Про такі відступи говориться окремо
Малі відносні деформації розглядають як нескінченно малі величини
4 Гіпотеза про ідеальну пружність матеріалу Припускається, що всі тіла абсолютно пружні Відхилення від ідеальної' пружності, які завжди спостерігаються при навантажуванні реальних тіл, неістот ні й ними нехтують до певних меж деформування
Більшість задач опору матеріалів вирішують у припущенні лінійно деформованого тіла, тобто такого, при якому справедливий закон Гука, що відбиває пряму пропорційність між деформаціями та навантажен нями
Прийнявши гіпотези про малість деформацій та про лінійну залеж ність між деформаціями і зусиллями, можна при розв’язуванні біль шості задач опору матеріалів застосовувати принцип суперпозиції (принцип незалежності й додавання дії сил) Наприклад, зусилля в будь якому елементі конструкції, спричинені різними факторами (кількома силами температурними впливами), дорівнюють сумі зусиль, що спричинені кожним із цих факторів, і не залежать від порядку прикладання їх Це справедливо також відносно деформацій
Зазначені гіпотези, а також деякі інші, про які йтиметься далі, дають змогу вирішувати широке коло задач щодо розрахунку на міцність, жорсткість та стійкість Результати розрахунків добре узгоджуються з даними практики
Глава 2. ГЕОМЕТРИЧНІ ХАРАКТЕРИСТИКИ
ПЛОСКИХ ПЕРЕРІЗІВ
Як уже зазначалось (§ і), основним об єктом, що його вивчають у курсі опору матеріалів, є стержень
Опір стержня різним видам деформації часто залежить не тільки від його матеріалу та розмірів, а й від обрису осі, форми поперечних перерізів та розташування їх Тому в цій главі, незважаючи на фізич ні властивості об’єкта, що вивчається розглянемо основні геометричні характеристики його поперечних перерізів, які визначають опір різ ним видам деформацій До них належать площі поперечних перерізів, статичні моменти та моменти інерції
$ 4 Статичні моменти площі.
Центр ваги перерізу
Розглянемо довільну фігуру (поперечний переріз стержня), зв яза-ну з координатними осями Ог та Оу (рис 9) Виділимо елемент площі йЕ з координатами г, у За аналогією з виразом для моменту сили від носко якої небудь осі можна записати вираз і для моменту площі, який називають статичним моментом Так добуток елемента площі 4Г на відстань у від осі Ог
аз, = уОЕ
називається статичним моментом елемента площі відносно осі Ог Аналогічно д8„ — гДЕ — статичний момент елемента площі відносно
Рис 9	Рис. 10
осі Оу Підсумувавши такі добутки по всій плоті Р фі гури, дістанемо відповідно статичні моменти відносно осей г та у
5, = У уйР, 8„ = гаР
(2 1)
Статичний момент вира мається в одиницях довжини в третьому степені (наприклад см*) Позначимо ?с> ус координати центра ваги (ц в ) фігури Продовжуючи аналогію а моментами сил, иа підставі теореми про момент рів надійної можна записатв такі виразні
5, = Рус, — Ріс,
(2 2)
де Р — площа фігури
Звідси координати центра ваги
ге ~ З^/Р. Ус = 8;Р	(2 3)
Із формул (2 2) випливає, що статичні моменти площі відносно цент ральних осей, тобто осей, що проходять через центр ваги дорівнюють нулю
Як приклад визначимо статичний момент площі трикутника (рис іО) відносно осі, яка проходить через основу Завдальшкн увіднеї виділимо елементарну площадку у вигляді смужки, паралельної осі? Площа смужки ар = Ь (у) ііу
Вважаючи, що
Ь(Й = (Ь#>)№ — й маємо
5, = (Г у (Л — »)
Простіше можна розв'язати цей приклад, використавши формули (2 2) Очевидно, що
р^-^-ЬН, ус^-^-Н,
отже,
«.-тИт^-т-
Для визначення статичних моментів складної фігури її розбивають на прості частини (рис 11), для кожної з яких відомі площа Рі та положення центра ваги г1 і у. Статичний момент площі всієї фігури відносно даної осі визначається як сума статичних моментів кожної
осі що проходять через центр ваги перерізу, називають головними центральними осями
Момент інерції' площі фігури виражається в одиницях довжини в четвертому степені (наприклад, см4)
Визначимо момент інерції прямокутника відносно центральних осей г, у, паралельних його сторонам (рис 15)
Для визначення моменту інерції відносно осі г елементарною площадкою будемо вважати безмежно вузький прямокутник, паралельний осі 2, заввишки Уу та завширшки Ь Отже
ОЕ = Ьау,
„	"І?	ййі
7, = \уЧЕ = Ь Г у‘<1у = 2Ь І уЧу(2 ІО) )	—ІЦ?	б
Очевидно, що
/, = Л68/і2	(2 1 і)
Зазначимо, що інтеграл не зміниться, якщо всі смужки йЕ = = Ьсіу перемістити паралельно осі а, відносно якої визначається момент інерції Отже, момент інерції паралелограма (рис іб) відносно цент ратьної осі 2, паралельної основі,
~ ЬЛ*/12	(2 І2)
Визначимо момент інерції трикутника відносно осі, яка проходить
Виділимо елементарну смужку, паралельну зазначеній осі 4Г = Ь (у) ііу Очевидно, ширина смужки, розташованої завдальшки у від осі ?, Ь(Й = (Ь/Л)(Л —И Отже, т?-.	(213)
Визначимо полярний момент інерції площі круга відносно його центра, а також момент інерції відносно центральної осі
При визначенні полярного моменту інерції виділимо елементарну площадку у вигляді безмежно тонкого кільця радіусом р завтовшки Лр (рис 18) Площа такого елемента
АР = 2яр4р
Полярний момент інерції =	=	(214)
>	6
Моменти інерції площі круга відносно центральних осей легко знайти, використавши формулу (2 8)
4 = 4 +
Унаслідок симетрії л=л. отже, = = <2І5>
Знайдемо осьовий момент інерції кругового сектора ОАВ (рис 19) відносно осі г
Використавши полярні координати р, <р, виділимо елементарну площадку <ІР = р&рсір Оскільки
у = рЗІПф,
Рас. їв
Рас. 19
Рис. 20
то
а = £ № = | р*зІпІ ф • (*мр = [(?—а) “а1п 2р 75ІП 2а ]
(2 16)
Для чверті круга а = 0, 0 = л/2 Тоді !, — лг*І\Ь Взявши Р = я, а = 0, знайдемо момент інерції площі півкруга відносно діаметра
У, = пг*/8
Визначимо момент інерції еліпса з півосями а, Ь (рис 20) відносно центральної осі г
Задачу можна розв'язати дуже просто, якщо розглядати еліпс як проекцію нахиленого круга При цьому
УІУХ - Ь/а
Покажемо момент інерції еліпса як суму моментів інерції елементарних прямокутників заввишки у та завширшки &
Останній інтеграл у правій частині є моментом інерції площі круга радіусом а відносно осі г він дорівнює ла4/4 Отже момент інерції еліпса
•' = -3-2ґ-=2Тї-	<2 17)
Очевидно,
$ 6 Моменти Інерції складних перерізів
При розв'язанні різних практичних задач часто виникає потреба визначити моменти інерції складних перерізів відносно тих чи інших осей що лежать у площині фігури Для стандартних поперечних пере-
Рнс 21
У
Рис 22	Рис 23
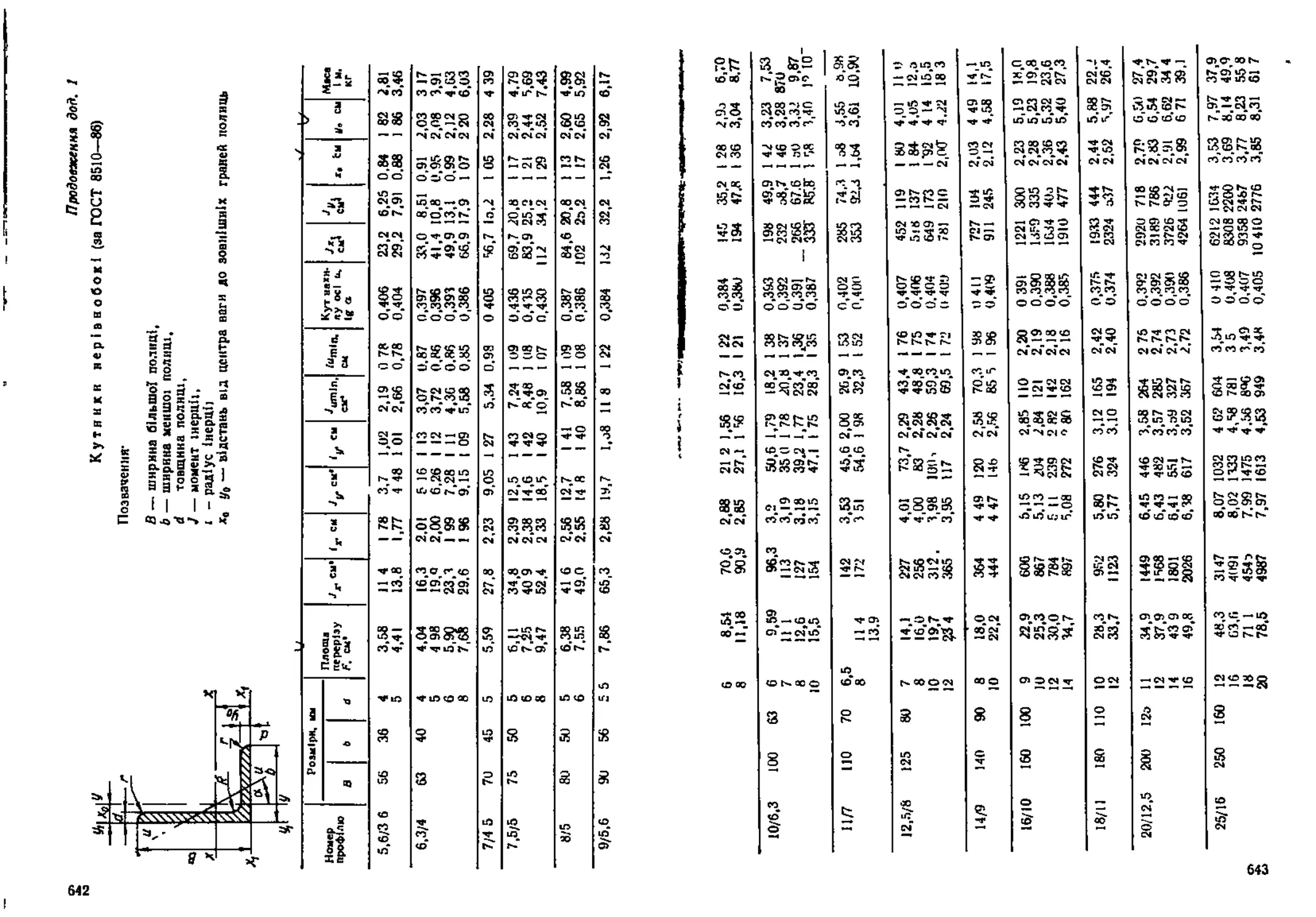
моменти інерції відносно різних осей наведено в таблицях сортаментів ГОСТ 8509-86, ГОСТ 85І0-86, _ ГОСТ 8239—89, ГОСТ 8240—89 по г ряд із розмірами, площами перері
зів положеннями центрів ваги та іншими характеристиками У сор таменп центральні осі перерізів позначені літерами х, у (рис 21)
При визначенні моментів інерції складних перерізів останні можна розбити на прості частини, моменти інерції яких відомі 3 основної властивості інтеграла суми випливає, що момент інерції складної фігури дорівнює сумі моментів інерції 11
складових частин
Нехай, наприклад, треба визначити момент інерції складної фігури відносно осі г (рис 22)

(2 і8)
Розбиваємо фігуру на прості частини 1, П> НІ, наприклад так як показано на рисунку інтегруємо (2 і8) послідовно по площах Ри Ріг Ра простих фігур
/, = ^ № + £ 1ЛО7 +1
Кожний із цих інтегралів є моментом інерції відповідної простої фігури Отже,
7,-7І + 7" + 7"'	(2 19)
Коли в перерізі є отвір, його зручно вважати частиною фігури з від’ємною площею Наприклад, переріз показаний на рис 23, можна розбити на прямокутник Ь х Л та отвір радіусом г від'ємної площі Тоді
/ _ і' і"	яг*
Л-Л - 12	4 •
§ 1. Моменти Інерції відносно паралельних осей
Нехай відомі моменти інерції фігури відносно центральних осей г у
1, - ( уЧР, 7, = | МР \	(2 20)
Треба визначити моменти Інерції відносно осей паралельних центральним (рис 24)
( г^сІР (2 2і)
Рис. 24
Рис 25
Рис 26
Координати будь якої точки в новій системі г^Уі можна виразити через координати в старих осях
г, = г 4- Ь; у, = у 4- а
Підставляємо ці величини у формули (2 2і) та інтегруємо почленно
/2| = Г у]ір = ([у 4- в)* сіР = [ уЧІР +аі[сІР 4- 2а ( удР, (2 22) >	Я	>	Е	>
7, =Гг;<ІЕ = Г(г+ »)•<(/’-(гМГ ЬР { ЛР 2Ь (гЛР (223) р	р	*	Е	р
( ^у^Р = | (г +Ь)(у +а)(1Р = і гуйР 4- яИ АР 4-
4- а У гіР 4-Й удР
(2 24)
Оскільки інтеграли | уйР = 5, та | гдР = 8* дорівнюють нулю як статичні моменти відносно центральних осей то формули (2 22) (2 23) (2 24) з урахуванням (2 20) набирають вигляду
« У, 4. а’Г
4. " 4- &Р;
4ж>Уг = х аЬР
(2 25)
(2 26)
Отже і) момент інерції фігури відносно довільної осі дорівнює мо менту Інерції відносно центральної осі, паралельної даній, плюс добуток площі фігури на квадрат відстані між цими осями 2) відцент ровий момент інерції відносно довільної системи взаємно перпендику лярних осей дорівнює відцентровому моменту інерції відносно цент рольних осей, паралельних даним, плюс добуток площі фігури на коор динати її центра ваги в нових осях
Зазначимо, що координати а, Ь у формулі (2 26) треба підставляти, враховуючи їхній знак
Формули (2 25) показують, що моменти інерції перерізу відносно центральних осей завжди будуть меншими порівняно з моментами інер ції відносно паралельних осей.
Визначимо момент інерції двотаврового перерізу відносно централь ної осі г (рнс 25).
Переріз, що складається з двох однакових полиць Ь х 6 та стінки Ні х і, розбиваємо на ці три прості частини Тоді
4 = 4 + 4' +4"
Момент Інерції ПОЛИЦІ ВІДНОСНО ОСІ 2 згідно з формулою (2 25)
4=4" - 4 + г -	и
Момент інерції СТІНКИ у/	"*1
Л	Ї2~’
Отже, момент Інерції двотавра
;,= 2[4 + М] + -^ Р 27)
Визначимо відцентровий момент інерції прямокутного трикутника відносно осей 2, у (рнс 26), що збігаються з катетами, а також відносно центральних осей г0, у0, паралельних їм
Елементарну площадку беремо у вигляді смужки завширшки Ь (у) та заввишки ду її площа
дР * Ь(у)ду = Л~у Ьду
Горизонтальна координата центра ваги смужки
Відцентровий момент інерції відносно осей 2, у - р-"’ = (-V * -4і	Р 
ьч*
причому
Тоді
(2 28)
Відцентровий момент інерції відносно центральних осей 2В, у, згідно з формулою (2 26)
7 ад, =	--^^вР•
ав = Л/3, Ь9 = Ь/3
24 ~ 2
Ж»
(2 29)
$ 8. Залежність між моментами Інерції при повороті координатних осей
Нехай відомі моменти інерції довільної фігури (рис 27) відносно координатних осей 2 у
1, = ( уЧГ, 1, = (ЛГ, = | гуле (2 ЗО)
Повернемо осі г, у на кут а проти годинникової стрілки, вважаючи кут повороту осей у цьому напрямі додатним Знайдемо тепер моменти інерції перерізу ВІДНОСНО повернутих осей 2и ух
,/г, = | Уі^Е, =	Л,кі "•	(2 Зі)
Координати довільної елементарної площадки в нових осях 2(, у, можна виразити через її координати 2, у в початковій системі за фор мулами
2, = ОС = ОЕ + ДО = гсоза 4-у$Іпа	334
Уі = ВС = ВІЇ—ЕА =усо$а — гзіпа
Підставивши ці значення у формули (2 Зі), матимемо
/ж, — £(усоза — 2 8ша)ягіГ = соз1 а £ /гіГ 4- зіп*а£ ЩЕ—
— зіп 2а ( гуііЕ,
((г соз а 4. у зіп а)’ <1Е = зіп8 а (у'іЕ 4- сої8 а $ ЩЕ 4-
’	'	>	(233)
4- зіп 2а £ гусІЕ,
уіі1(і == (гсоза 4-узіпа)(усоза — гзіпа)4Г «=
= (соз8 а — зіп8 а) гусіЕ 4- зіп 2а уя<іЕ — £ г’477^.
Ураховуючи формули (2 ЗО), остаточно знайдемо
соз1 а 4- зіп8 а —	зіп 2а;	34)
Л» ~ Л 5ІП’а + с05* ® +	8іп 2а,
Л>у,в^«сО52а—£-(/, —4)яіп2а	(2 35)
Зазначимо, що ні формули, здобуті прн повороті довільної системи прямокутних осей, звичайно справедливі й для / \ центральних осей -----‘ * — Додаючи почленно вирази (2 34), знаходимо
(2 36)
Отже прн повороті прямокутних осей сума осьових моментів інер-ції не змінюється і дорівнює полярному моменту інерції відносно початку координат
Прн повороті системи осей на кут а «= 90°	«
Ні =	/гм =
5 9. Визначення напряму головних осей Інерції. Головні моменти Інерції
Найбільше практичне значення мають голова! центральні осі, відцентровий момент інерції відносно яких дорівнює нулю Будемо позначати такі осі літерами и, V Отже,
^ = 0
Для визначення положення головних центральних осей несиметрич ної фігури повернемо довільну початкову систему центральних осей г, у (рис 28) на деякий кут а0, при якому відцентровий момент Інерції дорівнюватиме нулю
Аі*, = /«'в 0.
Тоді з формули (2 35)
]ііУі = Зщ соз2во —зіп2а0 = 0,	(2 37)
звідки
І? 2(2. = -^--	(2 38)
Добуті з формули (2 38) двоє значень кута а різняться між собою на 90е і дають положення головних осей Менший із цих кутів за модулем не перевищує я/4 Будемо далі користуватися тільки меншим кутом Проведену під цим кутом (додатним чи від'ємним) головну вісь будемо позначати літерою и Нагадаємо що від'ємні кути а0 відкла даються від осі г за годинниковою стрілкою Нарис 29 наведено деякі приклич п впачепия гшовних осей згідно із зазначеним правилом 11<і іиткчні осі ноліачсио літірімн г та у
Рис 29
Головні моменти Інерції можна знайти із загальних формул (2 341 переходу до повернутих осей, взявши а = «о
. І, соз8 а0 + зіп2 Оо — зіп 2а0, зіп8 а0 + ./у соз8 «о + /,в зіп 2а0 Перетворимо формули (2 39) для головних центральних моментів інерції, склавши вирази для їхніх суми та різниці Маємо
+ Л	(240)
^и—^в^=(^, — ^I/)со$2аI, — 2/ад5Ш2оо(У, — /*)	, (241)
причому у виразі (2 41) зроблено заміну із формули (2 38)
27аі = (/и-У,)ІЄ2а0
Тепер із формул (2 40) та (2 41) знаходимо більш зручні виразні
, , , <242>
а,-4-| у-їяЇег]-
Очевидно, що при У, > Л, момент
Використовуючи формулу (2 38), можна виключити з виразів (2 42) величину
75^-= ±/1 +ів*2«,= ± /і +
У результаті маємо
4 - 4-	± / (А - +«•'•І • і2 43»
/. = 4-	7«> т - Л)! + <4],
V	причому верхні знаки беремо при > }в, а
\И	нижні — при ,Іг < Л
V-** —\	Отже, формули (2 38), (2 43) і (2 44) дають
/у А/Ч змогу визначити положення головних осей та !	\	.хд	\а	головні центральні моменти інерції
і	І Г і/ Якщо тепер замість довільної початкової
\	І	системи центральних осей гОу взяти головні
X.	У	осі (рис ЗО), то формули (2 34), (2 35) пере-
------ХОДУ до повернутих осей спростятьсяі
Рве зо	= /и сов8 а + /в зіп1 а;
== /„ зіп8 а + /в соз1 а,	(2 45)
= 4" 8ІП 2а
Важливо зазначити, що головні моменти Інерції мають властивість екстремальності У цьому легко переконатися, проднференціювавши вираз для моменту інерції відносно довільної осі Ідив формули (2 34)1 по змінній а
47
зіп 2а + 4* зіп 2а — 2Л? соз 2а =
= — 2 соз 2а----------зіп 2а) = — 2/аді,
Звідси випливає, що похідна дорівнює нулю, коли = 0, а це означає, шо екстремальні значення мають моменти інерції від носно головних осей
Ураховуючи що сума моментів інерції відносно двох взаємно пер* пендикулярних осей — величина стала, можна зробити висновок, що відносно однієї з головних осей момент інерції має максимальне значення, а відносно іншої — мінімальне
Зауважимо, що площини, проведені через вісь стержня та головні осі його поперечного перерізу, називають головними площинами
$ 40. Графічне зображування моментів інерції
Визначення моментів інерції за формулами (2 45) чи (2 43) (2 44) можна замінити простою графічною побудовою При цьому розріз няють пряму та зворотну задачі Перша полягає у визначенні моментів інерції відносно довільних центральних осей г, у за відомими напряма ми головних осей та головними моментами інерції (формули (2 45)1 Найбільше практичне значення має друга задача Вона полягає у визначенні положення головних осей та значень головних центральних моментів інерції за відомими моментами інерції	відносно
будь якої системи прямокуїних центральних осей (формули (2 43), (2 44) і (2 38)]
Пряма задача. Нехай треба визначити моменти інерції Іц, відносно осей 2, у (рис. Зі, а) за відомими напрямами головних осей та величинами )а, Для певності вважаємо
Аналітичний розв’язок двється формулами $ 45)
Для графічної побудови введемо в розгляд геометричну плоти ну та віднесемо Ті до прямокутної системи координат По осі абсцис будемо відкладати осьові моменти інерції (Л А	), а по
осі ординат — відцентрові	)
У певному масштабі відкладаємо від початку координат О вздовж осі абсцис (рис 3(, б) відрізки ОА та ОВ, які дорівнюють головним моментам інерції Відрізок АВ ділимо навпіл, так що ВС = СА = = (]и—У„)/2 із точки С радіусом СА описуємо коло яке називаючи кругом інерції Для визначення моменту інерції відносно осі г, проведеної під кутом а до головної осі и, із центра круга під кутом 2а проводимо промінь СР, (додатні кути відкладають проти годинникової стрілки)
Покажемо що ордината точки Ря круга дорівнює відцентровому моменту інерції /ад, абсциса —моменту інерції відносно даної осі г Маємо
РХ = СР, зіп 2а = зіп 2а	(2 46)
Порівнюючи формули (2 46) та (2 45), бачимо, що РЯКЯ ==	Далі,
ОК, >=ОВ + ВС	+ ~	- Л) + -у Л — со52а =
=г -^-/„(1 + соз 2а)	— соз 2а) = /исо5*а + /озіп*а (2 47)
Згідно з формулою (2 45), ОК, = /я Отже, у певному масштабі абсциси точок круга інерції дають нам значення осьових моментів інерції, а ординати — відцентрових
а
Щоб визначити момент інерції відносно осі у, перпендикулярної до осі 2 і отже, проведеної під додатним кутом 0 == а + п/2 до головної осі и, проводимо із центра круга промінь СД„ під кутом 20 = 2 (а + т п/2) Очевидно, він є продовженням променя СД, Абсциса точки Д, (відрізок 0Лж) дорівнює моменту Інерції Ордината цієї точки дає нам значення відцентрового моменту інерції з протилежним знаком (—що відповідає повороту осей на 90°
Зазначимо, що двом взаємно перпендикулярним осям відповідають дві точки круга Д„ ОИ, що лежать на одному діаметрі
Проведемо Із точки Д, пряму (штрихова лінія на рис ЗІ, б), паралельну осі з, якій ця точка і належить Точку М перетину прямої з кругом називають полюсом круга інерції1 Легко показати, що лінія, яка сполучає полюс з будь якою точкою круга, дає напрям осі, якій ця точка круга належить
Покажемо, наприклад, що пряма МА дає напрям головної осі и За побудовою, кут АСД, дорівнює подвоєному куту а між осями и та г Кут й^МА як вписаний та обпертий на ту саму дугу АД* дорівнює половині центрального кута АСД„ тобто а. Отже, лінія МА, що утворює з напрямом осі 2 кут а, паралельна осі и Аналогічно пряма МВ паралельна головній осі о
Зворотна задача Нехай відомі моменти інерції	площі
перерізу стержня відносно деякої системи перпендикулярних осей 2, у (рис 32, а) Треба визначити головні моменти інерції та положення головних осей Для певності побудови припустимо ЩО /,>
>0
У геометричній площині (рис 32 б) будуємо точки Д, та Др які відповідають моментам інерції відносно осей г та у Абсцисами цих то ток е осі опі моменти інерції ОК, — ОКу = ординатами — від
 11 II ІІИ >  , їй пІї її  ч І  і -і ІЧ ія ЛЛі фіН.уі'' м я/іу <
Рис. 33
центровий момент інерції Уц,, Причому = і ід КуОу =—і.у Оскільки обидві точки належать одному діаметру, то, сполучивши їх матимемо центр С круга Інерції Із центра С описуємо коло радіусом
со. = со, _	+>!. Р
яке перетинає вісь абсцнс у точках А та В Очевидно, що абсциси цих точок — відрізки ОА та ОВ — і є шуканими головними моментами інерції /и Дійсно,
ол = о/с, + л,с + сл = /, +	)* + 4 =
= ~ [(Л + Л) +	+4-/ад] .
ОВ = ОКу + КуС -СВ	у +

= 4- [ іл+',) - Кіл - V н 4/ї,]
Для визначення напряму головних осей побудуємо фокус круга інерції Для цього з точкн	проведемо лінію, паралельну осі
г (у) до перетину з кругом у фокусі М Сполучаючи фокус з точками А В круга, дістанемо напрям головних осей и та© (рис 32,6)
Графічне розв'язання зворотної задачі відповідно до чотирьох схем, зображених на рнс 29, показано на рис 33
5 11. Поняття про радіус І еліпс Інерції
Момент інерції фігури відносно будь якої осі можна подати у вигляді добутку площі фігури на квадрат деякої величини, що називають радіусом Інерції
=	= Гі]	(2 49)
де Іг — радіус інерції відносно осі г
Із виразу (2 49) випливає, що
іг = \ҐТуЕ	(2 50)
Аналогічно радіус інерції площі перерізу відносно осі у
і,^ф	(2 51)
Головним центральним осям інерції відповідають головні радіуси інерції	____
‘, = УТ7р	(2 52)
Наприклад, для прямокутника, зображеного на рис 15, головні радіуси інерції
,	»	,=т/2Г________
* V Е т 126Л	21 3 * *	'	2 і З
Побудуємо на головних центральних осях інерції фігури еліпс а півосями, що дорівнюють головним радіусам інерції, причому вздовж осі и відкладаємо відрізки ів, а вздовж осі о — відрізки іи (рис 34) .	Цей еліпс, який називають еліпсом інерції,
X /	має таку властивість Радіус інерції віднос
\У	но довільної осі г визначається перпенди
куляром ОД, проведеним із центра еліпса -----\ р	на дотичну до еліпса, паралельну цій осі уТА \ \і Для визначення точки дотику досить про-/А хух' \ V вести паралельно даній осі г будь яку хор //х /\	ду Точка перетину еліпса з прямою, що
/ •	/	І	сполучає центр 0 із серединою хордн і є
\	I	ТОЧКОЮ дотику Вимірявши потім відрізок
______І	ОА — Ів, знаходимо момент інерції
Рис. 34	/, — РІІ.
5 12 Порядок розрахунку
.Можна рекомендувати такий порядок визначення положення головних осей та значень головних центральних моментів інерції складного поперечного перерізу, що складається з простих частин характерне?» ки яких легко дістати
І Проводимо довільну систему прямокутних координат Розбиваємо фігуру на прості частини та визначаємо за формулами (2 5) положення її центра ваги
2 Проводимо початкову систему центральних осей г, у так, щоб можна було найбільш просто визначити моменти інерції частин фігури відносно цих осей Для цього знаходимо моменти інерції частин фігури відно- но їхніх власних центральних осей, проведених паралельно осям а у, та користуємося формулами переходу до паралельних осей (2 25) та (2 26) Таким чином знаходимо значення
З Визначаємо із формули (2 38) кут нахилу головних центральних осей, причому вісь проведену під меншим кутом (додатним чи від'ємним), позначаємо літерою и, а перпендикулярну до неї —літерою ь
4 За формулами (2 43) та (2 44) визначаємо головні моменти інерції
Приклад 1 Для перерізу. показаною на рис 35, а, визначимо положення гО' лосних осей інерції головні моменти інерції та радіуси інерції Координати центра ваги цієї фігури в системі осей такі (табл /) га = 2,33 см у0 = 4,33 см
Проводимо початкову систему центральних осей г у паралельно сторонам кут ннка. Для визначення моментів інерції відносно них осей розбиваємо фігуру на прості частини — прямокутники І і 11 — та проводимо через їхні центри ваги власні центральні осі т, уд та у^ паралельно сторонам
Моменти інерції кожного прямокутника відносно власних центральних осей лег ко визначити за формулами (2 10) І (2 11)
,	2 10*	,	10 2*
1'гі “--12— = 166 7 см* У' = —{у— = 67 см*.
4>-ПГ-"5 33с>*' У" = -Ц^- = 85,3 см*
Моменти інерції кожної простої фігури відносно центральних осей г, у знаходимо ва формулами переходу до паралельних осей — (2 25) та (2 26) Наприклад
—	+	166,7 4-20 • 2 67* см«=- 308,1 см*
'«а =	“ 0 “ 20 2 67 1 33 см‘== — 71 см*
Результати обчислень зводимо в табл 2.
Підсумовуючи останні три колонки таблиці знаходимо моменти Інериії фігурн відносно центральних осей г, у
4 - 492,0 см* І72 0см«, 7^ = — 160,0 СМ*.
Кут нахилу головних центральних осей до осі г назначимо ва формулою (2 38)
2 2-2798
зві тки ?0 = 22® ЗО'
Головні центральні моменти інерції визначаємо за формулами (2 43) та (2 44)
Л, - 4" |(Л + + ‘ИУ«~А')’+ 47^| = 4*(664 0 і-45215) с“‘ =
=- 558 З сн‘
А>=4'|(/г‘і 4) -	+ М'гіІ) - 4- (664 0 - 452 5} см‘ =
= 105 8 см«
Головні центральні радіуси інерції ~*~аа’
'“-К?- /¥»”«" '-КУ-іЛтг»-1”»
Графічне розв язанпя задачі аокаїаио на рис 35 б
Глава 3. ЗОВНІШНІ Й ВНУТРІШНІ СИЛИ МЕТОД ПЕРЕРІЗІВ. ЕПЮРИ ВНУТРІШНІХ СИЛ
$ 13 Класифікація зовнішніх сил
Зовнішніми силами називають сили взаємодії між розглядуваним елечентом конструкції та пов'язаними з ним тілами
Якщо зовнішні сили е наслідком безпосередньої контактної нзаємо-дії даного тіла з іншими тілами то вони прикладені тільки до точок поверхні тіла в місці контакту і називаються поверхневими силами Поверхневі скли можуть бути неперервно розподілені по всій поверхні ті та або її частині, наприклад тиск пари в котлі вітрове та снігове навантаження, тиск газу в циліндрі двигуна
Навантаження, що припадає на одиницю площі, називається інтенсивністю навантаження її, як правило, позначають р й виражають у паскатях (Па) або кратних йому одиницях (кПа, МПа, ГПа) Часто навантаження, розподілене по поверхні (рис 36 а), зводять до голов іюї площини (рис 36, б), унаслідок чого створюється навантаження, розподілене по лінії, або лінійне навантаження Інтенсивністю такого навантаження у, Н/м, кН/м, МН/м, називають навантаження, що припадає на одиницю довжини лінії Інтенсивність може бути змінною по цій довжині Характер зміни навантаження, як правило, показують у вигляді епюри (графіка) у
У разі рівномірно розподіленого навантаження (рис 36, а) епюра у прямокутна (рис 36,6) При дії гідростатичного тиску епюра наванта женія у трикутна (рис 37) Бувають епюри у і більш складних ви дів трапецієвидна синусоїдна та ін.
Зазначимо, що рівнодійна розподіленого навантаження чисельно дорівнює площі його епюри і прикладена в центрі її ваги
Якщо навантаження розподілене по невеликій частині поверхні ті ла то його завжди замінюють рівнодійною, яку називають зосередженою силою Р, Н кН або МН Крім того бувають навантаження, які можна подати у вигляді зосередженого моменту (пари) Моменти М (Н м, кН м або МН м) будемо зображати одним із двох способів показаних на рис 35 а, б Іноді момент зручно подавати у вигляді вектора, перпендикулярно го до площини дії пари Вектор моменту домовимо ся завжди вважати право гвинтовим Для того щоб відрізняти його від векто ра сили, лінію вектора мо менту роблять хвилястою
(рис 38, г) або ставлять дві стріл ки (рис 38 в)
Бувають такі навантаження, які нее наслідком контакту двох а 5	0 а тіл, наприклад: власна вага.си
Рис 38	ли інерції тіла, ідо рухається та
ін Ці сили прикладені в кожній точці об'єму, який займаетіло і тому називаються об'ємними або масо вами силами Власна вага деталей або частин машин та споруд, як пра вило менша, ніж інші навантаження, що діють на них Тому якщо  немає особливого застереження, далі власну вагу не будемо брати до уваги
Залежно від характеру прикладання сил у часі розрізнюють навантаження статичні й динамічні Навантаження вважається статич ним, якщо воно відносно повільно Й плавно (хоча б протягом кількох секунд) зростає від нуля до свого граничного значення а далі зали шаеться незмінним При цьому можна знехтувати прискореннями деформованих мас, а отже, й силами інерції
Динамічні навантаження супроводжуються значними прискореннями як деформованого тіла, так і тіл, що взаємодіють з ним При цьому виникають сили інерції, якими неможна нехтувати Динамічні наван таження поділяють на миттєво прикладені ударні та повторно змінні
Навантаження вважається миттєво прикладеним, якщо воно зрос тае від нуля до свого граничного значення за дуже малий проміжок часу (частки секунди) Таким є навантаження при займанні пального в циліндрі двигуна внутрішнього згоряння або при зрушуванні з місця залізничного состава
Для ударного навантаження характерне те що в мить його прикла дання тіло яке спричинює навантаження, має певну кінетичну енергію Таке навантаження утворюється, наприклад при забиванні паль за допомогою копра, в деталях механічного коваїьського молота
Багато деталей машин (шатуни вали, осі залізничних вагонів то ’ що) зазнають дії навантажень які безперервно й періодично змінюються в часі. Такі навантаження називають повторно змінними Вони як І І	правило, пов’язані з рухами деталей, що циклічно змінюються Це
|	зворотно поступальні рухи штока поршня, коливання елементів конст
рукцій тощо
І § 14 Внутрішні скли. Метод перерізів. Епюри
11	Між сусідніми частинками тіла (кристалами, молекулами, ато-
|	мами) завжди є певні сили взаємодії, тобто внутрішні сили ЦІ
І	сили в усіх випадках намагаються зберегти тіло як єдине ціле,
І	протидіють усякій спробі змінити взаємне розташування частинок
1	Отже, внутрішні сили що діють між двома будь якими частинками, в
навантаженому та ненавантаженому тілі будуть різними.
Рис 39
Рис 40
В опорі матеріалів не розглядають та не беруть до уваги внутрішні сили, що діють в тілі, яке перебуває в своєму природному (ненавантаже-ному) стані, а вивчають й визначають тільки т: додаткові внутрішні сили, які з'являються внаслідок навантажування тіла Тому надалі, кажучи про внутрішні сили будемо мати на увазі власне ці додаткові сили взаємодії, що виникають внаслідок навантажування Внутрішні сили часто називають зусиллями
Для виявлення, а потім і визначення внутрішніх сил в опорі матеріалів широко застосовують метод перерізів
Розглянемо довільне тіло, навантажене самозрівноваженою системою сил У місці яке нас цікавить уявно розсічемо його деякою площиною на даі частини — А І В (рис 39 а) При цьому сам переріз тепер буде мати даа боки один, що належить частині А тіла (лівий), і др\гий, що належить частині В (правий) У кожній точці обох боків перерізу будуть діяти сили взаємодії (рис 39, б) Виходячи із введеної гіпотези про суцільність матеріалу, доводиться зважати на те що внутрішні сили діють в усіх точках проведеного перерізу і, отже, є розподіленим навантаженням Залежно від форми тіла і характеру зовніш піх навантажень інтенсивність внутрішніх сил у різних точках може бути різною
Треба підкреслити, що внутрішні сили, які діють по перерізу, що належить частині А тіла, відповідно до третього закону Ньютона, дорівнюють за модулем та протилежні за напрямом внутрішнім силам, які діють по перерізу що належить частині В тіла (рис 39,6) Інакше кнжучи, внутрішні сили, що діють на різні частини тіла, взаємні Як усяку систему сил їх можна звести до однієї точки (як правило, до центра ваги перерізу) внаслідок чого на кожному боці перерізу мати мемо головний вектор та головний момент внутрішніх сил у перері-
зу
Зокрема, стержень розсікають площиною перпендикулярною до осі, тобто поперечним перерізом (рис 40 а) Якщо головний вектор та головний момент внутрішніх сил спроекш'ювати «а вісь стержня х та головні центральні осі перерізу р та г го на кожному боні перерізу матимемо шість внутрішніх силових факторів (рис 40 б) три сили (Л1, (?ь (?г) і три моменти (Мх Му ЛІ,) Ці величини називають енугп ріщніми зусиллями в перерізі стержня
Зусилля Л/ спричиню? поздовжню деформацію стержяя (розтягання або стискання); чу та — зсув боків перерізу відповідно в напрямах осей у та г Мх — кручення стержня, Му та М, — згинання стержня в головних площинах (гх та уг) Тому для зусиль і моментів у перерізі домовилися про такі назви N —поздовжня або осьова (спрямована вздовж осі стержня) сила С)у р, — поперечні (рідше — перерізуючі) сили; Мх — Мир — крутний момент Му, Мг — згинальні моменти
Для зусиль та моментів у перерізі можна дати такі означення поз дозжня сила N — це сума проекцій усіх внутрішніх сил то діють у перерізі на нормаль до перерізу (або на вісь стержня) поперечні сили
та О» — не суми проекцій усіх внутрішніх си т 5 перерізі па готов ні центральні осі перерізу у та г відповідно крупний момент Мх (або
— це сума моментів усіх внутрішніх сил у перерізі відносно осі стержня, згинальні моменти Му та Мг — це суми моментів усіх внутрішніх сил у перерізі відносно головних центральних осей Перерізу у та 2 відповідно
Кожне з цих зусиль або моментів, як уже зазначалось, е наслідком взаємодії частинок розсіченого тіла, а тому повинно подаватись у вигляді двох протилежно спрямованих але однакових за модулем векторів або моментів (рис 40, б) Сукупність величин N (}у, (}г, прикладених до правого боку перерізу, замінює дію вилученої лівої частини стержня на праву частину сукупність зусиль та моментів що прикладені до лівого боку перерізу, визначають дію правої частини стержня на ліву
Для практичного обчислення зусиль та моментів у перерізі дово днться зважати на таке N чисельно дорівнює алгебраїчній сумі нроек цій ва вісь стержня (на нормаль до перерізу) всіх зовнішніх сил що діють на одну з частин (ліву чи праву) розсіченого стержня, <3Р — те саме, але на вісь р	—те саме але на вісь з; Мкр чисельно дорівнює
алгебраїчній сумі моментів відносно осі стержня всіх зовнішніх сил, що діють на одну із частин (ліву чи праву) розсіченого стержня, Му — те саме відносно осі у, М, — те саме але відносно осі г До цього вис новку легко дійти, якщо розглянути рівновагу кожної з частин розсі ченого стержня При цьому сума проекцій (або моментів) сил ліворуч від перерізу повинна бути прикладена до правої частини стержня, і навпаки
Отже, метод перерізів дає змогу знайти всі зусилля та моменти в будь якому перерізі стержня при дії будь якого навантаження Для цього треба»
І) знайти головні центральні осі поперечних перерізів стержня, 2) кислено провести поперечний переріз стержня в тому місці, де треба знайти зусилля та моменти,
3) визначити сили N. (}у С)г та моменти Лімр, Му М* як алгебраїчні суми проекцій та моментів зовнішніх сил, що діють на одну із частин (ліву чи праву відносно перерізу) розсіченого стержня (як правило, на ту, де проекції та моменти знаходяться простіше)
Як ілюстрацію до використання методу перерізів розглянемо такий приклад знайти зусилля та моменти в перерізі, що розташований посередині стержня (рис 41)
(Оскільки переріз стержня —це прямокутник то головними Цент ратьними осями перерізу вважатимуться осі симетрії прямокутника Зусилля та моменти в перерізі знаходимо як суми проекцій та моментів сил, що діють на ліву частину розсіченого стержняі
Я = ЮР, $у = Р-, <2,^ 0, Мкр = 0,
Мк = 0, мг~ — Р-^
Неважко перевірити, що, обчислюючи суми проекцій та моментів сил які діють на праву частину стержня, дістанемо гой самий результат Наприклад,
Зусилля та моменти в різних перерізах одного й того самого стержня різні Графіки (діаграми), шр показують, як змінюється внутрішнє зуіилля при переході від перерізу до перерізу, називають епюрами Зазначимо деякі правила що застосовують при побудові епюр
1	Вісь (базу), на якій будується епюра завжди вибирають так, щоб вона була паралельна або просто збігалася з віссю стержня
2	Ординати епюри відкладають від осі епюри по перпендикуляру
З Штрихують епюри лініями, які перпендикулярні до бази
4 Для зусиль та моментів вибирають певний масштаб Ординати відкладають суворо в масштабі Крім того, на епюрах проставляють числа, що показують значення характерних ординат а в полі епюри в кружку ставлять знак зусилля
5 1$. Епюри ПОЗДОВЖНІХ сил
Поздовжня (осьова) сила вважається додатною, якщо вона спричинює розтягання, та від'ємною, якшр спричинює стискання Зовнішні сили самі по собі ні додвтпі ні від'ємні, але кожна дає у виразі для N дода нок певного знака
Як приклад побудови епюр осьових сил розглянемо стержень (рис 42) навантажений у точках А В та С зосередженими силами
Ра> Рз уздовж ОСІ
Розпочинаючи будувати епюру стержень поділяють на ділянки Ділянкою називають частину стержня між точками прикладання зосереджених сил Якщо на стержень діє розподілене навантаження, ділянкою називають частину стержня, на якій розподілене навантажен ня змінюється за одним законом
У розглядуваному прикладі дві ділянки — 1 (АВ) та 11 (ВС)
Щрб побудувати епюри треба скласти вирази для осьових сил у довільному перерізі кожної* ділянки
Виберемо початок координат у крайній лівій точці стержня; вісь х спрямуємо вздовж його осі У довільному перерізі будь якої ділянки завдальшки х від початку координат знаходимо осьову силу як суму проекцій усіх зовнішніх сил ліворуч чи праворуч від перерізу, ЩО розглядається І ділянка (0 < х < а)
ліворуч N (х) — РІ =- 2 кН,
праворуч N (х) = Р, —	— (5 — 3) кН = 2 кН,
II ділянка (а < х І)
ліворуч (х) ж Р, — Р, = (2 — 5) кН = — 3 кН, праворуч N (х) = — Р9 = —3 кН
Оскільки ці величини не залежать від абсциси перерізу, то в усіх перерізах пер шої ділянки поздовжня сила # = 2 кН а для будь якого перерізу другої ділянки N = —3 кН Відкладаючи здобуті ординати від осі епюри, будуємо епюру N. Зазначимо, що штриховка епюри показує ординати, які відкладаються У перері-
Ряс 44
зах А В та С ми на епюрі маємо стрибки, що дорівнюють відповідно 2,5 та 3 кН, тобто тим самим силам, які прикладені до стержня в цих перерізах
Якщо на стержень діють тільки зосереджені сили то лінії епюри пзраіеіьні її осі (епюра N складається з прямокутників і має стрибки в тих перерізах де прикладені зовнішні сили) Так, неважко Перекопа тиси що для стержня зображеного на рис 43 епюра буде мати такий вигіяд як показано на рисунку
Якщо стержень розміщений вертикально і враховуєтеся його власна вага, то лінія епюри нахилена до осі (для циліндричного стержня) або криволінійна (для стержня з розмірами перерізів, що неперервно змі нюються)
Приклад 2 Побудуємо епюру N для східчастого стержня з урахуванням Ного в. іісноі ваги (рис 44) Площа перерізу верхньої частини стержня — Р1 нижньої — Гл Питома ваги у, ії/м3
Поіаток координат вибираємо а точці А (на рисунку показано тільки вісь х) Поздовжню ситу в будь якому перерізі находимо як суму зовнішніх сил (щоб спочину не визначати реакції я опорі) Тоді для ділянки Аб
N (х\ ~-Р-уІ\х (0<х<аі дія ВС
N (х) — —Р — уґ(в — уРв (х — а) (а < х < 0
Це рівняння похяткк прямих, отже епюра «V трапеиіевианв Проте оскільки піощі попере іііцх перерізів на ділянках різні нахнл епюри на ділянках АВ та ВС
неоднаковий
При х — І із другого рівняння знаходимо най Гі ьше за моду тем поздовжнє зусилля іУ ——[Р } ур,а -г- ур, (І — а)| Цій самій величині дорів нює й реакція а закріпленні
Приклад 3. Побудуємо епюру N для конічного цпержнч від його власної валі (рис 45)
Прн будь якому зна іенні х осьове зусалля в пе рсріїі дорівнює вазі нижньої відносно перерізу ча спіни конуса Діаметр основи цієї частини
4(х)- -р (1 -х)
Рас 46
тему
" М --у Т7Г ('“') Звідси видно що крива епюри буде кубічною параболою, причому
Отже в йнжній точці епюра торкається ссі При х « 0
'*пих 12
$ 16. Епюри крутих моментів
Деформація кручення найбільш поширена у валах Якщо навантаження на прямолінійний стержень (вал) складається тільки з моментів Лія, площини яких перпендикулярні до осі стержня то із шести зусиль та моментів у довільному перерізі залишається лише крутний момент Мкр
Внутрішній момент Ліф виражається через зовнішні Л4К ЛІкр у перерізі дорівнює сумі зовнішніх моментів Мк, розташованих по один бік від перерізу Якщо стержень (вал) обертається рівномірно то алгебраїчна сума всіх Мл дорівнює нулю Тому при визначенні Л4кр матимемо один і той самий результат, незалежно від того, чи будемо брати суму моментів М„ розташованих ліворуч або праворуч від перерізу
КрутниЙ момент Мкр вважається додатним, якщо при спостеріганні з торця вздовж осі розглядуваної частини він намагається обертати переріз за годинниковою стрілкою (рис 46)
Розглянемо як приклад будуваї трансмісійного вала (рис 47, а)
Розбиваємо стержень на ділянки /, 11, III, IV Вибираємо початок координат у крайній лівій точці ва ла Оскільки тертям у підшипниках нехтуємо то в будь якому перерізі на ділянці І (0 х < а)
^ = 0
епюр крутних моментів для
Рис. 46
Провівши довільні перерізи зі змінною абсцисою х нарешті ділянок вала дістанемо відповідно
II ділянка (0<х<2а) Л4кр = ЛІК| = 160 Н м (ліворуч)
III ділянка (2а<х<3а), Лїкр = Лїкі 4~ М>а = (160 + 60) Н м =
<= 240 Н м (ліворуч),
IV ділянка (За <х<5а), Л4кр = Мкі 4- Ліщ —	=
= (160 4- 80 — 300) Н м — — 60 Н м (ліворуч)
Лінр = —Мк<= — 60 Н м (праворуч)
Крутний момент на кожній ділянці не залежить від абсциси переріз) тому епюра крутинх моментів має вигляд трьох прямокутників (рис 47,6) У перерізах де прикладені зосереджені зовнішні моменти Л4„ утворюються стрибки на значення цих моментів Зазначимо, що в місці стрибка кратні моменти не визначають їх обчислюють на нескін ченно близьких відстанях ліворуч та праворуч від стрибка
Поб)довапа епюра (рис 47, б) показує що хоч до вала й прикла депо момент Млі ~ 300 Н м проте найбільший крутний момент у перерізі дорівнює лише 240 Н м Це значення й треба використовува ти при розрахунках на міцність та жорсткість Напрями крутних моментів у перерізах найбільш навантаженої' частини вала—ділян кн /// — показано на рис 47, в
На практиці часто задаються не моменти Мк, Н м прикладені до дисків (шківів або зубчастих коліс), а потужності К, Вт, що передаються на них або знімаються з них та частота обертання вала п Установимо залежність між цими величинами
Як відомо з курсу теоретичної механіки, момент здійснює роботу на куті повороту Позначивши кутову швидкість вала ш знайдемо, що за час І диск обернеться разом із валом на кут иґ, рад.
. ял .
ш'=То 1
і момент Мк здійснить роботу
А - М.аі М*1,
де Л — робота, Дж МЛ — момент Н м п — частота обертання хв 1 і — час с
Тоді потужність (робота за 1 с)
к __ А _ ллЛ4к
л ~ і ~ зо
Звідси випливає, шо
М, = 9,5494,	(ЗІ)
де К — потужність, Вт
Рис. 48
У старій технічній літературі використовувалася позасистемна одиниця потужності — кінська сила (і к в « 736 Вт) Якщо потужність, що передається або знімається, дорівнює к с , то К = 736# і з виразу (3 1)
М, -9,549 - 736 -ї- = 7028,8 —	(3 2)
п	п	' '
Приклад 4. Побудуємо епюру крутних моментів для бруса, який навантажено за схемою рис. 48, а
Легко побачити, що навантаження, яке діє на стержень еквівалентне розподі ленкм крутням моментам тк (рис. 48, б) інтенсивністю уЬ. Н м/м
Брус має дише одну ділянку в довільному перерізі якої
^кр (’)  -	- - дЬх, (0 < дг < /)
Л4кр(0)«0 Мкр(1)^-уЬІ
У результаті матимемо трикутну епюру (рнс 48 є) причому Мкв тв1 =• —уЬІ при х «“ І
$ 17 Валім І їхні опори
Балками будемо називати прямолінійні стержні шр працюють на згинання В опорі матеріалів термін єбалка» значно ширший, ніж у звичайному використанні цього слова з точки зору розрахунків на міцність, жорсткість та стійкість балкою є не тільки будівельна балка, а також і вал, болт, вісь залізничного вагона, зуб шестерні тощо
Спочатку обмежимося побудовою епюр для найпростішого ви падку згинання балок, при якому всі задані навантаження діють в одній площині, що називається силовою (на рис 49, а — площина П), причому ця площина збігається з однією із головних площин балки Та кий випадок будемо називати плоским згинанням 1
На розрахунковій схемі балку прийнято заміняти ії віссю (рив 49,6) При цьому всі навантаження природно, повинні зво
1 Детально плоске згинання розглядається а § 60
а
б
Риа 49

дитнсядоосі бачки, і силова площина буде збігатися з площиною рисунка
Як правило балки мають ті чи інші опорні пристрої — опори Конструктивні форми опор дуже різноманітні Для розра хунку їх схематизують у вигляді трьох ос новних типів опор
а)	шарнірно-рухома опора (рис 50, а), в якій може виникати тільки одна складова реакції — Кл, що спрямована вздовж опор ного стержня,
б)	шарнірно-нерухома опора (рис 50, б), в якій можуть виникати дві складові — вер тикальна реакція Ял та горизонтальна реак дія Нл
в| затиснення (жорстке затиснення або
закріплення), де можуть бути три складові —вертикальна/?л і гори дентальна На реакції й опорний момент Мл (рис 50, в)
Усі реакції та моменти вважаються прикладеними в точці А — центрі ваги опорного перерізу
Балка яку показано на рис 51, а, називається простою, або одно-прольотною, або двохопорною а відстань І між опорами — прольотом.
Консоллю називається балка, яка жорстко закріплена одним кінцем і не має інших опор (див рис 49, б), або частина балки що звисає за опори (частина балки 5Сна рис 51,6 частини ЛС та 52? на рис 51, в) Ьатки, які мають частини, що звисають, називаються консольними (рис 51, б, в)
Як відомо, для плоскої системи сил можна скласти три рівняння стятими для визначення невідомих реакцій Отже балка буде статично ниіначувана якщо кічькість невідомих опорних реакцій не перевищуватиме трьох у противному разі балка статично невизначувана Очевидно що балки, зображені на рис 49 та 51 статично визначувані
Бачка зображена на рис 52, а називається нерозрізною і е ста інчно невнзначуваною оскільки має п’ять невідомих опорних реакцій три в опорі А і по одній в опорах В та С Поставивши в перерізі балки Шарніри, наприклад в точках П і Е (рис 52, б), матимемо статично визначувану шарнірну балку бо кожний такий проміжний шарнір до трьох основних рівнянь статики додає одне додаткове рівняння сума
Рис 5)
Рис 52
моментів відносно центра шарніра від усіх сил, розташованих по один бік від нього, дорівнює нулю
Будування епюр для статично невнзначуваних балок потребує вміння обчислювати деформації а тому обмежимося поки що виключно статично визначуваними балками
$ 18. Визначення реакцій
Способи визначення опорних реакцій вивчають у курсі теоретичної механіки Тому тут зупинимося тільки на деяких практичних питаннях Для цього розгіяпемо просту балку (див рис. 51, а)
1 Опори як правито, позначають літерами А і В Три невідомі реакції знаходять з таких рівнянь рівноваги
а)	сума проекцій усіх сил на вісь балки дорівнює нулю
2Х-0,
звідки знаходять На,
б)	сума моментів усіх сил відносно опорного шарніра А дорівнює нулю
2МЛ = 0, звідки знаходять /?в.
в)	сума моментів усіх сил відносно шарніра В дорівнює нулю
2МВ = 0, звідки знаходять /?л
2 Для контролю можна використовувати або умову рівності нулю суми проекцій всіх сил на вертикаль
2К = 0, або умову рівності нулю суми моментів усіх сил відносно будь-якої точки С, що відрізняється від точок А і В, тобто
2Л1с = 0
Умовою 2К = 0 користуватися про стіше але вона дає надійну перевір ку тільки тоді, коли на балку не діють зосереджені моменти
З Перш ніж скласти рівняння рів новагн, треба вибрати (довільно) нап рями реакцій і зобразити їх на рисун ку Якщо внаслідок розрахунку яка небудь реакція буде від ємною, треба на рисунку поміняти її напрям на зворотний і надалі вважати цю реакцію додатною
4 Здебільшого навантаження перпендикулярні до осі балки Тоді На = 0, і рівнянням 2Х =- 0 не користуються
5 Якщо на балку діє розподілене навантаження, то для визначен ня реакції іі заміняють рівнодійною, яка дорівнює площі епюри на вантаження й прикладена в центрі ваги цієї епюри
Приклав 5 Визначимо опорні реакції балки (риє 53)
Перш ча все знаходимо ріанодійні Р, та Ра навантажень, розладі ієнах на ділян ках АС та СВ
Рх •= 20 2 = 40кН />, “4"20 3 = 30«Н
Сила Рг прикладена в центр! ваги прямокутника а Рх — в центрі вати трнкут ннка Знаходимо реакції
1МА -60 1-4-40 14-30 3 + 50 - Рв 5 — 0 Рв = 48 кН
Ї.МВ = РА 5-60 4 — 40 4 — 30 2 + 50 = 0 РА 82 кН
Перевірка
ЇМс- 82 2—60 1 —40 1 -|-30 1+50 — 48 3 =0
$ 19 Поперечні сили І моменти в перерізах балки
При плоскому згинанні все навантаження зосереджене в головній площині стержня ху (див рис 49, а), тому воно не дає проекцій на вісь г та моментів відносно осей х і у Отже, в будь якому перерізі балки
= Мх = Мкр = М„ =. 0, і не є нульовими тільки три величини АГ, рута Мг Надалі будемо позначати їх її, 0таЛ4 Ці зусилля діють також у перерізах елементів рам та криволінійних стержнів У балках при навантаженні, перпендику лярному до осі балки, поздовжня сила також дорівнюватиме нулю Тому надалі будемо вважати, що в будь якому перерізі балки можуть бути два внутрішніх зусилля поперечна сила <2 та згинальний мо мент М
Установимо такі правила знаків для <2 і М в балках
І) поперечна сила () у перерізі додатна, якщо її вектори иама гаються обертати частини розсіченої балки за годинниковою стрілкою (рис 54, а)
Рнс 54
2) згинальний момент М у перерізі додатний якщо вів спричинює стискання у верхніх волокнах балки і спрямований так, як показано на рис 54 а
Від'ємні напрями р та М показано на рис 54 б
Для практичних розрахунків можна рекомендувати таке
І Якщо зовнішня сила намагається повернути балку відносно розглядуваного перерізу за годинниковою стрілкою то у виразі для <2 в цьому перерізі вона дає додатний доданок Так, реакція Кл (рис 55, а) намагається повернути балку відносно перерізу С за годинниковою стрілкою, а сили Р та Я — проти Тому поперечна сила в перерізі С
Сіс—Рл—Р або
(& = — Рв
2 Якщо зовнішнє навантаження створює відносно розглядуваного перерізу момент, який спричинює стискання верхніх волокон балки, то у виразі для М в цьому перерізі воно дає додатний доданок Найпростіше з’ясувати знак М для консолі Так, на двох верхніх консолях, показаних на рис 58, а навантаження відгинає балку вгору; стисну тими будуть верхні волокна, тому згинальний момент додатний На рис 55, б стиснуті нижні волок на, і М < 0
У більш складних випадках (див , наприклад, рнс 55) можна уявити, що балка звільнена від усіх опор і затиснута в розгляду ваному перерізі Тоді вона перетворюється на дві консолі Треба розглядати ліву консоль, якщо згинальний момент визначається
як суча моментів сил розташованих ліворуч від перерізу (рис 55, б) Тоді
Мс = М (х) = Пах — Р(х —а)
Якщо ж М визначається як сума моментів сил, розташованих праворуч від перерізу (рнс 55, в), то
Мс = М(х) = Нв{1 — х) - М
§ 20 Побудова елюр 0 ІМ у балках
Розглянемо порядок побудови епюр0таЛ1для найхарактерніших випадків навантажування балок
Зосереджена сила на вільному кінці консолі (рис 57) Балка має лише одну ділянку Початок координат виберемо в крайній лівій точці А балки вісь х спрямуємо вздовж осі балки праворуч
Визначимо 0 та ЛІ в довільному перерізі з абсцисою х Праворуч від перерізу, що розглядається, діє тільки одна сила Р, тому (}(х) = Р М(х)^= — Р КВ = —Р(1-х)
Як видно з цих рівнянь, поперечна сила однакова в усіх перерізах балки, тому епюра 0 має вигляд прямокутника Функція М (х) ліній на Для побудови її епюри (графіка) досить знайти дві точки — на початку та в кінці ділянки
при х ~ 0 (переріз Л) Лід — — РІ, при х = І (переріз в) Мв > 0 За цими даними будуємо епюру М Зазначимо, що додаткові ординати епюр 0 та ЛІ відкладаються вгору від бази
На рис 57 штриховою лінією ДВі показано балку в деформованому стані Як бачимо з рисунка, стиснутими є нижні волокна балки Якщо сумістити базову лінію епюри згинальних моментів з віссю балки, то епюра М буде як би побудованою на стиснутих волокнах
Рівномірно розподілене навантаження інтенсивністю д, Цім на консолі (рис 58) Поперечну силу та згинальний момент у довільному перерізі К будемо визначати як наслідок дії розподіленого навантажен ия лізоруч від перерізу
0(х)=— д АК = — дх ---------------------------
Отже, поперечна сила 0(х) змінюється за за коном прямої лінії, а згинальний момент М (х) — за параболічним законом Для побудови еїно-ри 0 визначаємо ординати в двох точках при х = 0 0Л = 0 при х = І <2в = — ЦІ
Рис 57
і -І
Рис 58
Ряс 59
і проводимо пряму Враховуючи, що епюра М криволінійна, для її по* будови знаходимо ординати в трьох точках
при х = 0 Ма = 0, при х = Мс=~ , при х = І Мв = —
і проводимо через добуті три точки криву Це й буде епюра М.
Навантаження інтенсивністю д, Нім рівномірно розподілене по всій довжині прольоту двохопорної балки (рис 59) У цьому разі треба спочатку визначити опорні реакції Рівнодійна всього розподі леного навантаження дорівнює ді, і лінія її дії проходить через середину балки Тому
= Ялі — 9//2 = 0. ХМя = Яві - ?ї/2 == 0, звідки
Ял => Яв = дІ/2
Обчислюючи поперечну силу і згинальний момент у довільному пере* різі К як наслідок дії сил ліворуч від перерізу К, матимемо
<?(*) = Ял — дх^ -----дх,
М (х) = Ялх	-^-х-----
Очешідно що епюра буде прямолінійна а епюра М — параболічна Для побудови епюр знаходимо
М (0) = о,
м(-Ц-^ЬЛ_______<1* -	•
т 2 ) “ 2 2	8 ’
Л(1)= -Й-(--2^-=о
Щоб визначити екстремальне значення згинального моменту, прн рівняємо до нуля похідну від згинального моменту М (х) по абсцисі х перерізу
^=^-0.
звідси
х= 1/2
Оскільки друга похідна
а*м (х) ах» ~ У'
тобто від ємна, то в перерізі балки при х = 1/2 згинальний момент буде максимальний
Мтах ~ М (1/2) = дР/8
Епюри <2 та М наведено на рис 59.
Зосереджена сила Р, прикладена до двохопорної балки (рис 60) Перш за все знайдемо опорні реакції
2МН -= Рлі -РЬ^О, Рл= РЬ/1
їМл = Ра-РвІ = 0 Рв-= Ра/1
У цьому разі маємо на балці дві ділянки
Знаходимо 9 та Лі у довільному перерізі розташованому на ділянці АС (0<х<а)
Щх) -= РА -= РЬ/1
Отже, в усіх перерізах ділянки поперечні сили однакові й епюра С має вигляд прямокутника
Згинальний момент М (х) змінюється за лінійним законом
М (х) = Рлх = -у-х
Для побудови епюри визначимо ординати на межах ділянки
при х = 0 Ма = 0,
при х — а Мс — РаЬ/1
У довільному перерізі К% на ділянці СВ (а х І), розглядаючи дію сил, розташованих праворуч від нього, дістанемо
; М{х}-Кв К,В=~<І-х}
До такого самого результату ми дійшли б, розглядаючи дію сил розташованих ліворуч
(?(х) = /?д-Р, М(х) = РА АКг-Р СК,
Епюра <2 на ділянці СВ, як і на ділянці АС, має вигляд прямокутника Для побудови епюри М знайдемо значення ординат момен тів у перерізах С та В
при х = а Мс = —(1~а} =	\
при х = І Мв^О
У результаті дістанемо епюри, які наведено на рис 60 Вони показують, що при х = а функція С (х) розривається, і на епюрі С має місце стрибок що за модулем дорівнює зовнішній силі Р в цьому перерізі
Р& , Ра _ Р(а+ Ь) _ РІ __ о
І -і- -р------------ґ
на епюрі М в цьому перерізі є перелом (кутова точка)
Зосереджений момент у прольоті двохопорної балки (рис 61) Знаходимо опорні реакції, спрямувавши їх угору
їМв = РА1 + Мг = 0,
2ЛЦ = РВ1 - Мі =* 0, звідси
Яа^-Мі/1. Рн^Мі'і
Змінюємо напрям РА на зворотний Помітивши на ділянках АС і СВ довільні перерізи Кі і Кі, запишемо рівняння для функцій <2 (х) та М (х) для дітянки АС (0 < х а)
<г« = -Ял = --^; Л(») = -Я^ = -Ал,
для ділянки СВ {а х < І)
<}(*>=-Яв = -!%- ЛІ(х)=Яв К,В
На підставі цих рівнянь будуємо епюри С та М Епюра М розташована частково під віссю частково над віссю Оскільки вона побудована на стиснутих волокнах бачимо що на ділянці АС стиснутими є нижні вотокна, а на ділянці СВ — верхні Цьому відповідає зображена штриховою кривою деформована вісь балки У тому перерізі де згн нальний момент змінює знак на осі буде точка перегину
Неважко бачити, що
іда= ІеР ~
а тому прямі на епюрі М на ділянках АС та СВ паралельні
Звернемо увагу на те, що там, де прикладений зовнішній момент (переріз О на епюрі () ніяких змін немає, функція М (*) розривається, а на епюрі М має місце стрибок, що дорівнює значенню зовнішнього моменту
В окремому випадку, коли момент прикладений в опорному перері зі, на підставі наведених вище формул, при а = 0 дістанемо епюри, які показано на рис 62
Зосереджені моменти на опорах однопрольотної балки (рис 63) Знаходимо опорні реакції
ЇМв=РА1->-М — М~0, Яа=0,
ЇМА е=—ПвІ + М- М = 0 Кв = 0
Тоді для довільного перерізу завдальшки х від лівої опори
С (х) = /?л = 0; М (х) ® М == сопзі
Отже в будь якому перерізі р = 0 а згинальний момент однаковий по всій довжині балки Таке згинання балки має назву чистого згинання
$ 21 Диференціальні залежності при згинанні Деякі особливості епюр () ІМ
Визначимо деякі характерні особливості епюр поперечних сил С т.і згинальних моментів М знання яких полегшує побудову епюр і діє змогу певною мірою контролювати правильність їх
І
І і
Рнс 64
Розглянемо яку небудь баїку з довізьним навантаженням (рис 64, а) Розподілене навантаження умовимося вважати додатним, коли воно спрямоване вгору (таке навантаження дає додатну складову для зги кального моменту в будь якому перерізі)
Виділимо на ділянці, де немає зосереджених сил і моментів, малий елемент ОУО3 Він перебуває в рівновазі під дією зовнішнього навантаження, поперечних сил та згинальних моментів у перерізах О| і О(, розташованих завдальшки дх один від одного (рис 64 б) Оскільки взагалі 0 і М змінюються вздовж осі балки, то в перерізі О, маємо (х) і М (х), а в перерізі О3 маємо () (х) 1 Л? і М (х) 4- дМ Для виводу як завжди, будемо їх вважати додатними 3 умови рівноваги виділеної елементарної ділянки балки завдовжки гіх дістанемо
2У=(} + д<іх-((} (-Л?) = 0,
2Мо, *= Мл-І^х-і — (М + (ЇМ) = 0
Перше рівняння дає умову
4’=’	<33>
Із другого рівняння, нехтуючи членом дЛх (фхІЗ) другого порядку малості, знайдемо
На підставі формул (3 3) і (3 4) будемо мати
Коли на ділянці, яку ми розглядаємо, крім розподіленого наванта ження діє розподілений момент т Н м'м (рис 64 в) формула (3 4) набуває вигляду
(36)
при цьому формули (3.3) і (3.5) залишаються без змін
Співвідношення (3.3)	(3 6) називають диференціальними залеж
нестями при згинанні
Рис 65	Рис 66
Аналіз прикладів попереднього параграфа і добуті диференціальні залежності дають змогу встановити деякі особливості епюр поперечних сил та згинальних моментів
І На ділянках де немає розподіленого навантаження епюри С окреслюються прямими, паралельними базі, а епюри М в загальному випадку — похилими прямими (рис 65)
2	На ділянках де до балок прикладене рівномірно розподілене навантаження <?, епюра ^обмежується похилою прямою а епюра М — кв ідратичною параболою (рис 66) Оскільки епюр> ф будуємо на стис н} их волокнах, то опуклість параболи звернена в бік, протилежний напряму дії навантаження д (рис 67, а б)
З У перерізах, де р = 0, дотична до епюри М паралельна базі епюри (рис 66, 67)
4	На ділянках, де ф > 0, момент М зростає, тобто зліва направо додатні ординати епюри М збільшуються а від’ємні — зменшуються (див рис 65 66, ділянки АС та Вг) на ділянках, де 0 момент Л4 зменшується (див рис 66, 66, ділянки СО та ОВ)
5	У перерізах де до балки прикладені зосереджені сили
а) на епюрі <2 будуть стрибки на значення прикладених сил в напрямі їх дії' (на рис 66 та 66 ці стрибки показано товстими лініями зі стрілками)
Рис 71
на епюрі М будуть 58) причому вістря
переломи перелому спрямоване проти дії’сили (див також перерізи С, О та В на рис 65 та переріз В на рис 65)
6	У перерізах, де до балки прикладені зосереджені моменти, на епюрі М будуть стрибки на значення цих моментів (на епюрі <2 змін не буде) Напрям стрибка залежить від напряму зовнішнього моменту (рис. 69) Вітки епюри до стрибка і за ним паралельні Так, на рис 69 АВ (СО {ЕР (див також рис 61 та 70, а) Зазначимо, що це не стосується випадку, коли в одній точці прикладені сила і момент (рис 70, б) — сила спричинює перелом і порушує паралельність
7	Якщо на кінці консолі або в кінцевій опорі до балки прикладе ний зосереджений момент то в цьому перерізі згинальний момент до-рівнюезовнішньомумоменту (рис 71, перерізи В та С) Якщржукін цевій шарнірній опорі або на кінці консолі балка не навантажена зов нішнім моментом, то в них М — 0, що має місце найчастіше (див рис. 65 і 68, перерізи А та Е)
8	Епюра 0 е діаграмою похідної’від епюри моментів Отже орди нати епюри <2 пропорційні тангенсу кута нахилу дотичної до епюри М Для обгрунтування зазначених властивостей епюр розглянемо таке Якщо немає розподіленого навантаження, то
^- = ,^0
(їх 4
Інтегруючи, дістанемо
= С, = сопзі
(3 7)
Рис 72
ПІІІІІІІІКІІІІІІПІІІ
Отже,
ЗВІДКИ
М (х)« Сух + С,
0 8)
Рівняння (3 7) та (3 8) доводять властивість 1, оскільки для функції (З 7) графік буде мати вигляд горизонтальної' прямої, а для функції (З 8) — в загальному випадку — похилої прямої (якщо Сг 0) Два логічно доводиться й решта властивостей
Зазначимо однак, що поява стрибків на епюрі ф пов’язана із введенням умовного поняття про зосереджену силу Як уже зазначалося, зосередженою силою ми вважаємо навантаження, розподілене на не великій довжині Якщо завантажити балку таким дійсним навантаженням, то ніяких стрибків на епюрі <2 та переломів на епюрі М не бу де (рис 72) Це зауваження має відношення також і до дії зосередженого зовнішнього моменту
Розглянемо більш складні побудови епюр 2 та М
Приклад в Побудуємо епюри (і та М для простої балки, навантаженої за схемою, яку наведено на рис. 73
Перш за все визначимо опорні реакції РіанодіЙна всього розподіленого ваван гашення дорівнює уІ/2 і проходять через центр ваги вантажної епюри який віддалений на 1/3 від правої опори Тому
аі 2 ^“^-1—з*/в0-
8ВІДКК
Рис 74
Поперечну силу та згинальний момент у довільному перерізі К знайдено як па слідок дії сил, розташованих ліворуч від перерізу К,— реакції -?д та ріннодійної розподіленого навантаження (і/2) д (х) х З подібності трикутників
Я М = дх/1
V <*) =	— -^ї~ '
Тому
(з цих рівнянь ВИДНО то епюрі ф окрес леиа квадратичною параболою а епюра М —кубічною Для побудови їх визиа чнмо ординати в характерних точках
о/
при х«0 $А = у
л/
прн « « І Фв = — у ,
ТОбТ° ПРЯ «0 = -Т75-
Прн х
л	яі ?*о
ч = 0 прн -£—--------= 0,
„ <*$ прн х = 0 ”77
Отже, епюра д має такий вигляд як показано на рис 73 причому в перерізі А (х = = 0) дотична до ешорн (і пара тельна осі Далі, при х = 0 МА = 0 при х
І/УЗ похідна ІМ _ ді _ <?*р Ах 6	~2Г	4 (Х*
Л4.
перетворюється на нудь а
І А*М \	і дх\	<7
V	'х-//УЗ" I 1 )х-//у'зЯ“	РЗ <о
Отже у перерізі х = хе = І/УЗ маємо максимум М, причому
и л___________я і І Xі Яі*
б /з “ « \ л І ^ТТТ
Приклад 7 Побудуємо епюри ф та М для балки, яху показано на рис 74, Визиа іимо опорні реакції
2Ма = 30 2 5 0,7 - 50 - Кв 2,5 + 40 3 5 «= 0 Пв = 57,8 кН
ХЛІЙ = —ЗО 2,6 1,8+• 2,5 — 50 + 40 1 =0 Кд=6і)2кН.
Перевірка*
2Г= 60 2 —ЗО 2,64-57,8 - 40= 118 0 — ІіВО-О
Балка має п ять ділянок У довільних перерізах кожної з них записуємо вирази для (} і М перевіряючи при ньому чи виконується рівність () = іМІЛх, та обчислює мо 9 і Л4 у характерних перерізах.
Для ділянки РА (0 < х С 0 6 м)
ЗО*’
<2(*) = -ЗО* М (*) = — ——,
<2£ = (2 (0) = 0 М? = М (0) = 0
Сдд1а-= 0 (0 6) = — ЗО Об кН = - 18,0 кН,
ЗО 0.6і
Мл = ЛІ <0 6) = —--------2- м = — 5 4 кН м
Для ділянки АЕ (0 6 м < І 6 м)
ЗО*1
(?(*) = — ЗОх +60 2 М[х) = - —у— + 60,2(* —0 6),
<2. = (2 (0,6) (-30 0,6 + 60 2) кН = 42 2 кН Лпр
/ ЗО 0 6’ і
Лід ™ М (0 6) = І —---2---- ’-ОІкН м = — 5 4 кН м
ЧБ - 1 (1 6) = (— 30 І 6 Ь 60,2) кН = 12 2 кН
1	30 і 6і	1
Л4£л1в=Л4(1 6)= --------------+ 60 2(1 6 - 06)І кН м = 2І,8кН м
Для ділянки ЕО (І 6 м < 2,6 м)
ЗО*1
0 (*) = — ЗО* 4 60 2 М (х) = - —у- + 60 2 (* — 0 6)— 60
<2£ = <2(1 6) = (—30 І 6 + 60 2) кН « 12 2 кН
МЕ = Лї(! 6) = | —	д’--1 +60 2(1 6 - 06) - 5о|кН м = — 28 2 кН м
(2О = (2 (2 6) -= (— 30 2,6 + 60 2) кН «= — 17 8 кН
Мо = М (2 6)	— ^-д2 6- + 60 2 (2 6 — 06) — ^кН N = -31 «Н м.
Для ділянки ОВ (2 б м < х < З 1 м)
(2 (*) = (- 57 8 )- 40) кН = — 17 8 кН
М (*) = 57 8 (З І — х) — 40 (4 1 - *) = - 17 8* + 15 2,
Лїд = Лї(2 6) « (—17,« 2 6+І52)кН м —— ЗІкН м,
Ма = М(3 1) = (— 17 8 3 1 + 15 2) кН м = — 40 кН м
Дія ділянки ВС (З І м < * < 4 І м)
<2(х) = 40кН М (*) = -40(4 1 — *).
Рис 75
Мв <=М (3,1) — — 40(4 І — з і) «= = —40 кН м
Мс - М (4,1) — — 40 (4,1 — 4 І) = 0
Побудувавши за инцк ддиіши еаюру 0 бачимо що в деякому перерізі х0 па ділянці ЕО зусилля Ф дорівнює кутю, а от же, там дотична до епюри М бу хе горпзон талькою. Дія побудови епюри М необхідно ще обчисляти ординату М (хв1 Скори ставшись виразом для ф па дітяиііі Ей, знаходимо х0 з умови
<2(хв) = —30хг+б0 2«0, звідки
60 2 хв = —м = 2 0) м
Тоді
—	+ 60 2 (2 01 — 0 6) — 5о|кН м = - 25 7 кН м
За здобутими даними будуємо епюру М
Розглядаючи епюри З М та навантаження на балку з точки зору загачьшіх властивостей епюр виявляймо що побудовані епюри не містять принципових помилок наприклад усюди, деЗ>0 момент М зростає а там, де (} < 0 — зменшується в перерізі £ на епюрі М має місце стрибок на значення 50 кН м у перерізах Е та С момент М -= 0 і т. д.
Приклад 8 Побудуємо епюри ф та М для шарнірної балки, навантаженої за схемою яку наведено на рис 75
Ця бачка має чотири невідомі складові опорних реакцій — МА Нл Ив та Пв Наявність проміжного шарніра в точці С додає одне додаткове рівняння статики І перетворює балку на статично визначувану шарнірну
Визначимо опорні реакції
ЇХ — НА «= 0
2 Мс - 20 5 5 - Кв 4 + 60 2 5 = 0,	«= 65 кН
пр
#д-40— 60 + 65 — 20-0. КА-55 кН,
2А4с=-іИл + 55 2 — 40 І - 0, Л1д-70кН м, лі»
Перевірка
2Х, = —70 + 55 7 5 - 40 6 5 — 60 34-65 і 5=0
Тепер звичайним способом будуємо епюру поперечних сил 0, а потім визначаємо згинальні моменти а характерних перерізах
МА = —70 кН м, Л4В =70 + 55 • І) кН к — — 15 кН зг
Л1О = (—20 3 + 65 - 1 5) кН м— 37.5 кН м
<М€--20.15кН.м = -30кН м, М,-0
Користуючись цими даними будуємо епюру М.
Слід звернути увагу «а те, що иа епюрі М у перерізі, де розміщено проміжний шарнір згинальний момент завжди дорівнює нулю.
Іноді можна будувати епюри не складаючи виразів для фта М для довільних перерізів ділянок Досить лише обчислити величини 9 та Лі у характерних перерізах Для цих випадків можна рекомендувати такий порядок побудови епюр.
І Знайти опорні реакиїї (для консолі їх можна не знаходити}.
2 За стрибками та нахилами, Йдучи вздовж балки, обов’язково зііва направо, побудувати епюру (ніяких записів для цього робити не треба)
З Знайти характерні перерізи балки, тобто ті, в яких прикладені зосереджені снли та моменти, розпочинається або закінчується роз поділене навантаження, а також ті, в яких <2 перетворюється на нуль
4 Визначити в характерних перерізах моменти і за знайденими ординатами побудувати епюру М При цьому слід керуватися загаль ними властивостями епюр, а для консольних ділянок балок доцільно використати відомі для них епюри (див рис 57 і 66)
§ 22 Побудова епюр внутрішніх зусиль для рам
Рамами називають системи які складаються з прямолінійні х стержнів з'єднаних жорсткими вузлами Вертикально розміщені стержні рами називають стояками горизонтальні—ригелями Жорсткість вузлів виключає взаємний поворот скріптених стержнів, тобто у вузлових точках кути між осями з'єднаних стержнів залишаються незмінними
Вісь рами є ламаною лінією, а кожний прямолінійний елемент ра ми можна розглядати як балку Тому щоб побудувати яку небудь епюру для рами треба побудувати її для кожної окремої балки, що входить до складу рами На відміну від звичайних балок у перерізах стержнів рами крім згинальних моментів 44 і поперечних сит ф як правило, діють ще поздовжні зусилля N Отже, для рам доводиться будувати епюри N. (} та М
Для N та р зберігаються раніше введені правитазнаків
N > 0 яхи^о поздовжня сила спричинює розтягання
Р > 0, якщо її вектори намагаються обертати частини розсіченеЯ ра чи (відносно точок близьких до переріжу) за годинниковою стрілкою
Для згинальних моментів спеціального правила знаків не вста-новіюють а при складанні виразів для М (х) вибирають за влас ним розсудом який небудь момент додатним
Вирази для N (х)	(х) та М (х) записують дуже рідко — зде-
більшого для тих ділянок, де діють розподілені навантаження Найчастіше просто обчислюють значення N,^таМ у характерних перерізах (на межах ділянок та в екстремальних точках) а потім проводять лінії епюр зважаючи на їхні властивості, про які йшлося в§ 21.
Ординати епюр, як і завжди, відкладаємо перпендикулярно до осей стержнів рами, що утворюють базу, контур якої збігається з контуром рамн, причому додатні ординати N та — із зовнішнього боку рами,
2Р
Рис 76
а від’ємні — із внутрішнього (якщо звичайно рама має таку конфі гурацію що можна розрізнити її зовнішній і внутрішній боки) Гпюру М домовимося і для рам будувати на стиснутих волокнах
Якщо рамп має бііьіле ніж одну опору, то, починаючи будувати епюри, треба звичайними методами статики знайти опорні реакції
Побудуємо епюри Лї, Р та М для рами, зображеної на рис 76 За значимо, що оскільки немає розподілених навантажень всі епюри будуть окреслюватися прямими лініями
Щоб побудувати епюру V треба спроекціювати сили, прикладені до частини рами що лежить з одного боку від перерізу, на вісь стержня Отже, для будь якого перерізу матимемо /V — 0 на ділянці АВ N = = Р на ділянці ВД (розтяг) N = — 2Р на ділянці ОК (стиск) За ци ми даними будуємо епюру N Вона має вигляд двох прямокутників, розміщених на ригелі та лівому стояку
Тепер побудуємо епюру () Для будь якого перерізу на ділянці АВ сума проекцій сил що лежать внизу на перерізі, однакова, дорівнює Р і дає від ємні веіичину Р тобто <) = — Р Так само в будь якому перерізі стержня ка ділянці СК поперечна сила С = Р Щоб пояснити Знаки С в цьому прикладі на рис 77 показано напрями векторів (}, наприклад, в перерізах І і IV На рис 77 а вектори намагаються повернути частини розсіченої рами проти годинникової стрілки отже тут р < 0, а на рис 77, б — за годинниковою стрілкою, тому тут <?>о
У перерізі// як івбудь якому перерізі ділянки ВС, сума проекцій на переріз (на вертикаль) сил, прикладених до частини рами що лежить праворуч від перерізу (тобто одна сила Р) дорівнює нулю Отже, на ділянці ВС зусилля Р = 0
Для перерізу ІII і взагалі для будь якого перерізу ділянки СО проек ціюватися на переріз будетільки сила 2Р, тому в цих перерізах (? = 2Р
Отже, на ділянці АВ 0. = — Р, на ділянці —в д д* Д ......... ВС	Р = 0 на ділянці СД Р = 2Р, на ділянці
уу/	Р = Р Епюра Р на цих ділянках має вигляд
І	трьох прямокутників
0	' В Для побудови епюр моментів М будемо об
Рис 77 числюватв згинальні моменти в характерних точ
ках А В,С й Е та К Очевидно, Ма = 0 У перерізі В стержня АВ (тобто в перерізі І, нескінченно близькому до В) маємо
Мв = Р • АВ = РІП, причому від дії цього моменту стиснуті зовнішні (праві) волокна бо згинальний момент прикладений до верхнього боку перерізу /, спрямований проти годинникової стрілки Тому на епюрі М із точки В відкладаємо із зовнішнього боку ординату, що дорівнює РІ/2, і проводимо пряму аЬ
У перерізі В стержня ВО (тобто в перерізі //, нескінченно близь кому до В) маємо ту саму величину
М£ - Р • АВ = РІП
і стиснуті знову зовнішні (верхні) волокна Такий самий згинальний момент буде і в перерізі С
Мс = РІ/2
Відкладаємо в перерізах В та С із зовнішнього боку ординати, що дорівнюють РІ/2, і проводимо пряму Ь,е Продовжувати цю пряму далі ліворуч не можна, оскільки в цьому перерізі на епюрі М повинен бути перелом
У перерізі О стержня ОВ (перерізі //Лзгинатьний момент повинен бути обчислений від дії сил Р та 2Р Вважаючи наприклад, що для стержня ОВ додатним буде такий згинальний момент котрий спричинює, стискання верхніх волокон, знаходимо, що
МВ = Р А,О—2Р СО = Р-^-~2Р^-------------
Знак <мінус> свідчить проте, що в перерізі ПІ стиснуті нижні волокна. Відкладаємо вниз ординату що дорівнює РІ/2, і проводимо на епюрі М пряму
Переходимо до будування епюри М на стояку ОК, вважаючи, наприклад, що згинальний момент додатний, якщо він спричинює стискання внутрішніх (правих) волокон Тоді в перерізі /V
Мв = -Р А,о + !Р.СО-Р^- + 1Р±- = ^-
У перерізі Е на епюрі М повинен бути стрибок, тому значення М визначаємо окремо в перерізі V
Мц-Р-А1Е + 2Р-ЕС1 = Р-^- + гР-^--^-Р‘, а в перерізі VI
М'е^-Р А,Е-л-гР ЕС,-М = р4-+2Р-І—Р1=4-Р1
Нарешті в перерізі К
Мк-р-а^+ір-кс.-м =р4- + у>4—рі--^р‘
Усі моменти виявилися додатними Отже, в усіх цих перерізах, агідно з прийнятим для стояка ДЛ правилом знаків стиснуті праві волокна. Тому відкладаємо відповідні ординати і, проводячи пряні
та е£, закінчуємо побудову епюри М
Приклад 9 Побудуємо епюри N. (} та М для рами, зображеної на рис. 78
Оскільки ця рама не консольна, то перш за все знайдемо опорні реакції У кожному нерухомому опорному шарнірі А та В буде по дві складові реакції вертикальні і /?вта горизонтальні НА і Нв Дійсні напрями цих реакція ще не відомі, тому спрямуємо їх поки що довільно, наприклад, вертикальні реакції вгору, а горизон та.тьні — праворуч (чому реакції НА та Нв закреслено стане зрозуміло пізніше)
Для визначення чотирьох невідомих складових реакцій Яв НА, Нв, крім звичайних рівнянь статики маємо ще умову рівності нулю суми моментів відносно точки С усіх снл, розташованих по один бік від неї (інакше кажучи рівність нулю згинального моменту в перерізі С де е шарнір)
Взагалі можна вибрати різні варіант» чотирьох рівнянь статики для визначення реакцій Найзручніше розглядати суми моментів відносно шарнірів А. В та б При складанні рівнянь беремо до уваги закреслений варіант реакцій НА ти Нв
1МВ — 40 3 4- 20 І — ЯА . 2 — 0 КА “ 70 кН
2Ма » 40. 1 4- 20 . I + Яв 2 - 0 Пв “ — ЗО кН.
£МГ--7О	2+На 2-0- Ка--5 кН
2ЛІС—-20 1 —ЗО • І 4- Нв • 2 — 0 Яв = 25кН. пр
Реакції ЦА та Нв виявитися додатними, отже вони дійсно спрямовані так, як було вибрано НА — вюр> //„—праворуч реакції НА та /?„ від ємні отже мають напрям протилежний вибраному а саме НА спрямована ліворуч, а Нв — вниз Змінную на рисунку напрям ин т реакцій на протилежний і бу темо вважати всі реак ці додатними
Я^-70кН //Л=5кН «в-30кВ Нв-25кН,
Перевіримо чи правильно знайдено реакції
їЛ = -///4-204-Нв--5 — 20 4- 25 = 0
2У - НА — 40 - Яв - 70 — 40 - ЗО - 0
Тепер можна побудувати епюри Лі (} та N таким самим способом як небу то зроблено в попередньому прикладі, оскільки опорні реакції визначено а току відомі всі юанісипі си ти прикладені до рами.
Перш за все зробимо деякі зауваження щодо загального вигляду епюр ЛІ та (? Оскільки розводі іеного навантаження немає контури епюр Лі та фбудуть прямолі в пні, причому епюра () складатиметься з прямокутників У точці О на ній буде ерибок. а па епюрі Лі — перелом У точках А В,С та Р згинальний момсн _о рі ЦЮЄ И) 1К>
Для побудови епюри N знаходимо що
на ділянці ВК N	Нв = 30 КІІ
»	>	КЕ N =» НА = 5 кН
>	»	АЕ N = — НА — - 70	кН.
»	»	ЕЕ N = 0.
За цими даними будуємо епюру N
Для побудови епюрн (} визначаємо характерні ординати
на ділянці ВИ ф = — //„ — — 25 кН
>	»	ик	5	=	- Нв +	Х — (— 254-20) кН = — 5 кН
»	.	«£	(?	=	Лв= ЗО	кН,
>	*	ЕЕ	§	=	— 40 кН
>	»	АЕ	(і	=	НА — 5 кН,
За цими даними будуємо епюру Ф
Тепер визначаємо згинальні моменти
Ліо = Пв • 1 = 25 1 кН => 25 кН м (стиснуті праві волокна).
Лі, —//„ 2 — 20 1 —(23 2 — 20 І) кН > м =
«- ЗО кН м (стиснуті ліві волокна)
Мп = ЛІ, = ЗО кН м (стиснуті верхні волокна)
Мці^На 2-40 1 —(5 2 — 40 1) кН м =
= — 30 мН н (стиснуті нижні волокна) М!У^НА 2в5 2 кН м=10кН м (стиснуті ліві волокна) Му — «0 І кН м = 40 кН н (стиснуті нижні волокна) І будуємо епюру М
§ 23 Побудова епюр внутрішніх зусиль для криволінійних стержнів
У поперечних перерізах плоского кривого стержня можуть діяти як і в рамах, три внутрішніх силових зусилля /V, (?та М Найчастіше мають справу зі стержнями, вісь яких окреслена по дузі кола У цьому разі положення будь якого перерізу зручно визначати за допомогою полярної* системи координат тоді поздовжня поперечна сили та зги нальний момент будуть функціями кута ф N (ер), <3 (ф) та М (ф).
Для N та візьмемо звичайні правила знаків (див § 15 та 19) епюри М будемо, як і в рамках, будувати на стиснутих волокнах
Як приклад розглянемо плоский кривий брус схему якого наведено на рис 79, а. Запишемо вирази N (ф), ф (ф) та М (ф) для довільне го перерізу С Щоб дістати N (ф), треба визначити проекції сил Р, та Рл на напрям осі стержня в перерізі С тобто на дотичну КС Для зруч ності згадані проекції можна уявити перенесеними в точку С (на рис 79, а їх показано штриховими лініями) Тоді
N (<р) = Р( со$ ф 4- Р4 зіп ф
Щоб дістати $ (ф), треба знайти проекції сил, прикладених на ді ланці дуги АС, на площину перерізу тобто на напрям 051
<3 (ф) = Р| зіп ф — Р, СОЗ ф
Прн складанні виразу для згинального моменту в довільному перерізі домовимося, наприклад, вважати згинальний момент додатним, коли він спричинює стискання волокон, які лежать із внутрішнього боку стержня (тобто, якщо він збільшує кривизну стержня) Будемо мати
М (ф) = Р • Ай — Р, Сй = Р,/?(1 — созф) — Р,/?5ІПф
Таблиця З
	| >1пф ।	ео»ч	| 0»«ІП7	| 0 5 ео» ф |	«іф)/р |	іфі/Р |	М №УРЯ
0	0	1 000	0	0,500	1 000	—0 500	0
10	0 174	0 98о	0 087	0,498	1 072	-0 324	—0 072
20	0 342	0 910	0 171	0,470	1 III	—0 128	-0 111
ЗО	0 503	0866	0,250	0 433	1 116	0 067	—0 116
40	0 643	0 766	0 322	0 383	1 088	0,260	—0 088
50	0,766	0 643	0 383	0 322	1 026	0 444	-0 026
60	0,866	0,500	0,433	0 250	0,933	0,616	0 067
70	0 940	0 342	0.470	0,171	0 812	0 769	0 188
ПО	0,985	0 174	0 498	0,087	0 672	0 898	0,328
90	1 000	0	0 500	0	0,500	1 000	0,500
Добуті формули дають змогу будувати епюри И, $та М Візьмемо для певності РІ = Р та Р, — 0,5Р Тоді
N (ф) = (соз ф 4- 0,5 зіп ф) Р,
Сі (ф) = (зіп ф — 0,5 соз ф) Р,	(3 9)
М (ф) = РР (І — соз ф — 0,5 зіп ф)
Користуючись формулами (3 9), визначимо значення Лі, Ста М в деяких перерізах (табл 3)
Розмістивши вісь стержня, відкладаємо через 10° у масштабі по нормалі до осі стержню (тобто по радіусу) відповідні ординати для Лі, <2 (додатні — назовні, від'ємні — всередину) та для М (па стиснутих волокнах), сполучаємо кінці ординат плавною кривою і дістаємо епюри /V, С та М (рис 79, б)
Розглянемо деякі загальні питання побудови епюр внутрішніх зу сить для криволінійних стержнів
Зокрема зупинимося на побудові епюр внутрішніх зусильукривих стержнях при дії рівномірно розподіленого навантаження У цьому разі корисно мати на увазі таку теорему, рівнодійна рівномірно розподіленого навантаження, яке прикладене до дуги будь якого обрису, дорівнює добутку інтенсивності навантаження на довжину хорди яка стягує цю дугу перпендикулярна до цієї хорди і проходить через її се редину
Для доведення цієї теореми розглянемо довільний плоский стер* жень АВС навантажений рівномірно розподіленим навантаженням інтенсивністю у (рис 80)
Виділимо на цьому кривому брусі елемент завдовжки д$, центр яко го має координати х та у, а дотична до дуги в точці з координатами х, у утворює з віссю абсцис кута На цей елемент сіз діє сила фіз, складова якої по осі х дорівнюєфіз зіп а а по осі у — фіз соз а Але дз соз а =-— йх, а дз зіп а = ду, тому складові будуть відповідно дорівнювати фіу ла фіх (рис 80)
Позначимо рівнодійну навантаження (тобто елементарних снл<?Л) через Р Тоді проекція Рх рівнодійноі на вісь х
в о
рх = і = 1Н» -«І ‘іи - о
АСВ	А	6
Аналогічно знаходимо рівнодійну зусиль на вісь г/і в і
Р9 = Г Я<іх = я\^х= я\<іх~ Я1
АСВ	А 0
Звідси видно, що рівнодійна
р_р,=,/,
тобто дорівнює добутку інтенсивності навантаження на довжину хорди, що стягує дугу АСВ
Оскільки Рх == 0, то рівнодійна перпендикулярна до осі х, тобто до хорди, оскільки вісь х спрямована вздовж хорди
Тепер обчислимо суму моментів елементарних сил відносно початку координат
в в
ддх • х Ь у цйу • у »• <? у х&х Аг я \у<іу = АСВ	АСВ	А	Л
= ^'хЛ-г Ч^уіу = -3^-.
Нехай плече рівнодійноі відносно початку координат дорівнює Хр Тоді за теоремою про момент рівнодійноі
Рхр = 2МЛ або яі • хр = я№ звідки
хР = //2
Отже, рівнодійна проходить через середину хорди. Теорему доведено. 68
Як ілюстрацію застосування п!€і теореми розглянемо приклад побудови епюр внутрішніх зу сі ть та ЛІ для кривого стержня, навантаженого за схе мою яку наведено на рис 81, о (величини <?, /?, а та Р вважати мемо заданими)
У довільному перерізі Р1 на ділянці стержня АВ (О^ф <^а) визначаємо внутрішні зусилля як наслідок дії навантаження, прикладеного до дуги ЛР, Рів водіння цього навантаження Р1 перпендикулярна до хорди ЛР, і проходить через іі середину, огже, спрямована вздовж бісек трнси кута ЛОРі
Рх в д ЛР, = 2<?/?зіп(ф'2)
Для зручності визначення N та 0 па ділянці АВ (0 ч а) ріянодійну показано також у перерізі Р, Тоді будемо мати
N (ф) — — Р| зіп (ф/2) =
= — 2<?/? зіп2 (ф/2) =
= — дР(1 — созф),
З (ф) = Р\ СОЗ (ф/2) »
= 2дР зіп (ф/2) соз (ф/2) —
= дР зіп ф (3 10) М(ф) « Р, (ЛР,/2) «
= 2<?Я*зіп* (ф/2) (І — созф)
Рис 81
Зусилля та згинальний момент у довільному перерізі Р, ді ляпки ВС (а ф Р) е наслід ком дії всього розподіленого навантаження на ділянці АВ, рівнодійна якого
Рг = д • АВ « 2дР зіп (а/2)
перпендикулярна до хорди АВ і спрямована по бісектрисі кута АОВ Тому при а ф Р
(ф) = — Р, зіп (ф—а/2) = — 2дР зіп (а/2) зіп (ф — а/2),
Таблиця 4
Ч •	>1п<г	СО5 Ч	І -СО1Ф	V (ф)/фЯ	0 «П/еЯ	М Ог)/«Я>
0	0000	1 000	0 000	0 000	0,000	0 000
15	0 259	0 966	0 034	-0 034	0 259	0 0?4
ЗО	0 500	0 866	0 134	-0 134	0500	0 134
45	0 707	0 707	0 293	-0 293	0 707	0 293
60	0866	0500	0 500	-0 500	0 866	0 500
Таблиця	5					
Ч ’	Ф — ЗО"	*1л <? — — ЗО’)	СОІ (ф — — ЗО”)	N (ф)/еЛ		іЧ (ф)/«Я
60	зо	0 500	0 866	—0 500	0 866	0 500
75	45	0 707	0 707	—0 707	0 707	0 707
90	60	0866	0500	-0 866	0 500	0 866
105	75	0 966	0 259	-0 966	0 259	0 966
120	90	1 000	0 000	—1 000	0000	1 000
З (ф) = Р, со5 (ф — а/2) = зіп (а/2) соз (ф — а/2)	(3 11)
М (<р) » Р, 0,/С = Р,Р зіп (ф — а/2) = 2?/?’ зіп (а/2) зіп (ф — а'2) Вибравши кути а та р, обчислимо значення ЛІ (ф), З (ф) та М (ф) при різних кутах ф і побудуємо епюри Результати розрахунків при а --= 60° тар = 120° наведено в табл 4 та 5, а епюри, побудовані за цими даними, показано на рис 81 б
§ 24. Диференціальні залежності при згинанні плоских криволінійних стержнів
Нехай на криволінійний стержень 1 діє довільне навантаження (рис 82) Провівши два перерізи під кутами ф та ф + гіф, виді зимо елемент стержня АВ, на якому не буде зосереджених зусиль Довжина дуги виділеного елемента кривого бруса радіусом г буде бз = г<і<р До датний кут ф відкладаємо, як завжди, проти годинникової стрілки
У перерізах, що обмежують елемент стержня <і& діють поздовжні сили ЛІ та ЛІ -і- гіЛІ, поперечні сиіи 3 та 3 4- гіЗ а також згинальні моменти М та ЛЇ4- сіМ (рис 83) які замінюють дію відкинутих час тин кривого стержня
При виведенні диференціальних залежностей між внутрішніми зу силлями в кривих стержнях будемо вважати, що згинальний момент є додатним, якщо він спричинює стискання внутрішніх волокон стерж ня (волокон, розташованих на угнутому боці), а розподілене навангпа ження додатне, якщо воно спрямоване в центр кривизни
1 Обмежимося розглядом стержня, вісь якого не має точок перегину.
Рис. 82	Рис. 83
Розглянемо умови рівноваги елемента (із (рис 83) — суми про* екцій всіх сил на осі АВ та ОК відповідно та суму моментів сил від носно точки В
£пр ивлв — (З 4* гіС) зіп 4- (М + гі#) соз 4^- -і- з зіп -
— N соз = 0,
2пр Я.ОК = (3 4- Л2) СОЗ ---+ (Ж) зіп ~--------(} соз 4^--
-Л?5іп_^------9-ЛВ = 0	(312)
ХЛІв = — (М + <М1) 4- М -і- (? • ВС + /V • ЛС 4- «? • ЛВ = 0.
Ураховуючи, що
соз-^-аЯ,
АВ = 2г зіп —- « ггіф
АС = г (1 — соз гіф) т 0, ВС = т • зіп гіф » ггіф та нехтуючи добутком диференціалів, дістанемо]
<2гіф 4- гіМ = 0, гіф — Л/гіф — ^ггіф 0;
— гі/И + Зггіф = 0
Поділивши кожнеє цих рівнянь на гіф, матимемо
-$- = *+«<,	(3 14)
(3 15)
Це — шукані диференціальні заіежності при згинанні криволінійного стержня Оскільки гЛр — (із, іх можна записати ще й в такому внг-
«о и;
ТГ ' «	(3 18)
Залежності (З ІЗ) (3 15) дають змогу перевіряти правильність складання виразів для N (ер), Р (ер) та М (ер) при згинанні, зокрема, колового криволінійного стержня Отже, легко переконатися що та лежносп(3 9) .. (З 1!) у прикладах що розглядалися, складено вірно
із формул (З 13) та (3 15) випливає що в перерізах, де ЛІ та N дося гають екстремальних значень, 3= 0 Це дає змогу певною мірою кон трелювати справедливість побудови епюр N р та Лі Так на епюрах рис. 79, б у перерізі Е, де Ц = 0, момент М — Л1п,іп, а зусилля N = — Кгмх Екстремальні значення М та #можна знайти так із другого рівняння (3 9) видно що р = 0. копи
зіп ф — 0,5 соз ф = 0,
тобто, коли ф = 0 5, ф = 26е 34', зіп ф = 0 447, соз ф = 0,894 Підставивши ці значення зіп ф і соз ф у перше та трете рівняння (3 9), знайдемо*
Лїт1п = (І —0,894 — 0,5 0,447) РЯ-» 0 118РЯ,
/У™, = (0,894 4-0,5 0 447)Р = 1П8Р
Залежність (3 14) дає змогу знайти екстремальні точки на епюрі р У тих перерізах, де р = рт»« або р р піп
N= — 1?	(3 19)
якщо на цій ділянці стержня е й розподілене навантаження, або
N = 0	(3 20)
якщо розподіленого навантаження немає Внаслідок цього, на рис 79, наприклад, зусилля р ніде не досягає екстремального значення (дотич на до епюри р ніде не буде паралельна дотичній до осі стержня в тому самому перерізі), оскільки розподіленого навантаження немає а N ніколи не дорівнює нулю
Слід зазначити, що умови р — 0, (3 19) та (3 20) необхідні аіс не достатні для досягнення функціями N (ф), (ф) та М (ф) екстремаль*
них значень. ПРИ виконанні іх екстрему-у____хг5д\пПЖ\ ма може й не бути, але тоді на відповідній
Xй ^/Х,	\®к епюрі буде точка перегину причому до
./*	(м) тична до епюри обов'язково буде пара
К-х	лельна осі стержня в цьому перерізі
Рнс 84	Епюри Л, 3 та ЛІ для криволінійних
стержнів мають такі властивості ((части
на з них випливає із визначення Лі, 3 та Лі, решта —з форму і (З 13) (З 15)1
1) у кінцевій шарнірній опорі та на вільному кінці консолі, якщо вони не навантажені зовнішніми моментами, Лі — 0,
2)	у перерізах, де до стержня прикладений зосереджений момент, на епюрі М буде стрибок (рис 84) причому дотичні до епюри до стрибка га за ним будуть паралельні,
3)	у перерізах, де до стержня прикладені зосереджені сили пер псндикуляриі до осі стержня (тобто спрямовані по радіусу) на епюрі С) б>де стрибок, а на епюрах /И та Лі — переломи (рис 85),
4)	> перерізах де прикладені зосереджені сили, спрямовані по дотичній до осі стержня, па епюрі Лі будуть стрибки, а на епюрах () та М — переломи (рнс 86),
5)	у перерізах, де 0 = 0 на епюрах М та N будуть екстремуми, тобто дотичні до іпи р будхть паралельні дотичним до осі стержня в цих перерізах (рис 86)
6/ у перерізах де N — О, на епюрі 4? будуїь екстремуми (рис 85),
7) на ді іянках, де О 0, ЛІ зростає а N зменшується у напрямі ві ліку <р там де 3 < 0 М зменшується, а N — зростає (рис 85. 86),
8) на ділянках, де Л' > 0, Ф зростає в напрямі відліку <р а де Лі < < 0,— зменшується (рис 85 та 86)
Якщо стержень має прямолінійні та криволінійні ділянки, то на прямоіінійних ділянках епюри будують так само, як для балок або
Рис
цЦМР
рам, а на криволінійних — так, як було показано в попередніх прик ладах
Приклад ю Побудусно епюри Ь. Ста 41 для стержня, показаного на рис. 8? а. Склавши ріпняння І-МД = 0 2Х = 0 2У = 0 знаходимо РА = 0 ІО4Р; Ке •= І 104Р НА = Р
На ділянці С£ (йдучи справа) будуємо епюру так як для балки (рис 87,6), Потім вибираємо довільний переріз К, і записуємо для ділянки СВ
М (<?) = І 104Р (СЕ + Я зіп ф) - Р (СО 4- Я зіп ф) = (0 604 0 104 зіп (?) РЯ р (<?)=—0.104Р соз ф	{3 21)
Я (ф) = 0 Ю4Я зіп ф
Ураховуючи навантаження ліворуч від перерізу Я, записуємо для ділянки ВА М (ф) « [соз ф —0,104 (І — зіп ф)| ЯР,
Таблиця б
ч рад		ЄО»ф	Р/Р --0 ЮІЗІп Ф	М/РР — 0.604 4- 0 І34МП ф	ЧіР-~ —0 104 СО> ф
0	0	।	0	0 604	-0 104
0 0834л	0^о9	0,966	0 027	0.631	—0 100
0,166л	0,500	0 856	0,052	0656	-0 090
0,250л	0,707	0,707	0,074	0 678	- 0 074
Таблиця 7
(З 22)
(} (ф) — (зіп ф — 0 104 соз ф) Р N (ф) = (соз ф -і- 0 ІО4ф) Р
Перевіряємо иі вирази за форм> танк (З ІЗ) (3 15) і складаємо табл 6 для д • ляпки СВ та табл 7 для діїянкн АВ
За добутими значеннями М N та С будуємо епюрн на криволінійній дияниі стержня (рис 87 б)
§ 25 Побудові епюр внутрішніх зусиль для просторових рам
У багатьох конструкціях застосовуються стержні, осі яких не ле жать в одній площині, а також і плоскі системи що перебувають лід дією просторових навантажень У поперечних перерізах елементів таких систем можуть діяти всі шість внутрішніх силових факторів: А. <?», $г Ма, Му, Мг (див рис 40)
Методику побудови епюр у цьому разі розглянемо на прикладі стержня, осі якого становлять просторову ламану лінію (рис 86) Умовимося при переході від одного стержня системи до іншого сумі тати вісь х з віссю розглядуваного стержня відповідно розміщуючи
додатні напрями осей у та г (рве 88, а, б)
Епюри згинальних мо ментів як і раніше, буду нитимемо на стиснутих во юкнах, причому оріентува ти їх треба так, щоб пло щина епюри збігалася з пло щиною дії пари того зги на іьного моменту, для яко г<> и побудовано Знак зги нліьного моменту береться довільно І ДО ТОГО Ж ТІЛЬКИ у разі потреби записати від повідне рівняння (як для
Рис 89
плоских рам та криволінійних стержнів) Для поздовжніх сил і крут них моментів залишаються раніше взяті правила знаків Епюри N іа Мир можуть бути орієнтовані довільно але ординати завжди відкпа даються по нормалі до осі стержня Поперечні сили в перерізі вважа ються додатними якщо їхній напрям збігається з додатним напрямом осей у та г
Побудову розпочинаємо з ділянки АВ Для довільного перерізу завдальшки х від точки В визначаємо результат дії сил, розташованих ліворуч від перерізу (тобто сили Рта рівнодійноі розподіленого наван таження д)
N^0. <2у = -д(1,—х), 0,^ — Р Л1крЕ=0
М, = ?(/| ~(стиснуті нижні волокна), (3 23)
Му — Р(1і — х) (стиснуті ліві волокна) (3 24) У перерізі В (при х = 0)
N = 0,	=	<2, = - Р, Мкр = 0;
М, = Р/,
Користуючись цими даними, будуємо епюри для ділянки А В (рис 89) Момент Мг діє у вертикальній площині ху, в цій площині й орієнту ємо параболічну епюру Момент Му діє в горизонтальній площині лг в цій плошнні й орієнтуємо трикутну епюру
Переходимо до ділянки ВС Проекцію на вісь стержня дає тільки розподілене навантаження, отже, N =- д11г і епюра N на ділянці ВС прямокутна Легко бачити, що 3, = 0, а = — Р, тому епюра СУ прямокутна
Момент відносно осі стержня утворюється ТІЛЬКИ ВІД сили Р, при чому до верхнього боку будь якого перерізу він прикладений проти
годинникової стрілки (коли ДИВИТИСЯ ВНИЗ} вгору, тобто проти напряму осі х) Відповідно до правила знаків для кратних моментів на дітянці ВС, Лікр = Ріі, і епюра ЛКр тут прямокутна.
Епюри згинальних моментів Ми та Мг на ділянці ВС прямокутні, оскільки розподіленого навантаження на ній немає Отже, досить ви значити згинальні моменти в двох перерізах, наприклад у В та С У перерізі В момент Мг = 0, оскільки сила Рта рівнодійна розподіленого навантаження проходять через вісь г цього перерізу В перерізі С момент Л1,= РІЛ Рівнодійна розподіленого навантаження не дає в цьому перерізі моменту Мг, оскільки перетинає вісь г перерізу С За цими даними будуємо трикутник епюри Мг (рис 89) на стиснутих во локнях, розміщуючи його в площині ху, в якій діє згинальний момент Мг
Для згинального моменту Му в перерізах В та С
Сила Р не дає моменту відносно осей у в перерізах В та С, оскільки вона паралельна цим осям Отже, епюра Му на ділянці ВС прямокутна На рис 89 прямокутник побудовано на стиснутих волокнах і розмішено в площині хг.
Залишилося побудувати епюри на ділянці СР На вісь х проект-юється тільки сила Р, яка спричинює стискання Тому тут N — —Р, і епюра поздовжніх сил прямокутна.
У довільному перерізі ділянки = 0, а (2У — —<ік> тоиУ епюра прямокутна
Крутний момент відносно осі х утворюється тільки від дії розподіленого навантаження у (бо сила Р паралельна осі х), причому, згідно з взятим правилом знаків для крутних моментів, цей момент від ємний)
'М«р = -9',4=--Т--	(3 25)
Епюра Лікр знову буде прямокутною
Оскільки епюри згинальних моментів Му та Мг прямокутні, визна чнмо їхні значення тільки в даох перерізах — С та Р. у перерізі С
М( = Р • ВС = РІЛ (стиснуті нижні волокна),
МУ = Р АВ^РІі (стиснуті ліві волокна)1, у перерізі Р
Мг — Р ВС-і-уІі Сй = Р1г ~ уІі13 (стиснуті нижні волокна), Му — Р АВ<= РІ, (стиснуті ліві волокна)
За добутими даними будуємо епюру згинального моменту Му в гори зонтальчій площині та трапецієвидну епюру згинального моменту Мг у вертикальній площині
Рис 90
Рнс. 91
Користуючись побудованими епюрами (рис 89) можна в будь якому перерізі просторового стержня знайти згинальні та крутні моменти, поздовжні та поперечні сили та їхні напрями Як ілюстрацію на рис 90 показано внутрішні зусилля та моменти в перерізі О
Побудову епюр внутрішніх зусиль при просторовому навантаженні кривих стержнів покажемо на такому прикладі
Приклад 11 Побудуємо епюри внутрішніх зусиль для просліорового чаванта женого криволінійного стержня (рис 91 в), розташованого в горизонтальній площині
Перерізи стержня (наприклад який показано па рисунку заштрихованим прямокутником) такі що одна з головних центральних осей у збігається з напрямом радіу са проведеного в центр ваги перерізу а друга — а — вертикальна Дотична до кола тае для кожного перерізу напрям осі стержня (осі х) Сита Р вертикальна в зовиіш ній момент М прикладений в площині кінцевого перерізу А
Для побудови епюр /V <3 та 5( у кривому брусі треба ввести кутову кіюрдниа ту <р та записати формули тля зусиль І моментів. Прн тому ротгляїісмо проекцію стержня на горіпоитаїьну пташину (рис 91 б) Вісь г тоц чбЦаєтгсц з тоїкою Сі позначена точкою в кружку а сита Р — з точкою А й позначена хрестиком у круж ку діючий зовнішній моченг зображено у оигтяді вектора моменту
Унаслідок дії прикладених до стержня зовнішніх навантажень (сили Р га чомсії ту М) в будь якому довітьному перерізі С будуть такі внутрішні зуспіли
іУ(Ф)«.ЕХ==0	Ліг(Ф) = гМ, »0
Згинальний момент М = Мв та круглий момент Мкр “ М* від сили Р знав е_чо, помноживши силу Р на відповідне плече АО ~ зіп ф та АЕ * ОС “/?(! — Таблиця В
1	г	|	з	|	х	і				•
ф.'	1ІП ф	соїч	«О [3]		М — 800 |2) н и
0	0	і	800	200	0
15	0 259	0,966	773	173	207
ЗО	0 500	0,866	693	93	400
4о	0 707	0 707	566	-34	566
60	0866	0 500	400	—200	693
75	0,966 1	0 259	207	—393	773
90		0	0	-800	800
6001
— соз <р) Проекції цього вектора на осі у та г	200И
дадуть відповідно складові згинального та	рнс 93
крутиого моментів у перерізі С Дотримую
чксь взятого правила знаків для і вважаючи М яозатннн якщо він спричинює стискання нижніх волокон стержня, матимемо такі формули
М (<р) » Му (ф) ~ РР зіп ф 4- Мл зіп ф «® (РК + Мд) зіп ф
Мкр (ф) ш Мж (ф) « — РР (І — сої ф) 4- Мл соз ф = (Рр 4- Мл) созф — РР Прн Р - 2000 Н, Мл — 200 В м Я — 0 3 м
М (ф) = 800 зіп ф Н м, Лїкр (ф) = (800 соз ф - 600) Н м Користуючись цими формулами складаємо табл 81 і за добутими даними будує мо епюри 0 ТИ та /Икр (рис 92)
Іноді епюри для просторово навантажених кривих стержнів будують вв на про-екиіі стержня як ие зроблено на рис 92, а в верспектаві (рнс 93)
$ Н. Напруження в перерізі
Як уже зазначалося (див § 14), в перерізі навантаженого стерж ня діють неперервно розподілені по перерізу внутрішні зусилля Зводячи їх до центра ваги перерізу, дістаємо головний вектор % та голов ний момент М, проекції яких на головні центральні осі у, г перерізу та вісь х стержня дають величини (), N. Му, Мг Мх = Мкр, то називаються зусиллями та моментами в перерізі На рис 94, а пока зано розподілені по лівому перерізу зусилля, які є наслідком дії пра вої частини стержня (показано штриховими лініями) на ліву, їхні го ловний вектор /? та головний момент М Вектор/?е сумою зусиль, роз поділених по всій площі перерізу
Розглянемо нескінченно малий елемент площі (іГ (рис 94, б) Унас ділок малості елемента можна вважати, що внутрішні зусилля, які діють в його різних точках, однакові за модулем та напрямом Тоді їхня рівнодійна буде Проходити через центр ваги елемента еіР, ко-
1 . у і і далі цифри в квадр тних дужквх у головках таблиць вказують значення відповідної графи
”1
ординати якого у та г Отже, зводячи ці зусилля до центра ваги елемента АР, матимемо головний векторі/? та головний момент дМ, що
М """'"-у 1 торівнююгь нулю
І	Проекціями дЦ на осі х, у, 2 бу-
У а	дугь елементарна поздовжня силаДО
та елементарні поперечні сили
-Зи^ао, У	та ЙО* Оскільки, як було сказано,
зусилля на елементі АР можна вважати розподіленими рівномірно, то, поділивши гіф, таЛ^на ліо-ту дР, дістанемо значення поздовжніх та поперечних сил, які припа дають на одиницю площі
Ці величини називають напруженнями в точці у, 2 проведеного перерізу стержня, причому о — нормальне напруження, т — дотичне на-пруження. їх виражають у паскалях (Па) та кратних йому одиницях (кПа, МПа)
Отже, напруженням називається внутрішня сила, віднесена до оди ниці площі в даній точці розглядуваного перерізу
Іноді крім норма пьних напружень о та дотичних тг тг розгтядакгь ще й повне напруження
тобто повне зусилля, яке припадає на одиницю площі Очевидно,
р~ +	+ £
(3 28)
У загальному випадку навантажування тіла напруження в різних точках перерізу різні (як кажуть напруження розподілені по пере* різу нерівномірно), але бувають також і рівномірно розподілені на пруження
Поняття «напруження» відіграє дуже важливу роль у розрахунках на міцність Тому значна частина курсу опору матеріалів приділяється вивченню способів визначення напружень о та т
Неважко визначити загальні залежності між а та т, з одного боку, та (?„ Ми Мг та Ліх — з іншого Виходячи з означень з\силь та моментів (див $ 14) і враховуючи форм} ти (3 26), маемої
N - і Лї = {
(3 29)
щ = у т/Г.	(З ЗО)
= \т,гіг,	(ззп
Мц = ) гсіН = £	(3 32)
М, = £ уЛІЇ = ( ауйР.	(З 33)
Л<кр = І С/^х — ггіСв) = (ухг — гт,) гіГ = ртгіГ (3 34)
В останній формулі т е повним дотичним напруженням в точці перерізу з координатами у, гі
'~-зг=-------л/— =
ар- відстань від центра ваги перерізу до лінії дій (рис 94, в)
Добуті формули (3 29)	(3 34), які встановлюють зв'язок між
напруженнями та внутрішніми зусиллями, будемо називати статичними рівняннями, або інтегральними рівняннями рівноваги
Незважаючи на те, що компоненти внутрішніх зусиль в будь якому перерізі стержня, як правило, легко визначити наприклад з епюр, проте для практичних розрахунків добуті залежності безпосеред ньо використати не можна оскільки невідомий закон розподілу напружень по перерізу Отже задача обчислення напружень у перерізі завжди е статично невизнаяуванею Наприклад знаючи згинальний момент Мв у перерізі, не можна знайти нормальні напруження із формули (3 32) Однак, якщо скористатися тими чи іншими мірку ваіпіями вдається не тільки встановити закон розподілу а та % по пе-ремізу, але й за формулами (3 29)	(3 34) знайти самі напруження
Узагалі при виведенні формул для досліджування напруженого стану стержнів завжди будемо дотримуватися такої схеми
1	Розглядаємо статичний аспект задачі, тобто записуємо ті з рів нянь (3 29)	(3 34), котрі потрібні для розглядуваної задачі
2	Розглядаємо геометричний аспект задачі на базі експернменталь ного вивчення даного виду деформації стержня та певних гіпотез (зокрема гіпотези плоских перерізів) установлюємо залежності між переміщеннями точок стержня та їхнім положенням у перерізі відносно вибраної системи координат Ці залежності називають геометричними рівняннями
З	Розглядаємо фізичний аспект задачі на підставі експернменталь них досліджень фізичних властивостей матеріалу визначаємо залеж
ності між напруженнями та деформаціями (або переміщеннями) Ці залежності називають фізичними рівняннями
4	Виконуємо синтез, тобто разом розв’язуємо всі рівняння, здобуті в п 1 3, і шляхом виключення деформацій (або переміщень) діс таємо формули що виражають напруження через зусилля або моменти в перерізі
Глава 4. РОЗТЯГАННЯ І СТИСКАННЯ МЕХАНІЧНІ ХАРАКТЕРИСТИКИ МАТЕРІАЛІВ
$ 27. Напруження І деформації при розтяганні й стисканні Розрахунок на міцність І жорсткість
Розтягання або стискання стержня,спричинюється сигами, що ді .ють-уздовж його осі У цьому разі в поперечних"перерізах стержня Із шести внутрішніх силових факторів виникає лише один — поздовжня (осьова) сила N Найпростіший приклад розтягання стержня і епюру поздовжніх сил показано на рис 95 а б Осьова сила в перерізі є рівнодійною нормальних напружень, що виникають у кожній із точок перерізу Відсутність поперечних сил дає підставу припустити, що дотичні напруження в кожній точці поперечного перерізу дорівнюють нулю
Виведемо формулу для визначення нормальних напружень При розв'язанні цієї задачі будемо дотримуватися послідовності, наведе ної в § 26
Розсічемо стержень довільним поперечним перерізом п — п (рис 95. є) Статичний аспект задачі виражається вже відомим рівнянням (3 29)
N = £ адр	(4 І)
Із рівняння (4 І) не можна визначити напруження о, оскільки невідо мий закон розподілу їх в точках поперечного перерізу
Розглянемо геометричний аспект задачі При спостеріганні де формації розтягання стержня, на поверхні якого нанесено лінії, пер пенднкулярні до осі бруса (рис 95, а), можна помітити, шо иі лінії
зміщуючись паралельно самим собі, залишаються прямими і перпенди кулярними до осі бруса Припускаючи, що зазначена картин^леремі щупання перерізів має місце й усередині стержня, приходимо~дУгшо-теза плоских перерізів поперечні перерізи стержня, плоскі до дефор мани, залишаються плоскнми і після неї перемішимиїїг*
'вздовж осі стержня Поділимо тепер стержень ла''пдздовж»п’(гіаралель ні осі стержня) елементи нескінченно малих поперечних перерізів і будемо відтак називати їх «волокнами» На підставі гіпотези плоских перерізів можна зробити висновок, що всі волокна подовжуються на одну і ту саму величину і їхні відносні подовження є однакові
е = Д/// = сопзі	(4 2)
Це — аналітичний вираз геометричного аспекту задачі
Фізичний аспект задачі полягає у встановленні залежності дефор мацій від напружень При пружних деформаціях ця затежні##?™#* на і_як_віа£шо^назав^	І
8 — о/£. або о = Ев	(4 3)
де Е — коефіцієнт пропорційності, що називаються, ліодулелі поздовж ньоі пружності,. модулем пружності першого рсду^ або модулем Юнга Модуть прчжності — не одна зфпнчних констант матеріалу Виража ється модуль пружності в пасктіях
Ураховуючи сталість модуля пружності Е для однорідного й ізотропного матеріалу, а також вирази (4 2) і (4 3), знаходимо, що
о х= Ее — соп&і	(4 4)
Підставляючи вираз (4 4) у формулу (4 І), маємо
N = С ЕехіГ = Ее | АР = Ее.р = <зр,	(4 5)
9	є
ЗВІДКИ
О — М/Р	(4 6)
Знак напруження залежить від знака поздовжньої сили в розгляду ваному перерізі У разі стискання няпружрння ннлжають від'ємними
Зазначимо, що формула (4 6) справедлива лише для перерізів, досить віддалених від місць прикладання зосереджених навантажень Поблизу місць прикладання навантажень розподіл напружень має складний характер і потребує більш точних методів досліджування
Визначаючи напруження при розтяганні, стисканні й інших, видах деформування, в опорі хіатер.іаїіщ-я-такрж у соріі пружності широко користуються тя^мм ..їуукг важ 111ВИЧ по оженням яке має назв\ пріїн ципу Сен Взнана якщо тіло навантажується статично еквівалентна ми система ии сил, тобто такими, в яких головний вектор та головний момент однакові, й при цьому роз Міри зони прикладення навантажень невеликі порівняно з розмірами тіла, то в перерізах які достатньо від-дйлені від місць прикладення сил, напруження мало заіежапіь від
сдособу навантажування Загального теоретичного обгрунтування принципу Сен Венана немає, але його справедливість підтверджується численними теоретичними й експериментальними дослідженнями
Пояснимо цей принцип на такому прикладі Один І той самий стержень, закріплений верхнім кінцем (рис 96), навантажується на вільному кінці статично еквівалентними навантаженнями, рівнодійні яких визначаються вектором Р Навантаження прикладено різними слосо бами а — у вигляді зосередженої сили, б — у вигляді двох сил, в — у вигляді розподіленого навантаження Дослідження показують, що в усіх цих прикладах у поперечному перерізі віддаленому на ві істань, що перевищує в 1,5 2 рази його поперечні розміри напруження прак тпчно однакові Проте в перерізах поблизу місця прикладення сил напруження та характер розподілу їх різні
Перейдемо до визначення деформацій стержня Із виразу (4 5) мож на знайти відносне подовженню
—ег/
У межах призматичної ділянки стержня завдовжки І, виготовленого з однорідного матеріалу (£ = сопзі) І у перерізах якого діють однакові поздовжні сили тУ, подовження кожної одиниці довжини однакові й отже, .абсолютне подовження.
(4 8)
іОЗМІрНІСІЬ хи-
“Якщо на розглядуваній ділянці поздовжня сила та поперечний переріз змінні (рис 97 а в) то для елемента нескінченно малої дов жини (їх (рис 97 а) на підставі формули (4 8) можна записати
• . , , N (х) 4х
Повне подовження ділянки завдовжки І дістанемо, підсумувавши подовження всіх нескінченно малих відрізків
0
Рис 98
&

Зауважимо, що переміщення деякого перерізу відносно іншого до рівюое поздовжній деформації відрізка стержня між розглядуваними перерізами і позначається літерою А
Розтягання та стискання супроводжуються зміною поперечних роз мірів стержня (рис 98, а, б) При розтяганні вони зменшуються, а при стисканні збільшуються
За аналогією з поздовжньою деформацією різницю відповіли х по перечних розмірів після деформації й до неї назвемо абсолютною поперечною деформацією
Да — а, — а Дй = - Ь
(4 Ю)
При розтяганні поперечні деформації від ємні, а при стисканні - „г дати і
Поділивши абсолютну поперечну деформацію на вічповіднийпочат ковий розмір дістанемо відносну поперечну деформацію, яку лозначн мо е' Відносна поперечна деформація для ізотропних матеріалів в усіх поперечних напрямах однакова
е' — Да;а — ЬЬ/Ь	(4 11)
Між поперечною та поздовжньою відносними деформаціями при простих розтяганні та стисканні в межах застосування закону І у ка існує постійне співвідношення Абсолютне значений цього відношення має назву коефіцієнта Пуассона і позначається літерою ц
|х=|е'/е[	(4 12)
Коефіцієнт Пуассона — безрозмірна величина
Ураховуючи що поздовжня й поперечна деформації завжди мають протилежні знаки, маємо
в' = — це	(4 І 0
або згідно з формулою (4 3),
«' = -Н-г	(4 14)
При стисканні напруження у формулу (4 14)слідпідставлятизі знаком «мінус»
Коефіцієнт Пуассона р як і модуль пружності Е характеризує Пружні властивості матеріалу Для всіх ізотропних матеріалів значен ті коефіцієнта Пуассона перебуває в межах 0 0,5 Зокрема для корка
р наближається до нуля, для каучуку — до 0 5 для сталі р « 0,3 Значення модулів пружності Е та коефіцієнтів р для деяких матеріалів наведено в дод 9
$ 28 Умови МІЦНОСТІ і жорсткості, види розражунків
Основна задача опору матеріалів—забезпечити надійні розміри деталей, що зазнають того чи іншого силового, температурного (теп лсвого) або іншого впливу Такі розміри можна визначити з розрахунків на міцність та жорсткість Здебільшого основним буває розра хунок на міцність
Розглянемо умови міцності та жорсткості для простих розтягання та стискання
Зазначимо передусім, що небезпека початку руйнування характеризується не стільки значеннями внутрішніх зусиль та моментів у перерізі, скільки значеннями найбільших нормальних та дотичних на пружень, а також комбінаціями їх, які діють у небезпечних (тобто най більш напружених) точках перерізу
Фізично очевидно, що які завгодно великі напруження матеріал не може витримати. Тому найбільші напруження з умови ндд'йнеї рп боти деталі треба обмежувати- деякими попустимими чнячешіями Їх називають &пщ./пил<ижц напруженнями При розтяганні та стисканні допустимі напруження позначають відповідно Го\Гта~(<7_Т, прн зсуві — {ті •*;
.Якщо відомі допустимі напруження і є і|юрмули, щ© визначають напруження через Засилля і моменти в церцріл, то у принципі можна розрахувати на міцність будь яку деталь
У. пазі розтягання або стискання стержня знаходять діебезпещу Перерізи, в яких напруження досягають найбільших за_модулем зна-діепь, і для цих перерізів записують умову мшносхи
5—= |-^-|<ЮІ	(4 15)
При розтяганні в праву частину цієї умови підставляють допустимі .напруження на розтягання (о^І, а при стисканні — допустимі напру, ження'на_стисканни (о~Т
ЇВикористбвуючтг~уйову міцності (4 15), можна розв’язувати- три тини-задач—	"
1)_за відомими навантаженнями лля вибраного матеріалу знайти ЦаДійнід погляду міпності розміри поперечного пар^ріту стержня (про ектувальний розрахунок),
2) за піДДйими розмірами та матеріалом деталі перевірити, ди-вмо-вона аитрмматц чадан» ППППНТгЦЧЄННЯ (перевірний розрахунок);
1 Деякі мірк}ваиия щодо виборі допустимих напружень наведено в § 34
3) за відомими розмірами деталі, матеріалом і схемою навантажу «ВДНія- .визначити допустиме навантаження
іноді для забезпечення нормальної роботи машин та споруд розмі ри їхніх деталей треба вибирати так, щоб задовольнити умову жорсткості При розтяганні (стисканні) умова жорсткості має такий вигляд
АІ = Х(	<|ДІ)	(4 16)
де Д/ — зміна довжини деталі, [Д/і — допустиме значення цієї зміни Нагадаємо, що розрахунок за умовою жорсткості завжди слід до повнювати розрахунком на міцність Якщо умова жорсткості викону ється, а умова міцності ні, то задачу треба розв'язувати з умови міц пості
Аналогічно розраховують на міцність та жорсткість при інших простих деформаціях стержня Міркування щодо розрахунку на міцність прн складних напружених станах викладено в гл 7
$ 29. випробування матеріанів на розтягання
При проектуванні й розрахунках на міцність, жорсткість і стій кість елементів механізмів, машин та споруд треба знати властивості матеріалів Тому матеріали випробовують на розтягання, стискання, зсув, кручення згинання та твердість Докладні описи всіх видів механічних випробувань, а також машин та приладів, що прн цьому за стосовуються, наведено в спеціальних курсах і посібниках з лаборатор них робіт з опору матеріалів Обмежимося лише коротким описом деяких поширених видів механізмів випробувань та здобутих прн цьо му результатів
Одним із основних видів випробувань матеріалів є випробовування на розтягання, оскільки при цьому виявляються найбільш важливі їхні властивості 3 випробуваного матеріалу виготовляють спеціальні
У циліндричних зразках має витримуватися співвідношення між розрахунковою довжиною зразка Ів та діаметром у довгих зразків Іо — ІШо, у коротких — Іо = &40 Ці співвідношення можна виразити в дещо іншій формі Враховуючи, що
<1, = ]/' -!£•_ _ і.ізу"?;,
де Ро — площа поперечного перерізу зразка маємо для довгого зразка
4=113 1/?;	(4 17)
для короткого —	__
4 = 5 65 ^/%	(418)
Щоб дотриматися подібності при випробуваннях, ці співвідношення мають поширюватися і на плоскі зразки
Як основні використовують зразки з діаметром ф, = (0 мм; при цьому робоча довжина ї0 ~ 100 мм Допускається застосування зраз ків інших діаметрів за умови, що їхня робоча довжина /0 = ІО4о або /0 -- 5гі0 Такі зразки називають пропорційними
Діаграми розтягання Для випробувань на розтягання застосовують розривні машини що дають змогу в процесі випробування визна чити зусилля та відповідні до них деформації* зразка За цими даними будують початкову діаграму розтягання, в якій по осі ординат відкла дають зусилля, а по осі абсцис — відповідні до них подовження Діа і раму розтягання можна зняти її автоматиіно за допомогою спеці-атьних діаграмних апаратів Характер діаграми розтягання залежить від властивостей випробуваного маїеріату Типовий внгтяд такої діа грами для маловуглецевої стазі зображаю на рис 100
Розгіянемо характерні ділянки й гонки цієї діаірямп а також від повідні до них стадії деформування зразка
Від початку навантажування до певного значення розтягальної сили має місце прямо пропорційна залежність між подовженням зразка та силою Ця залежність на діаграмі визначається прямою ОА На цій стадії розтягання справедливий закон Гука
Позначимо силу за якої закон пропорційності припиняє свою дію. через РП11 Цьому значенню сили на діаграмі відповідає точка А На пруження спричинене силою Рад, називається границею пропорційнеє ті й обчислюється за формулою
Спа = /’пц/Ро	(4 19)
Отже, границею пропорційності називається напруження, після якого порушується закон Гука
Як уже зазначалося, деформація називається пружною, якшр вона повністю зникає після розвантаження Припустимо що поступово підвищуючи навантаження Р, будемо при кожному його значенні здійс нювати повне розвантаження зразка Доки сита Р не досягне певного значення, доти спричинені нею деформації будуть зникати прн роз
Рис 101
вантаженні Процес розвантажування прн цьому зобразиться тією самою лінією, що й навантажу вання
Позначимо через Рпр найбільше значення си ли, при якому зразок ще не дає при розвантажен ні залишкової* деформації Цьому значенню на діаграмі відповідає точка В а пружній стадії роз тягання зразка — ділянка ОВ
Найбільше напруження, до якого залишкова деформація при розвантаженні не виявляється, називається границею пружності Це напружен ня спричинюється силою РПр і визначається за формулою
Опр = Рпр/Рр	(4 20)
Границя пружності є характеристикою не пов язаною із законом Гука Точка В може бути як вище, так і нижче від точки А Ці точки а от
же і значення напружень опц та о„р близькі одна до одної, і, як правило, різницею між ними нехтують
Після точки А при далішому розтяганні зразка крива розтягай ня стає криволінійною і плавно піднімається до точки С деспостеріга еться перехід до горизонтальної ділянки СО, що називається плоіцзд кою текучості На цій стадії розтягання подовження зразка зростає при сталому значенні розтягальної сили, яку позначають Р, Такий процес деформації, що його називають текучістю матеріалу супроводжується залишковим (пластичним) подовженням яке не зникає після розвантаження
Отже границею текучості аг зветься найменше напруження, при якому деформація зразка відбувається при постійному розтягальному зусиллі Границя текучості визначається за формулою
а, - Р,!Р0
(4 21)
Початок пластичної деформації відповідає наставанню деякого критичного стану металу, який можна виявити не тільки за за тишко вими деформаціями але й за іншими ознаками При пластичній дефор манії підвищується температура зразка у сталі змінюються електропровідність та магнітні властивості При цьому на полірованій поверх пі зразків, особливо плоских, помітне гогьмянення що е наслідком появи густої сітки ліній Ці лінії мають назву ліній Чернова (ліній Лю-дерса) Вони нахилені до осі зразка приблизно під кутом 45° (рис 101 а) і становлять мікроскопічні нерівності, що виникають внаслідок зсувів у тих площинах кристалів, де діють найбільші дотичні напруження Внаслідок зсувів по похилих площинах зразок зазнає залишкових деформацій Механізм утворення їх спрощено показано на рис 101, б
І-----—-і Після стадії текучості матеріал знову набирає
Ц,____здатності збільшувати опір дальшому деформуванню
І сприймає зусилля щозростае до деякої границі
Рис 102 ЦьомувідповідаєвисхіднаділянкаДЕ(див рис 100) кривої розтягання що зветься ділянкою зміцнення
Точка Е відповідає найбільшому зусиллю Рт». яке може сприймати зразок
Напруження, що відповідає максимальній силі Рта, називається тимчасовим опором, або границею міцності, і позначається о, Його визначають за формулою
О» =	(4 22)
До цього моменту подовження розподілялися рівномірно ПО всій довжині /0 зразка площі поперечних перерізів розрахункової частини зразка змінювалися неістотно і також рівномірно по всій довжині. Тому для обчислення Опп, оПр, о, та а, у розрахункові формули вводитися початкові значення площі Ео
Після досягнення зусилля Рго„ при дальшому розтяганні зразка деформація відбувається, в основному на невеликій довжині зразка Це призводить до утворення місцевого звуження у вигляді шийки (рис 102) і до зменшення сили Р, незважаючи на те, що напруження у перерізі шийки неперервно зростає Зменшення розтягальної сили Р спостерігається лише при випробуванні зразка у машині яка обмежує швидкість зростання деформації При навантажуванні шляхом підвішування вантажів руйнування відбудеться при постійному навантаженні, але із все зростаючою швидкістю деформації
Позначивши через Ркр розтягальну силу в момент розриву, матимемо
Дкр = Рмр/Го	(4 23)
Визначене таким чином напруження при розриві зразка надто умовне і не може бути використане як характеристика механічних властивостей сталі Умовність полягає в тому, що його здобуто діленням сили в момент розриву на початкову площу поперечного перерізу зразка, а не на дійсну його площу при розриві яка значно меиша, ніж почат нова, внаслідок утворення шийки
Основними характеристиками пружності та міцності матеріалів що використовуються у практичних розрахунках є границя пружності сгОр, границя текучості ог та тимчасовий опір (границя міцності) а. Дія маловуглецевої сталі, що має площадку текучості, наприклад для сталі Ст2, ці характеристики такії ат = 200 МПа ат = 220 260 МПа, о, « 340 420 МПа
Для металів, що не мають площадки текучості, границю текучості визначають умовно як напруження, при якому залишкова деформація є величиною, регламентованою державним стандартом або технічними умовами Згідно з ГОСТ 1497—84, залишкова деформація становить 0.2 % від вимірюваної довжини зразка Умовні границі текучості по
значають нижнім індексом відповідно до заданогозначення деформації, наприклад оо.?
Ураховуючи, що практично важко встановити початок відхилення від закону пропорційності й початок появи перших залишкових дефор мацій, вводять також поняття умовних границі пропорційності та границі пружності
Умовною границею пропорційності називають найменше напружен ня при якому відхилення від лінійної залежності між напруженням та деформацією досягає деякого значення що встанов пояться техніч ними умовами (наприклад, 0 002 % від вимірюваної* довжини зразка)
Умовною границею пружності називають найменше напруження, при якому залишкова деформація досягає заданого значення (як правії ло 0,001 0 05 % від вимірюваної довжини зразка) її позначають нижнім індексом відповідно до заданого значення залишкової дефор* манії* (наприклад а0.ооі чи о00з)
Найважливіші механічні характеристики деяких матеріалів що широко застосовуються наведено в дод 2 8
Розвантаження та повторне навантажування. Як уже зазначалось, якщо при зусиллі розтягання, що спричинює напруження не вище за границю пружності припинити навантажування а потім розванта жувати зразок то процес розвантаження зобразиться на діаграмі лі нією, яка практично збігається з лінією навантаження Пісія оста точного розвантаження зразка його подовження повністю зникає Повторне навантажування на діаграмі піде по тій самій лінії ОВ, яку здобуто при першому навантажуванні зразка
Буде інакше, якщо до початку розвантаження напруження у зраз ку перевищує границю пружності Виконавши розвантаження на приклад, після досягнення силою значення, зображеного ординатою точки М (див рис 100), помітимо, що процес розвантаження на діа грамі описується вже не кривою яка збігається з кривою навантажу вання ОАВСОМ, а прямою МУ паралельною прямолінійній ділянці ОА діаграми Подовження ДҐ зразка до початку розвантаження при розвантаженні зникає не повністю Зникла частина подовження на діаграмі зобразиться відрізком ДЇПр. а та частина що залишилася,— відрізком Дїо Отже, повне подовження зразка за границею пружності складається із даох частин — пружної та пластичної
ДҐ = Дїлр + Д/о
Так буде до самого розриву зразка Після розриву пружна складова повного подовження в обох частинах зразка (відрізок Д4Р) зникає Подовження, що залишилося зображується відрізком Д1о
Будемо знову навантажувати зразок який був розтягнутий силою, що спричинила в ньому напруження вище за границею текучості а потім розвантажений При цьому виявиться, що лінія повторного навантажування майже збігається на діаграмі з лінією розвантаження МУ Границя пропорційності підвищиться й буде приблизно дорівню
м £_	вати тому напруженню, до якого
V	первісно був розтягнутий зра
я Г і	зок При дальшому підвищенні
й	;	І	роздягальної сил» крива ліагра
І	і	Д	ми збігається з МЕР Частина
/ о. й	л	діаграми ліворуч від ліпи ЯМ
І	4	/І	виявиться відсіченою тобто по
і/ і я і	1 чаток координат переміститься в
І/ 1 и	и! Іг точку N Залишкове подовження
СІ------ І И Л  -----------і—І	після розриву буде меншим ніж
— —1 а у зразку що не зазнав поперед-г------—’ й[	ньоі пластичної деформації
«•---------------  Отже попереднє витягування
Рис 103	за границю текучості змінюєдея
кі механічні властивості сталі — підвищує границю пропорційності й зменшує залишкове подовження після розриву, тобто робить її більш крихкою Зміна властивостей матерія ту внаслідок деформації’ за границею текучості зветься наклепом У деяких випадках це явище небажане, і його намагаються усунути, а інших же, навпаки, наклеп корисний, і його утворюють штучно
Відносні подовження та звуження після розриву. Повне подовжен ня, якого зазнав зразок перед руйнуванням, зменшиться після розри ву оскільки в частинах зразка зникнуть пружні деформації Віднос ним подовженням після розриву Ь, %, називають відношення приросту розрахункової довжини зразка після розриву до його початкової дов жнни
6 „^100	(4 24)
Відносне подовження після розриву характеризує пластичність матеріалу Залежно від цього подовження матеріали поділяють на плас тичні й крихкі. Для перших можна умовно взяти б > 5 %, а для других — б < 5 % До пластичних матеріалів належать маловуг тецева сталь, чавун, скло, камінь, бетон тощо Наприктад для вуглецевої сталі марки Ст2 відносне подовження після розриву б » Зі %
Відносне звуження зразка після розриву V, %, визначається ділен ням абсолютного зменшення площі поперечного перерізу в шийці на початкову площуі
V- -^=-100	(4 25)
Чим більше відносне звуження після розриву, тим пластичніший ма теріал Наприклад, для м’якої вуглецевої сталі марки Ст2 У — 55 65 %
Відносне подовження б й відносне звуження ¥ є характеристиками пластичності матеріалу Вони певною мірою умовні, оскільки приріст довжини у формулі (4 24) й зменшення площі поперечного пере
різу зразка у виразі (4 25) належать до початкової довжини й початкової площі поперечного перерізу Насправді пластична деформація відбувається на довжині зразка, що неперервно змінюється Позначивши через сії приріст довжини І зразка в даний момент випробування, знаходимо так зване дійсне відносне подовження
е = ^4--ІпТ7	(420
Тут і 4 — відповідно початкова та кінцева довжини зразка Оскільки
Їк = /О + Д( і « = Д///о то
е-Іп »-+^- = 111(1 +8) ‘в
Розкладаючи праву частину цієї формули в ряд за степенями 6, ді станемо
Є - 1П(1 хв)-.а—^-4 4-----------
Як бачимо, при матих значеннях 6 умовна та дійсна деформації прак тичнооднакові Так, ужеприб — 10 'о дійсне поювженняе -• 9,95 % Аналогічно можна визначити дійсне поперечне звуження
= = = <427>
Як свідчать експерименти, при пластичній деформації об’єм тіла не змінюється
або
Із цього випливає, що Т = е
Робота деформації Крім уже названих характеристик механічних властивостей матеріалу, діаграма розтягання дає змогу визначити ще й енергетичні його характеристики
Площа діаграми розтягання в координатах Р ~ характеризує роботу, яку витрачено на розрив зразка Це можна показати так
Нехай деякій розтягальній силі Р відповідає деформація X зразка (рис 103) Надамо силі Р нескінченно малого приросту сіР, при цьому приріст деформації буде 4Х Очевидно, робота зовнішніх сил на цьому переміщенні
4А = (Р+4Р)4Х«РА
Робота, яку витрачено на розтягання зразка до подовження X]
А = [ Рак (4 28) 6
Як видно з рис 103, інтеграї е площею ОАВСОМпО діаграми розтягання Робота яку витрачено на розрив зразка, буде дорівнювати всій площі ОАВСОЕРОО діаграми розтягання
У межах пружності повна робота де
формації визначається площею трикутника (рис 104, а)і
(4 29)
Поділивши повну роботу деформації А на об’єм робочої частини, зразка, знайдемо питому роботу деформації, тобто роботу, яку витрачено на деформування одиниці об'єму матеріалу!
апр = Д/И	(4 30)
Підставивши у формулу (4 ЗО) значення А із формули (4 29) та V — = Ро1о Дістанемо
Питома робота деформації у межах пружності визначається площею трикутника на діаграмі о **- е (рис 104, б)
Питома робота деформації характеризує здатність матеріалу чинити опір ударній дії навантаження чим більша питома робота деформації до розриву, тим краще матеріал чинить опір ударним навантаженням
Діаграма розтягання в координатах о **- в. Вигляд діаграми роз тягання в координатах Р ~ залежить не тільки від властивостей матеріалу, а й від розмірів випробуваного зразка
Щоб здобути діаграму, яка характеризує тільки механічні власти вості матеріалу, початкову діаграму розтягання перебудовують у координатах о ~ е Ординати такої діаграми дістають діленням розтя гальної сили на початкову площу поперечного перерізу зразка (о = = РіР»), а абсциси — діленням абсолютних подовжень розрахункової частини зразка на її початкову довжину (е = А///о) Зокрема для характерних точок діаграми ординати визначають за формулами (4 19)	(4 23)
Діаграму в координатах о ~ е, яка відповідає початковій діаграмі (див рис 100), зображено на рис 105 а Точкам О А В, С, О, Е, Р початкової діаграми відповідають точки О, а, Ь с, д, е, І діаграми о ~ е
(з діаграми а ~ в блчимо що
(§а = а/8 = Е,	(4 32)
тобто модуль пружності при розтяганні дорівнює тангенсу кута нахилу прямолінійної ділянки діаграми до осі абсцис
Площа діаграми напружень о~еу відповідному масштабі дорівнює питомій роботі деформації Низхідна ділянка є/ діаграми має умовний характер, оскільки дійсна площа поперечного перерізу зразка після утворення шийки та початкова площа за якою визначають ординати діаграми, значно відрізняються одна від одної Розділивши силу на дійсну площу поперечного перерізу зразка, можна знайти дійс не напруження та побудувати відповідну діаграму (рис 105 а — штрихова лінія)
Оскільки після утворення шийки відносна поздовжня деформація розподіляється по довжині зразка нерівномірно, то дійсні діаграми бу тують в таких координатах відносне звуження ¥ поперечного перерізу в шийці ~ дійсне напруження 5 де V = (Ро — Рі)/Р0, 5 = = а Р/ та Р, — відповідно зусилля та найменша площа поперечного перерізу в даний момент дослідження
Криву дійсних напружень при розтяганні маловуглецевоїсталі наведено на рис 105 б Точці В відповідає початок виникнення залишкової деформації й дійсне напруження що є границею текучості Точці Е відповідає найбільша сила Ям», яку витримав зразок під час випробування За нею визначається дійсний тимчасовий опір 5. Деформація зразка від початку розтягання до моменту, що відповідає точці Е, рівномірна по довжині зразка Абсциса точки Е (Ус) показує найбільше рівномірне звуження Точка А діаграми відповідає моменту розрн ву зразка її абсциса є найбільшим звуженням перерізу ¥к, орднна та — дійсним опором розриву 8к Як видно із дійсної діаграми, опір пластичному деформуванню зростає аж до моменту руйнування
Для визначення механічних характеристик на практиці використовують умовні діаграми розтягання в координатах а ~ е Побудови
Рис 106
о ооог ооой с Рис 107
діаграм дійсних напружень значно складні ші, вони потрібні здебільшого для теоретик них досліджень
Зазначимо що площадку текучості має порівняно небагато металів — маловуглецева стать латунь і деякі відпалені марганцевисті та алюмінієві бронзи Більшості металів при таманний поступовий перехід у пластичну зону Для порівняння на рис. 106 наведено діаграми позіягавия-кількох металів крива / — бронзи (о, '= 247МІЙ70 == 36 %), 2—вуглецевої сталі (ов = 358МІІа, б = 38 %), 3— нікелевої сталі (о„ = 715МПа, 6 =» 54 %) та 4 —марганцевистої сталі (оя = 916 МПа, 6 = ЗО %)
Розрив зразків із крихких металів відбувається при дуже невели кому подовженні й без утворення шийки На рис 107 наведено діа граму розтягання сірого чавуну СЧ 28 типову для таких матеріалів Діаграма не має вираженої початкової прямолінійної ділянки Однак, визначаючи деформації у чавунних деталях, користуються формулою закону Гука Значення модуля пружності Е знаходять як тангенс ку та нахилу прямої, проведеної через початкову точку О діаграми в точ ку В, що відповідає напруженню, при якому визначають деформацію Такий модуль називають січним
§ ЗО. Деякі інші види механічних випробувань
Випробування на стискання, незважаючи на їхню простоту, проводять рідше ніж на розтягання Це пояснюється так
Для пластичних матеріалів модуль пружності, границя пружності^ та границя текучості при стисканні тшб.інацо ті самі, що і при роз-^ тяганні Напруження, що відповідає руйнівній силі, при стисканні пластичних матеріалів дістати не можна, оскільки зразок не руйнується, а перетворюється на диск, а стискальна сила постійно арсогае. При випробуванні пластичних матеріалів на стискання_тааомцш можна здобути характеристик, аналогічних відносному подовженню й від_ 'носкому звуженню при РОЗРИВІ
Рис 108	Рис. 109	Рис. 110
Випробуванню на схискшміялиддаїоть-здебд.'идюгс) крихкі.матері алНіЩОд як правило, краще чинять опір стисканню, ніж розтяганню, і застосовуються для виготовлення елементів конструкцій, якГ працюють на стискання Для розрахунку їх на міцність треба знати харак теристики матеріалу, що дістають при випробуванні на стискання
Випробування матеріалів ия стискання виконують на спеціальних пресах-або універсальних випробувальних машинах Для цього ви готовляють зразки у вигляді циліндрів невеликої висоти (як правило, від одного до трьох діаметрів) або кубиків~Тертя, що виникає під час випробування на стискання між плитами машини і торцями "Зразка, Істотно впливає на результати випробування і на характер руйнування Циліндричний зразок із маловуглеиевої сталі набуває при цьому боч коподібної"форми (рис 108) Діаграму стискання, яку знято прн ви пробуванні зразка Із такого матеріалу, зображено на рис 109 На рис 110, а показано характер руйнування зразка із каменя під дією стискальних зусиль Р та сил тертя між плитами машини і торцями зразка Якщо зменшити сили тертя нанесенням шару парафіну на тор ці зразка руйнування відбудеться інакше (рис 110, б)і зразок дасть тріщини паралельні напряму стискальних сил, й розшарується. Як зразок із каменя руйнується і бетонний зразок
Руйнування при стисканні чавунного зразка вілбувядтьдя вняслЬ док зсуву однієї частини зразка відносно іншої (рио III). Діагр_аму
6 г—1		 ППй	р 300 	 200—і'-	 С'/уг	до/. -		 0 0002	0006 Є Рж НІ	Рнс. 112	/ґ /	—* лі Рис. 113
Деревина, то £ анізотропним матеріалом, при стисканні як і при розіясаиді, має різну мїцн їсть .залежно від напряму .стискальної сили відносно до напряму во-юкон На рис 113 зображено діаграми стис кання двох кубиків із деревини однієї поро ди Крива / ілюструє стискання кубика вздовж волокон а крива 2 — впоперек во-
локон ч£Іри стисканні вздовж волокон деревина значно міцніша, ніж діри стискаЯНІ Впоперек волокон І1ри_ стисканні вздовж волокон зразок руйнуєТЬСЯ-Епаслідок зсуву однієї’ частини відносно ГнійбТ’.’а при стисканні впоперек волокон деревиііа_має схильність до пресування, і незавждн вдається"виз~начити момент початку руйнування
У табл 5" наведено значення тимчасового опору при стисканні де яких матеріалів
Визначення твердості матеріалів Іноді для оцінки тимчасового опору можна скористатися непрямим методом зокрема вимірюванням твердості
Твердістю матеріалу називають здатність чинити опір механіч ному прониканню в його поверхню іншого, більш твердого тіла Для визначення твердості найчастіше в поверхню матеріалу з певного силою вдавлюють тіло (індентор) у вигляді кульки, конуса або піраміди На підставі розмірів здобутого відбитка роблять висновок про твердість випробуваного матеріалу
Найпоширенішим методом визначення твердості є метод Брінелля Статева загартована кулька діаметром О (рис III) удавлюється у випробуваний зразок (виріб) під цєю навантаження Р лриктаденого протягом певного часу Після віддалення иавашаженнн вимірюється діаметр відбитка, що залишився на поверхні зразка Число твердості за Брівеллем виражається відношенням заданого навантаження Р кгс, до площі поверхні сферичного відбитка Р, мм3 і може бути визначене за формулою
нв= <4-м>
де Р — навантаження, кгс, О — діаметр кульки, мм, д — діаметр відбитка, мм
Таблиця 9
2Р
Матеріал
мп*
Матеріал
а, сг МПв
Чавун сіоий звичайний ГраНІТ
Цегта
Бетон Текстоліт Гетинакс
600
120
130
150
1000 260
.30 50 250 160
Сосна (вологість 15 %)і уздовж волокон впоперек волокон
Дуб (вологість 15 %) уздовж волокон впоперек волокон
«О
50
Число твердості виражається у кілограм силі на міліметр квадрат ний (кгс/ммг), хоч, як правило, одиницю не вказують
Якщо твердість вимірюють кулькою діаметром О = 10 мм під на вантаженням Р = 3000 кгс із видержкою під навантаженням протягом часу і = |0с, то число твердості за Брінеллем супроводжується позна ченням НВ, наприклад 300 НВ При інших режимах випробування після літер НВ зазначають умови випробувань у такому порядку діа метр кульки навантаження і тривалість видержки під навантаженням Наприклад 200 НВ 5/250/30 означає 200 — число твердості, НВ — твердість за Брінеллем, 5 — діаметр кульки, мм 250 — навантажен ня кгс 30—тривалість видержки під навантаженням с
Якщо твердість матеріалу НВ 450 кгс/мм", то визначити її вдав люванням кульки не можна у зв'язку з помітною деформацією остан ньої Тоді замість кульки вдавлюють алмазний конус (метод Роквелла) або алмазну піраміду (метод Віккерса) Застосовують й інші методи Наприклад, твердість визначають за висотою відскоку бойка, що падає 8 певної висоти на поверхню випробуваного матеріалу, за періодом коливань маятника, що упирається у поверхню матеріалу
Твердість яку визначено різними методами, за допомогою спеці альних таблиць можна перевести у твердість за Брінеллем
Визначення твердості — вельми поширене випробування, що пояснюється його надзвичайною простотою Твердість можна визначити й безпосередньо в умовах виробництва на готових виробах, оскільки відбитки, що залишаються, здебільшого не псують виробів
Експериментальним шляхом установлено, що для деяких матеріа лів існує певний зв’язок між числом твердості за Брінеллем НВ та тимчасовим опором при розриві а. Наприклад, для маловуглецевої сталі о, «і 0,38 НВ, для сталевих виливків а. = (0,3 0,4) НВ для сірого чавуну ов== (НВ—40)/б
§ 31 Поняття про механізм утворення деформацій
Різні види механічних випробувань металів дають лише зовнішнє уявлення про характер пружної та пластичної деформації Наведемо короткий і спрощений виклад сучасних уявлень про процеси, що виникають у металах при таких деформаціях
Як відомо, метали мають кристалічну структуру При затвердиенні металу в розплаві одночасно виникають багато центрів кристалізації, внаслідок чого ріст кожного кристала обмежується сусідніми У результаті технічний метал складається з багатьох кристалів неправильної огранки, що їх називають кристалітами, або кристалічними зернами Відносно одне одного кристалічні зерна орієнтовані по-різному Разом з тим у кожному з них атоми розташовані цілком певно й утворюють так звані кристалічні решітки, які складаються з однакових комірок, що повторюються
Атоми електрично нейтральні, оскільки негативні заряди електро нів нейтралізовані позитивним зарядом ядра У металах при достатньому зближенні атомів виникає можливість відриву валентного електрона одного атома позитивно зарядженим іоном іншого Отже, частина ваіентних електронів починає переміщуватися Ці електрони назива ють вільними, оскільки вони не зв'язані з певними атомами
Метал можна уявити собі як структуру з нейтральних атомів та іонів, що перебувають в атмосфері електронного газу, який наче утри муе іони Зв'язок між атомами, що здійснюється електростатичними силами внаслідок взаємодії' позитивних іонів та електронного газу, на зивається металічним Оскільки ні атоми за своєю природою одна кові то розташовуватися вони повинні на таких відстанях один від одного та у таких точках простору де сили притягання й відштовху вання, що діють на них були б однакові У результаті відбувається закономірне розташування атомів яке спостерігається у кристалічних решітках
Кристалічну решітку утворюють уявні лінії й площини, що прохо дять крізь точки простору вякихрозташовані іони металу Правильніше пі точки визначити як центри найбільш імовірного розташування іонів, оскільки останні не залишаються нерухомими а котннаїоться навколо цих центрів Ці центри, як звичайно, називають вузлами кристалічної решітки Найпоширенішими типами таких решіток металів є кубічна обємноцентрована (рис 115, а}, кубічна гранснентрована (рис 115, 6) та гексагональна щільноупакована (рис 115, в) У них атоми перебувають у стійкій рівновазі й мають мінімальну потенціальну енергію
Коли метал деформується відстані між атомами під дією зовнішніх сил змінюються у певних напрямах, лінії та птощики що проходять крізь атоми, а отже, і кристатічна решітка викривлюються Оскільки при цьому рівнодійні сил притягання й відштовхування між атомами вже не дорівнюють нулю, то в решітках діятимуть внутрішні сили, що намагаються повернути атоми в положення рівноваги Залежність між малими зміщеннями атомів та силами взаємодії з певним ступенем наближення можна вважати лінійною Сумарно це виявляється в лі 100
Ряс. 116
ніііній залежності між зміщеннями точок тіла та зовнішніми силами, яка виражається законом Гука
При усуненні зовнішніх сил атоми знову займають свої попередні місця в кристалічних решітках внаслідок чого відбувається пружне відновлення форми металевого тіла Так пояснюється пружна дефор манія
Якщо зовнішні сили збільшуються, то зростають І внутрішні Тоді в зернах металу відбуваються зміщення однієї частини відносно ін шої, що зветься ковзанням Дослідженнями встановлено, що воно від б^вається по площинах і напрямах, уздовж яких атоми розташовують ся найбільш щільно У кожній з кристалічних решіток, які зображено на рис 115, одну таку площину заштриховано, а напрями ковзання показано стрілками Важливою характеристикою них площин та на прямів є напруження зсуву т, що спричинює ковзання
Розглянемо механізм утворення пластичної деформації в межах од ного кристала з довершеною кристалічною решіткою, спрощену модель якої показано на рис 116, а
Нехай у такій решітці верхній шар атомів зміщується відносно нижнього по площині А—А Якщо припустити, що в процесі зсуву кристалічна решітка не викривлюється -тобто у частинах її вище та нижче площини А—А відстані між атомами залишаються незмінними, то можна зробити висновок що всі атоми верхнього шару зміщуються відносно нижнього одночасно і на одне й тс саме значення Доки вза ємне зміщення и (рис 116, б), зростаючи, залишається меншим за по ловину відстані між атомами (а/2) доти сили взаємодії між ними пе решкоджають зсуву Як тільки це зміщення перевищить відстань а/2, си їй взаємодії почнуть сприяти зміщенню решітки в нове стійке положення рівноваги Пластична деформація відбудеться внаслідок зміщення частини решітки на відстані, кратні а (рис і 16, в) Найменша пластична деформація відповідає зміщенню на а Внаслідок таких змі щень кожний попередній атом займає місце наступного, всі атоми опи няються на місцях, що властиві даній кристалічній решітці Кристал зберігає свої властивості, змінюючи лише конфігурацію
Точні теоретичні розрахунки, що грунтуються на описаній карти пі деформації, дають змогу визначити максимальні дотичні напружен
Рнс 117
ня, які повинні виникнути в кристалі для того щоб з явилася пластин на деформація В дійсності вона починає утворюватися, коли напруження а сотні разів менші, ніж дає теорія Така розбіжність між теоретичним І дійсним опором зсуву в кристалах пояснюється тим, що перехід атомів з одного положення в інше здійснюється не одночасно, а у часі, подібно хвилі, з місцевими викривленнями решітки, що звуться дислокаціями
На рис (17, а показано так звану крайову дислокацію Верхня частина решітки зсунута відносно нижньої на одну міжатомну від стань, причому зафіксовано положення, коли зсув охопив ще не всю площину ковзання У результаті з явилося викривлення решітки од на вертикальна атомна площина верхньої потовими не має продов ження у нижній
Зазначимо, що реальні кристали або із самого свого виникнення містять дислокації, або мають якісь інші недосконалості, й у них дис локації утворюються вже при низьких напруженнях зсуву Тому прн низьких напруженнях дислокації рухаються через кристалічну ре щітку, що і спричинює пластичну деформацію кристала Після того, як дислокація вийде назовні кристала, форма його іміниться, але структура залишиться тією ж самою (рис 117, б) Виникають нові дислокації й рухаються крізь кристал Сумарно резу іьпіт цих ков зань у зернах виявляється у вигляді пластичної ц*<|іормлцІЇ ірвзка
Переміщення дислокації крізь кристал можна уподібнити руху складки по килиму Коли складка пройде крізь весь килим він буде дещо зміщений Сила, необхідна для переміщення і клпдкн Істотно менша, ніж та, яка потрібна для того, щоб зрушити весь килим цілком
Так теорія дислокацій пояснює механізм утворення пластичних деформацій та розбіжність між теоретичною і дійсною міцністю ме талів
При масовій пластичній деформації дислокації, які рухаються у кристалічній решітці по площинах, що перетинаються, утворюють нерухомі пороги, тому переміщення дислокацій гальмується Сумарно це виявляється як зміцнення металу після певної пластичної деформації
Поява зсувів у кристалічній решітці, що призводять до пластич мої деформації, не виключає викривлень кристалічної решітки, які 102
відповідають пружним деформаціям Це підтверджується тям, що иа будь якій стадії деформування зразка, аж до самого розриву, повна деформація складається з пружної та пластичної
Підвищення опору руху дислокацій приводить до збільшення міцності металу Цього досягають введенням у метал спеціальних домі шок, термічною обробкою, наклепом і т п Тепер уже зроблено перші кроки до створення металів, що не мають дефектів кристалічної ре* шітки Добуто бездислокаційні ниткоподібні металеві кристали («ву са»), що мають дуже велику міцність, яка наближується до теоретичної
§ 32. Поняття про концентрацію напружень
Теоретичні та експериментальні дослідження показали, що рівно мірний розподіл напружень по площі поперечного перерізу розтяг нугого або стиснутого стержня, який дає формула (4 б), буде виключно тоді, коли по довжині стержня поперечні перерізи однакові або зміївоються вельми плавно Різкі зміни площі поперечного перерізу внаслідок наявності поперечних отворів, викружок, канавок та надрі зів призводять до нерівномірного розподілу напружень спричинюють концентрацію напружень На рис 118, а показано графік розподілу розтягальних напружень у перерізі штаби який ослаблений круглим отвором, а на рис 118, б — у перерізі, ослабленому півкруглими
викружками
Зазначимо, що зображена тут І далі картина концентрації напру жень дещо спрощена, але в основному вірно відбиває суть явищ, що відбуваються Точні досліди показують, що напружений стан у міс цих концентрації має більш складний характер
Фактори, що спричинюють концентрацію напружень (отвір, надріз тощо), називають концентраторами напружень Максимального зна чення напруження досягають у безпосередній близькості від нього (наприклад біля краю отвору чи викружки) й обмежуються дуже не-
великою частиною площі лопереч но!о перерізу, тобто мають місце вни характер Тому напруження біля місць концентрації називають місцевими
Зупинимося на деяких поняттях та означеннях, що застосовуються при розрахунках на міцність у випадку концентрації напру жень
Номінальним напруженням називають напруження, визначене на підставі припущення про те, що концентрації напружень немає
Рис 119
У розглянутих лрик ладах (рис 118, а і б) но міна іьне напруження визначається як середнє напруження в ослабле* кому перерізі пластини
°и ~ М/Епі[п, (4 34) де N — поздовжня сила в ослабленому перерізі, ^тіп — площа ослаблено то перерізу, що зветься площею нетто
Іноді під номінальним
напруженням розуміють напруження, обчислене за площею Г суцільного поперечного перерізу без урахування його зменшення за рахунок отвору Цю площу називають площею поперечного перерізу брутто Тоді
ств = А'//7	(4 35)
У разі дуже малого отвору в штабі номінальні напруження, об числені за формулами (4 34) та (4 35), будуть практично однакові В інших випадках напруження можуть істотно відрізнятися Тому, використовуючи поняття номінального напруження, треба встановити, на базі якого поперечного перерізу його визначено
Теоретичний та ефективний коефіцієнти концентрації напружень. Кількісною характеристикою концентрації напружень є коефіцієнт концентрації а, який дорівнює відношенню нийбільшого місцевого напруження о»,, до номінального о,,
а = от.х/он	(4 36)
Найчастіше коефіцієнти концентрації напружень визначають ме тодами теорії пружності, що грунтуються на припущенні про однорідність, ізотропність та повну пружність матеріалу Такі коефіцієнти називають теоретичними коефіцієнтами концентрації
Місцеві напруження залежать від виду й розмірів концентратора Наприклад чим менший радіус отвору або викружки у штабі, тим більше максимальні напруження відрізняються від номінальних У ра зі дуже малого радіуса отвору в штабі (рис 118, о) біля країв отвору найбільше напруження дорівнює трьом номінальним (а * 3), а біля країв півкруглих вирізів (рис По, б) — приблизно двом номінали ним (а — 2) Надрізи з гострими вхідними кутами дають ще більші коефіцієнти концентрації напружень біля вершин кутів Для деяких поширених концентраторів напружень у штабі прямокутного поперечного перерізу значення теоретичних коефіцієнтів концентрації наве дено на графіку рис 119, а в стержнях круглого поперечного перерізу — в табл 10 Більш докладні дані про теоретичні коефіцієнти кон-
Таблиця 10
Вяд коячевтратора валружеаь	а	| Вяд концентратора напружень	•
Півкругла виточка при відио*		0 125	1 50
шенні радіуса до діаметра		025	І 20
стержня		05	1 10
0 1	2,0	Перехід під прямим кутом	20
05	1 6	Гостра V подібна виточка	ЗО
1 0	1 2	Отвір при відношенні діамет	
20	1 1	ра отвору до діаметра стерж	
Галтель при відношенні раді уса галтелі до діаметра стерж		вя 0 І . 0 33 Риски від різця на поверхні	20
ня 0 0625	і 75	виробу	12 14
центрації напружень містяться в довідниках з розрахунку на міцність та в спеціальних курсах
Визначивши номінальне напруження і знаючи коефіцієнт концент рації напружень для даного концентратора, знаходять максимальне напруження в місці концентрації
сгтпх = аок	(4 37)
Концентрацію напружень доводиться враховувати при конструю ванні й розрахунку на міцність деталей машин Слід по можливості уникати глибоких виточок, викружок, різних переходів перерізів, біля яких виникає концентрація напружень, яка в певних умовах сприяє передчасному руйнуванню матеріалу Треба також більш ста* ранно обробляти поверхні деталей, особливо виготовлених з високо* міцних загартованих сталей Навіть мілкі сліди від шліфувального круга можуть знизити границю міцності твердозагартованої сталі при розтяганні на 10 20 %
Теоретичні коефіцієнти концентрації напружень залежать від геометрії концентратора І не відбивають властивостей реальних матері алів Сумісний вплив геометрії концентратора й властивостей матеріалів можна визначити, випробовуючи зразки із даного матеріалудо руйнування При цьому дістають так звані ефективні (дійсні) коефі цієнти концентрації напружень Вони є відношенням граничного на вантаження зразка без концентратора напружень до граничного навантаження того самого зразка з концентратором напружень При статичному навантаженні
А = Р./Ри	(4 38)
де Р\ — руйнівне навантаження зразка без концентратора напружень, Р\\ — руйнівне навантаження зразка з концентратором напружень На міцність пластичних та крихких матеріалів концентрація на лружень впливає по різному Істотне значення прн цьому має також характер навантаження Якщо матеріал пластичний (діаграма па лружень має площадку теку чості чималої довжини) і навантаження ста
тичне, то прн збільшенні останнього зростання най* '	більших місцевих напружень припиняється, ЯК ТІЛЬ
кн вони досягнуть границі текучості У решті поперечного перерізу напруження будуть ще зростати до границі текучості от, при цьому зона пластичності біля концентратора буде збільшуватися (рис 120)
Отже, пластичність сприяє вирівнюванню напружень На цій підставі вважають, що прн статичному навантаженні пластичні матеріали мало чутливі до концентрації напружень Ефективний коефіцієнт концентрації для таких матеріалів близький до одиниці При ударних та повторно змінних наван Ряс 120 таженнях, коли деформації та напруження швидко змінюються в часі, напруження не встигають вирівнюватися, і шкідливий вплив концентрації напружень зберігається Тому в розрахунках на міцність треба враховувати концентрацію напружень
Для однорідного крихкого матеріалу нерівномірність розподілу напружень унаслідок концентрації зберігається на всіх стадіях навантажування й при статичному навантаженні У місцях дії максимальних напружень починається руйнування матеріалу (утворюються тріщини) Особливо чутлива до концентраторів загартована сталь і тим більше, чим вищі її характеристики міцності Ефективний коефіцієнт концентрації напружень для крихких однорідних матеріалів дуже близький до теоретичного Отже, для крихкого матеріалу в розрахуй ках на міцність при статичному навантаженні можна користуватися теоретичними коефіцієнтами концентрації напружень
$ 33. Вплив різних факторі* на механічні властивості матеріалі*
Механічні характеристики матеріалів залежать від багатьох факторів На властивості металів та сплавів істотно впливають хімічний склад, технологія добування їх, термічна та механічна обробка, умови експлуатації — температура середовище, характер навантаження тощо.
Останнім часом розвиваються нові види техніки реактивна авіація, ракетна техніка, атомні реактори тощо Матеріали, що застосовуються у несучих конструкціях нової техніки, зазнають дії високих темпера тур, великих швидкостей навантажування, агресивних рідких та га зоподібних сереаовищ, радіоактивних, особливо нейтронних, проникних випромінювань Для роботи в цих умовах створюють нові спеціальні сплави та композиційні матеріали
Нижче розглядається вплив деяких факторів на механічні характеристики найбільш важливих у машинобудуванні матеріалів — сталі, чавуну, алюмінію, різних сплавів
Вплив швидкості деформації При збільшенні швид б кості наростання навантаження, (отже, швидкості зро стайня напруження та деформації, всі матеріали, що перебувають у пластичному стані, виявляють загальну тенденцію до збільшення опору Деформуванню Чим вища швидкість деформування, тим вищі границя текучості та тимчасовий опір Особливо сильно залежать від швидкості навантажування механічні властивості пластичних мас та інших органічних матеріалів. У ме талів вплив швидкості навантажування помітний лише
при значній різниці у швидкостях
Порівняння результатів статичних та динамічних випробовувань маловуглецезих сталей на розтягання при нормальній температурі (рис 121) показує таке
!) крива / динамічного розтягання лежить вище, ніж крива 2 ста
тичного розтягання,
2)	максимум діаграми для динамічного навантаження зміщується в бік початку діаграми,
3)	тимчасовий опір при динамічному навантаженні підвищується, але менше, ніж границя текучості
4)	модуль пружності прн дннамічнсму навантаженні практично не змінюється
Вплив технологічних факторів Елементи сталевих конструкцій можна виготовити литтям або прокатуванням, куванням, штампуванням та волочінням Механічні властивості сталі одного А того самого складу дуже сильно змінюються залежно від способу її виготовлення та обробки
Під час лиття заготовки можливе утворення різних внутрішніх дефектів у вигляді порожнеч, раковин та включень, що знижують міцність виготовлюваних із них заготовок деталей У зв’язку з ним лотрі бен старанний контроль якості таких деталей рентгенівським, ультразвуковим або будь яким іншим способом
Прокатування робить сталь анізотропною Прокатна сталь має характерну структуру, в якій зерна що витягнуті в напрямі прока тування, утворюють свого роду волокна Механічні властивості сталі в напрямі прокат) вання істотно відрізняються від властивостей у напрямі, перпендикулярному до нього Зразки, які вирізано таким чином, що їхня вісь збігається з напрямом прокатування, виявляються міц нішими, ніж ті, в яких вісь перпендикулярна до напряму прокатування
Попереднє витягування у холодному стані за границю текучості (наклеп) дуже сильно підвищує границю текучості та границю міц ності, але знижує залишкове подовження після розриву Матеріал стає більш пружним та міцним, але менш пластичним
Волочіння у холодному стані, що є витягуванням з обтискуванням, ще сильніше впливає на механічні властивості сталі Статевий дріт
Рис 122
та сталеві стрічки, які виготовлено волочін ням, дуже МІЦНІ
Токарна обробка, обробка поверхні роликами, обдування дробом, хромування, ні келюваиня, алітування, азотування А інші види поверхневої обробки можуть істотно впливати на міцність деталей, особливо тих, що працюють при змінному навантаженні
Вплив термічної обробки Загартування сталі значно підвищує її твердість, грани цю текучості А границю міцності, але сильно знижує пластичність Модуль пружності сталі загартування практично не змінює поверхнева твердість із збереженням іншіх
Якщо потрібна висока _____г.... __.г______ „ ___(_______ _______
властивостей сталі, використовують поверхневе загартування токами високої частоти Для маловуглецевих сталей з цією метою застосову ють цементацію — збільшення у поверхневому шарі вуглецю —з подальшим загартуванням При цьому загартовується лише цей поверхневий шар, а основна частина матеріалу зберігає властивості маловуг-лецевої сталі
Для усунення наклепу використовують відпалювання Щоб ви рівняти Й поліпшити структуру, а також покращити механічні властивості сталі, застосовують нормалізацію Докладніше ці способи термічної обробки розглядають у металознавстві
Вплив температури Багато деталей сучасних машин (наприклад, парових та газових турбін, реактивних двигунів та ін ) працюють при високих температурах, що досягають 800 1000 °С Випробування по казали, що всі механічні характеристики металів істотно змінюють ся залежно від температури
На рис 122 наведено діаграми напружень вуглецевої сталі при різних температурах, а на рис 123— графіки залежності від темпе ратури границі текучості, тимчасового опору А відносного подовження при розтяганні В інтервалі температур 150 250 °С тимчасовий
~?00 -ЧООТ ’С
Рис. 123
опір досягає найбільшого значення, а відносне подовження після роз риву — найменшого, сталь, як кажуть, стає синьоламкою Прн більш високих температурах міцність вуглецевої сталі швидко зменшується, тому прн температурах, вищих за 350 400 °С таку сталь не застосо вують
При підвищенні температури також істотно зменшується модуль пружності Е (рис 124), а коефіцієнт Пуассона дещо збільшується Так при зростанні температури від кімнатної до 500 °С коефіцієнт Пуассона збільшується від 0,28 до 0 33
Вуглецеві сталі при високих температурах дуже окислюються, на їхній поверхні утворюється окалина У зв язку з цим застосовують спеціальні жаростійкі та жароміцні сталі, які містять у собі різні лі гуючі добавки Жаростійкістю називають властивість матеріалу протистояти хімічному руйнуванню поверхні при високих температу рах, а жароміцністю — здатність зберігати при високих температурах механічні властивості Останнім часом створено спеціальні сплави, а також металокерамічні матеріали, що надійно працюють при температурах до 1000 °С
Повзучість При високих температурах Істотне значення має явище повзучості матеріалів (крип), яке характеризується зростанням плас тичної деформації з часом прн постійному напруженні, що не сприяй нює пластичних деформацій при короткочасній дії навантаження За лежно від напруження та температури деформація, що виникає вна слідок повзучості може або припинитися, або продовжуватися до руйнування матеріалу
На рис 125, а наведено криві повзучості сталі прн постійній тем пературі для різних напружень Оі < а» < оа < о4 < о», а на рис 125 б— криві повзучості при постійному напруженні, але різ них температурах, причому 7\ < Тг < Т3 < Т4 < Ті Як видно із порівняння графіків збільшення напруження при постійній температурі й підвищення температури при постійному напруженні одна
ково впливають на повзучість матеріалу, а саме — швидкість повзучості збільшується
Окремі відрізки кривих рис 125 характеризують різні швидкості наростання деформації Розглянемо, наприклад, криву 4 Вертикаль ний відрізок Оа відображує подовження, здобуте відразу після навантажування Відрізок аЬ — це відрізок неусталеноі повзучості, оскільки швидкість її тут з часом зменшується Прямолінійний відрізок Ьс зветься відрізком усталеної повзучості, що характеризується її по стійною швидкістю Відрізок сд характеризує зростання швидкості повзучості, що закінчується руйнуванням зразка (точка Л)
Решта кривих повзучості відрізняються від кривої 4 тим, що в них немає того чи іншого відрізка Так, криві /, 2 та 3 зображують випадки, коли повзучість не спричинює руйнування (на них немає відрізка сії). Крива 5 не має відрізка усталеної повзучості (точки Ь на с збігаються) Ця крива відповідає випадку, коли період нсусталеної повзучості заміняється відразу періодом із зростаючою її швидкістю, який закінчується руйнуванням Межа між цими двома періодами внзначаєтся точкою перегину Ь
Границею повзучості називається найбільше напруження при якому швидкість або деформація повзучості при даній температурі за певний проміжок часу не перевищує встановленого значення (наприк лад, швидкості 0,0001 %/год або деформації І % за 10 000 год)
Якщо границю повзучості визначають за деформацією, то позначають її літерою о з трьома числовими індексами двома нижніми й одним верхнім Перший нижній індекс відображує задане подовження (сумарне або залишкове), %; другий нижній індекс — заданий чаа випробування, год, верхній індекс — температуру, °С Наприклад, запис оо’г/юо означає границю повзучості прн допуску на деформацію 0,2 % за 100 год випробування при температурі 700 °С При цьому треба додатково зазначити, за сумарною чи залишковою деформацією визначалася границя повзучості
_ Коли границя повзучості визначається за швидкістю повзучості, п слід позначати літерою о з двома числовими індексами одним верхнім А одним нижнім Нижній Індекс відображує задану швидкість повзучості, %/год, верхній — температуру випробування, °С Наприклад, 0^0-5 — це границя повзучості при швидкості її І 10“5 %/год при температурі 600 °С При цьому треба додатково зазначити час випробування, протягом якого було досягнуто задану швидкість лов зучості
Деталі, що працюють при високих температурах, розраховують на повзучість спеціальними методами з використанням експеримен тальннх даних, які характеризують повзучість матеріалу Метою та кнх розрахунків є визначення границь повзучості
За результатами експериментального визначення швидкості повзу чості о0 при розтяганні зразків будують графіки в логарифмічних ко
ординатах о ~ о0. Експериментальні точки добре групуються навколо деякої прямої (рис 126, а)
Зазначимо, що в деяких матеріалів (свинець, бетон, високополімер ні матеріали тощо) повзучість спостерігається й при нормальній тем пературі
Тривала міцність У разі високої температури й довгочасної дії навантаження відбувається руйнування матеріалу при напруженні, яке менше за тимчасовий опір матеріалу при даній температурі У зв язку з цим виникає потреба визначати тривалу міцність матеріалів
Границею тривалої міцності називається напруження, що спричи нює розрив зразка після заданого строку безперервної дії цього напруження при певній температурі Позначається границя тривалої мій. пості літерою о з двома числовими індексами Верхній Індекс дає тем пературу випробування, °С, нижній — задану тривалість випробування до руйнування, год Останню можна позначити кількістю годин або цифрою 10 з показником степеня Напр іклад, Ощ» або Оіооо — границя тривалої міцності за 1000 год Випробування при температурі 700 °С
Випробування на тривалу міцність полягає в тому, що зразки під дають різним напруженням при певній температурі й Дізнаються про час до іх розриву Результати подають у вигляді графіка (рис 126, б) Маючи криву тривалої міцності матеріалу, можна визначити руйнів не напруження за заданим строком роботи деталі прн заданій температурі Навпаки, за заданим напруженням можна визначити час до руйнування Наприклад, деталь, виготовлена з матеріалу, для якого криву тривалої міцності зображено на рис 126, б, при напруженні 30 МПа та температурі 500 °С зруйнується через 2550 год
Результати експериментального визначення тривалої міцності
час розриву, тим менше відносне подовження при розриві, тобто матеріал стає більш крихким Для низки матеріалів (наприклад, для висо» кополімерів) зазначений ефект виявляється й при кімнатній темпе ратурі
Релаксацією напружень називається зменшення їх а часом унаслідок повзучості в навантаженій деталі при незмінній П повній деформації У більшості металів релаксація помітна лише при великих температурах (рис 127) Для ілюстрації цього явища наведемо такі приклади.
Між розведеними кінцями розрізаного сталевого кільця вставимо пластинку (рис 128) Унаслідок деформації кільця в ньому виникнуть напруження, й кінні кільця, намагаючись зблизитися, з великою силою стиснуть пластинку Якщо це з'єднання видержати деякий час при високій температурі, то в кільці відбудеться релаксація напружень, сила затискання пластинки зменшиться, і її можна буде легко вийняти
Відомо, що початкове затягування болтів, які працюють при високій температурі, з часом слабішає, і це обумовлює необхідність підтягувати їх
Вплив низьких температур На механічні властивості деяких матеріалів істотно впливають низькі температури Це виявляється в тому, що матеріали, пластичні прн нормальній температурі, стають крихкими при низьких температурах Такі матеріали називають холодноламкими
Холодноламкість характерна для металів, що мають кристалічні решітки у вигляді об'ємноцентрованого куба або гексагональні До
них належать більшість чорних металів, зокрема сталі, а також цинкові сплави Виявляється холодноламкість як при статичній дії навантаження, так І, особливо, при динамічній. Як приклад на рис 129 наведено графіки зміни границі текучості, тимчасового опору, відносних подовженая й звуження при статичних випробуваннях вуглецевої сталі при низьких температурах
Метали, що кристалізуються в системі куба з центрованими гранями (мідь, алюміній, ні кель, срібло, золото гощо), не виявляють хо лодноламкості ні прн якому ратури Наприкад, алюміній
зниженні темпе-прн температурі
ППа\ /ООІ
600’С
1000	7000 і,год
Рве, 127
Рис. 123
о
рі'^ого азоту (—196 °С) збільшуеміцність приблизно в 2 рази, одночас но збільшуючи відносне подовження в 4 рази Аналогічно поводять себе мідь та нікель Багато сплавів алюмінію, міді, атакождеякі сталі не виявляють холодноламкості
§ 34 Допустимі напруження
Як уже зазначалося, деякі деталі машин та інших конструкцій мають задовольняти умови міцності та жорсткості Розміри деталей треба-лобирати такими, тпб під дією прикладених навантажень впни не руйнувалися й не зазнавали деформацій які перевищують допусти мі .у більшості мя|тіиип6упіпиму	-ійЛнпікппі яіЧрормації^к
звичайно, _н е_ допускаються
Помітні залишкові деформації з'являються у пластичних матері адахДкодй напруження досягають границі іекучості Руйнування на-сгає тоді, коли напруження досяґастБ грапяігі тимчасового’опору при пклму пАфґ>рмаіпі^дих2{пго~аламу можуть бути яевеликичи"Отже, ДЛЯ. деталей, ЯИГОТПВЛАНИУ а плябтіШнлго матерІДЛу,ШЄбЄЗДЄЧВИМИ.НЗ гіружеинями можна вважати границю текучості, а для деталей з крих кого матеріалу — границю міцності” (тимчасовий опір)
Цілком природно, що ці напруження не можуть вважатися допус тимими*_Слід зменшити їх настільки, щоб в умовах експлуатації діючі напруження яявжяи були меншими за границю пружності-Оике, ДОПУСТИМІ напруженняможна визначити за формулою
2 ~Ля/п^	(4 39)
де сти — небезпечне напруження (от або ав); п — коефіцієнт запасу міцпості,~що показує' у скільки разів допустиме напруження менше щж—небезпечне _
Вибір коефіцієнта запасу міцності залежить від стану матеріалу (крихкий або пластичний), .характеру прикладання навантаження (ста тичне, динамічне чи повторно змінне) й деяких загальних факторів, що мають місце майже д усіх випадках До таких факторів належать а)_неодно{мднють-мат0р4аду^-а отже, різні його механічні власти _вості у малих зразках та в деталях.
бГ_неточнтгть яяпйпямня зовнішніх навантажень;
в) наближеність розрахункових схем та певна наближеність. £рз рахункових формул.
—ТЗазнайейі-факторк-й-врахоауіоіьдя коефіцієнтом дапасу-мшносзхд* який іноді називають основним
Запас мишасті залежить від того, яке напруження вважати небез яєчним
Для пластичних матеріалів у разі статичного навантаження небез печним напруженням, як уже зазнач'алось. е границя текучості тобто' о, — ат, а п з.Лг Тоді
1С]
(4 40)
На підставі даних тривалої практики конструювання, розрахунку А експлуатації машин та споруд запас міцності лт для сталей при ста* тнчному навантаженні вибирають таким, що дорівнює 1,4 4,6 Оче-видно, менші значення лт слід брати тоді, коли матеріал більш однорідний, краще вивчено його властивості, повніше враховано наванта ження, точніші метод розрахунку й розрахункові схеми
Для крихких матрріяліп при статичних навантаженнях иебезпеч-ішм_няпручтням ч тимчасовий опір (границя міцності), і тоді
<44|)
Вибирають запас міцності я, = 2,5 3,0
Допустимі напруження М, що знаходять за формулами (4 40) та (4 41), як звичайно, називають основними допустимими напруженнями У зв’язку з тим, що тимчасовий опір визначити простіше, ніж границю текучості, іноді А для пластичних матеріалів при визначенні допусти мих напружень виходять з тимчасового опору, користуючись фор мулою
(а] = а^/п,	(4 42)
У цьому разі, враховуючи, що тимчасовий опір перевищує границю текучості на 50 .70 %, запас міцності ла для пластичних матеріалів вибирають 2,4 2,6 Це значення для пластичних матеріаіів беруть дещо меншим, ніж для крихких, оскільки пластичні матеріали, як правило, більш однорідні за своїми фізичними та механічними влас тивостямн
Іноді допустимі напруження на розтягання позначають як ІоД а на стискання — як |о_] Крихкі матеріали краще чинять опір стисканню, ніж розтяганню, і для них | [о_11 > | Іа+] | Для сталей та більшості інших пластичних матеріалів можна взяти | [о*11 = | Іо„11 та позначити допустимі напруження в цьому разі як (оі без індексу
Вибір допустимих напружень дуже важливий, оскільки від пра вильного визначення їхніх значень залежить міцність та безпечність проектованої конструкції, а також економічний аспект розрахунку — кількість матеріалу, що витрачається Тому встановленням допустимих напружень ДЛЯ основних цп-грр.рп?^~,ц?_вцкпрмгтпнуїоться у машинобудуванні та будівництві, займаються державні нормувальні установи ^Вони видають відповідні норми, якими й слід керуватись у звичайних умовах проектування В міру поліпшення якості матеріа лів і уточнення методів розрахунку допустимі напруження підвищу ють Орієнтовні значення основних допустимих напружень прнйня тих зараз для найпоширеніших матеріалів наведено в дод 10 Тоді, коли немає даних про допустимі напруження для того чи Іншого мате ріалу, їх треба визначати на підставі вище викладених міркувань та рекомендацій
Зупинимося коротко на складанні умов міцності у випадках що найчастіше трапляються
У пластичних матеріалах при статичному навантаженні концентра ція напружень не дуже впливає на міцність, тому діючим робочим на пруженням можна вважати середнє (номінальне) напруження в небез печному перерізі та записати умову міцності таким чином
о<(о]	(4 43)
У випадку однорідних крихких матеріалів (наприклад загартованих сталей) при статичному навантаженні треба враховувати концентрацію напружень та розраховувати на міцність за найбільшим місцевим напруженням У цьому разі умова міцності запишеться так
От»» = ава < [о)	(4 44)
До питання щодо вибору допустимих напружень ми будемо неодноразово повертатися, розглядаючи умовк міцності при різних деформаціях
Глава 5 РОЗРАХУНОК НА МІЦНІСТЬ І ЖОРСТКІСТЬ ПРИ РОЗТЯГАННІ Й СТИСКАННІ
$ 35. Приклади розрахунків при дії зосереджених сил
Розглянемо деякі задачі на розтягання і стискання стержнів
і Визначимо діаметр стержня однакового поперечного перерізу завдовжки і — 0,6 м (рис 130) Матеріал стержня — сталь СтЗ, модуль пружності Е = 2 І0*МПа Побудуємо також епюру переміщень поперечних перерізів стержня та визначимо зміну його початкової довжини
Перш за все будуємо епюру поздовжніх зусиль, з якої видно, що стержень має три відрізки У крайніх діють роїтягальні зуситля М\ —
= А^нї = Р = 12 кН а у се редньому—зусилля стискан ня = 2Р - 24 кН
Оскільки стержень, який проектується, повинен мати однаковий поперечний пере різ, то треба його добирати за найбільшим абсолютним зна ченням зусилля, що діє в середньому відрізку Напружен ня в поперечних перерізах цього відрізка
Умова міцності має вигляд он
або
2Р/Р < [о), звідки
Р>2РЛо]
Для сталі марки СтЗ допустимі напруження [а] на розтягання та стискання однакові При статичному навантаженні його можна взяти таким що дорівнює 150 МПа (див дод 10)
Підставивши числові значення дістанемо площу поперечного перерізу стержня
2 ‘ід,'0"3 м< = 1.5 10“* м!.|,5 см> та його діаметр
а = 4'р= 1	= 1.38 см
Діаметр треба змінити на найближчий найбільший згідно з держав ним стандартом Слід взяти і — 14 мм (Е = 1,54 см’)
Зауважимо, що розрахунок на міцність при стисканні є достатнім тільки для коротких стержнів, зокрема для сталевих круглих коли < 20 При стисканні довгих стержнів може втратитися стійкість 1 У розглянутому прикладі зазначена умова для стиснутої частини стерж ня виконується
Визначимо переміщення перерізів стержня Виберемо, наприклад, за початок відліку лівий кінець стержня (псрсрі і А), умовно вважаючи, що він нерухомий Нагадаємо що переміщення будь якого перерізу відносно початку відліку дорівнює зміні довжини відрізка стержня між нерухомим та розглядуваним перерізами
На першому відрізку переміщення перерізу, який розташований завдальшки х від лівого кінця стержня [0 х (ґ/3)),
X (х) = Рх/ЕЕ\ при х = 0
АЛ = 0;
при х = 1/3
і Р//3	12 І0-3 0,6	_ о іл—8	« пг\-?и
Хд = с'с »-------------------—~г м = 7,8 • 10 м = 0,0078 см
3 2 10» І 54 10-4
На другому відрізку (1/3 < х '21/3) переміщення перерізу х
при х — 1/3
Хв = ТГ “ °'0078 см'
1 Розрахунки стиснутих стержнів на стійкість наведено в гл 19.
при х = 21/3
і	Р//3	2РІ/3
Ас - ЕР	ЕР
0 0078 см
На третьому відрізку, де 2//3 х І,
і /и _ Р'/З 2РОЗ . Р(х~ 21/3) .
А {Х> ~ ЕР ЕР	ЕР ’
при х =* 21/3
ьс “ ігт = _ 0 0078 еч'
при X = І
.	РІ/3 ЇРЦЗ , и/з п
А° “ ЕР ЕР ' ЕР ~'і
Епюру поздовжніх переміщень наведено на рис 130 У цьому при кладі довжина всього стержня не змінюється, бо переміщення правого кінця відносно лівого дорівнює нулю
2 Побудуємо епюри поздовжніх сил, нормальних напружень відносних деформацій та переміщень для східчастого стержня (рис. 131)
Стержень складається з трьох відрізків У межах першого із них у перерізі, що розташований завдальшки х від закріпленого кінця (0 х /), поздовжня сила, нормальне напруження і відносне подов ження не залежать від координати х, тобто від положення перерізу, і мають такі значення

4Р	о _ 4Р
ЗР	Є “ Е ЗЕР
Переміщення перерізу, який розташований завдальшки х від закріпленого кінця стержня
, . ,	4Рк
1 (*) = !* = -тат
Отже переміщення змінюються за лінійним законом У початковій і кінцевій точках відрізка вони мають такі значення прн х = 0
Хл = 0, при X = І
І. *р1
Кв = ~5ер
Аналогічно на другому відрізку (/ < х < З/)
а-----£ = —£
Переміщення перерізу який розташований завдальшкн х від закріпленого кінця стержня,
- зер ЕР
Па початку другого відрізка, при х = І, і 4РІ *В = ~ЗЕР'
на кінці відрізка, при х = ЗІ,
Знак «міну» вказує на те що розглядуваний переріз переміщується в напрямі до перерізу який вибрано за початок відліку
На третьому відрі <ку (Зі х 40
Нт=Р о--£-. >=-я
Переміщення перерізу який розташований завдальшкн х від кінця А, ,/х]	2РІ , Р(х-3р
Л (х> -	ЗЕЕ Н ЕР
На початку третього відрізка, при х — ЗІ і _ ІРІ
на кінці третього відрізка, прн х = 4/, і _ Рі К[> ~ ЗЕР
Епюри N ст, в та X показано на рис 131 Епюра X дає змогу визначити зміну відстані між двома будь якими перерізами стержня, а отже, і зміну довжини будь якого відрізка
Визначимо, наприклад, зміну довжини другого відрізка стержня. Для цього від переміщення перерізу на кіпці відрізка (переріз С) треба відняти переміщення перерізу на початку відрізка (переріз В) Отже, 118
маємо

Знак «мінус» вказує на те, що довжина цього відрізка зменшилась
ео |  б Рис 132
---'Г — "2----------- ,	КИС 1-М
З Перевіримо міцність східчастого стерж ня круглого поперечного перерізу (рис 132) Матеріал стержня — загартована високовуглецева сталь з тимчасовим опором о, == 900 МПа Стержень розтягується силами Р = 80 кН
Унаслідок різкої зміни розмірів поперечних перерізів стержня ви никає концентрація напружень Оскільки загартовтна сталь чутлива до неї то перевірку міцності треба виконувати за найбільшим місце вим напруженням Для визначення цього напруження треба знати коефіцієнт концентрації напружень, який залежить від відношення радіуса галтелі до найменшого діаметра стержня У даному прикладі г і «= 5/20 = 0,25 3 табл 10 теоретичний коефіцієнт концентрації напружень а = 1,2
Номінальне напруження визначаємо за найменшою площею попе речного перерізу стержня
о. -	= „М0„,'°~3 МПа = 255 МПа
Гтіп	4
•«.	-І*! Ю-.
Найбільші місцеві напруження знайдемо на основі формули (4 37) Овівх «== аоа = 1,2 • 255 МПа = 306 МПа
Запас міцності
Для крихких матеріалів при статичному навантаженні вибирають, як уже зазначалося, коефіцієнт запасу міцності ла = 2,5 3 Отже стер жень при даному навантаженні має достатній запас міцності
4 Визначимо розміри поперечних перерізів стержнів АВ та ВС кронштейна (рнс 133 а) для кріплення блока, за допомогою якого підніматимуться вантажі вагою С = 20 кН, а також поперечний переріз підвіски ВО блока Стержень АВ і підвіска ВО (у верхній час тині) мають круглий поперечний переріз Матеріал — сталь СтЗ Стержень ВС виготовлятиметься із сосни він матиме квадратний попереч ний переріз Визначимо також вертикальне переміщення вузла В кронштейна
Конструкція кронштейна дає змогу наближено вважати кріплен ня стержнів до стіни та з єднання їх між собою шарнірними Розра хункову схему кронштейна наведено на рис 133, б
Насамперед визначимо зусилля у підвісці блока і зусилля що до рівнює йому і діє на вузол В Оскільки прн підніманні вантажу вагою С
Рис 133
До другої вітки троса перекинутого через блок, треба прикласти силу, яка дорівнює вазі (? вантажу, що піднімається (якщо знехтувати тертям), то у перерізі підвіски буде діяти зусилля Л^і ® 2Р = 40 кН Отже до вузла В кронштейна прикладено силу Р =	= 40 кН
Для сталі СтЗ допустиме напруження на розтягання [о+1 — = 160 МПа, для сосни допустиме напруження на стискання 1<т_1 — — 12 МПа. Модуль пружності для сталі — 2 10а МПа, для сосни Рл « 10* МПа
Знайдемо потрібну площу поперечного перерізу підаіскн ВО. Нормальне напруження в підвісці визначається за формулою
Умова міцності
а = Л'і/Р, <|а1, звідки потрібна площа поперечного перерізу підвіски с N1 40 10“° . о є . Е1^~І5Г= і® м ~2,5
Визначаємо діаметр підвіски
4,=	= 1,78 см = 17,8 мм
Вибираємо найближчий найбільший стандартний діаметр <і — = 18 мм (Р = 2 54 см2)
Оскільки ми припустили, що стержні прикріплені до стіни та з'єднані між собою шарнірами, а навантаження прикладене до вузлів (шарнірів), то стержні будуть зазнавати тільки поздовжніх (розтя-гальних або стискальних) зусвль Для визначення їх розглянемо рів повагу вузла В (рис 133, в), на який діє вертикальна сила Р і дві не відомі сили А/ата реакцій стержнів АВ і СВ на вузол
Визначаючи невідомі засилля в стержнях як правило вважають їх розтягнутими і відповідно до цього спрямовують вектори сил від вузла Якщо у розв’язку сила має знак <ллюо, то припущення про
напрям сили підтверджується Знак «мінус» покаже, що напрям сили треба змінити на протилежний, і відповідний стержень стиснутий Припускаючи, що обидва стержні розтягнуті, зусилля та спря мовуемо, як показано на рис 133 в
Для рівноваги вузла В у площині достатньо, щоб сума проекцій всіх скл, прикладених до вузла на координатні осі х та у дорівнювала нулю Вибраний напрям координатних осей показано на рис 133, в Тоді
2Х = —	— А^соза — 0,
ХУ = — Р— ЛГ(5Іла=0
Звідси знаходимо
л'.=-їК- = -ЛгкН-'~56’6кН'
N. = - N. соз а = (-у/-) -Й- кН - 40 кН,
тобто стержень АВ розтягнутий, а стержень ВС стиснутий Із умови міцності стержня АВ
о =	[а]
визначаємо потрібну площу його поперечного перерізу:
„	40 ю~3 4 п е .
-----і®— »* = 2.5 см’
У цьому рвзі вона виявилася такою, що дорівнює площі поперечного і ерерізу підвіски Отже діаметр стержня АВ має дорівнювати діа метру підвіски, тобто 4 = 18 мм
Потрібна площа поперечного перерізу дерев’яного стержня ВС
с Ь’,	56 6 10-3 <	„ 9
= юг  -----І2— м = 47 ™
Сторона квадрата поперечного перерізу а «== і 47 см = 6,85 см
Округлюючи до найближчого цілого числа, вибираємо а = 70 мм (£ _ 49 см2)
Визначимо вертикальне переміщення шарніра В кронштейна Стержень АВ подовжиться на величину
Л/, - -Й- ---------------------д-«= 0,118 см
8	2 10і 103 2 54 [О-*
Стержень ВС укоротиться на величину
56 6 1,5 /2 10* 10» 49 10~*
Д/а
м = 0,245 см»
Ураховуючи, що деформації малі, пере* Л \ оі	міщення вузла В можна визначити так
Н Н Припустимо, що стержні в шарнірі В роз'єд \ /	нані В*д точки & праворуч, у напрямі
\|/	стержня АВ відкладемо його подовження
Iе	О?	7	ВВ', а у напрямі ВС — укорочення ВВ"
| д |	|д	стержня ВС (рис 133, б, а) На рис 133, г
*—*	ІС/	це показано в масштабі, який значно біль-
Рнс. 134	ший, ніж масштаб довжини стержнів на
схемі конструкції Положення шарніра В після деформації збігається з точкою перетину дуг описаних з точок А ІС радіусами, які дорівнюють новим довжинам АВ' та СВ" стержнів Унаслідок малості деформацій стержнів дуги можна заміни ти перпендикулярами, які проведено з точок В' і В' до напрямів АВ та ВС Точка В, перетину перпендикулярів визначить нове положення вузла В після деформації кронштейна Відрізок ВВ, зобразить повне переміщення вузла В а відрізок В’В, *= І>у— вертикальну складову цього переміщення.
Із наведеної побудови легко встановити аналітичну залежність між переміщеннями точки і подовженнями стержнів Вертикаль не переміщення вузла (рис 133, г)
б, = В%-5^ + й’=^-+-^5.
Підставляючи числові значення, матимемо
8, = (0,118 + 0,245 2//2) си = 0,46 см
Приклад 12 Визначимо найбільші/ вагу вантажу С), який можна безпечно підві* сита до вузла В стержньової системи (рис 134). Матеріал стержнів — Ст2, до> пустине напруження на розтягання => 140 МПа Діаметр стержнів й в 3 ся. Найбільше безпечне нормальне аусятля яке можна допустиш в кожному стерж-ні підвіски,
N = [а]Ге 140 10* -2 (2 кН « 44 кН
Найбільшу допустиму вагу вантажу <і знаходимо з умова рівноваги вузла В Прирівнюючи до вуля суму проекцій на вертикаль ну вісь усіх сил, що діють на вузол В, з урахуванням симетрії системи маємо
ХУ — — <3 Ц- соз а = 0, звідки
<3 = М соз а -= 2 44 0,866 кН = 76 2 хН
Приклад ІЗ- Визначимо площу поперечного перерізу дерев’янт колони (рис 135) за умови, що вертикальне переміщення верхнього кінця колони пе повинно перевищувати [Ді| = 0,3 см Матеріал колона — сосна, модуль пружності (див дід 9) Е = 10і МПа
Для визначення площі холовя запишемо умову жорсткості
и -ТГ<5І4'І де N
Рис. 136
Звідси
„ М р> ’
Підставляючи числові значення матимемо
'-^г'ҐііД “-З-'О-3
Перевіримо чи буде виконуватися умова міцності при цій площі поперечною перерізу Допустиме напруження на стескання для сосни іо_| = 12 МПа (див дзд 10) Напруження спричниене силою N
а = 4- = 30 ,'°_з“ МПа = Ю МПа < |с_) = 12 МПа г 3 10
Отже умова міцності виконується
$ 36 Урахування власної ваги 1 сил Інерції
Власна вага матеріалу елементів конструкцій, а також сили Інерції рухомих частин машин і механізмів є зовнішніми навантаженнями розподіленими по об ему Далі розглянуто деякі задачі визначення напружень і переміщень при дії таких навантажень
Урахування власної ваги В машинобудуванні як правило, вплив власної ваги не враховують бо деталі машин мають порівняно неве ликі розміри, а отже, і вплив власної ваги не великий Проте в деяких інженерних конструкціях власна вага — це одне з основних наванта жеиь При розрахунку канатів шахтних підйомників штанг бурильних пристроїв, стояків мостів стін будівель, гребель вплив власної ваги слід враховувати
Припустимо що прямий стержень однакового поперечного перерізу великої довжини закріплено верхнім кінцем і навантажено на вільному кінці силою Р (рис 135 а) Визначимо як змінюються поздовжні сили та напруження в поперечних перерізах стержня, а також осьові пере міщений перерізів по довжині стержня, враховуючи вплив власної ваги
У довільному поперечному перерізі стержня, розташованому зав-дальшки х від вільного кінця, поздовжня сила
ЩхУ^Р+чЄх,	(5 1)
де у — питома вага матеріалу
Максимальне значення сила має у верхньому закріпленому пере* різі
Ит„ = Р + уГІ	(5 2)
Епюру поздовжніх зусиль зображено на рис 136, б
Нормальне напруження в розглядуваному перерізі о_-^- = -£.+їх	(53)
Максимального значення нормальне напруження набуває у верхньому закріпленому перерізі, який у цьому разі буде небезпечним
Отам = Р/Р + У/	(5 4)
V цій формулі перший доданок — це напруження від сили Р, а Другий—від власної ваги Глюру нормальних напружень наведено на рис 136 в
Умова міцності для небезпечного перерізу має вигляд
От„=Р/Г + т/<[аі	(5 5)
Із виразу (5 5) дістанемо формулу для визначення площі попереч* ного перерізу стержня з урахуванням впливу власної ваги»
(56)
Якщо навантаження на кінці стержня немає, тобто Р = 0, то на* лруження в небезпечному перерізі, спричинене тільки власною вагою, згідно з виразом (5 4),
Ощах = у/.	(5 7)
Умова міцності набуває вигляду
(5 8)
Звідси можна визначити довжину стержня, при якій напруження тільки від дії власної ваги досягає допустимого, і стержень не може нести корисне навантаження Цю граничну допустиму довжину знайдемо з умови (5 8)
А? = (о)/?	(5 9)
Від дії власної ваги може статися розрив стержня Це матиме місце, коли Опиа у виразі (5 7) досягне значення тимчасового опору Довжина стержня, при якій він розривається від власної ваги, називається кри тнчною їі знайдемо з формули (5 9), замінивши допустиме напружен ня тимчасовим опором матеріалу
(5 і0)
Гранична та критична довжини не залежать від площі поперечного перерізу стержня
Визначимо наприклад критичну довжину стержня Із сталі марки Ст2 у якої ав = 360 МПа Питома вага статі у =» 7,85 І0* Н/м* Підставивши у формулу (5 ГО} числові значення матимемо
-------“2’--------- -= 4580 м » 4 6 хм 7 85 10* 10“*
Для розглядуваного стержня (рис 136, а} визначимо переміщення перерізу розташованого завдальшкн х від вільного кінця Переміщення дорівнює подовженню частини стержня, розташованої вище цього перерізу
У перерізі стержня завдальшкн £ від вільного кінця (рис і 36, а) маємо N (|) — Р Ь уГБ За формулою (4 9) при Е = соті знаходимо
(5 1І)
Подовження Д/ стержня (чи переміщення % нижнього кінця стерж ця що дорівнює Д/) визначимо з виразу (5 11), взявши х = 0 д'=4+-&	є12)
Перший доданок у цьому виразі є подовженням стержня від сили Р, другий — від власної ваги
Ураховуючи, що повна вага стержня $ = уРІ, замість формули (5 12) матимемо
А' = 4+^-	<8‘3)
Отже абсолютне подовження стержня від власної ваги таке саме, як подовження від зосередженої сили, що дорівнює вазі стержня і прикладена в його центр ваги Епюру переміщень перерізів зображено на рис 136 г
Стержень однакового опору Як видно із розрахунку на міцність стержня однакового поперечного перерізу з урахуванням власної ва ги в усіх перерізах, крім небезпечного, нормальні напруження будуть меншими від допустимих, тобто матеріал недовантажений (див , на прикчад, рис 136 в) Проте можна спроектувати стержень такого змінного перерізу, в якого в усіх поперечних перерізах напруження будуть однаковими і дорівнюватимуть допустимому Такий стержень називають рівноміцним або стержнем однакового опору розтяганню чи стисканню Встановимо закон зміни площі його поперечного перерізу
Рис 137
Потрібна площа верхнього перерізу
Л = Р/Ю]	(5 14)
Площу поперечного перерізу завдальшки х від верхнього кінця стержня позначимо через Р (х) а вагу частини стержня завдовжки х — через (х). У цьому перерізі, як і в усіх інших, напруження повинно дорівнювати допустимому Рівняння рівноваги частини стержня завдовжки х має вигляд
Р+ С(х)« [а|Г(х)	(5 15)
Перейдемо до наступного перерізу, який проведено завдальшки гіх від першого Площа цього перерізу Р (х) 4- ар (х), а вага частини стержня завдовжки х + <іх становитиме <3 (х) + ур (х) Ох Умова рівноваги цієї частини стержня
Р + (2 (х) +	(х) Ох = [о] ІГ (х) + 4Р (х)1.	(5 16)
Віднявши вираз (5 15) із виразу (5 16), дістанемо
уР(х}4х = \а]4Р(х)	(5 17)
або, розділивши змінні
__ угі-Х (о| *
Проінтегрувавши це рівняння, знайдемо
1пГ(х) = ух/(о] 4-С.
Звідси
£(х)«еи’1+в.	(5.18)
Сталу інтегрування С визначимо з умови, що при х =» 0
Г(х)=Г0
Тоді з формули (5 18) дістанемо
Га = е°.
Підставляючи це значення у формулу (5 18), знайдемо закон зміни площі поперечного перерізу стержня однакового опоруї
(5 19)
Найбільша площа в місці закріплення (х =• /) х «_ г а’ЯА’О Гтм = Го®
або з урахуванням (5 14)
Р™.=-і5Г-е’мч.	(5.20)
Знайдемо повну вагу (} стержня однакового опору З умови рівноваги всього стержня маємо
Р + $ — М Япвх
Звідси
(2 = (аі - Р
Ураховуючи формулу (5 20), дістаємо
<г = р(еї"1’1 —і)
Легко визначити також укорочення стержня Ос кільки напруження в усіх поперечних перерізах одна нові і дорівнюють допустимому, то і відносна деформація е по довжині стержня однакового опору постійна і дорівнює іоГД Абсолютне укорочення стержня
Д<-ЄІ=М(
Рнс 138
(5 2 і)
Східчастий стержень. Стержень, який складається з окремих від різків (східців) з однаковою площею поперечного перерізу в межах кожного відрізка, називають східчастим Він займає проміжне місце між стержнем однакового поперечного перерізу і стержнем однакового опору
У східчастому стержні матеріал використовується краще, ніж у стержні однакового перерізу, але менш ефективно, ніж у стержні однакового опору. Проте виготовлення східчастого стержня значно простіше, тому такі стержні більш поширені, ніж стержні однакового опо ру Зазначимо, що опори мостів часто виготовляють у вигляді схід частих стержнів
Східчасті стержні проектують так, щоб у небезпечному перерізі, який розташований в кінці кожного східця, напруження дорівнювали допустимому
Складемо формули для визначення площі поперечного перерізу кожного східця (рис 138)
Площу поперечного перерізу першого східця знайдемо з формули (5 6)
До нижнього кінця другого східця прикладено склу, що дорівнює Гі [о! Тоді аналогічно
Ураховуючи формулу (5 22), дістанемо
е __________И21_
1 (И (Іоі — тУ
(5.23)
(6 24)
Рнс 139
До нижнього кінця третього східця прикладено силу Г, [о] Отже, площа поперечного перерізу третього східця
Підставляючи значення Р, із формули (5 24), матимемо
“ (ЮІ -їЧ <(»1-,Ч <1»І-їЧ 	(5 25)
Формула для площі поперечного перерізу п го східця має такий вигляд
Р______________________Р|ДІЯ-1________________
" (І<П - т/*> ([о| - у/,) (іо| - у/,) .. ({01 - у/п)
Якщо довжини всіх східців однакові, то
/і-»/,-/,-	„/„«і/т,	(5 26)
де / — загальна довжина стержня, т — число східців у стержні
Тоді
Г. - , Рм' ; у, = —т—-	.	(5 27)
(і’і-’-їг)
Урахування сил інерції Під силою інерції матеріальної' точки, яка рухається з прискоренням, розуміють силу, що дорівнює аа модулем добутку маси точки на іі прискорення Напрям сили інерції протилежний напряму прискорення У реальному тілі, яке можна розглядати як сукупність матеріальних точок, сили інерції розподілені по об ему тіла Вони складаються з іншими навантаженнями і впливають на значення напружень і деформацій, що виникають у тілі Часто сили інерції становлять основне навантаження на рухомі деталі конструкцій
При розв'язанні задач з урахуванням сил інерції користуються принципом Д’Аламбера Він полягає в тому, що рівнянням руху точ ки (або системи точок) можна надати вид рівнянь рівноваги, якщо до діючих заданих сил і динамічних реакцій зв'язків додати сили інерції
Визначення напружень і деформацій при дії сил інершї розгля немо на прикладі розрахунку тонкого [/і < (/720)1 кільця (рио. 139, а),
що вільно обертається зі сталою кутовою швидкістю навкою цент ральної осі, перпендикулярної до площини кільця
Нехай кутова швидкість обертання кільця,
ш =
пп зо
де п — частота обертання
Для тонкого кільця можна вважати, що всі його точки перебува ють на однаковій відстані від осі обертання, яка дорівнює радіусу г
При обертальному русі зі сталою кутовою швидкістю точки кільця зазнаватимуть лише доцентрового прискорення шгг а сили інерції будуть спрямовані від осі (відцентрові сили)
На елемент кільця завдовжки і діє сила інерції
, = Л,	(5 28)
де у —питома вага матеріалу, Р —площа поперечного перерізу кіль ця, г — радіус середньої лінії кільця
Отже, при рівномірному обертанні на кільце діють рівномірно розподілені по колу радіальні сили інерції інтенсивністю 4 Внаслідок калової симетрії системи і навантаження в усіх поперечних перерізах згинальні моменти і поперечні сили дорівнюють нулю
Для визначення поздовжніх зусиль Лї, що діють у поперечних (радіальних) перерізах кільця розглянемо рівновагу половини кіль ця (рис 139, б) На половину кільця діють дві сили Л, які прикладені в проведених перерізах, та сили інерції інтенсивністю д
Згідно з теоремою, що її доведено в § 23, рівнодійна розподіленого навантаження інтенсивністю д дорівнює добутку д на діаметр перпендикулярна до діаметра і спрямована по осі яка проходить через його середину, тобто по осі у
Умова рівноваги половини кільця при проекніюванні сил на вісь у має вигляд
2У - д2г == 0, звідки
И = дг	(5 29)
Нормальне напруження в поперечному перерізі кільця
о=П!Р = дгіР	(5 30)
Підставляючи значення д із формули (5 28), матимемо
О = -ГИМ	(531)
Напруження у кільці можна виразити через його колову швидкість в Ураховуючи, шр в = н>г, з виразу (5 31) маємо
а = -у- у*	(5 33)
Зауважимо, що напруження не залежить від площі поперечного перерізу кільця
Формули (5 Зі), (5 33) можна використовувати для наближеного (якщо знехтувати впливом спиць) визначення напруження в ободі маховика
З умови міцності кільця
(5 34) визначаємо допустиму колову швидкість
(5 35)
Відносне подовження в напрямі дотичних до середнього кола кіль ця (колове подовження), згідно із законом Гука та з урахуванням ви разу (5 31), в =	(5 36)
Розглядаючи геометричний аспект деформації (рис 139, а), бачи* мо, що відносне подовження по колу кільця дорівнює відносному подовженню радіуса . 2ят, — 2яг г, — г и	„
8 = —5К7------в —і—— в Т ’	& 37)
де « — радіальне переміщення точок середнього кола кільця
Із формул (5 37) і (5 36) знаходимо и = ег =	а»8/-8	(5 38)
$ 37. Статично нмизначувані конструкції
Статично невизначуваними називаються конструкції, зусилля в елементах яких не можна визначити тільки з рівнянь статики Крім рівнянь статики для розрахунку таких систем (конструкцій) треба використати також рівняння, що містять деформації елементів кон сгрукціі
Схеми деяких статично невизнану ваних конструкцій зображено на рис 140 а—стержньової підвіски б—стержня, закріпленого двома кінцями в — стержньового кронштейна г —складеного кіль ня д — залізобетонної колони; е — шарнірно стержньової системи 130
Усі статично невизначувані конструк ції мають додаткові або як ще кажуть «зайві» зв'язки у вигляді закріплень стержнів або інших елементів Зайвими такі зв язки називають тільки тому, шо вони не потрібні для забезпечення гео метричної незмінності та рівноваги кон струкціі при дії навантаження, хоч на явність їх випливає з умов експлуатації З умов міцності й жорсткості конструкції зайві зв'язки можуть стати необхідними
У статично невизначуваній системі
г д Є Рис 140
кількість невідомих зусиль, що треба
визначити більша, ніж кількість рівнянь статики, які для цього можна використати Різниця між кількістю невідомих і кількістю рівнянь статики визначає кількість зайвих невідомих або ступінь статичної невнзначуваності конструкції Коли є одна зайва невідома, конструкцію називають один раз статично невизначуваною, при двох — двічі статично невизначуваною і т д Конструкції, зо бражені на рис 140, а, б, г е, мають по одному додатковому зв'язку і є один раз статично невизначуваними, а конструкція, яку показано на рис 140 в має два зайвих зв’язки і є двічі статично невизнану
ваною
Розв'язання статично невизначуваних задач. Для розв язаиня ста тично невизначуваних задач розроблено загальні методи, деякі з яких наведено в гл 14
Найпростіші статично невнзиачувані конструкції, елементи яких працюють на розтягання або стискання будемо розраховувати шляхом сумісного розв язання рівнянь, здобутих у результаті розгляду ста тичного, геометричного і фізичного аспектів задачі При цьому зручно додержузатися такої послідовності
1	Статичний аспект задані Складаємо рівняння рівноваги відокремлених елементів конструкції, що мають невідомі зу силля
2	Геометричний аспект задачі Розглядаємо систему в деформованому стані, що дає змогу встановити зв’язки між деформаціями або переміщеннями окремих елементів конструкції. Здобуті рівняння називають рівняннями сумісності (нерозривності) деформації
З Фізичний аспект задачі На підставі закону Гука виражаємо переміщення або деформації елементів конструкції через невідомі зусилля, що діють у них У разі зміни температури до деформацій, спричинених зусиллями, додають температурні деформації
4	Синтез Розв’язуючи сумісно статичні, геометричні та фізичні рівняння, знаходимо невідомі зусилля
Розглянемо приклади розрахунку деяких простих статично невизначуваних конструкцій
Рис 141
і Нехай до стержня, закріпленого двома кінцями прикладено осьову силуР (рис і4і,а). Визначимо зусилля, що виникають у нижній та верхній частинах стержня
Статичний аспект задачі Оскільки сила Р діє вздовж осі стержня, в місцях його за кріплення виникають тільки вертикальні скла дові реакцій (РА і рв) Спрямуємо їх довіль но —так, як показано на рис 141, а Для системи снл, що діють по одній пря мій ліні? можна скласти лише одне рівняння рівноваги
2Х-Кд -) Рв-Р = 0	(539)
Отже, задача один раз статично невизначува на (дві невідомі реакції не можна визначити з одного рівняння)
Геометричний аспект задачі Оскільки кінці стержня жорстко закріплені, то його загальна довжина не змінюється Отже
Д/ = 0	(5 40)
Фізичний аспект задачі У поперечних перерізах верхньої частини стержня (ЛС) діють поздовжні зусилля N Ас Ра, а в поперечних перерізах нижньої" частини (ВС) —зусилля Nвс— —Рв Використовуючи закон Гука, виразимо деформації через ці зусилля
а, 1^ЛСа □_	РАа РдЬ
~ ЕР + ЕР - ЕР ~~ ЕР	(5
Синтез Підставляючи вираз (5 41) в рівняння (5 40), матимемо РАа РвЬ ЕР ~ ЕР ~ а звідси
Рла — РвЬ	(5 42)
Розв язуючи сумісно рівняння (5 39) і (5 42), дістанемо
Остаточну епюру поздовжніх зусиль показано на рис 14і, б
2 Добрати площі поперечних перерізів тригтержньовоі підвіски, розрахункову схему якої наведено на рис 142, а Довжина середньо ГО стержня її = і 5 м, кут між віссю середнього стержня і осями бокових стержнів а = 30е Усі стержні виготовлено із сталі марки Ст2 Площі поперечних перерізів бокових стержнів = Га Підвіска у вузлі А буде навантажуватися вертикальною силою Р -= 80 кН
із розрахункової схеми конструкції а також із припущення, що шарніри у вузлах ідеальні випливає, що при навантажуванні під
а
Рнс. 142
віски у вузлі А силою Р в стержнях виникатимуть тільки осьові зу силля, у даному прикладі — розтягальні
Площу поперечного перерізу стержня при розтяганні (проекту* вальний розрахунок) добирають з умови міцності
о = А7ГС(о-1,
звідки, якщо відоме зусилля АГ. визначають потрібну площуі
Знайдемо зусилля в стержнях підвіски
Статичний аспект задачі Рівняння рівноваги вузла (рио 142, б) мають виглад
2Х = АГазіпа — АГ, зіп а = 0,
2У = АГ, 4- А^соза ц-АГ,соза — Р = 0
із першого рівняння випливає, що 1^ = И, Із другого рівняння маємої
А^ + гЛГ.соза-Р	(5 43)
Отже, конструкція один раз статично невизначувана
Геометричний аспект задачі Оскільки система симетрична від* носко осі середнього стержня, а бокові стержні розтягуються ома* ковими силами, то вузол А при деформації підвіски опуститься по вертикалі на якусь величину 6 Нове положення вузла буде Лх (рис 142, в) Усі стержні подовжаться і займуть положення, що його показано на рис І42, в штриховими лініями
Подовження середнього стержня очевидно, буде Д/, = 6. По* довження бокових стержнів дістанемо, якщо з точок В і О радіусом, що дорівнює ВА (чи О А), проведемо дуги через точку А і зробимо за січки на нових довжинах стержнів ВЛ, і £)ЛХ Унаслідок того що пружні подовження дуже малі порівняно з довжинами стержнів (на рнс і42, є для наочності подовження дуже збільшено), можна вважа ти що кути а між осями стержнів не змінюються, а проведені дуги слід замінити перпендикулярами, опущеними з вузла А на нові
напрями стержнів Тоді, як видно з рисунка, Д/8 = Д/, = Д/(со8а	(5 44)
Фізичний аспект задачі Подовження стержнів виразямо за зако ном Гука через зусилля, що діють у них
4і" = -г?г- А/> = -иг-	і5 45»
Синтез Підставляючи значення Д/г і Д/2 з виразів (5 45) у формулу (5 44), дістанемо
Л'іб	,г .сх
-^---^соза	(546)
Звідси ЛГ, = ЛГ, сота або М, = -Й- со5 а,	(5 47)
де Сі —	, С2 =-^4- — жорсткості відповідно середнього і боко-
вих стержнів
Підставивши вираз (5 47) у рівняння (5 43) матимемо
N1	2 —*- N1 со$а а = Р,
звідки
п, --------£------- (5 48)
1 4-2 -р-соь*а ' «х
Ураховуючи вираз (5 47), знайдемо
Р “т—С05а 1.	(5 49)
І + 2	С051 а
Як бачимо, зусилля Л\ І Мг залежать від співвідношення жорст костей стержнів чим більша жорсткість стержня тни більшу частину п івантаження він сприймає У цьому полягає одна з особливостей статично невизначуваних систем Зауважимо, що в проектувальних розрахунках таких систем при визначенні зусиль треба задатися від ношенням жорсткостеЙ Якщо матеріал стержнів однаковий, то зада ються відношенням площ поперечних перерізів яке визначає і певне відношення жорсткостеЙ
Виберемо РІІР1 = к Тоді, враховуючи, що — Іг соь а, матимемо са ЕР,/,	сох а	ой а
Сі — І^ЕРі = ' \ЕР*Л к	*
Тепер зусилля в стержнях (5 48) і ЛГ, (5 49) визначатимуться такими виразами
;	(5 50)
І 4- сої* а
<550
Знайдемо ці зусилля, взявши, наприклад к = 2ї
Л,.=тда- = 48'5кИ 80 0,866»	, о о и
~ 204-0866») = 18'2кН
Доберемо площі поперечних перерізів стержнів, виходячи з при лущення що напруження в середньому стержні дорівнює допустимому [о] » 140 МПа Тоді
Площі поперечних перерізів бокових стержнів, згідно з взятим відношенням,
Р, = 4- = Цг =• І.73 см>
Напруження в цих стержнях
Он в 9(|І = Л- = |В,г—МПа = 105 МПа г» 1,73 10"4
Ці напруження менші, ніж допустиме тобто стержні мають надлишковий запас міцності
Якщо з умови міцності визначити площі поперечних перерізів бокових стержнів Гіг а потім, згідно з вибраним відношенням, взяти Г, = 2Гі, то напруження в середньому стержні перевищить допусти ме Отже, цей другий варіант добору площі поперечних перерізів слід відкинути.
Початкові й температурні напруження Вільне складання ста тично невнзначуваних систем можливе лише за умови точного виготовлення їхніх елементів У противному разі систему можна скласти, прикладаючи зусилля, які спричинюють деформації елементів Тому після монтажу в елементах конструкції виникають напруження, що називаються початковими, або монтажними У статично визначува них системах зазначені неточності розмірів елементів не заважають вільному монтажу Отже, після монтажу не виникають початкові на пруження в елементах.
Рнс 143
б
У елементах статично невизначуваних конструкцій зусилля і на лружеиня виникають також при зміні температури
і Припустимо що стержні конструкції, яку розглянуто в попередньому прикладі, виготовлено із заданими площами поперечних перерізів ?! та Г9 = Г9, а довжина середнього стержня /х виявилася меншою на відрізок Д (рис І43, а) Якщо значення Д мале порівняно з довжинами стержнів, то приклавши відповідні деформувальні зу силля, можна всі три стержні з'єднати у вузлі, що займе після монта жу якесь положення А (рис і43, б) Очевидно, при цьому середній стержень буде розтягнутий, а бокові —стиснуті Визначимо мон тажні зусилля в стержнях
Статичний аспект задані Рівняння рівноваги вузла (рис 143, а) мають вигляд
2Х = зіпа — АГ, зіпа =0
ЕУ = АГХ —А^соза — АГасоза =0.
Гз першого рівняння знаходимо, що АГ, = ЛГ9 Залишається одне рів ияння з двома невідомими
ЛГХ — соз а = 0	(5 52)
Геометричний аспект задачі 3 наведеної на рнс 143, б побудови випливає, що
Д/, =(Д —Д/^соза	(5 53)
Фізичний аспект задачі За законом Гука
Синтез Підставляючи значення Д/х і Д/а з виразів (5 54) у формулу (5 53), маємо
*«/« /* \
= -----етг)со5“
Звідси
Л,, = 'Т’(4_'Й")СМ“
або
=• с. (д —у^соза
Ввівши N1 у рівняння (5 52), матимемо
— 2с, (Д — Их/с,) соза а = 0
Звідси знаходимо розтиральне зусилля в середньому стержні*
Н,----------------- д	(5 55)
І 4- 2 соз» а
Стискальні зусилля в бокових стержнях визначаємо з рівняй* ня (5 52)
її* * АГ ,/2 соз а	(5 56)
Зусилля в стержнях залежать як від відношення жорсткостей так і від Д
Нехай у розглядуваній конструкції (рис і43> всі стержні виготовлено із сталі (£ = 2 • іО* МПа) Площі поперечних перерізів стержнів Рг = 3 сма, Рг = Р3 = 2 см\ проектна довжина стержня і =» 2 м, кути нахилу бокових стержнів а = 30° Після з’єднання крайніх стержнів виявилося що середній стержень коротший, ніж це треба для вільного складання, на Д = 0,15 см Знайдемо зусилля і напруження, що виникають після монтажу конструкції
За формулою (5 55) знаходимо розтягальне зусилля в середньому стержні
2 10» 10» 2 КГ4 0 866 паям
е ,0. ,0.1	.агт:—°’'5 І0"кН=
2 2 10» 10» З І4Г-*	1866
= 20,9 кіі
Стискальні зусилля в бокових стержнях, згідно з виразом (5 56), *, = *,= 2 кН = 12,06 кН
*=
Відповідно напруження в стержнях
а, = -ф- =	МПа = 69,7 МПа,
а, = а, = - -)г- =-------12,06 МПа - - ®.3° МПа
2	• Г» 2 КГ4
Отже, порівняно невелика неточність, яку допущено в довжині стержня при виготовленні, спричинює великі початкові (монтажні) Напруження
Рнс 144
2 Визначимо температурні напруження в стержні ДВ (рнс 144) зав довжкн І і площею поперечного перерізу Е Модуль пружності матерія лу Е, коефіцієнт лінійного температурного розширення а Стержень за кріплено кінцями в непіддатливих сті нах і нагріто так, що на кінці А температура його підвищилася до Та, на кінці В — До Тв, а по довжині стержня вона змінюється за законом
Т(х) = Тл+ Т,~—* У	(5 57)
При л = 0 температура по довжині стержня не змінюється і дорівнює Тв, прн п = 1 температура змінюється лінійно при п = 2 — за законом параболи другого порядку і т д
Визначимо реакції закріплень і напруження в стержні Статичний аспект задачі При підвищенні температури стержень намагається подовжитися Цьому перешкоджають жорсткі опори, внаслідок чого виникають реакції, спрямовані вздовж осі стержня (рис 144)
Для системи сил, які спрямовані по одній прямій, можна скласти одне рівняння рівноваги*
2Х = Дл_Двя0, звідки
Хл = К8 = К	(5 58)
Отже, задача один раз статично невизначувана Поздовжня сила в стержні N = —К
Геометричний аспект задачі Внаслідок закріплення кінців стержня його довжина не змінюється
Д/ = 0	(5 59)
Фізичний аспект задачі Укорочення вільного стержня, спричи нене поздовжніми силами, які дорівнюють реакціям закріплень, =-£г	(5 ед
Подовження вільного стержня внаслідок нагрівання визначимо так Завдальшки х від кінця А стержня виділимо елемент завдовжки сіх Будемо вважати, що в його межах підаищення температури Т (х) постійне Температурне подовження цього елемента
Ьйхт=а.Т{х)йх = а\ТА^-^~^- хАйх (56і)
Температурне подовження всього стержня знайдемо проівтегру-вавши вираз (5 61) по довжині стержня
И,-	+ Т‘~Т- ж")іх =-аі(Ті +	(5 62)
Повна зміна довжини стержня
Л1 = ЛІл + ЛІг=-тг + «і'тл + ^~^-)	(563)
Синтез Підставивши вираз (5 63) у формулу (5 59). матимемо
—+ а/(тл+	=».	(5 54)
звідки знайдемо реакції опор
/г = а(Гл+	(5 55)
і напруження в стержні
Т^4-)£	<5 66>
При п = 0 дві останні формули переходять у формули для випадку рівномірного нагрівання стержня по довжині на ДТ = Тв
Р = а.\ТЕР та а = — аЕЬТ
Розглянемо числовий приклад Визначимо осьову силу і напру ження в сталевому стержні, якшо І = 80 см, Е = 20 см’, Е = 2 X х 10і МПа а = 125 і0~7, Та - іО °С Тв « 55 °С Температура по Довжині стержня змінюється за законом параболи другого порядку (л = 2)
Підставляючи числові значення у формули (5 66) і (5 55), знайдемо Н = - 125 1<Г’(і0 + )а ІО‘.2О ІО^МН - - 125 кН, о - -ї_ .--------------К5- '2^. МПа = - 62,5 МПа
Р 20 ІО *
Зауважимо, що при зниженні температури в системі, яка подібна до зображеної на рис 144 виникають розтягальні напруження
На підставі розглянутих у параграфі прикладів можна зазначити такі особливості статично невизначуваннх систем
1	Розпотіл зусить між елементами статично невнзначуваних кон струкній залежить від жорсткої лей цих елементів Якщо збільшити Жорсткість якого небудь із них то він сприйме більше зусилля Змі нюючн співвідношення жорсткосте# елементів конструкції можна як завгодно змінювали розподіл зусиль в них
2	У статично невнзначуваних конструкціях при зміні температури їхніх елементів порівняно з температурою, при якій конструкції складалися виникають зусилля і напруження
З У елементах статично невнзначуваних конструкцій можуть іс нувати зусилля і напруження, коли немає зовнішнього навантаження Ці зусилля і напруження, що їх називають початковими (монтажни ми) виникають при складанні конструкції Початкові напруження або виникають внаслідок неточного виготовлення окремих елементів конструкцій, або утворюються з певною мстою (наприклад, затягуван-ня болтів, пресова посадка)
4	У статично невнзначуваних конструкціях у загальному випад ку в усіх елементах одночасно не можна дістати напруження, які до рівнюють допустимим Це треба мати на увазі при проектуванні та* ких конструкцій
$ 38. Розрахунок гнучких ниток
Абсолютно гнучкою називають нитку, яка здатна чинити опір тільки розтяганню В поперечних перерізах таких ниток лише осьова розтиральна сила не дорівнює нулю В інженерній практиці поширені системи, що з певним наближенням можна розглядати як гнучкі нит ки Це повітряні лінії електричних проводів проводи телеграфних мереж, контактні проводи електрефікованих залізниць і трамваїв, ланцюги висячих мостів, троси канатних доріг та кабельних кранів тощо
Точки підвішування нитки можуть бути на одному або різних рівнях (рис і 45)
При розрахунку на міцність довгих гнучких ниток крім інших навантажень, істотне значення має їхня власна вага Нехай вагому гнучку нитку однакового поперечного перерізу підвішено в двох точках на різних рівнях (рис 145 б) або на одному рівні (рис і45, а) Під дією власної ваги нитка провисає по деякій кривій
Введемо такі позначення ї, —відстань між точками А та В підвішування нитки, І — проліт, що дорівнює горизонтальній проекції відстані (]*, к — різниця між рівнями точок підвішування нитки / — віддалення нитки від прямої АВ що сполучає точки підвішування
а	б
Рнс, 145
нитки, виміряне посередині прольоту. £ — довжина непідвішеної нитки ч—інтенсивність навантаження
При підвішуванні нитки на одному рівні величина є віддаленням найнижчої точки нитки від горизонтальної лінії АВ і називається стрілою провисання Навантаження д. крім власної ваги, може вклю чати в себе також вагу льоду при обледенінні ниток, тиск вітру тощо Ці навантаження вважають рівномірно розподіленими по довжині нитки
Коли навантаження становить власну вагу нитки (провода) його інтенсивність
Ч -- ?п =	(5 67)
де дп — вага одиниці довжини провода, у — питома вага матеріалу Р — площа поперечного перерізу провода
При обледенінні ниток (проводів)
? = ?п і- Чп,	(5 68)
де дя — вага льоду на одиниці довжини нитки
Товщину корки льоду залежно від кліматичного району беруть 0,5 2 5 см
Зазначені навантаження діють у вертикальній площині, тиск же вітру на нитку —в горизопта іьній площині Його інтенсивність дЛ визначають як добуток тиску вітру р на площу діаметрального перері зу одиниці довжини провода
?. -або
<7В —	(5 69)
де (І —діаметр провода з урахуванням його обледеніння, к = і 2 — аеродинамічний коефіцієнт а — 0 85 — коефіцієнт нерівномірності вітру, Чшв — швидкісний напір
Виражаючи Н/м, через швидкість вітру ц маємо
ЧЛ О.бЗбоМ	(5 70)
Тут V —швидкість вітру, м/с <І — діаметр провода, м
Сумарну інтенсивність навантаження на нитку знаходимо як гео метричну суму вертикального та горизонтального навантажень
? _ і' <?» и.)"	(5 ті»
Зазначимо що площина дії сумарного навантаження, яка збігається з площиною провисання нитки, не буде вертикальною
На практиці провисання нитки найчастіше буває невеликим  таким, що довжина нитки по кривій провисання мало відрізняється від довжини прольоту (як правило, не більше, ніж на 10 %) Обмеж» мося розглядом тільки таких поюгих ниток У цьому разі для спро щення розрахунків з достатньою точністю можна вважати, що паваїї тажеїшя, яке діє на підвішену нитку рівномірно розподілене не по
Рнс. 146
довжині нитки, а по довжині лінії АВ, що з'єднує точки підвішування (рис 148, а)
Для зручності розрахунків це навантаження д заміняємо статично еквівалентним навантаженням д розподіленим уздовж прольоту І Очевидно,
?!- ?(,.
звідки
'5 72>
Статичний аспект задачі Розглянемо рівновагу нитки Оскільки виходимо з припущення, що нитка абсолютно гнучка то напрями розтягальннх сил у кожному поперечному перерізі повинні збігати ся з напрямом дотичної до кривоі провисання нитки В точках закріплення ці сили дорівнюють реакціям опор Позначимо останні відповідно через 7д та Тв Виберемо початок координат у лівій точці підвішування нитки і спрямуємо осі координат так, як показано на рис 146, а
Заміняючи реакції опор їхніми горизонтальними та вертикальними складовими, запишемо рівняння рівноваги нитки
= - Нл + Нв = 0,
2У = -Ра~Нв+чі=0.	(5 73)
= - НлН + Ял/ - ЯР/2 = 0
із цях рівнянь маємо
НА = Нв = Н,	(5 74)
(5 75)
К,=-£--Н±-.	(576)
Оскільки з трьох рівнянь рівноваги не можна визначити чотири невідомих (На, Рл, Нвча Рв), то задача є один раз статично невизна чувана
Розглянемо рівновагу частини нитки відсіченої довільним перерізом (рис І46, б)
IX - - Н + 7\ (х) = 0.	= - Ра чх -	(х) = 0
Звідси враховуючи формулу (5 75) маємо
Тх(х} = Н,	(5 77)
=	(578)
Як видно з виразу (5 77), горизонтальна складова розтягального зусилля в будь якому поперечному перерізі нитки постійна і дорів нює Н Зусилля Н називають горизонтальним натягом нитки
Отже, розтягальне зусилля в довільному перерізі нитки
ТМ - [/"7^М + 75(Х)_ рЛ« -ф'т +«(4 -*)]’ '579>
Як бачимо, найбільше розтягальне зусилля Тгавх діє у найвищій точці підвішування нитки (при х = 0)
Для пологих ниток різниця між найбільшим розтягальним зусил лям, що діє у найвищій точці підвішування, та натягом Н невелика Тому з достатньою для практики точністю можна вважати, що розтя гальне зусилля в нитці постійне і дорівнює натягу Н За цим зусил лям, як правило, і виконують розрахунок на міцність
Знайдемо форму кривої провисання нитки Для цього запишемо рівняння для згинального моменту в будь якому перерізі (рис 146 б). Оскільки нитка абсолютно гнучка, то в усіх іі перерізах згинальний момент дорівнює нулю
М (х) = РАх — Ну — <?х’/2 =. 0	(5 80)
Ураховуючи формулу (5 75), знаходимо
<68і>
ЗВІДКИ
-"=(-&+ЯХ—5Г'	<582)
тобто крива провисання нитки визначається квадратичною параболою
Зазначимо, що коли задачу розв'язувати точно, вважаючи навантаження розподіленим рівномірно по довжині нитки, а не по прольо
ту, то крива провисання нитки буде ланцюговою лінією Формула (5 82) є першим членом розкладання ланцюгової лінії у ряд Маклере* на за степенями х і дає достатнє наближення при розв’язуванні практичних задач
Визначимо можливі положення найнижчої точки кривої провисання нитки Координати цієї точки позначимо через х — а, у — ? (рис 147, а) У цій точні координата у має екстремальне значення Для його визначення візьмемо похідну від виразу (5 82)і
і прирівняємо її до нуля
£--° <5 84>
Звідси знаходимо значення абсциси, що визначає положення найнижчої точки
*=“=4+т	<5 85>
Найнижча точка кривої провисання нитки завжди розташована ближ че до найнижчої точки підвішування
Підставляючи вираз (5 85) у формулу (5 82), знайдемо екстремаль не значення ординати, тобто найбільше провисання нитки*.
„	, нл» , й	,к ясч
ртах « / = -5^- +	+ —	(5 86)
Будемо розрізняти три характерних випадки розташування най нижчої точки кривої провисання нитки
1	Найнижча точка кривої провисання розташована в межах прольоту, тобто а < І (рис 147 а) Згідно з виразом (5 85), це має місце, коли
(5 87)
2	Найнижча точка кривої провисання лежить за межами прольо ту, тобто а > І (рис 147, б) Це буде за умови що
(5М)
З Найнижча точка кривої збігається з найнижчою точкою підвішування, тобто а <= І (рнс 147, в) Необхідна умова для цього
(5 89)
У всіх трьох прикладах координати а та /' найнижчої точки визна чаються за формулами (5 85) і (5 85)
Установимо залежність між горизонтальним натягом Н і величн ною / Посередині прольоту х = 1/2. а у = й/2 4- / (див рис 145 б) Підставивши ці значення координат у формулу (5 82), дістанемо
І—(5 90» або
(5 91)
Виразимо натяг нитки Н через найбільше провисання [' Із фор мули (5 86) розв'язуючи квадратне рівняння відносно натягу Н, ма тимемо
з-±КГ<Г-8>]	(5 92)
Якщо найнижча точка кривої провисання перебуває в межах прольоту, то перед коренем беремо знак «мінус», якщо за межами прольоту,— знак «плюс», бо, як видно з виразів (5 87) та (5 88) в першому випадку натяг Н менший, ніж у другому
Геометричний аспект задачі Установимо зв язок між довжиною підвішеної нитки, прольотом та величиною /, яка характеризує про висання нитки
Довжина елемента кривої, як відомо,
<15 - V - <1уг = 11 + (-а7-)']'Я
Для пологої нитки величина {ду/іх}* мала порівняно з одиницею Роз кладаючи вираз 11 1- <<4г/Лг)*І,/8 У ряд за формулою бінома Ньютона і обмежуючись першими двома членами розкладання, дістанемо
85 = |1+4-(-Е-|’]л	(593)
Підставляючи сюди ду/сіх із виразу (5 83) та інтегруючи по всій дов жині прольоту, матимемо
5 = .([1 +-г(тй‘	—йЧ ]л,-' + -иг!~ + -й-
(5 94)
Підставляючи з формули (5 91) Н =-= дістанемо
5 = '+-3--?- + т	<5 95»
З геометричних міркувань подовження Д5 нитки завдовжки Ь після підвішу вання
Д5 = 5 — £ = І + +-^-+-а--£ <59е> Фізични і аспект задачі Установимо також фізичні залежності які виражають зміну довжини нитки від розтягального зусилля та від зміни температури Як зазначалося для пологих ниток розтиральне зусилля можна взяти таким що до рівнює натягу Н При виз наченні подовжень довжи
ну нитки замінимо довжиною що достатньо точно, коли провисання мале Тоді пружне подовження від розтягання
ЛЗя =
ніі________ні
ЕЕ ~ ЕЕ со$ З
(5 97)
Температурне подовження нитки визначається за формулою №=а(1(7'-Г^=-^-(Г-Т^,	(5 98)
де То — температура в момент підвішування нитки Т — температура, для якої виконується розрахунок нитки
Сумарна зміна початкової* довжини нитки
Д5 = Д5„+Д5г_-еІгї-+7^-(Т-Т,)	(5 99)
Формули (5 96) та (5 99) визначають одну і ту саму величину — подовження підвішеної нитки Прирівнявши праві частини цих рівнянь, знайдемо, що
—Й—Етап—=тг<7'-7'.>	<510<»
Рівняння (5 100) равом із статичним рівнянням (5 90) дає змогу визначити натяг нитки Н та стрілу провисання /
Визначивши з рівняння (5 100) натяг нитки Н, можемо за форму лою (5 79) знайти розтягальне зусилля в довільному перерізі нитки, а отже і Ттах Знаючи максимальне розтягальне зусилля можна перевірити міцність нитки
О = Тпих/Т ~ Н/р 1<т],
враховуючи формулу (5 91) діс-танемо
тут <1’1
Введемо позначення
(5 10!)
у = д/Р	Рнс 149
Цю величину у, що е відношенням інтенсивності лінійного навантаження до площі поперечного перерізу, називають питомим навантаженням Якщо діє тільки власна вага, питоме навантаження збіга ється з питомою вагою матеріалу нитки
Ураховуючи сказане, умову міцності можна записати у вигляд’
<5102>
Зауважимо, що при розрахунку електричних проводів переріз нитки визначають з електротехн чних міркувань, після чого вже ви конують перевірний розрахунок на міцність
Наведемо розрахункові формули для випадку нитки з точками під віщування, які розташовані на одному рівні (рис 148, а), тобто при сох р — 1 Таке буває дуже часто.
При такому підвішуванні Л = 0, реакції в точках підвішування однакові /?л == Рв -= ?//2, найбільше провисання / буде посередині прольоту Воно пов язане з натягом формулами (5 90) та (5 91)
/=-тг
„ '	(5 103)
П ц
Рівняння сумісності деформації (5 100) набуває вигляду
і = ,+ иї£— ТГ-<Ч(Г-Г^ (5104)
Вплив зміни температури і навантаження на напруження та стрілу провисання нитки В процесі експлуатації нитка може зазнавати дії різних навантажень та температур З'ясуємо, як змінюються на пруженкя та стріла провисання нитки при зміні цих факторів Для цього розглянемо два стани нитки т й і п й (рис 149)
Нехай у т му стані температура дорівнює Тт, лінійне наванта ження—дт, а стріла провисання—при цьому натяг Нт = =	а напруження в нитці а„ = Н„ІР
При зміні температури та навантаження в п му стані до значень Т„ та д„ стріла провисання стане /п натяг Н„ = ^чг/8/п а напружені я ол - Нп/Р
Установимо залежність між напруженнями та стрілами провисан ня нитки для цих двох станів Задачу легко розв язати, якщо записати
вираз для довжини нитки Ь до моменту підвішування через параметри обох станів Якщо точки підвішування нитки розташовані на одному рівні, то згідно з рівнянням (5 104) виходячи з параметрів т го та я го станів, відповідно матимемо
І = '+-Й------<5105>
і = '+^ї------(5 106)
Праві частини цих двох виразів які є однією і тією самою велнчи ною—довжиною нитки до моменту підвішування однакові Отже, , , А1- нті	И„І
*“ 24Н8 Ер	' ° ~~	24Я^ ер
— аЦТп — Т^
Звідси позначивши цпІР = ут, цп!р = та враховуючи що НтІГ — = Н^Р = знаходимо
«’/»£	V8 РЕ
О.----(5107’
Цю залежність Іноді називають рівнянням стану нитки Його можна записати також у вигляді
----^=0 (5Ю8)
Якщо виразити напруження через стріли провисання
то рівняння (5 106) можна записати так
д-[а+4-г"г.-ло -4- V =0 <5109)
Щоб дістати рівняння стану для ниток, підвішених на різних рів нях (рис 148, б), як вихідну формулу для довжини £ беремо формулу (5 100) Тоді рівняння стану (5 107) набуде вигляду
у£і*Е сод р 24а’	“ °т
у2тІ*Е сод р
+ аЕ(Тт-Тп)
(5 ПО)
Виразивши напруження через стріли провисання, матимемо
1___І/2	3	(7*п —7*лі)___3 улі<* І . З у„Р л
І Т5-«‘	64 "£/„ сод Р — 64 £соз Р ~
Здобуті кубічні рівняння можна розв'язувати у відомими способами в тому числі й графічним
При графічному розв'язанні наприклад, рів няння (5 109) яке має вигляд
й - аІ„ - Ь = 0,
де а та Ь — відомі числа, запишемо так	______1
Й =«/.+»	(5 112) "і----І------1 '
У прямокутних координатах будемо графіки Рис і5о у — & та у — а[п 4- Ь (рис 150) Очевидно що абс циса точки перетину кубічної' параболи з прямою лінією дає дійсний корінь рівняння, а отже шукану стрілу Два інших корені цього ку бічного рівняння уявні
Поняття про критичний проліт Установимо при якому сані нит ки в ній діє найбільше напруження Це можливо
а)	прн найбільшому навантаженні (ожеледь та помірний вітео або сильний вітер без ожеледі)
б)	при найнижчій температурі без ожеледі
Оскільки найбільше навантаження та найнижча температура у часі не збігаються то для розрахунку важко визначити, який з цих станів буде небезпечним З’ясуємо вплив навантаження та темпера тури на напруження залежно від довжини прольоту нитки
Виходимо з рівняння стану (5.107) У разі дуже малих прольотів поклавши в цьому рівнянні І = 0, знайдемо що
0п = ат + аЕ (Тт — Та)
тобто при малих прольотах зміна напруження залежить здебільшого від температури Зі зменшенням температури Тп напруження оп зрос тають і найбільше напруження в нитці буде при найнижчій темпера турі
Розглянемо тепер приклад дуже великих прольотів Поділивши рівняння (5 107) на Р та поклавши /-► оо матимемо
О» = а.
Отже якщо прольоти великі, то зміна напруження залежить в основ йому від навантаження на нитку Найбільші напруження будуть діяти при максимальних навантаженнях
Знайдемо таку довжину прольоту при якій напруження в нитці однакові в обох небезпечних станах тобто як при найбільшому наван таженні так і при найнижчій температурі Такий проліт називають критичним (і„р)
Нехай Тп відповідає температурі ожеледі, тобто Тп = Тож (як пра вило, Тож = —5 °С), при цьому уп — ут»х Т„ відповідає найнижчій
температурі тобто Тп = ТШ|ц, у цьому разі на нитку діє тільки власна вага отже,
При І -= /кр, згідно з означенням
«<тт = [о]
Вносячи ці дані у формулу (5 107) знаходимо
— !®11/ і -у .	(5 113)
’ ”пім У|
Порівнюючи розрахунковий проліт з критичним, можна встановити, за яких умов у нитці діє найбільше напруження Так, якщо І < Іф, то найбільше напруження буде при найнижчій температурі, якщо І > /кр, то небезпечний стан буде при найбільшому навантаженні
Приклад 14 Багатожильний мідний провід перерізам Р = 120 мм1 підвішують при температурі Т, =- 15 °С до опор, які розташовані на одному рівні вавдальшки І =з 100 м
Визначимо. а) яку стрілу провисання /в треба надати проводу, щоб напруження в найбільш небезпечному стані дорівнювало допустимому; б) висоту точок підвішу вання провода, щоб відстань його найнижчої точки від землі була не менша за 6 м Розрахунок провода виконаємо для таких випадків
І)	температура Тол = —5 °С прн цьому провід крім власної влгн навантажений шаром льоду завтовшки І см (ожеледь) а також горизонтальним тиском вітру р * = 240 Па
2)	температура = —40 °С, діє тільки власна вага провода,
3)	температура Т„ия = +40°С діє тільки власна вага провода
Перші два випадки можуть бути небезпечними з погляду міцності провода У третьому випадку може утворитися найбільша стріла провисання, за якою треба визначити мінімальну висоту точок підвішування провода
Згідно з сортаментом проводів багатожильний мідний провід перерізом Р = = 120 мм1 має діаметр 8 = 14 2 мм та вагу одиниці довжини = 10 9 Іі/м Модуль пружності матеріалу провода £	1,3 10й Па, коефіціевт лінійного температур-
ного розширення а в |7 10*~б (/°С Допустиме напруження для провода = = 80 МПа
Знайдемо навантаження <?тях у першому випадку Для визначення ваги льоду треба знати внутрішній та зовнішній діаметри льодового покрову Внутрішній діа метр дорівнює діаметру провода тобто Л = І 42 см зовнішній діаметр О прн товши ні льодової оболонки І см буде О = 3 42 см Птоша поперечного перерізу льодового покриття провода
л(О’ —<і*)	3 14 (3,42і -І 42’)	, _д ,
гл = —-------------------------------см’ «= 7 6 см*
Прн питомій вазі льоду ул = 9 10* Н'м3 навантаження від льоду на І м довжини провода 9 10* 7 6
4л =Улґл ” ----------Н/м — 6 84 Н/м
Тиск вітру иа і м довжини провода з льодовим покриттям „	240 3 42
4в = рО - ----їдо---Н,М = 8 21 Н/в,
Повне навантаження на І м довжини обледенілого провода
9ли> “ К(їп + Ялі* 4- 9, = ИІ09 + 684Р 4-821* Н/м =19 6 Н/м
З ясуємо, в якому (а перших двох станів провода напруження в ньому будуть більшими Для цього знаходимо
Гтм =	" ТЇПо-*' Н/М> = 16,3 І0* Н/М1'
у, = - 10 н/м» = 9 08 ю« Н/М»
За формулою (5 І ІЗ) визначаємо довжину критичного прольоту
. . , /24“І7'о« - ТтпІ .......... /• 2, ,7	5 -(-«)|
» м И	->® 10 V (ЇЇЗІ-9 0И-) іо*------------------
’ їпих її
= 70 6 м « 71 м
Оскільки дійсна довжина прольоту І = 100 м більша ніж довжина критичного прольоту, то найбільше напруження у проводі отах буде прн максимальному наван таженні = 19 6 Н/м і Тож = — 5 °С тобто в першому стані Взявши отм = = [ст] знайдемо стрілу провисання провода в цьому стані
19 6 100*
/і = а?і -----------------і--------м = 2 54 м
п ог |а)	8 і 2 і0~* 80 10*
Визначимо яку стрілу провисання треба надати проводу прн підвішуванні Для цього скористуємося залежністю 5 109) тявши = от„ ~ 19,6 Н/м. [т — = = 2 54 м Тт= Тож- -5°С он" Ю,9 Н/м Тп - То - І5°С /п =/0
Підставивши числові зиа іення в рівняння (5 109) д станемо
, І	З	3 19 6 100*	1
/о’-|234Ч-у,7 І0~» Ю.(І>т5,-и 2И |2	|0И]/.-
_______3 10 9 100*_________
~ 64 1,2 10“* І 3 10'* “
Виконавши розрахунки маємо
/3_541/в — 3 28 = 0
Рсов язавош рівняння знайдемо
/о -а 2 58 м
Визначимо тепер стріту г ровисання провода при Ттах = 40°С Для цього також скористуємося залежністю (5 109) взявши дт — </п — 10 9 Н/м /ст = /0 -= 2 58 м Тт = То= І5°С <?п = Чп= Ю9 Н/м Тп = 7гоад = 40 °С /п -=/»
Підставивши числові значення матимемо
/З —12 58*4-17 Ю-6 100* (40— 15) —
_________3 10 9 100*___________1	3 10 9 100*_______
~ 64 2 58 1 2 Ю-4 1,3 10“ I а" 64 І 2 10~* ІЗ 10" "°
або
3 28 = 0, звідки знаходимо, шо = 2 85 м
Стріла провисання в третьому стані більша, ніж після п!диіш>аання (при 7*в = = 15 °С) а також більша, ніж у першому випадку Очевидно вона бі іьша за стрілу провисання, яку матаме провід також у другому випадку (прн Гт|п = —40 °С)
Для того щоб найнижча точка проводе буде на відстані не меншій ніж 6 м від землі, треба щоб точки підвішування розташовувалися не нижче ніж 6 м 4- 2 85 м = - 8 85 м
Глава 6. ОСНОВИ ТЕОРІЇ НАПРУЖЕНОГО І ДЕФОРМОВАНОГО СТАНУ
$ 39. Напруження в точці
Напруження е наслідком взаємодії' частинок тіла при його наван тажуванні Зовнішні сили намагаються змінити взаємне розташував ня частинок, а напруження, що виникають прн ньому, перешкоджають зміщенню частинок обмежуючи його здебільшого деякою малою величиною
Відповідно до гіпотези про суцільність матеріалу слід вважати, що кожну частинку тіла 8 скільки завгодно малому околі в усіх напрямах оточують безліч інших частинок Розташована в даній точці час тинка по різному взаємодіє з кожною із цих сусідніх частинок Тому в одній і тій самій точці в різних напрямах напруження різні і тільки дуже рідко коли вони однакові в усіх напрямах
Досліджуючи напружений стан тіла в даній точці А поблизу неї як правило виділяють елемент об’єму у вигляді нескінченно малого паралелепіпеда (рнс 151 а), який у збільшеному масштабі показано на рис 151 б де початок координат суміщено з точкою А а коорди натні осі спрямовано вздовж відповідних ребер так що грані пара лелепіпеда перпендикулярні до напрямів декартових осей х у, г До цих граней прикладені внутрішні сили які замінюють дію відкинутої частини тіла Позначимо повні напруження на гранях елемента
5 Рве. 151
через/>, р, р, Тут ів-дексн означають нормалі до площадок на яких ді ють напруження Внаслідок малості виділеного елемента можна вважа ти що напруження на > кожній його грані розпо- А ділені рівномірно Повні
152
Рнс
напруження на гранях
елемента зображують у вигляді нормальних та дотичних складових — проекцій повних напружень на координатні осі (рис 151, в)
Нормальні напруження позначають літерою о з індексом, що від повідає напряму нормалі до площадки на якій вони діють Дотичні напруження позначають літерою т з двома індексами перший відлові дає напряму нормалі до площини а другий — напряму самого напру ження Так, на площадці перпендикулярній до осі х, діють напру ження ах хгухзх„ на площадках перпендикулярних до осей у та г відповідно маємо ар, Ту2 Тхх. т2{, (рис 151, в)
Отже на гранях елементарного паралелепіпеда виділеного в око-лі точки навантаженого тіла діють дев'ять компонент напружень За пишемо їх у вигляді такої квадратної матриці)
І
Тух	Оу	ХуХ 1 »
Тд»	Хуу О, |
де в першому другому та третьому рядках наведено складові напру жень відповідно на площадках перпендикулярних до осей х, у, г Цю сукупність напружень називають тензором напружень
Даті буде показано що кати відомий тензор напружень, тобто сукупність напружень на трьох взаємно перпендикулярних площадках то можна визначити напруження на будь яких площадках, проведених в околі точки
Введемо правило знаків для компонент напружень Нормальні напруження як уже зазначалося в гл 4 вважаємо додатними, якщо вони спричинюють розтягання, та від’ємними — якщо стискання
Нехай напрям зовнішньої нормалі V до площадки збігається з додатним напрямом будь якої координатної осі (рис 152, а) Тоді додат не нормальне напруження па цій площадці (на рисунку це ох) також збігається з додатним напрямом координатної осі Дотичні напружен ня на такій площадці вважаються додатними якщо вони спрямовані в бік відповідних додатних напрямів координатних осей Якщо зов нішня нормаль до площадки збігається з від’ємним напрямом коорди натних осей (рис 152, б), всі три складові напруження на площадці вважаються додатними, коли вони спрямовані в бік від'ємних напря мів відповідних координатних осей
Отже за цим правилом, компоненти напружень на рнс 152 а, б додатні Зазначимо також що всі напруження на гранях елемента, зображеного на рис 151, в в осях х у г додатні
$ 40. Закон парності дотичних напружень Головні площадки І головні напруження
Не всі дев ять компонент напружень які діють на гранях елементарного паралелепіпеда, незалежні В цьому легко переконатися, склавши умови рівноваги елемента щодо його обертання (див рис 151 в) Для цього прирівняємо до нуля суму моментів усіх сил, що прикладені до граней елемента відносно осей х, у г
2МХ <= 0 2МУ = 0, ХМ, = 0
Складемо рівняння моментів відносно осі 2 Скли які паралельні цій осі і перетинають Гі, в рівняння не увійдуть Моменти сил а^іусіг на двох гранях перпендикулярних до осі а зрівноважуються, так само як і моменти сил о^хдг на верхній та нижній гранях елемента Отже маємо тіуду<і2дх — хуіііхдаіу = 0 Звідси випливає
Тед = Тух
Аналогічно з двох інших рівнянь знаходимо
Тух = Т,„ Т„ = Тх,
Отже маємо рівності
тгу = Тух, Тух = Туу Тхх »Тхх,	(б /)
які виражають закон парності дотичних напружень дотичні напру* ження на двох будь яких, але взаємно перпендикулярних площадках, якл спрямовані перпендикулярно до лінії перетину площадок, однакові за модулем При цьому вони намагаються повернути елемент у різні боки Отже, завдяки властивості парності дотичних напружень кіль кість незалежних компонент напружень у кожній точці тіла зменшу* ється з дев яти до шести
При зміні орієнтації граней виділеного елемента змінюються також напруження що діють на його гранях При цьому можна провести такі площадки на яких дотичні напруження дорівнюватимуть ну лю Площадки, на яких дотичних напружень немає, називають голов* ними площадками а нормальні напруження що діють на цих площад ках - головними напруженнями В § 45 буде показано як би не було завантажене тіло, в кожній його точці є принаймні три головні пло щадки причому вони взаємно перпендикулярні Отже в кожній точ ці можуть діяти також три головних напруження, і вони теж взаємно перпендикулярні Напрями, паралельні головним напруженням, на зивають головними напрямами напружень або головними осями вданій точці
Рис 153
Головні напруження домовимося позначати о, о( оа При цьому індекси слід розстааляти так, щоб виконувалася нерівність
оа > аг > а,	(б 2)
Ця нерівність має алгебраїчний зміст Тому, якщо, наприклад, одне з головних напружень дорівнює нулю друге (розтягальне) становить 60 МПа третє (стискальне) дорівнює—140 МПа то їх позначають так
о, = 60 МПа, аа = 0, <т8 = —140 МПа
Отже в точках навантаженого тіла можна виділити елементарні паралелепіпеди на гранях яких діють тільки нормальні — головні — напруження
Напружений стан, в якому тільки одне головне напруження не є нульовим, а два інших дорівнюють нулю називається одновісним, або лінійним (рис 153, а) Якщо два головних напруження не є нульовими а одне дорівнює нулю, то такий напружений стан називається двовісним, або плоским (рис 153,6) Якщо всі три головних напружен ня не дорівнюють нулю, маємо тривісний, або об’ємний, напружений стан (рис 153 в)
Крім того, розрізняють однорідний та неоднорідний напружені стани В однорідному напруженому стані напруження однакові в кожній точні будь якого перерізу і всіх паралельних йому перерізів. При однорідному напруженому стані розміри виділених елементів не мають значення, оскільки напруження однакові в усіх точках однієї (будь якої) грані а отже, рівномірно розподілені по кожній грані
У неоднорідному напруженому стані елемент слід вважати иескін ченно малим Тоді припущення про рівномірність розподілу напру жснь по його гранях виконується з точністю до малих другого порядку Отже незалежно від того, однорідний чи неоднорідний напруже ний стан буде в усьому тілі виділені елементи розглядаємо як такі що перебувають в однорідному напруженому стані
При розрахунку елементів конструкцій на міцність визначають екстремальні значення нормальних та дотичних напружень в точках навантаженого тіла а також положення площадок, на яких вони ді югь Вирішуючи таку задачу вважають що напруження на гранях паралелепіпеда, виділеного в точці відомі й треба знайти напруження
на будь яких площадках, проведених в околі точки Задача легко роз* в’язується з розгляду рівноваги частини паралелепіпеда, відсіче* ноТ даною площадкою Найпростіше вирішити поставлену задачу, якщо вихідний елемент виділений головними площадками а вихід* ними е головні напруження
$ 41. Лінійний напружений стан
Елементи, які перебувають в лінійному напруженому стані можна виділити в околі деяких точок стержня що працює на згинання або складний опір, але в основному на розгягання чи стискання
Розглянемо призматичний стержень який зазнає простого розтя* гання силою Р (рис 154 а) В перерізах стержня досить віддалених від точок прикладання зовнішніх зосереджених сил напруження роз* поділяються рівномірно. В поперечних перерізах (довільної форми) нормальні напруження (див § 27)
= Ії/Ео = Р/Ео
Дотичні напруження тут дорівнюють нуію Отже, ці перерізи є голов* ними площадками
Перейдемо тепер до визначення напружень у неголовних, похилих площадках Відтак, стержень що перебуває в лінійному (а також у плоскому) напруженому стані будемо зображати у вигляді плоскої фігури (рис 154 б)
Припустимо, що зовнішня нормаль гидо похилої площадки утворює з віссю стержня (а отже і з лінією дії прикладеної сили) кут а Домовимося що кут а додатний якщо він відкладається проти годин* ннкової стрілки Очевидно такий самий кута утворює похила площадка з поперечним перерізом стержня тобто головною площадкою Р9. Проведемо також похилі осі хх, Уі, спрямовуючи вісь уг по нормалі дз площадки, а вісь х( — уздовж площадки
Проведену таким чином похилу площадку будемо називати а-пло-щадкою а повні, нормальні та дотичні напруження, що діють на ній, відповідно позначати ра, 0<х> та Для визначення цих напружень застосуємо метод перерізів Вважаючи, що похила площадка розсікла стержень на дві частини, відкинемо одну з них наприклад верхню, й розглянемо рівновагу ча стики, що залишилася (нижньої*)
Осьова сила в перерізі N = Р е рівнодійною пов
них напружень ра Вважаємо що вони спрямовані паралельно осьовій лінії' й рівномірно розподілені в точках проведеного похилого пе рерізу площа якого	т .Т>0
Ра = ^0/со8 а	*”	0
Отже	®
РаРч = Н,	Рнс
звідки N N ра = —р— = соза 4 о0со8а
155
(6 3)
Проекціюючи ра на нормаль Па і на площину перерізу, дістанемо формули для визначення нормальних і дотичних напружень гк> ді ють на похилій площадці (рис 154 є)
оа = рвсо8а,
(6 4)
Тв = ра ЗІП а,	'	'
або враховуючи (6 3)
ов = ов соз2 а,	(6 5)
Та = зіп 2а	(6 6)
Для напружень на похилих площадках можна взяти викладене в § 39 правило знаків але стосовно до похилих осей х, уг (рис 155 а, б) Зазначимо, що при повороті осей на 90° знак дотичних напружень змінюється на протилежний
У випадку лінійного та плоского напруженого стану як правило, виходять з більш простого правила знаків для дотичних напружень дотичне напруження на площадці вважають додатним, якщр воно на м мається повернути частину елемента, яка розглядається, відносно будь якої точки, взятої всередині її, за годинниковою стрілкою На рис 154, в напруження оа та та додатні
Як видно з формул (6 5) та (8 6) прн а = 0 в поперечних перері ззх стержня (див рис 154, а площадка /) та = 0 а оа = о#, тобто має найбільше значення При а — л/2 (див рис 154 а, площадка II) оа та то дорівнюють нулю
Аналогічно можна довести що в усіх перерізах, паралельних осі стержня нормальні та дотичні напруження дорівнюють нулю Отже при простому розтяганні (стисканні) в кожній точні тіла головні площадки перпендикулярні та паралельні його осі а головні напружен ня на них відповідно при розтяганні
ох =о0 =^/701 пІ=о8 = 0;
при стисканні
= а, = 0, а3 = — а0
!з формули (6 6) бачимо що дотичні напруження досягають свого найбільшого значення при а = ±45° при чому
Рис. 156
Тата, — О,/2
Приклад 15 Визначило нормальні та до тичні напруження на похилих площадках для елементів, показаних нарис. 156, а в
Дія елемента на онс 156. а в) = ал = 0 ст* = —50 МПа в = ЗО®, заїдки
аа = — 50 соз» ЗО* = — 37,5 МПа
Тв<=— —зіп60° = -21,7 МПа
Для елемента на рнс 156 б ст, = 50 МПа о, = а, = 0 а = —ЗО* отже ов = 50 соз» (— ЗО*) -= 37,5 МПа
50
тв = — 5<п (- 60*) = - 21 7 МПа
Для елемента на рнс 156 в ст, — о, = 0 СТ4 = —50 МПа а = —ЗО* отже, ав = —50соз»(—ЗО*) = — 375 МПа, 50
тв -----— зіп (— 60°) = 21 7 МПа
$ 42 Плоский напружений стан
Рис 157
Досліджуючи напружений стан елементів конструкцій, найчасті ше доводиться мати справу з плоским (двовісним) напруженим станом Він буває при крученні згинанні та складному опорі Тому на ньому мн зупинимося дещо докладніше
Усі означення та правила, які були введені в попередньому параграфі, залишаються в силі й для плос кого напруженого стану, але оскільки тут е два ненульових головних напру ження, треба уточнити умови для відлі чування кутів що характеризують на хил площадок Будемо вважати, що цей . кут завжди відлічується віднапряму ал 1 гебраїчно більшого з двох ненульових головних напружень до нормалі до похилої площадки причому завжди береться гострий кут, але з урахуванням його знака
Визначимо напруження на похилих площадках Розглянемо елемент
(рис 157) грані якого є головними площадками На них діють додат ні головні напруження і ст,. а трете головне напруження о8 •= 0 (головний напрям що відповідає о3, перпендикулярний до площини креслення)
Проведемо переріз /—/, який визначає площадку (а) що характеризується додатним кутом а Напруження ста і та по цій площадці бу дуть спричинюватись як дією а,, так і дією ст, Застосовуючи принцип суперпозиції тобто розглядаючи цей плоский напружений стан як накладання двох ортогональних одновісних напружених станів мо« жемо записати
°а = 0<* 4- Оа.
Та = Та 4- Та,
де Оа і 'Ч — напруження спричинені ДІЄЮ СТХ, Ста 1 Та —напруження, спричинені дією ст,
Щоб визначити <за 1 "4, використаємо безпосередньо формули (6 5) та (б б)
<4 = о: соз* а
Та = -у- зіп 2а
Для визначення ств та та треба враховувати що Па утворює з напря моч о, кут 90° — а Тоді, маючи на увазі, що
зіп 2 [—(90® — а)1 = — зіп 2а, соз*[—(90®—а)1 = зіп* а, дістанемо
Од = о, зіп* а
Та — —зіп 2а
Виконавши додавання остаточно знайдемо
ста = о, соз* а + ст, зіп* а,	(б 7)
ти « 01 зіп 2а	(8 8)
Нагадаємо, що стискальні головні напруження підставляють у ці формули Із знаком <мінус», а кут а відлічують від алгебраїчно більшого головного напруження
Скористаємося формулами (б 7) і (6 8) для визначення напружень на площадці, перпендикулярній до площадки (а). Домовимося таку площадку позначати (Р) Нормаль п$ до неї (рис 157 переріз //—//) утворює з напрямом ст, кут
р = — (90® — а)
Формули (6 7) і (6 8) справедливі для будь яких а Підставивши в них замість а вказане значення р матимемо
ар о1 зіп2 а т о, соз4 а	(6 9)
те — —~ 8іп 2а	(6 10)
Сукупність формул (6 7)	(6 10) дає змогузнаходіпи напруження
по будь яких взаємно перпендикулярних похилих площадках якщо відомі головні напруження Проаналізуємо ці формули
Склавши ліві та праві частини рівнянь (6 7) та (6 9) бачимо, що
Оа 4-ов "= °» + °ї«	(6.11)
тобто сума нормальних напружень по двох взаємно перпендикулярних площадках не залежить від нахилу цих площадок і дорівнює сумі головних напружень Інакше шо властивість можна сформулювати гак сума нормальних напружень по двох взаємно перпендикулярних площадках інваріантна щодо нахилу цих площадок
Із формул (6 8) та (6 10) бачимо що. як і прн одновісному напруженому стані, дотичні напруження досягають найбільшого значення прн а — ±45° тобто по площадках які нахилені до головних площадок під кутом 45°, причому
т._.(6 12)
Порівнюючи формули (6 8) 1 (6 10). знаходимо що
~ — Те	/6 13)
Ця рівність виражає закон парності дотичних напружень Знак «мі нус» в (6 13) відповідає введеному в § 39 правилу знаків для дотичних напружень, згідно з яким додатні дотичні напруження намагаються повернути елемент за годинниковою стрілкою
Нарешті з ясуємо, при якому нахилі площадок нормальні напруження що діють по ній, мають екстремальне (найбільше чи найменше) значення Для цього продиференціюємо вираз (6 7) по а і прирівняємо похідну до нуля
= — 2с, соз а зіп а 2а, зіп а соз а == — (О| — а,) зіп 2а = 0
Звідси або
о2 =- а, або
зіп 2а = 0
У першому (окремому) випадку (рівномірне всебічне розтягання в площині) з формул (6 7)	(6 10) маємо
Оа в Ов = О1> Та *= Тр — 0
Це означає, що будь яка площадка тут головна На всіх цих площад ках діють однакові напруження
У другому (загальному) випадку маємо
а = 0 а = 90°
Але площадки, що характеризу' ються цими кутами — головні площадки
Отже, приходимо до висновку, що екстремальними для нормальних напружень оа будуть значення
головних напружень причому
Оа т»х = Ор оскільки при а — 0 друга похідна
-^- = _2(Яі-а^со5 2<х від’ємна, та
Оа шіп = а», оскільки при а <= 90°
На всіх похилих площадках нормальні напруження мають проміжні значення між о1 та аа
Проведемо тепер ще два перерізи (рнс 157) переріз //!—///, па ралельний 1—1, та переріз IV—IV паралельний II—Н Оскільки напружений стан елемента однорідний, напруження по площадках,
утворених перерізами III—НІ та IV—IV, будуть такими самими як відповідно по площадках (а) та (0) Тому елемент аЬсЛ, виділений чотирма перерізами з елемента АВСО (рис 153, а), матиме вигляд який показано на рнс 158, б Обидва елементи визначають один і той самий напружений стан, але елемент АВСО подає його головними напруженнями, а елемент аЬаі — напруженнями на похилих площадках
У теорії напруженого стану можна розмежувати дві основні задачі, пряму і зворотну
Пряма задача В точці відомі положек ня головних площадок і відповідні до них головні напруження; треба знайти
6 2-2798
161
нормальній дотичні напруження що діють по площадках, які нахилені під заданим кутом а до головних Інакше кажучи дано елемент аЬсд (рис 159) з головними напруженнями, які діють на його гранях треба знайти напруження на гранях елемента агЬ1с1<11
Зворотна задача В точці відомі нормальні А дотичні напруження, які діють у двох взаємно перпендикулярних площадках що проходить через дану точку, треба знайти головні площадки і головні на пруження Інакше кажучи дано елемент (рис 159) з нормальними та дотичними напруженнями, що діють по його гранях треба визначити положення елемента аЬсд тобто кут Од І знайти головні напруження
Обидві ці задачі можна розв’язати як аналітично, так і графічно
§ 43. Пряма задача в плоскому напруженому стані Круг напружень
Аналітичне розв’язання прямої задачі дається формулами (6 7) . (6 10)
Проаналізуємо напружений стан, скориставшись простою графічною побудовою Для цього будемо розглядати геометричну площи ну і віднесемо її до прямокутної системи координат о ~ т тобто по осі абсцис будемо відкладати значення головних Оц о, а також йор мальних оа, ав напружень а по осі ординат — значення таі т& Порядок розв'язання задачі покажемо на конкретному прикладі напруженого стану, зображеного на рис 160.
Вибравши для напружень певний масштаб, відкладаємо по осі абсцис (рис І6І) відрізки
ОА = аІГ ОВ = <т, На відрізку АВ як на діаметрі будуємо коло з центром в точці С. По будоване таким чином коло називається кругом напружень, або кру
Рве. 160
гом Мора
Координати точок круга Мора відповідають нормальним та дотнч
Рас. 161
ним напруженням на різних площадках Так для визначення напру* жень на площадці, проведеній під кутом а (рис 160), з центра круга С проводимо промінь під кутом 2а до перетину з колом в точці Ра (додатні кути відкладаємо поотн годинникової стрілки) Доведемо, що абсциса точки (відрізок иХа) дорівнює нормальному напруженню ов, а її ордината (відрізок КаРаї — дотичному напруженню та
Радіус круга
о 6Я — 65 о, — о,
К«	2	=	2
Оскільки центр круга С лежить посередині між точками А та В, то
6Я 6В а, + о, ОС ~-----2------ —2—•
Крім того,
СК„ _ «а» 2а	си2а
Тоді абсциса точки Ра
ОКа = ОС + СКа =	+	+ Я17О1 соз 2а = О1 ‘+с2°і2а 4-
4-а, т — со» = соз»а 0( 8|п*а,	(6 14)
Із трикутника СОа^а ордината точки Ра буде
Йб;-«8Іп2а=-21^1-,Іп2а	(6 15)
Напруження на площадці, перпендикулярній до розглянутої, знайдемо, провівши промінь під кутом 2р = 2 Іа 4- (п/2)1 = 2а 4- я і діставши в перетині з колом точку Р$ Очевидно ордината точки Ц»
=	—^цр-лП2а =•,„	(біб)
1, нарешті, абсциса точки Ор
ОК, = б? _ ск( = -21А2!--С05 2а = Я15ІП1 а +
4- а, соз’ а <= ар.	(6 17)
Порівнюючи формули (6 14) (6 15) з формулами (6.7), (6 8), бачимо що дійсно
0Ка = КаРа в Те,
що й треба було довести
Слід зазначити, що дві точки круга — Рл та Ор, які характеризують напруження на двох взаємно перпендикулярних площадках (а) та (Р), завжди лежать на кінцях одного діаметра Р^Р^.
6*	ка
Побудований круг Мора цілком описує напружений стан елемента, зображеного на рнс 160 Якщо змінювати кут а в межах від —90° до +90° то похилі площадки (а) та (0) займуть послідовно всі можли ві положення, а точки 0а та 0В опишуть повне коло Зокрема лриа = -= 0 кати грані е/ та ет стануть головними площадками і по них бу дуть діяти ті самі напруження що і на гранях елемента аЬсі точка 0в збігається з А (рис 161) а 00 — з В
Як і у випадку круга інерції' найдемо на крузі напружень положення патюса Для цього з будь якої точки кола проведемо пряму паралельну нормальному напруженню на площадці якій ця точка належить Так провівши з точки 0в лінію паралельну ал Іу нашому прикладі (рнс 161) — горизонталь] до перетину з колом, знайдемо шуканий полюс — точку М Кати б при цьому ми виходили з точки 0р то треба було б провести лінію паралельно напруженню ов тобто вертикаль
Як і при розгляданні кругів інерції можна показати що лінія, яка сполучає полюс М з будь якою точкою круга паралетьна напря му нормального напруження на площадці котрій ця точка належить Так наприклад, лінія МА паралельна головному напруженню а» Дійсно ^.0аЛ1Л — 1/2 /_ОЛСА — а тобто він відповідає куту між »ормаллю до площадки /є і напрямом о. Очевидно, що лінія МВ па ралелька напряму головного напруження ал
Приклад ]в На головних площадках діють розтягальні напруження 90 МПа і 60 МПа Треба знайти нормальні її дотичні напруження на гранях елемента, одна з яких нахил на до горизонталі під кутом 20“ (рис 162, а)
Доаітьно лошача мо то датки (а) та (0) (її шриклад, так, як показано на ри судку) і промінно нормаль ла Тоді матимемо о,«- 90 МПа с, -= 60 МПа, о, = 0, в = — 70® КутвпідемкнП бо тут він підтічусгься за годинниковою стрілкою
Розв язуючн цю пряму задачу аналітично за форму тами іб 7)	(6 9) знаходимо
оа = а, соз’а + а, зіп* а = 90 0 117 + 60 0 83* МПі « 63 6 МПа
<гв = оІ зіп* а + о» соз» а - 90 0 884 + 60 0 117 МПа = 86 6 МПа,
та — -ТВ 1 2 в,зіп2а =---------2---(-0 6*3) МПа =—9 65 МПа
Ряс. 162
Ураховуючи знаки визначених напружень показуємо напруження на гранях елемента аЬаі (рис 162 а)
Графічний розв язок наведено на рис. 162 б Проводячи вимірювання дістанемо координати то чок Оа (3 16 см —0 485 см) та 0^ (4 33 см 0,485 см) Маючи на увазі взятий масштаб (І см — 20 МПа), приходимо до тих самих значень напружень, які були знайдені анелітичпо
Рис. 163
6
Зауважимо що одновісний напружений стан можна розглядати як окремий випадок плоского При цьому круг напружень буде проходам через початок координат (рис. 163) Нарешті, при всебічному розтяганні (оі = о») або стисканні (о, == Оа) в площині круг Мора перетворюється на точку В цьому разі, як уже зазначалося раніше, всі площадки будуть головними
$ 44 Зворотна задача в плоскому напруженому стані
При практичних розрахунках найчастіше вдається визначити (теоретично чи експериментально) нормальні та дотичні напруження на будь яких двох взаємно перпендикулярних площадках Припустимо, наприклад що відомі напруження ол іа ар, тр на взаємно перпенди кулярних площадках виділеного елемента (рис 104 а} За цими да ними треба визначити головні напруження і положення головних площадок
Спочатку розв’яжемо що задачу графічно Для певності припустимо що оа > ар, а та > 0 В геометричній площині 8 системі прямокутних координат о ~ т виберемо точку Оа з координатами оа, та точку Ор з координатами ор тр (рис 164, б) Як зазначалося при розгляді прямої задачі точки Оа та £>р лежать на кінцях одного
а	З
Рнс 164
діаметра круга напружень Отже сполучивши ці дві точки знаходимо центр круга Мора — точку С — і радіусом СОа — СО$ проводимо коло Абсциси точок перетину кола з віссю а — відрізки ОА та ОВ — дадуть відповідно значення головних напружень та оа
Для визначення положення головних площадок знайдемо полюс та скористаємось його властивістю 3 цією метою з точки Е>а проведе мо лінію паралельно лінії дії' напруження аа. тобто горизонталь Точ ка М перетину цієї лінії з колом і буде полюсом Сполучаючи полюс ЛІ з точками А та В, дістанемо напрям головних напружень о, та о( відповідно Головні площадки перпендикулярні до знайдених напря мів головних напружень Нарис 164 а всередині вихідного елемента виділено елемент обмежений головними площадками На гранях цього елемента показано головні напруження а, та о.
Використаємо побудований круг напружень для здобуття авалі тичних виразів головних напружень оа та оа, що відповідають відріз кам ОА та ОВ Маємо
аі = ОА =(£ + ~СА, о^ОВ^ОС-СВ Очевидно,
ос= ,
ЯС = СВ - СО« - У<М + ОМ - |/"(	7 *)' + £
Підставивши вирази (6 19) та (6 20) в (6 18) матимемо
(6 18)
(6 19)
(6 20)
(6 21)
або	___________
а1 = 4~[<’“ + 4 + V(Ч—Ч)’ + 4т«| ;
Ч = 4~|ч + Ч — Уоь — Ч)" + 4^|
Ураховуючи прийняте правило знаків знайдемо формулу для тангенса кута нахилу напряму головного напруження відносно осі а З рнс 164 б видно, що
МКВ	-тр
Ак*-----ОЛ-ОК^ ~ Оі
Отже
<622'
Ця формула й визначає єдине значення кута Од, на який треба повер нуги нормаль ла, щоб знайти напрям алгебраїчно більшого головного напруження Нагадаємо, що від’ємному значенню а відповідає поворот за годинниковою стрілкою Слід звернути увагу і на те що коли одне з головних напружень визначених за формулою (6 21), виявиться від'ємним а друге додатним, то їх треба позначити не о, та о, а о, 1 о$ якщо ж обидва головних напруження від'ємні — то а, і а,
Приклад 17 По гранях елемента (рис. /65, а) діють показані на рисунку напруження Треба знайти головні напруження та відповідні до них головні напрями
Якщо позначимо площадки так як показано на рисунку, та
Оа= 100 МПа, 0р=— 80 МПа
та — — 50 МПа Тр — 50 МПа
За формулою (6 21) знаходимо, що
®і - — [ а« + ор + У (ов — Ор)’ + +4 ] - 4" [ 1°0 — 80 +
+ /(100 4-80)* + 4.60*] МПа-Ц-(20 + 206) МПа- 113 МПа,
с, — -у (20 — 206) МПа——93,0 МПа
За формулою (6 22)
що відповідає
а0 = 14е 32'
Цей кут відкладаємо від горизонталі (напрям нормалі Пд) проти годинникової стрілки і знаходимо напрям напруження ор напрям аа перпендикулярний до нього На рис 165 виконано також графічне розв язання задачі відповідно до викладеного плану
§ 45	Об'ємний напружений стан
Напруження на довільній площадці
У загальному випадку напруженого стану при довільній орієнта ції елементарного паралелепіпеда виділеного в околі точки навантаженого тіла (див рис 151, а в), на його гранях діють шість незалежних компонент тензора напружень ох а, тху т„ Вважаючи ці напруження вихідними, обчислимо напруження на довільній площадці АВС проведеній в околі точки (рнс 166)
Нормаль V до площадки утворює з координатними осями х, у г кути, косинуси яких заради скорочення позначимо і т п
соз (V, х) = І соз (V, у) = т, соз (V, а) — п. (6 23)
На проведеній площадці АВС проекції повної о напруження р„ иа координатні осі х, у г позначимо відповідно через рУЛ р^и рчг Еони легко визначаються з умов рівноваги виділеного чотиригранника (рис 166 б) Зауважимо що відповідно до введеного в § 39 правила знаків компоненти напружень на рис 166 б додатні
Прирівняємо до нуля проекції на координатні осі всіх сил прикладених до елемента
2Х = 0, р^Ру —	— ЧцхйРу — ^и4Рг = 0,
2У=0, рчуііРу—- -ЬуііРх—ОуТіРд — Тц/СІРі — 0,	(624)
22 - 0, р^Р„ — Ххг(ІРІ — ХугїіРу — а^іРу « 0
Тут через АР-* йРх, ЛРу та <1Рг позначено площі граней елемента, нормалі до яких відповідно збігаються з напрямами V, х, у г тобто площі трикутників АВС, АОВ, АОС та ВОС
Очевидно що
•^- = С05(х~1)-/; -дг- = соз (вТч) = т, =
= соз (г, V) — п
Тоді з виразів (6 24) знаходимо
Рух в Ох^	Т^хП,
р^ =- хГу! 4- <ГуГП і- х,уп;	(6 25)
Рух = Т*аї +	"І" 0/1
Рис 166
Рис 167
Повні напруження на площадці
Л = 1'ХтЙ, + і>ї,	(6 26)
Нормальне напруження на довільній площадці знайдемо, склав ши суму проекцій на нормаль V складових повного напруження
«V — Рк* СОЗ (х, V) 4- соз &*) + Рог 005 (2, V)
Ураховуючи (6 25) та (6 23) матимемо
оу = о,/1 т СуПі1 г СжЛ8 4- 2тхкїт Ь 2хугтп 4- 2тІхлї (6 27)
Знаючи повне та нормальне а¥ напруження легко знайти дотнч не напруження на площадці
т. -- /рі-о1,	(6 28)
Отже, за відомими компонентами напружень на трьох взаємно перпендикулярних площадках можна визначити напруження на будь-якій площадці проведеній через дану точку
Визначення головних напружень та положень головних площадок. В окремих випадках лінійного та плоского напружених станів головні напруження та положення головних площадок були визнане ні (див § 41, 42) Розв'яжемо тегер цю важливу задачу в загальному випадку напруженого стану
Розглянемо в околі точки елементарний чотиригранник (рис 167) Нехай площадка Л5С — головна Нормаль V до неї є головною віссю Вона утворює з напрямами осей хуг кути, косинуси яких відповід но позначимо як і раніше через І т п Оскільки дотичного напру ження на головній площадці немає, то повне напруження рч на ній спрямоване вздовж нормалі і є головним нормальним напруженням на площадці Позначимо його через а Тоді проекції цього напружен ня на осі координат рух — о/, р„к = от р-п = ал	(6 29)
З іншого боку, проекції повного напруження на площадці виража ються через напруження на координатних гранях елемента формулами
(6.25) 3 них, ураховуючи (6 29), маємо:
(о, — о) І +	+ ХідП = 0,
Ххуі + (ау — о)т +	— 0;	(6 ЗО)
'іхгі +	4- (о, — сг) п ав 0
Система (6.30) становить три однорідних рівняння відносно нев! домих І, т, л, що визначають положення головної площадки Нульові розв'язки І = т = п = 0 неможливі внаслідок відомого співвід* ношення між напрямними косинусами
Р +?П* 4-Л* ав 1.	(6 31)
НеиульовІ розв'язки системи (6 30) бувають лише тоді, коли визнач ник, складений з коефіцієнтів при шуканих невідомих, перетворюється на нуль:
Іо,— а	т„ І
т,, о, — а Ь» І = 0	(6 32)
Ти	О. — О |
Розкриваючи визначник (6 32), дістаємо таке кубічне рівняння віднос но нормального напруження о на головній площадці
о» _ /10» 4. !^з — /, = 0,	(6 33)
де коефіцієнти І*, 19, які називаються інваріантами тензора напружень, визначаються за формулами
Л “О, 4-а, 4-а,,
«= а^у, + о^о, 4- <>Л —	— т», — т’д. (6 34)
/, - 0,0^, 4- 2т„т„т„ — о,%^ — о,%^ — о,х’.
Унаслідок симетрії елементів визначника (6 32) відносно його головної діагоналі розв язання рівняння (6 33) дає три дійсних корені, які є трьома головними напруженнями, що діють на трьох головних площадках Як зазначалося (див § 40) вони позначаються а,, о, та ав, причому алгебраїчно, як і раніше, > <т, > а9 Для визначен ня напряму будь якої головної осі, наприклад першої а рівняння (6 ЗО) підставляємо значення відповідного головного напруження, тобто О|, і з будь яких двох рівнянь знаходимо співвідношення між косинусами кутів
/1/л1 == вр = Ьг
Підставляючи ці величини в (6 31), знаходимо
'> = ±-і77^ПТ	(635)
після чого
= ахлх, г»! == Ь/ц	(6 36)
Рис 160
Аналогічно визначають напрямні косинуси другої та третьої головних осей Легко показати що три головні площадки взаємно перпендикулярні
Головні напруження в точці даного навантаженого певним чином тіла мають стаціонарні значення що не залежать від вибору початкової системи координатних осей х, у г тобто орієнтації в просторі ви діленого вихідного паралелепіпеда Отже, корені рівняння (6 33) так само як і коефіцієнти цього рівняння, інваріантні до вибраної системи декартових координатних осей тобто при повороті осей не змінюються Тож
ї, = СОПЛІ, ї, в СОПЗІ, 19 = С0П5(	(6 37)
Ці величини називають першим, другим та третім інваріантами тензора напружень
Рівняння (6 33) оскільки його корені дорівнюють о, о, та о, можна записати також у вигляді
(о — о,) (о — (о — Оа) — 0	(6 38)
Розкриваючи дужки, бачимо що інваріанти тензора напружень виражаються через головні напруження в більш простому вигляді
= О| -і- о, + а,
іх — о,а, т о,о, 4- о^о,,	(6 39)
- -	/з — °Іаг°3
Зауважимо що, досліджуючи напружений стан у точці, ми зиех тували дуже малою різницею напружень на нескінченно близько розіашованнх паралельних площадках а також об'ємними силами як малими вищого порядку Розглядаючи рівновагу елемента, ці малі зусилля слід ураховувати
Формули для визначення напружень на довільній площадці істот но спрощуються якщо за вихідний вибрати елементарний паралелепіпед, обмежений головними площадками
Сумістимо координатні осі х, у, г з головними напрямами 2, З (рис 168 а) та визначимо напруження на довільній площадці АВС,
Рнс 169
НОрМЯЛЬ ДО ЯКОЇ V (рнс 168. б) утворює З ГОЛОВНИМИ ОСЯМИ кути Оц сц, а, Тоді
/ = С05а1г /71 = С05О,	/1=С05<Х,
З формули (6 25) випливає, що
= о, соз а,, Руі = а, соз а,; р«з = о8со5а, (6 40) Повне напруження на площадці
р„ — V (01 соз а,)' |- (а, соз а,)8 +(а,соз а3)8	(6 41)
Нормальне напруження на площадці визначимо за формулою (6 27)
оУ = о, соз* О| +• о, соз8 о, 4- о, соз’ а,	(6 42)
Нарешті, дотичне напруження на підставі формул (6 28), (6 41) та (6 42) набуває вигляду
Ту = (ах соз сц)* + (°»соз аі)’ + (ОвСоз о,)8 — о8 (6 43)
Напруження на різних площадках у загальному випадку триви мірного напруженого стану можна визначити також за допомогою кругів Мора Нехай відомі головні напруження та положення голов них площадок Треба визначити нормальні та дотичні напруження на довільній площадці Спочатку розглянемо площадки, паралельні од йому з головних напружень, наприклад о, (рис 169, а) Нормалі до таких площадок лежать у площині ху і утворюють з напрямом о8 кут а, = п/2. Нехай кут між нормаллю до площадки й напрямом о, буде а (рис 169, б). Тоді а! = а, а, = (л/2) — а, і з формул (6 40) та (6 42) маємо
рв1=о1соза, рдц = а, соз (я/2—а) = а, зіп а,
Ра, = 0	(6 44)
= аа = ох соз8 а т а, зіп8 а
Дотичне напруження на площадці можна визначити з (6 43) Однак простіше спроекціюватн на напрям*, проекції повного напруження р^ та ра. Маємо
= Та =	5Ш а — Ра, С05 а =я
= _?і.~•?!. зіп 2а	(6 45)
Як видно з (6 44) та (6 45) голов не напруження а, не впливає на на пруження на площадках, паралельних напряму оа Отже, напруження на будь яких площадках, паралельних аа,
можна зобразити графічно за допомогою круга Мора £///, побудованого на головних напруженнях о, та а, (рис 170) Так само напружений стан
на площадках, паралельних головному напруженню о,, описується точ хами кола Ь/, побудованого на напруженнях о, та а3 Нарешті, сукупність точок кола Ди, побудованого на напруженнях о, та оа, описує напружений стан усіх перерізів, проведених в елементі паралельно о( Точки Оі О3 та (), на рис 170 є центрами кіл 1~ц, Ьт відповідно
Можна показати що напружений стан на площадках які перетинають усі три головних напрями, зображується точками Оа, розташованими в заштрихованій зоні (рис 170) Як видно з рнс 170, най бііьше нормальне напруження в точці дорівнює головному напружен ню о,, а найменше — головному напруженню а( Очевидно, точ кою яка характеризує напружений стан площадки, в котрій діє Тщіх, буде точка О (рис 170), оскільки вона має найбільшу ординату Ця точка лежить на колі І н, визначається кутом 45° і має ординату, яка дорівнює радіусу великого круга, побудованого на напруженнях о, та оа Отже, при будь якому об ємному напруженому стані найбільше дотичне напруження
тт„ - 0| у-»	(6 46)
і діє на площадках, паралельних головному напруженню о, й нахилених під кутом 45° до головних напружень о, та оа
Певний інтерес, особливо при вивченні пластичних деформацій, становить дотичні напруження, що діють по площадці, рівнонахнле-ній до всіх головних напрямів Така площадка називається октаед-ричною, оскільки вона паратеїьна грані октаедра, котрий може бути утворений з куба Нормаль до цієї площадки утворює однакові кути з головними напрямами
а, = а2 = а, а Ураховуючи, що
соз1 а, )-со53аа-г соз’а, = 1,
маємо
соз* а = 1/3
Тоді з формул (6 42) та (6 43) знаходимо!
,	(6 47)
Т<жт = £ о? + С] Оа —	~~	=
- "5" Н°і —	(°і — Оі)1 + (о8 — аі)а
Це дотичне напруження називається октаедричним Нормальне ок таедричне напруження а0Кг є ніби середнім напруженням для даного тривісного напруженого стану
У теорії пластичності виявилося зручним вводити в розрахунки так звану інтенсивність напружень о(, пов'язану а т0« залежністю
З
або виражену через головні напруження формулою
о» = /ої+оЗ+о?- 0,0, — о,оа — оао1 = і/2 е	.
Ґ(°і “ *і) +(’» —°х)* + (°а “	(6 48)
На закінчення зазначимо, що всі залежності А способи розв’язання задач, наведені в цьому і попередніх параграфах гл 6, справедливі для напружених станів, які відповідають як пружним, так і пластичним деформаціям
§ 46. Деформації при об'ємному напруженому стані.
Узагальнений закон Гука
Досліджуючи деформації А розглядаючи питання міцності при об* ємному та плоскому напружених станах, будемо відповідно до основ них гіпотез та припущень вважати, що матеріал відповідає закону Гука, а деформації малі
Вивчаючи просте розтягання-стискання, ми з'ясували, що від носна поздовжня деформація
в = о/Е,	(6 49)
а відносна поперечна деформація
(6 50)
Ці дві рівності виражали закон Гука (залежність між деформаціями 1 напруженнями) при простому розтяганні або стисканні, тобто
при лінійному напруженому	__Л_____ і£
стані Тепер установимо аа к лежкість між деформацією та напруженнями в загальному випадку об’ємного напруженого стану
Узагальнений закон Гука Розглянемо деформацію еле мента тіла, вибравши цей елемент у вигляді прямокутного паралелепіпеда розмірами ахйхс(рис 171, а) По гра нях паралелепіпеда діють головні напруження Оі, о, оа (вважаємо, що всі вони додатні) Внаслідок деформації ребра елементи змінюють свою довжину й дорівнюють а + До, Ь + ДЬ, с + Де Величини
е, = Да/а, в, = ДЬ/Ь, в, = Дс/с називаються головними подовженнями і е відносними подовженнями в головних напрямах
Застосовуючи принцип суперпозиції, можна записати
де 8| — відносне подовження В напрямі О], спричинене тільки напру* женням ох (о, = о, = 0), е[ — подовження в тому самому напрямі, спричинене дією тільки о,, в? — подовження, спричинене дією а,
Оскільки напрям ох для самого напруження а, є поздовжнім, а для напружень а, та <та — поперечним, то, застосовуючи формули (6 49) та (6 50), знаходимо, що
Склавши ці величини, матимемо
е, -	—нт—н(»< +’Л
Аналогічно дістанемо формули й для двох інших головних подов жень У результаті
Ві
Ч=4"^* — Р(°»+°і)Ь	(651)
в, = ~ І0» — Р (<Ч + °*)1
Формули (6 51) виражають узагальнений закон Гука для Ізотропного тіла, тобто залежність між лінійними деформаціями та головки*
ми напруженнями в загальному випадку тривісного напруженого ста ву Зауважимо, що стискальні напруження підставляють у ці формули із знаком <мінуо 3 формули (6 51) легко дістати формули закону Гу-ка для плоского напруженого стану Наприклад, при о» = 0
Єї = 4" ~
«,= —£-(>.+".);	(6 52>
- 7-і»! -1»,)
Формули (6 51) справедливі не тільки для головних деформацій, а А для відносних деформацій по будь яких трьох взаємно перпенди кулярних напрямах, оскільки при малих деформаціях вплив зсуву на лінійні деформації е величиною другого порядку малості Так, від носне подовження в напрямі дії оа та ое (рис 171, б)
(Ов _ род),
Об ємна деформація. Установимо залежність відносної зміни об'єму єу від головних напружень До деформації елемент займав об’єм У, = аЬс У деформованому стані його об єм
V ® (а + Да)(Ь + ДЬ) (с + Де) - аЬс(1 4- Да/а) (1 4- ДЬ/Ь) X
X (І + Дс/с) = Ио(1 + Є1)(1 +6^(1 -і-Єз) = Ио(| 4-е, 4-е, +е, 4-
+ Є>Ц + Є»Є» + Є8Є,1 + Є’1В«Вз)
Ураховуючи малість відносних лінійних деформацій, останніми чотирма членами можна знехтувати Тоді відносна зміна об’єму буде
Виразивши головні подовження через головні напруження згідно з (6 51), дістанемо
ву = 1	(о, -і- о, -і- о,)	(6 54)
Зокрема, при рівномірному всебічному стисканні, коли о, = о, = = а, = —р,
<6 65>
Величина К називається мо~	ь
дулем об’ємної деформації 3 фор-	і
мули (6 54) видно, що при дефор-муванні тіла, матеріал якого має Н і И коефіцієнт і [уассона р ® 0,5 (на *®а77іГ приклад, гума), об ем тіла незмі	Му іЛ н-
нюється	’—-§ **—
4н-
у ЛІПШІ
ІІІПІИІ
Рис. 172
Приклад 18. Брус щільно, але без напруження встановлений між двома нерухомими стінками і зазнав стиа.ан ня рівномірно розподіленими но горизонтальних гранях силами Р (рис 172) Нехтуючи тертям між брусам та стінками, знайдемо силу тиску його на стінки та зміну його розмірів, якщо £ та ц матеріалу бруса відомі
Унаслідок того шо при дії вертика тьного навантаження брус не може переміща тнея а горизонтальному напрямі (перешкоджають нерухомі стінки) у цьому напрямі виникають напруження стискання Введено для напружень позначення згідно з рнс 172 (ие будуть головні напруження оскільки на гранях бруса іенае дотичних напружень) Тоді маємо
°‘“и ” — -я- ’ — тг
Через N позначено тиск стінок на брус Оскільки аа умовою яяаачі розмір І ке ямі нюеться а, = 0 3 другої формули (6 51) маємо
Ч - -і-(я,-ро1)*=01 тобто
иР Оі=ма,—-а—.
Отже
N - — Ма, =. -&*-Далі
«-м—
Відносна зміна об ему згідно з форм лою (б 54)
. _ » - 2Я /о рР__________Р - (1 - 2ц) (1 +н) Р
у Е \ ЬІ ЬІ І	ЬІЕ
а зміна об'єму всього бруся
ЛИ _.„И -	_ (І - 2|І> (І + р) е±.
§ 47 Потенціальне енергія деформації
Потенціальною енергією деформації називається енергія, що на* колляється в тілі при його пружному деформуванні Коли під дією зовнішнього статичного навантаження тіло деформується, точки
Рис. 174
прикладення зовнішніх сил переміщуються 1 потенціальна енергія положення наванта ження зменшується на величину, яка кількісно дорівнює роботі, здійсненій зовніш німн силами Енергія, втрачена зовнішніми силами, не зникає, а перетворюється, в ос повному, на потенціальну енергію деформа ціїтіла Решта її (незначна частина) розсіюється здебільшого у вигляді теплоти за рахунок різноманітних процесів, які відбува ються в матеріалі при його деформуванні Потенціальна енергія деформації І! на копляється в оборотній формі — в процесі розвантаження тіла вона знову перетворюється на енергію зовнішніх сил або на кінетичну енергію Значення потенціальноїенер тії деформації, яка припадає на одиницю об'єму (1 см3) тіла, називають питомою по
тенціальною енергієюдеформацй і позначають и В різних точках тіла величина ц може бути різною залежно від напруження в цій точці Потенціальну енергію деформації можна легко визначити на шд ставі закону збереження енергії Оскільки при статичному наванта женні кінетична енергія системи залишається незмінною, то приріст потенціальної енергії деформації У дорівнює зменшенню потен щальної енергії положення зовнішніх сил Уп
Зменшення потенціальної енергії зовнішніх сил чисельно дорів нює роботі Ар, здійсненій ними при деформації
иа~Ар
Отже, потенціальна енергія деформації чисельно дорівнює роботі зовнішніх сил, затраченій прн пружному деформуванні тіла
У^Ар	(6 56)
При простому розтяганні або стисканні (рис 173) на підставі формули (4 29)
0--^.
Питома потенціальна енергія рм и “ ~2ГГ‘=
Ураховуючи, що в = оІЕ, матимемо
(6 57)
и==	.
(6 58)
па
Визначимо тепер питому потенціальну енергію в загальному ви палку об'ємного напруженого стану Для цього виріжемо елемент у вигляді кубика з довжинами ребер, що дорівнюють одиниці (рис 174), грані якого е головними площадками На цих площадках діють голов ні напруження о„ о, І о. Оскільки площі граней дорівнюють одиниці, ТО ЗУСИЛЛЯ, ЩО ДІЮТЬ На НИХ, ЧИСеЛЬНО ДОРІВНЮЮТЬ Оі О}, са Ці зу снлля здійснюють роботу на тих переміщеннях, які дістають грані внаслідок деформації кубика Ці переміщення в даному прикладі чисельно дорівнюють головним відносним подовженням е„ е,, еа, оскільки ребра мають одиничну довжину
Отже, на підставі формули (6 57) будемо мати
«--^-+-2*-+-^	(6 59)
• І Підставляючи в цю формулу вирази єІГ є,, % а формул (6 51), знай демо
и - -%г	+ оа 4- оа — 2р (о1а| + а,а3 +	(6 60)
Питома потенціальна енергія формозміни При деформуванні елемента (рнс 174) взагалі змінюються як його об'єм, так і форма (з кубика він перетворюється на паралелепіпед) Відповідно до цього можна вважати, що повна питома потенціальна енергія деформації
и = иУ+ііф,	(6 61)
де иу — питома потенціальна енергія зміни об ему, тобто енергія, накоплена за рахунок зміни об'єму, и$ — питома потенціальна енер гія формозміни, тобто енергія, яка нахопляється внаслідок зміни фор ми елемента
Безпосередньо обчислити цф важко, тому знайдемо спочатку енер гію иу Це можна зробити, виходячи з припущення про те, що в різ них елементах при дії різних головних напружень значення иу буде однакове, якщо в елементів буде однакова зміна об'ємів гу
Крім розглядуваного елемента (назвемо його 4) введемо ще допоміжний елемент А' Нехай А' —теж одиничний кубик, але по його гранях діють однакові головні напруження оі = <т3 = о3 = а' Для цього елемента, згідно з формулами (6 54), (6 61) та (6 60),
а И'=«,тв. = 21!^а.(ау
Але очевидно, що елемент А' прн деформуванні, спричиненому одна ковнми по гранях напруженнями, буде змінювати тільки свій об’єм, а його форма залишатиметься кубічною Тому — 0 і, отже,
Виберемо величину о’ такою, щоб ®= єу, тобто щоб
Звідси , _ а,+ 0,4-0,
З
Оскільки в обох елементів зміни об ємів однакові, на підставі прийнятого припущення можна стверджувати, що
иу - иу _ 3(1-аН	,
тобто
«к = -!-=^-(а1та, + я1)‘	(6 62)
Тепер, ЗГІДНО 8 формулою (6 61),
цф = и — «V
Підставивши сюди значення и та иу з формул (6 60) 1 (6 62), після простих перетворень остаточно знайдемо
“♦ “ *зе^' (°? + 4 + 4 “	=
"	1(<Л — «Ч)’ + (о, — О1)* + (». — »,)Ч	(6 63)
Це і є вираз для питомої потенціальної енергії 4>ормозміни
Глава 7. КРИТЕРІЇ МІЦНОСТІ
$ 48 Завдання теорій міцності
Найважливішим завданням інженерного розрахунку в оцінка міц пості елементів машин і споруд за відомим напруженим станом Най простіше ця задача розв’язується для простих видів деформації, зо крема для одповісних напружених станів, оскільки в цих випадках граничні (небезпечні) напруження можуть бути визначені безпосеред ньо експериментально
Як уже зазначалося, небезпечним вважають напруження, при яко му починається руйнування (при крихкому стані матеріалу) або з яв ляються залишкові деформації (у разі піастичного стану матеріалу) Так випробування зразків матеріалу на одновісне розтягання або стис кання дає змогу легко визначити небезпечні напруження
ов = о, або о„ = ов.
За небезпечним напруженням визначають допустимі напруження Іо+І при розтяганні або Іо_І при стисканні (див § 34), забезпечуючи відомий коефіцієнт запасу проти настання граничного стану Отже,
6 Рис. І7Б
умова міцності для одиовісного напруженого стану (рис 175, а) на буває вигляду
0,^10+} або | аа |	(о_]
Розглянемо тепер питання про міцність матеріалу при складних напружених станах, коли в точках деталей два чи всі три головних напруження Оі, о,, о8 не дорівнюють нулю (рис 175, б)
У цих випадках, як показують досліди, для одного і того самого матеріалу небезпечний стан може настати при різних граничних зна ченнях головних напружень О|Н, а2в, озн залежно від співвідношень їх Тому експериментально визначити граничні значення головних напружень дуже важко не тільки внаслідок складності постановки випробувань зразків матеріалів в умовах складних напружених ста нів при різних співвідношеннях значень головних напружень, а і в зв язку з великим обсягом випробувань
Інший спосіб розв язання цієї важливої задачі полягає у визна ченні на підставі низки теоретичних і практичних досліджень критерію міцності (критерію граничного напружено деформованого стану) Для цього вводять гіпотезу про переважний вплив на міцність матеріалу того чи іншого фактора вважають, що порушення міцності матеріалу при будь якому напруженому стані відбудеться тільки тоді, коли даний фактор досягне певного граничного значення і раничне значення фактора, що визначає міцність, знаходять з випробувань на просте розтягання або стискання, а іноді — на кручення Отже, введення критерію міцності дає змогу зіставити даний складний напружений стан з простим, наприклад, одновіспим розтяганням (рис 176), і знайти прн цьому такс еквівалентне (розрахункове) напруження, яке в обох випадках дає однаковий коефіцієнт запасу
Під коефіцієнтом запасу в загальному випадку напруженого ста ну розуміють число п, що показує, в скільки разів треба одночасно збільшити всі компоненти напруженого стану Оц оа, о8, щоб він став граничним
оІЯ == ло, а^н = паа, озв == пая
Вибрану таким способом гіпотезу часто називають механічною теорією міцності
Нижче розглянуто деякі з таких теорій
§ 49 Класичні крмткрії міцності {теорії міцності).
Критерій найбільших нормальних напружень [перша (І) теорія міцності] Згідно з цією теорією, переважний вплив на міцність справ ляє значення найбільшого нормального напруження Припускають, що руйнування матеріалу в загальному випадку напруженого стану виникає тоді, коли найбільше нормальне напруження досягає небез печного значення ов Останнє визначають при простому розтяганні або стисканні зразків з даного матеріалу
Умова порушення міцності при складному напруженому стані має вигляд
О) = о+н!
|о.|=о_,	(7 1)
Умова міцності з коефіцієнтом запасу п
а, < (о+[ або
|а»ІС(а-],	(7.2)
де
[о] = Ов/л
Отже, критерій найбільших нормальних напружень з трьох голов них напружень ураховує лише одне — найбільше, вважаючи, що два інших не впливають на міцність
Дослідна перевірка показує що ця теорія міцності не відбиває умов виникнення пластичних деформацій і дає при деяких напружених станах задовільні результати лише для дуже крихких матеріалів (наприклад, для каменя, цегли, кераміки, інструментальної сталі)
Критерій найбільших лінійних деформацій [друга (II) теорія міцності] Згідно з цією теорією, критерієм міцності вважають най більшу за абсолютним значенням лінійну деформацію Припускають, що руйнування матеріалу в загальному випадку напруженого стану виникає тоді коли найбільше лінійне відносне подовження е™» до сягає небезпечного значення ев Останнє визначають при простому розтяганні або стисканні зразків з даного матеріалу
Отже, умова руйнування має вигляд
Єпю в ®я>	(7 3)
а умова міцності з коефіцієнтом запасу п —
І вщ»х | С (е 1 = «в/л	(7 4)
Використовуючи узагальнений закон Гука [формули (6 51)], умо ву міцності (7 4) виразимо через напруження Нехай найбільше від носне подовження буде Тоді
Єпиі —	= [Ох — |Х (О# + О^].
Якщо при простому розтяганні допустиме напруження дорівнює [о], то для найбільшого відносного подовження ми цим самим допус каемо величину
(в] = (а]/£
Підставимо вирази для 8^ 1 [е] в умову міцності (7 4) Тоді
4- (°і — Н (“і + “Л < тг або
—Н(<Ч+<*1ХІ<П	(7.5)
Як видно з умови МІЦНОСТІ (7 5), згідно з цією теорією, з допустимим напруженням треба порівнювати не одне з трьох головних напру жень, а комбінацію їх Еквівалентне напруження в цьому разі
<7шц = — р (а, +	(7 6)
Дослідна перевірка цієї теорії свідчить про узгодженість у деяких випадках результатів лише для крихкого стану матеріалу (наприклад, для легованих чавунів та високоміцних сталей після низького від пускання) Зазначимо також, що застосування другої теорії міцності у вигляді (7 5) недопустимо для матеріалів, які не відповідають зако ну Гука або тих, що перебувають за границею пропорційності
Критерій найбільших дотичних напружень (третя (II і) теорія міцності] Тут критерієм міцності вважають найбільше дотичне на пруження Згідно з цією теорією, припускають, що граничний стан в загальному випадку напруженого стану виникає тоді, коли найбіль ше дотичне напруження Тпш досягає небезпечного значення т„ Остап нє визначають при досягненні граничного стану у випадку простого розтягання зразків з даного матеріалу
Умова руйнування має вигляд
Тщах ~ Ти,	(7.7)
умова міцності —
Тамх С М — Тц/Л	(7 8)
Оскільки, згідно з виразом (6 46),
Тщіх = ~2~ (^1	®і)>	3	= ~2~
то умови руйнування 1 міцності (7 7), (7 8) можна виразити через головні напруження такі
о, — о, = о„,	(7 9)
о\ — °а С Iа!	(7 Ю)
Отже, еквівалентним напруженням за третьою теорією є різниця алгебраїчно найбільшого і найменшого головних напружень
0«пШ = °1 — <?»	(7 11)
Третя теорія міцності взагалі добре підтверджується дослідами для пластичних матеріалів, у яких допустимі напруження на розтя гапня і стискання однакові Недоліком цієї теорії є те, що вона не враховує проміжного головного напруження о,, яке, згідно з дослі дами, спрааляє також деякий, хоч здебільшого і незначний, вплив на міцність матеріалу
Зазначимо, що критерій найбільших дотичних напружень, як зви чайно розглядають як умову початку утворення пластичних (залиш кових) деформацій Останні е наслідком ковзання шарів атомів у кристалі по певних кристалографічних площинах Це стає можливим тоді, коли на зазначених площинах ковзання дотичні напруження до сягають деякого граничного значення
Отже, як критерій, що визначає виникнення текучості матеріалу, можна взяти найбільше дотичне напруження
Вважаючи граничним станом настання текучості, з виразу (7 9) маємо
а,— о8 = от	(7 12)
Ця умова достатньо задовільно описує початок появи пластичної деформації при складному напруженому стані для багатьох металів і сплавів
Критерій питомої потенціальної енергії деформації формозміни [четверта (IV) теорія міцності] Як критерій міцності у цьому разі вибирають кількість питомої потенціальної енергії формозміни, на копленої деформованим елементом Згідно з цією теорією, небезпеч ний стан (текучість) у загальному випадку напруженого стану виникає тоді, коли питома потенціальна енергія формозміни досягає свого граничного значення Останнє можна легко визначити при простому розтяганні в момент настання текучості
Умова настання текучості —
=	(7 13)
Умова міцності —
(7 І4)
Припускаючи, що закон Гука справедливий аж до настання граничного стану, можна питому потенціальну енергію формозміни в за гальному випадку напруженого стану записати, згідно з виразом (6 63), у вигляді
«Ф - Іаі + о» 4- аз — («А + а30з + а/^)]	(7 і5)
При простому розтяганні в момент текучості (ч1 = <7Т, сг, = а, == 0) маємо

(7 16)
Отже, умова (7 13) після підставляння виразів (7 15) і (7 іб) перетворюється на таку
Уої +°2 4-оз — (0,0, + 0,о3 +од) “Ог (7 і7) або
/	((п, -	+ (о, - -Г (о, - а,)Ч = т, (7 181
Умова міцності має вигляд
Отже, еквівалентне напруження за четвертою теорією
4" И°і ~ огі)і + (°* ~ °»)я + (°» ~ сті)я1	ї7 2°)
Зауважимо, що оеквіу збігається з виразом (6 48) для інтенсивно сті напружень о.
Досліди добре підтверджують четверту теорію для пластичних ма теріалів, що однаково працюють на розтягання і стискання Поява в матеріалі малих пластичних деформацій четвертою теорією визиа чається більш точно, ніж третьою
Слід зазначити, що вираз (7 20) з точністю до постійного множника збігається з виразом для дотичного напруження токг на октаедричній площадці, рівнонахнленій до всіх трьох головних напружень (див § 45) Тому розрахункові рівняння четвертої теорії міцності можна ді стати, виходячи з критерію сталості октаедричннх дотичних напру жень
Тсжт [Токт], тобто пластична деформація незалежно від виду напруженого стану виникає при певному значенні октаедричного дотичного напруження Таке трактування звільняє розглядувану теорію міцності від обмежень, пов’язаних з межами дії закону Гука, і дає змогу встановити умови початку не тільки пластичних деформацій, а й руйнування Критерій Мора грунтується на припущенні, що міцність матеріа лів у загальному випадку напруженого стану залежить в основному від значення і знака найбільшого о, та найменшого оа головних напру жень Середнє за модулем головне напруження, як зазначалося вище, лише неістотно впливає на міцність Досліди з мідними, нікелевими і чавунними трубками показали, що похибка, яка пов’язана з тим, що не враховується ав, не вища за 12 15 % Виходячи з цього припущення, можна будь який напружений стан зобразити одним кругом Моря, побудованим на напруженнях а, І аа
Якщо при даних о, і о, міцність матеріалу порушується, то круг, побудований на цих навантаженнях, називають граничним Змінюючи співвідношення між головними напруженнями, дістанемо для
даного матеріалу сім'ю граничних кругів (рис 177) Досліди показують, що в міру пе реходу із зони розтягання в зону стискання С опір руйнуванню збільшується Цьому від ? повідає збільшення діаметрів граничних кругів у міру руху ліворуч
Обвідна АВСОЕ сім’ї граничних кру гів обмежує тону міцності (рис 177) Точка С відповідає всебічному рівномірному
розтяганню Оскільки і при рівномірному всебічному стисканні матеріал здатний, не руйнуючись, витримати дуже великі напруження то обвідна ліворуч затишається незамкіїеною
Якщо гранична обвідна відома, то обчислити міцність досить про сто За визначеними в небезпечній точці деталі значеннями головних напружень о, і а» будують круг Міцність буде забезпечена, якщо він цілком ляже всередині обвідної Збільшуватимемо пропорційно зна чення головних напружень доти дохи круг, що зображує даний напружений стан, не торкнеться граничних обвідних Відношення радіусів побудованого таким чином граничного круга і початкового визначить коефіцієнт запасу
Ма практиці, як звичайно, невелику ділянку обвідної будують на підставі двох дослідів — на розтягання і стискання відповідно до граничних напружень а, і овст, причому граничні криві заміняють прямими лініями дотичними до кіл (рис 178) Зменшуючи масштаб креслення в п разів (п — коефіцієнт запасу), дістанемо зону допустимого напруженого стану
На рис 179 показано таку зону для невеликої ділянки обвідної.
Легко здобути умову міцності для проміжного напруженого стану (°і> центр круга якого 03 розташований між точками Ог і Оя (рис 179) Проводимо прямі лінії ОЯМЯ і ОяМя, сполучаючи центри і точки дотику кіл з обвідними лініями, а також пряму Оха, паралельну М^Мг
З подібності трикутників дістанемо такі залежності о^ь _ б]о]	або б^мІ—о^м{ _ бб]—б%
б]д _ б]б] О«МЇ - брИ, " об] І- Об] Замінивши відрізки ліній значеннями відповідних напружень, матимемо
а, — о, - [ст.».] _ [д+] — (оі Ч-а»)
(а_|—Іа+1 —	(а+1-{о_1
Після перетворень, вводячи знак нерівності, маємо умову міц ності
---|^±ро,<(о+1	(7 21)
При (а+1 — !□_ 1 обвідна на цій ділянці проходить паралельно осі абсцис, і формула (7 21) збігається з формулою (7 10), яку складено за третьою теорією міцності
Грунтуючись цілком на дослідних даних, теорія Мора взагалі не потребує додаткової експериментальної перевірки Однак побудувати граничні обвідні для кожного матеріалу можна в результаті низки складних дослідів з плоскими і об ємними напруженими станами, що і обмежує її застосування Крім того, ця теорія, як І третя, не врахо вує вплив на міцність проміжного напруження а.
Щодо застосовності тієї чи іншої теорії міцності для практичних розрахунків можна сказати таке
Руйнування матеріалів відбувається шляхом відриву за рахунок розтягальних напружень або подовжень І шляхом зрізу під дією най більших дотичних напружень При цьому руйнування відривом може відбуватися при дуже малих залишкових деформаціях або зовсім без них (крихке руйнування) Руйнування шляхом зрізу має місце лише після деякої залишкової деформації (в язке руйнування) Отже, ясно, що першу і другу теорії міцності, які відображають руйнування відривом, можна застосувати лише для матеріалів, що перебувають у крихкому стані Третю та четверту теорії міцності, які добре відобра жають настання текучості і руйнування шляхом зрізу, слід застосовувати для матеріалів, які перебувають у пластичному стані
Теорія міцності Мора дає змогу визначити опір руйнуванню матеріалів, які мають різний опір розтяганню та стисканню При цьому вітка АВ (див рис 177) характеризує руйнування від зрізу, а вітка ВС — від відриву
Оскільки перша і друга теорії міцності мають істотні недоліки, то останнім часом панує думка про недоцільність застосування їх. Отже, для практичних розрахунків слід рекомендувати четвергу (або третю) теорію міцності для матеріалів з однаковим опором розтяганню та стисканню і теорію Мора — для матеріалів, опір яких розтяганню і стисканню різкий, тобто для крихких матеріалів (для них поки що застосовують і другу теорію міцності)
Слід підкреслити, що стан матеріалу (крихкий або пластичний) визначається не тільки його властивостями, а А видом напруженого стану, температурою І швидкістю навантажування Як показують досліди, пластичні матеріали при певних умовах навантажування і температурі поводять себе як крихкі, в той самий час крихкі матеріали в певних напружених станах можуть виявляти пластичні властивості Так, наприклад, при напружених станах, близьких до всебіч ного рівномірного розтягання, пластичні матеріали руйнуються, як крихкі Такі напружені стани називають <жорсткими» Дуже <м'я-кими» є напружені стани, близьк до всебічного стискання В цих ви палках крихкі матеріали можуть поводити себе, як пластичні При всебічному рівномірному стисканні матеріали витримують, не руй нуючись, дуже великий тиск
Зазначимо, що розглянуті теорії міцності непридатні для розра хунку міцності у разі всебічного стискання (ох = о, = о8 = —р) Вплив виду напруженого стану можна наближено врахувати за допомогою діаграм механічного стану, які розглядаються нижче
$ 50 Поняття про нові теорії міцності
Умови переходу матеріалу в граничний стан, а також умови міц иості за різними теоріями були виражені через головні напруження °і> які е інваріантами напруженого стану
Для тривимірного простору, спрямувавши осі координато головних напрямах, зазначені умови можна подати у вигляді деяких гра ннчних поверхонь
£(0,,^, <*5) = 0	(7 2/)
Так, гранична поверхня, що відповідає умові появи пластичних деформацій за теорією питомої потенціальної енергії формозміни [див формулу (7 18)], має вигляд
(О, - а,)1 + (а, - о,)" 4- (о. - а,)’ - 2а1 = 0	(7 23)
Гранична поверхня (7 23) е круговим циліндром, вісь якого рівно-нахилена до координатних осей (рис 180, а), радіусом г => V (2/3) о,. Для плоского напруженого стану, коли одне з головних напружень дорівнює нулю, умова (7 23) дає еліптичну граничну криву (рис 180,6) Критерію найбільших дотичних напружень відповідає гранична поверхня у вигляді правильної шестигранної призми, вписаної в ци ліидр (7 23) Критерію найбільших нормальних напружень відповідає куб з ребром, що дорів нюе
Рве |8С
Зазначимо, що всі точки які лежать усередині зони, обмеженої граничною поверхнею, відповідають напруженим станам з коефіцієн том запасу більшим за одиницю Напружені стани, які зображені точками поза цієї зони, мають коефіцієнт запасу менший за одиницю.
Недоліки розглянутих теорій, а також поява нових матеріалів були стимулами для розробки нових теорій міцності Більшість з них грунтуються на виборі такої форми граничної поверхні, яка дає змогу найповніше врахувати особливості опору даного класу матеріалів в умовах складного напруженого стану
Розглянемо деякі нові теорії
Теорія Ягна Ю І Ягн запропонував граничну поверхню (7 22) взяти у вигляді полінома другого степеня, симетричного відносно всіх трьох головних напружень
(Оі — о,)8 + (о, — а,)8 т (оа — Оі)8 + а (о, + а, + о,)8 +
+ &(»! •	&,)=€,	(724)
де сталі а, Ь і с для даного ізотропного матеріалу визначаються з до слідів на одновісне розтягання і стискання і чистий зсув
Визначивши допустимі напруження |о+), [о_1 і |т] відповідно для розтягання, стискання і зсуву, знаходимо вирази для сталих
6 |тр - 2(о^.Нд-1	.	б|т18(|о,1-К1)
с - 6 (т)8
Отже, теорія Ю і Ягна дає змогу врахувати неоднаковий опір матеріалу розтяганню і стисканню, а також опір матеріалу зсуву При певних співвідношеннях між введеними сталими а, о і с з виразу (7 24) можна здобути низку енергетичних критеріїв міцності, у тому числі і критерій питомої потенціальної енергії формозміни
Теорія Писаренка І Лебедева Виходячи з того що настання гра ничіюго стану обумов пене здатністю матеріалу чинити опір як дотнч ним, так і нормальним напруженням, автори запропонували шукати критерії міцності у вигляді інваріантних до напружених станів функ цій дотичних напружень і максимального нормального напруження Наприклад, один з таких запропонованих критеріїв має вигляд
Токт+^10;	(7 25)
Вираз для Токт дається формулою (6 47) Статі т1 і т, матеріалу можна виразити через граничні напруження ат1|, о_в прн одновісному розтяганні і стисканні Тоді умова (7 25) набуде вигляду
-Х)а, <о+„	(726)
де
х=->.
Рис 181
Для матеріалів, що перебувають у пластичному стані, он = а_н, X = І і формула (7 26) перетворюється на умову граничного стану за четвертою теорією міцності. Для ідеально крих кого матеріалу X » 0, і вираз (7 26) перетворюється на умову руйнування за першою теорією міцності Прн 0 ^Х^і (переважна більшість реальних матеріалів) гранична поверхня
(7 26) є рівнонахиленою до головних осей фігурою, в яку вписано шеоги-граніїу піраміду, що відповідає спрощеній теорії міцності Мора [\м> ва (7 21)1
Дослідна перевірка розглянутої теорії показала, що критерій (7 26) добре узгоджується з результатами випробувань широкого класу конструкційних матеріалів
Діаграми механічного стану (критерій Я. Б. Фрідмана) Вплив типу напруженого стану на характер порушення міцності матеріалів можна наближено врахувати за допомогою діаграм механічного стану Останні будують на підставі таких положень
1 Залежно від типу напруженого стану матеріали можуть руйнуватися від розтягальних напружень або подовжень шляхом відриву або від дотичних напружень шляхом зрізу Відповідно до цього розрізняють дві характеристики міцності — опір відриву 5»ц, який е нормальним напруженням на поверхні руйнування в першому випад ку, і опір зрізу т«, що є дотичним напруженням у другому випадку
2 Обидві характеристики міцності 5«ід і ?к не залежать від типу напруженого стану
З Крива деформування матеріалу в координатах Тщ» ~ та кож не залежить від напруженого стану
4 Порушення міцності шляхом відриву описується теорією най більших відносних подовжень
«екіп «= О'І — ц (о, + о,) «= 5»ід,	(7 27)
а порушення міцності шляхом зрізу — теорією найбідьшнхдотичних напружень
(7 28)
Діаграма механічногостану складається з двох діаграм (рис 18і)— власно діаграми механічного стану (ліворуч) і кривої деформування в координатах Там» ~ Ут»х При побудові діаграми по осі орди ват відкладають найбільше дотичне напруження тгах, а по осі абсцис— найбільше еквівалентне розтягальне напруження за другою теорією міцності 0сквп На діаграму наносять граничні лінії, що відповідають границі текучості тт при зсуві, опору зрізу і опору відриву 5«ід Відхилення лінії опору відриву праворуч вище за границю текучості
(рис 181) відповідає зростанню опору відриву з появою залишкових деформацій
Для характеристики типу напруженого стану вводять коефіцієнт <м якості», який становить відношення найбільшого дотичного напруження в точці до найбільшого еквівалентного розтягального напруження
«=-^-	(7 29)
0'Кп11
Отже, різні напружені стани із збільшенням навантаження зобра жуються на діаграмі променями, тангенси кутів яких дорівнюють відповідному значенню а Наприклад при всебічному розтяганні (о, = а, = а8) т™» = 0, а = 0 і промінь збігається з віссю абсцис при простому розтяганні (о( = а а9 = о3 = 0)
та,х=а/2, а«іп=о і а =1/2;
при простому стисканні (а, = о, = 0 аа = —а)
тш.х = а/2 оСК8ц = цо а = 1/(2ц)
Вибравши ц = 0,25, знаходимо, що а — 2
Розглядаючи промені, що відповідають різним типам напруженого стану матеріалу можна наблим єно визначити вид руйнування і ви брати придатну теорію міцності Наприклад, промінь / на діаграмі перетинає передусім лінію опору відриву Отже матеріал зруйнуеть ся шляхом відриву без попередньої пластичної деформації Промінь 2 перетинає спочатку лінію текучості, а потім лінію опору відриву Отже, при такому напруженому стані руйнування відбудеться шляхом відриву вле з попередньою пластичною деформацією Для напруженого стану, що відповідає променю 3, після пластичної деформації руйнування відбудеться шляхом зрізу
Тоді, коли промені, що зображують той чи інший складний напру жений стан перетинають передусім лінію опору відриву, розрахунок міцності слід виконувати за теорією Мора, другою або першою теорія ми міцності Якщо спочатку промені перетинають лінію границі текучості, то розрахунок міцності треба робити за четвертою або третьою теорією МІЦНОСТІ
Отже, діаграми механічного стану з певним наближенням відображають залежність форми руйнування від типу напруженого стану. Наближеність побудови полягає в тому, що границя текучості й опір руйнуванню непостійні Промені які зображають напружений стан, є прямими лише до досягнення границі текучості
Приклад 19 На гранях елемента (рис 182) вирізаного із циліндричної стінки резервуара, діють напруження а, — 150 МПа, а, — 75 МПа, <та = 0 Резервуар виготовлено з маловуглецевоі сталі марки СтЗ Допустиме напруження на розтягання [о+| = 160 МПа Перевіримо міцність стінки
Оскільки матеріал перебуває в пластичному стані, розраховувати слід за четвертою або третьою теорією міцності
Рис. Ш
Рис. 184
Умова міцності за четвертою теорією прн о, ” 0 має вигляд
У’оі + оа“°і‘’»<М	(7 30»
Підставляючи у вираз (7 ЗО) значення о, і а« знаходимо що
Оеміу “ /150*4-75’ —150 75 МПа - 129 9 МПа< 160 МПа
Виходячи з третьої теорії міино-ті маємо
в0* — або
°вміі) “• 150 — 0 < 160
Отже, міиність стіякя забезпечено
Приклад 20 У небезпечній точці чавуннії деталі на гранях виділеного елемента (рис 183) напруження оа = 5 МПа Ор «• —23 МПа тв«« —т^в 26 МПа. Пере-віримо міцність, якшр допустиме напруження на розтягання [о+] "" 35 МПа, а допустиме напруження на стискання (о_1«« 120 МПа
Визначимо головні напруження (див § 44)
[’« + °»+	“
= _1- [—20 + /30*4-4 26») МПа - 20 МПа,
а. в "Г [°* + “ V (о“ ” "В1* + *^] "
= .!_[—20 —/30*4.4 26») МПа«.-40 МПа
Оскільки опори чавуну розтяганню і стаскпнкю відрізняються то перевірку міцності виконаємо за теорією Мора. Цей напружений стан зображується на гранич ній діаграмі (див. рис. 179) між простим розтяганням і простим стисканням Отже, для розрахунку міцності можна використати формулу (7 21)
о» < 1
Маємо
<’ЄкаАі-’20-г-^-40«жЗ!,7 МПа <35 МПа.
Розрахунок за теорією найбі іьшях відносинх подовжень враховуючи, що о, в 0 аае
««кап в °і — М°з < (°І
Для ц “ 0 25
#ШІ1- 20Ц-0 25 40 ~ ЗО МПа < 35 МПа
Приклад 21 На гранях елемента (рис 184), виділеного в небезпечній точф стержня, який зазнав згинання, напруження
0ов0 °в”0
та "" г ТВ" т
Визначимо еквівалентні (розрахункові) напруження оз чотирма теоріями міцності
Обчислюємо головні напруження в небезпечній тачці за формулами (6 21)
о, «. (о ц- /о» 4-4т’)
а, = -і- (о — /о* 4-4т’)
Тоді еквівалентні напруження і умови міцності набувають такого вигляду а) ви першою теорією
Осхі) - Оі - -5-(о +	И1) < 1°1	П 3|І
б)	за другою теорією
”=..11 - "і - Н<». +	--ЦЛ ° +	•’'»* + 4,‘< 1°І <732>
або, взявше ц ж» 0 3 знаходимо що
в«»ц - 0,35с 4- 0 65 ҐагГ4Ї’ <	(7 33»
в)	аа третьою теорією
«'«•Ні - Сі — о, - /0*4- 4т»< (о)	(7 34)
г)	за четвертою теорією
<Ьму в |/І(о> - °а)* + (о, - о,)* 4- (о. — Оі)»! - /о»4-3т» < (о) (7.35>
Глава 8. ЗСУВ
$ М, Зсув. Розрахунок не зріз
Деформація зсуву відбувається годі, коли я шести компонент головного вектора сили та головного вектора моменту внутрішніх зусиль не дорівнюють нулю тільки поперечні сили або 3 достатнім ступенем наближення деформацією зсуву (зрізу) практично можна вважати випадок, коли на розглядуваний стержень з протилежних боків на вельми близькій відстані одна від одної діють дві однакові сили, перпендикулярні до осі стержня й спрямовані в протилежні 7 2-279»	193
Рис 185
Рнс 186
боки Прикладом такого навантаження може бути розрізання ножицями прутів штаби і т п (рис 185) Зазначимо що на практиці зсув у чистому вигляді спостерігати досить важко оскільки як звичайно деформація зсуву супроводжується іншими видами деформацій І найчастіше згинанням
Формули для напружень при розрахунку на зріз стержньовнх елементів конструкцій можна дістати, виходячи, наприклад, з випадку навантаження, наведеного на рис І85 Використовуючи метод перерізів, знаходимо, що на відрізку Ьс поперечна сила
(2в = Р	(8 1)
Опускаючи надалі індекс прн (}, установимо зв язок між поперечною силою й напруженням, яке діє в даному перерізі 3 формули (З ЗО)
(тД’-С	(82)
>
Вважаючи, що дотичні напруження т рівномірно розподілені по площі поперечного перерізу Г (рис і86), на підставі формул (8 І) та (8 2) будемо мати (} = Р = тГ звідки
т = Р/Р	(8 3)
Припущення про рівномірний розподіл дотичних напружень по перерізу, як буде показано пізніше, досить умовне Проте це припу щення в багатьох випадках справедливе, тому в інженерній практи ці його широко використовують при розрахунку болтових, заклепкових та зварних з'єднань, шпонок й інших деталей
$ 52. Чистий зсув
ііри розрахунках деяких елементів конструкцій бувають окремі випадки плоского напруженого стану, коти на чотирьох гранях прямокутного елемента діють тільки дотичні напруження (рис 187, а) Такий напружений стан називається числим з:узом
Знайдемо головні напруження та їхні напрями прн такому напру женому стані Для цього скористаємося побудовою круга напру жень (рис 187, б) Оскільки в цьому разі оя = ор = 0; тв = —-т; тр —
Рнс 187
Рнс 188
= т, то, побудувавши круг напружень знаходимо, що
о, = — аа = т,	(8 4)
а головні площадки нахилені до граней елемента на кут 45е
Третя головна площадка збігається з ненавантажеіюю фасадною гранню елемента, отже,
о, = 0	(8 5)
Розглянемо деформацію елемента аЬаі (рнс 187, а). Оскільки по гранях елемента немає нормальних напружень, то вздовж граней не має і лінійних подовжень Водночас діагональ ас, яка збігається з на прямом О] подовжується а діагональ М, що збігається з напрямом стискального напруження о,, укорочується Внаслідок цього квадрат аЬаі перетворюється на ромб а'ос'д.'
Отже деформація чистого зсуву характеризується зміною початко вих прямих кутів Заради більшої' наочності можна закріпити одну 8 граней елемента (рис 188) Малий круг у на який змінюється почат ковий прямий кут, називається кутом зсуву або відносним зсувом З рис 188 випливає, що
у = / ВАВІ
Абсолютне зміщення грані позначають Лз і називають абсолютним зсувом
З трикутника ВАВХ маємо
*б? = ї
враховуючи малість кута у, можна вважати, що
іб у = Дз/а тоді
у = Дз/а	(8 6)
Закон Гука прн чистому зсуві. Залежність між навантаженням та деформацією при зсуві можна простежити за так званою діаграмою зсуву (рнс 189) Для пластичних матеріалів вона схожа на діаграму
Рьс 189	Рис 190
розтягання На діаграмі рис 189 показано характеристики міцностії границю пропорційності т№. границю текучості тт та границю міц пості тв
Експериментально діаграму зсуву можна знятн при скручуванні тонкостінної труби (рнс 190) Дійсно, уявно виділений елемент стін ки труби (комірка ортогональної сітки яку попередньо нанесено на поверхню труби) перебуває в умовах чистого ісуву що характеризується напруженим станом, аналогічним показаному на рнс 188 Розглядаючи деформацію цього елемента в межах пружності, визна чимо, що між відносним зсувом та дотичним напруженням, що діють по гранях елемента, згідно з діаграмою зсуву (див рис і89), Існує лінійна залежність, яку можна виразити формулою
у => і/О або т = Оу	(8 7)
де О — коефіцієнт пропорційності, який називається модулем пруж~ пості при зсуві або модулем пружності другого роду, і виражається в мегапаскалях (або паскалях) Значення модуля О для деяких матеріа* лів навезено в дод 9
Для ізотропних матеріалів між модулем пружності 0 при зсуві та модулем пружності Е при розтяганні Існує певна залежність Для визначення її розглянемо деформацію елемента в умовах чистого зсуву (див рис 188) Знайдемо спочатку подовження &1 діагоналі АС завдовжки / = а 1^2
Розглядаючи геометричну картину деформації, матимемо
Д/ = 6,0, = СС, соз (я/4 — у/2) « ССЇ соз 45е = Дз/]/2
Тоді відносне подовження діагоналі
8 = .Дї. ии	= 1	____~ _Т_
І У 2а І 2	2 а 2	2
За законом Гука для чистого зсуву у = т/6, тому
є = т/(20)	(8 8)
Тепер скористаємось узагальненим законом Гука [формули (6 51)1 Оскільки головне напруження О[ діє в напрямі діагоналі АС, то відносне подовження в діагоналі це не що інше, як головне подовження Єі при плоскому напруженому стані що представлений чистим зсу вом Ураховуючи залежність (8 4), з першої формули (6 52) знаходи 196
мо, що
е-в,-.-Ц-ї-»	(8 9)
Зіставляючи праві частини формул (8 8) та (8 9), дістаємо шукану валежність
При и = 1/3 і /4 буде 0 = (0 375 0,4) Е
Запишемо вираз для зміщення однієї грані відносно іншої (тобто абсолютного зсуву Аз) при чистому зсуві Позначаючи площу грані А рівнодійну зсувальної сили = Гт та відстань між гранями, які зсуваються, через а (див рис 185), матимемо
А	т Ов
Д! = та_-в-а = ^-, тобто
(8 11)
Формула (8 11) і виражає закон Гука для абсолютного зсуву Повна потенціальна	енергія	деформації	елемента	прн	чистому зсуві
,,	У'а
2	2СР	»
а питома	потенціальна	енергія	деформації	при	зсуві
у 0*Д	0
V 2СР аР 2РЮ або
“ = -й-	<812>
Перевірка міцності й допустимих напружень при чистому зсуві Перевіримо міцність елемента, що зазнає деформації чистого зсуву (див рис 187, о) Дотичні напруження на гранях елемента дорівню* ють т, допустиме напруження для матеріалу при розтяганні —• [сі.
Як уже зазначалося, головні напруження при чистому зсуві а1=іт, о, = 0; о3 = — т
Умови міцності залежатимуть від вибору теорії (критерію) міц» ності
1 За другою теорією міцності
—(8 ІЗ)
Підставляючи значення головних напружень, знаходимо
Права частина формули (8 14) є допустимим напруженням при чистому зсуві
(Ч =	(8 15)
Для металів ц = 0,25 0,42 Отже за другою теорією міцності
[ті = (0 7	0 8) [о]	(8І6)
2 За третьою теорією міцності
о1 — оа [а] або
т — (— звідки
Т<№ = |т),	(8 і7)
тобто
(т1 = 0 5[с)	(8 і8)
З За четвертою теорією міцності
И°і -І °з —
Підставляючи в цю формулу головні напруження, матимемо т<(о|/)/3	(8(9)
Отже,
(т| - [а|//З я 0 6 (а|	(8 20)
Добуті значення допустимих напружень застосовують також і при розрахунках на міцність деталей, які пізнають деформації зрізу (бол ти, заклепки, шпонки тощо) Зазначимо що для пластичних матеріа лів найбіїьше підходить формула (8 20) яка випливає з енергетичної теорії формозміни При використанні цієї формули для допустимих напружень на розтягання слід вибирати відповідні значення Напри клад для сталі марки СтЗ допустиме напруження на розтягання та стискання при статичному навантаженні (о| = 160 МПа Тоді, згідно з формулою (8 20),
[т| —. 0 б 160 = 96 МПа* 100 МПа
' Умова міцності на зсув (зріз) може бути записана у звичайному вигляді.
Ттах = Цпах/Р [т]	(8 2 І)
Взагалі слід мати на увазі що значення допустимих напружень на зріз [ті залежать від властивостей матеріалу, характеру наванта ження та типу елементів конструкції Підстави для впборудогіустн мих напружень на зсув т наведено вище, а конкретні їхні значення для деяких матеріалів стосовно заклепкових та зварних з'єднань містяться в дод 11
Застосування наведеної теорії зсуву проілюструємо на прикладі розрахунку болтового з єднання (рис 191)
Рве 191
Сили Р намагаються зсунути листи один відносно одного Цьому перешкоджає болт на який з боку кожного листа передаються роз поділені по контактній поверхні сили (рис і91, а та б) Рівнодійні останніх, що дорівнюють Р спрямовані протилежно (рис 191, а) Зусилля намагаються зрізати болт по площині поділу листів т — п, оскільки в цьому перерізі діє найбільша поперечка сила <2 = Р (рис 191,в) Вважаючи що дотичні напруження розподілені попере* різу болта рівномірно, матимемо
Отже умова міцності болта на зріз набирає вигляду
(8 22)
Звідси можна знайти діаметр болта який забезпечує міцність болто вого з'єднання	_____
Слід зауважити, що сили Р, прикладені до болта, намагаються та кож зігнути його Проте згинальний момент невеликий, і спрнчинени ми ним нормальними напруженнями можна знехтувати тим більше що при збільшенні зовнішніх сил Р руйнування з’єднання відбудеться від зрізу болта
При розрахунку болтових, заклепкових та інших подібних з'єднань слід ураховувати те, що навантаження, прикладені до елемен тів з'єднань, крім зрізу спричинюють зминання поверхні болта в місті його контакту з листом Підзминанням розуміють пластичну де формацію яка виникає на поверхнях контакту
Розрахунок на зминання також виконують наближено оскільки закон розподіту тиску по поверхні контакту точно не відомий Як правило, вибирають криволінійний закон розподілу навантажень (рис 192) вважаючи що тиск д по діаметру й змінюється пропорційно
рнс |92	циліндричної поверхні на діа
метральну площину
ч ір
*” =
Тоді максимальне напруження зминання на циліндричних поверхнях
а» = Р/Р»», де — площа проекції поверхні контакту на діаметральну площину листа завтовшки б (рис і91, г)
/\, = <й	(8 23)
Умова міцності на вминання має вигляд
о» в І^аи]	(8 24)
Допустиме напруження на зминання визначають дослідним шляхом і вибирають його таким що дорівнює <тш = (2 2,5} Іо_]
На підставі залежності (8 24) маємо
Для забезпечення умов міцності на зріз та на зминання треба з двох знайдених діаметрів взяти більший, округливши його до стандартного значення
Ураховуючи, що отвори для болтів чи заклепок ослаблюють лис ти останні перевіряють на розрив в найбільш ослаблених перерізах У разі одного болта (див рис 191) умова міцності буде мати вигляд
’ = тАг = тчгаг<“’*і	<825)
Приклад 22 Визначимо юлокістозагслепок діаметрам <1 = 23 мм для закріплення розкосу ферми, який складається з двох нерівнобоких кутчикії 90 X 56 X 8 до флсон ного листа (косинки) завтовшки й в 1,2 см (рис 193) Розтягальне зусилля в розкосі N с= 300 кН матеріал — СтЗ, отвори для заклепок продавлено
Припускаючи шозусніля між заклепками розподіляються рівномірно і зважаючи на те, що вони звзнеють подвійного зрізу (одночасно по двох перерізах) кількість 200
заклепок з знайдемо з умови міцності на зріз N т== 2г я<р
або з умови міцності на зминання
“ "ібГ |а®“1
Ураховуючи що для сталі можна взяти [т) “ 100 МПа І (ош| = 280 МПа зиа-йдемо.
а)	з розрахунку па зріз
г > N в__________________300 10-3_________в 3 6
9 3 14(2 3 ІО-У ІП0 ” * '
4	4
б)	з розрахунку на зминання
г ’ь. N «=	300> 10-3	_ ч о
*	12 2 3 10* 280	'
Вибираємо кількість заклепок г =« 4
У розрахунку на зминання взято товщину фасонного листа б = 1 2 см оскільки сумарна товщина полинь іпох кутннкіп 26 = 1,6 см а отже напруження зминання в заклепках у місцях копіакіу з кутниками буде меншим ніж у місцях контакту з косинкою (вважається що матерія і нік юпок и нкішпй ніж матеріал з єднуввннх еземеїггів)
Приклад 23 Вал передав крутний момент = 27 кН . м за допомогою шіі цьового з'єднання (рис 194). Діаметр вала й ^80 мм, внутрішній діаметр й “ “ 68 мм, висота шліца її = 6 мм, ширина шліца 12 мм, довжина ^єднання і = = 100 мм Кількість шліців с 6 Визначимо напруження зрізу та зминання шліца
Вважаючи що всі шліци навантажені однаково знайдемо зусилля яке припадає на один шліц
Р, «. Мир. =--------27 2---- вН = 132 35 кН
_£ 2	6 8 10-’ 6
2
Напруження зрізу
т = А = , 13233 І0-3 МПа = ПО 25 МПа.
М 12 • 10~3 0.1
Напруження зминання
аак| = А == 132 35 10-3 МЛа « 220,5 МПа
Ік о.і ь ю-3
Рис 194
На зріз прийнято (також умовно) роз раховувати і деякі зварні з єднання Ви
Рнс 195
Рнс 196
Рнс 197
Рис 198
Рис 199
готовляючи металеві конструкції', як відомо, часто застосовують зварювання електричною дугою Якщо конструкцію з'єднання матеріали та технологію зварювання вибрано правильно, то зварне з'єднання за надійністю не уступає заклепковому прн діі як статичних, так і динамічних навантажень Крім того, з єднання елементів конструкцій за допомогою зварювання має багато переваг, основна з яких — економічність
Найпоширенішими є стикові з'єднання та за допомогою кутових, або валикових, швів Стикові з'єднання застосовують якщо листи розташовані в одній площині Якщо листи завтовшки б ^8 мм, їхні кромки не обробляють (рис 195, а), при 6 = 8 20 мм кромки ско шують і заварюють листи з одного боку (V подібний шов рнс 195, б), при 6 > 20 мм кромки скошують з двох боків (X подібний шов, рис 195, в) Розрахункову товщину шва вибирають такою що дорів нюе товщині листа 6 напливи не враховують
З єднання за допомогою кутових швів роблять коли з'єднувані листи паралельні або перпендикулярні До них належать з'єднання внапусток та таврові Якщо напрям кутового шва перпендикулярний до напряму дії зусилля то шов називається лобовим (торцевим) Шви паралельні зусилтям, мають назву флангових (бокових) Застосовують також скісні шви (рис 196), спрямовані під кутом до напряму дії зусилля На рно 197 показано з’єднання листів внапусток лобовими швами, на рис 196 — з'єднання з накладками які приварено фланговими швами а на рис 199 — таврове з'єднання
Якщо не враховувати напливи, тов розрізі кутовий шов має форму рівнобедреного прямокутного трикутника (рис 200, а) Руйнування шва відбуватиметься по його мінімальному перерізу АВСй (рис 200, б) заввишки
а = б соз 45° а? 0,76
Розрахункова площа перерізу шва
Рис 200
Ге= д/~ 0,76/, де І — розрахункова довжина шва
Зварні з єднання, як І заклеп кові, умовно розраховують в при лущенні рівномірності розподі ту напружень по перерізу шва
Допустиме напруження МПа
Вид вштружмхя
Помічений допустимого напруження
Ручне амрюмхя* електродами з тонкою обмазкою
ручне знарюванняРвл«ктродамн а тоаетою обмазкою
Розтягання	[ае]	100	130
Стискання	[ое|	ПО	145
Зріз	(те|	80	ПО
Примітка Індекс <е> означає що вироби зварюються електричною дугою.
В табл 11 наведено деякі значення допустимих напружень для зварних з'єднань Дані цієї таблиці можуть бути використані тільки для кой струкцій виготовлених із СтЗ
Не зупиняючись на розрахунках усіх видів зварних швів, розгля немо на прикладах розрахунок тільки лобових та флангових швів, тобто таких, які, в основному повинні протидіяти дотичним напру жениям
Враховуючи, що опір сталі зрізу менший, ніж розтяганню скла довою нормального напруження в лобовому шві нехтуємо і розраховуємо його умовно па зріз, припускаючи, що дотичні напруження рів номірно розподілені по площі перерізу ЛЛ1В(В (рис 20|) Прн цьому для з'єднання внапусток у розрахунок вводимо обидва шви — верхній і нижній Тоді, припустивши, що обидва шви працюють в однакових умовах, маючи загальну площу небезпечного перерізу
Г. = 2а/Т = 1,4&„
де 4— розрахункова довжина торцевого шва, умову міцності шва за пишемо в такому вигляді
(826>
Оскільки на початку та в кінці шва внаслідок непровару його якість погіршується, дійсну його довжину збільшуємо порівняно з розрахунком
Рис 201
Рнс 202
Рнс 203
на зріз у бісекторних перерізах
Зазначимо, що внаслідок иеве ликої деформативності матеріалу шва в напрямі дії сили лобові шви жорсткі,тому вони руйнуються прн дуже малих залишкових деформа иіях і погано протидіють повторно змінним та ударним навантаженням
Більш поширені на практиці флангові швн Вони належать до в язкнх, оскільки руйнуються ли ше після великих залишкових де формацій Флангові швн завжди ставлять парами; ці шви працюють )ис 202) Площа зрізу кожного шва
а/ф = 0,7б(/— 10) Умова міцності на вріз набирає вигляду
’ = і « (/- ІО) *ТїІ
(8 27)
Приклад 24. Визначимо потрібні розміри флангових швів, що Ревнують штаби (рис 202) Розтягальна сила Р =я 140 кН, а допустиме напруження на зрів для металу шва (тс] = ПО МПа, А « 1 см, в, « 0,8 см. Ь « 10 см, 5, « 12,5 см
З умови міцності (8 27) визначаємо потрібну довжин', шва
Р	/	140 10“9	\
' - -П5КЇ + 0 01 " " ( і ю~~1іо' +
Приклад 25. Знайдемо потрібні довжини її та і» флангових швів (рис 203), які Ґвднуюто рівнобокий кутник 26 5 з косинкою, при дії навантаження Р кН Вибираємо [те| = 90 МПа
Умова міцності на зріз двох швів має вигляд
(А + /і) І СОЗ 45*1	(8 28)
де А — товщина полиці кутника.
Загальна довжина швів прн А ™ 5 мм
'+- 6 £?£ я> “ - °'19 “ -19 “
Щоб забезпечити однакові умови роботи обох швів треба співвідношення для швів вибрати зворотним співвідношенню відстаней й, та й( що визначають положення центра ваги кутники, через який проходить сила Р тобто ІіІІ^ =я й^й, При й, =< = 3 6 см та й, « Н см
/і//, _ 1 4/3 6 « 0,4 і, = 19/1 4% 13 5 см і, « 19 — ІЗ б Б 5 см
На завершення розглянемо приклад розрахунку врубки, яку використовують для з'єднання дерев яких елементів конструкцій Де ревина — матеріал анізотропний, тобто її механічні характеристики
Вид нлружевяя	Ііоаяачев кя долу етимого напружся ця	Допустиме негру жевяя МПа	
		Сосна	Дуо
Розтягання	(аРІ	10	13
Зтнскдння вздовж волокон і зминання торця	ІЯстІ	12	15
Зминання у врубках уздовж волокон	[Озмі	8	11
Те саме перпендикулярно до волокон (на дов жині більшій, ніж 10 см)	І’шЯГІ	24	48
Сколювання у врубках уздовж волокон	|т«1	05.10	08.14
Те саме поперек волокон	1'4x90’1	06	08
Згинання	і<4г)	12	15
Сколювання прн агиканні	і’ск згі	2	2 8
залежать від напряму силових дій відносно орієнтації поздовжніх волокон (границя міцності для сосни вздовж волокон 40 впоперек — 5 МПа для дуба відповідно 50 та 15 МПа) Внаслідок цього допустимі напруження для різних напрямів діїсили доводиться вибирати різними (табл 12)
Приклад 28 Розрахуємо з єднання кроквяної ноги з кроквяною затяжкою {рис 204) Кут між осями кроквяної н<к.и і затяжки а. - ЗО' Зусилля, що дй вздовж кроквяної ноги М**50кН Матеріал — сосна допустимі напруження на зминання евдовяс волокон — 8 МПа Переріз ноги крокои ЛХо = 2О'<!Осм
Кінець затяжки зазнає сколювання вздовж волокон під дією горизонтальної проекції скли N
соз 30° = 50 0.866 = 43 3 кН
Довжину х затяжки що сгир іить за арубку визначимо з умови V,
Взявши (т| —= 08 МПа знаходимо лтощу сколювання м ач ч іл—З
<к [т|	0 8 тоді р	* Ґ^- І- =»гї 4 Рнс 204	— м* =в 0 0541 м’ 541 см* см = 27 І см 20 Потрібна лтоща зминання вр>б А	кіі ,	.	Л7,	43 3 ІО-"3 . Ч-	І-»І -	« р|	- 5 41 Ю“3 м’ = 54,1 см* 	і- Глибина врубки -4=т“-!71 “ беремо 8 - 3 04
Глава 9 КРУЧЕННЯ
§ $3. Напруження і деформації при крученні. Умови міцності й жорсткості
Як уже зазначалося (див §2), деформація кручення спричинюється парами сил, площини дії яких перпендикулярні До осі стерж ня Тому при крученні в довільному поперечному перерізі стержня з шести внутрішніх силових факторів має місце тільки один — крутний момент Мкр (рис 205) Як свідчать досліди, поперечні перерізи стерж ня при крученні повертаються один відносно одного навколо осі стерж ня, при цьому довжина стержня не змінюється
Стержні, що працюють на кручення, як правило, називають ва лами Розглядаючи кручення вала (наприклад, за схемою, наведеною на рис 206), легко визначити що під дією скручу вального моменту, прикладеного на вільному кінці, будь який переріз завдальшкн х від місця закріплення повертається відносно закріпленого перерізу на певний кут ф — кут закручування При цьом^ чим більший скручу-вальний момент Мк, тим більший і кут закручування Залежності Ф = / (Ми), які називаються діаграмами кручення, можна дістати експериментально на відповідних випробувальних машинах за допомогою спеціального записуючого пристрою Вигляд такої' діаграми (знятої при поступовому збільшенні навантаження аж до руйнування) для вала завдовжки І, виготовленого з пластичного матеріалу, наведено на рис 207
Розглядаючи діаграму кручення, неважко переконатися, що вона дещо подібна до діаграми розтягання — характерні ділянки та точки аналогічні тим які є на діаграмі розтягання Мпв — момент, до якого зберігається прямолінійна залежність між навантаженням та де-
формацією М, — момент, що відповідає початку текучості Мл — крутний момент, який спричинює руйнування вала
Надалі в цьому параграфі при виведенні формул для визначення
напружень та кута закручування насбу де цікавити відрізок діаграми кручення, який відповідає роботі матеріалу в ме-
Рис 206	Рис 207
Рис 208
жах пропорційності, тобто початковий прямолінійний відрізок, який характеризує лінійну залежність між крутним моментом і кутом за кручування, що має місце прн нормальних умовах роботи вала
Для визначення напружень у поперечних перерізах стержня розглянемо перш за все статичний аспект задачі Оскільки при кру ченні Мкр — єдиний внутрішній силовий фактор у поперечному перерізі вала є підстава вважати, що тут діють тільки дотичні напружен ня Тоді п ять інтегральних рівнянь (3 29) (3 33) тотожно перетво рюються на нуль а рівняння (3 34) набуває вигляду
ртйГ = Лїкр	(9 1)
де і — дотичне напруження, що діє на елементарній площадці <1Е розташованій на довільній відстані р від центра перерізу (рис 208 б)
Характер розподілу напружень по переріз) з ясуємо, розглянувши геометричну картину деформації вала прн крученні Для цього на поверхні круглого вата нанесемо ортогональну сітку, утворену ліні ями паралельними осі, та лініями, щр є паралельними колами (рис 208 о) Після прикладання скручу вального моменту спостері гаємо таке позловжні прямі ліні! перетворюються на гвинтові, тобто лінії однаково нахилені до осі стержня паралельні кола не викривляються і від стань між ними практично залишається незмінною, радіуси, проведені в торцевих перерізах, затиша ються прямими Вважаючи, що картина, яку ми спостерігаємо на поверхні вала, зберігається і все реднні, приходимо до гіпотези плоских перерізів перерізи, плоскі до деформації, залишаються плос кими при крученні круглого стержня повертаючись один відносно одного на деякий кут закручування
Розглянемо деякий відрізок вата завдовжки <1х (рнс 209) виділений з розглядуваного вала (див рис 206) Вал скручується зовнішнім моментом який спричинює в поперечних перерізах внутрішні крутні моменти Мир Нехай кут повороту полереч-
<1
Рис 209
<г ного перерізу т — т відносно нерухомого (місця за аг^~—кріплення вала) буде «р, тоді кут повороту перерізу п \ п — п, розташованого завдальшки сіх від перерізу т— н \	|\Г т, буде «р + Отже, кут закручування відрізка
\	стержня завдовжки сіх дорівнює <йр
Ь О1 а Розглянемо у зв язку з цим деформацію прямо-Рис 210 кутного елемента аЬ'д'с нескінченно малої товщини виділеного у поверхні вала Оскільки радіуси при деформації кручення залишаються прямими, то відрізок О'Ь' по вертаючись в площині поперечного перерізу на кут закручування гіф, займе положення О'Ь При цьому твірна аЬ' переміститься в нове положення аЬ, утворивши з початковим кут у Аналогічно твірна сЛ' перейде в положення аі Оскільки довжина цих відрізків практично залишається незмінною, то деформація прямокутного елемента аЬ'сі'с полягає в зміні початкових прямих кутів на кут у. Отже, розглянутий елемент перебуває в умовах чистого зсуву, і на його гра нях діють дотичні напруження (рис 209,210)
Отже, кут у є кутом відносного зсуву І
Ураховуючи, що аЬ' = сіх, а ЬЬ' = ніу, кут зсуву на поверхні скручуваного стержня можна подати у вигляді
(92)
Величина сі<$І<іх є відносним кутом закручування [виражається в сантиметрах у мінус першому степені (см-1)] і позначається в Враховуючи це, формулу (9 2) можна записати такі
у = Єг	(9 3)
Якщо уявити собі аналогічний елемент, виділений всередині стерж ня на довільній циліндричній поверхні радіуса р (див рис 209), то аналогічні міркування приведуть до висновку, що кут зсуву на цій поверхні
V» = в»	(9 4)
Тепер, дотримуючись прийнятих етапів розв’язання задач опору матеріалів, розглянемо фізичний аспект задачі Оскільки елемент стержня в будь якій точці поперечного перерізу завдальшки р від центра перерізу зазнає чистого зсуву, то з урахуванням (9 4) та (8 7) матимемо
тр « ОЄР	(9 5)
Формули (9 4) та (9 5) показують, що кути зсуву та дотичні напру ження в поперечному перерізі змінюються за лінійним законом прямо 208
пропорційно відстані р точок від центра перерізу (рис 211 а) Оче видно максимальні дотичні напру ження будуть на поверхні стержня прн р = г Отже, вираз (9 5) можна переписати у вигляді
Т, — Тим = Овг
Підставляючи (9 5) в (9 і), ді	Рис 2І1
станемо
Мкр = Ов ( рЧГ = Ов/р
Звідси виведемо формулу для визначення відносного кута закру чування круглого стержня
8=4!-=-^-	(96)
Тут 63 р — жорсткість поперечного перерізу стержня при крученні, Н м8, /р— полярний момент інерції круглого стержня, ЯКИЙ для суцільного стержня діаметром сі. як відомо (див § 5) виражається формулою /р = ла*/32, а для трубчастого стержня з внутрішнімдіа метром (ія і зовнішнім (і, я (4‘ -<ф
•'?“	32	~= 32 (
де
а =
На підставі (9 6) можна записати формулу для визначення взаєм ного кута закручування двох перерізів розташованих завдальшки І
Якщо в межах циліндричного відрізка стержня завдовжки І крут ні моменти в перерізах не змінюються, то
’=-в'=4г	(97>
Ця формула встановлює зв’язок при крученні між силовим фактором (Лїкр) та відповідною деформацією кручення (кутом закручування <р) і виражає закон Гука при крученні
Дія визначення дотичного напруження т в будь якій точці перері зу вала під дією крутного моменту досить у формулу (9 5) підставити вираз для відносного кута закручування в за формулою (9 6) Тоді
Максимальне дотичне напруження, яке діє в зовнішньому шарі матеріалу стержня
т -	- м«р
га“ ’
— полярний момент опору при крученні» см* Для суцільного круглого перерізу
16Л%
Тт« = п4з
Викладену теорію можна застосовувати також для круглого перерізу Тоді
_ ж? (!-«>
“'р--------ІЗ
І6М,Р
(!-«<>
(9 9)
(9 Ю)
трубчастого
(9 11)
Отже, максимальнедотичпе напруження в скручуваному круглому стержні пропорційне крутному моменту Мкр та обернено пропорційне кубу зовнішнього діаметра стержня
Діставши формули для визначення максимального дотичного на пруження та деформації при крученні, можна записати рівняння міц ності та жорсткості при крученні
Згідно з (9 9), умова міцності запишеться так
Ттм - Мнр/Ю’р’СІт],	(9 І2)
де |т) — допустиме напруження при крученні
Момент опору №р на підставі (9 12)
Ур>ЛЦт|	(9 13)
Умова жорсткості, згідно а (9 6),
=	(9 14)
ЗВІДКИ
016)
-рут (в] — допустимий відносний кут закручування
$ 54. Аналіз напруженого стану І руйнування при крученні
Аналізуючи загальну формулу (9.6) для визначення дотичних напру жень т при крученні, бачимо, шов будь якій точці площини перерізу вала напруження розподілені нерівномірно і залежно від радіуса змі нюються за лінійним законом від нуля в центрі перерізу до максимуму на Його периферії (риб 21і, а) Внаслідок закону парності дотичних напружень в поздовжніх перерізах, що проходять через вісь вала, також виникають такі самі за значенням дотичні напруження (рис 211, б) В елементі матеріалу, уявно виділеного із зовнішніх шарів матеріалу вала перерізами, паралельними та перпендикулярними до твірної (рис 212) циліндричного вала, по гранях діятимуть тільки дотичні напруження В перерізах, нахилених до осі, будуть діяти також і нор мальні напруження, як це зазначалося при розгляді напруженого стану елемента 8 умовах чистого зсуву Найбільші нормальні напруження діють на головних площадках, які нахилені під кутом 45° до площадок, де діють дотичні напруження чистого зсуву Іпри крученні під кутом 45° до осі вала (рнс 212)1
Отже, прн крученні круглих валів небезпечними можуть бути як дотичні напруження в поперечних та поздовжніх перерізах вала, так і нормальні напруження що виникають в площадках під кутом 45°до перших У зв'язку з цим характер руйнування вала при кручен ні буде залежати від здатності матеріалу протидіяти дотичним нормаль ним напруженням
Так, якщо матеріал погано чинить опір дотичним напруженням (дії зсуву, наприклад деревини вздовж волокон), то перші тріщини руйнування виникають по твірних в місцях дії максимальних дотич них напружень (рис 213) Якщо матеріал погано чинить опір дії нор мальних напружень наприклад чавун, то тріщини руйнування при крученні пройдуть по лініях, нормальних до дії головних розтягальних напружень, тобто по гвинтових лініях	г
дотичні до яких утворюють кут 45° 3	-----'Чй'
віссю вала (рис 214) Сталеві вали на / фІЇгХб //|\\ практиці часто руйнуються по попереч- +гк{ — уг—, ~~тгтзт йому перерізу, перпендикулярному ДО ОСІ	\ у
вала Цей тип руйнування обумовлений '4^------
ДІЄЮ В поперечному перерізі ДОТИЧНИХ	ркс 2|2
напружень
Рнс 213	Рнс 214
$ $$ Розрахунок валів на міцність І жорсткість при крученні
При проектуванні можна рекомендувати такий порядок розра хунку валів на міцність і жорсткість при крученні
За схемою вала і скручувальними моментами, що діють на нього, будують епюри крутних моментів по окремих відрізках (див § 16) Добирають матеріал для вала і визначають для цього матеріалу до пусті ме напруження [т] Записують умову міцності (9 12) для відрізка вала з максимальним значенням крутиого моменту (згідно з епюрою моментів)
Якщо вал досить довгий і по окремих його відрізках діють істотно різні за модулем крутні моменти то його слід конструювати східчас тим При цьому діаметр вала кожного східця розраховують, виходи чи з тієї самої формули (9 12), але крутні моменти при цьому будуть різні для різних відрізків відповідно до епюри крутних моментів
Ураховуючи, що для суцільного круглого вала ЙРр = ягі3/|6, мож-на на підставі виразу (9 13) записати розрахункову формулу для ви значення діаметра вала
3/~І6ЛГ“
(916>
При проектуванні порожнистого вала спочатку задаються співвідношенням внутрішнього та зовнішнього діаметрів, тобто коефіцієн том а = а потім з урахуванням (9 11) на підставі формули (9 ІЗ) знаходять зовнішній діаметр вала
і917)
Визначивши розміри вала з умови міцності, перевіряють вал на жорсткість, використовуючи для цього умову жорсткості (9 14) Допустиму відносну жорсткість вала яка характеризується відносним кутом закручування {в] вибирають залежно від умов навантаження Так при статичному навантаженні Ів] — 0,3° на кожний метр довжи ни вала при змінних навантаженнях (01 — 0 25 °/м а при ударних навантаженнях (в! = 0,5 °/м Ураховуючи, що в формулі (9 Ц) кут закручування виражений в радіанах, наведені допустимі значення ку* тів треба перевести в радіани, помноживши їх на л/180 Якщо прн перевірні виявиться що умова жорсткості (9 14) виконується, то на цьому, як правило, закінчують розрахунок вала В противному разі розміри вала треба добирати з умови жорсткості (9 15)
Підставляючи в що формулу вираз по лярного моменту інерції, знайдемо, що для суцільного вала
Рнс 215
(9 І8)
для порожнистого вала
*/ зЩТ
'•>1/ 0„,еі <,-«>	(9І9>
іноді при розрахунку вала відома потужність К, кВт, яка ним переда ється, та частота обертання п, хв~*
Тоді скручувальний момент у розрахункових формулах можна вира зити безпосередньо через потужність К. та частоту обертання л, вихо дячи з формули (З І)
Мк = 9549 Н м
(9 20)
Раніше, коли потужність N виражалася в кінських силах, скру чувальний момент визначався за формулою (3 2)
- 7028,8Н м	(9 21)
Приклад 27. Знайдемо потужність у кіловатах, яка передасться валом діамегг ромЛ=в 150 мм з частотою обертання п = 120хв~* Модуль зсуву 6 — 8,4 10* МПа кут закручування відрізка вала завдовжки 7,5 м дорівнює 1115 рад
З формули (9 7) _ яд* 8,м");".у мн..»»в. Тоді скориставшись формулою (9 21) визначимо потужність яка передається валом
Приклад 28 3 умов міцності та жорсткості визначимо діаметр суцільного вала (рис 215) при таких значеннях моментів, які передаються шківами МІ—0,бкНх X м Мг~ 0,8 кН м; Мг = 2 кН м М,— 0,6 кіі м. Допустиме напруження їх] - 20 МПа допустимий відносний кут закручування [в| = ІІ4еім, або ів| ~ = п'(18О 4) м~1 Модуль пружності сталі при зсуві 0 — 8 10* МПа
Будуємо епюру крутних моментів Найбільший момент діє на відрізку вала 2 З
«іфивк-^+М,-(0 6 + 08) кН м-НкЯ м
Доберемо діаметр вата з умови міцності використовуючи форму ду (9 16)
[7	.«„07.-7 »
|/ я [т)	|/ я 20
Тепер доберемо діаметр вала з умови жорсткості використовуючи формулу (9 18)
-І/ 32 14 '°7,І8° * м»0 08м = 8 »
У Ол(в| у 8 10* я*
Із двох діаметрів слід вибрати більший (8 = 8см) знайдений з умовк жорст-кості
Тепер визначимо відносні кути закручування ввла по окремих відрізках використовуючи формулу (9 6) Підставляючи в що формулу значення /Ихр для різних від* різків знайдемо що
„	М”'	°-6 10-3 32	, «л
®/= (У, = в ю* я (8 ІО"2)* ~186
=	14 ]0~3 У— в 4 з»
07р	8 10* я (8 10“2)«
ІО-3,
ю-3.
, _	»///	0 6 І0~3 32
‘ш- СУ, “8 10* я (8 ІО" г)‘ = ’
Знаючи відносні кути закручування по окремих відрізках можна побудувати епюри в< та кутів <р по довжині вала (рис 215) Епюру кутів закручування ф лобу ковано при і/ = Іц = 50 см та = 90 см При цьому один з перерізів нерухомий (нарис 215 це переріз І) Оскільки в межах кожного відрізка в ® сопзі то кут за чруїування на кожному відрізку змінюється за лінійним законом І
<рг_/ = 6/0 = І 86 ІО-3 0,5 рад = 0 93 І0—3 рад.
Фа_; - <рг_;+	(0 93 І0-34-2,|8 10“3) рад “З Ю ІО-3 рад,
Ф<-/= Фг_/+Фз-г+Фе-з™ (° 93 ІО-3 + 2.І8 10—3—1,67 Ю^рад^
— 1 43 10“3 рад
Прналад 29 Визначимо, на скільки процентів збільшиться максимальне напру ження вала при крученні, яким» у вали зроблено аксіальний отвір б, = 0,4 «і, (а = 0,4) На підставі формул (9 10) та (9 11) взявши = б знайдемо напруження суціль ного І порожнистого валів
Ьнах
16Л/^ тїХ = я<Р
ІбЛІ^
Шукана різниця в напруженнях
100
(0,4)* - і-ї'іо1,).
Прналад ЗО. Замінимо суцільний вал діаметром б = ЗОО мм порожнистим рів-неміцним валом із зовнішнім діаметром б* = 350 мм Знайдемо внутрішній діаметр порожнистого вала та порівняємо ваги цих валів
Максимальні дотичні напруження в обох валах мають бути однаковими
ІбЛ^ 16М,р т«»м" я<і8 * л<гЗ(1_о<)
Звідси визначимо коефіцієнт а
Внутрішній діаметр порожнистого вала
4, = а<і, = 0 78 350 = 273 мм
Співвідношення ваги дорівнює співвідношенню площ поперечних перерізів „ 4а,-Iа. _ зда-273-
4л<ї’	ЗОО’
З прикладів 29 та ЗО видно, що виготовлення порожнистих валів, тобто валів, у яких малонавантажену внутрішню частину вилучено — вельми ефективний засіб зниження затрат матеріалу, а отже, і зни ження ваги валів При цьому максимальні напруження,що виникають у порожнистому валу мало відрізняються від максимальних напру жень у ралу суцільного перерізу при тому самому зовнішньому діа метрі Так, у прикладі 29 за рахунок свердління при а = <44 = = 0,4 яке дає полегшення вала на 16%, максимальні напруження в зовнішніх волокнах порожнистого вала збільшилися лише на 2 6% У другому прикладі рівноміцний порожнистий вал, але з трохи біль тим зовнішнім діаметром (350 мм) порівняно з суцільним валом (300 мм), ьиявився легшим за суцільний на 53,4 % Ці приклади свідчать про раціональність застосування порожнистих валів, що ши роко використовуються в деяких галузях сучасного машинобудуван ня зокрема в моторобудуванні
Як приклад статично невизначуваного стержня який зазнає кручення» розглянемо круглий стержень, закріплений обома кінцями і навантажений скручувальним моментом Л4„ в якомусь перерізі вала С(рис 216, а). Побудхємо епюр) крутних моментів по довжині стерж ня (рис 216, б) і визначимо діаметр стержня
При такому навантаженні в місцях закріплення вала виникнуть реактивні моменти Ма та Мв в площинах, перпендикулярних до осі стержня
Статичний аспект задачі 3 умов рів поваги стержня
їМх = МА+Мв— Мк= 0 (9 22) бачимо, то задача один раз статично не визначувана
Геометричний аспект задачі Оскільки обидва Кіииі жорстко закріплені, то кут повороту перерізу В відносно А дорівнює

нулю
фв-л = фв-с + Фс-л = 0	(9 23)
Фізичний аспект задачі Використовуючи формулу (9 7), запишемо вирази для кутів закручування
Синтез Підставивши формули (9 24) у вираз (9 23), матимемо
=	(925)
Звідси з урахуванням (9 22) знайдемо, що
І926)
027)
Якщо а > Ь, то МКІітах ~Мв, і на підставі формули (9 16) діаметр вала
ЇЇ "***
Г (д + Ь) п [т|
$ 56. Кручення стержнів некруглого перерізу
В інженерній практиці досить часто кручення зазнають стержні, які мають не круглий переріз, а прямокутний, трикутний, еліптичний та ін У цих випадках гіпотеза плоских перерізів це може бути застосована, оскільки перерізи викривлюються (деплаиують) Точні розрахунки стержнів некруглого перерізу можна виконати методами теорії пруж ності Проте, оскільки в даному курсі немає змоги їх викласти, наведемо тут тільки деякі остаточні результати Зазначимо при цьому що в стержнях довільного перерізу як і в стержнях круглого перері зу, дотичні напруження при крученні спрямовані по дотичній до кон тура
Найбільші дотичні напруження, відносні та повні кути закручування за аналогією з крученням стержнів круглого перерізу прияня то визначати за формулами
мт
Твих =“	• >	(9 28)
Ф-	(9 29)
е = 4с-	<9 30>
Тут А І К’к — деякі геометричні характеристики, які умовно назива ють відповідно моментом інерції (см4) та моментом опору (см8) при крученні
Найчастіше застосовуються стержні прямокутного перерізу В цьому разі розподіл дотичних напружень має вигляд як на рис 217 Найбільші напруження виникають біля поверхні посередині довгих сторін прямокутного перерізу (в точках С та О) Визначаються вони за формулою (9 28) в якій
ІГк-аЛ68,	(9 Зі)
де Л — довга сторона прямокутного поперечного перерізу Ь — ко ротка його сторона, а — коефіцієнт, що залежить від співвідношен ня її і Ь
Напруження, які виникають біля поверхні перерізу посередині коротких сторін (в точках Д та В) менші їх можна виразити через Ттм таким чином
Т — уТгпах	(9 32)
де у— коефіцієнт, що залежить від співвідношення сторін прямонут ного перерізу
Для визначення відносного кута закручування прямокутного перерізу в формулах (9 29) та (9 ЗО) беруть
Л « 0Л&3	(9.33)
Значення коефіцієнтів а, у та 0 залежно від співвідношення сторін прямокутного перерізу НІЬ наведено в табл 13 У цій таблиці вміщено також формули для визначення максимальних дотичних напружень та кутів закручування деяких інших некруглих стержнів Запишемо умови міцності та жорсткості при крученні стержнів прямокутного перерізу
=	(9 34)
в-	< І8'	і935»
ііри крученні стержнів які мають форму рівнобедреноітрапеції', наближені значення максимальних дотичних напружень та кута закручування можна визначити, розраховуючи стержень з перерізом ек вівалснтного прямокутника Останній будується так (рис 2і8) Із центра ваги С трапеції опускають перпендикуляри СВ та СО на бо кові сторони, а потім проводять вертикалі через точки В та О Добу тий прямокутник аЬаІ і буде тим еквівалентним перерізом розгляду ваного трапецоїдного стержня до якого повинні бути застосовані фор мули (9 28) (9 33)
При крученні стержнів еліптичного поперечного перерізу макси маїьпі дотичні напруження виникають у крайніх точках, які лежать на малих півосях (рис 219) У цьому разі
Таблиця /З
форма переріжу	Момент Інерції при крученні .1* ем*	Момент опору При крученні О'к, см*	Точки з найбільшими доплаті напруженнями ^кр	Примітка
»’х - аКР
Посередині ювгих сторін
посередині коротких сторін
ївТГтах у кутах напруження дорівнюють нулю
МЬ )	а	1 |> 1 у	
І	0,208	0,141	1
1 5	0,231	0,196	0.859
1 75	0,239	0.214	__
2.0	0,246	0,229	0,795
2.5	0,256	0.249	__
3.0	0,267	0,263	0.753
4.0	0,282	0.281	0.745
6.0	0,299	0,299	0,743
8.0	0,307	0,307	0.743
10.0	0,313	0,313	0,743
оо	0,333	0,333	0.743
ГХІ 2Моб, 2Л#®в®«
Посередині довгих сторін
М
Є
посередині коротких сторін
У внутрішніх кутах має місце висока концентрація напружень, що досягають границі текучості матеріалу.
Якшо є заокруглення радіуса г, коефіцієнт концентрації
У зовнішніх точках малих півосей
,	= М<Ф
ябвл де у зовнішніх точках великих півосей
У кінці малих півосей
лт^і (1 —а4) 16 (т> + 1)
X (і — а4) т
у кінці великих півосей
т _ п^і/г
*к—	|6	.
де Ь та Н — відповідно розміри малої та великої осей еліпса Найбільші напруження в зовнішніх точках перерізу на великих півосях
Т* =
де т = Н/Ь
Умовний момент інерції при крученні стержня еліптичного перерізу
^ = -^-('’+<’’)	(9 36)
Значення та для деяких некруглих поперечних перерізів наведено в табл ІЗ
Якщо скручуються стержні складного незамкненого поперечного перерізу, який можна поділити на окремі частини з .Ікі та то для нього
=Ла + ^к2 + Аз +	• + Лої ~ ЇЛкІг (9 37)
де і — і, 2 3; . . п — номери найпростіших частин, на які поділена поперечний переріз
Оскільки кут закручування для всього перерізу і окремих його частин один і той самийі
Д _	_ ^крі	'Мхрл
° - ©4	0^ = ’ • • = 0^ •
то крутний момент розподіляється між окремими частинами склад ного перерізу пропорційно їхнім жорсткостям
Відповідно найбільше дотичне напруження в кожній частині (О перерізу
Рис 217	Рнс 218	Рис 219
Найбільшого значення напруження т досягне для того елемента, в якого відношення	буде найбільшим
(9 38)
(9 39)
Приклад ЗІ. Сталевий стержень прямокутного перерізу передав крутний момент Икр ~ 1000 Н м Знайдемо розміри перерізу стержня коли відомо, що допустиме напруження на кручення |т| = 40 МПа а співвідношення Іі/Ь ™ 2,5
З умовк міцності
’т.х -	< N
знаходимо момент опору крученню стержня
г.-^- іті0'°"  - 0 25 10- ..-ж»-,
а знаючи співвідношення сторін перерізу 1і/Ь ™ 2 5 та беручи з табл ІЗ відповідне значення а = О 2тС розміри перерізу знайдемо з формули (9 ЗІ)
Гк « аЛЬ» = 2 5ай»
Звідси	________________________
Ь = і/'	-- і/_	см = 3 38 см
У 2 5а У 2 5 0,256
Л = 2 5і = 2 5 3 38 см = 8 45 см,
Приклад 32 Знайдемо найбільше дотичне напруження та кут закручування дія сталевого стержня завдовжки 5 м, який мав поперечний переріз, показаний на рис 220 а Стержень скручується моментом Мкр = 500 Н м, прикладеним до обох його кінців
Розіб емо профіль перерізу на окремі елементи, як показано на рнс 220 б Мак* симатьне напруження визначимо за формулою (9 28)
Тт.х = Де
(ЛХі)т.х •
Відповідно до (9 37)
Л = •'кі + Лї*Г ^кЗ
Для елемента / перерізу стержня -= 45 м Ьх = — 35 мм, = і 285 УК| = Згідно з даними табл ІЗ прн = 1 285 ах = 0,221 р, = 0 172 Тоді
ГК|«ва,Мі-0 22і 4 5 3 5’ см’- 12 2 см8
7в1 = р,Л1^ = О 172 4,5 3 5’см4 = 33 2 см*
Лі 33 2
-----12У °* “ 2 72 °*
Рис. 220
Для елемента 2 перерізу стержня к. = 80 мм Ь. = 10 мм к^Ьг == 8 Згідно 9 табл |3 а, = 0 307 р, 0 307
«’й - а,Л,б| = 0,307 8
7^ => р,Л,&2" 0 307 8
1* см*
'кг
см
20 мм к^ІЬ3 «= 95/20 = 4,75
Для елемента 3 перерізу стержня /ц = = 0,288 р3 = 0 288 Аналогічно
= а,Мз - 0.288 9.5 • 2’ «** = *0.9 «“*•
= р*Л^ = 0,288 9 5 2* см* - 21,9 см*}
П7 * 1
ЇЙ" "
Отже
ук = 4І4-/|Є + ;к3 = 332 + 2,5 + 21 9 см«-57,в см«. Найбільше співвідношення Ук( відповідає елементу І перерізу тому максимальне дотичне напруження буде посередині Його довгих сторін Момент опору
/к|/№к1 =~2ТГ си*= 21 2 см* а максимальне напруження
- 4г - Д «п. - я-6 кп‘
21 2 І0-®
Кут закручування стержня Мкр1 500 10-0.5	......
» - ТЯГ * в. ,0* 57,0 - І0-* р“ " ° ЮК РЮ
$ 57 Кручення тонкостінних стержнів
Методи розрахунку тонкостінних стержнів на кручення залежать від того відкритий чи замкнений профіль їхнього поперечного перерізу
Замкнені профілі. Розглядаючи кручення замкнених тонкостінних профілів (рис 22і), будемо вважати товщину стінки стержня настільки малою, що дотичні напруження по ній можна прийняти однаковими, які дорівнюють напруженням посередині товщини стінки Йспрямова ними по дотичній до серединної лінії стінки
Щоб добути формулу для визначення цього напруження, виріжемо з тонкостінного замкненого стержня елемент завдовжки двома по перечними та двома довільними меридіональними перерізами (рис 222) Складаючи суму проекцій на вісь х всіх сил, прикладених до елемента, 222
222
маємо
» сопзі (9 40)
Момент сили т&і$ що діє на елемент профілю завдовж киЖ(див рис 221), відносно довільної’ точки О
аМ^ =
Ураховуючи що г<І$ е по
Рис 222
двоєною площею елементарного трикутника (на рис 221 заштрихова ний), тобто
гЛ$ = 2а&,
а тому
ам„ = 2т^а),
(9 41)
інтегруючи останній вираз по всьому контуру з урахуванням умови (9 40) знайдемо крутний момент який діє в поперечному перерізі тонкостінного стержня
Ліх„ = 2т&),	(9 42)
де ш- площа, яка окреслена серединною лінією тонкостінного перерізу
З формули (9 42) дістанемо
и 2шЛ
(9 43)
Ця формула вперше була виведена Бредтом
Якщо товщина профілю по контуру неоднакова, то максимальне напруження в стінці профілю визначається аа формулою
’- = тя^7’	(9 44)
де бшіп — мінімальна товщина стінки профілю
Щоб визначити відносний кут закручування тонкостінного стержня, розглянемо енергію деформації, яка нахопляється в елементарному об’ємі тонкостінного стержня розмірами а$, ах, б Враховуючи, що при крученні має місце чистий зсув, на підставі формули (8.12) маємої
аі) — баха$
Повну енергію деформації тонкостінного стержня завдовжки І знайдемо, проінтегрувавшн останній вираз по замкненому контуру з та по довжині І
V = -& |	- -нг # пг •
Тіш
Рнс 223
Підставляючи тб з формули (9 42) в праву частику останньої формули матимемо
20 <2ш)» У С
Цю енергію можна виразити також через роботу зовнішнього скручувального моменту Мк = Мир на шуканому куті закручування тобто
Н	А- икФ _ л;«рФ
и	А ~ 2	2
Тоді, прирівнявши праві частини останніх двох фор мул, знайдемо
с аз
Ф 40ш» у Л
Відносний кут закручування
Це друга формула Бредта її можна переписати у введених позначеннях для кручення:
При однаковій по довжині контура $ товщині
(9«)
Розглядаючи, наприклад, кручення тонкостінної труби (рис 223), при б = сопзі матимемо
гм Аз 2л/?
ш = "^'	------8“
За формулами (9 43) та (9 46) знайдемо
т = м*. е = Л}кр
т 2л/?’б ’	= 2пЯ»8О
Відкриті профілі Визначаючи при крученні напруження та де формації в тонкостінних стержнях відкритого профілю типу швелера двотавра (рис 224) або кутника, можна скористатися теорією розрахунку на кручення стержнів прямокутного перерізу В цьому разі незамкнені профілі розбиваються на прямокутні елементи, тов шина яких значно менша, ніж їхня довжина Як видно з табл ІЗ, для
таких прямокутних елементів (при К/Ь > іО) коефіцієнти а та & до рівнюють і/3 Тоді для складеного профілю на підставі формул (9 33) та (9 37)
(947)
Тут я — коефіцієнт, який враховує схематизацію реального профілю! для кутннкового перерізу Я =1.00
»	двотаврового	>	я	=	1.20
»	таврового	>	я	=	Ї.І5,
»	швелерного	»	я	=	1.І2
У тонкостінних відкритих профілях довжину елемента, як пра вило, позначають через з, а товщину стінки — через в Тоді, заміняючи в формулі (9 47) Н на з а Ь на в, дістанемо)
Л=Ч-з-26’«<	(9 48)
Кут закручування визначиться за формулою (9 ЗО), а найбільше дотичне напруження, яке виникає на ділянці, що має найбільшу товщину стінки бпих,— за формулою (9 28) При цьому для довгих прямокутників
Тоді
я бдаїх
.	(9 49)
Розглянемо приклади розрахунку тонкостінних стержнів від критого профілю
Приклад 33 Визначимо максимальне напруження та кут закручування стерж ня завдовжки 900 мм (рис 225) з поперечним перерізом у вигляді рівнобокого кутники 59 X 50 X 5, який зазнав дії крупного моменту Мкр = 50 Н м Модуль зсуву мате ріалу стержня 0 =8 • 10і МПа
максимальні дотичні напруження виникають посередині полиць (коацентранію напружень у вхідному куті не враховуємо) Ці напруження визначимо за форму лою (9 49)
‘Уікр°т.«
де
Л = п -у = 1 4"(5 0 £* • 4 5 ° 5’) см’ = 0 4 см4.
- М*?™* = М-1.Г0 0 5 '0~> МПа 5 ЧПа Л	0 4 І0-*
Кут закривання стержня мкр‘ 50 10“6 0 9 » —вт.-----------, 10. 0|4 ,0-. ' » ‘«25 Р» - 8- З'.
Приклад 34 Визначимо напруження та відносний кут закручування сталевої труби розрізаної вздовж твірної (рис. 226) Зовнішній діаметр труби й* = 90 мм, внутрішній да = 85 мм Труба зазнав ди крутного моменту М^ = 50 Н м Модуль зсуву матеріалу 0 = 8 10* МПа. Порівняємо добуті значення напружень та кута закручування розрізаної труби з відповідними даними для суцільної труби.
Дотичні напруження в розрізаній трубі визначимо за формулою (9 49)
де з — розгорнута довжина серединної лінії перерізу труби Тоді

угі»=уя 8 75 0 25» см4 = 0 143 си‘|
0 25 і О-2 ——5----- МПя = 87,5 МПа
Напруження в суцільній трубі визначимо за формулою (9 43)
Чср	50 І0-в 4
2«6 - 2„ 8 75 Ю-, 0 25 ,О-1 МПа-1,66 МПа
Відносний кут закручування розрізаної труби
Л Чці	50 Ю-8
®’ - ~33;— аіо-'опз ю-»- рм/" _ 0 ’37 "М"
Відносний кут закручування нерозрізаної труби визначимо за формулою (9 46)1 Л;хрд _________________50 10~* я 8 75 10~2________
с = 40и)*б = 4 8 10* [я/4 (8 75 ІО“2)»]’О25 10~2 рад/М = = 0,000475 рад/м
Отже у суцільній трубі прн крученні напруження менше у 52 5 разе акутзакру* чування — в 920 разів ніж у трубі розрізаній вздовж твірної
$ 58 Розрахунок гвинтових циліндричних пружин
Гвинтові пружини — це найпоширеніший тип пружин і у техніці Найчастіше їх виготовляють із сталевих стерж-нів (дроту) круглого поперечного перерізу В роботі вони зазнають дії розтягальних або стискальних сил
Точний розрахунок на міцність гвинтових циліндрич-них пружин досить складний, оскільки дріт пружини може зазнавати складного навантаження — одночасних кручен [ ня, зсуву та згинання Але прн малих к}тах нахилу вит- |р ків впливом згинання можна знехтувати Здебільшого як <г ± буде показано нижче, можна нехтувати також зсувом і, отже, з достатнім наближенням розраховувати такі пру-	—*
жиии на міцність та деформативність, виходячи з опору їх Рис 227
крученню
Розглянемо циліндричну гвинтову пружину а середнім діаметром О = 27? (рис 227), яка має п витків і діаметрів поперечного пере різу дроту Пружина зазнає розтягання центрально прикладеною силою Р Щоб вивести формули для визначення напружень у дроті з якого зроблено пружину, розріжемо її уявно на дві частини по будь якому витку площиною, що проходить через вісь циліндра, утворено го витками Застосовуючи метод перерізів (відкидаючи уявно нижню частину пружини), розглянемо умову рівноваги залишеної верхньої її частини (рис 228) Очевидно, вплив відкинутої частини пружини на розглядувану верхню може бути врахований прикладанням у міс ці розрізу витка поперечної сили = Р та крутного моменту Млр = РР Вважаючи, що приблизно кут нахилу витка дорівнює нулю, можна рештою силових факторів (поздовжня сила та згиналь ний момент) знехтувати
Огже, в розглядуваному перерізі пружини діють дві групи дотичних напружень напруження від зрізу, рівномірно розподілені по перерізу,
_»	0_
та напруження від кручення, максимальне значення яких -	16Р«
Тщіх » ~ір—
(9 50)
(9.51)
Розподіл напружень т' від зрізу показано на рис 229, а, а напружень і* від кручення — на рис 229, б
Як видно з наведеної картини розподілу напружень, в точні А перерізу витка на внутрішньому радіусі пружини дотичні напруження т' та і' за напрямом однакові Тому максимальні напруження в ній точці
- _і_	ІР 1вРР
т®“ “ т + т“» - “НЗГ ’	’
або
(9 52)
Здебільшого при розрахунку гвинтових пружин великого середнього радіуса Л виготовлених з тонкого дроту, при <Ї/4Л і напруження від кручення ігш значно вищі, ніж напруження зрізу і', тому останні можна не враховувати Тоді максимальні дотичні напруження у гвинтовій пружині з досить високим ступенем точності можна виз начнти за формулою
„ І6р/?
Хт»х -= -Гяї-
(9 53)
Зазначимо, однак, шо прн розрахунках потужних гвинтових ресор таких, наприклад, які застосовуються в залізничному транспорті, слід використовувати формулу (9 52), оскільки напруження від зрізу тут істотні внаслідок відносно великого значення І!# Досвід експлуатації гвинтових пружин свідчить про те, шо перші тріщини при руйнуванні як правило, виникають з внутрішнього боку витка, де діють найбільші сумарні дотичні напруження т' та т*
Виводячн формулу (9 52), мн не враховували, що на внутрішній та зовнішній поверхнях витків радіуси кривизни різні іноді, враховуючи це, замість формули (9 52) для визначення найбільших дотичних напружень використовують таку більш точну формулуї
Рас 230
16РЯ / 4т — і о 615 ) Тш.х = ла> (	_ 4 -І----„ ) ,
ДЄ
т = 2/?/гі
Неважко переконатися, що поправочний коефіцієнт в дужках збільшується ів змен шенням співвідношення т. наприклад, при т = іО він дорівнює 1,14. при т = 4 цей коефіцієнт становить ~ 1,4
Визначаючи розтяг або стиск К дружини, як правило беруть до уваги тільки кручення витків Розглянемо деформацію кручення уявно виділеного 8 пру жннн елементарного відрізка (із Ті витка
(рис 230), припустивши, що решта пружини абсолютно жорстка В перерізах А та В виділеного елемента проведемо радіуси витка 8 пло щині перпендикулярній до осі пружини, продовживши їх’до перетину з віссю пружини Добуті при цьому відрізки АС та ВС будуть раді усами пружніш По цих радіусах витка спрямуємо абсолютно жорст кі стержні, прикріплені до перерізів А та В витка Сили Р, що розтягують пружину по осі можна вважати прикладеними до кінців С і С жорстких стержнів АС та ВС
У таких умовах виділений елемент (із витка пружини зазнає деформації кручення Якщо вважати переріз А нерухомим, то переріз В при навантажуванні пружини повернеться відносно А на кут гіф, котрий визначається за формулою
де
М„~РК, У,»*-
Унаслідок повороту перерізу В «жорсткий» радіус ВС, поверну тиЙ на той самий кут гіф «перенесе» точку прикладення сили Р в нове поюження С Відрізок С С характеризує частину поздовжньої деформації витої пружини, спричинену закручуванням елемента гіз витка тобто
СС = /?гіф
Оскільки насправді скручуються всі витки пружини, які мають загаїьну довжину $ то переміщення нижнього кінця пружини від носко верхнього визначається формулою
ся	і)
Ураховуючи що наближено довжина дроту, з якого виготовлено циліндричну пружину з числом витків п буд
$ гіз = 2яЛл, «її
деформацію пружини визначимо за формулою
04 в або підставляючи в цю формулу М,
РР та = лгі*/32
МРП»п 6РО*п Осі* ~ Осі*
(9 54)
Формули (9 53) та (9.54) дають змогу перевірити міцність і визначити подовження (або осадку) циліндричної гвинтової пружини
Допустимі напруження на зріз при розрахунку сталевих пружин вибирають залежно від діаметра дроту пружини як правило, для загартованої пружинної' статі
{т| = 500 МПа при <і = 6 мм,
[т] — 400 МПа при і = іО мм,
[т| = 350 МПа при гі — 12 мм
Для хромонікелевих сталей при розтяганні пружин з діаметром дроту 12 16 мм беруть [ті -* 700 МПа Для фосфористої бронзи з модулем пружності при зсуві С = 4,4 І0* МПа при гі < іб мм вибирають |т] = іЗО МПа Такі допустимі напруження можуть братися тільки при постійних навантаженнях При повторно змінних або ударних навантаженнях допустимі напруження істотно менші
Часто, розраховуючи амортизаційні пружини (пружини для зни ження різких поштовхів) або ресори, за основу беруть енергію Т, яку повинна поглинати пружина (ресора) під час експлуатації При цьому виходять з того, що між зміщенням X пружини та силою Р, яка діє на неї, в межах пружності існує прямолінійна залежність Тому потенціальну енергію деформації пружини можна виразити фор мулою
З іншого боку, з формули (9 53) через напруження можна вирази ти крутний момент
,Мкр = Рй _
Тоді потенціальну енергію, яка накопляється в пружині, також мож на виразити через напруження
,, 2л Ял и ~ 40	4 Тт1’
Оскільки 2лРп — довжина дроту (з), з якого виготовлено пружину, а лй*/4 — площа його перерізу, то
іиі* 2лРп —5— = V
є об'ємом матеріалу пружини Враховуючи це, потенціальну енер* гію пружини можна виразити формулою
У = у	(9 55)
Отже задавшись значенням максимального напруження тпах -= » [т], можна визначити об'єм пружини який потрібний для погли нання заданої кінетичної енергії Т, з тим щоб не було перевищення
допустимого напруження!
Г = (/ = у, звідки
Конструюючи пружину за знайденим об'ємом її матеріалу, слід вибрати її параметри гі та п) з таким розрахунком щоб при перевірці осадки пру жини зазори між витками не закривалися
На закінчення зазначимо, що крім розглянутих циліндрич них гвинтових пружни постійного перерізу з пологим нахилом витків є багато інших конструкцій витих пружин конічні призматичні та різноманітні фасонні (параболічні, двійчасті конічні бочкоподібні тощо) При цьому крок витків пружини може бути як постійний, так і змінний, а переріз витка не тільки круглої а й прямокутної фор ми Методи розрахунку таких пружин досить складні й розглядаються в спеціальній літературі
Приклад 35 Запобіжний клапан діаметром 4К =* 75 мм повинен відкриватися при тиску пари р 0,6 МПа, мати змогу підніматися на висоту 1» = 20 мм. Діа метр дроту сталевої пружини 4 = 12 мм, середній діаметр пружини 2/? = 60 мм Якщр немає навантаження, крок витків пружини І = 17 мм; 0	8 10* МПа
Визначимо необхідну кількість витків пружини з тим щоб ари максимальному під нятті клапана іце залишався запас на дальше стискання не менший за X, =• /5 мм Знайдемо також початкове стискання пружини X, та напруження х при повному від критті клапана
Сипа яка піднімає клапан
Р = р = 06 10» —? ? 4'10 -і- кН = 2,65 кН
При цій силі пружина згідно з формулою (9 54) має таку початкову осадку
6зРЯ»л 64 2 65 10"З(3 )0~г)9л 0<і‘ и 8 то* (І 2 Ю-*)4
= 0 00276л м = 0,276л см
Повна осадка пружнни в навантаженому стані складається з А1о потрібного під* няггя X, та запасу к, Ця сума має дорівнювати різниці кроку пружини і та діаметра дроту пружин» помноженій на кількість витків тобто
Хі 4- X, _}. X, = л (І — 4) або
0,27б«4- 2 4- 1,5 = л(І 7—1,2), звідки
3,5 1Й л = ф 224 83 16 и,тк 3
Попередня осадка пружннн
Х| = 0 276л = 0,276 |6см=4 4см
Максимальне напруження з пружині прн повному відкритті клапана знайдемо пов язавши вирази для А та тт„ 3 формули (9 54)
р М<0 г “ 64Я»л '
Підставляючи це значення Р у формулу (9 53) для т^, знай* демо напруження прн повному відкритті клапана \46	6 4 12 10-4 8 10*	_______
,рі  =--------——ь '-------------- МПа я» 339 МПа.
4р«ля 4 (3 10“7)» |6ч
Приклад 36 Гвинтова пружина виготовлена з дроту 4 = 4 мм. внутрішній діаметр пружини = 46 мм. У напруженому стані зазор на просвіт між витками і, — І мм, 0=8 10* МПа Визна чимо, яка потрібна сила для стискання пружини, щоб зазора не було. Середній діаметр пружини
Рис 231	Я == 2Р = Я1 + <і = (46 + 4) мм » 50 мм
Зазор закривається якщо осадка одного витка буде дорівнювати йому, тобто 64РЯ»
звідки
04*1,	8 10» (0 4 І0-2)‘0 1 І0“2	,, _, „
'-ЯР"--------------,„-2„------------- «Н.205.10 акН=20,5Н
64 (2 5
Приклад 37 Дві пружини 112 (рис 231), які звиті з дроту однакового діаметра 4 = 10 мм і мають однакову кількість витків п •= 10, стискаються штоком клапана Висота зовнішньої пружини і у вільному стані на а = 60 мм більша, ніж внутрішньої пружини 2. Знайдемо зусилля, осадку та напруження кожної пружини, якщо радіус осьової лінії витка зовнішньої пружини = 50 мм, внутрішньої Р, = 30 мм, зусилля Р о 4 кН та модуль пружності при зсуві 6 = 8 10* МПа
Позначимо через Рх та Ра зусилля які припадають на кожну з пружин 3 рівнин ня рівноваги клапана вишиває що
(9 57)
Отже задача один раз статично кевнзнвчувана
Друге рівняння потрібне для визначення невідомих Рі і Р^ дістанемо з умов су місності деформацій
(9 58) де Лі та X, — осадки відповідно зовнішньої та внутрішньої пружин під дією сил Рі та Р, відповідно
54Рі^л Л1=	04*
6чР9/?|л ’ == —сиг- ’
Підставивши вирази для Лх та X, в (9 58) матимемо 64Р|/??в	64Р,/?|л
04* И 64*
або в числовому вираженні 54Рї(5 І0~2)»10 8 10* 10» (1 10-2)* звідки
64Р, (3 10~2)а 10
8 І0« 10» (І Ю“2)‘
І25Р, — 27Р, -=> 75
(9 59)
(9 60)
Розв язуючн останнє рівняння сумісно з (9 57) яке сліт переписати у вигляді
Р, (- Р, = 4, знайдемо
Рі » 1,2 кН Р, - 2 8 кН
Осадка зовнішньої пружний згідно з форму тою (9 59)
_ и 1,2 10~3|5 .0-^10 м_ОІ2и_І2см
о<*4	8 10* (1 10“2)*
Для внутрішньої' пружини
_ 64 2,6 Ю-З,з ю 2,40 , = 0М11 = ,„
О<1*	8 10* (І іо_ 2)‘
Максимальні дотичні напруження у витках зовнішньої та внутрішньої пружин, згідно з формулою (9 52) відповідно
16Р.Я, ( і \	16 і 2 10“3 0 05 (	0 01 \
’"	^+тяг)“ 3 14(1 10 ’> (І+ « 4В )мп,=
321 МПа
16 2 8 ІО-3 0 03
3 14(1 10~2)*
= 403 МПа
/	001 \
+ 4 6,ог) МПа“
$ 59. Концентрація напружень при крученні
Концентрація напружень або місцеве збільшення напружень, спричинюється різкою зміною форми деталі (наявністю надрізів отворів, різьби, різкою зміною перерізів стержнів та Ін )
Найбільше напруження прн крученні в зоні концентрації, обу мовлене зазначеними концентраторами, виражається як добуток номінального напруження тк на коефіцієнт концентрації напружень а,
Тт.х »- ахта	(9 61)
Тут тв обчислюється за формулами опору матеріалів, зокрема, для вала круглого перерізу

(9 62)
ах є відношенням максимального напруження в зоні концентрації обчисленого в припущенні абсолютної пружності матеріалу, до комі пального напруження тобто
ССх — Ттвх/Т-и
Як зазначалося раніше цей коефіцієнт називається теоретичним коефіцієнтом концентрації і визначається методами теорії пружності чи експериментально (поляризаційно-оптичним методом тензометру ванним за методом аналогій)
Таблиця 14
р мм	2 54	5,06	7,62	10 16	12 70	15 24	17 7В
а,	5,4	3 4	2 7	2 3	2,1	2 0	19
Зауважимо що коефіцієнт концентрації напружень для виточки (або надрізу) при даній її глибині і розмірах деталі залежить здебіль того від кривизни поверхні по дну виточки
Для ілюстрації впливу форми виточки на коефіцієнт концентрації напружень розглянемо паз (шпонкову канавку) з різко окресленими кутами (рис 232) Досліди, проведені з порожнистим валом зовніш-нього діаметра 4а = 254 мм та внутрішнього сі, =• 147 мм з глибиною паза /і = 25,4 мм та завширшки Ь — 63 5 мм при різних радіусах р викружкн в кутах, показали, що найбільші напруження в заокруглених кутах дорівнюють найбільшим в такому самому валу без паза, помноженим на коефіцієнт концентрації а., значення якого наведено в табл 14
Як видно з табл 14 концентрація напружень може бути знижена збільшенням радіуса заокруглення в кутах
Другий типовий приклад концентрації напружень, який часто буває на практиці,— це кручення валів змінного східчастого поперек ного перерізу (рис 233) Максимальна концентрація напружень має місце на початку заокруглення, тобто в точках т на рис 233 При цьому максимальне напруження залежить від співвідношень р 4 та Р 4 де р — радіус заокруглення а Р та 4 — діаметри спряжува них циліндричних частин східчастого вала Картина розподілу дотичних напружень при крученні в зоні концентрації тобто в місці спря ження двох діаметрів, має приблизно такий вигляд, як показано на рис. 234 для випадку р/4 = 1 2 та 2р/4 = 0 І Залежності а, = => / (2р/4) при різних співвідношеннях Р 4 наведено на рис 235
З аналізу наведених графіків видно, що при певному співвідношен ні діаметрів Р і 4 і малих значеннях радіуса заокруглення р місць спряження двох діаметрів вала коефіцієнти концентрації напружень можуть бути більше трьох
Слід мати на увазі що для пластичних матеріалів при статичних
навантаженнях концентрація напружень не є
Рве 232
Ркс 233
Рис 234
Рнс 236
Рнс 237
Рнс 235
розподіл (вирівнювання) напружень Проте у валах, виготовлених з крих ких матеріалів наприклад із загар тованої сталі, внаслідок концентра ції напружень в місцях заокруглек ня №ох суміжних діаметрів вала
навіть при статичних навантаженнях можуть з явитися тріщини, які призводять до руйнування вата Тому, конструюючи деталі з крихких матеріалів навіть за умови статичного навантаження їх слід більше уваги приділяти геометрії відповідних переходів, щоб запобіг ти великій концентрації напружень Щодо впливу концентрації напру жень при повторно змінних навантаженнях, то вона, як буде показано агл 21 має. істотне значення навіть для пластичних матеріалів
На закінчення розглянемо приктад концентрації напружень нав коло малого радіального отвору в порожнистому тонкостінному валу прн крученні (рис 236) Двома парами взаємно перпендикулярних площадок нахилених під кутом 45° до твірних вала виділимо навколо отвору якийсь елемент аЬаі (рис 237) Ці площадки для розгляду ганої задачі кручення будуть головними, а тому по гранях елемента аЬсіі діятимуть тільки норма іьні напруження о, та о8, які однакові за модулем, але різні за знаком Абсолютні значення \к, як відомо дорівнюють дотичним напруженням т, що діють в перерізі, де розта шований отвір, і які визна чаються у відповідних точ ках поперечного перерізу за формулами теорії кру чення
Аналізуючи напружений стан розглядуваного елемен та і враховуючи, що отвір маїий а стінки вала тонкі, легко переконатися що цей напружений стан аналогіч ний тому, який має місце в тонкій пластині з малим от вором розтягнутій в одно
Рнс 238
му напрямі деяким напруженням а = т та стиснутій таким самим за модулем напруженням в напрямі під кутом 90а до першого
Отже задвча про визначення концентрації напруження біля от* вору малого діаметра в стінці скручуваного трубчастого вата зводить ся до визначення концентрації напружень в тонкій пластині з малим отвором, яка зазнає у взаємно перпендикулярних напрямах розтягай ня та стискання напруженнями о -= т
Коефіцієнт концентрації' напружень в стінці вала з отвором знайдемо, взявши суму концентрацій у відповідних точках, яка має місце в двох окремих випадках показаних на рис 238
Як уже зазначалося (див § 32, рис 118, а) при навантажуванні за схемою рис 238, а значення максимальних розтягатьних напру жень в точках т в три рази вищі за напруження, які діють на конту рі пластинки, тобто а = З У той самий час в точках п, розташованих під кутом 90°, виникають стискальні напруження, які приблизно до рівнюють за модулем розтягальним напруженням, що діють на кой турі пластинки Очевидно при схемі навантажування рис 238, б картина напружень в точках т та п буде іншою Отже коли просу-муемо ці два напружених стани то в точках т матимемо
Спих = Зо + а = 4с а в точках п
Огпіп 35 “_’ Зо — о =: —— 4а, тобто коефіцієнт концентрації' в стінці трубчастого вата з малим от ВОрОМ От — 4
Отже
Ттах — «|Та
Такий високий коефіцієнт концентрації напружень при крученні валів з отвором (часто такі отвори роблять для мащення) зобов язує особливо обережно підходити до добору розмірів валів, які виготов ллються з крихких матеріалів, і крім того передбачати технологій ні засоби зниження концентрації напружень про які вже йшлося
Глава 10 ЗГИНАННЯ
$ 60 Нормальні напруження при плоскому згинанні прямого стержня
Розглянемо випадок чистого плоского згинання балки (рис 239, а) із шести внутрішніх силових факторів які можуть діяти в її по перечних перерізах в загальному випадку згинання прн чистому згн нанні не дорівнює нулю тільки згинальний момент М Вісь балки дефор* мується в площині, що збігається з силовою (на рис 239 — в площи-236
о
Рис 239	Рис 240
ні креслення) В § 17 було зазначено умовк необхідні для того, щоб згинання було плоским У цьому параграфі виведемо формули для обчислення напружень в будь якій точці перерізу Поки що не будемо вводити ніяких обмежень щодо форми та розташування силової' площи ни (за винятком того, що силова площина повинна проходити через вісь стержня)
Згідно із загальним планом (див $ 26), розпочнемо виведення із статичного аспекту задачі Проведемо поперечний переріз т — т на довільній відстані х від початку координат (рис 239, а) В пло щині перерізу (рис 239 б) проведемо координатні осі у та г вісь у сумістимо з силовою лінією (лінією перетину силової площини з пло* щиною перерізу), а вісь г проведемо на довільній поки що висоті, але перпедикулярно до осі у Вісь х спрямуємо перпендикулярно до площини перерізу Виділимо в перерізі елемент площі АР, координати якого у та а Взагалі на елемент могли б діяти напруження а та т Проте при чистому згинанні всі зусилля та моменти, пов язані з до* тичними напруженнями, — р, та МКр — дорівнюють нулю
Отже, в усіх умов рівноваги (3 29) (3 34) залишаться тільки три*
М,= (аг<ІГ	(ІО 1)
Але в даному прикладі в перерізах балки діє тільки один згинальний момент М*. тому
У-0, М,-0 М, = М	(10 2)
Із залежностей (іО і) та (іО 2) маємо
= 0 ] аггіґ = 0, ( ЩІЕ - М	(ІОЗ)
Переходячи до геометричного аспекту задачі, розглянемо картину деформацій тієї самої балки (рис 240) Досліди, проведені на еластин них (наприклад гумових) моделях, які дають змогу легко добути знач ні деформації, показують що коли на поверхню моделі нанести пря мокутну сітку ліній (рис 240, а) то прн чистому згинанні ця сітка деформується таким чином (рис 240, б) поздовжні лінії викривлю
ються по дузі кола, контури поперечних перерізів залиша ються плоскими, про ЩО свід мать поперечні лінії сітки, які залишаються прямими і перетинаються з поздовжніми лі ніями під прямим кутом і_і„ ______________________
На підставі сказаного мож на зробити висновок, що при чистому згинанні поперечні перерізи балки залишаються плоскими і повертаються так, що залишаються нормальними до зігнутої' осі балки Отже, прн чистому згинанні, як і при розтяганні (стисканні) та кру ченні круглих стержнів, буде справедлива гіпотеза плоских перерізів

<йг и>-
іа п
Рис *41
Вимірюючи відстані між аналогічними точками контура будь-яких двох перерізів, можна побачити, що при деформуванні ці від стані змінюються Так, виявляється, що ах < а і во > а (рис 240, а, б) Отже верхні поздовжні волокна банки укорочуються, а ниж ні — подовжуються Але можна знайти І такі волокна довжина яких прн згинанні залишається незмінною (ас == а). Сукупність волокон, які не змінюють своєї довжини при згинанні балки, називається нейтральним шаром (н ш ) Волокна що належать нейтральному шару до деформації* лежать в одній площині а в деформованому стані утворюють деяку циліндричну поверхню В обох випадках кожний поперечний переріз балки перетинається з нейтральним ша ром по прямій, яка називається нейтральною лінією (н л ) перерізу
При плоскому згинанні нейтральний шар виявляється перпеи днкулярним до силової площини, а отже, нейтральна лінія перпеи дикулярна до силової лінії в перерізі Будемо вважати що вісь г (див рнс 239, б) проведена в перерізі таким чином що вона збігається з нейтральною лінією (але положення останньої по висоті перерізу поки що невідоме)
Виділимо елемент балки двома суміжними поперечними переріза ми т — т та п — п, які розташовані один від одного завдальшки йх (рис 24і, а) та, взявши до уваги гіпотезу плоских перерізів, розглянемо його деформований стан (рис 241 б) Перерізи лі — літал— л повертаються одвн відносно одного на кут <іф і залишаються плос кимн Елемент а$Ь0 нейтрального шару перетворюється на дугу аоЬо з радіусом р а волокно аЬ, яке розташоване завдальшки у від нейт рального шару,— на криволінійне волокно ахЬх з радіусом кривизни 238
р + у Відносне подовження цього волокна
а,Ь, — аЬ
В~ аЬ
Але 6)6, = (р 4- у) <іф та аб — ііх, тому
(р+0*р-^	(І04)
Щоб спростити цей вираз, розглянемо волокно а^Ьа, яке належить нейтральному шару Його довжина а^ = йх Після деформації воно перетворюється на дугу лфо = (хі<р Але волокна нейтрального шару не змінюють своєї довжини при деформуванні, тому
Ох = ргіф	(10 5)
Підставивши (іО 5) у вираз (10 4) і скоротивши на <І<р, матимемо
е = у/р	(10 6)
Отже, розгляд геометричного аспекту задачі показав, що відносна поздовжня деформація пропорційна відстані волокна від нейтраль ної осі
Щоб записати закон Гука, що виражає фізичний аспект задачі, треба з ясувати, в якому напруженому стані перебуває волокно об На елементарній площадці ФЕ зрізу (див рис 239 б), як уже було ска зано, дотичних напружень немає. Припускається також, що волокна матеріалу, розташовані вздовж балки, не тиснуть одне на одне, а тому напруження між ними дорівнюють нулю Отже, волокно аЬ перебуває в лінійному напруженому стані—зазнає простого розтягання або стискання Тому для нього закон Гука (у відносних координатах) слід записати так.
в =« а/Е	(10 7)
Переходячи до синтезу результатів розгляду трьох аспектів зада чі виключимо е із залежностей (іО 6) та (іО 7)
(ІО 8)
Підставляючи (і0 8) у трете рівняння (іОЗ) та враховуючи, що Е і р як величини, що не залежать від положення елемента йЕ в перерізі, можна винести за знак інтеграла, матимемо
Згадавши, що $№Е = 7г е моментом інерції перерізу відносно осі г, можемо останню формулу переписати у вигляді
т-иг	<109)
Нарешті, підставивши внрвз (10 9) у формулу (10.8), знайдемо, то аоМр/7,	(10 10)
Ця формула, яку вперше було виведено французьким вченим К Навье, дає змогу визначати нормальні напруження при чистому згинанні балки в будь якій точці її перерізу
Тепер залишилося тільки з’ясувати, де в перерізі розташована вісь г — нейтральна лінія перерізу. Щоб відповісти на це запитання, внесемо вираз для о з формули (іО 10) у перші два рівняння (10 3)і
-^-рг<ІУг=0
Оскільки М//х Ф 0, а
уйр =	| угі? = Л»,
то
5, = 0,	(ІОН)
/и=0	(10 12)
На підставі рівності (І0 і 1) приходимо до висновку, шо вісь г — нейтральна лінія перерізу — проходить через центр ваги (ц. в) поперечного перерізу Силова площина проходить через вісь балки, а отже, силова лінія (вісь у) проходить через центр ваги перерізу Рів ність (10 12) показує що осі у та г — готовні центраіьні осі перері зу Цим визначається положення нейтральної лінії перерізу
Отже, якщо ситова лінія збігається з однією з головних централь них осей перерізу, то згинання буде птоским, і нейтральна лінія перерізу буде збігатися з іншою головною центральною віссю інакше ка жучи, якщо силова площина збігається з однією з головнях площин стержня, то нейтральний шар збігається з іншою головною площи кою.
Зазначимо що часто індекс г в позначенні моменту інерції випускають, пам ятаючи, однак, що ] обчислюється відносно нейтральної лінії перерізу
Тепер проаналізуємо добуті результати
Формула (10.9) в проведеному виведенні, хоч і була допоміжною, проте вона має і велике самостійне значення Її можна трактувати як закон Гука при згинанні, оскільки вона пов'язує деформацію (кривизну нейтрального шару 1/р) з силовим фактором — згинальним моментом, що діє в перерізі. Величина Е7 має назву жорсткості перерізу при згинанні, Н м* 3 формули (10 9) видно що коли балка виготовлена з однорідного матеріалу (£ — сопзі) і має постійний переріз (У — СОП5І), то при чистому згинанні (М — сопзі) її вісь викривля еться по дузі кола (і/р = сопзі і, отже, р = сопзі)
Формула (10 10) показує що незалежно від форми та розмірів перерізу балки, напруження в точках нейтральної пінії завжди до-
рівнюють нулю Величи на а лінійно зростає в міру віддалення від нейт ральної лінії Прн цьому напруження виявляють ся однаковими по шнри-ні перерізу (вздовж лінії у = сопзі) Отже, епюри а для будь яких перері
Рнс 242
зів що мають горизон-
тальну вісь симетрії, завжди будуть мати вигляд, показаний на рис 242 Всі волокна, розташовані вищеза нейтральну лінію виявляються стнс нутими, а нижче за неї — розтягнутими Якщо ж згинальний момент
матиме протилежний знак, то верхні волокна будуть розтягатися а нижні — стискатися
Максимальні напруження (От») мають місце в найбільш відда лених від нейтральної лінії волокнах, тобто у випадку симетричного перерізу відносно горизонтальної осі г при у = ±Н/2 Підставляючи це значеня у формулу (ІО 10) дістанемо
Позначимо відношення 7/(Л/2) через ІГ і назвемо його осьовим моментом опору, м8 Тоді
ОтіІ=М/й7	(іО 13)
Якщо переріз балки не має горизонтальної осі симетр її, то нейт ральна лінія зміщена відносно середини висоти перерізу (рис 243) і напруження Опах в крайніх верхніх та сг^* в крайніх нижніх волокнах не будуть однаковими
Отах «в М/У7, атал = М/^‘,	(10 14)
де
Здобуті результати двють змогу зробити певні висновки про раці* опальні форми перерізу балки при чистому згинанні На відміну від простого розтягання чи стискання при згинанні, як і при крученні, напруження в перерізі розподіляються нерівномірно Матеріал у зоні нейтрального шару навантажений мало Тому з метою економії матеріалу та зниження ваги конструкції, яка працює на згинання, слід вибирати такі форми перерізу, щоб більша частина матеріалу була віддалена від нейтральної лінії ідеальним з цього погляду е переріз, який складається з двох вузьких прямокутників (рис 245, а) Реально такий переріз нездійсненний, оскільки ці два прямокутники повинні бути зв'язані між собою, щоб утворювати один переріз Із застосову ваних на практиці профілів найближчий до ідеального двотавровий переріз (рис 245, б)
Згинальний момент, який переріз може витримати безпечно, залежить від моменту опору Ц7 Обмежуючи максимальне значення напруження О ПНІ, що діє в перерізі, допустимим (о] згідно з форму лою (10 ІЗ) визначимо допустимий згинальний момент
|М]-ою.хіГ = Іо|ІГ	(Ю16)
Затрата ж матеріалу пропорційна площі перерізу Р Отже, чим біль ще відношення Й7/Р, тим більший згинальний момент витримує переріз із заданою площею (тобто із заданою вагою стержня) і гнм менше матеріалу піде на виготовлення стержня що витримує заданий зги нальннй момент Тому відношення ж/Р може бути взято за критерій, що оцінює якість профілю
Грунтуючись на цьому критерії (або просто звернувши увагу на те яка частина матеріалу розташована поблизу нейтральної лінії бал ки), легко переконатися, що переріз, показаний на рис 245 більш раціональний ніж суцільний круглий, а розміщення двотавра та прямокутника наведене на рис 247, а при вертикальній силовій площині вигідніше за показане на рис 247, б
Усі формули цього параграфа виведено для випадку чистого згинання прямого стержня Для загального  випадку згинання дія поперечних сил при	‘“а4,	.	-
зводить до того, що гіпотеза плоских перері	з । Цтгг4
зів, на якій грунтується виведення формули н£	и 1 И
Рис 245
Рис 246
Рас, 247
Навьє для обчислення нормальних напружень порушується оскільки поперечні перерізи не залишаються плоскими а викривляються по здовжні волокна взаємодіють між собою, тиснуть одне на одне і отже, перебувають не в лінійному, а в плоскому напруженому стані Проте практика розрахунків показує, шо і при поперечному згинанні балок І рам, коли в перерізі крім М діють N та З, можна використовувати формули, виведені для чистого згинання Похибка при цьому дуже незначна
$ 61. Дотичні напруження при згинанні
При поперечному згинанні, коли в поперечних перерізах бруса діють С та М виникають не тільки нормальні напруження а а й дотичні т, для визначення яких виведемо відповідну формулу
Як уже зазначалося (днв $ 26) задача про визначення напружень у пружному тілі завжди статично невизначувана і потребує розгляду трьох аспектів задачі Проте можна прийняти такі гіпотези яро розподіл напружень, прн яких задача стане статично визначуваною тоді немає потреби використовувати геометричні та фізичні рівняння, а досить розглянути тіїьки статичний аспект задачі Саме так і будемо виводити формулу для визначення т прн згинанні
Будемо виводити на прикладі балки прямокутного поперечного перерізу (рис 248, а)
Двома близькими поперечними перерізами Л^та виділимо елемент балки (рис 248, б) завдовжки іх Як видно з епюр в обох
Рис 248
перерізах () та М додатні, причому в переріз!
<2 = <2 (х); М = М (х),
а в перерізі А,В»
<2 == <2 (х), М = М (х) + ам
Отже в проведених перерізах діють нормальні та дотичні напру* ження Нормальні напруження на лівому та правому торцях виділе ного елемента на підставі залежності (10 10) визначаться формулами
✓	(1017)
Введемо два припущення про характер розподілу дотичних напру жень у балках прямокутного перерізу
1) т скрізь паралельні поперечній силі ф,
2) в усіх точках перерізу на даному рівні (у — сопзі) т однакові (тобто і постійні по ширині і залежать тільки від відстані точки до нейтральної лінії)
Ці припущення справедливі, якщо Ь Л
Відсічемо частину елемента балки, провівши горизонтальну площину ті — пц завдальшки у від нейтрального шару (рис 248, в д) Очевидно в гранях ЛхЛаИцлі], СіС^/цлі та АіА£яСі взагалі немає ніяких напружень оскільки ці грані є частиною зовнішньої поверхні балки Обчислимо рівнодійну нормальних напружень, розподілених по грані АхСіПіПі На елементарну площадку ЛР — бей], проведену паралельно нейтральній осі г завдальшки і] від неї (рнс 248, г), діє елементарна осьова сила = о ЛР == (М (х)і]/У2) сіР Тоді шукана рівнодійна
п, - а'ЛЕ - -”^4 ЛГ -
Оскільки » 52 (у) е статичним моментом площі, що містить ся між рівнем у та краєм балки, то
(10 18)
Аналогічно в грані А^С^іутц рівнодійна нормальних напружень а*
ЛГ, _ ММ + .ІМ м	(|0 19)
Значення 5, (у) буде, очевидно таким самим, як і для лівого пере різу.
У грані піпупугіі діють нормальні напруження оскільки при поперечному згинанні волокна тиснуть одне на одне Однак цими иор мальними напруженнями нехтують як неістотними для розрахунку
Рис 250
Рис 249

наміцність Крімтого, згідно із законом парності дотичних напружень тут обов язково виникають і напруження т' — т, причому вони спря мовані так як показано на рис 248, д
Оскільки розмір грані Л|Л1лцпіІ елемента малий, можна вважа ти, що т' рівномірно розподілені по цій грані і отже дають зусилля
ЛТ = х'ЬНх — хЬіїх
Запишемо тепер умову рівноваги паралелепіпеда	Л|Лапігпі)
2Х = /V, — Л\ — 47 - 0
Підстав тяючи сюди зусилля дістаємо
\М (х) + <М4|	(у) _ М (х)	(у) __	__ 0
або
Поділивши це рівняння на Мхта враховуючи що ЛМ/іх — 3, остаточ но знайдемо формулу для визначення дотичних напружень у перерізі балки при згинанні
Ця формула вперше була виведена російським інженером Д І Журавським і носить його ім’я Незважаючи на те що покладе ні в основу її виведення гіпотези справедливі тільки для вузьких пря мокутних перерізів баїок (при Л/&> 2) на практиці нею можна кори стуватися для будь яких перерізів, крім тих місць у перерізі де є вузь кі прямокутники, розташовані перпендикулярно до 3 — полиці дво тавра, швелера
Дія довільного перерізу (рис 249) величини, які входять до фор мули (10 20), мають такий зміст 3 -	(х) — модуль поперечної сипи
в тому перерізі де визначаються дотичні напруження, У, — момент інерції цього перерізу відносно його нейтральної лінії Ь — Ь (у) ширина перерізу на рівні де визначаються дотичні напруження т
Рнс 25І
З, (у) — абсолютне значення статичного моменту відносно нейтральної* лінії тієї части ни площі Е (у), яка міститься між лінією, де визначається т, та краєм перерізу
Отже формула (іО 20) дає тільки модуль т Щодо напряму т то відповідно до вихідного припущення воно вважається паралельним ф і спрямованим у бік його Дії
Побудуємо епюру т для прямокутного перерізу (рис 250) Прове демо лінію тп, паралельну нейтральній лінії й віддалену від неї на довільну відстань у і знайдемо значення т в точках цієї лінії Лінія тп відсікає площу Е (у) = Ь (Л/2 — у) Статичний момент цієї площі
5ґ{у) = Е (у) ул, = Ь 1^- ~ у^у + -5"('Т “ *)]“
4»’ ї
Н1 )

(ІО 21}
Підставляючи (10 21) у формулу Журавського (10 20), а також зважаючи на те, що = ЬЛ’/І2, маємо
12
(10 22)
Змінна у входить до формули в другому степені, отже епюра т буде параболічною У найвіддатепіших від нейтральної лінії точках перерізу у — ±Н/2 і т - 0 Для точок нейтральної лінії прн у — 0 дотич ні напруження будуть максимальні
(Ю23)
За цими даними і побудовано епюру дотичних напружень в стержні прямокутного перерізу (рис 250)
Для круглого поперечного перерізу (рис 251) введені вище гіпо тези про характер розподілу дотичних напружень по перерізу не вн конуються Однак з певним ступенем точності можна вважати, що вертикальну складову дотичних напружень, які виникають у поперечному перерізі на рівні у від нейтральної лінії, можна визначити за форм)лою Ж) райського Для круглого перерізу матимемо
'І=ТЖг(!^’Й	(1024)
Виконавши відповідні обчислення статичного моменту 5, (у) згідно з рнс 251
Ь(у) — 2гсоз<р; 0=/-зіп<р,	»гсозфЛр;
5,М » ( уМ,
ЛГ = Ь (у) Лу аг 2га соз8 срг/ф я/г
З, (у) = ] уЛГ = 2г8 соз8 <р зіп <р 4<р =	,
обмежимося визначенням Тщах
_	5г&(і	<? 2Я 4 _ 4 (2	_М_Ио_0_ нп™
1п»х— Ьіу)^ _32ляН З № - З Р ~ 1,33 Р О025)
Епюра т знову параболічна причому максимальне дотичне напру ження т буде в точках нейтральної лінії* (у = 0) а мінімальне — в най віддаленіших від нейтрально» лінії точках (у == ±г)
Приклад 38 Побудуємо епюри зміни нормальних та дотичних напружень по висоті поперечного перерізу двотаврової балки М 12 якщо в перерізі діють згинальний момент М е= 2 кН м та поперечна сила 0. = 10 кН
За таблицею сортаменту (дод І) знаходимо основні розміри профіте (рнс 252) момент інерції' площі поперечного перерізу 1г ся 350 см* та статичний момент площі половини цього перерізу 5тлх = 33 7 см*
Нормальні напруження в точках попере того перерізу завдальшки у від нейтральної тінії (по лінії тт) инзна ідемо за формулою Навье (10 10)
Максимальні за абсолютним зна «енним напруження будуть прн уті* = й/2 Вн значимо їх
Тпжх =	“ 2 10-3 6 -10"2 МПа - 34 28 МПа
“х Л 350 І0“я
Епюри напружень а наведено на рнс 252 ліворуч від профілю перерізу балки
Дотичні напруження в точках поперечного перерізу балки завдальшки у аіт неитратьної лінії визначаємо за формулою Журавського (10 20)
Для побудови епюрн дотичних напружень обчислимо тв кііькох характерних точках а) в крайніх волокнах (по тіні: А В) б) \ місці спряження лотиць із стінкою
(в точках і і 2). причому будемо вважати що точки І і 2 розташовані нескінченно близько до межі полиці азе тежать по різні боки від цієї межі (для ясності це місце на рис 252 показано окремо) в) у точках нейтральної лінії
Для точок лінії АВ статичний момент 5, (и)	5, (Л/2) “ 0 оскітьки лінія АВ
не відсікає ніякої птоші Отже в точках лінії АВ напруження т са 0
Для точки І ширина перерізу Ь ва 6 4 см статичний момент визначатиметься статичним моментом полині 3 досить високим ступенем точності полито можна вва жати прямокутником з розмірами Ь X І Тоді
5, (У) “ 5гп = Ьі (*/2 ~	*= 6 4 0 73 (6 — 0 365) см» =» 26 З см»
Дотнчиі напруження в точці І
_ 10 10^ 26 3 10-° МПа _ , 18 мп>
6 4 ІО-7 350 10“8
Для точки 2 статичний момент залишається практично тим самим але ширина перерізу і 0 48 см Тому дотичні яапоуження в точці 2
1?ІІ..І2-3_26,3 А0-!. МПа= 15.67 МПа
0 48 ІО"2 350 ІО”8
Оти-е при переході від точки І до точки 2 дотичні напруження різко збільшуються.
Дія точки нейтральної тііііі ширина перерізу 4 ва 0,48 см а статичний момент сіід взяти для половини перерізу балки Очевидно це буде найбільша величина для даного перерізу — 5, тіж Тоді
т - 10 І0~3 33 7 10~9 ““	0 48 Ю“7 350 ІО"8
МПа “ 20 06 МПа
На підставі цих даних будуємо епюрні для нижньої половини ік рерізу Для верхньої ло-онннн внаслідок снм<. ірії профілю відносно осі г епюра буде симетричною Епюру і наведено на рис 252 праворуч від профілю балки
Побудована епюра дещо умовна оскільки дає справедливі значення т тільки для точок стінки досить віддалених від полинь Поблизу полиць дотичні напруження в стінці підвищуються внаслідок того що місце спряження позиці зі стінкоюеджерелом концентра!! і напруження
формула (10 20) та розглянуті приклади дають підставу зробити деякі загальні висновки щодо розводі ту дотичних напружень в перерізах при поперечному згинанні балок
1)	вигляд епюри т залежить від форми поперечного перерізу балки
2)	у крайніх найбільш віддалених від нейтральної лінії' точках т завжди дорівнює нулю,
3)	найбільшого значення дотичні напруження для більшості видів перерізів балок досягають ва нейтральній лінії перерізу, причому
<10 26)
де 5гиах — статичний момент половини площі перерізу формулу (10 26) можна подати також у вигляді
де к — коефіцієнт, який залежить від форми перерізу, для прямокут ного перерізу к = і,50 для круглого — к — 1,33;
4)	формулою Журавського можна користуватися для визначення дотичних напружень у будь яких точках масивних профілів Міркування щодо визначення дотичних напружень при згинанні
балок тонкостінних профілів викладено в § 72
$ 62 Розрахунок на міцність при згинанні
У попередніх параграфах ми вивели формули для обчислення нор мальних а та дотичних т напружень при плоскому поперечному згн нанні балок Ці формули дають змогу скласти умови міцності для перевірки та добору перерізів деталей що працюють на згинання Щоб здобути ці умови, з’ясуємо, в якому напруженому стані перебувають елементи стержня що зазнають плоского згинання Заради більшої конкретності розглянемо балку зображену на рис 253
На рис 253, а показано схему навантаженої балки, а також по будовано епюри М та ф На рис 253 б зображено фасад балки У різних зонах по висоті балки виділено елементарні кубики одна з граней яких збігається з пющиною поперечного перерізу балки На рис 253, в як приклад показано переріз А — А та виділені в ньому етементи 3 і ІЗ.
Елементи /, 2, /2 ІЗ та 14 виділені в крайніх точках перерізу Тут т — 0, а — От*» і елементи зазнають простого розтягання (/2 ІЗ) або стискання (/, !4), тобто перебувають в лінійному напруженому ста ні (рис 254, а)
Елементи 6,7 та 8 виділені біля точок нейтрального шару, де а = - 0, а т = Тпих, тому по їхніх гранях діють тільки дотичні напружен
Рис 253
Ттах т ня і, отже, вони перебувають в умо-Змн—1^** ІТИ 6 ІІ>* 6 вах чнстого зсуву (рнс 254, б) Г*~ п II ~*п ІГ~*~ У вертикальних гранях елемен дГ	тівЗ 4,5,9 /0 та//, що збігають-
0	0 ся з поперечними перерізами бал
Рас. 254	ки, виділених у довільних точках
балки, діють і о, і т тому елемен ти перебувають у плоскому напруженому стані (рис 254 а)
Значення а і т та їхні напрями залежать відзначень та напрямів М і З в розглядуваному перерізі та від поюження елемента по висоті перерізу Напрями напружень визначаються напрямами зусиль М та 3 Треба пам’ятати, що епюри М будують на стиснутих волокнах. Тому елементи /, 3, 10, 14 та // зазнають стискання, а елементи 9, 12, 13, 4 2 та 5 — розтягання
ІЦоб визначити напрям т слід звернути увагу на знаки З У відповідних перерізах Наприклад, у перерізі А —• А зусилля 3 від’ємне, а отже, намагаючись повернути обидві частини розсіченої' балки проти годинниковоїстрілки, 3 Діє на лівий бік перерізу вгору (рис 253 а). Саме так і будуть спрямовані т в правій грані елемента 3 у решті граней напрями т визначаються законом парності дотичних напружень Значення напружень у різних елементах можна знайти за формула ми виведеними в попередніх параграфах
а) для елементів / 2, 12, ІЗ та 14
Птах « А4/ЇГ,
6} для елементів б, 7 та 8
Тщ.х =	— Ч р .
в) для 2, 4, 5, 9, 10 та //
Якщо балка має наприклад, прямокутний переріз з розмірами, показаними на рис 253, в, при Ь = 5 см Н = 10 см, Г = 50 см1, к = = 1,5
см’-83,3 си>. У=-Ц^- см* = 417 см‘
Тоді для елементів 2 та 14 (] М | «= 18 кН  м)
~ в> МПа = 216 МПа'
для елемента 7 (| З І — кН)
Той - ’ 5Ю 1910Г~ МПа = 5,7 МПа;
для елемента З (М = 4,8 кН м | С | — і9 кН)
у = 3 см, 5 = (5 - 3)5 (з І- -Ц-5-) см’ =" 40 см’-
а = <» 10-3 з Ю~г МПа = з* 5 МПа 417 ю—•
т =	МПа = з 7 МПа
5 ІО”8 . 4|7 ІО-8 і Т д
Отже, прн поперечному згннапні балки її матеріат перебуває в неоднорідному плоскому напруженому стані Прн цьому умова міц пості повинна бути записана для так званої небезпечної точки балки тобто тієї точки, де матеріал перебуває в найбільш напруженому ста ні Небезпечною буде одна з таких трьох точок а) точка, де нормаль не напруження досягає найбільшого значення б) точка, де дотичне напруження досягає найбільшого значення, в) точка де а та т, хоч і не набувають найбільших значень але в своїй сукупності створюють найвипднішу комбінацію, тобто найбільше еквівалентне напруження за прийнятою для розрахунку теорією міцності При цьому таких то чок може виявитися кілька
Якщо орієнтуватися на першу небезпечну точку розташовану в крайніх волокнах того перерізу балки де згинальний момент М наби рає максимального значення, а елемент перебуває в лінійному напру женому стані (наприклад, точки 2 та 24 на рис 253), умову міцності можна записати у вигляді
Отих = М^/ГСІо]	(1028)
Друга небезпечна точка лежить на нейтральній лінії того перерізу де поперечна сила найбільша (на рис 253 це точка 6 і взагалі будь-яка точка на ділянці нейтрального шару де (2 = (2т»,;) У такій точ ці спостерігається чистий всув (рис 254, е), тому умова міцності набирає вигляду
(1029)
Щодо третьої небезпечної точки, то її положення не таке певне. Але де б її не було вибрано, в ній завжди буде плоский напружений стан при якому по гранях виділеного елемента діятимуть нормальні та дотичні напруження (рис 254, а) Головні напруження визначати маться за формулами
°і “ “Г(0 + °а + 4х*1
ст, = 0	(10 ЗО)
°з=4н° — а< + 4т*1
Підставляючи ці вирази у формули для еквівалентних напружень за різними теоріями міцності ((7 2) (7 6) (7 11), (7 20) (7 21)1, ді стаємо умови міцності
Оекві = 4" + ^°2 +	< м»	(10 31)
о™, =	V’	“4і І-	(10 32)
О..Ш =	И о* - 4т= < [ст|	(10	33)
о». IV =	Га*+ Зт=<1а|.	(1034)
а,..м -	+ -ТІЇ- к о1 + 4т- <|а),	(10	35)
де т = |<т+] / [о_]
Для розрахунку балок з пластичних матеріалів рекомендується користуватись умовами міцності виходячи з третьої або четвертої теорії міцності [формули (10 33) та (10 34)1
Зазначимо, що здебільшого небезпечною є крайня точка того перерізу, де ЛІ = Ліпші Тому на практиці перевірний розрахунок балок на міцність полягає ось в чому
1)	знаходять небезпечний переріз балки тобто той переріз в якому діє найбільший за абсолютним значенням згинальний момент
2)	за таблицею чи розрахунками визначають момент опору Ц? перерізу відносно нейтральної лінії
3)	застосовують тільки одну умову міцності (10 28), яку тому і називають основною
За цією схемою для більшості профілів легко можна виконати також проектувальний розрахунок, тоді умова міцності (10 28) зали сується у вигляді
И^МпахДо]	(10 36)
Визначивши потрібний момент опору балки та вибравши певний профіль поперечного перерізу, добирають його розміри
Розглянемо деякі приклади розрахунку балок за основною умовою міцності
Приклад 39 Для балки (рис 255) вважаючи заданими розміри І, й, <1 та допустиме напруження [о], знайдемо допустиме навантаження [Р]
Небезпечним перерізом буде, очевидно місце закріплення балки де діятиме мак симз іьннй згинальний момент =• Рі Момент опору в цьому разі
Небезпечними точками в балці будуть верхня та нижня точки перерізу в міси! закріплення умова міцності для яких запишеться так
„ - - аар<—^.О|
От» —— яО’ (І — а4) 101
ІР
ИІІІИІІІИІІІІІІН.І
ї,6н___________
Рнс 255
Звідси
Рі - лД‘(1 ^а-) |д|
Примаж 40 На балку (рис 256) дів навантаження 100 кН, рівномірно розподілене по прольоти Матеріал балки СтЗ (Іо) =» 160 МПа) Треба добрати різні варіанти перерізів балки На рис 256, а з горизонтальними осьовими лініями показано нейтральні
0 Є Ж З Рис. 256
лінії.
Небезпечний переріз розмяд>ваноі балки буде посередині прольоту в місці дії максимального згннаїьного моменту
ді* ді І
Л1гаах 8	8
Небезпечними точками нього перерізу будуть гочкн найбільш віддалені від иеЙ траіьноі лінії Умова міцності для них така
- М1Г1°' а; І°І - ібо мла
Звідси знаходимо потрібне значення моменту опору
",= 125
Знайдені розміри перерізу як звичайно округлюють до найближчих стандарт них тому фактичний момент опору V може відрізнятися від розрахункового <ГС01р. У результаті напруження а небезпечній точці бу .е відрізняіиен від (оі і отже, буде маги місце перенапруження (б0 > 0) або недоиапруження (б0 < 0) де
4„ = °т” ~|а| 100 „ -	~	100 % -
111	""іпах^розр
V —V ~	№ 100 %
Прн розрахунках на міцність відхилення розрахункових напружень від допу стимнх мають бути в межах ±5 °,Ь значення допустимих напружень
Щоб порівняти ваги балок різних варіантів перерізів, ураховуючи що вага пропорційна площі Р перерізу визначимо також і площу Р Для більшої наочності зло буті розрахунком розміри поперечних перерізів будемо округляти до найближчих бітьшнх цілих чисел, а для стандартних профілів брати найближчий профіль з біль шнм моментом опору.
Перейдемо до розрахунків
І Для перерізу показаного на рис 256 а
V =»	> 125 см» 4 > і/ 32 см “ 10 83 см
32	г я
Вибираємо 4 =» 11 см =» 110 мм тоді
?^.Р. - 130 5 см», 50 - 125100 % - - 4,2 %•
Р = я п* см’ - 95,0 см».
2 Для перерізу показаного на рнс 256 б
07 = 6І2й)* -4-5* >125 см», 5 > ^"ІвТЛ см - 5,72 см.
6 З
Вибираємо 5 =» 6 см =» 60 мм тоді
07 = А 6» см* - 144 см»,
З 125 — 144
бв =----------- 100 % - — 13 2 % Р - 6 . 12 см’ - 72 см’.
З Для перерізу показаного на ряс 256. в,
07 = 26--1-6»> 125 см», 5>у^375 см — 7,21 см 6 З
Вибираємо Ь = 7 5 см — 75 мм тоді
Г- -у 7,5» см» =» 140 5 см» 60 -	100	— II %
Р-7 5 15 см» - 112 5 см*
4	. Для перерізу у вигляді двотавра (вибираємо двотавр № 18) наведеного на рнс 256 г
V = 07, = |43см»; б„ -	‘.І3 100 % - - 12.6 %. Р - 23 4 ом»,
5	Для перерізу показаного на рве. 256 д, прийнятними виявляються профілі № 50 тн 55 перший з яких дає незначне перенапруження (1 6 %), а другий мве помітний надлишок міцності (16 7 %) вибираємо двотавр № 50 Тоді
07 = 07, = 123 см», 6„-	100 %- 1 6 % £= 100 см*
6	Для перерізу у вигляді двох двотаврів (рис. 256, е) прийнятним профілем буде двотавр № 14 У цього перерізу
07 = 207,- 2 8|,7 см» =» 163 4 см»,
6а = 'М 4 100 % - - 23,5 %,
Р<=2 17,4 см* — 34,8 см»
7	Для перерізу показаного на рнс 256, ж момент опору всього перерізу не дорівнює сумі моментів опору 07, кожного профілю а має визначатися діленням мо-
Таблиця 15
Переріз па рис 25В	Відхиленая «Ід розрахункової МІЦНОСТІ %	Площа перерізу ем*	Відносні вага
4,2	95	0	4	06
13,2	72	0	3	06
11,0	1|2	5	481
12 6	23,4	1	00
1,6	100	0	4	27
23 &	34,8	1	49
14 7	29,4	1	26
5,3	26,8	2	65
мейту інерції перерізу відносно нейтральної лінії на відстань від нейтральної лінії до крайніх волокон тобто на висоту одного профілю
т _ 2(4+04/2)*^)
йі
де Л, П7, — відповідно висота площа перерізу момент інерції та момент опору одного двотавра
Виберемо двотавр № 12 Для нього
Ц7 =а 2(350 4.6» 14 7) в 146 в см,
12
в. =» І28,Т І46.6 100 % “ — И 7 % Р « 2 . 14 7 см» « 29 4 см’
146 о
8 Для перерізу у вигляді двох рівнобоких кутників (рис 256, з) момент опору дорівнює сумі моментів опору кожного профілю Але в тиблицнх сортаменту для кут ників значення V немає Тому визначаємо момент опору перерізу як
П7=»2—А_
де З, Ь г» мають той самий зміст що і в таблицях сортаменту (небезпечними точками будуть нижні кінці кутників)
Безпосередньо визначити який саме профіль слід взяти важко, тому розглянемо два варіанти перерізів
і) для кутника 140 X 140 X 12
97-2	см» "• 119,3 см»
14 — 3,9
2) для кутника 160 X 160 х 10
»-2
Останній енріантз погляду міцності кращий Маємо
Г- 132 см» 5^2.31,4 см’^ 62 8 см».
а°° 125їа'32 %--53я
Результати розрахунків зведено в тнбл 15, котра дасть змогу вирішити які здобутих перерізів раціональні а які ні Так, з останньої графи бачимо в скільки
разів балка того чи іншого перерізу важча ніж двотаврова балка (рис. 256 е) вага якої виявилася найменшою тому взята за одиницю
Закінчуючи дослідження напруженого стану в балці прн згинанні, зробимо ще деякі додаткові зауваження та доповнення щодо згинання балки прямокутного поперечного перерізу (рис 257, а) Епюри нор мальних о та дотичних т напружень в перерізі п — п наведено відповідно на рис 257, б та а За значеннями напружень о та т в кожній точці по висоті перерізу п—л можна визначити головні напруження розтягальні Оі та стискальні о8, епюри яких наведено на рнс 257, г та д відповідно
За напруженнями о, та оа (або а та т) в кожній з точок по висоті балки можна знайти також максимальні та мінімальні дотичні напру ження, які діють в перерізах, нахилених під кутом 45е до перерізів з головними напруженнями 0! та аа в цій точці Ці дотичні напружен ня визначаються за формулою
Тгмх = ± А а> або Тви, = ± тіп	тіп *
Епюри дотичних напружень Тпих та Ттіп наведено на рис 257, етазю відповідно
Зазначимо що при поперечному згинанні (коли М 0, ф 0) в точках на нейтральній лінії абсолютні значення т, 0!, оа, ттІп, Тт« будуть однакові
Перевіряючи міцність балки, визначають головні напруження Іноді важливо знати також і напрями головних напружень в усіх точ ках балки Зокрема, це необхідно при конструюванні залізобетонних балок, в яких арматуру треба розміщати в напрямі дії найбільших розтягальних напружень, тобто в напрямі дії 0£
Щоб пояснити сказане розглянемо напрями головних напружень в різних точках деякого перерізу І балки (рнс 258) Тонкими лініями показано напрями а!, а товстими — о8 Продовжимо напрям 0! для точки 2 до перетину з суміжним перерізом в точці 2' У цій точці ви значимо знову напрям розглядуваного головного напруження і, далі робтячи так само, дістанемо ламану лінію 2 — 2 — 2і — 2" В гра
Рис 259
ниці ця ламана лінія перетвориться на криву, дотична до кожної точ кн якої буде збігатися з напрямом відповідного головного напружен ня в точні дотику Цю криву називають траєкторією головного напру ження Напрям траєкторії головних напружень залежить від виду навантаження та умов закріплення балки Очевидно, через кожну точ ку балки проходять дві траєкторії головних напружень (відповідно °і та аз) які перетинаються між собою під прямим кутом
У залізобетонних балках арматуру прагнуть розміщати приблизно в напрямі траєкторій головних розтягальних напружень (Ті (рис 259)
$ 63 Про раціональну форму перерізу балки
У § 60 вже йшлося про раціональну форму перерізу баток прн чнс тому згинанні Тут па підставі розглянутих прикладів розрахунку на згинання цю проблему розглянемо дещо докладніше
Іноді крім форми перерізу балки велике значення має його оріен тування відносно силової площини Як видно з табл 15, найбільш ра ціональним е двотавровий переріз, поставлений так, що його нейтрали на лінія збігалася з віссю, відносно якої .Ц — ./тв* Гірший буде переріз складений з двох двотаврів, поставіених поряд або один на інший Значно гірші будуть перерізи з двох рівнобоких кутників та прямокуїннй Нераціональний також круглий переріз оскільки вага балки такого перерізу майже в 4 рази перевищує вагу рівноміцної балки двотаврового перерізу, що має ту саму міцність Тому вибір круглого перерізу може бути виправданий тільки конструктивними або технотогічними міркуваннями (наприклад, для о юртових деталей) Зовсім нераціонаїьний переріз, орієнтований так, що нейтральна лі нія збігається з віссю Ут|0 (варіанти в та д на рис 258 та в табл 15)
Рис 260
Зазначимо також що коли в умові міцності
От»х = М/ЇР ^(0)
максимальне напруження близьке до допустимо го, то це не означає, що переріз добрано вдвю оскільки при іншій формі перерізу та значно меншим От.' балка може виявитися набагато легшою
Викладені висновки випливають з розгляду
прикладу 40 Ці висновки справеїливі для будь якої балки, яка за знає плоского згинання та виготовлена з пластичного матеріалу оскільки характер навантаження та схема балки впливають тільки на значення розрахункового згинального моменту
Для балок, виготовлених з крихкого матеріалу, висловлені рекомен дації втрачають силу оскільки для нього допустиме напруження па розтягання |о, 1 значно менше ніж допустиме напруження на стис канпя Іо І У цьому разі недоцільно вибирати перерізи нейтральна лінія яких є віссю симетрії перерізу і, отже максимальні напружен ня в розтягнутих та стиснутих зонах однакові Раціональний такий переріз В ЯКОГО Опи> У роЗТЯГНуТІЙ ЗОНІ ЗНЗЧН0 менше, НІЖ (Ттах В СТИСН) -тій зоні Досягти цього можна, вибираючи таку форму перерізу, при якій нейтральна лінія була б зсунута в бік розтягнутої зони Приклад такого перерізу та відповідну епюру напружень а показано на рис 260
У цьому параграфі було розглянуто деякі питання, пов язгчі з раціональною формою перерізу балки Якщо ж говорити про раціо на льність балки в цілому то слід мати на увазі, що М та ф неоднакові в різних перерізах по довжині балки Тому розміри, добрані за не безпечним перерізом, виявляються занадто великими для інших перерізів балки Ці обставини спонукають з мстою економії ваги та матеріалу застосовувати балки змінного перерізу Основи розрахунку таких балок розглянуто в § 69
$ 64 Повний розрахунок балок на міцність
Усі розглянуті приклади розрахунку на міцність при згинанні належать до тих випадків, коли небезпечною е одна з точок крайніх волокон балки (див рис 253, б) і напруженийстан в ній лінійний (див рис 254,а) Якужезазпачалося здебільшого такого розрахунку досить
Проте хоч і нечасто а ле буває таке, коли небезпечна точка належить нейтральному шару В ній матеріал зазнає чистого зсуву (див рис 253, б та 254. б) і для розрахунку слід використовувати умови міц пості (10 29) Така ситуація може бути тоді коли при великих попереч них силах в перерізах балки діють незначні згинальні моменти паприк лад при коротких прольотах і значному поперечному навантаженні
Приклад 41 Пабалку (рис 261) дів рівномірно розподілене навантаження ч -> — 120 кН м Прольот І - 70 см, переріз балки двотавровий матеріал СтЗ (|о| -= 160 \(Па |т] — 100 МПа) Треба добрати розміри балки
Виберемо переріз балки з умови міцності за нормальними напруженнями
Найбільший згинальний момент будевссреї ньому перерізі балки
М.....°	° 120 ? кН м = 7 35 кіі м
З і МОВИ МІЦНОСТІ
Г«—-ШДІ-	7 35 «* = 46 10“вм8 = 46см»
|о|	160 10а
За таблицею сортименту вибираємо двотавр № 12 в якого V — 58.4 см’ а 2	350 см*
Найбільша поперечна сила буде в опорному перерізі
“ 4-------«И “ <2 «Н
Перевіримо міцність балки ва дотичними напруженнями Умова міцності, згідно а формулою (10 29) має вигляд
Ширина перерізу по нейтральній лінії Ь — 0 48 см (у сортаменті вона позначена літе рою<0 За таблицею сортаменту знаходимо що 5т±х — 33 7 см* Підставивши числові значення в останню формулу матимемо
і_ак == 42	33 7 І0~8 мп _ 84 2- п ( _ 1(Х) МІЬ
так 0,48 10“2 360 ІО"8	‘
Отже розміри перерізу балки задовольняють умови міцності як за нормальним, так і за дотичним напруженнями
Приклад 42 Треба вибрати двотавровий переріз для балки, показана на рис 262, а Матеріал балки СтЗ (|а! = 160 МПа, |т] “ 100 МПа)
Побудувавши епюрн 5 та М, робимо висновок шо небезпечними можуть вияви тнся такі точки баткн
а)	крайні точки (рис 262 б точка /) перерізу С
б)	точка розташована в місці з єднання стжкн з полицею (рис. 262 б, точка 2) в перерізі праворуч від опори А.
в)	точка що лежить на нейтратьній лінії цього самого перерізу (рнс 232 б точка 5)
Доберемо поперечний переріз балки вважаючи небезпечною точку 1 в перерізі С, З умовк міцності (10 28) маємо
,0-4 «•“«»»•
За таблицею сортаменту знаходимо потрібний профіль № 33, в якого V — =» 697 см* Тоді напруження в точці 1
от„ 96 10~* МПа - 160,8 МПа “	597 ІО"8
Це більше за допустиме, але перенапруження становить всього 0 5 %
Тепер знаходимо геометричні характеристики двотвнра № 33, потрібні для перевірки міцності в точках 2 та 3 перерізу 4 Згідно з таблицею сортаменту
2- 9840 см4; 5тх-339 см»,
9*
259
ширина перерізу стінки що відповідає точкам 2 та ? 4 — 07см Знаходимо
$п = (4 і 12 15 94 см* = 250 см»
Перевіряємо міцність у точці З перерізу балки безпосередньо праворуч від опори А За умовою міцності (10 29) враховуючи що(?гпвх = 191 4 кН знаходимо
„ '8' <	1 ™	! МПа - 94 2 МП. < _
М 0 7 Ю"2 9640 ІО"8
100 МПа
Перевіряємо міцність у точці 2 цього самого перерізу Матеріал СтЗ пласгвчнвй, тому скористаємось умовою міцності (10 34) за четвертою теорією міцності
°«.ІУ “ И о’ 4- Зт» < [с]
У перерізі діють
М-87ІКН м та 0= Ст„ =191 4 кН
Тому в точи! 2
о =	= 871 1.07а (16 5-І 12) ІО-2 МПа и 136 !
'	9840 ІО"8
вім*5» „ І91Л Ю~3 25° Ю?
М 0 7 іО-2 9840 10-8
МПа = 69 З МПа
°«віу =• /а14-3? = о |/" І + З -2І. = 136,1 /Г+З 0,259 МПа =
= 131 4 МПа > {аі = 160 МПа
Отже у вибраній балці небезпечною виявилася точка 2 перерізу праворуч від опори А причому перенапруження в ній становить 14 % то недопустимо Тому за місгь профілю № 33 слід взяти профіти № 36
Слід зазначити що в балках з тонкими стінками (двотавр швелер) небезпечною може виявитися точка розташована в місці з’єднання стінки з полицею Це буває тоді, коли до балки прикладене значне поперечне навантаження, причому є перерізи, в яких М та ф одночасно великі Один з таких перерізів і буде небезпечний
Отже якщо баїка має тонкостінний переріз і до неі прикладені оіачні поперечні навантаження то слід виконувати повний розраху цок на мііиіїсті. Якщо розрахунок проектувать»»#. то спочатку міжіи іобрігн переріз за основною умовою міцності (10 28), а потім і іііс Ніни шрінірку п нсімп умовами міцності
$ 65 Концентрації напружень при згинанні
Прн згинанні як і при розтяганні або крученні, в місцях різко? зміни форми або розмірів поперечних перерізів спостерігається концентрація напружень Якщо навантаження статичне, то концентрація напружень в деталях з пластичного матеріалу не небезпечна завдяки перерозподілу напружень у зоні концентрації внаслідок текучості матеріалу При крихких матеріалах, коли не доводиться розрахову вати на обмеження максимальних напружень оскільки рівень остан ніх буде визначатися тимчасовим опором матеріалу, при розрахунку деталі на міцність слід ураховувати концентрацію напружень
Залежно від ступеня різкості порушення форми або суцільності матеріалу по довжині буде той чи інший ступінь концентрації напружень, тобто локальне підвищення напружень
На рис 263 наведено епюри нормальних напружень, які виникають в стержнях, якщо немає концентрації напружень (рнс 263, а) та якщо є концентрація (рис 263, б) В останньому випадку внаслідок різкої зміни перерізу вала в крайніх волокнах перерізу діють максимальні напруження
Оте* в СЮя, де о, = М№ — РІ/Ф — номінальні напруження, якщо немає концентрації а — теоретичний коефіцієнт концентрації, значення якого залежить від співвідношення діаметрів Л та й спряжуваних ділянок стержнів а також від радіуса заокруглення г у місці спряження цих ділянок
Значення а залежно від 4/£> та г визначаються методами теорії пружності і наводяться в довідковій літературі у вигляді відповідних графіків чи таблиць Зокрема, для круглої галтелі прн відношенні О/й “ 3 та 1,5 на рис 254 наведено графік залежності теоретичного . коефіцієнта концентрації а від відно*
шення гІЛ
Я 		_ * 3 		 || 1	1 ?те°0'" *	б Рнс 253	—	Розглянемо й інші типові випадки концентрації напружень при згинанні ’ <6=^4 		3 за — Кругла галтель 2 £	1 1111 —	а '	стффдф 0	0.1	0,2	0,3 Л4 -С а Рис 264
(рис 265) Із збільшенням глибини
двобічної' симетричної виточки ко	А/у
ефінієпт концентрації наближається
до свого граничного значення При	^нс
цьому внаслідок так званого закону
затухання згідно з яким чим більше максимальне напруження в місці концентрації тим різкіше затухання напруження при віддаленні від найбільш напруженої зони, істотно впливає на коефіцієнт концентрації тільки кривизна біля дна виточки Форма решти виточки мало впливає на коефіцієнт концентрації Враховуючи останнє і вважаючи, що вн точка має форму гіперболи, формулу для визначення максимальних напружень у зоні концентрації, виведену в теорії пружності для випад ку чистого згинання (рнс 265) можна записати у вигляді
Ощах =	4а'р^-------,	(І0 37)
в ЗІ^а'р + (а/р — 1)апійКа/р1
де аа =* ЗМІ2агсі — номінальне напруження (без урахування концентрації)
На рис 267 зображено залежність найбільшого напруження від а/р, а на рис 258 показано криві теоретичного коефіцієнта концентрації а для різних співвідношень НІН залежно від р/Л
Круглі та довгасті отвори в дуже широкому стержні (рис 269) Припускається, що велика вісь отвору збігається з віссю стерж ия або перпендикулярна до неї Нарис 269 наведено графіки розподі
лу напружень для випадку, коли //р — 25 При переміщенні від дна
па швидко зменшується Напруження показані штриховою лінією, відповідають результатам, здобутим на підставі елементарної теорії згн нання з урахуванням ослаблення стержня внаслідок висвердлювання отвору Для найбільшого напруження яке виникає біля дна виточки, форму па може бути записана у вигляді
= а» (1 + УЇІІЇ.	(10 38)
Де
_ ЗМІ
“ 266» ’
6 — товщина стержня
Залежність найбільшого напруження від 1/р показано на рис 270. Для круглого отвору Отая = 2о„ Якщо довгастий отвір розташований паралельно осі стержня концентрації напружень біля отвору немає
Глибока зовнішня кільцева виточка на тілі обертання (рис 271) Найбільше напруження при згинанні виникає на дні виточки, де ма теріал перебуває в плоскому напруженому стані Нарис 271 показано
Перерв ї о Рис 271
О 0,2 ОЬ 06 0,8 £ Рис 273
розподіл напружень а1т о8 і а3 в точках по поперечному перерізу в місці виточки а на рис 272 дається розподіл напружень ст1 та а, на дні виточки залежно від співвідношення а/и при різних коефіцієнтах Пуассона
Вельми поширеним концентратором напружень в машннобуду ванні є різні поперечні отвори в деталях круглого перерізу, які пра цюють на згинання При цьом) коефіцієнт концентрації напружень залежить від відношення діаметра поперечного отвору до діаметра деталі О Залежність а =- / (гі/О) наведено на рис 273
Поширеними концентраторами напружень у різних деталях машин е також різного типу мілкі виточки на круглих деталях, що приводять до східчастості стержнів Коефіцієнт концентрації в цьому разі зале жить в основному від співвідношення радіуса заокруглення г та мен шого діаметра східчастого стержня (діаметра виточки ф На рнс 274 наведено графік залежності а — / (гіф для розглядуваного випадку
Крім концентрації нормальних напружень при згинанні іноді спостерігається концентрація дотичних напружень, зокрема при по перечному згинанні кутниковнх, швелерних, таврових та двотаврових балок у цих випадках концентрація напружень обумовлюється різкою зміною товщини елементів перерізу балки в місцях з'єднання поли ці зі стінкою
Як свідчать детальні дослідження картини розподілу дотичних напружень при згинанні наприклад у балці двотаврового перерізу, фактичний розподіл дотичних напружень не відповідає картині, на веденій на рис 275, а, яку здобуто на підставі розрахунків за формулою (ІО 20) По лінії /—/, яка збігається з віссю симетрії перерізу, розпо діл дотичних напружень з достатньою точністю зобразиться графіком рис 275 б По лінії ж 2—2 яка проходить по самому краю перерізу, розподіл напружень г при мало
Іг_____1'	__ 2 2________ му радіусі заокруглення в місці
С Р А~~ з’єднання стінки з полицею зоб
—ЦІ  римі гдаД І ряаЛ	ражатиметься кривою, показа
І|І	І -/ І / |_ и І /	ноюна рис 275 в 3 цього графі
іТ”1 *—1'	-	— ка видно що в точках вхідних
г‘ а 6	г	кутів перерізу дотичні напружен
Рис 275	ня теоретично досягають дуже
великого значення На практиці ні вхідні кути округляють напружен ня при цьому різко падають, і їх розводі т в точках лінії’ 2—2 наближено можна зобразити кривою, наведеною на рис 275 г
В у сіх випадках значно зменшити концентрацію напружень можна, вводячи відповідні плавні переходи від одного розміру перерізу до іншого, закругляючи кути зменшуючи жорсткість масивнішої частини дтілі в місці переходу і т п
Якщо при статичному згинанні концентрація напружень не е небезпечною особливо для елементів конструкцій виготовлених з пластичних матеріалів, то при динамічних та повторно змінних навантаженнях питанням концентрації напружень слід приділяти особливо велику увагу (див гл 21)
$ 66. Диференціальне рівняння зігнутої осі балки
У попередніх параграфах було розглянуто питання, пов’язані з розрахунком балок на міцність Здебільшого при практичних роз рахунках деталей, які працюють на згинання, треба також виконувати розрахунок на жорсткість. Під розрахунком на жорсткість ми розу~ міємо оцінку пружної піддатливості балки під дією прикладеного навантаження та добір таких розмірів поперечного перерізу, при яких переміщення не буде перевищувати встановлених нормами границь Для виконання такого розрахунку треба навчитись обчислювати переміщення точок балки під дією будь яких зовнішніх навантажень Таке вміння необхідне також для розрахунків статично невнзначува них балок
Розглянемо деформацію балки при плоскому згинанні Вісь балки (рис 276) під дією навантаження в одній з головних площин інерції (в площині хОу) викривлюється в тій самій площині, а поперечні перерізи повертаються і одночасно дістають поступальне переміщення в напрямі осі у Викрив ієну вісь балки називають зігнутою віссю або пружною лінією На рис 276 та 277 зігнуту вісь зображено кривою лінією
Переміщення центра ваги перерізу в напрямі, перпендикулярному до недеформованої осі балки, називається прогином балки в даному перерізі й позначається літерою ш На рис 276 та 277 центр ваги довільного перерізу, взятого завдальшкн х від початку координат, перемістився по вертикалі з точки Оі в точку О, на відстань 0,0, Це пере-
Рнс 276
Рнс 277
Ряс 278	Рис. 279
міщення і є прогином балки ш (х) в перерізі з абсцисою х Найбільший прогин балки називається стрілою прогину і позначається літерою [
Кут 6. на який кожний переріз повертається відносно свого початкового положення, називається кутом повороту перерізу Кут повороту також може бути визначений як кут між дотичною до пружної' лінії й віссю х (рис 277)
Зазначимо, що довжина зігнутої осі що належить нейтральному шару, при викривленні бр>са не змінюється, отже при цьому від буваеться зміщення її точок також у напрямі осі х (переміщення О(Оа иа рис 278) Проте здебільшого зміщення V такі малі що ними можна нехтувати
Домовимось осі координат завжди розміщати так початок коорди нат поміщати на лівому кінні балки, вісьх спрямовувати по осі балки праворуч а вісь щ — вгору
Прогин Л) будемо вважати додатним якщо переміщення відповідної точки відбувається вгору тобто в напрямі осі ш Кут повороту в будемо вважати додатним при повороті перерізу проти годинникової стрілки
Внаслідок малості деформації балок можна вважати,що
Оскільки тангенс кута повороту е похідною від ординати прогину.
(10 39) то з достатнім ступенем точності можна вважати кут повороту в (х) в даному перерізі таким, що дорівнює похідній прогину иі (х) по абсци сі перерізу
(10 4°)
Отже, для визначення деформації балки в її довільному перерізі треба перш за все здобути рівняння пружної лінії
и> = Г (х)
Виходячи з фізичної природи зігнутої осі балки, можна стверджу вати що пружна лінія має бути неперервною та гладенькою (без будь яких зломів) кривою, отже, вздовж всієї осі бруса повинні бути неперервні функція ц> та її перша похідна Прогини та кути повороту і е переміщеннями перерізів балки прн згинанні Деформація тієї чи
іншої ділянки балки визначається викривленням її зігнутої осі, тоб то кривизною Оскільки вплив поперечної сили на кривизну балки незначний то в загальному випадку поперечного згинання рівняння (10 9) можна записати у вигляді
З курсу вищої математики відоме таке рівняння кривизни плоскої кривої)
№
(10 42)
Тепер для здоб) ття диференціального рівняння зігнутої осі балки зєли шається прирівняти праві частини рівнянь (10 41) та (10 42), з’ясував ши попередньо питання про знаки
Якщо згинальний момент додатний, то пружна лінія своїм угнутим боком повернута вгору (рис 279, а) і отже, при взятому напрямі координатних осей кривизна к — 1/р вважається додатною При від’ємному згинальному моменті кривизна теж від’ємна (рис 279, б) Якби вісь щ була спрямована вниз то при додатному згинальному моменті кривизна була б від ємною (рис 279, в) а при від ємному моменті — додатною (рнс 279 г)
Зберігаючи вибраний нами напрям осі ю вгору, маємо відповідність між знаком моменту та знаком кривизни, тому можна просто прирівня ти праві частини рівнянь (10 41) та (10 42) Тоді
(10 43)
Коли б вісь и> була спрямована вниз то в правій частині треба було б поставити знак «мінус»
Рівняння (10 43) називають точним рівнянням зігнутої осі балки (бруїа) Воно е нелінійним диференціальним рівнянням другого порядку, інтегрувати яке, як відомо досить важко Внаслідок цього та оскільки в переважній більшості розглядуваних на практиці задач прогини малі точне рівняння (10 43)замінююті наближеним — рівняй ням для малих переміщень
У знаменнику рівняння (10 43) стоїть сума двох доданків
 + Ш =1 ї
При малих деформаціях значення другого доданка в багато разів менше ніж першого Дійсно при розрахунках звичайних машино будівних чи будівних елементів норми допустимого прогину станов
лять 1/100 Л/ЮОО прольоту залежно від умов роботи балки а відповідні кути повороту не перевищують 1° На віть при максимальному прогині (/ = = //100) найбільший тангенс 6 буде такий
Отже, значення не перевищує 0 0004, тобто дуже мале порівняно з
одиницею Тому цими величинами можна знехтувати без відчутної для практичних цілей помилки ТодГ дістанемо спрощене диференці альне рівняння пружної лінії
Рнс 280
в якому згинальний момент М (х) визначається для недеформованої балки Відтак рівняння (10 44) будемо називати основним дифврен ціальним рівнянням пружної лінії балки (для малих деформацій) За його допомогою можна обчислювати лінійні та кутові переміщення в балках за будь яких умов навантаження
Розв'язуючи задачу аналітичним методом кути повороту 6 (х) та прогини иі (х) обчислюють послідовним інтегруванням основного диференціального рівняння (10 44) Проінтегрувавши рівняння пер ший раз матимемо вираз для кута повороту в (х)
Є«-ТГ=$-І7ІіН+С.	0045)
який містить у собі одну довільну сталу С Інтегруючи другий раз, знаходимо вираз для прогину о> (х)
»И-р«У-ІЩ-Д|: + Сх + О, (10 46)
де е дві сталі С та О Значення цих сталих визначають з умов закріп лення балки
а)	якщо балка має на кінці закріплення (рнс 280), то прогин та кут повороту в ньому дорівнюють нулю
щв = 0, 6в = 0,	(10 47)
б)	для балки на двох шарнірних опорах (див рис 277) дорівнюють нулю прогини на цих опорах
шд = 0 ща = 0	(10 48)
Зазначимо, що рівняння пружної лінії іноді зручно записати в іи шій формі вважаючи заданим не момент ЛІ (х), а навантаження д (х) Пригадавши, що сРМ (х)/4х* = д (х), та продиференціювавиїи рівняння
(10 44) двічі, матимемо
1?-|£;ИТ?-|-’И	(Ю49)
Рівняння пружної лінії у формі (10 49) використовують при роз рахунках балок на пружній основі та при розгляді коливань бачок
$ 67. Приклади визначення переміщень Інтегруванням диференціального рівняння зігнутої осі балки
Розглянемо кілька прикладів визначення деформацій балок методом безпосереднього інтегрування основного диференціального рів няння (10 44), а потім виведемо правила побудови епюр кутів по вороту та прогинів які потрібні прн дослідженні деформованого ста ну балок при складній системі навантажень
Визначимо бттмх та Шт,х ДЛЯ консолі постійного поперечного перерізу, навантаженої зосередженою силою Р на її вільному кінці (рис 280)
Згинальний момент у перерізі х будемо обчислювати як наслідок дії зовнішніх сил ліворуч від перерізу
М (х) = — Рх
Підставляючи вираз для М (х) в рівняння (10 44) маємо
_ Рх 4*» ~ ~ Е^
Інтегруємо двічі
Ш (X) = —	Сх + О
Для визначення сталих С та О маємо граничні умови
1) при х — І и> = 0,
2) при х = і Є — 0
З другої умови
е« = --йт-> с '*• звідки
С = ТҐГ	1'° 50>
Тоді
Рис гаї
З першої умови »«>--'Й7- + тЙт'-£’-0 звідки
О=--Й7	<‘051>
Остаточні рівняння прогину та кута повороту такі
І»М = --5£7(л>-ЗЛ<+2(,) = = ~ег[2-3т + (т)*| <10 52) е И = - -5І7 (X' - П г =^г['	<|053)
Як видно з (10 52), пружна лінія балкн є параболою третього порядку
Тепер можна визначити шш»» із ©т,і Легко переконатися, що №п«х та Отих мають місце на вільному кінці балки в точці А (при х = = 0) Отже,
№.... = !л = -	,	(10 54)
©гпхх «= ©Л = -257
(10 55)
Від’ємне значення /д показує, що прогин відбувається в напрямі, протилежному напряму осі ш (гобто вниз) Додатний кут повороту ©д показує, що переріз повертається проти годинникової стрілки
Порівнюючи вирази (10.60), (10 51) для довільних сталих з (10 55) та (10 54) для Є (0) та и> (0), переконуємося, що С дорівнює куту повороту на вільному кінці консолі (при х = 0), а О характеризує прогин вільного кінця консолі (при х — 0)
Побудуємо епюри прогинів та кутів повороту для простої балки постійного перерізу (рис 281) до якої прикладено суцільне рівномірно розподілене навантаження ц
Опорні реакції
Ял — Яв = <?//2
Згинальний момент у довільному перерізі
Складаємо диференціальне рівняння зігнутої осі .і /9/	є*1 \
£7 \ 2	2 ] •
Інтегруючи його двічі, маємо
('°ЗД
'»« = -і2їз-^-тгет"‘+с'-0	<І057>
Граничні умови такі
1) на лівому кінці-прогин дорівнює нулю тобто при х = 0 ш = 0, 2) на правому кінці прогин дорівнює нулю тобто прн х = і ш — 0 З першої умови маємо
ш(0)=й-0	(10 58)
Друга умова дає
“(') = -гап--ж-+с' = °,
ЗВІДКИ
С=~т^у-	(10 59)
Підставляючи здобуті значення довільних сталих у рівняння (10 56) та (10 57) дістаємо рівняння зігнутої осі балки
- м - -£г-&= - -&І [1 - 2 (т)‘ 1 (т)*1 “° м>
та рівняння куті повороту
«ги _	<&*	я**	о?
— іх ~~ Ш	ш	24£У =
(10 62)
“-тйф-Ч-т-Г И(тП о» 61)
Для побудови епюр Н(х) та и (х) визначимо кути повороту по кінцях балки а також проіин посередині прольоту и> (1/2) = [ Кути повороту на опорах знайдемо з рівняння (10 61) Прн х = 0 знайдемо кут повороту на лівій опорі
Єл~Є(0) = —
На правій опорі тобто при х — І
6(0 = 9,=.
Порівнюючи значення довільних стаїих С та й з виразами для 6(0) та ш (0) знову переконуємося що вони відповідно дорівнюють куту повороту і прогину на тій опорі де розташований початок коор динат
С-Є(0)---і-; 0-.»(0)=0
Рис. 282
Зазначимо, що таким буде геометричний зміст довільних сталих на ділянці, яка при* микає до початку координат для будь якої балки при до вільному навантаженні
Підставивши у формулу (10 60) х = //2, визначимо мак симальний прогин посередині прольоту
Г-~35Г-&	О»63)
З рівняння (10 60) пружної лінії випливає що балка згинається по параболічній кривій четвертого порядку Оскільки згинальний момент уздовж балки додатний, то це означає, що стиснуті верхні волокна і отже, балка згинається опуклістю вниз
Визначивши прогини в різних перерізах, відкладаємо їх у певному масштабі вниз від базисної лінії Сполучивши кінцеві точки відкла деких відрізків кривої, дістанемо епюру прогинів їй Ця епюра у вибраному масштабі відобразить зігнуту вісь розглядуваної балки
Для побудови епюри в відкладемо обчислені значення вд та ва від базисної лінії вниз та вгору відповідно 3 умови симетрії балки та навантаження випливає, що посередині прольоту балки (прн х » = 1/2) переріз балки повертатися не буде отже, 6(//2) = 0
Відповідно до рівняння (10 61) епюра кутів повороту по довжині балки буде окреслюватися параболою третього порядку Будуємо епюру по точках (рис 281), визначивши проміжні ординати
в(т)“—ЙГТ7"'
При цьому параболічна крива на лівій половині балки повернута угнутістю вгору а на правій — вниз
Розглянемо ше один приклад визначення переміщень Для простої балки постійного поперечного перерізу, навантаженої зосередженою силою Р в довільній точці С (рис 282), треба а) знайти рівняння пружної лінії та кутів повороту, б) обчислити прогини в точці С та посередині прольоту балки, а та кож визначити стрілу прогину / та її положення, в) обчислити кути повороту перерізів у точках А, В та С, г) побудувати епюри ЛІ в та и> взявши Р = 180 кН І = 6 м, а = 2,2 м, = 46 470 см4, £ = 2 104 МПа
Даємо змогу читачеві самостій но розв язати цей приклад За значимо лите, що на кожній з діля нок балки при інтегруванні диферен ціальних рівнянь пружної' лінії бу де знайдено по даі довільні сталі С|, Оі та Сц Для визначен ня їх до двох опорних умов балки иі (0) — 0 и. (/) -= 0 слід додати умо ви плавного та неперервного спря ження ділянок АС та СВ у точці С при х = а
0 (а)л1в «- © (а)Іф «'(а)лв=щ(а)пР Ці додаткові умови виражають від сутність розриву га злому пружної лінії' балки під силою Р
Для самоконтролю наводимо остаточні рівняння прогинів та кут
повороту для ділянки АС
И’(х)---^Г(а’+2а/>-хі)	(Ю64)
е(х) = --бйг<аІ“ 2о6-3хі)	(Ю65)
для ділянки ВС
«І (х) = -	1 - аЧ + («• + 2Р) X + х> - 31х>],	(10 66)
Є(х) = --Д1г(1.1 + 2Р-6ІХ -і-Зх")	(10 67)
Епюри С ЛІ, 0, © зображено на рис 283
Скористаємося результатами цього прикладу для того, щоб знайти абсциси перерізів з найбільшим прогином та значення І при різних поіоженнях вантажу Р на балці Найбіїьший прогин буде в перерізі з координатою х/ де
6(х/)=-^-=0	(10 68)
При а> Ь цей переріз розташовується на ділянці АС Прирівнявши до нуля рівняння (10 65), матимемо
=/2=2:	(1О69)
Простежимо, як буде змінюватись абсциса перерізу з найбільшим прогином при переміщанні сили Р від середини балки до правої опори При Ь -► 0 абсциса X/ = ІУ 3 » 0 577/ Отже навіть у граничному
випадку коли вантаж Р наблизиться до опори В, переріз Р з найбільшим прогином буде розташований від середини балки завдальшки
і -= 0 577/ — 0,5/ - 0 077/ = //13
Зазначимо що на такій самій відстані від середини прольоту має місце найбільший прогин і тоді коли баїка на двох опорах навантажена згинальним моментом, який діє на одну з опор (див рис 62)
Підставивши вираз (10 69) в рівняння (10.64) для пружної лінії на ділянці АС дістанемо формулу для и,™,, = /
і рь кг ,	«* 4 2а6 ) 1/ «Г+2вЛ
І = —---------------—) V —з—-
= р ь <а* 2аі>>3/г _ рь	(10 7П
913 Я «т»	9 3 £7	1	(	’
Прогин посередині пролюту знайдемо з рівняння (10 64) підста вивши в нього х = і/2
«(4)-—(Ю7)
Аналіз формул (10 69) та (10 64» показує, шо навіть при Ь -* 0 різниця між прогином посередині прольоту балки та максимальним прогином не перевищує 3 % Отже, прогин балки посередині прольоту (1/2) = / (//2) приблизно дорівнює найбільшому прогину І 1 (ей висновок справедливий при дії на батку будь яких навантажень, які сири чинюють згинання в отии бік
Здебільшого побудова епюр ш та в можіива і без складання ана літичних виразів для прогинів та кутів повороту по ділянках досить лише обчислити прогини та кути повороту для деяких характерних перерізів Проте при побудові епюр слід користуватися правилами, які можна здобути на підставі аналізу диференціальних залежностей, що існують між ш, 6 М та р Запишемо иі залежності в зручній для аналізу формі
З рівняння (10 44) з урахуванням виразу (10 40) знаходимо, що
Продиференціювавши рівняння (10 72) по х та враховуючи залежність дМ/іх — (}, дістанемо
_ <?иі “ Е]
(10 73)
Отже маємо дві групи диференціальних залежностей
гіе _ и (»)
йх “ Е1
<РЄ _ Р(Х)
Ах ~ Еі '
____________М (») Ах1 ~ Е]
(10 74)
(10 75)
аналогічних залежностям на підставі яких було здобуто правила по будови епюр 9 та М (див § 21)
Вирази (10 74), (10 75) а також зіставлення побудованих епюр д?є змогу встановити загальні для будь яких балок залежності між и, в, фтаЛІ, які далі будемо застосовувати як правила побудови епюр Зазначимо найголовніші з них правил
1	Оскільки М (х) є діаграмою похідної епюри кутів повороту в, то ординати епюри М пропорційні тангенсу кута нахилу дотичної’ до епюри в У перерізах, де М (х) = 0, дотична до кривої в - Р (х) має бути паралельна абсцисі (див рис 281 та 283 перерізи А та В). Стрибку на епюрі моментів відповідає кутова точка па епюрі 8 (рис 287, переріз С рнс 290, переріз О)
2	Якщо згинальний момент дорівнює нулю вздовж якоїсь ділянки балки то на цій ділянці епюра 8 прямокутна а епюра ш прямоліпій на, але. взагалі кажучи похила (рис 290 ділянка £>£)
З На ділянках, де діє постійний момент (на ділянках, що перебува ють в умовах чистого згинання) епюра 6 прямолінійна та похила, а епюра ці — параболічна (рис 290, ділянка ВО)
Тут виявляється протиріччя з висловленим вище твердженням що при чистому згинанні кривизна постійна (к = 1/р =- МІЕЛ = — сопьі) і балка згинається по дузі кола Це обумовлене наближеністю диференціального рівняння пружної лінії, кстрнм ми користуємося для виведення рівняння (10 72) Точно кажучи при чистому згинанні балка згинається по дузі кола яка в межах малих деформацій з дуже великою точністю може бути зображена квадратичною параболою
4	Друга похідна прогину
Д*№ М (х)
=—~еГ~
має знак моменту Коли момент додатний (стиснуті верхні волокна), то угнутість на епюрі а> буде повернута в бік додатних и> (вгору) При від ємному згинальному моменті угнутість параболи повернута вниз Оскільки ординати епюр згинальних моментів ми домовилися відкладати з боку стиснутих волокон (див § 20), то угнутість епюри прогинів и> завжди повернута в той бік з якого розташовані ординати епюри згинальних моментів У перерізах, де Діє зосереджений момент М маємо точку перегину пружної лінії (рис 287, точка С)
5	Друга похідна кута повороту
<?(х)
іх* ~ Е1
має знак поперечної сили Якщо 9 додатна, то опуклість на епюрі в буде повернута вниз (рис 283 ділянка АС рис 290, ділянки АС та СВ) При 9 < 0 опуклість спрямована в бік осі ш тобто вгору (рис 283, ділянка СВ) У перерізі, де 9 змінює знак, на епюрі 6 є точка перегину (рис 283, переріз С)
6	На тих ділянках балки де епюра М змінюється за лінійним за коном (ділянки АС та СВ на рис 283), епюра Є буде мати вигляд квадратичної параболи, а епюра и> — параболи третього порядку
7	Оскільки о є графіком зміни по довжині балки тангенсів кутів нахилу дотичних до пружної' лінії то можна стверджувати таке
а)	на ділянках, де в напрямі осі х прогин и> збільшується, кут нахн лу в додатний (рис 283. ділянка ВВ), при зменшенні ш кути нахилу в від’ємні (рис 283 та 290 ділянка АС)
6)	у перерізі, де 0 — 0 дотична до епюрн ш горизонтальна, тобто тут на епюрі ш має місце аналітичний максимум або мінімум (рис 283, переріз Г)
8	У тих перерізах, де на балці розмішено проміжні шарніри (рис 290 переріз О), на епюрі кутів повороту будуть стрибки На епюрі и> в цих перерізах мають місце переломи тобто кутові точки, в яких стрибкоподібно змінюється кут нахилу дотичної до епюри го
Зазначені особливості епюр дають змогу за їхнім виглядом з’ясувати, чи не допущено принципові помилки при побудові їх Кілька прикладів побудови епюр розглянуто в наступному параграфі
$ 68. Визначення переміщень у балках за методом початкових параметрів
Визначення переміщень в балках методом безпосереднього інтегрування диференціального рівняння пружної лінії у випадку балок з великою кількістю ділянок пов'язано із значними труднощами Ці труднощі полягають у техніці визначення довільних сталих інтег рування—складанні та розв'язанні систем лінійних алгебраїчних рівнянь Так, якщо балка за умовами навантажування розбивається на п ділянок то інтегрування диференціальних рівнянь для всіх ділянок балки дає 2л довільних сталих Додавши до двох основних опорних умов балки 2 (л — 1) умов неперервного та плавного сполу чення всіх ділянок пружної лінії можна скласти 2л рівнянь для ви значення цих сталих
Задача стає дуже трудомісткою вже при л = 3 Для зменшення великої обчислювальної роботи пов язаної з визначенням сталих інтегрування, останнім часом розроблено кііька методів До них у першу чергу, належить метод початкових параметрів, котрий дає змогу при будь якій кількості ділянок звести розв'язання ДО ВІДНІ 1 кання всього двох сталих — прогину та кута повороту на початку координат
Виведення загальних рівнянь та приклади застосування їх Роз глянемо якусь частину балки завдовжки (рис 284 а), обмежену двома перерізами, які проведено в точках К та Ь На рис 284, б зо бражено цей відрізок з прикладеними до нього найтнповішими наванта ЖЄіїНЯМИ
а)	зосередженим моментом М у перерізі з абсцисою а.
Рнс 284
б)	зосередженою силою Р у перерізі з абсцисою Ь
в)	навантаженням роз поділеним за законом тра пеціі від перерізу з абсци сою с до перерізу з абсци СОЮ (І, інтенсивністю
?(»)=?<+*(«- С)
де к —тангенс к^та 0 нахи ту дотичної до епюри наван таження (рис 284 а)
г)	крім того, по кінцях розглядуваної частини балки Ц прикладні поперечні сили та згинальні моменти, які замінюють дію уявно від кинутих частин балки
Виводячи рівняння напрями всіх навантажень виберемо такими, щоб вони спричинювали додатні згинальні моменти Зазначимо також що на розглядуваному відрізку може бути кілька зосереджених сил та згинальних моментів а також кілька ділянок розподіленого наванта ження На балці показано по одному із зазначених навантажень лише заради спрощення розрахунків
Щоб різко скоротити кількість невідомих довільних сталих, звівши розв'язання до визначення лише двох сталих інтегрування треба забезпечити рівність відповідних сталих на всіх відрізках балки Ця рівність може бути тільки тоді коли в рівняннях моментів кутів повороту та прогинів при переході від однієї ділянки до іншої повто рюються всі члени попередньої ділянки а доданки, що з'являються, перетворюються на нуль на лівих межах своїх ділянок Для забезпе чення цих умов при складанн днференціатьних рівнянь пружної лінії бачки за інтегруванні їх треба дотрим^ваїися таких правил
1	Початок координат слід вибирати в крайній лівій точці розгля дуваної балки та робити його загальним для всіх ділянок
2	Вираз для згинального моменту ЛІ (х) складати обчислюючи моменти сил ліворуч від розглядуваного перерізу
З При включенні в рівняння зовнішнього зосередженого моменту М його слід множити на множник (х — а)0, що дорівнює одиниці. Тут а — абсциса точки де прикладений момент М
4 У разі обривання розподіленого навантаження (наприклад у перерізі х = і рнс 284, б) його продовжують до кінця розглядуваного перерізу, а для відновлення дійсних вантажних умов введяїь «комленсувальне» навантаження зворотного напряму «Додаткове» та «комленсувальне» навантаження будемо показувати на кресленнях штриховими лініями
5 Інтегрувати рівняння на всіх ділянках слід не розкриваючи дужок
Отже, розглядаючи відрізок балки завдовжки та вибравши поча* ток координат у крайній лівій точці К (рис 284, б), складемо вираз для згинального моменту М (х) у довільному перерізі крайньої правої (У) ділянки, дотримуючись п 2 4 зазначених правил При цьому домовимося розбивати трапецієвидне навантаження на трикутне та рівномірно розподілене Згинальний момент запишемо так
М (х) - ЛІ,+ <?,»+М (г - ар+Р (г-»)+;,	-
(х —, ь <Х —<Р , (X — 4р	/1Л7Й1
— Ча---2---- *------6-----*----6---’	(10 7Ф
Розглядаючи рис 284, б, переконуємося в тому що вираз для зги пального моменту на ділянці IV легко дістати з рівняння (10 76), відкидаючи члени, які враховують навантаження лише на ділянці V
Дійсно вираз для згинального моменту на IV ділянці має вигляд
М (х) = Мо + Сох + М (х - 0)« + Р (х - Ь) +	+ А .
(10 77)
Слід пам’ятати, що вирази (х — а) (х — Ь), (х — с) , (х — /) можуть бути тільки додатними величинами Вираз (х — /)<0 означає що відповідне навантаження діє праворуч від розглядуваного перерізу і такий доданок має бути викреслений з рівняння
Згинальний момент Л1п та поперечну силу С}0, що діють в перерізі який збігається з початком координат, називають статичними початковими параметрами
Складемо диференціальне рівняння пружної лінії на ділянці Уі
-т£!- = тЯЛ’"+ <?’ + «(»-»>М Р(*-») +
. _	— ср (х — Ч)*	< іх ср , (х 4р |	/1П 7Я\
+ Чс---2------------6-----Ь * -б------*-----6---1
Проінтегруємо обидві частини рівняння двічі не розкриваючи дужок
е (х) =	- -±- [	4- <?. 4- и- М (х - о) + Р +
+ + + (»«)
«м - -Й- [«. 4+<г. -Т + «-4^ р 4^ -
+	4і (х 2/1 + * (ХІЯ)Х)— * т с',,:
(10 80)
Диференціальне рівняння пружної лінії на IV ділянці запишеться так
4.-^~ -‘-4—1	40 81)
Проінтегр>вавши його двічі матимемо
Є(х)-44 = 4|Л1«Л4-в.-4 «їх-»Н Р-Ц2-+
+ 4.41' ч к-^‘ +Сіу! (|о82>
"»(х)=4|лі.4-+<?»4ч м-4^- + р-4^--
+ 4. т ‘ -4г~ + Сі'х ь 0|ї]	<10 83>
Можна показати що дотримання правил складання та інтегрування рівнянь пружної лінії забезпечило рівність довільних сталих на IV та V ділянках Дійсно поклавши у виразах (10 79) та (10 82) х — д, з умов плавного сполучання ділянок IV та V дістанемо
р-4і!-+’'4а- +
+ ‘-42ї-с^]-Є(<Ч, =-4|м0<ї  ро 4- + М (4-а) |-
, „ (І-Ч- , . (1-е)’	_ (4-4Г . ь (4-а-
+ Р 2 + 4‘------б---41----6---+ ‘ й-----
-к +Су]	(10 84)
Отже
Су = Су
Поклавших — 4 у рівняннях (10.80) та (10 83), з умов неперервного сполучання ділянок и> (Фуі = ш(4)у знайдемо, що і О,у = Су
Виконавши аналогічні операції' для решти ділянок робимо висно вок, що відповідні довільні сталі однакові на всіх ділянках розгля дуваного відрізка балки
Сі = Сн — Сіп — Сіу = Су — С,	(10 85)
©і = ©ц = От — Оіу = £>у = О	(10 86)
Геометричний зміст цих двох сталих інтегрування визначимо, розглядаючи рівняння кутів повороту та прогинів на першій ділянці балки Викреслюючи в рівняннях (10 79) та (10 80) доданки які враховують навантаження прикладені на П V ділянках, дістанемо рівняння для першої ділянки
єи = ^!-=-^-[ліол: + <2,-4- + с]:	(Ю.87)
»М = -1-[м.4- + ‘?»4- + Сх + 0]	О»88)
Підставивши в ці рівняння х = 0, знайдемо
0 (0) = 60 = С/£/,	(10 89)
®(0)=щ0=О/£/	(10 90)
Отже довільні сталі С та О дорівнюють відповідно куту повороту та прогину на початку координат Прогин та кут повороту 0О е геомет ричними початковими параметрами
Підставивши сталі С та £) в рівняння (10.80) дістанемо загальне рівняння для прогину в довільному перерізі балки
»и=».+в^+ ^3-[ліс4-+й-ї- + Л’І;І^- +
+ Г 6	24	4 ~й 120 Я 120 І
(1091)
Для випадку кількох моментів і сил а також кількох ділянок розподіленого навантаження рівняння для а> (х) можна записати в такому загальному вигляді
» (х) » ш, + Є,х +	[ 1И,и.% £- + ЇМ +
> РП і* — Ь)1	V» (х ~ Є)*	V- (х—4)*
+	—зі------Т —їі-------^41 її----к
+	]	(>0 92>
Рівняння (10 92) як пра вн.то називають універсаль ним рівнянням пружної лінії При цьому мається на увазі що це рівняння придатне для будь яких розрахункових схем балок
Диференціюючи рівняння (10 92) дістаємо універсальне рівняння К)тів повороту пе рерізів
6 Рнс 285
+<2.4- + їм +ір +
+ £?. ‘У -ІЦ,	('7,СІ‘	‘-Т/*’] (109С)
У рівняння (10 92) та (10 93) підставляють тільки ті навантажеі ня які прикладені ліворуч від розглядуваного перерізу Знаки доданків визначаються знаками відповідних силових факторів
Отже визначення переміщень за методом початкових параметрів зводиться насамперед до визначення початкових параметрів Мц в0 Статичні початкові параметри С}0 та Л1о знаходять з умев рівноваги балки Геометричні початкові параметри Єота ш0 визначають з умов на опорах Рівняння (10 92) та (10 93), які виведено для довіль ного відрізка балки, придатні А для всієї балки в цілому Початок координат як правило будемо вибирати в крайній лівій точці балки
Розглянемо приклади визначення переміщень у балках за методом початкових параметрів
У консолі навантаженій рівномірно розподіленим навантаженням на половині довжини (рис 285, а) визначимо прогини в перерізах балки з абсцисами х — а та х — 2а
Запишемо рівняння пружної лінії для правої ділянки балки Оскільки розподілене навантаження обривається в точці С, продовжимо його до кінця бвлки одночасно вводячи компенсувальие наванта ження такої самої інтенсивності (рис 285 б) Рівняння пружної лінії в загальному випадку буде мати вигляд
ш (х) — ю0 + 6дХ —	-2|-	р0 —2і	д	д
(10 94)
З умов рівноваги балки визначаємо статичні початкові параметри
Ма = М„ = -4~. <2« = Кл=?а (Ю95)
шини
Й=~аІ	Оскільки початок координат
кв в " „ .2 збігається з жорстким закріплен ням балки, ю геометричні початкові параметри — кут повороту та прогин на початку координат — дорівнюють нулю
и>0 — 0, 60 =0	(10 96)
Підставивши в (10 94) значення початкових параметрів згідно з рівняння пружної лінії в остаточному
(10 95) та (10 96) матимемо вигляді
до1
^=1^] (10 97)
Поклавши в рівнянні (10 97) х -= 2а дістанемо формулу для прогину ВІЛЬНОГО КІНЦЯ консолі

Поклавши в рівнянні (10 97) х = а, дістанемо формулу для прогину в точці С
гВс~я — ~5ЕГ	(10 98)
У баші навантаженій за схемою рис 286 визначимо прогини та кути повороту в точках С та О
Запишемо рівняння пружної лінії' для крайньої правої ділянки балки (ділянка Вй де І < х 51/4) попередньо продовживши роз поділене навантаження до кіпця балки та приклавши компенсувальке навантаження
а> (х) = ша 4- ©(/ 4-	— Ял —з,- 4- Яв зі
. (х-02)* , . (х-04
-<?----ці----4 Я—зі—
Рівняння (10 99) записано з урахуванням того що статичні початкові параметри вже відомі
---Мо = 0
Для визначення геометричних початкових параметрів в0 та и>0 маємо }мовн на опорах
при х = 0	(0) — юд = 0
при х — £ и>(!) = и>в — 0
З першої опорної умови випливає що
= и>А = 0
Друга умова дає
* (/> - е„(+[ - х4 -, .ц®- ]=о, звідки
Тепер рівняння пружної лінії для ділянки ВО набирає вигляду , . І Г 57о/’	7 , ж* II (х — І)*
ш (х) — ЕУ [ 384 Х 8 Ч1 ЗІ + 8 91 ЗІ
+<?	(іо.іоо)
Щоб знайти переміщення точки О досить покласти в цьому рів* нянні х = 5/41 Тоді
<'Н^4-4Ж+тЖ-4(-І-)‘+
тобто
„-0,11(10 101)
Щоб обчислити переміщення точки С, треба записати рівняння пруж ної лінії для тієї ділянки де розташована ця точка Оскільки вона лежить на межі / та II ділянок, запишемо рівняння пружної лінії для першої ділянки Для цього в рівнянні (10 100) слід викреслити доданки що відповідають навантаженням які з’являються лишев//та/// ділянках Інакше кажучи в рівнянні має залишитися лише один силовий фактор —
Отже рівняння пружної лінії на першій ділянці має вигляд
“’М-’й-І-ж-»'’»—5-1'4]	(10102)
Поклавши тут х 1/2, дістанемо формулу для визначення прогину в точні С
” (т) = ТТ » 0 056 4 
Для визначення кута повороту будь якого перерізу балки треба мати вираз для кута повороту у відповідній ділянці балки Рівняння
кутів повороту для ділянки ВИ дістанемо диференціюванням рівняння ПО 100)
е(*)—	["ЯГ?*’ а 21 + 8 2І

(10 103)
Поклавши тут х = 5141 матимемо формулу для визначення кута повороту перерізу О
-Ж+-И-Ш —
отже,
Єо = -0,56-|ї.	(10 104)
Рівняння кутів повороту для першої ділянки (ділянки АС) дієта немо диференціюванням рівняння (10 102)
в«“-їт[-згг’',-т’'тґ]	<10105>
Звідси при х = 1/2 знаходимо формулу для визначення кута повороту перерізу С
= е (_П „	_____7_Л Л________>5_
°с \ 2 /	1 38*	8 2 2і/ Е2 384 Е2 М,ІМЗ Еі '
Розрахунок на жорсткість при згинанні Оволодівши методикою визначення прогинів та кутів повороту можна перейти до перевірки жорсткості балок, а також до добору розмірів перерізів балок з умови жорсткості
Позначивши абсолютне значення максимального прогину балки через /, а допустиму стрілу прогину через 1/1 дістанемо умову жорсткості балки
/СІЛ	(10 106)
Допустимий прогин визначають на підставі експериментальних та експлуатаційних даних
Приклад 43 Пля балки, навантаженої завдальшки а ™ 4 м від лівої опори зосередженим моментом М ™ 120 кН (рис 287), побудуємо епюри поперечних сил, зви нальних моментів, кутів повороту перерізів та прогинів, а також доберемо двотавровий переріз з умов міцності та жорсткості, (а| = 160 МПа; |/| = (ПбОО) І, Е = = 2-10' МПа
Визначивши опорні реакції будуємо епюри поперечних сил та згинатьннх моментів
Переміщення характерних перерізів бачки будемо визначати відповідно до рекомендованого вище порятк> розв язаиия задачі Запишемо рівняння прогинів для
ділянки СВ а> (*) •=»(,+ 0,* +
+ -^[-ТГ--------«(»-«>•]	<10 107)
Початок координат збігається з лівою опорою А отже ®0 — и>А = 0 Відповідно до умов на пра вій опорі а> (1} = №в = 0
З рівняння (10 107) при І = 6 м маємо
ЗВІДКИ
Є. - - -і-	<‘0 '®>
Підставивши вираз (10 108) в рівняння (10 107) запишемо рівняння пружної лінії нв ділянці СВ в остаточному випаді
а (х) =	80х +	- 60 (х - 4)*]
(10 109)
Рівняння пружної' лінії на ділянці АС запишеться так
’‘'>“-Й-(-№ + -ТІ)-Т7-[—Т-<И"Ч'
Проднференціювавши рівняння (10 109) дістанемо рівняння кутів повороту на ділянці СВ
Є (*) = —к. (— 80+ 10*’ — І20(х — 4)1	(10111)
Для побудови епюри 0 треба обчислити кути повороту на межах цієї ділянки
ес-е«>^ -ю+;° *
80
Є,-е,61 - А-|-К>+10 6- - 120в-ОІ _-12.
Оскільки в разе язакн{ розміри балки виражалися в метрах а сили — в к!лонью~ тонах то для визначення кута повороту в радіанах величини Ері треба виражати и кілопаскалях та метрах у четвертому степені відповідно
Диференціюючи рівняння (10 ПО) дістаємо рів іяння кутів повороту на ділянці АС
0(х)- -±.(-80 4. 10х»)	(10 112)
Кути повороту на межах цієї дітянки вже відомі Отже можна побудувати епюру 01.
На межах ділянки відкладаємо ординати рад а а — 80 а _____________________________ 80
< На епюрах в та ю відкладено ординати здобуті після остаточного розра лунку І = 7780 см4.
Вершини цих ординат відповідно до рівняння (10 112) сполучаємо параболічною кря вою Оскітьки ф > 0 то парабола в повинна бути повернута опуклістю вниз (див п 5 § 67) У точці А дотична до епюри має 6утн паратстьна осі абспнс (див п І). Аналогічно проводимо побудову на дітянці Св
Для побудови епюри прогинів обчислимо найбільший прогин Він має місце в пер різі де 0 (х) — 0 Запишемо цю умову
е (ж,) - .А. (-80+ ІО^>- 0, звідки
х, а 2 83 м
У цій точці прогин має екстремальне зна іеппя шПИІ = / Визначимо стріту прогину підставивши у вираз (10 110) х = хр
/ =	(24 -2 83») м~- 9 43 16 м=-^1и
3£/	ЕЗ	ЕЗ
Прогин буде виражений в метрах якщо £ та У як бузо зазначено — в кілопаскалях ти метрах у четвертому степені відповідно
Для побудови епюри прогинів треба ще визначити прогни у точці С, що є точ кою перегину гтя епюри прогинів (у ній точці на епюрі моментів змінюється знак) Поклавши в рівнянні (10 і 10) х = 4 м матимемо
(24~О) _______320_ ив__ІО6_ „
с	З ЕЗ	ЗЕЗ	ЕЗ
Відкладаємо знайдену ординату вниз від базисної лінії Відповідно до рівнянь (10 109) та (10 110) епюра прогинів повинна бути окреслена на обох ділянках кубічнн ми параболами На ділянці АС момент М > 0 тому парабола повернута угнутістю вгору на ділянці СВ момент М < 0 і парабола повернута угнутістю вниз (див п. 4). Перейдемо до вибору перерізу балки з умови жорсткості Умова жорсткості (10 106) набирає внглнд\
звідки
,	150,9
При £ = 2 • 10і МПа = 2 • 10е кПа ти допустамій стрілі прогину (/і = 1/600 ™ = 6/600 = 0 01 м потрібний момент Інерції
7 “ іо-’50?9 10-	“75,5 1[Н	“75,5
За каталогом сортаменту (дод. 1) знаходимо, що потрібний двотавр № 80а, момент інерції якого 3 = 7780 см»
Треба перевірити міцність вибраного двотавра № 30а момент опору якого V = 518 см3 Визначаємо максимальне напруження в балці
» 80 -10"* МІІа = 154,5 МПа<[о] = 180 МПа.
V	5(8 іо-в
Отже міцність балки забезпечено
Розрахунок балки з проміжним шарніром Універсальні рівняння пружної лінії та кутів поворогу було знайдено з розгляду ділянки д£ (див рис 284, б), на якій балка не має проміжних шарнірів, що
порушують плавність зігнутої осі Тому розглядаючи балку в цілому та залишаючи загальний для всіх ділянок початок координат застосу вати ці рівняння для безпосереднього визначення переміщень на ді лянці 5Г балки розташованій праворуч від шарніра 5, неможливо У цьому разі визначити переміщення можна лише розглядаючи балку по частинах (окремо частину С$ та окремо — 5Г)
Можна проте, показати спосіб узагатьнення рівнянь методу почат кових параметрів і для випадку баїки з проміжним шарніром (див рис 284). З цією метою записавши диференціальне рівняння дтя ді лянок 8$ та ЗГ проінтегруємо їх двічі для ділянки 88
ага>(х)__М (х)
ах* ~ Е^ '
О(х) = -^-=5-^-^4-Слів	(10 ІІЗ)
ш (х) = (іх (іх + Ся1вх 4- Олія. (10 114)
для ділянки 8Р
а{(е іх}_м (ж)
ах* е/ •
е« = Лг-=і-тт-‘'лг+с»:	(10115)
ю(х) =	(10116)
Унаслідок наявності шарніра кути повороту ліворуч та праворуч від точки 5 будуть відрізнятися на деякий кут а Для того щоб визна ЧИТИ зв’язок МІЖ сталими Сліп ОлівТаСпр Лпр. складемо умови спрЯ ження ділянок у точці 5
аг(а)лів = ш(5)пр.	(Ю 117)
О (5)л  — а — в (5)пр	(10 118)
Підставляючи в рівності (10 117) та (10 118) відповідні значення о; (з) та 6 (з) з виразів (10 114) (10 116) та (10 113) (10 115) при х = я дістанемо
Слш+а-Спр.	(10119)
СЛ1В5 4- ОЛІЯ - СпрЗ - Опр	(10 120)
З останніх двох рівностеи знаходимо
Опр -----05 ‘ Ол!»	(Ю 121)
Піставляючн рівності (10 119) та (10 121) в рівняння (10 ) 15) та (10 116) можна записати рівняння кутів повороту та прогинів на
IД' ,	1 &Г.4->тЧ-1
Рнс 286	Рнс 289
ділянці $Г у такому вигляді
е (х) - 5	Т Слів - а	(10 122)
ш(х) = \ <йг] -^х) СІХ 4- Слів* + ол!в | а(х — 5) (10 123)
Оскільки було визначено що ліворуч від шарніра 5 довільні сталі С та О на всіх ділянках однакові і є відповідно кутом повороту та прогином на початку координат приходимо до висновку що для перс різів праворуч від шарніра в універсальне рівняння прогинів слід ввести додатковий член а (х — в), а в рівняння кутів повороту — член а Отже при наявності шарніра ліворуч від розглядуваної ділянки універсальне рівняння методу початкових параметрів (10 92) набирає вигляду
и(х) = ®0 + Є„і -а(х — і)т	т ЇМ
+	-Т- т ?Ч,	-
-Зі |*~'||‘ [	(10 124)
Взаємний кут нахилу а е додатковою невідомою величиною в уні версальних рівняннях для иі (х) та 6 (х) Як і початкові параметри иі0 та 60 його ви нйчають з умов на опорах
Залежно від розрахункової схеми балки можливі два основних варіанти додаткових умов на опорах
1	Умова путьового прогину на правій опорі (рис 288) Звідси ви значають тільки кут а
2	Умова нульового прогину на опорах В та С (рис 289) Кут а тут визначають разом з 6 розв’язанням системи двох алгебраїчних рів нянь
Приклад 44 Для балки (рис 290) побудуємо епюри Ц, М. 6 та а; доберемо двотавровий переріз з умов міцності та жорсткості якшр М -» 160 кН м,а=2м (а] — 160 МПа, [/) -- 10 мм
Обчисливши реакції на опорах МА ЯА та Дв будуємо епюрн р і М Для лобу .ови епюр 0 та ю треба перш за все визначити їхні значення на межах усіх ді 288
Запишемо універсальне рів* ияння пружної лінії (10 124) для крайньої праве» ділянки балки йЕ враховуючи що геометричні початкові параметри 0О та <г0 дорівнюють нулю
• (*)  а (х- а) +
+тИ~'и‘ т+
4- Я .	— Я» (х - 20)1 -
~М	1
21	]
(10 125)
Значення взаємного кута по* вороту перерізу в шарнірі С — (ас) — знайдемо я умови нульо* вого прогину в перерізі над пра* вою опорою В
яваи (2а) = 0
Рівняння для прогину в пе рерізі В дістанемо з виразу (10 125). викресливши останній доданок та поклавши х ™ 2а
®8 ™ к (2а) » аа 4-
+-Г-ІГ-І-0-
ВВІДКИ
2 Ма
З Е^ '
(10.126)
Підставивши вираз (10 126) в рівняння (10 125), матимемо остаточне рівняввя пружної лінії для ділянки балки Ье
Р(Х)- » [2 МЯ(к-Я)-М-£+Л*
‘ ' Е1 [ 3	'	'	21 а ЗІ а ЗІ
— М-&Т:	(10.127)
З рівняння (10.127) можна дістати рівняння для решти ділянок балки.
Рівняння кутів повороту для всіх ділянок звайдемо диференціюванням рівнянь пружної лінії на відновіднях ділянках
Даємо читачеві змогу самостійно кнконати всі зазначені розрахунки та побудува ти епюрн 0 та и> Для самоконтролю ва рис 290 наведено епюри прогинів та кутів повороту
10 2-2784
Перейдемо до вибору перерізу бваки Найбільший згинальний момент Маих ™ = М = 180 кН м 3 умови міцності
V >	= .160 10-8 м* -= 10“8 м» = 1000 см»
[а]	180
За сортаментом вибираємо двотавр № 45 для якого V = 1231 см* І = 27 696 см*.
Перевіримо чи виконується умова жорсткості Знаходимо стрілу прогину
:а. Лнї - -25.	160 10-8 2*	„ в 012 и в ! 20 см.
24 Е^ 24 2 10» 27 696 ІО-8
Умова жорсткості (10 106) не виконується
І - 1.20 см > І/] - 1 см
Отже розміри перерізу балки треба збільшити виходячи з умови жорсткості
М і8°2	2‘	“-001 “	(10 12В)
З рівняння (10 128) знаходимо шо
7Х > —	10~3 4_ н» = 334 і0“8 я» » 33 400 см*.
24 0,01 2 10»
За сортаментом вибираємо двотавр № 50 (7 ™ 39 727 см»)
$ 69 Розрахунок балок змінного перерізу на міцність І жорсткість
Досі ми розглядали розрахунки на згинання стержнів, переріз яких був однаковий по всій довжині Такі стержні особливо ари знач ній їхній довжині, не можна вважати раціональними з погляду ваги та витрати матеріалу, оскільки розміри перерізу добираються за зу силлями які діють у небезпечному перерізі, в решті ж перерізів має місце значний надлишок міцності Крім того за конструктивними мір-
куваннями стержні які працюють на згинання часто мають поперечні
отвори, виточки східці тощо Внаслідок цього на практиці широко застосовуються стержні неоднакового по довжині поперечного пе-
рерізу
З погляду розрахунку на міцність та жорсткість всі такі стержні можна поділити натри основні групи
а)	стержні які мають місцеві зміни фор ми та розмірів перерізів (рис 291, а),
б)	стержні східчасто-змінного перерізу (рис 291, б)
в)	стержні, які мають розміри (іноді й форму) перерізів що неперервно змінюють ся по довжині (рнс 29і в)
Зрозуміло, що е багато деталей, в яких поєднуються різні типи порушень розмірів
та форми перерізів У цих випадках при розрахунках на міцність та жорсткість слід ураховувати всі особливості притаманні тому чи іншому виду пору шення форми й розмірів Розглянемо кожну групу окремо
Місцеві зміни форми та розмірів перерізів Отвори виточки й інші по
рушення форми та розмірів перерізів > спричинюють різку та значну зміну * характеру розподілу напружень та де4юрмацій Проте не збудження має місцевий характер і мало впливає на напружений та деформований стан стержня в цілому тому, визначаючи прогини та кути повороту перерізів
отвори й інші порушення перерізів локального характеру не врахову ють При розрахунках на міцність не беруть до уваги також дотичні напруження, а основну умову міцності записують для небезпечної точ ки, розташованої в одному з ослаблених перерізів, оскільки саме тут може мати місце концентрація нормальних напружень (див § 65)
Залежно від чутливості матеріалу до концентрації напружень умови міцності будуть мати різний вигляд, а саме для високопластичяих матеріалів (маловуглецева сталь, мідь, алюміній) та крихких неоднорідних матеріалів (чавун) концентрацію можна не враховувати і умову міцності записувати у звичайному ви гляді
ЛМ7«СІа],	(10 129)
де У — момент опору ослабленого перерізу, де діє згинальний момент М.
для однорідних крихких матеріалів (високоміцних нагартованих сталей)
а £ <1’1.	<10 130)
де а — теоретичний коефіцієнт концентрації, який береться з довід кових таблиць (див $ 65)
Прикаад 4В. Палець (нерухома вісь) із зовнішнім діаметром й = 15 мм, виготовлений з легованої сталі 20Х (о, = 600 МПа), має розміри, зазначені на рис 292, а, І навантажений силою 4 кН Посередині пальця е отвір діаметром сі = 3 мм для ма щення Перевіримо міцність, якщо коефіцієнт запасу міцності пч =* 1,6, та знайдемо прогин посередині пальця Розрахункову схему пальця та епюру згинальних моментів наведено на рис 292 6
Небезпе ікни буде переріз пальця посередині прольоту ослаблений отвором для мащення в якому діє Лі ™ 4 10—3 кН м Небезпечною точкою точно кажучи, буде точка а (рнс 292 а), але для розрахунку зручніше вибрати як небезпечну умовну точку Ь що, очевидно не внесе в розрахунок помітної похибки.
Момент інерції пальця  перерізі ослабленому отвором, * “ *а — ^яга»
/п = « 'Д>5<| р _ (44)*]си4 “ 0,228 “*•
,Втад2[ 0,3 10,35' +0.3 0,35 0 575» см‘ - 0,072 см»,
причому обчислюється для двох прямокутників розмірами 0,3 X 0,35 см Отже,
При заданому запасі міцності допустиме напруження
(а] » -2»_ » МПа » 375 МПа л, 1,0
Знайдемо номінальне напруження в небезпечній точці Ь
а. » *!_ - 4 І?"8 * ІР7?. МПа 192 МПа *	0 208 • 10~®
Оскільки небезпечна точка лежить коло конструктивного концентратора — отвору для мащення то максимальне напруження слід обчислювати з урахуванням концепт» рації напружень Теоретичний коефіцієнт концентрації напружень а знайдемо з гра фіка, наведеного на рнс 273. де прн ='0 3/1 5 ™ 0 2 коефіцієнт а ™ 1,87 Тоді максимальне напруження в небезпечній точці
°аих “ «о- “ 1 -87 • 192 МПв - 359 МПа < 375 МПа,
Отже міцність забезпечено
Переходимо до визначення прогину пальна Скориставшись універсальним рів* нянням пружної лінії (10 92), для правої Крайньої ділянки пальна матимемо
.м-' І*!—	У 1.
З умови що прогин иа правій опорі (х ™ 8 см) дорівнює нулю дістанемо рівняння для визначення початкового параметра
Звідси
Є.---------12-
Е^ Тепер для визначення прогину посередині прольоту запишемо рівняння
звідки при Е ™ 2,0 • ІО» МПа = 2 10* кПа та 7 = 7П = 0 228 см» знайдемо, що
, см » —" 0.0064 см. 0,228 .2 • 10» • 10“*	*
/=>0,064 мм та
_ 0.064 _	1
80	'1250 ’
Східчасті стержні. Вміс-цях спряження ділянок з різними розмірами перерізів виникає концентрація напружень Якщо матеріал чутливий до неї. то треба застосувати умову міцності (10 130) до всіх перерізів на межах ділянок Якщожма теріал нечутливий до концентрації' напружень, то треба застосувати умову міцності (10 129) до всіх імовірних небезпечних перерізів
Для визначення перемі щень у східчастому стержні можна або користуватися загальними методами, ви
Рис. 293
кладеними нижче (гл 13), або застосувати видозмінений метод початкових пара метрів Сутністьостаннього полягає в заміні східчастого стержня еквівалентним йому за деформаціями стержнем постійної жорсткості
Обгрунтуємо таку заміну на прикладі довільного багатосхідчастого стержня (ряс. 293. а) Розділимо стержень ва частини однакового перерізу (рис 293 б); у місцях розрізів діятимуть відповідні внутрішні силові фактори — 0 та М
Диференціальне рівняння пружної лінії для першої частина стержня ..................................................... (10	131)
4*»(х) М (х) Ох* = Е^
Аналогічно для всіх інших призматичних частин стержня
Л*а>(х) ___ М (х)	(х) М (х)
Дх» — Еіх ’	• ’ Лх* “ Е1„
(10 132)
Перетворимо заданий східчастий стержень на еквівалентний стер жень однакового перерізу з моментом інерції який дорівнює моменту
Інерції однієї з ділянок стержня, наприклад першої. Помноживши чисельникта знаменник правої частини останнього диференціального рівняння (10 132) для довільної ділянки п на дістанемо
<**»І*) М (х) У, М(х) _ .М(х) д ,1П іад.
</»*	Е2п29	Е29 2п “	р»’	(1°
де рп — коефіцієнт зведення
З (10 133) випливає, що помноживши згинальні моменти кожної частини стержня на відповідні коефіцієнти зведення та замінивши момент інерції на Уо дістанемо стержні однакового перерізу з моментом інерції Д пружні лінії яких тотожні пружним лініям відповідних частин заданого східчастого стержня
Оскільки згинальний момент лінійно залежить від навантаження, то для кожної частини стержня замість множення на коефіцієнт зведення згинальних моментів можна помножити на цей коефіцієнт усі навантаження цієї частини разом з внутрішніми зусиллями 9 та ЛІ в торцевих перерізах (рис 293, в)
Сполучаючи тепер окремі частини розрізаного стержня, дістаємо еквівалентний за жорсткістю стержень постійного перерізу Цей стержень зазнає дії зведених зовнішніх навантажень (тобто наванта жень. змінених в рп разів) Прн цьому в місцях спряження окремих частин стержня діють додаткові сили Лф та моменти &М, які внзна чаються різницею зведених внутрішніх силових факторів, прикладених до лівого та правого боків перерізу
АС?» = Рі(Р,-Рі).
Д<2, = <?,&-&). ДМ,- Лї.ф, —р>), Д/И^^фа-р»)
(10 134)
Отже, здобуто еквівалентний стержень (рнс 293 ?), пружна лінія якого повністю збігається з пружною лінією заданого східчастого стержня Для будь якої ділянки цього еквівалентного стержня пружна лінія визначається інтегруванням диференціального рівняння
м99(*) 4х* ~	Е29
(10 135)
де Мп (*) — момент від зведених зовнішніх навантажень та додаткових навантажень Др та ДЛЇ
Для визначення переміщень в еквівалентному стержні можна ви корнстати універсальне рівняння пружної лівії (10 92)
Примах 46. Визначимо кути повороту опорних перерізів та прогини для три східчасто/ балки яка мжить на двох опорах (рис. 294 а) Відношення моментів інерші перерізи окремих східців балки 2г 29 2,^1 3 2.
Визначаємо опорні реакції та будуємо епюрн згинальних моментів і поперечних сил Розрізаємо балку на три частини в місцях енряжеиня східців Нарис. 294 б зоб-
294
ражено окремі часта ин балки які перебувають під дією зовнішніх сил ти внутрішніх зусиль та Лі у місцях розрізів
Зведемо задану східчасту балку до еквівалентної балки постійного перерізу з моментом інерції Л що дорівнює моменту Інерції /, перерізу середньої ча стннн балки Коефіцієнти зведення відповідно такі
/. з
^“77 “ “ із®
Мвожнмо на вс х ділянках задані навантаження, а також (} та М у перерізах розрізів на від ПОВІДНІ коефіцієнти зведення 0л Усі три частини балки з црнкла деннмн до них зведеними наванта женнямн показано на рнс 294 в Тепер утворимо з них одну балку однакової жорсткості Еі9 = Е29 приклавши в перерізах слряжен ня додаткові сили Д(?. та додаткові момента ДЛі( та Дмв
Знаходимо додаткові енлн
«.-4'’-"’—4-'’.
або ДРі—-уР(1 —=
4р,. ‘3 р-^-р=-л.р 1в0	—2_Р
Обчислюємо додаткові моменти
МІ, = 3 ра — 7Ра — -у- Ра, або ДМ, = -у Ра (і — 3) — — -у- Ра,
ДЛІ, = 4Ра — -у- Ра = -д- Ра
або ЛЛ1, » Ра — |) »	ра
295
воТ балки перевіримо чи виконуються умови її рівноваги
=	2й4-Р	4« + ЗР 5а —
~~ТР 6а--у-Ра+4'^“(21-у--21-у-)/,л»0
Для визначення переміщень слористаемося методом початкових параметрів. Візьмемо переріз на крайній правій ділянці й запишемо для нього рівняння пружної лінії
п	її	м „	(* —2а)»	4 /х —4а)« х»
V (х) = ®в + Є,х +	1---3- Ра----2---+ "Т	Ра 2—2--+ 5Р “б--
(х-Д)*	4 „ (х —2а)* „ (х —За)*
“ ЗР § з Р б “Р 6	“
Початкові параметри знайдемо з умов на опорах прн х ™ 0 »(0) ™ 0. отже, ®в ™ 0; при х ™ І ™ оа ю(І)™ 0 Використаємо умову для визначення другого початкового параметра 0О
1 Ґ 14	(4а)»	4	(2а)’	{6а)»
• (0 “ Єеба +	[ - -з- Р* -4і- + -у Ра -Ц2- + 5Р -
Єв = _|0 68-^-	(10 138)
Для визначення кута повороту 0В правого кінця балки продиферевиіюемо рів* няиня пружної лінії (10 137) для крайньої прваоі ділянки балки (5а х < 6а) тв в здобуте таким чином рівняння для 6 (х) підставимо х = І = 6а Матимемо
0В ~ 0 (6а) = Єв 4-	-3“ Ра І6® — 2°) Ра (ва — 4а) 4-
.	(5ау*	(6а —о)*	4 „ (6а-2а)«	„ (6а-За)*
4-а/'	2	—№'	2	— з р 2	— р 2	—
наїдки знаходимо
Р (6а—4а)*	.„(6а — 5а)*
6	2 ~ЗР 2
Ра* Е/,
(10 139)
Визначимо, як приклад прогини в місцях прикладення зовнішніх навантажень Р, та Р( (тобто в перерізах х ™ а та х = За) При х = а
При х = За
а (За) =Є,За--у-	4" 4-5Р- ЗР-
4 а*	Ра*
— -у Р -^у- » (— «0,58 3 - 2,33 + 22 5 — 4 - 0 222)-£5—»
16 8ОРа*
Визначення лінійних та вутоанх переміщень будь яких інших перерізів балки також не е складним
Стержні, розміри перерізів яких неперервно ЗМІНЮЮТЬСЯ ПО ДОВЖИНІ Якщо розміри перерізу стержня неперервно змінюються по дов жині, то формули виведені на підставі гіпотези плоских поперечних перерізів стають взагалі невірними (як і сама гіпотеза) Проте деякі точні розв’язки теорії пружності показують, що тоді, коли кут нахилу твірної поверхні стержня до його осі малий (не перевищує 15 20°), з достатньою для інженерної практики точністю можна вважати роз поділ нормальних напружень по висоті перерізу прямолінійним Тоді, природно, можна користуватися звичайною умовою міцності та дифе ренціальннм рівнянням пружної' лінії тобто
і™.	(10 140)
Водночас дотичні напруження більш чутливі до нахилу твірних поверхонь стержня, тому формула Журавського стосовно до стержнів змінного поперечного перерізу дає значні похибки
Розрахунок на міцність та жорсткість стержнів змінного перерізу ускладнюється тим що момент опору те момент інерції* поперечного перерізу є функціями абсциси х перерізу На це вказують позначення в формулах (10 140) та (10 141) Останню формулу можна записати вде-що іншому вигляді
Позначимо через 70 момент інерції якогось перерізу (як правило, найбільшого чи найменшого) та введемо поняття зведеного згинального моменту
М„(х)-.М(г)^	(10 142)
Тоді, помноживши на Уо чисельник та знаменник правої частини фор мули (10 141), матимемо
Мм (х) 4х» “
(10 143)
Ця формула за своїм зовнішнім виглядом аналогічна формулі (10 135), але величини Лїм (х), які входять до формули мають різний зміст
Окремим випадком балок, розміри перерізів яких неперервно змінюються по довжині, є балки однакового опору згинанню, в усіх пере-
різах яких максимальне напруження дорівнює допустимому, тобто
И - -Ці,'}1 - І«|
Звідси знаходимо рівняння для визначення розмірів балки однакового опору*
(10144)
рве 295	Задавшись будь-якою формою перерізу
(причому таким чином щоб розміри його визначалися тільки одним параметром), з рівняння (10 144) знаходимо за кон зміни цього параметра по довжині балки Тим самим визначаємо розміри всіх перерізів Для визначення переміщень можна користуватися диференціальним рівнянням пружної лінії (10 143)
Знайдемо форму консолі однакового опору згинанню переріз якої прямокутний з постійною шириною Ь та змінною висотою (рис 295).
Позначимо висоту балки в довільному перерізі через К (х) Тоді
ГМ- И‘6М .
Крім того, очевидно,
|М(х)| — Рх
Тому, згідно з рівнянням (10 144),
звідки	______
Отже, висота розглядуваної балки однакового опору буде змінюватися за параболічним законом (рис 295, б) При цьому
Зазначимо, шо а околі кінцевого перерізу (х = 0) згинальні моменти малі, тому висоту перерізу слід визначати з умови міцності Ва Тта>1
З Р Ттім = — "Тд- ПІ.
ЗВІДКИ
ЗР 2*111 Побудована балка параболічного обрису найбільш раціональна з погляду економії матеріалу однак внаслідок складності форми не задовольняє технологічних вимог. Тому на практиці застосовують
не балки однакового опору, а близькі до них східчасті стержні
Аналогічно діють І у випадках двотаврового, круглого та інших форм перерізів Існує один тип балок однакового опору з дуже простим обрисом який застосовується в листових ресорах — це балки прямокутного перерізу з постійною висотою /і та змінною по дов жині шириною Ь(х)
Знайдемо форму такої балки однакового опору згинанню для схеми, показаної иа рнс 296 а
Унаслідок симетрії для визначення форми балки досить розглянути тільки ліву половину прольоту Тоді
«м =4*-
і.
Підставивши матимемо
звідки
ці вирази у формулу (10 144),
6Рх
26 (х) А'
= [01,

Рнс 296
ЗР
*(*)-
Л*(о]
Ширина перерізу змінюється за лінійним законом, і, отже, балка має вигляд показаний на рис 296, б Максимальна ширина балки Ьо буде посередині прольоту
Визначимо найбільший прогин / цієї балки Згідно з рівняннями (10 142) та (10 143), маємо
<Ра,	(х)
гіх’ =	є/,	•
де
Лї»(х) =	=Тх“7оо' ’
У нашому прикладі
отже,
а тому
Мп (х) « у X «а —у .
На рис. 296, б наведено епюри ЛТ та (?, а також епюру зведених згинальних моментів
Отже, дифаревціальне рівняння пружної лінії для лівої половини прольоту балки буде мати вигляд
а*а> РІ Ох* = 467. • Двічі проінтегруємо ЙОГО!
0(*)“-їМ-Т-* + с]:
ш в єів І”"®” ** 4" С1* 4- 
Для визначення сталих інтегрування Ста й використаємо симетрію пружної лінії ОТ показано штриховою лінією на рис 296, а) ш(0) =Є(//2)~ 0.
Звідси Тоді отже, а тому
Коли б балка мала однаковий по довжині переріз, то з умови міцності ми б знайшли, що вона буде прямокутного обрису в плані (балку завширшки Ьо по всій довжині на рис 296, б показано штриховим контуром) Для такої балки максимальний прогин
= 4&Б>, *	(10 145)
Отже, прогин балки постійного перерізу в півтора раза менший, ніж балки однакового опору, тобто
^=1,5/'	(10 146)
Нагадаємо, що ширина Ь перерізу опорних кінців балки однакового опору повинна визначатися з умови міцності ва ТпиХ з урахуванням конструктивних факторів, що забезпечують необхідні умови обпирання.
г
Рис 297
Розрахунок звичайної листової ресори (рис. 297. г) яка складається з пакета листів, зводиться до розрахунку щойно розглянутої балки
Балку однакового опору (рис 297, а) розріжемо па окремі штаби (рис 297, б), а потім складемо однакові штаби завширшки 1/2 У ре зультаті матимемо п штаб завширшки І = Ь0/п які зображено на рис 297 в Склавши ці штаби разом, одержимо показану на рнс 297 г листову ресору
Якщо всі листи з’єднати між собою (зварити або склепати), то вийде балка однакової ширини І і змінної висоти перерізу В ресорах листи не зв язані між собою (хомути, в яких вони розміщуються перешкоджають розсипанню їх) і мають змогу вільно прослизати один відносно одного Крім того наближено можна вважати що при деформації всі штаби однаково викривлюються Тоді сума штаб, з яких складе ється ресора з погляду напружень та деформацій буде еквівалентна сумі штаб показаних на рис 297 б, тобто балці однакового опору постійної висоти й змінної ширини (рис 297, о) Тому для такої ресори умова міцності (враховується, шо Ьв — Іп) матиме вигляд
“Ж®- <1’1.	(І0Л47)
а найбільший прогин
Г-ІЛҐ'1^.	(101«)
Де
7
= 12 “ 12
Для ресори, показаної на рис 298, а, відповідна балка однакового опору має форму трикутника (рис 298 б) і, очевидно,
РІ* _	.М(х) вРі
і зК77’ат“- Т(х) “ТЖ’’’
Тому умови міцності та жорсткості відповідно мають вигляд
ЯгСІ"!.	(10 149)
<Ю Ї50)
Зазначимо що взагалі ресори виготовляють з високоміцних ста* лей і допустимі напруження (а] досягають 400 МПа і більше Щодо прогину ресор, то на практиці (здебільшого внаслідок тертя між листа ми) він дещо менший, ніж у відповідній балці однакового опору, тому в формулах (10 148) та (10 150) замість коефіцієнта 1,5 беруть 0=12 1,4
Приклад 47 Ресоро (див рис 296, 297) завдовжки 100 см, яка складаєтеся Із семи штаб перерізом 60 X в мм, навантажена силою Р ^7.6 кН Перевіримо міцність ресори ([о] = 450 МПа) та знайдемо максимальний прогин.
У даному прикладі Л « 0 8 см. і ™ 6 см I “ 100 см, Р “ 7,5 кН, л = 7 Тоді
За умовою міпяості (10 147)
ЗР/ 3,75 10“8 • 1
-..-ВИг- г.6дЄ.,7(Ь..ІН'” мп-4'8 «"<« мп>
Отже, ресора міцва
Користуючись формулою (10 148) та ваніаюкки в яІВ коефіцієнт 15 на 0 = — 1,25 1,40, знаходимо що
Рі»	7.5 ІО"3 І
'“’иИ, “ І1'25 -..««І їй ,.79 10-» “ “
— (1.25 ... і 40) 4,16 . 10~2м-(і,25	. 1,40) 4 16 ем=»5 2 ., 5,8 см,
тобто ааббільший прогин становить 52 58 мм.
На закінчення зазначимо, що наведений спосіб розрахунку листових ресор певного мірою умовний, оскільки
а) не враховується тертя між листами ресор
<9 насправді листи ресори щільно прилягають один до одпого не всюди, а тільки в окремих точках внаслідок чого кривизна листів при деформації неоднакова, а отже, і напруження в них різні
$ 70 Розрахунок на дію сил Інерції при згинанні
Розрахунок на згинання з урахуванням сил інерції доводиться виконувати тоді, коли елементи конструкцій в процесі експлуатації набирають великих прискорень, які спричинюють значні Інерційні зусилля Класичним прикладом деталей, розміри яких слід добирати з умови міцності на згинання з урахуванням сил Інерції, е спарннки локомотивів та шатуни двигунів
Розглянемо спарник 4 В (рис 299>, що з'єднує два колеса, одне з яких (О,) є ведучим і на нього передається обертальний момент від машини Вточ ках А та В спарник приєднаний до коліс за допомогою циліндричних шарнірів, відстані 40, та ВО, дорівнюють радіусу кривошипа т, діаметр колеса — І> довжина спарника — І, ло-
Рнс 299
комотив рухається із сталою швидкістю і>
Беручи участь у переносному русі разом з локомотивом із сталою швидкістю о, спарник не маючи прискорення, не буде зазнавати інер ційних навантажень Прискорення він дістане тільки в процесі від лосного руху Оскільки в цьому русі точки А та В спарника леремі шаються однаково окреслюючи в одній плсщині кола радіусом г то цей рух буде плоским та поступовим Отже, всі точки спарника бу дуть мати ті самі швидкості й прискорення що і точки А та В
Точка А рухається разом з другим колесом окреслюючи коло ра діусом г При сталій швидкості руху локомотива кутова швидкість обертання колеса ш стала Отже, тангенціальне прискорення точки А дорівнює нулю а доцентрове прискорення иі„, спрямоване від точки А до точки 0„ дорівнює ш*г Будь який елемент спарника набуває такого самого прискорення спрямованого паралельно 0,4
Визначаючи згинальні моменти в спарнику, слід до рівномірно роз поділених сил інерції інтенсивністю
уГ	уЯ .
додати його власну вагу При цьому найбільш небезпечним положенням спарника очевидно буде крайнє нижнє, тобто положення, в якому до навантажень від сил інерції треба додати навантаження від власної ва ги Тоді повне навантаження на одиницю довжини спарника
Я = ур + -у-	= ур (1 +
При виборі розрахункової схеми спарник у даному випадку треба розглядати як балку, шарнірно обперту в точках 4 та В і навантежену рівномірно розподіленим по довжині навантаженням <?
Максимальний згинальний момент буде як відомо, посередині прольоту
а найбільше напруження в небезпечному перерізі
Матих Е	І 1 ,	\
Пш.> = —у-------у—+
Крім інерційних навантажень та алас-
Ці/Т/х.	ної ваги, які спричинюють згинання, спар-
ник при роботі зазнає дії осьової сили, яку ( лУ дСР[	д тежслідвраховувати в розрахунках на міц-
г- —«==г—1--------Дч • НІСТЬ Умову міцності при спільній дії зги*
\ І }	нання та осьової сили наведено в § 76
чІ ✓	Аналогічно можна виконати і розраху*
Рве. зоо	иок шатУаа (рис 300), шарнірно з’єднаного
в точці А з кривошипом ОА, який обертається навколо точки О з кутовою швидкістю
Якщо кривошип обертається із сталою кутовою швидкістю, то точкаА шатунанабуваєтільки доцентрового прискорення аточкаВ — тільки тангенціального Всі проміжні точки шатуна, розташовані між А та В, мають і ті й інші прискорення Обмежимося врахуванням тільки доцентрового прискорення
Прн такому положенні, кати кривошип утворює з шатуном кут 90°, напрям доцентрового прискорення буде перпендикулярний до осі шатуна Природно припустити, шо відцентрові скли інерції скрізь перпендикулярні до осі шатуна і по його довжині змінюються від Я = у точці А до я = 0 в точці В Це припущення тим ближче до істини чим більша довжина шатуна порівняно з довжиною кривошипа
Складаючи розрахункову схему, шатун слід розглядати як балку АВ на двох шарнірних опорах А та В з навантаженням, розподіленим за законом трикутника (див рис 73) Максимальний згинальний момент, як відомо, буде в перерізі завдальшки х = 1/^3 від точки Ві
Літах
9кЗ ’
а максимальне напруження від згинання
Ураховуючи, що знайдемо
(ТпМХ
і"г •
ЕуРа>*г
9«Г31Г

Зазначимо, що в розглядуваному прикладі, визначаючи напруження в спарнику та в шатуні, ми з усіх можливих положень, які неперервно змінюються в процесі експлуатації, вибирали положення елемента, який розраховується, що відповідає небезпечному положенню
Крім нормальних напружень, спричинених згинанням, прн розрахунку шатуна на міцність слід ураховувати також дію осьової сили (див. гл, 20)
Глава 11. ДОДАТКОВІ ПИТАННЯ ТЕОРІЇ ЗГИНАННЯ
$ 71. Про розрахунок складених балок
Складені балки широко застосовують у будівельній практиці судно- і літакобудуванні та інших галузях техніки Це здебільшого зварні (рис ЗО!) або .клепані (рис 302) балки двотаврового перерізу Вони складаються з двох поясів (полинь) та стінки Стінка 1 — це вертикальний лист (рис 301та302) Пояси Рзварноі балки (рис ЗОі) — це горизонтальні листи більшої порівняно із стінкою товщиною Пояс клепано! балки складається з кількох деталей — поясного листа 5 і поясних кутників 2 (рис 302) Окремі частини складеної балки з єднуються між собою в одне ціле З'єднувальним елементом зварної балки є зварний шов 3 ірис 301) У клепаній балці за з’єднувальні елементи правлять поясні заклепки 3 а також заклепки 4 шо з’єднують поясні листи з поясними кутниками (рис 302)
Здійснюючи розрахунок складених балок на міцність треба за довольннтн такі вимоги
1	Поперечний переріз у цілому повинен мати потрібну міцність
2	Листи поясів і особливо стінки складених балок е тонкостінними елементами і здатні прн стисканні (пояса) або при зсуві (стінки) втра чати стійкість, поробитися Чим менша товщина листів та чим більша довжина частини с поясних листів, що звисає тим менше навантаження може витримати балка без небезпеки дороблення листів Тому треба обмежувати вслкчннус(рис ЗО! та 302) і не вибирати для листів занад то малу товщину Щоб запобігти втраті стійкості стінки, застосовують кутники або ребра жорсткості
З З’єднувальні елементи повинні мати достатню міцність
Перша задача розв’язується методами, викладеними у попередній

главі, А зводиться до розрахунку перерізу за втік, до визначення товщн нн стінки з розрахунку за ттіж та іноді
Рис. ЗОЇ

до перевірки розмірів перерізу за теоріями міцності в місці переходу стінки в полицю (див §64, приклади 41, 42).
Друге питання, як і взагалі докладний розрахунок складених балок викладається в спеціальних курсах (наприклад, у курсі мс талевих конструкцій) Розглянемо тільки розрахунок з’єднувальних елементів
Двома близькими перерізами виділимо елемент завдовжки (їх зварної балки (рис 303, а) Нехай у лівому перерізі поперечна сила та згинальний момент дорівнюють $ та ЛІ, а в правому — відповідно ф 4- 4$ та М 4- (ІМ Тоді за формулою (10 18) нормальне поздовжнє зусилля в лівому перерізі пояса
де Зя — статичний момент пояса відносно нейтральної лінії перерізу.
У правому перерізі пояса
И'+'Ш,..	+	.
Нормальні зусилля у правому та лівому перерізах пояса відріз* няються на величину
Зусилля 4Л^0 намагається зсунути пояс відносно стінки, внаслідок чого зварні швн, що прикріплюють пояс до стінки (їх два), працюють на зріз як флангові (бокові) шви Умова міцності для них має вигляд (дав § 52)
Якщо позначити через катет шва (рис 303, б), то площа зрізу ^=2-0,7*^
Тоді дотичні напруження у небезпечному перерізі шва ,	5в ЛМ
т= <^»р =2 о,7М*ТГ
Але (іМі(іх = ф, тому остаточна умова міцності для шва має вигляд
Х = 2 0 7^ <	1 1)
Зазначимо, що знайдена вище різниця зусиль у двох перерізах пояса належить до випадку, коли відсталь між цими перерізами дорівнює (іх На одиницю ж довжини пояса нормальне зусилля дістає приріст, Н/м,
Рис 304
або
<1, =-~.	012)
Часто застосовують не суціль ні, а переривчасті (шпонкові) шви (рис 304) Розглянемо шпонкове зварне з єднання
На рис 304 4, — довжина шпонки, а — крок шва Розрахункову довжину шпонки з урахуванням непровару беруть Іш — І см На від різку АВ завдовжки а у поясі виникає різниця нормальних зусиль
=	(113)
Розраховуючи шпонку на це зусилля, дістанемо
,_________
(В 4)
2 0,7Лщ	— І) У
У клепаній балці (рис 305) зусилля ДЛ^П сприймає поясна заклеп ка / Цю заклепку розраховують на зріз та зминання Оскільки заклепка має дві площини зрізу, то площа зрізу Г,р = 2 (лгі*/4) Роз рахункова площа зминання = ІІУіі або = 2 Як правило, товщина стінки менша за подвоєну товщину полиці кутника Тому будемо вважати Е=а — Іе1<і
Умови міцності на зріз та зминання для поясних заклепок мають вигляд
лу„ _ 0^
Т Г,р 2 «/,)
О3У = —Vа- ~ і	ІОж]
(Н5)
(116)
Заклепки 2, що з еднують поясні листи з кутниками, розрахунку не підлягають, бо вони мають ті самі діаметр 4 та крок а, що й поясні, а навантаження на них менші, оскільки у формулі [П 3) замість 8П для них треба взяти 8п = 50 — 8«ун де 5^ — статичний момент кутників.
§ 72 Дотичні напруження при згинанні балок тонкостінного профілю. Центр згинання
Припущення, на підставі яких у § 61 було виведено формулу (10 20) для визначення дотичних напружень прн згинанні, здебіль шого справедливі якщо ширина перерізу Ь мала порівняно з висотою (розміром, перпендикулярним до нейтральної лінії перерізу) Так, в усіх перерізах, показаних на рис 306 (а д), ширина тп на рівні, де визначаються дотичні напруження, мала порівняно з й У цих випадках формула (10 20) дає правильні результати Якщо переріз є тонкостінним профілем (рис 306, в, г, д) то в полицях ширина пе* рерізу т,Пі значна і характер розподілу дотичних напружень тут істотно змінюється вони не тільки змінні вздовж середньої лінії по* лиці т^, а й напрям їх стає не паралельним, а перпендикулярним до зусилля ф
Зазначимо, що в полицях діють також дотичні напруження, па* ралельні (} Проте ці напруження такі малі порівняно з дотичними напруженнями, паралельними середній лінії полиці (позначимо їх Та), що їх можна не брати до уваги
Виведемо формулу для обчислення дотичних напружень тп у полицях тонкостінних профілів
Для певності будемо розглядати балку двотаврового перерізу На рис 307, а показано балку, її схему та епюри $ і М Двома близь кими поперечними перерізами 4,8, і «4,8, виділимо елемент балки завдовжки іх (рис 307, б)
Проведемо в перерізі балки А1в,О1Е1 у нижній полиці вертикальну лінію гпіПі на довільній відстані г від осі у В точках цієї лінії діють напруження о та тп Останні треба визначити
Ураховуючи, що полиця вузька (І мале порівняно з Ь), приймемо такі припущення
1) в усіх точках лінії дотичні напруження однакові, тобто т0 постійні по товщині полиці й залежать тільки від відстані г до вертикальної осі
2) скрізь у полиці тп паралельні середній лінії полиці
Відсічемо частину елемента балки, провівши через /п,л, верти кальну площину, паралельну осі балки (рис 307, б, в), та розглянемо тільки ті напруження, які діють у гранях відсіченої частини полиці і дають зусилля, що проекціюються на вісь х
Нормальні напруження спричинюють зусилля Згідно з форму лою (ІО !8),
дг М(х)5(гЧ .
Тут
5(г)= (&/2-2)ґ(й/2-'/2)	(Н 7)
— статичний момент площі 41С1/л1п1 відносно нейтральної лінії Він є функцією координати г
У грані	нормальні напруження спричинюють рівнодібне
вусилля
„ [ЛІ (х)-МЛ>1$(?) *	/(2)
причому значення 5 (?) таке саме, як і для першого перерізу
У грані /цяц/и/ц, згідно із законом парності дотичних напружень, виникають напруження т' = т,
Згідно з першим припущенням, вважаємо т' рівномірно розподіленими по товщині полиці І, авраховуючи, що розмір = пц/л, — сіх дуже малий, можна вважати, що т' рівномірно розподілені й полов жині йх грані п^гпугп^ Площа цієї грані дорівнює ііх, тому дотичні напруження, що діють у ній, дають зусилля
йТ = х'ійх — тп/4х
Напрям т' повинен бути таким, щоб зусилля йТ зрівноважило різ ницю зусиль
=	_ № (*) +<Щ| з Ж _ М (X) 5 (?) _ ам 5 (?)
Підставляючи в рівняння рівноваги
Рис. 308
вирази для ЛТ І Дії, матимемо
т,мх„ "рк
Поділивши це рівняння на ііх та маючи на уввзі, що йМІйх = <?, знаходимо
(118)
Напруження тп завади утворює єдиний потік з дотичними напру* женнями т у стінці профілю (рис. 308) Останні визначаються з формули Журавського та спрямовані в бік $
Формула (II 8) для дотичних напружень та у полицях та формула (10 20) для дотичних напружень т у стінці дають змогу обчислити до* тнчні напруження в будь якій точці тонкостінного профілю 1 побудувати повну епюру дотичних напружень При цьому, як звичайно, нех тують уклоном полиць у двотаврах і швелерах, вважаючи, що полиці мають постійну товщину Епюру т доводять до полиці, а епюру тп — до осі профілю
Приклад 48. Побудуємо повну епюру дотичних напружень для перерізу двом» ровоі балки № 20 в якому дів поперечна сила 5 = 100 кН (рис. 309)
За сортаментом знаходимо що 2 = 1840 см* 8 = 104 см*, та обчислюємо статичний момент полиці відносно нейтральної лінії
5п = ЬІ (-у
I 20	0.84 \
= 10 0,841-5--------І см»= 80 47 ом».
Тоді дотичні напруження в місці з'єднання стінка з полицею
05п
26
100 10"3 80,47 І0"3 „„ ---------~г-------------т	МПа
1840 • ІО-8 0,62 • 10"’
= 84,1 МПа,
а найбільші дотичні напруження в точках нейтральної лінії
Ч& Ю0 10"3 • 104 І0"3
“ 1840 10-8 0,52 • 10"’
МПа - 108,7 МПа
За цими даними будуємо параболічну епюру т дда стінки.
Для побудови епюри дотичних напружень тп у полицях двотавра звернемо увагу на те що згідно а виразами (11 7) та (11 8)
-Ж-Ж-)
Координата а точки де визначається тп входить до цього виразу у першому степені отже епюра прямолінійна.
Будемо обчислювати за формулою (11.8). Для краю полиш £ (Ь/2) = 0 отже, тп = 0 Для середини полиці (г = 0)
Рнс 309
5(0)«=-^-5п = 40 2 см>,
о-г5»
*В ШЛ И '"'/І	“
в 100 Ю-З 40 2 ЇЇГ* МПа = 26 МПа
1840 ІО""8 0 84 10~2
За цими даними будуємо трикутну епюру тп на правій половин) полиці На її лівій половині епюра буде симетрична оскільки статичні моменти за абсолютним значен иям такі самі як і на правій половині полиці Очевидно такий самий вигляд епюра має й для нижньої полиці
Наявність дотичних напружень у полицях тонкостінних профілів приводить до того, що в крайніх волокнах балки, де діють найбільші нормальні напруження 0^,, напружений стан буде плоский, а не лі нійний (рнс 310, а, б) Тому в таких балках імовірною небезпечною точкою буде не довільна точка крайніх волокон, а та точка, де тп = »* Тппах- Умову міцності для таких балок слід було б записати не в звичайному вигляді
Оп лій = М№ |О|, а користуючись теорією міцності, що має сенс для нестандартних про філів особливо при шн бта* роких полицях
*’ Дотичні напруження в полицях тонкостінних профілів можуть значно змінити характер напру женого стану стержня та вид його деформації
Якщо переріз має дві осі симетрії й силова площина проходить через од ну з них (наприклад у двотавра), то в ньому
Рис. ЗШ
ЗІ)
їй
Рис. 311
6
виникають дотичні напруження, показані на рис 311, а (див також рис 310) ЦінапруженнядаютьрівнодійнізусилляТст1Тп(рис 311,6) Унаслідок симетрії полиць відносно вертикальної осі зусилля Т„ взаєм-но зрівноважуються на кожній полиці
Інша справа, якщо головна центральна вісь перерізу, перпендикулярна до нейтральної лінії, не є віссю симетрії (рис 312) Дотичні напруження у стінці та полицях тут зводяться до зусиль Теч і Т„ показаних на рис 312, б (вертикальними дотичними напруженнями в полицях нехтуємо) Поперечна сила (}, що е рівнодійною цих зусиль, 0 = Т„
очевидно, спрямована вертикально вниз, але вона вже не буде проходити через центр ваги перерізу, оскільки дві снлн Т„ дають ще і пару сил Сила зміщується на деяку відстань 2$ (рис 312, б), перетинаючи нейтральну лінію в точці С
Відрізок 2с знайдемо, виходячи з того, що момент рівнодійної снли відносно будь якої точкч дорівнює сумі моментів складових сил відносно тієї самої точки
Отже, відносно точки С маємо
2МС = Ц(2с + Т„ (Н -/) = 0, звідки
гс=-§-(*-0-4-	<"9)
Залишається обчислити зусилля Та.
На елемент полиці Аг (рис 312, а) діє елементарне зусилля і АТа = х„іАг Отже,
Т'и = І § ТпіЙ
Користуючись виразом (!І 8)
І враховуючи, що
дістанемо
т..,^ ?	.ре-ай-*-
Підставляючи останній результат у формулу (II 9), остаточно маємо
г(Л-0«(>-4)« а гс =------------------
(II 10)
З'ясуємо тепер, яке значення має зміщення рівнодійної сили відносно центра ваги перерізу Для наочності розглянемо одян з найпростіших випадків, коли на консоль швелерного перерізу діє вертикальна сила Р в головній площині ху (рис 313, а) Це наванта* жйяня спричинює в перерізах балки змінні по довжині згинальні мо центи М (х) =я Рх та постійну поперечну силу ф (х) •= Р (рис 313, б) У поперечних перерізах, крій нормальних напружень, діють дотичні напруження т — в стінці та тп — в полицях Поперечна сила $ (х) = =я Р, щр е рівнодійною дотичних зусиль, в будь якому перерізі змі щена відносно геометричної ос! стержня (осі х) на одну і ту саму від стань г0 4- «с
Отже, ділянка балки між вільним кінцем та довільним перерізом (рис. 313, б) перебуває під дією сил Р, ф — Р І моменту М (х) = =• Рх Ця система сил задовольняє всі умови рівноваги, крім одного тут сума моментів відносно осі х не дорівнює нулю Але розглядувана ділянка балки перебуває в рівновазі Тому в перерізі х повинен діяти ще один силовий фактор — крутний момент Мкр = Р (Зо 4- £с), спря мованнй, як показано на рис 313, б Унаслідок цього, незважаючи на те, що навантаження перетинає вісь х, балка буде не тільки згина тися, а ще й скручуватися Досліди це підтверджують (рис 313, в) Отже, в поперечних перерізах балки виникає додаткове поле дотич
них напружень, яке разом з полем дотичних напружень від згинання зрівноважує силу Р
Як відомо, відкриті тонкостінні профілі погано працюють на кручення Крім того, якщо балка закріплена так, то депланація перерізу в закріпленні (жорсткозатискна опора) неможлива, то має місце так зване стиснене кручення, при якому в поперечному перерізі виникають не тільки дотичні, а й значні нормальні напруження Тому бажано вживати заходів для усунення кручення в балках відкритих прокатних профілів Як звичайно з цієї причини застосовують симетричні перерізи (наприклад, з двох швелерів) або балку навантажують у площині, що проходить через точку С паралельно головній площині (на рис 313, б таке положення навантаження показано штрихпункти* ром на рис 313, г зображено один з можливих варіантів конструктивного оформлення зміщення зовнішньої сили) У такому випадку ділянка балки завдовжки х повністю зрівноважена силами Р, $ (х) = = Р та моментом М (х) = Рх, кручення немає
Точка С, через яку проходить рівнодійна дотичних зусиль прн згинанні баїки, називається центром згинання (іноді — центром крУ’ чення, або центром жорсткості) Центри згинання всіх поперечних перерізів лежать на прямій, яку називають віссю жорсткості балки (рис 313, б).
Якщо на балку діє кілька сил то для виключення кручення вони повинні перетинати вісь жорсткості Коли переріз має дві (чи більше) осі симетрії то центр згинання лежить у точці перетину цих осей, тобто збігається з центром ваги перерізу
Приклад 49 Як приклад застосування формули (II10) визначимо положення центра злинання для швелера Лв 18а
Згідно з сортаментом Л = 18 см, Ь 7,4 см, 4 в» 0,51 см. /0 93 см і “ — Ц90 см4
Тол!
ЦК-1)ЧЬ-Л)*	8	,0 93 17 07» 6,89» . .Д
‘С---------ц----------г~-( "’Ч 1190---------о.
§ 73. Розрахунок балок ив пружній основі
Розглянемо балку (рис 314), що обпирається на суцільну пружну основу, реакцію якої на балку в кожній точці можна з певним набли жеиням вважати пропорційною пружному прогину в цій точці Це припущення відповідає моделі, в якій пружна основа е наборам не зв язаних між собою пружин
Позначивши коефіцієнт пропорційності літерою а і припустивши, що пружна основа однорідна по всій довжині балки, знайдемо, що інтенсивність реакції основи дорівнює — аи>, де коефіцієнт а внзпа чається дітенням силн на довжину в квадраті
Отже, повне розподілене навантаження р (х) що діє на балку, складається із заданого навантаження інтенсивністю у (х) та невідомої 314
Рес. 314	Рнс 315
реакції пружно? основи алу (ж)
р (х) = д (х) — сад (х) (11 II)
Для зручності додатний напрям осі прогинів та розподіленого наваи таження вибрано вниз
Розрахунок балки на пружній основі е статично невизначуваною задачею, оскільки лише рівнянь рівноваги недостатньо для визначення закону зміни інтенсивності реакцій основи по довжині балкн Інтен сивність реакції основи пов’язана з деформацією балки, тому для розв’язання задачі спочатку знайдемо рівняння пружної осі балки
Диференціальне рівняння зігнутої осі для балкн постійного попе речного перерізу на пружній основі, згідно з виразом (10 49), можна враховуючи вибрані напрями прогинів (о та інтенсивності «авантажем ця д, записати так
ООІХ)]	(1112)
Спочатку розглянемо ділянку балки (рнс 315), на якій немає зов нішнього розподіленого навантаження Диференціальне рівняння для цього прикладу спрощується Маємо
(1ПЗ)
Розмістимо початок координат у крайній лівій точці розглядуваної ділянки, вісь и> спрямуємо вниз та позначимо прогин, кут повороту, згинальний момент і поперечну силу в цьому Перерізі відповідно через і&о, в0, Ма 1 <?0- ЦІ величини будуть початковими параметрам» Позна чимо ЕЛо. *= Ь*/4, звідки
Ця'велнчина виражається в одиницях довжини (см) У рівнянні (І і ІЗ) незалежну змінну х замінимо безрозмірною абсцисою
(1115)
Тоді рівняння (11 13) з урахуванням виразів (II 14) і (II 15) набирає вигляду
ТР-+4І-0 •	(1116)
Загальний Інтеграл цього рівняння
ш = Де®соз£ 4-Ве® 8іп£ 4-Се~®соз5 4-Ле-® зіп^. (II 17) Послідовно диференціюємо цей вираз по 5, взявши до уваги диференціальні залежності між ш, в, <2, М та співвідношення (II 15)
ш1 =9£ = Де® (с08$ — зіп 5) + Ве® (соз£ 4-зіп5) —
— Се-®(соз£ 4-8іп£) 4-Ое-®(соз£—зіп5), (II 18) а»* _ _ м ($1.	_2(Де® зіп£ —Ве® соз 6 — Се-® зіп 6 4- Ле-*® соз|),
(11 19) ш"' = —= _ 2 [Де® (соз 5 + зіп 5) — Ве® (соз 6 — зіп 6) —
— Се-4 (соз 6 — Зіп а — Ое~» (соз 6 4- зіп ?))	(11 20)
Виразимо довільні сталі Д, В, С і О через початкові параметри ш0, бо, і Мо, поклавши для цього в рівняннях (1117) (1! 20) £ = 0.
ш0 => А 4- С -,
ІЄв«А+В-С + О-.
1»М9=*(— 2В + 2О)Е,І,	'	1
Ь»Лв = (2А — 2В - 2С - 20) Е.І.
З цієї системи лінійних алгебраїчних рівнянь маємо)
п іе, , і*м* рр, и - "Т“ КЕЗ —ЇЕҐ •
Підставивши ці вирази для довільних сталих у формули (II 17) .. (1120), знайдемо
«>м »®+£вог, ® - у> ® - у< ®; <'1
вм = в,Л®—(II 24)
М (х) = М,У, ® + 14'У, ® + аі-ш.У, ® + «Рв.У, ®, (І І 25)
<г«=<г.л®(п26)
Тут через ¥и У9, У,, У* позначено функції Крилова Ч
У^) =. сЬ£соз£ =-|-(е5 4-е-*)соз£, У, © - 4- <сЬ Е51п 5 + 5115 см 0 ’ = -^-[(Є* 4-е-1) ЗІП 5 + (Є* — Є-*)СО5$[,
у, ©=4- *і> е 5і" е=4-[4-<" - е-!>]зіп ь
^4 (5) = “ґ (сЬ £ ЗІП? — зИ ?СО8 5) =
=•	[(Є* + е-ї) зіп 5 — (еі — е-ї) соз 5]
(1127)
Зазначимо, що при диференціюванні функцій Крилова дістають такі прості, але важливі для практичного застосування залежності.
Перейдемо до виведення загальних рівнянь для ш, в, М І $ прн дії довільних розподілених або зосереджених зовнішніх навантажень
Нехай на відрізку х балки (рис 316) діють вертикальна зосереджена сила Р( у точці з абсцисою Ьь зосереджений момент М, у точці з абсцисою О( та рівномірно розподілене навантаження інтенсивністю ді на ділянці від х *= с до х = (і
Для виведення користуємося принципом незалежності ДІЇ сил, а також вважаємо, що переміщення малі Спочатку припустимо, що всі зовнішні навантаження на ділянці х дорівнюють нулю, тоді загальний інтеграл, або прогин иі (х), буде функцією початкових пара метрів і абсциси х за формулою (11 23) Нехай тепер усі початкові параметри дорівнюють нулю, але діють зосереджені навантаження Рі та Мі Очевидно, їх можна взяти як нові статичні початкові пара метри і визначити ч> (х) за формулою (11 23), підставивши Ліо = = Мі, = — Рі При цьому як початок координат треба вибрати не точку О, а відповідно до розташування кожного силового фактора точки з абсцисами а, та Ьі Тому аргументами функцій Крилова У„ У,, Ув, У4 будуть відстані від розглядуваного перерізу до нових силових факторів Рі та М/, тобто відрізки (х — а,), (х — Ь() і т п
Якщо сил І моментів кілька, то вводять їхні суми При розподілених навантаженнях суми перетворюються на інтеграли від елементарних силових факторів а прн кількох ділянках розподілених на вантажень — на суми інтегралів
1 Таблиці функцій О М Крилова можва знайти 8 (71
Обмежимося розглядом випадку дп рівномірно розводі леного навантаження Тоді, інтегруючи з урахуванням за лежності (1128), дістанемо просту формулу
---
-	с)|	(1129)
Отже, при одночасній дії всіх зазначених силових факторів і початкових параметрів повнив інтеграл и> (х) можна подати такі
“ (х) =	(і) + 9.ІГ, (і) + -Г {М.І-Г, (-£-) 4- О^У, +
+ СІМ,У,	- СгР,У4 (-Ц.—) +
+4-їМг'Р-гЧ-1'.(лА)])- (нзо)
Узагальнивши аналогічно вирази для в (х), М (х) і 0 (х), дістанемо такі універсальні рівняння методу початкових периметрів для балки на пружній основі*
в (х) - в,у, (-І-) + -і- {«.їх. (£•)+0.СУ, (-£-) +
+ ЧІЛ^У, (-£) + ІЛМ.У,	_ СЕР,У,	-
(ПЗІ)
М М - М,у, (-і.) + (?„£/,	4- аСч,.у, +
+ «І>е,у. (і) 4- гм,У,	- ьгр,у, 4-
+		(1132)
Таблиця 16
Умом вакріпяеява		Переміщеква та				плові фактори для			
лівого кіниа балки	правого кіпки	лівого кіная (х — 0>				іравого кіпи їх			-0
		а>(0)	Є (0)	М(Р)	5(0)	• <Л	| в т	М(Л	0(0
Вільний	Вільний			М.	ч»			Мі	с
	Обпертий	—	—	лвч		0		Мі	
	Затиснутнй	—	—	л<л	«?о	0	0		——
Обпертий	Обпертий	0	—	Лі,		0		м.	
	Затиснутнй	1)	—	Лі0		0	0	—•	—
Затиснутнй		0	0	—	—	0	0	—	—
(т) +	(£•)+«і’е.У. (т) - т'- г* (т) -
- -1- ЇМ,’/,	- ХР,У, +•
+ £!?,	у,(±=^)].	(1133)
Тепер обчислення» (х), в (х) М (х) та ф (х) у будь якому перерізі балки на пружній основі не викличе утруднень, якщо відомі початкові параметри »0, в0, <?0 і М9 У кожному конкретному випадку початкові параметри можна визначити з умов на кінцях балки Ці умови для різних випадків закріплення балки наведено в табл 16 (припускається, що початок координат суміщено з лівим кінцем балки)
У таблиці через М (І) і ф (/) позначено зовнішні зосереджений момент і силу на правій опорі Якщо на вільних кінцях балки зовніш піх сил і моментів немає, то треба покласти
Д40 =	= Мі = = 0
Як видно з таблиці при виборі початку координат на лівому кінці одпопрольотної балки два початкових параметри завжди відомі Для визначення двох інших параметрів треба розв'язати систему двох алгебраїчних рівнянь, які складаються з умов закріплення правого кінця балки
$ 74. Згинання балок, матеріал яких не відповідав закону Гунв
Викладені вище розрахунки на міцність та жорсткість при згинав ні, що грунтуються на гіпотезі плоских перерізів і законі Гука з од наковим модулем пружності при розтяганні А стисканні, не вичер пують усіх випадків, з якими доводиться зустрічатися конструкторам
Відомо, що закон Гука справедливий, поки напруження не перевищує границю пропорційності, а іноді розрахунки на міцність дово-
Рнс 317
днться виконувати при більш високих напруженнях з урахуванням пластичних деформацій Крім того, і в межах пружності залежність між напруженнями і деформаціями у низки матеріалів нелінійна, тобто не відповідає закону Гука До таких матеріалів належать ча вуй, камінь, бетон, деякі пластмаси У деяких матеріалів, що від Повідають закону Гука, модулі пружності при розтяганні та стисканні різні Тому останнім часом розрахунки на міцність для всіх зазначених випадків набувають все більшого значення
Розрахунки на міцність з урахуванням пластичних деформацій розглядатимуться в гл 19 Тут обмежимося лише визначенням нормальних напружень при згинанні балки прямокутного поперечного перерізу, матеріал якої не відповідає закону Гука протягом всього процесу навантажування, причому залежності між напруженнями і деформаціями різні при розтяганні й стисканні Розглянемо також випадок згинання при різних модулях пружності для розтягання і стискання Досліди показують, що в зазначнкх випадках гіпотеза плоских перерізів справедлива
Нехай балка зазнає чистого згинання Якщо припустити, як і равіше, що волокна при згинанні не тиснуть одне на одяе, то матеріал балки перебуває в стані простого розтягання і стискання
Діаграми розтягання 1 стискання для матеріалів, які не відпові дають закону Гука (чавун, камінь тощо), показують, що напруження зростають повільніше, ніж деформації, причому більшою мірою це відбувається прн розтяганні, ніж при стисканні (рис 317) У цьому разі нейтральна лінія поперечного перерізу не проходить через його центр ваги, а зміщується в бік центра кривизни осі балкн
На підставі гіпотези плоских перерізів та зазначеного характеру діаграми розтягання (стискання) матеріалу можна зобразити епюри відносних подовжень та нормальних напружень (рис 318) у попереч кому перерізі балкн Якщо позначити радіус кривизни нейтрального шару через р, то відносне подовження волокна, що розташовується завдальшкн у від нейтрального шару (рис 318, 319), виражатиметься аже відомою залежністю
в=»у/р
Для визначення відносних подовжень волокон балкн, а потім нормальних напружень треба знай ти положення нейтральної осі по перечного перерізу, радіус кривиз нн нейтрального шару та виразити аналітично чи графічно залежність між деформаціями та напру женнями
І Іроведемо який небудь попереч ний переріз балки перпендикуляр ний до п осі При згинанні баїкн парами сил внутрішні сили пруж ності в поперечному перерізі ПОВНІЇ ні звестися також до пари, отже, проекція нормальних зусиль на вісь х (рис ЗІ9) дорівнює нулю, а і
їх відносно нейтральної осі
г дорівнює згинальному моменту
Отже, дістанемо такі два рівняння статики
Іх=|а^-О,	(II 3-І)
ЇМ, = { ауЛ? - М = 0.
(І І 35)
Оскільки <ІР » Му, то відповідно
Ь Чрііу — <Тот^^ =» 0;	(II 36)
Єй.	\
Оруїіу + $ о^уОу І = м	(І [ 37)
о	/
Для багатьох матеріалів залежність між напруженнями ! деформа діями при розтяганні й стисканні з достатньою точністю можна зобразити степеневим законом
8„ = АрОр Свт^АстОсї,	(II 38)
деір, кег, піт — сталі, що характеризують фізичні властивості мате ріалу
Ураховуючи формулу (! І 34) для відносного подовження, з виразів (II 38) можна записати!
--(£Г-(^Г "ІИ>
Ці залежності та рівняння (II 38) і (II 37) дають змогу визначити положення нейтральної осі, радіус кривизни, а також напруження
<7р І Ост
II 2-2798
Підставивши формули (II 39) в рівняння (11 36), дістанемо
.) \ ЯР" І	і \ встР І І
ІО	0	З
а проінтегрувавши, матимемо
Далі, підставивши формулу (II 39) у рівняння (II 37), знайдемо, що
ь [І Ь&Г +) №ГН=м-
І після інтегрування дістанемо
М (1141)
Маючи иа увазі, що Ні + й2 — й, з рівнянь (і І 40) і (І І 41) знайдемо р. Ні і й,, а потім за формулами (11 39) — напруження ар та ост
Можна розв язати також зворотну задачу — визначити найбіль ший допустимий згинальний момент за допустимим напруженням на розтягання ІОр] або стискання [сст] Для цього запишемо за формулами (І! 39) напруження розтягання та стискання в крайніх волокнах балки завдальшкн Ні і /ц від нейтрального шару

(Н 42)
На підставі цього виразу формули (11 40) та (11 41) можна записати в такому вигляді
(1143)
(II 44)
(II 45)
Крім того, з формул (11 42) випливає, що
*• - 0^С7
Отже, з останніх трьох рівнянь, маючи на увазі, що Нг 4- й, — й,
можна визначити за допустимим напруженням [ор] чи [ост] положення нейтральної осі та допустимий згинальний момент За граничними значеннями напружень можна визначити граничний згинальний мо мент, який відповідає граничному значенню, досягнутому одним із напружень у найбільш віадатеннх від нейтральної осі волокнах у зоні розтягання або стискання
Так само, як це зроблено для балки прямокутного поперечного перерізу, можна розв’язати за дачу і для інших простих пере різів, наприклад складених з пря мокуїннків (таких, як двотавр, тавр тощо)	*
Ролгдяиемо ще -визначення нормальних напружень при згн панні у випадку, коли малеріал
відповідає закону Гука, але мо	рнс зго
дуті пружності при розтяганні га стисканні різні Нехай Ео — модуль пружності матеріалу прн розтяганні, £ст — при стисканні Для таких матеріалів, якзвичайно, Ееі>-> Ер Епюру нормальних напружень у перерізі балки для цього прик ладу зображено на рис 320
Для волокон, розташованих завдальшкн у від нейтрального шару в зоні розтягання та стискання
°р = — пст=-^-£от	(1146)
З рівняння (11 36) випливає, що
( ср4у = ас14у	(І І 47)
Підставляючи замість <з0 та аег їхні вирази (11 46), маємо (4 48) 6	о
звідки після інтегрування дістанемо
ЕГІЇ=.Е„І&	(1149)
або
Ураховуючи, що Ні + й, = й, знайдемо
К£РЧ-КСЄТ	(Ц50)
* \ГГр + \ГЕ^
Отже, положення нейтральної осі визначено
Тепер знайдемо напруження у крайніх волокнах балки в зонах розтягання ар і стискання а„. З епюри напружень (рис 320) випливає,
що сумарна розтягальна сила N9 в зоні розтягання і стискальна сила Л^ст в зоні стискання поперечного перерізу визначаються так
(1151)
Ці сили діють завдальшки (2/3) Л, та (2'3) Л, від нейтрального шару Оскільки зусилля в поперечному перерізі зводяться до пари сил, то Л/р => Плече пари дорівнює (2/3) Л Згинальний момент можна записати у вигляді
М=Н',-£-Ь
Ураховуючи вирази (11 51) та (11 50), маємо а« Орб/ц/і СрЬЛ1 /*ет -----------------о ~ ї - гтг- , , г-я— •
м =
оетЬЛ»
(1152)
звідки
(Н53)
Користуючись цими формулами, можна за згинальним моментом знайти найбільші розтягальні та стискальні напруження, якщо відоме відношення модулів пружності
Запишемо формули (11 53) в дещо іншому вигляді Згідно з виразом (II 50), маємо
_ Ур =
£„ лі УР	’
Підставляючи це відношення у формули (11 53), дістанемо
= V (* + 77) '	(11 54)
У цьому вигляді формули зручні для обчислення напружень у випад ку, коли в крайніх волокнах балки вимірюють відносні деформації за допомогою тензометрів
Глава 12 СКЛАДНИЙ ОПІР
Під скіадиич опором розуміють різні комбінації раніше розгляну тих простих напружених станів брусів (розтягання, стискання, зсуву, кручення та згинання)
У загальному випадку навантажування бруса (рнс 321, а, б) у поперечних пере різах можуть діяти шість компонент внутрішніх сил — її, $у, Му, М{, М*р, по в язаних з чотирма простими де4орманіямн стержня — розтяганням (стисканням), зсу вом крученням та згинанням
Чогось принципово нового задачі склад ного опору при достатньо жорстких брусах не вносять, оскі тькн спільна дія зазначених
Рис 321
зусиль призвод ґгь до напруженого стану, який можна здобути сумуван ням напружених станів, спричинених кожним видом простого навантажу вання окремо Вміючи визначати нормальні та дотичні напруження в різних точках стержня а також головні напруження, можна за тією ч» іншою теорією міцності перевірити міцність даного стержня Ана логічно може бути вивчена деформація або переміщення бруса шляхом відповідного складання переміщень, що дістають прн окремих більш простих навантажуваннях
Принцип сумування дії сил можна застосовувати в усіх випадках, коли деформації малі й відповідають закону Гука
На практиці одночасна дія всіх силових факторів спостерігається нечасто Частіше доводиться мати справу з різними комбінаціями їх, які й розглянемо нижче
$ 75 Складне І косе згинання
Складне згинання спричинюється силами або моментами, розта шованими в різних площинах, які проходять крізь вісь балки (рис 322, а) Таке згинання зветься також неплоским оскільки зігнута
вісь балки не є плоскою кривою
Якщо всі навантаження, які спричинюють згинання, діють в одній площині, що не збігається ні з однією з головних площин, то згинання зветься косим (рнс 323, а)
Як у випадку ііеплоского, так і у випадку косого згинання, най зручніше зводити згинання до двох плоских Для цього наван таження, що діють у довільних поздовжніх силових площинах, треба розкласти на складові, які розташовуються в готонних пло щинах ху та хг, тут осі у та г —
головні осі інерції' перерізу (рис 322 і 323) Отже, схеми навантажуван ня брусів при складному та косому згинанні можуть бути такими, які показано па рис 322, б та 323, б від повідно
При складному згинанні у по перечних перерізах бруса взагалі виникають чотири внутрішніх си лових фактори	ЛІ, та Ми
Розраховуючи на міцність при склад йому згинанні як правило, нехту ють впливом дотичних напружень
рис ззз	Обчислимо напруження в дея
кій точці (у, г) довільного попереч ного перерізу, розмістивши її для певності в першому квадранті (рис 324, а) Напрями головних осей показано на рисунку Згинальні моменти будемо вважати додатними, якщо вони спричинюють у точках першого квадранта розтягальні напруження
Виходячи з принципу суперпозиції, знайдемо напруження в зазна ченій точці, розглядаючи два плоских згинання Нехай спочатку діє тільки момент Лі, Тоді нормальне напруження в точці
Якщо ДІЄ ТІЛЬКИ момент Му, то
»«= "і
Очевидно, при одночасній ДІЇ обох згинальних моментів напруження
Формула (12 1) дає змогу визначити нормальні напруження в будь якій точці поперечного перерізу при складному, або, як ще кажуть, просторовому згинанні Згинальні моменти та координати точок, в яких визначають напруження, підстааляють в цю формулу із своїми знаками
У випадку косого згинання (рнс 325) згинальні моменти Мя та Му пов язані залежностями
ЛТ, ==/И соз а, М9 = М зіпа,	(12 2)
де М — згинальний момент у даному перерізі в силовій площині р — р (рис 325)
Тоді, використовуючи формулу (12 1), будемо мати
або 0 =	+	(123)
Рівняння нейтральної лінії при складному згинанні в будь-якому поперечному перерізі дістанемо з формули (12 1), поклавши а « 0 та позначивши координати точок нейтральної лінії через у9 та ц (рис 324, б) Тоді
о = -ІЬй- + Лй- _ 0.	(12 4)
'і	'V
Це рівняння е рівнянням прямої, що проходить крізь початок коор дннат (центр ваги О перерізу) Положення нейтральної лінії характеризується її кутовим коефіцієнтом
(125)
У загальному випадку складного (просторового) згинання кути нахилу нейтральних ліній уздовж осі бруса не залишаються однаковими, а змінюються відповідно до зміни співвідношення значень аги* нальних моментів /И2 та Му, як це випливає з виразу (12 5)
Якщо в деякому перерізі бруса, де діють найбільші згинальні моменти М, та Му (рнс 326, а), треба знайти положення нейтральної лінії, то зручно для більшої наочності спочатку показати положення силової лінії р — р Найпростіше це зробити, побудувавши векторну діаграму моментів (рис 326, б), яка показує напрям результуючого вектора моменту М і, отже, визначає кут а нахилу його площини дії (силової лінії р — р)
(12 6)
Тепер вираз (12 5) для кута нахилу нейтральної лінії з урахував нам формули (12 6) можна записати так
(12 7)
Аналізуючи цей вираз, бачимо, що на відміну від плоского (прямого) згинання при складному згинанні нейтральна та силова лінії взагалі (коли	не будуть взаємно перпендикулярні.
При косому згинанні відповідно до формул (12 2) відношення зги-вальних моментів Му та Мг однакові по всій довжині бруса (Му/М^ = — а) Тому з виразу (12 7) випливає, що й кут р нахилу нейтральної лінії' також однаковий Отже, поперечні перерізи бруса, залишаючись плоскими, повертаються навколо паралельних одна одній нейтральних ліній, як і при простому плоскому згинанні Викривлення осі бруса при цьому відбувається в одній площині л — п, нормальній до напряму нейтральної лінії (див рис 325) Ця площина називається площа ною згинання
Перевіряти міцність слід у тих перерізах, де згинальні моменти Му та /И, одночасно великі Таких перерізів у загальному випадку складного згинання може бути кілька
Якщо небезпечний переріз відомий, то в ньому треба відшукати небезпечні точки Наочне уяалення про розподіл напружень о (М?) та а (Л4Х) У поперечному перерізі бруса дають відповідні епюри, які па ведено на рис 326, б Для побудови епюри сумарних напружень ох слід провести базис епюри перпендикулярно до нейтральної лінії 3 формули (12 І) випливає, що епюра а лінійна Тому для її побудови, крім відомої нульової точки, досить визначити будь яку одну ординату, наприклад для точки А Очевидно, найбільш напруже цими точками перерізу будуть точки, найвіддаленіші від нейтральної лінії — точки А та В (рис 326, б) У даному випадку в точці А діє найбільше розтягальне напруження, а в точці В — найбільше стнс кальне
Отже, умови міцності для небезпечних точок мають вигляд
„	„ М*Л , МІІ^А
Оцих = &А — і +	—•
(12 8)

(12 9)
У випадку косого згинання, коли напрями згинальних моментів такі, як показано па рис 324, а, найбільші розтягальні напруження виникають у точці В, а найбільші стискальні — в точці б (див рис 324 б) Умови міцності набирають вигляду
Сів чіп а	ип соі а \
	 4*	[о^.],	(12 10)
Сго їіп а уп соі а \	.	.
]	4“ —~ 1	[О—)	(12 11)
Зокрема, для прямокутного перерізу
—І- _ -ІИ- _ ги -^2_ — -^2_ ги г0 «в — *• Уа — Уо
тому формули (12 10), (12 11) можна спростити .. І »іп а , соіа \	,
Отая “ °В — АІтах 1—5=------! ж—	(0+),
' *	* '	(12 12)
І $іп в , соз а \	,
Огаїп — Оо ~ — Літа» і 1$*"" 4“ —цр “ 1	[О_І
У загальному випадку неллоского згинання умова міцності на бираа вигляду
(12 13)
Аналогічно перевіряється міцність у точці, де діють найбільші стискальні напруження
Добір перерізів при неплоскому згинанні — задача більш складна, ніж при простому птоскому згинанні При іґ розв язуванні треба спо чатку задатися відношенням моментів опору й знаходити перерізи методом підбору
Якщо треба знайти дотичні напруження при неплоскому згинанні, можна скористатися формулами
т - <?А т
в~
Визначаючи переміщення, також виходимо з принципу незалеж ності дії сил та обчислюємо переміщення в кожній з головних площин Зберігаочи попередні позначення прогину в напрямі головної осі у через іа та позначаючи прогин у напрямі головної осі г через о, запи шемо диференціальні рівняння прогинів у площинах Х2 та ху в такому
Користуючись наведеними диференціальними рівняннями, безпосереднім інтегруванням іх або за методом початкових параметрів можна знайти відповідні переміщення Крім того, переміщення можуть бути визначені енергетичними методами, які розглянемо нижче
Повний прогин / перерізу визначиться як геометрична сума прогинів V та ш	______
(12 14)
Як приклад обчислимо прогин вільного кінця консолі, навантаженої силою Р, як показано на рис 327, а, б Розкладаючи силу Р у напрямах осей, дістанемо складові
Рк = Рсоза; Р, = Рзіпа	(12 15)
На підставі формули (10 54) визначимо прогини в головних площинах (рнс 327, в)
3£Л-	(1216)
Повне переміщення
І _	(|2 17)
Визначимо напрям повного прогину /, для чого знайдемо кут між відрізком ООц та віссю у
(12 18)
Порівнюючи формули (12 18) та (12 7), помічаємо, що кут між площиною згинання та віссю у за модулем дорівнює куту між нейтральною
лінією перерізу та ВІССЮ 2 Звід сн випливає, що повний прогин при косому згинанні перпендику лярний до нейтральної лінії пе рерізу (рис 327, в) Очевидно, відхилення повного прогину від силової' площини тим більше, чим більше відношення
Зазначимо, що, коли (це має місце для круглого пере
різу будь якого правитького многокут ика) сумарний прогин буде в силовій площині У цих випадках косе згинання неможливе
Приклад 50 Дерев який прогін перерізом 16 х 20 см (рис 328. б) вільно об-пиряється на кроквяні ферми (рис 328. а), відстань між якими 3 м Прогін наванта жений вертикальним рівномірно розподіленим навантаженням інтенсивністю д =□ = 4 кЯ>м Уклон верхнього пояса кросе ферми 1 2 Визначимо найбільші напруження стискання та розтягання в перерізі балки зазначимо точки перерізу де вони мають місце, та знайдемо повний прогин середнього перерізу балки
Макснматьний згинальний момент Який буде посередині баїкн
аР 4 3і
Л4т„ = —д— " —д— кН и = 4 5 кН м
Складові цього моменту що діють у головних площинах Інерції (вНіїосио осей г та у) визначимо за формулами
Л12 — Мтік еоа а = — 4 5 0 89ч кН м = — 4 025 кН м
М„ = — Л1тіх зіп а = - 4 5 0 447 кН м = — 2 0І2КІІ м
Кут пзхту нейтральної лінії л — п визначиться з формули (12 7) і Л’ і 20’
ійР = -~іва = --2- “5Г- = — у І6І = - 0 7813 - - (« 38°
Найбільшими будуть напруження стискання в точці В та розтягання в точці О, тобто в точках найбільш віддалених від нейтральної лінії
Лі, Му л / Лі, Му}	6
”8 ~ ІГ, +	“ 6 ( Мі’ 6’Л ) “ 16 20 ІО"4 Х
{ 4 025 ІО"3 2 012 І0~3\иг1
х ( м 10-> + І6" ,О-’ ) мп* - - 6-12
У точні О очевидно буде таке саме за модулем напруження розтягання оо «- 6 !2 МПа
Найбільший прогин має місце посередині прольоту Визначаємо його за форму лаю
Чді* ЗМЕ2
в яку замість інтенсивності розподіленого навантаження слід підставити Його складові в напрямах головних осей
4|і и 9 соз а = 4 0 844 = 3,576 кН'м
9,^ї8Іпа=>4 о 447 -= 1 788 кН м
а також моменти інерції відносно головних осей і та у Складові прогин) тоді
5 3 576 10-3 У 12
Ь)уІ* “ 3845У,
384 £Л
а повний прогин знайдемо як геометричну суму зазначених склидовнх прогину
/ = У о* + »’ = /О 28’ + 0 35’ см - 0 45 см
Прогни / лежить у площині яка перпендикулярна до нейтральної лінії
$ 76. Згинання з розтяганням (стисканням)
Розрахунки на спільну дію згинання та розтягання можна звести до таких двох видів
а)	розрахунки на дію поздовжньо поперечних навантажень;
б)	розрахунки на позаиентрове розтягання (стискання) Окремо має розглядатися згинання з розтяганням (стисканням) кривого бруса
Складне згинання з розтяганням (стисканням) прямого бруса Якшо на балку діють поздовжні та поперечні навантаження, що перетинають вісь бруса, то в загальному випадку (рис 329, а) в попереч них перерізах виникають згинальні моменти Лі, та М* в двох площинах, попречені силн та ф*,, а також поздовжня сила N (рис 329, б) Отже, в цьому разі буде складне згинання з розтяганням або стисканням Нормальні напруження в довільній точці перерізу
Згинальні моменти, поздовжню силу й координати точки, в якій визна чають напруження, підставляють сюди з їхніми знаками
Нехтуючи дотичними напруженнями від поперечних сил, можна вважати, що напружений стан у небезпечній точці лінійний Отже, умова міцності має більш простий вигляд
Якщо переріз має дні осі симетрії й кути, що стирчать, то небезпечною буде одна з ку тоаих точок Напруження в ній визначають за формулою (12 19) або ж так 1
N , мг , ми р ** г,
(12 21)
Рис 330
Знаки в цій формулі комбінують за змістом або на підставі порівняння з формулою (12 19)
У випадку плоского згинання в головній площині уОх з розтягай ням (стисканням) формула (12 21) спрощується
о-4-±-й-	<12 22>
Ці формули застосовують при розрахунку на міцність плоских рам та арок малої кривизни Небезпечними в цьому разі е ті перерізи, де Діє найбільший згинальний момент
При розрахунку брусів з поперечним переріюм довільної форми для визначення небезпечної точки переріжу треба насамперед знайти положення нейтральної лінії Спосіб визначення положення нейтральної лінії описано нижче при розгляді позацентрового стискання
Приклад 51. Доберемо двотавровий переріз пмекді сталю» рами (рис 330 а) при [а)	160 МПа
Визначивши опорні реакції та побудувавши епюри ЛІ, і N (рис 330 в, г) бачи но що небезпечний виваляється переріз правого стояка в якому
= 57 кН м N -= — 63,9 кН
Небезпечні точки в цьому перерізі розташовані ліворуч (рнс 330, б), оскільки тут арифметично додаються напруження від Мг та N Відповідно до формуїн (12 22) умова міцності запишеться так
атп = 57 уІ0~3 + -639. МПа< 160 МПа (12 23)
В умові міцності е дві невідомі величини — ІГі та Р. Здебільшого напруження ах від згинання більші ніж від поздовжньої сили тому прн доборі перерізу можна спочатку відкинута другий доданок і знайти наближене значення з розрахз яку ва згинання
ÄР> 57 [^|~ м8 = 356 Ю-с м8 ~ 356 см*
Далі за сортаментом (дод 1) треба вибрати двотавр з моментом опору дещо бі тьшнм ніж V Вибираємо двотавр № 27 для якого ІУ, — 371 см* Р = 40 2 см*
1 При згинанні із стисканням застосовувати наведені формули можна лише для коротких стержнів великої жорсткості, оскізькн у випадку тонкого доеюго стержня можлива втрата стійкості (див гл 20)
Далі перевіряємо міцність вибраного перерізу, обчислюючи максимальні нормаль ні напруження за формулою (12 22)
57 ІО"3 63 9
°тм“ 37[	[0-а + 40 2
І0~3
МПа -а (153 6+ 15 9) МПа
= 169 5 МПа
Перенапруження становить
169 5 — 160 ------------100 % ® 6 % > 5 %
тому необхідно збільшити розмір перерізу вибравши за сортаментом такий більший помер двогавра — № 27а аля якого
V, = 407 см* Г - 43 2 см*
Позацентрове розтягання (стискання) пргмого бруса Позацснтро ве розтягання (стискання) є окремим випадком складного згинання з розтяганням (стисканням), при якому брус розтягується силами паралельними осі бруса, так що рівнодійна їх не збігається з віссю бруса (рис 331), а проходить крізь точку р що називається полюсом сили
Нехай на брус довільного перерічу діє одна сила Р, яка паралельна осі бруса й перетинає довільний поперечний перерізу точці р(рис 331) Координати цієї точки в системі головних осей перерізу позначимо через ур та гр, а відстань цієї точки до осі х, яка зветься ексцентриситетом,— через е У довільному поперечному перерізі при даному навантаженні діють такі внутрішні силові фактори N — Р Му = Р?р
М, =- Ру»
Отже напруження в довільній точці перерізу будуть складатися з напружень осьового розтягання силою N га напру жень від чистого згинання моментами Ми та Мг
Підставивши сюди замість /V, Му та Мі їхні значення, дістанемо
"=40 -"442 1	<12 25>
Ця формула набере дещо іншого вигля ду якщо виразити головні моменти інер ції через радіуси інерції
>- -т(1 і--уг' 'Т' у) <12 26)
Для визначення небезпечної точки
Рис ззі	при складному профілі доцільно побуду
вати нейтральну лінію перерізу Небезпечною в перерізі буде точ ка, найвідддленіша від нейтраіь ноі лінії
Рівняння нейтральної лінії матимемо, прирівнявши до нуля праву частину рівняння (12 26) і позначивши координати точок на нейтральній лінії через у0 та я0
4-’о+Л-ї. = -1 (12 27)
Поклавши в цьому рівнянні по черзі го = 0 1 уа = 0, знайдемо відрізки ув та гк, що відсікають ся нейтральною лінією на осях у та я (рис 332)
Із залежностей (12 28) випливає, що нейтральна лінія перетинає координатні осі в точках, які належать квадранту протилежному тому, в якому лежить точка р
Тепер, провівши паралельно нейтральній лінії дотичні до контура перерізу знайдемо найбільш напружені точки А та В у розтягнутій та стиснутій зонах перерізу (рис 332) Напруження в цих точках та умови міцності мають вигляд
От» = <За =	+-Ц- яд +
р/ ?	?	\	(12 29)
Отл = Ов = — 1 4- ?а -1- -у- Ув} С |о-1
Тут яа, ул та —яв, —ув — координати точок А та В відповідно Епюру напружень а наведено на рис 332 Для прямокутного перерізу умову міцності зручніше записати в такому вигляді
Отож = -у 4-	4-	[о}	(12 30)
Формули (12 29) та (12 ЗО) справедливі й у випадку дії стискальної сили Р, якщо немає небезпеки виникнення поздовжнього згинання
Ядро перерізу Досі ми зображали нейтральну лінію як таку, що проходить крізь переріз Проте взагалі вона може проходити й поза перерізом Дійсно, якщо сила Р прикладена в центрі ваги то нейтральна лінія проходить у нескінченності, оскільки напруження в цьому разі розпаді ієні рівномірно
Ил2———————2
Рис. 333
Рис. 334
Із збільшенням ексцентриситета е (рис 333) нейтральна лінія буде наближатися до перерізу і при деякому положенні сили Р (на рнс 333, наприклад при положенні А8) вперше торкнеться контура перерізу При дальшому збільшенні ексцентриситета нейтральна лінія перети нає переріз причому нормальні напруження в перерві будуть обох знаків по один бік від нейтральної’ лінії — розтягальними. по інший — стискальними
Можна визначити зону таких віддалень сили Р від осі, при яких нормальні напруження по всьому поперечному перерізу будуть одного знака Така зона називається ядром перерізу Це важливо для брусів з матеріалів, що погано чинять опір розтяганню (наприклад для цегляної кладки, для бетону та сірого чавуну)
Отже, ядром перерізу називають зону навколо центра ваги попереч ного перерізу, яка мав таку властивість якщо позацснтрово прикладене навантаження розташоване в зоні ядра то нормальні напруження в усіх точках поперечного перерізу мають один знак
Для побудови ядра перерізу будемо задаватися різними положеннями нейтральної лінії, дотичними до контура перерізу й обчислювати координати відповідних точок прикладання сили Р за 'та кимн формулами що випливають з виразу (12 28)
=	2 --4-	(12'4)
Обчислені координати визначають точки, що лежать па межі яд,>а перерізу
Аби полегшити побудову ядра перерізу використаємо таку властивість нейтральної лінії при повороті нейтральної лінії навколо деякої фіксованої точки А контура перерізу точка прикладання сили переміщується вздовж деякої прямої Щоб обгрунтувати цю властивість досить підставити в рівняння (12 27) координати точки А (у^. гол), що лежить на нейтральній лінії Матимемо
Ум УоУол _	,
Р "Г і2-------------
(12 32)
Рнс 335	Рнс 336
Рнс 337
Дійсно рівняння (12 32) при гол = сопзі є рівнянням прямої' лінії відносно координат точок прикладання сили Р — [уг гр)
Отже для побудови ядра перерізу будь якої фігури треба провести кілька положень нейтральної лінії, що збігаються із сторо-нами перерізу, а також дотикаються до точок, які стирчать
Побудуємо, наприклад, ядро перерізу для прямокутника АВСЛ (рис 334) Сумістимо спочатку нейтральну лінію із стороною СО (положення 1 — 1) Очевидно в ньому разі
«. = И. г, = оо
Тоді із виразів (12 31)
Тут ураховано, що
12М

/і» .а___________1, _ ЛУ д»
12	” Р ~ 12ЙЛ “ 12
Отже, координати точки !' ядра перерізу визначені
Сумістимо тепер нейтрачьну лінію із стороною АЛ (положення 2 — 2) "Лаємо
Ун = 00 г„ — /1/2
Тод координати точки 2' ядра
„ л	Л* А
Ув и. гв -	- 6
Аналогічно визначаються координати точок 3' та 4 , що відповіла ють положенням 3—3 11 4 — 4 нейтральної іінії
Оскіїьки при переході нейтратьної іінії з одного боку на інший вона повертається навкото кутової точки перерізу то точка прикла дання сити перемішується по прямій утворюючи контур ядра Отже, ядро перерізу буде ромбом з діагонаїями, які дорівнюють одній третині відповідної сторони перерізу
Приклад 62 Для круглого перерізу побудуємо ядро перерізу (рис 335)
/ьіО
У колі всі центральні осі — голоа яі Тому при дотиканні нейтральної ті ніі 1—1 у будь якій точці А точка 1 ле жить на діаметрі, який також прохо дить крізь точку А її координати такі
Очевидно можна зробити висновок що внаслідок симетрії перерізу ядро пс рерізу також буде колом з радіусом
Ядро перерізу для двотавра (рис. 336), швелера (рнс 337) та трикутника (рнс 338) рекомендуємо читачеві побудувати самостійно
$ 77. Згинання з крученням
Круглі вали Сили, що діють на вали (тиск на зуб'я шестерен, на тяг ремнів, власна вага вала та шківів тощо) спричинюють у попереч них перерізах валів такі внутрішні силові фактори /ИКР « /Ия Ми, Фу та <Зг Отжа в будь якому поперечному перерізі одночасно ви никають нормальні напруження від згинання в двох птощинах а та кож дотичні напруження від кручення та згинання
Для розрахунку вала насамперед треба визначити небезпечні пе рерізи 3 цією метою слід побудувати епюри згинальних моментів Му, та крутного моменту /Ия
Навантаження що діють на вал, розкладаємо на ск задові вздовж координатних осей (рис 339, а), а потім будуємо епюри від сил Ріг, р2г, . . Рпг — еПЮру Му, ВІД СИЛ	Рпу — епюру М.
(рис. 339, б, а)
При згинанні вала круглого або кільцевого перерізу в кожному з його перерізів має місце пряме згинання під дією результуючого згинального моменту (рис 340)
Вектор моменту М у різних перерізах може мати різні напрями тому навіть якщо немає розподілених навантажень, епюра М може бути криволінійною (рис 339, а) Для загального випадку це легко доказати аналітично
Нехай Му = а 4- Ьх /И, = с + <іх (а Ь, с <1 — постійні коефі цієнти) Тоді
М = У (а т Ьх)г т(с г ^х)*
Вираз під радикаюм лише в деяких окремих випадках є повним квадратом (наприклад, при а - с = = 0) а здебільшого епюра криво лінійна, причому
т < гс= + ((' Ь , <Г)х
Це дає змогу будувати епюри М спрощеним способом, дещо за вищуючи значення сумарного зги наївного моменту М на ділянках між переломами епюри значення сумарного згинального моменту М обчислюють лише для тих перері зів у яких на епюрах Му та М, е перетоми Ці значення відкладають у масштабі по один бік від осі на епюрі М та сполучають прямою лі нією
Далі будуємо епюру /Икр — Мя (гне 339 д) та шукаємо небезпечні перерізи, в яких одночасно великі М та ЛЦр Порівнюючи епюри зна ходимо що небезпечним буде пере
Рнс 339
різ /—/ або 2—2.
Тепер у небезпечному перері зі треба знайти небезпечні точки Легко визначаємо положення нейт раїьноі лінії (0 а) та будуємо
епюри нормальних напружень а від результуючого згинатьного мо менту /И (рис 341) які змінюються пропорційно відстані точок від нейтральної лінії’ Очевидно небезпечними точками є точки А та В, які найбільш віддалені від нейтратьної ліпіі— в них одночасно і нормальні напруження від згинання і дотичні напруження мають най більші значення
л». = -£-!—4------;	(12 34)
т„.. - М„іф„	(12 35)
Бітя найбільш небезпечної точки В видіїимо елемент (рис 342) По чотирьох його гранях діють дотичні напруження а до даох із цих граней прикладені ще й нормальні напруження Решта граней вільні від напружень Отже при згинанні з крученням елемент у небезпечній точці перебуває в плоскому напруженому стані Аналогічні напруження на гранях ми мали у брусі що згинається (див гі 10), точу тут
Рис 340	Рнс 341	Рис 342
головні напруження треба визначати за тими самими формулами* о, -= (о 4- Уоа + 4т’)	— 0 аа - Ц- (о — Уа*~У~4Г2}
(12 36) Різниця між виразами (10 ЗО) та (12 36) лише в тому, що в останньому випадку дотичні напруження спричинюються крутним моментом, а при згинанні вони спричинюватися поперечною силою
Зазначимо, що в даному випадку сктадного напруженого стану впливом дотичних напружень від поперечних сил нехтуємо, оскільки вони значно менші, ніж дотичні напруження спричинені крученням
Для перевірки міцності елемента який виділено біля небезпечної точки треба, вибравши відповідну теорію міцності, скористатися однією з формул § 62, наприклад формутою (10 35) або (10 34) за теорією Мора
а т -Ц-2- /о2 + 4т" < [о];	(12 37)
за IV теорією	____
о».і»-/о,+Зт,«;і(И	(12 38)
Підставляючи у формули (12 37), (12 38) вирази (12 34), (12 36) для напружень та враховуючи що ЇРр = 2ЇГ, матимемо
V«;+«’+К «ї,+«5+
ОеквМ =	ІО],
______________ (12 39)
/о.’зм,2, о«квіу —................. |о]	(12 40)
Чисельники цих формул є зведеними моментами дія яких еквіва лентна спільній дії трьох моментів (згідно з вибраною теорією міц ності) Отже
= -Цр- т -Чг1 і-«;+«,’
______________ _________________ (12 41)
= V0,75/МЇ + м; т ]/ ЛГ т 0.75М2,	(12 42)
У разі потреби так само можна здобути форму ти для зведених моментів і за іншими теоріями міцності
Неважко помітити, що тепер умови міцності (12 37), (12 28) можна замінити однією простою форму тою
Огк. - м„№ С І°І	(12 43)
Отже при спільній дії’ згинання з крученням стержні круглого перерізу розраховують на згинання від зведеного моменту Л18,
Розв'язуючи нерівність (12 43) відносно V', дістанемо формули для визначення моменту опору
(12 44) та діаметра круглого вала
<і>|/ “ІЙоГ ~ V “Й-	<12 45)
Зазначимо, що наведені формули цілком придатні й для стержнів кільцевого перерізу
Розглянемо найпростіший приклад розрахунку вала на згинання з крученням
Приклад 63. На вал (рис. 343) насаджені три зубчастих колеса Колеса навал тажені силами Р\ = 4000 Н, Р, = 3000 Н Р3 = 2000 И, причому сила Р, вертикаль на а сили Р3 та Р3 горизонтальні Діаметри зубчастих коліс такі й, = 100 мм 300 мм О8 = 250 мм Допустимі напруження (а) — 60 МПа. Доберемо діа метр вала за четвертою теорією міцності
Замінимо діюче навантаження статично еквівалентною системою сил
Перенесемо сили Р, Р, та Р3 на вісь вала замінюючи кожну з них склою прн клиденою в точках В С або й відповідно й скручувальною парою си т Л11 = у Р^Пі Мг = у Р3О3 М3 = у відповідно Отже дістаємо розрахункову схему (рис. 343) На схемі наведено як значення прикладених зовнішніх навантажень (Р с, М^) так і значення спричинених Ними опорних реакцій
Розглядаючи окремо енлн в горизонтальній та вертикальній площинах (рис. 344 о та б), будуємо епюри згинальних моментів Для побудови сумарної епюри моментів М визначаємо ординати в характерних точках за формулою (12 33) у перерізі В
М = }/ГМ^ +МІ = /і60«-‘-501 Н м = /гГіоб Н м = 167 6 Н м у перерізі С
М = у440» + 562 5’ В м= ) 510006 Н м = 714 2 Н м у перерізі О
М « Ґ64О» + 250* Н м= Уч72 100 Н м = 687 і Н м
Епюру М побудовану за цими даними наведено на рнс. 344. а Як уже зазнача лося на ділянках ВС та Сй така епюра має завищені значення ординат (дійсні ана чеиия показано штриховою лінією)
Розглядаючи моменте що діють на вал будуємо епюру крутнях мочентін (рнс 344 а)
^'ігоон
№
V” р^Он"
Рнс 343
Рис. 344
м’ » 12 44 см*
Порівнюючи епюрн М та Л4кр знахо днмо що небезпечним е переріз 1—1 ліво* руч від точки С де одночасно діють М = = 714 2 Н ч та Л1кр = 250 Н м Згідно з IV теорією міцності зведений момент визначаємо за форм) тою (12 42)
Л1„ = /0 75 250і+ 714 2’ Н м =>
= ) 556 МІ 25 Н м =- 746 З Н м
Підстааяяючн зведений момент у фор мулу (12 44), знаходимо потрібний осьовий момент опору
М»» _ 746 З (о]	60
І поклавши ІГ яз 0 1(Р обчислюємо погрібний діаметр вата
4 > у/Тоі? =	12 44 см =. |/І24Л см =
Округтнвшн до найближчого стандартного діаметра вибираємо 4 = 50 мм
Брус прямокутного перерізу. На практиці часто зустрічаються стержні некруглого перерізу, які зазнають діі крутних та згинальних моментів Як приклад розглянемо брус прячок}тного перерізу (рис 345, а), навантажений силами Р, га Р9 що спричинюють у по перечних перерізах згинальні моменти Ми та Л14, а також поперечні си ли та Сг
Розраховуємо в такій послідовності Розкладаємо задані навзкта ження (сили Рі та Р*) на ектадові вздовж козрдннатних осей та зво
днмо їх до осі вала При цьому дістаємо в поперечних перерізах, у площинах яких лежать точки прикладання сил зовнішні скручуватьпі моменти Л4кі = /Мі* та ЛІК2 = Міг Добуту таким чином розрахункову схему наведено на рис 345
Для того щоб визначити положення небезпечного перерізу б) дуємо епюри згинальних моментів Му та Л12, а також епюру крутних моментів /ИХр (рис 345, б)
Зіставлення епюр показує, що найбільш небезпечним є переріз /—/ бруса ліворуч від гочки прикладення сили У цьому перерізі діють найбіїьші згинальні моменти /Иг, Му та максимальний крутний момент /Икр Щоб перевірити міцність бруса, треба в небезпечному пе рерізі знайти небезпечну точку обчистити для неї еквівалентне напру ження (за однією з теорій міцності) й порівняти його з допустимим напруженням
Для визначення небезпечної точки перерізу (рис 346, а) будуємо епюри напружень від усіх силових факторів (рнс 346,6 е) ах (Лі.) о2 (ЛІ,), т„ ((?,) т,х «?,) Т (Лікр)
Епюра т (МКр) для довгої сторони контура має максимум який позначимотт„ (/И„р) Найбільшу ординату епюри т (Лікр) на короткій стороні позначимо т' (;Мкр). Ці напруження можна знайти за відо мими формулами кручення брусів прямокутного перерізу (див гл 9)
Тща» (Л4«р) = Ті. — Т?	(12 46)
Епюри нормальних та дотичних напружень наочно показують що на відміну від круглого перерізу в даному випадку найбільші нор мальні напруження оа та найбільші дотичні напруження т (($ тат(ЛІ«р) мають місце не в одній і тій самій точці
Рис 316
Отже для визначення найнебезпечнішоі точки в перерізі треба порівняти еквівалентні напруження в кількох небезпечних точках Як правило, вважають за достатнє розглянути три точки перерізу одну кутову точку (А чи О одну точку посередині довгої сторони прямокутника (Ь або 71 та одну точку посередині короткої сторони (5 або К)
Елемент, виділений в окопі точки С (при вибраних на рис 346, а напрямах Му та Мг}, перебував в умовах простого розтягання напру жен іями, що дорівнюють сумі нормальних напружень від Ми та Тому умова міцності для цієї точки має бути записана як для випадку лінійного напруженого стану
ТГ ‘	112 47>
Елемент в околі точки А також перебуває в умовах лінійного напру женого стану — простого стискання, оскільки од відрізняється від Ос тільки знаком Якщо матеріал бруса має різні допустимі напру ження для розтягання та стискання, то перевіряти міцність за фор мулою (12 47) слід у кожній з цих точок
Елементи в околі точок Ь та К перебувають у плоскому напруже кому стані, й отже головні напруження в них, як і в круглому брусі можна обчислити за формулою (12 36) Взагалі дотичні напруження, що входять до формули (12 36), слід обчислювати як від дії крутного
моменту Л4кр, так і від дії поперечних сил
т. =
2 “	(12 43)
^ир . з Оу
Тк — V ~а№ ~ 2 Ьк
Однак дотичні напруження від поперечних сні та (}г, як зазнача лося, звичайно бувають дуже маті, а тому здебільшого їхнім вили вом нехтують
Для обчислення еквівалентних напружень у точках £. та X під ставляємо значення нормальних та дотичних напружень у формули (12 37) та (12 38) Одночасно дістанемо й відповідні умови міцності (за IV теорією та теорією Мора) у точці £.
О~ » = |/ (-Й-У + 3 ОЙ' < М. <12 49)
+	(1250)
у точці Я	_______________________
«~№|/(-^-)’ + з(т-^)'<М	(1251)
1 — т Мд , 1 4- т . / І Мд / , . І \*
-	2	+	2 у І + 4 (ї -аХ5§-) < І°1
(12 52)
Знаки моментів при підставлянні їх у рівняння (12 49) (12 52) не мають значення, оскі іьки до цих формул входять квадрати моментів
Отже, найнебезпечніша точка визначається тільки п результаті обчислення еквівалентних напружень в усіх трьох ті яках С, ї. та К за формулами (12 47) та (12 49) (12 52), причому в кожному окремому випадку положення найбільш небезпечної точки залежить від конкрет ного співвідношення значень моментів Мх Ми та Мг Для ілюстрації методики розрахунку розглянемо числовий приклад
Приклад 54. Перевіримо міцність бруса (див рис 345 а) за IV теорією міц нхт. якщо на брус діють такі сили Р] -7 21 кіі Р,-= ІЗ 4 кН. я віссю у вони утворюють кути а1 ™ 33^41' то а, = 2б°34 розміри поперечного перерізу к — 12 см Ь = 8 см довжини ділянок Іг = 300 см І, = 200 см Сила Р, прикладена до важеля закріпленого в торцевому перерізі бруса Довжина важеля і — 100 см Допустиме напруження (а] = 140 МПа
Розрахункова схема майже така сама, як і роїгтвдувана раніше (див рнс 345,6) Обчислюємо складові навантажень уздовж координатних осей
Рір = Р, сов -3,-7 21 0 832 кН = 6 кН
Ріу «- Р, сов а, = 13 4 0 894 кН = 12 кН,
Ріг = Р) аіп ец -= 7 21 0,555 кН = 4 кН, Рй = Р, віл-х, -» 13 4 0,477 кН=0кН.
Рис 347
рерізі діють моменти Лі,ф = 6.68 кЬ но до формул (12 47) (12 49) те (12 них точок С Ь та К перерізу (значе Матимемо
Звівши навантаження до осі. дістаємо крутні моменти
'Ч.рі “ - РіУ (<* + ~2") + Рч V “
= (— 6 1,06+4 • 004) кН м = = — 6,2 кН м
0 06 +
+ 6.0 04) кН м = — 0,48 кН м Епюри крутних та згинальних моментів побуло* ваио иа рис 347
Зіставлення епюр показує, шо небезпечним а переріз з абсцисою х = Іу = 300 см У цьому пе-I м Л1|, = 8кН м Лі,“ 12 кН м Відповід» 51) складемо умояи міцності для трьох иебезлеч ння коефіцієнтів а та у наведено в табл 13)
Ми М.	[ 8 ІО-1 12	10-3	\	„„
°с= Г»	+ V, Ю2 ІО-6	+ 128	10“6	)	8
= (41,7 + 93 8) МПа = 135 5 МПа < 140 МПа
= 69 9 МПа < 140 МПа
Отже, найбільш небезпечною е точка С але І в ній еквівалентне напруження менше за допустиме Міцність бруса забезпечено
Загальний випадок дії сил на брус Як приклад більш загального випадку складного опору розглянемо розрахунок колінчастого вала Для нього в деяких перерізах має місце одночасна дія осьових сил, крутних та згинальних моментів
Дослідимо роботу найбільш простого вала — вала, що має тільки одне коліно Вал (рис 348 а) складається із шатунної шийки 3 двох щік 2 та двох корінних шийок 1 що обпираються на корінні підшип иики Усі потрібні розміри вата наведено на рисунку
На шатунну шийку 3 з боку шатуна діє під кутом а - 15° до гори зонтальної осі у сита Ра — 10 кН Момент цієї сили відносно осі обер-
Рис 348
тання зрівноважується круглим моментом М на маховику Вага ма хоаика 6 = 5 кН
При заданих умовах треба визначити розміри перерізів вала та шатунної шийки, а також призначити розміри прямокутного перерізу щік залежно від більшого з діаметрів за співвідношеннями Л — 1,250. Ь — О 6Л, після чого виконати розрахунок на міцність Допустиме на юуження М = 80 МПа Розраховувати за IV теорією міцності
Від заданої конструкції переходимо до розрахункової схеми На самперед треба визначити реакції в підшипниках, а також скручуваль ний момент на маховику Для цього розкладемо силу Р, на горизон талану та вертикальну складові (Р& та Ріг)
Рід =_ рл соз а = 10 0,966 = 9,66 кН,
Р22 - Р.зша = 10 0,259 = 2,59 кН
Реакції в опорах також можна подати у вигляді двох проекцій — Рлц Каі та Рву. Рвг їхні значення знаходимо з рівнянь рівновагиі
ХЛІ ї0" - 9,66 16 - Кв, 43 = 0, Ко, = 3.59 кН,
ХЛІЇ0» = - 9,66 27 + йл, 43 = 0, Кл, = 6,07 кЙ.
ХМЇ0" „ 5  12- 2 59 16-Яв, 43 = 0 Ра, = 2,36 кН.
ХМЇ°” = 5 55 — йл, 43 - 2 59 27 = 0 йл, = 4 77 кН,
ХМ, - - ЛІ + 9,55 9 = 0; М- 86,9 кН . см = ВД69 кН м
Переходимо до побудови епюр згинальних моментів Обчислимо ординати епюри моментів Му (в площині хОг)
— для ділянки І (0 < х < 12 см)
Му(х) = — 5х М#(0)«-0 ^(12) — — 60 кН см = — 0,6 кН м, — для ділянки II (12 см х 23 5 см)
Л^(х) - —5х+4,77(х — 12), /И„(12) - — 60 «Н см = = — 0,6 кН м,
М,(23 5) = — 62 6 кіі- см----0,626 кН • м;
— для ділянки III (0 х 9 см)
Мр(х)-.—6 23 5 + 4,77 11,5 = 62,6 кН см = — 0 626 кН м, — для ділянки IV (23,5 см х 28 см)
Му (х) = — 5х 4,77 (х - 12) Му (23 5) = — 62,6 кН • см -= — 0 626 кН м,
^„(28) = —63 7 кН см = —0,637 кН м,
—	для ділянки V (28 см 5^ х 32,5 см)
Му (х) = - 2 36 (55 - х), Ми (28) = — 63,7 кН см = = — 0 637 кН м,
М/32 5) = -53 І кН см—0 531 кН • м,
—	для ділянки VI (0 х 9 см)
М,(х)-—236 22,5 =— 53 1 кН . см =—0,531 кН м,
—	для ділянки VII (32,5 см х 55 см)
Му (х) = - 2,36 (55 - х); Му (32,5) = — 53,1 кН . см = = —0,531 кН м,
Му (55) = 0
Відкладаючи обчислені ординати, будуємо епюру Му (рио 348, б)
Аналогічно визначаємо ординати й будуємо епюри згинальних моментів М{ та Мх, що діють у площинах хОу та уОг а також епюру крутнях моментів Мм
Зіставивши епюри бачимо, що небезпечними є такі перерізи для вала — переріз у нижнього кінця лівої щоки (рис 349), причому
Л4нр = 0 869 кН м, Му = 0,626 кН м, Мг = 0,698 кН м для щік — нижній переріз лівої щоки (рис 350), причому
Мг — 0 869 кН м Му =- 0,626 кН м Л4кр = 0,698 кН м, N =- 0,23 кН
для шатунної шийки — середній її переріз причому
Л4хр — 0 323 кН м, Му^ 0,637 кН м, Мх = 0 971кН м
Н^ІЗкН
Рис 349
на
Визначення діаметрів вала шатунної шийки Розрахунок міцність круглого бруса при згннан ні з крученням за IV теорієк. ,
+ М? + 0 75Лі^р
Рис 350 теорією виконується за формулою (12 40), звідки т /Л1* + Л1*+О75Л1* М„ >	М	= И1
При [о| == 80 МПа вал повинен мати момент опору
V _ Г05г8" + 0,698; + 075 08№	_ 15.10_.	_ 15 си.
Взявши наближено 1Г « 0 1 О8, знайдемо діаметр вала 10ІГ = у<І0 Ї5 см = у/ 150 см«5,31 см Шатунна шийка повинна мати момент опору
/0 637» +0 97.»+0 75 0323^	^ 95
(12 53)
Ї7>-тоді її діаметр
4>У10 14,92 см «5,31 см
Призначаємо для шатунної шийки та вала однаковий діаметр перерізу 4 = О = 54 мм
Перевірний розрахунок щоки. Відповідно до умови задачі доби раємо розміри перерізу щоки такими /і = 1 250 = 1,25 • 54 = 67,5 « яа 68 мм, б — 0,6 й « 41 мм Переходячи до перевірки міцності ви браного перерізу щоки, визначимо його геометричні характеристики
1, =	= 4 1126 8' = 107,4 см* ІГ, = 31,6 см"
/ =	= 68 ,4 '' - 39 0 см*; V, = 19,0 см"
Перевіряти на міцність прямокутну щоку в умовах згинання з крученням у небезпечному перерізі треба в кількох точках — К 5 та £ (рнс 350).
У точці К за формулою (12 51)
,»- |/+з(г^-)'-
= 1/^-'°7,У+з/о,839 °м і»"* V МПа _
V \ ЗІ 6 Ю~® /	\	0 234 6 8 4 1‘ 10“6 )
_= 1/2145 58 МПа - 46,4 МПа
У точці 5 за формулою (12 49)
/ м7'\* -з / М.
аек.іу|/	+3(^г) -
= ]/Г-°-626	МПа =
V \ 19.0 ІО"6 }	\ 0.234 6 8 4 1» ІО"6 )
= /3126,04 МПа - 65.9 МПа
У точці Ь за формулою (12 47)
/И* , Ми / 0 869 ІО-3 . 0 626 ІО-3 \ мп_
'V = X" + -к- = (тпр- + -їїїїї-1,—) МПа “
«У (27,5 + 32 8) МПа = 60 3 МПа < [о)
Отже найнебезпечнішою точкою в перерізі е точка £ але і в ній найбільше нормальне напруження менше за допустиме
Оцінка впливу поперечних та поздовжніх сил Урахування поздовжніх та поперечних сил лридоборі перерізу занадто ускладнило б розрахунок Оскільки додаткові напруження від дії поперечних сил, як звичайно, невеликі, то при виборі перерізу ними нехтуємо Най більш просто оцінити їхній вплив, перевіряючи переріз ПІСЛЯ ЙОГО добору
У небезпечному перерізі вала (див. рнс 349) крім урахованих при доборі перерізу моментів Л4Х. Му та Мг діють ще поперечні сили (}у • = 6,07 кН та = 0,23 кН Найбільші дотичні напруження від цих сил будуть відповідно в точках К та £ у точці К
-4-А	МПа =3,54 МПа
у точці £
^44- 4-	7^„- МПа -0.134 МПа
Небезпечну точку перерізу знайдемо, визначивши положення нейтральної лінії Остан ня перпендикулярна до площини дії результуючого зги пального моменту
М =У м1, +м’ =
= У 0 626’ -і 0,698а кН х
Хм— 0,938 кН м
Напрям нейтральної лінії лег ко визначити графічно (рис 351), оскільки він збіга еться з напрямом вектора М Небезпечною точкою в перерізі е точка 5 (рис 351) Природно, що в цій точці до
тичні напруження тих та Ьз будуть значно меншими, ніж обчислені више максимальні значення Вважатимемо наближено та з деяким запасом, що в небезпечній точці 5 до дотичних напружень від скручу вального моменту Мк
• _ М* _ о 869 ІО"3 16 5 “ ^0 ~ з 14 5 4» 10“8
МПа ~ 28,2 МПа
додається таке дотичне напруження від поперечних сил $в та ІЗ Й5 0,7 (Тутах “ Тдемх) ~ 2,4 МПа
Обчислимо еквівалентне напруження в точці 5 за IV теорією
Оеки IV = р/"	+ 3	+ Тз)’ =
- / (-?йНн-)‘+3 <28'2+2 4)1 МПа -
= /60,6а 4-3 28,2а МПа = 80,4 МПа
Еквівалентне напруження в тій самій точці без урахування впливу поперечних сил
<т5 - УбО.б’тЗ 28,2’ МПа яа 77,9 МПа
Отже, якщо врахувати дію поперечних сил, то напруження зростуть на
^^І-1ОО%^3%.
У небезпечному перерізі їдоки (див рис 350) діє тільки поперечна сита — 6 07 кН, поперечна сила <2,-0 Поперечна сита не дає дзтичних напружень у найбільш небезпечній точці £. Тому розглянемо 11 вплив у точці де спричинені нею дотичні напруження дося гають найбільшого значення
З (?«	3	6 07 І0~3 иг1 П су, иг1
Г, = -5--> = - 6 8	МПа = 3.27 МПа
й збігаються за напрямом з дотичними напруженнями від дії крупного моменту Мкр Значення останніх
0 698 І0-Тушм — аМ)1 = 0 236 б 8 4 [
Обчислимо еквівалентні напруження за IV теорією міцності а»,, IV - /о-+ 3 (т,+	_ /32,8" +3(3,27 +25,7)» МПа -
= /3597 МПа-60 МПа
У тій самій точці напруження без урахування <2^ нами вже внзна чено
МПа = 25,7 МПа
а'я = 55,9 МПа
Отже, поперечні сили збільшують напруження в точці 5Х на 60 5 ~ 55 9 100 % - 7,6 %
Якщо в перерізі діє осьова сила, згинальні моменти в головних площинах та крутний момент, то умова міцності, наприклад за IV теорією, в точці К (див рис 350) має вигляд
(-Й- І- 4)’ + 3 (т-да-)" <|а| <12 64>
Аналогічно в точці 5
- ]/ (-й-+4)’+зЬМ	<12
У розглядуваному небезпечному перерізі шийки діє поздовжня розтягальна сила V = 0 23 кН Спричинюване нею нормальне роз-тягальне напруження
о, • 4- = °м МПа »0,083 МПа
таке мале, що ним можна знехтувати
Глава 13. ЗАГАЛЬНІ ТЕОРЕМИ ПРО ПРУЖНІ СИСТЕМИ. ЗАГАЛЬНІ МЕТОДИ ВИЗНАЧЕННЯ ПЕРЕМІЩЕНЬ
$ 78. Узагальнені сили І переміщення
Однією а найважливіших задач опору матеріалів е оцінка жорсткості конструкції тобто ступеня її викрналення під дією наванта ження, зміщення зв язків, зміни температури Для розв’язання цієї задачі треба визначити переміщення (лінійні та кутові) довільно на вантаженої пружної системи (балки рами, криволінійного стержня, ферми тощо), гака сама задача постає прн розрахунку конструкцій на динамічні навантаження і при виявленні статичної кевизначува кості системи В останньому випадку, як уже зазначалося, складають рівняння спільності деформацій, які містять у собі переміщення певних перерізів
У попередніх главах розглядалися деякі окремі способи визначення переміщень зручні при розв ячанні найпростіших задач Нижче викладається загальний метод визначення переміщень у стержньових системах, який грунтується на двох фундаментальних принципах механіки початку можливих переміщень 1 законі зберігання енергії,
Я к відомо з теоретичної механіки, робота постійної сили Р на переміщенні Д за її напрямом дорівнює добутку значення сили на зазначене переміщення
А=Р&
У задачах опору матеріалів 1 будівельної механіки зовнішні навантаження відзначаються великою різноманітністю 1, як правило, становлять групи сил Вираз для роботи групи постійних сил також можна подати у вигляді добутку двох величині
А = Р&р,	(13 1)
у якому множник Р залежить тільки від сил групи 1 називається узагальненою силою, а Ар залежить від переміщень 1 називається узагальненим переміщенням
Отже, під узагальненою силою будемо розуміти будь-яке навантаження (зосереджені сили, зосереджені моменти, розподілене наванта ження), а тд узагальненим переміщенням — той вид переміщення, на якому узагальнена сила здійснює роботу
Розглянемо деякі приклади узагальнених сил 1 переміщень
1 На рис 352 показано узагальнену силу, яка складається а двох однакових за модулем протилежних сил Р прикладених у точках А та В 1 спрямованих по одній прямій Припустимо, що точки прикла дення сил перемістились у напрямі ВА на відрізки і Д». Очевидно, робота системи постійних сил на цих переміщеннях
4 = ^ —РДЇ=Р(Д1 —Д,) =.РДр, (132)
(2 2-8798
363
Ряс, 352	Рис 353
де Ар = А, — А, = А/ — зміна відстані І між точками прикладення сил
Отже, в цьому прикладі Р — узагальнена сила а зміна А/ довжини відрізка АВ — узагальнене переміщення
2 Нехай група сил складається з пари сил момент якої М = Ра (рис 353) Припустимо що елемент АВ повернувся на кут 46 Шляхи, пройдені ситами пари в напрямі їхньої Дії,
аа, = олае ввх = овае
Сумарна робота обох сил
А = Р АА| + Р ВВі=Р(ОА \-ОВ) № = Рас№ = М4Є (13.3) Отже, якщо узагальненою силою е момент М пари, то узагальненим переміщенням буде кут повороту 46 в площині дії пари.
Легко також довести, що при дії на елементи АВ і СО (рис 354) двох однакових за модулем і протилежно спрямованих пар з моментом М узагальненою силою є момент пари М, а узагальненим переміщен ням — зміна кута <р між елементами АВ і СІ) Інакше
Ар = 40! Ь 4в,
Умовимося надалі узагальнені переміщення (як лінійні, так 1 кутові) якого небудь перерізу стержня позначати літерою А або & з двома індексами Перший індекс відображує точку і напрям перемі щення, другий — указує причину цього переміщення Наприклад, Дрр означає переміщення точки прикладення сили Р у напрямі її Дії, спричинене цією самою силою (рис 356, а) На рис Зоб б зображено консоль, навантажену на вільному кінці зосередженим моментом Оче видно, кут повороту перерізу, де прикладений момент, слід позначити Амм Тут перший індекс означає переміщення в напрямі моменту М
Рис 354
Рас. 355
рис 356
Ряс. 357
Для позначення повного переміщення точки, спричиненого кілько ма зусиллями, прн Д зберігається тільки перший індекс Так, пов* ний прогин і кут повороту перерізу В балки, показаної на рнс 3&6 слід позначити відповідно через Д/> і Д«, прогин перерізу С — через Дд
Розглядаючи досить жорсткі лінійно деформівні конструкції (тобто системи, деформації яких відповідають закону Гука), можна на підставі принципу незалежності дії сил визначати повні перемі* щення точок як суму переміщень спричинених окремими наванта* женнями
Для зображеної на рис 356 балки прогин і кут повороту перерізу В можна записати у вигляді
Др = &Рр 4- ДРЧ + Дрлі,	цз
Дм = Дмр + Длю + Дмль
Д<! Лрр— переміщення ТОЧКИ В у напрямі СИЛИ Р ВІД СИЛИ Р те саме від сили (}, &рм ~ те саме від моменту М, Дмр — переміщення перерізу В у напрямі пари М (кут повороту) від сили Р, Дме — те саме від сили р Дмм — те саме від пари М
Переміщення спричинене одиничною силою (Р 1) або одиничною парою (М = 1), будемо позначати літерою б і називати питомим. При цьому умовимося вважати одиничні сили чн пари, які спричинюють переміщення 6, безрозмірними
Якщо одинична скла Р = І спричинила переміщення бр, то, згідно в принципом незалежності дії сил, повне переміщення, спричинене сплою Р,
Ьр*=Рбр	(13 5)
З виразу (ІЗ 5) легко визначити одиницю питимого переміщення
.« _ одиниця уаагальненого переміщення
* р' ~ одиниця узагальненої сили •	'	'
Зазначимо, що навантаження, яке діє на конструкцію, як правило, позначають літерами Р, М, X, з числовими індексами (наприклад, ) У цьому разі літерні індекси при Д або б заміняють від повідними числовими, тобто замість Ах, пишуть Дх (Д(,	)
На рис 357 показано позначення переміщень вільного кінця рами від дії різних сил (Р, Хи Ха, Ха) Повні переміщення перерізу С в горизонтальному і вертикальному напрямах (тобто в напрямах дії сил X] і Ха), а також кут повороту (переміщення в напрямі дії Х£ відповідно можна подати у вигляді
Ді = Д[? + Х1б11 4- Х2ви 4- Хав13,
Д, = Д,р 4- Х&, 4- ХД, 4- Хавм	(ІЗ 7)
Дв = Дзр 4- ХД, 4- Хаби 4- X Да Тут
ХДі = Дп, Ха6и = Ди; ХДа = Д„,	, ХДц « Д™/.
Для ОЦІНКИ ОДИНИЦІ переміщення вщс множимо останнє рівняння на Х„ Тоді
Х^^ = Х„Дт,
виражатиметься в одиницях роботи (Дж) Звідси переміщення
(«»/]==
Хт^ті______Дж	1
ІЛтНХ,] Н Дж = Н
і 79, Робота зовнішніх сип
При деформуванні конструкції її точки переміщуються Перемі вдуються також точки прикладення зовнішніх сил Унаслідок цього зовнішні сили здійснюють роботу
Обчислимо роботу деякої узагальненої сили Р прикладеної до будь якої пружної лінійно деформівної системи (рис 358 а) Прнпус кається що навантаження зростає від пули до заданого значення досить повільно, щоб можна було знехтувати силами інерції мас, що переміщуються Таке навантаження називатимемо статичним
Нехай в даний момент силі Р відповідає узагальнене переміщен ня Д Нескінченно мале збільшення сили на величину АР спричинює нескінченно малий приріст переміщення гіД Очевидно елементарна ро бота зовнішньої сили, якщо знехтувати нескінченно малими другого
^5?
Рас. 359
Повна робота здійснена статично прикладеною узагальненою сплою Р на спричиненому цією самою сплою узагальненому переміщенні А,
А - 5 Р<ІД	(13 8)
Інтеграл (13.8) становить площу діаграми Р ~ А для даної конструкції (рис. 358, б)
У лінійно деформівних системах переміщення пропорційні значенню сили (закон Гука):
Д = Р8РР1	(13.9)
де 8рр— переміщення, спричинене силою Р = 1
Диференціюємо вираз (ІЗ 9)
(ІД = 6Р6рр
Підставляючи цей вираз у формулу (13.8), матимемо
А-6„^Р<1Р--^-
Ураховуючи вираз (13 9), остаточно знайдемо
Л=Л^.=^..	(13.10)
Отже, дійсна робота при статичній дії узагальненої сили на пружну систему дорівнює половині добутку остаточного значення сили на остаточне значення відповідного узагальненого переміщення (теорема Кла нейрона)
У разі статичної дії на пружну систему кількох узагальнених сил Л’ » Лі (рис 359) робота деформації дорівнює половині суми добутків остаточного значення кожної скли на остаточне значення відповідного сумарного переміщення!
Д = -^-2Р(Ді	(13 11)
1 не залежить від порядку навантажування системи
$ 80 Робота внутрішніх сил
При пружній деформації тіла в деформівних елементах розвиваються внутрішні сили — сили пружного опору. Вони також здійснюють роботу Спочатку визначимо роботу внутрішніх сил пружності прн деформуванні плоскої стержньової системи
Двома суміжними перерізами виділимо елемент стержня завдовжки
(рис 350) Взагалі для плоского згинання дія відкинутих частин стержня на залишений елемент зводиться до поздовжніх М та поперечних сил 1 згинальних моментів М. ЦІ зусилля, зображені на
Рис 361
нодійиі внутрішніх
сил показано штриховими тініями
рисунку суцільними лі ніями відносно виділе ного елемента можна розглядати як зовнішні
Внутрішні сили перешкоджають розвитку деформації спричинюваної зовнішніми силами дорівнюють їм за значен ням і протилежні за на прямом На рис 350 рів
Ураховуючи напрям внутрішніх сил відносно деформацій, спричинених зовнішніми силами можна стверджувати що при навантажу ванні тіла сумарна робота внутрішніх сил завжди від ємна
Спочатку обчислимо роботу здійснену окремо внутрішніми поздовжніми силами, поперечними силами і згинальними моментами Нехай на елемент діють тільки поздовжні сили N (рис 361) Подов ження елемента внаслідок цього
л .
де ЕЕ— жорсткість поперечного перерізу на розтягання стискання Робота внутрішніх сил що поступово збільшуються від нуля до
N. на цьому переміщенні
=	(13 12)
Оскільки робота внутрішніх сил від’ємна в правій частині виразу (13 12) поставлено знак «мінус»
Розглянемо тепер елемент, який зазнає дії згинальних моментів (рис. 362) Внаслідок згинання перерізи тп і повернуться на кути 00 Моменти внутрішніх сил (показано штриховими лініями) на цих переміщеннях здійснюють роботу
<№* - —і- Мів —і- АМЄ - —1- ЛМф,	(13 13)
де гіф =	— взємний кут повороту перерізів елемента.
Як показано в гл 10,
Отже
. л, і	М Міз
(із 14)
Обчислимо, нарешті, роботу внутрішніх поперечних сил <?, що поступово зростають (рнс 363, а) Як зазначалося, поперечні сили
Рис. 362 е рівнодійними розподілених у точках перерізу дотичних напружень т Останні в будь якій елементарній площадці гіГ, паралельній нейтральній лінії (рис 363, б), згідно з формулою Журавського, мають вигляд
де З, — статичний момент відносно нейтральної осі г частини перерізу, розташованої між рівнем смужки і краєм перерізу
Взаємний зсув даох розташованих на одній висоті площадок <1Р
на торцях тп і (рнс 363 в)
у(І5=-5-(І5
Отже, робота внутрішніх елементарних сил чйР при зростанні їх від нуля до остаточного значення
----.-------------
Інтегруючи в межах перерізу Р, знайдемо роботу вил зсуву:
| 4-	~ ~	& =
С 5* .р .	.о ікч
----к>~20Г'	(1315)
де = (Г//Ї) (5г/Ь*) (ІР—коефіцієнт, який залежить ВІД форми поперечного перерізу; (ЗР — жорсткість поперечного перерізу стержня при зсуві
Для прямокутного перерізу Ь х Н
Г =	5,_
=	<13 >6)
Рнс. 364
Рис 365
Аналогічно визначають ко афіцІєнтА і для інших перері зів Наприклад для колового перерізу к = 32/27, для прокатних профілів наближено к^Г!Гв де Рв—площа стінки
У випадку чистого зсуву дотичні напруження розподіляються рівномірно ПО перерізу
Отже,
і = <№
(13 17)
При одночасній дії осьових і поперечних сил, а також згинальних моментів сумарну роботу можна знайти як суму робіт окремих скла дрвих Це пояснюється тим, що робота кожного з цих зусиль на переміщеннях, спричинених рештою сил, дорівнює нулю Наприклад, при подовженні спричиненому силами А/, поперечні перерізи зали шаються плоскими і паралельними, а тому пари М 1 сили (} роботу не здіснюють Аналогічно сили N не здійснюють роботи на переміщеннях, спричинених силами і парами М
Отже, в розглядуваному прикладі повна елементарна робота внутрішніх сил
2£/ 2ЕЕ к 2ОЕ

(13 18)
Інтегруючи вираз (ІЗ 18) в межах всього стержня 1 підсумовуючи за всіма стержнями системи, дістанемо формулу для роботи внутріш ніх сил у випадку плоского згинання
(13 19)
Коли стержень зазнає деформації кручення в поперечних перерізах, що обмежують виділений елемент завдовжки (і$, діють крутні моменти Мкр (рис 364), які відносно елемента є зовнішніми
Моменти сил пружності дорівнюють за модулем моментам Лїкр і спрямовані в протилежні боки Взаємний кут повороту перерізів
де — жорсткість поперечного перерізу стержкя при крученні.
Отже, прн крученні елементарна робота внутрішніх сил що посту-позо зростають
=- 4-<13 20>
Сумарна робота внутрішніх сил при крученні стержня
і^кр = У — Мкр£іф =	20Л	^3 21)
Нарешті в загальному випадку дії сил на стержень у перерізах маємо шість силових факторів (рис 365) осьову силу ІЇ, поперечні сили і крутний момент Мкр, згинальні моменти Му і Мг
Ураховуючи, що робота кожної з цих сил на переміщеннях, спри чинених рештою зусиль, дорівнює нулю, дістанемо таку формулу для роботи внутрішніх сил (сил пружності)
т	с мЬіз	с	с м* Лі
* “	] 2ЕІУ	З	З 20Л
сззд
Зазначимо, що вираз (ІЗ 22) справедливий також і для криволіній* них стержнів малої кривизни
$ 81. Застосування принципу початку можливих переміщень до пружних систем
Початок можливих переміщень, становлячи загальний принцип механіки, має важливе значення для теорії пружних систем Стосовно до них цей принцип можна сформулювати так якщо пружна система перебуває в рівновазі під дією прикладеного навантаження, то сума робіт зовнішніх і внутрішніх сил на можливих нескінченно малих переміщеннях точок системи дорівнює нулю, тобто
4-^ = 0,	(13 23)
де Рі — зовнішні сили Діт — можливі переміщення цих сил, 2Р/Д/Я — робота зовнішніх сил — робота внутрішніх сил
Оскільки пружні деформації дуже малі, то можливими переміщеннями мдіИна вважати пружні переміщення від положення рівноваги, які спричинені будь яким видом навантаження І відбуваються без порушення зв'язків Робота сил на можливих переміщеннях називається можливою або віртуальною роботою
Зазначимо, що коли системі надають можливого переміщення від стану її рівноваги, то вважають, що модуль І напрям зовнішніх та внутрішніх сил залишаються незмінними Тому при обчисленні мож*
переміщень
Покажемо, як визначається можлива робота зовнішніх і внутрішніх сил на прикладі плоскої системи Розглянемо два стани якої* небудь системи, що перебуває в рівновазі (рнс. 366) У стані а система деформується узагальненою силою Ра (рнс 366, а), у стані Ь — си лою Рь (рис 366, б)
Очевидно, переміщення в стані Ь можна розглядати як можливі для стану а, 1 навпаки, переміщення в стані а е можливими для стану Ь Тому робота сил стану а на переміщеннях стану Ь (Д^), так само, як І робота сил стану Ь на переміщеннях стану а (Діо). буде можливою Зазначені роботи зовнішніх сил відповідно
® Ра&аЬі Аьа = Р дДда
(13 24)
Обчислимо тепер можливу роботу внутрішніх сил стану а на переміщеннях, спричинених навантаженням стану Ь Для цього розгля немо довільний елемент стержня завдовжки гіз у цих даох станах Для плоского згинання дія відкинутих частин на елемент, як зазнача лося вище, зводиться до системи сил Л^а, ра, Л4а (рис 367 а) Внутрішні сили, що діють на елемент, мають напрями, протилежні зовнішнім, і показані штриховими лініями На рис 367 б зображено зовнішні сили Л74, С6, Мь що діють на елементну станів Деформації елемен та, спричинені цими зусиллями, показано на рис 368
Очевидно подовження елемента (із від дії сил іїц
Рас. 368
Робота внутрішніх осьових сил на цьому можливому переміщенні
(ІЗ 25)
Взаємний кут повороту граней елемента, спричине
ний парами М6,
<а<р)> =
Робота внутрішніх згинальних моментів Ма на цьому переміщенні
=	(13 26)
Взаємний зсув граней елемента, спричинений поперечними сила ми (&,
Робота внутрішніх поперечних сил С}а на цьому переміщенні
-Є.(ТЛ), = -*^!-	(13 27)
Підсумовуючи вирази (13 25), (13 26) і (13 27), знайдемо можливу роботу внутрішніх сил, прикладених до елемента (із стержня на переміщеннях спричинених іншим, цілком довільним навантаженням, позначеним індексом Ь
= —Ма (Лр)д — Л\ (Мз)ь — (?в (уйі)д (ІЗ 28) або
— еі ЕР------------------*—0?	(Іо29)
Підсумовуючи елементарні роботи в межах стержня а далі за всіма стержнями системи, знайдемо повне значення можливої роботи внутрішніх сил
= -|2 і	+ 2 (*>. Шч>). + 2 і 0. (7*)і] (із з»)
або
<1331>
Підставивши в рівняння (13.23) вирази для можливої роботи зовнішніх сил (першу з формул (13.24)] і внутрішніх сил (формулу (13 ЗО) або (ІЗ 31)] дістанемо загальний вираз принципу початку можливих переміщень для плоскої пружної стержньової системи
2 р.Ло - ^2 (м. (<*ф), + 2 (и. (л*)» + 2 (<?. (т*)» ]=о (із 32) або
+	+	=0 (,3 33)
Отже, якщо пружна система перебуває в рівновазі, то робота зовнішніх і внутрішніх сил у стані а на можливих переміщеннях, спричинених іншим, цілком довільним навантаженням, позначеним індексом 6, дорівнює нулю Вирази (13 32) і (13 33) можна застосувати і для стержнів малої кривизни Аналогічні вирази легко скласти також для загального випадку навантажування стержня, коли в його поперечних перерізах діють шість компонент внутрішніх зусиль
Якщо як можливі взяти дійсні переміщення Да, спричинені заданим навантаженням Ра, то вираз (13 33) набуває вигляду
+	(1334)
Поділимо вираз (13 34) на два Враховуючи, що
-1-ІР.Л^Л	(13 35)
е роботою зовнішніх сил у процесі статичної деформації (див формулу (13 11)1, а
— роботою внутрішніх сил (див формулу (13 19)1, маємо
А	(13 37)
тобто сумарна робота зовнішніх і внутрішніх сил при статичному деформуванні пружної системи дорівнює нулю Отже, дійсні значення роботи зовнішніх і внутрішніх сил однакові за модулем і протилежні ва знаком
$ 82. Теореми про взаємність робіт І переміщень
Розглянемо будь яку пружну систему наприклад балку, в двох станах У першому стані (рис 369 а) нехай діє узагальнене наванта ження, позначене індексом 1, переміщення відповідних точок системи будуть Дп, Ди, , Дл У другому стані (рис 359, б) на систему діє узагальнене навантаження позначене індексом 2, а переміщення від повідних точок системи від цього навантаження — Д„, Ли Дп
Запишемо вирази можливих робіт зовнішніх і внутрішніх сил для обох станів системи, взявши для першого стану як можливі переміщення, спричинені силами другого стану, а для другого — переміщення, спричинені силами першого Згідно з формулою (13 33) для першого стану
+	+	=	(‘338)
Рис. 369
Рис 370
6
Рис 371

п
для другого стану
+	+	<‘3 39>
Оскільки вирази для робіт внутрішніх сил однакові, то з рівнянь (13 38) і (13 39) випливає
^Д,, - Р^і	(13 40)
Вираз (13 40) має назву теореми про взаємність робіт (теореми Бет ті) Вона формулюється так можлива робота зовнішніх (або внутріш ніх) сил першого стану навантажування на переміщеннях спричинених силами другого стану дорівнює можливій роботі зовнішніх (або внут ріиініх) сил другого стану навантажування на переміщеннях, спричи нених силами першого стану
Розглянемо окремий випадок навантажування коли в обох станах системи прикладено по одній одиничній узагальненій силі = 1 та Рі = 1 в точках 1 і 2 (рис 370) На підставі формули (13 40)
~Р^ = Мі.
а оскільки Рі = Рі = 1, то
(13 41)
Цей вираз називають теоремою про взаємність переміщень (теоремою Максвелла) Формулюється зона так переміщення точки прикладення першої сили в напрямі її дії, спричинене дією другої одиничної сили, дорівнює переміщенню точки прикладення другої силі в напрямі її дії, спричиненому дією першої одиничної сили
Теореми про взаємність робіт і переміщень мають велике зна іення в загальній теорії дослідження напруженого і деформованого стану стержнів, пластинок оболонок та інших розрахункових об'єктів Застосування їх істотно спрощує розв язання багатьох задач буді вельноі механіки, а також визначення переміщень
Користуючись теоремою про взаємність робіт, визначимо прогин Дп балки посередині прольоту при дії на опорі моменту М (рис 371, а)
Розглянемо другий стан системи—балка навантажена в точці 2 зосередженою силою Р (рис 37 і б) За формулою (10 65) прн а =
Ь = 112 і х = 0 знайдемо кут повороту опорного перерізу А	Р1'
=	16£/
Згідно з теоремою про взаємність робіт, маємо МДц-РД,,.
звідки	Д31^=Л1-^1- =-------(13 42)
Приклад 55 Визначимо прогини в точках 1, 2 і 3 вала навантаженого силою Р у точці С (рис 372)
Замість у таїювлення прогниом'рів у зазначених точках, п ве показано на рис 372, а на підставі теореми про взаємність переміщень досить установити луо-гиномір у точці в а силу послідовно прнвладатн в точках 12 3 (рас. 372 б) Виміряні прн цьому а точці С прогини дорівнюють шуканим
Приклад 56 Покажемо що при навантажуванні балки з консоллю (рис 373 а) моментом М прикладеним завдальшки И}Гз від лівої опори А, понсоль ВС залишиться нерухомою
Якщо навантажити балку в опорному перерізі В моментом М (рнс 373 б) то максимальний прогин на відрізку АВ буде а перерізі Д завдальшки 1/^3 від опори А Отже кут повороту цього перерізу дорівнює нулю (&о = 0)
Якщо момент М прикласти в перерізі Д (рнс 373, а), то на підставі теореми про взаємність переміщень кут повороту Д перерізу на опорі В дорівнює нулю (ва = 0) Консоль ВС залишається нерухомою, оскільки її переміщення може відбутися тільки внаслідок повороту опорного перерізу В а він дорівнює нулю
$ 83 Загальне формула для визначення переміщень Метод Мора
Розглянемо спочатку довільну плоску стержньову систему (балку, раму, ферму тощо), навантажену заданими силами Р (рис 374, а) Зусилля в довільному перерізі системи позначимо через Лід, (}р, іїр Нехай треба визначити переміщення (узагальнене) будь якої точки системи в напрямі і —- І
Рис 374
Введемо допоміжний стан (рнс 374, б), що є заданою системою, навантаженою ли ще однією одиничною силою (узагальненою) = 1, прикладеною в тій самій точці т і в напрямі шуканого переміщення Д/р Зусилля в довільному перерізі допоміжно* го стану, спричинені дією.одиничної сили X, — 1, позначимо через М(, Аї, Застосуємо початок можливих перемі щень для допоміжного стану, взявши як можливі дійсні переміщення заданої систе мн Згідно з формулою (ІЗ 33), +	(1343)
Вираз (13 43) є загальною формулою для пружного переміщення плоскої стержньової системи
Якщо виходити з виразу початку мож ливих переміщень у формі (ІЗ 32),тозагаль
ну формулу для визначення пружного переміщення можна записати у вигляді
= 2 і Я, + 2 у Ж, (л*), + 2 У О, (V*)* (із«)
•	г	в
У загальному випадку дії сил (див рис 351) формула для перемі* щення містить шість доданків
+	(13 45)
Індекси у 2 у формулі (13 45) позначають головні осі, індекс «кр» — крутний момент Зазначимо що наведені формули можна застосувати і для кривих стержнів малої кривизни
Формули (13 43) та (13 45) вперше були виведені Мором Визна чення переміщень за цими формулами часто називають методом Мора Зазначимо, що метод Мора — це найчагальніший метод визначення переміщень стержньових систем Його значення особливо велике прн розрахунку статично невизначуваних систем
Здебільшого при визначенні переміщень у балках рамах та арках можна знехтувати впливом поздовжніх деформацій і деформа цій зсуву, враховуючи лише переміщення, спричинені згинанням і крученням Тоді формула (13 43) для плоскої системи наби* рає вигляду	_
(1346)
При просторозому навантажуванні, згід но з формулою (13 45),
+ $	|	(13 47)
При визначенні переміщень вузлів шар нірннх ферм, що складаються з прямих стержнів, у формулі Мора зберігається тіль ки один доданок
=	(13«в)

б
Рнс 375
Ця формула має назву формули Моксвелла
Можна запропонувати таку послідовність визначення переміщень за методом Мора.
1	Будують допоміжну систему, яку навантажують одиничним навантаженням у точці, де треба визначити переміщення Визначаючи лінійні переміщення, у заданому напрямі прикладають одиничну силу, визначаючи куюві переміщення,— одиничний момент
2	Для кожної ділянки системи записують вирази силових факто-рів у довільному перерізі заданої (Л4р,	(}р) і допоміжної (Л7Ь
систем
З Обчислюють інтеграли Мора (по ділянках в межах всієї системи) Як вже зазначалося, при розрахунку плоских балок, рам і арок ви ходять з формули (13 46), просторових систем — (13 47) ферм — (13 48)
4	Якщо обчислене переміщення додатне, то це означає, що його напрям збігається з вибраним напрямом одиничної сили Від'ємний знак свідчить про те що дійсний напрям шуканого переміщення протилежний напряму одиничної сили
Розглянемо приклади застосування методу Мора для визначення переміщень у різних стержньових системах
Нехай треба визначити прогин посередині прольоту та кут повороту на опорі шарнірно обдертої балки ^Е^ =- сопзі), навантаженої рів номірно розподіленим навантаженням інтенсивністю д (рнс. 375, а), а також дослідити вплив поперечних сил на максимальний прогин
1	Для визначення прогину посередині прольоту прикладаємо в цьому місці допоміжної балки (рис 375, б) одиничну зосереджену силу В довільному перерізі першої ділянки балки (0 х //2)
ЛІ1Мг-!-х
Ураховуючи симетрію дістанемо
Мі{х)Мр(х)Лх 2 ‘с х І ді * ЧХ*\Нг_ 5
=	— ЕЕ ] 2 \ 2 *	2 )аХ--з5Г ЕЕ
Урахуємо вплив дотичних напружень на шуканий прогин, припус каючн, що балка має прямокутний переріз Очевидно при0<х^//2 <?я (х) = -----------------чх Сі (х) = Ц-
На підставі формули (13 43) прогин, спричинений дією поперечних сил, аО пї А	2А Р і / ді X. . дР 2 ді*
Дір — 21 к еу. —	] 2 ( 2	= Л ВОГ = З ЕЕ
о	о
При цьому враховано, що коефіцієнт форми для прямокутного перерізу аС“ТПтЬг~Т*
Підсумовуючи вирази для переміщень, знаходимо, що А	5	ді* 2	вР____5_ ді*
Д,р=	384	£2	+ 5	ЕЕ	~ 384 ЬЕ	(	2,6 Р )
Другий член у дужках, що відображує вплив поперачної сили, при відношенні висоти перерізу до довжини прольоту МІ = 1/10 дорівнює 0,026 Отже прогин спричинений поперечною силою, становить мен ше ніж 3 % прогину, спричиненого згинальними моментами
2	Для визначення кута повороту опорного перерізу допоміжну балку навантажуємо одиничним моментом (рис 375, в) При 0 х І маємо
=	Зй,и)-1—7-;
С	Мр(х)ііх і Є / ді дх* \
------и-------8ґі(Т'—г)х
х(1--г)йх = -2^7-	<і3 49>
Рнс 376
Рис 377
Додатний знак свідчить про те, що напрям повороту збігається з напря мом одиничного моменту
Визначимо вертикальне переміщення вузла В шарнірно стержньо-воі системи (рис 376, а), яка складається з двох однакових стержнів АВ і ВС постійного поперечного перерізу Допоміжну систему зобра жено на рис 376, б
Розглядаючи рівновагу вирізаного вузла В, знаходимо зусилля в стержнях для обох станів
Стержень Кр
АВ Р 1
ВС -Р -1
З формули (13 48) маємо ,	^^р1	рі
й.\Р = \	1 р _ о -г‘
А ЕР	ЕР
(13 50)
Приклад 67 Розміщена в горизонтальній площині рама АВС (риє. 3/77, о) скла дається з двох стержнів однакового круглого поперечного перерізу Визначимо вертикальне переміщення точки С Допоміжну систему показано на рис. 872. б
Переміщення &ІР можна визначити з формули (ІЗ 45) Для довільній перерізів двох ділянок масно для / ділянки (0 < х < а)
Мр = Рх «^ = 0
М1кр = 0.
для Н ділянка (0 < х < І)
Мр^Рх МРкр = Ра,
^Ікр = а
С . Г 'Йі-Лркр* £7	+ ]	<Н„
[ РхЧх (• рх*0х С Ра*0х Р (°5 4- Р) РаЧ
= ] Еі ЕІ +] 07р “ ЗЕ^ +~С7Г (І35°
$ 84 Переміщення, спричинені дією температури
Припустимо, (ЦО довільний елемент сіз стержня нагріваеті єн внизу до температури Тв, авторі—до Та (рис 378, а б) Як звичайнії припускають, що по висоті перерізу температура змінюється за ліній ним законом, при цьому перерізи стержня переміщуються, залшнл ючись плоскими
Подовження нижнього і верхнього золокон (рис 378 б) ВІДПОНІДІЮ
ДЙ5Я аТа(із — аТвсІ5	(13 52)
де а — температурний коефіцієнт лінійного розширення
Подовження по осі стержня (середнє подовження)
Д<Ь, = а Г' Г*	(ІЗПІ)
Взаємний кут повороту перерізів елемента Л, спричинений ігеріп комірним нагріванням елемента,
(Д>)г-	(| |М)
Нехай тепер треба визначити переміщення (у <пм<імпчп) дппілинії ТОЧКИ к системи В будь-якому НЯІІрЯМІ / — І НІрІНіЩН'ІН* ДІОКі <і М|||> ратури 3 цією метою навантажуємо допоміжну ііиіему илннн'ііннії силою (узагальненою) X, = І (рік 378, о) Зііскнусмо нрннннн ції чатку можливих переміщень для допоміжного стану п-оївши як мож ливі дійсні переміщення, спричинені дією температури ІОДІ КІІДІКІ з формулою (і 3 44), маємо
= £ У м, (йє), + 2 («,л*с (її пв)
Підставивши формули (13 53) і (іЗ 54), дістанемо
Дт=2УЯ,а-?і=^* + 5;Уя,<хїЦ-Ї!-* (ІІПІІ)
Формулу (ІЗ 56) можна застосовувати також і для стержнів милої кривизни У фермах, де діють тільки поздовжні зусилля температурні
а>о
N>0
М>0
М<0
переміщення визначаються за формулою 6-а - ЇЙ&ТІ, (ІЗ 57) де Т = (Тя + Тв)/2—температура на осі стержня, однакова по йогодовжині. Під	?
сумовують за всіма стержнями ферми	Ря(Г до
Знак перед першим членом у формулі
(13 56) залежить від вибору правила знаків для згинального моменту Якщо вважати згинальний момент додатним, коди його напрям такий, як показано на рис 379, а, то перед першим членом у формулі (13 56) зберігається знак «плюо Іноді згинальний момент вважають додатним, якщо він спрямований, як зображено на рис 379, б Тоді перед пер шнм членом у формулі (13 56) треба поставити знак «мінуса
Нагадаємо, що в статично визначуваних системах температурні переміщення не спричинюють зусилля N ф і М в елементах системи.
У разі дії навантаження і температури на плоску систему загальна формула для переміщень складається з суми членів формул (13 43) і (13 56)
Д, -	= Е )+ X	+
+ Х Т'7-~	(13 58)
Приклад 58 Визначимо горизонтальне і вертикальне переміщення, а також кут повороту вільного кінця сталевої консолі (рис 380 а), спричинені нерівномірная на гріванням Довжина балки І = 2 м. висота перерізу Л = 10 см а =® Н8 ІО-1 Початкова температура балки Тв 5 °С; потім нижнє волокно нагріто до температу ри 55 °С. а верхнє — молоджено до температури — 5еС
Очевидно розрахункові температури волокон такі
Тя=.55— 5= 50 *0 Га=_5—5 = —Ю’С
Допоміжні стани для внзначевня вертикального і горизонтального переміщень та кута повороту показано на рис. 380, б е Маємо
М1 = — (І — х) = 0
ЛЇ,=0	Я,=-1,
М| = 1,	N,=0,
Отже на підставі формули (13 56) знаходимо а) прогин
0	6
або після підставляиня значень
іі8-'°~'27„	—1«»
б) горизонтальне переміщення
см =
4„ _ "" • '°~'о » р« - 0,0142 р>»
і 85. Обчислення Інтегралів Мера способом Верещагіна
Обчислення інтегралів Мора істотно спрощується, якщо одна з епюр (у дійсному чи одиничному стані) прямолінійна Ця умова вико* нується для систем, що складаються з прямих стержнів, оскільки при цьому епюри внутрішніх сил від одиничного навантаження (зосередженої сили або пари) завжди обмежені прямими лініями
Обчислимо інтеграл $ М)Мр(Іх для випадку, коли епюра від аада ного навантаження має довільну форму а від одиничного — прямолі нійна (рис 381) Позначимо через О площу епюри Мр, с— її центр ваги Ме — ординату епюри від одиничного навантаження під центром ваги епюри Мр Очевидно, що МРйх ~ ЛЙ е диференціалом площі епюри Мр, а М, = хі§а Тоді шуканий інтеграл
ЛІ|Лїр(£ї =	| хіЙІ	(іЗ 59)
Інтеграл у правій частині рівняння (13 59) є статичним моментом площі епюри Мр відносно осі О — Оі
хгіЯ = х£і,
де хе — абсциса центра ваги епюри Мр.
Рис 381
Тоді
_( ЛЇ,ЛІ,<1х=і(ахса =«И„ (13 60) І
оскільки
хД§а = Ме
Отже, інтеграл Мора дорівнює добутку площі епюри від зовнішнього навантажен ня на ординату прямолінійної епюри від одиничного навантаження розташовану під центром ваги епюри від заданого зовнішнього навантаження
Загальна формула (13 46) для визначен ня переміщень у системах з прямих стерж нів набирає вигляду
(13 61)
Описаний графоаналітичний спосіб визначення інтеграла Мора був запропонований О М Верещагіїїим і має назву способу Верещагіна Обчислення за цією формулою виконують по ділянках, на кожній з яких епюра від одиничного навантаження повинна бути прямоліній* ною (рис 382) Тоді коли обидві епюри прямолінійні можна множити люту будь якої* з них на ординату іншої під центром ваги першої
Якщо епюра Мр має сктадний вигляд, то її слід розбити на прості фігури (рис 383), для яких легко визначити площу і положення центра ваги При цьому кожну з площ треба множити на ординату одиничної епюри під центром ваги відповідної площі Ординати в цьому разі зручно позначати замість ЛЇе» літерами т]й, де к — і 2
Отже,
4-Е тр-	(13 62)
Переміщення від дії осьових і поперечних сил а також крутних моментів виражаються аналогічно
- 2. рр &ір$ — 2.* ~ср~ д^ч> —	.
де 2 — площа епюри Мр, або 0р або Ліркр від заданого навантаження, Мс> ^скр — ординати відповідних епюр осьових поперечних сил і крутних моментів від одиничного навантаження взяті під цент рами ваги епюр Мр 0Р Мркр
Якщо епюри від заданого і одиничного навантажень протилежні за знаком, то їхній добуток має знак «мінус»
Спосіб Верещагіна широко застосовують при розрахунку рамних кон сгрукцій (конструкцій, в яких кути В МІСЦЯХ з'єднання окремих стерж нів, жорсткі до дефор мації, залишаються жорсткими після неї)
Розглянемо деякі
приклади застосування Рис 382	Рис 383
способу Верещагіна для
визначення переміщень у різних стержньсвих системах
Визначимо прогин у точці О і кут повороту перерізу В консолі (рис 384, а) Відповідні допоміжні (одиничні) стани зображено на рис 384, б в	_
Будуємо епюри згинальних моментів Мр і М । Прогин у точці О балки за Верещагіним
л V
На ділянці АВ площа епюри МрЯ = (1/6) до* Центр ваги цієї площі, обмеженої квадратичною параболою д (а — х)*/2 (рис 384 а), розташований завдальшки (3'4) ввід точки В, у чому легко Перекопа тися застосувавши формулу (2 3) Ордината допоміжної' епюри
МЄ| — (7'4) а На ділянці ВД О =0 Отже .	І ра* 7	7 ра*
= У/ ~ГТ “б	Г а	24 ЕГ
Для визначення кута повороту допоміж ну систему навантажимо одиничною парою Очевидно, Ма = 1 Отже кут повороту пе рерізу В
Д2^ = 2.—77“ “ Ту ~ 1 = '6ЕГ-
Знайдемо повне переміщення точки С рами, зображеної на рис 385, а взявши ЕУ = соп5Ї Для визначення повного пере міщення Д — ССі обчислимо насамперед переміщення цієї точки у вертикальному та горизонтальному напрямах
Щоб визначити вертикальне переміщек ня точки С раму в допоміжному стані на вантажуємо силою — 1, спрямованою
Рнс 385
вертикально (рнс 385, б) Основну епюру Мр показано на рис 385, г, допоміжну — М, — на рис 385, д Маємо
Обчислюємо по ділянках
—	для ділянки СВ О, = Мі, т|і = 1/2,
—	для ділянки АВ Я, = МН г), = І
Для визначення горизонтального переміщення допоміжну систему навантажуємо в точці С горизонтальною силою X, = 1 (рис 385, в) Епюру показано на рис 355 е
Очевидно, на ділянці СВ ордината їй = 0, а на ділянці АВ ордината і], = Л/2 Отже
А _	_ Мк*
Дар -	- 2ЕІ
Повне переміщення точки С рами
Д = і/"Д,р 4- Д®р
Визначимо зміну відстані між точками А і В для рами, зображеної на рис 386, а Епюру згинальних моментів від заданого наванта
Ряс 387
ження Мр показано на рис 385,6 У допоміжному стані навантажуємо систему узагальненим навантаженням яке відповідає шуканому переміщенню (рис 385, а) 1 Таким навантаженням є одиничні зосереджені сиіи прикладені в точках А В Епюри Мр і М1 побудовано на стис нутих волокнах Маємо
О 1 РІ , РІ* т}
я “ Т 4 1 “ —— а Отже,
Визначимо опускання вільного кінця ламаної консолі круглого поперечного перерізу навантаженої на ділянці АВ вертикальним рів номірно розподіленим навантаженням (рис 387, о) Допоміжний стан та епюри згинальних і крутних моментів для основного і допоміжного станів зображено на рнс 387, б а Епюрн крутних моментів розташовані в горизонтальній площині, а їхні ординати зображено штриховими лініями
Обчислюємо по ділянках:
_ да / а« І* \ даЧ
3 /’’ 2О7р
1 Для скорочення кількості рисунків тут і в деяких прикладах далі епюри побудовано безпосередньо на осях стержнів, тобто схеми станів навантаження І епюрн суміщено на одному рисунку.
$ 86 Застосування способу Вероцагіна до стержнів змінного поперечного перерізу
Для визначення переміщень у балках змінного поперечного перерізу методом Мора перепишемо формулу (13 46) так
р М,МР<іх .і г мр (х) _
(1363)
/	І
де ] (х) — момент інерції’ довільного перерізу, /0 — момент інерції певного (характерного) перерізу
Позначимо величину МР (х)1 = Л4ав і назвемо її зведеним згинальним моментом у довільному перерізі Тоді інтеграл Мора можна записати у вигляді
Г м.м,.
Лір = і	(13 64)
Застосовуючи до формули (13 64) спосіб Верещагіна, знаходи-
мо що
О..7Ї.
Дір = —е7^~ ’	(13 65)
де Й,в — площа епюри Мав (тобто зведеної епюри); Мс — ордината одиничної епюри під центром ваги зведеної епюри
Визначимо прогин вільного кінця і кут повороту перерізу В консолі змінного перерізу (рис 386, а) якщо
У (х) =	,
де /0 — момент інерції перерізу в МІСЦІ затиснення
Поточна ордината епюри МР дорівнює
—Р(1 — *) Зведені ординати постійні, оскільки
М1в = Мр-Аї- = -Р1
Для визначення прогику будуємо допоміж ний стан (рис 386, б) Очевидно
О„ = РР,
.	РР
“ £/0 я 2Еі, ’
Щоб визначити кут повороту перерізу В, ^звантажуємо балку в допоміжному стані зосередженим моментом X, = і (рис 388, в) Ураховуючи, що епюра Л?> має дві ділянки, дістаємо
А %»а7> рл
Л2Р = Е^ - ~2Е^
і 87, Потенціальна енергія деформації
Згідно із законом зберігання енергії, робота зовнішніх сил не зникає, а трансформується в потенціальну енергію, яка накоплю-еться в пружному тілі Отже, накоплена потенціальна енергія де формації визначається роботою зовнішніх сил Ця енергія виявляеть ся у вигляді роботи, що здійснюють внутрішні сили при розвантажен ні Знімаючи, наприклад, частину гир прикладених до балки (рнс 389) бачимо, що балка трохи випрямляється і піднімає решту гир Отже, пружне тіло здатно акумулювати механічну енергію яку можна повернути при розвантаженні
Нехтуючи прн статичному навантажуванні змінами кінетичної енергії системи а також втратами енергії на внутрішнє тертя, зміну температури, магнітні та електричні явища, які мають місце при деформації, можна стверджувати що зменшення потенціальної енер гії навантажень дорівнює потенціальній енергії деформації, накопле-ної пружною конструкцією тобто
І/ = Ї7Р,
(ІЗ 66)
* де У — приріст потенціальної енергії деформації, Ур — зменшення
1 потенціальної енергії вивантажень
і Зменшення потенціальної енергії навантажень чисельно дорів
1 нює роботі зовнішніх сил при навантажуванні тіла Отже, потенці
і альна енергія деформації чисельно дорівнює роботі зовнішніх сил при навантажуванні системи або роботі внутрішніх сил у процесі
; розвантажування
На підставі формули (13 22) потенціальна енергія деформації ! в загальному випадку навантажування стержня
(ІЗ 67)
Як видно з формули, потенціальна енергія деформації становить квадратичну функцію узагальнених сил або узагальнених перем!
Ял_________в щень, оскільки останні пов’язані лінійно з узагалі»-
Я і неними силами Отже, потенціальна енергія деформації еЬ завжди додатна, не залежить від порядку навантажу-вання і цілком визначається остаточним значенням зу
Рис 389 силь і переміщень Зазначимо також, що потенціальна енергія деформації як квадратична функція узагальнених навантажень не відповідає принципу незалежності діїсил Цеозна-чає. що потенціальна енергія, накоплена внаслідок дії групи сил, не дорівнює сумі потенціальних енергій, спричинених дією кожного навантаження окремо Закон незалежності дії сил при обчисленні потенці альної енергії можна застосовувати лише тоді, коли переміщення в напрямі однієї узагальненої сили спричинене дією іншої сили, дорівнює нулю
<х<а)
М(х)
РЬ
0(х)«
РЬ
для іІ ділянкн (а<х^ /) Ра	Ра
І ) " Р’а’Ь* ь Р'аЬ Р'а'Ь' , 3 Р*аЬ НІР------в£Л ХЗРІ ЗЕЛ ТГ СРІ ’ ‘
Приклад 59 Визначимо потенціальну енергію деформації накоплену в шарнірно-стержньоЛй системі (рис 390), яка навантажена у вузлі В вертикальною силою Р. Стержні АВ і ВС мають однакові розміри і виготовлені з одного матеріалу
Розглядаючи рівновагу вузла В знаходимо що стержні розтягаються однаковії ми силами
оскільки для прямокутного перерізу <і=І2 Підставивши у формулу (ІЗ 72) М»
0 = 0,4£, 1 = -[з-, Р = ЬН
V) - V,- Р/И 3.
Отже, потенціальна енергія деформації системи
п в V в (Р/Ґ3)«/ РЧ £х~5еЕ~ ЕР *’ ЗЕЇ ’
(13 68)
(13 56)
знайдемо, що
2Р*а^ / З М__\
47 в ЕЬНЧ (1 + Т аЬ ) *
З іншого боку на підставі формули (ІЗ 10) потенціальну енергію деформації можна визначити як половину добутку силн прикладеної до вузла на вертикальне переміщення вузла Др тобто
Другий чтен у дужках виражає вплив поперечної силн При звичайних розмірах ба лок він не перевищує 2 3 % У зв’язку з ним при згинанні балки впливом попереч н<Я сили прн обчисленні потенціальної енергії, нк правило, нехтують
Бажаючи обчислити прогин балки а перерізі де прикладена сила потенціальну енергію деформації можна записати також у вигляді
(/=-5-РДр	(13 73)
и—Т-Рі,
(13.70)
Порівнюючи формули (13 69) і (13 70), можна знайти переміщення точки В у напрям! сили
А 2--^-
&р в З ЕР •
Порівнюючи вирази (13 73) та (13 72) нехтуючи впливом поперечної сили знай демо прогин у перерізі В
Ра*Ь* ДРв ЗЕЛ
(ІЗ 74)
$ 88. Теорема Каегільяно. Теорема Лвгранжа
Приклад 59 Визначимо потенціальну енергію накоплгну при деформації Лики постійного прямокутного перерізу Ь х А, навантажена як показано на рис 391.
Виходимо з формули (ІЗ 67). зберігаючи члени, які відповідають плоскому зги
нанню
и = Г м* (ж) ак л С О»(к)0ж
,) Ш + ] к? '
(13.7!)
Обчислюємо по ділянках. Вирази дня згинальних моментів ! поперечних сил у довільних перерізах ділянок ма ють такий вигляд для і ділкики (0 С
Рис. 390	Рис. 391
Нехай пружна система статично навантажена довільним навантаженням (? і деякою узагальненою силою Р (рис 392) Обчислимо потенціальну енергію, накоплену при деформації системи Для зруч-
ності виберемо такий порядок навантажу вання Спочатку навантажуємо систему силою Р Переміщення точки прикладен ня сили в її напрямі, спричинене цією самою силою, позначимо &рр. Потім прик ладаємо навантаження (? Внаслідок додаткової деформації сила Р дістане пере міщення Др<г Повне (узагальнене) пере-
0
Рис. 392
міщення точки прикладення сили
Ар — Арр + Ард.	(13 75)
Очевидно накоплена потенціальна енергія деформації чисельно дорівнює роботі зовнішніх сил
V = -у- Ррр + РАрд +	(13 76)
де 1/дд — енергія, накоплена внаслідок деформування системи тіль* ки силами яка чисельно дорівнює роботі цих сил на спричинених ними переміщеннях
Другий член у формулі (іЗ 76) не містить і/2, оскільки на переміщенні Ард сила Р, здійснюючи роботу не змінювала свого значен ня Оскільки Арр=РЬрр, то формулу (із 76) можна записати у вигляді
V - 4- РЧі>р +	(13 77)
Проднференціюемо вираз (іЗ 77) по силі Р, враховуючи вираз (ІЗ 75)
*^- = РЬрр + Ард = Арр + Ард — Ар
Отже,
(ІЗ 7в>
Переміщення точки прикладення узагальненої сили в напрямі її дії дорівнює частинній похідній від потенціальної енергії деформації по цій силі (теорема Кастільяно)
Зазначимо, що, згідно з формулою (іЗ 77), друга похідна від по* тенціальної енергії по узагальненій силі
завжди додатна
Для плоскої стержньової системи, виходячи із загальної формули (]3 67), потенціальну енергію деформації запишемо у вигляді
+	+	(1з 80)
де М (з), N (5), <2 (з) — зусилля в перерізі стержня
Застосовуючи правило диференціювання по параметру, знаходимо, що
. йи Г М(і)йз дМіа) , (* N («)Й» М (з) ,
= ] 2ЯТ------Їр +}ер-----------+
+ $*	(1381)
Рнс 393

Якщо знехтувати впливом осьових і поперечних сил на переміщення
.	Г дМ(ц
Др - з	Еі дР 
(ЇЗ 82)
Тоді коли треба розгля н}тнм способом визначити лінійне чи кутове перемі
щення в точці де узагальнена сила не діє в цій точці слід прикласти відповідну фіктивну узагальнену силу Далі записавши вираз для потенціальної енергії від системи сил, включаючи зазначену фіктив ну силу, слід взяти похідну по фіктивній силі і в здобутому виразі для переміщення покласти фіктивне навантаження таким, що дорівнюй нулю
Приклад 61 Виянашмо способом Кастільяно кут повороту вільного кінця пон солі, навантаженої рівномірно розподіленим навантаженням (рис 393. а)
У зазначеному перерізі балки як фіктивне навантаження прикладаємо М* (рис 393 б) Кут попороту герерізу А згідно з формулою (ЇЗ 78)
ои С М (х} <іх	дМ (х)
®л-дми- имо в] Е7
Взявша М9 ™ 0 дістанемо
Зазначимо, що загальна формула (13 45) для обчислення перемі щень у стержньових системах, яка не потребує складання виразів потенціальної енергії та диференціювання їх, витиснула з розрахункової практики спосіб Кастільяно Проте останній е загальним способом визначення переміщень у нестержньових системах (пластини, оболонки тощо)
Якщо виразити потенціальну енергію деформації як функцію незалежних узагальнених переміщень, то можна довести, що частин на похідна від потенціальної енергії по будь-якому переміщенню дорівнює відповідній узагальненій силії
03 83)
Ця теорема відома в літературі як теорема Лагранжа
Приклав 62 Симетрична шарнірно стержньоеа система навантажено у вузлі В вертикальною силою Р (рис 394). Визначимо значення сим Р якиу> вертикальне переміщення вузла дорівнює &р
Введемо ггозиачеикя. а< — кут некнлу стержня до вертикалі і/—довжина стержня. ЕіР/ — жорсткість поперечного перерізу стержая Стержні з однаковим на хн.юм до вертикалі мають однакові жорсткості
Очевидно ЩО подовження 1-ГО стержня Лі — Ар соз аі, в зусилля в ньому
Потенціальна енергія деформації системи
У — V Рі&> » V _ Д2 V
2	&	21/ р Ді 2І/
Диференціюючи по Др знаходимо
ОЦ	гч соз'аіЕіРі
и в “Зд^ “	2
і 89. Теорема про мінімум потенціальної енергії
Розглянемо довільну статично невианачувану систему (рнс 395, а), зусилля в елементах якої тільки а рівнянь рівноваги визначити неможна Так опорні закріплення зображеної балки дають шість реакцій а рівнянь рівноваги для довільної плоскої системи сил можяа скласти тільки три Перетворимо систему на статично визначувану, відкинувши відповідну кількість зв язків У даному прикладі (рнс 395, б) відкинуто три зв язки — шарнірно-рухомі опори В, С і О Дію відкинутих зв’язків замінимо відповідними реакціями Хі, Х3,	, які будемо розглядати як незалежні зовнішні на-
вантаження
Обчислимо за способом Кастільяно переміщення А,, Д„ А,, точок прикладення сил Хп X,, Х8, в напрямі їх дії Очевидно,
Д»=дх7’ д>в'33с7’ д’в-ЗхГ: •••
де У = У (Хп X,, Х8, . , Р) — потенціальна енергія деформації системи
Оскільки пі переміщення дорівнюють нулю, то
-Й7=0'	<'384>
Рівняння (13 84) — необхідна умова екстремуму функції У Легко бачити, що цей екстремум е мінімумом. Так, згідно з формулою (13 79), другі похідні функції У по Хп X,, Х9
д*Ц
8ХІ
-би,
д*Ц
дХ%
-б„.
дЧі
(13 85)
Переміщення Зп, 3„, Зю — зав жди додатні величини, отже, дру гі похідні функції и додатні, а умови (ІЗ 84) е умовами мініму му функції 0
Отже, приходимо до теореми про мінімум потенціальної енер еІЇ в апатично невизначуваних системах зайві невідомі зусилля
набирають таких значень, при яких потенціальна енергія деформації мав найменше значення (теорема Менабреа) Ця теорема відома також як теорема про найменшу роботу, оскільки робота зовнішніх сил чисельно дорівнює потенціальній енергії деформації
Приклад 63 Користуючись теоремою про мінімум потенціамнЛ енергії дефор мацП визначимо реакцію шарнірно рухомої опори стержня мажЯ кривизни, зображеного но рис 396 Стержень повантажений в опорному перерізі В зосередженим момен том М
Повиачвмо невідому реакцію через X Тоді яа підстеаі теорема про мінімум потенціальної еаергїї деформації
ви
-ИГ-О	(13 86)
С ЛІ*(ф)Л
Оскільки І! ™ І--— го формула (ІЗ 86) набирає вигляду
| у _<,	0387)
Маємо М (ф) — М + ХЛ зіп ф.	™ Я аіп ф де — Я4ф
Підставляючи ні значення у формулу (ІЗ 87) дістанемо ріваяння для визначення реакції X
П/2
(М + ХИ зіп ф) Р зіп ф^4ф п.	1
Еі	“ ’
Знак «мінус» у виразі для X свідчить про те, що нацрям реакції вибраний спочатку, треба змінити иа протилежний
На підставі викладеної теореми можна зробити висновок, що прн добавлянні яких небудь зв’язків потенціальна енергія деформації завжди зменшується
ІЗ г-зтва
385
Глав* 14. СТАТИЧНО НЕВИЗНАЧУВАНІ СИСТЕМИ
$ 90 Основи! поняття тв визначення
Етапи розрахунку статично невизначуваної системи
Як уже зазначалося, статично невизначуваними називаються системи силові фактори в елементах яких тільки з рівнянь рівноваги визначити неможна У таких системах ав язків більше, ніж необхід но для рівноваги Отже деякі зв язкн виявляються в цьому розумій ні так би мовити зайвими, а зусилля в них —зайвими невідомими За числом зайвих зв'язків або зайвих невідомих зусиль установлюють ступінь статичної невизначуваності системи
У § 37 було розглянуто найпростіші приклади статично невнзна-чуваних систем, елементи яких зазнавали лише осьового розтягання або стискання У цій главі розглянемо більш загальні випадки, причому основну увагу приділимо статично невизначуванкм балкам та рамам
На рис 397, а показано шарнірно обперту балку — систему статично визначувану і геометрично незмінювану Всі три реакції (Цд, Нл, На) визначаються з трьох умов рівноваги плоскої системи сил Використовуючи метод перерізів, легко знайти силові фактори (?, М у будь якому перерізі ба. кн
Додамо ще один зв'язок, наприклад шарнірно рухому опору в перерізі С (рис 397, 6) Хоч унаслідок цього система стала більш міцною та жорсткою проте з погляду геометричної незмінюваності цей зв’язок зайвий Тепер з трьох рівнянь рівноваги чотири реакції (На, На, Нв, Не) визначити неможна Отже, зображена на рис 397, б балка один раз статично невизначувана
На рис 398, а показано двічі статично невизначувану балку Для визначення п’яти реакцій е лише три рівняння рівноваги Отже, система має два зайвих зв’язки Вона може бути утворена, наприклад, із консолі (рис 398, б) установленням шарнірно-рухомих опор у перерізах В та С
У конструкціях часто застосовуються статично невизначувані балки з ламаною віссю — рами На відміну від фарм, де стержні з'єднані між собою шарнірами й навантажені силами, прикладеними у вузлах, рами мають один або кілька жорстких вузлів У жорсткому вузлі торці з еднуваних стержнів не дістають відносних поступальних переміщень а також відносних поворотів
Рамні конструкції можуть складатись як з пря молінійних.такі з криволінійних елементів На рис 399 показано двічі статично невизначувану плоску раму В цьому прикладі, як і в попередньо му. для визначення п’яти реакцій зовнішніх зв’язків маємо тільки три рівняння рівноваги
Рас 397
Рами можуть бути навантажені цілком довільним навантаженням, будь як орієнтованим
Статична невизначуваність може бути наслідком не тільки введен ня додаткових зовнішніх зв’язків, а й умов утворення системи Розгля немо раму, показану на рис 400, а Очевидно реакції На. На, Нв зов нішніх зв’язків (опор) легко визначити з рівнянь рівноваги Проте після цього рівняння рівноваги не дають змоги визначити всі силові фактори в елементах рами
Розріжемо раму на дві частини й розглянемо рівновагу однієї а частин (рис 400, б) Дію відкинутої частини на залишену замінимо в кожному з перерізів розрізу трьома силовими факторами* осьозою силою И, поперечною силою () та згинальним моментом М Отже, в трьох рівнянь рівноваги треба визначити дев’ять невідомих зусиль Система шість разів статично невизначувана Вона складається з двох вамкнених безшарнірних контурів, кожен з яких тричі статично не* визначуваний
Зазначимо, що встановлення шарніра на осі стержня (рис 401, а) перетворює на нуль згинальний момент у даному перерізі й, отже, внижуе ступінь статичної невизначуваності на одиницю Такий шарнір називають одиночним Очевидно
рама, показана на рнс 401 а, п’ять разів статично невизначу вана
Шарнір, розміщений у вуз лі, де вбігаються п стержнів ж (рис. 40і, в), знижує ступінь ста* тичної невизначуваності вал— 1.
™ б ™ І г Рас. 401
ІЗ*
38?
оскільки замінює собою таку саму кількість одиночних шарнірів (рис 401, г) Такий шарнір зветься загальним Рама зображена на рис 40і. б, чотири рази статично невизпачувана
Ступінь статичної невизначуваності плоских систем можна визна чати за формулою
5 = Зк - ш,	(І4 1)
де $ — ступінь статичної* невизначуваності, к — кількість замкнених контурів за умови повної відсутності шарнірів, ш—кількість шарні рів у перерахунку на одиночні
Основа (земля) розглядається як стержень Так наприклад, рама, наведена на рнс 400, має чотири замкнених контури, біля кожного шарніра вказано відповідну кількість одиночних шарнірів, при ньому група стержнів жорстко зв'язаних між собою, вважається одним стержнем
і Тож у розглядуваному прикладі к — 4, ш -»• і + 2 + 1 + І + + 1=6 Отже, 5=3 4 — 6 = 6
Як уже зазначаюся в § 37 для визначення зусиль у статично не-визначуваних системах додатково до рівнянь статики складають так звані рівняння сумісності деформацій Насправді зайві зв’язки обмежують переміщення тих перерізів, до яких вони прикладені Цю обставину й використовують для складання додаткових рівнянь, які разом з рівняннями статики дають змогу визначити всі силові фак тори в елементах системи
Розглянемо етапи розрахунку статично невизначуваної си стеми.
І Визначаємо ступінь статичної невизначуваності, тобто кількість зайвих зв'язків або зайвих зусиль
2 Усуваючи зайві зв’язки, заміняємо вихідну систему статично визначуваною, яка зветься основною системою Вибір зайвих зв’язків залежить від бажання того хто робить розрахунок Тому для однієї тієї самої статично невизначуваної вихідної системи можливі різні варіанти основних систем Однак треба стежити за тим щоб кожна з них була геометрично незмінюваною Раціональний вибір системи спрощує розрахунок
Отже основною системою називається будь-який із статично визначуваних варіантів розглядуваної системи, здобутої звільненням її від зайвих зв’язків
З Завантажуємо основну систему заданим навантаженням і зайвими невідомими зусиллями, що заміняють дію усунених зв язків Така система зветься еквівалентною системою
4 Для того щоб основна система була еквівалентною вихідній системі, невідомі зусилля треба добирати таким чином, щоб деформа ція основної системи не відрізнялася від деформації вихідної статично невизначуваної Для цього прирівнюють до нуля переміщення точок 388
прикладання невідомих зусиль у напрямі їх дії Із добутих таким чи» ном рівнянь знаходять значення зайвих невідомих
Визначати переміщення відповідних точок основної системи можна будь-яким способом, проте найкраще загальними методами — методом Мора або способом Верещагіна
Знайшовши вайві невідомі зусилля, визначаємо реакції, будуємо епюри внутрішніх силових факторів, а також добираємо перерізи та перевіряємо міцність звичайними способами
Наведена схема розрахунку має назву методу сил, оскільки як основні невідомі тут вибирають зусилля зайвих зв язків
б 91. Розрахунок простих статично невизначуваних балок
Як приклад розрахуємо балку, один кінець якої закріплений, а інший обпирається на шарнірно рухому опору (рис 402, а)
Затискання лівого кінця, еквівалентне трьом стержням, дає три реакції, шарнірно-рухома опора — одну реакцію Всього треба визначити чотири реакції Отже, балка один раз статично невн значувана Для побудови основної системи слід усунути один зв язок
Як зайвий зв'язок виберемо шарнірно рухому опору Основна єи стема, добута внаслідок усунення зайвого зв’язка, становить кон соль
Навантажуємо основну систему заданим розподіленим иавантажен ням, а замість відкинутої опори прикладаємо невідому реакцію Ив = Хх (рис 402, б) Надалі зайві зв'язки будемо позначати літерою X незалежно від того, си ла це чи момент
Повне переміщення точки В основної систе ми (від заданого навантаження й зайвого невідомого зусилля) у напрямі Хх, тобто у напрямі усуненого зв’язка, повинно дорівнювати нулю, оскільки в точці В вихідна система не має прогину. Отже, додаткове рівняння пере міщень запишеться так
Л,=0	(14 2)
Повний прогин Д{ можна визначити як су му прогинів від зовнішнього навантаження Дір = —(рис 402, в) та невідомої ре акції Д1Х = ХхР/3£/ (рис 402, г) (Методи визначення Дір та ДІХ наведено в гл іО і ІЗ) Тоді рівняння (і4 2) запишеться у вигляді
Дх = Дір + Дп = 0
Рнс 402
Рнс 403
Звідси шукана реакція
Тепер з рівнянь статики лег ко знайти решту реакцій, а потім звичайним способом побудувати епюри згинальних моментів і по перечних сил На рнс 403 наведено епюри ф та М, а також значення реакцій опор. Перевіряють міцність абодобирають.пе-рерізи також звичайним способом.
Нагадаємо, що вигляд основної системи залежить від того, які зв'язки (зусилля) вибрані як зайві Так взявши як зайве зусилля опорний момент Ма, дістанемо основну систему, замінивши затиснення шарнірно нерухомою опорою (рис 404, а} Тут основна система, крім заданого навантаження навантажується невідомим моментом Ма =• — Хи який визначається на підставі рівняння переміщень (І4 2). Під Д] у цьому разі слід розуміти пов ний кут повороту перерізу А
Нарис 404, 6 показано основну снсте му, здобуту в припущенні, що як зайву невідому взято реакцію Кд Така конструкція опори перешкоджає повороту й горизонтальному переміщенню, але до пускає вертикальне переміщення Уцьо му разі рівняння переміщень (і4 2) ви ражає рівність нулю в основній системі вертикального переміщення (прогину) точки А
Нарешті, основну систему можна ут ворнтий установленням проміжногошар-ніравякому небудь перерізі (рис 404 в) Таким чином дістаємо статично визначу вану шарнірну балку Тут вже усунено не зовнішній а внутрішній зв’язок Оскільки встановленням шарніра лікві дується згинальний момент у даному пе рерізі балкн, то для відновлення втрачених зв’язків прикладаємо два однакових за модулем та протилежно спрямованих моменти М = Лі, що станоалять дію
ііішшшц
В
шннші
а
б
ІЇЇІШПШІ
В
Рнс. 404
однієї на одну відокремлених шарніром частин балки Рівняння перемі* щень (і4 2) в цьому разі виражає рівність нулю взаємного кута поворо ту перерізів правої та лівої частин балки, які примикають до шарніра (рис 404, г)і
Аі = вілі« + Йіпр = 0, (14 3) оскільки у вихідній балці ці перерізи утворюють один переріз
Зазначимо, що прн побудові ос новної системи як зайві зв’язки не можна брати елементи, реакції яких визначаються безпосередньо з рівнянь рівноваги, наприклад горизонтальну реакцію На опори на рис. 403
Приклад М. Балка ЛВ, навантажена рівномірно розподіленим навантаженням (рис. 405, а), обпирається по кінця» на шар
нірні опори, а посередині підпирається пру	риь 405
жиною (пружною опорою). Визначимо зусил
ля, що стискав пружину побудуємо епюру згинальних моментів, якщо піддатливість пружини, тобто П осадка від одиничної сили (див § 68),
64К*п 68*
Розглядувана система один раз статично кеанзиачуваиа, Як зайве невідоме зусил яя візьмемо реакцію пружини На “ Хг Відлов дно до нього на рнс. 405, б побудова* ао основну систему Щоб вона деформувалась як задана балка, прогни точки С балкн повннеа дорівнювати осадці точки С пружини Інакше кажучи взаємне перемішений точок С та С тобто Да має дорівнювати нулю	-*
Отже, рівняння переміщення можна записятн так
де Д[р ™ (—5/384) (у'ЧЕІ) — переміщення точки С основної системи від заданого навантаження у Ди — (Х^/ІЗЕІ) 4- X — взаємне переміщення точки С балки і точки С" пружвин ТІЛЬКИ ВІД СИЛ Х[ причому переміщення точки С* пружини
Х-аХ]
Додатний напрям переміщень відповідає напряму Х( Отже, ___________________________________п
Звідси
— Ч>
№Еіа
При абсолютно жорсткій пружині а >= 0 І
Г”
Епюри поперечних сил та згинальних моментів на рис. 405 а побудовано для останнього випадку
і 92. Канонічні рівняння методу сип
Додаткові рівняння переміщень що виражають рівність нулю переміщень у напрямах зайвих невідомих, зручно складати в так зва-ній канонічній формі, тобто за певною закономірністю
Спочатку розглянемо систему, один раз статично невизначувану (рнс 406, а) Як зайву невідому виберемо шарнірно рухому опору В. Тоді, навантаживши основну систему заданим навантаженням і зайвою невідомою силою Хх (рис 406, б), прирівняємо до нуля повне переміщення точки В основної системи в напрямі Хі
Д, = Д, (/> Хі) ~ 0	(І4 4)
Обчислюючи А,, застосуємо принцип незалежності дії сил
Д] = Дір 4- Дп
де Дір — переміщення від заданого навантаження (рис 406, в}, Дц—переміщення від сили Х1
Якщобп —переміщення в напрямі Х: від сили Хі — і (рис 406 д' то
Дц !!= ^цХц
і рівняння переміщень (14 4) набирає вигляду
«„X, +Д|Р=0.	(І4 5)
а
І' І*
І'.
у Іі<
Це канонічна форма рівняння переміщень для один раз статично невизначуваної системи. З формули (і4 5)
X, =	(14 61
е
/[ІТТТТГттттт^
е
Рис 405
Рис. 407
або обчислюючи переміщення 6П та Дір, використовуючи формулу Верещагіна і дані рис 406, г, е, матимемо
д _	____!_ /* в > _ Р
°“ * Еі “ Е/ 2 З 3£У
ЮрЛІгр І	рр	І 5	А	ЬРР
“1Р — Е4	~ ЕЛ	4	6	48ЕГ'
Підставивши ці дані у формулу (14 6), остаточно знайдемо
X, =-^-Р
Для системи з двома зайвими зв'язками, як, наприклад, на рис 407, а, додаткові рівняння переміщень перерізу А основної системи (рис 407, б) мають вигляд
Д1 = 0, Дї = 0,
де Д, = Д, (Р, Хг, Х^ — повне переміщення точки А в напрямі Хі від заданого навантаження та зайвих невідомих сил Хх і Х„ А» = = Д, (Р, Хі, Хі) — повне переміщення точки А в напрямі X» від за значених навантажень
Виходячи з принципу незалежності дії сил, запишемо перемі щепня Ді та Да у вигляді сум переміщень, спричинених окремо кож пою з невідомих сил Х} та X, та заданим навантаженням Р Викорнсто вуючи вибрані раніше позначення переміщень (див § 78), знаходимо, що
Ді = Дц Дц 4*	=
Д, = Д,| + д„ + д!Р = о	(14 ”
Повне переміщення Д/* можна визначити як добуток питомого переміщення 5^, спричиненого дією одиничної сили, на відповідну уза гальнену силу
Дц ~ Дц ~	• • Дд = 5/*Хд
Отже, рівняння (14 7) набирають вигляду
ЗцХі 4-618Х, 4-Дір =-0,
6ИХ: 4-6пХ,4-Д2р = 0	04 в)
Це канонічна форма рівнянь переміщень для системи, двічі статично невизначуваної
За аналогією можна записати в канонічній формі рівняння переміщень для будь якої п разів статично невизначуваної системні
*" ®»ХІ + ' * • + «Л 4- Д|р = 0,
6пХх 4-6„Х, 4-	• +	+ Дгя = 0,
бщХх 4- 6пгХІ 4- ' • • 4* &плХа = 0
Переміщення Л/р та б/*, що входять до канонічних рівнянь найчастіше визначають за методом Мора або способом Верещагіна При цьому для балок та рам впливом поперечних та поздовжніх сил, як правило, нехтують і враховують лише згинальні моменти Однак, визначаючи переміщення в балках прямокутного поперечного перарізу, для яких відношення висоти перерізу до довжини прольоту п/1 >
1/5, поперечні силн враховувати обов'язково При розрахунку статично невязначуваних рам з великими зазначеними відношеннями (Л/О1/5) похибка, спричинена неврахуванням інтегралів поздовжніх та поперечних сил, також може стати істотною, особливо для високих рам Слід мати на увазі, що в реальних балочних, рамних та арочних конструкціях відношення М, як правило, менше за і/10 Тому при обчисленні переміщень у загальній формулі Мора цілком допустимо зберегти Інтеграл, що враховує лише згинальні моменти
Для визначення переміщень будуємо епюри згинальних моментів (див , наприклад, рис 406) в основній системі окремо від заданого навантаження (стан Р) і від кожної одиничної сили Хі = 1 (стан і), X, в і (стан 2),	,	= 1 (стан л) Ординати відповідних епюр
позначимо, як звичайно, через Л4/>, Мь Мг, , Мп Тоді на підставі формули (іЗ 46) знаходимо
ґ МіМраї А г МіМрОз	А С ЯяМріїз
-	е7—; •••:	- І и 
Питомі переміщення, що мають однакові індекси й називаються головними коефіцієнтами канонічних рівнянь, визначають таким чином:
гг"! 8«“)—є7~- •	ЕГ--
Очевидно, що ці переміщення додатні
Питомі переміщення, в яких Індекси не однакові, називають побічними коефіцієнтами А визначають за формулами
. Ґ Міїї.4» . . Г	я Г МіМ^з
Вони мажуть бути додатними або від’ємними, а також дорівнювати нулю
На підставі теореми про взаємність переміщень б,* =» б*^
Для систем, що складаються з прямолінійних елементів, обчислювати переміщення зручно за способом Верещагіна. Наприклад, для статично невизначуваної балки показаної на рис 406,
Дія
---ЕТ~‘ ««
°.мсі
о РІ* 77	5 ,
»4я = —§—, Мер — ~о~ і
«1=4-'
Отже .	5 й* . Р
*ІР-----48 “£Г ’	“ ~ЗЕГ •
З формули (І4 6)
Х-=4Р
Тоді, коли крім зовнішніх навантажень треба врахувати вплив температури, порядок розрахунку залишається попереднім Вільні члени канонічних рівнянь при цьому е переміщеннями в основній системі не тільки від заданих навантажень, а й від зміни температури
4-	®іЛ + '•• + ®і»Ля 4-Дір + Діг =0
бВІх1+впїх1+ ••• +М. + Д„Р + &пт = 0, <и де Літ — переміщення в основній системі в напрямі Х„ спричинені зміною температури
Визначивши коефіцієнти бд і вільні члени Д,р та Д^т, із «.истеми лінійних рівнянь (і4 10) знаходимо значення зайвих невідомих зу силь Хі. ....Хп Далі звичайним способом будуємо епюри внутріш-
ніх сил АІ,(},Мв елементах системи іноді будувати епюри зручно додаванням епюр Л4р до епюр ТІЇ।	, ~МЛ, попередньо помножених
на значення Хі, X»,	, Х„ відповідно*
М = ЛГ1Х14-Л41Х14- ...
=	+р,х«+ + 0*
# _ ^Х, +	+ ... 4- #р
Слід зазначити, що літерний вигляд канонічних рівнянь залиша еться незмінним при будь якому можливому варіанті основної системи Змінюється лише зміст зайвих невідомих та геометричний зміст пере міщень Наприклад, якщо як зайві невідомі вибирати внутрішні сили в будь яких перерізах, то коефіцієнти в канонічних рівняннях є від повідними взаємними переміщеннями перерізів у напрямах зайвих невідомих зусиль
На рнс 406 показано тричі статично невизначувану плоску раму (а) та два варіанти основної системи (б і а) Для будь-якої тричі ста тично невизначуваної системи канонічні рівняння мають вигляд
бпХі 4- 6ІІХа 4- Дір » 0;
бпХх 4- б^Х, 4. б„Х8 4- Ду> = °.	(І4 і і)
бмХх 4- 6МХ, 4- бдХр 4- Дал в 0.
рівняння (і4 1і) виражають вимогу рівності нулю переміщень перерізу А я напрямах невідомих сил Лі, Х„ Ха.
Другий варіант основної системи (рис 408, в) утворений розрізу ванням ригеля. Оскільки в плоскій системі в перерізах діють взагалі три силових фактори (осьова сила, поперечна сила та згинальний момент), то до сторін розрізу слід прикласти як зайві невідомі силові фактори Хь Х|, Х3, що визначають взаємну дію обох частин системи одна на одну в даному перерізі При такому виборі основної' системи рівняння (14 іі) виражають рівність нулю повних взаємних перемі щень сторін розрізу в напрямі зайвих невідомих Наприклад, трете рівняння системи (14 іі) означає рівність нулю переміщень у напрямі Х3, тобто взаємного кута повороту сторін розрізу під дією заданого навантаження та вайвих невідомих зусиль
Вибираючи як вайві невідомі внутрішні зусилля, здебільшого можна значно спростити розрахунок Наприклад, якщо вихідна система симетрична (за конфігурацією та розташуванням жорсткостеЙ), то основну систему слід будувати також симетричною, оскільки при цьому деякі побічні коефіцієнти канонічних рівнянь дорівнюватимуть нулю Так, прн розрахунку симетричної рами, показаної на рис 408, а, основну систему доцільно утворити розрізуванням горизонтального стержня (ригеля) посередині (рис 409, а) При цьому основна система також буде симетричною Тоді серед зайвих невідомих матимемо симетричні зусилля Х1( Ха та кососи^етричне X,. Епюри згинальних моментів від сил X, = і, Х3 = 1 та Х3 = 1 показано на рис 409, б г. Зазначимо, що епюри М3 та М3 симетричні, а епюра М3 кососимет-
ричпа Перемноження симетричної епюри на кососиметричку дає в результаті нуль
Визначимо переміщення 6Н = 6И Застосовуючи спосіб Верещагі* на, матимемо
’»=тт(—т4+44)=°	(’412>
Аналогічно ®83 =	= 0
Отже, система рівнянь (14 II) спрощується і набирає вигляду бцХі + бі>Х8 Дір = 0, 6иХ14-Д2р=0,	(14 13)
68|Х9 *• Дзз-Х, -т Дзр = 0
Якщо прн цьому задане навантаження Р кососнметричие (див рис 406, с), то епюра Мр також кососиметрична (рис 409, а) і перем! щення Дір — Дзр = 0 Тоді з першого та третього рівнянь (І4 13) випливає, що симетричні зусилля в місці розрізу дорівнюють нулю
X, = 0 Ха = 0
Зазначимо, що коли навантаження симетричне, епюра Мр теж симетрична І тому Дгр = 0 Тоді з другого рівняння (14 13) випливає, що косаснметрнчне зусилля X, = 0
Приклад 66. Побудуємо епюри силових факторів у елементах рами показаної на рис 410, а Рама навантажена рівномірно розподіленим навантаженням ч при кладеним до горизонтального стержня (ригеля)
Легко асбачити що система двічі статично нсиизяачуваиа Нарис 410 б ..г показано деякі можливі варіанти еквівалентної системи Для розрахунку візьмемо варіант рис 410 б Щоб обчислити два зайвих невідомих зусилля Хі та X, скори ставмося канонічними рівняннями (14 8)
+	ЬД2/> = 0
Для визначення переміщень Д(р розглянемо основну систему окремо заван важену заданим навантаженням та кожною з одиничних сил Х> = 1, Ха = 1
(рис. 411, о) Оскільки стержні прямолінійні. то переміщення зручно знаходь* ги способом Верещагіва Епюри згинальних моментів Мр "М^ показано на рис. 411 б
Для визначення Д1р та площі ешор МР перемножуємо ва ордянатн епюр Яг га Я* ідо відповідають центрам ваги ешор Мі
А_____
& ш •
з _2£_
Тут і далі заради спрощення вважаємо й — ІІ Е(/{ — Е^ “ Еі	__
Переміщеаня бц та б,, знайдемо аналогічним множенням ешор Л4, на Мі та Лі, на Я*
і	І	Л»	2	4 і»
б“ в Е^і	и,і + £♦•/»	2	З	Ь = З “ТТ	•
°« “	2 Т1 “ ЗЕі
Нарешті в,, визначаємо перемножевлям епюр Мі та М^
м-г
іе:
Підставляючи значення переміщень у кнновічні рівняння знаходимо
А. , ' х.__4-
Рис 412
Звідси
ді
Знак емінус» у виразі для X* показує, що спочатку вибраний напрям цієї сили {див ряс 410, б) слід зміните на протилежний
Розглядаючи тепер еквівалентну систему тобто статечно визначувану основну систему від дією заданого навантаження та знайдених сні Хг та X, легко побуду вати остаточні епюрн внутрішніх силових факторів та скласти умови міквості ене-ментів рами
Остаточні епюрн згинальних моментів поперечних та осьових сил наведено на рис 4І2
Доберемо прямокутний переріз для стержнів рами якщо д = 10 кН/м / = 2 м Матеріал стержнівСт2 [о] = 140 МЛа [т]*^ 90 МПа Відношення внеотиадошнрини Ь перерізу становить 2 1
Як видно з епюр внутрішніх сил (рис. 412) у небезпечному перерізі
Мг
—28~ «1» = 4 3 кН м (?„„ = — «1 = 11,43 кН
IV = -^-=,0 715 кН
Оскільки осьова сила незначна то розміри перерізу добираємо тільки а умови міцності на згинання
В-=2^, =	м»=308 Ю-6 м» = 30,6 см».
[о]	140
□*й в»
Оскільки 17 = —= 15-, то, округлюючи, дістаємо
а > ^І2—ЗО 6 см « 7,2 см. Ь — д/2 = 3,6см, 17 — 31,1см»
Найбільше нормальне напруження в поперечному перерізі визначається як сума напружень від дії згинального моменту та осьової сили
л	4 3 ІО-3 ,	0715
МПа
””	Р \ 31>1 10-е т 7,2 3 6 І0-4 ;
= (138 4-0 276) МПа — 138,3 МПа <140 МПа Найбільше дотичне напружений
4 -2^.- 3 11 ^-—^7 МПа = 6,55 МПа <90 МПа 2Р 2 • 7,2 • 3,6 • ІО"4
Приклад 86 Розрахуємо однопрольотну раму (рис 413 а) навантажену ао-Їизонтальною силою Р посередині лівого стояка Заради спрощення обчислень візьмемо = І. = £,/, = ЕЛ = £/
Система що становить один замкнений контур тричі статично невнзначуазна. Для утворення основної системи слід усунути три зв'язки Різні варіанта еквівалентної системи покеаано на рнс 413 б . г Зважаючи на симетрію рами, як основну ся стену доцільно вибрзта симетричний варіант (рис. 413 а) У цьому разі еайвкми невідомими будуть зусилля в розрізі.
Для визначення зайвих невідомих зусиль скористаємося канонічними рівняння ми (14 1!)
СцХ, + «цХ, + «зЛ» + *їР - 0 в»і Хг + бцХі + 2МХ, +	™ о,
+ виХ> + бмХ> +	= 0
У цих рівняннях переміщення в та Д е відповідними переміщеннями сторін розрізу Щоб визначите переміщення, застосуємо спосіб Верещагіна На рнс 414 покава но ешоря згинальних моментів для основної системи від зеааного навантаження та від одиничних узагальнених сил Х{ = 1 X, “ 1 X» = І Зазначимо що епюри та Мі симетричні а епюра Л4, — кососиметрична Як зазначалося побічні коефІЦІ
Рис 4И енти що визначаються перемноженням симетричної енюрн на кососиметричну, дорівнюють нулю Внаслідок цього би =- бц = 0	= 0
Канонічні рівняння набирають вигляду
б, »Хі + б18Х, 4-= 0, «лХ.+виХ.+ Дзр-О б„Х, 4-^ = 0	(14 15)
Перемножуючи відповідні енюрн знаходимо, що
1	РЛ* 5	5	РА*
ДІР = — £,7,	8	6 Л = “ 48	£7
І Рк*	І	РЬ*
*2Р =	£,7Ж	8	2	=	16£/
_______І	Рк*	Рк* ДВЯ=	£,7,	8	=	8Е7 •
І А» 2 І к* 2	2А»
°и “ £,7, 2 3 *+«,/, 2 З^Ш' 1 А» І А» А* 61»-0л«— £і7і 2	2	= — £7
1 і І І II І Р І 7 А' в«“ £,7, Й 2	2 2 +~£^7 2 8 3 = 12 £7 ’
А Л __	;	\ ЗА
°»»"“£Ї7Г+ Е^, +^7Г= Е2
Підставнашн в рівняння (14 15) та (14 14) знайдені значення б та Д, матимемо 4»х,-х,—^-РЛ
---5-ЛХі4-Х» = —^-РЕ	, 7 У РА»
ПГ Е2 Х*+ 16£7 ж=0
Звідси X, = 0,187Р X, < —0.107Р, X, = О 02ІРА На рнс. 415 показано екві валентну систему і побудовано епюри М, (}, N
Розрахуємо прямокутну раму (рнс 416, а), що складається з двох однакових поперечин та двох стояків Рама навантажена двома одна
Рнс 416
ковими протилежно спрямованими силами, прикладеними посередині поперечин Усередині рами температура Ти а вовні — Т, 7\ > Т, Жорсткість поперечини Е.Ц стояків — ЕЗі
Рама, що утворює замкнений контур без шарнірів, тричі статично невизначувана Задачу можна істотно спростити, використовуючи симетрію системи та навантажування Виберемо симетричну основну систему, розрізавши один із стояків по осі симетрії (рис 4і6, б) У місці розрізу прикладемо систему сил Х8| X». Як зазначалося, внаслідок симетрії навантаження поперечна сила X, = 0
Розсічемо тепер раму по осі Л—А (рис 416,6) Ураховуючи симет рію системи відносно осі В—В, з умов рівноваги відразу визначаємо силу Х8і
2Ха = Л Ха = Р/2
Залишається знайти лише один статично невизначуваний фактор Хі Канонічне рівняння переміщень має вигляд
+ Дія Діг — 0,
де Дір 4- Діг = Дір.г—взаємний кут повороту сторін розрізу, спричинений дією навантаження Р та температури Т.
Температурні переміщення визначаємо аа формулою (І3 56)
Л.г - £ | ">«	& + 2 і	<£,,
де —1—середня температура нагрівання елемен
та Т, — Та=Ті — Ті — різниця температур крайніх волокон Якщо деформації елемента йх від дії температури та одиничних силових факторів одного знака, то підінтегральні вирази додатні Якщо в межах ділянки температура постійна, то
Д*т = £ Г" І + а Гн7Г* ї =
Тут = У Муйх — площа епюри Мк	_
Для визначення переміщень будуємо епюри Мр, Мі (рис 416, в, а) Епюра дорівнює нулю Користуючись способом Верещагіна, зна ходимо
*	2 «і рії
~ ЕІ1 8 — 4£/і ’ д1г = -2«(і, + і,)-!1=А.
Тут у правій частині поставлено знак «мінус», оскільки при Тг > Тг внутрішні волокна елементів подовжені, а в одиничному стані (рнс 416, є) — стиснуті Далі, я 2/і , 2/« “ ет? + еіГ ’
отже, />/?	Т, _ т
---4/ї”	Л----
Х'~	2(-77 + ^	'
Прн = іі = І та ^^ = ^і =
X.-—
На рис 416, е, ж наведено епюри внутрішніх силових факторів за умови Тх — Ті = 0, Р 0
Прилад 67. Розрахуємо ферму, зображену на рис 417, а, в припущенні, шр всі стержні виготовлені з отого матеріалу І мають однакові перерізи Стержні 5 та 6 загального вузла нв мають.
Легко переконатися, що система один реа статично неанзначуазна. Основну ся стену упорену розрізуванням стержня 6, аоказаро на рис 417 б Зайве невідоме зусилля Хг визначаємо в канонічного рівняння яке в цьому реаі вярежае рівність нулю взаємного зміщення сторін розрізу
®іЛ+ Др=0.
Рис 417
Оскільки и елементах ферми діють тільки осьові зусилля то переміщення бп та Д1Р визначимо (див. § 83) за формулами
<*>«
(Н">
де Тії — зусилля в стержнях від навантаження Х( «а і, Кр — зусилля в стержвяа від заданого навантаження
Для визначення зусиль та Тії розглядаємо основну систему в стані Р (рис. 417 а) та в стані / (рнс 417, а)
Обчислювати зручно за допомогою таблиці (табл 17) Знак «мінус* при і?/ та ІЇР показує що у відповідному стержні зусилля стискальні У таблиці не наведено
Таблиця П
"ЇЇ*	До. стсрж ая 1		л>		
1	а	-Е1 2	2Р	-РауТ	а Т
2	а	_ ^2	р	—РвуТГ	а Т
3	а		0	0	а 2
4	а	_ №	2Р	-РоИ?	7
б	аі'7	і	-2Рі Т	—4Рд	
6	а) 2	і	0	0	
-р‘2^'.5+41 2) МІ+ИЇ>
жорсткості оскільки для всіх елементів вони однакові Отже, тйг(5+4ґ'г>’
.	2а(1
®«“-----ЕР--
Підставивша ці значення в канонічне рівняння, знаходимо
X °г ' ‘
* 2(2 +У 2)
1.56Я
$ 93. Багатопрольотні нерозрізні балки. Рівняння трьох моментів
Нерозрізнима називають балки, що обпираються на більше ніж дві опори й не мають проміжних шарнірів Такі балки, які широко вастосовуються в різних конструкціях, належать до статично невизна чуваних
На рис 418 показано балку, що обпирається на т шарнірних опор Одна з опор виконується шарнірно нерухомою для сприймання осьового навантаження, решта — шарнірно рухомими, що дає змогу балці вільно змінювати свою довжину із зміною температури
Опори нумерують зліва направо позначаючи крайню ліву номером 0 номер прольоту визначається номером правої опори, що належить йому.
При обпиранні на т шарнірних опор маємо стільки ж вертикальних реакцій Оскільки умов рівноваги можна скласти тільки дві, то така система (т — 2) разів статично невизначувана
Як видно, кількість зайвих зв'язків, з отже, і зайвих реакцій, дорівнює кількості проміжних опор Іноді крайня опора виконується у вигляді затиснення У цьому разі ступінь статичної невизначува ності збільшується на одиницю порівняно з шарнірною опорою
Рис 418
ніжних опор, замінивши їх дію невідомими реакціями X,, .. »Хт—а, прикладеними до основної системи додатково до заданого на* вантаження (рис 419) Додаткові рівняння переміщень
&! = 0 Д, = 0, ; Дт-2 = 0
виражають умови рівності нулю прогинів у точках прикріплення проміжних опор Однак такий спосіб розрахунку громіздкий, оскільки в кожне рівняння входять усі шукані невідомі зусилля Значно вигідніше будувати основну систему встановленням шарнірів у перерізах над усіма проміжними опорами (рис 420) Зайвими невідомими в цьому разі будуть згинальні моменти в опорних перерізах балки
Отже, еквівалентна система становить ряд простих шарнірно обпертих балок, навантажених заданим навантаженням та невідомими згинальними моментами
М1 = Хг =	.. . Л4п+1=Хп+1 . ,
прикладеними в перерізах де поставлено шарніри Напрямимоментів для певності вибрано додатними При такому виборі основної системи дія заданого навантаження поширюється тільки на той проліт, де воно прикладено вплив Його на інші прольоти визначається опорними згинальними моментами Мі
Складемо тепер додаткові рівняння переміщень Вони виражають рівність нулю переміщень опорних перерізів у напрямах дії невідомих моментів Л4(
Дійсно, кожна двохопорна балка основної системи під дією заданого навантаження та опорних моментів деформується незалежно від інших Це означає, що торці двох суміжних балочок, що примикають до однієї опори, наприклад п ї (рис 421), можуть повернутися на > лд	деякі кути Далі* та Допр Оскільки у вихідній
статично невизначуваній системі кожна пара та 1них перерізів становить один переріз, то з умов суцільності їх взаємний кут повороту має дорів нювати нулю Звідси для кожної проміжної опори
= Дпліа + Дппр = 0	(14 1®)
П	Оскільки основна система складається з окре*
Рис. 421 мих, не зв'язаних між собою двохопорних бало
чок, то для розкриття умови (14 18) слід розглянути лишедва прольоти основної системи, що примикають до п ї опори (рис 422).
Запишемо умову (14 13) у кано нічному вигляді
іХп_і 4*	-}
4- вл-л+іХ/ж 4-	= 0 (14 19)
Для визначення переміщень 8 та Д, що входять у це рівняння, бу дуємо епюри згинальних моментів у основній системі окремо від зада ного навантаження (рис 422, а) та від кожної із зайвих невідомих що дорівнюють одвннці (рис 422,6 г) Площі епюр від заданого навантаження на п та (п4* 1) У прольотах позначимо відповідно через Пп та Пп-н, а відстані центрів ваги цих площ від лівої та правої опор свого прольоту — через ап, Ьп аа+і та 6п+і відповідно
Застосовуючи спосіб Вереідагі на і вважаючи, що вздовж кожного
Рис. 422
прольоту балка має однаковий переріз, знаходимо
4-'=^П"-Й--'	(420)
6лл+і «	2 1 з — 6/7п ,	(14 21)
6т=	^+-£7—-Т-14'в-зЙг+-з^7> <14 22>
бл.л+1 = £/я+і	2-1 Т “ 6££+і 	(1423)
Підставляючи вирази (14 20) (14 23)уформулу (14 19) дістаємо таке рівняння

6 (। ^л-М^л+і \
\	Л»+іС«+1 )
(14 24)
Оскільки при такому виборі основної системи всі зайві невідомі * згинальними моментами в опорних перерізах балки, то в рівнянні (14 24) замістьХ»пншуть Мі Отже,
44.-, і І 2М,('А-+41±Ч+«.+!#±!--
*л	\ ’Л ^л+І /	'|»+І
= -6і'-ТТ!-+ 7Д+'*"~Н )	(14 25)
\ 'п'л	у
Рівняння (14 25) називається рівнянням трьох моментів Складаємо іх стільки, скільки вводимо шарнірів, утворюючи основну систему Щоб написати ні рівняння, досить у формулі (14 25) надати індексу п послідовно значень 1,2,3 і т д , що відповідають номерам проміжних опор Кожне з таких рівнянь містить не більше ніж три невідомих опорних моменти Л4л-і. М„, Мп+і, а перше та останнє рівняння — тільки по два невідомих моменти Розв'язати систему легко методом послі довного виключання невідомих
Для балки постійного поперечного перерізу (7 = сопзі) рівняння трьох моментів спрощується так
Мп—іІп 2Мл (/п	Л»+і) + Л^л+і/л+і =
» - б	1)	<14 26)
Розглянемо приклади складання рівнянь трьох моментів На рис 423 показано двопрольотну балку Це система один раз статично невнзначувана Рівняння трьох моментів слід написати один раз для проміжної опори 1
Поклавши в рівнянні (14 26) п = ), маємо
44.1, + 244,(1, + Ц + 44,1, = - 6	+ -Й&-)	(14 27)
Оскільки крайня ліва опора шарнірна 1 не навантажена зосередженим моментом, то
М„ = 0
Момент на крайній правійопорі дорівнює моменту від навантаження, прикладеного на консолі Отже,
ч—4-
Очевидно,
°і= "з~(4+ ^і = -з"(4 + 4)>
На — Ь» ~’ 2
Отже, рівняння (14 27) набирає вигляду
М1Й + щ._6(^Л±£. + 4)4і,
Звідси легко знайти момент Мі
Якщо лівий кінець балки затиснутий (рис 424, а), то затиснення можна замінити додатковим прольотом нескінченно великої жорсткості або нескінченно малої довжини (рис 424, б) Рівняння трьох моментів для І та 2 ї опор такі*
МЛ + 2Л4, (І, + І,) + М,І, - - 6 (-5ф- + -^1.) ;
М,1, + 2ЛІ, (І, + І,) + М,1, = - 6	.
Очевидно,
Я1 = й, = о, о, = -ді;
а» = Ьв =	; Ма = 0.
Крім того, в першому рівнянні системи слід покласти "0 Тоді гм^ 4- М& = 0,
МД + 2М. ((,+« =-6-^-.
|Д,	Аналогічно робимо, якщо за-
|||дди	тиснутий правий кінець балки.
Ц	Визначивши опорні моменти,
#|,	обчислення реакцій, побудову
г	епюр згинальних моментів та по-
перечних сил виконуємо звичайним способом
Спочатку визначаємо реакції опор кожної простої балочки від заданого навантаження та опорних моментів Позначимо ці реакції для п го прольоту через Ап та Вп (рис 425, а) Очевидно, що



(14 28)
де Вп — реакції тільки від заданого навантаження в прольоті. Повна реакція проміжної опори п (рис 425, б)
Н„ ~В„ +4,+, = я; —-------------------<11~Л<.2+'	(14 29)
‘л	'п+1
Тут Кп = В° 4- Дл+і — ревкція опори л, спричинена дією заданого навантаження, прикладеного в прольотах /в та 4-н
Визначивши реакції, будуємо епюри та М для кожної двохопорної балочки основної системи
Остаточну епюру згинальних моментів легко побудувати також як суму епюр моментів від навантаження та опорних моментів причому остання епюра має вигляд ламаної лінії, що сполучає відрізки, відкладені над опорами і які дорівнюють опорним моментам (див. приклад 68)
Можна рекомендувати такий порядок розрахунку нерозрізної балки Пронумерувавши опори та прольоти (опори — з нуля, прольоти — з одиниці), під вихідною балкою зображують основну систему, навантажену заданим навантаженням та невідомими опорними моментами Далі будують епюри М для окремих балочок основної системи тільки від заданого навантаження в прольотах Обчислюють площі цих епюр та координати а{, Ьі їхніх центрів ваги Для кожної проміжної опори записують рівняння трьох моментів
Розв'язуючи здобуту таким чином систему рівнянь, знаходять невідомі опорні моменти Потім визначають реакції і будують епюри поперечних сил та згинальних моментів Останню епюру, як зазначалося, можна побудувати як суму епюр моментів від навантаження та від опорних моментів
Приклад 68 Побддувмоеіиоразашашшхмоментівтаполеречміиаидмбами, зображеної на рис. 426, а
Для простота обчислень взято у = 2Р‘і Еквівалентну систему показано аа рас. 426, б, причому затиснення лівого кінця балка замінено додатковим прольотом, 410
Рнс 426
О1 = 0,-0,
Складаємо рівняння трьох моментів для трьох проміжних опор (в — 1, 3) З
2Лїг + Мі = — -д- Рі, (в-1),
Аї2-|-4А<І4-А<в--.-|-РІ, (в = 2),	(14 30)
+	+	(л-3).
Очевидно момент Мі дорівнює опорному моменту наванта ження, прикладеного до консолі тобто
Ряс. 427
(НЗІ)
Розв’язуючи систему рів-вянь (14 ЗО) а урахуванням внрвзу (14 ЗІ) дістаємо
Мі^—О.ШРІ Мі = — О.ОЗвР/, Лі,»- 0 053Р/
Від ємні значення моментів свідчать про те що насправді вони спрямовані про*, гнлежно наведеним на рис. 426, б.
Реакції опор (рис. 427) визначаємо за формулами (14 28) та (14 29)
Л, = 0,5Р4-0 ІЗР-0.63Р,
В, = О.йР — 0 іЗР = 0.37Р
= —0.015Р,
М,-Мі
	М.-М. В,*=—	—- = 0,01ЗР ді —	= 0.803Р, в4= V +• “7 * “ 2
Повні реакдІТ опор	« А, = 0.63Р Н, = В, + А, = 0 36Р. = 0.82Р В, = 2,20Р
Епюри поперечних сил та згинальних моментів наведено ва рис. 420, в.
$ 94 Вплив неточного розміщення опор ПО ВИСОТІ
У вже розглянутих прикладах вважалося, що всі опори розташовані на одному рівні На практиці, однак, бувають випадки зміщення опор від проектного рівня
У статично визначуваних системах зміщення опор не спричинюють додаткових зусиль у конструкції Проте в нерозрізних балках внаслі док їхньої статичної невнзначуваності ці зміщення спричинюють значні початкові напруження, котрі як показує розрахунок, залежать від зміщення опор та жорсткості балки, зростаючи прямо пропорційно зазначеним факторам
Нехай (л — 1), н та (л 4- І) а опори дістають зміщення по вертика лі відповідно на уа-\, уп, у»+і (рис 428) Унаслідок цього в основній 412
системі ділянки 1Л та /я+і повернуться иа м„..	м„.,
вороту за годннпнкозою стрілкою	рнс 428
Легко бачити, що таке зміщення спричн нюе взаємний кут повороту торцевих перерізів у п-і опори
д^ = Єп+і— ©я	(14 33)
Отже, канонічне рівняння (14 19) при розрахунку зміщення опор набирає вигляду
бя п~і 4* влдХлбп л+і-^п+і + Дл» = 0	(14 34)
] виражає вимогу рівності нулю взаємного кута повороту торцевих перерізів у п і опори, спричиненого дією всіх зайвих невідомих та зміщенням опор
Підставляючи в рівняння (14 34) значення б зрівнянь (14 21) (14 23) та Дя> з виразу (14 33), при » /„-і =	» сопзі дістаємо
таке рівняння трьох моментів
Мя_^„ 4- 2Ма (/„ + Ь+1) = Л4„+1/п+1	- № (Єя+1 - ©„) (14 35)
Для визначення опорних моментів, що виникають унаслідок вміщення опор, складають та розв'язують рівняння типу (14 35)
Зазначимо що початкові напруження від зміщення опор можуть бути використані для вирівнювання напружень від заданого наванта ження
Приклад 69 Визначимо напруження, що виникають у сталевому валу, встановленому на трьох підшипниках (рис 42$ а) при зміщенні вниз на 2 мм крайнього ярового підшипника Діаметр вала Л = 4 см. Відстань між підшипниками І 50 см.
Рнс 429
Підшипники будемо розглядати як шарнірні опори
Еквівалентну систему показано на рис. 429 б в Оскільки крайні опори шар нірні. тоА<в =ЛІ, = 0 крім того. 0! =0 От же рівняння трьох моментів поклавши в рів нянні (14 35) п = І можна записати в такому вигляді
2МХ2/ = — 6ЕУ0, звідки
* Індекс <з> при \ означає що узагаяь мене переміщення спричинене зміщенням опори
Оскільки
6-^.
Найбільше напружений в перерізі над опорою 1 Мі зел п„ее ба “ "|Г “	“ °>15Е
48 МПа,
§ 95 Розрахунок статично немзначуваних криволінійних стержнів
Статично иевизначувані системи, що містять криволінійні стержні, розраховують за методом сил у такій самій послідовності, як і системи, розглянуті в попередніх параграфах Але в цих випадках переміщення, що входять у канонічні рівняння, не можна обчислювати способом Верещагіна Для цього рекомендується застосовувати метод Мора
Як приклад розглянемо колове кільце постійного поперечного перерізу, що розтягується двома однаковими протилежно спрямованими силами (рис 430, а) Кільце як замкнена система тричі ста тично невизначуване Однак використання симетрії при виборі основної системи істотно спрощує розв’язання
Виберемо основну систему, розрізавши кільце по перерізу Ах (рис 430 б) 3 умов симетрії випливає, шо поперечне зусилля в цьому перерізі X, = 0 Розрізавши кільце на дві частини по осі АіАг (рис 430, а), з умов рівноваги відсіченої частини знаходимо, що осьове зусилля Р/2 Залишається тільки визначити невідомий згинальний момент у перерізі Остаточну еквівалентну систему показано на рис 430 а.
Канонічне рівняння переміщень, що виражає умову рівності нулю взаємного кута повороту граней розрізу, має вигляд
4* Дія = 0
Коефіцієнти цього рівняння визначимо способом Мора, спочатку розглядаючи основну систему під дією заданого навантаження, а по*
а	б	6	г
Рас. 430
тім — під дією зайвого невідомого одиничного моменту (рис 431) Впливом осьо вик та поперечних сил нех туємо Очевидно,
<ії)
Е4
вп
б
Ураховуючи симетрію в	РйСі 43]
станах Р та (основної системи (рис 431, а, б), при обчисленні переміщень Дір та 6и можна оби* житися розглядом однієї чверті кільци Маємо
(оСфС-5-): ЛЇ,= і
Додатний напрям для згинального моменту вибрано таким, при якому зовнішні волокна розтягнуті Отже,
,	/>/?•(!-сояч»аф 2РЦ* /я ,\
Дір=4^ --- --------““БГ’Р’“Т
Тоді

£
Отже, згинальний момент у перерізах А
Мл -= — 0.182Р/?
І спрямований у бік, протилежний вибраному. У довільному перерізі кільця згинальний момент
М (ф) = *^*(1 — созф) — МА = 0,5Р/?(1 — созф) —0.182Р/?
Найбільший згинальний момент діє в перерізах В, при ф •=• я/2, і становить
Мв-0,ЗІ8Р/?
Поперечна сила (ф) = 0,5Р зіп <р, осьова сила N (ф) = 0,5Р соз ф На рис 432 показано епюри внутрішніх силових факторів у перерізах кільця
$ 96 Визначення переміщень у статично невизначуваних системах
Визначивши зайві невідомі зусилля, переміщення в статично невизначуваних системах можна знайти звичайними способами При цьому слід користуватися методами, які в кожному окремому випадку найбільш просто приводять до результату Наприклад прогини та кути повороту перерізів статично невизначуваних балок, що несуть складне навантаження, зручно визначати за методом початкових параметрів Спосіб Мора, що е унікальним, може застосовуватися, звичайно, в усіх випадках Ним широко користуються при визначенні переміщень у балках, рамах, фермах
Обчислюючи переміщення за формулою Мора
у, С	у, с Я^рОа у,г
= Е )—и— + Е ) —ег~ + Е) —ог- • <14 36> слід розглянути задану систему під дією навантаження (остаточні епюри силових факторів Лі, N та р статично невизначуваної системи), а також під дією одиничного силового фактора, що відповідає шуканому □ *реміщенню(однничні епюри Л4<, N1, рі) Якщо при цьому одиничні навантаження прикладати безпосередньо до заданої статично невизна-чуваної системи, то кожен раз для побудови одиничних ешор М(, Рі знову доведеться розв’язувати статично невизначувану задачу Однак цього можна уникнути, якщо врахувати, що вихідна статично невизначувана система 1 основна статично визначувана, навантажена заданими силами та знайденими зайвими невідомими, повністю тотожні за умовами роботи Тому, визначаючи будь-яке переміщення, ми вправі прикладати одиничне навантаження до основної статично невизначуваної системи Остання може бути вибрана за будь яким можливим варіантом.
Як приклад обчислимо взаємні переміщення точок Аіг А, та Віг В, відповідно в горизонтальному та вертикальному напрямах для рами (рис 433, а) Визначимо лише переміщення, спричинені згинанням, оскільки переміщеннями від поздовжніх деформацій та зсуву можна знехтувати На рис 433, б показано складові сумарної епюри згинальних моментів у вигляді, зручному для застосування способу Верещагіна
Для визначення взаємного переміщення а горизонтальному напрямі точок/І!,/^прикладаємо до основної системи в цих точках (рис 433,а) одиничні сили “ 1 Перемножуючи епюри М та і вважаючи, ЩО 4 «а >= /, знаходимо
* А 1 / РІ* І , РІ* І Л РІ* І \ РІ* Дл.-л^Д,»-^-------16"—+ -у--2--2-зГТ)=-б457'
Щоб визначити изаємне вертикальне переміщення точок Вг та Віг прикладаємо до основної системи в цих точках дві одиничні сили X* = 1 (рис 433, г) Перемножуючи епюрн Л4 та Мл, знаходимо, шо
А а * / РІ* І РІ* і п , І* рі п\ 5 РР Дв,-в, =Д*-	16 —— 16 6 2+-5-“іб"2) =“іЗГТу“
Зазначимо, що у разі дії на статично невизначувану систему температури до переміщень основної системи, навантаженої знайденими зайвими невідомими, слід додати суто температурні переміщення При цьому формула (14 36) набере вигляду
+ £р,°—т'~ї-'-<ь <1437>
де Мт, N7, От — внутрішні силові фактори від зайвих невідомих, обумовлених дією температури.
14 9-іпя	> 417
§ 97 Контроль правильності розв'язанні статично невизначуваної системи
Остаточні епюри N. ф та М обов язконо треба перевірити Перевіряють при цьому умови рівноваги та деформацій
Для перевірки умов рівноваги слід вирізати вузол або яку небудь частину системи А переконатися в її рівновазі, тобто у виконанні умов рівності нулю суми проекцій або моментів усіх зовнішніх та внутріш ніх сил, прикладених до цієї частини
2Рж = 0 2Р1,«о. 2М=0
При цьому потрібні величини слід брати безпосередньо з остаточних епюр
Розглянемо, наприклад, як мають бути перевірені умови рівноваги для епюри згинальних моментів, показаної на рис 434 Виріжемо вузли В та С (рнс 436) Дію відкинутих частин рами на вузли заміни мо відповідно згинальними моментами Л4вл Мвс, Мав та Мсв, Мсо Напрями моментів відповідають розміщенню епюр на стиснутих волок нах
З умов рівноваги вузла В випливає що Мвл + Мвв — Мвс =» 0
З умови рівноваги вузла С випливає, що моменти Мса та Мсо повинні бути однаковими за модулем та протилежні за напрямом Аналогічно можна перевірити епюри # та (2
Зазначимо, що перевірка умов рівноваги не є достатньою, оскільки перевірка правильності побудови епюр за зайдепими значеннями зай вих невідомих зусиль не дає підстав для міркування про правильність самих величин
Загальним контролем є перевірка виконання умов нерозривності деформацій При цьому слід переконатися, що остаточні епюри уз годжуються з умовами опорних закріплень та нерозривності контура
Оскільки в заданій статично невизначувакій системі переміщення в напрямі будь якого зайвого зв'язку дорівнює нулю, то добуток оста точної епюри згинальних моментів на епюру моментів якого завгодно
і го стану основної системи повинен дорівнювати нулю, тобто
Рис. 434	Рис 435
Рнс 436
Як основну систему і го стану найкраще вибирати систему, від мінну від взятої прн розрахунку Кількість перевірок умов деформа цій має дорівнювати кількості зайвих зв'язків
Як приклад перевіримо умови деформацій для рами, розглянутої в § 92 (див приклад 66) Остаточну епюру М наведено також на рис. 436, а
Обчислимо взаємні переміщення в горизонтальному напрямі граней розрізу ригеля Для нього слід помножити епюру М на оди ничну епюру Йі (рис 436, б) Прн множенні часто зручно замінити епюру М її складовими
М = МР + Х/ї, Х,М,
Дістанемо
£/4, - З { М.М* - —™ 4 * +	Л _
— 0,021 РК  2Л ~ - РЛ" (— °. 1 04 + 0,125 — 0,021) =
= ££*(—0,125 4-0,125) -0
Тепер перевіримо, чи дорівнює нулю кут повороту перерізу Д вихідної системи 3 цією метою, множачи епюру М на одиничну епюру основної системи (рис 436, в), знаходимо помножений на £/0 кут повороту.
Тут Е-І^ — жорсткість поперечного перерізу якого-небудь елемента рами Оскільки в безшарнірній системі Мл *= 1, то
£М, “ХЇМ-Ц*
Інтеграл у правій частині е площею епюри М, помноженою на відношення Він зветься зведеною площею епюри М.
Отже, для замкнених безшарнірних контурів зведена площа епюри моментів дорівнює нулю, тобто
= 0	(1439)
У нашому прикладі враховуючи, що / =и сопзі, матимемо
Е.?ЬЯ =	+2-^-18^1 -002ІРЙЗ/1) = РЛ> (-0,125 +
п-0,187 -0,063) г- РИ1 (-0,188 +0,187) = — 0,001 Рй'
Оскільки при розрахунку системи зайві невідомі обчислюються з певною точністю, то Й результати перевірки, звичайно, мають деяку похибку — шукані переміщення не дорівнюють нулю Тому при перевірці рекомендується окремо обчислювати суми додатних та від ємних членів Якщо різниця між обома сумами, виражена в про* центах до меншої з них, невелика (до 5 %), то результат розрахунку можна вважати задовільним У нашому прикладі
Аналогічно контролюють правильність розрахунку нерозрізної балки
$ 98 Про розрахунок лросторолих рамних систем
У загальному випадку дії сил иа брус (див гл 12) у поперечних перерізах маємо шість внутрішніх силових факторів (рис 437) — N. Су, Мх, М* та Мя Для нерухомого прикріплення перерізу слід накласти шість зв'язків, зусилля в яких можна знайти з шести рівнянь рівноваги твердого тіла Кількість зв язків у просторових системах, що перевищує зазначену, дає ступінь статичної невизначу* ваяосп Так, просторова рама, зображена на рис 438, а, шість разів статично невизиачувана, оскільки для визначення дванадцяти неві
Рйс. 437	Рис. 438
7777 7т 7777,	7777.
а	б
Рис. 439
домих реакцій можна скласти тільки шість умов рівноваги Один з варіантів основної статично визначуваної системи показано на рис. 438, б Для визначення шести невідомих зусиль розв'я зуємо шість канонічних рівнянь звичайного вигляду (див § 92)
Показана на рис 439, а просторова рама 24 рази статично невизна чувана Це легко виявити за кількістю розрізів, які треба зробити, щоб утзорити основну систему (рис 439, б), причому кожний розріз вивільняє шість зв'язків
У машинобудівних конструкціях застосовуються плоскі рами, що працюють на просторове навантаження На рис 440, а показано плоску раму із затнснутими кінцями, навантажену перпендикулярно до площини рами
На підставі принципу взаємності можна показати, що в плоских системах, навантажених перпендикулярно до площини системи, силові фактори, які характеризують роботу рами в її площині, дорівнюють нулю Отже, з шести невідомих аусиль (рис 440, б) три дорівнюють нулю, тобто Х4 «• Ха = X» = 0
Ця обставина значно спрощує розрахунок плоских рам, наванта жених просторовим навантаженням Будь яке навантаження можна розкласти на складові в площині рами та перпендикулярні до неї Використовуючи принцип незалежності дії сил, можна розрахувати систему окремо від навантажень у площині рами та від перпендвкуляр них до неї
Як приклад розрахуємо раму, показану нарис 440 Шобвикориста ти її симетрію, утворимо основну систему, розрізавши стержень ВС посередині (рис 441) Такий варіант вигідніший, ніж зображений на рис 440, в
З міркувань симетрії основної системи випливає, шя кососиметричні силові фактори в перерізах розрізу (крутний момент X, та поперечна
сила Хд) дорівнюють нулю Невідомий згинальний момент Хі легко 'Найти з канонічного рівняння переміщень
виХ1 +	~ 0
Для визначення переміщень будуємо в основній системі епюри згинальних та крутних моментів
Рис 441	для Р го (рнс 442, а) та одиничного
Л1 = 1 (рнс 442, б) станів Епюри крутних моментів заштриховано штриховими лініями Переміщення обчислюємо за формулами Мора для просторового випадку дії сил, причому нехтуємо впливом осьових та поперечних сил Маємо
+ + <‘4«»
Ураховуючи, що одиничні епюри обмежені прямими лініями, переміщення Дір, бц можемо визначити ва способом Верещагіна Матимемо
і 2____1—
ЕЛ 2 3 2 *	04
Отже,
л„ «Ії ‘ + 6 03ГтУ ,1’
де
Р =
Остаточні епюри згинальних та крутних моментів наведено на рис 443
Глава II. РОЗРАХУНОК ПЛОСКИХ КРИВИХ БРУСІВ
§ 99. Визначення напружень у кривих брусах
У різних конструкціях часто застосовуються бруси з криволіній ною віссю. До них належать вантажопідйомні гаки, кільця ланцюгів, вушкк, обода шківів та коліс, арки тощо Осі цих брусів — плоскі криві Бруси з просторовою кривою віссю застосовуються нечасто і тут не розглядаються
У поперечних перерізах плоского кривого бруса взагалі е три внут рішніх силових фактори — /V, ф та Л4. Правила визначення іх та побудови їхніх епюр для кривих брусів розглянуто в § 23 У § 24 виведено диференціальні залежності (З 13) (3 15) між внутрішніми силовими факторами Й навантаженнями
У цій главі розглянемо визначення напружень та переміщень у кривих брусах, а також розрахунок їх на міцність При цьому об* межнмося розглядом брусів, що мають поздовжню площину симетрії (рис 444), в якій і діють зовнішні навантаження Внаслідок симетрії переміщення точок осі бруса також відбуватимуться в цій площині
Дослідження показують, що при згинанні розподіл нормальних напружень у поперечному перерізі, а також максимальні напруження в кривому брусі істотно відрізняються від тих, які мають місце в балці з прямою віссю За інших однакових умов ця відмінність тим більша, чим більше відношення висоти А поперечного перерізу до радіуса И кривизни його осі (рис 444)
У зз язку з цим розрізняють бруси малої кривизни, в яких МИ < < 1/5, та бруси великої кривизни, в яких МИ 1/5 При згинанні брусів малої кривизни нормальні напруження з достатньою для інженерних розрахунків точністю можна визначати за формулами (10 10), (10 ІЗ), виведеними для балок з прямою віссю Обчислення максимальних напружень за цими формулами для бруса прямокутного перерізу при МИ 1/15 дають різницю 2 % порівняно з напруженнями, визначеними за більш точними формулами, які виводитимуться нижче. При МИ — 1/Ю різниця зросте до 3 5 %, а при МИ — і/5 вона досягне 7 %
Виведення формули для нормальних напружень при згинанні бруса великої кривизни Розглянемо випадок чистого згинання кривого бруса (рис 444) Для прямого стержня ми спочатку вважали невідо мим положення нейтрального шару, а потім з ясували, що він розта шований на рівні осі стержня Тепер також припустимо, що нейтрали ний шар має поки що невідомий радіус кривизни гв, взагалі інший, ніж радіус И осі стержня
Виведемо формулу для напружень а при згинанні за тією самою схемою, яка застосовувалася для бруса з прямою віссю, 1 в його основу покладемо ті самі гіпотези гіпотезу плоских перерізів та гіпотезу про те, що поздовжні волокна не тиснуть одне на одне.
м
Рис. 445
Проведемо в перерізі осі у та г, як показано на рис 444 Вісь г вбігається з нейтральною лінією перерізу, положення іі поки що не визначене Додатним вважаємо напрям осі у до центра кривизни бруса
Для виведення рівнянь статичного аспекту задачі розсічемо кри вий брус на дві частини будь яким поперечним перерізом, наприклад аЬ (рис 444, о), і виділимо в перерізі елемент площі АР завдальшки у від нейтральної лінії (рис 444, б та 445, а) На елемент діє зусилля айР 3 умов(Ю 2) та (10 3) при N •= 0, /И, = М дістанемо
[п(^=0, їауАГ^М	(15 1)
Умова Мк <= £ сгАР = 0 виконується автоматично внаслідок симетрії перерізу відносно осі у
Розглядаючи геометричний аспект задачі, виділимо а кривого бруса (рис 444, а) двома нескінченно близькими перерізами аЬ те сА елементарну ділянку, якій до деформації відповідає кут <йр Після деформації кут між цими перерізами зміниться на деяку величину А (Лр) (рис 445 б) Спостерігаючи деформацію довільного волокна АВ, яке розташоване завдальшки у від нейтрального шару та має до деформації довжину (га — у) Л<р, легко помітити, що внаслідок деформації під навантаженням за рахунок взаємного повороту перерізів аЬ та сА розглядуване волокно подовжується на величину уА (шр) Тоді відносне подовження вибраного довільного волокна, очевидно.
уД (гіф) (Г« — У) *
05 2)
Фізичний аспект, як 1 для балки, якщо знехтувати тиском поздовж* ніх волокон одне на одне, можна виразити формулою Гука о = £е
Підставляючи в цю формулу вираз для е, згідно з формулою (15 2), матимемо
п = £А <4Ф)	У
=	<*ф	- У ’
Цю формулу, очевидно, не можна безпосередньо використати для визначення нормальних напружень при чистому згинанні кривого бруса, оскільки в ній поки що невідомі радіус га нейтрального шару та зміна кута А (йф) Для визначення г„ та А (Лф) скористаємося двома умовами (15 1) 3 першої умови маємо
“!*а_С_й£_=0. З <*ф	3 гв — у
Оскільки в ньому виразі £А (йф)/Лг 0, то
} г" — у
Друга умова відповідно запишеться у вигляді
) *	<*Ф	'.-У
Інтеграл в останньому рівнянні можна записати такі
(15 4)
(15 5)

(156)
Перший інтеграл у правій частині рівняння (15 6) є статичним моментом 5, площі поперечного перерізу відносно нейтральної осі г, тобто Р (—е) (див рис 444, б), а другий інтеграл, згідно з виразом ()5 4), дорівнює нулю Враховуючи це, вираз (15 6) запишемо так.
=	(157)
>
де е — відстань від центра ваги перерізу кривого бруса до нейтральної осі; р — плоіда поперечного перерізу бруса
Очевидно інтеграл у лівій частині виразу (15 7)— завжди величина додатна, а це означає, що статичний момент 5, — величина від’ємна. Оскільки статичний момент дорівнює добутку додатної величини р на координату е центра ваги площ відносно нейтральної осі г, то з
му можна стверджувати, що	Рнс 447
при згинанні кривого бруса нейтральна вісь завжди зміщується від центра ваги перерізу до центра кривизни бруса
Надалі у формулах, що містять е та 5Х, враховуємо їхні абсолютні значення
Підставляючи вираз (15 7) в умову (15 5), дістанемо
ЗВІДКИ .	(158)
аф ег	'
Ураховуючи вираз (15 8), формулу (15 3) для визначення напружень тепер можна записати так
де М — згинальний момент у перерізі, 5Х — статичний момент площі перерізу кривого бруса відносно нейтральної лінії
З аналізу формули (15 9) видно, що, як і в балці з прямою віссю, нормальне напруження по ширині перерізу однакове (не залежить
від 2) 1 змінюється тільки 13 зміною відстані точки від нейтральної лінії По висоті перерізу напруження в правому брусі (рис 446, а) змінюється за гіперболічним законом (рис 446, б) Найбільші за модулем напруження будуть у крайніх точках перерізу, розташованих біля угнутої поверхні бруса
Абсолютні значення напружень у крайніх точках перерізу кривого бруса, згідно з виразом (15 9), обчислюються за формулами
гаг- =	<1510)
де Яі га /?,— відповідно радіуси кривизни внутрішнього та зовнішнього волокон кривого бруса, Л5 та /ц—відстані від нейтральної лінії до цих волокон (див рис 444)
Знаки напружень легко визначити за напрямом згинального моменту в перерізі
Якщо на кривий стержень діє осьова сила N (рис 446, а), то в стержні, крім напруження, спричиненого згинальним моментом і яке ви зиачається за формулою (15 9), діятимуть нормальні напруження
о« - Л^/Р,
евюру яких наведено на рис 446, в
Підсумувавши напруження від згинання та розтягання (склавши ординати епюр напружень рис 446, б, а) знайдемо сумарне напруження в переріз) кривого бруса, епюру якого показано на рис 446, а
Визначення положення нейтральної осі в кривому брусі при чистому згинанні Для визначення напружень у кривому брусі при згинанні за формулами (15 9) та (15 10) треба насамперед обчислити значення ^(відстань від нейтрального шару до центра ваги) або радуіс гв нейтрального шару, оскільки
е = Я~ гя,	(15 11)
де/? — радіус шару, який містить центри ваги перерізів кривого бруса
Покажемо, як визначається положення нейтрального шару на прикладі бруса прямокутного поперечного перерізу заввишки А та завширшки Ь (рис 447) Для цього будемо виходити з рівняння (15 4) ^ТЙГ-0-
Зробимо в цьому рівнянні таку заміну змінних (рис 447) г = га — у, або у = гв — г
Тоді рівняння (15 4) можна переписати так*
( -^=^~ 4? = 0, або ги (	- Е 0 0,
ЗВІДКИ
Ураховуючи, що
??«ьн, ар = ьог,
будемо мети
_ Мі _	3__________А
Мг 1»-^-	2 303Ів-^-
Тут 2 303 — модуль переходу до десяткових логарифмів Скориставшись рядом
(15 12)
(15 13)
дістанемо
У першому наближенні ‘ 'і ‘ \	1+Т(1!Г) )
Друге наближення дає
Користуючись формулою (15 12), аналогічно можна знайти вираз для е при інших формах поперечного перерізу бруса
Приклад 70 Визначимо положення нейтрального шару для двотаврового перерізу (рис. 448).
Ураховуючи позначення на ряс. 448, значення е аля двотаврового перерізу маж на обчислити за формулою
(15 14)

Поклавши тут Ь, й, = 0 або ™ " 0, визначимо ексцентриситет е для таврового перерізу
Положення центра ваги перерізу знайдемо ва формулою
Приклад 71 Визначимо ексцентриситет нейтральнії лінії для тралецізеидного перерізу (рис 449)
Ь, + 6.
Р- 2 дГ~Ь(г)<іг
Положення пентра ваги перерізу визна чається за формулою
яку неважко дістати поділивши статичний момент перерізу відносно основи на площу
Із загальної формули (15 16). поклавши Ь, = 0 або 6, = 0. визначаємо ексцентрясн тег відповідно розташованих трикутних перерізів
Для круглого порожнистого перерізу (рис 450) аналогічно можна знайти
.-о_ /4Д*-<І*+/4Я»-О»
(15 17)
Рис 450
$ 100. Розрахунок на міцність кривих брусів
Якщо при згинанні кривого бруса крім згинального моменту в поперечному перерізі діє А поздовжня сила, то розрахунок на міцність виконують, ураховуючи напруження від обох цих силових факторів Дотичні напруження за дуже малим винятком (тонкостінні перерізи) не спрааляють помітного впливу на міцність, і іх, як правило, не визначають, хоч у разі потреби можна знайти іх наближено за форму лою Журавського
Для стержнів малої кривизни умова міцності має той самий ви гляд, що і для балок
=	(15 18)
Для стержнів великої кривизни на підставі формули (15 9) умова иіц ності запишеться так
=	(15 19)
При цьому треба розглядати перерізи в яких сумарні напруження від згинального моменту та від поздовжньої сили найбільші У цих перерізах небезпечною буде одна з крайніх точок. Для цих точок у формулу (15 19) слід підставити у = або у ~ /ц та відповідно г = або г -= /?»
У проектувальному розрахунку бруса великої кривизни для виз начення розмірів поперечного перерізу можна скористатись умовою міцності при згинанні балки з відповідною формою поперечного пере різу, а потім, дещо збільшивши здобуті розміри, перевірити міцність бруса за умовою (15 19) Якщо брус великої кривизни виготовлений з матеріалу, що має різні допустимі напруження на розтягання та стис кання (деякі чавуни, пластмаси тощо), то умова міцності має викону ватися для крайніх точок як у розтягнутій, так і у стиснутій зонах
Рис. 451
(<ц.) — —5—МПа — 18 МПа; (а□ - -у- МПа - ЗО МПа;
для волокніту
МПа — 10 МПа, (а_1 МПа = 40 МПа.
Перейдемо до назначений зусиль та моментів Розглянемо довільний переріз, проведений під кутом <р до горизонталі. Точка О — центр ваги цього перерізу — лежить ш осьовій дузі кільця, радіус яко/
Рівнодійна навантаження праворуч від перерізу
Р — рЬ • 2Я, аіп (ф/2)
Обчислюючи момент сили відносно точки О і проекцію»™ силу на дотичну до дуги в цій точці, дістанемо
Лі (ф) — РР зіп (ф/2) =рЬРгР (1 — соз ф);
N (Ф) — — Раїп (ф/2) — — р6К*(і — созф)
Згинальний момент та осьова сила досягають найбільшого значення в перерізі АВ, де кут ф — я, причому
Мац, - ІрЬР^Р - 2р • 0,8 • 3 • 2 • ІО-® - 9,6 . 10“*р МН • м.
ЛГт„- — р 0,8 3 - 2 10-* = — 4 8 • 10~*р МН
Висота перерізу й	= (3—1) см — 2 см та Л/Д = 1 > 1/5, тому слід
користуватися умовою міцності для кривого Сруса Оскільки осьова сила в небезпечному перерізі АВ стисяальва а матеріал кільця крихкий застосовуємо умову міц кості (15 !9) до двох імовірних небезпечних точок — А ти В.
Радіус нейтрального шару при чистому згинанні знаходимо м формулою (15 13)
й ----------~г~ 2 303 І, ' + ™ .
1—"2Я'
'	2 1,6- “ 2.303 20.<77	“
2,30318
Ексцентриситет нейтральної лінії при чистому згинанні
в =» Я — гл =» (2 — і ,82) см — 0,18 см Площа перерізу
Р — М — 0 «. 2 см» — 1,6 см» Статичний момент перерізу відносно нейтральної лінії 5 = ^-1,6 0,18 см» — 0 288 см» Відстань від нейтральної лінії та від центра кривизни для точки А ул == г, — /?, ™ (1 82 — І) см ™ 0 82 см гл =»	™ 1 см,
для точки В
ув— И, — гл —> (3— 1,82) см-1,18 см, гв =а Ц* — 3 см. Тоді
N„,1	~ 9 6 10~*р • 0 82 10“’ _
°л “ ВПі Р “	0,288 10-* І 10“3
-	----П.іц-Зр.------30,<р мп.,
ЧвмУа Урив 9,6 10“*р«1,18 10~~* __ °в “	Р “ 0,288.10-* • 3.10“’
—Рц—10^” ™ ІЗ.Ір —Зр = Ю Ір МПа
Крім того, пря г “ га
0 ™ 0 та а - Я^Р - — Зр
За цими даними для наочності на рнс. 451 побудовано етору <т
Тепер запишемо умом міцності й визначимо допустиме значення р у випадку вініпласту для точки А
30,4р < ЗО та р < 0,99 МПа, для точки В
10,ір< 18 та р< 1,78 МПа
у випадку волокніту для точки А
30,4р<40 та р< 1,32 МПа, для точки В
10,1р < 10 та р < 0 99 МПа.
Отже якщо кільце виготовлене з вініпласту, то рят ™ 0,99 МПа І небезпечною е точкаД якщо ж воно волокнітове, то рдоп 0,99 МІа І небезпечною е точна В, Отже незважаючи на помітну різницю в механічних характеристиках вініпласту та волокніту, рлм в обох нападках однакове й дорівнює приблизно 1,0 МПа
| 101. Визначення переміщень у кривих стержнях
Визначати переміщення в кривих стержнях необхідно для перевірки їхньої жорсткості, а також при розв'язанні статично невизначуваних задач Як у випадку стержнів малої, так і великої кривизни для ви значення переміщень зручно скористатися методом Мора У стержнях малої кривизни можна знехтувати поздовжніми деформаціями А де формаціями зсуву Тоді для плоского згинання формула Мора буде мати такий самий вигляд що і для балок:
(15 20)
У випадку плоского згинання бруса великої кривизни деформація елемента від дії зусиль Мр та М? (рнс 452, а, б) також складається з подовження А (4з) відрізка 45 осі й відносного повороту 46 перерізів, що обмежують елемент Взаємний кут повороту перерізів, спричинений згинальними моментами, як випливає з виразу (15 8),
ал	МрЛз
==	= -Щ?
Кут повороту перерізів, спричинений осьовими силами Мр, що виникає внаслідок неоднакової довжини волокон елемента (рис 452, б).
Рве. 452	Рнс. 453
Подовження осьового елемента, спричинене поворотом перерізів на кут гіві, ...	МрЛа Мр4і
Д (<&),=
Подовження осьового елемента внаслідок дії осьових сил
Повне подовження осьового волокна
д(<&) =д(<ь), +Д(<&), = тИг + тг"- <1522>
Підстааляючи формули (15 21) та (15 22) у вираз (13 44), знаходимо загальну формулу для визначення переміщень бруса великої кривизни
. V ГІ м.мр .. Я.Мр + ЛЇ.Л'р И.Ир .	.1
д- 2) №-*+ 1 дга.1 * + тг^ + т4]
(15 23)
Як звичайно, впливом поперечної сили нехтують Тоді останній
доданок у формулі (15 23) відкидається
Як приклад обчислимо кут повороту вільного кінця бруса великої кривизни, виконаного у вигляді чверті кільця постійного перерізу (рис. 453 а) Допоміжний стан показано на рнс 453, б
У довільному перерізі, що визначається полярним кутом <р, внут рішні силові фактори для дійсного та допоміжного станів такі
Мр =/’/?5ІПф, Мр = — РзіОф, фр=і°СО5ф,
М, = 1, ЛГ1 = О С1=0
Згідао з формулою (15 23), шукане переміщення
’У* ІЛіМрЛ^ ’р3 їїіНр/Му ] ’р3
Д*'=] -^+5 •—£>	Р/?8ІПЯ>^-
0	о	и
-ТЯгГрапфа,--^—(1524)
Як уже було показано (див § 99), для кривого бруса прямокутного поперечного перерізу в першому наближенні можна взяти е т Л*/12/?, Тоді с ь** і
5 — Га ~ [2Л — д
і формула (15 24) набирає вигляду
Д1'’=-їг(|-тг)
Для бруса малої кривизни, згідно з формулою (13 46), шукане переміщення
(18ад
Глава 16 РОЗРАХУНОК ТОВСТОСТІННИХ ЦИЛІНДРІВ І ОБЕРТОВИХ ДИСКІВ
§ 402. Товстостінний циліндр, що зазнав дН внутрішнього 1 ЗОВНІШНЬОГО тисків
Циліндр слід вважати товстостінним якщо товщина його стінки більша за одну десяту середнього радіуса циліндра
При розрахунку тонкостінних циліндрів припускається, що в тангенціальному (коловому) напрямі напруження постійні по товщині стінки, а в радіальному — їх взагалі немає Ці припущення неприйнят ні для товстостінних циліндрів
Розглянемо циліндр з внутрішнім радіусом Г| і зовнішнім Г1( що зазнає дії внутрішнього тиску />, та зовнішнього р% (рис 454) Внаслідок осьової симетрії циліндра та навантажень напруження і де* формації також симетричні відносна йога осі
Двома перерізами, перпендикулярними до осі циліндра і розташованими один від одного на відстані, що дорівнює одиниці, виріжемо кільце (рис 454) У цьому кільці виділимо елемент аЬсЛ двома площи нами, що проходять крізь вісь циліндра і утворюють між собою кут (рис 455, а), та двома сліввісними циліндричними поверхнями з радіусами г та г + & (рис 455, б) Нормальні напруження на цилінд ричній поверхні елемента радіусом г (радіальні напруження) позначи мо через а„ на радіусі г + дг напруження дістануть приросту і дорівнюватимуть а, + Лх, Нормальні напруження на плоских 2г гранях (тангенціальні, або колові, напруження) позна-
Рис. 454
чимо через Ое
Показані на рис 455, б напрями напружевь вважа* ються додатними і відповідають розтяганню елемента у двох взаємно перпендикулярних напрямах
Унаслідок осьової симетрії циліндра та навантажень елемент не буде перекошуватись, і дотичних напружень на його гранях немає Тому нормальні напруження о>та ов будуть головними напруженнями
Статичний аспект задачі Множачи напруження на площі гоаней, знайдемо зусилля, що діють на елемент (рис 455, в) а,п!В— на внутрішній циліндричній грань (<т, + <іаг) (г +йг)ііВ — на зовнішній циліндричній грані, а&іг — на бічних гранях
Рнс 455
Оскільки всі сили лежать в одній площині й перетинаються в од ній точці то для рівноваги елемента сума їхніх проекцій на дві вза ємно перпендикулярні осі повинна дорівнювати нулю Вісь х спрямує мо в напрямі бісектриси кута 46, а вісь у — перпендикулярно до неї Умовами рівноваги будуть
2Х=0, 2У = 0
Завдяки симетрії елемента друга умова задовольняється тотожно, а перша після підставлення виразів для зусиль має такий вигляд
2Х = — а/46 + (о, + (іо,) (г Ь дг) 46 — 2 (<3е& зіп (46/2)) = 0
Розкривши дужки дістанемо
— 0^46 + о/46 -и 40^46 і- о,дг(і9 і- 4о,4г4в — Іо^сіг зіп (46/2) = 0
У цьому рівнянні взаємно знищуються члени ±о,г46 Унаслідок малості кута 46/2 вважаємо, що зіп (40/2) - 46/2 Відкидаємо член вищого порядку малості <1а^іг(і9 і ділимо решту членів на 4г40 Після цього матимемо
г-^+о,-а«-0	(16 1)
Рівняння (16 1) містить два невідомих напруження о, та ое Для визначення їх, дотримуючись загального плану розв'язання статично невизначуваних задач, розглянемо ще геометричний та фізичний аспек ти задачі
Геометричний аспект задачі Деформація елемента симетрична відносно осі й тому спричинює радіальні переміщення всіх точок ци ліндра (рис 455, г) Позначимо радіальне переміщення циліндричної поверхні радіусом г через и, тоді переміщення циліндричної поверхні радіусом г + 4г буде и + (іи Абсолютне радіальне подовження елемента 4г дорівнюватиме 4и, а відносне подоаження
£	(16 2)
Відносне подовження в тангенціальному (коловому) напрямі і а радіусі г знайдемо таким чином. Довжина елемента по колу цнліндрич мої поверхні радіусом г після його приросту на величину и дорівнює
(г + и) йв Віднімаючи з останньої довжини початкову гдВ дістанемо абсолютний приріст довжини елемента на радіусі г у коловому на* прямі
(г 4- и) дВ — гйВ = ийВ
Поділивши абсолютне подовження на початкову довжину гйВ, знайдемо колове відносне подовження
ее = и/г	(16 3)
Фізичний аспект задачі При двосторонньому розтяганні, якого зазнає розглядуваний елемент, згідно Із законом Гука, напруження та деформації пов'язані між собою такими залежностями
о< -	(«Г + нее): - !£,,* («в + (•«,)
Ураховуючи формули (16 2) та (16 3), знайдемо
Підстааляючи вирази (16 4) у рівняння (16 1), для визначення переміщення и дістанемо лінійне диференціальне рівняння другого порядку із змінними коефіцієнтами (рівняння Ейлера)
-ЗД-+7-Т7—
Записавши це рівняння у вигляді
та інтегруючи його по г послідовно двічі, знайдемо загальний розв'я зок рівняння
и=>Аг+В-	(166)
Підставляючи розв’язок (16 6) у формули (16 4), дістанемо ви рази для напружень у точках завдальшки г від осі циліндра
а, “Т—гр1 _|*)Л-_ЧгЕв]’	(167)
°«= і1ц. [(І-Н)л+-Цід-в]	(168)
Сталі інтегрування А та В знаходимо з умов для а, на внутрішній та зовнішній поверхнях циліндра На внутрішній поверхні (/ = ці напруження дорівнюють внутрішньому тиску, тобто аг = —рь а на зовнішній поверхні (г = г«) — зовнішньому тиску, а, = —р* 438
Для визначення сталих А та В, згідно з рівнянням (16 7). виведемо два таких рівняння
-Л"-Г^г[(1+^-7Ьв|.
Розв'язуючи ці рівняння відносно А та В, знайдемо, що
„ і — н *?Р1 — /Ір«
Є	'
1 + н —л) Е
Підставляючи значення сталих у вирази (16 6), (16 7) та (16 8), дістанемо формули для визначення радіального переміщення та напру* жень (формули Ламе)
і — ц	і + р (Рі - Рі> і
£	т	г’
- 'іР» <Рі ~ Р|) І
О' '*
— 4рі ІЇз (Р1 - Рі>
(16 9)
(16 10)
(1611)
Склавши ліві та праві частини виразів для а, та ое, переконає мося в тому що сума радіального та колового напружень — величина стала
а, + аи = соті
Відносна деформація розглядуваного кільця в напрямі, паралель йому осі циліндра, також стала на будь якому радіусі, тобто
є, =-----(сг + о») = соп&і
На підставі цього циліндр можна розглядати як складений з окремих кілець, нанизаних на вісь Поперечні перерізи циліндра при деформа ції залишаються плоскими
Якщо циліндр крім радіальних тисків сприймає ще й поздовжню силу N (наприклад, коли е днища), в його поперечних перерізах ви никає напруження
«(4 —
(16 12)
а до виразу (16 9) для радіальних переміщень додається доданок Д0 = _р-^-г	(16 13)
Напруження о, та ое при цьому не змінюються.
Зазначимо, що всі наведені формули для деформацій та напружень о,, ое та а, справедливі для перерізів, досить віддалених від днищ. Поблизу закритих торців циліндра деформації та напруження дещо змінюються внаслідок впливу днищ
Розглянемо два окремих випадки навантажування циліндра
1	Циліндр навантажений тільки внутрішнім тиском, а зовнішнього тиску немає або він малий і тому ним можна знехтувати, тобто рі = р, р9 = 0 Формули (16 9)	(16 11) для напружень та
радіального переміщення набирають такого вигляду.
(16 14)
(16 15)
н 
(16 16)
Е ’І-'л Г+~Е ^,-ґі
Напруження а, скрізь стискальні, а а® — розтягальні Найбільші значення а, та о« будуть біля внутрішньої поверхні циліндра (прн
(16 17)
де
к = гі/г, Радіальне переміщення біля внутрішньої поверхні циліндра =-^(-ґ^- + н)р	(16 18)
Напруження та переміщення біля зовнішньої поверхні циліндра
такії
26-
(аг),_,,« 0, (ов),
(16 19)
р	(16 20)
Епюри напружень ог та ве для розглядуваного випадку при від ношенні к «= г/г, = 0,5 наведено на рнс 456, а Напруження змінюються за гіперболічним законом Найбільш небезпечною з догляду
міцності е точка, що лежить біля внут рішньої поверхні циліндра
Визначимо допустимий внутрішній тиск у циліндрі при безмежному збіль* шенні товщини стінки Поклавши г»-* <® та взявши у формулах (16 17) А =» 0, ма ТИМЄМО (□,),_, = —р (Ое),_, = Р
Використаємо наприклад, третю теорію міцності
о««» іп = 0і — о«С[о) У розглядуваному випадку о, = (ое),«е, = р та О| = (о,)г-л, = — р, і ця умова міцності набирає вигляду
Рис 456
звідки
Циліндр з дуже товстою стінкою не допускає внутрішнього тиску, більшого за певне значення Отже, збільшення товщини стінки цн ліндра не завжди е ефективним способом підвищення міцності
2	Циліндр навантажений тільки зовнішнім тиском рів р, />х = 0 У цьому разі формули (16 10) та (16 11) для напружень та формула (16.9) для переміщень набирають такого вигляду
—ч^-(’		(16 2і)
А /.		(16 22)
	+->)"•	
„ = ——г- Е 4“^	] —ц ’3і'&	1 Б 'З-'І '	(16 23)
Обидва напруження стискальні, причому за абсолютним значенням Ое > 0г> & радіальне переміщення спрямоване до осі циліндра (ра* діуси зменшуються)
Біля внутрішньої поверхні циліндра (г = гО
(а,)„.-0. (»«),-,, = - -іТГр-Л	(16 24)
.	Гі 2
---------
Біля зовнішньої поверхні циліндра (г = (От)г-г, = — р, (Ое)г-г, =---------------1 р>


(16 25)
(1626)
(16 27)
Епюри напружень а, та а» при к » г,/г, = 0.5 наведено на рнс 455, б Найбільшого значення напруження оте досягає біля внутрішньої поверхні циліндра Як і у випадку внутрішнього тиску* найнєбезпечнішою є точка біля внутрішньої поверхні циліндра
Зменшення зовнішнього радіуса суцільного циліндра (без внутріш* нього отвору) дістанемо поклавши у формулі (16 23) гх = 0 та г = г,. Тоді
(16 28)
$ 103 Розрахунок складених циліндрів
Міцність циліндра, що зазнає дії внутрішнього тиску, із збільшен ням товщини стінки зростає тільки до певної границі Вище було показано що навіть прн нескінченно великому зовнішньому радіусі внутрішній тиск у циліндрі не може перевищувати певного значення Виходячи з розрахунку на міцність за допустимими напруженнями А скориставшись третьою теорією міцності, ми прийшли до висновку, що ні при якому збільшенні товщини стінки циліндра його не можна виготовити на тиск, більший ніж р == ІоР2 Пояснюється це тим, що із збільшенням радіуса напруження ог та ое швидко зменшуються, і матеріал зовнішніх шарів циліндра працює малоефективно
Розподіл напружень можна поліпшити, розвантаживши внутрішні шари за рахунок більш інтенсивного використання зовнішніх Для цього треба зробити циііндр складеним надягнувши один циліндр на інший з натягом (як правило за допомогою гарячої посадки) У таких циліндрах допустимий внутрішній тиск може бути значно більшим ніж у суцільному циліндрі Так само виготовляють гарматні стволи
Прн насадженні одного циліндра на інший з натягом колові на пружекня се у внутрішньому циліндр) стають стискальними, а в зов нішньому — розгинальними (рнс 457 а) Якщо такий складений цн ліндр піддати внутрішньому тиску, то в ньому виникнуть додаткові розтягальні колові та стискальні радіальні напруження (рис. 457 б) Ці напруження визначаються за формулами (!6 14) та (16 15) як для
а	б	б
Рас. 457
суцільного циліндра Колові напруження від внутрішнього тиску будуть додаватися до напружень від посадки в зовнішньому циліндрі та відніматися від них у внутріш ньому циліндрі Радіальні напру ження від внутрішнього тиску та від тиску посадки додаються в обох ци ліндрах Сумарні епюри напружень після прикладання тнскубудуть ма тк вигляд як на рис 457, в Харак
терпим для них е стрибок на епюрі еге та перелом у епюрі о, на радіусі контакту циліндрів
Розглянемо розрахунок складених циліндрів Перш за все зна йдемо залежність тиску рв по контактній поверхні від натягу 6 — різ ниці між зовнішнім діаметром внутрішнього циліндра І та внутрішнім діаметром зовнішнього циліндра // (рис 456)
Оскільки після насадження одного циліндра на інший зовнішній радіус внутрішнього циліндра та внутрішній радіус зовнішнього ста ють однаковими то очевидно, то сума абсолютних значень радіальних переміщень обох циліндрів на радіусі поверхні контакту, слрн чинених контактним тиском, має дорівнювати половині натягу, тобто

(16 29)
Натяг б дуже малий порівняно з розмірами радіуса поверхні контакту, тому прн обчисленні переміщень будемо вважати, що гл = = Лп ® '’е (рис 458)
Позначимо через = ^/г, відношення внутрішнього радіуса циліндра до радіуса поверхні контакту, а через •» гв/г$ — відношення радіуса поверхні контакту до зовнішнього радіуса циліндра
Хоч здебільшого частини складених циліндрів виготовляють з одного матеріалу, будемо для спільності при розв'язанні задачі спочатку вважати ці матеріали різними
Контактний тиск р„ буде зовнішнім для внутрішнього циліндра та внутрішнім для зовнішнього циліндра Абсолютне значення раді ального переміщення внутрішнього циліндра на контактній поверхні знайдемо за формулою (16 27)
, / 1-х*?	\
<16 30)
в зовнішнього — за формулою (16 18)
(16 31)
Підставляючи значення цих переміщень у рівняння (16 29), будемо мати
, / І + *?	\	,71—4»	\	.
тг ~ ’ьр +	'• = т
Розв'язуючи рівняння відносно рс, дістанемо
л=—гггз——т—г-	<1&32>
, І * +*> І 7е / 5 “ *2	1
При однакових матеріалах спряжуваних циліндрів остання формула спрощується і набирає вигляду
„ - ЄЕ а-*?»и
^(Г-4>> + (І + ^(і_і;і • <1ЬЗЗ>
Напруження, спричинені тиском ре обчислюють за формулами (16 21) (16 22) ддя внутрішнього циліндра та за формулами (16 14), (16 15) для зовнішнього
Зазначимо таке Натяг визначають, вимірюючи діаметри спряжуваних деталей мікрометричними інструментами або іншими точними приладами Поверхні ж деталей ніколи не бувають абсолютно гладень кими на них завжди е сліди обробки — так звані гребінці, які зми маються при запресовуванні Внаслідок цього дійсний натяг дещо менший за виміряний, а дійсний контактний тиск менший ніж ви значений за формулою (16 32) або (16 33)
Крім цього треба мати на увазі, що формули (16 32) та (16 33) справедливі лише тоді, коли в жодній із спряжуваних деталей напру ження не перевищують границі пропорційності При появі ж пластичних деформацій контактний тиск буде менший ніж той, що визначається за цими формулами Знайти його можна методами теорії пластичності
$ 104. Температурні напруженні  товстостінних циліндрах
Якщо товстостінний циліндр нагрівається нерівномірно, то в ньому з’являються температурні напруження які додаються до напружень, спричинених тиском
Часто температурне поле симетричне відносно осі циліндра і постійне по його довжині За цієї умови також можна вважати, що поперечні перерізи, які лежать на достатній відстані від кінців циліндра, залишаються плоскими і деформація є, постійна
Для розв'язання температурної задачі можна скористатися тим самим методом, який було застосовано ори розрахунку циліндра на дію внутрішнього та зовнішнього тисків При цьому рівняння рівноваги
(16 1) не зміниться Геометричні співвідношення (16 2) та (16 3) також збережуться Дещо іншими будуть фізичні залежності
Позначимо через Т підвищення температури, яке залежить від радіуса г, а через а — температурний коефіцієнт лінійного розши * рення
Скористаємось узагальненим законом Гука, додавши до деформацій, обумовлених напруженнями, температурні розширення Тоді для е„ ее дістанемо такі -формули 1
є, =	(о, —	— рве) + аГ = сопзі,
в, = -^-(стг —— [Мві+аТ,	(1634)
вє = 4-(ое— ра,— ра,) + «7*
Розв'язуючи ці рівняння відносно напружень, знайдемо, що ”, “ (і+^п-гії) 1(1 — И)В. + |*е, + реє — (1 + и)аТ].
(і+и)11-4йі |(1~ц)ь +(“»+ (“-І* + Й“Л. (1635>
№ “	((> - Й «е + НЬ + Н». - (1 + Й «Л
Виражаючи в цих формулах деформації через переміщенням
а потім підставляючи добуті значення для о, та в’є в рівняння рівноваги (16 1)
^+а,-а. = 0.
дістанемо таке диференціальне рівняння для переміщення ці <Ри , І аи и 1-рр „ ІГ	/іс-иа
-зтг+—-зг—т—ї^га~гг-	<163®
З цього рівняння можна визначити переміщення, якщо відомий закон зміни температури Т (г) по товщині стінки циліндра
Останнє рівняння запишемо у вигляді
1 Модуль пружності Е залежить від температура. Тут не не вріхоаано, що долу сіймо якщо різним температур внутрішньої та зовнішньої поверхонь оиліадра не-велика У ньому разі модуль £ слід Орт тмам, Що дорівшое його знечеия» при середній температурі стінки кнліндра
Інтегруючи це рівняння двічі по г, знайдемо загальний розв’язок'
и = -^--і^-\аТп1г +АГ + Л-	(16 37)
Сталі А та В визначаються з умов для ог на внутрішній та зовніш ній поверхнях циліндра Оскільки ці поверхні вільні від навантаження, то
(о,),-,. = 0 і (о,},-,, = 0
Підставляючи у вираз (І6 35) для ог деформації е, = АиІАг та ее = и/г, а потім здобутий розв язок (16 37) для и, будемо мати
2_(аТл* + -гА------Ї- + Т-А-
г* )	' І — 2ц г* ‘ 1 — 2р
(16 38)
Прирівнюючи цей вираз до нуля при г = г„ г = г1( матимемо два рів* няння для визначення А та В розв'язуючи які, знайдемо, що
Підставивши ці значення у формули (16 35) визначимо
О, - -г^г[ —З-1!аГп1г • <і639> ое-гї—+ —; (1640)
а, = т^г[ ^ТШг + (1-Іі)в,-аТ	(1641)
В останньому виразі невідома величина вг Якщо циліндр має змогу вільно розширюватися, то є, знаходять 8 умови, що поздовжня скла в поперечному перерізі дорівнює нулю, тобто
ІЯ г,
N = | | о/4/тйр = 0,
або
| а/Аг = 0. л
(16 42)
(16 43)
Підставляючи сюди значення о, з виразу (16 41), знайдемо:
е, = --^аТгіІг.	(16 44)
Остаточний вираз для о, такий
с.=-Т^Г^-^Ьгїа7'г*-“7')	<1645>
Обчислити інтеграл $аТпіг та визначити напруження можна, якщо відомий закон зміни температури Т (г) по товщині стінки ци ліндра.
Найбільш простим та часто застосовуваним у технічних розрахунках законом зміни температури е лінійний закон Нехай Т* = = Ті — Тл означає перевищення температури внутрішньої поверхні циліндра над температурою зовнішньої поверхні Тоді лінійний закон зміни температури по радіусу циліндра виразиться формулою
Т(г) = Т*	(16 46)
Підставивши цей вираз у формули (16 39), (16 40), (16 45) для напружень та виконавши інтегрування, дістанемо
ог 8=
а» =
£«Т* 3(1 —р) (г,-п)
ЕаТ*
За-рН'і-П)
_ ЕаТ* Г -	М-/?) 1
1	і*-,*	]’
Біля внутрішньої поверхні циліндра (при г = гД (0^=0.
ЕаТ' їа, гі’ї-’і 1 (= з<і—ми,—гі) [Зг>-----------]•
Біля зовнішньої поверхні циліндра (при г =
(16 47)
(16 48)
(16 49)
(16 50)
(16 51)
(о,),^,=0, ЕаТ* Го — 1
(Пв)г-Л. = (<гА-г. = ї(і.ц)к,_Гі) |.3г.	^5-] •
Епюри розподілу напружень по товщині стінки циліндра з відношенням А = г\/Гі — 0,5 при у = 0,3 наведено на рис 459, а
/-ч	Іноді припускають, що в тов-
ґ \ у' \ стостіиних цвліндрах температура К \< хОИЯятХ. змінюється за логарифмічним зако-\ Ч /Тгабпгит* \ &. иом' яки® встановлюється теорією
•—	ка кТ/уЦ теплопередачі
\ (1в52)
’ч /	\ / Підставивши цей вираз у формули
а	б (16 39), (16 40), (16 45) та виконав
Рнс. 459	ши інтегрування, матимемо
	»7Г-Х^>'[1п-^ +	(1 -4)"-V •<І353) » =-----------------------------------[1 - ]"~Г—-(" + 4)1”-*- . (1««)
2(,ЛНМ^.)	<‘655І
Біля внутрішньої поверхні циліндра (а''7’=0;	, <іби>
(°в)'-' =	= 2|| - ц)	1	ІП ~ ’
Біля зовнішньої поверхні (ог)п-г,= 0;
(О8),«, =	= 2(| _М	1 ~
Епюри розподілу напружень по товщині стінки циліндра з відно* шенням « * Гі/г» ~ 0,5 при ц = 0,3 у разі зміни температури за ло* гарифмічним законом наведено на рис 459, б
Зазначимо, що поблизу торців циліндра напруження, які визначаються виведеними формулами, можуть мати місце лише тоді, коли торці будуть навантажені поверхневим навантаженням, що змінюється відповідно до формули для ог
$105 Приклади розрахунку товстостінних циліндрів
1. Товстостінний циліндр зазнає дії внутрішнього тиску рі = = 100 МПа та зовнішнього р, = 60 МПа Дослідимо, як будуть змінюватися напруження ок та Ов із зміною товщини стінки циліндра, що характеризується відношенням внутрішнього радіуса до зовніш нього к = г/г,
Напруження визначаються за формулами (16 10) та (16 11), які в цьому разі зручніше записати, ввівши відношення к = Гі/г»
°е- ‘’Г-"/' +-7^-4-	(І6 59)
При зміні товщини стінки циліндра напруження аг залишається стискальним і плавно змінюється за гіперболічним законом від значення —р) біля внутрішньої поверхні до значення —р( біля зовніш ньоі (рис 460 а)
Для обчислення напружень ае біля внутрішньої поверхні циліндра (г — /,) та біля зовнішньої (г = формулу (16 59) можна записати відповідно так
- ,2,. 1(1 + **) Рі — 2ра.
(те),.,, = -(2^,-12*4 - (1 + *2)Р.)
Підставляючи сюди різні значення к, можемо обчислити напруження ое біля внутрішньої та зовнішньої поверхонь циліндра при заданих значеннях р) та р.
На рис. 460, б .е показано епюрн Ое при значеннях к = 0,707, 0,655; 0,578 0,446 0,354
2 Сталева труба з внутрішнім діаметром 2<і = 40 мм зазнає дії внутрішнього тиску р = 250 МПа Визначимо товщину £ стінки труби за четвертою теорією міцності, якщо допустиме напруження для сталі [о] - 500 МПа
Небезпечними є точки труби біля внутрішньої поверхні, де головні напруження такі
4 -і 4 і + *« °і ”	= ,2_~Р = Ттр-Л
а,= а,»0. », = <,,»-/>	<1660)
Умова міцності за четвертою теорією

після підставляння напружень з формул (16 60) набирає вигляду
Оек.ІУ =	ОеОг І-О? <|о]
або	_________________________
/"/ 1 + Л* V 1 4- к* аеИ!У=1/ ( у2.-р-р) + і-ігР*+Р
ЗВІДКИ (Іо)’ _ р>) к* - 2 |а)‘ 4’ - (ІО)* - Зр’) =- 0
(16 61)
(16 62)
Розв язуючи відносно к*, маємо
Оскільки к* < 1, то перед коренем слід взяти знак «мінус* Тоді
Товщина стінки труби 5 — (55 — 20) мм = 35 мм
З Знайдемо оптимальний тиск ре натягу складеного циліндра з умови рівноміціюсті внутрішнього та зовнішнього циліндрів та допусти мий внутрішній тиск р{ Дано г1 = 40 мм, гЛ = 110 мм гс — 80 мм, [а] = 600 МПа Розрахунок виконаємо за четвертою теорією міц кості
Напруження у внутрішньому циліндрі будуть найбільшими при г = <! і такими за формулами (16 14). (16 15) та (16 24).
(СТеі)г«г,
(Огі)г_г, = — Рі, г%4- й	2г?
Рі ~ Ра = 1.31 Рі - 2,67рв
(16 63)
У зовнішньому циліндрі напруження будуть найбільшими при г = гв і такими за формулами (16 14), (16 15), (16 17)
и (	4 \
І |)'-'С =	І 1----— І Рі — Ра = — о, 136р| — ре,
(аеи)г-,с =	1 + рі + Ра = °.44Р1 + 3|25р«
Умова рівноміцності за четвертою теорією має вигляд
V (Оеі)8 — (Ові) (Од) + (в,і)а = /(О«ц)2~ (ОЖ1)(ОНІ) КОД])1
Підставивши вирази напружень череї тиски, звільнившись від радикалів та звівши подібні члени, лісгаїкмо
3,74рї~ 13,62р,рс — Т.ЖрІ = 0
Розв'язавши це рівняння відносно рс знайдемо, що
р1 = 4,12ре	(16 64)
Оптимальний тиск рй визначається умовою міцності / (Ові)* — (оеі) (ви) + (М1 = І°І
Використовуючи формули (іб 63) для а,і та ові та залежність (16 64), матимемо
(1,31 4,12 - 2,67)» р2 4- (1,31 • 4,12-2,67) р2 4- 4,12*р2 = |о),
звідки знаходимо, що ра — 114,5 МПа
Допустимий внутрішній тиск
Рі =-4,12рв = 4,12  П4,5 МПа = 472 МПа
4 Сталева труба з внутрішнім діаметром 2гг =? 4 см та зовнішнім 2г, = 8 см нагрівається так, що температура внутрішньої поверхні Т,“ 300вС, а зовнішньої 7^ = 200X3 Визначиш температурні напруження в трубі, вважаючи, іцо по товщині стінки температура змінюється за лінійним законом Прн розрахунку візьмемо Е = 2 х х 10і МПа, р — 0 3 а = 125 10_? Перевищення температури внут* рішньої поверхні над зовнішньою Т* = Тх—Тл » 100 °С.
За формулою (16 60) знаходимо колове та осьове напруження біля внутрішньої поверхні труби
2 10» 125 10-т 100 [о п	2 (4* — 2’) ]	1ПО
=	3(1-03)(4-2)— І3 2-----------4-—2ї— І МПа = - 198 МПа
За формулою (16 51) знаходимо напруження ае та а, біля зовніш* ньої поверхні
£аГ* | о,	[
ЛІ	‘	^-г2	|
(ав),_г, -- (а,),-,.
= 2 І0> 125 .‘Д 7 100 13 2 ---------1 МПа = 159 МПа
З (1 - 0 3) (4 - 2)	|	4» - 2» |
У інших точках поперечного перерізу труби напруження можна обчислити за формулами (16 47) (16 49)
| 106 Розрахунок обертових дисків
Обертові диски широко застосовують у парових та газових турбінах у компресорах вентиляторах та машинах хімічної промисловості Диски зазнають дії навантажень то спричинюють розтягання та згинання їх, а також дії високих температур Істотне значення мають відцентрові сили Як правило навантаження та температурне поле симет-
ричні відносно осі диска внаслідок чого і напруження є функціями тільки відстані від осі обертання
Рас 46І
Рнс 462
Обмежимося розглядом диска постійної товщини, який наванта* жено силами що діють паралельно його серединній площині й рів* номірно розподілені по його товщині Розглянемо також нагрівання диска при лінійному законі зміни температури вздовж радіуса
Будемо вважати, що диск тонкий 1 внаслідок цього напруження по його товщині не змінюються а в напрямах паралельних осі. взагалі їх немає (ох = 0) У такій постановці задача про визначення напружень у диску належить до так званої плоскої задачі теорії пружності, точ ніше— до задачі про плоский напружений стан
Розглянемо обертовий диск постійної товщини Н, що має централь ний отвір (рис 461, а) До позначень на рисунку додамо ще й такії — питома маса матеріалу диска ш — кутова швидкість обертання Як і в розглянутому вже прикладі розрахунку товстостінного циліндра, виріжемо уявно елемент диска даома меридіональними пло* шинами, кут між якими в серединній площині дорівнюєте і двома циліндричними поверхнями радіусами г та г + Ог (рис. 462, а)
Крім сил прикладених по гранях елемента (рис 462 б), на еле мент діють сили інерції у вигляді відцентрової сили, розподіленої по всьому об ему й зведеної до рівнодійної
{іта>*г “ -ї- НгсіОїіг^г
8
Ця сила також лежить у серединній площині диска й спрямована вздовж радіуса від осі обертання
Прирівнявши до нуля суму проекцій усіх сил на вісь х, що збі гається в бісектрисою кута гіб, дістанемо рівняная рівноваги в такому вигляді
г -п?2- + о, — ое 4- соМ = 0	(16 65)
(1г	8
Це рівняння відрізняється від рівняння рівноваги (16 І), злобу* того при розрахунку товстостінного циліндра, тільки доданком (у/£) а’г3, який обумовлений дією відцентрових сил. Геометричні та фізичні рівняння не відрізняються від рівнянь (16 2) (16.4), виведе них для товстостінного циліндра
Диференціальне рівняння для радіальних переміщень точок диска у цьому разі набирає вигляду
(і*и . 1 4и и	1 — Ц* V .	/і а як.
— —---------------<1666)
Це диференціальне рівняння відрізняється від рівняння (16 5) лише правою частиною Записавши його у вигляді
та проінтегрувавши послідовно двічі, знайдемо, що
>-А'(1668)
Підставивши цей розв’язок у вираз (16 4) для напружень, матимемо: аг=Л + 4—(1669) '	г* 8	/
од = А £—(16 70) де
Л=^_-Л„.В—^8,
Сталі А та В (а отже, Л1 та визначаються з граничних умов Найчастіше відомі радіальні напруження на зовнішньому та внутріш ньому контурах диска Тоді прн г = г\ аг = одр а при г = г, а, = = а,, Відповідно до виразу (16 69) ці умови дають два рівняння*.
,,,.л+-^х.Ч,
„,і=, л + 4-^±ьі<о-л
А, » І
розв'язуючи які відносно А та В, знайдемо
Л = -Д^а,,--Дт-а,,О6?!) Г2~ гі	гг~~'і	®
В = -Дга„--Д5-о„-------Цг.ХлИ (1672)
'І-'ї	8 •
Якщо на зовнішньому та внутрішньому контурах диска напружень немає, тобто о,, == 0 та о,, = 0, то
л .2+1Х<И(^+4	(1673)
(16 74) а е
Підставляючи останні значення А та В у формули (16 69) та (16 70), матимемо
<,г_-8+іЛ.ш.^+г;_-!у-г.),	(16 75)
’в - т (3 + Н) (н + А, +	- (1 + зн)г>] (16 76)
Взявши для короткості
^- = к, -Х-=р;	=	-Ші.= т, (16 77)
формули (16 75) та (16 76) можна переписати так:
<>,-ф + 4.(1__!г)_|).];	(16 78)
ае = ср +-±-)_тр.|,	(16 79)
Напруження о, додатне і, як неважко переконатися, досягає найбільшого значення при р = Н	Тоді
Огт.х = с(1—А)1	(1680)
Напруження од при всіх значеннях р також додатне і досягає найбільшого значення біля внутрішнього краю диска (при р = к)
Обпшх =с(2+ (1 — /п)*«|.	(16 8!)
Порівнюючи формули (16 60) та (16 81), переконуємося, ЩО ОД„щ іавжди більше ніж Отая Тому, перевіряючи міцність диска за енер г стичною теорією формозміни, умову міцності слід записати у вигляді
О„.І7 =овт„ =с[2+ (1 — /П) А’КІО]	(16 82)
У випадку крихких матеріалів перевірку слід виконувати за теорією Мора, яка при о8 = о, = 0 приводить до тієї самої формули (16 82)
Характер розподілу напружень о, та од уздовж радіуса диска з отвором при к = 0,2 та ц = 0,3 показано на рис. 461, б
Формули для напружень у суцільному диску (без отвору) можна дістати з формул (16 69) та (16 70), якщо взяти до уваги, що иа осі диска (прн г = 0)_ напруження повинні мати скінченні значення. Для виконання цієї умови стала В має дорівнювати нулю, 1 тоді формули наберуть такого вигляду:
О, = Л--Ц±--1-ВМ;	(16.83)
= Л --Шй.-І-«АЛ	(16 84)
Сталу А знайдемо з граничних умов на зовнішньому контурі (при г = /і) Якщо диск зазнає дії лише сил інерції власної маси, спричинених його обертанням, а зовнішнього навантаження на зовнішньому контурі немає, тобто од, = 0, то згідно з формулою (16 83),
А = -Г юі4	(16 85)
Підставляючи це значення А у формули (16 83) та (16 84), маємо: о, = с(1—р‘),	(16 85)
ОД-=с(1— дір»)	(16 87)
Обидна напруження додатні при всіх значеннях р та збільшуються в міру наближення до осі диска На осі диска, при р = 0
Огтвх «оетвх = с = 3~^ СоМ.	(16 83)
За знайденими напруженнями легко визначити переміщення та деформації в диску
Найбільш цікаво знати радіальне переміщення та збільшення ра* діуса, що дорівнює йому Згідно з виразом (16 3), « = евг	(16 89)
Оскільки
ее = -|-(ав —раг), то
а — (ав — ра,).	(169(0
Для визначення переміщення на зовнішньому контурі та збільшен* ня радіуса у формулу (16 90) треба підставити г = ае = ае, та а, = а,,
У разі нерівномірного нагрівання диска до напружень, спричинених відцентровими силами його власної маси та контурними навантаженнями, додаються температурні напруження
Визначимо окремо температурні напруження Хід розв'язання цієї задачі аналогічний щойно розглянутій. Рівняння рівноваги дістанемо з рівняння (16 65), поклавши ш = 0 Воно буде таким самим, як для розрахунку товстостінного циліндра [формула (16 1))
0	(1691)
Відносні деформації з урахуванням температурного розширення визначаються таким чином
е, = 4-(а, —рав) +«Г, ,	(16 92)
ее =	— рог) + аТ
Розв'язуючи спільно ці рівняння відносно напружень, дістанемо
"г =	І». + ИЗД - ( +
ь	(1693)
Ое » (ее + це, - (1 + р) О.Т]
Ураховуючи вирази (16 2) та (16 3), будемо мати
,	1	1	(1694)
".= -Г^г|-г + Н^--(1
Позначимо Т* = Т, — 7\ (див рис 451, а) При лінійній зміні температури вздовж радіуса диска Т = Т* (г — г^Цг% — гО, 1 останні 456
вирази набирають вигляду
о' = Т^?[-£+і‘-7--<1+>‘>"‘7'*-^77]'	('696)
<’в = -Г^г[-7-+і‘-г7--(‘-І‘)«‘7’*-^7-|-	П6 96)
Модуль пружності та коефіцієнт Пуассона вважаємо сталими, таки ми, що не залежать від температ} ри і дорівнюють їхнім значенням прн середній температурі диска
Підставляючи формули (16 95) та (16 96) у рівняння рівноваги (16 91), дістаємо таке диференціальне рівняння для визначення переміщень у температурній задачі
(16 97)
Записавши рівняння у вигляді
-г-|^--тг-]=4^’а7'* <іб9в> та проінтегрувавши його послідовно двічі, визначимо переміщення!
х = С,г +	4	(16 99)
Підставивши цей розв'язок у формули (16 95) та (16 95) для напружень, будемо мати
а, =С+-4- ..Г" ,, аВг,	(16 100)
ое= С—-------у- ГТ^_Г аЕг,	(16 101)
де
Сталі С та й можна визначити з граничних умов при г = Г) на □руження о,, = 0, при г = г, напруження ог, = 0
Якщо обертовий диск нагрівається нерівномірно, то напруження від відцентрових сил та температурні напруження слід складати. У разі лінійної зміни температури вздовж радіуса, склавши праві частини виразів (16 96) та (16 100), а також виразів (16 70) та (16 101), будемо мати
<., = «+	а£с (16102)
не = К - -і---Цг^—~т ,Д',,	(16 103)
де К = Д 4- С, Ь = В + О — нові ствлі, які також визначаються в граничних умов
Приклад 73. Знайдеш напруження в обертовому нерівномірно нагрітому диску постійної товщини з центральним отвором Зовнішній діаметр диска б, -= 500 мм. діаметр отвору = /00 мм, товщина диска Н -= /О мм і частота обертання п == = 3000 хв~1 На одиницю довжини зовнішнього контура диска при цій частоті обер тання діють відцентрові сили обода та лопаток Р, О І М Цім, внутрішній діаметр диска вважасмо вільним. Температура біля внутрішнього контура Ті = 200 °С, а бі ля зовнішнього Т, = 300 °С і змінюється вздовж радіуса за лінійним законом Матері ал диска — сталь з такими характеристиками Е-= 2 /О* МПа р = 0 3. у = = 78,5 кН/м*, а = /25 10~7.
Визначимо сумарні напружений від відцентрових сил та від нерівномірного на грівання Для цього скористаємося формутами (16 102) та (16 103) Обчислимо величини, ЩО ВХОДЯТЬ ДО ЦИХ формул
І+Зр у
78 5 і 3 14 3000 \* .....  ...
9,81 ( ЗО ) “325 МПа/м 78 5 / 3,14 3000
9 81 \ ЗО
Я^ = ~3(25 —5) 10-* 125	2 • 10* = 416 МПа/м,
“Г “ 4~ 3(25—-5) ІО"8 125 10~' 2	"833 МП№
ю1
187 МПа/м*.
Підставивши ді значення у формули (16 102) та (16 103), натанемо
о, = К + ~р- -325/*- 416г,
ов=К-------— 833/
Стазі К та і. знайдемо з граничних умов при є = є і — 5 см о, = о, = 0, при г « — 25 см а, “ <з,, в “ д*д^ МПа = 10 МПа.
Ці умови дають два таких рівняння
10 - К + -д-^г — 325 0,25» — 416 . Ог25,
0 - К + -д-др- - 325 • 0 05» — 416.0,05 або
625 10“4К+Д = 83945. 10“*, 25. ІО"4# 4-і - 540 10"4. Рове язавшн рівняний, знайдемо шо К = 139 МПа, а £ = —2935 ІО"4 МПа X X м’.
Рівняння для визначення напружень набирають такого вигляду о,-139- иО"4 , 325,3, 416г, ое = 139 + 2935д’-УҐ — 187Н — 833г,
Обчислимо напруженая прн середньому значенні радіуса
г, + ',	5 + 25
Г„----2-----2---“'*»
Матимемо
(із»—-ЗИ 0'5’-
— 416-0 Із|мПа = 56 МПа
Напруження 09 обчислимо при г= г, — 5 см г — гср — 15 см та г = г> = 25 см
(Ое>г-5=(>39+ в^ОБ»0"4 ~ 187 0 05*-833 -°05)МПа“2Н мп>
<°е)г-15^(139 + 293^151д°~4 - 187 0.15» -833 0 МПо = 23 МПа
(Ое),,» = (139 +	— 187 0 25»—833 0 25^ МПа = - 80 МПа
Епюри напружень показано на рис 463
Глава 17. ЕЛЕМЕНТИ ТЕОРІЇ ТОНКОСТІННИХ ОБОЛОНОК
$ 107. Вступ
У різних галузях техніки широко застосовують такі конструктивні елементи, які з погляду розрахунку їх на міцність І жорсткість можна віднести до тонкостінних оболонок, товщина яких значно менша ніж радіуси кривизни Це цистерни, водонапірні резервуари, повітряні й газові балони, куполи будинків, герметичні перегородки в літаках і підводних човнах, апарати хімічного машинобудування, частини кор пусів турбін і реактивних двигунів тощо
Розглянемо елемент оболонки (рис. 464) Взагалі у перерізах якими виділено елемент, діють лінійні (віднесені до одиниці довжини
Рнс 464
перерізу) зусилля (рис 464, а) 1 моменти (рис. 464, б)] нормальні зу силля Л\ та Л'а дотичні (зсувальні) зусилля 5і та 5, поперечні сили
та 9, згинальні моменти Мк та Міг крутні моменти Лі1кр та Вихідні диференціальні рівняння для розрахунку оболонок, здобуті з урахуванням усіх цих зусиль і моментів, виявляються такими склад ними, що інтегрування їх навіть для найпростіших задач пов’язане з великими математичними труднощами
Проте в багатьох окремих випадках вихідні диференціальні рів няиня і розв язаиня задачі значно спрощуються Цього можна досяг нути, по перше, враховуючи характер самої задачі Якщо оболонка становить тіло обертання і навантаження симетричне відносно осі оболонки, то задачу називають осесиметричною І в цьому разі в усіх перерізах, утворених площинами, що проходять крізь вісь симетрії, і в перпендикулярних до них перерізах
М1НР =	= 5, = 0; 9і = 0 (або 9, = 0)	(17 1)
По друге, якщо форма оболонки, характер навантаження та за-кріплень дають амогу вробити висновок, що які небудь зусилля або моменти всюди малі порівняно з рештою силових факторів, то виходять з припущення, що ці зусилля і моменти дорівнюють нулю Наприклад, часто вважають, що
М, = Лі, = М„р = Мї,р = 0; ^I = ^, = 0,	(17 2)
і в результаті приходять до так званої безмоментнт теорії оболонок
Ще більше спрощуються рівняння і розв язання їх, якщо поєднуються обидві зазначені обставини — розглядається осесиметрична задача е безмоментній теорії оболонок Тоді виконуються всі рів ності (17 1) та (17 2)
§ 108. Напруження в «несиметричній оболонці
_ Розглянемо резервуар (рис 465), що е осесиметричною оболонкою В ній меридіональні перерізи серединної поверхні утворюють плавні криві без зломів Товщина стінки й оболонки невелика порівняно з ра діусами кривизни Вільний край резервуара закріплений таким чином, що на нього можуть діяти тільки зусилля, дотичні до мерндіо* нальних кривих Тоді можна вважати, що оболонка перебуває в без моментному напруженому стані, для якого справедливі рівності (!7 2)
Нехай резервуар заповнений (частково або повністю) газом, рі даною чи сипкою речовиною Тиск р, МПа, в цьому разі може змінюватися по висоті (тобто вздовж осі резервуара), але буде однаковий в усіх точках площини, перпендикулярної до осі резервуара Тоді оболонка буде перебувати не тільки в безмоментному, айв осесиметрич йому напруженому стані
Виділимо прямокутний криволінійний елемент АВСО оболонки (рис 465) двома близькими осьовими перерізами та двома ортогональ 460
ними до них 1 до поверхні оболонки перерізами
(останні перерізи є двома конічними поверхнями «ІЩІ» з вершинами на осі резервуара) Довжини граней / елемента позначимо 4$, і яз,	І'яг^ \
Згідно з рівностями (17 1) та (17 2) уГраняхеле- /	-й \
мента діють тільки нормальні лінійні зусилля і І	р-т І
/V, і відповідні напруження а, і о, (розтягальні у разі внутрішнього тиску і стискальні —у разі зов нішнього) Отже, грані елемента — головні пло Ау. 1 щадки	у"т*І-----у
У гранях АВ і СО зусилля /V, можуть відріз хдО нятися на величину йМ* зусилля ж А\ у гранях ВС 1 АО внаслідок осьової симетрії однакові Рів- Рнс 4б5 нодійне зусилля в кожній грані елемента дорівнює добутку відповідного лінійного зусилля на довжину грані
Елемент АВСО серединної поверхні оболонки з прикладеними до нього зусиллями і тиском зображено на рис 466 Точка 0 — центр елемента, точки 0^ і 0, — центри головних кривизн серединної по* верхні, 00і — нормаль до поверхні елемента 1 оловиі радіуси кривизни серединної поверхні позначено через Рі і Рі, причому Рі — радіус широтної кривизни, ар, — радіус меридіональної кривизни Очевидно
4І8, р,4ф, 48, "• Р,4ф,	(17 3)
Запишемо умову рівноваги елемента, прирівнюючи до нуля суму проекцій усіх сил на нормаль до елемента Розглядаючи рис 465 і 467, дістаємо
2АЇ^8,510(^1/2)	N^1 зіп (4ф/2) + (У, 4- 4А7І)4$І 5Іп(4ф/2) —
— />45,48, — 0
Доданок 4^^$! зіп (4ф,/2) має більш високий порядок мвлості, і ним можна знехтувати Враховуючи також малість кутів 4фх та 4ф, і співвідношення (17 3), знаходимо, що
Підставляючи ці вирази в рівняння рівноваги і поділивши його на 4814$,, матимемо
^/Рі 1 А'1/Рі= Р	(17 4)
Вираз (17 4) встановлює залежність між днома зусиллями — та Оскільки невідомих зусиль дна то для визначення їх од ного рівняння недостатньо Додаткових рівнянь рівноваги елемента скласти більше не можна Тому запишемо рівняння рівноваги довільної скінченної частини ЛіС,в, оболонки (рис 465 І 468) Для цього проведемо переріз конічною поверхнею А їй іВь нормальною До середня ної поверхні оболонки, по контуру А,#,
Ряс 467
По контуру перерізу АіВі (по колу радіусом г) діють лінійні зусилля Наодиіінці довжини кон тура вони дають вертикальну проекцію Лі» соз а, де а — кут нахилу меридіональної кривої до осі
резервуара Тому сумарне вертикальне зусилля від дії Лі»спрямоване вгору 1 дорівнює 2лгЛі,со5а Вертикально вниз діють тиск ряг*, вага ррід рідини (чи сипкої речовини), що міститься в об'ємі /^£,8^ та вага частини резервуара Тоді з умови рівноваги
2лгЛІ,со8а — ряг2 — Срід — СР — 0
N	і +
*	2 соз а '	2яг соз а
(17 5)
Рівняння (17 4) і (17.5) дають змогу знайти всі зусилля в осесимег-ричній безмоментній оболонці Часто це рівняння записують у напруженнях
Вважаючи, що згинальних і крутних моментів в оболонці немає, припускаємо тим самим, що по товщині її напруження розподіляються рівномірно (як прн простому розтяганні-стисканні) Тому (рис 469)
N - а  й 1 = оН	(17 6)
Крім того, меридіональні напруження і радіуси кривизни часто позначають ат і рп, а не а» і р», широтні (колові) величини — о, і замість ах і Р; Відповідно до цього
ЛІ, = 0/й; ^-□„й	(177)
Підставляючи ці вирази в рівняння (17 4) та (17 5) і враховуючи заува ження щодо індексів, дістанемо
о<  От _ Р Рі Рт *
а - . " і + ™ 2Л соз а 1 2ялЛ соз а
(17 8)
(179)
Рис 468
Рис 469	Рис 470
Формула (17 8) має назву формули Лапласа формулу (17 9) іноді називають рівнянням рівноваги зони або просто рівнянням зони На пруження о„ зветься меридіональним нормальним напруженням, ст(— коловим (широтним, кільцевим) нормальним напруженням
Оскільки оболонка тонкостінна, то замість радіусів р/, рт і г се рединної поверхні оболонки у формули (17 8) та (17 9) можна підстав ляти відповідні радіуси зовнішньої чи внутрішньої поверхні
Слід звернути увагу ще й на те, що напружений стан в такій обо лонці мн визначали тільки з рівнянь рівноваги, не розглядаючи гео метричний та фізичний аспекти задачі Це пояснюється тим, що ми відразу постулювали закон розподілу напружень по товщині оболон кн — вважали їх постійними
Як уже зазначалося, напруження ат і о, — головні Трете головне напруження спрямоване нормально до поверхні оболонки в даній точці На одній з поверхонь резервуара (внутрішній чи зовнішній — залежно від того, з якого боку діє тиск) воно дорівнює тиску р, а на протилежній — нулю В тонкостінних оболонках завжди о,п і о, значно більші ніж р і, отже, третім головним напруженням порівняно з от і о, можна знехтувати, тобто вважати його нульовим
Отже, вважаємо, що матеріал оболонки перебуває в плоскому на пруженому стані Тоді для розрахунку на міцність у небезпечних точках залежно від стану матеріалу слід застосовувати відповідну теорію міцності Наприклад, для пластичних матеріалів за IV теорією міцності умова міцності має внгляд
«..ну -	1-а? —	(17 10)
Розглянемо приклади розрахунку безмоментних оболонок
Сферичний балон заповнено газом, тиск якого дорівнює р (рис 470) У цьому разі внаслідок центральної симетрії
=0.
Тому на підставі формули (17 8)
2.5_____£. абоо=^-
* Я “ й ’ ао° ° 2Л
Отже, головні напруження
Рис 471
Рнс 472
Умови міцності за першою, третьою і четвертою теоріями міцності мають однаковий вигляд
=	(17 12)
Циліндричний балон заповнено газом, тнск якого дорівнює р (рис 471) Тут
Р» = Я. Рт = ОО
Тоді з рівняння (17 8) С( , От _ а ~ІГ +	“ ІІ •
тобто
(17 13)
Для визначення о„ проведемо переріз а—а, перпендикулярний до осі циліндра, і розглянемо рівновагу будь якої з частин циліндра. В результаті, виходячи з формули (17 9) і поклавши <2Рід = <2Р = О та а = 0, матимемо
(17 14)
Отже, кільцеві напруження удвічі більші за меридіональні от Тому, наприклад, у клепаного резервуара поздовжній шов пови нен бути в два рази міцніший ніж поперечний
Зазначимо що здобуті результати справедливі тільки для центральної частини циліндра, оскільки ті частини, що примикають до днищ, не можна розрахувати за безмоментною теорією (докладніше про це розповідається нижче)
Резервуар у вигляді кульового сегмента (рис 472) заповнено рідиною (або сипкою речовиною) з густиною у Вводимо полярний кут ф, який визначає положення довільної точки А Тоді
а = 90е— ф рі =» рт = /?, г — /?зіпф, Н = /?(созф — со5 0); р=уН = уР (соз ф —соз Р)
З рівняння Лапласа (17 8) випливає, що от + «і =	<с03 *Р “ С03
Тепер скористуємося рівнянням (17 9) Величина фрід дорівнює вазі рідини в об’ємі кульового сегмен та АСВ
<?рід =	= V Ц- яНІ (З/? —
Висота кульового сегмента
/7С = /?(1 — СОЗ ф)
Тому
Рис 473
<2рід =	— СО8ф)®(2 і СО8ф)
Підставляючи в рівняння (17 9) вирази для р, г, <2рід, а і нехтуючи вагою резервуара дістаємо
=	Г1 4-соз ф 4-соз* Ф _ сюр 1	..7 .5.
т л зо+сюф) 2 • и/ю) Тоді
_ уЯ* [2соз*ф4- СОЗф— і СОЗР 1
Л І 3(1 4 созФ) 2 ]	(*' *о)
Максимальні напруження діють в точці С, де ф = О
На краю оболонки (ф = 0)
®_ ,о, уЯ1 2 —созр —соз*0 “-»<(?) = -„----------- (|7І6>
причому кільцеві напруження стають стискальними
Купол у вигляді кульового сегмента радіусом К з товщиною стінки Л (рис 473) виготовлений з матеріалу густиною у Вага одиниці площі поверхні купола у = ?Л її складову, нормальну до поверхні,
Уп~ у С08 ф = уЛ С05 ф можна розглядати як тиск, що діє на поверхню Всередині купола тиск дорівнює нулю, тому в рівнянні Лапласа слід покласти р = —уп, а в рівнянні зони р = О
Ураховуючи, що Рі=ря = Я, з рівняння Л.'піаса знаходимо
“< = т “	(П 19)
Щоб дістати додаткове рівняння, обчислимо вагу частини АСВ резервуара
<?р = уВдсв ~ ?Л5лев, де площа бокової поверхні кульового сегмента АСВ 8лсв = 2л/?//в = 2л/?® (1 — соз ф)
Отже,
СР = 2луЛ/?’ ( і — СО8 <р)
Підставивши тепер у формулу (17 9) вираз для СР і г = /? зіп <р; а = 90° — <р; р = 0, а також ураховуючи (знаком «мінус»), що в пе рерізі АВ вага частини АСВ купола спричинює стискання, знайдемо
а = — т—------
т і + см ф
(І7 20)
Тоді з рівняння (17 І9)
=	(П21)
Меридіональні напруження всюди стискальні і зростають в міру віддалення від вершини купола до краю Кільцеві напруження у верх ній частині купола від’ємні (стискальні), при <р = 5Г50' вони перетво рюються на нуль, а при <р > 51’50' стають розтягальними Здобуті результати справедливі, якщо опорна будова купола така, що в ньому можуть виникати тільки реакції, спрямовані по дотичній до меридіо кально кривої
$ 109. Розпірні гільця я оболонках
Досі ми розглядали оболонки, меридіональні перерізи яких ста новили плавні криві, кривизна яких не змінюється Розрахунок таких тонкостінних оболонок за безмоментною теорією дає цілком прийнятні для практики результати
Тепер дослідимо вплив переломів меридіональної кривої на напру жепнй стан оболонки Нехай у деякому перерізі А—А (рис 474) оболонка має такий перелом, що дотичні до меридіональної кривої ліворуч і праворуч від точки А утворюють між собою кут не 180’, а 180е— (а, 4- аа) Розглянемо меридіональні напруження аті і ам (рис 475) у перерізах В—В та С— С, нескінченно близьких до А—А (ці перерізи утворені конічними поверхнями ОіВВ і ОаСС, нормальними до серединної поверхні оболонки) Лінійні зусилля в цих перерізах дорівнюють Отійі і (рис 476), де йі і А» — товщини частин 1 і 2 оболонки
Рис 474
Рве 475
Рис 476
А
Рис. 477	Рис 478	Рис 479
З умови рівноваги кільця ВВСС випливає, що
Ои.Лі соз а)2лг = Отай, соз а£лг, тобто
оті/і1соза1 = ат2Л8С05а8	(17 22)
Отже, проекції зусиль і на вісь оболонки взаємно зрів доважуються інакше буде з проекціями цих зусиль на площину А—А (рис 476) Додаючись, вони дадуть лінійне радіальне зусилля
д = от|Л, зіпсц 4- ОпДзіпсц	(І7 23)
Зусилля д можна розглядати як місцеве навантаження, що стнс кає оболонку Це навантаження може спричинити в оболонці значні згинальні напруження Щоб зменшити згин, у резервуарах часто вста новлюють кільця жорсткості, або розпірні кільця (рис 477), які сприймають радіальні зусилля д
Розпірне кільце навантажене за схемою рнс 478 У ньому виника ють тільки стискальні напруження, і умова міцності для кільця має вигляд
-^С1с|	(17 24)
де /?к — рвліус осі кільця Г* — ллоша поперечного перерізу кільця а д визначається за формулою (І7 23)
Іноді замість розпірного кільця утворюють місцеве стовщення оболонки (рис 479), загинаючи краї диища резервуара всередину обичайки
Якщо оболонка зазнає зовнішнього тиску, то меридіональні напру ження будуть стискальними і, згідно з формулою (17 24), радіальне зусиїїя д спрямоване назовні Тоді кільце жорсткості чинитиме опір не стисканню, а роз тяганню При цьому, очевидно, умова міцності (17 24) залишається такою самою
Зазначимо, що розпірне кільце не лікві дує повністю згинальні напруження, а лише зменшує їх
Розглянемо як приклад циліндричний резервуар із сферичними днищами (рнс 480),
Рнс 480
заповнений газом, тиск якого дорівнює р, МПа У місці кріплення днищ до циліндра поставлено розпірні кільця Треба визначити тов щнии стінок і площу перерізу кільця, якщо допустимі напруження відомі
Товщину А] стінки днища знаходимо з формули (17 12)
Виходячи з четвертої теорії міцності І користуючись формулами (І7.10), (17 13) та (І7 14), запишемо умову міцності для циліндричної оболонки	________________
звідки

2и
Тоді меридіональне напруження в днищі
„ Р*
“ 'а? 
а в циліндричній оболонці
Підставляючи ці значення у формулу (і7 23) і враховуючи, що в даному прикладі «і = 90е — а а4 = 0, знаходимо радіальне зусил ля, прикладене до розпірного кільця
Я= -2%- сова
Нарешті, вважаючи, що радіус кільця /?в » г, з формули (І7 24) визначаємо потрібну площу поперечного перерізу кільця)
е _	рЯг сов а
’ ТаГ= 2І°1
$ 110. Крайова вадяча для тонкостінної циліндричної оболонки
Розглянемо одну з найпростіших задач моментної теорії оболонок* по краю тонкої напівнескінченної циліндричної оболонки (рис 48І) рівномірно розподілені лінійні поперечні СИЛИ Зо і згинальні моменти Мо, крім того на оболонку діє постійний внутрішній тиск р треба визначити переміщення точок оболонки і напруження в ній
Ця задача має деяке самостійне значення, і, крім того здобуті в ній результати в наступному параграфі будуть використані для визначення місцевих згинальних напружень
Виділимо з оболонки напівнескінченну	/У
смужкуодиничноїширини(рис 48! і482,а) к і _________________
двома осьовими перерізами Центральний . у^йг—7_ кут між ними малий і становить	гк^/Тр 1/^}*
ф - і//?	(17 25) ~ЧР7]І-------------4-
У кінцевому перерізі на смужку діють )тч.	І
зусилля (?0 і момент Мо по поверхні — Ц	/
тиск р, по поздовжніх краях — кільцеві	'
(широтні) зусилля ЛЛ,, змінні вздовж краю г |
Введемо осі координат и> та х вісь ш	рис 431
спрямуємо від ос> оболонки по радіусу, вісь х — по твірній (рис 482, а) Розподілене по поверхні й по поздовжніх краях навантаження можна звести до лінійного навантаження д (х), що діє в площині иіх паралельно осі и>
Виділивши в околі довільної точки /1 (рис 482, о) етемент смуж кн завдовжки одиниця і вважаючи що д(х)>0, якщо навантажен ня діє від осі оболонки назовні матимемо
<?(*) = — <М*) 4-Л
Ураховуючи малість кута <р і формулу (17 25) дістанемо
(х) = 2Л\ • і зіп (<р/2) = Л\<р — Л^/Я, « р | . 1 р
Отже, <?(*) = д-Л^/Я	(17 26)
Розподілене навантаження ?(х), а також Зв і Мо спричинюють плоске згинання смужки в площині сох Цю смужку можна назвати балкою-смужкою і далі розглядати її як напівнескінченну балку (рис. 482, а) прямокутного перерізу 1 х /і
Розглядаючи згинання балки смужки, треба врахувати, що, про гинаючись, вона взаємодіє з сусідніми смужками Один аспект цієї взаємодії враховується доданком — Л^//? у виразі (і7 26) для лі нійного навантаження д (х) Крім того, зазначена взаємодія приводить
до збільшення жорсткості балки смужки на згинання в площині шх порівняно із звичайною балкою З’ясуємо чому це відбувається і яким чином має враховуватися
При згинанні звичайної балки форма ії поперечних перерізів змінюється ширина перерізів у зоні, де поздовжні волокна стиснуті, збільшується, а в розтягнутій зоні — зменшується (штрихові лінії на рнс 483, б) Не змінюється лише ширина нейтрального шару В балці смужці внаслідок взаємодії її з сусідніми смужками таких змін поперечного перерізу не може бути Проте виникають напруження які перешкоджають зміні розмірів у напрямі, паралельному осі г, внаслідок чого г, = 0 Отже, в балці смужці, на відміну від звичайної балки, крім напружень ох у поперечному перерізі (рис 483, а), діють ще й напруження аг у поздовжніх перерізах, пер пендикулярних до нейтрального шару (рнс 483, б) Цим пояснюється збільшення жорсткості на згинання балки-смужкн
Кожний нескінченно тонкий шар матеріалу балки, паралельний нейтральному перебуває в плоскому напруженому стані (рис 483, в) Це треба враховувати при виведенні диференціального рівняння пружної лінії балки смужки
Диференціальне рівняння згинання для балки смужки можна дістати так само, як І для звичайної балки (див § 66) При цьому статичний і геометричний аспекти задачі виражаються тими самими залежностями (10 3) і (10 6), що і для звичайної балки, а саме
а)	статичне рівняння —
( 0,14г = МИ,	(17 27)
б)	геометрична залежність —
«бо	9	(17 28)
Фізичний аспект задачі (залежність між напруженням ох у поперечному перерізі та відносною деформацією для балки смужки на підставі узагальненого закону Гука з урахуванням того що = О, виражається так
ех = -^--р-^-,
ех =	— р -* = О або а2 = ра,
З цих формул знаходимо
(17 29)
Підставивши вирази (17 28) і (17 29) у рівняння(і7 27), матимемо
Для балки смужки з розмірами перерізу 1 х /і елемент площі йЕ = \йу Тоді
Ні/2
-М
І після обчислення інтеграла
Вводячи позначення для так званої циліндричної жорсткості И = >»	диференціальне рівняння згинання балки смужки за-
пишемо у вигляді
(17 30)
Двічі диференціюючи по х обидві частини цього рівняння і враховуючи, що (х)/сіх1 = <? (х), матимемо
=	(1731)
Отже, для балки смужки диференціальне рівняння пружної лінії має вигляд
<1732)
Тепер виразимо кільцеве (широтне) зусилля V! оболонки через прогин балки ш(х) (див рис 482, а) Одночасно ш (х) є також радіальним переміщенням
точок оболонки (рис 484) внаслідок дії (?в, Л1а і р Це переміщення спричинює в кільцевому напрямі відносне подовження
2я (Я -І- и> (х)| — 2лЯ » (х) 2яЯ “Я
Рнс. 484
(І7 33)
Вважаючи, що розтягальних меридіональних напружень в оболонці немає, знайдемо кільцеве напруження
а, = Еіі = и> (х)	(17 34)
і, нарешті, кільцеве зусилля «,-а,.(>.1-^-ш(х)	(17 35)
Підставляючи цей вираз у рівняння (І7 32), матимемо
<І73В>
Рівняння (17 36) ідентичне рівнянню (і 1 12) (див § 73), що описує згинання балки на пружній основі, якщо взяти
ет.	(17.37)
Тому перетворимо рівняння (І7 36) так само, як це зроблено в § 73. Поділивши рівняння (І7 35) на О, враховуючи вираз (І7 ЗО) і поз начившн	________
(>738> дістанемо
(*) »-у-	(17 39)
Введемо нову безрозмірну незалежну змінну 5 = ах	(17 40)
Оскільки
№ (х)	.* «І4® (6)	3(1— Ц1)	(6)
ах* ~а ау = яіл* ~4* ’
то рівняння (17 39) остаточно набере вигляду
Легко перевірити, що частинний розв’язок цього рівняння при постійній інтенсивності тиску р буде
ВД. =Т£-	(17 42)
Однорідне рівняння, шо відповідає рівнянню (17 4І), точно збіга ється з рівнянням (ІІ.16), і його загальний інтеграл має вигляд (І1 17) Тому загальний розв’язок рівняння (17 41) буде мати вигляд
ш(5) =	4-	(4 соз £ 4- ВзіпЕ) 4-е* (С соз £ 4-Ої зіп 5)	(і7 43
Четверту сталу позначено а ие О, щоб не переплутати і і з ци ліндричною жорсткістю
Очевидно, що в міру віддалення від краю, де діють лінійні лопереч ні сили Зо і згинальні моменти М9 вплив їх на переміщення ш повн нен зменшуватись і в нескінченно віддалених точках зовсім зникнути. Отже и> (оо) має бути скінченною величиною Оскільки е* безмежно збільшується із зростанням £ то щоб прогини смужки безмежно не вростали, треба покласти
С =» О, = О Тоді
ш (5) =4-е-5 (4 соз 5 4-В зіп 5)	(17 44)
Скориставшись відомими диференціальними залежностями для баЛок (замінивши жорсткість циліндричною жорсткістю О)
0 = -зг = <,-гг’
8 формули (17 44) дістанемо такі вирази для кутів нахилу пружної лінії згинальних моментів і поперечних сил
0 = ое-* (4 (соз 5 4- зіп 5) 4* В (соз 5 — зіп 5)},
М = Оа'е-* (24 зіп 1 — 2В соз 5).	(17 45)
З = Оа’е-* |24 (соз 5 — зіп 5) 4-25 (с03 5 4- зіп 5)]
Виразимо сталі А і В через <?0 і Мо Оскільки (див рис 482, б)
то з останніх двох формул (І7 45), поклавши £= 0, визначимо
- 2ВРа3« Мо, Оа*(2А
ЗВІДКИ
+ <-«.). в = -^ом>
Підставивши значення коефіцієнтів у вирази (І7 44) і (І7 45), остаточно знаходимо
» =	е~-|<?0 соз $ 4- аМ9 (соз Е — зіп £)],
0 =~ї^ое~і 1<2о(со5&4-5Іп£)4-2аЛ10со$Б].
М = —е-ї [<?0 зіп £ + аМ0 (соз £ + зіп £)].
<2 = Є-4 (Ра (соз £ — зіп ©—2аМ0 зіп £],
причому а дається формулою (17 38), = — формулою (17 40)
Здобуті формули є розв язками поставленої задачі, оскільки дають змогу обчислити в довільному поперечному перерізі оболонки радіаль* не переміщення и>, кут в нахилу деформовано? тиірно? до осі оболон-ки, лінійний згинальний момент М і лінійну поперечну силу 3 Додатні напрями цих величин збігаються з додатними напрямами и>л 60, Мо і (на рис 482, б ш0 > 0, Мо > 0, (?0 > 0, а 0в < 0)
Дослідивши згинальні напруження в балці смужці, виділеної з тонкостінної циліндричної оболонки, ми дістали розв'язок і для всієї оболонки Напруження ах у балці смужці е згинальними напруженнями а„ в меридіональному напрямі оболонки (в Ті поперечних перерізах), а напруження о, — згинальними напруженнями о, в кільцевому напрямі (в поздовжніх перерізах)	і
Епюри ст і о( показано на рис 485 На- СрТТтЧ'ї'ЇЇІГИ І пруженням от відповідає згинальний мо	у ♦ І	♦ 14 ♦ №
ментМ а напруженням а, — момент Мі МлГЇ”і і лиши Г
50 І- бітам
,4 6 В Ю л.см Рис 486
Вите було показано, що аг — ц<7а, тобто аі = |іот Тоді, очевид но, М1 = цЛ!	(17 47)
У поздовжніх перерізах оболонка також зазнає розтягання або огискання (залежно від того,'зсередини чи ззовні діє тиск)
Максимальні напруження визначаються за формулами _ М	. М, , лч
Ощ пах “	• О/ пих = І т ‘~р~' >
ДЄ	*
и7 = ЛА-. р = і л
Отже, 6М	6М, , N1	,і-г лйі
Ощ шах — Л*, О< пій =	4* —•	( * 7 4о)
Величини Л4, і N1 знаходимо за формулами (17 47) і (17 35) після обчислення за формулами (17 43) до і Лі Знаючи максимальні напру* ження і вибравши ту чи іншу теорію міцності, можна виконати роз рахунок иа міцність При цьому треба правильно вибрати знак у формулі для а(пих
З’ясуємо тепер, як далеко від краю оболонки поширюється вплив крабових моментів Мо Зробимо це иа числовому прикладі
п Приклад 74 Сталева труба (Е = 2  10* МПа. р «= 0,3) радіусом Н = 40 мм а товщиною стінки Н — 2 мм зазнав дії рівномірного внутрішнього тиску р «= 2 5 МПа І крабових моментів Мо = 33,3 Н мім (рис 486) Побудуємо епюри зміни макси мольних меридіональних і кільцевих напружень уздовж осі труби
При відсутності крайових моментів у всіх перерізах було б
ат~0. а< д* МПа = 50 МПа	(17.49)
Поклавши 0, = 0 з формул (17 46) знайдемо
+ (1Л50)
М~Мое-І (СО864-8ІПЄ)
і, згідно з формулами (17 48), (17 35), (17 38), (17 ЗО) і (17 47) в точках біля внутрішньої поверхи
6-М	6-М.	,
«я них “ -дГ" «= —ЙГ- »“* («з Е + зіо 6) ________________________________________ (17 51)
«, » -	+ 4- ’ - -і- +1”« — + ТГ- «-* '“•* - «" В
Підставивши числові значеная р Ц МЛ її, р, матимемо
а( ти *=• 50 + 42,Ба-6 соз 5 — 12,5а-6 ЗІП 6 —
= 25 (2 + 1,7е—* соз 6 — 0,5а-6 зіп 6)	(17.52)
Таблиця 18
' 1 1		, і .		6	в				10
X ем		X СО5{		їй	°тп'пх“ -50 |5]	І 7 ПІ	0 5 [4]		— 25 [91
0	0	1 000	0	1 000	500	1 700	0	3,700	92.5
0,21	03	0 708	0 219	0 927	46.4	1 204	0,110	3 094	і І А
0 49	07	0 371	0 329	0,700	350	0 631	0,165	2,476	61,9
0 76	। і	0 151	0 297	0 448	22 4	0 257	0 148	2,109	52 7
1 04	1 5	0 016	0 222	0238	II 9	0 027	0,111	1,916	47 9
1,32	1 9	—0 048	0 141	0 093	47	-0 082	0,071	1 847	48,2
1 60	23	—0 067	0 075	0 008	04	-0 114	0 038	1,848	46 2
1 88	2,7	-0 081	0 029	—0 032	-1 6	-0 104	0,014	1 882	47,0
2 15	3,1	—0 045	0,002	—0 043	—2,2	-0 076	0 001	1 923	48 1
243	35	-0 028	-0 011	-0 039	—2 0	-0,048	0,006	1 958	49,0
2 71	39	-0 015	-0 014	0 029	-1 5	-0 026	-0 007	1 981	49 5
2,99	4 3	-0 005	-0 013	-0 018	-0 9	-0 006	-0 007	1 999	500
3.27	47	0 000	—0 009	—0 009	—0 4	000	—0 004	2,004	50 1
3 54	5 1	0 002	-0 005	-0 003	—02	0,003	-0 003	2,000	50,0
382	5 8	0003	0,003	0000	0	0005	-0,002	2,008	50,2
4.Ю	5,а	0 003	0,001	0 002	0 1	0,005	—О 001	2,006	50,2
Нарешті, згідно з формулами (17 40) і (17 38),
.,1» і= -ЛІЗЬ і- о «е “ И З (І - И’>	у з—д-дї
Користуючись таблицями функцій	(соз Е + сіп <Нои( і є“ЕзіяВ
(табт 18 і дод 12), обчислюємо значення <тшПцХ і а(твх для ряду значень 6 (табл 18) і за цими даними будуємо епюри зміни по довжині оболонки максимальних меридіональних і кільцевих напружень у точках біля внутрішньої поверхні в поперечних і поздовжніх перерізах оболонки (рис. 486)
Ці епюри показують, що прикладені до краю оболонки згинальні моменти Мо впливають на напружений стан оболонки тільки в безпосередній близькості від місця прикладання їх Вже на деякій відстані від краю напруження практично не відрізняються від добутих у результаті розрахунку оболонки за безмоментною теорією Такий характер розподілу напружень, спричинений в даному разі дією розподіленого моментного навантаження на краю оболонки, називають крайовим ефектом Швидко затухаючі місцеві напруження виникають також при дії поперечних сил Зо, розподілених по краю оболонки (див рис 481)
§111. Приклади врахування згинальних напружень  оболонках
1 Введене поняття крайового ефекту в оболонках здебільшого спрощує розрахунок конструкцій, які за своєю розрахунковою схемою належать до циліндричних оболонок Слід зазначити, що виведені
Рис 487	Рис 488
в попередньому параграфі формули для напівнескін ченноі циліндричної оболон кн можна застосувати і для скінченних оболонок, якщо тільки їхня довжина значно перевищує розміри зони крайового ефекту
Припустимо що до дов гого тонкостінного цилінд ра (рис 487) в перерізі
А — А прикладене рівномірно розподілене по периметру перерізу навантаження інтенсивністю д, Н/м. У цьому разі крайовий ефект симетричний відносно перерізу А — А Тому
а) навантаження розподіляється порівну на ліву та праву части ни циліндра, тобто (див рис 481)
с.---г-
причому початок координат вибираємо в точці 0 (рнс 487), б) дотична до пружної лінії балки смужки в перерізі А — А пара
лельна осі цнііндра, тобто (див рис 482)
0О = 0 ((.о = 0
Тоді з другого рівняння (І7.48) знаходимо, що
Підставляючи значення <?0 і Мо у формули (І7.46), враховуючи, що р — 0, дістаємо
ш _ тйг<соа Е +5ІП 0> е”-таг^-ішЕ.
М = е-і (соз 5 — зіп £);
Звідси, зокрема для перерізу А — А (В = 0), = Ч, = -	^3 (і-и«)
“	‘/3(1 - из
(і 7 53)
(І7 54)
(17 55)
Максимальні напруження обчислюються за формулами (17 48)
Нехай на тонкостінну трубу (рнс 488) насаджено з натягом тонке кільце, площа поперечного перерізу якого дорівнює Рк, модуль пружності £к
Якщо позначити через д інтенсивність радіального зусилля, що ви никає між кільцем і трубою, а через б — натяг (різниця між зовнішнім радіусом труби і внутрішнім радіусом кільця до насадження), то з умови сумісності деформацій
| І 4- І Шщах І = б, де и>к =	----збільшення радіуса кільця після запресування;
Шпих — максимальний прогин труби, тобто прогин у перерізі посадки кільця
Труба перебуває в умовах близьких до умов попереднього прикладу, тому штах визначається за формулою (17 54) Підставивши вира зи для і Шпш в умову сумісності деформацій знайдемо
звідки визначимо д Потім за формулами (17 55) і (17 47) знайдемо згинальні моменти а за формулами (17 48) — напруження Переміщення обчислимо за формулою (17 54)
Глава 18 РОЗРАХУНОК КОНСТРУКЦІЯ
ЗА ГРАНИЧНИМИ СТАНАМИ
$ 112. Основні відомості про граничний стан
Розрахунки на міцність окремих стержнів, балок та конструкцій, розглянуті в попередніх розділах курсу, грунтуються на оцінці міцності матеріалу в небезпечній точці При таких розрахунках найбільші нормальні, дотичні або еквівалентні напруження (залежно від виду напруженого стану та вибраної теорії' міцності) у небезпечному перерізі та в небезпечній точці порівнюються з допустимим напружен ням Якщо найбільші розрахункові напруження не перевищують допустимих, то вважають, шо належний запас міцності конструкції забезпечено. Такий спосіб розрахунку на міцність називають розра-хунком за допустимими напруженнями
Метод розрахунку на міцність за допустимими напруженнями, без перечно, забезпечує міцність конструкції проте здебільшого не дає змоги раціонально використовувати всі її можливості й часто приз водить до завищеної ваги
При розрахунку за допустимими напруженнями небезпечним, або граничним, станом конструкції вважається такий її стан, при якому найбільше напруження хоч би в одній точці матеріалу конструкції досягає небезпечного значення — границі текучості (для пластичного
матеріалу) або тимчасового опору (для крихкого матеріалу) Стан решти маси матеріалу не враховується
Проте при нерівномірному розподілі напружень (наприклад, при згинанні, крученні) у статично невизначуваних конструкціях, виготовлених з пластичних матеріалів, поява місцевих напружень, які дорівнюють границі текучості, здебільшого не е небезпечною для всієї конструкції Практика показує, що при появі місцевих пластичних деформацій конструкція ще може задовольняти вимоги, що ставляться до неї, і дія переходу її в граничний стан потрібне дальше зростагая навантаження Отже, насправді конструкція має запас міцності більший, ніж при розрахунку за допустимими напруженнями
У зв'язку з цим недоліком методу розрахунку на міцність за допустимими напруженнями виникла поіребавновому підході до оцінки міцності конструкцій Було запропоновано метод розрахунку кон струкцій за граничним станом
Під граничним станом конструкції розуміють такий її стан, при якому вона втрачав здатність чинити опір зовнішньому навантажен цю або перестав задовольняти експлуатаційні вимоги
Наведемо деякі приклади, що характеризують граничні стани
Випробування слабкоармованнх залізобетонних балок показують, що як тільки напруження в арматурі досягають границі текучості, балка сильно і необоротно провисає а також покривається багатьма тріщинами Зрозуміло, що дальша експлуатація такої балки немож лива, хоч для руйнування її й потрібне ще деяке збільшення наван тажения Отже, залізобетонна балка переходить у граничний стан як тільки напруження в арматурі досягають границі текучості
Сталеві стержньові конструкції можуть перетворитися на кіне мзтично змінювані після утворення достатньої кількості так зва них пластичних шарнірів, тобто появи в стержнях таких перерізів, у всіх точках яких напруження дорівнюють границі текучості Проте в деяких типах конструкцій цей процес може відбуватися таким чином, що після утворення перших пластичних шарнірів (задовго до перетворення цих конструкцій на кінематично змінювані) дальша експлуатація їх стане неможливою внаслідок значних залишкових деформа цій, що виникають У цих випадках мають місце граничні стани конструкції
Розрізняють три види граничних станів
а)	перший граничний стан — за несучою здатністю (міцністю, стійкістю та опором втомленості при змінних напруженнях),
б)	другий граничний стан — за розвитком надмірних деформацій (прогинів перекосів та ін ),
в)	третій граничний стан —за утворенням або розкриттям тріщин
Розрахунки за граничними станами широко застосовуються при проектуванні будівельних конструкцій та споруд Поширюються методи цих розрахунків і в машинобудуванні, причому і тут виявляється їхня прогресивна роль вони дають змогу використати резерви міц-
Рис. 489
Рис 491
ності, які не використовуються при розрахунках за допустимими напруженнями розрахунок за граничними станами дає змогу зменшити вагу конструкцій
Тут розглядатимуться деякі приклади розрахунків за несучою здатністю конструкцій з пластичних матеріалів, які мають площадку теку чості на діаграмах розтягання, стискання і чистого зсуву
Площадку текучості мають діаграми напружень матовуглецевих сталей та деяких інших матеріатів ірис 489) Наприклад, крива на діаграмі напружень алюмінію (рис 490) за межею дії закону і ука має дуже слабкий нахил, і при розрахунках її можна вважати горизон талькою прямою
Щоб спростити розрахунки, діаграми розтягання, стискання та чистого зсуву для пластичних матеріалів схематизують таким чином, що пряма закону Гука безпосередньо сполучається з горизонтальною прямою без плавного переходу (рнс 491) Саме цим приймається рівність між границями пропорційності та текучості Довжина горизон тальноі ділянки діаграми не обмежується, тобто матеріал вважається таким, що не зміцнюється (ідеально пластичним) Така діаграма має назву дюграми Прандтля
Зазначена схематизація досить точна для матеріалів типу алюмінію і цілком допустима для матеріалів, що мають діаграми з обмеженою довжиною площадки текучості (див рис 489) Це випливає з таких міркувань При наявності такої площадки текучості, як, наприклад, у м яких вуглецевих сталей, відносне подовження на початку зміцнення єй у кілька разів перевищує відносне подовження ее на початку появи пластичної деформації Тому навіть при нерівномірному почат ковому розподілі напружень (згинання, кручення, наявність кон центраторів), але дальшому послідовному поширенні пластичної зони з вирівнюванням напружень, граниш текучості вони досягнуть одночасно по всьому перерізу раніше ніж почнеться зміцнення матеріалу в точках з найбільшою пластичною деформацією Отже, граничний стан, що визначається значною пластичною деформацією, настане до початку зміцнення матеріалу, і граничне навантаження може бути обчислене за границею текучості
Для складного напруженого стану, як зазначалося в гл 6, запропоновано різні теорії переходу матеріалу в пластичний стан Найбільш
просто розрахунки виконуються при використанні теорії пластичності Сен Венана Згідно з цією теорією, пластичний стан матеріалу прн складному напруженому стані настає тоді, коли найбільші дотичні напруження досягають граничного значення — границі текучості при зсуві
Тта» = Тт	(18.1)
Наведеними вище положеннями й будемо користуватися надалі
$ 113. Розрахунки при розтяганні й стисканні
При розтяганні та стисканні напруження по площині поперечного перерізу стержня розподіляються рівномірно Внаслідок цього роз рахунок на міцність статично визначуваних систем за допустимими напруженнями і за граничним станом дає один і той самий результат У разі статично невизначуваних систем результати різні
Покажемо це на прикладах
Визначимо запас міцності тристержньової підвіски (рис 492, а, б), навантаженої силою Р Площі поперечних перерізів стержнів однакові Матеріал пластичний з границею текучості пт
Розрахунок за допустимим напруженням Задача один раз статично невнзначувана Її розв язання розглянуто в §37 Прн г\ = Г, коефіцієнт к = 1, І тоді з формул (5 50) та (5 51) знайдемо
N. -	- Р,
1	1 +2«в»а ’
(18 2)
= = <183>
Очевидно завжди > М, = тобто більше зусилля виникає в середньому стержні Отже, в середньому стержні буде й найбільше напруження
° = "Т* = 1 -І- 2см1 а "Р-
Запас міцності при розрахунку за граничним напруженням а, (1 4-2ай* о) Ра,
«т =__ = -------------- (18 6)
Розрахунок за граничним станом Граничний стан конструкції буде характеризуватися вичерпуванням несучої здатності, яке настане тоді, коли в усіх стержнях напруження досягнуть границі текучості. Знайдемо граничне навантаження для конструкції.
Оскільки напруження в стержнях при пружній роботі їх неодиа кові (у середньому стержні більші ніж у крайніх), то границі теку чості напруження досягнуть не одночасно в усіх стержнях Спочатку при навантаженні Рі, настане пластична деформація в середньому стержні Зусилля в ньому
(18 6)
16 3-27М
481
При цьому, згідно з виразом (18 2),
Рн-Ц +2со5«а)атГ	(187)
Після появи пластичного течіння в середньому стержні конструк шя ще зберігає здатність сприймати навантаження, що зростає При цьому зусилля в середньому стержні залишається постійним і дорів нюс ЛГІТ Конструкція перетворюється на статично визначувану, і зусилля в крайніх стержнях визначається з умови рівноваги вузла (рис 493)
«, = N =	(18 8)
’	* 2с<йа	‘	'
Несуча здатність конструкції вичерпується тоді, коли йу крайніх стержнях напруження досягнуть границі текучості Навантаження, що відповідає цьому моменту, буде
Ргр = Ь 2Готсо8а — (1-| 2со5а)отГ (189)
Запас міцності при розрахунку за граничним станом
Очевидно, що Лгр > пт Наприклад, при а = 30° ЛпА, = 1,19. Отже, розрахунок за граничним станом дає змогу виявити захований запас працездатності конструкції
Визначимо запас міцності трисхідчастого бруса (рис 494), виготовленого з пластичного матеріалу
Розрахунок за допустимим напруженням Задача один раз статпч но невизначувана Умова рівноваги має такий вигляд
(і8 іі) умову
/?Л + /?а - 2Р = 0
Деформації ділянок бруса повинні задовольняти
Звідси випливає, що
/?х=-2-Л«	(18 12)
Підставляючи значення /?л у вираз (18 Н), знайдемо, що /?в = -5-Р	(18 13)
Ревкція верхнього закріплення
«л-4р
(18 14)
Ділянки І та НІ бруса стиснуті зусиллями N1 ==	(4/5) Р,
а ділянка Ні розтягнута зусиллям Мін = (6/5) Р.
Найбільші напруження виникають у поперечних перерізах верх ньої ділянки Ці напруження
Запас міцності за границею текучості
Л,= -Ь------Г-ЧА-	(18 16)
°ІІІ	0 Н
Розрахунок за граничним станом Насамперед з'ясуємо, який стан для розглядуваної системи буде граничним 3 розрахунку випливає, що в межах пружності ащ> о/ > он Тому при зростанні навантаження границі текучості спочатку досягнуть напруження на верхній ділянці Цей стан не призведе до вичерпання несучої здатності системи, оскільки нижні ділянки, що перебувають у пружному стані, будуть чинити опір навантаженню, яке зростає. Зусилля, що сприймається верхньою ділянкою, прн ньому постійне
Nиігр=“ Рл =	(18 17)
Ділянки і та II стиснуті зусиллям
У/ =Иіі~Кв=*2Р-Ка = 2Р—огР
(18 18)
При дальшому зростанні навантажень Р пластичний стан настане в нижній ділянці /, де напруження більші, ніж на ділянці Н Цей момент і відповідає вичерпанню несучої здатності системи, оскільки середня ділянка між пластично деформованими зонами не зустріне зрос таючого опору переміщенню
Отже, граничний стан системи характеризується появою текучості одночасно у верхній та нижній ділянках
Граничне навантаження знайдемо з умови
Звідси
Л’/гр Оіп>--------р~ в р
Ргр =
(18 19)
(І8 20)
Іб*
Запас міцності системи, навантаженої силами Р,
(18 21)
Порівнюючи формули (18 16) та (18 21), бачимо, що запас міц ності виявився більшим ніж прн розрахунку за допустимим напруженням
$114 Розрахунки при крученні
При крученні стержнів з круглим поперечним перерізом дотичні напруження в пружній зоні пропорційні відстаням точок перерізу від осі стержня (рис 495) і визначаються за формулами
а Ттах = Р	(18 23)
Коли крутний момент збільшується то пластичні деформації з’являються не відразу по всьому поперечному перерізу, а поступово, І із зростанням моменту поширюються від найвідда.леніших точок до осі стержня Внаслідок цього розрахунки на міцність за напружен рями в найбільш небезпечних точках і за граничним станом дають різні нез}льтати навіть у статично визначуваних системах Розрахунок аа граничним станом і в цьому разі дає змогу виявити додаткові резерви міцності
Розглядаючи кручення в пластичній зоні, будемо припускати, що залежність між дотичними напруженнями й відносним зсувом для на теріалу відповідає ідеалізованій діаграмі з необмеженою горизон тальною ділянкою (рис 496)
При деякому значенні крутного моменту = тт®’р напруження Тіш у найбільш віддалених точках перерізу досягнуть границі теку чості Внаслідок збільшення напружень в усіх точках що лежать ближче до осі, стержень збереже здатність сприймати зростаючий крутний момент У міру дальшого збільшення останнього зростання напружень припиняється в тих точках де вонидосягли границі теку чості, а в решті точок які утво рюють так зване пружне ядро, напруження зростають Епюру напружень, що відповідає цьому стану стержня наведено на рис 497, а Пружне ядро має радіус Г|
Коли пластична зона поши риться на весь переріз, несуча
Рис 495	Рнс 496
а	б	б
Рнс. 497
вдатність стержня буде вичерпана, оскільки далі він буде закручу ватися без збільшення крутного моменту Епюру напружень у цьому стані стержня зображено ня рнс. 497, б
Обчислимо граничний крутний момент ЛТгр, що відповідає вичер панню несучої здатності стержня
Виділимо в поперечному перерізі елементарну площадку у вигляді кільця завширшки (Ір (рис 497, е) Розмір площадки, ня якій діють дотичні напруження тт, становить ііЕ =» 2лр<ір, а момент від цих напружень відносно осі стержня буде т, 2лрагір
Крутний момент у перерізі дорівнює сумі всіх елементарних моментів внутрішніх сил Тому
лп
МГр = Ч2л ї рМр о або
Л1,р = т,~	(18 24)
Величина
(18 25)
називається пластичним моментом опору при крученні Тоді Мг, = ^впл	(18 26)
Знайдемо відношення граничного моменту Мгр та моменту Мг, при якому в перерізі вперше виникнуть напруження текучості
М V
-П> =	(18 27і
Підставивши значення ІР'рм = я^/12 та ІГр = шР/Іб, дістанемо
-Ж-= 4-	08 28)
або
Мг^^-М*'* 1.33М„	(1829)
Такий захований запас працездатності круглого стержня, що виявляється при переході від розрахунку за допустимими напруженнями до розрахунку за гранич ним станом
У скручуваних стержнів кільцевого поперечного перерізу розподіл напружень у пружній стадії'ближче до рівномірно* го, точу різниця в запасах міцності, що виявляється при розрахунку за гранич ним станом та за допустимими напруженнями, буде меншою
Як приклад розглянемо стержень круглого поперечного перерізу, КІНЦІ якого жорстко затиснуті (рис 498, д) У проміжному перерізі стержня прикла
дений скручувальний момент Мк Визначимо запас міцності при розрахунку за допустимим напруженням та за граничним стаї ом
Розрахунок за допустимим напруженням Розкриємо статичну не-визначуваиість при пружному стані матеріалу Позначивши реактивні моменти через Ма та Мв, дістанемо рівняння рівноваги в та кому вигляді
Мл + Мв Мл
Деформації повинні задовольняти таку умову ? =	=0
або Мла М$2д =
Звідси
Мл = 2МВ
Розв'язуючи разом рівняння (18 ЗО) та (18 32), знайдемо, що мя = мк, - і м„ мв = м„„ - 4"
Епюру скручувальних моментів показано на рис 498, б Найбільші дотичні напруження будуть на ділянці І.
— М'^ М* 2Мк _ 32ЛІК Тип» — в Гр = я<і» ~ Злі»
3-Ї6“
Розраховуючи за допустимими напруженнями, маємо
(18.33)
(18 30)
(18 31)
'Звідси запас міцності за границею текучості
Розрахунок за граничним станом При збільшенні скручувального моменту найбільші напруження на ділянці І досягають границі текучості, і далі зона текучості буде поширюватися до осі стержня Коли текучість охопить вбсь переріз, реактивний момент Ма досягне свого граничного значення
Млгр-т.Уял	(18 35)
або
Млгр = і,-^.	(18 36)
Цей стан не буде граничним для всього стержня, оскільки ділянка II, що перебуває в пружному або в пружно-пластичному стані (з пружним ядром), вбереже здатність чинити опір зростаючому моменту Мя Несуча здатність стержня вичерпається, коли й на ділянці II зона пластичності пошириться на весь переріз Реактивний момент Мв при цьому досягне свого граничного значення
А^отХ.,	(18 37)
або
(18 38)
Епюру крутних моментів у граничному стані стержня зображено на рио 498, в
Граничне значення скручувального моменту для всього стержня знайдемо з умови рівноваги (18 30)і
Мк гр = АІДгр 4- М&р
або з урахуванням виразів (18 36) та (18 36)
)Иьп, = т,^-.	(18 39)
Запас міцності
Отже, розрахунок за граничним станом показав, що запас міц ності стержня значно вищий ніж той, який дає розрахунок за допустимим напруженням (формула (18 34)] Відношення цих запасів міц ності Пгр/Лт ~ 1,78
Слід зазначити, що розрахунки за несучою здатністю цілком прийнятні при дії постійних крутних моментів
§115. Розрахунки при згинанні
У поперечних перерізах балки при згинанні нормальні напружен» ня в пружному стані матеріалу розподіляються нерівномірно, лінійно змінюючись по висоті балки (рис 499, а) Найбільші нормальні на* пруження в найвіддаленіших від нейтральної лінії точках поперечного перерізу визначаються за формулою
Птах в М№
При розрахунку міцності за допустимими напруженнями запас мш ності визначається як відношення границі текучості матеріалу до найбільшого напруження Цим самим як небезпечний вибирається стан балки, що відповідає досягненню найбільшими нормальними на пруженнями в небезпечних точках границі текучості Такий стан лише умовно можна вважати небезпечним Балка ще зберігає здатність сприймати згинальний момент, що збільшується
Визначимо граничний згинальний момент у разі чистого згннан ня Розглянемо спочатку балку, поперечні перерізи якої мають даі осі симетрії Границі текучості при розтяганні та стисканні будемо вважати однаковими
Після появи текучості в найвіддаленіших від нейтральної осі точ* ках перерізу при дальшому збільшенні згинального моменту пластичний стан матеріалу поширюється в напрямі до нейтральної осі До повного вичерпання несучої здатності балки в її поперечних перерізах будуть даі зони — пластична та пружна (рис 499, б) Граничний стан настане тоді, коли текучість пошириться на весь поперечний переріз, оскільки після цього дальша деформація балки відбувається без збільшення згинального моменту Епюру нормальних напружень у попереч ному перерізі для граничного стану показано на рис 499. в У розгля дуваному поперечному перерізі утворюється так званий пластичний шарнір, який передає постійний момент, що дорівнює граничному згинальному моменту
Граничний момент можна обчислити як суму моментів відносно нейтральної осі сил у поперечному перерізі (рис 499, в)
Мгр =	в °Т2 І У(іР = От25тах,	(18 41)
де 5ти — статичний момент площі половини поперечного перерізу відносно нейтральної осі
Величину 25л>іх називають пластичним момек том опору та позначають ІГ<и Тоді
Мг^а^пл	(18 42)
Для прямокутного поперечного перерізу зав ширінки Ь та заввишки А
Рнс 500

(18 43)
Небезпечний згинальний момент при розрахунку за допустимими напруженнями
М, = отГ
Відношення
(18 44) характеризує ступінь збільшення запасу міцності балки при переході до розрахунку за граничним станом Для балки прямокутного перерізу
упл _ ЬМ/4 . -1Г Ьй’/6 = ‘ 0
Для двотаврових прокатних балок у середньому їРпл/їР = 1,18 Якщо переріз балки має тільки одну вісь симетрії в площині на вантаження (рис 500), то в граничному стані нейтральна вісь не лрой де крізь центр ваги поперечного перерізу Положення нейтральної осі визначається з рівності нулю суми проекцій на вісь белки всіх сил а^Р, розподілених по її перерізу
(мг= (<миЧ	= 0,	(18 45)
де Т7! — площа розтягнутої зони перерізу Ря — площа стиснутої зони Звідси
— Ря = 0, або Рх = Ря,
тобто в граничному стані нейтральна вісь перерізу повинна ділити його площу навпіл
Граничний згинальний момент
МРр = |	= І + { (— От) (— У) АР — о, (5Р + 5ст), (18 46)
де — статичний момент розтягнутої зови перерізу відносно нейт ральної осі, 5сТ — статичний момент стиснутої зони перерізу віднос но тієї самої осі
У цьому разі пластичний момент опору
5р + «5с»	(18 47)

л
ІШІІШШШИ

Наведені міркування щодо визначення граничного стану, еквівалент ного утворенню пластичного шарніра > в поперечному перерізі балки, точно кажучи, справедливі лише для чистого згинання коли немає дотичних напру жень Визначення граничного стану 1 з урахуванням поперечної сили більш складне Це питання тут не висвітлюється
л Розглянемо приклад розрахунку - балки на згинання за допустимими напруженнями та за граничним ста ном без урахування впливу поперечної снти
Балка прямокутного поперечного Рис	перерізу, затиснута по кінцях, несе
рівномірно розподілене по довжині навантаження інтенсивністю? (рис 501 а) Визначимо найбільшу ін тенснвність цього навантаження, допустиму згідно з розрахунком за допустимими напруженнями та за граничним станом при одному і тому самому запасі міцності п
Розрахунок за допустимими напруженнями Балка статично невиз начувана її розрахунок істотно спрощується завдяки симетрії. Ви користовуючи методи гл 14, легко знаходимо зайві невідомі та будує мо епюру згинальних моментів (рис 501, а) Найбільший згинальний момент діє в опорних затнснутнх перерізах Мтвх = ?/8/і2
(18 48)
При збільшенні навантаження ? максимальні напруження в цих самих перерізах першими досягають границі текучості Вибираючи запас міцності за границею текучості таким що дорівнює п, знайдемо найбільшу допустиму інтенсивність навантаження з умови міцності]
Мтвх/Г^о^л	(18 49)
Ураховуючи, що V = ЬЛ’/6, а Мтіх =	12, маємо
=	(18 50)
Розрахунок за граничним станом Після появи пластичних деформацій у найбільш віддалених від нейтральної осі точках опорних перерізів дальше зростання навантаження призведе До утворення в цих перерізах пластичних шарнірів, а згинальний момент при цьому досягне граничного значення Мгр Тепер уже балка працює як шарнірно обперта, до якої на опорах прикладені постійні моменти (рис 501, б)
(18 51)
При дальшому збільшенні навантаження ці моменти зберігають своє значення, і задача стає статично невизначуваною В довільних перерізах балки згинальні моменти будуть зростати доти, доки посере дині прольоту момент не стане дорівнювати тому самому значенню ЛЛР, тобто доки не утвориться пластичний шарнір При цьому три пластичних шарніри розмістяться на одній прямій, тому дальше зрос тання навантаження неможливо Несуча здатність балки вичерпується
Умова рівності згинальних моментів в опорних перерізах та по середині прольоту має вигляд
І^-Мгр= Мгр,	(1852)
звідки знаходимо, що
(18 53)
Прирівнюючи праві частини формул (18 51) та (18 53), знайдемо
= 4а,	(18 54)
Вибираючи запас міцності таким, що дорівнює п, знайдемо най більшу допустиму інтенсивність навантаження
(18 55)
Відношення найбільших допустимих навантажень прн розрахуй ках аа граничним станом та за допустимими напруженнями
»Лі = 2
Розрахунок за граничним станом часто дає змогу виявити додат коні резерви міцності Як зазначалося вище, він дістав поширення при розрахунках будівельних конструкцій І дрцрлі більше застосовується в машинобудуванні Однак цей метод не слід вважати універсальним, здатним повністю замінити розрахунки за допустимими напруженнями
Розрахунок за граничним станом з певним запасом міцності не гарантує від появи місцевих пластичних деформацій Останнє ще до пустимо при постійних навантаженнях, які мають місце переважно в будівельних конструкціях При змінних навантаженнях на які найчастіше розраховують машинобудівні конструкції, поява піастич них деформацій здебільшого недопустима Тому в таких випадках розрахунок слід виконувати за допустимими напруженнями
Глава 19. СТІЙКІСТЬ СТИСНУТИХ СТЕРЖНІВ
$ 119 Стійка га нестійка пружна рівновага
' Виконуючи розрахунки на міцність та жорсткість при різних де формаціях, ми вважали що під час деформації будь якої системи мне місце лише одна наперед відома форма рівноваги Насправді ж у і‘‘-
^-^9* Р^ка формованому стані рівновага між зов-і	нішніми та спричиненими ними виутріш
м м ц |	німи силами пружності може бути не
।	'•X	тільки стійкою, а й нестійкою
И ! \ Пружна рівновага буде стійкою, якії	і що деформоване тілопри будь якому ма-
I	। | лому відхиленні відстану рівноваги на-
її	। / магаеться повернутися до початкового
х* 11 І/ стану й повертається до нього після при пинення зовнішнього впливу, який пору л /7 и шив початковий стан рівноваги “	0	0	Пружна рівновага нестійка якщо
Р«С- 8СЙ	Деформоване тіло, виведене з неї будь
якою зовнішньою Дією продовжує деформуватися в напрямі наданого йому відхилення й після припинен ня зовнішньої дії у вихідний стан не повертається
Між цими двома станами рівноваги існує перехідний стан, який зветься критичним при якому деформованетілоперебуваєубайдужій рівновазі) воно може зберегти вихідну форму, але може й втратити її внаслідок самого незначного впливу
Стійкість форми рівноваги деформованого тіла залежить від прикладених до нього навантажень Наприклад, якшосили, що стискають стержень, невеликі, то вихідна форма рівноваги залишається стійкою (рис 502, а) Прн зростанні прикладених сил досягається стан бей-дужої рівноваги, при якому поряд з прямолінійною формою стержня можливі суміжні з нею злегка викривлені форми рівноваги (штрихові лінії на рис 502, б) При дальшому найнезначнішому збільшенні на вантаження характер деформації стержня різко змінюється — стер жень випучується (рис 502, а), прямолінійна форма рівноваги перестає бути стійкою Це означає, шо навантаження перевищило критичне значення
Навантаження, перевищення якого спричинює втрату стійкості вихідної форми тіла, зветься критичним І позначається Р^
Можна стверджувати, що досягнення навантаженнями критичних значень рівнозначно руйнуванню конструкції, оскільки нестійка форма рівноваги неминуче буде втрачена, що пов'язано з практично необмеженим зростанням деформацій та напружень Особлива небезпека руйнування внаслідок втрати стійкості полягає в тому, що, як правило, воно відбувається раптово й при низьких значеннях напружень, коли міцність елемента ще далеко не вичерпана
До моменту настання критичного стану пружні деформації за моду лем зовсім невеликі, І зростання їх майже непомітно для ока Проте з моменту настання критичного стану до моменту руйнування залиш кові деформац ії наростають надто швидко, й практично немає часу вжи ти заходів щодо запобігання катастрофи, яка загрожує Отже, при розрахунку на стійкість критичне навантаження подібне руйнуваль-492
йому при розрахунку на міцність Для забезпечення певного запасу стійкості необхідно, щоб задовольнялася умова
(19 1)
ТїІ	|Р|	(19 2)
де Р — діюче навантаження Пс? — коефіцієнт запасу стійкості
Отже щоб розрахувати стиснуті стержні на стійкість треба ви вчити способи визначення критичних навантажень Ркр
З усієї різноманітності розрахунків на стійкість пружних систем докладно розглянемо лише приклад втрати стійкості прн стисканні довгого тонкого стержня, або так зване поздовжнє згинання
$ 117. Формула Ейлера для визначення критичної сили стиснутого стержня
Припустимо, шо ПІД дією сили Р, яка дещо перевищує критичну силу Ркр, стержень з шарнірно закріпленими кінцями (рис 503, а) трохи зігнувся (рис 503 б) Віднесемо викривлену вісь стержня до прямокутної системи координат, вибравши початок координат у точ ці О
Припустимо що критична сила Рхр ис спричинює в стержні напружень які перевищують границю пропорційності і що розглядаються лише малі відхилення від прямолінійної форми Тоді для визначення поздовжньої сили можна скористатися наближеним диференціальним рівнянням (10 44) пружної лінії
ЕЛ.І. =±ММ	(19 3)
Тут Лпіп — найменший момент Інерції пе рерізу стержня
Ураховується найменша жорсткість стержня £Лпіп оскільки, очевидно, прогин відбудеться перпендикулярно до осі най меншої жорсткості, якщо решта умов для згинання в усіх площинах однакові, як у розглядуваному прикладі
На відміну від поперечного згинання при поздовжньому в правій частині цього рівняння слід ставити знак «мінус», оскільки абсолютне значення згинального моменту
|М(Х)| -|Й0|,	094)
а знак прогину завжди протилежний знаку другої похідної, тобто знаки моменту М (х) та другої похідної (РиіІйзР протилежні при будь якому напрямі ш
Рис, 503
Підставивши в рівняння (19 3) вираз (19 4) для згинального момен-		
ту, дістанемо		(19 5)
або	Й’® . Р	п V +	“ “°	(19 6)
Ввівши позначення	с^тіп	(19 7)
перепишемо рівняння (19 6)і		
		(\9 В)
Ми дістали однорідне лінійне диференціальне рівняння загальний інтервал якого, як відомо, можна виразити гармонічною функцією
ш = .4 зіп Ах + В соз Ах	(19 9)
Сталі інтегрування А та В повинні добиратися так, щоб задовольнялися граничні умови
ш(х)|х-о = О, »(х)|г»/«»0
З першої граничної умови випливає, що В = 0, тобто
и>(х) = А$їпкх	(19 10)
Із другої умови знайдемо
АгіпйівО	(19.И)
Якщо припустити, що А 0, то прогин буде тотожно дорівнювати нулю, тобто
Ш (х) а 0
Цей розв'язок відповідає одній з можливих форм рівноваги стиснутого стержня, а саме — прямолінійній формі Нас же цікавить значення сили Р, при я кому стає можливою друга форма рівноваги — криволінійна Оскільки А =£ 0, то при викривленій формі стержня повинна виконуватися рівність
зіп кі = 0
Корінь цього рівняння кі може мати нескінченну кількість значень! 0; я, 2я ; ял, тобто
кі = ля, де л — довільне ціле число
Однак перший корінь кі == 0 відкидається, оскільки він не відповідає вихідним даним задачі Отже,
А’/’-л’я1	(19 12)
Тоді з рівняння (19 7) дістанемо вираз для стискальної сиди
(19 13)
Рівняння (19 13) є формулою що впер ше була виведена Ейлером
Практично нас цікавить найменше значення поздовжньої стискальної' сили, при якому стає можливим поздовжнє зги нання Найменше значення критичної сили Рпр дістанемо при п = І та АІ — л
(19 Н)
Повертаючись до рівнянь (19 10),
(19 12), запишемо рівняння зігнутої осі Рнс 504 Рнс 505 стержня прн малих деформаціях
, , Л . лях ш(х) — А 51П ——
Найб ЯЬШНЙ прогин стержня Мін } при 5ІП (лях/і) = І Тоді и> (х) = и>пах = }= А Отже рівняння пружної лілії стиснутого стерж ня має вигляд
о> =- / $іп	(19 15)
Графік цієї залежності показано на рис 504 Максимум ш має місце при такому значенні х для якого = 0, тобто
Найменше значення аргументи при якому хосипус дорівнює нулю, буде л/2, отже пххії - п/2, звідки
ж =4-	(19 16)
Якщо п = І, тох = 112, а максимуми» має місце посередині стержня, що відповідає так званому основному випадку, показаному на рис 503
Із '’піввідношення (19 16) або з рівняння (19 15) та рнс 505 випли ває, що п є числом півхвиль синусоїди, які розташовані на довжині зігнутого стержня
§ 118. Вплив умов заерЬілення кінців стержня на значення критичної сили
У § 117 розглянуто так званий основний випадок навантажування й закріплення кінців стиснутого стержня — стержня з шарнірно обпертими кінцями Як було показано, після втрати стійкості на довжи
а
Рис
506
ні стержня укладається тільки одна півхви-ля (л = і)
Розглянемо інші приклади закріплення кінців стержня
1 Стержень завдовжки / закріплений од ним кінцем та стиснутий поздовжньою силою, прикладеною до вільного кінця (рис 506, а) Порівнюючи рис 506, атаб бачимо, що зігну та вісь стержня, закріпленого одним кінцем, перебуває в тих самих умовах, що і верхня половина стержня завдовжки 21 з шарнірно закріпленими кінцями Отже, критична сила Для стержня з одним закріпленим а іншим вільним кінцем така сама, як І для стержня з шарнірно обпертими кінцями при довжині 1 = 2/ тобто
Р*
(»)• її1
(19 17)
При цьому зігнута вісь стержня (рис 506, а) має вигляд половина півхвилі синусоїди
2 Стержень завдовжки І, в якого обидва кінці жорстко закріплені (рис 507) Після втрати стійкості стержня внаслідок симетрії його середня частина завдовжки 1/2 працює в тих самих умовах, шо і стер жень при шарнірно обпертих кінцях При цьому утворюються дві півхвилі середня завдовжки 4 = і/2 та дві крайні половинки лів-хвилі завдовжки 1/4
Критичну силу в цьому разі знаходимо з рівняння (19 14) яри
гнр ------Ті---
(19 18)
З Стержень завдовжки / закріплений одним кінцем та шарнірно
обпертий на іншому (рис 506) Після втрати стійкості права частина СВ стержня має вигляд півхвилі синусоїди Порівнюючи рис 508 та 506, б, бачимо що ділянка СВ завдовжки 4 =
0,71 перебуває в тих самих умовах, що і стер-
0,71
Рис. 608

Рас. 507
Рас. 510
жень з шарнірнозакріпленими кінцями Отже,
Р^ = -7БЯГ- 09 19)
Співвідношення (19 14), (19 17)	(19 19) можна об єднати в одну
формулу
де V/  ізл ~~ зведена довжина стержня, І — фактична довжина стерж ня V- коефіцієнт зведення довжини
Отже р’^ні випадки обпирання та навантажування стержня зводяться до основного випадку введенням у формулу для Рйр так зва лої зведеної довжини = уі Це поняття вперше було використано Ф С Ясннським
З формули Ейлера (19 20) видно, то критичне навантаження за лежить від найменшої жорсткості £7т|л, Довжини стержня / та коефіцієнта V
На рис 509 наведено значення V для розглянутих стержнів Проте такі розрахункові схеми на практиці нечасто зустрічаються в чис тому вигляді Найчастіше закріплення кінців бувають пружними Найбільш поширені такі випадки пружного закріплення кінців
а)	один кінець стержня жорстко закріплений, а інший пружно обпертий
б)	обидва кінці пружно закріплені
Розглянемо перший випадок (рис 510) Після втрати стійкості пружно обпертий кінець стояка переміщується у вертикальному на прямі на величину (в, при цьому виникає пружна ревкція Рв Ця реакція пропорційна відхиленню (в
Яв - с(в,
де с — коефіцієнт пружності опори В
Складемо диференціальне рівняння пружної лінії стиснутого стержня після втрати стійкості
= РпЯа-иіу-сІоіІ-х)	(19 21)
Поділивши почленно на та позначивши, як звичайно е У- = «*п»іп = А*, дістанемо
т£-‘’т£г<'~'> або
ТГ^ + Р-^-х	(19 22)
Загальний інтеграл цього диференціального рівняння
ю = СзіпАх Ч-ОсозЛхЧ- /в/і-4-/ех (19 23)
\ Г«ф І *хр
Для визначення сталих інтегрування і критичного навантаження маємо такі граничні умови прн х = 0
ш(0) = шд = 0;	(19 24)
^- = Є(0) = Є„.= 0,	(1925)
При X = /
ш (/) = шв«» /в	(19 26)
Використовуючи граничну умову (19 24), з рівняння (19 23) знаходимо
Ч-Чг')-
Щоб застосувати граничну умову (19 25), обчислимо похідну від переміщення ш
“• = кС соя кх— кО зіп кх + -у—/в, ах	г«р
звідки при х = 0
ІіС + ^Іа^О, або С =-----~ Ів
гмр	ч/кр
Підставивши добуті вирази для довільних сталих у формулу (19 23), дістанемо остаточне рівняння зігнутої осі стиснутого стержня ш(х)=_-^.;в3іп^л_/вр--------------2__/)со8*х і-
+ /41 --5Г- +	(1927)
\ гнр / “кр
Граничну умову (19 26) використаємо щоб вивести рівняння, яке дає змогу визначити критичне навантаження Поклавши в рівняній
(19 27) х = Л знаходимо, що
а>(0 = —/взіпйі —Мр — -£~ 1)совМ +
+ М(1--7Г^)+-7Г^М'=М. або
— -ту—зіп Я -{1 —-4—Ае<к6| =0, \	'«р і
ВВІДКИ
(19 28)
Якщо розв'язати ае рівняння, тобто визначити найменший корінь к то тим самим можна знайти значення критичного навантаження. ОСКІЛЬКИ
Лф — РЕЛіІп
Розглянемо два граничних випадки Поклавши с — 0 матимемо кі = оо, тобто кі = п/2,
і приходимо до такої розрахункової схеми стержня, коли один кінець (лівий) жорстко закріплений, а інший (правий) вільний Критична сила
Поклавши с •= оо (дууе жорстка опора), дістанемо визначальне рівняння
тобто кІ~ 4,493 = л/07
Критична сила
що дає формулу для стержня, один кінець якого закріплений, а ін ший — шарнірно обпертий
Отже якщо коефіцієнт пружності опори с змінюється від нуля до нескінченності, то це можна врахувати коефіцієнтом зведення V, який при цьому відповідно змінюється від 2 до 0,7
$ 119 Поняття про втрату стійкості при напруженнях, що перевищують границю пропорційності
Виведення формули Ейлера грунтується на застосуванні диферен ціального рівняння пружної лінії Тому скористатися цією формулою можна лише тоді коли справедливий закон Гука, тобто доки критичне напруження (напруження стискання, що відповідає критичній силі)
О Я ЮО іІОк Рис 511
пе перевищує границі пропорційності
а*Р ~ р °пи	(19 29)
Дійсно якщо прямолінійна форма стержня залишається стійкою й ори напруженнях, що перевищують границю пропорційності, то диференціальне рівняння (19 3), що передбачає спра
вадливість закону Гука, вже непридатне
Виведемо формулу для критичного напруження окр Відповідно до виразів (19 29) та (19 20)
гт ^хр __ ЛІ^тИі _
Скр= р —
Тут Iі = Ліп = ^іп/Р — квадрат найменшого з головних інерції стержня, Е ~ Евр — площа брутто поперечного стержня
Ввівши безрозмірну величину
X — УІ/І,
що називається гнучкістю стержня, остаточно знайдемо
(19 ЗО) радіусів перерізу
(1931)

(19 32)
тобто критичне напруження стержня залежить тільки від пружних властивостей матеріалу (модуля пружності Е) та гнучкості стержня 1
Функціональна залежність (19 32) становить видозміну формули Ейлера У системі координат акр ~ цю залежність можна подати у вигляді гіперболічної кривої, що зветься гіперболою Ейлера Як приклад наведемо такий графік (рис 511) для стержня із стелі марки СтЗ для якої модуль пружності Е = 2,1 10і* МПа, границя текучості ат = 240 МПа, а границя пропорційності Огт 200 МПа Графік показує, що в міру зростання гнучкості стержня критичне напруження прямує до нуля і навпаки, в міру наближення гнучкості стержня до нуля критичне напруження прямує до нескінченності
Однак з умови (19 29) застосованості формули Ейлера відповідно до формули (19 32) маємо
я*Е
Окр — 	' ^<Тпц,
І, отже,	____
^і/хг	<19 33>
Це означає, що формула Ейлера стає непридатною при гнучкості стерж ня, меншій за граничне значення Ігр, яке залежить тільки від властивостей матеріалу, тобто в розглядуваному прикладі прн
Таблиця 19
Матеріал		а	Ь	
		МП1	
Ст2 СтЗ	100	310	1 14
Стб	100	464	326
Сталь 40	90	321	1 16
Кремениста сталь	100	589	3 82
Деревина (сосна)	ПО	293	0 194
Чавун	80	776	12 0
Те саме можна дістати і графічно Якщо на осі ординат (окр) від класти значення границі пропорційності (ага — 200 МПа) і провести із здобутої точки К. пряму, паралельну осі абсцис, то вона в перетині з гіперболою Ейлера дасть точку М, абсциса якої і є Лгр Ліворуч від точки М гіперболу Ейлера показано штриховою лінією ос кільки вона тут дає значення напружень, вищі за границю пропорційності, тобто такі що не відповідають умовам й застосування
Проте явище поздовжнього згинання продовжує існувати й за границею пружності Дослідами встановлено, що дійсні критичні нап руження для стержнів середньої та малої гнучкості	менші,
ніж визначені за формулою Ейлера Отже, в цьому разі формула Ей лера дає завищені значення критичної сили тобто завжди переоцінює дійсну стійкість стержня Тому використання формули Ейлера для стержнів, що втрачають стійкість за границею пружності, не тільки принципово невірно, а й дуже небезпечно за своїми наслідками
Теоретичне розв язання задачі про стійкість за границею пропор ційності складне, тому, як звичайно, користуються емпіричними формулами здобутими в результаті обробки багатьох дослідних да них
Ф С Ясинсьхий зібрав та обробив великий дослідний матеріал щодо поздовжнього згинання стержнів, у результаті чого склав таблицю критичних напружень залежно від гнучкості для низки матері злів та запропонував просту емпіричну формулу для обчислення кри тичних напружень за границею пропорційності
Окр=д_ІХ	(19 34)
Значення коефіцієнтів а та Ь для деяких матеріалів наведено в табл 19
Для чавуну користуються параболічною залежністю
Окр = а—614- сХ1,	(1935)
де с = 0 53
За цими даними для кожного матеріалу при 0 < 1 < Хгр можна побудувати графік залежності критичних напружень від гнучкості стержня
При деякому значенні гнучкості (позначимо його Ід) напруження а<р, обчислене за формулою (19 34) або (19 35), стає таким що дорівнює граничному напруженню при стисканні, а саме для пластичних матеріалів
окр = ат,
а для крихких матеріалів
Окр = о,	(19 36)
Стержні, в яких X < Хд, називають стержнями малої гнучкості» їх розраховують тільки на міцність
У розглядуваному прикладі (рис 511) частина графіка критичних напружень за границею пропорційності (прн 40 < Х< 100) має вигляд злегка нахиленої прямої 5 Л1, а частина (при 0 < X < 40) — горизонтальної лінії ^5 Отже, графік амр == / (X) для сталі СтЗ скла дається з трьох частик гіперболи Ейлера при X 100, похилої прямої при 40 < X < 100 та майже горизонтальної прямої прн X < 40 Похила пряма 8М відповідає напруженням між границею пропорційності і границею текучості Горизонтальна пряма 8М відповідає напруженню, що дорівнює границі текучості
$ 120 Розрахунки иа стійкість за допомогою коефіцієнтів зменшення основного допустимого напруження
Можна вважати що центрально стиснуті стержні втрачають свою несучу здатність від втрати стійкості раніше, ніж від втрати міцності, оскільки критичне напруження завжди менше за границю текучості або границю міцності
О«р Оц,
де о„ = от — для пластичних матеріалів, ов = <т» — для крихких матеріалів
Слід нагадати, що для стержнів малої гнучкості (X < Хд) важко казати про явище втрати стійкості прямолінійної форми стержня, як це має місце для стержнів середньої та великої гнучкості Несуча здатність стержнів малої гнучкості визначається міцністю матеріалу
Критичне напруження для центрально стиснутих стержнів середньої та великої гнучкості, мабуть, більш небезпечне, ніж границя текучості для пластичних матеріалів або границя міцності для крих них матеріалів при простому розтяганні Очевидно, що при практик йому вирішенні питання щодо стійкості стержня не можна припустити виникнення в ньому критичного напруження, а слід взяти відповідний запас стійкості
Щоб визначити допустиме напруження на стійкість, треба вибрати коефіцієнт запасу п„ Тоді
[ост] — Окр/Псї	(19 37)
Таблиця 20
Рвучкість	Коефіцієнт ф				Гнучкість	КоефІ ііінт ф			
	Ст? СтЗ Сті	Сті	Чавун	Дере екна		Ст? СтЗ сн	Ст9	Ч« уа	"іинТ
О 43 — 0,25 О 36 — 0 22
10 20 ЗО 40 ЬО 60 70
60 90
100
1,00 0 99 0,96 0,94 0,92 0,89 086 0 8!
0.75,
085 0,82 0 76 0 70 082 0 51
0,97 0,91 0 81 0,69 0 67 0,44 0 34 0 26 0,20 О 16
0 97 093 0,87 060
0,48 038 0,31
120 130
140 160 150
170 180 190 200
0,45' 0,401.
0,26
0,19
0,24	-	0,12
021	-	0 11
0,19	—	0,10
0 17	-	0 09
0 16	—	0 08
Коефіцієнт запасу на стійкість беруть дещо більшим, ніж основний коефіцієнт запасу на міцність (л^ і» л). Це обумовлено тим, що для центрально стиснутих стержнів низка обставин, неминучих на практи ці (ексцентриситет прикладання стискаїьинх сил початкова кривизна і неоднорідність стержня), сприяють поздовжньому згинанню, тоді як при інших видах деформації ці обставини майже не відбиваються Коефіцієнт запасу стійкості для сталей вибирають у межах 1,8 3 0, для чавуну — 5 0 5,5, для деревини — 2,8 3,2 Зазначимо, що менші значення п„ вибирають для більшої гнучкості
Допустиме напруження на стійкість [<т6Т1 « та допустиме напруження на міцність при стисканні [о ] = ая/п взаємно лов я-зані Складемо відношення і
•£т = ЧЛІ--	093»
Позначивши
аи Леї “ф’ матимемо
1ост]=<р[а_]	(19 39)
Тут ф — коефіцієнт зменшення основного допустимого напруження прн розрахунку на стійкість Цей коефіцієнт для кожного матеріалу можна обчислити при всіх значеннях гнучкості X й подати у вигляді таблиці або графіка залежності ф від X Значення коефіцієнта ф для сталей, чавуну та деревини наведено в табл 20 Користуючись аналогічними таблицями, можна досить просто розрахувати стержні на стійкість
Складемо умову стійкості стиснутих стержнів О Сієсті
(19 40)
Оскільки о = ЛГ/Лср, а їсте] = ф то умова стійкості набирає вигляду о =» Л0Гвр<фІа_}
При розрахунку на стійкість місцеві ослаблення_
практично не змінюють значення критичної сили, тому в розрахункові формули вводиться повна площа Евр поперечного перерізу
Розглянемо два види розрахунку на стійкість стиснутих стержнів—перевірний та проектувальний
Перевірний розрахунок стиснутих стержнів. Порядок перевірного розрахунку на стійкість при використанні таблиці коефіцієнтів ф такий
1) виходячи з відомих розмірів та форми поперечного пе-
(19 41) перерізу
Рис 512
рерізу, визначаємо найменший осьовий момент інерції /тш» площу Р&-,, обчислюємо мінімальний радіус інерції
та гнучкість
Ітіп — V Етіп/Евр в ТЇ/Їщіп»
2) за таблицею знаходимо коефіцієнт ф та обчислюємо допустиме напруження на стійкість за формулою
кет] = ф
3) порівнюємо дійсне напруження а ® Р/Ее? з допустимим напруженням кет] на стійкість
о<(о„|
Приклад 75 Перевіримо на стійкість стиснуту дерев'яну колону (рис, 612) квадратного поперечного перерізу (а = 15 см) завдовжки і = 5 м. якщо основне допустиме напруження і<гЛ = 10 МПа, а стискальна сила Р = 100 кН
Визначаємо такі величини
— площу —
— момент ІнероЛ —
— радіус Інерції —
Р = в1« 225 см*, а* 15* 1 ®	“ —$  см* = 4210 см*,
С«К77р«в/КП-4,34 см
— зведену довжину — =• V/« 0,11 - 0,7 • 5 м = 3.5 м « 350 см,
— гнучкість —
—ЇХ-80’6’
За табл 20 Інтерполяцією знаходимо що
0.48 — 0.38
<р = 0,48 - ‘	ц*” 0,6 = 0,474
Тоді
[0„] “ ФІО-]“ 0.474 . 10,0 = 4 74 МПа
Р	100 10-3
в - ТГ - ТТг ,гд- МПа = 4,44 МПа а	225 10“*
Оскільки о = 4,44 МПа < 4 74 МПа то стійкість колона забезпечено.
Проектувальний розрахунок У розрахунковій формулі на стій* кість	~
□ =^<10.1 або	(1942)
е дві невідомі величини — коефіцієнт ср та шукана площа брутто АсР поперечного перерізу Тому при доборі перерізів слід користуватися методом послідовних наближень, варіюючи значення коефіцієнта ф Як правило, в першій спробі беруть ф, — 0,5 0,6 Вибираючи будь-яке з цих значень фь визначають потрібну площу Гвр та добирають переріз Вибраний переріз перевіряють та визначають фактичне зна чення фі Якщо фі значно відрізняється від ф( то й напруження відрізняється від допустимого Тоді слід повторити розрахунок, тобто вробити другу спробу, взявши середнє за модулем значення між ф1 та фі
У результаті другої спроби визначають ф, Якщо потрібна третя спро-бе, то
Ф* + Ф2
Фз =-----7-----
1 т д Як правило, при доборі перерізів потрібно не більше ніж ДВІ-три спроби
Приклад 7в Доберем за сортаментом двотавровий лоперлний переріз стержня завдовжки 5 м, що зазнав дії центрального стискального навантаження ЗгО кН Обидва кінці стержня затиснуті Матеріал — СтЗ Основне допустиме напруження = 160 МПа
Визначаємо розрахункову зведену довжину стержня
(а = VI = 0,5 500 см = 250 см
Добираємо поперечний переріз за методом послідовних наближень
Перша спроба вибираємо Фі = 0 5 потрібна площа поперечного Перерізу
Г ~ фКЇ “ ЇМ ‘ ’ 10-3
За озртамектом вибираємо двотавр № 27 з площею Р = 40,2 см’ та мінімальним радіусом Інерції' 1т[п = Іт = 2 54 см Гнучкість стержня
1—98-5-
За табл 20 при лінійній Інтерполяції
_	0 54-0614
Перейдемо до другого наближення взявши ф, =---------я> 0,657. Потріб-
на наоша поперечного перерізу стержня „	320	_
^“0557 16-10» и, = 3’в 10-3 “ “36 см*
За сортаментом вибираємо двотавр № 24а з площею Е “ 37,5 см* та мінімальним радіусом Інерції Іт|0 “ /„ = 2 63 см Гнучкість стержня
За табл 20 знаходимо коефіцієнт <рг
Ф2 = 0,69-------зд-2— 5 = 0 645 > Ф» ав 0.557.
Переходимо до третього наближений, взявши 0 557 + 0 645
------і-------- а. ҐІ ЯЛ
3,33 - ІО-3 м»
Фз =
Обчислюємо Потрібну площу 320 Р “ 0.60_1,6 10»
За сортаментом вибираємо двотавр № 24 з площею Р =• 34,8 см* та мінімальним радіусом інерції /Ш|П = і„ = 2,37 см Гнучкість стержня
{аа 250
* “ '»|. " 2.37 “ "®
Для Х= 105 коефіцієнт
0,60 — 0,52 ІЗ
Обчислюємо напруження Р 320 10“3 ------------------------------------ МПа = 164 МПа.
° = <РР = 0,66 - 34 ;
Перенапруження становить 164—160 _ -------------------------------100 % » 2 5 %
Остаточно вибираємо для стержня двотавр № 24.
9 121. Про добір матеріалу І раціональних форм поперечних перерізів дяа стиснутих стержнів
Для стержнів великої гнучкості (X > Хгр). коли критичні напру ження не перевищують границі пропорційності матеріалу, модуль пружності Е е єдиною механічною характеристикою, що визначає опірність стержня втраті стійкості У цьому разі недоцільно застосо вувати сталь підвищеної міцності, оскільки модулі Е для різних сталей практично однакові
Для стержнів малої гнучкості застосування спеціальних високосортних сталей доцільно, оскільки в цьому разі підвищення гра іиці текучості сталі збільшує критичне напруження, а отже, І запас стій кості
З погляду економічності раціональніша така форма поперечного перерізу стержня, при якій найменший радіус Інерції ітіп при пев ній площі е найбільшим Для зручності порівняння різних перерізів введемо безрозмірну характеристику
- Е, яку можна назвати питомим радіусом Інерції Нижче наведено значення £ для деяких перерізів
Переріз
1 рубчастий (а* = 0,95.. 0,8) » (а = 0,7 0,8)
Кутник Двотавр Швелер Квадрат Коло Прямокутник (А = 26) 1 а =
2,25 .1,64
1,2 1,00 0 5 0,3 0,41 0 27 0 41 0.29
0,289 0 293
0204
Аналіз даних показує, що найбільш раціональні трубчасті тонкостінні перерізи Так само раціональні й коробчасті тонкостінні перерізи Однак слід зазначити, що при проектуванні тонкостінних трубчастих та коробчастих перерізів необхідно передбачати встановлення діафрагм (ребер жорсткості) на певних відстанях уздовж стержня Ці діафрагми перешкоджають появі місцевих деформацій (жолоблення стінок) Найменш раціональні суцільні прямоку'ні перерізи
При розрахунку стиснутих стержнів на стійкість слід прагнути до того, щоб вони були рівностійкнми в усіх напрямах Для цього проектувати перерізи треба таким чином, щоб моменти інерції були по можливості однаковими Трубчасті перерізи раціональні й з цієї точ ки зору Цьому критерію відповідають також квадратні та круглі перерізи. Нераціонально застосовувати двотаврові перерізи та перерізи у формі прямокутника
Однак якщо зведені довжини в головних площинах різні, то й головні моменти інерції також слід проектувати різними, з тим шоб гнучкості стержнів в обох головних площинах були однаковими або хоч би близькими між собою Якщо не вдається зробити гнучкості однаковими, то розраховувати слід за максимальною гнучкістю
9 122. Поздовжньо-поперечна згинання
Згинання прямого бруса зветься поздовжньо-поперечним, якщо в його поперечних перерізах виникають згинальні моменти як від поздовжніх так і від поперечних навантажень (рис 513) При розрахунку на поздовжньо-поперечне згинання згинальні моменти в поперечних перерізах обчислюють з урах$ ванним прогинів осі бруса
|Ма|=|М|+[5®п|,
(19 44)
де М„ — повний згинальний момент; М — момент від поперечного навантаження, — додатковий згинальний момент від дії осьової сили $
Обчислення повного згинального моменту Ліо ускладнюється тим, що в цьому разі принцип незалежності дії сил застосувати немож на Дійсно, повний прогин иь можна розглядати як такий, що склада ється з прогину и>, спричиненого дією тільки одного поперечного на вантаження та додаткового прогину ш„ — спричиненого силою 5 Очевидно що кати осьові сили стискальні, повний прогин більший за прогин від одного тільки поперечного навантаження
Точний спосіб розрахунку Визначення повного згинального моменту Мп за цим способом проілюструємо на консольній балці (рис 514) Нехай на балку діє стискальна сила 5 та поперечні наван таження момент Мо та сила Ро прикладені на вільному кінці, який збігається з початком координат
У цьому разі диференціальне рівняння (10 44) пружної лінії запишеться так
де Мп (х) — повний згинальний момент у довільному перерізі балки

9^2
Рис 513
Рис 514
При складанні виразу Ма (х) який підставляється в праву частину рівняння (19 45і для згинальних моментів, спричинених поперечини навантаженням, зберігається звичайне правило знаків, а момент від стискальної сили £ записується із знаком «мінус», оскільки (Рив/іІх* та ш завжди мають протилежні знаки Для нашого прикладу вираз (19 44) слід переписати так
И - М (») - 8ш„ - М„ -г Р„х і- З (», — ш„)	(19 46)
Продиференшювавши вираз (19 46) по х двічі, матимемо
(*)   о	(*)	/іп д-чк
і? д	а?
Підставивши сюди вираз для <і*шп/4х* із рівняння (19 45), запише мо
- — З "•$	(19 48)
Ввівши позначення
тг -	(19 49)
дістанемо диференціальне рівняння для згинальних моментів
4>Л4„«~0	((9 50)
Загальний інтеграл рівняння (19 50) буде такий
М„(х) — А соз Ах + В зіп кх	(і9 51)
Продиференціювавши рівняння (19 51) по х, дістанемо рівняння для поперечних сил
0п(х) = — Л48ІпАх + ВАсозАх	(1952)
Фізнчіпіи зміст ста тих інтегрування визначимо, розглядаючи початкові 5 мови при х = 0
Ма(0)^А	(19 53)
<?П(О)-ВА	'	(19 54)
Ці початкові значення Мп та назвемо початковими параметрами * позначимо через М„оч та фпоч відповідно Тоді рівняння згинальних моментів при поздовжньо поперечному згинанні набере вигляду
ЛГВ (х) = Мпоч соз кх + зіп кх	(19 55)
Щоб здобути загальне рівняння дія згинальних моментів при дії стискальної сили та різних зосереджених або розподілених зовніш ніх навантажень, можна застосувати метод початкових параметрів Дійсно, рівняння (19 55) складено з урахуванням одночасної дії поз довжньої сили та поперечних навантажень і, отже, тут можна засто
Рис 515
суватк принцип незалежності та додаваная дії сил.
Розглянемо балку, навантажену такими поперечними наван х таженнями (рис 515) силами Ро та Р|, моментами Мо та Мь роз-поділеним навантаженням Прикладемо також стискальну осьову силу $
Щоб знайти вираз для згинальних моментів Мп (х) на крайній правій (тобто V) ділянці бал ки, будемо міркувати таким чином Спочатку припустимо, «ю ніяких навантажень (Р{, М, та 9і), за винятком початкових, не-
має Тоді момент .Мп (х) виражатиметься як функція від початкових параметрів М»,, <?по« та абсциси х за формулою (19 55) Нехай тепер початкові параметри дорівнюють нулю, але діють зосереджені навантаження Р( та Мі Виходячи з геометричного та статичного змісту цих силових факторів, приходимо до висновку, що їх можна вибрати за нові початкові параметри, якщо перемістити початок координат відповідно розташуванню цих силових факторів — у точки з абсцисами а» чи відповідно Тоді аргументами тригонометричних функцій у формулі (19 55) будуть відрізки
(х —я,) (х— Ьі),
і рівняння для згинальних моментів иабаре вигляду р,
Ма (х) = Мі соз к (х — аі) +	зіп к (х — Ьі)	(19 5б)
Якщо сил та моментів на ділянці х кілька (т), то слід ввести суми. Тоді матимемо
Ма(х) = ^М1созЛ(х — а,)+ 5,зіпк(х —	(19 57)
При дії розподіленого навантаження д (х) друга складова перетворюється на інтеграл від елементарних силових факторів дйц (рис 515)
У -р зіп к (х — п) (соз к (х — 4) — соз к (х — с>]. (19 58)
Ураховуючи одночасну дію всіх зазначених силових факторів, у тому числі й початкових параметрів Мт>ч та От», здобудемо уні нереальне рівняння для моментів прн поздовжньо-поперечному 510
вгинанні
ЛТв(х) = Мпо. СО5^Х-+- -^р-зіпйх + £м, соз к (х~аі) +
І	— м+ £тгІсиі(х~<У-е<»*(ж-<:,)| (19 59)
Продиферениіювавши це рівняння по х, дістанемо рівняння для поперечних сил
30(х) — — Мпо,Й51п£х + <?пояСО$йХ — 2] ЛїіАзіпЛ(х—в|)4-
+ £р(созЬ(х -ь,)— £-^-(зіпй(х—гі,) — зііій(х — с()] (19 60) Порядок застосування цнх рівнянь для розв язання задач принципово такий самий, що і в розглянутих раніше прикладах застосування початкових параметрів (див гл 10)
Початкові параметри визначаються з крайових умов балки За
гальний вигляд цих умов такий
а) для шарнірно обпертої балки
М„(0) »	(19 61)
М„ (Л=МП0,(ї)	(19 62)
при відсутності зовнішніх моментів на кінцях балкн (М (0) « М х X (/) = 0), б) для консольної балки з лівим затиснутнм кінцем
Мп(П“Мпоч(П.	(19	63)
^(О)-^^,	(19	64)
в) для консольної балки із затисненням праворуч
Мп(0) = Мпоч(0)	(19	65)
<2П(П = <М)	(19	55)
Нагадуємо, що тут М(0), М(і) та <?(/) — моменти та поперечні сили в кінцевих перерізах балки тільки від поперечного навацта ження
Умови (19 64) та (19 55) випливають з того, що в місці затиснення поздовжня сила 5 не дає поперечної складової, оскільки дотична до осі балкн тут горизонтальна
Після того як знайдено початкові параметри Мх» та (?по„ легко визначити загальний (повний) згинальний момент Мп у будь якому перерізі балки Знаючи згинальні моменти, можемо обчислити най більше нормальне напруження
5 Мв д,,
Оща» = р	•	(19 67)
Для визначення прогинів скористаємося рівнянням (19 44), звідки знайдемо
ч>, « - «<*>-”<*)	(19 68)
Лришид 77 Вибравши для балки (див рис 514) такі навантаження. 5 = ** ІООРь; М9 — 2РпІ, Р„ = 2,5 кН, визначимо найбільші нормальні напруження в перері» В. якщо І= 200 см Поперечний переріз квадратний площею Р = 10 X X 10 см* 1 = а*//2 => 835 см*, Г — аЧб = 157 см*, Е = 2.10> МПа
Складаємо рівняная моментів та поперечник сил
А*п (*) = М^ соз кх + зіп Ах,
^а М = ~ А<почА *|п ** + Споч С05 **
Граничні умови розглядуваної балки такі
Ма (0) = Ліо = 2Р»/ <?п (0 = <2 (0 =
З першої1 граничної умови знаходимо
Л1п (0) =	= 2Р,1
Друга гранична умова дає
<?в (0 = ~ 2Р0/А яіп кі + соз кі = Ра, ВВІДКИ
Ра + 2Р0/А зіп кі
*поч = соз кі
Тепер запишемо остаточний вираз для Лїв (х)
+ 2Р„1 зіп кі
Ма (х) = 2Р„1 соз Ах -1--------—-------зіп Ах.
соз кі
Оскільки нам треба визначити згинальний момент Ма у перерізі В то при
А« ]/"-А- « ]/" 100 2 5 10~\ И-1 „зетз ю-3 с-1
У ВЗ У 2 10* 835 І0-®
зіп М « зіп 200А = зіп 0,775 =* 0,700
соз кі в соз 200А = соз 0 775 = 0,713
кі = 200А = їй 0 775 = 0 983 знайдемо що
Ма (/) = ЛІЯ= 2Р01 ^соз кі +	+ зіп Аї^ ів А/ 20,35 кН  м.
Найбільше напруження обчислюємо за формулою (19 67)
0т>і » 25 + 121 9 МПа = 146,9 МПа.
Наближений розрахунок У практичних розрахунках поширені наближені способи розв'язання, які грунтуються на припущенні, що зігнута вісь балки при поперечному навантаженні набирає форми 512
синусоїди, тобто
ф (х)« / зіп	(19 69)
При наявності поздовжньої снли також наближено вважають, ш» иі0(х)«/п5Іп-2-	(19.70)
Це припущення дає змогу добути практична досить точні результати для шарнірно обпертих балок при дії поперечних навантажень, спрямованих в один бік, особливо якщо деформація балки виявляється симетричною ВІДНОСНО її середини, де Шп (1/2) & /„
Диференціальне рівняння пружної лінії
<Г*а> (х) М (х)
(19 71)
при поздовжньо-поперечному згинанні балки з урахуванням виразу (19.46) запишеться тат
Д»«м(х) М (х) 5иа	/ю
З?	= ~еГ	ЕҐ •
Виключивши із рівнянь (19 71) та (19 72) М (х) та врахувавши припущення (19 69) та (19.70), знаходимо, що
(19.73)
Тоді піеля диференціювання
(19.74)
Введемо позначення
«а назвемо Рв ейлеровою силою. Ця вила чизельно дорівнює Ркр, яка визиачаєтьєя за формулою (19 14) Із рівняння (19.74) знайдемо вирва для прогину посередині прольоту балки при епільній дії по* вдовжнього та поперечного навантажень)
/. -		<19.76)
Застосовуючи цю формулу, олід мати на увазі, що ейлерова сила РЛ, введена виразом (19 75), вуто формальна Тому на відміну від критичної сили Р>р сила рв повинна обчислюватися за формулою (19 14) при будь якій гнучкості балки (навіть меншій за граничну) Визначаючи ейлерову силу, момент інерції слід брати відносно тієї в головних осей інерції перерізу, яка перпендикулярна до площини дії поперечного навантаження.
17 8-27М
Б13
Вираз (19 76), як звичайно, застосовують й ори інших типах опор* них закріплень стсяуто-зігнутих балок У цьому разі ейлерова сила має обчислюватися аа формулою (19 20)і
р **&
•в (*')’
Вираз (19 76) дає задовільні результати, якщо стискальна сила 5 ве перевищує 0,8Ркр
Припускаючи, що згинальні моменти пропорційні прогинам, дістанемо просту формулу для наближеного визначення найбільшого
І моменту при поздовжньо-поперечному згинанні
'	М.™=(19 77)
Тоді для обчислення напружень, згідно з виразами (19 6?) та (19 77), і дістанемо формулу
! (	Оп т«ж в — + г {1 -.5/р^	(19 78)
і	Приклад 78. Визначимо максимальний момент та найбільше нормальне яалру-
і	ясеямя в балці, яку показано ма рис 316. Поперечний переріз балки — двотавр № 10,
1	бля нього ?=• 12 см*, 1Г, » 39,7 см*, 7» » 193 см*
Обчислюємо Р9 ча формулою (19 78і
1	Р. _	й, - >08,К »Н.
1	Вианачвеко момент посередині прольоту для випадку поперечного згянаквя
а потім за формулою (19.77) знаходимо найбільший момент прн поздовжвьо-попере*. ] йому згинанні
.. І І М	1,28	„	і.№
( А*а І -у) ~	5 “	|(Ю. 0& «н • м «• |_о,71Й	“
1 РГ 1	108746
= 5,9 кН • м.
Найбільше напруження визначаємо за формулою (19 67)
86 - 10-8	6,9 > ІО"3
°““ “ 12 . ІО-4 + 39,7 •
МПа «> 219,4 МПа.
Визначення допустимого навантаження при поздовжньо-поперечному згинанні Розрахунок на поздовжньо поперечне згинання мав ту особливість що напруження при збільшенні навантаження зростає значно швидше, ніж останнє (рнс 617) [Графік на рисунку побудовано за формулою (19 78) відповідно до даних прикладу 78 ) Така сама не лінійна залежність напружень від навантажень має місце в будь якій задачі поздовжньо-поперечного згинання
Із графіка випливає якщо для пластичного матеріалу напруження От» У стержні дорівнюють допустимим напруженням ІоІ, то забезпечено запас міцності за напруженнями
ПвмоЛоІ в‘п	(19.79)
Здавалося б, що при цьому міцність стиснуто-зігнутої балки забезпечено Проте з графіка також випливає, що в цьому разі коефіцієнт запасу за навантаженнями значно менший ніж п, тобто
Пр >=> Рт/Р[а] < п	(19 80)
Це означає, що достатньо незначного збільшення навантаження (нз величину Рг — А«])» щ°б напруження досяглн границі текучості, а це практично відповідає руйнуванню балки Звідси робимо висновок, що стиснуто-зігнуті балки слід розраховувати не за допустимим напруженням, а ва допустимим навантаженням
[/>]=. Р^п	(19 81)
Зрозуміло, що при цьому напруження Ощ., будуть значно менші за допустимі [оі
Отже, для визначення допустимого навантаження треба спочатку знайти небезпечне (руйнувальне) навантаження Р, Це можна зроби ти, скориставшись формулою (19 67) або (19 78), якщо припустити, що границя пропорційності та границя текучості збігаються. При застосуванні формули (19 67) з обчисленням Ма точним способом задача розв'язується методом послідовних наближень, прн цьому доцільно скористатися побудовою графіка, подібного до зображеного на рис 517. Застосовуючи формулу(19 78). результат можна здобути скоріше Для цього достатньо розв'язати квадратне рівняння відносно Р,
Глава 20 ПРУЖНІ КОЛИВАННЯ
$ 123. Вступ Класифікація механічних колиаак-»
Вивчення коливальних процесів має дуже важливе значення для різних розділів механіки, фізики та техніки Вібрація елементів машин та будівельних споруд електромагнітні коливання в радіотехніці й оптиці, звукові та ультразвукові коливання — всі ці не схожі один на інший процеси об’єднуються методами математичної фізики в одне загальне вчення про коливання.
Тут ми обмежимося розглядом тільки механічних коливань з яки* ми доводиться мати справу в машинобудуванні та інженерному будівництві Вивчення механічних коливань важливе насамперед для розв'язання задач міцності при змінних напруженнях
Для того щоб те чи Інше тіло здатне було здійснювати коливання, воно повинне мати певні масу та пружність Якщо пружне тіло (на вантажена балка, скручений вал або деформована ресора) буде виве дене з положення рівноваги якою-небудь сторонньою причиною (уда ром, раптово прикладеною силою) то сила пружності цього тіла в новому положенні вже не зрівноважиться навантаженням, і виникнуть коливання
Усі коливальні процеси в техніці можна класифікувати за зовнішніми ознаками, формі того закону за яким певна величина що бера участь у процесі, змінюється в часі Таку класифікацію можна назвати кінематичною
Розрізняють два класи коливальних процесів періодичні та неперіодичні В теорії коливань істотне значення має проміжний клас — майже періодичні коливання
Періодичним називається такий процес при якому коливна величина, взята в будь-який момент часу через певний відрізок часу Т (період) має те саме значення Математичне означення періодичної функції таке функція І (і) називається періодичною з періодом Т, якщо Існує така стала величина Т для якої
при будь якому значенні змінної і
Неперіодичними функціями називаються решта функцій, які не задовольняють зазначену умову
Майже періодична функція визначається умовою
при будь якому і, де т та в — певні сталі величини Величина т, що, взагалі кажучи, є функцією в, називається майже періодом. Очевидно, якшр в дуже мале порівняно із середнім модулем функції /і (0 за час і, то майже періодична функція буде близькою до періодичної
Серед класу періодичних коливань дуже важливі гармонійні, або синусоїдні, коливання прн яких фізичні величини з часом змінюються за синусоїдою (або косинусоідою)
Неперіодичні коливання набагато різноманітніші ніж періодичні. Найчастіше з неперіодичних коливань мають місце затухаючі (або наростаючі} коливання. Коливання х що відбуваються за законом затухаючої синусоїди, або, як іноді їх називають, затухаючі гармоній ні коливання показано на рис 518, а Математично вони виражаються так
х = Д^’соз (ші 4- ф), де А, ф, б та ш — сталі величини, і — час
Наростаючі гармонійні коливання показано на рис 518 б Мате* матично вони описуються останнім виразом з тією різницею, що має бути змінений знак величини б на протилежний Про такі коливання слід було б сказати затухаючі (або наростаючі) коливання близькі до гармонійних при досить малих значеннях б Тому назва «затухаючі синусоїди» або «затухаючі періодичні коливання» не зовсім логічна, оскільки гармонійні коливання не можуть затухати Але ж такий тер* мін у літературі про коливання використовується, і ми теж будемо його застосовувати
Наведених зовнішніх ознак коливальних процесів, звичайно, не* достатньо для систематизації та аналізу можливих типів коливань Тому їх доцільно класифікувати також за основними фізичними ознаками розглядуваних коливальних систем
Взагалі пружна система може мати коливання різних типів На приклад струна або балка під час коливань може набирати різких форм залежно від кількості точок перегину, що поділяють довжину розглядуваного стержньового об’єкта Досліджуючи коливальні рухи пружних систем, важливо знати, яка кількість незалежних параметрів визначає положення системи в кожний даний момент часу Кількість таких параметрів називають числом ступенів вільності У найпростіших випадках положення системи може визначатися тільки однією величиною Такі системи називають системами з одним ступенем вільності
Розглянемо найпростіший випадок (рис 519) Якщо механічна система така, що можливі тільки вертикальні переміщення вантажу (і, і якщо маса пружини мала поріввяво з масою вантажу р, то таку коливальну систему можна роз глядати як таку, що має один ступінь вільності Положення іг може бути визначене одним _	параметром — вертикальними
,<*	переміщеннями вантажу р,
Цш що висить на пружині.
•>.	Системоюз двома або кіль-
> кома ступенями вільності
т( тг
б
Рнс біа
Рве, 619	Рнс 520
будемо називати таку систему положення якої в довільний момент часу можна охарактеризувати двома або кількома незалежними параметрами. Два ступені вільності має, наприклад невагома балка, що несе дві зосереджені маси (рис 520, а) Незалежними параметрами в цьому разі будуть переміщення мас /и1 та т, відносно положення рівноваги балки
розглядаючи поперечні коливання такої балки, можна поступово збільшувати кількість зосереджених мас доти, доки не утвориться балка з розподіленою по всій довжині масою тобто балка перетвориться на вагому (рис 520, б) У результаті матимемо коливальну систему з нескінченним числом ступенів вільності При цьому прогин у будь якому перерізі балки змінюється за певним законом 3 одного боку, прогин балки при коливаннях є функцією абсциси х (збігається з віссю балки), а з іншого — неперервною функцією часу і
Класифікуючи механічні коливання за іншими ознаками, розрізняють такі чотири типи можливих коливань: аласні, вимушені, параметричні та автоколивання
Власними (вільними) називаються коливання, які виникають в ізольованій системі внаслідок зовнішнього збудження (^поштовхів»), що спричинює в точок системи початкові відхилення від положення рівноваги або початкові швидкості, і тривають потімзавдяки внутріш нім пружним силам, які відновлюють рівновагу
Класичним прикладом власних коливань пружної системи є вертикальні коливання вантажу відвішеного до кіння пружмви Іднь рис 519), якщо верхній кінець її закріплений, а вантаж спочатку від тягнутий вниз а потім відпущений
При власних коливаннях характер коливального процесу в основному визначається тільки внутрішніми силами системи, які залежать від її фізичної будови Потрібна енергія що забезпечує процес коли вань, надходить ззовні в початковий момент збудження коливань Найбільше значення відхилень вантажу С) від його рівноваги в процесі коливань тобто амплітуда власних коливань та їхня швидкість, внзна чаються з початкових умов При цьому період коливань (чрс одного повного коливання) або частота коливань (кількість коливань за секунду), тобто величина протилежна періоду, залежить від самої системи Ця величина є певною для кожної системи і називається частотою власних коливань системи
Власні коливання можуть відбуватися не тільки біля положення стійкої рівноваги а й відносно стійкого руху наприклад крутильні коливання рівномірно обертового вала
Унаслідок того, що в усіх реальних механічних коливальних системах діють сили опору коливальному руху (опір середовища, в якому відбуваються коливання тертя в підшипниках, тертя в з єд наннях конструкції сили внутрішнього тертя в матеріалі циклічно деформованого пружного елемента системи), власні коливання завжди затухаюіь Й припиняються В цьому полягає важлива особливість
власних коливань порівняно з іншими типами коливальних рухів
Заради спрощення при теоретичному дослідженні власних коливань на початку розв'язання задачі силами

Рас. 52)
опору як правило, нехтують
Вимушеними називають коливання пружної системи, які відбуваються при дії на систему (протягом усього періоду коливань) заданих зовнішніх збуджувальних сил, що періодично змінюються і діють неперервно незалежно від коливань у системі Хараитер коливального процесу при цьому визначається не тільки властивостями системи, з А також істотно залежить від зовнішньої сили
Прикладом вимушених коливань механічної системи можуть бути поперечні коливання балки (рнс 521), що править за опору для елек гродвигунз якщо в нього обертові маси не повністю зрівноважені. Період вимушених коливань дорівнює періоду зміни збуджувальної сили Амплітуда вимушених коливань від початкових умов не зале жить
На відміну від власних вимушені коливання не затухають, хоч у механічній системі мають місце сили опору Це пояснюється тим, що при вимушених коливаннях у систему з боку збуджувальної сили неперервно підводиться енергія, яка й витрачається на подолання існуючих у коливальній системі сил опору
У певних умовах коли частота збуджувальних сил близька до час тоти власних коливань розглядуваної системи або збігається з нею, вимушені коливання супроводжуються значним (часто небезпечним) збільшенням амплітуди, що спричинює недопустимі для конструкції деформації (напруження) Це явище, як відомо має назву резонансу.
Параметричними називають коливання пружної системи, в процесі яких періодично змінюються фізичні параметри системи, тобто величини, що характеризують масу системи або її жорсткість Важливою особливістю параметричних коливань е те, що зовнішні силн впливають не безпосередньо на коливальний рух, а на фізичні пара метри системи
Отже, параметричні коливання відрізняються від вимушених видом зовнішнього впливу При вимушених колиханнях ззовні задано силу або іншу величину що спричинює коливання, а параметри при цьому залишаються сталими Параметричні коливання спричинюються періодичною зміною ззовні певного фізичного параметра системи Так наприклад обертовий вал некруглого перерізу, який має від носко різних осей перерізу різні моменти інерції що входять до ха рактеристнки жорсткості при згинанні, зазнає поперечних коливань у певній площині внаслідок згинної жорсткості вала, яка періодично змінюється за кожний оберт зала Зміна фізичного параметра (згинної жорсткості) обумовлюється зовнішніми силами У наведеному прикладі зовнішнім силовим фактором є двигун, що здійснює обертання вала
Параметричні коливання не затухають коли е'сили опору Підтримуються параметричні коливання за рахунок підведення енергії зов иішніми силовими діяннями які змінюють фізичні параметри системи
Автоколиваннчми, або самоколиваннями, пружна системи називають незатухаючі коливання, шр підтримуються такими зовнішніми силами, характер дій яких визначається самими коливальними процесами механічної системи
Автоколнвання виникають у системі без зовнішньої періодичної дії Характер цих коливань визначається виключно будовою системи. Джерело енергії, яка компенсує втрати її в системі при коливаннях (в основному на теплоту), як правило, е невід’ємною частиною системи
Із сказаного випливає, що автоколивання відрізняються від власних коливань, оскільки останні є затухаючими. тоді як аетоколивання не затухають Автоколнвання відрізняються також від вимушених та від параметричних коливань оскільки ті і інші так чи інакше спричинюються зовнішніми силами характер дії яких заданий У цьому розумінні автоколивання можуть бути названі також самозбуджува-ними, оскільки процес коливань тут керується самими коливаннями Джерело додаткової енергії, яка підтримує коливання системи, розміщується поза пружною системою Наприклад, енергія повітряного потоку, який набігає на вібруючі частини літака, спричинює особливий вид аатоколивань, що називається флатером
Крім того, коливання класифікують за характером деформації пружних елементів конструкцій Зокрема стосовно стержньових систем розрізняють поздовжні поперечні та крутильні коливання.
До поздовжніх коливань належать такі коливальні рухи системи, зокрема пружного стержня, при яких переміщення всіх точок перерізу стержня спрямовані вздовж осі стержня прн цьому має місце деформація його подовження або укорочення Нормальні напружен ня, що виникають при таких коливаннях, розподілені рівномірно по поперечному перерізу Отже, поздовжні коливання інакше можна назвати коливаннями розтягання стискання
Поперечними коливаннями називають коливання згинання, при яких основні компоненти переміщень (у даному випадку прогини) спрямовані перпендикулярно до осі стержня Напружений стан при поперечних коливаннях очевидно буде такий самий, як і при статичному згинанні балки Тому поперечні коливання інакше можна назвати коливаннями при згинанні
Крутильними називають коливання стержнів, які супроводжуються змінними деформаціями кручення 3 цими коливаннями в ма шннобудуванні доводиться мати справу здебільшого при аналізі деформацій різного типу валів, які працюють переважно на кручення
При розгляді тонкостінних конструкцій, зокрема елементів кой струкції літаків, часто доводяться мати справу з коливаннями змішаного типу, прн яких одночасно відбуваються деформації згинання та кручення, тобто так звані згинно крутильні коливання
б 124. Власні гармонійні коливання пружної системи з одним ступенем вільності
Задача про гармонійні коливання системи з одним ступенем віль ності розглядається в курсі теоретичної механіки Тут як пружну систему розглянемо вантаж, підаішений до нижнього кінця вертикально розміщеної пружини (рис 522)
Диференціальне рівняння коливань вантажу вагою (? (нехтуючи масою пружини) можна дістати, користуючись принципом Д’Аламбе-ра Прирівнюючи до нуля суму проекцій на вертикальну вісь усіх сил що діють на вантаж матимемо
<? + «-(<?--звідки
або
х ~ <л‘х = 0	(20 1)
ТУТ х = -да- І - час
=-^	(20 2)
де с — жорсткість пружини (чисельно дорівнює силі яка спричинює розтягання пружини що дорівнює одиниці довжини). Є — прискорен ня вільного падіння 60 — статичне подовження пружини під дією підвішеного вантажу вагою р
Рівняння (20 1) має. очевидно такий загальний розв'язок який визначає залежність між вертикальним переміщенням х вантажу та часом І
х — А соз ш/ + В зіп ш/	(20 3)
де № — колова частота власних коливань А та В — сталі інтег^/ вання, що залежать від початкових умов
За початок відліку переміщень вибирається положення вантажу яке відповідає стану рівноваги
Якщо задані початкова координата вантажу Хд та початкова швидкість^, ~ л при і — 0 то з рівняння (20 3) визначаються сталі інтегрування
А—х0, В	(20 4)
Поклавши х0 — а зіп а та Од/ш == а ссе а рівняв ня (20 3) можна переписати також у вигляді
X = а зіп (а/ + а), при цьому амплітуда коливань
а = / Л’ + Д*	Рис. 522
(?*СХ
або	________
а а |/хо 4- оц/со*.
Величина сої 4- а зветься фазою коливань, а величина а — зсувом фази
На підставі (20 4) & можна визначити з умови
З рівняння (20.2) колова частота власних коливань
и ~	(20 5)
Маючи на увазі, що (?/§ в масою т підвішеного вантажу р, колову частоту можна також визначити за формулою
<£> =я )/с/т.
Нагадаємо, що під коловою частотою розуміють кількість коли» вань, здійснюваних протягом 2л с
Знаючи колову частоту коливань можна знайти період коливань Т (час одного повного коливання) за формулою
Т=-^--2п/І_2я)/ї	(20 6)
Величина, зворотна періоду коливань визначає кількість коливань за одиницю часу (секунду) і має назву секундної частоти.
. І _ ю
^“Т 2я
Секундна частота коливань, як правило, виражається в герцах число герц дорівнює кількості коливань за секунду
Реальною пружною коливальною системою з одним ступенем вільності можна вважати механічну систему, що складається а пружного тонкого стержня, верхній кінець якого жорстко закріплений а до нижнього підвішений вантаж Очевидно в цьому разі, коли маса стержня значно менша за масу вантажу, така система не буде відрізивти си від раніше розглянутої (рис 522) Тому, щоб знайти частоту, період та амплітуду власних коливань вантажу.підвішеного до пружного стержня, можна скористатися виведеними вище формулами для важ тажу, підвішеного на пружині При цьому треба визначити жорсткість стержня, еквівалентну жорсткості с пружини
При розтяганні стержня завдовжки і та площею поперечного перерізу г абсолютне подовження стержня при статичному навантаженні (), як відомо, визначається формулою
Зусилля, що відповідає статичній деформації бе яка дорівнює одиниці, е шуканою жорсткістю
с = -^-	(207)
Тоді на підставі формули (20 5) частота власних коливань підвішеного вантажу	____ __________
Р°8)
Маючи на увазі, що С?/# е масою вантажу, формулу (20 8) можна за Писати у вигляді
<20 9>
З формул (20 8) та (20 9) видно, що частота власних коливань розглядуваної системи зростає із збільшенням жорсткості, або, шо те саме із зменшенням статичної деформації спричинюваної підвішеним вантажем Легко переконатися, що вантаж, підвішений до пружного стержня має значно більшу частоту власних коливань ніж той самий вантаж, підвішений де стержня з більшою поздовжньою жорсткі
При цьому відношення частот власних коливань вантаж), при кріпленого до двох різних стержнів, обернено пропорційне кореню квадратному з відношення статичних подовжень стержнів
Приклад 19 Визнтимо частоту власних коливань вантажу вагою ()=/),2 кН, підвішеного до кінця сталевого стержня завдовжки 40 см і площею коперечногв юрерізу Р = 1 см*. при модулі пружності матеріалу Е = 2 10і МПа -= 2 10* кпа
Колова частота коливань згідно з формулою (20 8)
Отже відповідна секундна частота вааских коливань вантажу
.	«	>570
/= 2л 2 З М Га
250 Гд
Приклад 80. Визначимо. як зміниться частота власних коливань вантажу Р, якою від першого способу закріплення його перейти до другого, розрізавши пружину на дві однакові частини й закріпивши вантаж посередині (рис 523)
Частота власних коливань вантажу підвішеного на кінці дружняя
.	. 4РЯ*п Р
°с “ * “	“ “Г •
де — середній радіус витка пружини л — Кількість витків О — модуль пружності при зсуві г — радіус дроту пружини с — жорсткість пружини
Рис. 623	Рис. 524
Для першої схеми
Ог*
‘‘"Ж*
Прн другій схемі кожна пружина буде мата більшу жорсткість
У першому випадку переміщення вантажу «і = Р/с».
У другому випадку кожна пружина сприймає навантаження РІ2 Тешу . Р р -**-
2с,	2-2с, =Т'
Частота власних коливань вантажу, підвішеного за першою схемою.
Частота власних коливань вантажу підвішеного за другою схемою,
Співвідношення частот коливань при двох різних схемах підвішування вантажу Мі-2.
тобто при ааміві способу закріплення підвішеного вантажу частота власних коливань збільшується вдвічі
Викладена вище теорія розрахунку поздовжніх коливань вантажу, підвішеного на пружному стержні, може поширюватися також і на розрахунки поперечних та крутильних коливань Наприклад, розглядаючи невагому балку із зосередженим вантажем (рис. 524) з одним ступенем вільності, дістанемо рівняння руху у вигляді (20.1). У цьому разі замість змінної х слід взяти переміщення вантажу р у напрямі, перпендикулярному до осі, тобто прогин ш Вирази для власної частоти та періоду коливань залишаються в тому самому вигляді (20 5) та (20 6) При цьому \ буде прогином під вантажем 3 при ста тичному його прикладанні
Для прикладу, показаного на рис 524
Приклад 81. Визначимо частоту власних поперечних коливань сталевого диска вагою <? = і кН (рис. 625), насадженого на сталевий вал діамет ром 6 = 50 мм
Частота власних коливань такої системи а одним ступенем вільності визначиться за форму ЛОЮ (20 5) й>» = /ї7бс.
—[|£---------*
а=40см	Ь-бОсм
Рис 525
де Сс —
в місці насадження диска
,	Оа»Ь»	1 0 4» 0 6» 64	„ „ ______.
вс = ®с = ЗЕЛ - з 2 10» 3,14 0,05* І “" 3,12 • 10 м
Тоді
= / 3.,2,8Ю^	“ 177 С-'’
а секундна частота
І—к--тттг=28г“
Прикладом пружної системи, здатної здійснювати крутильні коли вання може бути диск, з'єднаний із стержнем за схемою рис 526 Якщо до диска в його площині прикладена а потім раптово знята пара сил, то виникнуть власні крутильні коливання диска разом з валом, прн яких вал буде правити за пружину а характер крутильних коли* вань такої системи з одним ступенем вільності визначатиметься ку* том <р повороту диска
Позначимо крутильну жорсткість стержня (скручувальний момент потрібний для закручування стержня в місці закріплення диска на 1 рад) через с = СпЛ*Ц 32 (д. — діаметр стержня, І — його дозжи на), а повний кут закручування стержня (поворот диска) — через ф Крутний момент у циклічно закручуваному при коливаннях стержні в довільний момент часу буде сф Нехтуючи силами інерції маси стерж* ня порівняно з масою диска та прирівнюючи крутний момент у пере різі стержня до моменту сил інерції диска дістаємо таке диферен
'//А/7/ ціальне рівняння руху диска
/-^+4-0,	І2010)
Рис. 526
де У — момент інерції маси диска відносно осі стерж* ня перпендикулярної до площини диска.
Для круглого диска постійної товщини К діаметром О (питома вага матеріалу у)
де С — вага диска
Ряс. 627
На випадок диска змінної товщини Н (р)
С ’і (Р) ЇР’^Р
Позначивши ш* = с!і, рівняння (20 10) можна переписати у вигляді (20 1)і
? Д. М*т = П
загальний розв’язок якого
Ф =» А соз со/ + В зіп ш/
Звідси бачимо, що період власних крутильних коливань диска на кінці стержня
Т = — = йіТ^—. СО тс
Для стержня постійного перерізу діаметром Л період та частота аласних крутильних коливань диска відповідно
І-т-г/тв? (М11>
Здобуті результати можна використовувати й при розгляді системи з двома обертовими дисками (рнс 527) Дійсно, якщо закрутити дав диски один відносно одного а потім моментально зняти прикладені зовнішні моменти, то диски почнуть здійснювати крутильні коливання назустріч один одному Прн цьому деякий проміжний переріз вала залишиться нерухомим Положення цього так званого вувлового перерізу т — т можна знайти з умов рівності частот коливань обох дисків з примикаючими до них ділянками вала завдовжки а та Ь, для яких придатні формули (20 11)
і 1 -]/~яо5г і -і / яоа*
' = 2л V 32.1	= 1п V 32/^ ’
звідки
а/Ь = </^</1,
де .Ц та А —моменти інерції мас відповідно першого та другого дисків
Використовуючи останнє сиіввідношення, а також ураховуючи, що а + Ь = І, знайдемо
“-ТТ+ТГ’ Ь~-^+7Г
Тоді період та частота власних крутильних коливань розглядувано? системи, згідно з формулами (20 11) в яких замість і слід підставити вирази для а (чи Ь), будуть визначатися так
_ і/ ^‘(Л+ЛГ
1 м V ява* (/> + А) * ' ~~ ТіГ V
Зазначимо, шо розглянуте тут коливальна система має велике практичне значення, оскільки вона е прототипом коливальної системи, до якої можуть зводитися численні пружні системи що зустріче ються в інженерній практиці, зокрема вали а двома обертовими ма сами
$ 125 Вимушені коливання пружних систем з одним ступенем ВІЛЬНОСТІ
Вважаючи, що крім постійної ваги вантажу 3 (дяв рис 522) на нього діє періодична збуджувальна сила Р, то на відміну від розгля кутих в останньому параграфі власних коливань будемо мати вимушені коливання Рівняння цих коливань дістанемо з виразу (20 і), додавши до його правої частини силу Р (0
-2-х + «=Р(0	(20(2)
Поділивши всі члени останнього рівняння на 0/д, знаходимо
ї +	= Р|р8--	(20 ІЗ)
Розглянемо окремий випадок, коли Р (0 « Рі соарі, тобто коли період сили Ті •• 2л/д, а частота Д «= р/2я
Позначивши
Р д*8 = -|г рі соз рі = <7 соз рі, перепишемо рівняння (20 ІЗ) у вигляді
х 4- со’х = <? соз рі.	(20 14)
При повільній зміні зовнішньої сили Р (0, тобто при р, мвлому порівняно з ш можна знехтувати інерційним членом х і на підставі (20 14) знайти статичну деформацію
 <20|5>
8 амплітудою д/со8
Для визначення динамічної деформації треба розв язати диферен ціальне рівняння (20 і4) Цей розв’язок як відомо, можна дістати, якщо до розв’язку однорідного рівняння (20 1)
х = А соз со/ + В зіп со/	(20 іб)
додати окремий розв’язок рівняння (2і 14)
х = С со$ рі	(20 17)
Підставляючи окремий розв’язок (20.17) у диференціальне рівняная (20 14) і враховуючи, шо
х — — рС зіп ріі
х = — р*С соз р/, знайдемо
— р*Ссоьрі + ®*Ссьзрі — дсо&рі
Звідси після скорочення на соз рі
С(<о*^р*)—д, тобто амплітуда
с“ щ*—р* •	(20.18)
Тоді загальний розв’язок рівняння (20 14) остаточно набере вигляду
х — А соз<аі 4- В зіпш/ +'^1.рГС08/^	(20.19)
Перші два доданки правої частини рівняння (20 19) характеризують власні коливання, що, як прванло, швидко затухають останній доданок характеризує вимушені устелені коливання системи, які відбуваються з частотою зовнішньої збуджувальної свли Р
Амплітуда С вимушених коливань, як випливає з формули (20 18), залежить від частоти цих коливань р Відношення амплітуди С до амплітуди статичної деформації (20 15) визначає так званий коефіцієнт наростання коливань рі
Р=-^-^г-^---5І$їг---г=да- <20 2’> або
(20 2!) дв
Тд «= 2п/р, Т 2л/а
З формули (20 20) випливає, що при малому відношенні р!ч> коефіцієнт Р близький до одиниці й амплітуда вимушених коливань лише небагато відрізняється від статичної деформації Якщо ж частота вимушених коливань наближається до частоти власних коливань системи, амплітуда вимушених коливань прямує до нескінченності, тобто при рі<о -> 1 амплітуда С При р « ш має місце стан резонансу відповідна частота збуджувальної сили називається критичною
Розглядаючи залежність (20 20), графічне зображення якої наведене ва рнс 528, бачимо, що при частоті збуджувальної сили р, більшій за власну часіоту со коливальної системи, тобто р > ш, амплітуда С динамічного переміщення зменшується І прн р ш робиться дуже малою порівняно із статичним переміщенням У цьому разі вантаж ф можна розглядати як нерухомий
о 1 Р
Рви 52Й
Рис. 629
При р < © вимушені коли* ванна і збуджувальна сила сере* бувають в одній фазі, тобто зсув фез а = 0 Це означає, що в мо* мент, коли коливний вантаж
(див рис 522) досягає сзого найбільшого відхилення припустимо вниз збуджувальна сила набирає найвищого значення в цьому самому на прямі При р > <и різниця фаз вимушених колнваньта збуджувальної сили становить а = я, тобто коливання відбуваються в прогифезі із збуджувальною силою Це означає, що в той час, коли збуджувальна сила має максимальне значення в напрямі вниз, коливний вантаж до* сягає свого найбільшого відхилення вгору
Таке явище можна добре зрозуміти на прикладі вимушених коли вань математичного маятника (рис 529), збудження якого здійснюють горизонтальним зворотнопоступальним періодичним переміщенням точки підвісу з різною частотою Положення маятника, що колива еться водній фазі із збуджувальним фектором Показано на рис 529, а; коливання маятника в протифазі із збуджувальною силою показано на рис 529, б
Амплітуду власних (незалежних) коливань можна визначити із загального розв'язку (20.19) при розгляді початкових умов Так, по* клавши, що в початковий момент (прн і = 0) переміщення та швид кість дорівнює нулю, тобто Мі-о «= 0 та <= 0, з рівняння (20 19) будемо мати
В-0; Л
Підставляючи ці значення в рівняння (20 19), остаточно знаходимо
х “ (соз р/ - соз ио	(2022)
На початку дії збуджувальної сили виникають вимушені коливання та власні коливання однієї амплітуди
Якщо частота збуджувальної сили наближається до частоти власних коливань, має місце биття Нехай
© — р == 2Д
Рис 530
Тоді рівняння (20 22) при
^ = 4’1<а~Р> з урахуванням відомого співвідношення соз а — сО5р = — 2зіп-£-і£- аш можна переписати таким чином:
х/5шЛЦї>Г=-^«-5і„-!г±ї11,	(20 23)
тобто дістанемо рівняння синусоїдного коливального руху з періодом
та змінною амплітудою
‘,=-зг!Ьг5іп'а’
період зміни якої, або період биття, характеризується величиною
Т6 2л/Д
Графічну картину коливань з биттям наведено на рнс 530 3 формули (20 23) випливає, що період биття збільшується в міру наближення частоти збудження р до частоти власних коливань ш і стає нескінченним при резонансі (при р = ш) В останньому випадну, коли р-ь- «о та Д-> 0 рівняння (20 23) можна записати так
’” -м%+Т) 5І" -'"Л*” “ТГ5І"<2° 24>
тобто амплітуда коливань з часом зростає безмежно Зазначимо, що останній висновок справедливий тільки тоді, коли в коливальній системі немає снл опору Однак таких реальних коливальних систем не існує
БЗО
§ ЇМ. Власні коливання а а'ямсмм демпфуаанням
Розглянемо коливання системи з одним ступенем вільності (рис 531) коли сили опору прн коливанні пропорційні швидкості руху Для виведення диференціального рівняння коливань вантажу підві шеного на пружині в якомусь рідкому середовищі (рис 531) скориста емося принципом Д’Аламбера (умову динамічної рівноваги вантажу розглядаємо прн відхиленні його на відстань х від положення статичної рівноваги, враховуючи силу інерції маси вантажу 0)
Є--2-і-ої = Є+«,
де а — коефіцієнт пропорційності ах — сила тертя, пропорційна швидкості що діє в напрямі, протилежному рухові
Звідси диференціальне рівняння коливань системи з урахуванням розсіяння енергії можна записати у вигляді
х = 2пх + ш*х = 0.	(20 25)
де
2п _ Л, « и Л	(20 26)
Позначивши
п»	(20 27)
дістанемо загальний розв'язок диференціального рівняння (2і 25) х ®(Л віл 4- В соз соїО.	(20 28)
де е = 2 718
із цього рівняння випливає що період коливань розглядуваної системи з демпфуванням
<202<"
тобто він залежить від зату хання, що характеризується коефіцієнтом п
Загадімийразв’язок(20 28) можна подати також у вигляді зіп^ґ + ф), (20 30) де Я та ф деякі сталі, що залежать від початкових умов і можуть бути знайдені так са мо як і в § 124
При л <о різниця між коловою частотою оі! системи

8 демпфуванням та власного частотою ш, тобто в — о>і — а, е велнчи ного другого порядку малості, тому період Т буде мало відрізнятися від періоду власних коливань
Т = 2я/ш, тобто можна вважати що невелика сила опору не впливає на період (частоту) коливань системи
Розглядаючи розв’язок (20 28), бачимо, що через множник е~ЛІ амплітуда коливань з часом зменшується Сталі інтегрування А та В, які входять до розв'язку, визначимо з початкових умов Так, поклавши в початковий момент (при і = 0) х = х0 та х = х0, з рівняння (20 28) знайдемо, що
В = х0, А =*	(х0 + пХд)
Підставивши ці дані в рівняння (20 28) матимемо
X «= Є’п' зіп	+ Ха ^СО8	+ -і- 5ІП }
В окремому випадку, коли А = 0, тобто, коли
-І8_ ц. Л*ї_ = 0, ®1 С0і ’ останнє рівняння набирає вигляду
х = хое~п/ соз ©і/.	(21.31)
Цю залежність на рнс 531 подано у вигляді графіка Рівняння верхньої та нижньої обвідних наведеної затухаючої віброграми відповідно х = х^г"* та х = — хое~'1/
Точки т1г Шг, пц, дотику обвідної до віброграми мають координати часу і = 0; і = Т, І = 2Т, , а точки ті, т?, тз, . дотику до нижньої обвідної кривої — координати І = Т/2, і = 3772 і т д При цьому зазначені точки не збігаються з точками крайніх переміщень системи з положення рівноваги Легко переконатися, що внаслідок затухання коливань час для переміщення системи із середнього положення до наступного крайнього положення менший ніж час, потрібний для повернення з крайнього в наступне середнє положення
Інтенсивність затухання коливань системи залежить від сталої п (характеристики затухання) Амплітуда коливання після кожного циклу зменшується у відношенні е~п‘ * І, що видно з рівняння (20 Зі), тобто зменшення амплітуди відповідає геометричній прогресії Дійсно, послідовні амплітуди при І = 0,1 -= Т, І = 2Т і т д мають значення ав = х0, а, = хое_,,г, а, = х0е~2лТ,
Відношення якої небудь амплітуди коливань до амплітуди, шо безпосередньо йде за нею через один період
«в	«і , ... Д» _ х>е~*лГ _ _
Д1	«в	Д*+І хое_(*+1,пГ
звідки
Іп ) = Іп е”г = пТ = 8	(2032)
Величина б називається логарифмічним декрементом затухання коливань і взагалі е основною характеристикою затухання коливань як наслідку демпфування їх обумовленого наявністю в будь якій реальній механічній системі сил опору механічним коливанням У техніці, зокрема в машинобудуванні, значення декремента істотно від різняється від одиниці й становить, наприклад для таких коливальних систем, як турбінні лопатки, приблизно 0,03, тобто 3 %
Крім сил опору, пропорційних швидкості руху, демпфування коли вань у реальних конструкціях може обумовлюватися й іншими причи нами, зокрема втратами енергії гістерезисного типу в самому матеріа лі пружного елемента коливальної системи внаслідок його пружної недосконалості, значення яких залежить не від швидкості а від ам плітуди коливань (циклічних повторно змінних напружень в «пружи ніж) іншим поширеним джерелом втрат енергії в реальних колнваль них системах е розсіяння енергії внаслідок сил тертя в з єднаннях елементів конструкції витоку енергії у фундамент тощо
Тут ми не маємо змоги зупинятися на розрахунку коливань елемен тів конструкцій з урахуванням різних видів розсіяння енергії1 й обмежимося лише випадком вимушених коливань, коли розсіяння енергії пропорційне швидкості руху
$ 127. Вимушені коливання механічної системи з в’язким демпфуванням
Розглянемо вимушені коливання системи з одним ступенем віль ності, якщо е сили опору механічним коливанням, пропорційні швид кості Диференціальне рівняння коливань для такої системи дістанемо, якщо додатково до сили опору 5 = ах на вантаж у вертикальному напрямі (рис 53і) буде діяти якась періодична сила Р зіп рі
Позначивши
Я = Є?®, дістанемо рівняння коливання для даного прикладу, додавши в праву частину рівняння власних коливань Із затуханням (20 26) член д зіп рі
1 Докладно це питання висвітлено в монографіях Г. С Писаренка «Колебанкя упругих систем с учетом рассеянкя звергни в материале» (К . Изд во АІІУССР 19об) «а «Обобщающая нелиненная модель учета рассеянкя знергки прн коїебаниях» (К Наук думка 1985)
При цьому
х + 2лх + ©’х » д зіп рі	(20 38)
Загальний розв’язок цього рівняння знайдемо, якщо до розв’язку однорідного диференціального рівняння (20 28) додамо окремий роз* в'язок
х = К 5ІП рі + с соз рі	(20 34)
Тоді, маючи на увазі, що
х •= Кр соз рі — Ьряп рі;
х => — Кр* зіп рі — Ьр* соз рі,
1 підставляючи вирази х, х та х в диференціальне рівняння (20 33), а потім прирівнюючи коефіцієнти прн зіп рі та соз рі правої та літо? частин, матимемо
—	Ьр* + 2Крп + £©* = 0;
—	Кр* — 2Ьрп + Ка* = д
Розв’язуючи разом здобуту систему двох рівнянь відносно невідомих сталих К та Д, знайдемо, що
(щ* — р»)ї 4р‘п’
Тоді загальний розв’язок рівняння (20 33) можна записати у вигляді
X = в-" (4 зіп а,І + В соз аД -	соз рі +
+ (^Л-У,ГД.-ЯІ трі.	(20 36)
Перші доданки що мають множник є-*, з часом зменшуються (за* тухають), два інших доданки, пропорційні д, які характеризують ви* мушені коливання, з часом не затухають Період цих незатухаючих коливань
Ті = 2п/р.
а Тхня амплітуда пропорційна збуджувальній силі Ця амплітуда, як легко переконатися, залежить також від характеристики п демлфу-вання, а також від співвідношення періодів вимушених 7) та власних Т •=• 2л/© коливань
Якщо ввести таку заміну
= «>-«	<М37)
°яс°5'х’	<2оз8>
<0 вимушені коливання можна виразити дещо простіше
х =И(со8а$іпр/— зіп а соз рО — Ж зіп(р/ —а) (20 39)
Амплітуда Я вимушених коливань на підставі (20 37) та (20 38) визначиться з виразів
__?*(со>-р*і*	-я» соз» а
І(ш«-рЧЧ-<р>аЧ‘ _В “
склавши які й розв язуючи відносно Я, знаходимо
_ у&р'п*	___________я	,2040)
(й» _ р>)« + 4р^ УІ&-рі)* + 4№	’
Кут а зсуву фаз иа підставі рівнянь (20 37) та (20 38) можна внзна* Чити, поділивши перше з них на друге
І2041)
При ш > р кут а додатний і менший за я/2 тобто 0 < а < я/2 З рівняння (20 39) випливає що при цьому вимушені коливання від стають за фазою від збуджувальної силн Коли ш < р л/2 < а < л, тобто вимушені коливання відстають більше ніж на а = л/2 Коли (о = р, (§ а = оо тобто під час коливального руху система займає своє середнє положення в той момент, коли збуджувальна сила дося гає максимального значення
Аналізуючи формулу (20 40), маючи прн цьому на увазі що
знаходимо ^=^г=4 = 6-	<2042>
де 6С — переміщення, яке виникло б при статичному навантаженні пружини Зусиллям, що дорівнює амплітудному значенню збуджу вальної сили Р
Ураховуючи формулу (20 42) і поділивши чисельник та знаменник виразу (20 40) на квадрат колової частоти власних коливань ш2 зна ходимо
а- .	----------- , (20 43)
де у = 2л/(в — коефіцієнт, який залежить від сили опору в колива ть вій системі.
При дуже великому періоді вимушених коливань їхня амплітуда наближається до статичного переміщення (Я -> -► бо) При 7, -► Г та малому затуханні И -*• оо
Як зазначалося, при розрахунках амплітуд вимушених коливань зручно користуватися коефіцієнтом наро-
стання амплітуди коливань р, що становить відношення амплітуди Я вимушених коливань до статичного переміщення 60
(20 44)

Побудувавши графіки залежності р = [ (р/ш), дістанемо так зва-ні резонансні криві при різних демпфувальних характеристиках снсте ми, що визначаються коефіцієнтом у (рис 532).
Графічне зображення зсуву фез а = {р!и>} при різних значеннях коефіцієнта у наведено на рис 533 3 цих графіків видно, що в зоні збудження коливань з частотами близькими до власних, має місце дуже різка зміна фази вимушених коливань тоді коли коефіцієнт у малий
або
Приклад 82 Електродвигун вагою <) = 4 кН з частотою обертання ротора п = ел 1000 хе-1 установлений на двох консольно закріплених в стіні швелерах Доберемо переріз швелерів якшр відстань «ід стіни до центра ваги двигуна Iе 1 м, вертикальна складова відцентрової сили що виникав внаслідок неврівноваженості двигуна» дорівнює Р зіп аі де амплітуда відцентрової сили Р становить 25 % ваги двигуна»
Переріз швелерів має бути такий вюб частота власних коливань систем» при близно на VI % була більша ав частоту збуджувельноТ сили, тобто л, = 1,3л = 1 3 • 1000 » 1300 хв“1
ял, 3 14 1300	...	,
° ЗО =	30 с—ІЗбс,
а напруження, що виникає в швелерах, не перевищувало допустимого [о| Ю0МПа< Коливальну систему що складається з електродвигуна иа швелерах, з досить внсоилм ступенем точності можна розглядати як систему з одним ступенем вільності, для якої класна частота може бути знайдена за формулою (20 5)
шп — Ґ в/бс = 136 с“*.
звідки

981
-[^ГСМ»ОО53 о»
Статичний прогин двох консольно закріплених швелерів
X /
° ° ЗЕ • 2/, •
Звідси визначимо момент інерції одного швадера ОР	4 1»
7, = Лі.. а —-------------------—г = 6 29 10-6 м* = 629 см*
* 6£вс 6-2. 10». 5 З ІО-1 ’ м
Згідно з таблицею сортаменту найближчий за розмірами швелер № 16 з мсіієн том інерції
Для швелера № 16 частота власних вмивань системи

ЗО®» 30.(47 іллп
° я.м- * І«а> ” ’
що більше за частоту збуджувальної сили за
‘••^іЬоо000 іоо«°40«
Перевіримо напруження що виникають у небезпечному перерізі швелерів, урахуванням вібраційного навантаження Статичне напруження під дією ваги адекі родвигуна
2.^-» МП-21 6
Коефіцієнт наростання амплітуди коливань згідно а (20 20) ’
2,04
Тоді напруження з урахуванням динамічності
мпа-±и мп.
а максимальне напруження в швелері
§ 128 Критична швидкість обертанні вала
З практики експлуатації машин відомо, що при деякій цілком пев ній для даної машини частоті обертання, прн якій робота вала стає динамічно нестійкою, настає так званий резонанс При цьому можуть виникати великі поперечні коливання вала Частота обертання, при якій настає резонанс, називається критичною Легко показати, що критична швидкість для вала відповідає частоті обертання вала за секунду, яка дорівнює частоті його власних поперечних коливань
Для доказу розглянемо обертання вертикально розміщеного вала з одним диском вагою 0 посередині (рис 534, а)
Припустимо, що центр ваги С диска розташований завдальшки е від його осі (при насадженні диска на вал уникнути ексцентриситету «практично не вдається) Прн обертанні такої системи на вал буде діяти відцентрова сила, що спричинює його згинання
т
де <і> — кутова швидкість обертання вала ш — прогин вала в місці насадження диска
Знайдемо реакцію на опорах вала від дії відцентрової сили
Р — СІІ)
де с — згинна жорсткість вала, котра, наприклад для вала постійного перерізу при розміщенні диска посередині між опорами
с =	(20 45)
З умови рівноваги очевидно що Т = Р Підставляючи замість Т та Р їхні вирази дістанемо таке рівняння для визначення прогину ип
-2- (а» 4- в) цЛ -= си>	(20 46)
звідки
Ураховуючи [див формулу (20 26)1, що
становить квадрат частоти власних поперечних коливань вала рівняння (20 47) можна переписати так
(2048>
З цього рівняння видно що прогин вата ш швидко зростає в міру наближення кутової швидкості обертання вале а до частоти ш, власних поперечних коливань вала з диском Критична швидкість обертання вала	____
о>кр = ш. =-	(20 49)
При цьому знаменник у формулі (20 48) дорівнює нулю, а тому прогин теоретично дорівнює нескінченності тобто повинен безмежно збільшу ватись аж до руйнування В реальних умовах внаслідок втрат енергії
в системі які в наведеному розрахунку не враховуються на практиці при попаданні вала в резонанс прогини не завжди набирають значень, небезпечних для експлуатації
цікаво, що при швидкостях обертання вала, більших за критичні, амплітуда згинних коливань істотно зменшується, коливання затуха югь Досліди показують, що при ш > ш, центр ваги диска розміщу ється між лінією, що з еднуе опори та викриаленою віссю вала (рис 534, б) У цьому разі рівняння для визначення прогину вала буде мати вигляд
ЗВІДКИ
ш »
(ш — е) = си>
«Г
(20 50,
зменшу великих опори і
"а?"
Отже, із зростанням швидкості обертання вала прогин а> ється І наближається до ексцентриситету е, тобто при дуже швидкостях центр ваги диска досягає лінії, яка сполучає зігнутий вал обертається навколо центра ваги С диска
Приклад 83 Визначимо діаметр вам турбогенератора потужністю N = = 73,6 кВт, щр несе посередині прольоту завдовжки 100 см диск вагою <? = = 15кН у двох випадках 1) для жорсткого вам з критичною частотою обертання вииуно ніж п^ 3000 хв~1 на 35 %. 2) для гнучкого вам з критичною частотою обер такая, нижчою ніж робоча частота втричі Масою вам порівняно з масою диска знех тусмо Відомо иу> ексцентриситет е = 0,01 см; [сі =- 80 МПа Е=2 /0* МПа
Для першого випадку визначимо частоту власних коливань системи (жорсткою вала з диском)
3,14 3000 36
зо
424 е“‘

Діаметр жорсткого вала знайдемо з аирачу
заїдки
/48й£я^* “ОТ"’
.	,‘/~^40І»	424* 4 15 ІО-3 І»
V ЗаВя‘ у З 9 81 2 10» 3 14
Максимальний прогин вала при коливаннях
= 8 75 • 10~8
1.35*—і
Нормандії напруження від згинання
_ бЕа/ = 0 2 10» 8 75 ІО-8
|0_< м
-12-А МПа = 12 8 МПа
Дотичні напруження від скручування

9549/1/	9549 73 6 - 10-8 • 16
—з:-------	1  1" -....*	МПа "1.8 МПа.
я** „ 3 14 (8,75 • ІО'2)» 3000	’
16 п
Еквівалентні напруження за третьою теорією міцності
’еквііі = /<»* + <** “ Ґ128» + 4 1 8« МПа = ІЗ 3 МПа < [о] = 80 МПа. У другому випадку частота власних коливань системи а гнучким валом
Діаметр гнучкого вада
. ‘/фрі» */~ 105» 4 1,5 10—’• 1	, ае -
‘"V	3-981.2 10.814 ——
Длкамічний прогин е	0 01 • І0~2
1 = 1 — (сохр/ш)’ ° 1 —(1/3)* и = 1,13 * 10 “ = 1 ІЗ • 10“ см.
Нормальні напруження від згинання
о _	_ Є.2.|0‘.4,35 ІО-8 • 1,13»І0~- „щ, _ 6 9 мій
Дотичні напруження від кручення
т_ Л|-р - 35ИА' - ™ ”6 10-«.1в „п.„и?мп. В'є ягі* „	3,14 (4 35 • 10~2)а3000
16 "
Екаївелеятві напруження за третьою теорією міцності <>емШ ° /с* +	“/5 9*4-4 • 14,6»МПа = 29 8 МПа <[оі = 80 МПа,
§ 129. Власні коливання системи з двома або кількома ступенями вільності
Системою з двома трьома і т д ступенями вільності називають» як зазначалося вище, таку систему, положення якої в будь-який момент часу може визначатися відповідно двома трьома і т д незалежними параметрами
До коливальних систем такого типу, які часто застосовуються в т „	а машинобудуванні, належать вал з
К3^ кількома дисками (рис 535), що здійс-
нюе крутильні коливання вал з кількома зосередженими масами (рис 536), що здійснює поперечні коливання тощо У першому ви падку рух описується кутом повороту навколо поздовжньої осі ва >а а в другому —вертикальним переміщенням зосереджених мас у напрямі, перпендикулярному до осі вала Прикладом коливальної системи, в якій рух маси визнана еться одночасно лінійним зміщен-
Ряс. 537
ням та кутом повороту, може бути кузов автомобіля, схему якого наведено на рнс 537
Розглядаючи коливання пружних систем з кількома ступенями вільності диференціальні рівняння руху здебільшого можна дістати, як і у випадку систем з одним ступенем вільності, користуючись прин ципом Д Аламбера Розглянемо загальний підхід до складання рівняння руху маси в просторі
Рух маси т у просторі розглянемо в координатній системі хуг Складаючи рівняння рівноваги, до рівнодійних х, у та г усіх зовнішніх сил які діють на масу т і спрямовані відповідно вздовж осей х, у та г слід додати сили інерціТ Складові сил інерції у напрямах х, у та г дорівнюють відповідно —тх, —ту, —пй Тоді рівняння руху маси т у просторі
X — шх = 0, У—яц} — 0. 2 — пй=0	(20 51)
Якщо .розглядається система з кількох мас, вільних у просторі, то рівняння (20 5і) треба написати для кожної маси системи
Тепер розглянемо застосування принципу Д’Аламбера для скла дання рівнянь руху коливальної системи (рис 538, а) з кількома сту-п'нями вільності, яка складається з двох мас ті та /я, та двох пружив з жорсткостями ск та с, Будемо вважати, що ці дві маси можуть переміщатися без тертя тільки в горизонтальному напрямі вздовж осі х Переміщення першої маси т позначимо через хп а другої — через х,
У процесі коливань на масу Ші як зовнішні сили діють сила натягу першої пружини та сила с, (х, — х0 натягу другої пружини. Силами опору тертя нехтуємо Тоді, користуючись принципом Д’Алам-
Рве. 638
Сера, рівняння руху першої маси
X = т1х = 0 запишемо у вигляді
—с^і + с, (Ха — х,) — ГГ^Хі = 0 або
т,х,+С|Х, —с,(х,-х0 =0	(20 52)
На масу /п, діє тільки сила натягу другої пружини —са (х^ — Л0, а рівняння руху маси лц буде
т,ха + с, (х, — X!) = 0	(20 53)
Коли б система мала не дві, а три чи більше послідовно в'едааннх мас, то рівняння руху для кожної з мас містило б три чи більше не відомих координат Так наприклад, сили пружності пружини, що діюгьна ї-у масу, цілком визначаються переміщеннями х,та хі+і (рис. 538, б)
Складаючи диференціальні рівняння руху розглядуваної системи, можна було б користуватися й іншим методом Дійсно, при розгляді цієї системи можна було б вважати, що є даі зв'язані між собою пру жини (рис 538, в), які зазнають дії сил інерції —та —при* кладених відповідно в місцях віддалених мас (точки / і 2) Тоді перша пружина навантажується силою —т,х, — а друга — силою —т^х* При цьому переміщення першої маси що дорівнює подовженню першої пружини
х, =	~~ т*х»
а переміщення другої маси визначиться сумарним подовженням обох пружин
Дещо перетворивши останній вираз, остаточно матимемо
х^Сі +	+ т^х, = О,	(20 54)
*АС» + сі («Л + ш»*ї) + сі^хі « 0	(20 55)
Здобута система рівнянь руху (20 54) та (20 56) еквівалентна системі рівнянь (20 52) та (20 53), але відрізняється своєю структурою
Зазначимо що другий метод дещо громіздкий, оскільки зміщення наприклад кінцевої точки залежить від сил інерції всіх мас, а отже, виразиться через другі похідні від зміщень усіх точок
Крім розглянутих двох способів складання диференціальних рів нянь коливань систем з багатьма ступенями вільності, існує третій найбільш загальний метод що грунтується на використанні відсмих з теоретичної механіки рівнянь Лагранжа другого роду, які при від
сутності сил опору та зовнішніх збуджувальних сил мають вигляд
ТГ«-)~£- = —ЯГ’ « = і:2.з. • :») (2056) де Т та и — відповідно кінетична та потенціальна енергія системи Застосовуючи рівняння Лагранжа для складання рівняння руху двомасовоТ системи (рис 538, а), перш за все запишемо вирази кіне тичної та потенціальної енергії цієї системні
Т /п*лч , /л**г 1 =3—2	1	2~1
и =
2
2
Відповідні похідні які входять до рівнянь (20 56),
Тоді рівняння (20 56) стосовно до випадку, що розглядається» буде мати вигляд
/п,х, 4-сл =>с,(х, — ж,) = 0, т^х, 4*М*і— х») = 0
Зазначимо, що рівняння, здобуті з рівнянь Лагранжа, завжди збігаються з рівняннями, виведеними при використанні принципу Д’Аламбера Іноді, зокрема для системи ланцюгової структури типу розглядуваної, з міркувань простоти викладок слід користуватися першим методом, при розрахунку згинних коливань виявляється більш зручним другий
Отже, припустимо, що рівняння руху системи з двома ступенями вільності одчим із розглянутих способів здобуті Нехай пі рівняння ма ють вигляд (20 52) та (20 53) Розв'язання системи цих даох лінійних диференціальних рівнянь можна шукати в такій формії
« 1г зіп (<йґ 4- а), х, «=Х,5Іл (со/ 4-а),
(20 57)
Де Хр А,, а* та а — сталі, які треба вибрати такими, щоб задовольнити рівняння (20 52) та (20 53).
Підставляючи розв'язок (20 57) у ці рівняння, матимемо
—4- ^Х, — (А, — Х0 = 0;
—/п^со* 4- с, (X, — Хі) = 0,
або
Х1 (гі + с» — т^ш*) — 4е» в 0»
—V» + X, (с, —/я,®’) — 0.
(20 58)
Рівняння (20 58) містить три невідомі: амплітуди X,. X, та частоту ш З цих двох рівнянь знайти зазначені три величини неможливо, проте з них можна визначити частоту Дійсно, розглядаючи систему рівнянь (20.58), бачимо, що випадок коливального руху, коли X, 0 та X, ?ь ^ь0, можливий тоді, коли дорівнює нулю визначник указаної системи двох однорідних рівнянь відносно та X,, тобто коли
с, +с. — т.и*	—с. І
1	. -0
—4,	/Я,®*)
Записавши пей визначник у розгорнутому вигляді, після деяких пере* творень матимемо
+.ч + Лі-) + -аа_ _ 0. \ т, т, /	’ «т^т,
Це рівняння е квадратним відносно и’, І легко показати, шо воно має два дійсних додатних коренії
г(-а^ +-§г)-‘И-аїг1 +-£•)
Відповідно можна знайти і дві власні частоти:
(20.6(9
Відновідво до (20 60) двочастогний коливальний процес в загально* му вигляді слід записати такі
Хі = X,, зів (ШіІ + сц) + Хц «Іп Ш	0
х, «в X,, зіп (ш(/ + сц) + Ч, зіп № + сц) С ) Тут перший індекс біля амплітуди X показує номер координати, а другий — номер доданка в рядку або номер частоти
Амплітуди коливань пов'язані відношенням, яке визначається з першого або другого рівняння (20 58)і
2х- =	+е» ~ "і01? X, е»
X»	ві ‘ Хі С1 — пцШз
або відповідно до прийнятої індексації:
„ х« «»+*,-«!<>? .
*« •
с,-т^ '
Тещі рівняння (20 бі) можна записати у вигляді
X, - X,, 5ЇП (а,І + »Ч) + Х„ 5ІП (и^ + сч),
X, = Х^Хц 4-00 +хяХп5ІП(й)^ 4-сц)	'	}
При цьому власні частоти а, та (в,, а також відношення амплітуд хц та Хм залежать від параметрів коливальної системи
Щодо значень амплітуд Хц та Хц, а також кутів зсуву фаз ец та а,, то їх слід визначати з чотирьох початкових умов, що виражають значення зміщень та швидкостей обох мас у початковий момент часу
Якщо рух системи спричинений ударом по масі т, що відповідає таким початковим умовам при І = О
х,(0)=0, х,(0) = 0;
х, (0) = 0; і, (0) = о„
з рівнянь (20 62) матимемо
Хп зіп а, -р Хм зіп а, = 0; х„Хп зіп а, 4- КмХ(І зіп а, = 0, Х^и, соза, 4- Х,»®і соза, > 0;
«мХц^соза, +хпк1(ш|соза1*»о0 Звідси, оскільки соц ш,, хм і Хм відомі, знаходимо, що
а, = а, = 0
і = «6	1
ц »і	«и - Х*1
Добираючи штучно початкові умови так щоб амплітуда Хп= 0, можна знайти одночастотні коливання, які описуються однією гармонікою
х(| = Хп зіп(<!>[/ 4-а,), Хм = ХцХц зіп (а,/ 4-
(20 63)
Коливання що описуються однією гармонікою, називаються пер-тими нормальними коливаннями Оскільки відношення амплітуд хц не залежить від початкових умов, то одночасні коливання характеризуються досить певним співвідношенням амплітуд, яке залежить від параметрів системи Отже, х„ визначає першу нормальну форму коливань
Друга форма коливань очевидно, визначатиметься відношенням тоді, коли початкові умови вибрано такими, при яких
18 2-2798
646
Ці = О, І здійснюються другі нормальні коливання, що описуються формулами
•*і« = Ьц*іп(<>М І «»)• Хм =ХЯХ118ІП(«1/ і сц)
(20 64)
Зазначимо, що кількість нормальних форм коливань та така сама кількість власних частот збігаються з числом ступенів вільності коли* вальної системи та що дві нормальні форми коливань ортогональні, ообго має місце співвідношення

Виявивши загальні принципи визначення основних параметрів коливань пружних систем з кількома ступенями вільності перейдемо до розгляду дуже важливих видів коливань які часто мають місце в інженерній справі
§ 130. Крутильні коливання валів І систем передач
Уявимо собі механічну систему, яка складається з пружного вала з насадженими на нього дисками (рис 539 а) і здійснює крутильні коливання Нехай Л ./), .І3, /я - моменти інерції маси дисків відносно осі вала; фп ф», Фі < фп — кути повороту дисків при коли ваннях, си с(, с,, , сп — жорсткості різних ділянок вала між диска ми прн крученні
де І, — довжина відповідної ділянки
Оскільки с|( Сі с3, є крупними моментами, які спричннюютьза* кручування відповідних ділянок вала на І рад то с, (фі — фі); с3 (ф, — — фд), — крутні моменти, що виникають у перерізах вала прн вза ємному повороті першого та другого дисків на кут ф| — <р, другого та третього — на кут ф1 — ф» і т д (рис 539, б)
Нехтуючи моментом інерції маси обертового вала порівняно з мо* ментами Інерції .1* обертових мас дисків кінетичну енергію
Рис 639
Рис 640
коливної системи можна виразити як
7'-4-Ат?+-5-4Й + т'/«Й+	(20.65)
Потенціальна енергія розглядуваної системи а л ступенями вільності за рахунок пружної деформації вала
або
у = ІМФ, —Фі)* +-5-«»(ф« — фі)’ Ч^^-ФіГ +	ї2065)
Підставляючи вирази (20 65) та (20 Ьб) в рівняння Лагранжа (20 58), дістанемо таку систему диференціальних рівнянь вільних кру тильних коливань вала з насадженими на нього дисками
Афі +сі(Фі“ Фі) =°>
•'Д +Мфі —Ф#>—МФі —Фі)
Аф» + сі (ф» — ф*) — с« (ф, — Ф.) = о, .............................. (20 67)
А—іфл—і + Л|-1 (ф«-і — фп) — Сп-2 (фя-е + Ф«-1) = 0
Афп — С”-1 (фи-1 — фд) = 0
Складаючи ці рівняння, матимемо
АФі + Аф» + •	+ пф» = 0,
звідки, Інтегруючи одвн раз, знайдемо
Афі + Аф» + Аф> + ••• +Афп=сопзі, тобто момент кількості руху системи навколо осі вала при вільних коливаннях залишається сталим
Надалі будемо вважати, що цей момент кількості руху дорівнює нулю Цим самим виключаємо з розгляду будь яке обертання вала як твердого тіла і будемо розглядати лише коливальні рухи, що слричи нюються скручуванням вала
Користуючись загальними методами розв'язання добутої системи диференціальних рівнянь (20 67), розв'язок шукаємо у вигляді
Ф, = А., соз(ш/ + Ч7), ф, «»Лїсоз(й»/ + V). (20 68)
Підставляючи розв’язок (20 68) у рівняння (20 67), будемо мати
ААХ©»— а (А — А)-0;
+ сх (X, — А) — с, (А — А) •	(20 69)
Виключивши з цих залежностей X,. X,, X,, ., Х„ дістанемо рівняння для визначення частот
Так, у випадку трьох дисків (рнс 540) система рівнянь (20 69) буде мати вигляд
АХ,<о’ — с2 (X, — X,) = 0,
А\»*4 сі(Хі — Х,)-е,(Х,— X,) «=0	(2070)
+ сг (X, - X,) = 0
Склавши ці рівняння, дістанемо
/1Х1 + АЧ + АХ, « 0	(20 71)
З першого та третього рівнянь системи (20 70) знайдемо, що  *“—Т^г-	(2(>72)
Підставляючи вираз (20 72) у формулу (20 71), будемо мати
ЛУі- (о‘ _	+	+ (/, + 7, + /,) = о
(20 73)
Розв'язуючи це рівняння відносно 03е. можна знайти два корені та о>2 що відповідають двом головним видам коливань Підстав ляючи здобуті при цьому значення о? та с>4 у рівняння (20 72), знайдемо відношення Х,/Х, та Х^Х, для двох головних видів коливань і тим самим визначимо стан системи під час коливань Зазначені два види коливань для тримасової системи показано на діаграмах І та II (рис. 540) відповідно для одновузлової та двовузлової форм коливань
У разі чотирьох обертових масивних дисків рівняння частоти дістанемо, прирівнюючи до нуля визначник рівнянь (20 67) при л = 4. Розв'язуючи його знайдемо чотири корені рівняння, з яких один унаслідок вільного обертання вала як твердого тіла навколо його осі виявиться нульовим, а решта (відмінні від нуля) дадуть частоти трьох головних коливань розглядуваної системи
§ 131 Поперечні коливання стержнів Із зосередженими масами
Поперечні коливання стержнів досить часто мають місце в машинобудуванні. і зокрема в турбобудуванні, де застосовуються вали з прямолінійними осями, що несуть низку дисків Оскільки такі вали мають значні прольоти, то дуже важливо вміти визначати критичні швидкості обертання таких ввлів, що пов'язано з вивченням їхніх поперечних коливань
Вивчення поперечних коливань валів із зосередженими масами роз почнемо з розгляду пружної бвлки на двох опорах, що несе довільну КІЛЬКІСТЬ зосереджених (точкових) М8С ЛІ], /П,,	, Шп (рнс 54І)
Розв’язуючи поставлену задачу, ско- & %	, Дд
ристаємося другим способом (див § І29), .ДЛ * * п~* ЗГІДНО З ЯКИМ до пружної системи, ЩО не	Т''7,
має часи треба прикласти сили інерції	Рис-
—яцші,—яци», — . тлі0я<деш1( а»і, ,ш„ — відповідно поперечні переміщення (прогини) осі бвлки в місті прикладення мас тх, /л,	, т„.
аиі| Ш| ,ил — другі похідні цих переміщень по часу
Вирази для зазначених переміщень можуть бути узагальнені й подані в канонічному вигляді
иі, = —т^бц—т,ю,би— ••• —тпа>пбі„,
= ——пциіД,— ••• — нпшпб2п,	4)
= — тДвяі — т^і^пз — ... — т„шпб=, де б» — переміщення в напрямі і, спричинене одиничною силою, що діє в напрямі к
Ці коефіцієнти при згинанні визначаються за методом Мора
де Мх (х) та Мк(х) — згинальні моменти, спричинені відповідними одиничними силами
Рм = —ткшм = І
Ці коефіцієнти можуть бути обчислені також за допомогою фор мули Верещагіна
де Я;—площа епюри М{ (або частини Мх), Мец — ордината епюри М/, розташована напроти центра ваги площі епюри Я(
Нагадаємо також, що, згідно з теоремою про взаємність переміщень (теоремою Максвелла) б<* =
Основна система рівнянь (20 74) в найпростішому випадку для коливальної системи з одним ступенем вільності приводить до одвоп рівняння з однією невідомою
ц>1 -в — що еквівалентне відомому рівнянню ти> +	= 0,
оскільки с = 1/би
Для системи з двома ступенями вільності на підставі основних рів* нянь (20 74) дістанемо систему двох рівнянь з двома невідомими функціями прогину м>і та ш,і
ш, в — тІиі]б11 —
ш, = —	— т1ш16п
При розв’язанні системи рівнянь (20 74) функцію прогину можна взяти у вигляді
и>і = Х( зіп (<аІ + а) Підставляючи ці вирази в основні рівняння (20 74), матимемо таку однорідну систему алгебраїчних рівнянь відносно невідомих амплітуд X, та частот ш(
Хі (лцбцв* — і) 4- А^л,бцй* + ... 4. Хлтабіпй>в <» 0;
+ ^-і(лцбцШ* І) -[• • • • 4* Хп/Яд®2л®* = 0ї ^20 7&)
Хгт1бяіш‘ 4- Х./пДгСо* ц. • • - 4- Хп (тпбплй>* — І) = 0
Прн наявності коливань амплітуда X, не перетворюється на нуль, якщо визначник, складений з коефіцієнтів системи рівнянь (20 76), дорівнює нулю, тобто
і пцбиа* .. Пдвисв* ті®н®> лцбм<а* — І ... тпб2лсі)’
/п1бяі«* тДап* ... табмсй* — 1
В окремому випадку системи з двома ступенями вільності рівняння (20 7&) наберуть вигляду
X, (тД^* — І) 4- Х/Ми®** = 0'
Хі/гцбцШ* 4* X, (лцбмсйа — 1) = 0
Визначник (20 7б) при цьому буде
І/п^цФ* — І т1б„а* лцб^ю* т,бйй)я — І
Записавши визначник у розгорнутому вигляді, знайдемо частотне рів* няиня
®4 (®н®м — б’з)	(битх +	4 1 = 0,	(20 77)
звідки перша та друга частоти коливань визначаються відповідно фор* мулами
“* = |/	1’“ + +
“0-	(20.76)
= 0
+ V(»„ + Ь, %}’ - 4 (»„»» - вЬ) -£-| .	(20 78)
“’= /-2)»..^'-^., і"”+°"^- -
~У і»„4	(20 79)
Приклад 84 Визначимо частоту власних коливань балки (рис 542) що несе три однакових зосереджених вантажі масою т кожний
Перш запасе визначимо переміщення точок прикладення вантажів під дією ода 1ІНЧНИХ СИЛ Р, = 1	= 1 і Рі и і Для цього побудуємо епюри згинальних момен
тів від зазначених одиничних сил (рис 543) Користуючись формулою Верещагіна знайдемо переміщення від одиничних навантажень
бц-бм-»75* би = 243* б,, = дІЯ =	= в„ = ІП*; б1г = в„ = 51*
де	І*
* = 9 1296£7
Маючи значення 6(л складемо визна іник аналогічний виразу (20 76)
175/п*®* — 1	117т*ш*	51т*ш* І
117т*ш*	243*тш* — 1	1І7т*м* 1=0
5іт*ш* 1 17т*ш»	75т*®* — 11
Записавши здобутий визначних у розгорнутому вигляді знайдемо рівня пня частоти
77 760 (т*м*)» — 12 096 (т*ш*)* + 393т*®» — 1=0
Це рівняння має такі три корені що відповідають трьом значенням власних катових частот коливань розглядуваної пружної системи
(20 80)
§ 132. Коливання пружних тіл і розподіленими масами
Поперечні коливання струни. Виведемо диференціальне рівняння поперечних коливань струни як найтиповішого об’єкта коливальної системи а розподіленими параметрами Для цього розглянемо відхи-денна струни, закріпленої в точках А та В (рис 544, о) Початковий натяг струни позначимо через Р Будемо вважати відхилення малим, а зміною зусилля натягу Р при цьому знехтуємо, тобто Р = сопзі Довжина струни І
Припускаючи що при відхиленні всі точки струни лежать у площині ху, розглянемо елемент струни масою (іт кінцеві точки його х та х + (їх, тобто (іт = рР(іх де р — густина Р — площа поперечного перерізу Проведемо дотичні до елемента струни в його крайніх точках, кути нахилу дотичних до осі х відповідно а та ац (рнс 544, б) Вважаємо їх також малими
Складова натягу струпи, паралельна осі Оу, в точні х
У => — Р$іпа, а в точці х + йх
У +дУ ~Рі\паі.
Унаслідок малості кутів можна взяти
8іпа«І£а = -|£- ;
зІпа^Іеаі •	+ -зрг^-
Сума проекцій натягу на вісь у
'У-р-%-*
Щоб знайти рівняння руху струни при долиаанні, треба, користуючись принципом Д’Аламбера, що силу прирівняти до сили інерції елемента струни, яка дорівнює (іт (<Ру!д(*), що дає
(20 83)
Позначивши через (1 вагу всієї струни, знайдемо йт = -Я-йх, в»
де § — прискорення вільного падіння
Тоді рівняння (20 83) набере вигляду
Позначаючи
рівняння (20 84)
(20 85)
запишемо так
- „і дх* •
Це і є диференціальне рівняння плоских поперечних коливань натяг* нугоГ струни
Виходячи з рівняння (20 85). треба знайти відхилення як функцію двох незалежних параметрів х та І тобто
У = Р(х. ()
Ця функція повинна відповідати
1)	диференціальному рівнянню (20 85);
2)	граничним умовам, тобто прн х •= 0 та х = І ордината у = 0 або
^(О, ґ)=0, Г(/. 0 = 0.	(2086)
3)	початковим умовам, тобто при І = 0 вона повинна перетворюва тнся на задану функцію прогинів
Г&,0)=ї(х)	(20 87)
Крім того, частинна похідна по і при / = 0 повинна перетворюватися на задану функцію о (х) (початкова швидкість)
-°<*>	(20 88)
Умова (20 87) означає, що в початковий момент, тобто при І = 0, струна має задану форму, наприклад таку якої вона набере, якщо буде відтягнута штифтом 5 (рис 545) У момент і = 0 штифт убирають, і струна розпочинає свої коливання
Умова (20 88) означає, що в початковий момент усі точки струни мають задану швидкість, зокрема можуть перебуиати в стані спокою, як це має місце у прикладі, показаному на рнс 545
Розв’язок рівняння (20 85), застосовуючи метод Фур’е, шукаємо у вигляді
у = ХТ,	(20 89)
де X та Т відповідно функції х І І
Х = Цх}, Т = {я(0 Продиференціювавши рівняння (20 89) по х і і, дістанемо 8»у _ У дТ д'у т д*Х Л» ~Л ді* ’ '5*г в ‘ дх* ’
Після підстановки цих виразів у рівняння (20 8?) останнє набере ви гляду
‘ дх*
де С„ та тя — сталі, рівняння (20 94) запишемо у вигляді	л=/
У = сп 5іп х соз (/ - т„) (20 95)
Здобуте рівняння характеризує рух як періодич
ний, тобто коливальний Період коливань т = 2,1 =—,	(20 96) л=3
аяя	Рис 546
або
І в*Т а*	а*х
Т ді* = X	0л*
(20 90)
Прирівнявши праву та ліву частини останнього рівняння до однієї і тієї самої сталої величини — к\ дістанемо два рівняння
_^_==_/еіт	**=_±_х
4Г«	'Г/ ’	4*1 а» •
або
-^ + *т-о. т£ + -£*-о-	<209'>
Окремі розв'язки цих двох звичайних диференціальних рівнянь другого порядку такі
7\ = соз кі Т, = зіп кі, у к у . к	(20 92)
д1=соз —х, д, ваш — х
У щюму легко переконатися, підставивши їх у рівняння (20 91)
З функції (20 92) слід виключити соз (А/а) х як вираз, що ке перетворюється на нуль прн х = 0 Щоб зіп (к/а) х дорівнювався нулю при х — І, треба, щоб кі = апл звідки к = апя/1, де п — ціле число Рівність кі «= для називається рівнянням періодів або рівнянням частот. Воно виводиться безпосередньо з граничних умов
Тепер маємо два окремих розв’язки рівняння (20 85) ,___________ ЛЯ	ЛЛЛ ,	ЛЛ	апп , /пп
Ні = зіп—хсоз—р- і, уг = зіп —— хзіп—2—і	(20 93)
Помноживши кожне з цих рівнянь на невизначені коефіцієнти А і В та склавши ці два розв'язки, дістанемо загальний розв’язок рівняння (20 85) у вигляді
ї = зіп-¥-х/л„сда-^-<+а.їіп-^ і) (20 94) або, позначивши
Лл = С„соз-7-тп, В. = Сп5іп^-т„,
а секундна частота коливань
?""-7Г=-ЇГ	<2097>
При п — І струна коливається в основному тоні (з однією півханлею) При п = 2 струна коливається, утворюючи дві півхвилі, при п = 3 — в трьома півхвилями (рис 546)
Взагалі характер коливань струни залежить від початкових умов. Наприклад, струна буде коливатися в основному тоні, якщо при ( — 0 вона мала форму першої кривої (п = І) і всі її точки були в спокої Якщо ж початкова форма струни інша то крім основного тону з'яв ляються обертони, оскільки коливання струни становлять сукупність окремих коливань, що накладаються одне на одне Рівняння руху в цьому разі буде мати вигляд
у = 2(Лпсозп-уї-/ + В„5іпп -^2- /)$іпл-^£-.	(20 98)
Для остаточного розв'язання задачі треба з початкових умов (20 87) та (20.88) визначити коефіцієнти А та В рівняння (20 98)
З умови (20 87)
(У)<-о = 2 Лп8іп-^ = /(х),	(20 99)
а з умови (20 88)
(тН =2в.-^г-!іп-!2-і=1,(») (голос) \ ІІшЛ Л—0
Тут / (х) та о (х) — функції, задані в інтервалі 0 < х < І
Для визначення коефіцієнтів А„ і В„, які входять до залежностей (20 99) та (20 100), треба розкласти функції / (х) та о (х) в ряди, члени яких є тригонометричними функціями кутів, кратних пх/1 Ця задача розв'язується методом Фур’є, який полягає в тому, що рівність (20.99) множать на зіп т (гіх/І} та інтегрують по всій довжині струни від 0 до І. У результаті такого інтегрування знаходять
Їтях	г . плх тпх _
/(х)5іл ~~~і— дх = 2 \ Аа зіп —і—зіп—і—дх (20 101)
554
555
Прн цьому всі члени правої частини цього рівняння, крім одного, перетворюються на нуль, оскільки при л
т
с . пзис тях . п
\ зіп —— 51П—1~~Ох =0, (20 102)
а при л = т
рІП-^5іп-2^-Л = -і-
°	(20 103)
Рис 547	Для доказу рівностей (20 102) та
(20 103) пригадаємо, що
соз (а — 0) = соз а соз 0 4- зі л а зіп 0, соз (а + 0) = соз а соз р — зіпазіпр 2 зіп а зіп 0 = соз (а — 0) — соз (а 4- 0) Тоді
У зіп п -у- зіп т -у- 0х = ~%- С соз	<& —
д	о
І Г (л 4- /п) л* .
— -у у СОЗ -*	— Ох
6
Розглядаючи другий інтеграл правої частини останнього рівняння, бачимо, що він становить площу, обмежену кривою
у = соз(л4- от)-у-
та ординатами х = 0 і х = / Якщо п + т — парне число, то крива має вигляд, як на рнс. 547, а, якщо ж п 4- т — непарне число, то як на рис 547, б Площі окремих частин в обох випадках взаємно знищуються Інтеграл
соз(л — т)-~<іх
також перетворюється на нуль для всіх значень л у» т, в прн л » т дорівнює І
Отже, в правій частині рівності (20 101) тільки один член, що входить до рівності (20 103), не перетворюється на нуль Він, як доведено, дорівнює Ап1!2, а тому
4о = ~-( /(х)зіп-^у-Дк	(20 104)
Рис. 548
Аналогічно
’,«5іп-Т-*'	(20 І05>
0
За допомогою цих рівностей цілком можна визначити ряд (20 98)» а разом з тим і рух струни
Поздовжні коливання стержня Розглянемо поздовжні коливання призматичних стержнів, що на відміну від струни мають значну поперечну жорсткість Перш за все нагадаємо, що розрізняють три типи коливань поздовжні, крутильні та поперечні
Прн поздовжніх коливаннях усі частини стержня рухаються паралельно його осі (рис 548, а) Стискання та розтягання по черзі відбу ваються одне за одним як у часі, так і в просторі
Виведемо диференціальне рівняння поздовжніх коливань пружного стержня Для цього розглянемо умову динамічної рівноваги ділян ки коливного стержня, обмеженої перерізами а га Ь (рнс 548, б), завдовжки Ох Переміщення довільного перерізу стержня а з координа тою х позначимо через и = [ (х і) Переміщення перерізу 6 буде и + 4- (ди/дх) Ох Тоді відносні подовження в зазначених двох перерізах будуть такі в перерізі а е = диїдх, а в перерізі Ь —~	X
X	Розглядаючи зусилля, що діють на елемент стержня ’яч
довжки Лх, бачимо осьова сила в перерізі а
N... Ег = ЕЕ , •	дх
у перерізі Ь
= N. +	= ЕЕ + 4- іх] .
Для динамічної рівноваги рівнодійна цих іусиль має дорівнювати силі інерції маси розглядуваного елемента стержня
т д*и .
1
Тоді рівняння динамічної рівноваги елемента стержня буде
Рнс 549
Після скорочення на <іх та введення нового позначен ня тії? = р (т — маса стержня р — густина матеріалу) дістанемо диференціальне рівняння поздовжніх коливань в такому остаточному вигляді
с д*и д*и
Е дх» = р ~дїг
(20 107)
Це рівняння варте уваги тим що рух який воно виражає, не залежить від розмірів стержня Якщо покласти £7р = а2, то рівняння (20 107) буде цілком збігатися з рівнянням (20 85) руху струни
=	(20І08)
Тому формули здобуті при розгляді коливань струни, можуть бути автоматично використані при розрахунку поздовжніх коливань стержня При цьому тільки треба підставити відповідне значення для коефіцієнта а
Крутильні коливання стержнів. При коливаннях кручення якого-«ебудь наприклад циліндричного, стержня його циклічний рух найкраще характеризувати хвилястою лінією, креслячи іі на розгорнутій поверхні стержня (рис 549 а)
Нехай переріз завдальшкн х закручується відносно нерухомого перерізу на кут <р, а переріз завдальшкн х + <іх — на кут <р + ^.(дір/дх) Лх (рис 549, б) Тоді відносний кут закручування елемента завдовжки йх буде дуїдх, і крутні моменти в кінцевих перерізах відло-відво
Прирівнюючи рівнодійну цих крутних моментів до моменту Інерції обертання елемента завдовжки <іх, що дорівнює
І — Р^о (б’ф/гі/2) <іх, дістанемо рівняння руху
яке після скорочення на та Ох буде мети вигляд
(20 109)
Позначивши С/р через а2, знову дістаємо диференціальне рівняння у формі коливань струни
» д*ч> ді* ~0 дх* •
Тому в цьому разі формули, виведені при розгляді коливань струни, залишаються придатними
$133 Поперечні коливання призматичних стержнів
Розглянемо поперечні коливання призматичного стержня (рнс 550 в) в площині хи> яка «площиною симетрії для йогопопереч-ного перерізу
Позначимо через и> поперечне переміщення осі стержня на відстань х від лівого кінця На відміну від згинної жорсткості струни Е.І, якою нехтували внаслідок їі малості, при розгляді поперечних коли вань стержня цього робити неможна, оскільки тут зона відіграє ви рішальну роль
Для виведення диференціатьного рівняння поперечних коливань стержня розглянемо умови динамічної рівноваги сил, що діють в напрямі елемента стержня завдовжки сіх, обмеженого перерізами зав дальшкп х та х + сіх від лівого кінця стержня (рнс 550, б) Проек ціюючи всі сили, що діють на елемент стержня (враховуючи сили інер ції), на вертикальну вісь ш, матимемо
* “ (° + Тії І ~	= °-
(20 І І І)
де р — густина матеріалу, Р — площа поперечного перерізу стержня
Ураховуючи зв'язок між поперечною силою ($ та згинальним мо ментом М
рівняння (20 ІІ1) можна переписати у вигляді
Р0ІІ2)
Ураховуючи відомий з теорії згинання стержнів зв язок між згнналь ним моментом М та прогином нейтральної осі х батки ш

Рас 550
рівняння (20 112) можна переписати у вигляді
сгопз>
Це і буде загальне диференціальне рівняння власних поперечних коливань стержня
В окремому випадку призматичного стержня постійного перерізу, коли жорсткість при згинанні від х залежати не буде (Е^ = сопзі), рівняння (20 І ІЗ) матиме вигляд
+	(20 114)
або
(20)15)
д*	____
с-У-^Г	(20 116)
— швидкість поширення хвилі деформації по стержню
Якщо стержень коливається в поперечному напрямі за однією з форм аласних коливань, його прогин у довільному перерізі буде змінюватися з часом за гармонічним законом
ш « X (4 соз и/ + В зіп <і)ґ)	(20 117)
Тут для зручності запису випущено індекс і, який позначає і у форму коливань
Підставляючи (20 Н7) в (20 ІІ4), після відповідних скорочень матимемо
Ц£-Х = 0	(20118)
або
де
(20 119)
Поклавши в рівнянні (20 118)
Х=/“.	(20 120)
дістанемо (п* — *«) = 0, звідки видно, що величина п може набирати таких значень = к, л, — —к, Пз = ік, л« = — ік, де і* = —і Тоді загальний розв'язок рівняння (20 120) запишеться так
X = Се“ + О~*' + £«“* + Л~““	(20 121)
або в еквівалентній формі
X •= С1 зіп кх + С9 сов кх + С, зЬ кх 4-+ С4сЬ4*.	(20 122)
де Сх С„ Са та С4 — довільні сталі, які по винні визначатися в кожному конкретному випадку відповідно до так званих крайо вих умов, тобто умов, заданих на кінцях стержня
Взагалі кількість крайових умов дорівнює кількості довільних сталих (по даі на кожний кінець) Всі вони виражаються рівністю нулю двох із таких чотирьох величин X, X' Xі Хт, у тому числі на вільному кінці X' = Xм =»= 0, на вільній опорі X = X' = 0, на жорстко закріпленому кінці X = X' = 0
Для прикладу розглянемо поперечні коливання простої балки, вільно обпертої на дві опори (рис 551, а) Умови на кінцях балки такі при х = 0 X = 0, X = 0, при х = І X •= 0, X' = 0
Запишемо ці умови, виходячи з формули (20 122)
С, 4- С4 = 0; С1 зіп кі + С, зН кі = 0, — С, + С4 -0; — С4зіпМ 4-С,зЬ« = 0, звідки
С, = С, = С4 = 0,
Сх зіп кі = 0
Оскільки для нетривіального розв’язку В =/= 0, то
зіп кі = 0	(20 123)
Звлежаість (20 123) І буде рівнянням частоти для розглядуваного прикладу коливань балки шарнірно обпертої на дві опори 3 рівняння (20 123) випливає, що
кІ = іп(і= 1, 2, 3,. .), вле оскільки
*•-
де т = рР, то колова частота коливань балки
Р°124> а секундна частота коливань
Л =	<20 125>
Для власних коливань балки, ягідно з формулою (20 122), рівняння прогинів буде мати вигляд
•X	.	(20 126)
Ю 2-27М
561
Графіки перших трьох форм власних коливань наведено на рис 551, б Загальний розв июк диференціального рівняння власних коливань (20 114) стосовно до балки на двох опорах має вигляд
»(* 0= У. (а( С05 0),/ -{ Ьі ЗІП СО|0 51П •££-
Коефіцієнти а( та Ь, знаходять з початкових умов ш (х 0) = = / (х) а> (х, 0) = V (х) за методом, викладеним у § 132
Глава 21. ОПІР МАТЕРІАЛІВ ДІЇ
ПОВТОРНО-ЗМІННИХ НАПРУЖЕНЬ
$ 134 Явища втомленості матеріалів
Опір матеріалів дії навантажень, що змінюються в часі за моду лем або за модулем та знаком, суттєво відрізняється від опору дії статичного навантаження При цьому під дією змінних навантажень елементи конструкцій руйнуються при значно менших напруженнях, ніж під дією статичних навантажень Типовим прикладом детаїі що зазнає змінних навантажень е шток поршневої машини, знак напру жень в якому змінюється відповідно до змін напряму руху поршня
Практикою встановлено якщо елемент конструкції багаторазово піддавати змінному навантаженню певного рівня, то після деякої кількості змін напружень у ньому з явиться тріщина, яка поступово буде розвиватися Урешті решт дета ть зруйнується, не давши при цьому помітних залишкових деформацій навіть тоді, коли її матеріал високопластичний
КІЛЬКІСТЬ циклів до появи першої тріщини і до повного руйнування буде тим більша чим менше напруження Характерно що руйнування матеріалу під дією повторно змінних навантажень може відбу тися при напруженнях, нижчих за границю текучості
Руйнування матеріалу під дією повторно змінних напружень називається руйнуванням від втомленості
Взагалі ж втомленістю матеріалів (зокрема, металів) називають явище руйнування внаслідок поступового нагромадження в них пошкоджень що призводять до виникнення тріщини при багаторазовому повторенні навантажень
Здатність металів чинити опір руйнуванню при дії повторна змін них напружень називається опором втомленості матеріалу
Вивчення питань втомленості в опорі матеріалів має дуже велике значення Такі важливі деталі, як осі залізничних вагонів колін часті вали шатуни моторів гребні гвинти пружини клапанів, по вітряні гвинти поршневі пальці й багато інших деталей, виходять з ладу здебільшого внаслідок руйнувань атомленісного характеру
Руйнування від втомленості відбувається якщо має місце одна з таких двох особливостей прикладання навантаження
І)багаторазовеприкладання на* вантаження одного знака напри* клад періодично змінюваного від нуля до максимуму (рис 552 а), рИ£ К2	2) багаторазове повторення на
вантаження, шо періодично змінюється не тільки за модулем, а й за знаком (знакозмінні навантаження), коли на опір втомленості матеріалу одночасно впливають як повтор* вість, так і змінність навантажування Прн цьому розрізняють зміну навантаження за симетричним циклом (рис 552, б) та за несиметрнч ним (рис 552, в, г)
Для руйнування від втомленості недостатньо змінності напружень Треба також, шоб напруження мали певне значення.
Максимальне напруження, при якому матеріал здатний чинити опір, не руйнуючись, при будь якій довільно великій кількості повторень змінних напружень, називається границею витривалості (гра ницею втомленості)
Злом деталі від втомленості має характерний вигляд (рис 553) На ньому майже завжди є даі зони Одна з них (4) гладенька, притер та, утворена внаслідок поступового розвитку тріщини друга (В) — крупнозерниста що утворилася при остаточному зломі перерізу деталі ослабленого під час розвивання тріщини Зона В у крихких де талей має крупнокристалічну будову, а у в язких — волокнисту
Коротко зупинимося на механізмі явища втомленості
Усі метали, які застосовуються в техніці, е полікристалічничи ре новинами що складаються з окремих зерен і не становлять однорід ний моноліт, яким вважають матеріал згідно з основними гіпотезами опору матеріалів Зерна технічних металів є сукупністю кристалів що мають неправильну огранку, їх, як правило, називають криста літами І Іолікристалічність матеріалу та неминуча його пеоднорід ність призводять до того, що лід дією тих чи інших навантажень в
19*
563
окремих червах виникають перенапруження і створюються умови для появи мікротріщин При ньому в разі напружень, спричинених ста тичним навантаженням, подібні мікротріщини не небезпечні Якщо ж напруження змінні у часі, то має місце тенденція розвитку мікротрі щин, що призводить урешті решт до злому деталі
Крім зазначеної гіпотези існує й дещо інший підхід до пояснення фізичної природи явища втомленості Зокрема виникнення тріщин від втомленості можна пояснити вичерпанням здатності кристалічних зерен чинити опір зсуву
Зерна більшості металів складаються з низки елементарних куби ків з розмірами сторін (3 6) І0~* см Кубики в свою чергу, склада ються з системи атомів що взаємодіють між собою, розташованих у цілком певному для даного матеріалу порядку, утворюючи так звану просторову атомну решітку Форма та розміри елементів останньої залежать віл сил взаємодії атомів та визначають характерні аласти вості даної речовини
Деформація матеріалу звичайно пов язана із спотворюванням кристалічної решітки та зміною міжатомних відстаней При цьому в разі невеликих напружень взаємодія між атомами не порушується, і при дальших розвантаженнях зазначені викривлення решіток зни кають Якщо ж напруження великі, то в кристалічних зернах пластич них матеріалів по деяких площинах що звуться площинами ковзання Кристаліту відбуваються необоротні зсуви Зсунуті відносно один одного групи атомів уже не утворюють єдиної атомної решітки Нове утворення, що при цьому виникло виявляється більш міцним унаслЬ док посилення площини коазання всередині окремих зерен Тепер для його руйнування потрібне більше зусилля
Однак зміцнення при зсувах супроводжується зниженням міцності (розпушуванням) Тому процес зсуву обов'язково супроводжується появою зон, де атомні зв'язки порушуються, а нові не утворюються Це проявляється в тому, що утворюються дуже дрібні мікротріщини, кожна з яких у певних умовах (наприклад, прн сусідстві кількох зерен, послаблених тріщиною) може стати осередком розвитку тріщини від втомленості, яка в результаті призводить до руйнування від втомленості
Отже, із сказаного випливає, що механізм утворення тріщин при повторно*змінних навантаженнях дуже складний і не може вважатися повністю вивченим
із безумовних положень теорії втомленості можна зазначити такі
і) процеси що відбуваються в металі при повторно*змінних на вантаженнях, носять різко виражений місцевий характер
2) із двох видів напружень — нормальних та дотичних — внрі шальннй вплив на процеси втомленості до утворення першої тріщини включно маютр дотичні напруження, які спричинюють пластичні зсуви та руйнування
Розвиток тріщини від втомленості, безумовно, може прнскорюва тись, якщо є розтягальні напруження як у пластичних, так і особлн* 564
а во, в малопластичних та крихких матеріалів типу чавуну в яких поява тріщини відриву значно підвищує чутливість до розтягальних напружень Тріщини найчастіше утворюються в зернах які лежать ближче до поверхні дегалі Пояснюється це тим, що поверх неві шари матеріалу певною мірою мають сліди пошкоджень різними технологічними операціями при обробці деталі (внутрішні напружен ня, сліди механічної обробки), не кажучи вже про ті випадки, коли зовнішні шари прн повторно*змінних навантаженнях зазнають най більших напружень (при згинанні та крученні)
Границю витривалості визначають експериментально Вона залежить від цілої низки факторів, вокрема від форми та розмірів деталі, способу н обробки, стану поверхні деталі, виду напруженого стану (розтягання стискання, кручення, згинання тощо), закону зміни навантаження в часі прн випробуваннях
При розгляді опору матеріалів дії змінних напружень у більшості випадків інженерної практики припускається, що ці напруження є періодичними функціями часу р = / (0 з періодом Т1.
Сукупність усіх значень напружень за час одного періоду назива ють циклом напружень (рис 554, а). На опір втомленості в основному впливають максимальні ртш та мінімальні раїп напруження циклу. Крім них в опорі матеріалів вводять поняття постійного, або середнього, напруження циклу р (рнс 554, б)
_	4" Ртіп	ті ««
Рср =------§------- "
1 У даному підручнику не розглядаються розрахунки на опір втомленості під дією випадкових змінних навантажень, що має місце в деяких випадках експлуатації конструкцій
та поняття про амплітуду ра циклу, що характеризує змінність напру жень
Ро__^2±!ї_	(212)
Середнє напруження може бути як додатним так і від'ємним, ам плітуда ж циклу — абсолютна величина (знак не враховується) Від повідно до виразів (21 і) та (21 2)
Рп\п = Рср + Ра» Ртіп = Рср — Ра
Подвоєне значення амплітуди коливань напружень називається розмахом циклу Відношення мінімального напруження циклу до мак симального з урахуванням знаків цих напружень називається харак теристикою циклу, або коефіцієнтом асиметрії циклу, і позначається літерою г тобто
Г — РаіпІРшлж	(2І 3)
Найнебезпечнішим є так званий симетричний цикл, коли р^- = = —Рпііп та Дер = 0, при якому
С = РпйоІРта = — І
Границя витривалості при симетричному циклі е мінімальною для даного типу деформації й позначається через р-і. У випадку напру ження, що змінюється від нуля до максимуму, тобто при віднульово* му (пульсуючому) ЦИКЛІ, КОЛИ Ртіп = 0,
г = 0/Рт.і = 0, а границя витривалості, що відповідає даному циклу, позначається через р0
При до = сопзї, тобто коли діє постійне статичне навантаження, р-.. = ргаїп = р і характеристика циклу
Г = Ротіп/Рпмі — р/р = і
У самому загальному випадку границю витривалості, здобуту при характеристиці циклу г, позначають рг границю витривалості, визна чеку при якомусь певному значенні г, наприклад прн г = —0,5, по* значають відповідно р^ь
Цикли, що мають однакові характеристики г, називаються подібними Характеристика циклу, або коефіцієнт асиметрії може зміню ватися від —оо до 4-оо
Значення коефіцієнтів асиметрії циклу для різних видів циклів наведено в табл 21 Очевидно для повного висновку про характер дії циклічного навантаження крім характеристики циклу г повинно бути відомим хоча б максимальне чи мінімальне напруження циклу
Зазначимо, що в окремих випадках, коли мова йтиме про нормаль ні або дотичні напруження (у першому випадку при циклічному роз тяганні стисканні або при згинанні, у другому — при циклічному крученні), літера р у прийнятих вище позначеннях повинна бути за Б66
Таблиця 21
мінена відповідно на а або т при збереженні відповідних індексів Так наприклад, при циклічному розтяганні стисканні або згинанні замість Дгтш, Ртіп, Рср ТВ ра ПОВИННІ ВІДПОВІДНО фігурувати От». Отіп, 0ср та ал, тоді границя витривалості при характеристиці циклу г буде позначатися сг, а наприклад, при симетричному циклі, тобто при г = = —1 буде о_| У разі кручення з циклічною зміною напружень характерні напруження циклу будуть відповідно позначатися через Тшах> Тгоіп, тСр, тв а границя витривалості — через т,, Т_|, т0 і т д.
$ 13$. Методи визначений границі витривалості. Діаграма втомленості
Для визначення границі витривалості того чи іншого матеріалу треба на відповідній випробувальній машині випробувати партію зразків з даного матеріалу в кількості 6 І2шт Для цього найчасті ше беруть гладенькі циліндричні зразки діаметром 7 ІО мм
Границі витривалості матеріалу при вибраній характеристиці цик лу г, зрозуміло будуть різними залежно від виду деформації, при якій випробовують зразки, тобто залежно від того, прн змінних.напруженнях розтягання стискання, змінному крученні, згинанні або ж в умовах складного напруженого стану їх випробовують Тому, ставлячи перед собою мету визначити границю витривалості, слід наперед зазначити при якому виді деформації та характері зміни напружень за цикл треба визначити границю витривалості
Відповідно до посгаалених вимог вибирають потрібну випробу вальну машину Для випробування матеріалу на опір втомленості при змінному розтяганні стисканні можна взяти машину, схему якої на ведено на рис 555
У лабораторних умовах симетричний цикл здійснити найбільш просто Схему найпростішої установки для визначення границі витри валості при ротаційному згинанні у разі симетричного циклу показано на рис 556 При обертанні зразка його зовнішні волокна будуть за ввавати навперемінного розтягання (коли вони знизу), то стискання (прн повороті зразка на (80°)
Частота обертання найбільш поширених машин для визначення опору втомленості, як правило, дорівнює 3000 хв~> (50 Гц) Тому випробування на опір втомленості з метою знайти границю витривалості погребує багато часу, що становить тижні неперервної роботи машини Останнім часом при дослідженні матеріалів та конструктивних деталей на опір втомленості застосовують більш швидкохідні ма
шини з частотою 100 150 Гц а іноді й 20 000 Ги (ультразвукові частоти) В останньому випадку час випробування становить тільки десятки хвилин.
Прн випробуванні партії зразків з метою визначити границю ви тривалості треба давати такі навантаження на окремі зразки, щоб вони не руйнувалися, витримавши різну кількість циклів навантажу
вання.
Обробка здобутих експериментальних даних, як правило, супроводжується побудовою кривої втомленості, яку в літературі часто Називають кривою Веллвра (рис 557) Криву втомленості будують по точках у координатах кількості циклів N та напруження ртп Кожному зразку, що зруйнувався, на діаграмі відповідає одна точка з координатами N (кількість циклів до руйнування) та (напруження) тобто крива втомленості є функцією = / (Л0
Порядок прикладання навантажень на випробувані зразки здебільшого вибирають спадаючим, тобто на перший зразок дають наванта ження, що значно перевищують границю витривалості, а наванта ження на наступні зразки поступово знижують Зрозуміло, що кожний з менш навантажених зразків буде витримувати дедалі більшу кількість циклів Можна вибрати й інший порядок навантажування
Будуючи криву втомленості по точках зруйнованих зразків легко
переконатися, що, наприклад при випробуванні сталі (рис 557, крива /), при висо кому рівні напруження крива стрімко падає, а в міру зик ження іх крутість зменшуеть ся і крива асимптотично на блнжається до деякої горизон тальної прямої, що відсікає на
Рис 557

N
Рис 558
осі ординат відрізок, величиною якого й визначається границя витри валості Ордината точки на кривій, де остання практично починає збі гатись із зазначеною асимптотою, відповідає такому напруженню, при якому зразок не зруйнується пройшовши кількість циклів, що від повідає наперед заданій величині, так званій базі випробувань
Легко зрозуміти, що за базу випробувань Мо і вибирають ту кіль кість циклів, прн якій правий кінець кривої втомленості практично проходить паралельно осі абсцис Виходячи з цього, базою випробу вань на опір втомленості називається найбільша кількість повторно змінних навантажень, перевищення якої не повинне призводити до руйнування від втомленості випробуваного зразка при даному напруженні
Для чорних металів (сталі, чавуну тощо) за базу випробувань, як звичайно, беруть 10 млн циклів, а для кольорових (міді, алюмінію і т п ) — число, в 5 10 разів більше із розгляду характеру кривої втомленості для кольорових металів (рис 557, крива 2) видно, що на більшій ділянці вона спадає дуже поступово, тобто крива прямує до асимптоти повільно, тому й доводиться в цьому разі за базу випробу* вань брати більшу кількість циклів Взагалі для таких металів можна казати тільки про деяку умовну границю витривалості Умовною ера кицею витривалості називається максимальне напруження, при якому при здійсненні певної наперед заданої кількості циклів, що відлові дав тій чи іншій базі випробувань, зразок не руйнується
У зв’язку а тим що за кривою втомленості, побудованою в коорди натах N ~ р, або, що те ж саме, N ~ а (рис 558, а) часто буває важ* ко визначити границю витривалості, застосовують два інших способи побудови діаграм втомленості
Перший спосіб полягає в тому, що по осі абсцис відкладають величину, зворотну кількості циклів (рис 558, б) Границю витрива лості тоді визначають як ординату в місці перетину кривої втомленості з віссю напружень
Другий спосіб грунтується на зображенні результатів випробувань у півлогарифмічних (рис 558, в) або логарифмічних (рис 556, а) координатах Як видно а рнсувків, критерієм для висновку про границю витривалості є перелом кривої
Зазначимо, що, згідно з численними експериментальними даними, для деяких матеріалів можна помітити певні співвідношення між границями витривалості при різних видах деформації й, зокрема між границями витривалості при згинанні о-цг, крученні т-і та розтя 570
ганні стисканні а_|Р при симетричних циклах
Для гладеньких зразків ці співвідношення прнблиз но такі для сталі о_|р = = 0,7а_|ЇГ, для чавуну о_ір = 0,65о_імг для ста лейта легких сплавівх-і» = 0 55а_)9г для чавуну т_| = 0,8а-ік
Знаючи тимчасовий опір а., границю витривалості сталі при симетричному циклі можна наближено знайти за такими емпірич ними співвідношеннями від повідно для розтягання стискання згинання та кру чення
а_ір = 0,28ав,
О—ііг =- 0,40ст., т_| = 0 22а.	(21 4)
Для кольорових металів співвідношення між границею витривалості та границею міцності менш стійке згідно з експериментальними даними. о_ІЇГ = (0,24 0 50) а.
Діаграма граничних напружень Щоб охарактеризувати опірність матеріалу дії змінних напружень з різною асиметрією циклу, будують так звану діаграму граничних напружень (рис 559) В ній по осі ординат відкладають найбільші оетм та найменші Отш напруження цнк лу, а по осі абсцис — середнє напруження циклу (діаграма Сміта) їхні граничні значення Огтіх агт1П1 о, С[/визначаються приданій характеристиці циклу дослідним шляхом у результаті побудови крн вих втомленості
Як звичайно починають з симетричного циклу (г = —і) Граиич ним напруженням у цьому разі буде границя витривалості о_| Отже,
О—| п>іх = ®—1 О—і а>|ц я 0—1,	О—| ер = 0
Цьому циклу на діаграмі відповідають точки А та А', що лежать на осі ординат
Випробувавши партію зразків з даного матеріалу при певному значенні характеристики циклу г = ©тіп/отм, визначимо найбільше та найменше значення напружень, при яких матеріал працює на границі витривалості а, тобто
ти “Ь
О< тах = Ог Оггоіа = ГОГ, Огер = ————— .
Нанесемо на діаграму точки М та Л7, абсциси яких дорівнюють огср, а ординати — відповідно а, тах та о, т>п- Роблячи так само для інших значень г, дістанемо точки Ми N1, М,, і т д
Сполучимо лініями всі точки, що зображують максимальні та міні мальні граничні напруження циклів Очевидно крайня права точка діаграми (точка О) відповідає циклу, при якому ат«» = огаіо = г =* і, тобто постійному навантаженню Граничним напруженням у цьому разі є границя міцності матеріалу Отже, абсциса і ордината точки О дорівнюють границі міцності матеріалу, а ординати точок лінії АО відповідають границям витривалості матеріалу при різних значеннях коефіцієнта асиметрії циклів
Легко переконатися, що промені, які проходить крізь початок ко ординат діаграми граничних напружень, є геометричним місцем точок, що характеризують цикли з однаковим коефіцієнтом асиметрії Г Оспіп/Цшдх ДІЙСНО,
10 я = °'п*ж = 2°ПІ1К = 2 °ср ®пих4’°т1г>	•+*
Для визначення границі витривалості матеріалу при даному зна ченні коефіцієнта асиметрії г треба обчислити за наведеною формулою кут (і і провести промінь під цим кутом до перетину з лінією А, орди ната точки перетину дорівнює о,
У разі циклічного кручення діаграма будується по один бік від осі ординат і має такий вигляд, як показано, наприклад, для конструкційної сталі на рнс 560
Діаграму граничних напружень можна будувати також у коордн натах с0 ~ аср (діаграма Хейя), тобто по осі орданат відкладати гра ннчну амплітуду оо циклу, а по осі абсцис — середнє напруження Сер циклу (рис 561) На цій діаграмі пряма, проведена з початку координат під деяким кутом, також характеризує цикли з однаковою аси метрією, оскільки
®яіі> ~ ®тіп
®ер ®яі»х Ч* ®тіп І Ч" г
§
Отже, при сталому £ сталим е і коефіцієнт асиметрії г
При плоскому та об'ємному напружених станах опір втомленості можна охарактеризувати, виходячи з відповідних гіпотез міцності, що узгоджуються з експериментальними даними
Для дослідження дійсної поведінки матеріалу в умовах складного напруженого стану, наприклад при згинанні з крученням, використовують спеціальні випробувальні машини, що дають змогу одночасно навантажувати зразок змінним згинальним та крутним моментами
За результатами випробувань, здобутими при різних комбінаціях змінних о та т, будують діаграми в координатах ав ~ тв або у віднос-572
них величинах со/о^ та та/т_і Точки таких діаграм визначають на пружені стани, що характеризуються величинами а0 та т0 при складно му напруженому стані Типову діаграму для конструкційних сталей, побудовану за експериментальними даними, показано на рис 562 (крива 1) Вона відповідає дузі ката Для високоміцних сталей та ча вунів експериментальні дані розміщуються ближче до еліптичних дуг (рис 5б2, крива 2)
При симетричному циклі з додержанням синхронності та синфаз ності напружень умова міцності в амплітудах головних напружень відповідно до гіпотези найбільших дотичних напружень запишеться так
010 — 03о = 0-1
Виходячи з теорії міцності енергії формозміни, умову міцності можна записати в такому вигляді
(010 — О2о)* + (Оіо — Озо)* 4- (030 — Оіо)’ = 2аІ_,	(21 5)
Для складного напруженого стану, що характеризується спіль ною дією розтягання та кручення або згинання та кручення, із по* правкою на співвідношення границь витривалості умова міцності виражається так
[/^+1-^-4-0-1	(216)
Остання умова збігається'з раніше наведеною експериментально здобутою залежністю, що характеризується в координатах оа/о_і, Тв/т-і дугою кола
§ 136. Вплив конструктивно-технологічних факторів на границю витривалості
На значення границі витривалості зразків або деталей, виготов люваних з того чи іншого матеріалу, крім характеристики циклу впли ває ціла низка різних факторів До них належать форма зразка, розмі ри, стан поверхні, середовище, в якому відбуваються випробування,
температура випробовувань, режим циклічного/силового впливу (тренування, паузи, перевантаження, частота навантажування тощо), попередня внутрішня напруженість матеріалу /а ін
Для з’ясування впливу того чи іншого фактора як еталон беруть границю витривалості р-\, здобуту випробовуванням на повітрі при симетричному циклі партії гладеньких полірованих зразків діаметром 7 ІО мм Тоді вплив різних факторів на опір втомленості можна оці* нити відхиленням границі витривалості р~\ партії розглянутих зраз ків від границі витривалості р_і еталонних зразків
Вплив концентрації напружень Найбільш важливим фактором, що знижує границю витривалості, е концентрація напружень, спри чинена різкою зміною перерізу деталі Концентраторами напружень на практиці е шпонкові канавки, отвори в деталі, нарізки на поверхні, малі радіуси заокруглень у місцях різкої зміни розмірів перерізів тощо Концентрація напружень, як правило, сприяє зародженню тріщини від втомленості, яка, розвиваючись, призводить урешті решт до руйнування деталі
Як показують досліди, при дії змінних напружень границя витривалості з концентрацією напружень більша, ніж частка від ділення границі витривалості гладенького зразка на теоретичний коефіцієнт концентрації напружень а„ (див § 33), тобто
Р-1« Р-і/Оа
Така розбіжність пояснюється тим, що теоретичний коефіц єнт концентрації а, відображує характер розподілу напружень лише для ідеально пружного матеріалу у реальних матеріалах унаслідок плас тичних деформацій у мікрозоні місця концентрації напружень дещо перерозподіляються й згладжуються Враховуючи це, разом з теоретичним коефіцієнтом концентрації при розгляді питань опору втомленості використовують поняття ефективного, або дійсного, коефіцієнта концентрації, який є відношенням границі витривалості гладенького зразка без концентрації напружень до границі витривалості зразка з концентрацією напружень, що має такі самі абсолютні розміри пере різів Ці коефіцієнти надалі позначаються так для нормальних на пружень
для дотичних напружень
де 0-і та т_] — границі витривалості для гладеньких зразків, а_ін та т_|к — границі витривалості зразків з концентрацією напружень
Далі міркувати будемо стосовно до нормальних напружень, маючи на увазі, що дія дотичних напружень усе сказане залишається в силі, тільки слід індекс а при коефіцієнтах замінити на т
Ефективні коефіцієнти концентрації напружень мають менші зна чення, ніж коефіцієнти концентрації Оа, що визначаються теоретично в припущенні «пружного» розподілу напружень
кількісно оцінити зазначену різницю коефіцієнтів к0 та а<і мо»нз введенням так званого коефіцієнта чутливості матеріалу до концентра ції напружень
Знаючи коефіцієнти чутливості дв, для яких у довідковій літера турі є відповідні графіки (рис 563). можна за а? обчислити значення ефективних коефіцієнтів концентрації
Л<І = І + ?о(Ла — І)	(21 7)
Очевидно для матеріалу, не чутливого до концентрації напружень, тобто при = 0,	— 1 При — і к0 тобто матеріал має
повну чутливість до концентрації напружень
Як видно з графіків (рис 563), чутливість матеріалу до концентра ції напружень залежить насамперед від його властивостей При цьо му чим вища міцність сталі, тям вища її чутливість до концентрації на лружень Тому застосування високоміцних сталей прн змінних напру женнях не завжди виявляється доцільним
Чутливість металу до концентрації напружень у крупнозерннстих сталей менша, ніж у дрібнозернистих Метали та сплави з неоднорід нею структурою, наприклад сірий чавун, мають знижену чутливість до концентрації напружень внаслідок того, що структурна иеоднорід ність є внутрішнім джерелом концентрації напружень і знижує гра ницю витривалості гладеньких зразків, тому зовнішні концентратори вже мало знижують границю витривалості
Коефіцієнти чутливості до концентрації напружень, як показують експерименти, залежать не тільки від механічних властивостей, а й
від конструктивної форми самої деталі, а також розподілу в ній напружень	/
Вплив концентрації напружень у розраху/ках деталей машин, що зазнають дії змінних напружень з асиметричним циклом, слід враховувати на основі експериментальних даних, оскільки теоретично це питання досі не вирішено	/
Згідно з експериментальними даними, здобутими на лабораторних зразках невеликого перерізу, відношення граничних амплітуд гладеньких зразків та зразків з концентрацією, що відповідають одному і тому самому середньому напруженню, не залежить від амплітуди циклу Цю обставину використовують для розрахунку деталей машин на опір втомленості при асиметричних циклах
Вплив концентрації напружень прн згинанні з крученням, як звичайно, оцінюють на підставі відповідних випробувань на машині, яка дає змогу створювати одночасно навантажування зразка круг ними та згинальними моментами при різному співвідношенні їх На рис 564 наведено результати експериментів при синфазніЙ зміні нормальних та дотичних напружень прн симетричному циклі (о_|К, т_ік — границі витривалості при симетричному циклі для зразків з концентрацією при згинанні та тільки прн крученні відповідно, о», твк — граничні амплітуди для зразків з концентрацією при одночасній дії згинання та кручення).
Розглядаючи рис 564, бачимо, що більшість експериментальних даних цілком відповідає еліптичній залежності
'+('йг)' = '	(2|8)
тобто такій самій залежності, як і без концентрації напружень.
Вплив розмірів (масштабний фактор). Ефективність концентрації напружень пов'язана з абсолютними розмірами перерізу деталі, а саме із збільшенням розмірів деталі при збереженні її геометричної подібності значення ефективних коефіцієнтів концентрації напружень збільшуються
Як показують результати експериментів, при збільшенні діаметра зразка більше ЗО 40 мм дальше зростання ефективних коефіцієнтів концентрації практично припиняється Можна вважати, що при досяг ненні деякого розміру перерізу ефективний коефіцієнт не відрізняєть ся від теоретичного, тобто «о -= аа Для легованих сталей з границею міцності <7В > і200 МПа рівність зазначених коефіцієнтів при >ееред ніх рівнях концентрації напружень «о = 2 3 досягається вже при
== 40 50 мм Щодо вуглецевих сталей, то в них граничний розмір, після якого к,, = а0, значно більший
Абсолютні розміри перерізів деталі, впливаючи на ефективність кон центрації напружень, істотно впливають також на границю витрива лості зразків без концентрації напружень При цьому із збільшенням абсолютних розмірів перерізів границі витривалості знижуються Від-576

Рис 566
ношення границі витривалості деталі розміром А до границі витрнва лості лабораторного зразка подібної конфігурації, що має малі розміри (гі0 — 7 ІО мм), називають коефіцієнтом впливу абсолютних розмірів перерізу і позначають стосовно до нормальних напружень так
Коефіцієнти впливу абсолютних розмірів перерізу можна визна чиги й на зразках з концентрацією напружень У цьому разі
(2110)
причому деталь розміром А та зразок малого розміру повинні бути геометрично подібні
Для розрахунку елементів машин з урахуванням впливу розмірів деталі як при наявності концентраторів напружень, так і без них, Існують спеціальні графіки типу наведених на рис 565 (тут шкала А — логарифмічна), побудовані на основі експериментів Тут крива 1 відповідає деталі з вуглецевої сталі без джерела концентрації напру жень, а крива 2 — деталі з легованої сталі (ов — І000 1200 МПа) при відсутності концентрації напружень та вуглецевої сталі при наяв ності помірної концентрації напружень Крива 3 відповідає деталі з легованої сталі при наявності концентрації напружень, а крива 4 — будь якій сталі прн сильному концентраторі (типу нарізки)
Як показують експерименти, при збільшенні діаметра до і50 200 мм зниження границі витривалості зразків при ротаційному згинанні (див рис 556) може досягати ЗО 45% Дослідні дані свід чать про малий вплив абсолютних розмірів на опір втомленості при однорідному напруженому стані — розтяганні стисканні При кру ченні, як і при згинанні, зниження границі витривалості із збіль шенням розмірів деталі проявляється значно більше Це пояснюється впливом градієнта напружень
Зниження границь витривалості із збільшенням абсолютних роз мірів деталі можна пояснити також впливом таких факторів
о зменшенням механічної міцності матеріалу /з збільшенням діа метра заготовок навіть за умови додержання належної термічної обробки їх	/
2) зміною властивостей поверхневого шару після механічної обробки, оскільки ці зміни виявляються різни&и при різних розмірах деталі;	/
2>) неоднорідністю механічних властивостей та напруженістю різ них зерен у ав язку з полікристалічною структурою металу і як на слідок підвищенням імовірності більш раннього руйнування від втомленості із збільшенням розмірів деталі, цей фактор, мабуть, є головним
Зниження міцності із зростанням розмірів особливо сильно вияв ляється в неоднорідних металів, наприклад у сірого чавуну із збіль шенням розміру з 5 10 до 50 мм зниження о, та о_і для нього може досягати 60 70 % Виходячи з імовірності руйнування від втомленості, яку с. ід вважати пропорційною кількості небезпечних дефектів на одиницю об'єму найбільш напруженого шару металу, можна визиа Чити вплив абсолютних розмірів перерізу ма міцність На ряс наведено епюри напружень при згинанні для зразків різних діаметрів без концентрації напружень Заштриховані зони становлять шар, в якому напруження перевищують границю витривалості а_1р (яка має місце при однорідному розподілі напружень), визначену або при розтяганні стисканні, або при згинанні на зразках досить вели кого розміру 3 рнс 566 видно, що із зростанням діаметра зразка збільшується об'єм небезпечно напруженого шару, а отже, і ймовір кість руйнування від втомленості, що призводить до зниження грани ці витривалості Прн збільшенні діаметра зразків з 7 до 150 мм зни ження границі витривалості для вуглецевої сталі досягає 45 %
Пояснення залежності границь витривалості від розмірів перері зів, як й інших закономірностей та характеристик втомленості, дають статистичні теорії втомленості Ці теорії висвітлюють питання змі ни ефективних коефіцієнтів концентрації залежно від градієнтів на пружень та абсолютних розмірів
Гіпотези, що пояснюють ослаблення ефективності концентрації напружень порівняно з тим, яке повинне випливати з розподілу на пружень у пружній воні, та залежність коефіцієнтів к^, кх від ннзки факторів (розмірів, властивостей матеріалу тощо), висловлені різни ми авторами, поки що не дають змоги обчислювати значення цих кое фіцієнтів для різних випадків розрахункової практики виходячи з початкових властивостей металу Тому для розрахунку деталей ма шин слід використовувати експериментальні дані, застосовуючи у разі потреби інтерполяцію
Опір втомленості матеріалів оцінюється ва границею витривалості яка визначається на гладеньких лабораторних зразках малого діаметра, а для висновку про міцність деталі при змінних иапружен нях треба анати її границю витривалості Тому вводять додатко-
ве поняття ефективного коефіцієнта концентрації напружене деталі
(2ІІІ)
Коефіцієнт Ь04 враховує сумарний вплив концентрації напру жень та абсолютних розмірів на опір втомленості й визначається за да ними випробувань зразків та моделей різних перерізів
Якщо ефективний коефіцієнт концентрації коі визначається на зраз ках досить великого діаметра д (після якого дальше збільшення його розмірів небезпечно впливає на значення коефіцієнта), то
= °~ІД« — °-|< _ к°а їм 6оа°~ їм е<м
Зазначимо, що ступінь впливу концентрації напружень на границю витривалості залежить від виду напруженого стану Прн циклічному крученні, наприклад, ефективні коефіцієнти концентрації виявляються, як правило, меншими, ніж при згинанні для одних і тих самих конструктивних форм (рис 567 та 568) Співвідношення між коефіціен тами при згинанні та крученні (рис 687 та 566) можна виразити наближеною формулою
А. = і + 0.6(Ло - І)	(2І І2)
Щодо ефективного коефіцієнта концентра: іі при розтяганні стисканні, то він, як звичайно, дорівнює коефіцієнтам концентрації при згинанні або перевищує їх (рис. 557 та 569)
Вплив стану воверхні. Здебільшого поверхневі шари елемента конструкції, який зазнає дії циклічних навантажень, виявляються більш напруженими, ніж внутрішні (зокрема, це має місце при зги нанні та крученні) Крім того, поверхня деталі майже завжди має дефекти, пов’язані з якістю механічної обробки, а також з корозією внаслідок впливу оточуючого середовища Тому тріщини від втомле ності, як правило, починаються з поверхні, а погана якість останньої призводять до зниження опору втомленості
Вплив стану обробленої поверхні на втомленість оцінюється коефіцієнтом р, що дорівнює відношенню границі витривалості випробу ваного зразка з левкою обробкою поверхні д</ границі витривалості старанно полірованого зразка Залежності коефіцієнтів {} від границі міцності ов для різних видів обробки наведено на рис 570, де крива / відповідає полірованим зразкам 2—шліфованим, 3—зразкам з тонкою обточкою, 4-а грубою обточкою 5 — з окалиною Як ба чимо, границя витривалості сталевих зразків при грубій обточці зни жується на 40 %, а при наявності на поверхні окалини — на 70 %
Шкідливий вплив мікроперівностей поверхні здебільшого пом як шується пластичною деформацією, що спричинюється у поверхневому шарі механічною обробкою і поширюється на деяку глибину, ця гли б іна залежить від режимів різання і, зокрема, від подачі При грубій обточці вона може досягати І мм і більше, а при шліфуванні й поліру ванні не перевищує сотих часток міліметра Пластична деформація поверхневого шару може підвищити границю витривалості на 10 20 %
На границю витривалості істотно впливає корозія Цей вплив буде різним тоді, коли метал, що зазнав корозії до випробування на опір втомленості, не зазнає її під час випробовувань, і тоді, коли метал зазнає корозії під час випробовувань В обох зазначених випадках, особливо в другому, корозія спричинює різке зниження границь ви тривалості (до 70 60 %) При цьому зниження границі витривалості при корозії виражене тим більше, чим вища границя міцності металу і чим бііьше останній схильний до корозії
Вплив корозії при розрахунках можна врахувати коефіцієнтом 0В, який становить відношення границі витривалості о-і» королева ного зразка до границі витривалості полірованого зразка, тобто 0В = = а_!В/а_! Вплив корозії в процесі випробування на границю витри валості сталевих зразків при ротаційному згинанні показано на рис 571, де крива і характеризує вплив корозії у прісній воді при на явності концентрації напружень, 2— у прісній воді при відсутності концентрації або в морській воді при наявності концентрації 3 — у морській воді при відсутності концентрації
Причиною такого різкого зниження границі витривалості внаслідок корозії є корозійне пошкодження поверхні, яке спричинює значну концентрацію напру жень, а також послаблення опору ут
воренню трішки
Рнс 570
Зменшити вплив' стану поверхні на границю витривалості можна відповідними технологічними методами обробки, які приводять до зміцнення поверхневих шарів До таких методів належать, наклеп поверхневого шару накатуванням роликом, обдування дробом тощо, хіміко термічні методи — азотування, цементація, ціанування термічні — поверхневе гартування токами високої частоти або газовим полум ям Зазначені методи обробки приводять до збільшення міцності поверхневого шару й утворення в ньому значних стискальних залишкових напружень, які стають на перешкоді утворенню тріщин від втомленості, а тому підвищують границю витривалості
Прн наявності концентрації напружень крім глибини шару та його абсолютних розмірів на ефект зміцнення істотно впливають рівень концентрації напружень і градієнт напружень біля поверхні Ефект зміцнення зростає із збільшенням концентрації
Вилив пауз На границю витривалості впливають паузи (перерви в навантажуванні) При цьому в одних випадках цей вплив невели кий, а в інших кількість циклів до руйнування збільшується за рахунок пауз на 15.. 20 % Збільшення кількості циклів тим більше, чим частіше паузи й чим вони довші (останній фактор впливає менше)
Вплив перевантажень тобто навантажень, вищих за границю ви тривалості, залежить від характеру перевантаження При малих перевантаженнях до певної кількості циклів границя витривалості підвищується, при великих перевантаженнях після певної кількості циклів — знижується
Вплив тренування Якщо до зразка прикласти напруження, дещо нижчі за границю витривалості і потім поступово підвищувати змінне навантаження, то опір втомленості можна значно підвищити Це явище, що його називають тренуванням матеріалу, широко вико ристовуеться в техніці
Зміцнення можна досягти при відносно короткочасних тренуван нях [ял 50 000 циклів), але значних перевантаженнях Досліди показують якщо спочатку діє менше перевантаження, а потім більше, то опір втомленості матеріалу виявляється більш високим, ніж тоді, коли спочатку діє більше навантаження, а потім менше
Вплив температури. З підвищенням температури границя витри валості, як правило, зменшується, а із зниженням її — зростає як у гладеньких зразків, так і в зразків з коянентоатора* н
Для сталі прн температурі, вищій за 300 X, спостерігається зни ження границі витривалості приблизно на 15 20 % на кожні 100 СС підвищення температури. Правда, у деяких сталей при підвищенні температури від 20 до 300 °С границя витривалості підвищується Од нак це підвищення, мабуть, пов язане з фізико хімічними процесами, що відбуваються при одночасному впливі нагрівання та змінних на пружень
При підвищених температурах навіть при дуже великій кількості циклів крива втомленості не має горизонтальної ділянки Так, для
гладевькнх зразків навіть при 100 млн циклів горизонтальна ділянка не спостерігається Вплив концентрації напружень з піданщенням тем ператури взагалі зменшується, однак для деяких сталей, мабуть, знову таки внаслідок фізико хімічних процесів чутливість сплаву до надрізу збільшується При температурах порядку 500 500 °С у сталі починаються пронеси повзучості, які мають місце також при змінних навантаженнях навіть при симетричному циклі
При зниженні температури з 20 до —І90 °С границя витривалості в деяких сталей збільшується більше ніж удаічі, хоч їхня ударна в яз-кість при цьому знижується
Це ще раз свідчить про принципову різницю між руйнуванням від втомленості та руйнуванням від відриву при статичному та ударному навантаженнях
$ 137. Розрахунок на міцність при повторно*змінних навантаженнях
У разі простих видів деформації при зміні напружень у деталі за симетричним циклом запас міцності при дії, наприклад, нормальних напружень можна обчислити за формулою
де о-ш — границя витривалості деталі при розтяганні стисканні або при згинанні оа — номінальні фактично діючі знакозмінні напру ження
Для розрахунку на міцність при змінному навантаженні у разі складного напруженого стану можна використати відповідні теорії міцності Прн цьому для матеріалів у пластичному стані, як відомо, застосовують третю та четверту теорії міцності У розглядуваному ви падку ці теорії повинні бути записані у такому вигляді
о-, - /<Й + 4ії,	(21 13)
О-і - /’.+ Зт2.	(21 14)
Відповідно до експериментальних даних умова міцності у формі еліптичної залежності (див рис 682) при згинанні й крученні вира мається формулою (2і 6), а стосовно до деталі досить великих розмі рів з концентрацією напружень — формулою
о_1м - )/Г°2+	<2І і5>
або
Таблиця 22
МПа			*»
350	550	0	0
520	750	0,05	0
700	1000	0,10	0 05
1000	1200	0 20	0 10
1200	1400	0 25	0 ІЗ
Тоді, маючи на увазі що Па ~ — а-м/аа — коефіцієнт, який харак г теризуе запас міцності тільки за нор-ба мальними напруженнями, та /ц = = т-іхАв — коефіцієнт, що харак теризуе міцність тільки за дотич ними напруженнями, на підставі співвідношення (21 16)будемо мати
п»
звідки запас міцності п при складному напруженому стані, наприклад При спільній дії згинання та кручення, визначиться формулою
Визначаючи запаси міцності при асиметричних циклах для будь якого виду циклічного навантажування (згинання, розтягання-стис канни, кручення), виходять із схематизованої діаграми графічних напружень для зразків без концентрації напружень (рис 572)
Аналітично криву граничних напружень у координатах Опих ~ °сР можна виразити рівнянням прямої, що проходить через даі точки А та В з координатами (0 о_і) та (о0/2 ов)
От*х= <и.і+
де, згідно з рис 572,
Ов — ‘8“=—5^ї-
Тоді
І. 2°_| — О, \
□вам - а-! н-5^5— <т«р «* о_і -Ці---Сф
Позначивши
У8 = —(2І.І8)
запишемо рівняння кривої граничних напружень для зразка без кон центрації напружень
0пи« - 0-1 + (1 - Чо) Оер	(21 19)
При дії дотичних напружень відповідне рівняння має аналогічний вигляд
Тщ»ж = т_і 4- (1—'Рт) тср	(21.20)
Значення та для деяких сталей при різних видах деформації залежно від границі міцності наведено в табл 22
Ураховуючи вплив на границю витривалості прн асиметричному циклі різних факторів, у тому числі концентрації напружень, абсолютних розмірів перерізу, стану поверхні тощо, виходять з експериментально встановлених закономірностей, які полягають у тому, що відношення граничних амплітуд напружень гладенького зразка та розглядуваної деталі залишається сталим незалежно від середнього напруження циклу На підставі цього можна побудувати схематизо вану діаграму граничних напружень для деталі (рис 573)
Цю побудову можна дістати також, виходячи з таких аналітичних уявлень Відповідно до виразу (21 19) гранична амплітуда напружень зразка виражається формулою
Ов = Спи* — Сер = ІО—1 + (1 — ^рОср] —- Оер = 0—1 ~ V Оер.
а гранична амплітуда напружень для деталі а0Іщ на підставі зазначеної вище закономірності щодо впливу різних факторів тільки на змінну складову напружень буде в кда разів менша, тобто
Тоді рівняння кривої граничних напружень для деталі можна записа* ти в такому вигляді
Одні &ср = ®ср 4-----І---= “Т-------Ь П----1 ° ! Оср (21 22)
яоа	яоа І яоа І
Припустимо, що деталь у небезпечній точці зазнає дії змінних на пружень З коефіцієнтом асиметрії Г, причому ВІДОМІ ВІДПОВІДНО Ота! та (тср циклу Як зазначалося вище, всі цикли, що відповідають г » = сопзі, лежать на одній прямій За наведеними даними на діаграмі рис 574 заданий напружений стан характеризується точкою М Ог же, всі точки, що лежать на промені, проведеному з початку коорди нат крізь дану точку М, мають коефіцієнт асиметрії, який дорівнює г Точка перетину цього променя з кривою втомленості має ординату, що дорівнює границі витривалості Ппиґ Отже, коефіцієнт запасу
^_2ї.=-ЇЙ-_Лї«.=_Ьї-,	(2123)
°М °пчх серМ °оМ
де <Ггк4 — границя витривалості деталі при асиметричному циклі, а™ = ои —• максимальне напруження деталі
При перетині променя ОО з прямою АВ граничних напружень у точці N максимальне напруження 0™*» збігається з максимальним граничним напруженням сц = Сща, тобто
З іншого боку, на підставі рівняння (21 23),
'	°м
°т»« = ———
а	о	ш	1	(2124)
о*»	О_І	Г.	”я	1	’	'
—----Перм — —Т  4- 1---------[Перл.
°ЄРМ	«см	[	ярЛ	|
Звідси знаходимо абсцису точки N
__________°-1__________________°-1дерМ______
** "7 |~ °М . , У0 Т	(°м ~0 ери) + ^ЛрМ
Оскільки см — Оерм = аам, остання формула перетворюється на таку
„	_	°-1°СРМ
- «й* + »Лн
Підставляючи здобутий вираз аСр^ у формулу (21 24), знайдемо вираз максимального граничного напруження для деталі (ординату точки №).
а.„ - а» -	- ,„Л + То<,ад •
Тоді остаточний вираз для запасу міцності буде такийі
(21 25)
0М~ *0^а + ¥0<тС(>м Аналогічно при крученні
=	+ ’л,м	121
Якщо асиметрія циклу дуже велика, то роль змінних напружень прн оцінці міцності може виявитися несуттєвою, і розраховувати слід за граничним станом, як при статичному навантаженні У зв'язку з цим поряд з запасом міцності за втомленістю [формули (21 25), (21 26)1 слід визначати запас міцності й за несучою здатністю при статичному навантажуванні
Аналогічно розраховують і при складному напруженому стані При асиметричному циклі коефіцієнт запасу при змінних навантажен нях визначається за формулою (21 17), у якій По та /ц обчислюються відповідно за формулами (21 25) та (21 26) Запас міцності за статичною несучою здатністю визначається за методикою, викладеною в гл 18 При цьому міцність оцінюється за найменшим із запасів за втомленістю і за статичною несучою здатністю
Запаси міцності прн розрахунку на опір втомленості залежать від точності визначення зусиль та напружень, від однорідності матеріал в, якості технології виготовлення деталі та інших факторів При підвищеній точності розрахунку (з широким використанням експеримен тальних даних щодо визначення зусиль, напружень та характеристик міцності), прн достатній однорідності матеріалу та високій якості технологічних процесів береться запас міцності л — 1,3 14 Для звичайної точності розрахунку (без належної експериментальної перевірки зусиль та напружень) при помірній однорідності матеріалу я = 1,4 1,7 При зниженій точності розрахунку (якщо немає експериментальної перевірки зусиль та напружень) і зниженій однорідності матеріалу, особливо для литва та деталей великих розмірів, п — 1,7 . ЗО
Найвірогідніші дані про потрібні запаси міцності деталі можна здобути на підставі результатів натурних випробувань деталей або досвіду експлуатації машин з деталями цього типу
Приклад 86 Шатун поршневого двигуна, що в стержнем круглого перерізу, вздовж осі зазнав повторно-змінних навантажено щз змінюються без ударів від Рщак = =• +200 к.Н до Рт|п = +50 кН Стержень мав радіальний отвір 03 мм матеріал стержня — сталь 12ХНЗА з такими характеристиками міцності о» = 950 МПа, а, = 720 МПа о_1 = 430 МПа та 'У •= О І Поверхня шатуна грубо шліфована Визначимо його діаметр з розрахунку на опір втомленості та здобуті розмі ри порівняємо з визначеними з розрахунку на статичне навантаження що дорівнює максимальному навантаженню в циклі
У ньому прикладі треба виконати так званий проектувальний розрахунок, тобто за відомими зусиллями що діють на детаїь, визначній її розміри
Вяалачаемо небвутечиий переріз вам Таким слід вважати переріз у місці раді ального отвору
Оскільки співвідноишяя розмірів шатуна та радіального отвору не відоме то не відома й величина аоі Тому, маючи па увазі що ией коефіцієнт при малих отворах та крупких деталях машин близький до двох задаємося значенням теоретичного коефіцієнта концентрації а0 = 2
Користуючись графіком риє. 563 знаходимо коефіцієнт чутливості до концепт рації напружень прн аа “ 2 та ож = 920 МПа коефіцієнт д0 •= 0,77
Скориставшись формулою (21 7) визначимо ефективний коефіцієнт концентрації
Ао=1+<?„(%-!) = і 4-0,77(2-1)- і,77
Із графіка рис. 570 пе кривою З знаходимо коефіцієнт, що враховує якість ос» робки поверхні р = 0 82
} Задаємося коефіцієнтом, що враховує розміри стержня в =• 0,8.
Ефективний воефівІвкт кавцеитраиїї деталі з урахуванням розмірів та ставу по-.	верхні
1	*«* " 75“" °-8 0 62 “ 2,70
І	Виберемо зайве міцності л 2 1.
1 Визначимо переріз шатуна за формулами (21 25) |	а—і	і?
і	8 *ои°в "і"	ь ^пих “ ^яіп ‘ ш ^тах + тіа
*	каі '	2 	"т" тв у
заїдки
0,2 — 0,05
і
Визначаємо діаметр стержня з формули Р ~ Х&/4 ~!®^£2_м«37.10-3 м = 37 мм.
Перевіримо значення раніше вибраного коефіцієнта. який враховує абсолюті розміри. Для цього скористаємося графіки* рнс 565 згідно з яким при б » 37 мм а — 0 8) тобто величина в наближається до прийнятого значення в •= 0,8.
Знаходимо діаметр шатуна із стетнчного розрахунку тобто з умова Ощ^ =« “ РпЛ? < І °+1 І
а = ЗЕ _ р/" <Лз 1'4°~* “ ~ 2 31 1°-г м - 23,\ му
Візьмемо б = 24 мм, тобто діаметр виявився у 37/24 = і 54 раза меншим ніж при розрахунку з урахуванням змінності навантаження
Приклад 86 Східчастий сталевий шток водяного насоса (рис 375) зазнав повторно-змінного розтямкня стискання динамічними зусиллями з характеристикою циклу г -* —0,5 Матеріал штока — маловуглецева сталь з тимчасовим опором ая —
» 400 МПа, границею текучості ог = = 330 МПа і границею витривалості при симетричному циклі о_( ж 204 МПа Поверхня стержня оброблена різцем Визначимо допустимі зусилля, що діють на шток.
У даному прикладі виховуємо перевірний розрахунок Є розміри деталі, треба вю-начнти допустиме навантаження при заданій характеристиці циклу Як розрахунковий слід взяти небезпечний переріз у місці спря ження двох діаметрів	,
Визначимо теоретичний коефіцієнт концентрації прн р/й >" 5/50 = 0,1 можна взяти а„ = 1 6 (див § 32)
За графіком рис. 563 знаходимо коефіцієнт чутливості до концентрації напружень: “ 0.39
Визначаємо дійсний коефіцієнт концентрації
йо«і+90(о0-1)«1 +
4- 0 39 (1,6 — 1) = і ,234
Рнс 675	Рнс 576
За графіком рис 555 знаходимо коефіцієнт впливу абсолютних розмірів **= = 0 75
Коефіцієнт що враховує якість обробки поверхні, визначимо за графіком рис 570 Р =• 0 875.
Вибираємо коефіцієнт запасу міцності з урахуванням динамічності (див гл 23) Пд З
Знаходимо ефективний коефіцієнт концентрації напружень для деталі , кс Ь834	. м
лав -	= 0,875 • 0,75 “ 1
Визначаючи амплітуду напружень з формули ®—і
дістенемо
Маючи на увазі що для даного матеріалу (о* =* 400 МЛа) згідно з табл 22,коефіцієнт 0, за останньою формулою знайдемо
О-1	204
-----М МП»»Ю МП.
Ввзначаємо допустимі зусилля що діють на шток амплітудне значення зусилля
Ра - А». = оа > 3	10	40 МН-78 6 кН,
середнє значення зусялія
рср = ра і - 78.6 1 + «Н =» 26 2 кН,
мінімальне зусилля
Ртіп“Ли.«'“-0’5 Ю4.8 кН — 52.4 кН максимальне зусилля
Рщ,, - Рв + Рер - (78 6 4- 26 2) кН - 104,8 кН
Приклад 87 Обертовий круглий порожнистий вал (рис 576) у небезпечному перерізі ослабленому отвором для мащення (0 3 мм). зазнав змінного згинання з моменточ М-=І5кН м Одночасно вал зазнав змінного кручення з кое фіщвнтом асиметрії є •= —0 25 та Мкр — 1,8 кН м Діаметри вала зовніш ній О = 70 мм внутрішній 35 мм Матеріал — сталь 45 (ав =» 700 МПа, аТ =• 320 МЛа о_( = 300 МПа, т—1 = 180 МПа) Поверхня вам шліфована Ви значимо запас міцності вала.
Визначимо номінальні напруження у валу від згинання та кручення
М 32М	32.1,5 10“3	.. ............
ж	3,14(70 Ю~*)* (І—0 5*) МПа”473‘ЧПа
= 47,3 МПа 0^ = 0.
^ярпмх 1Ж ІМІкрмак в 7р іф»!! — (й/О)*\
16 • 1 8 • 10-3 »-------———---------------МПа = 28 3 МПа
3.14(70 ІО"3)« (1 - 0 5‘)
тш(п = гггаіх - — 0,25 28 3 МПа-—7 1 МПа,
_ Чі». = 28.3 +7.» МПа - 17 7 МПа, “	2	2
Тер =	= МЯ — У МПа = 10,6 МПа
Визначимо коефіцієнт концентрації ари згинанні. При 0/О — 3/70 = 0 04 коефіцієнт (див $ 65, рнс. 273) ав <= і 5 Згідно а графіками рис. 563, коефіцієнт чутли вості до концентрації напружень ра — 0 65 Ефективний коефіцієнт концентрації прн згинанні
*«а 1 Н(«.-1) = । + 0.65 (2.5- 1) = 1.975
Коефіцієнт янкй враховує абсолютні розміри, згідно з графіками (див рис. 565), мож на взяти таким що дорівнює в = 0 ТО коефіцієнт, що враховує стан поверхні вала (див ряс 570, крива 2). Р = 0,92 Тоді ефективний коефіцієнт концентрації вала
.	*0	1 975	- .
=	076.0,92	’
Обчислимо запас мінності ма згинання
п„ =	—_	—	- 2 05
’	"«’.-’Л,	3,1.47,3 + 0
Визначимо коефіцієнти концентрації при крученні Теоретичний коефіцієнт кон* нентрації візьмемо ат= 3 коефіцієнт чутливості до концентрації напружень візьмемо такий самий як і прн згинанні тобто = 0,65 Тоді ефективний коефі
ціеят концентрації прн крученні 1+ %(«,- І)-1+0 65(3-І)-2 8,
Взявше як і при згинанні, в—О7Ота0 — 0 92 знайдемо
“	- О,7<?3О.» “ 3 60
Визначимо запас міцності при крученні
Обчислимо загальний запас міцності ари спільній аії змінного згинання та кручення
2 05 2 77 - 1 65 /27О5> + 2,77*

л —
Отже загальний коефіцієнт запасу міцності виявився значно меншим ніж запаси міояості окремо на згинання та кручення
Глава 22. РОЗРАХУНКИ ПРИ УДАРНИХ
НАВАНТАЖЕННЯХ
$ 13В Розрахунок при осьовій дії ударного навантаження
Явище удару має місце тоді, коли швидкість розглядуваного еле мента конструкції або стичних з ним частин протягом дуже малого проміжку часу змінюється на скінченну величину Великі прискорен ня (сповільнення), що виникають при цьому приводять до появи знач них сил Інерції, які діють у напрямі протилежному напряму прискорень, тобто в напрямі руху тіла У випадку падаючого вантажу силу удару (динамічну силу Рд) можна обчислити за формулою
ВД-2-/Л	(22 І)
де 5 — вага падаючого вантажу, § — прискорення вільного падіння, І (/) — прискорення падаючого вантажу після зіткнення його з перешкодою
Проте визначення сили удару Р* (0 за формулою (22 1) пов язане з великими труднощами, оскільки не відомий час співударяння, тобто час, протягом якого швидкість рухомого тіла зменшується від свого максимального значення в момент зіткнення з тілом що ударяється (початок удару) до нуля після деформації останнього (кінець удару)
У зв'язку із зазначеними труднощами, що виникають при визиа ченні динамічних напружень та деформацій, в Інженерній практиці виходять з так званої технічної теорії удару, яка грунтується на таких припущеннях
1 При співударянні тіло що ударяє, рухається разом з тілом, що зазнає удару, до розвитку кав більших деформацій При цьому немає пружних хвиль у тілах І пов'язаних з ними відскоків тіла що ударяє (такий удар називають нгпружним)
2 За проміжок часу співударяння деформації поширюються по всьому об єму тіла, що зазнає уда ру, а залежність між силами та деформаціями, що виникають відповідає закону Гука
З Прн співударянні рухомих тіл зменшення кінетичної енергії системи дорівнює збільшенню потенціальної енергії деформації тіл При цьому,
як звичайно, нехтують втратами енергії на місцеві пластичні дефор мації, а також інерцією маси тіла, що зазнає удару
4 Вважають, що система тіл при співударянні має один ступінь вільності, тобто положення системи визначається однією координатою
Формули для визначення динамічних напружень та деформацій при осьовому ударі будемо виводити на прикладі системи (рис 577), що складається з вертикально розміщеного пружного призматичного стержня з жорсткістю при розтяганні (стисканні) с = ВЕН, на то рець якого з висоти Н вільно падає вантаж <2
Припустимо що вантаж прикладається до стержня статично тобто навантаження повільно наростає від нуля до максимального зна чення (рис 577, а) і стискає стержень на величину 6С При падінні вантажу з висоти Н унаслідок удару на стержень буде діяти дика мічна сила Р., більша ніж сила (?, і укорочення стержня 6Д буде більше за 6„ (рис 577, б)
Зміна переміщень та деформацій при ударній дії навантаження 0 порівняно з переміщеннями (деформаціями) при статичній дії того самого навантаження характеризується коефіцієнтом динамічності
=	(22 2)
авідки динамічну деформацію через статичну можна виразвти форму лою
6д-*я60	(22 3)
Ураховуючи лінійний зв'язок між напруженнями та деформація ми, а також припускаючи, що модулі пружності при статичній і удар ній дії навантаження однакові що з достатньою точністю підтверджу ється експериментом можна за аналогією з формулою (22 3) встановити зв язок між статичним та динамічним напруженнями
Од = АдОс,	(22 4)
де
ав = Р/Г	(22 5)
— напруження, яке виникає в стержні при стисканні силою, що до рівнюе вазі падаючого вантажу.
Щоб використати формули (22 3), (22 4), треба визначити коефі цієнт динамічності Будемо розраховувати на підставі технічної теорії удару, маючи на увазі, що залежність між силами та деформа діями має один і той самий вигляд як при статичних, так і при дииа мічних навантаженнях, тобто
6е =- Р^с,	(22 6)
6д=Рд/с,	(22 7)
де Рс — статичне навантаження що дорівнює вазі падаючого вантажу \ (у цьому разі Ре — 0) Ра — динамічне навантаження що е силою інерції тіла яке ударяє в перший момент його зіткнення зі стержнем
Виходимо із закону збереження енергії, нехтуючи як зазначалося вище втратами енергії на місцеві пластичні деформації при співуда рянні тіл а також інерцією маси тіла, що зазнає удару Падаюче на стержень тіло в момент зіткнення має найбільшу швидкість Після зіткнення (початок удару) відбувається динамічне укорочення стержня до найбільшого значення 6Д У цей момент швидкість вантажу дорівнює нулю (кінець удару), на стержень діє стискальна сила Ря і потенціальна енергія деформації досягає найбільшого значення
Отже, при ударі кінетична енергія Т падаючого тіла перетворюється на потенціальну енергію деформації тіла, що зазнає удару
Утрачена кінетична енергія чисельно дорівнює роботі вантажу при його падінні й деформуванні стержня
Т«0(й+6в).	(22 8)
а потенціальну енергію деформації пружного тіла при ударі, враховуючи, що динамічна свла за проміжок часу удару аростае від иуля до Рд можна записати у вигляді [див (13 10) та (22 7)1
=	(22 9)
Отже,
4-а£ = <г(«+б„)	(22 10)
Оскільки 6а = %/с, рівняння (22 10) можна записати так:
6І-26Д-2У2 =0.
Звідси визначаємо динамічну деформацію
(22 П)
Знак мінус перед радикалом треба відкинути, бо знак динамічної деформації не може бути протилежним знаку статичної
Записавши формулу (22 11) у вигляді
6Д - бс (1 + V 1 + 2ЙА)	(22 12)
і зіставивши ії з формулою (22 3), знаходимо вираз для коефіцієнта динамічності
*д = 1 +У І 4-2///6ь	(22 13)
Маючи на увазі, що Н = сЯ/2£ (о — швидкість падаючого вантажу в момент початку удару), коефіцієнт динамічності можна записати у вигляді	________
«І-1 + / 1 + -^-.	,22'14)
Ураховуючи, що 2Д дн _ «с “ і п. ~ V' ’
-5-Обе
коефіцієнт динамічності можна виразити такі 4,- 1 +И1 +тА,	(2215)
де Те = <2Н — кінетична енергія падаючого вантажу в момент початку удару, иа— потенціальна енергія деформації стержня що зазнає удару, при статичній дії сили, яка дорівнює вазі ударяючого вантажу
(22 16)
Якщо Н — 0, тобто коли вантаж не падає на стержень, а прикла і дається раптово, то згідно з (22 13), коефіцієнт динамічності £.= 2 І Оскільки висота падіння вантажу Н завжди значно більша за о0, то здебільшого при визначенні коефіцієнта динамічності у виразах під ! коренем одиницею порівняно з другим доданком нехтують Тоді на підставі виразу (22 13) матимемо
!	4,= 1 + К2«Ж	(22.17)
і або, згідно з формулою (22 15),
*« = 1 + Утуг.	(22 18)
Тепер, виходячи Із залежності (22 4), вапишемо вираз для напру жень прн ударі
ад == ідО0 = о.(| + К1 + 2Я/6.)	(22 19)
або
’. = <’.(1 + Кт~)~г+/:^Г	(22 20)
Аналогічно визначаємо зусилля при ударі
Рд = ОаР = Ро (1 + /1 + 2/7/6.)	(22 21)
Розглянута наближена теорія удару має певні межі застосування. Вони обумовлені швидкістю падаючого вантажу до моменту удару
692
20 2-2798
693
І жорсткістю конструкції, що виражається у формулі (22 13) або (22 15) відношенням 2л/6е або Та/У^ Так якщо 2й г* Т7"І4<1ІХІ’
то похибка розрахунку не більша ніж 10 % Урахування маси конструкції, що зазнає удару, розширює межі застосуван ня наближеної теорії
З аналізу формул (22 19) 1 (22.20) ба чимо, що при рівномірно розподілених напруженнях однакових в усіх попереч них перерізах стержня динамічні напру від площі Г поперечного перерізу, як це
ження залежать не тільки	,	.г.. .
має місце прн дії статичного навантаження в статично визначуваних
системах, а й від довжини І і модуля пружності Г матеріалу стержня Отже, можна сказати, що динамічні напруження в стержні прн ударі за лежать як від об'єму так і від якості матеріалу стержнів При ньому чим більший об єм пружного стержня, що зазнає удару (чим більша «енергоємність» стержня) тим менші динамічні напруження, а чим більший модуль пружності матеріалу стержня тим динамічні напруження більші
Сказане справедливе для призматичних стержнів (стержнів одна нового поперечного перерізу)
Інша картина — прн ударі стержнів окремі ділянки яких мають різні площі поперечного перерізу У цьому разі (рис 578 а) найбіль ше номінальне напруження в стержні (без урахування концентрації) буде в перерізах з найменшою площею (у місці виточки) При ударі воно залежить від деформативності всього стержня, а не тільки його ослабленої частини Зменшити динамічні напруження в цьому разі можна двома способами збільшенням поперечного перерізу в місці виточки або зменшенням площі поперечного перерізу стовщеної час тини стержня і, отже підвищенням піддатливості всього стержня в цілому що приводить до зниження максимальних динамічних напру жень у місці виточки Якщо виготовити весь стержень однакового діа метра, що дорівнює діаметру виточки то при цьому збільшиться де
формативність стержня, а отже, зменшиться динамічне напруження ая Проілюструємо сказане на прикладі визначення максимальних дина нічних напружень, що виникають у трьох типах стержнів при поздовж ньому ударі вантажем (? який падає з однакової висот.і/7 (рис 578)
Нехай співвідношення між окремими розмірами стержнів такі
Гі/Гї = а, = Р
Динамічні напруження в кожному стержні визначаємо за загальною формулою
де
г — кількість східців
Для східчастого стержня (рис 578, а)
Для стержня постійного перерізу з розмірами стовщеної частини східчастого стержня (рис 578, б)
Для стержня постійного перерізу, що дорівнює мінімальному пе* рерізу східчастого стержня (рис 578, в),
°с(й ££, Е^а *
Тоді співвідношення між деформаціями трьох стержнів будуть такі
був) в (1 — Р + Р/о) 1 і 1/®	(22,22)
Нехтуючи у виразі (22 17) одиницею порівняно а коренем, що при великій висоті падіння Н і малій статичній деформації Й, можна допустити, вираз для коефіцієнта динамічності запишемо у вигляді
Виходячи з цього і враховуючи вираз (22 22), дістанемо співвідиошен ня між коефіцієнтами динамічності для розглядуваних випадків
&ЯЮ &АІ® 1	“ / «(.Л+Г 1	І2223)
Виходячи з виразів
°дс® = йДІ)4ае(4 = каш =	»
ад(б> = ^а<п°в(« = Йдій ;
Чия = ^ді*>°м« “ Адю ~р~ = Я£ 1 враховуючи співвідношення (22 23), матимемо
Оди»: вам ’ Од<в = (і — р) + яр 1	(22 24)
Припустимо, наприклад, що коефіцієнти а та р дорівнюютьі
а <= р^рх= 0,5, р =	= 0,4.
20»
695
Тоді за формулою (22 24) знаходимо таке співвідношення)
°дм> °а(Л =17.1 1,41
Отже максимальні напруження виникають у стержні з виточкою (рис 578, а) а мінімальні — 8 стержні постійного перерізу найбіль шої площі (рис 578, б) У стержні ж постійного найменшого перерізу (рис 578, в) напруження мають деяке проміжне значення
Проведений аналіз показує що характер опору стержнів удару якісно відрізняється від опору їх статичному навантаженню При ста тичному стисканні (або розтяганні) стовщення одіїісї частини стержня не спричинює змін напружень у перерізах іншої частини, при ударі воно підвищує їх Місцеве зменшення площі поперечного перзрізу на невеликій довжині стержня різко підвищує напруження
Для зменшення напружень треба намагатися в основному збільши ти піддатливість стержня шляхом збільшення його довжини, встанов лення буферної пружини заміни матеріалу на Інший, з меншим мо* дулем пружності, вирівнювання площ поперечних перерізів з метою дістати всі ділянки стержня з однаковою мінімальною піощею перерізу Ось чому, конструюючи стержні, що праьюоть на удар, требз добиватися постійної площі перерізу по всій довжині Місцеві стовщення допустимі лише на невеликих ділянках довжини місцеві ви точки малої довжини вельми небажані
Умова міцності ори ударі має вигляд
Коефіцієнт запасу міцності п, можна вибрати таким як і при статичному навантаженні (1 4 1,6), оскіїькн динамі шість вже відобра жена у розрахункових формулах коефіцієнтом ка Однак, враховуючи наближеність розглянутого методу розрахунку, цей коефіцієнт беруть дещо більшим («т — 2)
Ми розглянули розрахунок динамічних напружень і деформацій при ударному стисканні Однак усі наведені формули також справед ливі й для ударного розтягання, зокрема для прикладу, показаного на рис 579
Приклад 88 вантаж 0 вагою 50 Н. прикріплений до сталевого дроту діаметром З мм (рис 580) вільно подій від точки А з прискоренням а Знайдемо напруження в дрояи, якщо його верхній кінець раптово зупинено Масою дроту знехтуємо
Напруження в точи! А після раптової зупинки дроту визначимо за формуймо (22 20) прн довжині дроту І = Н
а ~ 0 І	4 0 05 1°~* ।
л р + V рі я (о з ю-2)* +
+	4 ? • 0105 .‘°~3 12 І0? = (7,08 + 1720) МПа « 1727 МПа
V	я (О З І0“2)’
Оскільки в розілккуваному прикладі кінетична енергія падаючого ті та збільшу, еться в тій самій пропорції що І об ем дроту, то напруження не залежить від висоти падіння вантажу ().
Рнс 578
Рнс. 580	Рнс 581
Рас. 582
Приклах 88. Визначимо динамічні напруження, ир виникають у стержнях під вісхи (рис 561) при падінні вантажу 0= 0,25 кН з висоти Н 1 см Площр поперечного перерізу мідних похилих стержнів АС і ВС = 0,2 см*, площа поперечного перерізу сталевого стержня 0 25 см* довжина сталевого стержня 2,4 м. довжина похилих стержнів 2 м.
Динамічні напруження в сталевому стержні визначимо за формулою о, — 43ос
Напруження в стержнях при статичній дії навантаження ос с, =	= -0 25 І0~* МПа = 10 МПа)
'•'*	0 25 ІО-4
О	О.ЗД 10~~*
^„созЗО0 = 2 0,2 10~* 0,866
МПа = 7 2 МПа.
Переміщення перерізу О при статичній дії навантаження
/ 025 10“3 2,4	0,125 . 10-3 2	\	„а„
ж І -	4- -	,	— )м =28,7 • 10—3 см.
2 10» 0 25 Ю~*т 1 10» 0 2 Ю^-О.ТЗу
Динемічннй коефіцієнт
йд = і + і/” 1 + 2^_ « 1 + |/~ 1+ _2_2 ‘	=94,
' ТГ V 28 7 • 10-3
Отже,
Одст = Мах» - 9«4 • ю МПа = 94 МПа, °*.м = йд°е в “ 9’4 • 7.2 МПв = 67 7 МПа
На практиці буває, що за здобутими вище формулами динамічні напруження визначити неможливо До таких задач належить, напри клад визначення динамічних напружень у сталевому тросі, що піднімає вантаж $ зі швидкістю о, при раптовому гальмуванні підйомника (рис 582}.
Позначимо вільну довжину троса в момент зупинки через Г, а площу його поперечного перерізу через р
Нехтуючи масою троса та вважаючи, що кінетична енергія рухомого вантажу цілком перетворюється на додаткову потенціальну енер гію деформації троса, дістанемо таке рівняння для визначення най більшого подовження 6 троса
?-+<?(«-«.
звідки, враховуючи, що
р-ЕрЛ.,
матимемо
Звідси	_____
6=6.+л?-
Отже, розтягальні напруження в тросі прн раптовому гальмуванні зростають у відношенні
‘22 28> тобто
4=1+-^.
Приклад 90- Визначимо напруження в сталевому канаті, іцо опускав вантаж вагою <2	45 кН зі швидкістю о = 1 м/с при раптовому гальмуванні в поменш поли
вантаж опуститься на 18 м Переріз каната Р •= 16 см*. модуль пружності Е >* - 105 10* МПа.
Обчислимо статичну реформацію канап
1,^-Тб”1^  - °',8г
Згідно а формулою (22 25) коефіоіевт динамічності
к. » 1 + • в 1 +	ь 1 в 5,6
И 0,482 ІО-2-9 81 і динамічні напруження л <5 І0~3
« ка_У_ в5,в — [-^р- МПа - 157 5 МПа.
Зробугі високі напруження при раптовому.гальмуванні можуть призвести до руйнування підйомного каната
Приклад 91 Розв'яжемо попередню задачу зо умови що між тросом і вантажем розміщено пружину яка під дією вантажу 45 кН дав статикнв подовження 12 см 596
Статична деформація пружного елемента (каната і пружини 6^
ое = 6СК+бс п = (0,482 + 12) см = 12,482 см
Підставляючи це значення у формулу (22 25) знайдемо що
Й“ “ *	“ 1 +	ІО-®.»,»! “ 1‘92’
Динамічне напруження в канаті
О	45 10-4
а, « к,ос » к. -в- в І 92	т- МПа в 54 МПа
а а ' д г	16 ІО”4
Як бачимо розміщення пружини між канатом і вантажем Істотно (майже в 3 ра ан) знизило динамічні напруження при раптовому гальмуванні вантажу У цьому разі пружина стала тик амортизаторам який часто застосовують у техніці для пом'якшення поштовхів а отже і зменшення дннемічвнх напружень, що виникають прн поштовхах
Урахування маси стержня, що зазнав удару. Іноді маса стержня Істотно впливає на динамічні напруження в стержні, що зазнає удару Це пов'язане з тим, що кінетична енергія вантажу частково витрачається на наданії певної швидкості масі стержня
Для наближеного врахування впливу інерції маси стержня, що зазнає удару, в процесі удару розрізняють два етапи Перший починається з моменту зіткнення падаючого вантажу, який має найбільшу швидкість V, з верхнім кінцем нерухомого стержня і закінчується, коли внаслідок зминання матеріалу в місці зіткнення швидкість вантажу знизиться до а верхній кінець стержня набере за цей час такої самої швидкості ц2 Другий етап починається з моменту спільного ру ху вантажу і кінця стержня що зазнає удару Деформація стискання поширюється по всій довжині стержня з певною швидкістю від най більшої Сі на верхньому кінці до нуля в нижньому перерізі, тобто В місці закріплення
Припустимо що швидкість руху довільного перерізу стержня ЗМІНЮЄТЬСЯ по його довжині І за лінійним законом (рис 583) Отже, швидкість перерізу завдальшки х від нижнього закріпленого кінця
Кінетична енергія маси елемента завдовжки <іх

Повна кінетична енергія стержня визначається так
Рнс. 583
Позначимо власну вагу стержня через Тоді формулу для внзна-чення кінетичної енергії стержня в момент початку другого етапу мож на записати у вигляді
Ост °?
(22 26)
Отже, якщо в момент початку першого етапу удару падаючий вантаж мав кінетичну енергію то втрата енергії до початку другого етапу внаслідок місцевих пластичних деформацій
ЛТ =
О»1	/
Т»---\ТГ
АГ=тН'’"-“ї(1+-Тг)|-	(22 27>
З іншого боку, цю саму втрачену кінетичну енергію можна обчислити, виходячи з того, що швидкість вантажу в перший етап удару змінюється на величину и— 14, внаслідок чого кінетична енергія ван тажу зменшується на величину (ф/2$) (о — 0^® Стержень, що зазнає удару, за перший етап удару дістає запас кінетичної енергії (Рог/3) X х 1(0 — о0а/2£І Тоді сумарна втрата кінетичної енергії вантажу що падає, або
(2228) Прирівнюючи праві частини виразів (22 27) та (22 28) матимемо £[»’-41 +4-4-)і=т5-[‘’,-2™-+<1 +4-»| Звідси визначаємо швидкість вантажу в момент початку другого етапу удару
»,=----ї-д—	(22 29)
+ з -£
Зазначимо, що цей вираз можна дістати також, використовуючи закон збереження кількості руху
Отже, кінетична енергія системи в момент початку другого етапу удару визначається формулою
~ + Т “ "2? V + “З" ~0~)Щ
або остаточно
т------г^і 122 301
Ця енергія згідно із законом збереження енергії, трансформуєм ся в потенціальну енергію деформації пружного стержня Тому вираз (22 ЗО) треба підставити замість То у формулу (22 15) для визначення коефіцієнта динамічності тобто
або
кл = 1 + V 1 ^Т/Уо
Ураховуючи, що і;8/2£ = Н і Н<1 — То а також позначаючи = Р, формулу для визначення коефіцієнта динамічності запишемо у вигляді
а максимальне напруження в стержні, що зазнає удару,
(22 ЗІ)
або
2ЕЕН
І. і Еуі з 0
З останніх формул бачимо що коли відношення ваги стержня до ваги падаючого тіла (коефіцієнт Р) порівняно з одиницею не мале, то врахування маси стержня помітно знижує напруження при ударі
Удар стержня по жорсткій плиті Іноді виникає потреба визначити напруження в тілі що ударяє, зокрема розраховуючи шток куваль ного молота Прн цьому найбільш небезпечним для міцності штока е момент закінчення кування коли виріб майже не деформується і вся енергія удару поглинається штоком Схематично такий приклад по казано на рис 584, де призматичний стержень завдовжки І попереч ного перерізу Е і вагою (} падає з висоти Н на жорстку плиту А Ос кільки плита ке деформується, то весь запас кінетичної енергії Го — = падаючого стержня до моменту удару по плиті цілком трансформується в потенціальну енергію деформації стержня, що падає
Рве. 564 Рис. 585
У момент удару, коли швидкість стержня раптово зменшується до нуля, частинки стержня дістають значних прискорень, спрямованих угору Припусти мо, що їхня інтенсивність однакова в об'ємі стержня Отже, на частинки стержня діють розподілені сили інерції однакової інтенсивності, напрям яких протилежний напряму прискорень(рнс 585), і задача зводиться до визиа1 ення динамічних на-
пружень від такого навантаження Ця задача подібна до задачі про визначення напружень у перерізах призматичного стержня від дії власної ваги (див гл 5 § 36) При такому навантаженні нормальні напруження по довжині стержня змінюються за лінійним законом Вважаємо, що і при дії динамічних навантажень постійної інтенсивності залежність напружень по довжині стержня має той самий вигляд.
Отже, в довільному перерізі з абсцисою х (рнс 585) динамічне на пруження можна виразити через максимальне напруження в нижньому перерізі
°д (*) = ад пив ~ •
Потенціальна енергія деформації в елементі стержня завдовжки Лс лі. - 4зг № =	4-
Потенціальна енергія деформації всього стержня
О, -	ЕІ	(22 32)
0
Знаючи запас кінетичної енергії Та падаючого стержня і нехтуючи втратами енергії на місцеві пластичні деформації, деформації плити тощо, вважаємо, що
т.-и„ звідки на підставі формули (22 32)
Максимальне напруження при ударі
(22 33)
Ураховуючи, що Т, = уРІН, дістанемо
(22 34)
Підставляючи в (22 34) вираз Н = о*/2^. де V — швидкість у момент удару, знаходимо
Формулу (22 33) можемо записати у вигляді
(22з5)
Порівнюючи формули (22 35) і (22 20), нехтуючи в останній форму* лі статичним навантаженням, бачимо що динамічні напруження в стержні, який ударяє, будуть такі самі, як би він зазнав удару від іншого стержня з кінетичною енергією, що втричі більша за енергію розглядуваного стержня, який падає на жорстку плиту
$ 139. Напруження при скручувальному ударі
При ударному крученні (рис 585) можна, виходячи з енергетичного балансу (С/ — Т), дістати формулу для визначення максимальних дотичних напружень аналогічну тій, що була здобута при поздовжньо*
му ударі
Тд П»х •* 4дТ0
(22 36)
Тут, як і раніше,
ід=1 + 1/1+2ВДс,
де 6е — переміщення точки співудару в напрямі удару під дією статично прикладеної сили ф
Нехтуючи деформацією кривошипа і вважаючи, що внаслідок малості переміщення точки співудару його проекція на вертикаль дорівнює довжині дуги, маємо
бв-ф/? = -57^-л = -с77«< тобто
Якщо вантаж раптово прикладається до кривошипа (Н «= 0), то коефіцієнт динамічності => 2
У машинобудуванні ударне кручення найчастіше спричинюється не падінням тих чи інших вантажів, а силами інерції мас, що оберта ються з великими прискореннями Це має місце в основному при галь муванні швидкообертових валів що несуть маховики
Для виведення розрахункових формул розглянемо вал із закріп леним маховиком, що обертається із сталою кутовою швидкістю ш Подібну систему, наприклад, показано на рис 587 Раптово загаль муемо вал завдальшки І від маховика, приклавши деякий момент Мл, який треба визначити При цьому маховик завдяки запасу кінетичної енергії продовжує рух, скручуючи вал Отже, ділянка вала завдовжки І скручується моментами Мл (момент гальмування і момент сил інерції маховика).
Динамічні скручувальні моменти, напруження тд і кути закручу вання фд визначимо, виходячи із закону збереження енергії То = І7Д
Кінетична енергія маховика при обертальному русі
де /рн — полярний момент інерції маси маховика, ф — вага маховика, Д — його діаметр
Потенціальна енергія деформації Кручення
<4 = т “ 'и/7 •
де = лгі4/32 — полярний момент інерції круглого перерізу вала діа метром (І
Підставляючи значення йа і То в умову збереження енергії, знай демо динамічний момент
Тепер можі а визначити максимальне дотичне напруження та дина мічннй кут закручування
т	«а	т _ Млі
Тд те*	у- • фд----»
де ЇРр =	== -2^—полярний момент опору круглого перерізу.
Ураховуючи вираз для Мл формулу для максимальних дотичних напружень можна записати у вигляді
т»™, -і/тг-	(22 38)
де Р —• площа поперечного перерізу вала. 604 /
Приклад 92. Диск діаметром й = 20 ся і вагою <і=0,5 кН жорстко насадже ний на вал АВ завдовжки І - / мі діаметром і = 6 см (рис 587), обертається із сталою кутовою швидкістю, що відповідав п = 120 хе-1. Визначимо найбільші дотич ні напруження у ваш при раптовій зупинці кінця А Масою вала нехтуємо Модуль зсуву 0 = 8 10* МПа
Для визначення максимального напруження при ударному крученні скорнста емося формую» (22 38)
*тах ' у ,
№і - <?<?’ ( я:я\' -	( лд ?-
2	4£ \&И	16й \ ЗО )
0.5 0.2* 3 14* 120* .. 16 9,8| 900
ІО"2 кН м.
Л — - п^- —	|0-.^- и* = 28,26 10~* м»
Отже.	_________________
т = 2 1/-І&. - 2 }/'-2 01-	? !°* МПа » 47 6 МПа
У ІР у 1 28 26 10“’
Приклад 93 Гвинтова пружина що працює на стискання, виготовлена із ста~ левого дроту квадратного перерізу Ь = 6 мм Середній діаметр витка пружини О °-= 12 см, кількість витків п= 18 Знайдемо статичне навантаження, яке стисне пружину на X — 2 5 см Припускаючи що той самий вантаж падав на ненаваипаже-ну пружину з висоти Н = їй см, визначимо осадку пружин і найбільше дотичне напруження при ударі 0=8 10* МПа
Вагу вантажу визначимо з виразу для статично? осадки аружикн і —їаі я,
(Ух де
Лікр“«в / = 2л/?а А-ДО
Тоді
, _ 0К’2пп
С0ЙІ» ’ авідки
п«	25_ 10~2 6 _10< 0 НН6 Ю^)4 МН = 15 Н
2яЯ’л	2 3 14(6 10“*)* 18
Згідно а табл ІЗ, при Ь7Ь =» І (Л “ Ь) коефіцієнт Р =• 0.141
Визначимо осадку пружини прн падінні вантажу 0 = 15 Н з висоти Н = 10 см.
Хд = к*Зе	(22 39’
дв
»,-!+ К‘ + Т7= ' +
Підставляючи значення ЬЛ1 бс в (22 39) знайдемо
Ад=*4 2 5 см » 10 см Максимальні дотичні напруження у витку пружини т* л >дТе.
де
Для квадратвого перерізу згідно з табД ІЗ коефіцієнт а “ 0 208 Тоді _ оп _ 25№^6ШІ мп. - 20 мгь.
0,208 (б . Ю”8)» а максимальне динамічне напруження тд = йдТс = 4 20 МПа  80 МПа
$ 140. Напруження і деформації прн згинальному ударі
Виходячи з технічної теорії удару і прийнятих вище припущень, переміщення і напруження при ударі, що згинає стержень, можна визначити за формулами, аналогічними виразам, здобутим при ударному розтяганні або стисканні
ч>л = ки)а /.«у.	(22 40)
Од «= Адов,	(22 41)
‘« => + /> + -V	(22 42)
Тут а>0 — відповідно динамічний і статичний прогини в довільному перерізі балки; /д, /0 — те саме в перерізі зіткнення вантажу з балкою динамічний коефіцієнт можна визначити також за формулами (22.14), (22 15), (22 ) 7), (22 і8) в яких 60 треба замінити на /в
Так, наприклад, для шарнірно обпертої балки з прольотом /, яка зазнає посередині прольоту удару від падаючого з висоти Н вантажу 5 (рис 588), / =-^- гт =-21_ «о ЗЕ^ ’ Ос «пак = 2У
Для консолі, що зазнає удару від вантажу (2, який падає на її вільний кінець, і	Я* . ~	&
••	48£/” ’ авт”	V ‘
Підставляючи значення у формулу (22 42), знаходимо коефіцієнт динамічності кя, а далі з формул (22 4і) і (22 40) — динамічні напруження та деформації
Так, для балки на двох опорах (рис 588) найбільші динамічні напруження
„	Ч1 (> . і/Т", 96Н£/\
Оц так = к»Ре чи в  ^І + у і + —) > або
+	(22 43)
де То = 0Н — енергія падаючого тіла в момент зіткнення
Умова міцності в цьому разі має вигляд
Рнс 58а
де лд— запас міцності з урахуванням ди намічності навантаження
Опір балки ударним навантаженням за лежить як від осьового моменту опору попе речного перерізу, так і від її згинальної
жорсткості Чим більша піддатливістьбалки гим більшу кінетичну енер гію удару вона може витримати при таких самих допустимих напружен нях Найбільшу піддатливість мають балки однакового опору згинай цю (див § 69). в яких От» однакові в усіх перерізах Тому ресори і виготовляють у формі балок однакового опору
Обчислюючи напруження в балках прн згинальному ударі, ми не враховували вплив маси самої' балки, який іноді може бути великим Інерцію маси балки будемо враховувати, як і при поздовжньому ударі наближено, замінивши розподілену масу зосередженою в місці зіт кнення при ударі Позначимо останню через ти назвемо іі зведеною і визначимо з умови що кінетичні енергії розподіленої і зосередженої мас однакові
Нехай у момент удару вантаж Р має швидкість о а швидкість ма сн ті внаслідок інерції дорівнює нулю, тобто балка нерухома Швид кість вантажу зменшується внаслідок місцевих непружних деформа цій Цей період закінчується, коли швидкість вантажу І стержня в місці зіткнення (тобто маси стають однаковими і дорівнюють і>]( і починається другий період — згинання балки під дією вантажу & що рухається зі швидкістю разом з перерізом балки в місці зіткнення
У цій фазі удару, коли згинається вже вся балка, кінетична енергія вантажу і балки перетворюється на потенціальну енергію деформації згинання Отже, спочатку знайдемо зведену масу балки Для певності розглянемо балку, зображену на рис 588 Рівняння пружної лінії аігнутоі балки на двох опорах статично навантаженої посередині прольоту має вигляд
да = ЦР 0Рх — 4х»), (0 < ж < //2), де / = ЗР/48Е/ — прогин посередині прольоту
Припустимо, що при ударі балка згинається по кривій такої самої форми Отже, якщо іот» — прогин при ударі посередині прольоту, то
® (X) -	(3(*х — 4«*>. (0 < х < //2).
1 швидкість руху цього перерізу
»м - -тг- - -т-
Тоді кінетична енергія елемента балки завдовжки Лх о^РАх уРАх І *•»»« І	и„л1*
1,г«=—55—= 25-1.—а—г <ЗЛ - 4хЧ)  а кінетична енергія всієї балки //2
т‘ “ 2	(тг)‘ Т <ЗЛ-<*>• * = -£$- (тї 
'.-«(V)’-	<*«
У кінці першого періоду удару, коли
ДИ>"І»Я о р„
кінетична енергія балкн визначається формулою т 17 уРі з
“ “5Г 2Г 0|
Зведена маса повинна мати таку саму кінетичну енергію
Стіо? 17 уРІ і
2 = 35 2е Иі
(22 45)
(22 46)
де (?б —вага балки
Швидкість V] системи вантаж — балка знайдемо, використовуючи за кон збереження кількості руху для цієї системи
До моменту зіткнення вантаж $ мав швидкість о а швидкість зве* деної маси дорівнювала нулю В кінці першого етапу удару вантаж і зведена маса мають швидкість Отже,
звідки
о <2
-р =--рі +
. . _£Ь.
’+ а
__________о_________ 17 У/?/ 35 Сі
(22 47)
о
Тепер визначимо кінетичну енергію системи (вантаж — балка), яка перетворюється при ударі на потенціальну енергію деформації балки:
, 17 уРі »_ /и , 17 _Л
Підставляючи в цю формулу вираз (22 47) для ц, знайдемо '
Т* ~ "І 17	=	17 &_ ’
*+ 35 Ч *+ 35 С де
Т0=-^-~СІН	(22 49)
Отже, Для визначення динамічних напружень у балці при ударі з урахуванням маси балки у формулу (22 43) замість Тв треба підставити Т* в формули (22 48)"
Оі (г 1/, . ^Т«Є4 \
Одвів* ~ -цу- (І + у 1 4- дч* І
тобто в цьому разі коефіцієнт динамічності
*. = 1+1/’Ц--------1	„ V 	Р25о>
Розглядаючи вирази (22 48) і (22 50). бачимо що. коли відношення (ЩО) =* не мале порівняно з одиницею, то енергія удару Т* може бути значно меншою, ніж Го => тобто врахування маси балки знижує розрахункові напруження при ударі 3 формули (22 50) також видно, що при даному запасі кінетичної енергії тіла що уда ряє, максимальні напруження зменшуються при збільшенні маси балки
Зазначимо, що для інших схем закріплення і навантажування балок вираз для коефіцієнта динамічності можна записати у вигляді
де х — коефіцієнт зведення маси балки до точки співудару, для розглянутого випадку х » 17/35
Приклад 94 Визначимо напруження і осадку ресори автомобіля якщо його колесо а невеликою швидкістю попадав в канаву завглибшки Н -= 200 мм Навантаження на ресорц Р = 7 кН Ресора становить балку однакового опору згинанню. Складається ресора зп = і! листів. її довжина і = 1020 мм. Ширина листа Ь — 65 мм. висота Ііабш Модуль пружності мітеріалу ресори £*=> 2 І 10* МПа
Визначимо статичну деформацію ресори
. $РР =а РРР12 в РЯ» «£/в " 48£лМ’ ІЕпЬН*
де Р - деякий коефіцієнт Ф =• 1,20 • 1.40), що враховує ступінь наближення прак тнчно внкоиаг оТ ресори до балки однакового опору
Підставляючи в останню формулу відомі величини і сяявши Р = і 35 знаходимо що
/ - Рр/* -
4£лМ’
4 2,1 10* 11 65 10“ 3(6 ІО-3)»
Статичне напруження
2 11 65 ІО-3 (6 10~3)*
м « 7,7 10-* м » 7 7 см
ЗРІ _
2лМ* =
МПа = 417 МПа
Визначимо коефіцієнт динамічності
Осадка ресори прн попаданні колеса в канаву
/д = ^ = 3 5 • 7,7 см = 27 см
Динамічне напруження в ресорі
Од Лдас = 3,5 > 417 МПа = 1460 МПа
Приклад 95. Визначимо динамічні нормальні напруження в сталевому стержні при його надійні з висоти Н = 10 см таким чином що залишаючись горизонталь ним він ударяв кінцями об жорсткі опори Довжина стержня 1= 100 см, діаметр 4= 1 см, питома вам матеріалу у = 7.6 10* Н/м*
Розв язати шо задачу виходячи з наведеної формули для £д прн згинанні бал кн, неможливо В момент удару стержень, що падає, навантажений силами інер ції своєї маси інтенсивністю які невідомі, оскільки невідомі прискорення елемен гів стержня при ударі Припустимо що сили інерції розподілені по довжині стержня рівномірно Для визначення їх скористаємося евкоиом збереження евергії вважаючи що вся кінетична енергія Т падаючого стержня повністю перетворюється на потенціальну енергію його деформації и при ударі об жорсткі опори (втратами енергії на місцеві деформації, терти тощо нехтуємо), тобто
Т =» V
Потенціальну енергію стержня на диох опорах навантаженого рівномірно розподі-ленима силами, обчислимо за формулою
С М* (х) Лх
У 2Еі
•бо _________________________64_____________4 23 ІО-1^ 2405/	240 2 КРл (1 ІО”2)*
Кінетична енергія стержня
Т = (}Н = НуН = я (|	1 • 7 8 • 10* . 0,1 Дж = 0,612 Дж.
Тоді 0 612 = 4 25 10“*^,
’<-/тї^-н'"-120Н'"
Максимальний згинальний момент
мт.,_Л£._ » '•.н-.-ібн.. тм 8	д
Визначимо максимальне динамічне напруження в стержні
V п (1 10“а)»
$ 141 Механічні властивості матеріалів при ударі
Для перевірки здатності матеріалу чинити опір ударним наванта женням застосовують особливий вид випробувань ударним згинанням — визначення ударної в'язкості надрізаних зразків Ці випробування здійснюють на маятникових копрах (рис 589) на зразках матеріалу стандартної форми з надрізом з одного боку На рис 590 показано схе* му такого зразка і напрям удару бійка маятника. Різниця висот положення маятника до і після удару дає змогу обчислити роботу А, затрачену на руйнування зразка
Ударною в'язкістю матеріалу КС називають роботу, затрачену на руйнування зразка, віднесену до площі його поперечного перерізу в місці надрізу
КС = -£- =	(22 51)
Хоч дані про ударну в'язкість матеріалу ие можна використати при розрахунках на міцність, але вони дають змогу оцінити особливу властивість металу — його схильність до крихкого руйнування при динамічних навантаженнях в умовах складного напруженого ставу в зоні надрізу і прийняти рішення про застосування того чи іншого матеріалу для даних умов роботи Саме в таких умовах працюють бе« гаго деталей машин, що мають отвори, канавки для шпонок різні вхідні кути тощо.
Рнс. 589	Рис. 591
Низька ударна в’язкість є підставою для бракування матеріалу Так, наприклад сталі, що застосовуються для виготовлення деталей, які працюють при динамі чннх навантаженнях повинні мати ударну в’язкість не меншу ніж 8 10і 8 10е Дж/м8
Ударна в’язкість однієї і тієї самої сталі залежить від її структури, причому цю залежність при статичних випробуваннях виявити немож ливо У табл 23 наведено результати визначення ударної в'язкості для дрібнозернистої та крупнозерннстої ствлей марки Ст2 (0,і5 % вуглецю) Ці сталі мають майже однакові пластичні властивості при статичних випробуваннях, але дуже різняться ударною в’язкістю
При низьких температурах більшість чорних металів стають крих кими, їхня ударна в’язкість також знижується Для таких металів при ударних випробуваннях з поступовим зниженням температури можна встановити так звану критичну температуру крихкості — тем лературу, при якій раптово зменшується ударна в’язкість Критична
Таблиця 23
%
Сталь дрібнозерниста Сталь крупноаерниста
375	35,3	72 2	13 І 10*
345	36,9	66 7	2 6 10»
температура крихкості різних металів різна Нижче Цій температури метал стає непридатним для роботи при динамічних навантаженнях
Ударна крихкість може з’являтися і при підвищених температу* рах Наприклад, ударна в’язкість вуглецевих сталей значно знижу еться в інтервалі температур 200 550 °С (рис 591)
Глава 23. КОНТАКТНІ НАПРУЖЕННЯ
§ 142 Основні поняття
Деформації і напруження, що виникають при взаємному натискай ні двох стичних тіл, обмежених криволінійними поверхнями, нази вають контактними Внаслідок деформацій у місцях зіткнення елементів конструкцій передача тиску відбувається по дуже малих пло-щад ках Матеріал поблизу такої площадки, не маючи змоги вільно де* формуватися, зазнає об’ємного напруженого стану (рис 592). Як по казують розрахунки, контактні напруження мають явно місцевий ха рактер і дуже швидко зменшуються в міру віддатяння від місця кон такту Незважаючи на це досліджувати контактні напру-кенпя і деформації необхідно для вирішення питань міцності багатьох важли вих деталей До таких деталей належать наприклад, шарикові й ро ликові підшипники, зубчасті колеса елементи кулачкових механіз мів, котеса рухомого складу, рейки кульові й циліндричні катки тощо
Уперше правильний розв’язок основних випадків стискання пруж них тіл дано методами теорії пружності в працях німецького фізика Г Герца (і881—1882 рр) Далі контактну проблему розвивали в ос новному вчені нашої країни
Нижче наведено деякі результати, здобуті методами теорії пруж пості прн таких припущеннях
1) навантаження спричинюють в зоні контакту тільки пружні деформації, що відповідають закону Гука.
2) площадки контакту маті порівняно з поверхнями стичних тіл, 3) силн тиску розподілені по поверхнях контакту, нормальні до цих поверхонь
$ 143 Формули для визначення контактних напружень
Стискання куль. При взаємному стисканні силами Р двох куль, радіуси яких Рі і (рис 593), утворюється кругла площадка контакту, радіус якої визначається за формулою
“ =	<23 0
де £, і £а — модулі пружності матеріалів куль.
Нормальні (стискальні) напруження на площадці контакту розподілені по півсфері Найбільше напруження діє в центрі площадки кон такту
о, = -|,_„і = -і.5т£г 	:
(23 2) два Інших головних напруження в центрі площадки
О[ = О; « - 0,8 | СГщах |
Отже, в найбільш напруженій точці площадки контакту матеріал зазнає напруженого стану, близького до рівномірного стискання Завдяки цьому в зоні контакту матеріал може витримати без появи залишкових деформацій вельми великий тиск (див § 49)
Обчислимо, наприклад, напруження в центрі площадки контакту, при якому вперше виникають залишкові деформації Скористаємося для цього четвертою теорією міцності
V 4- №>• — "Л" + (о, — ”•)’ + (“і —
Підставивши значення головних напружень, знайдемо, що 0,2ат„ = от, або ошах = 5а,
Для загартованої хромистої сталі, з якої виготовляють шарикові підшипники, замість границі текучості візьмемо границю пропорційності апц - 1000 МПа Отже, — 5000 МПа
Найбільш небезпечна точка лежить на осі г на глибині, що приблизно дорівнює половині радіуса площадки контакту Головні напруження в цій точці	р
Рис. 592	Рис 593
Рнс 594	Рнс. 595	Рнс 596
Де сгтах — найбільше напруження в центрі площадки контакту, що визначається за формулою (23 2)
Найбільше дотичне напруження в небезпечній точці
Т„.Х =	= 0,31а™	(23 4)
Змінивши у формулі (23 2) знак при на зворотний, дістанемо значення а™., у випадку тиску кулі на угнуту сферичну поверхню (рис 594).
= о 3881/АР (£,СД|. £^')*-	<23 5>
При взаємному натисканні кулі й площини (рис 595), взявши — = со, знаходимо
а™ = 0,388 |/«Р	(23 6)
Стискання циліндрів При взаємному натисканні двох циліндрів з паралельними твірними рівномірно розподіленим навантаженням інтенсивністю д, Н/м (ряс 596), площадка контакту має вигляд вузь кого прямокутника, ширина якого визначається за формулою
6 = 2’і5/’-ітШ?	<237>
Найбільше напруження стискання, що діє в точках осі площадки контакту,
а... = 1.274-^ 0.4І8	(23 8)
Аналіз напруженого стану показує, що небезпечна точка лежить на осі г на глибині, що дорівнює 0,4 ширини площадки контакту Го ловні напруження в цій точці мають такі значення
ох = — О.ІбООаая,
о, = -0 288атак, (23 9) а, — —0,780от#11
Найбільше дотичне напруження в небезпечній точці
тго„ =0,3ога„	(23 10)
Змінюючи у формулі (23 8) знак при /?а на зворотний, знайдемо нап руження у випадку тиску циліндра на деталь з угнутою циліндричною поверхнею Такі напруження діють у місцях контакту циліндричного шарніра та балансирів (рис 597)
При взаємному тиску циліндра
і площини, взявши у формулі (24 8) Ні — оо, знаходимо с„„ =0 418]/^- -1^,'	(23 11)
Наведені вище формули здобуті при ц = 0,3, Однак для практмч* них розрахунків ними можна користуватись і при інших значеннях коефіцієнта Пуассона
Загальний випадок контакту двох тіл Наведемо формули для за гального випадку контакту двох тіл з однакового матеріалу
Припускається, що обидва тіла в точці дотику мають загальну до тичну площину АЙ і загальну нормаль г, уздовж якої спрямовані сили Р (рис 598) Позначимо радіуси кривизни в точці дотику першого ті ла р1 1 рі, другого тіла •— ра і рі, причому Рі < рі, ря < рі Нагадаємо, що головними кривизнами називають найбільшу і найменшу кривизни, розташовані в даох взаємно перпендикулярних площинах, що про ходять через центр кривизни Радіуси кривизни вважаються додатки мн, якщо центри кривизни розташовані усередині тіла Позначимо че* рез <р кут між головними площинами кривизни тіл в яких лежать менші радіуси рі і р.
У загальному випадку площадка контакту становить еліпс з пів осями
‘-•>1/ - , -	—гт
Де И — коефіцієнт Пуассона біб
(23 І2)
(23 ІЗ)
Таблиця 24
ф •	«	Р	| Ф •		а |	В	
20	3 778	0 408	60	1,486	0 717
ЗО	2 731	0 493	65	1.378	0 759
35	2 397	0530	70	1,284	0,802
40	2 136	0 567	75	1 202	0 846
45	1 926	0,604	80	1,128	0,893
50	1 754	0 641	85	1 061	0 944
55	1 611	0 678	90	1 000	1 000
Значення коефіцієнтів а і 0 наведено в табл 24 як функції допо міжного кута % що визначається за формулою
±|/г(4г--і;)+
№’*' = ---------_1_ _1_-------------------
Р. + р; + Р. + р2	(23 14)
При цьому знак чисельника у формулі (23 14) вибирають так, щоб соз V був додатним
Найбільше напруження стискання в центрі площадки контакту
Отм —(23 і5)
Найбільш небезпечна точка лежить на осі г на деякій глибині, яка залежить від відношення (Ь/а) півосей еліптичної площадки контак ту Однак найбільше дотичне напруження в небезпечній точці майже не залежить від зазначеного відношення розмірів площадки, і можна взяти
тт„«0,32ат„	(23 іб)
З наведених формул видно, що контактні напруження залежать від пружних властивостей матеріалів і ке є нелінійною функцією на вантаження Із збільшенням навантаження швидкість наростання на пружеиь зменшується Це обумовлено тим, що із збільшенням каван таження збільшуються і розміри площадки контакту
б 144 Перевірка міцності прн контактних напруженнях
Ураховуючи <м якість» напруженого стану в небезпечних точках (всі три головні напруження стискальні), перевіряти міцність при контактних напруженнях слід за третьою або четвертою теорією
міцності (формули (7 іО), (7 19)]
Оскіїи =“ <Т1 —<7,	[а],
СТсквІУ = ]/ 4“ Иа1 — О»)’ + («ї — О»)’ + {°а — °1)2] С ІО)
Підставляючи в ці формули значення головних напружень у небезпеч ній точці, виражені через найбільше напруження атах в центрі площадки контакту, умови міцності можна записати в такому вигляді
0ека = ^Оамх |О],	(23 17)
ЗВІДКИ
Отвх ІО] [Окоиті	(23 І 8)
Тут ІОковтІ = [оі/т — допустиме значення найбільшого напруження в місці контакту.
Значення коефіцієнта т залежно від відношення півосей еліптичної площадки контакту і вибраної теорії міцності наведено в табл 25
Можна запропонувати таку послідовність розрахунку на міцність елементів конструкції в місці контакту
і Визначити головні радіуси кривизни контактуючих тіл (рн Рі, Ра. Рг) > кут ф між головними площинами кривизни одного та іншо го тіла.
2 Обчислити за формулами (23 12) і (23 13), враховуючи формулу (23 14), розміри півосей еліптичної площадки контакту
З Визначити за формулою (23 15) найбільше напруження стискан ня Ота, в центрі площадки контакту У випадау круглої та прямокутної площадок контакту Оп», визначають безпосередньо з формули (23 2) або (23 8), не обчислюючи розмірів площадки
4 Розраховують на міцність за формулою (23 18) Значення коефіцієнта т беруть з табл 25 При цьому рекомендується виходити з четвертої теорії міцності
Допустимі максимальні напруження в місці контакту [акмті для роликових і шарикових підшипників з хромистої сталі вибирають до _	3500...5000 МПа, для рейкової сталі —
Таблиця 25	до 800 .1000 МПа
У табл 26 наведено значення допустимих максимальних тисків на площадці контакту при первісному контакті по лінії (т = 0,557) і статичній дії наван таження У випадку первісного контакту в точці значення [ошжті треба збільшити в і,3 і,4 раза
Приклад 96. Упорний шариковий підшипник з плоскими кільцями без жолобів (рис 599) ста-точно стиснутий силами Ц 6,4 кН Визнано-
в	1 Е	ііг 1 Е
1 (коло)	0 620	0,620
) 75	0,625	0.6І7
) 50	0,649	0,611
525	0,646	0,587
0 (смуга)	0,600	0.557
мо розміри площадки контакту між шариком і кільцем та найбільше напруження на цій плоищдці перевіримо ,. л міцність. Діаметр шарика 6 = 15 мм кількість шари У//Лс/Л ків і => 20 коефіцієнт нерівномірності розподілу новак-таження між окремими шариками підшипника — 0 8	-4 +--4 
Матеріал шариків і кілець — хромиста сталь допусти ме найбільше напруження в місці контакту |аконт| = = ЗЯЮ МПа, модуль пружності Е= 2,12 10* МПа.
Ураховуючи нерівномірність розподілу наванта ження між окремими шариками визначаємо найбіль ше зусилля шо стискає шарик
о
Рис. 599
6*
У місцях зіткнення кілець І шариків (рис 599 точки К) утворюється кругла площадка, радіус якої згідно з формулою (23 1),
а = 0,86 у/"2^- - 0 860,4 ‘^2 ‘-у 10 - и = 0,0268 см
При цьому /?і = 8/2 = 0 75 см, /?, “ оо Е1 = Ег  Е Найбільше напруження на цій площадці на підставі формули (23 2)
О та* в
Отже
5 и *-5 03 10 3 МПа = 2657 МПа я®*	3 14 (0.0268 ІО"7)»
°<п«» < І°кпвт1
Приклад 97, Циліндричне ходове колесо крана передає на рейку тиск Р=- 70 кН (рис 600) Діаметр зовнішнього обода колеса О =• 700 мм Радіус поперечного перерізу головки рейки г = 300 мм. Визначимо розміри площадки контакту І найбільше напруження на цій площадці Модуль пружності 2 10* МПа. коефіцієнт Пуассона ц = 0 3
Таблиця 26
Марка иегму
ТимчасоелЗ опір Од, МПа
Твердість ва Бріхеллем НВ
Допустимі найбільший пек ва площадці контакту ІОцдщі.
МПа
Сталь
30
40
50 50Г 15Х 20Х 15ХФ
ЩХІ5
Чавун
СЧ21 СЧ24 СЧ28 СЧ32 СЧ35
СЧ38
480	600	180
670	.700	200
630	800	230
650.860	240
620	750	240
700	860	240
1800	.1800	240
850 . 1050
1000 1350
1050 1400
1100 .1450
1050 1600
1200 1450
1350...1800
3800
960	180	.	207
1000	187	217
1100	170	241
1200	170	241
1300	197	255
1400	197	„255
900
1000
1100
1200
1300
800
900
1000
1100
1200 ______
1300...1400
Рнс 600
а
Рис. 801
Відповідно до зазначеної вище послідовності розрахунку випишемо головні ра діуся крианзнк
— для колеса р, =• 350 мм р, = <®.
— для рейки р, 300 мм р2 = оо
Кут між головними площадками в яких містяться Рд І Ря як вадно з рисунка <р а л/2 Годі а формули (23 14) знаходимо
Рі
-у-= 0 077.
Рі Ря	35 ЗО
Отже, допоміжний кут V = 85,5“
За табл 24 виконавши лінійну Інтерполяцію знаходимо значення коефіцієнтів « Р
а = 1,055, £=0960
За формулами (23 12) і (23 ІЗ) визначаємо ровмірн півосей еліптичної площадки контакту	________________________
2 10» (1/0.35 + 1/0 ЗО)
З 0 91 70 І0“3 2~16* (1/0 35“+ 1/0 ЗО)
Найбільше напруження на площадці контакту 1.5 70 • 10-3
МПа = 1180 МПа
= 1 5
Приклад 68 При статичній дії навантаження для радіального однорядною підшипника (рис 60!) визначимо розміри еліптичної площадки контакту найбільш навантаженого шарика з доріжками кочення внутрішнього і зовнішньою кілець та найбільше напруження на площадці контакти. Розміри підшипника. внутрішній діаметр 4 = 130 мм. зовнішній діаметр О = 380 мм. ширина 8 = 58 мм, діаметр шарика </ш =- 44 5 мм Радіус найменшого кола доріжка кочення внутрішнього кільця 80 мм, Радіус найбільшого кола доріжки кочення зовнішньою кільця /?а =
= 125 мм Радіус поперечного профілю доріжка кочення г == 23,4 см Найбільший розрахунковий тиск на шарик Р — 40 кН Матеріал шариків I кілець — хромиста сталь Модуль пружності Е=2,!2 М МПа, коефіцієнт Пуассона ц = 0.3 Допустим’ найбільше напруження в місці контакту [о^овті = 5000 МПа.
Головні радіуси кривизни поверхонь тіл у точках Сі І С> первісного контакту їх такі для шерикв
Рі = дщ/2 == 22,25 мм; р, = дщ/2 22 25 мм-для внутрішньої доріжки коиення
р, «ж — г = — 234мм рд = Яв  80 мм
для зовнішньої доріжки кочення
Рі “ — г “ 23,4 мм р^ = — /?а = — 125 мм
Спочатку розглянемо зіткнення шарика а внутрішньою доріжкою кочення Формула (23 14) прн рі > р,’ набирає вигляду
соз Т = ± —і---------"------— ,	(2319)
5Т+7Г+^+7Г
Підставимо значення кривизни Тоді „	-0,0427 - 0 0125	„
соз V = ± 0,0895 — 0 0427 4-0 0І25 = 0 931
І У— 21е 25'.
За табл 24 виконуючи лінійну Інтерполяцію, знаходимо, що а — 3 629, Р = = 0 420
З анразін (23 12) і (23 ІЗ) визначаємо розміри площадки дотику
V £(’й"+7Г+’Г+'й')
Ь = Р 1 Л —------3£11 ~|>’1---;-г- - 0,420.0,206 І0~2 м — 0 087 о,.
V £(—+7Г’,^+ТГ)
Максимальне напруження на площадці контакту
Оаил = 1,5	=-------1 5 • 40 > ІО"3-- МПа = 2970 МПа
3,14 (0,740 ІО”8) (0 087 . ІО-8)
Аналогічно в місці контакту шарика із зовнішньою доріжкою кочення маємо — 0,0427 4- 0,0080	. м,
соз V = ± 0>0895 _ 0,0427 _ 0,0080 “ 0,895
Звідси V = 26° ЗО*.
З табл 24 знаходимо
а » і 097, Р — 0 463
Тоді	________________
°-здаІ/-2°г' ПГ-мҐ "-0 732 “
‘-"•4ИІ/ %,їі9' зЛ~*
Найбільше напруження на площадці контакту
амі =. 215Р и--------1 5 40 ІО"3----- МПа - 2400 МПа
«в*	3,14 (0 732 Ю-*9) (0,109 ІО-2)
Як бачимо найбільш небезпечною е точка С,
Для шарикових підшипників із загартованої хоомистої сталі допустиме значення найбільшого напруження на площадці контакту 1оковті" 6000 МПа Отже, міцність аабезпечено
Глава и ОСНОВИ МЕХАНІКИ РУЙНУВАННЯ
6 141. Загальні поняття
Механіка руйнування, або теорія тріщин, як складова частина науки про міцність твердого тіла виникла порівняно недавно (прнблиз но в останні 50 років) і займається вона визначенням законів розді лення твердих тіл на частини під дією зовнішніх силових факторів та інших причин
Руйнування може бути частковим і повним Часткове руйнування тіла характеризується пошкодженням матеріалу внаслідок виникнен ня в ньому окремих тріщин або розподілених по об’єму дефектів, що знижують його міциісні властивості При повному руйнуванні відбу ваеться розділення тіла на частини Отже, руйнування є найбільш характерним показником порушення міцності твердого тіла
Розрізняють два типи руйнування — пластичне та крихке. Плас тичне руйнування відбувається після істотної пластичної деформації по всьому об ему тіла або його значній частині і є результатом внчер-пання здатності матеріалу чинити опір пластичній деформації. Крих ким називається руйнування, що відбувається без пластичної деформа ції Розрізняють також квазікрихке руйнування, прн якому має місце деяка пластична зона перед краєм тріщини Квазікрихке руйнування відбувається в найбільш ослабленому перерізі при напруженні, ви щому за границю текучості, але нижчому, ніж границя міцності При крихкому руйнуванні швидкість поширення тріщини становить 0,2 . 0,5 швидкості звуку, тобто досить велика, а злом має кристалічний вигляд При пластичному руйнуванні швидкість поширення тріщини мала і становить не більше ніж 0,05 швидкості звуку, а злом має волокнистий вигляд
Важливе місце в теорії руйнування займає руйнування від втомленості, яке відбувається внаслідок поступового розвитку тріщини при повторно змінному циклічному навантажуванні. Руйнування від втомленості, як про це вже було сказано (див гл 21), виникає внаслідок нагромадження в матеріалі необоротного пошкодження під дією ба гаторазового прикладання повторно змінного навантаження При ньому тріщини в матеріалі починають розвиватися задовго до повного руйнування незалежно від того, пластичне це буде руйнування чи крихке
Особливо велике практичне значення в інженерній справі має вив чення крихкого руйнування конструкцій, що відбувається від швид кого поширення тріщини при середніх напруженнях, нижчих за гра ницю текучості, які здаються безпечними Останнє свідчить про те, що розглянутих до цього класичних методів розрахунку на міцність за пружним і пластичним станами недостатньо Ось чому класичні методи необхідно доповнити новими методами розрахунку на міцність, враховуючи закони зародження та розвитку тріщин, а також внести нові характеристики матеріалів за якими можна було б оцінювати його тріщиностійкість
Зазначимо, що для побудови теорії руйнування методів опору матеріалів недостатньо Треба застосовувати методи теорії пружності та пластичності, тобто більш точні методи
$ 146. Крихке руйнування. Теорія Гріффітса
Практика експлуатації інженерних конструкцій показує, що окремі їхні елементи з часом можуть руйнуватися внаслідок концентрації напружень, дефектів технології обробки та складання, впливу середо вища, що призводить до виникнення та поступового розвитку тріщи ни Іноді процес розвитку тріщини від початку виникнення її до ос таточного руйнування може становити до 90 % часу <життя» деталі Тобто деталь може працювати майже протягом всього часу експлуата ції і при наявності тріщини Отже, практично важлива не так наяв ні'сть тріщини, як швидкість її поширення в тих чи інших умовах У зв'язку з цим одними з основних задач механіки руйнування є ви вчення міцності тіл з тріщинами з урахуванням геометрії тріщин та впливу на розвиток тріщини різних факторів (характер навантажування, напружений стан, середовище, температура тощо), а також розробка критеріїв несучої здатності елементів конструкцій з тріщи нами
Розрізняють три найпростіші типи розвитку тріщин з погляду змі щення їхніх берегів один відносно ОДНОГО ВІДПОВІДНО до дії різних зовнішніх навантажень (рис 502) При деформації розтягання (схема /) виникає тріщина відриву, коли її поверхні зміщуються в напрямах, перпендикулярних до поверхні тріщини, при деформації поперечного зсуву (схема її) поверхні берегів тріщини зміщуються поперек її
Ряс. 602
передньої кромки; при навантаженні за схемою /// утворюються тріщини поздовжнього зсуву, при якому точки поверхні тріщини зміщують ся вздовж її передньої кромки Очевидно, якщо на тіло з тріщиною діє довільне навантаження в межах застосування закону Гука, на підставі принципу суперпозиції будь яке зміщення берегів тріщини, що розвивається, можна подати у вигляді суми зведених трьох типів змі-
щень
Отже, крихке руйнування пов язане з виникненням у матеріалі тріщин, спричинених дефектами в структурі матеріалу, станом поверх ні деталі внаслідок обробки чи корозії, дією повторно змінних наван тажень Тріщини, що виникли, спочатку розвиваються в часі повіль но, а потім — швидко Розвиток тріщин з часом може відбуватись І при постійному навантаженні
Перші основоположні дослідження щодо розвитку тріщин при крих кому руйнуванні пов язують з ім'ям англійського вченого А Гріффіт
са, який розглянув умови розвитку одиночної тріщини в пластині при її розтяганні (рнс 603) При цьому треба було визначити, при якому значенні розтягального зовнішнього напружен ня о = акр, прикладеного на нескін ченності, тріщина з початковою дов жиною 21 стане нестійкою, тобто почне швидко поширюватися при постійному зовнішньому напруженні, яке назива ють критичним (Довжину тріщини, при якій починається нестійкий роз виток її, називають критичною їкр )
Для здобуття відповідних розра хункових формул у теорії тріщин ви ХОДЯТЬ з того, що для розширення тріщини треба затратити певну роботу на подолання сил взаємодії сусідніх шарів матеріалу Позначимо через у густину поверхневої енергії, тобто ро-
боту, потрібну для утворення одиниці нової поверхні. Тоді поверхнева енергія розглядуваної пластини, обумовлена утворенням тріщини,
Г = 4уї	(24 1)
Густину поверхневої енергії у, яка визначається експериментально 1 для різних матеріалів буде різна, можна вважати константою матеріалу
Потенціальна енергія деформації пластини після виникнення в ній тріщини зменшиться на величину
що становить різницю потенціальної енергії деформації пластини беа тріщини 1 з тріщиною у вигляді витягнутого еліпса
Згідно із законом збереження енергії, А Гріффітс запропонував таке формулювання критерію руйнування, тріщина починав поширю-ватися тоді, коли при варіації її довжини б/ > 0 приріст поверхневої енергії компенсується відповідною кількістю потенціальної енергії де-формації (припускають, що Інших видів енергії немов)'
б(Г4-ЇГ)в0,	(24 3)
де з урахуванням (24.1) та (24.2),
вГ----^Г(4уІ)61 = 4у61,
8Г=тг(—------------------(244)
Приріст поверхневої енергії 6Г — величина додатка! вона характеризуй збільшення внутрішньої енергії тіла, тоді як приріст потенціальної енергії деформації бІГ — величина від’ємна, оскільки ця частина енергії виділяється тілом (завдяки релаксації напружень у зв язку в виникненням нових, вільних від навантажень поверхонь тіла). Підставивши (24 4) в (24 3), дістанемо
2,—-0	(24.5)
Звідси для плоского напруженого стану знайдемо
<24е)
При плоскій деформації (коли є, = 0) в останній формулі замість модуля пружності Е слід підставити £7(1 — р.*), тобто формула (24 6) буде мати вигляд	__________
’ = V•	<24 7>
Зміну співвідношення енергій, що входять у доданки рівняння (24 3), при збільшенні довжини тріщини можна подати у вигляді
21 «-ї«8	62Б
графіків Г = /і (І) та У -= Д (О (рис 604) Максимальному значенню повної енергії відповідає критична довжина тріщини /НР
Користуючись формулами (24 6) та (24 7), можна визначити кри тнчне напруження окр прикладене до пластини, при якому ві'дбува ється самочинне, без додаткової роботи зовнішніх сил, поширення тріщини початкової довжини 21 Графічну залежність між напружен ням що діє на пластині, і довжиною трішини наведено на рис 605
Розглянута теорія Гріффітса не враховує некритичного росту трі щини, який спостерігається експериментально Проте ця теорія за слуговує великої уваги, оскільки вона дає змогу виразити крихку міц ність через фізичні та механічні властивості матеріалу І свідчить, що максимальне руйнувальне навантаження має місце не при виникненні тріщини, а після досягнення нею певного критичного розміру Останнє свідчить про те, що існують безпечні тріщини, які не розвиваються, але можуть перетворитися на небезпечні внаслідок підвищення крих кості матеріалу, зниження температури дії динамічного навантажен ня, старіння матеріалу та ін
Огже, з теорії і ріффітса випливає, що наявність у тій чи іншій деталі тріщини ще не є свідченням негайного виходу її з таду В прин цнпі, можливо за критичним значенням довжини тріщини і характером зовнішнього навантаження, вводячи відповідний запас на наяв ність тріщини, визначати допуск на розмір тріщини, з якою деталь може працювати заданий час Оскітьки не кожна тріщина небезпеч на, механіка руйнування може розвиватись як наука що створює надійні методи захисту конструкцій від крихкого руйнування
Теорію Гріффітса можна застосовувати також для матеріалів, що мають деяку пластичність При цьому слід враховувати енергію, яка
,і~йг	витрачається на пластичне деформу
б-У*,,	вання в кінці тріщини Як показують
6*4	/ /V / гн 	1	— \ \ £ \ » Рнс. 604	досліди, пластична деформація розвивається поблизу вершини тріщини у порівняно тонкому шарі, що оточує її Товщина шару пластично деформова б \ \ Рцх  Рнс 605
ного металу залежить від умов навантажування, властивостей матеріалу і може становити від кількох десятків мікрометрів до десятих часток міліметра
Скориставшись концепцією енергетичного балансу А Гріффітса, Е Орован і Д Ірані запропонували додатково врахувати енергію птастичного деформування уп, ввівши у формулу (24 6) замість дійсної ПИТОМОЇ поверхневої енергії У ефективну поверхневу енергію Уеф в = V + їл, Де уп — робота пластичного деформування при утворенні одиниці поверхні
Отже, умови квазікрихкого руйнування металів Для плоского на пруженого стану та плоскої деформації відповідно можна записати так
Досліди показують, шо, наприклад, для сталі у = 0,1 Дж/м*, у„ = = 200 Дж/м*, тобто ?п ~ 10®?, тому величиною у можна знехтувати і вважати, що у«ф — ул Тоді останні формули наберуть вигляду
°.р =	•	(2« «)
- V	<2<9>
$ 147. Силові критерії руйнування
Руйнування матеріалу внаслідок розвитку тріщини зосереджене в малому околі вершини тріщини, де дуже висока концентрація напружень, обумовлена малим радіусом заокруглення Напружений стан у цій зоні при різних схемах навантажування, користуючись метода ми теорії пружності, можна в загальному вигляді виразити формулою
‘7" = Т&Г/"-0)'	(24І0)
де І, І = х, у
Коефіцієнт К, який залежить від виду навантажування, значення навантаження, а також форми тріщини, називається коефіцієнтом інтенсивності напружень (одиниця К — сила/довжнна’/г) Залежно від виду навантаження (див рнс 602) коефіцієнти інтенсивності напружень позначають відповідно індексами /, Ц чи ї/ї, тобто Кг, Кн, Кін г та 0 — полярні координати з полюсом у вершині тріщини (рис 606) [ц —деяка функція кута 6
Зокрема, при плоскому напруженому стані для навантажування за схемою І формули (24 І0) мають вигляд
“'“Т^Г005^1+5іп-г’іп-т-)’	<241»
К] е , 6 зв
т" = ТяГ т ~ 5|п т см—•
Переміщення и та V в напрямі осей х та у відповідно визначаться за формулами
2/С/(і +н)	б / 1-н , , . 8\
« =----Е---- У -5Н-СО8-3- Т+Т +5ІП*т)
Ь ' 2п 2 К 1+н	2 >	(24 12)
2К/(1 +р) т/ г .6/2	. 6 'і
—і—V йг5,п-2-(т+іг-с°3'-2-)
У випадку плоскої деформації, коли є, « 0, у формулах (24 12) слід замінити (1 — ц)/(1 + ц) та 1/(1 + ц) на 1 — 2ц та 1 — ц відповідно.
Епюри напружень біля вершини тріщини відриву (0	6 я)
у декартовнх і полярних координатах показано на рис 607, а, б За означенням коефіцієнт інтенсивності напруження біля вершини трі щнни при плоскій деформації
Кі = Ііт ИБйо^г, Є),	(24 13)
г-»0
що випливає з аналізу напруженого стану біля вершини тріщини Так при розтяганні пластини а тріщиною завдовжки 21 за схемою рис 606 цей аналіз дає змогу записати вираз для нормального напру* ження в перерізі пластини в околі тріщини
а*°°-І^Г °° Аї+'‘ 	12414>
де х — координата, що відлічується від середини тріщини, г = х — І.
Біля вершини тріщини, при х-* 1, г-+ 0, напруження необмежено зростає за модулем Підставляючи ці значення в (24 13) 1 обчислюючи
границю, знаходимо:
Кі» &У п/
Аналогічно можна здобути формули для коефіцієнтів інтенсивності напружень Ки та Кін відповідно до схем навантажування //та НІ нарис 602 Отже,
Кі =аУ~яї
Кп^іУяї (24 15)
Кін л
У лінійній механіці руйнування виходять з припущення Д [рвіна, що тріщина буде поширюватися тоді, коли коефіцієнт інтенсивності напружень досягне критичного значення, характерного для даного матеріалу Так, критерій розвитку тріщини нормаль-
ного відриву має вигляд	и	{
Кі=Кіс (24 16)
Аналогічно можна записати Два інших	Рвс> 607
критерії Кис та Кніс для тріщин поперечного та поздовжнього зсувуї Кн = Кис та Кін = Кще
Критичні значення коефіцієнтів інтенсивності напружень Кіс, Кін, Кип визначають експериментально, користуючись певною методикою, регламентованою відповідними стандартами Критерій руйнування Ірвіна (24 16) у літературі називають силовим, оскільки він грунтується на аналізі напруженого стану біля вершини тріщини
Для пластин обмежених розмірів при різних видах навантажування І розташування тріщин критичні значення коефіцієнтів інтенсивності напружень визначаються за формулами
Кіс ~	УЯІкр
Кне в ///ирТкр І^л/ир,	(24 17)
Киїс ™ ////ирТир |/"л/кр,
Де //ир, Л/Кр, Л//ир —* деякі поправочні коефіцієнти Вирази для //кр наведено в табл 27
Можна довести, що силовий критерій руйнування еквівалентний критерію Гріффітса
У тілі з симетричною тріщиною завдовжки 21 прн її розвитку в кожний бік на величину 61 вивільняється пружна енергія —
Таблиця ТІ
Вид навантажумиия І розташуванні тріщини	Схемі	Поправочні функція
Розтягання необмеженої пластини з поли лою трі щниою в середині
Розтягання півнескінчен ноі пластннн з однобіч пою тріщиною
Розтягання пластннн зав ширінки 26 з поперечною тріщиною посередині
Те саме з двома бокови мн тріщинами
Згинання в площині пла стннн завширшки В і зав* товшкн Н з поперечною тріщиною посередині
Чисте згинання тієї самої пластини розподіленим моментом т
Продовження табл. 71
Вид навахтажумвкя і рпзтвшумі і» тріщини	Сдем.	Поправочна функція
Дія внутрішнього тиску р на циліндри іну трубу діаметром 2/? зантовш кн Н при поздовжній наскрізній тріщині
+ *61 -т-
— 2 (дИГ/дїї 61. Позначивши вивільнену енергію —дф/ді на одиницю плоді через О, дістанемо
6Г = 206/	(24 18)
З іншого боку, на утворення нових поверхонь потрібна енергія
6Г = 4^61,	(24 19)
де, як і раніше, через V позначено поверхневу енергію, віднесену до одиниці площі Отже на підставі (24 18) та (24 19) будемо мати
6 = 2?	(24 20)
Потік енергії у вершину тріщини при збільшенні її можна визна* читн як роботу, потрібну для .закриття» тріщини, виходячи з таких міркувань
Уявимо собі, що вздовж тріщини (рис 608) е розріз, на поверхні якого діють напруження, що виникають у зоні концентрації напру жень від дії зовнішнього навантаження Тоді шуканий потік енергії при просуванні тріщини на одиницю довжини уявного розрізу, згідно із схемою рис 608, визначиться як
б/ = — |	(24 21)
де нормальне напруження аи та переміщення и при плоскій деформації беруться з формул (24 11) та (24 12) відповідно при 0 = 0 та Є = я
При цьому
[) = 4<!^К;|/2_«	(2423)
Підставляючи (24 22) та (24 23) в (24 21) та інтегруючи, знайдемо
(24 24) для плоскої деформації та
о, = -Її-	(24 25)
для плоского напруженого стану.
Отже, маємо два еквівалентних формулювання критерію руйну вання
І) енергетичне, згідно з яким припускається, що тріщина може поширюватися тоді, коли інтенсивність вивільненої енергії б досягає критичного значення
в,, =	= 2у = сопзі,	(24 26)
2) силове, згідно з яким тріщина може розвиватися при досягненні коефіцієнтом інтенсивності напружень К свого критичного значення
Ке - сопзі	(24 27)
Ця еквівалентність випливає з формул (24 24) та (24 25) для плоскої деформації та плоского напруженого стану відповідно.
=	Ол = 4	(24 28)
Зазначимо, що формули (24 28) справедливі для ідеально крихкого руйнування Насправді, як уже зазначалось, у більшості матеріалів у малій зоні вершини тріщини внаслідок пластичних деформацій про являються нелінійні властивості багатьох реальних матеріалів Од нак унаслідок малості зони пластичної деформації порівняно з довжи ною тріщини вважають, що розміри цієї зони і ступінь пластичної де формації, що відбувається в ній, контролюються коефіцієнтом інтенсивності напружень К та границею текучості ат Тому для квазікрнх кого руйнування залишають у силі обидва критерії руйнування Кс і Се вважаючи, що вони залежать від характеру опору матеріалу пластичній деформації
Отже, співвідношення (24 26) та (24 27) у лінійній механіці руйну вання є основними За допомогою їх можна розраховувати граничний стан елементів конструкцій з тріщиною, а також оцінювати механічні властивості матеріалу і його здатність гальмувати розвиток тріщин.
У загальному випадку навантажувань, коли можливі зміщення берегів тріщин відносно один одного одночасно аа трьома розглянутими схемами (днв рис 602), знаходимо для плоскої деформації о = ЇЇ + -Ц4- ІЄ„ +	К‘,„ = О, + О„ + О,„, (24 29)
для плоского напруженого стану
а - 4- К' + к" + к'"> = °' +	(24 30>
§ 148. Оцінка розмірів пластичної зони вздовж тріщини
Енергетичний критерій для нестабільного розвитку тріщини, виражений умовою (24 26), з урахуванням (24 І5) можна записати у вигляді
=	(2431)
де ус — критична енергія деформації, потрібна для утворення віль ної поверхні тріщини при наявності* пластичних деформацій.
Наведений раніше вираз (24 ІЗ) для коефіцієнта інтенсивності напружень з урахуванням (24 14) дає змогу наближено визначити дов жину пластичної зони гт уздовж тріщини Так, при =* от для напру женого стану, що характеризується коефіцієнтом інтенсивності Кі, 8 пластині необмежених розмірів
<24 32>
або з урахуванням виразу Кі —
= 4'(-£)’•	(24 33)
Для пластини скінченної ширини
'.=4<24 34>
Тоді половина довжини тріщини з урахуванням пластичної зони г,-( + гІ = ;[і+ 4(-і-у].	(24 38)
Користуючись величиною /т, за наведеними вище формулами можна визначити Кіс, а потім і переміщення V біля вершини тріщини Так, для плоского напруженого стану прн г = г„ 6 = я
<24 33)
Подвоєна величина V дорівнює роз крипто тріщини б (рис 609)
Ряс 610
в - 2»,-,,-2	11/ 1+4-(-£-)’
(24 37)
У випадку крихкого руйнування при о < ог розкриття тріщини наближено можна знайти за формулою
(24 38)
Результати обчислення розкриття тріщини б за формулою (24 38) при а 0,8а, підтверджуються експериментально
При плоскому деформованому стані внаслідок того, івд г і 6 менші, Довжина пластичної зони зменшується в кілька разів порівняно з такою прн плоскому напруженому стані
Слід мати на увазі, що розміри пластичної зони біля вершини трі щинн для одного і того самого матеріалу залежать від ступеня дефор мації вздовж переднього краю тріщини Тим часом ступінь стиснення деформації залежить від товщини зразка, із збільшенням якої напру жений стан змінюється від плоского, при якому о, = 0, до об ємного при плоскій де^юрмації, коли о, -- ц (о4 + о*) При цьому на боковій поверхні плоского зразка за умови відсутності тут зовнішнього тиску
завжди має місце плоский напружений стан, а тому розміри пластичної зони бі ля вільної поверхні зразка завжди більші, ніж у середній частині Пластична зона спереду вершини тріщини в досить товстому плоскому зразку приблизно має форму котушки (рис 610)

*
Оскільки в середній частині зразка має місце об'ємний напружений стан, а отже, більш жорсткий, ніж у зоні тріщин, які
примикають до бокових поверхонь, то опір руйнуванню в цій зоні буде менший, а тому і фронт просу вання тріщин буде видаватися вперед, маючи язикоподібний вигляд Для зразків різної товщини співвідношення пластичних зон і переду тріщини різне Уяв язку з цим змінюється зна чення енергії' затраченої на руйнування, а отже, існує залежність від товщини зразка характеристик тріщиностійкості — коефіцієнта інтен сивності напружень Кг (рис 611) та інтенсивності звільнюваної енер гіі 6е Як видно, із збі іьшснням товщини зразка значення Кс (а отже, Сг) зменшується і прямує до свого граничного, асимптотичного зна чення Ке при об ємному напруженому стані в умовах плоскої дефор маиії
§ 149 Методика експериментального визначення тріщиностійкості конструкційних матеріалі*
Як міру тріщиностійкості матеріалу стосовно до найбільш небез печиих і поширених тріщин нормального відриву найчастіше викорис товують критичне значення коефіцієнта інтенсивності напружень Кіс, шо відповідає моменту старту тріщини при виконанні в її вершині умов плоскої деформації
Для експериментального визначення характеристики Кіс кон кретного матеріалу використовують спеціальні компактні зразки СТ (рис 612) із заздалегідь вирощеною циклічними навантаженнями тріщиною, що задовольняють такі розмірні вимоги
В (и — /) > 2 5	(24 39)
де В — товщина зразка І — довжина тріщини (ш — І) — ширина робочої' частини зразка ав,г — границя текучості матеріалу зразка
Режим вирощування і довжина тріщини повинні відповідати лев ним вимогам, що забезпечують здобуття вірогідних значень характеристики тріщиностійкості матеріалу
Навантажуючи зразок зростаючим зусиллям, знімають діаграму навантаження Р'-»-зміщення берегів тріщини V Критичний коефіцієнт інтенсивності напружень КІе випробуваного матеріалу розраховують за навантаженням Р, що відповідає на діаграмі Р ~ і> старту тріщи нн, з використанням деякої залежної від конфігурації зразка функції його розмірів та довжини тріщини
= ,24 4О) де
у(~) =»6(4)°Б- >85.5ЦІ! + 665.7(-ір-.
-1ОП(-Ь)“ + (Ї38.9(-Ь)“.	(2441)
Рас. 612
Якщо обчислене за формулою (24 40) значення Кіс задовольняє роз* мірні вимоги (24 39), то воно вважається шуканим У противному разі треба повторити випробування на зразках збільшених розмірів.
Зауважимо, що оскільки значення навантаження на діаграмі Р ~ ~ о не залежить від місця вимірювання зміщень, то останні доцільно вимірювати поблизу точок дії навантаження або поблизу середньої точки лінії фронту тріщини За діаграмами Р що реєструються синхронно, можна додатково до силової характеристики Кіс визна чати і деформаційну характеристику тріщиностійкості б/е
Такий підхід дає змогу комплексно, з єдиних методичних позицій, оцінювати тріщиностійкість матеріалу як у крихкому, так і пластич йому станах Зазначимо однак, що наведена методика визначення ха рактеристики Кіс точно обгрунтована тільки при випробуванні крих ких матеріалів, що руйнуються в лінійно пружній зоні
Приклад 99 Визначимо запас міцності циліндричної посудини діаметром О «= 480 ми і товщиною стінки Н = 8,5 мм, що працює в умовах кімнатної темпера тури під внутрішнім тиском р = 28 МПа і в якій при обстеженні було виявлено
Рис. 613
з внутрішнього боку твеліптичну тріишну завглибшки І = 3 мм та завдовжки вздовж твірної 2а = 8,5 мм (рис 613. а) Матеріал посудини — сталь (границя текучості о, ** - 1000 МПа; границя міцності о, = 1200 МПа)
Для визначення характеристики тріщнно-стійкості сталі було проведено внпробовуван ня відповідних зразків в умовах кімнатної температури при статичному навантажуванні аа схемою рнс 613 б Зразки зазшнршкн 2В та товщиною що дорівнювала товщині стінки
посудини (8 5 мм) мали центрально розташовані тріщини завдовжки 21 = 10 мм Номінальне напруження прн якому зразки руйнувалися по мінімальному перерізу, дорівнювало ак — 720 МПа Наслідки випробувань показали, що прн вибраній тов шині зразка його матеріал перебував у крихкому стані, а тому запас міцності в цьому ЇазІ можна розраховувати використовуючи теорію лінійної механіки руйнування
Ому критичне значення коефіцієнта інтенсивності напружень К/с ножна знайти користуючись першою формулою системи (24 17)
-1»&, У ”5.
де/Лр — поправочний Коефіцієнт, що враховує схему навантажування тип розміри зразка і характер тріщини окр — номінальне руйнувальне напруження в ^ослабленому перерізі (т — довжина тріщини з урахуванням пластичної зони в її вершині Напруження о*? знайдемо через номінальне напруження в ослабленому перерізі
”"Р -	- ’ (' - т) - 720 (‘ - ж) - 5,0 мп*
Умовна довжина тріщини І, на підставі (24 35)
,’='|1-|',5(^)’|-5І,+05(таг)’І = 57!““
Поправочний коефіцієнт відповідно до табл 27
Тоді згідно з формулою (24 42),
К/( = //мЛ<р И літ " 1 04 540/я 5 72 = 2290 МПа / м
Пей коефіцієнт використовують для обчислення номінального руйнувального на пруження в посудині із зазначеною вище тріщиною Номінальне головне напруження в стінці посудннн (вважаємо її тонкостінною) яке намагається зруйнувати посудину по твірній згідно з формулою Лапласа
мп<
Коефіцієнт інтенсивності напруження К Іе аля розглядуваної тріщини згідно з формулою (24 17) без урахування пластичної деформації
ЧІе = /кр п1
де о/кр — критичне руйнувальне напруження для посудннн (— глибина тріщини Поправочний коефіцієнт для ненаскрізноі півеліитнчної поверхневої тріщини
завглибшки І (мала піввісь) і завдовжки на поверхні 2а (а — вели за піввісь) в пласти ні зааговшки Н
•а-й-іЛ+Н-й-)- <««> де Фо —величина, що залежить від співвідношення На (при збільшенні На від 0 І до І Фа рівномірно збільшується від І до л/2)
Отже при і/а — 3/4 25 = 0 71 співвідношення становить 1 39 Тоді підставля ючн в (24 43) відомі величини знайдемо
''«“Тй 11+012(1-07111 х
* V-081
Критичне напруження для посуаняя
Глибина тріщини з урахуванням пластичної деформації що виникла в н верши ні, згідно з (34 35)
Вважаючи шо розмір тріщини 2а зростає пропорційно знайдемо
вт = А. а 	8 5 г- 12 1
Поправочний коефіцієнт //кр згідно з (24 43)
''""“ТТ5-"+оі2('-”7'1і!<
х 1/" 255 [ _т______4,25 і/" | _|_ ] 6і-12	= о 91
И ч 4,25	2 8,5 V	240 8 5
Тоді значення уточненого руйнувального напруження з урахуванням пластично? деформації и, = 4 25 та //кв = 0,91
к'с	2290
о,ь„ ™	г^=~ =	у”~г тг‘ — = 695 МПа
0 91 /я 4.25
Для визначення руйнуватьного напруження аІкр у другому иаближенн слід у фср мулі .24 43) другого наближення урахувати скорнговані розміри тоіщнпи
(т = 3|і 4-0 5 (695/1000)»] » 3 74 мм.
о, = (/,//) а = (3 7ч/3) 8,5 = 10 6 мм
Тоді поправочний коефіцієнт
'/„--ГуІІ+О.ЬІО-ОППх
Руйнувальне напруження в другому наближенні
2293
з7.--75ОМП<
Дальше наближення не дає істотного уточнення
Отже здобуте критичне напруження о/1ф порівняно з номінальним напружен вам у стінці о/н дає змогу визначити запас міцності стінки посудини з тріщиною
п «= °/ІСР «= 760 я 0,948 о,н 79)
Оскільки п < 1 то експлуатація посудний із зазначеним дефектом недопустима
640
гІЙ?	“яй	(• © яг ©,© ©, "* ЗЙЯЗЙяг^	§3	© © © ь*«— ©© ЙЙ588ІЇ&	$3	©© — Р5©© ©88833=
5338	газ	© « © Ь-’кЛ п ° Я «стяг и5© ь-		Й553£85		'ч8©8=3»
	пстео	Ч- Т ЯГ ЯГ « « яг	ЯГ яг	иа іл © © іл © ©	©©	<3 © ©"»-. Гя Г~ ь.
3853 іьсіо	35 8	§І§5=|І	??© з а	8Й83ЙЗЗ ©Зй5ЙфЗ	і!	О^О --И ЯГ •»
2.47 2,46 2,45 2,44	©СОФ	© 00 Ґя © ^ <*5 © ПППППП^	83	3,99 3.98 3,97 3,96 3,93 3.91 3,89	88	^.838©88 * я» ^Гяг ЯГ ч-^>
	8=§	© СО ©	ь- © ЗЯЙ3533		ші§!!		®2« ©©Ь;ф® 325&323 “ечеіечечгаЛ
2ЙЙК	§ї-?	6,25 6,24 6,23 6.20 6,17 6,13 6,10	83	3852Р.88	38	9,78 9,75 9,72 9,69 9.84 9,59 9.56'
	888	ІШІІЯ	іі	8233833 азййЗзз	II	ІЗ§8§Яа
8882	ЗйЗ	ЙЙЗЙ^&Ж	<%©	21-,8^8§	8©	Кй-®2г®
		* ” * * * * *	©©		©©	Г— (я. Г>~ Г" Є- (я. Гя
8«§§	ш	2323582 Ь-Лоф — сяяг			8 п	= 58§8^Р: ЇЙЙЗйР:©
зНЙв’	с5&Й		8*5	— ©© о ©я © 5833^3*=	8'8	ЯййїїяІ
2222		© — © я£© ® £	=її	Є4С0 ^© © по меч л	22	228К888
	2	8	3	а	§	а
	2	2	2	8	8	а »
64)
2	Продовження дод. І
Кутники нер і в вобокі (за ГОСТ 8510—«6)
Позначення*
В — ширина більшої полиці, Ь — ширина меншої полиці.
<1 товщина полиш,
7 — момент інерції, і - радіус інерції х« Уц — відстань від центра ваги до зовнішніх граней полиць
															
Номер профілю	Розміри, мм		Площа перерізу	У, см*	см			4тІп.	й'тіп.	Кут из>н- ЛУ ОСІ іе а	&		з, Ьм	V» СМ	Меса їм. кг
	' 1.	О													
5,6/3 6	56	36	4	3,58	11 4	1 78	3,7	1,02	2,19	0 78	0,406	23,2	6,25	0 84	1 82	2 81 5	4,41	13,8	1,77	4 48	1 01	2,66	0,78	0,404	29,2	7,91	0,88	186	3,46 6,3/4	63	40	4	4,04	16,3	2.01	5 16	1 ІЗ	3,07	0.87	0,397	33.0	8.51	0 91	2,03	3 17 5	4 98	19,0	2,00	6.26	112	3,72	0,86	0,396	41,4	10,8	0,95	2,08	3.91 6	5,90	23,3	1 99	7,28	1	11	4,36	0.86	0,393	49,9	13,1	0,99	2,12	4,63 8	7,68	29.6	1 96	9.15	1	09	5,58	0.85	0,386	66.9	17.9	1 07	2 20	6,03 7/4 5	70	45	5	5,59	27.8	2,23	9,05	1	27	5.34	0.98	0 405	56,7	Іо,2	1 05	2.28	4 39 7,5/5	75	50	5	6.11	34,8	2,39	12,5	1	43	7,24	1 09	0.436	69,7	20,8	117	2 39	4 79 6	7.25	40 9	2,38	14,6	142	8,48	1 08	0,435	83,9	25,2	1 21	2,44	5,69 8	9,47	52.4	2 33	18,5	1 40	10,9	1 07	0.430	112	34.2	1 29	2.52	7.43 8/5	80	50	5	6,38	41 6	2,56	12,7	1 41	7.58	1 09	0,387	84,6	20,8	1 13	2,60	4,99 6	7,5.5	49.0	2.55	14 8	1 40	8,86	1 08	0.386	102	2з,2	1 17	2.65	5,92 9/5,6	90	56	5 5	7,86	65,3	2,88	ІУ.7	І,а8	118	122	0.384	Ш	32,2	1,26	2,92	6,1?															
	6 8			8,54 11,18	70.6 90.9	2,88 2.85	21 2 1.56		12.7 16,3	1 22 1 21	0,384 0,380	145 194	35.2 47.8	1 28 1 36	2,9а 3,04	6,70 8.77
							27,1	1 56								
10/6.3	100	63	6	9,59	96,3	3,2	50,6	1,79	18,2	1 38	0,393	198	49,9	1 42	3,23	7,53
			7	11 1	113	3.19	35 0	1 78	20,8	1 37	0,392	232	о8,7	1 46	3,28	870
			8	12,6	127	3.18	39^2 1.77		23,4	1,36	0.391	266	67.6	1 аО	3,32	9,87
			10	15,5	154	3,15	47.1	1 75	28,3	1 35	0,387	ЗХГ	85.8	1 58	4,40	Р 10
11/7	110	70	6,5		142	3.53	45,6	2,00	26,9	1 .53	0,402	285	74.3	1 о8	3,55	6.98
			8	11 а	172	3 51	54.6	1 98	32,3	1 52	0,400	353	924	1,64	3,61	10.90
				13.9												
12,5/8	125	80	7	14,1	227	4,01	73,7	2,29	43,4	1 76	0,407	452	119	1 80	4,01	11 0
			8	16,0	256	4,00	83	2,28	48,8	1 75	0.406	5і8	137	і 84-	4.05	12.0
			10	19,7	312.	3,98	10(Ь	2,26	59,3	1 74	0.404	649	173	(92	4 <4	15,5
			12	#4	365	3,95	117	2,24	69,5	1 72	О40У	781	210	2,0(1	4.22	18 3
14/9	140	90	8	18,0	364	4 49	120	2,58	70,3	1 98	О 411	727	ІО4	2,03	4 49	>4,1
			10	22,2	444	4 47	146	2,.56	В6 5	1 96	0.409	9)1	245	2.12	4.58	17,5
16/10	160	100	9	22,9	606	5,15	186	2,85	ПО	2,20	0 391	1221	300	2.23	5,19	18,0
			10	25,3	867	5.13	204	2,84	121	2.19	0,390	1359	335	2,28	5,23	19,8
			12	30,0	784	А 1 1	239	2 82	142	2,18	0,388	1634	40а	2,36	5,32	23.6
			14	34,7	897	5.08	272	>80	162	2 16	0,385	1910	477	2,43	5,40	27.3
18/11	180	110	10	28,3	952	5,80	276	3,12	165	2,42	0.375	1933	444	2.44	5.88	22.2
			12	33.7	1123	5.77	324	3.10	194	2,40	0,374	2324	а37	2.62	5,97	26.4
20/12,5	200	12о	11	34,9	1449	6,45	446	3,58	264	2 75	0.392	2920	718	2.7Р	6,50	27.4
			12	37,9	1568	6,43	482	3 57	285	2,74	0.392	3)89	786	2.83	6.54	29,7
			14	43 9	1801	6.41	551	З.оУ	327	?,7.і	0,390	3726	Я22	2,91	6.62	34 4
			16	49,8	2026	6,38	617	3,52	367	2.72	0,386	4264 1061		2,99	6 71	39.1
25/16	250	160	12	48,3	3147	8,07	1032	4 6?	604	3,54	0 410	6212 1634		3,53	7,97	37,9
			16	63,6	4091	8,02	1333	4,58	781	3 5	0,408	8308 2200		3.69	8,14	49,9
			18	71 1	454о	7,99	1475	4.56	8°0	3,49	0,407	9358 2487		3,77	8,23	558
			20	78.5	4987	7,97	1613	4.53	949	3.48	0,405	10 410 2776		3,85	8,31	61 7
40	400	155
45	450	160
50	500	170
55	550	130
60	600	190
8.3	13,0	72,6	19062	953	16,2	545	667	86,1	3,03	57,0
9	14,2	84,7	27 695	1231	18,1	708	808	101	3,09	66,5
(0	15,2	100	39727	1589	19,9	919	1043	123	3,23	78,5
	16,5	118	55962	2035	21 8	1181	1356	151	3,39	92 6
12	17,8	138	76806	2560	23,6	1491	1725	182	3,54	108*
Позначення
Ш в е і е р и (за ГОСТ 8240—89)
Л — висота швелера, Ь — ширина полиці <і — товщина стінки, < — середня товщина полнаі — чонеат терші
V — момент «тору, і — радіус інерції З — статичний момент півпереріау. «о — відстань від осі у до зовнішньо? грані стінки
о>
профілю	Розміри ми	Піо<« 1 «рері.у 1 1, см* Л гм»	*	Те см»	Ігси	5Г см1! і у, см*	см1	(Г£“	см	Маеа 1 м. «т
	.|.и,								
665	55 Іб 1'1 ?’? ті? ??•’	?•'	1 ®	5'61 275 ю~™-«~Й—Й--.Й8	89:4	8^ 18:“ и !“ » Й Й 1Н Ж	8$ • й 1	•' 7» «	."-з }?	160	84	8,0	8,4	18 1	747	93	4	6 42	64 1	АЧ к	іч я 18й	180	тп	1'?	я’?	19 5	823	103	6'49	59^	783	ЇМ Я>	яо	7Л	по	™’7	1040	121	7.24	69,8	66	17,0 20^	от ті Н оп	1,90	132	7,32	76.1	105	20.0 ТОН	М—«Г -г4—	-	152	8.07	87.8	113	20Л- 200 8°^ °2 77	ЖТ	1670	167	8,15	95,9	139	24 2							0,054	1 16	4,84 1,08	1 24	5.90 1,19	1,31	7,05 1,37	1.44	8,59 1,53	1.54	10,4 1 70 і 67	12,3 1 84	1 67	13,3 1 87	1 80	14,2 2,01	2,00	15,3 2.04	1 94	16,3 2.18	2,13	17,4 -2,20	2.07	18,4 2,35	2,28	19,8		
профілю	Розміри мм				Площа перирізу 1	с“‘		'г		*г см*	ІР см*	•у «	«0. см	Мми 1 м.
	а	ь	4											
Додаток 2
матеріалів
Границі міцності а,, МПа, хеяхих
Матеріал	Розтягання	Стисканні	1	Матеріал	| Розтягання	Стискання
Чавун сірий			ялина вздовж волокон	65	35
звичайний	140 180	600 1000	> поперек І	—	4
дрібнозернистий	210 250	до 1400	дуб уздовж волокон	95	50
Пластмаса:			» поперек »		15
бакеліт	20 ЗО	80 100	Камінь:		
целулоїд	60 70	—	граніт	3	120 260
текстоліт	85 100	130 250	пісковик	2	40 150
гетинакс	150 170	150 180	вапняк	—	50 150
бакелізована фанера	130	115	цегла	—	7,4 ЗО
Деревина (прн вологості 15 %)			бетон	—	5 35
сосна вздовж волокон	80	40	кам яна кладка па розчині	0,2 0,з	2,5. 9
» поперек »	—	5			
Додаток З
Механічні характеристики чавуну
		Границя кіііност	МІІа, при			Границя витривалості МПа при	
Марка чавуну	розтяганні 1 ’• 1	стасквині 1 ”• 1	згинанні "• 1	крученні	Твердість аа брінеллем НВ	згинявні »-Ьг	крученні т_ і
СЧ 12 СЧ 15 СЧ 18 СЧ 21 СЧ 24 СЧ 28 СЧ 32 СЧ 35 СЧ 36 ВЧ 40 10 ВЧ 50 І 5 ВЧ 60 2 (1 рам 1 т кх.	120 160 180 210 240 280 320 350 380 400 600 600 'раииця текучост	500	280 650	320 700	360 750	400 850	440 1000	480 1100	520 1200	560 1400	600 1600	1700	— 1860	2000	— 2040	2290	— о для ВЧ <0-10 становить 380		240 280 300 350 390 400 450 480 510 740 790 660 810 для ВЧ 50-1 5	143	229	— 163	229	70 170	229	— 171	241	100 187.	217	120 170	241	140 167.	255	140 197.	269	150 207.	269	150 156	197	150	170 187 .	255	230	270 197	269	170	230 - 380 та для ВЧ 60-2 - 420 МПв.		50 80 100 110 110 115 115 198 170. 210 150 150
Додаток 4
Механічні характеристики, МІІа вуглецевих конструкційних сталей
	Марка сталі	" 1 ’’ 1 ’’			Відносне полов ження 6 %, при 1 " ЇМ	Ударна в яз-кість КС. кДж/м*	°-1зг		°-1р		т—Ікр	
		ае менше										
	10	340	210	140	31	2400	160	220	120	150	60	120
	20	420	250	160	25	__	170	220	120	160	100	130
	25	460	230		23	900	190	250				
	ЗО	500	300	170	21	800	200	270	170	210	ПО	І4О
	35	540	320	190	20	700	220	300	170	220	130	180
	40	560	340	—	19	600	230	320	160	240	І4О	190
вв менше
Відносне по-довженна в.
Ч. прн І» ш
45	610	360	220	16
50	640	380		
55	660	390		
60	690	410		
20Г	460	280		24
80 Г	550	320		20
50Г	660	400		
20Х	800	650		
40Х	1000	800		
45Х	1050	350		
80ХМ	950	750		
35ХМ	1000	850		
40ХН	1000	800	390	
50ХН	1)00	900		
40ХФА	900	750		
38ХМЮА	1000	850		
І2ХНЗА	950	700	400	
20ХНЗА	950	750		12
ЗОХНЗА	1000	800		
40ХНМА	1000	950		
ЗОХГСА	1109	850	—	10
 їсть КС. кДж/м1
500 400	250 340 270 350	190 250 200 260	150 200 160 210
—	310 380	220 280	180 220
800	220 320		—
400	290 360			
600	380			170. 230
600	350 380	250	225
500	400 500		
800	310 410	370	230
800	470 510		
700	400	290	240
500	660		
900	380 490		
900	420 550		
900	390 470	270 320	220 280
1000	430 450	300 320	245 255
800	520 700		320 400
1000	500 700			270 380
500	510 540	500 535	220 245
ДОбїТО “ пал1ром“’ Зрежнн. 2 Прн ввкористиші стеле» м ГОСГ 380-аа слід урахумтн
Додаток 5
Механічні характеристики жароміцних ставів
Спліав	Марка сплнау		°о,г		Е	в	•	КС, кДж/м’
			мп					
Аустенітні сталі	ЗИ734	1000	600		172 000	20	25	300
	ЗИ589	918 1020	795			211000	15	15. 25	300
	ЗИ590	785 856	336 408	—	—	31 44	40 49	1000
Сталі на нікелевій ос	ХН77ТЮ	1000	600	367	194 000	25	28	800
нові прн 20 °С	ЗИ826	1050	720	388	204000	10	12	200
	ВЖ96	750	388	310	—	40	—	—
Сталі на залізонікеле	ХН35ВТЮ	1350	940		223000	14	15. 29	350 700
вій основі прн 20 °С	ЗПІ05	950	700	—	190000	10	13	250
	ХН35ВТР	800	450	—	214000	20	36	1000
Титанові у відпаленому	ВТ5	770	720	459	107 000	8.5 ІЗ	40	400
стані	ОТ4	800	680	388 438	110000		25. 50	400
	ВН 2 прн 7 = 20 °С	650 750	530 700	480	112000	25. 30	60. 70	2700
Ніобієві	»	>7=І200’С	180 200	110 12С			109000	30 35	100	—
	>	»7=1600°С	40 50	20	—	107000	60 60	100	—
	ВМ 1 при Т - 20 °С	760	500	500	328000	25	55	20
Молібденові	>	> 7 = 1200’С	250	200			259000	22	90	—
	>	» 7 = 1600 °С	60	400	—	212000	55	100	—
	Та + 10 % V прн Т = 20 Те саме прн 7 = 1250 °С	°С 600	480 500			184 000	36,0	96	—
Танталові		185	100		155000	45.0	94	——
	> прн Гя 1500 °С	150	85	—	147000	60 53	95	—
		200 240					360 000	45. 48	80 90	—
Вольфрамові	>	» 7= 1500 °С	140 150			—	840000	48 58	90 95	—
	»	» 7 =2000 °С	80 .85	—	—	280000	60 70	9а. 96	—
Додаток 6
Механічні характеристики, МПа, пружинних сталей
Сталь	Розтягання			Стискання	1 риниця витри, аалості т. іружини при иіднульово-му циклі
	“в	°т |	°гга	£•10—	’ 1 ’’ 1	
Середвьовуглецева	1500	1600	1І100	1200	750
Внсоковуглепева	1450	1700	950	і 350	800
Хромова шшєва	1600	1750	1500	1600	900
Кремлемарганнева	1600	1700	1400	1500	900
Кремневаиадієма	1400	1500	950	1050	боо
Примітка Границя витривалості пружини дається при ирактерезуетка коефіцієнтом V, е 04
900	2.1	850	1100	600	800	8.1	500	650
1000	2,0 2,2	1100	1400	650	900	7.6 8,3	500	700
1000	2,01	1700	1300	9Х>	1000	8,0	550	600
УХ)	2,05	1 130		950	1000	7,6	100	660
650	2.3	1200	1260	«00		8,3	450	500
		»_| ДІ					ДЛЯ с	
Додаток 7
Механічні характеристики деяких кольорових сплавів
Сплав |	Матеріал	| «і;, і «я. і '	НЬ |	Галуїь аастосуииия
Мід"1 Латунь	Л58	91. 52С 320	660	об: ЗО 55; 150	Труби дріт листи Латунь	алюиініева	ЛЛ77	2	140. _ 400 .	650	бо; 12 60.170	Труба трубіи и^аеисатоаі Латунь марганцева	ЛМцбб 2	156, _ 400. 700 4Л 10 55 75 Пр™ , Рлн "і	Р Бронза слон яка	БрШО	_ 250 _	11 _ (к/ _	Л™,, и	,	БрОФІО 1	140, — 2<И) 300 — 3 80, 100 Шестірні підшипники Бронза алюмінієва	БрА5	160, 500 380 400	65, 4	60, 200 Стрічки штаби Бронза кремінна	БрКЗ	-	250 - 10 20	- Литво Алюмі Дуралюиїн нормальний	ДІ	Цщ 240 2Ю. 120	18. Із	45; їм Труби пресовані	профілі мкЕГ“ п1Д8НЩен01 Д6	Я- 380 |80- “0 в! 20 50. 125 тКби "Йфі“ ** Алюмінієво-магнієвий сплев АМг	100 , 210 180, 260 6; 23 45; 60 Труби, листи Примітка. Перші цифри дано для м якого етану матеріїшу, другі — для твердого		
Додаток 8 м...и.ии. іапактепистнкм основних мдіа пластмас						
Матеріали	Характернетика	Густина кг/м‘	Граииия міцності ов при рот- стискан і згкнвв-генні [	"1	| н|	В	а	°ВР
МПа
Сктоплалії	На основі тканини, ниток орієнтованих у двох вза ємно перпендикулярних нварнмах	1400 1700	1850 260 1900 300		400 і 00 300 130				150 460	18000 24 000	22 000 35000
					500	-	230					
Текстоліти	На основі бавовняних тканин	1300	1400	60	110 130		150	90	160	6000	10000
Деревні	На основі деревини	1200			220 120		155 165		220	12000	34 000
пл аттики Гетинакс	На основі паперу, просоченого фанолформальде гідною смолою	1300	1400	70	100			80	140	10000	18000
ФібрЄ	На основі спецсортів па	1100	1250	55	100	80	140	60	95	7000	
Волокніт	Наповнювачі										
	бавовняні пачоси, азбо-волокно, скловолокно	1350	1°00	ЗО	130 110		130	40	100	5000	8500
Прес по рошкк тер моревктіївш	Наповнювачі деревне, кварцове борош но, слюда На основі полімерів ме-	1400	1900	35	60	150	180	50	80		
Скло орга		1180		71	92			99	153	2900	4100
нічиє	такрнлової кислоти			1°	60			12.	100	150	700
Термоп.іастн	Лінійні полімери			0 4	25*	0.17	. 4.50,7		ь.с	37.	200
Пі’копластн	Неаркоаані			14			20	п	14	470	850
Фторпласт 4	—	П40 1140		35	70	60	80	45	70	1400	2000
Капрон	Литво			60	80	70	80		90	700	1050
	Полікапрол актам			45	50	45	50	70	90		
Поліамід 68	—		1400	40	60	80	І6С		90	3000	4000
Вініпласт	— Поліетилен НД	—		1380	1400	25	35	28	40		зо	550	880
Полістирол блоковий	—	1050	1070		35		100	95	юс	1200	3200
3500 4000 0,22.. 0,25
_	0 25-0.28
2500	0.25 0.30
800 2600 0.25-0,30
800 2500 0,20.. 0,30
_	0,20 0.30
_	0,25-	0,30
_	0,3	0,4
_	0.1	0,16
_	0.15..	0,2
15. 19	-
4X1. 480
Додаток 9
МакулІ пружності і коефіцієнти Пуаесоя* для деяких матеріалі»
Матеріал	Модуль пружності МПі		Коефіцієнт Пуассоае м
	£	0	
Чавун білий, сірий	(1,15 1,60)10»	4,5 10»	0,23 0,27
» КОВКИЙ	1,55 10»			——
Сталь вуглецева	(2 0 2 1) 10»	(8,0 8,1) 10»	0,24 0 28
і легована	(2,1 2 2) 10»	(8,0 8,1) 10»	0 25 0,30
Мідь прокатана	І 1 10»	4,0 10»	0,31 0,34
> холоднотягвуте	1 3 10»	4,9 10»	—
• лита	0 84 104	—-	
Бронза фосфориста катана	1,15 10»	4,2 10»	0,32 0,35
Бронза маргзацееиста катана	1.1 10»	4,0 10»	035
Бронва алюмінієва лнта	1,05 10»	4,2 10»	
Латунь холодиотягиута	(0,91 .0,99) 10»	(3,5 3 7) 10»	0,32 ..0,42
Латунь корабельна катана	1,0 |0»	—	036
Алюміній катаний	0,69 104	(2 6 2 7)10»	0.32 0,36
Дріт алюмінієвий тягнутий	0,7 104	—	—
Дуралюміи катаний	0,71 |0»	2,7 10»	
Цинк катаний	0,84 10»	3,2 10»	0,27
Свинець	0,17 10»	0 70 10»	0,42
Лід	0,1 ЇМ	(0,28 0,3) 10»	
Скло	0,56 10»	2,2 10»	0,25
Граніт	0,49 10»	—-	
Вапняк	0,42 10»	_—	
Мармур	0,56 10»		
Пісковик	0,18 10»		
Каи яна кладка з граніту	(0 09 0,1) 10»	—	—
Кам яка кладка з вапняку	0 06 10»		
Кам'яна кладка а цегли	(0,027 0,030) 10»	—	
Бетон прн границі міадлсті,			
МПа,			
10	(0,146 0,196)10!		0,16 0,18
15	(0,184 0,214) 10»		0 16 0,18
20	(0,182 0,232) ЇМ		0,16 0,18
деревина вздовж волокон	(0,1 0,12) ЇМ	0,055 10»	
» поперек волокон	(0,005 ..0,01) 10»	—	*
Каучук	0,00008 10»		0,47
Текстоліт	(0,06 0,1) ЇМ	—	
Гетинакс	(0,1 0,17) ІМ	—	—.
Бекеліт	(2 3)10»		0,36
ВІсхомлІт (ИМ 44)	(40 42) 10*	—	0,37
Целулоїд	(14,3.27,5) 104	—	0,33 0,38
Додаток 10 Орієнтовні значення основних аоаустнмях напружень на розтягання 1 стискання		
Матеріал	Допустяни вапружешп МПа ві	
	розтягали	|	спкиакя
Чавун сірнА у відливках	25 .60	120 150
Сталь Ст2		140
. СтЗ		160
» СтЗ у мостах		140
Сталь машинобудівна (конструкційна)		
вуглецева		60 250
Те саме легована	і 00	400 і вище
Мідь		ЗО 120
Латунь		70 140
Бронза		60 120
Алюміній		30 60
Бронза алюмінієва		60 120
Дуралюмін		60 150
Текстоліт		ЗО 40
Гетинакс		50 70
Фанера бахелізозава		40 60
Сосна вздовж волокон	7 10	10 12
в поперек волокон	—	1,5 2
Дуб уздовж волокон	9 ІЗ	13 15
» поперек волокон	—	2 3.5
Кам'яна кладвв	до 0,3	0,5 4
Цегляна кладка	до 0.2	0,6 2,5
Бетон	0 1 0,7	1,0 9
Додаток 11 Допустимі вапруження на зріз для ваклеекомх і зварних	з’єднань
Тип  «двивя	1 Напруженая на арі», МПа
Заклепкове основні елементи із сталі 20 ваклепка в розсвердлених отяорах (клас В) ваклепка в продавлених отворах (клас С) Зварне зварювання ручне електроди з тонкою обмазкою те саме електроди з товстою обмазкою зварювання автоматичне	100 140 100 60 110 110
653
Податок /2
Значення функцій Т]( і],
0 0 1	і 0000 0 9907	1 оооо 08100	—1 0000 -0 9003	0,8 09	0 6354 0 5712	-0,0093 —0 0657	-0 3131 0 2527
0 2	0 9651	0,6398	—0 8024	і 0	0 5083	-0 1108	0 1988
п,з	0 9267	0 4888	-0 7077	1 1	0 4476	—0 1457	—0 1510
04	0 8784	0 3564	-0 6174	1.2	0 3899	—0 1716	-0 1091
05	0 8231	0 2115	-0 5323	1 3	0 3355	-0 1897	-0 0729
06	0 7628	0 143)	-0 4530	1 4	0 2849	—0 201!	-0 0419
0 7	0 6997	0 0599	-0 3708	1 5	0 2384	-0 2068	-0 0158
1/4.1	0,6448	ООООО	-0 3224	1.2	0 2079	-0 2079	ооооо
1 6	Ц 1959	-0 21)77	0 0059	4 4	-0 01546	0 СМ791	0,00377
1 7	0 1576	—1» 2047	0 0235	45	—0 01320	0 00852	0 00234
1,8	0 1234	—0 (985	0 0370	46	-0,41112	0 00886	0 00113
1.9	0 0932	-0 1890	00434	4,7	—0 'Ю921	0 00898	0 00011
2 0	0 0667	-0 1794	О.ОобЗ	6/4л	—0 00893	0,00898	0 00000
2 1	0,0439	—0 1675	0О6|8	4 8	—0,00748	0 00892	-0,00072
2 2	0 0244	-0 1548	0 0652	4 9	-3 00593	0,00870	-0,00139
2,3	0 0080	-0 1416	00668	50	-0 00455	0 00837	—0 00191
3/4л	ооооо	-0 1340	0,0670	5 1	—0 00334	0 00795	-0,00230
24	—0 0056	—0 1282	0 0669	52	—0 00229	0,00746	—0 002з9
25	—0 0166	-0 1)49	0 0658	53	—ОИОІ39	0 00692	—0.00277
26	—0 1)254	-0 10)9	00636	5.4	—0 00-753	0,00636	-0 00287
2 7	—0 0320	-0 0895	0 0608	7/4л	—о ооооо	0 00579	-0 00290
28	—0 П369	—0 0777	0 0573	55	0,00001	0 00578	-0 00290
2 9	-о ічоз	- О 0666	0 0534	56	0 00053	0,00520	-0 00287
ЗО	—0 04226	—0 С5632	0 04929	57	0,00095	0,00464	-0 00279
з,і	-0 С43Н	—0 04688	0 0450]	58	0,00127	0 00409	-0,00268
і	—0 04121	—0 04321	0,04321	59	0,00152	0 00356	—0 00254
3 2	—0 04307	-0 03831	0,04069	6,0	0 00169	0 00307	-0 00238
33	—0 04224	—0 03060	0 03642	6 1	0 00180	0,00261	-0,00221
34	—0 04079	-0 02374	0,03227	6.2	0 00185	0 00219	-0 00202
35	—0,03887	-0 0)769	0 02828	8/4л	000187	0 00187	-0,00187
3 6	—01'3659	-0 01241	0 02450	63	0 00187	0 00181	-0 00194
3 7	—1' 03407	-0 00787	0,02097	6,4	0,00184	0 00146	-0 00165
38	—0 03138	—0 00401	ООІ77О	65	0 00179	0,00Н 5	—0,00)47
3,9	-0 02882	—0,00077	0,01469	66	0 00)72	0,00087	—0,00129
5/4л	-0 02786	0,0000	0,01393	6.7	0,00162	0,00063	-0,00113
4 0	—0 02583	0 00189	001197	6.8	0 00)52	0,00042	—0,00097
4 1	—0 02309	0 00403	0 00953	6.9	0 00141	0 00024	-0,00082
4 2	—01'2042	0 00672	0,01'735	7,0	000129	0,00009	—0,00069
4 3	—0 01787	0 00699	0 (0544	9/41	0,00120	000000	-0,00060
СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ
1	Бир&р И А , Мавлютов Р Р Сопротнвленне матерналов — М Наука 1986 — с
2	Опір матеріалів і Г С Писаренко. П М Варвак А М. Васкленко С. Е Гарф В В Хііьчевський За ред Г С Писаренка — К Вища шк Головне вндво 1974 - 304 с
З Писаренко Г С . Мокаржкий Н С Уравнеиия в краевне аадачи творим піас тичности н ползучестн — К Наук думка 1981 — 496 с
4	Посацький С Л Опір матеріалів Львів Вид во Львів унту 1973 — 404 с
Б Прочность катерна, оа н ваемеитов коїіструкций в акстрематміик условмях ВЗт'Подред Г С Писаренко—К Наук думка 1960 —Т 1—2
б ФеаЬсьее В И Сопротивленне магериа-юв — М Наука 1986 —512 с
7	Прочность. устой інвость. колебання Справ.. В 3 т./ІІод ред И А Бнргера Я Г Наковко—М Машнностроенне 1968 —Т І — 831 с