Text
А.Н. Матвеев
Электричество
и магнетизм
Допущено
Министерством высшего и среднего
специального образования СССР
в качестве учебного пособия
для физических специальностей вузов
Москва
«Высшая школа»
1983
ББК 22.23
МЗЗ
УДК 537+538@75)
Рецензенты:
первая кафедра общей физики Ленинград-
Ленинградского государственного университета им.
А. А. Жданова (зав. кафедрой проф. Н. И. Ка-
литсевскнй); акад. АН УССР А. И. Ахнезер
(Харьковский физико-технический институт)
Матвеев А. Н.
МЗЗ Электричество и магнетизм: Учеб.
пособие.—М.: Высш. школа, 1983.—
463 с, ил.
В пер.: 1 р. 50 к.
Изложение курса начинается с экспериментального
обоснования теории электричества и магнетизма и
базируется на релятивистских представлениях, извест-
известных студентам из предшествующих разделов курса
общей физики Связь между электрическими и магнит-
магнитными полями выявляется на самой ранней стадии
изложения. Наряду с традиционными достаточно под-
подробно изложены новые вопросы курса' флуктуации
тока в Цепях, аномальный скин-эффект, волноводы
и резонаторы и др.
Книга представляет собой третий том курса общей
физики для университетов и вузов. Первый том «Меха-
«Механика и теория относительности» вышел в 1976 г.,
второй том «Молекулярная физика» — в 1981 г.
Для студентов физических факультетов вузов.
-.1704040000-285.,-. __„„,,
М 42-83 ББК 22.33
001@1)-83 537
Издательство «Высшая школа», 1983
Оглавление
l
Заряды,
поля,
силы
Предисловие 11
Введение 13
§ 1. Микроскопические носители электрических
зарядов 16
Классификация. Электрон. Протон. Нейтрон. Что
означает непрерывное распределение электрического
элементарного заряда? Спин и магнитный момент
§ 2. Заряженные тела. Электризации 20
Термоэлектронная работа выхода. Энергетический
спектр электронов. Энергия Фермн. Контактная
разность потенциалов. Электризация
§ 3, Элементарный заряд и его инвариантность 28
Опыты Милликена. Резонансный метод измерения
заряда. Отсутствие дробного заряда. Равенство
положительных и отрицательных элементарных за-
зарядов. Инвариантность заряда
§ 4. Электрический ток 32
Движение зарядов. Непрерывное распределение за-
зарядов. Объемная плотность зарядов. Концентрация
зарядов. Поверхностная плотность зарядов. Плот-
Плотность тока. Сила тока через поверхность
5. Закон сохранения зарида 37
|ва аспекта понятия сохранения заряда. Интеграль-
Интегральная формулировка закона сохранения заряда. Дивер-
Дивергенция. Формула Гаусса —Остроградского. Диффе-
Дифференциальная формулировка закона сохранения заряда
§ 6. Закон Кулона 44
Экспериментальные проверки закона Кулона. Метод
Кавендиша. Проверка закона для больших рас-
расстояний. Проверка закона для малых расстоя-
расстояний. Полевая трактовка закона Кулона. Электри-
Электрическое поле. О границах применимости классической
концепции поля
§ 7. Принцип суперпозиции 52
Принцип суперпозиции для взаимодействия то-
точечных зарядов. Полевая формулировка принципа
суперпозиции. Пробные заряды. Границы примени-
применимости принципа суперпозиции
§ 8. Магнитное поле 55
Необходимость возникновения магнитного поля при
движении зарядов. Взаимодействие точечного заряда
и бесконечной прямой заряженной нити. Реляти-
Релятивистская природа магнитного поля. Силы взаимо-
взаимодействия параллельных проводников с током. Еди-
Единица силы тока. Магнитное поле
§ 9. Сила Лоренца. Сила Ампера ?]
Преобразование сил. Сила Лоренца. Индукция маг-
магнитного поля. Сила Ампера. Переход от объемных
токов к линейным. Магнитное поле прямолинейного
тока
§ 10. Закон Био-Савара ?б
Взаимодействие элементов тока Об эксперименталь-
экспериментальной проверке закона взаимодействия. Полевая трак-
трактовка взаимодействия. Закон Био —Савара. Сила
взаимодействия прямолинейных токов
Оглавление
Постоянное
электрическое
поле
§ 11. Преобразование полей 72
Инвариантность выражения для силы в электро-
электромагнитном поле. Преобразование полей. Применения
формул A1.15). Поле точечного заряда, движуще-
движущегося равномерно и прямолинейно
Задачи 77
§ 12. Постоянное электрическое поле 80
Неподвижный заряд. Существо модели. Границы
применимости модели
§ 13. Дифференциальная формулировка закона Кулона 81
Теорема Гаусса. Измерение заряда. Физическая
основа справедливости теоремы Гаусса. Дифферен-
Дифференциальная формулировка закона Кулона. Уравнение
Максвелла для div E. Силовые линии. Источники
и стоки вектора Е. Инвариантность заряда
§ 14. Потенциальность электростатического поля 86
Работа в электрическом поле. Потенциальность
кулоновского поля. Ротор вектора. Формула Стокса.
Дифференциальная формулировка потенциальности
поля. Градиент. Скалярный потенциал. Неодно-
Неоднозначность скалярного потенциала. Нормировка. Вы-
Выражение работы через потенциал. Потенциал поля
точечного заряда. Потенциал поля системы точечных
зарядов. Потенциал поля непрерывного распределе-
распределения зарядов. Потенциал поля поверхностных за-
зарядов. Бесконечность потенциала поля точечного за-
заряда Конечность потенциала при непрерывном рас-
распределении заряда с конечной плотностью. Непре-
Непрерывность потенциала Теорема Ирншоу
§ 15. Электростатическое поле в вакууме 98
Постановка вопроса Прямое использование закона
Кулона. Вычисление потенциала. Использование
теоремы Гаусса. Уравнения Лапласа и Пуассона
Бесконечный равномерно заряженный круглый чи-
линдр
§ 16. Электростатическое поле при наличии
проводников 104
Дифференциальная форма закона Ома. Классифи-
Классификация материалов по проводимости. Отсутствие
электрического поля внутри проводника. Отсутст-
Отсутствие в проводнике объемных зарядов. Электриче-
Электрическая индукция. Поле вблизи поверхности провод-
проводника. Механизм образования поля вблизи поверх-
поверхности проводника. Зависимость поверхностной плот-
плотности зарядов от кривизны поверхности. Стекание
заряда с острия. Электроскопы и электрометры.
Металлический экран. Потенциал проводника Ем-
Емкость уединенного проводника Система проводни-
проводников. Конденсаторы. Проводящий шар в однород-
однородном поле. Поле диполя. Метод изображений
§ 17. Электростатическое поле при наличии
диэлектриков 134
Дипольный момент непрерывного распределення за-
зарядов. Поляризация диэлектриков. Молекулярная
картина поляризации. Зависимость поляризованиости
от напряженности электрического поля. Влияние
поляризации на электрическое поле Объемная и
поверхностная плотное!и связанных зарядов. Элек-
Оглавление
трическое смещение. Электростатическая теорема
Гаусса при наличии диэлектриков. Граничные усло-
условия. Граничные условия для нормальной состав-
составляющей вектора D. Граничные условия для
тангенциальной составляющей вектора Е. Преломле-
Преломление силовых линий на границе раздела диэлектри-
диэлектриков. Знаки связанных зарядов на границе раздела
диэлектриков. Метод изображений. Диэлектрический
шар в однородном поле
§ 18. Энергия электростатического поля 152
Энергия взаимодействия дискретных зарядов. Энер-
Энергия взаимодействия прн непрерывном распреде-
распределении зарядов. Собственная энергия. Плотность
энергии поля. Энергия поля поверхностных зарядов.
Энергия заряженных проводников. Энергия диполя
во внешнем поле. Энергия диэлектрического тела
во внешнем поле
§ 19. Силы в электрическом поле 161
Природа сил. Сила, действующая на точечный
заряд. Сила, действующая на непрерывно распре-
распределенный заряд. Сила, действующая на диполь.
Момент сил, действующих на диполь. Объемные
силы, действующие на диэлектрик. Силы, дейст-
действующие на проводник. Поверхностные силы, дейст-
действующие на дизлекгрик. Объемные силы, действую-
действующие на сжимаемый диэлектрик. Вычисление сил из
выражения для энергии
Задачи 174
Диэлектрики
Постоянный
электрический
ток
§ 20. Локальное поле 178
Отличие локального поля от внешнего. Вычисление
напряженности локального поля
§ 21. Неполярные диэлектрики 180
Молекулярная диэлектрическая восприимчивость.
Разреженные газы. Плотные газы
§ 22. Полярные диэлектрики 183
Зависимость поляризованности от температуры. По-
Поле насыщения. Разреженные газы Квантовая ин-
интерпретация поляризованности полярных газообраз-
газообразных диэлектриков. Плотные газы. Полярные жидкос-
жидкости. Ионные кристаллы
§ 23. Сегиетоэлектрики 189
Определение. Петля гистерезиса. Точка Кюрн. Мо-
31екулярный механизм спонтанной поляризованности.
Диэлектрические домены. Антисегнетоэлектрики
§ 24. Пьсзоэлектрики 193
Свойства пьезоэлектриков. Продольный н попереч-
поперечный пьезоэффекты. Механизм пьезоэффекта. Обрат-
Обратный пьезоэффект. Отличие обратного пьезоэффекта
от элек1 рестрикции. Пироэлектрики
Задачи 196
§ 25. Электрическое пою прн наличии постоянных
токов 198
По ie внутри проводника. Вопрос об источниках
поля. Поле вне проводника. Поверхностные заряды.
Объемные заряды. Механизм осуществления посто-
постоянною тока. Изменение потенциала вдоль провод-
проводника с током
Оглавление
§ 26. Сторонние э. д. с. 202
Сущность сторонних э. д с. Механическая сторонняя
э. д. с. Гальванические элементы. Элемент Вольта.
Область действия сторонних э. д. с. Закон сохранения
энергии. Поляризация элемента. Способы деполяри-
деполяризации. Аккумуляторы
§ 27. Дифференциальная форма закона
Джоули-Ленца. Работа, совершаемая при прохождении
тока, н развиваеман мощность 209
Работа, совершаемая при прохождении тока. Мощ-
Мощность. Дифференциальная форма закона Джоуля —
Ленца. Источник энергии для работы электриче-
электрического тока Вывод закона Ома исходя из элек-
электронной картины электропроводности. Вывод за-
закона Джоуля — Ленца исходя из электронной теории
электропроводности. Недостатки классической тео-
теории электропроводности. Основные черты квантовой
трактовки электропроводности
§ 28. Линейные цепи. Правила Кирхгофа 213
Изолированная замкнутая цепь. Разветвленные це-
цепи. Правила Кирхгофа
§ 29. Токи в сплошной среде 217
Постановка задачи Вывод формулы. Условия при-
применимости B9.6). Коаксиальные электроды. Неодно-
Неоднородная среда
§ 30. Заземление линий передач 220
Постановка задачи. Расчет сопротивления. Экспери-
Экспериментальная проверка. Напряжение шага
Задачи 223
§ 31. Электропроводность металлов 226
Д
Ч n№TnnimnRnmini<TL Доказательство отсутствия переноса рещества элек-
ОЛеК1р0Пр0В0ДН01ГЬ О Т
у р
^ током в метаЛлах. Опыты Толмена и
Стюарта. О зонной теории. Зависимость сопротив-
сопротивления от температуры. Эффект Холла. Магнето-
сопротнвление. Подвижность электронов. Сверх-
Сверхпроводимость. Критическая температура. Критиче-
Критическое поле. Эффект Мейсснера. Поверхностный ток.
Сверхпроводники первого и второго рода. Объяс-
Объяснение сверхпроводимости
§ 32. Электропроводность жидкостей 234
Диссоциация. Расчет электропроводимости. Зависи-
Зависимость электропроводимости от концентрации. Зави-
Зависимость электропроводимости от температуры. Элек-
Электролиты
§ 33. Электропроводность газов 237
Самостоятельный и несамостоятельный ток. Не-
Несамостоятельный ток. Плотность тока насыщения.
Характеристика тока. Самостоятельный ток. Дей-
Действие пространственного заряда. Подвижность за-
зарядов. Сравнение выводов из C3.18) с экспери-
экспериментом
§ 34. Электрический ток в вакууме 241
Термоэлектронная эмиссия. Характеристики элек-
электронного облака. Плотность тока насыщения. Закон
трех вторых
Задачи 248
Оглавление
Стационарное
магнитное поле
§ 35. Закон полного тока 250
Постановка задачи. Интегральная формулировка
закона полного тока. Дифференциальная форма
закона полного тока. Экспериментальная проверка
закона полного тока. Вывод дифференциальной
формулировки непосредственным дифференцирова-
дифференцированием формулы Био — Савара
§ 36. Уравнения Максвелла для стационарного
магнитного ноля 255
Уравнение для div В. Уравнения Максвелла. Тип
решаемых задач
§ 37. Векторный потенциал
Возможность введения векторного потенциала.- Не-
Неоднозначность векторного потенциала. Калибровка
потенциала. Уравнение для векторного потенциала.
Закон Био-Савара. Поле элементарного тока
§ 38. Магнитное иоле при наличии магнетиков
Определение. Механизмы намагничивания. Намаг-
Намагниченность. Векторный потенциал прн наличии маг-
магнетиков. Объемная плотность молекулярных токов.
Поверхностные молекулярные токи. Однородно на-
намагниченный цилиндр. Напряженность магнитного
поля. Уравнение для напряженности. Зависимость
намагниченности от напряженности. Поле в магне-
магнетике. Постоянные магниты. Граничные условия для
векторов поля. Граничное условие для нормаль-
нормальной составляющей вектора В. Граничное условие
для тангенциальной составляющей вектора Н. Пре-
Преломление магнитных силовых линий. Измерение
индукции магнитного поля. Поля бесконечного со-
соленоида и однородно намагниченного бесконечно
длинного цилиндра. Измерение магнитной проницае-
проницаемости, нндукцни и напряженности поля внутри
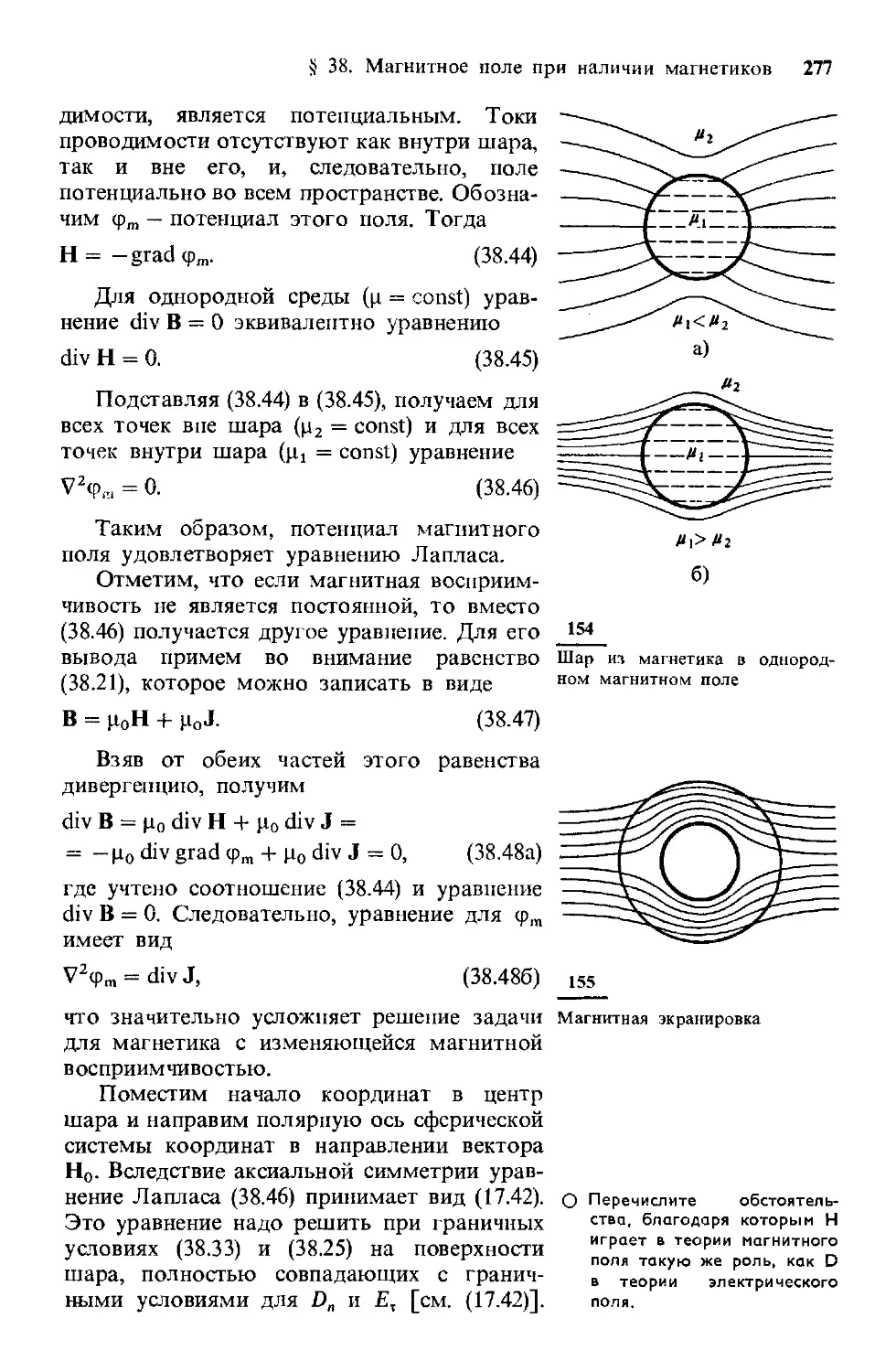
магнетика. Шар из магнетика в однородном поле.
Магнитная экранировка
257
264
Магнетики
§ 39. Силы в магнитном поле 280
Силы, действующие на ток. Сила Лоренца. Силы
и момент сил, действующие на магнитный мо-
момент. Объемные силы, действующие на несжимае-
несжимаемые магнетики
Задачи 284
§ 40. Диамагнетики 288
Ларморова прецессия. Диамагнетизм. Диамагнит-
Диамагнитная восприимчивость. Независимость диамагнитной
восприимчивости от температуры
§ 41. Парамагнетики 292
Механизм намагничивания. Зависимость парамагнит-
парамагнитной восприимчивости от температуры. Магнитные
моменты свободных атомов. Магнитные моменты
молекул. Магнетизм, обусловленный свободными
электронами. Парамагнитный резонанс
§ 42. Ферромагнетики 298
Определение. Кривая намагничивания и петля гис-
гистерезиса. Кривая магнитной проницаемости. Клас-
Классификация ферромагнитных материалов. Взаимо-
Взаимодействие электронов. Элементарная теория фер-
ферромагнетизма. Закон Кюри—Вейсса. Анизотропия
намагничивания. Домены. Границы. Перемагничива-
Оглавление
8
Электромагнитная
индукция
и квазистационарные
переменные
токи
ние. Антиферромагнетизм. Ферримагнетизм. Ферро-
Ферромагнитный резонанс
§ 43. Гиромагнитные эффекты 306
Соотношение между механическими и магнитными
моментами. Опыт Эйнштейна — де Гааз. Эффект
Барнетта
Задачи 310
§ 44. Индукция токов в движущихся проводниках 312
Возникновение э. д. с. в движущемся проводнике.
Обобщение на произвольный случай Генераторы
переменного тока Закон сохранения энергии
§ 45. Закон электромагпитяой индукции Фарадея 316
Определение. Физическая сущность явления. Движу-
Движущийся проводник в переменном магнитном поле.
Применение электромагнитной индукции к генера-
генераторам переменного тока
§ 46. Диффереициальная формулировка закоиа
электромагнитной индукции 318
Формулировка. Непотенцнальность индукционного
электрического поля. Векторный и скалярный по-
потенциалы в переменном электромагнитном поле.
Неоднозначность потенциалов, калибровочное пре-
преобразование
§ 47. Энергия магнитного поля 321
Энергия магнитного поля изолированного контура
с током. Энергия магнитного поля нескольких
контуров с током. Энергия магнитного поля прн
наличии магнетиков Плотность энергии магнит-
магнитного поля. Индуктивность. Поле соленоида. Энер-
Энергия магнетика во внешнем магнитном поле. Вы-
Вычисление енл из выражения для энергии. Объемные
силы, действующие на сжимаемые магнетики. Энер-
Энергия магнитного момента во внешнем поле
§ 48. Цепи квазистациоиариого неремеаиого тока 335
Определение. Самоиндукция. Включение и выклю-
выключение постоянной э. д. с. в цепи с сопротивлением
и индуктивностью. Получение прямоугольных им-
импульсов тока. Емкость в цепи. Включение и вы-
выключение постоянной э. д. с. в цепи с емкостью
н сопротивлением. Цепь с емкостью, индуктив-
индуктивностью, сопротивлением и источником сторонних
э. д. с. Переменный ток. Векторные диаграммы. Пра-
Правила Кирхгофа. Последовательное и параллельное
соединения нмпедансов. Метод контурных токов
§ 49. Работа и мощность переменного тока 346
Мгновенная мощность Средняя мощность. Эффек-
Эффективные значения силы тока и напряжения. Коэф-
Коэффициент мощности. Электродвигатели. Синхронные
двигатели. Асинхронные двигатели. Создание вра-
вращающегося магнитного поля. Согласование на-
нагрузки с генератором. Токи Фуко
§ 50. Резоиаисы в цепи переменного тока 356
Резонанс напряжений. Резонанс токов. Колеба-
Колебательный контур
§ 51. Цепи с учетом взаимной индукции
Роль взаимной индукции. Уравнения для системы
проводников с учетом самоиндукции и взаимоин-
359
Оглавление
дукцин Случай двух контуров. Трансформатор.
Векторная диаграмма холостого хода трансфор-
трансформатора Векторная диаграмма нагруженного транс-
трансформатора. Автотрансформатор. Трансформатор как
элемент цепн. Реальный трансформатор
§ 52. Трехфазный ток
Определение. Получение трехфазного тока. Соеди-
Соединение обмоток генератора звездой. Соединение об-
обмоток генератора треугольником. Соединение нагру-
нагрузок. Получение вращающегося магнитного поля
§ 53. Скии-эффект
Сущность явления. Физическая картина возникно-
возникновения. Элементарная теория. Толщина скин-слоя.
Зависимость омического сопротивления проводника
от частоты. Зависимость индуктивности проводни-
проводника от частоты. Закалка металлов токами высокой
частоты Аномальный скин-эффект
§ 54. Четырехполюсники
Определение. Уравнения. Теорема взаимности. Со-
Сопротивление четырехполюсника. Простейшие че-
четырехполюсники. Входное и выходное сопротив-
сопротивления. Коэффициент передачи
§ 55. Фильтры
Определение. Фильтр низких частот. Фильтр вы-
высоких частот. Цепочка из фильтров. Полосовой
фильтр
§ 56. Бетатрон
Назначение Принцип действия. Бетатронное усло-
условие. Радиальная устойчивость. Вертикальная ус-
устойчивость. Бетатронные колебания. Предел энергий,
достижимых в бетатроне
Задачи
9 § 57. Ток смещения
ЭлектппмагНИТНЫе Сущность процесса. Почему скорость изменения
^icMjmmiu пш вектора смещения называется плотностью тока?
ВОЛНЫ Уравнение Максвелла с током смещения. Реля-
Релятивистская природа тока смещения
§ 58. Система уравнений Максвелла
Система уравнений Максвелла. Физический смысл
уравнений Условия применимости уравнений. Пол-
Полнота и совместность системы уравнений
§ 59. Закон сохранения энергии
электромагнитного поля. Поток энергии
Формулировка. Поток энергии
§ 60. Движение электромагнитной энергии вдоль
линий нередач
Механизм компенсации потерь энергии на джоуле-
ву теплоту Движение энергии вдоль кабеля. Линия
передачи для переменного тока. Уравнения для
силы тока и напряжения. Характеристический им-
импеданс и постоянная распространения. Характерис-
Характеристическое сопротивление Скорость распространения.
Отражение
§ 61. Излучение электромагнитных воли
Уравнение для векторного потенциала. Выбор ка-
калибровочной функции Уравнение для векторного
потенциала Решение волнового уравнения. Запазды-
366
369
373
377
380
383
388
393
396
398
405
10
Оглавление
вающие и опережающие потенциалы Вибратор
Герца. Скалярный потенциал диполя, изменяюще-
изменяющегося со временем Векторный потенциал Электри-
Электрическое и магнитное поля Поле вибратора в вол-
волновой зоне. Мощность, излучаемая вибратором
Излучение рамкн с током. Излучение ускоренно
движущегося электрона Сила торможения излу-
излучением
§ 62. Распространение электромагнитных волн
в диэлектриках 418
Плоские волны. Уравнения для векторов поля
волны. Векторы волны. Фазовая скорость Длина
волны. Свойства волн. Плотность потока энергии
§ 63. Распространение электромагнитных воли
в проводящих средах 422
Комплексная диэлектрическая проницаемость Глу-
Глубина проникновения. Физическая причина погло-
поглощения. Интерпретация скин-эффекта. Фазовая ско-
скорость и длина волны в проводящей среде Соот-
Соотношение между фазами колебаний векторов поля.
Соотношение между амплитудами векторов поля
§ 64. Инвариантность плоской волны 426
Преобразование полей Иварианты преобразований
электромагнитного поля. Анализ инвариантов поля
§ 65. Давление электромагнитных волн. Импульс
фотона 428
Механизм возникновения давления. Давление. Им-
Импульс цуга электромагнитных волн Объемная плот-
плотность импульса электромагнитных волн. Импульс
фотона
§ 66. Волноводы и резонаторы 431
Участок цепи. Участок проводника. Катушка ин-
индуктивности. Конденсатор. Излучение. Волноводы.
Прямоугольный волновод Граничная частота. Фа-
Фазовая скорость. Длина волны в волноводе. При-
Применение метода изображений к анализу волново-
волноводов. Дискретность направлений распространения
плоских волн от системы излучателей. Граничная
длина волны. Длина волны и фазовая скорость
в волноводе. Групповая скорость. Соотношение
между групповой и фазовой скоростями. Магнитное
поле Классификация волн в волноводах. Резо-
Резонаторы
Задачи
10 § 67. Флуктуации в контуре с током. Шум
Флуктуации И шумы сопротивления
Теорема о равнораспределении энергии по степеням
свободы. Применение теоремы о равнораспределе-
равнораспределении энергии к свободному гальванометру. Флук-
Флуктуации в колебательном контуре. Распределение
флуктуации по частотам. Шум сопротивления. Экви-
Эквивалентный генератор шума. Мощность шума гене-
генератора. Максимальная чувствительность. Эквива-
Эквивалентная шумовая температура приемника. Коэффи-
Коэффициент шума приемника. Отношение сигнал — шум
§ 68. Дробовой шум и шум тока 451
Источник дробового шума. Распределение шума
по частотам. Шум тока. Методы уменьшения
шумовых помех
Задачи 455
Приложение 455
Предметный указатель 460
441
444
Предисловие
Данный курс отражает современный уровень науки и образования
и учитывает изменения в программе общей физики.
Поскольку основные положения теории относительности известны
из курса механики, можно при изложении электричества и магнетизма
с самого начала опираться на релятивистскую природу магнитного
поля и представить электрическое и магнитное поля в их взаимной
связи и единстве. Поэтому изложение материала в данной книге начи-
начинается не с электростатики, а с анализа основных понятий, связанных
с зарядами, силами и электромагнитным полем. При этом определен-
определенный запас сведений о законах электромагнитных явлений, имеющийся
у студента из курса физики средней школы, преобразуется в совре-
современное научное знание, а обоснование теории анализируется в свете
современного состояния экспериментальных основ электромагнетизма
с учетом пределов применимости используемых понятий. Это приводит
иногда к необходимости выхода за пределы теории электромагнетизма
в строгом смысле этого слова. Например, вопрос об эксперименталь-
экспериментальном обосновании закона Кулона для больших расстояний не может
быть изложен без упоминания о его связи с нулевой массой покоя
фотонов. И хотя полностью и строго этот вопрос излагается в кван-
квантовой электродинамике, его основные общие черты целесообразно
изложить в классической теории электромагнетизма. Это создает
у студента общее представление о проблеме и о связи изучаемого
материала с материалом будущих курсов. Последнее обстоятельство
имеет немаловажное методическое значите.
Основной задачей курса является изложение экспериментального
обоснования теории электромагнетизма и формулировка теории в ло-
локальной форме, т. е. в виде соотношений между величинами в одной
и той же пространственно-временной точке. В большинстве случаев
они имеют дифференциальную форму, но существенна не их диффе-
дифференциальная форма, а их локальный характер. Поэтому конечным
продуктом курса являются уравнения Максвелла как результат обобще-
обобщения и математической формулировки установленных в эксперименте
закономерностей. Следовательно, главный метод изложения индуктив-
индуктивный. Однако это не исключает, а предполагает его сочетание с дедук-
дедуктивным методом изложения в соответствии с принципами научного
познания физических закономерностей. Поэтому уравнения Максвелла
выступают в книге не только как результат математической форму-
формулировки установленных в эксперименте закономерностей, но и как
инструмент исследования этих закономерностей.
Выбор экспериментальных фактов, которые могут быть взяты
в экспериментальное обоснование теории, неоднозначен. В книге изло-
изложено обоснование теории электромагнетизма без теории относитель-
относительности и с теорией относительности. Последнее обоснование более
предпочтительно, поскольку в нем теория относительности выступает
12 Предисловие
как общая теория пространства-времени, на которой должны базиро-
базироваться любые физические теории. Такое обоснование стало возможным
в рамках новой программы общей физики.
Существенной частью теории является вопрос о границах ее при-
применимости и области применимости используемых в теории понятий
и моделей. Эти излагаемые в книге вопросы имеют принципиальное
значение. В частности, анализ силового взаимодействия зарядов уже
в рамках классической теории, без какого-либо привлечения квантовых
представлений, показывает, что классическая теория электричества и
магнетизма не может быть применена к анализу взаимодействия от-
отдельных заряженных частиц.
Автор благодарит своих коллег по Московскому университету
и другим университетам и вузам за плодотворное обсуждение вопросов
курса. Автор благодарен акад АН УССР А. И. Ахиезеру и проф.
Н. И. Калитеевскому с сотрудниками возглавляемой им кафедры за
внимательное рецензирование рукописи и ценные замечания.
А. Матвеев
Введение
В настоящее время в физике известны четыре вида взаимодействий
материальных объектов: гравитационное, сильное, слабое и электро-
электромагнитное Эти взаимодействия проявляются в различных простран-
пространственных масштабах и характеризуются своей интенсивностью.
Гравитационное взаимодействие заметно лишь между телами астро-
астрономических масштабов. Сильные взаимодействия проявляются лишь
между определенными частицами при их сближении на весьма малые
расстояния A05 м). Слабое взаимодействие осуществляется при
взаимопревращении определенных сортов частиц. При удалении частиц
друг от друга оно несущественно. И лишь электромагнитные взаимо-
взаимодействия проявляются в тех пространственных масштабах, в которых
осуществлена наша повседневная жизнь Практически все «силы»,
обусловливающие физические явления в нашем повседневном окруже-
окружении, за исключением силы тяготения, являются в конечном счете
электромагнитными. Конечно, все многообразные связи и явления,
обусловленные электромагнитными взаимодействиями, не могут быть
описаны законами электродинамики, поскольку на каждом уровне
явления существуют свои специфические черты и закономерности, не
сводимые к закономерностям другого уровня. Однако электромагнит-
электромагнитные взаимодействия на всех уровнях являются в определенном смысле
элементарной связью, с помощью которой образуется вся цепь связей.
Этим определяется практическое значение электромагнитных явлений.
Чрезвычайно велико значение теории электромагнитных явлений.
Эта теория является первой релятивистски инвариантной теорией. Она
сыграла решающую роль в возникновении и обосновании теории
относительности и явилась тем «полигоном», на котором проходили
проверку многие новые идеи. Квантовая электродинамика является
лучше всего разработанной квантовой теорией, предсказания которой
согласуются с экспериментом поразительно хорошо, хотя в настоящее
время она еще и не является внутренне непротиворечивой и завер-
завершенной Очень существенно общефилософское и мировоззренческое
значение электромагнетизма Например, в рамках электромагнитных
явлений отчетливо проявляются особенности полевой теории сущест-
существования материи, хорошо прослеживается взаимопревращение ее раз-
различных форм и взаимопревращение различных форм энергии
В книге излагаются два пути обоснования теории. При обоснова-
обосновании без теории относительности в качестве экспериментальных основ
теории электричества и магнетизма взяты инвариантность элементар-
элементарного заряда, закон Кулона, принцип суперпозиции для электрического
поля, закон Био — Савара, принцип суперпозиции для магнитного поля,
сила Лоренца, закон электромагнитной индукции Фарадея, токи сме-
смещения Максвелла, закон сохранения заряда и закон сохранения энергии.
При обосновании с теорией относительности закон Био —Савара,
14 Введение
принцип суперпозиции для магнитного поля и сила Лоренца перестают
играть роль независимых экспериментальных фактов в формулировке
теории. Второй путь обоснования теории электричества и магнетизма
изложен не в виде основного магистрального пути, а в виде побочного
пути, выбранного с расчетом максимального упрощения математи-
математической стороны дела. Он включает в себя следующие этапы.
Релятивистская природа магнитного поля демонстрируется в § 8.
Там выводится формула взаимодействия прямолинейных токов, теку-
текущих по параллельным бесконечно длинным проводникам, и получается
сила Лоренца исходя из электрического взаимодействия зарядов. Поле-
Полевая интерпретация этих результатов позволяет найти индукцию маг-
магнитного поля тока, текущего по прямолинейному бесконечно длинному
проводнику. Принцип суперпозиции для магнитного поля является
теперь следствием принципа суперпозиции для электрического поля.
Переход к индукции магнитного поля произвольных токов и вывод
соответствующих уравнений производится в § 35, где существенно
используется независимость локальных соотношений от значений фи-
физических величин в других точках. Затем в § 37 теоретически выво-
выводится закон Био — Савара и тем самым завершается анализ связи,
которая существует в рамках релятивистских представлений о простран-
пространстве и времени между инвариантностью элементарного электрического
заряда, законом Кулона, принципом суперпозиции для электрического
поля и законом Био — Савара, силой Лоренца и принципом супер-
суперпозиции для магнитного поля.
§ 1
Микроскопические носители
электрических зарядов
1
§2
Заряженные тела
Электризация
§3
Элементарный заряд
и его инвариантность
§4
Электрический ток
§5
Закон сохранения заряда
§6
Закон Кулона
Заряды,
поля,
силы
Принцип суперпозиции
Магнитное поле
Сила Лореица. Сила Ампера
Закон Био—Савара
Заряд — источник и объект действия
электромагнитного поля.
Поле — материальный носитель элект-
электромагнитных взаимодействий зарядов,
форма существования материи.
Сила — количественная мера интенсив-
интенсивности взаимодействия зарядов.
Заряды, поля и силы существуют
в неразрывной связи с пространст-
пространством, временем и движением материи.
Их взаимоотношение не может быть
понято без учета связи с пространст-
пространством, временем и движением.
Преобразование полей
16 1. Заряды, поля, силы
§ 1. Микроскопические носители
электрических зарядов
Описываются свойства основных микроско-
микроскопических носителей электрических зарядов.
Обсуждается распределение электрического
заряда в протоне и нейтроне и анализиру-
анализируется его физический смысл.
классификация. Под микроскопическими носителями зарядов пони-
понимаются заряженные частицы и ионы. Они могут нести как поло-
положительный, так и отрицательный заряд. По числовому значению он
может быть лишь в целое число раз больше элементарного:
| е\ = 1,6021892D6)-109 Кл. A.1)
К настоящему времени не обнаружено микроскопических носителей
с дробным зарядом, несмотря на значительные экспериментальные
усилия (см. § 3).
Известно около 200 частиц и громадное число ионов, атомов и
молекул. Большая часть частиц после возникновения существует не-
непродолжительное время, по истечении которого распадается на другие
частицы, т. е. частицы имеют конечное время жизни. В большинстве
случаев оно чрезвычайно мало и составляет ничтожные доли секунды.
Существует лишь небольшое число заряженных частиц с бесконечным
временем жизни. Это электрон, протон и их античастицы. В состав
ядер атомов входят протоны, а в состав электронной оболочки ато-
атомов — электроны. Именно эти частицы обусловливают почти все явле-
явления, изучаемые в курсе электричества и магнетизма. В состав ядер
кроме протонов входят также нейтроны. Они электрически нейтральны
и их время жизни в составе ядер неограниченно. Однако вне ядер они
живут в среднем около 17 мин, распадаясь на протоны, электроны
и антинейтрино.
Заряженность ионов обусловливается тем, что в электронной обо-
оболочке соответствующего атома или молекулы недостает одного или
нескольких электронов (положительные ионы) или, наоборот, имеются
лишние (отрицательные ионы). Поэтому вопрос об ионах как микро-
микроскопических носителях зарядов сводится к вопросу о зарядах электронов
и протонов,
^лектрон. Электрон является материальным носителем элементарного
отрицательного заряда. Обычно принимается, что электрон явля-
является точечной бесструктурной частицей, т. е. весь электрический
заряд электрона сосредоточен в точке. Такое представление внутренне
противоречиво, так как энергия электрического поля, создаваемого
точечным зарядом, бесконечна, а следовательно, должна быть беско-
бесконечной и инертная масса точечного заряда, что противоречит' экспери-
эксперименту, поскольку масса электрона равна т„ = 9,1 • 10~31 кг. Однако
§ 1. Микроскопические носители электрических зарядов 17
с этим противоречием приходится мириться вследствие отсутствия
более удовлетворительного и менее противоречивого взгляда на струк-
структуру (или отсутствие структуры) электрона. Трудность бесконечной
собственной массы успешно преодолевается при вычислениях различных
эффектов с помощью перенормировки массы, сущность которой заклю-
заключается в следующем. Пусть требуется рассчитать некоторый эффект,
причем в расчет входит бесконечная собственная масса. Получаемая
в результате такого вычисления величина бесконечна и, следовательно,
лишена непосредственного физического смысла. Чтобы получить физи-
физически разумный результат, проводится еще одно вычисление, в котором
присутствуют все факторы, за исключением факторов рассматриваемого
явления. В последний расчет также входит бесконечная собственная
масса и он приводит к бесконечному результату. Вычитание из пер-
первого бесконечного результата второго приводит к взаимному сокра-
сокращению бесконечных величин, связанных с собственной массой, а остав-
оставшаяся величина является конечной. Она характеризует рассматриваемое
явление. Таким способом удается избавиться от бесконечной собствен-
собственной массы и получить физически разумные результаты, которые
подтверждаются экспериментом. Такой прием используется, например,
при вычислении энергии электрического поля (см. § 18).
PJ. Носителем положительного элементарного заряда является
протон. В отличие от электрона, он не рассматривается как точеч-
точечная частица. Экспериментально хорошо изучено распределение электри-
электрического заряда внутри протона. Метод изучения аналогичен исполь-
использованному в начале текущего столетия Резерфордом для исследования
структуры атомов, в результате которого было открыто существование
ядра. Анализируется столкновение электронов с протоном. Если пред-
представить себе протон в виде сферически симметричного распределения
заряда в конечном объеме, то траектория электрона, не проходящего
через этот объем, не зависит от закона распределения заряда. Она
точно такая же, как если бы весь заряд протона был сосредоточен
в его центре. Траектории электронов, проходящих через объем протона,
зависят от конкретного вида распределения заряда в нем. Эти траек-
траектории могут быть вычислены. Поэтому, проведя достаточное число
наблюдений за результатами столкновений электронов с протонами,
можно сделать заключение о распределении заряда внутри протона.
Поскольку речь идет об очень малых областях пространства, для
экспериментов пришлось воспользоваться электронами очень боль-
больших энергий. Такая необходимость диктуется квантовой теорией.
По соотношениям де Бройля материальные частицы обладают
волновыми свойствами, причем длина волны частицы обратно про-
пропорциональна импульсу. Чтобы «прощупать» некоторую простран-
пространственную деталь, необходимо, очевидно, пользоваться частицами,
длина волны которых меньше соответствующих пространственных
размеров детали, а это соответствует достаточно большим импуль-
импульсам. Поэтому исследование электромагнитной структуры протона
18
1. Заряды, поля, силы
М(Г15М
б)
1
Электромагнитная структура
протона. Почти весь заряд про-
протона сосредоточен внутри шара
радиусом г0
Электрон рассматривает-
рассматривается как точечная частица,
хотя это и приводит к
трудностям. Эксперимен-
Экспериментально обнаружить внут-
внутреннюю электромагнит-
электромагнитную структуру электрона
пока не удалось.
Непрерывное распределе-
распределение элементарного элект-
электрического заряда не свя-
связано с его разбиением на
части, а означает учет за-
закона движения этого за-
заряда в пространстве.
стало возможным лишь после создания
электронных ускорителей на энергии в не-
несколько миллиардов электрон-вольт. На
рис. 1, а приведен результат этих экспери-
экспериментов. По оси ординат отложена не плот-
плотность р заряда на расстоянии г от центра
протона, а величина 4лг2р, представляющая
плотность суммарного по всем направлени-
направлениям заряда на расстоянии г от центра,
поскольку 4лг2 р (г) dr — полный заряд в сфе-
сферическом слое толщиной dr. Из рисунка
видно, что практически весь заряд протона
сосредоточен в шаре радиусом «10~15 м.
После первого максимума 4лг2р(г) не убы-
убывает монотонно, а имеется еще один мак-
максимум.
иейтрон. Аналогичные эксперименты были
проведены также по рассеянию электро-
электронов на нейтронах. Они показали, что ней-
нейтрон обладает электромагнитной структурой
и не является точечной электрически ней-
нейтральной частицей. Распределение электри-
электрического заряда внутри нейтрона показано
на рис. 2, а.
Очевидно, что вблизи центра нейтро-
нейтрона располагается положительный заряд,
а дальше от центра — отрицательный.
Площади, ограниченные кривыми и осью
абсцисс, равны, следовательно, положитель-
положительный заряд равен отрицательному, и в целом
нейтрон электрически нейтрален. Размеры
областей, в которых сосредоточены электри-
электрические заряды, у протона и нейтрона при-
примерно одинаковы.
11то означает непрерывное распределение
электрического элементарного заряда?
Площадь, ограниченная кривой и осью
абсцисс (см. рис. 1, а), численно равна
заряду протона, а заштрихованная пло-
площадь — заряду внутри протона в шаровом
слое толщиной dr на расстоянии г от центра
протона. Ясно, что этот заряд составляет
лишь небольшую часть от полного заряда
протона, т. е. небольшую часть элементар-
элементарного заряда. Однако в природе не удалось
обнаружить физических объектов, заряд ко-
которых равен дробной части от элемен-
§ 1. Микроскопические носители электрических зарядов 19
тарного. Спрашивается, каков смысл утверж-
утверждения, что в объеме 4кг2 dr находится не-
небольшая часть элементарного заряда?
В настоящее время предполагается, что
протон состоит из двух точечных кварков
с зарядом + 2 \е |/3 и одного — с зарядом
— | е [/3 (см. рис. 1,6). Кварки в протоне
движутся. Их относительное время пребыва-
пребывания на различных расстояниях от центра
протона может быть эффективно представ-
представлено в виде размазанности заряда по объему
протона, как показано на рис. 1, а. Нейтрон
состоит из двух кварков с зарядом — | е |/3
и одного — с зарядом + 21 е |/3 (рис. 2, б).
Объяснение распределения заряда в нем
(рис. 2, а) аналогично.
В свободном состоянии кварки не обна-
обнаружены, несмотря на значительные экспери-
экспериментальные усилия. В настоящее время счи-
считается, что их в принципе нельзя обнаружить
в свободном состоянии, поскольку для этого
надо затратить бесконечную энергию, а
внутри протона они все же существуют.
Такое допущение позволяет объяснить мно-
многие явления и поэтому принимается физи-
физиками в качестве вероятной гипотезы.
Прямое экспериментальное доказатель-
доказательство наличия кварков внутри протона от-
отсутствует.
и магнитный момент. Кроме заряда
частицы могут обладать моментом им-
импульса или спином. Спин не обусловлен
вращением частицы, поскольку для такого
объяснения при разумных предложениях о
размерах частиц пришлось бы допустить
наличие линейных скоростей при вращении,
превосходящих скорость света, что невоз-
невозможно. Поэтому спин рассматривается как
внутреннее свойство частицы.
Со спином связано наличие у заряженной
частицы магнитного момента, который так-
также не может быть объяснен движением
заряда и рассматривается как первоначаль-
первоначальное свойство.
В классической электродинамике магнит-
магнитный момент может быть лишь результатом
Движения зарядов по замкнутым траекто-
б)
Электромагнитная структура
нейтрона Вблизи центра нейт-
нейтрона располагается положитель-
положительный заряд, а дальше от цент-
центра — отрицательный. Положи-
Положительный и отрицательный заряды
взаимно компенсируют друг дру-
друга и поэтому в целом нейтрон
электрически нейтрален
О Не существует заряда, мень-
меньше элементарного Каков
смысл представления о рас-
распределении заряда в п ротоне,
если его полный заряд равен
элементарному'
С какой основной трудно-
трудностью связано представление
об электроне как о точечной
частице' Каким искусствен-
искусственным приемом эта трудность
преодолевается I
20 1 Заряды, поля, силы
риям. Поэтому спиновый магнитный момент частиц не может быть
описан в классической теории электричества и магнетизма. Однако
магнитное поле, обусловленное спиновыми магнитными моментами,
может быть при необходимости описано феноменологически. Как
правило, напряженность этого поля очень мала. Лишь в случае
постоянных магнитов оно достигает больших значений. Классическая
теория не в состоянии описать механизм возникновения этого поля,
но само поле вне постоянных магнитов полностью описывается
классической теорией (см. § 38).
§ 2. Заряженные тела.
Электризация
Выясняется физическое содержание процес-
процессов, приводящих к электризации тел при
соприкосновении. Сообщаются некоторые
сведения об энергетическом спектре элект-
электронов в твердых телах.
Термоэлектронная работа выхода. Силы, удерживающие нейтральные
атомы в молекуле и нейтральные молекулы в твердом теле, рас-
рассматриваются в молекулярной физике. Сам факт существования твер-
твердых тел свидетельствует о наличии сил, удерживающих электроны
внутри твердого тела. Для извлечения из него электрона необходимо
затратить определенную работу против сил, удерживающих электроны
внутри твердого тела. Представим себе, что твердое тело вместе
с прилегающим к нему пространством заключено в адиабатическую
оболочку и поддерживается при постоянной температуре Т. Вследствие
теплового движения и распределения электронов по скоростям внутри
тела найдутся электроны, кинетическая энергия которых достаточна
для преодоления сил, удерживающих их внутри тела, и выхода за его
пределы. Благодаря этому у поверхности тела образуется «газ» из
электронов. Электроны этого «газа» при своем движении приближаются
к поверхности твердого тела и захватываются внутрь него. Термо-
Термодинамическое равновесие достигается тогда, когда число покидающих
объем тела электронов в среднем равно числу электронов, поступающих
в объем тела из прилегающего к его поверхности слоя электронного
«газа». При этом концентрация электронов у поверхности тела име-
имеет определенное значение пй. Этот электронный газ не вырожден и
его плотность может быть представлена в виде распределения Больц-
мана:
B1)
где А зависит только от температуры Т, Ф — термоэлектронная ра-
работа выхода.
По смыслу распределения Больцмана термоэлектронная работа
выхода представляет собой разность энергий электрона вне твердого
§ 2. Заряженные тела. Электризация 21
тела и внутри него. Однако внутри твердого тела электроны име-
имеют различные энергии, и о какой энергии идет речь при определе-
определении Ф, становится ясно лишь из анализа энергетического спектра
электронов.
Г^нергетический спектр электронов. Законы движения микрочастиц
даются квантовой механикой, которая позволяет рассчитать спектр
энергий электронов, если известен закон изменения их потенциальной
энергии. Эти расчеты усложняются тем, что необходимо принимать
во внимание также и взаимодействие электронов между собой. Точное
решение такого рода задач не по силам даже современным ЭВМ
и вряд ли когда-либо будет возможно в будущем. Но в этом и нет
необходимости, потому что удается разработать методы приближенного
решения задачи, вполне удовлетворяющие практические потребности.
Важно констатировать, что спектр существует и является дискретным
для электронов, заключенных в конечной области пространства. Он
определяет различные свойства тела, изучая которые экспериментально
можно сделать заключение об его особенностях. Следовательно, энер-
энергетический спектр может быть изучен как теоретически, так и экспе-
экспериментально.
Энергетический спектр электронов в твердых телах исследован
достаточно подробно и его основные особенности сводятся к следую-
следующему. В изолированном атоме энергетические уровни составляют
дискретный набор энергий.
На рис. 3 изображена идеальная схема уровней водородоподобного
атома. В аналитическом виде энергия электрона на п-м уровне дается
формулой
Wn=-A/n\
где А — положительная величина, выражаемая через элементарный
заряд, массы ядра и электрона и постоянную Планка. Наименьшей
энергией электроны обладают на уровне и = 1. Расстояние между уров-
уровнями составляет несколько электрон-вольт, причем эти расстояния
с увеличением п уменьшаются.
Поскольку электроны подчиняются статистике Ферми — Дирака,
в каждом квантовом состоянии может находиться лишь один электрон.
Квантовое состояние характеризуется не только энергией. В водородо-
подобном атоме оно характеризуется также моментом импульса элект-
электрона при орбитальном движении в атоме, его ориентировкой в прост-
пространстве и ориентировкой спина электрона. Эти последние характери-
характеристики также квантованы, т. е. имеют дискретный набор числовых зна-
значений. В результате получается, что на каждом энергетическом уровне
имеется не один электрон, а несколько. Как показывают расчеты, на
уровне п = 1 могут находиться два электрона, отличающиеся ориенти-
ориентировкой спина (возможны только две ориентировки спина). Момент
импульса на этом уровне может быть равным только нулю. На сле-
следующем уровне п = 2 момент импульса электрона, кроме нулевого,
22
1. Заряды, поля, силы
-0
-2
-4
-6
-8
-10
-12
-13
-13,53
:^"-4
¦_п~2
—
—
—
— л-1
эВ
3
Энергетический спектр атома во-
водорода
Схема образования энергетиче-
энергетических зон
У диэлектриков работа
выхода зависит от чисто-
чистоты состава и состояния
поверхности.
Прн контакте тел проис-
происходит переход электронов
от тела с меньшей ра-
работой выхода к телу с
большей работой выхода.
может иметь также одно отличное от нуля
значение. При нулевом значении момента
импульса не имеет смысла говорить о его
ориентировке в пространстве. При отличном
от нуля значении момента импульса можно
говорить об его ориентировке в простран-
пространстве. При п = 2 имеем три возможные ори-
ориентировки. Таким образом, всего по абсо-
абсолютному значению момента импульса и его
ориентировкам в пространстве на уровне
п — 2 имеется четыре квантовых состояния.
В каждом из них спин электрона может быть
ориентирован двумя способами и, следова-
следовательно, всего на энергетическом уровне п = 2
имеется восемь различных квантовых со-
состояний. Это означает, что всего на этом
уровне может быть восемь электронов. Ока-
Оказывается, что на последующих уровнях мо-
могут находиться 18, 32, 50 и т. д. электронов.
Так как устойчивому состоянию атома
(основное состояние) соответствует состоя-
состояние с наименьшей энергией, то энергетиче-
энергетические уровни должны заполняться начиная
с уровня п — 1, а переход к заполнению
следующего уровня происходит после того,
как предшествующий уровень оказывается
полностью заполненным электронами. Со-
Совокупность электронов с определенным зна-
значением п называется оболочкой атома. Обо-
Оболочки принято обозначать буквами К, L,
М, N и т. д. по следующей схеме:
12 3 4 5
Название
обочочки К L М N О
Например, вместо «электрон на уровне п = 2»
говорят «электрон L-оболочки» и т. д.
Если атомы составляют кристаллическую
решетку твердого тела, то ситуация изме-
изменяется. Само существование кристаллической
решетки свидетельствует о том, что между
атомами имеется взаимодействие, которое
и обусловливает возникновение решетки.
Следовательно, атомы уже нельзя считать
изолированными, надо всю кристаллическую
решетку рассматривать как единую систему
и говорить об энергетических уровнях этой
системы. Оказывается, что энергетический
§ 2. Заряженные тела. Электр1тция 23
спектр кристаллической решетки связан с энергетическим спектром
изолированных атомов простым соотношением, а именно: в результате
взаимодействия между атомами каждый из энергетических уровней
п=1, 2, ... расщепляется на большое число очень близко расположен-
расположенных между собой подуровней, на которых в состоянии разместиться
все электроны, находившиеся первоначально на соответствующем уров-
уровне изолированных атомов. Например, К-оболочку изолированного атома
занимают два электрона. Если атомы входят в кристаллическую
решетку, состоящую из No атомов, то уровень п = 1 расщепляется на
No подуровней, на каждом из которых может находиться по два
электрона с различной ориентировкой спинов, т. е. всего в кристалли-
кристаллической решетке образуется 2N0 различных квантовых состояний, кото-
которые заняты 2N0 электронами, ранее принадлежавшими К-оболочкам.
Совокупность близко расположенных энергетических уровней, обра-
образовавшихся в результате расщепления некоторого энергетического
уровня изолированного атома, называется энергетической зоной или
просто зоной. Говорят о Х-зоне, L-зоне и т.д. по их соответствию
оболочкам К, L, ... изолированных атомов. Схема образования зон
изображена на рис. 4. Как было сказано, внутри зон расстояние между
различными уровнями чрезвычайно мало. Расстояние же между различ-
различными зонами остается значительным, по порядку величины равным
расстоянию между энергетическими уровнями изолированных атомов.
Промежутки между энергетическими зонами, которые не могут зани-
заниматься электронами, называются также зонами. Эти зоны называются
запрещенными, поскольку в них электроны не могут находиться.
Таким образом, энергетический спектр электронов твердого тела
состоит из разрешенных и запрещенных зон. Расстояние между
энергетическими уровнями внутри каждой из разрешенных зон чрез-
чрезвычайно мало по сравнению с шириной запрещенных зон. Рассмотрен-
Рассмотренная схема энергетических уровней изолированного атома является
идеализированной. Если более полно учесть взаимодействие электронов,
то окажется, что энергия электронов в оболочке не одинакова, а за-
зависит, например, от момента импульса. При этом энергия электрона
с более высоким значением п может быть не больше, а меньше
энергии электронов на предшествующем уровне. В результате изме-
изменяется последовательность заполнения электронами оболочек. Соот-
Соответственно изменяется и структура энергетических зон кристалла и их
заполнение электронами. Однако общий характер спектра твердого
тела не изменяется.
"^нергия Ферми. Основным состоянием твердого тела является со-
состояние с наименьшей энергией. Поэтому при температуре О К
должны быть заполнены последовательно без промежутков все кванто-
квантовые состояния электронов начиная с уровня с наименьшей энергией.
Ввиду конечного числа электронов имеется конечный заполненный
уровень с наибольшей энергией, а последующие уровни свободны.
Таким образом, при О К существует резкая граница между заполнен-
заполненными и свободными уровнями.
24 1. Заряды, поля, силы
При температуре, отличной от О К, эта граница размывается,
поскольку в результате теплового движения у некоторых электронов
энергия оказывается больше граничной энергии при Г=0К, ау неко-
некоторых — меньше. Таким образом, некоторые уровни энергии, бывшие
при Г = 0 К свободными, станут заполненными, а бывшие заполнен-
заполненными — свободными. Ширина переходной области от практически пол-
полностью заполненных до практически полностью свободных энергети-
энергетических уровней имеет порядок кТ. Распределение электронов по энер-
энергиям при этом характеризуется функцией Ферми —Дирака:
/(?, Г) = {1 + ехр [(? - n)/(fer)]}- \ B.2)
где Е — энергия электрона; ц — энергия Ферми, зависящая от темпера-
температуры. Энергия Ферми определяется как энергия, при которой функция
Ферми — Дирака равна /2-
Для металлов понятия об энергии Ферми очень наглядны. В этом
случае энергия Ферми является энергией электронов на уровне, кото-
который заполнен при Т = О К и выше которого уровни свободны. Это
определение является точным при Г = О К и достаточно точным для
всех температур, когда «размывание» распределения Ферми мало (для
большинства металлов это утверждение справедливо вплоть до темпе-
температур плавления и выше).
Для диэлектриков энергия Ферми приходится на середину запрещен-
запрещенной зоны (при Г=0 К), лежащей выше последней, полностью запол-
заполненной зоны, а на этом уровне электрон не может находиться, т. е.
энергия Ферми не соответствует энергии какого-либо реального элект-
электрона в диэлектрике. Но это, конечно, не уменьшает ее значения для
описания статистических свойств электронов в диэлектриках в соот-
соответствии с формулой B.2).
Как показывает теория, термоэлектронная работа выхода Ф, входящая
в формулу B.1), связана с энергией ц уровня Ферми соотношением
Ф = Ео - ц, B.3)
где Ео — энергия покоящегося электрона вне проводника в вакууме.
Таким образом, Ф равна работе перемещения электрона с уровня
Ферми за пределы твердого тела. Для металлов это утверждение имеет
буквальный смысл, для диэлектриков несколько условный, поскольку
на уровне Ферми нет реальных электронов. Однако в обоих случаях —
это есть работа для извлечения электрона из твердого тела, произ-
произведенная против сил, удерживающих электроны в твердом теле.
Существование работы выхода проявляется, например, в фотоэффекте,
когда энергия поглощаемого в металле фотона полностью передается
электрону. По длинноволновой границе фотоэффекта можно непосред-
непосредственно определить работу выхода. Поэтому можно сказать, что элект-
электроны внутри твердого тела находятся в потенциальной яме глубиной
Ф. Вид потенциальных ям для металлов (а) и диэлектриков (б) показан
на рис. 5 (энергетические уровни, занятые электронами, заштрихованы).
Промежуток между уровнями ЕП и Ев является запрещенной зоной.
§ 2. Заряженные тела. Электризация 25
Потенциальная яма для электро- ===)
на в металле (а) и диэлект-
диэлектрике (б). Термоэлектронная
Е„
.-ft
работа выхода Ф является раз- =Н;;=::ёёг:==:Ш-:=Я !ШЩПП=ПШП| "
иостью между энергией ?0 по- Ш=ПШШШ1ШШ| ЙЙШНШНШИ!
юящегося электрона в вакууме ;;;:--: -:=~===-=i "IIIIIiIIi=II====i=a
и энергией ц^уровия Ферми a) gN
Следует отметить, что у диэлектриков работа выхода сильно зависит
от чистоты состава. Даже небольшие примеси могут существенно
изменить работу выхода. Кроме того, работа выхода зависит от самых
ничтожных загрязнений поверхности. У чистых металлов она имеет
порядок нескольких электрон-вольт. Например, 4,53 эВ у вольфрама,
4,43 эВ у молибдена, 4,39 у меди и т. д.
|?онтактная разность потенциалов. Силы, удерживающие электроны
в твердом теле, — электрического происхождения. Они обусловлива-
обусловливаются разностью потенциалов между точками вне тела и внутренними
точками или, другими словами, на электронный газ вблизи поверхности
действуют электрические силы, стремящиеся втянуть электроны внутрь
тела. Эти силы тем значительнее, чем больше работа выхода Ф. Они
действуют в очень тонком слое молекулярных размеров (d « 100 м).
Поэтому эффективная напряженность электрического поля, обусловли-
обусловливающего возникновение этих сил, весьма велика:
Езф~Ф/(М<О~Ю10 В/м, B.4)
где учтено, что работа выхода равна по порядку величины нескольким
электрон-вольтам.
Сблизим поверхности двух тел настолько, чтобы в промежутке
между ними произошло перекрытие слоев электронного газа, находя-
находящихся у поверхности тел. Благодаря этому тела начинают обмени-
обмениваться электронами. Поскольку силы, увлекающие электрон в тело,
больше у тела, имеющего большую работу выхода, после сближения
поверхностей начнется переход электронов от тела с меньшей работой
выхода к телу с большей работой выхода, в результате чего первое
тело будет заряжаться положительно, а второе отрицательно. Воз-
Возникающее вследствие этого электрическое поле между поверхностями
тел препятствует движению электронов, в результате которого оно
возникло. Напряженность этого поля достигает определенного значе-
значения, дальнейший переход электронов от одного тела к другому
прекращается и устанавливается равновесное состояние. Поверхности
оказываются заряженными противоположными по знаку, но равными
по абсолютному значению зарядами. Между поверхностями, как между
обкладками конденсатора, устанавливается некоторая разность потен-
потенциалов, называемая контактной.
26 1. Заряды, поля, силы
Контактная разность потенциалов может быть найдена на основа-
основании следующих соображений. Поскольку между телами устанавливается
электронное равновесие, энергии Ферми тел должны быть равными,
в результате чего верхние точки потенциальных ям смещаются отно-
относительно друг друга. Следовательно, между ними, т. е. между поверх-
поверхностями тел, возникают разность потенциалов и напряженность
электрического поля.
На рис. 6 показаны схемы образования контактной разности по-
потенциалов между двумя металлами (рис. 6, а), между металлом и ди-
диэлектриком (рис. 6, б), между диэлектриками (рис. 6, в). Отличие в об-
образовании контактной разности потенциалов между металлами и между
металлом и диэлектриком состоит в том, что электрическое поле
не проникает внутрь металла, но проникает на небольшую глубину
в диэлектрик (на рис. 6, б, в глубина проникновения обозначена d\ и d2).
Поэтому у диэлектриков падение потенциала происходит не только между
поверхностями, но и частично в тонком слое внутри диэлектрика
вблизи его поверхности. Однако толщина этого слоя обычно мала
по сравнению с расстоянием между поверхностями и с большой
точностью это обстоятельство можно не принимать во внимание.
Как видно (см. рис. 6), разность между энергиями верхних точек
потенциальных ям равна Ф2 — Ф1 и поэтому контактная разность
потенциалов между поверхностями тел, находящихся в электронном
равновесии, задается формулой
| Аф | = | Ф2 — Ф, |/| е |. B.5)
Заметим, что потенциал уменьшается в направлении от положительно
заряженных тел к отрицательно заряженным. Поэтому изменение
потенциала противоположно изменению потенциальной энергии элект-
электрона, т. е. потенциал уменьшается от первого тела ко второму.
^лектризация. Если плоские поверхности тел, между которыми обра-
образовалась контактная разность потенциалов, удалить друг от друга,
сохраняя строгую параллельность между ними, то находящиеся на
них заряды останутся на телах и тела окажутся разноименно
заряженными. Однако развести строго параллельно поверхности прак-
практически невозможно, так как различные их участки удаляются
с различной скоростью. Результат разведения поверхностей для про-
проводников и диэлектриков принципиально различен.
При разведении плоских поверхностей проводников находящиеся
на них заряды могут перемещаться вдоль поверхности. Если одни
участки поверхности развести раньше других, то на них, так же как
в конденсаторе, при той же разности потенциалов плотность заряда
уменьшится. В результате между телами осуществится обмен зарядами
для восстановления электронного равновесия, причем он происходит
посредством обмена электронами через электронное облако на данном
участке поверхности и вследствие движения зарядов вдоль поверхности
на других участках. Те участки поверхности проводников, которые
§ 2 Заряженные тела. Электризация 27
а)
разведены достаточно далеко и потеряли при
этом электронный контакт через приповерх-
приповерхностное электронное облако, оказываются
практически лишенными зарядами. Заряд
сохраняется лишь на тех участках поверх-
поверхности, которые еще находятся в электронном
контакте. Наконец наступает момент, когда
электронный контакт сохраняется на ничтож-
ничтожно малой площади поверхности, содержащей
очень малый заряд. Поэтому при оконча-
окончательном разведении проводников на них не
остается зарядов.
Результат разведения диэлектриков иной.
У них заряды не могут перемещаться вдоль
поверхности и сам потенциал вдоль поверх-
поверхности может быть различен. При разведении
участков поверхности разность потенциалов
между ними не остается постоянной, а уве-
увеличивается точно так же, как увеличивается
разность потенциалов между обкладками
конденсатора, когда заряд обкладки постоя-
постоянен, а расстояние между обкладками увели-
увеличивается. Плотность зарядов на поверх-
поверхностях существенно не изменяется. После
потери электронного контакта через при-
приповерхностное электронное облако на участ-
участках поверхности сохраняются электрические
заряды. В результате полного разведения
поверхностей диэлектриков они оказываются
носителями разноименных, равных по абсо-
абсолютному значению зарядов. Этот процесс
называется электризацией.
Для достижения более тесного сближения
поверхностей диэлектриков и образования
контактной разности потенциалов тела обыч-
обычно трут одно о другое и говорят об
Образование контактной разнос-
разности потенциалов в промежутке
между поверхностями мстачл —
металл (а), металл — диэлектрик
F), диэ 1ектрик — диэлектрик (в)
ф Расстояние между энерге-
энергетическими уровнями внут-
внутри каждой из разрешен-
разрешенных зон чрезвычайно ма-
мало по сравнению с ши-
шириной запрещенных зон.
В диэлектриках энергия
Ферми не соответствует
энергии кокого-либо ре-
реального электрона в ди-
диэлектрике.
Термоэлектронная работа
выхода равна работе пе-
перемещения электрона с
уровня Ферми за пределы
твердого тела.
О Каково соотношение между
энергетическими /ровнями
изолированного атома и
энергетическими зонами
твердого тела? За счет каких
факторов образуются энерге-
энергетические зоны?
Какова наглядная интер-
интерпретация энергии Ферми в
металлах?
Почему эта интерпретация
не подходит для диэлектри-
диэлектриков?
Как определить знаки заря-
зарядов соприкасающихся тел?
Почему нельзя произвести
электризацию металлов со-
соприкосновением?
28 1. Заряды, поля, силы
электризации трением. Однако трение при этом никакого отношения
к электризации не имеет. Более правильно было бы сказать об электри-
электризации посредством контакта тел. Терминология установилась раньше,
чем была выяснена физическая природа явления.
§ 3. Элементарный заряд
и его инвариантность
Описываются эксперименты, доказывающие
существование элементарного электрическо-
электрического заряда и отсутствие зарядов, дробных
относительно элементарного. Обсуждаются
экспериментальные свидетельства одинако-
одинаковости абсолютных значений положительных
и отрицательных элементарных зарядов и
инвариантности заряда.
Опыты Милликена. Мысль о дискретности электрического заряда
была в ясной форме высказана уже Б. Франклином в 1752 г., однако
она носила умозрительный характер. Как экспериментальный резуль-
результат дискретность зарядов в принципе следует из открытых в 1834 г.
М. Фарадеем A791 — 1867) законов электролиза. Однако такой вывод
из законов электролиза был сделан лишь в 1881 г. Г. Л. Гельмгольцем
A821-1894) и Д. Стонеем A826-1911). Вскоре после этого в 1895 г.
Г. Лоренц A853 — 1928) разработал теорию электромагнетизма, основы-
основывающуюся на представлении о реально существующих элементарных
зарядах (электронах). Числовое значение элементарного заряда было
теоретически вычислено на основании законов электролиза, поскольку
значение постоянной Авогадро было известно. Прямое эксперименталь-
экспериментальное измерение элементарного заряда было выполнено Р. Э. Милли-
кеном A868-1953) в 1909 г.
Схема опытов Милликена изображена на рис. 7. Маленькие шаро-
шарообразные частицы движутся в вязкой жидкости при наличии одно-
однородного электрического поля Е. На частицу действуют подъемная сила,
направленная против силы тяжести (плотность частицы больше плот-
плотности жидкости), и сила вязкого трения /тр, направленная против
скорости.
Сила вязкого трения в соответствии с формулой Стокса пропор-
пропорциональна скорости. При постоянной скорости частицы сумма дей-
действующих на нее сил равна нулю.
Все силы, за исключением действующей на частицу со стороны
электрического поля, могут быть измерены экспериментально при дви-
движении частицы в среде без электрического поля. Изучив затем движе-
движение частицы в электрическом поле, найдем силу дЕ. Это позволит
вычислить заряд q частицы, поскольку напряженность Е поля известна.
Можно также изменять напряженность электрического поля и до-
добиться, чтобы частица находилась в покое. В этом случае сила
§ 3. Элементарный заряд и его инвариантность
29
трения также отсутствует, а остальные
силы известны. Поэтому, зная Е, можно
определить q.
Заряд частицы с течением времени изме-
изменяется, что отражается на движении частицы.
Определив заряды ?i и^2 частицы в различ-
различные промежутки времени, можно найти из-
изменение заряда
Aq = qi-qi- C-1)
Произведя большое число измерений заря-
зарядов, Милликен нашел, что Aq является всегда
целым, кратным одной и той оке величине
И:
Aq = n\e\, n = ±1, +2, ..., C.2)
И = 1,6-КГ19 Кл. C.2а)
резонансный метод измерения заряда.
В дальнейшем методы прямого изме-
измерения элементарного заряда были усовер-
усовершенствованы. В настоящее время точность
измерений такова, что позволяет обнару-
обнаружить десятые доли элементарного заряда.
Наиболее эффективным является резонанс-
резонансный метод, схема которого изображена на
рис. 8. Шарик достаточно малой массы т
укреплен на очень тонком упругом стержне.
Под влиянием сил упругости, возникающих
при изгибе стерженька, шарик колеблется
около положения равновесия с собственной
частотой соо, которая может быть измерена
экспериментально. Если на шарике есть не-
некоторый заряд q, то под действием пере-
переменного электрического поля шарик осу-
осуществляет вынужденные колебания, ампли-
амплитуды которых зависят от соотношения меж-
между частотами со и соо- Максимальная ампли-
амплитуда колебаний достигается в резонансе
(со и соо)- Амплитуда колебаний шарика в ре-
резонансе равна
C.3)
***
'тр
' Гт%
'- ~ - - - -1
Схема опытов Милликена
где Q — добротность системы, Ео — ампли-
амплитуда напряженности электрического поля.
Оценим возможности метода. Предполо-
Предположим, что т = 1 мг = 10 кг; Ео « 105 В/м;
Е— E0cosco0t
Схема резонансного метода изме-
измерения элементарного заряда
9 Поиски кварков позволи-
позволили с большой точностью
доказать отсутствие в при-
природе дробных зарядов.
Отсутствие кварков в сво-
свободном состоянии не до-
доказывает их несущество-
несуществование в связанном состоя-
состоянии внутри элементарных
частиц.
О В чем состоит принцип ре-
резонансного метода измерения
элементарного заряда! Како-
Какова современная точность
этого метода? Приведите чи-
числовые оценки.
30 1. Заряды, поля, силы
д=1,6-1(Г19 Кл; coo = lO с; Q х 100, тогда
1,6-10-19105-102 4 ... ....
Ара « 10-6 10_2 м « 1,6 • 10 4 м = 160 мкм. C.4)
Величина 160 мкм является очень большой и легко измерить ее
небольшую часть. Следовательно, таким способом можно измерить
заряды много меньшие, чем 1,6 -10"9 Кл. Этот метод доведен до
такого совершенства, что позволяет в принципе обнаружить и измерить
заряд в десятые доли элементарного, если бы он существовал.
При изменении заряда шарика на A<j амплитуда резонансных
колебаний изменяется скачком:
ДЛрез = AqE0Q/(mo>20). C.5)
Измерения позволили с большой точностью установить, что заряд
шарика изменяется всегда на целое число элементарных зарядов
и что не существует зарядов, меньших элементарного.
Отсутствие дробного заряда. Были предприняты интенсивные поиски
дробных зарядов. Это было инициировано предсказанием существо-
существования кварков. Предполагается, что кварки являются частицами, из
которых построено большинство тяжелых элементарных частиц (про-
(протоны и др.). Было предсказано, что электрический заряд кварков
должен составлять */з и 2/3 элементарного заряда (с соответствую-
соответствующими знаками). Поиски кварков проводились многими учеными раз-
различными методами, в том числе и резонансным. Все они дали отри-
отрицательный результат. Таким образом, в настоящее время эксперимен-
экспериментально с большой точностью установлено, что дробных зарядов
в свободном состоянии не существует.
Мы выделяем слова «в свободном состоянии», поскольку экспери-
эксперименты были направлены именно на поиск свободных кварков. Однако
отсюда не следует, что и в связанном состоянии внутри элементар-
элементарных частиц кварки отсутствуют. Однако прямая экспериментальная
проверка этого утверждения неизвестна.
равенство положительных и отрицательных элементарных зарядов.
В описанных выше опытах измерялся как отрицательный элементар-
элементарный, так и положительный заряд. Результаты этих опытов доказали
их равенство с той же точностью, с какой измеряют значение зарядов.
Эта точность не велика. Например, можно сказать, что по абсолют-
абсолютному значению положительный и отрицательный элементарные заряды
отличаются не больше, чем на одну десятую часть своей величины, т. е.
И«+1-1«-И <±, C.6)
|е1 Ю
Эта точность совершенно неудовлетворительна, потому что теория
предполагает полное равенство абсолютных значений отрицательных
и положительных элементарных зарядов.
§ 3. Элементарный заряд и его инвариан шость 31
Неизмеримо более точную оценку можно получить, не измеряя
непосредственно значение элементарного заряда. Как известно, в атомах
имеется одинаковое число протонов и электронов. Тела также содер-
содержат одинаковое число протонов и электронов. Поэтому оценка ра-
равенства зарядов протона и электрона может быть проведена по
результатам измерения нейтральности тел. А это можно сделать
чрезвычайно точно, поскольку даже очень небольшое ее нарушение
приводит к возникновению громадных сил электрического взаимодей-
взаимодействия между телами, которое легко заметить. Пусть, например, два
железных шарика массой по 1 г, находящихся на расстоянии 1 м друг
от друга, не нейтральны из-за того, что заряды протона отличаются
от заряда электрона на одну миллионную долю заряда. Оценим, какая
сила отталкивания возникнет между шариками. В 1 г s^Fe имеется
6-1023-26/56 зарядов каждого знака. Следовательно, при нарушении
нейтральности всего на 10~6 на каждом шарике появится заряд
g = [i;6-10-19 • 10~б- 6-1023-26/56] Кл = 4,46-1(Г2 Кл. C.7)
Сила отталкивания между шариками равна
г.2
~ = D,46 ¦ 10J ¦ 9 • 109 Н = 1,8 • 107 Н = 18 МН. C.8)
Это означает, что между шариками возникает сила отталкивания,
равная силе, с которой тяжеловесный железнодорожный состав массой
почти 2 тыс. т давит на рельсы. И это всего-навсего при отличии
зарядов протона и электрона на 10 часть заряда в 2 г железа.
Ясно, что можно легко измерить силы между железными шариками,
в громадное число раз меньшие C.8). А если в эксперименте таких сил
не обнаруживается, то это означает соответствующее увеличение точ-
точности, с которой заряд электрона по абсолютному значению равен
заряду протона. В настоящее время экспериментально установлено, что
отрицательный элементарный заряд электрона равен по абсолютному
значению положительному заряду протона с относительной точ-
точностью 10~21, т. е.
C.9)
Изложенное доказательство равенства абсолютных значений поло-
положительного и отрицательного элементарных зарядов может показаться
недостаточно строгим. Можно представить себе тело, состоящее из
атомов или молекул, в которых элементарные заряды по абсолютному
значению не равны друг другу, хотя их числа в каждом атоме или
молекуле одинаковы. В этом случае атомы или молекулы должны
обладать зарядом, однако тело в целом может оставаться нейтраль-
нейтральным, если в нем наряду с этими атомами и молекулами находятся
в нужном числе свободные электроны или положительные ионы
(в зависимости от знака заряда атомов или молекул). Однако при
32 1. Заряды, поля, силы
таком допущении возникают осложнения, с которыми трудно прими-
примириться. Например, приходится отказаться от представления об одно-
однородной структуре тел и принять зависимость их структуры от разме-
размеров и т. д. Тем не менее желательно иметь более прямое и непосред-
непосредственное доказательство равенства абсолютных значений положитель-
положительных и отрицательных элементарных зарядов в атомах. Такое дока-
доказательство было получено.
Нейтральность отдельных атомов проверялась прямыми экспери-
экспериментами: исследовалось отклонение пучка нейтральных атомов в
электростатических полях. По отклонению можно судить о заряде
атома и сделать заключение о равенстве зарядов электронов и про-
протонов в атоме. Исследования с пучками цезия (Z = 55) и калия (Z = 19)
доказали, что абсолютные значения зарядов электрона и протона
равны с относительной точностью 3,5-10~19.
Мнвариантность заряда. Независимость числового значения элемен-
элементарного заряда от скорости также доказывается фактом нейтраль-
нейтральности атомов. Из-за различия масс электронов и протонов можно
заключить, что электроны в атомах движутся значительно быстрее
протонов. Если бы заряд зависел от скорости, нейтральность атомов
не могла бы соблюдаться. Например, электроны в атоме гелия дви-
движутся примерно в два раза быстрее, чем в молекуле водорода,
а нейтральность атома гелия и молекулы водорода доказаны с боль-
большой точностью. Можно заключить, что с той же точностью заряд
не зависит от скорости вплоть до скоростей электронов в атоме гелия.
В атоме гелия скорость электронов равна примерно 0,02 с. В более
тяжелых атомах, нейтральность которых доказана, электроны движутся
во внутренних оболочках со скоростями, равными примерно половине
скорости света. Тем самым экспериментально доказано, что элементар-
элементарный заряд инвариантен вплоть до 0,5 с. Нет оснований предполагать,
что он не инвариантен при более высоких скоростях. Поэтому
инвариантность электрического заряда принимается в качестве одного
из экспериментальных обоснований теории электричества.
§ 4. Электрический ток
Обсуждаются основные понятия и величины,
характеризующие распределение и движение
электрических зарядов.
Движение зарядов. Движение электронов и протонов обусловливает
движение их зарядов. Поэтому можно говорить просто о движении
зарядов, не оговаривая каждый раз их носителя. Это не только удобно,
но и придает общность рассуждениям, поскольку многие явления зави-
зависят только от зарядов, их движения и т. д. и не зависят от свойств
носителей этих зарядов, например массы носителей зарядов. Если
существен не только заряд, но и свойства носителя заряда, например
§ 4. Электрический ток 33
масса носителя заряда, то необходимо принимать во внимание не
только заряд, но и другие характеристики носителя.
В теории электричества элементарный заряд считается точечным,
в том числе и заряд протона. Положение заряда, его скорость и уско-
ускорение имеют такой же смысл, как и в случае материальных точек.
ХТепрерывное распределение зарядов. Элементарный заряд весьма мал.
Поэтому в большинстве макроскопических явлений, изучаемых
в электричестве, участвует громадное число электрических зарядов
и их дискретность никакого проявления не имеет. Например, на каж-
каждой из обкладок плоского конденсатора емкостью 10 мкФ при разности
потенциалов 100 В содержится около 7-Ю15 элементарных зарядов.
При токе 1 А через поперечное сечение проводника проходит при-
примерно 6-1018 элементарных зарядов в секунду. Поэтому в большинстве
случаев можно считать, что заряд как бы непрерывно распределен
в пространстве, и не принимать во внимание его дискретность.
фбъемная плотность зарядов. Объемной плотностью непрерывного
распределения зарядов называется отношение заряда к объему:
D.1)
где е, — элементарные заряды в объеме Д7Ф (с учетом их знака); Ag —
полный заряд, заключенный в ДКф. Объем ДКф является малым, но
не бесконечно малым в математическом смысле. Мы говорим о ДКф
как о бесконечно малом объеме в физическом смысле, понимая под
этим, что он очень мал и, следовательно, его положение в простран-
пространстве достаточно точно характеризуется какой-то координатой точки,
расположенной внутри него, т. е. у р в левой части D.1) можно взять
в качестве аргумента координаты (х, у, z) любой точки внутри АКф
и написать р(х, у, г). Однако в объеме ДКФ должно находиться доста-
достаточно много элементарных зарядов, так что небольшое изменение его
не приводит к существенному изменению плотности р, вычисляемой
по формуле D.1). Следовательно, АКф зависит от конкретных условий.
В одних случаях малый объем AV может удовлетворять необходимым
условиям и считаться бесконечно малым физическим объемом, а в дру-
других случаях его нельзя считать таковым. Наконец, возможны условия,
когда вообще не существует никакого объема AV, который может быть
назван бесконечно малым физическим объемом. В этом случае невоз-
невозможно пользоваться представлением о непрерывном распределении
заряда и нельзя определить р по формуле D.1) как объемную плотность.
Однако в большинстве случаев, которые рассматриваются в класси-
классической теории электричества, представление о непрерывном распределе-
распределении заряда справедливо.
При определении объемной плотности р по формуле D.1) ее можно
рассматривать как обычную математическую функцию, а заряд непре-
I Л Н Матвеев
34 1. Заряды, поля, силы
рывно размазанным по объему. Тогда из D.1) следует, что полный
заряд, заключенный в объеме F, равен
D.2)
v
где d V— дифференциал объема.
концентрация зарядов. Концентрацией зарядов определенного знака
называется отношение числа зарядов к занимаемому ими объему:
¦, - ^
где Ап± — число зарядов соответствующего знака в объеме АКф. Тогда
[см. DЛ)]
1 V (+
Р Д7 //
ф // + АКф //' ДКф + АКф
= е( + )п( + ) + е'-'и,-) = р< + ) + р(~\ D.4)
где е< + ) — элементарный точечный заряд с соохветствующим знаком,
р(±) = eti'n^j — объемная плотность зарядов. Физический бесконечно
малый объем должен содержать достаточно много зарядов, чтобы
определение концентрации имело смысл.
р[оверхностная плотность зарядов. Иногда заряд распределяется
в очень тонком слое вблизи некоторой поверхности. Если нас
интересует действие заряда на расстояниях, много больших, чем тол-
толщина слоя, а не процессы в этом слое, то можно предположить, что
весь заряд сосредоточен на поверхности, или, другими словами, этот
очень тонкий слой можно считать поверхностью. Поверхностная
плотность заряда определяется формулой
D.5)
где Д5ф — бесконечно малая площадь в физическом смысле, AQ —
заряд, приходящийся на площадь AS^ поверхности в тонком слое
около нее.
У ст в качестве аргумента можно поставить координаты точек
поверхности и рассматривать ее как функцию эгих координат. Обосно-
Обоснования и смысл этого точно такие же, как и для объемной плотности р
в D.1). Поэтому полный заряд на поверхности S равен
Q = J сг dS, D.6)
s
где dS — дифференциал площади поверхности.
§ 4. Электрический ток 35
ТТлотность тока. Заряды, находящиеся в объеме ДКф, движутся с раз-
различными скоростями, отличающимися не только по модулю, но
и по направлению. Движение заряда приводит к переносу заряда
в направлении скорости. Поэтому в результате различных движений
зарядов, заключенных в объеме ДКф, образуется некоторый средний
Перенос заряда, заключенного в этом объеме. Интенсивность этого
переноса характеризуется плотностью тока, определяемой формулой
D.7)
где Vj — скорость заряда е,.
Разбив сумму в D.7) на суммы по положительным и отрицательным
зарядам, получим
АЪ 1??"¦ D8)
Формула D.8) будет более наглядна, если входящие в нее величины
выразить через средние скорости и концентрации зарядов:
I
где
v<+> = д„<+> __L_ \ у<+> = Ап(+)
поскольку Лп< + ) — число зарядов, сумма скоростей которых стоит под
знаком ?. Аналогично преобразуется сумма по скоростям отрицатель-
отрицательных зарядов. С учетом этого формула D.8) приобретает вид:
e<->n(-> (v'"') = p<+) <v<+)> + p1'» <v<-)>, D.9)
где приняты во внимание соотношения D.3) и D.4). Таким образом,
отрицательные и положительные заряды создают каждый свою плот-
плотность тока:
D.10)
36 1. Заряды, поля, силы
dS
Направление плотности тока положи-
положительных зарядов совпадает с направлением,
их средней скорости, а отрицательных заря-
зарядов противоположно ей.
Формулы D.10) для упрощения написания
обычно представляют в виде
= pv,
D.11)
К вычислению силы электри-
электрического тока через элемент по-
поверхности
10
Электрический ток через по-
поверхность
В большинстве макроско-
макроскопических явлений, изучае-
изучаемых в электричестве, уча'
ствует громадное число
электрических зарядов и
их дискретность никак не
проявляется.
Какой-то конкретный па-
палый объем в одних случаях
может считаться бесконеч-
бесконечно палым физическим
объемом, а в других — его
нельзя считать таковым.
Возможны условия, когда
вообще не существует ни-
никакого объема, который
может быть лринят за
бесконечно малый физи-
физический объем. Тогда нель-
нельзя перейти к картине не-
непрерывного распределе-
распределения зарядов в объеме.
где р и v — объемная плотность и скорость
зарядов соответствующего знака. Если ток
создается зарядами обоих знаков, то в пра-
правой части имеется в виду сумма двух чле-
членов, относящихся к положительным и отри-
отрицательным зарядам. Однако в большинстве
случаев, рассматриваемых в теории электри-
электричества, ток обусловлен лишь движением
отрицательных зарядов электронов и по-
поэтому правая часть D.11) содержит лишь
произведение отрицательной объемной плот-
плотности заряда электронов на их среднюю
скорость. Перенос отрицательного заряда
против скорости эквивалентен переносу по-
положительного заряда в направлении скорости.
При различных рассуждениях удобнее пред-
представлять себе, что ток обусловливается
движением положительных зарядов, по-
поскольку их пространственное перемещение
совпадает с направлением плотности тока.
тока через поверхность. Бесконечно
малый элемент поверхности характери-
характеризуется вектором dS, модуль которого равен
площади элемента поверхности и направлен
по нормали к поверхности, принятой за
положи телыгую.
Вычислим заряд, который в течение вре-
времени ck пересекает элемент поверхности dS
(рис. 9). Перемещение заряда за это время
равно v dr. Следовательно, заряд, пересекаю-
пересекающий dS, равен объемной плотности заряда,
умноженной на объем косого цилиндра
(рис. 9). Площадь основания и высота косого
цилиндра равны 6S и h = v At cos 0. Поэтому
заряд, пересекший dS, равен
dq = pv df dS cos 9 = df j dS cos 9 = df j ¦ dS,
D.12)
§ 5. Закон сохранения заряда 37
Л
где j - dS = j dS cos (j, dS). Силой тока через поверхность называется
отношение заряда, пересекающего поверхность, ко времени. Поэтому
бесконечно малая сила тока 61, протекающего через элемент поверх-
поверхности dS [см. D.12)], равна
dl - uQ/dt = j • dS. D.13)
Сила тока, протекающего через конечную поверхность S (рис. 10),
равна интегралу по этой поверхности от элементов силы тока D.13):
D.14)
Если постоянный электрический ток течет по проводнику, то фор-
формула D.14) сводится к определению силы тока как количества электри-
электричества, протекающего через поперечное сечение проводника в секунду.
§ 5. Закон сохранения заряда
Обсуждаются два аспекта понятия сохра-
сохранения заряда. Даются интегральная и диф-
дифференциальная формулировки закона сохра-
сохранения заряда.
Два аспекта понятия сохранения заряда. В понятие «сохранение
^заряда» включаются две группы совершенно различных фактов:
1) электрон и протон являются материальными частицами с бесконеч-
бесконечным временем жизни, а их элементарные электрические заряды ин-
инвариантны и не зависят от скорости. Следовательно, их заряды
существуют без изменения столь долго, сколь долго существуют про-
протоны и электроны, независимо от того, как они движутся, т. е. при
любых движениях заряд сохраняется. В этом аспекте закон сохране-
сохранения заряда является просто следствием неуничтожимости носителей
заряда как физических объектов и инвариантности заряда; 2) кроме
Протонов и электронов существует большое число других заряженных
элементарных частиц. Все они порождаются, порождают другие части-
частицы и уничтожаются в различных процессах взаимопревращений. Весь
громадный экспериментальный материал свидетельствует, что каков бы
НИ был процесс взаимопревращения частиц, суммарный заряд частиц
до взаимопревращения равен суммарному заряду частиц после взаимо-
взаимопревращения. Например, при C-распаде до испускания электрона ядро
имеет некоторый положительный заряд 2е( + ). После испускания элект-
электрона положительный заряд ядра увеличивается на один элементарный
положительный заряд и становится равным (Z + 1) е<+). Однако в сумме
с отрицательным зарядом испущенного электрона система «ядро +
+ электрон» имеет прежний заряд (Z + 1) е(+) ~ | е<"> | = Ze(+\ В ка-
38 1. Заряды, поля, силы
честве другого примера можно привести порождение у-квантом пары
электрон — позитрон. Исходная частица — 7-квант — нейтральна. Она
превращается в пару частиц, суммарный заряд которых равен нулю,
что доказано с большой точностью при измерении положительного
заряда позитрона. Исследовано громадное число взаимопревращений
элементарных частиц и во всех процессах соблюдается равенство сум-
суммарного заряда до процесса и после процесса, или, иначе говоря,
соблюдается закон сохранения заряда. Благодаря этому заряд приобре-
приобретает в некотором смысле существование, независимое от носителей,
и закон его сохранения может быть сформулирован следующим об-
образом: заряд сохраняется при всех процессах и движениях, связанных
с носителями зарядов.
Однако, несмотря на относительную самостоятельность, заряд не
может существовать независимо от носителей заряда или вне про-
пространства и времени. Это означает, что заряд не является самостоя-
самостоятельной сущностью, независимой от материи, он выражает одно из
свойств материи. Выяснение природы этой связи — одна из трудней-
труднейших проблем современной физики. Еще не ясно, почему существует
только один элементарный заряд и почему он равен | е |, а не какому-то
другому значению.
ЭДнтегральная формулировка закона сохранения заряда. Исходя из
закона сохранения заряда как экспериментального факта, выразим
его в виде утверждения о том, что изменение заряда в некотором
объеме Vможет произойти только в результате втекания или вытекания
заряда через замкнутую поверхность S, ограничивающую объем:
E.1)
Левая часть E.1) определяет скорость изменения заряда в объеме,
а правая — силу тока через поверхность, ограничивающую объем. Знак
минус учитывает, что если положительный заряд внутри объема
уменьшается, то плотность тока направлена из объема V. Напомним,
что у замкнутых поверхностей положительной нормалью считается
внешняя нормаль. Следовательно, вектор dS в E.1) направлен по внеш-
внешней нормали к поверхности (рис. 11).
Т? ивергенция. Для описания процессов, связанных с порождением,
^ уничтожением и сохранением физических величин, важную роль
играет математическое понятие дивергенции.
Пусть имеется вектор А(х, у, z), определенный во всех точках
пространства. Рассмотрим некоторую поверхность 5 (рис. 12). Интеграл
ФЛ = J А • dS E.2)
s
называется потоком вектора А через поверхность S. Причина для
такого названия состоит в следующем. Предположим, что име-
§ 5. Закон сохранения заряда 39
11
ется внешняя нормаль
ется костер, плотность дыма от которого
равна р, а скорость дыма в различных
точках пространства есть v. Выберем в ка-
качестве вектора А величину pv. Тогда ин-
интеграл E.2) с учетом рис. 9 определяет
массу дыма, проходящего сквозь поверх-
поверхность S в секунду. В применении к элект-
электрическому заряду аналогичное представление
уже использовалось В равенстве D.14). По Положительной нормалью у
аналогии с E.1) заключаем, что поток век- замкнутых поверхностей явля-
тора А сквозь замкнутую поверхность ха-
характеризует интенсивность порождения или
уничтожения А внутри объема, ограничен-
ограниченного поверхностью. Таким образом, поток
вектора pv сквозь замкнутую поверхность
характеризует интенсивность порождения
дыма внутри объема, ограниченного замкну-
замкнутой поверхностью. Такую же интерпретацию
имеет равенство E.1) в применении к элект-
электрическим зарядам. Можно сказать, что ин-
интеграл E.2) характеризует суммарную мощ-
мощность источников вектора А внутри объема.
Дивергенция характеризует мощность
источников и определяется формулой
§ A-dS
12
Поток вектора А сквозь поверх-
поверхность
divA= lim
AV
E.3)
где AS — бесконечно малая замкнутая по-
поверхность, ограничивающая бесконечно ма-
малый объем АУ.
Найдем выражение для div А в декарто-
декартовых прямоугольных координатах. Для этого
вычислим поток вектора А сквозь поверх-
поверхность куба (рис. 13) со сторонами Ах, Ау,
Аг, центр которого имеет координаты (х, у,
z). Координаты середин граней равны (х +
+ Дх/2, у, z), (х - Axil, у, z), (х, у + Ay/2, z),
(х, у - Ау/2, г), (х, у, г + Аг/2), (х, у, г - Дг/2).
Подынтегральное выражение E.3) в коорди-
координатах имеет вид
A • dS = Ax dSx
тде
dSx = + dy dz,
Aj, dSy + Az dSz,
E.4)
= +dzdx,
Sz = ±dxdy,
E.5)
О Каким требованиям должен
удовлетворять бесконечно
малый физический объем ?
При каких условиях можно
пользоваться понятием не-
непрерывного распределения
зарядов? Всегда ли можно
определить объемную плот-
плотность заряда? Приведите
примеры.
При каких условиях мож-
можно пользоваться представле-
представлением о поверхностных заря-
зарядах!
В каком соотношении на-
находится направление векто-
вектора плотности тока к на-
направлению вектора скорости
заряда >
40
1. Заряды, поля, силы
z
i
dS
L
P
IdS
d,S
dS
*
13
Поток вектора сквозь поверх-
поверхность куба сводится к сумме
потоков через его грани
причем знак этих величин определяется на-
направлением внешней нормали к грани отно-
относительно положительного направления соот-
соответствующей оси. Например, dSy по правой
грани (х, у + Ay, z) имеет положительное
значение, а по левой грани — отрицательное.
Интеграл по поверхности куба сводится
к сумме интегралов по ее граням.
Вычислим, например, интеграл по гра-
граням, перпендикулярным оси У. На этих гра-
гранях dSx = 0, dSy = +dzdx, dSz = 0 и, следо-
следовательно, сумма в правой части E.4) сво-
сводится к одному слагаемому AydSy. Обозна-
Обозначив площади поверхностей граней ASyl (ле-
(левая) и ASyl (правая), запишем:
A-dS= f
AydSy
(x,y-Ay/2,z)dxdz
{x,y + Ay/2, z) dx dz.
14
К выводу формулы Гаусса — Ост-
Остроградского
E.6)
Знак минус у первого интеграла в пра-
правой части E.6) учитывает, что внешняя нор-
нормаль к левой грани ASyl направлена в сто-
сторону отрицательных значений у. Для даль-
дальнейших вычислений представим Ау в виде
ряда Тэйлора по Ау:
Ау (х, у + Ау/2, г) = А (х, у, z) +
+ (Ау/2) дАу (х, у, z)/dy + О [(АуJ],
Ау (х, у - Ау/2, г) = А (х, у, г) -
- (Ау/2) дАу (х, у, z)/dy + О [(ДуJ],
E.7)
где О [(АуJ] - члены высшего порядка ма-
малости по Ду. Подставляя E.7) в E.6), находим
, = Ау
E.8)
AS,
где учтено, что площади поверхностей АБуг
и ASy2 равны и имеют одинаковые коор-
координаты по осям X, Z.
Интеграл в E.8) можно вычислить,
разложив подынтегральное выражение в ряд,
§ 5. Закон сохранения заряда 41
считая z и х переменными интегрирования, а отнюдь не коор-
координатами центра граней. Если под х и у понимать координаты
центра граней, то переменные удобно заменить по формулам:
х -»х + ?,, z-* z + г|, dx dz -> 6t, dr|, E.9)
E10)
J Sy J ду
AS, AS,
где x, z в правой части E.10) — координаты центра граней, т. е.
постоянны при вычислении E.10). Выражение ВАу/ду можно разложить
в ряд по %, ц:
дАу (х + 5, У, z + л) _ 8Ау (х, у, г) 52Лу (х, у, z) |
Sy ду ёхду
+ ^^ё^+ое112)' EЛ1)
где Ъ, и г| при интегрировании изменяются от 0 до ±Дх/2 и +Az/2
и имеют, следовательно, тот же порядок малости, что и Дх и Az.
Подставим E.11) в E.10):
AS, AS, AS,
^йц + ... = ^-АхАуА2 + 0 [(АхJ, (AzJ]. E.12)
dzdy
AS,
Тогда для E.8) получаем
Iy ^ BA,(x,y,z) Ax AyAz + Q г_(Дх Ау AzJj_ E.13)
Аналогично вычислим потоки через другие пары граней:
<?а • dS = (Ц±- + Ц?- + Ц±) Дх Ay Az + 0 [(Дх Ау ДгJ]. E.14)
J \ дх ду dz J
s
Подставляя E.14) в E.3) и учитывая, что объем куба равен
&.V = Дх Ду Az, находим
div A = lim I-^L + M)L + 8А- + о [(Дх Ау ДгJ]ДДх Ду ДгI =
ДК-.0 | дх ду dz J
дх ду dz
поскольку слагаемое, зависящее от (Дх Ay Az), при переходе к пределу
обращается в нуль. Формула
42 1. Заряды, поля, силы
E.16)
позволяет вычислить дивергенцию в декартовых координатах,
формула Гаусса — Остроградского. Эта формула связывает мощность
источников с потоками порождаемых ими векторов и играет важ-
важную роль в теории электричества. Разобьем объем V, ограниченный
поверхностью S (рис. 14, а\ на большое число малых объемов AVh
поверхности которых AS,-.
Формулу E.3) можно представить в виде
(divA)iAK;« $A-dS, E.17)
AS,
где (div А)( означает div А в i-м объеме. В E.17) поставлен знак прибли-
приближенного равенства, поскольку ДК; хотя мал, но конечен. При неограни-
неограниченном уменьшении AV, соотношение E.17) становится точным. Про-
Просуммируем обе части E.17) по всем ячейкам объема V:
А),ДК;«? $A-d& E.18)
i AS,
Сумма в правой части может быть преобразована следующим
образом. Соседние между собой ячейки имеют общую поверхность
соприкосновения. Все внутренние ячейки находятся в соприкосновении
всей своей поверхностью с соседними ячейками. Поэтому в сумму
правой части E.18) интеграл по каждой поверхности внутри объема V
входит дважды как интеграл по соприкасающимся частям соседних
ячеек (рис. 14,6; dS,- противоположно dSy). Поскольку направление
нормалей в каждой паре этих интегралов противоположно, а вектор А
имеет один и тот же модуль, эти интегралы равны по абсолютному
значению, но противоположны по знаку. Следовательно, в сумме они
дают нуль, и соответственно в правой части E.18) все интегралы
по поверхности соприкосновения ячеек внутри объема V в сумме дают
нуль и остается лишь сумма интегралов по тем частям ячеек на гра-
границе объема V, которая не соприкасается с другими ячейками. Сумма
площадей этих внешних поверхностей ячеек, лежащих на границе объема
V, составляет площадь поверхности S, ограничивающей объем V
Следовательно,
? $A-dS = JA-dS, E.19)
¦ AS, s
причем это точное равенство, справедливое при любом разбиении
объема V на ячейки hV{.
Левая часть E.18) при ДК;->0 может быть выражена в виде
интеграла:
lim Y(divA),AFi = fdivAdK E.20)
Подставив E.19) в E.18) и перейдя к пределу, получим формулу
dS,
§ 5 Закон сохранения заряда 43
E 21)
которая называется формулой Гаусса — Остроградского. Она связывает
интеграл по объему от дивергенции вектора с потоком этого вектора
сквозь замкнутую поверхность, ограничивающую объем В математике
указываются условия применимости этой формулы, которые здесь
не перечисляются, поскольку в большинстве физически реальных си-
ситуаций они автоматически выполняются
Дифференциальная формулировка закона сохранения заряда. В фор-
формуле E 1) объем V и поверхность S не изменяются с течением
времени Следовательно, производную по времени в левой части E 1)
можно ввести под знак интеграла С другой стороны, правую часть
равенства можно по формуле Гаусса — Остроградского преобразовать
в интеграл по объему
E22)
Перенося все члены в E.1) в левую часть и принимая во внимание
E 22), получаем
-^-+divjW=O E 23)
Jt J
v
Это равенство справедливо для любого объема Очевидно, что
подынтегральное выражение тождественно равно нулю Доказательство
производят от противного Если в некоторой точке подынтегральное
выражение не равно нулю, то в качестве V можно взять маленький
объем вблизи этой точки, в пределах которого подынтегральное вы-
выражение сохраняет знак Интеграл по этой области не равен нулю,
что противоречит исходному равенству E 23) Поэтому подынтегральное
выражение равно нулю во всех точках. Тогда
dt
+ divj = O.
E 24)
Равенство E 24) является выражением закона сохранения заряда
в дифференциальной форме Оно называется также уравнением непре-
непрерывности.
Пример 5.1. Вычислить поток радиус-вектора сквозь поверхность круглого
цигиндра (рис 15) Расчет произвести непосредственно и с помощью формуаы
Гаусса — Остроградского
Поместим начало координат в центр основания цилиндра и направим
ось Z вдоль оси цилиндра (см рис 15) Тогда
Jr dS= Jr dS+ Jr dS + J r dS,
44
1. Заряды, поля, силы
где S,,, SB и S50K ~ соответственно площади ниж-
нижнего и верхнего оснований цилиндра и боковой
поверхности. Имеем:
j г • dS = 0, | г ¦ dS = hna2,
поскольку для точек на поверхности нижнего
Л .
и верхнего оснований г • dS = r dS cos (r, dS) = 0,
Л
r-dS = rdScos(r, dS) = /i4S. Наконец, для интег-
интеграла по боковой поверхности J г • dS = cunah,
s6ok
поскольку для точек на боковой поверхности
г ¦ dS = a dS. Следовательно,
Jr-dS = 3rca2fc. E.25)
15
¦ По теореме Гаусса — Остроградского
К вычислению потока радиус-
вектора через поверхность пря- J r- dS = J div t dV — 2na2h,
мого цнлнндра S У
E.26)
# Заряд сохраняется при
всех движениях и взаи-
взаимопревращениях носите-
носителей заряда.
Дивергенция характеризу-
характеризует мощность источников.
Формула Гаусса — Остро-
Остроградского связывает сум-
суммарную мощность источ-
источников в объеме с лото-
ком порождаемого источ-
источим ка'нм вектора через по-
поверхность, ограничиваю-
ограничивающую объем.
Заряд не является само-
самостоятельной сущностью,
независимой от материи,
он — одно из свойств ма-
материи.
О Какие две группы различных
фактов описываются поня-
понятием сохранения заряда ?
В чем физический смысл
равенства, выражаемого тео-
теоремой Гаусса—Остроград-
Гаусса—Остроградского?
Выполнение какого условия
необходимо потребовать,
чтобы из равенства нулю
интеграла следовало равен-
равенство нулю подынтегрально-
подынтегрального выражения?
где div г = 3, V — na2h (объем прямого круглого
цилиндра).
§ 6. Закон Кулона
Обсуждается точность эксперименталь-
экспериментальных проверок закона Кулона.
Экспериментальные проверки закона Ку-
Кулона. Закон Кулона для силы F взаимо-
взаимодействия двух точечных зарядов qx и q2,
находящихся на расстоянии г, имеет вид
Е1
4тге0
F.1)
где б0 = 1/Dл • 9 • 109) Ф/м. Он был установ-
установлен Ш. О. Кулоном A736-1806) в 1785 г.
посредством прямых измерений сил взаимо-
взаимодействия между заряженными телами, раз-
размеры которых много меньше расстояния
между ними. Точность опытов была неболь-
небольшой. Лишь из общих соображений, осно-
основанных на аналогии с силами тяготения,
существовала уверенность в абсолютной
правильности этого закона.
Закон Кулона F.1) входит в число основ-
основных экспериментальных фактов, на которых
построено учение об электричестве. Про-
Проверка его справедливости и установление
§ 6 Закон Кулона 45
границ применимости являются важнейшими задачами, на решение
которых были направлены значительные усилия экспериментаторов.
Проверка закона F.1) посредством прямого измерения сил взаимо-
взаимодействия с очень большой точностью затруднительна, поскольку
в распоряжении экспериментаторов нет покоящихся точечных зарядов.
Поэтому с результатами экспериментов обычно сравниваются след-
следствия из закона Кулона и на этой основе делаются заключения
о границах его применимости и точности
Первая экспериментальная проверка закона была проведена в 1772 г.
Г. Кавендишем A731 — 1810) за 13 лет до открытия его Кулоном.
Однако он не опубликовал своей работы и тем самым потерял приори-
приоритет на открытие. Рукопись, содержащая описание его опытов, была
найдена в архивах лишь примерно в конце 60-х годов XIX столетия.
Метод Кавендиша широко применялся и в последнее время позволил
проверить закон Кулона с большой точностью.
Задача экспериментальной проверки формулируется следующим
образом Закон взаимодействия представляйся в виде
F = const/r2 + *. F.2)
Требуется найти порядок малости а. Чем меньше | а |, тем ближе
закон взаимодействия к закону Кулона. Поэтому результат экспери-
эксперимента выражается в форме ограничения на а. | а [ ^ 8. Задача экспе-
эксперимента состоит в определении значения 5.
]у/|етод Кавендиша. Свободные заряды в однородном проводнике
располагаются на его поверхности. На первый взгляд это является
следствием отталкивания одноименных зарядов, в результате которого
они стремятся разойтись на максимальные расстояния, устремляясь
к поверхности проводника. Однако это неверно. Такая ситуация
возникает из-за того, что сила взаимодействия точечных зарядов убы-
убывает точно обратно пропорционально квадрату расстояния между ними,
а не по другому закону.
Из теории тяготения известно, что сферический однородный слой
вещества в полости, окруженной этим слоем, не создает никакой силы.
Отсюда следует, что если точечные электрические заряды взаимо-
взаимодействуют по закону обратных квадратов расстояний, то сферический
слой зарядов не создает никакой силы в этой полости.
Пусть заряд равномерно распределен по поверхности сферы с
поверхностной плотностью а (рис. 16). В точке Р внутри сферы
заряды, находящиеся на элементах поверхности dSx и dS2, создают
противоположно направленные силы dFt = a dS i/Dneorf) и dF2 =
= a dS2/DKE0rl). Из свойства касательных к концам хорды следует,
что углы 0Х и 82 между перпендикулярами к хорде и элементам
поверхности dSt и dS2 равны друг другу. Тогда dSx = dS'2/cos 8
и dS2 = dS/cos 8 Следовательно, dFx = a dS",/D7rEori cos 8), dF2 =
= ст dS'2/DnE0rj cos 8), где dS\/r\ = dQt и dS'2/r2 = d?22 — телесные углы,
под которыми dSi и dS2 видны из точки Р (они равны друг другу
по построению) Таким образом, равные по модулю силы dFt и dF2
46 1. Заряды, поля, силы
К теории метода Кавендиша
17
Возникновение силы со стороны
шарового слоя в точках внутри
сферы
противоположно направлены вследствие од-
Е5\ в ноименности зарядов на dSj и dS2. В ре-
' ,2„ зультате происходит взаимная компенсация
1 сил от всех пар противоположно располо-
расположенных элементов поверхности и полная
сила, действующая на пробный заряд в точ-
точке Р, равна нулю.
Если проводящему шару сообщить заряд,
то он вследствие сферической симметрии
равномерно распределится по поверхности
сферы. Отсутствие зарядов в объеме дока-
доказывается так. Пусть внутри шара имеются
некоторые заряды. Из-за сферической сим-
симметрии их распределение должно быть сфе-
сферически симметричным. Рассмотрим некото-
некоторый сферический слой зарядов. На заряды
слоя не действуют никакие силы со стороны
зарядов, находящихся вне полости, ограни-
ограниченной сферическим слоем, но на них дей-
действуют силы отталкивания со стороны за-
зарядов, находящихся в полости, ограниченной
сферическим слоем. А это означает, что
сферический слой зарядов начнет движение
от центра к периферии. Таким образом, при
равновесном распределении заряды внутри
проводящего шара отсутствуют.
Иначе обстоит дело, если закон взаимо-
взаимодействия отличается от кулоновского.
В этом случае в точке Р со - стороны
зарядов odSj и odS2, расположенных на
элементах поверхности dSt и dS2, действуют
силы:
dSj a const ¦
const
18
UF-, = const
dS2a
„2+а :
Метод Кавеидиша проверки за-
закона Кулона
cos 9
const ¦ а
cos 0
а 1
l 7f'
1
равнодействующая которых
F.3)
FА)
Если строго выполняется „.*.,-
закон Кулона, то заряд не равна нулю. В формуле F.4) А обозна-
праводящега шара рас- чает одинаковые множители перед \/г\ и
лределяется на его по- ]Д-« в ф 3)
ниРиХНотТИзакоРнИа ^Га Н™е СИ™ AF прИВОДИТ К В03М0Ж-
имеется заряд и в объеме ности равновесного распределения зарядов
шара. по всему объему проводящего шара, по-
§ 6. Закон Кулона 47
скольку на заряд внутри шара действуют силы не только со стороны
внутренних сферических слоев, но и внешних, причем характер их
действия зависит от знака ос.
Рассмотрим случай, когда ос > 0. При этом сила со стороны заряда
(а > 0), расположенного от точки Р (рис. 16) на более отдаленном
элементе поверхности, меньше, чем со стороны заряда на более
близком элементе поверхности. Следовательно, сила направлена в сто-
сторону более отдаленного элемента поверхности. Суммируя возможные
пары элементов поверхности, приходим к заключению, что результи-
результирующая сила F направлена к центру О (рис. 17). Следовательно, внутри
сферы радиусом ОР можно создать такое распределение заряда, при
котором сила в точке Р со стороны этого распределения компенсирует
силу со стороны зарядов во внешних сферических слоях. В результате
слой зарядов на сфере радиусом ОР может находиться в равновесии.
Нужно подобрать такое распределение плотности зарядов по радиусу,
чтобы в каждой точке внутри шара сила была равна нулю. Такое
распределение будет равновесным. Таким образом, при ос > 0 в заря-
заряженном проводящем шаре заряды присутствуют не только на поверх-
поверхности, как при ос = 0, но и в объеме. Аналогичный вывод получается
и при ос < 0. Можно произвести более детальный математический
подсчет и найти заряд в объеме шара как функцию от ос. Метод
Кавендиша состоит в измерении заряда в объеме шара и последующем
вычислении значения ос.
К проводящему шару (рис. 18) плотно примыкает разъемная про-
проводящая сферическая оболочка, состоящая из двух полусфер. Когда
она надета на шар, системе сообщается электрический заряд. Затем
оболочка с помощью изолирующих ручек отъединяется от шара и
исследуется оставшийся в нем заряд.
Если закон Кулона справедлив, то весь заряд находится на оболочке
и удаляется вместе с ней. Остающийся на шаре заряд равен нулю.
Если имеется отклонение от закона Кулона, то часть заряда
сосредоточится в объеме шара, а часть находится на оболочке. После
удаления оболочки на шаре остается некоторый заряд. Определив его,
можно оценить ос. Конечно, в экспериментах непосредственно можно
измерить не заряд, а потенциалы, что не меняет сути дела.
Кавендиш получил, что | ос | ^ 0,02. Примерно через сто лет
аналогичные опыты произвел Максвелл и нашел | ос | < 5 • 10~5.
В 1971 г. метод Кавендиша был усовершенствован. Опыт проводился
не в статическом режиме, а с помощью переменных по времени
потенциалов. Установка состоит из двух концентрических проводящих
сфер. На внешнюю подавалось переменное напряжение +10 кВ отно-
относительно земли. В случае отклонения от закона Кулона потенциал
внутренней сферы должен меняться относительно земли. Исследователи
могли фиксировать разность потенциалов меньшую, чем 1 пВ. Они
не обнаружили колебаний потенциала внутренней сферы, что позволило
принять | а | ^ | 2,7 ± ЗД | • 10~16.
48 1. Заряды, поля, силы
Этими опытами справедливость закона Кулона с указанной чрезвы-
чрезвычайно большой точностью подтверждена для расстояний от нескольких
миллиметров до десятков сантиметров.
|~[роверка закона для больших расстояний. Применить метод Кавен-
диша для проверки закона Кулона уже для расстояний, равных
нескольким метрам и больше, затруднительно. Для больших расстоя-
расстояний используют косвенные методы, обоснование которых лежит вне
классической теории электричества. Они используют квантово-механи-
ческие представления о взаимодействии частиц с учетом их волновых
свойств. Каждое взаимодействие обусловливается конкретным видом
частиц. Закон взаимодействия зависит от свойств частиц, обусловли-
обусловливающих взаимодействие и в первую очередь от их массы. Если масса
покоя частиц, ответственных за взаимодействие, равна нулю, то сила
взаимодействия обратно пропорциональна квадрату расстояний, а по-
потенциал взаимодействия обратно пропорционален расстоянию. Если же
у частиц, осуществляющих взаимодействие, масса покоя отлична от
нуля, то потенциал изменяется по закону ~A/г) ехр( — цг), где ц зави-
зависит от массы покоя частиц. При нулевой массе покоя ц равно нулю
и потенциал изменяется обратно пропорционально расстоянию, как
это должно быть при законе Кулона и законе тяготения Ньютона.
По современным представлениям электромагнитные взаимодействия
обусловливаются фотонами. Поэтому вопрос о справедливости закона
Кулона сводится к вопросу о равенстве массы покоя фотонов нулю.
Все частицы наряду с корпускулярными обладают также и волно-
волновыми свойствами. Энергия Еф фотонов связана с частотой и массой
соотношениями еф = йш и ц = игтс2, где h = 1,05 • 104 Дж • с — посто-
постоянная Планка, тщ — масса фотона. Эта масса больше массы покоя,
если таковая у фотона имеется. Поэтому, найдя верхний предел для
иг7, получим ограничение на массу покоя фотона. Доказав экспери-
экспериментально существование электромагнитных волн достаточно большой
длины, можно утверждать, что значение ту достаточно мало. Если бы
удалось продемонстрировать существование электромагнитных волн
бесконечной длины волны, то можно было бы утверждать, что масса
покоя фотона равна нулю и, следовательно, закон Кулона справедлив
абсолютно.
Наиболее длинные электромагнитные волны, которые удается
в настоящее время наблюдать, образуются в виде стоячих волн
в пространстве между поверхностью земли и ионосферой. Они назы-
называются резонансами Шумана. Наименьший резонанс Шумана соответ-
соответствует частоте v0 = 8 Гц. На основании этого с учетом расстояния
от поверхности земли до ионосферы и условий образования стоячих
волн для массы фотона получаем игт < 10~48 кг. Эта оценка показы-
показывает, что закон Кулона выполняется с чрезвычайно большой точностью,
поскольку неравенство | а | ^ 10~16 эквивалентно ту < 10~50 кг.
Проведены эксперименты, связанные с исследованием магнитного
поля с помощью спутников в околоземном пространстве и позволяю-
позволяющие определить точность выполнения закона Кулона на больших
§ 6. Закон Кулона 49
расстояниях. Установлено, что закон Кулона выполняется с чрезвы-
чрезвычайно большой точностью вплоть до расстояний порядка 107 м. Нет
сомнений, что и для больших расстояний закон Кулона также хо-
хорошо выполняется, однако прямых экспериментальных проверок не про-
проводилось.
Проверка закона для малых расстояний. Для малых расстояний
закон Кулона проверяется в экспериментах по взаимодействию эле-
элементарных частиц. Уже опыты Резерфорда позволили заключить, что
закон Кулона справедлив с большой точностью вплоть до расстояний
105 м. Последующие эксперименты по упругому рассеянию электро-
электронов при энергиях в несколько миллиардов электрон-вольт показали, что
закон Кулона справедлив вплоть до расстояний 107 м.
При интерпретации этих экспериментов используется квантовая
электродинамика.
Полевая трактовка закона Кулона. До работ Фарадея закон Кулона
трактовался с позиций дальнодействия, т. е. считалось, что одно
тело действует на другое как бы без посредников. Поэтому и назы-
называлась эта концепция как действие на расстоянии. В первой половине
XIX в. выработалась другая точка зрения на механизм взаимодействия,
согласно которой взаимодействие между телами осуществляется лишь
посредством непрерывной «передачи сил» через пространство между
телами. Такое представление получило название концепции близко-
действия. Она была введена в науку Фарадеем A791 — 1867) в ряде
работ, опубликованных в период с 1831 по 1855 г. Вместе с идеей
близкодействия в науку вошло представление о поле как посреднике,
осуществляющем взаимодействие. Первоначально функции посредника
приписывались среде, которая заполняет все мировое пространство. Эта
среда получила название Мирового эфира. Состояние эфира характери-
характеризовалось определенными механическими свойствами, такими, как упру-
упругость, натяжение, движение одних частей среды относительно других
И т. д. По этой трактовке сила, действующая на тело, является
следствием взаимодействия тела со средой в той точке, в которой
находится тело. Таким образом, механизм взаимодействия формули-
формулируется в виде локальных соотношений. Попытка математической фор-
формулировки этой механической картины передачи взаимодействий была
предпринята в 1861-1862 гг. Максвеллом A831-1879), пытавшимся
представить силы электромагнитного взаимодействия в виде механи-
механических сил, обусловленных натяжениями и давлениями в эфире. Затем
он перешел к феноменологической формулировке взаимодействия,
характеризуя состояние среды с помощью векторов Е, D, Н, В, кото-
которым, однако, не дается какой-то механической интерпретации. Следует
отметить, что при этом Максвелл не исключал возможности механи-
механического истолкования феноменологических уравнений. В 1864 г. он
сформулировал уравнения электромагнитного поля — уравнения Макс-
Максвелла. В дальнейшем выяснилось, что нельзя приписывать эфиру
механических свойств и нельзя говорить о движении относительно
50 1. Заряды, поля, силы
эфира. Надежда на механическое истолкование электромагнитных
взаимодействий потеряла право на существование. Но идея локальной,
формулировки взаимодействия и необходимость существования в про-
пространстве поля, которое осуществляет это взаимодействие, сохрани-
сохранились. Поле становится первоначальной сущностью и характеризуется
величинами, которые не могут быть интерпретированы в рамках
механических представлений. Это утверждение в наиболее четкой форме
было высказано в 1889 г. Герцем A857 — 1894), экспериментально
открывшим электромагнитные волны и сформулировавшим уравнения
Максвелла для вакуума в современном виде. Ясно, что поле существует
в пространстве и времени наряду с материей в виде атомов, молекул
и т. д.
Следовательно, поле есть также вид материи, обладающий свой-
свойственными для всякой материи характеристиками — импульсом, энер-
энергией и т. д.
Электрическое поле. Обозначим: F12 —силу со стороны заряда qx на
заряд q2; F21 —силу со стороны заряда q2 на заряд q,; r12 и r2i —
векторы, проведенные из точки нахождения первого заряда в точку
нахождения второго заряда, и наоборот. В соответствии с этим запишем
закон Кулона в виде:
q2, (a) F.5)
Лг
По своему физическому содержанию эти две формулы различны
и определяют силы, действующие на второй и первый заряд в точке
их нахождения, т. е. описывают силы в различных пространственных
точках. Но механизм возникновения этих сил одинаков. Заряды qi и q2
создают в окружающем их пространстве электрическое поле, которое
характеризуется напряженностью Е. Напряженность поля является
локальным понятием и имеет определенное значение в каждой точке
пространства. Напряженностью электрического поля в точке называется
величина^ равная отношению силы, с которой поле действует на
положительный заряд, помещенный в данную точку поля, к заряду.
Отсюда, однако, не следует, что для измерения напряженности поля
достаточно в точку пространства поместить положительный заряд
и измерять действующую на него силу.
Во многих случаях внесение заряда в данную точку сопровождается
сильным изменением напряженности электрического поля в ней и
результат измерения оказывается сильно искаженным (см. § 7).
С учетом сказанного формулы F.5) можно представить в виде:
Е2 = -±- 4^ —, (a) F, 2 = F2 = q2E2, (б) F.6)
<471Б0 Г12 Г12
§ 6. Закон Кулона 51
4пе0 г|, г.
21
-, (a) F21 = F, = 9lEu (б)
F.7)
Формула F.6а) описывает напряженность
электрического поля, образуемого точечным
зарядом qu а формула F.66) характеризует
силу, с которой поле с напряженностью Е2
действует на заряд, находящийся в точке
поля. Аналогичный смысл имеют и форму-
формулы F.7).
Таким образом, действие одного заряда
иа другой разделено на два этапа:
1. Точечный заряд q создает в окружаю-
окружающем его пространстве электрическое поле,
напряженность которого
где г — радиус-вектор, проведенный из точки
нахождения заряда до точки, в которой
определяется напряженность (рис. 19).
2. Точечный заряд q, находящийся в точке
поля с напряженностью Е, подвергается
со стороны этого поля действию силы
Е(<7<0)
F.9)
Формулировка второго этапа взаимодей-
взаимодействия, выражаемая формулой F.9), является
локальной: напряженность Е, заряд q и сила
F определяются в одной и той же точке.
Формулировка же первого этапа взаимодей-
взаимодействия, выражаемая формулой F.8), не явля-
является локальной: напряженность Е в левой
части F.8) зависит не только от точки, где
она определяется, но и от точки нахождения
источника поля. Другими словами, F.8)
является соотношением между величинами,
относящимися к различным точкам прост-
пространства, т. е. имеет нелокальный характер.
Локальная формулировка дана в § 13.
О границах применимости классической
концепции поля. Выше предполагалось,
что напряженность Е непрерывно и доста-
достаточно плавно изменяется в пространстве
и во времени. Однако в рамках квантовых
19
Полевая трактовка закона Ку-
Кулона
# Представление о класси-
классической непрерывном взаи-
подействни справедливо
лишь при условии мало-
малости действия отдельных
квантов по сравнению с
совокупным действием,
т. е. когда рассматривае-
рассматриваемое явление зависит от
одновременного действия
громадного числа квантов
и когда действие отдель-
отдельных квантов не проявля-
проявляется.
Определение напряженно-
напряженности электрического поля
не связано с малостью
пробных зарядов.
О На каком физическом зако-
законе основан иетод Кавенди-
ша для проверки закона Ку-
Кулона? Какова точность про-
проверки закона Кулона совре-
современными средствами по ме-
методу Кавендиша? Для каких
расстояний эти проверки
справедливы?
В чем состоит метод про-
проверки закона Кулона для
больших расстояний? До ка-
каких расстояний имеются пря-
прямые результаты проверки?
Каковы они?
На чем основана проверка
справедливости закона Ку-
Кулона для очень малых рас-
расстояний? Каковы результаты
проверки?
В чем отличие понятий элек-
электромагнитного поля и эфира?
52 1. Заряды, поля, силы
представлений сила взаимодействия между заряженными телами воз-
возникает в результате обмена фотонами. Отсюда следует дискретность
взаимодействия. А это означает, что напряженность Е нельзя пред-
представлять себе как непрерывную величину, плавно изменяющуюся
в пространстве и времени. Спрашивается, при каких условиях все же
можно считать ее непрерывной? Ясно, что это возможно лишь при
условии малости действия отдельных квантов по сравнению с сово-
совокупным действием, т. е. когда рассматриваемые явления зависят от
одновременного действия громадного числа квантов. Такая ситуация
осуществляется наиболее часто. Например, электрическая лампочка
мощностью 200 Вт на расстоянии 2 м дает поток фотонов видимого
света, равный примерно 1015 фотоновДсм2 • с). Площадь зрачка глаза
много меньше 1 см2, тем не менее число фотонов, попадающих в глаз
за 1 с, велико. Поэтому поток фотонов воспринимается как непрерыв-
непрерывный. Однако уменьшением интенсивности света можно добиться такого
положения, чтобы в глаз попадало лишь небольшое число фотонов
в секунду. При специальных условиях глаз способен воспринимать
отдельные фотоны в виде раздельных вспышек. В этом случае уже
нельзя пользоваться представлением о непрерывном потоке света.
Радиостанции ультракоротковолнового диапазона в СССР работают
на частотах 60 — 70 МГц. На расстоянии 10 км такая радиостанция
мощностью 200 Вт дает поток около 4-Ю1* квантовДсм2• с). Это
соответствует плотности 104 квантов/см3. Следовательно, в объеме,
равном кубу длины волны («64 м3), находится более 1011 квантов
излучения. При этих условиях также является затруднительной фикса-
фиксация поля отдельного кванта. В тех случаях, когда действие отдельных
квантов не проявляется, применимо классическое описание. Это воз-
возможно, когда число квантов велико, а импульс отдельного кванта мал
по сравнению с импульсом материальной системы. Например, излу-
излучение отдельного атома нельзя рассматривать классически, потому что
число фотонов до излучения равно нулю, а после излучения имеется
только один фотон.
§ 7. Принцип суперпозиции
Анализируется физическое содержание прин-
принципа суперпозиции и обсуждаются границы
'его применимости.
Лринцип суперпозиции для взаимодействия точечных зарядов. Силы
взаимодействия двух точечных изолированных зарядов определя-
определяются законом Кулона F.1). Изменится ли эта сила, если вблизи
двух взаимодействующих зарядов имеется еще один точечный заряд?
Чтобы вопрос имел однозначный смысл, необходимо уточнить, что
понимается под силами взаимодействия двух зарядов в присутствии
третьего заряда (все заряды предполагаются неподвижными).
Если под силами взаимодействия понимать силу, направленную
вдоль линии, соединяющей взаимодействующие заряды, то эти силы
§ 7. Принцип суперпозиции 53
зависят от третьего заряда и к тому же не удовлетворяют требованию
равенства действия и противодействия. Трудность состоит в том, что
можно измерить силу, действующую на заряд, но не ясно, как разли-
различить в ней вклады от отдельных зарядов. Однако третий точечный
заряд ничем не отличается от рассматриваемых двух зарядов и все
три заряда равноправны. Поэтому постановку вопроса можно изменить.
Имеются три взаимодействующих заряда. Экспериментально измеряе-
измеряемыми величинами являются силы, действующие на каждый из зарядов.
Закон сложения сил по правилу параллелограмма известен. Спраши-
Спрашивается, равна ли измеряемая сила, действующая на каждый из зарядов,
сумме сил со стороны двух других зарядов, если эти силы вычислять
по закону Кулона F.1)"? Отметим,* что здесь говорится об экспери-
экспериментальном измерении силы и о математическом вычислении сил по
закону F.1) и их сложении по правилу параллелограмма. В такой
постановке вопрос имеет вполне определенный смысл и ответ на него
можно получить из эксперимента. Исследования показали, что всегда
измеряемая сила равна сумме вычисляемых по закону Кулона сил
со стороны двух зарядов. Этот экспериментальный результат выра-
выражается в виде следующих утверждений:
а) сила взаимодействия двух точечных зарядов не изменяется
в присутствии других зарядов;
б) сила, действующая на точечный заряд со стороны двух точеч-
точечных зарядов, равна сумме сил, действующих на него со стороны каж-
каждого из точечных зарядов при отсутствии другого.
Это утверждение называется принципом суперпозиции. Оно отражает
экспериментальный факт, составляющий одну из основ учения об
электричестве. По своей роли в учении об электричестве он столь же
важен, как, например, закон Кулона. Обобщение на случай многих
зарядов очевидно.
Полевая формулировка принципа суперпозиции. Рассмотрим силу F3,
действующую на точечный заряд qb при наличии двух других
зарядов ql и q2 (рис. 20). Обозначим F13 и F23 - силы, действующие
на заряд q3 со стороны зарядов qt и q2, когда нет зарядов q2 и qt.
Принцип суперпозиции утверждает, что
F3 = F13 + F23. G.1)
Обозначим: Е13 и Е23 - напряженности электрического поля, созда-
создаваемого зарядами qx и q2 в точке с зарядом q3 при отсутствии
заряда q2 или qr соответственно. По формуле F.9) имеем:
. G-2)
Перепишем выражение G.1):
G.3)
Сила в электрическом поле возникает в результате действия поля
на заряд. Следовательно, сила F3 в G.3) свидетельствует о на-
54 1. Заряды, поля, силы
линии в точке нахождения заряда q3
электрического поля с напряженностью Е3,
которая обусловливает эту силу [см. F.9)],
т. е.
F3 =
G.4)
20
Принцип суперпозиции
Подставляя G.4) в G.3) и сокращая получен-
полученное выражение на общий множитель qz,
находим
Е3 = Е13 + Е23. G.5)
Равенство G.5) является полевой формули-
формулировкой принципа суперпозиции: напряжен-
напряженность поля двух точечных зарядов равна сум-
сумме напряженностей, создаваемых каждым из
зарядов при отсутствии другого. Она яв-
является локальной, поскольку все величины
относятся к одной точке пространства.
Обобщение на случай многих зарядов
очевидно:
Сила взаимодействия двух
точечных зарядов не из-
изменяется в присутствии
других зарядов, а сила
взаимодействия заряжен-
заряженных тел, вообще говоря,
изненяется в присутствии
других заряженных тел.
Пробный заряд предпо-
предполагается достаточно ма-
малым. Однако это требо-
требование не имеет отношения
к принципу суперпозиции,
который остается справед-
справедливый при любых значе-
значениях пробного заряда.
О Почему сила взаимодействия
двух заряженных тел, вооб-
вообще говоря, изменяется в при-
присутствии третьего заряженно-
заряженного тела? Является ли это
нарушением принципа супер-
суперпозиции?
Какие экспериментальные
факты позволяют судить о
справедливости принципа су-
суперпозиции вплоть до очень
больших напряженностей
электрического поля?
G.6)
т. е. напряженность поля любого числа то-
точечных зарядов равна сумме напряженно-
напряженностей полей каждого из точечных зарядов
при отсутствии всех других.
Дробные заряды. Из определения напря-
напряженности электрического поля следует,
что ее измерение сводится к измерению
силы, действующей на точечный заряд. То-
Точечный заряд, с помощью которого опреде-
определяется напряженность, называется пробным.
Возникает вопрос о величине пробного за-
заряда. Если предположить, что все точечные
заряды, суммарная напряженность поля ко-
которых вычисляется, закреплены неподвижно
в точках пространства, то пробный заряд
может быть любым. Если же положения
точечных зарядов не фиксированы в прост-
пространстве, то пробный заряд своим действием
на эти заряды может сместить их в другие
точки пространства. В этом случае будет
найдена не та напряженность, которая была
в точке нахождения пробного заряда при
первоначальном положении всех зарядов,
§ 8. Магнитное поле 55
а другая напряженность, возникшая в результате перемещения за-
зарядов в новое положение под влиянием пробного заряда. Во избе-
избежание этого надо уменьшить воздействие пробного заряда на заряды,
создающие исследуемое поле. Поэтому пробный заряд должен быть
достаточно малым. Однако необходимо отметить, что это требование
не имеет отношения к принципу суперпозиции, а лишь обеспечивает
соблюдение условий, при которых напряженность исследуемого поля
существенно не изменяется самим актом измерения.
р'раницы применимости принципа суперпозиции. Экспериментальными
свидетельствами справедливости принципа суперпозиции является
согласие полученных с его помощью выводов с результатами экспе-
экспериментов. Установлено, что принцип суперпозиции соблюдается вплоть
до очень больших напряженностеи полей. Его правильность для
напряженностеи полей в несколько миллионов вольт на метр (электро-
(электротехника, ускорители, высоковольтные разряды и т. д.) хорошо подтверж-
подтверждается всей инженерной практикой. Более значительные напряженности
поля имеются в атомах и ядрах. На орбитах электронов в атомах
они равны Е « 10п-1017 В/м. Рассчитанные в соответствии с прин-
принципом суперпозиции разности энергетических уровней атомов подтверж-
подтверждены экспериментально с большой степенью точности (относительная
погрешность не более 10). Это означает, что и принцип суперпози-
суперпозиции при напряженности внутриатомных полей соблюдается с большой
точностью. На поверхности тяжелых ядер напряженности достигают
громадных значений (Е « 1022 В/м). Экспериментальные данные сви-
свидетельствуют, что и для этих громадных напряженностеи принцип
суперпозиции выполняется. Однако в этом случае появляются другие
эффекты, а именно, при напряженности около 1020 В/м возникает
поляризация вакуума в результате возникновения электронно-позитрон-
ных пар. Это приводит к квантово-механической нелинейности взаимо-
взаимодействия.
§ 8. Магнитное поле
Анализируется релятивистская природа маг-
магнитного поля. Из закона Кулона с помощью
релятивистских преобразований выводится
закон взаимодействия параллельных провод-
проводников.
Леобходимость возникновения магнитного поля при движении заря-
зарядов. Взаимодействие точечных неподвижных зарядов полностью
описывается законом Кулона. Однако закон Кулона недостаточен для
анализа взаимодействия движущихся зарядов, причем такой вывод сле-
следует не из конкретных особенностей кулоновского взаимодействия,
а обусловливается релятивистскими свойствами пространства и времени
и релятивистским уравнением движения.
56 1. Заряды, поля, силы
Это утверждение в принципе вытекает из таких соображений.
Релятивистское уравнение движения
= F (8.1)
инвариантно и имеет одинаковый вид во всех инерциальных системах
координат, в частности в системе координат К', которая движется
равномерно и прямолинейно относительно К:
dp'/dt' = F. (8.2)
Буквы со штрихами обозначают величины, относящиеся к К'.
В левые части этих уравнений входят чисто механические величины,
поведение которых при переходе из одной системы координат в другую
известно. Следовательно, можно связать между собой некоторой фор-
формулой левые части уравнений (8.1) и (8.2). Но тогда оказываются
связанными между собой стоящие в правой части этих уравнений силы.
Наличие такой связи обусловливается требованием релятивистской
инвариантности уравнения движения. Поскольку в левые части урав-
уравнений (8.1) и (8.2) входят скорости, заключаем, что сила взаимо-
взаимодействия движущихся зарядов зависит от скорости и не сводится
к кулоновской силе. Тем самым доказывается, что взаимодействие
движущихся зарядов осуществляется не только кулоновской силой, но
также силой другой природы, называемой магнитной. Ее существование
выявляется из следующего примера взаимодействия зарядов.
взаимодействие точечного заряда и бесконечной прямой заряженной
нити. Конечно, самым простым является кулоновское взаимодей-
взаимодействие двух точечных зарядов, которые покоятся в системе координат К'.
Однако в другой системе координат К, движущейся относительно К',
эти заряды движутся с одинаковыми скоростями и их взаимодействие
усложняется, поскольку из-за движения зарядов электрическое поле
в каждой точке пространства переменно. Поэтому целесообразно
выбрать ситуацию, которая является достаточно простой как в системе
координат К', где заряды покоятся, так и в системе координат К,
где они движутся. Сравнительно простым является взаимодействие
точечного заряда и бесконечной прямой заряженной нити.
В системе координат К' нить покоится и направлена вдоль оси X'
(рис. 21). Точечный заряд q расположен на оси У на расстоянии у'о
от нити. Обозначим' S'o — площадь поперечного сечения нити, счи-
считая его линейные размеры очень малыми по сравнению с расстоянием
до точечного заряда. Если объемная плотность заряда р', то на эле-
элементе длины dx' нити находится заряд dg' = p'S'o dx'. Для определен-
определенности предполагаем, что заряд нити и точечный заряд положительны.
В этом случае силы, действующие на точечный заряд со стороны
заряда в элементе нити, направлены так, как показано на рис. 21.
По закону Кулона
dFx = "Ру cQs = gPSodx
4тгео(/о2 + х'2) " 4тге0 (у'о2 + х'2) v '
§ 8 Магнитное поле 57
Принимая во внимание, что cos ot = -х'/(у'о2 + х'2I/2, sm ot = у'0/(у'о +
+ х'2I'2, для комполент силы получаем
* 4яв0 J (^ + x'2K'2 ' ** 4us0 J (>tf + x'2K'2
Первый интеграл равен нулю, поскольку в подынтегральном выра-
выражении стоит нечетная функция, а для вычисления второго интеграла
целесообразно произвести замену переменных х' = — у'о ctg ос, dx' —
— у'о doc/sm2 ос, 1 + ctg2 ос = 1/sin2 ос Тогда
(8 5)
Кроме того, F'z = 0 Принимая во внимание, что заряд в данный
момент покоится, и обозначая т0 массу носителя заряда, получаем для
ускорения заряда в системе К' следующие выражения
а'х = О, а'у = F'y/m0 = qp'S'o/Bneoy'omo), a'z = 0 (8 6)
Теперь рассмотрим это взаимодействие в системе координат К,
движущейся относительно системы К' со скоростью v в направлении
отрицательных значений оси AT'. Направим ось X вдоль нити так,
чтобы ее положительное направление совпадало с положительным
направлением оси X', и будем считать эту систему неподвижной.
В системе координат К система К', нить и заряд движутся в направ-
направлении положительных значений оси X со скоростью v
Вычислим силу кулоновского отталкивания со стороны движущейся
нити на движущийся заряд Вследствие инвариантности заряда
точечный заряд q неизменен В результате сокращения движущихся
масштабов на метр длины движущейся нити приходится большее число
зарядов, чем на метр длины неподвижной, т е тотность зарядов
движущейся нити больше, чем неподвижной В предшествующих рас-
расчетах плотность зарядов неподвижной нити обозначалась р' Поэтому
плотность зарядов движущейся нити в системе координат К равна
р = p'/l/l - t;2/c2, (8 7)
где |/1 — у2/с2 учитывает релятивистское изменение движущихся мас-
масштабов Все дальнейшие вычисления совершенно аналогичны расчетам
для покоящейся нити Поскольку длины в перпендикулярном скорости
v направлении остаются неизменными, то площадь поперечного сече-
сечения движущейся нити и расстояние от нити до точечного заряда будут
неизменными Поэтому вместо (8 5) получаем
/« = 0, /, = qpS0/Bmoyo), /. = 0, (8 8)
58 1. Заряды, поля, силы
dF'
причем здесь кулоновская сила обозначена
маленькой буквой, чтобы отличить ее от
полной силы, действующей на заряд, кото-
которая не сводится к кулоновской силе. Под-
Подставляя (8.7) во второе из уравнений (8.8),
находим
X'
fy = qp'S0/Bneoy0 ]/l - v2
21 = <7р'?о/BтгеоУо 1/1 - v2/cl) = F'y/tfl - v2/c2,
К вычислению силы взаимоден-
ствия точечного заряда и бес- где S = S> у = у „ принята во внимание
конечной прямой заряженной формула (g 5)
Найдем полную силу, действующую на
точечный заряд в системе координат К.
Вследствие симметрии сила направлена
d*2 _? вдоль оси У и связана с импульсом урав-
I \ ~х2 нением движения
/,Г \>^ F, = dp,/dt. (8.10)
| —*¦ „i^* ^ " системе координат К' эта связь имеет
dx, AT, вид
22 F'y = dp'y/dt'. (8.11)
Взаимодействие двух параллель- т-г i ?¦
ных токов ' По формулам преобразования теории от-
относительности
Р'у =РУ, х" = * " , 2 (Р = "/с), (8-12)
• Для описания взаимодей- "Г 1 "*" т*1с
ствия движущихся заря- где и'х — компонента скорости частицы в
^улоГТтГГвод^сГ системе к°°РДинат К\ причем в данном
дует не из конкретных случае и'х = 0. С учетом (8.12) из (8.10) на-
особенностей кулоновско- ХОДИМ
го взаимодействия, а обус-
ловливается релятивист- р = d /d[ = (dp'/d/') (dt'/dt) =
скнми свойствами про- у у у
странства и времени и ре-
релятивистским уравнением „ .. . о _ч
движения. Сравнение (8.13) с (8.9) показывает, что
Магнитное взанмодейст- г _ /1 _ R2\ f (ЧЛА\
вие сравнимо с злектри- Г у ~ У1 Р ) J y> IP-1V
ческим лишь прн доста- т е кулоновская сила отталкивания f боль-
^аГ^м силы Fy, действующей па движущийся
не менее оно может про- заряд со стороны движущейся нити. Следо-
являться и прн очень вшпелъно, кроме кулоновской силы отталкива-
малых скоростях, если ку- ния на зарЯд действует еще другая сила,
сутствует. случае является силой притяжения. Она
§ 8. Магнитное поле 59
возникает в результате движения зарядов и называется магнитной.
Полевая трактовка взаимодействия для магнитной силы формули-
формулируется аналогично полевой трактовке электрического взаимодействия:
движущийся заряд создает в окружающем его пространстве магнитное
ноле; на движущийся заряд со стороны магнитного поля действует сила.
релятивистская природа магнитного поля. Из (8.14) видно, что маг-
магнитная сила равна
FyM = Fy-fy= -v2fy/c2. (8.15)
Знак минус означает, что сила направлена к заряженной нити, т. е.
является силой притяжения. Как видно из (8.15), эта сила описывается
величиной второго порядка малости по v/c относительно кулоновского
взаимодействия. Следовательно, магнитное взаимодействие сравнимо
по величине с электрическим лишь при достаточно больших скоростях
заряженных частиц. Тем н е менее оно заметно и при малых ско-
скоростях зарядов, если кулоновское электрическое взаимодействие по
каким-то причинам не проявляется. Такая ситуация осуществляется,
например, при наличии электрического тока в проводнике. В этом
случае электрическое поле движущихся зарядов нейтрализуется элект-
электрическим полем зарядов проводника противоположного знака, т. е.
экранируется. В результате остается одна лишь магнитная сила,
ничтожно малая по сравнению с кулоновской силой, если бы она
не была экранирована. Например, при типичных скоростях дрейфа
электронов в металлическом проводнике (см. § 31) магнитная сила
меньше кулоновской более чем в 1020, тем не менее она достаточно
большая и проявляется в виде взаимодействия проводников с током.
Поэтому чисто релятивистский эффект возникновения магнитного
поля проявляется при любых скоростях и не только при достаточно
больших.
уы взаимодействия параллельных проводников с током. Представим
себе, что заряды движутся в тонкой цилиндрической проволоке,
которая в целом электрически нейтральна Тогда кулоновские силы
со стороны движущихся зарядов, образующих электрический ток,
экранируются зарядами противоположного знака проволоки и вне
проволоки действует лишь магнитная сила (8.15). Следовательно, вокруг
проводника с током проявляется действие магнитной силы на движу-
движущиеся заряды, которые образуют электрический ток. При этом возни-
возникает магнитное взаимодействие токов. Это получается как результат
релятивистского анализа взаимодействия движущихся зарядов. Однако
магнитное взаимодействие токов было открыто задолго до создания
теории относительности.
Предположим, что движущиеся заряды составляют линейный ток,
текущий по проводнику, параллельному исходному току, текущему
вдоль оси X и расположенному на расстоянии г от него (рис. 22).
Величины, относящиеся к исходному току, обозначим с индексами 1,
а к линейному — с индексами 2. На каждый заряд тока 12 со стороны
60 1. Заряды, поля, силы
тока /j действует магнитная сила притяжения Fm (8.15), которую
удобно с учетом (8.8) представить в виде
ту с2 2neor 2ne0c2 r 2neoc2 r '
где PlvSol =It [cm. D.11) и D.14)], r = y0 [см. (8.8)].
Обозначим «2 линейную концентрацию зарядов на втором провод-
проводнике. На элементе длины dxz находится пг dx2 зарядов, на которые
действует магнитная сила
dFm = Fm,H2 dx2. (8.17)
Подставляя в (8.17) выражение (8.16), находим
-, (8.18)
где qvn2 = /2. Кроме того, в теории магнетизма вместо постоянной е0
принято использовать ц0 = 1/(е0с2) — магнитную постоянную. Тогда
[см. (8.18)]
(8.19)
Она характеризует взаимодействие прямолинейных токов в беско-
бесконечных параллельных проводниках. Необходимо отметить, что условием
применимости (8.19) является малость поперечных размеров проводни-
проводников по сравнению с расстоянием между ними (тонкие проводники,
линейные токи).
Единица силы тока. Из формулы (8.19) видно, что на длину /2 про-
проводника приходится сила
Fml=-~- ^-12. (8.20)
2п г
Знак минус показывает, что при одинаковых направлениях 1Х и 12
между проводниками действует сила притяжения. Если же направления
токов /, и 12 различны, то возникает сила отталкивания.
На основе (8.20) дается определение единицы силы тока: ампер
есть сила постоянного тока, который, будучи поддерживаемым в двух
параллельных прямолинейных проводниках бесконечной длины и ничтож-
ничтожно малого кругового сечения, расположенных на расстоянии 1 м один
от другого в вакууме, вызывает между этими проводниками возникно-
возникновение силы, равной 2-Ю'1 Н на метр длины. Полагая в (8.20)
/, = 12 = 1 А, г = 1 м, /2 = 1 м, Fm, = -2- 10 Н, находим
цо=4я-1О-7 Н/А2. (8.21)
Как было отмечено [см. (8.19)],
= 1/с2, (8.22)
§ 9 Сила Лоренца. Сила Ампера 61
где с — скорость света в вакууме. Это соотношение отражает глубокую
связь, существующую между электрическими и магнитными полями
и характеризуемую фундаментальной физической константой с, равной
скорости света. Природа этой связи станет ясной при изучении электро-
электромагнитных волн (см. гл. 9).
]У[агнитное поле. В полной аналогии с полевой трактовкой кулонов-
ского взаимодействия (см. § 6) можно переформулировать процесс
возникновения силы (8.18) в виде двух этапов: порождение током It
магнитного поля в окружающем ток пространстве и действие магнит-
магнитного поля на движущийся заряд или ток. Однако законы возникнове-
возникновения магнитного поля и действия силы оказываются более сложными,
чем в законе Кулона, так как зависят от взаимной ориентации тока
и скорости заряда. Кроме того, текущий по бесконечно длинному
проводнику ток h не подходит для роли элементарного объекта,
взаимодействие точечного заряда с которым можно считать элемен-
элементарным актом. Поэтому необходимо вернуться к анализу действия сил
на точечные движущиеся заряды или элементы тока.
§ 9. Сила Лоренца. Сила Ампера
Обсуждаются релятивистские свойства сил
Лоренца и Ампера.
преобразование сил. В § 8 на частном примере было показано, как,
исходя из предположения о релятивистской инвариантности уравне-
уравнения движения, можно получить закон преобразования силы при пере-
переходе от одной системы координат к другой. Обобщим этот метод
на более общий случай.
Как обычно, система координат К' движется относительно системы
К в направлении положительных значений оси X со скоростью v.
Рассмотрим движение материальной точки под действием заданных
сил. Пусть проекции силы в системе координат К' равны (F'x, F'y, F'z),
а в К — (Fx> Fy, Fz). В общем случае соответствующие проекции
этих сил в различных системах координат не равны между собой.
Однако между ними имеются вполне определенные соотношения, обеспе-
обеспечивающие инвариантность уравнений движения, т. е. их одинаковый вид
в различных системах координат:
dpjdt = Fx, dpjdt = Fy, dpjdt = Fz, (9.1)
dp'Jdf = F'x, dp'Jdt' = Fy, dp'Jdt' = F'z. (9.2)
Левые части этих уравнений преобразуем с помощью формул
теории относительности для импульса и преобразований Лоренца:
p'x + {E'/c2)v
Р* = ^~~ > Ру = Ру Р* = Р» (9.3)
62 1. Заряды, поля, силы
где Е = т'с2 — полная энергия материальной точки, р = v/c. Формулы
(9.1) приводятся к виду:
dt
_ p>
dp, dt' d Г pi + (E'/c2) v "I dt'
~ dt' dt ~ dt' |_ л/\ _ q2 J dt ~
vu'Jc2
F =
dPy dP;
y dt dt' dt
dt' dt 1 + vu'Jc2
(9.4)
(9.5)
(9-6)
где (u'x, u'y, u'2) — скорость точки в системе К'; F'x, F'y, F'z в правые части
(9.4)-(9.6) вошли в результате использования уравнений движения (9.2).
При вычислении (9.4) принята во внимание формула
dF
^r = F'-"', (9-7)
выражающая закон сохранения энергии в системе координат К'.
С помощью формул сложения скоростей
и, =
(9.8)
(9.9)
Для упрощения (9.5) и (9.6) необходимо важное соотношение, ко-
которое получается из формул для преобразования скоростей. Запишем
прямые и обратные преобразования, например ^'-проекции скорости:
1 + vujc1 ' "z 1 + vu'Jc1
выражение (9.4) приведем к виду
F =F' + --"~ " ¦ mJc2
1 + vujc1
-, «у =
1 - vujc2 '
Перемножая почленно левые и правые части этих равенств и сокра-
сокращая полученные равенства на общий множитель иуи'у, находим
1 +
VU.
= 1 -
Учитывая (9.10), преобразуем формулы (9.5) и (9.6):
1 - vujc2
-F'
Г у,
(9.10)
(9.11)
§ 9. Сила Лоренца. Сила Ампера 63
1 - mjc2
Таким образом, с помощью формул (9.9), (9.11) и (9.12) сила в си-
системе координат К выражена через силу в системе К'. По принципу
относительности нетрудно написать и обратные формулы преобразо-
преобразования.
При выводе этих формул не делалось никаких предположений
о свойствах исходных сил — они могут зависеть от координат, времени
и скорости. Кроме того, не предполагалось, что в какой-то из систем
координат частица является покоящейся, поскольку на скорость частиц
не налагалось ограничений. Полученные формулы показывают, что
зависимость сил от скорости в релятивистской теории неизбежна:
даже если в какой-то системе координат ее нет (например, F'x, F'y, F'z),
в других системах координат она неизбежно появляется (в данном
случае Fx, Fy, F2 зависят от скорости их, иу, и, частицы).
Запишем формулы преобразования сил в векторной форме. Для
этого введем следующие обозначения:
Ф = (F'x, F;//l - р2, Fzf\/\ - р2), (9.13)
G = [0, -(vie2) Fi/j/l - р2, (р/с2) F',/\/l - Р2]. (9.14)
Нетрудно проверить, что с помощью (9.13) и (9.14) формулы (9.9),
(9.11) и (9.12) записываются в виде векторного равенства
F = Ф + и х G. (9.15)
Так как F — вектор, то и вся правая часть — век гор. Равенство
справедливо для произвольных и. Следовательно, каждое из слагаемых
в правой части является вектором. Поскольку u x G и и — векторы,
заключаем, что G тоже вектор. Тем самым доказано, что определяемые
равенствами (9.13) и (9.14) величины Фи G являются векторами.
(^ Лоренца. Предположим, что в системе координат К' имеется
только электрическое поле и, следовательно, сила (F'x, F'y, F'z) не зави-
зависит от скорости и' частицы. Тогда Ф [см. (9.13)] не зависит от ско-
скорости и частицы и представляет собой электрическую силу в системе
координат К.
Аналогично заключаем, что вектор G также не зависит от скорости
и частицы, а может зависеть лишь от координат и времени. Поэтому
зависимость силы от скорости частицы содержится во втором слагае-
слагаемом (9.15):
Fm = и х G. (9.16)
Это магнитная сила, направленная перпендикулярно скорости части-
частицы и вектору G, представляющему магнитное поле, которое действует
на движущуюся частицу.
64 1. Заряды, поля, силы
Поскольку Ф в формуле (9.15) представляет электрическую силу,
действующую на заряд q, то напряженность
Е = Ф/q. (9.17)
Аналогично, индукция магнитного поля
B=G/q. (9.18)
С учетом (9.17) и (9.18) формула (9.15) для силы, действующей на
точечный заряд, записывается в виде
F = ^Е + qu х В.
(9.19)
Это — сила Лоренца. Первое слагаемое в правой части характеризует
силу, действующую на точечный заряд со стороны электрического поля,
а второе — со стороны магнитного.
ЭДндукция магнитного поля. Поскольку сила, действующая со стороны
магнитного поля на движущийся заряд, описывается вектором В,
то естественно назвать этот вектор напряженностью магнитного поля.
Однако историческое название напряженности магнитного поля закре-
закрепилось за другим вектором, который обозначается Н. Этот вектор
не является полевой характеристикой магнитного поля, он учитывает
свойства материальной среды, в которой поле существует. В частности,
при заданном Н вектор В, а следовательно, и сила, действующая на
движущийся заряд, могут иметь самые различные значения (см. § 38).
За вектором В установилось название индукции магнитного поля.
Ампера. Пусть имеется совокупность точечных зарядов, кон-
концентрация которых равна п. Тогда в элементе объема dV имеется
ndV зарядов. Если все они движутся со скоростью и и на каждый
из них действует магнитная сила, определяемая вторым слагаемым
в (9.19), то на заряды в элементе объема dV действует сила
dFm = nq dVu х В. (9.20)
В дальнейшем нет необходимости у силы писать индекс т, пока-
показывающий, что эта сила «магнитная». Сила действует одинаково на
заряд независимо от своего происхождения. Учитывая, что
щ = р, nqa = pu = j, (9.21)
где р и j — плотность зарядов и плотность тока [см. D.4) и D.11)],
запишем формулу (9.20) в виде
dF=puxBd7, (9.22)
или
(9.23)
dF = j х BdK
Соотношение (9.23) называется законом Ампера и определяет силу,
§ 9. Сила Лоренца. Сила Ампера 65
действующую на элемент электрического
тока с плотностью j, заключенного в объ-
объеме dV.
|"|ереход от объемных токов к линейным.
Формулу (9.23) можно представить и
в другом виде. Допустим, что электрический
ток течет по тонкому проводнику, площадь
поперечного сечения которого So. Рассмот-
23
„ , _„. Переход от объемных токов к
рим элемент длины d/ проводника (рис. 23). яа^иым: jdc
Объем этого элемента dF = SQ dl. Из-за
малости площади поперечного сечения про-
проводника можно считать, что плотность j
тока через сечение проводника постоянна и,
следовательно,
= Sq/.
(9.24)
Пусть dl совпадает по направлению с
вектором плотности тока, текущего по этому
участку проводника. Тогда
jdF=jSodi = IdL (9.25)
Электрический ток в каждой точке про-
странства имеет, вообще говоря, различную
плотность и поэтому называется объемным.
Сила, действующая на такой ток в элементе
объема dV, определяется формулой (9.23).
Если же ток проходит по тонким провод-
проводникам (в пределе бесконечно тонким в фи-
физическом смысле), то он называется линей-
линейным. В этом случае можно говорить об
элементе тока на длине dl проводника.
Переход от формул, выведенных для объем-
объемных токов, к формулам для линейных токов
дается соотношением (9.25), которое целесо-
целесообразно представить в виде °
jdF?±/dL
(9.26)
Стрелки показывают, что эта замена
позволяет перейти как от формул для
объемных токов к формулам для линейных
токов, так и наоборот.
В частности, формула (9.23) для линейных
токов принимает вид
= /dlx В.
(9.27)
Формулы преобразования
силы получаются из тре-
требования инвариантности
релятивистского уравне-
уравнения движения.
В релятивистской теории
неизбежна зависимость
сил от скорости. Даже
если в какой-то системе
координат сила не зависит
от скорости, в другой си-
стене координат, движу-
движущейся относительно пер-
первой, появляется зависи-
зависимость силы от скорости.
Если формулы преобразова-
преобразования силы получаются из
требования инвариантности
релятивистского уравнения
движения, то нельзя ли от-
отсюда заключить, что закон
преобразования силы являет-
является физически бессодержа-
бессодержательный утверждением, про-
простой тавтологией требования
релятивистской инвариант-
инвариантности ?
Почеиу непосредственно из
вида формул (9.13) и (9. 14)
нельзя заключить, что Ф
и G — векторы!
3 А. Н. Матвеев
66 1. Заряды, поля, силы
Формула (9.27) отражает основную идею Ампера — свести взаимо-
взаимодействие контуров с током к взаимодействию бесконечно малых
элементов токов.
]у1агнитное поле прямолинейного тока. Сравнивая формулы (9.27) и
(8.19), заключаем, что ток, текущий по бесконечному прямолиней-
прямолинейному проводнику, создает магнитное поле, силовые линии которого
являются окружностями, концентрическими току и лежащими в
плоскостях, перпендикулярных току. Индукция магнитного поля на
расстоянии г от центра проводника с током выражается формулой
*-?? (9.28)
полученной с помощью теории относительности из закона Кулона
с учетом принципа суперпозиции для напряженности электрического
поля и инвариантности заряда. Из принципа суперпозиции для напря-
напряженности электрического поля можно сделать заключение о справед-
справедливости также и принципа суперпозиции для индукции магнитного поля.
§ 10. Закон Био — Савара
Рассматриваются полевая трактовка взаи-
взаимодействия токов и закон Био — Савара.
взаимодействие элементов тока. Закон взаимодействия токов был
открыт экспериментально задолго до создания теории относитель-
относительности. Он значительно сложнее закона Кулона, описывающего взаимо-
взаимодействие неподвижных точечных зарядов. Этим и объясняется, что
в его исследовании приняли участие многие ученые, а существенный
вклад внесли Био A774-1862), Савар A791-1841), Ампер A775-1836)
и Лаплас A749-1827).
В 1820 г. X. К. Эрстед A777—1851) открыл действие электрического
тока на магнитную стрелку. В этом же году Био и Савар сформули-
сформулировали закон для силы dF, с которой элемент тока / d/ действует на
магнитный полюс, удаленный на расстояние г от элемента тока:
dF~/d/cp (ос) /(/•), A0.1)
где а — угол, характеризующий взаимную ориентацию элемента тока
и магнитного полюса. Функция <р(<х) вскоре была найдена эксперимен-
экспериментально. Функция /(г) теоретически была выведена Лапласом в виде
/(г) ~ 1/г2. A0.2)
Таким образом, усилиями Био, Савара и Лапласа была найдена
формула, описывающая силу действия тока на магнитный полюс.
В окончательном виде закон Био — Савара — Лапласа был сформули-
сформулирован в 1826 г. в виде формулы для силы, действующей на магнит-
магнитный полюс, поскольку понятия напряженности поля еще не суще-
существовало.
§ 10. Закон Био - Савара 67
В 1820 г. Ампер открыл взаимодействие токов — притяжение или
отталкивание параллельных токов. Им была доказана эквивалентность
соленоида и постоянного магнита. Это позволило четко поставить
задачу исследования: свести все магнитные взаимодействия к взаимо-
взаимодействию элементов тока и найти закон их взаимодействия как
фундаментальный закон, играющий в магнетизме роль, аналогичную
закону Кулона в электричестве. Ампер по своему образованию и
склонностям был теоретиком и математиком. Тем не менее при
исследовании взаимодействия элементов тока он выполнил очень
скрупулезные экспериментальные работы, сконструировав ряд хитро-
хитроумных устройств. Станок Ампера для демонстрации сил взаимодей-
взаимодействия элементов тока и их зависимости от углов до сих пор исполь-
используется на лекциях. В результате Ампер открыл закон взаимодействия
элементов тока. К сожалению, ни в публикациях, ни в его бумагах
не осталось описания пути, каким он пришел к открытию. Однако
формула Ампера для силы отличается от A0.3) наличием в правой
части полного дифференциала. Это отличие несущественно при
вычислении силы взаимодействия замкнутых токов, поскольку интеграл
от полного дифференциала по замкнутому контуру равен нулю. Учи-
Учитывая, что в экспериментах измеряется не сила взаимодействия эле-
элементов тока, а сила взаимодействия замкнутых токов, можно с полным
основанием считать Ампера автором закона магнитного взаимодействия
токов. Используемая в настоящее время формула для взаимодействия
элементов тока была получена в 1844 г. Грассманом A809—1877) и имеет
в современных обозначениях вид
A0.3)
где dF12 — сила, с которой элемент тока /j dlt действует на элемент
тока /2d/2; г12 — радиус-вектор, проведенный от элемента тока /t dlt
к /2 dl2 (рис. 24); пунктиром обозначены замкнутые контуры, взаимо-
взаимодействие элементов тока в которых не рассматривается.
Сила dF21, с которой элемент тока /2dl2 действует на /х dll5
дается, конечно, той же формулой A0.3), но с заменой индекса 2 на 1:
На рис. 24 единичными векторами п21 и п12 показано направление
сил dF21 и dFl2, перпендикулярных соответствующим элементам тока.
Эти силы, вообще говоря, не коллинеарны друг другу. Следовательно,
взаимодействие элементов тока не удовлетворяет третьему закону
Ньютона:
dF21+dF12^0. A0 5)
68 1. Заряды, поля, силы
\
I
Сила, с которой ток /ь текущий по
замкнутому контуру. Lu действует на замк-
замкнутый контур L2 с током /j, на основании
A0.3) равна
р МЛ Г Г dl2 х (dh x r12)
4тс
я*
г\г
A0.6)
Силы токов 1и 12 вынесены за знак
интеграла, поскольку постоянны во всех
точках соответствующих контуров Lj и L2
интегрирования. Аналогичный вид. имеет
формула для силы F2b действующей на
замкнутый контур с током /t. Для сил
взаимодействия замкнутых контуров с то-
Взаимодействие элементов тока ком третий закон Ньютона (см. § 39) вы-
выполняется:
24
21
Fu = 0.
A0.7)
25
Магнитная индукция прямоли-
прямолинейного участка тока конечной
длины
Экспериментальное под-
подтверждение формул для
магнитного поля, получен-
полученных с помощью реляти-
релятивистских преобразований
из формул для электри-
электрического поля, служит не
только доказательством
существования ногнитно-
го поля, но :И подтверж-
дает его релятивистскую
природу.
Г\б экспериментальной проверке закона
взаимодействия. Строго говоря, закон
взаимодействия элементов тока A0.3) нель-
нельзя проверить экспериментально, потому что
не существует изолированных элементов
тока / dl, силу взаимодействия между кото-
которыми можно было бы измерить. Каждый
элемент тока — это часть замкнутого кон-
контура тока и поэтому экспериментально про-
проверяется лишь закон взаимодействия замкну-
замкнутых токов A0.6). Из справедливости A0.6)
не следует, однако, справедливость A0.4),
потому что к A0.4) можно добавить любую
функцию, которая при интегрировании по
замкнутым контурам после подстановки
в A0.6) дает нуль.
Электрический ток обусловлен движением
зарядов. Поэтому формула A0.4) выражает
также закон магнитного взаимодействия дви-
движущихся зарядов, который из нее нетрудно
получить и проверить экспериментально,
поскольку силу взаимодействия между дви-
движущимися зарядами можно измерить. Наи-
Наиболее же полной экспериментальной провер-
проверкой этой формулы является согласие с
опытом ее следствий, которые весьма много-
многочисленны.
§ 10. Закон Био - Савара 69
ролевая трактовка взаимодействия, в полной аналогии ? электроста-
электростатикой взаимодействие элементов тока представляется двумя стадия-
стадиями: элемент тока It dlt в точке нахождения элемента тока I2 dl2 создает
магнитное поле, взаимодействие с которым элемента I2 dl2 приводит
к возникновению силы dF12. Действие магнитного поля с индукцией
В на /dl описывается формулой (9.27). С ее учетом две стадии
взаимодействия описываются так:
1) элемент тока Ii dlx создает в точке нахождения элемента тока
l2 dl2 магнитное поле с индукцией
A0.8)
dB12 =
Цо
4тг
/xd
i x
3
Г12 .
J
2) на элемент тока /2dl2, находящийся в точке с магнитной ин-
индукцией dB12, действует сила
х dB, 2.
A0.9)
^ Био-Савара. Соотношение A0.8), описывающее порождение
магнитного поля током, называется законом Био —Савара. Для
замкнутого тока I
A0.10)
где г — радиус-вектор, проведенный от элемента тока / dl к точке,
в которой вычисляется индукция В магнитного поля. Интегрирование
в A0.10) производится по замкнутому контуру тока. Ток предполагается
линейным. Переход к объемным токам совершается в соответствии
с правилом (9.26). Для объемных токов закон Био — Савара A0.10)
принимает вид
A0.11)
Здесь интегрирование производится по всем областям пространства,
где имеются объемные токи, характеризуемые плотностью тока j.
i взаимодействия прямолинейных токов. Элемент тока /t dxi
(рис. 22) в точке нахождения элемента /2 dx2 создает поле с индук-
индукцией dB12, которая направлена перпендикулярно плоскости чертежа
к нам, а по модулю равна
Но h d*i sin « nn n,
dB12 = -7IT Z2 ¦ A0-12)
Следовательно, индукция магнитного поля, создаваемого прямо-
70 1. Заряды, поля, силы
линейным током 1и текущим по бесконечному проводнику в точке
нахождения элемента тока I2dx2 [см. A0.10)], выражается формулой
(ШЗ)
Mi Г sinadxt _'ц0 Ii
где для вычисления интеграла используется замена переменных, про-
проведенная при получении формулы (8.5). Формула A0.13) совпадает с (9.28).
Формула Ампера приводит к заключению, что сила dF12 в магнит-
магнитном поле с индукцией A0.13) действует на элемент тока I2 dl2 пер-
перпендикулярно проводнику с током 12 и направлена к току 1и т. е.
является силой притяжения:
dFl2 = ^I-^dx2. A0.14)
Формула A0.14) совпадает с (8.19).
Пример 10.1. Определить индукцию магнитного поля, создаваемого конечным
прямолинейным участком проводника длиной I, по которому течет ток I
(рис. 25).
Напряженность поля от каждого элемента проводника направлена перпен-
перпендикулярно плоскости чертежа и в соответствии с законом A0.10) равна
4л г3
поскольку dl х г перпендикулярно плоскости чертежа. Тогда
| dl х г | = dlr sin (dlfV) = ulr sin p = dyd,
поэтому
4k
a
\
С помощью этой формулы можно вычислить индукцию поля любого кон-
контура с током, состоящего из прямолинейных отрезков.
Пример 19.2. Определить индукцию магнитного поля на оси кругового тока
I радиусом г0 (рис. 26).
Воспользуемся законом A0.11):
__ ц0/ fdlxr
где г = г0 + h, dl х г = dl х r0 + dl х h. При интегрировании модуль г не изме-
изменяется, поэтому
В = ^—(f dl x r0 + $ dl x h). A0.15)
§ 10. Закон Био - Савара 71
Поскольку h — постоянный вектор, находим
L L
так как § dl = 0 Другой интеграл, входящий в
A0 15), вычисляется следующим образом
| dl х г0 = § w0 dl = nr0 § dl = пго2яго,
L L L
где п - единичный вектор, перпендикулярный
плоскости, в которой протекает ток /
Тогда /"
в* = "^у- — Г°2г/2а A0Л6) 26
Магнитная индукция на оси вит-
Пример 10.3. Кольцами Гельмгопца называ- ка с током
ют два коаксиальных кольцевых проводника оди-
одинакового радиуса, расположенных в параллельных
плоскостях, расстояние d между которыми равно
радиусу колец.
Доказать, что магнитное поле на оси колец
Гельмгольца на середине расстояния между ними
однородно с высокой точностью.
Поместим начало декартовой системы коор-
координат в центр одного из колец и ось Z направим
вдоль оси колец (рис 27) Индукция поля на оси
колец в точке с координатой z в соответствии
с A0.16) равна
A0 17)
где / — сила тока в кольце.
Неоднородность В2 в первом приближении
характеризуется первой производной
z-d 1
BBZ = 3n0Jrg Г
dz 2 L
-z
27
К расчету взаимодействия двух
круговых токов
A0 18)
При z = d/2 получаем дВ2/дг = 0, тогда
S2BZ _ Ъ\1п1г1 f 5z2
dz2 ~
2 K^ + rgO'2 (z2 +
5(z-dJ 1
- dJ
-dJ
Для колец Гельмгольца d = r0 и при z =
= d/2 (82B2/Sz2) = 0 Это показывает, что поле
вблизи точки z = d/2 на оси колец Гельмгольца
действительно однородно с высокой степенью
точности.
A0 19) 0 Силы взаимодействия эле-
элементов тока не удовлетво-
удовлетворяют третьему закону
Ньютона.
Силы взаимодействия
замкнутых контуров с то-
током удовлетворяют треть-
третьему закону Ньютона.
72 1. Заряды, поля, силы
28
Соленоид конечной длины
Пример 10.4. Имеется прямой круглый соле-
соленоид длиной L, состоящий из п витков тонкого
провода, прилегающих плотно друг к другу. Найти
индукцию на оси соленоида, если через его витки
течет ток I.
Поскольку витки очень плотно прилегают
друг к другу, можно с достаточной точностью
считать, что каждый виток создает поле на оси
соленоида в соответствии с формулой A0.16).
Плотность намотки равна njL. Можно принять,
что на длине dz соленоида течет ток (In/L)dz.
Помещая начало системы координат в точку оси
соленоида на половине его длины (рис. 28),
находим с помощью формулы A0.16), что ин-
индукция на оси соленоида в точке z
L/2
ЦОп1
2L
2L
f
z +
-L/2
-z + L/2
- w? + ri:
L/2 }
г + r2]3/2
11/2" h "
q Поскольку элементов тока
в изолированном виде не су-
существует, в каком смысле
можно говорить о прямой
Жспериментальной проверке
формулы для взаимодейст-
взаимодействия элементов юка?
Какой вывод можно сделать
из того факта, что силы
взаимодействия элементов
тока не удовлетворяют
третьему закону Ньютона,
а замкнутых токов — удов-
удовлетворяют?
A0.20)
Для очень длинного соленоида (L-> oo) в
точках z <K L/2 иэ A0.20) получаем
Нт Вг = \ionl/L. A0.21)
Поле бесконечно длинного соленоида не
только постоянно вдоль оси, но и однородно
по его сечению [см. (8.38)].
§ 11. Преобразование волен
Исходя из инвариантности уравнения дви-
движения заряда в электромагнитном поле
выводится закон преобразования полей.
Инвариантность выражения для силы в
электромагнитном поле. Выражение (9.19)
для силы Лоренца, действующей на точеч-
точечный заряд в электромагнитном поле, полу-
получено из требования инвариантности реляти-
релятивистского уравнения движения. Следователь-
Следовательно, это выражение также должно быть
§ 11. Преобразование полей 73
релятивистски инвариантным, т. е. иметь одинаковый вид во всех систе-
системах координат. Таким образом, в системах координат К и К' выраже-
выражения для сил имеют вид:
F = <z(E+uxB), A1.1)
F = g(E' + u'x В'). A1.2)
Используя релятивистскую инвариантность выражения для силы,
представленной формулами A1.1) и A1.2), и учитывая (9.9), (9.11) и (9.12),
можно получить соотношения между векторами электрических и маг-
магнитных полей в различных системах координат.
Частный случай преобразования векторов полей уже был рассмот-
рассмотрен ранее, а именно: было показано, что если в системе координат К'
имеется только электрическая напряженность, то в системе К появляется
Также и магнитная индукция. Можно было бы аналогично показать,
что если в некоторой системе координат имеется только магнитная
индукция, то в другой появляется, вообще говоря, и напряженность
электрического поля. Рассмотрим связь между электрическими и маг-
магнитными полями в общем случае.
^^образование полей. Подставим в формулу (9.11) вместо Fy и Fy
их выражения из A1.1) и A1.2):
Е, + (мА - uxBz) = 1^1^ [Е; + (u'zB'x - u'xB'z)l A1.3)
Исключая из A1.3) величины и'х и u'z с помощью формул сложения
скоростей
их - v uz l/l - р2
«х = г~ тт. и'г = -Р- rV A1.4)
1 - vux/c2 1 - vux/c2 v '
И группируя все члены в левой части A1.3), находим
A1.5)
Это равенство справедливо при произвольных значениях их и uz.
Следовательно, выражения, стоящие в скобках A1.5), по отдельности
равны нулю. Приравнивая их нулю, получаем формулы преобразования
для векторов поля:
Е'у + vB'z _ B'z + (v/c2)Ey
t = (ll(>> Bx-Bx,[l\.l) Bz = ¦ ^ . (U.8)
y ^f> (> xx,) z ^
Аналогично, исходя из (9.12), получаем формулы преобразования
Для других компонент:
Е, = Е\ ~ vB>> , (U.9) В» = Bi, A1.10) Ву д *> ~М?}_Ъ_. A1.11)
74 1. Заряды, поля, силы
Вывод преобразования х-проекции силы удобно обосновать на
формуле (9.4), записанной: в виде
Fr =
A1.12)
Поступая так же, как и в предыдущих случаях, приводим равенство
A1.12) к форме
+ ~f) Iе* + ("А - «АИ - К + W - «ВД = ^-(Е' • «4 (П.13)
где F • и'= #Е'¦ и'. Воспользовавшись формулами A1.8) и A1.11), нахо-
находим, что
Е* = Е*. A1.14)
Таким образом, формулы преобразования для векторов электро-
электромагнитного поля имеют вид:
A1.15)
? - ?*Н
-db;
я» = в'х,
в _в;-
в -в; +
(Р/С
(f/c
. -
2)Е,
—- 9
2)Е'У
Обратные формулы преобразования векторов поля по принципу
относительности получают из формул A1.15) заменой v-* —v, величин
со штрихом на величины без штриха и наоборот.
Применения формул A1.15). формулы A1.15) позволяют найти векторы
электромагнитного поля в любой инерциальной системе координат,
если только они известны в какой-либо одной из них.
В качестве примера изучим поле заряженной бесконечной нити.
Нить неподвижна и расположена в системе координат К' вдоль оси X'.
Следовательно, в этой системе координат имеется только электрическое
поле, напряженность которого дается формулами (8.5) с учетом опре-
определения напряженности. Поэтому вместо (8.5) для напряженности
электрического поля получаем выражения:
Е'х = О, Е'У = p'So/Bneoy'ol Е'г = 0. A1.16)
Ось Y может иметь любое направление, перпендикулярное нити.
Из формулы A1.16) заключаем, что напряженность электрического поля
заряженной бесконечной нити направлена по перпендикулярам к нити
и убывает обратно пропорционально первой степени расстояния от нее.
Магнитное поле в системе координат К' отсутствует, поскольку заряды
неподвижны.
§ 11. Преобразование полей 75
В системе координат К нить движется вдоль своей длины в направ-
направлении положительных значений оси X со скоростью v. Напряженность
электрического поля на основании A1.15) равна
Ех = О, ЕУ = Еу/}/1 - р2 = p'S'o/Bneuy'o ]/i - р2), Ег = 0, A1.17)
что эквивалентно (8.8), поскольку напряженность равна отношению
силы к заряду.
Формулы A1.15) показывают, что наряду с электрическим полем
движущаяся заряженная нить создает в окружающем ее пространстве
также и магнитное поле, индукция которого
-о в -
iv/c2)E'y vp>s'°
— ¦ = —
l/l-p2
что эквивалентно формуле (8.15) с учетом (8.9), если только от силы/у
перейти к индукции магнитного поля в соответствии с формулами
(9.18) и (9.16), т. е. разделить /, в (8.15) на qv. Очевидно, что магнитные
силовые линии являются концентрическими окружностями, лежащими
в перпендикулярных нити плоскостях (рис. 29); центр окружностей
лежит на нити.
При решении конкретных задач необходимо выбрать такую систему
координат, в которой электромагнитное поле было бы наиболее
простым, что упрощает решение задачи. Не следует думать, что
всегда существует такая система координат, где поле сведется либо
к электрическому, либо к магнитному. Существуют такие конфигура-
конфигурации электромагнитного поля, когда в любой системе координат
существуют одновременно и электрическое и магнитное поля. Общее
рассмотрение данного вопроса производится с помощью анализа
инвариантов электромагнитного поля относительно преобразования
Лоренца (см. § 62).
|"|оле точечного заряда, движущегося равномерно и прямолинейно.
Совместим начало декартовой системы координат К' с точечным
зарядом q. В этой системе напряженность электрического поля описы-
описывается законом Кулона, а магнитное поле отсутствует:
Е' = -2- ~, В = 0, A1.19)
4тс? г'3
где г'г = х'2 + у'г + z'2. В системе координат К заряд q движется
со скоростью v в направлении положительных значений оси X. Оси
координат системы К' ориентированы таким образом, что в момент
времени t' = t = 0 они совпадают с соответствующими осями системы
К. Подставляя A1.19) в A1.15) и используя преобразования Лоренца,
получаем
FP,i^l gy(x-vt)
^l
г'3 " 4я?0 [у2 (х - vtJ + у2 + z2]3'2 '
76 1. Зарвды, поля, силы
где
- v2/c2)m -
A1.21)
Обозначая xq координату заряда q в си-
системе К в момент t, когда определяется
напряженность поля в точке (х, у, z), пере-
перепишем A1.20) в виде
г, Ч У (х- хд)
о [у2 (х - х„J +
z2-]3/2 »
A1.22)
29 поскольку х, = vt — закон движения заряда
Силовые линии магвитного по- В системе К.
ля движущейся вдоль своей дли- Аналогично находим и две другие ком-
ны заряженной нити поненты напряженности электрического по-
поля:
Л
Если в некоторой системе
координат имеется только
электрическое поле, то в
другой появляется также
и магнитное, и наоборот.
Подходящий выбором си-
системы отсчета можно по-
постараться добиться наибо-
наиболее простой конфигурации
электрического и магнит-
магнитного полей или устронить
одно из них. Однако не
всегда существует такая
система отсчета, где поле
сводится либо к электри-
электрическому, либо к магнит-
магнитному.
Какими способами можно,
исходя из формул преобра-
преобразования величин от системы
К' к системе К, получить
формулы преобразования
тех же величин от системы К
к системе К'? На примере
формул A1.15) проверьте,
что оба способа приводят
к одинаковому результату.
Является ли поле быстро
движущегося точечного за-
заряда центральным? цент-
центрально-симметричным?
Л П
4пе0 [у2 (х - xqf +y2 + z2]3'2 '
4пе0 [у2 (* - xqJ
(Ц23)
П12
Индукция магнитного поля определяется
с помощью формул A1.15). Результат удоб-
удобнее записать в векторной форме:
B = (l/c2)vxE, A1.25)
где Е определяется формулами A1.22)—
A1.24). Видно, что линии В образуют кон-
концентрические окружности с центром на
оси X, вдоль которой движется заряд q.
Конфигурация поля заряда, движущегося
равномерно и прямолинейно, с течением
времени не изменяется, а меняется лишь
положение этой конфигурации относительно
неподвижной системы координат К, т. е.
неизменная конфигурация поля движется
вместе с зарядом. Изучим ее в тот момент,
когда заряд находится в начале системы
координат К, т. е. при xq = 0. В этом случае
[см. A1.22)-A1.24)]
Е =
Ч
уг
4пг0 {ух2 + у2 + z2K'2 '
A1.26)
где г — радиус-вектор, проведенный от точки
нахождения заряда q в точку, где определя-
определяется Е. Таким образом, напряженность на-
Задачи 77
правлена вдоль радиус-вектора, однако ее значение зависит от направ-
направления радиус-вектора. Обозначим 8 — угол между направлениями скоро-
скорости v заряда и радиус-вектора. Тогда х = г cos 8, уг + z2 = г2 sin2 8, ух2 +
+ у1 + z2 = jr2y2 (* - Р2 sin2 8), р = с/с и формула A1.26) принимает вид
- г 1 - р2
Е =
4та0 г3 A - р2 sin2 0K/2
Отличие электрического поля движущегося заряда от поля непод-
неподвижного заряда сводится к сильной зависимости напряженности поля
движущегося заряда от направления. По линии движения заряда
(9 = 0; 9 = л) и перпендикулярно ей (8 = ±тг/2) напряженность соот-
соответственно равна:
(П.27)
4кеог2
При релятивистских скоростях (р « 1) напряженность поля движу-
движущегося Заряда на заданном от него расстоянии мала по линии движения
заряда и велика в перпендикулярном направлении, т. е. поле как бы
концентрируется вблизи плоскости, проведенной через заряд перпенди-
перпендикулярно его скорости.
Задачи
1.1. Вычислить div r.
1.2. Вычислить grad (г • А), где А —
постоянный вектор.
1.3. Вычислить div (со х г), где со -
постоянный вектор.
1.4. Вычислить div (г/г).
1.5. Вычислить div [A х (r х В)], где
А и В — постоянные векторы.
1.6. Чему равна индукция магнитного
поля в центре квадратного кон-
контура со стороной а, по которому
протекает ток П
1.7. Проводник намотан по спирали
на цилиндрический изолятор ра-
радиусом а и образует п полных
витков. Угол подъема спирали ра-
равен а. Определить магнитную
индукцию в центре цилиндриче-
цилиндрического изолятора, если по обмотке
течет ток /.
1.8. Два точечных заряда q и — q
расположены соответственно в
точках (а, 0, 0), (-о, 0, 0) Найти
напряженность электрического по-
поля в точке (х, у, z).
1.9. Заряд распределен с линейной
плотностью т на длине L вдоль
радиус-вектора, начинающегося в
точке нахождения точечного за-
заряда q Расстояние от q до бли-
ближайшей к нему точки линейного
заряда равно R. Найти силу, дей-
действующую на линейный заряд
1.10. Два заряда распределены с оди-
одинаковой линейной плотностью т
на длине L параллельно и нахо-
находятся на расстоянии I друг от
друга (рис. 30). Найти силу взаи-
взаимодействия между ними.
30
Два участка проводника ко-
конечной длины
78 1. Заряды, поля, силы
1.11. Диск имеет поверхностный заряд
с плотностью <т = аг2, где г —
расстояние от центра диска. Ра-
Радиус диска равен г0. Найти напря-
напряженность поля на перпендикуляре
к плоскости диска, проведенном
через его центр на высоте h.
1.12. Две равномерно заряженные по-
поверхности параллельны плоско-
плоскости X, Y и пересекают ось Z
в точках zi = a-i и z2 = сц > «i-
Поверхностные плотности заря-
зарядов одинаковы, но противопо-
противоположны по знаку (стА = — <т2). Най-
Найти напряженность электрического
поля во всех точках пространства.
V
31
Обозначения углов в выбран-
выбранной системе координат
1.13. Найти напряженность электри-
электрического поля в точке Р, создан-
созданного заряженной нитью длиной
L (рис. 31). Линейная плотность
заряда т. Точка Р лежит в
плоскости Z, Y, что, однако, не
ограничивает общности решения,
поскольку поле аксиально сим-
симметрично.
1.14. Бесконечно длинный цилиндр
кругового сечения заряжен рав-
равномерно с поверхностной плот-
плотностью ст. На оси цилиндра
расположена бесконечно длинная
нить, равномерно заряженная с
линейной плотностью т. При ка-
каком условии напряженность
электрического поля вне ци-
цилиндра равна нулю?
1.15. Внутри шара радиусом а распре-
распределен заряд с объемной плот-
плотностью р = а ]/г. Найти напря-
напряженность электрического поля.
1.16. Пучок круглого сечения радиу-
радиусом 1 мм, состоящий из прото-
протонов, ускорен разностью потен-
потенциалов 10 кВ. Предполагая, что
плотность протонов по сечению
пучка постоянна, найти объемную
плотность электрического заряда
в пучке при токе 5-10~6 А.
Ответы
1.1. 3. 1.2. г-А/г. 1.3. 0. 1.4. 2/г. 1.5. 2 (А-В). 1.6. 2\/2цо1/(п1).
17 ^°1п 1 18 Е- q ( <* ~ Q>j* + У'г (x + a)ix + yiy \
Ъа
1.9. F =
4гсе0К (К + L)
2h2
¦?)¦"-]¦ ¦•"•
г2 + 2й2 1
° 2 1/2— 2й . 1.12. Ег = 0 при z < аг и z > а2; Ez =
при аг < z < a2.
1.14. т = -2гсгст.
1.13. Е = —-—[(sin Q(i + sin а2) i» - (cos а, - cos а2) ij.
4яеог
1.15. Е = — ]/г г, 0 < г < а; Е = — \- при г> а. 1.16. р = 1,15 х
7е0 7е0 Г
хГб Кл/м3.
§12
Постоянное
электрическое поле
§13
Дифференциальная
формулировка
закона Кулона
§14
Потенциальность
электростатического поля
§15
Электростатическое поле
в вакууме
Постоянное
электрическое
поле
§
Электростатическое поле
при наличии проводников
§17
Электростатическое поле
при наличии диэлектриков
§
Энергия электростатического
поля
§19
Силы в электрическом поле
Постоянные электрические поля не су-
существуют в природе, поскольку нет не-
неподвижных элементарных зарядов. Од-
Однако если в бесконечно малом физи-
физическом объеме сумма элементарных за-
зарядов каждого знака примерно по-
постоянна, а средняя скорость близка
к нулю, то порождаемое ими поле на
достаточно большом расстоянии от
объема почти постоянно. Оно назы-
называется постоянным электрическим по-
полем. Моделью заряда, порождающего
такое поле, является неподвижный то-
точечный заряд. Совокупность точечных
зарядов может образовывать объем-
объемный, поверхностный и линейный за-
заряды. При переходе к модели не-
непрерывного распределения заряда эти
совокупности характеризуются объем-
объемной, поверхностной и линейной плот-
плотностями заряда.
80 2. Постоянное электрическое поле
§ 12. Постоянное
электрическое поле
Обсуждается идеальная модель постоянного
электрического поля и границы ее примени-
применимости.
Неподвижный заряд В электростатике изучаются электрические поля
¦неподвижных зарядов. Предполагается, что заряды удерживаются
в различных точках пространства силами неэлектростатического про-
происхождения, природа которых в рамках электростатики не уточняется.
Например, в электростатике исследуются распределение зарядов на
поверхности проводника, создаваемое ими электрическое поле, дей-
действующие силы, но не рассматривается, почему эти заряды не покидают
поверхности проводника. Природа сил, удерживающих заряды на
поверхности проводника, не изучается в рамках электростатики. Ана-
Аналогичный смысл имеет выражение «заряд q находится в точке (х, у, z)
в вакууме». Предполагается, что заряд q как бы закреплен в точке
(х, у, z) пространства, причем в непосредственной близости от заряда
нет никаких материальных частиц (вакуум). Ясно, что такое представ-
представление является идеализацией.
?ущество модели.Неподвижных элементарных зарядов не существует,
а потому не существует и постоянных полей. Однако в большинстве
явлений, изучаемых в классической теории электричества, наблюдается
не поле отдельного элементарного заряда, а суперпозиция полей многих
зарядов. Вклад поля отдельного элементарного заряда в суперпозицию
полей весьма мал. К этому следует добавить, что напряженность
электрического поля определяется как средняя величина по некоторому
физически малому объему и физически малому отрезку времени.
Флуктуации среднего значения напряженности поля весьма малы.
Именно эти средние значения и являются предметом •изучения класси-
классической теории электричества и магнетизма. Поэтому, строго говоря,
существенным для электростатики является не неподвижность зарядов,
а постоянство во времени электрического поля. Другими словами,
в модели постоянных полей идеализацией является не постоянство
поля, а неподвижность порождающих его зарядов.
ураницы применимости модели. Поскольку модель основывается
на существовании полей с очень малыми флуктуациями средних
значений, а не на существовании неподвижных зарядов, ее границы
определяются требованиями малости вклада от отдельных элементар-
элементарных зарядов в наблюдаемое поле. Отсюда, например, следует, что
электродинамика не применима к движению отдельных электронов
в атоме. Их движение в атомах описывается квантовой теорией.
§ 13. Дифференциальная формулировка закона Кулона 81
§ 13. Дифференциальная формулировка
закона Кулона
Анализируются физические факторы, обу-
обусловливающие справедливость теоремы Га-
Гаусса. Дается дифференциальная формули-
формулировка закона Кулона и обсуждаются ее
следствия.
Теорема Гаусса. Электростатическая теорема Гаусса устанавливает
математическую связь между потоком напряженности сквозь замкну-
замкнутую поверхность и зарядом, находящимся в объеме, ограничиваемом
этой поверхностью.
Пусть точечный заряд q находится внутри объема V, ограниченного
замкнутой поверхностью S (рис. 32). Рассмотрим поток N напряжен-
напряженности Е сквозь эту поверхность:
tf = §E-dS. A3.1)
s
Напомним, что для замкнутых поверхностей в качестве положи-
положительного всегда выбирается направление в сторону внешней нормали.
Это означает, что элемент площади поверхности dS в A3.1) направлен
во внешнюю сторону от объема (рис. 32). По закону Кулона
— 1 я г
е0
Т* г
Следовательно, интеграл в A3.1) можно представить так:
A3.3)
s
Учтем соотношение
— dScos(ifdS) = dS', A3.4)
где dS' — проекция площади элемента dS на плоскость, перпендику-
перпендикулярную радиус-вектору г. Из геометрии известно, что
d?2 = dS'/r2, A3.5)
Где dfi — телесный угол, под которым элемент площади dS' виден
из начала отсчета радиус-векторов, в данном случае совпадающим
с местонахождением точечного заряда q. С учетом A3.4) и A3.5) выра-
выражение A3.3) принимает вид
4ле0 J
A3.6)
S
Полный телесный угол, под которым видна замкнутая поверхность
из точек внутри ограничиваемого ею объема, равен 4тс, т. е.
82 2. Постоянное электрическое поле
и поэтому из A3.6) получаем
N = ф0.
A3.7)
A3.8)
32
Вычисление потока вектора на-
напряженности сквозь замкнутую
поверхность в случае нахожде-
нахождения точечного заряда внутри объ-
объема, ограничиваемого поверх-
поверхностью
D
Поток Е сквозь замкнутую поверхность,
если точечный заряд находился вне объема,
ограничиваемого поверхностью, вычисляется
аналогично (рис. 33) и определяется форму-
формулой A3.3). Однако теперь подынтегральное
выражение принимает как положительные,
так и отрицательные значения: в тех точках
поверхности, где угол (г, dS) меньше я/2, оно
положительно, а где больше — отрицательно.
Это означает, что на поверхности ADB
подынтегральное выражение положительно,
а на АСВ — отрицательно. Поэтому элемен-
элементы телесного угла A3.5) на поверхности
ADB положительны, а на АСВ — отрицатель-
отрицательны. Обозначим телесный угол при вершине
конуса, образованного касательными из точ-
точки О к рассматриваемой поверхности, По
(рис. 33). Тогда
33
Вычисление потока вектора на-
напряженности сквозь замкнутую
поверхность в случае нахожде-
нахождения точечного заряда вие объема,
ограничиваемого поверхностью
¦ Теорема Гаусса выражает
связь между потоком на-
напряженности электриче-
электрического поля сквозь замкну-
замкнутую поверхность и заря-
зарядом в объеме, ограничен-
ограниченном этой поверхностью.
Физической основой тео-
теоремы Гаусса является за-
закон Кулона или, иначе,
теорема Гаусса является
интегральной формули-
формулировкой закона Кулона.
S ADB ЛСВ
= По-П0=0, A3.9)
поскольку поверхности АСВ и ADB видны
из точки О под одним и тем же телесным
углом По, но входят в интеграл с разными
знаками. Когда точечный заряд находится
вне объема, поток напряженности Е сквозь
замкнутую поверхность равен нулю:
N = 0. A3.10)
Объединяя результаты A3.8) и A3.10),
можно для A3.1) окончательно написать:
q/s0, когда q находится
внутри объема,
ограничиваемого S;
когда q находится
вне объема,
ограничиваемого S.
Утверждение, содержащееся в A3.11),
составляет содержание электростатической
теоремы Гаусса для точечного заряда.
0,
A3.11)
§ 13. Дифференциальная формулировка закона Кулона 83
Ее обобщение на систему точечных зарядов производится с помощью
принципа суперпозиции. Если имеются точечные заряды д;, то напря-
напряженность Е поля в каждой точке является суммой напряженностей
Е,- полей, создаваемых каждым из точечных зарядов:
A3.12)
Следовательно,
f U jo Vilr Лв И 1 1 1\
S ' S
При вычислении каждого из интегралов, стоящих под знаком суммы
в правой части A3.13), надо принять во внимание A3.11): для точеч-
точечного заряда внутри объема соответствующий интеграл равен qjzo,
а для заряда вне объема — нулю. Поэтому A3.13) принимает вид
E-dS=— У«,= — Q, A3.14)
?о / j Ео
s v
где V у знака суммы означает, что в сумму входят только заряды,
находящиеся внутри объема V. Полный заряд внутри объема V
обозначен в A3.14) Q:
v
Формула A3.14) с учетом определения D.1) для объемной плотности
р при непрерывном распределении зарядов сразу переписывается в виде
A3.16)
(|)E-dS= — fpdF= — Q,
J Eo J Ео
где
A3.17)
v
— полный заряд, заключенный в объеме, ограниченном замкнутой
поверхностью S. Утверждение, содержащееся в формуле A3.16), состав-
составляет содержание электростатической теоремы Гаусса для непрерывного
распределения зарядов. Очевидно, что эта формула включает в себя
также и выражения A3.14) и A3.11) как частные случаи.
ГТзмерение заряда. Теорема Гаусса позволяет определить полный
заряд, заключенный внутри объема, посредством измерения потока
напряженности сквозь поверхность, ограничивающую объем. Другие
определения заряда не дают удовлетворительных результатов. Напри-
Например, нельзя найти этот заряд, измерив силу, с которой он действует
на находящийся вне этого объема пробный заряд, поскольку сила
зависит не только от. общего заряда, но и от распределения его
по объему, которое, вообще говоря, неизвестно. Можно определить
заряд, измерив действующую на него силу в известном однородном
внешнем электрическом поле. При этом важно обеспечить однород-
84 2. Постоянное электрическое поле
ность поля. Ясно, что этот способ применим лишь тогда, когда внешнее
однородное поле существенно не изменяет распределения зарядов
внутри объема.
физическая основа справедливости теоремы Гаусса. Из вывода тео-
теоремы Гаусса видно, что ее справедливость обусловливается возмож-
возможностью сведения подынтегрального выражения A3.3) с помощью A3.4)
и A3.5) к дифференциалу телесного угла dQ. Это возможно только
в том случае, когда Е(г) убывает обратно пропорционально квадрату
расстояния от точечного заряда. При другой зависимости Е(г) в фор-
формуле A3.6) под- интегралом должна стоять кроме дифференциала телес-
телесного угла также и некоторая функция от г, не позволяющая выразить
поток напряженности через поверхность в виде функции заряда, что
означает несоблюдение теоремы Гаусса. Поэтому физической основой
теоремы Гаусса является закон Кулона или, иначе, теорема Гаусса
является интегральной формулировкой закона Кулона.
Дифференциальная формулировка закона Кулона. Уравнение Макс-
велла для div Е. Поток Е сквозь замкнутую поверхность можно
с помощью математической формулы Гаусса — Остроградского E.21)
преобразовать в интеграл по объему от divE:
|E-dS = jdivEdK A3.18)
s v
в результате чего формула A3.16) принимает вид
\ (div Е - р/е0) d V = 0. A3.19)
v
Равенство нулю интеграла выполняется при произвольном объеме
V. Следовательно, подынтегральное выражение тождественно равно
нулю, т. е.
div Е = р/е0.
A3.20)
Выполнимость A3.20), так же как и теоремы Гаусса, обусловлена
справедливостью закона Кулона. Следовательно, A3.20) является диф-
дифференциальной формулировкой закона Кулона. Линейность уравне-
уравнения A3.20) отражает справедливость принципа суперпозиции для
напряженности поля. Оно выведено здесь для неподвижных зарядов.
Принимается, что оно справедливо для произвольного движения зарядов.
/"¦* иловые линии. Силовой линией электрического поля называется
линия, касательная к которой в каждой точке совпадает с напря-
напряженностью Е. С помощью силовых линий удобно графически изобра-
изображать поле. Условились напряженность поля характеризовать числом
силовых линий, пересекающих 1 м2 площади поверхности, перпенди-
перпендикулярной направлению силовых линий в соответствующей точке: чем
больше плотность линий, тем больше напряженность поля. На рис. 34
изображено электрическое поле, напряженность которого возрастает
слева направо.
§ 13. Дифференциальная формулировка закона Кулона 85
34
р| сточники и стоки вектора Е. Как видно
из уравнения A3.20), силовые линии начи-
начинаются там, где div E > 0, и оканчиваются
там, где div E < 0, т.е. начинаются на по-
положительных зарядах и оканчиваются на
отрицательных. Говорят, что положитель-
положительные заряды являются источниками вектора
Е, а отрицательные — стоками. Конечно та-
такое различие между зарядами чисто условно,
оно исходит из определения направления
напряженности ПОЛЯ. По ИХ роли В обраЗО- Силовые линии поля, напряжен-
ВаНИИ Электрического ПОЛЯ положительные ность которого возрастает спра-
ва налево
и отрицательные заряды совершенно экви-
эквивалентны. На рис. 35 изображены силовые
линии двух разноименных зарядов.
Инвариантность заряда. Найдем поток Е
сквозь замкнутую поверхность, окружаю-
окружающую движущийся равномерно и прямоли-
прямолинейно точечный заряд q. Напряженность
поля этого заряда определяется формулой
A1.26). Поток напряженности равен
N = $ Е- dS = §Er2 dS2 = §Er2 sin 0d6 dq>,
A3.21)
где в качестве поверхности интегрирования
взята сфера с центром в точке нахождения
движущегося заряда в некоторый момент
Времени и учтено, что Е и dS коллинеарны
радиус-вектору г; 0 и (р — соответственно
полярный и аксиальный угол сферической
Системы координат, полярная ось которой
совпадает с осью X неподвижной системы
координат. Подставляя A1.26) в A3.21), на-
находим
35
Силовые линии двух разноимен-
разноименных зарядов
2е0
sin 9 d9
-P2sin29K/2>
A3.22)
где произведено интегрирование по углу dp,
от которого подынтегральное выражение
в A3 21) не зависит. Так как sin2 8 = 1— cos2 6,
sin8d9 = -dcosG, то
A -
sin 6 d9
p2 sin2 9K/2 ~
Силовой линией электри-
электрического поля называется
линия, касательная к кото-
которой в каждой точке сов-
совпадает с напряженностью
электрического поля.
Положительные заряды
являются источниками на-
напряженности электриче-
электрического поля, а отрицатель-
отрицательные—стоками. Однако это
различие между зарядами
чисто условно. Их роль в
образовании электриче-
электрического поля абсолютно оди-
одинакова.
86 2, Постоявное электрическое поле
Г
dx 2 ' A ' * где a2 = A -
о
— Р2)/Р2. Тогда соотношение A3.22) принимает вид
N = q/so, A3.23)
совпадающий с A3.8). Это доказывает, что теорема Гаусса справедлива
также и для точечного заряда, движущегося равномерно и прямо-
прямолинейно. Если заряд в объеме определить посредством потока Е
сквозь замкнутую поверхность, ограничивающую объем, то равенство
A3.23) выражает инвариантность заряда.
§ 14. Потенциальность
электростатического поля
Обсуждаются интегральная и дифференци-
дифференциальная формулировки потенциальности поля.
Вводится скалярный потенциал и рассматри-
рассматриваются его свойства. Вычисляется потен-
потенциал зарядов, распределенных в конечной
области пространства. Доказывается тео-
теорема Ирншоу.
работа в электрическом поле. Так как сила, действующая в электри-
электрическом поле на точечный заряд q, равна F = qE, то при перемещении
заряда на dl совершается работа
dA = ?-dl = qE-dl A4.1)
Удельная работа при перемещении заряда определяется как отно-
отношение работы к заряду:
E-dl A4.2)
Она выражается в джоулях на кулон. Из A4.2) видно, что работа,
совершаемая полем, считается положительной, а внешними относи-
относительно поля силами — отрицательной. Это условие знаков аналогично
тому, которое используется в термодинамике для работы системы.
При перемещении заряда из точки 1 в точку 2 по траектории L
(рис. 36) удельная работа равна
А' =
A)
L
Потенциальность кулоновского поля. Поле сил называется потенци-
потенциальным, если работа при перемещении в этом поле зависит лишь
от начальной и конечной точек пути и не зависит от траектории.
Другим эквивалентным определением потенциальности является требо-
требование равенства работы нулю при перемещении по любому замкнутому
контуру.
§ 14. Потенциальность электростатического поля 87
Известно, что сила тяжести точечной массы, убывающая обратно
пропорционально квадрату расстояний, является потенциальной, при-
причем ее потенциальность обусловлена именно этой зависимостью от
расстояния. Поскольку кулоновская сила точечного заряда убывает
по такому же закону, она потенциальна. Вся математическая часть
учения о потенциале была разработана в рамках теории тяготения.
Понятие о потенциале возникло в работах Ж. Л. Лагранжа A736 — 1813)
в 1777 г., хотя для функции, являющейся потенциалом, он еще не
употребил этого названия. Термин «потенциал» был введен в науку
в 1828 г. Дж. Грином и независимо К. Ф. Гауссом A777 — 1855).
Большой вклад в теорию потенциала был внесен П. С. Лапласом
A749-1827) и С. Д. Пуассоном A781-1840).
На основании принципа суперпозиции из потенциальности поля то-
точечного заряда следует потенциальность произвольного электростати-
электростатического поля. Математическое доказательство этого утверждения
O, A4.4)
где
Е = ?ЕЬ fE,-dl = O. A4.5)
ротор вектора. Критерий потенциальности поля, который был ис-
использован до сих пор, не является дифференциальным и применять
его не всегда легко и эффективно. Его применение сводится к про-
проверке утверждения о том, что работа по любому замкнутому пути
равна нулю. Это означает необходимость исследования бесконечного
числа замкнутых путей, что в общем случае невозможно. Критерий
можно применить лишь тогда, когда известно общее выражение для
работы по любому пути в виде аналитической формулы. Получить
такую формулу удается только в редких случаях. Поэтому желательно
найти другой критерий потенциальности, который легко и удобно
использовать на практике. Таким критерием является дифференциаль-
дифференциальная формулировка, которая дается с помощью ротора вектора.
Прежде всего рассмотрим векторное определение ротора А, обозна-
обозначаемого rot А. Вектор определяется тремя составляющими, не лежа-
лежащими в одной плоскости. Выберем некоторое направление, характе-
характеризуемое единичным вектором п. В плоскости, перпендикулярной п,
ограничим площадь AS очень малым замкнутым контуром L (рис. 37).
На контуре L направление положительного обхода обычно связано
с п правилом правого винта. Ротором называется вектор, проекция
которого на направление п определяется формулой
Ротор характеризует интенсивность «завихрения» вектора, что отра-
отражено в названии операции. Пусть, например, вектор А равен скорости
88 2. Постоянное электрическое поле
v точек твердого тела, вращающегося с уг-
угловой скоростью со вокруг оси, коллинеар-
2 ной с п. Найдем rotn v для точек оси вра-
вращения. В качестве контура L выберем окруж-
окружность радиусом г с центром на оси и лежа-
лежащую в плоскости, перпендикулярной оси.
Очевидно, имеем v = юг, AS = кг2 и А • dl =
= v dl, где d/ — скалярное значите элемента
окружности. Поэтому на основании A4.6)
получаем
Работа в электрическом поле -
при перемещении точечного за- . _ j- юг ? dl _ j- юг2лг
РВД* " г->0 КГ2 Г-.П
36
КГ'
> 2со, A4.7)
.rotnА
где §dl = 2nr — длина окружности. Таким
образом, ротор линейной скорости точек
вращающегося абсолютно твердого тела
равен удвоенной угловой скорости его вра-
вращения. Можно показать, что это утвержде-
утверждение справедливо не только для точек на оси
вращения, но и для всех точек.
При практическом вычислении ротора
удобнее вместо A4.6) пользоваться коорди-
координатными формулами. Найдем проекции
rot А в прямоугольной декартовой системе
координат. Возьмем для примера ось Z
(рис. 38). Контуром L является прямоуголь-
ник со сторонами Дх, Ду. Направление
К~~1ектоРиому определению положительного обхода указано на рисунке.
ротора В этом случае
(х + Дх, у, Z)
|A-dI= J Ax(x,y,z)dx +
Z L (x, у, z)
37
(х -|- Дх, у + Ду, z)
+ j Л, (х + Дх, у, z) dy +
(х + Дх, у, г)
(х, у + &у, г)
+ j Ах (х, у + Ду, г) dx +
(x+Axor.2) (х+Дх,>+Д>.г) <*+**'+^ •>
(х, л г)
38 + 1 Лу(х, у, z)dy,
^"¦"^ (х, у + Ду, г)
К определению ротора в ко-
координатах где интегрирование производится вдоль сто-
сторон прямоугольника между его вершинами,
координаты которых обозначены в A4.8) как
пределы интегрирования. Учитывая, что Дх
и Ду являются сколь угодно малыми, мож-
A4.8)
§ 14. Потенциальность здектростатического поля 89
но в подынтегральных выражениях второго и третьего интегралов
произвести разложение Ау и Ах в ряд по Ах и Ау и ограничиться
линейными членами:
Ах(х, У + АУ, z) = АЛх, у, z) + АуМ(у г) + ... (а)
Л, (х + Дх, у, z) = Л, (х, у, z) +¦ Дх 8АЛ^хУ' Z) + ... (б) A4.9)
Вычислим сумму первого и третьего интегралов:
(х + Ах, у, г) (х, у+Ду, г)
Л = Л*(х, ^z)dx+ Лх(х, у + Ду, z)dx =
(*, У, г) (х + Дх,
х + Дх, у, z) (х+Дж. у, z)
J j
(х, У, z) (х. у, z) (Мл0)
где при вычислении второго интеграла в A4.10) использована фор-
формула A4.9а), а знак минус появился вследствие изменения направления
интегрирования на обратное. В A4.10) члены, содержащие в подын-
подынтегральных выражениях Ах (х, у, z), взаимно уничтожаются и поэтому
sAA^jA A4U)
Аналогично вычисляем сумму второго и четвертого интегралов
в A4.8):
A4.12)
По формуле A4.6) находим
Аналогично вычисляем проекции на другие оси координат:
Обозначая, как обычно, \х, \у, \ — единичные векторы осей коорди-
координат, запишем вектор rot А в виде
формула Стокса. Формула Стокса связывает циркуляцию вектора
по контуру, ограничивающему поверхность, с потоком его ротора
через поверхность. Ее вывод основан на определении A4.6). Вычислим
поток вектора rot А сквозь поверхность S, ограниченную контуром L
90 2. Постоянное электрическое поле
(рис. 39), которую разобьем на элементы ASt:
-s \ sWv JrotA-dS = ? JrotA-dS.
A4.16)
as,-
39
К доказательству
Стокса
формулы
—const
40
Направление grad
Поскольку ASi очень малы, для каждой
из них на основании A4.6) имеем
J rot A • dS = J (rot А)„ dS *
AS,- AS;
* (rot А)„ AS « § Adi, A4.17)
где L, — контур, ограничивающий ASf. По-
Поэтому A4.6) может быть представлено в виде
frotA-dS»? $A-dl. A4.18)
S ' Ц
Части контуров L-t, являющиеся грани-
границами между AS,-, входят в два члена суммы
A4.18): один раз — при интегрировании по
контуру данной площадки AS<, а другой
раз — по контуру соседней площадки. Ин-
Интегралы равны по модулю, но противо-
противоположны по знаку, поскольку пути вдоль
границы при вычислении интегралов про-
проходят в противоположных направлениях.
Таким образом, в сумме A4.18) все части
интегралов по границам между AS; взаимно
сокращаются и остается лишь сумма ин-
интегралов по тем частям контуров Lh кото-
которые не образуют границы между AS;, т. е.
остается интеграл по контуру L, ограничи-
ограничивающему площадь S. При AS; -* О прибли-
приближенное равенство A4.18) превращается в точ-
точное:
Условие знаков: совер-
совершаемая полем работа счи-
считается положительной, а
внешними относительно
поля силами — отрица-
отрицательной.
Дифференциальная фор-
формулировка потенциально-
потенциальности электростатического
поля: rot E =0.
Знак минус в выражении
Е = —gradip выбран по со-
соглашению дли та го, что-
чтобы Е было направлено в
сторону уменьшения ф.
| rot А • dS = $ А • dl,
S L
A4.19)
которое называется формулой Стокса.
JT ифференциальная формулировка потенци-
альности поля. Независимость работы от
пути при перемещении заряда в электро-
электростатическом поле выражается равенством
|E-dl=jEdl, A4.20)
где L-i и L2 — различные пути между точ-
§ 14. Потевциальвость электростатического поля 91
В А
ками А и В. Учитывая, что | Е • dl = — | Е • dl, представим A4.20)
А В
L2 L2
в виде
| Е• dl+ jE-dl = $E-dl = O, A4.21)
Л В L
где L= L-i + L2. Формула A4.21) является математической формули-
формулировкой утверждения о том, что в электростатическом поле работа при
перемещении заряда по любому замкнутому контуру равна нулю.
С помощью A4.19) из A4.21) получаем
JrotEdS
s
A4.22)
где S — поверхность, ограничиваемая контуром L. Ввиду произволь-
произвольности S из A4.22) следует, что
rot E = 0. A4.23)
Это равенство является дифференциальной формулировкой потенци-
потенциальности электростатического поля.
^радиент. Пусть ф (х, у, г) является скалярной функцией точки. Гра-
Градиентом ф называется вектор
A4.24)
Чтобы выяснить смысл этого вектора, вычислим полный дифферен-
дифференциал функции q> при перемещении на dr = \хйх + уйу + ijdz:
d(p = |Ldx +8JLdy+^.dz = grad ф. dr. A4.25)
Таким образом, бесконечно малое приращение d<p при перемещении
в некотором направлении равно компоненте grad ф по этому направ-
направлению, умноженной на модуль перемещения. Начертим семейство
поверхностей <р = const (рис. 40). При перемещении вдоль поверхности
Ф = const имеем dq> = 0. Поэтому [см. A4.25)] grad ф ± dr, т. е. вектор
grad ф направлен перпендикулярно поверхности ф = const. По модулю
он равен производной от ф по пути в направлении, перпендикулярном
поверхности ф = const.
(^калярный потенциал. Поскольку работа при перемещении заряда
в потенциальном поле не зависит от траектории, а зависит лишь
от начальной и конечной точек пути, ее можно выразить через коор-
координаты концов траектории. Это делается с помощью потенциала.
92 2. Постоянное электрическое поле
Непосредственной проверкой можно убедиться, что всегда имеет
место тождественное равенство
rot grad ф = 0. A4.26)
Поэтому уравнение A4.23) будет удовлетворено, если Е представить
в виде
Е= — grad<p.
A4.27)
Знак выбран так, что напряженность Е направлена в сторону
убывания ф. Скалярная функция ф, связанная с напряженностью Е
поля формулой A4.27), называется скалярным потенциалом электри-
электрического поля.
Напряженность можно измерить экспериментально. Потенциал ф
не имеет определенного числового значения, и бессмысленно говорить
об экспериментальном определении его значения.
Неоднозначность скалярного потенциала. Из формулы.A4.27) видно,
что если к ф прибавить некоторую постоянную, то описываемое
потенциалом поле не изменяется, поскольку производные по коорди-
координатам от постоянной величины равны нулю. Следовательно, потен-
потенциал ф заданного электрического поля определен лишь с точностью
до аддитивной постоянной.
ВДормировка. Пользуясь неоднозначностью скалярного потенциала,
можно в любой одной наперед заданной точке приписать ему любое
наперед заданное значение. После этого во всех других точках потен-
потенциал имеет вполне определенное значение, т. е. будет однозначным.
Эта процедура придания однозначности потенциалу путем приписывания
ему определенного значения в одной из точек называется нормировкой
потенциала. При изучении электрических полей вблизи поверхности
земли за нулевой принимается обычно потенциал земли. При исследо-
исследовании общих вопросов, когда заряды находятся в конечной области
пространства, удобнее считать потенциал равным нулю на бесконечном
удалении от зарядов. Такая нормировка часто применяется в этой
книге.
||ыражение работы через потенциал. Если заряд перемещается между
точками 1 и 2, то удельная работа равна
B) B) B)
А'= jE-dI= - Jgrac^-dr= - |с!ф = фA)-фB)( A4.28)
A) ID A)
где использована формула A4.25) и dl = dr. Из A4.28) видно, что
работа действительно зависит от конечной и начальной точек траек-
траектории и не зависит от формы траектории. Из этой же формулы
следует, что разность потенциалов между двумя точками имеет ясный
физический смысл и может быть измерена экспериментально. Таким
образом, физический смысл имеет не сам потенциал, а разность
потенциалов между, различными точками.
§ 14. Потенциальность электростатического поля 93
Потенциал поля точечного заряда. Будем нормировать потенциал на
нуль в бесконечности. Считая, что в формуле A4.28) точка 2 нахо-
находится в бесконечности, полагаем ф B) = ф (оо) = 0 и получаем следую-
следующее выражение для потенциала в точке 1:
ФA)ь= jE-dl. A4.29)
A)
Путь из точки / в бесконечность может быть любым. Однако его
надо выбрать так, чтобы максимально упростить вычисления.
Поле точечного заряда q сферически симметрично. Потенциал на
расстоянии г от точечного заряда по формуле A4.29) равен
ф(г) =
-4-U--
4яе0 I r \ г
Наиболее подходящим является путь интегрирования вдоль радиус-
вектора, исходящего из точечного заряда. Тогда (г • dl/r) = dr и из A4.30)
следует, что
A4.31)
Рекомендуется в качестве упражнения проверить, что из этой фор-
формулы получается закон Кулона:
1 \ SI Г
Е = -grad ф = - —2—grad— = % . A4.32)
4пЕ0 г 4ле0 г2- г
Лотенциал поля системы точечных зарядов. По принципу суперпози-
суперпозиции потенциал поля системы точечных зарядов равен сумме потен-
потенциалов, создаваемых в рассматриваемой точке каждым из зарядов. Это
очевидно:
Е = Et + Е2 = -grad фх - grad ф2 = -grad (ф, + <р4).
Следовательно, с помощью формулы A4.31) для потенциала, созда-
Вгаемого системой точечных зарядов qu можно написать выражение
A4.33)
где г; = |/(х — X;J + (у - уд2 + (z — z,J — расстояние от точечного за-
заряда &, находящегося в точке (х() yh z,), до точки (х, у, z), в которой
вычисляется потенциал.
Потенциал поля непрерывного распределения зарядов. Предполагаем
по-прежнему, что все заряды расположены в конечной области прост-
пространства и потенциал нормирован на нуль в бесконечности. Обозначая
94 2. Постоянное электрическое поле
р (х', у', z1) — объемную плотность заряда, получаем для потенциала
вместо A4.33) выражение
Ф(х, Л z, = -±- Г PV-y-WW" _. A4.34)
4тео J ]/(x - х'J + {у - у'I + (z - z'J
Эту формулу можно записать иначе, не указывая подробно пере-
переменных:
A4.35)
где AV — элемент объема, по которому производится интегрирование.
Такая краткая форма записи часто используется в последующем
изложении.
Р[отенциал поля поверхностных зарядов. Если заряд расположен на
поверхности, то распределение характеризуется поверхностной плот-
плотностью заряда ст. На элементе площади dS (это скаляр, а не век-
вектор элемента поверхности) находится заряд crdS и, следовательно,
потенциал в некоторой точке аналогично A4.35) дается формулой
A4.36)
где г — расстояние между элементом площади dS и точкой, в которой
вычисляется потенциал. Интеграл A4.36) распространяется на все по-
поверхности, несущие поверхностные заряды.
бесконечность потенциала поля точечного заряда. Из A4.31) сле-
следует, что при г->0 потенциал ср (г-*())-» оо. Это связано с тем,
что точечный заряд формально имеет бесконечную объемную плот-
плотность, поскольку его объем равен нулю. Именно бесконечная объемная
плотность заряда и обусловливает обращение в бесконечность потен-
потенциала.
^онечность потенциала при непрерывном распределении заряда с
конечной плотностью. При непрерывном распределении заряда с ко-
конечной плотностью потенциал нигде не обращается в бесконечность.
В этом можно убедиться при вычислении потенциала по формуле A4.34).
Примем точку (х, у, г) за начало координат (х = у = z = 0) и будем
вести расчет в сферической системе координат. Элемент объема в ней
выражается формулой dx' d/ dz' = г'2 sin 8' d9' da' &r', где г' =
= Ух'2 + у'2 + г'2. Тогда [см. A4.34)]
Ф @, 0, 0) = -—-- р (г1, а', в1) г' sin 0' d6' da' dr'.
4тс0 J
Следовательно, если р конечно, то и потенциал ср конечен, что
и требовалось доказать.
§ 14 Потенциальность электростатического поля 95
жхепрерывность потенциала. Производная от потенциала по декарто-
** вой координате дает соответствующую компоненту напряженности
электрического поля. Ясно, что напряженность не может быть беско-
бесконечной. Следовательно, производные по координатам от потенциала
должны быть конечными. А это означает, что потенциал является
непрерывной функцией. Таким образом, потенциал ср является непре-
непрерывной и конечной функцией с конечными производными по координа-
координатам. Эти условия важны при решении дифференциальных уравнений
для потенциала.
тгеорема Ирншоу. Эта теорема утверждает, что не существует такой
конфигурации неподвижных зарядов, которая была бы устойчивой,
если нет других сил, кроме сил кулоновского взаимодействия между
зарядами системы.
Доказательство теоремы Ирншоу следует из формулы Гаусса.
ДопустимГ что равновесие устойчиво. Тогда при смещении любого
из зарядов системы из его положения равновесия в любом направ-
направлении на него должна действовать сила, стремящаяся возвратить
заряд в прежнее положение. А это означает, что напряженность поля,
создаваемого вблизи каждого из покоящихся зарядов всеми другими
^зарядами, направлена вдоль радиусов, исходящих из точки нахождения
этого заряда. Поток напряженности этого поля сквозь замкнутую
поверхность вокруг заряда отличен от нуля, поскольку напряженность
направлена вдоль радиусов в одном направлении (вблизи положитель-
положительного заряда — к заряду, вблизи отрицательного — от заряда). По теореме
Гаусса поток сквозь замкнутую поверхность создается зарядом, нахо-
находящимся в ограничиваемом ек? объеме. Это противоречит исходному
предположению о том, что он создается зарядами, находящимися вне
объема. Тем самым отвергается допущение об устойчивости конфигу-
конфигурации неподвижных зарядов, и теорема Ирншоу доказана.
Устойчивые конфигурации неподвижных зарядов могут существовать
лишь тогда, когда кроме сил взаимодействия между ними имеются
какие-то посторонние силы, удерживающие заряды в положениях
равновесия. Устойчивые состояния движущихся зарядов возможны,
как, например, движение двух разноименных зарядов по эллипсам
вокруг центра масс (если, конечно, пренебречь излучением).
Пример 14.1.
Имеем:
grad ф = i* ~ +
д(р дф дг
дх дг дх
Аналогично
по аргументу
Вычислить
. 5ф . 5с
h~dJ+h~d
Ф'— г = 1/
дх' *
вычисляем
grad ф (г).
Р_
z
' 2 i 2 | 2
х у z
ёц>/ду, <3ф/дг
ёг
г Учитывая, что —
дх
рд
2х х
=—, получаем
% 2. Постоянное электрическое поле
В частности, при ф(г) = г grad г — г/г, а при q>(r)=l/r grad(l/r) = — г/г3.
Пример 14.2. Вычислить циркуляцию вектора <о х г по окружности L
радиусом г0, расположенной в плоскости, перпендикулярной постоянному век-
вектору (О, как непосредственно, так и с помощью теоремы Стокса. Центр
окружности совпадает с началом координат.
Вектор (о х г0 направлен в каждой точке по касательной к окружности.
Следовательно,
§<о х r-dl = coro( d/ = Inovl. A4.38)
L L
Направление обхода выбрано таким, что векторы и х г и dl в каждой
точке коллинеарны. При обратном направлении обхода изменится знак ин-
интеграла.
С помощью теоремы Стокса задача решается по-другому:
| и х г • dl = J rot (и х г) • dS,
L S
где S — поверхность, ограниченная окружностью L. Прн и = const rot (u> x r) =
= 2и и
J rot (и х г) • dS = 2 J о> • dS = 2w J dS = 2itwrg, A4.39)
s s s
что, как и должно быть, совпадает с A4.38).
Нетрудно видеть, что поверхность S может быть любой поверхностью,
ограниченной окружностью, а не только плоской. Имеем
Jrot(« х r)dS = 2 Je>-dS = 2<o- JdS. A4.40)
Примем во внимание, что
O, A4.41)
где S" — замкнутая поверхность, состоящая из поверхности Si в A4.40) и по-
поверхности S круга в A4.39), т. е. S" = St + S. Из A4.41) получим
JdS=-njirj5, A4.42)
s,
где п — единичный вектор, перпендикулярный плоскости круга. В A4.42) учтено,
что в A4.41) элемент dS направлен по внешней нормали к замкнутой поверх-
поверхности. Подставляя A4.42) в A4.40), получаем формулу, идентичную A4.39).
Пример 14.3. Найти потенциал и напряженность поля, создаваемого в ок-
окружающем пространстве равномерно заряженной нитью конечной длины 2L.
Линейная плотность заряда нити равна х.
Поместим начало декартовой системы координат в середине нити (точка О)
н ось Z направим вдоль нити (рис. 41). Вследствие аксиальной симметрии
потенциал зависит только от г н координаты z.
14. Потенциальность электростатического поля 97
На рис. 41 изображена плоскость, проходя-
проходящая через точку (г, z) и ось Z. Находящийся на
элементе длины dz' нити заряд rdz' создает
в точке (г, z) потенциал
1 rdz'
dm = - =-.
4Я8О |Д2 + (Z - Z'f
Следовательно, потенциал, создаваемый всей
заряженной нитью, равен
™o J ]/r2 + (z - :
— L
-L+j/r
dz1
г
-Z,
4ле0
41
A4.43) Линейный заряд конечной длины
Компоненты напряженности электрического поля
даются формулами:
5ф__ т { 1
Е,
dz
I
4ree0
z + L
(z - LJ
A4.44)
A4.45)
При L -> оо получаем
?, = 0, ?, = т/Bл80г).
Потенциал при L-
нечности:
т
оо стремится к беско-
2яе0
-pnr-lnBL)]-»oo.
Это является следствием того, что заряд не
сосредоточен в конечной области пространства
и поэтому применять формулу A4.43) для вы-
вычисления потенциала в случае L -> оо нельзя.
При очень больших расстояниях от центра
нити [R = ]/г2 + z2 » L) из A4.43) находим
t2L I Q
Ф ~ 4ree0R 4ле0 R '
где Q «= 2tL — полный заряд нити. Таким образом,
на больших по сравнению с линейными разме-
размерами нити расстояниях поле близко к кулонов-
скому.
Ф Использование уравнения
Пуассона для решения
задачи не предполагает
определенной нормировки
потенциала и отсутствия
зарядов иа бесконечности.
Потенциал является не-
непрерывной и конечной
функцией, с конечными
производными ло коорди-
координатам.
О Какие методы определения
напряженности поля по за-
заданному распределению за-
зарядов вы знаете? Чем оп-
определяется в каждом кон-
конкретном случае выбор ме-
метода решения задачи?
Какими преимуществами по
сравнению с другими ме-
методами обладает нахожде-
нахождение напряженности поля пу-
путем решения уравнений Лап-
Лапласа и Пуассона?
Какими свойствами облада-
обладает потенциал, как решение
соответствующих дифферен-
дифференциальных уравнений?
Какие формулировки потен-
потенциальности электростатиче-
электростатического поля вы знаете? В чем
преимущество дифференци-
дифференциальной формулировки?
Какие физические обстоя-
обстоятельства обусловливают воз-
возможность нормировки ска-
скалярного потенциала? Какие
нормировки наиболее упо-
употребительны и когда они
целесообразны?
4 А. Н. Матвеев
98 2. Постоянное электрическое поле
42
Поле на оси равномерно заря-
заряженного дисха
тип,
чишш
чтиши.
iinmii
У-1
^v
IB
И
"ft*
43
К вычислению напряженности
поля бесконечной заряженной
иити с помощью теоремы Гаусса
Ф Нахождение напряжен-
напряженности попя по заданному
распределению зарядов
пряным применением за-
закона Кулона является наи-
наиболее естественным, ио не
самым простым.
Нахождение напряженно-
напряженности поля с помощью тео-
теоремы* Гаусса обычно це-
целесообразно при наличии
симметрии распределения
заряда.
q Что можно сказать о фи-
физическом смысле потенциала
в рамках электростатики?
Какой физический смысл
имеет разность потенциалов?
§ 15. Электростатическое поле
в вакууме
Излагаются основные методы расчета по-
потенциала и напряженности электростати-
электростатического поля и анализируются примеры вы-
вычислений.
Лостановка задачи. Решим одну го задач
электростатики:
определить напряженность электрическо-
электрического поля, создаваемого известным распреде-
распределением зарядов.
Эта задача может быть решена не-
несколькими методами. В принципиальном
смысле все они равноценны, в практическом
в зависимости от обстоятельств различны,
так как связаны с неодинаковым объемом
вычислительной работы. Целесообразно вы-
выбрать тот метод, который приводит к иско-
искомому результату наиболее простым путем.
ГЖрямое использование закона Кулона.
В этом случае напряженность поля в точ-
точке вычисляется как сумма напряженностей,
полей, создаваемых всеми элементами pdF
и cjdS объемных и поверхностных зарядов.
Этот метод является наиболее естественным,
но не самым простым, поскольку приходится
суммировать векторы, что значительно ус-
усложняет вычисления. Пример использования
этого метода был рассмотрен в § 8 при
вычислении силы взаимодействия точечного
заряда и бесконечной прямой заряженной
нити.
Вычисление потенциала. Формулы A4.35)
и A4.36) можно использовать только при
распределении заряда в конечной области
пространства и нормировке потенциала на
нуль в бесконечности.
Рассмотрим в качестве примера поле
в точках перпендикуляра к плоскости равно-
равномерно заряженного диска радиусом а, про-
проходящего через его центр (рис. 42). Полный
заряд диска равен Q. Для потенциала на
расстоянии h от поверхности диска имеем
[см. A4.36)]
§ 15. Электростатическое поле в вакууме 99
1 Г adxdy
4яв0 J 1Д2 + у2 + h2 '
s
•»2\
где <т = 6/(яя ) — поверхностная плотность заряда на диске. Интеграл
удобно вычислять в полярных координатах, полагая х2 + у2 = г2,
dx dy = dS = г &r da. Тогда [см. A5.1)]
2л a
<р(h) = -т?— fda f /dr = x-^— -%(j/a2 + h2 - h). A5.2)
о о
Из аксиальной симметрии распределения заряда следует, что вектор
напряженности электрического поля направлен вдоль оси диска и равен
dh 2яв0 а2
Для ft»o можно считать, что
. f,2 l/i _l ^2/J,2 2 ft
И, следовательно,
как это можно было ожидать и без вычислений, поскольку на боль-
больших расстояниях напряженность поля заряженного тела близка к на-
напряженности поля точечного заряда.
Использование теоремы Гаусса. При наличии симметрии в некоторых
случаях наиболее эффективным методом определения напряженности
поля является применение теоремы Гаусса. Пусть, например, требуется
найти напряженность поля бесконечной заряженной прямой нити
с линейной плотностью т. Построим круглый цилиндр радиусом г,
ось которого совпадает с нитью (рис. 43). Обозначим h — высоту
цилиндра. Применим к объему цилиндра теорему Гаусса:
jE-dS = Q/E0, A5.6)
Где Q — заряд в объеме цилиндра, S — поверхность цилиндра. Очевид-
Ио, что Q = xh. Поток Е сквозь основания цилиндра равен нулю так
гак вектор Е параллелен основаниям. Поток Е сквозь боковую
Поверхность легко вычисляется, поскольку на ней вектор Е совпадает
По направлению с нормалью к поверхности, а по модулю он постоя-
постоянен. Тогда
jE-dS= J E-dS = E-2nrh. A5.7)
S s6ok
4*
100 2. Постоянное электрическое поле
Таким образом, теорема Гаусса приводит к равенству
Е ¦ 2nrh = тй/е0, A5.8)
из которого получаем
Е = ~ -. A5-9)
2к?0 г
В поле с такой напряженностью сила, действующая на точечный
заряд, имеет значение (8.5), полученное прямым применением закона
Кулона.
уравнение Лапласа и Пуассона. Во многих случаях предпочтительным
методом нахождения напряженности поля является сведение задачи
к решению дифференциального уравнения для потенциала. Чтобы его
получить подставим в
divE = p/e0 A5.10)
выражение
E=-gradcp. A5.11)
Тогда
div grad q> = — р/в0. A5.12)
Учтем, что
SS5 V4 A5.13)
'Y дх2 " By2 ' 8z2 ' ^
где V2 — оператор Лапласа, являющийся суммой вторых производных
по координатам. Иногда он обозначается А = V2. С использованием
A5.13) равенство A5.12) записывается в виде
?2Ф=-р/80 A5.14)
и называется уравнением Пуассона. В тех областях пространства, где
заряды отсутствуют (р = 0), оно превращается в уравнение
?2Ф = 0, A5.15)
называемое уравнением Лапласа.
После нахождения потенциала ф как решения A5.14) можно вычис-
вычислить напряженность электрического поля по формуле A5.11). Решение
должно удовлетворять требованиям, которые были сформулированы
для потенциала (см. § 14): потенциал ф является непрерывной и конеч-
конечной функцией, с конечными производными по координатам.
Если все заряды сосредоточены в конечной области пространства,
то решением A5.14) будет A4.35), что следует из однозначности реше-
решения задач электромагнетизма (см. § 58).
Наиболее важным преимуществом нахождения напряженности поля
с помощью дифференциального уравнения Пуассона для потенциала
является большая общность этого метода и его очень широкая при-
§ 15. Электростатическое поле в вакууме 101
менимость. Формулы A4.35) и A4.36) предполагают, что все заряды
находятся в конечной области пространства, благодаря чему имеет
смысл нормировка потенциала на нуль в бесконечности. Уравнение же
Пуассона не предполагает определенной нормировки потенциала и отсут-
отсутствия зарядов на бесконечности.
бесконечный равномерно заряженный круглый цилиндр. Найдем с по-
помощью уравнения Пуассона потенциал, создаваемый бесконечным
круглым цилиндром радиусом а с объемной плотностью заряда
р = const.
Направим ось Z по оси цилиндра. Вследствие аксиальной симмет-
симметрии распределения заряда потенциал ср также аксиально симметричен,
т. е. Ф = ф (г). Поэтому удобно использовать цилиндрическую систему
координат, аксиальный угол которой обозначим а. В ней оператор
Лапласа имеет вид
4*?& A5.16)
уФ-!? + !?+4?+&.
дг* г дг г да. oz
Так как в данном случае потенциал ф зависит только от г, то
Выражение A5.16) упрощается:
I dq> ^ 1 d / dq>
A5.17)
а уравнение Пуассона A5.14) записывается так:
г
1 d / dф
Общие решения A5.18) находятся интегрированием:
= --г — r2 + A1\nr+B1,
4 ?0
A5.19)
где Аи А2, Bt и В2 — постоянные интегрирования. Поскольку потенциал
во всех точках должен быть конечным, a In г -> оо при г -»0, необхо-
необходимо в решении A5.19) положить А^=0. Удобно потенциал норми-
нормировать условием фх @) = 0, и тогда Вг = 0.
Поскольку поверхностные заряды отсутствуют, напряженность элект-
электрического поля на поверхности шара непрерывна, т. е. непрерывна
производная от потенциала. Условия непрерывности потенциала и его
производной при г = а дают два алгебраических уравнения для опре-
определения двух оставшихся пока неизвестными постоянных А2 и В2:
A2lna + B2= --L-?-a2, ^-= --J--2-O, A5.20)
4 е0 а 2 е0
102 2. Постоянное электрическое поле
Отсюда следует, что
n i n A521)
Тогда
1 p a2 <15-22>
"t -, — -z i? 5= я).
ст 2 ?q r
Учитывая, что рла2 = т — заряд, приходящийся на 1 м длины ци-
цилиндра, можно второе из равенств A5.22) переписать в виде
Ег = -^~ —. A5.23)
2ГС?0 Г
Сравнение A5.23) с A5.9) показывает, что поле вне однородно
заряженного цилиндра таково, как если" бы весь его заряд был
сосредоточен на оси.
Пример 15.1. Найти напряженность поля прямой нити конечной длины,
равномерно заряженной с линейной плотностью заряда т (рис. 44). Принять:
х = 10'10 Кл/м; / = 1 м; d = 0,5 м; а = 0,5 м.
По закону Кулона
_ т dy cos a dxdy
* ~ 4яе0 (у2 + d2) ~ 4яе0 (у2 + d2K'2 '
, _ т dy sin а _ ту dy
" ~ 4яе0 (у2 + d2) 4яе0 (у2 + d2K'2 '
откуда
а а
Р id Г dy х__ Г ydy
4jce0 J (У2 + d2K12 ' " 4яе0 J (у2 + d2K12 '
-A-0) -A-о)
Произведя замену переменных у = d tg a, dy = d da/cos2 a, 1 + tg2 a = 1/cos2 a
и вычислив интегралы, получим:
(sin a2 + sin ai) = 1,27 В/м,
4ne0d
x A5.24)
E. = (cos a2 — cos aj = 0.
4яе0я
Для бесконечной нити (f-> оо) ai = a2 = я/2 и поэтому Еу = 0, Ех = т/Bяео(/).
Пример 15.2. Определить с помощью потенциала напряженность поля
в точках перпендикуляра к плоскости диска, если по нему равномерно
распределен заряд Q. Радиус диска а (рис. 45).
Принять: Q = 10 10 Кл; а — 10 см; h = 20 см
(расстояние до точки от плоскости диска).
По формуле A4.36) имеем
§ 15. Электростатическое поле в вакууме 103
Y dE,-_ dE
ф(*) =
о dx dy
4яе0 J ]/x2 + y2 + h2
s
-, о =
Q
„г •
Для вычисления интеграла перейдем к поляр-
полярным координатам в плоскости диска: х2 + у2 =
= г2, dx dy = r dr da,
44
К вычислению напряженности
электрического поля линейного
заряда конечной длины
2яе0 а1
откуда
A5.25)
У а2 + h2
A5.26)
Формула A5.26) совпадает с A5.3).
Пример 15.3. Найти напряженность электри-
электрического поля, создаваемого поверхностным заря-
зарядом сферы радиусом R. Полный заряд сферы Q,
поверхностная плотность заряда а = Q/DnR2).
Потенциал, создаваемый элементом заряжен-
заряженной поверхности (рис. 46) в точке, характеризуе-
характеризуемой г, равен
1 aK2 sin 9 d9 da
dcp =
4яе0
A5.27)
dcp =
4яе0
-dp da.
A5 28)
45
К вычислению напряженности
электрического поля заряжен-
заряженного диска
где R2 sin 9 d9 da — элемент поверхности сферы
в сферических координатах, полярная ось которых
совпадает с вектором г; угол a — аксиальный
угол. Из рисунка видно, что р = R — г. После
возведения обеих частей равенства в квадрат,
находим р2 = R2 + г2 — 2Rr cos 9. Взяв дифферен-
дифференциалы от обеих частей этого равенства, имеем
2р dp = 2Rr sin 9 d9,
откуда следует, что R2 sin 9 d9 = (р-R/r) dp. Тогда
[см. A5.27)]
46
К вычислению напряженности
поля поверхностного заряда
сферы
104 2. Постоянное электрическое поле
Интегрируя A5.28) по всей поверхности сферы, находим
стК Г da | dp = -i —Гр]Г+к, , = < е°Г 4яе° Г
J J 2 r Jl'-Rl
О |r-R|
Отсюда получаем напряженность электрического поля
Е, = - -^= < 4яе0 г2
0 (г < Л),
т. е. вне равномерно заряженной сферы напряженность поля такая же, как
если бы весь заряд был сосредоточен в ее центре, а внутри объема, ограни-
ограниченного сферой, поле отсутствует.
§ 16. Электростатическое поле
при наличии проводников
Рассматривается влияние проводников на
электрическое поле. Описываются основ-
основные физические явления, обусловленные рас-
распределением зарядов на поверхности провод-
проводника (стенание зарядов с острия и т. д.).
Обсуждаются количественные характери-
характеристики электрических свойств уединенных
проводников и систем проводников. Излага-
Излагается суть метода изображений.
Дифференциальная форма закона Ома. Проводниками называются
материальные тела, в которых при наличии электрического поля
возникает движение зарядов, т. е. электрический ток. Закон, связываю-
связывающий силу тока, протекающего по проводнику, с разностью потенциалов,
приложенной к его концам, был открыт экспериментально в 1827 г.
Г. С. Омом A787-1854) и имеет вид
/ = U/R, A6.1)
где R — величина, называемая сопротивлением проводника. Закон Ома
в дифференциальной форме получается в результате записи соотноше-
соотношения A6.1) для плотности тока. Рассмотрим бесконечно малый эле-
элемент проводника (рис. 47; А1 - длина; AS — поперечное сечение про-
проводника, к концам которого приложена разность потенциалов Дер).
Пусть у — удельная электрическая проводимость вещества, которая
является величиной, обратной удельному электрическому сопротивле-
сопротивлению. Электрическое сопротивление элемента проводника и сила тока,
текущего по нему, равны
Я=--^-, (a) /T=jtAS, (б) A6.2)
§ 16. Электростатическое поле при наличии проводников 105
где индекс т означает, что берется состав-
составляющая плотности тока вдоль элемента
проводника. Закон Ома для этого элемента
проводника записывается так:
Аф =jz AS ——-. A6.3)
Принимая во внимание, что (Дср/Д/) =
= Е, - компонента напряженности электри-
электрического поля в направлении рассматривав- к выводу дифференциальной
МОГО элемента, ИЗ A6.3) получаем формы закона Ома
h = yK A6.4)
Это соотношение справедливо при любой
ориентировке элемента проводника и по-
поэтому может быть записано в векторной
форме:
47
A6.5)
Равенство A6.5) является дифференциаль-
дифференциальной формой закона Ома.
классификация материалов по проводимо-
проводимости. Удельная электрическая проводи-
проводимость у зависит от свойств материала.
По ее значению материалы делят на три
Класса: диэлектрики, полупроводники и про-
проводники. Резкой границы между ними нет.
Принимается следующее деление этих ма-
материалов по проводимости:
а) диэлектрики — вещества с малой элект-
электрической проводимостью. Идеальный ди-
диэлектрик характеризуется отсутствием про-
проводимости. Однако это может осуще-
осуществиться лишь при 0 К. При температуре,
отличной от 0 К, все материалы обладают
определенной проводимостью и, следова-
следовательно, идеальных диэлектриков нет; ди-
диэлектриком принято называть материал,
удельная электрическая проводимость кото-
которого у < 10~5 См/м;
б) полупроводники имеют удельную
электрическую проводимость более
10 См/м, но менее 103 См/м;
в) проводники характеризуются удельной
электрической проводимостью, большей
103 См/м. В основном — это металлы. Наи-
¦ В электростатике поля
внутри проводника нет,
а объемные заряды отсут-
отсутствуют. Вблизи поверхно-
поверхности проводника напряжен-
напряженность электрического по-
поля направлена по норма-
нормали к поверхности и про-
пропорциональна поверхност-
поверхностной плотности заряда.
На выпуклой поверхности
проводника поверхност-
поверхностная плотность зарядов и
напряженность поля уве-
пичиваются с увеличени-
увеличением кривизны поверхности,
т. е. с уменьшением ради-
радиуса кривизны. На вогну-
вогнутой поверхности провод-
проводника поверхностная плот-
плотность заряда уменьшает-
уменьшается.
Закон Ома в дифферен-
дифференциальной форме справед-
справедлив не только при посто-
постоянной электропроводимос-
электропроводимости, но и при изменяю-
изменяющейся, независимо от
причин и характера ее
изменения.
О Следствием какого свойства
электростатического поля
является отсутствие танген-
тангенциальной составляющей на-
напряженности поля вблизи
поверхности проводника?
106 2. Постоянное электрическое поле
более хорошими проводниками среди них являются медь и серебро,
у которых удельная электрическая проводимость имеет порядок 107 См/м.
Отсутствие электрического поля внутри проводника, в электростатике
рассматривается случай неподвижных зарядов, когда j = 0. Равен-
Равенство A6.5) в этом случае дает
Е = 0, A6.6)
т. е. внутри проводника при электростатическом равновесии электри-
электрическое поле отсутствует.
/Отсутствие в проводнике объемных зарядов. Из уравнения
div E = р/?0 A6.7)
при Е = 0 следует, что
р = 0, A6.8)
т. е. внутри проводника отсутствуют объемные заряды. Это означает,
что заряд проводника концентрируется на его поверхности в слое
атомарной толщины. Конечно, внутри проводника имеются как поло-
положительные, так и отрицательные заряды, но они взаимно компенси-
компенсируются и в целом внутренние области проводника нейтральны [см. A6.8)].
Установление нейтральности происходит чрезвычайно быстро. Пред-
Предположим, что в некотором объеме внутри проводника в момент
времени t = 0 плотность свободных зарядов отлична от нуля (р @) ф 0).
Уравнение непрерывности E.24) с учетом A6.5) принимает вид
Ц- + div (уЕ) = 4г- + У div Е = 0,
ot ot
где у = const (для однородного проводника). С учетом A6.7) отсюда
получаем уравнение для изменения р во времени:
др _ у
1 ^р
решение которого имеет вид
т. е. плотность уменьшается экспоненциально. По общему правилу
можно считать, что образовавшийся объемный заряд «рассасывается»
в течение промежутка времени т = ео/у, называемого временем релак-
релаксации. Для металлов оно чрезвычайно мало. Например, для меди
(у = 6-107 См/м) т« 109 с. Такой промежуток времени чрезвычайно
мал даже в масштабах внутриатомных процессов. Поэтому в неста-
нестационарных ситуациях, когда поля изменяются со временем, при не
слишком больших частотах с большой точностью можно считать, что
в проводнике свободные заряды распределены по поверхности, а объемные
заряды отсутствуют. Данное заключение остается справедливым также
§ 16. Электростатическое поле при наличии проводииков 107
при учете зависимости проводимости у от частоты, хотя при этом
получается увеличение времени релаксации на несколько порядков.
Установление нейтральности связано с токами, которые, однако,
не создают заряда в тех областях, где они протекают. Чтобы это
понять, рассмотрим простой пример. Имеется шар радиусом а2, ве-
вещество которого характеризуется диэлектрической проницаемостью е
и удельной проводимостью у. В начальный момент t = 0 шаровая
область радиусом at < a2 заряжена равномерно с плотностью заряда
р0. Сферический слой между радиусами at и а2 нейтрален. Рассмотрим
процесс нейтрализации заряда в объеме шара.
Изменение плотности заряда в различных точках шара дается
формулой
где т = с/у. Полный заряд шара Qo = */эпа1ро остается постоянным,
но заряд шаровой области радиусом at уменьшается по закону
Этот заряд током проводимости через сферический слой между
радиусами а^ и а2 переносится к поверхности шара, где концентри-
концентрируется в виде поверхностного заряда.
Распределение заряда в любой момент времени сферически сим-
симметрично и поэтому по теореме Гаусса получаем следующее выраже-
выражение для напряженности электрического поля:
(О < г < aj,
4кга[
(ai < г < а2),
Поверхностный заряд шара возрастает. Он может быть рассчитан
по закону сохранения заряда или исходя из граничных условий.
В первом случае
Во втором случае
=а2 = Д-1г=„2 + 0 — А-1г=а2-0 =
где значения функции с аргументами г = а2 + 0 и г = а2— 0 берутся
соответственно с внешней и внутренней сторон поверхности шара.
103 2.. Постоянное электрическое поле
Плотность тока проводимости равна
(О < г < а,),
Л = уЕг =
Убое
(а, < г < а2),
Апгг2
О (а2 < г < оо).
Сила тока проводимости, протекающего через сферическую поверх-
поверхность радиусом г, определяется формулой
Ir=jr4nr2 =
-— @<г<
a-i
< г < а2),
О
(а2 < г < оо).
Таким образом, полный ток в области 0 < г < at возрастает с уве-
увеличением радиуса. Это обусловлено тем, что каждая точка этого
объема является источником тока проводимости. В, области ах<г <аг
источников тока проводимости нет и поэтому полный ток, проходящий
через сферическую поверхность, не зависит от радиуса.
Электрическая индукция. Если нейтральный проводник помещается
во внешнее электрическое поле, то поверхностные заряды на
проводнике перераспределяются так, что создаваемое ими внутри
проводника поле полностью компенсирует внешнее поле, в результате
чего суммарная напряженность поля внутри проводника равна нулю.
Явление перераспределения поверхностных зарядов на проводнике при
его помещении во внешнее электрическое поле называется электри-
электрической индукцией. Если проводник заряжен, то под влиянием внешнего
поля происходит также перераспределение и заряда проводника.
р^олс вблизи поверхности проводника. Выделим на поверхности
проводника элемент поверхности AS и построим прямой цилиндр
высотой п, пересекающий поверхность (рис. 48). Применим к этому
цилиндру теорему Гаусса:
jE-dS = Q/?0, A6.9)
s
где S — поверхность цилиндра, Q — заряд в объеме цилиндра.
Внутри цилиндра заряд имеется только на поверхности проводника
и характеризуется поверхностной плотностью а и, следовательно,
Q = aS. Внутри проводника поле равно нулю и поэтому поток Е через
часть поверхности цилиндра, находящуюся в объеме проводника,
равен нулю. Поток через часть поверхности цилиндра, находящуюся
вне проводника, слагается из потоков через основание цилиндра и его
боковую поверхность. В пределе высоту h цилиндра возьмем сколь
угодно малой (h -* 0), следовательно, и площадь боковой поверхности
§ 16. Электростатическое поле при наличии проводников 109
dSj
цилиндра и поток Е через боковую поверх-
поверхность будут сколь угодно малыми. Поэтому
в пределе h -> 0 останется лишь поток через
основание цилиндра:
jE-dS = EBAS, A6.10)
AS
где Е„ — нормальная компонента Е. Напом-
Напомним, что положительным направлением нор-
нормали в теореме Гаусса считается внешняя
нормаль к замкнутой поверхности. В рас-
рассматриваемом случае это означает, что по-
положительная нормаль направлена во внеш-
внешнюю сторону от поверхности проводника.
При h-*0 с учетом A6.10) равенство A6.9) к выводу формулы для нормаль-
ной составляющей напряжен-
48
принимает вид
откуда
?„ = ст/е0.
ности электрического поля вблн-
A6.11) зи поверхности проводника
A6.12)
Таким образом, нормальная компонента
напряженности поля у поверхности провод-
проводника однозначно определяется поверхност-
поверхностной плотностью зарядов.
Теперь возникает вопрос о тангенциаль-
тангенциальной компоненте напряженности поля. Пока-
Покажем, что она должна быть равна нулю
исходя из невозможности существования
вечного двигателя. Рассмотрим замкнутый
контур L, пересекающий поверхность про-
проводника, верхняя часть которого идет парал-
параллельно поверхности вне проводника, а внут-
внутренняя часть — внутри проводника (рис. 49).
Внутри проводника напряженность Е поля
равна нулю, а следовательно, отсутствует
и тангенциальная компонента поля. Допус-
Допустим, что вне проводника тангенциальная
компонента поля не равна нулю. Возьмем
положительный заряд и будем перемещать
его по замкнутому контуру в направлении,
указанном на рис. 49 стрелками. На участке
АВ поле совершает положительную работу.
Участок ВС в пределе может быть сделан
сколь угодно малым, поскольку участки АВ
и CD расположены сколь угодно близко
к поверхности проводника. Следовательно,
¦у
Ш
t
Д
1 .
49
К доказательству отсутствия тан-
тангенциальной составляющей на-
напряженности электрического по-
поля вне проводника
50
Механизм образования поля
вблизи поверхности проводника
110 2. Постоянное электрическое поле
перемещение на участке ВС связано с работой, которая может быть
сделана сколь угодно малой. Для перемещения заряда на участке CD
никакой работы не затрачивается, поскольку поле внутри проводника
отсутствует. Работа, связанная с перемещением заряда на участке DA,
так же, как и на участке ВС, может быть сделана сколь угодно малой.
Таким образом, в результате перемещения заряда по замкнутому
контуру электрическое поле произведет положительную работу и
больше в системе никаких изменений не произойдет. Можно повто-
повторить этот цикл и получить еще раз такую же работу и т. д. Таким
образом, осуществлен вечный двигатель первого рода, что невозможно.
Этот вечный двигатель совершает работу за счет тангенциальной
компоненты напряженности электрического поля вблизи поверхности
проводника. Следовательно, эта компонента должна быть равна нулю.
Другими словами, равенство нулю тангенциальной компоненты элект-
электрического поля у поверхности проводника является следствием потен-
потенциальности электростатического поля и отсутствия поля внутри
проводника.
Равенство
Et = 0 A6.13)
означает, что напряженность электрического поля вблизи поверхности
проводника направлена по перпендикуляру к поверхности и равна ст/е0
[см. A6.12)].
"[Механизм образования поля вблизи поверхности проводника. Един-
Единственными источниками электрического поля в электростатике
являются заряды. Поэтому поле вблизи поверхности проводника созда-
создается всеми поверхностными зарядами данного проводника и всеми
зарядами, находящимися вне проводника. Выделим бесконечно малый
элемент AS поверхности проводника (рис. 50). Напряженность Е поля
вблизи поверхности проводника состоит из двух частей: напряжен-
напряженности Et поля, создаваемого зарядами, находящимися на элементе AS,
напряженности Е2 поля, создаваемого всеми остальными зарядами вне
элемента AS. Ясно, что заряды элемента поверхности AS создают поле
с обеих сторон элемента. Поскольку обе стороны элемента AS экви-
эквивалентны, можно заключить, что векторы Et и Ei противоположно
направлены и равны по модулю | Ех | = | Ei |. Поле Е2 создается всеми
зарядами, находящимися вне элемента AS. Ясно, что эти заряды
создают не только напряженность Е2 вне проводника, но и напряжен-
напряженность Ег внутри проводника. Поскольку это есть электрическое поле
в пространстве вне зарядов, которые его создают, оно должно быть
непрерывным, и, следовательно, Е2 = Е'2. Напряженность полного поля
внутри проводника равна нулю, т. е. Е' = Ei + Е'2 = 0. Отсюда следует,
что Ei = — Е'2. Учитывая также равенство | Ei | = | Ei |, заключаем, что
|Eil=|E2|.
Отсюда следует
Ei = Е2 = '/гЕ, A6.14)
§ 16. Электростатическое поле при наличии проводников Ш
т. е. напряженность поля вблизи поверхности
проводника состоит из двух равных частей:
одна часть создается поверхностными заря-
зарядами прилегающего элемента поверхности,
а другая — всеми остальными зарядами, ле-
лежащими вне этого элемента поверхности.
зависимость поверхностной плотности за-
зарядов от кривизны поверхности. Заряд по
поверхности проводника распределяется не-
неравномерно, поверхностная плотность заря-
заряда зависит от кривизны поверхности. Чтобы
в этом убедиться, проанализируем распре-
распределение напряженности поля вблизи некото-
некоторого элемента поверхности (рис. 51). В слу-
случае малой кривизны поверхности (рис. 51, а)
находящиеся вне dS заряды создают вблизи Si
ЭТОГО Элемента малую нормальную СОСТаВ- Зависимость поверхностной
ляющую напряженности Е'2. Следовательно, плотности заряда от кривизны
для ее компенсации заряды, находящиеся поверхности
на элементе поверхности, должны создать
Сравнительно малую напряженность поля
Ei = — Е'2. В соответствии с формулами
A6.14) и A6.12) заключаем, что на этом
Элементе поверхностная плотность заряда
должна быть сравнительно малой, равной
а = 2?0?i. Если же кривизна поверхности
вблизи рассматриваемого элемента велика,
то напряженность Е2, создаваемая зарядами,
находящимися вне элемента AS поверхности,
велика и соответственно должна быть зна- 52
чительно больше напряженность, создавав- Стекание зарЯдОВ с octpaa
мая зарядами, лежащими на элементе по-
поверхности. А это означает, что поверхност-
поверхностная плотность зарядов на этом элементе
должна быть больше. Таким образом, мож-
можно заключить, что поверхностная плотность
зарядов увеличивается с ростом кривизны
поверхности, т. е. увеличивается с уменьше-
уменьшением радиуса кривизны.
С помощью аналогичных рассуждений
можно убедиться, что на вогнутой внутрь
проводника поверхности плотность заряда
уменьшается.
Увеличение поверхностной плотности за-
заряда на выпуклых поверхностях особенно
наглядно проявляется В СТекаНИИ заряда С Электрическое сегнерово колесо
острия.
©—?(+)
112 2. Постоянное электрическое поле
? текание заряда с острия. Рассмотрим, что происходит вблизи острия
заряженного проводника (рис. 52). Напряженность Е вблизи острия
очень велика. В окружающем воздухе имеются заряды (ионы, элект-
электроны), на которые в поле с напряженностью Е действует сила.
В соответствии с третьим законом Ньютона равная, но противопо-
противоположно направленная сила действует на заряды острия. Поэтому в ре-
результате взаимодействия заряды в воздухе вблизи острия и острие
получают равные, но противоположно направленные импульсы. Заряды
в воздухе, которые под влиянием действующей на них силы движутся
к острию, при попадании на острие передают ему свой импульс и заряд.
Этот импульс равен по модулю импульсу, полученному острием в ре-
результате взаимодействия с соответствующим зарядом, но имеет проти-
противоположное направление. Следовательно, в результате попадания
зарядов на острие эти импульсы взаимно компенсируются и итоговый
результат взаимодействия равен нулю.
Таким образом, взаимодействие зарядов острия с разноименными
зарядами окружающего воздуха не приводит к возникновению какой-либо
силы, действующей на острие.
По-другому обстоит дело для одноименных зарядов: сила, дей-
действующая на заряды острия, все время направлена в сторону про-
проводника (на рис. 41 эта сила обозначена — F+). Если острие заряжено
положительно, то отрицательные заряды, попадающие на острие, как
это изображено на рис. 41, нейтрализуют соответствующие положи-
положительные заряды. Это выглядит так, как будто бы положительные
заряды покидают острие, или, как говорят, стекают с острия. Сила — F+,
действующая при этом на острие, эквивалентна реактивной силе
отдачи, возникающей в результате стекания зарядов с острия. Если
острие заряжено отрицательно, то электроны покидают его факти-
фактически, т. е. фактически стекают с острия. Механизм возникновения
«реактивной силы» в этом случае совершенно аналогичен описанному
выше.
Это означает, что «реактивная сила» возникает не только в мо-
момент «старта» электронов с поверхности проводника, но и во все
последующие моменты времени, когда электрон ускоряется полем
зарядов, оставшихся на острие.
Эффектной демонстрацией наличия «реактивной силы» вследствие
стекания заряда с острия является вращение электрического сегнерова
колеса (рис. 53). Пунктирными стрелками показано направление стека-
стекания зарядов, в результате чего возникает «реактивная сила» и горизон-
горизонтальный отрезок проводника приходит в быстрое вращение вокруг
вертикальной оси.
Электроскопы и электрометры. Наиболее простым прибором для
обнаружения электрических зарядов является вертикальный метал-
металлический стержень или пластинка, к которому одним концом при-
прикреплена легкая проводящая фольга или стрелка (рис. 54). При
отсутствии заряда на металлическом стержне и фольге (стрелке) послед-
последняя висит вертикально, параллельно стержню. При наличии за-
§ 16. Электростатическое поле при наличии проводников 113
ряда силы отталкивания между одноимен-
одноименными зарядами на стержне и фольге (стрелке)
отклоняют фольгу от вертикального поло-
положения на некоторый угол. Таким образом,
прибор может служить индикатором на-
наличия заряда — электроскопом. Угол откло-
отклонения стрелки от вертикали тем больше,
чем больше заряд стержня. Это позволяет
проградуировать электроскоп и по углу
отклонения определять количество электри-
электричества на нем. Такой приспособленный для
количественных измерений электроскоп на-
называется электрометром. Заряд зависит от
потенциала стержня и стрелки. Поэтому
с помощью электрометра можно измерять
разности потенциалов. Электрометр заклю-
заключен в корпус (рис. 54).
Зависимость поверхностной плотности
заряда от кривизны поверхности проводника
демонстрируется с помощью электрометра
следующим образом. Небольшим проводя-
проводящим шариком, закрепленным на непрово-
непроводящей ручке, касаются соответствующего
участка поверхности проводника (рис. 55).
При этом на шарике образуется тем боль-
больший заряд, чем больше поверхностная плот-
плотность заряда на той части поверхности
проводника, в соприкосновении с которой
находится шарик. После этого шарик отде-
отделяется от поверхности проводника и приво-
приводится в соприкосновение со стержнем элект-
электрометра. На электрометр при этом пере-
переходит тем больше заряда, чем его было
больше на шарике. Поэтому по отклонению
стрелки можно судить о поверхностной
плотности заряда того участка поверхности
проводника, с которой взят заряд, перене-
перенесенный на электрометр. По соотношению
углов отклонения стрелки можно судить
о соотношении поверхностных плотностей
заряда на соответствующих участках поверх-
поверхности проводника. В зависимости от кри-
кривизны поверхности поверхностная плотность
заряда изменяется весьма значительно.
]у[еталлический экран. Механизм уничто-
уничтожения поля внутри проводника распре-
распределением зарядов на его поверхности пока-
54
Схема электроскопа и электро-
электрометра
55
Демонстрация зависимости плот-
плотности поверхностного заряда на
проводнике в зависимости от
кривизны поверхности с по-
помощью электрометра
114 2, Постоянное электрическое поле
56
Металлический экран для внеш-
внешних полей
——л
57
Заряд, окруженный замкнутой
проводящей оболочкой
-О
зывает, что внутренние части проводника
к нему не имеют никакого отношения и их
можно удалить. В результате этого остается
проводящая замкнутая оболочка (рис. 56).
В пространстве, окруженном оболочкой,
электрическое поле равно нулю. Замкнутая
оболочка называется экраном. Она экрани-
экранирует внутреннее пространство от внешнего
электрического поля. Экраны используются
для защиты технических устройств от влия-
влияния внешних электрических полей. Обычно
их изготовляют не из сплошного проводя-
проводящего материала, а из сетки с мелкими
ячейками. Как показывают опыт и расчет,
экранирующая способность такой сетки чуть
меньше сплошного экрана, но значительно
меньше затраты материала и проще устрой-
устройство экрана.
Экранирует ли замкнутая проводящая
оболочка внешнее пространство от зарядов,
находящихся внутри полости? Иначе говоря,
проникает ли поле зарядов, имеющихся
в объеме, окруженном замкнутой проводя-
проводящей оболочкой, во внешнее пространство?
Да, проникает. Чтобы в этом убедиться,
необходимо подробнее проанализировать си-
ситуацию.
Пусть в объеме V внутри полости распре-
распределен заряд
Q = JpdF. A6.15)
v
По закону электростатической индукции
на внутренней поверхности оболочки образу-
образуется заряд противоположного знака (рис. 57).
Чтобы найти его значение, воспользуемся
теоремой Гаусса, примененной к объему
внутри замкнутой оболочки:
A6.16)
внут
где SBliyT — внутренняя поверхность оболочки.
Обозначая ст — плотность поверхностно-
ка экранирует внешнее прост- го 3аРяДа на внутренней поверхности, ДЛЯ
ранство от зарядов внутри объ- напряженности Е поля вблизи поверхности
ема [см. A6.12)] получаем
58
Заземленная замкнутая оболоч-
§ 16. Электростатическое поле при наличии проводников 115
Е = — п, A6.17)
?о
где п — нормаль к внутренней поверхности оболочки, направленная
внутрь объема, ограниченного оболочкой. Учтем, что dS в A6.16)
направлен по внешней нормали к объему V, т. е. противоположно п,
и, следовательно,
n- dS = dScos(n, dS) = dScos к = -dS. A6.18)
Интеграл в левой части A6.16) с учетом A6.17) и A6.18) равен
E-dS= adS. A6.19)
^внут SBHyr
Тогда теорема Гаусса A6.16) принимает вид
- J adS = $pdV=Q. A6.20)
Следовательно, на внутренней поверхности оболочки образуется
заряд, равный по абсолютному значению заряду внутри полости и
противоположный ему по знаку.
Внутри оболочки напряженность поля равна нулю, поскольку обо-
оболочка является проводником. На внешней поверхности оболочки рас-
расположен заряд, знак которого противоположен знаку заряда на
внутренней оболочке, а абсолютное значение по закону сохранения
заряда равно абсолютному значению заряда на внутренней поверхности.
Для доказательства существования электрического поля во внешнем
пространстве воспользуемся теоремой Гаусса. На рис. 57 пунктирной
кривой изображена замкнутая поверхность, окружающая оболочку.
Полный заряд в объеме, ограниченном этой замкнутой поверхностью,
равен заряду внутри полости, ограниченной оболочкой, поскольку заряд
оболочки равен нулю. Следовательно, теорема Гаусса имеет вид
= 0, A6.21)
s v
т. е. напряженность Е поля в окружающем оболочку внешнем прост-
пространстве не равна нулю.
«Заземлим» оболочку, т. е. соединим ее проводником с очень боль-
большим удаленным проводящим телом. Обычно таким телом является
Земля (рис. 58). Для упрощения анализа представим это тело в виде
бесконечной проводящей среды, заполняющей все пространство вне
оболочки и соприкасающейся с оболочкой. Все заряды с внешней
поверхности оболочки уйдут на бесконечность и останется лишь заряд
внутри полости и заряд на внутренней поверхности оболочки. Напря-
Напряженность поля внутри проводящей среды, окружающей оболочку, равна
нулю. При этом роль среды сводится лишь к тому, чтобы обеспечить
удаление заряда с внешней поверхности оболочки на бесконечность.
Поэтому роль областей среды на конечном расстоянии от оболочки
116 2. Постоянное электрическое поле
может выполнить тонкий проволочный проводник, который обеспечи-
обеспечивает возможность обмена зарядом между оболочкой и достаточно
удаленными областями среды. Ясно, что после удаления проводящей
среды из области, окружающей оболочку, напряженность поля в точка;;
области по-прежнему равна нулю. Таким образом, заземленная замкну-
замкнутая оболочка экранирует внешнее пространство от зарядов, находя-
находящихся в объеме, окруженном этой оболочкой. Незаземленная оболочка
такой экранировки не создает.
Потенциал проводника. Из равенства нулю напряженности Е поля
внутри проводника следует, что во всех точках проводника потен-
потенциал имеет одно и то же значение, т. е. разность потенциалов между
точками 1 и 2 проводника [см. A4J28)] равна
B)
срB)-фA)= J Е • dl = 0. A6.22)
A)
Одинаковое во всех точках проводника значение потенциала назы-
называется потенциалом проводника.
Пусть имеется изолированный заряженный проводник. В окружаю-
окружающем проводник пространстве имеется электрическое поле, создаваемое
зарядом проводника. Будем нормировать потенциал на нуль в беско-
бесконечности. Тогда [см. A4-29)] потенциал проводника может быть выра-
выражен формулой
Ф= J E-dL A6.23)
/поверхностью
^ проводника}
В формуле A6.23) путь интегрирования начинается в любой точке
проводника и заканчивается на бесконечности.
|?мкость уединенного проводника. От чего зависит потенциал уеди-
уединенного проводника? Из формулы A6.23) видно, что по принципу
суперпозиции потенциал должен быть прямо пропорционален заряду,
поскольку Е в подынтегральном выражении A6.23) прямо пропорцио-
пропорциональна заряду. Далее очевидно, что потенциал зависит от размеров
и формы проводника, которые учитываются его емкостью.
Емкостью проводника называется отношение заряда Q уединенного
проводника к его потенциалу ср:
с = е/Ф.
A6.24)
Емкость проводника выражается в фарадах (Ф). Из A6.24) находим:
1 Ф = 1 Кл/В. A6.25)
В системе СГС емкость выражается в сантиметрах, а формула для
емкости совпадает с A6.24). Поскольку 1 В = A/300) СГС, 1 Кл =
= 3 • 109 ед. СГС, из A6.24) следует, что
1 ф = 91011 см. A6.26)
§ 16. Электростатическое поле при наличии проводников 117
Фарад является очень большой единицей. Вычислим, например,
емкость шара, радиус которого R, а заряд Q. Поскольку напряжен-
напряженность поля такого шара в окружающем его пространстве равна
,-J
Е=г т, A6.27)
4ле0 г2 г
то потенциал и емкость выражаются формулами:
?dr=—1—%, A6.28)
R
С = й/ф = 4jie0R. A6.29)
При радиусе шара 1 см находим
С = 10" 2/(9 • 109) » 10-12 Ф. A6.30)
Поэтому емкость обычно выражают в дольных единицах.
?|истема проводников. Если имеется несколько проводников, то по-
потенциал каждото из них зависит не только от заряда проводника,
но и от напряженностей полей, создаваемых другими проводниками,
или, другими словами, от зарядов других проводников, причем по
принципу суперпозиции он прямо пропорционален этим зарядам.
Рассмотрим для определенности два проводника (рис. 59). На ос-
основании сказанного можно написать
A6.31)
где a,j — потенциальные коэффициенты, зависящие от формы и разме-
размеров проводников и от их взаимного расположения. Теоретическое
Вычисление этих коэффициентов является сложной математической
задачей. Обычно они определяются опытным путем.
Потенциальные коэффициенты не являются независимыми друг от
друга. В этом можно убедиться следующим образом. Пусть: а^
и ст2 — поверхностные плотности зарядов; гп — расстояние от элемента
интегрирования dSt на поверхности первого проводника до некоторой
фиксированной точки внутри него; г12 — расстояние от элемента поверх-
поверхности dS2 второго проводника до той же точки. Тогда потенциалы
первого и второго проводников равны (смысл г22 и г21 аналогичен
Гц и г12):
1 Г a dS 1 Г dS
<Pi = l — ~+ ~л ——-, A6-32)
4гсе0 J Гц 4яе0 J rl2
s, s2
1 Г jo i Г jc
Ф2 = 7 — -+ — L. A6.33)
S2 Si
Заряды проводников равны:
б! = Jc^dSt, Q2 = Jc2dS2. A6.34)
118 2. Постоянное электрическое поле
Предположим, что заряды проводников изменились:
Qi = | ai dSb Q2 = f a'2 dS2. A6.35)
S, Si
Умножим обе части A6.32) на Qi, a A6.33) на Q2 и сложим почленно
полученные равенства:
61Ф1 •
Г\2
s, s, s, s2
л Г Г _ Jtr 1 С Г ~ AQ
+ I ст'2 dS2 I ь -; IC72 dS2 I =
4ле0 J J г22 4ле0 J J r2i
S2 Si S2 Si
if f oi dS, if Г CTi dS,
= -. CTt dS1 —i + ст2 dS2 +
4яе0 J J «"и 4яе0 J J r12
4ts0
s s2 s" s2 A6.36)
где порядок интегрирования изменен, поскольку интегрирование про-
проводится по разным независимым переменным. Величины (pi и ср'2
являются потенциалами проводников, когда заряды их равны Q\ и Q'2.
Полученное в A6.36) соотношение
+ б'гФг = б1ф1 +
A6.37)
называется теоремой взаимности. Из нее получается условие, которому
удовлетворяют потенциальные коэффициенты ау.
Если заряд второго проводника равен нулю (Q2 = 0, Qi Ф 0), то
[см. A6.31)]
Ф1 = «пбь Фг = «2i6i- A6.38)
Если заряд первого проводника равен нулю (Qi =0, Q2 ф 0), то
[см. A6.31)]
Ф1 = «12G2, Ф2 = «22Q'2. A6.39)
Теорема взаимности A6.37) для этих двух случаев принимает вид
б'2Ф2 = Qi<fi. A6.40)
Подставл5м в A6.40) выражения ср2 и cpi [см. A6.38) и A6.39)]
и сокращая обе части полученного равенства на общий множитель
Q'iQi, находим
ai2 = a2i, A6.41)
т. е. потенциальные коэффициенты симметричны относительно своих
индексов.
§ 16. Электростатическое поле при наличии проводников 119
Все вычисления нетрудно провести для любого числа проводников,
записав исходные соотношения A6.31) для и проводников в виде
ф| =
Все дальнейшие вычисления аналогичны вычислениям от A6.32) до
A6.37) и вместо A6.37) приводят к следующей формуле, выражающей
теорему взаимности в общем случае:
I й'Ф, = ? QM- A6-43)
i=i 1=1
Из A6.43) вместо A6.41) получается общее условие симметрии по-
потенциальных коэффициентов:
О,; = ОС;;. A6.44)
Система уравнений A6.42) может быть решена относительно Q,:
& = L C,jq>j. A6.45)
Здесь Су = Ay/D, где D — детерминант из коэффициентов системы урав-
уравнений A6.42), Ai} — дополнение элемента Оу в этом детерминанте.
На основании A6.44) заключаем, что коэффициенты Су удовлетворяют
условию
Су = С,, A6.46)
где Су — емкостные коэффициенты, Сц — емкостной коэффициент i-ro
проводника, а Су — емкостной коэффициент между i-м и j-м проводни-
проводниками. Емкостной коэффициент уединенного проводника называется
просто емкостью проводника.
Поскольку положительный заряд на уединенном проводнике создает
положительный потенциал, можно заключить, что все емкостные
коэффициенты с одинаковыми индексами (Сц, С22> —) положительны.
Чтобы в этом убедиться, заземлим все проводники, за исключением
i-ro, а на i-м проводнике оставим положительный заряд, т. е. будем
считать, что Qt > 0. Тогда, очевидно, ф( > 0 и фу = О при j ф L Следова-
Следовательно, уравнение A6.45) для Q принимает вид
Qi = С„Ф>-. A6.47)
Так как ф( > 0 и Qi > 0, то Си > 0, что и требовалось доказать.
Аналогично можно доказать, что емкостные коэффициенты с различ-
различными индексами не могут быть положительными — они либо отрица-
отрицательны, либо равны нулю. Рассмотрим, например, два проводника, из
которых один заземлен, а другой изолирован и заряжен положительно.
Этот положительный заряд вследствие явления электростатической
индукции наведет на заземленном проводнике отрицательный заряд.
Формула A6.45) для заряда на втором проводнике принимает вид
Qi = С21ф1. A6.48)
120 2. Постоянное электрическое поле
59
Система проводников
Так как Q2 < 0, ф, > 0, то С21 < 0. Такой
вывод не исключает возможности, что коэф-
коэффициент может быть равным нулю, но этот
коэффициент безусловно не может быть по-
положительным.
Рассмотрим три проводящие сферы
(рис. 60). Их потенциалы и заряды обозначим
соответственно срь ср2, ср3 и Qu Q2, Q3.
Для определения С^ имеем уравнения A6.45),
которые в данном случае принимают вид:
A6.49)
60
К нахождению емкостных коэф-
коэффициентов в случае двух сфер
61
К вычислению емкостных коэф-
коэффициентов двух проводящих ша-
шаров
Емкость уединенного про-
проводника зависит только
от его формы и размеров.
Потенциальные и емкост-
емкостные коэффициенты зави-
зависят только от геометри-
геометрических характеристик про-
проводников и их взаимного
расположения.
Емкостные коэффициенты
с одинаковыми индексами
всегда положительны, а
с различными — либо рав-
равны нулю, либо отрица-
отрицательны.
Qi = Cn<Pi + С12ф2 + С13ф3,
Q2 = С21ф1 + С22ф2 + С23Фз,
из = С31Ф1 + С32ф2 + СззФз-
Чтобы определить коэффициенты Су,
необходимо иметь достаточное число урав-
уравнений A6.49) с известными Qt и ф(, из
КОТОРЫХ ВЫЧИСЛЯЮТСЯ Cij.
Предположим, что Q3 = 0 и вторая сфера
заземлена. При этом ф3 = ф2 = 0 и уравне-
уравнения A6.49) принимают вид:
Qi = Сцфь Qi = С21фь 0 = С31ф!. A6.50)
Тогда C3i = С13 = 0, т. е. емкостной
коэффициент между заэкранированными
проводниками равен нулю.
Предположим, что первая и вторая сфе-
сферы заземлены, т. е. ф! =0, ф2 = 0, но заряд
Qi Ф 0. Уравнения A6.49) в этом случае
принимают вид:
Qi = 0, Q2 = С23ф3, бз = СззФз- A6.51)
Как было показано, на внутренней по-
поверхности заземленной проводящей оболоч-
оболочки индуцируется заряд, равный по абсолют-
абсолютному значению заряду в полости ограничи-
ограничиваемой оболочкой, но противоположный ему
по знаку, т. е. Q2 = —из- Из уравнений A6.51)
получаем
С23=-С33. A6.52)
Таким образом, емкостной коэффициент
между двумя проводниками, один из кото-
которых полностью окружает другой, равен взя-
взятому с обратным знаком емкостному ко-
коэффициенту внутреннего проводника, что
играет важную роль для конденсаторов.
§ 16. Электростатическое поле при наличии проводников 121
Предположим, что имеются два шара, расположенных на большом
по сравнению с их радиусами а расстоянии г друг от друга (рис. 61).
Обозначим: а — радиусы шаров и г — расстояние между их центра-
центрами. Поскольку а <§: г, можно для расчета напряженности поля вдали
от шаров пренебречь перераспределением зарядов на шарах из-за их
взаимной электростатической индукции. Тогда формулы для потенциа-
потенциалов шаров принимают вид:
где Qi и Q2 — заряды первого и второго шаров. Уравнения A6.53)
можно решить относительно Gi и Q2:
а2г
О, = 4яе0^ 5-фх — 4яе0 -j г Фг»
аг2
= С22 = 4яе0 2_ 2 =С>0, A6.55)
-=у<0. A6.56)
Представим A6.54) с учетом A6.55) и A6.56) в виде:
Qi = Сфх + уфг» 0,г = УФ1 + СФ2- A6.57)
При г-* со получаем Сп = С22 = 4яЕоа, С12 = С21 = 0, т. е. электри-
электрическая связь между шарами прекращается и каждый из них ведет
себя как изолированный проводник, а коэффициент емкости каждого
из шаров становится просто емкостью изолированного шара.
Рассмотрим теперь типичную задачу.
Напомним, что емкостные коэффициенты при неизменной конфигу-
конфигурации проводников и их взаимного положения постоянны, независимо
от изменения их зарядов и потенциалов. Поэтому надо рассмот-
рассмотреть столько различных ситуаций, сколько имеется неизвестных
емкостных коэффициентов, и решить систему уравнений.
Пусть шарам сообщаются некоторые заряды, в результате чего их
потенциалы будут равны фх и ф2. После этого второй шар заземляется.
Чему равны заряды и потенциалы шаров после заземления?
До заземления заряды и потенциалы шаров связаны уравнениями
A6.57). Поскольку потенциалы известны, заряды могут быть вычислены
по этим формулам. После заземления второго шара его потенциал
равен нулю (ф2 = 0), а заряд Q'2 неизвестен; заряд первого шара по-преж-
по-прежнему равен Q\ = Gi> поскольку он изолирован. Потенциал q>\ неиз-
неизвестен. Запишем уравнения A6.57) для случая, когда второй шар
заземлен:
6i = Сф'ь Й2 = уфь Gi = Gi- A6.58)
122 2. Постоянное электрическое поле
Решение этих уравнений:
^-l-^-p. + lft.ft-rl. A6.59)
Из A6.55) и A6.56) следует, что
у/С = ~а/г, A6.60)
поэтому выражения A6.59) принимают вид
4>'i = Ф» - (а/г)ср2) & = _ (а/г)б,, A6.61)
т. е. после заземления второго шара потенциал первого шара изменяется
на долю а/г от потенциала второго шара, а на втором шаре остается
индуцированный заряд, равный доле а/г от заряда первого шара и
имеющий знак, противоположный знаку заряда первого шара.
Прервем заземление второго шара, заземлим после этого первый
шар и определим потенциал второго шара и заряд первого.
Очевидно, что после заземления первого шара его потенциал будет
равен нулю (<р'[ = 0), а заряд Q'[ неизвестен. Поскольку второй шар
изолирован, его заряд не изменяется при заземлении первого шара
F1 = Q'l)- Уравнения A6.57) после заземления первого шара имеют вид:
Q'i = Y<P2, Q'i = Cq>, Q'i = Q'2, A6.62)
откуда
_. Q'i
\— J Ф2»
A6.63)
(
Эти примеры иллюстрируют методы расчета емкостных коэффициен-
коэффициентов, зарядов и потенциалов при наличии нескольких проводников в
электростатическом поле.
^онденсаторы. Конденсатором называется совокупность двух любых
проводников с одинаковыми по абсолютному значению, но противо-
противоположными по знаку зарядами. Проводники называются обкладками
конденсатора. Полагая в A6.31) 6i = б, Qi = -Q, получаем cpt = 6(ceu -
— anh Фг =Q(«2i — Я22). Тогда разность потенциалов между провод-
проводниками
Лф = Ч>1 - Ч>2 = е(«11 + «22 - «12 - «2l)- A6.64а)
Это означает, что разность потенциалов между обкладками конден-
конденсатора пропорциональна заряду на обкладке и, следовательно, конден-
конденсатор характеризуется одним параметром, называемым емкостью.
Емкость конденсатора определяется соотношением
С=^-, I A6.646)
I ^Ф I
§ 16. Электростатическое поле при наличии проводников 123
62
Конденсаторы: общий случай
(а), сферический F), цилиндри-
цилиндрический (в), плоский (г)
причем, по определению, емкость считается положительной величиной,
т. е. в A6.64) как Q, так и Лф должны иметь одинаковый знак.
Сравнение A6.646) с A6.64а) показывает, что емкость конденсатора
выражается через потенциальные коэффициенты формулой
С = (аи + а22 - 2ai2)~1, A6.64в)
где at2 = 0С21- Поскольку а^2 и а21 отрицательны, емкость С в A6.64в)
всегда положительна [см. A6.646)]. Принимая во внимание смысл потен-
потенциальных коэффициентов из A6.64в), заключаем, что емкость конден-
конденсатора зависит только от геометрических характеристик обкладок кон-
конденсатора и их взаимного расположения.
Исходя из A6.45) и пользуясь определением A6.646), получаем выра-
выражение емкости конденсатора через емкостные коэффициенты:
С =
A6.64Г)
22
В большинстве случаев форма обкладок конденсатора и их взаим-
взаимное расположение подбирают таким образом, чтобы внешние поля
не влияли существенно на электрическое поле между ними, и силовые
линии, начинающиеся на одной из обкладок, обязательно заканчивались
на другой. Благодаря этому всегда обеспечивается равенство абсолют-
абсолютных значений зарядов на обкладках.
Конденсатор может быть представлен в виде проводника, помещен-
помещенного в полости, окруженной замкнутой оболочкой (рис. 62, а). Если
внутренний проводник является шаром или сферой, а замкнутая обо-
оболочка — концентрическая ему сфера, то конденсатор называется сфери-
сферическим (рис. 62, б). Если внутренний проводник — прямой сплошной
цилиндр, а оболочка — полый прямой цилиндр, коаксиальный внутрен-
внутреннему, то конденсатор называется цилиндрическим (рис. 62, в). Совокуп-
Совокупность двух параллельных плоских проводящих пластин является плоским
конденсатором (рис. 62, г).
124 2. Постоянное электрическое поле
U
a)
Вычисление емкости конденсатора сво-
сводится к определению разности потенциалов
между обкладками конденсатора при извест-
известном заряде на обкладках. Например, если на
внутренней обкладке сферического конденса-
конденсатора имеется заряд Q, то напряженность
поля между внутренней и внешней обклад-
обкладками равна Е = 6/Dяеог2) и направлена по
радиусу. Поэтому разность потенциалов
между обкладками
63
Последовательное (а) и парал-
параллельное (б) соединения кон-
конденсаторов
!- Ф2 "" Ф1 =
64
Поле внутри однородно заря-
заряженного шара
65
К вычислению напряженности
поля сдвинутых друг относитель-
относительно друга шаров
4пе0
dr
4^0^! Г2)
A6.65)
Отсюда по формуле A6.646) получаем, что
емкость сферического конденсатора равна
С = 4яеог1г2/(г2 -rt). A6.66)
Аналогично находим емкости цилиндри-
цилиндрического и плоского конденсаторов:
С = 2яеог/1п (г2/гД С = e0S/d.
Определим емкость плоского конденса-
конденсатора, площадь обкладок которого 1 см2 =
= 10 м2, а расстояние между обкладками
if=lMM = 10
1
м:
-1-4
С =
Ф«10
~12
Ф =
пФ.
A6.67)
4п-9-109 10
Конденсаторы можно соединять последо-
последовательно (рис. 63, а) и параллельно (рис. 63, б).
При последовательном соединении склады-
складываются разности потенциалов, а при парал-
параллельном — заряды на обкладках.
При последовательном соединении
U = U1 + U2,U = QIC, U, = Q/Cu
U 2 = Q/C2, A6.68)
где U — разность потенциалов между край-
крайними обкладками конденсаторов; t/t и U2 —
разности потенциалов между обкладками
каждого из конденсаторов; Q — модуль за-
заряда на каждой обкладке конденсаторов
(модули заряда на всех обкладках конден-
конденсаторов равны); С — емкость двух конден-
конденсаторов; Ct и С2 — емкости каждого из кон-
16. Электростатическое поле при наличии проводников 125
денсаторов. Из A6.68) следует, что
A6.69)
Таким образом, при последовательном соединении складываются
обратные значения емкостей.
При параллельном соединении
б = Qi + Qi, Q = VC, Q1 = UCU Q2 = UC2. A6.70)
Тогда
С2,
A6.71)
т. е. при параллельном соединении складываются емкости конден-
конденсаторов.
^"|роводящий шар в однородном поле Напряженность поля, которое
возникает в результате внесения проводящего шара во внешнее
однородное электрическое поле, может быть найдена элементарными
методами.
Прежде всего определим напряженность внутри однородно заряжен-
заряженного шара радиусом R (рис. 64), который, конечно, не является провод-
проводником. Пусть объемная плотность заряда внутри шара равна р. Тогда
в сферическом объеме радиусом r<R находится заряд Qr = 4/3nr3p.
Применяя к сферическому объему теорему Гаусса, получаем (е0 — ди-
диэлектрическая проницаемость материала шара)
Е(гLяг2 = Qr/Eo = 4яг3р/(Зб0) A6.72)
и, следовательно, напряженность поля внутри однородно заряженного
шара в точке, характеризуемой радиус-вектором г, равна
Е(г) = [(Р/(Зб0)]г, A6.73)
причем началом отсчета радиус-вектора является центр шара.
Теперь представим, что имеются два шара одинакового радиуса с
одинаковой объемной плотностью заряда разных знаков (рис. 65).
Допустим, что отрицательно заряженный шар сдвинут влево. Вектор,
проведенный из его центра в центр другого шара, обозначим I. Найдем
напряженность поля во внутренних точках шаров. Напряженности,
создаваемые зарядом каждого из шаров, равны:
Е(+) = [| р|/Cео)] г(+), Е<_) = -[I Р|/(Зб0)] г,_„ A6.74)
где Е(+) и Е(_) — напряженности, создаваемые зарядами шаров соот-
соответствующего знака; г(+) и г(_) — радиус-векторы, проведенные в рас-
рассматриваемую точку из центров шаров с зарядами соответствующего
знака. Суммарная напряженность равна
Е = Е<+) + Е,-, = [1р1/(Зво)](г(+) - г(_)) = -[| pl/ЗеоД >, A6.75)
126 2. Постоянное электрическое поле
где
г(_) = I + г(+, A6.76)
(см. рис. 65). Таким образом, внутри шаров напряженность поля постоян-
постоянна и направлена вдоль линии, соединяющей их центры.
В точках пересечения объемов шаров плотность заряда равна нулю,
поскольку положительная и отрицательная плотности заряда взаимно
компенсируют друг друга. Заряженными являются лишь непересекаю-
непересекающиеся части шаров серповидной формы (см. рис. 65). Максимальная
ширина этих серповидных областей, равная /, может быть сколь угодно
малой.
Теперь представим, что проводящий шар помещен во внешнее одно-
однородное поле с напряженностью Eq. Электростатическая индукция при-
приведет к возникновению поверхностных зарядов. Знаки этих зарядов и
направление напряженности внешнего поля показаны на рис. 66. Внутри
шара поле должно быть равным нулю, т. е. распределение поверх-
поверхностных зарядов будет такое же, как на рис. 65, а возникающее при
этом поле внутри шаров компенсирует внешнее поле. Тогда [см. A6.75)]
(|р|/38оI = Ео. A6.77)
Таким образом, центры воображаемых заряженных шаров сдвинуты
друг относительно друга по линии напряженности внешнего поля.
Поскольку I в A6.77) совпадает по направлению с Eq, для скалярных
величин можно написать
|р| / = 3?0?0-
Очевидно, что сдвиг I центров шаров может быть сколь угодно
малым, если |р| достаточно велико. Поэтому возникающие здесь заряды
можно действительно считать поверхностными с изменяющейся поверх-
поверхностной плотностью.
Найдем распределение поверхностной плотности заряда в зависи-
зависимости от угла 0. Расстояние между поверхностями шаров в направ-
направлении угла Э равно 8 = 1 cos Э (рис. 65). Если объемный заряд между
поверхностями шаров трактовать как поверхностный и обозначить его
поверхностную плотность сг, то
о-AS = pAS5, A6.78)
где слева стоит выражение для заряда, приходящегося на элемент
поверхности AS, через поверхностную плотность, а справа - через
объемную. Следовательно [см. A6.78)],
сг = р5 = р/ cos 0 = 3?0?0 cos 9, A6.79)
где 5 = I cos 0.
Теперь можно найти напряженность поля у поверхности проводя-
проводящего шара:
Еп = ст/?о = 3?0 cos 9, A6.80)
откуда видно, что она изменяется от нуля до утроенного значения
напряженности однородного поля. Конечно, во всех точках поверхности
§ 16. Электростатическое поле при наличии проводников 127
шара напряженность направлена по нормали
к поверхности.
Вне шара на конечном расстоянии от его
поверхности она равна сумме напряжен-
напряженностей внешнего поля и полей, создаваемых
сдвинутыми друг относительно друга заря-
заряженными шарами или, что то же самое, соот-
соответствующими поверхностными зарядами.
Поле вне равномерно заряженного шара та-
таково же, как если бы весь его заряд был
сосредоточен в центре. Таким образом,
необходимо найти напряженность поля двух
разноименных точечных зарядов с одинако-
одинаковым абсолютным значением, находящихся
на небольшом расстоянии один от другого.
Такая совокупность зарядов называется ди-
диполем (рис. 67). Вектор 1, проведенный от
отрицательного заряда к положительному,
называется плечом диполя. Вектор
р = q\ A6.81)
называется моментом диполя. В формуле
A6.81) q — абсолютное значение каждого из1
зарядов диполя. Для определения напряжен-
напряженности поля вне проводящего шара необхо-
необходимо найти напряженность поля диполя, за-
заряды которого сосредоточены в центрах
сдвинутых шаров. Из A6.77) следует, что
момент диполя равен
4Я8П
(+)
однородном
0-
= 4я8оЯ3Ео, A6.82)
где R — радиус шара.
Г|оле диполя. Напряженность поля диполя
слагается из напряженностей составляю-
составляющих диполь зарядов. Плечо диполя сколь
угодно мало и поэтому его можно считать
много меньшим расстояния до точек, в ко-
которых вычисляется напряженность. Найдем
потенциал диполя. В точке Р (рис. 68) по-
потенциал, очевидно, выражается формулой
1
I7-Y.
/cos А
A6.83)
Так как / «: г, то можно считать г(_, —
- г(+) я* /cos в, г(_)Г(+)«г2 и характеризо- w
вать местоположение точки Р радиус-векто- к вычислению поля
диполя
128 2. Постоянное электрическое поле
ром г с началом в любой точке диполя, поскольку диполь имеет сколь
угодно малые геометрические размеры.
Тогда [см. A6.83)]
Ф(г) =
1
4я?0
A6.84)
где ql cos Q = (p-r)/r, откуда
1*} <16-85>
Напряженность поля диполя убывает обратно пропорционально
третьей степени расстояния, т. е. быстрее, чем напряженность куло-
новского поля заряда. Силовые линии поля диполя изображены на
рис. 69.
Формула A6.85) позволяет построить линии напряженности поля,
когда проводящий шар помещен во внешнее однородное поле. В каж-
каждой точке напряженность равна сумме напряженности Ео однородного
внешнего поля и напряженности Е, создаваемой индуцированными на
поверхности проводящего шара зарядами. Линии напряженности этого
поля изображены на рис. 66.
]у/|етод изображений. При решении задачи о проводящем шаре во
внешнем однородном поле было сделано одно предположение,
справедливость которого не доказывалась, а именно: было построено
некоторое поле, удовлетворяющее всем условиям задачи, и считалось,
что другого поля, удовлетворяющего тем же условиям задачи, не
существует, т. е. предполагалось, что решение задачи является единствен-
единственным. Если бы это было не так, то найденное конкретное решение
не обязательно было бы тем решением, которое фактически реализуется.
В теории электричества и магнетизма доказано, что решение задач,
удовлетворяющее всем необходимым условиям, является единственным.
Позднее будет рассмотрено, о каких всех условиях идет речь и как
в общих чертах проводится доказательство этого утверждения, здесь же
пока примем его справедливость без доказательства. Это позволяет
найти решение задачи с помощью некоторых догадок или построений
и на основании теоремы об единственности заключить, что найденное
таким способом поле дает решение задачи. Примером удачной догадки
является рассмотренное выше решение о проводящем шаре во внешнем
однородном электрическом поле.
Существует наглядный метод построения поля, удовлетворяющего
условиям задачи, называемый методом изображений. Его суть состоит
в следующем. Поле точечного заряда хорошо известно. Стараются
подобрать такую систему точечных зарядов, суммарное поле которых
удовлетворяет всем условиям задачи. Из теоремы об единственности
решения заключаем, что это поле дает искомое решение. Матема-
Математически задача сводится к нахождению потенциала, удовлетворяющего
§ 16. Электростатическое поле при наличии проводников 129
условиям задачи. Напряженность Е направле-
направлена перпендикулярно эквипотенциальным по-
поверхностям и вычисляется как взятый с об-
обратным знаком градиент от потенциала.
Получить форму эквипотенциальных поверх-
поверхностей системы точечных зарядов в принци-
принципе легко. Рассмотрим, например, поле двух
положительных точечных зарядов q, распо-
расположенных на расстоянии 2d друг от друга
(рИС. 70). Так как потенциал Точечного За- Силовые линии вблизи диполя
ряда на расстоянии г от него равен
Ф = q/Dne0r), то потенциал системы двух
одинаковых точечных зарядов (см. рис. 70)
в точке (х, у, z) определяется выражением
Ф (х, у, z) = (
69
4Я80
1
У(х -
I + У2 + Z2
¦>
A6.86)
Из A6.86) получаем уравнение эквипотен-
эквипотенциальных поверхностей:
1 1
_ 70
|/(х - dJ + у2 + z2
]/(х + dJ + у2 + z2
= const.
Каждая из них характеризуется соответст-
соответствующим потенциалом фх = const, ф2 = const.
На рис. 70 изображены линии пересечения
плоскости XY с эквипотенциальными поверх-
поверхностями. Сами эквипотенциальные поверх-
поверхности получаются в результате вращения
картины, изображенной на рис. 70, вокруг
оси X.
Пусть проводящая изолированная поверх-
поверхность совпадает с одной из эквипотенциаль-
эквипотенциальных поверхностей, потенциал которой ф0.
Если принять, что на этой поверхности
находится заряд 2q, а ее потенциал равен сро>
то система эквипотенциальных поверхностей
и соответствующее ей поле полностью
удовлетворяют условиям задачи о поле за-
заряженной поверхности. Потенциал во всех
внешних относительно поверхности точках
определяется формулой A6.86). Таким обра-
образом, нахождение характеристик поля, создан-
созданного заряженным проводником, свелось к
Эквипотенциальные поверхности
A6.87) двух одинаковых точечных за-
зарядов
5 А Н Матвеев
130 2. Постоянное электрическое поле
определению характеристик поля, двух одно-
одноименных равных точечных зарядов. В этом и
состоит суть метода изображений. Проис-
Происхождение названия метода станет очевидным
из рассматриваемых ниже примеров.
Потенциал двух разноименных точечных
зарядов определяется аналогично A6.86):
W 1
4яео \]/(х - d)z + у1 + z2
71
Эквипотенциальные поверхно-
поверхности двух разноименных разных
по абсолютной величине точеч-
точечных зарядов
A6.88)
72
К нахождению эквипотенциаль-
эквипотенциальных поверхностей двух точеч-
точечных зарядов различной величины
73
К определению поля конден-
конденсатора с непараллельными плас-
пластинами
Форма эквипотенциальных поверхностей
В этом случае показана на рис. 71. Потен-
Потенциал вдоль оси Y равен нулю и, следова-
следовательно, он равен нулю в плоскости X = 0.
Представим себе, что все бесконечное
полупространство X < 0 заполнено провод-
проводником, границей которого является плос-
плоскость YX, и имеется заряд +q там, где он
изображен на рис. 71. Ясно, что этот заряд
посредством электростатической индукции
наведет на поверхности проводника заряд
—q. Потенциал проводника при этом дол-
должен быть равен ф = 0, а силовые линии
в каждой точке поверхности должны быть
нормальны к ней. Ясно, что картина силовых
линий в полупространстве X > 0, изображен-
изображенная на рис. 71, полностью удовлетворяет
этим условиям. Следовательно, задача опре-
определения характеристик поля точечного заря-
заряда + q, находящегося на расстоянии d от
плоской поверхности проводника, заполняю-
заполняющего полупространство X < 0, свелась к на-
нахождению характеристик полей двух точеч-
точечных зарядов q и — q. Заряд —q расположен
в точке, которая является изображением
местоположения точечного заряда q, если бы
плоскость X = 0 являлась зеркалом. Отсюда
и произошло название метода изображений.
Вместо проводящего тела, занимающего
полупространство X < 0, можно взять за-
заземленную проводящую пластину, парал-
параллельную плоскости X — 0. Метод расчета и
поле остаются без изменения. Если пласти-
пластина не заземлена, то на стороне пластины
§ 16 Электростатическое поле при наличии проводников 131
обращенной в сторону отрицательных значений оси X, индуцируются
поверхностные положительные заряды, которые полностью изменяют
характер поля: поле при этом не является суперпозицией полей заряда
q и его изображения.
Определим напряженность поля заряда q, расположенного в точке
X = d при наличии заземленной проводящей плоскости X = 0. Потен-
Потенциал поля во всех точках х > 0 дается формулой A6.88). Напряжен-
Напряженность электрического поля в плоскости Z = 0 равна
_ дФ д f x-d x + d ]
Ех ~ ~ дх ~ 4яе0 \[(х - df + у2У'2 [_(х + df + у2?11]'
F _ Эф g [ у у ]
*">- ду~ 4яе0 \ [_(х - df + у2?*2 [(х + dJ + у2У>21 ¦ ( '
В плоскости X = 0 компонента Еу исчезает, а
Поверхностная плотность заряда на плоскости X = 0 [см. A6.12)]
равна
„ _ _ JL t A6.92)
° ~ 2я (z2 + у2 + d2K12 ' К '
Полный поверхностный заряд на плоскости X = 0 дается формулой
т. е. индуцированный на проводнике заряд равен индуцирующему заряду
с обратным знаком [см. A6.20)].
Сила взаимодействия точечного заряда q с зарядом на поверхности
х — 0 равна силе взаимодействия q с его изображением:
F = -q2/A6iteod2). A6.94)
Знак минус указывает, что точечный заряд притягивается к проводящей
заземленной поверхности.
Метод изображений, конечно, не сводится во всех случаях в букваль-
буквальном смысле к нахождению зеркального изображения зарядов. Рассмот-
Рассмотрим картину эквипотенциальных поверхностей, создаваемых двумя
различными по модулю зарядами. Для удобства введем полярную
систему координат с началом в точке О (рис. 72). Полярная ось
проходит через местоположение точечных зарядов qt и q2. Полярные
координаты qt и q2 равны 0t = 0, rt = d\ и 92 = 0, гг = di соответственно.
Потенциал в точке Р выражается формулой
d\ - 2rdi cos 9 + ]/r2 + d22 -2rd2 cos 9
Г* ~ 4яе^ \у2 + d\ 2d 9 + ]/2 + d2 2d 9 /"
132 2. Постоянное электрическое поле
Если dx = a2/d2 (a < d2) и q2 = -aq2/d2, то ср (а, 9) = 0, т. е. потенциал
на сфере радиусом а равен нулю. Следовательно, эта сфера является
эквипотенциальной поверхностью с нулевым значением потенциала.
Если на ее место поместить реальную проводящую заземленную сферу,
то поле не изменится. Таким образом, если имеется проводящая
заземленная сфера радиусом а и точечный заряд q2 вне ее на расстоя-
расстоянии d2 от центра сферы, то поле вне сферы таково же, как и поле,
создаваемое зарядом q2 и его «изображением» — зарядом qi = —aq2/d2,
помещенным в точку с координатами di = a2/d2, 9 = 0 внутри сферы.
Сила взаимодействия между зарядом q2 и сферой равна
* - 4я80 (d2 - dtf ~ 4*80 (dl - a2J ' (Ь)
Пример 16.1. Найти силу взаимодействия между проводящей сферой радиу-
радиусом а и точечным зарядом q2, находящимся на расстоянии d2 от центра
сферы, если на сфере распределен заряд Q.
Схема расположения сферы и заряда изображена на рис. 72. Заряд q2
индуцирует в проводящей сфере свое изображение в виде заряда qy = —a2ajd2
на расстоянии dj = a2/d2 от центра сферы. Однако теперь взаимодействие
не сводится к силе притяжения между зарядом q2 и его изображением, потому
что по условию сфера имеет заряд Q, а не q\. Следовательно, для описания
взаимодействия необходимо добавить еще одно «изображение» заряда, которое
создает на сфере постоянный потенциал и в сумме с qt составляет Q.
Поэтому надо в центр сферы поместить заряд Q — qt = Q + q2a/d2. Взаимо-
Взаимодействие точечного заряда q2 со сферой, имеющей заряд Q, слагается из
взаимодействия q2 с «изображениями» qt и Q + q2ajd2. Таким образом, сила
взаимодействия равна
+ Ч1Ф1
A697)
F = qi Г
4iteo|_ 4
Пример 16.2. Найти силу взаимодействия между проводящей сферой ра-
радиусом а, поддерживаемой при постоянном потенциале ф0, и точечным заря-
зарядом q2, находящимся на расстоянии d2 от центра сферы.
Схема расположения сферы и заряда изображена на рис. 72. Заряд q2
и его изображение q\ создают нулевой потенциал сферы. Чтобы он стал
равным ф0, необходимо в центр сферы поместить «изображение» Q = 4яеояфо.
Сила взаимодействия между точечным зарядом q2 и сферой, поддерживаемой
при потенциале ф0, равна
F = _2а_ [_?. W ] A6.98)
Aldl d^dtfX
Пример 16.3. Две проводящие плоские пластины образуют угол а0 (рис. 73).
Длина пластин, перпендикулярных плоскости рисунка, бесконечна. Между пласти-
пластинами поддерживается постоянная разность потенциалов Uo. Найти напряжен-
напряженность поля между пластинами и емкость, приходящуюся на длину I. Ширина
пластины Ь — а. Принимается, что пластины не соприкасаются в точке О,
но сходятся достаточно близко, и поэтому можно пренебречь краевыми
эффектами.
§ 16. Электростатическое поле при наличии проводников 133
Поле аксиально симметрично. Поэтому удобно пользоваться цилиндри-
цилиндрической системой координат, ось Z которой направлена перпендикулярно
плоскости рисунка. Обозначим: а — аксиальный угол, г — расстояние от оси.
Тогда уравнение Лапласа имеет вид
где учтено, что 52q>/5z2 = 0 из-за цилиндрической симметрии поля. Решение
ищем в форме
ср(г, а) = Я(г)Ф(а). A6.100)
Подставляя A6.100) в A6.99), находим — — [ г—) + 4-^г = 0.
г dr \ dr J r2 dor
Умножая обе части этого уравнения на г2/ЯФ, получаем
(г).
R dr V dr ) Ф da2
Левая и правая части A6.101) зависят от разных независимых переменных.
Следовательно, равенство может быть удовлетворено лишь в том случае,
когда его левая и правая части равны по отдельности одной и той же
постоянной. Поэтому полагаем:
ii(rf) = n\j^r=-n\ A6.102)
R dr\ dr / Ф da2
где п2 — постоянная. Решение уравнения для Ф очевидно:
Г1М + В2 пр„„ = 0,
[ Ai sin па + А2 cos na » » т °-
Решение уравнения для R ищем в виде R = Аг* (р ф 0).
Подставляя это выражение в первое из уравнений A6.102), получаем ра-
равенство
Э2 = л2, A6.104)
из которого следует, что Р=±п. При п = 0 первое из уравнений A6.102)
упрощается:
dR
г = const
dr
и может быть удовлетворено функцией
R = Dilnr + D2.
Следовательно, окончательно решение уравнения A6.102) может быть
представлено в виде
\Di\nr + D, при п = 0,
Попытаемся найти решение задачи, не зависящее от г, т. е. при п = 0,
Di =0, тогда [см. A6.103)] ср(а) = В^ + В2. Граничные условия для ср имеют
134 2. Постоянное электрическое поле
вид: ср(О) = 0, ф(а0) = Uo, т. е. О = В2, Uo = B^q. Следовательно,
A6.106)
Напряженность электрического поля равна
?» = ~Чг = -1/о/Ио). A6.107а)
Поверхностная плотность зарядов на пластинах
<Т! = еЕл(а = 0) = -zUQ/(m0), ст2 = -е?„(а = а0) = sUa/(m0). A6.1076)
Заряд каждой из пластин (по модулю) на длине I выражается формулой
ъ
б = /J <rdr = (коио/*оIп(Ь/а). A6.108)
а
Емкость, приходящаяся на длину /, равна
и о а0
§ 17. Электростатическое поле
при наличии диэлектриков
Рассматриваются влияние диэлектрика на
электрическое поле и различные механизмы
поляризации. Выводится соотношение между
плотностями объемных и поверхностных свя-
связанных зарядов и поляризованностъю. Об-
Обсуждаются явления на границе между ди-
диэлектриками.
Т1ипольный момент непрерывного распределения зарядов. Влияние
вещества на электрические и магнитные поля было экспериментально
открыто и исследовано Фарадеем. Результаты этих работ привели
Фарадея к идее близкодействия и концепции поля. Электростатическая
индукция была им открыта в 1837 г. Тогда же он ввел в науку
термины «диэлектрик» и «диэлектрическая постоянная».
Пусть в некотором объеме V (рис. 74) имеется непрерывно распре-
распределенный с объемной плотностью р заряд, причем в целом объем
электрически нейтрален. Однако это не означает, что в каждой точке
внутри объема положительный и отрицательный заряды взаимно
компенсируются. Если положительные и отрицательные заряды распре-
распределены в объеме по разным законам, то в одних точках объема
суммарная плотность р заряда положительна, а в других отрицатель-
отрицательна. Математически условие нейтральности объема V имеет вид
JpdF=O. A7.1)
у
§ 17. Электростатическое поле при наличии диэлектриков 135
Если во всех точках . объема р = 0, то
материальная система в объеме V электри-
электрически нейтральна: на нее не действует внеш-
внешнее электрическое поле и сама она не порож-
порождает электрического Поля. Однако если плот-
плотность р заряда в одних частях объема V
положительна, а в других отрицательна, то
хотя в целом заряд в объеме V равен нулю,
система обладает электрическими свойст-
свойствами: на нее действует внешнее электри-
электрическое поле и сама она порождает электри-
электрическое поле. В первом приближении электри-
электрические свойства нейтральной системы харак-
характеризуются ее дипольным моментом. Для
двух точечных зарядов определение диполь-
дипольного момента дается формулой A6.81). При
непрерывном распределении зарядов ди-
польный момент (рис. 74) определяется фор-
формулой
74
К определению дипольного мо-
меита непрерывного распреде-
распределения зарядов
= |prdF
v
A7.2)
Радиус-вектор г в A7.2) отсчитывается от
любой точки О, принятой за начало отсчета.
Очевидно, что A7.2) не зависит от того, ка-
какая точка выбрана за начало системы отсче-
отсчета. Для доказательства этого примем за на-
начало отсчета точку (У, положение которой
относительно точки О характеризуется ра- _!?_
диус-вектором г0 (см. рис. 74). Относительно к вычислению дипольного мо-
моточки О' формула A7.2) имеет ВИД мента ДВУХ точечных зарядов
A7.3)
по формуле для непрерывного
распределения зарядов
Преобразуем A7.3):
p' = fp(r-ro)dF=jprdF-fropdF =
V V V
= |prdF=p,
A7.4)
что и требовалось доказать. Здесь г = г0 + г'
и [см. A7.1)]
fropdF=r<JpdF=O. A7.5)
76
Применим формулу A7.2) ДЛЯ вычисления' Поляризация ненолярных ди-
ДИПОЛЬНОГО Момента Двух Точечных Зарядов, электриков в электрическом поле
136 2. Постоянное электрическое поле
которые можно рассматривать как заряды, находящиеся в сколь угодно
малых объемах AFt и kv2 (рис. 75):
p = JprdF= fprdK+ f prdK=ri f pdK+r2 f pdF= r^ + t2Q2,
V Д|/, ДК2 ДК, &V2
A7.6)
где Qb 62 — заряды в объемах AFi и AF2 соответственно, r1( r2 —
радиус-векторы этих объемов. Пусть, например, в объеме &V2 находится
положительный заряд Q2 — Q. Тогда вследствие электрической нейтраль-
нейтральности системы Qi = —Q и формула A7.6) принимает вид
A7.7)
что аналогично A6.81).
Напряженность поля нейтральной системы с дипольным моментом
р определяется формулами A6.84) и A6.85).
ТТоляризация диэлектриков. Диэлектриками называются вещества, в
которых под действием электрического поля не возникает переме-
перемещения зарядов, как, например, в проводниках. Однако это не означает,
что в диэлектриках заряды под действием электрического поля вообще
не двигаются. Они сдвигаются, но не перемещаются на большие
расстояния.
Рассмотрим электрически нейтральный объем диэлектрика (рис. 76).
Внешнее электрическое поле стремится сдвинуть положительные заряды
в направлении напряженности поля, а отрицательные — в противополож-
противоположном. Поэтому в направлении напряженности в диэлектрике образуется
избыток положительного заряда, а в противоположном — недостаток.
Диэлектрик приобретает дипольный момент. Этот процесс называется
поляризацией.
Степень поляризации диэлектрика характеризуется поляризован-
ностыо, определяемой как отношение дипольного момента Ар элемен-
элемента диэлектрика к его объему AF:
р =
АР
A7.8)
]yt олекулярная картина поляризации. Диэлектрик состоит из атомов
и молекул, причем любой его бесконечно малый физический элемент
объема является электрически нейтральным. Положительный заряд
сосредоточен в ядрах атомов, а отрицательный — в электронных обо-
оболочках атомов и молекул. Положительные и отрицательные заряды
расположены в различных точках пространства, и, следовательно,
атомы и молекулы могут обладать электрическими дипольными мо-
моментами, которые изменяются с частотой колебаний электронов в ато-
атомах порядка «1015 с.
Если в атоме при отсутствии внешнего электрического поля
электронное облако распределено сферически симметрично относительно
ядра, то атом не обладает электрическим дипольным моментом.
§ 17. Электростатическое поле при наличии диэлектриков 137
Аналогично, в молекулах полоокителъные и отрицательные заряды могут
обладать такой симметрией распределения, когда у них не возникает
дипольный момент. Такие молекулы и атомы называются неполярными,
например атом гелия, двухатомные молекулы, состоящие из одинаковых
атомов (Н2, N2, O2, ...), симметричные многоатомные молекулы СО2,
СН4 и др. При отсутствии внешнего поля такой диэлектрик не поля-
поляризован.
Молекулы и атомы, обладающие электрическим дипольным момен-
моментом при отсутствии внешнего поля, называются полярными, например
СО, N2O> SO2 и др. Постоянный дипольный момент у них имеет
порядок 10~29 —10~30 Кл-м. Это соответствует диполю, состоящему
го двух элементарных зарядов 1,6-109 Кл, расстояние между кото-
которыми 100 м, т. е. порядка атомных размеров.
При отсутствии внешнего электрического поля постоянные диполь-
дипольные моменты отдельных молекул ориентированы беспорядочно и, сле-
следовательно, их сумма в физически бесконечно малом объеме равна
нулю, т. е. диэлектрик неполяризован.
Во внешнем электрическом поле положительные заряды стремятся
сместиться по направлению напряженности поля, а отрицательные —
противоположно. В результате неполярные молекулы приобретают
дипольный момент и диэлектрик поляризуется. Полярные молекулы
также приобретают дополнительный индуцированный внешним полем
дипольный момент и благодаря этому также поляризуются, но эта
поляризация играет для них лишь незначительную роль. Главный ме-
механизм поляризации для них другой: во внешнем электрическом
поле на постоянные дипольные моменты молекул действуют моменты
сил [рис. 77; см. A9.7)], стремящиеся ориентировать дипольные
моменты в направлении напряженности поля. В результате молекулы
переориентируются так, что бесконечно малые физические элементы
объема диэлектрика приобретают дипольные моменты, т. е. диэлектрик
поляризуется. Поляризованность за счет переориентации молекул зна-
значительно больше, чем вследствие образования дополнительных диполь-
ных моментов, индуцированных внешним полем.
Наряду с этими механизмами поляризации существует еще один.
В ионных кристаллах под влиянием внешнего электрического поля
положительные ионы смещаются в направлении напряженности поля,
а отрицательные — противоположно. В результате происходит некото-
некоторая деформация кристаллической решетки или относительное смещение
подрешеток, что приводит к возникновению в диэлектрике дипольных
моментов, т. е. поляризации диэлектрика. Такая поляризация называ-
называется ионной решеточной поляризацией.
Во всех случаях поляризация количественно характеризуется поляри-
зованностью Р. Механизм поляризации проявляется лишь при изучении
зависимости Р от напряженности внешнего поля и других факторов
(см. гл. 3). При этом фррмула, связывающая между собой напряжен-
напряженность электрического поля, электрическое смещение и поляризованность,
остается неизменной [см. A7.29)].
138 2. Постоянное электрическое поле
Поляризованность неполярных молекул равна
1 ^ A7-9)
где АКпод символом суммы указывает, что суммирование распростра-
распространяется на все молекулы в объеме AV; N — концентрация молекул;
р0 — индуцированный дипольный момент (одинаков у всех молекул),
совпадающий по направлению с напряженностью Е внешнего электри-
электрического поля. При отсутствии внешнего поля р0 = 0 и, следовательно,
Р = 0, т. е. поляризация отсутствует.
У полярных молекул главным механизмом поляризации является
переориентация направлений постоянных дипольных моментов под
влиянием внешнего поля. Формула для поляризованное™ имеет вид
где <р> — среднее значение дипольных моментов, равных друг другу по
абсолютному значению, но различно направленных в пространстве.
В изотропных диэлектриках средние дипольные моменты совпадают по
направлению с напряженностью внешнего электрического поля. В ани-
анизотропных диэлектриках, т. е. таких, электрические свойства которых
различны в различных направлениях, такого совпадения не наблюдается.
В них связь между поляризованностью и напряженностью более слож-
сложная (см. гл. 3). У полярных диэлектриков вклад в поляризованность
от индуцированных дипольных моментов значительно меньше вклада
от переориентации постоянных дипольных моментов и обычно не учи-
учитывается. При необходимости его учета в правую часть формулы
A7.10) надо добавить правую часть равенства A7.9).
Ионная решеточная поляризация описывается формулой A7.10),
в которой под <р> надо понимать среднее значение дипольных моментов
в объеме AF, возникших в результате смещения ионов в узлах кристал-
кристаллической решетки. В подавляющем большинстве случаев эта поляриза-
поляризация является анизотропной.
Зависимость поляризованное™ от напряженности электрического поля.
У электретов и сегнетоэлектриков поляризованность может быть
отлична от нуля при отсутствии электрического поля (Е = 0, Р Ф 0).
У остальных диэлектриков при отсутствии электрического поля поляри-
поляризованность равна нулю. Ее зависимость от напряженности может быть
в общем случае представлена в виде
Pi = ?o Z *UEJ + ?oX*y*?j?* + -.
J j,t
где индексы i, j, к, ... нумеруют компоненты величин по осям декарто-
декартовой системы координат (i = х, у, z; j = х, у, г, ...). Поэтому поляризо-
поляризованность в общем случае зависит не только от первой степени напря-
напряженности электрического поля, но и от ее высших степеней. Если
зависимость от высших степеней существенна, то диэлектрик назы-
§ 17. Электростатическое поле при наличии диэлектриков 139
вается нелинейным. Такая нелинейность
проявляется обычно лишь в очень сильных
электрических полях, хотя имеются неко-
некоторые специальные материалы, в которых
нелинейность наблюдается и при сравнитель-
сравнительно небольших полях.
Если нелинейность несущественна, то по-
ляризованность выражается через первые
степени компонент поля:
Pi = е<>2>1 А--
J
Такой диэлектрик называется линейным.
Если свойства такого диэлектрика различны
по направлениям, то диэлектрик называют
анизотропным. Совокупность девяти величин
Hij называется тензором диэлектрической
восприимчивости. Он полностью характери-
характеризует электрические свойства диэлектрика.
Если свойства диэлектрика по всем направ-
направлениям одинаковы, то диэлектрик называ-
называется линейным изотропным. У него диэлектри-
диэлектрические свойства характеризуются одной ска-
скалярной величиной — диэлектрической вос-
восприимчивостью.
Для линейного изотропного диэлектрика
Р = И80Е, A7.11)
где и — диэлектрическая восприимчивость.
В абсолютной системе единиц Гаусса ди-
диэлектрической восприимчивостью и назы-
называется величина, в 4л раз меньшая у, в фор-
формуле A7.11):
и' = х/Dя). A7.12)
Диэлектрическая восприимчивость боль-
большинства твердых и жидких диэлектриков
выражается числами порядка нескольких
единиц. Диэлектрическая восприимчивость
большинства газов составляет десятитысяч-
десятитысячные доли единицы и в большинстве случаев
практически может не приниматься во вни-
внимание. Однако имеются диэлектрики, у ко-
которых восприимчивость достигает очень
больших значений. Например, у воды х = 80,
у спирта х = 25 - 30, у сегнетоэлектриков
(сегнетовая соль, титанаты бария и т. д.)
диэлектрическая восприимчивость достигает
нескольких тысяч единиц.
Поляризация полярных диэлект-
диэлектриков в электрическом поле
78
Механизм ослабления поля при
поляризации
Вычисление заряда, пересекаю-
пересекающего элемент поверхности при
поляризации
dS
80
К нахождению выражения для
связанного объемного заряда
140 2. Постоянное электрическое поле
||лияние поляризации на электрическое поле. Дипольный момент
элемента объема dV в соответствии с формулой A7.8) равен
A7.13)
т. е. совпадает по направлению с напряженностью Е, поскольку и > 0.
Поэтому напряженность поля, создаваемого дипольным моментом,
направлена противоположно напряженности внешнего поля и ослабляет
его (рис. 78). Таким образом, в результате поляризации напряжен-
напряженность в диэлектрике ослабляется. Роль поляризации при этом сводится
лишь к разделению положительных и отрицательных зарядов, в резуль-
результате чего в объеме диэлектрика, как и на его поверхности, образуются
заряды. Эти заряды называются поляризационными или связанными,
так как они как бы привязаны в различных местах диэлектрика и не
могут свободно перемещаться по его объему или поверхности. Свя-
Связанные заряды порождают электрическое поле точно так же, как и
свободные заряды, и в этом отношении ничем не отличаются от них.
Таким образом, наличие диэлектрика учитывается тем, что принимается
во внимание электрическое поле, создаваемое связанными зарядами,
возникающими в результате поляризации. Поэтому необходимо найти
выражение связанных зарядов.
(^бъемная и поверхностная плотности связанных зарядов. Рассмотрим
элемент dS поверхности (рис. 79), проведенной внутри неполяризо-
ванното диэлектрика. При поляризации электрические заряды приходят
в движение сквозь этот элемент поверхности. Вычислим заряд, пересе-
пересекающий элемент dS при возникновении поляризованности Р. Для упро-
упрощения формул будем считать, что движутся только положительные
заряды. Обозначим: q — заряд диполя; / — плечо диполя, соответствую-
соответствующее поляризованности Р; N — концентрацию зарядов. Площадку dS
(см. рис. 67) при возникновении поляризованности Р пересекут все
положительные заряды, которые до движения, обусловленного поляри-
поляризацией, находились в объеме dF= dSh = dSJcosG косого цилиндра с
основанием dS. Следовательно,
dQ = Ngl cos 9 dS = P dS cos 9 = P • dS. A7.14)
Рассмотрим теперь некоторый объем V (рис. 80). В результате поля-
поляризации поверхность S, ограничивающую объем V, пересекают заряды.
В зависимости от баланса втекающих и вытекающих из объема зарядов
в нем образуется связанный заряд, объемная плотность которого р^.
С учетом A7.14) запишем закон сохранения заряда в объеме V в виде
f pCBdK=-fP-dS. A7.15)
у ?
Знак минус показывает, что в объеме возникает заряд, противополож-
противоположный по знаку тому, который вытекает через ограничивающую объем
поверхность. Перепишем равенство A7.15), применив к правой его части
теорему Гаусса — Остроградского:
J(pCB-divP)dK = O. A7.16)
§ 17. Электростатическое поле при наличии диэлектриков 141
Если равенство A7.16) тождественно выпол-
выполняется при любых V, то подынтегральная
функция будет тождественно равна нулю.
Следовательно,
рсв= -divP.
A7.17)
Таким образом, объемные связанные за-
заряды возникают лишь в том случае, когда
поляризованностъ Р изменяется от точки
к точке. Это понятно и без вычислений,
поскольку при однородной поляризованно-
сти заряды переходят на новое место, зани-
занимая места ушедших в таком же количестве
зарядов, в результате чего соответствующие 81
части объема диэлектрика остаются электри- к выводу выражения для по-
ЧеСКИ нейтральными. верхностной плотности связан-
На границе двух различных диэлектриков ных заРядов
возникают поверхностные заряды. Это оче-
очевидно из следующих соображений. При од-
одной и той же напряженности электрического
поля в различных диэлектриках поляризо-
ванность различна. Следовательно, гранич-
граничная поверхность пересекается разным чис-
числом поляризационных зарядов со стороны 82
каждого из диэлектриков. В результате
вблизи Границы СОСреДОТОЧИТСЯ некоторый Поле в конденсаторе при на-
связанный заряд, который называется по- личии диэлектрика
верхностным связанным зарядом. Обозначим
СТсв-его поверхностную ПЛОТНОСТЬ. Для ее « Поляризационные (или
Нахождения Проще Всего ИСХОДИТЬ ИЗ фор- связанные) заряды возни-
Мулы A7.17). Построим на границе раздела как>т в иестах изменения
между диэлектриками прямой цилиндр с
ПЛОЩадЬЮ Основания AS И ВЫСОТОЙ h электрического поля па-
(рис. 81) И проинтегрируем обе части урав- термальные тела сани ста-
НенИЯ A7.17) ПО объему ЭТОГО цилиндра: новятся источниками элек-
электрического поля, в реэуль-
J pCBdK= — JdivPdK A7.18) тате чего наблюдаемое
v v поле изменяется. При этом
В левой части A7.18) СТОИТ ПОЛНЫЙ заряд электрические поля в от-
_ u ношении своих источни-
внутри объема, т. е. поверхностный заряд ков ведут се6я так> как
асв AS. Правую часть равенства преобразуем будто дело происходит
по теореме Гаусса - Остроградского в ин- • »<"<ууме и никаких на-
теграл по поверхности: термальных тел нет.
Поляризацией называется
J div P d V = J P • dS = J P2 • dS2 + f Pt ¦ dSb процесс образования ди-
y $ sz s польных нонентов у мак-
макроскопических объемов
A7.19) диэлектрика.
142 2. Постоянное электрическое поле
где индексами 1 и 2 обозначены величины, относящиеся к первому
и второму диэлектрикам по разные стороны границы раздела. Поток
поляризованности вектора Р слагается из потоков через основания
и через боковые поверхности цилиндра. Потоки через боковые поверх-
поверхности полагаются равными нулю, поскольку в пределе высота h
цилиндра стремится к нулю. Выберем в качестве положительной
нормали к границе раздела направленную от первого диэлектрика
ко второму. Следовательно, dS2 направлен по положительному направ-
направлению нормали, a dSj — по отрицательному. Поэтому
$P-dS = P2nAS-PlnAS. A7.20)
s
Напомним, что интеграл по боковой поверхности не учитывается.
Принимая во внимание значение интеграла в левой части уравне-
уравнения A7.18), окончательно получаем
A7.21а)
Поэтому, обозначая п2 — единичный вектор нормали, направленной
во вторую среду, формулу A7.21а) можно представить в виде
ас„= -
A7.216)
Полезно заметить, что вакуум также можно рассматривать как
диэлектрик, поляризованность которого равна нулю. Формула A7.21)
может быть применена к границе между диэлектриком и вакуумом.
Принимая в этом случае положительной нормалью внешнюю нормаль
к диэлектрику [т. е. считая диэлектрик в формуле A7.21а) средой 2],
положим Р2п = 0. Следовательно [см. A7.21)],
где Р„ — нормальная компонента поляризованности диэлектрика на его
границе с вакуумом.
Формулы A7.17) и A7.21) позволяют полностью учесть влияние
диэлектрика на электрическое поле. Создаваемая связанными зарядами
напряженность поля вычисляется по тем же формулам, по которым
определяется напряженность в вакууме, порождаемая свободными за-
зарядами. В частности, потенциал <рд, создаваемый связанными зарядами
диэлектрика, дается формулами A4.35) и A4.36) с заменой в них сво-
свободных зарядов на связанные:
ф = _L_ fpc*df , J_ fq-ds =
фд 4ice0 J г 4ice0 J r
V S
_ 1 f^Pdll+ 1 fZi-Z-dS. A7.23)
4ics0 J r 4rcs0 J r
§ 17 Электростатическое поле при наличии диэлектриков 143
Этот потенциал слагается с потенциалом, создаваемым свободными
зарядами.
Теперь полезно еще раз в явном виде сформулировать основную
идею учета влияния вещества на поле, которая была прослежена на
примере проводников и диэлектриков: при наличии внешнего электри-
электрического поля вещество само становится источником электрического
поля, в результате чего внешнее поле изменяется.
Рассмотрим этот процесс на примере образования поля в плоском
конденсаторе, пространство между обкладками которого заполнено
диэлектриком (рис. 82). Будем считать, что на обкладках конденсатора
находится заряд с поверхностной плотностью ст. Если между обклад-
обкладками конденсатора будет вакуум, то Е = <у/е0 [см. A6.12)]. Вследствие
поляризации диэлектрика напряженность поля уменьшается. Определим
лоляризованность диэлектрика по формуле A7.11), учитывая, что
Е ф ст/е0. Вследствие однородности диэлектрика и однородности поля
между параллельными заряженными пластинами заключаем, что поля-
ризованность диэлектрика однородна, т. е. объемные связанные заряды
отсутствуют. Имеются лишь связанные поверхностные заряды, поверх-
поверхностная плотность которых [см. A7.22)]
Сто = xso?, A7.24)
где Е — проекция напряженности по внешней нормали диэлектрика.
Известно, что напряженность направлена от положительно .заряженной
пластины конденсатора к отрицательно заряженной. Поэтому из A7.24)
следует, что поверхностная плотность связанного заряда на границе
с положительно заряженной пластиной отрицательна, а на границе
с отрицательно заряженной — положительна. Поэтому напряженность
поля в диэлектрике между пластинами конденсатора равна напряжен-
напряженности поля в вакууме между теми же пластинами, но при поверхност-
поверхностной плотности заряда ст — Ста,. На основании этого можно написать
уравнение для определения неизвестной величины
Е = (а- CTj/eo = (ст - xs0E)/e0. A7.25)
Решение этого уравнения имеет вид
Е = о/[е0 A + х)] A7.26)
Электрическое смещение Уравнение A3.19) с учетом связанных заря-
зарядов как источников поля может быть записано, очевидно, следую-
следующим образом:
div Е = р/е0 + рсв/?о. A7.27)
Заменяя в A7.27) ро выражением из A7.17), получаем
div(s0E + P)=p. A7.28)
Вектор
D = ?0Е + Р A7.29)
144 2. Постоянное электрическое поле
называется вектором смещения. Он не является чисто полевым векто-
вектором, поскольку учитывает поляризованность среды. Запишем с его
помощью уравнения A7.28) в виде
div D = р.
A7.30)
Припоминая смысл дивергенции вектора, из A7.30) можно заклю-
заключить о преимуществах использования D. Видно, что единственным
источником D являются свободные заряды, на которых этот вектор
начинается и заканчивается. В точках без свободных зарядов он
непрерывен, включая точки со связанными зарядами. Изменения
напряженности поля, обусловленные связанными зарядами, учтены уже
в самом векторе D [см. A7.29)].
Выразив Р в A7.29) по формуле A7.11), находим
D = (ё0 + ие0) Е' = ёЕ, е = A + и)г0, A7.31)
где s - диэлектрическая проницаемость. Использование D значительно
упрощает анализ поля при наличии диэлектрика. Наряду с е удобно
использовать также безразмерную величину
?г = e/s0, A7.32)
называемую относительной диэлектрической проницаемостью.
Электростатическая теорема Гаусса при наличии диэлектриков. Ум-
Умножая обе части A7.30) на dV и интегрируя по объему V, получаем
JdivDdF= JpdF. A7.33)
v v
Справа в A7.33) стоит полный заряд Q внутри объема, а левая часть
преобразуется в интеграл по поверхности с помощью теоремы Гаусса —
Остроградского. В результате находим формулу
A7.34)
которая называется электростатической теоремой Гаусса при наличии
диэлектриков. Она справедлива при любом расположении диэлектри-
диэлектриков и граничных поверхностей: часть или весь объем может быть
заполнен различными диэлектриками, а поверхность S может прохо-
проходить как в вакууме, так и пересекать диэлектрики.
Применив формулу A7.34) к точечному заряду q, находящемуся
в безграничной однородной диэлектрической среде, и взяв в качестве
поверхности интегрирования сферу радиусом г с центром в точке
нахождения точечного заряда, получим закон Кулона в однородной
диэлектрической среде:
§ 17. Электростатическое поле при наличии диэлектриков 145
Напряженность поля в среде в е, раз
меньше, чем в вакууме. Во столько же раз
меньше и потенциал точечного заряда. Фор-
Формула A7.26) показывает, что напряженность
поля между обкладками конденсатора при
наличии диэлектрика также уменьшается в sr
раз по сравнению с напряженностью поля
в вакууме. Емкость конденсатора увеличи-
увеличивается в s, раз.
Тираничные условия. Граничными условиями
называется связь между векторами поля
по разные стороны поверхности, разграничи-
разграничивающей две области. Эта поверхность может
разделять вещества с различными свойства-
свойствами, быть границей тела в вакууме, а может
быть, вообще говоря, просто воображаемой
поверхностью в однородной среде. Во всех
случаях граничные условия позволяют
определить изменение векторов поля при
переходе через границу. Они выводятся
с помощью уравнений поля.
Тираничные условия для нормальной со-
составляющей вектора D. Выведем это усло-
условие аналогично тому, как было получено
граничное условие A7.21). Однако теперь
надо исходить из уравнения A7.30), а не
A7.17):
D2n - l>i. = о,
п2 ¦ (D2 - Dt) = a,
или
Еп = а/е.
-»/ L+ .в
/ гГг ¦
шшшш
83
К выводу граничного условия
для тангенциальной составляю-
составляющей вектора Е
84
Преломление силовых линий иа
границе между диэлектриками
A7.36)
где а — поверхностная плотность заряда на
границе. Нормаль п2 направлена в сторону
среды 2. Из A7.36), в частности, можно
получить напряженность поля у поверхности
заряженного проводника. Приняв внешнюю
к проводнику нормаль положительной, мы
должны считать в формуле A7.36) вакуум
средой 2, а проводник — средой 1. В про-
проводнике напряженность Е. поля равна нулю,
т. е. ?Iп = 0- Следовательно,
Dn = a A7.37)
A7.38)
Нормальная составляю-
составляющая напряженности элек-
электрического поля терпит
разрыв на границе меж-
между различными диэлектри-
диэлектриками и поэтому силовые
линии преломляются.
146 2. Постоянное электрическое поле
Эта формула совпадает с формулой A6.12) для вакуума, но с заменой
г0 на е, т. е. напряженность поля у поверхности проводника при на-
наличии диэлектрика уменьшается в е, = е/б0 раз.
Формула A7.38) дает также непосредственно решение задачи о поле
в плоском конденсаторе, выраженное соотношением A7.26). При этом
нет необходимости учитывать в явном виде связанные поверхностные
заряды в диэлектрике между пластинами конденсатора, как это дела-
делалось при выводе A7.26).
р^раничные условия для тангенциальной составляющей вектора Е. По-
Построим вблизи границы раздела диэлектриков 1 и 2 замкнутый
контур (рис. 83). Вследствие потенциальности электрического поля
циркуляция Е по замкнутому контуру равна нулю:
| E-dl = 0. A7.39)
ABCDA
Интегралы по участкам ВС и DA сколь угодно малы, так как АВ
и CD расположены бесконечно близко к поверхности раздела. Знаки
интегралов по АВ и CD противоположны ввиду того, что пути интегри-
интегрирования проходят в противоположных направлениях. Поэтому [см.
A7.39)]
?2t-Elt = 0.
A7.40)
Преломление силовых линий на границе раздела диэлектриков.
Допустим, что на границе раздела диэлектриков нет свободных
зарядов. Тогда
et?ln = ?2Е2п, Еи = Е2г A7.41)
Если е2 > Si, тогда E2n < Eln и, следовательно, силовые линии ведут
себя так, как показано на рис. 84, т. е. силовые линии удаляются от
нормали, входя в диэлектрик с большей диэлектрической проницае-
проницаемостью.
3 наки связанных зарядов на границе раздела диэлектриков. Рассмот-
Рассмотрим нормальные компоненты напряженности поля и поляризован-
ности на границе раздела диэлектриков. Запишем формулу A7.11)
с учетом A7.31) для диэлектриков по разные стороны границы в виде
(рис. 85):
Рщ = (е2 - во) Е2т Ри = (е, - s0) Eu. A7.42)
Преобразуем формулу A7.21) для поверхностной плотности заряда
с учетом A7.32):
- е2Е2п - s0 (Eln - E2n). A7.43)
A7.44)
Если свободные заряды на поверхности отсутствуют, то
— Е2Е2п = 0 и формула A7.43) упрощается:
§ 17. Электростатическое поле при наличии диэлектриков 147
е2>е,
?2
85 EzJi!
Знак поверхностного заряда и ====-|
поведение нормальных состав- Ё==Ё=|
ляющих напряженности поля и =====
поляризованности при пересече- гЕЕЕ:
ниях границы в различных на-
правлениях
"-\п
а)
б)
Для определенности по-прежнему будем считать, что е2 > et, a E
направлено из первой среды во вторую. Напомним, что в качестве
положительной выбрана нормаль, направленная во вторую среду. Тогда
в формуле A7.44) Е1п и Е2п положительны, причем Е1п > Е2п. Поэтому
связанный заряд на границе отрицателен (рис. 85, а). Величины Р1я
и Р2„ также обе положительны и, следовательно, Р2„ > Р^п, как это
видно из A7.43) при <тсв < 0 (рис. 85, а).
С помощью аналогичных рассуждений можно изучить изменение
нормальных составляющих напряженности поля, поляризованности
и знака поверхностной плотности заряда, когда напряженность поля
направлена в сторону диэлектрика с меньшей диэлектрической прони-
проницаемостью (рис. 85, б).
Гетод изображений. Идея метода при применении к диэлектрикам
такая же, как и при применении к проводникам (см. § 16).
Пусть имеются две бесконечные диэлектрические среды (проницае-
(проницаемости 8i и е2) с плоской границей раздела. В первой среде на рас-
расстоянии d от границы расположен точечный заряд q. Утверждается,
что потенциал в первой среде такой же, как от заряда q и его изобра-
изображения q' ¦= q (ед — 42)/(et + e2), расположенного во второй среде на рас-
расстоянии d от границы (рис. 86, а), причем расчет ведется так, как
будто диэлектрическая проницаемость сред равна st. Потенциал во вто-
второй среде равен потенциалу, создаваемому зарядом q" = 2s2^/(s1 + e2),
Находящимся на месте заряда q в первой среде (рис. 86, б), причем
расчет ведется так, как будто диэлектрическая проницаемость сред
равна е2. Таким образом, потенциалы в первой и второй средах равны:
Ф. " ^T-L '. .+ !'Т!2 , '. Л A7-45)
Ф2 =
]/(х + dJ + у2
2г2
+ ?2 |/(х - df + у2 У
s2
+У
Нетрудно проверить, что <pt и ф2 удовлетворяют уравнению Лап-
Лапласа и граничным условиям:
148 2. Постоянное электрическое поле
f,(*<0)
q>
Ж*
q"
и
Y
«2
Ч>г(х>0)
X
а)
б)
86
Метод изображений в примене-
применении к диэлектрикам
дх
= s2
дх
= 0,
: = 0
A7.46)
выражающим непрерывность нормальных компонент D и непрерыв-
непрерывность тангенциальных компонент Е. Кроме того, удовлетворяется также
требование конечности потенциала:
Ф11*--о=. -*0, ф2|х- + 00->0. A7.47)
По теореме единственности формулы A7.45) представляют искомое
решение.
Сила, действующая на заряд q, равна силе взаимодействия этого
заряда с изображением [(8t — 82)/^ + s2)] q, расположенным на рас-
расстоянии 2d от заряда q:
F =
1
г2 Ad2
A7.48)
При st < 82 значение F отрицательно, т. е. q притягивается к гра-
границе раздела диэлектриков. Если et > s2, то F положительно и, сле-
следовательно, q отталкивается от границы.
ТТ иэлектрический шар в однородном поле. Найдем с помощью урав-
нения Лапласа напряженность электрического поля при внесении
диэлектрического шара в первоначально однородное электрическое
поле. Если линейные размеры обкладок плоского конденсатора доста-
достаточно велики, то даже при сравнительно большом расстоянии между
ними поле во внутренних областях вдали от краев однородно с боль-
большой точностью. Если размеры обкладок увеличиваются до бесконеч-
бесконечности с одновременным увеличением до бесконечности расстояния
между ними при постоянной поверхностной плотности зарядов на
обкладках, то во всем пространстве создается однородное электри-
электрическое поле. Поместим в это поле проводящий диэлектрический шар.
Ясно, что вследствие поляризации напряженность поля вблизи шара
изменится, а на бесконечности останется без изменения. Определим
напряженность электрического поля во всем пространстве, включая
область внутри диэлектрического шара.
Допустим, что шар радиусом R состоит из диэлектрика с ди-
диэлектрической проницаемостью si, а окружающее пространство за-
§ 17. Электростатическое поле при наличии диэлектриков 149
Ео
87
Ориентировка системы коорди-
координат в случае диэлектрической
сферы в однородном поле
полнено диэлектриком с диэлектрической проницаемостью гг (рис. 87).
Напряженность однородного поля направлена параллельно оси Z.
Вследствие аксиальной симметрии задачи удобно пользоваться сфери-
сферической системой координат с полярной осью по оси Z.
Для однородного диэлектрика с диэлектрической проницаемостью
е уравнение Пуассона A5.14) имеет вид
V29=-p/s, A7.49)
чгго очевидно из сравнения уравнения A5.10) для вакуума с уравне-
уравнением A7.30), имеющим для однородного диэлектрика вид
div E = р/6. A7.50)
В сферической системе координат уравнение Пуассона записывается
так:
д { ду\ 1 с^ср р
А~ —— I i —— i -г —*—:—-—^г-1 Sin U .„ ) + —^—;—5-х—i—т" = —
59
sirr 9
где а — аксиальный угол. В данной задаче свободные заряды отсут-
отсутствуют (р = 0) и в результате аксиальной симметрии Зф/Зос = 0. По-
Поэтому задача сводится к решению уравнения Лапласа
1 5
дг
17
+
2 ¦ Q -is
г1 sin 9 39
. дф ,
sln6 -55- =0
39 ,
A7.52)
во всем пространстве с соблюдением следующих условий:
1) потенциал ф всюду непрерывен и конечен;
2) нормальные компоненты вектора D = — s grad ф непрерывны на
границах раздела сред, т. е. на поверхности шара;
3) тангенциальные компоненты вектора Е = —grad ф непрерывны
на поверхности шара.
Величины, относящиеся к внутренней области шара, обозначим
с индексом 1, а к внешней — с индексом 2. В математике известно
общее решение уравнения A7.52). В данном случае оно значительно
упрощается. Непосредственной проверкой можно убедиться, что функ-
функции
(?! = А^cosQ + A2r~2cosQ, ф2 = -?0rcos9 + B2r~2cosQ A7.53а)
150 2. Постоянное электрическое поле
удовлетворяют уравнению A7.52), где Аъ
А2 и В2 — постоянные, Ео — модуль напря-
напряженности однородного поля (на бесконеч-
бесконечности).
Поскольку (pi и ф2 удовлетворяют урав-
уравнению A7.52), они представляют потенциал,
если удовлетворяют всем требованиям зада-
задачи. Потенциал <pt относится к внутренней
области шара, а ф2 — к внешней. Из A7.53а)
видно, что ф1 -> со при г -» 0. Поэтому сле-
следует считать, что А2 — 0. Условие непре-
непрерывности ф на границе имеет вид
AiR cos 9 = -E0R cos 9 + B2R~2 cos 9,
откуда
A1=B2R~3-E0.
A7.536)
A7.54)
88
Линии вектора смещения D для
диэлектрического шара во внеш-
внешнем однородном поле
Тангенциальная компок-нта вектора Е
на поверхности шара равна
A7.55)
Условие Е1е = Е2в удовлетворяется, если
выполняется условие A7.536), т.е. между А1
и В2 существует соотношение A7.54).
Нормальные составляющие вектора на-
напряженности равны:
Ещ = Еи = - Eф!/аг)г=к - -At cos 9,
Е2п = Е2г = - (dip2/8r)r=R = A7.56)
= Ео cos 9 + 2B2R~3 cos 9.
Из условия slElr = ?2?2r следует, что
Ai=- {еМФо + 2B2R~3). A7.57)
Решение системы A7.54) и A7.57):
3s2 ,, n ei - е2
-Еп, В-> =
R3E0.
(
Точечный заряд, окруженный
концентрическим с ним слоем Потенциалы внутри и вне шара равны:
диэлектрика 3s
q>i = - , *„ ?Qrcose, A7.59)
?i +
Ф2 = - A -
2s2
R3
-e2
2s2
Eor cos Q. A7.60)
§ 17. Электростатическое поле при наличии диэлектриков 151
Очевидно, что внутри шара напряженность поля постоянна и па-
параллельна оси Z:
El =_^L= 8J?l = 3?* Еп A7-61)
Liz 8z д (г cosG) ?l+2s2 °-
Она является суммой напряженности внешнего поля и напряжен-
напряженности поля, созданного связанными зарядами, возникшими на поверх-
поверхности шара. Следовательно, напряженность поля, созданного внутри
шара связанными зарядами, равна
Есв = Е1й -Ео = (s2 - et) E0/(Sl + 2е2). A7.62)
Она постоянна и направлена по оси Z. Распределение зарядов на
поверхности шара, которое приводит к постоянной напряженности
внутри шара, определяется формулой A6.75). Поэтому можно заклю-
заключить, что напряженность A7.62) создается связанными зарядами на
поверхности шара, плотность которых изменяется с углом 9 так же,
как в формуле A6.79), т. е. а ~ cos 9.
Из A7.62) видно, что при et > г2 напряженность E^ направлена
противоположно Ео и, следовательно, напряженность внутри шара
меньше, чем в исходном однородном поле. При е2 > ?i напряженность
Есв совпадает по направлению с Ео и усиливает ее внутри шара.
На рис. 88 показаны линии вектора D для случаев et > г2 (а) и
6i < г2 (б) и знаки связанных зарядов, которые при этом образуются
на поверхности шара. Отметим, что на рис. 88 изображены линии
вектора D, а не Е, поскольку именно вектор D при отсутствии сво-
свободных зарядов непрерывен. При вычерчивании линий вектора Е не-
необходимо изменять их плотность на поверхности шара, где имеются
связанные заряды.
Пример 17.1. Найти связанные заряды, поляризованностъ и напряженность
поля, индуцированного точечным зарядом q, помещенным в центре двух кон-
концентрических сфер радиусами ах и а2. Сферический слой заполнен веществом
с диэлектрической проницаемостью е (рис. 89).
Поле сферически симметрично. Выбрав в качестве S поверхность сферы
радиусом г с центром в точке нахождения заряда q, по формуле Гаусса
j D • dS = Dr4nrz = q определяем электрическое смещение
s
Dr= 47^'
непрерывное во всем пространстве. Напряженность электрического поля
Ег = — = ~ ПРИ г < а,,
е0 4ле0 г*
^J4- » ai<r<a2, A7.63)
4ле
е0 4яе0 г
терпит разрыв на поверхностях сферического слоя при г = at и г — а2.
= Dr- eo?r =
<г < а2, A7.64)
152 2. Постоянное электрическое поле
Поляризованность дается выражениями
О при г <аъ
(e-eo)g
4яе-2
О » а2 < г
и, следовательно, поверхностная плотность связанных зарядов равна:
стсв1 = ~Р, (г = oi) = - (е - so)q/Dneaj),
<*св2 = Р, (г = а2) = F - е0) д/Dя6а1). AХ65)
Связанные заряды на поверхности сферического слоя вычисляются по
формулам:
<2СВ1 = 4яа?стсв1 = - (е - б0) q/e, q^ = 4ла|стсв2 = (е - so)q/e.
Они равны по абсолютному значению и противоположны по знаку.
Объемная плотность связанных зарядов везде равна нулю, поскольку
Ре = -div Р = - 4~ ~(Г2РГ) = 0. A7.66)
г2 дг
Поле внутри сферического слоя создается точечным зарядом q и связан-
связанным зарядом qCBl, находящимся на внутренней поверхности слоя. Связанный
заряд, расположенный на внешней поверхности сферического слоя, не создает
электрического поля в ограничиваемом им объеме. Поэтому напряженность
поля точечного заряда q внутри сферического слоя уменьшена на значение
напряженности, созданной связанным зарядом qCBi = — (б —so)g/e. При а(-»0
заключаем, что точечный заряд q в диэлектрике действует как эффективный
точечный заряд
Чэф = q + 9св1 = ЧФ- A7-67)
Это приводит к ослаблению напряженности электрического поля в диэлектрике.
§ 18. Энергия
электростатического поля
Рассматриваются энергия взаимодействия
и собственная энергия зарядов и ее связь
с плотностью энергии электрического поля.
Выводятся формулы для энергии заряжен-
заряженных проводников и энергии диэлектрического
тела во внешнем поле.
взаимодействия дискретных зарядов. Допустим, что имеются
заряженные шары очень малого диаметра, который меньше рас-
расстояния между центрами шаров. Распределение заряда в шарах сфе-
сферически симметрично. Физический смысл формулы A4.32) позволяет
заключить, что величина
W>=J_QlQ2L A8.1)
4гсе0 г
§ 18. Энергия электростатического поля 153
равна работе, которая совершается при разведении зарядов Qx и Q2
от расстояния г между ними до бесконечного. Эта работа положи-
положительна, когда заряды одноименны и между ними действуют силы
отталкивания. Между разноименными зарядами действуют силы при-
притяжения и работа отрицательна. В последнем случае необходимо
совершить работу за счет внешних источников энергии. Поэтому
в соответствии с общим определением A8.1) есть энергия взаимо-
взаимодействия заряженных шаров. Поскольку оба заряда входят в фор-
формулу A8.1) симметрично, ее целесообразно записать в виде
w> -т Ыв+ &)
где <p'i — потенциал, созданный вторым зарядом в центре первого шара;
ф'2 — потенциал, созданный первым зарядом в центре второго шара.
Формула A8.2) легко обобщается на случай нескольких заряженных
шаров с зарядами Qt:
2 /
2 /j 4tcs0 гц 2
Она дает энергию взаимодействия системы зарядов.
^нергия взаимодействия при непрерывном распределении зарядов.
Пусть в элементе объема dV находится заряд dQ= p dV. Для опре-
определения энергии взаимодействия элементов заряда dQ можно приме-
применить формулу A8.3), перейдя в ней от суммы к интегралу:
A8.4)
где ф — потенциал в точке элемента объема dV.
Собственная энергия. На первый взгляд формула A8.4) кажется
аналогичной A8.3). Однако между ними существует принципиальное
различие. Формула A8.3) учитывает лишь энергию взаимодействия
между заряженными шарами, но не учитывает энергии взаимодействия
элементов заряда каждого шара между собой. Формула A8.4) учиты-
учитывает как энергию взаимодействия между шарами, так и энергию
взаимодействия элементов заряда каждого шара между собой, назы-
называемую собственной энергией заряженного шара. При расчете энергии
взаимодействия заряженных шаров A8.4) сводится к интегралам по
объемам Vt шаров:
| L A8.5)
В любой точке объема i-го шара потенциал ф, слагается из двух
частей: ф}1', созданной зарядами других шаров, и хр}соб), созданной
154 2. Постоянное электрическое поле
зарядами i-ro шара:
<ft = Ф«!1) + Ф,(со6)-
Тогда [см. A8.5)]
W = V- f cppp dF + У у L(co6)P dV. A8.7)
Так как заряды на шарах распределены сферически симметрично, то
где ф| — потенциал в центре шара, Qt = J pd К —полный заряд шара.
Доказательство A8.8) в принципе аналогично доказательству эквива-
эквивалентности электрического поля, порождаемого сферически симметрич-
симметричным распределением заряда в шаре и соответствующим точечным
зарядом, расположенным в центре шара (для области вне шара).
Теперь A8.7) можно записать в виде
^У [Ф(СО6)Рd^ = W + У
A8.9)
где W,! дается формулой A8.3).
Собственные энергии и*7,'006* шаров зависят от законов распределе-
распределения заряда в шарах и значений зарядов. Пусть, например, по поверх-
поверхности шара равномерно распределен заряд Q. Потенциал в этом слу-
случае определяется формулой A6.28) и, следовательно
A8Л0)
При R -+ 0 величина jy(co6) -*¦ оо. Это означает, что собственная энер-
энергия точечного заряда равна бесконечности. Это приводит к серьезным
трудностям при использовании понятия точечных зарядов.
Таким образом, формулу A8.3) можно применять для анализа
взаимодействия точечных зарядов, поскольку она не содержит их
бесконечных собственных энергий. Формула A8.4) для непрерывного
распределения заряда учитывает всю энергию взаимодействия, а фор-
формула A8.3) —лишь часть. Поэтому A8.4) является более полной и со-
содержательной формулой по сравнению с A8.3).
("(лотность энергии поля. Воспользовавшись уравнением
divD=p, A8.11)
запишем A8.4) в виде
W = ~ LdivDdK A8.12)
§ 18. Энергия электростатического поля 155
Принимая во внимание формулу векторного анализа
«р div D = -Dgrad ф + div (<pD), A8.13)
представим A8.12) в виде суммы двух интегралов:
W
= у | Е• DdV + у Jdiv(cpD)dV, A8.14)
где Е=—gradф. Второй интеграл в A8.14) по теореме Гаусса —
Остроградского равен
JdivtoD)dF = ^D-dS, A8.15)
v s
где S — замкнутая поверхность, охватывающая объем V. Предполага-
Предполагается, что все заряды расположены в конечной области пространства.
На далеких расстояниях г от зарядов ф ~ 1/r, D ~ 1/г2, т. е. ф?> ~ 1/г3.
Площадь S поверхности растет прямо пропорционально г2. Следова-
Следовательно, интеграл A8.15) имеет порядок ф?>5 ~ 1/г и при удалении
поверхности интегрирования на бесконечность стремится к нулю.
Поэтому для всего пространства формула A8.14) принимает вид
A8.16)
Энергии W, вычисленные по формулам A8.16) и A8.4), равны, но
физическое содержание этих формул совершенно различно. Предста-
Представим себе, что заряды находятся в тонких поверхностных слоях шаров.
В этом случае интеграл A8.4) сводится к сумме интегралов по поверх-
поверхностным слоям шаров, а в пространстве между шарами он равен
нулю. Интеграл же A8.16) сводится к интегралу по пространству между
шарами, где имеется поле Е. Следовательно, в A8.4) носителем энер-
энергии выступают заряды и энергия представляется локализованной на
зарядах. В A8.16) носителем энергии считается электрическое поле
и энергия представляется локализованной во всем пространстве, где
имеется электрическое поле. Плотность электрической энергии [см.
A8.16)] равна
w=
A8.17)
Таким образом, плотность энергии в A8.17) положительна, по-
поскольку E-D = eE2>0. Следовательно, и полная энергия в A8.16)
и A8.4) положительна. Однако энергия взаимодействия A8.3) между
дискретными зарядами может быть и положительной, и отрицательной.
Причина этого видна из равенства A8.9), которое целесообразно пред-
представить в виде
W' = W - %,Щсо6)- A8.18)
156 2. Постоянное электрическое поле
Таким образом, энергия взаимодействия между дискретными заря-
зарядами положительна тогда, когда их собственная энергия (всегда
положительная) меньше полной энергии поля, и отрицательна — когда
их собственная энергия больше полной энергии поля.
Допустим, что все заряды, за исключением одного, зафиксированы
на своих местах. Тогда энергия взаимодействия выделенного заряда
с другими зарядами называется его потенциальной энергией. На осно-
основании сказанного, это есть просто часть энергии электрического поля.
Изменение потенциальной энергии связано с изменением энергии поля.
Закон сохранения энергии для частицы в потенциальном поле, утверж-
утверждающий постоянство суммы ее кинетической и потенциальной энергии,
означает, что уменьшение кинетической энергии частицы сопровожда-
сопровождается соответствующим увеличением энергии поля, и наоборот.
Выражение A8.17) сформулировано в локальном виде и определяет
плотность энергии как функцию напряженности электрического поля
и свойств среды в данной точке, учитываемых смещением D. Ясно,
что справедливость этой формулы не может зависеть от того, каким
способом создано электрическое поле в данной точке. Поэтому выра-
выражение A8.17) справедливо не только для постоянных полей, но и для
переменных. Другими словами, эта формула выражает плотность энер-
энергии электрического поля, а не только электростатического,
^нергия поля поверхностных зарядов. Поскольку формула A8.17)
не зависит от того, какие заряды являются источниками поля, она
справедлива также и при наличии поверхностных зарядов. Формула
A8.16) также дает полную энергию поля независимо от того, какими
зарядами это поле порождено. Следовательно, формула A8.16) пра-
правильно учитывает не только объемные, но и поверхностные заряды.
Формула A8.4) при наличии поверхностных зарядов несколько
изменяется. Однако это изменение самоочевидно. Подынтегральное
выражение в A8.4) равно (ppdK=(pdq и имеет смысл потенциальной
энергии, которой обладает элемент заряда dq, находясь в точке с по-
потенциалом ф. Эта потенциальная энергия не зависит от того, является
ли dq элементом объемного или поверхностного заряда. Поэтому
выражение A8.4) применимо и к поверхностным зарядам, но при
этом dq = a dS и интегрировать надо по всем поверхностям S, на
которых имеются заряды. Следовательно, с учетом поверхностных
зарядов формула A8.4) принимает вид
A8.19)
Все, что было сказано об энергии взаимодействия и собственной
энергии, справедливо также и относительно поверхностных зарядов.
Надо лишь учесть их вклад как в полную энергию, так и в собственную.
Это обстоятельство уже было использовано при выводе собственной
энергии [см. A8.10)].
§ 18. Энергия электростатического поля 157
Энергия заряженных проводников. Поскольку на проводниках име-
имеются лишь поверхностные заряды и потенциал в разных точках
проводника имеет одно и то же постоянное значение, формула A8.18)
принимает вид
W = ~JcpadS = ±УГф(о,dS; = А^ср, LdSt = A YФ,&. A8.20а)
S i S; I S; 1
Подставляя в эту формулу выражение A6.42), получаем соотношение
A8-206)
С помощью A6.45) преобразуем A8.20а) к виду
A8.20b)
Из A8.20а) имеем
^ = ~е(Ф1-ф2)=у^, A8.20т)
где С = Q/(q>i — Ф2) — емкость конденсатора, Q — заряд на одной из
обкладок.
3 нергия диполя во внешнем поле. Эта энергия равна сумме энергий
зарядов диполя (см. рис. 77):
(г)]. A8.21)
Разложим ф (г + 1) в ряд по 1:
= Ф (г) - AХЕХ + 1уЕу + 1ZEZ) = Ф (г) - 1 • Е, A8.22)
где вследствие чрезвычайной малости / сохранены лишь члены первого
порядка по /. Формула A8.21) принимает вид
W= -p-E.
A8.23)
3 нергия диэлектрического тела во внешнем поле. Дипольный момент
элемента объема dV тела равен dp = P dV. Энергия этого элемента
во внешнем поле с напряженностью Е равна [см. A8.23)] dW = —Р • Е dK
Кажется, что энергия диэлектрического тела равна интегралу от dW
по объему тела. Однако это неправильно. Дело в том, что каждый
поляризованный элемент объема dV диэлектрического тела становится
источником электрического поля, благодаря чему в расчет энергии
входит дважды: один раз как дипольный момент, находящийся во внеш-
158 2. Постоянное электрическое поле
нем поле, а другой раз как источник поля, в котором находятся
другие дипольные моменты.
Поэтому для определения его энергии удобно исходить из полной
энергии поля. Кроме того, предположим, что диэлектрик является
однородным и заполняет все пространство, что значительно упрощает
математические расчеты.
Пусть электростатическое поле создается некоторым распределением
зарядов в свободном пространстве. Как обычно, заряды считаются
расположенными в конечной области пространства. Обозначим: Ео
и D = Б0Е0 — векторы поля, создаваемого распределением заряда в сво-
свободном пространстве. Полная энергия поля [см. A8.16)] равна
Wo = ~ ГЕо • Do dV, A8.24)
где интеграл распространен на все пространство. Теперь предположим,
что все пространство заполняется диэлектрической средой, заряды же
при этом как источники поля остаются неизменными. Поле во всем
пространстве изменяется. Обозначим: е, Е, D = бЕ — диэлектрическая
проницаемость и векторы поля в среде. Полная энергия после запол-
заполнения пространства диэлектриком равна
{e-D6V. A8.25)
Следовательно, энергия диэлектрика, помещенного во внешнее поле
с напряженностью Ео> равна
Wa=W-W0=~\(E-D-E0-D0)dV. A8.26)
При заполнении всего пространства однородным диэлектриком
с проницаемостью е напряженность во всех точках поля уменьшается
в s/e0 раз. Следовательно,
Е = s0E0/s. A8.27)
Поэтому подынтегральное выражение в A8.26) можно преобразо-
преобразовать:
Е D - Ео • Do = еЕ2 - z0El = - (е - е0) — El = -Р • Ео, A8.28)
с
где
(в - е0) ^-Ео = (е - е0) Е = Р. A8.29)
Тогда [см. A8.26)]
Wa= -у fp.EodK A8.30)
Можно показать, что формула A8.30) справедлива также и для энер-
энергии диэлектрика конечных размеров во внешнем поле Ео.
Из A8.30) можно получить энергию диэлектрического тела с про-
проницаемостью е2, находящегося в среде с диэлектрической проницае-
§ 18. Энергия электростатического поля 159
мостью et. Запишем формулу A8.30) для энергии диэлектрического
тела с проницаемостью ех:
Vai= ~T K8i-8o)Ei
где Ei — напряженность поля в теле. Для упрощения расчетов по-
прежнему считаем, что диэлектрик заполняет все пространство. Энер-
Энергия диэлектрика с проницаемостью е2 аналогично выражению A8.31)
равна
= - \ [& - е0) Е2 • Ео dV. A8.32)
Отсюда следует, что разность энергий диэлектрика с проницае-
проницаемостью е2 и диэлектрика с проницаемостью et равна
- Wal = - — [(s2 - e0) E2 • Eo - (et - s0) Et • Eo] dV. A8.32a)
Преобразуя подынтегральное выражение с помощью формул
Е2 = s0E0/s2, Et = 80E0/Sl) A8.33)
находим
г -1
(е2 - б0) Е2 • Ео - (st - s0) Et • Ео = — (s2 - е0) —(et - г0) El =
I 2 81 I
?2
= (s2 - e,) ^--Eo = (e2 - e,) E2 • E,. A8.34)
Тогда A8.32) принимает вид
A8.35)
где Wa2i — энергия диэлектрика с диэлектрической проницаемостью е2,
помещенного в среду с диэлектрической проницаемостью ги поле
в которой Et создается фиксированными свободными зарядами в среде.
Можно показать, что эта формула справедлива и для конечного
диэлектрика, если в A8.35) понимать интегрирование по объему
диэлектрика. В этом случае: Et —напряженность поля, которая суще-
существовала бы в объеме диэлектрика, если его диэлектрическая прони-
проницаемость была бы равна диэлектрической проницаемости et окружаю-
окружающей среды; Е2 — напряженность поля в объеме диэлектрика после вне-
внесения его в поле при фиксированных зарядах, создающих поле.
Формула A8.35) важна для понимания сил, действующих на диэлектрики.
Из A8.35) следует важное утверждение: увеличение диэлектрической
проницаемости среды ведет к уменьшению полной энергии поля. Дока-
160 2. Постоянное электрическое поле
зательство проводится следующим образом.
Пусть напряженность исходного поля Et =E,
а диэлектрическая проницаемость среды ev
При увеличении диэлектрической проницае-
проницаемости среды на 5s = S2 — Ei напряженность
равна Е2 = Е + 5Е и, следовательно, измене-
изменение энергии дается формулой
90
Двухслойный цилиндрический
или сферический конденсатор
Собственная энергия за-
заряда — это энергия взаимо-
взаимодействия различных эле-
элементов заряда между со-
собой. Собственная энергия
точечного заряда беско-
бесконечна.
Энергия взаимодействия
дискретных зарядов — это
полная энергия поля га
вычетом собственной
энергии зарядов. Она по-
положительна, когда их соб-
собственная энергия (всегда
положительная) меньше
полной энергии поля, и
отрицательна — когда
больше полной.
Закон сохранения энергии
для частицы в потенци-
потенциальном поле, утверждаю-
утверждающий постоянство сунны
ее кинетической и потен-
потенциальной энергий, означа-
означает, что уменьшение кине-
кинетической энергии частицы
сопровождается соответ-
соответствующим увеличением
энергии поля, и наоборот.
Увеличение диэлектриче-
диэлектрической проницаености среды
ведет к уменьшению пол-
полной энергии поля.
Чем обусловлено различие
множителей в формулах для
энергии диполя [см. A8.23)]
и энергии диэлектрического
тела [см. A8.30)]?
1 Г
dV
A8.36)
(член 5s8E • Е высшего порядка малости от-
отброшен). Формула A8.36) доказывает выска-
высказанное утверждение.
Пример 18Л. Найти энергию, накопленную
в цилиндрическом двухслойном конденсаторе на
длине I. Данные о конденсаторе приведены на
рис. 90.
Считая, что на внутренней обкладке кон-
конденсатора на длине / находится заряд Q, и при-
применяя к цилиндрической поверхности радиусом г,
коаксиальной с осью конденсатора, теорему
Гаусса, находим для радиальной составляющей
напряженности поля выражение
-— при
г
< г < а,
У- » а<г < г2,
2пк2
О
» гг < г < оо.
-if'
Энергию поля находим по формуле
E-DdF,
принимающей в данном случае вид
e,
4л/
е2 а
§ 19. Силы в электрическом поле 161
§ 19. Силы в электрическом поле
Рассматриваются силы, действующие на за-
заряды, проводники и диэлектрики в электри-
электрическом поле. Анализируется возникновение
объемных и поверхностных сил.
Природа сил. Все силы, возникающие в
электростатическом поле, являются в ко.-
нечном счете силами, действующими на
Заряд.
Г^ила, действующая на точечный заряд.
Она равна
I ? = qE= -ggradcp.
Сила и момент сил, действую-
A9.1) щих на диполь
\ ила, действующая на непрерывно распре-
распределенный заряд. Она равна
dF=pEdF.
A9.2)
Следовательно, объемная плотность сил
A9.3)
<
а, действующая на диполь. Она равна
сумме сил, приложенных к зарядам ди-
диполя (рис. 91):
F = F(+) + F(_, = q [Е(г + I) - E(r)]. A9.4)
Здесь Е (г + V) можно представить в виде
ряда по lx, ly> lz и ограничиться линейными
членами:
8z
8х у 8у
(r) + (l-V)E(r), A9.5)
7\ 7\ ?\
где (I • V) = / ^— + \у -г- + 1Х -г-- С учетом
8х 8у 8z
A9.5) формула A9.4) принимает вид
= (p-V)E.
A9.6)
В однородном поле сила, действующая
на диполь, равна нулю, поскольку к зарядам
Силы в электрическом по-
поле являются в конечном
счете силами, действую-
действующими на заряды, хотя в
выражении для силы зна-
значение зарядов присутст-
присутствует не всегда.
Формула для силы, дей-
действующей на абсолютно
жесткие диэлектрики,
справедлива также и для
сжимаемых диэлектриков
при условии, что их по-
ляризованность линейно
зависит от плотности мас-
массы.
Силы, действующие иа
диэлектрик, зависят от
соотношения диэлектри-
диэлектрической проницаемости те-
тела и диэлектрической про-
проницаемости окружающей
среды. На поверхности
раздела между диэлектри-
диэлектриками сила всегда направ-
направлена в сторону диэлектри-
диэлектрика с меньшей диэлектри-
диэлектрической проницаеиостью.
6 А Н. Матвеев
162 2. Постоянное электрическое поле
диполя приложены противоположно направленные и равные по мо-
модулю силы.
iyf омент сил, действующих на диполь. Силы, приложенные к зарядам
диполя (см. рис. 91), составляют пару сил с моментом
М = р х Е. A9.7)
Объемные силы, действующие на диэлектрик. Сила, приложенная
к элементу объема dV диэлектрика, равна сумме сил, действующих
на элементарные диполи внутри этого объема. Поэтому формула A9.6)
принимает вид
dF = ?F( = ?(p(-V)E& A9.8)
AV AV
где AV означает, что суммирование проводится по всем элементарным
диполям в объеме AV. В макроскопической картине напряженность Е
считается медленно изменяющейся величиной. Поэтому в сумме A9.8)
Е( можно заменить на одинаковую для всех членов суммы напря-
напряженность Е. Тогда суммирование в A9.8) сведется к вычислению
Ip, = PAF. A9.9)
AV
Поэтому из A9.8) для объемной плотности силы, действующей
в диэлектрике, получаем
dF
f=^ = (P-V)E. A9.10)
Примем во внимание, что Р = ие0Е = (е - е0) Е, и используем
известное из векторного анализа тождество
(E-V)E= 72grad?2-Ex rotE, A9.11)
в котором ввиду потенциальности электростатического поля, rot E = 0.
Тогда [см. A9.10)]
A9.12)
Эта формула справедлива как для абсолютно жестких диэлектриков,
так и для сжимаемых диэлектриков при условии, что их поляризо-
ванность линейно зависит от плотности массы или, иначе говоря, при
условии, что дипольные моменты индивидуальных молекул и атомов
при сжатии и растяжении элемента объема не изменяются, а диполь-
дипольные моменты, обусловленные смещением ионов, либо отсутствуют,
либо их вклад в поляризованность может считаться несущественным.
Эти условия выполняются у газов и в большинстве случаев у жидкостей.
Эта формула очень наглядна, поскольку показывает, что на элемен-
элементарные объемы диэлектрика действуют силы, стремящиеся сдвинуть эти
объемы в направлении максимальной скорости возрастания модуля
напряженности электрического поля. Иногда это чвыражают в биде
§ 19 Силы в электрическом поле 163
утверждения, что элемент объема диэлектрика увлекается в направле-
направлении роста модуля напряженности.
Формула для объемной плотности сил, справедливая для изотроп-
изотропных сжимаемых диэлектриков, имеет вид [см. A9.41)]
\) \ A9.13)
где рт — плотность массы диэлектрика. Эта формула справедлива
и тогда, когда е ф const. Если Р линейно зависит от рш, то е = D/E =
) = Е-е0, и формула A9.13) пере-
°Рт/
ходит в A9.12). Если внутри диэлектрика имеются свободные заряды
и гидростатическое давление, то в A9.13) добавляется объемная плот-
плотность рЕ сил, действующих на свободные заряды, и гидростатическое
давление.
Применим эти формулы для определения сил, действующих на
диэлектрический шар в однородном поле (см. рис. 88). Для применения
формулы A9 12) необходимо считать, что переход от внешней области
с диэлектрической проницаемостью е2 к внутренней области с ди-
диэлектрической проницаемостью гх совершается не скачком на поверх-
поверхности шара, а непрерывно в некотором тонком сферическом слое.
В этом слое напряженность Е изменяется непрерывно от ее значения
вне шара до значения внутри шара. В каждой точке сферического слоя
для вычисления силы можно использовать формулу A9.12).
В случае ег > е2 напряженность поля внутри шара меньше, чем вне
шара. Поэтому сила в каждой точке слоя направлена во внешнюю
сторону шара. Вследствие симметрии равнодействующие этих сил по
разные стороны шара стремятся растянуть шар по линии напряжен-
напряженности внешнего поля (см. рис. 88, а), однако результирующая всех сил
равна нулю и шар как целое остается в покое. При ех < е2 силы
в переходном сферическом слое направлены внутрь шара и их равно-
равнодействующие по разные стороны шара стремятся его сплющить по
линии напряженности внешнего поля. Результирующая сила, действую-
действующая на шар в целом, как и ранее равна нулю (рис. 88,6).
Однако если внешнее поле неоднородно, то результирующая сила,
действующая на шар в целом, не равна нулю. Легко видеть, что при
ех > е2 она направлена в сторону возрастания напряженности поля
в среде Этим объясняется, что легкие диэлектрические предметы при-
притягиваются к наэлектризованным телам, поскольку для воздуха е2 = е0
и всегда соблюдается условие ех > е0. Если же ?i < e2, то она направ-
направлена противоположно, т. е. в сторону уменьшения напряженности поля
в среде Поэтому в среде с достаточно большой диэлектрической
проницаемостью диэлектрические предметы с меньшей диэлектрической
проницаемостью отталкиваются от наэлектризованных тел.
При исследовании поведения напряженности электрического поля
на границе между двумя диэлектриками (см. рис. 84 и 85) было
6*
164 2. Постоянное электрическое поле
92
Механизм возникновения силы
притяжения со стороны заряда
на нейтральные диэлектрические
тела
Диэлектрическое тело в виде вы-
вытянутого эллипсоида занимает
положение вдоль поля своей наи-
наибольшей осью
F.
©
94
Механизм возникновения силы
отталкивания со стороны заряда
на нейтральное диэлектрическое
тело, помещенное в диэлектри-
диэлектрическую среду с большей, чем у
тела, диэлектрической проницае-
проницаемостью
Вытянутый эллипсоид в среде с
большей, чем у него, диэлектри-
диэлектрической проницаемостью распола-
располагается поперек поля своей длин-
длинной осью
замечено, что Е2 всегда возрастает в сторо-
сторону диэлектрика с меньшей диэлектрической
проницаемостью. Поэтому из формулы
A9.12) с помощью рассуждений, аналогичных
использованным в случае диэлектрического
шара, приходим к выводу, что на незаря-
незаряженной границе между двумя диэлектри-
диэлектриками сила всегда направлена в сторону ди-
диэлектрика с меньшей диэлектрической про-
проницаемостью. Этим объясняются многие
явления. Например, диэлектрические тела,
кусочки бумаги и т. д. притягиваются к заря-
заряду. Конечно, в любых частях поверхности те-
тела, кусочка бумаги и т. д. силы направлены
во внешнюю сторону, однако эти силы
больше в частях поверхности, находящихся
ближе к заряду. В результате возникает
суммарная сила притяжения (рис. 92).
Такое поведение диэлектриков может
быть понято, исходя из выражения A8.35)
для энергии диэлектрика с проницаемостью
е2, находящегося в среде с проницаемостью
ех. Очевидно, что при е2 > ?i эта энергия
отрицательна. Она уменьшается из-за увели-
увеличения е2 и Ej и уменьшения е^ Так как
система стремится к минимуму энергии, то
при е2 > ех тело будет втягиваться в области
с большей напряженностью поля или с мень-
меньшей диэлектрической проницаемостью tv
Если же е2 < ?i, то диэлектрик с е2 будет
выталкиваться из области с большей напря-
напряженностью в область с меньшей напряжен-
напряженностью.
Допустим, что диэлектрическое тело в
виде вытянутого эллипсоида, помещено в по-
поле, изображенное на рис. 93. Так как во всех
точках поверхности эллипсоида силы, дей-
действующие во внешнюю сторону, больше там,
где больше градиент квадрата напряженно-
напряженности, то возникает момент сил, стремящийся
развернуть эллипсоид длинной осью в на-
направлении силовых линий. Это особенно
ясно, если вспомнить, что все части ди-
диэлектрика увлекаются в область наибольшей
напряженности.
Если диэлектрическая проницаемость те-
тела меньше диэлектрической проницаемости
§ 19 Силы в электрическом поле 165
среды, то силы в поверхностном слое тела направлены во внешнюю
сторону. Поэтому направление результирующей силы изменится. Ди-
Диэлектрические тела, кусочки бумаги и т. д. вместо притяжения к на-
наэлектризованному телу отталкиваются. Картина сил в этом случае
показана на рис. 94. Вытянутый диэлектрический эллипсоид в среде
с большей, чем у него, диэлектрической проницаемостью распола-
располагается своей длинной осью не в направлении силовых линий, а
перпендикулярно их направлению (рис. 95). В этом случае части ди-
диэлектрика выталкиваются из области с ¦большей напряженностью
в области с меньшей напряженностью.
Г* илы, действующие на проводник. На заряд dq = a dS, находящийся
на элементе поверхности dS проводника, действует лишь половина
напряженности поля, имеющегося у поверхности проводника, поскольку
вторая половина создается самим зарядом элемента поверхности
и не может на него действовать (см § 16, рис. 39). Следовательно,
поверхностная плотность силы равна
f _^=5^=^1„ A914)
пов ~ dS 2 2г ' { '
где п — единичный вектор внешней нормали к поверхности провод-
проводника; е — диэлектрическая проницаемость среды, с которой граничит
проводник [см. A7.28)]. Таким образом, на поверхности проводника
сила всегда действует в направлении внешней нормали и как бы стре-
стремится увеличить его объем.
Результирующая сила, действующая на проводник в целом [см.
A8.24)], равна
где S — поверхность проводника.
Выражение A9.15) позволяет сразу же вычислить силу, приходя-
приходящуюся на участок площадью S обкладки плоского конденсатора,
заполненного диэлектриком:
F = \~S, A9-16)
поскольку поле при этом однородно, т. е. ст и е в подынтегральном
выражении A9.15) являются постоянными. Эта сила направлена внутрь
конденсатора.
Р|оверхностные силы, действующие на диэлектрик. Объемные силы
электростатического происхождения в состоянии равновесия не при-
приводят в движение соответствующие элементы объема. Они вызывают
деформацию среды, в результате которой возникают объемные силы
упругости, полиостью уравновешивающие объемные электростатические
силы. Аналогичное равновесие возникает в объеме жидкости, находя-
находящейся в поле тяжести. На каждый элемент объема действует сила
166 2. Постоянное электрическое поле
тяжести жидкости, находящейся в элементе объема, однако она урав-
уравновешивается силой, возникающей в результате давления соседних
участков жидкости на поверхность элемента объема. Объемные элект-
электрические силы приводят в движение элементарные объемы лишь при
достаточно быстрых изменениях полей, когда упругие силы не уравно-
уравновешивают электрические силы в каждый момент времени. Равнодей-
Равнодействующая всех объемных сил приложена к диэлектрику в целом
и может вызвать его движение, если только она не уравновешена
какой-то другой силой.
Наряду с объемными у диэлектриков имеются также поверхностные
силы, которые возникают в поверхностном слое диэлектрика. Они дей-
действуют наряду с объемными. При их выводе будем исходить из пер-
первого начала термодинамики.
При изотермических процессах термодинамическим потенциалом
является свободная энергия F, связанная с работой соотношением
йА = -dF. A9.17)
Поскольку термодинамические соотношения при отсутствии электри-
электрического поля были изучены в молекулярной физике, ограничимся
учетом лишь тех величин, которые зависят от электрического поля.
Поэтому в A9.17) рассматриваются лишь работа и изменение свобод-
свободной энергии, обусловленные электрическим полем. Работу и изменение
свободной энергии, обусловленные деформациями и силами упругости,
не учитываем, т. е. считаем диэлектрик недеформируемым. Кроме того,
ограничимся изотропными диэлектриками.
Свободной является та часть внутренней энергии, которая не свя-
связана в системе и доступна для получения работы. Ее величина зависит
от условий осуществления процесса.
Рассмотрим плоскую границу между диэлектриками с диэлектри-
диэлектрическими проницаемостями ех и е2. В качестве конкретной модели
физической системы можно взять плоский конденсатор, пространство
между обкладками которого заполнено жидкими диэлектриками с
плоской границей раздела. Граница раздела может проходить либо
параллельно, либо перпендикулярно обкладкам. С помощью этой
модели можно получить выражения для поверхностной плотности сил,
действующих на границе между диэлектриками. Так как соотношения,
которые будут получены, имеют локальный характер, они не зависят
от конкретного вида нелокальной модели, в рамках которой получены,
т. е. имеют общий характер.
Рассмотрим плоскую границу, параллельную обкладкам конденсато-
конденсатора (рис. 96). Напряженность Е поля перпендикулярна границе. В качестве
положительной нормали выберем ту, которая направлена во второй
диэлектрик. При бесконечно малом смещении границы производится
работа за счет изменения свободной энергии. Вычислив независимо
работу и изменение свободной энергии, найдем из A9.17) поверх-
поверхностную плотность сил. Конечно, смещение Ах следует рассматривать
как виртуальное, т. е. не обязательно фактически осуществляемое.
§ 19. Силы в электрическом поле 167
Работа при смещении элемента поверх-1
ности AS по нормали на dx равна
dA = ASfndx, A9.18)
где /п — поверхностная плотность силы.
При вычислении dF учтем, что на грани-
границе между диэлектриками D2 = ?>ь т. е. сме-
смещение границы происходит при D = const.
Это соответствует условию постоянства' за-
заряда на обкладках конденсатора, поскольку
D = о. Следовательно, надо вычислить dF
при постоянном заряде q обкладок, т. е.
(dF)Tq. При смещении границы на dx объем
ASdx, первоначально заполненный электри-
электрической энергией с плотностью E2D2/2, станет
заполненным энергией с плотностью EiDJl.
Других энергетических факторов, участвую-
участвующих в процессе при производстве работы,
нет. Следовательно, разность энергий в объ-
объеме ASdx после перемещения границы и до
ее перемещения и составляет изменение
свободной энергии:
\tdx
96
Возникновение
натяжений
максвелловскнх
A9.19)
где индекс п означает, что рассматриваются
нормальные компоненты D и Е.
С учетом A9.18) и A9.19) соотношение
A9.17) принимает вид
/п = 7г E2nD2n - Х1г E,nDln. A9.20)
Поверхностная плотность силы направ-
направлена по нормали к границе раздела. Из
A9.20) видно, что поверхностная плотность
силы /п слагается из двух частей:
1) поверхностной плотности силы
f^=lj2E2nD2n, A9.21)
возникающей под влиянием электрического
поля второй среды и направленной в сто-
сторону второй среды;
2) поверхностной плотности силы
fin^~l/2ElnDlm A9.22)
возникающей под влиянием электрического
поля первой среды и направленной в сто-
сторону первой среды.
97
Возникновение максвелловскнх
давлений
Компонента поля, нор-
нормальная к поверхности
раздела диэлектриков, как
бы притягивает к себе по-
поверхность с поверхност-
поверхностной плотностью силы, рав-
равной объемной плотности
электрической энергии по-
поля, связанной с этой ком-
компонентой.
Компонента поля, танген-
тангенциальная к поверхности
раздела диэлектриков, как
бы давит на поверхность,
причем давление равно
объемной плотности элек-
электрической энергии поля,
связанной с этой компо-
компонентой.
Всегда, независимо от
ориентации поля, поверх-
поверхностная сила действует в
сторону диэлектрика с
меньшей диэлектрической
проницаемостью.
168 2. Постоянное электрическое поле
Таким образом, в данном случае электрические тюля, находящиеся
по разные стороны от границы раздела как бы притягивают к себе
поверхность раздела с поверхностной плотностью силы, равной объем-
объемной плотности электрической энергии, приходящейся на нормальную
компоненту напряженности поля.
Равнодействующая двух сил, приложенных к поверхности раздела
от полей по разные стороны от границы, является полной силой,
действующей на границу раздела. Так как D2n = Dln = ?>„, то [см. A9.20)]
При г2 < ei поверхностная плотность силы /п > 0. Это означает, что
на границу раздела сила действует в сторону диэлектрика с меньшей
диэлектрической проницаемостью, т. е. в направлении большей объем-
объемной плотности электрической энергии. Заметим, что объемная плот-
плотность силы [см. A9.12)] также направлена в сторону увеличения
объемной плотности электрической энергии.
Теперь рассмотрим диэлектрики, плоская граница между которыми
перпендикулярна обкладкам плоского конденсатора (рис. 97). В этом
случае на границе соблюдается условие Е2х = Еи = Ет, поскольку на-
напряженность поля направлена параллельно границе. Индекс т означает
тангенциальные к поверхности раздела компоненты векторов. Смещение
границы происходит при условии ЕТ = const, т. е. при постоянной раз-
разности потенциалов. Следовательно, необходимо вычислить изменение
свободной энергии (dF)Tip. Для поддержания неизменной разности
потенциалов необходимо изменить плотность зарядов на той части
обкладок конденсатора, которая соответствует смещению поверхности
раздела на dx. Для этого затрачивается энергия по перемещению
заряда, равная dq (<р2 — срх) = dqEJ, где ?, и I- напряженность поля
и расстояние между обкладками конденсатора. Поверхностные плот-
плотности заряда в области соприкосновения обкладок с первым и вторым
диэлектриком равны соответственно Oi = ei?x = ^Е, и о2 = е2Е2 =
= z2Ev Глубина диэлектрика в направлении, перпендикулярном плоско-
плоскости рис. 97, равна AS//. Следовательно,
dq = (стх - ст2) (AS//) dx. A9.24)
При данных условиях для производства работы доступна лишь
разность между энергией поля и энергией, которая затрачивается для
поддержания постоянства потенциалов. Поэтому изменение свободной
энергии равно
- (а2 - a1)(AS/0dx?t/. A9.25)
Так как о2 = ег^т и CTi = ei^r то
(dF)T ф = - C/2EiTDu-l/2E2f>2T)ASdx. A9.26)
С учетом A9.18) и A9.26) соотношение A9.17) принимает вид
/п= -72E2tD2t+
§ 19. Силы в электрическом поле 169
Эта поверхностная плотность силы также направлена по нормали
к поверхности раздела. Из A9.27) видно, что она слагается из двух
частей:
1) поверхностной плотности силы
/2n=-72E2TD2t, A9.28)
действующей на границу раздела в направлении первой среды со сто-
стороны электрического поля второй среды. Напомним, что положитель-
положительная нормаль выбрана из первой среды во- вторую и, следовательно,
знак минус в A9.28) свидетельствует о направлении силы из второй
среды в первую:
2) плотности силы
/,„=72^1,, A9-29)
действующей на границу в направлении положительной нормали со
стороны электрического поля первой среды.
Таким образом, за счет тангенциальной компоненты напряженно-
напряженности электрическое поле как бы давит на граничащую с ним поверх-
поверхность раздела, причем давление равно объемной плотности энергии,
приходящейся на тангенциальную компоненту напряженности поля.
Равнодействующая сил давления, приложенных к поверхности раз-
раздела со стороны полей по разные стороны границы, является полной
силой, приложенной к границе. Поскольку ?1т=Е2х = .Е„ формула
A9.27) принимает вид
/n=72??Fi-e2). A9.30)
При е2 < 8t плотность силы /п > 0. Следовательно, поверхностная
плотность силы направлена в сторону диэлектрика с меньшей ди-
диэлектрической проницаемостью. Таким образом, всегда, независимо от
ориентации поля относительно поверхности раздела, поверхностная
плотность силы направлена в сторону диэлектрика с меньшей ди-
диэлектрической проницаемостью [см. A9.12)]. Справедливость и общность
этого утверждения также следуют из равенства A8.36), если принято
во внимание, что система стремится перейти в состояние с наимень-
наименьшей энергией.
Объемные силы, действующие на сжимаемый диэлектрик. Исходим
из формулы A8.36), в которой 5е обусловливается деформацией,
изменяющей плотность массы. Процессы предполагаются изотерми-
изотермическими (Т= const). Диэлектрическая проницаемость изменяется от
точки к точке, являясь функцией от г, и, кроме того, может зависеть
от плотности рт массы диэлектрика, т. е. е = е (г, рт). Пусть при де-
деформации элемент объема dF смещается на 1 и при этом происходит
изменение плотности массы диэлектрика. Элемент объема, который
после смещения находится в точке с радиус-вектором г, до смещения
находился в точке г — 1. Следовательно,
de = -1 grade + ^5pm, A9.31)
где 8pm — изменение плотности массы диэлектрика.
170 2. Постоянное электрическое поле
Можно показать, что элемент объема dF' после деформирования
равен
dF=(l + divl)dF'. A9.32)
Закон сохранения массы для элемента объема имеет вид
pmdF=P;dF' A9.33)
или
pm(l+divl)dF' = p^dF', A9.34)
где рт и р'т - плотности массы после деформации и до деформации.
Из A9.34) следует, что для бесконечно малого смещения
5pm=pm-p^= -pmdivl. A9.35)
Подставляя A9.31) и A9.35) в A8.36), находим
[F?2id ?2^diIldl/ A9-36)
По формуле (П.12) имеем
Тогда [см. A9.36)]
5W = у f Ге2 grad 8 - grad U29m -~-\\ ¦ 1 dF + у f div
A9.38)
При обычных предположениях о непрерывности подынтегральных
выражений можно второй из интегралов преобразовать по теореме
Гаусса — Остроградского в интеграл по поверхности, ограничивающей
рассматриваемый объем. Считая для упрощения рассуждений, что
диэлектрик занимает все пространство, а порождающие поле заряды
распределены в конечной области пространства, убеждаемся, что вто-
второй интеграл равен нулю, поскольку Е2 ~ 1/г4, где г — расстояние от
заряда до поверхности интегрирования и, следовательно,
2pmep7bds"a A9-39)
Объемная плотность сил f описывает действие электрического поля
на диэлектрик. Объемная плотность совершаемой этой силой работы
при деформации равна f • 1. Поэтому закон сохранения энергии при
деформации с учетом A9.38) и A9.39) имеет вид
f f • I dV= - i- f [e2 grad e - grad (e2Pm ~j\ ¦ 1 dK A9.40)
§ 19. Силы в электрическом поле 171
Так как равенство A9.40) справедливо при произвольных смещениях
A9.41)
Эта формула справедлива для изотропных сжимаемых диэлектриков
при произвольной зависимости е от плотности массы рт [см. A9.13)].
Если поляризованность линейно зависит от объемной плотности
массы, то
рт^=е-?о A9.42)
ОР
f = - -тг- E2 grad e + grad ?2p
и A9.41) переходит в A9.12). Следовательно, формула A9.12) справед-
справедлива не только для жестких диэлектриков, но и для сжимаемых
с Р ~ рт.
Хотя формула A9.41) для упрощения рассуждений при преобразо-
преобразованиях A9.39) была выведена в предположении, что диэлектрик зани-
занимает все пространство, она справедлива всегда, поскольку является
дифференциальным соотношением, справедливость которого не может
Зависеть от того, что происходит в других точках пространства.
"Пычисление сил из выражения для энергии. Для того чтобы перенести
заряд d<? в точку с потенциалом <р, необходимо совершить работу
fpdq. Поэтому полное изменение энергии системы зарядов при изме-
изменении зарядов на dqt равно
5>,d?r A9.43)
j
Оно сопровождается изменением энергии электрического поля на AW
И производством работы зарядами. Если конфигурация системы харак-
характеризуется параметрами !;,, то, по определению, обобщенной силой,
связанной с этим параметром, называется величина Fb такая, что
F.-d^j является работой, которую производит система при изменении
параметра %t на d^,. Закон сохранения энергии имеет вид
YJq>}dq} = dW+YjFidt,i. A9.44)
Рассмотрим прежде всего виртуальные процессы, в которых заряды
сохраняют постоянные значения, т. е. dg, = 0. В этом случае уравне-
уравнение A9.44) принимает вид
+ XF,d^. A9.45а)
I
Здесь (dPFL зависит только от ^ и поэтому
Сравнение A9.45а) и A9.456) с учетом независимости d^ приводит
к равенству
172 2. Постоянное электрическое поле
A9.46)
где индекс q у частной производной в явном виде показывает, что
сила вычисляется при постоянных зарядах. Для использования этой
формулы энергия W должна быть выражена в виде функции от за-
зарядов и параметров ?(.
Можно обобщенную силу выразить также через производную при
постоянном потенциале. Для этого принимаем во внимание выражение
2 / v«<- A9-47)
Изменение энергии при постоянных потенциалах равно
Lj
i
поэтому [см. A9.45а)]
О = (dW),-1Л<Н;,. A9.49)
Учитывая независимость di^, получаем
A9.50)
где индекс ср у частной производной в явном виде показывает, что
она вычисляется при постоянных потенциалах. Для использования этой
формулы энергия W Ъолжна быть выражена в виде функции от
потенциалов q>j и параметров %t- Ясно, что формулы A9.46) и A9.50)
эквивалентны и получаются одна из другой. Какой из них пользо-
пользоваться, зависит от обстоятельств.
Пусть, например, требуется вычислить силу, с которой притяги-
притягиваются друг к другу пластины плоского конденсатора. Энергия плоского
конденсатора равна
где С = e0S/x; S и х - площадь обкладки конденсатора и расстояние
между обкладками.
Вычисление силы по формулам A9.46) и A9.50) дает:
F ..АЩ -.filJJlV-^^-- A9 51)
х~ 8x\2C)q" 2 dxycj'lcr дх' У }
8С A9.52)
дх'
п, д (Дф) С I
§ 19. Силы в электрическом поле 173
Принимая во внимание определение емкости С = б/Аф, заключаем,
что F'x = Fx.
Пример 19.1. Исходя из результатов решения примера 16.3, найти момент
силы, который сближает пластинки конденсатора, изображенного на рис. 73.
Энергия конденсатора [см. A6.109)] равна
w
2 2ас0
Обобщенной силой для угла поворота является* момент силы М относи-
относительно оси, совпадающей в данном случае с линией пересечения пластин
конденсатора. Поэтому с учетом A9.50) получаем
, A9.54)
2a2,
где знак минус свидетельствует о том, что момент сил стремится уменьшить
угол а0. Другими словами, между пластинами конденсатора действуют силы
притяжения. Конечно, между пластинами конденсатора всегда действуют силы
притяжения и результат A9.54) лишь подтверждает, что момент сил получился
с неравным знаком. Такая проверка правильности результата бывает полезной
при использовании обобщенных координат и обобщенных сил, когда эти пере-
переменные не имеют достаточно наглядной интерпретации.
Получим этот результат другим способом. Поверхностная плотность силы,
действующей на проводник, равна / = ст2/Bе). Поэтому на слой длиной / между
г и г + dr действует сила
-^!-/dr, A9.55)
где для ст использовано значение A6.1076). Знак минус учитывает, что эта сила
стремится уменьшить угол а0' Результирующая сила, действующая на пластину,
равна
v
Линия приложения сил находится от оси вращения на расстоянии г0,
которое определяется условием
ь
= fr
J
r0F= frdF-- -^г-1" -, A9.57)
J 2aJ a
откуда
r0 = -r^— In —. A9.58)
о — a a
Момент силы относительно оси вращения равен
=--^|-In A, A9.59)
2a2, a
что совпадает с A9.54).
174 2. Постоянное электрическое поле
Задачи
2.1. Найти напряженность электриче-
электрического поля в шаровой полости
радиусом а внутри равномерно
заряженного шара радиусом R.
Объемная плотность заряда р
(рис. 98).
2.2. Найти напряженность поля в бес-
бесконечной круглой цилиндрической
полости, ось которой параллельна
оси бесконечно длинного равно-
равномерно заряженного круглого ци-
цилиндра. Объемная плотность за-
заряда р (рис. 98).
2.3. Расстояние между пластинами
плоского конденсатора равно d.
В пространство между обклад-
обкладками конденсатора вносится ме-
металлическая пластина толщиной
5, поверхность которой парал-
параллельна о&кладкам. Пластины кои-
Цилиндрическая полость в ци-
лиидре или шаровая полость
в шаре
У,
99
Проводящая пластина в плос-
плоском конденсаторе
денсатора имеют потенциалы (pj
и ф2 (рис. 99). Найти потенциал
металлической пластины.
2.4. Определить силу, действующую
на заряд q, расположенный на
расстоянии d от центра незаря-
незаряженной изолированной проводя-
проводящей сферы радиусом r0 (d > rQ).
2.5. Найти силу, действующую на за-
заряд q, помещенный внутри ме-
металлической сферы на расстоянии
г от ее центра. Радиус сферы
равен а.
2.6. Имеются две концентрические
проводящие сферы радиусами rt
и r2 (rt < r2). Между сферами
на расстоянии d от их общего
центра (rj < d < г2) помещен . то-
точечный заряд q. Определить за-
заряды, индуцированные на сфе-
сферах.
2.7. На расстоянии d от центра за-
заземленной сферы помещен точеч-
точечный заряд q. Определить отно-
отношение / заряда, индуцированного
на части сферы, видимой из точ-
точки нахождения заряда q, к заряду
невидимой части сферы. Радиус
сферы равен a, d > а.
2.8. Два конденсатора емкостью Ct
и С2 и с зарядами qi и q2 (qi
и q2 — абсолютное значение за-
зарядов пластин первого и второго
конденсаторов) соединены парал-
параллельно. Вычислить изменение
энергии конденсаторов и объяс-
объяснить полученный результат.
2.9. Диэлектрическая проницаемость
среды между пластинами плос-
плоского конденсатора площадью S
равномерно изменяется от е1 до
б2. Расстояние между пластинами
равно d. Определить емкость кон-
конденсатора.
2.10. Цилиндрический конденсатор с
радиусами пластин ri и г2 опу-
опущен вертикально в диэлектри-
диэлектрическую жидкость с диэлектри-
Задачи 175
ческой проницаемостью е. Ниж-
Нижний конец конденсатора нахо-
находится в жидкости, верхний — в
воздухе, диэлектрическая про-
проницаемость которого б0. Плот-
Плотность массы жидкости равна р.
Определить высоту h, на кото-
которую поднимается жидкость меж-
между пластинами конденсатора, ес-
если разность потенциалов между
ними U.
2.11. Проводящий шар, плотность
которого рь плавает в жидкости,
имеющей плотность р2 (р2 > 2pi)
и диэлектрическую проницае-
проницаемость б. Шар погружен в
жидкость менее чем иа поло-
половину. Какой заряд надо ему
сообщить для того, чтобы он
погрузился в жидкость до поло-
половины? Радиус шара равен а.
2.12. Обкладки плоского конденсатора
имеют форму квадрата со сто-
стороной а. Расстояние и разность
потенциалов между пластинами
соответственно равны d и V.
В пространство между обклад-
обкладками частично вдвинута пластина
толщиной Д в форме квадрата
со стороной а. Ее поверхности
и стороны параллельны поверх-
поверхностям и сторонам обкладок, а
диэлектрическая проницаемость
равна е. Найти силу, с которой
пластина втягивается в простран-
пространство между обкладками конден-
конденсатора.
2.13. На расстоянии d от оси беско-
бесконечного проводящего цилиндра
радиусом г находится равномер-
равномерно заряженная бесконечная нить,
параллельная оси цилиндра. Ли-
Линейная плотность заряда т. Опре-
Определить силу, действующую на
длину / нити (d > г).
2.14. Методом изображений найти си-
силу, приходящуюся на длину / каж-
каждого из двух бесконечных про-
проводящих цилиндров, расстояние
между параллельными осями ко-
которых равно d. Радиусы цилинд-
цилиндров г\ и г2. Один из цилиндров
заряжен с линейной плотностью
заряда т.
2.15. Найти дипольный момент заря-
заряда, равномерно распределенного
по поверхности сферы радиусом
а. Одна из полусфер имеет заряд
Q, а другая - Q.
2.16. Точечный диполь с моментом р
находится, на расстоянии d от
центра заземленной проводящей
сферы радиусом а. Найти инду-
индуцированный дипольный момент
сферы.
2.17. К обкладкам плоского воздуш-
воздушного конденсатора, имеющим
форму квадратов со стороной 1,
приложена постоянная разность
потенциалов Uo. Определить си-
силу, необходимую для того, чтобы
сдвинуть одну из пластинок па-
параллельно самой себе в направ-
направлении, перпендикулярном какой-
либо стороне квадрата, при не-
неизменном расстоянии d между
пластинами.
2.18. Имеется проводящий шар ради-
радиусом гх и концентричный с ним
сферический проводящий слой,
внутренняя поверхность которо-
которого имеет радиус гг (r2 > rt), a
внешняя радиус r3 (r3 > rz)- Про-
Пространство между rt и г2 сво-
свободно. Заряды шара и слоя рав-
равны соответственно Qi и Q2, при-
причем Qt Ф —Q2 (как это не бы-
бывает в конденсаторе). Найти энер-
энергию этой системы зарядов.
2.19. Найти напряженность электриче-
электрического поля в центре прямого
круглого цилиндра длиной / и ра-
радиусом а, поляризованность ко-
которого Р параллельна оси и од-
однородна.
2.20. Поляризованность Р в задаче
2.19 направлена перпендикулярно
оси цилиндра. Найти напряжен-
напряженность поля в центре цилиндра.
2.21. Бесконечный проводящий ци-
цилиндр кругового сечения радиу-
радиусом а и проводящая плоскость,
расположенная на расстоянии d
от оси цилиндра, образуют кон-
176 2. Постоянное электрическое поле
денсатор. Найти емкость, при-
приходящуюся на длину / цилиндра.
2.22. Воспользовавшись результатом
решения задачи 2.21, найти силу,
действующую со стороны зазем-
заземленной бесконечной плоскости на
участок длины I прямолинейной
заряженной иити, параллельной
плоскости. Линейная плотность
заряда нити равна т.
2.23. Молекула представлена модель-
ио зарядом — 21 q | в начале ко-
координат и двумя зарядами | q |,
расположенными в точках, ха-
характеризуемых радиус-векторами
14 и г2, причем | Г! | = | г2 | = /.
Угол между rt и г2 обозначим 6.
Найти эффективный заряд | q l^
для молекулы воды Н2О, у ко-
которой / = 0,958 • 100 м, 6 = 105°,
р = 6,14-ИГ30 Кл-м.
2.24. Между двумя параллельными
бесконечными проводящими за-
заземленными плоскостями, рас-
расстояние между которыми d, по-
помещен точечный заряд q на рас-
расстоянии х от одной из них.
Найдя изображения заряда q,
вычислить действующую на него
силу.
Ответы
2.1. Е = рг/Cео). 2.2. Е = рг/Bе0). 2.3. V = Vl-
d-6v
- <р2). 2.4. F=-
. 2.5. F =
q2ar
4mo{a*-r2f
2.7. / = ]/(d + a)l(d - a). 2.8. AW = (C2?1 -
tC2 (Ct + C2)]. 2.9. С =
S E2-El
. 2.10. h--
In(e2/ei) (rl—2
(s-
—. 2.11.
2.12. F^gf- (S E°|A -g-t/2. 2.13. /--x
2 (d — Д) e + Дб0 d
3(e-Eo)
-r2)]. 2.14. / =
2. 2.15. p = Qo. 2.16. рннд = ра3/<*3.
2.17. F= -4^-1/а. 2.18. W=-l_rf-L--L+-L)Q2+2eiG-ti
2.19. E = -(l/e0) P(l - /Д/4а2 + I2). 2.20. E = - Ii/Beo)] "*. 2.21. С =
/4а2 + I2
; при а «; d имеем С *
= _
- * *
t2/
. 2.23. Р =
= 5,26- Ю-20 Кл= 0,328 |e|. 2.24. F=-
X Ь2 + Hind + xJ (nd-xf\\-
16яе0
§20
Локальное поле
§21
Неполярные диэлектрики
§22
Полярные диэлектрики
Диэлектрики
§23
Сегнетоэлектрнки
Основной физический фактор, опре-
определяющий характер взаимодействия
диэлектрика с электрическим полем,—
электрический дипольный момент ато-
атомов и молекул.
Основные механизмы поляризации —
возникновение индуцированных ди-
польных моментов атомов и молекул
или переориентация и перераспреде-
перераспределение в пространстве имеющихся.
Существует также и ионная реше-
решеточная поляризованность.
§24
Пьезоэлектрики
178 3. Диэлектрики
§ 20. Локальное поле
Обсуждаются причины, обусловливающие от-
отличие локального поля от внешнего, и вы-
вычисляется напряженность локального поля
для простейших условий.
Отличие локального поля от внешнего. В результате поляризации
диэлектрика, помещенного во внешнем поле, сам диэлектрик стано-
становится источником электрического поля. Следовательно, поле внутри
диэлектрика, которое действует на его молекулы, отличается от
внешнего. Оно называется локальным. Отличие локального поля от
внешнего особенно существенно для диэлектриков с большой плот-
плотностью — жидкостей и твердых тел.
вычисление напряженности локального поля. Выделим в объеме
диэлектрика физически малую сферу, в центре которой вычисляется
напряженность локального поля (рис. 100). Возникающая в центре сферы
в результате поляризации диэлектрика напряженность состоит из напря-
напряженности Еь порождаемой частью диэлектрика, расположенной вне
объема, ограниченного сферой, и напряженности Е2, создаваемой той
частью диэлектрика, которая расположена в объеме, ограниченном
сферой.
При вычислении Ех можно предполагать, что диэлектрик — сплош-
сплошная среда, поскольку расстояние между центром сферы, в которой
вычисляется напряженность локального поля, и источниками поля срав-
сравнительно велико. Так как сфера имеет физически малый объем, то
среду вблизи ее поверхности с внешней стороны можно считать одно-
однородно поляризованной. В объеме, ограниченном сферой, необходимо
учесть атомарную структуру диэлектрика, т. е. вычислять вклад в напря-
напряженность локального поля от дипольного момента каждого атома
отдельно, а сферу считать границей между средой вне объема сферы
и вакуумом в объеме, ограниченном сферой.
Напряженность в центре сферы создается связанными зарядами на
ее поверхности, как на границе раздела между средами с различной
диэлектрической проницаемостью. Поверхностная плотность связанных
зарядов равна [см. A721)]
осв= -(P2n-Pin)= -Р-ь, B0.1)
где Р2п — нормальная компонента поляризованности с внешней сто-
стороны поверхности сферы; Р1п = 0 — с внутренней. Направив ось Z вдоль
вектора постоянной поляризованности Р, получим
<*» = -P2n = PcosQ. B0.2)
В телесном угле dQ расположен поверхностный заряд
B0.3)
где г - радиус сферы. Этот заряд в направ-
направлении оси Z в центре сферы создает поле
с напряженностью
сШ2 = - ?-cos 0. B0.4)
4яе0 г2
Видно, что отличной от нуля является
только компонента напряженности поля
вдоль оси Z. Из B0.4) с учетом B0.3) получаем
1
-
4пе0
Р cos2 9 dQ = Ei =
1
И
4пе0
о о
или в векторной форме
cos29sinede= -—1
Зе0
§ 20. Локальное поле
Z
179
гп
К вычислению локального поля
B0.5)
B0.6)
Формула B0.6) справедлива лишь для бес-
бесконечного однородного диэлектрика. Если ди-
диэлектрик конечен, то напряженность поля в
нем зависит, вообще говоря, от его размеров
и формы. У однородного диэлектрика объем-
объемные поляризационные'заряды равны нулю,
поскольку рсв = — divP = — xeodivE = 0. По-
Поэтому отличие напряженности поля конеч-
конечного диэлектрика от напряженности Ei бес-
бесконечного диэлектрика обусловливается на-
напряженностью полей связанных зарядов, воз-
возникающих на внешней поверхности тела. Это
поле называют иногда деполяризующим,
поскольку оно уменьшает напряженность
поля.
Напряженность Е2 зависит от распределе-
распределения дипольных моментов молекул внутри
выделенной физически малой сферы и не мо-
может быть представлена какой-то универсаль-
универсальной формулой. Вычислим напряженность для
случая, когда молекулы расположены в узлах
кубической кристаллической решетки, а все
дипольные моменты имеют одинаковое на-
направление в пространстве. Это условие вы-
выполняется для индуцированных дипольных
моментов. Напряженность Е2 надо найти
в точке расположения одной из молекул,
Ш Молекулярная диэлектри-
диэлектрическая восприимчивость
не зависит существенно
ат плотности вещества и
тенперотуры.
Диэлектрическая прони-
проницаемость неполярного ди-
диэлектрика от температуры
может зависеть лишь не-
неявно, посредством зависи-
зависимости концентрации поле-
кул от температуры.
Локальное поле, дейст-
действующее на молекулы ди-
диэлектрика, отличается от
внешнего потому, что сам
диэлектрик во внешнем
поле становится источни-
источником дополнительного по-
поля.
О Какие основные факторы
обусловливают различие
между диэлектрическими
свойствами разреженных и
плотных газов? В чем эти
различия состоят?
Какие физические факторы
обусловливают независи-
независимость диэлектрической про-
проницаемости неполярных диэ-
диэлектриков от температуры
в достаточно широких пре-
пределах?
180 3. Диэлектрики
т. е. в узле кристаллической решетки. Поместим начало координат
в эту точку, а оси X. Y, Z направим по ребрам решетки. Восполь-
Воспользуемся формулой A6.85), которая в данном случае для х-проекции
напряженности имеет вид
F - Рх \ ' + ' + Ру > ^ + Рг \ -^5. B0 71
4ЯЕ0 /_j Г; 4ЯЕ0 ?_j rf 4П8О 2_J r«?
i i i
Здесь суммирование проводится по всем молекулам физически ма-
малого объема внутри сферы. Аналогичные формулы можно написать
также для у и z-компонент поля.
В формуле B0.7) можно сначала вычислить сумму по всем моле-
молекулам, находящимся в малом сферическом слое радиусом г, а затем
вычислить сумму по сферическим слоям, соответствующим различным г.
При первом суммировании вследствие кубической симметрии имеем:
I х? = I У? = I г? = 4" I rf, ? х1У1 = 5>( = ? ад = 0. B0.8)
Следовательно, B0.7) с учетом B0.8) принимает вид
Е2х = 0. B0.9)
Аналогично доказывается, что Е2у = E2z = 0. Поэтому окончательно
получаем
Е2=0. B0.10)
Таким образом, напряженность локального поля, действующего на
молекулу внутри диэлектрика, равна
Е* = Е + Р/(Зе0). B0.11)
Эту формулу надо рассматривать лишь как первое приближение,
поскольку реальный диэлектрик отличается от модели, с помощью ко-
которой эта формула получена. В частности, электрические поля моле-
молекул могут существенно отличаться от полей диполей, решетка диэлект-
диэлектрика может иметь другую симметрию, дипольные моменты молекул
могут иметь неодинаковые направления и т. д.
Локальное поле, действующее на молекулы диэлектрика, отличается
от внешнего потому, что сам диэлектрик во внешнем поле становится
источником дополнительного поля.
§ 21. Неполярные диэлектрики
Описываются основные свойства неполярных
диэлектриков.
iyf олекулярная диэлектрическая восприимчивость. Из механизма обра-
образования индуцированного дипольного момента молекулы [см. § 17]
следует, что его направление совпадает с направлением напряженности
электрического поля. В первом приближении дипольный момент мо-
§ 21. Неполярные диэлектрики 181
лекулы можно считать пропорциональным напряженности поля:
р = ое?0Е*, B1.1)
где а характеризует «полязируемость» молекулы (или атома) и назы-
называется молекулярной (или атомной) диэлектрической восприимчивостью.
Она определяется внутренними свойствами молекулы. Ввиду большой
величины собственных внутренних электрических полей в молекуле мо-
молекулярная диэлектрическая восприимчивость мала и не зависит су-
существенно от плотности вещества и температуры. Значение а можно
оценить, исходя из следующей модели молекулярной поляризации.
Молекула представляется в виде проводящей сферы, радиус которой
примерно равен радиусу молекулы (а = 100 м). В постоянном поле
Е* эта сфера приобретает дипольный момент [см. A6.82)], равный
р = 4яеоа3Е*. B1.2)
Сравнивая B1.2) с B1.1), находим для молекулярной диэлектри-
диэлектрической восприимчивости выражение
а = W. B1.3)
Если для радиусов молекул пользоваться значениями, полученными
из кинетической теории, то формула B1.3) дает для а несколько за-
завышенные, однако по порядку величины правильные значения. Поэтому
для оценки порядка величины такая модель молекулярной поляризации
вполне подходит.
Из B1.1) находим, что поляризованность равна
р = -ШI «?оЕ*= «?оЕ* -г^ Е 1 = aeQNE*. B1.4)
Здесь
?1 = AVN, B1.5)
&v
где N — концентрация молекул.
разреженные газы, в этом случае напряженность Е* локального поля
весьма незначительно отличается от напряженности Е внешнего поля.
Поэтому [см. B1.4)]
Р = <хе0ЛГЕ. B1.6)
Сравнивая B1.6) с A7.11) заключаем, что диэлектрическая восприим-
восприимчивость равна
•л = odV. B1.7)
Относительная диэлектрическая проницаемость er = s/e0 с учетом
A7.31) представляется в виде
ег = 1 + aN. B1.8)
Значение ег отличается от единицы на величину aJV, которая для
газов весьма мала. Например, концентрация молекул воздуха при
нормальных условиях равна JV = 2,6- 102S м~3. Считая в соответствии
182 3. Диэлектрики
с B1.3) для молекул а да 109 м3, находим
B1.9)
С увеличением размеров молекул а и, следовательно, и аЛГ увели-
увеличиваются, оставаясь по порядку величины малыми.
Величина ег может зависеть от температуры лишь неявно, посредст-
посредством зависимости N от температуры. Обозначим: Л?д, рт, т — соответст-
соответственно постоянная Авогадро, плотность газа, масса молекулы и напишем
очевидное равенство
N = NApJm. B1.10)
С помощью B1.10) перепишем соотношение B1.8) в виде
(sr-l)m/pm = uNA. B1.11)
Следовательно, (еР — 1)/рт является постоянной, не зависящей от
температуры и давления, величиной, если только давление достаточно
мало. При увеличении давления плотность растет и возникает необходи-
необходимость учета отличия локального поля от внешнего.
Плотные газы. В этом случае в формуле B1.4) надо для Е*
использовать выражение B0.11):
Р = ае0АГ[Е + Р/(Зе0)], B1.12)
откуда
Подставляя B1.13) в A7.29), находим
° = ?Е = ?°Е+Т^/з-Е' BL14)
откуда
^&—?- = aN. B1.15)
е, + 2
Эта формула называется формулой Клаузиуса — Моссотти. Ее с по-
помощью B1.10) можно представить в виде
^=i>^ = aiVA. B1.16)
?г + 2 рт
Левая часть равенства B1.16) не зависит от температуры и давле-
давления в тех пределах, в которых молекулярная восприимчивость остается
постоянной. Для газов такие давления могут быть большими (порядка
100 МПа). В жидкостях и твердых телах при больших плот-
плотностях а зависит от давления. Формула B1.16) проверена эксперимен-
экспериментально в широком диапазоне давлений. Например, для углекислого
газа СО2, являющегося неполярным, справедливость соотношения
Клаузиуса-Моссотти B1.16) была проверена с большой точностью до
давлений примерно 100 МПа при 100° С. Во всем интервале этих
§ 22. Полярные диэлектрики 183
давлений относительное отклонение левой
части B1.16) от постоянного значения не пре-
превышает нескольких сотых, причем до давле-
давлений примерно в 20 МПа наблюдается не-
небольшой рост, а выше — небольшое умень-
уменьшение значения левой части B1.16). Относи-
Относительная диэлектрическая проницаемость ег
при этом изменяется довольно значительно,
примерно в полтора раза в интервале дав-
давлений от 1 МПа до 100 МПа.
Пример 21.1. Оценить атомную диэлектри-
диэлектрическую восприимчивость а атома водорода. Напря-
Напряженность электрического поля направлена перпен-
перпендикулярно плоскости движения электрона (рис. 101).
Запишем условие равновесия движущегося
электрона при наличии внешнего поля:
101
К вычислению атомной диэлект-
диэлектрической восприимчивости во-
водорода
еЕ =
471ЁО (X2 + Г2)
4тге0 (х2 + г2K'2
,B1.17)
При х «: г получаем х/(х2 + г2K'2 = х/г3 и поэто-
поэтому [см. B1.17)]
ех = 4теог3Е = />,
откуда
а = 4тгг3« 1,57-100 м3,
что дает правильный порядок атомной диэлект-
диэлектрической восприимчивости атома водорода.
§ 22. Полярные диэлектрики
Описываются основные свойства полярных
диэлектриков,
Зависимость поляризованности от темпе-
температуры. Постоянный дипольный момент
у большинства молекул имеет порядок
10~29-10~30 Кл-м. Например, у СО он
равен 0,36-100 Кл-м, у SO2-
5,3- 10° Кл-м, у КС1 - 3,5 • ИГ29 Кл-м.
Дипольные моменты большинства молекул
измерены и имеются в таблицах.
Дипольный момент р, находящийся в
электрическом поле Е, обладает потенциаль-
потенциальной энергией
W=-p-E. B2.1)
Эта величина достигает минимального
значения, когда направление диполя совпа-
Ш Поля насыщения, когда
полярнэованность поляр-
полярного диэлектрика дости-
достигает максимально возмож-
возможного значения, в типич-
типичных условиях составляют
сотни миллионов вольт на
метр.
Вклад в поляризованность
от индуцированных ди-
польных моментов при-
примерно в сто раз меньше,
чем ат постоянных, и им
можно пренебречь в боль-
большинстве случаев.
Механизм поляризации
плотных полярных газов
и жидкостей с учетом ло-
локального поля не может
быть понят как переориен-
переориентация дипольных момен-
моментов в этом поле.
О Почему моменты диполя по-
полярных молекул стремятся
повернуться до совпадения с
направлением напряженнос-
напряженности электрического поля?
При каких условиях поляри-
поляризованность полярных диэлек-
диэлектриков достигает насыще-
насыщения?
Каким расстояниям между
элементарными зарядами со-
соответствуют постоянные ди-
дипольные моменты молекул?
184 3. Диэлектрики
102
Ориентировка диполя в сфери-
сферической системе координат
р
103
Функция Ланжевена
дает с направлением напряженности электри-
электрического поля. Поскольку устойчивым являет-
является состояние системы с наименьшей энер-
энергией, моменты диполей полярных молекул
стремятся повернуться до совпадения с
направлением напряженности электриче-
электрического поля. Этот поворот осуществляется
парой сил, действующих на диполь (см.
рис. 91). Однако тепловое движение расстраи-
расстраивает упорядочивающее действие электри-
электрического поля. В результате устанавливается
некоторое равновесие.
Совместим ось Z с направлением напря-
напряженности Е электрического поля (рис. 102).
Потенциальная энергия молекул B2.1) зави-
зависит от угла между направлениями их диполь-
ного момента и напряженности:
W = ~рЕ cos 9 = -pzE B2.2)
и, следовательно, распределение Больцмана
в данном случае характеризует распределе-
распределение направлений дипольных моментов мо-
молекул по углам. Число молекул dn, диполь-
ные моменты которых расположены в телес-
телесном угле dil, равно
p?cos0 pEcos0
dn = Ае кт dQ = Ae kT " da sin 9 d9. B2.3)
Тогда среднее значение компоненты мо-
момента диполей по оси Z равно
2л л
Ар\ dajepcosecosesinede
О Позволяет ли современная
экспериментальная техника
разделить вклад в поляри-
зованиость от постоянных
и индуцированных диполь-
дипольных моментов? Объясните,
как это можно сделать в
принципе.
Какие физические факторы
приводят к невозможности
рассмотрения поляризации
плотных полярных ди-
диэлектриков, как результат
переориентации дипольных
моментов в локальном поле?
Vz/ ~ idn ~ 2ж " '
J A Jda|epcosesinede
о о
B2.4)
где pz=pcos9, и введено обозначение
р = рЕ/(кТ). B2.5)
Прежде всего необходимо вычислить
внутренний интеграл в знаменателе B2.4):
/ = Je^osesinede! B2.6)
о
поскольку внутренний интеграл в числителе
выражается формулой
J ep cos e cos9 sin 9d9 =
о
B2.7)
§ 22. Полярные диэлектрики 185
Интеграл B2.6) вычисляется легко:
= | epcosesinede = - -|-
о
p
B2.8)
откуда
(l) B2.9)
Таким образом, формула B2.4) с учетом B2.8) и B2.9) принимает вид
<pz> = pL(p), B2.10)
где L(p) = cth р - 1/р — функция Ланжевена (рис. 103).
При не очень больших напряженностях поля, когда рЕ <8С кТ,
т. е. р «: 1, разлагая гиперболический котангенс в ряд
cth р = 1/р + р/3 - р3/45 + ... B2.11)
и ограничиваясь в выражении для L(p) линейным по р членом
Щ = р/3, B2.12)
получаем
<Р*> = Р2ЩЗкТ). B2.13)
Поле насыщения. С увеличением напряженности поля дипольные мо-
моменты все более интенсивно ориентируются в направлении напряжен-
напряженности и при рЕ » кТ, т. е. при р » 1, можно считать, что все ди-
дипольные моменты параллельны между собой и имеют направление
напряженности поля. Следовательно,
<Р*> = Р- B2.14)
Соотношение B2.14) получается из B2.10), если учесть, что при
р :» 1 функция L(p) близка к единице:
L(P -юо) -> 1. B2.15)
При выполнении условия B2.14) достигается максимально возмож-
возможная поляризованность и дальнейшее увеличение напряженности поля не
приводит к ее увеличению. Напряженность поля, при которой дости-
достигается максимально возможная поляризованность, называется напряжен-
напряженностью поля насыщения. Считая порядок величины дипольных моментов
равным 109 Кл-м, заключаем, что при Т =300 К напряженность
поля насыщения равна
?нас ккТ/р^ 4,2 • 108 В/м. B2.16)
Отсюда видно, что условие рЕ «: кТ, при котором справедлива
формула B2.13), выполняется вплоть до напряженностей полей, равных
миллионам вольт на метр. Поэтому в большинстве практически важных
случаев можно пользоваться формулой B2.13).
186 3. Диэлектрики
Разреженные газы. В этом случае напряженность локального поля
можно считать равной напряженности внешнего и представить поля-
ризованность [см. B2.13)] в виде
Р = Np2E/{3kT). B2.17)
Далее, в полной аналогии с ходом вычислений по формулам
B1.6)*- B1.8), получаем, что относительная диэлектрическая восприимчи-
восприимчивость равна
е, = 1 + Np2/(lkTe0). B2.18)
Наряду с поляризованностью из-за переориентировки постоянных
дипольных моментов полярные диэлектрики обладают также поляризо-
поляризованностью, обусловленной индуцированными дипольными моментами,
которая описывается формулой B1.8). Поэтому с учетом обоих меха-
механизмов поляризации выражение для ег полярных газообразных диэлект-
диэлектриков при не слишком большом давлении имеет вид
еР = 1 + N [ос + р2/(ЗШ0)]. B2.19)
Как видно из B1.3), а = 10~29 м3. С другой стороны, при комнат-
комнатной температуре &Т«4-10~21 Дж и поэтому при р х 10~29 Кл-м
p2/CfcTe0) ~ 10~27 м3, т. е. вклад в поляризованностъ от индуцирован-
индуцированных дипольных моментов примерно в сто раз меньше, чем от постоян-
постоянных, и им можно пренебречь. Однако в принципе современная точность
измерений такова, что позволяет разделить вклад в поляризованностъ
от постоянных и индуцированных дипольных моментов. Для этого изме-
измеряют ег в широком интервале температур и пользуются формулой
B2.19). Зависимость ег от \/Т на графике представлена прямой линией.
Ее пересечение с осью ординат при \/Т = О дает г, = 1 + <xN. Отсюда
по формуле B2.19) вычисляется ое = (er — l)/N. После этого по результа-
результатам измерения при других значениях 1/Г с помощью формулы
B2.19) можно вычислить постоянный дипольный момент, поскольку все
остальные величины в этом уравнении известны.
^вантовая интерпретация поляризованное™ полярных газообразных
диэлектриков. В квантовой теории, как и в классической, возникно-
возникновение поляризованное™ полярных диэлектриков объясняется преиму-
преимущественной ориентировкой постоянных магнитных моментов молекул
в направлении напряженности электрического поля. Для диэлектри-
диэлектрической проницаемости получается формула B2.19). Однако в трактовке
переориентации постоянных дипольных моментов имеется существенное
различие с классической теорией.
В квантовой теории необходимо принять во внимание вращение
молекул. Момент импульса вращающихся молекул ориентируется в
пространстве во всевозможных направлениях, а его проекции на любое
выделенное направление составляют дискретный набор значений,
причем среднее значение проекции равно нулю. Электрический диполь-
дипольный момент жестко связан с молекулой и изменяет свою ориентацию
в пространстве вследствие вращения молекулы.
§ 22. Полярные диэлектрики 187
Дипольный момент молекулы можно разложить на две составляю-
составляющие: вдоль оси вращения и перпендикулярно ей. Вторая составляю-
составляющая вследствие вращения молекулы изменяет свою ориентацию в
пространстве в плоскости, перпендикулярной оси вращения молекулы.
Среднее значение этой составляющей в системе координат, в которой
молекула вращается, равно нулю. Среднее значение составляющей
дипольного момента по оси вращения молекулы также равно нулю
из-за того, что момент инерции молекулы проквантован и среднее
значение его проекции на любое направление равно нулю независимо
от того, имеется ли электрическое поле или нет. Следовательно,
молекулы с отличным от нуля моментом импульса не дают вклада
в поляризованность. Поляризованность образуется только иевращаю-
щимися молекулами с нулевым моментом импульсов в результате
переориентации их постоянных электрических дипольных моментов.
Проекции дипольного момента на направление электрического поля
образуют дискретный ряд значений со средней величиной, отличной
от нуля, благодаря чему возникает поляризованность.
Длотные газы. В этом случае необходимо учесть отличие локального
поля от внешнего и принять во внимание различную ориентацию
дипольных моментов, которая зависит от взаимодействия между ди-
диполями. Все это чрезвычайно сильно усложняет вычисление.
Считая, что напряженность локального поля много меньше напря-
напряженности поля насыщения, разумно для поляризованное™ вместо
B2.17) написать:
п - Np2 г,*. B2.20)
Однако напряженность Е* локального поля в ней нельзя выразить
через напряженность внешнего поля по формуле B0.11). В этом можно
убедиться из следующих соображений.
Представим себе, что в центре сферической полости радиусом а,
образованной в плотном диэлектрике с относительной диэлектрической
проницаемостью е,, помещен диполь р. Поле этого диполя вызывает
поляризацию среды вне сферы. Благодаря этому в сферической
полости возникает дополнительная напряженность
2 О — 11 о
доп 2ег + 1 4кеоа3 '
т. е. в полости возникает постоянная напряженность, по направлению
совпадающая с направлением дипольного момента. Эта дополнительная
напряженность вызывает появление дополнительного индуцированного
дипольного момента, совпадающего по направлению с направлением
постоянного дипольного момента и, следовательно, не может переориен-
переориентировать постоянный дипольный момент. Поэтому поляризацию нель-
нельзя интерпретировать как переориентацию дипольных моментов в локаль-
локальном поле.
188 3. Диэлектрики
Формула B2.20) с учетом B0.11) принимает вид
р = ^Е1|е + т^-Л B2.22)
откуда
Р = 1 - Np2/(9kTe0) Е ( ' 3)
При То = Np2/(9ke0) знаменатель в правой части обращается в нуль.
При Т> То поляризованность Р имеет конечное значение, а при
Т = То она обращается в бесконечность. Это означает, что при Т< То
соответствующее вещество должно обладать спонтанной поляри-
поляризацией. Например, по формуле B2.23) можно ожидать, что пары воды
под большим давлением должны быть спонтанно поляризованы, что
заведомо неверно. Аналогично ошибочные результаты получаются и
для других веществ. Поэтому для описания плотных газов с поляр-
полярными молекулами и полярных жидкостей необходимы другие модели.
Полярные жидкости. Онзагер предложил для полярных жидкостей
модель, которая лучше согласуется с экспериментом, хотя и дает
весьма приблизительные числовые результаты. В модели принимается,
что каждый диполь находится в центре реальной сферической полости,
объем которой равен среднему объему, приходящемуся на одну моле-
молекулу. Учитывается ориентировка диполей дальнодействующими силами
и возникновение дополнительного дипольного момента под влиянием
напряженности B2.21). В результате получено соотношение
(f — Р \(?F 4- Р ^ ЛГп2
У^г ЬиндД'^г Т Ь,иид| _ 14 р
р/с 4- Т»2 ~ 04-Тс ' y.i..tJ*)
?f V гиид "т" AJ -"^ * ?о
где ?г — относительная диэлектрическая проницаемость; ?гинд — относи-
относительная диэлектрическая проницаемость, обусловленная индуцирован-
индуцированными дипольными моментами. Для воды ?гиня = 4,9, р = 2,16-10" 29 Кл-м
и формула B2.24) при Т = 273 К дает ег = 105. Экспериментальное
значение ?г = 88. Лучшего согласия с экспериментом трудно ожидать.
Лучшее количественное согласие с экспериментом получается для
сильно разбавленных растворов полярных диэлектриков в неполярном
растворителе. В этом случае полярные молекулы растворенного ве-
вещества расположены достаточно далеко друг от друга и взаимодейст-
взаимодействие между ними можно не принимать во внимание. С помощью
модели Онзагера можно учесть взаимодействие полярных молекул с
неполярным растворителем. В результате получается теория, достаточно
хорошо согласующаяся с экспериментом.
р|онные кристаллы. Их можно себе представить состоящими из двух
подрешеток с положительными и отрицательными ионами. Под влия-
влиянием внешнего электрического поля эти решетки смещаются друг отно-
относительно друга, в результате чего возникает значительная поляризован-
поляризованность, что дает сравнительно большие значения относительной ди-
диэлектрической проницаемости ег. Например, у поваренной соли NaCl
величина гг = 6, у КО — ?г = 5, и т. д.
§ 23. Сегнетоэлектрики 189
§ 23. Сегнетоэлектрики
Обсуждаются физические свойства сегнето-
электриков и природа сегнетоэлектричества.
{"Определение. Сегнетоэлектриками называются полярные диэлектрики,
которые в определенном интервале температур спонтанно поляри-
поляризованы, т. е. обладают поляризованностью при отсутствии электри-
электрического поля. На границах интервала температур сегнетоэлектрик в
результате фазового перехода превращается в полярный диэлектрик.
Относительная диэлектрическая проницаемость сегнетоэлектриков
чрезвычайно велика (er ~ 104) и зависит от напряженности поля, не
являясь, однако, однозначной функцией напряженности. Значение s,
зависит от того, как изменялась напряженность до достижения данного
значения.
Сегнетоэлектрики иногда называют ферроэлектриками ввиду фор-
формальной аналогии, которая существует между их свойствами и свой-
свойствами ферромагнетиков. Примерами сегнетоэлектриков являются, сег-
нетова соль NaKC4H4O6-4H2O (от которой и произошло название
этого класса диэлектриков), титанат бария BaTiO3 и др.
J1 етля гистерезиса. Так как е зависит от Е, то D = еЕ нелинейно
зависит от Е. Кроме того, поскольку е зависит от предыстории
изменения Е, D неоднозначно зависит от Е. Поместим между обклад-
обкладками плоского конденсатора сегнетоэлектрик и будем измерять е,
в зависимости от напряженности Е поля, изменяющейся по гармони-
гармоническому закону.
Схема установки показана на рис. 104. К крайним клеммам двух
последовательно соединенных плоских конденсаторов подсоединен гене-
генератор, создающий между ними гармонически изменяющуюся разность
потенциалов. Она распределяется между конденсатором С с сегнето-
электриком и конденсатором Ci, между обкладками которого нет ве-
вещества. Полагая, что площади всех обкладок конденсаторов равны,
и обозначая d — расстояние между обкладками, имеем
Е = а/е, Ех = а/е0, B3.1)
откуда
U = Ed = ad/e, Ut = Е^/г0 B3.2)
и, следовательно,
tg Ф = UJU = s/s0 = еЕ/(?0Е). B3.3)
Поэтому если напряжение U подать на горизонтальную разверт-
развертку осциллографа, a [/t на вертикальную, то на экране осциллографа
при изменении Е будет прочерчена кривая, абсцисса точек которой
равна в некотором масштабе е0Е, а ордината — еЕ = D в том же
масштабе. Эта кривая называется петлей гистерезиса (рис. 105). Стрелки
190 3. Диэлектрики
Схема установки для снятия пет-
петли гистерезиса: tgq> = е/ео =
105
Петля гистерезиса
Температура Кюри-Вейс-
са не совладает с темпе-
температурой Кюри, однако
близка к ней. Во многих
случаях нет необходимос-
необходимости делать различия между
ними.
Большинство сегнето-
электриков имеют лишь
одну (верхнюю) точку
Кюри. Но есть некоторое
число сегнетоэлектриков с
двумя точками Кюри.
на кривой показывают направление движе-
движения точки по кривой при изменении напря-
напряженности поля. Отрезок ОА характеризует
остаточную поляризацию, т. е. ту поляри-
поляризацию, которую образец имеет тогда, когда
напряженность внешнего поля обратилась в
нуль. Отрезок ОБ характеризует напряжен-
напряженность, имеющую противоположное поляри-
зованности направление, при которой обра-
образец полностью деполяризуется, т. е. его оста-
остаточная поляризация исчезает. Чем больше
j О А |, тем более значительна остаточная
поляризация сегнетоэлектрика. Чем больше
| ОБ |, тем лучше остаточная поляризация
удерживается сегнетоэлектриком.
Т1 очка Кюри. При повышении температуры
выше некоторого значения Тк, характер-
характерного для каждого сегнетоэлектрика, его сег-
нетоэлектрические свойства исчезают и он
превращается в обычный полярный диэлект-
диэлектрик. Точка фазового перехода из состояния
сегнетоэлектрика в состояние полярного
диэлектрика называется точкой Кюри, а
соответствующая ей температура Тк — тем-
температурой Кюри. В некоторых случаях име-
имеются две точки Кюри - сегнетоэлектри-
ческие свойства исчезают также и при пони-
понижении температуры. Например, у сегнетовой
соли имеются две точки Кюри, характери-
характеризуемые температурами tK.B = 24° С, tK.H =
= —18 °С. Сегнетоэлектриков с двумя точка-
точками Кюри сравнительно немного. Большинст-
Большинство имеет лишь верхнюю точку, называемую
просто точкой Кюри.
В точке Кюри осуществляется переход
диэлектрика из сегнетоэлектрического сос-
состояния в состояние полярного диэлектрика.
При этом диэлектрическая проницаемость
изменяется непрерывно от значения, соот-
соответствующего сегнетоэлектрическому со-
состоянию, до значения, соответствующего
состоянию полярного диэлектрика. Закон из-
изменения диэлектрической восприимчивости к
вблизи температуры Кюри имеет вид
к =
B3.4)
§ 23 Сегнетоэлектрики 191
где А — некоторая константа; То —температура Кюри —Вейсса, близкая
к температуре Кюри Тк (в большинстве случаев в формуле B3.4)
вместо TQ используют Тк, что не вносит сколько-нибудь существен-
существенных погрешностей в х для температур, отличных от Тк). Закон,
выражаемый формулой B3.4), называется законом Кюри — Вейсса.
Если имеется также и нижняя точка Кюри, то вблизи нее закон
Кюри —Вейсса имеет вид
х=-Ар B3-5)
1 о — 1
Как уже говорилось, у кристаллов диэлектрические свойства различны
по различным направлениям и поэтому их диэлектрическая восприим-
восприимчивость характеризуется не скалярной диэлектрической восприимчи-
восприимчивостью х, а тензором диэлектрической восприимчивости хи Однако
зависимость компонент тензора от температуры имеет тот же харак-
характер, что и в B3.4) и B3 5).
[ олекулярныи механизм спонтанной поляризованности. Теория сегне-
тоэлектричества лежит вне рамок курса общей физики. Поэтому ог-
ограничимся лишь качественным описанием процессов на молекулярном
уровне. Очень сильное взаимодействие между дипольными моментами
молекул может привести к тому, что возникает конечная поляризован-
ность Р при сколь угодно малой напряженности Е поля или, что то
же самое, возможна поляризованность Р при отсутствии внешнего
поля. Другими словами, при сильном взаимодействии между диполь-
дипольными моментами молекул возникает спонтанная поляризация, при
которой отдельные диполъные моменты ориентируются в одном и той
оке направлении. Принимая во внимание, что постоянные дипольные
моменты во много раз больше, чем индуцированные [см. B2.19)],
можно заключить, что спонтанная поляризация характеризуется очень
большой поляризованностью. А это приводит к тому, что соответст-
соответствующие восприимчивость х и диэлектрическая проницаемость е значи-
значительно больше значений, наблюдаемых у полярных и неполярных
диэлектриков. Состояние спонтанной поляризации и есть сегнетоэлект-
рическое состояние. Переход из сегнетоэлектрического состояния в
состояние полярного диэлектрика является переходом из состояния
спонтанной поляризации в состояние, когда спонтанная поляризация
исчезает и - диэлектрик становится обычным диэлектриком с молеку-
молекулами, обладающими постоянными дипольными моментами, т. е. пере-
переходом в состояние полярного диэлектрика. Физические факторы, приво-
приводящие к этому переходу, сводятся к механизмам, ослаб хяющич
взаимодействие дипольных моментов молекул.
Диэлектрические домены. Спонтанная поляризация является источни-
источником очень больших электрических полей. Поэтому, если макроско-
макроскопический объем сегнетоэлектрика поляризован спонтанно в некотором
направлении, вокруг этого объема возникает очень большое электри-
электрическое поле, с которым связана большая энергия поля. Такое состояние
192 3. Диэлектрики
энергетически невыгодно. Система стремится перейти в такое состоя-
состояние, чтобы, с одной стороны, существовала спонтанная поляризация,
а с другой стороны, энергия поля была бы минимальной. Это может
осуществиться в результате разделения объема сегнетоэлектрика на
малые области, в каждой из которых имеется спонтанная поляризация
в некотором определенном направлении, различном для различных облас-
областей. Средняя поляризованность объема, включающего достаточное
число малых областей с различными направлениями спонтанной поля-
поляризации, равна нулю и поэтому напряженность внешнего электрического
поля, порождаемого этим объемом, близка к нулю. Малые области со
спонтанной поляризацией называются диэлектрическими доменами или
просто доменами. Таким образом, неполяризованный сегнетоэлектрик
является совокупностью доменов с беспорядочно ориентированными
спонтанными поляризованностями.
Очевидно, что для уменьшения электрической энергии выгодно умень-
уменьшать объемы доменов. Однако процессу уменьшения размера доменов
препятствует другой фактор, связанный с наличием поверхностной
энергии на границе между соседними доменами. Ясно, что суммарная
поверхность границ между доменами увеличивается при уменьшении
объема доменов и, следовательно, увеличивается также и поверхност-
поверхностная энергия. Поэтому объемы доменов могут уменьшаться лишь до
определенных пределов, когда это приводит к уменьшению полной
энергии системы. При дальнейшем уменьшении объема доменов за счет
поверхностной энергии происходит не уменьшение, а увеличение полной
энергии. Тем самым фиксируются размеры доменов. Эти размеры имеют
порядок тысяч межмолекулярных расстояний. Существование доменов
доказывается в экспериментах прямым наблюдением с помощью поля-
поляризованного света, а также в опытах по травлению поверхности
сегнетоэлектрика, поскольку различные части домена при травлении
разрушаются с различной скоростью.
Процесс изменения поляризованное™ сегнетоэлектрика во внешнем
электрическом поле состоит в переориентации дипольных моментов
отдельных доменов, в изменении объемов и движении границ между
доменами. Эти процессы усиленно изучаются, поскольку сегнетоэлектри-
ки имеют многочисленные практические применения. Известно более
ста различных чистых сегнетоэлектриков и очень большое количество
сегиетоэлектрических твердых растворов.
Д нтисегнетоэлектрики. При определенных условиях в кристалле возни-
возникают одновременно две спонтанные поляризации, направленные про-
противоположно друг другу. Одна из спонтанных поляризаций возникает
в результате ориентировки дипольных моментов молекул одной из
подрешеток кристалла в одном направлении, а другая — в результате
ориентировки дипольных моментов молекул другой из подрешеток
кристалла в противоположном направлении. При этом полная поляри-
поляризованность любого физически малого объема такого кристалла равна
нулю. Таким образом, доменов с различными направлениями спонтан-
спонтанной поляризации нет, хотя спонтанная поляризация в любом физически
§ 24 Пьезоэлектрики 193
малом объеме присутствует. Такие вещества
называются антисегнетоэлектриками. Они по
своей структуре аналогичны антиферромаг-
антиферромагнетикам и поэтому иногда называются анти-
ферроэлектриками.
В достаточно малых полях антисегнето-
электрики ведут себя как обычные диэлект-
диэлектрики с линейной зависимостью поляризован-
ности от напряженности внешнего поля.
В достаточно сильных пблях возможен пере-
переход в сегнетоэлектрическое состояние со
всеми вытекающими отсюда последствиями,
в частности наблюдается петля гистерезиса.
Переход осуществляется при большой ПО Двойные петли гистерезиса у ан-
МОДУЛЮ Напряженности ЭЛектрИЧеСКОГО ПОЛЯ, тисегнетоэлектриков, переходя-
ПОЭТОМУ ПРИ бОЛЬШОЙ амплитуде КОЛебанИЙ ЩИХ В болы™х полях в сегнето-
напряжения в схеме на рис. 104 с антисег-
нетоэлектриком вместо сегнетоэлектрика
наблюдаются две петли гистерезиса (рис. 106).
106
электрическое состояние
§ 24. Пьезоэлектрики
Описываются механизмы пьезоэффекта и
обратного пьезоэффекта. Обсуждается соот-
ношение между обратным пъезоэффектом
и электрострикцией. Даются основные сведе-
сведения о пироэлектриках.
(Двойства пьезоэлектриков. Имеются много-
многочисленные кристаллы, на поверхности ко-
которых при деформациях возникают электри-
электрические заряды. Такие кристаллы называются
пьезоэлектриками. Поскольку деформации
сами по себе не в состоянии изменить об-
общий заряд кристалла, образующиеся при
деформации поверхностные заряды имеют
различные знаки на различных частях поверх-
поверхности. К числу пьезоэлектриков относят
кварц, турмалин, сегнетову соль и многие
другие.
Как показывает опыт, заряды на поверх-
ности пьезоэлектрика возникают в резуль-
результате однородных деформаций сжатия или
растяжения во вполне определенных направ-
направлениях, называемых полярными осями пьезо-
пьезоэлектрика. На противоположных гранях,
перпендикулярных полярной оси, при одно-
7 А Н Матвеев
При возникновении усло-
условий для спонтанной поля-
поляризации диэлектрик стре-
стремится перейти в такое со-
состояние, чтобы, с одной
стороны, существовала
спонтанная поляризация, а
с другой стороны, энергия
поля была бы минималь-
минимальной. Благодаря этому про-
происходит образование до-
доменов.
Исчезновение спонтанной
поляризации и переход из
сегнетоэлектрического со-
состояния в состояние по-
полярного диэлектрика вы-
вызываются факторами, ос-
ослабляющими взаимодей-
взаимодействие дипольных момен-
моментов молекул.
Чем отличается температура
Кюри от температуры Кю-
Кюри—Еейсса!
Каков механизм возникно-
возникновения доменов? Почему до-
домены не могут быть очень
большими?
Что такое антисегнетоэлек-
трики?
194 3. Диэлектрики
родных деформациях возникают заряды противоположного знака,
причем знаки зарядов изменяются при изменении знака деформации,
т. е. если, например, при сжатии вдоль полярной оси на данной гра-
грани образовался положительный заряд, то при растяжении эта грань
заряжается отрицательно. Пьезоэлектрический эффект наблюдается не
только при чистом сжатии или растяжении вдоль полярной оси, но
при любой деформации кристалла, сопровождающейся сжатием или
растяжением вдоль полярной оси.
Поскольку на разных гранях, перпендикулярных полярной оси,
возникают заряды различного знака, различные направления вдоль по-
полярной оси неэквивалентны. А это означает, что если кристалл повер-
повернуть на 180° вокруг оси, перпендикулярной полярной, то полярная
ось совместится сама с собой, но кристалл сам с собой не совмес-
совместится. Поэтому кристаллы с центром симметрии не могут быть
пьезоэлектриками. Для существования пьезоэлектрического эффекта при
однородной деформации необходимо отсутствие у кристалла центра
симметрии. Полярные оси определяются свойствами симметрии кристал-
кристаллической решетки. Вообще говоря, кристалл имеет несколько полярных
осей.
Пьезоэлектрические свойства зависят от температуры. Если при
некоторой температуре кристаллическая решетка перестраивается так,
что образуется центр симметрии, то при этой температуре исче-
исчезают пьезоэлектрические свойства кристалла. Например, у кварца до
температуры 200 °С пьезоэлектрические свойства изменяются незначи-
незначительно, а затем до температуры 576 °С начинают медленно ослабе-
ослабевать. При 576 °С происходит перестройка кристаллической решетки
кварца, в результате которой пьезоэлектрические свойства у него исче-
исчезают. При понижении температуры изменение свойств кварца происхо-
происходит в обратном направлении,
продольный и поперечный пьезоэффекты. Возникновение зарядов на
гранях, перпендикулярных полярной оси, при однородной деформа-
деформации кристалла вдоль этой оси называется продольным пьезоэффектом.
Однако можно вызвать появление зарядов на тех же гранях, сжимая
или растягивая кристалл перпендикулярно полярной оси, если только
при этом происходит растяжение или сжатие кристалла вдоль полярной
оси. Это явление называется поперечным пьезоэффектом. Его существо-
существование обусловливается связью между продольными и поперечными
деформациями твердого тела'.
]У[еханизм пьезоэффекта. Пьезоэлектрическими свойствами могут
обладать только ионные кристаллы. Пьезоэлектрический эффект воз-
возникает в том случае, когда под действием внешних сил кристаллическая
подрешетка из положительных ионов деформируется иначе, чем кристал-
кристаллическая подрешетка из отрицательных ионов. В результате происхо-
происходит относительное смещение положительных и отрицательных ионов,
приводящее к возникновению поляризации кристалла и поверхностных
зарядов. Поляризованность в первом приближении прямо пропорцио-
пропорциональна деформации, которая, в свою очередь, прямо пропорциональна
§ 24 Пьезоэлектрики 195
силе. Следовательно, поляризованность прямо пропорциональна при-
приложенной силе. Между разноименно заряженными гранями деформиро-
деформированного диэлектрика возникает разность потенциалов, которую можно
измерить, а по ее значению сделать заключение о величине деформа-
деформаций и приложенных силах. Использование этой связи находит много-
многочисленные практические применения. Например, имеются пьезоэлектри-
пьезоэлектрические датчики для измерения быстропеременных давлений. Известны
пьезоэлектрические микрофоны, пьезоэлектрические датчики в автома-
автоматике и телемеханике и т. д.
Q братный пьезоэффект. Он состоит в том, что во внешнем электри-
электрическом поле пьезоэлектрик будет деформироваться. Необходи-
Необходимость его существования следует из наличия прямого эффекта и за-
закона сохранения энергии. При деформировании пьезоэлектрика работа
затрачивается на образование энергии упругой деформации и энергии
возникающего при этом в результате пьезоэффекта электрического
поля. Следовательно, при деформировании пьезоэлектрика необходимо
преодолевать дополнительную силу, кроме силы упругости кристалла,
которая препятствует деформации и является фактором, обусловливаю-
обусловливающим обратный пьезоэффект. Чтобы компенсировать эту дополнитель-
дополнительную силу, надо приложить внешнее электрическое поле, противопо-
противоположное тому, которое возникает в пьезоэффекте. Следовательно, для
получения некоторой деформации пьезоэлектрика под влиянием внеш-
внешнего электрического поля необходимо, чтобы оно было равно, но про-
противоположно направлено тому полю, которое при данной деформации
возникает в результате прямого пьезоэлектрического эффекта. Напри-
Например, если при некоторой деформации пьезоэлектрика вдоль полярной
оси между его гранями, перпендикулярными оси, возникает некоторая
разность потенциалов, то для осуществления такой же деформации
без приложений механических сил необходимо к этим граням прило-
приложить такую же разность потенциалов, но с противоположным знаком.
Механизм обратного пьезоэлектрического эффекта аналогичен меха-
механизму прямого: под действием внешнего электрического поля кристал-
кристаллические подрешетки положительных и отрицательных ионов деформи-
деформируются различным образом, что и приводит к деформации кристалла.
Обратный пьезоэлектрический эффект также имеет многочисленные
практические применения, в частности широкое применение получили
кварцевые излучатели ультразвука.
JJ ироэлектрики. У некоторых пьезоэлектриков подрешетка положи-
положительных ионов оказывается смещенной относительно подрешетки
отрицательных ионов в состоянии термодинамического равновесия,
в результате чего такие кристаллы оказываются поляризованными при
отсутствии внешнего электрического поля. Таким образом, такие
кристаллы обладают спонтанной электрической поляризацией.
Обычно наличие такой спонтанной поляризации маскируется свобод-
свободными поверхностными зарядами, оседающими на поверхность кристал-
кристалла из окружающей среды под действием электрического поля, свя-
196 3. Диэлектрики
занного со спонтанной поляризацией. Этот процесс происходит до тех
пор, пока электрическое поле не будет полностью нейтрализовано,
т. е. до тех пор, пока наличие спонтанной поляризации не будет
полностью замаскировано. Однако при изменении температуры образ-
образца, например при нагревании, происходит смещение ионных подреше-
ток друг относительно друга, в результате чего изменяется спонтан-
спонтанная поляризованность и на поверхности кристалла появляются электри-
электрические заряды. Возникновение этих зарядов называется прямым пиро-
пироэлектрическим эффектом, а соответствующие кристаллы называются
пироэлектрикам и.
Всякий пироэлектрик является пъезоэлектриком, но не всякий пьезо-
электрик является троэлектриком. Это связано с тем, что у пиро-
электрика имеется выделенное направление, вдоль которого существует
спонтанная поляризация, а у пьезоэлектрика такого выделенного направ-
направления, вообще говоря, нет.
Имеется также и обратный пироэлектрический эффект: изменение
электрического поля в адиабатно изолированном пироэлектрике сопро-
сопровождается изменением его температуры. Необходимость его суще-
существования может быть доказана на основе термодинамического ана-
анализа процесса и продемонстрирована экспериментами.
Задачи
3.1. Вычислить относительную ди-
диэлектрическую проницаемость ге-
гелия при р= 101,3 кПа, t= 15 °С,
если его атомная диэлектрическая
восприимчивость а=2,48-100 м3.
Экспериментальное значение е, =
= 1,000074.
3.2. Рассчитать диэлектрическую про-
проницаемость аммиака при t = 27 °С;
а =1,37-КГ29 м3; р = 0,46 х
х 109 Кл-м. Указание:
воспользоваться формулой B2.19).
3.3. Постоянный дипольный момент
молекулы воды 6,2 ¦ 100 Кл ¦ м.
Определить поляризованность на-
насыщенного водяного пара при
t = 100 °С и атмосферном дав-
давлении.
3.4. Воздух состоит в основном из мо-
молекул N2 и О2. По формуле
Клаузиуса —Моссотти найти коэф-
коэффициенты их атомной восприимчи-
восприимчивости, принимаемые для упро-
упрощения одинаковыми. Найти ра-
радиус молекул.
3.5. Принимая для молекулы азота
значения а и га, полученные в за-
задаче C.4), вычислить изменение
расстояния между зарядами, обра-
образующими диполь, в поле напря-
напряженностью 1 МВ/м.
Ответы
3.1. ?, = 1,000067. 3.2. е, = 1,0076. 3.3. 1,2 10 Кл/м2. 3.4. а =1,1-10"
г0 = 0,96-100 м. 3.5. 0,87-106 м.
§25
Электрическое поле
при наличии
постоянных токов
§ 26
Сторонние э д с
§27
Дифференциальная форма
закона Джоуля — Ленца
Работа, совершаемая
при прохождении тока
и развиваемая мощность
Постоянный
электрический
ток
§28
Линейные цепи
Правила Кирхгофа
Постоянный ток невозможен при на-
наличии лишь сил электростатического
происхождения. Для его осуществления
необходимы силы неэлектростатиче-
неэлектростатического происхождения, называемые сто-
сторонними электродвижущими силами.
Основной закон —закон Ома в локаль-
локальной формулировке.
$ 29
Токи в сплошной среде
§ 30
Заземление
линий передач
198 4. Постоянный электрический ток
§ 25. Электрическое поле
при наличии постоянных токов
Обсуждаются особенности электрического
поля при наличии постоянных токов и роль
поверхностных и объемных зарядов. Анализи-
Анализируется роль различных факторов, обеспе-
обеспечивающих существование постоянного тока.
|у внутри проводника. Закон Ома (см. § 16) в дифференциальной
форме имеет вид
j = УЕ. B5.1)
При наличии тока j ф 0 и, следовательно, Е Ф 0. Таким образом,
внутри проводника с током имеется электрическое поле. Напомним, что
в электростатике поле внутри проводников отсутствует.
Плотность постоянного тока по сечению проводника распределена,
вообще говоря, неравномерно. Чтобы в этом убедиться, рассмотрим
участок искривленного проводника с круговым поперечным сечением
[речь идет об однородном проводнике (у = const)]. Изогнутый участок
проводника следует представить себе вырезанным из недеформирован-
ного куска материала, поскольку в изогнутой проволоке имеется дефор-
деформация и условие однородности для нее, строго говоря, не выполняется,
а вся картина распределения плотности тока усложняется.
Вблизи поверхности проводника плотность тока можетбыть направ-
направлена только по касательной к поверхности. Это означает [см. B5.1)J,
что напряженность Е поля вблизи поверхности проводника касательна
поверхности. Следовательно, эквипотенциальные поверхности перпенди-
перпендикулярны его поверхности. Если участок проводника изогнут, то, оче-
очевидно, две близкие эквипотенциальные поверхности не могут находиться
на неизменном расстоянии друг от друга во всех точках внутри
проводника. Например, в кольцевом проводнике круглого сечения
расстояние между эквипотенциальными поверхностями на внутренней
части кольца меньше, чем на внешней. Поскольку расстояние между
соседними эквипотенциальными поверхностями изменяется, изменяется
и напряженность электрического поля в соответствующих точках экви-
эквипотенциальной поверхности. Отсюда [см. B5.1)] заключаем, что в одно-
однородном проводнике плотность постоянного тока, вообще говоря, изме-
изменяется по сечению проводника. В круговом цилиндрическом прямоли-
прямолинейном проводнике бесконечной длины эквипотенциальные поверхности
внутри проводника являются плоскостями, перпендикулярными оси про-
проводника. Поэтому по всему сечению такого однородного проводника
как напряженность электрического поля, так и плотность тока постоянны.
В дальнейшем в основном рассматриваются лишь проводники с
очень малой площадью поперечного сечения, называемые линейными.
Для них с большой точностью можно пренебречь изменением плотности
§ 25 Электрическое поле при наличии постоянных токов 199
электрического тока по сечению проводника, считая, что в каждой точке
этого сечения плотность тока постоянна по модулю и направлена
вдоль элемента длины dl проводника. Сила тока, текущего по провод-
проводнику, в этом случае равна / = j AS, где AS — площадь поперечного
сечения проводника.
Таким образом, в общем случае вопрос о напряженности электри-
электрического поля и плотности постоянного тока внутри толстых проводни-
проводников является сложным. Распределение плотности тока по сечению за-
зависит от ряда факторов и, в частности, от формы проводника.
О напряженности поля вблизи поверхности проводника можно высказать
более определенные суждения. Вблизи поверхности как напряженность
поля, так и плотность тока направлены касательно поверхности.
Нормальные к поверхности составляющие этих величин внутри провод-
проводника отсутствуют. Из граничного условия A7.30) заключаем, что
вблизи поверхности вне проводника имеется электрическое поле, танген-
тангенциальная составляющая напряженности Ег которого равна тангенциаль-
тангенциальной составляющей напряженности Е, поля внутри проводника (рис. 107).
Однако о нормальной составляющей напряженности электрического
поля вне проводника отсюда никаких выводов сделать нельзя.
JJonpoc об источниках поля. Чем же порождается электрическое поле
внутри проводника, что является источником этого поля? Так как
существование постоянного тока в цепи обеспечивается соответствую-
соответствующим источником постоянного тока, например гальваническим элемен-
элементом, то ясно, что он имеет какое-то отношение к порождению электри-
электрического поля. Однако непосредственно он не может породить это поле.
Такое утверждение очевидно в случае очень длинного проводника для
участков цепи, удаленных от батареи на очень большое расстояние,
например на сотни километров. Напряженность электрического поля,
которую могут создать заряды полюсов батареи, на этом расстоянии
ничтожно мала. Следовательно, батарея не может быть непосредствен-
непосредственным источником электрического поля внутри проводника.
Единственным источником постоянного электрического поля может
быть только электрический заряд. Поэтому обсуждаемая проблема
сводится к вопросу о том, какими зарядами порождается поле внутри
проводника и где эти заряды находятся?
Поле вне гтроводника. Для ответа на этот вопрос необходимо изучить
электрическое поле вне проводника. Поместим проводник с током в
плоскую ванночку с тонким слоем диэлектрического порошка (рис. 108).
Отдельные крупинки порошка при этом располагаются цепочками вдоль
силовых линий электрического поля (см. § 19). На рисунке изображены
два участка проводника с током и силовая линия между ними.
Видно, что силовые линии электрического поля не касательны к
поверхности проводника. Это означает, что вне проводника вблизи его
поверхности наряду с тангенциальной составляющей напряженности Е,
электрического поля имеется также нормальная составляющая Е„.
Однако внутри проводника Е„ = 0. Поэтому из A7.26) заключаем, что
на поверхности проводника должны существовать заряды, поверхностная
200 4. Постоянный электрический ток
плотность которых
а = Ео?„.
B5.2)
it
107
Поле внутри проводника и тан-
тангенциальная составляющая на-
напряженности поля вблизи поверх-
поверхности вне проводника
108
Демонстрация наличия нор-
нормальной составляющей напря-
напряженности поля вблизи поверх-
поверхности проводника
9B)
9@
109
В формуле B5.2) предполагается, что про-
проводник находится в вакууме. Если его погру-
погрузить в диэлектрическую среду, то вместо е0
в формулу B5.2) войдет диэлектрическая про-
проницаемость s среды.
[Поверхностные заряды. Таким образом, на
поверхности проводника, по которому те-
течет постоянный электрический ток, имеются
электрические заряды. Они и являются источ-
источниками электрического поля, которое су-
существует в проводнике и обеспечивает нали-
наличие постоянного тока. Поверхностная плот-
плотность заряда на различных участках провод-
проводника может иметь различные знаки. Напри-
Например, левый и правый участки проводника
на рис. 108 имеют соответственно положи-
положительную и отрицательную поверхностную
плотность заряда.
Объемные заряды. В однородных провод-
проводниках имеются только поверхностные за-
заряды. В неоднородных проводниках, когда
проводимость изменяется от точки к точке,
возникают также заряды в объеме провод-
проводника. Это непосредственно следует из закона
сохранения заряда E.24). В рассматриваемом
стационарном случае (Sp/St) = 0 и уравнение
E.24) принимает вид
divj = O. B5.3)
Объемный заряд в веществе в принципе
может быть как свободным, так и связан-
связанным. Нас интересует суммарная объемная
плотность р + рсв заряда, наличие которой
приводит к изменению напряженности элект-
электрического поля вдоль проводника. Поэтому
[см. A7.27)] суммарная объемная плотность
заряда равна
р + рсв = div (е0Е) = е0 div (j/y), B5.4)
где Е = j/y. Учитывая B5.3) и выражение
B5.5)
К вычислению разности по- div (j/y) = A/у) div j + j • grad A/y),
тенциалов между двумя точка-
точками проводника с током ИЗ B5.4) НЭХОДИМ
Р+ Рс=?оГ grad A/у).
B5.6а)
§ 25 Электрическое поле при наличии постоянных токов 201
Направляя ось X вдоль прямолинейного участка проводника и
считая, что его свойства изменяются лишь в этом направлении, пере-
перепишем формулу B5.6а) в виде
B5.66)
Если в направлении тока проводимость уменьшается, то объем-
объемная плотность зарядов положительна. Причина этого заключается в
следующем. При постоянной площади сечения проводника плотность
тока вдоль проводника должна быть постоянной. Если проводимость
в направлении тока уменьшается, то для поддержания постоянства
тока необходимо увеличивать напряженность электрического поля.
Увеличение напряженности и обеспечивается объемными положитель-
положительными зарядами. Аналогично объясняется и возникновение отрицатель-
отрицательных объемных зарядов при увеличении проводимости в направлении
тока.
Д/^еханизм осуществления постоянного тока. Источник тока называется
источником сторонних электродвижущих сил (сторонних э. д. с;
см. § 26). По результатам своего действия он представляет собой
процесс или устройство, отделяющее положительные заряды от отрица-
отрицательных. После разделения заряды перемещаются на электроды и по
закону Кулона действуют на заряды проводника вблизи электродов,
- которые в свою очередь действуют на другие заряды, и т. д. В ре-
результате этих коллективных взаимодействий в цепи на поверхности
проводников возникает такое распределение зарядов, которое обеспечи-
обеспечивает существование внутри проводника соответствующего электри-
электрического поля. Таким образом, роль зарядов на полюсах источника
сторонних э. д. с. состоит не в том, чтобы создавать во всех провод-
проводниках непосредственно соответствующее электрическое поле, а в том,
чтобы обеспечить такое распределение поверхностных зарядов на провод-
проводниках, которое создает нужное электрическое поле внутри них. А это
и обеспечивает существование постоянного тока. Поскольку взаимо-
взаимодействие между зарядами осуществляется посредством электромагнит-
электромагнитных сил, процесс образования постоянного тока в цепи после ее замы-
замыкания характеризуется скоростью распространения электромагнитных
волн, зависящей от распределения емкостей, индуктивностей и других
характеристик цепи. В свободном пространстве скорость распростра-
распространения электромагнитных взаимодействий равна скорости света.
потенциала вдоль проводника с током. Поскольку в про-
проводнике при наличии постоянного тока Е Ф 0, потенциал изменяется
вдоль проводника, т. е. в отличие от электростатики потенциал не
является постоянным во всех точках проводника. Однако поле внутри
проводника создается неподвижными, постоянными по времени поверх-
поверхностными зарядами и поэтому так же, как в электростатике, является
потенциальным. Следовательно, разность потенциалов между двумя
точками проводника (рис. 109) по формуле A4.28) равна
202 4. Постоянный электрический ток
B)
ФB)-ФA)=- jE-dl, B5.7)
A)
где интеграл вычисляется по любому пути, соединяющему точки 1
и 2. Для удобства вычислений целесообразно в качестве пути выбрать
одну из линий тока, соединяющих некоторую точку в сечении 1 про-
проводника, с соответствующей точкой в сечении 2. Вдоль линии тока
Е и dl коллинеарны и поэтому Е • dl = E d/, причем положительный знак
обусловливается тем, что ток течет в направлении от большего потен-
потенциала к меньшему. Кроме того, если площадь сечения проводника
постоянна, то вдоль проводника Е = const. Следовательно [см. B5.7)],
ФA)-срB) = И, B5.8)
где I — длина проводника между сечениями 1 и 2. Разность потен-
потенциалов между сечениями называется напряжением и обозначается
Ui2 = фA) ~ фB). Из дифференциальной формулировки закона Ома
(j = уЕ) находим
( B5.9)
где ! — сила тока. С учетом B5.9) соотношение B5.8) принимает вид
U12=U/(yS) = IR12, B5.10)
где R12 = l/(yS) — омическое сопротивление участка проводника. Форму-
Формула B5.10) является законом Ома для участка проводника.
§ 26. Сторонние э. д. с.
Обсуждается роль сторонних э. д. с. в цепях
тока и описываются конкретные источники
сторонних э. д. с.
Сущность сторонних э. д. с. Сторонняя электродвижущая сила не
может иметь электростатического происхождения по той простой
причине, что электростатическое поле является потенциальным. Следо-
Следовательно, работа поля по замкнутому контуру, по которому течет
ток, равна нулю, т. е. при этом условии ток не мог бы существо-
существовать, поскольку он должен совершать работу для преодоления омиче-
омического сопротивления проводников. Существование постоянного тока
доказывает, что сторонние электродвижущие силы имеют неэлектроста-
неэлектростатическое происхождение.
Сторонняя электродвижущая сила может быть, в частности, меха-
механической или электрической силой, но не силой электростатического
происхождения. Например, такой э. д. с. является сила, действующая
на заряд в электрическом поле, возникающем по закону электромагнит-
электромагнитной индукции Фарадея (см. гл. 8).
§ 26. Сторонние э.д.с. 203
ХД еханическая сторонняя э. д. с. Схема
простейшего источника тока, в котором
сторонняя э. д. с. имеет механическое проис-
происхождение, изображена на рис. 110. Между
электродами А и В имеется нейтральная
среда с равным числом положительных и
отрицательных зарядов. Сторонняя сила
неэлектростатического происхождения пере-
перемещает положительные заряды к электроду
В, а отрицательные — к электроду А. В ре-
результате этого электрод А заряжается отри-
отрицательно, а электрод В — положительно. Во
внешней цепи от В к А течет электрический
ток, производящий соответствующую рабо-
работу. Необходимая для этого энергия сообща-
сообщается системе сторонними силами, которые
затрачивают работу для разделения зарядов
между электррдами А и В и доставки этих
зарядов на электроды против сил электри-
электрического поля с напряженностью Е, сущест-
существующего между электродами. Ток между
электродами А и В внутри источника э. д. с.
замыкает ток во внешней цепи. Если направ-
направление тока характеризовать относительно
электродов, то во внешней цепи ток течет
от положительного электрода к отрицатель-
отрицательному, а внутри источника тока — от отри-
отрицательного электрода к положительному.
Практической реализацией механической
сторонней э. д. с. является электростати-
электростатическая машина, схема которой показана на
рис. 111. Заряды Q+ и <2~ создают электро-
электростатическое поле в пространстве между ними.
Изолированные друг от друга проводящие
пластины С и D движутся по окружности
вокруг оси О под влиянием сторонних ме-
механических сил. В положении 1 пластины
оказываются соединенными между собой
неподвижным проводником (сплошная ли-
линия со стрелками на концах). В результате
электростатической индукции пластины С и
D в этом положении заряжаются соответст-
соответственно отрицательно и положительно. При
дальнейшем вращении их контакт с провод-
проводником прерывается и в положении 2 плас-
пластины изолированы друг от друга, но несут
на себе разноименные заряды. В положении
В
110
Схема действия сторонних э.д.с.
механического происхождения
111
Схема электростатической ма-
машины
Сторонней э. д. с. называ-
называется сила неэлектростатн-
ческого происхождения,
производящая разделение
зарядов.
Работа, совершаемая в це-
цепи при прохождении элек-
электрического тока, равна
работе сторонних э. д. с.
Плотность постоянного
тока по сечению провод-
проводника распределена, вооб-
вообще говоря, неравномерно.
На поверхности провод-
проводника с током имеются по-
поверхностные заряды, яв-
являющиеся источниками
электрического поля, ко-
которое существует в про-
проводнике и обеспечивает
наличие постоянного тока.
204 4. Постоянный электрический ток
Zn
112
Возникновение разности потен-
потенциалов между твердым телом
и жидкостью
Си
Zn
ИЗ
Элемент Вольта
Поверхностные заряды
на различных участках
проводника могут иметь
различные знаки.
Роль зарядов на полю-
полюсах источника сторонних
э. д. с состоит не в том,
чтобы создавать во всех
проводниках непосред-
непосредственно соответствующее
электрическое поле, а в
той, чтобы обеспечить
такое распределение по-
поверхностных зарядов на
проводниках, которое соз-
создает нужное электриче-
электрическое поле внутри них.
Объемные заряды возни-
возникают лишь в неоднород-
неоднородных проводниках.
3 они вступают в контакт с электродами
Л и В, на которые переходит заряд с С и D.
Между электродами по цепи BGA течет
электрический ток. Если имеется одна пара
вращающихся проводников CD, то ток по
цепи протекает импульсами, по два импульса
за оборот. Если же взять достаточно боль-
большое число пар пластин С, D, чтобы они
вступали в контакт с электродами А, В
последовательно с ничтожно малыми пере-
перерывами, то по внешней цепи течет практи-
практически постоянный ток. Такая машина реали-
реализует стороннюю э. д. с. механического проис-
происхождения, возникающую за счет механиче-
механических сил, обеспечивающих движение пластин
С, D по окружности.
Цепь взаимопревращений энергии здесь
выглядит следующим образом. Сторонние
механические силы, перемещая пластины
С, D, производят работу против сил электри-
электрического поля, существующего между заря-
зарядами Q+, Q~, и переносят заряды на пласти-
пластинах С, D к электродам А, В. В результате
этого изменяется энергия электрического по-
поля, т. е. происходит превращение энергии из
механической формы в энергию электриче-
электрического поля. Затем эта энергия в результате
протекания тока по цепи BGA превращает-
превращается в джоулеву теплоту и другие формы
энергии, обусловленные работой тока во
внешней цепи.
Гальванические элементы. Очень распрост-
распространенными источниками постоянного тока
являются гальванические элементы и акку-
аккумуляторы. Электрический ток был открыт
в 1791 г. Л. Гальвани A737-1798). Однако
Гальвани не сумел дать правильное толкова-
толкование своим опытам. Это сделал в 1792 г.
А. Вольта A745—1827). Элементы постоян-
постоянного тока, о которых идет здесь речь, полу-
получили название по имени Гальвани.
Разность потенциалов (см. § 2) возникает
не только при контакте твердых тел, но и
твердых тел с жидкостями. При этом могут
происходить химические реакции. Например,
если цинковую пластину Zn опустить в
раствор серной кислоты H2SO4, то цинк
§ 26 Сторонние э. д с. 205
растворяется (рис. 112). Однако в раствор уходят не нейтральные
атомы цинка, а положительные ионы Zn++, в результате чего
раствор заряжается положительно, а цинковая пластина — отрицатель-
отрицательно. При этом между раствором и пластиной возникает разность
потенциалов. При некотором потенциале металла относительно раство-
раствора, называемом электрохимическим, переход ионов цинка в раствор
прекращается. Он зависит от свойств металла, жидкости и от кон-
концентрации ионов металла в растворе. При контакте металла с водой
металл заряжается более отрицательно, чем при контакте металла
с раствором соли, содержащим ионы металла. При большой концентра-
концентрации ионов в растворе может произойти обратный процесс, при кото-
котором положительные ионы начнут осаждаться на металле и он заря-
зарядится положительно. Таким образом, при различных комбинациях
металлов, жидкостей и концентраций ионов в растворах могут возни-
возникать различные электрохимические потенциалы.
Поскольку электрохимический потенциал зависит от концентрации
ионов металла, условились брать раствор, содержащий в 1 л раствора
моль ионов металла, деленный на валентность иона. Электрохимический
потенциал металла относительно такого раствора называется абсолют-
абсолютным нормальным электрохимическим потенциалом. Например, для
растворов в серной кислоте этот потенциал для Zn равен -0,5 В, а для
Си равен +0,6 В.
Если два различных металла погружены в раствор, то между ними
возникает разность потенциалов, равная разности их электрохимических
потенциалов. Совокупность двух металлов и раствора называется галь-
гальваническим элементом, а разность потенциалов между металлами —
электродвижущей силой элемента.
Элемент Вольта. Ои состоит из медной и цинковой пластинок,
погруженных в раствор серной кислоты (рис. 113). Принимая во вни-
внимание электрохимические потенциалы цинка и меди, заключаем, что
э. д. с. элемента Вольта равна [0,6 — (—0,5)] В = 1,1 В.
Г)бласть действия сторонних э. д. с. Не следует думать, что сторонние
э. д. с. возникают в пространстве между медной и цинковой пластин-
пластинками. В данном случае имеются две сторонние э. д. с. сосредоточен-
сосредоточенные в поверхностных слоях соприкосновения цинковой и медной пласти-
пластинок с раствором. Эти слои имеют молекулярную толщину. Во всем
остальном объеме раствора никаких сторонних э. д. с. нет. При соеди-
соединении пластин элемента проводником по нему течет ток от медной
пластины, являющейся положительным электродом элемента, к цинко-
цинковой пластине, являющейся отрицательным электродом. В растворе
между электродами ток течет от цинковой пластины к медной. Таким
образом, как это и должно быть, линии постоянного тока замкнуты.
Рассмотрим изменение потенциала в цепи с током. В направле-
направлении тока потенциал падает на омическом сопротивлении проводника.
На рис. 114 изображено изменение потенциала по замкнутому контуру
с элементом Вольта в качестве сторонней э. д. с. Точки А и В соот-
соответствуют поверхностным слоям контактов медной и цинковой пласти-
206 4. Постоянный электрический ток
114
Изменение потенциала в цепи
с гальваническим элементом
нок с растворами, в которых действуют сторонние электродвижущие
силы. Их разность и составляет стороннюю э. д. с. элемента. Она
равна полному падению потенциала на омическом сопротивлении
внешней цепи на участке AGB и на омическом сопротивлении элект-
электролита на участке BDA. Омическое сопротивление электролита назы-
называется внутренним сопротивлением элемента. Обозначим: ^СтоР, R и г —
соответственно сторонняя э. д. с. элемента, сопротивление внешней цепи
и внутреннее сопротивление элемента. Запишем закон Ома для всей
цепи в виде
%mp = l{R + r). B6.1)
Сторонняя э. д. с. элемента определяется свойствами элемента и не
зависит от силы протекающего по цепи тока. Из формулы B6.1)
видно, что падение напряжения на внешней цепи (U = IR) не равно
электродвижущей силе элемента и всегда меньше ее. Это есть напря-
напряжение между клеммами работающего элемента, когда по цепи течет
ток. С увеличением силы тока напряжение во внешней цепи уменьша-
уменьшается, причем тем значительнее, чем больше внутреннее сопротивление
элемента. При использовании элемента всегда желательно, чтобы напря-
напряжение во внешней цепи как можно меньше зависело от силы тока,
т. е. от нагрузки. Поэтому важной характеристикой элемента является
внутреннее сопротивление. Чем оно меньше, тем при прочих равных
условиях лучше качество источника сторонних э. д. с.
Закон сохранения энергии. Проанализируем закон сохранения энергии
в цепи с током, изображенной на рис. 114. Обозначим: Ах —работа
электрического поля при движении заряда q по замкнутой цепи;
А2 — работа сторонних э. д. с. Электрическое поле производит работу
на участках, на которых потенциал падает от фх до ср2 (внешняя
цепь) и от (рз Д° Ф4 (за счет омического сопротивления раствора
току внутри элемента). Она равна
(ф3-Ф4)Я- B6-2)
Работа сторонних э. д. с. в слоях молекулярной толщины приводит
к увеличению потенциалов от ф+ до ф! (на медной пластине) и от ф2
§ 26. Сторонние э. д, с. 207
115
Элемент Даниэля
Си
|1-_Си+^
CuSO4'--
4- 4
4- 4
4 4
4-4
4 ~4
Л,
1
—.
— —
- -
- ~
Zn
до ф3 (на цинковой пластине). Поэтому работа сторонних э. д. с. дает-
дается выражением
(фз-ф+)?, B6.3)
где второе равенство получилось в результате перегруппировки членов.
Из сравнения B6.2) и B6.3) видно, что
А, = А2, B6.4)
т. е. работа, совершаемая в цепи при прохождении тока, равна работе
сторонних э. д. с.
Выведем еще раз закон Ома B6.1) для всей цепи, пользуясь законом
Ома B5.10) для участка цепи:
<Pi - Фг = JR. Фз - Ф+ = 1г, B6.5)
откуда
IR + Ir = (ф! - ср2) + (ф3 - ф+) = (ф! - ф+) + (фз - ф+) = %тор. B6.6)
Поляризация элемента. При прохождении тока в цепи элемента Вольта
ионы Zn++ переходят в раствор, где соединяются с отрицательными
ионами SO^ ~, на которые наряду с ионами Н++ диссоциирует серная
кислота. В растворе происходит реакция Zn++ + SO4 ~ = ZnSO^, про-
продукты которой выпадают в виде осадка. Положительные ионы водо-
водорода устремляются к медной пластине и там нейтрализуются электро-
электронами тока проводимости в пластине. В результате на поверхности
медной пластины образуется пленка водорода, которая, с одной сто-
стороны, увеличивает внутреннее сопротивление элемента, а с другой,
создает дополнительный электрохимический потенциал, направленный
против потенциала, существовавшего там до образования пленки.
В результате всех этих ¦ процессов э. д. с. элемента уменьшается. Такие
процессы называются поляризацией элемента.
Q] пособы деполяризации. Чтобы избежать падения э. д. с, используют
различные способы деполяризации.
1. Использование двух жидкостей, подобранных так, что на электро-
электродах не происходит выделения новых веществ. Для каждого электрода
208 4. Постоянный электрический ток
подбирается подходящая жидкость. Жидкости разделяют перегородкой,
которая, с одной стороны, предохраняет их от смешивания, а с другой
стороны, не препятствует обмену ионами. Например, в элементе Да-
Даниэля в качестве жидкостей берутся медный купорос CuSO4 и раствор
ZnSO4 (рис. 115), причем в медный купорос опускается медная пласти-
пластина, а в раствор ZnSO4 — цинковая. Цинк переходит в раствор серной
кислоты в виде иона Zn++. Электроны с медной пластины перехо-
переходят в раствор медного купороса и нейтрализуют ион Си + +, в резуль-
результате чего медь осаждается из раствора на медную пластинку. Остав-
Оставшиеся в растворе ионы SO4 ~ проникают через перегородку в другую
часть элемента, соединяются там с Zn++, а образовавшийся в резуль-
результате этого избыток ZnSO4 выпадает на дно в виде осадка. Таким
образом, при работе элемента никакой поляризации не возникает, а
лишь происходит обеднение раствора медного купороса CuSO4. Его
требуется пополнять.
2. Использование сильных окислителей, которые связывают водород
и кислород с образованием воды.
Дккумуляторы. Это гальванический элемент, в котором вещества,
расходуемые при работе в качестве источника тока, накапливаются
при пропускании через аккумулятор тока от постоянного источника.
Такая процедура называется зарядкой аккумулятора.
Наиболее распространенным является свинцовый аккумулятор,
состоящий из двух свинцовых пластин, опущенных в раствор серной
кислоты. При этом на электродах образуется сернокислый свинец
PbSO4, которым насыщается весь раствор. Пропускание через аккуму-
аккумулятор тока при зарядке сопровождается окислением свинца электрода,
соединенного с положительным полюсом заряжающего устройства, до
перекиси РЬО2 и восстановлением другого электрода до чистого свинца.
Таким образом, заряженный аккумулятор имеет одну пластину с пере-
перекисью РЬО2, а другую из чистого свинца и электролит, состоящий из
раствора H2SO4, насыщенного сернокислым свинцом PbSO4. При ра-
работе аккумулятора его пластина с перекисью РЬО2 является положи-
положительным полюсом и постепенно восстанавливается с образованием
PbSO4. Отрицательная пластина, состоящая из чистого свинца, при
работе аккумулятора постепенно покрывается сернокислым свинцом.
В результате этого аккумулятор разряжается. Э. д. с. свинцового акку-
аккумулятора при максимальной зарядке равна примерно 2,7 В. Однако
уже при небольшой разрядке она падает до 2,2 В и на этом уровне
сохраняется длительное время, лишь медленно уменьшаясь при работе
аккумулятора. Минимально допустимая э. д. с, при которой зарядка
полностью восстанавливает свойства аккумулятора, считается равной
1,85 В. При разрядке до меньших э. д. с. аккумулятор портится.
Важной характеристикой аккумулятора является его емкость, опреде-
определяемая как полный заряд, который может отдать аккумулятор при
разрядке, и выражаемая в ампер-часах.
27 Дифференциальная форма закона Джоуля — Ленца 209
§ 27. Дифференциальная форма
закона Джоуля — Ленца. Работа,
совершаемая при прохождении тока,
и развиваемая мощность
Вводятся формулы для работы, совершаемой
при прохождении тока, и развиваемой мощ-
мощности. Дается дифференциальная формули-
формулировка закона Джоуля — Ленца. Описывается
классическая эгектронная картина электро-
электропроводности и обсуждаются ее недостатки.
Излагаются общие черты квантовой трак-
трактовки электропроводности.
Работа, совершаемая при прохождении тока. Мощность Если между
точками с разностью потенциалов U переносится заряд dQ, то совер-
совершается работа
dA = dQU. B7.1)
Пусть по проводнику протекает ток /. Рассмотрим участок провод-
проводника, между концами которого имеется разность потенциалов U. В те-
течение времени dt на участке перемещается заряд dQ — I dt и, следо-
следовательно, совершаемая работа равна
dA = IU dt. B7.2)
Следовательно, мощность, развиваемая током на этом участке, опре-
определяется формулой
Г Р = dA/dt = IU.
B7 3)
Форма выделяемой при этом энергии зависит от природы физических
факторов, обусловливающих падение потенциала. Падение потенциала
на омическом сопротивлении проводов сопровождается выделением
теплоты, падение напряжения на клеммах двигателя постоянного тока
обусловлено производством механической работы и т. д. Формула
B7.3) дает полную мощность, развиваемую током на участке с паде-
падением потенциала U. Если все падение потенциала происходит на
омическом сопротивлении проводника, то по закону Ома U = IR, где
R — сопротивление участка В этом случае вся энергия выделяется в
виде теплоты с мощностью
р = W = I2R.
B7.4)
Формула B7.4) выражает закон Джоуля —Ленца. Он был открыт
в 1841 г. Дж. Джоулем A818-1889) и в последующем подробно
исследован Ленцем.
210 4. Постоянный электрический ток
Т\ ифференциальная форма закона Джоуля —
Ленца. Применив закон B7.4) к бесконеч-
бесконечно малому цилиндру (рис. 116), ось кото-
которого совпадает с направлением тока, полу-
получим
АР = (/А*J у^' <27-5>
К выводу закона Джоуля-Лен- где / = jAS, } - ПЛОТНОСТЬ тока. Сопротивле-
ца в дифференциальной форме ,ше бескоНечНо малого цилиндра равно
AR = Al/(yAS). Принимая во внимание, что
ASA/ = AV - объем цилиндра, из B7.5) на-
находим
72/y, B7.6)
где Pv — объемная плотность тепловой мощ-
мощности, выделяемой в проводнике, т. е. тепло-
теплоты, образующейся в 1 м3 проводника в 1 с.
Формула B7.6) является дифференциальной
формой закона Джоуля — Ленца, поскольку
все величины относятся к одной и той же
точке.
Пользуясь законом Ома в дифферен-
Работа, совершаемая при циальной форме, преобразуем B7.6):
прохождении тока, не яв-
пяется результатом прев- р Av— vF1 = i • F B7 7^
ращен ня кинетической V —} П ~ I J У • )
энергии электронов в дру- nmfiOp из чтих пяиенгтп когття н ттенпй
гие формы энергии. Носи- J»°ooe из этих равенств, когда в левой
телеи энергии, эатрочи- части стоит Ру, является записью закона
ваемой на совершение ра- Джоуля — Ленца в дифференциальной форме,
боты, являются не элект- Хотя формула B7.6) и выведена для бесконеч-
ноГполе. ЛншГГчаст- н0 малого цилиндрического участка провод-
проводном случае выделения ника, ее справедливость не связана с фор-
джоупева тепла кииетиче- МОЙ бесконечно МЭЛОГО объема, ПОСКОЛЬКУ
екая энергия электронов входящие в нее величины зависят лишь от
Ф^ПрЯмойЯэнергиив1г1осреНстЙ- их значений в точке и не зависят от других
вом которой энергия элек- факторов.
рГщГтГ.т;„лотувд;у: и
гих случаях кинетическая ческого тока. Падение потенциала в цепи
энергия электронов ни- тока компенсируется соответствующим
какой роли не играет, подъемом потенциала, возникающим в ре-
своКбоДнСоМгоСпРГегаТввклаМсЯ. 3УЛЬТаТе Д^СТВИЯ СТОРОННИХ ЭЛеКТроДВИЖу-
сической теории эпектропро- Щи* сил на заряды (см. 26). При прохожде-
водности? нии тока производится работа и выделяется
Какие основные трудности энергия, например в форме теплоты. Сторон-
РопСроИводСности^ОрИИ ЭЛеКТ" ние электродвижущие силы совершают ра-
Как они в общих чертах боту над зарядами, сообщая им соответст-
преодопеваются; вующую энергию. Поэтому получается, что
§ 27. Дифференциальная форма закона Джоуля — Ленца 211
вся работа, совершаемая током, производится за счет энергии сторон-
сторонних электродвижущих сил.
Оывод закона Ома исходя из электронной картины электропровод-
электропроводности. Механизм прохождения тока по проводнику и его нагревание
в рамках классических представлений выглядит так.
Свободный электрон ускоряется полем, которое имеется внутри
проводника. Закон Ньютона для движения электрона имеет вид
та = еЕ, B7.8)
где т, а, е — соответственно масса, ускорение и заряд электрона.
Действительное движение электрона очень сложно, поскольку электро-
электроны находятся в хаотическом тепловом движении. Под влиянием внеш-
внешнего поля все они получают одинаковое ускорение и приобретают
дополнительную скорость в одном и том же направлении. В резуль-
результате образуется упорядоченное движение электронов, т. е. электрический
ток. Нас интересует здесь только это упорядоченное движение
электронов, которое накладывается на их хаотическое тепловое движе-
движение. При своем движении электроны взаимодействуют между собой
и с атомами кристаллической решетки проводника. При взаимодейст-
взаимодействии с атомами кристаллической решетки электроны обмениваются с
ними небольшой частью своей энергии, которая в среднем является
энергией, приобретенной ими за счет электрического поля, потому что
при отсутствии электрического поля свободные электроны и атомы
находятся в тепловом равновесии. Эту сложную картину приобрете-
приобретения электронами энергии под влиянием электрического поля и после-
последующую ее передачу атомам при взаимодействии можно представить
в следующем виде. Допустим, что электрон в соответствии с урав-
уравнением B7.8) ускоряется в течение времени т, затем сталкивается с
атомом и отдает ему всю приобретенную кинетическую энергию.
Затем он снова начинает ускоряться, через время т снова сталкива-
сталкивается с атомом и т. д., т. е. т — время релаксации неравновесного
распределения электронов к тепловому равновесию с кристаллической
решеткой. В модели предполагается, что в течение этого времени
средняя кинетическая энергия электронов возрастает под действием
внешнего электрического поля выше их средней тепловой энергии,
затем избыток над средней тепловой энергией передается кристалли-
кристаллической решетке и снова восстанавливается тепловое равновесие. В дейст-
действительности, конечно, этот процесс происходит непрерывно и его сту-
ступенчатость введена лишь для упрощения математических расчетов.
Время т характеризует скорость возвращения к тепловому равновесию
совокупностей электронов и кристаллической решетки проводника, если
совокупность электронов какими-то причинами (не только внешним
электрическим полем) выведена из этого равновесия.
В этой картине результат многих актов передачи энергии от
электрона к атомам заменяется одним актом и поэтому х имеет смысл
среднего промежутка времени между столкновениями. Если I — средняя
длина пробега между столкновениями, a v - средняя скорость электро-
212 4. Постоянный электрический ток
на, обусловленная его тепловым движением, то по определению
т = l/v. B7.9)
Путь, проходимый электроном из состояния покоя при ускорении
электрическим полем, равен
,_??!?* B7.10)
2 2 те
Это путь, на который в среднем электрон смещается в направлении
действия электрического поля за время т между соударениями. Упоря-
Упорядоченное смещение обусловливает дрейф электронов со скоростью
va = s/T = eEl/Bmev). B7.11)
Скорость дрейфа обратно пропорциональна частоте v/l соударений
и, следовательно, уменьшается при росте температуры.
Если п — концентрация электронов, то
j = етд = e2lnE/Bmev). B7.12)
Сравнивая B7.12) с законом Ома j = yE, находим следующее выра-
выражение для удельной электрической проводимости:
2 mev
Таким образом, получена правильная зависимость плотности тока
от напряженности электрического поля и выражение удельной электри-
электрической проводимости через характеристики движения свободных элект-
электронов.
рывод закона Джоуля — Ленца исходя из электронной теории электро-
электропроводности. Скорость, которая теряется электроном при столкно-
столкновении, равна
еЕ I
у, = ах= . B7.14)
те v
Поэтому при каждом столкновении атомам проводника передается
приобретенная между столкновениями кинетическая энергия
Частота столкновений каждого электрона с атомами равна v/l,
а частота столкновений п электронов с атомами — nv/l. Поэтому
объемная плотность мощности выделения теплоты дается выражением
где учтены равенства B7.13) и B7.15). Тем самым, исходя из элект-
электронной теории электропроводимости, получено правильное выражение
закона Джоуля-Ленца в дифференциальной форме.
§ 28. Линейные цепи. Правила Кирхгофа 213
Недостатки классической теории электропроводности. Классическая
теория электропроводности весьма наглядна и дает правильную
зависимость плотности тока и количества выделяемой теплоты от
напряженности поля. Однако она не приводит к правильным количествен-
количественным результатам. Главные расхождения теории с экспериментом
состоят в следующем:
1) для того чтобы по формуле B7.13) получить правильные зна-
значения у, надо I принять очень большим (/ в тысячи раз превосходит
межатомные расстояния в проводнике). Понять возможность таких
больших свободных пробегов затруднительно в рамках классических
пре дет авл ен ий;
2) эксперимент для зависимости удельной проводимости у от темпе-
температуры приводит к закону у ~ 1/Т. Объяснить это формулой B7.13)
невозможно, поскольку кинетическая теория газов дает v ~ уТ, допус-
допустить же зависимость I ~ 1/уТ невозможно в классической картине
взаимодействия;
3) по теореме о равнораспределении энергии по степеням свободы
следует ожидать от свободных электронов очень большого вклада в
теплоемкость проводников, которая в эксперименте не наблюдается.
/Основные черты квантовой трактовки электропроводности. Лишь
квантовая теория позволила преодолеть указанные только что труд-
трудности классических представлений. Квантовая теория учитывает вол-
волновые свойства микрочастиц. Важнейшей характеристикой волнового
движения является способность волн огибать препятствия благодаря
дифракции. В результате этого при своем движении электроны как
бы огибают атомы без столкновений, и длины их свободного про-
пробега могут быть весьма большими. Из-за того что электроны подчи-
подчиняются статистике Ферми — Дирака, в образовании электронной тепло-
теплоемкости может принимать участие лишь незначительная часть электро-
электронов вблизи уровня Ферми. Поэтому электронная теплоемкость провод-
проводников совершенно незначительна. Решение квантово-механической зада-
задачи о движении электрона в металлическом проводнике приводит к
зависимости у ~ 1/Т, как это и наблюдается действительно. Таким
образом, непротиворечивая количественная теория электропроводности
была построена лишь в рамках квантовой механики.
§ 28. Линейные цепи. Правила Кирхгофа
Формулируются правила расчета линейных
цепей.
Изолированная замкнутая цепь. Этот случай уже был рассмотрен
в § 26 и результат представлен формулой B6.1): если в изолированной
замкнутой цепи имеется один источник сторонних э. д. с, то сила
тока в цепи должна быть такой, чтобы суммарное падение напряже-
напряжения на внешнем сопротивлении и внутреннем сопротивлении источника
было равно сторонней э. д. с. источника. Если имеется несколько источ-
214 4. Постоянный электрический ток
пиков сторонних э. д. с, то надо взять их сумму со знаками, приняв
в качестве положительной э. д. с. некоторого направления.
Чтобы не ошибиться в знаках, удобно поступить следующим
образом. Принимаем за положительное направление обхода цепи либо
обход по часовой стрелке, либо против часовой. На рис. 117 за поло-
положительный выбран обход по часовой стрелке. Электродвижущие силы
элементов обозначены &и <я2, &з- В каком направлении течет ток,
заранее неизвестно. Поэтому за направление тока выбираем любое,
например на рис. 117 оно совпадает с положительным направлением
обхода.
Теперь необходимо условиться о знаках. Знак э. д. с. берется поло-
положительным, если при движении по контуру в положительном на-
направлении первым встречается отрицательный полюс источника. Если
же первым встречается положительный полюс, то соответствующая
э. д. с. будет с отрицательным знаком. Знак силы тока считается поло-
положительным, если направление тока совпадает с направлением обхода.
В противном случае знак отрицателен. Таким образом, как э. д. с,
так и сила тока являются алгебраическими величинами, принимающими
как положительные, так и отрицательные значения. Теперь нетрудно
обобщить уравнение B6.1) на произвольное число источников сторон-
сторонних э. д. с. в изолированном замкнутом контуре: произведение алгебраи-
алгебраического значения силы тока на сумму внешних и внутренних сопротивле-
сопротивлений всех участков замкнутой цепи равно сумме алгебраических значений
сторонних э. д. с. в замкнутом контуре:
B8.1)
где + перед / и ^ означает, что знак должен быть выбран в
соответствии с приведенными выше правилами. Например, для случая,
изображенного на рис. 117, уравнение B8.1) имеет вид
ri+r2 + r3) = «>i - %г + ?3, B8.2)
где гг, гг,г3 — внутренние сопротивления источников сторонних э. д. с,
R - полное сопротивление всех участков цепи вне источников. Если
бы при том же направлении обхода, принятого за положительный,
стрелка, изображающая ток /, была ориентирована противоположно,
то вместо уравнения B8.2) получилось бы следующее:
-/ (R + »Ч + г2 + г3) =?!-?,+ «з- B8.3)
Уравнения B8.3) надо решать относительно I. Если в конкретном
случае / положительно, то ток течет, как указывается стрелкой, если
же отрицательно, то в противоположном направлении,
разветвленные цепи. Во многих практически важных случаях электри-
электрические цепи являются более сложными, как, например, на рис. 118.
Однако в цепь любой сложности входят элементы двух простейших
видов:
§ 28. Линейные цепи Правила Кирхгофа 215
1) узлов, в которых встречается более чем
два проводника (рис. 119; точки Си/));
2) замкнутых контуров (рис. 119; контуры
ABDCA, CDFEC, ABFEA).
Правила Кирхгофа. Правила Кирхгофа слу-
служат для составления системы уравнений,
из которой находятся силы тока для развет-
разветвленной цепи любой сложности. Они являют-
являются записью закона Ома B8.1) для каждого из
замкнутых контуров и закона сохранения за-
заряда в каждом узле. Правила знаков для сил
тока и э. д. с. в каждом из замкнутых конту-
контуров такие же, как для изолированного кон-
контура [см. B8.1)]. Направление положитель-
положительного обхода для всех контуров выбирается
одинаковым. Закон сохранения заряда в уз-
узлах требует, чтобы сумма сил токов, входя-
входящих в узел, была равна сумме сил токов,
выходящих из него, иначе говоря, сумма
алгебраических значений сил токов в узле
должна быть равной нулю. При составлении
суммы силы токов, изображаемых стрелками
с направлением от узла, берутся, например,
со знаком минус, а силы токов, изображае-
изображаемых стрелками с направлением к узлу, со
знаком плюс. Можно, конечно, брать обрат-
обратные знаки, это не изменит соответствующих
уравнений, важно лишь для всех узлов при-
применять одно и то же правило.
Таким образом, правила Кирхгофа гла-
гласят:
1) сумма произведений алгебраических
значений сил токов на сопротивление соот-
соответствующих участков каждого из замкну-
замкнутых контуров равна сумме алгебраических
значений сторонних э. д. с. в каждом замкну-
замкнутом контуре:
B8.4)
117
Изолированный замкнутый кон-
контур
2) сумма алгебраических значений сил то-
токов в каждом узле, равна нулю;
B8.5)
118
Электрическая цепь
К определению замкнутых кон-
контуров и узлов разветвленной
цепи
О Как выбираются знаки в
правилах Кирхгофа?
Какими соображениями надо
руководствоваться, чтобы не
выписывать лишних уравне-
уравнений Кирхгофа?
216 4. Постоянный электрический ток
Можно показать, что получающаяся при этом система уравнений
для любой разветвленной цепи является полной и позволяет опреде-
определить все токи.
Эти законы вывел Г. Кирхгоф A824—1887). Он дал общее решение
задачи о разветвленных цепях постоянного тока в 1847 г., хотя сами
правила сформулировал в 1845 г.
Применим правила Кирхгофа к цепи, изображенной на рис. 119.
1. По первому правилу Кирхгофа:
а) 11г1 + I1R1 - I2R2 - hr2 = ?i + ?2 (контур ABDCA).
б) I2R2 + I2r2 ~ I3R3 ~ hr3 = -%2- $3 (контур CDFEC).
в) h*i + /1R1 - /3R3 - I3r3 = ?t- ?3 (контур ABFEA).
2. По второму правилу Кирхгофа:
а) -71-/2-/3=0 (узел С);
б) 1г + 12 + 13 = 0 (узел D).
Здесь гь г2, г3 — внутренние сопротивления источников сторонних
э. д. с. Уравнения для узлов совпадают друг с другом, а из трех
уравнений по контурам независимыми являются лишь два. Например,
если сложить почленно первых два уравнения, то получается третье.
Таким образом, имеется система трех уравнений для трех неизвестных
сил тока 1и 12, /3. Решив эту систему, найдем силы тока и их истин-
истинные направления. Но даже не решая ее, можно сказать: на рис. 119
мы наверняка ошиблись в выборе направлений тока, потому что в узлах
при выбранных направлениях тока закон сохранения заряда заведомо не
может выполняться — в узле С должен накапливаться отрицательный
заряд, а в узле D — положительный. Но это нас не должно беспо-
беспокоить, потому что решение автоматически подскажет, какими должны
быть направления токов.
Таким образом, пример показывает, что если выписать правила
Кирхгофа для всех контуров и всех узлов, то получится больше урав-
уравнений, чем необходимо, поскольку не все уравнения независимы. Чтобы
не усложнять работы, желательно не выписывать лишних уравнений.
Для этого можно руководствоваться такими правилами. Выписывая
очередное уравнение для замкнутых' контуров, необходимо следить,
чтобы оно содержало хотя бы одну величину, не вошедшую в пред-
предшествующие уравнения; если все величины уже встречались в предшест-
предшествующих уравнениях, то это уравнение лишнее. Аналогично поступаем
и при выписывании уравнений для узлов. Например, выше в уравне-
уравнениях по первому правилу Кирхгофу не следовало выписывать уравне-
уравнение в), поскольку все входящие в него величины уже содержатся в
уравнениях а) и б). В уравнениях по второму правилу Кирхгофа
не следовало выписывать уравнение б), поскольку все входящие в него
величины уже вошли в уравнение а). Дальнейший контроль правиль-
правильности выписанной системы уравнений состоит в проверке ее полноты -
число уравнений должно быть равным числу неизвестных.
§ 29. Токи в сплошной среде 217
§ 29. Токи в сплошной среде
Излагается метод расчета сил токов в
сплошных средах.
Постановка задачи. Электрический ток может существовать не только
в проводах. Например, почва (особенно сырая) является проводни-
проводником электрического тока. Спрашивается, какое сопротивление электри-
электрическому току окажет почва, если в нее на некотором расстоянии друг
от друга погружены концы двух проводников, соединенных с полюсами
источника э. д. с? Или каково сопротивление очень массивной металли-
металлической плиты, к которой припаяны два проводника от полюсов источ-
источника э. д. с? Под сопротивлением массивной пластины или среды
электрическому току понимается отношение разности потенциалов
между подводящими ток электродами к силе тока. Хотя удельная про-
проводимость среды известна, вычисление сопротивления не является
простой задачей. Измерение же этого сопротивления легко провести
стандартными методами, найдя разность потенциалов и силу тока.
Вывод формулы. Рассмотрим однородную сплошную среду с погру-
погруженными в нее электродами, между которыми протекает электри-
электрический ток. Линии плотности тока совпадают с линиями напряжен-
напряженности электрического поля в среде, поскольку
j = уЕ. B9.1)
Сила тока сквозь замкнутую поверхность S, окружающую один из
электродов, равна
/ = $ j-dS = y$E-dS. B9.2)
S 5
Теперь представим себе, что проводящая среда удалена, а электроды
рассматриваются как обкладки конденсатора. По определению емкости
С конденсатора имеем
Q = CU, B9.3)
где Q — заряд электрода, U — разность потенциалов между электродами.
По теореме Гаусса получаем
$ Е • dS = G/?0, B9.4)
s
где Е — напряженность поля конденсатора, S - та же поверхность, что
и в B9.2). Однако вследствие единственности решения задач электроста-
электростатики заданная разность потенциалов между заданными электродами
однозначно определяет напряженность поля. Следовательно, напряжен-
напряженность поля в проводящей среде, по которой протекает ток [см. B9.2)],
совпадает с напряженностью поля, создаваемого в вакууме между теми
же электродами при той же разности потенциалов [см. B9.4)]. Поэтому
из B9.2) и B9.4) с учетом B9.3) заключаем, что
= ТС{//с0. B9.5)
218 4. Постоянный электрический ток
120
К вычислению сопротивления
среды между коаксиальными
электродами
ф Наиболее важный свойст-
свойством заземления линий пе-
передач является неэовисн-
мость сопротивления от
расстояния между элект-
электродами. Главный вклод
в сопротивление дают
участки среды, непосред-
непосредственно граничащие с
электродани.
Формула, выражающая
сопротивление среды че-
через емкость конденсатора,
обкладками которого явля-
являются электроды, справед-
справедлива лишь при условии,
что при наличии тока по-
потенциал во всех точках
каждой из обкладок с до-
достаточно большой точно-
точностью постоянен и в среде
не возникают объемные
зоряды.
Для этого удельная элек-
электропроводимость материа-
материала электродов должна
быть много больше удель-
удельной электропроводимости
среды, а среда должна
быть электрически одно-
однородной.
О В чем состоит условие при-
применимости формулы для со-
сопротивления среды между
электродами через емкость
конденсатора, образуемого
электродами?
Тогда сопротивление однородной среды
току дается формулой
R = U/I = ео/(уС). B9.6)
Отметим, что все эти рассуждения непри-
неприменимы для неоднородной среды, поскольку
в ней при прохождении тока образуются
объемные заряды, которые являются источ-
источниками электрического поля. В этом случае
электрическое поле в среде при прохождении
постоянного тока не совпадает с полем в ва-
вакууме, хотя электроды и поддерживаются
при той же разности потенциалов,
"условия применимости B9.6). Формула
B9.6) позволяет вычислить сопротивление
среды току, если известна емкость конден-
конденсатора, обкладками которого являются
электроды. Результаты получаются тем
точнее, чем лучше соблюдается постоянство
потенциала электрода при прохождении
через него тока. Если последнее требова-
требование не удовлетворяется достаточно хорошо
и потенциалы разных точек электрода при
прохождении по нему тока существенно
различаются, то расчет сопротивления нель-
нельзя свести к расчету емкости конденсатора,
поскольку у конденсатора потенциал всех
точек обкладки одинаков. Поэтому, в част-
частности, необходимо, потребовать малости
удельного сопротивления электродов по
сравнению с удельным сопротивлением сре-
среды. Если электроды достаточно малы по
размерам, то это требование отпадает,
коаксиальные электроды. Рассмотрим в ка-
качестве примера два коаксиальных элект-
электрода. Между ними находится проводящая
среда (рис. 120), сопротивление которой необ-
необходимо вычислить. Для применения форму-
формулы B9.6) удельную проводимость материала
жилы и оболочки надо считать много
большей удельной проводимости среды.
Ток в среде протекает во всем объеме сре-
среды по радиусам между центральной жилой
и оболочкой. Поскольку емкость цилиндри-
цилиндрического конденсатора С = 2nh0j\n{r2lr1), со-
сопротивление среды равно
)/Bл/7). B9.7)
§ 29. Токи в сплошной среде 219
Неоднородная среда. Если удельная проводимость не постоянна, то
задача значительно усложняется, поскольку возникают объемные
заряды и необходимо принимать во внимание порождаемое ими
электрическое поле.
Рассмотрим в качестве примера электрические токи в атмосфере.
Как показывает эксперимент, вблизи поверхности Земли имеется элект-
электрическое поле с напряженностью Е<0) » -100 В/м, направленной по
радиусу к центру Земли. Она является достаточно хорошим провод-
проводником, и поэтому можно считать, что на ней присутствует поверх-
поверхностный заряд
СТ0 = 80?;@) = - 8,85 • 100 Кл/м2. B9.8)
Измерения показывают, что удельная проводимость земной атмос-
атмосферы возрастает с высотой. Главная причина этого состоит в дейст-
действии космического излучения, вызывающего ионизацию. На больших
высотах главным источником ионизации становится солнечное излуче-
излучение. На высоте около 50 км атмосферу можно считать практически
идеальным проводником. Как показывают измерения, зависимость
удельной проводимости от высоты может быть- с достаточной точ-
точностью представлена в виде
y(r) = Yo + A(r-roJ. B9.9)
Здесь г0 — радиус Земли, г — расстояние от центра Земли до рассматри-
рассматриваемой точки, 7о = У (ro) ~ удельная проводимость у поверхности Земли,
А — постоянная, причем
Уо = 3-КГ1+ См/м, B9.10)
А = 0,5- Ю-20 См/м3. B9.11)
Поле в атмосфере Земли в среднем стационарно и сферически
симметрично. Поэтому уравнение непрерывности для плотности тока
принимает вид
-^(r2;,) = 0, B9.12)
откуда
J,(r)=M20/r2, B9.13)
где j0 - плотность тока у поверхности Земли (г = г0), равная
Jo = YcA@> = - 3 • 102 А/м2. B9.14)
Поскольку радиус Земли г0 » 6 • 106 м, сила тока из атмосферы
в Землю равна / = \j0 \ 4nrl & 1400 А. Напряженность электрического
поля в атмосфере на расстоянии г от центра Земли равна
Е,= Щг B9.15)
У (г)
220 4. Постоянный электрический ток
и поэтому разность потенциалов U между поверхностью Земли и верх-
верхней атмосферой, удельная проводимость которой практически беско-
бесконечна, определяется формулой
B9.16)
Го 'о
Здесь область интегрирования расширена до бесконечности, поскольку
у (г) на высотах, больших примерно 50 км, практически обращается
в бесконечность, а подынтегральное выражение в нуль. Однако доста-
достаточную точность при вычислении можно получить также, взяв для у
выражение B9.9). В этом случае вклад в интеграл от области интегри-
интегрирования для г > г0 + 50 км очень мал по сравнению с вкладом от
области интегрирования от г0 до г0 + 50 км и им можно пренебречь.
Поэтому вместо B9.16) получаем
Го
Этот интеграл легко вычисляется в элементарных функциях, одна-
однако результат получается довольно громоздким и здесь не приводится.
С достаточной точностью до величины порядка [уоД^о^)] •« 1 он может
быть представлен в виде
^]/l B9.18)
2 у yoj
Подставляя в B9.18) значения j0, у0, А из B9.14), B9.10) и B9.11),
находим U л 400 кВ.
Благодаря постоянно протекающему через атмосферу току силой
около 1400 А эта разность потенциалов должна уменьшаться, а по-
поверхностный заряд земли — нейтрализоваться. Время релаксации для
этого процесса имеет порядок х = ео/уо х 300 с. Однако как сила тока,
так и разность потенциалов в среднем стационарны. Поэтому сущест-
существуют причины, поддерживающие эту стационарность. Ими являются
главным образом нестационарные процессы в атмосфере, такие, как
бури, грозы и др.
§ 30. Заземление линий передач
Выясняется физическая основа возможности
заземления и обсуждаются требования к
заземлению.
^остановка задачи. Поскольку удельная электрическая проводимость
грунта довольно значительна, возникает вопрос об использовании
земли в качестве проводника электрического тока. Электрическая цепь
в этом случае показана на рис. 121 (А и В — электроды, зарытые в
землю). Ясно, что при этом можно сократить расход проводов примерно
в два раза.
§ 30. Заземление линий передач 221
р асчет сопротивления. Найдем сопротивле-
сопротивление сплошной среды, считая электроды
сферами радиусами г0. Расстояние между
центрами электродов обозначим d. Для упро-
упрощения расчета допустим, что среда неогра-
неограниченная (рис. 122), а заряд на электродах
распределен сферически симметрично.
Пусть х — расстояние от центра левого
электрода до некоторой точки, лежащей на
линии, соединяющей центры электродов.
Напряженность поля в этой точке
?(+> + ?<->=4^(^+(^k, t
C0.1)
Разность потенциалов между электро-
дами
d-r0
и- Г
J
121
Схема заземления линии пере-
передачи
I
а — r0 r0 r0 a -
C0.2)
В большинстве практически важных слу-
случаев расстояние между электродами много
больше размеров электродов, т. е. d » г.
Поэтому равенство C0.2) принимает вид
и = -Л—-. (зо.з)
2гсе0 г0
На основании сказанного в § 29 имеем
/ = jj-dS = y|E dS = yG/?o, C0.4)
s s
где / - сила тока в среде; S - замкнутая
поверхность, окружающая один из электро-
электродов. Из C0.3) и C0.4) для сопротивления
среды получаем
Я = и/1 = Bпуго)-\ C0.5)
Наиболее важным свойством сопротивле-
сопротивления C0.5) является его независимость от
расстояния между электродами. Это физи-
физически объясняется тем, что при увеличении
расстояния между электродами соответст-
йенно увеличивается эффективная площадь
среды, через которую протекает ток. Увели-
Увеличение расстояния между электродами увели-
122
К расчету сопротивления среды
при сферических электродах
Независимость сопротив-
сопротивления от расстояния меж-
между электродами в неогра-
неограниченной среде обуслов-
обусловлена тем, что эффективное
поперечное сечение пло-
площади, сквозь которую те-
течет ток, пропорционально
расстоянию между элект-
электродами.
222 4. Постоянный электрический ток
Y
К расчету сопротивления сре-
среды при сферических электродах
чивает сопротивление, а увеличение площади — уменьшает. Как пока-
показывает формула C0.5), эти два фактора практически компенсируют
друг друга, и сопротивление оказывается независимым от расстояния.
Следовательно, главный вклад в сопротивление среды дают участки,
непосредственно граничащие с электродами. Поэтому особенно важно
обеспечить их хорошую проводимость. Для этого пользуются элект-
электродами, имеющими большую площадь поверхности, и закапывают их
на достаточно большую глубину, где наличие подпочвенных вод
обеспечивает хорошую проводимость грунта.
"^ кспериментальная проверка. В слабо проводящую жидкость, напри-
например речную воду (рис. 124), опускают два плоских электрода,
соединенных с полюсами элемента сторонних э. д. с. По цепи протекает
некоторый ток. Изменяя расстояние между электродами, замечаем,
что при достаточно больших расстояниях (по сравнению с линейными
размерами электродов) это не оказывает влияния на показания ам-
амперметра. Следовательно, сопротивление среды при указанных условиях
не зависит от расстояния между электродами.
Дапряжение шага. Поскольку в среде течет ток, то имеется электри-
электрическое поле и изменяющийся в пространстве потенциал.
Предположим, что произошел обрыв высоковольтной линии пере-
передач и конец провода длиной L лежит на земле. В прилегающих к про-
проводу участках в грунте имеется электрический ток. Если по соседству
идет человек, то между точками соприкосновения его ног с землей
существует разность потенциалов, называемая напряжением шага.
В результате через тело человека проходит электрический ток, сила
которого зависит от этой разности потенциалов.
Рассчитаем напряжение шага. Вследствие большой длины провода
можно считать, что от него ток в глубь земли течет по направлениям,
перпендикулярным проводу. Эквипотенциальные поверхности — по-
поверхности полуцилиндров, оси которых совпадают с проводом (рис. 124).
Пусть человек идет в направлении, перпендикулярном проводу, рас-
расстояние его ближайшей к проводу ноги от провода d, а длина
шага I. Считая, что ток от провода растекается равномерно в полу-
полуцилиндрическую область, для плотности тока на расстоянии г от
провода получаем
j = 1/(шЦ. C0.6)
§ 30. Заземление линий передач 223
Тогда напряженность поля вдоль ра-
радиусов, перпендикулярных проводу, равна
Er=J/Y = I/(nrLy). C0.7)
Следовательно, напряжение шага
d + l
d + l
иш= ?rdr = -^-ln
J nyL
C0.8)
124
Например, при / = 500 A, d = 1 м, I = 65 см,
L = 30 м находим Um = 270 В. При других
условиях и конфигурациях проводов могут
возникать гораздо более значительные на-
напряжения. Поэтому при падении высоковольт-
высоковольтных проводов на землю возникает опасная Демонстрация независимости со-
ситуация не только в результате прямого ZlZT^ZTZ^™*'
касания провода и человека, но и в резуль-
результате возникновения напряжений типа напря-
напряжения шага.
Пример 30.1. Полусферический заземли-
тель погружен в землю вровень с ее поверх-
поверхностью (рис. 125). Найти напряжение, под
которым может оказаться человек, прибли-
приближающийся к заземлителю (напряжение ша-
шага). Сила тока I, протекающего через зазем-
литель, задана. Длина шага равна I, расстоя-
расстояние от ближней к заземлителю ноги чело-
человека до заземлителя равно г0. Рассмотреть
числовой пример: у = 10~2 См/м, / = 1 А,
г0 = 2 м, I = 1 м.
Сила тока от заземлителя равномерна по
всем направлениям и поэтому вектор плотности
тока направлен по радиус-векторам от заземли-
заземлителя и равен
Л = 1/Bкг2).
Напряженность электрического поля по за-
закону Ома равна
Следовательно, напряжение шага
2лу J г2 2лу \r0 r0
125
К расчету напряжения шага при
приближении к полусфериче-
"скому заземлителю
2,7 В.
224 4. Постоянный электрический ток
Задачи
4.1. Медный шар диаметром 10 см
опускают в полусферическую мед-
медную чашу диаметром 20 см,
наполненную водой, так что шар
и чаша концентричны. Удельная
проводимость воды равна у =
= 10~3 См/м. Определить элект-
электрическое сопротивление между ша-
шаром и чашей.
4.2. Маленький сферический электрод
радиусом а помещен в среду с
удельной проводимостью у на
расстоянии d от другого электрода
в виде большой пластины с хо-
хорошей проводимостью. Найти
сопротивление среды электри-
электрическому току, текущему между
электродами.
4.3. Найти сопротивление среды току
между двумя концентрическими
электродами, радиусы которых г,
и г2. Удельная проводимость сре-
среды равна у.
4.4. Найти сопротивление между точ-
точками А и В цепи, изображенной
на рис. 126. Сопротивление сторон
малых квадратов равно R.
126
4.1. R = 1590 Ом.
4.5. Между двумя плоскими электро-
электродами площадью S каждый, линей-
линейные размеры которых много боль-
больше расстояния d между ними, нахо-
находится проводящий материал,
удельная проводимость которого
изменяется линейно от yt у поверх-
поверхности одного электрода до у2 у
поверхности другого. Найти со-
сопротивление среды между элект-
электродами.
4.6. Найти сопротивление конического
проводника кругового сечения,
размеры которого указаны на
рис. 127. Удельная проводимость
материала проводника у.
4.7. Пространство между плоскими
бесконечными параллельными
электродами, находящимися на
расстоянии d друг от друга,
заполнено двумя слоями вещест-
вещества, граница между которыми плос-
плоская, параллельная электродам.
Проводимости и диэлектрические
проницаемости веществ слоев рав-
равны соответственно уь ъг и у2, е2,
а толщины слоев а и d - а. К
электродам приложены потенциа-
потенциалы ф1 и ф2. Найти потенциал
и поверхностную плотность заря-
заряда на границе между слоями.
Ответы
4.2. R = [1 - o/Bd)]/Dnyo). 4.3. R
4.4. Rab = ~R. 4.5. R =
S(Y2-Yi)'
4.7.
y, (d-a) + y2a
5 31
Электропроводность
металлов
§32
Электропроводность
жидкостей.
Электро-
Электропроводность
§33
Электропроводность
газов
Механизмы электропроводности мно-
многообразны. Общим между ними яв-
является лишь неразрывная связь с дви-
движением зарядов. В зависимости от ме-
механизма электропроводности, свойств
вещества и условий осуществления
электрического тока закономерности,
описывающие электропроводность,
варьируются в широких пределах.
§34
Электрический ток
в вакууме
8 А Н. Матвеев
226 5. Электропроводность
§ 31. Электропроводность
металлов
Описываются основные экспериментальные
факты, связанные с электропроводимостью
металлов, и их теоретическая интерпре-
интерпретация.
Доказательство отсутствия переноса вещества электрическим током
в металлах. Еще задолго до открытия электронов было экспери-
экспериментально показано, что прохождение тока в металлах не связано,
в отличие от тока в жидких электролитах, с переносом вещества
металла. Опыт состоял в том, что через контакт двух различных
металлов, например золота и серебра, в течение времени, исчисляемого
многими месяцами, пропускался постоянный электрический ток. После
этого исследовался материал вблизи контактов. Было показано, что
никакого переноса вещества через границу различных металлов не
наблюдается и вещество по различные стороны границы раздела имеет
тот же состав, что и до пропускания тока. Эти опыты доказали,
что атомы и молекулы металлов не принимают участия в переносе
электрического тока, но они не ответили на вопрос о природе носи-
носителей заряда в металлах.
(Лпыты Толмена и Стюарта Прямым доказательством, что электри-
электрический ток в металлах обусловливается движением электронов, были
опыты Толмена и Стюарта, проведенные в 1916 г. Идея этих опытов
была высказана Мандельштамом и Папалекси в 1913 г.
Представим себе проводящую катушку, которая может вращаться
вокруг своей оси. Концы катушки с помощью скользящих контактов
замкнуты на гальванометр (рис. 128). Если находящуюся в быстром
вращении катушку резко затормозить, то свободные электроны в про-
проволоке продолжают движение по инерции, в результате чего гальвано-
гальванометр должен зарегистрировать импульс тока.
Обозначим v — линейное ускорение катушки при торможении. Оно
направлено по касательной к поверхности катушки. При достаточно
плотной намотке и тонких проводах можно считать, что ускорение
направлено вдоль проводов. При торможении катушки к каждому
свободному электрону приложена сила инерции — mev, направленная
противоположно ускорению (те — масса электрона). Под ее действием
электрон ведет себя в металле так, как если бы на него действовало
некоторое эффективное электрическое поле:
Еэф=-теи/е. C1.1)
Поэтому эффективная электродвижущая сила в катушке, обусловлен-
обусловленная инерцией свободных электронов, равна
l=-^-vL, C1.2)
§ 31. Электропроводность металлов 227
где L — длина провода на катушке. Все точки
провода тормозятся с одинаковым ускоре-
ускорением и поэтому 6 в C1.2) вынесена за знак
интеграла.
Обозначая: 1 — силу тока, протекающего
по замкнутой цепи, R — сопротивление всей
цепи, включая сопротивление проводов ка-
катушки и проводов внешней цепи и гальвано-
гальванометра, запишем закон Ома в виде
IR = mei>L/e. C1.3)
Количество электричества, протекающее
через поперечное сечение проводника в тече-
течение времени At при силе тока J, равно
Поэтому в течение времени торможения
катушки от начальной линейной скорости v0
до полной остановки через гальванометр
пройдет количество электричества
о
, те L
dv = -r-b~vo- C1-5)
(* те L
128
Опыт Толмена и Стюарта
Значение Q находится по показаниям галь-
гальванометра, а значения L, R, v0 известны.
Поэтому можно найти как знак, так и абсо-
абсолютное значение е/те. Эксперименты показа-
показали, что е/те соответствует отношению за-
заряда электрона к его массе. Тем самым до-
доказано, что наблюдаемый с помощью галь-
гальванометра ток обусловлен движением элект-
электронов.
Q зонной теории. В основе квантовой тео-
теории электропроводности твердых тел ле-
лежит зонная теория, базирующаяся на анали-
анализе энергетического спектра электронов
(см. § 2). Электрический спектр разбивается
на зоны, разделенные запрещенными проме-
промежутками. Если в верхней зоне, где еще имеют-
имеются электроны, ими заполнены не все кван-
квантовые состояния, т. е. в пределах зоны имеет-
имеется возможность для перераспределения энер-
энергии и импульсов электронов, то соответст-
соответствующее вещество является проводником
электрического тока. Зона при этом назы-
+ + +
©в -
©в -
1
а)
|
б)
J
j
j
+ +
+ ++ + +
в)
129
Эффект Холла
Большое различие в про-
проводимости проводников,
полупроводников и ди-
диэлектриков обусловлива-
обусловливается не различней в под-
подвижности носителей заря-
зарядов, а главный образом
большим различней кон-
концентрации носителей.
8*
228 5. Электропроводность
вается зоной проводимости, а соответствующее вещество является про-
проводником электрического тока с электронным типом проводимости.
Если в зоне проводимости много электронов и свободных квантовых
состояний, то электропроводимость достаточно велика. Только элект-
электроны в зоне проводимости являются носителями зарядов, осуществляю-
осуществляющими электрический ток. Их движение подчиняется квантовым законам.
Число этих электронов составляет лишь небольшую часть от общего
числа электронов. Благодаря этому устраняются трудности классической
теории электропроводимости (см. § 27).
Зависимость сопротивления от температуры. Не только в металлах
главный вклад в электропроводимость вносит движение электронов.
Например, в полупроводниках с электронным типом электропроводи-
электропроводимости основной вклад в перенос электрического заряда также вносится
движением электронов. Одним из наиболее характерных различий
электропроводимости в этих двух случаях является характер зави-
зависимости удельной проводимости от температуры.
Эксперимент показывает, что у металлических проводников удель-
удельное сопротивление растет с повышением температуры, т. е. удельная
проводимость уменьшается. При не слишком низкой температуре зави-
зависимость проводимости от температуры имеет вид 7 ~ 1/T.
Однако у некоторых веществ, например стекол, полупроводников,
электролитов и т. д., проводимость увеличивается с температурой.
Хотя механизмы возрастания проводимости различны, они сводятся
в конечном счете к увеличению числа носителей электрических
зарядов, благодаря движению которых осуществляется ток. В металлах
число носителей, т. е. свободных электронов, практически не зависит
от температуры и сопротивления току, определяется лишь их способ-
способностью образовывать упорядоченное движение под действием электри-
электрического поля, т. е. их подвижностью. А она с увеличением темпера-
температуры уменьшается.
ЗФфюст Холла. На заряды, движением которых обусловливается ток,
действует сила Ампера (9.23). Плотность силы Ампера может быть
записана в виде
f=j х В = пе\д х В, C1.6)
где п, е — концентрация и заряд, движение которого обусловливает
ток, V, — скорость дрейфа заряда.
Под действием силы с плотностью f заряды в проводнике при
наличии магнитного поля, индукция которого перпендикулярна плот-
плотности тока j, стремятся сместиться в направлении силы (рис. 129, а).
В результате на соответствующей части поверхности проводника обра-
образуется избыток зарядов того же знака, что и знак зарядов, осуществляю-
осуществляющих ток. Поэтому если ток обусловливается движением положитель-
положительных зарядов, то создается распределение поверхностной плотности за-
зарядов, изображенное на рис. 129, б, а при движении отрицательных —
§ 31. Электропроводность металлов 229
на рис. 129, в. Между противоположными сторонами проводника
появляется разность потенциалов и такое электрическое поле, напря-
напряженность Е которого нейтрализует действие плотности силы C1.6).
Направление напряженности зависит от знака зарядов, осуществляющих
ток, а модуль определяется теми факторами, от которых зависит
плотность силы C1.6). Возникновение разности потенциалов в провод-
проводнике с током в магнитном поле называется эффектом Холла. Он
был открыт в 1879 г.
Индукция В поля и скорость va зарядов взаимно перпендикулярны.
Отношение плотности силы C1.6) к заряду аналогично C1.1) может
рассматриваться как эффективная напряженность электрического поля,
называемого полем Холла:
?3ф = идВ. C1.7)
Следовательно, между поверхностями проводника создается раз-
разность потенциалов (рис. 129,6)
d
U = J vaB dx = vaBd, C1.8)
о
где d - толщина проводника. Принимая во внимание, что j = nev,
перепишем C1.8) в виде
U = djB/{ne) = RjBd, C1.9)
где
R = 1/(ие) C1.10)
— постоянная Холла. Разность потенциалов может быть измерена.
Остальные величины, за исключением концентрации п зарядов и их
знака, известны. По знаку разности потенциалов можно определить
знак заряда носителей, движение которых осуществляет ток, а по раз-
разности потенциалов — их концентрацию.
Заметим, что формулы C1.9) и C1.10) совпадают с соответствую-
соответствующими формулами более полной теории эффекта Холла, когда учиты-
учитывается распределение электронов по скоростям, статистические характе-
характеристики их столкновений и т. д. Однако расчеты при этом оказываются
очень громоздкими и здесь не приводятся.
Результаты измерений показали, что в металлах ток осуществляет-
осуществляется движением отрицательных зарядов. Концентрация носителей пример-
примерно равна концентрации атомов, т. е. один заряд, участвующий в обра-
образовании тока, приходится примерно на один атом металла, хотя это
число и изменяется в определенных пределах. Носителями зарядов,
осуществляющих ток в металлах, являются электроны. Сказанное
означает, что в металлах на один атом приходится в среднем около
одного свободного электрона. Например, на один атом серебра при-
приходится 0,7 электронов; меди — 0,8; золота — 0,9, а алюминия — около
двух электронов. Напомним, что у металлов обычно концентрация
атомов, а следовательно, и свободных электронов близка к п ~ 1028 м~3.
230 5. Электропроводность
Исследование эффекта Холла в других случаях показало, что он не
всегда обусловлен движением отрицательных зарядов. Когда знак раз-
разности потенциалов в эффекте Холла соответствует движению поло-
положительных зарядов, то эффект называется аномальным.
Эффект Холла является одним из гальваномагнитных явлений. Под
этим термином объединяются явления, возникающие в проводнике
с током, находящимся в магнитном поле. Физическая сущность всех
этих явлений состоит в том, что электропроводимость проводника
во внешнем магнитном поле является не скаляром, а тензором. Напря-
Напряженность поперечного электрического поля, называемого холловским,
складывается с напряженностью электрического поля, которое обуслов-
обусловливает существование тока при отсутствии магнитного поля. В резуль-
результате этого напряженность электрического поля образует с плотностью
тока некоторый угол — угол Холла. Значит, направления плотности
тока и напряженности электрического поля не совпадают. Эти вели-
величины связаны тензорной формулой
2
в которой у** — тензор электропроводимости. В анизотропных вещест-
веществах проводимость описывается тензором электропроводимости также
и при отсутствии внешнего магнитного поля.
IVf агпетосопротивление. Другим важным гальваномагнитным явлением
является изменение сопротивления проводника, помещенного в попе-
поперечное магнитное поле (эффект магнетосопротивления). Как показы-
показывает опыт, относительное изменение электропроводимости А7/7 при
не очень сильных полях выражается формулой
Ду/у = -ХХВ2,
где хх — коэффициент поперечного магнетосопротивления, зависящий от
свойств материала; В — индукция магнитного поля.
Это явление — следствие тензорного характера электропроводимости
проводника, помещенного в магнитное поле. В результате возникает
компонента напряженности электрического поля, коллинеарная току,
что и вызывает изменение его силы, проявляющееся в изменении
сопротивления.
П одвижность электронов. Закон Ома j = yE может быть записан
в виде
neva = yE. C1.11)
Подвижностью Ь электронов называется отношение скорости дрейфа
к напряженности электрического поля:
Ъ = vJE. C1.12)
Принимая во внимание C1.11), получаем
Ь = у/(пе). C1.13)
Удельная проводимость металла известна, а пе может быть найдена
из эффекта Холла, т. е. измерение эффекта Холла позволяет найти
§ 31 Электропроводность металлов 231
подвижность электронов в проводнике. В металлах подвижность элект-
электронов имеет порядок
Ь~ 10- 1(Г3 м2/(В-с). CU4)
Таким образом, скорость дрейфа электронов в металлах очень
мала по сравнению с обычными скоростями движения микрочастиц.
Большая удельная проводимость металлов обусловлена главным обра-
образом большой концентрацией носителей заряда {п ~ 1028 м~3), а не их
большой подвижностью [см. C1 13)]:
у = епЪ ~ 10~19 • 1028 • 10 См/м = 106 См/м.
У диэлектриков большинство электронов жестко привязано к атомам
и очень мало свободных носителей заряда. Поэтому, хотя подвиж-
подвижность этих носителей заряда не сильно отличается от подвижности
свободных электронов в металлах, удельная проводимость диэлектриков
очень нала. Концентрация носителей в полупроводниках изменяется в
широких пределах от 1019 до 1025 м~3, а подвижности заключены
примерно от 10 до 10~4 м2/(В-с), т е велики. Благодаря таким
широким пределам изменения концентрации носителей и их подвиж-
ностей удельная проводимость полупроводников изменяется в широких
пределах, на много порядков величин. Однако не удается получить
у полупроводников столь же большую проводимость, как у металлов,
сохранив, конечно, при этом характерную для полупроводников зави-
зависимость проводимости от температуры (увеличение проводимости
с температурой).
(Сверхпроводимость. В 1911 г. К. Оннес обнаружил, что при Г=4,2 К
ртуть, по-видимому, полностью теряет сопротивление электрическому
току. Уменьшение сопротивления происходит очень резко в интервале
нескольких сотых градуса В дальнейшем потеря сопротивления наблю-
наблюдалась и у других чистых веществ и у многих сплавов. Само
явление получило название сверхпроводимости. Температуры перехода
в сверхпроводящее состояние различны, но всегда очень низки.
"критическая температура. Возбудив электрический ток в кольце из
сверхпроводника с помощью электромагнитной индукции, можно
наблюдать, что его сила в течение нескольких лет не уменьшается.
Это позволяет найти верхний предел удельного сопротивления сверх-
сверхпроводников (менее 10~25 Ом-м). Это на много порядков меньше,
чем, например, удельное сопротивление меди при низкой температуре
A0~12 Ом-м) Поэтому принимается, что электрическое сопротивление
сверхпроводников равно нулю. Сопротивление до перехода в сверхпро-
сверхпроводящее состояние бывает самым различным. Многие из сверхпро-
сверхпроводников при комнатной температуре имеют довольно высокое сопро-
сопротивление. Переход в сверхпроводящее состояние совершается всегда
очень резко. У чистых монокристаллов он занимает интервал темпе-
температур меньший, чем одна тысячная градуса.
Сверхпроводимостью среди чистых веществ обладают алюминий,
кадмий, цинк, индий, галлий. Свойство сверхпроводимости зависит от
232 5. Электропроводность
структуры кристаллической решетки. Например, белое олово является
сверхпроводником, а серое — нет; ртуть обладает свойством сверхпро-
сверхпроводимости только в а-фазе.
критическое поле. В 1914 г. К. Оннес обнаружил, что сверхпроводящее
состояние разрушается магнитным полем, когда магнитная индукция
В превосходит некоторое критическое значение. Критическое значение
индукции зависит от материала сверхпроводника и температуры.
Критическое поле, разрушающее сверхпроводимость, может быть
создано и самим сверхпроводящим током. Поэтому имеется крити-
критическая сила тока, при которой сверхпроводимость разрушается.
т Мейсснера. В 1933 г. Мейсснер и Оксенфельд обнаружили,
что внутри сверхпроводящего тела полностью отсутствует магнит-
магнитное поле. При охлаждении сверхпроводника, находящегося во внешнем
постоянном магнитном поле, в момент перехода в сверхпроводящее
состояние магнитное поле полностью вытесняется из его объема.
Этим сверхпроводник отличается от идеального проводника, у которого
при падении удельного сопротивления до нуля индукция магнитного
поля в объеме должна сохраниться без изменения. Явление вытеснения
магнитного поля из объема проводника называется эффектом Мейссне-
Мейсснера. Эффект Мейсснера и отсутствие электрического сопротивления
являются важнейшими свойствами сверхпроводника.
у|оверхностный ток. Отсутствие магнитного поля в объеме проводника
позволяет заключить из общих законов магнитного поля (см. гл. 6),
что в нем существует только поверхностный ток. Он физически реален
и поэтому занимает некоторый тонкий слой вблизи поверхности.
Магнитное поле тока уничтожает внутри сверхпроводника внешнее
магнитное поле. В этом отношении сверхпроводник ведет себя формаль-
формально как идеальный диамагнетик (см. § 41). Однако он не является
диамагнетиком, поскольку внутри него намагниченность равна нулю,
/^верхпроводники первого и второго рода. Чистые вещества, у которых
наблюдается явление сверхпроводимости, немногочисленны. Чаще
сверхпроводимость бывает у сплавов. У чистых веществ имеет место
полный эффект Мейсснера, а у сплавов не происходит полного вытал-
выталкивания магнитного поля из объема (частичный эффект Мейсснера).
Вещества, проявляющие полный эффект Мейсснера, называются сверх-
сверхпроводниками первого рода, а частичный — сверхпроводниками второго
рода.
У сверхпроводников второго рода в объеме имеются круговые то-
токи, создающие магнитное поле, которое, однако, заполняет не весь
объем, а распределено в нем в виде отдельных нитей. Что же касается
сопротивления, то оно равно нулю, как и у сверхпроводников
первого рода.
Объяснение сверхпроводимости. По своей физической природе сверх-
сверхпроводимость является сверхтекучестью жидкости, состоящей из
электронов. Сверхтекучесть возникает из-за прекращения обмена энер-
энергией между сверхтекучей компонентой жидкости и ее другими частями,
§ 31. Электропроводность металлов 233
в результате чего исчезает трение. Существенным при этом является
возможность «конденсации» молекул жидкости на низшем энергети-
энергетическом уровне, отделенном от других уровней достаточно широкой
энергетической щелью, которую силы взаимодействия не в состоянии
преодолеть. В этом и состоит причина выключения взаимодействия.
Для возможности нахождения на низшем уровне многих частиц необхо-
необходимо, чтобы они подчинялись статистике Бозе —Эйнштейна, т. е. обла-
обладали целочисленным спином.
Электроны подчиняются статистике Ферми —Дирака и поэтому не
могут «конденсироваться» на низшем энергетическом уровне и обра-
образовывать сверхтекучую электронную жидкость. Силы отталкивания
между электронами в значительной степени компенсируются силами
притяжения положительных ионов кристаллической решетки. Однако
благодаря тепловым колебаниям атомов в узлах кристаллической ре-
решетки между электронами может возникнуть сила притяжения и они
тогда объединяются в пары. Пары электронов ведут себя как части-
частицы с целочисленным спином, т. е. подчиняются статистике Бозе —
Эйнштейна. Они могут конденсироваться и образовывать ток сверхте-
сверхтекучей жидкости — электронных пар, который и образует сверхпроводя-
сверхпроводящий электрический ток. Выше низшего энергетического уровня имеется
энергетическая щель, которую электронная пара не в состоянии
преодолеть за счет энергии взаимодействия с остальными зарядами,
т. е. не может изменить своего энергетического состояния. Поэтому
электрическое сопротивление отсутствует.
Возможность образования электронных пар и их сверхтекучести
объясняется квантовой теорией.
Пример 31.1. Зависимость сопротивления от температуры весьма существен-
существенна для работы многих приборов, что хорошо видно на примере функциониро-
функционирования обычной лампы накаливания. Нить накаливания делают из вольфрама. При
температурах между 300 и 3000 К удельная проводимость вольфрама и энерге-
энергетическая светимость М, т. е. поверхностная плотность потока излучения с
поверхности, могут быть представлены формулами: у = 0,95-1010 Т'2 См/м;
М = 6,6-102 Т5 Вт/м2, где Т — термодинамическая температура. Рассчитать
диаметр d и длину I нити накаливания, чтобы лампа излучала мощность Р при
напряжении U и температуре Т нити. Потери энергии на теплопроводность
от нити накашвания пренебрежимо малы Оценить требования на точность
изготовления нити накаливания.
Имеем:
R = —, R = -1- 4/, , Р = nMld,
Р у nd2
откуда
4Р2 У/3 (уРУ2уз
^n2yU2M) ' ~\4кМ2) '
Поскольку уМ ~ Г3'8, у/М2 ~ Т1'2, зависимость длины н толщины нити
от температуры весьма сильная. Поэтому погрешность в соблюдении диаметра
и длины нити накаливания при изготовлении сильно сказывается на темпера-
температуре и, следовательно, на спектральном составе излучаемого света. К допускам
предъявляются достаточно жесткие требования.
234 5. Электропроводность
§ 32. Электропроводность жидкостей
Описывается механизм электропроводности
жидкостей и зависимость электропроводи-
электропроводимости от различных факторов.
Диссоциация. Чистые жидкости в основном являются плохими провод-
проводниками электричества. Это обусловлено тем, что они состоят из
электрически нейтральных атомов и молекул, движение которых не
может осуществить электрический ток. Однако растворы солей, кислот
и щелочей в воде и некоторых других жидкостях хорошо проводят
ток. Это связано с тем, что молекулы растворенного вещества
диссоциируют, т. е. распадаются на положительные и отрицательные
ионы. Упорядоченное движение ионов обеспечивает перенос электри-
электрических зарядов, т. е. ток. Если при растворении не происходит диссо-
диссоциации молекул, то раствор не является проводником электричества.
расчет электропроводимости. Обозначим N = JV( + ) = N{~) — концент-
концентрация ионов каждого знака в растворе. Для плотности тока можно
написать формулу
C2.1)
где q — модуль .заряда ионов, />(+) и Ы~) — подвижности положительных
и отрицательных ионов [см. C1.12)].
На основании C1.12) скорость дрейфа ионов пропорциональна
напряженности:
»<±> = #*>?. C2.2)
Подвижности положительных и отрицательных ионов, вообще гово-
говоря, различны. Подвижность ионов в жидкостях невелика и обычно
составляет десятимиллионные доли метра в квадрате на секунду-вольт.
Концентрация ионов зависит от степени диссоциации, характери-
характеризующейся коэффициентом диссоциации а, который определяется отно-
отношением концентрации N ионов к концентрации No молекул растворен-
растворенного вещества, т. е.
N = odV0. C2.3)
Следовательно, концентрация недиссоциированных молекул
ЛГ=A-а)ЛГ0. C2.4)
В растворе одновременно и непрерывно происходит как диссоциация
молекул, так и молизация ионов, т. е. соединение ионов в нейтральные
молекулы. При равновесии интенсивности этих двух процессов, изменяю-
изменяющих состав раствора в противоположных направлениях, равны. Ско-
Скорость изменения (dN/dt) концентрации ионов каждого знака в резуль-
результате диссоциации молекул пропорциональна концентрации N' недиссо-
недиссоциированных молекул:
§ 32. Электропроводность жидкостей 235
= p A - а) АГо, C2.5)
где р — коэффициент пропорциональности.
Скорость изменения (diV/dt) концентрации .недиссоциированных мо-
молекул в результате ионизации ионов пропорциональна произведению
концентраций положительных и отрицательных ионов:
{dN'/dt) = ла2Л^, C2.6)
где ц - коэффициент пропорциональности. При равновесии
C2.7)
Отсюда с учетом C2.5) и C2.6) получаем формулу, связывающую
коэффициент диссоциации с концентрацией растворенного вещества:
^-=-^0- C2.8)
Очевидно, что коэффициент диссоциации зависит от концентрации
растворенного вещества. При очень слабой концентрации (No as 0)
равенство C2.8) дает
а - 1, C2.9)
т. е. диссоциация близка к полной. Если а<1, то из C2.8) получаем
C110)
т. е. а уменьшается при увеличении концентрации растворенного ве-
вещества.
Формула C2.1) с учетом C2.3) может быть записана в виде
. C2.11)
Подвижность ионов в очень широких пределах напряженностей элект-
электрических полей не зависит от напряженности. Лишь при очень большой
напряженности порядка миллионов вольт на сантиметр наблюдается
отклонение от прямой пропорциональности между напряженностью
поля и скоростью дрейфа носителей зарядов, что, согласно C2.2), озна-
означает зависимость подвижности от напряженности. Значение а также
в очень широких пределах не зависит от Е. Следовательно, вплоть
до напряженностей в миллионы вольт на сантиметр формула C2.11)
выражает закон Ома. Поэтому удельная электрическая проводимость
раствора равна
y = g(b(+> + b<->)aN0. C2.12)
Зависимость электропроводимости от концентрации. При небольшой
концентрации раствора коэффициент диссоциации [см. C2.9)] является
величиной постоянной, сумма подвижностей ионов b(+) + bi~) также
приблизительно постоянна. Следовательно, при малой концентрации
раствора электропроводимость пропорциональна концентрации, а при
236 5. Электропроводность
большой зависимость значительно усложняется. С одной стороны,
необходимо учитывать зависимость коэффициента диссоциации от кон-
концентрации [см. C2.8), C2.10)], а с другой стороны, подвижность ионов
.также начинает заметно зависеть от концентрации и в концентриро-
концентрированных растворах уменьшается, поскольку начинает играть роль элект-
электрическое взаимодействие ионов друг с другом. Поэтому при большой
концентрации прямой пропорциональности между электропроводи-
электропроводимостью и концентрацией раствора не наблюдается.
Зависимость электропроводимости от температуры. При повышении
температуры коэффициент диссоциации увеличивается, поскольку бо-
более энергичное движение молекул затрудняет молизацию и облегчает
диссоциацию (при столкновениях). При нагревании вязкость жидкости
уменьшается и, следовательно, увеличивается подвижность ионов.
Поэтому [см. C2.12)] удельная проводимость электролитов с увеличе-
увеличением температуры растет, причем этот рост может быть весьма
значительным (во много тысяч раз).
Электролиты. Так как прохождение тока через растворы обусловлено
движением ионов, то в результате происходит разделение молекул
растворенного вещества на составные части, которые выделяются на
электродах. Это явление называется электролизом. Изучение электро-
электролиза сыграло большую роль в развитии учения о строении вещества.
Законы электролиза были открыты М. Фарадеем и подробно изучаются
в средней школе. Проводники электрического тока, которые при про-
прохождении по ним тока испытывают электролиз, т. е. разлагаются на
составные части, называются электролитами. Из сказанного следует,
что электролитами являются многие растворы солей, кислот и щело-
щелочей, а также ряд химических соединений как в жидком, так и в твердом
состоянии.
Примером твердого электролита может служить стекло, которое по
своей физической природе является сильно переохлажденной жидкостью
с очень большой вязкостью. Можно показать на опыте, что в стекле
заметной подвижностью обладают ионы Na+, движение которых и
обусловливает электропроводимость стекла. При нагревании стекла его
сопротивление может уменьшиться в миллионы раз. Это позволяет
показать очень эффектную демонстрацию. Первоначально стеклянная
палочка разогревается пламенем горелки. Ток в цепи выделяет джоуле-
ву теплоту, чем способствует повышению температуры палочки. При
некоторой температуре, которую следует подобрать на опыте, горелка с
пламенем убирается, а дальнейшее повышение температуры палочки
обеспечивается уже только омической теплотой.. Скорость изменения
температуры палочки все время увеличивается, поскольку с температу-
температурой увеличивается удельная проводимость, что в свою очередь обуслов-
обусловливает еще более энергичное повышение температуры. В результате
такого лавинообразного возрастания температуры происходит энергич-
энергичное расплавление стекла и палочка перегорает с яркой вспышкой.
§ 33. Электропроводность газов 237
§ 33. Электропроводность газов
Обсуждаются различные механизмы осу-
осуществления тока в газах, характеристика
тока и роль пространственного заряда.
Самостоятельный и несамостоятельный ток. Газ, в котором отсутст-
отсутствуют заряженные частицы, не является проводником электричества.
Он становится проводником лишь при наличии ионизации, когда
появляются носители электрических зарядов в виде свободных электро-
электронов и ионов. В зависимости от числа потерянных электронов поло-
положительные ионы могут быть однозарядными и многозарядными. Отри-
Отрицательные ионы, образующиеся в результате присоединения к атому
электрона, бывают обычно однозарядными.
Для того чтобы газ стал проводником, необходимо наличие ка-
какого-либо постороннего фактора ионизации (высокая температура газа,
ультрафиоlemoeoe или рентгеновское излучение и т.д.). Если напря-
напряженность поля не велика, то ток через газ прекращается, как только
перестает действовать посторонний фактор ионизации. Такой ток назы-
называется несамостоятельным.
Если напряженность достаточно велика, то поле само может вызвать
ионизацию, в результате которой газ становится проводником. Возни-
Возникающий при этом ток называется самостоятельным. Какой-либо одной
универсальной функциональной зависимости силы тока от напряжения
для самостоятельного тока не существует. Все определяется конкрет-
конкретными условиями. В частности, нередко бывает, что сила самостоятель-
самостоятельного тока при росте напряжения уменьшается.
1-1 есамостоятельный ток. Рассмотрим более подробно несамостоя-
несамостоятельный ток. Обозначим: N — концентрация зарядов каждого знака,
(dW/dt)ogp — скорость изменения концентрации зарядов внешним источ-
источником ионизации. Наряду с процессом образования зарядов происходит
процесс их ликвидации в результате рекомбинации, т. е. взаимной
нейтрализации. По прошествии достаточно большого промежутка вре-
времени устанавливается динамическое равновесие, когда скорость образо-
образования зарядов и скорость рекомбинации взаимно нейтрализуются.
При этом, очевидно,
N = N<+> = ND C3.1)
где. для простоты, ионы предполагаются однозарядными.
Ясно, что скорость рекомбинации должна быть пропорциональна
произведению концентрации зарядов, т. е. N2. Следовательно, при рав-
равновесии
(uN/dt)o6p=-rN\ C3.2)
где г — коэффициент рекомбинации.
Плотность тока, по определению, равна
j =/+) +/-> = q (JV<+4+) + JV<-ty->) = qN(ita+) + v^). C3.3)
238 5. Электропроводность
Скорость дрейфа заряда в электрическом поле пропорциональна
его напряженности:
vu = ЬЕ, C3.4)
Подвижности Ь(+) и Ь(~> положительных и отрицательных зарядов,
вообще говоря, различны. Равенство C3.2) с учетом C3.4) принимает
вид
b('))NE. C3.5)
Эта формула напоминает закон Ома. Однако она является экви-
эквивалентной закону Ома лишь в том случае, когда множитель при Е не
зависит от ? и j. В газах, вообще говоря, этот множитель зависит,
как правило, от указанных величин и поэтому формула C3.5) не эквива-
эквивалентна закону Ома.
В том случае, когда число рекомбинирующих ионов в газе в 1 с вре-
времени много больше числа ионов, попадающих за 1 с на электрод,
можно для определения N в C3.5) воспользоваться ее выражением
C3.2) для условий равновесия. Тогда
Е. C3.6)
обр
Для выяснения условий применимости этой формулы необходимо
иметь в виду, что подвижность ионов в газах при нормальном давле-
давлении имеет порядок десятитысячных долей метра в квадрате на вольт-
секунду, а коэффициент рекомбинации г да 1 м3/с. Например, если dN/dt
имеет порядок 1016 ионовДм3-с), а Е = 103 В/м, то число ионов,
падающих на 1 м2 электрода за 1 с, равно
; /l
±_ = ш+) + ь("') /—
e V r
dN_\
dt )
обр
E«2-1013 m^. C3.7)
Если расстояние между плоскими электродами равно 0,1 м, то в
пространстве между электродами на 1 м2 поперечного сечения рекомби-
нируют 1015 ионов, т. е. условие применимости формулы C3.6) в данном
случае выполнено. Аналогично проверяется применимость этой формулы
и при других значениях параметров.
Плотность тока насыщения. Обозначим d — расстояние между плоски-
плоскими электродами. Если напряженность поля достаточно велика, так
что все образующиеся внешним источником ионы попадают на электро-
электроды раньше, чем они успеют рекомбинировать, то возникает ток насы-
насыщения, плотность которого
) . C3.8)
t /обр
Характеристика тока. В области промежуточных электрических полей
часть ионов до попадания на электроды успевает рекомбинировать.
Баланс потерь и образования ионов записывается в виде
§ 33. Электропроводность газов 239
+
сШЛ /dN\ _
)
рек
C3.9,
Принимая во внимание равенства C3.2),
C3.3) и C3.8), получаем
j»Jq - rN2d - N (b( + > + b(->) Е = 0. C3.10) о
Учитывая, что 130
j = qN (b ' + D ) ?, C3.11) Характеристики самостоятель-
самостоятельного и несамостоятельного то-
перепишем C3.10) в виде уравнения относи- ков
тельно j:
f + 2а/ + 2а/нас = 0,
C3.12)
где
а = | q | (b<+) + &<->J Е2/Bг4 C3.13)
Положительный корень уравнения C3.12)
равен
j = a (/l + 2;нас/а - 1). C3.14)
График плотности тока в зависимости от
а показан на рис. 130. В предельных случаях
(а<с./нас и а^-Унас) C3.14) переходит соот-
соответственно в формулы C3.6) и C3.8).
Выражение C3.14) называется характерис-
характеристикой несамостоятельного тока. Оно нахо-
находится в хорошем согласии с эксперимен-
экспериментом, если дополнительно учесть потери
ионов вследствие диффузии.
(Самостоятельный ток. Если при плотности
тока, почти равной плотности тока насы-
насыщения, продолжать увеличивать напряжен-
напряженность электрического поля, то плотность
тока снова начинает возрастать. Это проис-
происходит потому, что имеющиеся в газе
электроны до рекомбинации с ионами газа
успевают ускориться благодаря большой
напряженности поля до энергий, при кото-
которых они ударом ионизуют молекулы газа.
В результате скорость ионизации начинает
зависеть от напряженности. Возникающий
при этом ток называется самостоятельным.
Начальная часть характеристики этого тока
на рис. 130 обозначена пунктиром. Она
начинается при конечном значении а.
# Для того чтобы газ стал
проводником, необходимо
наличие какого-либо по-
постороннего фактора иони-
ионизации (высокая температу-
температура газа, ультрафиолетовое
или рентгеновское излуче-
излучение и т. д.). Однако при
достаточно большой на-
напряженности электриче-
электрического поля ионизация га-
газа возникает в результате
действия поля. Возникаю-
Возникающий при этой ток назы-
называется самостоятельным.
В случае посторонних фак-
факторов ионизации ток назы-
называется несамостоятель-
несамостоятельный.
О Что такое самостоятельный
и несамостоятельный ток?
Почем/ между электродами
возникает пространственный
заряд? Каково его действие?
За счет каких факторов под-
подвижность отрицательных за-
зарядов оказывается большей,
чем положительных?
240 5. Электропроводность
Действие пространственного заряда. Как было отмечено, подвижность
положительных и отрицательных носителей зарядов различна и
обычно Ь{') > Ь(+). В связи с этим плотность тока, обусловленного
движением положительных зарядов, меньше плотности тока, связанного
с движением отрицательных зарядов. Поэтому число положительных
зарядов, попадающих в течение фиксированного интервала времени
на катод, меньше числа отрицательных зарядов, попадающих на анод,
хотя число образующихся и рекомбинирующих ионов за этот интервал
времени одинаково. Очевидно, что такое состояние не может быть
равновесным. Равновесное состояние достигается следующим образом.
В результате движения положительных зарядов к катоду и отрицатель-
отрицательных к аноду у катода образуется избыток положительных зарядов,
а у анода — отрицательных. Однако ввиду большей подвижности отри-
отрицательных зарядов избыток отрицательного заряда у анода будет
меньше избытка положительного заряда у катода. В результате
такого перераспределения концентрации зарядов и связанного с этим
изменения напряженности электрического поля устанавливается равно-
равновесие, при котором число попадающих на электроды положительных
и отрицательных зарядов становится равным.
ТТодвижность зарядов. Ион с массой т и зарядом q в однородном
поле Е движется с постоянным ускорением
а = qE/m C3.15)
и в течение времени т при начальной нулевой скорости проходит
путь
s = qEz2/Bm). C3.16)
Если I — средний свободный пробег иона в газе при беспорядочном
тепловом движении, a v — средняя скорость, то можно принять, что
т = l/v. Время и средний свободный пробег определяются таким обра-
образом, чтобы можно было считать, что при каждом столкновении ион
полностью теряет свою энергию упорядоченного движения. Поэтому
для скорости дрейфа как средней скорости упорядоченного движения
в направлении, коллинеарном направлению напряженности поля, на
основании C3.16) можно написать:
»д = s/x = qEx/Bm) = qlE/Bmv). C 3.17)
Уточнения, вносимые статистическим распределением I, приводят
лишь к небольшому изменению числового коэффициента в C3.17).
Поэтому подвижность ионов равна
Ь = ql/{2mv). C3.18)
Из этой формулы видно, что подвижность положительных и отри-
отрицательных ионов с равными массами должна быть одинаковой. Однако
средняя подвижность отрицательных зарядов больше подвижности
положительных, потому что подвижность отрицательных зарядов обра-
образуется не только за счет вклада от отрицательных ионов, но и
вклада от электронов. Подвижность же электронов ввиду их малой
§ 34. Электрический ток в вакууме 241
массы весьма значительна, что и обусловливает в конечном счете
большую подвижность отрицательных зарядов.
/уравнение выводов из C3.18) с экспериментом. Из C3.18) видно, что
подвижность обратно пропорциональна плотности газа, поскольку
длина свободного пробега обратно пропорциональна плотности. Этот
вывод подтверждается на опыте.
Однако в целом формула C3.18) не объясняет всей совокупности
экспериментальных фактов. В частности, эксперимент дает для подвиж-
подвижности меньшее значение, чем теория. Чтобы объяснить расхождения
между теорией и экспериментом, Ланжевен учел поляризованность
ионов при приближении друг к другу при столкновении, благодаря
которой ионы приобретают дипольные моменты и характер их столкно-
столкновения изменяется. Учет этого обстоятельства вносит существенные
поправки в формулы. Однако изложение этой теории выходит за
рамки настоящего курса.
§ 34. Электрический ток
в вакууме
Обсуждаются основные закономерности
термоэлектронной эмиссии и их проявление
при прохождении тока между электродами
в вакууме.
Термоэлектронная эмиссия. В вакууме не может существовать электри-
электрический ток, если в нем нет носителей электрических зарядов. Если
же в нем имеются электроны, то их движение обусловливает возникно-
возникновение тока, называемого током в вакууме.
В металле имеется электронный газ. В условиях термодинамического
равновесия распределение электронов по энергетическим уровням опре-
определяется статистикой Ферми —Дирака и дается формулой
п: \ И4Л
д, ехр[р(?,--ц)]+1' 1 ''
где р = 1/(кТ); щ — число электронов, имеющих энергию Е{; gt — число
квантовых состояний, соответствующих энергии Et\ ц — энергия Ферми
при температуре Т, которая при Г->0 К стремится к энергии Ферми
ц0 при Т = О К в соответствии с формулой
Принимая во внимание, что во всех практически интересных слу-
случаях ц » кТ, можно в C4.1) величину ц считать равной ц0.
Пусть Ео — энергия покоящегося электрона вблизи поверхности вне
металла (рис. 131). Формула C4.1) позволяет вычислить вероятность
того, что электрон имеет энергию Ео, если вместо Е, подставить в нее
242 5. Электропроводность
?0. Эта вероятность не равна нулю и тем больше, чем выше темпера-
температура (т. е. чем меньше р). Таким образом, вблизи поверхности металла
имеется электронное облако, которое находится в равновесии с электрон-
электронным газом внутри металла. Это равновесие динамическое: электроны
внутри металла, обладающие достаточно большой кинетической энер-
энергией, преодолевают силы, удерживающие их внутри металла, и выходят
за его пределы; электроны вблизи металла при соответствующих
направлениях их скоростей и местоположения захватываются силами,
удерживающими электроны внутри металла. Таким образом, в условиях
динамического равновесия сквозь поверхность металла протекают про-
противоположно направленные токи, силы которых равны по модулю.
Суммарная сила тока сквозь поверхность равна нулю. Явление обра-
образования электронного облака вблизи поверхности металла из-за тепло-
теплового движения свободных электронов называется термоэлектронной
эмиссией. При О К никакой термоэлектронной эмиссии не наблюдается,
т. е. электронное облако вблизи поверхности металла отсутствует.
Электроны с кинетической энергией WK вблизи поверхности металла
имеют полную энергию ?; = WK + ?0 и формула C4.1) принимает для
них следующий вид:
А = _J__ C4.3)
где Ф = ?0 — ц — работа выхода электронов из металла. Из фор-
формулы C4.3) видно, что плотность электронного облака вблизи поверх-
поверхности металла сильно зависит от работы выхода Ф и резко умень-
уменьшается с ее увеличением.
Если вблизи поверхности металла существует электрическое поле,
то электроны облака приходят в движение и образуется электрический
ток, называемый термоэлектронным. Таким образом, если в вакууме
имеются две металлические пластины, между которыми приложена
разность потенциалов, то между ними возникает термоэлектронный
ток. Очевидно, что сила тока должна расти с увеличением разности
потенциалов. Существует максимальная сила тока, когда все электро-
электроны, попадающие через поверхность катода в электронное облако, увле-
увлекаются внешним электрическим полем к аноду и никакого обратного
тока электронов через поверхность внутрь катода не существует.
Эта максимальная сила тока называется силой тока насыщения: при
дальнейшем увеличении разности потенциалов между анодом и като-
катодом сила тока не изменяется, поскольку все электроны, поставляемые
в результате термоэлектронной эмиссии из катода, задействованы для
образования электрического тока и других носителей заряда для даль-
дальнейшего увеличения силы тока нет.
Для металлов Ф составляет несколько электрон-вольт. Энергия
кТ даже при температуре в тысячи Кельвинов составляет доли
электрон-вольта. Следовательно, рФ » 1 и exp [P(W, + Ф)] » 1. По-
Поэтому в C4.3) можно в знаменателе пренебречь единицей по сравнению
с exp [p (WK + Ф)] и записать эту формулу в виде
§ 34. Электрический ток в вакууме 243
^ е-ФЛ*Ле
-WJ(kT)
C4.4)
Таким образом, сила тока насыщения
очень сильно зависит от работы выхода
и температуры, поскольку эти величины вхо-
входят в экспоненту. Для чистых металлов
значительный ток может быть получен лишь
при температуре порядка 2000 К, т. е. в ка-
качестве катодов необходимо использовать ме-
металлы с высокой температурой плавления.
Одновременно желательно, чтобы их работа
выхода была как можно меньше. Например,
чистый вольфрам, работа выхода которого
4,5 эВ, должен эксплуатироваться при темпе-
температуре 2500 К. Для уменьшения рабочей
температуры катода и понижения работы
выхода используются оксидные катоды, ког-
когда на подложку (керн) с помощью соот-
соответствующих технологических процессов на-
наносится слой окислов щелочноземельных
металлов (например, BaO, SrO и др.).
Затем катод активируется при пропускании
через него термоионного тока при темпе-
температуре катода около 1300 К. В результате
образуется моноатомный слой щелочнозе-
щелочноземельных атомов, значительно понижающий
работу выхода. Например, бариево-стронци-
евые оксидные катоды имеют работу выхода
около 1,8 эВ, благодаря чему значительные
токи удается получить уже при температуре
около 1100 К. При этой температуре дости-
достигается плотность тока порядка 104 А-м~2.
Слой бариево-стронциевого окисла наносит-
наносится обычно на никелевую трубку, внутри
которой в качестве нагревателя использу-
используется вольфрамовая нить. Такая конструкция
имеет дополнительное преимущество по
сравнению с использованием нагретой
вольфрамовой нити в качестве катода, по-
поскольку в последнем случае вдоль нити
возникает значительное падение потенциала
и ее поверхность не будет эквипотенциаль-
эквипотенциальной. В оксидном катоде слой окислов яв-
является эквипотенциальной поверхностью, что
улучшает весьма существенно условия ра-
работы катода в целом.
Со
Вакуум Метам Вакуум ®
131
Энергетические уровни свобод-
свободных электронов в металле
132
К расчету силы тока насыщения
МТ
133
Зависимость между силой тока
насыщения и температурой
О В чем состоит механизм
термоэлектронной эмиссии!
Чем обусловлено существова-
существование тока насыщения? От ка-
каких факторов зависит его
сила?
При каких условиях наблю-
наблюдаются отклонения от закона
трех вторых?
244 5. Электропроводность
^Характеристики электронного облака. Облако электронов вблизи
поверхности металла описывается формулой C4.4). Число квантовых
состояний в элементе фазового объема dx dy dz dpx Ару dp2
д = -Q^f dxdydz dpx dpy dpz. C4.5)
Поэтому число электронов, заключенных в элементе фазового
объема dx dy dz dpx dpy dp2, представляется в виде
dn = OnK^е-фдет)е""р2/B^Т) dx dy dz dPx dPy dPz, C4.6)
где WK = p2lBme).
Интегрирование выражения C4.6) no dxdydz дает в качестве мно-
множителя объем V. Поэтому число электронов в объеме V, импульсы
которых заключены в элементе объема dpx dpy dpz, вблизи импульса
Рх, РУ, Pz Равно
dnp = [27/BяЙK] ехр [-ФДкГ)] exp [-р2/Bт«*Г)] dPxdpydpz, C4.7)
где'р2 = p\ + Py + pi. Отсюда для концентрации электронного облака
вблизи поверхности металла получаем выражение
у К " [ W*f] гар ( - w) if jsxp ( ~
00
w) if js
Средняя кинетическая энергия электронов
Длотность тока насыщения. Направим ось Z прямоугольной декар-
декартовой системы координат нормально к поверхности металла (рис. 132).
Электроны дают вклад в плотность тока насыщения компонентой vz
скорости по оси Z. Вклад в плотность тока от одного электрона
равен evz = epz/me. Следовательно, плотность тока насыщения опреде-
определяется формулой
emjk2 ., , .. ,
тч —. i C4.10)
§ 34. Электрический ток в вакууме 245
или
C4.11)
где постоянная
А = етек2/BпЧ3)=1,2-106 Ам^-К. C4.12)
Равенство C4.11) называется формулой Ричардсона — Дешмана.
Для экспериментальной проверки эту формулу удобно представить
в виде
In (/нас/Г2) = In А - Ф/(кТ). C4.13)
На графике зависимость 1п(/нас/Т2) от 1/Г по формуле C4.13)
выражается прямой линией (рис. 133). Эксперимент подтверждает такую
зависимость с учетом небольшого изменения Ф, которое обусловлено
уменьшением |х с температурой [см. C4.2)]. По углу наклона прямой
в соответствии с формулой C4.13) определяется работа выхода Ф.
По пересечению прямой с осью ординат вычисляется In А. Величина А
по формуле C4.12) должна быть универсальной постоянной, одинаковой
для всех металлов. Это заключение не подтверждается экспериментом.
Имеется некоторое различие в А для различных металлов. Например,
для меди А = 1,1-106 А-м- К, для никеля А = 1,2-106 А-м-К,
а для платины А = 0,3- 106 А-м • К. Это изменение А обусловлено
поверхностными эффектами. Кроме того, у кристалла плотность тока
насыщения несколько различается для разных граней.
*1 акон трех вторых. Рассмотрим зависимость силы тока, протекающего
в вакууме между электродами, от приложенной разности потенциа-
потенциалов. Электроды будем считать плоскими, а ось X направим нормально
поверхности электродов (рис. 134). Потенциал катода примем за нуль
(фк = 0), а потенциал анода обозначим U.
Главным физическим фактором, влияющим на движение электронов
между катодом и анодом, является объемный заряд: силы взаимо-
взаимодействия с ним затрудняют движение электронов от катода к аноду
под действием приложенной разности потенциалов.
Допустим, что площади пластин катода и анода достаточно велики
и при расчете плотности тока вблизи линии, соединяющей центры
электродов, можно пренебречь изменением величин в направлениях,
перпендикулярных этой линии, т. е. рассматривать одномерную задачу,
когда все величины зависят только от координаты х. Уравнение
Пуассона для потенциала имеет вид
&-t-^ <3414)
где п — концентрация электронов. Закон сохранения энергии для дрейфа
электронов имеет вид
72»V>5 = M<P, C4.15)
где !-'д — скорость дрейфа в точке с потенциалом ср. Объемная плотность
тока в этой точке
246 5. Электропроводность
\j\=n\e\va.
C4.16)
Р=0
134
Все величины в правой части C4.16)
являются положительными. Вычислив ско-
рость ид из C4.15) и подставив полученное
уравнение в C4.16), находим
«МНЛКЛ2МФ)]1/2. C4.17)
С учетом C4.17) уравнение C4.14) пре-
К выводу закона трех вторых образуется К ВИДУ
d2q>/dx2 = а
C4.18)
О с
135
где а = (|j |/е0) j/me/B \ е |). Умножая обе ча-
части C4.18) на (dcp/dx) = ф, получаем
C4.19)
C4.20)
ф'ф =
где точками обозначено дифференцирование
по х. Учитывая, что
Тх фф = (ф*)/2, ф/1/ф = 2
запишем C4.19) так:
объемного заряда на (Ф ) =4аA/ф).
C4.21)
распределение потенциала между Теперь можно проинтегрировать обе ча-
катодом л анодом сти C421) по х в пределах от 0 до того
значения х, при котором потенциал равен ф.
Тогда
(М-22)
где учтено, что ф @) = 0. Производная
(с!ф/с1х)о характеризует напряженность элект-
электрического поля у катода, а — пропорцио-
пропорциональна j. Поэтому объемная плотность тока
j достигает максимума при (d<p/dxH = 0 и
тогда [см. C4.22)]
-^- = 2[/йф1/4, C4.23)
их
ИЛИ
1/4
ф- ' C424)
Интегрируя обе части C4.24) в пределах
от х = 0, ф = 0 до х = d, ф = U, получаем
\d]fa. C4.25)
§ 34. Электрический ток в вакууме 247
Возводя обе части C4.25) в квадрат и учитывая, что
« = (L/l/eo)l/WB|eD, C4.26)
получаем
Ш = Р1/3/2, C4.27)
где
В = ^fliiLV'2 C4.28)
Расчет аналогичной задачи для коаксиальных цилиндрических элект-
электродов, для концентрических сферических электродов приводит к тако-
такому же виду зависимости объемной плотности тока от разности
потенциалов в степени три вторых. Впрочем, такую зависимость можно
было бы ожидать и без расчетов с помощью анализа размерностей.
Коэффициент р во всех случаях имеет одинаковую размерность, как
это следует из уравнения Пуассона, записанного в различных системах
координат.
При отсутствии объемного заряда между катодом и анодом изме-
изменение потенциала происходит по линейному закону (рис. 135; прямая 1).
Объемный заряд изменяет этот ход. Ясно, что вблизи катода объемный
заряд уменьшает силы, действующие на электроны при отсутствии
объемного заряда, а вблизи анода увеличивает. Поэтому изменение
потенциала между электродами с учетом объемного заряда характери-
характеризуется кривой 2.
Вывод формулы C4.27) приведен в предположении, что электроны
покидают катод с нулевой скоростью. Однако они могут покидать
катод с конечной скоростью эмиссии. В этом случае ток будет
существовать даже в том случае, если вблизи катода имеется неболь-
небольшое обратное поле. Следовательно, объемная плотность заряда может
измениться до таких значений, при которых потенциал вблизи катода
уменьшится до отрицательных значений. В результате этого ход по-
потенциала вблизи катода будет характеризоваться пунктирной кривой С.
При достаточно большой разности потенциалов наблюдается откло-
отклонение от закона трех вторых. Оно наступает тогда, когда объемная
плотность заряда уменьшается настолько, что поддержание нулевого
электрического поля у поверхности катода оказывается невозможным
и, следовательно, будет невыполнимым условие (dcp/dxH = 0, при кото-
котором был введен закон трех вторых. При дальнейшем увеличении
напряженности объемная плотность тока становится независимой от
разности потенциалов (ток насыщения).
Закон трех вторых здесь рассмотрен в качестве примера нелиней-
нелинейного соотношения между силой тока и напряжением. Он не имеет
универсального характера и даже в приведенном случае справедлив
лишь в сравнительно узком интервале напряжений и токов. Нелиней-
Нелинейность вольтамперной характеристики является наиболее важной осо-
особенностью многих элементов радио- и электротехнических схем, вклю-
включая элементы твердотельной электроники.
248 5. Электропроводность
Задачи
5.1. Концентрация электронов прово-
проводимости в меди равна п0 =
= 8,5 • 1022 см. Определить сред-
среднюю скорость дрейфа электронов
проводимости при плотности тока
j = 10 А/мм2.
5.2. Через электролит прошло | Q | ку-
кулонов электричества. Подвижно-
Подвижности ионов равны Ь(+) и Ь(~\ Ка-
Какое количество электричества пе-
перенесено положительными и от-
отрицательными ионами?
5.3. Две электролитические ванны с
растворами AgNO3 и CuSO4 со-
соединены последовательно. Опре-
Определить массу серебра, выделив-
выделившегося за то время, в течение
которого выделилось 10 мг меди?
5.4. Электролиз AgNO3 проводится
при разности потенциалов 4 В.
Какая электрическая энергия рас-
расходуется для выделения 100 мг
серебра?
5.5. Проводящая металлическая лента
толщиной а = 0,1 мм и шириной
d = 5 см помещена в однородное
магнитное поле с индукцией В =
— 1 Тл, направленной перпенди-
перпендикулярно поверхности ленты. По
ленте течет ток силой I = 1,6 А.
Найти холловскую разность по-
потенциалов.
5.6. В газоразрядной трубке между
электродами с площадью по-
поперечного сечения 1 см2, располо-
расположенными на расстоянии 3 см друг
от друга, сила тока насыщения
равна /н = 10~7 А. Разряд неса-
несамостоятельный. Какое число эле-
элементарных зарядов каждого из
знаков возникает ежесекундно в
1 см3 объема трубки.
Ответы
5.1. va = 0,0736 см/с. 5.2. | Qi + ) \ = -^
5.4. 360 Дж. 5.5. 10 B. 5.6. JV«2-10'
i,. I
-. 5.3. 34 мг.
§ 35
Закон полного тока
§ 36
Уравнения Максвелла
для стационарного
магнитного поля
§37
Векторный потенциал
§38
Магнитное поле
при наличии магнетиков
Стационарное
магнитное
поле
Стационарное магнитное поле обу-
обусловлено электрическими токами. Его
нельзя осуществить движением отдель-
отдельного заряда, поскольку в этом слу-
случае магнитное поле неизбежно пере-
переменно. Тем не менее с помощью
принципа суперпозиции делается за-
заключение о создании поля отдель-
отдельным движущимся зарядом.
§39
Силы
в магнитном поле
250 6. Стационарное магнитное поле
§ 35. Закон полного тока
Дается вывод дифференциальной формы за-
закона полного тока. Обсуждается экспери-
экспериментальная проверка закона полного тока.
Постановка задачи. Так же как и в электростатике, нам необходимо
получить дифференциальную формулировку законов магнитного
поля. В электростатике это было сделано, исходя из закона Кулона
и принципа суперпозиции как экспериментальных положений. Их
интегральная формулировка дается теоремой Гаусса, из которой следует
дифференциальное уравнение A3.20).
В случае магнитного поля можно, в принципе, поступить аналогично,
а именно, можно исходить из закона Био —Савара A0.10) или A0.11)
и принципа суперпозиции для магнитного поля как экспериментальных
факторов. Их интегральная формулировка называется законом полного
тока (в данной главе для случая стационарных полей), из которых
получается соответствующее дифференциальное уравнение. Однако
можно поступить по-другому и продолжить теоретический вывод
законов магнитного поля из законов электрического поля с помощью
теории относительности (см. § 8, 9). Поэтому исходим из формулы (9.28)
для индукции магнитного поля тока, текущего по прямолинейному
бесконечному проводнику, которая была получена теоретически.
р^нтегральная формулировка закона полного тока. Линии индукции
магнитного поля, порождаемого током, текущим по прямолинейному
бесконечному тонкому проводнику, являются концентрическими окруж-
окружностями, центр которых лежит на линии тока. Значение индукции
дается формулой (9.28). Вычислим циркуляцию вектора В
fB-dl C5.1)
L
по некоторому замкнутому вокруг тока / контуру L (рис. 136).
Поскольку линии В лежат в плоскостях, перпендикулярных линии тока
/, контур L следует выбрать лежащим в одной из плоскостей.
Используя при вычислении интеграла C5.1) обозначения, показан-
показанные на рис. 137, а, получаем
B-dl = Bdlcos(lCdI) = Bdl1. C5.2)
По определению, da = 6l±jr. Принимая во внимание формулу A0.3),
перепишем C5.2) в виде
Тогда
|5b = jio', C5.4)
35. Закон полного тока
251
где учтено, что интеграл от da по замкну-
замкнутому контуру, окружающему начало коор-
координат, равен 2п. Следовательно, циркуляция
вектора В по замкнутому контуру вокруг
тока не зависит от вида контура и опреде-
определяется только силой тока.
Если замкнутый контур L не охватывает
ток / (рис. 137, б), то
и
C5.5)
т. е. циркуляция вектора В по замкнутому
контуру, не охватывающему ток, равна
й\
НУЛЮ. ПОЭТОМУ полученные результаты м? Вычисление циркуляции вектора
у у ре
тут быть сформулированы так:
цо1 (контур интегрирова-
I ния охватывает ток),
iВ • dl = < Л ,
7 ) О (контур интегрирова-
охватывает
В по замкнутому контуру
О
C5.6)
d)
ния
ток).
не
Представим себе, что имеется большое
число токов и контур охватывает часть из
них (рис. 138). Индукция магнитного поля
в каждой точке контура по принципу супер-
суперпозиции равна сумме индукции магнитных
полей, создаваемых каждым из токов:
В = ?В,. C5.7)
Подставляя В в левую часть C5.6), по-
получаем
V
1 L
137
Ток / направлен перпендикуляр-
перпендикулярно плоскости чертежа вверх.
Положительный обход контура
C5.8) против часовой стрелки
где индексом к обозначены лишь токи,
охватываемые контуром L. Токи, не охваты-
охватываемые L, не дают вклада в интеграл. Сле-
Следовательно, сила тока / в C5.8) есть сумма
всех сил токов, охватываемых контуром.
Поэтому в общем случае закон полного тока
может быть сформулирован в виде
Обобщение закона полного тока
на произвольную совокупность
252 6. Стационарное магнитное поле
где / — сила полного тока, охватываемого контуром L. Если сила
полного тока равна нулю, то и циркуляция равна нулю. Этот случай
реализуется не только тогда, когда контур не охватывает никакого
тока, но и тогда, когда охватываемые токи текут в противоположных
направлениях и в сумме дают нуль. Например, циркуляция В по кон-
контуру, охватывающему два равных по силе тока, текущих в противо-
противоположных направлениях, равна нулю. В формуле C5.9) знак тока /
учитывается по общему правилу (см. § 14): если направление обхода
контура L и направление Тока связаны правилом правого винта, то
знак ) положителен.
В противном случае знак / отрицателен.
Выражение C5.9) закона полного тока для вакуума в стационарном
случае является непосредственным следствием соотношения (9.28) и
может быть проверено экспериментально. Этот закон выше был вы-
выведен для тока, текущего по прямому бесконечному проводнику, но
сейчас станет очевидным, что он справедлив и для произвольного тока.
Дифференциальная форма закона полного тока. Перепишем форму-
формулу C5.9) для объемных токов. Обозначим S — поверхность, охваты-
охватываемую контуром L. Как обычно, положительная нормаль к поверх-
поверхности связана с направлением обхода контура L правилом правого
винта.
Сила полного тока /, протекающего через поверхность, равна
/ = J" j - dS, C5.10)
s
где j — объемная плотность тока. Следовательно, закон полного тока
C5.9) принимает вид
jB-dI = n0Jj-dS. C5.11)
L S
Левую часть равенства C5.11) можно преобразовать по теореме
Стокса в интеграл по поверхности:
jB-dl = JrotB-dS C5.12)
L S
и представить равенство C1.11) в виде
J[rotB-n0j]-dS = 0. C5.13)
s
Равенство нулю интеграла C5.13) должно соблюдаться при произ-
произвольном выборе поверхности S. Следовательно, подынтегральное вы-
выражение равно нулю:
rot В = noj.
C5.14)
Равенство C5.14) является дифференциальной формой закона полного
тока. Оно имеет дифференциальный характер и справедливо в каждой
§ 35. Закон полного тока 253
точке. Отсюда следует, что оно справедливо для произвольного поля,
хотя и выведено для поля, порождаемого током, текущим по прямо-
прямолинейному бесконечному проводнику.
Теперь можно доказать, что закон полного тока C5.9) справедлив
для произвольных токов, а не только для прямолинейных. Для дока-
доказательства возьмем произвольные токи и проведем произвольную
поверхность S, ограниченную замкнутым контуром L. Умножая обе
части C5.14) на элемент dS этой поверхности и интегрируя по dS,
находим
-dS = HoJj'dS. C5.15)
Левую часть C5.15) преобразуем по теореме Стокса C5.12) в ин-
интеграл по контуру, а правую часть с помощью C5.10) выразим через
полный ток /, пересекающий поверхность. В результате C5.15) прини-
принимает вид C5.9). Это доказывает, что закон C5.9) справедлив для
произвольных токов и произвольных контуров. Отметим также, что
при вычислении силы полного тока по формуле C5.10) можно выбрать
любую поверхность S, натянутую на контур L. Отсюда следует, что
уравнение C5.14) было получено, исходя из закона Кулона, принципа
суперпозиции для напряженности электрического поля, Инвариантности
заряда и формул теории относительности. Закон Био — Савара в форме
A0.10) или A0.11) получается из C5.14) как решение этого уравнения
в случае отсутствия токов на бесконечности [см. C7.11в)].
Экспериментальная проверка закона полного тока. Для демонстрации
закона полного тока и для его экспериментальной проверки с пе
очень большой точностью можно воспользоваться поясом Роговского.
Он представляет собой гибкую проволочную спираль, выполненную
в виде пояса (рис. 139), концы которой присоединены к гальванометру.
Действие пояса основано на законе электромагнитной индукции Фара-
дея (см. гл. 8): при изменении магнитного поля в цепи спирали пояса
Роговского возникает электрический ток. По показаниям гальванометра
можно определить
jB-dl, C5.16)
L
где L — контур, совпадающий с осью спирали пояса Роговского.
Для демонстрации закона полного тока C5.9) достаточно располо-
расположить пояс Роговского в виде замкнутого контура, совпадающего с кон-
контурами Lu L' (см. рис. 137). При включении тока в случае, показанном
на рис. 137, а, наблюдается отклонение стрелки гальванометра, по кото-
которому можно убедиться, что интеграл равен \хо1. В случае, изображенном
на рис. 137, б, отброс гальванометра отсутствует, что означает равенство
нулю циркуляции вектора В по контуру L'.
дифференциальной формы непосредственным дифференци-
дифференцированием формулы Био — Савара. Формула C5.14) получается
254 6. Стационарное магнитное поле
139
Пояс Роговского
140
Коаксиальный кабель
фазу, если взять операцию rot от обеих
частей формулы A0.11), выражающей закон
Био — Савара. В правой части операция rot
применяется только к подынтегральному
выражению, поскольку объем V интегриро-
интегрирования не зависит от переменных, по кото-
которым выполняется операция. От этих пере-
переменных j в подынтегральном выражении
не зависит, а зависит лишь гиг. Вычислив
rot и проведя интегрирование, получим
формулу C5.14). Эти вычисления можно про-
провести в качестве упражнения.
Пример 35.1. С помощью закона полного тока
найти индукцию магнитного поля в коаксиальном
кабеле, который используется для передачи посто-
постоянного тока (рис. 140). Ток течет по централь-
центральной жиле радиусом гг и возвращается по оболочке,
внутренний и внешний радиусы которой равны г2
и г3. Пространство между жилой и оболочкой
заполнено диэлектриком.
Учитывая осевую симметрию магнитного
поля, по закону полного тока получаем
где 1Г — сила тока, охватываемого круговым кон-
контуром радиусом г. Плотность тока в жиле jx =
= I/(nr\). Поэтому при 0 < г < гг имеем /, =
= j1nr2 = Ir2/r{ и, следовательно,
В = ]xlr/Bnrl).
При j-j < г <г2 имеем I, = I = const и, следо-
следовательно,
В = ц//Bяг).
При г2 < г < г3 контур охватывает встречный
ток, плотность которого
Если магнитная проницае-
проницаемость тела больше чем сре-
среды, то оно ведет себя как
парамагнетик, если мень-
меньше — как диамагнетик.
Циркуляция вектора ин-
индукции по замкнутому кон-
контуру вокруг тока не за-
зависит от вида контура и
определяется только силой
тока.
Тогда сила тока, охватываемого контуром
при гг < г < г3, и индукция магнитного поля
равны:
/, = /-/
г1-Л
Л-Л'
1 -
,2 „2
Г3 — Г2
Вне кабеля индукция поля обращается в нуль.
§ 36. Уравнение Максвелла для стационарного магнитного поля 255
§ 36. Уравнения Максвелла
для стационарного магнитного поля
Дается формулировка уравнений Максвелла
для частного случая стационарного маг-
магнитного поля и обсуждаются типы решае-
решаемых задач.
\ равнение для div В. Вычислим div В, исходя из формулы Био — Са-
г вара A0.11):
divB= ir|div(jx -rld7, C6.1)
v
где операция div введена под знак интеграла на том основании, что
пределы интегрирования (объем V) не зависят от переменных, по ко-
которым производится дифференцирование при вычислении div. Для даль-
дальнейших преобразований формул целесообразно выписать в явном виде
переменные в уравнении C6.1). Пусть В — индукция поля в точке
(х, у, z), т. е. В = В (х, у, z). Вычисление div сводится к дифференциро-
дифференцированиям по х, у, z. Текущие координаты точек интегрирования в подын-
подынтегральном выражении C6.1) обозначим х', у', z'. Тогда
j = j(х'; У, Л r=ix(x' - x) + iy(/ - у) + iz(z' - z),
C6.2)
г = |/(X' - xJ + (у' - уJ + (z' - zJ, dV = Ax' dy' dz'.
По формуле (П. 15) имеем
div I j x — I = —• rot j — j ¦ rot -j- = 0, C6.3)
поскольку первый член в правой части равен нулю из-за независимости
j от координат (х, у, z), по которым выполняется дифференцирование
при вычислении rot. Равенство второго члена нулю доказывается
прямым вычислением rot (г/г3) = 0. Равенство нулю rot (г/г3) является
следствием центральной симметрии поля вектора г/г3. Нетрудно пока-
показать, что любое центрально-симметричное поле потенциально. Реко-
Рекомендуется это проделать в качестве упражнения.
Таким образом, подынтегральное выражение в C6.1) тождественно
равно нулю и, следовательно,
div В = 0.
C6.4)
Из равенства C6.4) заключаем (см. § 13), что линии В не имеют
источников. Это означает, что нет магнитных зарядов, которые созда-
создавали бы магнитное поле, как электрические заряды создают электри-
электрическое поле. Линии В не имеют ни начала, ни конца. Они являются
либо замкнутыми линиями, либо уходят на бесконечность. Отсут-
Отсутствие начал и концов у таких линий очевидно. Однако могут су-
256 6. Стационарное магнитное поле
141
При иррациональном отношении
длины окружности тора к шагу
спирали силовая линия ие замк-
замкнута
• Уравнение div B = 0 по-
показывает, что линии век-
вектора ие имеют ни начала,
ни конца; они либо замк-
замкнуты, либо уходят в бес-
бесконечность, либо сосредо-
сосредоточены в конечной обла-
области пространства, но на-
начала и конца не имеют.
Это означает, что нет
магнитных зарядов, кото-
которые создают магнитное
поле так, как электриче-
электрические заряды создают
электрическое поле.
Для определения трех про-
проекций вектора магнитной
индукции имеются четы-
четыре скалярных уравнения
C6.5) и C6.6). Однако это
не делает систему урав-
уравнений переполненной (см.
§ S8).
О Можете ли вы привести при-
пример линии, которая вся на-
находится в конечной области
пространства, но не имеет
ни начала ни конца?
шествовать незамкнутые линии, заключен-
заключенные в конечной области пространства и
тем не менее не имеющие ни начала, ни
конца. Рассмотрим, например тор (рис. 141),
на поверхность которого наматывается спи-
спираль. Если отношение длины большой ок-
окружности тора к шагу спирали является
иррациональным числом, то линия никогда
не замкнется и будет бесконечное число раз
обвивать тор. Такая линия является приме-
примером незамкнутой линии без начала и конца,
заключенной в конечной области простран-
пространства. Линии В такого типа нетрудно реа-
реализовать на опыте. Для этого перпендику-
перпендикулярно плоскости тора по его оси необходимо
пропустить ток 1Ь а по большой окружно-
окружности, совпадающей с осью спирали тора, ток
1г. При определенных соотношениях между
1У и 12 будут реализованы указанные выше
условия незамкнутости линии В.
уравнения Максвелла. Уравнения C5.14)
и C6.4) составляют систему уравнений
Максвелла для магнитного поля, порож-
порожденного постоянными токами в вакууме:
rot В = Цо
div В = 0.
C6.5)
C6.6)
Решение этих уравнений позволяет найти
В, если известна j. Число неизвестных ска-
скалярных величин в этих уравнениях равно
трем (Вх, Ву, Bz), а общее число скалярных
уравнений для их определения равно четы-
четырем [три скалярных уравнения, получаю-
получающихся из первого векторного уравнения и
еще рдно скалярное уравнение C6.6)]. Таким
образом, число уравнений больше, чем число
неизвестных, однако это не делает систему
переполненной (см. § 58).
'рип решаемых задач. С помощью урав-
уравнений C6.5) и C6.6) можно решить две
задачи:
1. Зная индукцию магнитного поля, найти
объемную плотность токов.
Для этого надо вычислить rot В по урав-
уравнению C6.5).
§ 37. Векторный потенциал 257
2. Зная плотность токов, найти индукцию магнитного поля, которое
они порождают. Для этого надо решить эти уравнения при неизвест-
неизвестных j. Методы решения уравнения будут рассмотрены позднее, а сейчас
заметим, что для случая, когда все токи сосредоточены в конечной
области пространства, решение дается формулой Био — Савара A0.11):
«34
Из-за сложной структуры подынтегрального выражения и его век-
векторного характера вычисления получаются довольно громоздкими. Для
их упрощения целесообразно ввести векторный потенциал.
§ 37. Векторный потенциал
Обсуждаются свойства векторного потен-
потенциала и его калибровка. Вычисляется ин-
индукция поля элементарного тока.
JJ озможность введения векторного потенциала. Известное из вектор-
векторного анализа тождество div rot = 0 показывает, что решение урав-
уравнения
divB = 0 C7.1)
может быть представлено в виде
В = rot A, C7.2)
где А — векторный потенциал магнитного поля.
Неоднозначность векторного потенциала. Поле с заданной индукцией
В может быть описано не каким-то одним векторным потенциалом,
а многими векторными потенциалами. Чтобы в этом убедиться,
докажем, что если потенциал А описывает поле с индукцией В, то
и другой потенциал
А' = А + grad х C7.3)
при произвольной функции х описывает то же самое поле В. Для
доказательства вычислим индукцию поля В', описываемого потенциа-
потенциалом А':
В' = rot A' = rot A + rot grad % = rot A = В, C7.4)
поскольку rot grad = 0.
Неоднозначность векторного потенциала аналогична неоднознач-
неоднозначности скалярного потенциала в теории электростатического поля,
только там потенциал был определен с точностью до произвольной
постоянной, а здесь — с точностью до произвольной функции опреде-
определенного класса.
9 А. Н. Матвеев
258 6. Стационарное магнитное поле
калибровка потенциала. Пользуясь неоднозначностью в выборе по-
потенциала, можно наложить на потенциал определенное условие.
В магнитостатике чаще всего оно выбирается в виде
divA = 0 C7.5)
и называется условием калибровки потенциала. Его роль аналогична
роли нормировки скалярного потенциала в электростатике. В частности,
произвол в выборе векторного потенциала показывает, что векторный
потенциал имеет лишь вспомогательное значение и не может быть
измерен экспериментально.
Уравнение для векторного потенциала. Подставляя C7.2) в C6.5),
получаем
rot rot A = noj- C7.6)
Из векторного анализа известно, что
rot rot A = grad div A - V2A C7.7)
и поэтому C7.6) принимает вид
V2A=-Hoj, C7.8)
где принята во внимание калибровка C7.5). Распишем уравнение C7.8)
в координатах:
V2AX = -но/*, VM, = -Цо/Я V2AZ = -ЦоЛ- C7.9)
Таким образом, каждая из компонент векторного потенциала под-
подчиняется уравнению Пуассона (см. § 15). В частности, если все токи
сосредоточены в конечной области пространства, то по аналогии
с функцией A4.35), являющейся решением A5.14), можно написать
решение уравнений C7.9) в виде:
J А J А J C7Л
_ Но (hd
или в векторной форме
C7.11а)
Для линейного тока
L i Lf
где Li — контуры токов. В каждом из них сила тока /,-, вообще говоря,
различна. При интегрировании по замкнутому контуру конкретного
тока Lf силу тока 1( можно вынести за знак интеграла, как это
обозначено в сумме C7.116).
Найдя векторный потенциал, можно по формуле C7.2) определить
соответствующую ему индукцию магнитного поля.
§ 37. Векторный потенциал 259
Био — Савара. Из C7.11а) по формуле C7.2) получаем следующее
выражение для индукции магнитного поля:
* у, z) = ? f rot Г
/x - x'f + (y -
где в явном виде выписаны координаты точки наблюдения, в которой
вычисляется ротор, и текущие координаты (х', у', z') точки интегриро-
интегрирования. Операция ротор включает в себя вычисление частных произ-
производных по (х, у, z). Учитывая формулу векторного анализа rot (cpA) =
= ф rot A + grad ф х А, получаем
i 1 . , 1 . i х г
rot — = — rot j + grad — x j = j!
г г г г
где rot j = 0, поскольку j не зависит от переменных, по которым
вычисляется ротор, и grad(l/r)= -т/г3. Следовательно, получаем фор-
формулу
C7.11b)
выражающую закон Био-Савара. Тем самым завершается вывод ос-
основных законов магнитостатического поля из законов электростати-
электростатического поля с помощью теории относительности.
ТТоле элементарного тока. Вычислим векторный потенциал и индук-
индукцию поля элементарного замкнутого тока, т. е. линейного тока,
обтекающего поверхность с бесконечно малыми линейными размерами
в физическом смысле. Контур, по которому течет линейный ток /,
выберем в виде параллелограмма со сторонами lu l2, l$, U (рис. 142).
Начало координат поместим в точку О поверхности, обтекаемой током.
Выбор точки О не имеет значения, поскольку контур и поверхность
бесконечно малые. Потенциал вычисляется в точке, характеризуемой
радиус-вектором г. По формуле C7.116) получаем
C7.12)
где произведен переход к линейным токам (jdK->/dI)-
Поскольку длины сторон параллелограмма бесконечно малы, при
интегрировании в C7.12) по каждой из его сторон значение г может
считаться постоянным и равным, например, расстоянию от точки,
в которой определяется поле до середины стороны. Поэтому [см. C7.12)]
dl =
4л \rt
9*
C7ЛЗ)
260 6. Стационарное магнитное ноле
Учитывая, что lt =
ходим:
' 1 1
-/Y7/
142
Элементарный ток
-13 и 12 = — Ц, на-
на(Ь ¦ г)
= h
• г)
C7.14)
143
Вычисление разности расстояний
от двух точек
где принято во внимание, что при вычисле-
вычислениях можно пренебречь бесконечно малыми
высших порядков. Например, на рис. 143
показаны геометрические построения, ис-
использованные при вычислениях второй серии
равенств C7.14):
г4 = li + r2) C7.15)
откуда
г\ = 1\ + r| + 21t -г2 C7.16)
и, следовательно,
,.2 _
' 2 -
Тогда
/2
= Н
-±^- * \ ¦ г/г.
C7.17)
C7.18)
к расчету потенциала от ко-
гГтока УЧаСТК" прямо"тшнейно'
Здесь сохранены лишь члены первого по-
порядка малости по It. С помощью равенств
вида C7.18) получаются формулы C7.14).
С учетом C7.14) выражение для потенциала
C7.13) принимает вид
А = ~- 4~[>2 (I • г) - h a2 • г)]. C7.19)
4л: г
Из векторной алгебры известно разложе-
разложение двойного векторного произведения:
А х (В х С) = В(А-С)-С(А-В), C7.20)
которое показывает, что выражение в квад-
квадратных скобках в C7.19) можно представить
в виде
12 (li • г) - li (Ij • г) = г х A2 х \t) =
= (>i х 12) х г. C7.21)
§ 37. Векторный потенциал 261
Принимая во внимание, что
h х 12 = S C7.22)
- вектор элемента поверхности, обтекаемой током, перепишем C7.19)
с учетом C7.21) и C7.22):
jtoJSx г C723)
An г3
Величина
/S = рт C7.24)
играет чрезвычайно важную роль в магнетизме и называется магнитным
моментом элементарного тока. Он по модулю равен произведению силы
тока в контуре на площадь, охватываемую контуром. По направлению
он совпадает с направлением положительной нормали к поверхности.
Представим векторный потенциал элементарного тока в виде
Рт X Г
An r3
откуда
В = rot t
. Но
i An
Г з(Pm¦
1 г5
r)r
__Pml
C7.25)
C7.26)
Формула C7.26) показывает, что индукция поля магнитного момен-
момента убывает обратно пропорционально третьей степени расстояния,
в то время как индукция поля элемента тока убывает обратно про-
пропорционально квадрату расстояний. Это обусловлено тем, что индукция
поля магнитного момента слагается из индукций полей элементов
тока, текущих в противоположных направлениях на очень малых рас-
расстояниях друг от друга.
Пример 37.1. Найти вектор-потенциал и индукцию поля, создаваемого
прямолинейным участком линейного проводника длиной L, по которому про-
протекает ток I.
Имеется в виду, что данный участок составляет часть замкнутой цепи.
По принципу суперпозиции этот потенциал войдет слагаемым в полный по-
потенциал от тока по замкнутой цепи и поэтому его вычисление имеет физи-
физический смысл, хотя незамкнутого постоянного тока не существует.
Поместим начало координат в середине рассматриваемого участка про-
проводника, направив ось Z вдоль проводника (рис. 144). Поскольку магнитное
поле прямолинейного тока аксиально симметрично, достаточно вычислить
индукцию в точках плоскости ZY. Координаты точки в этой плоскости будем
характеризовать расстоянием г от оси Z и координатой г. Из формулы C7.116)
следует, что отличной от нуля является только компонента Az, поскольку ток
течет в направлении оси Z. Тогда
dz' ц0/
An J [(г-г') +r]' 4jt
-L/2
C7.27)
262 6. Стационарное магнитное поле
Индукция вычисляется по формуле
В = rot A,
которую надо расписать в цилиндрических координатах. Единственной
отличной от нуля проекцией индукции В является Вф, где <р —
аксиальный угол цилиндрической системы координат, причем
Bv=-8AJdr. C7.28)
На рисунке в точках плоскости ZY Вф является компонентой,
направленной перпендикулярно этой плоскости в сторону отрица-
отрицательных значений оси X. По формуле C7.28) с помощью C7.27) полу-
получаем
_ я. .„ МГ -z + L/2 z + L/2 1
Для бесконечного прямолинейного проводника из C7.27) и C7.29)
находим:
Аг (L- оо) = - ^In r + const, C7.30)
Lit
B,(L-»oo)=^. C7.31)
Пример 37.2. Найти векторный потенциал и индукцию, создаваемые током,
текущим по коаксиальному кабелю (рис. 140). Материал проводников и простран-
пространство между ними немагнитны.
Потенциал подчиняется уравнению C7.8). Из-за аксиальной симметрии
задачи удобно пользоваться цилиндрической системой координат, ось Z кото-
которой совпадает с осью кабеля. Очевидно, что от г и аксиального угла ф
потенциал не зависит, т. е. А = А (г). Кроме того, если от нуля отлична лишь
компонента jz плотности тока, то отличной от нуля будет компонента Аг
векторного потенциала, которую необходимо найти. Обозначим эту компонен-
компоненту А. Индекс показывает область, к которой эта компонента относится.
Таким образом, Аи А2, А3, АА —векторные потенциалы соответственно в об-
областях @, )¦]), (ги гг\ (г2, г3), (г3, оо). Тогда [см. C7.8)]
r dr \ dr J nr\
V4 =0 (r, < r < r2),
^^ = -~~(>-^~)=--7Г^-2Г ('2<r<r3), C7.32)
r dr \ dr J n (r3 — rj)
где jl = //(nrf), j2 = 0, Л = ll\r\ - rl)l h = 0.
Решение уравнений C7.32) таково:
Аг = С3 In r + С4 (г, < г < г2), C7.33)
§ 37. Векторный потенциал 263
-+C5lnr + C6 (r2<r<r3),
Ал = С7 In г + С8 (г3 < г < оо).
Индукцию магнитного поля находим по формуле В = rot А, которая
в данном случае сводится к выражению В,, = —SA/Sr.
Поскольку В9 — единственная, отличная от нуля, проекция магнитной
индукции, индекс ср в дальнейшем не будем выписывать. Индекс обозначает
область, к которой относится значение В. Тогда
1 til 1Л\
1КГ\ Г
Из конечности В1 при г = О заключаем, что С[ = 0. Выберем в качестве
условия нормировки у4!@) = 0. Это дает С2 = 0 и поэтому выражения для А2
и В2 принимают вид:
А1 = -цо/г2/Dлг?), В, = iiolr/Bnr2). C7.35)
Для области rt <г <г2 получаем
В2=-С3/г. C7.36)
Пользуясь граничными условиями для В и учитывая, что ц = цо> получаем
B2(ri) = Bv (rv) = —C3Ai = Ио*/Bгоч). Следовательно, Сэ = — цо//Bл).
Запишем условие непрерывности векторного потенциала при r = r, в виде
С3 In rj + C4. = - цо//Dя), что приводит к равенству С4 = — Цо-Wit) +
+ Q'oWSt)] In rj. Поэтому выражения для векторного потенциала и магнитной
индукции при гх < г < гг принимают вид
2 = — ш , i>2 = . Ei.ii)
2л г, 4я 2лг
Индукция в оболочке кабеля (г2 < г < г3) равна
В, =
С5
йг 2л (г| - r^) r
Из граничных условий В2(г2) = В3(г2) и А2(г2) = А3(г2) находим:
откуда
э -П гъ- г2
М (rj - г2)
2кг (г\ - r\) '
3 2к (r23-rl
Пользуясь граничными условиями, • при г = г3 находим для векторного
потенциала и индукции магнитного поля для г3 < г < оо выражения
А4 = — —-———In (- In — = const,
2л L r3 - r2 r2 r, J C7 39j
B4 = 0.
264 6. Стационарное магнитное поле
§ 38. Магнитное поле
при наличии магнетиков
Рассматриваются влияние магнетика на маг-
магнитное поле и различные механизмы намаг-
намагничивания. Выводится соотношение между
объемной и поверхностной плотностями мо-
молекулярных токов и намагниченностью. Об-
Обсуждаются явления на границе между маг-
магнетиками и измерение индукции магнитного
поля в магнетике. Выясняется сущность
магнитной экранировки.
/Определение. Магнетиками называются вещества, которые при вне-
внесении во внешнее поле изменяются так, что сами становятся
источниками дополнительного магнитного поля. При этом полная
индукция магнитного поля равна сумме индукций внешнего магнитного
поля и магнитного поля, порождаемого магнетиком. Изменение состоя-
состояния магнетика под влиянием внешнего магнитного поля, в результате
чего сам магнетик становится источником магнитного поля, называется
намагничиванием магнетика. Это явление для широкого класса ве-
веществ было открыто экспериментально Фарадеем в 1845 г. Им же
было установлено существование диа- и парамагнитных тел, для кото-
которых он ввел эти термины.
|^Теханизмы намагничивания. Существуют различные механизмы на-
намагничивания. В соответствии с ними магнетики подразделяют на
диа-, пара-, ферро- и ферримагнетики. Антиферромагнетики также
относят к магнетикам, хотя они и не создают магнитного поля
в окружающем их пространстве (см. гл. 7).
Количественно интенсивность намагничивания во всех случаях харак-
характеризуется одинаково, а именно, под действием магнитного поля все
элементы объема приобретают магнитный момент. Это может быть
обусловлено следующими механизмами:
1. При внесении во внешнее магнитное поле в молекулах и атомах
движение электронов изменяется так, что образуется' определенным
образом ориентированный суммарный круговой ток, который харак-
характеризуется магнитным моментом [см. C7.24)]. Можно сказать, что
молекулы при внесении в магнитное поле приобретают индуцированный
магнитный момент. Благодаря этому они становятся источниками
дополнительного поля, индукция которого определяется формулой C7.26),
т. е. вещество намагничивается. Такие вещества называются диамаг-
нетиками.
2. Движение электронов в молекулах может быть таково, что мо-
молекулы будут обладать магнитным моментом и при отсутствии маг-
магнитного поля, т. е. молекулы обладают постоянным магнитным мо-
моментом. Благодаря этому каждая молекула является источником
§ 38. Магнитное поле при наличии магнетиков 265
магнитного поля. Если внешнего поля нет, то магнитные моменты
различных молекул ориентированы совершенно беспорядочно, благо-
благодаря чему суммарная индукция поля, создаваемого ими, равна нулю,
т. е. физически бесконечно малые элементы тела не являются источ-
источниками магнитного поля и тело не намагничено. При внесении такого
магнетика во внешнее поле постоянные магнитные моменты отдель-
отдельных молекул переориентируются в направлении индущии поля, в резуль-
результате чего образуется преимущественное направление ориентации маг-
магнитных моментов. При этом бесконечно малые физические объемы
приобретают магнитный момент, равный сумме магнитных моментов
молекул, заключенных в объеме, и становятся источниками магнитного
поля — магнетик намагничивается. Такие вещества называются пара-
парамагнетиками.
3. Намагничивание ферромагнетиков и ферримагнетиков связано
с тем, что электроны обладают магнитным моментом, находящимся
в определенном соотношении с их механическим моментом — спином.
Намагничивание такого класса магнетиков связано с определенной
ориентировкой спинов и поэтому называется спиновым. Объяснение
спинового магнетизма выходит за рамки классической теории электри-
электричества и магнетизма и возможно лишь в рамках квантовой теории.
Поэтому в данной книге описаны лишь наиболее важные свойства
этого класса магнетиков без количественной теории. Вся излагаемая
ниже теория магнитного поля в присутствии магнетиков относится
лишь к диа- и парамагнетикам, если только не оговорено противное.
Намагниченность. Эта величина определяется отношением магнитного
момента элементарного физического объема к объему:
>mi, C8.1)
AV
где AV — элементарный объем; pmi — моменты молекул; суммирование
распространяется на все молекулы в объеме AV.
Другими словами, определение C8.1) для намагниченности может
быть сформулировано так: намагниченность есть объемная плотность
магнитного момента магнетика. Из C8.1) следует, что магнитный
момент элемента объема dV равен
dpm = J dV. C8.2)
векторный потенциал при наличии магнетиков. Он равен сумме по-
потенциала Ао, создаваемого токами проводимости, и потенциала Ам,
создаваемого магнетиком в результате намагничивания:
А = Ао + Ам, C8.3)
причем на основании C7.11), C7.25) и C8.2) можно написать:
—э—dV. (р) t-io л\
266 6. Стационарное магнитное поле
Объемная плотность молекулярных токов. Как было сказано, возник-
возникновение магнитных моментов связано с наличием круговых токов.
Токи в элементарных объемах, приводящие к возникновению магнит-
магнитного момента требуемой величины, получили название молекулярных.
Однако не следует придавать этому выражению слишком буквальный
смысл. Молекулярные токи в строгом смысле слова могут течь только
внутри молекул. При определении намагниченности и других величин
подразумеваются усредненные величины, благодаря чему магнитные
моменты молекул представляются как бы непрерывно размазанными
по всему объему, а молекулярные токи — текущими по объему магне-
магнетика, как в непрерывной среде. Тем не менее за ними сохранилось
название молекулярных.
Рассмотрим бесконечно малый замкнутый контур L, ограничиваю-
ограничивающий AS (рис. 145), и вычислим циркуляцию намагниченности по контуру:
JJ-dI = f/td/, C8.5)
L L
где JT — тангенциальная составляющая J вдоль контура интегрирования.
Она создается за счет токов, текущих по замкнутым контурам вокруг
линии, вдоль которой производится интегрирование C8.5) (рис. 145;
5S — площадь, обтекаемая током в плоскости, перпендикулярной линии
интегрирования). Умножив числитель и знаменатель в C8.5) на 5S, про-
проведем следующие преобразования:
где принята во внимание формула C8.2). По определению магнитного
момента, имеем dpmt = 675S (8/ — сила тока, обтекающего площадку
8S на длине d/, причем 67 пересекает AS по нормали). Поэтому
L L L
где А/„ — нормальная составляющая силы тока, пересекающего пло-
площадку AS. Таким образом, C8.5) с учетом C8.6) и C8.7) принимает вид
JJ-dI = A/B. C8.8а)
L
Найде2м составляющую rot J в направлении нормали к площадке AS.
Воспользовавшись определением A4.6) для ротора и равенством C8.8а),
находим
fJdI A/
rot»J = 2J?/as— №-?-*"> {ЖЩ
Величина
C8-9)
§ 38. Магнитное поле при наличии магнетиков 267
является, очевидно, нормальной составляю-
составляющей плотности молекулярных токов, по-
поскольку именно эти токи ответственны за
возникновение намагниченности. Равенство
C8.86) справедливо при произвольной ориен-
ориентировке площадки AS, т. е. для любых ком-
компонент rotJ и jM. Поэтому имеет место
векторное равенство
jM = rotJ. C8.10)
Эта формула дает выражение объемной
платности молекулярных токов, порождаю-
порождающих намагниченность J.
Доверхностные молекулярные токи. Моле-
Молекулярные токи могут течь также и по
поверхности раздела между магнетиками
или по поверхности раздела между магне-
магнетиком и вакуумом.
На рис. 146 обозначена поверхность
раздела между магнетиками 1 и 2. Все
величины, относящиеся к магнетику 1, обо-
обозначим с индексом /, а к магнетику 2 —
с индексом 2. Проведем в плоскости, пер-
перпендикулярной поверхности раздела, контур
L. Параллельные поверхности раздела части
контура равны I, а перпендикулярные очень
малы и стремятся к нулю. Этот контур
ограничивает площадь поверхности S, пер-
перпендикулярной поверхности раздела магне-
магнетиков. Пусть dS - элемент этой площади,
который при выбранном на рис. 146 направ-
направлении обхода контура направлен от нас.
Умножая обе части C8.10) на dS и интегри-
интегрируя по S, находим
JrotJ-dS = JjM-dS. C8.11)
s
Левую часть C8.11) можно преобразовать
по теореме Стокса в интеграл по контуру
L и вычислить
I rot J ¦ dS = | J ¦ dl = (J2l - Jlx) / + < J>6oK A/60K,
L L
C8.12)
где Ju и J2* ~ тангенциальные к контуру
интегрирования составляющие в первой и
второй средах, причем знак минус у Ju
Нахождение выражения для объ-
объемной плотности молекулярных
токов
146
К выводу формулы для поверх-
поверхностной плотности токов
Г1 Ии=
147
К выводу векторной запнсн для
поверхностной плотности моле-
молекулярных токов
J2-0
148
Поверхностные молекулярные то-
токи по однородно намагниченно-
намагниченному цилиндру
268 6. Стационарное магнитное поле
появился из-за изменения направления интегрирования на обратное
во второй среде. Величина <^>бок^'бок учитывает интегралы по
вертикальным участкам пути. Нет необходимости их более подробно
выписывать, поскольку они обращаются в нуль при стягивании гори-
горизонтальных участков интегрирования к поверхности. Правая часть C8.11)
дает проекцию тока по направлению нормали к поверхности S.
Это направление также тангенциально поверхности раздела магнетиков,
поэтому
JjM-dS = A/Mn0B. C8.13)
С учетом C8.12) и C8.13) равенство C8.11) после деления на /
принимает вид
Ju~ Jlr + <-Обок Л'бок/* = А/м. пов/' = «м. пов, C8.14)
где
»„.пов= А*м.повА C8.15)
— проекция поверхностной плотности тока на направление, перпен-
перпендикулярное поверхности S. Сжимая в C8.14) контур к поверхности
(Д/6ок->0), получаем
¦/21-^1 = („.Пов. C8.16)
Такая формула справедлива при произвольной ориентировке кон-
контура относительно различных направлений вдоль поверхности раздела.
Поэтому более удобно записать ее в векторном виде. Обозначим п —
единичный вектор нормали к поверхности раздела, направленный
во вторую среду (рис. 147). Из построения на рис. 147 и смысла
входящих в предшествующие формулы величин видно, что форму-
формула C8.16) в векторном виде записывается следующим образом:
iM = n х (J2 - J,). C8.17)
0днородно намагниченный цилиндр. В качестве примера вычисления
по формуле C8.17) найдем поверхностную плотность молекулярного
тока однородно намагниченного цилиндра (рис. 148), который» может
быть реализован в виде постоянного магнита. Хотя природа ферро-
ферромагнетизма, обусловливающего существование постоянных магнитов,
не может быть понята в рамках классической теории магнетизма,
создаваемое намагниченными ферромагнетиками в пространстве поле
может быть описано классической теорией. При этом предполагаемая
известной намагниченность ферромагнетика рассматривается как ис-
источник магнитного поля в том же смысле, в каком является источ-
источником магнитного поля намагниченность диа- и парамагнетиков.
Намагниченность диа- и парамагнетиков существует лишь при наличии
внешнего поля. Намагниченность ферромагнетиков сохраняется при
отсутствии внешнего поля, а порождаемое этой намагниченностью
поле существует самостоятельно. Задача состоит в том, чтобы это
поле описать.
§ 38. Магнитное поле при наличии магнетиков 269
Однородный намагниченный цилиндр можно себе представить также
в виде диа- или парамагнетика, помещенного во внешнее поле, которое
с достаточной точностью обеспечивает постоянную намагниченность.
В этом случае в пространстве вне цилиндра определяется индукция
не полного поля, а лишь его части, обусловленная намагниченностью.
Намагниченность Jx цилиндра показана на рис. 148 стрелкой,
в вакууме J2 = 0, а нормаль п — к поверхности раздела является
внешней нормалью к цилиндру. По формуле C8.17) плотность поверх-
поверхностного молекулярного тока, текущего по цилиндру, равна
iM= -n х Ji = Ji x n. C8.18)
Одна из линий этого тока показана на рис. 148 окружностью
со стрелками. Очевидно, что намагниченность Jt с текущим по поверх-
поверхности цилиндра током составляет правовинтовую систему. Форму-
Формула C8.10) показывает, что молекулярные объемные токи внутри ци-
цилиндра отсутствуют, поскольку rot Jx = 0. Следовательно, все поле вне
цилиндра создается поверхностными токами, текущими по окруж-
окружностям. Тем самым доказана эквивалентность полей постоянного
цилиндрического магнита и круговых токов (поля соленоида). Это
утверждение справедливо для любых магнетиков, включая ферро-
ферромагнетики.
Напряженность магнитного поля. При отсутствии магнетиков вы-
выполняется соотношение
n0j, C8.18)
описывающее порождение магнитного поля токами проводимости. При
наличии магнетиков наряду с токами проводимости j поле порожда-
порождается также и молекулярными токами jM [см. C8.10)]. Следовательно,
C8.18) при наличии магнетиков должно быть записано в виде
rot В = ц0 (j + jj = ц0 G + rot J). C8.19)
Разделим обе части C8.19) на ц0 и перенесем rot J в левую часть:
rot(B/no-J)=i C8.20)
где
Н = В/цо - J C8.21)
— напряженность магнитного поля. Она не является чисто полевой
величиной, поскольку включает в себя вектор J, характеризующий
намагниченность среды. Поэтому по своему значению вектор Н играет
в теории магнитного поля такую же роль, как вектор D в теории
электрического поля, и его не следовало бы называть напряженностью.
Тем не менее такое название закрепилось за ним исторически.
уравнение для напряженности. С учетом C8.21) уравнение C8.20)
принимает вид
rot Н = j. C8.22а)
Это уравнение очень удобно для вычисления напряженности поля
при наличии магнетиков.
270 6. Стационарное магнитное поле
Закон полного тока при наличии магнетиков выводится так же,
как он был получен при отсутствии магнетиков, исходя из C5.14),
с последующим переходом к C5.15):
jH-dl = /. C8.226)
L
Зависимость намагниченности от напряженности.По тем же причинам,
по которым вектор Н был назван напряженностью магнитного поля,
было принято считать, что источником намагничивания является не В,
а Н. Поэтому зависимость J от Н представляем в виде
J = ХН, C8.23)
где % — магнитная восприимчивость. Зависимость В от Н принято
записывать в виде
В = цН, C8.24)
где ц — магнитная проницаемость среды. Эти величины для диа-
и парамагнетиков не зависят от В и Н. Чтобы найти соотношение
между ними, подставим C8.23) и C8.24) в C8.21) и сократим обе части
полученного равенства на Н:
1 = ц/цо - X, C8.25)
или
X = (Ц - Цо)/йо = Иг - 1, C8.26)
где \ir = ц/цо — относительная магнитная проницаемость среды. Заме-
Заметим, что в системе единиц Гаусса магнитная восприимчивость выра-
выражается числом, в 4я раз меньшим, чем в СИ.
Различные механизмы намагничивания приводят к разным зависи-
зависимостям J от Н (см. гл. 7). Сейчас лишь отметим, что у диамагне-
тиков намагниченность направлена против Н. У диамагнетиков % < 0
[см. C8.23)] и, следовательно, в соответствий с C8.26) магнитная про-
проницаемость ц < |х0 (цг < !)• Это означает, что порождаемое диама!нети-
ком поле направлено против первоначального, т. е. диамагнетик
ослабляет внешнее поле. Модуль их восприимчивости |xl очень мал
и имеет порядок ~10~5. Восприимчивость не зависит от температуры.
Диамагнетизм имеется у всех веществ.
У парамагнетиков J совпадает по направлению с Н. Для них %>0,
ц > |х0, Иг > 1. Дополнительное поле у парамагнетиков совпадает по
направлению с первоначальным. Следовательно, парамагнетик усили-
усиливает поле. Восприимчивость % парамагнетиков зависит от температуры.
При комнатной температуре парамагнитная восприимчивость веществ
в твердом состоянии имеет порядок ~10~3, т.е. примерно на два
порядка больше диамагнитной восприимчивости. Поэтому у парамагнит-
парамагнитных веществ роль диамагнитной восприимчивости относительно мала
и ею можно пренебречь.
§ 38. Магнитное поле при наличии магнетиков 271
У ферромагнетиков J совпадает по направлению с Н и является
очень большой. Для них % » 1, ц »|х0. Характерно, что % и ц зависят
от поля и от предыстории намагничивания. Благодаря этому у них
имеется остаточная намагниченность, т. е. намагниченность образца
в целом сохраняется и после того, как внешнее поле стало равным
нулю. По своим формальным свойствам ферромагнетики аналогичны
сегнетоэлектрикам (см. § 23).
Поле в магнетике. В вакууме J = 0, и формула C8.21) позволяет
определить напряженность поля в вакууме равенством Но = В/(х0.
В безграничном однородном магнетике токи проводимости порождают
поле Н [см. C8.22)]. В вакууме те же самые токи проводимости
порождают поле Но [см. C5.14)]. Уравнение C5.14) можно переписать
в виде
rot Но = j. C8.27)
Сравнивая C8.22) с C8.27), заключаем, что одинаковые токи про-
проводимости возбуждают одинаковые напряженности магнитного поля
в вакууме и однородном безграничном магнетике:
Н = Но. C8.28)
Следовательно, индукции в магнетике и вакууме В и Во находятся
в таком соотношении:
В = цВо/ио = щВ0. C8.29)
Это равенство показывает, что в диамагнетиках (ц, < 1) индукция
поля уменьшается по сравнению с индукцией в вакууме, а у пара-
парамагнетиков (|хг > 1) — увеличивается.
Если все магнетики и токи проводимости расположены в конечной
области пространства и известны как токи проводимости, так и на-
намагниченность всех магнетиков как функция точки [J = J (x, у, z)], то
индукция магнитного поля в принципе всегда может быть просто
найдена. Векторный потенциал представляется в виде формул C8.3),
C8.4а) и C8.46), которые целесообразно записать по-другому. Можно
сказать, что векторный потенциал А является суммой потенциалов,
созданных токами проводимости C8.4а), молекулярными токами C8.10)
и поверхностными молекулярными токами C8.17), причем все токи
создают потенциал по одному и тому же закону C8.4а). Поэтому
формула для потенциала имеет вид
где последний интеграл учитывает поверхностные молекулярные токи,
a S означает совокупность поверхностей раздела между магнетиками.
Однако простота нахождения потенциала с помощью C8.30а) только
кажущаяся, потому что так его можно найти только в том случае,
272 6. Стационарное магнитное поле
если известна J. Однако во многих случаях эта величина неизвестна
и ее определение является трудной задачей.
Постоянные магниты. Они являются либо ферро-, либо ферримагне-
тиками и к ним излагаемая теория непосредственно неприменима.
Тем не менее по полученным выше формулам можно формально вы-
вычислить потенциал поля, порождаемого постоянными магнитами в
окружающем их пространстве. Магнитные свойства постоянных магни-
магнитов, как и магнетиков, характеризуются их намагниченностью Jro
порождающей поле точно так же, как если бы она была намагни-
намагниченностью дна- или парамагнетика. Поэтому, используя C8.30а), можно
для векторного потенциала, порождаемого постоянными магнитами,
написать формулу
? f i^JL. C8.ЗОб)
4я J г 4к J r
V S
В частности, если намагниченность постоянного магнита одинакова
по всему объему, первый член в C8.306) обращается в нуль и все
магнитное поле как бы создается токами, текущими по поверхности
магнита в соответствии со вторым интегралом C8.306). Однако никаких
реальных токов, текущих по поверхности постоянного магнита, нет,
они в данном случае являются лишь вспомогательной величиной для
вычисления напряженности поля. Физический смысл вспомогательного
характера этой величины можно понять из следующего примера.
Представим себе постоянный магнит в виде длинного цилиндра,
создающий некоторое поле в окружающем его пространстве. Если
взять цилиндрический соленоид такого же диаметра и длины с доста-
достаточно плотной намоткой и сердечником из пара- или диамагнетика,
то подбором силы тока можно добиться, что индукция поля в окру-
окружающем соленоид пространстве будет практически совпадать с индук-
индукцией поля постоянного магнита. Ток, текущий в соленоиде по тонким
проводам, может рассматриваться как поверхностный ток, эквивалент-
эквивалентный фиктивному току, текущему по поверхности постоянного цилинд-
цилиндрического магнита. В этом и состоит математический смысл,, наличия
второго слагаемого в правой части C8.306). Фиктивность тока обнару-
обнаруживается тогда, когда возникает вопрос о поле внутри магнетика
и внутри соленоида. Эти поля различны.
При учете постоянных магнитов уравнение для индукции остается
без изменения (div В = 0), но уравнение, выражающее связь индукции
с напряженностью магнитного поля, несколько изменяется. Дополни-
Дополнительным источником магнитного поля является постоянный магнит
и поэтому вместо C8.21) надо написать уравнение
В = ц0Н + М + Mm C8.31a)
где Jn — намагниченность постоянного магнита. Учитывая, что ц0Н +
+ \i0J — цН, получаем
В = цН + Мп- C8.316)
§ 38. Магнитное поле при наличии магнетиков 273
Заметим, что в этой формуле ц является лишь диа- и парамагнит-
парамагнитной восприимчивостью вещества, а не ферромагнитной восприимчи-
восприимчивостью, которая учтена уже членом |x0Jn- Поэтому если под Jno7H
понимать полную намагниченность (JnonH = J + JJ, то формулу C8.31а)
лучше представить в виде
Рассмотрим для примера постоянный магнит в виде плоской
пластины конечной толщины и бесконечной площади (рис. 149). Посто-
Постоянная намагниченность Jn направлена перпендикулярно поверхности
постоянного магнита. Диа- и парамагнитные свойства постоянного
магнита не учитываем.
Пусть вне постоянного магнита имеется магнитное поле с напря-
напряженностью Но, направленной перпендикулярно его поверхности. Индук-
Индукция поля одинакова как вне магнита, так и внутри него и равна
В = ц0Я0. Тогда [см. C8.31в)] ц0Я0 = ЦОЯ + Мп- Отсюда напряжен-
напряженность поля внутри постоянного магнита равна (см. рис. 149):
Н = Но — Jn.
Тираничные условия для векторов поля. На границе между магнети-
ками с различными и векторы В и Н испытывают скачкообразные
изменения, характеризующиеся граничными условиями. Для их вывода
исходим из уравнений C6.4) и C8.22), которые справедливы как для
вакуума, так и для среды, заполненной магнетиком. Методически
вывод граничных условий проводится точно так же, как и в случае
электрического поля [см. § 17; A7.21> и A7.30)].
Тираничное условие для нормальной составляющей вектора В. Оно
выводится аналогично A7.21), исходя из A7.17), только теперь
вместо A7.17) надо использовать уравнение
div В = 0. C8.32)
В результате получаем
C8.33)
Т раничное условие для тангенциальной составляющей вектора Н. Оно
выводится аналогично A7.30) исходя из A7.29), только теперь вместо
A7.29) надо использовать уравнение
J H-dl = fj-dS, C8.34)
ABCDA
которое получается из C8.22), если его части умножить на dS и про-
проинтегрировать по площади, ограниченной контуром ABCDA (см. рис. 83),
преобразовав левую часть по теореме Стокса. В результате получаем
Н2Т - Ни = inm, C8.35)
274 6. Стационарное магнитное поле
Но
t
А
149
Магнитное поле в присутствии
ферромагнетика
в
где гпов — поверхностная плотность тока в
направлении, перпендикулярном тому, в ко-
котором выбираются тангенциальные состав-
составляющие напряженности магнитного поля.
Необходимо также иметь в виду, что это
поверхностные токи проводимости, а не по-
поверхностные молекулярные токи iM [см.
C8.16)].
Преломление магнитных силовых линий.
На границе между магнетиками силовые
линии испытывают преломление, которое
определяется с помощью граничных условий
аналогично тому, как это было сделано при
анализе формулы A7.31).
тжзмерсние индукции магнитного поля,
Наиболее простой и наглядный метод
измерения индукции основан на использо-
использовании закона электромагнитной индукции
Фарадея. Если проводник в виде маленькой
петли (рис. 150), замкнутый на гальванометр,
ориентировать в плоскости, перпендикуляр-
перпендикулярной В, а затем повернуть на 90° вокруг оси,
лежащей в этой плоскости, то через гальва-
~ нометр пройдет импульс тока, по которому
Измерение индукции с помощью r r J ' г j
закона Фарадея можно определить В в области петли (см.
гл. 8). Таким методом измеряется средняя
индукция поля на площади, ограниченной
петлей. Вместо поворота рамки можно вы-
выключить поле.
Р~[оля бесконечного соленоида и однородно
намагниченного бесконечно длинного ци-
цилиндра. Пусть поле создается током, теку-
текущим по обмотке бесконечного соленоида
(рис. 151). Число витков провода на 1 м
длины, силу тока и магнитную проницае-
проницаемость сердечника обозначим соответственно
п, I и ц. Магнитное поле аксиально сим-
симметрично и может иметь лишь компоненту,
параллельную оси соленоида (витки намо-
намотаны очень плотно).
Для нахождения напряженности поля вос-
воспользуемся C8.22а) и, произведя интегриро-
интегрирование по контуру ABCDA, получаем
J H-dl = 0, C8.36)
ABCDA
150
В
шш
н=о
стшшшшш
D
н=о
А
151
Поле бесконечного соленоида
О Какая величина в теории
электрического поля соответ-
соответствует магнитной проницае-
проницаемости и, в теории магнит-
магнитного поля?
Почему молекулярные токи
нельзя представлять текущи-
текущими лишь в объеме молекул?
§ 38. Магнитное поле при наличии магнетиков 275
поскольку по противоположным сторонам соленоида токи текут в про-
противоположных направлениях, и, следовательно, суммарная сила тока
через поверхность, натянутую на контур ABCDA, равна нулю. Вклад
в интеграл от участков интегрирования ВС и DA равен нулю, по-
поскольку вектор Н может быть направлен только перпендикулярно ВС
и DA. Поэтому остается лишь вклад от участков АВ и CD:
HBCl ~ HADl = О, C8.37)
где Нвс и HAD — напряженности поля на участках ВС и AD; I — длина
этих участков. Знак минус появился из-за того, что направления
интегрирования на участках противоположны. Растягивая контур вдоль
АВ и CD, например удаляя AD от цилиндра, замечаем, что для тож-
тождественной справедливости C8.37) необходимо, чтобы Н не зависело
от расстояния, т. е. Н вне соленоида должна быть постоянной вели-
величиной. На бесконечно большом расстоянии от соленоида поля не бу-
будет, следовательно, оно отсутствует во всем пространстве вне соле-
соленоида.
Для определения напряженности поля внутри соленоида применим
закон C8.22а) к контуру ABXCXDA (рис. 151). Интеграл не равен нулю
только на участке В\С± и поэтому
HBiCl = nil, C8.38)
поскольку поверхность, ограниченную контуром AB^^DA, пересекают
nl витков с током /. Из C8.38) видно, что поле внутри соленоида
однородно и его напряженность равна
Я = nl. C8.39)
Эта формула позволяет измерять напряженность магнитного поля
в ампер-витках, что часто используется в технике. Из C8.39) видно,
что напряженность магнитного поля внутри соленоида не зависит от
его материала и при прочих равных условиях одинакова для всех
материалов. Индукция же поля внутри соленоида с учетом C8.24)
и C8.39) равна
В = цН = цп1 C8.40)
и зависит от материала сердечника. Для диамагнетиков она меньше,
чем индукция в полом соленоиде, а для парамагнетиков — больше.
Индукция поля бесконечно длинного однородно намагниченного
цилиндра находится аналогично с той лишь разницей, что поверх-
поверхностные токи отсутствуют. Соотношение C8.37) не изменяется и
напряженность поля вне цилиндра, так же как и в случае бесконечно
длинного соленоида, равна нулю. Вместо формулы C8.38) получаем
HI = 0 или Н = 0. Это означает, что напряженность поля внутри
бесконечно длинного однородно намагниченного цилиндра равна нулю,
в то время как в соленоиде она не равна нулю. Однако индукция
внутри цилиндра не равна нулю (В = ц0Л). Если длина цилиндра
276 6. Стационарное магнитное поле
конечна, напряженность магнитного поля
отлична от нуля как внутри, так и вне
р^змерение магнитной проницаемости, ин-
индукции и напряженности поля внутри
магнетика. Представим себе бесконечный
соленоид, в сердечнике которого параллель-
параллельно оси соленоида сделан бесконечно узкий
канал (рис. 152). Поле внутри соленоида
создается током в обмотке. В канал вводится
измерительная катушка, соединенная с галь-
гальванометром. Граничное условие C8.35) по-
показывает, что напряженность в канале равна
нитиого поля внутри магнетика напряженности в магнетике. Индукция в ка-
нале равна В, = ц0Н. Ее можно измерить,
повернув петлю на 90° или включив поле.
Напряженность поля внутри магнетика вы-
вычисляется по формуле
Н = Вц/К. C8.41)
Измерение напряженности маг-
Для измерения индукции внутри магне-
магнетика сделаем небольшой поперечный разрез
в бесконечном соленоиде (рис. 153). Гранич-
Граничное условие C8.33) показывает,. что в этом
разрезе индукция В L равна индукции В
внутри магнетика. Поэтому достаточно из-
измерить индукцию в поперечном разрезе.
Зная индукцию и напряженность поля
в магнетике, можно определить магнитную
проницаемость:
Вц. C8.42)
Измерение индукции магнитного
поля внутри магнетика
О Почему диамагнетизм пара-
парамагнетиков мал по сравне-
сравнению с парамагнетизмом?
Дайте количественные оцен-
оценки.
Каким образом можно из-
измерить индукцию и напря-
напряженность магнитного поля
внутри магнетика?
Щар из магнетика в однородном поле.
Допустим, что шар радиусом R из магне-
магнетика с магнитной проницаемостью nt поме-
помещен в бесконечную среду с магнитной про-
проницаемостью ц2» в которой создано одно-
однородное магнитное поле с напряженностью
Но (рис. 154, а, б). Требуется определить
напряженность магнитного поля как внутри
шара, так и вне его. Предполагается, что
токи проводимости отсутствуют.
Уравнение C8.22) в этом случае имеет вид
rot H = 0, C8.43)
т. е. магнитостатическое поле в простран-
пространстве, в котором отсутствуют токи прово-
§ 38. Магнитное иоле при наличии магнетиков 277
димости, является потенциальным. Токи
проводимости отсутствуют как внутри шара,
так и вне его, и, следовательно, поле
потенциально во всем пространстве. Обозна-
Обозначим фт — потенциал этого поля. Тогда
H=-grad(pm. C8.44)
Для однородной среды (ц = const) урав-
уравнение div В = 0 эквивалентно уравнению
div H = 0. C8.45)
Подставляя C8.44) в C8.45), получаем для
всех точек вне шара (ц2 = const) и для всех
точек внутри шара (ц! = const) уравнение
У2фга = 0. C8.46)
Таким образом, потенциал магнитного
поля удовлетворяет уравнению Лапласа.
Отметим, что если магнитная восприим-
восприимчивость не является постоянной, то вместо
C8.46) получается другое уравнение. Для его
вывода примем во внимание равенство
C8.21), которое можно записать в виде
В = ц0Н + М- C8.47)
Взяв от обеих частей этого равенства
дивергенцию, получим
div В = ц0 div Н + Цо div J =
= -|х0 div grad q>m + u0 div J = 0, C8.48a)
где учтено соотношение C8.44) и уравнение
div В = 0. Следовательно, уравнение для фт
имеет вид
V2q>m = divJ, C8.486)
что значительно усложняет решение задачи
для магнетика с изменяющейся магнитной
восприимчивостью.
Поместим начало координат в центр
шара и направим полярную ось сферической
системы координат в направлении вектора
Но. Вследствие аксиальной симметрии урав-
уравнение Лапласа C8.46) принимает вид A7.42).
Это уравнение надо решить при граничных
условиях C8.33) и C8.25) на поверхности
шара, полностью совпадающих с гранич-
граничными условиями для ?>„ и ?, [см. A7.42)].
154
Шар ю магнетика в однород-
однородном магнитном поле
155
Магнитная экранировка
О Перечислите обстоятель-
обстоятельства, благодаря которым Н
играет в теории магнитного
поля такую же роль, как D
в теории электрического
поля.
278 6. Стационарное магнитное поле
Поскольку поверхностные токи проводимости отсутствуют, в C8.35)
можно положить in0B = 0. Поэтому решение этой задачи аналогично
решению задачи о диэлектрическом шаре в однородном электрическом
поле. Надо лишь в решении уравнения A7.42) заменить <р-крт, Е-»Н,
D -> В, е -» ц.
Напряженность магнитного поля внутри шара постоянна и анало-
аналогично A7.51) равна
Я** = „ Уз,, Я°- C8'49)
Hi + 2Иг
Она является суммой напряженностей внешнего поля Но и поля,
созданного шаром в результате его намагничивания. Поле, созданное
внутри шара за счет его намагничивания, называется «размагничи-
«размагничивающим полем Нразм». Это название условно, поскольку никакого
«размагничивания» нет, а есть просто намагничивание магнетика во
внешнем поле и создание этим намагниченным магнетиком дополни-
дополнительного поля, складывающегося с первоначальным. Но поскольку
название поля Яразм установилось, приходится им пользоваться. Тогда
Яразм = Hlz -Но= ^~^2 "о- C8.50)
Это выражение можно записать в ином виде. На основании C8.26)
с учетом C8.26) имеем
Ji = WHo - 1) Н1в J2 = (И2/И0 - 1) Яо, C8.51)
j j (Иг ~ Hi) (Но + 2ц2) „ пят
J2- Jt = —г—г Яо. C8.52)
Н (H + 2Н)
откуда
Hi) (Но + 2ц2)
—г—г
Но (Hi + 2Нг)
Следовательно, формула C8.50) может быть представлена в виде
Яраэм = [ноЛНо + 2н2)] (Jz ~ Ji). C8.53)
В частности, если шар находится в вакууме, то ц2 = Но и ^2 = 0,
поэтому
|У|агнитная экранировка. Из C8.50) видно, что при Hi > H2 магнитное
поле внутри шара ослабляется, т. е. шар как бы экранирует свою
внутреннюю часть от внешнего магнитного поля. Если рассчитать
индукцию поля внутри полости, окруженной оболочкой из магнетика
с достаточно большой проницаемостью (хь то получается, что магнит-
магнитные линии концентрируются в основном в оболочке (рис. 155), не
проникая внутрь полости. Это означает, что оболочка из магнетика
с большим ц действует как экран, не допускающий проникновения
магнитного поля в пространство, ограничиваемое оболочкой.
Пример 38.1. Вдоль оси бесконечного прямого круглого цилиндра радиусом
а течет линейный ток силой I. Магнитная проницаемость вещества ци-
§ 38. Магнитное поле при наличии магнетиков 279
линдра ц. Вне цилиндра — свободное простран-
пространство. Найти напряжешюстъ магнитного поля,
индукцию и намагниченность во всех точках
пространства.
Направим ось Z декартовой системы коор-
координат вдоль оси цилиндра в направлении тока /
(рис. 156). Выберем в качестве контура интегри-
интегрирования L окружность радиусом г, концентри-
концентрическую с током и лежащую в плоскости, перпен-
перпендикулярной току. Тогда напряженность магнит-
магнитного поля во всех точках определяется из закона
полного тока:
| Н • dl = Яр2яг = /,
L
откуда
Я, = 1/Bпг) C8.54)
— напряженность магнитного поля, направленная
по касательной к окружности. Линиями напряжен-
напряженности являются окружности, концентрические
с током.
Индукция равна
^ @ < г < а),
C8.55)
(а < г).
2кг
2пг
Но
Мо
2яг
(а < г).
jM = rot J = -ir
8z
_ _j_ i
r
dr
(У- ~ Цо)
К определению поля
кутего по цилиндру
тока, те-
кругового
Намагниченность удобно найти из соотношения
C8.21):
C8.56)
Объемиую плотность молекулярных токов
найдем с помощью C8.10). Принимая во внима-
внимание, что намагниченность дана в C8.56) в ци-
цилиндрических координатах, удобно вычисление
ротора в C8.10) также проводить в цилиндриче-
цилиндрических координатах. Имеем
C8.57)
Таким образом, объемные молекулярные то-
токи отсутствуют. Однако имеется поверхностный
молекулярный ток, плотность которого на основе
C8.17) с учетом C8.56) равна
C8.58)
Молекулярные токи в бук-
буквальной смысле могут
течь только внутри моле-
молекул. Однако в подели не-
непрерывной среды речь
идет об усредненных по
бесконечно малый объе-
объемам величинах и поэтому
молекулярные токи пред-
представляются текущими по
объеиу магнетика, как в
непрерывной среде.
По своему значению на-
напряженность магнитного
поля играет такую же
роль в теории магнитного
поля, как смещение в тео-
теории электрического поля.
У диамагнетикоВ намагни-
намагниченность направлена про-
против напряженности маг-
магнитного поля, а индукция
внешнего поля умень-
уменьшается.
У парамагнетиков намаг-
намагниченность направлена по
напряженности магнитно-
магнитного поля, а индукция внеш-
внешнего поля усиливается.
Классическая теория не
может объяснить ферро-
ферромагнетизм, но она в со-
состоянии описать магнит-
магнитное поле вне ферромагне-
ферромагнетиков, если считать на-
намагниченность ферромаг-
ферромагнетика известной.
280 6. Стационарное магнитное поле
§ 39. Силы в магнитном поле
Рассматриваются силы, действующие на то-
токи, и объемные силы, действующие на несжи-
несжимаемые магнетики.
, действующие на ток.
dF = j x BdF=/dl x В,
= Jj x BdF=f/dl x В.
C9.1а)
C9.16)
Лоренца. На точечный заряд q, движущийся со скоростью v,
действует сила
F = q\ х В,
C9.2)
причем q включает в себя знак заряда, т. е. может быть как поло-
положительной, так и отрицательной величиной. Формула C9.2) получается
из C9.16), если учесть, что j = nq\dV= pvdF, где р - объемная плот-
плотность зарядов и, следовательно, pdF заряд в объеме dV, a JpdF=<j.
? и момент сил, действующие на магнитный момент. Допустим,
что круговой элементарный ток, создающий магнитный момент,
течет по квадратной рамке со стороной /. Поместим начало коорди-
координат в центр квадрата и направим ось Z перпендикулярно плоскости
рамки (рис. 157). Направление тока / в рамке указано стрелками.
Магнитное поле произвольно, посторонние токи и ферромагнетики
в области рамки отсутствуют (div В = 0, rot В = 0). Определим силу
и момент сил, действующих на магнитный момент рамки с током.
Размеры рамки малы и необходимо учитывать изменение индукции
магнитного поля в пределах рамки лишь до величин первого порядка
малости относительно размеров рамки.
В соответствии с формулой C9.1а) на стороны АВ, ВС, CD, DA
рамки со стороны магнитного поля действуют силы:
FAB = Iliy х В (У/2), FBC = П [-ix х В(у/2)],
Fcd = Л [-i, х B(-U/2)], FDA = II [ix x В (-у/2)],
где ix, ij, — единичные векторы в направлении осей X и У. В аргу-
аргументах В указаны расстояния от центра рамки до соответствующих
сторон с учетом направления. Полная сила, действующая на рамку,
равна
F = ?АВ + FBC + FCD + FDA = 1Пу x [В(У/2) - B(-i,//2)] +
+ /fixx[B(-y/2)-B(y/2)]. C9.3)
§ 39. Силы в магнитном поле 281
Учитывая, что с сохранением лишь чле-
членов первого порядка малости
преобразуем C9.3) к виду
8В
дх
су
157
C9.4) к расчету действия силы на
магнитный момент
Учитывая, что II2 = рт — абсолютное зна-
значение магнитного момента рамки с током,
а также принимая во внимание хорошо
известные соотношения между единичными
координатными векторами (ix х \у = iz, i, x
х \z = ix, \z x ix = iy), преобразуем C9.4) к
виду.
F = (Pra X 1J X —r + (pm X ly) X —-,
6Л Cy
где pm = ijpm — магнитный момент рамки.
С помощью разложения двойного вектор-
векторного произведения по формуле векторной
алгебры А х (В х С) = В (А • С) - С (А • В) по-
получаем
F = 1Л Р„
дх
дх
дВ
дх
¦ +
C9.5)
где ix • (дВ/дх) = 8Вх/8х, i, ¦ {бВ/ду) = дВу/8у.
Так как div В = dBJdx + 8Ву/8у + 8BJ8z =
= 0, то
~V
дх ду
Л_
" dz
дВ
= 1ИРт' я,
• Сила на магнитный мо-
момент действует лишь в не-
неоднородной нагнитнон
поле.
Момент, сил, возникаю-
возникающий в результате дейст-
действия магнитного поля на
нагнитный момент, стре-
стремится повернуть нагнит-
нагнитный нонент до совпаде-
совпадения с векторон магнит-
магнитной индукции поля.
Объемные силы, действу-
действующие на парамагнетик,
направлены в сторону уве-
увеличения индукции магнит-
магнитного поля, а у дианагие-
тиков — в сторону умень-
уменьшения.
О Как изменяется действие сил
иа магнетик, если магнитная
проницаемость среды отли-
отличается от магнитной по-
постоянной и становится боль-
больше или меньше магнитной
проницаемости магнетика?
282 б. Стационарное магнитное поле
откуда
C9.6)
Эта формула показывает, что на магнитный момент сила действует
лишь в неоднородном поле. Поскольку формула C9.6) выражает силу
через магнитный момент рт, выбранная выше специальная форма
контура тока не играет роли и C9.6) справедлива для произвольного
магнитного момента, пространственные размеры которого достаточно
малы.
Для вычисления момента сил, действующих на магнитный момент,
поступаем аналогично. Помещаем начало координат в центр рамки
и вычисляем момент сил по формуле
М = / J г х (dl х В). C9.7)
L
Однако теперь вычисления упрощаются, поскольку расстояние г
имеет порядок размеров I рамки и величину В надо учитывать только
в нулевом порядке по размерам рамки, т. е. считать постоянной.
В результате получаем
М = рт х В.
C9.8)
Эта формула показывает, что момент сил стремится повернуть
магнитный момент до совпадения с вектором магнитной индукции поля.
Объемные силы, действующие на несжимаемые магнетики. Поскольку
элемент объема dV магнетика с намагниченностью J обладает
магнитным моментом
dPm = J dV, C9.9)
на него [см. C9.6)] действует сила
dFx = J• —-dV, dF., = J • ~^-dV, dFz = J • ~^dV. C9.10)
ex oy cz
Очевидно, что эти выражения справедливы во всяком случае для
жестких магнетиков, поскольку формула C9.6) получена в результате
дифференцирования при pm = const.
Представим C9.10) в векторном виде. Учитывая, что
C9.11)
B,
Wo
находим для объемной плотности силы выражение
dFx ц - ц0 дВ 1 ii-по дВ2
f*-~dv = -^ в^ = Т1и7Г"^Г C9Л2)
и т. д. Таким образом, объемная плотность силы, действующей на
магнетик, равна
§ 39. Силы в магнитном поле 283
1 И-Но
grad В2.
158
Выталкивание диамагнитного те-
C9.13)
Это означает:
а) у парамагнетиков ц > ц0 « поэтому
объемная плотность силы направлена в сто-
сторону увеличения индукции поля;
б) у диамагнетиков ц < ц0 и поэтому
объемная плотность силы направлена в сто-
сторону уменьшения индукции поля.
Различное поведение пара- и диамагнети- ла из области максимального
ков в одном и том же поле очень наглядно поля
демонстрируется многими опытами. Пусть
магнитное поле создается в вакууме между
полюсами сильного магнита (рис. 158). Ясно,
что между полюсами магнита индукция поля
убывает от центральной линии, соединяю-
соединяющей полюса, к периферии. Легкий висмуто-
висмутовый шарик, являющийся диамагнитным те-
телом, выталкивается из области поля с мак-
максимальной индукцией (рис. 158). Парамаг-
Парамагнитная жидкость, например водный раствор
хлорного железа, втягивается в область поля
с максимальной индукцией (рис. 159).
Если пространство между полюсами маг-
магнита заполнено материальной средой, то
направление сил зависит от соотношения 159
магнитных проницаемостей среды и тела.
г, г Втягивание парамагнитной жид-
Если магнитная проницаемость тела больше, кости в область максимального
чем среды, то оно ведет себя как парамаг- поля
нетик, если меньше — то как диамагнетик.
Например, если между полюсами магнита
поместить парамагнитную жидкость с доста-
достаточно большой проницаемостью (рис. 160),
то на парамагнитный шарик, проницаемость
которого меньше, чем жидкости, сила дей-
действует так же, как на диамагнитный шарик
в вакууме.
Пример 39.1. По кольцу радиусом г0 из очень
тонкой проволоки течет ток силой I. Прочность
проволоки на разрыв равна /0. Кольцо помещено 160
в магнитное поле, индукция которого перпендику-
' . „ г Парамагнитное тело в парамаг-
лярна плоскости кольца, так, что действующие нитной среде с большей> чем
силы стремятся разорвать кольцо. Определить у тела> магнитной проницаемос-
индукцию, при которой кольцо разорвется. Ври- тью ведет себя как диамаг-
нять, что /0 = 1,5 Н; г0 = 15 см; / = 10 А. нитное тело
284 6. Стационарное магнитное поле
Силы на кольцо действуют по радиусу. Обозначая dl — элемент длины
кольца, находим, что элемент силы, действующей на элемент dl в радиальном
направлении, равен dF = / dl х В. Проведем через центр кольца в его плоскости
ось X. Проекция элемента силы dF на ось X равна dFx = dF cos a = IB d/ cos а,
где а — угол между осью X и радиусом, проведенным к элементу dL
Так как dl = r0 da, то выражение для силы, действующей на полукольцо
я/2
в направлении положительных значений оси X, равно Fx = IBr0 J cos a da =
-я/2
= 2IBr0. Эта сила распределяется на два сечения провода в местах его пере-
пересечения с осью Y. Поэтому условие разрыва имеет вид 21Вг0 = 2/0 и, сле-
следовательно, В = fo/(Iro) = 1 Тл.
Задачи
6.1. Имеется медная спираль радиусом
а и плотностью п витков на 1 м.
Витки намотаны так, что между
ними имеются очень маленькие
зазоры. Верхний конец спирали
закреплен, а нижний конец соеди-
соединен с проводящим грузом массой
т, лежащим на металлическом
столе. Никакие силы упругости
со стороны спирали на груз в этом
положении не действуют. Считая,
что зазоры между витками спира-
спирали уменьшаются равномерно, оп-
определить силу тока, который дол-
должен быть пропущен через спираль
для того, чтобы поднять груз со
стола. Массой спирали пренебречь.
6.2. Два маленьких магнита с одина-
одинаковыми магнитными моментами
рт и массами т подвешены на
легких длинных нитях. Расстояние
d между точками подвеса очень
велико. Длины нитей одинаковы.
Показать, что магниты сориенти-
сориентируются так, что будут притяги-
притягиваться друг к другу. Определить
угол отклонения нитей от верти-
вертикального направления. Влиянием
магнитного поля Земли пре-
пренебречь.
6.3. Сфера радиусом я, равномерно
заряженная с поверхностной плот-
плотностью заряда сг, вращается вокруг
оси, проходящей через центр сфе-
сферы, с угловой скоростью со. Найти
магнитную индукцию в центре
вращающейся сферы.
6.4. Чему равен магнитный момент,
создаваемый точечным зарядом q,
движущимся по окружности ра-
радиусом г0 с постоянной угловой
скоростью со?
6.5. В пространство между полюсами
постоянного магнита, в котором
существует магнитное поле Но,
вдвинута пластина из магнетика
с магнитной проницаемостью ц
(рис. 161). Найти силу, действую-
действующую на магнетик.
К вычислению силы взаимо-
взаимодействия между магнитами
6.6. Найти силу в задаче 6.5, если
пластина является постоянным
магнитом, намагниченность кото-
которого Jn совпадает по направлению
с Яо.
Задачи 285
6.7. Найти силу, с которой однород-
однородный поверхностный ток плот-
плотностью in0B, текущий по беско-
бесконечной плоскости, действует на
длине / параллельного ему тока
силой /, протекающего по беско-
бесконечному линейному проводнику
на расстоянии d от плоскости.
Обозначить п — нормаль к пло-
плоскости в направлении линейного
проводника.
6.8. Ток силой /х течет по кольцевому
проводнику радиусом а, лежащему
в плоскости (х, у) с центром а на-
начале координат, и составляет пра-
правый винт с положительным на-
направлением оси Z. Ток силой /2
течет по бесконечно длинному
прямому проводнику параллельно
оси X в направлении ее положи-
положительных значений, пересекая ось
Z в точке z = d. Определить силу,
действующую на прямолинейный
ток.
6.9. Найти магнитную индукцию в
центре соленоида длиной L с п
витками, имеющего квадратное
сечение со стороной а. Сила тока,
текущего по обмотке соленоида,
равна /.
6.10. Диск радиусом г вращается с уг-
угловой скоростью со вокруг оси,
перпендикулярной поверхности
диска и проходящей через его
центр. Найти индукцию магнит-
магнитного поля на оси вращения диска
на расстоянии h от его плоскости.
Поверхностная плотность заряда
равна ст.
6.11. Поляризованный диэлектриче-
диэлектрический шар радиусом а вращается
с угловой скоростью ю вокруг
оси, проходящей через его центр.
Поляризованность Р постоянна и
совпадает по направлению с со.
Найти магнитную индукцию в
точках пересечения поверхности
шара с осью вращения.
6.12. Бесконечный прямолинейный ци-
цилиндрический пучок кругового
поперечного сечения радиусом а
с постоянной объемной плот-
плотностью заряда р движется в
направлении своей оси со ско-
скоростью v. Найти магнитную
индукцию.
6.13. По бесконечному прямолинейно-
прямолинейному цилиндрическому проводнику
радиусом а, ось- которого совпа-
совпадает с осью Z декартовой систе-
системы координат, течет ток силой /
в положительном направлении
оси Z. Найти векторный потен-
потенциал.
6.14. Найти аксиальную составляю-
составляющую векторного потенциала в
центре спирали, по которой течет
ток силой /. Данные о спирали
приведены в задаче 1.7.
6.15. Диэлектрический шар радиусом
а вращается с угловой скоростью
со вокруг оси, проходящей через
его центр. Постоянная объемная
плотность заряда шара равна р.
Найти индукцию внутри шара на
оси вращения.
6.16. Однородно заряженный круглый
цилиндр радиусом а и длиной /,
заряд которого Q, вращается с
угловой скоростью со вокруг сво-
своей оси. Найти его дипольный
магнитный момент.
6.17. Найти в диполыюм приближении
взаимную индуктивность двух
круговых токов радиусами а^ и
а2, лежащих в одной плоскости.
Расстояние между витками рав-
равно г.
6.18. Ось прямого круглого цилиндра
совпадает с осью Z декартовой
системы координат, начало кото-
которой находится в центре цилиндра.
Цилиндр однородно намагничен.
Вектор намагниченности совпа-
совпадает с положительным направ-
направлением оси Z: J = Лг. Найти
магнитную индукцию па оси ци-
цилиндра, если радиус его попереч-
поперечного сечения а, а длина /.
6.19. Сферический слой из магнетика,
радиусы внутренней и внешней
концентрических поверхностей
которого равны гг и г2, одно-
однородно намагничен. Вектор на-
намагниченности параллелен оси Z
286 6. Стационарное магнитное поле
декартовой системы координат,
центр которой совпадает с цент-
центром поверхностей, и равен Jiz.
Найти напряженность магнит-
магнитного поля на оси Z для поло-
положительных значений г.
6.20. Прямой цилиндр, длина которого
/, а радиус кругового сечения а,
однородно намагничен. Вектор
намагниченности параллелен оси
цилиндра и равен J. Найти маг-
магнитную индукцию в центре ци-
цилиндра, считая / » а.
6.21. Сфера с поверхностной плот-
плотностью заряда а вращается во-
вокруг своего диаметра с угловой
скоростью со. Найти ее магнит-
магнитный дипольный момент.
6.22. Ток силой / течет по бесконеч-
бесконечному прямолинейному провод-
проводнику, параллельному плоской по-
поверхности раздела между средой
с магнитной проницаемостью ц0,
в которой находится проводник
с током, и средой с магнитной
проницаемостью ц. Найти силу,
6.23.
6.24.
действующую на участок I про-
проводника. Расстояние от провод-
проводника до поверхности раздела
равно d.
На поверхность деревянного ша-
шара намотаны очень плотно в
один слой витки тонкой прово-
проволоки. Плоскости всех витков мож-
можно считать перпендикулярными
одному и тому же диаметру
шара. Витки покрывают всю по-
поверхность шара. Радиус шара а,
полное число витков п. По об-
обмотке протекает ток силой /.
Найти магнитную индукцию в
центре шара.
В цилиндрическом проводнике
радиусом а имеется цилиндри-
цилиндрическая полость радиусом Ь, ось
которой параллельна оси про-
проводника и расположена на рас-
расстоянии d от нее. По провод-
проводнику протекает ток с объемной
плотностью j. Найти магнитную
индукцию в точках диаметра по-
полости, совпадающего с диамет-
диаметром проводника.
6Л. / =
Ответы
l
/
па у яц0
6.5. Fx = 7г (И - Но
. 6.2. 8=——^— . 6.3. В=73иостасо. 6.4. pm = qar2,/2.
2 тгцо<Г mg
6.6. Fx = ц0</. (Яо + Jn) Id. 6.7.
6.9.
F= -'
В = \ionlA arcsin l2u г
при 0 < г < а, В =
х r/r2 при а < г < со. 6.13. Аг =
— — ^т r-+ const при r < a, Az~ ^—In r + const при a < r < со, где г =
Л.ТР .т^ /it
6.17. L12 = 7tuoa?a2/Dr3). 6.18. Вг=-^-
+ Jt2n2tg2a). 6.15. 0. 6.16. Qa2<a/4.
z + l/2 z- 1/2
2 \ \/a2 + (z + 1/2J l/72 + (z-//2J
6.19. H2 = 0 при 0 < z <ru Hz = -
J(g
при
< z < n, Hz = 2J (rl -
-r?)/Cz3) при rz<z< oo. 6.20. B = u0J(l -a2//2). 6.21.
6.22. f = - HeL ^ ~ ^o ji 623 ИоП/д4а). 6.24. Ha/d/2.
§ 40
Диамагнетики
§41
Парамагнетики
Магнетики
§42
Ферромагнетики
Феноменологически свойства магнети-
магнетика в магнитном поле учитываются
посредством магнитной проницаемости
р.. Зависимости ц от различных па-
параметров весьма многообразны, как
многообразны сами магнетики. Эти за-
зависимости интерпретируются построе-
построением моделей магнетиков, учитываю-
учитывающих особенности их поведения в
магнитном поле.
§43
Гиромагнитные эффекты
288 7. Магнетики
§ 40. Диамагнетики
Обсуждаются физическая природа диамаг-
диамагнитной восприимчивости и ее свойства.
Л арморова прецессия. В магнитном поле частота вращения электронов
в атоме отличается от их частоты вращения при отсутствии маг-
магнитного поля. Чтобы в этом убедиться, рассмотрим простейший слу-
случай, когда при отсутствии магнитного поля электрон движется вокруг
ядра по круговой орбите радиусом г и частота его вращения равна ю0
(рис. 162). Уравнение Ньютона для движения электрона имеет вид
Fu, D0.1)
где Fu - центростремительная сила, возникающая в результате притя-
притяжения электрона ядром. Эта сила весьма велика по сравнению с сила-
силами, которые могут действовать на электрон со стороны внешних
полей, поэтому радиусы орбит электронов при помещении атома во
внешние поля не изменяются. Атом в отношении действия внешних
полей можно с большой точностью рассматривать как жесткий.
Теперь пусть атом находится во внешнем поле, вектор индукции
В которого перпендикулярен плоскости орбиты электрона. Сила Лорен-
Лоренца действует. вдоль радиуса, а по направлению либо совпадает с
центростремительной силой, либо противоположна ей в зависимости от
относительной ориентировки векторов угловой скорости движения
электрона по орбите и магнитной индукции. Эта сила равна по абсо-
абсолютному значению
F = | е | (огВ, D0.2)
где е — заряд электрона; ю — частота вращения электрона по орбите в
магнитном поле, отличная от ю0.
Уравнение движения электрона в магнитном поле имеет вид
тю2г = Fu ± | е | югВ, D0.3)
где радиус г орбиты электрона тот же, что и в D0.1), а знаки (±)
выбираются в соответствии с относительной ориентировкой векторов
угловой скорости движения электрона по орбите и магнитной индукции.
Центростремительная сила Fn в D0.3), конечно, та же самая, что и в
D0.1), поскольку это сила притяжения со стороны ядра, а расстояние г
не изменилось. Исключая из D0.1) и D0.3) Рц, получаем
тю2г — та^г = ± \ е \ ожВ. D0.4)
Учитывая, что ю2 — Юц = (со — ю0) (ю + ю0) « 2Дюю, где | Дю | =
= | ю — ю0 | <с ю, из D0.4) находим
Дю = + | е | В/Bт). D0.5)
§ 40. Диамагнетики 289
Таким образом, в магнитном поле элект-
электрон приобретает дополнительную угловую
скорость движения, характеризуемую часто-
частотой
= | в | В/{2т),
D0.6)
которая называется ларморовой. Направле-
Направление вектора угловой скорости определить
нетрудно. Например, если индукция В (см.
рис. 162) направлена противоположно угло-
угловой скорости движения электрона вокруг
162
Возникновение дополнительной
угловой скорости вращения элек-
ядра, то сила F направлена против Fu и,
следовательно, скорость электрона и частота ;ро11ов в мгагнит1!огм"поле^
вращения должны уменьшиться. Это озна-
означает, что oL совпадает с направлением В.
Если направление В противоположно перво-
первоначальному, то придем к такому же заклю-
заключению. Поэтому можно записать
,,= -еВ/Bт\
D0.7)
где учтено, что заряд электрона е отрица-
отрицателен. Образование этой дополнительной
угловой скорости вращения без изменения ра-
радиуса орбиты можно себе представить в виде
дополнительного вращения атома как целого
с частотой mL в магнитном поле. Полная
частота вращения электрона равна сумме его
частоты вращения о>0 в атоме и частоты вра-
вращения a>L атома. Все это справедливо лишь
для случая, когда векторы угловой скорости
и индукции магнитного поля коллинеарны.
Поскольку скорость электрона в атоме,
помещенном в магнитное поле, изменяется,
то изменяется и его кинетическая энергия.
С другой стороны, поскольку г остается
неизменным, потенциальная энергия не изме-
изменяется. Спрашивается, за счет чего измени-
изменилась энергия электрона в атоме, если извест-
известно, что магнитное поле действует всегда
перпендикулярно скорости и не производит
работы? Ответ на этот вопрос может быть
дан только в рамках теории электромагнит-
электромагнитной индукции (см. гл. 8): при возникновении
магнитного поля порождается электрическое
поле, под действием которого изменяется
скорость движения электронов в атоме.
10 А. Н. Матвеев
163
Ларморова прецессия (а); воз-
возникновение парамагнитного ре
зонанса F)
290 7. Магнетики
Чтобы представить себе, каким будет движение атома при произ-
произвольной взаимной ориентации угловой скорости вращения электрона
вокруг ядра и индукции внешнего поля, обобщим полученные резуль-
результаты на произвольный случай. Атом с движущимся в нем по окруж-
окружности электроном можно рассматривать как гироскоп, обладающий
магнитным моментом. Момент импульса электрона равен тюг2. Дви-
Движущийся по орбите электрон эквивалентен круговому току силой
е/Т = ео)/Bл) и, следовательно, магнитный момент атома равен
пг2с(а/Bп). С учетом направления механического и магнитного момен-
моментов атома, обусловленных движением электрона, запишем:
L = mr2w, pm = (er2/2)o). D0.8)
Здесь учтено, что заряд е электрона отрицателен, а механический мо-
момент L и магнитный момент рт имеют противоположные направле-
направления (рис. 163, а).
Уравнение движения атома, рассматриваемого как гироскоп, имеет
вид
~ = М, D0.9)
где М — момент сил [см. C9.8)]. Из D0.8) следует, что
pm = eL/Bm) D0.10)
и, следовательно, уравнение D1.9) принимает вид
^=АхВ=-^-Вх1. D0,11)
dt Ъп 2т
Сравнение D0.11) с уравнением движения точек абсолютно твер-
твердо! о тела, вращающегося с угловой скоростью о,
v = dr/ck = »х г D0.12)
показывает, что конец вектора L движется вокруг направления вектора
индукции с частотой
oL= -eB/Bm). D0.13)
Следовательно, атом совершает в магнитном поле, подобно гироскопу,
прецессионное, движение (рис. 163,6). Оно называется ларморовои пре-
прецессией.
Диамагнетизм, в результате ларморовои прецессии от каждого элект-
электрона в атоме возникает круговой ток, который с направлением вектора
индукции магнитного поля составляет левовинговую систему. Следо-
Следовательно, создаваемая этим круговым током дополнительная индукция
магнитного поля направлена навстречу вектору индукции внешнего
магнитного поля. Магнитный момент атома, возникающий в резуль-
результате прецессии, и намагниченность также направлены противоположно
вектору индукции внешнего магнитного поля. Эта картина возникнове-
§ 40. Диамагиетикн 291
ния ларморовой прецессии и связанных с
ней магнитного момента и дополнительно-
дополнительного магнитного поля составляет сущность яв-
явления диамагнетизма. Очевидно, что диамаг-
диамагнетизмом обладает любое вещество. Вопрос
заключается лишь в оценке его величины.
/Т иамагнитная восприимчивость. Каждый
электрон в атоме совершает ларморовское
движение вокруг оси, совпадающей с направ-
направлением магнитного поля (рис. 164). Возни-
Возникающий вследствие этого магнитный момент
равен
pmi. = S,l, = nrfe/T = erfiajl,
164
откуда
D0.14) к вычислению
юсприимчивости
диамагнитной
где N — концентрация атомов. В D0.15) ис-
использовано выражение для ларморовой час-
частоты, а под знаком среднего стоит сумма
квадратов расстояний электронов в атоме от
оси ларморовой прецессии. На рис. 164
видно, что
Rf = xf + yf + zf, D0.16)
где Rj — расстояние электрона от ядра. При-
Принимая во внимание беспорядочную ориенти-
ориентировку атомов в пространстве, имеем
<А?> = <У.2> = <z,2> = Я,?>/3 D0.17)
и, следовательно,
<'¦?> = <4 + yf) = 2 <R?>/3 = 2 <R2>/3,
откуда
D0.18)
D0.19)
где Z — число электронов в атоме. Поэтому
окончательно для намагниченности получаем
формулу
J = -~NZ(R2) цН. D0.20)
J =
от
Сравнивая D0.20) с формулой
D0.21)
Изменение частоты вра-
вращения электронов в ато-
атоме, обусловливающее диа-
диамагнетизм, возникает при
изменении индукции маг-
магнитного поля во время
внесения атома в магнит-
магнитное поле или во время
возникновения магнитного
поля. Сап о по себе маг-
магнитное поле не произво-
производит работы и не в со-
состоянии изменить ско-
скорость движения электро-
электронов в атоме.
Диамагнитная восприим-
восприимчивость не зависит от
температуры, поскольку
тепловое движение и стол-
столкновения атомов не выво-
выводят их на сколько-нибудь
заметное время из состоя-
состояния ларморовой прецес-
прецессии.
10*
292 7. Магнетики
получаем для диамагнитной восприимчивости выражение
2
Хд= -^-#2<Кг>ц0, D0.22)
глс учтено, что ц % ц0, поскольку у диамагнетиков проницаемость
лишь незначительно отличается от проницаемости вакуума. Формула
D0.22) хорошо согласуется с экспериментом, если под (Я2) понимать
средний квадрат расстояния электронов от ядра в атоме, вычислен-
вычисленный по квантовой теории. Для твердых тел и жидкостей диамагнитная
восприимчивость имеет порядок ~10~5, а для газов она значительно
меньше из-за меньшей концентрации атомов [т. е. меньших значений N
в формуле D0.22)].
Независимость диамагнитной восприимчивости от температуры.Фор-
температуры.Формула D0.22) показывает, что %д не зависит от температуры, потому
что ни одна из входящих в эту формулу величин не может зависеть
от температуры. Это объясняется тем, что ларморовское движение
электронов устанавливается очень быстро, за характерные для атомных
процессов промежутки времени. Поэтому тепловое движение и столкно-
столкновения атомов не выводят их ни сколько-нибудь заметное время из
состояния ларморовой прецессии. Это хорошо подтверждается экспери-
экспериментом. Независимость диамагнитной восприимчивости от темпера-
температуры была открыта экспериментально в 1895 г. П. Кюри A859-1906).
§ 41. Парамагнетики
Обсуждаются физическая природа парамаг-
парамагнитной восприимчивости и ее свойства. Опи-
Описываются магнетизм, обусловленный сво-
свободными электронами, и парамагнитный ре-
резонанс.
{У^ намагничивания. Парамагнетиками являются вещества,
молекулы которых обладают постоянными магнитными моментами.
Энергия магнитного момента во внешнем магнитном поле равна
W = - pm В. D1.1)
Минимум энергии достигается при совпадении рт с направлением
вектора индукции, благодаря чему при внесении парамагнетика в маг-
магнитное поле в соответствии с распределением Больцмана возникают
преимущественная ориентация магнитных моментов его атомов в
направлении индукции и соответствующее намагничивание. Индукция
дополнительного магнитного поля за счет намагничивания совпадает
по направлению с индукцией внешнего поля и усиливает ее. Однако
угол между направлением магнитного момента атома и индукцией
магнитного поля под действием поля не изменяется: магнитный
момент испытывает лишь прецессионное движение вокруг направления
вектора индукции без изменения угла между ними [см. D0.11)].
§ 41. Парамагнетики 293
Переориентировка магнитных моментов в соответствии с распреде-
распределением Болъцмана происходит в результате столкновений и взаимо-
взаимодействий атомов между собой.
'i ависимость парамагнитной восприимчивости от температуры. Меха-
Механизм намагничивания парамагнетиков аналогичен механизму электри-
электризации полярных диэлектриков (см. § 22). Различие заключается лишь
в использовании формулы D1.1) вместо формулы B2.1). Поэтому фор-
формулы для парамагнитной восприимчивости получаются заменой вели-
величин р -> pm, E -> В в формулах § 22 для диэлектрической восприим-
восприимчивости,
Вместо B2.10) получаем формулу
<?«.>= РтЬф), D1.2)
где Цр) - функция Ланжевена (см. § 22) при р = ртВ/(к'Г). При сравни-
сравнительно высоких температурах и малых полях, когда ртВ <к кТ, т. е. Р <к 1,
вместо B2.13) получаем формулу
<pms> = Р2тВ/(ЗкГ) № p2mix0HfCkT), D1.3)
где ц г fi|), поскольку отличие магнитной проницаемости парамагнети-
парамагнетиков от |!0 очень небольшое. Для намагниченности получаем формулу
, D1.4)
сравнение которой с равенством
J = Х„Я D1.5)
приводит к следующему выражению для парамагнитной восприимчи-
восприимчивости:
Хп = plNno/CkT) = С/Т, D1.6)
где С — постоянная Кюри.
Зависимость /п ~ 1/Т называется законом Кюри, так как впервые
была экспериментально обнаружена в 1896 г. П. Кюри.
Величина атомных магнитных моментов имеет порядок
рт ~ 10" 23 А • м2, поэтому при комнатной температуре %П ~ 10, т. е. %п
на два порядка больше диамагнитной восприимчивости. Это означает,
что у парамагнитных веществ диамагнитной восприимчивостью обычно
можно пренебречь.
Теория Ланжевена достаточно точно описывает лишь газы, у ко-
которых взаимодействие между молекулами пренебрежимо мало вследст-
вследствие больших расстояний между ними. В жидкостях и твердых телах это
взаимодействие может быть значительным. Учет этого взаимодействия
во многих случаях модифицирует зависимость D1.6) восприимчивости
от температуры. Эта зависимость принимает вид закона Кюри —Вейсса:
х„ = const/(T - То), D1.7)
где температура То характерна для вещества и определяется его свойст-
свойствами.
294 7. Магнетики
]У|агнитные моменты свободных атомов. Магнитные моменты атомов
возникают за счет двух факторов:
1) орбитального движения электронов. Полный орбитальный маг-
магнитный момент атома является суммой орбитальных магнитных момен-
тов отдельных электронов;
2) наличия у каждого электрона собственного магнитного момента,
связанного со спином электрона, т. е. собственным механическим мо-
моментом электрона.
Магнитные моменты отдельных электронов связываются между со-
собой, образуя полный спиновый магнитный момент атома. Каждый
электрон, двигаясь в магнитном поле, создаваемым орбитальным
движением всех остальных электронов, благодаря наличию спинового
магнитного момента взаимодействует с этим полем. Это взаимодейст-
взаимодействие называется спин-орбитальным. Благодаря ему полный орбитальный
момент электронов связывается с их полным спиновым магнитным
моментом, образуя полный магнитный момент атома. О таком пути
образования полного магнитного момента атома говорят как о LS-связи.
В принципе возможен и другой путь возникновения полного магнит-
магнитного момента атома: сначала спиновый магнитный момент каждого
электрона связывается с орбитальным моментом того же электрона,
образуя полный магнитный момент электрона, а затем полные магнит-
магнитные моменты электронов связываются между собой и получается пол-
полный магнитный момент атома. Однако в большинстве случаев, за
исключением самых тяжелых элементов, такой путь не реализуется,
поскольку интенсивность взаимодействия спинового магнитного момен-
момента электрона с его собственным орбитальным движением оказывается
слабее, чем его взаимодействие со спиновыми магнитными моментами
других электронов и полный магнитный момент отдельно для
каждого электрона не возникает. Поэтому в большинстве случаев
реализуется LS-связь.
Вопрос о сложении полного магнитного орбитального момента с
полным спиновым моментом требует учета того обстоятельства, что
коэффициент пропорциональности в линейном соотношении между пол-
полным орбитальным магнитным моментом и полным орбитальным меха-
механическим моментом отличается от коэффициента пропорциональности
в линейном соотношении между полным спиновым магнитным момен-
моментом и полным спином. По правилу сложения векторов в атоме скла-
складываются полные механические моменты, а сложение магнитных мо-
моментов получается как следствие сложения механических моментов.
В результате полный магнитный момент атома может быть неколли-
неарным с его полным внутренним механическим моментом.
Проблема магнитных моментов свободных атомов упрощается бла-
благодаря тому, что энергетически выгодным является такое заполнение
атомных оболочек электронами, при котором полный момент имеет
минимальную величину. Благодаря этому полный орбитальный и спи-
спиновый моменты замкнутых полных оболочек атома, а также полный
момент полностью заполненных оболочек равны нулю. Следовательно,
§ 41. Парамагнетики 295
магнитный момент атома определяется лишь электронами не пол-
полностью заполненных оболочек. В большинстве случаев такие оболочки
являются внешними. Дальнейшее упрощение картины получается за счет
того, что спины электронов и орбитальные моменты во внешней обо-
оболочке стремятся ориентироваться в противоположном направлении,
чтобы максимально компенсировать друг друга. Поэтому магнитный
момент свободного атома определяется в основном нескомпенсирован-
ными спинами внешних электронов.
]У[агиитные моменты молекул. Магнитный момент молекулы не равен
сумме магнитных моментов атомов, поскольку осуществление хими-
химической связи между атомами требует определенной перестройки внеш-
внешних атомных оболочек. Например, молекула азота N2 осуществляется
ковалентной связью и два обобществленных электрона имеют антипа-
антипараллельные спины. Орбитальные моменты также скомпенсированы и
равны нулю. В результате получается, что молекулы N2 не обладают
постоянным магнитным моментом, т. е. азот не является парамагнети-
парамагнетиком. В молекулах с ионной связью наблюдается та же тенденция к
скомпенсированное™ магнитных моментов. Например, молекула пова-
поваренной соли NaCl осуществляется ионной связью между Na+ и С1~.
Оба иона обладают замкнутыми электронными оболочками, в резуль-
результате чего полный магнитный момент равен нулю. Можно сказать, что
общая тенденция при образовании молекул состоит в обеспечении нуле-
нулевого полного момента. Из распространенных газов парамагнитными
свойствами обладают только кислород О2, у которого спины обоб-
обобществленных электронов нескомленсированы, и NO и NO2, у которых
общее число электронов нечетно и, следовательно, спин одного из
электронов оказывается нескомпенсированным.
Большинство твердых веществ состоит из ионов с замкнутыми
оболочками, благодаря чему они не обладают парамагнитными свойст-
свойствами, а являются лишь диамагнетиками. Главное исключение из этого
правила составляют соединения, в которые входят «переходные эле-
элементы». Электронная оболочка этих элементов заполнена лишь частич-
частично, благодаря чему они многовалентны, а их ионы обладают постоян-
постоянными магнитными моментами. Таким образом, пара.магнетизм соеди-
соединений переходных элементов обусловлен магнитными моментами их
ионов. Ионы с близкими конфигурациями внешних электронных обо-
оболочек приводят к близким парамагнитным свойствам соединений.
]У[ агнетизм, обусловленный свободными электронами. Хотя свободные
электроны в магнитном поле под действием силы Лоренца дви-
движутся по окружностям, классическая теория предсказывает отсутствие
диамагнитного эффекта вследствие отражения электронов на границах
области, а квантовая теория утверждает его существование. Диамагнит-
Диамагнитная восприимчивость оказывается равной
е2 (Ъп\13
296 7. Магнетики
где m* — эффективная масса свободных электронов; п — их концентра-
концентрация. При не очень большой индукции магнитного поля диамагнит-
диамагнитная восприимчивость является постоянной и не зависит от температуры.
Другой магнитный эффект, связанный с электронами проводимости,
обусловлен взаимодействием спинового магнитного момента электрона
с магнитным полем, благодаря чему возникает избыток электронов,
магнитные спиновые моменты которых ориентированы по направлению
индукции поля по сравнению с электронами с противоположными
спиновыми магнитными моментами. Это явление называется парамагне-
парамагнетизмом электронов проводимости. Как показывают расчеты, парамагнит-
парамагнитная восприимчивость электронов проводимости в лабораторных усло-
условиях практически не зависит от температуры. Наиболее сильно пара-
парамагнетизм электронов проводимости проявляется у переходных ме-
металлов. В лабораторных условиях диамагнитная восприимчивость
электронов проводимости практически всегда меньше их парамагнит-
парамагнитной восприимчивости (примерно в три раза) и поэтому их суммарная
восприимчивость оказывается положительной (парамагнитной).
Парамагнитный резонанс. Представим себе, что в парамагнетике, поме-
помещенном в магнитное поле, создается дополнительное периодическое
магнитное поле, вектор индукции которого перпендикулярен вектору
индукции постоянного поля. За счет постоянного магнитного поля
(рис. 163,6) магнитные моменты атомов совершают ларморову пре-
прецессию. В результате взаимодействия магнитного момента рт атома с
индукцией В дополнительного переменного магнитного поля создается
момент сил М, стремящийся изменить угол между рт и В. Если частота
переменного магнитного поля отличается от частоты ларморовой пре-
прецессии, то часть времени этот момент стремится увеличить угол
между рт и В, а часть времени — уменьшить, и в среднем никакого
эффекта не наблюдается. Если же частоты переменного магнитного
поля и ларморовой прецессии совпадают, то созданный переменным
магнитным полем момент сил либо все время увеличивает угол
между моментом атома и индукцией постоянного магнитного поля, либо
уменьшает, в зависимости от соотношения фаз ларморовой прецессии
и индукции переменного магнитного поля. В результате такого сравни-
сравнительно длительного действия момента сил происходят переориентация
магнитного момента атома и изменение угла между ним и вектором
индукции постоянного магнитного поля. Это явление называется пара-
парамагнитным резонансом. Переориентация магнитного момента в соот-
соответствии с формулой D1.1) связана с изменением энергии магнит-
магнитного момента в постоянном магнитном поле, что по закону сохра-
сохранения энергии сопровождается обменом энергией с переменным магнит-
магнитным полем. Это поле осуществляется в виде стоячих электромагнит-
электромагнитных волн, магнитный вектор которых перпендикулярен вектору индукции
постоянного магнитного поля. Таким образом, обмен энергией происхо-
происходит с электромагнитной волной.
В результате этого создаются группы атомов с ориентировкой
магнитных моментов, параллельной индукции магнитного поля и анти-
§ 41. Парамагнетики 297
параллельной, т. е. обладающих согласно D1.1) различной энергией
взаимодействия с магнитным полем,- Энергии атомов с антипараллель-
антипараллельной ориентацией больше, чем с параллельной.
Кроме механизма переориентировки магнитных моментов перемен-
переменным электромагнитным полем постоянно действует механизм пере-
переориентировки магнитных моментов тепловым движением и взаимо-
взаимодействием между атомами. В условиях одновременного действия этих
механизмов тепловое движение и взаимодействие атомов производит
преимущественно переориентировку магнитных моментов, антипарал-
антипараллельных вектору индукции. Выделяющаяся при этом энергия превра-
превращается в теплоту. Переориентировка параллельных индукции поля
магнитных моментов осуществляется преимущественно в результате
поглощения энергии электромагнитной волны. Поэтому наблюдение
парамагнитного резонанса сводится к измерению интенсивности электро-
электромагнитной волны, прошедшей через парамагнетик, находящийся в маг-
магнитном поле. С экспериментальной точки зрения проще использо-
использовать электромагнитную волну постоянной частоты, а резонанса доби-
добиваться изменением индукции магнитного поля. В тот момент, когда
соответствующая индукции поля ларморова частота будет равна часто-
частоте электромагнитной волны, наблюдается резкое ослабление ее интен-
интенсивности, свидетельствующее о наступлении парамагнитного резонанса.
Парамагнитный резонанс позволяет получить большую и разнооб-
разную информацию о свойствах парамагнетика и широко исполь-
используется в научных исследованиях.
Эта классическая картина возникновения парамагнитного резонанса
имеет лишь качественный характер. Более строгий подход возможен
в рамках квантовой теории, которая основана на представлении о
поглощении и испускании квантов электромагнитного излучения атом-
атомными системами с соответствующей скачкообразной переориентировкой
магнитных моментов, обеспечивающих соблюдение закона сохранения
энергии. В рамках этих представлений удается получить количествен-
количественные соотношения, характеризующие парамагнитный резонанс.
Из формулы D0.13) следует, что при индукции магнитного поля
1 Тл частота парамагнитного резонанса имеет порядок 1010 Гц, а при
уменьшении индукции эта частота соответственно уменьшается и можно
надеяться наблюдать парамагнитный резонанс при сравнительно низких
частотах. Однако его не удается наблюдать на частотах ниже 108 Гц,
т. е. при индукции постоянного поля, равной примерно 0,01 Тл.
Это находится в соответствии с квантовой теорией парамагнитного
резонанса, предсказывающей значительное уменьшение поглощения
электромагнитных волн при уменьшении их частоты, благодаря чему
резонанс на сравнительно низких частотах выражен очень слабо.
Наиболее используемыми в исследованиях являются частоты порядка
1010 Гц (длина волны 3 см).
298 7. Магнетики
§ 42. Ферромагнетики
Обсуждаются основные экспериментальные
факты ферромагнетизма и дается их элемен-
элементарная теоретическая трактовка. Вводится
общее представление об антиферромагне-
антиферромагнетизме, ферримагнетизме и ферромагнитном
резонансе.
Определение. Магнетики, магнитная проницаемость которых дости-
достигает больших значений и зависит от внешнего магнитного поля
и предшествующей истории, называются ферромагнетиками. Они обла-
обладают остаточной намагниченностью, т. е. их намагниченность может
быть отличной от нуля при отсутствии внешнего магнитного поля.
В этом случае они являются постоянными магнитами. Таким обра-
образом, по своим формальным проявлениям ферромагнетики аналогичны
сегнетоэлектрикам (см. § 23). Следует заметить, что ферромагнетизм
был открыт и изучен значительно раньше сегнетоэлектричества. Намаг-
Намагничивание ферромагнетиков было исследовано А. Г. Столетовым
A839 — 1896) в 1878 г. Им была построена кривая магнитной прони-
проницаемости (рис. 168), названная позже кривой Столетова. Гистерезис
был открыт в 1880 г. Варбургом A846-1931).
^ривая намагничивания и петля гистерезиса. Магнитная восприимчи-
восприимчивость ферромагнетиков является функцией напряженности внешнего
поля, а зависимость J(H) имеет вид, показанный на рис. 165. Намагни-
Намагниченность не увеличивается безгранично при увеличении напряженности,
а имеет предел, называемый намагниченностью насыщения. Ее существо-
существование по аналогии с парамагнетиками указывает, что намагничен-
намагниченность ферромагнетиков обусловливается также переориентировкой неко-
некоторых элементарных магнитных моментов.
Поскольку
В = ц0Н + M0J, D2.1)
кривая зависимости В(Н) не выходит на насыщение, хотя J испытывает
насыщение. График этой зависимости называется кривой намагничива-
намагничивания (рис. 166).
Если производить перемагничивание образца в периодическом маг-
магнитном поле, то в полной аналогии с сегнетоэлектриками кривая
зависимости В (Я) имеет вид петли, называемой петлей гистерезиса
(рис. 167). Участок ОА является кривой намагничивания, поскольку
включение поля производится при нулевом значении индукции, т. е. при
отсутствии постоянной намагниченности. Замкнутая кривая ACDFGKA
является петлей гистерезиса. Ее демонстрация производится по схеме,
аналогичной схеме демонстрации петли гистерезиса сегнетоэлектриков
с заменой конденсаторов на катушки (см. § 23).
42. Ферромагнетики 299
165
О
166
При уменьшении напряженности Н маг-
магнитного поля от некоторого значения (точка
А) до нуля индукция В поля уменьшается
лишь немного, до значения индукции, описы-
описываемой отрезком ОС. Эта индукция назы-
называется остаточной. Ферромагнетик в чтом
состоянии называется постоянным магни-
магнитом.
Для ТОГО чтобы Ликвидировать ОСтатОЧ- Насыщение намагниченности
ное поле, необходимо приложить обратное
поле, напряженность которого задается от-
отрезком OD. Эта напряженность называется
задерживающей или коэрцитивной силой фер-
ферромагнетика. Форма петли гистерезиса, оста-
остаточная индукция и коэрцитивная сила зави-
зависят от материала ферромагнетика и изме-
изменяются для различных материалов в широ-
широких пределах.
кривая магнитной проницаемости. Относи-
тельная магнитная проницаемость цг =
- ц/Цо = В/(ц0Н) как функция от Я может Кривая ™м«™™вания
быть построена по данным кривой намаг-
намагничивания (рис. 166) и имеет вид, показан-
показанный на рис. 168. При росте Н значение
цг достигает максимума и ^атем при дости-
достижении насыщения намагниченности быстро
спадает. У ферромагнетиков цг порядка 10* в
максимуме не являются редкостью.
классификация ферромагнитных материа-
материалов. Ферромагнитные материалы можно
разделить на две группы:
1) мягкие в магнитном отношении ма-
материалы с большой магнитной проницае-
проницаемостью, легко намагничивающиеся и размаг-
размагничивающиеся, с малой коэрцитивной си-
силой;
2) жесткие в магнитном отношении ма-
материалы с относительно низкой магнит-
магнитной проницаемостью, очень трудно намагни-
намагничивающиеся и размагничивающиеся, с боль-
большой коэрцитивной силой.
Материалы первой группы используют-
используются главным образом в электротехнике пере-
переменных полей, в частности в трансформато-
трансформаторах, а второй группы - для создания посто-
ЯННЫХ Магнитов.
н
Я
167
Петля гистерезиса
И
168
магнитной проницаемо-
проницаемости (кривая Столетова)
300 7. Магнетики
взаимодействие электронов. Ферромагнетизм может быть рассмотрен
только в рамках квантовой теории. В рамках классической теории
магнетизма можно лишь описать свойства ферромагнетиков и обсу-
обсудить качественно механизм его возникновения.
Экспериментально было установлено впервые в опытах Эйнштейна
и де Гааз, что ферромагнетизм обусловлен спинами электронов.
Ферромагнетики обладают свойством спонтанной намагниченности, ког-
когда при отсутствии внешних магнитных полей под действием внутрен-
внутренних причин спины электронов стремятся ориентироваться в одном
общем направлении. Однако образцу в целом быть намагниченным
энергетически невыгодно. Поэтому он разбивается на малые намагни-
намагниченные области — домены. Каждый домен намагничен в определенном
направлении, но направление вектора намагниченности в соседних до-
доменах различно и поэтому магнитный момент малых физических
объемов оказывается равным нулю, т. е. магнетик в целом не намаг-
намагничен.
Сказанное показывает, что основной вопрос теории ферромагнетизма
состоит в объяснении стремления спинов электронов сориентироваться
в одном общем направлении. Поскольку в системе реализуется состоя-
состояние с наименьшей энергией, задача состоит в том, чтобы найти такое
взаимодействие, при котором энергетически выгодным была бы парал-
параллельная ориентировка спиновых магнитных моментов различных ато-
атомов. Для этого надо, чтобы полная энергия была минимальной
при параллельной ориентировке моментов.
Возникновение такой ситуации связано с обменным взаимодейст-
взаимодействием. Вследствие того что электроны подчиняются статистике Ферми —
Дирака, которая не допускает нахождения двух частиц в одном и том
же состоянии, электроны с параллельными спинами оказываются как
бы раздвинутыми в пространстве, благодаря чему уменьшается их
энергия кулоновского взаимодействия по сравнению с электронами с
антипараллельными спинами, когда они могут располагаться в прост-
пространстве более тесно. Энергией обменного взаимодействия называется
разность энергий между конфигурациями с параллельными и антипа-
антипараллельными спинами.
Однако такая ситуация сама по себе не обеспечивает возникно-
возникновения ферромагнетизма, поскольку с уменьшением кулоновского взаимо-
взаимодействия при параллельных спинах происходит увеличение их кинети-
кинетической энергии. В большинстве случаев оно перекрывает уменьшение
потенциальной энергии и полная энергия конфигураций с параллель-
параллельными спинами оказывается невыгодной. Лишь в редких случаях, когда
уменьшение потенциальной энергии при параллельных спинах более
значительно, чем увеличение кинетической энергии, полная энергия
уменьшается. При этом конфигурации с параллельными спинами стано-
становятся энергетически выгодными и возникает ферромагнетизм. Исследо-
Исследование условий, при которых такая ситуация возможна, составляет
предмет теории ферромагнетизма. При этом главную роль играет
правильный выбор выражения для энергии взаимодействия.
^ 42. Ферромагнетики 301
Элементарная теория ферромагнетизма. Обменная энергия в теории
ферромагнетизма выражается формулой
Wo6= -2/o6SrS2, D2.2)
где Sx и S2 — спины взаимодействующих электронов, 7об — инте1 рал
обменного взаимодействия. Из D2.2) видно, что при /о6 > 0 потенциаль-
потенциальная энергия достигает минимума при параллельных спинах. Эта энергия
обусловлена взаимодействием магнитного момента электрона с магнит-
магнитным полем и выражается формулой вида D1.1), в которой, однако, под
индукцией В понимается индукция Во6 обменного поля. Собственный
магнитный момент pl?] электрона связан с его собственным механи-
механическим моментом или спином S соотношением вида D0.10), однако
с коэффициентом пропорциональности, в два раза большим:
№ = (e/m)S. D2.3)
Поэтому, представляя энергию взаимодействия D2.2) как энер1ию
магнитного момента второю электрона, находящегося в магнитном
поле, созданном за счет обменного взаимодействия первым электроном,
имеем
Wo6 = - ?^L. 1- S2 = - PZ ¦ Во5, D2.4)
где
Воб = B/o6m/e) S,. D2.5)
Полная индукция магнитного поля складывается из индукции В поля
при отсутствии обменного взаимодействия и индукции В^ обменного
поля. Соотношение C8 21) с учетом C8.23) может быть представлено
в виде
Ш> A + X) J = ХВ, или XoJ = [X/A + X)] В. D2.6)
Это соотношение обобщается при наличии обменного взаимодейст-
взаимодействия формулой
HoJ = [х/0 + X)] (В + Вой), D2.7)
причем магнитная восприимчивость у. в этой формуле считается равной
ее значению в D2.6) для парамагнетика при отсутствии обменного
взаимодействия.
Дальнейшее рассмотрение ведется в приближении среднего поля,
основное предположение которого состоит в том, что индукция обмен-
обменного поля пропорциональна намагниченности:
Воб = W, D2.8)
где X — постоянная обменного взаимодействия. Подставляя D2.8) в
D2.7), находим соотношение
= [X/A + х - *О)] В, D2.9)
302 7. Магнетики
которое целесообразно представить в виде, аналогичном D2.7):
MoJ = [х'/A + X')] В, D2.10)
где
Х'/A + X') = X/U + X - *О) D2.11)
характеризует восприимчивость с учетом обменного взаимодействия.
Из D2.11) находим
[Л 1 ")\
Г^г Т^гхс I42-12)
где х = С/Т.
В области температур Т> ХС тело ведет себя как парамагнетик с
характерным уменьшением магнитной восприимчивости с увеличением
температуры. При приближении к Т = ХС восприимчивость %' -* ос. Это
означает, что сколь угодно малые поля вызывают конечную намагни-
намагниченность. Другими словами, при Т = ХС происходит возникновение спон-
спонтанной намагниченности, т. е. переход в ферромагнитное состояние.
Изложенная элементарная теория не позволяет количественно проана-
проанализировать изменение спонтанной намагниченности при дальнейшем
уменьшении температуры в области Т < ХС. Более точная теория пока-
показывает, что спонтанная намагниченность лри Т = ХС возрастает скачком
до конечного значения, а затем при уменьшении Т продолжает возрас-
возрастать, но скорость роста постепенно уменьшается. Таким образом, при
Т < ХС магнетик находится в ферромагнитной фазе.
3 акон Кюри — Вейсса. Для всякого ферромагнетика существует темпе-
температура, при переходе через которую он испытывает фазовый переход
(второго рода) и превращается в парамагнетик. Магнитная восприим-
восприимчивость в парамагнитной области вблизи температуры перехода, назы-
называемой температурой Кюри, описывается соотношением вида D2.12),
называемым законом Кюри —Вейсса. Величина ХС = 0 называется тем-
температурой Кюри —Вейсса. Теория показывает, что фазовый переход со-
совершается не при температуре Кюри —Вейсса, а при температуре, близ-
близкой к ней.
Поэтому иногда допустимо не делать различия между температу-
температурой Кюри, при которой происходит фазовый переход, и температурой
Кюри — Вейсса.
Диизотропия намагничивания. При исследовании кривых намагничива-
намагничивания ферромагнитных монокристаллов было показано, что при раз-
различных ориентировках намагничивающего поля относительно осей
кристалла кривые намагничивания получаются различными, т. е. ферро-
ферромагнитные свойства кристалла зависят от направления намагничивания.
Направление, в котором намагниченность при данном поле максимальна,
называется направлением или осью легкого намагничивания, а направле-
направление, в котором намагниченность при данном поле минимальна, назы-
называется направлением или осью трудного намагничивания.
§ 42. Ферромагнетики 303
169
Идеализированные структуры
доменов в монокристалле
t
I
I
1
1
1
1
/
1
\
1
t 1
/is,
ii
ti
а)
б)
в)
г)
Домены. Идеализированные структуры доменов в монокристалле
"тюображены на рис. 169 (стрелками показаны направления намаг-
намагниченности):
а — индукция внешнего магнитного поля велика;
б — внешнее поле сосредоточено в основном около верхней и ниж-
нижней стенок и имеет значительно меньшую энергию, чем в случае а;
в — нет свободных полюсов и поле не выходит из области домена;
г — осуществляется та же ситуация, что и в случае в, но при разбие-
разбиении структуры на более мелкие домены.
Границы. Для минимизации энергии магнитного поля выгодным
является максимальное уменьшение размеров домена. Однако этому
препятствует необходимость затраты энергии на образование границ
между доменами, поскольку намагниченность по разные стороны гра-
границы имеет различное направление. Граница между доменами имеет
конечную толщину d, в пределах которой намагниченность постепенно
изменяет свое направление от ориентации в одном домене к ориента-
ориентации в другом, т. е. границы между доменами являются стенками
конечной толщины, Стенки классифицируются по особенностям пово-
поворота вектора намагниченности в них. Если перпендикулярная стенке
составляющая намагниченности в процессе его поворота не изменяется,
то стенка называется стенкой Блоха. Другими словами, в стенке Блоха
вращение намагниченности происходит в плоскости, параллельной стен-
стенке (рис. 170, а). Если изменение направления намагниченности происхо-
происходит с изменением ее составляющей, перпендикулярной стенке, то стенка
называется стенкой Нееля (рис. 170,6).
ТТеремагыичивание. Увеличение намагниченности образца при росте
напряженности магнитного поля происходит сначала из-за обрати-
обратимого смещения границ и поворотов граничных стенок (рис. 171; участок
ОА). На участке АС осуществляется необратимое смещение границ и
исчезновение некоторых доменов и, наконец, на участке CD, предшест-
предшествующем насыщению, наблюдается изменение направления намагничен-
намагниченности внутри доменов,
А нтиферромагнетизм. При определенных условиях обменное взаимо-
взаимодействие приводит к такой ситуации, что энергетически выгодным
является антипараллельная ориентировка спинового момента соседних
атомов. Для этого необходима реализация условий, аналогичных
условиям возникновения ферромагнетизма, но для конфигураций
304 7. Магнетики
а)
¦--уаи-тг-т—
б) */ .
170
Изменение намагниченности в
стенке: Блоха (а); Нселя (б)
171
Области различных механизмов
неремагничивания
¦ ¦
172
Антиферромагнетизм
Характерной особенно-
особенностью кривой намагничива-
намагничивания ферромагнетиков яв-
является существование на-
насыщения, а кривой пере-
иагничивания — петля ги-
гистерезиса.
с антипараллельными спинами. В резуль-
результате этого спиновые магнитные моменты
соседних атомов оказываются ориентиро-
ориентированными в противоположных направлениях
(рис. 172).
Такую ситуацию можно интерпретиро-
интерпретировать как одновременное наличие двух подре-
подрешеток, которые спонтанно намагничены в
противоположных направлениях с одинаковой
интенсивностью. Суммарная намагничен-
намагниченность равна нулю. Эта ситуация называется
антиферромагнетизмом, а тела, в которых она
осуществляется, — антиферромагнетиками.
У антиферромагнетиков вектор индукции
обменного поля направлен противоположно
вектору намагниченности J. Поэтому вместо
D2.8) для них справедливо соотношение
Во6 = -X*MoJ. D2.13)
Произведя такие же вычисления, которые
от D2.8) привели к D2.12), получим для
восприимчивости антиферромагнетика фор-
формулу D2.12), но с заменой X на — Ха:
Х„ = С/(Т + ХаС) = С/(Т + 0), D2.14)
где 0 = ХаС — температура Кюри —Вейсса.
Так же как и в случае ферромагнетиков,
переход в антиферромагнитное состояние
происходит при температуре, отличающейся
от температуры Кюри —Вейсса. Температура
перехода в антиферромагнитное состояние
называется температурой Нееля TN.
Ниже температуры Нееля в нулевом поле
полная спонтанная намагниченность анти-
антиферромагнетика равна нулю, поскольку про-
противоположные намагниченности подрешеток
полностью компенсируются. При наложении
внешнего поля возникает небольшая намаг-
намагниченность, соответствующая положитель-
положительной восприимчивости.
Модель двух подрешеток достаточна для
объяснения антиферромагнетизма во мно-
многих случаях. Однако иногда, когда дело
не сводится лишь к коллинеарным магнит-
магнитным моментам и необходимо обеспечить
равенство нулю векторной суммы несколь-
нескольких магнитных моментов, что является
§ 42. Ферромагнетики 305
а)
t
14 ¦'
1,1.1,
в)
173
Простейшие возможности
осуществления ферримагне-
тизма
характерным признаком антиферромагнетизма, приходится пользо-
пользоваться моделью более чем двух подрешеток.
Ф ерримагнетизм. Может случиться, что подрешетки обладают спон-
спонтанной намагниченностью противоположного направления, но раз-
различной интенсивности, из-за чего не происходит, как у антиферро-
антиферромагнетиков, полной ликвидации намагниченности. У таких веществ
имеется спонтанная намагниченность, хотя и менее интенсивная по
сравнению с. веществами, все магнитные моменты которых были бы
ориентированы в одном направлении. Такие материалы обладают свойст-
свойствами, аналогичными свойствам ферромагнетиков, в частности обладают
остаточной намагниченностью, характеризуются коэрцитивной силой
и т. д. Они называются ферримагне гиками или ферритами. Иногда о
ферримагпетизме говорят как о нескомпенсированном антиферромагне-
антиферромагнетизме.
Очень существенные преимущества ферритов по сравнению с ферро-
ферромагнетиками связаны с их чрезвычайно малой электропроводимостью,
в то время как ферромагнетики являются хорошими проводниками
электрического тока, поскольку хорошая электропроводность ферро-
ферромагнетиков является недостатком при использовании в радиотехнике.
Под подрешеткой понимается совокупность всех ионов внутри крис-
кристалла, которые эквивалентны друг другу как в кристаллографическом
смысле, так и в смысле электростатических и магнитных взаимодейст-
взаимодействий с окружающими ионами. Отсюда следует, что для существования
ферримагнетизма необходимо существование по меньшей мере двух
неэквивалентных подрешеток. Простейшие возможности осуществления
ферримагнетизма показаны на рис. 173, а— в.
ферромагнитный резонанс. Он обусловлен взаимодействием спиновых
магнитных моментов электронов с переменным электромагнитным
полем. Однако в ферромагнетиках этот резонанс значительно сложнее,
чем в парамагнетиках. Это вызвано тем, что в ферромагнетике имеются
спонтанная намагниченность и доменная структура, а спины электро-
электронов очень сильно связаны обменным взаимодействием. Поэтому в
ферромагнетике явление резонанса с самого начала имеет коллек-
коллективный характер, а прецессия спинов обусловливается не только внеш-
внешним полем, но и эффективным полем, зависящим как от внешнего
поля, так и от внутренних полей ферромагнетика, таких, как, напри-
например, поле анизотропии.
Ферромагнитный резонанс наблюдается при частотах в несколько
тысяч мегагерц. Если сверхвысокочастотное поле однородно по ампли-
306 7. Магнетики
туде, то во всем образце ферромагнетика наблюдается однородная
прецессия спинов, вызывающая появление соответствующего резонасно-
го пика. Однако наряду с ним образуются дополнительные резо-
резонансные пики, обусловленные доменными стенками (резонанс доменных
стенок). Неоднородность поля сверхвысоких частот приводит к воз-
возникновению дополнительных резонансных пиков, обусловленных фор-
формой и размерами образца. Расшифровка этой довольно сложной кар-
картины ферромагнитного резонанса позволяет получить ценную инфор-
информацию о свойствах ферромагнетика и измерить многие характеризую-
характеризующие его величины, такие, как намагниченность насыщения, гиромагнит-
гиромагнитное отношение, константу анизотропии и др.
Так же как и ферромагнетизм, ферромагнитный резонанс может быть
описан только с помощью квантовой теории.
§ 43. Гиромагнитные эффекты
Описываются гиромагнитные эффекты и их
экспериментальное наблюдение.
(Соотношение между механическими и магнитными моментами. На-
Намагничивание магнетика всегда связано с переориентировкой магнит-
магнитных моментов в определенном направлении. Лишь в явлении диамагне-
диамагнетизма образуются новые магнитные моменты, ориентированные с само-
самого возникновения одинаково. Магнитный момент орбитального движе-
движения электрона связан с механическим моментом этого движения соот-
соотношением D0.10). Собственный магнитный момент электрона связан
с его собственным механическим моментом также линейным соотно-
соотношением. Поэтому ясно, что и магнитный момент атома связан с его
механическим моментом определенным соотношением. Это означает,
что переориентировка магнитных моментов происходит одновременно
с переориентировкой соответствующих механических моментов.
Полный магнитный момент атома складывается из магнитных мо-
моментов орбитальных движений электронов и их спиновых магнитных
моментов. Аналогично суммируются и механические моменты. Однако,
учитывая, что коэффициенты пропорциональности между магнитными
и механическими моментами у орбитального движения и у спина раз-
различны, полный магнитный момент атома, вообще говоря, не колли-
неарен его механическому моменту, а составляет с ним некоторый
угол (рис. 174). Механический момент изолированной системы сохра-
сохраняется. Следовательно, в свободном атоме Ln сохраняет свое направ-
направление в пространстве. Поэтому pmn в результате движения электронов
в атоме прецессирует вокруг направления полного механического
момента, причем угловая скорость этой прецессии определяется време-
временами внутриатомных процессов, т. е. очень велика. Поэтому при
взаимодействии магнитного момента с внешними полями эффективное
значение имеет только компонента рт5ф е направлении полного
механического момента атома. Эффективным магнитным моментом
§ 43 Гиромагнитные эффекты 307
атома при взаимодействии с внешними
полями является момент рга:)ф, коллинеарныи
Ln. Таким образом, во всех случаях соотно-
соотношение между моментами можно представить
в виде
pm = geh/Bm), D3.1)
где е и т — масса и заряд электрона; д —
гиромагнитное отношение. Для орбитального
движения электрона д — 1, для спина д = 2,
а для атомов эта величина имеет промежу-
промежуточное значение между 1 и 2 в зависимости
от того, в какой пропорции и как в полных
моментах присутствуют вклады от орбиталь-
орбитального движения электронов и их спинов.
Напомним еще раз, что для атома в D3.1)
nod pm понимается не истинный полный маг-
магнитный момент атома, а его проекция на
направление полного механического момента,
обозначенная на рис. 174 как ртэф-
Опыт Эйнштсйна-дс Гааз. Рассмотрим
цилиндр из магнетика, подвешенный на
упругой нити (рис. 175). Соотношение D3.1)
между механическим и магнитным момен-
моментом показывает, что намагничивание цилинд-
цилиндра вдоль оси сопровождается не только
приобретением атомами магнитного мо-
момента вдоль оси цилиндра, но и приобрете-
приобретением ими также и соответствующего ме-
механического момента, направленного вдоль
оси. Полный механический момент стержня
слагается из механических моментов отдель-
отдельных атомов и механического момента стерж-
стержня как целого. До намагничивания полный
механический момент стержня равен нулю.
Для изолированной системы полный момент
сохраняется. В рассматриваемом случае изо-
изолированная система состоит из стержня
и намагничивающего поля, создаваемого
токами в соленоиде.
Отметим без доказательства (см. гл. 9),
что момент импульса электромагнитного
поля относительно оси цилиндра равен нулю
и, следовательно, не влияет на закон сохра-
сохранения момента импульса рассматриваемой
системы. Это означает, что постоянной
'тор.
Pmn
174
Схема сложения магнитных и
механических моментов в атоме
175
Опыт Эйнштейна-де Гаа>
О По каким причинам полный
механический и полный маг-
магнитный моменты атома не-
коллинеарны?
Какая величина играет роль
эффективного полного мо-
момента атома при взаимодей-
взаимодействии с внешними магнит-
магнитными полями?
Почему в опыте Эйнштей-
Эйнштейна — де Гааз используется пе-
ремагиичивание в периоди-
периодическом внешнем поле? Каки-
Какими требованиями определяет-
определяется частота внешнего поля?
Какова природа намагни-
намагниченности в эффекте Бар-
нетта!
308 7. Магнетики
должна быть сумма механических моментов всех атомов и механическо-
механического момента стержня как целого, т. е. и после намагничивания эта
сумма должна быть равна нулю. Но поскольку в результате намаг-
намагничивания механический момент атомов изменяется, изменяется и
момент стержня как целого. Из D3.1) следует, что при намагничи-
намагничивании выполняется соотношение
Лр™ = Я |>/Bт)] ALZ, D3.2)
где ALZ и Др, — механический и магнитный моменты, приобретаемые
каждым атомом при намагничивании вдоль оси Z. Суммируя обе
части равенства D3.2) по всем атомам, получаем
VJ^YJ^pmz^g{e|{2m)-\lJ^Lz, D3.3)
где J — намагниченность стержня, V — его объем. По закону сохранения
момента импульса, приобретаемый в результате намагничивания момент
импульса стержня как целого равен
Lz = - X ALz = - [2т/(ед)] VJ. D3.4)
Угловая скорость со вращения стержня связана с его моментом
импульса L, относительно оси вращения и моментом инерции Iz соот-
соотношением
Lz = 12а>. D3.5)
Кинетическая энергия вращения равна
W = '/212со2. D3.6)
С другой стороны, модуль кручения D нити связан с частотой соо
свободных крутильных колебаний стержня соотношением
Iz(al = D. D3.7)
В результате приобретения кинетической энергии D3.6) стержень
закрутит нить на угол 0, определяемый из закона сохранения энергии:
7,/гсо2 = l/2D92. D3.8)
Из D3.8) с учетом D3.7), D3.4) и D3.3) получаем
7гсо = D82/co = - 2mVJ/(eg), D3.9)
откуда
д = -2mVJ(a/(eQ2D). D3.10)
Все величины в правой части или известны, или могут быть, в прин-
принципе, измерены, что позволяет определить д.
Эффект закручивания нити при намагничивании невелик. Поэтому
фактически опыт проводился не однократным намагничиванием, как
это было описано выше, а многократным перемагничиванием образца
с частотой соо- В результате происходит наращивание крутильных
колебаний образца, причем амплитуда вынужденных колебаний в ре-
§ 43. Гиромагнитные эффекты 309
зонансе при достаточно хорошей добротности может быть уже легко
и надежно измерена. В принципиальном отношении переход к резо-
резонансной раскачке в приведенные рассуждения не вносит изменений.
Опыты Эйнштейна — де Гааз были поставлены с ферромагнитными
стержнями, у которых эффект намагничивания особенно заметен.
Экспериментально было получено
9=2. D3.11)
Это значение в два раза больше того, которое следовало ожидать,
если бы магнетизм обусловливался орбитальным движением электро-
электронов в атоме. Когда выполнялись впервые эти опыты A915) о спине
электрона еще ничего не было известно и получившийся результат
был загадочным. В дальнейшем был открыт спин и было показано,
что для него д = 2. После этого стало ясно, что результат опыта
Эйнштейна — де Гааз является прямым экспериментальным указанием
на то, что ферромагнетизм обусловливается собственным магнитным
моментом электронов, а не их орбитальным движением.
Для других магнетиков гиромагнитное отношение в аналогичных
опытах получилось заключенным между 1 и 2. Знак во всех случаях
свидетельствовал о том, что магнетизм обусловливается движением
электронов.
^ффект Барнетта. Любой магнетик обладает диамагнетизмом. Если
он является парамагнетиком, то его диамагнетизм вызван процессией
магнитных моментов атомов вокруг направления вектора индукции
магнитного поля, созданного в системе координат, где магнетик как
целое покоится. Другими словами, его диамагнетизм является резуль-
результатом прецессии атомов относительно кристаллической решетки маг-
магнетика. Приведем во вращательное движение магнетик как целое.
Отдельные атомы представляют собой маленькие гироскопы, которые
стремятся сохранить направление своей оси вращения в пространстве.
Поэтому направление магнитных моментов отдельных атомов в прост-
пространстве сохраняется неизменным. Следовательно, относительно кристал-
кристаллической решетки магнетика эти магнитные моменты будут совершать
прецессионное движение с частотой вращения магнетика. Но такая
упорядоченная прецессия атомов относительно магнетика как целого
приводит к намагничиванию. Следовательно, в результате вращения
магнетик намагнитится. В этом состоит эффект, впервые наблюдав-
наблюдавшийся Барнеттом в 1909 г.
Из изложенного ясно, что при вращении магнетика с частотой со
его намагниченность такая же, как при внесении диамагнетика в маг-
магнитное поле с индукцией
В = 2тесо/(\ е\д). D3.12)
Подчеркнем, что при вращении парамагнетика у него возникает
лишь диамагнитная намагниченность. Она примерно на два порядка
меньше, чем намагниченность в результате парамагнитного эффекта
(переориентировки магнитных моментов).
310
7. Магнетики
Задачи
7.1. Диамагнитная восприимчивость
меди (в твердом состоянии) рав-
равна Хд=-8,8-Ю~8. Определить
среднее расстояние электронов от
ядра в атоме меди.
7.2. Магнитный момент молекулы кис-
кислорода равен рт = 2,6- 103 А-м2.
Определить парамагнитную вос-
восприимчивость кислорода при нор-
нормальных условиях.
7.3. Магнитный дипольный момент
молекулы имеет порядок одного
магнетона Бора ц = eh/Bme) =
= 9,27-104 А-м2. Принимая,
что молекулы идеального газа
имеют постоянный магнитный
момент ц, найти максимально
возможную намагниченность при
t= 100 °С и р= 101,3 кПа.
Ответы
7.1. 1/<Л2> = 1/-6тхд/(е22цо^) = 0,9-100 м. 7.2. х„ =
7.3. iMaKC = 182 А/м.
§ 44
Индукция токов
в движущихся
проводниках
§45
Закон электромагнитной
индукции Фарадея
§ 46
Дифференциальная
формулировка закона
электромагнитной индукции
8
§47
Энергия
магнитного поля
§ 48
Цепи квазистационарного
переменного тока
§ 49
Работа и мощность
переменного тока
§ 50
Резонансы в цепи
переменного тока
§51
Цепн с учетом
взаимной индукции
S 52
Трехфазный ток
§53
Скин-эффект
§ 54
Четырехполюсники
§55
Фильтры
§ 56
Бетатрон
Электромагнитная
индукция
и квазистационар-
квазистационарные переменные
токи
Квазистационарное приближение спра-
справедливо при описании электромагнит-
электромагнитных полей и токов в областях, ли-
линейные размеры которых много мень-
меньше длины волны, и когда можно
пренебречь токами смещения. Электри-
Электрическое поле, порождаемое изменением
магнитного поля, учитывается, а маг-
магнитное поле, порождаемое изменением
электрического поля, не принимается
во внимание. Линии плотности тока
проводимости замкнуты, поскольку то-
токами смещения пренебрегают. Магнит-
Магнитное поле определяется мгновенными
значениями плотности токов проводи-
проводимости в тот же момент времени.
Плотности токов проводимости зависят
от изменения магнитного поля и, сле-
следовательно, от изменения плотности
токов проводимости.
312 8. Электромагнитная индукция и квазистационарные переменные токи
§ 44. Индукция токов
в движущихся проводниках
Дается количественная формулировка индук-
индукции токов в движущихся проводниках. Опи-
Описываются физические процессы в генерато-
генераторах переменного тока.
g озникновение э. д. с. в движущемся проводнике. При движении про-
проводника в магнитном поле его свободные электроны под действием
силы Лоренца приводятся в движение относительно проводника, т. е.
в проводнике возникает электрический ток. Это явление называется
индукцией токов в движущихся проводниках.
Рассмотрим прямолинейный участок DG проводника (рис. 176),
который, двигаясь со скоростью v, скользит по проводникам СК и AL
как направляющим, постоянно сохраняя контур AGDCA замкнутым.
Индукция внешнего однородного магнитного поля перпендикулярна
плоскости, в которой лежит контур. На заряды в движущемся про-
проводнике действует сила Лоренца
F = fvxB, D4.1)
коллинеарная DG. Силы, действующие на положительные и отрица-
отрицательные заряды проводника, показаны соответственно векторами F(+)
и F(_). Свободные электроны приходят в движение и образуют
электрический ток. Его направление принимается за положительный
обход контура и, следовательно, положительной нормалью к поверх-
поверхности, в которой лежит контур, является вектор п на этом рисунке.
Наличие силы F [см. D4.1)] эквивалентно тому, что в проводнике
действует на заряды эффективное электрическое поле
Еэф = F/e = v х В D4.2)
и поэтому э. д. с. индукции между некоторыми точками 1 и 2 провод-
проводника равна
B) B)
(Д g""uJ1 = J Еэф ¦ dl = J v х В • dl. D4.3)
A) in
В рассматриваемом случае эта э. д. с. возникает между точками
D и G:
(D)
(Д^ИНДЬС= ]vBdl = vBl. D4.4)
(С)
На неподвижных участках замкнутого контура электродвижущая
сила не образуется. Поэтому электродвижущая сила индукции в замкну-
замкнутом контуре AGDCA, вызванная движением его части DG во внешнем
поле, равна
Гинл= J E^-dl = vBI. D4.5)
AGDCA
§ 44. Индукция токов в движущихся проводниках 313
Выразив скорость проводника DG в виде
v = dx/dt, D4.6)
где х — координата его контактов в точках
D и G с направляющими проводниками,
запишем D4.5) в виде
?отл = dx IB/dt. D4.7)
Примем во внимание, что
Ф= -х№ D4.8)
176
Индукция токов в движущихся
проводникак
— поток магнитной индукции сквозь поверх-
поверхность, ограниченную контуром AGDCA. Знак
минус в D4.8) показывает, что направления
В и dS противоположны. Поэтому оконча-
окончательно D4.5) можно записать в форме
D4.9) /
т. е. при движении замкнутого проводника
во внешнем магнитном поле в его контуре
возникает электродвижущая сила индукции,
равная скорости изменения потока индукции
внешнего магнитного поля сквозь поверх-
поверхность, натянутую на замкнутый контур.
Формула D4.9) выведена для частного
случая, когда движется лишь часть провод-
проводника в плоскости, перпендикулярной индук-
индукции магнитного поля. Если движется не-
несколько участков проводника, то электро-
электродвижущая сила индукции в замкнутом кон-
контуре равна алгебраической сумме э. д. с.
индукции, возникших на участках. Поэтому
формула D4.9) без всяких дальнейших вы-
вычислений обобщается на случай произволь-
произвольного движения проводника в плоскости,
перпендикулярной направлению вектора ин-
индукции магнитного поля. При этом движе-
движении контур проводника может, конечно,
произвольно деформироваться.
Обобщение на произвольный случай. Рас-
Рассмотрим элемент длины проводника dl,
движущийся со скоростью v = dr/dt (рис. 177).
На этой длине в соответствии с форму-
формулой D4.3) создается электродвижущая сила
177
Обобщение формулы для ин-
индукции токов в движущихся про-
проводниках на произвольный слу-
случай
При движении и дефор-
деформации замкнутого провод-
проводника во внешней магнит-
магнитной поле в его контуре
возникает электродвижу-
электродвижущая сила индукции, чис-
численно равная скорости из-
изменения потока индукции
внешнего магнитного по-
поля через поверхность, на-
натянутую на замкнутый
контур.
Вся работа, совершаемая
током, индуцированным в
движущемся проводнике,
осуществляется эо счет
работы сил, приводящих
проводник в движение.
314 8. Электромагнитная индукция и квазистациопарные переменные токи
а)
d^«fl = vx B-dl= ^-(drx B-dl). D4.10)
at
Смешанное произведение в D4.10) пре-
преобразуется следующим образом:
dr х В • dl = dl x dr • В = - dr x dl • В =
= -dSB=-5O, D4.11)
где §Ф — поток магнитной индукции сквозь
элемент поверхности dS = dr x dl, образо-
образованный элементом длины dl при его дви-
движении. Положительное направление норма-
нормали к этому элементу поверхности выбира-
выбирается совпадающим с положительным на-
направлением нормали к поверхности, ограни-
ограничиваемой замкнутым контуром.
Подставляя D4.11) в D4.10), получаем
d^™= -бФ/df. D4.12)
Для нахождения полной электродвижу-
электродвижущей силы индукции в замкнутом контуре
надо просуммировать э. д. с. индукции от
всех элементов d/ этого контура:
^и„д = _ _L(|)§o = _ ^°_
dt Т df
где
D4.13)
?> = dФ D4.14)
— изменение потока индукции сквозь по-
поверхность, ограниченную замкнутым конту-
контуром.
Формула D4.13) совпадает с D4.9). Тем
самым доказано, что D4.9) справедлива при
произвольных движениях и деформациях
замкнутого контура.
Генераторы переменного тока. Если замк-
замкнутый проводник движется в магнитном
поле так, что охватываемый им поток маг-
магнитной индукции непрерывно изменяется,
то в нем непрерывно генерируются электро-
электродвижущая сила индукции и соответствую-
соответствующий переменный ток, т. е. такой замкнутый
О Каковы физические явления, контур является генератором переменного
лежащие в основе действия ТЖ& Простейшая схема генератора пере-
генераторов переменного то- r r *
ка! Опишите основные схе- менного тока изображена на рис. 178, а.
мы генераторов. Если магнитное поле однородно, а рамка
178
Схема генератора переменного
тока
§ 44. Индукция токов в движущихся проводниках 315
вращается в нем с постоянной угловой скоростью, то возникающая
в рамке $"ииа является гармонической электродвижущей силой, частота
которой равна частоте вращения рамки в магнитном поле. В замкну-
замкнутом контуре возникает переменный ток соответствующей частоты
(рис. 178,6).
Если вместо одного витка в магнитном поле движутся два парал-
параллельных последовательно соединенных витка, то электродвижущая сила
индукции возрастает в два раза. Поэтому при практическом осуще-
осуществлении генераторов используются намотки из многих витков. Вопро-
Вопросы о наиболее целесообразном осуществлении намоток, о создании
магнитного поля, о снятии тока с движущихся обмоток и т. д.
подробно рассматриваются в электротехнике. Отметим лишь, что сня-
снятие тока с движущихся проводников при большой силе тока является
не простой задачей. Поэтому часто вместо движения проводников
с током осуществляют движение источников магнитного поля при
неподвижных проводниках, В простейшей схеме (рис. 178, в) это означает
движение постоянных магнитов вокруг неподвижной рамки с током,
В неподвижной рамке при этом возбуждается электродвижущая сила
индукции. Количественно эта э. д. с. индукции при одинаковых относи-
относительных скоростях магнитов и рамки одна и та же. Однако физиче-
физическая сущность происходящих при этом явлений в этих двух случаях
различна (см. § 45).
Первыми генераторами были машины с постоянными магнитами,
но уже в 1866 г. был сконструирован генератор, в котором магнитное
поле создавалось электромагнитом. После этого конструкция генера-
генераторов быстро совершенствовалась.
3 акон сохранения энер] ии. При прохождении тока по цепи с омическим
сопротивлением выделяется джоулева теплота. Энергия, выделяемая
в форме теплоты, получается в результате работы механических сил
в генераторе электрического тока.
При переходе энергии из одной формы в другую соблюдается,
конечно, закон сохранения энергии. Проследим за этим на простейшем
примере (рис. 176).
Пусть R - сопротивление в контуре AGDCA, л I — сила тока в цепи.
Следовательно, в цепи током в форме теплоты выделяется энергия
с мощностью
/\ = I2R. D4.15)
С другой стороны, при движении участка проводника DG с током
силой / необходимо преодолевать силу Лоренца
F = IIB. D4.16)
Следовательно, силы, осуществляющие движение проводника, долж-
должны развивать мощность
Р2 = Fv = IlBdx/dt = -/Г1™» = -I2R, D4.17)
316 8. Электромагнитная индукция и квазистационарные переменные токи
где учтена формула D4.9) и принято во внимание, что '4тл — IR. Знак
минус в D4.17) показывает, что работа производится над системой.
Сравнение D4.15) и D4.17) показывает, что Р1 + Р2 = 0. Это означает,
что энергия, выделяемая в форме теплоты, в контуре равна работе
сил, приводящих проводник в движение, т. е. сторонними электродвижу-
электродвижущими силами в данном случае в конечном счете являются механические
силы, осуществляющие движение проводника.
§ 45. Закон электромагнитной
индукции Фарадея
Обсуждаются физическая сущность и мате-
математическая формулировка закона электро-
электромагнитной индукции Фарадея. Анализиру-
Анализируется соотношение между электромагнитной
индукцией Фарадея и индукцией тока в
движущихся проводниках.
Определение. В 1831 г. Фарадей экспериментально открыл явление
электромагнитной индукции, состоящее в возникновении электри-
электрического тока в замкнутом проводнике при изменении потока магнит-
магнитной индукции, охватываемого контуром. Правило, определяющее
направление э. д. с. индукции, было сформулировано в 1833 г. Э. X. Лен-
цем A804—1865): индукционный ток направлен так, что создаваемое
им поле препятствует изменению магнитного потока. Иначе говоря,
направление возникающего в контуре тока составляет с направлением
изменения потока магнитной индукции левовинтовую систему (рис. 179).
В 1845 г. Ф. Э. Нейман A798—1895) дал математическое определение
закона электромагнитной индукции в современной форме:
?-<•> = -dO/df, D5.1)
причем контур считается неподвижным.
физическая сущность явления. По внешнему виду формула D5.1)
полностью совпадает с D4.9), но физическое содержание ее совер-
совершенно иное. Возникновение э. д. с, учитываемое формулой D4.9), свя-
связано с действием силы Лоренца на движущиеся заряды. В возникно-
возникновении э. д. с, учитываемой формулой D5.1), никакая сила Лоренца
не участвует, поскольку проводники неподвижны. Однако в проводнике
возникает электрический ток, поэтому можно заключить, что в нем
имеется электрическое поле. Следовательно, закон Фарадея D5.1) вы-
выражает новое физическое явление: изменяющееся магнитное поле
порождает электрическое поле. Таким образом, электрическое поле
порождается не только электрическими зарядами, но и изменяющимся
магнитным полем.
Строго говоря, наличие тока в замкнутом проводнике показывает,
что электрическое поле имеется лишь внутри проводника. Однако про-
проводник в данном случае играет роль устройства для обнаружения элект-
§ 45. Закон электромагнитной индукции Фарадея 317
рического поля. При отсутствии проводника
изменяющееся магнитное поле также порож-
порождает электрическое поле. Это можно пока-
показать, например, тем, что на заряд в изменяю-
изменяющемся магнитном поле действует электри-
электрическая сила (см. § 56). Это доказывает, что
электромагнитная индукция является всеоб-
всеобщим фундаментальным законом природы,
устанавливающим связь между электриче-
электрическими и магнитными полями. Различное
физическое содержание описываемых форму-
формулами D4.9) и D5.1) явлений очевидно из
такого примера. Предположим, что провод-
проводник DG на рис. 176 движется со скоростью
v, но одновременно магнитная индукция В
уменьшается. Вследствие движения провод-
проводника в замкнутом контуре появляется э. д. с.
индукции, которая вызывает ток (рис. 176).
Изменение В по закону электромагнитной
индукции Фарадея вызывает в контуре также
э. д. с. индукции, которая в данном случае
направлена противоположно той, которая
возникает в результате движения участка
проводника DG. Можно подобрать такую
скорость изменения В (dB/dt), что эти две
э. д. с. будут взаимно компенсироваться.
В результате в замкнутом контуре не будет
тока, потому что полная э. д. с. индукции
равна нулю. Однако эта взаимная компен-
компенсация э. д. с. индукции происходит в замкну-
замкнутом контуре в целом, а не в каждой точке
контура. Э. д. с. индукции за счет движения
проводника возникает только на участке DG,
а э. д. с. индукции Фарадея возникает как
на участке DG, так и на остальных участках
проводника DC, С А и AG. В результате
движения на элементе проводника dl возни-
возникает э. д. с. индукции, зависящая только от
В и скорости v движения этого элемента,
но не зависящая от dB/dt. В результате
изменения индукции на элементе проводника
dl появляется э. д. с. индукции Фарадея, кото-
которая не зависит от индукции В и скорости v
движения этого элемента, а зависит только
от dB/dt. Это и доказывает, что физическая
природа э. д. с. индукции в этих двух случаях
различна.
179
Закон электромагнитной индук-
индукции Фарадея
180
Демонстрация электромагнитной
индукции Фарадея
Электрическое поле по-
порождается не только элек-
электрическими зарядами, но
и изменяющийся магнит-
магнитный полем.
Э. д. с. индукции выража-
выражается формулой D5.1), при-
причем под dO/dt понимает-
понимается полная скорость изме-
изменения потока индукции,
охватываемого проводни-
проводником, в результате дви-
движения и деформаций про-
проводника и изменения маг-
магнитного поля.
318 8. Электромагнитная индукция и квазистационарные переменные токи
ТТвижущийся проводник в переменном магнитном поле. Если замкну-
^ тый проводник движется в переменном магнитном поле, испытывая
при этом произвольные деформации формы, то э. д. с. индукции в нем
возникает как за счет движения и деформации, учитываемой форму-
формулой D4.9), так и в результате изменения индукции магнитного поля,
учитываемого аналогичной формулой D5.1). Поэтому можно сказать,
что э. д. с. индукции в проводнике определяется формулой D5.1), причем
под dO/df понимается полная скорость изменения потока индукции,
охватываемого проводником, как за счет его движения и деформации,
так и в результате изменения магнитного поля.
|~урименение электромагнитной индукции к генераторам переменного
тока. Теперь ясно, почему электрический ток можно генерировать
не только движением проводников в магнитном поле, но и движением
магнитов при неподвижных проводниках. На рис, 180 изображена схема
демонстрации электромагнитной индукции.
§ 46. Дифференциальная формулировка
закона электромагнитной
индукции
Дается дифференциальная формулировка за-
закона электромагнитной индукции и обсуж-
обсуждаются свойства векторного и скалярного
потенциалов переменного электромагнит-
электромагнитного тюля.
формулировка. Запишем закон электромагнитной индукции Фарадея
[см. D5.1)] в виде
Edl = - ~ BdS, D6.1)
1 s
где L — контур, S — поверхность, натянутая на контур L. В D6.1) учтены
определения:
ёта = { Е • dl, Ф = J В • dS. D6.2)
L S
Заметим, что между направлением обхода контура Ьи вектором dS
соблюдается правовинтовое соотношение. Необходимо также обратить
внимание на то, что в определении потока индукции Ф [см. D6.2)]
поверхность S, сквозь которую вычисляется поток, является произволь-
произвольной, натянутой на контур L поверхностью. Такое, определение пред-
предполагает, что этот интеграл не зависит от формы поверхности, важно
лишь, чтобы поверхность была ограничена контуром L или, как гово-
говорят, натянута на контур L. Докажем это. Выберем две какие-либо
поверхности St и S2, натянутые на контур L. Их совокупность
составляет замкнутую поверхность S = Si + S2, ограничивающую не-
некоторый объем V между ними. Поток вектора В сквозь замкнутую
§ 46. Дифференциальная формулировка закона 319
поверхность S равен нулю, поскольку по теореме Гаусса — Остро-
Остроградского он равен интегралу по объему V, ограниченному поверх-
поверхностью S, от div В = 0. Из этого следует утверждение о равенстве
потоков через Si и S2 (знаки потоков одинаковы при одинаковой
относительно направления обхода контура ориентировке положитель-
положительных нормалей к этим поверхностям).
Преобразуем левую часть D6.1) по формуле Стокса:
jE-dl = JrotE-dS. D6.3)
L S
В результате получаем
Гав
rot E • dS = - — • dS, D6.4)
L S
причем производная по t внесена под знак интеграла на том осно-
основании, что площадь интегрирования не зависит от времени. Так как
S произвольна, то из D6.4) следует, что
rot E = -dB/dt.
D6.5)
Уравнение D6.5) является дифференциальной записью закона электро-
электромагнитной индукции Фарадея. Оно описывает закон порождения элект-
электрического поля в некоторой точке за счет изменения индукции магнит-
магнитного поля в той же точке. Поле Е часто называют индукционным.
J-Jепотенциальность индукционного электрического поля. В неременном
магнитном поле dB/dt ф 0 и, следовательно, в соответствии с D6.5)
rot E Ф 0. D6.6)
Это означает, что индукционное электрическое поле в отличие от
электростатического, порождаемого неподвижными зарядами, не явля-
является потенциальным. Работа перемещения заряда q в нем по замкну-
замкнутому контуру, вообще говоря, не равна нулю:
А = q %™а = q\ Е • dl Ф 0. D6.7)
L
Отсюда, в частности, следует, что это поле не может быть пред-
представлено в виде градиента от некоторой функции, т. е. не может быть
представлено в виде A4.27). Необходимо использовать отличное от
A4.27) представление.
^екторный и скалярный потенциалы в переменном электромагнитном
поле. Поскольку закон электромагнитной индукции не затрагивает
законов порождения магнитного поля, уравнение C6.4) для диверген-
дивергенции магнитного поля остается без изменения, т. е. div В = 0. Следова-
Следовательно, без изменения остается и формула C7.2), связывающая вектор-
векторный потенциал с индукцией магнитного поля:
В = rot A. D6.8)
Связь скалярного потенциала с напряженностью электрического
320 8. Электромагнитная индукция и квазистационарные переменные токи
поля изменяется. Выражая В в D6.5) с помощью D6.8), получаем
rot Е = - --—rot A = -rot ~, D6.9)
от dt
где последовательность дифференцирований по времени и координатам
изменена вследствие их независимости. Уравнение D6.9), переписанное
в виде
| D6.10)
показывает, что вектор Е + dA/dt является потенциальным и, следова-
следовательно, может быть представлен в виде градиента некоторой функции
Е + дА/dt = -grad cp, D6.11)
где ф — скалярный потенциал. Таким образом, в случае переменных
полей напряженность электрического поля выражается не только через
скалярный, но и через векторный потенциал формулой
Е = -grad ф -
D6.12)
Первое слагаемое в правой части D6.12) учитывает порождение
электрического поля электрическими зарядами, а второе — порождение
поля по закону электромагнитной индукции Фарадея.
иеоднозначность потенциалов, калибровочное преобразование. уак же
как и в стационарном случае, скалярный и векторный потенциалы
являются неоднозначными, т. е. одно и то же электромагнитное поле
может быть описано многими скалярными и векторными потенциалами.
Пусть поле Е, В описывается потенциалами А, ср по формулам D6.8)
и D6.12) и имеется некоторая произвольная функция % (х, у, z, t). Ут-
Утверждается, что потенциалы
А' = А + grad х, ф' = ф — <3ф/5г D6.13)
характеризуют го же самое поле Е, В, что и потенциалы А, ф. Для
доказательства найдем Е', В', описываемые потенциалами А', ф' по
формулам D6.8) и D6.12):
В' = rot A' = rot A + rot grad x = в, D6.14)
где учтено, что rot grad = 0 и принята во внимание формула D6.8).
Для поля Е' получаем
Е' = —grad ф' — oA'/dt = —grad ф — grad (oyjdt) —
- cA/ct - д (grad yJ/Л = - grad Ф - cA/ct = E. D6.15)
Таким образом, действительно потенциалы D6.13) описывают то же
самое поле, что и потенциалы А, ф. Преобразования D6.13) называют
калибровочными. Они позволяют «калибровать» потенциалы, т. е. нало-
наложить на них некоюрое условие, пользуясь их неоднозначностью
(см. § 14, 37, 63).
§ 47. Энергия магнитного поля 321
§ 47. Энергия магнитного поля
Выводятся формулы для энергии магнитного
поля контуров с такой и выражение для
плотности энергии. Приводятся выражения
для энергии магнетика во внешнем магнит-
магнитном поле и объемных сил, действующих на
сжимаемые магнетики.
Энергия магнитного поля изолированного контура с током. Для
того чтобы в неподвижном контуре создать электрический ток,
необходимо включить в цепь источник сторонних э. д. с. Если в цепи
течет постоянный ток, то энергия, поступающая в цепь из источника
сторонних э. д. с, расходуется на выделение джоулевой теплоты и на
совершение работы в потребителе энергии. Индукция магнитною поля,
как и его энергия, при этом неизменна. Индукция изменяется с изме-
изменением силы тока. Следовательно, источник сторонних э. д. с. передает
в цепь энергию па создание магнитного поля в процессе увеличения
силы тока. Вычислив работу, совершаемую источником сторонних
э. д. с. для увеличения силы тока от нуля до конечного значения,
получим энергию магнитного поля, которое связано с этим током.
При изменении потока магнитной индукции, охватываемого конту-
контуром, в контуре возникает э. д. с. индукции в соответствии с зако-
законом D6.1). У изолированного контура поток электромагнитной индук-
индукции Ф возникает за счет магнитного поля, создаваемого током
в контуре (рис. 181). При увеличении силы тока возрастает поток Ф,
охватываемый током, и в контуре по закону Фарадея возникает э. д. с.
индукции, которая в данном случае называется э. д. с. самоиндукции.
По правилу Ленца, она направлена так, что препятствует увеличению
силы тока. Для увеличения силы тока необходимо, чтобы сторонняя
э. д. с. источника была направлена противоположно э. д. с. самоиндук-
самоиндукции и равна ей. Таким образом, в процессе роста силы тока источник-
сторонних э. д. с. совершает работу против э. д. с. самоиндукции.
За промежуток времени dt по контуру проходит количество электри-
электричества dQ = I dt и, следовательно, против э. д. с. самоиндукции источник
сторонних сил в течение dt совершает работу
АА = - %тЧ dt = (dO/dt) ldt = l №, D7.1)
где для 'ёк"Л использована формула D6.1). При совершении этой ра-
работы происходит превращение энергии источника сторонних э. д. с.
в энергию магнитного поля тока в контуре. Поэтому изменение энергии
магнитного поля связано с изменением потока соотношением
dW = Id<S>. D7.2)
Индукция магнитного поля тока в соответствии с законом
Био — Савара A0.10) линейно зависит от силы тока. Поэтому при
11 АН Матвеев
322 X. Электромагнитная индукция и кванилащюнарпые переменные токи
181
При увеличении тока источник
сторонних э.л.с. совершает ра-
работу против ч д.с. самоиндукции
182
К вычислению индуктивное ги
контура
Почему взаимная индук-
индуктивность может быть рас-
рассчитана по формуле, в ко-
которую входят линейные
токи, а индуктивность не
может быть выражена че-
через линейные токи?
Какое свойство магнитно-
магнитного поля обусловливает по-
постоянство индуктивности
жесткого контура с током?
Индуктивности и взаим-
взаимные индуктивности зави-
зависят только от геометри-
геометрических характеристик кон-
контуров с током и их
взаимного расположения.
переменной силе тока, протекающего по
жесткому неподвижному контуру, карти-
картина силовых линий остается прежней, а ин-
индукция в каждой точке растет пропорцио-
пропорционально силе тока. А это означает, что
поток магнитной индукции Ф сквозь фикси-
фиксированную неподвижную площадь также про-
пропорционален силе тока, и поэтому
Ф = L1, D7.3)
где L — постоянный коэффициент пропор-
пропорциональности, не зависящий от силы тока
и индукции магнитного поля. Этот коэффи-
коэффициент называется индуктивностью контура.
Подставляя D7.3) в D7.2), находим
dW = LIdI = d(l/2LI2). D7.4)
Интегрируя обе части D7.4) от / = О до
некоторого значения /, получаем формулу
W=l/2LI2, D7.5)
которая определяет энергию Mai нитного поля,
создаваемого током силы /, текущим по
контуру с индуктивностью L.
^нергия магнитною поля нескольких кон-
контуров с током. Аналогично можно найти
энергию магнитного поля двух контуров
с током (рис. 183). При этом надо,, учесть,
что э. д. с. индукции в каждом контуре воз-
возникает не только за счет изменения потока
индукции магнитного поля, создаваемого то-
током этого контура, но и за счет изменения
потока индукции магнитного поля, создавае-
создаваемого током, текущим в другом контуре.
Обозначим: /j и 12 — силы токов в первом
и втором контурах, Фм и Ф12 — охваты-
охватываемые первым контуром потоки магнитной
индукции полей, создаваемых соответствен-
соответственно токами /t и 12. Аналогичные величины
для второго контура обозначим Ф22 и Ф2,.
Полные потоки, охватываемые каждым из
контуров, равны
<Х>1 = Фи + Ф12, Фг = Ф21 + Фг2> D7.6)
Пусть Z.n и L22 — индуктивности конту-
контуров. Тогда [см. D7.3)]
Фи =/,„/„ Ф22=Ь2212. D7.7)
§ 47. Энергия магнитного поля 323
ев
183
К вычислению энергии магнит-
магнитного поля двух контуров с
током
Из тех же соображений, которые были изложены при получении
формулы D7.3), заключаем, что поток Ф12, охватываемый первым
контуром, за счет магнитного поля, создаваемого током во втором
контуре, пропорционален силе тока 12 во втором контуре:
Ф12 = Ll2I2, - D7.8)
где L12 — постоянная, называемая взаимной индуктивностью первого
и второго контуров. Аналогично, для второго контура получаем
d>2,=Wi. D7.9)
Поэтому [см. D7.6)]
Ot = L,,/! + Ll2/2, Ф2 = L21/i + L22I2. D7.10)
Э. д. с. индукции в первом и втором контурах равны:
dФ2
dt
l +L
г ь1
= - L
df
-+ L
22
df
df
D7.11)
Вся работа, совершаемая источниками сторонних э. д. с. контуров
в течение df, аналогично D7.1) равна
dA=dAl+dA2= - %Fnh df -
= (L, tIt d/t
/t d/z
2 dt =
d/, + L12/2 d/2
D7.12)
где использованы соотношения D7.10).
Для дальнейших вычислений докажем, что L12 = L21. С этой целью
вычислим Ф21 и Ф12:
Ф21= jB,-dS2, Ф12= jB2-dSb D7.13)
s2 s,
где Bt и В2 — индукции полей, создаваемых соответственно токами
1! и I2; S, и S2 — поверхности интегрирования, натянутые на контуры.
Индукция поля в каждой точке равна Bj + В2. Обозначив At и А2 —
векторные потенциалы, описывающие поля Bt и В2, имеем
Bj = rot Аь В2 = rot A2
II*
324 8. Электромагнитная индукция и квалтлационарные переменные токи
и, следовательно, равенства D7.13) принимают вид:
ф21 = JrotAj-dSj = jAi-db,
s* Ll D7.14)
Ф12 = jrot A2-dS! = JA2-dlb
где Lj и L2 — контуры с током. Переход к интегрированию по кон-
контурам произведен в соответствии с формулой Стокса. Формула C7.116),
выражающая векторный потенциал через ток, в данном случае прини-
принимает вид
L, L2
Подставляя D7.15а) в D7.14), получаем:
^-^-, D7.156)
L2 L, /., L2
где г!2 =г21 — расстояние между элементами d]1 и dl2 первого и вто-
второго контуров. Сравнивая D7.156) с D7.8) и D7.9), получаем:
D7.16а)
Формулы D7.16а) показывают, что взаимная индуктивность зависит
только от геометрических характеристик контуров и от их взЬимного
расположения. Поскольку dlt и dl2 — независимые переменные интегри-
интегрирования, можно изменить порядок интегрирований. Учитывая также,
что г12 = г21 и dlj ¦ dl2 = dl2 ¦ dlb заключаем, что
L12=L21, D7.166)
т. е. взаимная индуктивность первого контура со вторым равна взаим-
взаимной индуктивности второго контура с первым. С учетом этого можно
написать
L12/! d/2 + L21/2 d/t = d ("
и, следовательно, представить D7.12) в виде
? ti + l/iL2iI2Ii + Чг^1211). D7.17a)
Учитывая, что затрачиваемая на увеличение силы тока работа равна
энергии образовавшегося при этом магнитного поля, после интегри-
интегрирования обеих частей равенства D7.17а) от нулевых значений силы
тока в контурах It = 0, /2 = 0 до их значений 1^ и 12 получаем
2
V
L12ItI2 + L21/2/j + L22/|) =i- V Цки\к. D7.176)
if 47. Энер| ия магшпною поля 325
Эта формула определяет энергию магнитного поля, создаваемого
токами /j и 12. Она легко обобщается на случай N контуров:
JV
khh, D7.18)
где Lik при i = к называется индуктивностью j'-ro контура, а при хфк —
взаимной индуктивностью г-го, и к-то контуров. Выражения для этих
коэффициентов даются формулами D7.16а), принимающими вид
' " Aфк), D7.19)
L, L,
где dl,, dlt — элементы длины i-ro и к-то контуров Ц и Lk, rik — рас-
расстояние между ними. Из D7.19) следует равенство
Lik = Lu, D7.20)
являющееся обобщением D7.166) на случай многих контуров с током.
"^нергия магнитного поля при наличии магнетиков. Если все про-
пространство заполнено однородным магнетиком, то создаваемая за-
заданными токами индукция поля изменяется в (i/Ио раз по сравнению
с индукцией в вакууме [см. C8.29)]. Следовательно, во столько же раз
изменяются потоки Ф и dФ в формуле D7.1). Все последующие
вычисления аналогичны, но везде Ф изменяется в ц/Но раз. Из фор-
формул D7.7) и D7.8) заключаем, что индуктивность контура и взаимные
индуктивности увеличиваются в ц/ц0 раз. Это означает, что форму-
формулы D7.16а) для взаимной индуктивности при наличии магнетика
имеют тот же вид, но с заменой ц0 на ц. Такая же замена происходит
и в формулах D7.15а) и D7.156). Выражения D7.5) и D7.17) для энергии
магнитного поля остаются без изменения, но в них индуктивности
и взаимные индуктивности увеличиваются в ц/ц0 раз. Следовательно,
И энергия магнитного поля токов, протекающих в неограниченном
однородном магнетике, изменяется в ц/р.о раз по сравнению с энергией
поля тех же токов в вакууме.
Плотность энергии магнитного поля.Магнитное поле заданных токов
распределено по всему пространству. Выразим энергию поля D7.5)
изолированного контура с током через векторы поля. Формула D7.5)
с помощью D7.3) может быть представлена в виде
^=72^Ф- D7.21)
Здесь
Ф = j В • dS = J rot A • dS = J A • dl, D7.22)
S S L
где L и S — соответственно контур тока и поверхность, натянутая на
этот контур. В D7.22) потенциал А создается током /. Таким образом,
326 8. Электромагнитная индукция и квазистационарные переменные токи
замкнутый ток взаимодействует со своим собственным магнитным
полем. Физическая сущность этого взаимодействия состоит в том, что
каждый из элементов тока / dl создает в пространстве магнитное поле,
с которым взаимодействуют другие элементы тока. Подставляя D7.22)
в D7.21), находим
Adl AjdF D7.23)
l v
где с помощью соотношения (9.26) произведен переход к объемным
токам. Теперь преобразуем подынтегральное выражение так, чтобы
в него входили только векторы поля и векторный потенциал. Для этого
воспользуемся формулами В = rot A, j = rot H, а также известным из
векторного потенциала соотношением div (А х Н) = Н • rot А — А ¦ rot H.
В результате получаем А • j = Н • В — div (A x H) и, следовательно, фор-
формула D7.23) принимает вид
W = -y HBdF- div(AxH)dK. D7.24)
Второй интеграл по теореме Гаусса — Остроградского преобразуется
в интеграл по поверхности, ограничивающей объем интегрирования:
JdivA х HdK= JA x H • dS. D7.25)
V S
Если все токи расположены в конечной области пространства, то
на больших расстояниях г от. этой области А ~ 1/г, Н ~ 1/г2, т.е.
подынтегральное выражение убывает как ~1/г3. Поверхность интегри-
интегрирования при этом растет как г2 и, следовательно, интеграл умень-
уменьшается как 1/г. Поэтому для всего пространства, когда г —> од, второй
интеграл в D7.24) обращается в нуль и полная энергия поля представ-
представляется формулой
D7.26)
Можно сказать, что энергия поля распределена по всему прост-
пространству с объемной плотностью
D7.27)
т. е. объемная плотность энергии магнитного поля в каждой точке опре-
определяется значением векторов поля в этой точке, при этом, конечно,
несущественно, какими источниками созданы эти поля.
1/?ндуктивность. В равенстве D7.23) представим потенциал А с по-
помощью C7.11а) в виде
dr' D7'28)
§ 47. Энергия м.иншного поля 327
где плотность тока и элемент объема отмечены штрихами, чтобы
не путать их с теми же величинами в подынтегральном выражении D7.23):
это разные элементы объема одного и того же тока, расстояние между
которыми обозначено в D7.28) г (см. рис. 183). Подставляя D7,28)
в D7.23), находим
±JLl[\l± D7.29)
2 4я J J r 2 4я /2 J J r
V V V V
где в последнем равенстве числитель и знаменатель формулы умно-
умножены на I2. Сравнивая D7.29) с D7.5), получаем
L^-^-^-W^-dVdV. D7.30)
4л: / J J r
VV
Формулы D7.16а) для взаимной индуктивности при переходе к объ-
объемным токам (/dl^jdF) принимают вид
^dF,dKt. D7.31)
аналогичный D7.30). Однако формула D7.30) не можег быть выражена
через линейные токи. Если это сделать формально, то подынтеграль-
подынтегральное выражение в D7.30) принимает вид I2 dl • dt/r и обращается
в бесконечность при совпадении элементов интегрирования, когда dl =
= dl', поскольку при этом г = 0. Поэтому интеграл расходится и фор-
формула для индуктивности теряет смысл. Эта ситуация аналогична си-
ситуации при вычислении собственной энергии заряда, когда собствен-
собственная энергия обращается в бесконечность для точечного заряда.
|~[оле соленоида. В качестве примера использования полученных
в этом пара1рафе формул рассмотрим поле соленоида. Как было
показано, индукция поля вне соленоида равна нулю, а внутри соленоида
определяется равенством C8.40), т. е.
В = ]xnl, D7.32)
где п — число витков на 1 м длины соленоида. Поток индукции поля,
охватываемый одним витком соленоида, равен
ф1 = BS = \xnIS, D7.33)
где S — площадь поперечного сечения соленоида. Поток, охватываемый
N витками соленоида, которые занимают длину соленоида / = N/n,
равен
фм = ф^ = \inISN = \iISN2/l. D7.34)
Следовательно, индуктивность N витков соленоида равна
LN = Фы/1 = nSN2//. D7.35)
328 8. Электромагнитная индукция и квазистационарные переменные токи
Энергия, сосредоточенная на длине /, равна
W = ~LNP=-^^^S=^m2I2Sl = ^HBK D7.36)
где \хп2!2 = НВ, SI = V — объем участка соленоида, в котором вычисля-
вычисляется энергия поля. Формула D7.36) позволяет определять энергию поля
как через ток и индуктивность, так и через плотность энергии поля.
Найдем вектор-потенциал бесконечно длинного соленоида. Целесо-
Целесообразно исходить из формулы D7.22). Вследствие аксиальной симметрии
задачи будем вести расчет в цилиндрической системе координат
с аксиальной осью, совпадающей с осью соленоида. Обозначим: ср —
аксиальный угол, а г — расстояние от оси до точки, в которой вы-
вычисляется потенциал. В качестве контура L в D7.22) выберем окруж-
окружность радиусом г, лежащую в плоскости, перпендикулярной оси
соленоида, и с центром на оси. Тогда
Ф = J В • dS = § А • dl = § A9r d«p = 2nrA9,
S L L
где принято во внимание, что Av = const при г = const. Следовательно,
вектор-потенциал равен
s
где S — площадь круга, ограничиваемого окружностью радиусом г.
Отсюда
]mJr/2 @ < г < а),
цП1а2/Bг) {а < г < да).
^ йергия магнетика во внешнем магнитном поле. Пусть имеется фик-
фиксированное распределение токов, которое в свободном пространстве
создает магнитное поле, индукция которого Во (х, у, z) = \i0H(x, у, z),
а энергия
JHBdF D7.37)
Предположим, что все пространство заполнено однородным маг-
магнетиком с магнитной проницаемостью ц = const, а поле создается
тем же распределением токов. Как было показано [см. C8.22)], напря-
напряженность магнитного поля в магнетике не изменится (Н = Но), а ин-
индукция будет равна В = цН. Следовательно, при наличии магнетика
энергия поля
HBdK D7.38)
Это означает, что при заполнении всего пространства магнетиком
энергия поля увеличивается. Источником этой энергии являются,
§ 47. Энергия машитксно поля 329
в частности, сторонние электродвижущие силы, с помощью которых
поддерживаются неизменными токи при заполнении пространства
магнетиком. Поскольку после заполнения пространства магнетиком все
источники, благодаря которым возникло дополнительное поле, иден-
идентичны тем, которые создавали поле до заполнения пространства,
можно считать, что энергией магнетика во внешнем поле Но является
величина
WM = W - Wo = у f (Но В - Но Во) dK D7.39)
Подынтегральное выражение можно преобразовать:
Н0-В-Н0-В0=(ц-Цо)Яго= —-^В-Во = J-Bo, D7.40)
Ийо
где
"JlJ^B. D7.41)
zH R
Но И ЦЦо
Следовательно, энергия магнетика в магнитном поле равна
D7.42)
Это выражение аналогично формуле A8.30) для энергии диэлектрика
во внешнем электрическом поле, но отличается знаком в правой части.
Формула D7.42) выведена для магнетика, заполняющего все про-
пространство с ц = const. Однако она имеет вид интирала от плотности
энергии магнетика и поэтому следует ожидать ее справедливости
в произвольном случае. Соответствующие вычисления подтверждают
этот вывод. Ввиду их громоздкости они здесь не приведены.
Теперь можно вычислить энергию магнетика с магнитной прони-
проницаемостью ць находящегося в среде с магнитной проницаемостью \и2-
Будем опять рассматривать бесконечный магнетик и исходить из фор-
формулы D7.42) так же, как при выводе формулы A8.30), с той лишь
разницей, что в электростатике данное распределение зарядов создает
в различных средах одинаковое поле D, а в теории стационарного
магнитного поля данное распределение токов создает в различных
средах одинаковое поле Н. Тогда
WM ,2 = WM, - Wm2 = J (ц, - й2) Н, • Н2 d V, D7.43)
где
W», = у | (В, - Н, - Во • Но) d V. D7.44)
Выражение D7.43) аналогично формуле A8.31) с измененным знаком
перед интегралом. Хотя эта формула и выведена для бесконечного
магнетика, она справедлива и для ограниченного магнетика. В этом
случае интеграл распространяется по объему магнетика. Напряженность
330 8. Электромагнитная индукция и квазистационарные переменные токи
Н2 является напряженностью поля, создаваемого в точках объема
магнетика, если бы его проницаемость была равной магнитной про-
проницаемости Цг среды; Hj — фактическая напряженность в магнетике
с магнитной проницаемостью ць погруженном в среду с магнитной
проницаемостью \х2-
Предположим, что магнитная проницаемость среды изменяется на
бесконечно малую величину 5ц. При этом энергия магнетика, находя-
находящегося в магнитном поле Н, изменяется на bWM. Полагая в D7.43)
5ц = р.! - ц2, Н2 = Н, Н] = Н + 5Н и отбрасывая 5ц6Н • Н как величину
высшего порядка малости, получаем
D7.45)
где ц может быть функцией точки и других параметров. Эта формула
отличается от аналогичной формулы A8.36) для диэлектриков лишь
знаком.
П ычисление сил из выражения для эиерг ии. Рассмотрим систему
контуров, по которым текут токи. При перемещении и деформации
контуров за счет сторонних электродвижущих сил производится меха-
механическая работа. Энергия источника сторонних электродвижущих сил
расходуется на создание магнитного поля и на совершение механи-
механической работы. Работа сторонних электродвижущих сил определяется
формулой D7.2), а механическая работа при изменении параметра ?,,-,
характеризующего конфигурацию системы, равна по определению F] dE,,-,
где Fj — обобщенная сила, отнесенная к параметру ?,t. Закон сохранения
энергии записывается в виде
X/;d<Dy = dW+?F,dSi. D7.46)
i i
Рассмотрим прежде всего виртуальные процессы, в которых сохра-
сохраняются магнитные потоки, т. е. dOj = 0. Уравнение D7.46) принимает
вид
D7.47)
откуда с учетом независимости d^; получаем
D7.48)
где индекс Ф у частной производной в явном виде показывает, что
она берется при постоянных значениях потоков Фу. Чтобы пользоваться
формулой D7.48), необходимо энергию магнитного поля выразить
в виде функции от Ф; и ?,; как независимых параметров.
Для практических применений во многих случаях удобнее выразить
обобщенную силу в виде производных от энергии по обобщенным
параметрам при постоянных токах. Энергия магнитного поля D7.18)
i) 47. Энергия магнитного поля 331
с учетом того, что [см. D7.6)]
Ф. = I Uh, D7.49)
выражается в виде
1
'7" D150)
При постоянных силах токов (/( = const) из D7.50) следует, что
(dW), =-i V/,dO,, D7.51)
i
и поэтому формула D7.46) приводится к виду
(dW), = ?F,dS,. D7.52)
i
Отметим, что эта формула справедлива лишь при постоянных токах.
Принимая во внимание независимость \t, находим выражение для
обобщенных сил:
D7.53)
где индекс / у частной производной показывает, что она берется при
постоянных токах. Для использования D7.53) W должна быть выражена
в виде функции от сил токов и параметров !;,¦.
Рассмотрим в качестве примера два взаимодействующих контура
с токами, энергия магнитного поля которых определяется формулой
D7.17). Рассчитаем по D7.53), например, х-ю компоненту силы, которая
действует со стороны первого контура на второй. В качестве обоб-
обобщенной координаты возьмем значение координаты х некоторой точки
второго контура, считая первый контур неподвижным. В качестве
виртуального перемещения, связанного с этой координатой, необходимо
взять смещение второго контура вдоль оси X без деформаций и вра-
вращений и выразить энергию магнитного поля через эту координату
и дру1ие независимые параметры, которые нас сейчас не интересуют.
Вся зависимость энергии магнитного поля от х содержится во взаим-
взаимной индуктивности L12 = L2i, поскольку индуктивности LH и L12
не зависят от изменения взаимного расположения контуров. Обоб-
Обобщенная сила, связанная с декартовой координатой х, есгь проекция
обычной силы Fx. Поэтому D7.53) принимает вид
^ = М2~-. D7.54)
Аналогично определяются и другие компоненты силы. Индуктив-
Индуктивное ib L12 является геометрической величиной и ее зависимость от х
можно найти с помощью формулы D7.19).
332 8. Электромагнитная индукция и квазистационарные переменные токи
Ясно, что значение силы не зависит от того, по какой формуле ее
вычислять. Поэтому к значению силы D7.54) мы придем также, если
ее вычислять по формуле D7.48). Проведем это вычисление. В D7.48)
в качестве выражения для W нельзя взять D7.17), поскольку в него
входят в явном виде силы тока. Исключим их с помощью формул D7.10),
из которых следует:
Ь22Ф1 - ЬУ2Ф2 LnO2 -Ь21Ф1
li = —j—j Тг—> 1г = —г—j Ji—¦ D/.55)
Ь11^22 ~ Ь12 ^11^22 ~ ^12
Подставляя D7.55) в D7.17), находим
Ьр\ D7.56)
Теперь энергия магнитного поля выражена в явном виде через
потоки и можно применить формулу D7.48) при Ф, = const. Единствен-
Единственной величиной, зависящей в D7.56) от х, является L12, поэтому
- (LtlL12 + Lf2) Ф1Ф2 + Ll2Lll<bl-]^=I1l1 ^-, D7.57)
где учтены равенства D7.55). Как и ожидалось, D7.57) совпадает с D7.54).
Формулами D7.48) и D7.53) следует пользоваться в зависимости от
обстоятельств и выбирать ту из них, которая приводит к более
простым выкладкам.
фбъемные силы, действующие на сжимаемые магнетики. Имея выра-
выражение D7.45) для энергии магнетика в магнитном поле, можно,
пользуясь соотношением между силами и энергией, получить выраже-
выражение для сил точно так же, как это было сделано для диэлектриков
в § 19. Исходим из выражения D7.45) и рассуждаем так же, как при
переходе от A8.36) к формуле A9.41). Все вычисления также аналогичны,
надо лишь учесть, что для диэлектриков сила находится при постоян-
постоянных зарядах, т. е. по формуле A9.46), а для магнетиков — при посто-
постоянных токах, т. е. по формуле D7.53). Это означает, что при вычислении
производных энергию надо брать с различными знаками. В результате
вместо формулы A9.41) получается следующая формула:
D7.58)
Напомним, что все рассмотрение проводится для изотермических
процессов и, следовательно, производная йц/йрт в D7.58) должна
вычисляться при Т = const.
Формулу D7.58) целесообразно переписать по-другому:
, D7,9)
= - — #2gradu + — grad [H2pm
§ 47 Энергия viai питого поля 333
где учтено, что Н2 = В2/ц2 и -—( — ] = rJi- и т. д. В этом
виде D7.59) является более близким аналогом формулы A9.41), по-
поскольку роль полевого вектора в магнетизме играет В, а аналогом е
выступает 1/ц.
Запишем формулу D7.41) в виде
1 1 J
Пусть намагниченность J линейно зависит от плотности рт,
т. е. J ~ рт. Тогда из D7.60) следует, что
D7.61)
При этих условиях формула D7.59) принимает вид
D7.62)
что совпадает с C9.13). Таким образом, формула C9.13) справедлива
не только для жестких, но и для сжимаемых магнетиков, у которых
намагниченность линейно зависит от плотности массы. Это соблю-
соблюдается у газов и у некоторых жидкостей.
^ нергия магнитного момента во внешнем поле. Так как работа,
необходимая для увеличения потока магнитной индукции сквозь
поверхность, натянутую на контур с током I, равна / d<t> (йФ — поток
магнитной индукции, создаваемый не током /, протекающим по кон-
контуру, а другими источниками магнитного поля), то энергия, затрачи-
затрачиваемая для создания потока Ф сквозь поверхность, ограничиваемую
контуром тока /, равна /Ф. В случае бесконечно малого контура
Ф = В • S, 1Ф = рт • В, где рт = IS — магнитный момент тока. Следова-
Следовательно, энергия магнитного момента во внешнем магнитном поле
W= -р,„В.
D7.63)
Минимального значения эта величина достигает при совпадении
направлений рт и В. Это означает, что внешнее магнитное поле стре-
стремится повернуть магнитный момент до совпадения с вектором индук-
индукции [см. C9.8)].
Пример 47.1. Вычислить силу, с которой один соленоид втягивается или
выталкивается из другого (рис. 184). Плотности намотки и сила токов в них
равны ль 11 и п2, 1г соответственно, а площади поперечных сечений одинаковы.
Соленоиды достаточно длинные, а намотка достаточно плотная, поэтому поле
вдали от их концов можно описывать формулами для бесконечно длинного
соленоида. Значение х велико, вследствие чего можно пренебречь краевыми
эффектами.
334 8. Электромагнитная индукция и квазистаинопарныс переменные юки
184
К расчету силы взаимодействия
соленоидов
^p
шшЁЯЯш
н
х X
185
К расчету силы взаимодействия
соленоида и магнита
Найдем взаимную индуктивность, пользуясь
формулами D7.48) —D7.49). Первый соленоид
создает через каждый виток второго соленоида
поток HqUj/jS, а весь ноток через п2х витков
второго соленоида в области пересечения равен
Ф21 = \lonJiSll2X,
откуда получаем взаимную индуктивность
L2l = Ф21/Л = Mo"i,S.v (L12 = L2,)- D7.64)
Тогда сила равна
дх
D7.65)
Если токи имеют одинаковое направление,
то ItI2 > О, Fx > 0 и, следовательно, соленоиды
отталкиваются. При различных направлениях то-
токов Iil2 < О, Fx < О, что означает притяжение
соленоидов.
Пример 47.2. В соленоид, площадь кругового
сечения которого S, длина I, имеющего п витков
на 1 м длины, вдвинут магнетик с магнитной
проницаемостью ц (рис. 185). Найти силу, дей-
действующую на магнетик, пренебрегая краевыми
эффектами, если по соленоиду течет ток силой I.
Поскольку магнитная восприимчивость маг-
магнетика х **; '. в первом приближении напряжен-
напряженность везде можно считать равной HJU| = Нх =
= nl. Следовательно, энергия магнитного поля
системы равна
W = [НхВх/2 + НХО)ВХО) (I - x)/2] S,
где Вх и В,[о) — индукция соответственно в магне-
магнетике и вакууме, Учитывая, что Вх = \iHx, BXQ) =
= ц0Н^0), получаем
W = (n2l2/2) [их + цо (* - х)] S
и, следовательно, сила равна
где
) = 4- (И - Но) n2I2S = (vv - w0) S, D7.66)
дх /i 2
= HxBx/2, w0 =
— плотности энергии магнитного поля по разные
стороны границы, на которую действует сила,
Таким образом, поверхностная плотность силы
fx = Fx/S является суммой двух сил, действующих
с разных сторон на границу раздела. Поверхност-
Поверхностная плотность каждой из сил paei.a плотности
энергии магнитного поля.
§ 48. Цепи квазиспщпонарпого переменного юка 335
Пример 47.3. Вычислить индуктивность коаксиального кабеля длиной I,
центральная жила которого имеет радиус ги а оболочка радиусы г2 (внутрен-
(внутренний) и г3 (внешний) (см. рис. 140). Магнитная проницаемость проводников
равна \i, а пространство между жилой и оболочкой заполнено диэлектриком.
Прежде всего найдем индукцию магнитного поля. Ясно, что поле акси-
аксиально-симметрично и силовые линии индукции являются окружностями
с центром на оси кабеля. Из закона полного тока имеем (см. пример 35.1):
JL
2л
Но
2л
~2п
О
(О < г < г,),
(г, < г < г2),
оо).
D7.67)
Для вычисления самоиндукции участка кабеля воспользуемся соотношением
W = L1112, Так как W = — Н • В dK, то [см. D7.67)]
-—• 2wdr +
~Ь ~Г"
2 8л 2 2л
откуда
L =
'
2 2л
-'2
- ' Г,. In H + ^ In
2 (r? -
D7.68)
§ 48. Цепи квазистационарного
переменного тока
Излагаются основные методы расчета цепей
квазистационарного переменного тока.
Определение. При изучении переменных полей и токов необходимо
принять во внимание два фактора:
1) конечную скорость распространения электромагнитных полей
(см. § 61);
2) порождение магнитного поля изменяющимся электрическим по-
полем. Величина /см = OD/dt называется объемной плотностью тока сме-
смещения (см. § 57).
336 8. Электромагншная индукция и квазистационарные переменные юки
При не очень большой частоте переменного тока этими факторами
можно пренебречь, т. е. считать, что электромагнитные поля распростра-
распространяются в пространстве мгновенно, а токи смещения не существуют или,
другими словами, магнитное поле порождается только токами проводи-
проводимости. Токи и поля, удовлетворяющие этим условиям, называются
квазистационарными. Выразим критерии квазистационарности математи-
математически.
1. Если имеется периодический процесс, распространяющийся от
источника со скоростью с, то длина волны этого процесса, т. е. расстоя-
расстояние, на которое развертывается один период Т изменения процесса
во времени, равна
Пренебречь пространственным изменением некоторой величины, ха-
характеризующей процесс, можно только в том случае, если она рассмат-
рассматривается в областях, линейные размеры / которых много меньше длины
волны (/ <к X). Это и есть критерий пренебрежения конечной скоростью
распространения электромагнитных полей.
2. Если D = Do exp (tot), то jcu = dD/dt = imD = теЕ. Поэтому пре-
пренебречь эффектом токов смещения по сравнению с эффектом токов
проводимости можно при условии
17см I макс <^~ 17 1макс*
Поскольку j = yE, j.M = шшЕ, это условие может быть записано в
виде ^Л- = ^<<1.
IЛ макс Y
Принимая во внимание, что для металлических проводников е « е0,
у « 107 См/м, получаем, что токи смещения несущественны в области
частот
со «с —« 1018 с,
?о
т. е. вплоть до частот, больших частот колебаний, соответствующих
ультрафиолетовой части спектра. Эта оценка приближенная, поскольку
она не учитывает инерционных свойств среды, которые играют сущест-
существенную роль при высокой частоте. Учет инерционных свойств вещества
ослабляет эту оценку на несколько порядков, однако и после этого
диапазон частот, при которых можно пренебречь токами смещения по
сравнению с токами проводимости, остается очень большим.
Однако для переменных электромагнитных полей в вакууме и
диэлектрике учет токов смещения как источника магнитного поля
является необходимым при всех частотах, поскольку там токи прово-
проводимости отсутствуют. Наличие токов смещения обусловливает су-
существование электромагнитных волн (см. гл. 9).
Что касается первого критерия, то его роль определяется отно-
относительной величиной частоты и пространственных размеров области,
§ 48. Цепи квазистацнонарного переменною гока 337
в которой изучается процесс. Например, для технического тока часто-
частотой 50 Гц длина волны X я: 6 тыс. км. Поэтому если нас интересуют
вопросы, связанные с распределением тока по проводникам в преде-
пределах электростанции или даже города, то ток можно считать квази-
квазистационарным. Но если речь идет о передаче тока на многие тысячи
километров, то необходимо принять во внимание его переменность
вдоль линии передачи и нельзя считать его квазистационарным. Ток
очень больших частот с длиной волны в несколько метров нельзя
принимать за квазистационарный даже в пределах квартиры.
^амоиндукция. Электродвижущая сила индукции D6.1) возникает при
любых причинах изменения потока Ф, охватываемого контуром тока.
В частности, сам линейный замкнутый ток создает поток магнитной
индукции сквозь поверхность, которую он ограничивает. Следовательно,
при изменении силы тока в контуре возникает электродвижущая сила.
Это явление называется самоиндукцией. Поскольку ток создает вокруг
себя магнитное поле по правилу правого винта, а электродвижущая
сила в контуре связана с изменением потока по правилу левого винта,
из рис. 186 заключаем, что электродвижущая сила самоиндукции
направлена так, что препятствует изменению силы тока, которое ее
вызывает (правило Ленца).
Сила тока в контуре связана с охватываемым им собственным по-
потоком магнитной индукции формулой D7.3)
Ф = LI, D8.1)
где L — индуктивность контура. Поэтому формула D6.1) для э. д. с.
самоиндукции принимает вид
^с.„нл= _L—. D8.2)
at
включение и выключение постоянной э. д. с. в цепи с сопротивлением
и индуктивностью. Если в момент t = 0 в цепь (рис. 187) включается
источник сторонней э. д. с. постоянной величины, например батарея, то
сила тока / в цепи начинает расти. Однако за счет роста индукции
поля в контуре возникает э. д. с. самоиндукции, действующая противо-
противоположно сторонней э. д. с. В результате рост силы тока в цепи
замедляется. Для каждого момента времени соблюдается закон Ома,
который с учетом D8.2) записывается в виде уравнения
IR = и о - Ldl/dt, D8.3)
где R — полное сопротивление в цепи (включая внутреннее сопротив-
сопротивление источника). Это уравнение необходимо решить при начальном
условии / @) = 0. Говоря о том, что в каждый момент соблюдается
закон Ома, мы предполагаем, что сила тока во всех участках цепи
одна и та же, т. е. ток квазистационарен. Решение уравнения D8.3)
элементарно:
()! D8-4)
338 8. Элеюромапштиая индукция и квазистационариые переменные токи
R
График I (t) изображен на рис. 188. Уста-
Установившееся значение силы тока /(оо) = Uo/R,
соответствующее закону Ома для постоян-
постоянного тока, достигается лишь в смысле пре-
предела при бесконечном времени. Учитывая
экспоненциальную зависимость силы тока от
времени, можно как обычно за время на-
*синд растания силы тока в цепи принять такое
" значение т., при котором показатель экспо-
186 ненты обращается в минус единицу, т. е.
Возникновение самоиндукции. т = [_,/Ц_ D8,5)
Правило Ленца
При большой индуктивности в цепи на-
нарастание силы тока происходит медленно.
Например, если в цепь включить большую
катушку индуктивности и лампу накали-
накаливания, то после замыкания цепи проходит
значительный промежуток времени, в тече-
течение которого лампа разгорается до своего
полного постоянного накала.
При выключении постоянного источника
Цепь с сопротивлением и „ндук- э_ ( Ш) ш ицер Зако-
гивностью г ** \r h г г г
ротив его, можно наблюдать, что сила тока
не падает мгновенно до нуля, а уменьшает-
уменьшается постепенно. Уравнение для силы тока в
этом случае, очевидно, имеет вид
IR = - L d//df D8.6)
и решается при начальном условии / @) =
= VJR:
187
Up
R
О t
188
Нарастание силы тока в цепи
после включения постоянном сто-
сторонней э.д.с.
= ^° cxp(-Rt/L).
D8.7)
I
График этой функции показан на рис. 189.
Время убывания силы тока дается той же
формулой D8.5). При достаточно больших
индуктивностях после выключения сторон-
сторонней э. д. с. лампа накаливания в цепи гаснет
лишь постепенно в течение заметного про-
промежутка времени. Электродвижущей силой,
которая обеспечивает существование тока в
цепи в течение этого промежутка времени,
является электродвижущая сила самоиндук-
~ ЦИИ, а ИСТОЧНИКОМ Энергии — ЭНЬрГИЯ МаГНИТ-
Убывание силы тока в цепи после ' г г
выключения постоянной сторон- НОГО ПОЛЯ катушки ИНДукТИВНОСТИ. ВопрО-
ней э.д.с. сы включения и выключения э. д. с. в цепи
о
189
$ 48 Цепи квазистационариого переменного тока 339
с самоиндукцией впервые рассмотрел Гельм- i /
гольц в 1855 г.
ТТолучение прямоугольных импульсов тока.
Ьсли имеется источник прямоугольных
импульсов напряжения, то наличие в цепи
явления самоиндукции препятствует полу-
получению прямоу1 ольных импульсов тока. i
Импульсы тока имеют форму, показанную 190
на рис. 190. Для максимального прибли-
1 ч г Форма импульсов тока при пря-
жения их формы к прямоугольной необхо- моуРгольныхУ импульсах на%яже.
димо сделать возможно меньшей индуктив- Яия
ность контура.
р мкость в цепи. Наличие в цепи конден-
конденсатора исключает возможность протека-
протекания по ней постоянно: о тока. В этом случае
разность потенциалов между обкладками
конденсатора, на которых располагаются
соответствующие заряды, полностью ком-
компенсирует действие сторонней э. д. с. Одна-
Однако переменный ток в цепи при наличии
конденсатора протекать может, поскольку в
этом случае заряд на обкладках конденса-
конденсатора переменен, что и позволяет существо-
существовать току в цепи. Кроме того, разность
потенциалов на обкладках конденсатора не
компенсирует действия сторонней э. д. с,
благодаря чему и поддерживается соответ-
соответствующая сила тока.
Закон Ома при наличии в цепи конден-
конденсатора и сопротивления (рис. 191) записы-
записывается в виде уравнения
IR = U о - QIC, D8.8)
где Q — заряд на обкладке конденсатора,
Q/C — разность потенциалов между обклад-
обкладками конденсатора. Уравнение D8.8) удобно
продифференцировать по t и записать в виде
191
Цепь с емкостью и сопротив-
сопротивлением
192
Цепь с емкостью, индуктивнос-
индуктивностью, сопротивлением и источ-
источником сторонних э д.с
R
dl dUc
dt
dt
I,
D8.9)
где / = dg/df.
В ключение и выключение постоянной э. д. с.
в цепи с емкостью и сопротивлением.
Пусть постоянное напряжение Uo включа-
включается в момент t = 0. Из уравнения D8.8)
видно, что / @) = Uo/R, а уравнение D8.9)
Индуктивность и емкость
характеризуют свойство
цепи накапливать энер-
энергию в форме энергии элек-
электрического и магнитного
полей. Они «сглаживают»
кривые изменения силы
тока в сравнении с кри-
кривыми изменения напряже-
напряжения в зависимости от вре-
времени.
340 8. Электромагнитная индукция и квазисмационарные переменные токи
принимает при t > 0 вид
*?--тИ- D8Л0)
Решение этого уравнения при начальном условии I @) = Uo/R выра-
выражается формулой
^ D8.11)
т. е. с течением времени сила тока в цепи убывает от максимального
значения Uo/R до нуля. График / (t) аналогичен графику, показанному
на рис. 189, а время убывания силы тока х = RC. Поэтому если
емкость С достаточно велика, то ток после выключения постоянного
напряжения может существовать заметное время. Лампа, включенная
в цепь, сначала вспыхнет, а затем постепенно погаснет.
После того как сила тока упала до нуля, конденсатор оказывается
заряженным до разности потенциалов, равной сторонней э. д. с, но
противоположно направленной. Они компенсируют друг друга. При
выключении сторонней э. д. с, например путем закорачивания полю-
полюсов батареи, разность потенциалов на обкладках конденсатора ока-
оказывается нескомпенсированной. По цепи начинает течь ток, начальная
сила которого равна Uo/R, а закон уменьшения силы тока полностью
совпадает с D8.11) с тем же временем убывания силы тока.
Цепь с емкостью, индуктивностью, сопротивлением и источником
сторонних э. д. с. Эта цепь показана на рис. 192. На основании
D8.8) и D8.6) уравнение для тока в цепи имеет вид
IR = U - L^-~-Q. D8.12)
dt С
Дифференцируя обе части D8.12) по t, перепишем уравнение в виде
L*l- + R*L + ±l = -d-U. D8.13)
dt2 dt С dt
Различные частные случаи решения этого уравнения были рассмот-
рассмотрены раньше.
Переменный ток. Наиболее важным является анализ гармонического
переменного тока, поскольку с помощью представления произволь-
произвольной функции в виде ряда или интеграла Фурье к этому случаю
может быть сведен и любой другой.
Для рассмотрения этих вопросов целесообразно пользоваться комп-
комплексной формой представления гармонически изменяющихся величин.
Будем рассматривать установившийся режим.
Если сторонняя э.д.с. изменяется по закону
U = Uoeiat, D8.14)
то очевидно, что сила тока в D8.13) также должна изменяться со
временем по закону
§48. Цепи ква^истационарного переменного тока 341
1 = 10еш, D8.15)
причем /, U, Io, Uo в формулах D8.14) и D8.15) являются, вообще
говоря, комплексными величинами. Из D8.14) и D8.15) следует, что
~=iaU, ~=Ы, D8.16)
ш at
и поэтому уравнение D8.13) принимает вид
(-oJL + /сой + 1/С) / = mU. D8.17)
Разделив обе части уравнения D8.17) на ico, представим его в виде
IZ = U, D8.18)
где
Z = R + i [coL - 1/(й)С)] D8.19а)
называется импедансом. Уравнение D8.18) имеет вид закона Ома,
в который входит импеданс. Для переменного тока импеданс играет
роль сопротивления, однако, будучи комплексной величиной, он
посредством D8.18) позволяет учесть не только соотношение между
амплитудами силы тока и напряжения, но и соотношения между их
фазами.
В уравнении D8.18) все величины являются, вообще говоря, комплекс-
комплексными. Взяв модули от обеих частей этого уравнения, найдем связь
между амплитудами силы тока и напряжения:
\I\\Z\ = \U\, D8.196)
где
] Z | = ]/R2 + [coL - 1/(соС)]2. D8.19b)
Таким образом, если интересоваться только амплитудами силы тока
и напряжения, то уравнение D8.196) полностью эквивалентно закону
Ома для постоянного тока, однако величина | Z |, играющая роль
сопротивления, зависит от частоты тока в соответствии с D8.19в).
Оекторные диаграммы. Представим комплексные числа векторами на
комплексной плоскости. Гармонически изменяющаяся величина
изображена вектором, вращающимся с частотой со вокруг своего на-
начала против часовой стрелки. Длина этого вектора равна амплитуде
колебаний соответствующей физической величины.
Графический метод решения уравнения D8.18) очевиден из рис. 193,
если учесть, что умножение комплексной величины на i означает ее
поворот на я/2 против часовой стрелки без изменения длины, а умно-
умножение на ( — i) — поворот на я/2 по часовой стрелке.
Из рис. 193 видно, что угол ср определяется из уравнения
D,20)
342 8. Электромагнитная индукция и квачистационарпые переменные токи
J(»LI
193
Векторная диаграмма напряже-
напряжений в цепи переменного тока
194
Метод контурных токов
Импедансом учитывается
ие только омическое со-
сопротивление цепи, но и ее
индуктивное и емкостное
сопротивления. Будучи
комплексной величиной
импеданс позволяет учесть
не только соотношение
между амплитудами силы
тока и напряжения, но и
соотношения между их фа-
фазами.
Следовательно, ф изменяется в пределах
( + я/2, —я/2) в зависимости от соотношения
между импедансами различных элементов
цепи и частотой, при этом внешнее напря-
напряжение U по фазе может изменяться от
совпадения с напряжением на индуктивности
до совпадения с напряжением на емкости.
Более удобно это выразить в виде соотно-
соотношения между фазами напряжений на элемен-
элементах цепи и фазой внешнего напряжения:
1) фаза напряжения на индуктивности
(U, = i<x>LI) всегда опережает фазу внешнего
напряжения на угол между 0 и я;
2) фаза напряжения на емкости \UC =
= — ;//(<вС)] всегда отстает от фазы внеш-
внешнего напряжения на угол между 0 и —я;
3) фаза напряжения на сопротивлении
может как опережать, так и отставать от
фазы внешнего напряжения на угол между
+ я/2 и —я/2, причем отстает при преиму-
преимущественно индуктивной нагрузке, когда coL>
> 1/(соС), а опережает при преимущественно
емкостной нагрузке, когда coL < 1/(ojC).
Диаграмма (рис. 193) позволяет также
сформулировать следующие утверждения о
соотношении между напряжениями и силами
токов на различных элементах цепи, причем
отсчет удобно вести от силы тока, посколь-
поскольку он на всех элементах цепи имеет одну
и ту же фазу:
1) фаза напряжения на индуктивности
опережает фазу силы тока на я/2;
2) фаза напряжения на емкости отстает
на я/2 от фазы силы тока;
3) фаза напряжения на сопротивлении
совпадает с фазой силы тока;
4) фаза внешнего напряжения может- как
опережать, так и отставать от фазы силы
тока, что определяется нагрузкой.
|~[равила Кирхгофа. Уравнение D8.18)
позволяет решать все задачи, касаю-
касающиеся переменного тока в цепи с индук-
индуктивностью, емкостью и сопротивлением
аналогично тому, как соответствующие за-
задачи решаются с помощью закона Ома
для цепи с сопротивлением в случае
постоянного тока. Анализ разветвленных
§ 48. Цепи квачиспационарного переменней о тка 343
цепей переменного тока аналогичен анализу цепей постоянного тока
(см. § 28). Так как для переменного тока в замкнутом контуре спра-
справедлив закон D8.19), а в каждом узле справедлив закон сохранения
заряда, то правила Кирхгофа B8.4) и B8.5) для постоянного тока
обобщаются на переменные токи следующим образом:
1) для всякого замкнутого контура
i = YJ(±)Vk; D8.21)
k
2) в каждом узле
(+)/, = 0. D8.22)
Это обобщение правил Кирхгофа на разветвленные цепи перемен-
переменного юка было осуществлено в 1886 Д. У. Рэлеем A842-1919).
Следует сделать замечание о знаках величин в D8.21) и D8.22). Хотя
каждая из величин /,-, Uk, входящих в эти формулы, является комплекс-
комплексной и содержит в себе фазу (а следовательно, и знак), при составлении
уравнений необходимо проставлять знаки, потому что один и тот же
участок может принадлежать разным контурам и, следовательно,
проходится при составлении уравнений в противоположных направле-
направлениях. Аналогичное замечание касается и знака Uk. Решение уравнений
позволяет найти как амплитуды, так и фазы всех сил токов. Ввиду
комплексности всех величин число существенных уравнений при этом
в два раза больше, чем было бы в аналогичном случае постоянных
токов.
Последовательное и параллельное соединения импедансов. Из фор-
формулы D8.18), аналогично случаю постоянных токов, следует, что при
последовательном соединении
D8.23)
а при параллельном
D8.24)
Эго обстоятельство делает анализ элекхрических цепей переменного
тока аналогичным анализу цепей постоянного тока и нет необходи-
необходимости более подробно останавливаться на этом вопросе.
Величина, обратная импедансу, называется проводимостью:
Y = 1/Z. D8.25)
Поэтому можно сказать, что при параллельном соединении скла-
складываются проводимости:
Y=Yl + Y2. D8.26a)
С помощью проводимости закон Ома записывается в виде
/ = YU. D8.266)
344 8. Электромагнишая индукция и квазистационарные переменные токи
iyf етод контурных токов. При расчете сложных цепей значительные
упрощения вносит метод контурных токов, который является пря-
прямым следствием правил Кирхгофа. Сложный контур состоит из системы
простых замкнутых контуров. На рис. 194 изображен сложный контур,
состоящий из трех простых контуров. В уравнении Кирхгофа при
обходе замкнутого контура на каждом его участке между узлами
берется сила тока, действительно протекающего по этому участку.
На каждом участке контура сила тока, вообще говоря, различна. В ме-
методе контурных токов принимается, что на всех участках каждого
замкнутого контура течет один и тот же ток. Эти токи называются
контурными. Полная сила тока, текущего по участку контура, равна
при этом алгебраической сумме сил контурных токов, для которых
этот участок является общим. Уравнение Кирхгофа для каждого кон-
контура пишется с учетом этого обстоятельства, т. е. выражается через
контурные токи. Полный импеданс для каждого участка контура между
узлами (рис. 194) обозначен соответствующим индексом. Положительное
направление обхода взято по часовой стрелке.
Уравнения для контурных токов, число которых совпадает с числом
простых контуров, имеют вид:
Z23/3 = 0,
D8'27)
где Zlb Z22, Z33 — собственные импедансы контуров, равные сумме
импедансов участков соответствующих контуров:
2ц = Zj + Z2 + Z3, Z22 = Z4 + Z5 + Z6 + Z2, Z33 =
= Z3+Z6 + Z2, D8.28)
a Z12, Z13 и т. д. — взаимные импедансы контуров, равные импе-
дансам участков, принадлежащих двум контурам. Их знак зависит от
того, проходится ли соответствующий участок током, стоящим у взаим-
взаимного импеданса сомножителем, в положительном или отрицательном
направлении по сравнению с контурным током, для которого пишется
уравнение. Так, например,
Zl2 = -Z2, Z21 = -Z2 и т. д. D8.29)
Нетрудно видеть, что
Z,j = Zj,. D8.30)
Изложенное делает почти очевидным тот факт, что уравнения D8.27)
объединяют в себе оба правила Кирхгофа. Более строго это можно
доказать, если D8.27) получить из уравнений Кирхгофа D8.21) и D8.22),
перейдя к контурным токам. Читатель может попытаться проделать
эти алгебраические выкладки.
Число уравнений D8.27) для контурных токов равно числу неиз-
неизвестных токов. Система уравнений решается по общему правилу
tj 48. Цепи квазистационарного переменного тока 345
с помощью теории определителей:
где
Д =
), 1г = U(Al2/A), I3 = U(A13/A),
D8.31)
Zl2 Z13
Z22 Z23
Z32 Z33
D8.32)
— определитель системы; Д1Ь Д12, Д13 —
дополнения элементов Zlb
определителе Д:
12
и Z,
Аи =
Z22
Z32
Z21
Z31
Z23
Z33
z22
Z32
Z21
Z3i
Z23
Z33
195
Тороид прямоугольного сечения
D8.33)
Тем самым задача решена. Обобщение
изложенного метода контурных токов на
произвольное число элементарных контуров
очевидно. При этом необходимо вниматель-
внимательно следить, чтобы все элементарные контуры
проходились в одном и том же направлении
и были все учтены в уравнениях.
Пример 48.1. Найти самоиндукцию п витков
обмотки, намотанных на тороид прямоугольного
сечения, внутренний и внешний радиусы которого
равны соответственно rL и г2, а высота а (рис. 195).
Выбирая в качестве контура интегрирования
Lo окружность радиусом г, концентричную с осью
симметрии тороида, и применяя закон полного
тока, получаем
H-dl =
по обмотке
где / — сила тока,
тороида.
Магнитный поток, охватываемый одним вит-
витком, равен
ч ч
ГЛЪ* I I /1И Г *•
D8.34)
1 - ип [и н- ^anI fdr Или/. гг
h - V-a Hvur= —— —= ——In —
J 2л J r 2it rj
откуда самоиндукция равна
L= (n<bjl) = [цаи2/Bл)] In
D8.35)
Хотя в случае перепенных
токов электродвижущие
силы и силы токов пред-
представлены комплексными
величинами и, следова-
следовательно, содержат в себе
фазу (и знак) при состав-
составлении уравнений Кирхго-
Кирхгофа необходимо простав-
проставлять знаки, потопу что
один и тот же участок
может принадлежать раз-
разным контурам и проходит-
проходится при составлении уравне-
уравнений в противоположных
направлениях.
В методе контурных токов
принимается, что на всех
участках каждого замкну-
замкнутого контура течет один и
тот же ток, называемый
контурным. Полная сила
тока, текущего по участ-
участку контура, равна при этом
алгебраической сумме сил
контурных токов, для ко-
которых этот участок явля-
является общим.
Каков физический смысл кри-
критериев квазистационарности?
Чем определяются знаки в
уравнениях, выражающих
правила Кирхгофа, в случае
переменных токов?
В чем преимущества метода
контурных токов и когда его
целесообразно применять?
346 8. Электромагнитная индукция и квазистационарные переменные токи
§ 49. Работа и мощность переменного тока
Выводятся формулы работы и мощности,
развиваемой переменным током. Обсуж-
Обсуждаются основные физические явления, связан-
связанные с работой электродвигателей.
TVI1 новенная мощность. Энергия источника сторонних э. д. с. в цепи
с током испытывает следующие превращения:
а) превращается в теплоту в результате джоулева нагрева провод-
проводника [см. B7.4)]. Если в цепи имеется потребитель, который за счет
энергии источника сторонних э. д. с. совершает механическую работу,
то его мощность выражается формулой, аналогичной B7.4). Поэто-
Поэтому предположим, что в цепи имеется лишь омическое сопротивле-
сопротивление R, а мощность, развиваемую на этом сопротивлении, обозначим
p,r = i2R;
б) превращается в энергию магнитного поля. Поскольку энергия
магнитного поля определяется формулой D7.5), мощность, развиваемая
источником сторонних э. д. с. для изменения энергии магнитного поля,
равна
Индуктивные свойства цепи характеризуются индуктивностью L.
В отличие от PtR, мощность PlL может быть как положительной
(dl/dt > 0), так и отрицательной (dl/dt < 0). Это означает, что источник
сторонних э. д. с. отдает энергию для увеличения энергии магнитного
поля и получает энергию при уменьшении энергии магнитного поля;
в) превращается в энергию электрического поля при его изменении.
Электрические свойства цепи характеризуются ее емкостью С. Посколь-
Поскольку энергия конденсатора, на пластинах которого имеется заряд Q,
определяется формулой A8.20г), мощность источника сторонних э. д. с.
для изменения энергии электрического поля равна
AW Q AQ Q
где / = dQ/df — сила тока в цепи. Эта мощность может быть как
положительной, так и отрицательной: при увеличении напряженности
электрического поля энергия источника сторонних э. д. с. превращается
в энергию электрического поля, при уменьшении напряженности —
энергия электрического поля превращается в энергию источника сторон-
сторонних э. д. с.
Полная мощность, развиваемая источником сторонних э. д. с. в цепи,
равна
,c D9.3)
§ 49. Работа и мощность переменного тока 347
Часто Р, называют мощностью, развиваемой током, или мощностью
тока. Мы будем использовать это выражение, помня, однако, о его
условном характере. Аналет ично P,R, Р,ь Р1С называют мощностями
тока на сопротивлении, индуктивности и емкости. Для наглядности
допустим, что омическое сопротивление, индуктивность и емкость
сосредоточены в разных частях цепи (см. рис. 192).
Стороннюю э. д. с. U называют напряжением.
На омическом сопротивлении происходит изменение потенциала на
UlR = IR, поэтому UlR принято называть потерей напряжения на сопро-
сопротивлении. Между пластинами конденсатора разность потенциалов равна
UtC = QIC. Поэтому в цепи на конденсаторе напряжение изменяется
на UtC. В индуктивности возникает э. д. с. самоиндукции ^иид= — Ldl/dt,
на компенсацию которой источник сторонних э. д. с. затрачивает соот-
соответствующую часть сторонней э.д.с. (U,L— Ldl/dt — изменение напря-
напряжения на индуктивности).
Поэтому формулы D9.1) и D9.2) принимают вид:
Pl,.= U,J,PlC=UtCI. D9.4)
Тогда [(см. 49.3)]
Pl=U,RI+U,LI+U,cI = UI. D9.5)
Пусть сила тока в цепи изменяется по закону
/ = /0 sin cot. D9.6)
В соответствии с рис. 193 для действительных значений U,L, U,c и U,R
запишем:
UlL = /ocoLsin (oaf + я/2), D9.7)
U,c = [/оДюС)] sin (of - я/2), D9.8)
UlR = I0Rsiniat. D9.9)
Следовательно, мгновенные мощности, развиваемые током на раз-
различных элементах цепи, определяются формулами:
PtL = JqCoL sin cof sin (cof + я/2) = J^coL sin u>t cos cot, D9.10)
Pic = t/o/(wC)] sin cot sin (cot - я/2) = - [/,V(oaC)] sin cut cos cot, D9.11)
PlR = I20R sin2 cot, D9.12)
которые показывают, что лишь на сопротивлении R мощность тока
все время положительна, т. е. ток совершает положительную работу.
Мгновенная мощность, развиваемая током на индуктивности и емкости,
знакоперемеииа: часть времени ток совершает положительную работу,
т. е. передает свою энергию в эти элементы; часть времени работа
отрицательна, т. е. энергия из этих элементов возвращается к источ-
источнику сторонних э. д. с. Таким образом происходит обмен энергией между
индуктивностями, емкостями и источниками сторонних э. д. с, в про-
процессе которого емкости и индуктивности играют роль источников
электродвижущих сил.
348 8. Электромагнитная индукция и квазистационарные переменные токи
С мощность. Для получения средней мощности тока за период
колебаний необходимо усреднить выражения D9.10) — D9.12) па пе-
периоду колебаний силы тока. При этом необходимо учесть, что
<sin Ш cos со(> = 0, <sin2 Ш} = 1/2. D9.13)
С учетом D9.13) из D9.10) - D9.12) находим:
Pl = <P,l> = 0, D9.14)
>с = <Р,с> = 0, D9.15)
Pr = <PtR> = №*. D9.16)
Средняя мощность отлична от нуля лишь на сопротивлении R.
Средние мощности на индуктивности и емкости равны нулю, т. е. на
этих элементах током никакой работы не совершается, они в среднем
энергетически нейтральны. Поэтому сопротивление R называется актив-
активным элементом цепи (активным сопротивлением), а емкости и индук-
индуктивности — реактивными сопротивлениями.
Эффективные значения силы тока и напряжения. Из рис. 193
видно, что
I0R = U0 cos cp, D9.17)
и поэтому формула D9.16) может быть представлена в виде
Pr = 4ihhR = '/г'о^о cos ф, D9.18)
где Io, Uo — амплитуды силы тока и внешнего напряжения; ср — раз-
разность фаз между силой тока и напряжением [см. D8.20)]; cos cp —
коэффициент мощности, от которого зависит, насколько эффективно
производится передача мощности от источника тока к потребителю.
У постоянного тока мгновенная мощность совпадает со средней
[см. D9.2)]. Так как у постоянного тока cos cp = 1, то формулу D9.18)
можно сделать идентичной B7.3), если вместо амплитудных значений
/0 и Uo использовать их эффективные значения:
D9.19)
Тогда
Л* = 'эфС/эфСО5ср. D9.20)
Использование /^ и С/Эф позволяет рассматривать мощность перемен-
переменного тока формально так, как будто нет колебаний мощности. Лишь
присутствие cos cp напоминает о том, что речь идет о переменном токе.
Когда в электротехнике говорят о силе переменного тока и напря-
напряжении, то имеют в виду их эффективные значения. В частности,
амперметры и вольтметры градуируют обычно на эффективные зна-
значения. Поэтому максимальное значение напряжения в цепи перемен-
переменного тока почти в полтора раза больше того, которое показывает
вольтметр. Это необходимо принимать во внимание при расчете изо-
изоляторов, анализе вопросов безопасности и т. д.
§ 49. Работа и мощность переменного тока 349
J? оэффициент мощности. Одним из главных назначений цепей пере-
переменного тока является передача энергии. Поэтому при проектирова-
проектировании линий передач необходимо учитывать cos ф.
Предположим, что в линии имеется лишь активная нагрузка.
Тогда cos ф = 1 и отдаваемая в нагрузку мощность при заданных /эф и
{УЭф максимальна. Если в цепь включить реактивную нагрузку, например
индуктивность, то cos ф станет меньше единицы и для обеспечения
передачи прежней мощности необходимо соответственно увеличить
/эфGЭф, т. е. к потребителю энергии по линии передачи подводить
больший ток. Это приводит к увеличению потерь энергии на джоулеву
теплоту в линии передачи. Поэтому всегда стремятся распределить
нагрузки так, чтобы было ф « 0, т. е. cos ф « 1.
Рассмотрим, например, линию передачи для питания лампы нака-
накаливания (рис. 196), когда в цепи последовательно с лампой имеется
большая индуктивность и переменная емкость. Пусть в начальный
момент емкостное сопротивление равно нулю (С = оо). В этом случае
при достаточно больших Leo по сравнению с сопротивлением R лампы
угол ф достигает значений, близких к я/2, и cos ф очень мал. Поэтому,
если даже абсолютное значение [/-,ф в цепи достаточно велико, на
лампе выделяется очень малая мощность и лампа горит очень тускло
или даже совсем не светится. При уменьшении емкости С коэффи-
коэффициент мощности возрастает (угол ф уменьшается, приближаясь к нулю)
и накал лампы постепенно увеличивается. Эффективное напряжение
на клеммах генератора остается неизменным, мощность, передаваемая
генератором в линию, возрастает. Таким образом, увеличение коэффи-
коэффициента мощности введением реактивных, не потребляющих мощности
или, как говорят, безваттных, нагрузок в цепи позволяет улучшить
эффективность работы линии передачи.
Электродвигатели. Одним из важнейших применений электрического
тока является преобразование передаваемой им энергии в механи-
механическую работу, осуществляемую электродвигателями. Их работа осно-
основана на использовании силы Ампера, которая действует на проводник
с током в магнитном поле. Первый электродвигатель, положивший
начало применению электричества для производства работы, был
сконструирован в 1839 г. Б. С. Якоби A801-1874).
Для выяснения принципиальной стороны дела рассмотрим простей-
простейший электродвигатель постоянного тока (рис. 197). Источник постоянной
электродвижущей силы Uo включен в цепь ACDFA. Прямолинейный
проводник DC может скользить вдоль проводников FG и АК. Он
находится в однородном магнитном поле, индукция которого направ-
направлена вверх от плоскости чертежа. Когда по этому проводнику течет
ток, то на него действует сила Лоренца F = ПВ. Под ее действием
проводник движется и совершает механическую работу, т. е. осуществля-
осуществляет функцию электродвигателя.
Рассмотрим баланс энергий. При перемещении проводника на dx
совершается работа
350 8. Электромагнитная индукция и квазистационарные переменные гоки
196
Повышение коэффициента мощ-
мощности
О
197
Схема работы
электродвигателя
простейшего
d/4 = F dx = IIB dx D9.21)
и, следовательно, мощность равна
Pa = dAldt=IBlv, D9.22)
где v = dx/dt — скорость проводника.
С другой стороны, при движении провод-
проводника в контуре возникает электродвижущая
сила индукции
— d<l> IB dx'
?инд = —— = — = _iB D9.23)
df dt
направленная против сторонней электродви-
электродвижущей силы, которая генерирует токи и со-
совершает работу по преодолению действия
силы D9.23). Затрачиваемая при этом источ-
источником сторонних э. д. с. мощность равна
рст= Гинл/= -IBvI. D9.24а)
Сравнение D9.24) и D9.22) показывает, что
вся развиваемая электродвигателем мощ-
мощность обеспечивается источником сторон-
сторонних э. д. с. Кроме полезной мощности D9.22)
источником сторонних э. д. с. развивается
мощность, расходуемая на выделение джоу-
левой теплоты в омическом сопротивлении
проводов, по которым течет ток, и внутрен-
внутреннем сопротивлении источника. Обозначив
R — суммарное омическое сопротивление
проводов и внутреннее сопротивление источ-
источника, получим следующий баланс напряже-
напряжений для замкнутого контура (первое прави-
правило Кирхгофа):
IR = Uo
=U0- IBv.
D9.246)
Умножим обе части этого равенства на /:
I2R = U0I -IlBv = U0I -Pn, D9.25)
198 где использовано выражение D9.22). Оконча-
Схема работы синхронно, о лви- тельно формулу D9.25) целесообразно запи-
гателя сать в виде
= IU0 = I2R + Ря, D9.26)
Мгновенная мощность,
развиваемая током иа ии-
дуктивиостях и емкостях,
энакопеременна, а на со-
сопротивлении — положи-
положительна.
т. е. мощность, развиваемая источником сто-
сторонней э. д, с, расходуется на выделение
джоулевой теплоты с мощностью I2R и ра-
работу электродвигателя с мощностью Рл.
§ 49 Работа и мошноси. переменною тока 351
Для переменного тока расчет баланса энергий несколько сложнее,
но физическая суть явлений остается без изменения.
/"'инхронные двигатели Для обеспечения непрерывности работы дви-
двигателя необходимо создать некоторый периодический режим. Наибо-
Наиболее простой является схема, изображенная на рис. 197, в которой
индукция изменяется периодически со временем.
После того как проводник CD переместится на некоторое расстоя-
расстояние вправо и совершит определенную работу, направление индукции
изменяется на обратное. При одном и том же направлении тока и
сила F изменит свое направление на обратное. После этого проводник
замедляется и начинает двш аться влево, снова совершая работу, и т. д.
В результате получается электродвигатель, рабочая часть которого
(проводник CD) движется синхронно с изменяющимся внешним магнит-
магнитным полем Такой двигатель называется синхронным. В указанной
схеме можно, конечно, индукцию поля оставить постоянной, а пе-
периодически изменять направление тока в движущемся контуре. При
этом движение проводника будет происходить синхронно с изменениями
тока в нем. Такой двигатель тоже является синхронным. Можно
также одновременно изменять соответствующим образом и индукцию
и силу тока в проводнике, осуществляя при этом синхронно с ними
соответствующее движение проводника CD.
Используемые в технике синхронные двигатели в принципиальном
отношении работают так же, как схематический двигатель. При этом
в технике используются все три возможности осуществления синхрон-
синхронного двигателя. Однако фактическая реализация этих принципиально
простых схем осуществляется довольно сложными конструкциями. Как
правило, при этом используется вращательное движение.
Простейшая схема работы синхронного двигателя с вращательным
движением изображена на рис. 198. В постоянном магнитном поле
находится рамка, по которой течет переменный ток. Силы Лоренца,
действующие на проводники рамки, перпендикулярные индукции маг-
магнитного поля, создают вращательный момент, под действием которого
рамка вращается. Чтобы этот момен! действовал все время в одном
направлении, частота вращения рамки должна быть равна частоте
текущего по ее проводам переменного тока, т. е. должно соблюдаться
условие синхронизма. Можно осуществить также такие схемы двига-
двигателей, когда частота вращения рамки будет в целое число раз меньше
частоты питающего электродвигатель переменного тока.
Основными недостатками синхронных двигателей являются труд-
трудность запуска, в процессе которого частота вращения рамки стано-
становится синхронной с частотой переменного тока, и возможность потери
синхронизма при резком изменении нагрузки. В технике разработаны
способы достаточно эффективного преодоления эгих недостатков.
Асинхронные двигатели. Изменяющееся магнитное поле по закону
электромагнитной индукции Фарадея создает электрическое поле
[см. D6.5)]. Если такое вихревое поле существует в проводнике, то
352 8. Электромагнитная индукция к квазистационариые переменные токи
возникают соответствующие электрические токи, плотность которых в
каждой точке проводника определяется законом Ома (j = yE). Эти
токи взаимодействуют с магнитным полем. Следовательно, перемен-
переменное магнитное поле не только создает в проводнике токи, но и
действует на него с соответствующими силами.
Представим себе, что переменное магнитное поле создается магни-
магнитами А и С, которые закреплены на оси и могут вращаться вокруг
нее под действием внешнего момента сил (рис. 199). Диск D из сплош-
сплошного проводника также закреплен на оси и может вокруг нее вра-
вращаться. При движении магнитов в каждой точке диска D существует
переменное магнитное поле и возникает соответствующая плотность
тока, на который со стороны магнитного поля действует сила Ампера.
Таким образом, на диск D со стороны вращающихся магнитов дейст-
действуют определенные силы. Вычислим результирующее действие этих
сил. По закону Ленца, токи, возникающие в проводнике вследствие
электромагнитной индукции Фарадея, стремятся уменьшить дейст-
действие факторов, которые их вызывают. В данном случае фактором,
вызывающим индукционные токи в диске D, является относительное
движение магнита и диска. Следовательно, силы, действующие на диск,
должны стремиться уменьшить скорость относительного движения маг-
магнита и диска. Это означает, что к диску приложен момент сил,
стремящийся его вращать в том же направлении, в каком вращаются
магниты. Поэтому диск приходит во вращение в направлении движе-
движения магнитов, как бы увлекается вращающимся полем магнитов.
Момент сил существует лишь тогда, когда угловая скорость вра-
вращения магнитов отличается от угловой скорости вращения диска, т. е.
между вращающимся магнитным полем и диском существует «проскаль-
«проскальзывание». Чем оно меньше, тем меньше момент сил, действующих
на диск. Поэтому при увеличении нагрузки на ось диска увеличивается
«проскальзывание». При неизменной скорости вращения магнитного
поля и его индукции это означает уменьшение скорости вращения
диска.
Этот механизм приведения диска во вращение составляет принци-
принципиальную основу работы асинхронных двигателей. Однако для того,
чтобы двигатель мог именоваться электродвигателем, необходимо
обеспечить вращение магнитного поля без механического привода. Для
этого используются электромагниты, питаемые переменным током,
(^оздание вращающегося магнитного поля. Два электромагнита,
создающих взаимно перпендикулярные магнитные поля (рис 200),
питаются переменным током с разностью фаз я/2. На схеме (рис. 200)
это в достаточной степени достигается введением в цепь электро-
электромагнитов индуктивности L и сопротивления R. В результате этого
в пространстве между полюсами электромагнитов создаются два
переменных магнитных поля, индукции которых изменяются по гармо-
гармоническому закону с разностью фаз, близкой к я/2. Сумма индукций
Bj и В2 этих полей является вектором В, который вращается вокруг
точки О (рис. 201).
§ 49. Работа и мощность переменного тока 353
Если в пространстве между магнитами
(рис. 200) поместить массивный проводник,
например цилиндр с осью вращения, перпен-
перпендикулярной плоскости рисунка, то во вра-
вращающемся поле он будет приведен во вра-
вращение в направлении вращения поля. Проис-
Происходящие при этом физические процессы ана-
аналогичны тем, которые осуществляются при
создании поля вращающимися постоянными
магнитами. Вместо сплошного цилиндра
употребляется короткозамкнутый ротор
(рис. 202).
Вращающееся магнитное поле гораздо
удобнее создавать с помощью трехфазного
тока, поскольку в этом случае не требует-
требуется искусственно создавать разность фаз
между силами токов, питающих различные
электромагниты (см. § 52).
Ясно, что скорость вращения асинхрон-
асинхронного двигателя может изменяться непрерыв-
непрерывно и ни в каком кратном соотношении
с частотой питающего тока не находится,
поэтому двигатель и называется асинхрон-
асинхронным, а возможность непрерывного измене-
изменения скорости вращения составляет одно из
его очень существенных преимуществ.
Сила тока в обмотках электромагнита
зависит от «проскальзывания»: чем оно боль-
больше, тем больше сила тока. Поэтому в
момент запуска, когда проскальзывание
максимально, через обмотки двигателя про-
проходит очень большой ток, который может
их повредить. Для избежания этого в цепь
питания вводится переменный реостат, ко-
который в момент включения устанавливается
на достаточно большое сопротивление.
По мере увеличения частоты вращения
двигателя сопротивление реостата умень-
уменьшают.
Так же как и в случае синхронных
двигателей, техническое осуществление асин-
асинхронных двигателей характеризуется боль-
большим разнообразием и не является простой
задачей. Однако даже в самых сложных
конструкциях основополагающие принципы
остаются неизменными.
199
Схема возникновения враща-
вращательного момента в асинхронном
двигателе
200
Схема установки для создания
вращающегося магнитного поля
[
\ °
B^Bos
в
у
inu/
В
\
I-B0COS4)J
/
201
Сложение двух взаимно перпен-
перпендикулярных гармонических коле-
колебаний с разностью фаз я/2
202
Короткозамкнутый якорь асин-
асинхронного двигателя
12 А. Н. Матвеев
354 8. Электромагнитная индукция и квазистационарные переменные токи
Асинхронные двигатели могут работать не только при вращающем-
вращающемся магнитном поле, но и при пульсирующем. Это очевидно, если
принять во внимание, что пульсирующее поле эквивалентно двум по-
полям, вращающимся в противоположных направлениях. Одно из полей
обеспечивает вращение ротора асинхронного двигателя, а вращаю-
вращающееся в противоположном направлении поле в среднем никакого
действия на вращение ротора не оказывает.
(Согласование нагрузки с генератором. Генератор переменного тока,
создающий электродвижущую силу, сам обладает определенным
внутренним сопротивлением, емкостью и индуктивностью, т. е. обладает
определенным импедансом:
Zr = RT + iXT, D9.27)
где Rr — активное сопротивление; Хт — реактивное сопротивление, яв-
являющееся разностью индуктивного и емкостного сопротивлений. На-
Нагрузка, на которую работает генератор, также характеризуется импе-
импедансом :
ZH = RH + iXH, D9.28)
причем мощность выделяется лишь на активном сопротивлении RH.
В цепи генератор и нагрузка стоят последовательно. Ur — электро-
электродвижущая сила генератора.
Мощность, развиваемая на нагрузке Rm в соответствии с форму-
формулой D9.16) равна
рн = 72/оД„, D9.29)
где /о — квадрат амплитуды силы тока, протекающего через нагрузку.
На основании D8.196) имеем
\Ur\2 \Ur\2
С помощью D9.30) запишем формулу D9.29) в виде
II/ I2 R
Рн= ~?~Tr .2 (х—Y\r- D9.31)
Выясним, при каких условиях эта мощность максимальна.
Реактивные сопротивления Хт и Хк могут принимать как положи-
положительные, так и отрицательные значения. Ясно, что для достижения
максимальности D9.31) необходимо выполнение условия
Х\ + Хк = 0.
D9.32)
Оно означает, что коэффициент мощности должен иметь макси-
максимальное значение (cos ср = 1). При соблюдении условия D9.32) выражение
D9.31) принимает вид
I ir |2 p
Р ' Urlн (лд зт)
§ 49. Работа и мощность переменного тока 355
Мощность изменяется с изменением активного сопротивления
нагрузки и достигает максимума при условии cPHjdRH = 0, т. е. когда
D9.34)
При соблюдении условий D9.32) и D9.34) генератор отдает нагруз-
нагрузке максимальную мощность. В этом случае говорят, что нагрузка
полностью согласована с генератором.
С учетом D9.34) максимальная мощность, выделяемая на нагрузке
генератора, равна
Р = |t/r|2 — = ^^- D9 35)
^нмакс 2 4Л AR ' \~>'-J->)
где <1/о> — средний квадрат амплитуды напряжения генератора.
Вопросы согласования нагрузки с генератором имеют большое зна-
значение во всех случаях, когда требуется передать на нагрузку макси-
максимальную мощность. Например, входное сопротивление приемника
желательно согласовать с сопротивлением антенны (генератор) и линии
передачи (см. § 54).
'J1 оки Фуко. Индукционные токи, возникающие в массивных проводниках
в переменном магнитном поле, называются токами Фуко. Иногда
они играют полезную роль, а иногда вредную.
Токи Фуко играют полезную роль в роторе асинхронного двига-
двигателя, приводимого в движение вращающимся магнитным полем,
поскольку само осуществление принципа работы асинхронного дви-
двигателя требует возникновения токов Фуко. Являясь токами проводи-
проводимости, токи Фуко рассеивают часть энергии на выделение джоулевой
теплоты. Эта потеря энергии в роторе асинхронного двигателя является
бесполезной, но с ней приходится мириться, избегая лишь чрезмер-
чрезмерного перегревания ротора. Но одновременно с этим в сердечниках
электромагнитов асинхронного двигателя, выполненных обычно из
ферромагнетиков, являющихся проводниками, также возникают токи
Фуко, которые не имеют никакого значения для принципа работы
электромагнитов, но нагревают эти сердечники, ухудшая тем самым
их характеристики. С ними необходимо бороться, как с вредным фак-
фактором. Борьба заключается в том, что сердечники изготовляют из
тонких пластин, отделенных одна от другой слоями изолятора, причем
их устанавливают так, чтобы токи Фуко были направлены поперек
пластин. Благодаря этому при достаточно малой толщине пластин токи
Фуко не могут развиваться и имеют незначительную объемную
плотность.
Джоулева теплота, выделяемая токами Фуко, полезно используется
в процессах разогрева или даже плавки металлов, когда это оказы-
оказывается более выгодным или целесообразным по сравнению с другими
методами разогрева. Если производить разогрев металла токами очень
высокой частоты, то в результате скин-эффекта (см. § 53) раскаляется
только поверхностный слой проводника.
12*
356 8. Электромагнитная индукция и квазистационарные переменные токи
§ 50. Резонансы в цепи
переменного тока
Рассматриваются резонансы в цепи перемен-
переменного тока и свойства колебательного кон-
контура.
Резонанс напряжений. Рассмотрим цепь, в которую последовательно
с генератором включены R, L, С (см. рис. 192), и определим зави-
зависимость амплитудного значения тока силы /0 и разность фаз ф между
током и внешним напряжением от частоты. На основании D8.18)
и D8.20) имеем:
10= . ^ , E0.1)
YR2 + [Leo - 1/(шС)]2
tg Ф = ^—'-. E0.2)
Графики зависимостей /0 (ю) и ср (со) изображены на рис. 203 и 204.
Сила тока 10 достигает максимума при частоте
соо = 1/l/Ec, E0.3)
которая называется резонансной частотой контура. При этом амплитуда
силы тока равна Uo/R, а разность фаз ср = 0, т. е. получается, что в цепи
как бы нет ни емкости, ни индуктивности. Иначе говоря, при этой
частоте напряжения на емкости и индуктивности полностью взаимно
компенсируются, будучи равными по значению (по фазе они противо-
противоположны всегда). Поэтому этот резонанс называют также резонансом
напряжений. Векторная схема резонанса напряжений изображена на
рис. 205. При резонансе (со = соо) контур ведет себя как чисто актив-
активное сопротивление.
Если через контур пропускается ток постоянной частоты со, то при
изменении, например, индуктивности /0' также имеет резонансный
характер изменения. Максимальное значение /о достигается при
L= 1/(а>2С) [см. E0.1) и E0.3)]. Если в цепь включена лампа накали-
накаливания, то ее яркость при приближении к резонансу увеличивается,
достигает в резонансе максимума, а затем уменьшается.
Резонанс токов. Рассмотрим цепь, изображенную на рис. 206. Очевидно,
что сила тока, текущего в цепи, равна
Следовательно, при условии
coL - соС (Я2 + ©2L2) = 0 E0.5)
цепь ведет себя как чисто омическое сопротивление. Сдвиг фаз между
§ 50. Резонансы в цепи переменного тока 357
Зависимость силы тока от час-
E0.7) тоты при резонансе напряжений
внешним напряжением и силой тока равен
нулю. Разделив все члены уравнения E0.5)
на co2LC, запишем его в виде
1 R2
—-—coL=-j-. E0.6)
соС coL v '
В большинстве практически важных слу-
случаев соблюдается условие coL »йи поэтому
решение уравнений E0.6) и E0.5) может быть 3
представлено в виде
ю0 = 1/ J/L С.
При этой резонансной частоте импеданс
между точками А и D достигает максимума,
а сила тока /0 в цепи — минимума. Однако
силы тока IL и /с при этом не являются
минимальными. Векторная диаграмма сил
токов в контуре между точками А и D при-
приведена на рис. 207. При приближении к
условиям резонанса диаграмма токов прини-
принимает вид, показанный на рис. 208. Таким
образом, внутри контура, ограниченного точ-
точками А и D, циркулируют очень большие - —
токи по сравнению с токами, которые подво- ^
дятся к этому контуру. Заряд внутри кон- 204
тура, ограниченного точками A, D, протекает
ОТ еМКОСТИ К ИНДУКТИВНОСТИ И наоборот, Зависимость сдвига фаз <р
- частоты при резонансе напря
т. е. в этом контуре происходит колебание ний
силы тока. В резонансе друг с другом, как
это видно на рис. 208, находятся силы токов
в емкости и индуктивности. Они компенси-
компенсируют друг друга. Поэтому сам резонанс
называется резонансом токов.
колебательный контур. В обоих рассмот-
рассмотренных случаях контур, изображенный на
рис. 192, ведет себя как резонансная систе-
система, совершающая вынужденные колебания
под действием внешней силы. Колебания
тока в LC-контуре впервые рассмотрел
Томсон в 1853 г. Тогда же он получил
формулу E0.7), названную позже формулой
Томсона (Т =2я ]/LC). Для анализа колеба- 205
ний силы тока в контуре можно непосредст- Векторная днаграмма напряже-
веННО ИСПОЛЬЗОВать результаты Теории ВЫ- ний при резонансе напряжений
нужденных механических колебаний точки.
Для этого необходимо выяснить, какие ве-
величины в электрических колебаниях соот-
от
при резонансе напряже-
?¦
358 8. Электромагнитная индукция и квазистационарные переменные токи
Hh
л
ветствуют силе, отклонению и скорости для
механических колебаний. Запишем уравнение
для вынужденных механических колебаний:
х + 2ух + <а%х = F/m, E0.8)
где х — отклонение точки от положения рав-
равновесия; т — ее масса; F — внешняя сила;
у = Ь/Bт) - декремент затухания; Ъ - коэф-
коэффициент трения. Точками обозначены произ-
производные по времени.
Теперь преобразуем уравнения D8.12) и
D8.13) для электрического контура. Прини-
Цеш», в которой осуществляется мая во внимание, что / = dQ/dt, запишем
резонанс токов уравнение D8.12) в виде
206
R+icoL
207
Векторная диаграмма токов в
цепи с параллельными емкос-
емкостью и индуктивностью
lc~imCU
208
fL-U/(ia>L)
Векторная диаграмма токов при
резонансе токов
+ R
d^"^r-^ = - E0-9)
Разделив обе части E0.9) на L, получаем
уравнение
G + (R/L) Q + [1/(LC)] Q = U/L, E0.10)
аналогичное E0.8). Роль отклонения в элект-
электрическом контуре играет заряд Q на пласти-
пластинах конденсатора, роль массы — индуктив-
индуктивность L, роль силы — электродвижущая сила
U, роль коэффициента трения - омическое
сопротивление R. Частота собственных коле-
/—'
баний контура равна ш0 = 1/J/LC [см. E0.3)].
Сила тока I = dQ/dt играет роль скорости.
Поскольку для механических колебаний точ-
точки обычно рассматривают ее отклонение от
положения равновесия, амплитуду колебаний
и т. д., при анализе электрических колеба-
колебаний удобно пользоваться уравнением E0.10),
а не D8.13). Кроме того, вместо заряда Q на
пластинах конденсатора целесообразно поль-
пользоваться напряжением на конденсаторе
(U с — Q/C). Относительно этой величины
уравнение E0.10) принимает вид
E0.11)
где у = R/BL), соо = 1J/LC. Все свойства этих
колебаний получаются простым сопоставле-
сопоставлением величин у, ш0, U, Uc электрического
колебательного контура соответствующим
величинам, характеризующим механические
колебания точки. Частота собственных ко-
§ 51. Цепи с учетом взаимной индукции 359
лебаний контура при отсутствии сопротивления (R = 0) равна
со0 = (LC)~1/2. Колебания незатухающие. При наличии трения колеба-
колебания становятся затухающими, причем время затухания равно
^ат = 1/Y = 2L/R. E0.12)
В качестве частоты затухающих колебаний в общепринятом услов-
условном смысле принимается частота
E0.13)
Логарифмический декремент затухания равен
0 = уТ, E0.14)
где Т = 2тс/со0 — период собственных колебаний.
Амплитудная и фазовая резонансные кривые аналогичны соответст-
соответствующим кривым для механических колебаний.
Добротность определяется равенством
и
Срез
«О WOb I /L
U0 -2," R -R]/ С E0Л5)
где U0Cpe3 — амплитуда напряжения на конденсаторе при резонансе;
Uo — амплитуда приложенной к контуру сторонней э. д. с. Таким обра-
образом, в достаточно добротном контуре амплитуда колебаний напряже-
напряжения на конденсаторе может быть во много раз больше амплитуды
приложенного к контуру напряжения.
Ширина резонансной кривой равна
2Дсо = roo/G = R/L. E0.16)
Напомним, что ширина 2Дк> резонансной кривой определяется не
относительно амплитуды колебаний, а относительно квадрата ампли-
амплитуды.
§ 51. Цепи с учетом взаимной индукции
Излагаются основные методы расчета цепей.
Обсуждается работа трансформатора.
роль взаимной индукции. Каждый из контуров, по которому течет
переменный ток, является источником переменного магнитного поля.
По закону электромагнитной индукции Фарадея оно индуцирует в дру-
других контурах, находящихся в этом поле, электродвижущие силы, кото-
которые изменяют силу тока в этих контурах. Таким образом, контуры
оказываются связанными между собой посредством электромагнитной
индукции.
¦у Ранения для системы проводников с учетом самоиндукции и взаимо-
взаимоиндукции. Полный магнитный поток, пронизывающий fc-й контур,
определяется выражением
E1.1)
360 8. Электромагнитная индукция и квазистационарные переменные токи
которое является непосредственным обобщением формул D7.6) и D7.10)
на случай многих контуров с током на основании принципа суперпо-
суперпозиции. Здесь Lkk — индуктивность fc-ro контура, a Lki при к Фг — взаим-
взаимная индуктивность fc-ro и 1-го контуров. Общее число проводников
равно N.
Для упрощения предположим, что емкости в цепях отсутствуют.
Тогда с учетом электромагнитной индукции для силы тока в к-ы конту-
контуре получаем уравнение
hRk = Uk- <№»/*, E1.2)
где Uk — сторонняя электродвижущая сила в к-ы контуре. Подставляя
E1.1) в E1.2), получаем для определения силы тока во всех контурах
следующую систему уравнений:
N
IkRk =Uk- Vlh ^ (k=l,2, ...,N). E1.3)
Эта линейная система из N уравнений для N неизвестных сил то-
токов 1к является полной и, в принципе, ее всегда нетрудно решить.
Единственной нетривиальной задачей является определение взаимных
индуктивностей и индуктивностей контуров. В уравнениях E1.3) эти
величины представляются известными.
^лучай двух контуров. Рассмотрим в качестве примера систему
уравнений для двух проводников:
E1.4)
E1.5)
где Ln и L22 — индуктивности первого и второго контуров; Ц2 и /^ —
взаимные индуктивности контуров.
Дальнейшее решение будет достаточно простым, если рассмотреть
ситуацию, которая с достаточной точностью осуществляется в трансфор-
трансформаторе переменного тока (рис. 209).
'Т рансформатор. В трансформаторе имеется два проводника, намотан-
намотанных в виде катушек на замкнутый сердечник из материала с боль-
большой магнитной проницаемостью, благодаря чему потоки магнитной
индукции, создаваемые текущими по проводам токами, сосредоточены
практически полностью внутри сердечника. Проводники называют
обмотками трансформатора. Обмотка, к которой присоединяется источ-
источник сторонних э. д. с, является первичной, а обмотка, к которой при-
присоединяется нагрузка,— вторичной.
Величины, относящиеся к первичной и вторичной обмоткам, обозна-
обозначим соответственно с индексами 1 и 2. Запишем уравнения E1.2) в виде:
E1.6)
§ 51. Цепи с учетом взаимной индукции 361
I2R2 = -
E1.7)
где./?! — омическое сопротивление первичной
обмотки; R2 — сумма омических сопротивле-
сопротивлений вторичной обмотки и нагрузки, кото-
которая для простоты предполагается чисто оми-
омической; Фх и Ф2 — полные потоки магнитной
индукции, охватываемые соответственно
первичной и вторичной обмотками; Ui —
сторонняя э. д. с, приложенная к первичной
обмотке.
Сопротивление Rx первичной обмотки
достаточно мало и падение напряжения на
ней за счет омического сопротивления мо-
может быть принято значительно меньшим
Uu т. е. I10Ri «; Uw, гДе *ю и U10 -
амплитуды силы тока и напряжения в пер-
первичной обмотке. Поэтому в соотношении
E1.6) можно пренебречь произведением /jRi
по сравнению с 1/[ и записать его в виде
Ux = dФ1/dг. E1.8)
В обычных условиях омическое сопро-
сопротивление нагрузки много больше омического
сопротивления вторичной обмотки. Поэтому
R2 в E1.7) равно с большой точностью
сопротивлению нагрузки. Следовательно,
I2R2 в левой части E1.7) равно напряже-
напряжению U2 на клеммах вторичной обмотки
трансформатора. Поэтому E1.7) может быть
записано следующим образом:
U а = -дФ2/й1. E1.9)
Поскольку сторонняя э. д. с. изменяется по
гармоническому закону [L^ ~ exp (iotf)], все
величины изменяются по такому же закону.
Следовательно, dФ1/dt = *'соФь dФ2/df =
= 1'соФ2. Так как весь поток магнитной
индукции заключен внутри сердечника, то
каждый из витков первичной и вторичной
обмоток охватывает один и тот же магнит-
магнитный поток Фо. Следовательно, потоки, охва-
охватываемые первичной и вторичной обмот-
обмотками, равны
фх = <&ONU E1.10)
209
Трансформатор
Ф2 =
E1.11)
210
Векторная диаграмма трансфор-
трансформатора при холостом ходе
О Каковы физические условия
реализации резонанса токов
и резонанса напряжений?
Какое соответствие сущест-
существует между параметрами, ха-
характеризующими колеба-
колебательный контур с сопротив-
сопротивлением, емкостью и индук-
индуктивностью, и параметрами
механической колебательной
системы с трением?
В чем физический смысл
условий согласования нагруз-
нагрузки с генератором?
Перечислите случаи, когда
токи Фуко играют полезную
роль и когда они нежела-
нежелательны?
362 8. Электромагнитная индукция и квазистационарные переменные токи
где Nt и N2 — число витков соответственно первичной и вторич-
вторичной обмоток. С учетом E1.10) и E1.11) уравнения E1.8) и E1.9) при-
принимают вид:
?/!=«*>#!<&„, E1.12)
U2= -koW200. E1.13)
Разделив почленно левые и правые части E1.12) и E1.13) и перейдя
к модулям, получим
\U1\/\U2\=NJN2. E1.14)
Учитывая, что | L^ | = Ui0, | U2 | = U20 — амплитуды напряжения на
первичной и вторичной обмотках, запишем E1.14) в виде
l/io/JVi = U20/N2, E1.15)
т. е. амплитуда напряжения во вторичной обмотке во столько раз
больше (меньше) амплитуды напряжения в первичной, во сколько раз
число витков вторичной обмотки больше (меньше) числа витков первич-
первичной обмотки.
Если пренебречь потерями энергии в трансформаторе, то закон
сохранения энергии имеет вид
IiU1=I2U2. E1.16)
Переходя в E1.16) к модулям, получаем на основании E1.15) соот-
соотношение
11ON1=12ON2, E1.17)
где /10 и /2о — амплитуды силы токов в первичной и вторичной
обмотках.
Формулы E1.15) и E1.17) описывают закон преобразования ампли-
амплитуд напряжений и сил токов в трансформаторе. Они строго спра-
справедливы для идеального трансформатора, в котором нет рассеяния
магнитного потока и потерь энергии. Для реального трансформатора
они соблюдаются с большой точностью.
Иекторная диаграмма холостого хода трансформатора. Холостым
ходом трансформатора является его работа при разомкнутой
вторичной обмотке. Будем пренебрегать запаздыванием фазы потока
магнитной индукции по сравнению с фазой силы тока в первичной
обмотке из-за некоторой инерции перемагничивания материала сердеч-
сердечника. Это запаздывание пренебрежимо мало. Поэтому поток можно счи-
считать совпадающим по фазе с током в первичной обмотке, который
называется током холостого хода. Ток во вторичной обмотке равен
нулю. Из формулы
[/инД= _do/df E1.18)
следует, что С/инд отстает на я/2 от потока Ф. Поэтому векторная
диаграмма ненагруженного трансформатора имеет вид, изображенный
на рис. 210: Ui — внешнее напряжение, приложенное к первичной
обмотке; С/"нд — напряжение в первичной обмотке в результате самоин-
самоиндукции; С/2НЯ — напряжение на вторичной обмотке в результате взаим-
t) 51. Цепи с учетом взаимной индукции 363
ной индукции; /0 — сила тока холостого хода; Фо — поток холостого
хода, охватываемый каждым из витков обмоток трансформатора. Как
и раньше, потерями и рассеянием потока в трансформаторе пренебре-
пренебрегаем.
По закону электромагнитной индукции
^P E1.19)
at
** E1.20)
at
поскольку полные потоки индукции, пронизывающие первичную и вто-
вторичную обмотки, равны:
ф1 = фо^ь ф2 = фо^2. E1.21)
Необходимо учесть, что сила тока холостого хода очень мала, как
и омическое сопротивление первичной обмотки по сравнению с ее индук-
индуктивным сопротивлением. Поэтому (см. рис. 210)
С/, а C/'i « - Щня, E1-22)
т. е.
иГл « - U1. E1.23)
Разделив почленно левые и правые части равенства E1.20) на соот-
соответствующие части равенства E1.19) и принимая во внимание E1.23),
находим
E1.24)
Иекторная диаграмма нагруженного трансформатора. В нагруженном
трансформаторе поток Фо, охватываемый каждым из витков обмо-
обмоток, создается токами как первичной, так и вторичной обмоток.
Э. д. с. самоиндукции в первичной обмотке должна все время компенси-
компенсировать внешнее напряжение, т. е. сумма потоков ФA) и ФB), создаваемых
токами первичной и вторичной обмоток, должна быть примерно равна
потоку Фо холостого хода, т. е. Фо = ФA) + Ф<2). А это приводит к тому,
что напряжение во вторичной обмотке будет удовлетворять условию
E1.24) и для нагруженного трансформатора.
Следует обратить внимание, что потоки ФA) и Ф<2) не являются
полными потоками Ф! и Ф2, охватываемыми первичной и вторичной
обмотками. Потоки ФA) и ФB) являются потоками, охватываемыми
одним витком каждой из обмоток, созданными в сердечнике соответст-
соответственно токами Ii и 12. Полные потоки, охватываемые первичной
и вторичной обмотками, равны Ф^ = JVt (ФA) + ФB)), Ф2 = N2 (ФA) +
B>)
)
Векторная диаграмма нагруженного трансформатора изображена
на рис. 211. Силы токов /t и 12 значительно больше силы тока /0
холостого хода, поэтому и создаваемые ими потоки ФA) и ФB)
значительно больше потока Фо. Так как ФA) + Ф<2) = Фо (комплексные
числа), то
364 8. Электромагнитная индукция и квазистационарные переменные токи
.Ф^яНФ^М- E1.25)
Примем во внимание равенства
| ФA) | = const | /t | Nu | ФB) | = const 1121 N2,
E1.26)
которые будут очевидными, если учесть, что
ф'1' и ФB) - потоки, создаваемые каждой из
обмоток. Тогда E1.25) принимает вид ра-
равенства
\Ii\Nl = \I2\N2, E1.27)
которое удобнее записать в форме
Векторкая диаграмма нагружен- , г
\12
ного трансформатора
El
N2
E1.28)
212
Автотрансформатор
О Почему сердечник авто-
автотрансформатора должен
быть замкнутый?
Каковы принципиальные
преимущества и недостатки
синхронных и асинхронных
двигателей?
Какова роль «проскальзы-
«проскальзывания» в асинхронном дви-
двигателе? От чего она зависит?
Как должен быть включен
трансформатор для согла-
согласования генератора с на-
нагрузкой, если сопротивление
нагрузки слишком мало?
Чем реальный трансформа-
трансформатор отличается от идеаль-
идеального?
что, как и должно быть, совпадает с E1.17).
Первые трансформаторы были созданы
П. Н. Яблочковым A847-1894) в 1877 г.
и Ф. И. Усагиным A855-1919) в 1882 г.
А вгогрансформатор. Очень экономичной
конструкцией трансформатора, помогаю-
помогающей сберечь обмоточные провода, является
автотрансформатор, изображенный на рис.
212. Физические принципы его работы и
формулы аналогичны рассмотренным выше.
Эксплуатационное отличие состоит в том,
что первичная и вторичная обмотки авто-
автотрансформатора находятся между собой в
электрическом контакте, а обмотки транс-
трансформатора изолированы. Поэтому, напри-
например, статические электрические заряды могут
перейти из первичной обмотки автотранс-
автотрансформатора во вторичную, а в трансформа-
трансформаторе это исключается. Эти особенности
трансформаторов и автотрансформаторов в
ряде случаев приходится принимать во
внимание.
Трансформатор как элемент цепи. Сила
тока во вторичной цепи равна (рис. 209)
I2 = U2/R.
Учитывая, что IiNt = I2N2,
= U2/N2, из E1.29) получаем
E1.29)
E1.30)
§ 51. Цепи с учетом взаимной индукции 365
Ц
213
Схема реального трансфор- "
матора
Следовательно, сопротивление R во вторичной цепи трансформатора
представляется со стороны входа эффективным сопротивлением
.2
iV,
R.
E1.31)
Это означает, что трансформатор можно использовать для согла-
согласования источника мощности с нагрузкой для получения максимальной
отдачи мощности [см. D9.34)]. Например, с его помощью можно
согласовать большое внутреннее сопротивление усилителя с малым
сопротивлением громкоговорителя. Комплексные импедансы преобра-
преобразуются также аналогично E1.31).
реальный трансформатор. Из E1.31) видно, что идеальный трансфор-
трансформатор со стороны первичной обмотки представляется в виде чистого
сопротивления. Индуктивность первичной обмотки никак не проявляет-
проявляется, что обусловлено взаимным уничтожением магнитных потоков,
создаваемых токами в первичной и вторичной обмотках, т. е. трансфор-
трансформатор в цепи выступает как преобразователь эффективного сопротивле-
сопротивления, не обладающий собственной индуктивностью.
Приведенные соотношения справедливы для идеального трансфор-
трансформатора. Реальный трансформатор обладает как индуктивностью, так
и емкостью. Эквивалентная схема его представлена на рис. 213. Индук-
Индуктивности Lx и L2 первичной и вторичной обмоток обусловлены
рассеянием магнитного потока, в результате которого нет полной ком-
компенсации магнитных потоков, создаваемых токами первичной и вто-
вторичной обмоток. Сопротивления Rt и R2 являются омическими
сопротивлениями проводников обмоток. Индуктивность Lq в первичной
обмотке обусловлена магнитным потоком, соответствующим току хо-
холостого хода в первичной обмотке. Емкости Сх и С2 в обмотках
возникают за счет емкостной связи между витками проводников этих
обмоток.
Из эквивалентной схемы трансформатора можно заключить, что
на очень малых частотах трансформатор перестает работать из-за того,
что индуктивное сопротивление coLo становится очень малым и боль-
большая часть тока идет через индуктивность Lo. На достаточно больших
частотах трансформатор также не работает, поскольку ток в основном
идет через емкость Сь минуя витки трансформатора. В технической
характеристике трансформатора всегда указываются пределы его нор-
нормальной эксплуатации.
366 8. Электромагнитная индукция и квазистационарные переменные токн
Генератор трехфазного тока
215
Схематическое изображение об-
обмоток генератора трехфазного
тока
О Каковы основные преиму-
преимущества использования трех-
трехфазного тока по сравнению
с однофазный?
Начертите схемы соединения
нагрузок и генераторов звез-
звездой и треугольником и пере-
перечислите соотношения между
фазными и линейными на-
напряжениями и токами.
§ 52. Трехфазный ток
Описываются основные физические явления в
цепях трехфазного тока.
{"Определение. Рассмотренный до сих пор
ток характеризовался амплитудой и фа-
фазой и назывался однофазным. Совокупность
трех одинаковых однофазных токов, сдвину-
сдвинутых друг относительно друга по фазе на
одну третью часть периода, называется
трехфазным током.
ТТолучение трехфазного тока. Рассмотрим
генератор переменного тока с тремя от-
отдельными обмотками, в которых генери-
генерируется ток, расположенными под углом 120°
друг относительно друга (рис. 214). Вращаю-
Вращающееся магнитное поле, возникшее вследствие
вращения постоянного магнита, создает в
обмотках генератора одинаковые, но сдвину-
сдвинутые по фазе напряжения:
Ux = Uo sin Ш, U2 = Uo sin (cot + 2тг/3), U3 =
= Uо sin (cot - 2тг/3). E2.1)
Обмотки генератора удобно изобразить
в виде схемы рис. 215.
Соединение обмоток генератора звездой.
Если три обмотки генератора использо-
использовать без связи друг с другом, то генератор
трехфазного тока становится просто со-
совокупностью трех отдельных генераторов
однофазного тока и никаких новых элемен-
элементов не содержит. В частности, для передачи
электроэнергии к потребителю требуется три
пары проводов.
Если обмотки соединить между собой
определенным способом, то у трехфазного
тока обнаруживаются специфические свойст-
свойства, очень полезные для технических приме-
применений. Существует два вида соединения об-
обмоток генератора — звездой и треугольником.
Схема соединения звездой и векторная
диаграмма напряжений на обмотках пока-
показаны на рис. 216, а, б. В этом случае имеется
общая точка О одинакового потенциала.
Напряжение на каждой из обмоток назы-
называется фазным. Проводник, соединенный с
§ 52. Трехфазный ток 367
г
i
Щ
о]
\
Гф
"ф
ил
•
б)
216
точкой общего потенциала, называется нуле-
нулевым проводом; проводники, соединенные со
свободными концами обмоток, называются
фазными проводами. Таким образом, фазные
напряжения являются напряжениями между
нулевым и фазными проводами. Напряжение
между фазными проводами называется ли-
линейным. Из векторной диаграммы видно,
что амплитуды 1/ол и U^ линейных и фазных
напряжений находятся в следующем соотно-
соотношении друг с другом:
Um = 21/Оф sin 60° = С7оф1/3. E2.2)
В частности, если [7Оф = 127 В, то
UOJI = 220 В. Ток /ф, текущий через обмотки,
называется фазным током, а ток /л, текущий
в линии,— током линии. При соединении
звездой фазные токи равны токам в линии
(/ф = /л). ЕСЛИ К каждой ИЗ обмОТОК при- Соединение обмоток трехфазно-
СОеДИНИТЬ Одинаковые нагруЗКИ R, ТО сум- го генератора звездой (а); со-
Марная СИЛа ТОка Через нулевой ПРОВОД рав- ответствующая векторная диа-
на нулю, поскольку грамма напР™ений W
Il+I2+h=^(U1 + U2 + U3) = 0, E2.3)
так как из векторной диаграммы видно, что
S ui = °-
Соединение обмоток генератора звездой
позволяет для передачи электроэнергии
вместо шести проводов использовать только
четыре, что является немаловажным преиму-
преимуществом.
(Соединение обмоток генератора треуголь-
треугольником. Схема такого соединения и вектор-
векторная диаграмма изображены на рис. 217, а, б.
В этом случае ?/Оф = Uox. Из векторной
диаграммы токов (рис. 218) находим:
'ол = 2/офcos 30° = /оф|/3. E2.4)
ЛФ + Ы + 7зФ = h- E2.5)
При соединении обмоток генератора без
нагрузки треугольником ток замыкания в об-
обмотках отсутствует. Но это справедливо
только для основной гармоники. Токи выс-
высших гармоник, всегда возбуждаемые в ре-
результате нелинейности колебаний, в обмот-
а)
б)
217
Соединение обмоток трехфаз-
трехфазного генератора треугольником
(а); соответствующая векторная
диаграмма напряжений (б)
368 8. Электромагнитная индукция и квазистационарные переменные токи
А
Л>2 ках присутствуют. Поэтому обмотки мощ-
мощных генераторов, как правило, не соединяют
треугольником.
Соединение нагрузок. Нагрузки между со-
собой также можно соединить звездой и
треугольником и затем подключить к трех-
/л фазному генератору, обмотки которого меж-
218 ду собой связаны по схеме звезды или
Векторная диаграмма токов при треугольника. Таким образом, имеется че-
соединении обмоток треуголь- тыРе возможные комбинации соединения ге-
ником нератора и нагрузок (рис. 219 — 222).
Каждое из таких соединений имеет свои
особенности.
При соединении звезда-звезда (рис. 219)
на всех нагрузках имеется разное напряже-
напряжение. При приблизительно равных нагрузках
1 ' в соответствии с E2.3) сила тока по нуле-
219 вому проводу очень мала. Тем не менее
" нулевой провод нельзя убрать, поскольку без
Соединение звезда-звезда J r J г > «jr
него на каждую из пар нагрузок действует
линейное напряжение 11ОЛ = [/оф |/з, которое
распределяется между нагрузками в соот-
соответствии с их сопротивлениями. Однако та-
такая зависимость напряжений от нагрузок
недопустима, поэтому необходимо всегда
сохранять нулевой провод и не вводить
в него предохранители.
Соединение звезда - треугольник При соединении звезда — треугольник
(рис. 220) на каждую нагрузку действует
линейное напряжение Uon = U,^ |/з неза-
независимо от сопротивления нагрузки.
При соединении треугольник - треуголь-
треугольник (рис. 221) на всех нагрузках действует
фазное напряжение независимо от сопро-
22j тивления нагрузок.
При соединении треугольник — звезда
Соединение треугольник - треу- (рис 222) напряжение на каждой нагрузке
ГОЛЬИИК 1— я *
равно 1/офД/З.
ГТолучение вращающегося магнитного по-
поля. Если к обмоткам генератора (см.
рис. 214) подвести трехфазный ток, то в
пространстве между ними возникает вра-
вращающееся магнитное поле, соответствующее
полю вращающегося магнита, который гене-
рировал ток. Если вместо магнита устано-
Соединеиие треугольник-звезда ВИТЬ КОроткОЗаМКНутыЙ ротор, То ОН будет
i) 53. Скин-эффект 369
приведен во вращение, т. е. генератор будет работать как асинхрон-
асинхронный двигатель. Таким образом, при использовании трехфазного тока
конструкция о гектродвигателей значительно упрощается, что является
также большим преимуществом.
Первым получил вращающееся магнитное поле с помощью трех-
трехфазного тока Доливо-Добровольский A862—1919), им же в 1889 г. был
построен первый асинхронный двигатель и затем осуществлена пере-
передача электрической энергии с помощью трехфазного тока на большое
расстояние. Трехфазный ток обеспечил широкое и эффективное приме-
применение тока в технике.
§ 53. Скин-эффект
Обсуждаются физическая картина возникно-
возникновения и элементарная теория скин-эффекта
и его следствий. Дается понятие об ано-
аномальном скин-эффекте.
явления. Постоянный ток распределяется равномерно по
поперечному сечению прямолинейного проводника. У переменного
тока благодаря индукционному взаимодействию различных элементов
тока между собой происходит перераспределение плотности тока по
поперечному сечению проводника, в результате чего ток сосредоточи-
сосредоточивается преимущественно в поверхностном слое проводника. Концентра-
Концентрация переменного тока вблизи поверхности проводника называется
скин-эффектом.
физическая картина возникновения. Рассмотрим цилиндрический про-
проводник, по которому течет ток (рис. 223). Вокруг проводника с
током имеется магнитное поле, силовые линии которого являются
концентрическими окружностями с центром на оси проводника. В ре-
результате увеличения силы тока возрастает индукция магнитного поля,
а форма силовых линий при этом остается прежней. Поэтому в
каждой точке внутри проводника производная dB/dt направлена по
касательной к линии индукции магнитного поля и, следовательно,
линии дЪ/St также являются окружностями, совпадающими с линиями
индукции магнитного поля. Изменяющееся магнитное поле по закону
электромагнитной индукции
rotE= -дЪ/dt E3.1)
создает электрическое индукционное поле, силовые линии которого
представляют замкнутые кривые вокруг линии индукции магнитного
поля (рис. 223). Вектор напряженности индукционного поля в более
близких к оси проводника областях направлен противоположно вектору
напряженности электрического поля, создающего ток, а в более даль-
дальних — совпадает с ним. В результате плотность тока уменьшается
в приосевых областях и увеличивается вблизи поверхности провод-
проводника, т. е. возникает скин-эффект.
370 8. Электромагнитная индукция и квазистационарные переменные токи
223
Элементарная теория. Прежде всего необ-
необходимо получить уравнение, описываю-
описывающее скин-эффект. Исходим из уравнения
Максвелла
rot В = (ij E3.2)
и уравнения E3.1). Подставляя в E3.2) вы-
выражение для j по закону Ома
j = YE E3.3)
и дифференцируя обе части полученного
уравнения по времени, находим
ев 6Е
Физическая картина возникнове- ot "t
ния скин-эффекта или с учетом E3.1)
—rot rot Е =
BE
ИГ
Поскольку
rot rot E = grad div E - V2E
и div E = 0, окончательно имеем
224
Скин-эффект в бесконечном про-
проводнике с плоской границей
Ф У переменного тока бла-
благодаря индукционному вза-
взаимодействию различных
элементов тока между со-
собой происходит перерас-
перераспределение плотности то-
тока по поперечному сече-
сечению проводника, в резуль-
результате чего ток сосредоточи-
сосредоточивается преимущественно в
поверхностном слое про-
проводника.
О В чей физическая причина
зависимости сопротивления
и индуктивности провод-
проводника от частоты перемен-
переменного тока?
При каких условиях возни-
возникает скин-аффект!
E3.4)
E3.5)
E3.6)
7VL~dT' E17)
Для упрощения решения этого уравнения
предположим, что ток течет по однородному
бесконечному проводнику, занимающему по-
полупространство у > 0 вдоль оси X (рис. 224).
Поверхностью проводника является •плос-
•плоскость Y = 0. Таким образом,
J«=J»(y,t),J,=J« = O. E3.8)
Ex = Ex(y,t), Ey = Ez = 0. E3.9)
Тогда [см. E3.7)]
^Л- = Ч»Цг- E3-10)
Поскольку все величины в E3.10) гармо-
гармонически зависят от t, можно положить
Ех(у, t) = E0(y)eim. E3.11)
После подстановки E3.11) в E3.10) и
сокращения обеих частей уравнения на
exp(icof) получаем уравнение для Е0(у):
d2E0
dy
= iy\i(oE0.
E3.12)
§ 53. Скин-эффект 371
Общее решение уравнения E3.12) таково:
=Aie~kr + A2ekr. E3.13)
Учитывая, что
к = ]/iy\uo = а A + i), а = ]/уцю/2, E3.14)
находим
Ео (у) = А^-^е-™ + А2е*уё*у. E3.15)
При удалении от поверхности проводника (у -» оо) второе слагаемое
в E3.15) неограниченно возрастает, что является физически недопусти-
недопустимой ситуацией. Следовательно, в E3.15) А2 = 0 и в качестве физически
приемлемого решения остается только первое слагаемое. Тогда решение
задачи с учетом E3.11) имеет вид
Ех (х, t) = A^-^e'^-^. E3.16)
Взяв действительную часть этого выражения и перейдя с помощью
соотношения j = yE к плотности тока, получим
]Лу, t) = уА^-™ cos (art - ay). E3.17)
Принимая во внимание, что /,@, 0) = j0 — амплитуда плотности
тока на поверхности проводника, приходим к следующему распределе-
распределению объемной плотности тока в проводнике:
Ш t) =№-" cos (cot - ay). E3.18)
Толщина скин-слоя. Объемная плотность тока максимальна у поверх-
поверхности проводника. При удалении от поверхности она убывает и на
расстоянии Д = I/a становится меньше в е раз. Поэтому практически
весь ток сосредоточен в слое Д, называемом толщиной скин-слоя.
Она на основании E3.14) равна
Д = [2/(уцсо)]. E3.19)
Очевидно, что при достаточно большой частоте со толщина скин-слоя
может быть очень малой. Например, для хорошего проводника типа
меди у = 107 Ом~1-м~1 и при со = 104 с толщина А = 4 мм. Если
частота со увеличивается в 100 раз до со = 10б с, то толщина скин-слоя
уменьшается в 10 раз (Д ж 0,4 мм). Это означает, что при достаточно
большой частоте в не очень тонких проводниках весь ток течет лишь
в небольшой части поперечного сечения проводника, вблизи его поверх-
поверхности. Поэтому ничего не изменится, если убрать проводящий материал
из цилиндрической области внутри проводника и оставить лишь его
цилиндрическую оболочку толщиной скин-слоя. Если проводник доста-
достаточно толстый, а частота тока не очень велика, то ток течет по всему
поперечному сечению, лишь немного ослабевая к его оси. Например,
при техническом токе частотой 50 Гц скин-эффект в обычных проводни-
проводниках выражен очень слабо.
372 8. Электромагнитная индукция и квазистационарные переменные токи
Зависимость омического сопротивления проводника от частоты. Так
как эффективная площадь поперечного сечения, по которому течет ток,
с увеличением частоты уменьшается, то сопротивление проводника с
увеличением частоты увеличивается.
Зависимость индуктивности проводника от частоты. Энергия магнит-
магнитного поля, по которому течет ток, равна
Wm = V2U2. E3.20)
Если ток течет по полому цилиндру, то поле вне цилиндра такое
же, как и у такого же тока, текущего по сплошному цилиндру, а
поля в полости цилиндра нет. Поэтому энергия поля тока, текущего по
полому цилиндру, меньше энергии поля такого же тока, текущего
по сплошному цилиндру. Это означает, что за счет скин-эффекта
энергия магнитного поля Wm уменьшается. Отсюда на основании
E3.20) следует, что с увеличением частоты индуктивность проводников
уменьшается.
Эакалка металлов токами высокой частоты. Благодаря скин-эффекту
на высоких частотах джоулева теплота выделяется преимущественно
в поверхностном слое. Это позволяет раскалить проводник в тонком
поверхностном слое без существенного изменения температуры внутрен-
внутренних областей. Это явление используется в важном с технологической
точки зрения методе закалки металлов в промышленности.
Д^номальный скин-эффект. Изложенный механизм возникновения скин-
эффекта предполагает, что при своем движении электрон непрерывно
теряет энергию на преодоление омического сопротивления проводника,
в результате чего происходит выделение джоулевой теплоты. Ясно,
что такая идеализация возможна лишь в том случае, когда движение
электронов происходит в областях, линейные размеры которых много
больше средней длины свободного пробега электрона между столкнове-
столкновениями с атомами вещества. Поэтому изложенная теория справедлива
лишь при условии, что толщина скин-слоя много больше средней длины
свободного движения электронов. Такое соотношение между ними
соблюдается в весьма широких пределах. Например, даже при частоте
10 ГГц и температуре 300 К толщина скин-слоя в меди равна примерно
1 мкм, а длина свободного пробега составляет около 0,01 мкм. Однако
при очень низкой температуре ситуация резко меняется, поскольку
проводимость сильно повышается, а следовательно, увеличивается
длина свободного пробега и уменьшается толщина скин-слоя.
Например, при температуре жидкого гелия D,2 К) проводимость
чистой меди увеличивается приблизительно в 104 раз. Это приводит
к увеличению средней длины свободного пробега электронов в 104 раз
и уменьшению толщины скин-слоя в ]/104 = 102 раз. Таким образом,
длина свободного пробега и толщина скин-слоя становятся соответ-
соответственно равными 100 и 0,01 мкм. При этих условиях механизм, при-
приводящий к образованию скин-эффекта, уже не действует. Эффективная
толщина слоя, в котором сосредоточен ток, изменяется. Такое явление
называется аномальным скин-эффектом.
§ 54. Четырехполюсники 373
В условиях аномального скин-эффекта в пределах нормального
скин-слоя в течение всего свободного пробега могут двигаться только
те электроны, скорости которых почти параллельны поверхности про-
проводника. Все другие электроны в процессе свободного движения успе-
успевают покинуть «нормальный» скин-слой и значительно изменить направ-
направление движения. Из-за этого уменьшается проводимость материала
и изменяется эффективная «аномальная» толщина А' скин-слоя. Для
того чтобы ее приближенно оценить, можно принять, что доля
электронов проводимости имеет порядок А'/l от того числа электронов,
которые осуществляли бы проводимость в рамках «нормального»
скин-эффекта (/ — средняя длина свободного пробега электронов). Умень-
Уменьшение этой доли приводит к уменьшению проводимости, учиты-
учитываемой приближенно заменой в формулах у -> Ру (А'//), где Р — числовой
коэффициент порядка единицы. Производя эту замену в формуле E3.19),
находим
А' = [2//(Pyuco)]. E3.21)
§ 54. Четырехполюсники
Излагаются терминология и основные поло-
положения теории четырехполюсников.
Определение. Электрическая цепь с двумя входными и двумя выход-
выходными клеммами, через которую передается электрическая энергия,
называется четырехполюсником. Его символическое изображение пока-
показано на рис. 225. Примерами четырехполюсников являются преобразо-
преобразователи амплитуд колебаний, фильтры частот, трансформаторы и т. д.
Требуется найти связь между напряжениями и силами токов на входе
и выходе четырехполюсника. Если в четырехполюснике отсутствуют
источники энергии, то он называется пассивным, если присутствуют —
то активным. Предполагается, что сила тока, выходящего из клеммы 2,
равна силе тока, входящего в клемму 1, и аналогично, сила тока,
выходящего из клеммы 3, равна силе тока, входящего в клемму 4.
¦уравнения. Пусть в четырехполюснике имеется п независимых конту-
контуров. Тогда для них можно составить п уравнений для контурных
токов вида D8.27):
t Znh = Uи t zrti =-U3, t z*^ = 0 (fc = 3, 4, ...,«). E4.1)
i = i i=i i=i
Знак минус во втором из уравнений E4.1) у U2 появился вследствие
того, что при написании этих уравнений при избранном направлении
положительного обхода напряжения Ui и U2 проходятся в противопо-
противоположных направлениях (см. рис. 225). Решение этой системы уравнений
таково:
» Ац г. ^21 г; . А12 ,. А22 Г, ,,. «>
Ii=—r-U1---^U2,l2 = ——U1-—-U2> E4.2)
374 8. Электромагнитная индукция и квазистационарные переменные токи
—
Четырехполюсник
1^^
YI2
226
Продольно-симметричный П-об-
разный четырехполюсник
где Д и Atj — определитель и соответствую-
щие дополнения системы уравнений E4.1).
Следовательно, между силами токов и на-
напряжениями пассивного четырехполюсника
имеются линейные зависимости вида E4.2),
которые удобно записать так:
I1=BnU1+Bl2U2, I2=B21U1+B22U2.
E4.3)
Коэффициенты Btj имеют размерность
проводимостей. Поэтому E4.3) называются
уравнениями четырехполюсника с коэффици-
коэффициентами в виде проводимостей.
Нетрудн.0 решить уравнения E4.3) отно-
относительно напряжений:
ZI2
ZI2
227
Продольно-симметричный Т-об-
Т-образный четырехполюсник
+ А\212, V2 —
"Ь
E4.4)
где коэффициенты Atj имеют размерность
сопротивлений (импедансы). Уравнения E4.4)
называются уравнениями четырехполюсника
с коэффициентами в виде сопротивлений.
Теорема взаимности. Поскольку у пассив-
пассивного четырехполюсника коэффициенты Zi;-
в уравнениях E4.1) симметричны [см. D8.30)]:
Zy = zJb E4.5)
можно показать, что коэффициенты Atj в
E4.4) в этом случае также симметричны:
Ai2 = A2l. E4.6)
Отсюда следует, что
228
г,-о, E4.7)
т. е. выходное напряжение на разомкнутой
Несимметричный п-образный че- паре клемм при заданной силе входного тока
тырехполюсник це изменяется, если входные и выходные
клеммы четырехполюсника поменять места-
местами (теорема взаимности для пассивного че-
четырехполюсника).
(Сопротивление четырехполюсника. Сопро-
Сопротивление А2г называется взаимным сопро-
сопротивлением четырехполюсника, поскольку при
229 разомкнутой выходной цепи A2 = 0) из вто-
рого уравнения E4.4) следует, что
Несимметричный Т-образиый че-
четырехполюсник Ац = ^гД !• E4.8а)
§ 54. Четырехполюсники 375
При этом же условии первое из уравнений E4.4) дает:
/In = UJh. E4.86)
Это означает, что Ац является входным сопротивлением четырех-
четырехполюсника при разомкнутой выходной цепи. Аналогичный смысл имеют
коэффициенты А12 и А22 в соответствии с теоремой взаимности.
ТТростейшие четырехполюсники. С помощью уравнений E4.3) и E4.4)
напряжение и силу тока на входе четырехполюсника можно связать
с этими же величинами на выходе:
Ui = DrlU2 + Dl2I2, h = D21U2 + D22I2, E4.9)
где DtJ легко выражаются через BXl и Ац, входящие в уравнения
E4.3) и E4.4); коэффициент D12 имеет размерность сопротивления,
D2i —проводимости; коэффициенты Z)n и D22 безразмерны.
Четырехполюсник называется продольно-симметричным, если при
перемене местами входных и выходных клемм силы токов и напряже-
напряжения в присоединенных к клеммам цепях не изменяются. Из возмож-
возможности такой замены с помощью E4.9) получаем для симметричных
четырехполюсников
Z)n = ZJ2. E4.10)
Простейшие симметричные четырехполюсники П- и Т-образной фор-
формы показаны на рис. 226 и 227, а несимметричные — на рис. 228 и 229.
Коэффициенты Dtj для четырехполюсника проще всего найти методом
контурных токов. Для этого составляется система уравнений, затем из
нее исключаются силы контурных токов внутренних контуров. Остав-
Оставшиеся два уравнения, в которые входят Ult U2 и Iu 12, преобра-
преобразуют к виду E4.9) и из сравнения с E4.9) фазу же получают Д,-.
Для продольно-симметричного П-образного четырехполюсника
(рис. 226) находим:
/>и = 1 + ZY/2, Dl2 ~Z, Dll= Y(l + Zr/4). E4.11)
Для продольно-симметричного Т-образного четырехполюсника
(рис. 227) имеем:
Du = 1 + ZY/2, Д12 = Z(l + ZY/4), D21 = Y. E4.12)
Непосредственной проверкой убеждаемся, что
Dh-Di2D2i = \, E4.13)
т. е. детерминант коэффициентов преобразования E4.9) равен единице
в случае продольно-симметричных П- и Т-образных четырехполюсников.
Выражения коэффициентов для несимметричных четырехполюсников
несколько сложнее и здесь не приведены.
Иходное и выходное сопротивления. Для четырехполюсника они опре-
определяются как отношения соответствующих напряжений к силам тока:
ZBX = UJIlt ZBbIX = Ujh- E4.14)
376 8. Электромагнитная индукция и квазистационарные переменные токи
Из E4.9) с учетом E4.10) - E4.13) находим
Таким образом, четырехполюсник преобразует выходное сопротивле-
сопротивление на входное. При коротком замыкании выхода (ZBbIX = 0) входное
сопротивление четырехполюсника равно
¦ZOm=Dl2/Dlb E4.16)
а при разомкнутом выходе (ZBbIX = оо) оно определяется выражением
E4.17)
коэффициент передачи. Преобразование напряжений и сил токов ха-
характеризуется отношением их значений на выходе к значениям на
входе. Аналогично E4.15) получаем:
V2/U1 = ZBb!X/(ZBblxZ>u + Dn\ E4.18)
+ ZmD21). E4.19)
Если четырехполюсник работает без преобразования сопротивления,
т. е. когда входное и выходное сопротивления одинаковы, то говорят
что выходное сопротивление согласовано с системой. Подставляя в
E4.15) значение сопротивления
Zx = ZBX = ZBbIX, E4.20)
находим для него значение
Z. = \/D12/D21. E4.21)
Эта величина называется характеристическим (волновым) сопротивле-
сопротивлением четырехполюсника. Следовательно, четырехполюсник согласован
с линией передачи, если его входное и выходное сопротивления равны
характеристическому. В этом случае соотношения E4.18) и E4.19)
принимают вид:
U2/U, = !/(/>„ + \/Dl2D2l), E4.22)
/2//1 = 1/(D11+]/d12ZJ1).
С помощью соотношения
cbg = D11
определим коэффициент передачи д. Тогда на
shд = |/ch2д - 1 = ]/Dl2D21.
Используя E4.24) и E4.25), преобразуем
к виду
тт тт ~—д
и 2 — и 1& ,
12== и ^е *
основании E4.13)
формулы E4.22)
E4.23)
E4.24)
получим
E4.25)
и E4.23)
E4.26)
E4.27)
§ 55 Фильтры 377
Отметим, что выражения E4.26) и E4.27) справедливы только в
условиях полного согласования. При отсутствии согласования необхо-
необходимо пользоваться формулами E4.18) и E4.19).
С помощью коэффициента передачи и характеристического сопро-
сопротивления формулы E4.18) и E4.19) можно представить так:
U2/U1 = ZBhtJ(ZBm chg + Zx shg), E4.28)
I2/h = ZJ(ZK chg + ZBb[X shg). E4.29)
Как и все величины, входящие в формулы E4.26) —E4.29), коэффи-
коэффициент передачи является комплексной величиной:
д = а + ф. E4.30)
Как видно из E4.26) и E4.27), в условиях согласований действи-
действительная часть коэффициента передачи определяет изменение амплитуд
напряжения и сил токов на выходе четырехполюсника по сравнению
с их входными значениями, а мнимая часть — изменение фаз. Действи-
Действительная часть коэффициента передачи есть просто логарифм отношения
амплитуд:
a = In(J71/l72). E4.31)
Поскольку д зависит от частоты, при проходе через четырехполюс-
четырехполюсник сигнала, включающего в себя многие частоты, его спектральный
состав, а следовательно, и форма изменяются. Характер изменения
частотного и фазового спектра сигнала может быть найден с помощью
полученных в этом параграфе формул.
§ 55. Фильтры
Описываются принцип действия и свойства
фильтров.
Определение. Фильтром называется устройство, изменяющее ампли-
амплитуду колебаний в зависимости от их частоты. Если фильтр осу-
осуществлен в виде четырехполюсника, то коэффициент передачи должен
существенно изменяться с частотой.
фильтр низких частот. Рассмотрим Т-образный четырехполюсник,
изображенный на рис. 230. Из сравнения с рис. 227 видно, что
в полученных формулах надо положить:
Z = icoL, Г= гсоС. E5.1)
Характеристическое сопротивление на основании E4.24) и E4.11)
равно
Для коэффициента передачи g [см E4.24)] с учетом E4.11) находим
378 8. Электромагнитная индукция н квазистационарные переменные токи
LI2
230
Фильтр низких частот
231
Характеристика фильтра низких
частот
chg = 1 - co2LC/2. E5.3)
Учитывая для д его выражение E4.30),
перепишем уравнение E5.3) в виде
ch (a + ip) = ch а cos р + i sh а sin p =
= 1 - co2LC/2,
откуда
choc cos 0= 1 -ю2?С/2,
sh a sin P = 0.
Уравнение E5.6) имеет решения:
p = nn (и = 0, 1, 2, ...), E5.7)
при которых cos p = +1. Однако гиперболи-
гиперболический косинус всегда больше или равен еди-
единице, т. е. ch a > 1. Поэтому из E5.5) следует,
что cos Р = — 1, и можно положить р = я.
При этих условиях уравнение E5.5) прини-
принимает вид
CI2
CI2
232
Фильтр высоких частот
О шг ш
233
Характеристика фильтра высоких
частот
E5.4)
E5.5)
E5.6)
1 + ch a = co2LC/2.
E5.8)
Поскольку ch a > 1, E5.8) имеет решение
лишь для достаточно больших частот
со > сог, E5.9)
где
со, = 2/|/LC E5.10)
— граничная частота. С учетом E5.9) из
E5.2) заключаем, что характеристическое
сопротивление является чисто мнимым:
Tl/~o7Zc ~~
— i = j I/
С
= »' I/ ^г
-1.
E5.11)
Действительная часть коэффициента пе-
передачи определяется из уравнения E5.8).
Видно, что с увеличением частоты она очень
быстро возрастает. А это на основании
E,4.26) и E4.27) означает, что амплитуды
колебаний на выходе четырехполюсника при
со ^ юг быстро уменьшаются с увеличением
частоты.
Другое решение уравнения E5.6) имеет
вид:
shoc = 0, a = 0. E5.12)
§ 55. Фильтры 379
234
Фильтр в виде цепочки Т-образ-
Т-образных звеньев
Тогда уравнение E5.5) имеет вид
cos р = 1 - co2LC/2. E5.13)
Оно имеет решение лишь для cos р ^ — 1, т. е. при частотах
со ^ сог = 2/]/Ес, E5.14)
для которых первое решение не подходило. Характеристическое сопро-
сопротивление в этом случае является действительным:
Ц/~^Щг. E5.15)
Поскольку здесь а = 0, частоты со < сог пропускаются без затухания
по амплитуде. Однако имеется зависящий от частоты сдвиг фаз, опреде-
определяемый уравнением E5.13).
Зависимость амплитуды колебаний на выходе от амплитуды на
входе приведена на рис. 231. Рассмотренный четырехполюсник является
фильтром, пропускающим низкие частоты, меньшие некоторой гранич-
граничной частоты сог. Частоты выше граничной очень быстро затухают. Для
частот, значительно больших граничной, этот фильтр действует как
затвор. Область частот со < сог называется полосой пропускания,
фильтр высоких частот. Четырехполюсник, показанный на рис. 232,
рассчитывается аналогично предыдущему случаю и действует как
фильтр высоких частот с частотной характеристикой, показанной на
рис. 233.
IIепочка из фильтров. Если к выходным клеммам четырехполюсника,
^изображенного на рис. 230, подключить входные клеммы такого же
четырехполюсника и продолжить этот процесс, то получится четырех-
четырехполюсник, изображенный на рис. 234. К его рассмотрению могут
быть применены те же методы. Однако и без детального расчета
можно выяснить основные свойства этого четырехполюсника, поскольку
последовательные ячейки, из которых он состоит, имеют одинаковые
характеристические сопротивления и работают в режиме согласования
на каждой данной частоте. Граничная частота у всех ячеек одинакова.
Следовательно, у этого четырехполюсника будет та же полоса пропуска-
пропускания со ^ со,, а затухание частот со > сог будет значительно усилено.
Частотная характеристика имеет вид, аналогичный рис. 231, но с более
крутым спаданием амплитуд при со > сог (рис. 235).
Колосовой фильтр. Полосовым называется фильтр, пропускающий лишь
полосу частот между некоторой минимальной и максимальной
частотами:
Юг мин < Ю < Юг макс- E5.16)
380 8. Электромагнитная индукция и квазистационарные переменные токи
\Ui
Его частотная характеристика показана
на рис. 236.
В принципе, такой фильтр можно осу-
осуществить в виде последовательности низко-
низкочастотного и высокочастотного фильтров.
Высокочастотный фильтр должен отсеять
все частоты, меньшие югмин, и пропустить
большие частоты, а низкочастотный фильтр
должен пропустить все частоты, меньшие
согмак© и отсечь все частоты, большие <огмакс.
Однако на практике обычно используют бо-
Характеристика фильтра из це- лее сложные схемы (см., например, рис. 237).
почки т-образных звеньев Такой фильтр также является четырехпо-
четырехполюсником и может быть рассмотрен анало-
,, гичными методами.
иг
235
0>г
W г. макс
236
Характеристика полосового
фильтра
с2
J
1
=с2
237
Полосовой фильтр
О Объясните физические jipo-
цессы. лежащие в основе
действия фильтров высоких
и низких частот.
Как устроен полосовой
фильтр?
§ 56. Бетатрон
Рассматриваются принцип действия бе-
бетатрона и основные положения теории
устойчивости движения электронов в нем.
Обсуждается предел энергий, достижимых в
бетатроне. ¦
ХХазначение. Бетатрон является примером
устройства, в котором вихревое индук-
индукционное электрическое поле действует на
свободные электроны в вакууме. Он предназ-
предназначен для ускорения электронов до больших
энергий порядка нескольких сотен мегаэлект-
рон-вольт. Ускорению до более значитель-
значительных энергий препятствуют потери энергии
на тормозное излучение, возникающее
вследствие движения' электронов с ускоре-
ускорением по круговым орбитам. Используемый
в бетатроне механизм ускорения не в состоя-
состоянии компенсировать эти потери и цикл уско-
ускорения прекращается.
р^ринцип действия. Основная идея: подо-
подобрать такие условия, при которых элект-
электрон в нарастающем магнитном поле уско-
ускорялся бы вихревым электрическим полем
и одновременно магнитным полем удержи-
удерживался бы на круговой орбите постоянного
радиуса.
Оказывается, что такое условие возмож-
возможно. Оно называется бетатронным условием.
§ 56. Бетатрон 381
ретатронное условие. Запишем уравнение
движения электрона по окружности
постоянного радиуса в растущем магнит-
магнитном поле, считая, что такое движение воз-
возможно. Решение даст условия, при которых
это движение может быть осуществлено.
Обозначим: г0 — радиус орбиты; р — им-
импульс электрона, направленный все время по
касательной к круговой орбите (рис. 238).
Закон электромагнитной индукции для опре-
определения напряженности электрического поля
на орбите дает уравнение
2пг0Е= -йФ/dt. E6.1)
С другой стороны, уравнение движения
имеет вид
dp/dt = eE. E6.2)
Из E6.1) и E6.2) следует, что
е с!Ф
dp/dt = --
238
К выводу бетатронного условия
E6.3)
2яг0 dt
Поскольку r0 = const, можно обе части
уравнения проинтегрировать по t от 0 до t:
Р, ~ Ро = - [е/Bяг0)] (Ф, - Фо), E6.4)
где индексами t и 0 обозначено значение
соответствующих величин в момент времени
г и в начальный момент t = 0. Уравнение
Ньютона для центростремительного ускоре-
ускорения запишем в виде
mv2/r0 = -evB, E6.5)
где т — релятивистская масса. Из E6.5) сле-
следует, что р = mv = — eBrQ. Тогда [см. E6.4)]
1 ( Ф« Фо
239
Схема бетатрона
, — в0 =
E6.6)
240
К выводу условия радиальной
устойчивости электронов в бе-
бетатроне
Так как вектор индукции В направлен
перпендикулярно плоскости орбиты и поток
магнитной индукции равен
Ф = |В-с15 E6.7)
s
(S = ягд — площадь, ограниченная орбитой),
то
Ф/(пг20) = <В> E6.8)
241
Схема обеспечения вертикальной
устойчивости движения электро-
электронов в бетатроне
382 8. Электромагнитная индукция и квазистационарные переменные токи
— средняя индукция поля на площади S, охватываемой орбитой. Счи-
Считая, что в начальный момент поле отсутствует (Во = О, Фо = 0), из E6.6)
с учетом E6.8) находим
В,= 1/г<В,У E6.9)
Это есть бетатронное условие: магнитная индукция на орбите элект-
электрона равна половине величины средней магнитной индукции, охватывае-
охватываемой орбитой. Следовательно, надо индукцию магнитного поля сделать
уменьшающейся от центра к орбите по какому-либо закону, лишь
бы выполнялось условие E6.9). Для этого необходимо соответствую-
соответствующим образом подобрать форму полюсов электромагнитов, создающих
магнитное поле (рис. 239). Поскольку при заданной форме полюсов
магнитов форма силовых линий не зависит от силы тока и индукции
магнитного поля, условие E6.9) оказывается выполненным для любой
силы тока в электромагните. А это означает, что нет необходимости
заботиться о законе изменения силы тока. Единственный вопрос,
вызывающий беспокойство, — устойчивость движения; если некоторые
причины выведут электрон го режима движения строго по окружности
радиусом г0, то возникнут ли силы, стремящиеся удержать его в режиме
ускорения вблизи окружности, или он выйдет го режима ускорения и
будет потерян?
Имеются две возможности отклонения электрона от орбиты: либо
по радиусу, либо по вертикали из плоскости его движения,
радиальная устойчивость. Индукцию магнитного поля в области орби-
орбиты принято представлять в виде
В = const//" E6.10)
и характеризовать скорость ее изменения величиной п. Центростреми-
Центростремительная сила F|Jco6x, необходимая для обеспечения движения электрона
по окружности радиусом г, и фактически возникающая центростреми-
центростремительная сила Fnc на том же расстоянии г от центра равны:
Fjjeo6x = mv2/r = Ajr> pac = evB = 42/у.; E6.Ц)
где Ai и А2 - постоянные (v = const). Графики этих величин при п > 1
и 0 < п < 1 показаны на рис. 240. При г = г0 выполняется равенство
E6.5) и осуществляется движение по окружности радиусом г0. Если по
каким-то причинам произойдет смещение электрона на радиус г > г0,
то при п > 1 центростремительная сила Fuc < F?co6\ Это означает, что
возникают факторы, стремящиеся удалить электрон.от орбиты радиу-
радиусом г0. Поэтому при п > 1 движение оказывается неустойчивым. При
п < 1 центростремительная сила Fuc > F^o6x и возникают факторы,
стремящиеся возвратить электрон на орбиту радиусом г0, в результате
чего достигается радиальная устойчивость. Рассмотрение случая г <г0
приводит к тому же заключению. Следовательно, условие радиальной
устойчивости движения имеет вид
0 < п < 1. E6.12)
Задачи 383
Иертикальная устойчивость. Она обеспечивается всегда при спадании
индукции магнитного поля к периферии (п > 0), поскольку в этом
случае силовые линии выпуклы наружу (рис. 241) и при отклонении
электрона от средней плоскости возникает составляющая силы Лоренца,
стремящаяся вернуть его к ней (рис. 241). Таким образом, при выполне-
выполнении условия E6.12) обеспечивается также и вертикальная устойчивость
движения, т.е. неравенство E6.12) является общим условием устойчи-
устойчивости движения электрона в бетатроне.
Сетатронные колебания. При небольших отклонениях от равновесной
орбиты (г = г0) электроны совершают около нее небольшие гармо-
гармонические колебания как в радиальном, так и в вертикальном направ-
направлениях. Эти колебания называются бетатронными. Их амплитудой
определяется сечение кольцевой вакуумной камеры, в которой осу-
осуществляется движение электрона. Обычно линейные размеры попереч-
поперечного сечения этой камеры составляют примерно 5 % от радиуса орбиты.
Дредел энергий, достижимых в бетатроне. Как было уже сказано,
этот предел обусловливается потерями энергии электронов на тор-
тормозное излучение (см. гл. 10). Практически в бетатронах можно полу-
получить максимальные энергии, не превышающие 300 МэВ.
Задачи
8.1. Вычислить индуктивность участка
длиной I двухпроводной линии,
пренебрегая внутренней индуктив-
индуктивностью проводов, Радиусы прово-
проводов одинаковы и равны г0, рас-
расстояние между проводами равно d.
8.2. По прямому бесконечному круг-
круглому цилиндрическому проводни-
проводнику течет ток плотностью j. В про-
проводнике имеется цилиндрическая
полость круглого сечения. Оси
цилиндра и полости параллельны
(см. рис. 98). Найти индукцию
магнитного поля внутри полости
(ц = Но)-
Указание: См. задачу 2.9.
8.3. Имеется очень длинный соленоид
с плотностью намотки п витков
на 1 м длины. Площадь попереч-
поперечного сечения соленоида равна S.
Через обмотку соленоида течет
ток силой /. В соленоид с двух
сторон вдвинуты очень длинные
железные стержни с магнитной
проницаемостью ц. Стержни плот-
плотно прилегают к обмотке соленои-
соленоида. Между стержнями внутри со-
соленоида имеется очень маленький
промежуток. Определить силу, с
которой стержни притягиваются
друг к другу.
8.4. Имеется электромагнит U-образ-
ной формы, обмотка которого
состоит из и витков. Площадь
поперечного сечения, длина, маг-
магнитная проницаемость материала
магнита и расстояние между по-
полюсами равны соответственно S,
I, ц и d. Сила тока, текущего
через обмотку магнита, равна /.
К полюсам магнита приложили
полосу из того же материала
и с тем же поперечным сечением,
что и магнит. Определить силу,
с которой полоса притягивается к
магниту.
8.5. Горизонтальный металлический
стержень вращается около верти-
вертикальной оси, проходящей на рас-
расстоянии 1/fe его длины от одного
384 8. Электромагнитная индукция и квазистационарные переменные токи
из концов, с частотой V. Длина
стержня равна /. Определить раз-
разность потенциалов между конца-
концами стержня, если он вращается
в вертикальном однородном маг-
магнитном поле с индукцией В. Счи-
Считать, что к = 3; / = 1,2 м; v = 6 с;
В = 10-2 Тл.
8.6. Между круглыми полюсами боль-
большого электромагнита, питаемо-
питаемого переменным током частотой
v = 1 кГц, образуется синусо-
синусоидально изменяющееся со време-
временем магнитное поле с амплиту-
амплитудой индукции Во = 0,5 Тл. Считая
магнитное поле однородным,
определить максимальную напря-
напряженность электрического поля в
зазоре между магнитами на
расстоянии г = 0,1 м от центра.
8.7. Замкнутый на себя соленоид ра-
радиусом Ъ с п витками вращается
с угловой скоростью ш вокруг
диаметра одного из витков в
однородном магнитном поле с ин-
индукцией В. Ось вращения перпен-
перпендикулярна вектору индукции. Со-
Сопротивление и индуктивность со-
соленоида равны R и L соответст-
соответственно. Определить силу тока, те-
текущего через соленоид, как функ-
функцию времени.
8.8. Сверхпроводящее кольцо, которое
может двигаться лишь в верти-
вертикальном направлении, лежит на
столе над витком проводника.
Через виток проводника начинает
течь ток силой /. В результате
этого сверхпроводящее кольцо
поднимается. Взаимная индуктив-
индуктивность витка и кольца, поднятого
на высоту х, равна L12 (х). Индук-
Индуктивность сверхпроводящего коль-
кольца равна Ьц, масса кольца т,
ускорение свободного падения д.
Определить высоту й, на которую
поднимается сверхпроводящее
кольцо.
8.9. Через катушку Ах пропускается
ток силой /0 sin ал. В катушке А2
индуцируется соответствующая
сила тока. Индуктивности и
взаимоиндуктивность равны Ll5
L2, L12. Сопротивление катушки
А 2 равно R2. Пусть ^ — некото-
некоторая обобщенная координата, ха-
характеризующая положение катуш-
катушки А2. Найти обобщенную сред-
среднюю силу F(, которая связана с
обобщенной координатой (^.
1.10. В плоскости лежат бесконечно
длинный прямолинейный про-
проводник и проводник в виде
окружности радиусом а (рис. 242).
Расстояние от центра кольцево-
кольцевого проводника до прямолиней-
прямолинейного d. Найти взаимную индук-
индуктивность.
Z
о
242
Взаимное расположение вза-
взаимодействующих прямого и кру-
кругового токов
5.11. По прямолинейному и кольце-
кольцевому проводникам, описанным в
задаче (8.10), протекают токи си-
силой Ii и 1г. Какая сила дейст-
действует на кольцевой проводник?
1.12. Найти взаимную индуктивность
обмотки тороида (рис. 195) и
прямолинейного проводника бес-
бесконечной длины, совпадающего с
аксиальной осью симметрии то-
тороида.
1.13. Найти индуктивность обмотки
тороида круглого сечения радиу-
радиусом гсп витками. Большой
радиус тороида равен R.
!.14. Коаксиальный кабель, жила и
оболочка которого имеют беско-
бесконечную проводимость и радиусы
rt и г2, замкнут накоротко под-
подвижной диафрагмой (рис. 243).
Найти силу, которая действует на
подвижную диафрагму, когда по
кабелю протекает ток силой /.
Задачи 385
243
Кабель с подвижной диафраг-
диафрагмой
U5. Полый цилиндр радиусом гг и
коаксиальный с ним цилиндриче-
цилиндрический проводник радиусом гх
очень большой проводимости
опущены в проводящий жидкий
магнетик с магнитной прони-
проницаемостью ц и плотностью массы
р (рис. 244). В цепи идет ток
силой /. Найти высоту подъема
жидкого магнетика в цилиндре.
244
Втягивание магнетика в прост-
пространство между коаксиальными
проводниками с током
8.16. Диэлектрический цилиндр ра-
радиусом а вращается вокруг своей
оси с угловой скоростью ш, па-
параллельно которой направлен
вектор индукции В постоянного
магнитного поля. Найти поляри-
зованность цилиндра и поверх-
поверхностную плотность связанного
заряда. Диэлектрическая прони-
проницаемость вещества цилиндра рав-
равна е.
8.17. Тонкий проводящий диск с про-
проводимостью у расположен в пе-
13 А. Н. Матвеев
ременном магнитном поле, ин-
индукция которого равна В =
= В cos (at + ф) и направлена
перпендикулярно плоскости дис-
диска. Найти плотность токов Фуко,
индуцируемых в диске.
8.18. Найти индуктивность обмотки
тороида из п витков квадрат-
квадратного сечения со стороной а. Боль-
Большой радиус тороида равен R.
8.19. Круглая петля радиусом а вра-
вращается вокруг своего диаметра с
постоянной угловой скоростью (о
в однородном магнитном поле
с индукцией В. Ее омическое
сопротивление равно R, а ось
вращения перпендикулярна В.
Найти силу тока I(t), момент
тормозящих вращение рамки сил
М (t) и среднюю мощность <Я>,
которая расходуется на поддер-
поддержание постоянной угловой ско-
скорости вращения рамки. В ка-
качестве начала отсчета t = О при-
принять момент, когда плоскость
петли перпендикулярна В.
8.20. Участок цепи состоит из двух
цилиндрических коаксиальных
трубок радиусами at и а2 (а2 > аг)
длиной I. На одном конце труб-
трубки соединены проводящей плос-
плоской пластиной. Найти индуктив-
индуктивность участка цепи.
8.21. Два плоских замкнутых круглых
витка проволоки радиусами ах
и а2 лежат в одной плоскости
на расстоянии d друг от друга.
Считая, что расстояние d доста-
достаточно велико и можно восполь-
воспользоваться дипольным приближе-
приближением, найти взаимную индуктив-
индуктивность контуров.
8.22. Магнитная индукция Во между
плоскими параллельными полю-
полюсами электромагнита может счи-
считаться однородной и постоян-
постоянной. В пространство между по-
полюсами вдвигается пластина пло-
площадью S из парамагнитного ма-
материала с парамагнитной вос-
восприимчивостью Хп- Ее поверх-
поверхности параллельны поверхностям
386 8. Электромагнитная индукция и квазистационарные переменные токи
полюсов электромагнита. Найти
действующую на пластину силу.
8.23. Найти радиальную силу, дейст-
вующую на тороид, данные ко-
торого приведены в задаче 8.13,
если по нему течет ток силой /.
8.24. Два идентичных контура с индук-
тивностями L=Ln =Ъгг распо-
ложены так, что их взаимная
индуктивность L^l = 0. В конту-
pax протекают сверхпроводящие
токи силой /0. После этого изме-
няется взаимное положение кон-
туров, в результате чего их
взаимная индуктивность стано-
вится равной L12. Найти силу
токов в конечном состоянии.
8.25. Электрический контур состоит из
четырех узлов. Три узла совпа-
дают с вершинами равносторон-
него треугольника, а четвер-
тый - с его центром (точка пере-
сечения медиан или биссектрис).
Между вершинами треугольника
емкости участков равны С (R = 0,
L = 0), а между вершинами тре-
угольника и его центром вклю-
чены индуктивности L (R = 0,
С = 0). Найти резонансную час-
тоту системы.
Ответы
8.1. L = i^/ln i-.g.2. В = W2)j х г. 8.3. F =4 fc
2. 8.4. F =
(/ + аJ
Но
к-^-В=9Л В. 8.6. ?=Вошг/2=156 В/м. 8.7.
х (R2 + <o2L2)-1/2 sin (ом + ф0). 8.8. h = i — — {[L12 (О)]2 - [Li2 (й)]2}. 8.9. F, =
2 тд Ь
In (
2re V 2R - a
- e0) Bcoa. 8.17. j = G2) ушВ0 x r sin (cot + ф). 8.18.
8.19. /(,) ^L
хмп(а*-ф); <p>-i-/jn=i.-^!™3Lji. 8.20. L= [цо//Bя)]
8.21. L12 = n07Cfl2ai/DA 8.22. F = Хп^/[2Цо d + Х„I 8.23. F=-no/V
x (R/\/R2 - ? - 1). 8.24. / = I0L/{L+ L12). 8.25. coo
§57
Ток смещения
§58
Система
уравнений Максвелла
§59
Закон
сохранения энергии
электромагнитного поля.
Поток энергии
§ 60
Движение
электромагнитной энергии
вдоль линий передач
§ 61
Излучение
электромагнитных волн
§ 62
Распространение
электромагнитных волн
в диэлектриках
§ 63
Распространение
электромагнитных волн
в проводящих средах
§64
Инвариантность
плоской волны
§65
Давление
электромагнитных волн.
Импульс фотона
§66
Волноводы и резонаторы
Электромагнитные
волны
Изменяющееся магнитное поле поро-
порождает изменяющееся электрическое
поле, которое, в свою очередь, по-
порождает изменяющееся магнитное по-
поле, которое, в свою очередь, порож-
порождает изменяющееся электрическое по-
поле, и т. д. В результате образуются
сцепленные между собой электриче-
электрическое и магнитное поля, составляю-
составляющие электромагнитную волну. Она
«отрывается» от зарядов и токов, ко-
которые ее породили. Способ сущест-
существования электромагнитной волны де-
делает невозможным ее неподвижность
в пространстве и постоянство напря-
напряжен ностей ее полей во времени.
13*
388 9. Электромагнитные волны
§ 57. Ток смещения
Обсуждается физическое содержание тока
смещения. Проводится учет тока смещения
в уравнениях Максвелла.
Сущность процесса. Постоянный ток не протекает в цепи с конден-
конденсатором, а переменный ток протекает. Сила квазистационарного
тока проводимости во всех последовательно соединенных элементах
цепи является одной и той же. В конденсаторе ток проводимости,
связанный с движением электронов, не может существовать, поскольку
обкладки конденсатора разделены диэлектриком. Поэтому необходимо
заключить, что в конденсаторе происходит некоторый процесс, ко-
который как бы замыкает ток проводимости, т. е. в некотором смысле
обеспечивает обмен зарядом между обкладками конденсатора без
переноса заряда между ними. Этот процесс называется током сме-
смещения.
Рассмотрим цепь переменного тока с плоским конденсатором
(рис. 245). Между обкладками конденсатора имеется электрическое поле
с напряженностью Е = а/г, где а — плотность заряда на обкладке;
е — диэлектрическая проницаемость вещества между обкладками. Элект-
Электрическое смещение между обкладками конденсатора равно D = а = Q/S,
где Q — заряд на каждой из обкладок конденсатора; S — площадь
обкладки. Сила тока в цепи равна / = dQ/dt. Отсюда следует, что
E7.1)
т. е. процессом, замыкающим ток проводимости в цепи, является изме-
изменение электрического смещения между обкладками конденсатора, при-
причем в формуле E7.1) величина / дана с индексом «см» («смещение»),
чтобы показать, что это не ток проводимости между обкладками,
хотя / = /см. Плотность тока смещения в пространстве между обклад-
обкладками равна jCM = IaJS = dD/dt. Учитывая, что направление jCM в каж-
каждой точке между обкладками плоского конденсатора совпадает с
направлением dD/dt, можно вместо E7.1) написать следующее диффе-
дифференциальное соотношение:
jCM =
E7.2)
Из локального характера этого соотношения следует ожидать его
независимость от нелокальной модели (плоский конденсатор), в рамках
которой оно получено. Так оно и есть на самом деле. Формула
E7.2) определяет объемную плотность тока смещения jCM. Существова-
Существование тока смещения теоретически было постулировано Максвеллом
в 1864 г. и в последующем экспериментально подтверждено другими
учеными.
§ 57. Ток смещения 389
почему скорость изменения вектора смещения называется плотностью
тока? Само по себе математическое равенство величины SdD/dt,
характеризующей процесс между обкладками конденсатора, и силы тока
проводимости вне обкладок конденсатора, т. е. равенство двух величин,
относящихся к разным областям пространства и имеющим различную
физическую природу, не содержит в себе, вообще говоря, какого-то
физического закона. Поэтому называть SdD/dt «током» можно только
формально. Для того чтобы придать этому названию физический
смысл, необходимо доказать, что SdD/dt обладает наиболее характер-
характерными свойствами тока, хотя и не представляет движения электри-
электрических зарядов, подобного току проводимости. Главным свойством тока
проводимости является его способность порождать магнитное поле.
Поэтому решающим является вопрос о том, порождает ли ток сме-
смещения магнитное поле так же, как его порождает ток проводи-
проводимости, или, более точно, порождает ли величина E7.2) такое же
магнитное поле, как равная ей объемная плотность тока проводи-
проводимости? Максвелл дал утвердительный ответ на этот вопрос.
Экспериментальная проверка правильности этого ответа состоит в
следующем. По закону полного тока циркуляция вектора В по охва-
охватывающему ток контуру равна ]iol- Циркуляция может быть измерена
с помощью пояса Роговского. Перемещая его вдоль контура, отме-
отмечаем, что циркуляция не изменяется и тогда, когда пояс Роговского
охватывает конденсатор. А это как раз и означает, что ток смещения
в конденсаторе порождает такое же магнитное поле, как соответствую-
соответствующий ток проводимости. Однако наиболее ярким подтверждением по-
порождения магнитного поля током смещения является существование
электромагнитных волн. Если бы ток смещения не создавал магнит-
магнитного поля, то не могли бы существовать электромагнитные волны.
"уравнение Максвелла с током смещения. Порождение магнитного
поля током проводимости описывается уравнением
rotH = j. E7.3)
Учитывая порождение поля током смещения, необходимо обобщить
это уравнение в виде
j + jCM. E7.4)
Тогда, принимая во внимание E7.2), окончательно получаем урав-
уравнение
rot H = j + dD/dt,
E7.5)
являющееся одним из уравнений Максвелла.
релятивистская природа тока смещения. При преобразовании полей
от одной системы координат к другой электрическое и магнитное
поля обусловливают друг друга (см. § 11). Если в некоторой системе
координат имеется неоднородное магнитное поле, то в другой системе
390 9. Электромагнитные волны
t/
246
Двухслойный плоский конден-
конденсатор с утечкой
координат это поле представляется перемен-
переменным по времени и одновременно появля-
появляется электрическое поле. А это как раз
и есть свидетельство того, что переменное
электрическое поле порождает магнитное
поле. Однако отсюда не следует, что порож-
порождение магнитного поля переменным электри-
электрическим полем не является новым фундамен-
фундаментальным явлением в физике электричества
и магнетизма. Ситуация здесь аналогична
той, которая была подробно разобрана в
связи с электромагнитной индукцией в § 45,
46. Порождение магнитного поля перемен-
переменным электрическим полем является фунда-
фундаментальным явлением природы.
Пример 57.1. Между обкладками плоского
конденсатора имеются два слоя слабо проводя-
проводящего материала с удельными проводимостями yt
и у2 и диэлектрическими пронщаемостями et и s2.
Толщины слоев равны соответственно ах и а2
(рис. 246). Площади обкладок конденсатора S.
Исследовать процесс установления силы тока в
цепи, если в момент t = 0 к обкладкам конден-
конденсатора приложена постоянная разность потенциа-
потенциалов Uo. Рассмотреть процессы, возникающие при
размыкании цепи и при шунтировании источника
сторонних э. д. с.
В момент включения напряжения на границе
между слоями не может мгновенно возникнуть
поверхностный заряд. Поэтому в начальное мгно-
мгновение рассматриваемая система ведет себя так, как
будто проводимость вещества между пластинами
равна нулю, т. е. как идеальный конденсатор.
Поэтому в пространстве между пластинами возни-
возникает смещение
# Формальное равенство то-
тока смещения в конденса-
конденсаторе н тока проводимости
в присоединенных к его
обкладкам проводах не со-
содержит в себе какого-ли-
какого-либо физического зокона.
Новый физический закон
состоит в том, что ток
смещения создает такое
же магнитное поле как н
соответствующий ему ток
проводи мости.
= ?lE1 =s2?2,
E7.6)
где Et и Е2 - напряженности электрического
поля в первом и втором слоях соответственно.
В E7.6) учтена непрерывность D. Так как разность
потенциалов между пластинами равна Uo, то
B)
E-dl
E7.7)
где в качестве пути интегрирования от первой
пластины ко второй взят путь по нормали к
пластинам. Из E7.6) и E7.7) следует, что
D = e1e2U0/(e2a1
E7.8)
§ 57. Ток смещения 391
Весь ток в начальный момент является током смещения. Он равен беско-
бесконечности, поскольку разность потенциалов включается мгновенно и D мгно-
мгновенно возрастает от 0 до значения, определяемого по формуле E7.8). Поверх-
Поверхностная плотность заряда на пластинах также возрастает мгновенно от О
до <?! = —аг = D.
Мгновенные изменения электрического смещения от нуля до конечного
значения обусловлены очень большой скоростью возникновения поляризован-
ности вещества под влиянием внешнего поля. Поляризованность возникает
за время, характерное для внутримолекулярных процессов.
В последующие моменты времени после включения начинает возрастать
сила тока проводимости и по прошествии достаточного времени ((-> оо)
устанавливается равновесное значение плотности тока:
j = Yi?i = У2Е2 = YiY2^o/(Y2«i + yia2), E7.9)
где учтено соотношение E7.7). Поскольку проводимость неоднородна, на поверх-
поверхности раздела между слоями существует заряд с поверхностной плотностью
а = D2n - Du = е2?2 - s,?, = (s2y, - е,у2) 1/0/(у2а, + у,а2), E7.10)
где использовано граничное условие A7.36), так как напряженность электри-
электрического поля не зависит от времени.
В переходном режиме, до достижения стационарных значений E7.9) и E7.10),
токи проводимости в первом и втором слоях различны, а плотность
заряда на границе раздела между слоями возрастает со временем. Одинаковое
значение в обоих слоях в переходном режиме имеет сумма объемных плот-
плотностей токов проводимости и смещения, называемая полной объемной плот-
плотностью тока:
h = У1Б1 + JJ-Mi) = У2Е2 + ^(^Е2). E7.11)
Исключив Ег из E7.11), с помощью E7.7) получаем уравнение для Et:
E7Л2)
+
dt т
где
т = (s^ + c2a1)/(yla2 + y2ai). E7.13)
Аналогичное уравнение получается и для Е2.
Решение этих уравнений при начальном условии E7.8) таково:
-.,Tj E7 14)
-,„ш E7 15)
При t -* 00 эти решения, как и должно быть, принимают вид E7.9).
Поверхностная плотность заряда между слоями изменяется по закону
а = s2?2 - Ё1?, = 82Yl ~ SlY2 A - e-'/l) Uo. E7.16)
уО + ya
392 9. Электромагнитные волны
При t = 0 поверхностная плотность заряда о = 0, а при t -* оо она, как
и следовало ожидать, стремится к E7.10).
Полная плотность тока находится из E7.11) с учетом E7.14) и E7.15):
1 + M0 Y2?2 +
62 Y2
&{t)\U0, E7.17)
где S (t) — дельта-функция. Она возникла из-за того, что смещение D при t = О
возросло мгновенно от 0 до E7.8). Другими словами, при вычислении
производной по времени в E7.17) имеем
E7.18)
а при вычислении SE^/et в E7.18) пользуемся выражением E7.14), справедли-
справедливым для всех t > 0.
Проведенный анализ показывает, что распределение напряжений по различ-
различным участкам цепи в момент включения внешнего напряжения может существен-
существенно отличаться от распределения в установившемся режиме. Это обстоятельст-
обстоятельство необходимо принимать во внимание при расчете цепей.
При размыкании цепи уп = 0 и, следовательно, уравнения E7.11) принимают
вид:
- = 0, т.*. + 5J^- = 0- E7.19)
Поля распадаются независимо. В установившемся режиме, как это видно
из E7.14) и E7.15),
?20 = Yi^o/(Y2ai + Yi^)- E7.20)
Решение уравнений E7.19) при начальных условиях E7.20) имеет вид:
Yl«2
где t! =e!/Yi, т2
Разность потенциалов между разомкнутыми клеммами изменяется так:
= а,?, + а2?2 = ^ baie^1 + Y^e"*2]. E7.22)
Ya + Y^
Поверхностная плотность заряда на границе между слоями в конденсаторе
определяется формулой
а = г2Ег - М, = ^ [eaY.e' - ElY2e']. E7.23)
Ya + Ya
При шунтировании источника сторонних э. д. с. Uo = 0 и уравнения E7.7)
и E7.12) принимают вид:
atEi + а2Е2 = 0, E7.24)
^-+^- = 0, E7.25)
dt 1
§ 58. Система уравнений Максвелла 393
где т — определяется выражением E7.13). Начальное условие при t = 0 нахо-
находится из E7.10) с учетом E7.24):
Е2?2О - El?10 = - f^L + еЛ ?10 = е^' ~ s^ и о. E7.26)
\ а2 ) уа + YO
Решение уравнения E7.25) с начальным значением Е10 из E7.26) таково:
, = -Е2а2/а1 - - М.-;.^А ., E7.27)
Сила тока в контуре и поверхностная плотность заряда между слоями
равны:
_\Э . тг _ _ т г ~1
E7.28)
E7.29)
Член с 5-функцией в E7.28) появился из-за того, что в момент шунти-
шунтирования источника сторонних э. д. с. вектор смещения D скачком изменился от
значения, соответствующего формуле E7.9) для установившегося режима, к
значению, соответствующему начальным условиям при t = 0 по формуле E7.26).
§ 58. Система уравнений Максвелла
Обсуждаются физический смысл, условия
применимости, полнота и совместность
системы уравнений Максвелла.
^истема уравнений Максвелла. Полученные в предыдущих парагра-
параграфах в результате обобщения экспериментальных фактов уравнения
E7.5), D6.5), C6.4), A7.30) составляют систему уравнений Максвелла:
rot Н = j + dD/dt, (I) div В = 0, (III)
rotE=-oB/St, (II) divD = p. (IV) E8.1a)
Эти уравнения, называемые полевыми, применимы для описания всех
макроскопических электромагнитных явлений. При рассмотрении конк-
конкретной ситуации необходимо учесть электромагнитные свойства мате-
материальных сред. Во многих случаях это достигается соотношениями
A7.31), C8.24), A6.5):
D = sE, В = цН, j = yF (V), E8.16)
называемыми обычно материальными уравнениями. Однако существует
много явлений, когда материальные уравнения имеют другой вид
(например, нелинейные явления) и их установление составляет самостоя-
самостоятельную научную задачу.
394 9. Электромагнитные волны
физический смысл уравнений. Уравнение (I) выражает закон, по
которому магнитное поле порождается токами проводимости и
смещения, являющимися двумя возможными источниками магнитного
поля.
Уравнение (II) выражает закон электромагнитной индукции и ука-
указывает на изменяющееся магнитное поле как на один из возмож-
возможных источников, порождающих электрическое поле. Вторым источни-
источником электрического поля являются электрические заряды, порождение
поля которыми описывается уравнением (IV), выражающим закон
Кулона. Физический смысл уравнения (III) подробно обсуждается
в связи с C6.4).
Материальные уравнения (V) являются соотношениями между векто-
векторами поля и токами, учитывающими свойства материальной среды.
Учет диэлектрических свойств, феноменологически описываемых поля-
ризованностью, содержится в диэлектрической проницаемости s; учет
магнитных свойств, феноменологически описываемых намагничен-
намагниченностью, содержится в магнитной проницаемости ц; учет проводящих
свойств среды содержится в удельной проводимости у.
Уравнения поля являются линейными, учитывающими принцип
суперпозиции, который является независимым экспериментальным
фактом,
-условия применимости уравнений. По ходу обоснования уравнения
E8.1) видно, что они справедливы при следующих условиях:
1) материальные тела в поле неподвижны;
2) материальные константы е, ц, у могут зависеть от координат,
но не должны зависеть от времени и векторов поля;
3) в поле отсутствуют постоянные магниты и ферромагнитные
тела.
Для того чтобы учесть движение среды, проще всего поступить
так. Наличие среды для электрических и магнитных явлений сводится
в конечном счете к наличию зарядов среды и их движениям. Поэтому
можно исходить из уравнений Максвелла для вакуума (s = ?о> И = Но)»
а среду учесть точно так же, как это делалось в § 17 и 38, но
приняв во внимание движение зарядов. В результате получается, что
уравнения поля E8.1) сохраняют без изменения свой вид, а весь учет
движения среды сводится к модификации материальных уравнений
E8.16), которые становятся зависимыми от скорости среды и значи-
значительно усложняются. При этом они перестают быть соотношениями
между двумя величинами (например, между D и Е и т. д.), а «за-
«зацепляются» друг за друга. Например, плотность тока проводимости
начинает зависеть от индукции магнитного поля, а не только от
напряженности электрического поля и т. д.
Поле вне постоянных магнитов и ферромагнетиков в предположе-
предположении, что известна их намагниченность, можно описать с помощью
уравнений Максвелла. Однако решить задачу при наличии ферромагне-
ферромагнетиков в пространстве, когда, например, заданы токи, с помощью
уравнений Максвелла нельзя. Они неприменимы для этого случая.
§ 58. Система уравнений Максвелла 395
гтолнота и совместность системы уравнений. С помощью материаль-
материальных уравнений E8.16) можно исключить из полевых уравнений E8.1а)
величины D, Н и j, в результате чего они становятся уравнениями
относительно векторов Е и В, т. е. относительно шести неизвестных
независимых компонент этих величин. С другой стороны, число ска-
скалярных уравнений в E8.1а) равно восьми. Получается, что имеется
восемь уравнений для шести неизвестных величин, т. е. число уравне-
уравнений превышает число неизвестных, что недопустимо, поскольку систе-
система уравнений кажется переполненной.
Однако в действительности система не переполнена и никаких
трудностей не возникает. Это обусловлено тем, что уравнения (I)
и (IV) и (II) и (III) имеют одинаковые дифференциальные следствия
и потому связаны между собой, хотя и нельзя сказать, что какие-то
из них являются следствиями других.
Для доказательства одинаковости дифференциальных следствий
уравнений (II) и (III) применим к обоим частям уравнения (II) опера-
операцию div, а обе части уравнения (III) продифференцируем по времени.
В обоих случаях получается одно и то же уравнение д divB/d/ = 0.
Докажем, что с учетом закона сохранения заряда
^ + divj = O E8.2)
уравнение (IV) можно рассматривать как дифференциальное следствие
уравнения (I). Для доказательства применим операцию div к обеим
частям уравнения (I):
ddivD/St=O, E8.3)
где div rot H = 0. Сравнивая E8.3) с E8.2), находим, что должно выпол-
выполняться равенство
div D = р, E8.4)
совпадающее с уравнением (IV). Тем самым доказано, что (IV) является
дифференциальным следствием уравнения (I) с учетом закона сохране-
сохранения заряда.
Наличие двух дифференциальных связей между уравнениями (I —IV)
делает эту систему совместной. Более подробный анализ показывает,
что система уравнений является полной, а ее решение однозначно
при заданных граничных и начальных условиях. Доказательство един-
единственности решения в общих чертах сводится к следующему. Если
имеется два различных решения, то их разность вследствие линейности
уравнений Максвелла является также решением, но при нулевых заря-
зарядах и токах и нулевых начальных и граничных условиях. Отсюда,
пользуясь выражением для энергии электромагнитного поля и законом
сохранения энергии, заключаем, что разность решений тождественно
равна нулю, т. е. решения одинаковы. Тем самым единственность
решения уравнений Максвелла доказана.
396 9. Электромагнитные волны
§ 59. Закон сохранения энергии
электромагнитного поля. Поток энергии
Дается математическая формулировка за-
закона сохранения энергии и обсуждается по-
понятие потока электромагнитной энергии.
формулировка. Энергия электрического и магнитного поля опреде-
определяется формулами A8.16) и D7.26). В § 19 и 39 были исследованы
силы в электрическом и магнитном полях, под действием которых
совершается работа. В § 49 была определена работа переменного
тока, в § 27 изучено тепловое действие тока. Закон сохранения
энергии требует, чтобы все эти процессы были сформулированы в
виде закона сохранения и превращения различных форм энергии друг
в друга. Поскольку при этом источники производства электромагнит-
электромагнитной энергии пространственно отделены от мест ее потребления, возни-
возникает представление о движении энергии, характеризуемом ее потоком.
Рассмотрим некоторый замкнутый объем V, в котором имеются
электромагнитное поле и токи (рис. 247). Джоулева теплота, выделяе-
выделяемая токами в этом объеме, равна
E9.1)
v
Для упрощения расчета предполагается, что других превращений
энергии в этом объеме нет. Подставляя в E9.1) выражения для j из
уравнения E8.1а), получаем
= |*ErotHdF- |E~
v
E9.2)
По формуле (П. 15) имеем
divEx H=rotE-H-E-rotH E9.3)
и, следовательно,
^ E9.4)
Р=- Nj5-HdF- E-^-dF- divExHdK
где rotE=-5B/3f. Учитывая, что Н—г- = -г- —~г—- и—'-— =
ct 2 at ot
= — —-—-, и преобразуя последний интеграл в E9.4) по теореме
Гаусса — Остроградского в интеграл по поверхности а, ограничиваю-
ограничивающей объем V, окончательно получаем
Н)с1К -jExH-dcr.
Jo
Р= - -|-Г1|(Е-В + В-Н)с1К -jExH-dcr. E9.5)
§ 59. Закон сохранения энергии электромагнитного поля. Поток энергии 397
Здесь поверхность обозначена о для того,
чтобы букву S сохранить для обозначения
плотности потока электромагнитной энер-
энергии.
ТТоток энергии.
Величина
1
E9.6)
характеризует электромагнитную энергию,
заключенную в объеме V. Величина
= ExH
E9.7)
dW
dt
= -P-jSdcr,
К формулировке закона сохра-
сохранения энергии
является плотностью потока энергии сквозь
поверхность, ограничивающую объем V, и
называется вектором Поннтинга. Она была
получена Д. Г. Пойнтингом A852—1914)
в 1884 г. Однако на десять лет раньше, в
Г874 г. Н. А. Умовым A846-1915) было
проведено общее исследование движения
энергии в телах, которое характеризовалось
соответствующим потоком энергии. Поэтому
вектор E9.7) называется также вектором
Умова —Пойнтинга. Равенство E9.4) удобнее
переписать в виде
E9.8)
т. е. изменение энергии электромагнитного
поля в объеме происходит за счет работы
токов проводимости в этом объеме и потока
энергии сквозь поверхность, ограничивающую
объем. Если энергия электрического поля не
изменяется dW/dt = 0, то [см. E9.8)]
P=-jS-d«r. E9.9)
Следовательно, вся производимая в замк-
замкнутом объеме работа совершается за счет
потока электромагнитной энергии сквозь по-
поверхность, ограничивающую объем.
Равенство E9.8) выражает закон сохране-
сохранения энергии электромагнитного поля.
Следует подчеркнуть, что E9.8) является
именно выражением закона сохранения энер-
энергии, а не его доказательством.
Закон сохранения энергии
как всеобщий закон при-
природы предполагается дан-
данным при построении тео-
теории электричества и маг-
магнетизма. Исходя из закона
сохранения энергии как
всеобщего закона можно
найти математическое вы-
выражение для объемной
плотности энергии элек-
электрического и магнитного
полей и плотности энер-
энергии электрического и маг-
магнитного полей и плотности
потока электромагнитной
энергии, а также устано-
установить связь между ними,
выражающую идею дви-
движения электромагнитной
энергии. В формуле E9.8)
физическая величина Р
учитывает возможность
взаимопревращения раз-
различных форм энергии друг
в друга.
398 9. Электромагнитные волны
§ 60. Движение электромагнитной энергии
вдоль линий передач
Обсуждаются физическая картина движения
энергии вдоль линий передач и основные
характеристики линий передач.
ДДеханизм компенсации потерь энергии на джоулеву теплоту. Рас-
Рассмотрим участок проводника круглого сечения радиусом г, вдоль
которого течет постоянный ток с объемной плотностью j (рис. 248).
По закону Ома в дифференциальной форме напряженность электри-
электрического поля, параллельная оси проводника, равна
E = j/y- F0.1)
Вследствие граничного условия непрерывности тангенциальных
составляющих напряженности электрического поля точно такое же поле
существует вне проводника около его поверхности.
Вычислим по формуле E9.9) поток электромагнитной энергии
сквозь замкнутую поверхность цилиндра, боковая поверхность которого
совпадает с поверхностью проводника длиной I, а основаниями являют-
являются круглые сечения проводника.
Напряженность магнитного поля на поверхности проводника направ-
направлена по касательной к поверхности в плоскости, перпендикулярной
оси проводника (и вектору j) (рис. 248), и равна
Я-;яг2/Bяг)=;/Bг). F0.2)
Таким образом, вектор Пойнтинга E9.7) направлен по радиусу к оси
проводника и равен
S = EH =fr/By). F0.3)
Это означает, что электромагнитная энергия втекает в проводник
из окружающего пространства через его боковую поверхность. Поток
энергии через основания цилиндра отсутствует. На участке проводника
длиной / за 1 ев проводник втекает энергия
P = S-2ml = {j2li)nr2l F0.4)
По закону Джоуля—Ленца на длине I проводника в 1 с выделяется
количество теплоты
P' = (j2/y)nr2l. F0.5)
Сравнение F0.4) с F0.5) показывает, что вся выделяемая в провод-
проводнике при прохождении электрического тока в виде теплоты энергия
поступает из окружающего пространства через боковую поверхность
проводника. Следовательно, передаваемая с помощью электрического
тока энергия движется в окружающем проводник пространстве. Про-
Провода играют роль направляющих, вдоль которых движется электро-
электромагнитная энергия, причем плотность потока энергии в любой точке
пространства определяется вектором Пойнтинга.
§ 60. Движение электромагнитной энергии вдоль линий передач 399
движение энергии вдоль кабеля. По цент-
^фальному проводу ток движется в одном
направлении, а по оболочке кабеля - в про-
противоположном (рис. 249). Между централь-
центральной жилой и оболочкой находится диэлект-
диэлектрик. Для упрощения расчетов предположим,
что сопротивление проводов кабеля ничтож-
ничтожно мало и им можно пренебречь, т. е. мож-
можно считать, что энергия передается без по-
потерь. Тогда потенциал вдоль центральной
жилы и оболочки постоянен, а изменение
потенциала между ними происходит на
потребителе энергии и на источнике (сто-
(сторонняя э. д. с). Пусть падение потенциала на
потребителе энергии равно U. Это означает,
что разность потенциалов между жилой и
оболочкой равна U. Следовательно, между
ними существует электрическое поле. Вслед-
Вследствие аксиальной симметрии задачи и того,
что ток течет вдоль кабеля без сопротивле-
сопротивления, напряженность этого поля направлена
по радиусу, а касательная составляющая Еа
отсутствует. Ось Z цилиндрической системы
координат совпадает с осью кабеля. Сило-
Силовые линии магнитного поля являются кон-
концентрическими окружностями с центром на
оси кабеля. Напряженность поля отлична от
нуля только в пространстве между жилой
и оболочкой, а вне кабеля она равна нулю.
Радиальная составляющая вектора Пойнтин-
га равна нулю. Уравнение Максвелла
div D = р для пространства между жилой
и оболочкой принимает вид
248
Механизм компенсации потерь
тока на выделение джоулевой
теплоты
div Е = у ~
= 0,
F0.6)
где использована запись операции диверген-
дивергенции в цилиндрических координатах и при-
принято во внимание, что аксиальная и каса-
касательная составляющие вектора Е отсутству-
отсутствуют. Из F0.6) получаем
Ег = яо/г, F0.7)
где а0 — постоянная интегрирования, опреде-
определяемая условиями задачи. Разность потен-
потенциалов между жилой и оболочкой равна
U = f Е, dr = a0 In (r2/ri),
F0.8)
Передача электромагнитной
эцергии с помощью тока по
кабелю
О Передаваемая с помощью
электрического тока энер-
энергия движется в простран-
пространстве, окружающем про-
проводники. Проводники иг-
играют роль направляю-
направляющих, вдоль которых дви-
движется электромагнитная
энергия. Джоулева тепло-
теплота в проводнике выделя-
выделяется за счет электро-
электромагнитной энергии, по-
поступающей в проводник
через его поверхность из
окружающего простран-
пространства.
О Что такое характеристиче-
характеристический инпеданс линии и по-
постоянная распространения?
Опишите физические про-
процессы, приводящие к отра-
отражению энергии от нагруз-
нагрузки. При каком условии от-
отражение отсутствует и вся
передаваемая по линии энер-
энергия поглощается нагрузкой?
400 9. Электромагнитные волны
которая позволяет найти значение постоянной а0 = t//ln (r2/rj). С уче-
учетом этого значения формула F0.7) принимает вид
Ег = , .U. .-. F0.9)
In(rjr,) г
Напряженность магнитного поля в кабеле равна
Я. = 1/Bкг), F0.10)
как это фазу следует из закона полного тока, с учетом аксиаль-
аксиальной симметрии поля. Из F0.9) и F0.10) получаем
S = EH = ^ У' ~. F0.11)
r2
Эта величина представляет собой плотность потока электромагнит-
электромагнитной энергии, направленного параллельно оси кабеля в пространстве
между жилой и оболочкой. Вне кабеля, а также в центральной
жиле и в оболочке никакого потока энергии нет, поскольку там
вообще отсутствует электрическое поле при принятом допущении об
отсутствии сопротивления. В 1 с времени через поперечное сечение
кабеля проходит электромагнитная энергия
2л '2
Р = fSz da = — [da f —• ™ = UI. F0.12)
a 0 r0
При силе тока /, протекающего через нагрузку при разности
потенциалов U, развивается мощность
Рн = /[/. F0.13)
Сравнение F0.12) с F0.13) показывает, что вся используемая
потребителем энергия движется вдоль кабеля в пространстве между
жилой и оболочкой в виде электромагнитной энергии.
Ничего не изменяется в принципиальном отношении и для пере-
переменного тока не очень высокой частоты. Если ток в кабеле меняет
направление на обратное, то составляющие Ег и На векторов поля
также изменяют направление на обратное, а направление вектора
Пойнтинга остается прежним. Поэтому хотя направление тока меняется
на обратное, направление движения электромагнитной энергии сохра-
сохраняется: она все время движется от источника к потребителю.
В других линиях передачи в принципиальном смысле картина
движения энергии не изменяется, лишь усложняется конфигурация по-
полей и пути, по которым движется энергия.
т|иния передачи для переменного тока. При не очень больших часто-
частотах и достаточно малых расстояниях, когда можно считать выпол-
выполненными условия квазистационарности, токи в линии полностью опи-
описываются методами, изложенными в гл. 8. При несоблюдении усло-
условий квазистационарности картина усложняется, что очевидно уже из
того обстоятельства, что сила тока в один и тот же момент времени
60. Движение электромагнитной энергии вдоль линий передач 401
-O~*v-r~-'4Z>|
250
Эквивалентная схема линии пе-
передачи переменных токов
в различных участках линии различна. Любой участок проводника
имеет определенную индуктивность и емкость, что делает всю линию
передачи электрической цепью с непрерывно распределенными сопро-
сопротивлениями, емкостями, индуктивностями.
уравнения для силы тока и напряжения. Прежде всего необходимо
найти закон, по которому сила тока и напряжение между проводни-
проводниками изменяются вдоль линии. Эквивалентная схема распределения
индуктивности, емкости и сопротивления показана на рис. 250. Индук-
Индуктивность, емкость и сопротивление, приходящиеся на 1 м длины
линии, обозначим L, С, R. Импедансы Zl и Zi также отнесены к 1 м
длины. Участок Ах линии обладает последовательно включенным
импедансом, дающим комплексное сопротивление
Z t Ах = (R! + icoL) Ax, F0.14)
и параллельно включенным импедансом Z2, дающим комплексную
проводимость
1
Z2
Дх =
+ icoC ) Дх.
}
F0.15)
Пусть к началу участка линии Дх приложено напряжение U, а сила
тока равна I. В конце участка эти величины равны соответственно
U + AU, / + А/. Утечки через изоляцию здесь и в последующем не
учитываются.
Применим правило Кирхгофа для внешнего контура всего участка,
взяв в качестве положительного направления обход против часовой
стрелки:
-Z, 4p(' + M)-Zi~I = U + AU - U. F0.16)
Разделив F0.16) на Дх, получим
-ZiAI/2-ZJ = AU/Ax. F0.17)
Если Дх -* 0, то первое слагаемое в левой части F0.17) стремится
к нулю (Д/ -» 0). Тогда
dx
F0.18)
14 А. Н. Матвеев
402 9. Электрома1нитные волны
Аналогично, правило Кирхгофа, применяемое к левому контуру,
включающему импеданс Z2/Ax, дает
^M-Z2^-I=~V, F0.19)
откуда при Ах -»0 получаем
-^=--L[/. F0.20)
dx Z2
Дифференцируя обе части F0.18) по х и выражая d//dx с помощью
F0.20), находим следующее уравнение для U:
Аналогично, дифференцирование F0.20) по х и использование F0.18)
приводит к уравнению для силы тока:
Уравнения F0.21) и F0.22) называются уравнениями линии передачи.
Характеристический импеданс и постоянная распространения. Общее
решение уравнений линии передачи имеет вид (например, для U):
U = Ае'** + ?е« F0.23)
причем для а, называемой постоянной распространения, после подста-
подстановки F0.23) в F0.21) находим выражение:
<х = ]/zjZ2. F0.24)
Аналогичный вид имеет также и решение уравнения F0.22):
/ = Л1е-" + В1еса. F0.25)
Подставляя решения F0.23) и F0.25) в F0.18) и F0.20), находим
связь между постоянными А, В, Аи Bt:
A1 = A/ZmBl=-B/Za, F0.26)
где
Za = ]/z^Z~2 F0.27)
— характеристический импеданс линии. Чтобы выяснить его смысл,
предположим, что линия длиной / оканчивается нагрузкой, импеданс
которой равен характеристическому (рис. 250). На основании равенств
F0.23) — F0.27) для напряжения на выходе линии, т. е. на нагрузке Zat
можно написать:
UH = 1„2Л, F0.28)
или
Ае- + Be = zj — e- - —е"). F0.29)
§ 60. Движение электромагнитной энергии вдоль линий передач 403
Отсюда следует, что В = 0, А = UBX, где Un — напряжение на входе
в линию при х = 0. Таким образом, напряжение и сила тока в линии
определяются выражениями:
U = 1/„е-« / = 1/„е-«/гл. F0.30)
Следовательно, входной импеданс линии равен характеристическому:
Zn=UJIn = Za. F0.31)
Это означает, что если линия оканчивается нагрузкой с характеристи-
характеристическим импедансом, то ее входной импеданс равен характеристи-
характеристическому, независимо от длины, т. е. в этом случае ток передается
по линии без изменения отношения напряжения к силе тока.
характеристическое сопротивление. В большинстве практически важ-
важных случаев омические сопротивления элементов линии значительно
меньше соответствующих индуктивных и емкостных сопротивлений
(i?! <s: toL, 1/R2 *к юС) и ими можно пренебречь. При этом условии
характеристический импеданс
*' + iaL 1/T F0.32)
1/Д2 + icoC ]/ С
является действительной величиной, т. е. сопротивлением, и называется
характеристическим сопротивлением.
Характеристическое сопротивление зависит от формы и размеров
проводников, от расстояния между ними и других факторов, от которых
зависят емкость и индуктивность участков линии. Например, характе-
характеристическое сопротивление параллельных цилиндрических проводников
радиусом а, расстояние между осями которых D, равно
Zn = 216\og(D/a). F0.33)
Принимается, что проводники расположены в среде, относительная
диэлектрическая проницаемость которой близка к единице (вакуум,
воздух и т. д.).
/скорость распространения. Выше было рассмотрено распределение
силы тока и напряжения вдоль линии передач в некоторый момент
времени. Если на входе сила тока и напряжение периодически изме-
изменяются с частотой со, то и во всех участках линии они изменяются
с той же частотой. При тех условиях, когда характеристический
импеданс является вещественной величиной F0.32), постоянная а
[см. F0.24)] является чисто мнимой:
F0.34)
Поэтому, взяв зависимость величин от времени в виде exp i(at,
можно на основании F0.30) написать:
U (х, г) = U0 exp [i (cot - ш j/Ec x)],
I (x, t) = (Uo/\/T/C) exp [i (cot - со ]/LC x)] . F0.35)
14*
404 9. Электромагнитные волны
Формула F0.35) описывает волну с частотой со, распространяющую-
распространяющуюся вдоль оси X со скоростью
F0.36)
Напомним, что в этой формуле L и С являются емкостью и индук-
индуктивностью линии передачи, отнесенными к 1 м длины. Для двух
тонких цилиндрических проводников радиусами а, находящихся в
вакууме на расстоянии D один от другого, емкости и индуктивности
1 м длины линии равны:
С = Ео/[2 In (D/a)~], L = 2ц0 In (Dfa) F0.37)
и поэтому скорость распространения волны рарна
v = 1/l/LC = 1/J/e^ = с, F0.38)
/"Отражение. Если сопротивление нагрузки равно характеристическому,
то вся передаваемая по линии энергия поглощается нагрузкой.
Говорят, что нагрузка и линия передачи согласованы между собой.
Если такого согласования нет, то часть энергии отражается от нагруз-
нагрузки и движется по линии навстречу первоначальному потоку энергии.
Рассмотрим в качестве примера закороченную на конце линию
передачи, т. е. когда UH = 0. Уравнения F0.23) и F0.25) принимают вид:
0 = Ae~ifil + Beif", F0.39)
/„ = Ае - ifW/p - Be'V/p, F0.40)
где для упрощения написания формул введены обозначения: р = co|/LC,
р = у L/C. Разрешая эти уравнения относительно А и В, получаем
А = /„ре'^/2, В = -/„ре-""/2. F0.41)
Поэтому выражения F0.23) и F0.25) для напряжения и силы тока
вдоль линии передачи записываются следующим образом:
U = /«,-у О-'*1-" - е""*], F0.42)
/ = -^-[е~'«*"'> Ч-е'^]. F0.43)
Поскольку зависимость величин от времени характеризуется мно-
множителем exp(itot), можно заключить, что первые слагаемые в правой
части этих формул описывают волну, распространяющуюся в положи-
положительном направлении оси X, а вторые — в отрицательном (т. е. опи-
описывают отраженную от закороченного конца линии волну). Отсюда
можно заключить, что не только невозможность полностью передать
энергию в нагрузку при отсутствии согласования с линией диктует
желательность согласования. Если сигналы передаются в виде импуль-
импульсов, то последовательные отражения от нагрузки, а затем снова от
входа, настолько искажают сигнал, приходящий в нагрузку, что с ним
становится трудно работать.
§ 61. Излучение электромагнитных волн 405
§ 61. Излучение электромагнитных волн
Дается решение задачи об излучении линей-
линейного осциллятора. Полученное решение обоб-
обобщается на случай произвольно ускоренного
нерелятивистского электрона. Обсуждается
реакция излучения.
уравнение для векторного потенциала. Индукция и напряженность
переменных полей выражаются формулами D6.8) и D6.12) через век-
векторный и скалярный потенциалы, для нахождения которых необходимо
иметь уравнения.
Исходим из уравнения Максвелла E8.1,1), которое удобно записать
в виде
. дЕ п
rot В = uj + ue , F1.1)
ot
где для упрощения предполагается, что и и е не зависят от коорди-
координат. Подставляя D6.8) и D6.12) в F1.1), получаем
rot rot A = uj + це — ( — grad m ). F1.2)
ot \ ot J
Принимая во внимание, что rot rot A = grad div A — V2A, преобразуем
F1.2) к виду
V2A — us 2 = — uj + grad I div A + ue -=— I. F1.3)
Пользуясь неоднозначностью потенциалов, определенных с точ-
точностью до калибровочного преобразования D6.13), можно на них
наложить некоторое условие. Для максимального упрощения уравне-
уравнения F1.3) это условие выбирается в виде равенства
div A + |is -^-= 0,
F1.4)
называемого условием Лоренца. В результате ?см. F1.3)] получаем
V2A-?n-|A=-w F1.5)
— уравнение Даламбера.
JD ыбор калибровочной функции JC- При наложении на потенциалы
условия Лоренца F1.4) функция х, с помощью которой осуществля-
осуществляется калибровочное преобразование потенциалов D6.13), не может быть
выбрана произвольно; необходимо, чтобы условие Лоренца F1.4)
сохранялось при калибровочных преобразованиях. Имеем
div А' + \хг —^—= div (A + grad у) + це — (<р - oyjdt) =
406 9. Электромагнитные волны
Таким образом, условие Лоренца инвариантно лишь при калибро-
калибровочных преобразованиях с функцией х. удовлетворяющей уравнению
82у
Vx-MB-^O. F1.6)
Уравнение такого вида называется волновым уравнением или одно-
однородным уравнением Даламбера.
¦уравнение для векторного потенциала. Подставляя D6.12) в уравнение
Максвелла E8.1, IV), находим
div I -grad ф ;
Исключая отсюда div А, с помощью F1.4) окончательно получаем
следующее уравнение для скалярного потенциала:
V2<p — ец —=~ = • F1.8)
дг ?
Таким образом, для декартовых проекций векторного потенциала
F1.5) и для скалярного потенциала получается одно и то же уравне-
уравнение вида
У2Ф - р- 4т~= -f(T> t), F1-9)
где вместо Ф можно подставить Ах, Ау, Az, (p, а вместо / соответ-
соответственно ц/„ ц/у, ц/„ р/е. Выясним смысл ?ц = 1/t;2.
решение волнового уравнения. Прежде всего рассмотрим решения
уравнения F1.9) при / = 0, т.е. однородного уравнения. Возьмем
одномерный случай Ф = Ф (х). Уравнение F1.9) имеет вид
—5 j *-=0. F1.10)
дх v* dt
Непосредственной проверкой убеждаемся, что решением F1.10) яв-
является любая функция Ф от аргумента t — x/v или Г + x/v. Проверим
это, например, для функции Ф (г - x/v):
dt ' dt2 ¦ ' дх v дх2 v2
где Ф' — производная по аргументу функции. Из F1.11) следует, что
произвольная функция Ф (f — x/v) действительно удовлетворяет уравне-
уравнению F1.10). Аналогично доказывается, что и функция Ф (t + x/v) также
удовлетворяет этому уравнению.
Смысл этих решений очень прост. Функция Ф (г — x/v) представляет
собой волну, движущуюся в направлении положительных значений оси
X со скоростью v. Действительно,
Г _ x/v = t + At - (х + hx)/v F1.12)
при Ax/At = v. Это означает, что если в момент времени t функция
Ч7 (Г — x/v) представляется некоторой кривой (рис. 251), то в момент
§ 61. Излучение Электромагнитных волн 407
времени t + Дг она изображается той же кривой, но сдвинутой
в направлении положительных значений оси X на v At, т. е. это волна,
движущаяся в направлении положительных значений оси X со скоростью
v. Вот почему было введено обозначение ец = 1/v2.
Аналогично показывается, что функция <&(t + x/v) представляет
собой волну, распространяющуюся со скоростью v в направлении отри-
отрицательных значений оси X.
Рассмотрим решение волнового уравнения в сферически симметрич-
симметричном случае, т. е. считая, что в F1.9) / = 0, а Ф = Ф (г), где г - расстоя-
расстояние от начала координат до рассматриваемой точки. В этом случае Ф
от углов не зависит и оператор Лапласа имеет вид
дф\_ <ЯФ_ 2_дФ _\_8_
дг J дг2 г дг г дг
Поэтому волновое уравнение для Ф записывается в виде
Решением этого уравнения для гФ, как и в предыдущем случае,
являются произвольные функции от аргументов t — r/v и t + r/v, т. е.
общее выражение для Ф таково:
Ф(г,0-*'('-'-/'1+Ч'»<' + ^>. F1.15)
г г
Функция Ч*! (г — r/v) представляет волну, движущуюся в радиальном
направлении от начала координат со скоростью v. Форма волны при
этом не изменяется, а амплитуда уменьшается как 1/г. Эта волна
называется расходящейся. Функция Ч*2 (t + r/v) представляет сходящуюся
к началу координат волну.
Возвращаясь к F1.5) и F1.8), видим, что потенциалы поля, а сле-
следовательно, и сами поля распространяются в свободном пространстве
(р = 0) со скоростью v = 1/]/ец. В вакууме ц = ц0, е = е0, поэтому ско-
скорость распространения полей равна скорости света с = \[\/го\хо. Таким
образом электромагнитные волны и всякие изменения электрического
и магнитного поля распространяются в вакууме со скоростью света.
А это означает, что электромагнитные взаимодействия распространя-
распространяются со скоростью света. Например, если два точечных заряда покоятся
на расстоянии г друг от друга и один го зарядов в некоторый
момент сдвинут со своего места, то другой заряд «почувствует» этот
сдвиг лишь спустя время т = г/с.
'2 апаздывающие и опережающие потенциалы. Учитывая свойства
решений волнового уравнения, следует ожидать, что решение урав-
уравнений F1.5) и F1.8) для потенциалов переменных полей отличается от
решений уравнений C7.11а) и A4.35) для потенциалов постоянных полей
только тем, что надо учесть конечную скорость распространения
электромагнитных взаимодействий. Другими словами, движущийся
408 9. Электромагнитные волны
г+Дг
2S1
Изменение со временем решения
одномерного волнового урав-
уравнения
252
Модель вибратора
253
К вычислению
поля
потенциала ди-
заряд и элемент переменного тока создают
в каждой точке окружающего пространства
такой же потенциал, как если бы заряд был
неподвижным, а ток постоянным, но с тем
различием, что такой потенциал в каждой
точке создается не в тот же момент вре-
времени, а позднее на время запаздывания, т. е.
на время, необходимое электромагнитному
полю для распространения от источника до
точки наблюдения. Поэтому для зарядов и
токов, находящихся в конечной области
пространства, получаем вместо формул
C7.11а) и A4.35) следующие формулы:
''<-|r-r'^dK', F1.16)
г-г'
p(r',r-|r-r'|M
r-r'
dV, F1.17)
где v = lfye\i; | г — г' | — расстояние между
точкой, в которой вычисляется потенциал,
и элементом dV' объема интегрирования.
В данный момент времени в данной точке
потенциал обусловлен не положением и ве-
величиной зарядов и сил токов в данный
момент времени, а их положениями и вели-
величинами в предшествующие моменты вре-
времени, определяемыми с учетом скорости
распространения электромагнитного поля.
Например, пусть некоторый электрический
заряд быстро приближается к какой-то точке.
Скалярный потенциал, созданный зарядом
в точке, определяется не расстоянием от
заряда до точки в данный момент времени,
а расстоянием в некоторый предшествую-
предшествующий момент времени, т. е. большим расстоя-
расстоянием. При скорости заряда, близкой к ско-
скорости света, различие в расстояниях может
быть весьма значительным.
Здесь не приводится формальная про-
проверка того, что формулы F3.16) и F1.17)
удовлетворяют уравнениям F1.5) и F1.8).
В принципе это делается так же, как и для
решений A4.35) и C7.11а).
Потенциалы вида F1.16) и F1.17) называ-
называются запаздывающими, потому что они опи-
описывают потенциалы в более поздний момент
§61. Излучение электромагнитных волн 409
времени t по сравнению с моментом времени t — | г — г' \/v для
зарядов и токов, которые этот потенциал создали. Формально
решениями уравнений F1.5) и F1.8) являются также решения, анало-
аналогичные F1.16) и F1.17), но с заменой временных аргументов t-\r —
— т1 \/v на t + | г — г' \/v, что соответствует двум возможным знакам
в аргументах решений F1.15) волнового уравнения. Решение со знаком
« + » в аргументе не имеет ясного физического смысла, поскольку оно
формально соответствует ситуации, в которой сначала создается по-
потенциал, а потом появляются соответствующие ему заряды и токи,
т. е. ..потенциал опережает заряды и токи. Поэтому он называется
опережающим. Для получения решений задач с граничными условиями
опережающим потенциалом приходится пользоваться наряду с запаз-
запаздывающим. Это можно понять из следующего. Пусть надо найти
электромагнитное поле, удовлетворяющее некоторым условиям на
границе. Ясно, что в точках внутри объема поле должно быть
таким, чтобы, достигнув в более поздний момент времени границы,
иметь значения, предписанные граничными условиями. Ясно, что при
решении таких задач необходимо руководствоваться не только про-
прошедшим, но и принимать во внимание, что должно произойти
в будущем, т. е. необходимо использовать опережающие потенциалы.
Но это ни в какой степени не означает нарушения принципа причин-
причинности, как это непосредственно видно из проведенного выше рассуж-
рассуждения. С физической точки зрения это есть просто ответ на вопрос
о том, что должно было произойти в прошлом, чтобы настоящее
являлось таким, каким оно есть при известных законах развития.
D ибратор Герца. Это электрический диполь, момент которого изме-
изменяется со временем. Реальным прототипом вибратора Герца может
служить совокупность двух металлических шариков (рис. 252), соеди-
соединенных проводником. Если шарикам сообщить равные, но противо-
противоположные по знаку, заряды и предоставить систему самой себе, то
будет происходить колебательный процесс перезарядки шариков. Коле-
Колебания тока будут затухающими. Если сопротивление проводников мало
и потери на излучение за один период невелики, то в течение
достаточно большого числа периодов затуханием можно пренебречь.
Тогда на расстояниях, много больших /, система может рассматри-
рассматриваться как диполь, момент которого изменяется со временем. Таким
вибратором пользовался Герц, впервые экспериментально получивший
электромагнитные волны. Поэтому он называется вибратором Герца.
/скалярный потенциал диполя, изменяющегося со временем. Потен-
Потенциал диполя определяется формулой F1.17), которую удобно перепи-
переписать в виде
где предполагается, что диполь расположен в вакууме (е = е0, ц = Цо)-
При вычислении F1.18) начало координат целесообразно поместить
410 9. Электромагнитные волны
в области распределения заряда; местоположение начала в пределах
области распределения заряда несущественно, потому что размеры
диполя предполагаются сколь угодно малыми по сравнению с расстоя-
расстояниями до точек, в которых рассматривается его поле. Положение
точки, в которой вычисляется потенциал поля, характеризуется радиус-
вектором г; § — радиус-вектор элемента объема d V^, a / — есть рас-
расстояние между элементом объема AV^ и точкой наблюдения (рис. 253).
Рассмотрим потенциал на больших расстояниях от диполя {tjr <sc 1).
Учитывая, что
г' = г - ? г' = l/r2 - 2г • 4 + ^2, F1.19)
можно выражение для г' разложить в ряд по %jr и ограничиться
линейным членом разложения
='--—+••• F1-20)
Пользуясь этой формулой, разложим подынтегральное выражение
в F1.18) в ряд Тэйлора в точке г:
pfe t - r'jc) = pfe t - r/c) г-g д Tpfe t - r/c)l
t> r r dr |_ r J
Подставляя F1.21) в F1.18), находим
b F1.22)
<P= -A-— f
где принято во внимание, что г является при интегрировании посто-
постоянной величиной. Вследствие электрической нейтральности системы
первый интеграл в правой части F1.22) равен нулю, а второй пред-
представляет собой момент диполя [см. A7.2)]
- г/с) dK5 = p(f - г/с). F1.23)
Поэтому окончательно потенциал диполя, изменяющегося со временем,
определяется формулой
|[ F1.24)
4яе0 г dr | r J
Пользуясь выражением для дивергенции в сферических координатах,
формулу F1.24) можно представить в виде
секторный потенциал. Он вычисляется разложением подынтеграль-
подынтегрального выражения F1.16) в ряд вида F1.21):
§ 61. Излучение электромагнитных волн 411
Электрическое и магнитное поля. Для упрощения написания после-
последующих формул введем обозначение
Р^^), F1.27)
где ро — постоянный вектор, характеризующий направление колебаний
диполя. Исходя из F1.25) и F1.26), получаем:
B = rotA=^rot^-=^-|-rotri, F1.28)
4я й 4j ft
_ , дА 1 ц0 д2П
Е = -grad ф —- = grad div П
dt 4ле
= grad div П j
dt 4ле0 4л <Эг
—— (grad div П - \ 4?-l = -r^~ rot rot П, F1.29)
4ле0 \ <r от1 у 4яе0
где принято во внимание, что uoeo = 1/с2, учтена формула (П. 10),
а вектор П удовлетворяют волновому уравнению
vn4?r 0- ()
с от
Значение rot П вычисляется по формуле (П.16):
rot П = rot р0Ф = gradO х р0 = — —— г х р0. F1.31)
Дальнейшие вычисления удобнее провести в сферической системе
координат. Направим полярную ось Z вдоль вектора р0, поместив
начало координат в центре диполя. Полярный и азимутальный углы
обозначим соответственно 9 и а (рис. 254). Очевидно,
(г х ро)г = (г х р0)о = 0, (г х ро)„ = -rp0 sin 9, F1.32)
поэтому
rotr П = rote П = 0, rot;, П = -sin 9 . F1.33)
dt
Отсюда на основании F1.28) получаем:
Вг = Вв = 0, Ва = ^-^-тоКП = - H2_sin9 1^-. F1.34)
4л от 4л от дг
Проекции вектора Е вычисляются с помощью формулы для
ротора в сферической системе координат:
1 1 д ,. л л. 1 cose гя
? (etn)
6L35
е0 г sin 9 59 " 2ле0 т дг
1 1 д , „ I sinG 5 / дП
(tn
4ле0 г Вг 4яе0 г д
Формулы F1.34) и F1.35) показывают, что вектор напряженности
электрического поля лежит в меридиональных плоскостях, а вектор
412 9. Электромагнитные волны
индукции магнитного поля перпендикулярен меридиональной плоскости,
проведенной через соответствующую точку, причем магнитные силовые
линии совпадают с параллелями рассматриваемой сферической системы
координат. Векторы электрического и магнитного полей в каждой
точке взаимно перпендикулярны.
Формулы F1.34) и F1.35) справедливы при произвольной зависи-
зависимости функции Ф (t, r) в F1.27) от времени. Считая, что момент диполя
изменяется по гармоническому закону
р = рое1Ю1, F1.36)
получаем
101 (Г- Г/С)
П = ро . F1.37)
Выполняя соответствующие дифференцирования в формулах F1.34)
и F1.35), находим выражения для отличных от нуля проекций:
¦ Л ICO \ „ 1 /1 1@ \
in 9 I h — Я, Ег=^ cos 9 (-Т-+— Я,
" 4к
Е„=- sinGl -4-+ '-^--~)П. F1.38)
4я?0 у г сг с J
Поле в непосредственной близости к осциллятору на расстояниях,
меньших длины волны X = сТ = 2кс/а>, одинаково с полем статического
диполя и тока. На расстояниях, много больших длины волны, поле
осциллятора принципиально отличается от поля постоянного диполя
и тока. Соответствующая область называется волновой зоной.
ГТоле вибратора в волновой зоне. Расстояние г до точек волновой
зоны удовлетворяет, по определению, следующему неравенству:
— <s—. F1.39)
ГС
Поэтому в формулах F1.38) можно пренебречь 1/г и 1/г2 по срав-
сравнению с со/с и со2/с2. В результате получаем следующие выражения
для проекций векторов поля:
Но ю2
Ba=-i^ nsinQ, В, = Вв = 0; F1.40)
4к с
Ео= - ^-Я sin 9, Ег = Е* = 0. F1.41)
4яе0 с2
В этих формулах в качестве Я можно взять либо действительную,
либо мнимую часть выражения F1.37), например:
Я = Ро cos Иг-г/с) F1 42)
Поэтому окончательно напряженность и индукция электромагнит-
электромагнитного поля в волновой зоне вибратора могут быть представлены
61 Излучение электрома!нитных волн 413
следующим образом:
Ее = сВ„ =
1
со
sin G / г
р0 cos m f
г V с
4ке0 с
?г = ?„ = О, В, = Во = 0.
F1.43)
254
Эти формулы показывают, что в волно-
волновой зоне электрический и магнитный век-
векторы перпендикулярны друг другу и радиус-
вектору Г. Векторы Е, В, Г СОСТаВЛЯЮТ Выбор сферИческой системы ко-
праВОВИНТОВую Тройку Векторов В каждой ординат при вычислении поля
точке. Напряженность поля убывает об- диполя
ратно пропорционально первой степени рас-
расстояния. Представляемая формулами F1.43)
волна называется сферической. Она распро-
распространяется в направлении радиус-вектора.
Поверхности постоянной фазы этой волны
являются сферами. Скорость волны (фазо-
(фазовая) равна скорости света. Поскольку ?в =
= сВт малые участки поверхности сфери-
сферической волны могут рассматриваться как
плоские электромагнитные волны.
]у^ощность, излучаемая вибратором. Плот-
Плотность потока электромагнитной энергии 255
характеризуется вектором Пойнтинга E9.7).
ПОЭТОМУ ПОТОК электромагнитной Энергии Рамка с током
Р сквозь поверхность S сферы радиусом г,
окружающую вибратор, равен
= Ex HdS= \
/ \ I
cos2co|t- — I sin39d9 x
da =
- cos со t
•— ). F1.44)
Это есть мощность потока, т. е. энергия
излучения вибратора в 1 с. Средняя за пе- 256
риод излучения мощность излучения равна
1
12кеп
Соотношение между смещением
электрических зарядов, создаю-
F1.45) щих дипольный эпеюрический
момент, и током в рамке, со-
создающим магнитный момент
414 9. Электромагнитные волны
Эта формула показывает, что мощность излучения вибратора очень
сильно зависит от частоты и пропорциональна ее четвертой степени.
Это означает, что для увеличения мощности излучения целесообразно
переходить к более коротким длинам волн.
Так как вектор Пойнтинга убывает обратно пропорционально
квадрату расстояния, а площадь поверхности сферы растет прямо
пропорционально квадрату расстояния, то полный поток энергии,
пересекающий поверхность сферы, не изменяется с расстоянием, сле-
следовательно, энергия без потерь переносится от вибратора в отдален-
отдаленные участки пространства в виде электромагнитных волн. Плотность
потока излучения уменьшается с увеличением расстояния обратно
пропорционально квадрату расстояний. Благодаря потери энергии на
излучение колебания вибратора должны быть затухающими. Чтобы
иметь незатухающие колебания вибратора, необходимо к нему извне
постоянно подводить энергию. Вибратор является простейшим излу-
излучателем электромагнитных волн.
Мз лучение рамки с током. Другим простейшим излучателем электро-
электромагнитных волн является рамка с током, которая характеризуется
магнитным моментом pm = /S (рис. 255). Ее излучение аналогично
излучению диполя. Приведем лишь результат. Магнитный момент
рамки с током изменяется по закону
Pm = Pm0 COS Wt. F1.46)
Поместим начало сферической системы координат в центр рамки,
а ось Z направим вдоль магнитного момента, т. е. на рис. 254 следует
себе представлять ток текущим в плоскости z = 0, а магнитный момент
тока рт расположенным как р. Для поля излучения рамки с током
получаются следующие формулы:
г. Цо (о2 sin6 / г \
?*= "СВ.- 4^ — —**«»»{*-т)' F1.47)
Е, = Ев = О, В,=В, = 0.
Сравнение формул F1.47) и F1.43) показывает, что если между
магнитным моментом pmQ тока и дипольным моментом р0 соблюдается
соотношение (рис. 256)
Рт0 = ср0, F1.48)
то напряженность электрического поля и магнитная индукция излуче-
излучения диполя равны по модулю соответствующим модулям векторов
поля излучения рамки с током, изменяется лишь их направление
в пространстве. У диполя напряженность электрического поля направ-
направлена по меридианам, а у рамки перпендикулярно меридиональным
плоскостям по параллелям. Соответствующим образом изменяется
и ориентировка векторов магнитного поля. Как видно из F1.47) и F1.43),
векторы поля излучения диполя и рамки с током находятся между
собой в следующем соотношении:
S 61. Излучение электромагнитных волн 415
?„ (рамки) = —сВ« (диполя), сВв (рамки) = Ео (диполя). F1.49)
Мощность излучения рамки с током определяется формулами F1.44)
и F1.45) с заменой в них дипольного момента на магнитный момент
по формуле F1.48).
Вибратор и рамка с током являются элементарными излучателями
электромагнитных волн. Излучение более сложных систем может быть
сведено к элементарным излучателям с помощью принципа супер-
суперпозиции.
^злучение ускоренно движущегося электрона. Поместим мысленно
в начало координат положительный заряд, равный по величине
заряду электрона. Он неподвижен и по закону Кулона создает
в окружающем пространстве постоянное по времени электрическое поле,
напряженность которого убывает обратно пропорционально квадрату
расстояния. Совокупность движущегося электрона и неподвижного
положительного заряда составляет диполь, момент которого изменя-
изменяется со временем. Векторы поля излучения диполя являются перемен-
переменными и убывают обратно пропорционально первой степени расстояния.
Ясно, что постоянное электрическое поле неподвижного заряда ком-
компенсируется электрическим полем электрона и какого-либо отношения
к полю излучения иметь не может, т. е. поле излучения является полем
излучения колеблющегося электрона. Положительный заряд помещен
в начало координат лишь мысленно, что позволяет воспользоваться
полученными выше формулами для излучения диполя с переменным
во времени моментом.
Возникающий при отклонении электрона от начала координат на
z{t) дипольный момент равен
p(t)=-\e\z(t)iz, F1.50)
где iz — единичный вектор вдоль оси Z. Знак минус возник из-за того,
что дополнительный момент направлен от отрицательного заряда
к положительному. Принимая, что
z = bcos(ut, F1.51)
где b — амплитуда колебания электрона, для дипольного момента F1.50)
получаем
р= -ije|fccoscot. F1.52)
Сравнение F1.52) с действительной частью F1.36) для диполя пока-
показывает, что момент Ро в формуле F1.36) связан с величинами, харак-
характеризующими движение электрона, соотношениями:
Ро= ~1г\е\Ь, р„ = ИЬ. F1.53)
Формула F1.43), характеризующая векторы поля излучения, прини-
принимает теперь вид:
^1() FL54)
416 9. Электромагнитные волны
?„ = ?,= О, Вг = Вв = О,
где т — время прихода волны в точку наблюдения на сфере радиусом г.
Переменная t = т — г/с зарезервирована для времени, характеризующего
движение электрона. Из формулы F1.51) следует, что
'z = -(o2bcos(nt, F1.55)
и поэтому F1.54) можно переписать:
Ee(r,T) = cBa(r,z) =
г = т - г/с
4яеос2
sine
г
F1.56)
где учтено, что заряд электрона отрицателен. Формула F1.44) для
мощности излучения принимает следующий вид:
F1.57)
т.е. мощность излучения пропорциональна квадрату ускорения элект-
электрона. Равномерно движущийся заряд не излучает.
Формулы F1.56) и F1.57) получены для модели колеблющегося
электрона. Однако они зависят только от ускорения электрона в любой
данный момент времени. Следовательно, описываемое ими поле излу-
излучения не зависит от того, как электрон двигался до данного момента
и как он будет двигаться после этого момента. Поэтому они всегда
применимы и представляют выражения для напряженности и индукции
поля излучения и мощности излучения в зависимости от ускорения
при любом движении. Однако при этом скорости электрона должны
быть малы, поэтому, строго говоря, это формулы для покоящегося
электрона, обладающего ускорением, что очевидно из определения
диполя, занимающего бесконечно малую область пространства и
покоящегося в ней.
Однако обобщение этих формул на произвольные скорости не
составляет труда. Для этого надо просто перейти в ту систему
координат, где электрон движется с произвольной скоростью, и вос-
воспользоваться формулами преобразования полей и ускорений. В резуль-
результате получаются формулы, справедливые для произвольных скоростей
и ускорений заряда. Здесь они не приводятся.
?ила торможения излучением. Из-за излучения электрон теряет свою
энергию и замедляется, т. е. на него действует тормозящая сила.
Найдем ее. Очевидно, что уравнение колебаний электрона с учетом
силы торможения имеет вид
ml + rm>2z = F, F1.58)
где со — частота свободных колебаний при отсутствии силы торможе-
торможения излучением. Умножая обе части этого уравнения на г, получаем
§ 61. Излучение электромагнитных волн 417
Fz. F1.59)
В правой части F1.59) стоит работа силы торможения излучением,
отнесенная ко времени. По определению она равна мощности излу-
излучения [см. F1.57)], поэтому
Fz=--1— ~-z\ F1.60)
6яе0 с
Равенство F1.60) выражает закон сохранения энергии при излучении.
В общем виде из него нельзя найти силы F в виде функции от z
и ее производных. Это можно сделать лишь приближенно, предполагая,
что:
1) излучение, а следовательно, и затухание колебаний не очень
велики, так что в течение некоторого числа периодов движение можно
считать практически периодическим;
2) из закона сохранения энергии для средних величин, относящихся
к небольшому числу периодов, можно вывести заключения о равенстве
мгновенных значений соответствующих величин.
Исходим из очевидного равенства:
F1.61)
Усредняя ('zz)' по одному периоду и пользуясь первым из предпо-
предположений, имеем
((ЩУ = 1 [(zz)I = r - (zz)t=0] = 0. F1.62)
Тогда F1.60) с учетом F1.61) и F1.62) принимает вид
_ 1 е2
6ЯЕ0 С3
На основании второго допущения находим
1 е1 ...
F1.63)
F1.64)
F = 4z.
6ле0 с
Эта формула определяет силу торможения излучением. Уравнение
колебаний электрона с учетом силы торможения имеет вид
mz + nm2z - [е2/Fлеос3)] z" = 0. F1.65)
В электродинамике выражение для силы торможения обобщается
на произвольное движение. Оно там тоже описывается третьей произ-
производной по собственному времени от соответствующих величин, харак-
характеризующих движение электрона. Получаемое при этом уравнение
релятивистски инвариантно. Долго считалось, что оно правильно
описывает реакцию излучения. Однако недавно был проведен расчет
на ЭВМ ряда простых случаев движения и были получены заведомо
бессмысленные результаты. Поэтому вопрос о релятивистски инвари-
418 9. Электромагнитные волны
антном классическом описании движения электрона с учетом реакции
излучения в настоящее время не может считаться решенным.
Наличие силы торможения подтверждено экспериментально в уско-
ускорителях. Как уже было сказано, заряженные частицы в ускорителе
испытывают небольшие гармонические колебания около равновесной
орбиты, называемые бетатронными (см. § 56). Кроме того, заряд при
своем движении интенсивно излучает. Сила торможения излучением
вызывает затухание бетатронных колебаний.
§ 62. Распространение электромагнитных
волн в диэлектриках
Рассматриваются основные свойства и осо-
особенности распространения электромагнит-
электромагнитных волн в диэлектриках.
гт лоские волны. Электромагнитная волна называется плоской, если
вектор волны имеет одну и ту же величину во всех точках любой
плоскости, перпендикулярной направлению распространения волны. От
плоскости к плоскости эти векторы, конечно, изменяются. Можно
сказать, что поверхностями постоянной фазы в плоской волне являются
плоскости, перпендикулярные направлению распространения. Волна
называется монохроматической, если векторы волны изменяются со вре-
временем по гармоническому закону с определенной одной частотой.
Например, если плоская электромагнитная волна распространяется
вдоль оси Z, то векторы поля волны имеют вид:
E(z, «) = E(z)e>wl; В (z, t) = В (г) е'ш. F2.1)
Если поверхности постоянной фазы совпадают с поверхностями
постоянной амплитуды, то волна называется однородной.
¦уравнения для векторов поля волны. Будем исходить не из потенциа-
потенциалов, как в § 61, а непосредственно из векторов поля. Рассмотрим
случай однородной неограниченной среды е = const, ц = const. Прово-
Проводимость диэлектрика у = 0. Уравнения Максвелла имеют вид:
rot В = це —, F2.2)
rot Е = - 43-. F2.3)
ct
Дифференцируя обе части уравнения F2.2) по времени и исключая
в левой части полученного равенства производную dB/dt с помощью
F2.3), получаем
- rot rot E = ец —у-. F2.4)
Воспользовавшись формулой (П. 10) и учитывая, что div E = 0, по-
поскольку свободные заряды отсутствуют, находим уравнение для Е:
§ 62. Распространение электромагнитных волн в диэлектриках 419
V2E - ец ^r-f- = 0. F2.5)
Аналогично находим уравнение для В:
V2B - ец -уу- = 0. F2.6)
Таким образом, векторы поля удовлетворяют волновому уравнению,
в котором скорость распространения равна
v = l/j/ец = c/j/mv F2.7)
Формула F2.7) показывает, что в диэлектрике скорость распространения
волн меньше, чем в вакууме.
Оекторы волны. Совместим ось Z с направлением распространения
электромагнитной волны. Векторы поля при этом определяются
формулами вида F2.1). Подставляя в F2.5) выражение для Е [см. F2.1)]
и сокращая обе части уравнения на е1Ш| после дифференцирования,
находим для E(z) уравнение
d2E(z)/dt2 + /c2E(z) = 0, F2.8)
где к = со |/ец. Общее решение этого уравнения таково:
1? (-\ _ V o-iki | р -i*z if.") Q\
где Ео1 и Eo2 — постоянные. Подставляя F2.9) в F2.1), находим
Mz> ч = ^oie + ^ог6 - (oz.iu)
Первое слагаемое в правой части F2.10) представляет собой волну,
распространяющуюся в направлении положительных значений оси Z,
а второе — в отрицательном направлении [см. F1.12)].
Аналогично находим и решение для В. Допустим, что волна
распространяется в положительном направлении оси Z. Тогда
E(z, t) = Еоег «--ад; В (г, t) = Boef ^~kz\ F2.11)
Такая волна является плоской, монохроматической и однородной.
фазовая скорость. Формулы F2.11) показывают, что плоские волны
в однородном диэлектрике распространяются без изменения ампли-
амплитуды, т. е. без поглощения. Скорость движения плоскости постоянной
фазы называется фазовой. Она находится дифференцированием по вре-
времени условия постоянства фазы:
at - kz = const, F2.12)
которое дает
co-fc^-=0, F2.13)
, = ^ = ^= 4=- --?=- F2-14)
dt к л/Z. i/
420 9. Электромагнитные волны
Формулы F2.11) записаны при специальном выборе системы коор-
координат, когда ось Z совпадает с направлением распространения волны.
От этого ограничения можно освободиться с помощью волнового
вектора к, который направлен вдоль распространения волн, а по модулю
определяется F1.8). По определению плоской волны, распространяю-
распространяющейся в направлении вектора к, векторы Е и В в любой точке плоскости,
перпендикулярной этому направлению, а в данном случае оси Z, одни
и те же. Пусть г — радиус-вектор некоторой точки на такой плоскости
постоянной фазы.
Очевидно, kr = kz (рис. 257), и вместо F2.11) можно написать:
E(r, t) = Еое'<ю'-к г>; B(r, t) = Вое'<ш'-к г>. F2.15а)
Длина волны. По определению, это расстояние, на которое точка
постоянной фазы перемещается за один период колебаний:
X = vT= аТ/к = 2к/к, F2.156)
где
к = 2тгА F2.15b)
— волновое число.
Двойства волн. Для исследования свойств плоских волн подставим
выражения F2.15а) в F2.2) и F2.3). Для упрощения вычислений
целесообразно воспользоваться символическим операторным представ-
представлением векторных операций. Исходным является векторный оператор
набла:
V = i^+i^+'^' F2Л6)
где ix, iy, \z — единичные векторы в направлении осей координат.
Нетрудно проверить, что с помощью этого оператора основные
операции векторного анализа представляются так:
grad ф = Уф, div А = V • A, rot = V х А, F2.17)
где V • А и V х А — скалярное и векторное произведения оператора V
на вектор А. Учтем, что
Ve-'k r= -ike-'k '. F2.18)
С помощью уравнений Максвелла и выражений F3.15а) можно
исследовать свойства плоских волн. Уравнение Максвелла div E = 0 дает
divE = V-E= -ik-E = 0. F2.19)
Это означает, что вектор напряженности Е волны перпендикулярен
к, т. е. перпендикулярен направлению ее распространения. Аналогично,
уравнение Максвелла
divB = V В = -ik-B = 0 F2.20)
62 Распространение электромагнитных волн в диэлектриках 421
показывает, что и В также перпендикулярно
направлению распространения волны. Под-
Подставляя выражения F2.15а) в F2.2) и F2.3),
находим:
-к х В = ецшЕ, F2.21)
к х Е = юВ. F2.22)
Пусть п — единичный вектор в направ-
направлении распространения волны. Тогда на ос-
основании F2.8) можно написать
к = псо ущ = nco/i>. F2.23)
Поэтому [см. F2.22)]
п х Е = vB. F2.24)
С помощью F2.19) и F2.20) было пока-
показано, что векторы Е и В перпендикулярны
п. Формулы F2 21), F2.22) и F2.24) показы-
показывают, что эти векторы также перпендикуляр-
перпендикулярны друг другу. Взяв от обеих частей ра-
равенства F2.24) модули величин, находим
Е = vB. F2.25)
Из соотношения F2 24) можно заклю-
заключить, что в однородном диэлектрике векторы
Е и В изменяются в одной фазеЛВсе фор-
формулы этого параграфа справедливы для
вакуума, если положить е = е0, ц = ц0> v =
= с — скорость света. Изменение векторов
плоской волны в пространстве показано
на рис. 258.
р[лотность потока энергии. Она определя-
определяется вектором Пойнтинга, модуль кото-
которого в случае плоской волны равен
|S| = |E х Н| = |Е||Н| =
1 1
kz-k-t
257
Поверхность постоянной фазы
плоской волны
(E-D + В Н),
F2.26а)
где 1/]/ец = v — скорость распространения
волны, а
w = 4-(E-D+B-H)
258
Гармоническая плоская электро-
электромагнитная волна
F2.266)
— объемная плотность энергии в ней. Вы-
Выражение для потока энергии может быть
0 Электромагнитные волны
излучаются лишь перемен-
переменными токами и ускоренно
движущимися электриче-
электрическими зарядами. Постоян-
Постоянные токи и заряды, дви-
движущиеся равномерно и
прямолинейно, не излу-
излучают.
О В чем состоят физические
процессы, приводящие к воз-
возможности существования
электромагнитных волн?
Какова структура плоской
волны и чему равна ско-
скорость ее распространения
в вакууме'
422 9. Электромагнитные волны
представлено в виде
S = wv. F2.27)
Это означает, что скорость переноса энергии плоской волной в одно-
однородном диэлектрике равна фазовой скорости волны.
§ 63. Распространение электромагнитных
волн в проводящих средах
Рассматриваются основные свойства и осо-
особенности распространения электромагнит-
электромагнитных волн в проводящих средах.
1? омплексная диэлектрическая проницаемость. Рассматривается случай
однородной среды: ц = const, ? = const, у = const (у Ф 0, т.е. среда
является проводящей). Уравнения Максвелла при этом имеют вид:
Vx B = nj + |ie — = цуЕ + ЦЕ —, F3.1)
дВ
V х Е = - —, F3.2)
где использованы символические обозначения векторных операций и
учтено, что j = уЕ. Подставляя в эти уравнения выражения F2.15а) для
векторов поля, находим:
- кш х В = соц [е + y/(to)] Е, F3.3)
к„хЕ = <вВ, F3.4)
причем к в F2.15а) обозначено кт = k@)fcm, где к@) — единичный вектор.
Уравнение F3.3) переходит в уравнение F2.21) для диэлектриков
при у = 0. Уравнение F3.4) не отличается от соответствующего урав-
уравнения для диэлектриков. Таким образом, проводящая среда в мате-
математическом отношении отличается от диэлектрика лишь тем, что
в уравнении для нее вместо диэлектрической проницаемости е входит
комплексная диэлектрическая проницаемость
?ш = е + y/(icu) = е - iy/ш. F3.5)
Все последующие вычисления совпадают с вычислениями для ди-
диэлектриков, надо лиШь вместо е пользоваться ет. Таким образом,
вместо действительного волнового числа к появляется комплексная
величина кт причем
kl = <В2?ШЦ = С02ЕЦ - 1ЮУЦ. F3.6)
Представив fcm в виде комплексного числа:
К = к- is, F3.7)
перепишем равенство F3.6) в виде
к2 — 2iks — s2 = оJец — ia>y[i. F3.8)
§ 63. Распространение электромагнитных волн в проводящих средах 423
Приравнивая действительные и мнимые части F3.8), находим:
к2 -s2 = со2ец = а, F3.9)
2ks = m[i = b. F3.10)
Решение этой алгебраической системы уравнений таково:
F3.11)
F3.12)
Глубина проникновения. Исследуем амплитуду плоской волны, рас-
распространяющейся в направлении положительных значений оси Z:
Е = ?ое''(ю<~*шг) = Eoe-sV(ml-4 F3.13)
Таким образом, амплитуда волны в процессе распространения
уменьшается, т. е. в проводящей среде электромагнитная волна рас-
распространяется с затуханием амплитуды. На пути
Д = 1/s F3.14)
амплитуда напряженности поля волны уменьшается в е раз, поэтому
Д называется глубиной проникновения плоской волны в проводящую
среду.
Оценим глубину проникновения волн различной длины волны.
Для видимого света длина волны равна
X = @,4 -f- 0,75) 10 м, F3.15)
что соответствует частоте со порядка 5-Ю15 с. Проводимость ме-
металлов имеет порядок 107 Ом^'-м, а значение е может быть при-
принято равным е0. Таким образом,
уДеш) « 2 • 102 » 1. F3.16)
При длинах волн, больших, чем световая, это неравенство усили-
усиливается. Поэтому в формуле F3.12) можно пренебречь единицей по
сравнению с уДесо) и записать выражение для s в виде
s = j/coyh/2. F3.17)
Следовательно, глубина проникновения равна
Д = 1/5 = |/2/(шуц). F3.18)
Поскольку длина волны X связана с частотой ш соотношением
со = 2п/(Х j/ец), формулу F3.18) можно переписать:
F3.1У)
424 9. Электромагнитные волны
где 1/ц/е имеет размерность сопротивления и является характеристи-
характеристическим сопротивлением среды. Для вакуума оно равно
= 377 Ом. F3.20)
Рассмотрим, например, медь, для которой у = 5 • 107 Ом^-м,
ц * fi0, е « е0. При 1= 1 м глубина проникновения равна Д як 4 • 10~6 м.
Поэтому ни о каком проникновении волны в проводящую среду,
в сущности, не может быть и речи, есть просто поглощение в очень
малом поверхностном слое. Даже для очень коротких волн это заклю-
заключение остается справедливым. Например, для длин волн порядка све-
световых (Хяк10~6 м) глубина проникновения составляет Дяк4-10~9 м.
ф изическая причина поглощения. Физической причиной такого быст-
быстрого затухания электромагнитных волн в проводящей среде явля-
является преобразование электромагнитной энергии волны в джоулеву
теплоту: напряженность электрического поля волны возбуждает в про-
проводящей среде токи проводимости, которые по закону Джоуля — Ленца
нагревают вещество среды.
14 нтерпретация скин-эффекта. Теперь можно дать интерпретацию
скин-эффекта. Формула E3.19) для толщины скин-слоя совпадает
с формулой F3.18) для глубины проникновения электромагнитной
волны в проводник, что имеет глубокую физическую основу.
Энергия, переносимая током, движется в пространстве вокруг про-
проводников в виде электромагнитной энергии. Часть ее через поверх-
поверхность проводника проникает внутрь проводника, чтобы поддержать
движение электронов, и там превращается в кинетическую энергию
электронов, которая, в свою очередь, превращается в джоулеву теп-
теплоту. Поэтому ток может поддерживаться в тех частях проводника,
в которые из окружающего пространства поступает электромагнитная
энергия Поскольку эта энергия может проникнуть в проводник лишь
на глубину Д [см. F3.18)], то только в пределах такой глубины
около поверхности проводника и может существовать ток, т. е. А есть
толщина скин-слоя.
ф азовая скоршль и длина волны в проводящей среде. Формула F2.14)
с учетом F3.13) и F3.11) принимает вид:
Эта скорость меньше скорости волн в непроводящей среде с теми же
значениями ц и е, т. е. наличие в среде проводимости уменьшает
фазовую скорость. Длина волны в проводящей среде равна
' F122)
т. е. уменьшается по сравнению с длиной волны в непроводящей среде
с теми же значениями ц и г.
§ 63. Распространение электромагнитных волн в проводящих средах 425
Формула F3.22) показывает, что в проводящей среде фазовая ско-
скорость зависит от частоты, т. е. наблюдается явление дисперсии. Поэтому
проводящая среда всегда является диспергирующей. Наиболее суще-
существенной особенностью распространения сигналов в диспергирующих
средах является изменение их формы в процессе распространения.
(Соотношение между фазами колебаний векторов поля. Комплексную
величину кш в F3.7) удобно представить в экспоненциальной форме:
fc.= |fcje". F3.23)
Формула F3.4) может быть представлена в виде
В = 1^1е'Фк«» х Е, F3.24)
со
где к@> — единичный вектор в направлении распространения волны,
в данном случае в направлении оси Z. Векторы Е и В перпендикулярны
этой оси.
Пусть напряженность электрического поля волны в соответствии
с F3.13) выражается формулой
Е=Еое-"е;(м-*г>, F3.25)
где без ограничения общности можно считать вектор Ео действитель-
действительным, поскольку выбор начала отсчета времени f всегда произволен.
Подставляя F3.25) в F3.24), находим
В = !М.к@> х Еое-"е' «"•-"-- + ф>. F3.26)
Определив действительные части выражений F3.25) и F3.26), найдем
формулы для действительных колебаний векторов поля в плоской
волне, распространяющейся в проводящей среде:
Е = E0e"szcos(cut -kz),
В = 1^Ц«>) х Е е-« cos ,ш -kz + <p). F3.27)
ш
Следовательно, фазы колебаний электрического и магнитного век-
векторов плоской волны различны. Из F3.7) находим
tg Ф = - s/k = \fcfr - /ГЙец/уJ, F3.28)
т. е. угол ф отрицателен. Это означает, что фаза В достигает некото-
некоторого значения позднее, чем фаза Е. Это проявляется двумя путями.
Если рассматривать колебания векторов волны в фиксированной
точке, мимо которой движется волна, то В достигает своего, например,
максимального значения позднее, чем Е, т. е. В как функция времени
отстает от Е.
Если рассматривать волну в фиксированный момент времени, то
В достигает своего, например, максимального значения при меньших
значениях г, чем Е, т. е. В как функция от z опережает Е.
426 9. Электромагнитные волны
Эти утверждения взаимно дополняют друг друга и находят свое
единство в том факте, что бегущая электромагнитная волна движется
в направлении своего распространения (в данном случае в направлении
положительных значений оси Z).
/^оотношение между амплитудами векторов поля. Из F3.25) и F3.26)
следует, что
Щ = !М = ]/^ {1 + [7/(eil)]2]W. F3.29)
Сравнивая F3.29) с F2.25), видим, что в проводящей среде | В |
относительно | Е | больше, чем в непроводящей среде с теми же зна-
значениями ц и е.
§ 64. Инвариантность плоской волны
Обсуждаются инварианты преобразований
электромагнитного поля и следствия из ана-
анализа инвариантов.
ТТреобразование полей. При переходе от одной инерциальной системы
отсчета к другой напряженности полей изменяются. Формулами
преобразования являются равенства A1.15).
Может случиться, что в одной инерциальной системе отсчета
имеются электрическое и магнитное поля, а в другой — только электри-
электрическое и т. д.
Плоская электромагнитная волна характеризуется вполне определен-
определенными свойствами: векторы Е и В взаимно перпендикулярны и их
модули связаны соотношением Е = сВ. Спрашивается, сохраняются ли
эти свойства векторов поля при переходе в другую инерциальную
систему отсчета? Если сохраняются, то понятие плоской электромаг-
электромагнитной волны является релятивистски инвариантным, отражающим
внутренние свойства электромагнитного поля плоской волны. Если нет,
то это понятие зависит от случайного выбора той или иной инерци-
инерциальной системы отсчета и не определяет объективно существующего
физического объекта. С помощью формул A1.15) нетрудно проверить,
что векторы напряженностей электромагнитного поля, удовлетворяю-
удовлетворяющие условию плоской волны в одной системе координат, удовлетво-
удовлетворяют этим условиям в любой другой системе координат, т. е. плоская
волна является релятивистски инвариантным понятием, определяющим
объективно существующий физический объект. Вместо прямой проверки
частного утверждения об инвариантности плоской волны целесообразно
проанализировать более широкий вопрос об инвариантах преобразова-
преобразований электромагнитного поля и утверждение об инвариантности плоской
волны обосновать как частный вывод, наряду с которым, однако,
получаются и многие другие важные выводы.
I/Тнварианты преобразований электромагнитного поля. Инвариантами
преобразований электромагнитного поля называются такие вели-
величины, составленные из векторов поля, которые не изменяют своего
§ 64. Инвариантность плоской волны 427
значения при переходе от одной инерциальной системы отсчета
к другой. Векторы поля в разных системах координат связаны между
собой преобразованиями A1.15).
Существуют способы нахождения инвариантов преобразований.
С помощью формул A1.15) прямым вычислением можно проверить,
что при переходе от одной инерциальной системы отсчета к другой
не изменяют своей величины следующие инварианты:
h = с2В2 - Е2, 1\ = Н2 - c2D2; F4.1)
/2 = ВЕ, Г2 = Н D; F4.2)
/3 = Н B-DE. F4.3)
Проверим, для примера, что величина 12 является инвариантом.
По формулам A1.15) имеем
В Е' = В'ХЕ'Х + В'Е'У + В'Л = ВХЕХ
Zz = В Е F4.4)
Аналогично доказывается инвариантность и других величин.
Плоская волна определяется равенством нулю инвариантов 1Х = О
и 12 = 0, а ее инвариантность не требует дальнейшего доказательства,
поскольку /х и 12 - инварианты. Однако инвариантность величин
F4.1)-F4.3) позволяет сделать и некоторые другие важные выводы
о поведении электромагнитных полей при переходе от одной системы
отсчета к другой.
Анализ инвариантов поля. Из инвариантности величин F41) —F4.3)
можно сделать следующие выводы:
1) если в некоторой инерциальной системе отсчета с2В2 > Е2 и
В IE, то можно выбрать такую инерциальную систему отсчета, где
электрическое поле отсутствует, а магнитное отлично от нуля. Если же
В не перпендикулярно Е, то такой инерциальной системы отсчета
не существует;
2) если в некоторой инерциальной системе отсчета с2В2 < Е2 и
ВХЕ, то можно выбрать такую инерциальную систему отсчета, 1де
магнитное поле отсутствует, а электрическое отлично от нуля. Если же
В не перпендикулярно Е, то такой инерциальной системы отсчета
не существует;
3) если в какой-либо инерциальной системе отсчета имеется только
электрическое поле или только магнитное, то при переходе к другой
инерциальной системе отсчета имеется, вообще говоря, как электриче-
электрическое, так и магнитное поля, которые перпендикулярны друг другу;
4) плоская волна, для которой Е = сВ, EJ_B, во всех инерциальных
системах отсчета остается плоской волной.
428 9. Электромагнитные волны
§ 65. Давление электромагнитных волн.
Импульс фотона
Описывается механизм возникновения дав-
давления электромагнитных волн. Вычисляется
объемная плотность импульса электромаг-
электромагнитной волны и определяется импульс фо-
фотона.
\/1еханизм возникновения давления. Если плоская волна распростра-
распространяется в проводящей среде, то ее электрическое поле возбуждает
в среде объемную плотность тока проводимости по закону Ома:
j = YE. F5.1)
На элемент тока jdFco стороны магнитного поля волны действует
сила (рис. 259):
dF = jx BdK=yE x BdF, F5.2)
направленная по вектору Е х В, т. е. в сторону распространения волны.
Обозначив п — единичный вектор в направлении распространения вол-
волны, можно написать:
dF = yEx BdV=nyEBdV=njEdV/v = ndP/v, F5.3)
где использовано соотношение между модулями векторов плоской
волны (Е — vB) и принят во внимание закон Джоуля —Ленца dP = jEdV.
Следует обратить внимание, что в формуле F5.3) величина dP - погло-
поглощенная энергия, отнесенная ко времени.
ГТавление. Пусть из вакуума на проводящую среду падает поток
^"энергии электромагнитных волн, который весь поглощается. В 1 с
на элемент поверхности dS падает в соответствии с формулой F2.27)
энергия
dP = vw dS, F5.4)
которая поглощается и создает на нормали к поверхности силу F5.3),
на основании F5.4) равную
dF = nw dS. F5.5)
Поэтому давление по нормали к поверхности равно
dF
Рд=-^-=™. F5.6)
Величина
w = 7г (Е • D + В • Н) F5.7)
есть объемная плотность энергии электромагнитных волн.
румпульс цуга электромагнитных волн. Допустим, что энергия W,
заключенная в некотором объеме в цуге электромагнитных волн,
поглощается в некотором объеме проводящего тела в течение проме-
промежутка времени At. Тогда в соответствии с F5.3) на этот объем тела
§ 65. Давление электромагнитных волн. Импульс фотона 429
действует сила
W
1 дГ
W 1
F-ч-г--. F5.8)
им-
At v
По закону Ньютона, сила, действующая на объем, связана с
пульсом, приобретенным объемом, соотношением
F = р/Дг. F5.9)
Подставляя F5.9) в F5.8), получаем
W
р = п—. F5.10)
Формула F5.10) содержит фундаментальное утверждение: цуг элект-
электромагнитных волн, обладающий энергией Wи движущийся со скоростью
v, обладает импульсом р, связанным с энергией соотношением F5.10).
Импульс направлен в сторону распространения волн.
Объемная плотность импульса электромагнитных волн. Разделив обе
части F2.10) на объем, в котором содержится энергия W, получим
для объемной плотности импульса электромагнитных волн формулу
G = p/V=aw/v, F5.11)
где w = W/V — плотность электромагнитной энергии в плоской волне.
С помощью F2.27) выражение F5.11) может быть записано в виде
G = S/u2, F5.12)
где S — вектор Пойнтинга, v — скорость движения волн.
Давление электромагнитных волн может рассчитываться по изме-
изменению их импульса. Например, если электромагнитные волны падают
по нормали к поверхности и полностью поглощаются, то давление,
в соответствии с формулой F5.12), равно
рЛ = vG = S/v = w, F5.13)
что, конечно, совпадает с F5.6). Если же волна полностью отражается,
по телу передается двойной импульс и давление равно
pa = 2vG = 2w. F5.14)
Аналогично может быть рассчитано давление при частичном погло-
поглощении, при косом падении на поверхность и т. д.
Впервые экспериментально давление световых волн было обнару-
обнаружено в 1900 г. П. Н. Лебедевым A866-1912). Как видно из F5.14),
давление очень мало. Например, при потоке 1,4 кВт/м2, что прибли-
приблизительно равно потоку солнечной энергии на орбите Земли, световое
давление составляет около 5 мкПа. Поэтому потребовалась разработка
очень тонких методов измерения.
Омпульс фотона. В соответствии с квантовыми представлениями
свет представляет собой совокупность квантов энергии, называемых
фотонами. Энергия фотона связана с частотой света соотношением
430 9 Электромагнитные волны
Эйнштейна
VW
[—¦AS
259
Схема возникновения давления
электромагнитной волны
Б = ~h(u,
F5 15)
где Л — постоянная Планка Наличие свето-
светового дав пения заставляет признать что
фотоны обладают также и импульсом
В соответствии с F5 10) импульс фотона
равен
р = ийсо/с, F5 16)
где с — скорость распространения света в
вакууме Перепишем формулу F5 16) с уче-
учетом F2 23)
р= Лк
F5 17)
Соотношение F5 17) является наряду с
F5 15) фундаментальным уравнением кван-
квантовой теории света
260
К вычислению давления элект-
электромагнитного излучения на аб-
абсолютно отражающую сферу
ф Напряженность электри-
электрического поля плоской вол-
волны возбуждает в прово-
проводящей среде токи проводи-
проводимости, в результате взаи-
взаимодействия которых с ин-
индукцией магнитного поля
волны возникает сила Ло-
ренца, проявляющаяся в
виде давления электромаг-
электромагнитной волны
О Что представляет собой в
классической подели сила
приводящая к воэникнове
нию давления при погло
шении электромагнитной
волны в проводящей среде'
Чем определяется плотность
импульса электромагнитной
волны'
Пример 65.1. Определить силу с которой
фотоны объемная плотность потока энергии ко
торых S действуют на абсолютно отражающую
сферу радиусом i (рнс 260)
Вследствие аксиачьнои симметрии распреде
ления дав 1ений от нуля отлична только состав
ляющая силы в направтении первоначатьною
потока фотонов На элемент поверхности do
(рис 260) в соответствии с формулой F5 13)
действует направленная к центру сферы сита
AF = BS/c) cos 9 do а состав ияющая этой снты
в направлении оси Z равна
df = -BS/Ocos29da
Площадь лемента поверхности в сфериче
ской системе координат dcr = i2 sin в d9 dot где
a — аксиатьныи угол в тоскосги, перпендикуляр
ной оси Z Для полной си ты вдоль оси Z
получаем
F. = -
н-уп-
3 с
т е сила в 4/з раза бо гьше чем в случае когда
вся энергия потока пог ющается сферой
§ 66. Волноводы и резонаторы 431
§ 66. Волноводы и резонаторы
Описываются основные характеристики вол-
волноводов и особенности распространения
электромагнитных волн в них. Дается клас-
классификация волн в волноводах. Обсуждается
принцип действия резонатора.
\/часток цепи. Любой участок цепи обладает омическим сопротивле-
нием, емкостью, и индуктивностью. Эквивалентная схема участка цепи
изображена на рис. 261,.а. Омическое сопротивление R всегда имеется
потому, что провода обладают омическим сопротивлением. Емкость
возникает потому, что на участке цепи всегда имеются поверхностные
или объемные заряды и электрические поля, в которых запасается
энергия электрического поля. При протекании тока по участку цепи
возбуждается магнитное поле, в котором запасается энергия. Следова-
Следовательно, участок цепи обладает также индуктивностью. Относительная
роль R, С и Lзависит от конкретных свойств участка цепи и от частоты.
х/ часток проводника. На небольшой прямолинейный участок провод-
ника приходятся очень небольшой поверхностный заряд и энергия
магнитного поля. Это означает, что емкость и индуктивность его
достаточно малы. Поэтому на малых частотах емкостное сопротивле-
сопротивление участка оказывается больше омического, а индуктивное — меньше,
т. е. имеет место неравенство 1/(юС) »Л> coL. Поэтому на схеме,
изображенной на рис. 261, а, ток протекает главным образом по
участку R, L, а емкость как бы отключается. Поскольку coL <s R,
индуктивное сопротивление не имеет существенного значения и участок
-проводника на малых частотах изображается так, как показано на
рис. 261, б.
С увеличением частоты сопротивление R растет. Поскольку толщина
скин-слоя уменьшается как 1/]/ш, можно считать, что сопротивление
растет как |/ш. Индуктивность L при росте частоты уменьшается
незначительно и поэтому индуктивное сопротивление coL растет как со.
Следовательно, с увеличением частоты относительная роль индуктив-
индуктивности участка проводника возрастает и его уже нельзя считать просто
участком с омическим сопротивлением. С увеличением частоты умень-
уменьшается емкостное сопротивление 1/(соС). Поэтому на достаточно боль-
больших частотах значительная часть тока осуществляется в виде токов
смещения. Это означает, что на больших частотах эквивалентная схема
участка проводника имеет вид, показанный на рис. 261, а, причем как
R, так и L, С должны быть приняты во внимание. Их относи-
относительная роль зависит от частоты. При крайне больших частотах
определяющую роль играет емкость.
|?атушка индуктивности. На малых частотах у катушки 1/(шС)»
»a>L».R. Ток в основном протекает через R, L (рис. 261, а), и
поскольку R <e QiL, эквивалентная схема катушки индуктивности на
малых частотах имеет вид, показанный на рис. 261, в.
432 9. Электромагнитные волны
261
1,В,Е
ДЕ
При увеличении частоты индуктивное
сопротивление катушки растет, а емкостное
уменьшается. Поэтому все большая часть
тока проходит в виде тока смещения через
емкости, имеющиеся между отдельными вит-
витками катушки. Наряду с индуктивностью
и омическим сопротивлением начинает су-
существенную роль играть емкость. В резуль-
результате эквивалентная схема катушки индуктив-
индуктивности превращается в схему, изображенную
на рис. 261, а, причем относительная роль
R, L, С зависит от частоты. При очень
Эквивалентные схемы участка большой частоте почти бесь ток идет в виде
цепн при различных частотах тока смещения, как бы перескакивая с витка
на виток, а индуктивность как бы выключа-
выключается из цепи.
тлонденсатор. На малых частотах у конден-
конденсатора емкостное сопротивление меньше,
чем омическое и индуктивное [1/(шС) <s: R,
1/(соС) <? <bL]. В результате на схеме
(рис. 261, а) участок R, ?как бы отключается
и эквивалентная схема конденсатора имеет
вид, показанный на рис. 261, г.
При увеличении частоты ситуация изме-
изменяется. Чтобы выяснить, что при этом про-
происходит, рассмотрим для примера плоский
конденсатор.
В плоском конденсаторе при росте часто-
частоты увеличивается отклонение электрическо-
электрического поля от однородного. Причиной этого
является взаимодействие электромагнитной
индукции и токов смещения. На первый
взгляд кажется, что здесь картина явления
должна быть аналогичной той, которая при-
приводит к возникновению скин-эффекта
(рис. 223), но это не так. Различие обуслов-
обусловливается другими фазовыми соотношениями
между векторами полей.
Рассмотрим векторную диаграмму полей
и токов в случае скин-эффекта (рис. 223).
Индукция магнитного поля находится в фазе
с силой тока и напряженностью порождаю-
порождающего его электрического, поля. Производная
от индукции магнитного поля опережает
их на к/2, а порождаемая изменением маг-
Соотношение между напряжен- ' Г
ностями полей в конденсаторе НИТНОГО ПОЛЯ напряженность ДЕ ДОПОЛНИ-
непосредст-
б)
«в
АЕ
262
на высоких частотах
тельного электрического поля,
§ 66. Волноводы и резонаторы 433
венно приводящего к скин-эффекту, отстает на к/2 от напряженности
Е поля. Поэтому при более строгом подходе на рис. 223 необходимо
было бы принять во внимание не только пространственное распределе-
распределение полей, но и фазы изменения напряженностей.
Векторная диаграмма возникновения скин-эффекта показана на
рис. 262, я.
Расчетные формулы автоматически учитывают соотношение между
фазами векторов.
В конденсаторе (рис. 262, б) соотношение между фазами векторов
поля другое. Поскольку магнитное поле порождается токами смещения
по закону
дЕ
rot В = це —,
его индукция находится в фазе с dE/dt и, следовательно, опережает
на п/2 напряженность Е (рис. 262, в). Поэтому возникающая по закону
электромагнитной индукции напряженность ЛЕ, приводящая к пере-
перераспределению напряженности поля Е в конденсаторе, находится в фазе
с напряженностью Е (рис. 262, в). Главное различие с явлениями,
происходящими при возникновении скин-эффекта, состоит в разном
соотношении фаз между Е и В: при образовании скин-эффекта их
фазы совпадают, а в конденсаторе индукция магнитного поля опере-
опережает по фазе напряженность электрического поля на п/2. Поэтому,
например, при нулевом электрическом поле в картине скин-эффекта
индукция магнитного поля равна нулю, а в конденсаторе она имеет
максимальное значение. При росте напряженности Е поля при скин-
эффекте от нулевого значения индукция магнитного поля растет и ли-
линия dB/dt составляет с Е правовинтовую систему (рис. 223), а в кон-
конденсаторе она уменьшается и поэтому линии dB/dt составляют с Е
левовинтовую систему (рис. 262, б). Следовательно, напряженность ДЕ
вихревого электрического поля направлена так, что увеличивает напря-
напряженность электрического поля в центре конденсатора и ослабляет на
периферии, т. е. в конденсаторе поле ослабляется от центра к пери-
периферии. На некотором расстоянии от центра напряженность обращается
в нуль, а затем изменяет свое направление на обратное (рис. 262, г).
Количественная характеристика этого явления может быть получена
в результате решения уравнения для напряженности Е поля, исходя
из F2.5). В данном случае имеется одна компонента Е и осевая
симметрия задачи, т. е. Е = Е (г), где г — расстояние от оси конденса-
конденсатора до точки, в которой определяется напряженность. Полагая, как
обычно,
E(r, t) = E0(r)ee*
и считая, для определенности, что между обкладками конденсатора
е = е0, A = (i0, получаем для Ео (г) уравнение
0 . 1 d?0 ю2
z r dr с2
15 А. Н. Матвеев
434 9. Электромагнитные волны
записанное в цилиндрических координатах. Это уравнение называется
уравнением Бесселя с нулевым индексом, решение которого записы-
записывается в виде Jo (wr/c). Функции Бесселя хорошо изучены. На рис. 277, г
показан ход функции Jo (иг/с). Наименьшими корнями функции с ин-
индексом нуль являются %i = 2,40; \2 = 5,52; \ъ = 8,65; .... Учтем, что
со/с = 2к/к, где X — длина электромагнитной волны с частотой ю
в вакууме. Поэтому расстояния, на которых напряженность поля
в конденсаторе обращается в нуль, равны
г, = Ц,/Bя).
В частности, первый раз напряженность обращается в нуль на
расстоянии r-i = X^JBk) = O,38L Благодаря такому поведению напря-
напряженности конденсатор уже перестает играть роль чистой емкости.
Ясно, что магнитные поля в конденсаторе становятся существенными,
а это означает, что вступает в игру индуктивность. Другими словами,
конденсатор также теряет на высоких частотах свои первоначальные
функции емкости.
разлучение. В § 61 было показано, что мощность излучения вибра-
вибратора растет пропорционально четвертой степени частоты (~ш4),
т. е. очень быстро. А это означает, что при прохождении по проводам
токов высокой частоты имеет место интенсивное излучение электро-
электромагнитной энергии. При высокой частоте потери становятся столь
значительными, что передача по проводам становится нецелесообраз-
нецелесообразной. Необходимо найти другие способы передачи электромагнитной
энергии с высокой частотой, поскольку разработанные для низких
частот методы генерирования и передачи электромагнитных колебаний
неприменимы для очень высоких частот.
цолноводы. Основная идея волновода состоит в том, чтобы напра-
направить электромагнитные волны по некоторому каналу, сведя к мини-
минимуму возможные потери в процессе распространения. Для этого,
очевидно, надо по возможности избежать возбуждения токов прово-
проводимости и исключить проникновение электромагнитной энергии за
стенки канала. Простейшей моделью волновода является полая труба,
внутри которой распространяются электромагнитные волны. Основные
особенности этих электромагнитных волн рассмотрим на простейшем
примере — прямоугольном прямолинейном волноводе.
жтрямоугольный волновод. Стенки волновода предполагаются иде-
идеально проводящими, размеры волновода и положение системы
координат даны на рис. 263. В волноводах, вообще говоря, могут
распространяться многие типы волн. Рассмотрим один из них.
Допустим, что электрический вектор волны направлен вдоль оси Y.
Для упрощения ситуации примем длину волновода вдоль оси Y бес-
бесконечной. Это избавляет от необходимости учета граничных условий
для вектора Е на поверхностях волновода, параллельных плоскости
XZ, и значительно облегчает решение задачи. Кроме того, при беско-
бесконечной протяженности волновода в направлении оси У задачу можно
§ 66. Волноводы и резонаторы 435
рассмотреть методом изображений, что позволяет прояснить физиче-
физическую ситуацию и суть процессов, которые происходят при распростра-
распространении волн в волноводе.
Таким образом, задача сводится к двум измерениям. Волновое
уравнение для напряженности электрического поля имеет вид
д2Е д2Е 1 32Е . ,„,.
!?-+-&*" ^Ж"* F6-1)
где Е = Еу (х, z, О-
Поскольку стенки волновода идеально проводящие, граничное усло-
условие для Е имеет вид
Е (х, О, t) = О, Е (х, a, t) = 0. F6.2)
Будем искать решение уравнения в виде
E«E08m*,2e<*~k"x), F6.3)
причем для удовлетворения граничным условиям F6.2) надо положить
кга = пп (п = 1, 2,...). F6.4)
Очевидно также, что решение F6.3) удовлетворяет условию отсут-
отсутствия свободных зарядов в волноводе: div Е = дЕу/ду = 0, Ех = Ег = 0.
Подставляя F6.3) в F6.1), получаем
(-к2, - к2 + и2/с2)Е = 0. F6.5)
Это равенство может быть удовлетворено лишь при условии
-к2х-к2 + а2/с2 = 0, F6.6)
из которого следует, что
кх = j/co2/c2 - п2п2/а\ F6.7)
Г'раничная частота. Электромагнитная волна распространяется в вол-
волноводе без затухания, если в F6.3) величина кх действительная.
Это означает, что в F6.7) подкоренное выражение не должно быть
отрицательным. Отсюда получаем условие, при котором в волноводе
распространяются волны:
Т-^О F6-8)
или
и > — п. F6.9)
а
Таким образом, при заданном значении п, характеризующем форму
волны в направлении оси Z, имеется граничная частота. Электромаг-
Электромагнитные волны с меньшей частотой не могут распространяться в волно-
волноводе. Значение этой частоты получается из F6.9) при п — 1:
и0 = пс/а. F6.10)
Наличие граничной частоты означает, другими словами, существование
волны с максимальной длиной волны, которая в состоянии распро-
15*
436 9. Электромагнитные волны
страняться в волноводе. Учитывая, что X = сТ — 2кс/(л, получаем для
граничной длины волны
Хо = 2яс/ш0 = 2а. F6.11)
Это равенство имеет очень ясный геометрический смысл: в рассмат-
рассматриваемом волноводе могут распространяться лишь волны, длина волны
которых меньше удвоенного поперечного сечения волновода.
Наличие граничной частоты является характерной чертой всех
волноводов, хотя ее конкретное значение различно для различных
волноводов.
фазовая скорость. Согласно выражению F6.3) эта скорость находится
из условия
eat — kxx = const, F6.12)
откуда
dx и и со
у& = —~- = — = —= — = с —?= - > с, F6.13)
Ф dt kx yV/c*-n2/a2 ]А2 - n2c2/a2
т. е. фазовая скорость электромагнитных волн в волноводе больше ско-
скорости света. Это также является характерной чертой волноводов,
хотя конкретное значение фазовой скорости зависит от свойств волно-
волновода и типов волн.
С учетом выражения F6.10) и F6.11) формулу F6.13) удобно пред-
представить в виде
F6.14)
]/l- (©о/соJ 1/1 -
Следовательно, и > ю0, X < Хо, поскольку в противном случае фазо-
фазовая скорость становится мнимой, т. е. распространение волн невоз-
невозможно.
ТТлина волны в волноводе. По определению длины волны имеем
... -,. ]/vz
где X = cT* Длина волны в волноводе всегда больше длины волны
в свободном пространстве. Возведя обе части F6.15) в квадрат и взяв
от них обратные величины, получим
1Д2 = 1/Х2 - 1/A.i. F6.16)
Соотношение F6.16) справедливо для волноводов любой формы,
хотя и было выведено здесь для частного случая.
Применение метода изображений к анализу волноводов. Для более
четкого выяснения физической картины распространения волн в вол-
волноводе и смысла полученных соотношений проанализируем рассмот-
рассмотренный пример методом изображений. В качестве элементарного
§ 66. Волноводы и резонаторы 437
излучателя можно себе представить бес-
бесконечный прямой проводник, по которому
течет переменный ток частоты ю. Этот
излучатель аналогично вибратору Гер-
Герца испускает волны, электрический вектор
которых направлен параллельно проводнику.
В случае бесконечно длинного проводника
волны будут, очевидно, цилиндрическими.
Однако на достаточно большом расстоя-
расстоянии от излучателя их можно считать пло-
плоскими.
На рис. 264 показаны проекции стенок
волновода на плоскость XZ, электрический
вектор волн направлен перпендикулярно
плоскости чертежа. Расположим первый из-
излучатель в середине волновода, на расстоя-
расстоянии а/2 от каждой из его перпендикулярных
плоскости чертежа стенок. Фаза колебаний
излучателя обозначена точкой, т. е. ток в
данный момент течет к нам. Излучатель
испускает по всем направлениям волны,
и поэтому на стенках волновода напряжен-
напряженность поля отлична от нуля. Задача состоит
в том, чтобы так подобрать сисгему излу-
излучателей, чтобы суммарная напряженность
их полей на стенках волновода все время
была равна нулю. Удовлетворяющее этому
условию поле и будет искомым полем в
волноводе. Конечно, когда волны распро-
распространяются от воображаемых излучателей,
стенки волновода тоже считаются вооб-
воображаемыми и через них без препятствий
проходят воображаемые волны.
Для того чтобы на стенке At волно-
волновода ликвидировать поле, порождаемое
излучателем 0, необходимо на расстоянии
а/2 от нее поместить излучатель /, кото-
который колеблется со сдвигом колебаний на
полпериода относительно излучателя 0. Сле-
Следовательно, излучатель 1 должен коле-
колебаться в противоположной излучателю 0
фазе, что обозначено знаком ( + ) («ток
от нас»). Волны от излучателя 1 приходят
в точки стенки Ах волновода через тот же
промежуток времени, что и от излуча-
излучателя 0. Так как фазы волны от 0 и J на
стенке А± отличаются на я, то сумма
263
Прямоугольный волновод
264
Рассмотрение прямоугольного
волновода методом изображений
Характерной особеннос-
особенностью любого волновода
является наличие гранич-
граничной частоты. В любой
волноводе фазовая ско-
скорость электромагнитных
волн больше скорости
света.
438 9. Электромагнитные волны
напряженностей этих волн равна нулю. Аналогично излучатель 2 гасит
на стенке А2 излучение 0.
Однако излучатель / создает поле на стенке А2, а излучатель 2 —
на стенке Ах. Необходимо добавить следующие излучатели, которые
погасили бы эти поля. Для того чтобы погасить излучение от* 1 на
стенке А2, необходимо взять излучатель 4, а для погашения излучения
от 2 на стенке А± служит излучатель 3 и т.д. до бесконечности.
Напряженность поля от бесконечной системы этих излучателей равна
нулю на стенках Ах и А2. Следовательно, полученное поле удовлетво-
удовлетворяет уравнениям Максвелла, будучи суперпозицией полей, каждое из
которых удовлетворяет этим уравнениям, и представляет собой искомую
электромагнитную волну в волноводе. Поле вне волновода имеет
вспомогательное значение и нас не интересует.
тт искретность направлений распространения плоских волн от системы
^ излучателей. От индивидуального излучателя плоские волны рас-
распространяются во всех направлениях. Однако от системы излучателей
плоские волны могут распространяться лишь во вполне определенных
направлениях, а не в любых. Такими направлениями могут быть лишь
те, в которых плоские волны отдельных излучателей взаимно усили-
усиливаются. Это возможно лишь в том случае, когда разность хода вол»,
излученных соседними излучателями, равна целому числу длин волн
с половиной, поскольку соседние излучатели испускают волны в про-
тивофазе. В результате получается, что в обсуждаемом направлении
от всех излучателей распространяются волны с разностью фаз в целое
число периодов и, следовательно, эти волны усиливают друг друга.
На рис. 264 направление распространения волн характеризуется углом 0.
Условие взаимного усиления волн имеет вид
a sin 9 = X (т + 1/2) (от = 0, 1, 2,...). F6.17)
Аналогичное условие можно записать для волн, распространяющихся
в другую сторону от оси волновода, т.е. для отрицательных углов 9.
Р'раничная длина волны. Условие F6.17) показывает, что для каждой
длины волны имеется минимальный к оси угол, распространения,
достигаемый при т = 0, а также максимальное значение числа т, при
котором угол равен 9 = п/2, т. е. волна распространяется перпендику-
перпендикулярно длине волновода. При достаточно большой длине волны уже
т = 0 приводит к условию sin0 = 1, т. е. эта волна может распростра-
распространяться только перпендикулярно оси волновода. Это означает, что волны
с такой длиной волны и большими длинами в волноводе распростра-
распространяться не могут. Это есть граничная длина волны Хо, определяемая
из F6.17) при sin 0 = 1, т = 0:
а = 10/2, F6.18а)
что совпадает с F6.11). Этой длине волны соответствует граничная
частота F6.10).
й 66. Волноводы и резонаторы 439
Длина волны и фазовая скорость в волноводе. Фазовой скоростью
^ является скорость точек поверхности постоянной фазы волны в на-
направлении волновода, т. е. скорость точки пересечения фронтом плоской
волны стенок волновода. Из рис. 264 видно, что она равна
уф = c/cos 9. F6.186)
Взяв в F6.17) волну с т = 0, получим sinG = X/Ba) и представим
формулу F6.186) в виде
с с с с
J/1 - sin2 9 ]/\ - |>/Bа)]2 ]/l - (ХД6J |/Пч
F6.19)
что совпадает с F6.14). Таким образом, фазовая скорость не связана
с движением в пространстве какого-либо физического объекта и энергии.
Можно себе представить, что на рис. 264 ось X изображает кромку
письменного стола, а линия, изображающая фронт волны, является
линейкой. Тогда при угле G, достаточно близком к к/2, малые скорости
перемещения линейки перпендикулярно ее длине приводят к скоростям
точки соприкосновения линейки с кромкой стола, превосходящим ско-
скорость света. Ясно, что наличие этой скорости не находится в противо-
противоречии с ограничением, налагаемым теорией относительности на ско-
скорость движения физических объектов и распространения взаимо-
взаимодействий.
Длина волны Хв также определяется в результате геометрического
построения на рис. 264:
К = —^г = , F6.20)
в cos е 1/1. -' к '
что совпадает с F6.15). Из F6.20) следует также и F6.16).
т-фупповая скорость. Ясно, что фазовая скорость не представляет
скорости движения энергии волны вдоль волновода. Энергия в пло-
плоской волне движется в вакууме со скоростью с перпендикулярно фронту
волны. В направлении оси волновода скорость движения энергии
определяется проекцией скорости с на ось. Эта скорость называется
групповой. Как видно на рис. 264, она равна
IV = с cos 9 = с )/l - (kfkoJ- F6.21)
Групповая скорость всегда меньше скорости света. Свое название
она получила потому, что равна скорости пика суммарной амплитуды
группы волн с близкими частотами, распространяющимися с различ-
различными фазовыми скоростями, зависящими от частоты. Совокупность
волн с различными частотами в волноводе составляет такую группу
волн, зависимость фазовых скоростей которых от частоты определяется
формулой F6.14). Важнейшее физическое свойство групповой скорости
уже было сформулировано - это скорость движения энергии, связанной
с волнами.
440 9. Электромагнитные волны
Соотношение между групповой и фазовой скоростями. Перемножая
почленно F6.21) и F6.19), получаем
iy>r = с2.
F6.22)
Это соотношение является фундаментальным в теории распростране-
распространения волн и имеет универсальный характер, хотя и получено для част-
частного примера и специальным методом.
агнитное поле. Индукция магнитного поля плоской волны перпенди-
перпендикулярна напряженности ее электрического поля. Поэтому векторы
магнитной индукции расположены в плоскостях, параллельных плоско-
плоскости рис. 264. Поскольку плоские волны распространяются под углом
к оси волновода, индукция магнитного поля каждой из плоских волн
имеет компоненты вдоль оси волновода и перпендикулярно ей.
То же можно сказать и о индукции магнитного поля суперпози-
суперпозиции плоских волн, составляющих волну в волноводе. Это означает,
что электромагнитные волны, движущиеся в волноводе, не являются
чисто поперечными, они имеют составляющую индукции магнитного
поля в направлении распространения. В других случаях возможны
типы волн, когда имеется компонента напряженности электрического
поля вдоль направления распространения, и т. д. Следует также отме-
отметить, что волны в волноводе, вообще говоря, не являются однородными.
ХЛлассификация волн в волноводах. Общепринятой является следую-
следующая классификация волн в волноводах:
1. Поперечно-магнитные волны (ТМ-волны), определяемые требова-
требованием Нх = 0, т. е. отсутствием составляющей напряженности магнитного
поля в направлении распространения волн. Можно показать, что в этом
случае все характеристики волн выражаются только через Ех.
2. Поперечно-электрические волны (ТЕ-волны), определяемые тре-
требованием Ех = 0. В этом случае решения выражаются только через Нх.
3. Поперечные электромагнитные волны (ТЕМ-волны), определяемые
требованиями Ех = 0, Нх = 0.
4. Гибридные волны, когда одновременно Нх Ф0, Ехф 0. Они воз-
возникают в том случае, когда граничные условия требуют, чтобы отлич-
отличными от нуля были одновременно и Ех и Н„ что осуществляется
в реальных волноводах, проводимость стенок которых конечна.
резонаторы. Рассмотрим конденсатор, график изменения напряжен-
напряженности поля которого на высоких частотах изображен на рис. 277, г.
На цилиндрической поверхности радиусом гх электрическое поле отсут-
отсутствует. Это означает, что вектор Пойнтинга на этой поверхности
равен нулю и, следовательно, отсутствует движение электромагнитной
энергии через нее. Будем считать эту цилиндрическую поверхность
идеальным проводником, соединяющим обкладки конденсатора. Элект-
Электрическое поле на его поверхности по-прежнему останется равным нулю.
Магнитное поле не равно нулю и его силовые линии являются окруж-
окружностями, концентрическими с точками оси цилиндра. Вдоль цилиндри-
Задачи 441
ческого проводника текут токи от одной пластины конденсатора
к другой, как это следует из граничного условия C8.35) для танген-
тангенциальной составляющей вектора Н. Теперь весь цилиндрический замк-
замкнутый объем, ограниченный идеально проводящими стенками, может
быть изолирован и предоставлен самому себе. Электрическое поле
в нем будет колебаться с частотой ш и с такой же частотой будет
происходить перезарядка пластин конденсатора. Замкнутый объем,
внутри которого происходят колебания электромагнитного поля, назы-
называется резонатором. Частота колебаний поля при отсутствии потерь
электромагнитной энергии называется собственной частотой резонатора.
Такой резонатор называется цилиндрическим. В резонаторе, так же как
и в волноводе, могут существовать колебания и стоячие волны раз-
различных .типов. Они обладают различными резонансными частотами.
Для того типа колебаний в цилиндрическом конденсаторе, который
только что рассмотрен, резонансные частоты а, колебаний равны
<°i — \iclroi гДе ?>; ~ корни функции Бесселя с нулевым индексом. Таким
образом, резонатор для этого типа колебаний имеет не одну резо-
резонансную частоту, а бесчисленное множество. Для других возможных
типов колебаний получаются'другие резонансные частоты. В реальном
резонаторе имеются потери энергии и колебания являются затухаю-
затухающими. Терминология и понятия, связанные с колебаниями в резонато-
резонаторах, полностью совпадают с употребляемыми при рассмотрении меха-
механических колебаний.
Задачи
9.1. Определить среднюю мощность плоских электромагнитных волн
излучения рамки с током I = не очень большой частоты насту-
= /0 cos fflf• Площадь рамки равна пает пробой в воздухе?
ст. Считать, что /0 = 10 А, а = 9.5. Плоская поляризованная электро-
= 100 см2, <о = 108 с. магнитная волна с круговой ча-
9.2. Используя данные задачи 9.1, най- стотой со = 106 с падает с ребра
ти максимальную плотность пото- на рамку из проводника, причем
ка излучения в плоскости рамки вектор индукции волны направлен
с током на расстоянии 200 м от перпендикулярно плоскости рам-
нее. ки. Линейные размеры рамки ма-
9.3. Определить плечо диполя, если лы по сравнению с длиной волны,
мощность его излучения равна Площадь рамки а = 100 см2, сред-
мощности излучения рамки с то- няя плотность потока энергии
ком в задаче 9.1. Частота колеба- в волне <S> = 1 Вт/м2. Найти
ний диполя равна частоте колеба- максимальную э. д. с. индукции,
ний силы тока в рамке, а каждый наводимую в контуре.
из зарядов диполя равен \q\= 9.6. На орбите Земли поток солнечной
= 10~4 Кл. энергии излучения равен примерно
9.4. Пробей в воздухе происходит при S = 1,4 кВт/м2. Найти радиус аб-
напряженности электрического по- солютно черной шарообразной
ля, равной ? г; 30 кВ/см. При ка- частицы с плотностью р = 5 г/см3,
кой плотности потока энергии для которой световое давление
442 9. Электромагнитные волны
в межпланетном пространстве
равно солнечному притяжению.
Масса Солнца равна тс — 2 х
х 1030 кг, гравитационная посто-
постоянная G = 6,7-10"" Н-м2/кг2.
Расстояние от Земли до Солнца
R = 150-106 км.
9.7. Плоский конденсатор с круглыми
пластинами радиусом а подсоеди-
подсоединен к постоянному источнику сто-
сторонних э. д. с. ?СТОр- Расстояние
между пластинами медленно из-
изменяется по гармоническому за-
закону d = d<> + Д sin cot. Найти на-
напряженность магнитного поля
между пластинами, порождаемого
токами смещения.
9.8. Рамка из п витков, охватывающая
площадь S, лежит в плоскости
XZ. В направлении оси X рас-
распространяется плоская электро-
электромагнитная волна, электрический
вектор которой параллелен оси
У: Еу = Ео cos (wf - кх). Найти
электродвижущую силу, индуци-
индуцируемую в рамке. Длина волны
много больше линейных разме-
размеров рамки.
9.9. Поток солнечной энергии на ор-
орбите Земли равен S = 1340 Вт/м2.
Чему равны амплитуды Ео и Во
плоской электромагнитной волны
с такой плотностью потока энер-
энергии?
9.10. Как следует из формулы F5.14),
давление электромагнитной вол-
волны на идеально отражающую по-
поверхность при угле падения 9
равно рв = 2и> cos2 9, где и> —
плотность электромагнитной
энергии в падающей волне. До-
Допустим, что на поверхность па-
падает изотропное излучение, т. е.
плотность потоков энергии, при-
приходящих со всевозможных на-
направлений, одинакова. Найти
давление волны на поверхность.
9.11. Найти амплитуду напряженности
электрического поля излучения
электрического диполя в плоско-
плоскости, проходящей через диполь
перпендикулярно его направле-
направлению, на расстоянии 10 км от
диполя при мощности излучения
диполя 10 кВт.
9.12. Среда между обкладками плоско-
плоского конденсатора имеет диэлект-
диэлектрическую проницаемость е и
обладает небольшой электро-
электропроводимостью у (неидеальный
диэлектрик). Емкость конденса-
конденсатора С. К обкладкам конденса-
конденсатора прикладывается разность
потенциалов U, после чего они
изолируются. Найти закон изме-
изменения величины заряд* со вре-
временем на каждой из обкладок
конденсатора и ток смещения,
протекающий через конденсатор.
Ответы
9.1. <Р> = Ho©4/go2/A2jtc3) = 0,124 Вт. 9.2. SmM = цо(о4%а2/A6к2с*г2) = 0,47 х
х 10 Вт/м2. 9.3. I =/оа/(| <j | с) = 3,3 ¦ 10 м = 0,33 мм. 9.4. <S> =
= [eo/D(io)]1/2?j = 1,2-Ю3 кВт/см2 =12 ГВт/м2. 9.5. ^мак = l^2 <s> I1» x
-5CD2
х (еоцоI/4 ош = 9 мВ. 9.6. г = = 0,5 • 10 м. 9.7. Н„ = -е0 ^CTop<oAr x
х cos cof/[2 {d0 + A sin югJ]. 9.8. 2 инд =* nft;S?0 sin cot. 9.9. Eo = 1005 В/м, Bo =
= 3,35 10 Тл. 9.10. р = и-пол/3. 9.11. Eo = 0,095 В/м. 9.12. Q = i
10
§ 67
Флуктуации
в контуре с током.
Шум сопротивления
и шумы
Шумы в контуре с током обусловлены
дискретным характером носителей за-
заряда и фпуктуациями тока. Шумы
принципиально полностью неустрани-
неустранимы, но могут быть уменьшены. В оп-
определенных условиях возможно детек-
детектирование полезных сигналов ниже
уровня шумов.
§68
Дробовой шум
444 10. Флуктуации и шумы
§ 67. Флуктуации в контуре с током.
Шум сопротивления
Обсуждаются физические причины, обуслов-
обусловливающие существование шума, и рассмат-
рассматриваются количественные характеристики
шума в цепях с током.
о равнораспределении энергии по степени свободы. В ста-
статистической физике важную роль играет положение о том, что
в состоянии термодинамического равновесия на каждую степень сво-
свободы системы приходится одна и та же энергия, равная к Т/2 (к —
постоянная Больцмана, Т — термодинамическая температура). Нагляд-
Наглядным проявлением справедливости этого утверждения является броунов-
броуновское движение. Средняя кинетическая энергия поступательного движе-
движения <(mu2/2)> броуновской частицы удовлетворяет соотношению
(mv2/2y = ЗкТ/2, поскольку имеется три степени поступательного
движения.
{Применение теоремы о равнораспределении энергии к свободному
гальванометру. Если на упругой нити свободно подвешено зеркаль-
зеркальце, то по теореме о равнораспределении оно не может быть абсолютно
неподвижным. В результате взаимодействия зеркальца с тепловым
движением молекул воздуха возбуждаются его крутильные колебания
и на каждую степень свободы при этом должна приходиться энергия
кТ/2. Напомним, что теорема о равнораспределении энергии по сте-
степеням свободы относится не только к кинетической, но и к потенциаль-
потенциальной энергии осциллятора.
Обозначим D — модуль кручения нити, ср — угол отклонения зер-
зеркальца от положения равновесия (рис. 265). Уравнение крутильных
колебаний имеет вид
7ф = -йф, F7.1)
где J — момент инерции зеркальца относительно оси кручения. Умно-
Умножая обе части F7.1) на ф и интегрируя полученное выражение, находим
закон сохранения энергии:
+ 7г Dtp2 = const. F7.2)
Поскольку на каждую степень свободы приходится энергия кТ/2,
из F7.2) получаем
<72./ф2> = <72tf<P2> = ЧгЪТ F7.3)
и, следовательно,
<Ф2> = kT/D. F7.4)
Это означает, что зеркальце не может находиться в положении
равновесия, а колеблется около него со средним квадратом угла
отклонения F7.4). Таким образом F7.4) характеризует отклонение угла
§ 67. Флуктуации в контуре с током. Шум сопротивления 445
265
266
Флуктуации крутильных колеба- ^Шк Флуктуации в колебательном кон-
ний ^рг туре
от средней величины, т. е. описывает флуктуации. Ясно, что если
имеется некоторое крутильное колебание, то по принципу суперпозиции
можно заключить, что F7.4) характеризует флуктуацию квадрата
амплитуды.
флуктуации в колебательном контуре. В колебательном контуре
(рис. 266) происходят колебания с частотой со = 1/J/LC, физическая
сущность которых заключается во взаимопревращении энергии элект-
электрического поля в конденсаторе и энергии магнитного поля в индук-
индуктивности. Закон сохранения энергии имеет вид
67BС) + LP/2 = const, F7.5)
где Q — заряд на обкладках конденсатора, / - сила тока в контуре.
Нельзя себе представить контур, в котором абсолютно отсутствуют
токи, а на обкладках конденсатора не возникают заряды. Точнее
говоря, такую ситуацию можно себе представить лишь при темпе-
температуре О К. При температуре, отличной от О К, тепловое движение
электронов приведет к возникновению зарядов на обкладках конденса-
конденсатора и токов в контуре. По теореме о равнораспределении имеем
<б2/BО> = <LI2/2> = кТ/2. F7.6)
Следовательно, средний квадрат заряда на обкладках конденсатора
и средний квадрат силы тока равны
<@2>=/сТС, <(/)*>= kT/L.
F7.7)
Исходя из принципа суперпозиции, можно сказать, что F7.7) пред-
представляет собой средние квадратичные флуктуации величин заряда и
силы тока в колебательном контуре.
распределение флуктуации по частотам, формула F7.7) дает лишь
полную среднюю квадратичную величину флуктуации и ничего
не говорит о том, как она распределяется по частотам. Чтобы
ответить на этот вопрос, необходимо решить уравнение колебаний
для контура, на который действуют случайные силы, представив их
в виде ряда (интеграла) Фурье по частотам:
С = I UJ". F7.8)
446 10. Флуктуации и шумы
Уравнение E0.10) доя колебаний заряда конденсатора принимает вид
IQ + RQ + QIC = X VJ~, F7.9)
откуда
что проверяется дифференцированием. Для среднего квадрата ампли-
амплитуды <| QQ* |> = <| Q |2>, отсюда находим
<\Q\2> = <QQ*> = \^ (_L(B2 + Ж(В +Ш1/с)(-?ю2 - 1Кш + I/O /'
F7.11)
Электродвижущие силы, возбуждающие колебания различных частот,
являются независимыми и некоррелированными между собой. Поэтому
при усреднении в F7.11) члены с со Ф а' пропадают и остается
<е2> = <i q I2>=^
где <22> и <17щ> — средние значения от действительных квадратов
амплитуд соответствующих величин.
Теперь перейдем к непрерывному спектру частот, поскольку пред-
предшествующие вычисления проделаны для дискретного спектра лишь
с целью упрощения вычислений. Фактический спектр является непре-
непрерывным. От средних квадратичных величин для частот дискретного
спектра необходимо перейти к плотностям соответствующих величин.
Средний квадрат полного заряда составляется из вкладов отдельных
частот. Поэтому
^§Ld^' F7.13а)
о
где d <2ш>/с1со — плотность квадратов амплитуд колебаний заряда;
d <бш) — средний квадрат амплитуды колебаний заряда, приходящейся
на интервал частот (со, со + doo). Под знаком суммы в F7.12) произ-
произведем замену:
<Ctf>-^p-d«o, F7.136)
понимая под d <U*>/doo — плотность распределения квадратов ампли-
амплитуд напряжений по частотам. После такой замены можно в F7.12)
перейти от суммы к интегралу. В результате получаем
§ 67. Флуктуации в коигуре с током. Шум сопротивления 447
откуда
d<G2>=(L(D2-l/C)" + K2a>2- F7Л5)
HI ум сопротивления. Средняя энергия гармонических колебаний про-
пропорциональна квадрату амплитуды. Поэтому плотность среднего
квадрата амплитуды колебаний характеризует плотность их энергии.
Дальнейший анализ основывается на предположении, что средняя плот-
/d<[72> \
ность квадратов амплитуд — = А не зависит от частоты. Обос-
V dco ;
нование его справедливости основывается на случайном характере
электродвижущих сил. Поэтому F7.14) можно записать в виде:
о
Интеграл вычисляется элементарными методами и приводит к ра-
равенству
dco nC
( 7)
J (L&2-Т/СJ +R2a2 2R'
о
Из F7.7) с учетом F7.16) и F7.17) находим
d <C/2> = B/п)IcRTdw. F7.18)
Отсюда на основании F7.15) следует, что
.,,«24 B/71)/СТО dco
(Leo2 - 1/СJ
F7.19)
Необходимо обратить внимание на то, что — ш определяет
плотность среднего квадрата амплитуды, отнесенную к интервалу
круговых частот со. Очень часто пользуются плотностью среднего
квадрата амплитуды, отнесенной не к круговой частоте со = 2п/Т,
а просто к частоте v = 1/Г, т. е. величиной —- v . Учитывая, что
со = 2nv, do = 2л dv, находим
^iEA. = _L d <У "> . F7.20)
dco 2л dv
Тогда [см. F7.18)]
d <{72> = 4kTR dv, F7.21)
— формула Найквиста: средний квадрат амплитуды напряжения флук-
флуктуации пропорционален интервалу частот и зависит только от сопро-
сопротивления в контуре и температуры. Экспериментально существование
448 10. Флуктуации и шумы
таких флуктуации было обнаружено Джонсоном. Эти флуктуации
называют шумом сопротивлений или шумом Джонсона.
Г^ квивалентный генератор шума. Флуктуации, обусловленные сопро-
^тивлением R, средний квадрат напряжения которых определяется
формулой F7.21), могут быть представлены как результат действия
генератора э. д. с. Uv и внутреннего сопротивления R. Эквивалентный
генератор тока шунтирован сопротивлением R и характеризуется
(в соответствии с законом Ома) средним квадратом силы тока:
d </2v> = 4kTdv/R. F7.22)
A/I ощность шума генератора. Антенна, с помощью которой прини-
принимаются радиосигналы, направляющиеся затем в приемник, по
своей роли в цепи эквивалентна генератору с соответствующим
внутренним импедансом. Ее согласование с приемником состоит в том,
чтобы сделать сумму реактивных составляющих импедансов антенны
и приемника равной нулю, а их активные сопротивления равными
между собой (см. § 49). При этом максимальная мощность, которую
генератор (антенна) может отдать в приемник [см. D9.35)], равна
Л,.макс=<^>/DЯ), F7.23)
где <1/2> — средний квадрат э. д. с. антенны; К — ее внутреннее сопро-
сопротивление, равное сопротивлению нагрузки.
Пусть нагрузочное сопротивление R са_мо по себе не производит
шума и является, например, омическим сопротивлением, поддерживае-
поддерживаемым вблизи температуры О К. Можно также представить себе в ка-
качестве нагрузки идеальный приемник, который сам по себе не обладает
никаким внутренним шумом. Тем не менее, в принимаемом с антенны
сигнале будет содержаться шум, мощность которого в соответствии
с F7.23) и F7.21) равна
^р F7.24)
Этот шум в наушниках при достаточном усилении будет слышен
и никакими усовершенствованиями приемника от него избавиться
нельзя. Его можно также увидеть на экране осциллографа. Увеличение
коэффициента усиления приемника пропорционально увеличит на вы-
выходе из приемника как полезный сигнал, так и шум F7.24), поданный
на его вход, не изменив соотношения между ними.
аксимальная чувствительность. Сигнал можно детектировать, если
его мощность будет больше мощности шума. Поэтому из F7.24)
для минимальной мощности детектируемого сигнала получается выра-
выражение
dP0 = kTdv, F7.25)
справедливое для идеального приемника. Эта мощность представляет
порог чувствительности приемника.
§ 67. Флуктуации в контуре с током. Шум сопротивления 449
Единственной возможностью повышения чувствительности (при
фиксированной температуре) является уменьшение ширины полосы
используемых частот dv. Однако при этом уменьшается количество
информации, которую несет с собой сигнал, и в каждом случае имеется
нижний предел, до которого можно сужать полосу. Например, для
передачи речи по радио с помощью амплитудной модуляции без очень
большого искажения необходимо иметь полосу порядка dv = 10 кГц.
При комнатной температуре (Т = 290 К) это для минимальной детек-
детектируемой мощности дает
dP0 = 1,38- КГ23-290-104 Вт = 4- КГ17 Вт. F7.26)
Для передачи телевизионных изображений минимальная ширина
полосы должна быть порядка 4 МГц, поскольку объем информации
для восстановления изображения значительно больше, чем для восста-
восстановления речи. При этих условиях минимальная мощность сигнала,
подаваемого на идеальный приемник, составляет 1,6-10~14 Вт.
Г^ квивалентная шумовая температура приемника. Фактически прием-
приемник сам является источником дополнительных шумов, которые
накладываются на шумы антенны. Поэтому мощность dPj минималь-
минимального сигнала, который может быть детектирован, больше, чем dP0,
на мощность йРщ, внутреннего шума приемника:
dP1=dP0 + dPnp. F7.27)
Мощность dPnp внутреннего шума приемника принято выражать
по формуле F725) посредством эквивалентной шумовой температуры
Тэ в виде
dPnp = fcT3dv. F7.28)
У идеального приемника Тэ = 0 К. Однако очень близко подходить
к этому пределу в практике нет необходимости. Достаточно эквива-
эквивалентную температуру сделать примерно раз в десять меньше соот-
соответствующей температуры генератора (антенны), чтобы дополнительный
шум приемника был практически несуществен.
коэффициент шума приемника. При комнатной температуре на
интервал частот dv = 1 в соответствии с F7.26) приходится мощ-
мощность dP01 = 4-10~21 Вт. Шумовая характеристика приемника описы-
описывается коэффициентом шума
F7.29)
Обычно он выражается в децибелах.
/"Отношение сигнал — шум. Сигнал детектируется тем надежнее, чем
больше он превышает уровень шума, что особенно важно, напри-
например, для качественной передачи и воспроизведения музыкальных
произведений. Эта характеристика приемных и воспроизводящих
устройств определяется отношением амплитуды напряжения сигнала к
450 10. Флуктуации и шумы
амплитуде напряжения шума. Поскольку это
отношение в обычных условиях составляет
очень большое число, его выражают в де-
децибелах по формуле
ЛГ = 20log -^-=10log Ж,
267
К вычислению шума на сетке
вакуумного триода
О При полном согласовании
нагрузки с генератором от-
отношение сигнал —шум не
является самым лучшим.
При рассогласовании на-
нагрузки с генератором по-
посредством увеличения со-
сопротивления нагрузки R2
можно улучшить это отно-
отношение примерно в два
раза. К такому же заклю-
заключению можно прийти и
через оценку чувствитель-
чувствительности — при рассогласова-
рассогласовании нагрузки с генератором
посредством увеличения со-
сопротивления нагрузки R2
чувствительность увеличива-
увеличивается.
F7.30)
где Uc и Um — соответственно амплитуды
напряжения сигнала и шума.
Рассмотрим для примера отношение сиг-
сигнал — шум у вакуумного триода (рис. 267).
Сигнал подается на вход в цепь между
сеткой и катодом. Источник сигнала харак-
характеризуется электродвижущей силой UT и
внутренним сопротивлением Rt. Мощность
шума сопротивления генератора на основа-
основании F7.21) равна
4/cTdv = VlJRi, F7.31)
где иш1 — э. д. с. эквивалентного генератора
шума, который включен в цепь последова-
последовательно с Rh и генератором GГ.
Другим источником шума является со-
сопротивление R, с которого снимается на-
напряжение. Мощность шума этого источника
равна
4fcTdv = Uli/R, F7.32)
где иш2 — э. д. с. эквивалентного генератора
шума.
Для вычисления мощности шума на сет-
сетке примем во внимание, что нагрузкой для
генератора шума иш\ является сопротивле-
сопротивление R2, а для генератора шума Um2 —
сопротивление R^. Ясно, что генераторы
шума действуют независимо и поэтому сред-
средний квадрат напряжения полного шума ра-
равен сумме средних квадратов напряжений
шумов, создаваемых каждым из генераторов.
Поэтому для среднего квадрата шумово-
шумового напряжения на сетке получаем
2
= 4kTdv
R2R\
R,
F7.33)
§ 68. Дробовой шум и шум тока 451
Примем во внимание, что средний квадрат амплитуды сигнала
на сетке равен
4 F734)
Из F7.33) и F7.34) получаем отношение среднего квадрата напря-
напряжения сигнала к среднему квадрату напряжения шума на сетке:
и\ т r2 1_р r2 F735)
Ul 4kTdv Rt+R2 Ri kTdvR1+R2'
где P = I72r/DR1) — максимальная мощность сигнала, отдаваемого гене-
генератором во внешнюю цепь [см. F7.23)]. Из формулы F7.35) видно,
что при полном согласовании нагрузки с генератором (R2 = Ri) отно-
отношение сигнал — шум не является самым лучшим. Наоборот, при
рассогласовании путем увеличения сопротивления нагрузки R2 можно
улучшить это отношение примерно в два раза.
К такому заключению можно прийти и через оценку чувстви-
чувствительности. Минимальная мощность сигнала генератора, который на
сетке еще можно отличить от шума, получается из F7.35), если
u?/ul = u
Ri+R2. F7.36)
Очевидно, что минимальная детектируемая мощность при согласо-
согласовании нагрузки с генератором (R2 =Ri) равна 2/cTdv, а при рассогла-
рассогласовании (R2 » Rt) — kTdv, т.е. при рассо?. пасовании уогрузки с генера-
генератором чувствительность увеличивается.
Если генератором в рассматриваемой схеме является антенна, то
все эти заключения применимы к системе антенна — приемник.
§ 68. Дробовой шум и шум тока
Рассматривается физическая причина воз-
возникновения дробового шума и анализируется
его распределение по частотам. Даются
основные характеристики шума тока.
жжсточник дробового шума. Электрический ток представляет собой
движение дискретных элементарных зарядов, а не непрерывный
поток заряда. Поэтому он дает последовательность импульсов тока,
каждый из которых обусловлен прибытием в рассматриваемую точку
отдельного электрона. Ток через некоторую площадку подобен потоку
дробинок через нее, выброшенных из некоторого устройства и распре-
распределенных по времени хаотически. Ясно, что число дробинок, пере-
пересекающих поверхность в последовательные одинаковые малые проме-
промежутки времени, будет испытывать значительные флуктуации. Анало-
Аналогично, из-за дискретного характера зарядов будет флуктуировать
и сила тока. Эти флуктуации называются дробовым шумом.
452 10. Флуктуации и шумы
распределение шума по частотам. Прибытие каждого электрона
эквивалентно импульсу тока, продолжительность которого чрезвы-
чрезвычайно мала. При точечном электроне ее следует считать нулевой,
а импульс тока бесконечным, т. е. импульс представлять 8-функцией.
Поскольку заряд, содержащийся в импульсе тока, равен заряду элект-
электрона е, можно представить ток, обусловленный прибытием электрона
в момент времени tt, в виде
i(t) = eb(t-td. F8.1)
Пусть Т — большой интервал времени, в течение которого прибы-
прибывает в среднем N электронов. Средняя сила тока, обусловленного
прибытием одного электрона на этом интервале времени, равна
<!> = е/Т, а средняя сила тока, обусловленного прибытием N электро-
электронов, определяется выражением </> = N <i> = Ne/T. Однако электроны
прибывают неравномерно, вследствие чего возникают флуктуации тока,
порождающие шум. Для определения спектрального состава шума
представим силу тока i(t) в виде ряда Фурье на интервале ( — Т/2, Т/2):
i (t) = ao/2 + Y, (ап cos nat + bn sin nat) (ш = 2п/Т), F8.2)
я = 1
где
Г/2
2 Г
а„ = у i(t)cosncatdt (п = 0, 1, 2, ...), F8.3a)
-Г/2
Г/2
/
К = y ' Wsi
sin nm dt (" = 1,2,...). F8.36)
-T/2
Учитывая правило интегрирования с 8-функцией
из F8.3а) и F8.36) с учетам F%Л) получаем
2е 2е
а„ = —cos nati, Ь„ = —sin ncot,-. F8.4)
Тогда [см. F8.2)]
00
i (t) = y + Цг У cos па (t - ti). F8.5)
n=l
Среднее значение квадрата силы тока n-й компоненты равно
,.2v 4е2 / , 2кп \ 2е2
<'»> = уг\cos2 -jr-t> = yt- F8-6)
Поскольку отдельные электроны движутся беспорядочно и некорре-
некоррелированно друг с другом, их вклады в разложение в ряд Фурье для
§ 68. Дробовой шум и шум тока 453
силы тока будут отличаться фазами. При вычислении квадрата флук-
флуктуации силы тока усреднение по фазе обратит в нуль все члены
с неравными частотами и в ряду останутся лишь члены с одинаковыми
частотами. Поэтому для среднего квадрата флуктуации n-й компоненты
Фурье силы тока N электронов, прибывающих в течение времени Г,
имеем
<7*„> = N <in2> = 2e2N/T2 = 2eI0/T, F8.7)
где /0 = eN/T — средняя сила тока.
Число компонент ряда Фурье, частоты которых заключены между
v и v + dv, равно Tdv, поскольку эти компоненты отстоят друг от
друга на равных расстояниях по частотам на 1/Г. Интервал Т можно
считать очень большим, а расстояние между соседними частотами
[(п + 1)/Т] - (п/Т) = 1/Г- очень малым.
Суммируя вклады от этих компонент в интервале частот dv полу-
получим на основе формулы F8.7) для средней квадратичной флуктуации
силы тока следующее выражение:
d </2> = </„2> Tdv = 2elo dv. F8.8)
Эта формула описывает дробовой шум.
Соотношение F8.8) называется формулой Шоттки. Заметим, что если
в спектральный интервал частот v включить их отрицательные значе-
значения, то множитель 2 в формуле F8.8) пропадает. Так обычно посту-
поступают при использовании экспоненциальной формы рядов или интегра-
интегралов Фурье.
щум тока. На очень малых частотах возникают шумы, обусловленные
различными неоднородностями сопротивлений. Средний квадрат
амплитуд напряжений этого шума убывает обратно пропорционально
частоте.
Экспериментальное изучение этого шума, называемого шумом тока,
приводит к формуле
<(Д17J> = <xll/v, F8.9)
где а — эмпирическая постоянная, зависящая от геометрии сопротив-
сопротивления и его материала. В массивных металлических проводниках шум
практически отсутствует. В различного рода композиционных сопро-
сопротивлениях он очень велик.
Природа этого шума в настоящее время еще до конца не выяснена.
Однако с увеличением частоты его роль во всех случаях становится
пренебрежимо малой.
]у[етоды уменьшения шумовых помех, Шумовые помехи искажают
форму полезного сигнала и их желательно уменьшить. Количе-
Количественно соотношение между сигналом и шумом характеризуется от-
отношением сигнал — шум. Задача состоит в том, чтобы увеличить это
отношение.
Усиление сигнала для этой цели не подходит, поскольку усилитель
в одинаковое число раз изменяет как сигнал, так и шум, подаваемые
454 10. Флуктуации и шумы
/\ -
(а)
(а)
(a) t
а)
б)
Иллюстрация процесса выделе-
выделения сигнала на фоне сильного
шум»
на его вход, а, кроме того, в процессе прохождения сигнала добавляет
к нему свой внутренний шум. Поэтому усиление уменьшает отноше-
отношение сигнал — шум, т. е. ухудшает этот показатель и не может служить
методом уменьшения шумовых помех.
Шум сопротивления может быть уменьшен за счет уменьшения
температуры, при которой работают соответствующие устройства.
Этот метод широко применяется, однако он имеет свои пределы.
Во-первых, он значительно усложняет работу и, во-вторых, при силь-
сильных охлаждениях элементы устройств изменяют свои электрические
характеристики, причем иногда необратимо.
Дробовой шум и шум тока ослабляются при уменьшении силы тока,
а шум тока уменьшается еще и при увеличении частоты сигнала.
Увеличение частоты сигнала ограничено высокочастотными характе-
характеристиками контуров и элементов цепи.
Все виды шумов уменьшаются при уменьшении полосы пропуска-
пропускания. Однако ширина полосы пропускания ограничена свойствами сиг-
сигнала, поскольку любой сигнал имеет конечную ширину и уменьшение
полосы пропускания ниже этой ширины существенно искажает сигнал,
т. е. вводит новый шум.
Таким образом, улучшение технических характеристик устройств для
приема сигналов позволяет улучшить отношение сигнал — шум, но
наталкивается на ограничения принципиального порядка. Поэтому раз-
разработаны методы приема сигналов, позволяющие преодолевать эти
ограничения. Один из распространенных методов состоит в следующем.
Пусть имеется некоторый периодически повторяющийся сигнал,
очень сильно искаженный шумовым фоном (рис. 268, а). Период сиг-
сигналов может быть определен с достаточной точностью, поскольку
шум не искажает периода. После этого можно синхронизировать момент
измерения сигнала с периодичностью его изменения, т. е. производить
измерение значения сигнала много раз в одной и той же точке его
периода, например, точке а на рис. 268, а. Каждое измерение из-за
наложения шума дает различное значение, но среднее значение боль-
большого числа измерений приводит с соответствующей точностью к ве-
величине сигнала в этой точке периода. В принципе, эта точность может
быть беспредельно повышена, если только соответствующим образом
увеличить число измерений. Проделав такие измерения для различных
точек периода, получим форму сигнала на одном периоде без шумовых
искажений (рис. 268, б).
Приложение 455
ПРИЛОЖЕНИЕ
I. Единицы СИ, используемые в книге
Величина
наименование
Длина
Масса
Время
Сила тока
Температура
Количество вещества
Сила света
обозна-
обозначение
размерность
Освоение единицы
/
т
t
I
Т
V
/
L
М
Т
I
0
N
J
Производные единицы
Скорость
Ускорение
Сила
Давление
Импульс
Энергия
Мощность
Момент инерции
Момент силы
Момент импульса
Электрический заряд
Плотность заряда объемная
Плотность заряда поверхност-
поверхностная
Плотность заряда линейная
Абсолютная диэлектрическая
проницаемость
Электрическая постоянная
Относительная диэлектричес-
диэлектрическая проницаемость
Напряженность электрическо-
электрического поля
о» и
а
F
Р
Р
W, U, Е
Р
J
М
L
Q,q
Р
<7
Т
Е
Ео
е,
Е
LT-1
LT-2
LMT-2
L-'MT-2
LMT-1
L2MT ~2
L2MT
L2M
L2MT-2
L2MT-1
TI
L-2TI
L-'TI
L^M-'Ttl-
L-3M-iT4i
Единица
наименование
метр
килограмм
секунда
ампер
кельвин
моль
кандела
метр в секунду
метр в секунду
в квадрате
ньютон
паскаль
килограмм-метр в
секунду
джоуль
ватт
килограмм-метр
в квадрате
иьютон-метр
килограмм-метр
обозначе-
обозначение
м
кг
с
А
К
моль
кд
м/с
М/С2
н
Па
кг-м/с
Дж
Вт
кг-м2
Нм
кг • м2/с
в квадрате в се-
секунду
кулон
кулон иа кубичес-
кубический метр
кулон на квадрат-
квадратный метр
кулон иа метр
'¦ фарад на метр
- фарад иа метр
Кл
Кл/мЗ
Кл/М2
Кл/м
Ф/м
Ф/м
безразмерная величина
LMT-3!-'
вольт на метр
В/м
456 Приложение
Продолжение
Величина
наименование
обозна-
обозначение
размерность
Единица
наименование
обозначе-
обозначение
Поток напряженности элект- N
рического поля
Потенциал электрического по- ср
ля
Электрический момент диполя р
Поляризованность Р
Электрическое смещение D
Поток электрического сме- Ч*
щения
Электрическая емкость
Объемная плотность энергии
электрического и магнит-
магнитного полей
Электрическое напряжение U
Электрическое сопротивление R
Подвижность носителей за- Ъ
рядов
Плотность объемного тока j
Магнитный момент электри- рт
ческого тока
Магнитная индукция В
Магнитный поток Ф
Напряженность магнитного Н
поля
Индуктивность
Абсолютная магнитная про-
проницаемость
Магнитная постоянная ца
Относительная магнитная про- цг
ницаемость
Намагниченность /
Частота колебаний v
Круговая частота колебаний со
Плотность потока энергии S
электромагнитного поля
вольт-метр
В м
В
LTI
L-2TI
LTI
TI
кулон-метр Кл • м
кулон на квадрат- Кл/м2
ный метр
кулон на квадрат- Кл/м2
ный метр
кулон Кл
С L-2M-lrT4I2 фарад Ф
w L~'MT~2 джоуль на куби- Дж/м3
ческий метр
L2MT-3I-' вольт В
L2MT~3I~2 ом Ом
М ~ 'Т21 квадратный метр м2/(В • с)
на вольт-секун-
вольт-секунду
L ~Ч ампер на квадрат- А/м2
ный метр
L4 ампер — квад- А • м2
ратный метр
MT~2I-1 тесла Тл
L2MT-2I-1 вебер Вб
L~"'l ампер на метр А/м
L L2MT I ~2 генри
ц LMT~2I~2 генри на метр
ц0 LMT ~Ч ~2 генри на метр
цг безразмерная величина
Mi
-з
ампер на метр
герц
секунда в минус
первой степени
ватт на квадрат-
квадратный метр
Гн
Гн/м
Гн/м
А/м
Гц
с-1
Вт/М2
Приложение 457
П. Соотношение между формулами СИ и системы Гаусса
Хотя в настоящее время уже почти везде произведен переход к СИ,
умение переводить формулы из записи в одной системе единиц к записи в другой
все еще иногда требуется. Для этого используется следующая таблица:
Наименование
величины
Сила тока
Плотность тока
Электрический
заряд
Плотность за-
заряда
Проводимость
Емкость
Напряженное гь
электрическо-
электрического поля
Электрическое
смещение
Напряженность
магнитного
поля
Магнитная ин-
индукция
Поток магнит-
магнитной индукции
Индуктивность
Поляризован-
ность
Намагничен-
Намагниченность
Электрическое
сопротивле-
сопротивление
СИ
/
;
Q
р
У
с
Е
D
Н
В
Ф
L
Р
J
R
Система
Гаусса
DяеоI/2/
Dяе0I^
D7ГЕ0)'/2 Q
D*еоI/2Р
4яЕ0у
4яе0С
Dяеа)-1/2?
[цо/Dя)]'/25
ЫDп)]У2Ф
Dяеа)-12,
4кеоР
Dк/иаI/2/
Dтао)-'Л
Наименование
величины
Электрический
дипольный
момент
Магнитный
момент тока
Скалярный
потенциал
Векторный
потенциал
Скорость све-
света
Магнитная во-
сприимчи-
сприимчивость
Диэлектричес-
Диэлектрическая воспри-
восприимчивость
Диэлектричес-
Диэлектрическая проница-
проницаемость
Магнитная
проница-
проницаемость
Относитель-
Относительная диэлек-
диэлектрическая
проницае-
проницаемость
Относитель-
Относительная магнит-
магнитная прони-
проницаемость
СИ
Р
Рт
Ф
А
X
ш
8
Ц
<=г
Система Гаусса
(.4пеоI'2р
Dя/цо)'/2/>т
Dя80)-1'/2ср
MW]ll2A
с
4кХ
4яж
??о
Wo
е/е0
Ц/Цо
Правила пользования таблицей. Для того чтобы перевести соотношение,
записанное в СИ, в соответствующую формулу в системе Гаусса, необходимо
символ, обозначенный в колонке «СИ», заменить символом в колонке «Система
Гаусса». Пользуясь этим правилом в обратном направлении, можно перейти
от формул в системе Гаусса к формулам в СИ. При этих переходах механи-
механические и другие неэлектрические и немагнитные величины остаются неизме-
неизмененными. Неизменны также производные по координатам и времени.
458 Приложение
Примеры использования таблицы
1. Записать уравнение Максвелла
(СИ)
в системе Гаусса. Имеем
rot [DяцоГ1/2 Н] = D7Г60I'2 j + ^
т. е.
rot H = —j + —.
с с 8t
2. Записать вектор Пойнтинга
S = [с/Dл)] Е х Н (система Гаусса)
в СИ. Имеем
S = (ti°e°^ [DяеоI/2 Е х D71Цо) Н] = Е х Н.
Примечание. Переход из СИ в систему Гаусса всегда приводит к правиль-
правильному результату. При переходе из системы Гаусса в СИ возможны ошибки,
если формула в системе Гаусса написана для вакуума. В этом случае D — Е,
В = Н и одна из величин в формуле может оказаться замененной другой,
а коэффициенты перевода для этих величин различны. Поэтому прежде чем
переводить формулу из системы Гаусса в СИ, необходимо позаботиться о том,
чтобы она была записана в форме, справедливой для среды, а не только
для вакуума.
Перевод числовых значений величин из одной системы единиц в другую
производится с помощью таблиц, приводимых в книгах по системам единиц.
III. Формулы векторной алгебры и анализа
1. Свойство смешанного произведения векторов:
А(ВхС) = (АхВ)С. (П.1)
2. Разложение двойного векторного произведения:
Ах(Вх С) = В(АС)-С(АВ). (П.2)
3. Определение векторного оператора набла:
V=iJc^+i,^+is^-, (П.З)
дх ду dz
где ix, i,,, iz — единичные векторы декартовой ортогональной системы координат.
4. Определение операции градиента:
grad ф = Уф. (П.4)
5. Определение оператора дивергенции:
div А = V • А. (П.5)
6. Определение операции ротора:
rot А = V х А. (П.6)
Приложение 459
7. Векторные тождества:
дх2 дуг 8z2 '
V х Уф = О, (П.8)
V • (V х А) = О, (П.9)
Vx(Vx A) = V(V-A)-V2A, (П.10)
x(Vx A) + A x (V x В), (П.13)
V(A-B) = B(V-A) + A(V-B) + (Bx V) x A + (A x V) x В, (П.14)
V-(AxB) = B-(Vx A)-A-(VxB), (П.15)
V x (фА) = ф (V x A) + (Уф) x А, (П.16)
Vx(Ax B) = (B-V)A-(A-V)B + A(V-B)-B(V-A). (П.17)
8. Теоремы Гаусса: замкнутая поверхность S окружает объем V. Вектор dS
элемента поверхности направлен по внешней нормали к ней:
J(V-A)dF=$A-dS, (П.18)
v s
J (V x A) dV = § dS x А. (П.20)
v s
9. Теоремы Стокса: замкнутый контур L ограничивает поверхность S.
Вектор dl элемента контура L совпадает с направлением положительного
обхода, который связан с направлением положительной нормали к поверхности
S правилом правого винта:
J(Vx A)-dS = §A-dl (П.21)
s l
J dS x Уф = § ф dl, (П.22)
S L
J(dS x V) x A = $dlx А. (П.23)
S L
10, Теоремы Грина:
J (q>V2i|/ - \|/У2ф) dV=§ (cpVvJ/ - х|/Уф) • dS, (П.24)
V S
I
v
(Уф x Vv|/)dV = -j фdS x (фУ\[» - »|/Уф), (П.25)
s
1
(П.26)
460 Предметный указатель
Предметный указатель
Автотрансформатор 364
Аккумуляторы 208
Ампер 60
Анизотропия 302
Антисегнетоэлектрики 193
Антиферромагнетики 304
Атомы 22
— неполярные 137
— полярные 137
Бетатрон 380
Вектор Пойнтинга 397
— смещения 143
Взаимодействие спин-орбитальное
294
Вибратор Герца 409
Волноводы 434, 440
Время релаксации 106
Газы плотные 182, 187
— разреженные 181, 186
Генератор тока переменного 314
— шума 448
Глубина проникновения 423
Градиент 91
Давление волн электромагнитных 428
Двигатели асинхронные 351, 353
— синхронные 351
Декремент затухания логарифмический
359
Диамагнетизм 291
Диамагнетики 264, 283, 288
Дивергенция 38, 39
Диполь 124
Диссоциация 234
Диэлектрики 22, 25, 139
— изотропные 139
— линейные 139
— нелинейные 139
— неполярные 180
— полярные 183
Добротность 359
Домены диэлектрические 191
Емкость 116
— конденсатора 122
— проводника 120
Жидкости полярные 188
85
Заряд 16, 29, 30, 31, 32, 44, 83,
— неподвижный 80
— объемный 200
— поверхностный 200
связанный 141
— пробный 54
— связанный 146
Закон Ампера 64
— Био - Савара 69, 259
— — — Лапласа 66
— Джоуля - Ленца 210, 212
— индукции электромагнитной 316,
318
— Кулона 44, 47, 48, 49, 84, 98, 144
— Кюри 293
Вейсса 191, 293, 302
— Ома 104, 105, 211
— сохранения заряда 37, 38, 43
— — энергии 206, 315
Закон тока полного 251, 252, 253
— трех вторых 245
Импеданс 341
Импульс фотона 429
— цуга волн электромагнитных
Индуктивность 322, 327
— взаимная 323, 324
Индукция взаимная 359
— поля магнитного 274, 301
— — обменного 301
— — электрическая 312
— электромагнитная 312
Кварк 19
Колебания бетатронные 383
Конденсатор 122, 123
Контур колебательный 357
Концентрация зарядов 34
428
Концепция близкодействия 49
— дальнодействия 49
Кристаллы ионные 188
Линии силовые 84, 85
Магнетики 264
Магнетосопротивление 230
Магниты 272
Метод измерения заряда резонансный
29
— изображений 128, 131, 147
— Кавендиша 45
— токов контурных 344
Момент дипольный 127, 135
— магнитный 19, 261, 282, 290, 294,
295
— сил 162
Мощность тока 209
— — переменного 346
— шума генератора 448
Намагниченность 265
— спонтанная 302
Напряжение 347
— шага 222
Напряженность задерживающая 299
— поля диполя 128
— — локального 178
— — магнитного 270, 276
— — насыщения 18
электрического 50, 109, ПО, 111,
125
Нейтрон 18
Нормировка потенциала 92
Облако электронное 136, 244
Оператор Лапласа 101
Опыт Эйнштейна — де Гааз 307
Опыты Милликена 28, 29
— Толмена и Стюарта 226
Отношение гиромагнитное 307
Парамагнетики 265, 283, 292
Перемагничивание 303
Петля гистерезиса 189, 298
Пироэлек грики 195
Плотность диполя 127
Предметный указатель 461
Плотность заряда объемная 33, 140,
161, 162
— — поверхностная 34, 111, 113, 140,
200
— потока энергии 397, 421
— сил поверхностная 167, 169
— силы Ампера 228
— тока 35, 36, 198, 237
— — насыщения 238, 244
— — объемная 266, 267, 335
— — поверхностная 269
— — смещения 378
— энергии поля магнитного 325
— — — электрического 155
Подвижность зарядов 240
— электронов 230
Подрешетка 305
Поле квазистационарное 336
— критическое 232
— локальное 178
— магнитное 55, 59, 61, 66, 255, 411,
440
— — вращающееся 353, 368
— насыщения 186
— потенциальное 201
— сил потенциальное 86, 90, 91
— соленоида 327
— тока элементарного 259
— Холла 229
— центрально-симметричное 255
— электрическое 50, 411
Поляризация 136
— ионная решеточная 137
— спонтанная 191
— элемента 207
Поляризованность 136
Потенциал 91, 92, 93, 94, 98", 100
— векторный 257, 265, 319, 405, 406,
410
Потенциал запаздывающий 408
— опережающий 409
— поля 409
— — проводника 116
— скалярный 320, 409
Поток вектора 38
Правила Кирхгофа 213, 342
Правило Ленца 337
462 Предметный указатель
Прецессия ларморова 290
— магнитная 288
Принцип суперпозиции 53, 54, 55
Проводимость электрическая 343
— — удельная 105
Протон 17
Пьезоэлектрики 193
Пьезоэффект 194, 195
Работа выхода термоэлектронная 24
— тока 209
Разность потенциалов 92
контактная 25, 26, 27
Распределение Больцмана 20
Резонанс напряжений 356
— парамагнитный 296
— токов 357
— ферромагнитный 305
Резонаторы 440
Ротор 87
Самоиндукция 337
Сверхпроводимость 231, 232
Сверхпроводники 232
Сегнетоэлектрики 189
Сила Ампера 64
— взаимодействия токов прямолиней-
прямолинейных 69
— Лоренца 63, 64, 72
— объемная 162, 165, 169, 282, 332
— поверхностная 165
— тока 37
— — насыщения 242
— электродвижущая сторонняя 202,
205
Скин-эффект 369, 424
— — аномальный 372
Скорость групповая 439, 440
— дрейфа 238
— фазовая 419, 424, 436, 439, 440
Спектр электронов энергетический
21, 22, 23
Спин 19
Среда неоднородная 218, 219
— однородная 217
Температура критическая 231
— Кюри 190
Вейсса 190, 191, 202, 304
— Нееля 304
Теория зонная 227
Теорема взаимности 118
— Гаусса 81, 82, 84, 99, 108, 114
— Ирншоу 95
Толщина скнн-слоя 371
Ток квазистационарный 336
— несамостоятельный 237
— однофазный 366
— переменный 340
— поверхностный 232
— — молекулярный 267
— самостоятельный 237, 239
— смещения 388, 389
— трехфазный 366
Токи Фуко 355
Точка Кюри 190
Трансформатор 360
— реальный 365
Угол Холла 230
Уравнение Даламбера 405, 406
— для потенциала векторного 258
— Лапласа 100
— непрерывности 43
— Пуассона 97, 100
Уравнения линяй передачи 402
— четырехполюсника 374
Условие бетатронное 380, 381, 382
— калибровки потенциалов 258
— Лоренца 405
Условия граничные 145, 146
Устойчивость вертикальная 383
— радиальная 382
Ферромагнетики 298
Ферримагнетизм 305
Фильтры 377
Флуктуации 445
Формула Гаусса — Остроградского
42, 43
— Клаузиуса — Моссотти 182
— Найквиста 447
— Ричардсона — Дешмана 245
— Стокса 89, 90
— Томсона 357
Предметный указатель 463
Функция Ланжевена 185
— Ферми — Дирака 24
Цепи разветвленные 214
Цепь замкнутая 213
Частота граничная 485
— ларморова 289
Четырехполюсники 373
Число волновое 420
Чувствительность максимальная 448
Шум дробовой 451
— сопротивления 447
— тока 453
Экран металлический 114
Экранировка магнитная 278
Электризация 26, 27
Электродвигатели 349
Электроды коаксиальные 218
Электролиты 236
Электропроводимость 234, 235, 236
Электропроводность 213
Электрон 16, 18
Элемент Вольта 205
— Даниэля 207
Элементы гальванические 204
Эмиссия термоэлектронная 241
Энергия взаимодействия обменного
300
— диполя 157
— зарядов 152, 153
— магнетика 328, 329
— момента магнитного 333
— поля зарядов поверхностных 156
— — полная 326
магнитного 321, 322, 325
— проводников заряженных 157
— собственная 153, 154, 160
— тела диэлектрического 157
— Ферми 23
— электромагнитная 398
Эфир мировой 49
Эффект Барнетта 309
— Мейсснера 232
— Холла 229
Алексей Николаевич Матвеев
Электричество и магнетизм
Зав. редакцией Е. С. Гридасова
Редактор Г. Н. Чернышева
Мл. редакторы С. А. Доровских,
Н. П. Майкова, Н. Г. Закалюкина
Художественный редактор В. И. Пономаренко
Технический редактор 3. А. Муслимова
Корректор В. В. Кожуткина
ИБ № 3590
Изд. № ФМ-678. Сдано в набор 04.08.82. Подп. в печать
25.05.83. Формат 60х90]/16. Бум. кн.-журн. Гарнитура
тайме. Печать высокая. Объем 29 усл. печ. л. 58,25 усл.
кр.-отт. 29,90 уч.-изд. л. Тираж 30 000 экз. Зак. № 555.
Цена 1 р. 50 к.
Издательство «Высшая школа»,
101430, Москва, ГСП4, Неглинная ул., Д. 29/14
Ордена Октябрьской Революции, ордена Трудового Крас-
Красного Знамени Ленинградское производственно-техниче-
производственно-техническое объеднненне «Печатный Двор» имени А. М. Горького
Союзполиграфпрома при Государственном комитете
СССР по делам издательств, полиграфии и книжной
торговли. 197136, Ленинград, П-136, Чкаловский пр., 15.