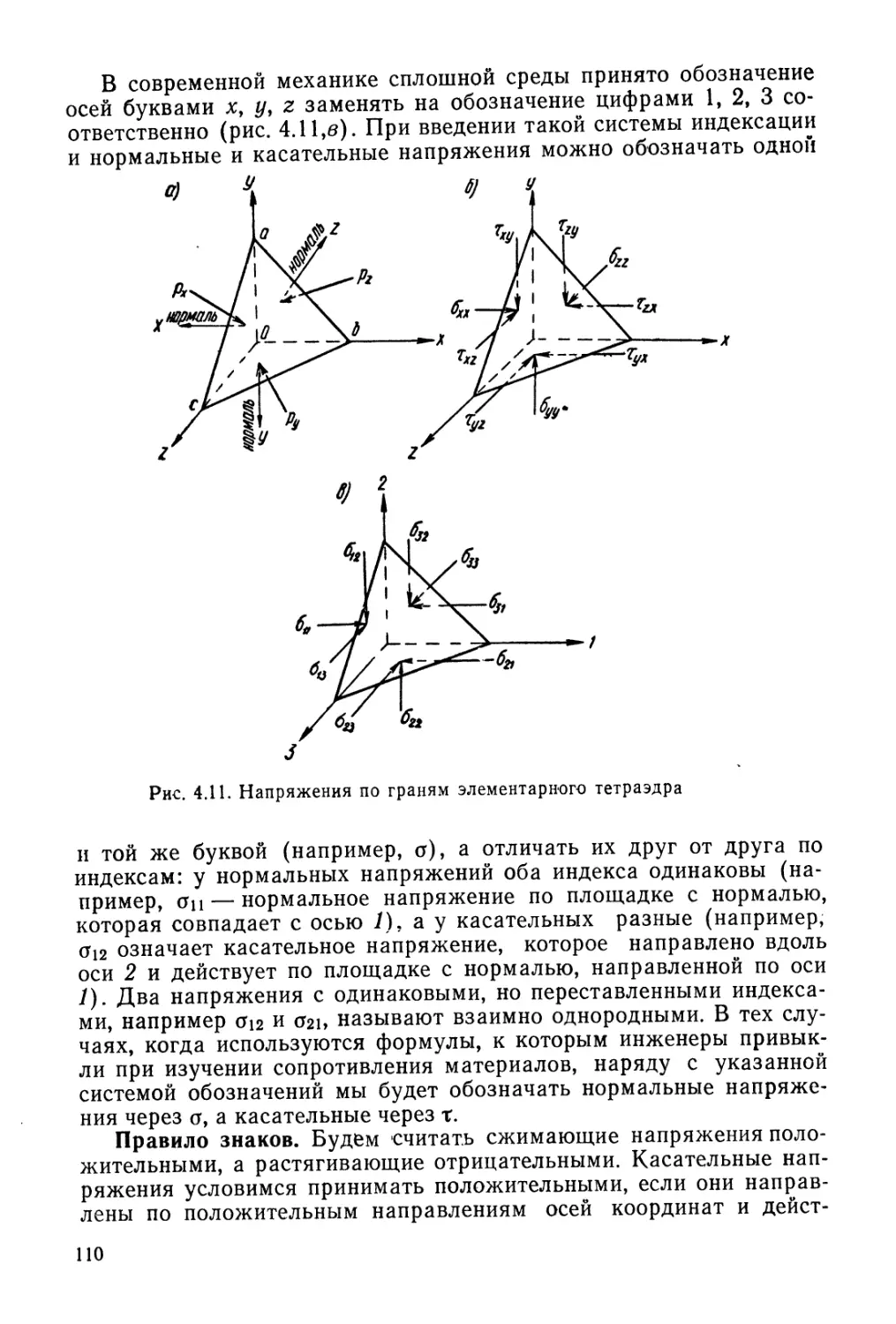
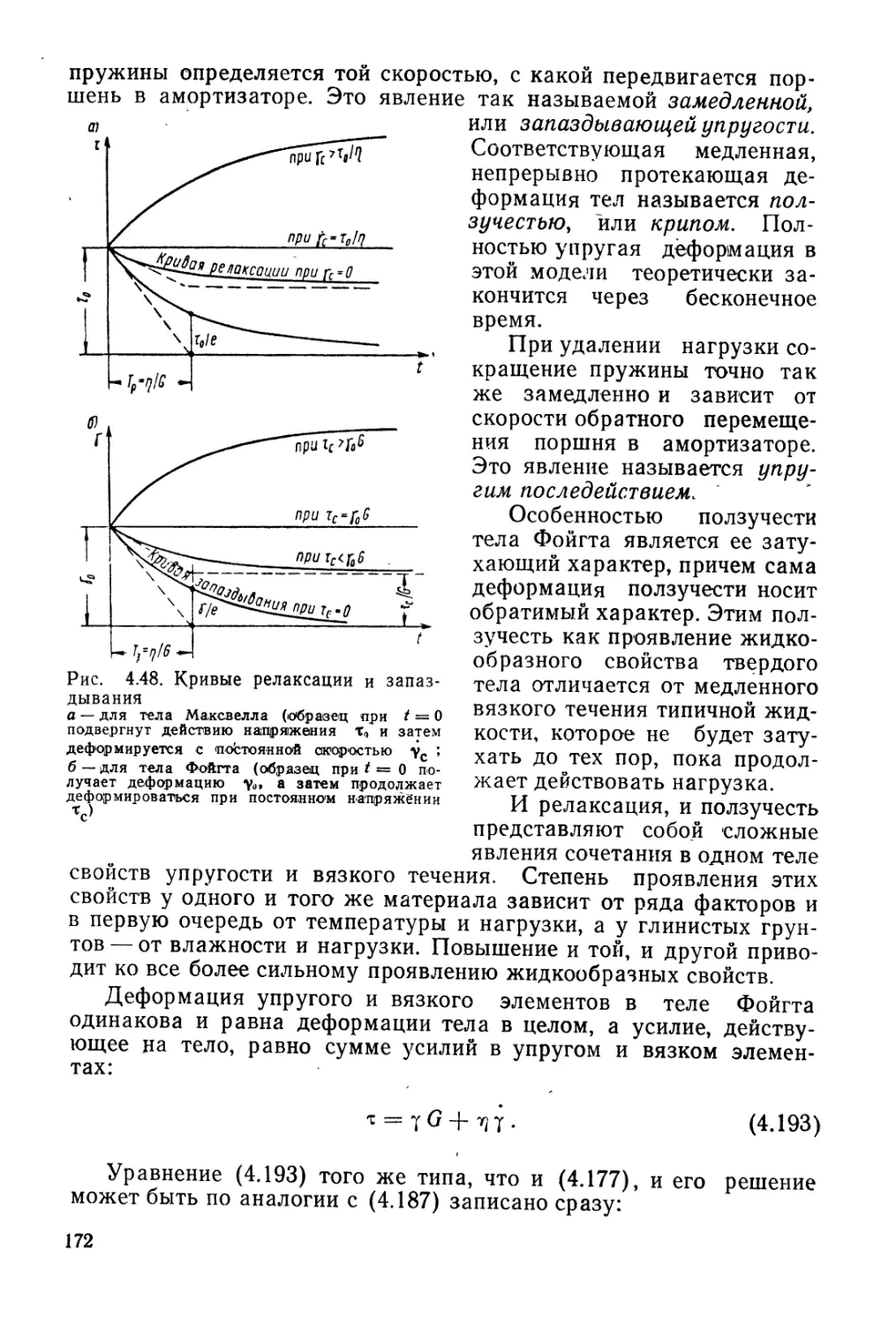
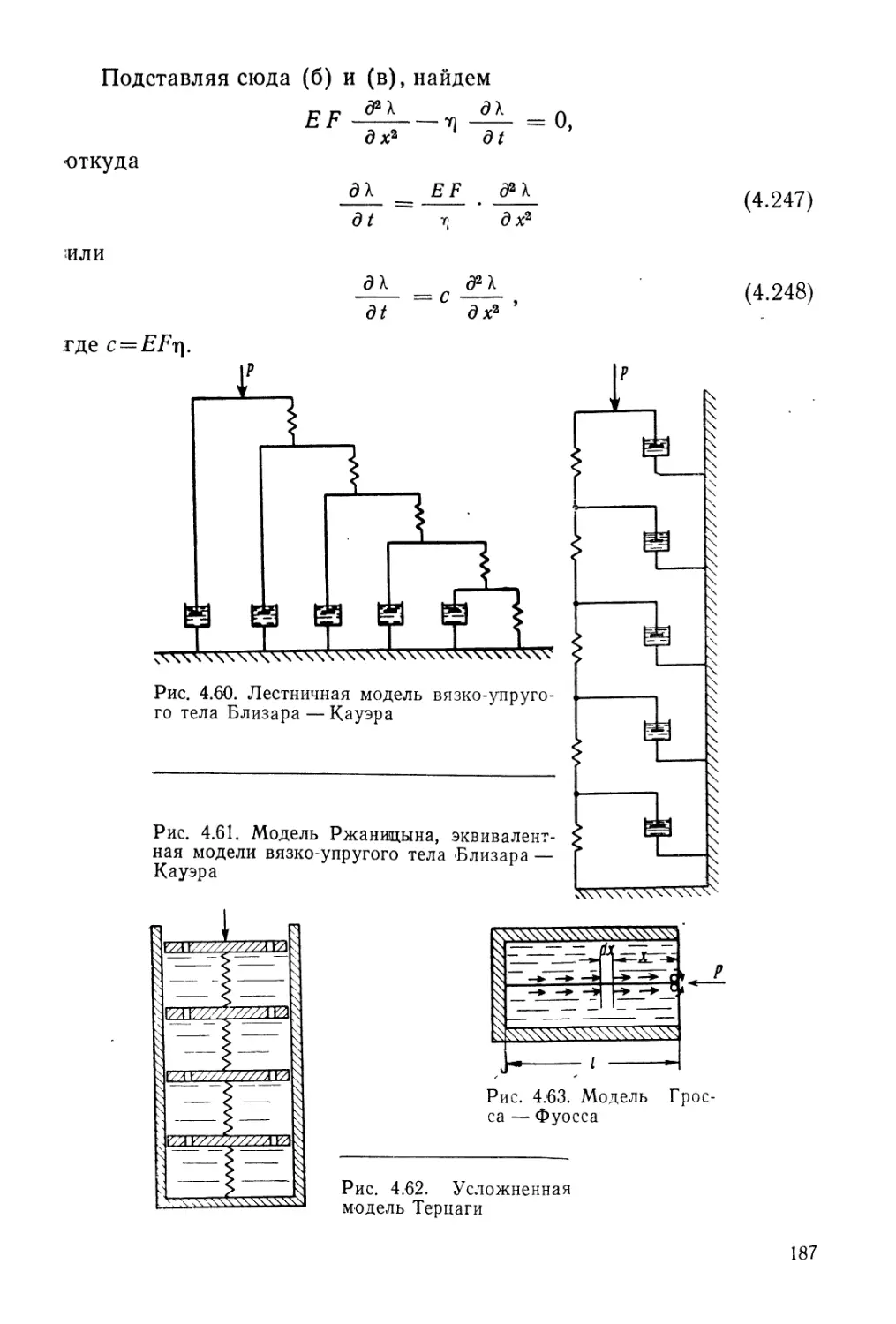
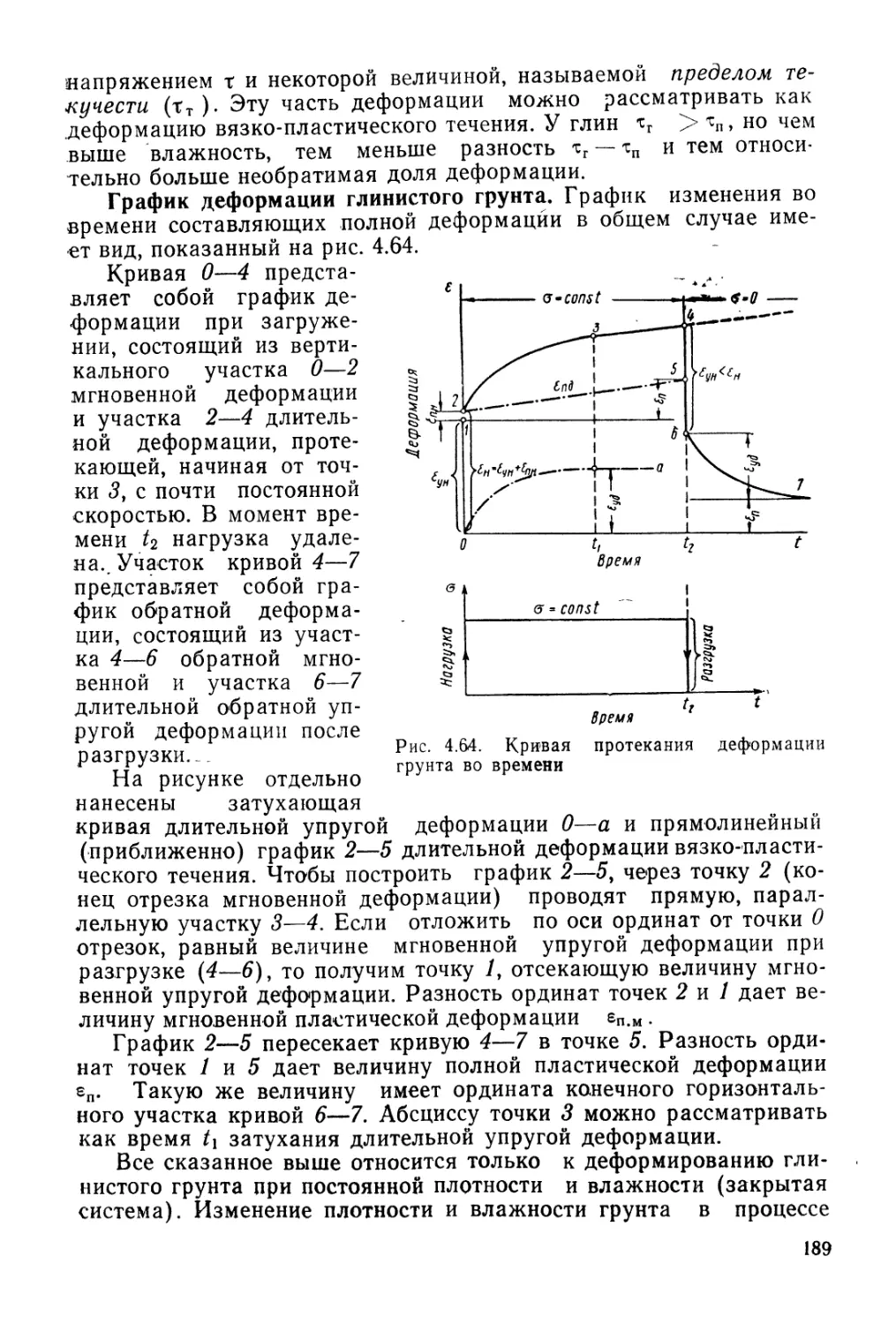
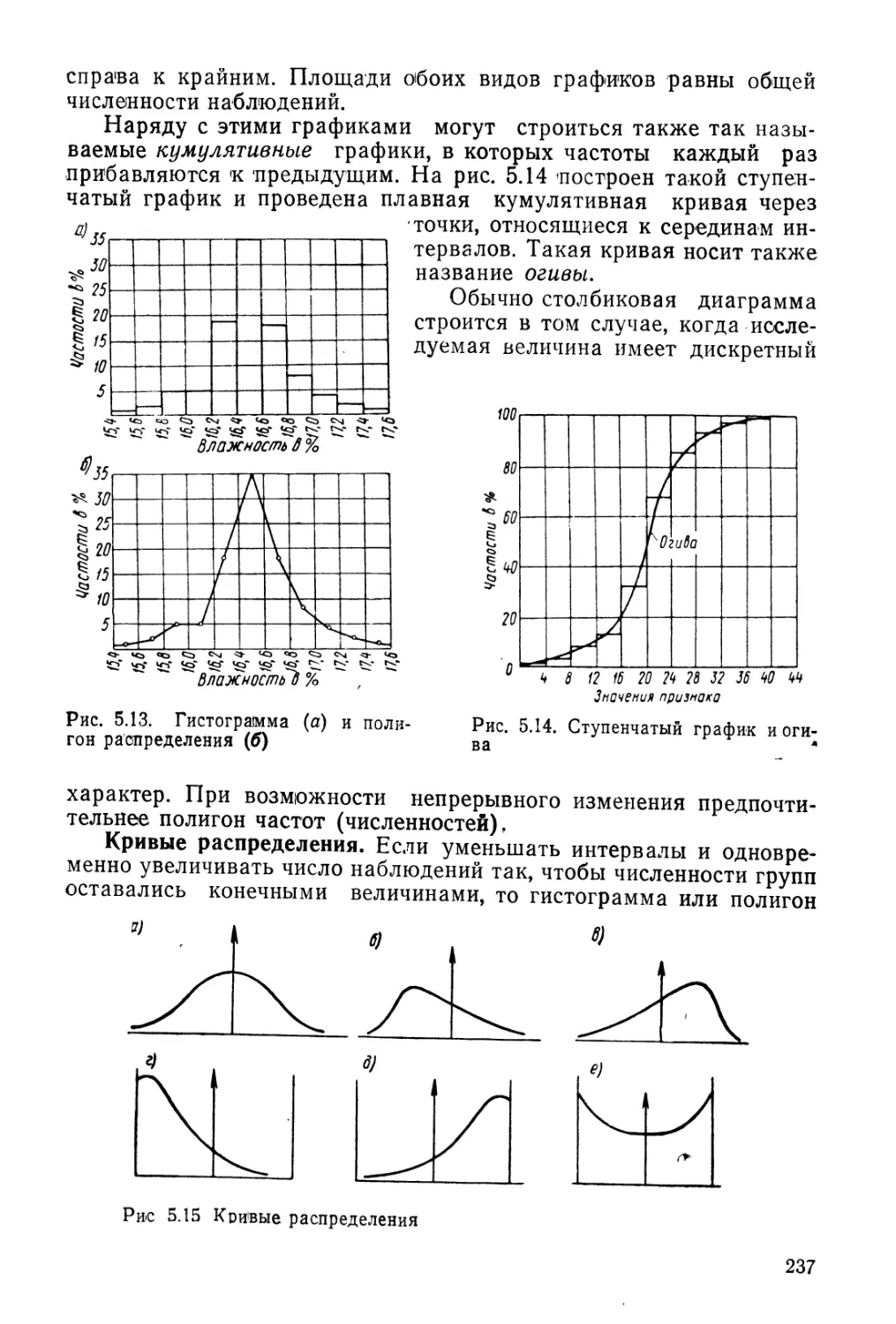
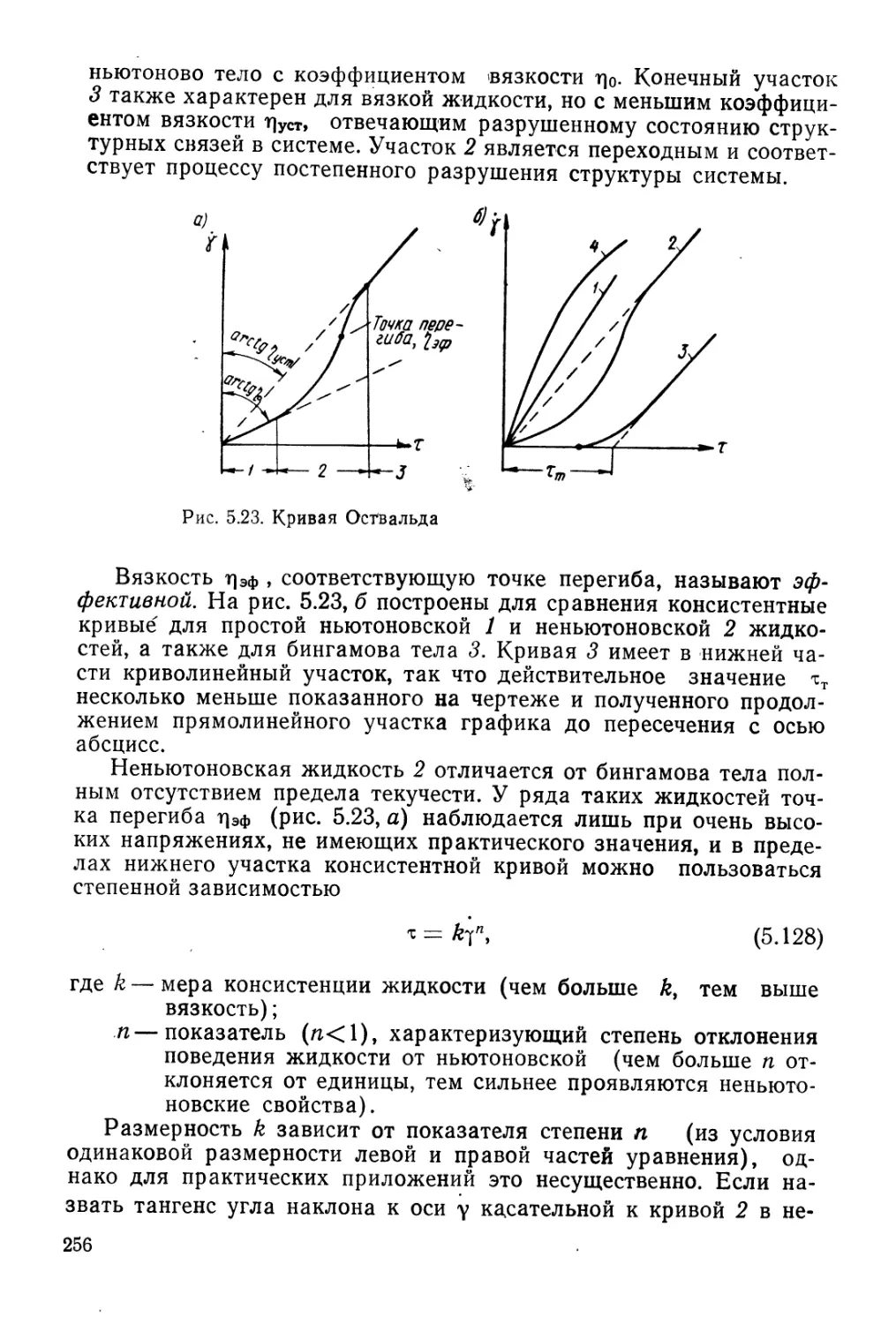
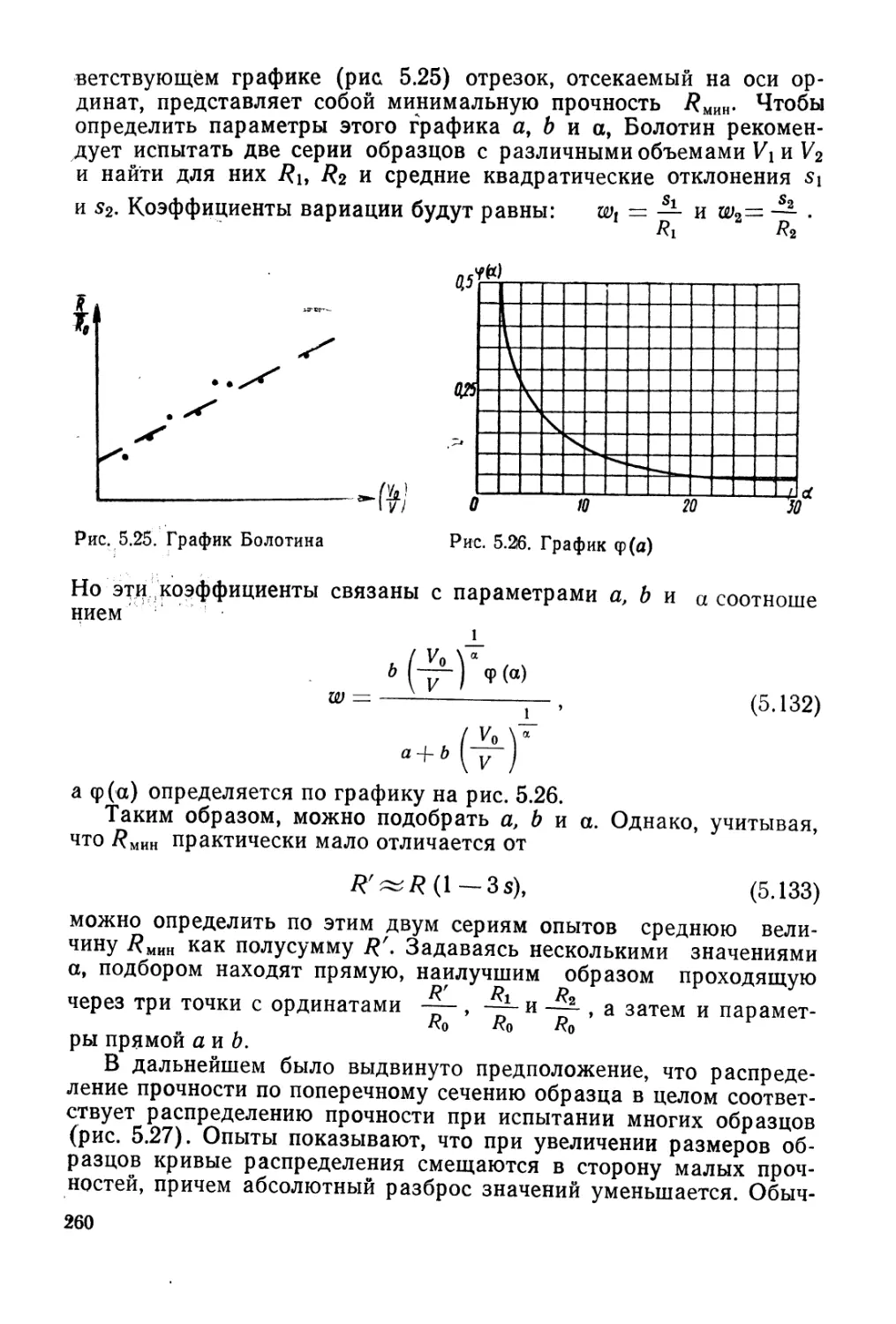
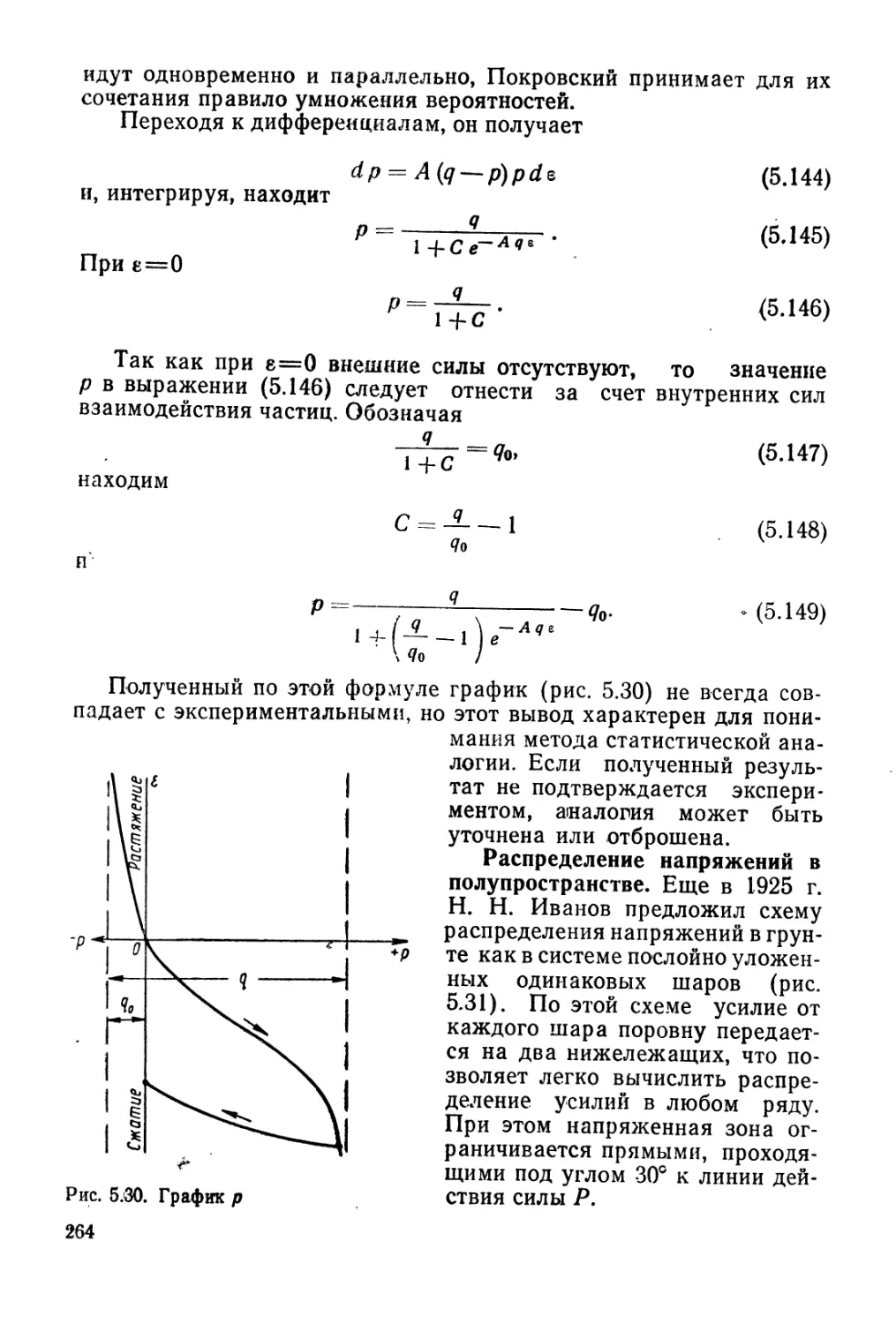
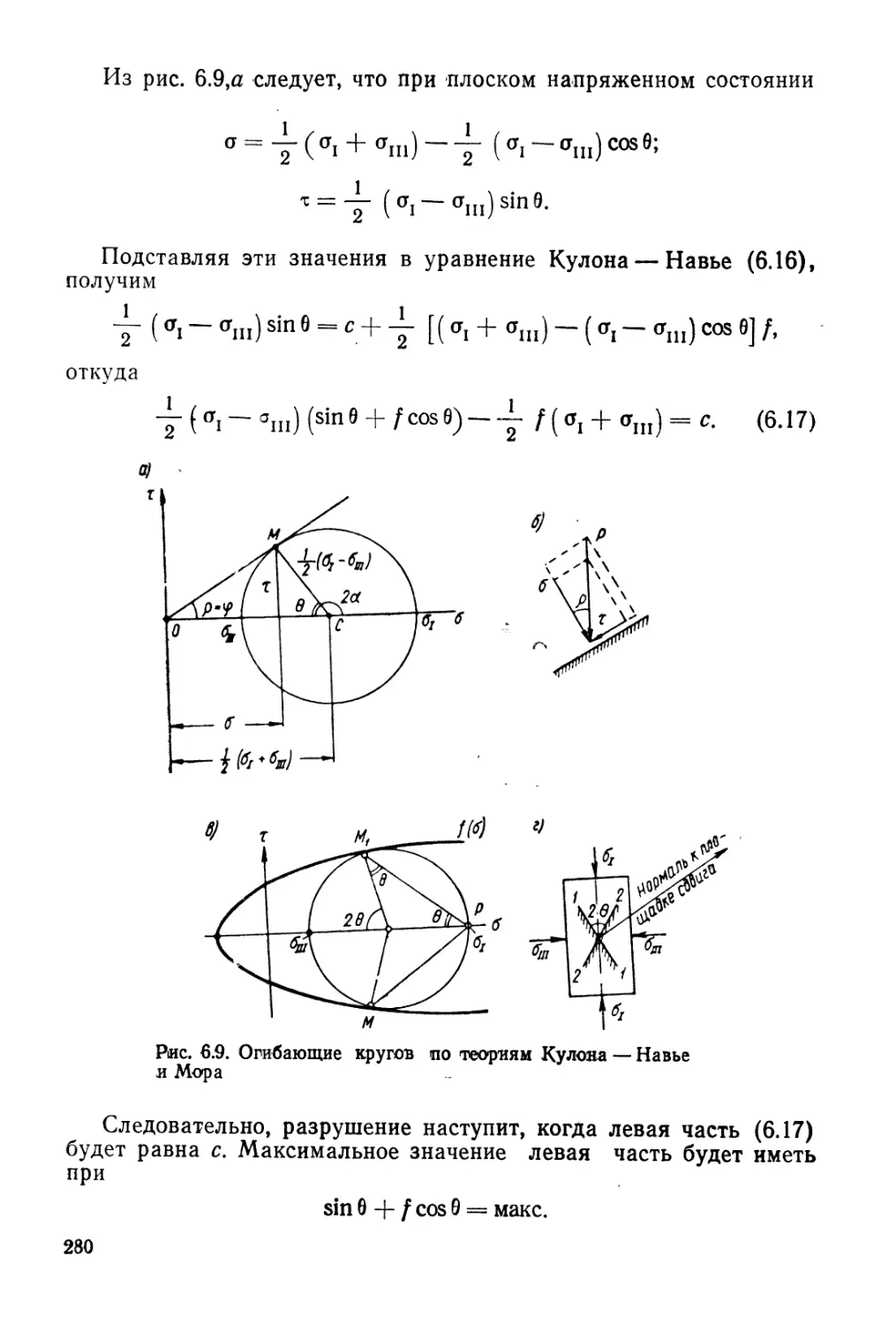
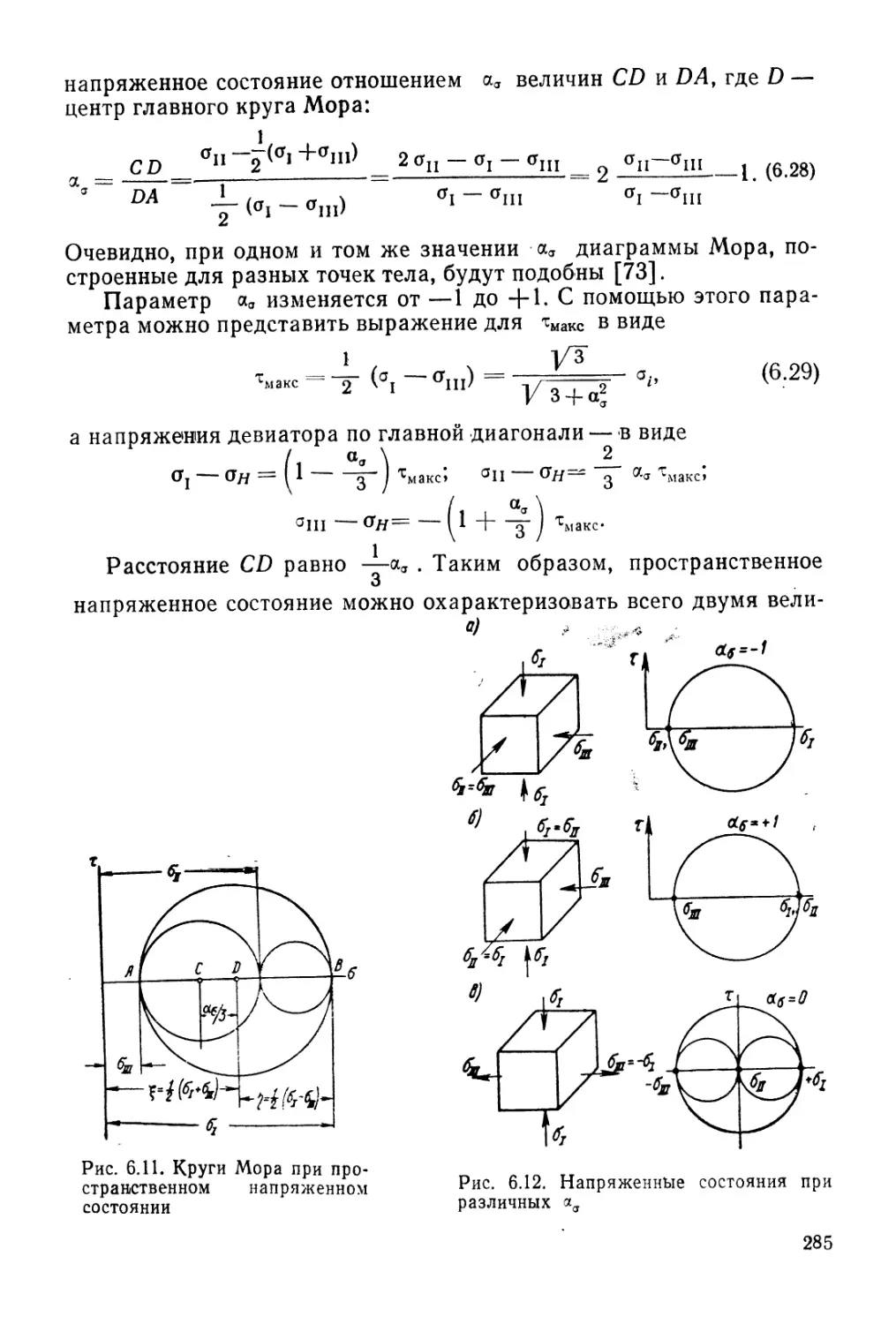
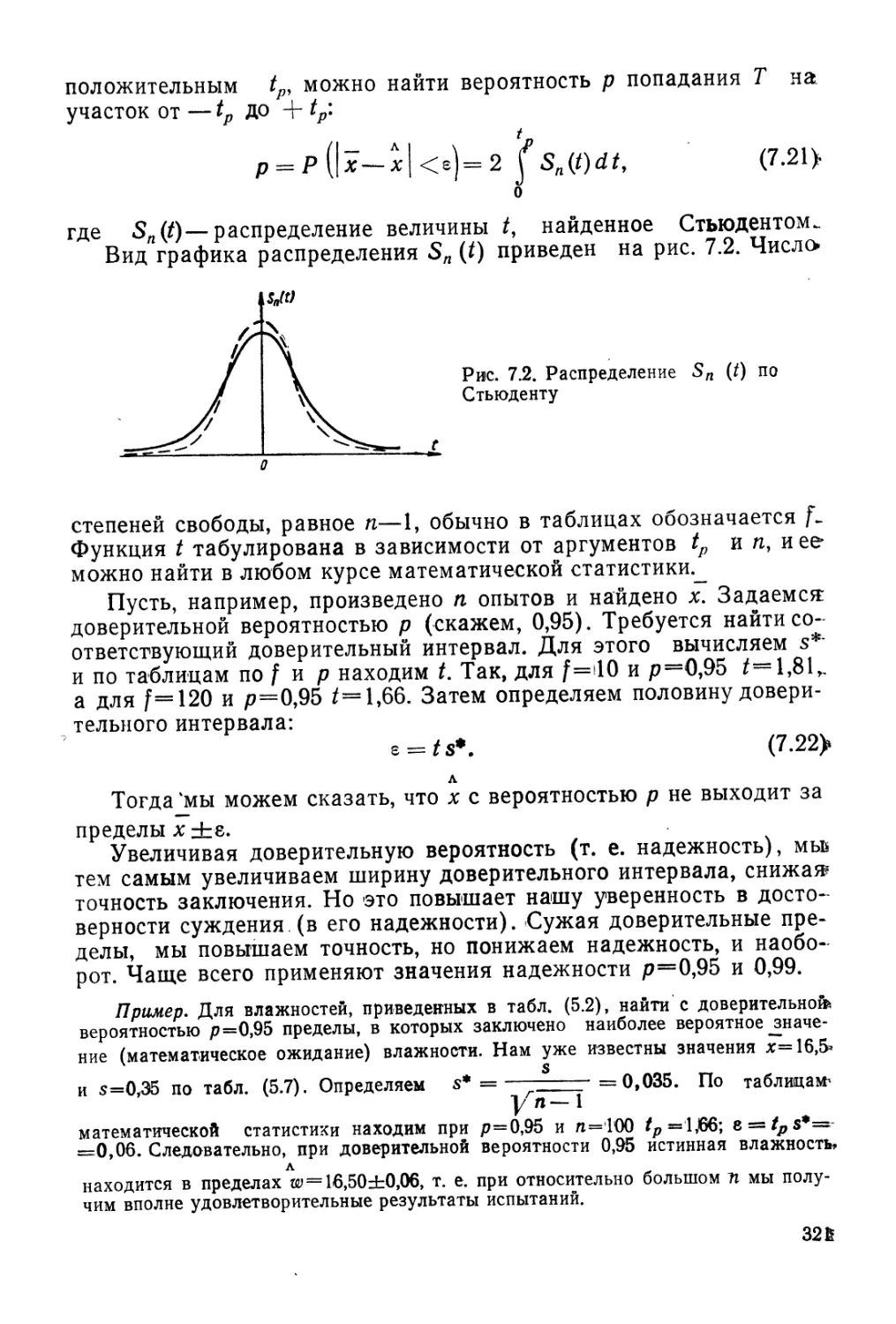
Author: Гольдштейн М.Н.
Tags: подземное строительство земляные работы фундаменты строительство тоннелей строительство механика грунтов грунты
Year: 1971
Text
М. Н. ГОЛЬДШТЕЙН
МЕХАНИЧЕСКИЕ
СВОЙСТВА
ГРУНТОВ
Второе издание, переработанное
ИЗДАТЕЛЬСТВО ЛИТЕРАТУРЫ ПО СТРОИТЕЛЬСТВУ
Москва—1971
УДК 624.131.431
Эта книга является первой частью труда, посвя-
щенного мето дико-теоретическим основам исследова-
ния механических свойств грунтов в строительных це-
лях.
В ней рассматриваются: связь механики грунтов с
теологией; основные положения теории сплошной среды,
термодинамики и статистической механики в приложе-
нии к исследованию грунтов; условия, обеспечивающие
правильную постановку и проведение испытаний.
Книга рассчитана как на лиц, непосредственно за-
нимающихся испытанием грунтов, так и на инжене-
ров, работающих в области инженерной геологии и
фундаментостроения. Она может быть использована
также как пособие для углубленного изучения фи-
зических основ современной строительной механики
грунтов.
3-2-6
106—70
ПРЕДИСЛОВИЕ
Эта книга выходит почти через 20 лет после первого изда-
ния — срок достаточно большой для истории любой науки, а в
особенности столь быстро развивающейся, как механика грунтов.
За эти годы состоялось пять международных конгрессов по
механике нескальных и два по механике скальных грунтов, про-
шел ряд региональных конференций и симпозиумов по отдельным
проблемам механики грунтов, опубликованы тысячи статей и де-
сятки монографий. Значительная часть этих работ посвящена
изучению физико-механических свойств грунтов, так как этот
вопрос является ключевым для развития как строительной ме-
ханики грунтов, так и инженерной геологии. Естественно, что
обзор всех этих исследований — задача совершенно безнадежная.
Автор не ставил также перед собой задачу создать лабораторный
справочник или руководство по испытанию грунтов, тем более что
прекрасные методические пособия такого рода уже имеются.
Цель этой работы совершенно иная, а именно:
изложить теоретические основы постановки исследований фи-
зико-механических свойств таких разнородных и сложных по сво-
им свойствам материалов, как грунты;
помочь испытателю правильно оценивать получаемые резуль-
таты и делать из них выводы и рекомендации для практического
использования;
показать необходимость отхода в ряде случаев от традицион-
ных испытательных методик, когда последние могут вести к явно
неверным результатам;
облегчить лицам, занимающимся испытаниями грунтов в про-
изводственных целях, проведение самостоятельных исследований
тех механических свойств грунтов, которые еще недостаточно изу-
чены и требуют разрешения чисто методических вопросов.
Соответственно книга предназначена, в первую очередь для
тех, кто непосредственно занимается изучением свойств грун-
тов в связи с теми или иными теоретическими и практическими
проблемами механики грунтов, фундаментостроения и геотехни-
ки. Кроме того, она может быть использована и как пособие для
углубленного изучения физических основ современной строитель-
ной механики грунтов.
Принципы, на которых основана существующая практика ла-
бораторных и полевых испытаний грунтов, соответствуют боль-
шей частью весьма упрощенным расчетным моделям, выдвинутым
классической механикой грунтов. Между тем многие современные
теории существенно отличаются от первых, довольно элементар-
1* Зак. 530
3
пых представлений. Широко развилось изучение реологических
свойств, появились различные вероятностно-статистические (стоха-
стические) модели грунтов, далеко вперед шагнуло изучение ме-
ханических свойств различных специфических видов грунтов, та-
ких как лёссы, вечномерзлые грунты, насыпные грунты и т. д.
Если в 1948 г. Терцаги мог писать, что «в настоящее время
объем проводимых испытаний и утонченность техники их выпол-
нения далеко превосходят практические потребности с точки зре-
ния использования получаемых результатов», то сейчас положе-
ние изменилось коренным образом, и методы испытаний грунтов
заметно отстают от достижений теоретической механики грунтов
и требований проектирования. Действительно, большинство выд-
вигаемых практикой новых важных проблем механики грунтов
требует для своего решения гораздо более сложных физических
и математических методов, чем те, которые были достаточны на
варе развития механики грунтов.
Естественно, что исследователи и экспериментаторы должны
Но своей подготовке отвечать уровню подобных требований, и ав-
тор попытался отразить в этой книге хотя бы частично те измене-
ния в постановке исследований грунтов, которые вытекают из все
более широкого использования методов реологии, термодинамики,
тоерии вероятностей, математической статистики и физико-химиче-
ской механики.
В той мере, в какой это допускал объем книги, автор попутал-
ся все изложение построить «замкнутым» образом, изложив и те
чисто теоретические вопросы, которые необходимы для пони-
мания книги. При этом автор исходил из уровня той подготовки,
которую получает по математике, строительной механике, меха-
нике грунтов и инженерной геологии подавляющее большинство
инженеров.
Эта книга посвящена описанию физико-теоретических основ
современной механике грунтов.
В главе 1 книги дается краткое изложение основных све-
дений о происхождении и условиях формирования свойств грун-
тов и грунтовых толщ. Главная задача этой главы — привлечь
внимание инженеров-строителей к столь часто недооцениваемой
ими геологической стороне проблемы использования грунтов в
строительных целях. Вместе с тем автор стремился подчеркнуть
всю сложность и многообразие природных условий, которые опре-
деляют механические свойства грунтов.
В главе 2 характеризуется современная дифференциация наук,
изучающих грунты: приводятся некоторые существенные данные
по истории развития механики грунтов и, в особенности, ее связей
с инженерной геологией; рассматриваются основные положения, на
которые должно опираться изучение механических свойств грун-
тов.
Глава 3 посвящена изложению основ термодинамики в том
объеме, который понадобится для понимания второй части книги
4
Глава 4 представляет собой введение в теорию напряженно-
деформированного состояния грунтов, рассматриваемых как
сплошная среда. В этой,главе описываются также различные ре-
ологические модели, используемые в современной механике
грунтов.
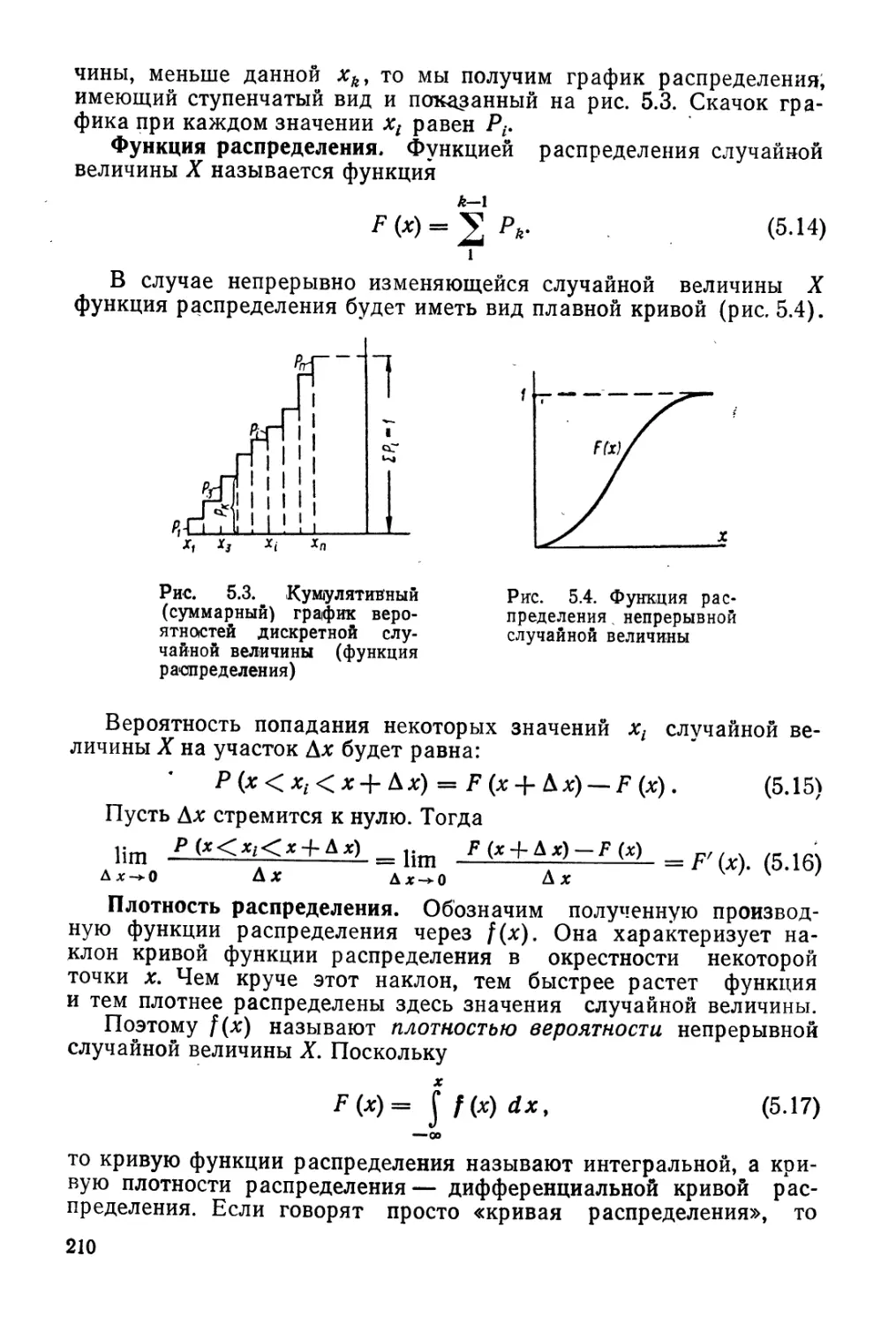
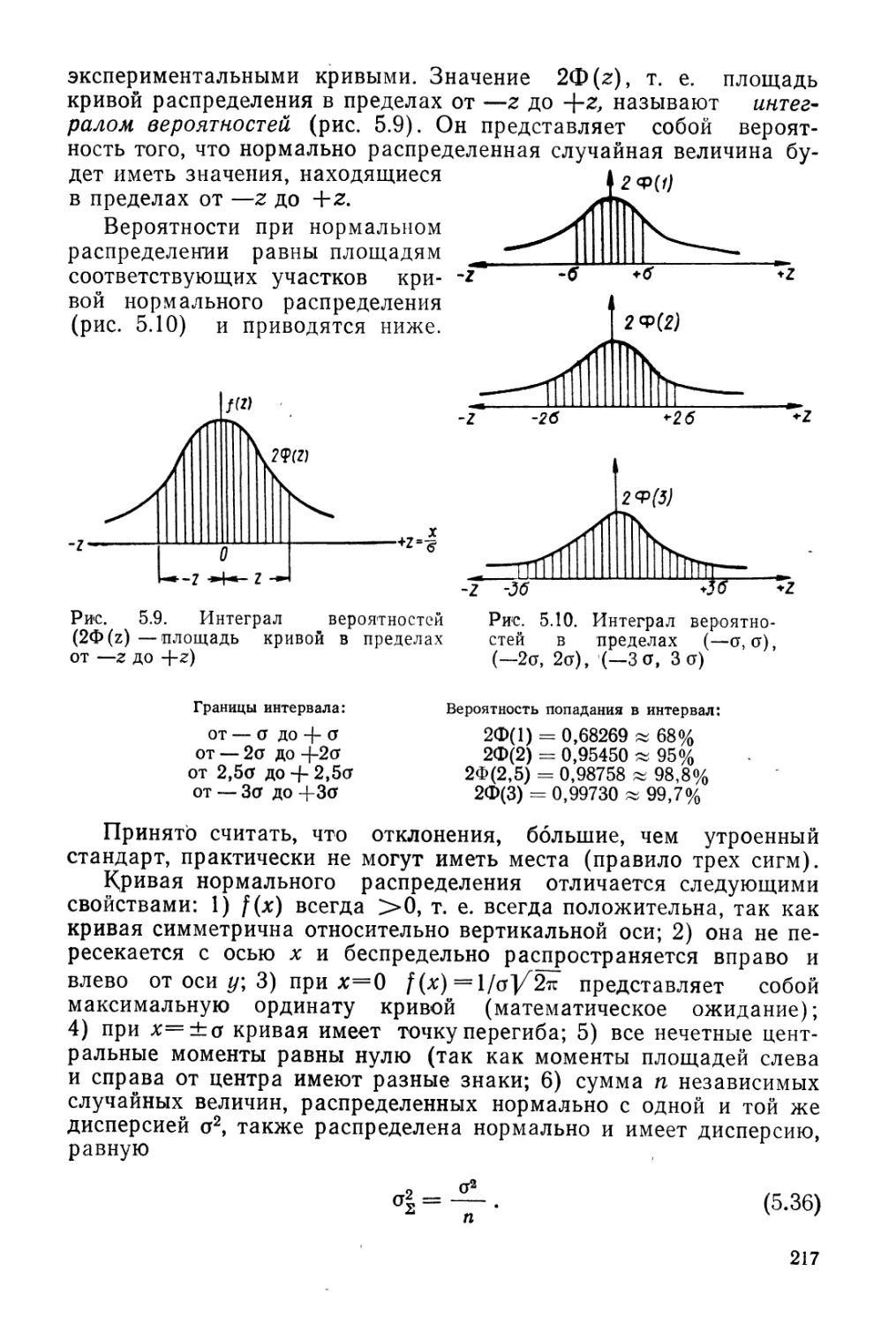
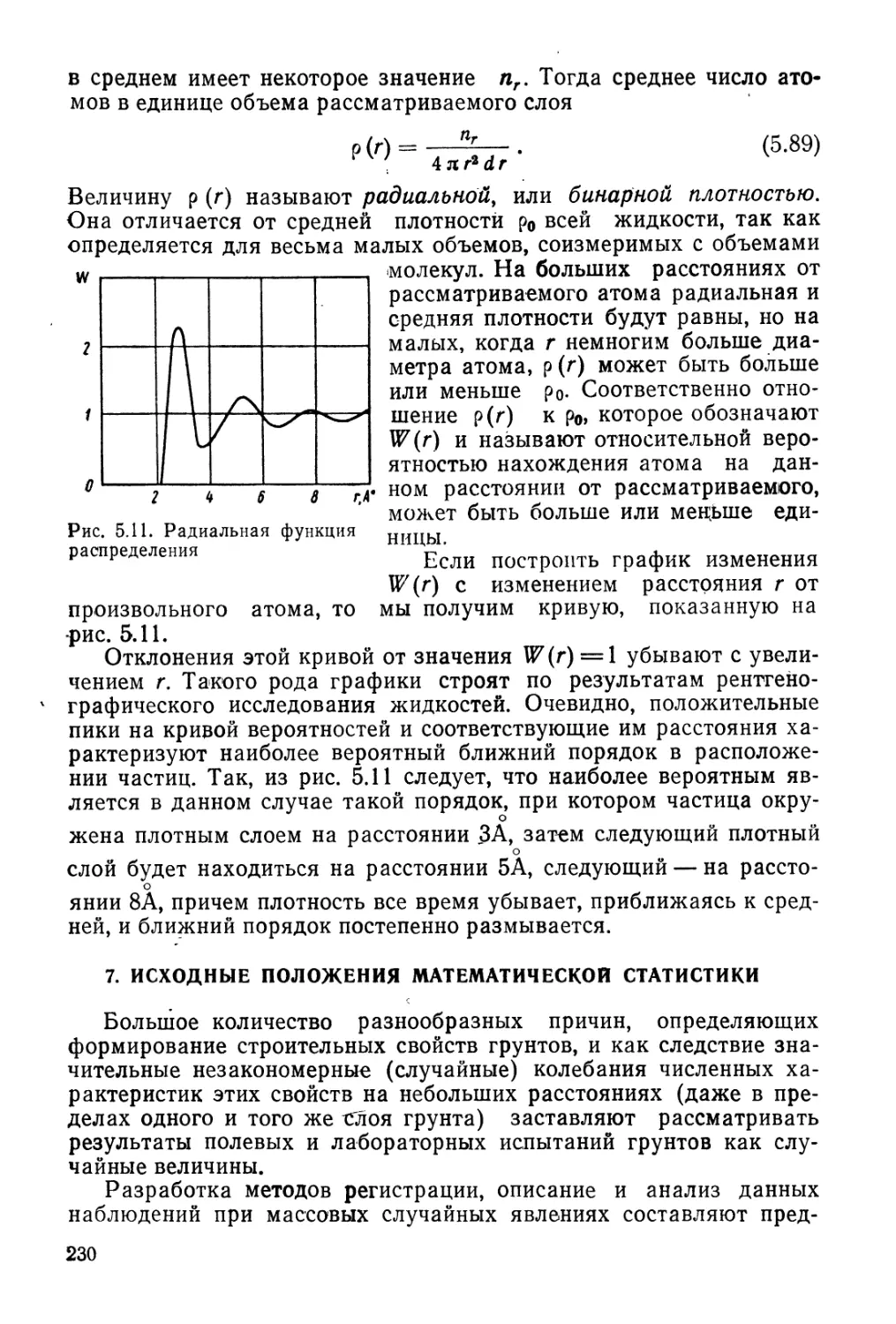
В главе 5 изложены исходные понятия теории вероятностей и
математической статистики и рассматриваются основы статисти-
ческой теории внутреннего трения и вязкости в жидкостях и га-
зах, особенности сыпучих тел, вопросы структуры дисперсных сис-
тем с точки зрения физико-химической механики грунтов
П. А. Ребиндера и И. М. Горьковой и, наконец, приложение ста-
тистических методов к описанию свойств грунтов как дисперсных
сред, успешно развитое Г. И. Покровским и И. И. Кандауровым.
Основным понятиям теории прочности грунтов посвящена гла-
ва 6, в которой рассматриваются энергетические теории прочности,
теория Кулона — Мора, теория Филоненко-Бородича, динамиче-
ская теория прочности, длительная прочность, прочность структу-
рированных систем. Вопросы прочности различных видов грунтов
(теории Н. Н. Маслова, Скемптона и др.) анализируются во второй
части книги.
Общие вопросы постановки и проведения испытаний грунтов,
выполнения измерений и обработки их результатов излагаются в
главе 7. В этой главе освещены также теория моделирования и
размерностей, принципы классификации грунтов, основные поло-
жения методики испытаний механических свойств. Дальнейшее
развитие вопросов, затронутых в первой части книги, читатель най-
дет во второй части, которая будет посвящена подробному рассмот-
рению механических свойств грунтов и принципов, на которых
строится методика исследования этих свойств.
Автор выражает свою искреннюю благодарность проф.
Н. Н. Маслову, который внимательно ознакомился с рукописью
и советы которого помогли устранить ряд ее недостатков, и зара-
нее признателен всем тем, кто сообщит ему свои замечания
по книге после ее выхода в свет.
Автор приносит благодарность сотрудникам лаборатории меха-
ники грунтов и кафедры «Основания и фундаменты» Днепропет-
ровского института инженеров транспорта за помощь в подготовке
рукописи к изданию.
Глава 1
ГРУНТЫ, ГОРНЫЕ ПОРОДЫ И СООРУЖЕНИЯ
1. ДВА ОСНОВНЫХ КЛАССА ГРУНТОВ
Термин «грунт* в строительном деле. Нередко один и тот же
предмет или явление в различных областях производства или в
различных науках называют по-разному. К таким профессиональ-
ным синонимам относится термин «грунт», который обычно приме-
няется в строительном деле вместо принятого в геологии названия
«горная порода».
Термин «грунт» в инженерной геологии. В инженерной геоло-
гии грунтом обычно называют всякую горную породу, когда она
становится объектом тех или иных строительных мероприятий. В
курсе инженерной геологии Н. В. Коломенского [27] грунт опре-
делялся как горная порода или почва, изучаемая в естественных
условиях залегания с целью определения физико-технических
свойств с учетом непрерывного изменения их во времени. Однако
в учебнике, изданном с участием того же автора позднее, термин
«грунт» вообще исключен, и авторы пользуются только термином
«горная порода» [28].
В работах по инженерной геологии имеются и иные определе-
ния грунта. Так, некоторые авторы называют грунтами горные
породы, слагающие верхние слои зедной коры, независимо от то-
го, являются ли они объектами строительного производства или
нет, поскольку они всегда могут стать такими объектами. Другие
авторы называют грунтами только верхние слои осадочных по-
род.
Е. М. Сергеев [71] понимает под термином «грунт» любые гор-
ные породы, которые залегают преимущественно в зоне выветри-
вания и могут быть использованы в качестве оснований, матери-
алов или среды для различных сооружений.
Мы будем далее называть грунтами любые горные породы,
когда они рассматриваются с точки зрения использования в строи-
тельно-технических целях.
В строительной технике все грунты обычно подразделяют на
два класса, резко различающиеся по основным строительным
свойствам: скальные и нескальные.
Скальные грунты. Скальными (скалистыми по Н. Н. Масло-
ву), или просто скалой, называют такие грунты, которые пред-
ставляют собой твердые тела, отличаются относительно высокой
6
прочностью и не изменяют или очень мало изменяют свои свой-
ства при, длительном насыщении водой. Все изверженные и ме-
таморфические горные породы являются скальными грунтами.
Изверженные или магматические породы возникают при осты-
вании расплавленной магмы, выжимаемой либо в земную кору
(например, гранит, сиенит), либо на ее поверхность (например,
базальт, трахит, диабаз). Эти породы обладают большой плот-
ностью и прочностью в' образцах, но в массиве разбиты обычно
трещинами па отдельные крупные блоки, в ряде случаев содержа-
щие местные сильно ослабленные зоны раздробленной породы.
Метаморфические породы — продукт преобразования осадоч-
ных и магматических пород под влиянием высокой температуры,
высоких давлений и действия химически активных веществ. К
метаморфическим относятся такие распространенные породы, как
гнейсы, сланцы, кварциты, или такой строительный материал, как
мрамор. Метаморфизм, как правило, ухудшает механические
свойства изверженных пород, увеличивает их анизотропность (не-
одинаковость свойств по различным направлениям), трещино-
ватость, водопроницаемость, понижает устойчивость против вы-
ветривания. Наоборот, свойства осадочных пород метаморфизм
обычно улучшает — сильно уплотняет их, повышает прочность,
но в некоторых случаях может придавать им также и такие свой-
ства, как, например, сланцеватость, приводящую к резкой анизо-
тропии по прочности и легкой выветриваемое™.
К скальным грунтам относятся также многие осадочные по-
роды, прочная связь между частицами которых создается либо с
помощью постепенно выпадающих из водных растворов цементи-
рующих веществ, либо в результате непосредственного химическо-
го взаимодействия в точках контакта минеральных частиц. В за-
висимости от прочности связей и характера их распределения по
поверхности частиц прочность скальных грунтов осадочного
происхождения может быть самой различной — от весьма высо-
кой до очень низкой.
Нескальные грунты. Эти грунты в литературе иногда назы-
вают также рыхлыми, рушенными или землистыми (эти термины
не привились). Они представляют собой легко распадающееся в
воде несцементированные или очень слабо сцементированные
скопления частиц и обломков различных горных пород и имеют за
немногими исключениями осадочное происхождение.
Твердые минеральные частицы, слагающие нескальный
грунт, называют его скелетом. Скелет состоит в большинстве слу-
чаев из частиц различного размера, а у многих грунтов имеет
и разнородный минералогический состав. Соответственно частицы
скелета могут обладать неодинаковыми физико-механическими
свойствами. В зависимости от состава скелета и относительного
расположения его частиц, а также характера связей между ни-
ми механические свойства нескальных грунтов колеблются в са-
мых широких пределах. Если однородный по минералогическому
7
составу грунт содержит незначительное количество частиц совер-
шенно иного состава и происхождения (например, органические
вещества), то их называют примесями.
Промежутки между частицами скелета, называемые порами,
могут содержать воду, лед, пар, воздух и другие Газы. Вещест-
во, заполняющее поры, называется поровой средой или заполни-
телем.
Благодаря наличию интенсивного физико-химического взаимо-
действия между минеральными частицами скелета и поровой во-
дой, а также примесями и содержащимися в воде ионами раство-
ренных веществ изменение содержания воды в порах, состава й
концентрации ионов в поровом растворе и количества примесей
оказывает значительное влияние на механические свойства
грунтов.
Грунт и скала. Иногда в работах по механике грунтов предла-
гают называть грунтами только нескальные породы, не применяя
этот термин по отношению к скальным, иными словами, подраз-
деляют все породы на грунты и скалу. Так, в работе Ионга и
Уоркентина [95] грунт определяется как продукт выветривания
скалы и разложения органического вещества, который может со-
держать как частицы микроскопических размеров, так и круп-
ные обломки пород вплоть до валунов, диаметром во много де-
сятков сантиметров.
В ряде работ авторы предлагают различать механику грунтов
и механику скалы. В основе этих предложений лежит, во-первых,
стремление к унификации международной терминологии, так как
на других языках для обозначения скальных и нескальных грун-
тов пользуются различными терминами (по-английски грунт —
«сойл», скала — «рок»; по-французски — «соль» и «рош»; по-не-
мецки — «боден» и «фельс»; по-испански — «суэло» и «рока» и
т. д.). Во-вторых, механические свойства и особенности этих двух
типов пород и их поведение в сооружениях существенно отлича-
ются друг от друга и соответственно совершенно различны ме-
тоды их лабораторных и полевых испытаний, а также и теорети-
ческие основы расчета деформаций и прочности. В-третьих, тре-
буются совершенно различные способы производства работ при
разработке скальных и нескальных грунтов.
Однако в соответствии с принятым в отечественной строитель-
ной практике и приведенным в начале параграфа широким опреде-
лением термина «грунт» как инженерного понятия мы будем в этой
книге называть грунтами любые горные породы, подразделяя их на
скальные и нескальные грунты. Е. М. Сергеев [71] предлагает
подразделять все горные породы на два класса: породы с жест-
кими связями и без них. Первые являются с точки зрения строи-
теля скальными грунтами, вторые — нескальными.
Граница между скальными и нескальными грунтами. Грани-
цу между скальными и нескальными грунтами трудно провести
абсолютно строго. Принято считать, что в отличие от скалы обра-
8.
зец нескального грунта при встряхивании с водой легко распадает-
ся на отдельные мелкие частицы. Другой способ испытания за-
ключается в том, что образец грунта сначала высушивают при
105°С, а затем погружают в воду на 24 ч. Если это скальный
грунт, то образец не должен обнаружить никаких признаков рас-
пада или размягчения.
1Строители обычно разграничивают эти два типа грунтов по
чисто производственному признаку. Они называют скальными та-
кие грунты, которые требуют при разработке применения взрыв-
ных работ, а те грунты, которые можно непосредственно разра-
батывать с помощью механического оборудования (например,
скреперов, бульдозеров), относят к нескальным.
Трудность подобного подразделения пород объясняется тем, что
некоторые грунты в одном состоянии практически не отличаются от
скалы, а в другом являются нескальными. Соответственно следует
различать скальное и нескальное состояние таких грунтов.
Почва. Необходимо упомянуть и другой специальный термин,
но уже чисто агрономический,— «почва». Почвой называют непос-
редственно примыкающий к дневной поверхности слой земли, ес-
ли он пригоден для произрастания растений. Почвы образовались
из горных пород в результате их изменений под влиянием воды,
воздуха и, что особенно важно и специфично именно для почв,
различного рода организмов — растительных, животных и бакте-
рий. Почвы всегда содержат примеси органических остатков или
продукты их разложения.
В тех случаях, когда почвенные слои покрыты последующими
отложениями осадочных пород и залегают на известной глубине
от поверхности, эти слои называют погребенной почвой.
Горная порода, из которой образовалась данная почва, назы-
вается по отношению к последней материнской породой. В поч-
воведении пользуются также термином «грунт», обозначая им
породы, непосредственно подстилающие почвенный слой.
2. нескальные грунты как осадочные горные породы
Образование осадочных горных пород. Под действием физико-
механических и химических процессов выветривания различные
горные породы разрушаются и затем, при соответствующих усло-
виях, могут переоткладываться, образуя слоистые толщи, мощ-
ность которых местами достигает сотен и даже тысяч метров.
Эти отложения носят названия осадков. Несмотря на относитель-
но низкие давления и температуры, господствующие в верхнем
слое земной коры, осадки постепенно уплотняются и изменяют
свой минералогический состав, переходя в горные породы, на-
зываемые осадочными. К ним относятся такие, очень сильно раз-
личающиеся по своим механическим свойствам породы, как
глина, мергель, песок, известняк, доломит, мел, гипс, песчаник,
9
толщи вулканического пепла, различные естественные химические
продукты вроде каменной соли или такие полезные ископаемые,
как торф и уголь.
Все нескальные грунты представляют собой осадочные горные
породы.
Состав пород. Физико-механические свойства тех осадочных
пород, которые относят к категории нескальных грунтов, опреде-
ляются, во-первых, относительным содержанием частиц различ-
ных минералов и крупностью этих частиц, а во-вторых, свойства-
ми веществ, заполняющих поры грунта.
Простое перечисление веществ, образующих грунт, характе-
ризует его качественный состав, но обычно указывается также
относительное содержание по весу или объему различных состав-
ляющих грунта, неодинаковых по своим свойствам.
Основные типы осадочных пород. В литологии —учении об
осадочных породах, эти породы по происхождению подразделя-
ются на следующие четыре типа [74]:
1) пирокластические, образованные при вулканических извер-
жениях (вулканические бомбы, пепел и т. д.);
2) обломочцые или кластические — крупно- и мелкозернистые
продукты выветривания горных пород, сложенные химически не-
измененными зернами минералов или обломками материнских по-
род (валуны, галька, щебень, песок, пыль и т. п.);
3) глинистые — продукты химического разрушения и преобра-
зования исходных минералов; частицы глинистых минералов
имеют размеры, измеряемые микронами и долями микрона;
4) химические и биохимические, выпавшие из растворов хи-
мическим путем или при содействии организмов,— представлены
обычно скальными грунтами.
Во многих случаях частицы и минералы пород этих четырех
групп перемешаны в различных соотношениях и образуют обилие
разновидностей смешанных осадочных пород.
Горные породы не являются неизменными образованиями, по-
стоянно сохраняющими приобретенные при возникновении свой-
ства. Под влиянием как внутренних процессов, так и внешних воз-
действий они непрерывно преобразуются с той или иной интен-
сивностью, причем преобразования могут быть очень глубокими
и приводить к коренному изменению минерального состава и
структуры пород.
Генезис горных пород. Совокупность всех процессов, ведущих
к образованию горных пород, называется генезисом пород, или
петрогенезисом. Так как генезис породы в значительной мере пре-
допределяет ее свойства, то в геологии это обстоятельство широ-
ко используется для того, чтобы по характерным особенностям
породы выяснять условия, имевшие место в период ее возникно-
вения или последующего преобразования, поскольку главной и
основной целью геологии является изучение истории и эволюции
Земли.
10
При инженерно-геологических изысканиях механические свой-
ства естественных толщ горных пород обычно исследуются лишь
в отдельных точках, а затем результаты экстраполируются на
весь массив. Но, как известно, всякая экстраполяция таит в се-
бе опасность серьезных ошибок, а тем более когда к ним прибе-
гают для оценки строительных свойств пород на больших участ-
ках, да еще при сложном геологическом строении.
В этих условиях детальное знание геологических условий и
генезиса пород в пределах данного района и участка существен-
но облегчает правильную оценку инженерно-механических свойств
рассматриваемого массива.
Стадии образования. В литологии различают в общем случае
следующие стадии образования осадочных пород [68]:
а) образование осадочного материала — выветривание;
б) перенос ]
в) отложение (образование осадка) / се иментогенез>
г) превращение осадка в осадочную горную породу (уплотне-
ние и удаление избыточной поровой воды, минералогические и
структурные изменения)—диагенез;
д) дальнейшие изменения осадочной породы под действием
значительного давления от веса вышележащих толщ и цемента-
ции, приводящие к окаменению породы,— эпигенез.
Стадии диагенеза и эпигенеза часто объединяют под общим
названием литификации, что означает окаменение (литое — по-
гречески камень).
В ряде случаев образовавшиеся осадочные породы в резуль-
тате поднятия земной коры и эрозии покрывающих слоев могут
снова подвергаться выветриванию. Сумму геохимических явле-
ний, происходящих в поверхностных горизонтах, включая процес-
сы химического выветривания и почвообразования, называют
пергенезом.
В других случаях осадочные породы по мере отложения
следующих слоев и в результате тектонических процессов
гружаются на столь большие глубины, что под воздействием
рактерных для таких глубин очень высоких давлений и темпера-
тур их минералогический состав и структура резко меняются.
Эта стадия называется метагенезом, или метаморфизмом, в ре-
зультате которого осадочные породы, как таковые, уже переста-
ют существовать, переходя в метаморфические.
Выветриванием называют возникающие при определенных ус-
ловиях естественные механические и химические процессы рас-
слабления и разрушения горных пород. Выветриванию подверга-
ются слои горных пород, выходящие на дневную поверхность и
близкие к ним. Однако в поверхностных слоях могут при извест-
ных условиях происходить противоположные выветриванию и
противодействующие ему процессы механического уплотнения и
химического упрочнения пород.
Важным элементом выветривания является выщелачивание,
ги-
по-
по-
ха-
11
т. е. удаление с водой растворимых веществ, входящих в состав
породы. Ряд пород при выщелачивании сохраняет свой внешний
вид, но внутренние связи в них так резко ослабляются, что по-
роды могут испытывать внезапные катастрофические деформации
и подвижки даже при незначительных механических воздейст-
виях—происходит структурное разупрочнение, своеобразная ес-
тественная дестабилизация грунта.
Выветривающаяся порода проходит через ряд стадий, начиная
с общего ослабления внутренних связей в монолитной породе, за-
тем образования системы трещин выветривания и постепенного
распада породы на крупные глыбы, кончая превращением ее в
мелко раздробленную массу (дезинтеграция породы).
Производственная деятельность человека (действие на поро-
ды отходов химического производства; взрывы, вызывающие да-
леко распространяющееся растрескивание породы; изменение гид-
рологического режима при строительстве каналов и плотин и
т. п.) может в ряде случаев заметно влиять на скорость и ха-
рактер процессов выветривания.
Элювий. Продукты конечных стадий выветривания и выщела-
чивания материнских пород, остающиеся на месте, образуют так
называемый элювий, или элювиальные грунты, которые в зави-
симости от состава и структуры исходной породы, характера
процессов разупрочнения и причин, его вызывающих, рельефа,
климата, наличия и степени встречных явлений упрочнения могут
весьма сильно различаться по своим механическим свойствам.
Исследованиями строительных свойств элювиальных грунтов
занимались Н. Н. Маслов [33], Л. И. Корженко [26], В. Б. Швец
и ряд других ученых. В связи со строительством большого моста,
опоры которого закладывались в мощном слое первичных каоли-
нов, обстоятельное ^изучение свойств этих элювиальных грунтов
провела в лаборатории ДИИТ А. Я. Туровская [80]. Она отме-
чает, что так как в отличие от других осадочных пород в образова-
нии элювия нет стадии переноса и отложения, то отсутствуют
и дифференциация частиц по величине и весу и седиментаци-
онная слоистость. Исчезает при формировании элювия и стадия
диагенеза в ее обычном понимании. Если обычные осадочные
толщи растут, накапливаясь постепенно, так что их поверхность
непрерывно перемещается вверх, то элювиальный процесс, нао-
борот, постепенно распространяется сверху вниз, и? более молодые
элювиальные слои находятся внизу, а наиболее полно разложив-
шиеся — сверху. При наличии в материнской породе участков с
различным сопротивлением выветриванию мощность элювиаль-
ных грунтов может весьма сильно меняться, переходя от тонких
покровных слоев в мощные карманы, простирающиеся в глубь
подстилающей породы.
Кора выветривания. Так называется поверхностный слой гор-
ных пород, претерпевших в той или иной степени выветривание.
Если возникшая некогда кора выветривания перекрывается затем
12
более поздними осадочными отложениями, она сохраняется как
подстилающий слой, называемый древней корой выветривания, в
отличие от современной коры выветривания, выходящей на по-
верхность. Мощность древней коры выветривания может местами
доходить до 100—150 м и более. На территории СССР древняя
кора выветривания занимает огромные пространства на Украине,
Урале, в Казахстане, Сибири и других районах страны.
Продукты выветривания, которые переносятся водой, ветром,
ледниками или перемещаются под действием силы тяжести, от-
кладываются на новых местах, образуя перемещенные грунты.
Процессы переноса, за исключением ледникового, сопровожда-
ются большей или меньшей сортировкой материала по весу и
крупности, а также обработкой и сглаживанием поверхности час-
тиц в результате истирания и соударений.
Стадия отложения перемешенных грунтов. Перемещенные про-
дукты выветривания после выпадения и оседания входят в но-
вую стадию существования, для которой вначале характерны вы-
сокая подвижность осадка и большой объем пор, заполненных
веществом той среды, в которой осадок образовался. В процессе
осаждения частицы могут соединяться друг с другом в микро-
агрегаты и хлопья благодаря действию поверхностных сил и фи-
зико-химическим процессам. Частицы могут прочно удерживать
на своей поверхности как мельчайшие частицы минералов, так и мо-
лекулы воды и других веществ из окружающей среды, ионы ра-
створенных в воде солей и т. п. Эти поверхностные оболочки иг-
рают важную роль в образовании сил сцепления между частица-
ми осадка.
Образующийся осадок с самого начала имеет сложные состав
и структуру, и в нем сразу же начинаются медленные физико-хи-
мические и коллоидно-химические превращения и преобразования,
ведущие к изменению характера первично возникших связей, мед-
ленному относительному перемещению зерен и миграции воды и
химических и минералогических компонентов.
Сингенез. Начальные явления образования из воздушной или
водной взвеси системы взаимно контактирующих частиц и созда-
ние первичных структур называют в литологии сингенезом или
ранним диагенезом. Это первый шаг в последующей длительной
истории преобразования осадка в породу. Сингенетические из-
менения начинаются уже на стадии седиментогенеза.
Грунт на стадии сингенеза рассматривается в литологии не
как горная порода, а как осадок с неустановившимися свойствами,
которому еще предстоит превратиться в стабильную в данных
термодинамических условиях осадочную горную породу в резуль-
тате процессов диагенеза.
Однако процессы сингенеза могут длиться многие тысячеле-
тия, и строители, часто закладывающие свои сооружения в са-
мых молодых осадочных отложениях и на небольших глубинах,
нередко встречаются именно с осадками на ранних стадиях их
13
преобразования, задолго до превращения в горные породы. До-
статочно привести в качестве примера строительство крупных и
тяжелых портовых сооружений на мощных толщах морских илов,
которые в литологии рассматриваются как сингенетическая ста-
дия образования глин. Таким образом, термин «грунт» охваты-
вает не только горные породы, но и геологические осадки, если
они являются объектом строительно-технических мероприятий.
Стадии диагенеза. Процесс формирования породы- в литоло-
гии обычно рассматривается лишь в геохимическом и минерало-
гическом аспектах, т. е. с точки зрения происходящих в породе
химических и минералообразующих процессов, так как основной
целью литологии является выяснение тех условий, в которых про-
исходит образование и концентрация полезных ископаемых. Толь-
ко с появлением инженерной геологии возник интерес к изучению
формирования и изменений физико-механических свойств осад-
ков и пород. В. А. Приклонский [54] впервые поставил вопрос об
изучении диагенеза пород в физико-механическом отношении и
ввел понятие о физико-механическом диагенезе.
Исследования И. М. Горьковой, Н. Я. Денисова, В. А. Ломтадзе
и др. показали, что формирование физико-механических свойств
осадочной породы происходит вначале под влиянием главным
образом коллоидно-химических и физико-химических процессов,
к которым лишь по мере накопления осадка добавляется дейст-
вие уплотняющего давления от веса вышележащей толщи (в ос-
новном на стадии эпигенеза). Плотность и прочность пород, обра-
зующихся на умеренных глубинах, существенно зависит от со-
отношения между скоростью упрочнения межчастичных связей
скелета и скоростью роста внешнего давления.
Характерной особенностью процессов сингенеза является ин-
тенсивная и очень существенная роль, которую играют в них мик-
роорганизмы и, вообще, биологические факторы, почти полностью
прекращающие свое действие, когда порода перемещается на
значительную глубину.
Весьма важное различие между продуктами сингенеза и ди-
агенеза, между осадком и породой заключается в том, что перво-
начальная структура осадка может сама собой полностью восста-
новиться после ее нарушения (при неизменной плотности и влаж-
ности), а следовательно, осадок обладает обратимостью струк-
турно-механических свойств (так называемое тиксотропное вос-
становление). Между тем порода, которая претерпела в той или
иной степени диагенетические изменения, как правило, уже не-
способна к полному восстановлению своих первоначальных меха-
нических свойств после нарушения ее структуры (например, пе-
реминанием), даже если не произошло ни уплотнения, ни разрых-
ления породы и сохранилась ее начальная плотность. Именно
это обстоятельство позволяет отличать с механической точки зре-
ния породу от осадка.
Но главной особенностью диагенеза является изменение ми-
14
нерального состава осадка из-за разложения органических ве-
ществ и появления условий для восстановительных химических
реакций, причем в исходных минералах одни химические эле-
менты замещаются другими, характер кристаллической решетки
изменяется, происходит потеря воды и кислорода. Химические
процессы превращения минералов особенно энергичны на на-
чальных стадиях диагенеза.
Процессы диагенетического изменения осадка на конечной
своей стадии характеризуются глубоким преобразованием мало-
устойчивых минералогических составляющих, входящих главным
образом в самые тонкие фракции осадка.
Хотя большинство сформировавшихся на стадии диагенеза
пород благодаря наличию цементационных связей гораздо проч-
нее осадка, однако не все породы переходят при этом в состоя-
ние окаменения, за исключением карбонатных , (известняк) и
кремнистых пород, а также сцементированных крупнообломочных,
которые уже на стадии диагенеза образуют плотные каменистые
массы. Особенно сильное упрочнение и окаменение нескальные
грунты испытывают на стадии эпигенеза.
Грунтовые воды содержат на глубоких горизонтах значитель-
ное количество солей (до 250—300 г/л), имеют высокую темпера-
туру и, попадая в крупнозернистые отложения или циркулируя под
давлением по трещинам, вызывают минералогические изменения в
омываемых ими породах.
Из-за циклических поднятий и опусканий земной поверхности
и соответствующих изменений окружающей среды указанные вы-
ше стадии преобразования пород могут прерываться, некоторые
могут совсем отсутствовать (например, перенос), другие повто-
ряться несколько раз, а процессы выветривания и литификации
нередко тесно переплетаются. На каждой из этих стадий среди уже
имеющихся в породе минералов могут возникать новые, зави-
сящие от термодинамических и химических условий окружающей
среды. Поэтому квалифицированное петрографо-минералогическое
изучение породы в сочетании с другими геологическими методами
исследований, раскрывающими происходившие в прошлом про-
цессы, позволяет выяснить историю образования и существова-
ния пород и дать ключ к оценке их физико-механических свойств
и начального напряженно-деформированного состояния. Особен-
ный практический интерес представляет такое изучение пород для
их искусственного химического закрепления.
Фации. Весьма важным фактором, определяющим физико-ме-
ханические особенности осадочных пород, являются условия их
отложения. С этой точки зрения в геологии говорят о фациях, т. е.
относящихся к одному и тому же геологическому времени физико-
географических условиях какой-либо зоны или области, иногда
очень узкой (например, русло реки или даже его часть), которая
представляет собой среду переноса и отложения и определяет
характер образующихся осадков. Этим же термином обозначают
15
и сам состав (фациальный состав) и особенности обстановки его
формирования {фациальная обстановка).
Именно фациальная обстановка определяет те мельчайшие
особенности геологического строения площадки, которые так
трудно непосредственно обнаружить при инженерно-геологичес-
ких изысканиях и которые могут оказаться роковыми для устой-
чивости сооружений. На это обстоятельство обращал внимание
К. Терцаги [103, 104], назвавший мельчайшими геологическими
деталями такие особенности строения грунтовой толщи, которые
не могут быть вскрыты никакими современными методами раз-
ведки, например точное положение и колебания ширины трещин
в грунтах оснований; колебания водопроницаемости тонкозер-
нистых аллювиальных отложений. Весьма интересное исследова-
ние связи неоднородности горных пород и их свойств с условия-
ми осадконакопления опубликовал недавно М. В. Рац [59].
Подразделение осадочных горных пород по условиям их на-
копления. Условия накопления горных пород являются важным
генетическим признаком, так как обстановка, в которой происхо-
дило накопление осадка, всегда определяется специфическими
свойствами окружающей среды, а также климатическими и гео-
морфологическими особенностями, влияющими на характер за-
легания, текстурные и основные структурные свойства пород. С
этой точки зрения выделяют три основные группы отложений —
морские, континентальные и переходные, а в пределах этих ос-
новных групп существуют частные генетические и фациальные
подразделения.
Характер морских отложений существенно зависит от условий
образования (расстояния от береговой линии, колебаний уровня
моря, морских течений и т. д.).
Среди древних морских отложений широко распространены
плотные глины и хорошо отсортированные плотные пески. Для
этих отложений характерна правильная, относительно тонкая
слоистость. Косая слоистость наблюдается редко. Мощность
морских отложений измеряется обычно десятками и сотнями мет-
ров. Для типичных морских отложений характерна высокая со-
леность воды, в которой происходит образование осадка, состав-
ляющая в среднем 35 г/л. Это вызывает интенсивную коагуля-
цию глинистых взвесей, причем оседающие частицы захватыва-
ют ионы растворенных в воде солей. В результате морские глины
приобретают характерную микроагрегатную структуру, а поровая
вода в них отличается повышенным содержанием солей.
Морские глины содержат некоторые малостойкие минералы,
легко разлагающиеся .в окислительной среде. Поэтому откосы
выемок в таких глинах должны обязательно защищаться от вы-
ветривания.
В зависимости от агентов переноса и условий осадконакопле-
ния континентальные отложения подразделяются на такие на-
16
иболее распространенные типы: ледниковые, аллювиальные, делю-
виальные, эоловые и аэральные, озерные и др.
Отложения, образованные непосредственно ледником, назы-
ваются моренными. Они характеризуются разнородностью меха-
нического состава, чаще всего невысокой пористостью и незначи-
тельной сжимаемостью, легкой размокаемостью в откосах вы-
емок, значительным и неравномерным пучением при промерзании.
Типичным ледниковым образованием являются валунные гли-
ны, в которых глины, пыль, песок, гравий и валуны беспорядочна
перемешаны. ;
Алювиальные (речные) отложения характерны своей неодно-
родностью и нейфавильной слоистостью. Среди них встречаются
и слабо уплотненные прослойки, и линзы очень слабых илистых
грунтов с невысокими механическими свойствами, и слои с доста-
точно высокой несущей способностью (например, глинистые
пласты, испытывавшие в прошлом уплотнение при высыхании,
или крупнообломочные гравелисто-галечниковые пласты).
Специфическими отложениями приледниковых озер являются
так называемые ленточные глины, встречающиеся в северных
районах. Они представляют собой чередующиеся светлые слои
пылеватого материала средней плотности и более темной глины.
Толщина слоев обычно измеряется несколькими миллиметрами, хо-
тя иногда бывают ленты толщиной в несколько сантиметров. Для
озерных отложений характерен также так называемый озерный
мергель — белый тонкозернистый известковистый грунт.
Делювиальными грунтами называют отложения продуктов
выветривания, оползающие по склону к его подножию. Для де-
лювия характерно содержание в глинистой массе большего или
меньшего количества обломков исходной породы. Делювиальные
отложения могут образовывать многометровые толщи. С этими
грунтами особенно часто приходится встречаться при строитель-
стве дорог. Откосы глинистого делювия обычно малоустойчивы
и легко оползают.
Наиболее важными для строителей эоловыми отложениями
являются лёссы, образующиеся в результате накопления в пу-
стынных и степных засушливых районах мощных толщ мелких
пылеватых частиц, перенесенных ветром на большие расстояния.
Лёссы отличаются высокой пористостью, так как относительна
прочные, хотя и неводостойкие связи между частицами, возник-
шие в период образования породы, не позволили откладывавшим-
ся выше слоям уплотнить своим весом грунт
Строение грунтовой толщи. Условия залегания различных
грунтов в осадочной толще, характер границ между ними, мощ-
ность и протяженность отдельных слоев, их относительное рас-
положение и порядок чередования, наличие и характер всевоз-
можных нарушений закономерности условий залегания — все эти
характеристики грунтовой толщи объединяют под общим поняти-
ем ее строения.
17
В прошлом строители выделяли в грунтовой толще так назы-
ваемый материк, понимая под ним те слои грунта, которые от-
личаются высокой плотностью и прочностью и могут служить на-
дежным основанием для сооружения. С появлением механики
грунтов и инженерной геологии этот чисто описательный термин
вызвал справедливую критику и был забыт. Однако в последнее
время он вновь начинает использоваться в строительном произ-
водстве, возрождаясь в связи с широким распространением свай.
Как известно, сваи подразделяются на висячие и сваи-стойки, и
для различия между ними оказалось удобным вновь вернуться к
понятию о материке, но в новой его трактовке, понимая под ма-
териком те слои поверхностной толщи земной коры, которые рез-
ко отличаются высокой несущей способностью и малой сжимае-
мостью от вышележащих слоев и могут служить надежным осно-
ванием для фундаментов и свай-стоек, причем материк не должен
иметь слабых прослоек и пропластков.
Породы, покрывающие материк и отличающиеся низкими ме-
ханическими свойствами, называют надматериковыми или нано-
сами. Использование их в качестве оснований всегда требует спе-
циальных мероприятий, позволяющих безопасно передавать на-
грузку от сооружения на слабые грунты.
Так как инженеры-геологи также ощущали необходимость со-
ответствующего подразделения грунтовой толщи, то И. В. Попов
в 1959 г. [52] предложил понятие о так называемой коренной
основе для обозначения тех пород, которые прошли стадии диаге-
неза и эпигенеза или метаморфизма еще до крупных тектоничес-
ких движений в данном районе. Коренную основу И. В. Попов
отличает от поверхностных отложений.
До последнего времени грунтовую толщу обычно подразделя-
ли на коренные и четвертичные отложения, считая, что все по-
роды старше четвертичного возраста резко отличаются в лучшую
сторону от четвертичных, так как они уже прошли эпигенети-
ческие изменения. Однако в некоторых случаях сама граница
между третичными и четвертичными породами не может быть
точно установлена.
Очевидно, такое подразделение исходило из предположения,
что силы, способные в достаточной степени уплотнить относитель-
но молодые четвертичные отложения, отсутствовали. Однако
строителей вполне устраивает и то уплотнение, которое во мно-
гих случаях четвертичные отложения уже испытали. Четвертич-
ный период начался около миллиона лет тому назад. За это вре-
мя в отдельных местах толща четвертичных отложений достигла
большой мощности, и их нижние слои могли достаточно хорошо
уплотниться под тяжестью вышележащих пород, оказывавших
давление в десятки кГ/см2. В некоторых случаях четвертичные
глинистые породы, выходя на поверхность, подвергались в за-
сушливых районах длительному высыханию, сопровождавшемуся
интенсивным усадочным уплотнением грунтов, эквивалентным
18
действию довольно значительного давления. Ледники, наступав-
шие в четвертичный период, уплотняли своим огромным весом
подстилающие грунты (так называемая донная морена, которая
отличается прекрасными строительными свойствам»). Поэтому во
многих районах нижние слои четвертичных и верхние слои тре-
тичных пород практически не отличаются по строительным свой-
ствам. Именно поэтому и рационально введение вновь понятия
о материке или коренной основе, с одной стороны, и о наносах
или поверхностных отложениях — с другой. В ряде случаев грани-
ца между ними совпадает с нижней границей пород четвертич-
ной системы, в других местах она проходит глубже — по третич-
ным отложениям, в верхней их части, а в третьих — находится
в четвертичной толще.
Слоистость. Более или менее четко отграниченные друг от
друга различные по составу породы образуют так называемые
слои или пласты. Тонкие слои называют пропластками или прос-
лойками, а очень тонкие — лентами. Группу слоев породы, свя-
занную между собой в том или ином отношении, часто называют
пачкой.
В пределах каждого слоя состав, цвет и другие характерные
признаки той или иной породы могут колебаться. Таким образом,
слоистость грунтов осадочйого происхождения выражается как
сменой вещественного и минералогического состава, так и сме-
ной характера строения скелета грунта. Причиной слоистости
могут быть, во-первых, циклическая смена опусканий и поднятий
земной коры и соответствующие периодические изменения в со-
отношении процессов размыва, сноса и отложения осадков, что
приводит к определенному ритму в строении ряда осадочных толщ,
и, во-вторых, периодическая и случайная изменчивость факторов
выветривания и агентов переноса (ветра, временных потоков, ручь-
ев и рек, морских течений).
Характерное расположение слоев различных пород и границ
между ними в общей толще имеет важное строительное значение.
Глинистые слои при обжатии выделяют поровую воду, которая
отводится через легко проницаемые крупнообломочные и песча-
ные слои. Жесткие песчано-пылеватые прослойки препятствуют
поперечным деформациям и выпиранию в стороны зажатых меж-
ду ними глинистых слоев, заставляя последние более равномерно
уплотняться под сооружениями. С другой стороны, наличие тон-
ких песчано-пылеватых прослоек в глинистой толще облегчает
возникновение горизонтальных сдвигов в этой толще по контак-
ту с прослойками и не раз служило причиной расползания на-
сыпей и дамб, отсыпанных на подобных толщах.
При однородных строго выдержанных по толщине и имеющих
почти горизонтальнее границы слоях пород можно достаточно
точно предсказать поведение оснований под нагрузкой от соору-
жений. Такое строение грунтовой толщи обычно называют пра-
вильным или регулярным (рис. 1.1,а). Термин «согласное зале-
19
гание», принятый в геологии, применяется для обозначения на-
пластований с параллельными границами, причем последние могут
быть и наклонными.
От правильного типа строения грунтовой толщи или, как еще
говорят, от правильного грунтового профиля отличают неправиль-
ное (беспорядочное или эрратическое) строение1, образованное
а) 6}
Рис. 1.1. Правильное (а) и неправильное (б) строение грунтовой толщи
1 — скважины
слоями, незакономерно меняющими границы и толщину и содержа-
щими всевозможные линзы и прослои (рис. 1. 1,6). Эрратичес-
кие профили встречаются чаще, чем правильные, и вызывают
обычно большие трудности при строительстве. При беспорядоч-
ном строении свойства каждого пласта также отличаются значи-
тельными колебаниями. При подобных профилях необходимо об-
ращать особое внимание на получение правильной картины строе-
ния толщи.
Влияние условий накопления на строение осадочных пород.
Относительно правильное строение имеют пойменные и эоловые, а
также морские отложения, образовавшиеся на больших глубинах
и на значительных расстояниях от берега и отличающиеся одно-
родностью состава. Однако плотность и физико-механические
свойства даже таких отложений могут колебаться так, что иног-
да образцы одной и той же породы, отобранные буквально в нес-
кольких сантиметрах друг от друга, обладают неодинаковой
прочностью и сжимаемостью.
Алювиальные отложения отличаются обычно своей беспоря-
дочностью. Особенно неправильный характер имеют дельтовые
отложения, в которых слои песка и гравия могут самым неожиг
данным образом перемежаться со слоями и карманами ила, гли-
1 В геологии принят термин «несогласное залегание».
20
ны и торфа. Наиболее неправильными являются ледниковые от-
ложения, часто содержащие значительное количество валунов.
На практике могут встретиться грунтовые толщи с самыми
разнообразными видами строения и свойствами. Поэтому инже-
нерно-геологическое изучение района строительства имеет ис-
ключительно важное значение для избежания различных неожи-
данных затруднений, которые могут возникнуть при производстве
работ.
Тектонические процессы. Существенные изменения прочност-
ных свойств всех пород вызываются тектоническими процессами.
При этих процессах, являющихся проявлением внутренней дина-
мики Земли, породы испытывают действие как мгновенных мощ-
ных ударов, так и длительно действующих огромных растягива-
ющих, сжимающих и сдвигающих усилий, вызванных движения-
ми и деформациями земной коры. В результате изменяется харак-
тер залегания горных пород, в них возникают значительные на-
пряжения, происходят смещения и разрывы, образуются всевоз-
можные складки и зоны дробления.
Денудационные процессы. Эта группа мощных процессов яв-
ляется проявлением внешней геодинамики, определяемой в пер-
вую очередь энергией Солнца. Процессы вызываются действием
атмосферных осадков, рек, морей, ледников, ветра, колебаний тем-
пературы и ведут к выравниванию, сглаживанию земной поверх-
ности. Происходящие при этом явления можно разделить на две
группы: 1) выветривание и разрушение пород и их перенос водой и
ветром, эрозия и 2) перемещения поверхностных слоев, происходя-
щие в виде оползней, обвалов, оплывов, лавин и т. п. и называемые
геологическими процессами. Эти процессы протекают медленно,
периодически сменяясь катастрофическими движениями, которые
подготавливаются малозаметными предшествующими измене-
ниями.
В результате геологических процессов, а также мощных сило-
вых воздействий, которым подвергаются грунты в современной
технике (например, взрывов), в них возникают нарушения пер-
воначальных условий залегания, появляются трещины, поверхнос-
ти скольжения и другие нарушения, которые мы будем называть
атектоническими.
Основной закон связи между свойствами грунтов и условия-
ми их образования. Этот закон, впервые четко сформулирован-
ный Н. Н. Масловым [33], гласит, что горные породы, одинако-
вые по своим составу, происхождению и условиям залегания и
претерпевшие одинаковые последующие изменения, обладают
одинаковыми инженерно-геологическими свойствами.
Таким образом, при инженерно-геологических исследованиях
необходймо постоянно вскрывать связь между свойствами грунтов
и условиями их образования и залегания, а накопленный таким
образом изыскательскими организациями материал должен сис-
тематически обобщаться специалистами в области инженерной
21
геологии. В этом направлении в Советском Союзе уже проделана
значительная работа и интенсивно ведутся дальнейшие исследо-
вания.
3. ОСОБЕННОСТИ РАБОТЫ ГРУНТА
В РАЗЛИЧНЫХ СООРУЖЕНИЯХ И УСЛОВИЯХ
Грунты в основаниях сооружений. Грунты, на которые опира-
ется сооружение, образуют его основание. Под влиянием прило-
женных нагрузок грунты основания деформируются, и сооруже-
ния соответственно испытывают вертикальные перемещения —
осадки, при неравномерных осадках — наклоны (крены), а под
действием горизонтальных сил — сдвиги (рис. 1.2). Эти переме-
щения сооружений никогда не происходят сразу же и полностью
по приложении нагрузки, а длятся некоторое время, зависящее от
ряда факторов. Очевидно величина перемещений не должна
превосходить предельно допустимой для сооружения по условиям
его эксплуатации. Таким образом, возникает задача прогноза ве-
личины указанных перемещений, а также продолжительности их
протекания во времени, для чего нужно знать соответствующие
механические характеристики грунтов.
Если нагрузка на основание оказывается слишком большой,
она может вызвать разрушение основания, которое проявляется
в виде выжимания грунта из-под сооружения и обычно называет-
ся выпором. Соответствующее моменту разрушения предельное
давление на основание, называемое его несущей способностью,
зависит от механических свойств грунта. Правильное решение
всех этих задач требует рассмотрения работы основания и соору-
жения как единого неразрывного целого с учетом непрерывного
22
перераспределения усилий в них по мере деформирования. Эта за-
дача сейчас только начала разрабатываться.
Строительная и активная толщи. В грунтовом массиве, на ко-
тором возводится сооружение, необходимо выделить строитель-
ную толщу. В свою очередь, ее следует разбить на два различ-
Рис- 1.3. Строительная толща (прорезаемая и
рабочая)
чем 2—2.5 шиоины фундамента или
ных участка — на проре-
заемую и рабочую толщи
(рис. 1.3); последняя со-
стоит из двух перекрыва-
ющихся слоев: активного
и несущего. Рабочая тЛл-
ща залегает ниже подош-
вы фундаментов, и дефор-
мации ее активного слоя
определяют собой величи-
ну и степень неравномер-
ности осадок сооружений.
Несущим называется
слой, оказывающий соп-
ротивление выпиранию-.
Обычно мощность ак-
тивной толщи не больше,
сооружения, опирающегося на грунт. Если представить се-
бе огромное здание на сплошной плите шириной порядка
200 м, то активная толща будет иметь мощность около
400—500 м. Если до такой большой глубины весь этот слой будет
представлен только нескальным грунтом, то полное давление от
его собственного веса в нижней части активной толщи составляет
около 100 кГ1см2. Однако в подавляющем большинстве случаев
размеры сооружений гораздо меньше, и суммарные напряжения
в активной толще не превосходят 10—30 кГ/см2, а максимальные
дополнительные напряжения от сооружения чаще всего составля-
ют 2—6, но при плотных грунтах и глубоком заложении фунда-
ментов могут доходить до 8—12 кГ!см2.
Глубокие фундаменты. Для заложения фундаментов на боль-
шой глубине прибегают к сваям, опускным колодцам и кессонам.
Производство работ по сооружению таких фундаментов выдви-
гает перед механикой грунтов ряд специфических задач.
Анкерные устройства. Ряд сооружений требует заделки в
грунте специальных конструкций, называемых анкерными, ко-
торые должны воспринимать значительные выдергивающие уси-
лия (рис.1.4). При проектировании анкерных устройств требуется
определить такую глубину заделки в грунт, которая обеспечит их
полную незыблемость при действии растягивающих или сдвигаю-
щих сил.
Устойчивость склонов и откосов. В этих случаях возникают
многообразные проблемы, связанные с прочностью грунтов. К
ним близко примыкает сложная задача — обеспечить устойчи-
23
вость огромных масс земли в оползневых склонах и в откосах
глубоких дорожных выемок или глубоких карьеров при открытой
разработке полезных ископаемых (рис. 1.5). Кроме того, инжене-
ры постоянно встречаются с аналогичной, хотя и гораздо проще
V' решаемой задачей обеспече-
л, ния устойчивости откосов
' всевозможных строительных
Рис. 1.4. Анкерный массив висячего моста
1 — поверхностные слои; 2 — «прочные слои
котлованов и траншеи.
Грунт как материал зем-
ляных сооружений. Грунт
может служить также мате-
риалом, из которого отсыпа-
ются такие ответственные
инженерные сооружения,
как плотины и дамбы. При
больших земляных плоти-
нах (высотой порядка 300 м)
давление в их нижней части
составляет около 60—70
кГ/см2. Здесь задача заклю-
чается в том, чтобы обеспе-
чить устойчивость как осно-
Рис. 1.6. Откос глубокой выемки
вания, так и тела сооруже-
ния, а также искусственно
придать ему необходимую
плотность и прочность.
При строительстве до-
рожных насыпей необходи-
мо гарантировать не только
их общую устойчивость, но и
достаточную прочность и от-
сутствие недопустимых де-
формаций в верхней части,
непосредственно несущей
жесткие покрытия автомобильных дорог или рельсо-шпальную
решетку железнодорожного пути (рис. 1.6).
Давление грунта. Давление грунта необходимо определять при
устройстве различных подпорных стен, шпунтовых ограждений и
креплений котлованов (рис. 1.7). Особые и притом весьма слож-
ные задачи возникают при проектировании подземных сооруже-
ний и тоннелей в связи с расчетом давления пород на их обделки
(горное давление). При этом обычно приходится рассматривать
совместную работу массива грунта и обделки и определять со-
противление окружающего массива изгибанию погруженных в не-
го упруго деформирующихся конструкций (упругий отпор породы).
Разработка грунта. При строительстве любых сооружений
строителям приходится иметь дело с разработкой грунта, его
транспортированием, обратной засыпкой грунта в пазухи котло-
24
ванов и его искусственным уплотнением. И здесь возникает но-
вая специфическая проблема — определение сопротивления грунта
разработке и обработке раз-
личными строительными ма-
шинами и механизмами.
Динамические воздейст-
вия. Особые и вместе с тем
очень сложные проблемы
связаны с действием на
грунт фундаментов под ма-
шины и взрывов различного
характера, с распростране-
нием в нем колебаний и по-
ведением оснований при ви-
брациях и землетрясениях,
с сопротивлением грунта
ударному и вибрационному
погружению свай. Все эти
задачи требуют изучения ди-
намических свойств грунтов
и их отклика на различные
виды динамических воздей-
ствий.
Упрочнение грунтов. Во
многих случаях можно обе-
спечить необходимые техни-
ческие свойства грунтов с
помощью их искусственного
преобразования. Соответст-
вующие строительные рабо-
ты требуют применения осо-
бого оборудования и вы-
полняются специализиро-
ванными строительными ор-
ганизациями. Для оценки
возможности и эффективно-
сти упрочнения грунтов на-
до проводить специфические
исследования их свойств до
Рис. 1.6. Железнодорожная насыпь
1 — основная 'площадка; 2 — насыпь; 3 — основание
Рис. 1.7. Подпорные стены и крепление кот-
лована
а — гравитационная бетонная стенка; б — уголко-
вая железобетонная стенка; в — анкерное 'Крепле-
ние стенки котлована
1 — глубина промерзания; 2 — дренажная засып-
ка; 3 — анкерное устройство
и после упрочнения.
Проблемы, выдвигаемые исследованием космоса. В наше вре-
мя ко всем перечисленным выше «земным» проблемам прибави-
лась задача исследования физико-механических свойств грунтов
на других планетах с целью не только выяснения условий посад-
ки на них космических кораблей, но и хозяйственно-технического
их освоения в недалеком будущем — задача, недавно еще занимав-
шая только воображение писателей-фантастов, а теперь ставшая
вполне реальной.
25
4. ОСНОВНЫЕ ВИДЫ НЕСКАЛЬНЫХ ГРУНТОВ
В дальнейшем мы подробно рассмотрим классификации грун-
тов, основанные на количественных физических и механических
характеристиках. Однако для того чтобы читатель получил не-
обходимое начальное представление об основных типах нескаль-
ных грунтов, относительно резко различающихся по своим стро-
ительным свойствам, приведем краткое их описание и названия,
которыми чаще всего пользуются практики-строители.
Галечником называют скопления несцементированных относи-
тельно крупных окатанных обломков размером в несколько сан-
тиметров, с трудом поддающихся разработке. Образцы галечника
практически невозможно отобрать с сохранением естественно?!
плотности, и его деформативные и прочностные свойства обычно
приходится определять полевыми испытаниями. В большинстве
случаев не требуется даже этих испытаний, так как в естествен-
ном залегании галечник обладает весьма малой сжимаемостью и
является хорошим основанием (если защищен от размыва). Более
мелкий материал — гравий и дресва — обычно рассматривается
как промежуточный по своим свойствам между галечником и
крупным песком.
Песчаные грунты состоят в основном из кварцевых частиц раз-
мером от десятых долей миллиметра до 2 мм и лишены сцепления.
Строительные свойства песка существенно зависят от его
плотности. В плотном состоянии это превосходное малосжимае-
мое основание для сооружений, обладающее высокой несущей
способностью. При больших по площади и заложенных на доста-
точной глубине фундаментах оно может свободно выдерживать
давление в десятки килограммов на квадратный сантиметр. Нао-
борот, в рыхлом состоянии песок, особенно мелкий, сильно сжи-
маем, дает большие осадки под нагрузкой, а будучи водонасыщен-
ным, под влиянием динамических воздействий или при значи-
тельных сдвиговых деформациях резко понижает свою устойчи-
вость и разжижается, растекаясь подобно густой жидкости.
Наиболее характерным свойством песчаных грунтов являет-
ся малая изменяемость их объема при изменении влажности; ины-
ми словами, они почти не обладают способностью сжиматься (да-
вать усадку) при высыхании или расширяться (набухать) при ув-
лажнении. Однако насыщение водой заметно снижает их сопро-
тивление действию нагрузки от сооружений. Это объясняется в ос-
новном уменьшением собственного веса частиц грунта, испыты-
вающих под водой выталкивающую силу (взвешивание) в соот-
ветствии с законом Архимеда. Соответственно уменьшается тре-
ние между частицами и облегчается их относительный сдвиг.
Сцепление между частицами, возникающее у влажного песка, ис-
чезает при его высыхании и затоплении песка водой. Однако ес-
ли это сцепление создано за счет цементационных связей и но-
26
сит стабильный характер, оно может играть существенную роль
в механических свойствах песка.
Плывунами строители называют грунты, которые легко те-
ряют устойчивость, превращаясь в текучую, расплывающуюся
массу. Это явление особенно часто встречается у водонасыщенных
тонкозернистых грунтов, представляющих собой смесь очень
мелкого песка, пылеватых и глинистых частиц, а также и у не-
которых высокопористых глин. Такие грунты даже при слабых
сотрясениях или при небольших деформациях, происходящих, на-
пример, при выпучивании стен котлована под действием собствен-
ного веса, переходят в состояние, напоминающее густую жид-
кость. Эти плывуны обычно очень плохо «отдают» воду, т. е.
не осушаются при откачке воды из котлованов и приямков на-
сосами. Их называют истинными плывунами или просто плыву-
нами.
С другой стороны, средне- и мелкозернистые пески, не явля-
ющиеся плывунами, могут переходить в плывунное состояние под
влиянием высокого давления фильтрующей сквозь них под боль-
шим напором воды. В подобных случаях грунт редко называют
плывуном, но говорят о «выносе» или «размыве» или о явлении
«кипения» грунта, как бы бурлящего под действием направлен-
ного вверх давления просачивающейся воды.
К глинистым грунтам относят тонкозернистые грунты, ко-
торые в маловлажном состоянии обладают высоким сопро-
тивлением нагрузке и небольшой сжимаемостью, но при высокой
влажности резко понижают свою прочность и дают большие и
долго продолжающиеся осадки сооружений. При увлажнении гли-
нистые грунты увеличивают свой объем (набухают) ц могут по-
этому впитывать большие количества воды, переходя в некото-
рых случаях в текучее состояние. Наоборот, при высыхании они
уменьшаются в объеме, давая значительную усадку, и приобре-
тают при полном высыхании высокую плотность и камневидное
состояние. Характерным свойством глинистых грунтов во влаж-
ном состоянии является их пластичность, проявляющаяся в спо-
собности сильно изменять свою форму под действием сдвигающих
сил, причем тем легче, чем выше влажность. При этом глина не
трескается и не крошится.
Таким образом, на строительные свойства этих грунтов влия-
ет их влажность, причем степень этого влияния сильно зависит от
их минералогического состава. Эти грунты способны испытывать
длительные незатухающие деформации под постоянной нагрузкой
и изменять свои прочностные свойства в процессе деформирова-
ния. В зависимости от плотности и прочности глинистых грунтов,
которая приближенно оценивается сопротивлением разработке,
строители на практике делят глины на твердые, мягкие и текучие.
Название «органический» в применении к грунтам не совпа-
дает с литологическим термином «органогенный», означающим
органическое происхождение. Строители называют органическими
27
как органогенные нескальные, так и любые другие грунты с боль-
шой примесью органического вещества, представляющего собой
остатки животных и растений на разных стадиях разложения. Эти
грунты имеют обычно темно-серый или черный цвет и нередко ха-
рактерный болотный запах, обычно усиливающийся при нагрева-
нии. Примесь тонко раздробленного органического вещества прида-
ет грунтам свойства, близкие к свойствам почв, а именно: большую
вязкость, сжимаемость и более низкую прочность в водонасыщен-
ном состоянии, чем у тех же грунтов без органических примесей.
В сухом состоянии, наоборот, они имеют очень высокую проч-
ность.
В термины «ил и илистые грунты» геологи и строители часто
вкладывают совершенно различное содержание. Так, иногда на-
зывают илом отложения (независимо от их влажности) тонко-
пылеватых частиц, содержащие лишь незначительную примесь
песчаных и глинистых частиц. В литологии и инженерной геоло-
гии илом называют сингенетическую стадию образования глины,
т. е. свежевыпавший тонкозернистый осадок на дне водоемов,
обладающий высокой влажностью и способный превратиться в
результате диагенетических изменений в глину. В просторечии
илом обычно называют тонкозернистый слабый водонасыщенный
грунт с высоким содержанием органических примесей, придающих
грунту темный цвет.
В строительной практике часто термином «ил» обозначают
придонный весьма рыхлый и текучий тонкозернистый грунт с
любым соотношением пылевато-глинистых частиц. Если в нем
преобладают глинистые частицы и ил проявляет четко выражен-
ные пластические свойства, его называют пластичным или глинис-
тым илом, а если преобладают пылеватые частицы и пластичес-
кие свойства выражены слабо — непластичным, пылеватым (алев-
ритовым) илом. Ил с большим содержанием органических при-
месей называют органическим илом. Чтобы отличить глинистый
и алевритовый илы друг от друга, пользуются таким простым при-
емом. Лепешку насыщенного водой ила встряхивают на ладони.
Если при этом поверхность оказывается глянцевитой из-за выс-
тупающей влаги, но затем при сгибании лепешки между пальца-
ми вода снова впитывается и поверхность делается матовой, то
мы имеем дело с непластичным илом. Когда лепешка непластич-
ного ила высыхает, она становится хрупкой и легко растирается
пальцами в пыль. Характерной особенностью илов является их
высокая сжимаемость и очень низкая прочность.
Торф — это органический грунт, представляющий собой волок-
нистый материал, который образовался в результате разложе-
ния под водой отмерших растений. Торф отличается очень боль-
шой сжимаемостью, причем нередко линзы его встречаются в ал-
лювиальных грунтах, и тогда на этих участках могут возникнуть
большие и неравномерные осадки, нередко разрушающие соору-
жения.
28
Растительным грунтом строители называют почвенные слои,
обычно прорезаемые фундаментами, но часто используемые в до-
рожном строительстве.
Лёссы представляют собой почти чисто пылеватые по сос-
таву связные грунты, обычно светло-желтого или палевого цве-
та, маловлажные. Лёссы (в основном эоловые отложения) отли-
чаются высокой пористостью, легко и сильно уплотняются при
замачивании под действием внешней нагрузки или собствен-
ного веса. Образцы лёсса, опущенные в воду, бурно распада-
ются.
Если толщи лёсса за свою историю не испытывали уплот-
нения, а затем при строительстве обводняются, то они дают
быстро протекающие осадки, измеряемые многими десятками
сантиметров (просадки).
Лёссовидные грунты по составу и происхождению (лёссовид-
ные супеси, суглинки, глины) могут отличаться от типичных лёс-
совых, но обладают подобно последним способностью давать при
замачивании под нагрузкой большие просадки.
Деградированные лёссы и лёссовидные грунты — это лёссы
и лёссовидные грунты, потерявшие свойство просадочности в ре-
зультате затопления, размыва и переотложения, химического
разложения или искусственного уплотнения (искусственно дегра-
дированный лёсс).
Насыпными называют искусственно образованные отложения
грунтов, вывезенных из котлованов, выработок метро и т. п., а
также отвалы из других материалов (типа заводских шлаков,
пустой породы и т. д.). С течением времени эти грунты слежива-
ются, т. е. естественным путем постепенно уплотняются.
К насыпным относят также всевозможные свалки.строительного
мусора, утиля, отходов производства и т. д., не поддающиеся уп-
лотнению и с трудом пробиваемые обычными сваями. В подоб-
ных случаях устройство фундаментов бывает сопряжено с больши-
ми трудностями и затратами.
От настоящей скалы строители отличают так называемые
полу скальные грунты — окаменевшие (ломовые) грунты, размяг-
чающиеся в воде.
Строители обозначают этим термином литифицированные поро-
ды типа аргиллитов, алевролитов или очень плотных окаменевших
смесей песка, гравия и глины. Название «ломовые» объясняется
тем, что эти грунты вручную можно разрабатывать только с по-
мощью лома и кирки. К этому классу грунтов часто относят и мер-
гель.
29
Глава 2
ГРУНТЫ КАК ОБЪЕКТ ИССЛЕДОВАНИЯ
1. НАУКИ, ИЗУЧАЮЩИЕ ГРУНТЫ
Науки, изучающие грунты, можно разделить на три основные
группы: науки, изучающие горные породы в первую очередь с
естественно-исторической точки зрения; науки, рассматривающие
решение чисто прикладных, главным образом строительно-техни-
ческих задач, связанных с расчетом, конструированием и возведе-
нием различных сооружений и, наконец, науки промежуточные
между этими двумя группами, как бы перебрасывающие мост
между двумя различными подходами к грунтам.
Геологические науки. В этих науках, входящих в первую из
указанных трех групп, грунты рассматриваются прежде всего как
горные породы, слагающие земную кору. Геологические науки
изучают естественные условия формирования и изменения горных
пород и выясняют различные природные факторы, определяю-
щие характер, направление и скорость соответствующих явлений и
процессов.
Прикладные строительно-технические науки. Эти науки изуча-
ют грунты как материалы, непосредственно используемые в тех
или иных технических целях. Это в первую очередь «Основания и
фундаменты»—прикладная наука, которая до 1925—1930 гг. была,
пожалуй, единственной, рассматривавшей вопросы использования
грунтов в строительных целях. Затем к ней присоединилась «Ме-
ханика грунтов», являющаяся ветвью строительной механики и
изучающая распределение напряжений в нескальных грунтах и
деформативные и прочностные свойства последних. С ее появле-
нием изучение грунтов стало быстро продвигаться вперед. В рам-
ках механики грунтов сейчас уже оформились такие разделы, как
«Физико-механические свойства грунтов», «Теория предельного
равновесия», «Теория балок на грунтовом основании», «Динамика
грунтов» и т. д., развившиеся, в сущности, в самостоятельные на-
уки.
Механика грунтов превращается теперь, с одной стороны, в
учебную дисциплину, излагающую в едином комплексе основные
положения этих разделов, а с другой,— в обобщающую науку,
анализирующую с общей точки зрения выводы всех этих частных
наук, устанавливающую связь между ними и изучающую общие
30
для всех них вопросы и, в частности, принципы построения раз-
личных расчетных моделей.
В последние годы все более определяется как наука геотех-
ника, изучающая использование грунтов в качестве материала для
различных искусственных земляных сооружений — дорожных на-
сыпей, плотин и дамб.
В настоящее время бурно развивается наука, изучающая фи-
зико-химические методы искусственного преобразования грунтов и
придания им наперед заданных свойств, называемая технической
мелиорацией грунтов. Об интересе к этой науке и интенсивности, с
которой ведутся исследования в этой области, свидетельствует
хотя бы то, что за последние десять лет прошло уже шесть всесо-
юзных конференций, посвященных ее проблемам.
Следует иметь в виду, что в этой области разрабатываются не
только методы искусственного улучшения, но также и способы
искусственного расслабления грунтов, снижения их прочности,
которое используется для облегчения производства строительных
работ (например, электроосмос при погружении свай в глинистые
грунты). Изучение сопротивления грунтов разработке и перера-
ботке различными строительными машинами и механизмами
оформляется в самостоятельную науку — «Механическую геотех-
нологию» (или просто «Геотехнологию»).
Под механикой горных пород понимают обычно науку о горном
давлении нескальных и скальных пород на крепления подземных
выработок [72]. В последнее время к ней также относят проблемы
разрушения горных пород при бурении.
В связи с проблемой образования снежных лавин были широко
развернуты исследования в области механики снега и льда. Изу-
чение механического поведения этих материалов в широкой степе-
ни основывается на использовании методов механики грунтов
[93,96].
Уже первые попытки измерить4 напряжения и деформации
грунтов под действием нагрузок от сооружений показали, что ме-
тоды, применяющиеся при аналогичных исследованиях строи-
тельных конструкций, как правило, неприложимы к грунтам. По-
требовались разработка и создание специальной аппаратуры для
этой цели. Соответствующие вопросы составили столь обширную
область исследований, что в настоящее время она оформляется в
самостоятельную прикладную науку—«Терраметрику». Она охва-
тывает вопросы натурного измерения колебаний и давления
грунтов на подземные сооружения, осадок и сдвигов сооружений,
распределения напряжений по подошве фундаментов и в глубине
оснований, давления в минеральном скелете и поровой воде. Тер-
раметрика разрабатывает более совершенную аппаратуру для из-
мерения и автоматической записи деформаций грунтов при их ис-
пытаниях в лаборатории и поле.
Совсем недавно появилось еще одно направление в изучении
грунтов — террамеханика, рассматривающая грунты с точки зре-
31
ния их проходимости для различных машин. Эта наука усиленно
развивается как в связи с проблемой движения строительных ма-
шин на новостройках при отсутствии удовлетворительных дорог,
так и под влиянием потребностей военной техники, поскольку
военным машинам и орудиям часто приходится передвигаться в
условиях полного бездорожья.
Быстро развиваются также особые разделы всех перечисленных
выше наук, относящиеся к категориям нескальных грунтов со
специфическими свойствами — к мёрзлым, лёссовидным, аллюви-
альным и др.
Основы всевозможных технологических процессов, в которых
имеют дело с раздробленными порошкообразными веществами,
рассматриваются в микроме ритике. Это название [90] происходит
от греческих слов «микрос»—малый и «мерос» — часть. Многие
исследования и данные микромеритики очень близки к проблемам,
которые рассматриваются в механике грунтов.
Наряду с механикой нескальных быстро развивается механика
скальных грунтов. Ранее, в течение многих лет она занималась
главным образом вопросами давления на крепления подземных
выработок и обделки тоннелей («Механика горных пород»), а
также некоторыми проблемами, связанными с деформациями гор-
ных пород и земной поверхности при подземной разработке по-
лезных ископаемых (так называемая «Теория сдвижения горных
пород»). Однако недавние аварии нескольких крупных гидротех-
нических сооружений, основанных на скале и потому не вызыва-
вших ни у кого особых опасений, а также грандиозные оползни
скальных откосов заставили обратить внимание на устойчивость
скальных массивов в основаниях сооружений и в склонах. В ре-
зультате оформилась как самостоятельная наука механика скаль-
ных пород [75]. В 1966 г. состоялся Первый всемирный конгресс
по механике скальных пород, который подвел итоги современному
состоянию изученности этой проблемы и наметил первоочередные
задачи для дальнейших исследований.
Инженерная геология. К естественно-историческим наукам о
горных породах, с одной стороны, и к чисто техническим наукам
о грунтах, с другой, примыкает инженерная геология с ее разветв-
лениями. Она появилась ранее механики грунтов и имела целью
изучение естественно-исторических условий формирования тех
свойств различных грунтов, которые имеют значение для строи-
тельства. Эта наука устанавливает влияние геологических факто-
ров на поведение грунтов как оснований и материала инженерных
сооружений, а также на устойчивость сооружений в целом. Так,
Ф. П. Саваренский [69] определял инженерную геологию как от-
расль геологии, трактующую вопросы приложения геологии к ин-
женерному делу.
С другой стороны, существует точка зрения, согласно которой
задачей инженерной геологии является исследование явлений на-
рушения строительством и эксплуатацией сооружений естествен-
32
ного течения природных процессов. Эти исследования должны не
только выяснять характер подобных изменений, но и дать воз-
можность направить их таким образом, чтобы это отвечало на-
роднохозяйственным интересам. И. В. Попов [53] писал, что
«инженерная геология как наука является отраслью геологии, изу-
чающей динамику верхних горизонтов земной коры в'связи с ин-
женерной деятельностью человека».
Обобщающее определение современной инженерной геологии
предложил Н. Н. Маслов [36]: «Инженерная геология представ-
ляет собой ветвь геологии, изучающую в динамическом разрезе
и во всех возможных и необходимых случаях на количественной
основе процессы и явления, возникающие во взаимодействии ин-
женерных сооружений с местной природной обстановкой, а также
методы их прогноза и пути возможного на них воздействия в же-
лательном для нас направлении».
Особенно большое внимание в современной инженерной гео-
логии привлекают вопросы формирования свойств осадочных по-
род от момента образования осадка и до позднейших стадий
литогенеза. В этой области уже получены весьма интересные и
важные экспериментальные и теоретические результаты. Для этих
исследований характерно широкое использование методов колло-
идной химии, реологии, физической химии, физики поверхностных
явлений и физико-химической механики.
От инженерной геологии по мере ее развития отпочковывался
ряд новых наук. Так появилось «Грунтоведение», связывающее
физико-механические свойства грунтов с условиями их возникнове-
ния и соответствующей геологической обстановкой. Оформляются
в самостоятельные крупные научные дисциплины «Инженерная
гидрогеология», «Инженерное мерзлотоведение», «Инженерная ге-
одинамика»— учение о различных геологических процессах, важ-
ных в инженерном отношении: оползнях, селях, обвалах, карсте,
переработке берегов, тектоно-сейсмических процессах, образова-
нии коры выветривания.
Некоторые исследователи предлагают выделить и назвать
«Геомеханикой» науку, объединяющую и обобщающую механику
нескальных грунтов и механику скалы в связи с проблемами под-
земного строительства и горного дела, в то время как другие рас-
сматривают ее как механико-теоретическую базу тектоники, гео-
физики и инженерной геологии, иными словами, как науку о
механизме геологических процессов [78, 107].
В настоящее время многие инженерные сооружения достигли
столь гигантских размеров, что передают на грунты усилия, соиз-
меримые с усилиями геологического масштаба, действовавшими
на земную кору в процессе ее формирования, а некоторые воздей-
ствия, вроде сверхсильных взрывов .создают в земной коре усилия
и колебания, близкие к наблюдаемым при землетрясениях. Соот-
ветствующие проблемы одни авторы относят к геомеханике, дру-
гие считают их изучение основной задачей инженерной геологии.
2 Зак. 530
33
Е. М. Сергеев, например, считает, что современная инженерная
геология представляет собой целый комплекс геологических дис-
циплин, среди которых основными являются грунтоведение, ин-
женерная геодинамика и региональная инженерная геология.
Одна из важных новых задач инженерно-геологической нау-
ки — изучение истории изменения напряженного состояния горных
пород в ходе их формирования и в результате участия в дефор-
мациях земной коры. Соответствующую науку следовало бы наз-
вать «Палеогеомеханикой» .Палеогеомеханическая реконструкция
атектонических дислокаций была недавно осуществлена по пред-
ложению автора в связи с изучением одного крупного оползня [80].
Современное состояние геомеханики и геологии позволяет во
многих случаях проводить подобные палеогеомеханические изыска-
ния и реконструкции. Чтобы изучение сохранившихся следов
древних деформаций и дислокаций не носило чисто описательного
характера, необходимо связывать это изучение с анализом напря-
жений в породе, как остаточных, так и тех, которые действовали
ранее и нашли свое отражение в физико-химических и структур-
ных изменениях, испытанных породой под влиянием возникших в
ней усилий. Этим вопросам посвящены интересные монографии
А. В. Артемьева [2] и В. Т. Терновской и др. [76].
2. ВОЗНИКНОВЕНИЕ МЕХАНИКИ ГРУНТОВ
Развитие практического опыта. В течение многих веков чело-
веческой истории методы проектирования и строительства основы-
вались почти целиком на практическом опыте. Сведения об удач-
ных конструкциях и способах производства работ передавались
из поколения в поколение, а за неудачи строителей жестоко на-
казывали. В далекой древности, когда еще не существовало и не
могло существовать, естественно, никаких строительных норм,
вавилонский царь Хаммурапи издал за 18 веков до н. э. законы,
гласившие, что если постройка разрушится, то строитель обязан
ее за свой счет восстановить, а если при аварии будет убит хозяин
дома или кто-либо из членов его семьи, то должен быть обезглав-
лен строитель или член его семьи. При строительстве Великой
Китайской стены длиной 4000 км в IV—III вв. до н. э. виновных
тут же казнили, если в шов между камнями входил ноготь.
Таким образом, профессия строителя в те далекие времена бы-
ла сопряжена с немалым риском, и поэтому закладка каждого
сооружения сопровождалась кровавыми жертвами богам, а в сред-
ние века — торжественными богослужениями и церемониями. На-
дежда на милость фантастических потусторонних сил, естественно,
не могла заменить отсутствия знаний, и, несмотря на накапли-
вавшийся практический опыт, аварии при сколько-нибудь слож-
ных геологических условиях продолжали повторяться.
И тем не менее от прошлых веков сохранились творения ге-
34
ниальных зодчих прошлого — огромные сложные сооружения, вы-
зывающие удивление и восхищение своей технической смелостью.
Уже за тысячи лет до нашего времени появились сваи и опускные
колодцы, строились огромные каналы и земляные плотины, тех-
нически безупречно устраивались фундаменты многих сооружений.
Теоретические исследования. Только применение теории наряду
с использованием практического опыта позволяет обеспечивать
надежность ответственных сооружений, возведенных в сложных
геологических условиях. Аналогичную роль в развитии строитель-
ных конструкций сыграли возникшие в XVII—XVIII вв. механика
и теория сооружений. Но область проектирования оснований и
земляных сооружений еще долго отставала от строительной меха-
ники, упорно не поддаваясь усилиям исследователей, несмотря на
то что к началу XX в. уже накопилось значительное количество
теоретических исследований и испытаний, в том числе и очень
крупных (достаточно назвать хотя бы работы Кулона, Ренкина и
Буссинеска). К этому времени уже были проведены важные ис-
следования на моделях (например, опыты В. И. Курдюмова в Рос-
сии в 1890 г.), выполнялись испытания оснований пробной на-
грузкой (например, с помощью возведения высоких кирпичных
столбов), для разведки грунтов применялось шурфование и буре-
ние, существовали понятия о предельном и допускаемом давлении
на основание. Были установлены региональные эмпирические зна-
чения допускаемого давления для ряда грунтов, предложены
различные формулы для расчета давления на подпорные стены,
несущей способности оснований и устойчивости откосов.
Теперь, после работ Терцаги, уже ясно, что создание механики
грунтов задерживалось из-за отсутствия, во-первых, способов
безошибочной идентификации грунтов, а во-вторых, надежных
методов количественного определения их механических характе-
ристик, пригодных для использования в расчетах на устойчивость.
Любопытно в качестве иллюстрации привести высказывание одно-
го из крупных инженеров того времени — проф. Франциуса в его
книге «Der Grundbau»: «Угол трения <р не следует смешивать с
углом естественного откоса ввиду совершенной невозможности
определить действительное значение <р». Нужно добавить, что в
то время не существовало понятия о ненарушенной структуре
грунтов, никто еще не думал о грунтоносах, и пробы грунта от-
бирались с помощью спиральных буров и желонок в совершенно
перемятом состоянии.
Из-за отсутствия каких бы то ни было методов расчета оса-
док и оценки влияния неравномерности осадок на деформации
в проектировании оснований и земляных сооружений по-прежнему
имели место просчеты, приводящие к авариям и катастрофам,
при которых терялись материальные ценности, а иногда гибли
люди.
В первые десятилетия нынешнего века почти одновременно
в нескольких странах были созданы комиссии для изучения при-
2* Зак. 530
35
чин этих аварий и выработки методов рационального решения со-
ответствующих проектно-строительных проблем. В январе 1913 г.
Американское общество гражданских инженеров создало специ-
альный Комитет по нормированию несущей способности грунтов,
а в декабре того же года в Швеции была создана Геотехническая
комиссия Шведских государственных железных дорог для выра-
ботки мер по борьбе с многочисленными деформациями земляного
полотна и оползнями. К работе в этих комиссиях привлекались
крупные специалисты и по ряду вопросов были достигнуты извест-
ные успехи. Так, в Швеции были разработаны способы отбора
ненарушенных образцов грунтов и, в частности, предложена пене-
трация, получившая теперь широкое распространение; разработан
метод расчета устойчивости откосов в предположении круглоци-
линдрической поверхности скольжения и т. д. Однако в целом ра-
бота этих комиссий не оправдала возлагавшихся на них надежд.
Наиболее значительные результаты были получены К. Терцаги
(1883—1963 гг.), работавшим в одиночестве в маленькой, прими-
тивно оборудованной лаборатории. Свои исследования Терцаги
опубликовал в 1925 г. в книге «Строительная механика грунтов на
основе их физических свойств», которая быстро получила мировую
известность. С ее появлением оформилась как самостоятельная
наука новая ветвь строительной механики — «Механика грунтов»1.
Заголовок книги подчеркивал, что новая наука целиком опирается
на исследования физических свойств грунтов.
После опубликования книги Терцаги методы эксперименталь-
ного и теоретического изучения напряжения и деформаций в
грунтах стали бурно развиваться, и многим уже казалось, что
только чисто математические трудности сдерживают прогресс ме-
ханики грунтов и нужно лишь преодолеть их, чтобы все препятст-
вия к дальнейшему движению вперед были сняты. Однако практи-
ка вскоре показала всю необоснованность подобных надежд, за-
ставив обратить особое внимание на развитие инженерной гео-
логии.
Инженерная геология и механика грунтов. Представляется
поучительной история постепенного пересмотра создателем меха-
ники грунтов К. Терцаги своего отношения к инженерной геологии.
С этой историей, как нам кажется, небесполезно будет познако-
миться многим специалистам в области механики грунтов, уси-
ленно превращающим ее в чисто строительную или даже расчет-
но-математическую дисциплину, оторванную от своей геологиче-
ской основы.
Уже в 1929 г. в статье «Влияние мелких геологических осо-
бенностей на безопасность плотин» К. Терцаги писал о важной
роли деталей геологического строения для устойчивости сооруже-
1 Самый термин «механика грунтов» впервые появился в опубликованной в
1846 г. французским инженером Александром Коллэном монографии «Экспери-
ментальные исследования оползней в глинистых грунтах, сопровождаемые рас-
смотрением некоторых принципов механики грунтов».
36
ний. Одновременно он выпустил в соавторстве с крупными геоло-
гами Редлихом и Кампе «Инженерную геологию» (1929 г.), в ко-
торой писал: «При современных условиях инженеры не в состоя-
нии еще согласовать результаты своего опыта с данными геолога
и бурового мастера». Вся книга посвящена, в сущности, попытке
решения проблемы такого согласования. В этот период Терцаги
еще видел главную задачу во внедрении открытий^ механики грун-
тов в практику инженерно-геологических изысканий.
Однако позднее он вынужден был по-иному оценить соотноше-
ние между механикой грунтов и инженерной геологией. В 1948 г.
в своей книге «Механика грунтов в инженерной практике», напи-
санной совместно с Р. Пэком, он отметил, что в результате увлече-
ния теорией от внимания ряда исследователей и ученых стали ус-
кользать многочисленные ограничения, налагаемые природой на
приложение математики к проблемам оснований и земляных соо-
ружений. Терцаги считал, что при сложных геологических условиях
многие задачи вообще не могут быть решены теоретически, и пола-
гал, что стремление получить необходимые данные с помощью бу-
рения и испытаний образцов приводит в этом случае лишь к на-
прасной трате средств и чаще всего оказывается безуспешными. Со-
ответственно для подавляющего большинства практических задач
достаточно ограничиваться, по его мнению, лишь приближенными
решениями, которые должны достигаться простыми способами, ос-
нованными на надежной картине общего строения основания и
характеристике его свойств. Эту картину надлежит устано-
вить в первую очередь с помощью методов инженерной гео-
логии.
В 1955 г. он снова публикует работу, специально посвященную
одной из основных проблем инженерной геологии: «Влияние гео-
логических факторов на инженерные свойства отложений». Резю-
мируя в 1961 г. в своей статье «Прошлое и будущее прикладной
механики грунтов» обзор аварий и катастроф, все еще продолжа-
ющихся, несмотря на применение методов современной механики
грунтов, К. Терцаги объясняет их либо недостаточным объемом и
качеством инженерно-геологической информации, полученной при
изысканиях, либо же недостатками в технике и методике отбора
образцов и их испытаний.
Так как эта статья не публиковалась в переводе на русский
язык, мы позволили себе привести из нее несколько, хотя и
длинных, но весьма любопытных цитат и прежде всего характер-
ное признание К. Терцаги: «Когда я опубликовал книгу «Строи-
тельная механика грунтов», я еще не сознавал той неопределен-
ности, которая связана с интерпретацией результатов бурения,
а мои методы испытания были еще очень примитивны. Поэтому я
сам прошел через период, в течение которого моя деятельность мо-
жет быть охарактеризована как «злоупотребление механикой
грунтов». Я и сейчас еще поражаюсь, когда вспоминаю смелые
заключения, которые я в то время делал на основании опытов,
37
проведенных на примитивных приборах над недостаточным коли-
чеством, да к тому же еще и нарушенных образцов.
Однако этот период был кратким. Он закончился вскоре после
1926 года, когда я впервые получил возможность изучить оса-
дочные толщи различного происхождения и добыть близко распо-
ложенные монолиты из отдельных буровых скважин. Я узнал, как
велико влияние методики отбора образцов и испытаний на полу-
чаемые результаты».
Далее он писал, что по мере того, как время шло и его кон-
сультационная деятельность распространялась на все большие и
большие территории, он увидел, что осадочные отложения с не-
правильным строением гораздо более часты, чем он ранее предпо-
лагал, и что такое строение исключает возможность точных рас-
четов.
«В подобных условиях важно знать колебания в горизонталь-
ром направлении средних свойств неблагоприятных слоев. Опыт
подтверждает, что удовлетворительные решения могут быть полу-
чены исходя из основных принципов механики грунтов, дополнен-
ных умеренным объемом буровых работ и испытаний. Но имеют
место и такие геологические условия, которые исключают возмож-
ность получения до начала строительства существенной информа-
ции, требующейся для надежного проектирования. В подобных
случаях разумно исходить из наиболее неблагоприятных предпо-
ложений, совместимых с результатами инженерно-геологических
изысканий».
Однако неправильно было бы сделать вывод, что при сложных
геологических условиях следует ограничиваться только изучением
литологического строения площадки. К сожалению, некоторые
строители считают, что большего им и не нужно, что достаточно
испытать образцы грунтов и поступать в соответствии с нормами,
чтобы все было в порядке. Соответственно они рассматривают
более глубокие геолого-генетические исследования как хотя и
интересное, но практически ненужное занятие. В крайнем случае,
они готовы согласиться на полезность подобных исследований
только при строительстве таких сооружений, как большие плоти-
ны или тоннели. К сожалению, современные строительные нормы
во многих странах построены таким образом, что поддерживают
эти ошибочные представления.
С другой стороны, специалисты в области инженерной геоло-
гии, правильно протестуя против метафизичности подобных взгля-
дов и связанного с ними узкого эмпиризма, не всегда еще могут
указать, как правильно использовать генетические данные для
прогноза поведения сооружений с тем приближением к действи-
тельности, которое необходимо строителям. Некоторые недоста-
точно квалифицированные инженеры-геологи иногда сами дискре-
дитируют инженерную геологию в глазах проектировщиков-строи-
телей, когда начинают с ними пресловутый спор о «четверти
килограмма», т. е. о возможности немного увеличить расчетное
38
давление на основание, и при этом вынуждены оперировать в
споре аргументами, взятыми из тех же строительных норм, кото-
рые строители знают отнюдь не хуже геологов.
Таким образом, неотложной задачей инженерной геологии с
точки зрения строительной практики является уточнение методов
качественного прогноза поведения оснований в тех случаях, когда’
сложность геологического строения площадки и неоднородность
свойств грунтов исключают возможность сколько-нибудь точного
расчета осадок и несущей способности способами современной
механики грунтов. Методы инженерной геологии должны в подоб-
ных случаях позволить оценить степень приближенности выпол-
ненных расчетов и указать порядок возможных отклонений
результатов расчета от действительности с тем, чтобы при проек-
тировании можно было предусмотреть возможные неожиданности
и внести в проект соответствующие коррективы [35, 36, 37].
Технические науки и производственный опыт. Важная осо-
бенность прикладных наук, к каковым относятся и сама строи-
тельная механика грунтов, и ее физико-геологические основы,
заключается в непосредственной связи с производственным опы-
том, из которого эти науки черпают многие свои выводы и ут-
верждения, нередко носящие характер чисто практических пра-
вил и рекомендаций. С развитием теоретических знаний эти
«рецептурные» приемы уступают место научно обоснованным ре-
шениям.
Относительно не так давно, в двадцатые годы, в строительных
вузах читался курс «Строительное искусство»; теперь это название
вызывает лишь улыбку. Однако вопрос о том, на чем же основа-
но современное фундаментостроение — на научном знании или на
искусстве строителей, поднимается иногда еще и сейчас. Это
вызвано значительной сложностью соответствующих проблем и
все еще недостаточно совершенной техникой инженерно-геологи-
ческих изысканий, что порождает известное разочарование в тео-
рии даже у крупнейших специалистов в области механики грун-
тов. В 1948 г. К. Терцаги во вступительной статье к первому но-
меру журнала «Geotechnique» писал, что по отношению к пробле-
мам фундаментостроения и геотехники роль точной науки «го-
раздо ближе к ее роли в области медицины, чем в области мосто-
строения или машиностроения» и что «хорошо документированное
описание различных практических случаев стоит не меньше, чем
целый десяток искусно построенных гипотез, а результаты лабо-
раторных исследований не должны привлекать к себе слишком
много внимания, пока значение этих результатов не проверено
надлежащими наблюдениями за сооружениями в натуре»/В 1957 г.
в своем выступлении на международной конференции по механи-
ке грунтов Терцаги заявил, что специалисты в области механики
грунтов должны уметь приходить к правильным решениям ин-
туитивно «без предшествующих логических заключений».
В 1958 г. А. Лосье опубликовал во французском журнале
39
«Genie Civil» статью под названием «Кризис доверия к механике
грунтов», а Р. Пек в 1962 г. опубликовал статью «Искусство и
наука в основаниях и фундаментах», в которой проводится мысль
о том, что поскольку механика грунтов дает указания на поведе-
ние грунтов лишь для простейших условий, близких к идеальным,
то вообще задача этой науки сводится лишь к тому, чтобы дать
удобную и логическую основу для анализа и систематизации на-
капливаемого практического опыта, всегда протекающего в гораз-
до более сложных реальных условиях, чем идеализированные по-
строения механики грунтов. Цо его мнению, механика грунтов
только помогает установить, что именно следует наблюдать на
практике, и лишь намечает путь, по которому нужно следовать
при решении новых проблем, не имевших прецедентов в прош-
лом.
Нам представляется, что ни в коем случае нельзя согласиться
с подобного рода умалением значения теории и отведением ей
столь ограниченной роли по отношению к практике. Значение
теории, как известно, заключается прежде всего в предсказании,
предвидении. Без этого она не представляет никакой ценности.
Вопрос о правильном соотношении между теорией и практикой
давно уже не является проблемой и окончательно решен диалек-
тическим материализмом.
Теория возникает и развивается на основе практики, является
научным обобщением этой практики. Однако теория не ограничи-
вается только регистрацией результатов опыта, а на основе
абстрагирующей деятельности человеческого мышления способна
давать представления и о таких явлениях, которые не только не
были известны ранее, но которые невозможно непосредственно
наблюдать. Теория после ее создания используется для дальней-
шего развития практики, развития производства; на этом прове-
ряется ее истинность, уточняются пределы применимости и откры-
ваются пути ее дальнейшего развития.
В связи со сказанным представляет интерес приводимое Тер-
цагй высказывание автора одного старинного строительного по-
собия: «При изложении современного уровня наших знаний о
прочности строительных материалов я многократно получал воз-
ражения со стороны дельных и опытных инженеров, говоривших,
что попытки создания научных основ в этой области должны
быть признаны безнадежными, так как в действительности не су-
ществует ни однородных материалов, ни однородных напряжен-
ных состояний».
Нечто аналогичное в 1916 г. писал один из воздухоплавателей,
убежденный в том, что никакая теория неприложима к столь не-
постоянной среде, как воздух. Это говорилось как раз в то время,
когда Н. Е. Жуковский опубликовал свои знаменитные «Теоре-
тические основы воздухоплавания».
История науки уже не раз доказывала полную несостоятель-
ность любых сомнений в возможности развития теории в области
40
самых сложных проблем, с которыми сталкивалось человечество.
Несомненно, будут созданы и надежные теоретические методы
оценки возможных деформаций оснований и сооружений даже в
самых сложных геологических условиях [12].
Необходимо подчеркнуть, что ошибки в проектах, аварии и
большие перерасходы средств, послужившие причиной выступления
Р. Пека, происходят в основном из-за неправильной или неточной
оценки механических свойств грунтовых толщ. Возможные ошибки
и неудачи из-за несовершенства существующих методов расчета
или погрешностей в методике испытания отдельных образцов
имеют гораздо меньшее значение, и многие рафинированные ма-
тематические теории механики грунтов не находят практического
приложения потому, что требующиеся для них расчетные пара-
метры грунтовой толщи в целом определяются еще слишком
грубо или вообще не определяются.
Без преувеличения можно сказать, что современная механика
грунтов позволяет для подавляющего большинства задач, кото-
рые ставит перед собой строительная практика, определять толь-
ко порядок искомых величин, причем даже в самых благоприят-
ных условиях ошибка может доходить до 100%. Известно, что
если при расчете разность осадок двух соседних опор оказалась
равной 4,5 см, то это означает, что разность будет измеряться сан-
тиметрами, а не десятками сантиметров, но какова она будет в
точности — совершенно неизвестно (она может оказаться равной,
например, и 6, и 9 см).
Чем сложнее геологическое строение площадки, тем менее то-
чен расчет. Грамотное техническое решение в подобных случаях
может быть принято только при консультации квалифицирован-
ного инженера-геолога, который, оценивая все особенности ин-
женерно-геологической обстановки, может дать справедливую
оценку точности расчетных прогнозов и надежности проектных ме-
роприятий.
Развитие механики грунтов и инженерной геологии в СССР.
Огромный размах строительства в СССР, широко развернувшего-
ся начиная с 1925 г. после решения XIV съезда партии об инду-
стриализации страны, выдвинул неотложную проблему возведения
грандиозных гидротехнических и инженерных сооружений на сла-
бых грунтах, которая была смело и успешно решена в короткие
сроки. И, несомненно, одна из основных причин этого успеха за-
ключалась в интенсивном развитии одновременно всех направле-
ний исследований, обеспечивающих правильное понимание взаи-
модействия грунта и сооружения: инженерно-геологических, меха-
нико-теоретических и физико-грунтоведческих.
О высоком уровне этих исследований в СССР свидетельству-
ют многие работы, появившиеся в двадцатых и тридцатых годах.
Наиболее значительные среди них: капитальная монография со-
здателя советской школы инженерной геологии Ф. П. Саваренско-
го «Инженерная геология», вышедшая в 1937 г.; две друг друга
41
дополняющие работы Н. М. Герсеванова — основателя отечест-
венной школы механики грунтов — «Опыт применения теории уп-
ругости к определению допускаемых нагрузок на грунт на основе
экспериментальных работ» (1930 г.) и знаменитые «Основы дина-
мики грунтовой массы» (1931—1937 гг.); обширная монография
Н. П. Пузыревского «Фундаменты» (1934 г.), содержавшая много
новых идей и методов расчета; первые в мире учебники Н. А. Цы-
товича «Основы механики грунтов» (1934 г.), Н. Н. Иванова и
В. В. Охотина «Дорожное почвоведение и механика грунтов»
(1934 г.) и И. В. Попова «Механика грунтов» (1937 г.); серия ста-
тей Н. Н. Маслова в 1934—1936 гг. по вопросам геотехнических ис-
следований, опубликованная в сборниках Свирьстроя; работы в
области грунтоведения М. М. Филатова «Почвы и грунты в дорож-
ном деле» (1932 г.) и «Основы дорожного грунтоведения» (1936 г.)
и А. Ф. Лебедева «Почвенные и грунтовые воды» (1930 г.) и, нако-
нец, многочисленные исследования их учеников.
Главной особенностью всех этих работ было стремление как
можно лучше и глубже оценить роль и влияние естественно-геоло-
гической обстановки, возможней более полный и всесторонний
учет физико-механических и физико-химических свойств грунтов
и рассмотрение работы грунта и сооружения в их единстве и
взаимодействии.
На перечисленных выше и других работах (в сочетании с
непосредственным участием в решении задач, выдвигавшихся
практикой строительства) была воспитана и выросла большая
группа выдающихся советских исследователей, продолжающих в
наше время славные традиции своих учителей и обеспечивающих
этой области советской науки мировое признание.
3. О ФИЗИКО-ГЕОЛОГИЧЕСКИХ ОСНОВАХ
МЕХАНИКИ ГРУНТОВ
Раздел механики в физике. В известных «Лекциях по физике»
(1965 г.) Ричард Фейнман заметил: «У физиков есть привычка
брать простейший пример какого-то явления и называть его «фи-
зикой», а примеры посложнее отдавать на растерзание других
наук, скажем прикладной математики, электротехники, химии или
кристаллографии. Даже физика твердого тела для них только
«полуфизика», ибо ее волнует слишком много специальных воп-
росов».
Действительно, хотя основы механики представляют собой
важную часть физики, тем не менее тот объем вопросов механики,
который рассматривается в физике и исследуется физиками, со-
ставляет лишь весьма небольшую часть обширной и разветвлен-
ной науки, которую представляет собой современная механика,
получившая «на растерзание», по выражению Фейнмана, огром-
ное количество весьма сложных и слишком специальных для фи-
42
зикии вопросов, выдвинутых развитием техники. Таким образом,
раздел механики в физике, который можно было бы назвать
физическими основами механики, представляет собой исследова-
ние фундаментальных законов механики применительно к про-
стым задачам, не требующим привлечения громоздких и сложных
вычислений, затемняющих ясную физическую суть явлений.
Физика и изучение свойств грунтов. Хотя изучение физико-
механических свойств грунтов и не является разделом физики,
оно не входит непосредственно и в собственно механику грунтов, а
служит введением в нее, образуя ее физико-механическую основу.
При исследовании физико-механических свойств грунтов не ста-
вятся в отличие от механики грунтов задачи, непосредственно свя-
занные с взаимодействием сооружений и оснований или с пове-
дением земляных сооружений и т. п., но рассматриваются отдель-
ные простейшие стороны этого взаимодействия, его физическая
суть, основанная на общих законах физики и лежащая в основе
больших групп сложных задач, решаемых современной механикой
грунтов.
Формально-феноменологический и структурно-динамический
подход к исследованию грунтов. Для феноменологического (от
греческого «феноменов» — являющееся) подхода к изучению яв-
лений характерно то, что он не требует исследования структуры
тех сред, в которых происходят изучаемые явления.
Естественно, что обойтись совершенно без тех или иных допу-
щений о структуре сред не удается, однако эти допущения носят
характер существенной идеализации структуры и достаточны
лишь для того, чтобы как-то объяснить соответствие между на-
блюдаемыми явлениями и формальным математическим аппара-
том, который предлагается для их описания. Нередко эти допу-
щения вводятся для облегчения понимания и усвоения феномено-
логической теории при преподавании. Так, в теории упругости или
гидродинамике вводятся допущения о том, что вещество представ-
ляет собой идеальную непрерывную среду, способную делиться до
бесконечности на элементы, обладающие теми же свойствами, что
и среда в целом. Феноменологическое направление в физике ведет
свое начало от Ньютона и позволяет успешно решать многие зада-
чи механики твердых тел, жидкостей и газов.
Критерием правильности феноменологических теорий служат
непосредственные эксперименты или наблюдения в натуре, с по-
мощью которых устанавливаются численные параметры, харак-
теризующие отклик данной среды на данный вид внешних воздей-
ствий при прочих равных условиях.
Основным требованием к этим параметрам среды является
их неизменность при количественном изменении внешних воздейст-
вий данного типа. Таким параметром, например, при растяжении
упругого, стержня является модуль упругости (модуль Юнга), по-
стоянный для данного материала, но имеющий различную вели-
чину для различных материалов. Вычислить величину этого моду-
43
ля исходя из каких-либо данных о структуре материала и взаи-
модействии атомов и молекул, из которых он состоит, феноменоло-
гическая теория не в состоянии, да и в принципе не позволяет
ставить подобную задачу.
Феноменологическое направление называют поэтому формаль-
но-математическим, и оно отказывает при решении таких задач,
в которых учет действительной структуры материала и характера
взаимодействия ее элементов является обязательным.
В подобных случаях феноменологический подход должен усту-
пить место молекулярно-кинетическому или структурно-динамиче-
скому, который требует изучения физических явлений в тесной
связи со структурой соответствующих сред, причем для расчета
макроскопического движения среды широко используется стати-
стическое рассмотрение взаимодействий огромного количества
элементарных частиц, образующих тело. Этот путь в физике был
проложен исследованиями Максвелла и Больцмана, а в наше вре-
мя он получил дальнейшее развитие в квантовой теории вещества.
Именно структурно-динамический подход дал возможность ре-
шить задачу предвычисления, например, различных констант ве-
щества по его структурно-молекулярным свойствам.
Физико-химическая механика. До недавнего времени при ре-
шении задач, стоявших перед механикой сплошных сред, можно
было ограничиваться чисто феноменологическим подходом, ис-
пользуя лишь несколько весьма простых физических моделей,
вроде идеального упругого тела, идеального пластического тела,
идеальной сжимаемой жидкости (газа) или вязкой жидкости не-
изменного химического состава и т. п.
Проблемы, поставленные развитием новой техники за послед-
ние 15—20 лет и связанные главным образом с большими скоро-
стями, высокими температурами, огромными нагрузками и глубо-
ким вакуумом при одновременной необходимости учета физико-
химических превращений, сопровождающих механические процес-
сы в этих условиях, потребовали изучения гораздо более тонких и
глубоких свойств материалов. Это привело к обогащению механи-
ки сплошных сред ранее чуждыми для нее представлениями и
идеями квантовой механики, статистической физики, кинетики и
т. д. В результате «стыкования» всех этих наук возникла новая
наука, которую одни называют физико-химической механикой, а
другие — физической механикой.
Задача этой новой науки заключается в исследовании природы
механических свойств сред и материалов, используемых в технике,
исходя из микростроения вещества. Важной целью этой науки
является изучение проблемы создания новых искусственных мате-
риалов с наперед заданными свойствами.
Применение идей физико-химической механики к грунтам. В
настоящее время быстро и успешно развивается направление, ис-
пользующее те исключительно ценные сведения о взаимодействии
частиц дисперсных систем между собой и с поровой средой, ко-
44
торые дают современная физическая и коллоидная химия и в осо-
бенности работы школ П. А. Ребиндера и Б. В. Дерягина. Следу-
ет указать, что в почвоведении уже давно и широко используется
подобное направление (школы В. Р. Вильямса, И. Н. Антипова-
Каратаева, А. Ф. Иоффе, Н. А. Качинского). В работах Н. Я. Де-
нисова, С. В. Нерпина, И. М. Горьковой и их учеников в области
исследования механических свойств грунтов были получены очень
интересные и важные результаты, показывающие, какие широкие
горизонты открывает это направление перед исследователями в
области физико-геологических основ механики грунтов. Большую
роль во внедрении в практику исследования грунтов методов фи-
зико-химической механики сыграли систематические исследова-
ния различных генетических типов осадочных пород, проведенные
И. М. Горьковой [15].
Следует указать, что и за рубежом в работах И. Розенквиста,
Т. Лэмба, Г. Уинтеркорна и ряда других исследователей в послед-
ние годы также уделяется значительное внимание связи физико-
механических свойств грунтов с современными представлениями
физической и коллоидной химии и реологии. Эти проблемы об-
стоятельно рассматриваются и в таких монографиях, как «Ин-
женерные свойства грунтов» Д. Леонардса (1969 г.), «Введение
в поведение грунтов» Р. Ионга и П. Уоркентина [95] и «Принци-
пы механики грунтов» Р. Скотта (1963 г.).
Физико-геологическая механика грунтов. Подобно физико-хи-
мической механике материалов изучение физико-механических
свойств грунтов находится на стыке нескольких наук — физики,
геологии и строительной механики грунтов. Соответственно на-
уку о физико-механических свойствах грунтов можно было бы с
полным правом назвать физико-геологическими основами строи-
тельной механики грунтов, или просто физико-геологической ме-
ханикой грунтов. В наше время, когда появляются все новые
и новые науки на стыке нескольких старых, подобные «много-
членные» названия становятся все более привычными, так же как
стали привычными такие названия, как физическая химия, мате-
матическая физика, инженерная геология и т. д., хотя в свое время
эти сочетания резали слух ортодоксальных теоретиков и нередко
бывали предметом острых дискуссий.
Требуется, однако, пояснить, почему приведенное выше назва-
ние связано с геологией. Дело в том, что главная цель физической
или физико-химической механики материалов сводится к созданию
новых материалов с необходимыми свойствами, между тем как в
физико-геологической механике грунтов наряду с исследованием
возможности искусственного преобразования свойств грунтов в
нужном направлении основная задача заключается в правильной
оценке строительных свойств, разнообразных по строению и неод-
нородных в физико-механическом отношении таких сложных пре-
образований, какими являются естественные грунтовые толщи.
Поэтому необходимо обратить особое внимание на тесную
45
зависимость физико-механических свойств грунтов от характера
геологических процессов, которые ведут к образованию и форми-
рованию горных пород.
В последние годы в этой области появился ряд интересных и
обнадеживающих работ, в особенности школ, возглавляемых
И. В. Поповым, В. Д. Ломтадзе, А. К. Ларионовым и рядом дру-
гих исследователей. Нельзя при этом не вспомнить о блестящих
исследованиях безвременно скончавшегося Н. Я- Денисова.
Обобщение всех этих разнообразных по направлению иссле-
дований й задача оформления физико-геологической механики
грунтов в самостоятельную науку, стоящую на стыке инженерно-
геологических, физико-химических и механико-строительных наук
о грунтах, еще ждут своего осуществления.
4. ПРИНЦИПЫ ПОСТРОЕНИЯ РАСЧЕТНЫХ
И СТРУКТУРНЫХ МОДЕЛЕЙ ГРУНТА
Понятие о модели. Моделью обычно называют систему, кото-
рая обладает отдельными свойствами, подобными свойствам мо-
делируемого. объекта (оригинала или прообраза). Модели пред-
назначены для изучения поведения оригинала в тех или иных ус-
ловиях, в кдторых проявляются указанные свойства.
Чтобы создать как мысленную (или воображаемую), так и
материальную, (физическую) модель, мы должны иметь достаточ-
ный объем предварительных сведений о свойствах и поведении
моделируемого объекта; знать, какие именно свойства являются
существенными, .и определяющими для рассматриваемых явлений.
Действительный объект и его модель—системы не тождест-
венные; а лишь аналогичные, обладающие подобием свойств, по-
зволяющим, имитировать поведение оригинала и прогнозировать
его реакцию на. те или иные воздействия. Таким образом, в ос-
нове моделирования лежит аналогия.
В технической литературе встречаются также несколько иные
определения понятий, связанных с моделированием. Так, моделью
назьгаают иногда только систему, изготовленную из того же мате-
риала, что и оригинал, полностью подобную ему по своим очерта-
ниям и отличающуюся лишь масштабом. Если же модель в физи-
ческом отношении отлична от прообраза и сходна с ним лишь
своим поведением при определенных условиях, то такую модель
называют симулятором. Характерным примером применения тако-
го симулятора является электрическое моделирование механиче-
ских явлений или, например, использование аналогии между осты-
ванием нагретой пластины и уменьшением влажности пласта грун-
та, обжимаемого нагрузкой.
Материальные модели. Если модель представляет собой неко-
торую реальную физическую систему, то кроме основных, интере-
сующих нас свойств она будет обладать дополнительными собст-
венными свойствами. Однако последние не должны оказывать
46
сколько-нибудь заметного влияния на течение исследуемого про-
цесса, иначе модель окажется непригодной. Таким образом, обра-
щение к материальным моделям производится не для исследова-
ния общефизических закономерностей, которые должны быть по-
лучены из наблюдений над оригиналом или экспериментов с ним
непосредственно, а для детального изучения некоторых конкрет-
ных процессов, протекающих в прообразе при определенных его
геометрических характеристиках и физических свойствах и при
заданном режиме взаимодействия с внешней средой. В частности,
в СССР широко и успешно применяется для этой цели центробеж-
ное моделирование.
Выше уже отмечалось, каким разнообразием свойств отлича-
ются грунты. Наряду с этим мы видели, что они могут быть разби-
ты на определенные классы с более или менее общими строитель-
ными характеристиками. При рассмотрении тех или иных видов
механического взаимодействия грунта с сооружением и вообще его
поведения под действием нагрузок мы можем объединять в одну
группу многие виды грунтов (например, при рассмотрении устой-
чивости откосов земляных сооружений все песчаные грунты можно
рассматривать как качественно одинаковые, подчиняющиеся од-
ним и тем же закономерностям, определяющим устойчивость, и
различающиеся между собой лишь количественными значениями
коэффициентов, входящих в уравнения).
Каждая такая группа близких видов грунта при рассмотрении
тех или иных механических задач заменяется одной общей идеали-
зированной моделью, обладающей теми же определяющими свой-
ствами, что и реальные грунты данной группы. Соответственно
один и тот же грунт может изображаться множеством различных
моделей в зависимости от характера рассматриваемой задачи и
учитываемых условий его работы.
Воображаемые модели. Одним из распространенных видов
воображаемых моделей деформаций грунтов являются механиче-
ские модели. Простейшим примером таких моделей является пру-
жина (как модель упругих свойств грунта) или амортизатор (как
модель его вязких свойств).
Структурные модели грунта. Чтобы объяснить характер реак-
ции тех или иных грунтов на различные воздействия, мы должны
обращаться к анализу взаимодействия между отдельными части-
цами грунта. При этом приходится делать определенные предпо-
ложения о свойствах этих частиц и силах, действующих между
ними, — создавать так называемую структурную модель. Так, что-
бы объяснить пластичность глин, было сделано предположениё.--о
плоско-чешуйчатой форме их частиц. При этом исходили из двух
предпосылок: 1) песок, обладающий округлыми зернами, не про-
являет пластичных свойств; 2) искусственные смеси из песка-и
плоских чешуек слюды обладают пластичностью.
Таким образом, первое наблюдение производилось над систе-
мой, которую можно было бы назвать антимоделью, а второе —
47
над системой, подобной по своим свойствам оригиналу, т. е. над
моделью. Исследования антимоделей часто являются важным
средством для объяснения свойств оригинала. Интересно, что по-
следующие исследования, проведенные после появления электрон-
ного мйкроскопа, полностью подтвердили предположение о пло-
ской форме частиц глины.
Структурные модели могут быть как абстрактными, так и ма-
териальными, вроде указанной выше модели глины в виде смеси
песка и слюды.
Математическое моделирование. Создавая математическую тео-
рию (или, как иногда говорят, математическую модель) некото-
рого явления, мы всегда имеем дело с определенной абстракцией, с
упрощением действительности. Характерной особенностью мате-
матической модели является изображение поведения оригинала в
терминах математических символов и операций, причем в основу
кладется, во-первых, представление о некоторых элементарных
объектах, образующих структуру оригинала (например, понятие о
материальной точке в теоретической механике), а во-вторых,
представление о характере взаимодействия между этими элемен-
тарными объектами (понятие о связях). Исходя из этих основных
понятий можно затем построить определенную систему уравне-
ний, позволяющую найти изменения системы, возникающие при
тех или иных воздействиях на нее. Как показывает опыт, эти
уравнения оказываются совершенно аналогичными для ряда раз-
нообразных систем и явлений, отражая то общее, что имеется
между ними в рассматриваемом отношении, и тем самым позво-
ляют значительно расширить наши представления об изучаемом
объекте, направляют мысль на поиски дальнейших аналогий и
более глубоких связей между различными действительными объ-
ектами.
В результате нередко удается распространить на изучаемую
систему те зависимости, которые ранее уже были выведены для
других объектов.
Если удается найти общее решение составленной системы диф-
ференциальных уравнений, мы получаем возможность прогнозиро-
вать поведение оригинала при различном характере внешних
воздействий (лишь бы только они не выходили за пределы приня-
тых исходных предпосылок). Если же такое решение получить не
удается, тогда для каждой новой частной задачи приходится заново
решать систему уравнений, прибегая в необходимых случаях к
использованию вычислительной техники. При этом существует
возможность, получив решение ряда частных задач, попытаться
обобщить эти решения, выявляя зависимость между найденными
результатами и изменениями тех параметров, которые привели к
изменению решений.
Идеализация свойств грунтов. Как известно, и в теоретической
механике, и в теории упругости, и в гидравлике, и вообще во всех
науках принято пренебрегать второстепенными для данного круга
48
проблем свойствами тел и сохранять за ними лишь основные, ре-
шающие для рассматриваемых процессов свойства. Таким обра-
зом, мы заменяем реальные тела и явления некоторыми идеали-
зированными представлениями о них. В теоретической механике,
например, все тела рассматриваются как абсолютно жесткие, не-
деформируемые; в теории упругости — как абсолютно упругие; в
теории пластичности — как объемно несжимаемые и т. д.
На подобную «идеализацию» материала мы имеем право, одна-
ко, лишь до тех пор, пока результаты расчетов, основанных на
принятых допущениях, оправдываются опытом, имеют практиче-
ски приемлемую точность.
Механика грунтов для возможности решения стоящих перед
нею задач также вынуждена допускать известное упрощение
свойств грунтов и рассматривать вместо реальных идеализиро-
ванные материалы, обладающие лишь некоторыми, основными для
данного круга задач свойствами действительных грунтов.
Одним из видов идеализации материала является замена пе-
ременных характеристик постоянными. С идеализацией свойств
материала не следует смешивать упрощение в постановке задачи,
когда рассматриваемое явление заменяется более простым. В
качестве примера можно привести замену действительной карти-
ны распределения напряжений в основаниии равномерным рас-
пределением. Такого рода упрощения в постановке задач наряду
с идеализированными представлениями о свойствах материала
составляют в комплексе то, что называют расчетной моделью за-
дачи. Расчетная модель объединяет в себе исходные предпосыл-
ки для математического моделирования, представляющего собой
следующий шаг в решении задачи.
В качестве примера можно назвать расчетную модель грунта
в виде„линейной упругой сплошной среды. При этом понятие
о линейной упругости предполагает использование деформатив-
ной модели Гука, а понятие о сплошной среде связано с опреде-
ленным структурным представлением, которые мы подробно рас-
смотрим несколько ниже. При этом одной и той же модели строе-
ния среды могут соответствовать различные деформативные мо-
дели, но одной и той же деформативной модели, как правило,
отвечает только одна модель строения.
Другим примером являются расчетные модели в теории балок
на грунтовом основании: модель Винклера, модель упругого по-
лупространства, модель упруго-слоистой среды Власова, дискрет-
ная модель Гельфандбейна, двухпараметрическая модель Пас-
тернака.
Исследователь, изучающий физико-механические свойства
грунтов, должен быть хорошо знаком с различными расчетными
моделями механики грунтов, чтобы иметь возможность, с одной
стороны, правильно поставить испытания, дающие основные рас-
четные характеристики грунтов применительно к тем или иным
4$
моделям, а с другой, — способствовать постоянному их совер-
шенствованию и приближению к действительности.
Следует иметь в виду, что при исследовании одной и той
же расчетной модели можно воспользоваться различными матема-
тическими моделями, например построить для нее дифференци-
альные или интегральные уравнения, прибегнуть к методу функ-
ций комплексной переменной, рассматривать задачу в координат-
ной или векторной постановке и т. д.
Таким образом, расчетные модели представляют собой мыс-
ленно конструируемые структуры, подчиняющиеся определенным
упрощенным физическим закономерностям. Они позволяют далее
воспользоваться для исследования изучаемого явления той или
иной математической моделью, наиболее пригодной для решения
задач, относящихся к данной расчетной модели.
Сравнение результатов расчета модели с поведением реально-
го грунта в сооружении покажет, насколько удачно был сделан
ее выбор, каковы пределы ее применимости и в каком направле-
нии должно вестись дальнейшее ее совершенствование.
Два основных класса расчетных моделей грунта. Несмотря на
то что в зависимости от характера рассматриваемых задач ис-
пользуются различные модели грунта, все они могут быть раз-
биты на два основных класса: 1) модели сплошной и 2) модели
дискретной среды.
Грунт как сплошная среда. Сплошной называется такая среда,
которая непрерывным образом заполняет рассматриваемую часть
пространства. Плотность р такой среды определяется как предел
отношения массы Ат, содержащейся в некотором малом объеме
Д7, к величине этого объема, когда он стремится к нулю:
Д т dm
р = 11Ш “ ~— .
Г ДК->0 dV
Сплошная среда может представлять собой либо твердое тело,
либо жидкость, либо такой материал, который может проявлять
при одних условиях свойства твердого тела (или, как говорят,
твердообразные свойства), при других — свойства жидкости
(жидкообразные свойства), при третьих — сочетание тех или дру-
гих вместе. Соответствующие разновидности моделей сплошной
среды называются реологическими моделями, или телами.
Введение в строительную механику такой модели, как сплош-
ная среда, имело то преимущество, что позволяло рассматривать
напряжения и деформации бесконечно малых элементов объема
тела, переходя от них к напряженному состоянию и деформациям
(к напряженно-деформированному состоянию) всего тела, исполь-
зуя методы математического анализа. Наука, изучающая механи-
ческое поведение сплошных сред, называется механикой сплошной
среды.
Модель сплошной среды использовалась как при изучении
твердых тел, так и в теории жидкостей и газов. В результате до-
50
стигли высокого уровня развития такие разделы механики сплош-
ной среды, как теория упругости, теория пластичности, гидродина-
мика и др.
Использование модели сплошной среды в механике грунтов
позволило сразу же перенести в последнюю целый ряд решений,
полученных в механике сплошной среды. Как показывает имею-
щийся опыт, приложение к задачам механики грунтов решений,
найденных в теории упругости, теории пластичности и в других
разделах механики сплошной среды, во многих случаях позволяет
правильно оценить порядок ожидаемых деформаций оснований и
земляных сооружений и получить примерное распределение в них
внутренних усилий.
В механике сплошной среды принято рассматривать поведе-
ние среды под действием различных нагрузок как нарушение
первоначального состояния равновесия между взаимодействую-
щими внутренними элементами среды и как переход к ее новому
состоянию равновесия в результате изменения сил, действующих
между элементами. Таким образом, задачи решаются исходя из
того, что должны удовлетворяться условия равновесия для бес-
конечно малых элементов среды. Кроме того, ставится добавочное
условие, что при относительных перемещениях этих элементов в
процессе деформирования среды в последней не должно насту-
пать внутренних разрывов и нарушений сплошности.
Термодинамический метод. Во многих случаях предыдущий
подход к решению задач связан со значительными трудностями,
и гораздо более легким оказывается термодинамический (или
энергетический) метод решения. Этот метод основан на том, что
всякое изменение, происходящее в некоторой системе, рассматри-
вается с точки зрения выделения или поглощения энергии, преоб-
разования одних видов энергии в другие.
Как показывают исследования, энергетический анализ во мно-
гих случаях не только существенно облегчает решение различных
задач механики грунтов, но и делает гораздо более ясной физиче-
скую сущность рассматриваемых проблем.
Вместе с тем необходимо помнить, что чисто энергетический
подход, отражая лишь одну, хотя и чрезвычайно важную сторону
процессов, еще не исчерпывает всей глубины задачи, так как
одному и тому же энергетическому состоянию соответствует мно-
жество различных путей, которыми тело может в это состояние
перейти.
Поэтому энергетический метод позволяет с достаточной опре-
деленностью находить конечные состояния среды при тех или
иных воздействиях на нее, но промежуточные ее состояния в про-
цессе деформирования могут быть установлены лишь при неко-
торых ограничениях, накладываемых на течение процессов.
Грунт как дискретная среда. Дискретные модели грунта отра-
жают те или иные предположения о структуре грунта и о механи-
ческих свойствах элементов этой структуры.
51
При исследовании поведения дискретных моделей под дейст-
вием внешней нагрузки учитываются не только совершенно раз-
личные механические свойства скелета и заполнителя, но грунт
рассматривается как система, состоящая из бесчисленного мно-
жества частиц, от свойств которых и условий их взаимодействия
переходят к механическим свойствам грунта в целом. Хотя в ряде
случаев анализ дискретных моделей дает более ясное представле-
ние о природе тех или иных характерных особенностей поведения
грунта, однако модели сплошной среды обладают рядом преиму-
ществ в расчетном отношении. Нередко приходится прибегать
к использованию моделей обоих этих типов для взаимной коррек-
тировки и уточнения получаемых выводов.
Изучением поведения макроскопических сред как результата
взаимодействия огромного числа отдельных частиц, из которых
эти системы состоят, занимается наука, называемая статистической
механикой, которая опирается на теорию вероятностей и матема-
тическую статистику. Впервые обстоятельное рассмотрение грун-
тов как статистических систем в 1935 г. предпринял Г. И. Покров-
ский [50]. В тех случаях, когда частицы грунта испытывают ин-
тенсивные колебательные движения и перемещаются друг отно-
сительно друга, как это имеет место, например, при прохождении
сейсмических волн или действии различных вибрационных меха-
низмов, Г. Винтеркорн в 1953 г. [106] предложил рассматривать
колеблющиеся частицы грунта по аналогии с молекулами газов
или жидкостей, находящихся в тепловом движении. Эта идея еще
мало использовалась [14], однако представляет значительный ин-
терес и может найти немало приложений, особенно в динамике
грунтов.
Границы применимости расчетных моделей. Все расчетные ме-
тоды и формулы механики грунтов относятся к тем или иным мо-
делям грунта в основании или земляном сооружении. Поэтому
при пользовании формулами механики грунтов необходимо посто-
янно иметь в виду те допущения относительно свойств моделей,
которые принимаются при выводе ради упрощения математиче-
ских выкладок либо ради самой возможности получения этих
формул.
Соответственно различные формулы механики грунтов имеют
определенные границы применимости, знать которые необходимо
во избежание грубых ошибок при проектировании.
Кроме того, правильный выбор расчетной модели оснований и
земляных сооружений зависит в первую очередь от того, позволя-
ют ли материалы изысканий составить верную модель инженер-
но-геологического строения, отражающую основные особенности
грунтовой толщи, важные в строительном отношении.
Испытание грунта и модели. Основные расчетные характери-
стики грунтов определяются с помощью испытаний, которые
должны проводиться по методике, соответствующей принятой
расчетной модели. Поэтому лаборатории, выполняющие испыта-
52
ния, должны быть всегда непосредственно связаны не только с
изыскателями, но и с проектировщиками, а последние, в свою
очередь, должны непосредственно интересоваться методикой и тех-
никой проведения испытаний и участвовать в обсуждении получа-
емых результатов. Расчетная модель или модели (когда выполня-
ется несколько вариантов расчета по различным моделям) долж-
ны устанавливаться совместно строителем-проектировщиком, ин-
женером-геологом и специалистом по физико-геологической ме-
ханике, проводящим испытания. Особенно важно выполнять это
требование при проектировании ответственных сооружений и
сложном геологическом строении площадки.
Глава 3
О ТЕРМОДИНАМИЧЕСКИХ СИСТЕМАХ
1. СВОЙСТВА и состояния СИСТЕМ
Системы, строение, структура. Любая, мысленно выделенная с
помощью воображаемой граничной поверхности часть матери-
ального мира, представляющая собой комплекс так или иначе
связанных между собой объектов, называется в термодинамике
системой. Свойства системы, т. е. особенности поведения, прояв-
ляющиеся в процессе ее взаимодействия с другими системами, об-
разующими окружающую среду, непосредственно связаны со свой-
ствами ее более элементарных составляющих и, следовательно,
зависят от состава системы. Свойства элементов, образующих
систему, в свою очередь, проявляются в особенностях взаимодей-
ствия между собой этих элементов. Закономерность относитель-
ного расположения частей системы (строение системы) и законо-
мерности связей (взаимодействий) в ней (связность системы)
обычно обозначают общим термином структура. Таким образом,
каждая система определяется составом, строением и связностью.
Строение и связность систем взаимозависимы, влияют друг на
друга, образуя диалектическое единство.
Всякая система всегда является частью, элементом другой си-
стемы более высокого порядка (структурного уровня), и, наобо-
рот, каждый элемент системы данного порядка, каждое тело само
представляет собой систему более низкого структурного уровня.
Таким образом, существует определенная иерархия структур.
Взаимодействие между элементами у различных по характеру си-
стем данного уровня, а также у систем различного порядка под-
чиняется закономерностям различного характера.
В некоторых случаях один и тот же элемент может одновре-
менно входить в несколько систем, однако одна из них является
для него главной, определяющей. Вместе с тем на той или иной
стадии развития могут сосуществовать различные структуры од-
ного и того же уровня, составленные из одних и тех же элементов
более низкого структурного уровня. Структуры не являются не-
подвижными, застывшими. Они развиваются, видоизменяются,
распадаются, порождают новые.
Совокупность всех свойств системы, характеризующих ее не
только с качественной, но и с количественной стороны, называ-
ется состоянием системы. Возможность количественной оценки
54
свойств системы позволяет выражать ее состояние с помощью ма-
тематических соотношений, называемых уравнениями состояния.
Исследование предметов обычно начинают с изучения их
внешних отношений и взаимодействий, т. е. их связей с другими
элементами той системы, в которую они входят, и лишь потом
переходят к исследованию состава, строения и взаимодействия
между внутренними элементами самого предмета, к его сущност-
ному познанию как некоторой системы.
Когда реакция (или отклик) системы на внешние воздействия
исследуется как функция ее состава и структуры, то говорят о
структурном изучении системы. Если при взаимодействии системы
с окружающей средой какой-либо из элементов этой системы ис-
пытывает изменения, то это сказывается как на других элементах,
так и на системе в целом в силу их взаимообусловленности и
взаимосвязи. При этом не следует забывать, что свойства системы
несводимы к свойствам ее элементов и не являются простой сум-
мой их свойств.
Свойства системы обладают следующей важной особен-
ностью: они не зависят от пути перехода системы из одного со-
стояния (начального) в другое (конечное в данном процессе). И,
наоборот, если при переходе системы из одного состояния в дру-
гое изменение некоторых величин, характеризующих систему, за-
висит от пути перехода, то эти величины не являются свойствами
системы. Иными словами, свойства системы — это такие ее ха-
рактеристики, которые не зависят от пути перехода из одного со-
стояния в другое (инвариантны относительно этого пути). Однако
все свойства системы или их часть изменяются при переходе си-
стемы в новое состояние, т. е. являются функциями состояния
системы.
Количественные характеристики свойств системы называются
ее параметрами. Условно рассматривая некоторую систему как
неизменную и придавая ее свойствам не только качественное, но
и количественное постоянство, устанавливают состояние системы
в данный момент, называемое условно покоем системы. Всякое
изменение параметров системы, изменение ее состояния означает
ее движение в широком смысле слова, причем изменение какого-
либо одного параметра влечет за собой большее или меньшее из-
менение всех остальных.
Так как каждую точку некоторой системы можно характеризо-
вать с помощью значений тех или иных параметров системы, на-
пример температуры, плотности, концентрации, объема и т. п., то
систему можно рассматривать как некоторую область значений
данного параметра.
Если значения параметров в каждой точки области остаются
постоянными во времени, систему называют стационарной, а если
изменяются — нестационарной по отношению к данному пара-
метру.
Соответственно если некоторый процесс протекает при пара-
55
метрах, хотя и неодинаковых в разных точках пространства, но
неизменных во времени, то такой процесс называют стационар-
ным, или установившимся, а в противном случае нестационарным
(или переходным, если в результате процесса осуществляется пе-
реход системы из одного стационарного состояния в другое).
Однородность и неоднородность систем. Если значения некото-
рого параметра во всех точках системы одинаковы, ее называют
однородной по данному параметру, а если различны — неоднород-
ной, У систем, сохраняющих однородность в течение всего изучае-
мого процесса, свойства не зависят от размеров и конфигурации
и, следовательно, не являются функциями пространственных коор-
динат, которые таким образом выпадают из рассмотрения.
Основные, или агрегатные, состояния вещества, с которыми
встречаются в механике грунтов, — твердое, жидкое и газообраз-
ное.
Находясь в одном из состояний, вещества могут обнаруживать
при определенных условиях также и некоторые свойства, специфи-
ческие для других состояний, причем это «смешение» агрегатных
свойств носит различный характер у различных материалов.
Нескальные грунты представляют собой тела, для которых в
зависимости от состава, плотности и влажности степень проявле-
ния тех или иных свойств, характерных для твердых или жидких
тел, может быть совершенно различной.
2. ИЗМЕНЕНИЕ СОСТОЯНИЯ СИСТЕМЫ
Обобщенные заряды. Всякое изменение состояния материаль-
ной системы определяется изменением некоторых характеристик
параметров системы, которые называют координатами состояния,
или обобщенными зарядами системы. Координатами состояния
могут являться линейные перемещения, углы поворота, количество
движения, объем, плотность, масса, тепловой (термический) и
электрический заряды и т. д. Если, например, сжимать грунт
всесторонним давлением, то его объем будет изменяться, и пос-
ледний можно рассматривать как координату состояния при дан-
ном механическом процессе. Будем обозначать координаты со-
стояния (заряды) буквой Е с соответствующими индексами.
Каждой форме движения материи соответствуют свои определен-
ные обобщенные координаты, свои заряды.
Потенциалы. Опыт показывает, что любой процесс взаимодей-
ствия связан с некоторыми физическими величинами, при равен-
стве которых вне и внутри системы данный вид взаимодействия не
может иметь места. Такие физические величины называют обоб-
щенными потенциалами. Будем обозначать эти потенциалы бук-
вой Р. Разность величин потенциалов данного вида вне и внутри
системы является причиной изменения координат состояния си-
стемы (переноса обобщенного заряда). Поэтому потенциалы на-
зывают иногда также движущими силами. Величина потенциала
56
характеризует интенсивность процесса переноса заряда через
границу системы при ее взаимодействии с внешней средой.
Примером потенциалов могут служить температура (тепловой
или термический потенциал), давление, электрический потенциал,
концентрация раствора и т. д. Разность потенциалов по обе сто-
роны граничной поверхности системы считают положительной,
если под действием этой разности соответствующая координата
состояния системы увеличивается. Так как при действии сжимаю-
щих сил (давления) объем тела уменьшается, то это означает,
что если принять объем за координату состояния, то разность по-
тенциалов (давлений) следует считать отрицательной.
Следует иметь в виду, что при изменении какого-либо потен-
циала изменяются в той или иной мере все координаты состояния.
Однако одна из координат, называемая главной, или сопряженной
с данным потенциалом, изменяется во много раз больше, чем все
остальные.
Одним из критериев при выборе физической величины, являю-
щейся главной координатой состояния при данном взаимодейст-
вии, является ее относительное постоянство при отсутствии этого
взаимодействия.
Предмет термодинамики. Определенным типам связей и вза-
имодействий отвечают соответственные формы движения материи.
Количественное и качественное изучение свойств материи, прояв-
ляющихся в процессе движения и взаимного превращения форм
движения друг в друга, составляет предмет современной термоди-
намики.
Термодинамика возникла как наука, изучавшая взаимопревра-
щения механической работы и теплоты, но современная термоди-
намика значительно шире, по своему содержанию. Она рассматри-
вает взаимосвязи и взаимопревращения различных видов энергии
при любых физических и химических процессах и явлениях и
влияние этой связи и переходов на изменение свойств физических
тел. Поэтому современную термодинамику можно рассматривать
как энергетический метод изучения явлений природы [16, 31].
Особенностью классического термодинамического метода ис-
следования является то, что он позволяет установить общее на-
правление процессов и найти конечное состояние исследуемых
систем, но не позволяет рассмотреть течение процессов изменения
состояния во времени, скорости этих процессов, методы управле-
ния этими скоростями. Другой особенностью термодинамического
метода является то, что он не связан с какими-либо определен-
ными конкретными представлениями о внутреннем строении си-
стем и о характере взаимодействия образующих системы внутрен-
них элементов. Термодинамика оперирует с макроскопическими
характеристиками систем исходя из экспериментально установлен-
ных, весьма общих законов термодинамики. Термодинамические
методы начинают широко применяться при исследовании грунтов.
Изолированные и открытые системы. Если при исследовании
57
некоторой системы можно принять, что она практически не обме-
нивается зарядами с окружающей внешней средой, то систему
называют изолированной, или обособленной. Если происходит об-
мен любыми зарядами, кроме массы, то систему называют закры-
той; если же возможен обмен с внешней средой зарядами любого
вида, то систему называют открытой.
Равновесность и неравновесность. Если значения внешних и
соответственных внутренних потенциалов (например, температу-
ры) системы во всех ее точках одинаковы, то система называется
равновесной, а в противном случае — неравновесной.
Изменение состояния системы в результате внешнего воздейст-
вия на нее требует известного времени. Во всякой системе через
то или иное время после ее полной изоляции от внешней среды
прекращаются все процессы, вызванные воздействием на нее этой
среды, которое имело место до момента изоляции и наступает со-
ответствующее состояние равновесия—макроскопическое равнове-
сие.
Время, которое требуется для перехода в это состояние равно-
весия, называют временем релаксации.
Состоянию равновесия не обязательно соответствует покой;
например, при равновесии сил, действующих на тело, оно может
находиться в состоянии равномерного прямолинейного движения.
Обратное, однако, неверно, и всякому состоянию покоя соответ-
ствует равновесие.
Флуктуация. Равновесие никогда не бывает абсолютным, и не-
большие меняющиеся во времени отклонения в разных точках си-
стемы от состояния равновесия называют флуктуациями системы.
Термин «флуктуация» применяется и в более широком смысле
для обозначения отклонений значений любого физического пара-
метра системы L от среднего значения этого параметра L. Мерой
флуктуации является среднее значение квадрата отклонений
(AL)2= (L—L)2, что можно записать в виде
(ДЬ)2 = L2 —2LL + (L)2 = Г2 — 2LL + (L)2 ж=
= Р —(Г)2>0. (3.1)
Из этой записи следует, что (Д£)2 никогда не может быть отри-
цательной величиной (меньше нуля). Черта над выражением оз-
начает, что имеется в виду его среднее значение. Величину (ДЬ)2
т. е. среднее значение квадратов L, называют квадратичной флук-
туацией.
Влияние флуктуаций на колебание значений параметра L
оценивается так называемой относительной флуктуацией 8L , ко-
торая представляет собой отношение корня квадратного из квад-
ратичной флуктуации к среднему значению параметра:
8t=.
58
Пусть рассматриваемая система отделена от окружающей сре-
ды некоторой граничной поверхностью, действительной или во-
ображаемой, через которую система и среда обмениваются заря-
дами. Эту граничную поверхность называют также контрольной
поверхностью, так как на ней производят измерения количества
зарядов, проходящих из системы в среду и в обратном направле-
нии. Если эти количества строго равны друг другу или отличают-
ся лишь в бесконечно близких точках и в бесконечно малые проме-
жутки времени, то говорят, что система и окружающая среда
находятся в динамическом равновесии. В таком равновесии на-
ходятся, например, жидкость и насыщенный пар над ней. Всякое
равновесие в природе носит динамический характер. Система, на-
ходящаяся в динамическом равновесии с внешней средой, может
рассматриваться так, как будто она является изолированной.
Термодинамические параметры. Сопряженные параметры (т. е.
сопряженные заряд и потенциал) относят к одной и той же форме
движения. Так как каждой координате состояния соответствует
свой сопряженный потенциал, то системе с п координатами
Е%.. Еп соответствуют п потенциалов Pi, Pz£., Рп. Координаты
состояния называют также параметрами состояния, а координаты
состояния и потенциалы в совокупности называют термодинамиче-
скими параметрами системы. Потенциалы системы являются одно-
значными функциями координат состояния:
Е2, ..., Е„), (3.3а)
где Pi перед скобками — обозначение функции, и наоборот,
любую координату можно однозначно выразить через потенциалы
Е^ЕДРь Р2........Р„). (3.36
Уравнения состояния. Если состояние системы определяется п
параметрами состояния, то это состояние можно в общем случае
охарактеризовать зависимостью между п+1 термодинамическими
параметрами в виде некоторой функции F:
F{ZU Z* ..., P/t Et...Zn, Zn+i) = 0, (3.4)
где величины Z могут быть как координатами, так и потенци-
алами, но одна пара из них (Р/ , Ei ) будет сопряженной.
Уравнения вида (3.4.) или системы уравнений (3.3а) называют
уравнениями состояния системы. Каждой системе отвечает свое
определенное уравнение состояния, однако установить вид этого
уравнения (вид соответствующей функциональной зависимости)
средствами самой термодинамики невозможно.
Эти уравнения могут быть найдены чисто экспериментальным
путем на феноменологическом уровне либо могут быть установле-
ны с помощью микроструктурных исследований, исходя из струк-
туры системы и внутреннего взаимодействия между ее элемента-
ми, т. е. опять-таки на основе опыта, но уже на микроструктур-
ном уровне. В ряде случаев в процессе микроструктурных иссле-
дований непосредственный эксперимент заменяется сначала чисто
59
теоретическим исследованием некоторой мысленной модели. Од-
нако окончательно полученные результаты могут быть приняты
только после их прямого подтверждения экспериментом или на-
блюдениями. Уравнения состояния являются алгебраическими.
Экстенсивные и интенсивные параметры. Все термодинамиче-
ские параметры можно подразделять на две категории в зависи-
мости от того, как эти параметры связаны с размерами системы.
Первая категория — это экстенсивные параметры, которые за-
висят от размеров системы (ее объема) и изменяются аддитивно
с изменением этих размеров (аддитивно означает, что параметры
некоторого целого равны сумме параметров его частей). Экстен-
сивными параметрами (или факторами экстенсивности) являются
координаты состояния.
Вторая категория — это интенсивные параметры (факторы-
интенсивности), которые от размеров системы не зависят и не
являются аддитивными, т. е. не связаны с размерами системы.
К ним относятся все потенциалы — силы, температура и т. п.
Наименьшее число независимых термодинамических парамет-
ров, необходимых для полной характеристики состояния системы
(объемы, температуры, давления и т. д.), представляет собой коли-
чество термодинамических степеней свободы системы. Таких сте-
пеней свободы в уравнении (3.4) п, так как это уравнение можно
решить относительно одного из параметров, выразив его как
функцию всех остальных, например
Pi = Pi(Zlt z2, ..., Zn).
3. ЭНЕРГИЯ
Обобщенный заряд, поступающий извне в данную систему, не
только изменяет состояние данной системы, но и влияет на ее
взаимодействие с другими системами. При этом характеры заря-
дов, получаемых данной системой и передаваемых ею следующей,
могут быть различными. Так, система может получить термиче-
ский заряд, а передать электрический, произведя соответствующее
преобразование зарядов. Так как перемещение каждого вида за-
рядов определяется соответствующим сопряженным потенциалом,
то это означает, что в системе происходит также преобразование
потенциалов.
Энергия. В целом эти преобразования можно определить как
превращение одной формы движения в другую. Несмотря на всю
глубину качественного различия всевозможных форм движения,
оказывается, что переход одной формы в другую подчиняется
строгой закономерности. Она заключается в том, что существует
некоторая физическая скалярная величина, являющаяся общей
количественной мерой любых видов движения. Эту величину на-
зывают энергией.
Одним из основных законов природы является закон сохране-
ния энергии (первый закон термодинамики), гласящий, что энер-
60
гия во всякой изолированной системе не исчезает и не создается
вновь и что в любом процессе взаимодействия систем происходит
лишь обмен энергии между ними. Следовательно, энергия являет-
ся наиболее общей количественной характеристикой движения,
обобщающей понятия и зарядов, и потенциалов. Именно поэтому
в термодинамике энергия избирается в качестве исходной харак-
теристики, а затем математически устанавливают связь с нею
всех других характеристик движения и изменения системы.
Количественную меру всех форм движения, проявляющихся во
взаимодействии внутренних элементов системы, образующих
структуру данного уровня, называют внутренней энергией систе-
мы. Так как количество различных форм движения у любой си-
стемы неограниченно, то при ее исследовании всегда рассматрива-
ют лишь некоторые виды движения, характерные для изучаемого
процесса. Соответственно им определяют и изменение внутренней
энергии системы.
Но формы движения определяются обобщенными зарядами, и,
следовательно, мы можем аналитически представить внутреннюю
энергию U как функцию этих зарядов:
U = U(Elt Е2, ..., Еп). (3.5)
Обобщенная работа. В результате переноса зарядов через
граничную поверхность системы происходит изменение ее внут-
ренней энергии, измеряемое произведением потенциала на величи-
ну перенесенного заряда. Это произведение именуют обобщенной
работой, или просто работой.
Элементарное количество работы dA может быть записано в
виде
dA = PdE, (3.6)
где Р— разность потенциалов;
dE — передаваемый заряд.
Различают работы механическую, электрическую, химическую
и по аналогии с ними термическую.
Работа не является свойством системы и относится лишь к
процессу переноса заряда через контрольную поверхность. Как
только кончается процесс переноса, работа прекращается. Поэто-
му, когда применяют обозначение dA, его следует рассматривать
не как дифференциал А и не как приращение А, а лишь как не-
которое малое количество работы.
Правило знаков для потенциалов и зарядов принимают таким,
чтобы получить при их умножении друг на друга положи-
тельное произведение (положительную работу), когда внутрен-
няя энергия системы в результате совершения этой работы воз-
растает. Возрастанию внутренней энергии соответствует таким об-
разом увеличение обобщенных зарядов системы.
61
Механическая работа. Механической называется работа, в ре-
зультате совершения которой изменяется механическое движение
тела, его положение по отношению к другим телам либо его объ-
ем. Механическая работа при линейном перемещении равна ска-
лярному произведению вектора силы F на вектор перемещения
точки ее приложения dr
d 4 = F dr = F ds cos a = ds (3.6a)
или в декартовых координатах
d А = Fx dx + Fy dy + Fz dz, (3.66)
где г— радиус-вектор точки;
х, у, г — декартовы координаты точки;
а— угол между векторами F и dr;
ds==|dr|—длина пути точки вдоль траектории движения;
Ft = F cos а—проекция силы F на касательную к траектории
движения.
В выражении^(3.6а) dr представляет собой обобщенный заряд;
проекция силы F на направление движения Fx является потен-
циалом. _ _ _
При действии на тело группы сил F1; F2,..., F„ работа будет
равна:
d4 = 2^^’ (З.бв)
1
где drt — элементарное перемещение точки приложения силы F/.
В случае вращательного перемещения тела зарядом является
угол поворота dq> (измеряется в радианах), потенциалом — ре-
зультирующий момент М всех сил относительно сил вращения. Ра-
бота будет равна:
dA = Md<f. (3.6г)
Количество работы, очевидно, зависит от того пути, по ко-
торому совершается переход из первоначального положения или
состояния тела в новое.
Основной единицей работы в международной системе (СИ)
является джоуль (дж). При механической работе линейного пе-
ремещения джоуль измеряется как произведение силы в 1 ньютон
(1 м) на путь в 1 м (ньютон — сила, сообщающая массе 1 кг
ускорение 1 м/сек2). Принятому в технике измерению силы в 1 кГ
соответствует в системе СИ сила 9,81 н«10 н. Применяются так-
же единицы эрг либо (в технической системе единиц) кило-
граммометр. 1 эрг равен работе силы в 1 дину на пути 1 см
(дина — сила, которая сообщает массе в 1 г ускорение 1 см/сек2)*
62
1 н=105 дн\ 1 эрг=10"7 дж. Работа силы в 1 кГ на пути 1 м равна
9,80665 дж (1 кГм &10 дж).
В случае механической работы изменения объема системы за-
рядом является приращение объема (положительное или отрица-
тельное) dV в jm3, потенциалом — давление р в
н/м2. Работа равна:
йА = рдУдж. (3.7а)
Рассмотрим в качестве примера работу, со-
вершаемую при сжатии грунта в цилиндрической
обойме с помощью поршней (рис. 3.1).
Пусть первоначальный объем системы равен
V. Под действием давления р, приложенного ж
поршням площадью/7 (сжимающая силаР=pF),
высота h столбика грунта сокращается на dh =
=h—hi. Работа силы Р
dA = Pdh (3.76)
Рис. 3.1. Сжатие
или грунта в обойме
dA — pFdh. (3.7в)
Изменение объема системы в данном процессе
dV = Fdh,
откуда
dA = pdV.
В выражениях (3.76) и (3.7в) величины Р и р представляют
собой движущие силы процесса сжатия и являются потенциалами,
а величины dh и dV — приращениями координат состояния сис-
темы, ее обобщенными зарядами.
Потенциальные силы. Силы, действующие на систему, назы-
вают потенциальными (говорят еще, что силы имеют потенциал),
если работа, совершаемая ими, зависит только от начального и
конечного положения системы в пространстве. Такова, например,
работа сил тяготения, совершаемая над некоторым телом, кото-
рое перемещается в поле этих сил. Так как направление двух
сил между любыми двумя неподвижными друг относительно дру-
га точками поля всегда постоянно, то при движении тела между
этими точками поля в одну сторону работа имеет один знак, а при
движении тела в противоположную сторону знак работы меняется
на противоположный.
Поэтому работа потенциальных сил на замкнутом пути равна
нулю независимо от того, каков этот путь.
С другой стороны, как бы ни двигалось тело от одной точки по-
ля к другой, суммарная работа .будет оставаться постоянной и
определится лишь положением начальной и конечной точек дви-
жения. Иными словами, работа сил, имеющих потенциал, не за-
63
висит от пути, а определяется только начальным и конечным сос-
тоянием (в частном случае механического движения в виде пе-
ремещения — начальным и конечным положением) системы.
Если же работа сил зависит от пути, по которому движется
система, то такие силы называют непотенциальными (или не
имеющими потенциала). Примером могут служить силы трения,
которые в любом месте траектории всегда* направлены в сторону,
противоположную движению.
Механическая энергия. Механической энергией называют
энергию W механического движения и взаимодействия тел. Эта
энергия состоит соответственно из двух частей — кинетической К и
потенциальной П:
W = K + n. (3.8)
Кинетическая энергия тела измеряется той энергией, которую
необходимо затратить, чтобы затормозить движущееся тело
вплоть до его полной остановки. Так как при изменении скорости
тела изменится скорость его движения, то изменится и количест-
во движения k, равное произведению массы тела на его скорость:
k = tn v я • сек.
Количество движения можно рассматривать как заряд'систе-
мы, а скорость — как потенциал. Соответственно работа при этой
форме движения, совершенная за счет приращения заряда dk—
— mdv, будет равна
dA — vdk дж.
Подставляя сюда значение dk, найдем
d А = v tn d v.
Интегрирование дает изменение кинетической энергии системы
р m (t>2—eg)
К = j mvdv -------------, (3.9)
Vo
представляющее собой меру механического движения, способно-
го превращаться в другие формы движения.
Напомним, что все системы между собой и все элементы каж-
дой системы друг с другом взаимодействуют через окружающие
их силовые поля. При изменении относительного положения тел
в силовом поле изменяются и силы, с которыми тела действуют
друг на друга. Так, при перемещении в-поле тяготения изменяет-
ся сила взаимного притяжения тел. Соответствующая энергия
взаимодействия тел, зависящая от их относительного положения
и есть потенциальная энергия. Она определяется способностью те-
ла совершать работу, перемещаясь под влиянием потенциальных
сил. Так как внутренние частицы тела как некоторой системы так-
64
же взаимодействуют между собой через соответствующие поля, то
относительное изменение положения этих элементов при изменении
объема системы сопровождается изменением суммарной потенци-
альной энергии элементов системы.
Консервативные системы. Системы, у которых изменение кине-
тической энергии движения полностью переходит в изменение по-
тенциальной энергии, называются консервативными. Примером
консервативной системы является идеально-упругое тело. Изменяя
объем такого тела, внешние силы сообщают его частицам кине-
тическую энергию, которая затем превращается в потенциальную
энергию упругой деформации тела, когда относительное переме-
щение частиц прекращается. По снятии нагрузки потенциальная
энергия расходуется на восстановление объема тела, превращаясь
в кинетическую энергию упорядоченного перемещения его частиц
в первоначальное положение (до действия нагрузки).
В случае неконсервативной системы часть энергии расходу-
ется при деформации на нагревание тела, превращаясь в кинети-
ческую энергию беспорядочного (теплового) движения частиц
тела.
Если бы грунт, сжимаемый в опыте по рис. 3.1, был идеально-
упругим материалом, то работа, затраченная на его сжатие, пол-
ностью пошла бы на изменение потенциальной энергии частиц
грунта, и при снятии нагрузки грунт совершил бы работу расши-
рения на величину dh, раздвинув поршни. Однако если проде-
лать соответствующий опыт, можно увидеть, что столбик грунта
при разгрузке примет меньшую, чем h, высоту. Следовательно, ра-
бота расширения грунта будет меньше работы, затраченной на
его сжатие. Если во время опыта создать тщательную тепловую
изоляцию грунта от окружающей среды, то можно заметить по-
вышение его температуры.
Таким образом, грунт в описанном опыте представляет собой
систему неконсервативную.
Полный дифференциал. Напомним, что дифференциалом назы-
вают главную линейную часть приращения функции f (х) одного
переменного, а полным дифференциалом — главную линейную
часть приращения функции f(xb х2,..., хл) нескольких переменных.
Полный дифференциал равен сумме частных дифференциалов, по-
лучаемых при изменении каждой из независимых переменных в
отдельности. Следовательно, если
/(х) = /(хп х2..хп),
то всегда можно написать дифференциал f (х) в виде
d f (х1= dxl f (х) + dx2 f (x) + ... + dxn f (x),
где dx£— частные дифференциалы f (x), или в виде
df(.x) = -^dx1 + ~^-dx2+...+ 4LdXn. (3.10)
dXi дхг dx„ ' ’
3 Зак. 530
65
Если мы имеем выражение для некоторого линейного прира-
щения функции от двух переменных в виде, например,
df — Mdx± + N dx2, (3.11)
где M = и N = являются функциями от х{ и х2, то
дхг дх2
выполняется условие
, (3.12)
д х2 д Xi
которое вытекает из очевидного равенства смешанных произ-
водных:
дМ _ a2/ dN _ d2f
дх2 дх±дх2 ’ дхг dx2dxt
Таким образом, если в выражении вида (3.11) величины М и
N удовлетворяют условию (3.12), то (3.11) представляет собой
полный дифференциал.
Если df является полным дифференциалом, то значение ин-
теграла от df находится сразу и равно разности значений функ-
ции f при начальных и конечных значениях координат системы
(обозначены верхними индексами), например
2
f df = /(42), x^)~f(x{l\ -4°). (3.13)
1
Если система в результате ряда изменений вернулась в пер-
воначальное состояние (соответствующий процесс называют кру-
говым циклом), то х)1) = х<12); = х<2>, и интеграл (3.13) будет
равен нулю. Таким образом, интеграл от полного дифференциала
по замкнутому контуру всегда равен нулю. Это записывается так:
jdf^O, (3.14)
где df должно быть полным дифференциалом.
Важной особенностью полного дифференциала является то,
что его значение не зависит от порядка изменения координат: сна-
чала изменялось а потом х2 или наоборот, т. е. зависит не
от пути, а только от начальных и конечных значений координат.
И, наоборот, если приращение какой-либо функции зависит от
пути изменения, то это приращение не является полным диффе-
ренциалом, и его во избежание путаницы обозначают знаком д
(читается «дельта-круглое»).
66
Так как внутренняя энергия системы есть функция только ее
состояния и не зависит от предшествующей истории деформиро-
вания или характера протекания других процессов, которые пе-
ревели систему из исходного состояния в данное, то всякое при-
ращение внутренней энергии представляет собой полный диф-
ференциал.
Связь между потенциалами и внутренней энергией. Внутренняя
энергия U является функцией зарядов системы:
Е2, Е„);
dU = ^kdE1+ ~^dE2+---+~^dEn- (ЗЛ5)
Вместе с тем приращение внутренней энергии равно сумме про-
изведений потенциалов на приращение сопряженных зарядов:
d U - Рх d Ег + Р2 d Е2 + ... + Рп d Еп. (3.16)
Уравнения вида (3.16) являются дифференциальными уравне-
ниями состояния.
Из сравнения (3.15) и (3.16) следует, что
р = ди • р = ди • • р = ди
1 dEi ’ 2 Э£3 ’ ' ’ ' ’ " дЕп
(3.17)
Таким образом, потенциалы представляют ’ собой частные
производные первого порядка от внутренней энергии по сопря-
женным координатам состояния.
Из того что обобщенному заряду присуща способность само-
произвольно распространяться в системе в направлении убывания
др.
сопряженного с ним потенциала, следует, что —> 0, т. е. част-
ная производная от некоторого потенциала по сопряженной с ним
координате состояния при неизменности всех остальных координат
должна быть всегда положительна (больше нуля).
Модули системы. Рассмотрим теперь производные от U и Е
более высоких порядков. Ради упрощения примем во внимание
только два каких-либо заряда Еги Е2, так что
U = U(Elt £2).
(3.18)
В соответствии с (3.16)
dU ~ Р^Е^ P2dE2)
(3.19)
где
Р,= ^; Р, = -^-.
дЕг дЕ2
Так как, согласно (3.3а),
Pi — рх (Elf Е2\, Р2 = Р2 (Еъ Е2),
то, исходя из (3.10), мы можем написать:
3* Зак. 530
67
dP± — Си d Ei *4“ £12 d Ez, |
d P2 = C21 d Ei + C22 d E2, /
где коэффициенты имеют значения:
dPi __ д » ( ди \ __ д2и
dEi д Ei \ д Ei ) дЕ\
= дР' - d*U •
>12~ дЕ2 “ dEidE2 5
г _ дР2 _ d*U .
G22 "" л с “ a е-2 ’
о Е2 д Е2
, _ дР2 = д2 U
'21~ aEi ~ dEtdE2
(3.21)
(3.20)
Так как при смешанном дифференцировании непрерывной функ-
ции порядок переменных, по которым берут производные, не иг-
рает роли, то
d2U _ &U
д Eid Е2 дЕ2д Ei
и, следовательно,
С12 = С21. (3.22)
Из выражений (3.20) читатель легко увидит, что первый индекс
при коэффициенте С всегда совпадает с индексом величины, стоя-
щей в левой части выражений, а второй индекс такой же, как у
величины, при которой С стоит в качестве коэффициента.
Величины С, играющие роль коэффициентов пропорциональ-
ности между потенциалами и зарядами, называют модулями
системы. Если Р и Е представляют собой сопряженные парамет-
ры и имеют одинаковые индексы, то соответствующие модули
имеют повторяющиеся индексы и их называют главными (или
основными) (С1ь С22 и т. п.) либо сопряженными с соответству-
ющими координатами состояния.
Если же индексы у Р и Е различны, то и индексы при С не-
одинаковы, и тогда коэффициенты называют перекрестными, или
побочными модулями.
Модули С являются частными производными второго порядка
от U по соответствующим зарядам и, в свою очередь,являются
функциями обобщенных зарядов:
Cij — CiJ(E1, Е2).
Тогда, повторяя те же рассуждения, что и при выводе соотноше-
ний (3.21), найдем
68
dCU — d Ci2 — d С22 — дси дЕг д С12 дЕг dC2i дЕ± д С22 дЕ± dEr + dEr + dE± 4- dE1 -f- 4~dE2, . (3.23)
dE2
^-dE2,
dE2 -™*l-dE2,
d E2
-^-dE2.
dE2
Коэффициенты Dm ^112 ЗСц дЕ± д£ц ~ дЕ2 — д2Р1 = ~ дЕ2. ~ 1 — д Ег д Е2 dE3x ’ = _JPU_ dE2xdE2 > (3.24)
^121 _ д £12 дЕ± д E^dEi ~ dE2dE2 ИТ. Д.
представляют собой частные производные третьего порядка от
внутренней энергии по соответствующим зарядам. Таким же об-
разом можно получить характеристики систем, представляющие
собой частные производные от внутренней энергии более высокого
порядка.
Так как
г) _____ г) ______ Г) _____ д3 &
Р112 - ь>121 - ь>211 - е*
п _____ п ____ Г) ___ д3
Ь>122- ь>212- Ь>221 - дЕ^дЕ,
(3.25)
то с учетом (3.22) можно утверждать, что любые перекрестные
коэффициенты, содержащие одинаковые индексы в любых пере-
становках, равны друг другу. Перекрестные коэффициенты харак-
теризуют количественное влияние данной формы движения на не-
сопряженные с ней свойства системы (например, влияние измене-
ния объема тела под действием давления на электрическое соп-
ротивление материала и т. п.). Это влияние, как мы видим, явля-
ется взаимно эквивалентным (соответствующие перекрестные ко-
эффициенты равны).
Термическая работа'. Рассматривая передачу энергии между
системами в виде теплоты как некоторую работу, которую назы-
вают термической, мы легко придем к выводу, что разностью по-
тенциалов (термическим потенциалом) в этом случае должна
служить разность температур Т. Соответствующий заряд должен
быть назван термическим (dti ). Термическая работа обычно обоз-
начается буквой Q. Очевидно,
dQ = Td9. (3.26)
69
Распространение любого обобщенного заряда всегда сопро-
вождается выделением или поглощением термического заряда. -
Если обобщенный заряд перемещается в направлении убывания
сопряженного с ним потенциала, то при этом термический заряд
выделяется (нагревание системы), а при распространении заряда
в направлении возрастания сопряженного потенциала термичес-
кий заряд поглощается (охлаждение системы). Этот эффект пре-
вращения части энергии при движении любого вида в термичес-
кую носит название диссипации и объясняется наличием внешних
и внутренних сопротивлений распространению заряда. Термиче-
скую работу обычно называют теплотой.
Первое начало термодинамики. Это начало является проявле-
нием всеобщего закона сохранения и превращения энергии. Оно
гласит, что если телу передан извне некоторый термический за-
ряд, то соответствующая термическая работа Q расходуется на
повышение внутренней энергии тела U и на работу Л, которую
тело, расширяясь при нагревании против действующего на него
внешнего давления, совершит по отношению к внешней среде:
t>Q = dU + %A. / (3.27)
Отсюда следует, что изменение внутренней энергии равно
dU — §Q — М. (3.28)
Изменение внутренней энергии представляет собой полный
дифференциал и обозначено знаком d, тогда как величины 6Q
и бЛ в общем случае не являются полными дифференциалами и
обозначены поэтому знаком 6, как мы условились выше. Дейст-
вительно, оба эти вида работы не являются свойствами системы
и функциями ее состояния и поэтому зависят от характера вза-
имодействия системы с внешней средой при различных путях
процесса. Но хотя систему можно перевести из определенного со-
стояния в одно и то же другое, заставляя ее по-разному взаимо-
действовать с окружающей средой и при этом получать каждый
раз иные значения 6Q и бЛ, разность их все время будет оста-
ваться постоянной и равной dU.
Адиабатический процесс. Работа перевода системы из одного
состояния в другое определяется только ее начальным и конечным
состояниями в тех случаях, когда отсутствует обмен термическим
зарядом с окружающей средой и 6Q=0. Такие процессы называ-
ются адиабатическими. В этом случае из (3.28) следует, что
ВЛ = — dU9 (3.29)
и работа является полным дифференциалом.
Другие виды процессов. Если при взаимодействии системы с
внешней средой ее объем остается неизменным, то такой процесс
называют изохорным. Если неизменным поддерживается давле-
ние, то процесс называют изобарным. Если, наконец, процесс про-
70
текает таким образом, что температура системы все время под-
держивается постоянной, то процесс называется изотермическим.
Уравнение состояния в частном случае^ Пусть некоторая тер-
модинамическая система характеризуется двумя зарядами (V и
0) и двумя сопряженными с ними потенциалами (р и Г), где
V — объем; 9 — термический заряд; Т—абсолютная температу-
ра, ар — давление.
В общем виде уравнение состояния этой системы будет пред-
ставлять собой, согласно (3.4), функцию (n+1) = (2+1) =3 па-
раметров, в качестве которых выберем р, V и Т:
F (р, V, Т) = 0. (3.30)
Практически пользуются уравнениями состояния, представлен-
ными в явном виде, причем в физике преимущественно выбирают
в качестве независимых переменных температуру и объем, в хи-
мии удобнее пользоваться температурой и давлением, так как
эти величины легче измерять и ими легче управлять в ходе хи-
мических реакций, в механике в большинстве случаев при изуче-
нии деформаций тел можно принимать температуру постоянной
и интересоваться только зависимостью между давлением и объ-
емом.
Напишем уравнение состояния (3.30) системы в явном виде:
p=p(V, Г). При изменении V и Т будет изменяться и внутрен-
няя энергия U (V, Т). В соответствии с общей формулой (3.10)
для полного дифференциала находим
dU = (-^-\ dV +
\ dV )т
(3.31)
V
Здесь необходимо сделать следующее замечание. Когда берет-
ся частная производная по некоторой независимой переменной, то
при этом не учитывается влияние изменения всех остальных не-
зависимых переменных, которые условно или временно принима-
ются неизменными. Однако когда в термодинамике берут час-
тную производную по некоторому параметру и необходимо ука-
зать, какие именно параметры вообще приняты во внимание и рас-
сматриваются временно как постоянные, их обозначают нижни-
ми индексами у частной производной.
С учетом (3.27) и (3.7а) получим
\ дТ /у
(3.32)
так как &A=pdV. В (3.32) круглые скобки можно было бы
опустить, так как при наличии всего двух независимых перемен-
ных недоразумений не возникает, и ясно, что раз частная произ-
водная берется по одной из них, значит вторая переменная при-
нимается постоянной.
71
Если разделить термическую работу на соответствующее из-
менение температуры
dT
то это отношение будет представлять собой термическую работу,
которую нужно совершить для изменения температуры системы
на 1° (теплоемкость системы). Эта работа будет, очевидно, зави-
сеть от условий опыта, так как она не является полным диффе-
ренциалом. Делая путь процесса строго определенным, мы мо-
жем получить значение теплоемкости, соответствующее данным
условиям опыта.
При постоянном объеме V (изохорный процесс) dV=0 и из
(3.32) следует, что
GQ) / dU \
—L = ---------- . (3.33)
dT \ дТ /у 7
При постоянном давлении (изобарный процесс) p = const и
Vdp=0. Следовательно,
V>Q)p = dU + pdV==d(U + pV),
(3.34)
т.е. термическая работа становится полным дифференциалом, рав-
ным линейной части приращения внутренней энергии и механи-
ческой работы.
4. ЭНТРОПИЯ
Рассмотрим циклический или круговой процесс, например про-
цесс загружения и разгрузки образца при испытании.
Если по окончании циклического процесса, испытанного систе-
мой, как сама система, так и окружающая среда полностью воз-
вращаются в первоначальное состояние, то такой процесс называ-
ется обратимым. Если же после окончания процесса для возвра-
щения системы в первоначальное состояние необходимо произвес-
ти какие-либо изменения в окружающей среде (например, отнять
у нее энергию и сообщить ее системе), то такой процесс являет-
ся необратимым. Все реальные процессы в природе необратимы,
однако в ряде случаев можно без особой погрешности рассматри-
вать необратимый процесс как обратимый, что существенно уп-
рощает анализ.
Примером необратимых процессов являются выравнивание в
системе конечных разностей температур, давлений и концентра-
ций, процессы трения, пластического деформирования, вязкого
течения И'Т. д. Необратимые процессы всегда приводят к рас-
сеянию механической энергии, в результате которого упорядочен-
ное механическое движение превращается в хаотическое тепло-
вое движение молекул тела.
Если необратимый процесс происходит интенсивно (напри-
мер, когда деформация тела совершается со значительной ско-
ростью или когда газ устремляется в вакуум), в системе возни-
72
кают макродвижения в виде колебаний либо завихрений. Когда в
естественных условиях какая-либо система сама собою внезапно и
быстро переходит к новому состоянию термодинамического равно-
весия, то процессы перехода такого рода называются обычно спон-
танными (что означает самопроизвольные) и должны пониматься
как процессы, свойственные природе системы. В действительнос-
ти все спонтанные процессы вызываются той или иной причиной.
Примерами таких процессов в грунтах являются просадки лёссов
при замачивании или разжижение рыхлых водонасыщенных пес-
ков при динамических воздействиях. При спонтанных процессах
всегда выделяется энергия, большая, чем затраченная на «пуск»
этого процесса.
Если представить себе предельный случай — бесконечно мед-
ленное течение процесса, то можно считать, что практически в
каждый момент времени между системой и внешней средой су-
ществует термодинамическое равновесие; такого рода процесс
называют квазистатическим. Этот процесс можно на каждом
этапе провести в обратном направлении путем бесконечно малых
изменений во внешней среде. В термодинамике для обозначения
обратимых процессов предпочитают пользоваться термином «ква-
зистатические процессы», оставляя название «обратимые» для
чисто механических движений. Очевидно, при квазистатическом
процессе система находится в нестационарном равновесном сос-
тоянии.
Энтропия. Механическое равновесие достигается тогда, когда
потенциальная энергия системы минимальна, а тепловое равно-
весие имеет место, когда все части системы приобрели одинако-
вую температуру.
Если же температура, например, внешней среды Тс будет вы-
ше, чем температура тела Тт, то последнее получит извне энер-
гию, передаваемую в форме термической работы. Это вызовет
изменение некоторой координаты состояния тела, в данном слу-.
чае термического заряда, сопряженного с термическим потенци-
алом. В частном случае равновесных нестационарных (квазиста-
тических) процессов эту координату называют энтропией и обоз-
начают буквой S. Если термическая работа равна 6Q, а темпера-
тура тела (абсолютная в градусах Кельвина) — Г, то энтропия
= (3.35)
Пусть от тела, температура которого перешло в тело с
температурой Т2 некоторое количество теплоты 6Q. Тогда в со-
ответствии с (3.35) мы можем сказать, что термическая коор-
дината состояния первого тела — его энтропия — уменьшилась
на величину
dS1 = ^~, (3.36)
11
73
а энтропия второго тела возросла на величину
dS2=-^-. (3.37)
7*2
Общее изменение энтропии двух тел будет равно сумме энтро-
пий, взятых с их знаками:
dS^dS2 — dS1. (3.38)
Так как Т{>Т2, то из (3.36) и (3.37) легко видеть, что dS{<
<dS2, и, следовательно, из (3.38) заключаем, что
dS>Q. (3.39)
Таким образом, поскольку теплота сама собой всегда перехо-
дит только от более нагретого тела к более холодному, постоян-
но будет иметь место соотношение (3.39), т. е. при любом процес-
се теплообмена в закрытой системе энтропия системы возрастает;
иными словами, выравнивание термических потенциалов в систе-
ме сопровождается увеличением ее энтропии.
При любом неравновесном состоянии термодинамические па-
раметры в различных частях системы неодинаковы: имеют место
различия в давлении, плотности, температуре и т. д.
При равновесном состоянии, когда Т2 отличается от 7\ на бес-
конечно малую величину, можно принять, что | dSx | = | dS21,
и энтропия системы остается постоянной, а сам процесс, протека-
ющий бесконечно медленно, будет квазистатическим, т. е. пред-
ставляющим собой последовательную систему бесконечно близких
друг к другу состояний равновесия.
При адиабатическом процессе 6Q—О, и, следовательно, в случае
равновесного процесса энтропия системы не изменяется. Поэтому
адиабатические обратимые процессы называют также изоэнтро-
пийными.
Второе начало термодинамики. Итак, если бы мы захотели от-
нять теплоту у более холодного тела и передать ее более нагре
тому, то должны были бы затратить на это некоторую допол-
нительную энергию. Это положение составляет сущность второго
начала термодинамики, которое формулируется так: невозможен
самопроизвольный переход теплоты от более холодного тела к те-
лу более теплому.
Другая формулировка этого начала связана с использованием
понятия об энтропии: в изолированной системе возможны только
такие процессы, при которых энтропия системы возрастает.
Так как в изолированной системе процессы идут в направле-
нии возрастания энтропии, причем состояние системы все более
приближается к равновесному, то условием наступления равно-
весия в закрытой системе является достижение максимума
энтропии.
Основное уравнение термодинамики. Подставим в выражение
(3.28) первого начала термодинамики TdS вместо 6Q и pdV
вместо 6А. Тогда
74
dU = TdS~pdV (3.40)
в случае квазистатического процесса.
При нестатическом (неравновесном) процессе
TdS>dU + pdV (3.41)
или в общем виде
TdS>dU + pdV. (3.42)
Уравнение (3.42) называют основным уравнением термодина-
мики, так как оно обобщает оба ее начала.
Из (3.40) сразу следуют соотношения:
при постоянном V (т. е. при dV=0)
(3-43)
- \ О О /у
при постоянном S (т. е. при dS=0)
(З-44)
\ dV )s
Запишем (3.40) в виде
dS = -у- dU + -у- pdV. (3.45)
Представим теперь полный дифференциал dU функции U от
Т и V следующим образом:
dU = dT + dv.
\ дт }v 1 \ dV )т
Тогда из (3.45) получим
dS =
1 / $U \ , 1 Г/ ди
-- --- а / Ч ----
Т\дТ)у Т [\ дУ
+ p\dV.
т J
(3.46)
Так как dS представляет собой полный дифференциал, то для
соответствующих величин, входящих в правую часть (3.46), долж-
но выполняться условие (3.12). Сопоставляя (3.11) и (3.46), по-
лучим:
df - dS*,
м=л.(^\ ;
Т \ дТ Jv
Xi — Т\
х2 = V.
Следовательно,
дМ __ д Г 1 / dU \ 1 _ 1 d2U .
дх2 ~ dV L Т \ дТ /J ~ Т дУдТ 1
75
откуда
(4Я ==г(~й~)~р- (3-47)
\ О V ] т \ и Т /у
Это выражение называют термодинамическим уравнением сос-
тояния.
Теплота диссипации. При движении заряда сквозь
систему (проводник) потенциал вдоль этой системы падает вслед-
ствие различных сопротивлений движению заряда, которые
можно объединить общим понятием «трение». Количество тепло-
ты диссипации, выделяемой на некотором участке проводника,
равно разности потенциалов на этом участке (падению потен-
циала вследствие трения), умноженной на количество перене-
сенного заряда.
Все формы движения превращаются в результате трения толь-
ко в одну — термическую. Этот вид превращения называют дисси-
пативным. Точно так же процессы превращения различных форм
движения, обусловленные переносом зарядов, всегда сопровожда-
ются диссипативными превращениями.
Если падение потенциала на некотором участке проводника
равно dP, а перенесенный заряд dE, то работа диссипации
d<2ДИС = dPdE дж. (3.48)
Приравнивая это выражение термической работе, легко найдем
соответствующее изменение энтропии системы
d Олис = TdS дж,
откуда
dS = dP*E (3.49)
В результате диссипации энтропия системы возрастает на ве-
личину, пропорциональную разности потенциалов dP и количест-
ву перенесенного заряда dE и обратно пропорциональную темпе-
ратуре Т.
Количество энтропии, которое возникает за счет диссипации в
единице объема и за единицу времени (возникновение энтропии):
(3.50)
dV at
5. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
Из условия, что внутренняя энергия U является функцией состо-
яния, т. е. функцией обобщенных координат системы, в п. 3 главы
76
3 было показано, что любой из потенциалов системы равен про-
изводной от ее внутренней энергии по сопряженной координате
состояния.
Кроме внутренней энергии существуют и другие функции, про-
изводные от которых дают параметры, сопряженные с теми, по
которым производится дифференцирование. Такие функции ф на-
зывают характеристическими. Рассмотрим систему с п степеня-
ми свободы и характеристическую функцию для нее от k потенци-
алов Pi и п—k координат Ер
ф = Л, • • •, Pk , Ek+i, Ek+2l .. ., Еп).
(3.51
Очевидно,
дф
TpJ
n x ।
X dE; 1
/=*+1 1
Можно доказать, что при этом
-^- = -£г (i = 1, 2, '
=Pj (j = k+\, k + 2, n).
Таким образом, частная производная от характеристической
функции по какому-либо из потенциалов равна сопряженной ко-
ординате состояния, взятой с обратным знаком, а производная от
ф по координате равна сопряженному с ней потенциалу.
Характеристические функции для систем с двумя степенями
свободы. Пусть параметры системы E"i=S (энтропия), E2=V
(объем), Р\ = Т (температура), Р2 = р (сжимающее давление).
Если рассматривать системы с двумя степенями свободы, то
вид характеристической функции ф будет зависеть от того, какие
две из величин Т, S, р и V мы выберем за независимые пере-
менные, что определяется характером решаемой задачи.
Если за независимые переменные выбрать энтропию и объем,
то ф (S, V) будет представлять собой внутреннюю энергию U.
Характеристические функции от других независимых переменных
получили следующие названия и обозначения:
ф (S, р)— энтальпия И;
ф (Т, 7) — свободная энергия F;
ty(T,p)—функция Гиббса или свободная энтальпия G (иногда
обозначается Ф).
Рассмотрим наиболее распространенные характеристические
функции подробнее.
Внутренняя энергия как характеристичес-
кая функция. Из соотношений (3.43) и (3.44) следует, что
температуру можно найти как частную производную от внутрен-
ней энергии по энтропии при постоянном объеме, а давление —
77
как взятую с обратным знаком производную от внутренней энер-
гии по объему при постоянной энтропии.
Свободная энергия. Характеристическую функцию ф
(Г, V) называют также функцией Гельмгольца, который ввел ее
в термодинамику. Чтобы найти эту функцию, преобразуем урав-
нение (3.40) таким образом, чтобы вместо независимой перемен-
ной S в него вошла независимая переменная Г.
Вычтем из правой и левой частей (3.40) дифференциал произ-
ведения
d(TS) = TdS + SdT. (3.52)
В результате получим
dU~ d(TS) = — SdT~ pdV (3.53)
и найдем искомую зависимость
d(U — TS) = — SdT — pdV. (3.54)
Разность
F — U — TS (3.55)
называется функцией Гельмгольца; отсюда
dF — dU — ТdS — Sdt — — Sdt ~рdV. (3.56)
Сравнивая правую часть (3.56) с исходным уравнением (3.40),
мы видим, что переменные S и Т поменялись местами.
Любое преобразование, в результате которого независимые
и зависимые переменные меняются ролями, называют преобразо-
ванием Лежандра.
Так как, согласно общему правилу (3.10),
dF = (-~-]dT+ (-^-)dv’ (3-57)
\ О 1 / у \ и V / т
то, сравнивая (3.56) и (3.57), получим
В случае изотермического процесса (T=const) dT=0, и тогда из
(3.56) следует, что
dF = — pdV = — dA. (3.59)
Следовательно, при изотермическом процессе система соверша-
ет работу только за счет убывания свободной энергии, составляю-
щей часть внутренней энергии системы. Другая ее часть, равная
TS, должна рассматриваться как связанная энергия, т. е. энергия,
которая может превратиться только в теплоту, рассеивающуюся в
окружающей среде при изотермическом процессе.
Энтальпия. Произведем преобразование Лежандра ос-
новного уравнения (3.40), прибавив к обеим его частям d (pV):
dU + d(pV)— Т dS —pdV + (pdV + Vdp).
78
Тогда
(3.61)
(3.62)
(3.63)
d(U + pV) = TdS + Vdp. (3.60)
Из (3.60) следует, что U+pV—функция независимых переменных
5 и р, названная выше энтальпией, фавна:
H = U + pV;
dH = TdS + Vdp,
где
I дН \ = т, / дН \ = у
[ dS )р ’ \ др )s
При изобарном процессе, при котором p=const и dp=0,
dH = TdS = ZQ, (3.64)
т. е. энтальпия равна количеству теплоты, которое система по-
лучает из внешней среды или отдает последней. Поэтому энталь-
пию называют также теплосодержанием.
Функция Гиббса. Если искать выражение для характе-
ристической функции от независимых переменных Т и р, то
удобнее всего преобразовать по Лежандру энтальпию, вычтя из
обеих частей уравнения (3,62) rf(TS):
dH — d(TS) = TdS+ Vdp — (TdS + SdT)-,
d(H— T S) = — SdT + V dp.
Обозначая
G = H — TS,
получим
dG = — SdT + Vdp.
С другой стороны, согласно (3.10),
(3.65)
(3.66)
(3.67)
(3.68)
(3.69)
(3.70)
и, сравнивая выражения (3.68) и (3.69), находим
\ дТ )р ’[ др
Из (3.67) и (3.70) получаем уравнение, связывающее энтальпию
Н с функцией Гиббса:
H = G — т(-^-\ . (3.71)
\ дТ
Функцию G называют также термодинамическим или изобар-
но-изотермическим потенциалом.
Дифференциальные соотношения термодинамики. Эти соотно-
шения, называемые также соотношениями взаимности или урав-
79
нениями Максвелла, непосредственно вытекают из условия (3.12)
полного дифференциала dpi dEt и могут быть трех типов: дР> - — (первый тип); (3.72) д Е j
dEf др£ dEi ~ ~дР (ВТ°РОЙ ™П)’ (3.73)
ЭЕ; f dEf ' f д Pf у < ЭР< / дЕ, 1 дР, \ или —— = — (третий тип), (3.74) \ dPj J
где Ei и Ej—обобщенные координаты, а Р, и Ру— соот-
ветственно сопряженные с ними потенциалы.
С помощью этих соотношений при исследовании можно заме-
нять одни термодинамические параметры другими. Так, для слу-
чая рассмотренной выше системы с двумя степенями свободы мы
можем получить, исходя из этих соотношений, дифференциальные
зависимости вида
и ряд других.
Из полученных соотношений легко установить связь между
различными характеристическими функциями. Так, свободная
энергия
Р = U~ TS,
а при постоянном объеме, согласно (3.58), энтропия
5 = -(—•
\ дТ )v
"Таким образом,
и = . (3.77)
\ дТ )v
Связь между функцией Гиббса и энтальпией выражается урав-
нением (3.71).
Уравнения типа (3.71) и (3.77) называют уравнениями Гиб-
бса — Гельмгольца. Они связывают между собой различные харак-
теристические функции.
Мнемонический квадрат. Нет смысла запоминать многочислен-
ные аналитические соотношения термодинамики. Достаточно знать
основное уравнение (3.40) и определения характеристических
функций:
dH = d(U + рV) - TdS + Vdp\
80
d F = d(U — T S) = ~ S dT ~ pdV-,
dG = d(H— T S) — ~ SdT + Vdp,
а также правило перехода от одних переменных к другим.
Очень удобно пользоваться следующим мнемоническим пра-
вилом [58]. В квадрате из четырех клеточек (рис. 3.2) размеще-
ны обозначения температуры Т, давления р, объ-
ема V и энтропии S. Снаружи обозначения ха- ----------
рактеристических функций распределены таким т р
образом, чтобы независимыми переменными для
них были величины, стоящие внутри квадрата с w F
противоположной стороны. Размещение букв, ес- v s
тественно, следует запомнить. Так, для энталь- _______
пии Н независимыми переменными являются р и '6
S, для свободной энтальпии G — независимые
переменные Т и р и т. д. Рис- 32; Мнемо-
ПравилсА. Связь между парамет- нически квадрат
рами и термодинамическими функ-
циями. Любая из величин внутри квадрата равна частной произ-
водной от расположенной рядом снаружи квадрата функции по не-
зависимой переменной, стоящей накрест от искомой величины.
Постоянной при этом является величина, соседняя с независимой
переменной. Знак производной—минус, если величина, по которой
берется производная, лежит левее искомой.
Например, Т может быть выражено только через соседние
функции U и Я; S — только через F и G:
- / дб \ . т ( дн \ s - ( dG \ S - I dF }
V dS )у k dS Ip к дТ ]р к дТ /у
Правило Б. Связь между характеристи -
ческими функциями. Любая из функций Н, U, F и G равна
функции, расположенной у соседней стороны квадрата, плюс про-
изведение величин, лежащих на диагонали, соединяющей концы
этих сторон квадрата. Если величина, которая является первым
слагаемым, лежит левее той, для которой пишется уравнение, бе-
рется знак минус. Например, выражая Н через U, получим Я=
= U+pV (аналогично H=G + TS-, F=G—pV и т. д.).
Правило В. Имея эти уравнения, легко получить все урав-
нения Гиббса—Гельмгольца. Так, в зависимости U=H—pV мож-
но выразить V через производную от Н и р по правилу А:
v = ('-™-\,
к др !s'
и тогда
U = H~p(-^L.\ .
к др ls
81
Таким образом, чтобы получить уравнение Гиббса—Гельмголь-
ца, нужно функцию, стоящую вне квадрата, выразить через функ-
цию, стоящую у смежной стороны, и через ее производную, которая
берется по переменной, стоящей у противоположной стороны
квадрата рядом с искомой функцией. Эту производную нужно
умножить на независимую переменную и произведение вычесть. На-
пример, нужно выразить U через F и производную от F. Значит, U
(dF\
— на Г, так как именно Т стоит со
стороны, противоположной F, и рядом с U. Получаем
и = F — Т (.
дТ )v
Выражая G через Н} по указанному правилу получим
G = H — S .
V 9S )р
Правило Г. Полные дифференциалы харак-
теристических функций. Полный дифференциал характе-
ристической функции равен алгебраической сумме произведений
каждой из величин, расположенных в квадрате рядом с этой функ-
цией, на дифференциалы величин, расположенных накрест от них.
Если величина со знаком дифференциала стоит левее величины, на
которую этот дифференциал умножается, берется знак минус. На-
пример,
dU = TdS — pdV' dG^—SdT + Vdp.
Правило Д. Уравнения Максвелла. Следует
взять две величины, стоящие в одном вертикальном или горизон-
тальном ряду, и записать их частные производные по перемен-
ным, стоящим в соседнем ряду (не накрест с ними). Затем берет-
ся смешанная частная производная от соответствующей характе-
ристической функции по тем же переменным. Между всеми тре-
мя производными ставится знак равенства. Например, чтобы по-
лучить уравнение (3.75), находим производные Т и р по стоящим
не накрест переменным V и S; и ( as") ’ ^атем берем
смешанную производную от U (которое соответствует по правилу
А переменным Т и V) по тем же переменным 5 и V: -—— и
д S д V
окончательнд получаем:
/ дТ \ _ ( 'дР \ — д2и
\ dv М \ dS )v~ dSdV ’
Перед частной производной ставится знак минус, если вели-
чина, остающаяся постоянной, стоит слева от той, по которой
берется производная.
32
Физический смысл характеристических функций. Изменение
характеристических функций, которые называют также функция-
ми состояния системы, всегда определяет собой максимальную
работу, которую система может совершить при изменении пара-
метров, принятых в данном процессе независимыми переменны-
ми. Поэтому функции U, Н, F и G называют еще термодинамичес-
кими потенциалами. Внутренняя энергия является термодинами-
че^ским потенциалом при постоянной энтропии, а свободная энер-
гия— при постоянной температуре. Не следует, однако, смеши-
вать понятие о термодинамическом потенциале с понятием о по-
тенциале как о движущей силе, которое было дано в п. 2 главы
3. Поэтому далее во избежание путаницы будем называть функ-
ции ф характеристическими.
Приведем без доказательств следующие важные положения,
поясняющие смысл и значение термодинамических функций при
анализе поведения различных систем [58].
1.. Максимальная внешняя работа, соверщаемая системой при
адиабатическом процессе, равна убыли внутренней энергии систе-
мы U.
2. Максимальная внешняя работа, совершаемая системой при
изотермическом квазистатическом процессе, равна убыли свобод-
ной энергии системы F.
3. Если независимые переменные, определяющие ту или иную
характеристическую функцию, поддерживать постоянными в хо-
де некоторого процесса, то соответствующая характеристическая
функция получает экстремальное значение. Так, например, если
система находится при постоянной температуре и постоянном объ-
еме, то она стремится к минимуму свободной энергии F, являю-
щейся функцией Т и V.
4. Количество теплоты, получаемой системой при неизменном
объеме, равно приросту внутренней энергии U системы.
5. Количество теплоты, получаемой системой в квазистатичес-
ком процессе при постоянном давлении, равно приросту энталь-
пии Н системы.
6. Если квазистатический процесс протекает при одновремен-
но постоянных температуре и давлении, то функция Гиббса (сво-
бодная энтальпия G) остается постоянной.
7. Если состояние системы определяется не только параметра-
ми р и V, но и какими-либо другими параметрами, то в обратимом
процессе разность между совершаемой системой работой при по-
стоянных р и Т и работой расширения р(У\—V2) равна убыли сво-
бодной энтальпии G.
8. Для твердых тел и жидкостей величины U и Н практически
одинаковы. Для этих тел можно пренебречь также различием в из-
менении функций F и G. При исследовании следует пользоваться
только той термодинамической функцией, которая соответствует
независимым параметрам данного процесса.
83
6. ХИМИЧЕСКИЙ ПОТЕНЦИАЛ. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
Химический потенциал. Если, например, в изолированный сосуд
с водой и паром над ней поместить гигроскопическое вещество, ко-
торое поглощает пар, то в результате отбора части пара его давле-
ние упадет и испарится добавочное количество воды. Этот процесс
будет продолжаться до тех пор, пока гигроскопическое вещество не
насытится водой. Таким образом, в системе произойдет ряд внут-
ренних процессов без всякого обмена с внешней средой. Эти про-
цессы связаны с увеличением массы одной части системы за счет
уменьшения массы другой ее части.
Именно такого рода изменения в соотношении масс частей си-
стемы происходят при химических реакциях и агрегатных прев-
ращениях. То, что при этом температуры и давления в любой точ-
ке системы могут быть совершенно одинаковыми, заставляет пред-
положить, что в системе должны существовать градиенты како-
го-то специфического потенциала, являющегося движущей силой
указанных процессов. Гиббс впервые постулировал существование
такого потенциала, назвав его химическим. Химический потен-
циал обозначают буквой ц. Если в рассмотренном выше примере
равновесие между паром и водой установится так, что массы их
больше изменяться не будут, то это означает, что химические по-
тенциалы для пара и жидкости должны быть одинаковыми.
Так как в данном случае координатой состояния (обобщен-
ным зарядом) является масса т, то сопряженный с ней потенци-
ал должен определяться, согласно общему условию (3.18), из
выражения
Н = (, (3.78)
\ dm )s, V
где через U обозначена внутренняя .энергия.
Следовательно, химический потенциал представляет собой из-
менение внутренней энергии системы при изменении ее массы
на единицу, причем в качестве такой единицы может быть выбран
1 г, 1 моль, масса одной частицы, концентрация частиц и т. п.
В соответствии с формулой (3.54) для характеристических
функций можно написать также
( dG \ [ дН \ I dF \
I1 — ----- = ---------- = --------- • (3.79)
\ дт )т, р \ dm jp,s \ дт ]т, v
Фазы. Фазовые превращения. Фазой называется часть систе-
мы, однородная во всех точках по химическому составу и физи-
ческим свойствам и отделенная от других частей системы поверх-
ностями раздела. Вода и лед, например, представляют собой две
фазы, так как хотя у них и одинаковый химический состав, но
различны физические свойства.
Различные фазы одного и того же вещества могут одновре-
менно сосуществовать, находясь в динамическом равновесии
друг с другом. Изменение условий равновесия вызывает переход
84
одной фазы в другую. При этом изменение их масс равно по
величине, но противоположно по знаку. Такой переход называют
фазовым превращением.
Однофазные системы физически однородны (гомогенны),
многофазные — физически неоднородны (гетерогенны).
Не всякое различие в свойствах при одинаковом химического
составе является фазовым различием. Так, существуют вещества,
кристаллы которых можно получать с двумя различными струк-
турами, представляющими собой как бы зеркальное отображение
друг друга. Такие зеркально симметричные кристаллические
структуры поворачивают плоскость поляризации света в противо-
положные стороны, но, несмотря на это физическое различие, их
следует считать одной фазой, так как никакими изменениями тер-
модинамических условий их нельзя перевести друг в друга.
Причиной фазовых превращений является разность химичес-
ких потенциалов различных фаз.
Компоненты. Составные части системы, различные по своим
химическим свойствам и независимые друг от друга, называются
компонентами системы. Например, при реакции образования во-
ды из водорода и кислорода имеются три вещества — водород,
кислород и вода:
2Н2 + О2 -> 2Н2О,
но независимых компонент только две: Н2 и О2, так как третье
вещество Н2О образуется из первых двух.
Но если температура смеси такова, что реакция соединения
водорода и кислорода не происходит, то кислород, водород и во-
да образуют три компоненты системы. Таким образом, число
компонент системы — это наименьшее число веществ, с помощью
которых можно описать состав каждой фазы системы в отдельно-
сти.
Приведенные выше определения фаз и компонент были вве-
дены в связи и в соответствии с задачами химической термоди-
намики. Однако этими же терминами пользуются и в физике дис-
персных систем, гдо они получают несколько иное определение,
соответствующее изучаемым там взаимодействиям.
Направление процесса. Будем обозначать массы, химические
потенциалы и внутренние энергии каждой из компонент или облас-
тей, в пределах которых система может рассматриваться как од-
нородная, следующим образом:
заряды (массы) т2,..., пгп\
химические потенциалы
внутренние энергии t7b I72,..., U п.
Размерность химического потенциала определяется тем, что
произведение pdm должно иметь размерность работы (дж).
В условиях равновесия
(3.80)
85
а при химических и фазовых превращениях
2|izdmz<0. (3.81)
Из сопоставления (3.79) и (3.81) следует, что каковы бы ни
были характеристические функции, избранные для анализа по-
ведения системы, всегда химические реакции и фазовые превраще-
ния могут протекать только таким образом, что характеристичес-
кие функции убывают.
Если же условия таковы, что эти функции не могут уменьшать-
ся, то система находится в устойчивом равновесии, и ни химичес-
кие реакции, ни фазовые превращения в ней невозможны.
Основные частные случаи взаимодействия. Рассмотрим систе-
му, которая подвергается извне деформационному и термическому
воздействию и в которой одновременно протекают фазовые и хи-
мические превращения, как это часто бывает в грунтах. В этих
условиях изменение внутренней энергии может быть представлено
следующей суммой:
d U = Т d S — р d V + S ft т/, (3.82а)
где TdS— изменение внутренней энергии системы в результате
термического взаимодействия с внешней средой и не-
равновесных химических и фазовых превращений;
pdV — то же, в результате деформации;
2 p-z dm,i — то же, в результате обмена массой с окружающей сре-
дой.
В случае если система состоит из N фаз и k компонент, в урав-
нении (3.82а) следует просуммировать все члены по фазам, а член,
связанный с химическим потенциалом, еще и по компонентам:
^dU ^^TdS — ^pdV + (3.826)
N N N N k
Перепишем уравнение (3.82а) для одной фазы в виде
2 ^idmi — dU — (TdS — pdV) (3.83)
и рассмотрим следующие основные частные случаи взаимодействия
системы с окружающей средой.
1. Взаимодействие, при котором сохраняются постоянные энтро-
пия и объем (S=£onst, V=const). При V=const деформационное
взаимодействие отсутствует, а теплообмен с внешней средой регу-
лируется так, чтобы энтропия оставалась постоянной.
Уравнение (3.83) принимает вид
2 Pi dtni~ d U. (3.84)
Так как 2p.zd/nz<0, то
dU<0, (3.85)
т. е. пока идет процесс химических или фазовых превращений,
внутренняя энергия системы в рассматриваемом процессе все вре-
мя убывает и в конце процесса, когда достигается состояние рав-
новесия, она минимальна: U = £7МИН.
86
2. Взаимодействие при постоянной энтропии 8 и постоянном
давлении р. В этом случае dS=0 и dp=0. Следовательно, добав-
ляя к правой части уравнения (3.83) величину Vdp, равную нулю,
мы можем преобразовать его к виду
Zpdm — dU + (pdV + Vdp) — dU d(pV) ~
= d\U + pV) = dH, (3.86)
где H — энтальпия.
Из условия 2pt/m<0 получаем, что в данном процессе энталь-
пия системы стремится к минимуму.
3. Взаимодействие при постоянном объеме и потенциале (тем-
пературе) Т. Объемная деформация отсутствует, но имеет место
теплообмен в условиях T=iconst. В этом случае pdV—0, a TdS =
= d(TS ), так как SdT=0. Следовательно,
2 рь dm = d U — d (Т 8) = d (U — Т S) = d F, - (3.87)
где F — свободная энергия.
Так как 2pzdmz <0, то в данном, процессе dF<0 и F Гмин.
4. Взаимодействие при постоянных потенциалах Тир. При этом
TdS=d(TS), a pdV=d(pV). Следовательно,
2 pi d tn = d U — d (Т 8) + d (р V) =
= d (U — Т 8 + р V) = d G, (3.88)
где G — функция Гиббса.
Рассуждая аналогично предыдущим случаям, получаем, что в.
данном процессе G
Так как, согласно (3.68), dG=—SdT-\-Vdp, а Т и р при агре-
гатных превращениях постоянны, то это означает, что при них
функция Гиббса системы остается постоянной. Итак, во всех рас-
смотренных случаях характеристические функции, соответствую-
щие данным условиям взаимодействия, стремятся к минимуму, что-
и определяет направление происходящих процессов.
Условия равновесия в многофазной системе. Из основных поло-
жений термодинамики следует, что если многофазная система на-
ходится в равновесии, то: 1) температуры всех ее фаз равны между
собой; 2) давления во всех фазах одинаковы; 3) химические по-
тенциалы различных фаз каждой из компонент также одинаковы.
Вычисление химического потенциала. Из приведенных выше со-
отношений
S d mi ~ d U\ 2 uzdm-^d H\ 2 p.zdm^d F;
2 p-zdmt~dG
следует, что химический потенциал может быть вычислен по урав-
нению
где ф — характеристическая функция;
mi — масса компоненты или части системы (подсистемы) /,
потенциал которой ищется;
mk, inv— индекс, означающий, что массы всех остальных ком-
понент или подсистем (кроме z-той) остаются неизмен-
ными.
Химический потенциал для компоненты /, находящейся в сильно
разбавленном растворе при концентрации Mi , вычисляется по
формуле
ft- = /?Т1пМ/( (3.896)
где р.?— потенциал, зависящий только от свойств вещества /-той
компоненты;
R — газовая постоянная.
Правило фаз Гиббса. Обозначим количество веществ в системе
через В, а количество условий, определяющих изменение относи-
тельного содержания этих веществ в ходе тех или иных процессов,
через У. Такого рода условием является, например, то, что при хи-
мической реакции число независимых компонент уменьшается на
единицу, так как зависимость между относительным содержанием
веществ, участвующих в реакции, определяется уравнением реак-
ции, например 2Н2+О2=2Н2О.
Таким образом, можно заключить, что число компонент k си-
стемы равно числу веществ В минус число уравнений У, определя-
ющих связи между относительным содержанием веществ.
Гиббс показал, что в многофазной системе существует равнове-
сие между фазами только в том случае, если число фаз в ней
/Уф < k + 2. (3.90а)
Это правило называется правилом фаз Гиббса. Несмотря на фазо-
вое равновесие в системе, некоторые параметры ее состояния
могут меняться, например можно менять температуру системы во-
да— насыщенный пар, не нарушая равновесия между фазами.
Количество таких параметров, которые могут меняться без нару-
шения фазового равновесия системы, представляет собой число
степеней свободы системы.
Число фаз /Уф и число компонент k в системе связаны с-числом
ее степеней свободы п соотношением
n = k — /Уф + Al, (3.906)
где М — число независимых переменных, равное двум, если этими
переменными являются, например, давление р и темпера-
тура Т.
Независимая переменная — число частиц. В ряде задач термо-
динамики удобно рассматривать не изменение массы, а изменение
числа частиц или молекул /V в системе. Тогда вместо термодина-
мического параметра m в предыдущие уравнения надлежит ввести
переменную N.
88
Химический потенциал в этом случае следует рассматривать как
величину, относящуюся к одной молекуле, и, соответственно, заме-
нить соотношение (3.906) на
Термодинамические величины, зависящие от числа частиц в си-
стеме, являются, очевидно, аддитивными, как, например, энергия
системы, ее объем и ее энтропия, которые пропорциональны числу
частиц в системе. Температура и давление — величины неаддитив-
ные, так как в любой части равновесной системы они будут иметь
одно и то же значение, независимо от числа частиц в системе.
Аддитивные величины, отнесенные к одной молекуле, принято
называть удельными молекулярными (например, объем воды при
данной температуре, приходящейся на одну молекулу воды, назы-
вают удельным молекулярным объемом).
Если представить внутреннюю энергию как функцию не только
3 и V, но и N, то мы должны получить выражение
U = (3.92)
Соответственно, выражение (3.82а) примет вид
dU = TdS~pdV + ?dN. (3.93)
Аналогичным образом мы получим для других характеристиче-
ских функций:
dH = TdS + Vdp+ v-dN;
dF = — SdT — pdV + vdN;
dG = — SdT + Vdp+ v-dN.
(3.94)
Отсюда можно получить для химического потенциала выражения
/ дН \ ( dF \ ( dG \ /о пс:\
и = ------ = ---------- = ----------- . (3.95)
\ dN )siP \ dN Jt.v \ ON )т, р
Если тело состоит из частиц одинаковой массы, то из (3.95) сле-
дует, что химический потенциал
(3.96)
т. е. равен функции Гиббса, отнесенной к одной частице. Так как Т
и р величины неаддитивные, то химический потенциал системы,
выраженный через эти величины, не зависит от числа частиц и, сле-
довательно, может быть представлен как
d? = — 5Уд d Т + Гуд d р, (3.97)
где 3Уд и Руд— значения энтропии и объема, приходящиеся на
одну молекулу системы.
89
7. ПОНЯТИЕ О ТЕРМОДИНАМИКЕ НЕОБРАТИМЫХ
ПРОЦЕССОВ
Изучением стационарных необратимых (неравновесных) про-
цессов с энергетической точки зрения занимается термодинамика
необратимых процессов. Особенный интерес представляет возмож-
ность ее успешного применения к таким системам, в которых про-
текание необратимых процессов вызывает появление сопряженных
с ними новых эффектов. Таким эффектом является, например, элек-
троосмос — фильтрация жидкости, возникающая при пропускании
электрического тока через насыщенную жидкостью пористую среду,,
причем явления электропроводимости системы и фильтрации вза-
имосвязаны, так как движение ионов переносит ток и одновремен-
но определяет перемещение воды.
Далее излагаются получившие широкое распространение идеи
термодинамики необратимых процессов.
Термодинамические силы. Термодинамика необратимых процес-
сов устанавливает зависимость между скоростями процессов раз-
личных видов и величинами вызвавших их градиентов потенциалов
(температуры, электрического напряжения, химического потенциа-
ла, давления и т. п.). Эти последние рассматриваются как своеоб-
разные «силы», которые в отличие от сил в механике называются
термодинамическими. Далее рассматриваются лишь такие явления,
скорость которых может, хотя бы приближенно, считаться прямо
пропорциональной величине соответствующих сил. Эта линейная
связь хорошо осуществляется во многих случаях.
Обозначим термодинамические силы через Xi . Тогда
Xt = , (3.98)
d х
где dP — разность потенциалов на участке dx.
Обобщенные скорости и силы. Пусть Е//г — некоторая коорди-
ната (например, термический или электрический заряд, масса и т.
д.) состояния системы, отнесенная к единице ее поперечного сече-
ния. Назовем скорость ее изменения Vik обобщенной скоростью
или потоком:
dE/f?
= (3.99)
a t
Линейная связь между потоком при стационарном процессе и
вызвавшей его термодинамической силой может быть представле-
на уравнением
vlk=LlkXk, (3.100а)
где Xk —сила, вызвавшая данный поток (обобщенная сила);
Lik — коэффициент пропорциональности.
Удобно ввести понятие о термодинамическом направлении, по-
нимая его не в геометрическом смысле, а подразумевая под ним
90
тот или иной вид скоростей любых изменений. Индексами при обоб-
щенных силах и скоростях обозначаются соответствующие термо-
динамические направления. Так, символ Vik следует понимать как
обобщенную скорость по направлению обобщенной силы Xi , вы-
званную обобщенной силой Xk. Исходя из этого отношение (3.100)
можно сформулировать следующим образом: обобщенная скорость
vik по направлению z, вызванная действием некоторой обобщенной
силы Xk, действующей по направлению k, прямо пропорциональна
величине этой силы.
В случае электроосмоса, например, направлением i можно обоз-
начить явление движения воды, а направлением k — явление элек-
тропроводности. Тогда Xi будет обобщенной силой, обычно вызы-
вающей фильтрацию (разность напоров), a Xk — обобщенной си-
лой, вызывающей электрический ток (разность потенциалов). Со-
ответственно Vik будет представлять собой скорость движения
жидкости, вызванного пропусканием электрического тока (явление
электроосмоса), a Vki —электрический ток, вызванный фильтраци-
ей жидкости, переносящей ионы, или так называемый ток переноса
(явление потенциала протекания).
При наличии п различных обобщенных сил суммарная обоб-
щенная скорость по направлению i
vt = ^Lik-Xk, k= 1, 2....................(3.1006)
n
В этой сумме член вида LaXi мы будем называть главным,
а вида LikXk—побочным. Соответственно, и коэффициенты Lu
будут главными, a Lik — побочными.
Полагая Xk в (3.100а) равным 1, мы видим, что коэффициент
Lik представляет собой не что иное как обобщенную скорость при
единичной обобщенной силе, и мы будем называть далее эти коэф-
фициенты удельными скоростями — главными и побочными.
Особенность главной скорости состоит в том, что она непосред-
ственно сопряжена с данной обобщенной силой. Если, например,
обобщенной силой является разность напоров, то главная обоб-
щенная скорость будет относиться к току жидкости-, а побочная —
к электрическому току (току переноса). Если же обобщенной силой
является разность электрических потенциалов, то главная обобщен-
ная скорость будет относиться к электрическому току, а побоч-
ная — к электроосмотическому течению жидкости.
Таким образом, побочные скорости возникают в результате из-
менений, вызванных в системе главными скоростями. Те побочные
скорости, которые совпадают с направлением градиентов, соответ-
ствующих им по термодинамическому направлению главных сил,
мы будем считать положительными, а если их направления расхо-
дятся на 180° — отрицательными.
Соотношение взаимности. Одно из основных положений термо-
динамики необратимых процессов, установленное Онзагером и но-
91
сящее его имя, представляет собой так называемое соотношение
взаимности:
L„, = LU. (3.101)
Пользуясь принятой терминологией, его можно сформулировать
следующим образом: удельная скорость по направлению z, вызван-
ная единичной обобщенной силой Xk = l, действующей по на-
правлению k, равна удельной скорости по направлению k, вызван-
ной единичной обобщенной силой X/ =1, действующей по на-
правлению z.
Скорость возрастания энтропии. Возникновение энтропии. Клас-
сическая термодинамика обычно не идет далее формулировки не-
равенства
dS>0 (3.102)
в случае необратимых процессов.
Термодинамика необратимых процессов исходит из очевидного
положения, что раз система изолирована от внешней среды и эн-
тропия ее не может меняться за счет взаимодействия с этой средой,
то условие (3.102) означает, что приращение энтропии возникает
внутри системы.
Если взять производную от приращения энтропии в единице
объема изолированной системы по времени, то она будет, очевид-
но, представлять собой скорость возрастания энтропии. Так как эта
скорость представляет собой приращение энтропии в необратимом
процессе в единицу времени, то ее называют возникновением энтро-
пии и обозначают обычно символом ог$ (3.50):
= <3J03>
В случае обратимого процесса
= (3.104)
где 6Q — количество тепла, получаемого системой при температу-
ре Т в течение времени dt за счет взаимодействия с окружающей
средой.
В случае необратимого процесса
dS>-^-,’ (3.105)
и можно рассматривать dS как сумму двух величин
+ (3.106)
где &Q' — называют по Клаузиусу некомпенсированным теплом.
Очевидно, 6Q'>0, т. е. является величиной существенно положи-
тельной.
92
В случае адиабатически изолированной системы, т. е. системы,
не обменивающейся теплом с окружающей средой,
8Q = 0, (3.107)
и тогда
dS = _^L. (3.108)
есть приращение энтропии, возникающее внутри изолированной
системы.
Очевидно, некомпенсированное тепло 6Q' внутри изолирован-
ной системы может возникнуть (в соответствии с законом сохране-
ния энергии) лишь за счет превращения в теплоту других видов
энергии, содержащихся в системе.
Но если внутри системы совершается какая-либо работа, то она
может быть представлена как сумма произведений обобщенных
сил Xt на соответствующие обобщенные перемещения (коорди-
наты) :
(ЗЛ09)
и,следовательно,
dS = ^Х^Ее . (3.110)
Возникновение энтропии, согласно (3.103) и (3.110), будет
равно:
или с учетом (3.99)
^ = 4" <ЗЛ11>
Т^^Х, (3.112)
Таким образом, возникновение энтропии пропорционально сум-
ме произведений обобщенных сил на обобщенные скорости.
В случае неизолированной системы энтропия ее может либо
уменьшаться, либо возрастать в зависимости от того, теряет или
получает тепло рассматриваемая система. Но если процесс в этой
системе протекает необратимо, то это означает, что внутри системы
происходит возникновение энтропии в соответствии с уравнением
(3.112).
Канонические уравнения для обобщенных сил. В общем случае
при действии п обобщенных сил можно описать возникающие по-
93
токи системой уравнений первой степени (каноническими уравнени-
ями для обобщенных сил):
^11 + ^12 -Х'з + • • • + Цп *п — ^1*,
^21 -^1 + ^22 А*2 + • • • + ^2п — ^2»
(3.113)
^nl I ^п2 %2 “Ь • • • 4" ^пп *п ^гт ,
В сжатой записи эту систему уравнений можно представить в
виде i уравнений:
= (i, k=l, 2, .... n). (3.114)
k
В силу соотношений взаимности (3.101) из общего числа п2
членов левых частей системы п уравнений различными будут лишь
п . п(п — 1) __ п(п+1)
2 2
членов.
Канонические уравнения для обобщенных скоростей. Если си-
стему уравнений (3.113) решить относительно обобщенных сил
Х2,..., Хл, то мы получим линейные уравнения вида:
К11 + К12 V2 + • • • + Kin vn —
К 21 V1 + K22 V2 + • • • + Kzn Vn ~
(3.115)
Knl V1 + Kn2 ^2+ • • • + Knn Vn — Xn,
где коэффициенты представляют собой определенные алгебраиче-
ские комбинации из .
Аналогично исходной системе уравнений (3.114) здесь также
будет иметь место соотношение взаимности
Klk = Kk, (3.116)
Легко видеть, что Kik представляет собой удельную обобщен-
ную силу, действующую по направлению z, вызванную обобщенным
перемещением по направлению k при скорости, равной единице.
В сокращенной записи систему (3.115) можно представить в
виде z уравнений
2^ = */ (i, k=l, 2, ..., п). (3.117)
k
Можно показать, что из свойств системы уравнений (3.113) вы-
текают очень важные соотношения:
LuLkk>L2ik, (3.118)
означающие, что произведение любых двух главных скоростей
всегда больше квадрата соответствующей им взаимной побочной
скорости (при действии единичных обобщенных сил).
94
Эти соотношения могут быть с успехом, использованы для конт-
роля экспериментальных результатов.
Возникновение энтропии как квадратичная функция. Как было
показано выше, при умножении обобщенных сил на соответствую-
щие им по направлению обобщенные скорости должны получаться
произведения, сумма которых пропорциональна возникновению
энтропии в единице объема системы. Подставляя в (3.112) значе-
ние Vi из (3.114), получим
Tas = ^LikXkX, (3.119)
ik
Это означает, что возникновение энтропии является однородной
•функцией второй степени (квадратической) от обобщенных сил.
Подставляя (3.17) в (3.112), получим
T^^XikvkVi, (3.120)
1 ik
т. е. возникновение энтропии является однородной квадратической
функцией обобщенных скоростей.
Из уравнений (3.100) и соотношений взаимности Онзагера сле-
дует, что при /
Линейность соотношений (3.100) означает приложимость к рас-
сматриваемым задачам принципа независимости действия термо-
динамических сил. Это позволяет сформулировать следующее по-
ложение, которое может быть названо принципом взаимности воз-
никновения энтропии: «В линейно-изменяемой системе сумма про-
изведений обобщенных сил состояния i на соответствующие по
направлению обобщенные скорости состояния k равна сумме про-
изведений обобщенных сил состояния k на соответствующие по на-
правлению обобщенные скорости состояния /, т. е. взаимно равны и
соответствующие величины возникновения энтропии» [11].
Для доказательства напишем в развернутом виде величины воз-
никновения энтропий при различной очередности приложения к
системе обобщенных сил XL и Xk.
Если сначала прикладывается сила Xt, а затем Х*,-то соот-
ветствующее возрастание энтропии равно:
Д41)=До£7) + Да^’+Да^’. (3.122)
При противоположном же порядке загружения
Д42) = Да^А)+До£7) + Д4*°. (3.123)
Так как возрастание энтропии не зависит от порядка загруже-
ния в случае независимых обобщенных сил, то
Да^1)=Д^2), (3.124)
95
откуда следует, что
АаГ = Д4‘*>,
(3.125)
что и требовалось доказать.
Продифференцируем (3.112) по Xt:
Т S = —- (Ц1Хх + О2 Х2 + • • • + vn ^п)<
и Х^ О X
т
dXt
дщ dv2
= Vi 4- Xx ———h X2 ———|-... + Xn
и X и A-
dvn
dXt
(3.126)
Так как из (3.100a) следует, что
д V,-
= Lik = Lki, (3.127)
то, согласно (3.126) и с учетом (3.100),
Т s = v. -f- Хх Lxx4- Х2 LX2 4-... 4- Х„ Lln; (3.128)
и Xj
д Go
Т—-^-=2vz, (3.129)
т. е. частная производная от возрастания энтропии по обобщенной
силе равна удвоенной величине соответствующей обобщенной ско-
рости, деленной на Т.
Продифференцировав (3.112) по vit аналогичным образом по-
лучим соотношение
д По
Т-^- = 2Х1, (3.130)
т. е. частная производная от возрастания энтропии по обобщенной
скорости, умноженная на абсолютную температуру, равна удвоен-
ной величине соответствующей обобщенной силы, деленной на Т.
Следовательно, если для какой-либо системы мы найдем воз-
никновение энтропии, то соответствующим дифференцированием
этого выражения мы получим величину обобщенной скорости по
направлению любой из сил, либо величину обобщенной силы по на-
правлению любой из имеющих место скоростей.
Принцип наименьшего возникновения энтропии. Как известно из
теории линейных уравнений, если система (3.113) имеет единст-
венное решение, то и квадратичная функция имеет один экстре-
мум. Если при этом линейная система положительно определена,
то этот экстремум является минимумом. Отсюда можно сформули-
ровать следующий принцип, который следовало бы назвать прин-
ципом наименьшего возникновения энтропии: если в какой-либо
замкнутой системе под действием группы постоянных обобщенных
сил происходят необратимые процессы, то направление и интенсив-
96
ность последних таковы, что скорость возникновения энтропии ми-
нимальна [Н].
Изложенное выше позволяет получить еще одно важное соотно-
шение.
По Онзагеру потоки — суть производные по времени парамет-
ров состояния (3.99):
(3.131)
а термодинамические силы представляют собой производные энтро-
пии по параметрам состояния
Хе =-/§- (3.132)
Подставляя в (3.130) Д- вместо о,-, получим
д По
Т —— = 2XZ. (3.133)
а 4
Сопоставляя^ (3.132) и (3.133), найдем уравнение, совпадающее
по форме с известным в динамике уравнением Лагранжа 2-го рода:
(3.134)
d f dS \ dS
T ---- /-----I-------= Xi .
dt \ dEt J dE;
В то время как в динамике число уравнений Лагранжа равно
числу степеней свободы механической системы, здесь число этих
уравнений равно числу независимых параметров состояния. При
этом энтропия S играет роль потенциальной функции, а ее возник-
новение os —диссипативной (функции рассеяния).
Правило выбора зарядов и потенциалов. Для данной формы
движения заряд устанавливается на основе опытных данных, а со-
пряженный потенциал может быть вычислен, если известно изме-
нение энергии системы в результате поступления в нее заряда.
Если известна формула для работы
dA^PidEi,
то заряд легко найти, так как он всегда находится под знаком диф-
ференциала.
4 Зак. 530
97
Глава 4
ГРУНТЫ КАК ОБЪЕКТ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
1. МЕХАНИЧЕСКОЕ ВЗАИМОДЕЙСТВИЕ
МЕЖДУ ЧАСТИЦАМИ ТЕЛА
Различным состоянием вещества соответствует различный ха-
рактер взаимодействия между молекулами тела. Это взаимодейст-
вие имеет электрическую природу и упрощенно может рассматри-
ваться как проявление притяжения разноименных зарядов и оттал-
кивания одноименных. Всякое устой-
Рис. 4.1. Условия равновесия и по-
тенциальная энергия
П& — потенциальный барьер; П & —
энергия активации
чивое расположение частиц в теле
означает наличие определенного
равновесия между силами притя-
жения и отталкивания, которое мо-
жет быть нарушено и изменено дей-
ствием внешних силовых полей.
Устойчивое положение частиц
всегда связано с минимумом потен-
циальной энергии системы. Если
представить себе холмистую поверх-
ность (рис. 4.1,я), на разные точки
которой положено шарообразное те-
ло, то, очевидно, на дне впадины (по-
ложение а) шар будет находиться в
наиболее устойчивом состоянии, со-
ответствующем относительному ми-
нимуму его потенциальной энергии.
Действительно, чтобы переместить
в другое положение этот шар, необ-
ходимо поднять его, произведя ра-
боту для преодоления действия силы тяжести. При этом по-
тенциальная энергия шара (энергия положения) возрас-
тет. С другой стороны, в точке б равновесие будет неустойчи-
вым, и достаточно небольшого толчка, чтобы шар скатился
вниз, уменьшив свою потенциальную энергию. В положе-
нии в равновесие будет безразличным, и горизонтальное переме-
щение шара происходит здесь без изменения его потенциальной
энергии. При бесконечно медленном движении нужно преодолевать
только сопротивление трения.
98
Если изобразить в виде условного графика потенциальную
энергию частицы в зависимости от занимаемого ею положения
(рис. 4.1,6), то в устойчивом состоянии энергия будет минималь-
ной /7МИН (как бы потенциальная «яма»), а для перевода частицы
в новое устойчивое состояние путем перемещения из положения а
в положение б необходимо сообщить ей добавочную энергию Пб~~
—- Лмин, чтобы частица могла перевалить через «бугорок» Пб, на-
зываемый потенциальным барьером. Энергия, которую следует со-
общить частице, чтобы преодолеть потенциальный барьер, назы-
вается энергией активации. Эту энергию частица в общем случае
может получить за счет действия внешних сил, нагревания или
электромагнитной энергии. Преодоление потенциальных барьеров
характерно для случаев, когда под влиянием внешних сил проис-
ходит перестройка структуры тела.
Силы. Любое механическое взаимодействие между телами пред-
ставляет собой, в сущности, взаимодействие различных по своей
природе силовых полей, окружающих тела и их частицы. Соответ-
ственно, понятие о силе является чисто условным, введенным для
обозначения причины таких механических явлений, как изменение
скорости и направления движения тел или как относительное пере-
мещение внутренних частиц тела, в результате которых последнее
изменяет свои объем и форму. Количественно силы определяют и
сравнивают между собой по произведенному эффекту, например
по ускорению движения, которое они сообщают телу, или по вели-
чине и характеру изменений формы и объема, испытанных телом
под их действием.
Силы, действующие на грунт, могут быть поверхностными и
объемными. В первом случае, как показывает само название, силы
приложены к поверхности грунта, во втором они распределены по
всему его объему.
К поверхностным относятся, например, разнообразные по вели-
чине и направлению нагрузки от сооружений, передающиеся через
фундаменты на основание. Примером объемных сил являются гра-
витационные и центробежные силы; гидродинамическое или фильт-
рационное давление, оказываемое движущейся сквозь грунт водой
на обтекаемые ею частицы грунта; сейсмические силы, определяе-
мые ускорением, сообщаемым частицам грунта при землетрясении.
Объемная сила, приходящаяся на единицу объема тела, называет-
ся удельной объемной силой. Если распределение сил по объему
тела зависит от характера распределения в нем масс, то такие
силы называют также массовыми (например, гравитационные и
сейсмические силы). При равномерном распределении массы тела
по всему его объему удельные значения объемной и массовой сил
совпадают. Всякая сила характеризуется не только величиной,
но и направлением действия и является поэтому вектором.
Для упрощения решения некоторых задач о распределении на-
пряжений в грунтах вводится понятие о сосредоточенных силах,
которые рассматриваются как приложенные в точке (в действи-
4* Зак. 530 по
дельности они всегда распределены на некотором участке поверх-
ности (рис. 4.2), так что сосредоточенная сила Р представляет со-
бой равнодействующую распределенного давления р(х).
Сосредоточенные силы измеряются в кГ и Т либо в к, а распре-
деленные нагрузки — в T/jw2 либо в н/м2.
Поверхностную силу Р можно разложить на две составляющие:
одну, действующую по касательной к поверхности и называемую
касательной или сдвигающей силой Т, и другую, действующую пер-
пендикулярно поверхности N и называемую нормальной (рис. 4.3).
Силы, которые действуют со стороны одного тела на другое, на-
пример со стороны сооружения на основание, являются по отно-
шению к последнему внешними, а силы, с которыми частицы тела
взаимодействуют друг с другом, — внутренними.
Р
Рис. 4.?< Распределенная
нагрузка р(х) заменена
сосредоточенной силой Р
Рис. 4.3. Ка.сательная и
нормальная: составляю-
щие силы Р
Рис. 4.4. Изменение сил взаимо-
действия между частицами тела
в зависимости от расстояния меж-
ду ними (точка 1 соответствует
отсутствию внешних сил)
Прилрженце к грунту внешних сил оказывает возмущающее
влияние на взаимодействие между частицами. Если внешние силы
сжимадод тело, приближая частицы друг к другу, между ними
усиливается отталкивание, которое препятствует сближению под
действием внешних сил, и наоборот. На рис. 4.4 показан график
изменения сил взаимодействия между частицами тела при измене-
нии расстояния между ними.
Следует заметить, что в первое мгновение нагрузка от соору-
жения, приложенная к грунту, действует на поверхностные части-
цы, расположенные непосредственно по площадкам контакта с
100
нагрузкой, а затем эти частицы, смещаясь, оказывают, в свою
очередь, воздействие на соседние, и возмущение постепенно, с оп-
ределенной скоростью распространяется от точки к точке в глубь
тела.
Сплошная среда. Проследить за перемещениями каждой из
частиц под действием сил, приложенных к телу, невозможно, по-
этому прибегают к мысленной замене тела воображаемой сплош-
ной средой, в которой вещество распределено равномерно по всему
объему без разрывов и промежутков.
Следует иметь в виду, что когда грунт теоретически рассматри-
вается как сплошная среда, то это не означает, что он не должен
иметь пор или не может быть многофазной системой. Однако в
данном случае все свойства грунта, связанные с его пористостью и
многофазностью, предполагаются одинаковыми и в бесконечно
малом мысленно выделенном элементе объема грунта и в конечном
его объеме.
Таким образом, если мы установили, что в грунте содержится
70% скелета и 30% пор, то при использовании модели сплошной
среды предполагается, что это же соотношение между скелетом и
порами сохранится и в бесконечно малом объеме грунта, хотя та-
кой бесконечно малый объем неизмеримо меньше действительных
размеров одной частицы скелета.
Такое предположение приводит к правильным результатам,
когда зависимости, установленные для бесконечно малого эле-
мента сплошной среды, в результате интегрирования соответству-
ющих дифференциальных уравнений распространяются на доста-
точно большие однородные массивы грунта. Иногда, чтобы избе-
жать логических трудностей, связанных с подобным переходом,
говорят не о бесконечно малом элементе грунта, а об элементе, до-
статочно малом по сравнению со всем рассматриваемым массивом.
2. НАПРЯЖЕНИЯ И ДЕФОРМАЦИИ
Напряжение. Внутренние силы в сплошной среде принимают
непрерывно распределенными по сечениям, мысленно проведенным
внутри тела (рис. 4.5). Пусть по некоторой площадке &F такого' се-
чения действуют внутренние силы, равнодействующая которых
равна АР. Отношение р— называется средним напряжением
по рассматриваемой площадке. Оно представляет собой вектор, на-
правленный параллельно силе АР, или, согласно терминологии
векторного исчисления, коллинеарный \Р.
Система обозначений. Будем прибавлять в необходимых случа-
ях к обозначению напряжений р индекс v, показывающий направ-
ление нормали к сечению. Разложим напряжение р на нормальную
и касательную к сечению составляющие. Нормальную составляю-
щую обозначим буквой о, а касательную (тангенциальную) — г.
101
Чтобы отличить среднее напряжение от его составляющих, это на-
пряжение называют полным.
Если полное напряжение р раскладывают на составляющие, ко-
торые направлены по трем осям координат (в дальнейшем всюду
Рис. 4.5. Внутренние си-
лы в сплошной среде
принята правая прямоугольная система ко-
ординат), причем нормаль к площадке не
совпадает ни с одной из этих осей, т. е. со-
ставляющие не являются ни нормальными,
ни касательными напряжениями по пло-
щадке, то каждую составляющую обозна-
чают обычно той же буквой р, но с двумя
индексами, из которых первый указывает
нормаль к площадке, а второй — ось, по на-
правлению которой действует составляющая
напряжения (рис. 4,6,а). Например, р^г
означает напряжение, направленное вдоль
оси z и действующее по площадке, имею-
щей нормаль, идущую в некотором направ-
лении, которое условно обозначено v. В литературе встречаются
также и обозначения вида p2v, где нормаль обозначена вторым
индексом.
В том случае, если нормаль совпадает с какой-либо осью коор-
динат, индекс повторяют. Например, если направление v совпадает
с осью г, то нормальное напряжение будет иметь обозначение ozz.
102
Касательные составляющие по той же площадке вдоль осей х и у
тогда обозначатся tzx и тгу (рис. 4.6,6).
При системе двойной индексации отпадает необходимость в
обозначении нормальных и касательных напряжений разными бук-
вами, и все напряжения обозначают одной и той же буквой, напри-
мер о (рис. 4.6,в), а о характере действия напряжений судят по
индексам — два одинаковых индекса (или один индекс) означают
нормальные напряжения (например, охх, оуу, огг или ау>
сг),адва разноименных — касательные (например, оху, ох23 оуг
и т. д.). В тех случаях, когда необходимо выделить нормаль-
ные и касательные напряжения, не указывая их направление в про-
странстве, мы будем обозначать первые буквой о, а вторые буквой
т без координатных индексов.
Истинные напряжения. Среднее напряжение представляет со-
бой равнодействующую внутренних сил, действующих между час-
тицами, расположенными по обе стороны от рассматриваемого се-
чения в реальном несплошном теле. Площадки контактов между
этими частицами в зависимости от их формы и структуры мате-
риала ориентированы относительно проведенного сечения самым
различным образом (рис. 4.7). Очевидно, и силы, с которыми час-
Рис. 4.7. Истинные на-
пряжения
тицы действуют друг на друга, будут иметь в разных точках се-
чения различные направления и величины. Соответствующие им
напряжения по площадкам контакта частиц называются истин-
ными.
Истинное напряжение может быть найдено из выражения
г \Р
оист = hm ——
A F-^Q /X F
Вектор напряжения имеет размерность силы, деленной на пло-
щадь, обычно кГ/см2 (~ 10 н!см2).
Условия сплошности. Как теоретические, так и эксперименталь-
ные исследования [87, 10, 55] показывают, что сторона единичной
квадратной площадки, для которой рассчитывается среднее напря-
жение, должна превосходить диаметр частиц грунта не менее чем
в 20—30 раз. Только в этом случае можно при расчете условно рас-
сматривать грунт как сплошное тело. Условие сплошности означа-
ет, что при стороне единичной площадки 1 см грунт должен иметь
частицы не крупнее 0,5—1 мм. Гравелистый грунт с частицами
диаметром около 5 мм может рассматриваться как сплошное тело
при минимальном размере единичной площадки не менее 5—10 см,
и, следовательно, измерение средних напряжений в таком грунте
103
должно производиться с помощью приборов, воспринимающих дав-
ление по площадке не менее 1 дц2. Только с результатами таких
измерений можно сравнивать расчеты средних напряжений, произ -
веденные в предположении о сплошности грунта.
Перемещения. Переход под действием нагрузки отдельных то-
чек тела в новое положение в пространстве называется перемещен
нием этих точек относительно их первоначального положения. Ве-
личина перемещений в общем случае определяется не только вели-
чиной приложенных усилий, но и продолжительностью их действия.
Перемещения вдоль осей х, у, z обычно обозначают u, v, w соот-
ветственно.
В результате действия нагрузки на грунт как его поверхность,
так и стоящие на нем сооружения получают соответствующие пере-
мещения, которые свидетельствуют о том, что происходят переме-
щения и внутренних, глубоко расположенных частей массива
грунта.
Связи. В некоторых методиках расчета, используемых механи-
кой грунтов, массив разбивают мысленно на отдельные несжимае-
мые жесткие блоки (отсеки). Затем предполагают, что эти блоки
смещаются друг относительно друга и относительно остального
массива грунта и исследуют возникающие при этом силы взаимо-
действия между самими блоками и между блоками и примыкаю-
щим массивом. В подобных случаях приходится включать в рас-
смотрение связи: либо тела, ограничивающие свободу перемещений
элементов рассматриваемой системы (геометрические связи), либо
силы, с которыми элементы действуют друг на друга (динамиче-
ские связи). Усилия, возникающие в связях при действии на си-
стему внешних сил, называют реакциями связей, или пассивными
силами, а внешние силы, которые могут вызвать ускорение точек
систем, — активными.
Связью является, например, массив, по которому происходит
движение оползня. В этом случае связь допускает одни переме-
щения (сдвиг оползня) и не допускает другие (например, переме-
щение сползающей массы вертикально вниз параллельно самой
себе). Если поверхность, по которой происходит смещение, не яв-
ляется идеально гладкой, то по ней действуют силы трения, и такая
связь называется нецдеалъной. Связи без трения называют идеаль-
ными.
Кроме связей в виде поверхностей контакта или жестких стерж-
ней (неподвижно закрепленных или вращающихся относительно
некоторых точек — шарниров) в некоторых случаях могут при-
ниматься воображаемые связи в виде гибких, но нерастяжимых не-
весомых нитей. Нити в отличие от стержней работают только на
растяжение (односторонние связи). Связи, препятствующие пере-
мещению во взаимно противоположных направлениях, называют
двусторонними, или удерживающими.
В силовой механике Ньютона, в которой механическое движение
тел или их взаимодействие рассматривается как результат дейст-
104
вия сил, принято при расчете связи отбрасывать, заменяя их дейст-
вие действием сил, совпадающих с реакциями отброшенных связей.
Если связи не изменяются во времени, то они называютя ста-
ционарными, или склерономными, а если изменяются —'нестацио-
нарными, или реономными. Связи, которые не влияют непосредст-
венно на скорости элементов системы, называют голономными, а
если влияют — неголономными. Так, стержень, связывающий в
маятнике качающийся груз с точкой подвеса, является голономной
стационарной связью. Если груз подвешен на нити, длина кото-
рой в процессе качания маятника меняется (например, нить нама-
тывается на ось), то подобная связь является голономной неста-
ционарной. При качении шара по шероховатой поверхности силы
трения влияют на скорость качения, и связь является неголоном-
ной, если же поверхность идеально гладкая, то связь является го-
лономной.
Очевидно, равновесие системы не нарушится при наложении на
нее новых связей. Точно так же не нарушится равновесие системы,
если, не изменяя размеров, формы, веса и положения в простран-
стве, мысленно превратить ее в абсолютно твердое несжимаемое
тело.
Внутренние силы. Из третьего закона Ньютона следует, что
каждый элемент действует на другой с такой же силой, с какой
второй элемент действует на первый, причем направления этих
равных сил противоположны. Соответственно внутренние силы
должны быть взаимно Уравновешенными, и при составлении урав-
нений равновесия их не следует учитывать. Сказанное, однако,
справедливо только по отношению к элементам жесткой неизменя-
емой системы. Следовательно, если, рассматривая равновесие грун-
тового массива, мы будем считать его несжимаемым и мысленно
разобьем на отдельные жесткие блоки, то силы взаимодействия
между блоками в условия равновесия всего массива в целом не
войдут.
Возможные перемещения. В механике принято называть дейст-
вительными те перемещения системы, которые происходят под дей-
ствием приложенных к ней сил.
От действительных отличается другой вид элементарных пере-
мещений, рассматриваемый в механике, — так называемые возмож-
ные, или виртуальные перемещения системы. Это чисто воображае-
мые (т. е. не вызванные приложенными к системе данными сила-
ми) перемещения, которые являются бесконечно малыми и допу-
скаются связями системы. Их всегда относят к некоторому опре-
деленному состоянию системы, в котором она находится в некото-
рое мгновение. Представим себе, например, проволочное кольцо,
находящееся на провисшей нити, причем эта нить вращается на-
подобие детской скакалки вокруг двух точек подвеса. Тогда воз-
можными следует называть бесконечно малые перемещения кольца
вдоль нити в обе стороны от его первоначального положения.
Однако действительное перемещение кольца будет более сложным
105
и определится изменением его положения в пространстве вместе с
движущейся нитью.
Следовательно, понятие о виртуальном перемещении является
понятием чисто геометрическим, характеризующим свойства весьма
малой окрестности рассматриваемой точки в зависимости от ха-
рактера наложенных на эту точку связей. Работу на виртуальном
перемещении силы, приложенной к телу, называют виртуальной
работой. Пользуясь понятием о виртуальной работе, можно сфор-
мулировать следующее необходимое и достаточное условие равно-
весия, предложенное еще Бернулли и Лагранжем: «Для равновесия
системы материальных точек с идеальными стационарными удер-
живающими связями необходимо и достаточно, чтобы сумма
элементарных работ всех действующих на систему активных сил
при любом возможном перемещении была равна нулю». Этот
принцип возможных перемещений был распространен также на
случай нестационарных и неудерживающих (т. е. таких, при кото-
рых тело может покидать поверхность или линию, по которой оно
движется) связей.
Если не все связи, наложенные на систему, являются идеаль-
ными, то к внешним силам следует добавлять силы трения и вклю-
чать в сумму элементарных работ также и работу сил трения на
возможных перемещениях системы.
Использование принципа возможных перемещений весьма силь-
но упрощает решение задач механики для систем со связями.
Обобщенные координаты и обобщенные силы в механике. Вы-
ше мы уже ознакомились со значением этих понятий в термодина-
мике. В частном случае механического движения обобщенными ко-
ординатами называют независимые параметры, однозначно опре-
деляющие положение точек некоторой системы. Количество
обобщенных координат в случае идеальных и голономных связей
равно количеству степеней свободы и, которое определяется по
формуле
п = 6 m— k,
•
где m — количество элементов, образующих систему; каждый из
элементов имеет шесть степеней свободы: три линейных
составляющих перемещения вдоль осей х, у и z и три угла
поворота вокруг каждой из этих осей;
k — количество связей.
Если элементы тела рассматриваются как точки, каждая из ко-
торых имеет только три степени свободы (линейные перемещения),
то количество степеней свободы системы равно 3m — k.
Обобщенными силами называют силы, которые могут произве-
сти работу на приращениях обобщенных координат системы.
Если силы, действующие на систему, имеют потенциал, то обоб-
щенные силы равны взятым с обратным знаком частным производ-
ным от потенциальной энергии системы по соответствующим обоб-
щенным координатам. Это правило знаков следует из того, что при
106
убывании потенциальной энергии обобщенная сила возрастает, и
наоборот. Так, если тело падает с высоты на землю, то его потен-
циальная энергия уменьшается, а сила притяжения к Земле уве-
личивается.
Деформации и течение. В результате изменения расстояния
между частицами и их относительного положения под действием
внешних сил изменяются как объем, так и форма тел (происходит
их деформация).
В процессе деформации внутренние силы в теле постепенно
возрастают, и когда между внутренними и внешними силами на-
ступает равновесие, то его деформирование прекращается, хотя
нагрузки и продолжают действовать. Если же внутренние силы не
в состоянии уравновесить внешние, тело испытывает непрекращаю-
щиеся изменения под действием внешних сил, и такой процесс на-
зывают течением. Течение прекращается только, если убрать внеш-
нюю нагрузку.
Виды деформаций. Различают линейные и угловые деформации.
Линейные деформации могут проявляться в виде как увеличения,
так и уменьшения линейных размеров тела. В первом случае их
называют растяжением, во втором — сжатием (рис. 4.8, а, б).
Рис. 4.8. Деформации растяжения (а), сжатия (б) и сдви-
га (в)
Угловая деформация (сдвиг) представляет собой изменение
первоначального угла между какими-либо двумя осями, мысленно
проведенными в теле до деформации (рис. 4.8,в).
В общем случае деформации могут иметь сложный вид: растя-
жение в одном направлении и сжатие в другом сочетаются с дейст-
вием сдвигающих напряжений, причем в разных точках массива
грунта они могут быть различны по величине и направлению.
Однако какова бы ни была деформация тела, ее всегда можно
разделить на две основные части: изменение объема — объемную
деформацию (как результат чисто линейных деформаций) и изме-
нение его формы — формоизменение (как результат чисто угловых
деформаций).
107
В теории сплошной среды предполагается, что как при дефор-
мации, так и при течении сплошность тела не нарушается. Если в
результате деформации в теле возникают трещины, и разрывы, по
которым прекращается или резко изменяется характер Действия
внутренних сил, то говорят о разрушении дела. Разрушение пред-
ставляет собой протекающий с большей или меньшей скоростью
процесс, который может закончиться распадением тела на отдель-
ные части — обломки.
Если деформации настолько малы, что их квадратами и произ-
ведениями можно пренебречь по сравнению с первыми степенями,
то их можно рассматривать как бесконечно малые, что существен-
но облегчает математический анализ соответствующих задач. Не-
которые материалы могут переносить без разрывов относительно
большие деформации, которые при исследовании уже нельзя ради
упрощения рассматривать бесконечно малыми. Такие деформации
называют конечными.
Геологические дислокации. Горные породы под влиянием мощ-
ных сил внутренней динамики Земли испытывают весьма значи-
тельные (по сравнению с толщинами деформируемых слоев)
перемещения. Эти перемещения могут совершенно изменить перво-
а)
начальное положение и форму
слоев пород, вызвать их изгиба-
ние и смятие, срезывание и раз-
рыв. Такого рода смещения гор-
ных пород называют уже не де-
формациями, а геологическими
дислокациями (рис. 4.9). Они де-
Рис. 4.10. Напряжения по различным
сечениям в одной и той же точке
Рис. 4.9. Геологические дислокации
а—пластическая; б — хрупкая
лятся на два основных типа — пластические (складчатые) и хруп-
кие (разрывные). Последние сопровождаются появлением трещин,
по которым могут происходить весьма большие смещения пород.
Дислокации, происходящие в земной коре при действии текто-
нических сил, называют тектоническими; возникающие в результа-
тов
те денудационных процессов — атектоническими, или гравитаци-
онными, а происходящие под действием нагрузок от сооружений
или горных работ — техническими.
Напряженное состояние. Через любую точку загруженного тела
можно провести бесчисленное множество по-разному ориентиро-
ванных площадок, и на каждую из них будет действовать иное по
величине и направлению напряжение (рис. 4.10). Совокупность
всех этих одновременно действующих напряжений характеризует
собой напряженное состояние в данной точке.
Однородным напряженным состоянием называется такое рас-
пределение напряжений в теле, при котором напряженное состоя-
ние во всех точках совершенно одинаково, т. е. по параллельным
площадкам действуют параллельные между собой и одинаковые
по величине напряжения. В качестве примера можно .привести со-
стояние цилиндрического стержня, у которого по нормальным к оси
торцам приложены равномерно распределенные сжимающие или
растягивающие усилия (рис. 4.8,а). По любому сечению, перпенди-
кулярному оси стержня, будут действовать равномерно распреде-
ленные напряжения, нормальные к сечению и равные напряжениям
по торцам. Этот случай называется простым (или одноосным) на-
пряженным состоянием либо простым сжатием (или растяжением).
Напряжения в точке. Чтобы охарактеризовать напряжения в
любой точке массива грунта, необходимо, во-первых, привести ис-
ходные данные для определения напряжения по площадке любого
направления, проходящей через данную точку, а во-вторых, указать
правило, по которому такое определение может быть произведено.
Выделим в некоторой точке загруженного массива грунта ^бес-
конечно малый объем с помощью трех взаимно перпендикулярных
плоскостей и произвольно проведенной четвертой плоскости, секу-
щей все три оси (рис. 4.11,а). Мы получим тетраэдрический элемент
Oabc. Если известны напряжения по трем взаимно перпендикуляр-
ным граням этого элементарного объема, то из условия равновесия
тетраэдра легко вычислить напряжения по любой наклонной пло-
щадке abc, представляющей собой четвертую грань тетраэдра.
Следовательно, заданными напряжениями по трем взаимно пер-
пендикулярным (ортогональным) площадкам в окрестности неко-
торой точки полностью характеризуется напряженное состояние .в
ней.
Обозначение напряжений. Обозначим напряжения, действую-
щие по ортогональным граням тетраэдра, буквой в с двумя числен-
ными, индексами внизу, причем первый индекс отнесем к оси,
перпендикулярной площадке, по которой действует напряжение, а
второй индекс — к оси, параллельно которой направлено напряже-
ние. Если читатель внимательно сравнит рисунки 4.11,а и 4.11,6,
ему станет понятной эта система обозначений. Следует заметить,
что часто удобнее другой порядок расстановки индексов, t когда
первый индекс обозначает направление напряжения, а второй —
нормаль к площадке.
109
В современной механике сплошной среды принято обозначение
осей буквами х, у, z заменять на обозначение цифрами 1, 2, 3 со-
ответственно (рис. 4.11,в). При введении такой системы индексации
и нормальные и касательные напряжения можно обозначать одной
J
Рис. 4.11. Напряжения по граням
элементарного тетраэдра
и той же буквой (например, о), а отличать их друг от друга по
индексам: у нормальных напряжений оба индекса одинаковы (на-
пример, стц — нормальное напряжение по площадке с нормалью,
которая совпадает с осью 1), а у касательных разные (например,
012 означает касательное напряжение, которое направлено вдоль
оси 2 и действует по площадке с нормалью, направленной по оси
1). Два напряжения с одинаковыми, но переставленными индекса-
ми, например 012 и 021, называют взаимно однородными. В тех слу-
чаях, когда используются формулы, к которым инженеры привык-
ли при изучении сопротивления материалов, наряду с указанной
системой обозначений мы будет обозначать нормальные напряже-
ния через о, а касательные через т.
Правило знаков. Будем считать сжимающие напряжения поло-
жительными, а растягивающие отрицательными. Касательные нап-
ряжения условимся принимать положительными, если они направ-
лены по положительным направлениям осей координат и дейст-
110
вуют по площадке, нормаль к которой также совпадает с положи-
тельным направлением координатной оси.
. Если нормаль имеет направление, противоположное положи-
тельному направлению оси, то касательные напряжения положи-
тельны, если они направлены вдоль отрицательных осей (см. рис.
4.11,6).
3. ОДНОРОДНЫЕ ДЕФОРМАЦИИ
Однородной называется такая деформация, при которой все
линии, прямые и параллельные до деформации, остаются прямыми
и параллельными после нее, хотя их общее направление может
измениться (см. рис. 4.8). Следовательно, при однородной дефор-
мации все подобные по форме и подобно расположенные фигуры
во всех точках тела деформируются подобно, и окрестности всех
точек тела деформируются одинаково по одинаковым на-
правлениям.
В практике лабораторных испытаний грунтов постоянно встре-
чаются следующие виды однородных упругих деформаций: простое
сжатие, всестороннее равномерное сжатие, простой и чистый сдвиг.
Простое сжатие. По предложению Коши, отношение величины
Д/, на которую изменяется в результате деформации расстояние
между параллельными сечениями стержня при простом сжатии, к
первоначальному расстоянию между ними Zo рассматривается как
количественная мера линейной деформации е элемента тела между
двумя точками (см. рис. 4.8,а\.
Если элемент сжимается, то е называют относительным сжати-
ем, или укорочением, а если растягивается, то относительным рас-
тяжением, или удлинением. Деформацию сжатия в механике грун-
тов принято считать положительной, а деформацию растяжения —
отрицательной.
Если к стержню последовательно прикладывается несколько
сил, то в случае бесконечно малых деформаций от каждой из них
суммарную деформацию можно определить, относя сумму удлине-
ний или укорочений к одной и той же первоначальной длине Zo-
При простом сжатии одновременно с продольным укорочением
образца происходит его поперечное расширение, как показано на
рис. 4.12,а. Если первоначальная ширина образца Ьо, а его ширина
после деформации Ь, то поперечное расширение будет равно &Ь —
= Ь—Ьо, Его отношение к первоначальной ширине Ьо называют
поперечной деформацией. Чтобы отличить продольную деформацию
стержня от поперечной, выберем оси координат, как показано на
рис. 4.12,6, и обозначим деформацию стержня вдоль оси z через
ег, вдоль оси х через гх и вдоль оси у через ev. В случае изо-
тропного тела = еу.
111
Обычно поперечную деформацию выражают как некоторую
долю от основной продольной:
— ех= ~$у = — VSZ>
(4.2)
а коэффициент v называют коэффициентом Пуассона.
Рис. 4.12. Деформации при сжатии
а —простое сжатие; б — правая система координат; в — всесто-
роннее равномерное сжатие niapa
Всестороннее равномерное или гидростатическое давление. Если
шар из любого твердого материала (например, из стали) подверг-
нуть всесторонним равномерным сжимающим напряжениям
то он несколько сожмется и его радиус соответственно уменьшит-
ся, однако форма останется по-прежнему шарообразной
(рис. 4.12,в), а по снятии нагрузки шар примет первоначальные
размеры. То же произойдет у твердых тел любой другой формы,
подвергнутых всестороннему равномерному сжатию (например, с
помощью сжатого газа или жидкости).
Приложенные к поверхности тела сжимающие напряжения
обычно называют давлением. Оказывается, что при всестороннем
равномерном давлении не только твердые тела, но и тела из любых
сплошных однородных материалов (например, пластилин или во-
да) будут вести себя точно так же, как типично упругие, не испы-
тывая ни течения, ни разрушения.
При этом, конечно, не имеются в виду такие высокие давления,
которые могли бы полностью изменить внутреннюю структуру и
свойства материала, т. е. материал после разгрузки должен иметь
те же физические свойства, что и до нагрузки. Если же при сжатии
внутренние связи между частицами разрушатся, то всестороннее
давление вызовет объемную остаточную деформацию тела и необ-
ратимое его уплотнение.
Если в теле, подвергнутом всестороннему сжатию или растя-
жению, выделить элементарный объем любой формы, то по всем
его граням будут действовать только нормальные напряжения
(сжимающие или растягивающие), а касательные будут отсутство-
вать. Подобное напряженное состояние называют гидростатиче-
ским, а также чистым сжатием, или чистым растяжением. При этом
112
напряженном состоянии упруго изменяется лишь объем тела, а его
форма остается неизменной.
Отношение бесконечно малого изменения объема dV к перво-
начальной его величине V называют относительным объемным
сжатием или объемной деформацией и обозначают 9:
dV
V
(4.3)
С точностью до бесконечно малых высшего порядка 0 представ-
ляет собой сумму линейных деформаций по трем взаимно перпен-
дикулярным направлениям (рис. 4.13):
9 “ гх + £у + £г • (4.4)
Изменение объема при простом сжатии. Нетрудно видеть, что
относительное изменение объема стержня при простом сжатии с
учетом (4.2) будет равно:
6 = + гу + гг = ег — 2 v гг = (1 — 2 >). - (4.5)
При v=0 поперечная деформация отсутствует, и 9 —- ег (ха-
рактерно, например, для пробки). Когда v = 0,5, 9 =0, т. е. увели-
- чение объема стержня за счет поперечного расширения в точности
равно уменьшению объема стержня за
счет продольного сжатия. Поэтому мате-
риалы, у которых v=0,5, условно назы-
вают несжимаемыми.
Простой сдвиг. Рассмотрим теперь
призматический упругий элемент, кото-
рый находится под действием только ка-
сательных напряжений тху, приложен-
ных к противоположным граням и рав-
ных по величине друг другу (рис. 4.14, а).
Пара касательных напряжений, дейст-
Рис. 4.13. Линейные дефор-
мации -по трем взаимно пер-
пендикулярным направле-
ниям
вующих на две противоположные грани,
вызывает так называемый простой сдвиг,
при котором бесконечно тонкие слои сдви-
гаются относительно друг друга, сохра-
няя свою длину и толщину (рис. 4.14,6).
В результате объем элементов не меняется, искажается лишь
форма тела.
Аналогичную деформацию сдвига дадут касательные напряже-
ния тух (рис. 4.14,в), приложенные к двум другим противополож-
ным граням элемента.
Показанные на рис. 4.14,6, в две пары касательных напряже-
ний стремятся вращать элемент вокруг его центра тяжести в про-
тивоположные стороны. Поэтому, если при их одновременном дей-
ствии деформированный элемент не испытывает вращения, то сум-
ма моментов от двух пар напряжений тху и тух должна быть
равна нулю. Из этого условия вытекает
Хху Хух • (4.6)
ИЗ
В этом и заключается так называемый закон парности или вза-
имности касательных напряжений, известный из теории упругости.
При простом сдвиге, когда действует только одна пара касатель-
ных напряжений, возникающий момент во избежание вращения
рассматриваемого элемента должен уравновешиваться моментом
от неравномерно распределенных нормальных напряжений, дейст-
вующих на элемент сверху и по его основанию. Таким образом, хо-
тя так называемое испытание на простой сдвиг широко применяет-
ся в механике грунтов, напряженное состояние при нем является
весьма сложным, что затрудняет как проведение испытания, так и
интерпретацию его результатов. На рис. 4.15,а показана деформация
Рис. 4.15. Деформация образца при
сдвиге
а—«когда ab смещается параллельно cd\
б— (при растяжении ‘вдоль оси у и сжатии
вдоль оси х
образца в приборе без боковых стенок (равнодействующие сдвига-
ющих сил Т и нормальных напряжений Р дают противоположные
по знаку моменты).
114
Обозначим через du перемещение (рис. 4.14,в) при простом
сдвиге. Отношение du к высоте dh, равное
(4-7>
dh
удобно избрать в качестве меры деформации сдвига.
По малости угла у2, называемого углом сдвига,
tgT2~T2» (4-8)
и поэтому деформацию сдвига обычно измеряют самим углом
сдвига.
Чистый сдвиг. Наложение друг на друга двух простых беско-
нечно малых сдвигов, показанных на рис. 4.14, б, в, дает деформа-
цию, изображенную на рис. 4.14,г (чистый сдвиг, так как при этом
по всем внешним граням элемента отсутствуют нормальные на-
пряжения). Величина, на которую уменьшается в результате сдви-
га первоначально прямой угол между гранями,
Тху = 71 + 72 • (4.9)
При однородном и изотропном материале у1=у2 = у и
7ху = 2ь (4.10)
Таким образом, угол уху при чистом сдвиге складывается из
двух углов, каждый из которых равен “Ъу» причем один из
них возникает за счет простого сдвига, вызванного напряжениями
тжу, а второй — за счет действия напряжений тул..
При чистом сдвиге одна диагональ квадрата, не изменяя своего
положения в пространстве, удлиняется, другая укорачивается на
одну и ту же величину (рис. 4.15,6). Поэтому рассматриваемую
деформацию можно представить как результат действия сжимаю-
щих напряжений вх вдоль оси Ох и равных им растягивающих
напряжений оу вдоль оси Оу. При этом по площадкам, накло-
ненным к этим осям под углом 45°, действуют только касательные
напряжения т=ог = сгу; объем деформируемого тела не изме-
няется, меняется только его форма.
Из сказанного выше следует, что объемная деформация без
формоизменения в чистом виде осуществляется только при всесто-
роннем равномерном (гидростатическом) сжатии, а формоизмене-
ние без объемной деформации происходит лишь при чистом сдвиге.
Простое сжатие в общем случае вызывает как объемную деформа-
цию, так и формоизменение.
Связь между перемещениями и деформациями. Выразим в при-
нятых выше обозначениях зависимость между деформациями и
перемещениями (рис. 4.16,а). Если перемещение точки О тела
вдоль оси х равно и, то перемещение точки А, лежащей на беско-
нечно близком от точки О расстоянии dx, будет равно и-\- ^—dx,
d х
115
так как с приращением координаты х функция и(х.) получает при-
ращение-—^- dx. Соответственно относительное удлинение по на-
правлению х равно
dx\ : dx, т. е. . Следовательно,
dx дх
С помощью аналогичных рассуждений легко найти
Рис. 4.16. Зависимость между перемещениями и деформациями
а — элементарный объем;
б — изменение положения ребер ОА и ОВ
Найдем теперь сдвиг ^ху (рис. 4.16,6), который представляет
собой искажение угла АОВ. Перемещение точки А в направлении
оси у отличается от перемещения точки О в том же направлении
dv 1 п
на величину -у- dx, а перемещение точки В в направлении оси х
будет отличаться от перемещения точки О в том же направлении
на dy. Соответствующие изменения угла АОВ, очевидно, рав-
ду
ны -уу и -у- (по малости углов тангенсы равны углам). Следо-
вательно, общее изменение угла АОВ
Чху д и ду + дх (4.11в)
Аналогично найдем
Туг dv дг dw (4.11г)
7zx “ dw дх . ди »—— • дг (4. Ид)
Обозначение деформаций. В дальнейшем будем обозначать де-
формации аналогично напряжениям с помощью численных индек-
116
сов, например Еп или ё2з и т. д. Деформация Е12, соответствующая
в прежних обозначениях sxy, представляет собой деформацию
при простом сдвиге, которую мы ранее обозначили (см. рис. 4.14,6)
через уь Деформация e»2i соответствует в прежних обозначениях
еух; на рис. 4.14,в она обозначена через Из (4.9) следует, что
—612+^21, и так как у1=у2, то ei2 = 82i=> — . Поступая ана-
логично, мы можем записать, что
__ 1 . _ _ 1
£23 “ £32 — g Туг» £13 — £31 — 2 Tzx *
4. ТЕНЗОР НАПРЯЖЕНИЙ
Матрица напряжений. Выпишем напряжения по трем ортого-
нальным площадкам на рис. 4.11,в в виде таблички. Напряжения в
каждой строке относятся к одной и той же площадке, а располага-
ются они в строках так, чтобы в каждом столбце друг над другом
стояли напряжения, направленные по одной и той же оси, а имен-
но, по оси 1 — в левом столбце, по оси 2 — в среднем и по оси 3 —
в правом (т. е. в строках совпадают первые индексы при напряже-
ниях, а в столбцах — вторые): k
^11 ^12 а13
<Т21 О22 #23
^31 а32 0Г3з
® х Хху Xxz
Хух ®у
Xzx xzy az .
(4-12)
Справа приведена тождественная табличка напряжений в слу-
чае обозначения осей координат через х, у, z.
Всякая прямоугольная табличка, в которой выписаны какие-
либо величины, называется матрицей, а сами величины — ее эле-
ментами. Таким образом, (4.12) представляет собой матрицу на-
пряжений, определяющих напряженное состояние в окрестности
точки О.
Напряженное состояние в данной точке зависит от величины и
распределения внешней нагрузки, от физических свойств материа-
ла и от геометрии тела, но не зависит от выбора координатных
плоскостей, с которыми затем совмещаются ортогональные грани
тетраэдра. Можно повернуть координатные оби, заменить прямо-
угольные координаты косоугольными, но от этого напряжения по
одним и тем же площадкам, проведенным в точке, не могут изменить-
ся, если не изменились внешние силы. Однако исходные площадки—
грани тетраэдра — будут при таких преобразованиях каждый раз
другими. Следовательно, другим будет и тот набор напряжений,
которым характеризуется одно и то же напряженное состояние в
точке. Соответственно элементы матрицы (4.12) при преобразова-
ниях координат будут изменяться, так как они как раз и представ-
ляют собой исходные напряжения по граням тетраэдров.
Очевидно, можно установить правило, позволяющее вычислять
117
новые элементы матрицы напряжений при любых изменениях си-
стемы координат, если, разумеется, напряженное состояние оста-
ется одним и тем же.
Тензор напряжений. Матрица напряжений, элементы которой
преобразуются по определенному правилу при изменении системы
координат, так что новая матрица продолжает характеризовать
то же самое напряженное состояние в точке, называется тензором
напряжений в данной точке Тн. Элементы матрицы (4.12) назы-
вают компонентами тензора напряжений. Тензор изображается ма-
трицей своих компонентов:
^11 012 013
021 022 023
031 032 033
(4.13)
В соответствии с принятой системой обозначений на пересе-
чениях строк и столбцов с одинаковыми порядковыми номерами
(например, вторая строка сверху и второй столбец слева) стоят
напряжения, у которых первый индекс совпадает со вторым. Та^
ким образом, по главной диагонали матрицы, идущей слева
сверху и вправо вниз, всегда стоят нормальные напряжения (у
них первый индекс совпадает со вторым).
Громоздкую запись (4.13) можно заменить более краткой:
= (*,7 = 1, 2,3), (4.14)
если условиться, что каждому из значений I, равных последова-
тельно 1, 2 и 3, соответствует своя строка, а каждому из значений
/=1, 2, 3—свой столбец. Фигурные скобки означают матрицу из
элементов aZy.
Общее количество компонентов этого тензора равно числу
размещений с повторениями из трех элементов (1, 2, 3) по два,
т. е. равно 32 = 9 (1,1; 2,2; 3,3; 1,2; 1,3; 2,3; 2,1; 3,1; 3,2).
В соответствии с законом парности (взаимности) касательных
напряжений
012 ~ 0215 013 = 031; 023 == 032 • (4.15)
Отсюда следует, что элементы матрицы (4.13) симметричны
относительно главной диагонали. Такие матрицы напряжений и
соответственно тензоры называются симметричными. Матрицу в
этом случае обычно записывают в виде
0ц 012 01з
• 022 023
• 0зз
(4.16)
Здесь точки замещают симметричные компоненты, и вид мат-
рицы показывает, что для характеристики напряженного состоя-
ния в точке нам достаточно знать всего шесть компонентов тен-
зора напряжений.
118
Напряжения по наклонной площадке. Обозначим направление
нормали к наклонной грани тетраэдра через v и составляющие
напряжения по этой грани, направленные вдоль осей координат
/, 2 и <?, через рн, р^2 и /н в соответствии с указанным выше
правилом индексов (рис. 4.17,а). Пренебрегая собственным ве-
сом тетраэдра и рассматривая его в состоянии равновесия, полу-
чим из трех уравнений равновесия при действии по трем ортого-
нальным граням напряжений, как это показано на рис. 4.16,в,
следующие выражения для напряжений по наклонной площадке:
Рч = Он cos (v, 1) + 012 cos (у, 2) + Ou cos (у, 3) ;
р,2 — о21 cos (у, 1)4- о22 cos (у, 2) 4- о^з cos (у, 3);
р v3 = о31 cos (у, 1)4" Оз2 cos (у, 2) 4~ <*33 cos (v, 3),
(4.17)
где cos (v, i) — означает косинус угла
между направлениями v и i.
Выводя соотношения (4.17), площадь
каждой грани трехгранного угла при на-
чале координат получают умножением
площади f наклонной площадки abc на
косинус угла между нормалями к ним,
т. е. площадь
Д аОс = f cos (у, 1);
Д ЬО с = f cos (у, 2) и Д а О b — f cos (у, 3)
(рис. 4.12, б).
Косинусы этих углов называются на-
правляющими. Часто обозначают cos (v,
1) через /, cos (v, 2) через mncos (v, 3)
через n. 1
Нормаль v к площадке abc проходит
через начало координат. Возьмем на этой
нормали некоторый произвольный отре-
зок длиной d, начинающийся от начала
координат, и спроектируем его на оси 1,
2 и 3. Длины этих проекций будут равны
а) 2
Рис. 4.17. Напряжения по
наклонной площадке
соответственно
dx = d cos (у, 1) = dl; d2 = d/n; d3 — dn,
а величина d2 определится из выражения
d2 = d\ 4- d2 4” ^3.
Подставляя сюда значения db d2 и d3 из предыдущих соотноше-
ний и сокращая полученное равенство на d2 найдем, что
/24-т24-и2 = 1. (4.18)
119
Однако удобнее для направляющих косинусов воспользовать- .
ся индексационной системой, обозначивших через avi:
cos (v, i) = av/ (i = 1, 2, 3),
и тогда вместо (4.18) получим
2 + з “ 1 • . (4.19)
Теперь мы можем все три члена в каждом из уравнений (4.17)
заменить одним, придав ему общий вид для всех трех уравнений,
которые отличаются друг от друга только значением i:
з
P,i = 2 ацач 2- 3)-
/=1
Если условиться далее, что суммирование при подобной запи-
си производится только по тому индексу, который повторяется
дважды в правой части (в данном случае по /), то можно не пи-
сать знака суммы. Тогда запись
р . = о., a .
I I} М /
(4.20)
будет означать систему трех уравнений, первое из которых выпи-
сывается для i=l, второе— для i — 2 и третье— для i—З, т. е.
каждое из уравнений относится к индексу, который повторяется
при р и при o'. Следовательно, формула (4.20) представляет со-
бой сокращенную запись следующих трех уравнений:
Р.Х — all ! + ^12 2 °13 з ’>
Рч 2 “ °21 % J + °22 av 2 “Ь a23 3 ’ (4-21)
РчЗ — °31 av 1 + a32 av 2 °33 з •
Индексы, по которым производится суммирование, называют-
ся немыми (или скользящими), так как сумма не меняет значе-
ния, если немую букву заменить какой-нибудь другой, посколь-
ку она все равно должна пробежать значения 1, 2 и 3. Осталь-
ные индексы называются свободными, В качестве индексов обыч-
но используют буквы латинского алфавита, начиная с L При
этом принимается, что уравнение имеет силу при всех значениях
свободных индексов, т. е. каждому значению (1, 2 или 3) отве-
чает новое уравнение. Так, уравнение
rik = Pt/ Ч/k
со свободными индексами i и k заключает в себе девять уравне-
ний вида
ГИ = Pllflil + Р12<?21 + Р13 Чз1 (£=1,^=1);
120
Г12 “ Pll 712 + P12 ?22 + P13 7з2 (* = 1 > & = 2)
r2i = P21Q11 + P22Q21 + P23Q31 G “2, k = 1);
гзз — Р31713 + Р32 723 + Рзз 7зз 0 — 3, k = 3) .
Индексы, сохраняющиеся неизменными во всех уравнениях
[например, индекс v в выражениях (4.20) и (4.21)], называются
постоянными, и это обстоятельство иногда оговаривают в тексте
или в скобковой записи (например, v = idem, i= 1,2,3).
Поясним правило записи еще на нескольких примерах, понят-
ных из предыдущего:
1) выражение = bt заменяет сразу три равенства:
Ct} — bi J — ^2, «3 ~ ^3 •
Выражения ak — bk ; ап = bn ; aq — bq и т. п. совершенно равно-
сильны;
2) выражение а/у означает любую из девяти величин
°11> ^22, а33, ^12, а23, СГзЬ а21, а32, ^13»
3) выражение обозначает сумму Оц + о22 + о33.
Повторение одного и того же немого индекса более двух раз
(например, аш) запрещается;
4) выражение означает сумму вида (Гцвц + о22 £22+^33 £зз+
+ 2 (а12 £12 + п23 s23 4- а31 s3i) . Здесь множитель 2 отвечает
условию симметрии а =а и г. = г..; выражение atj^kt
означало бы лишь какое-либо одно из произведений, входящих в
приведенную выше сумму. Выражение аД означает сумму «1ДЧ-
+ #2 &2 “Ь #3 ^3 ;
дии диц ди22 ди33
5) выражение ------- означает сумму-----------1------1-----.
дх- д %! д х2 дх3
Коротко оно записывается в виде uiiy где запятая означает диф-
ференцирование по координате xz. Соответственно, производная
-ди д2 и
--- записывается в виде и,,-, а -ч—5------как а,н;
dxi 1 dx^dxj 'Ч'
6) уравнение б/, ,• =0 с немым индексом / и свободным i за-
ключает в себе сразу три уравнения вида u UZ/ (| Q тл ouun •
— V, d именно. dxi
А ^11 | а12 | (Т13 д %! д х2 дх3 = 0;
д 021 j д 0^22 j 023 dxi д х2 д х3 = 0;
д 031 । д 032 । д 033 д дх2 дх3 = 0.
Преимущество тензорной записи заключается в том, что она
гораздо компактнее координатной и, главное, существенно сокра'
121
щает время, необходимое для преобразования громоздких систем
уравнений в координатной записи. При решении пространственных
задач механики грунтов это преимущество становится особенно на-
глядным [19].
Так как все три напряжения ри образуют прямые углы друг
с другом, то их равнодействующая, или полное напряжение по
наклонной площадке, будет отвечать соотношению
Р? = ^1+^2+Р?з- (4-22)
Нормальные и касательные напряжения по наклонной пло-
щадке. Напряжения р^ t не являются ни нормальными, ни каса-
тельными к наклонной грани тетраэдра. Это составляющие пол-
ного напряжения по этой грани, направленные вдоль осей 1, 2 и
3. Чтобы найти нормальную составляющую полного напря-
жения по наклонной площадке, нужно спроектировать все
напряжения на ось v:
<\ = Pvlcos(v, 1) + pv2 cos (л 2) + pv3cos(v, 3) (4.23)
или
а = р. i i (v = idem’ * = 2> 3)- (4.24)
Величина касательного напряжения найдется из уравнения
т2 = _ a2 t (4.25)
Главные напряжения. Как известно из теории упругости, в
каждой точке напряженного тела существуют три взаимно орто-
гональные площадки, по которым отсутствуют касательные на-
пряжения и действуют только нормальные. Эти площадки назы-
ваются главными, а напряжения по ним носят название главных
напряжений. При этом наибольшее из них обычно обозначается
индексом 1(о*1 ), наименьшее по величине — индексом III (ош)
а промежуточное — оц , т. е.
ai > ан > °ш •
В случае всестороннего равномерного сжатия Oj = оп = сгш =
= он, и любая площадка является главной, так как касательные
напряжения в теле вообще отсутствуют.
При механических испытаниях грунтов часто создают напря-
женное состояние, при котором 04 > ап , оп = ош (рис. 4.18,я).
Существуют также испытания (рис. 4.18,6), при которых
ai “ an » an > аш •
Главный тензор напряжений. Если выбрать в качестве орто-
гональных граней тетраэдра на рис. 4.11 главные площадки, то
в матрице (4.12) исчезнут касательные напряжения, и соответст-
вующий тензор напряжений, называемый главным, примет вид
122
(Ji О О
ТЙ = 1 0 °-j О
I 0 ® стш
(4.26)
Координатные оси, совпадающие с направлениями aj , оц,
напряжений.
осями тензора
Рис. 4.18. Напряженные состояния
а - ’i > ’и* ’п = ’ш = 6 - °1 = ’п; ’и > ’ш
Ош , называются главными
Матрицы вида (4.26)
называют диагональны-
ми. У них равны нулю все
элементы, кроме стоящих
на главной диагонали
(слева сверху — вправо
вниз). Так как здесь толь-
ко три элемента не равны
нулю, то для характери-
стики напряженного со-
стояния с помощью глав-
ного тензора нужно знать
еще три геометрические
величины, характеризую-
щие положение главных
площадок. Положение главных площадок и величины главных на-
пряжений в данной точке тела при данном напряженном состоя-
нии не зависят от выбранной системы координат и сохраняются не-
изменными при любых преобразованиях координат, т. е. инвариан-
ты по отношению к этим преобразованиям.
Определение главных напряжений в точке.
ряжения в точке по трем взаимно
определяемые тензором
Пусть даны нап-
ортогональным площадкам,
Т =
1 н
Oil °r12 °r13
°r21 °r22 °r23
°r3i °r32 °33
и требуется найти главные напряжения в этой точке. Примем эти
площадки за грани тетраэдра и проведем наклонную к ним пло-
щадку. Если бы эта площадка была главной, то полное напряже-
ние по ней было бы нормально и являлось главным напряжени-
ем. Подставляя в левые части выражений (4.21) проекции пол-
ного напряжения на оси координат:
р. 1 = av 1;
Рч2~ P'i av 2 »
(4.27)
находим
123
(СТц — р„) а„ ! + 012 «, 2 + 013 а, 3 = 0 ;
021 а, 1 + (а22 Р,) а, 2 "Ь °23 а, 3 — 0 :
О31 а, 1 + о32 а,2 4- (Озз —р„) а,3 = 0 .
В этих уравнениях четыре неизвестных: р, , а„ ь а,2 и а,3. При*
соединяя к ним в качестве четвертого уравнения (4.19), получим
после исключения величин а, ь а, 2 и а, 3 с учетом того, что =
= оу7, кубическое уравнение относительно , называемое
характеристическим, или вековым:
р? —+ —4 = 0,
коэффициенты которого
Л — <*н 4“ <*22 + <*зз ’» (4.28)
А = <*11 <*22 + <*22 <*33 + <*33 <*11 — <*12 ~ <*23 ~ <*31 ’ (4-2Э)
Л = <*11 <*22 <*33 4" 2 0*12 (*23 <*31 <*11 <*23 <*22 <*31 <*33 <*12 ’ (4.30)
Три корня уравнения (4.27) являются главными напряжения-
ми Qi , Оц и ощ. Зная их, найдем нормальное напряжение по на-
клонной площадке
= +OIiav2 + ffin av3 (4-31>
и, касательное напряжение
Л = 2 + <*?п °? 3 - • (4.32)
Эллипсоид напряжений. Если три ортогональные грани тетра*
эдра являются главными площадками, то уравнения (4.21) при-
нимают вид
р,1 = %1^; p,2 = a,2an; Pv3 = av3CTni’ (4-33)
откуда
Р» 1 Ру 2 РмЗ
, av2 — , з — .
ai <*п <*iii
Подставляя эти значения в (4.19), получим
т. е. уравнение эллипсоида с полуосями щ , ац и ощ . Следова-
тельно, если построить в данной точке такой эллипсоид на глав-
ных осях, то радиусы-векторы, проведенные из его центра к по-
верхности, будут представлять собой полные напряжения дей-
ствующие по площадкам, касательным к эллипсоиду в точках пе-
ресечения с радиусами-векторами.
Если одно из главных напряжений равно нулю, мы получим
плоское напряженное состояние, и эллипсоид напряжений прев-
ратится в эллипс напряжений (рис. 4.19). Если два главных на-
124
пряжед^я равны нулю, то напряженное состояние будет одно-
осным. Оси, совпадающие с* направлениями ненулевых главных
напряжений, называются осями напря-
женного состояния.
Инварианты тензора напряжений. Так
как главные напряжения в данной точке
при неизменной внешней нагрузке, оче-
видно, не могут меняться, если произ-
вольно менять положение ортогональных
площадок, то коэффициенты (4.28) —
(4.30) не должны зависеть от выбора ко-
ординатной системы. Поэтому их называ-
Рис. 4.19. Эллипс напряже-
ний
ют инвариантными, т. е. неизменяемыми
при преобразовании координат. Из их ин-
вариантности следует, что какова бы ни была выбранная система
координат, в данной точке /i = const, /2=const, /3=const.
Первый инвариант (4.28) является линейным выражением и
представляет собой сумму нормальных напряжений по любым
трем взаимно перпендикулярным направлениям. Легко заметить,
что первый инвариант равен также сумме трех главных напряже-
ний, поскольку они действуют по трем взаимно, ортогональным
площадках (см. далее стр. 149)
Л = #! + #п + а1П = Ai, (4.35)
и, следовательно, при любой системе координат
+ #22 + #зз = #i + #ц + #ш — Ai. (4.36)
Третий инвариант, который называют также кубическим,
представляет собой развернутый в строку определитель, состав-
ленный из компонентов тензора напряжений (4.13):
/3 — (Гц
#22 #23
#32 #33
#12
#21 #23
#31 #33
#21 #22
#31 #32
— #11 (#22 #33 #23) #12 (#12 #33 #23 #13) #13 (#12 #32 ~~ #22 #1з) • (4.37)
Если рассматривать главный тензор напряжений, то его детер-
минант (поскольку все при i^=j равны 0)
/3 — (jj сГц #щ , (4.38)
т. е. третий инвариант можно выразить как произведение трех глав-
ных напряжений.
Второй инвариант можно представить как сумму трех опреде-
лителей:
#22 #23 #11 #13
+
#32 #33 #31 #33
#11 #12
#21 #22
(4.39)
125
Определители в правой части (4.39) представляют собой так
называемые миноры определителя матрицы (4.12), разложенно-
го по главной диагонали. Это означает, что каждый определи-
тель здесь получается, если вычеркнуть элементы матрицы, на-
ходящиеся в строке и столбце, которые пересекаются у соответст-
вующего элемента главной диагонали.
Выражая напряженное состояние с помощью главного тензо-
ра напряжений и раскрывая определители типа (4.39), написан-
ные для этого тензора, т. е. при =0 (£=#/), получим второй
инвариант в виде квадратичного выражения:
h = Oj а„ + ап <тш + СТП1 ст,, (4.40)
где индексы образуют так называемую
Рис. 4.20. Площадки главных касательных на-
пряжений (три взаимно перпендикулярные
площадки, делящие пополам углы между глав-
ными площадками)
циклическую, или круго-
вую перестановку цифр I,
II, III. Второй инвариант
называется квадратиче-
ским.
Инварианты тензора
напряжений имеют важ-
ное значение, так как яв-
ляются основными харак-
теристиками напряженно-
го состояния в точке, не
зависящими от системы
координат.
Г л явные касательные
напряжения. Проведем в рассматриваемой точке тела три взаимно
перпендикулярные площадки, делящие пополам углы между глав-
ными площадками / и //, // и III и III и I (рис. 4.20).
Касательные напряжения по каждой из этих площадок боль-
ше, чем касательные напряжения по любым соседним площад-
кам, проведенным по обе стороны от данной. Эти напряжения на-
зываются главными касательными. Но в отличие от площадок
главных нормальных напряжений, по которым действуют толь-
ко нормальные и отсутствуют касательные напряжения, по пло-
щадкам главных касательных напряжений в общем случае дей-
ствуют также и нормальные напряжения, которые отсутствуют
только при чистом сдвиге. Поэтому правильнее называть эти каса-
тельные напряжения экстремальными. Величины этих касатель-
ных и нормальных напряжений запишутся так:
т1/п — ± 2 - CTn) а1/П “ 1 , 1 у (°1 + стп);
х = + — п/ш — 2 ап/ш ~ (СТП + аш) > (4.41)
1 ^П/! - ± 2 аШ/1 ~ у (°jn + CTi)«
126
где индекс I/II означает площадку, проведенную в промежутке
между главными площадками напряжений с?! и оп, индекс
П/Ш — площадку между главными площадками II и III и т. д.
Легко заметить, что максимальное из этих касательных нап-
ряжений по абсолютной величине тмакс ~ — аш), так как Hi
наибольшее, а ощ наименьшее из главных напряжений.
Октаэдрические напряжения. Повернем оси координат таким
образом, чтобы координатные плоскости совпадали с главными
площадками. Проведем равно наклоненную к ним плоскость и рас-
смотрим полученный тетраэдри-
ческий элемент abc (рис. 4.21).
Направляющие косинусы наклон-
ной грани будут равны друг дру-
гу, и из условия (4.19) найдем:
а т = а тт — а тт. — —. (4.42)
V I V II V ш 1Л з v
Если провести такие равнона-
клоненные к координатным плос-
костям площадки во всех восьми
внутренних углах, образуемых пе-
ресечением трех координатных
плоскостей, мы получим восьми-
гранник, или октаэдр. Поэтому
площадки, имеющие равные меж-
ду собой направляющие косинусы
(4.42), называют октаэдрическими
Рис. 4.21. Октаэдрические площадки
Эти площадки обладают рядом особенностей,
упрощающих
рассмотрение напряжений по этим площадкам при анализе
условий разрушения (прочности) материала.
Найдем нормальное напряжение по октаэдрической площадке.
Подставляя в (4.23) значения из (4.33), получим
О' = a m = сгт а2 т 4- сгтт а2 4- (Гттт а2 Т1Т
v ОКТ I v I 1 II vll 1 III V III
и с учетом (4.42) найдем
СТокт = 4 (*! + <*ц + <*ш) <4-43>
О
Правая часть (4.43) называется средним нормальным (или
гидростатическим) напряжением ан в данной точке тела. Тог-
да мы можем это выражение сформулировать следующим обра-
зом: нормальное напряжение по октаэдрической площадке равно
среднему нормальному напряжению в данной точке.
Но так как сумма главных напряжений в данной точке пред-
ставляет собой первый инвариант тензора напряжений Д, то
%кт = v А = vA1- (444)
127
Для касательного напряжения по октаэдрической площадке
получим с учетом (4.25)
-2 ^р2 — о2 (4.45}
или, подставляя сюда (4.43) и учитывая, что, согласно (4.22),
4т = у (°1 + *11 + *?ц) - (4’46>
получим
1 Г 1 П2
4т = у (*! + 4 + *?и) - у (ст1 + *п + *1и) I • (4-47>
□ L ° J
Раскрывая скобки, находим
токт = У /(*1 - *ц)2 + (*п - *ш)2 + (*ш - *i)2 (4.48}
или, согласно соотношениям (4.41), выражая т0КТ через экстре-
мальные касательные напряжения, получим
2 ____________________
Токт з V ^1/ц + тп/ш + (4.49)
или
Токт = (Ti/ii "Ь тп/ш + » (4.50)
и, следовательно, квадрат октаэдрического касательного напря-
жения равен 4/э от суммы квадратов экстремальных напряжений
в данной точке.
Из (4.47) с учетом (4.35) и (4.40) получаем, что токт выра-
жается через инварианты тензора напряжений следующим об-
разом:
(4.5i)
Вместо касательного октаэдрического напряжения токт в не-
которых случаях удобно рассматривать пропорциональную ему
величину, обозначаемую обычно oz:
Q 1г_____________________________________
*/ = —— %кт = —7= т <*i - *п)2 + (*п — *ш)2 + (*111 — *i)2> (4.52)
V 2 V 2
которую называют интенсивностью напряжений или обобщенным
напряжением. '*
При оп=аш =0, т. е. при одноосном напряженном состоя-
нии, есть не что иное, как сжимающее или растягивающее
напряжение. Как показал В. В. Новожилов [45], токт равно
среднему значению касательного напряжения в данной точке с
ТОЧНОСТЬЮ ДО ПОСТОЯННОГО множителя I =------- ТСР) •
128
Шаровой тензор и тензор-девиатор. Согласно правилам тен-
зорного исчисления, чтобы сложить два тензора, нужно сложить
элементы, стоящие на одинаковых местах (т. е. на пересечениях
одинаковых у обоих тензоров по порядковым номерам строк и
столбцов). Соответственно мы можем представить тензор напря-
жений (4.13) как сумму двух тензоров:
СГц 012 ^13 аи — оя 012 а1з сг„ 0 0
а21 ^22 а23 — О21 О22 О„ о23 • — ' 0 0 Г1 , (4.53)
0*31 0'32 Озз <*31 °32 а33 0 0 ан
где
~ (аИ + а22 + а3з) = °окт •
«5
На рис. 4.22 показаны напряженные состояния, соответствую-
щие каждому из тензоров в правой части (4.53). Первый тензор
Рис. 4.22. Разложение тензора напряжений
отвечает чистому сдвигу (см. рис. 4.14,г и 4.16), а второй тен-
зор— равномерному всестороннему сжатию по схеме, аналогич-
ной приведенной на рис. 4.12.
Следовательно, первый тензор в правой части (4.53) вызыва-
ет только формоизменение, а второй — только изменение объема.
Первый тензор обычно называют тензором-девиатором напряже-
ний, или просто девиатором напряжений, и обозначают его D н
а второй — шаровым, или гидростатическим тензором напряже-
ний ^ обозначают Нп. Следовательно,
П = DH + Нп, (4.54)
и любое напряженное состояние может быть представлено как
результат действия двух тензоров напряжений — девиатора и
шарового:
(о. — о„ 0 0 1 1 /1
Da = 0 <УП ан 0 ; (4.55)
0 0 стш ан
5 Зак. 530
129
Нн
ан О О
О ан О
О О ан
п
(4.56)
Связь между октаэдрическими напряжениями и инвариантами
шарового тензора и девиатора. Нетрудно убедиться в том, что
первый инвариант тензора напряжений Ц совпадает с первым
инвариантом шарового тензора, равным = Зоокт, а первый ин-
вариант девиатора равен нулю (Ло=0). Второй инвариант де-
виатора напряжений
= (4-57)
т. е. квадрат октаэдрического касательного напряжения отлича-
ется от второго инварианта девиатора напряжений постоянным
множителем. Таким образом аОкт и токт инвариантны.
1/^2*
Подставляя сюда из (4.53) вместо хокт величину ctz, найдем
= (4-58)
(4-59)
Если выразить /2 d через главные напряжения, а именно
4 d ~ [(ffi стц)а + (Gn стш)а 4~ (стш °i)a]»
и подставить его в (4.58) и (4.59), придем к формулам
4т = у [(°i ~ стп)а + (стп ~ аш)а + (стш ~ CTi)a] > (4-60)
CTz = у [(ai — стп)а + (ffn - °ш)а + (стш ~ ai)a]- (4-61)
Третий инвариант шарового тензора
4н = <4т. (4-62)
а третий инвариант девиатора
4 D = 4 4 Н А 4 £> ~ (аХ °окт) (аП Стокт) (Стш СТокт). (4-63)
Тензор деформаций. Аналогично представлению напряженно-
го состояния в окрестности точки деформированное состояние
также может быть охарактеризовано соответствующим тензором
деформаций, который в общем случае будет иметь вид
е11 е12 е13
= е21 е22 е23
. S31 е32 е33 ,
(4.64)
130
Здесь еп, ©22 и езз — относительные удлинения или укороче-
ния элементарной призмы вдоль осей х, у и г, а е12 = т1а;
1 1 ж
®1з = ®8i = Т13; s23 = ®зз = — Тгз — деформации простого
Л Хй
сдвига.
Если сложить компоненты по главной диагонали, мы получим
объемную деформацию 9:
Величина
е11 + е22 + е33 — ® •
О
з _£с₽
называется средней деформацией.
Шаровой тензор деформаций будет равен:
еср О О
0 еср О
О 0 еср
а девиатор тензора деформации
811----scp s12 s13
* s22 — scp e23
• ’ £33 £cp
Sj sCp 0 0
0 £n £cp 0
0 0 SIII Scp
(4.65)
(4.66)
(4.67)
(4.68)
где точки означают, что тензор является симметричным относи-
тельно главной диагонали.
Инварианты тензора деформации J имеют вид, аналогичный
инвариантам тензора напряжений:
Л = SU + s22 + s33 = SI + sn + sm ~ ® »
= Sj еп + еп £ш + £ш £T;
^3 = SI SII eHI ’
(4.69)
где ei, вц и еш — главные деформации по нормалям к тем пло-
щадкам, по которым сдвиги равны нулю (т. е. по нормалям к
площадкам главных напряжений).
Октаэдрические деформации. Деформация в направлении,
нормальном к октаэдрической площадке, равна */з объемной де-
формации: 1
8окт = "з~ (ei + sn еп1)= тт = ~» (4-70)
О О О
5. Зак. 530
131
Рис. 4.23. Плоское и одноосное
напряженное состояние
а октаэдрический сдвиг
Т.„ - Т V (. - •..) + !•„ - ",„н ,)“. (4.71)
о
В некоторых случаях удобно рассматривать так назыйаемую
интенсивность деформации (обобщенную деформацию)
Ток, “ -Кг V ('. - •..)’+ (•« - 'и.)* + («1,1 (4.72)
у 2 6
которая отличается от октаэдрического сдвига лишь числовым
множителем.
При испытаниях материалов в условиях сложных напряжен-
ных состояний, когда известны главные напряжения и главные
деформации, удобно изображать результаты испытаний в виде
графиков зависимости между тъкт (4.48) и у0Кт (4.71).
Пространственное и плоское напряженные состояния. Нап-
ряженное состояние элементарного параллелепипеда, по всем
шести граням которого действуют на-
пряжения, называется пространствен-
ным или объемным (см. рис. 4.22). Ес-
ли по каким-либо противоположным
граням (например, параллельным ко-
ординатной плоскости 1 0 3 (рис. 4.23,а)
напряжения будут отсутствовать, то
напряженное состояние называется
плоским или двухосным. Очевидно, пе-
ремещения ненагруженных граней мо-
гут происходить только за счет пуассо-
новой деформации. Поэтому при плос-
ком напряженном состоянии паралле-
лепипед деформируется по направле-
ниям всех трех осей. То же имеет место
и при одномерном (одноосном) на-
пряженном состоянии, когда на две
противоположные грани действуют
только нормальные напряжения, а ос-
тальные грани свободны от усилий
(рис. 4.23,6). Иногда такое напряжен-
ное состояние называют линейным, од-
нако этот термин неудачен, ибо им пользуются также для характе-
ристики линейной зависимости между напряжениями и деформа-
циями.
Тензор напряжений при плоском напряженном состоянии
представлен матрицей из двух столбцов и двух строк, которая в
зависимости от того, какие грани загружены, имеет вид
f °11 °12 1 ( °22 °23 ] | а11 <^13
j f ИЛИ f ИЛИ ।
t °21 &22 J t °32 °33 J I О”з1 а33
132
Пространственная и плоская деформация. Если загруженное
тело деформируется по направлениям всех трех координатных
осей, деформация называется пространственной. При одноосном
и плоском напряженном состоянии всегда имеют место попереч-
ные пуассоновы деформации тела. Поэтому, чтобы получить
плоскую или линейную (одноосную) деформацию, необходимо
приложить к незагруженным граням параллелепипедов на
рис. 4.23,6/, б дополнительные напряжения, вызывающие переме-
щения этих граней, обратные по направлению и равные по вели-
чине пуассоновым.
Если, например, сжимать грунт в кольцевой обойме (рис. 4.24),
исключающей возможность его поперечного расширения, мы по-
лучим одноосную деформацию. Но по боковой поверхности об-
разца будет действовать соответствующее реактивное давление
сг обоймы, и напряженное состояние образца одноосным не бу-
дет.
Круг Мора. При плоском и напряженном состоянии очень удоб-
ным и наглядным способом характеристики напряженного сос-
тояния в точке является графический прием, предложенный
О. Мором и носящий название круга Мора, или круга напряже-
ний. Рассмотрим его применение в случае плоского напряженно-
го состояния.
Выделим в сечении тела, находящегося в плоском напряжен-
ном состоянии, трехгранную призму (рис. 4.25,а)
чтобы по ее взаимно перпендикулярным
граням abb'a', abc и cbb'c' действовали
главные напряжения. Составляя урав-
нение равновесия призмы и проектируя
все силы на направления ас, аа' и нор-
маль к плоскости асс'а', найдем напря-
жения по грани асс'а'. Так как напряже-
ния оц, нормальные к плоскостям abc и
таким образом,
«)
'а
аУ
К построению круга
Рис. 4.25.
Мора
(5Г
Рис. 4.24. Сжатие образ-
ца грунта в кольцевой
обойме
1 — обойма; 2 — грунт
а'Ь'с', взаимно уравновешены, то они не войдут в суммы проекций,
и мы можем далее ограничиться рассмотрением равновесия тре-
133
угольника abc по рис. 4,25,6 (точнее, призмы с длиной, равной еди-
нице) .
Обозначим найравление нормали к стороне ас через v, а угол
наклона ас к площадке большего главного напряжения ai через
а. Примем направления главных напряжений за оси координат.
Очевидно, угол между нормалями к ас и Ьс будет также ра-
вен а, а между нормалями к ас и ab ---------а. Косинусы этих уг-
лов (направляющие косинусы) cos (7, v) = cos а и cos (777, v) = sin а.
Обозначив длину ас буквой I и проектируя напряжения на нор-
маль v, получим
0^1==^ cos а . /cos а + (Тп1 sin а • /sin а, (4.73)
откуда
<т, = Oj cos2 а + (тП1 sin2 а, (4.74)
а проектируя напряжения на площадку ас, найдем
\ I = (Tj sin а • / cos а — стш sin а • / cos а, (4.75)
откуда
gl~gin sin2a. (4.76)
Преобразуем формулу для а, , выразив в ней ai и а|Ц через
их полусумму и полуразность:
ffI + °Ш . в1 ~ сш .
Gl = ----------+ ----------;
(4.77)
_ ai + аш CTi — ain
aiu “2 2
Тогда
0 = . (cos2 a + sin2 a) + _Zl_ . (cos2 a — sin2 a),
откуда
a, - °'+2"‘" + 2 “ • I4.7S)
Главные напряжения в данной точке — величины постоянные,
и, следовательно, т, и а, являются функциями только угла а, ко-
торыи может меняться от 0 до — и от 0 до-----в зависимости от
2 2
положения площадки (рис. 4.26,а), по которой мы ищем напря-
жения (рис. 4.26,6). Но постоянный радиус-вектор г какой-либо
площадки (рис. 4.26,в) при изменении удроенного полярного уг-
ла 2a в пределах соответственно от 0 до я и от 0 до—я должен
описать окружность (рис. 4.26,г).
Сопоставим значения проекций радиуса г на оси х и у, приве-
денные на рисунке, с выражениями для т, и о, . Можно видеть,
134
что эти две последние величины определятся через проекции ра-
диуса-вектора, равного Vs(Oj—ош) на оси координат, причем для
получения а, нужно к проекции на ось добавить постоянную
величину, -у (ffj + оП1). Эту величину, очевидно, можно рассмат-
ривать как абсциссу центра С, из которого исходит радиус-
вектор.
Рис. 4.26. Круг Мора в случае плоского напряженного состояния
Следовательно, если отложить на оси абсцисс величину
(Oj о1П) и из полученной точки описать окружность радиу-
сом (о1 — а1П), то координаты точек последней будут представ-
лять собой значения а-, и х, для площадки в данной точке, на-
клоненной под углом а к площадке ai (рис. 4.26,3).
Построенный нами круг и есть круг Мора (или круг напряже-
ний), с помощью которого очень просто, как мы видим, находить
напряжения по любой площадке, проходящей в данной точке.
Очевидно, ось х можно рассматривать как ось нормальных на-
пряжений (а или аа), а ось у — как ось касательных напряже-
ний (т или atj).
Если напряжения Oj и оц не даны, но известны напряжения
Оц, 022 и 012, то круг Мора строят следующим образом. Откла-
дывают по оси о значения оц и 022 и на перпендикулярах к оси
135
напряжения
Рис. 4.27. Построение круга Мора
напряжениям на взаимно перпендикуляр-
ных площадках
по
аналогичное построение для какой-
о в полученных точках — значения ±ois, как это показано на
рис. 4.27. Соединяя концы полученных отрезков, находим центр
С и из него описываем окружность радиусом СМ, которая бу-
дет кругом Мора. Пересечения этого круга с осью дают сра-
зу главные напряжения oj и ощ .
Правило знаков для круга Мора. Как и раньше, сжимающие
будем считать положительными, а растягивающие —
отрицательными. Касательные
примем положительными, если
они вращают элемент относи-
тельно его центра тяжести про-
тив часовой стрелки, и отрица-
тельными, если вращение на-
правлено по часовой стрелке
(рис. 4.27,6).
Полюс круга Мора. Если
через точку Л1 провести пря-
мую, параллельную площадке,
по которой действуют напряже-
ния, изображаемые проекция-
ми точки М на оси координат,
то она пересечет окружность в
некоторой точке Р. Повторим
нибудь другой точки Mi, и снова
прямая, параллельная площадке, пройдет через ту же точку Р. Эта
точка носит название полюса круга Мора. Зная положение этой
точки, можно сразу находить напряжения по любой площадке, не
откладывая угла 2 а, как это было описано ранее, а проводя через
полюс прямую, параллельную площадке, по которой мы хотим
узнать напряжения. Координаты точки пересечения этой прямой
с кругом Мора и дадут нам искомые значения и .
Пусть, например, главное напряже-
ние Qi действует по некоторой площад-
ке (рис. 4.28). Проводим на круге Мо-
ра через точку сп прямую, параллель-
ную этой площадке, и находим полюс
Р. Прямая Р Ош будет параллельна
второй главной площадке III. Пусть
нам нужно знать напряжение по пло-
щадке ab. Проводим через Р прямую,
параллельную ab, и находим точку М,
изображающую напряжения по пло-
щадке ab.
Сложение напряженных состояний
с помощью круга Мора. Допустим, что
нам известен для некоторой точки те-
ла круг Мора при напряженном сос-
тоянии, вызванном некоторой системой
Рис. 4.28. Полюс круга Мора
136
сил I (круг с центром в Ci на рис. 4.29). Пусть к телу приложена
вторая система сил //, для которой напряженное состояние в той же
точке изображается вторым кругом Мора (с центром С2), при-
чем направления главных площадок от обеих нагрузок не сов-
падают. Требуется для той же точки построить круг Мора для
суммарного действия системы сил / и II. Г. И. Тер-Степанян ис-
пользовал свойство полюса круга Мора, чтобы получить удоб-
ный и простой графический способ решения этой задачи [77].
I+IL
-т
----------------------------------------------------------------------------------------- <5р
Рис. 4.29. Сложение напряжений с помощью круга Мора
При этом должны быть известны какие-либо данные, позволяю-
щие найти полюса Pi и Р2 обоих кругов Мрра.
Проводим через Pi и Р2 вертикальные и горизонтальные пря-
мые. Координаты точек Di и D2 в осях т — а дадут нам напряже-
ния по горизонтальным площадкам, вызванные в данной точке
тела обеими системами сил. Складывая алгебраически соответст-
венные компоненты, получим для той же горизонтальной пло-
щадки суммарные значения компонентов напряжения от обеих
систем сил:
а£> G D 1 + ° D 2 >
= Ъ1 "Ь ( г) •
(4.79)
Аналогичным образом поступают и для вертикальной пло-
щадки:
°м °mi + °м 2 >
ТМ 1 “Ь 2 •
(4.80)
Откладывая в той же системе координат найденные значе-
ния суммарных напряжений для двух площадок, получаем точки
М и D суммарного круга Мора. Соединяя точки М и D прямой,
найдем на пересечении с осью о центр суммарного круга Мора
С. Пересечение вертикальной прямой, проходящей через точку М,
и горизонтальной, проходящей через точку £>, дает полюс Р сум-
137
мирного круга Мора. Если в построениях и вычислениях не бы-
ло ошибок, точка Р должна лежать на окружности.
Круг Мора при пространственном напряженном состоянии.
Решая совместно систему уравнений (4.31), (4.32) и (4.19), най-
дем направляющие косинусы площадки, наклоненной к главным
площадкам:
(<Тц — <т„ ) (<тш —- _
(gj — an) (ст, — <тП1)
(qin — ) (gi ~ .
(ап — а1П) (<тп а1 ) ’
(qi _ ) (g,, _ ) +
(аш — CTi) (стш ~ стп)
(4-81)
(4.82)
(4.83)
Будем менять наклон площадки так, чтобы изменялись толь-
ко ее углы с двумя координатными плоскостями, а третий направ-
ляющий косинус сохранялся постоянным. Если, например, ос-
тавлять неизменным avl, то мы получим из (4.81)
(стп — CTv) (СТШ - О + = а? 1 (ст1 — стц) (ст1 - стш) (4-84)
или
[1 I2 1
°, - у <стп + aHi)j = Y (ап-стш)2 +
+ 1 (qi — ац) (CTI - °ш) • (4-85)
Это уравнение семейства окружностей с центром Оз в точке
— (ст„ + стш) на оси о. При а,! =0 имеем окружность с радиусом
У (ап аш)’
Аналогичным образом получим уравнение семейства окруж-
ностей с центром Oi в точке -у (ffj + <тш)прй а, 2 = const и с цент-
ром О2 в точке (ст, + ст„) при а,з — const.
Если av 2=0, радиус окружности г равен -у (ст, — стП1), а при
а,3=0 г=-у(ст,—ст„). На рис. 4.30,а построены эти три окруж-
ности, представляющие собой три круга Мора.
Чтобы показать, как пользоваться подобным построением, по-
ступим следующим образом. Опишем вокруг точки тела О, в ок-
рестности которой мы рассматриваем напряженное состояние,
сферу единичного радиуса (рис. 4.30,6) и проведем координатные
плоскости, совпадающие с главными площадками. Очевидно,
138
положение любой, как угодно ориентированной площадки можно
представить плоскостью, касательной к сфере в соответствующей
точке Af, через которую проходит нормаль у к поверхности
сферы. Точкам А, В и С соответствуют главные площадки.
Точки экватора АВ характеризуют касательные к сфере пло-
щадки, нормали к которым лежат в плоскости <Ti~CTh. Напря-
жения по этим площадкам не зависят от <з1П и определяются
Рис. 4.30. Пространственное напряженное состояние
главными напряжениями th и Стц, т. е. точками круга Мора с
диаметром CTi — Стц. Точки на меридиане АС характеризуют пло-
щадки, по которым напряжения определяются через erj и стщ,
т. е. большим кругом Мора, имеющим диаметр ctj—стш. Нако-
нец, напряжения по площадкам, соответствующим меридиану
ВС, определяются напряжениями стп и стш, т. е. точками круга
Мора с диаметром Он — «Ни-
какими же точками на построении (рис. 4.30,6) изображают-
ся напряжения по остальным площадкам, скажем, по площадке,
проходящей через точку М? Чтобы ответить на этот вопрос, обоз-
начим через 9 угол, образуемый с осью х нормалью у в точке Н,
а через <р угол, образуемый с осью z нормалью у в точке D.
Очевидно, что нормали к любой точке на окружности GMH
соответствуют 9= const, причем в точке Н имеем ауП1 =
= cos (v, z) = 0; a, i = cos 9 ; av n = cos — 9 j = sin 9 . В точке G
равен нулю направляющий косинус a, „. Точке Н на рис. 4.30,6
соответствует точка Н на рис. 4.31, засекаемая радиусом, проведен-
ным под углом 29 к оси ст. Если провести через М горизонтальное
сечение, параллельное плоскости хОу, то получим на сфере окруж-
ность FMD, которой соответствует q>=const, а направление OD
определяется направляющими косинусами av j = 0; ay ш = cos <p;
ауП = cos^- —<pj = sin <p. Точке D на рис. 4.30,6 соответст-
вует точка D на рис. 4.31, засекаемая радиусом, проведенным под
углом 2<р к оси ст, отложенным по часовой стрелке.
139
Проводя через точку D на рис. 4.31 дугу окружности с цен-
тром в 4 и через точку Н дугу окружности с центром в В, полу-
чим на пересечении дуг точку М, координаты которой дают зна-
чения напряжений а, и т, по площадке, касательной к сфере в
точке М на рис. 4.30. На рис. 4.32 показано семейство таких ок-
ружностей, а числа на них означают величины углов 0 и <р в
Рис. 4.31. Построение для Рис. 4.32. Построение кругов Мо-
определения напряжений в ра к схеме на рис. 4.30
точке при пространственном
напряженном состоянии
градусах. Таким образом, точки площади между большим и дву-
мя малыми кругами Мора на рис. 4.32 характеризуют напряже-
ния по всем площадкам, касательным к ’/в части сферы, пока-
занной на рис. 4.30. В качестве примера здесь показаны напря-
жения в точке М. с углами 6=60° и <р=45°. Построение на
рис. 4.32 называют тензорной диаграммой для точки О с данны-
ми главными напряжениями си , оц, Щп-
5. ЗАВИСИМОСТЬ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ
Однородность и изотропия грунта. Грунт называется одно-
родным, если свойства его во всех точках совершенно одинаковы.
Если, кроме того, свойства его (например, сжимаемость) одина-
ковы по любому направлению, то грунт называется изотропным.
В противном случае грунт называется анизотропным. В слоис-
той грунтовой толще отдельные слои могут быть однородными,
однако вся толща в целом является неоднородной.
Упругие и пластические деформации. Течение. Если бросить
на пол резиновый шар, он отскочит вверх. В момент удара о пол
шар несколько сплющится, но, отскочив, снова восстановит свою
первоначальную форму. Такая восстанавливающаяся сама по
себе или обратимая деформация носит название упругой. Де-
формируя тела, внешние силы совершают работу, которая при
упругой деформации обращается в накапливаемую телом потен-
циальную энергию деформации. По снятии нагрузки эта энергия
расходуется на восстановление первоначальной формы и разме-
ров тела. Если упругая деформация пропорциональна действую-
щему усилию, то максимальное напряжение (например, растяже-
ние), при котором еще сохраняется эта линейная зависимость.
140
называется пределом пропорциональности. Пределы пропорцио-
нальности при сжатии и растяжении грунта обычно не совпадают.
Однако деформация может быть не только упругой. Если мы
бросим на пол шар, скатанный из глиняного теста, то в отличие
от резинового, он не отскочит вверх, а расплющится. Деформа-
ция шара из глины уже не может исчезнуть сама собой, и полу-
чившаяся лепешка сохранит свою форму, если не затратить внеш-
нюю энергию на то, чтобы снова сформовать из нее шар. Подоб-
ная остаточная (или необратимая) деформация носит название
пластической. Работа, совершаемая при пластической деформа-
ции, рассеивается, обращаясь в теплоту, вследствие чего тело
нагревается. Свойства пластичности и упругости характерны для
твердых тел.
Необратимые деформации могут достигать значительных раз-
меров и возникают при напряжениях, превосходящих некоторый
предел, называемый пределом упругости.
Течение возникает при действии напряжений, превосходящих
некоторое критическое значение, называемое пределом текучести.
Оно продолжается непрерывно до тех пор, пока не удаляется
вызвавшая его нагрузка или пока напряжения не станут ниже
предела текучести. Таким образом, между пределом упругости и
пределом текучести грунт испытывает хотя и необратимые, но за-
тухающие пластические деформации, не переходящие в течение.
Скорость течения тем больше, чем больше действующие напряже-
ния.
Упругий и пластический сдвиг. Малые касательные напря-
жения вызывают лишь упругое искажение структуры в виде вос-
станавливающегося скашивания (упругий сдвиг), а при больших
напряжениях происходит скольжение одной части тела относи-
тельно другой — пластический сдвиг. Это скольжение легче все-
го происходит по таким поверхностям и в таких направлениях,
при которых имеет место минимальное нарушение внутренней
структуры и требуется, следовательно, затрата минимальной
энергии.
Во многих случаях у грунтов нет четко выраженного предела
упругости, и тогда за условный предел упругости принимают на-
пряжение, при котором пластическая деформация достигает не-
которой заранее обусловленной величины. При этом оговаривает-
ся также и скорость загружения, от которой зависит величина де-
формации.
Остаточные и начальные напряжения. У многих грунтов в си-
лу неоднородности их механических свойств одни зоны деформи-
руются упруго, а другие при тех же напряжениях — пластически.
Между этими участками могут появляться трещины скола и раз-
рыва, перераспределяться напряжения. Точно так же после уда-
ления внешней нагрузки некоторые зоны стремятся восстановить
первоначальный объем и форму, обладая упругостью, а другие
(пластические), наоборот, сохраняют приобретенную деформацию.
141
В результате такая упруго-пластическая система может после
разгрузки лишь частично восстановить свое первоначальное сос-
тояние, и в ней останутся внутренние ( остаточные) напряжения,
так как одни элементарные объемы, стремясь расшириться и встре-
чая сопротивление со стороны окружающих зон, сохраняют в себе
остаток прежних упругих сжимающих напряжений, тогда как
примыкающие к ним зоны будут испытывать растягивающее воз-
действие со стороны соседних упругих областей, стремящихся
ликвидировать свои деформации.
Остаточные напряжения представляют собой систему взаим-
но уравновешенных внутренних напряжений, беспорядочно рас-
пределенных по объему грунта. Если грунт может испытывать
деформации течения даже при малых напряжениях, то в резуль-
тате' медленного внутреннего течения остаточные напряжения
могут постепенно полностью рассеиваться. В результате дейст-
вия тектонических и атектонических сил остаточные напряжения
в горных породах нередко достигают значительных величин.
Таким образом, во многих случаях в грунте могут действовать
напряжения, сохранившиеся в итоге прошлой истории его за-,
гружения и деформирования. Эти напряжения, являющиеся оста-
точными по отношению к прежней нагрузке, обычно называют
начальными по отношению к напряжениям от нагрузки, вновь
приложенной. ‘
Закон Гука. Установленная экспериментально для большинст-
ва упругих тел линейная связь между напряжениями и деформа-
циями при простом растяжении или сжатии стержня называется
законом Гука. Согласно этому закону между продольной дефор-
мацией е и средним напряжением о по поперечному сечению стерж-
ня существует прямая пропорциональность
а = Ее, (4.86)
где Е — коэффициент пропорциональности, называемый модулем
упругости (измеряется в кГ/см2).
Для случая упругого сдвига закон Гука имеет вид
t = Gy, (4.87)
где коэффициент G называется модулем (кГ/см2) сдвига, а у —
деформацией сдвига.
Упругая бесконечно малая объемная деформация 9 при все-
стороннем нормальном давлении на тело интенсивностью ан так-
же прямо пропорциональна этому давлению:
= К 9, (4.88)
где коэффициент пропорциональности К. называют объемным мо-
дулем упругости (кГ/см2).
Напряженное состояние в любой точке упругого изотропного
тела характеризуется шестью компонентами напряженного (<Гц,
а22, <*зз, <*12, <*2з, <*з1) и шестью компонентами деформированного
142
состояния (бц, $22, £зз, е12, ®2з, £3i) • В общем случае каждый из
компонентов напряженного состояния должен зависеть от всех
шести компонентов деформации, что может быть выражено соот-
ветствующими уравнениями:
°il — /11 (£11, £22, £33, 812» е23» £31) = /11 (£/у)
а22 = /22 (£//)j °33 = /зЗ (8/;) »
°12 = /12 (8//) j °23 = /23 (£Zj) 5 °31 — /з1 (£/у)
(4.89)
и вообще
°ki = fki > причем okl = alk; е/у = е;7. (4.90)
Разлагая правые части (4.89) в степенные ряды и ограничи-
ваясь только членами первой степени, представим напряжения в
виде линейных функций компонентов деформации, как это при-
нято в классической или линейной теории упругости.
При объемном упругом напряженном состоянии связь между
напряжениями и деформациями дает так называемый обобщен-
ный закон Гука, по которому в любой точке упруго деформиро-
ванного тела каждый из шести компонентов тензора напряжений
является линейной функцией шести компонентов тензора дефор-
маций, и наоборот. В случае упругого анизотропного материала
между напряжениями и деформациями при объемном напря-
женном состоянии будут иметь место следующие линейные зави-
симости:
(4.91)
Оц = Си + С12 822 + С13 833 + С14 82з + С15 831 + Ci6 812
(Г22 — C2i еп + С22 е22 + С23 S33 + С24 s23 + С25 e3i + C2e si2 \
°33 = £з1 £11 + С32 ^22 + С33 833 Ц- С34 823 Ц- С35 831 Ц- С36 812 »
°23 = С41 $н + С42 ^22 + С4з 833 -|- С44 823 С45 831 С46 812 *,
О31 C5i еп + С52 £22 + С53 833 + С54 е23 + С55 e3i + С56 8i2;
012 = Cei 8п -|- Сб2 822 + С63 е33 -|- Сад 823 4~ Сб5 е31 Сб6 е12
(при этом = а/, е/у = е/7).
При коэффициентах пропорциональности С лучше ставить че-
тыре индекса, повторяющих индексы при о в левой части и при
е, стоящем рядом с С, например
#23 = С2311 £11 + С2322 е22 + ^2333 £33 4“ ^2323 £23 “Г С2331 S31 -|“ С2312 84 2.
Тогда всю систему уравнений (4.91) можно сокращенно записать
в виде
= ^tjki > (4.92)
где матрица величин С//л/ называется тензором модулей уп-
ругости.
Таким образом, анизотропное тело характеризуется 36 упру-
гими постоянными Cijki- Но если то остается
21 независимая постоянная. При этом направления главных на-
пряжений и главных деформаций совпадают.
143
Частные случаи. Если координатные плоскости совпадают с
плоскостями симметрии свойств грунта (т. е. грунт будет
обладать одинаковыми свойствами по осям 1, 2, 3), то количест-
во независимых упругих постоянных еще уменьшится и станет
равным девяти. Уравнения (4.91) примут вид
ан — сп еп 4- С12 £22 + С13 е33;
0*22 — С21 811 4" С22 s22 + С23 S33 J
О'ЗЗ = ^31 S11 + С32 е22 4“ С33 s33 J
°2з = С44 е23; о31 = С55 е31; а12 = С6в si2;
(Cig = С21; С23 == С; С31 = С13).
(4.93)
Такой материал называется ортотропным. Для грунтов меха-
нические свойства по всем горизонтальным направлениям обыч-
но одинаковы, но отличаются от свойств в вертикальном направ-
лении. Этот материал, называемый трансверсально-изотропным,
характеризуется уже только пятью независимыми упругими по-
стоянными
Си, С33 , С44, С6в и С13.
Следовательно,
<Уц = Си + (Си — 2 Сев) s22 + С13 8зз >
а22 = (Си — 2 Свв) eu -J- Сп е22 + С1Э вад;
азз = Ci3 еи + С13 е22 4' С33 833 ;
O23 — С44 е23; о31 = С44 е31; о12 = Свв е12.
(4.94)
Наконец, в случае изотропного материала остается всего два
независимых коэффициента Си и Ci2:
Оц == Си еи 4- С12 е22 + С12 833 ;
о22 — С12 еи Си е22 + С12 езз; I
а33 — С12 8П 4- С12 е22 + Си 833 ;
0*23 = С44 е23; о31 = С44 е31; а12 = С44 ei2.
Здесь С44 является функцией Си и Ci2:
С44 = — (Сц — СХ2).
Отнесем уравнения (4.92) к главным осям:
— Си 8j 4- СХ2 8jj 4- С13 е1П ;
(Уц — Си Sj 4- С22 еи 4- Сгз еш ;
~ С31 Sj 4- С32 бу 4" С33 Sjjj .
(4.95)
(4.96)
(4.97)
144
В случае изотропного тела обозначим C11 = C%t=Ca3 = a;C12—
= С1з = C2i = С23 = C3i =С32=6. Подставляя в (4.97) новые обоз-
начения, получим:
Oj =аг1 + Ь (еп + еП1);
°П = аеп + (SHI
Ош = аеш + b (8j
(4.98)
Прибавим и вычтем в первом уравнении , во втором bsn ив
третьем 6ещ. Например,
Oj = (а — ft) Sj + b (е, + е„ + еш). (4.99)
Аналогичный вид примут и другие два уравнения. Обозначая
а — b = 2|л* b — £j -f- sji ~ ® ’ (4. 100^
получим
cTj — \ 0 4~ 2 р* ©J
(*п = х 6 + 2еп ;
<*щ = X 6 Ц- 2 р^ £jjj .
(4.101>
Постоянные Ляме. Упругие постоянные К и jjl называют посто-
янными Ляме. Для произвольно выбранных декартовых координат
мы получим в случае изотропного тела:
(Гц = X 6 + 2 р 8ц;
0*22 — X 6 Ц- 2 р- ^22>
(*зз — X 6 + 2 р е33;
(4.102>
Из этих уравнений легко вывести:
012 — р е12;
<*23 = I1 ®23 ’>
<*з1 = Iх S31 •
Л4-Р , ГГ-- - А (<*22 Ч~ <*3з) 5
£11 — |x(3X-|-2p) а11 2 р (3 X 4- 2 р)
е22 — X -|- р- <*22 X (<*33 + <*11) (4.103)
НЗХ4-2р) 2р (ЗХ4-2р)
<*зз — х 4- р- . (Т X (<*11 + <*22) •
Р (ЗХ4-2р) и33 2р (ЗХ4-2Х)
Обозначим величину, обратную коэффициенту при в пер-
вом члене правой части уравнений (4.103), через Е:
Е = р (ЭХ-f-2р.) . (4.104)
+ Iх
Так как е—величины безразмерные, то размерность Е долж-
на быть такой же, как у <т.
145
(4.105)
(4.106)
Обобщенный закон Гука для изотропного материала. Обоз-
начая
__ к
V ~ 2 (X + [л) ’
получим
1 N / I \
£11 — ~ ~ (°22 + а3з) >
Е Е
__ 1 V . .
е22 — — °22---~ (а33 I °11/ 5
, Е Е
£33 = “^33-----— (а11 + а22) ,
Е Е
где Е — модуль упругости или модуль Юнга;
v — коэффициент Пуассона.
Уравнения (4.106) представляют собой выражение обобщен-
ного закона Гука для изотропного материала.
В системе так называемых технических упругих постоянных,
принятой в сопротивлении материалов, коэффициент пропорцио-
нальности ц в (4.101) обозначают через G и называют модулем
сдвига.
Складывая уравнения (4.106), мы получим
£н + е22 + £зз ==-~— (ап + а22 + азз) • (4- Ю7)
Е
В левой части этого выражения стоит объемная деформация
0, а в скобках правой части — первый инвариант"тензора напря-
жений /ь
Таким образом,
6= (4.108)
Е
В случае равномерного гидростатического давления (<Тц = а22 =
= Озз = ая):
0„ =--------- 6 = К 6, (4.109)
н 3(1—2ч) z 7
т. е. объемная деформация в точке пропорциональна всесторон-
нему давлению <зн.
Выражение
дает соотношение между модулем объемной деформации или
объемным модулем упругости К и величинами Е и v.
Из приведенных выше различных производных упругих посто-
янных обычно пользуются модулем Юнга Е и коэффициентом
Пуассона v, так как в технике широко распространены стержневые
конструкции, а для сжатых или растянутых стержней Е и v не-
посредственно характеризуют продольную и поперечную дефор-
146
мации. Кроме того, определение этих упругих постоянных при
испытании образцов в виде стержней и призм осуществляется
очень просто. Однако при исследованиях деформаций грунтов во
многих случаях удобнее пользоваться системой упругих постоян-
ных К и G. Вообще выбор наиболее удобных для расчета постоян-
ных зависит от характера конструкции и поставленной расчетной
задачи, но в случае изотропных материалов это всегда только два
независимых друг от друга параметра.
Приводим для справок таблицу соотношений между различны-
ми упругими постоянными.
Постоянные - Основная пара
X, G, v K, G E, v E, G
X X 2Gv I О СЧ 1 co X vE G(E—2G)
1—2v (1+4(1-24 3G—E
Р- р* G G E 2(1+4 G
G р- G G E 2(1+4 G
Е (ЗХ 4“ 2р*)р* 2G(l +n) 9KG E E
X + р- 3K + G
К 2р. 2G(l+4 3(1—2^) К E 3(1— 24 EG 3(3G—E)
4 X 2(Х -J-р.) V 3K — 2G 6K + 2G s-'
В системе технических упругих постоянных шесть равенств
(4.102) можно записать в виде одной тензорной формулы:
Р / м \
. «1П>
где через (символ Кронекера) обозначена величина, ко-
торая может принимать только два значения: при i=/
8Z/-= 1, а при i=^=j 8Z/=0. Следовательно, для напряжений <Уц>
о22 и озз по главной диагонали тензора напряжений (4.13) умно-
жение на 8/у равносильно умножению величины —-— 8 на 1, а
1 — 2 v
для напряжений а// при i^=j—умножению на 0. Решая (4.111)
относительно е//, получим с учетом (4.108) тензорное представ-
ление шести уравнений для деформаций одним уравнением:
*0 = у КН- V) vSyZJ, (4.112)
где /1 — первый инвариант тензора напряжений.
147
упругие постоянные
(4.113)
= Gs3i. (4.114)
= 2G, (4.115)
Если выразить соотношения (4.101) чере
G и v, получим
Он = 2 G eu -Е -—-— б] ;
1 — 2 v J
о22 — 2 G Ге22 + г— \
L 1 — 2 м J
°зз = 2 G Гг33 + -—— б! ;
L 1 — 2 м J
012 — G si2 > °*2з == G е23; а31 =
Из (4.113) вытекают зависимости
о 11 — Ogg _ Ogg — O33 == Озз — Оц
е11 — eg2 £gg — е33 е33 — £11
что дает способ непосредственного вычисления G по результа-
там экспериментов на всестороннее негидростатическое сжатие.
Зависимость между интенсивностью напряжения и интенсив-
ностью деформации. Между октаэдрическими напряжениями и
деформациями существует, согласно закону Гука, следующая за-
висимость:
Токт = Токт (4. 116)
Подставляя сюда т0КТ из (4.48), а уОкт из (4.71), найдем
(Oj Оп)2 + (оп 0Ш)2 + (Ojjj Oj)2 =
= 2G + (S„ - еш)* + (Вш-si)2 • (4-117)
Пользуясь выражениями (4.42) и (4.72), представим (4.117)
в следующей простой записи:
az = 3Gez, (4.118)
т. е. при упругих деформациях интенсивность напряжения равна
интенсивности деформации, умноженной на утроенный модуль
сдвига.
Зависимость между тензорами напряжений и деформаций.
Пользуясь зависимостями (4.55) и (4.68), можно (4.117) пред-
ставить в виде
£>Н = 2С£>Д, (4.119)
т. е. девиатор напряжений прямо пропорционален девиатору де-
формаций.
Аналогичная зависимость существует и между шаровыми
тензорами напряжений и деформаций:
Я„ = КНд. (4.120)
Обобщенные инварианты напряженного состояния. Главные
напряжения в точке От , оц5 0щ (величина и направление кото-
148
рых не зависят от выбора системы координат, т. е. условий сис-
темы отсчета, а зависят только от характера распределения внеш-
ней нагрузки) называют исходными инвариантами.
Очевидно, любые аналитические выражения, составленные из
исходных инвариантов, будут независимы относительно преобра-
зования координат. Таким образом, можно составить бесчисленное
множество инвариантов напряженного состояния. Из инвариан-
тов, например /1, Л, h (п. 4 главы 4), только Ц имеет опре-
деленный физический смысл, т. е. с точностью до постоянного
множителя— представляет собой нормальное или гидростатичес-
кое напряжение в точке
1 г
— 4 = о„.
з н
Желательно квадратический и кубический инварианты подо-
брать таким образом, чтобы и они имели ясное физическое ис-
толкование. При этом можно исходить из того, что формоизмене-
ние определяется отклонением напряженного состояния от гидро-
статического и выбрать второй и третий инварианты такими,
чтобы они характеризовали среднее квадратическое и кубическое
отклонения напряженного состояния от гидростатического. Обоз-
начим эти инварианты Л2 и Л8 и примем их в виде следующих
комбинаций вторых и третьих степеней исходных инвариантов.
л| = + oj, + <т2„ + а (а, + а„ <тш 4- аП1 aj; (4.121)
Лз = а1 + ап aiii "Ь Р (CTi ап + стп а1П Н- °П1 CTi +
4* Oj Cjj ~|- (Гц <Tjjj 4* ^iii 4- 7 ^ii °ni» (4.122)
где a, P и у — численные параметры.
Эти инварианты М. М. Филоненко-Бородич [83] назвал обоб-
щенными.
Приняв а=—1, из (4.121) мы легко получим
Ai = 4 [(*! - + (<тп - <тш)2 + (<тш - а,)2], (4.123)
а приняв р=—2~ и Y—6, из (4.122)
А| = 4 1(°! - + (стп - + (°Ш - стн)8Ь (4.124)
Так как среднее квадратическое отклонение тензора напряже-
ний от гидростатического напряжения равно среднему значению
квадратов отклонения Д главных напряжений от среднего гидро-
статического ~н, то
Ai = 4 - ая)2 + (ап - °я)2 + (°-1п ~ <Ъ)21; (4-125>
о
А2 = -/(а, - он)2 + (<тп - Оя)2 + (аш - о„)2. (4.126)
]/з
14Э
Сравнивая (4.123) и (4.125), видим, что Л2 отличается от Л2
только постоянным множителем. Вместе с тем и (4.123) отлича-
ется от квадрата касательного октаэдрического напряжения
(4.60) только постоянным множителем. Следовательно, обобщен-
ный квадратический инвариант получает двойное истолкование и
имеет четкий физический смысл.
Выражение (4.124) для Л8 представляет собой среднее куби-
ческое отклонение тензора напряжений от гидростатического на-
пряженного состояния. Таким образом, можно заменить систему
инвариантов Ц, /2 и 1з системой обобщенных инвариантов Ль
Л2 и Л3:
Л1 = Oj -J- стп + <тш; (4.127)
Ла = —— (<Tj — <тя)2 4' (сГщ О/у)2 + (tfjn О/у)2! (4.128)
V 2
Аз = V (<т, - он)з + (<тп - + (<тш - Of]y , (4.129)
/ 3
которые мы будем называть инвариантами Филоненко-Бородича.
6. ЖИДКОЕ И АМОРФНОЕ СОСТОЯНИЯ
. Жидкое состояние. При нагревании твердых тел и их расшире-
нии, связанном с увеличением амплитуды колебательных движе-
ний частиц, эти тела по своим механическим свойствам все бо-
лее приближаются к жидкостям. Наконец, при температуре плав-
ления вещество переходит в жидкое состояние, и кристаллическая
структура тела исчезает. При этом расстояние между частицами
изменяется, и они могут теперь легко обмениваться местами со
своими ближайшими соседями. Длительность пребывания моле-
кул в «оседлом» состоянии зависит от температуры и, следова-
тельно, от энергии тепловых колебаний частиц. Чем выше темпе-
ратура, тем меньше время «оседлой жизни» частиц, тем чаще
они меняются местами и тем интенсивнее происходит перемеши-
вание жидкости.
Если принять объем вещества при наиболее плотной укладке
частиц и абсолютном нуле температуры за 1, то при плавлении
объем вырастает примерно до 1,21, а при кипении — до 1,42.
Частота, с которой молекулы жидкости могут менять своих
соседей, определяет сопротивление жидкостей течению, называе-
мое вязкостью. Чем подвижнее частицы, тем меньше вязкость
жидкости щ тем больше скорость ее течения при одном и том же
усилии. Следует заметить, что колебания частиц наблюдаются и
в кристаллах, однако в жидкостях, кроме того, перемещаются и те
центры равновесия, относительно которых совершаются колеба-
ния.
Эти перемещения центров колебаний, представляющие собой
150
как бы самодиффузию молекул жидкости, Я. И. Френкель [84]
образно назвал дрейфом. Частота колебаний молекул жидкости в
среднем равна 1013 гц. Молекула жидкости за 1 сек меняет место
(совершает дрейф) около 100 млн. раз, причем в промежутках
между переходами она успевает совершить до 100 тыс. колебаний.
По мере повышения температуры жидкости, расширяясь, все
более приближаются по своим свойствам как бы к сильно уплот-
ненным газам. При охлаждении до точки замерзания жидкости
постепенно уменьшаются в объеме, все более приближаясь по
своим свойствам к твердым телам.
Твердообразные и жидкообразные свойства реальных мате-
риалов. Понятия о твердых и жидких телах являются весьма упро-
щенными представлениями о действительных свойствах реальных
материалов, у которых напряжения могут зависеть в той или иной
степени и от скоростей деформаций (что характерно для жидко-,
стей) и от абсолютных величин последних (что характерно для
твердых тел). У таких материалов, как глинистые грунты, если они
не испытывают вязкого течения при данных нагрузках, текуйесть
при тех же нагрузках может появиться в результате изменения их
влажности. Однако характерным отличием тел, которые называ-
ют твердыми, от тех, которые называют жидкими, является нали-
чие у первых предела текучести, тогда как у вторых течение вызы-
вается даже при бесконечно малых напряжениях. С другой сторо-
ны, жидкости могут проявлять свойство упругости при очень крат-
ковременном действии сил или при всестороннем равномерном
сжатии, а у некоторых твердых тел предел текучести может сильно
уменьшаться в зависимости от продолжительности действия на-
грузки. Характерной особенностью твердых тел является также
способность испытывать мгновенные пластические деформации, на-
пример при ударных нагрузках.
Таким образом, у реальных тел следует различать твердооб-
разные и жидкообразные свойства, каждое из которых в отдель-
ных случаях имеет преобладающее значение. При тех или иных
условиях эти свойства могут одновременно влиять на характер
протекающих деформаций, причем одно и то же тело может
обладать одновременно и упругостью, и пластичностью, и теку-
честью.
Необходимо помнить, однако, что проявление упругих свойств
у жидкостей отличается от упругости твердых тел, а проявление
вязких свойств у последних иное, чем у жидкостей, что объясня-
ется различием в их молекулярном строении. Поэтому некото-
рые авторы [62] предлагают, например, вязкость у твердых
тел называть пластической вязкостью, псевдовязкостью и т. д.
У многих материалов сочетание твердообразных и жидкообраз-
ных свойств носит весьма сложный характер [56].
Твердые аморфные тела. Так называются тела, занимающие
промежуточное положение между кристаллическими телами и
жидкостями. У них, как и у жидкостей, существует ближний по-
151
рядок в размещении частиц, но отсутствует дальний. При этом
ближний порядок представляет собой элемент кристаллической
Рис. 4.33. Структура кристаллическо-
го и аморфного кварца
решетки, однако в отличие от
кристаллических тел эти элемен-
тарные кристаллические образо-
вания не построены в единую
симметричную систему, а рассея-
ны беспорядочно. Вместе с тем
между элементами сохраняются
атомные связи.
На рис. 4.33 (сверху вниз)
приведено схематическое изобра-
жение структуры кристалличе-
ского и аморфного кварца [58].
В обоих случаях основным струк-
турным элементом является тет-
раэдр с ионом кремния в центре
и ионами кислорода по углам.
Но в кристалле эти тетраэдры
размещены закономерно, а в
аморфном кварце — беспорядочно, хотя между любыми двумя
ионами кремния сохраняется связь через ион кислорода, что созда-
ет прочный каркас во всем теле.
Особенностью перехода из жидкого состояния в твердое
аморфное является постепенное и непрерывное изменение при
этом свойств вещества, тогда как при переходе в кристалличес-
кое состояние изменения совершаются скачками.
7. НАПРЯЖЕНИЯ В ФАЗОВОЙ МОДЕЛИ ГРУНТА
Фазы грунта. В главе 3 было приведено определение фазы,
принятое в' химической термодинамике. В механике грунтов по-
нятие о фазах несколько отлично от предыдущего, так как в за-
висимости от рассматриваемого комплекса свойств грунта под-
разделение на фазы в одной и той же системе может меняться.
Если, например, в некотором случае важно только то, что все
частицы минерального скелета грунта являются твердыми тела-
ми, то весь скелет независимо от минералогического состава рас-
сматривается как одна твердая фаза грунта (так называемая
смешанная фаза по терминологии химической термодинамики).
Если же представляют интерес, например, геохимические яв-
ления в грунте, которые зависят от минералогического состава, то
каждый из минералов будет образовывать отдельную фазу со
своими характерными свойствами, например кристаллы кварца —
одна фаза, полевого шпата — другая и т. д., как это и принято в
термодинамике химических процессов.
Опыт показывает, что если в порах грунта отсутствует вода, то
воздух и газы в порах не оказывают практически никакого влия-
152
ния на поведение грунта под статической нагрузкой. Поэтому су-
хой грунт в механическом отношении можно рассматривать как
однофазную систему.
Если заполнителем пор является только вода, то такой насы-
щенный водой грунт называется двухфазным: твердая фаза —
скелет, жидкая фаза — вода. Если же в порах грунта одновре-
менно находятся и вода и газ (или пар), то влиянием последне-
го на свойства грунтов уже нельзя пренебрегать, и грунт назы-
вается трехфазным: к двум указанным выше фазам добавляется
третья — газообразная. Примеси кристаллов солей и органичес-
кого коллоидного вещества относят обычно к твердой фазе.
В ряде случаев требуется учитывать изменение свойств части
объема указанных основных фаз под влиянием тех или иных при-
чин, например при переходе воды в порах в лед, и тогда может
возникнуть необходимость выделения дополнительных фаз.
Фазовая модель грунта. Назовем фазовой разновидность мо-
дели сплошной среды, когда последняя рассматривается состоя-
щей из частиц скелета и порового заполнителя, причем соотноше-
ние между этими составляющими и все свойства, связанные с фа-
зовым строением, сохраняются в данной точке при переходе к
бесконечно малому элементарному общему. Иными словами, в этой
модели мы не интересуемся конкретными размерами отдельных
частиц и пор, но считаем, что в любых объемах грунта, включая
сколь угодно малые, соотношение между объемом частиц и
объемом пор остается одним и тем же.
Фазовая модель грунта была предложена К. Терцаги в 1925 г.
для расчета осадок сооружений. Терцаги принял, что скелет
грунта образован из жестких несжимаемых твердых частиц.
Точно так же несжимаемой принимается и жидкость (вода), за-
полняющая поры грунта. Соответственно его объемные деформа-
ции могут происходить только за счет изменения относительно-
го содержания в грунте различных фаз. При сжатии объем пор
уменьшается и на столько же увеличивается объем скелета (на
единицу объема грунта). Если поры грунта заполнены водой, то
уплотнение сопровождается выжиманием из пор соответствующе-
го ее количества. Таким образом, изменение объема фазовой мо-
дели грунта при сжатии равно изменению объема пор грунта. В
случае двухфазной модели изменение объема грунта равно из-
менению объема жидкой фазы.
Фазовую модель сплошной среды называют также уплотня-
ющейся моделью сплошной среды.
Отсыпем на дно сосуда слой песка и зальем сосуд водой
(рис. 4.34,а). Передадим на воду через поршень давление интен-
сивностью Р. Очевидно, можно было бы вместо поршня с нагруз-
кой просто налить в сосуд добавочное количество воды, высота
столба которой определялась бы выражением
h = см,
153
где 8В — удельный вес воды;
h— высота эквивалентного давлению р столба (эквивалент-
ная высота).
Добавочное давление р в жидкости от нагрузки на поршень
будет действовать и в жидкости, находящейся в порах слоя пес-
ка. При этом каждая песчинка получит добавочное всестороннее
равномерное давление р (рис. 4.34,6). Так как частицы грунта в
Рис. 4.34. Напряжения в системе грунт — вода
фазовой модели принимаются несжимаемыми, то никакой дефор-
мации песчаного слоя не произойдет.
Теперь допустим, что в поршне имеются тонкие отверстия, че-
рез которые будет продавливаться вода, так что он сможет посте-
пенно опускаться (рис. 4.34,в), пока не коснется слоя песка. В те-
чение всего процесса движения поршня напряженное состояние
песка не будет изменяться, и деформации его будут отсутство-
вать, хотя в воде будет существовать некоторое давление, кото-
рое можно принять по-прежнему равным р. Когда поршень опус-
тится на песчаный слой, начнется обжатие последнего, сопровож-
даемое уменьшением пористости системы и выжиманием из него
Рис. 4.35. Механиче-
ская модель Терцаги
воды (явление консолидации грунта).
Для наглядного представления явлений,
происходящих в двухфазной системе, К. Тер-
цаги предложил механическую модель, изобра-
женную на рис. 4.35. В ней роль слоя грунта
на дне сосуда играет стальная пружина, а
роль воды в порах — вода, окружающая пру-
жину, причем последняя может сжиматься
лишь по мере выхода воды через отверстие в
поршне.
По мере сжатия пружины будет возрас-
тать ее реакция и соответственно убывать дав-
ление на воду, равное давлению на поршень, за вычетом реакции
пружины, моделирующей реакцию скелета грунта. Когда пружи-
на сожмется настолько, что ее реакция полностью уравновесит дав-
ление на поршень, давление в воде станет равным нулю. Таким
образом, в процессе' деформации модели происходит непрерывное
перераспределение нагрузки между водой и пружиной. Вначале
154
вся нагрузка воспринимается водой, а в конце — пружиной. Ана-
логично этой модели в двухфазном грунте (насыщенном водой) в
первый момент после приложения нагрузки все давление воспри-
нимается поровой водой, а в конце — скелетом.
Напряжения, действующие в скелете, называются эффектив-
ными, межчастичными, скелетными, а в поровой воде — нейт-
ральными, или поровым давлением. Сумма этих напряжений дол-
жна равняться средним суммарным напряжениям в точке от
внешней нагрузки, определенным как для однородной сплошной
среды. Для обозначения этих суммарных напряжений существует
ряд терминов — общие, полные, тотальные. Мы будем далее
пользоваться первым из них
Если_обозначить напряжения в скелете (эффективные) через
аэ или о, напряжения в жидкости (нейтральные) через и, а
общие через о, то для двухфазной модели Терцаги должно вы-
полняться условие
а = оэ-|-и, (4.130)
причем в первое мгновение по приложении нагрузки (/=0) а=и,
а в конце процесса деформирования (/=<х>)<т=стэ.
Если рассматривать трехфазную систему скелет — вода — воз-
дух, то напряжения будут передаваться также и на воздух. Одна-
ко сжимаемостью воздуха уже нельзя пренебрегать, и по своему
поведению под нагрузкой трехфазная модель будет отличаться от
двухфазной. Как показал Бишоп [88], для таких систем характер-
на следующая зависимость (в ходе деформирования):
о = огэ-Н«а — X (“а — «в)]. (4.131)
гДе иа— давление в поровом воздухе (кратко газовое давление);
ив— давление в воде;
% — параметр, зависящий от соотношения между объемами
воды и воздуха в порах.
Параметр % равен 0 при совершенно сухом грунте и 1 при пол-
ностью водонасыщенном, когда выражение (4.131) переходит в
(4.130).
8. РЕОЛОГИЧЕСКИЕ СВОЙСТВА ГРУНТОВ
Реология (от греческих слов «рео» — течь и «логос»— уче-
ние) представляет собой раздел физики, изучающий законы де-
формирования и течения различных материалов и условия поте-
ри ими прочности. Однако в строительной механике под реологи-
ческими обычно понимают только закономерности протекания
деформаций материалов во времени.
Фундаментальные реологические свойства. Вообще фундамен-
тальными называют такие свойства, физическая природа которых
не может быть объяснена исходя из любых других свойств, кото-
рые можно было бы рассматривать как более элементарные, на
данном структурном уровне. Фундаментальные свойства характе-
155
ризуются фундаментальными константами — постоянными, кото-
рые не могут быть вычислены исходя из других характеристик
данного структурного уровня. Все остальные константы, коэффи-
циенты, модули данной системы являются производными от ее
фундаментальных констант.
В реологии в качестве фундаментальных свойств тел рас-
сматривают: 1) упругость; 2) пластичность и 3) вязкость. Все
другие механические свойства являются сложным сочетанием в
различных комбинациях этих трех фундаментальных свойств.
Основными явлениями, составляющими объект изучения в
реологии, являются: 1) релаксация; 2) ползучесть и 3) длитель-
ная прочность материалов.
Под релаксацией понимают процесс постепенного перехода при
длительном действии нагрузки упругой деформации в пластиче-
скую (необратимую остаточную). Подобное явление означает
понижение с течением времени в деформированном материале
предела упругости, т. е. его расслабление.
Ползучесть означает свойство материала испытывать длитель-
но протекающие деформации при постоянной нагрузке.
Под длительной прочностью понимают прочность материала
при длительном действии на него нагрузки. Эта прочность по-
степенно снижается, причем у различных материалов процесс
постепенного падения прочности под нагрузкой протекает с раз-
личной интенсивностью.
В реологии все процессы обычно рассматриваются как проте-
кающие в изотермических условиях.
Реологические модели. В реологии для наглядного представле-
ния характера указанных комбинаций фундаментальных свойств
различных материалов широко применяются простые механичес-
кие модели (реологические). Естественно, что простейшие из
этих моделей слишком упрощают действительные свойства ре-
альных материалов, однако приближенные к действительности
модели настолько сложны, что теряют целиком свое главное до-
стоинство — наглядность.
Простейшие или основные реологические модели облегчают
понимание реологических свойств материалов, а при своем появ-
лении сыграли и определенную эвристическую роль, позволив ус-
тановить ряд зависимостей, количественно характеризующих осо-
бенности поведения многих реальных материалов. В настоящее
время они используются в основном лишь при преподавании как
удобное по своей наглядности вспомогательное методическое
средство, так как гораздо легче представить себе поведение ма-
териала по реологической модели, чем по аналитическим зависи-
мостям.
Идеальные материалы, отвечающие по своим свойствам тем
или иным реологическим моделям, называют реологическими те-
лами, и им обычно присваивается имя ученого, исследовавшего
впервые их поведение.
156
Аналитическая зависимость между напряжениями, с одной
стороны, и величиной и скоростью деформаций, с другой, назы-
вается реологическим уравнением данного реологического - тела.
Реологические уравнения устанавливаются на основе экспе-
риментов. Входящие в них скалярные параметры, различные для
каждого материала, обычно называют реологическими коэффици-
ентами или модулями (вроде, например, модуля упругости Е или
коэффициента Пуассона у для упругих тел).
Материалы, обладающие качественно одними и теми же свой-
ствами, отличающимися лишь количественно, считаются одним и
тем же реологическим телом и изобража-
ются одинаковыми, но имеющими различ-
ные по величине коэффициенты или модули
моделями.
Каждый материал характеризуется дву-
мя реологическими уравнениями: одно опи-
сывает скорость объемных деформаций, дру-
гое — скорость формоизменения.
Упругое тело Гука. Упругое тело называ-
ют телом Гука и обозначают символом Н.
Свойства упругости условно изображают
Рис. 4.36. Модель упру-
гого тела (модель Гука)
механической моделью в виде пружины
(рис. 4.36,а). Точки приложения к модели внешних сил называют
конечными точками модели.
График зависимости между напряжениями и деформациями
у тела Гука прямолинеен, причем графики загрузки и разгрузки
совпадают (рис. 4.36,6). Работа, затраченная на сжатие пружи-
ны,' накапливается в ней в виде потенциальной энергии деформа-
ции и полностью возвращается при снятии нагрузки с пружины.
Понятие о скорости деформации. Скоростью деформации на-
зывается изменение деформации во времени:
• d е
8 — ~dT'
(4-132).
котррое зависит, во-первых, от скорости загружения, а во-вто-
рых, от свойств самого материала и особенностей его «отклика»
на возмущающее действие нагрузки.
Упругие деформации в телах с кристаллическим строением,
а также в жидкостях распространяются со скоростью звука в дан-
ном материале, которая измеряется сотнями метров в секунду.
Поэтому в большинстве случаев распространение в теле упругих
деформаций может практически рассматриваться мгновенно сле-
дующим за загружением (встречающийся в литературе термин
«условно мгновенная деформация» излишен, так как само по-
нятие о мгновении уже является условным).
В полимерах, обладающих сложной пространственной струк-
турой из переплетающихся и свернутых гибких цепочек макромо-
лекул, упругая деформация кроме мгновенной составляющей име-
157
ет также обратимую замедленную составляющую, проявляющую-
ся как при загрузке, так и при разгрузке. Эту составляющую в
теории деформаций полимеров и физико-химической механике на-
зывают также эластической.
Пластическое тело Сен-Вейана. Идеально-пластическим или
жестко-пластическим называют тело, которое не испытывает ни-
каких деформаций (является жестким) до тех пор, пока напря-
жения не превзойдут определенного предела, после чего разви-
вается пластическая деформация.
При жестко-пластической деформации объем тела принима-
ется неизменным. Изменяется лишь его форма подобно тому, как
это имеет место при чисто упругом сдвиге, однако от последнего
пластическая деформация отличается своей необратимостью.'
Пластическая деформация представляет собой остаточную
деформацию сдвига, происходящую при напряжениях, превос-
ходящих предел, называемый пределом пластичности жестко-
пластического тела и обозначаемый через тпл- Следовательно,
условие наступления пластической деформации в таком теле
можно представить в виде предельного соотношения
* = *пл» (4.133)
где т — касательное напряжение (рис. 4.37,в).
Идеально-пластическое тело называют телом Сен-Венана»
обозначают символом StV и схематически изображают в виде
Рис. 4.37. Пластическое тело Сен-Венана
г
модели ползуна (рис. 4.37,а или 4.37,6). Между элементами мо-
дели действует сухое, или кулоново, трение. Это трение остается
постоянным при постоянном нормальном давлении.
В действительности процесс пластической деформации разви-
вается несколько сложнее. Как только начинается эта деформа-
ция, первоначальное сопротивление материала, называемое верх-
ним пределом пластичности тПл. макс, падает и по достижении
некоторого значения, называемого нижним, или установившимся
пределом пластичности тпл. уст, остается постоянным (рис. 4.38).
Такое падение сопротивления реальных тел пластической дефор-
мации связано со структурными изменениями материала.
158
Характерной особенностью пластического тела Сен-Венана яв-
ляется независимость деформации от скорости загружения. Ра-
Рис. 4.38 Падение сопротивления ма-
териала при пластической деформа-
ции (условная аналогия с трением
покоя и трением движения).
бота, затраченная на пластическую деформацию, идет на преодо-
ление внутреннего трения и полностью рассеивается, обращаясь
в теплоту.
У ряда тел при пластической деформации наблюдается посте-
пенное увеличение сопротивления деформации — так называемое
упрочнение. Это явление может быть условно представлено се-
рией моделей Сен-Венана, соединенных свободными от натяже-
ния нитями, непрерывно включающими в работу по мере сдвига
одну модель за другой (рис. 4.39).
Рис. 4.39. Пластическое тело с упрочнением
Скорость деформации в точке. Скорость деформации в неко-
торой точке тела по любому направлению определяется тремя
взаимно перпендикулярными направлениями главных осей ско-
рости деформации I, II и III и соответствующими тремя глав-
ными скоростями удлинений Ci , Си, Сщ. Вдоль этих главных
осей направления скоростей деформаций совпадают с направле-
ниями нормалей к соответствующим площадкам.
Величина
с = 2- (С/+С// + М (4.134)
О
называется средней скоростью деформации, а положительная ве-
личина
- -k V(4 - С„)2 + (Сп - Ч»)2 + - Ч)2 <4-135)
У 6
интенсивностью скоростей деформаций сдвига.
159
Если ввести безразмерный параметр Соколовского [73]
£ц ~ £щ ___ ।
а = 2
^111
удобный для обработки экспериментальных данных, то макси-
мальная скорость деформаций сдвига выразится следующим обра-
зом:
(4.136)
3 Lz
(4.137)
функцией от
(4.138)
изотропных
и скоростей
2
v ......
'W7^7/^V7777/77777777777777777777777
У
Рис. 4.40. Течение между двумя параллельны-
ми пластинами
тм.кс = - (Ч-Сп) =
2
Интенсивность напряжений является некоторой
интенсивности скоростей сдвига:
az = F(Lz).
Эксперименты показывают, что у однородных и
материалов главные оси напряжений, деформаций
совпадают, а экстремальные касательные напряжения и главные
скорости деформаций сдвига пропорциональны друг другу.
Вязкое тело Ньютона. Если для поведения твердых тел под
действием нагрузки характерны упругие и пластические дефор-
мации, то для жидкостей
характерно вязкое тече-
ние, которое начинается
при бесконечно малых
сдвигающих напряжени-
ях. Скорость вязкого те-
чения пропорциональна
величине этих напряже-
ний.
На рис. 4.40 показано
течение жидкости, находящейся между двумя параллельными плас-
тинами, верхняя из которых смещается под действием горизонталь-
ной силы параллельно самой себе, увлекая за собой жидкость.
Вследствие вязкости жидкости скорость ее течения с глубиной убы-
вает. Вязкость рассматривается как проявление внутреннего тре-
ния в жидкости (так называемое жидкостное трение).
Обозначим скорость жидкости на некоторой глубине через v.
Тогда изменение скорости с глубиной z (градиент скорости) бу-
о dv
дет выражаться производной ---.
dz
Если обозначить перемещение верхней пластины за время dt
через du, а глубину, на которой скорость течения нижнего слоя
равна нулю, через h, то скорость верхнего слоя жидкости v =
d и
а градиент скорости
dу v 1 du
dz h h dt
dt
(4.139)
160
Величина — представляет собой градиент смещения. Обоз-
h
начим его через у. Таким образом, из (4.139) следует, что гра-
диент скорости равен производной по времени от градиента сме-
щения
-г- (4.140)
где точкой над у обозначена производная по времени.
По закону Ньютона касательное напряжение т, действующее
между слоями жидкости, пропорционально отношению разности
скоростей слоев к расстоянию между ними. Если выделить два
соседних бесконечно тонких слоя с расстоянием dz между их се-
рединами и считать в пределах каждого такого слоя, скорость
постоянной, изменяющейся на величину dv только при переходе
через границу между слоями, то
^ = 7)—, (4.141)
dz
где dv — разность скоростей соседних слоев;
dz — расстояние между слоями.
Коэффициент т], называемый динамической вязкостью при
сдвиге, или просто вязкостью, представляет собой касательное
напряжение, необходимое для того, чтобы вызвать движение сло-
ев относительно друг друга со скоростью, равной единице, и
имеет размерность напряжения, помноженного на время.
С учетом (4.140) формулу (4.141) можно записать в виде за-
висимости, которая носит название закона вязкости Ньютона:
т = . (4.142Х
Единицу вязкости иногда называют пуазом (пз):
1 п: = 1 дн-сек/см2 = 0,1 н-сек/м2 = 10,2 г-сек/м2 = 0,01 кг-сек/мК
Коэффициент вязкости воды т| = 0,01, этилового спирта 0,012,
ртути 0,016 и касторового масла 10 пуаз.
Вязкая жидкость, подчиняющаяся закону (4.142), называет-
ся реологическим телом Ньютона^ обозначается символом W и
имеет своей моделью так называемый амортизатор в виде порш-
ня с тонкими отверстиями, движущегося в цилиндре, заполненном
жидкостью (рис. 4.41,а). Здесь скорость перемещения поршня
пропорциональна приложенной силе Р в соответствии с зависи-
мостью (4.142), которая графически преставлена на рис. 4.41,6.
Работа сил, вызывающих вязкое течение, полностью расхо-
дуется на преодоление вязкого (жидкостного) трения, превра-
щаясь в теплоту, и является необратимой.
6 Зак. 530
161
Рис. 4,41. Модель реологического тела
Ньютона (вязкое течение)
I
Рис. 4.42. Движение вязкой жидкости
Ньютона в цилиндрической трубке
Движение вязкой жидкости
Ньютона в цилиндрической
трубке. Эта задача имеет важ-
ное значение для теории фильт-
рации воды в грунте. В случае
достаточно тонкой трубки и не-
большой скорости течения дви-
жение жидкости будет лами-
нарным. Это значит, что в
жидкости отсутствуют завихре-
ния и линии тока параллельны
оси трубки. Скорость течения
жидкости максимальна по оси
трубки (у0) и убывает к пери-
ферии.
Боковая поверхность ци-
линдрического столбика жид-
кости радиусом г и длиной I
равна 2лг/ (рис. 4.42). При ин-
тенсивности касательных на-
пряжений вдоль поверхности т
общее сопротивление движе-
нию равно 2лг/т. Если интенсивность давления на торец жидкого
столбика радиусом г равна р, то общее давление равно рлг2. Усло-
вие равновесия столбика жидкости имеет вид
р т: г2 — 2 к г / т ~ О,
откуда
= (4.143)
Заменяя в уравнении (4.139) z на г, получим
dv = ^dr. (4.144)
Из уравнения (4.141) с учетом (4.143) и (4.144) находим
dv —-— г d г
2/т}
и, интегрируя, получаем
v = —-— г2 + С.
4 Z т]
Произвольную, постоянную С находим из граничных условий,
полагая, что жидкость «прилипает» к стенкам трубы, т. е. что при
r=R скорость v=0. Тогда
С =-------/?2, (4.145)
4 17}
162
и, следовательно,
v=-------(№ — г2}. (4.146)
4 Z 77
Знак минус означает, что течение идет в сторону убывающего
давления р. Запомнив это, можно в дальнейшем знак опускать.
Из выражения (4.146) следует, что распределение скорости по
сечению имеет параболический характер с максимумом скорости
по оси трубки (при г = 0):
^акс= R2. (4.147)
4 / 7]
Формула Пуазейля. Расход жидкости определяется по форму-
ле для объема параболоида вращения
С=у^01(аш> (4.148)
откуда, подставляя уМакс , получаем
Q = ^--~Ri. (4.149)
О I 7]
Это равенство носит имя Пуазейля, который, изучая законы
движения воды по капиллярам, опытным путем нашел зависи-
мость вида
Q = k-^~, (4.150)
где k — эмпирический коэффициент.
Приведенный выше вывод показывает, что эмпирический ко-
эффициент Пуазейля
(4.151)
Неудобство формулы (4.149) заключается в том, что расход
при данном давлении зависит не только от вязкости жидкости,
но и от размеров трубки R и /. Этот недостаток можно устранить
следующим образом.
Из уравнения (4.142)
т = (4.152)
а из уравнения (4.149)
(4-153)
о I Q
Подставляя в (4.152) т из (4.143) при г=7?, найдем
‘ (4Л54)
а с учетом (4.153)
(4-155>
6* Зак. 530
163
Рис. 4.43. График зависимо-
сти у от т
Так как для данной жидкости коэффи-
циент вязкости т| — величина постоянная,
то, меняя размеры трубки и получая раз-
личные значения расхода, мы должны
каждый раз получать одно и то же зна-
чение т]. Соответственно на графике зави-
симости у ют т (рис. 4.43) точки для всех
таких опытов должны лежать на одной
прямой, тангенс угла наклона которой
оси т
tg«=^- = y (4.156)
не будет зависеть от /? и I. Величину — называют коэффициен-
том текучести и обозначают буквой ф:
. (4.157)
Заменяя в (4.149) давление р весом эквивалентного столба
жидкости
Р = Тв^
и замечая, что 2L представляет собой гидравлический градиент
I, можно представить формулу Пуазейля в виде
Q = — /?< = —• (4.158)
8 7] 8 7]
где F=xR2 — площадь поперечного сечения капилляра.
Введем понятие о гидравлическом радиусе сечения /?г, который
представляет собой отношение живого сечения потока жидкости
к смоченному периметру U канала (живым называется се-
чение, нормальное к направлению оси потока):
П ___
—7Г-
Так как для кругового сечения потока f7=2n/?, а F* = ~R2 ,
то в этом случае
= = (4.159)
Отсюда следует, что (4.158) можно представить в виде
Q = (4.160)
164
Таким образом, при замене R на Rr получаем формулу, отли-
чающуюся от формулы Пуазейля (4.149) только численным ко-
эффициентом.
Движение вязкой жидкости через канал с произвольной фор-
мой сечения. Рассмотрим канал с произвольной формой сечения
площадью Гис периметром U. Условие равновесия жидкости в
таком канале длиной I при разности давлений по обоим концам
Др будет иметь вид
kpF = (4.161)
откуда
Д р г т = . UI Заменяя Др весом столба жидкости h и замечая, h ношение — есть гидравлический градиент i, получим и (4.162) , что от- (4.163)
Согласно (4.144), dv = — dz = -К dz л или с учетом (4.159) dv = Rvdz. У (4.164)' (4.165)
Так как понятие о гидравлическом радиусе можно также к любому элементарному сечению, выделенному сечении потока, мы можем заменить dz на dz = adRr и выразить смоченный периметр потока через Rr: где аир — некоторые коэффициенты. Тогда = ; JkL RrdRr отнести в живом (4.166) (4.167)
и после интегрирования Ув i Я* V = а, —- . Т] 2 (4.168)
Поскольку расход равен Q = J vdF F и так как, согласно (4.140) и (4.167), F = URr = $R?T (4.169) (4.170)
165
и
dF = 2p/?rd7?r,
то
Q = ар 111 f $ = _a£ . YbJ_ r4
oJ 4 Z'
или, подставляя сюда F из (4.170), получим
Q = C^^i-R*F, (4.171)
где коэффициент Сф = зависит только от формы сечения и на-
зывается коэффициентом формы. В этом виде формула пригодна
для канала любой формы и носит название обобщенной формулы
Пуазейля.
9. СЛОЖНЫЕ РЕОЛОГИЧЕСКИЕ ТЕЛА
Сложными реологическими телами называют модели, сочетаю-
щие в себе различные фундаментальные реологические свойства,
и, таким образом, более точно (хотя и все еще очень приближен-
но) описывающие поведение реальных материалов.
Они составляются путем последовательного или параллельно-
го соединения фундаментальных моделей. В символической запи-
си последовательное соединение двух моделей обозначается гори-
зонтальной чертой между их символами (например, Н—N), а па-
раллельное— вертикальной чертой (например, H|N).
Как показывает опыт, фундаментальные реологические свойст-
ва у разных материалов проявляются в различных условиях по-
разному. При сочетании этих свойств упругое начало сказывается
прежде всего на обратимости деформаций, вязкое — на особенно-
стях их протекания во времени, пластическое — на появлении оста-
точных, необратимых деформаций только по достижении некото-
рого предельного значения напряжений. В результате сочетания
появляются такие, например, свойства, как растянутые во времени
упругие деформации — прямая и обратная (при разгрузке), или
неодинаковый характер отклика различных материалов на мгно-
венные и длительно действующие нагрузки. Первым в названии
этих тел ставится наименование вида деформации в первое мгно-
вение после приложения нагрузки.
Модель упруго-пластического тела. Она представляет собой
последовательное соединение моделей Гука и Сен-Венана
(рис. 4.44,а). На рис. 4.44\б приведен график зависимости
для этого тела, ведущего себя при напряжениях, меньших тпл, как
упругое, а при больших — как пластическое. Это тело называют
телом Прандтля и обозначают символом Рг:
Рг = Н —StV. (4.172)
Модели упруго-вязких тел. Эти модели получают путем соеди-
166
нения между собой упругих и вязких элементов (моделей Гука и
Ньютона).
Если следуя по ветвям (элементарным моделям), соединяю-
щим между собой конечные точки, можно найти такой путь, ко-
торый будет проходить только по пружинам, то такая связь на-
зывается непрерывной упругой связью (рис. 4.45,а); если путь
й г
Рис. 4.44. Модель упруго-пластическо-
го тела Прандтля
Рис. 4.45. Непрерывные и смешанные
реологические связи
между конечными точка-
ми содержит только вяз-
кие элементы (амортиза-
торы), то такая связь на-
зывается непрерывной
вязкой связью (рис.
4.45,6). Связь же по пути,
содержащему как упру-
гие, так и вязкие элемен-
ты, называется смешан-
ной [64].
В зависимости от ха-
рактера связей различа-
ют два вида так называе-
мых основных моделей
упруго-вязких тел, обра-
зованных из двух элемен-
тов — одного упругого и
одного вязкого:
1) модель, у которой
имеется только смешан-
ная связь, называемая мо-
делью Максвелла (рис.
4.46,а), или моделью уп-
руго-вязкой жидкости;
Рис. 4.46. Модель упруго-вязкого тела Макс-
велла (релаксация напряжений)
Рис. 4.47. Модель вязко-упругого тела Фойгта
(запаздывание деформаций)
167
2) модель* у которой имеются одновременно непрерывные уп-
ругая и вязкая связи, называемая моделью Фойгта (рис. 4.47,а),
или моделью вязко-упругого твердого тела.
МЪдели, содержащие более двух элементов, могут иметь одно-
временно непрерывные и смешанные связи.
Модель упруго-вязкой жидкости Максвелла. Модель Максвелла
представляет собой последовательное соединение моделей Гука и
Ньютона и обозначается буквой М (рис. 4.46,а).
На рис. 4.46,6 показан график изменения во времени внутрен-
них усилий в максвелловом теле после того, как к нему прило-
жена некоторая сила Р. В первое мгновение произойдет растяже-
ние пружины (деформация будет носить чисто упругий харак-
тер). Если концы растянутой модели закрепить, т. е. поддержи-
вать деформацию постоянной, то поршень в амортизаторе начнет
медленно двигаться вверх и одновременно длина пружины будет
сокращаться за счет исчезновения в ней упругого удлинения. В
конце концов пружина примет первоначальный размер, и усилие
в ней исчезнет. Поршень сдвинется на соответствующее расстоя-
ние и тоже остановится, раз прекратится действие на него усилия
со стороны пружины. Следовательно, общая деформация сохра-
нится, а напряжения в теле исчезнут. Произошло явление, кото-
рое называют релаксацией («расслаблением») напряжений. По-
этому модель Максвелла называют также моделью релаксиру-
ющего тела.
Так как течение в максвелловом теле происходит при самых
малых усилиях, его рассматривают как жидкость и называют
также упруго-вязкой жидкостью. При мгновенном приложении на-
грузки эта жидкость деформируется упруго наподобие твердого
тела, проявляя твердообразные свойства.
Получив под постоянной нагрузкой упругую деформацию, те-
ло Максвелла будет испытывать затем непрерывное вязкое тече-
ние, идущее с постоянной скоростью. Это течение необратимо, так
как полученная деформация сохраняется после снятия нагрузки.
Деформация е модели Максвелла представляет собой, очевид-
но, сумму удлинений упругого элемента зу и вязкого элемента
ев‘
s = ey + eB. (4.173)
Согласно (4.86),
еу = -^-, (4.174)
Е
а в соответствии с (4.142) для вязкого течения со скоростью е
имеем (подставляя ст вместо т и е вместо у )
ёв = —, (4.175)
где ij, — коэффициент вязкости при продольной деформации.
168
Дифференцируя (4.173) по времени и учитывая (4.174) и
(4.175), получаем
ё = ёу + ёв = 4 ° + — ст- (4.176)
Е ’Is
Это выражение называется уравнением релаксации напряже-
ний в модели Максвелла. В случае чистого сдвига удлинению мо-
дели в соответствует сдвиг у, а напряжениям о соответствуют ка-
сательные напряжения т. Соответственно (4.176) перепишется в
виде
т = — Т + — т, (4.177)
° ’1-
где G — модуль упругости;
— коэффициент вязкости при сдвиге. Когда ясно, о какой
деформации идет речь, индекс при ц можно опускать.
Уравнение (4.177) можно переписать в виде
= (4.178)
т. е. это линейное неоднородное (с правой частью) дифференци-
альное уравнение первого порядка, имеющее постоянный коэффи-
циент при т. Это одно из простейших линейных дифференциаль-
ных уравнений первого порядка, которое имеет вид
-^"+^ = Q> (4.179)
а х
где Р и Q могут быть либо непрерывными функциями от х, либо
постоянными. Для интегрирования подобных уравнений представ-
ляют у как произведение двух функций от х, а именно
- у = и (х) v (х).
В обозначениях уравнений (4.178) получим
= ии, (4.180)
где и и v — некоторые неизвестные функции от t. Дифференцируя
последнее, найдем
d т
~dt
(4.181)
dv . du
-----Ну ---
dt dt
Подставляя т из (4.180) вместо у и — из (4.181) вместо —— в
dt дх
уравнении (4.179), получим
dv . du . n
dt dt 4
dv , (du . n '
И-----р v------р Ри
dt \ dt
(4.182
169=
Найдем функцию и, при которой второй член в левой части
обращается в нуль:
— +Ри = 0. (4.183)
d t
Интегрируя это уравнение, в котором переменные и и t разде-
лены, найдем
In и + J Р d t = In Ci,
откуда
— J pdt
u~C1e . (4.184)
В дальнейшем выражения вида ех мы будем записывать в
виде ехр х (читается «экспонента х»).
Подставляя значение и из (4.184) в (4.182), получим (посколь-
ку это значение обращает скобку в нуль)
откуда
Ci exp (-J Pdt] = Q,
d v = -5- (exp J Р dt] dt-,
v = J (exp J Pdt] dt + С.
(4.185)
Подставляя (4.184) и (4.185) в (4.180), находим решение урав-
нения (4.179):
т = exp (—Pdt) [q (exp J Pdt] dt + c]. (4.186)
Заменяя P на-у, Q на Gy и подставляя значение С=то, кото-
рое находится из (4.186) при /=0, получим решение (4.178) в
виде
t
т = |\0 + G J у ^exp J — dt^ dt^ exp --------— (4.187)
о
Если у = 0 и деформация поддерживается постоянной, то из
последнего выражения получаем уравнение релаксации:
Т = ТОехр (4.188)
\ ч /
где То — начальное упругое напряжение сдвига при мгновен-
ном нагружении.
170
Уравнение (4.188) показывает, как падает
времени. Величину имеющую размерность
ют временем релаксации и обозначают Тр :
напряжение т во
времени, называ-
= (4.189)
Таким образом,
т = т0 exp f------------------------—. (4.190)
За время t= Тр напряжение в системе уменьшится в е раз. При
/-^оо т становится равным нулю, и напряжения в теле полностью
исчезают.
Чем короче время релаксации Тр , тем слабее проявляются
твердообразные свойства максвеллова тела^
Если скорость деформирования у постоянна и равна некоторой
величине ус, то из (4.188) находим
т + (то —тПс) ехр ; (4.191)
\ 1 р /
ПрИ — это дает т=т0, т. е. при скорости деформирования,
и Тл
равной ——, напряжения в системе остаются неизменными.
При большей скорости напряжения в системе растут, при
меньшей убывают, как это видно из рис. 4.48. Релаксация пред-
ставляет собой характерную особенность систем со смешанными
твердообразными и жидкообразными свойствами.
Больцман обобщил соотношение (4.190), указав, что убывание
происходит не обязательно по экспоненциальному закону. Больц-
ман считал, что механическое поведение твердого тела является
функцией всей предшествующей истории его деформирования, и
допускал, что действие каждой из предыдущих деформаций на
свойства тела не зависит от других. Поэтому общий результат
можно определить простым суммированием всех этих независимых
эффектов. Больцман указывал, что сдвиг и объемная деформация
релаксируют по-разному, и это сильно осложняет анализ явлений
при сложных напряженных состояниях.
Модель вязко-упругого тела Фойгта. Упругий Н и вязкий N
элементы в реологической модели этого тела соединены парал-
лельно (см. рис. 4.47,а). Символическое обозначение модели
F = H|N. (4.192)
На рис. 4.47,6 приведены графики изменения деформаций в
этой модели как после приложения, так и после снятия нагрузки
Р. Приложенная сила не может вызвать мгновенного удлинения
пружины, так как этому препятствует амортизатор. Удлинение
171
пружины определяется той скоростью, с какой передвигается пор-
шень в амортизаторе. Это явление так называемой замедленной,
а} или запаздывающей упругости.
Рис. 4.48. Кривые релаксации и запаз-
дывания
а — для тела Максвелла (образец при t = О
подвергнут действию напряжения и затем
деформируется с постоянной скоростью ус ;
б — для тела Фойгта (образец при t = 0 по-
лучает деформацию а затем продолжает
деформироваться при постоянном напряжении
Соответствующая медленная,
непрерывно протекающая де-
формация тел называется пол-
зучестью, или крипом. Пол-
ностью упругая деформация в
этой модели теоретически за-
кончится через бесконечное
время.
При удалении нагрузки со-
кращение пружины точно так
же замедленно и зависит от
скорости обратного перемеще-
ния поршня в амортизаторе.
Это явление называется упру-
гим последействием.
Особенностью ползучести
тела Фойгта является ее зату-
хающий характер, причем сама
деформация ползучести носит
обратимый характер. Этим пол-
зучесть как проявление жидко-
образного свойства твердого
тела отличается от медленного
вязкого течения типичной жид-
кости, которое не будет зату-
хать до тех пор, пока продол-
жает действовать нагрузка.
И релаксация, и ползучесть
представляют собой сложные
явления сочетания в одном теле
свойств упругости и вязкого течения. Степень проявления этих
свойств у одного и того же материала зависит от ряда факторов и
в первую очередь от температуры и нагрузки, а у глинистых грун-
тов — от влажности и нагрузки. Повышение и той, и другой приво-
дит ко все более сильному проявлению жидкообразных свойств.
Деформация упругого и вязкого элементов в теле Фойгта
одинакова и равна деформации тела в целом, а усилие, действу-
ющее на тело, равно сумме усилий в упругом и вязком элемен-
тах:
т = у G + у 7 .
(4.193)
Уравнение (4.193) того же типа, что и (4.177), и его решение
может быть по аналогии с (4.187) записано сразу:
172
t
Г । 1 f* I G A i ,“| / G A
T = To H--------------I T exP — 4 dt \ exp------------------------------/ .
L J \ Ъ ) J \ 7] /
0
(4.194)
При постоянном напряжении (T=const=rc) находим
Т=_~ + (то----------М ехр (4.195)
G \ G ) \ ^ /
Если тс = joG, у — Yoi деформация остается постоянной; если тс>
> "(0G, деформация возрастает, а если тс < y0G, деформация убы-
вает, приближаясь к величине — асимптотически. При уо=О по-
G
лучаем
где
— ехр
Т3^ ~
G
(4.196)
(4.197)
Рис. 4.49. Упруго-вязкое те-
ло Кельвина
В начальный момент, когда / = 0, ехр (------— j = l и у по фор-
\ Т'з /
муле (4.196) равно 0. Во избежание путаницы величину Т3 для
тела Фойгта называют не временем релаксации (это понятие от-
носят только к напряжениям), а временем запаздывания дефор-
мации или временем последействия.
Вырожденные модели. Если в теле Максвелла модуль упру-
гости пружины Е обращается в бесконечность, иными словами,
если пружина превращается в жесткий
стержень, то модель вырождается в мо-
дель ньютоновой жидкости, а если коэф-
фициент вязкости т| -> оо , то амортиза-
тор становится твердым телом и модель
Максвелла вырождается в модель Гука.
Упруго-вязкое тело Кельвина. Из двух
пружин и амортизатора можно сделать
две эквивалентные невырожденные моде-
ли, показанные на рис. 4.49 и отвечаю-
щие так называемому телу Кельвина. У
этого тела имеются одновременно непре-
рывная упругая и смешанная связи. В отличие от тела Фойгта мо-
дель Кельвина испытывает при загружении мгновенную упругую
деформацию, а затем уже развивается явление ползучести. Реоло-
гическая формула тела Кельцина
K-H — F или К = Н|М.
(4.198)
Общий вид реологических уравнений для обеих этих моделей
одинаков и записывается так:
173
Рис. 4.50. Упруго-вязко-пластическое тело Бин-
гама
Л + Вт = С+ D-r, (4.199)
d t dt
где Л, В, С и D — выражения, составленные из Еь Е2 и ц,
причем эти выражения для систем а и б на
рис. 4.49 различны.
Вообще, когда невырожденная модель состоит более чем из
двух элементов, то для данной реологической зависимости между
напряжением и деформацией она не будет единственной. Если в
невырожденной модели, содержащей более двух элементов, ме-
нять как угодно расположение этих элементов, сохраняя, однако,
характер связей (упру-
гая, вязкая, смешанная),
реологическое уравнение
сохранит свой вид, но ко-
эффициенты в этом урав-
,нении будут изменяться.
Таким образом, такие мо-
дели реологически экви-
валентны.
Тело Кельвина не-
сколько ближе к поведе-
нию реальных твердых
материалов, чем тело
Фойгта.
Упруго - вязко-пласти-
ческое, или бингамово те-
ло. В телах Максвелла и Фойгта твердообразные и жидкообраз-
ные свойства проявляются одновременно, накладываясь друг на
друга. В отличие от этих тел, тело Бингама сначала проявляет уп-
ругие свойства твердого тела, а затем, по достижении усилием не-
которого предельного значения, превращается в жидкое тело, ха-
рактеризуемое вязким течением, скорость которого возрастает с
увеличением внешнего усилия. Таким образом, модель должна
быть составлена объединением простых реологических моделей Гу-
ка, Сен-Венана и Ньютона, как показано на рис. 4.50,а. Структур-
ная формула тела Бингама
В - Н — NI Stv.
(4.200)
На рис. 4.50,6 показан график зависимости между напряже-
ниями и скоростью течения у бингамова тела. Как видно из гра-
фика, зависимость между т и у имеет вид
т = тт + т] у , (4.201)
где тг — предел текучести; T] = tg р.
Рассмотрим движение бингамова тела в цилиндрической труб-
ке (рис. 4.51), подобно тому, как мы это делали при выводе урав-
174
нения Пуазейля (4.149). Подставляя в реологическое уравнение
(4.201) для бингамова тела значения (4.143) и (4.144)
d v
dr
и
получаем
dv __ р г
dr 2 1
(4.202)
откуда интегрированием при граничном условии г=/? и и=0 на-
ходим
v = — Г р ('R2~-r2}- — Тт (7? — г)1, (4.203)
7) L 4 I
которое отличается от уравнения для вязкой жидкости (4.146)
наличием второго члена в правой части. Распределение скоростей
v и напряжений т по сечению трубки показано на рис. 4.51,6.
В центре движущегося цилиндрического объема т=0 и по ме-
ре удаления от центра напряжения возрастают. В средней части,
где т< тт , образуется цилиндрическое ядро, показанное штри-
ховкой, которое движется вместе с окружающим материалом как
одно целое с постоянной по сечению скоростью. Напряжения
внутри этого ядра будут чисто упругими.
При хт =0 упругое ядро исчезает, и материал в трубке пред-
ставляет собой вязкую ньютоновскую жидкость, движение которой
подчиняется закону Пуазейля.
Кривые зависимости скорости течения v от напряжения в
пристеночном слое трубки т (при испытании в одном и том же
приборе) называются в реологии консистентными кривыми, или
кривыми течения. Если консистентная кривая не проходит через
начало координат, то материал является твердым телом (рис. 4.52).
Обратное утверждение может быть неправильным. Если кон-
систентная кривая, построенная по данным опытов с движением
материала в трубке, проходит через начало координат, то ма-
териал может быть как жидкостью, так и твердым телом, кото-
рое не «прилипает» к. стенке трубки и проскальзывает по ней.
175
Тело Шведова. Это упруго-вязко-пластическое твердое тело,
отличающееся от тела Бингама способностью к релаксации на-
пряжений (рис. 4.53). Его реологическая формула имеет вид
Sch w = Н — (М | StV), (4.204)
Рис. 4.52. Консистент-
ные кривые
1 — жцдкое телю; 2 — твер-
дое тело
Рис. 4.53. Реологическая модель упруго-
вязко-пластического релаксирующего тела
Шведова
а реологическое уравнение
7 = т° 4- . (4.205)
Первый член правой части характеризует скорость вязкого те-
чения, а второй — скорость упругой деформации, пропорциональ-
ную скорости изменения напряжений. Благодаря наличию преде-
ла текучести напряжения в теле Шведова релаксируют лишь
частично. Вместо формулы (4.190), характеризующей релакса-
цию максвеллова тела, для тела, изображенного на рис. 4.53,
Шведов получил формулу
т = Тт + (т0 — Тт) ехр (-, (4.206)
\ 7 р /
где to — мгновенное (начальное) напряжение;
Тр— время релаксации.
При t -+ со напряжение т релаксирует до остаточного нере-
лаксирующего напряжения тт.
Реологическое уравнение Шведова часто используется при
исследовании устойчивости грунтов [17].
Общее правило. Мы видели, что при выводе реологического
уравнения для модели с последовательным соединением элемен-
тов общая деформация системы в каждый момент времени равна
сумме деформаций ее элементов, а усилия в последних такие же,
как и усилие, приложенное к системе в целом (например, в слу-
чае тела Максвелла).
176
При этом удобно заменить модуль Е обратной ему величиной
•/=у, (4.207)
называемой упругой податливостью. Упругая податливость сис-
темы из последовательно соединенных элементов равна сумме по-
датливостей этих элементов. Точно так же суммируются вели-
чины, обратные коэффициенту вязкости (4.157) и называемые ко-
эффициентами текучести (не смешивать с пределом текучести тт);
г|>= — + — + . (4.208)
^1 ^2 Чп.
В случае параллельного соединения элементов в модели, на-
оборот, деформации элементов одинаковы и равны деформации
системы в целом, а сумма сил, действующих на элементы систе-
мы, равна общей силе, приложенной к телу (например, в случае
тела Фойгта).
Эти правила сохраняются при анализе любых реологических
тел, образованных последовательным и параллельным соедине-
нием простых моделей.
Физическая нелинейность. Выше мы молчаливо предполага-
ли, что реологические коэффициенты систем — модуль упругости,,
коэффициент вязкости, время релаксации и т. п. — остаются не- -
изменными в процессе деформирования. Такого рода реологичес-
кие тела называются физически линейными. Однако у реальных
материалов в ходе деформации изменяется структура, уменьшает-
ся или увеличивается плотность, нарушаются в той или иной ме-
ре внутренние связи и соответственно должны изменяться реоло-
гические коэффициенты, которые зависят и от абсолютной вели-
чины деформаций, и от скорости их развития. Такого рода систе-
мы называются физически нелинейными.
При этом реологические уравнения становятся уравнениями с
переменными коэффициентами, или квазилинейными. Графики за-
висимости напряжений от деформаций перестают быть прямыми
и становятся криволинейными. Упругие физически нелинейные
тела называют обобщенными телами Гука, а физически нелинейные
жидкости — обобщенными или ненъютоновыми жидкостями. Пере-
менную вязкость таких жидкостей В. Оствальд назвал структурной
вязкостью.
Геометрическая нелинейность. Характерное для большинства
реальных материалов отсутствие линейной связи между напря-
жениями и деформациями или скоростями деформаций может
вызываться не только изменением физических свойств материалов
в процессе деформирования, т. е. нелинейность может быть не
только физической .Во всех случаях, когда деформации нельзя
считать бесконечно малыми, существует и другой источник нели-
нейности, а именно, наличие деформации второго и более высоких
порядков малости, учет которцх требует перехода к рассмотрению
конечных деформаций.
177
Если обозначить первоначальную длину элемента до деформа-
ции через /0, конечную через Z, а отношение через X (эту вели-
ко
чину, называют главной частью деформации), то можно определять
конечную деформацию одним из следующих соотношений:
е77 — Ink = (к— 1)--(к— I)2 4~... — мера Генки;
= 1------ = (к — 1) — (к — 1 )2 + ... — мера Свейнгера; (4.209)
к
= у (к2- 1) = (к—+ (к—1)2 —мера Грина; (4.210)
= (к—1)-----(к—I)2— мера Алманси. (4.211)
Чтобы оценить количественную разницу между различными
мерами деформации, допустим, что растягиваемый стержень уве-
личил свою длину в два раза. Тогда по Коши ес =100%; по Ген-
ки вя =66%; по Свейнгеру es =50%; по Грину eG =150% и
по Алманси =37,5%.
Меры Алманси и Грина удобны для описания больших (ко-
нечных) упругих деформаций, однако для пластических деформа-
ций и течения следует пользоваться мерой Генки.
Большинство задач механики грунтов нелинейно как в фи-
зическом, так и в геометрическом смысле, и применение к их
исследованию методов линейной классической механики сплошных
сред связано со значительными погрешностями. Однако на это
идут ради упрощения выкладок, когда повышение точности
решений при учете нелинейности «съедается» неточностью в оценке
исходных характеристик, приближенностью модели литолого-тек-
стурного строения массива и незнанием его начального напряжен-
ного состояния.
Общее реологическое линейное уравнение. Общее реологиче-
ское уравнение, пригодное для всех рассмотренных выше как про-
стых, так и сложных линейных реологических тел, было предло-
жено Гогенэмзером и Прагером и может быть представлено в виде
Т — Тт — G Y + Y — Т^р т = G ("[ + Тр 7) — т\) т. (4.212)
При равенстве нулю некоторых параметров этого уравнения
можно получить как частные случаи уравнения для тел Гука,
Ньютона, Сен-Венана, Прагера, Максвелла, Фойгта, Кельвина,
Бингама, Шведова.
Термодинамическая классификация Ирме. Пользуясь безраз-
мерным отношением
у __ 7*р
и ” 7
1 з
времени релаксации к времени запаздывания, Ирме произвел
178
термодинамическую классификацию линейных реологических тел
следующим образом [62, 63]:
1) тела, у которых при циклической нагрузке не происходит
рассеивания энергии (чисто упругие), имеют Ти=1 и могут
быть названы гомотермическими ;
2) тела, у которых Ти<1, упругая деформация меньше, чем у
чисто упругих тел, и часть энергии, затраченной на деформирова-
ние, рассеивается, как у N-, F- и М-тел, могут быть названы экзо-
термическими',
3) тела, у которых Ти>1, деформация сопровождается осво-
бождением части внутренней энергии за счет изменения структу-
ры; эти тела могут быть названы эндотермическими.
10. СПЕКТРАЛЬНЫЕ РЕОЛОГИЧЕСКИЕ МОДЕЛИ
Как показывает опыт, реальные грунты, даже если они вполне
однородны, не следуют простым экспоненциальным зависимостям,
установленным для элементарных реологических тел Максвелла и
Фойгта. Поэтому для более точного моделирования реологических
свойств грунтов прибегают к сочетанию множества элементарных
упруго-вязких моделей, каждая из которых подчиняется экспонен-
циальному закону, но имеет иные по величине реологические ко-
эффициенты. Такого рода модели называются спектральными.
Единичная функция и внезапное загружение. Прежде чем пе-
рейти к рассмотрению основных спектральных моделей, необходи-
мо познакомиться с некоторыми математическими понятиями.
Пусть усилие изменяется во времени, как некоторая функция
F (/), изображенная графиком на рис. 4.54.
Рис. 4.55. График единичной функции
Допустим, что мы хотим изучить поведение какби-либо
системы, начиная с момента, когда к ней внезапно приложена
нагрузка, изменяющаяся по этому графику. Существует способ
сокращенной записи того факта, что до некоторого времени
нагрузка на систему не действовала (иными словами, для систе-
мы она до этого была равна нулю) и что отсчет времени начина-
179
ется с момента приложения нагрузки. Для этого пользуются так
называемой единичной функцией (называемой также функцией
Хевисайда, просто хевисайдом и, наконец, единичным прерыва-
телем). Эта функция, обозначаемая H(t) или e(t), имеет график,
изображенный на рис. 4.55, т. е. равна нулю при i<0 и единице
при />0, что записывается в таком виде:
(О, t <0; 1
^>0.} (4-213>
Ясно, что если мы умножим силовую функцию F[t) на H(t),
то все ординаты F(t) при /<0, умноженные на нуль, исчезнут,
при t >0 ординаты функции F(t), умноженные на единицу, сохра-
нят свое первоначальное значение. Полученный перемножением
график F(t) -H(t) показан на рис. 4.56.
Дельта-функция и мгновенная нагрузка.
Аналитическое представление внезапно при-
ложенной и сразу же снятой нагрузки
(мгновенное воздействие) осуществляется с
помощью так называемой дельта-функции
Рис. 4.56. График
Рис. 4.57. Дельта-функция
Дирака
Дирака, которая обычно обозначается через 6(0- Эта функция
имеет следующие особенности:
1) при всех t>0 и всех она равна нулю;
2) при /=0 она бесконечна;
3) интеграл от этой функции, взятой в пределах от —оо до
+ оо, равен 1.
Так как 6(0=0 при всех //0, то из этого свойства функции
следует, что интеграл от произведения из 6(0 на некоторую функ-
цию F(t) можно записать в виде
4-00 4-е
/ = J 8(0 F(t) dt = J 8(0 F (0 dt, (4.214)
------OO --c
где e — сколь угодно малая величина (рис. 4.57).
Так как пределы интегрирования очень малы, то на интерва-
ле от —8 до 4-е можно считать, что F(t)=F(O). Следовательно,
4-е 4-е ' -
I = J 8 (О F (0 dt = J 8 (О F (0) dt. (4.215)
180
Величина F(0) является некоторой постоянной, и ее можно
вынести за знак интеграла:
+е
I = F (0) j 8 (0 dt = F (0) 1 ,= F (0).
------------£
Итак,
4-00
J = J 8 (0 F (0 dt = F (0). (4.216)
— 00
Если дельта-функция равна бесконечности не при £=0, а в
точке t=a, то, рассуждая по предыдущему, получим
4-00
J 8(/ — a) F (t) dt = F (а). (4.217)
--00
Приведем без вывода еще некоторые важные формулы, связан-
ные с дельта-функцией:
8(а/) =—*— 8 (/) при а = const 0 ; (4.218)
|а|
о [F (/)] = ----------—
v ’ F' (0)
8 (f), если F (t) = 0 лишь при t = 0; (4.219)
F (0 8 (t^ а) = F (а) 8 (t — а). (4.220)
С помощью дельта-функции любую сосредоточенную в точке
нагрузку Ра можно представить как распределенную, интенсив-
ность которой меняется по закону
р (х) = Рас> (х —а). (4.221)
Действительно, интеграл
«4-£ а4-£
j р (х) dx — Ра j 8(х — a) dx = Ра1 = Ра . (4.222)
а—е а—£
Ударно приложенное усилие с импульсом J Pdt можно пред-
ставить как распределенное во времени по закону
5 + £
I = J Р 8 (/ — /у) dt = Р, (4.223)
'у“е
где /у — момент удара.
Согласно этой записи сила Р отлична от нуля только в момент
/у:
Р(0 = /8(/ —/у). (4.224)
Единичная функция Хевисайда H(t) связана с дельта-функ-
цией соотношением
181
H(t) = J 8(0 dt. (4.225)
--00
Так как при /<0 получим H(t) =0, а при />0
н (0 = 1,
то //(/) представляет собой разрывную функцию, испытывающую
скачок от 0 до 1 при t = 0. Интегрируя получим
t
J H(f) dt = tH(t). (4.226)
О
Согласно закону количества движения,
t
mv = J Р (0 dt (4.227)
— 00
(если начальная скорость равна нулю при t=— оо ). Если
сила действует ударно, то, подставляя (4.224) в последнее выра-
жение, получаем
t
v(/)= — [/8(/-L)d/ = -H(f-L), (4.228)
m т
т. е. скорость равна нулю до удара (при /</у) и равна — после
т
удара.
Дифференцируя H(t), получим, согласно (4.225),
~dH (Z) = 8 (/). (4.229)
d t
Таким образом, дифференцируя разрывную функцию Н(t), мы
пришли к дельта-функции.
Для обозначения знака функции пользуются функцией sign t
(читается «сигнум /»), которая равна —1 при /<0 и +1 при />0.
Очевидно, ее можно представить как
sign t = —. (4.230)
111
Между H(t) и sign / существует следующая зависимость:
sign/= 2Я(/)—1 , (4.231)
и интеграл от Н(/) равен
р (0 при / < 0 ;
( t при />0. 4 ’
Спектральная модель Фойгта. Эта модель (рис. 4.58) составле-
на из п элементов Фойгта, причем первый элемент получен при ус-
182
ловии, что в нем коэффициент вязкости rji равен нулю и, следова-
тельно, первый элемент превращается в модель тела Гука. У вто-
рого элемента, наоборот, Е=0 и он превращается в модель тела
Ньютона. Вместе эти элементы образуют тело Максвелла, что со-
77—<х»
Рис. 4.58- Спектральная модель Фойгта
общает спектральной модели Фойгта свойство релаксации напря-
жений. Значения соответствующих реологических коэффициентов
каждого из элементов спектральной модели различны [5].
Ползучесть при внезапно приложенной постоянной силе. Пусть
к ненапряженной модели прикладывается в момент t = 0 усилие
о(/) =РН(/), где Р — постоянная, a H(t)—единичная функция.
Согласно закону Гука,
е (0 = 4 Н (0 . (4.233)
£
Для вязкого тела Ньютона, согласно (4.216),
De (/) = — #(/), (4.234)
где через D обозначена операция дифференцирования по времени;
ds(0 = 4t-
a t
Интегрируя (4.233) от 0 до t, получим
е(0= у tH (t), (4.235)
так как при/=0 е=0.
Для тела Максвелла из (4.176) найдем
De = — £><г + — а; (4.236)
Вт;
De = 4 D[PH(t)] + — [PH(f)]-
E 7]
E>e = 4 8(0 + Z. Я(О,
В т;
183
так как, согласно (4.229),
DH(t) = §(/).
Интегрируя (4.236), найдем
t
t
•откуда
е
(4.237)
так как при t=0 е=0.
Для тела Фойгта
Es + flDe = PH (t).
Умножая на интегрирующий множитель
(4.238)
, находим
т]£) ехр
(4.239)
« после интегрирования получаем
(4.240)
так как при/=0 е=0.
Поскольку при последовательном соединении деформации скла-
дываются, то с учетом (4.237) и (4.240) найдем [5]
* (t) = р(4~ + ~Ч Н (0 + Р S 441 ~ехР (- — *У1Я(0- (4.241)
\ ~ Ei L \ *1* / J
Если из удлинения, вызванного единичной силой H(t). вычесть
мгновенное удлинение и удлинение, соответствующее установив-
шемуся вязкому течению, то оставшаяся часть при Р=1 будет
равна:
JL 1 г / Е- \1
2 "Г 1 —ехр H(t). (4.242)
s Е‘ L \ ъ Л1
Обозначенная через ф функция называется функцией ползу-
чести.
Величина — есть упругая податливость Jt. Вводя вместо
время запаздывания Т3 z перепишем (4.242) в виде
Ei
^(0= У Л [1-ехр(--М1 Я(0- (4.243)
£з L V Гз< 'J
184
Если число п составляющих спектральной модели Фойгта неог-
раниченно возрастает, так что для всех i, но сумма
«=з
при п со стремится к постоянной, то функция ползучести приоб-
ретает вид
= J /(Тз)
о
1 —ехр
3
(4.244)
Непрерывная функция j(T3) заменяет собой дискретный ряд
физических постоянных JiT\i и показывает, какая доля упругой
податливости системы имеет время запаздывания, находящееся в
соответствующем интервале dT3.
Функция /(Т3) называется функцией распределения времен
запаздывания, или спектром запаздывания.
Спектральная модель Максвелла. В случае спектральной моде-
ли Максвелла (рис. 4.59) изменение внутренней силы при релакса-
ции определяется уравнением
Рис. 4.59. Спектральная модель Максвелла
Р (/) = е Et H(t) + e ^ 8 (0 + е У Et ехр (/) (4.245)
\ Ч/ /
Если действует единичное удлинение &(t) то изменение
силы без учета первых двух элементов, образующих при тр = оо
и Е2— °° элемент Фойгта, называется функцией релаксации и
обозначается
" р \
х(о=2 £« ехр I—%-
(4.245а)
Когда п -> оо , это выражение принимает вид
Х(0 = Я(0 f у(Тр) ехр7-^И dTp, (4.246)
о \ Тр J
185
где у(Т^ ) называется функцией распределения времен релаксации,,
или спектром релаксации [5].
Так как у реальных тел спектры времен запаздывания и релак-
сации распределены непрерывно и характеристикой тел являются
формы соответствующих функций распределения, то использова-
ние функций ф(/) и %(/) для описания реологического поведения
материала существенно упрощает исследования. Они могут быть
найдены и экспериментальным путем [9, 38].
Между функциями ф(/), х(0, /(^з) и У(ГР ) существует тесная
связь, и они могут быть получены друг из друга чисто математи-
ческими приемами [57, 19, 64].
Лестничная модель вязко-упругого тела Близара — Кауэра.
Эта модель с непрерывной упругой связью, параллельно которой
распределены вязкие сопротивления, показанная на рис. 4.60, мо-
жет быть заменена эквивалентной реологической моделью, пока-
занной на рис. 4.61 [64]. Она эквивалентна также усложненной
реологической модели Терцаги (рис. 4.62), предложенной им для
иллюстрации протекания во времени процесса сжатия водонасы-
щенной глины.
При бесконечном увеличении числа элементов модели и умень-
шении каждого из них так, что распределение вязких элементов
становится непрерывным, мы придем к схеме упругого стержня,
деформирующегося в вязкой среде, оказывающей вдоль стержня
сопротивление деформации в каждой его точке, пропорциональное
скорости деформирования в данной точке (рис. 4.63). Эта модель
предложена Гроссом и Фуоссом [92].
Пусть упругое напряжение в некоторой точке х по длине стерж-
ня равно:
ау — » - (а)
где F — площадь поперечного сечения стержня;
Рх — усилие в стержне на расстоянии х от начала.
Тогда в соответствии с законом Гука
где X — перемещение в точке х к моменту времени t. Приращение
упругой силы Рх в данной точке с течением времени будет опреде-
ляться уменьшением за то же время силы Рв вязкого сопротивле-
ния деформации со стороны окружающей среды:
<)
где т) — коэффициент вязкости.
Составляя дифференциальное уравнение равновесия элемента
стержня dx, получим
186
Подставляя сюда (б) и (в), найдем
EF
д х2
7) ----- = О,
1 dt
S-T’Z—rfx_zT_z-_
SpZSSSISSSZ
р>---I ----
Р
Рис. 4/63. Модель Грос-
са — Фуосса
Рис. 4.62. Усложненная
модель Терцаги
187
Если продифференцировать уравнение (4.248) по х и подста-
вить в него значение напряжения в упругом стержне ау из (а)
и (б), то мы получим
да? _ с , (4.249>
dt дх*
т. е. дифференциальное уравнение, описывающее изменение уп-
ругих напряжений в стержне по его Длине и во времени.
Для двухфазной системы, в модели которой по рис. 4.63 пру-
жины изображают упругий скелет, оу представляет собой напря-
жение в последнем и, следовательно, является эффективным на-
пряжением.
Составляющие деформации глинистых грунтов. Исследования
[13] показывают, что полная сдвиговая деформация глинистого
грунта в общем случае состоит из четырех составляющих: 1) не-
медленной обратимой деформации (упругой); 2) немедленной
остаточной деформации (необратимой); 3) длительной обратимой
деформации (упругой) и 4) длительной остаточной деформации
(необратимой).
Немедленная деформация протекает с относительно высокой
скоростью* и ее часто называют также мгновенной. Немедленная
упругая деформация протекает в материалах со скоростью, равной
скорости распространения упругих колебаний в данном материале.
Вопрос о скорости немедленной пластической деформации в грун-
тах пока исследован недостаточно.
Остаточная деформация тем больше по величине, чем больше
действующая нагрузка. Эта деформация развивается одновремен-
но с обратимой, и величина ее может быть установлен^ только
как разность между полной и обратимой деформациями.
Немедленная остаточная деформация сдвига глины по своей
абсолютной величине тем больше, чем больше разность между
приложенным сдвигающим напряжением т и некоторой его вели-
чиной тп> называемой пределом упругости.
Прямая (при загружении) длительная упругая деформация,
как показали опыты, практически линейно связана с напряжени-
ями и поэтому подчиняется принципу независимости действия сил
так же, как и мгновенная упругая деформация. Скорости прямой
и обратной (при разгрузке) длительных упругих деформаций с
большой точностью подчиняются закону вязкости, и эти деформа-
ции могут быть названы вязко-упругими. Они протекают неодина-
ково, образуя петлю гистерезиса, и носят энтропийный характер
подобно эластической деформации полимерных материалов. Пос-
ле того как нагрузка превзойдет некоторый предел, называемый
пределом упругости, часть деформации после разгрузки сохраня-
ется, являясь необратимой (пластической) деформацией. Дли-
тельная остаточная деформация протекает со скоростью, которая
возрастает с увеличением разности (т — тт) между сдвигающим
188
напряжением т и некоторой величиной, называемой пределом те-
кучести (тт). Эту часть деформации можно рассматривать как
деформацию вязко-пластического течения. У глин тг >^п, но чем
выше влажность, тем меньше разность т:г — т:п и тем относи-
тельно больше необратимая доля деформации.
График деформации глинистого грунта. График изменения во
времени составляющих полной деформации в общем случае име-
ет вид, показанный на рис. 4.64.
Кривая 0—4 предста-
вляет собой график де-
формации при загруже-
нии, состоящий из верти-
кального участка 0—2
мгновенной деформации
и участка 2—4 длитель-
ной деформации, проте-
кающей, начиная от точ-
ки 3, с почти постоянной
скоростью. В момент вре-
мени t2 нагрузка удале-
на.. Участок кривой 4—7
представляет собой гра-
фик обратной деформа-
ции, состоящий из участ-
ка 4—6 обратной мгно-
венной и участка 6—7
длительной обратной уп-
ругой деформации после
разгрузки.
На рисунке отдельно
Рис. 4.64. Кривая протекания деформации
грунта во времени
нанесены затухающая
кривая длительной упругой деформации 0—а и прямолинейный
(приближенно) график 2—5 длительной деформации вязко-пласти-
ческого течения. Чтобы построить график 2—5> через точку 2 (ко-
нец отрезка мгновенной деформации) проводят прямую, парал-
лельную участку 3—4. Если отложить по оси ординат от точки О
отрезок, равный величине мгновенной упругой деформации при
разгрузке (4—6), то получим точку /, отсекающую величину мгно-
венной упругой деформации. Разность ординат точек 2 и 1 дает ве-
личину мгновенной пластической деформации вп.м.
График 2—5 пересекает кривую 4—7 в точке 5. Разность орди-
нат точек 1 и 5 дает величину полной пластической деформации
вп. Такую же величину имеет ордината конечного горизонталь-
ного участка кривой 6—7. Абсциссу точки 3 можно рассматривать
как время t\ затухания длительной упругой деформации.
Все сказанное выше относится только к деформированию гли-
нистого грунта при постоянной плотности и влажности (закрытая
система). Изменение плотности и влажности грунта в процессе
189
деформации вносит существенные отклонения в характер рассмот-
ренного графика.
Реологическая модель связного грунта. Принцип действия ме-
ханической модели двухфазного сплошного тела Терцаги, рас-
смотренной в п. 7 этой главы, полностью сохранится, если пру-
жину из сосуда (рис. 4.35) вынести наружу и соединить ее попе-
речным стержнем с поршнем так, чтобы они перемещались парал-
лельно самим себе без перекосов (рис. 4.65,а). При этом мы
Рис. 4.65. Реологические модели консолидации грунтов
а — Терцаги — Фойгта; б — Денисова; виг— Тана; д — Бюргерса; е — Мураямы
получим реологическую модель Фойгта. Таким образом эти две
модели совпадают между собой. Модель глины типа Кельвина ис-
следовалась А. И. Ксенофонтовым [30]. Хорошо отвечает свойст-
вам реальных глинистых грунтов модель Денисова [18], которую
можно представить как параллельное соединение моделей Бинга-
ма и Максвелла (рис. 4.65,6). Модель Тана [101], изображенная
на рис. 4.65,г, реологически эквивалентна модели Бюргерса. По-
следняя имеет реологическую формулу Bu = М — F (рис.
4.65,6). Модель Мураямы [98], показанная на рис. 4.65,е, явля-
ется несколько упрощенной моделью Денисова. На рис. 4.65,в
показана модель, также принадлежащая Тану и отличающаяся
излишней громоздкостью.
Все эти модели глинистого грунта предлагались для изобра-
жения процесса уплотнения водонасыщенной глины, которое про-
исходит за счет выжимания воды из пор грунта и представляет
собой объемную деформацию (консолидация глины).
Однако и чисто сдвиговые деформации глинистого грунта при
неизменной влажности протекают как реологический процесс. Со-
ответствующая реологическая модель, предложенная автором,
приведена на рис. 4.66. Она представляет собой последовательное
соединение моделей Кельвина и Шведова. Пружина 1 дает при
приложении нагрузки мгновенную упругую деформацию. Следую-
190
щий за пружиной элемент Фойгта моделирует длительную упру-
гую деформацию.
Как только будет превзойден предел текучести тт (элемент
5), произойдет мгновенная остаточная деформация в виде смеще
ния люфтового элемента 4. После этого начнется длительная
необратимая (остаточная) деформация. В случае закрепления
деформации, часть усилия т,.равная г—гТ, бу-
дет релаксировать до значения тт.
Коэффициент релаксации. На рис. 4.67 при-
ближенно показана связь между явлениями
релаксации и ползучести в глинистом грунте.
Если при некоторой скорости деформирования,
изображаемой кривой /, довести деформацию
; до значения d и сохранять ее далее постоян-
ной, то напряжение постепенно релаксирует
до значения Т2, соответствующего той же де-
формации по кривой более медленного дефор-
мирования 2 и может продолжать падать даль-
ше, имея пределом значение
вующее кривой 3 бесконечно
?
Рис. 4.66. Реологическая
модель сдвига грунта
1—7 — элементы модели
'Ср.п, соответст-
медленного за-
Lpn
Рис. 4.67. Связь между релакса-
цией и ползучестью
По лз учесть
Релаксация
£
гружения. Напряжение тр,п называется пределом релаксации.
Наоборот, если сохранять постоянным напряжение Ть то будет
происходить деформация ползучести, которая постепенно достига-
ет значения 82 и может расти далее, теоретически имея пределом
опять-таки кривую 3, хотя экспериментальные кривые ползучести
и релаксации при t -> оо не совпадают. При достаточно высо-
ком значении напряжения т, большем, чем некоторое значение
*ср.п, деформация будет возрастать вплоть до разрушения образ-
ца.
В опытах, проведенных в лаборатории механики грунтов
ДИИТ В. А. Мизюмским, было доказано, что при всестороннем
равномерном сжатии глинистых грунтов без возможности консо-
лидации, явления ползучести и релаксации отсутствуют. При трех-
осном сжатии релаксирует лишь та часть напряжений, которая
представлена девиаторной составляющей тензора напряжений.
191
В. А. Мизюмский [41] получил следующую эмпирическую
формулу, хорошо описывающую процесс релаксации напряжений:
——
х -I- т0 (1 — £р) е , (4.250)
где т — напряжение в сечении через время t после начала
релаксации;
То — начальное напряжение;
тр — предел релаксации напряжений;
b и т — параметры процесса,релаксации.
Величину
= (4.251)
*0
назовем коэффициентом релаксации.
Оказалось, что kp не зависит от то и является величиной по-
стоянной для данного глинистого грунта при данном его физи-
ческом состоянии. Это означает, что с изменением то в некотором
отношении в таком же отношении меняется и конечное напряже-
ние .
П. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
Удельная потенциальная энергия. При линейной зависимости
между напряжениями и деформациями потенциальная энергия
упругой деформации тела равна полусумме произведений всех
компонентов напряжения на сопряженные с ними деформации.
Эту энергию, отнесенную к единице объема, называют удельной
потенциальной энергией упругой деформации или удельным уп-
ругим потенциалом:
77 = yCTv£O’ (4.252)
(следует иметь в виду, что под при i j подразумеваются
деформации сдвига, равные — т0 ).
В общем виде можно записать
п = ± ТНТЛ.
(4.253)
Через главные напряжения и главные деформации энергия
выразится так:
~ ~2~ £1 + °н £п “Ь °ш еш) • (4.254)
Заменяя в (4.253) деформации через напряжения и пользуясь
обобщенным законом Гука, получим
П “ТБ" а22 + а|з — 2 v (аи а22 + <^22 п'зз + (Тзз аи) +
2 £ _ .
+ 2(1+>) (с^ + ^з + п*,)] (4.255)
или в главных напряжениях
п = l°i + сти + — 2 v (а, ап + ап а„, + ащ а,)]. (4.256)
192
При других упругих постоянных (G и К)
„ (<Ч - О„)а + (<ГП - <Tni)2 + (ffin - 0J )S (<h + <*П + ffIIl)2 9[.-4
n= J2G r- 18/< 1,4.207)
. Аналогичным образом найдем энергию упругого формоизмене-
ния, используя выражения для девиатора напряжений и девиато-
ра деформаций:
п — (Од ~ qi^2 + (qn ~ Ст1")2 + (q,n ~ q^2 = Зт°кт /4 258)
D ~ 12 G 4G ' ' ‘ 7
Энергия объемной деформации, соответствующая шаровому
тензору напряжений, будет равна:
_ (gl + qn + ^щ)2 _
н~ 18 К ~ 18 К
Сопоставляя (4.257) с двумя последними выражениями, видим,
что
(4.259)
n = nD + nH. (4.260)
Уравнение (4.258) можно представить также в виде
П = 3 (1+") Т2 . (4.231)
£> 2 f окт’ 4 /
(4.262
т. е. упругая работа интенсивности напряжений на интенсивности
деформации в данной точке равна удельной энергии формоизме-
нения в той же точке. Эта зависимость объясняет удобство вве-
дения понятий об интенсивности напряжений и деформации.
Вместо (4.259) можно написать *
(4-263)
и в общем виде
no=~DnD^ (4-264)
Пн = — НН..
п 2 н А
Из последнего выражения следует, что удельная упругая ра-
бота внутренних сил, идущая на изменение объема, равна поло-
вине работы компонентов шарового тензора напряжений на ком-
понентах шарового тензора деформаций и что аналогичное соот-
ношение существует и для работы формоизменения. Распределе-
ние напряжений в упругом теле всегда таково, что потенциальная
энергия деформированного тела минимальна.
Предельные значения упругих постоянных. Выразим удельный
упругий потенциал через деформации:
7 Зак. 530
193
х[—4- (£н + £22 + езз)2 + в?! + + в|з + 2 (£Ь + е23 + е31)1' (4-265)
Так как потенциальная энергия упруго-деформированного те-
ла не может быть отрицательной, то из (4.265) следует необходи-
мость неравенств
—— > 0 и ---------> 0.
1 + 1 —2 v
Это означает, что Е не может быть отрицательной величиной,
a v не может быть ни отрицательным, ни больше чем 0,5 и долж-
но находиться в пределах 0 *<Д5 при упругом деформировании.
Из (4.265) следует также, что удельный упругий потенциал
является однородной квадратичной функцией от компонентов тен-
зора деформации.
Соотношения Грина. Так как удельная потенциальная энергия
упругой деформации является функцией
П — П (ец, 822, egg, е12, 833, е31), (4.266)
то полный дифференциал <1П имеет вид
dn=-^~ dsu + дП - de22 + дП A . дП d £33 + d ®i2 4~
V £11 д £2з д £33 д £1а
+ дП d е2з 4- - дП de31 (4.267)
9 £33 д £31
или в краткой записи dn = - j- (4.268)
С другой стороны, это приращение потенциальной энергии
равно элементарной работе напряжений на приращениях соответ-
ствующих упругих деформаций:
dn = <Тц d 4" <т22d 832 4* O33 d 8gg -f- O12 d si2 “I- ^2s d 833 Ogj d egj (4.269)
или кратко
dn = Scry dst). (4.270)
Сравнивая правые части полученных выражений (4.267) и (4.269),
найдем соотношения, полученные Грином:
= П11; 4^- = ; ~~ = и т. д„ (4.271)
0 £ц 0 £33 0 S33
или в сокращенной записи
дП
д 4 ‘
Таким образом, производная от потенциальной энергии дефор-
(4.272)
194
маций по любой компоненте тензора деформаций дает сопряжен-
ную компоненту тензора напряжений. Эти соотношения действи-
тельны и в том случае, если материал не подчиняется закону Гука.
Согласно теореме Эйлера об однородных функциях, произведе-
ние показателя однородной функции на саму функцию равно
сумме произведений частных производных однородной функции по
всем независимым переменным на эти переменные. В данном слу-
чае показатель равен двум, и, следовательно,
0 гг д П . д П । д П
2П= ----------------------------
(7 8ц о 0 £33
, дП . дП
s88 + "7-------- е12 +
О 812 0 £23
s23 +
+:-^~ (4.273)
или в сокращенной записи
П = — S е/;.. (4.274)
Выразив в (4.265) деформации е/у через напряжения azy с
помощью закона Гука, мы увидим, что П является однородной
квадратичной функцией от компонентов тензора напряжений.
Тогда, согласно теореме Эйлера, можно записать, что
д==±2-££_(Т (4.275)
2 дау 4 v ’
Сопоставляя это выражение с (4.252), получим
= (4.276)
т. е. частные производные от удельной потенциальной энергии де-
формации по компонентам тензора напряжений равны сопряжен-
ным компонентам тензора деформаций (теорема Кастилиано).
Эти соотношения действительны только в том случае, если ма-
териал следует закону Гука.
12. РАССЕЯНИЕ ЭНЕРГИИ
ПРИ НЕОБРАТИМЫХ ДЕФОРМАЦИЯХ
Внутреннее трение в твердых телах. Представим себе, что
упруго сжатое всесторонним давлением твердое тело внезапно
освобождено от нагрузки. Оно начнет расширяться, и упругая по-
тенциальная энергия, накопленная в теле при его деформирова-
нии, преобразуется в кинетическую энергию движения частиц те-
ла, возвращающихся в первоначальное положение, не встречая
сопротивления внешних сил.
В тот момент, когда тело примет первоначальную форму и раз-
меры, потенциальная энергия системы станет равной нулю, а ки-
нетическая энергия частиц достигнет максимума, и частицы будут
продолжать свое движение, что вызовет расширение тела. Этому
7* Зак. 530
195
расширению теперь начнут сопротивляться внутренние силы свя-
зи, а в теле вновь начнет накапливаться потенциальная энергия
деформации растяжения, в которую будет переходить кинетиче-
ская энергия движения частиц.
Когда деформация прекратится, тело снова начнет сжиматься
и опять пройдет через первоначальное состояние. Затем оно будет
расширяться и т. д. Таким образом, возникнут упругие колебания
тела, которые должны были бы продолжаться бесконечно, если бы
во время движения не происходило рассеивания энергии, приво-
дящего к постепенному затуханию колебаний. Так как в действи-
тельности подобные колебания реальных тел затухают, то это оз-
начает, что в реальных материалах происходит рассеяние (дисси-
пация) энергии. Но из этого следует, что в системе существует
трение между частицами, которое называют внутренним трением
твердого тела. При этом направленное колебательное движение ча-
стиц постепенно перейдет в беспорядочное по ориентации колеба-
тельное движение теплового характера. Тело нагреется, в резуль-
тате чего произойдет соответствующее тепловое расширение, кото-
рое затем исчезнет из-за постепенной теплоотдачи в окружающую
среду.
Исходя из закона сохранения энергии мы должны заключить,
что
77 + К Н- Q = const, (4.277)
где П — потенциальная энергия деформации;
К—кинетическая энергия упорядоченного движения частиц
(при колебаниях тела);
Q — кинетическая энергия беспорядочного (теплового) коле-
бательного движения частиц.
Диссипация энергии деформаций. Рассеивание энергии проис-
ходит как при пластических деформациях, так и при вязком тече-
нии. В первом случае внутреннее трение пропорционально вели-
чине деформации и называется сухим, или кулоновым. Во втором
случае диссипация вызвана вязкостью и пропорциональна скоро-
сти деформации (жидкостное трение). Обычно в реальных телах
диссипация энергии существует в обеих этих формах.
Логарифмический декремент колебаний. Так как из-за внут-
реннего трения колебания постепенно затухают и их амплитуды
уменьшаются, удобно характеризовать этим явлением внутреннее
трение системы. Обычно в качестве меры внутреннего трения ис-
пользуют так называемый логарифмический декремент, представ-
ляющий собой логарифм отношения амплитуд а двух последова-
тельных колебаний:
О = In . (4.278)
Эта величина связана с рассеиваемой энергией простой зависи-
мостью
196
(4.279)
где Д№—потерянная (рассеянная) энергия, равная 6Q;
W— полная энергия колебаний.
Релаксационная диссипация энергии. Диссипация энергии за
счет вязкостных свойств системы существенно зависит от частоты
колебаний. При очень малых частотах, когда время деформирова-
ния гораздо меньше времени релаксации, диссипация энергии
практически отсутствует, и процесс протекает как квазистатиче-
ский и чисто обратимый (упругий). При очень больших частотах
релаксации не происходит, и колебания большинства частиц со-
храняют постоянную амплитуду. В том случае, если период коле-
баний Т и время релаксации Тр соизмеримы, затухание носиг
особенно интенсивный характер, причем максимальное внутреннее
трение соответствует такой частоте ®, при которой произведение
(оТр ~1.
Внутреннее трение, связанное с явлением релаксации, т. е. с
жидкообразными свойствами системы, не зависит от амплитуды
колебаний тела. Исследования показывают, что вязкое трение в
твердых телах непосредственно сопряжено с перемещением точеч-
ных дефектов, их диффузией. Вместе с тем перемещение дислока-
ций в значительной мере связано с рассеиванием энергии, завися-
щим от амплитуды колебаний (сухое внутреннее трение).
Снижение сопротивления деформации. Рассеивающаяся часть
энергии деформации вызывает в материале еще до начала течения
два процесса, ведущих к снижению сопротивления материала де-
формациям:
1) необратимую перестройку структуры материала. При этом
по площадкам сдвига и отрыва расположение и ориентировка ча-
стиц становятся такими, что разрушение требует минимального
усилия. Это стадия как бы расслабления материала, и расходуе-
мая на него часть энергии представляет собой энергию активации;
2) нагревание материала, которое ведет, как правило, к сни-
жению сопротивления разрушению.
В процессе течения практически вся энергия диссипации рас-
ходуется на нагревание материала. Если процесс идет медленно,
то получаемая теплота рассеивается в окружающее пространство,
и повышение температуры тела может не улавливаться, т. е. про-
цесс следует рассматривать как изотермический.
Если кроме постоянного деформирующего усилия приложить
также небольшую пульсирующую нагрузку, вызывающую колеба-
ния тела, то благодаря явлению диссипации энергии сопротивле-
ние материала течению или разрушению от постоянной нагрузки
резко снижается. Это явление в грунтах быдо исследовано в лабо-
ратории ДИИТ В. И. Стороженко.
Интенсивность процесса затухания колебаний зависит как от
их частоты и амплитуды, так и от свойств материала. У материа-
197
лов с интенсивным затуханием колебаний влияние последних на
прочность особенно значительно.
Объемная вязкость. Явление затухания колебаний при раз-
грузке после всестороннего сжатия тела говорит о том, что при
чисто объемной деформации также имеет место вязкое сопротив-
ление. Соответственно необходимо ввести понятие об объемной
вязкости твердого тела т|об) и при учете явления объемного
вязкого течения мы должны внести поправку в соответствии с
законом Ньютона (4.142) в формулу (4.88), заменив ее выраже-
нием
a„ = K6 + W, (4.280)
где 6— скорость объемной деформации.
Мощность деформации. Работу деформирования, отнесенную к
единице объема и выполняемую за единицу времени, называют
удельной мощностью деформаций и обозначают Л:
А=~=аЬ. (4.281)
Подставляя сюда (4.280), получим удельную мощность дефор-
мации при всестороннем сжатии упруго-вязкого тела:
Л = К66 + т]о662. (4.282)
Первый член в правой части представляет собой обратимую
или консервативную часть работы напряжений, а второй — рассе-
ивающуюся или диссипативную часть этой работы. Общая работа
напряжения за время t равна:
t t * 2
А = J Adt = К J 6 6dt + т]об J Odt. (4.283)
0 0 о
Вязкое течение при всестороннем сжатии происходит за счет
заполнения макропор и пустот в материале, а при высоких напря-
жениях также и за счет его общего уплотнения вследствие пере-
стройки внутренней структуры.
Изменение внутренней энергии и энтропии при деформации.
Изменение свободной энергии в изотермическом обратимом про-
цессе равно работе, совершенной внешними силами над системой.
В п. 3 главы 3 было показано, что с учетом принятого правила зна-
ков для работы и при площади сечения, равной единице,
— dA = pdh, (4.284)
где р — давление;
dh — перемещение.
198
(4.285)
Согласно (3.70)
/ dA \ =Г dF \
\ dh )т )т’
т. е. давление (напряжение) равно изменению свободной энергии
на единицу сжатия. При ненапряженном состоянии (при р=0)
свободная энергия минимальна. Следовательно,
=0 при h — hf). (4.286)
При малых р можно принять скорость изменения F прямо про-
порциональной ускорению этого изменения:
(-Tri -(-TS-i <4-287)
\ dh /„ \ dh2 /
' ‘т 4 'т
и тогда давление можно рассматривать как линейную функцию
деформации, причем коэффициент пропорциональности определя-
ется кривизной графика свободной энергии. При больших дефор-
мациях эта зависимость не будет линейной.
С другой стороны, производная от F по h при Т=const
—Т (4.288)
\dh }т k dh )т к dh )т’
откуда .
р= —Т , (4.289)
Р \dh )т \ dh )т’
где первый член представляет собой изменение внутренней энер
гии, а второй — изменение энтропии при деформации
Если процесс неизотермический (dT=£0),
dF = dU~ TdS — Sdt.
Подставляя сюда dU, получим
dF = —pdh — SdT.
Используем известное свойство производных
d IdF\ d [ dF\
dh \dT )“ dT \ dh /
h 4 ZT
и подставим сюда значения производных от F из
(3.58). Тогда
/ dS \ _ ( др \
\ dh L \ dT
\ JT \ /Л
Величина представляет собой температурный коэф-
' 'л
фициент напряжения, т. е. напряжение, которое возникает в зажа-
том по длине стержне (ft=const) при изменении температуры на
(4.290)
(4.291)
(4.292)
соотношений
(4.293)
199
1°. Эту величину легко измерить, и численно она равна изменению
энтропии при деформации в изотермических условиях. На рис.
4.68 показан график зависимости р от Т при постоянной длине h.
Таким образом, тангенс угла наклона касательной к этой кри-
вой в некоторой точке i равен энтропии при изотермической де-
формации с температурой Т<. Отрезок ОА, равный, согласно
(4.289) и (4.293),
р-Т ,
\dT)h \dh )т
(4.294)
определяет изменение внутренней энергии при единичной дефор-
мации. Следовательно, кривые, подобные изображенным на рис.
4.68, позволяют судить о соотношении между внутренней энергией
Рис. 4.68. График зависимости
напряжения от температуры
при постоянной длине образца
Рис. 4.69. Гистерезис эла-
стической деформации
и энтропией и об их изменении в ходе деформирования. Если
график зависимости изображается прямой,тони (7, ниХ не зависят
от температуры, а если эта прямая проходит через начало коор-
динат, то упругие напряжения в теле возникают только вследст-
вие изменения энтропии. Последнее характерно для эластических
деформаций, которые полностью обратимы, но обнаруживают
гистерезис при нагрузке и разгрузке (рис. 4.69).
Таким образом, энергия, затраченная на прямое деформирова-
ние, не равна энергии, выделяемой при обратном деформировании
(последняя меньше). В ходе процесса обратной эластической
деформации происходит некоторая необратимая потеря энергии
деформирования, поглощаемая материалом. Это может 'быть объ-
яснено только тем, что при прямой деформации изменение струк-
туры происходит в виде обратимого изменения ориентировки ча-
стиц, тогда как у обычных твердых тел упругость связана в пер-
вую очередь с изменением внутренней энергии, и при деформации
свободная энергия возрастает. У эластических материалов увели-
чение деформаций сопровождается уменьшением энтропии, т. е.
200
увеличением степени упорядоченности строения. Следовательно,
согласно уравнению (3.59)
dF = — SdT-pdV,
мы должны заключить, что в случае упругой деформации свобод-
ная энергия тела изменяется за счет второго члена, а в случае эла-
стической — за счет первого члена.
Поперечная ползучесть. В опытах по исследованию поперечных
деформаций при ползучести бетона, проведеных Глэнвилем и
Томасом (1939 г.), оказалось, что при наличии продольной ползу-
чести сжатия образца бетона поперечная ползучесть практически
почти отсутствует, и коэффициент Пуассона в этих опытах был
всего 0,044. Очевидно, при ползучести бетон затекал в имеющиеся
в нем пустоты, почти не давая поперечного расширения образца,
и общая объемная плотность материала за счет уменьшения
объема пустот возрастала. Аналогичный результат для некоторых
видов грунтов был получен Е. И. Медковым.
Это означает, что при объемной деформации пористых материа-
лов кроме упругой деформации возникает также и объемное тече-
ние. С другой стороны, при сдвиговых деформациях подобных
материалов одновременно также меняются их объемы (за счет
перестройки структуры) и пористость.
Дилатация и контракция. Если при сдвиге материал увеличи-
вается в объеме вследствие перестройки структуры, то такая объ-
емная деформаций называется дилатацией (или дилатансией).
Если же объем материала при сдвиге уменьшается, то объемная
деформация называется отрицательной дилатацией, или сдвиговой
контракцией. Термин «дилатация» был введен Рейнольдсом, впер-
вые обратившим внимание на это явление [100].
13. ФЕНОМЕНОЛОГИЧЕСКИЕ РЕОЛОГИЧЕСКИЕ МОДЕЛИ
Если спектральные модели появились как результат усложне-
ния более простых реологических моделей с целью приведения их
в соответствие с экспериментальными данными, то модели, о кото-
рых пойдет речь далее, возникли как результат непосредственно-
го поиска таких аналитических зависимостей, которые бы наилуч-
шим образом описывали наблюдаемые в действительности соотно-
шения между напряжениями, деформациями и их скоростями.
Эти модели получили не очень удачное название теорий, ко-
торое мы, однако, сохраним, как сохраняется применяемое в ана-
логичном аспекте название «теория» по отношению к различным
критериям прочности.
Таких реологических теорий, выдвинутых специалистами по
механике сплошной среды, несколько, но мы остановимся в этой
главе на трех основных: теории упрочнения, теории старения и тео-
рии наследственности.
Теория упрочнения. Согласно этой теории скорость деформации
зависит от величины действующих напряжений и от абсолютной
201
величины уже достигнутой деформации. Соответствующая зави-
симость в неявном виде запишется так:
Фу (а, е, е) = 0 (4.295)
или в виде, разрешенном относительно е:
ё = /у (а) фу (е).
Вид этих функций подбирается так, чтобы наилучшим образом
описать экспериментальные данные. Если рассматривать явление
затухающей ползучести, то при постоянном о получается, что ско-
рость деформации убывает по мере возрастания самой деформа-
ции, т. е. материал как бы упрочняется по мере деформирования,
что и отражено в названии теории.
Теория старения. В этой теории рассматривается непосредст-
венно величина деформации как функция не только напряжения,
но и времени в виде:
Ф (о, е, 7) = 0 (4.296)
или в виде е = 0, (4.297)
как, например, . е= у+<*''* (9 (4.298)
где r(t) — некоторая функция времени, например
-с (0 = е~а — и др.
Так как эта теория позволяет непосредственно учитывать изме-
нение свойств материала во времени и приводит к положению, по
которому затухание скорости деформации связывается с увеличе-
нием вязкости жидкообразной «составляющей» материала (как бы
с загустеванием последней), то ее называют теорией старения. По-
добный термин уже давно применяется По отношению к изменению
во времени механических свойств бетона. Значение функции x(t}
при t -> со называют обычно мерой ползучести, прибавляя имя
автора, предложившего тот или иной вид функции r(t).
Теория наследственности. Теория наследственности ведет свою
историю от Больцмана, который впервые предложил считать, что
протекание деформации материала в данный момент определяется
предшествующим ходом деформирования и является результатом
как бы «наследования» изменений свойств материала, вызванных
историей его деформации.
Обычно предполагают, что при наличии в прошлом многократ-
ных деформаций, их влияние на деформацию, протекающую в на-
стоящее время, может быть установлено простым суммированием
соответствующих эффектов (принцип суперпозиции).
202
Если к некоторому времени т произошла деформация е(т),
длившаяся время Дт и затем задержанная, как это имеет место
при релаксации, то напряжение в момент времени t>x будет по
Больцману равно:
<Т (/, е) = Е е (f) — f (t — т) е (1) Д т •,
где f(t—т) —монотонно убывающая функция, характеризующая
уменьшение со временем влияния прошлой деформации.
При наличии в прошлом нескольких деформаций, используя
принцип суперпозиции, мы получим
о (/, s) = Е е (/) — S f (t — nz) е (tz) Д .
При непрерывном процессе деформирования следует перейти
от суммы к интегралу
t
ст(/, e) = Ee(f) — J f (t — т) е (т) dz. (4.299)
------------------00
Это выражение и называется уравнением Больцмана.
Вид функции f(t—т), характеризующей реологические свойст-
ва материала, находят либо теоретически на основе микрострук-
турного анализа, либо непосредственно из опыта, подобно тому
как определяют модуль Е или вязкость т|. Функцию f(t — т) назы-
вают ядром интегрального уравнения (4.299).
Сам Больцман выбрал для ядра функцию > н0 по-
лучил решение, не совпадающее с данными опыта. К настоящему
времени предложен ряд видов функций f(t — т), полученных в
результате экспериментов с различными материалами. Соответст-
вующие результаты для грунтов будут нами рассмотрены во вто-
рой части книги.
Указанные выше три модели служат основой для дальнейшего
развития феноменологических теорий, которое идет в направлении
учета переменности модулей материала в ходе деформирования и
уточнения вида функций, определяющих временное поведение ма-
териала.
Глава 5
ГРУНТЫ КАК ОБЪЕКТ СТАТИСТИЧЕСКОЙ МЕХАНИКИ
1. ИСХОДНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Теория вероятности оперирует следующими основными терми-
нами.
Испытание — осуществление некоторого комплекса воздействий
на заданную систему, которое может быть повторено сколь угодно
большое число раз. Искусственное осуществление такого воздейст-
вия с целью выяснения его результатов называется опытом, или
экспериментом.
Исход испытания — любое явление, происходящее в результате
реализации некоторого воздействия на систему. Приведем в каче-
стве примера бросание жребия с помощью монеты. Это испытание
состоит из ряда подготовительных этапов: выбор монеты (напри-
мер, монета не должна быть погнутой и т. п.), выбор места для ее
подбрасывания и способа подбрасывания, выбор условий оценки
результата (например, если монета упала на ребро и покатилась,
это испытание исключается) и т. д. Исход испытания — появление
сверху герба или решки.
Событие — появление некоторого заданного или ожидаемого ис-
хода, например именно герба или именно решки. Часто понятие
«событие» применяют в том же смысле, что и исход.
Достоверное событие — которое происходит неизбежно в каж-
дом испытании.
Невозможное событие — которое не может произойти ни в од-
ном из испытаний, как бы ни было велико число повторений.
Случайность, или случайное событие — которое может либо
произойти, либо не произойти при испытании, либо в каждом ис-
пытании может происходить несколько по-иному. Соответственно
случайной величиной, или стохастической переменной, называют
величину, значение которой изменяется случайным образом.
Несовместимые события. Случайные события называются не-
совместимыми, если они не могут появиться одновременно. Случай-
ные события образуют группу попарно несовместимых событий, ес-
ли при каждом испытании появляется одно и только одно из них.
Полная группа событий представляет собой минимальное число
попарно несовместимых событий, причем одно из них должно
обязательно осуществиться при испытании.
204
Частота и частость. Рассмотрим серию из W испытаний. Пусть
нас интересует некоторое событие А. Если это событие произошло
Па раз, то отношение
^Л=Л- (5.1)
называется частостью события А в данной серии испытаний. В
тех случаях, когда это не будет вызывать сомнений, мы будем
употреблять обозначения п и W без индексов. Величину п обычно
называют частотой, или повторяемостью.
Очевидно, W представляет собой величину, которая может
принимать любое значение в пределах между 0 (когда п = 0) и1
(когда n=N):
0<№<1.
В случае, если событие А невозможно, №=0; а если оно до-
стоверно, №=1.
Вероятность. Случайное событие всегда является результатом
одновременного действия ряда причин, каждая из которых так
или иначе взаимодействует с другой, и, кроме того, в свою очередь,
есть следствие многих других причин. Поэтому, когда самое на-
ступление того или иного результата всей это разветвленной цепи
взаимосвязанных воздействий либо его количественное значение
невозможно заранее предвидеть, говорят о случайности, о случай-
ном событии. Тем не менее из наблюдений за случайными собы-
тиями выяснилось, что существует определенная закономерность
их поведения при массовых испытаниях, позволяющая установить
с достаточной надежностью среднее число появления или общий
результат массы случайных событий. Однако при этом остается
невозможным предсказание индивидуального случайного события
в данном конкретном испытании или при малом числе таких испы-
таний.
При достаточно большом количестве опытов частость будет
мало отклоняться от некоторой устойчивой величины, количествен-
но характеризующей возможность реализации случайного события
А в данных условиях и называемой его вероятностью, которую мы
будем обозначать Р или Р (Д) (читается «вероятность Д»). Со-
гласно классической теории вероятностей Лапласа, для того что-
бы определить численное зачение вероятности, необходимо иметь
результаты испытания в виде полной группы N событий и знать,
что некоторое случайное событие А может произойти в М случаях
из N. Тогда вероятность события Р (Д) по аналогии с частостью
можно определить как M)N, т. е. как отношение числа случаев,
«благоприятствующих» событию, к общему числу случаев. Так как
достоверное событие это такое событие, которое при данном комп-
лексе условий должно обязательно произойти, то для него значе-
ние вероятности всегда равно 1. Вероятность невозможного собы-
тия всегда равна 0.
205
Таким образом, вероятность случайного события лежит в пре-
делах между 0 и 1:
О < Р (Л) < 1.
. Приведем следующий пример. В урне N одинаковых шаров, из
них М белых. Испытание заключается в извлечении на ощупь одно-
го шара. Здесь испытание — это вынимание шара, случайное со-
бытие — извлечение белого шара.
Так как мы обязательно извлечем какой-либо из шаров, то об-
щее количество возможных событий равно N. Возможное количе-
ство благоприятствующих событий, заключающихся в извлечении
белого шара, очевидно, М. Вероятность извлечения белого шара в.
этом случае определяется строго и будет равна:
Р (Л) = . (5.2)
Если, однако, общее количество шаров в системе очень велико
и среди них мало белых, то может случиться, что при N ис-
пытаниях белый шар, например, не будет вытащен ни разу, так
что частость окажется равной O/N=0, тогда как теоретическая
вероятность для системы, содержащей белые шары, нулю не рав-
на. Таким образом, экспериментально мы находим только часто-
сти и можем лишь случайно получить частость, совпадающую с
вероятностью.
Тем не менее опыт показывает, что, повторяя такое испытание
очень много раз, получим частость, очень близкую к вероятности,
которую можно подсчитать теоретически, не производя испытания,
если исходить из положения о равновероятности исходов, знать
общее количество событий в полной группе и если известно воз-
можное количество М интересующих нас событий А.
Однако важно помнить, что даже при очень большом количест-
ве испытаний могут существовать отклонения частости от веро-
ятности.
Самым трудным в реальных задачах является определение чис-
ла благоприятствующих случаев М, которое нам заранее не мо-
жет быть точно известно в силу самой природы массовых слу-
чайных явлений. Поэтому в современной аксиоматической теории
вероятностей, созданной А. Н. Колмогоровым, вводится чисто
формально понятие о вероятности, как о некотором числе, удов-
летворяющем определенным немногим правилам (аксиомам), и
разрабатываются и исследуются различные математические опе-
рации над вероятностями. Вопрос же о том, как определить это
самое число — вероятность некоторого интересующего нас реаль-
ного случайного события — оставляют окрытым, справедливо по-
лагая, что этот вопрос к собственно математической теории веро-
ятностей отношения не имеет. Математики поступают точно таким
же образом и во многих других случаях. Например, установив, что
площадь прямоугольника равна произведению его сторон axb, ге-
ометры совершенно не интересуются вопросом о том, как найти
206
конкретные значения а и 6 для данного прямоугольника. Это уже
дело прикладных наук, как например геодезии, но не математики.
Численное значение вероятностей реальных случайных собы-
тий, как указывалось выше, можно приближенно найти исходя из
их частости в длинной серии испытаний. Эту вероятность называют
экспериментальной, или эмпирической, однако ее значение само
носит вероятностный характер.
Частости отличаются от теоретической вероятности потому, что
при массовых реальных испытаниях на их результаты накладыва-
ются дополнительные факторы, не учитываемые в априорном пред-
ставлении о вероятности данного события. Практическим изучени-
ем вероятностей реальных случайных событий занимается матема-
тическая статистика.
2. СЛОЖЕНИЕ И ПРОИЗВЕДЕНИЕ ВЕРОЯТНОСТЕЙ
Если событие С состоит в осуществлении одного из двух не-
совместимых событий А и В, оно обозначается как С = А + В и
подразумевается как А или В. Вероятность события С
Р(С) = Р(Л + В) = Р(Л) + Р(В), (5.3)
т. е. Вероятность наступления какого-либо события из группы не-
совместимых событий Л и В равна сумме их вероятностей. Если
случайные события Ль Л2,..., Ап попарно несовместимы, то
Р(С) = Р(Л1 + Л2+... + Лп) = Р(Л1) + Р(Л2) + ... + Р(Л„). (5.4)
Если попарно несовместимые события Ль Л2,...,ЛЯ образуют
полную группу, то сумма их вероятностей
2Р(Л,)=1. (5.5)
Если же полная группа состоит из двух несовместимых собы-
тий, то наступление одного из них равносильно ненаступлению
другого. Такие события называются взаимопротивоположными.
Обозначим одно из пары взаимопротивоположных событий А, а
другое Л (читается «не Л»). Тогда по условию сумма вероятнос-
тей двух этих противоположных событий
Р(Л)4-Р(Л)=1, (5.6)
откуда
Р(Л)=1— Р(А). (5.7)
Поэтому, если непосредственное определение вероятности со-
бытия Л проще, чем определение вероятности события Р (Л), то
последней формулой часто пользуются для вычисления Р (Л), на-
ходя сначала Р (Л).
Вероятность совмещения случайных событий (произведение
событий). Совмещением случайных событий Л и В называется
случайное событие С, заключающееся в том, что в результате ис-
207
Рис 5.1.
ятностей
сти совмещения событий
пытания произойдет и событие А, и событие В. Совмещение обоз-
начается как произведение событий (подразумевается и А и В):
С = АВ. (5.8)
В выражении (5.8) подразумевается, что события А и В неза-
висимы, т. е. появление одного из них не влияет на возможность
появления второго.
Пусть событие А появится М раз из N возможных исходов, а
событие В наступит К раз из L исходов. Тогда совмещение собы-
тий будет сочетанием каждого из М событий А с каждым из К со-
бытий В и может произойти МК раз. Всего исходов будет NL, и
тогда вероятность совмещения
Р(С) = Р(ЛВ) = -^- = А =Р(Л) Р(В), (5.9)
т. е. вероятность совмещения событий А и В равна произведению
их вероятностей.
Правило сложения вероятностей в общем случае (жри воз-
можности совмещения). Рассмотрим полную группу событий А.
В, А и В. Так как А и Л, В и В взаимно противоположны, то это
означает, что когда произойдет одновременно событие АВ, то как
событие Л, так и событие В при этом исключаются. Следова-
тельно,
Р(Л + В) = 1— Р(АВ), (5.10)
откуда
Р(Л + В)= 1-[1-Р(Л)] [1 — Р (В)] =
= Р(Л) + Р(В) —Р(Л) Р(В). (5.11)
Полученное соотношение можно проиллюстрировать геометри-
чески следующим образом. Пусть на участке плоскости F даны
два пересекающихся контура А и В. Испы-
тание заключается в выборе наудачу какой-
либо точки плоскости F (рис. 5.1).
Вероятность случайного выбора точки
на какой-либо из площадок А или В равна
отношению суммы этих площадей ко всей
площади F. Но при суммировании общая
площадь АВ (и Л, и В), заштрихованная на
чертеже, войдет два раза — один раз с Лг
другой раз с В, поэтому ее следует один раз
вычесть, как это сделано в выражении (5.11).
При этом вычитается произведение Р (Л) Р (В), так как попа-
дание точки на заштрихованную площадь означает совмещенное
событие — точка оказывается одновременно и на площадке А и
на площадке В.
в
f Г
Сложение веро-
при возможно-
208
3. РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ
Пусть некоторая величина может принимать ряд случайных
значений. Такой случайной величиной может быть, например,
ошибка при измерении. При повторении измерений одного и того
же объекта мы будем под влиянием различных случайностей по-
лучать каждый раз другой результат, так как величина ошибки
при каждом измерении будет меняться. При этом, как правило,
малые ошибки будут встречаться чаще, большие—реже, иными
словами, вероятность малых ошибок будет больше.
Если некоторая случайная величина X может принимать лишь
конечное число значений х2, х3 и т. д. (например, результаты
измерений или число попаданий в мишень при стрельбе), то она
называется прерывной, или дискретной. Каждому отдельному зна-
чению дискретной случайной величины соответствует определен-
ная вероятность, с которой мы можем ожидать ее появления.
Если нам известны вероятности,
ям случайной величины, то тем
самым известно и распределение
этой величины. Если значения
случайной величины изменяются
непрерывно, то случайная величи-
на называется непрерывной.
Закон распределения. Так на-
зывается соотношение, устанавли-
вающее зависимость между зна-
чениями случайной величины и их
вероятностями. Закон распреде-
ления может быть задан либо в табличной форме, либо графически,
либо аналитически. При графическом представлении закона рас-
пределения по оси абсцисс откладывают значения случайной вели-
чины, а по оси ординат — их вероятности (рис. 5.2). Будем далее
обозначать вероятности отдельных значений xz некоторой дискрет-
ной случайной величины X через P(xt) или просто Pz. Очевидно,
сумма вероятностей всех п значений рассматриваемой случайной
величины
п
2Р*=1- (5-12)
1
Вероятность того, что значения xt случайной величины X ока-
жутся меньше некоторого выбранного значения xk, обозначается
как Pk или как Р (xt < хк) и будет равна:
л—1
= Р (Xi хк) = Р . (5.13)
1
Если откладывать по оси ординат при построении графика
распределения случайной величины не просто вероятности а
суммы вероятностей Р(х,<хА) всех значений случайной вели-
соответствующие всем значени-
ям
Xf *n-t х
Рис. 5.2. Графическое представле-
ние распределения дискретной слу-
чайной величины
209
чины, меньше данной xk, то мы получим график распределения,
имеющий ступенчатый вид и показанный на рис. 5.3. Скачок гра-
фика при каждом значении xz равен Pz.
Функция распределения. Функцией распределения случайной
величины X называется функция
А—1
F(x) = 2^- (5-14)
1
В случае непрерывно изменяющейся случайной величины X
функция распределения будет иметь вид плавной кривой (рис, 5.4).
Рис. 5.3. Кумулятивный
(суммарный) график веро-
ятностей дискретной слу-
чайной величины (функция
распределения)
Рис. 5.4. Функция рас-
пределения , непрерывной
случайной величины
Вероятность попадания некоторых значений xz случайной ве-
личины X на участок Дх будет равна:
’ P(x<xz<x+ Дх) = F(x + Дх) — F (х). (5.15)
Пусть Дх стремится к нулю. Тогда
lim Р(х<хг<х + Дх) =Иш F(x + Ax)-F(x)=r( }
Ах->0 Дх Дх—*0 Ах
Плотность распределения. Обозначим полученную производ-
ную функции распределения через /(х). Она характеризует на-
клон кривой функции распределения в окрестности некоторой
точки х. Чем круче этот наклон, тем быстрее растет функция
и тем плотнее распределены здесь значения случайной величины.
Поэтому f(x) называют плотностью вероятности непрерывной
случайной величины X. Поскольку
F(x)=p(x)dx, (5.17)
-------------------------00
то кривую функции распределения называют интегральной, а кри-
вую плотности распределения— дифференциальной кривой рас-
пределения. Если говорят просто «кривая распределения», то
210
обычно подразумевают дифференциальную кривую. Так как для
построения кривой распределения требуется непрерывная диффе-
ренцируемость функции, то дифференциальная кривая распреде-
ления существует только для непрерывных случайных величин.
Рассмотрим некоторую кривую плотности распределения f(x),
показанную на рис. 5.5.
Вероятность попадания случайной величины X на участок
Рис. 5.5. Кривая плотности рас-
пределения fM
Дх между и Х2 равна площади соот-
ветствующего участка кривой
Р (хх < х < х2) = J f (х) dx. (5.18)
Вероятность того, что значение X
будет в точности равно некоторому xz>
не рассматривается, так как вероят-
ность любого отдельного значения не-
прерывной случайной величины равна
нулю, поскольку эта вероятность опре-
деляется не как ордината кривой рас-
пределения, а как площадь ее участка
при длине основания по оси абсцисс, равной нулю.
Функция распределения F(x) для любого значения xz слу-
чайной величины X будет равна площади кривой распределения,
соответствующей всему участку абсциссы левее xz (рис. 5.5):
F (х) = J7 (х) dx = Р (— < х < xz). (5.19)
Так как максимальное значение
F(x) = J f(x) dx=l, (5.20)
—00
то это означает, что вся площадь кривой распределения равна 1.
Функция распределения, представляющая собой сумму веро-
ятностей,— величина безразмерная. Плотность распределения
f(x) имеет размерность, обратную размерности случайной вели-
чины dx.
Числовые характеристики распределения. В зависимости от
конкретных особенностей тех или иных случайных величин кри-
вые их распределения могут иметь самый различный вид. В боль-
шинстве случаев вероятности распределяются неравномерно и
притом так, что самые малые и самые большие значения случай-
ной величины имеют малые вероятности, тогда как некоторым
промежуточным значениям случайной величины соответствуют
максимальные вероятности, как это видно, например, из рис. 5.5.
Приведенная на этом рисунке кривая распределения характер-
на тем, что большим отклонениям случайной величины от сред-
ней части кривой соответствуют меньшие вероятности, т. е. малые
211
отклонения встречаются гораздо чаще, чем большие. В тех слу-
чаях, когда вероятности равных по абсолютной величине отрица-
тельных и положительных отклонений будут одинаковы, кривая
распределения получается симметричной.
Кривая распределения полностью характеризует случайную
величину. Однако во многих случаях нет необходимости знать
вид функции распределения или кривой плотности случайной ве-
личины. Достаточно располагать лишь некоторыми числовыми
показателями распределения, позволяющими оценить его харак-
тер. Даже в тех случаях, когда кривая распределения известна,
использование таких показателей оказывается полезным и удоб-
ным, так как позволяет обобщить и сжато представить все рас-
пределение в виде нескольких числовых величин, по которым лег-
ко сравнивать между собой различные распределения. Наиболее
важными из этих показателей являются те, которые характеризу-
ют, во-первых, расположение относительно узкого интервала зна-
чений случайной величины, которому соответствуют максимальные
вероятности («центр группирования» случайной величины), и, во-
вторых, особенности распределения вероятностей относительно это-
го центра.
Математическое ожидание. Центр группирования случайной
величины в теории вероятностей называют математическим ожи-
данием случайной величины X, и его обозначают символом Л4(Х)
или Е(Х} или х. Математическое ожидание определяется совер-
шенно аналогично тому, как находится центр
тяжести.
Пусть мы имеем некоторое распределение
дискретной случайной величины (рис. 5.6). Со-
ставим сумму моментов относительно на-
oj чала координат, рассматривая вероятности Pz
как некоторые массы, сосредоточенные в точ-
ках по оси х, а соответствующие значения xz
как плечи:
2M = 2Pzxz = 0,1 -0 + 0,15-1 +0,25-2 +
+ 0,25-3 + 0,15-4 + 0,1-5 = 2,5.
Так как моменты взяты относительно неко-
Рис. 5.6. Начальный торой точки, принятой за начало координат, то
момент 2Л1 в этом случае называется начальным мо-
ментом.
Сумма всех масс равна:
2 Pz = 0,1 +0,15 + 0,25 + 0,25 + 0,15 + 0,1 = 1 .
Деля 2Л4 на 2 Pz, получаем математическое ожидание слу-
чайной величины X:
м (X) = + = 2,5,
имеющее ту же размерность, что и сама случайная величина.
212
Таким образом, математическое ожидание находится по пра-
вилу
М(Х)=-^~. (5.21)
Так как SPZ = 1, то
M(X) = ZPixi. (5.22)
В случае непрерывной в интервале ab случайной величины
М (X) определяется аналогичным образом, только вместо вероятно-
стей (%) рассматривается плотность распределения f(x). Соот-
ветственно получаем (рис. 5.7)
ь
§ W (*) dx] х ь
М (X) = —ь--------= J f(x)xdx. (5.23)
J f (х) dx а
Рис. 5.7. Математическое ожи-
дание при непрерывном распре-
делении
Вообще, если случайная величина изменяется в пределах от
— оо ДО 4-00,
М (Х) = J f (х) xdx. (5.24)
-00
При этом мы предполагаем, что интеграл сходится абсолют-
>оо
но, т. е. что интеграл J f(x)\x\dx имеет конечное значение,
—оо
не зависящее от того, каким образом пределы а и b стремятся к
бесконечности.
В механике широко используется понятие момента для ха-
рактеристики распределения масс (статические моменты, момен-
ты инерции и т. д.).
Если представить (5.21) в виде М (X) SPz = SPzxz, то, поль-
зуясь известным положением механики о том, что сумма моментов
сил относительно некоторой точки равна моменту равнодействую-
щей относительно этой же точки, мы можем рассматривать сум-
марную массу SPZ как равнодействующую, а Л4(Х) как ее плечо.
Следовательно, математическое ожидание представляет собой абс-
циссу центра тяжести кривой распределения, отсчитываемую от
той точки, которая принята за начало координат при вычислении
моментов.
Дисперсия. Аналогично тому, как мы это делали при определе-
нии математического ожидания, возьмем сумму произведений ве-
213
роятностей на квадраты расстояний от математического ожида-
ния. Мы прлучим снова моменты, у которых массы умножаются
на квадраты плеч. Сумму этих моментов называют вторым цент-
ральным моментом (моментом второго порядка), или дисперсией
случайной величины. Центральным момент назван потому, что
он получен относительно математического ожидания, являющегося
центром тяжести кривой распределения. Дисперсию обозначают
D(X) или о2.
Согласно определению для дисперсных случайных величин
D(X) = S(x(--x)2 Р(-, (5.25)
а для непрерывных величин
D(X)= J (х-х)2 f(x) dx. (5.26)
-00
Дисперсия случайной величины характеризует распределение
(разброс) случайной величины относительно ее математического
ожидания аналогично моменту инерции площади, характеризую-
щему ее распределение относительно оси, проходящей через центр
тяжести площади.
Корень квадратный из дисперсии называют среднеквадрати-
ческим отклонением (или флуктуацией) и обозначают о(х):
о(.г) = /Ж. (5.27)
Если D(X)=O, то это означает, что величина X не является
случайной, так как с вероятностью, равной 1, принимает лишь
единственное значение, совпадающее с математическим ожидани-
ем. Обратно, постоянная величина имеет дисперсию, равную
нулю.
Во многих случаях для сопоставления друг с другом различ-
ных распределений используют также центральные моменты
третьего и четвертого порядка. Моменты более высоких поряд-
ков на практике не применяются, так как сами обладают очень
высокой дисперсией, и сколько-нибудь точное определение их
требовало бы очень большого количества измерений случайной
величины.
4. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Рассмотрим непрерывную случайную величину, распределение
которой имеет следующие две особенности: 1) кривая плотности
имеет один максимум; 2) кривая плотности симметрична относи-
тельно максимума.
Это требование означает, во-первых, что отклонения случайной
величины X от ее наиболее вероятного значения, которому со-
ответствует максимум кривой, встречаются тем реже, чем эти от-
клонения больше; во-вторых, отклонения, равные по абсолютной
214
величине и противоположные по знаку, встречаются одинаково
часто.
Этим условиям, например, соответствует рассеяние точек по-
ражения мишени при стрельбе в цель или распределение случай-
ных ошибок при многократном измерении одного и того же объ-
екта. Непрерывное распределение, отвечающее этим условиям,
носит название нормального.
Первое из условий означает, что вероятность появления слу-
чайной величины при нормальном распределении представляет со-
бой убывающую функцию ее отклонения от вероятнейшего значе-
ния, которое при нормальном распределении обозначают а, а
второе, что функция f(x—а) должна быть четной по отношению
к х—а, так как перемена знака не должна влиять на величину
функции, т. е.
f {х — а) = f (а — х).
Первое условие означает, что
f(-oo) = f(oo) = 0.
При этом, очевидно,
J f (х — a) dx = 1.
— со
Функция Гаусса. Функция, отвечающая этим условиям, была
найдена Гауссом и носит его имя. Она имеет вид
X*
f(x)= -7Х- е 2а‘ =—X- ехр (-------------(5.28)
У2тса l/2ica 2о® у
где о — флуктуация (среднеквадратическое отклонение);
е—основание натуральных логарифмов.
Это уравнение называют центрированным, так как ось ординат
проходит через середину кривой, совпадающую с ее центром тя-
жести (кривая симметрична). График этой функции называется
кривой Гаусса (рис. 5.8).
Если начало координат сместить так, чтобы расстояние до се-
редины кривой распределения равнялось х0 ,то мы получим урав-
нение в виде
f (х) = —ехр { - . (5.29)
V 2 л а у 2 а2 у
215
Положив в уравнении центрированной кривой распределения
(5.28) х=0, получим значение максимальной ординаты х кривой
распределения:
Л 1 / 0 \ 1 ,е оп.
х = —==— ехр-------------) = . (5.30)
У 2 it в \ 2 а2/ У 2 л о
Нормированное, или стандартное распределение. Флуктуация
о при нормальном распределении называется стандартом. Если
Принять масштаб по оси х кратным стандарту, т. е. принять о за
единицу измерения оси абсцисс, то мы получим так называемое
нормированное, или стандартное уравнение кривой. Обозначая
x=zo, найдем
1 / \
/(z)=—ехр • (5.31)
К 2 л \ 2 )
Площадь кривой нормированного распределения в пределах от
— со до г
* 1 р / z2 \
F (z) = f / (z) dz = - _ ехр----------] dz. (5.32)
-I И 2л J, V 2/
В пределах от — co до 0 интеграл от f (z) обозначают
Ip / z2 \ 1
Ф (0) = —^=- ехр I------I dz = —.
у 2 л \ 2 } 2
Следовательно,
F (z) = Ф (0) + J f (z) dz,
о
F (z = — + —L=r С ехр (— — ) dz = — + Ф (z), (5.33)
2 У2л \ 2/ 2
где
1 2 / 2 \ '
Ф (z) = —т==- С ехр I —— I dz. (5.34)
/2 k J \ 2 )
Площадь кривой распределения от ее середины до абсциссы
z=3 (т. е. х=3о) равна
з
ф (2 = 3) = J f (z) dz = 0,49865. (5.35)
о
Это уравнение дает площадь кривой распределения от ее се-
редины до так называемого трехсигмового предела. Значения f(z)
по (5.31) и Ф(г) по (5.34) табулированы. Ф(з) обычно называют
функцией Лапласа. Таблицами пользуются для построения стан-
дартной кривой нормального распределения при ее сравнении с
216
экспериментальными кривыми. Значение 2Ф(г), т. е. площадь
кривой распределения в пределах от —z до +z, называют интег-
ралом вероятностей (рис. 5.9). Он представляет собой вероят-
ность того, что нормально распределенная случайная величина бу-
дет иметь значения, находящиеся
в пределах от —z до +z.
Вероятности при нормальном
распределении равны площадям
соответствующих участков кри-
вой нормального распределения
(рис. 5.10) и приводятся ниже.
Рис. 5.10. Интеграл вероятно,
стей в пределах (—о, о)
(—2а, 2а), (—За, 3 о)
Рис. 5.9. Интеграл вероятностей
(2Ф(г) —площадь кривой в пределах
от —z до 4-г)
Границы интервала:
от — а до + а
от — 2а до +2а
от 2,5а до + 2,5а
от — За до Н-За
Вероятность попадания в интервал:
2Ф( 1) = 0,68269 « 68%
2Ф(2) - 0,95450 95%
2Ф(2,5) = 0,98758 98,8%
2Ф(3) = 0,99730 99,7%
Принято считать, что отклонения, большие, чем утроенный
стандарт, практически не могут иметь места (правило трех сигм).
кривая нормального распределения отличается следующими
свойствами: 1) f(x) всегда >0, т. е. всегда положительна, так как
кривая симметрична относительно вертикальной оси; 2) она не пе-
ресекается с осью х и беспредельно распространяется вправо и
влево от оси //; 3) при х=0 f (х) = 1/ог]/2к представляет собой
максимальную ординату кривой (математическое ожидание);
4) при х=±сг кривая имеет точку перегиба; 5) все нечетные цент-
ральные моменты равны нулю (так как моменты площадей слева
и справа от центра имеют разные знаки; 6) сумма п независимых
случайных величин, распределенных нормально с одной и той же
дисперсией о2, также распределена нормально и имеет дисперсию,
равную
а1=~- (5.36)
217
Из этого вытекает очень важное следствие, широко используе-
мое в математической статистике: если из нормального распреде-
ления некоторой величины отобрать п случайных значений, то
для такой выборки получим также нормальное распределение, но
с дисперсией, в п раз большей, чем для всей случайной величины
в целом.
5. ТЕРМОДИНАМИЧЕСКАЯ ВЕРОЯТНОСТЬ
Макро- и микрораспределения. В термодинамике состояния
систем (макросостояния) определяются небольшим числом термо-
динамических параметров. В микроскопической (молекулярной)
теории состояние системы тогда определенно, когда известно со-
стояние каждой молекулы. Если каждая молекула имеет г степе-
ней свободы, т. е. г независимых параметров состояния, то каждой
степени свободы соответствует кроме пространственной координа-
ты также и определенная составляющая скорости v или импульса
mv. Следовательно, микросостояние системы из п молекул опреде-
ляется 2гп параметрами. Однако рассмотрение микросостояний
можно’ существенно упростить, если применить к анализу состоя-
ния системы статистические методы.
Охарактеризуем каждое микросостояние вероятностью его на-
ступления. Воспользуемся так называемым методом ячеек Больц-
мана. Будем считать для упрощения, что частицы характеризуются
только скоростью движения и имеют только три степени свободы
поступательного движения. Состояние частицы опишем положени-
ем изображающей ее точки (так называемая фигуративная точка)
в воображаемом трехмерном пространстве скоростей. Все это про-
странство мысленно разобьем на элементарные ячейки
d<о = du dv dw, (5.37)
где и, v, w—компоненты скорости по направлениям, соответ-
ственно х, у и z.
Состояние частиц в каждой ячейке примем одинаковым. Веро-
ятность для п частиц находиться в одной и той же ячейке (т. е.
вероятность иметь одну и ту же скорость) равна произведению ве-
роятностей каждого из этих независимых событий. Так, если вероят-
ность для одной молекулы попасть в ячейку i равна Pt, то для
п молекул она будет равна Р", а вероятность того, что в каждой
/-той ячейке находится i молекул,
PZZ = P? р* ... рд, (5.38)
где Рр — означает вероятность того, что в f-той точке будет ров-
но i молекул.
Эта величина, соответствующая определенному распределению
218
скоростей, есть вместе с тем и вероятность микросостояния с дан-
ным распределением скоростей.
Вероятность макросостояния. Найдем теперь вероятность со-
ответствующего макросостояния. Каждому микросостоянию соот-
ветствует одно макросостояние, но одному макросостоянию может
соответствовать множество микросостояний, если данное распре-
деление скоростей реализуется с помощью разных частиц. Общее
число перестановок из п частиц равно и!. Из этого числа переста-
новок надо исключить внутренние перестановки в каждой из яче-
ек. Соответственно одно и то же макросостояние можно реализо-
вать -------—------ способами перестановок частиц по ячейкам.
«1! ns I... nr!
Согласно (5.38)), вероятность некоторого маркосостояния X в этом
случае будет равна:
Рх = Р?« Р2«»... Р"г ——. (5.39)
пг I Л2 I • • • пг 1
Если объем всех ячеек одинаков и равен dco, а общий объем
равен rdco, то вероятность попадания одной частицы в некоторую
ячейку равна d<sy!rd<&—\/г и одинакова для всех частиц. Это озна-
чает, что
= ]
, (5.40)
Рх = Г~П-------------- .
П1 ! п21 • • • пг • J
Термодинамическая вероятность. Так как определить Рх. по
формуле (5.40) трудно, то пользуются так называемой термодина-
мической вероятностью, представляющей собой отношение вероят-
ности Рл данного макросостояния к вероятности некоторого ус-
ловного нормального макросостояния Ро, в качестве которого
может быть выбрано любое из макросостояний:
Рт = -^-. (5.41)
* о
Удобно принять за условное нормальное состояние такое, при
котором все частицы имеют одинаковую скорость, т .е. все изобра-
жающие точки находятся в одной ячейке, например 1. Тогда
Их — п; п2 = Пз = ... = пт = 0;
Ро = г~п----------------= г“л,
п ! о ! . . . о !
(5.42)
так как 0! = 1. Но вероятность Ро весьма мала, и следовательно,
Рт»1.
Таким образом, термодинамическая вероятность может быть в
отличие от математической больше 1 и притом во много раз, по-
казывая, во сколько раз вероятность данного макросостояния боль-
219
ше вероятности нормального. Подставляя (5.40) и (5.42) в (5.41),
получим
Ро ! . . . п?! । у
П
1
где знаком П обозначено произведение.
Термодинамическая вероятность равна, следовательно, числу
перестановок, которыми может быть реализовано данное макро-
состояние, т. е. представляет собой число микросостояний, при
каждом из которых в данных условиях осуществляется данное
макросостояние.
Энтропия и термодинамическая вероятность. Формула Больц-
мана. Рассмотрим систему, состоящую из двух подсистем. Энтро-
пия системы равна сумме энтропий ее частей, и, следовательно,
5 = + S2. (5.44
С другой стороны, термодинамическая вероятность для всей
системы Рт равна произведению вероятностей подсистем:
Предположим, что энтропия системы является функцией веро-
ятности. Так как энтропии подсистем складываются, а вероятности
умножаются, то указанное предположение приводит к выводу, что
энтропия должна быть пропорциональна логарифму вероятности:
Si = k In Pi, S2 = k lnP2
и только в этом случае
5i + S2 = k (1пР1 + 1пРа) = JfelnPi P2,
откуда
S = klnPT.
Постоянная k, равная 1,38-IO-23 дж/град, называется постоян-
ной Больцмана.
Последнее выражение представляет собой известную форму-
лу Больцмана, согласно которой энтропия пропорциональна лога-
рифму термодинамической вероятности данного макросостояния.
Следовательно, увеличению энтропии системы отвечает увеличе-
ние числа ее микросостояний. Отсюда может быть сделан вывод,
что энтропия является мерой неупорядоченности системы. Чем
хаотичнее, беспорядочнее состояние системы, тем больше вероят-
ность возникновения различных ее микросостояний, тем больше ее
энтропия. Чем больше, например, температура, тем интенсивнее
тепловое движение молекул газа, тем менее упорядочена система и
больше ее энтропия. При сокращении объема газа упорядочен-
ность в расположении молекул растет, а энтропия системы убы-
вает.
220
При этом следует иметь в виду статистический характер полу-
ченных выводов и то, что они неприменимы для систем, размеры
которых сравнимы с размерами частиц.
Распределение Максвелла. Классическое понятие вероятности
исходит из того, что нам известны (или могут быть установлены
путем логического анализа) все равновозможные исходы (собы-
тия), появляющиеся в результате некоторого опыта. Хотя в боль-
шинстве реальных вероятностных ситуаций либо все возможные
исходы нам заранее неизвестны, либо не может быть принята их
равновероятность, тем не менее в ряде случаев принципы класси-
ческой теории вероятностей могут быть с успехом применены к
анализу поведения большого количества индивидуально непред-
сказуемых случайных событий, которые в своей массе подчиняются
определенным закономерностям (например, поведение молекул
газа).
Газ представляет собой систему хаотически движущихся моле-
кул, непрерывно сталкивающихся между собой и разлетающихся в
стороны, и предсказать поведение одной какой-либо молекулы,
очевидно, невозможно. Таким образом, газ представляет собой ти-
пичную статистическую систему. Давление газа на стенки сосу-
да— результат ударов летящих молекул газа об эти стенки. Если
бы мы могли замерить одновременно скорости, массы и направле-
ние движения всех молекул газа в момент столкновения их со
стенками сосуда, то это позволило бы вывести закон Бойля —
Мариотта. Осуществить такое измеренйе нельзя, но можно приме-
нить статистические методы, не производя измерений, а построив
мысленно некоторую модель газа и рассмотрев различные рас-
пределения скоростей отдельных молекул. При этом путеводной
звездой в подобном исследовании будет служить известная из опы-
тов над газом в целом зависимость*между его давлением и объе-
мом. Если бы удалось решить эту задачу, придя в конце концов к
закону Клапейрона, то можно было бы затем использовать най-
денные зависимости для теоретического исследования целого ряда
других вопросов о поведении газа, которые не могут быть столь
просто получены экспериментально.
Эта задача была решена Максвеллом, который исходил из того,
что в макроскопическом объеме газа содержится весьма большое
количество молекул, а размеры их столь малы по сравнению с про-
межутками между ними, что их,можно рассматривать как матери-
альные точки. Молекулы находятся в непрерывном движении, при-
чем каждая из них движется прямолинейно до столкновения, ко-
торое происходит по закону упругого соударения. Принимается
также, что газ достаточно разрежен для того, чтобы за время
между двумя соударениями каждая молекула при движении не
испытывала никакого влияния со стороны других молекул (в виде,
например, сил притяжения). Газ, отвечающий всем этим идеализи-
рованным условиям, получил название идеального.
Простые рассуждения приводят прежде всего к выводу, что в
221
общей массе рассматриваемого газа молекулы распределены рав-
номерно.
Можно затем полагать, что в газе содержатся молекулы с са-
мыми различными скоростями, но число молекул с очень большими
скоростями, так же как и с очень маленькими, невелико, и что чем
ближе скорость к некоторой средней величине, тем большее число
молекул ею обладает. Далее предполагается, что при установив-
шемся, стационарном состоянии газа скорости равной величины и
противоположных направлений встречаются одинаково часто, и со-
ставляющие скорости молекулы по одному какому-либо направле-
нию не зависят от составляющих скорости по другим направлени-
ям. Соответствующий закон распределения скоростей, найденный
Максвеллом, записывается так:
____________________________________
4 л са
dnc = ry^-‘~%e dc’ (5.45)
где dnc—количество молекул, обладающих скоростями между
с и c+dc и приходящихся на единицу объема газа;
п — общее число молекул в единице объема;
сн — наивероятнейшая скорость молекул.
Если описать вокруг центра мишени кольца одинаковой толщи-
ны и подсчитать количество попаданий в каждое такое кольце, то
получится распределение, аналогичное максвеллову.
Зная распределение скоростей, можно рассчитать число уда-
ров молекул за единицу времени о единицу площади стенки и по-
казать, что давление газа пропорционально числу ударов.
Вероятность того, что молекула имеет скорость в пределах от
с до c-i-dc:
dPe=-^~. (5.46)
Введем обозначение
« = 4- (5-47)
для отношения квадрата скорости молекулы к квадрату наиверо-
ятнейшей скорости.
Тогда dPc— г— е Уа da —f (a) da, (5.48) у тс
где функция /(а)=-^ ё~а УТ (5.48а) V тс
представляет собой плотность вероятности.
222
Распределение Максвелла несимметрично и показывает, что в газе
при тепловом равновесии относительно мало медленных молекул и
очень немного молекул с весьма высокими скоростями. Большая
часть молекул движется со скоростями, близкими к наивероятней-
шей.
/ с \*
Умножив знаменатель и числитель выражения I— , входяще-
\ сн /
го в закон (5.45), на величину
тических энергий:
мы получим отношение кине-
(5.49)
Легко видеть, что от подстановки (5.49) в формулу (5.45) по-
следняя не изменится; следовательно, она характеризует и распре-
деление молекул газа по кинетическим энергиям.
Закон Клапейрона — Менделеева. Постоянная Больцмана. Из
курса физики известен закон Клапейрона — Менделеева, представ-
ляющий собой уравнение состояния идеального газа:
= const, или pV — RT, (5.50)
где р — давление газа;
V — объем, занимаемый! молем газа (при Т=273,2°Сир=
= 1 ат, V=22,4 л);
—универсальная газовая постоянная, равная
8,31 дж/моль -град-,
Т — абсолютная температура.
С другой стороны, давление газа зависит от средней скорости
молекул с, массы молекулы пг и их числа п в единице объема и
выражается формулой
1 ' —2
р— — тс п.
3
Так как средняя кинетическая энергия молекулы
—2
К = (5.51)
ТО
О —
(5.52)
Количество молекул в одном моле определяется числом Аво-
гадро No=6,O2-1023, и, следовательно,
4- No^ = v (5.53)
О 3
где W — средняя энергия No молекул.
223
Из сопоставления (5.50) и (5.51) находим
К = — . — Т =— kT, (5.54)
2 N„ 2 1
где через &=1,38-10~23 дж)град обозначена постоянная Больцма-
на, равная отношению 7?/N0. Эта постоянная представляет собой
приращение кинетической энергии одной молекулы газа при уве-
личении температуры на 1 град.
Из (5.50) с учетом (5.51) и (5.54) следует, что
p=A£=nAT, (5.55)
т. е. давление идеального газа при данной температуре определя-
ется только числом молекул в единице объема и не зависит от ро-
да молекул.
Наиболее вероятная скорость молекул сн в формуле (5.45)
связана с постоянной Больцмана отношением
Л 1/2kT -1/2RT
—<5-56>
где m — масса молекулы;
М — масса 1 моля газа.
Входящее в формулы (5.52) — (5.54) число 3 — число степеней
свободы молекул газа, движущихся в пространстве без вращения.
Таким образом, из (5.54) следует, что на каждую степень свободы
молекулы приходится в среднем кинетическая энергия, равная
l/2 kT.
Распределение молекул в силовом поле. В поле тяготения (на-
пример, Земли), которое можно считать однородным, потенциаль-
ная энергия молекул газа на различной высоте над землей
неодинакова. Разность давлений столба газа на высотах z и dz
dp = — nmgdz, (а)
где п — среднее число молекул в единичном объеме на высоте z\
m — масса молекулы;
g — ускорение силы тяжести;
mg — вес молекулы.
С другой стороны, согласно (5.55),
dp = kTdn. (б)
Сопоставляя (а) и (б), получим
d п ms j
= — dz,
п--------kT
откуда
где nQ — среднее число молекул в единице объема газа на высоте
z=0.
224
Формула (5.57) называется формулой Лапласа — Больцмана^
В данном случае распределение молекул по скоростям не зави-
сит от их распределения по высоте. Давление газа пропорциональ-
но числу молекул, и, следовательно, на высоте z давление газа
р = роехр(--^, (5.58)
где ро — барометрическое давление на высоте z=0.
Формулу (5.58) можно обобщить для любого силового поля.
Так как величина mgz есть потенциальная энергия Д77 молеку-
лы в поле тяготения, то (5.57) принимает вид
п = По ехр j. (5.59)
Формула (5.59) называется законом Больцмана распределения
частиц по энергиям в силовом поле. Относительное число частиц в
единичном объеме, энергии которых отличаются на величину Д/7,
равно
дп
6. ВНУТРЕННЕЕ ТРЕНИЕ И ВЯЗКОСТЬ В ГАЗАХ И ЖИДКОСТЯХ
Процессы переноса в газах. Выделим в объеме газа два смеж-
ных плоских слоя. При переходе молекул через границу между
этими слоями из слоя в слой будет переноситься кинетическая
энергия, количество движения и вещество (масса). В состоянии ди-
намического равновесия перенос имеет характер эквивалентного
обмена, однако при неравновесном процессе он принимает преоб-
ладающее одностороннее направление. Перенос кинетической энер-
гии происходит в форме теплоты при наличии градиента темпера-
туры и носит название теплопроводности, перенос вещества имеет
место при градиенте концентрации (плотности) и носит название
диффузии.
Перенос количества движения возникает при наличии движения
(сдвига) слоев друг относительно друга. В этом случае молекулы
из слоя, который движется медленнее, попадая в слой, который
движется быстрее, тормозят его. Наоборот, переход более быстрых
молекул в слой, движущийся медленнее, ускоряет его. Таким обра-
зом, между слоями действует как бы касательная сила, стремя-
щаяся выравнять их скорости. Явление обмена молекулами с пере-
носом количества движения вызывает явление внутреннего трения
в газах.
Если обозначить переносимую величину, приходящуюся на одну
молекулу, через ф, то при переходе от слоя к слою изменение ф
будет равно:
Дф = 7, (5.61)
d г
8 Зак. 530
225
где i _ толщина элементарного слоя, равная средней длине сво-
бодного пробега молекул до столкновения друг с другом;
d ib
—— — градиент переноса.
d z
Если общее число молекул, проходящих через границу между
слоями в одну сторону, N, то-результирующее количество перене-
сенной величины
В = Н(4/Щ)- N ($ — Aip) =22VA^. (5.62)
(в одну сторону) (в другую сторону)
Если число молекул в единице объема п, размер площадки,
через которую происходит перенос, $, и средняя скорость теплового
движения молекул с, то за время t через площадку может пройти в
одну сторону количество молекул
N = _L ns с t. (5.63)
Здесь коэффициент */б показывает, что из всех молекул, нахо-
дящихся в беспорядочном хаотическом движении, в заданном на-
правлении может пройти в среднем лишь Vs. причем лишь половина
из них пройдет в одну сторону. Из (5.62), подставляя (5.63) и
(5.61), найдем
В= _L п~с 11 fst, (5.64)
3 dz
а разделив на 5 и /, получим удельный поток переносимой величи-
ны (скорость переноса через единицу площади):
= (5-М)
3, dz
Количество движения, перенесенного одной молекулой,
= т v,
где т — масса молекулы;
v — ее скорость.
Подставляя
d ib d v
—X. = tn —
dz dz
в (5.65), получим
= (5-66>
Согласно экспериментально установленному Ньютоном закону,
называемому законом вязкого течения, касательные напряжения т,
действующие между слоями жидкости или газа, движущимися с
различной скоростью, пропорциональны градиенту скорости:
226
d v
Т — 71 -- ,
' dz
где т] — коэффициент пропорциональности, называемый коэффи-
циентом динамической вязкости.
Согласно второму закону Ньютона, поток количества движения
должен быть равен импульсу силы внутреннего трения f за время t:
B = ft. (5.67)
Вместе с тем касательное напряжение равно удельной силе тре-
ния:
Т = 2-. (5.68)
S
Из (5.67) и (5.68) следует ,
В — ust',
= (5.69)
S г
откуда с учетом (5.66) и (4.70) находим
т] = — nmcl = — pel, (5.70)
3 3
где р— плотность газа, равная пт.
Таким образом, коэффициент внутреннего трения газа не зави-
сит от нормального давления, а зависит только от плотности газа и
его температуры.
Аналогичным образом можно найти закон переноса кинетиче-
ской энергии молекул. Коэффициент теплопроводности
k= — nmclCv, (5.71)
3
- где Су — теплоемкость газа при постоянном объеме, измеряемая
в дж)кг • град или дж]кмоль град.
Точно так же можно найти значение коэффициента диффузии:
D = ±-cl. (5.72)
Сравнивая выражения (5.70), (5.71) и (5.72), найдем следую-
щие зависимости:
n = Dp; (5.73)
Х = 7]С/, (5.74)
(5-?5>
Молекулярно-кинетическая теория вязкости жидкостей. В отли-
чие от газов молекулы жидкости длительное время остаются на
8 Зак. 530
227
своих местах, и поэтому механизм внутреннего трения у них отли-
чен от газов, у которых внутреннее трение связано с переносом ко-
личества движения при соударении молекул. Под влиянием усилий,
вызванных действием внешней нагрузки, молекулы в жидкости со-
вершают более частые скачки в направлении общего перемещения,
вызываемого силой. Соответственно молекулы приобретают ско-
рость в этом направлении [58], равную
о = Д/8, (5.76)
где Д/ — разность между числами скачков в направлении силы и
в противоположном;
б — длина скачка.
Градиент — при движении с различной скоростью двух слоев
d г
жидкости, находящихся на расстоянии Дб друг от друга, равен:
^ = А/. (5.77)
Д о
Согласно закону вязкости Ньютона,
dv А .
т==
аг
откуда
(5.78)
Зависимость частоты скачков молекулы от температуры можно
выразить приближенной формулой
/ = /оехр ( — q/kT), (5.79)
где q — энергия активации;
Т — абсолютная температура;
k — постоянная Больцмана.
Пусть работа касательных напряжений на пути, который совер-
шает молекула, преодолевая потенциальный барьер, равна а. Тогда
энергия активации уменьшается на величину а при скачке в сторо-
ну действия силы и увеличивается на а при скачке в противопо-
ложном направлении. Разность скачков молекулы в обоих направ-
лениях, следовательно, равна:
Д / = -£-/ ехр (— q/k Т) [ехр (a/k Т) — ехр (— a/k 71)]. (5.80)
Коэффициент Ve учитывает, что скачки молекул возможны по
трем пространственным координатам (по каждой из них в обе сто-
роны). Так как
-e-~9g~X- = shx, (5.81)
то, заменяя выражения в скобках’гиперболическим синусом, кото-
рый раскладывается в ряд
228
shx=x + -^- + -^- + ..., (5.82)
3! о!
получим при а< <.kT, ограничиваясь первым членом ряда,
alkT _ e-alkT = 2 s h ± ~ 2 JL , (5.83)
kT kT
и тогда
Д; = ±/е-«‘>- (5.84)
Подставляя (5.84) в (5.78), получим
Работа а, совершаемая напряжением т, очевидно, пропорцио-
нальна этому напряжению:
а = Ьх,
и, следовательно,
3 k Т ofk т
т] =-----е
‘ b jo
Так как величина первого множителя в правой части 3kT/bj0
с изменением Т меняется гораздо медленнее, чем ef<lkT , где Т
входит в показатель степени, можно для не очень большого диа-
пазона изменения Т принять первый множитель постоянным. Обо-
значая его А, получим формулу Френкеля:
4 = Aexp(q/kT), (5.86)
дающую приближенную зависимость коэффициента вязкости жид-
костей от температуры.
Между коэффициентом диффузии D и вязкостью жидкостей Ч
зависимость тоже иная, чем у газов [формула (5.73)], а именно:
^ = ±£.-1-, (5.87)
Cf U
где сг— величина, зависящая от радиуса молекул жидкости.
Радиальная функция распределения. В современной физике
структура жидкостей и все их физические свойства определяются
некоторыми функциями распределения частиц, причем наибольшее
значение имеет радиальная функция распределения. Она позволяет
охарактеризовать ближний порядок не только в жидкостях, но и в
кристаллах и аморфных твердых телах.
Возьмем какой-либо атом в жидкости и опишем вокруг него две
концентрические сферы радиусами г и r-\-dr. Объем dV слоя между
двумя сферами будет равен разности объемов этих двух сфер.
Д17 = 4кгМг. (5.88)
Число атомов в этом слое меняется из-за теплового движения и
229
в среднем имеет некоторое значение пг. Тогда среднее число ато-
мов в единице объема рассматриваемого слоя
р(0 =
fir .
4 л г2 d г
(5.89)
Величину р (г) называют радиальной, или бинарной плотностью.
Она отличается от средней плотности р0 всей жидкости, так как
определяется для весьма малых объемов, соизмеримых с объемами
молекул. На больших расстояниях от
рассматриваемого атома радиальная и
средняя плотности будут равны, но на
малых, когда г немногим больше диа-
метра атома, р (г) может быть больше
или меньше ро- Соответственно отно-
шение р(г) к ро, которое обозначают
W(г) и называют относительной веро-
ятностью нахождения атома на дан-
. ном расстоянии от рассматриваемого,
может быть больше или меньше еди-
ницы.
Если построить график изменения
W(г) с изменением расстояния г от
w
2
1
2 4 6 8 г,А<
Рис. 5.11. Радиальная функция
распределения
о
произвольного атома, то мы получим кривую, показанную на
•рис. 5.11.
Отклонения этой кривой от значения 1Г(г) = 1 убывают с увели-
чением г. Такого рода графики строят по результатам рентгено-
графического исследования жидкостей. Очевидно, положительные
пики на кривой вероятностей и соответствующие им расстояния ха-
рактеризуют наиболее вероятный ближний порядок в расположе-
нии частиц. Так, из рис. 5.11 следует, что наиболее вероятным яв-
ляется в данном случае такой порядок, при котором частица окру-
жена плотным слоем на расстоянии ЗА, затем следующий плотный
слой будет находиться на расстоянии 5А, следующий — на рассто-
янии 8А, причем плотность все время убывает, приближаясь к сред-
ней, и ближний порядок постепенно размывается.
7. ИСХОДНЫЕ ПОЛОЖЕНИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Большое количество разнообразных причин, определяющих
формирование строительных свойств грунтов, и как следствие зна-
чительные незакономерные (случайные) колебания численных ха-
рактеристик этих свойств на небольших расстояниях (даже в пре-
делах одного и того же х!лоя грунта) заставляют рассматривать
результаты полевых и лабораторных испытаний грунтов как слу-
чайные величины.
Разработка методов регистрации, описание и анализ данных
наблюдений при массовых случайных явлениях составляют пред-
230
мет математической статистики. Данные, полученные при таких
наблюдениях, называются статистическими.
Динамические и статистические законы. В физике принято на-
зывать количественные законы, связывающие между собой одно-
значно независимые и зависимые переменные и, в частности, про-
странственно-временные координаты со свойствами и параметрами
движения систем, динамическими законами. Таким образом, дина-
мические законы дают возможность по известным начальным дан-
ным определять движение системы и ее состояние в любой задан-
ный момент времени.
В отличие от динамических законы случайных, явлений, уста-
навливаемые на основе вероятностного изучения этих явлений,
носят название вероятностных законов, а законы, выведенные на
основе наблюдений за массовыми случайными явлениями, — ста-
тистических.
I В динамические законы, которые однозначно определяют со-
стояние системы в некоторый момент времени, исходя из данных о
Се состоянии в другой момент времени, причина изменения состоя-
ний может в явной форме не входить (это обычно имеет место в
функциональных зависимостях, когда одна величина зависит от
другой, отнюдь не являющейся причиной ее изменений, например
изменение пройденного пути в функции времени, которое, конечно,
не является причиной изменения пути). Однако строгая детерми-
нированность предполагает определенность и однозначность соот»
ветствующих причинно-следственных отношений.
В реальной действительности, когда переплетается действие
многих взаимосвязанных причин, всегда есть различные дополни-
тельные влияния, вызывающие даже при динамических законо-
мерностях большие или меньшие флуктуации, носящие случайный
характер. Поэтому статистические законы, охватывающие инте-
грально весь многообразный комплекс причинных отношений, шире
динамических. И, действительно, в науке имеется много примеров,
когда динамическая закономерность получается как частный слу-
чай статистических законов.
Ярким примером такого рода является кинетическая теория
газов, в которой многие динамические закономерности, установлен-
ные ранее экспериментально, выводятся из общих статистических
закономерностей для газа, рассматриваемого как скопление очень
большого количества молекул. Подобные закономерности все шире
используются и в инженерной геологии, и в механике грунтов.
Систематизация и сводка статистических данных. Первичный
статистический материал может содержать сотни и тысячи цифро-
вых данных. Первый шаг в их обработке заключается в системати-
зации их. Однако человеческий ум не в состоянии уловить никаких
закономерностей в явлении, характеристика которого представлена
в виде большой массы цифр. Необходимо произвести такую обра-
ботку, которая позволила бы представить их в удобной, легко обо-
зримой форме, в виде относительно небольшого количества обоб-
231
щающих итоговых данных. Такая обработка называется сводкой
статистических данных. Сводка осуществляется путем группировки
данных по тем или иным признакам. Выбор признаков, по которым
производится группировка, является одним из решающих условий,
определяющих результат последующего анализа и обобщения ста-
тистических данных.
С самого начала исследования, еще при составлении программы
массовых наблюдений и измерений и разработке методики их про-
ведения, а затем при отборе необходимых первичных данных для
анализа, наиболее важная задача заключается в том, чтобы из
всей массы разнообразных явлений и факторов отобрать те, кото-
рые действительно типичны, характерны для изучаемого вопроса.
В противном случае можно не только допустить грубые ошибки, но
и получить ложные выводы. <
Формы представления экспериментального материала. В ре4
зультате измерений некоторой величины мы имеем ряд чисел, обыч-j
но записанных в порядке их получения в виде таблицы. Назовем
эту совокупность данных первичной совокупностью, или первичг
ным материалом. Каждое число в такой совокупности называют
вариантой.
Приведем в качестве примера табл. 5.1 определения влажности
100 образцов грунта.
Таблица5.1
Влажность в % (первичные данные)
16,4 16,7 16,7 16,5 16,3 16,8 17,2 16,5 16,3 16,2
16,0 15,4 16,2 16,2 16,5 16,2 16,4 16,4 16,7 16,6
17,1 16,6 16,5 16,7 16,5 15,9 16,8 16,5 16,5 16,4
16,4 16,8 17,0 16,5 16,6 16,7 16,6 15,8 16,4 16,3
16,3 16,2 16,6 16,1 16,4 16,2 16,4 16,5 16,3 16,1
15,9 15,8 16,5 17,1 16,5 16,9 16,3 16,4 16,3 16,4
16,4 16,6 16,4 16,5 17,2 16,7 16,6 16,6 15,8 16,2
16,6 15,7 16,4 16,2 16,0 16,5 17,1 16,4 16,5 16,3
16,7 16,8 16,9 16,0 16,4 15,6 16,9 16,5 16,3 16,8
16,6 16,5 16,3 16,5 17,5 16,4 16,7 16,3 16,4 16,5
Анализ чисел, собранных в таком виде, представляет большие
трудности, особенно если количество их велико.
Действительно, уловить какую-либо закономерность в распре-
делении влажностей, пользуясь непосредственно табл. 5.1, невоз-
можно, хотя количество данных в ней относительно невелико.
Таким образом, возникает задача представления результатов на-
блюдений в удобообозримом виде.
Простейшим способом является перестройка этой исходной
таблицы таким образом, чтобы приведенные в ней величины были
расположены в возрастающем порядке (табл. 5.2). Данные измере-
ний, расположенные таким образом, обычно называют упорядочен-
232
ним, или ранжированным, а также вариантным рядом. В таком
виде они более пригодны для изучения, чем в виде случайного рас-
пределения в первой таблице.
Таблица 5.2
Влажность в % (ранжированный ряд)
15,4 16,0 16,2 16,3 16,4 16,5 16,5 16,6 16,7 16,9
15,6 16,1 16,3 16,3 16,4 16,5 16,5 16,6 16,7 16,9
15,7 16,1 16,3 16,4 16,4 16,5 16,5 16,6 16,7 16,9
15,8 16,2 16,3 16,4 16,4 16,5 16,5 16,6 16,7 17,0
15,8 16,2 16,3 16,4 16,4 16,5 16,5 16,6 16,7 17,1
15,8 16 2 16,3 16,4 16,4 16,5 16,5 16,6 16,8 17,1
15,9 16,2 16,3 16,4 16,4 16,5 16,5 16,6 16,8 17,1
15,9 16,2 16,3 16,4 16,4 16,5 16,6 16,7 16,8 17,2
16,0 16,2 16,3 16,4 16,4 16,5 16,6 16,7 16,8 17,2
16,0 16,2 16,3 16,4 16,5 16,5 16,6 16,7 16,8 17,5
Легко увидеть, что минимальная влажность составляет 15,4, а
максимальная— 17,5%; что влажность большинства образцов ко-
леблется от 16,2 до 16,7% и что разность между максимальным и
минимальным значением ряда, называемая размахом варьирова-
ния, или широтой распределения, равна 17,5—15,4 = 2,1%.
Однако это все еще слишком общая характеристика ряда, из
которой трудно уловить какую-либо закономерность. Желательно
заменить этот ряд еще более удобным для анализа и прежде всего
содержащим меньшее количество чисел — произвести так называ-
емую группировку ряда. Для этого весь размах варьирования делят
на несколько интервалов (обычно при предполагаемом нормальном
распределении принимают 10—12 интервалов, хотя иногда берется
меньшее-или большее их количество).
Чтобы определить размер интервала, берут из таблицы размах
варьирования и делят на принятое количество интервалов. Прини-
мая в данном случае 10 интервалов, найдем
17,5-15,4
10
— =0,21.
10
Округляя, принимаем размер интервала равным 0,2.
Прежде чем приступить к группировке данных, следует уста-
новить границы интервалов. Удобнее всего это сделать, определив
сначала приближенно среднее значение измеренной величины. Для
этого берут из первичной таблицы небольшую выборку, отбирая
числа случайным образом. Посмотрим, как это делается.
Образование случайных выборок при помощи таблиц случайных
чисел. Такие таблицы обычно состоят из четырехзначных чисел,
расположенных совершенно случайно и притом так, что каждая
цифра встречается на каждой странице таблицы приблизительно
233
Таблица 5.3
Случайные числа
2182 1666 7373 4982 2368 2613 9025 2836 8493 8207
1549 8441 3351 3079 0026 4161 6224 4184 2633 2736
5118 4796 7035 2010 3449 7061 3847 9508 4528 1226
6848 3420 6583 7520 4809 1575 3209 9070 0644 3614
3309 4853 4021 8644 3980 5318 1959 4783 1810 2020
2050 3603 1812 4020 6573 0312 7799 9374 4788 4350
6817 6736 4591 9037 2949 7406 4238 4279 6206 1699
8310 3044 0433 1322 7664 3310 2487 3926 2233 8260
7050 7670 1848 5173 2146 1289 8504 0911 2001 5804
5637 5325 9367 5939 3191 5930 3361 6743 5995 4194
8251 3537 5139 5050 1516 8792 5513 5583 6103 9872
6129 7391 0429 2836 5284 5485 2643 4035 3089 4991
1311 4847 2317 3561 4533 6655 7354 1903 6909 9776
5151 2477 3250 7859 1764 1590 3309 2555 9334 3869
4245 4289 9301 ' 4788 3937 9122 9301 4741 0683 0253
3395 7157 1084 0561 8388 7575 7513 0431 9659 8204
6542 9575 7896 7029 4986 6632 8145 7080 3287 3336
8068 1543 2019 3678 9248 2452 1224 0260 4158 3735
3370 3763 4713 4726 7010 3736 2412 9066 8663 5408
9306 0691 3231 ЗОЮ 5948 5659 4145 2452 3340 5540
2166 2583 6878 3080 6318 6494 8057 7173 5753 3592
6844 3518 1638 7438 6106 2268 6361 7008 7995 8010
1479 7233 3827 9134 1023 6356 5108 3033 3546 0827
6342 6329 1364 1015 3892 5611 7390 2421 9873 9796
0485 7584 6030 2040 8568 3539 6208 9450 7613 4591
3603 9141 3778 1939 2596 5841 0528 4948 3849 4894
6736 5786 4356 9390 7245 7645 6476 1022 3393 5062
3044 9355 5064 6508 6771 2173 0511 7104 6753 6486
7670 6721 2387 4220 9357 2070 ' 8506 9126 4729 1798
5325 7972 3664 8187 2040 3668 4930 9203 0248 8489
3537 8129 6485 3472 3915 2040 4353 8415 4506 3644
7391 3452 6919 3520 1417 7784 0734 7174 2648 6464
2066 3343 8506 9336 8366 9748 9925 4961 6179 0922
5120 2905 3163 6449 2833 2971 3390 4915 8231 6403
4058 0542 7260 9652 0310 5901 5420 9443 8654 5492
0079 8768 8409 2949 4751 5945 6473 7475 9696 2861
5609 9172 4284 2793 1333 2760 8276 6593 2346 7244
7070 3543 3812 8478 3696 8015 4970 1574 1636 6966
4748 0896 . 3758 6368 9968 6245 3108 9344 4513 0218
1093 8312 0310 1512 0178 6667 2966 0873 0582 7541
9818 4719 8187 6589 8807 2195 1160 4756 6503 1341
5690 7934 8875 9796 0520 7012 6355 5557 2070 5013
0943 8798 6149 5385 2884 1816 5453 8893 3695 4625
2166 5084 9117 0199 7127 4378 2940 2861 4690 5711
6702 2902 6365 7014 6121 5108 7369 7804 6732 3310
3208 4252 1361 8838 6770 9128 7183 8966 8292 9768
9692 1021 2415 6337 6060 5803 8205 2398 5607 0046
1211 1918 0260 7193 7633 8314 2891 9541 2529 6572
3230 7073 1890 4899 6533 4839 2512 0938 0233 7302
5969 3070 6557 9925 1969 4212 3052 4238 4210 6860
234
одинаковое число раз. Для дальнейшего использования приводим
выписку из таблицы, взятой из пособий по математической стати- •
стике и содержащей 500 чисел (см. табл. 5.3).
Отберем из этой таблицы подряд 10 случайных величин, начи-
ная с любого числа. В данном случае начнем с числа 6848 (четвер-
тое сверху в первом столбце) и будем отбрасывать две последние
цифры в каждом четырехзначном числе (так как их общее количе-
ство в табл. 5.1 равно 100), опуская повторяющиеся числа, если они
встретятся.
Теперь рассмотрим их как порядковые номера искомых чисел
выборки из табл. 5.2 и выпишем соответствующие этим номерам
десять значений наблюденных величин:
случайные числа .68 33 20 83 70 56 82 61 13 51
варианты .... 16,6 16,4 16,2 16,7 16,6 16,5 16,7 16,5 16,1 16,5
Среднее их значение
16,6+16,4+16,2 + 16,7+16,6+16,5+16,7 + 16,5+16,1 + 16,5 _
10
= 16,49%
Примем это число за середину среднего интервала. Так как мы
выбрали интервал равным 0,2, то средний интервал окажется меж-
ду 16,39 и 16,59. Примем 16,39 за конец предыдущего интервала.
Теперь, отсчитывая по 0,2 единицы в обе стороны от 16,40 и 16,59,
определим границы интервалов, охватывающих всю широту варьи-
рования, и сгруппируем наблюденные величины по этим интерва-
лам в виде таблицы (табл. 5.4).
Таблица 5.4
.№ интервала Граница интервала Частота в интер- вале п. i Середина интервала Частости п^п
1 15,40—15,59 1 15,50 0,01
2 15,60—15,79 2 15,70 0,02
3 15,80—15,99 5 15,90 0,05
4 16,00—16,19 5 16,10 0,05
5 16,20—16,39 19 16,30 0,19
6 16,40—16,59 35 16,50 0,35
7 16,60—16,79 18 16,70 0,18
8 16,80—16,99 8 16,90 0,08
9 17,00—17,19 4 17,10 0,04
10 17,20—17,39 2 17,30 0,02
11 17,40—17,59 1 17,50 0,01
п=100
Мы получили 11 интервалов вместо 10, так как взяли несколько
меньший размер интервала, чем полученный при вычислении, а
именно 0,2 вместо 0,21. Кроме того, обращаем внимание читателя
на то, что границы интервалов взяты с большим на единицу числом
Десятичных знаков, чем в данных наблюдений (табл. 5.1). Это сде-
235
лано для того, чтобы избежать затруднений при отнесении к тому
или иному интервалу тех чисел, которые совпадают с границей
интервала. Подсчет частот производится по табл. 5.2, в которой
подчеркиваются границы интервалов. Величина интервалов должна
быть одинаковой для возможности сравнения численности групп.
Рис. 5.12. Точечная диаграмма
частот щ в интервале к общему объему выборки п (сумма частот),
равной в данном случае 100.
Вычислением частостей заканчивается первый этап статисти-
ческой обработки материала, который носит название «группиров-
ки данных».
Графическое представление данных. Иногда удобнее предста-
вить первичные материалы графически. Для этого на миллиметров-
ке отмечается в виде точки по вертикали каждая наблюденная
величина, размер которой помечен на абсциссе графика. Таким
образом, по оси ординат оказываются отложенными частоты
(рис. 5.12). Такой график носит название точечной диаграммы. Ее
преимуществом является значительная наглядность по сравнению
с вариантным рядом. Графики облегчают сравнение величин, не
утомляют внимания, позволяют легко находить требуемые данные
и быстро обнаруживать наличие максимумов, минимумов, точек пе-
региба, установить характер изменений на различных участках, пе-
риодичность и ряд других важных характеристик [36].
Если вычислено распределение численностей, то его можно
представить графически двумя способами: с помощью столбиковых
диаграмм — гистограмм (рис. 5.13,а) или полигонов распределе-
ния (рис. 5.13,6). При построении гистограммы проводится гори-
зонтальная прямая в пределах каждого интервала на высоте,
соответствующей численности наблюдений (частоте). При построе-
нии полигона (многоугольника) частоты откладываются против
середин интервалов, и полученные точки соединяются прямыми. За
нули принимают середины интервалов, примыкающих слева и
236
справа к крайним. Площади обоих видов графиков равны общей
численности наблюдений.
Наряду с этими графиками могут строиться также так назы-
ваемые кумулятивные графики, в которых частоты каждый раз
прибавляются к предыдущим. На рис. 5.14 построен такой ступен-
чатый график и проведена плавная кумулятивная кривая через
точки, относящиеся к серединам ин-
тервалов. Такая кривая носит также
название огивы.
Обычно столбиковая диаграмма
строится в том случае, когда иссле-
дуемая величина имеет дискретный
Ч 8 12 16 20 2Ъ 28 52 56 W Ы
Значения признака
Рис. 5.14. Ступенчатый график и оги-
ва
Рис. 5.13. Гистограмма (а) и поли-
гон распределения (б)
характер. При возможности непрерывного изменения предпочти-
тельнее полигон частот (численностей) .
Кривые распределения. Если уменьшать интервалы и одновре-
менно увеличивать число наблюдений так, чтобы численности групп
оставались конечными величинами, то гистограмма или полигон
Рис 5.15 Кривые распределения
237
‘станут все более приближаться к плавной кривой. Такая предель-
ная кривая носит название кривой распределения частот. Площадь
кривой распределения между двумя ординатами равна числу на-
блюдений в соответствующем интервале значений исследуемой ве-
личины. Таким образом, можно условно заменить дискретное рас-
пределение непрерывным, анализ которого значительно проще.
В качестве основных элементарных типов кривых распределения
следует назвать: 1) симметричное (рис. 5.15,а); 2) умеренно сим-
метричное, или скошенное (рис. 5.15, б, в); 3) крайне асимметрич-
ное, или /-образное (рис. 5.15,г, д) и 4) {/-образное распределение,
называемое также антимодальным (рис. 5.15,в). Многие распреде-
' ления являются комбинациями этих элементарных и называются
составными.
8. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ
Средняя арифметическая. Аналогично теоретическим характе-
ристикам распределения случайной величины в теории вероятно-
стей (математическому ожиданию, дисперсии, моментам различ-
ных порядков) существуют подобные же характеристики для ста-
тистических распределений. Эти характеристики обычно называют
статистиками. Математическому ожиданию случайной величины в
теории вероятностей соответствует в статистике арифметическая
средняя, которая обозначается х и равна
пг
х.п.
i i
П
где xt— среднее наблюденное значение признака в z-том интер-
вале;
nt— частота в r’-том интервале;
m — количество интервалов;
п — общее количество вариант (объем выборки).
Арифметическая средняя аналогично математическому ожида-
нию является центром тяжести статистического распределения. Вы-
числим в качестве примера х для данных по распределению влаж-
ностей, приведенных выше (табл. 5.5).
Характерно, что найденная средняя очень близка к значению
16,49, полученному ранее для выборки в 10 величин, сделанной с
помощью таблицы случайных чисел.
Для упрощения процесса вычисления средней можно воспользо-
ваться следующим приемом. Из определения средней арифметиче-
ской следует, что алгебраическая сумма отклонений отдельных ве-
личин ряда от средней равна нулю:
пг __
2 (xz-x)nz=0, (5.91)
238
Таблица 5.5
Интервал влажности Середина ин- тервала X. Частота п. i х, nt X
15,40—15,69 15,50 1 15,5
15,60—15,79 15,70 2 31,4
15,80—15,99 15,90 5 79,5
16,00—16,19 16,10 5 80,5 1650,4 _ _ х < ™ —16,50 100
16,20—16,39 16,40—16,59 16,30 16,50 19 35 309,7 577,5
16,60—16,79 16,70 18 300,6
16,80—16,99 16,90 8 135,2
17,00—17,19 17,10 4 68,4
17,20—17,39 17,30 2 34,6
17,40—17,59 17,50 1 17,5
п = 100; 2 = 1650,4
Поэтому если определять отклонения не от средней х, а от
какой-то другой величины а, которая сама отклоняется от х на
d (а=х—d), то, зная a nd, легко получить
х — а + d. (5.92)
Подставляя в (5.91) значение х, получим
У — (а + d)J П. = 0;
1
т т
2 (х.— а)п{~£^ = 0;
1 1
т
2 (xz — а) п. _ п d = 0, (5.93)
1
где п — общее число вариант.
Из (5.92) получим
2 (xz — а)^
d = —1-------------. (5.94)
п
Величину а называют рабочей средней, или условной средней.
Таким образом, вычисляя не непосредственно х, как мы это де-
лали в табл. 5.4, а величину d. легко затем находим х по формуле
как сумму a + d.
Так как отношения njn представляют собой частости, то
(5.94) есть ни что иное как суммарный момент относительно точки
а в том смысле, как это излагалось в п. 3 главы 5. Обычно за а
принимают середину какого-либо интервала вблизи от центра
распределения.
239
Поскольку интервалы распределения одинаковы по величине, то
мы можем вместо величин х1— а вычислять величины di =——
(где h — ширина интервала), а так как и xt и а представляют
собой середины интервалов, то их разность, деленная на ширину
интервала, — это просто-напросто количество интервалов между
xz и а. Следовательно, мы можем искать не сумму разностей
xz — а, а сумму интервалов между ними, что резко упрощает вы-
числения. Естественно, при определении d мы должны результат
умножить на h:
т
м h У\ П; di
d = А 2 =-----!-----= hdn, (5.95)
п 1 ' h п
где
т
2 ni
dn = . (5.96)
п
Итак, для расчета следует:
1) сгруппировать варианты в таблицу распределения частот и
разбить их на равные интервалы шириной h;
2) выбрать в качестве условного начала а срединную точку од-
ного из интервалов вблизи от центра распределения;
3) вычислить отклонения dt от условного начала в терминах
интервалов d. = (х. — а}:1г;
4) умножить отклонение каждого интервала на частоту nz с
учетом знаков ;
5) найти алгебраическую сумму '^nidl;
6) разделив эту сумму на общую сумму вариант п, получить по-
правку dn, выраженную в терминах интервалов;
7) умножив поправку dn на действительную величину интер-
вала h и прибавив к условному среднему а, получитй
~x = hdn + а. (5.97)
Приводим в табл. 5.6 соответствующие вычисления (за а при-
нята середина интервала 16,20—16,39).
Итак, значение х, вычисленное по сокращенному способу, так-
же равно 16,50%.
Медиана и мода. Медианой Me называется такое значение на
оси абсцисс, которое делит площадь кривой распределения на две
равные части. Иными словами, это такое значение х, которое делит
количество вариант, соответствующих большим и меньшим, чем Me,
значениям, пополам. Значит, медиана есть срединное значение при-
знака в ранжированном ряду его значений (по табл. 5.5 это 16,50 —
середина шестого интервала). Если число вариант четное, то за
240
Таблица 5.6
Интервал влажностей Середина ин- тервалов xi Частота п. i Отклонение в терминах ин- тервалов di ni di Вычисления
15,40—15,59 15,50 1 —4 —4 а = 16,30
15,60—15,79 15,70 2 —3 —6 h = 0,2
15,80—15,99 15,90 5 —2 —10 , 102 , no
16,00—16,19 16,10 5 —1 -5 d„ = — = 1,02 п 100
16,20—16,39 16,40—16,59 16,30 16,50 19 35 0 1 0 35 d = 1,02 0,2 = 0,2
16,60—16,79 16,70 18 2 36 x = 16,30 + 0,2 =
16,80—16,99 16,90 8 3 24 = 16,50
17,00—17,19 17,10 4 4 16
17,20—17,39 17,30 2 5 10
17,40—17,59 17,50 1 6 6
и =100 +127
-25
+102
медиану принимают среднюю арифметическую из двух срединных
значений. _
Модой Мо называется то значение признака, которое соответст-
вует максимальной ординате теоретической кривой, наиболее близ-
кой к кривой действительного распределения. В качестве моды при-
нимают измерение с наибольшим числом повторений (в табл. 5.4
это 16,50 для 35 повторностей). При симметричном распределении
средняя арифметическая, медиана и мода совпадают. При скошен-
ном распределении между модой и медианой существует следую-
щее приближенное соотношение:
Мо = х — 3(7— Me), (5.98>
т. е. медиана лежит на ’/з расстояния от средней арифметической до
моды, будучи ближе к средней арифметической (рис. 5.16,а).
Показатели рассеяния. Второй важной числовой характеристи-
кой является мера рассеяния вариант относительно средней ариф-
Рис. 5.16. Медиана и мода (а); размах колебаний и точность (б). Наблюдения
по кривой 2 более точные, чем по кривой 1
241
метической. Очевидно, что при одном и том же значении последней
может быть совершенно различный разброс данных. Чем больше
размах колебаний ряда, тем менее точно проведены измерения
(рис. 5.16,6), тем больше разброс.
Чаще всего в качестве показателя изменчивости используется
та же величина, что и в теории вероятностей, а именно флуктуация,
которую обычно называют средним квадратическим отклонением и
обозначают в математической статистике через $. Оно представля-
ет собой корень квадратный из суммы квадратов отклонений ва-
риант от среднего арифметического, деленной на число вариант:
или
п
(5.99)
(5.100)
где т — число групп (интервалов);
щ— число вариант в группе.
Сумма квадратов отклонений от средней арифметической будет
минимальна по сравнению с суммой квадратов отклонений от лю-
бого другого значения х.
Квадрат среднего квадратического отклонения называется, как
и в теории вероятности, дисперсией.
Если воспользоваться условной средней а, равной х — d, и вы-
числить отклонения от нее dt = xi — а, то момент второго поряд-
ка относительно этой условной средней будет равен:
2 «z(xz -0)2
D = s2a = —----------. (5.101)
Подставим в (5.101) вместо а его значение х—d, тогда
т т
2 Пг (хг- — а)2 2 ni [ xt — pz — d)]2
Проведем следующие преобразования:
2^2 ni{xi — х)
1
п
242
Так как сумма отклонений случайной величины от средней арифме-
тической равна нулю, то второй член в правой части также равен
т
нулю, а так как —п, то третий член равен просто d2. Следо-
1
вательно,
2 лДх,-*)2
s2 = J----------- + d\
п
Сравнивая с (5.100), получаем
4 = «2 + ^2,
откуда
s2=s2 — <Р. (5.102)
Если при вычислениях выражать отклонения в терминах интер-
вала h, как мы это делали при определении средней арифметиче-
ской, то получим
- s2 = (s2 — &]h*. (5.103)
Это соотношение позволяет упростить вычисление s. Использу-
ем в качестве примера уже знакомую нам таблицу распределения
влажности и определим моменты распределения до четвертого по-
рядка включительно. Моменты вычисляются относительно некото-
рого произвольного начала а, за которое принята середина интер-
вала 16,20—16,39, т. е. а= 16,30. Соответственно моменты называ-
ются начальными, и для них принято обозначение у, с числовым
индексом, указывающим порядок момента. Моменты, приведенные
в табл. 5.7, вычисляются по формулам (5.104) — (5.107).
Таблица 5.7
Интервал влажностей в % Середина интервала xi Часто- та п. i Отклонение от условного начала в тер- минах интер- вала d. п. d. i i п. г/2? i i \з ni nd*
15,40—15,69 15,50 1 —4 16 —64 256
15,60—15,79 15,70 2 —3 —6 18 —54 162
15,80—15,99 15,90 5 —2 —10 20 —40 80
16,00—16,19 16,10 5 —1 —5 5 —5 5
16,20—16,39 16,30 19 0 0 0 0 0
16,40—16,59 16,50 35 1 35 35 35 35
16,60—16,79 16,70 18 2 36 72 142 284
16,80—16,99 16,90 8 3 24 72 216 648
17,00—17,19 17,10 4 4 16 64 256 1024
17,20—17,39 17,30 2 5 10 50 250 1250
17,40—17,59 17,50 1 6 6 36 216 1296
п = 100; 102; 388; 951; 5040
Условные начальные моменты
102 1 ™ 388 951 5040
= Too = 1,02: >Х2 = ^ = 3>88: ^=wo = 9’51; ^ = 1Го = 50’4-
243
(5.104)
(5.105)
(5.106)
(5.107)
Легко видеть, что порядок момента равен степени, в которую
возводятся «плечи» dt.
Условными начальные моменты здесь названы потому, что они
определены не для абсолютных значений отклонений, а для зна-
чений , вычисленных, когда интервал принят за единицу. Так
как а= 16,30, /г = 0,2 и, согласно (5.96),
dn = — = 1,02,
л 100
то на основании (5.99) и (5.103>
x = a + dnh = a + p1h = 16,30+ 1,02-0,2= 16,50%;
s2 = (Sa — 4) /t2= ta— ) й2 = (3,88 — 1,022) 0,22 = 0,12;
s = ]/0jJ= 0,35.
Таким образом, при размахе, равном 17,5—15,4 = 2,1, среднее
квадратическое отклонение равно $=0,35.
Поправка Шеппарда. Так как значения х разбросаны по каждо-
му интервалу обычно неравномерно и их средние значения по
интервалу не могут быть в точности отнесены к его середине, то
это вносит в определение дисперсии систематическую ошибку, из-
за которой вычисленная дисперсия будет больше истинной.
Шеппард установил, что при более или менее симметричном
распределении ошибка в дисперсии по этой причине равна 712
квадрата величины интервала. Обозначая величину интервала
244
через h, получим поправку Шеппарда в виде /г2/12. С учетом этой
поправки
s2 = Sp-fJ, . (5.108)
где $р — дисперсия без учета поправки.
В нашем примере
s2 = 0,12 — -^-=0,117,
12
т. е. в данном случае поправкой можно пренебречь (0,117^0,12).
Чтобы оценить относительную степень изменчивости, среднее
квадратическое отклонение сопоставляют со средней арифметиче-
ской.
Такой показатель относительной изменчивости называется
коэффициентом вариации и представляет собой отношение среднего
квадратического отклонения к средней арифметической, выражен-
ное в процентах:
w = 100. (5.109)
X
В нашем случае
а) = 0?35 100~2%
16,50
В практике исследования грунтов обычно считают, что при w С
20 грунт по соответствующему показателю является однород-
ным, а при w>20% — неоднородным.
Сложение средних и дисперсий. Если мы имеем, например, три
средних %1, %2, х3, найденных по выборкам из пъ и п$ элементов
(частные средние), то общая средняя для всех п = П1+п2+п3 эле-
ментов будет равна
х _ П1 Х1 ~1~ п2Х2 П3 Х3 _ 2 til xi /£ НО)
“ п — п ’ К • /
т. е. общая средняя равна средневзвешенному значению частных
средних, а общая дисперсия
s2
«1 «? •+ П2 $2 + П3 $3
П1 + П2 + п3
(%1 — * )2 + П2 (*2 — * )2 + П3 (%3 — Х)2
~h п2 п3
или в общем виде
2 ni (xi — х )2
п
(5.111)
2 л. s2
S2 = ----—
п
т. е. общая дисперсия равна средневзвешенной дисперсии плюс
дисперсия частных средних относительно общей средней.
Показатель скошенности. Обычно распределение характеризу-
ют тремя величинами: средней арифметической, дисперсией и по-
казателем скошенности, который позволяет оценить степень
245
симметричности кривой. Самым простым показателем скошенности
кривой распределения является отношение разности между сред-
ней арифметической и модой к среднему квадратическому откло-
нению:
к = х-М?... (5.112)
Для симметричного распределения разность х — Мо = 0 и Х = 0.
Так как моду не всегда легко определить, то более точно пока-
затель скошенности находят, используя момент третьего порядка,
т. е. момент, взятый относительно среднего арифметического значе-
ния случайной величины.
Момент третьего порядка относительно условного начала выше
был обозначен через ц3. Чтобы перейти от него к центральному
моменту т3, взятому относительно средней арифметической, поль-
зуются формулой
/»3= [1*з — Зр-2 1*, 4-2рЗ] h. (5.113)
Когда «длинная» часть распределения расположена справа от цент-
ра, т3 будет положительным, так как сумма кубов положительных
отклонений превзойдет сумму кубов отрицательных, и, наоборот,
когда длинная часть распределения находится слева от центра, т3
будет отрицательным. Таким образом, центральный момент третье-
го порядка может характеризовать асимметрию распределения.
Критерием скошенности служит отношение
(5-114)
Знак pi соответствует положительной или отрицательной скошен-
ности кривой.
Показатель крутизны. Часто применяется еще четвертый пока-
затель, указывающий на степень концентрации частот около сред-
ней и на концах распределения, называемый показателем крутиз-
ны (его называют также показателем эксцесса или куртозиса).
Этот показатель (32 равен отношению центрального момента четвер-
того порядка к квадрату центрального момента второго порядка,
который представляет собой дисперсию:
= (5.115)
ml s<
Центральный момент четвертого порядка определяют по фор-
муле
т4 = + 4 р3 + 6 — 3 р.4] h*, .(5.116)
где — условные начальные моменты i-ro пооядка.
Для нормального распределения 02=3. Если р2>3, то это ука-
зывает на более тесное сосредоточение частот около центра, чем
при нормальном распределении, и, наоборот, если р2<3, то кривая
246
распределения положе нормальной. Часто пользуются показате-
лем у2=02—3, характеризующим эксцесс относительно нормально-
го распределения.
С помощью 01 и 02 можно точно вычислить основной показа-
тель скошенности % по формуле
1^ + 3) . 117
2№-6|М-9)
Из (5.117) следует, что расстояние между средней арифметиче-
ской и модой (х—Мо) будет равно
k = ls. (5.118)
Соответственно легко определить моду:
Mo = x — k. (5.119)
В нашем примере
т3 = 0,23 (9,51 — 3-3,38 -1,02 + 2-1,023) = — 0,0019;
mi = 0,24 (50,4-4-9,51 • 1,02 + 6 • 3,88 • 1,023 — 3 • 1,024) = 0,0661;
0Х = = _ 0,045; 02 = = 4,71; X = 0,059;
s3 ml
k = \s = 0,024; Mo = х — k = 16,50 — 0,024 = 16,48 16,50.
Понятие о степенях свободы в статистике. Когда мы имеем
только одно измерение случайной величины, у нас нет никаких
данных для оценки изменчивости. Если измерений два, то одно
добавочное уже позволяет как-то судить об изменчивости. При
трех измерениях основание для суждения растет. В статистике го-
ворят, что два измерения дают одну степень свободы для оценки
изменчивости случайной величины, три измерения—две степени
свободы и т. д. Если бы мы заранее знали из какого-нибудь дру-
гого источника информации величину средней арифметической, то
даже одно измерение давало бы возможность судить об изменчи-
вости, и мы бы не теряли степени свободы. Но так почти никогда
не бывает, и мы используем одну степень свободы для подсчета
средней арифметической. Следовательно, при п измерениях ос-
тается п—1 степеней свободы для вычисления среднего квадрати-
ческого отклонения. Соответственно сумму квадратов отклонений
в (5.100) нужно делить не на п, а на оставшееся количество степе-
ней свободы n—1. Если и больше 100, то можно пренебрегать раз-
ницей между п и п—1, но при малых выборках это имеет сущест-
венное значение. Количество степеней свободы обычно обозначает-
ся буквой f.
Вся проделанная до сих пор вычислительная работа представ-
ляет собой по существу лишь количественное описание явления.
247
Следующий важный шаг заключается в анализе полученных ре-
зультатов с целью вскрытия причин явления и выяснения роли
различных факторов . Так, установив, например, прочность грунта
по испытанию ряда образцов, далее необходимо выяснить, в какой
мере на искомой величине сказались те или иные факторы, напри-
мер скорость загружения, колебания плотности и влажности и
т. п.
9. СЫПУЧИЕ ТЕЛА
Особыми свойствами, как бы промежуточными по своему ха-
рактеру между твердыми и жидкими телами, обладают так назы-
ваемые сыпучие тела, к которым относятся многие нескальные
грунты.
Если твердое тело (например, камень) раздробить на относи-
тельно мелкие части, то каждая из них также будет твердым те-
лом, но куча из частиц уже не будет обладать свойством послед-
него. Насыпь из таких частиц не может сохранять любое очер-
тание без ограждающих стенок, но в отличие от жидкостей имеет
ряд устойчивых форм, не требующих для своего поддержания
внешнего воздействия. Если поместить такой материал в желоб и
постепенно увеличивать его наклон, то при некотором угле накло-
на материал начнет двигаться по желобу вниз, и это движение
вначале будет напоминать течение жидкости.
Таким образом, хотя сыпучая масса является продуктом раз-
рушения твердого тела, ее поведение под действием нагрузок су-
щественно отличается от поведения твердых тел. Вместе с тем
движение сыпучего тела отличается от движения жидкости, так как
у сыпучих тел отсутствует характерное свойство жидкостей — вяз-
кость.
Деформации и разрушение сыпучих тел. Так как эти тела со-
стоят из отдельных зерен и обломков, представляющих собой оса-
дочные горные породы, и уже являются продуктом разрушения
других пород, то возникает вопрос, что считать деформацией и
разрушением сыпучих тел. Чтобы ответить на этот вопрос, необхо-
димо обратиться к понятиям о дальнем и ближнем сложении та-
ких грунтов.
Беспорядочным или случайным называют такое расположение
предметов, в котором отсутствует какая-либо система. Если в рас-
положении предметов можно установить известную закономер-
ность, то говорят о наличии определенного порядка, как это имеет
место, например, в расположении атомов у кристаллов, где они
образуют определенные структурные ячейки, характерные для
данного кристаллического вещества. Эти ячейки повторяются
закономерно через одинаковые расстояния в пределах
всего кристалла. Такое строго повторяющееся одинаковое относи-
тельное расположение частиц, образующих данную систему, назы-
248
вается дальним порядком. Дальний порядок характеризуется тем
или иным ритмом, т. е. определенным периодом повторяемости
ячеек, образующих систему.
Беспорядочный характер расположения отдельных частиц име-
ет место в газе, молекулы которого находятся в непрерывном
движении, постоянно сталкиваясь друг с другом и резко изменяя
при этом направление. Газ, как известно, стремится всегда рас-
шириться, распространившись равномерно по всему доступному
объему. В жидкостях энергия движения частиц гораздо меньше, чем
у газа, и они располагаются достаточно плотно относительно друг
друга. Вместе с тем молекулы жидкости испытывают гораздо более
энергичные колебания, чем атомы в узлах кристаллической решет-
ки, претерпевая непрерывные относительные смещения. Однако при
этом количество и относительная укладка частиц, соседствующих
друг с другом, в общем остаются неизменными, и, если зафиксиро-
вать некоторое мгновенное состояние жидкости, можно говорить
о наличии известного ближнего порядка в ней (рис. 5.17,6).
По мере удаления от некоторой частицы, выбранной в качест-
ве центральной, порядок как бы «размывается» (рис. 5.17,6), и в
отличие от кристаллов
дальний порядок в жид-
костях полностью отсутст-
вует.
-Если рассмотреть на-
сыпь из отдельных об-
ломков горных пород, то
эта система с самого на-
чала беспорядочная, и
понятие о дальнем поряд-
ке к ней совершенно не-
применимо. Будем называть относительное расположение частиц,
которое возникло при их отложении, сложением грунта. Первона-
чальное сложение грунта сохранится до тех пор, пока оно не будет
нарушено действием внешних сил.
Рассматривая любую небольшую группу отдельных соседних
частиц, можно увидеть, что при небольших деформациях «старые»
соседи сохраняются и ближнее сложение практически не нару-
шается. Но если охватить большую группу частиц, достаточно уда-
ленных от некоторой центральной, то, двигаясь по некоторому не-
изменному лучу, заметим, что последний после деформации пере-
секает уже новые частицы, а прежние сместились относительно
радиуса тем больше, чем дальше они отстояли от центральной ча-
стицы (рис. 5.18,а). Таким образом, дальнее сложение при не-
больших деформациях нарушается, а ближнее сохраняется.
Теперь представим себе, что одна часть обломочной массы сдви-
нулась относительно другой так, что в зоне сдвига частицы пол-
ностью поменяли своих соседей, нарушив ближнее сложение
(рис. 5.18,6). Такого рода перемещения в обломочной породе мы
249
будем называть уже не деформацией, а разрушением (сдвигом
грунта).
Тело Кулона. К трем простейшим реологическим телам, рас-
смотренным в главе 4, необходимо добавить четвертое, характер-
ное для сыпучих тел, которое можно назвать телом Кулона
Рис. 5.18. Деформация и сдвиг грунта
(Coulomb) или Кулона—Навье, впервые исследовавших его меха-
нические свойства. По своему поведению оно. очень близко к пла-
стическому телу Сен-Венана. Его сопротивление формоизменению
зависит от сопротивления сдвигу между отдельными частицами,
которое, по Кулону, определяется линейным соотношением
s = <rf + c, (5.120)
Где о — нормальное давление по некоторой площадке внутри тела,
по которой происходит сдвиг;
f — осредненный коэффициент трения по площадке;
с — сопротивление сдвигу, не зависящее от нормального дав-
ления и называемое сцеплением.
Если с=0, то сопротивление кулонова тела сдвигу зависит
только от нормального давления по площадке сдвига:
s = of. (5.121)
После того как касательное напряжение т от внешней нагрузки
достигнет предельного значения
^ = s (5.122)
или незначительно превзойдет его, начинается безостановочный
сдвиг по площадке а—а (см. рис. 5.18, б), аналогичный пластиче-
скому течению тела Сен-Венана.
Трение в сыпучем теле называют внутренним, чтобы отличить
его от поверхностного трения между сыпучим телом и поверхно-
стью уложенного на него какого-либо твердого тела.
Трение между частицами, по Кулону, подчиняется такому же
закону, как трение по поверхности соприкосновения двух твердых
тел, которое прямо пропорционально нормальному давлению по
этой поверхности (кулоново, или сухое трение). Кулоново тело при
с=0 называют несвязным, или сыпучим, а подчиняющееся закону
(5.120) можно было бы назвать связно-сыпучим, чтобы подчерк-
нуть, что оно обладает и кулоновым трением и сцеплением.
Реологическая модель связно-сыпучего кулонова тела (или те-
250
ла Кулона—Навье с реологическим символом С1) показана на рис.
5.19, а, б), а графики зависимости между з и о даны на
рис. 5.19, в, г.
Чисто сыпучее тело (с=0) обозначим CL, а связно-сыпучее —
С1с ф-
Из рис. 5.19, в следует, что
f = tg<p, (5.123)
где ф — угол внутреннего трения грунта-.
Работа, затрачиваемая на деформацию кулонова тела, пол-
ностью обращается в теплоту и является необратимой.
Правило эквивалентности. Сцепление связно-сыпучего тела
можно представить в виде эквивалентного по величине внутренне-
го трения, как это предложил впервые А. Како [89]'. Если продол-
жить влево график s ~ а на рис. 5.19, в до пересечения с осью абс-
цисс (рис. 5.20), то отрезок ординаты
(5.124)
Рис. 5.19. Модель реологического тела Кулона
Следовательно, если перенести условно начало координат на
графике сдвига в указанную точку пересечения, то сыпуче-связное
Рис. 5.20. Правило эквивалентности
тело можно рассматривать как сыпучее, но с добавочным нормаль-
ным давлением по площадке сдвига:
(5.125)
Так как площадки сдвига в разных точках тела могут быть
ориентированы различным образом, то для возможности такого
251
рассмотрения необходимо, чтобы давление <тЭкв было приложено к
телу всесторонне и равномерно распределенным.
Этот же результат можно получить непосредственно из
(5.120), если вынести за скобки в левой части f=tg <р:
s = (° + tg<p = (о + <тэкв) tg <р. (5.126)
Возможность подобной замены отличает сыпуче-связное тело*
от истинно связных тел, какими являются,, например, чисто глини-
стые грунты.
10. ДИСПЕРСНЫЕ СИСТЕМЫ
Если раздробить твердое тело на очень мелкие частицы, размер
которых измеряется тысячными долями миллиметра, то в резуль-
тате взаимодействия между молекулами окружающей среды и по-
верхностью тонких частиц поведение системы в целом будет отли-
чаться и от свойств сыпучего тела, и от свойств окружающей ча-
стицы среды.
Такие системы называются дисперсными телами и состоят из
двух и более различных веществ, из которых одно является сплош-
ной средой (обычно воздух или жидкость) и называется дисперс-
ной средой, а другие представляют собой распределенные в первом
раздробленные частицы, называемые дисперсным веществом. Это
вещество может состоять как из твердых частиц, так и из пузырь-
ков жидкости либо газа. Свойства дисперсных систем представля-
ют собой сложное сочетание свойств твердых и жидких тел, но на-
ряду с этим они приобретают и совершенно новые качества.
Классификация дисперсных систем. Дисперсные системы мож-
но подразделить на зернистые, частицы которых имеют размеры
>0,01 мм, грубодисперсные с размером частиц от 0,01 до»
0,0001 мм\ коллоидно-дисперсные, частицы которых находятся и
пределах от 100 до 1 ммк (миллимикрон). Далее начинается об-
ласть молекулярно-дисперсных систем, в которых частицы распре-
деленного вещества состоят из отдельных или нескольких ассоции-
рованных молекул.
Зернистые системы по своим свойствам могут быть отнесены к
сыпучим телам, и, таким образом, сыпучие тела являются одним из
видов дисперсных систем. В воде зернистые частицы довольно бы-
стро оседают на дно, тогда как грубодисперсные частицы оседа-
ют гораздо медленнее, практически не испытывая при этом броу-
новского движения.
Взвесь твердых частиц грубодисперсных размеров в жидкости
называется суспензией.
Трение в дисперсных системах. Дисперсные системы, пред-
ставляющие собой дисперсию твердых частиц в жидкой среде, мо-
гут содержать частицы различной крупности и обладать одновре-
менно свойствами как вязкой жидкости, так и сыпучего тела, про-
являя при деформациях оба вида внутреннего трения — вязкое и
кулоново.
252
Поверхность дисперсных частиц. Взаимодействие дисперсных
частиц между собой и с дисперсионной средой осуществляется по
их поверхности, и влияние этого взаимодействия на поведение си-
стемы в целом в большой степени зависит от общего размера по-
верхности частиц, приходящегося на единицу объема или веса си-
стемы. Обычно суммарную поверхность, приходящуюся на 1 г, на-
зывают удельной. Удельная поверхность шарообразных зернистых
частиц диаметром от 2 до 0,2 мм в среднем равна около 45 см2. а
коллоидных частиц кварца диаметром от 1 • 10“4 до 1 • 10“6 мм дохо-
дит до 10 млн.см21г.
Благодаря огромным величинам удельной поверхности колло-
идно-дисперсных частиц и малым их размерам в их взаимодей-
ствии практически никакой роли не играет масса отдельной части-
цы, но все определяется поверхностными силами.
Если вещество при растворении в жидкости распадается на от-
дельные молекулы или ионы, то раствор называют истинным; если
же в жидкости распределены частицы колоидных размеров, то та-
кая система называется коллоидным раствором.
Отдельная частица дисперсной фазы в коллоидном растворе
называется мицеллой, а жидкая среда — интермицеллярной жид-
костью.
Коллоидные частицы в воде оседают чрезвычайно медленно.
Так, частица диаметром 10 ммк оседает в спокойной воде со ско-
ростью около 1 см!год, а частица диаметром 1 ммк — со скоростью,
в 100 раз меньшей (0,01 см)год), Коллоидные частицы, распреде-
ленные в жидкости, испытывают интенсивное броуновское движе-
ние.
Большая межфазная удельная свободная энергия, которой об-
ладают коллоидные частицы вследствие сильно развитой поверх-
ности раздела фаз, является причиной невысокой устойчивости та-
ких систем. Они стремятся довести свою поверхностную энергию
до минимума, либо слипаясь в агрегаты частиц, либо притягивая
к поверхности различные вещества из дисперсионной среды. Про-
цесс слипания и укрупнения частиц называется коагуляцией.
Коллоидные растворы можно получать двумя способами: 1) ди-
сперсионными (или диспергационными), когда более крупные ча-
стицы дробятся на мелкие в результате механического воздейст-
вия, и 2) конденсационными, когда объединяются более мелкие
частицы (агрегация).
Коллоидные растворы с жидкой дисперсионной средой, облада-
ющие ярко выраженными жидкообразными свойствами (предел
текучести практически равен нулю), называют золями. Золи, как
правило, представляют собой вязкие неньютоновские жидкости.
Если коллоидная система с жидкой дисперсионной средой обла-
дает таким характерным твердообразным свойством, как заметный
предел текучести, то система называется гелем. Если дисперсион-
ной средой является вода, то говорят о гидрозолях и гидрогелях.
Обычно гели образуются в результате коагуляции и агрегирова-
253
ния коллоидных частиц золя. При этом гель может существовать
в виде осадка выпавших на дно крупных коагулированных частиц
(коагель), но возможна и такая структура геля, когда частицы зо-
ля, не выпадая в осадок, соединяются друг с другом в пространст-
венную структуру, пронизывающую весь объем коллоидного рас-
твора. Дисперсионная среда заполняет ячейки и поры этой струк-
туры и является полностью иммобилизованной, а такие гели назы-
вают также лиогелями.
Объемная концентрация. Важной характеристикой дисперсных
систем является объемная концентрация дисперсных частиц Су,
которая определяется как отношение:
q объем дисперсных частиц в данном объеме системы |
V объем системы ’ \ /
Любая реологическая характеристика такой системы является
функцией реологических свойств дисперсной и дисперсионной
фаз. Реологические коэффициенты при одних и тех же компонентах
системы существенно зависят от объемной концентрации.
У разбавленных золей реологические параметры можно при-
нимать изменяющимися линейно с концентрацией. Это справедли-
во до значений Су, не превосходящих примерно 2—3%. В этом
случае на поведение системы форма частиц дисперсной фазы прак-
тически не оказывает влияния, поскольку объем, занимаемый ча-
стицами, мал по сравнению со всем объемом системы.
У высококонцентрированных систем уже нельзя пренебрегать
формой частиц, находящихся близко друг к Другу и непосредст-
венно взаимодействующих между собой. Реологические свойства
таких систем существенно зависят от плотности упаковки твердых
частиц.
В физико-химической механике П. А. Ребиндера структуры
дисперсных систем делятся на два основных типа, носящих дву-
членные названия: 1) коагуляционно-тиксотропные и 2) конденса-
ционно-кристаллизационные. Первое слово в этих терминах ха-
рактеризует особенности процесса структурообразования, вто-
рое—особенности связей между частицами.
Коагуляционно-тиксотропная структура. В коагуляционных
структурах частицы дисперсной фазы образуют беспорядочную
Рис. 5.21. Тиксотропное восстановление
пространственную сетку
(рис. 5.21, б), причем по
микроплошадкам контак-
та остаются очень тонкие
прослойки жидкой среды.
В этих структурах сцепле-
ние между частицами от-
носительно слабое и соз-
дается силами притяже-
ния между поверхностны-
ми ионами частиц с уча-
254
стием ионов солей раствора. Связи этого рода между частицами
обычно называют коллоидными.
При механическом воздействии в виде перемешивания или
встряхивания происходит разрушение коагуляционной структуры,
называемое тиксотропным (от греческих слов «тиксис» — встря-
хивание, «тропос» — поворот, направление). Связи между части-
цами нарушаются (рис. 5.21,а), и образуется концентрированный
золь или бесструктурный гель. Если после этого систему оставить в
покое, в ней постепенно снова восстанавливается структурный кар-
кас.
Таким образом, тиксотропные превращения полностью обрати-
мы. Коагуляционно-тиксотропные структуры следует считать вяз-
кими жидкостями, отличающимися, однако, от ньютоновой наличи-
ем внутренней структуры, разрушающейся и перестраивающейся
в процессе деформирования. Их называют также структурирован-
ными, или неньютоновскими жидкостями.
Не следует смешивать явления тиксотропии и структурной вяз-
кости, хотя оба эти явления связаны с обратимым падением вяз-
кости при деформации сдвига. Однако структурная вязкость вос-
станавливается практически мгновенно, без запаздывания, тогда
как тиксотропное восстановление требует известного времени пре-
бывания системы в покое. Упрощенной реологической моделью
для этих структур является модель Бингама или модель Шве-
дова.
Эрмит (1949 г.) обнаружил явление увеличения вязкости неко-
торых материалов в результате течения и назвал его антитиксо-
тропией (рис. 5.22). После отдыха системы
вязкость постепенно падает до первоначаль-
ного значения. В литературе описан случай,
когда после сдвига вязкость раствора поли-
мера увеличивалась в три с половиной раза.
В некоторых жидкостях, у которых ин-
тенсивные сдвиги вызывают тиксотропное
нарушение, обратное восстановление струк-
туры происходит значительно скорее, если
система находится не в покое, а подверга-
ется медленным и незначительным сдвиго- Рис- 5-22- Антитиксотро-
вым деформациям. Это явление, обнаружен- пия
ное, например, у суспензии бентонита, полу-
чило название реопексии. Реопексией называют также явление по-
степенного замедления начавшегося сдвига в результате структуро-
образования, происходящего в процессе течения.
В результате деформации и разрушения структурного каркаса
вязкость коагуляционно-тиксотропных систем уменьшается, и их
поведение все более приближается к поведению ньютоновских
жидкостей. Консистентная кривая для структурированной жид-
кости называется кривой В. Оствальда (рис. 5.23). Начальный уча-
сток 1 кривой прямолинеен, и здесь материал ведет себя как
255
ньютоново тело с коэффициентом вязкости т)0- Конечный участок
3 также характерен для вязкой жидкости, но с меньшим коэффици-
ентом вязкости г]Уст, отвечающим разрушенному состоянию струк-
турных связей в системе. Участок 2 является переходным и соответ-
ствует процессу постепенного разрушения структуры системы.
Вязкость т]эф , соответствующую точке перегиба, называют эф-
фективной. На рис. 5.23, б построены для сравнения консистентные
кривые' для простой ньютоновской 1 и неньютоновской 2 жидко-
стей, а также для бингамова тела 3. Кривая 3 имеет в нижней ча-
сти криволинейный участок, так что действительное значение хт
несколько меньше показанного на чертеже и полученного продол-
жением прямолинейного участка графика до пересечения с осью
абсцисс.
Неньютоновская жидкость 2 отличается от бингамова тела пол-
ным отсутствием предела текучести. У ряда таких жидкостей точ-
ка перегиба т]Эф (рис. 5.23, а) наблюдается лишь при очень высо-
ких напряжениях, не имеющих практического значения, и в преде-
лах нижнего участка консистентной кривой можно пользоваться
степенной зависимостью
x=kr, (5.128)
где k—мера консистенции жидкости (чем больше k, тем выше
вязкость);
п—показатель (п<1), характеризующий степень отклонения
поведения жидкости от ньютоновской (чем больше п от-
клоняется от единицы, тем сильнее проявляются неньюто-
новские свойства).
Размерность k зависит от показателя степени п (из условия
одинаковой размерности левой и правой частей уравнения), од-
нако для практических приложений это несущественно. Если на-
звать тангенс угла наклона к оси у карательной к кривой 2 в не-
256
которой ее точке кажущейся вязкостью , то из предыдущей фор-
мулы следует, что
т)к = 4- (5.129)
Y
и так как п<1, то кажущаяся вязкость убывает с увеличением
скорости.
Консистентная кривая 4 на рис. 5.18,6 характеризует жид-
кость, у которой в отличие от жидкости 2 кажущаяся вязкость не
убывает, а возрастает с увеличением скорости сдвига. В этом слу-
чае также пригоден степенной закон (5.129), но с показателем
степени п+1. Эти жидкости впервые были исследованы Рейнольд-
сом, который считал их суспензиями с очень высокой концентра-
цией дисперсной фазы. При сдвиге происходит увеличение объема
системы (дилатация), на что требуется затрата дополнительной
энергии, и это воспринимается наблюдателем как увеличение вяз-
кости в ходе деформации.
Конденсационно-кристаллизационная структура. В конденса-
ционно-кристаллизационных структурах связи между частицами
возникают в результате химического соединения их поверхностных
атомов (нередко с участием атомов дисперсной среды). В резуль-
тате образуется гораздо более прочный каркас, чем у коагуляци-
онно-тиксотропных структур. Такого рода связи между частицами
иногда называют цементационными. Конденсационно-кристаллиза-
ционные структуры могут возникать из коагуляционных в резуль-
тате обезвоживания, уплотнения и возникновения цементационных
связей.
После разрушения конденсационно-кристаллизационные струк-
туры сами собой не восстанавливаются, их разрушение носит хруп-
кий и необратимый характер. Эти структуры обладают хорошо
выраженными упругими свойствами. Характерной для них яв-
ляется реологическая модель Прандтля либо модель Прандтля с
включением вязкого элемента.
Реотропия. Если тиксотропия является характерным свойством
неньютоновских жидкостей, то реотропия представляет собой свой-
ство твердых бингамовых тел. Явление реотропии заключается в
том, что у бингамова тела в результате деформации (формоизме-
нения) понижается как предел текучести, так и 'Вязкость, однако
предел текучести не падает до нуля, и обращения в ньютоновскую
или неньютоновскую жидкость не происходит (рис. 5.24). После
отдыха структурные связи восстанавливаются полностью или ча-
стично.
На рис. 5.24 показана первичная консистентная кривая реот-
ропного тела 1. Если в точке А снять нагрузку, а затем сразу же
снова подвергнуть систему сдвигу, то консистентная кривая будет
иметь форму 2 с пониженным пределом текучести Если же
9 Зак. 530
257
после разгрузки предоставить телу отдых, то его кривая снова
совпадет, с кривой /. Реологическая модель реотропного тела
представляет собой спектральную бингамову модель. Реотропные
свойства характерны для многих грунтов.
11. ПРИЛОЖЕНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
К ОПИСАНИЮ НЕКОТОРЫХ СВОЙСТВ ГРУНТОВ
Грунты, состоящие из множества частиц, подвергавшиеся в
процессе своего образования и существования многочисленным
случайным воздействиям, могут несомненно исследоваться веро-
ятностно-статистическими методами. Первые исследования в этом
направлении были проведены Г. И. Покровским [48—50], зало-
жившим основы статистической механики грунтов.
Приложение статистических методов к грунтам может осущест-
вляться по трем направлениям.
1. Непосредственное приложение методов математической ста-
тистики к явлениям, носящим случайный характер. Сюда отно-
сятся, например, задачи, связанные с характером разброса ре-
зультатов определения физико-механических свойств грунтов. Так,
экспериментальная проверка показала, что большинство основных
физико-механических характеристик грунтов имеет нормальный
закон распределения. Второй пример — задача об оценке влияния
случайных структурных неоднородностей на механические свой-
ства грунта/подверженного механическому воздействию, в зависи-
мости от его объема (задача о масштабном факторе).
2. Метод статистической аналогии. Он заключается в том, что
некоторое явление в грунте рассматривается как случайное, и к
нему применяются математические зависимости теории вероятно-
стей и математической статистики. В качестве примера можно на-
звать предположения о распределении напряжений в грунтах по
тому или иному закону распределения случайных событий.
3. При анализе какого-либо явления делаются упрощения, ха-
рактерные для статистического подхода. На основе этого анализа
составляются дифференциальные уравнения процесса, интегриро-
вание которых приводит к искомому результату.
В ряде случаев можно сочетать эти три подхода.
258
Влияние неоднородностей на распределение механических
свойств. В любом материале имеются те или иные начальные де-
фекты и неоднородности: в монокристаллах — дислокации и блок-
мозаичная структура; в аморфных телах — микронеоднородности в
строении, плотности и химическом составе; в сыпучих материалах
и структурированных дисперсных системах — колебания плот-
ности, неравномерное строение, неодинаковая ориентация частиц,
наличие случайно расположенных микро- и макроагрегатов раз-
личных размеров и строения. Все эти неоднородности и нарушения
порядка приводят к неравномерному распределению в материале
деформативных и прочностных свойств, с одной стороны, а с дру-
гой,— к локальным отклонениям от теоретического распределения
по объему напряжений, вызванных внешней нагрузкой. Кроме то-
го, в материалах неравномерно распределены остаточные напря-
жения и отдельные перенапряженные или, наоборот, разгружен-
ные микрообъемы. В результате в отдельных точках напряжения
от нагрузки могут превосходить сопротивление материала разру-
шению, тогда как в других еще будет иметься значительный запас.
Первые попытки построить теорию прочности, учитывающую не-
постоянство механических свойств в различных точках, относились
к хрупким материалам и исходили из того, что разрушение начи-
нается в самом слабом месте, причем оно может либо блокиро-
ваться соседними, более прочными^ участками, либо распростра-
няться далее. Чем больше объем или поверхность образца или
элемента конструкции, тем вероятнее встретить в этом образце на-
иболее опасный дефект, влияющий на прочность. Следовательно,
чем больше размеры образца, тем меньшей должна быть его удель-
ная прочность (отнесенная к единице площади сечения).
Соответственно, исследования ставили своей целью решение за-
дачи о переходе от результатов испытаний малых образцов к
оценке прочности материала в конструкциях реальных размеров.
Обобщая результаты проведенных ранее работ Вейбулла и других
исследователей, В. В. Болотин [6] предложил для такого перехо-
да формулу
Я=/?о а
(5.130)
где Я — средняя прочность материала в объеме V;
/?о — то же, образцов в объеме Vo;
а, b и а — эмпирические величины.
Из этой формулы следует, что
(5.131)
и — является линейной функцией от
На соот-
259
ветствующем графике (рис 5.25) отрезок, отсекаемый на оси ор-
динат, представляет собой минимальную прочность /?мин. Чтобы
определить параметры этого графика а, Ь и а, Болотин рекомен-
дует испытать две серии образцов с различными объемами и V2
и найти для них R2 и средние квадратические отклонения $i
и $2- Коэффициенты вариации будут равны: wt = — и w2= ~ .
°i “г
Рис. 5.25. График Болотина
Но эти коэффициенты связаны с параметрами а, b и а соотноше
нием
1
/ |/п \ а
6 ) ф (а)
W = —------------— , (5.132)
а±Ь у j
а <р(а) определяется по графику на рис. 5.26.
Таким образом, можно подобрать а, b и а. Однако, учитывая,
что /?мин практически мало отличается от
R'^R(l-3s),
(5.133)
можно определить по этим двум сериям опытов среднюю вели-
чину R„ин как полусумму R'. Задаваясь несколькими значениями
а, подбором находят прямую, наилучшим образом проходящую
через три точки с ординатами и , а затем и парамет-
ре Ро Ро
ры прямой а и Ь.
В дальнейшем было выдвинуто предположение, что распреде-
ление прочности по поперечному сечению образца в целом соответ-
ствует распределению прочности при испытании многих образцов
(рис. 5.27). Опыты показывают, что при увеличении размеров об-
разцов кривые распределения смещаются в сторону малых проч-
ностей, причем абсолютный разброс значений уменьшается. Обыч-
260
но принимают, что распределение прочности подчиняется нормаль-
ному закону [67].
В своем решении задачи о масштабном факторе В. Н. Быков-
ский [8] предложил исходить из соотношения между дисперсией
некоторого признака в материале конструкции в целом (генераль-
ная совокупность) и дисперсиями в образцах (частные выборки).
Рис. 5.27. Распределение прочно-
сти (Fi, F2, F3 — площади сечений
образцов)
Это соотношение заключается в следующем: генеральная диспер-
сия D равна средневзвешенной величине дисперсий частных выбо-
рок, сложенной с дисперсией арифметических средних этих выбо-
рок по отношению к математическому ожиданию (см. стр. 245).
Если количество элементов в каждой выборке постоянно и рав-
но N, то средневзвешенная дисперсия частных выборок равна s2.
Дисперсия частных средних по отношению к математическому
D
ожиданию генеральной совокупности равна —, и, следовательно,
D = s2 + y, (5.134)
откуда
s2 = D /1 — у). (5.135)
Так как N нам неизвестно, примем его пропорциональным не-
которой величине R, характеризующей размер образца (линейный
размер, поверхность, объем, площадь поперечного сечения и т. п.),
и тогда
s2 = D (1--------Ц
\ Л/?/
(5.136)
где k — коэффициент пропорциональности, соответствующий наи-
меньшему объему, в пределах которого материал можно
считать однородным.
Извлекая из обеих частей (5.136) квадратный корень и деля их
на генеральное среднее данного признака Л1ген:
М ~ Л4 11-4- и>макс \
ген ± угк)'
(5.137)
261
получим зависимость коэффициента вариации w от размеров об-
разца:
w~w + -1/1-----(5.138)
маке - ykR J |/ kR
где знак ~ означает корреляционную связь;
wMaKc — максимальное значение ш, характеризующее гене-
ральную совокупность.
Практически, при использовании этого метода за генеральную
совокупность принимается весь объем проведенных испытаний, ко-
торый затем делится на ряд случайных выборок. При этом, естест-
венно, общий объем испытаний должен быть достаточно велик.
На рис. 5.28 приведен график, асимптотически приближающий-
ся к значению wMaKC» и прилегающая к графику область наиболее
вероятных значений w.
Понятие о структоре. Принимая в качестве характеристик струк-
туры плотность у и сцепление с, Покровский [50] характеризует
кривые распределения этих величин двумя параметрами
(рис. 5.29): значением, соответствующим максимуму кривой рас-
пределения (обозначается индексом 0), и значением, соответству-
ющим ординате, равной половине максимальной (обозначается ин-
дексом Д). Таким образом, структура может быть охарактеризова-
на матрицей значений
Тео
Со
Тед
Сд
(5.139)
где точками обозначены любые другие параметры, которые могут
быть введены для описания структуры. Эту матрицу характеристик
Покровский назвал структором.
Чтобы учесть влияние ориентировки структурных элементов
грунта, Покровский предложил [50] сравнивать механические
свойства образцов по двум взаимно перпендикулярным направ-
лениям — горизонтальному и вертикальному. Если в первом слу-
чае структор обозначить через Srop , а во втором — через 5верт , то
разность матриц Srop —SBepT будет характеризовать влияние
ориентировки на механические свойства. Очевидно, выраженная
ориентировка отсутствует, если
Sop = Srop — SBepI = 0. (5.140)
Величину Sop Покровский называл структором ориентировки.
Нетрудно видеть, что структор ориентировки зависит не от абсо-
лютных значений соответствующих параметров, а от их флукту-
262
аций. С учетом влияния ориентировки полный структор
вид - . .
примет
fro I с А верт * г А гор*
С0 верт
^А гор
(5.141)
Рис. 5.28. График вариации прочности
Рис. 5.29. Распределение
свойств грунта
Сопротивление грунта сжатию. Если рассмотреть процесс уплот-
нения грунта, то в нем можно увидеть два явления, противополож-
ных по своему влиянию на сопротивление грунта деформации.
Первое представляет собой увеличение плотности, а следовательно,
и количества точек контакта между частицами. Этот процесс ве-
дет к увеличению сопротивления грунта деформации. Можно при-
нять, что приращение сопротивления пропорционально давлению
р, уплотнившему грунт, и величине 8 деформации:
Д1Р^ Д1РАз, (5.142)
где А1 — постоянная.
С другой стороны, в результате относительного сдвига частиц
одновременно с уплотнением происходит разрушение первоначаль-
ных связей между ними и ослабление грунта. Падение сопротивле-
ния максимально в первые моменты сдвига, а далее сопротивление
падает все меньше по мере продолжающегося деформирования
грунта.
При одноосном сжатии образец испытывает поперечное расши-
рение, равное vAe (где v—коэффициент Пуассона), благодаря ко-
торому как плотность, так и прочность его соответственно убывают.
Таким образом, если прочность грунта на одноосное сжатие обо-
значить через q, то падение сопротивления следует принять про-
порциональным как разности между q и приложенным давлением
р, так и деформации vAe:
Д2р = Л2(<? —р)Де, (5.143)
где А2 — постоянная (включающая в себя v).
Так как оба процесса — упрочнение за счет уплотнения и раз-
упрочнение за счет внутренних сдвигов и поперечного расширения—
263
идут одновременно и параллельно, Покровский принимает для их
сочетания правило умножения вероятностей.
Переходя к дифференциалам, он получает
dp = А (7 — р)pde (5.144)
и, интегрируя, находит
Р~1+С'-*- <5Л45>
При е=0
р~Т+с- (5'146)
Так как при е=0 внешние силы отсутствуют, то значение
Р в выражении (5.146) следует отнести за счет внутренних сил
взаимодействия частиц. Обозначая
-Г~ = <7о> (5.147)
1 -J- и
находим
C = _L —1 (5.148)
<7о
И*
Р =----------Я-----------<?0. . (5.149)
\ Я о /
Полученный по этой формуле график (рис. 5.30) не всегда сов-
падает с экспериментальными, но этот вывод характерен для пони-
мания метода статистической ана-
логии. Если полученный резуль-
тат не подтверждается экспери-
ментом, аналогия может быть
уточнена или отброшена.
Распределение напряжений в
полупространстве. Еще в 1925 г.
Н. Н. Иванов предложил схему
распределения напряжений в грун-
те как в системе послойно уложен-
ных одинаковых шаров (рис.
5.31). По этой схеме усилие от
каждого шара поровну передает-
ся на два нижележащих, что по-
зволяет легко вычислить распре-
деление усилий в любом ряду.
При этом напряженная зона ог-
раничивается прямыми, проходя-
щими под углом 30° к линии дей-
ствия силы Р.
264
Г. И. Покровский [49, 50] исследовал распределение напряже-
ний исходя из общего предположения, что грунт состоит из непра-
Рис. 5.31. Распределение усилий в системе шаров
вильных по форме частиц, случайным образом опирающихся друг
на друга (рис. 5.32).
F^F —
1 ——
L
Если рассматривать частицу / как
балочку, то ее левая опорная реакция
будет равна:
. (5.150)
Если же перейти к слою грунта
толщиной, равной единице, содержа-
щему множество подобных частиц, то
при действии на участке dx поверхно-
сти этого слоя силы F давление по этой
площадке (рассматривается плоская
задача, и размер в плоскости, перпен-
дикулярной чертежу, равен единице),
находящейся на глубине у и на рас-
стоянии х от направления F, выразится
зависимостью
dF = F(l — ^-\ f(x)dx. (5.151)
Р.ис. 5.3Й. Распределение давле-
ний между частицами грунта
по Покровскому
Введение функции f (х) Покровский объясняет следующим об-
разом: так как величины х и L могут быть в различных точках
грунта различными, то каждому значению х будет соответствовать
сила, пропорциональная вероятности того, что осуществится имен-
но данное значение х. Следовательно, f(x) является функцией ве-
роятности. Покровский принимает ее в форме нормального за-
кона распределения:
/ (х) = Ае~в (5-152)
Подставляя (5.152) в (5.151), обозначая 1-= W и полагая х0
достаточно малым, получаем
dF = We^Bxtdx
265
откуда
a = d_I=We~Bx*. (5.153)
X
Покровский приходит к следующему важному выводу: если раз-
меры частиц или структурных элементов грунта, а также парамет-
ры, определяющие их взаимное расположение ^в данном случае
отношение j , подчиняются какому-либо определенному зако-
ну распределения, то этому же закону должно следовать и распре-
деление давления в грунте. Далее он показывает, что если для не-
которой глубины принята определенная функция распределения
напряжений, то это же распределение должно осуществляться и
на всех других глубинах.
Сопоставляя результаты расчета с опытами, Покровский при-
ходит к выводу, что статистический метод более надежен, чем ме-
тод теории упругости.
И. И. Кандауров в 1958 г. предложил использовать аналогич-
ную схему случайного характера распределения точек контакта
между дискретными элементами зернистой среды. Им была созда-
на стройная схема расчета напряжений в таких средах при раз-
личных условиях загружения и различных характеристиках са-
мой среды [22].
Приводим основные положения схемы его расчета, несколько
упростив ВЫВОДЫ.
Рассмотрим сначала плоскую задачу о распределении напря-
жений в модели из продольных элементов типа швеллеров, каждый
из которых опирается на два нижележащих (рис. 5.33). Легко
Рис. 5.33. Распределение напряжений в симметричной швел-
лерной модели
266
21
чисто арифметически подсчитать усилия, воспринимаемые каж-
дым швеллером, если сила Р равна единице. Эти усилия на рис.
5.33 показаны в виде чисел, которые нужно умножить на коэффи-
циент где п — порядковый номер ряда, считая сверху вниз
и рассматривая верхний швеллер как нулевой.
Числа, стоящие на швеллерах, образуют известный треугольник
Паскаля и являются коэффициентами биномиального ряда (соче-
тания из /г по т, где п — номер ряда, т — порядковый номер
швеллера в ряду, причем в каждом ряду п=Шмакс):
Сочетание С™ часто обозначают (”). Таким образом, распре-
деление усилий в швеллерах является биномиальным. Усилие в
каждом швеллере можно кратко записать в виде
Ш"- (5Л55)
По формуле Стирлинга факториал числа п
n\^=V2ni (5.156)
\ е /
Подставляя (5.156) в (5.154), а затем (5.154) в (5.155), полу-
чим при больших п
<5Л57>
Если сила, приложенная к верхнему швеллеру, равна Р, то
. <5158)
Пусть швеллеры имеют высоту а, ширину, вдоль оси х рав-
ную Ь, и вдоль оси у, равную 1. Тогда координаты каждого швел-
лера
z = an*t x = b — = dm
2
и
_ 2 а х2
Q = Р 1/г d*
^п,т Г V лп 6
или, переходя к напряжениям,
_ *п, т г, 1 f 2 а I 8 а
Максимальное значение <г2, х будет иметь при х=0:
267
<*макс —oZtX=0—P У яг& '
Введем безразмерные величины:
а . а ь
а = — ; р = — .
z z
Тогда
аг = Р ехр .
г Г лр2г2 F\ z2 Р2 )
Обозначим =т) и назовем эту величину коэффициентом рас-
пределения. Тогда
аг = Р ехр (—(5.159)
В случае пространственной задачи, когда линейные элементы в
модели заменены кубами, можно по аналогии написать
Q„..-p “") <5'160’
Рассуждая по предыдущему, получим для пространственной за-
дачи
| л 2 Я Z2 \ Z2 /
Примем = т] и обозначим х2 + у2 — г2.
Тогда
^ехр Ь4,1Я- (5Л62)
Обозначая
-3-ехр (-47) 4) = Кк, (5.163)
где К к — коэффициент Кандаурова, придем к выражению
аг = Кк4’ (5.164)
отличающемуся от известной формулы Буссинеска значением коэф-
фициента К. Для различных значений т] при — =0 получим:
при т) = 4 Кк = 1,27;
» т)=1,5 К„ = 0,48; = 0,48,
где Кб — коэффициент распределения Буссинеска для упругой
среды.
268
Глава 6
ОСНОВЫ ТЕОРИИ ПРОЧНОСТИ
1. ПОНЯТИЕ О ПРОЧНОСТИ
Разрушение материала. При возрастании напряжений, действу-
ющих на твердые материалы, возможны два исхода: либо начнется
пластическая деформация, переходящая в течение, при котором
деформации могут стать сколь угодно большими, либо материал
при сравнительно небольших деформациях растрескается и разру-
шится, распавшись на отдельные части. Во втором случае говорят
о хрупком разрушении и разрушающих напряжениях. И течение и
хрупкое разрушение выводят конструкции из строя. Оба эти случая
рассматриваются как потеря материалом прочности.
Таким образом, прочность можно определить как свойство ма-
териала сопротивляться хрупкому разрушению или наступлению
состояния неограниченного деформирования (течения).
Величина предшествующих хрупкому разрыву остаточных де-
формаций, связанных с вязким течением (для аморфных материа-
лов) или пластическим деформированием вещества (для кристал-
лических материалов), зависит от скорости загружения. При обыч-
ных достаточно высоких скоростях остаточные деформации очень
невелики, и сечение образца в месте разрыва не испытывает
сужения, характерного для разрушения при течении материала.
Нарушение прочности может происходить также в виде соче-
тания обоих указанных выше процессов — сначала происходит
пластическая деформация, переходящая в течение, которое закан-
чивается разрывом. Однако в большинстве случаев уже переход в
состояние течения недопустим для конструкций.
Виды прочности. В зависимости от особенностей материала
его прочностные свойства могут проявляться по-разному при раз-
личном характере приложения и распределения действующих
усилий.
Однако все случаи потери прочности сводятся, в сущности, к
потере прочности вследствие объемной деформации и к потере
прочности при формоизменении. В первом случае нарушение проч-
ности происходит только в виде хрупкого разрыва под действием
нормальных напряжений по площадкам отрыва, во втором — в виде
пластического сдвига вдоль площадок скольжения и течения ма-
териала. Однако возможны также случаи как объемной пластиче-
ской деформации (течения), так и хрупкого сдвига, называемого
269
сколом. Сопротивление грунта разрушению за счет отрыва
объясняется наличием между его частицами сил притяжения, ко-
торые называют сцеплением при растяжении (адгезией). Сопротив-
ление грунта разрушению за счет сдвига обычно складывается
из двух частей — одной, не зависящей от нормального давления по
площадке скольжения и называемой сцеплением при сдвиге, и дру-
гой, зависящей от нормального давления и называемой внутренним
трением. Если эти две составляющие не выделяют, то говорят
просто о сопротивлении грунта сдвигу.
Основные виды режимов загружения. Характер деформирова-
ния (и, особенно, разрушения) материала, его прочность и долго-
вечность существенно зависят от режима загружения. Различают
шесть основных режимов загружения грунтов — три статических и
три динамических. К статическим режимам относят действие по-
стоянной нагрузки, действие ступенчатого загружения, испытание
на заданную деформацию. Особенностями статических режимов
является медленное приложение нагрузки или медленное деформи-
рование с последующим сохранением созданных напряжений или
деформаций.
К динамическим режимам относят непрерывное загружение или
деформирование с высокой скоростью, быстрое периодическое или
циклическое загружение и ударное воздействие.
Виды разрушения. При растяжении возможны следующие
основные или элементарные типы разрушения (рис. 6.1): разрыв
(/), сдвиг (II), разрыв со сдвигом (III), разрыв со сдвигом в на-
правлении растяжения (IV), пластическое течение с образованием
шейки (V).
Элементарные виды разрушения при сжатии, показанные на
рис. 6.2, представляют собой: сдвиг (Г), продольный разрыв (II),
сдвиг с продольным разрывом (III) и пластическое течение с об-
разованием «бочки» (IV).
Деформации кристаллической решетки. В твердом теле все
частицы размещаются так, что образуют систему с минимальной
суммарной потенциальной энергией. Этому соответствует опреде-
ленное закономерное расположение частиц, образующих кристал-
лическую решетку твердого тела. Следует иметь в виду, что у ре-
альных кристаллов имеются многочисленные отклонения от строго-
го теоретического строения идеальной пространственной решетки.
Атомы в кристаллической решетке всегда совершают колебания
малой амплитуды вокруг положений равновесия, которыми явля-
ются узлы решетки. Атомы, обладающие высокими уровнями энер-
гии, преодолевают силы, удерживающие их в положении равнове-
сия, и выскакивают из своих мест, образуя так называемые
точечные дефекты кристаллической структуры. Эти дефекты пред-
ставляют собой либо свободные, не занятые атомами узлы решетки
(«дырки», вакансии»), либо межузельные атомы, стоящие «не на
месте», внедрившиеся в межузельное пространство.
Переход в межузельное положение существенно облегчается за
270
счет внешних источников энергии — нагрева, внешней нагрузки,
столкновения с частицами высоких энергий.
Рис. 6.1. Элементарные типы разрушения при растяже-
нии
Рис. 6.2. Элементарные типы разрушения при
сжатии
Эти перемещения атомов носят название самодиффузии. В ре-
шетке могут иметься также чужеродные атомы, которые вносят
возмущение в правильность ее строения. Отдельные точечные де-
фекты могут -сосредотачиваться в группы, образуя двойные,
тройные и более крупные вакансии. Возможны скопления чужерод-
ных атомов и в виде отдельных групп.
Кроме точечных имеются также линейные дефекты, нарушаю-
щие правильное чередование атомных плоскостей (дислокации),
вроде приведенной на рис. 6.3,6 дислокации, называемой краевой.
Дислокации повышают свободную энергию решетки и делают ее
менее термодинамически устойчивой. Плотность дислокаций, т. е
их количество на единицу площади поверхности кристалла, может
быть огромной — до 1012 на 1 с;и2.
Встречаются и другие дефекты в виде неправильного срастания
271
отдельных блоков кристалла, наклоненных* друг к другу или по-
вернутых относительно друг друга под малыми углами, неправиль-
ного чередования отдельных слоев атомной решетки, их пропусков.
Дефекты структуры оказывают существенное влияние на механи-
ческие свойства твердых тел.
(a); KpiaeBiafl дислокация i(6) и решетка после
сдвига (в)
Наблюдения показывают, что существует диффузия дефектов
(например, равномерное рассеяние вакансий по объему), которая
определяется некоторым градиентом, аналогично тому, как это бы-
вает при обычной диффузии в растворах под влиянием градиента
концентрации. Тогда удельный поток атомов через единицу пло-
щади сечения за единицу времени при градиенте, равном единице,
можно назвать коэффициентом самодиффузии. Этот коэффициент
зависит от характера строения кристаллической решетки и может
быть разным в различных направлениях. Интересно, что коэффи-
циент самодиффузии вблизи точки плавления у всех металлов
примерно одинаков. Диффузия имеет место не только внутри ре-
шетки, но и по поверхности кристаллов, и тогда она называется
поверхностной.
Если в некотором направлении действуют постоянные напря-
жения от внешней нагрузки, то атомы в какой-либо плоскости
решетки могут перескакивать друг за другом в новое положение,
в результате чего происходит сдвиг одной части кристалла отно-
сительно другой. Если напряжения достаточно велики для соответ-
ствующей активации частиц, эти микросдвиги приведут к суще-
ственным деформациям и разрушению тела.
Если бы для сдвига нужно было одновременно сместить весь
ряд атомов относительно другого, то для этого потребовалась бы
во много раз большая энергия, чем для последовательного переме-
щения атомов друг за другом при наличии дислокаций. Таким
образом, сдвиг в этом случае можно рассматривать как перемеще-
ние дефектов.
Облегчение сдвига благодаря дефектам очень наглядно иллю-
стрируется передвижением складки на ковровой дорожке
(рис. 6.4), которое происходит гораздо легче, чем сдвиг всей
дорожки сразу на такую же величину [82].
Влияние дислокаций и неоднородностей на разрушение. Дисло-
кации, нарушая регулярность внутреннего строения, вносят возму-
272
щение в потенциальные поля и поэтому приводят к зарождению
микронеоднородностей, являющихся концентраторами напряжений.
Когда точки концентрации напряжений совпадают с точками мест-
ных ослаблений межчастичных связей и напряжения превосходят
сопротивление этих связей, в этих точках зарождаются и растут
зоны пластических деформаций. Неоднородность в величине и ско-
0
1 г /7 X 2 2* %
----Г7777 2ДХ--------------------------------------
Рис. 6.4. Сдвиг как перемещение складки на ковровой дорожке
роста развития пластических деформаций в соседних точках приво-
дит к появлению микротрещин, которые затем начинают быстро
расти под влиянием нормальных растягивающих напряжений.
Если прочность кристаллических твердых тел определяется
в первую очередь дислокациями и элементарными пластическими
сдвигами, то прочность хрупких аморфных тел — различного рода
дефектами и микротрещинами. У нехрупких твердых материалов
трещины и сдвиги обычно распространяются от поверхности
в глубь материала, тогда как у хрупких материалов опасные тре-
щины могут зарождаться как на поверхности, так и во всем их
объеме. Существует аналогия между влиянием температуры на
прочность твердых тел и влажности на прочность глинистых грун-
тов. Как известно, при повышении температуры механические свой-
ства твердых тел изменяются. Так, соотношение между пределом
текучести и пределом хрупкой прочности твердого тела при измене-
нии температуры характеризуется графической схемой, предложен-
ной физиком А. Ф. Иоффе (рис. 6.5). Кривая 2 на этом рисунке ха-
рактеризует изменение предела текучести; график 1 — изменение
предела хрупкой прочности. Пока температура остается ниже неко-
торого предельного значения Ткр предел хрупкой прочности будет
ниже предела текучести, и материал разрушается только хрупко,
причем прочность несколько падает с повышением температуры.
Когда температура становится выше 7кр , хрупкое разрушение уже
невозможно, и материал разрушается путем течения. Особенностью
графика на рис. 6.5 является то, что он действителен только для оп-
ределенной скорости загружения.
Аналогичный характер имеет и влияние влажности на прочность
связных грунтов. Чем выше температура твердого тела и чем выше
влажность глинистого грунта, тем сильнее у того и у другого про-
являются жидкообразные свойства. Чем выше влажность, тем ниже
прочность грунта. При влажности, меньшей некоторого критическо-
го значения для данной скорости загружения, прочность тем выше,
чем выше скорость приложения нагрузки;
273
Поверхностно-активные вещества. Так называют вещества, ко-
торые снижают поверхностное натяжение материала, облегчая тем
Рис. 6.5. Зависимость между
характером разрушения и тем-
пературой
самым образование поверхностей раз-
дела, так как при этом уменьшается
необходимая для их формирования
энергия. Структура материала при дей-
ствии на него поверхностно-активных
веществ не меняется.
Поверхностно-активные вещества
облегчают возникновение и развитие
микротрещин, делают материал более
хрупким и ослабляют также его со-
противление сдвигу. При циклических
нагрузках поверхностно-активные ве-
щества входят в раскрывающиеся тре-
щины и не успевают из них выжимать-
ся при изменении направления сил, что ускоряет разрушение ма-
териала.
Теории прочности. Теории, связывающие течение или хрупкое
разрушение с напряженно-деформированным состоянием образца
или конструкции, называют механическими теориями прочности.
Если в теории прочности не учитывается влияние на величину
разрушающих'усилий скорости деформирования, то такая теория
прочности называется статической, а если учитывается — динами-
ческой. Структурный анализ явлений разрушения материалов
(вроде, например, влияния дислокаций) носит название физиче-
ских теорий прочности.
2. ЭНЕРГЕТИЧЕСКАЯ ТЕОРИЯ ПРОЧНОСТИ
Разрушение и энергия формоизменения. Впервые идею о связи
разрушения с энергией формоизменения высказал еще Максвелл
в одном из своих писем: «Когда энергия искажения формы дости-
гает известного предела, элемент выходит из строя». Это письмо не
было опубликовано, и гораздо позже (в 1904 г.) Губер выступил с
работой, в которой наступление разрушения материала связывалось
с моментом, когда удельная энергия упругого формоизменения до-
стигает предельного значения, характерного для данного материа-
ла. Мизес (1913 г.) и Генки (1924 г.) предложили такой же крите-
рий для случая пластического течения.
Генки образно пояснил свою идею, символизируя максимальное
количество энергии, которое может быть накоплено телом при уп-
ругом формоизменении, жидкостью, заполняющей весь объем
некоторого сосуда. Если количество энергии превосходит этот
объем, то она уже не может поместиться в «сосуде» и расходуется
на разрушение материала.
Выражение упругой работы формоизменения через главные на-
274
пряжения. Упругая работа формоизменения, как было показано
ранее, равна:
По = — о. eit
D 2
где о, и е/ определяются по формулам (4.52) и (4.72).
Подставляя в (4.72) значения главных деформаций, выражен-
ные через главные напряжения с помощью обобщенного закона
Гука, найдем:
= У <СТ1 - СТп)2 + (СТП — аш)2 + (аШ - CTl)2 • <6Л)
о с
Из (4.262), (4.52) и (6.1) находим
- [(’I-’в)’+ (6-2)
Если предположить, что предельное количество упругой энергии
формоизменения, которое тело может накопить без разрушения,
не зависит от характера напряженного состояния, то проще всего
определять эту энергию испытанием при одноосном напряженном
состоянии.
В этом случае Оц = (Гщ =0, а предельное (разрушающее)
значение Qi обозначим через в# (различное при растяжении и
сжатии).
Тогда из (6.2) получим
nDR = 2 <?R = . (6.3)
DR 6Е 3£ - л
Условие прочности Губера. В соответствии с критерием прочно-
сти Губера разрушение не наступает до тех пор, пока
< ^DR * (6-4)
Подставляя сюда значения из (6.2) и (6.3), получим, что в пре-
дельном состоянии
(СТ1 ~ °п)2 + ( - стш)2 + ( стш - ст02 = 2 . (6.5а)
Для чистого растяжения получаем
а, = аЛ. (6.56)
Это и есть условие разрушения по энергетической теории проч'
ности Губера.
Условие наступления течения Мизеса—Генки. В случае если
разрушение происходит за счет течения, вместо в (6.5а) следует
подставить предел текучести при растяжении- от:
(CTi стп) CTni) + (аш CTi) ==2ст2. (6-6)
Для чистого сдвига, когда о, = — стш = тт и оц = 0, получаем
из (6.6), что ат = ]ЛЗ\Т.
275
Условие (6.6) носит имя Мизеса — Генки и экспериментально
подтвердилось, тогда как условие (6.5а), как показывают опыты,
не оправдывается при сложных напряженных состояниях. Иными
словами, определив gr из опытов, например, на простое сжатие,
нельзя считать, что мы имеем право подставить его в выражение
(6.5а) в случае других напряженных состояний. Обычно теории
Губера и Мизеса — Генки рассматриваются как единая энергети-
ческая теория прочности Губера — Мизеса — Генки. Она относится
к статическим теориям, и ее не следует смешивать с динамическими,
которые будут рассмотрены далее.
Условие Мизеса — Генки называют также условием постоянства
максимального касательного напряжения, поскольку ни в одной
точке тела касательные напряжения не должны 1превосходмть пре-
дельного значения хт, постоянного для данного материала в дан-
ных условиях его работы.
Так как
°? = т [ (~ стп )‘ + ( СТП - СТ1п)* + ( °1П -
то из сравнения этого выражения с (6.6) следует, что
= <гт, (6.7)
т. е. при пластическом течении интенсивность напряжений посто-
янна.
Обобщением этого вывода является следующее условие плас-
тичности, предложенное Мизесом и Шлейхером: при пластическом
течении интенсивность напряжений является функцией от среднего
нормального напряжения (равного нормальному октаэдрическому
напряжению)
Ъ = f (ОЪкт)- (6.8)
Это условие оправдывается для горных пород.
Предельная поверхность текучести. В декартовых осях Qi , оц,
ош уравнение (6.6) представляет собой некоторую пространст-
венную поверхность, зависящую от параметра от. Рассмотрим
сначала особенности выбранной системы координат. Очевидно, что
точки на осях координат изображают простое растяжение или
сжатие вдоль соответствующих направлений, а на координатных
плоскостях лежат точки, изображающие плоские напряженные со-
стояния (<Ti =0), (011=0), (ощ =0). Началу координат соот-
ветствует отсутствие напряжений в теле.
Если после приложения нагрузки напряженное состояние неко-
торого элемента тела будет характеризоваться напряжениями си ,
Он и Ош , то точка в координатном пространстве с этими коор-
динатами будет изображать напряженное состояние в элементе, и
ее можно назвать изображающей» или фигуративной точкой. Если
плавно изменять напряженное состояние тела, то фигуративная
точка будет перемещаться в координатном пространстве, и ее тра-
276
ектория будет показывать, как менялось напряженное состояние
данного элемента тела (рис. 6.6,6).
Фигуративная точка, относящаяся к случаю равных главных
напряжений, должна лежать на прямой, точки которой имеют рав-
ные между собой координаты ст, = ап = ош. Это случай гид-
ростатического напряженного состояния.
Если увеличивать все эти три напряжения так, чтобы они оста-
вались равными, то фигуративная точка будет перемещаться по
прямой, равно наклоненной ко всем трем осям координат (так на-
зываемая пространственная диагональ) (рис. 6.6,а). Три ее направ-
ляющие косинуса т, п и I будут равны друг другу:
l/TT 1
т = п = I = -— = —. (6.9)
3 уз
Точки с координатами (oj , сгц, <Тш ), соответствующие пре-
дельным значениям этих напряжений, при которых наступает пла-
стическое течение, должны удовлетворять уравнению (6.6). Мно-
жество этих точек образует предельную поверхность с уравнением
ф(ар оп, <тш)=0. (6.10)
Любая точка, лежащая внутри пространства, окр) женного этой
поверхностью, соответствует прочному состоянию ра» сматриваемо-
го элемента материала.
Предельная поверхность Мизеса — Генки. Для критерия проч-
ности Мизеса—Генки (6.6) уравнение предельной поверхности
(6.10) примет вид
( ~ ап)’ + ( стп - стш)* + ( аш - а,)* - 2а? = 0 (6-11 >
или после раскрытия скобок
а1 + СТ?1 + аП1 - а1 ап - стп аш - СТШ а1 = °Т. (6Л2>
Эта поверхность представляет собой круговой цилиндр с радиу-
сом -|- стт ж 0,82 стт, ось которого совпадает с пространствен-
ной диагональю (6.9). Этот цилиндр называют цилиндром Мизе-
са— Генки (рис. 6.7,а). Так как он наклонен по отношению к
координатным плоскостям, то в пересечении с последними он дает
эллипсы. На рис. 6.7,6 показан такой эллипс, образованный пере-
сечением с плоскостью (oi , Ош) и соответствующий двухосному
напряженному состоянию (оц =0). Координаты точек этого эллип-
са характеризуют соотношения между Щ и Ощ, при которых
наступает в данном случае пластическое течение. Уравнение этого
эллипса
of—Giffni +стш = (6.13)
Связь между прочностью и деформативными свойствами мате-
риала. Еще не так давно эта связь совершенно отрицалась, так
277
как казалось, что в основе таких свойств, как упругость, с одной
стороны, и сопротивление разрушению, с другой, лежат различные
молекулярные механизмы. Однако чисто экспериментальные ис-
следования указывали на наличие довольно тесной корреляцион-
ной зависимости между этими двумя свойствами.
Рис. 6.6. Изображающая точка
Рис. 6.7. Поверхность теку-
чести (цилиндр) по Генки—
Мизесу
В физической теории прочности твердых тел, выдвинутой Гриф-
фитсом, разрушение рассматривается как результат развития
микротрещин под действием приложенных напряжений. При обра-
зовании трещины и ее расширении происходит перераспределение
напряжений в сечении, часть материала над и под трещиной раз-
гружается и потенциальная энергия упругой деформации мате-
риала уменьшается. Одновременно возрастает поверхностная
энергия за счет образования свободных поверхностей разрыва
(стенок трещины). Если уменьшение потенциальной энергии упру-
гой деформации происходит быстрее, чем увеличение поверхност-
ной энергии, то избыток первой расходуется на развитие трещины,
приводящее в конце концов к разрушению. Таким образом, кри-
тическим условием служит равенство этих изменений энергии,
которое приводит к выражению вида
<Г« = /(СТПОВ. а1, “2, •••,%), (6-14)
278
где апов — поверхностное напряжение материала в кГ1см2\
Е — модуль упругости в кГ/см2-,
ае — другие параметры (например, начальный размер тре-
щины, коэффициент Пуассона и т. д.).
Часть энергии разрушения расходуется на необратимые поте-
ри — затухающие колебания частиц после разрыва связей, вязко-
пластическое течение в местах перенапряжений и т. п.
Так как <Tr зависит не только от Е, но и от ряда других пара-
метров, естественно, что связь между и Е носит корреляцион-
ный характер.
Имеется ряд работ, авторы которых пытаются установить вид
функции (6.14). Несмотря на различие исходных предпосылок,
почти все они приходят к выводу, что зависимость между oj? и Е
при прочих равных условиях должна иметь вид
gr = AVE, (6.15)
где А — эмпирический коэффициент, соответствующий данным ус-
ловиям испытания данного материала и зависящий от
оПов и параметров а,- .
3. ТЕОРИЯ ПРОЧНОСТИ КУЛОНА —МОРА
Теория Кулона. Кулон полагал, что разрушение материала на-
чинается в точке, в которой наибольшие касательные напряжения
достигают некоторого значения, называемого предельным значени-
ем прочности данного материала при сдвиге. Максимальное каса-
тельное напряжение тмакс , определяемое выражением (4.41),
действует в плоскости, нормаль к которой делит угол между Qi и
Ош пополам (рис. 6.8,а). При одноос-
ном сжатии (<rii=ain =0), когда Qi =
= ви (гдеая —предельное значение ai
соответствующее разрушению), полу-
чается, что площадки сдвига наклоне-
ны к ai под углом в 45° (рис. 6.8,6).
Однако у большинства материалов
этот угол оказывается меньше 45°.
Навье видоизменил эту теорию,
приняв, что сопротивление сдвигу ма-
териала при действии нормального
давления возрастает на величину, ко-
торая составляет некоторую долю f от
нормального напряжения по площад-
ке. Если нормальное и касательное на-
пряжения по площадке равны от и т, то
разрушение наступает тогда, когда
+ (6.16)
где с — сопротивление материала сдви-
гу при а==0.
Рис. 6.8. Схема разрушения по
Кулону
279*
Из рис. 6.9,а следует, что при плоском напряженном состоянии
а = у (gi + стш)-у (<71-<тш)совв;
т = у (ai-Msin9-
Подставляя эти значения в уравнение Кулона — Навье (6.16),
получим
у- (СТ1 - ^ш)sine = с + у [(CTi + °ш) - (~ "in)cos е] а
откуда
Следовательно, разрушение наступит, когда левая часть (6.17)
будет равна с. Максимальное значение левая часть будет иметь
ПРИ
sin 0 + /cos 9 — макс.
280
Беря производную по 9 и приравнивая ее нулю, получим
cos 9 — f sin 0 = О,
откуда
tg6=-L. (6.18)
Следовательно, разрушение наступит в виде сдвига по той пло-
щадке (6.9, а, б), наклон которой отвечает условию (6.18).
Теория прочности Мора. Мор принял, что сопротивление мате-
риала сдвигу зависит от нормальных напряжений по площадкам
сдвига. Чем больше нормальные напряжения, тем больше это
сопротивление. Таким образом, величина касательных напряжений,
которые могли бы вызвать сдвиг, будет зависеть от нормальных
напряжений по площадкам сдвига, что может быть представлено в
виде некоторой функции
т = /(о). (6.19)
Теория Кулона — Навье является частным случаем теории Мора
при функции (6.19) в виде (6.16).
Если построить круги Мора для момента разрушения некоторо-
го материала при различных напряженных состояниях, как пока-
зано на рис. 6.9, в, г, то уравнение огибающей этих кругов и будет
представлять собой искомую функцию f(o) для данного материала.
Эту огибающую обычно называют предельной кривой Мора. Сам
Мор в своей работе указывал, что такая кривая должна быть полу-
чена экспериментально для каждого материала.
Как показывают опыты, общий вид этих кривых близок к пара-
боле, ординаты которой возрастают с увеличением <т, а наклон
rftn
касательной с увеличением расстояния от начала координат
стремится к нулю.
Круги Мора, касающиеся предельной кривой, называются пре-
дельными кругами Мора, а напряженное состояние в точке, харак-
теризуемое предельным кругом Мора, — предельным состоянием.
Координаты точки касания дают значения касательного и нор-
мального напряжений в момент разрушения (сдвига) в данной
точке, для которой построен круг Мора. С помощью соответствую-
щего весьма простого построения, которое было изложено в раз-
деле, посвященном кругам Мора, можно легко найти наклон
площадки сдвига. Предельное состояние в точке характеризуется
радиусом предельного круга Мора и положением его центра.
Так как огибающая имеет две ветви (в положительной и отри-
цательной полуплоскости), то предельный круг Мора касается оги-
бающей в двух точках (Afj и М2 на рис. 6,в), и, следовательно, й
каждой точке тела имеются две взаимно наклоненные площадки,
по которым одновременно достигается предельное состояние, непо-
средственно предшествующее разрушению (рис. 6.9,г).
Условие разрушения (6.19) мозкно заменить в соответствии со
281
сказанным выше эквивалентным условием г=Г(о), так как вели-
чина радиуса предельного круга Мора г изменяется в зависимости
от абсциссы его центра ОС (рис. 6.9,а). Радиус круга
ai ~ аш
г ~ 2
а абсцисса центра
ai + аш
Следовательно, условие прочности Мора можно представить
в виде
g, ~-qin = F ( j, (6.20}
причем вид функции F будет отличаться от f по уравнению (6.19).
Особенности теории прочности Кулона—Мора. Теория прочно-
сти Мора имеет две характерные особенности. Первая заключается
в том, что абсолютные значения нормального и касательного на-
пряжений ino площадке сами по себе не оказывают влияния на
прочность, и решающее значение имеет отношение этих напряже-
ний. В самом деле, из рис. 6.9,а следует, что T=otg р , и если уве-
личить пропорционально значения тио, как показано пунктиром,
то отношение их т/oi остается без изменений и будет равно танген-
су угла р (отклонения равнодействующей напряжений р от норма-
ли к площадке) (см. рис. 6.9,6). Этот угол р называют углом
отклонения. Очевидно, что чем больше этот угол, тем меньше при
том же р величина о и больше т и тем ближе к моменту разруше-
ния будет система. Значение угла р, при котором наступает сдвиг,
называется предельным углом отклонения и обычно обозна-
чается <р.
Вторая особенность теории Мора заключается в следующем:
проекция напряжений, нормальных к плоскости чертежа (см.
рис. 6.9, а) на эту плоскость, равна нулю. Поэтому эти напряжения
не оказывают влияния на величины г и в в рассматриваемой плос-
кости, а следовательно, и не влияют на их отношение. Если рас-
сматриваемая плоскость является плоскостью главных напряже-
ний, например (oi , а1П ), как показано на рис. 6.9,а, то на зна-
чения о и t по площадке сдвига не будет оказывать влияния третье
главное напряжение Оц, перпендикулярное плоскости чертежа.
Легко сообразить, что наибольшее значение угол р имеет тогда,
когда рассматривается плоскость действия наибольшего и наи-
меньшего главных напряжений. Следовательно, вторая особенность
теории Мора заключается в том, что она по самой своей сути не
может учесть влияния на прочность третьего главного напряжения,
хотя в формулу энергетической теории прочности это напряжение
входит.
Опыты показывают, что для одних материалов можно, действи-
тельно, пренебрегать влиянием третьего главного напряжения в
282
силу незначительности этого влияния, тогда как для других это
напряжение необходимо учитывать [32].
Положение площадок сдвига. Пользуясь свойствами полюса
круга Мора, можно легко найти положение площадок сдвига в раз-
рушающемся теле, как показано на рис. 6.9,в, г. Из этого построе-
ния отчетливо видно, что угол а между двумя площадками сдвига
в данной точке зависит при криволинейной огибающей, от напря-
жений Oi и ош , так как при изменении этих напряжений угол
G наклона линий МР будет изменяться.
У материалов с одинаковым сопротивлением на растяжение и
сжатие огибающие кругов Мора превращаются в две параллель-
ные прямые, и углы наклона площадок сдвига к площадкам глав-
ных напряжений 0i и <гш становятся одина-
ковыми и равными 45°.
Прямолинейные огибающие. Простейши-
ми огибающими предельных кругов Мора
являются прямые линии (рис. 6.10) с урав-
нением
т = с + a tgcp. (6.21)
Обозначая tg ф через Д мы приходим к
условию прочности Кулона — Навье (6.16).
Таким образом, материалу, для которого
огибающая предельных кругов Мора вы-
рождается в прямую, отвечают как теория
теория прочности Кулона—Навье, которые в этом случае совпа-
дают.
4. ОБОБЩЕНИЕ ТЕОРИИ ПРОЧНОСТИ МОРА.
УСЛОВИЕ ПРОЧНОСТИ ФИЛОНЕНКО-БОРОДИЧА
Новые теории прочности. Для учета влияния на прочность всех
трех главных напряжений рядом авторов были предложены пре-
дельные условия, содержащие первый и второй обобщенные инва-
рианты:
Ф(АХ, Д2) = С. (6.22)
При этом функцию ф они выбирали в виде многочлена второй сте-
пени
Af+ 4A? + BAX = C. (6.23)
Чтобы определить три параметра этого уравнения, необходимо
провести по меньшей мере три опыта при различных напряженных
состояниях (например, на растяжение, сжатие и кручение). Чтобы
можно было ограничиться простыми опытами только на растяже-
ние и сжатие, предлагалось положить 4=0 [3] или внести неко-
торое уравнение связи между параметрами уравнения (6.23), что
уменьшает число неизвестных параметров до двух [43].
Рис. 6.10. Прямолиней-
ные огибающие Мера при
наличии сцепления
Мора, так и
283
Октаэдрическое условие прочности. Представим предельное ус-
ловие (6.22) разрешенным относительно Л2 [83]:
Л2 = ср (Лх). (6.24)
Если принять ось абсцисс в декартовой системе координат за
ось Ап а ось ординат — за ось А2, то (6.24) изобразится на плос-
кости (Ль А2) некоторой кривой, точки которой будут отвечать
условию прочности тела. Так как Лх и А2 являются функциями
трех главных напряжений (oi , 0ц, (Тщ ), то представлению ус-
ловия прочности в виде некоторой поверхности в трехмерном про-
странстве 0j , 0ц, 0ц1 отвечает его изображение в виде кривой
на плоскости Ль А2. Очевидно, каждой линии в пространстве ai ,
0п, 0ш соответствует точка на плоскости Аь Л2. Исключение
составляет пространственная диагональ 0i = 0ц = (Тщ , кото-
рой на плоскости Ль Л2 соответствует также прямая, а именно
ось Аь точки которой изображают всестороннее равномерное сжа-
тие или растяжение. На прямой Ах =0, т. е. на оси А2, лежат
точки, соответствующие чистому сдвигу (кручению).
Так как Ах и А2 связаны с компонентами 0ОКт и т0КТ полно-
го октаэдрического напряжения:
АХ 3 OqktJ
л 3
7'2 — %кт 0/,
/2
(6.25)
то, подставляя эти выражения в (6.24), получим условие предель-
ного состояния в виде
^окт / (®окт)>
(6.26)
аналогичное условию прочности Мора (6.19), но исходящее из ок-
таэдрических напряжений. Так как —Атокт равно оу (интенсив-
на
ности напряжений), то условие прочности (6.24) можно предста-
вить также в виде
«7 = f (*окт). (6.27)
Обобщенное условие прочности Мора. Как условие Мора, так и
условие (6.26) могут быть изображены в одной и той же системе
координат о, т. Хотя эта система не инвариантна, условие (6.26)
выделяет кривую (ст0Кт, 'окт), инвариантную относительно пре-
образования координат. Так как условие (6.26) или (6.27) учиты-
вает (в отличие от условия Мора) все три главных напряжения,
Филоненко-Бородич предложил называть его обобщенным услови-
ем прочности Мора.
Пространственное напряженное состояние, как мы знаем, изо-
бражается тремя кругами Мора (рис. 6.11). Будем, как это предло-
жил Надаи [44], характеризовать численно пространственное
284
напряженное состояние отношением аа величин CD и DA, где D —
центр главного круга Мора:
а _ СР 011 2 ^ffi ~^qni) 2 <тп — — <т1п °ц—gjii । (6.28)
DA у (<Tj - am) ffl “ G'11 01 “Gl11
Очевидно, при одном и том же значении а3 диаграммы Мора, по-
строенные для разных точек тела, будут подобны [73].
Параметр а0 изменяется от —1 до +1. С помощью этого пара-
метра можно представить выражение для ^макс в виде
тмакс = ~2 (ai gni) = 2~ (6.29)
а напряжения девиатора по главной диагонали — в виде
__ I ] ао \ _ 2
0^ I * 3 / ^макс> О'// — £ ^макс»
„ fl ! а-}
аШ — = — у1 ‘ ~з / тмакс-
Расстояние CD равно — аа . Таким образом, пространственное
3
напряженное состояние можно охарактеризовать всего двумя вели-
а) ? у:,** z
Рис. 6.11. Круги Мора при про-
странственном напряженном
состоянии
Рис. 6.12. Напряженные состояния при
различных
285
чинами: аа и тмакс, если известны направления главных нормаль-
ных напряжений. Очевидно, любой девиатор напряжений в точке
можно получить при изменении , когда оно будет пробегать все
значения от —1 до +1. При =—1 имеем случай, когда оц =
= Ош (рис. 6.12,а)\ при = + 1 оп = От (рис. 6.12,6), а
CFj О'j j j
при <ха =0 °r1I==----§----=0, и центР главного круга сов-
падает с началом координат (рис. 6.12,в), т. е. случай чистого
сдвига (<*! = —<*1П; <тп= 0).,
Испытание на прочность при а3 =—1 называют испытанием на
обобщенное сжатие, а при aa =-}-1 — на обобщенное растяжение.
Знак а зависит от принятого правила знаков для нормальных на-
пряжений. Если растягивающие напряжения считать положитель-
ными, а сжимающие — отрицательными, то а=—1 соответствует
обобщенному растяжению, «= + 1 обобщенному сжатию.
Обозначим величину -у (щ + <тш ) через стц. Тогда оОКт =
= у (°1 + ап + ctiii) бУдет
П Т
~ । 5 макс //? onv
^окт Н" , (6.30>
а
Токт = —• У( °1 <*ц)2 + ( <ТП ^т)2 + ( аш ^l)2
будет
^окт з ^макс* (6.31)
При некотором постоянном полном октаэдрическом напряжении
постоянны и его компоненты аОкт и токт , чему соответствует се-
мейство напряженных состояний, характеризуемое главными кру-
гами Мора (с параметрами ац и т^акс) и параметром aa вида
напряженного состояния. Тогда из уравнений (6.30) и (6.31) по-
лучим
Чу *^ОКТ
Чц ~ ^ОКТ ' >
Г2(Э + а2)
_______-----3 т0КТ_
тмакс _/___________г-«V- •
V 2 (З + а*)
(6.32)
(6.33)
Мы видим, что при постоянных <т0КТ и т0КТ положение главно-
го круга Мора изменяется в зависимости от значения параметра
При а, =1 вместо выражений (6.32) и (6.33) получим
286
.а при aa = — 1
<Гц ^окт
^макс”
__ Tqkt .
2 ]/2 ’
3 Токт
2 У 2
(6.34)
______ I %кт
°Ц t'OKT I
2 У 2
_________3 т0КТ
тмакс____— >
(6.35)
т. е. радиус главного круга Мора будет оставаться постоянным, но
при переходе от аа =1 к аа =—1 этот круг сместится вправо на
величину
2 / т°кт । — ^°кт 35)
у 2 У2 } у2 '
Постоянство тмакс означает постоянство разности од—Ош
и, следовательно, смещение главного круга определяется только,
средним главным напряжением ац. Отсюда следует вывод, что
для оценки влияния промежуточного главного напряжения ац на
прочность достаточно провести два испытания на прочность при
аа, равном +1 и —1. Если полученные круги Мора сольются или
будут очень близки друг к другу, то <тц на прочность не влияет
и можно пользоваться обычным условием Мора x=F (ai , Ощ)
В противном случае необходимо учитывать третье главное напря-
жение. В этом случае возникает неопределенность, связанная с тем,
что одним и тем же значениям аокт и токт соответствует не один
круг Мора, а их семейство. Чтобы избежать этой неопределенности,
Филоненко-Бородич [83] предлагает выделять семейства, дающие
определенный тип напряженного состояния. Для этого можно при-
нять семейства при аа =1, =—1 и аа =0 с наложенными на
них гидростатическими напряженными состояниями.
Следовательно, обобщенная теория прочности Мора означает,
что нет единого предельного семейства главных кругов для всех
видов напряженного состояния, а каждому виду напряженного сос-
тояния соответствует свое семейство кругов со своей огибающей,
являющейся предельной кривой (если предельное состояние при
данном виде напряженного состояния вообще существует).
Три предельные кривые Мора. Обобщенная теория Мора дает
три предельные кривые для каждого основного вида напряженного
состояния. При испытании в случае аа = + 1 уравнение предель-
ной кривой можно представить в виде
(^окт, Токт) — 0, (6.37)
а при испытании в случае аа =—1 — в виде
287
F (о т Л = 0, (63
где индексы при F соответствуют знаку а3 .
Условие прочности Филоненко-Бородича. В случае сложного на-
пряженного состояния Филоненко-Бородич предлагает приближен-
ную зависимость, основанную на простой линейной интерполяции
и объединяющую оба случая (6.37) и (6.38) в виде
F+ ( °окт ’ Хокт) + —F- ( °ОКТ’ Ъкт) = 0 (6-39>
или
~2~ Р"-|- ( ^окт’ Зкт) "Г F— ( ^окт’ Токт)] +
4-^ [F (а , Т )— F (a , г )] = 0. (6.40)'
1 2 L +\ окт окт/ — \ окт окт/-* v 7
Таким образом, вместо условия прочности (6.26) Филоненко-Бо-
родич предлагает принять условие
Fla , т , а)=0, (6.41>
зависящее не только от октаэдрических напряжений, но и от вели-
чины параметра аа . Это условие прочности будем называть усло-
вием Филоненко-Бородича.
5. ДИНАМИЧЕСКАЯ ТЕОРИЯ ПРОЧНОСТИ
Величина скорости деформирования. Как показывает опыт, ско-
рость загружения (или связанная с нею скорость деформации тела)
оказывает существенное влияние на прочность. Поэтому изложен-
ные выше теории прочности, являющиеся чисто статическими, не
могут дать во многих случаях сколько-нибудь удовлетворительных
результатов. При хрупком разрушении тел возникают колебания,
энергия которых по мере затухания превращается в теплоту. Сум-
марная поверхность обломков разрушенного тела всегда больше,
чем первоначальная поверхность тела, что приводит к увеличению
поверхностной энергии. Как энергия, идущая на колебания, так и
приращение поверхностной энергии имеют своим источником потен-
циальную энергию упругой деформации тела.
Общая энергия деформирования реальных тел всегда больше,
чем потенциальная энергия чисто упругой доли деформации, так
как она расходуется также на необратимую вязко-пластическую
деформацию тела. Чем медленнее загружение, тем больше относи-
тельная величина необратимой деформации.
Динамическая теория прочности является обобщением статиче-
ской энергетической теории прочности. Она исходит из того, что
разрушение материала наступает, когда удельная работа упругих
деформаций достигает определенного предела. Работа упругой де-
формации равна общей работе за вычетом энергии диссипации,
288
т. е. энергии, расходующейся на необратимые вязко-пластические
деформации.
Условие разрушения при равномерном всестороннем напряжен-
ном состоянии. Реологическое уравнение объемной деформации
изотропного твердого тела имеет вид
ая=К9 +W- (6.42)
Вязкая объемная деформация, характеризуемая вторым членом
правой части, задерживает развитие упругой деформации, вызыва-
ет затухание колебаний, но в отличие от течения жидкости носит
затухающий характер, и объемная вязкость ^об является функци-
ей объемной деформации. Соответственно (6.42) является прибли-
женной зависимостью.
Удельная работа деформации (на единицу объема)
0 t
w = J /cede + J* т}об edt. (6.43)
О 6
Когда первый член в правой части уравнения, представляющий
собой работу упругого деформирования, достигает некоторого пре-
дельного для данного материала значения, которое мы обозначим
наступает разрушение. Таким образом, условие разрушения
запишется так:
е
С = (6.44)
о
Интегрируя это выражение при постоянном К, находим для пре-
дельного состояния
откуда объемная деформация в момент разрушения
<6.45)
является величиной, не зависящей от скорости деформирования.
Подставляя (6.45) в (6.42), получим динамическое разрушаю-
щее всестороннее напряжение:
. <н - К + ^об6. (6.46)
При 0 = 0 величина будет, очевидно, представ-
лять собой статическое разрушающее напряжение о^т . Тогда
одя = + т|об0. (6.47)
Отсюда следует, что с увеличением скорости деформирования
О разрушающее напряжение возрастает.
10 Зак. 530
289
При объемном сжатии плотность материала растет, и сжимае-
мость и вязкость его изменяются, однако и в этом случае
~дин стат
VRH > &RH •
Условие разрушения при простом сдвиге. В случае упругого
твердого тела работа деформации при простом сдвиге
(6.48)
О
и в предельном состоянии должна быть равна некоторому предель-
ному значению W# , откуда
(6-49)
-r=+G^= + V^W^G. (6.50)
Эта величина, очевидно, не зависит от скорости загружения или
деформирования.
Модель Рейнера. Для иллюстрации поведения жидкообразных
тел Рейнер модифицировал модель Генки (рис. 6.13). Жидкость,
Рис. 6.13. Модель Рейнера
динамической теории проч-
ности
втекающая в сосуд, изображает энергию
упругого формоизменения некоторого те-
ла. Если деформация идет так медленно,
что поступающая в тело энергия — вли-
вающаяся в сосуд жидкость — успевает
вытекать через отверстия в дне, то это
означает, что скорость деформации мень-
ше или равна скорости релаксации на-
пряжений и разрушения от сдвига не
произойдет. Материал будет испытывать
деформацию ползучести.
При достаточно большой энергии де-
формации за единицу времени (большой
мощности деформации) сосуд постепенно
заполняется жидкостью, пока она не дойдет до сливного отверстия,
что соответствует пределу текучести. Вся поступающая далее энер-
гия будет расходоваться на развитие течения материала.
Если необратимо рассеивающаяся энергия, идущая на релакса-
цию и течение, меньше, чем энергия, поступающая в тело в резуль-
тате действия внешних сил, то сосуд переполнится и произойдет
хрупкое разрушение.
Различные реальные материалы будут вести себя по-разному.
Для одних моделью будет служить сосуд без отверстий в дне и без
сливной трубы. Такие материалы разрушаются только хрупко. Для
других модель должна будет иметь такое большое сливное отвер-
стие, что вся поступающая жидкость будет выливаться. Такой ма-
290
териал не может разрушиться хрупко, а будет только течь. Если
модель имеет отверстия не в дне, а в стенках сосуда (выше неко-
торого уровня), то тело может сначала накопить некоторое коли-
чество упругой энергии, прежде чем начнется релаксация (реоло-
гическое тело Шведова). Ньютоновская жидкость может рассеи-
вать энергию с любой скоростью (чем больше поступающая энер-
гия, тем больше скорость течения). Это как бы сосуд без дна, хотя,
конечно, жидкость не может выдерживать любые, сколько угодно
большие касательные напряжения, сохраняя постоянную вязкость.
Динамическое условие прочности максвеллова тела. Работа де-
формации этого тела
W - т 7;
скорость приращения этой работы во времени определяется ско-
ростью деформирования
dW d у
d t dt
Подставляя вместо у его значение (4.177), получим
W = — + —. (6.51)
G Ъ
В этом выражении работе сил упругости соответствует первый
член правой его части. Обозначая предельное значение накоплен-
ной телом энергии упругой деформации, при котором произойдет
разрушение, через Wr , получим условие прочности в виде
J V dt~ l -^dx = WR <6-52>
о о
или с учетом (6.51)
При постоянном G из условия (6.52)
откуда, согласно формуле (6.51),
(6.53)
Найдем величину постоянного усилия т, при котором скорость
деформации достигнет критического значения, ведущего к разру-
шению. При постоянном т значение т=0, и из (6.53) находим
(в.54)
10* Зак. 530
291
Из закона Ньютона следует
и критическое стационарное значение
xR = V2GW*. (6.55)
Таким образом, максвеллово тело разрушается при сдвиге
тогда, когда касательные напряжения достигают предельного зна-
чения. У этого тела не существует предельного значения деформа-
ции сдвига у, но есть предельное значение скорости сдвига у^ ,
при которой наступает разрушение, причем критическое значение
у^ тем больше, чем больше скорость приложения нагрузки т.
Динамическая теория прочности тела Фойгта. Подставляя в
выражение для скорости приращения работы деформирования
значение
т = G 7 + iq 7,
получим
VT = G 7 7 + 72- (6.56)
Условие прочности заключается в том, чтобы работа упругой
деформации за время t не превосходила предельного значения
j Gy ydt = j* (r — ny*)dt — WR. (6.57)
0 0
Если значение r=yG, при котором материал разрушается во
время статических испытаний (у = 0), обозначить тдт, то из вы-
ражения (4.193)
хдин _ Тстат +тп. (6 58)
Из условия (6.57) при постоянном G следует, что
G f 7 dt = G = WR,
.1 1 dt 2 R
О
и предельное значение деформации сдвига
, /2^7
<6-59)
. При этом значении деформации сдвига тело Фойгта разрушает-
ся. Для него не существует предельной или опасной скорости при-
292
ложения нагрузки, причем величина разрушающего напряжения
возрастает с увеличением скорости деформации у.
Влияние на прочность вязких свойств материала. У чисто упру-
гих тел Гука работа напряжений полностью переходит в потенци-
альную энергию деформации, тогда как у ньютоновской жидкости
только работа объемной деформации превращается в потенциаль-
ную энергию, а работа формоизменения полностью рассеивается.
Соответственно ньютоновская жидкость имеет бесконечную
прочность при всестороннем сжатии и значительную прочность при
всестороннем растяжении (в случае отсутствия в жидкости пузырь-
ков воздуха), но ее прочность при сдвиге равна нулю.
Все остальные тела занимают промежуточное положение между
этими двумя крайними случаями, и прочность их зависит от скоро-
сти загружения или скорости развития деформаций.
6. ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ
Экспериментальные исследования ползучести материалов пока-
зали, что в общем случае могут быть выделены три стадии разви-
тия этого процесса во времени (рис.
6.14)
1. После условно мгновенной де-
формации, возникающей сразу же по
приложении нагрузки, с большой ско-
ростью начинается явление ползуче-
сти (кривая /), быстро, однако, замед-
ляющееся и переходящее в установив-
шуюся стадию ползучести (кривая II),
которая протекает с постоянной ско-
ростью.
2. На стадии установившейся пол-
зучести, скорость которой увеличивает-
ся с увеличением действующей нагрузки, деформация имеет в ос-
новном характер вязкого течения. Эта стадия может перейти либо
в стадию затухающей, либо в стадию ускоряющейся ползучести.
3. На стадии ускоряющейся ползучести (кривая III) (по Н. Н.
Маслову — прогрессирующая ползучесть) деформации развива-
ются со все возрастающей скоростью и заканчиваются либо хруп-
ким разрушением материала, либо разрушением в виде течения с
высокой скоростью (кривая III).
Стадия ускоряющейся ползучести наступает только по дости-
жении некоторой предельной величины сдвигающих напряжений.
Пока напряжения ниже этого предела, ползучесть не приводит к
разрушению материала и в конце концов замедляется и затухает.
При более высоких напряжениях процесс ползучести обязательно
заканчивается разрушением, если только он не сопровождается
какими-либо другими явлениями, ведущими к упрочнению матери-
ала и затуханию ползучести. Время, протекающее до момента раз-
293
рушения, уменьшается с увеличением скорости загружения.
Прочность материала при длительном действии нагрузки назы-
вается длительной, долговременной (или текущей) прочностью, а
прочность при бесконечно большой продолжительности действия
нагрузки — пределом длительной прочности или асимптотической
прочностью (рис. 6.15).
Прочность материала при непрерывном быстром загружении в
процессе испытания или при кратковременном действии нагрузки
называется начальной прочностью. Скорость загружения при та-
ких испытаниях- обычно задается инструкциями и техническими
условиями на приемку материала и потому является стандартной.
График длительной прочности. Л. М. Качанов [23], считая, что
ползучесть и хрупкое разрушение имеют в основе различные мик-
роструктурные механизмы, получил следующую зависимость:
/ =/„-_ h _ /В> (6.60)
L п *i J
где t# — время до разрушения;
t\ — время вязкого разрушения для данного напряжения;
п А вп
(6.61)
t2 — время хрупкого разрушения при напряжении о
(1+6') В а*
(6.62)
Когда n=k, хрупое разрушение происходит всегда при одной и
той же величине деформации.
Если построить график длительной прочности в осях 1g о ~
~ 1g/ (рис. 6.16) и провести прямые вязкого t—ti (о) и хрупкого
Рис. 6.15. Длительная проч-
ность
Рис. 6.16. График дли-
тельной прочности (по
Качанову)
и хрупкого t=t2 (о) разрушений, то переход от одной прямой к
другой определится кривой, построенной по уравнению (6.60).
294
13
Закономерность длительной прочности у различных материалов.
Как показывают исследования [4], длительная прочность метал-
лов, пластмасс и полимерных волокон выражается формулой
/ = Де—аа, (6.63)
где t — продолжительность действия нагрузки до момента разру-
шения (долговечность);
А и а — константы, зависящие от вида материала и температуры;
о — действующее растягивающее напряжение.
Зависимость долговечности при данном значении в от темпера-
туры выражается экспоненциальной зависимостью
и
t = toekT, ' (6.64)
где /о — долговечность при £7=0;
U — энергия активации процесса разрушения;
k — постоянная Больцмана;
Т — абсолютная температура.
Для ряда твердых тел зависимость энергии активации от напря-
жения (рис. 6.17) имеет вид
£7 = £70 —ра,
где Uo — энергия активации при о=0;
Р — коэффициент, зависящий от природы и структуры мате-
риала.
Подставляя (6.65) в (6.64), получим
, , / U о — Р а \
Сравнивая выражения (6.63) и (6.66), находим
и»
A = tQekT ;
а=А.
kT
(6.65)
(6.66)
(6.67)
(6.68)
Из (6.66) следует, что в полулогарифмической сетке координат
lg/ = lg/0 + --°—Р ?- . ±
2,ЗА Т
зависимость между 1g / и — выражается на рис. 6.18 прямой (при
постоянном ст). Однако в действительности соответствующие
графики для многих материалов имеют в этих осях координат кри-
волинейный характер, что объясняется в первую очередь зависи-
мостью параметра £ от напряжений и изменением структуры мате-
риала в ходе деформации. Кроме того, на to влияют также структу-
(6.69)
295
ра и термодинамические свойства материала и характер напряжен-
ного состояния.
В настоящее время не существует общепринятой теории дли-
тельной прочности [57], и вопрос о зависимости величины разру-
Рис. 6.17. График энер-
гии активации
1
--------------------.г
Рис. 6.18. График зави-
симости lg/~l/T
рукции, вероятностью
тающих напряжений от продолжительности действия нагрузки ре-
шается обычно чисто экспериментальным путем.
О допускаемых и безопасных напряжениях. Понятие о допуска-
емых напряжениях было выдвинуто в свое время практикой инже-
нерных расчетов и относилось к напряжениям в элементах конст-
рукций, работающих под нагрузкой. В последние годы от этого по-
нятия отказались, перейдя к оценке работы конструкций по так
называемым предельным состояниям, численные характеристики
которых определяются эксплуатационными требованиями к конст-
тех или иных условий ее работы в процессе
эксплуатации и степенью достоверности со-
ответствующих расчетных прогнозов.
Однако это не исключает применения
понятия о безопасном напряжении, которое
является характеристикой не конструкции,
а ее материала при данных условиях работы.
Если построить экспериментальную зависи-
мость 1g/ от o', то оказывается, что она име-
ет линейный характер, но эта линейность
нарушается при малых напряжениях (рис.
6.19). Зависимость стремится к вертикаль-
ной асимптоте, соответствующей напряжению ог0, которое можно на-
звать безопасным в том смысле, что при любой длительности дей-
ствия напряжений о0 разрушение не наступает. Таким обра-
зом, безопасное напряжение, в сущности, представляет собой не что
иное, как предел длительной прочности материала.
7. ПРОЧНОСТЬ СТРУКТУРИРОВАННЫХ СИСТЕМ
Прочность коагуляционных структур. Некоторые авторы пола-
гают, что основным отличием жидкости от твердого тела является
отсутствие в первой и наличие у второго пространственной струк-
турной сетки [29]. Из этого следует, что гели, представляющие со-
296
Рис. 6.19. Эксперимен-
тальный график tg/~o
бой связнодисперсные системы и обладающие в отличие от свобод-
нодисперсных систем (золей) пространственной структурной сет-
кой, уже не могут рассматриваться как жидкости. Вместе с тем
резкий переход от золей к гелям отсутствует. Соотношение между
твердообразными и жидкообразными свойствами у гелей зависит от
концентрации дисперсной фазы, формы ее частиц и характера их
силового взаимодействия друг с другом и дисперсной (поровой)
средой. Чем больше форма частиц отклоняется от изометрической
(т. е. имеющей одинаковый порядок размеров по всем направле-
ниям) и чем меньше расклинивающее действие поровой среды, тем
меньше концентрация дисперсной фазы, при которой возникает
пространственная структурная сетка. Глинистые частицы с их ани-
зометричной формой и характерными поверхностными свойствами
могут образовывать связнодисперсные системы при очень малых
концентрациях. Взвесь бентонита (монтмориллонитовая глина) в
воде дает, например, пространственную сетку при концентрации
всего 0,01 %.
Существуют коагуляционные структуры (в частности, большин-
ство свежевыпавших гелей), обладающие пространственной сеткой
и проявляющие течение (хотя и чрезвычайно медленное) при са-
мых малых напряжениях. Предел текучести у таких структур
можно принять равным нулю; они являются типичными неньюто-
новскими жидкостями. Если такого рода структура испытывает
при длительном пребывании в покое постепенное необратимое уп-
рочнение связей, она превращается в твердое (точнее, твердооб-
разное) тело с четко выраженным пределом текучести. При на-
пряжениях ниже предела текучести такие тела проявляют харак-
терные для твердых тел упругость и пластичность и обладают пре-
делом упругости. Таким образом, классификацию структуриро-
ванных систем по характеру их образования и исходным свойствам,
созданную Ребиндером, необходимо дополнить для целей механи-
ки грунтов классификацией по характеру последующих изменений
при состоянии покоя под статическим давлением и в условиях фи-
зико-химического взаимодействия с окружающей средой. Испыты-
ваемая при этом медленная перестройка структуры, ее уплотнение
и упрочнение приводят к преобразованию структурированной дис-
персной системы в горную породу. При этом тиксотропные струк-
туры переходят сначала в реотропные, а затем в результате диаге-
нетических и эпигенетических изменений (через образование
цементационных связей) — к литифицированному состоянию [60,
Очевидно, условием разрушения коагуляционно-тиксотропных
систем ”следует считать разрушение структуры, образованной дис-
персной фазой. Это разрушение может происходит как плавно, так
и скачкообразно в зависимости от величины и скорости приложе-
ния сдвигающих напряжений.
Рассмотрим на примере движения структурированной системы
в цилиндрической трубке вопрос о том, в каком случае разрушение
297
движения жидкости в такой
• R2.
(4.143) касательное напряже-
(6.70)
структуры при вязком течении связано с наступлением турбулент-
ного режима течения, а в каком случае это разрушение может
наступать ранее, еще на стадии ламинарного режима.
Средняя скорость. ламинарного
трубке по формуле Пуазейля:
Q 1
Ucp “ л R2 “ 8
Подставляя сюда из зависимости
ние т (при г=/?), получим
%=4~- — я-
4 7]
Обозначим максимальное значение т, при котором наступает
разрушение структуры жидкости, тмакс. Тогда
4’ = т~Я <6-71>
Критическая скорость перехода ламинарного движения в тур-
булентное, согласно критерию Рейнольдса,
Re т]
2 ’ р R’
у(2) =
кр
где 7? — радиус трубки.
Обозначим величину
Re
— буквой С и запишем
V(2) = . JL
кр р R ‘
следует, что скорость, при которой раз-
(6.72)
Из выражения (6.71)
рушается структура жидкости, тем больше, чем больше -радиус
трубки, а из выражения (6.72) получаем, что скорость, при кото-
рой начинается турбулентное движение, тем выше, чем меньше
радиус.
Приравнивая (6.71) и (6.72), получим
-1. А. = _£. 2L
4 7] макс Р R *
Отсюда радиус трубки, при котором обе критические скорости
равны друг другу,
— 2 т]
С
р т
г макс
На рис. 6.20 показаны графики обеих скоростей. При 7?</?Кр
разрушение структуры дисперсной фазы в жидкости наступит
раньше, чем начнется турбулентное движение, тогда как при /?>
> /?кр турбулентное движение структурированной жидкости на-
чнется при той скорости движения, которая еще безопасна для
устойчивости структуры.
(6.73)
298
Основные свойства коагуляционных структур. В физико-хими-
ческой механике свойства коагуляционных структур оцениваются
исходя из следующих предположений: 1) частицы глины на участ-
ках контакта разделены остаточными тонкими прослойками водной
среды; 2) наличие этих прослоек резко ос-
лабляет сцепление между частицами (осу-
ществляемое благодаря силам Ван-дер-Ва-
альса) и облегчает относительную подвиж-
ность частиц — пластичность и ползучесть
структур — даже при самых незначительных
сдвиговых напряжениях; 3) структуриро-
ванные системы обладают эластическими
свойствами, напоминающими свойства поли-
меров; 4) прочность коагуляционных струк-
тур определяется удельным (на единицу
объема системы) числом точек контакта
между частицами или (что, в сущно-
сти, то же) удельным числом частиц,
ранственную структурную сетку; 5) чем
Рис. 6.20. Критические
скорости движения стру-
ктурированной системы
образующих прост-
больше толщина вод-
ных прослоек между частицами, тем меньше прочность струк-
турной сетки. Наибольшую толщину эти прослойки имеют в су-
спензиях натриевых глин. Кальциевые глины лучше связывают во-
ду, чем натриевые, обладают большей теплотой смачивания и, сле-
довательно, более гидрофильны, чем натриевые. Однако они обра-
зуют гораздо более тонкие диффузные слои ионов, чем натриевые
бентониты, и обладают более компактными контактами через тон-
чайшие прослойки водной среды. Литиевый бентонит более гидро-
филен, чем натриевый, и приближается к кальциевому, однако
ионные диффузионные слои у него развиты так же, как у натрие-
вых глин, что способствует более полной пептизации (распаду аг-
регатов частиц) и, следовательно, более интенсивному коагуляци-
онному структурообразованию. Управляя с помощью электролитов,
поверхностно-активных веществ и защитных коллоидов (т. е. пре-
пятствующих агрегированию) явлениями пептизации и коагуляци-
онного сцепления, можно в широких пределах регулировать меха-
нические свойства структурных и тампонажных растворов при бу-
рении [46]; 6) характер соотношения между твердообразными и
жидкообразными свойствами коагуляционных структур непрерыв-
но изменяется в ходе деформирования; изменяются их реологиче-
ские модели, и. соответственно механические свойства таких струк-
тур отличаются значительной сложностью. Реологические харак-
теристики структурированных систем были подробно рассмотрены
в работе [42], а грунтов — в работе [15].
Упругие характеристики коагуляционных структур. Такими ха-
рактеристиками являются:
1) условно мгновенный модуль сдвига GM, соответствующий
условно мгновенной (упругой) деформации уо, развивающейся
сразу по приложении нагрузки и исчезающей немедленно по ее сня-
299
тии (объясняется обратимым поворотом частиц вокруг точек кон-
такта и вытягиванием структурной сетки);
2) эластический модуль
Уобр ~ Yo
(6.74)
где уобр— полная обратимая деформация (сумма условно мгно-
венной и медленно развивающейся
эластичной деформации, происходящей
за счет обратимого смещения частиц в
точках контакта);
т — напряжение сдвига;
3) равновесный модуль
бм бэ .
Рис. 6.21. Графики механиче-
ских свойств структурирован-
ных систем
а — зависимость £ ~ Т; б — зависи-
мость 7] т
G _-------------------,
Уобр Ом + Сэ
бр GM G3
(6.75)
ь;
42 — на-
с которого
характеризующий суммарную обрати-
мую деформацию.
Прочность структуры. Сопротивле-
ние структурной сетки разрушению оп-
ределяют следующими характерными
значениями напряжений (рис. 6.21):
1) истинным пределом текучести
(совпадает с пределом упругости) ч ь
При вязкое течение не может
иметь места;
2) условной границей, до которой
сохраняется начальная (неразрушен-
ная) структура — начальной структурной прочностью
3) условным (бингамовским) пределом текучести
чинается лавинообразное разрушение структуры;
4) пределом структурной вязкости тт, начиная
имеет место постепенный переход к ньютоновской жидкости;
5) условной границей предельного разрушения структуры (пре-
дельной структурной прочностью) При т> т/ система ведет
себя как ньютоновская жидкость, и продолжение кривой проходит
через начало координат.
Вязкостные характеристики. Чтобы избежать путаницы, необ-
ходимо различать истинную вязкость, которая определяется накло-
ном касательной к некоторой характерной точке консистентной
кривой, и эффективную вязкость, которая определяется наклоном
радиуса вектора, проведенного к данной точке кривой из начала
координат. В соответствии с характерными точками кривой на
300
рис. 6.21,а следует различать такие вязкостные характеристики
структурированных систем:
1) наибольшую эффективную вязкость при практически не-
разрушенной структуре (напряжения сдвига i < х < );
2) наименьшую эффективную вязкость , относящуюся к
предельно разрушенной структуре (следует иметь в виду, что пол-
ностью структура не разрушается и в суспензиях всегда остаются
ее обрывки), которую можно условно называть бесструктурной,
соответствует напряжениям т > т/ и представляет собой ньюто-
новскую вязкость;
3) наибольшую истинную вязкость (шведовскую) при т > 4 i
—
(6.76)
где у'—скорость деформации на участке консистентной кривой
между 4 i и тг ;
4) наименьшую истинную вязкость (бингамову) при > 4 2
X~Xk2
(6.77)
=------
У'
где 4 2— условный (бингамов) предел текучести;
5) вязкость упругого последействия ~qK , определяющую ско-
рость длительной упругой (эластической) деформации (кельвино-
ву вязкость).
К прочим характеристикам относятся:
1) период истинной релаксации
та = ; (6.78)
<3м
2) период упругого последействия (эластичности)
Л = V-; (6.79)
3) деформируемость
1 1 1 .
’ G3’ G ’
4) эластичность
5) текучесть —;
6) подвижность ----;
7) пластичность по Воларовичу и ; f
8) прочность по Ребиндеру пластично-вязких систем с не-
301
разрушенной структурой — определяется по предельному погруже-
нию стандартного конуса под некоторой определенной нагрузкой.
Определение прочности по Ребиндеру. Пусть металлический
конус с утлом заострения а вдавливается в грунт под действием
силы Р (рис. 6.22).
Если обозначить площадь соприкасания кону-
са с грунтом F, то предельное напряжение сдви-
га по этой поверхности будет равно:
а
Р cos ~2~
F *
Так как боковая поверхность конуса
а
л Л2 tg —
F = лг/=-------
а
cos —
2
где h — глубина погружения конуса, то среднее
касательное напряжение т R по поверх*
ности контакта конуса с грунтом
а „ а
Р cos — Р cos2 —
2 2
л /i2 tg ~
(6.81)
Рис. 6.23. Испытание плоским
клином
По опытам Ребиндера значение остается неизменным при
данной консистенции вязко-пластического тела независимо от дей-
ствующей нагрузки Р.
Формулу (6.81) можно представить
в виде
то = К —, (6.82)
где Кл = 1,108 при а=30°; 0,658 при
а=45°; 0,413 при а—60° и 0,159 при
а=90°.
Если считать, что между штампом
и грунтом течения не возникает, то для
плоского клинообразного штампа (рис. 6.23) сопротивление вдав-
ливанию, по В. В. Соколовскому, равно:
Р = 2с(л + 2 —2Р)а, (6.83)
где с — сцепление в кГ1см2\
Р — нагрузка на 1 пог. см штампа;
0— угол, образованный гранью штампа с горизонталью;
а — полуширина клина на расстоянии h от острия клина (й —
глубина погружения).
302
Так как
PJt (X / i (X
~---------и а ~ h tg —,
2 2 S 2
ТО
Р = 2 с (2 + a) A tg,
откуда
с =-------f. (6.84)
2(2 + <x)fttg J
Сопоставим значение с со значением касательного напряжения
т по поверхности соприкосновения клина с грунтом:
a
Р cos2 “2”
= 2Л
с 2
Отношение — будет равно -------------------, а при a = 30°
т (2 + a) sin а
с= 1,58 т. (6.85)
Приведенные выше многочисленные характеристики позволяют
полностью описать поведение структурированных систем с учетОхМ
изменения структуры в ходе деформирования. Однако во многих
случаях можно ограничиваться изучением лишь одной-двух из
этих характеристик в соответствии с характером рассматриваемой
задачи.
Глава 7
НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ
ИССЛЕДОВАНИЯ ГРУНТОВ
1. ОШИБКИ ИЗМЕРЕНИЙ
Измерения. Измерить какую-либо величину — значит сравнить
ее с другой, заранее принятой за единицу меры, и выразить числом
отношение между ними. Вместе с числом всегда указывается и на-
именование соответствующей единицы меры. Термином «мера» на-
зывают тела, вещества или приспособления, воспроизводящие либо
единицу измерения, либо ее кратные или дробные значения.
Измерение может быть прямым или косвенным. При прямом
измерении непосредственно определяется интересующая нас вели-
чина. Значение измеряемой величины находится путем сравнения
либо с однородной ей величиной, которая известна, либо с помощью
градуированного измерительного прибора (например, длина стерж-
ня сравнивается с длиной, непосредственно прикладываемой к не-
му линейки, разделенной на миллиметры). При прямом измерении
процесс собственно измерения заканчивается отсчетом по измери-
тельному прибору.
При косвенных измерениях определяют непосредственно не ту
величину, которая нас интересут, а некоторые другие, связанные с
первой определенной зависимостью, позволяющей вычислить ее
значение. Примером может служить вычисление удельного веса по
результатам измерения веса и объема скелета грунта. Косвенные
измерения производятся в тех случаях, когда прямое измерение
сложно или даже невозможно осуществить и когда косвенное изме-
рение дает более точный результат, чем прямое.
Измерительные приборы — это устройства, служащие для пря-
мого или косвенного сравнения измеряемой величины с единичной
мерой. Проверка правильности мер и измерительных приборов
производится путем сравнения их показаний с эталонами, т. е. осо-
бо точными единичными мерами, выполненными в виде 'какого-
либо предмета, или с другими аналогичными мерами и прибора-
ми, сверенными, в свою очередь, с эталонами. Эталоны для непо-
средственных измерений не применяются, а служат лишь для про-
верки так называемых рабочих мер и приборов. Промежуточное
по точности место между теми и другими занимают образцовые
меры и приборы первого, второго и третьего разрядов. Образцо-
вые приборы могут применяться для внутрилабораторной проверки
304
менее точных рабочих приборов только в том случае, если первые
не используются для работы и хранятся в надлежащих условиях.
Рабочие измерительные приборы делятся на два типа: для лабора-
торных и производственных измерений (последние имеют более
низкий класс точности).
В зависимости от характера измеряемых свойств и носителей
этих свойств применяются различные измерительные приборы, од-
нако, каковы бы ни были их тип и конструкция, во всех случаях
возникает один и тот же вопрос, имеющий исключительно важное
значение, — вопрос об ошибках или погрешностях измерения.
Субъективные и объективные ошибки. Любое измерение подвер-
жено влиянию ряда разнообразных факторов, приводящих к иска-
жению результатов, появлению различного рода ошибок. Эти фак-
торы могут зависеть от самого наблюдателя, и тогда соответствую-
щие ошибки называются субъективными, или личными, но могут и
не зависеть от него и определяться чисто внешними обстоятельства-
ми. Такие факторы и соответствующие им ошибки называются объ-
ективными.
Обычно пользуются термином «ошибка» по отношению к ре-
зультатам измерения, а термином «погрешность» по отношению к
вычислениям. Ошибки делят на абсолютные и относительные.
Абсолютной ошибкой называют абсолютную величину разности
между данным результатом измерения или вычисления и истинным
значением измеряемой величины. Если последнее неизвестно, то
устанавливают предельную абсолютную ошибку или погрешность,
т. е. некоторое минимальное значение абсолютной ошибки.
Относительной ошибкой называют отношение величины пре-
дельной абсолютной ошибки к значению измеряемой величины.
Погрешность прибора и поправка. Тарировка и калибровка.
При проверке мер и приборов различают номинальную меру АИ,
указанную на ней (соответственно номинальное показание прибо-
ра), и действительную Лд меру (действительное показание прибо-
ра), определяемую сравнением с образцовой мерой или прибором.
Разность между ними
Д = ЛН —Лд - (7.1)
называют погрешностью прибора (меры), а взятую с обратным зна-
ком — поправкой и обычно обозначают буквой
С = ~ А = ЛД — Лн. (7.2)
Следовательно,
Лд = Лн + С. (7.3)
Поправки обычно указываются в паспорте прибора или опреде-
ляются при проверках и должны учитываться при проведении из-
мерений. Иногда поправки бывают различными на различных уча-
стках шкалы или диапазона измерений прибора.
И Зак. 530
305
Проверку и регулировку приборов объединяют под общим на-
званием тарировки приборов. Нанесение делений шкал измеритель-
ных приборов при помощи сравнения с эталоном называют калиб-
ровкой.
Различают правильность, точность, чувствительность и постоян-
ство измерительных приборов. Под правильностью понимают сте-
пень приближения показания прибора к действительному значению
измеряемой величины, определяемому образцовым прибором. Не-
правильным называют прибор, погрешность которого при сравне-
нии с образцовым оказывается больше, чем указанная в паспорте
поправка.
Точность прибора — это характеристика достоверности резуль-
тата измерения, оцениваемая величиной ошибки, которая может
быть сделана при измерении правильным прибором. Если, напри-
мер, три измерении силы тока данным прибором мы можем сделать
ошибку в ±'0,01 а, то эта величина и представляет собой точность
измерения. Если истинное значение измеряемой величины неизвест-
но, то точность прибора можно иначе определить как ошибку, кото-
рая представляет собой разность между его показаниями и пока-
заниями образцового прибора, которые мы считаем точными. Точ-
ность правильного прибора оценивается паспортной величиной по-
правки С к его показаниям.
Чувствительностью прибора называют отношение линейного или
углового перемещения указателя прибора (например, стрелки) к
изменению измеряемой величины. Если малым изменениям послед-
ней отвечают значительные перемещения указателя, то прибор яв-
ляется чувствительным. То максимальное изменение измеряемой
величины, которое еще не вызывает перемещения указателя, назы-
вают порогом чувствительности прибора. Чувствительность иногда
определяют как отношение количества делений шкалы, на которые
переместился указатель, к изменению измеряемой величины. Если,
например, стрелка пружинных весов под влиянием груза в 20 г
пробежала два деления, то чувствительность весов будет 2 :20=0,1
деления на 1 г. Чувствительность не следует смешивать с ценой
деления шкалы, под которой понимают изменение измеряемой ве-
личины, соответствующее одному делению шкалы (в данном слу-
чае 10 г). Чувствительность обратно пропорциональна цене де-
ления.
Постоянство измерительного прибора характеризует сходимость
повторных измерений этим прибором одной и той же величины,
или, как еще говорят, степень устойчивости показаний прибора.
Постоянство характеризуют вариацией показаний, т. е. наибольшей
разностью показаний при многократных повторных измерениях
одной и той же величины в неизменных условиях.
Методы измерения. Среди различных методов измерения мож-
но выделить метод непосредственного определения, дифференци-
альный и нулевой методы, а также методы совпадения и заме-
щения.
306
Метод непосредственного определения состоит в том, что изме-
ряемая величина непосредственно определяется с помощью измери-
тельного прибора (например, при взвешивании на весах или при
измерении различного рода величин стрелочными приборами).
Этот метод наиболее распространен, особенно в технике, и отли-
чается простотой и быстротой выполнения. Однако он обладает
меньшей точностью, чем другие. Одной из причин ошибок стрелоч-
ных приборов является параллакс — кажущееся смещение проек-
ции стрелки относительно шкалы при перемещении глаза наблю-
дателя. Чтобы облегчить нахождение правильного положения гла-
за при взятии отсчета по шкале, прибегают к различным приемам.
Например, если конец стрелки сделан широким (в виде лезвия но-
жа), то глаз помещают так, чтобы плоскость ножа не была видна
и проектировалась в тонкую линию. Если на шкале имеется зерка-
ло, то при отсчете следят за тем, чтобы стрелка и ее изображение в
зеркале сливались. Следует не смешивать приборы с зеркальной
шкалой с зеркальными приборами (например, зеркальными галь-
ванометрами), в которых указателем является вращающееся зер-
кальце, отбрасывающее луч света на шкалу, находящуюся на неко-
тором расстоянии. Это позволяет существенно повысить точность
взятия отсчетов (чувствительность) при весьма малых перемеще-
ниях зеркальца.
При нулевом методе действие на прибор измеряемого предмета
уравновешивается с помощью другого предмета, величина которо-
го известна, так как указатель равновесия остается в начальном
положении. Типичным примером является взвешивание на равно-
плечих весах или измерение электрического сопротивления с по-
мощью электрического моста. Нулевые методы отличаются высо-
кой точностью, а нуль-приборы — высокой чувствительностью и
широко применяются в практике научных измерений.
Точность нулевого метода теоретически беспредельна, а прак-
тически зависит только от чувствительности указателя нуля. Если
равновесие осуществляется не полностью и отклонение от нуля из-
меряется тем или иным способом, то такой метод называют мето-
дом ложного нуля, а по отношению к измерениям электрическим
мостом — методом неуравновешенного моста. Для устранения по-
грешностей нулевого метода часто прибегают к так называемому
методу замещения, при котором измеряемая величина заменяется
другой, равновеликой ей в отношении измеряемого свойства (на-
пример, когда взвешиваемое тело уравновешивается на противопо-
ложной чашке весов какой-либо тарой, а затем взвешиваемое тело
заменяется гирями). Этот прием позволяет правильно взвешивать
даже в случае неравноплечих весов.
Дифференциальный метод — это метод, при котором с помощью
прибора измеряется не сама искомая величина, а разность между
нею и некоторой другой известной величиной. Он может давать вы-
сокую относительную точность даже при малых разностях и по
существу является развитием метода ложного нуля. В последнее
11* Зак. 530
время этот метод в сочетании с нулевым получает все большее рас-
пространение.
Метод совпадения заключается в том, что при измерении долж-
ны совпасть отметки двух шкал или вообще каких-либо двух ве-
личин. На нем основаны измерения с помощью всем известного
нониуса, позволяющего определять десятые или даже сотые доли
миллиметра. На этом же методе основано измерение усилий с по-
мощью струнных (акустических) датчиков, когда добиваются сов-
падения частоты тока от лампового генератора и собственной ча-
стоты струны, натягиваемой под влиянием измеряемого усилия. Во
многих случаях, подобных этому, метод совпадений оказывается
незаменимым.
Основные виды ошибок при измерениях. Если результаты по-
следовательных измерений можно считать совершенно независи-
мыми друг от друга и они получены при абсолютно одинаковых
условиях, то такой ряд измерений называется идеальным. Выдер-
жать эти требования полностью на практике не удается, причем
легче всего их выполнить в чисто лабораторных условиях и гораз-
до труднее в натурных исследованиях, когда приходится мириться
с большим числом различных внешних влияний, непрерывно меня-
ющихся во времени и пространстве.
В зависимости от причин ошибок при измерениях и наблюдени-
ях они подразделяются на три типа: 1) грубые ошибки (промахи
и просмотры), 2) случайные и 3) систематические.
Грубые ошибки. Грубые ошибки можно разделить на логи-
ческие ошибки, просмотры при измерениях и промахи при вычис-
лениях.
Логические ошибки вызываются обычно недостаточным понима-
нием выполняемой работы. Отсюда вытекает необходимость тща-
тельной подготовки и инструктажа всех участников эксперимента.
Даже если и не допускаются логические ошибки, неподготовлен-
ный наблюдатель может не обратить внимания на непредусмот-
ренные заранее, но существенные обстоятельства.
Просмотры при измерениях заключаются в основном во взятии
неправильных отсчетов по приборам и в описках при записи отсче-
тов в журнал наблюдений. Эти ошибки, к сожалению, непоправи-
мы, и если они обнаруживаются, следует браковать результаты
опыта. Чтобы исключить такие ошибки, возможные при усталости
даже у очень внимательного человека, необходимо каждый отсчет
повторять дважды, обязательно вслух, а в ответственных случаях
контролировать их вторым наблюдателем. Еще лучше везде, где
возможно, переходить на автоматические самозаписывающие при-
боры, особенно при таких испытаниях, когда необходимо брать ча-
стые отсчеты при непрерывно движущейся стрелке прибора.
Промахи при вычислениях обычно связаны с путаницей в раз-
мерностях, с чисто арифметическими ошибками, с погрешностями
при установке движка и ползунка на логарифмической линейке и
при определении и записи результата вычислений на ней, с ошиб-
308
Измеренный ре-
зультат в мм
№ измерения
ками в постановке запятой, в неправильном округлении и отбрасы-
вании нужных значащих цифр и т. п. Эти ошибки легко обнару-
живаются и исправляются при проверке вычислений другим ли-
цом. Такая проверка должна быть обязательной.
Очевидно, грубые ошибки могут быть исключены при надлежа-
щей подготовленности, внимательности и тщательности работы ис-
полнителей и при осуществлении необходимого контроля.
Случайные ошибки. Допустим, что 12 раз измерена
длина одного и того же стержня с помощью одной и той же линей-
ки, имеющей деления через 0,5 мм, и что десятые доли миллиметра
были определены на глаз. В результате получен ряд чисел, приве-
денный в таблице.
Из этой таблицы видно, что из-
меренная длина колеблется от 41,7
до 42,3 мм, причем некоторые ре-
зультаты измерений повторяются
чаще, некоторые — реже.
Различие между результатами
измерений в данном случае вызвано
какими-то неизвестными причинами,
по-разному проявляющимися в каж-
дом отдельном измерении и носящи-
ми случайный характер по отноше-
нию к процессу измерения. Очевид-
но, величина случайной ошибки в
каждом измерении представляет со-
бой разность между его результа-
том и истинным значением измеряв
вестна, но которую хотят найти в результате измерений. Для этого
следует каким-то образом исключить случайные ошибки при после-
дующей обработке.
Характерной особенностью случайных ошибок является незави-
симость результатов последовательных измерений друг от друга.
Это означает, что любая из них имеет одну и ту же свою постоян-
ную вероятность появиться независимо от того, сколько измерений
и с каким результатом было сделано до этого. То обстоятельство,
что одинаковые ошибки разных знаков при большом количестве
измерений встречаются одинаково часто, означает, что сумма та-
ких ошибок (отклонений в ту и другую сторону от истинного зна-
чения измеряемой величины) равна нулю.
Благодаря этим свойствам случайных ошибок можно считать
наиболее вероятным (истинным) значением измеряемой величины,
или по крайней мере наиболее близким к нему (наилучшим значе-
нием), среднее арифметическое всех результатов измерений.
Очевидно, разность между средним арифметическим ограничен-
ного количества измерений и истинным значением измеряемой
величины, найденным как результат достаточно большого количе-
1
2
3
4
5
6
7
8
9
10
11
12
42,3
41,8
41,7
42,0
42,1
41,9
41,8
41,9
41,9
41,8
41,9
42,0
величины, которая неиз-
309
ства измерений, также носит случайный характер, т. е. будет раз-
личной для различных групп одинакового числа измерений.
В приведенном выше примере измерений среднеарифметиче-
ское значение двенадцати измерений длины стержня будет равно:
, 42,3 + 42,1 +42,0-2 4-41,9-4.+ 41,8-3 + 41,7 .1П
/ = ------------------------------------ — 41 ч ММ,
12
Если считать, что это значение представляет собой с известной
вероятностью истинную длину стержня, то мы можем оценить от-
клонения от нее результатов измерений. Вычитая из значений, при-
веденных в табл. 7.1, это истинное значение, получим отклонения:
0,4—1 раз; 0,2—1 раз; 0,1—2 раза; 0—4 раза; (—0,1)—3 раза и
(—0,2)—1 раз. Легко видеть, что точность наших измерений было
бы логично оценить средним значением отклонений, но оно оказы-
вается равным нулю, так как суммы положительных и отрицатель-
ных отклонений от среднеарифметического равны друг другу. Гаусс
предложил возводить сначала эти отклонения в квадрат, а затем
извлекать из среднего значения этих квадратов квадратный корень,
назвав результат средней квадратической, или стандартной ошиб-
кой. Для рассматриваемого случая эта ошибка равна:
„ _ 1/ 0,16 + 0,04 + 0,01 • 2+ 0-4+ 0,01-3 +0,04 п 1К.
о — у -------------------------------------- = и, 10 ММ»
Чем меньше стандартная ошибка, тем выше точность измерений.
Таким образом, определение среднеарифметического значения поз-
воляет исключить случайные ошибки, а результат будет тем точ-
нее, чем больше сделано повторных измерений. Величина стан-
дартной ошибки позволяет оценить качество выполнения изме-
рений.
Систематические ошибки. Ошибки измерений, которые
проявляют видимую закономерность в последовательном чередо-
вании величин и знаков или сохраняют постоянно свой знак (по-
ложительный или отрицательный) при всех измерениях, называют-
ся систематическими. Если, кроме того, их абсолютная величина
не меняется от измерения к измерению, то они называются посто-
янными.
Систематические ошибки искажают не только каждое измере-
ние, но и наилучшее значение, вычисляемое как среднеарифмети-
ческое по результатам всех измерений. Они не могут быть выявле-
ны никакой последующей обработкой результатов измерений и об-
наруживаются обычно лишь путем сравнения с измерениями, вы-
полненными при коренном изменении методики эксперимента и
иной аппаратуре.
Систематические ошибки в той или иной мере присутствуют в
каждом измерении и каждом эксперименте, и задача исследовате-
ля обнаружить их и свести к пренебрежимому минимуму. Иногда
наличие систематической ошибки обнаруживается много времени
спустя лишь при сравнении результатов с данными других иссле-
дователей.
310
В качестве некоторых источников систематических ошибок
можно назвать:
1) дефекты измерительной аппаратуры, особенно: а) неточную
тарировку приборов или тарировку в условиях, отличных от ус-
ловий, в которых приборы будут работать; б) трение и износ в
движущихся частях приборов; в) неправильную установку нуля;
г) конструктивные недостатки приборов — люфты, деформации,
инерционность (запаздывание), термоэлектрические и иные анало-
гичные эффекты; д)1 неуравновешенность подвижных деталей,
приводящую к появлению ускорений и динамических перегрузок;
е) изменение механических характеристик деталей приборов со
временем (например, жесткости пружин и т. п.);
2) использование при создании принципиальной схемы и изме-
рительных устройств приборов недостаточно точных зависимостей
и уравнений. Так, при определении гранулометрического состава
по скорости оседания частиц в воде всегда имеют место отклоне-
ния от закона Стокса при падении мельчайших частиц, что дает
постоянную систематическую ошибку в содержании самых тонких
фракций. Вообще в опытах чаще всего измеряют не непосредствен-
но интересующую величину, а какую-то другую, функционально
связанную с первой. Однако закон, связывающий между собой эти
величины, может быть известен лишь приближенно, а предполагае-
мая линейная зависимость между ними может быть в действитель-
ности нелинейной или линейной лишь в некотором, неизвестном
диапазоне. При измерении электрическими методами неэлектриче-
ских величин возникают различные дополнительные емкости и ин-
дуктивности, паразитные сопротивления и т. п., появляющиеся в
ходе измерения, если наблюдаемый объект сам входит в электри-
ческую цепь или контур, как это бывает, например, при измерении
влажности грунтов емкостным методом или по изменению их эле-
ктрического сопротивления;
3) неудовлетворительное обеспечение постоянства условий из-
мерения: а) влияние изменений температуры и давления в окру-
жающей среде на самый опыт и измерительную аппаратуру; б) не-
одинаковую или вообще неправильную установку приборов, чувст-
вительных к положению в пространстве (например, недостаточную
регулировку по отвесу или уровню); в) колебание тока в сети;
г) непредвиденные изменения во времени свойств материалов;
д) недостаточную химическую чистоту реактивов; е) испарение
или конденсацию влаги; ж)' работу в неустановившемся режиме;
з) недостаточную виброустойчивость приборов;
4) пренебрежение необходимыми паспортными и иными поправ-
ками к показаниям приборов, например поправками на изменение
атмосферного давления с высотой, на изменение силы тяжести в
различных пунктах земного шара, на мениск в жидкостных указа-
телях и т. д.;
5) ошибки самого исследователя (личные систематические
ошибки) при взятии отсчетов между делениями шкалы на глаз
311
или из-за параллакаса, бессознательного стремления улучшить ре-
зультат запаздывания реакции на сигнал при взятии отсчета и т. п.
Из приведенного перечня причин систематических ошибок вид-
но, что они могут быть в значительной мере устранены путем тща-
тельной подготовки и постановки опыта, а обнаружить их можно
сравнением результатов измерений с результатами, полученными
с помощью других приборов или по другой методике. Если
же эта ошибка меняется со временем, то она может быть установ-
лена при изучении изменения средней арифметической во времени.
Главной заповедью экспериментатора должны быть тщательное со-
держание и уход за аппаратурой, систематическая проверка ее ра-
боты, выдерживание строго постоянных условий эксперимента,
обеспечение высокой квалификации операторов и т. д. Нередко
приходится совершенно менять методику эксперимента либо при-
бегать к повторным исследованиям, изменяя те или иные условия
опыта.
Но если грубые ошибки сравнительно легко устранить и если
систематические ошибки, хотя и с трудом, но также в принципе уст-
ранимы, то устранить случайные ошибки при отдельных измерени-
ях принципиально невозможно. Однако эти ошибки подчиняются
определенным закономерностям при массовых измерениях, что по-
зволяет в той или иной мере уменьшить их влияние на значение из-
меряемой величины и найти последнюю с достаточно высокой на-
дежностью как среднее арифметическое значение результатов из-
мерений.
Возникает вопрос, как меняется это среднее значение при уве-
личении количества опытов. Естественно, что слишком большого
числа испытаний достичь невозможно, однако можно определить то
количество, при котором получаемый результат .можно считать до-
стоверным с той или иной определенной степенью вероятности. На
этом вопросе мы остановимся далее.
Точность и тщательность измерений. Следует различать точность
и тщательнрсть измерений. Точность определяется случайными
ошибками и тем выше, чем они меньше, а тщательность характери-
зуется систематическими ошибками и тем больше, чем эти ошибки
меньше.
Различие между двумя результатами измерений, сообщаемыми
двумя различными наблюдателями, или между наблюденным зна-
чением некоторой величины и приводимым в справочниках, назы-
вают расхождением, а различие между рядом результатов при по-
вторных измерениях в относительно одинаковых условиях — раз-
бросом. Расхождение не является само по себе ошибкой, хотя, по
крайней мере, одно из двух данных несомненно ошибочно, но появ-
ляется в результате того, что одна или обе из сравниваемых вели-
чин имеют различные по величине ошибки, которые следует уста-
новить, чтобы объяснить расхождение.
Округление результатов измерений. Остановимся несколько под-
робнее на вопросе о неправильном округлении чисел как о причи-
312
не ошибок. Значащей цифрой называется всякая цифра, входящая
в число, выражающее результат измерения с определенной точно-
стью. Существует ряд правил для назначения последней значащей
цифры. Например, американское «Общество испытания материа-
лов» допускает ошибку в последней значащей цифре не более чем
на 15 единиц последнего разряда в числе, т. е. если приводится,
например, число 63,7 см, то это означает, что результат измерения
находится между 63,7—1,5 = 62,2 и 63,7-Н 1,5=65,2 см. Однако во
многих случаях ограничивают ошибку 10 единицами и даже менее.
Иногда рекомендуют записывать приближенные числа так, чтобы
только последняя значащая цифра была сомнительной, но не более
чем на одну единицу. Обычно включают в результат измерения по-
следнюю не вполне точную цифру (взятую, например, на глаз
между двумя соседними делениями шкалы прибора), но записы-
вать ее следует несколько ниже всех остальных цифр числа, на-
пример 63,7.
За последнюю надежную значащую цифру принимают также ту
последнюю цифру в ряде результатов измерений, которая является
инвариантной (неизменной). Например, в ряду 325,5, 321,4, 327,7,
320,ь 326,8, 324,2, 324,з такой инвариантной цифрой будет число де-
сятков. Так как среднее арифметическое равно здесь 324,26, то
этот результат следует записывать (округляя до десятых) в виде
324,з или 324,3, надчеркнув две последние цифры, чтобы показать,
что это средний результат ряда измерений, в которых первые две
цифры оставались неизменными.
Если производится вычислительная обработка результатов из-
мерений, рекомендуется при промежуточных выкладках и в окон-
чательном результате сохранять число значащих цифр на одну
больше, чем в измерениях, и считать последней надежной цифрой
следующую за инвариантными, т. е. в данном примере мы бы по-
лучили 324,28- Эта рекомендация исходит из того, что среднее
всегда точнее каждого отдельного измерения. Приведя подобную
запись, необходимо, кроме того, указать стандартную ошибку. Во-
обще оценка требуемой точности измерений в каждом отдельном
случае зависит от характера задачи и, естественно, может несколь-
ко меняться.
Округление чисел представляет собой отбрасывание одной или
нескольких значащих цифр и замену их нулями и обычно делается
при вычислениях, в которые входят измеренные количества. Пра-
вила такого округления широко известны, и при постоянном их вы-
полнении в вычисления не вносятся никакие дополнительные
ошибки. Все числа следует округлять до одного и того же порядко-
вого места, считая от запятой, причем если заменяемое нулями
число больше, чем 5 с нулями, то предыдущая цифра увеличивает-
ся на 1, а если точно равно 5, то перед пятеркой увеличивается
яа 1 только нечетная цифра. Во всех других случаях цифра, пред-
шествующая отбрасываемым, остается без изменения.
При умножении и делении чисел, имеющих неодинаковую точ-
313
.ность, но одинаково существенных для результата, надлежит поль-
зоваться следующим правилом: сохранять с самого начала в самом
точном из чисел на одну значащую цифру больше, чем их содер-
жится в наименее точном из чисел, а затем округлять окончатель-
ный результат в соответствии с этим последним числом. При сло-
жении и вычитании в наиболее точном числе также удерживается
на один десятичный знак больше, чем их содержится в самом не-
точном числе (десятичными знаками называют цифры справа от
запятой независимо от количества их слева от последней).
Все изложенные выше соображения справедливы только при
независимых друг от друга измерениях.
2. СТАТИСТИЧЕСКИЙ АНАЛИЗ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ
Кривая распределения частот, найденная в результате серии
испытаний, называется экспериментальной. Получив такую кривую,
исследователь обычно проверяет, не является ли она близкой к ка-
кому-либо типу теоретических кривых распределения, хорошо изу-
ченных в теории вероятностей. Такое сравнение нередко позволяет
сделать определенные выводы относительно тех закономерно-
стей, которые обусловили найденное экспериментальное распреде-
ление.
Наиболее распространенным в естественных условиях, хотя и
далеко не единственным, является нормальное распределение^
подробно рассмотренное в п. 4 главы 5.
Нормальное распределение. Чтобы экспериментальное распре-
деление непрерывной случайной величины можно было считать,
нормальным, оно должно отвечать следующим условиям:
1) среднеарифметическая х и среднеквадратическое отклоне-
ние $ должны быть связаны соотношением
s]/2n 2,5 s
2) кривая симметрична, и, следовательно, показатель скошен-
ности 01 = 0;
3) если определить момент /П4 четвертого порядка площади
кривой распределения относительно ее центра (умножая элемен-
тарные площади на четвертую степень «плеча») и разделить этот
момент на четвертую степень стандарта, то мы должны получить
значение эксцесса р2, характеризующего крутизну кривой распре-
деления, равным 3. Если распределение случайной величины х яв-
ляется нормальным, то сокращенно это записывают так:
А
х: jV(x, о).
Нормальное распределение чаще всего встречается на практике.
В 1900 г. Ляпуновым была доказана теорема о том, что: «Случай-
ная величина, состоящая из большого числа взаимно независимых
слагаемых, среди которых нет ни одного, резко выделяющегося
314
большой величиной дисперсии, имеет нормальное распределение
вероятностей».
Таким образом, если случайная величина
х — xi + х2 + • • • + хп, (7.4)
то при соблюдении условий Ляпунова плотность вероятности стре-
мится к нормальному закону (5.28).
Следовательно, каковы бы ни были распределения вероятностей
для каждой из случайных величин X/ , входящих в сумму (7.4), ве-
роятности возможных значений как их средней, так и суммы х
распределяются нормально, если только этих величин достаточно
много.
Практически считают, что условие Ляпунова соблюдается даже
при малом числе слагаемых, лишь бы они были сравнимы друг с
другом по своим дисперсиям.
Теорема Ляпунова называется центральной предельной теоре-
мой теории вероятностей. Таким образом, нормальное распределе-
ние имеет место во всех случаях, когда наблюдаемая величина яв-
ляется результатом действия многих случайных причин, ни одна
из которых не выделяется по своему влиянию по сравнению со всей
суммой. Но если имеются превалирующие слагаемые, которые са-
ми распределены не по нормальному закону, то могут возникать су-
щественные отклонения суммарного распределения от нормального.
Особенно важен тот факт, что даже если случайная величина
распределена не по нормальному закону, обычно арифметические
средние и дисперсии серий испытаний распределены приблизитель-
но нормально. Это обстоятельство лежит в основе всех методов ста-
тистического анализа реальных случайных событий.
В некоторых случаях сама величина х распределена асиммет-
рично, но некоторая функция от нее, например 1g х или х2 и т. п.,
приближенно следует нормальному закону. Тогда прибегают к со-
ответствующему функциональному преобразованию наблюденных
величин, чтобы воспользоваться нормальным распределением их
функций. *
Логарифмически нормальное распределение. Это распределение
особенно часто встречается при механических испытаниях материа-
лов. Нормальное распределение при этом имеют логарифмы слу-
чайной величины (результатов испытаний). Такое распределение
называется логарифмически нормальным, или логнормальным. Вме-
сто самой случайной величины х рассматривают случайную вели-
чину y=lgx, пересчитав соответственно и все исходные данные.
Как показал анализ [40], логнормальное распределение возника-
ет, когда исследуемая случайная величина является произведением
положительных случайных величин xi:
п
X = П х1’ (7-5)
Z=1
315
откуда
п
£/ = lg* = 2lgX/- <7-6>
1
Согласно теореме Ляпунова, r/=lgx распределено нормально, а
следовательно, х распределено логнормально. Точно так же, если
разность между i-той и (I—1)-й случайной величины прямо пропор-
циональна (i—4)-й величине, так что
Х1 Х1— 1 ~ xi— 1
(7.7)
где ki — независимые случайные коэффициенты, то при малых
х, —х£._, можно написать
lim У
п—« **
xi — xi—\ с" dx . ,
“——— — 1 — 1g хп 1g *в»
xi-\ J «
(7.8)
откуда с учетом (7.7)
lg х„ = 1g х0 + + • • • + kn. (7.9)
Следовательно, х, распределено логнормально.
Таким образом, ® тех случаях, когда мы получаем в результа-
те наблюдений логнормальное распределение, мы можем видеть
его причину в проявлении закономерности (7.5).
На рис. 7,1 показаны кривые логнормального распределения
при различных математических ожиданиях х и среднеквадратиче-
ских отклонениях а. Логнормальное распределение часто обозна-
А
чают символом А(х, <т).
Другие виды распределений при исследовании грунтов встреча-
ются редко, и мы их здесь рассмат-
ривать не будем.
Генеральная совокупность и вы-
борка. Назовем все количество пред-
метов, о котором мы должны су-
дить по результатам испытаний, ге-
неральной совокупностью, а то ко-
личество их, которое непосредствен-
но подвергается испытанию, — вы-
боркой, или случайной выборкой.
Опыт показывает, что при анали-
зе выборки не может быть получено
точное значение характеристик ге-
неральной совокупности. Однако
Рис. 7.1. Логнормальные распре-
деления
теория позволяет установить с определенной вероятностью, кото-
рая называется доверительной и которой мы задаемся, те пре-
3 16
делы (их называют доверительными), в которых может при этом
находиться искомая величина.
Например, мы можем установить, что с вероятностью 0,99 иско-
мая величина лежит между значениями 4,6 и 5,2, а с вероятностью
0,95 — между значениями 4,8 и 5,0. Очевидно, более узким довери-
тельным пределам должна соответствовать меньшая доверитель-
ная вероятность, т. е. в этом примере в среднем в 1% случаев (при
обязательном условии массовости события) искомая величина мо-
жет оказаться менее 4,6 и более 5,2, а в 5% случаев — менее 4,8
и более 5,0.
Ясно, что если мы поставим задачу о том, какова должна быть
величина выборки для характеристики генеральной совокупности,
то на этот вопрос можно ответить, лишь задавшись определенной
доверительной вероятностью, с которой мы хотим охарактеризо-
вать генеральную совокупность. Чем выше доверительная вероят-
ность, тем шире получаются пределы, в которых находится искомая
величина, и если мы хотим сузить эти пределы при данной вероят-
ности, то тем большим должно быть количество испытаний, тем
большей должна быть выборка и выше точность измерений. Рас-
смотренная выше задача является наиболее важной задачей мате-
матической статистики, которая разрабатывает способы, позволяю-
щие характеризовать генеральную совокупность по результатам
испытания выборки.
Задача экспериментатора существенно усложняется, если ошиб-
ки измерения накладываются на естественные колебания самой из-
меряемой величины, когда повторным испытаниям подвергаются
каждый раз новые объекты. Это всегда имеет место в случаях,
когда в процессе испытания объекты выходят из строя, разрушают-
ся (например, при испытании образцов грунта на прочность). В по-
добных случаях мы сталкиваемся с задачей оценки свойств некото-
рого массива грунта по результатам испытаний сравнительно огра-
ниченного количества образцов.
Закон больших чисел. Этот закон представляет собой теоретиче-
скую основу математической статистики. Он был доказан Чебыше-
вым в виде следующей теоремы: «Можно утверждать с вероятно-
стью, близкой к 1, что средняя арифметическая из ряда независи-
мых случайных переменных с ограниченной дисперсией при доста-
точно большом их количестве будет сколь угодно мало отличаться
от математического ожидания».
Таким образом, из этого закона следует, что при очень боль-
шом числе случайных явлений средний их результат практически
перестает быть случайным.
Частным случаем теоремы Чебышева является теорема Бернул-
ли, которая гласит, что «при достаточнобольшом числе независи-
мых испытаний можно утверждать с вероятностью, близкой к еди-
нице, что частость появления события сколь угодно мало отличает-
317
ся от вероятности его появления в отдельном испытании». Это мож-
но записать в виде
Р (|Г-р|<8)-1, (7.10)
п-*оо
где Р —вероятность данного события;
п — количество испытаний;
р — вероятность появления события в отдельном испытании;
W — частость;
е —сколь угодно малое число.
Если вероятность некоторого утверждения о результатах испы-
таний при большом количестве испытаний сколь угодно мало отли-
чается от 1, то в этом случае говорят о сходимости по вероятности.
Теорема Вернули была выведена для постоянных условий опыта,
когда вероятность появления события в каждом опыте одна и та
же и равна р. Если же условия опыта, а следовательно, и величи-
на р каждый раз меняются, то. для этого случая Пуассоном была
доказана следующая теорема: «Если производится п независимых
опытов и вероятность появления события А в i-том опыте равна pi„
то при увелиличении п частость события А сходится по вероятности
к среднему арифметическому значению вероятностей pi ».
Выборочное распределение. Теорема Гливенко. Назовем распре-
деление случайных величин в выборке выборочным, или эмпириче-
ским в отличие от неизвестного нам распрёделения генеральной со-
вокупности, которое для краткости будем называть генеральным.
Обозначим случайную переменную в выборке через хв , а в гене-
ральной совокупности через х.
Чтобы найти генеральное распределение исходя из выборки, ма-
тематическая статистика опирается на теорему Гливенко, говоря-
щую о том, что при количестве испытаний п — °о можно утверж-
дать с вероятностью 1, что максимальная разность между функ-
циями распределения х и хв стремится к нулю. Это значит, что с
увеличением объема выборки выборочное распределение все более
приближается по характеру к генеральному. _
Статистическая оценка. Согласно закону больших чисел, х и s,
найденные для некоторой выборки, сходятся по вероятности к ма-
А
тематическому ожиданию х и к среднему квадратическому откло-
нению генеральной совокупности о, т. е.
Р (рё —х| < s)1; (7.11)
Д-э-оо
Р (|s —а|<е)-1, (7.12)
Л->00
где е — сколь угодно малая величина.
318
Но если число наблюдений не очень велико, приходится ограни-
Л
чиваться приближенными значения х и о, которые называют.
оценками, и определять их точность и надежность. При этом сами
оценки являются случайными величинами.
Если математическое ожидание (т. е. наиболее вероятное значе-
ние) оценки будет как раз равно искомому параметру, го оценку^
называют несмещенной. Оказывается, что средняя арифметическая
является именно несмещенной оценкой математического ожидания/
а дисперсия — смещенной, так как ее математическое ожидание
Л1(52) = Ст2 (7.13)
п
несколько меньше дисперсии генеральной совокупности о2. Поэтому
при переходе от s к о компенсируют эту ошибку, умножая $2 на
-----и получая, таким образом, несмещенную оценку,.для о2:
п — 1
о2 = —— s2. (7.14)
п — 1
При большом п разница между в и s будет несущественна.
_________ л
Приняв х за х и s за ст, мы должны оценить возможную ошибку.
Здесь исходят из того, что если определять по ряду выборок из од-
ной и той же генеральной совокупности величины х и s, то они ока-
зываются распределенными по нормальному закону. Поэтому при
большом кцличестве наблюдений можно пользоваться непосредст-
венно нормальным распределением. Покажем, как это делается.
Как мы видели в п. 4 главы 5, вероятность того, что значение
непрерывной случайной величины отклоняется от математического
ожидания не больше чем на некоторую величину 1а, равна удвоен-,
ному значению интеграла вероятностей Ф(£) согласно формуле,
(5.35). Например, вероятность того, что величина отклонения бу-
дет не более 2<т, равна 2Ф (2) =0,9545 «95 % (в данном случае
1=2). Таким образом, задаваясь вероятностью 2Ф(/), с которой мы
можем допустить данное отклонение, по таблице интеграла Лап-
ласа находим соответствующее значение t. При этом границы ин-
тервала, которые определят возможное максимальное отклонение,
будут равны:
±е=±/а=±/-^, (7.15)
]/ п
где s — среднеквадратичное отклонение совокупности выборок,
причем каждое на’блюде1ние мы условно считаем за сред-
ний результат испытания какой-то случайной выборки
(всего п наблюдений).
Значения 2Ф(/) и 2© называются соответственно доверительной
319
вероятностью р и доверительным интервалом. Следовательно, для
нашего примера (см. главу 5), когда х—16,50; п=100, а $=0,35,
истинное значение влажности в генеральной совокупности лежит в
пределах 16,50 + t—=16,50±0,07%, т. е. между 16,43 и 16,57%
Уп
при доверительной вероятности р=0,95.
Доверительная вероятность и доверительные пределы. Метод
Стьюдента. Выше мы обозначили через р веооятность того, что
Л
ошибка в определении х и а не превзойдет ±е:
р(|х — х|<е) = р; (7.16)
P(|s-<T|<e) = p. (7.17)
Величина р представляет собой доверительную вероятность.
Поставим задачу таким образом: каков должен быть доверитель-
ный интервал от —в до +е, чтобы с заданной доверительной веро-
Л
ятностью р можно было утверждать, что искомая величина х или о
не выйдет за этот интервал. Доверительный интервал называют
также доверительной оценкой, а его границы — доверительными,
границами.
Итак, требуется найти вероятность неравенства
| х — х | < е, (7.18)
если известно, что х подчинено нормальному закону с центром рас-
сеивания х и средним квадратическим отклонением о/]/п соглас-
но формуле (5.36). При малом количестве наблюдений мы не мо-
жем непосредственно воспользоваться нормальным законом, как
это делали выше. Для этих случаев Стьюдент предложил заменить,
случайную величину х другой случайной величиной Т:
(7.19)
——7-----р— • (7.20)
r n(n-l) v ?
Распределение этой случайной величины Т не зависит от неиз-
Л
вестных нам х и <т, а только от некоторого аргумента t и числа на-
блюдений п. При (л->-оо) распределение Стьюдента сходится к
нормальному (практически при п>100). Задаваясь произвольным
320
положительным tp, можно найти вероятность р попадания Т на
участок от — ip до + ip-
р = р(|х — х|<е)=2 Sn(f)dt, (7.21>
где S„(£)—распределение величины t, найденное Стьюдентом^
Вид графика распределения S„ (£) приведен на рис. 7.2. Число-
Рис. 7.2. Распределение S„ (/) по
Стьюденту
степеней свободы, равное п—1, обычно в таблицах обозначается
Функция t табулирована в зависимости от аргументов tp и п, и ее
можно найти в любом курсе математической статистики._
Пусть, например, произведено п опытов и найдено х. Задаемся
доверительной вероятностью р (скажем, 0,95). Требуется найти со-
ответствующий доверительный интервал. Для этого вычисляем s*-
и по таблицам по f и р находим t. Так, для f=JO и р=0,95 £=1,81,.
а для f=120 и р=0,95 £=1,66. Затем определяем половину довери-
тельного интервала:
s = £s*. (7.22>
Л
Тогда^мы можем сказать, что х с вероятностью р не выходит за
пределы х ±8.
Увеличивая доверительную вероятность (т. е. надежность), мы
тем самым увеличиваем ширину доверительного интервала, снижая?
точность заключения. Но это повышает нашу уверенность в досто-
верности суждения, (в его надежности). Сужая доверительные пре-
делы, мы повышаем точность, но понижаем надежность, и наобо-
рот. Чаще всего применяют значения надежности р=0,95 и 0,99.
Пример. Для влажностей, приведенных в табл. (5.2), найти с доверительной*
вероятностью р=0,95 пределы, в которых заключено наиболее вероятное значе-
ние (математическое ожидание) влажности. Нам уже известны значения х=16,5*
s
и s=0,35 по табл. (5.7). Определяем s* —-— = 0.035. По таблицам^
Уп— 1
математической статистики находим при р=0,95 и п=100 /р=1,66; 8 = /ps*=
=0,06. Следовательно, при доверительной вероятности 0,95 истинная влажность
Л
находится в пределах t<y=16,50±0,06, т. е. при относительно большом п мы полу-
чим вполне удовлетворительные результаты испытаний.
321
Отбор элементов выборки. Результаты исследования случайных
величин в высокой степени зависят от качества отбора данных, на-
пример от правильности отбора образцов грунта, направляемых
на испытание. Эти образцы должны как можно более близко ха-
рактеризовать исследуемую генеральную совокупность, быть, как
говорят, представительными или репрезентативными.
Для того чтобы произвести представительный отбор проб, нуж-
но иметь известное, иногда довольно подробное представление о
свойствах генеральной совокупности. Так как такое представление
заранее не всегда можно составить, нередко приходится вести ис-
следования в неколько последовательных этапов, каждый раз уточ-
няя требования к репрезентативности.
Это условие относится ко всем стадиям исследования и в поле,
и в лаборатории; на каждой из них должны приниматься меры к
обеспечению представительности получаемых материалов.
Необходимое количество испытаний. Для определения необхо-
димого количества испытаний п используют критерий Стьюдента,
рассчитывая по нему заранее для данной доверительной вероятно-
сти и доверительных пределов необходимое количество образцов,
обеспечивающее определенный доверительный интервал. Так как
для этого необходимо знать дисперсию, то сначала берут неболь-
шую пробную выборку и по ней находят s*. Затем, задаваясь е
(половиной доверительного интервала), по (7.22) вычисляют t и
далее для этого значения t и принятого р находят по таблицам п.
Число испытаний можно существенно сократить, если по мере
получения каждого ihoboto результата испытания производить ста-
тистический анализ имеющегося материала методом так называемо-
го последовательного анализа Вальди. За подробностями отсылаем
читателей к литературе по математической статистике, а также к
методическому пособию по инженерно-геологическому изучению
горных пород [71].
Выбор доверительных величин. Вопрос о выборе необходимой
величины доверительной вероятности выходит за рамки статисти-
ческого анализа выборочных данных, так же как и вопрос о том.
каким значением полученной величины пользоваться в практиче-
ских расчетах (средним, минимальным или каким-либо другим, на-
ходящимся в пределах доверительного интервала).
Ответ на этот вопрос определяется ответственностью проекти-
руемого сооружения, наличием неучтенных факторов, имеющимся
опытом поведения сооружений в близких условиях и т. д.
События с очень малыми вероятностями принято считать прак-
тически невозможными. В частности, принято считать невозмож-
ными события или случайные величины, отклоняющиеся от средне-
го значения (математического ожидания) более чем на Зег (так на-
зываемый трехсигмовый предел). Опыт показывает, что при малом
количестве испытаний следует принимать значения измеряемой ве-
личины, равные доверительным границам при доверительной веро-
ятности 0,95, причем, естественно, принимается та из двух границ,
322
которая идет в запас устойчивости (например, Для нагрузок —
верхняя, для показателей прочности материала — нижняя).
Если распределение является нормальным или близким к нему,
то можно принять, что доверительный интервал уменьшается про-
порционально корню квадратному из числа испытаний (наблюде-
ний). Следовательно, для уменьшения ошибки в два раза количе-
ство испытаний следует увеличить в четыре раза.
Оценка генеральной дисперсии. Оценка дисперсии генеральной
совокупности по дисперсии выборки производится методом, анало-
гичным определению доверительного интервала для математиче-
ского ожидания, но при этом используется распределение выбороч-
ной дисперсии, называемое %2 (хи-квадрат-распределением) или
распределением Пирсона, которое также табулировано.
Если обозначить доверительную вероятность через р=1—р (на-
пример, при доверительной вероятности р=0,95; р=0,05), то по
величине р и числу степеней свободы f по таблице для %2 находят
значения %2, соответствующие (1—’/^Р) и V2P- Величины (1—V2P)
и V2P называют уровнями значимости. Затем доверительные пре-
делы для о определяются по формуле
S
f
Тл—912
(7.23)
Имеются также таблицы величин
•=v, что еще более уп-
рощает вычисления.
Пример. Для нашего примера при р=0,90 и — — pj = \— =0,95^
и -- р=0,05 получим значения %2 соответственно 18,5 и 43,8 (при максимальном
f, равном 30). Соответствующие значения
== 0,83, и тогда
равны:
-Ми ^2
S v3/2 < 0 < S Vl— 3/2-
(7.24)
Подставляя сюда числа, найдем:
0,35 • 0,83 0,35-1,3, т. е. а = 0,375 ± 0,085.
При f>30 распределение Пирсона уже близко к нормальному с
математическим ожиданием а и дисперсией Определяя до*
верительные пределы по Стьюденту, следует пользоваться вместо
s значением о, найденным по приведенному здесь методу.
Критерии согласия. Если мы предполагаем, что результаты ис-
пытаний соответствуют какому-либо теоретическому распределе-
нию вероятностей для генеральной совокупности, то следует про-
32а
верить, согласуются ли эмпирические данные с предполагаемым
распределением. Ответ на этот вопрос получают при помощи так
называемых критериев согласия, которые позволяют определить,
является ли расхождение между опытным и теоретическим распре-
делением случайным или существенным. Имеется ряд таких крите-
риев, и они подробно рассмотрены в курсах математической стати-
стики.
Дисперсионный анализ. Если какая-либо исследуемая величина
испытывает колебания (например, прочность образцов грунта из
одного и того же пласта), то возникает вопрос: присущи ли эти ко-
лебания самому грунту или они связаны с лабораторными погреш-
ностями? Ответ на этот вопрос дает так называемый дисперсион-
ный анализ. Описание методики этого анализа заняло бы слишком
много места, и мы отсылаем читателей к специальным пособиям по
математической статистике.
Зависимость между случайными величинами. Если каждому
значению какой-либо величины (независимая переменная) соответ-
ствует одно значение другой величины (зависимая переменная), то
связь между этими величинами называется функциональной. Если
же обе величины являются случайными, но изменения одной влия-
ют на распределение другой, то связь между ними называется сто-
хастической. Степень, или сила стохастической связи между величи-
нами оценивается коэффициентом корреляции г, который равен:
г = . (7.25)
(n—\)sxsy v ’
где xi и yi — наблюденные значения двух случайных величин,
_ _ зависимость между которыми исследуется;
х, у — их средние значения;
sx и sy — их среднеквадратические отклонения;
п — количество испытаний, в каждом из которых заме-
рялись xt и yi, т. е. количество пар выборочных
значений (xj, у\), (х2, Уг) и т. д.
При г=0 связь отсутствует, а при г=1 она является функциональ-
ной. Сильной («тесной») связью считаются значения г>0,8. При
этом следует иметь в виду, что коэффициент корреляции характе-
ризует только линейную связь, так что при нелинейной зависимо-
сти (например, квадратичной) г может быть меньше 1, а связь в
действительности является функциональной. Поэтому лучше всего
Рис. 7.3. Виды корреляций
324
наносить опытные значения на график в координатах х и у и на
глаз оценивать характер их распределения.
На рис. 7.3,а распределение данных соответствует сильной, или
тесной корреляции, на рис. 7.3,6—слабой, на рис. 7.3, в корреляция
отсутствует, а на рис. 7.3, г коэффициент корреляции не характери-
зует силу связи.
Регрессия. Если построить график зависимости от х средних
значений уг при каждом xi, то получим кривую регрессии, уравне-
ние которой называется уравнением регрессии. Это уравнение мож-
но найти и не строя кривой, а исходя из принципа наименьших
квадратов, согласно которому сумма квадратов отклонений значе-
ний yi от наиболее вероятных значений у должна быть минималь-
ной.
Отсылая за подробностями к курсам математической статисти-
ки, отметим здесь только, что найденное уравнение регрессии долж-
но быть подвергнуто дополнительному анализу с целью оценки сте-
пени его приближенности (регрессивный анализ) и силы связи
между yi и х/ (корреляционный анализ).
В случае линейной регрессии отрезок, отсекаемый прямой на
оси ординат, называется свободным членом регрессии, а тангенс
угла наклона прямой к оси абсцисс — коэффициентом регрессии.
Если найти доверительные пределы
для у, то можно построит^ довери-
тельную область, в которой с веро-
ятностью (1—£)2 лежит линия ис-
тинной регрессии (рис. 7.4).
В случае нелинейной, регрессии
видом уравнения задаются, а затем
вычисляют его параметры, пользу-
ясь методом наименьших квадратов.
Уравнение регрессии считают окон-
чательным лишь в том случае, если р.ис. 7.4. Лин ih регрессии
соответствующая ему дисперсия D
незначительно отличается от дисперсии наблюденных величин s2.
При нелинейных зависимостях метод наименьших квадратов
приводит обычно к столь громоздким вычислениям, что практиче-
ски удобнее подбирать формулы, выражающие экспериментальную
зависимость между х и у с помощью графических приемов, даю-
щих гораздо быстрее результат, очень мало отличающийся от най-
денного по методу наименьших квадратов.
Графический подбор экспериментальных формул. Прежде всего
необходимо нанести точки, имеющие координатами эксперимен-
тально найденные значения х/ и yi, на график. В случае одинако-
вых размерностей х и у масштабы осей ординат и абсцисс графика
должны быть одинаковы. Затем на график ребром накладывается
гибкая прозрачная линейка, которую изгибают так, чтобы экспери-
ментальные точки по обе стороны от линейки лежали к ней ближе
325
всего, и проводят по линейке кривую. Если ее кривизна мала и экс-
периментальную зависимость можно без большой ошибки при-
нять за прямую, то на графике проводят такую прямую, чтобы
опять-таки экспериментальные точки лежали к ней ближе всего
Рис. 7.5. Построение эксперимен-
тальной зависимости
(рис. 7.5). Затем прямо по чертежу
определяют параметр b и угловой
коэффициент k:
A = tga==±r±., (7.26)
где у и х — координаты какой-ли-
бо произвольной точки
на проведенной йрямой.
Если искомая зависимость, не
может быть принята за прямолиней-
ную, то надо ввести такие новые пе-
ременные, чтобы в них зависимость
стала линейной. Это делают мето-
дом попыток. Прежде всего пробу-
ют построить график в осях 1g х и 1g у. Когда полученные точки
лежат практически на прямой, то мы получаем уравнение
1g Уч — 1g У1 = (1g х2 — 1g Xi)'tg a, (7.27)
откуда
lg^. = jfelg^; y = lh_xk = bxk, (7.28)
У1 xr
причем b определяют для значений yx и Xi в самом начале прямой,
проведенной через все экспериментальные точки.
Если же при таком построении график не получается прямым,
то пробуют полулогарифмическую сетку координат (у~1пх), и если
при этом получают прямую, то ее уравнение (рис. 7.6) запишется
так:
Уч. ~ Hi = (In хг — In Xi) tg a;
Уч — y^kln^-, (7.29)
откуда
Уч = У1 + k In — ,
*1
где A = tg a.
Логарифмическое уравнение можно представить в виде экспо-
ненциальной зависимости.
326
Нормативные и расчетные харак-
теристики грунтов по строительным
нормам и правилам 1962 г. Прочност-
ные и деформатнвные характеристики,
установленные непосредственно испы-
таниями, называют нормативными. Эти
характеристики определяют с учетом
природного состояния грунта и того
давления (бытового), под которым он
находится в условиях естественного за-
легания, а также тех изменений, кото-
рые возможны в процессе строитель-
ства и эксплуатации. При этом за нор-
Рис. 7.6. Построение к фор-
муле
мативную характеристику принимают
среднеарифметическое значение, полученное при испытании образ-
цов, количество которых определяется по методу, описанному вы-
ше, и должно быть во всяком случае не менее шести.
При расчетах пользуются, однако, не нормативными, а так на-
зываемыми, расчетными характеристиками, которые представляют
собой произведение нормативной характеристики на коэффициент
однородности k, учитывающий возможное отклонение характеристи-
ки в неблагоприятную сторону вследствие физико-механической не-
однородности материала. Этот коэффициент по СНиП 1962 г. опре-
деляется по формуле
А = ‘-Г
(7.30)
где s — среднее квадратическое отклонение;
Ая — нормативная характеристика грунта.
Нетрудно видеть, что коэффициент однородности представляет
собой разность между единицей и коэффициентом вариации, выра-
женным в ее долях. Если умножить Аа на k, то получим расчет-
ную характеристику
ЛР = ЛЛН = ЛН -^=^-=Лн-5. (7.31)
-Ян
Таким образом, расчетная характеристика по СНиП равна нор-
мативной за вычетом среднего квадратического отклонения.
В тех случаях, когда условия действительной работы грунта в
сооружении не отражаются в расчетах прямым путем, расчетные
характеристики получают умножением Лн не только на коэффици-
ент однородности, но и на коэффициент условий работы, который
обычно приводится в соответствующих нормативных документах.
3. ИСПОЛЬЗОВАНИЕ ТЕОРИИ РАЗМЕРНОСТЕЙ
И ПОДОБИЯ ПРИ ИССЛЕДОВАНИЯХ
В ряде задач механики грунтов до сих пор отсутствует удовлет-
ворительная математическая постановка, что определяется слож-
327
ностью этих задач, и тогда на первое место выдвигается испытание
соответствующих моделей. Однако проведение таких испытаний до-
статочно сложно и для получения приемлемых результатов необ-
ходимо выдержать ряд условий как при проектировании экспери-
мента, так и при обработке его результатов. Эти условия могут
быть установлены с помощью теории размерностей и подобия (69,
25].
Техника использования этой теории отличается простотой и
даже элементарностью, однако от исследователя требуется пони-
мание сущности изучаемых явлений и знание тех факторов, кото-
рые определяют их протекание.
Размерности. Единица измерения. Количественный анализ яв-
лений и возможность численной их характеристики требуют прове-
дения соответствующих измерений как исходных величин, так и по-
лучаемого конечного результата. Опыт показывает, что все вели-
чины, с которыми вы встречаемся при экспериментах и наблюдени-
ях, могут быть охарактеризованы через некоторое ограниченное
число простых основных понятий.
В эти понятия должны входить длина и время, так как измене-
ние пространственно-временных координат и состояние систем оп-
ределяются в первую очередь этими параметрами, а также мас-
сой, от которой зависит отклик систем на механические воздейст-
вия, вызывающие их перемещения. Соответственно говорят о неза-
висимых размерностях длины, времени или массы, причем единицы
измерения можно выбирать численно различными (например сан-
тиметр, метр и т. п.). Таким образом, понятия о размерности и
единицах измерения не совпадают, и одна и та же размерность мо-
жет быть представлена в различных единицах измерения. Размер-
ность отражает физические особенности системы и предопределяет
способ измерения параметров этой системы, тогда как единицы из-
мерения характеризуют масштаб, принятый при данном способе
измерения для определения численного значения данного пара-
метра.
В качестве единицы меры длины [L] обычно принимают метр,
времени [Г] — секунду, массы [Af] — килограмм. Скорость, выра-
женная через отношение м/сек, а также сила, определяемая произ-
ведением массы на ускорение (кг-м/сек2), являются производными
величинами. Однако можно выбрать в качестве основной размер-
ность не массы, а силы (например, ньютон), и тогда размерность
массы выразить через силу, деленную на ускорение, т. е. как
н-сек2/м. Таким образом, выбор основных велич!ин является услов-
ным. Необходимо лишь, чтобы эти величины были независимыми
друг от друга, т. е. чтобы изменение масштаба измерения одной не
влекло за собой изменения масштаба другой. Кроме того, основ-
ные размерности должны быть удобны для измерения.
Размерность некоторой производной величины [К] в общем
виде записывается как
328
[К)=ГТ?Л1\ (7.32)
где квадратные скобки означают размерность, а величины а, р и
у — показатели степени. Формула (7.32) называется формулой раз-
мерности. Обычно показатели а, р и у называют размерностями,
хотя они выражают, собственно, связь между последними.
Условие однородности физических формул. Как показал впер-
вые Фурье, размерности левой и правой частей любой физической
формулы должны быть одинаковы (так называемое свойство од-
нородности формул). Иногда при сопоставлении размерностей ле-
вой и правой частей уравнения нужно обращать внимание на ве-
личины, измеряемые в относительных (безразмерных) единицах,
например в радианах, герцах и т. п. Действительно, если в раз-
мерности углового ускорения рассек2 опустить обозначение рад,
физический смысл записи 1!см2 будет неясен. Заметим попутно, что
в формулах, содержащих углы, следует выражать последние через
радианы, а не градусы, если требуется непосредственно определять
условные размеры в числах (например, вычислять длину дуги как
произведение длины радиуса на угол).
_ „du „ и
Размерность производной есть размерность дроби — , вто-
рой производной
а3 и и „и
---размерность дроби , третьей------------
и т. д. Размерность интеграла J ydx равна размерности выражения
ух. В трансцендентных выражениях, например sinx, ех или 1g х,
под х следует подразумевать безразмерные значения —, где х0 —
единица размерности. '
Любую физическую величину можно рассматривать как основ-
ную и выражать через нее размерность других величин. Более то-
го, число основных величин можно произвольно увеличивать, но
при этом в формулах появятся дополнительные размерные кон-
станты, что в большинстве случаев только усложняет запись. Если,
например, считать основной величиной вместо длины [L] скорость
[о], то можно путь (размерность L) выразить как
L = vT,
(7.33)
но. чтобы выполнить основное требование — одинаковые размерно-
сти левой и правой частей, мы должны ввести в формулу констан-
ту С, имеющую размерность [L/vT], и тогда
L = CvT.
Физически эта константа представляет собой путь, проходимый те-
лом при о=1 и T=il.
Подобные системы. Рассмотрим две каких-либо системы 1 и 2
(например, два откоса одинакового заложения, но различной вы-
соты) и допустим, что путем мысленной равномерной деформации
одной из этих систем можно добиться их совмещения при наложе-
329
нии. Все точки систем 1 и 2, которые при этом совпадут, будем на-
зывать сходственными. Расстояния между сходственными точками
в обеих системах также называют сходственными.
Если между двумя системами одинаковой физической природы
существует подобие, то это означает, что соответствующие обоб-
щенные координаты Ei обеих систем для любых сходственных то-
чек систем и сходственных моментов времени пропорциональны
друг другу:
где индекс «о» означает оригинал, индекс «м» — модель, а величи-
на а представляет собой коэффициент подобия. Если известен ко-
эффициент подобия и значения координат Eiw, то легко вычис-
лить соответствующие координаты Ei 0 для оригинала, что и со-
ставляет основную цель моделирования.
Системы, в которых для сходственных точек существует посто-
янное отношение масс
----= const,
называют динамически подобными.
Если в соотношениях
^10 ^2 О о О Л /7 ол\
= —- = = а (7.34)
м £2м м сп м
разделить все члены равенства на какой-нибудь из членов, напри-
Е-
мер —— =а, то (7.34) перейдет в безразмерное равенство:
Егм
ф- = ф- = ... = -^- = 1, (7.35)
Е1 м Е2 м Еп м
в котором все величины представляют собой безразмерные коор-
динаты, выраженные в единицах сходственных величин Ei 0 и
Eiu, причем числитель каждой дроби равен знаменателю той же
дроби, т. е. безразмерные сходственные величины численно равны
между собой.
Безразмерные комплексы. Пусть в результате наблюдений нами
установлено чисто качественно наличие зависимости между груп-
пой физических величин п/:
f (th, Th, ..., nk) = 0. (7.36)
Эти величины могут быть как постоянными, так и переменными,
причем их размерность должна быть нам известна.
330
Если мы определим по (7.36) какую-либо из величин nt, на-
пример
«й = ф («1. «2, • • • . Л*_1).
то легко видеть, что численное значение tik будет зависеть от вы-
бранной системы единиц измерения величин п/. Так, если Пй
представляет собой скорость, то ее численная величина будет раз-
лична в зависимости от того, будет ли она выражена в м/сек или
в км/ч.
Вместе с тем в обоих случаях речь будет идти об одной и той
же физической величине, и возникает вопрос, возможно ли и в
каких случаях, чтобы численное выражение этой величины остава-
лось неизменным (инвариантным) при любом преобразовании еди-
ниц измерения. Очевидно, что инвариантными относительно преоб-
разования единиц могут быть только безразмерные величины или
комплексы, составленные из размерных параметров таким образом,
чтобы их размерности сократились, т. е. безразмерные комплексы.
Изменение единиц измерения какой-либо величины есть, в сущ-
ности, изменение масштаба, в котором изображается эта величи-
на в результате измерения. Например, можно измерить некоторую
длину (допустим, 100 см) отрезком, равным 11 см, и установить,
что он .помещается на этой длине ровно 100 раз. Отношение изме-
ренной длины к длине измерительного отрезка будет представлять
собой безразмерную величину — число 100. Представим себе те-
перь, что измеряется длина, в два раза большая (200 см), с по-
мощью линейки длиной, также в два раза большей и равной 2 см.
Снова отношение измеряемой длины к длине измерительного от-
резка будет равно 100. Таким образом, в данном случае масштаб
остался неизменным, так как в равное число раз изменились изме-
ряемая длина и измерительный отрезок.
Очевидно, все безразмерные соотношения размерных величин
можно рассматривать как масштаб, который остается неизменным,
если все входящие в безразмерный комплекс величины изменяются
в одинаковое число раз.
Если вдуматься в это положение, то нетрудно увидеть, что оно
должно играть весьма важную роль при моделировании. Если по-
ведение оригинала определяется рядом параметров, то поведение
модели будет подобно поведению оригинала только в том случае,
если все безразмерные комплексы однородных величин, составлен-
ные для оригинала и модели, будут численно совпадать. Это поло-
жение широко используется при проектировании модельных экспе-
риментов. При этом следует иметь в виду, что величина различных
коэффициентов и модулей, входящих в определяющие уравнения,
должна определяться непосредственно из соответствующих опытов,
и теория размерностей не может дать их численные значения.
Сколько же можно составить независимых безразмерных комп-
лексов из величин, входящих в выражение (7.36)? На этот вопрос
331
отвечает так называемая л-теорема (пи-теорема), называемая
иногда также теоремой Бакингема, по которой из k величин, имею-
щих неодинаковую размерность, можно составить k — т безраз-
мерных комплексов, где т—число основных размерностей, опреде-
ляющих данную систему (например, длина, время, масса в зада-
чах механики). Каждый из безразмерных комплексов обычно обо-
значают буквой л с численным порядковым индексом внизу. Если,
например, значение k в (7.36) равно 6, а число основных единиц—3,
то можно составить всего (6—3)=3 независимых безразмерных
комплекса, которые обозначают Ль Лг и лз.
Покажем на примере, как составляют безразмерные комплексы.
Рассмотрим задачу о гидравлическом сопротивлении Q, возникаю-
щем при течении вязкой жидкости внутри круглой трубы. Это со-
противление, как показывают различные наблюдения, можно пред-
ставить в виде функции следующих пяти величин:
Q = f(o,'n,P,Z,d), (7.37)
где v — средняя скорость течения;
т] — коэффициент вязкости;
р — плотность;
I — длина рассматриваемого участка трубы;
d— диаметр трубы.
Исходя из понятия об однородности физических формул, не-
трудно сообразить, что должно иметь место соотношение
[Q] = MWlPlW[<- (7.38)
При этом I и d, хотя и измеряются в одинаковых единицах, яв-
ляются независимыми величинами, так как они выражают различ-
ные пространственные свойства системы. В частности, I измеряет-
ся вдоль одной оси, a d — вдоль другой оси координат. Таким об-
разом, нельзя сокращать одинаковые размерности двух функций,
если их физическая природа различна.
Подставим в (7.38) размерности, выраженные через размерно-
сти массы [М], длины [L] и времени [Т]. При этом, поскольку ис-
комая величина Q имеет размерность давления, выразим ради уп-
рощения массу через силу по соотношению [А4] = где а —
[<»]
ускорение, имеющее размерность [LT-2]. Тогда получим
[Q] = PL-2 н/м\
[о] = L Т~1 м/сек:,
h) = рт L~2 н-сек/м2-,
332
[р] = РТ21~4нсек2/м2-,
[/] = L м\
[d] = L м
и соответственно
P L~2 = (L T~x)’ (PT IT2)* [P T2 L~4f (L)y (L)\ (7.39)
Из условия однородности следует, что показатели степени при
однородных единицах измерений (т. е. при Р, L и Т) в левой и пра-
вой частях равенств должны быть одинаковыми, что дает следую-
щие уравнения для определения неизвестных показателей степени:
(Р) 1=/+х;
(L) — 2 = s — 2t — 4 х + г/ + z;
(Т) 0 = — s + t + 2x.
Эта система уравнений содержит пять неизвестных s, t, х, у, г. Ре-
шая ее относительно s, t, х, получаем
s = у + z 4- 2;
t = — у — z;
x = ^ + z+ 1.
Подставляем эти значения в (7.38) и переходя от размерностей к
самим величинам, вводим безразмерный коэффициент пропорцио-
нальности С:
Q = C vy+z+2 тГУ~г Ру+г+1 ly <?. (7.40)
Чтобы получить безразмерный комплекс в левой части, подби-
раем из величин, входящих в правую часть, комплекс, имеющий
размерность Q (т. е. PL-2), например произведение р а2:
и разделим обе части (7.39) на это произведение. Получим
= С тГ(и+г} Ру+г 1У d2 .
рО»
Теперь нетрудно подобрать безразмерные комплексы в правой
части:
£Ь=с(-^-\У+г f—Y. (7.41)
ри2 \ т] / \ d )
О v р d I
Три безразмерных комплекса ——, и — должны иметь
р я2 т) d
для модели те же значения, что и для оригинала. Тогда явление те-
333
чения вязкой жидкости в модельной трубе будет во всем подобно
течению жидкости в натурной трубе и по испытанию на модели мож-
но будет определить коэффициент С. Неизвестные пока показатели
степени у и z также должны определяться из опыта. Безразмер-
/ I \У
ные отношения вида — , т. е. отношения двух величин с одина-
\ а /
ковыми размерностями, называют симплексами.
Другой способ получения безразмерных комплексов заключает-
ся в том, что за основные размерности принимают любые три из
входящих в (7.38) величины, например v, т] и р. Затем делят каж-
дую величину в (7.37) на произведение oS; , rfi и рж* , где значе-
ния степеней s/, tt и X/ различны для каждой из величин и
должны быть найдены из условий безр азмерности полученных от-
ношений. Так, из уже найденного выше решения мы видим, что
величину Q нужно делить на произведение t^-q’p1:
Vs* т/* рх‘ Vs 2 if* р*1 t)S> rf* р*’
Следовательно:
Q ly #
=------------; =-------------; -з =--------------• (7.43>
OS* 7]'1 p*1 t>S2 tf* p*’ Vs’ if* pX*
В каждом из этих отношений размерности числителя и знамена-
теля должны быть равны:
Ch) PL~2 (PTL~2)tl (РТ*Ь~*}Х'-,
(ъ) Ly= ( L T~' )s’ (PT L-2)'2 (PT® L-4/2;
(it8) lY = (L T~l )s> (P T L~2/’ (PT® L~*Y‘ ,
откуда получаем уравнения для показателей степени: {
(^i) 1 = /1 Хь — 2 = Si —• 2 ti — 4 Xij 0 = — Si 4~ /i 2 x^
(^2) 0 = /2 + -^2> У = ^2 — 2/2 — 4 x2; 0 = — ^2*4”/2 + 2xgj
(^3) 0 = ^3 4~ X39 2 === S3 ~ 2 /3 4 X3, 0 = S3 4- ^3 4~ 2 х^»
Решая эти системы уравнений, находим:
(^1) Si = 2; = 0; = 0;
(к2) s2 = — у\ h = хг = — у\
(^з) S3 == 2, /3 = 2, Хд = Z.
334
Из выражения (7.42) теперь получаем:
I» „у ?у _ / Ivp у
рг / dv р V
Здесь вид безразмерных комплексов несколько иной, однако он
легко может быть представлен в виде (7.41).
Критерии подобия. Если известны только основные параметры,
определяющие изучаемое явление, то можно найти соответствую-
щие безразмерные комплексы, позволяющие утверждать, что при
одинаковой физической природе и равных численных значениях
комплексов у оригинала и модели явления в них должны характе-
ризоваться одинаковыми численными коэффициентами. Если чис-
ленные коэффициенты у оригинала и модели одинаковы, мы сразу
находим, что различные величины, входящие в безразмерные ком-
плексы, могут отличаться у оригинала и модели лишь таким об-
разом, чтобы безразмерные комплексы оставались неизменными.
Так, из (7.44) следует, что если при модельном испытании будет
взят иной, чем у оригинала, диаметр трубы d, то ее длина должна
быть также пропорционально изменена, чтобы отношение lid оста-
валось тем же. Но этого мало. Величина d входит и в другой без-
размерный комплекс. Следовательно, если мы хотим, чтобы сопро-
тивление Q у модели точно равнялось сопротивлению Q у оригина-
ла, нам необходимо пропорционально d изменить также и вязкость
ЖИДКОСТИ Т].
Из изложенного ясно, почему безразмерные комплексы называ-
ют критериями подобия. Оригинал и модель подобны, если у них
одинаковы численные значения всех безразмерных комплексов, в
которые должны входить также граничные условия.
Моделирование при наличии дифференциальных уравнений.
В тех случаях, когда изучаемое явление описано дифференциаль-
ными уравнениями (например, процесс консолидации), моделиро-
вание обычно используется для нахождения решений конкретных за-
дач. При этом должны соблюдаться следующие условия: 1) гео-
метрическое подобие модели и оригинала; 2) описание изучаемого
явления и в оригинале, и в натуре одними и теми же дифференци-
альными уравнениями; 3) тождественное совпадение начальных и
краевых условий, представленных в безразмерном виде; 4) равен-
ство соответственных безразмерных параметров модели и ориги-
нала.
В тех случаях, когда дифференциальные уравнения процесса от-
335
сутствуют, прибегают к установлению критериев подобия в виде
безразмерных комплексов, получение которых было описано выше.
Для того чтобы из дифференциального уравнения получить кри-
терии подобия, следует опустить в уравнении знаки дифференци-
рования и поделить все члены уравнения на один из них [1]. В ка-
честве примера приведем уравнение одномерной консолидации
(7.44)
dt д* v
где о — давление в скелете грунта [PL~2 ];
t —время [Г];
z — глубина [L];
с—коэффициент консолидации [L2T-1].
В соответствии с приведенным правилом отбрасываем знаки
производных и находим
Г о
с “]•
z2 J
Делим обе части на о// и получаем безразмерный комплекс
К = — . (7.45
г2 v
Следовательно, если у модели (индекс 1) и оригинала (индекс
2) значения л одинаковы, т. е.
АА = АА ( (7.46)
А 4
то и процессы изменения о во времени и по глубине в сходственных
точках будут в обеих системах протекать одинаково.
Если в модели и оригинале грунт один и тот же. т. е. ci = c2, из
(7.46) мы-получим, что >
А. = А.
откуда
t —t
‘2 — ‘1 ~Т »
А
и легко вывести (подставляя вместо z мощности пластов) извест-
ное соотношение: продолжительность консолидации прямо пропор-
циональна квадрату мощности пласта при прочих равных усло-
виях. Приведем другой пример [1] из теории колебаний фундамен-
тов под машины. Дифференциальное уравнение вынужденных ко-
лебаний фундамента при учете вязкого сопротивления грунта (за-
тухания) записывается так:
т + k — + сх= Fesina>/, (7.47)
d /а dt
336
где т — масса фундамента [Af];
х —его перемещение [L];
t — время [Т];
k — коэффициент вязкого сопротивления основания [МТ-1];
Fosin<oZ—возмущающая сила с амплитудным значением Fq[MLT~2]
и частотой <о[Т-1];
с —коэффициент упругого сопротивления основания [Л4Т-2].
Отбрасывая знаки дифференциалов, получаем
+ *£ + с = о sin щ (7.48)
Размерность — будет . Следовательно, если разде-
/2 Т2
лить это выражени на Fo, имеющее такую же размерность, то по-
лучим первый безразмерный комплекс:
т х
К1 =
а умножая и деля это выражение на х и замечая, что x!t — v, мы
исключим из критерия время t и найдем, что
тх х т v2
7^1 ------— — ------ .
t2 F х xF
Выражение kx/t имеет размерность MLT~2.
Следовательно, деля его на F^ снова получим
комплекс:
k х kv
(7.49а)
безразмерный
(7.496)
Выражение сх имеет размерность MLT~2. Делим его на Fo ста»
кой же размерностью и находим
’'3=-^. (7.49b)
Наконец, величина at является безразмерной, и ее можно непо-
средственно принять за
Tzi = at = u>t^- = '^. (7.49г)
Для подобия между оригиналом и моделью в начальный момент
- мы должны подставить в безразмерные комплексы начальные зна-
чения Х = Хнач и V = ЦНач (при t — 0):
__т ^нач . цнач С *нач ш *нач
— z тг > яз — — ; пз = —- ; ^4 —------. (7.50)
хначТ То То V
Следовательно, если мы захотим исследовать процесс колеба-
ния фундамента на модели, должны быть выполнены следующие
12 Зак. 530
337
критерии (индекс «ф» относится к фундаменту, индекс «м» — к
модели):
отм^.м = стф Цн.ф . МндМ = *ф рн.ф .
*н.м Л>м *н.ф^0ф Л) м *0ф
См *н.м _ сф хн.ф . * ШМ *н.м _ щф *н.ф (7 51)
Л) м Л)ф ун.м ун.ф
Кратко эти критерии подобия записывают так:
т kvR схн ш хн
-----= idem; = idem; —— = idem; -= idem. (7.52)
Fo-------------------------------------------F° Fo-7
Если под x и t понимать текущие значения координаты и вре-
мени, то по соотношениям
mv2 .j kv ., ex .j wx ..
-----= idem; — = idem; -------= idem и — — idem
x Fo Fq Fo Fq
можно установить связь между координатами и временем для
оригинала и модели.
После наступления установившегося состояния начальные усло-
вия xQ и уо уже не оказывают влияния на поведение систем, и по-
этому условия подобия можно упростить, например, приняв два ус-
ловия:
k . . т со2 . j
----= idem и-----------= idem,
т со с
которые получаются делением второго из комплексов (7.49) на
первый и четвертый и умножением квадрата четвертого на первый
и делением на третий.
Центробежное моделирование. Во многих задачах, связанных с
поведением грунтов, решающее значение имеет собственный вес
грунта (например, в задаче об устойчивости откосов). Можно при-
нять, что предельная устойчивость откоса определяется уравнением
f (Я, m, ;г, ф, с) = 0, (7.53)
где Н — высота откоса;
т — его заложение — отношение высоты откоса Н к его гори-
зонтальной проекции В(т = Н!В)\
уг — объемный вес грунта [PL“3], равный
7г = ря; (7-54)
Р —плотность [ML-3];
g — ускорение силы тяжести [LT-2];
<р —угол внутреннего трения;
с —сцепление [PL-2].
Уравнение (7.53) зависит от двух основных размерностей (М и
L), и в него входят три размерных величины (Н, у,, с). Таким об-
разом, в данном случае можно составить (3—2) = 1 безразмерный
338
комплекс, который почти очевиден, а именно с/утН. Величины т и
ср — симплексы. Очевидно, критериями подобия будут
—-—^idem; m=idem; q) = idem.
Уг Я
Из условия m = idem вытекает, что заложение откоса у модели
и в натуре должно быть одинаковым. Из третьего критерия следу-
ет, что углы внутреннего трения у модели и у оригинала также
должны быть одинаковыми. Но если взять для модели тот же грунт,
что и в натуре, то будут одинаковы и с, и уг, и из первого крите-
рия получается, что высота модели должна равняться высоте на-
турного откоса (Нм = //0), иными словами, моделирование невоз-
можно. Однако выйти из этого затруднения можно, взяв для моде-
ли тот же грунт, что и в натуре, и потребовав вместе с тем, чтобы
объемный вес грунта в модели отличался от объемного веса грун-
та в натуре в соответствии с соотношением
1 _ 1
Ум #м У о //о
или
= (7.55)
п
т. е. ум должно быть во столько же раз больше у0, во сколько вы-
сота натурного откоса больше высоты модели.
Очевидно, это можно сделать при условии, что модель будет
помещена в поле сил, отличающихся соответственным образом от
гравитационного. Так как ум и у0 можно заменить произведения-
ми плотности на соответствующие ускорения (/— для модели и
g— для натуры), то мы получим
/ = g (7.56)
Ускорение j технически легко получить с помощью центробеж-
ной машины, дающей ускорение, равное / (рис. 7.7). Так как при
этом
/
1__Рис. 7.7. Схема центробежной машины
Л'4--3 для моделирования
1 — коромысло; 2 —каретка с моделью
Ф
где v — скорость вращения;
R — расстояние от тела до оси вращения,
то мы находим, что при данном радиусе вращения R круговая ско-
рость v должна быть равна:
р-57>
12* Зак. 530
339
На рис. 7.8 показан общий вид помещения и установки для
центробежного моделирования в лаборатории механики грунтов
Днепропетровского института инженеров транспорта.
Рис. 7.8. Центробежная машина ДИИТ
4. О ПРИНЦИПАХ КЛАССИФИКАЦИИ ГРУНТОВ
Полезность любой классификации определяется прежде всего
тем, что она представляет собой удобный вид систематизации име-
ющихся знаний о той или иной группе предметов. При наличии
классификации достаточно лишь суметь правильно отнести данный
предмет к тому или иному классу или, как говорят, произвести его
идентификацию (отождествление), чтобы сразу получить представ-
ление о его особенностях и свойствах, характерных для того клас-
са, к которому принадлежит рассматриваемый предмет, и о его
соотношении с представителями других классов.
Из сказанного следует, что классификация должна, во-первых,
распределять классифицируемые предметы по их характерным
свойствам,’ а во-вторых, позволять по определенным признакам лег-
ко устанавливать принадлежность рассматриваемого объекта к со-
ответствующему классу.
Признаки, называемые идентификационными, представляют со-
бой как бы «входы» в классификацию, а «выходами» являются
описания характерных особенностей и свойств того класса предме-
тов, к которому относится. идентифицируемый объект. Чтобы
произвести идентификацию, необходимо знать, какие именно при-
знаки позволяют установить s принадлежность рассматриваемого
объекта к тому или иному классу, и уметь определять эти признаки.
Как известно, одни и те же объекты можно классифицировать
по различным признакам в зависимости от целей, которые пресле-
дуются при классификации. Таким образом, одновременно и па-
340
раллельно может существовать ряд различных классификаций
грунтов, друг друга не только исключающих, но и дополняющих.
Рассматривая в последующем различные свойства грунтов, мы бу-
дем попутно останавливаться и на классификации грунтов по этим
свойствам.
Однако необходимо, чтобы свойства, положенные в основу лю-
бой из классификаций, были важными и существенными, определя-
ющими поведение объектов в рассматриваемом отношении. Опыт
показывает, что все классификации, основанные на случайных не-
существенных признаках, быстро выходят из употребления и забы-
ваются.
Многообразие видов грунтов в природе и значительное различие
между ними требуют соответствующих классификаций, которые
позволяли бы объединять в отдельные группы близкие по свойст-
вам грунты и вместе с тем указывали на основные различия меж-
ду ними.
Все существующие инженерные классификации грунтов могут
быть разбиты на следующие группы: 1) инженерно-геологические;
2) почвенно-дорожные; 3) физико-технические.
Любая рациональная классификация грунтов должна иметь в
качестве выходов характерные для соответствующей области тех-
ники особенности поведения грунтов. Что же касается входов ( в
классификацию, то различают прямые и косвенные идентификаци-
онные характеристики.
Казалось бы, что логичнее всего идентифицировать грунты по
таким входным характеристикам, которые непосредственно связа-
ны с поведением грунтов в сооружении, а именно, по деформатив-
ным и прочностным характеристикам. Подобные характеристики
называют прямыми. Однако непосредственное нахождение прямых
характеристик оказывается сложной и дорогостоящей задачей, а
кроме того, их надо знать далеко не во всех случаях.
Почти все классификации широко используют наличие корре-
ляции (статистической зависимости) между некоторыми просто и
легко определяемыми физическими характеристиками грунтов и
прямыми характеристиками, от которых непосредственно зависят
строительные свойства оснований и грунтовых сооружений. Такого
рода характеристики, находящиеся в корреляционной связи с пря-
мыми, называются косвенными. Классификации, ограничивающиеся
установлением связи между косвенными и прямыми характеристи-
ками без выхода к строительным свойствам, называются промежу-
точными, или вспомогательными.
Входные и выходные характеристики могут быть как качествен-
ными, описательными, так и количественными (в физико-техниче-
ских классификациях).
Инженерно-геологические классификации горных пород. В гео-
логии породы классифицируют либо по происхождению и истории
формирования, либо по вещественному составу. Существует также
ряд классификаций, стремящихся сочетать оба эти фактора, при-
341
нимая, однако, в качестве ведущей генетическую характеристику
пород. В литологии, кроме того, существует классификация пород
по степени литификации. Несомненно, генетические классификации,
отражающие идею развития, возможны только при высоком уров-
не развития науки.
В инженерно-геологических классификациях поведение грунтов
во взаимодействии с сооружениями связывается с геолого-генети-
ческой характеристикой пород, с условиями их формирования и
преобразования. Эти классификации позволяют оценить особенно-
сти строительства, зависящие от геологических условий площадки,
помогают установить объем разведочно-изыскательских работ, не-
обходимых для получения достаточно полной характеристики стро-
ения и свойств грунтовой толщи.
Почвенно-дорожные классификации. Разновидностью инженер-
но-геологических являются так называемые почвенно-дорожные
классификации. Они развились из чисто агрономических и агрохи-
мических классификаций почв, которые строились исходя из оцен-
ки состава почв и характера почвообразующих факторов. Почвен-
но-дорожные классификации применяются в тех областях строи-
тельства, которые связаны с использованием поверхностных поч-
венных слоев грунта при сооружении дорог и аэропортов и осуще-
ствлении некоторых градостроительных мероприятий.
Физико-технические классификации. Эти классификации связы
вают строительные свойства грунтов с их физическими свойствами.
Идентификационные признаки в различных физико-технических
классификациях различны. В одних случаях они легче и проще оп-
ределяются, но хуже коррелируются со строительными ствойства-
ми грунтов, в других корреляция гораздо теснее, но сложнее оп-
ределение входных признаков. Входные признаки в этих класси-
фикациях всегда носят количественный характер.
Практические классификации. Первые классификации грунтов,
составлявшиеся строителями еще до появления механики грунтов
и инженерной геологии, были чисто описательными и исходили из
местных общепринятых названий различных грунтов, выделявших-
ся в практике строительства на основе сопоставления чисто внеш-
них (визуальных) признаков грунтов с поведением построенных на
них или из них сооружений. При этом отсутствовал какой-либо оп-
ределенный и четко выраженный принцип построения классифика-
ции. Одни виды грунтов выделялись по составу, другие — по ха-
рактеру изменений, вызываемых климатическими и атмосферными
воздействиями, третьи — по обоим этим факторам вместе, четвер-
тые— по стадии генетических изменений, претерпеваемых грун-
том в данный период. Подобные классификации часто называют
практическими или визуально-описательными. Они играют важную
роль на первых этапах изучения какого-либо явления или в нача-
ле развития той или иной отрасли техники, когда к научно направ-
ленным исследованиям соответствующих проблем еще только при-
ступают.
342
Указание на тип грунта по практической классификации дает
инженеру-строителю общее представление о характерных особен-
ностях этого грунта, однако каждое наименование здесь охваты-
вает большие группы грунтов с разнообразными физико-механиче-
скими свойствами и существенно различающимися количественны-
ми показателями этих свойств, что в ряде случаев приводит к круп-
ным ошибкам <в оценке строительных качеств материала. Кроме
того, один и тот же грунт может встречаться в различных физиче-
ских состояниях, которым отвечает и различное поведение его в со-
оружении.
Однако главный недостаток подобных классификаций заключа-
ется в том, что определение грунта производится на основании до-
вольно неопределенных признаков, носит субъективный характер,
и поэтому один и тот же грунт разные специалисты могут относить
к различным классам. Это чрезвычайно затрудняет обмен опытом
использования тех или иных грунтов в качестве оснований или ма-
териала сооружений.
Большинство практических классификаций носит узко местный
характер, определяемый инженерно-геологическими особенностями
данного района. В одних классификациях грунты имеют названия,
совпадающие с принятыми в инженерно-геологической терминоло-
гии, в других — чисто местные названия, неизвестные за пределами
данной местности. Поэтому даже простое их сопоставление друг с
другом обычно приводит к самым противоречивым результатам.
Однако такого рода практические региональные классификации
нередко используются строителями для первоначального описания
грунтов в качестве основы для составления программ дальнейших
идентификационных испытаний грунта, после которых уже можно
использовать более строгие инженерно-геологические и физико-тех-
нические классификации.
Полевые классификации. По своей терминологии и разбивке на
классы они обычно следуют той или иной основной инженерной
классификации, но входами в них служат простейшие косвенные
признаки, легко определяемые на глаз в полевых условиях и нахо-
дящиеся в корреляционной связи с прямыми входными признака-
ми основной классификации.
Таким образом, рациональные полевые классификации являют-
ся приближенными и упрощенными вариантами тех или иных ос-
новных классификаций, названия которых они обычно носят, но с
добавлением к ним слова «полевая».
К визуальным признакам относят те, которые могут быть опреде-
лены непосредственно с помощью органов чувств человека без
приборов и измерений или в крайнем случае с помощью каких-ли-
бо подручных простейших принадлежностей. В некоторых случаях
можно прибегать также к зарисовкам и черно-белому или цветно-
му фотографированию образцов и обнажений грунта.
Выполнение визуальной оценки совершенно необходимо при
проведении инженерно-геологической разведки, осмотре обнаже-
343
ний и полевом описании образцов грунта, извлеченных из разве-
дочных выработок.
Несмотря на кажущуюся простоту визуальной оценки грунтов,
для правильного ее выполнения требуется определенный опыт. Не-
обходимо, чтобы тем, кто производил визуальное описание грунта
в поле, обязательно направлялись затем для ознакомления данные
лабораторных испытаний этого же грунта и его идентификации по
более строгим классификациям. Опыт, полученный в результате
сравнения соответствующих данных, позволяет полевым работникам
резко повысить точность визуальной характеристики грунтов и об-
наруживать такие их особенности, которые иначе не бросились бы
в глаза. Автор на основании собственного опыта считает, что неза-
висимое визуальное описание грунта должно обязательно произво-
диться также старшим персоналом грунтовых лабораторий, кото-
рый обязан присутствовать при вскрытии каждого монолита, посту-
пающего в лабораторию на испытания. Это позволит существенно
облегчить последующий анализ результатов испытаний и сделать
из них более правильные выводы. Постоянное сопоставление визу-
альных и количественных характеристик грунтов позволяет раз-
виться и закрепиться весьма важному для каждого, кто занима-
ется исследованием грунтов, интуитивному умению приближенно
оценивать строительные свойства грунта по его визуальным при-
знакам.
Значение классификаций грунтов. Подразделение грунтов на
различные классы по их строительно-техническим свойствам име-
ет важное значение, так как облегчает выбор конструкций соору-
жения ^фундаментов, способа расчета осадок и несущей способно-
сти оснований, назначение рациональных способов производства
работ, прогноз поведения выстроенных сооружений. Накопление
данных наблюдений за основаниями и земляными сооружениями и
анализ этих данных бесполезны без отнесения грунтов к тому или
иному классу, так как только в этом случае можно определенным
образом систематизировать результаты наблюдений и использовать
их в строительной практике.
С другой стороны, классификация грунтов связана с результа-
тами инженерно-геологических исследований, позволяет предви-
деть такие особенности поведения оснований и сооружений, кото-
рые не могут быть пока охвачены никаким расчетом и оцениваются
лишь качественно.
Именно поэтому во всем мире не прекращаются настойчивые
исследования по улучшению и развитию существующих и созданию
новых классификаций грунтов.
5. ПОКАЗАТЕЛИ СВОЙСТВ ГРУНТОВ
Для возможности сравнения различных грунтов друг с другом
их свойства следует оценивать численными величинами, которые
называют обычно параметрами, характеристиками или показате-
ли
ляма свойств. Следует заметить, что эти показатели не являются
физическими константами, так как их значения изменяются в зави-
симости от условий, в которых находится тот или иной грунт.
Н. Н. Маслов подразделяет все показатели на два класса: к перво-
му он относит те, которые непосредственно используются в расчет-
ных формулах (физико-механические показатели), ко второму — те,
которые характеризуют породы по их составу и строению (физичес-
кие показатели).
Основные виды свойств грунтов. Основным и наиболее важным
эффектом, вызываемым действием нагрузки на основания и земля-
ные сооружения, является относительное перемещение частиц грун-
та, причем величина и характер возникающих деформаций сущест-
венно зависят от пористости грунта и от сил взаимодействия между
частицами в точках их взаимного контакта. Если под действием
нагрузки происходит только уплотнение грунта, то соответствующие
деформации всегда носят затухающий характер, и сопротивление
грунта этим деформациям быстро растет с увеличением последних.
Если же деформации связаны с формоизменением загружен-
ного массива, то они могут носить как затухающий, так и незату-
хающий характер, и в последнем случае говорят о нарушении проч-
ности грунта.
Очевидно, при проектировании необходимо знать как начальные
показатели соответствующих свойств грунта, так и характер их из-
менения под действием нагрузки.
В подобных изменениях большую роль играют особенности
взаимодействия частиц скелета не только между собой, но и с по-
ровой средой, а также характерное для грунтов перераспределение
напряжений в ходе деформирования между скелетом и водой, на-
ходящейся в порах.
Из указанных соображений вытекает необходимость не только
определения количественных показателей механических свойств
грунтов, но и исследования степени стабильности и возможных пре-
делов вменений этих показателей при действии нагрузок и других
факторов.
Изучение тех физико-геологических свойств грунтов строитель-
ной площади, от которых зависят их деформации и прочность, сле-
дует вести в тесной увязке с геологическим строением площадки,
с литогенетической характеристикой грунтов. Это позволит суще-
ственно ускорить и удешевить изыскания, используя наличие опре-
деленной корреляции между теми свойствами грунтов, которые оп-
ределяются достаточно легко и просто, и деформативно-прочност-
ными свойствами, определение которых требует сложного оборудо-
вания и высокой квалификации исполнителей.
Все свойства грунтов, представляющие интерес для механики
грунтов, можно с известной условностью подразделять на следую-
щие пять основных видов: физические, механические, химико-мине-
ралогические, физико-химические и коллоидные.
345
К физическим относят пространственно-весовые характеристи-
ки грунтов (размер и форму как отдельных частиц, так и агрегатов,
образованных из этих частиц, структуру, плотность и пористость,
вещественный состав грунта), показатели гидравлических свойств,
свойств пара и газов в порах грунта, а также показатели тепловых,
электрических и магнитных свойств. Из физических характеристик
для механики грунтов основное значение имеют состав, структура,
плотность грунта и его весовые показатели.
Механическими называют те свойства, которые определяют ве-
личину деформаций грунта под нагрузкой и его прочность (вклю-
чая и реологические свойства). К ним относят также механическое
взаимодействие между частицами скелета и движущейся сквозь
поры грунта водой (гидродинамическое давление).
Химико-минералогические свойства грунтов определяются их
химико-минералопическим составом и теми химическими реакциями,
которые протекают или могут протекать в грунтах при взаимодей-
ствии минеральных частиц друг с другом и с поровой средой в раз-
личных термодинамических условиях. В комплекс исследований
этой группы свойств входит также изучение агрессивного действия
грунтовой воды на материал сооружений.
Физико-химические свойства определяют физические закономер-
ности протекания в грунтах химических процессов, а также связь
физических свойств грунтов с микроструктурой их компонентов и
с химическими свойствами этих компонентов.
Коллоидными называют свойства грунта, проявляющиеся как
результат высокой степени раздробленности минеральных частиц
скелета, когда важную роль начинает играть взаимодействие по-
верхности частиц с окружающей средой.
Во многих случаях строгую границу между всеми этими свойства-
ми провести нельзя и, в зависимости от характера той или иной
технической проблемы, нередко приходится рассматривать различ-
ные свойства грунтов в их совокупности. Каждая такая проблема
предопределяет свой особый подход к изучению грунтов, причем
выбор соответствующей методики осложняется огромным разно-
образием как видов горных пород, так и условий их залегания и
режимов окружающей среды. Следует иметь в виду, что задача
исследования свойств грунтов имеет свои отличительные особенно-
сти в каждой из областей строительной техники—при строитель-
стве шахт, возведении 'земляных сооружений, устройстве основа-
ний, производстве строительных материалов и др.
Хотя для механики грунтов основной интерес представляют пер-
вые две группы свойств — физические и механические, однако для
того чтобы правильно понять природу этих свойств, необходимо
обращаться также к исследованию физико-химических, коллоидных
и химико-минералогических свойств грунтов.
Те свойства грунтов, которые определяют устойчивость и долго-
вечность возведенных на них или из них сооружений, а также усло-
346
вия производства работ, объединяют под общим название строи-
тельных свойств грунтов.
Особенности исследований скальных и нескальных грунтов. Так
как скальные грунты обладают высокой прочностью и сопротивляе-
мостью внешним воздействиям, то их испытания в строительных
целях предпринимаются только в случае возведения особенно тя-
желых и ответственных сооружений. При этом основное внимание
уделяется изучению всевозможных тектонических нарушений, раз-
рывов сплошности грунтов, их трещиноватости, словом, всему тому,
что создает местные ослабления массива и разбивает его на отдель-
ные блоки, так как устойчивость скального массива в целом опре-
деляется в основном'взаимодействием между блоками, сопротивле-
нием их относительному смещению.
Чрезвычайно разнообразные по своим свойствам нескальные
грунты отличаются от скальных не только неизмеримо меньшей
прочностью и гораздо большей деформируемостью, но и тем, что
под влиянием насыщения водой сопротивление механическому воз-
действию у многих таких грунтов может сильно падать.
Поэтому испытания физико-механических свойств нескальных
грунтов часто приходится производить даже при строительстве
относительно небольших сооружений. Нередко, чтобы обеспечить
надлежащее качество основания из нескальных грунтов, приходит-
ся прибегать к весьма дорогостоящим мероприятиям, и поэтому к
правильности определения механических характеристик грунтов
предъявляются высокие требования.
В зависимости от вида сооружений и характера действия на-
грузки, от того, используется ли грунт в его естественном залегании
или извлекается и применяется как материал для земляной плотины
или дорожной насыпи, а также от тех строительных операций, кото-
рым подвергается грунт, в его строительные свойства может вхо-
дить иной комплекс физических, механических и других свойств
грунтов.
Изменчивость свойств грунтов. В связи со строительством все
более тяжелых и ответственных сооружений и значительной слож-
ностью и высокой стоимостью исправления их повреждений важ-
ное значение приобретает стабильность во времени тех количест-
венных характеристик грунтов, которые определяют долговечность
сооружений. При этом нельзя ограничиваться изучением только
реологических явлений, происходящих при длительном действии
нагрузки на грунт. Не следует забывать, что и в ненагруженных
грунтах непрерывно протекают разнообразные внутренние процес-
сы, связанные с проявлением физико-механического взаимодействия
частиц друг с другом и с внешней средой. При изучении этих про-
цессов и их влияния на механические свойства грунта следует иметь
в виду, что соответствующие изменения протекают в естественных
условиях иначе, чем в лаборатории. Это объясняется прежде все-
го неоднородностью состава, структуры и строения грунтовой тол-
347
щи. Приложение нагрузки от сооружений и вообще изменение
естественных условий, вызванное строительством и эксплуатацией
сооружений, в свою очередь отражается на характере протекания
различных физико-химических процессов.
При этом одни грунты обнаруживают высокую степень лабиль-
ности (неустойчивости) физико-механических свойств, тогда как
другие грунты с большим трудом поддаются изменениям. Одни из-
менения происходят сравнительно быстро и являются почти мгно-
венной реакцией на процессы в окружающей среде, другие требу-
ют длительного времени для своего осуществления. Некоторые из
этих явлений обратимы, другие — нет (остаточные явления); одни
проходят почти незаметно, от других остаются резкие следы. Та-
ким образом, изучение в строительных целях физико-механичес-
ких свойств грунтов должно охватывать не только их состав, стро-
ение и внутренние связи между частицами, но также и степень из-
менчивости всех этих свойств во времени под влиянием окружаю-
щей среды.
Образец и массив грунта. Свойства всякого тела определяются,
с одной стороны, его составом и строением, т. е. относительным
пространственным расположением составляющих элементов, а с
другой, внутренними и внешними связями, т. е. взаимодействием
этих элементов между собой и взаимодействием данного тела с
другими. Поэтому свойства тела в целом представляют собой не
сумму свойств его составных частей, а качественно новое диалек-
тическое единство. Можно, например, детально изучить полевой
шпат, кварц и слюду, но этого совершенно недостаточно, чтобы
правильно представлять себе свойства гранита, который из них
состоит.
В свою очередь, свойства отдельного образца гранита еще не
позволяют с уверенностью судить о поведении гранитного массива
при опирании на него, например, плотины, так как огромную роль
будут играть его трещиноватость и тектонические нарушения, о
которых отдельный образец не может дать полного представления.
Вследствие трещиноватости модуль деформации основания в це-
лом окажется в несколько раз меньше модуля деформации отдель-
ного образца, а борьба с фильтрацией 'воды по трещинам потребует
проведения весьма дорогих работ (например, нагнетания в них
тампонирующего раствора).
Вместе с тем изучение грунтовой толщи не только не исключает,
но и предполагает исследование свойств ее отдельных составля-
ющих, так как эти свойства являются важным фактором, знание
которого необходимо для правильной оценки особенностей толщи
в целом.
Определение физико-механических характеристик грунтов про-
изводится в настоящее время лишь для отдельных точек массива
путем испытания извлеченных из этих точек образцов грунта. По
результатам испытаний судят о свойствах всего объема грунта в
целом. Несмотря на указанную выше ограниченность подобного под-
348
хода, создание методики соответствующих испытаний и иссле-
дований позволило заложить основы современной теоретической
механики грунтов с ее многочисленными и разнообразными расчет-
ными моделями и существенно продвинуло вперед развитие тех-
ники фундаментостроения.
Вместе с тем изучение свойств грунта даже по отдельным образ-
цам наталкивается на специфические и нередко трудно преодоли-
мые препятствия. Это, прежде всего, сложность отбора образцов
грунта с больших глубин, из-под воды и из очень слабых или,
наоборот, из чрезвычайно прочных пород. Нередко образцы грунта
разрушаются, прежде чем их удается извлечь на поверхность, а в
других случаях требуется специальное тяжелое оборудование, спо-
собное развить значительные усилия, чтобы отделить образцы от
окружающей породы. Во многих случаях состояние образцов после
отбора оказывается настолько измененным, что их испытание уже
не может дать надежной информации о действительных свойствах
грунта.
Но если даже и удается ценой высокой тщательности работы и
с помощью особых методов отобрать и испытать образцы в почти
ненарушенном состоянии, то и тогда остается нерешенной чрез-
вычайно важная проблема правильной оценки строительно-механи-
ческих свойств всего массива грунта в целом, а не его отдельных
точек, что, очевидно, далеко не одно и то же.
Между тем в большинстве строительных задач важное значение
имеют не только характерные, притом часто весьма сложные, ес-
тественные особенности грунтовой толщи, но и неизвестные на-
чальные, 'напряжения в ней, которые являются результатом дли-
тельных и не всегда ясных геологических процессов. Особенности
напластования грунтов, наличие всевозможных, иногда тончайших
ослабляющих прослоев, различные тектонические и атектоничес-
кие нарушения, история напряженного состояния и изменений гид-
рогеологического режима, неоднородность и анизотропность фи-
зико-механических свойств — все это оказывает решающее влияние
на строительные свойства массива основания.
Компонентный и фазовый состав. Ранее было дано общее опреде-
ление фаз и компонентов, принятое в термодинамике. В механике
грунтов, рассматривающей чисто механические явления в грунтах,
фазами принято называть твердую (минеральный скелет), жидкую
(поровая вода или, точнее, поровый раствор) и газовую (поровый
воздух) составляющие, резко различающиеся по своим механичес-
ким свойствам, главным образом вследствие различногб характе-
ра взаимодействия отдельных частиц, образующих эти фазы.
Если песок содержит частицы неоднородные по своим механи-
ческим свойствам (например, кварцевые и глауконитовые зерна),
то их следует рассматривать как два компонета песка. Но и при
одинаковом химическом составе частицы могут заметно отличать-
ся друг от друга по размерам, что также сказывается на свойствах
грунта в целом (например, крупнозернистый или тонкозернистый
349
пески), и тогда следует говорить о компонентах скелета по круп-
ности.
Пар и газы в порах грунта образуют одну общую фазу — га-
зовую, но являются различными компонентами этой фазы. С дру-
гой стороны, пар и вода, будучи двумя различными фазами, пред-
ставляют собой один компонент грунта. Из приведенных примеров
видно, что отличительной чертой различных компонентов являют-
ся их невозможность перехода друг в друга при изменениях термо-
динамического состояния системы.
При уплотнении некоторого объема грунта под действием сжима-
ющих напряжений происходит уменьшение относительного (на
единицу объема грунта) объема пор и соответственное увеличе-
ние объема скелета. Если поры были заполнены водой, то при
сжатии системы относительный объем жидкой фазы уменьшится,
а относительный объем твердой фазы на столько же увеличится.
Таким образом, изменение плотности грунта может характеризо-
ваться изменением соотношения его твердой и жидкой фаз.
Для нескальных грунтов характерна относительно высокая
прочность и малая сжимаемость отдельных зерен скелета по срав-
нению с грунтом в целом. Поэтому изучению механических
свойств отдельных зерен минералов, образующих твердую фазу
грунта, в физико-геологической механике нескальных грунтов
почти не уделяется внимания, и основной интерес сосредоточен
на особенностях контактного взаимодействия частиц скелета ме-
жду собой и с поровой средой. При этом следует иметь в виду
исключительно большое, во многих случаях решающее влияние,
которое оказывает на свойства нескальных грунтов их влажность.
Механические свойства дисперсных систем, к которым отно-
сится и большая часть нескальных грунтов, могут быть кратко
охарактеризованы следующим образом:
а) остаточные объемные деформации дисперсных систем
происходят за счет изменения в них объема пор: сопротивление
этим деформациям определяется сопротивлением относительному
смещению частиц скелета, которое по мере уплотнения системы
возрастает;
б) сопротивление остаточным деформациям формоизменения
дисперсных систем определяется сопротивлением относительному
смещению частиц скелета, которое по мере деформирования мо-
жет убывать, оставаться постоянным либо (гораздо реже) возрас-
тать;
в) упругие деформации дисперсных систем складываются из
упругих деформаций скелета, воды и газа в их порах, причем
относительное их значение в общей деформации зависит от фазо-
вого состава системы, ее структуры и упругих свойств компонен-
тов, образующих фазы.
Соотношения между напряжениями и деформациями, величины
деформаций и скорость их протекания могут быть исследованы не-
посредственно путем соответствующих лабораторных и полевых ис-
350
пытаний. Однако сложность, длительность и высокая стоимость та-
ких испытаний всегда ограничивает их количество. Это заставляет
прибегать к широкому использованию различных косвенных приз-
наков, и тогда возникает проблема оценки по этим признакам непо-
средственно интересующих нас механических свойств грунтов.
При этом надлежит опираться на изучение инженерно-геоло-
гических условий района строительства и строительной площадки
и на связь между механическими свойствами грунта, как системы,
и свойствами его фаз и компонентов.
Необходимо особо подчеркнуть следующее обстоятельство,
имеющее важное практическое значение — у большинства нескаль-
ных грунтов величины механических показателей весьма невысо-
ки, и эти грунты значительно уступают по своей прочности и соп-
ротивлению деформациям таким строительным материалам, как
сталь или бетон. При низких значениях этих показателей сущест-
венную роль начинают играть колебания прочности всего на нес-
колько десятых кГ/cjw2, а модуля деформации на несколько десят-
ков кГ!см2. Между тем -в эксплуатационных условиях под влиянием
различных факторов механические характеристики грунтов могут
испытывать относительно большие изменения как *в сторону сни-
жения, так и, наоборот, повышения, и эту возможность необходимо
учитывать при проектировании сооружений для обеспечения их
надежности.
Все изложенные выше соображения предопределяют (в случае
ответственных сооружений и слабых оснований) необходимость
детального исследования физико-химических свойств как отдель-
ных составляющих, так и грунта в целом. Совершенно необходи-
мы такие исследования в тех случаях, когда приходится рассмат-
ривать механическое взаимодействие фаз, например скелета грун-
та и фильтрующей сквозь грунт воды, или когда проектируются
и осуществляются мероприятия по технической мелиорации (за-
креплению) грунтов.
Изложенные выше соображения приводят к выводу, что физи-
ческие основы механики грунтов являются гораздо более слож-
ными, чем, например, сопротивления материалов или гидравлики.
Чисто качественная характеристика фазового и компонентного
состава грунта, ограничивающаяся лишь перечислением назва-
ний его составляющих, совершенно недостаточна, когда ’требует-
ся сопоставить друг с другом состав и свойства грунтов. В этом
случае необходимо прибегать также и к количественным характе-
ристикам грунта, определяя весовое или объемное содержание
различных его фаз и компонентов.
При исследовании грунтов широко используются два основных
вида количественных характеристик компонентного состава грун-
тов— гранулометрический или механический состав — относитель-
ное содержание в грунте частиц различной крупности (по весу) и
минералогический состав — относительное весовое содержание в
грунте различных минералов.
351
Три основных вида свойств грунтовой толщи. Из сказанного
выше следует, что строительные свойства грунтов зависят, во-пер-
вых, от свойств минеральных частиц скелета, поровой среды и
примесей, во-вторых, от относительного расположения частиц
скелета в грунте, характера связей между ними и взаимодействия
частиц с поровой средой иг в-третьих, от геологических и гидро-
геологических особенностей грунтовой толщи в целом.
Мы 'будем называть первую группу свойств—компонентными,
вторую — агрегатными и третью — ситуационными или форма-
ционными свойствами грунта.
6. ОСНОВНЫЕ ПРИНЦИПЫ ИСПЫТАНИЙ
МЕХАНИЧЕСКИХ СВОЙСТВ ГРУНТОВ
Для механических испытаний грунтов на современном уровне
необходимо располагать сложным и дорогостоящим оборудовани-
ем, а проведение испытаний требует от исполнителей большого
опыта. В то время как выполнение таких испытаний для крупных
ответственных сооружений является вполне оправданным, оно
совершенно излишне в случае легких и малочувствительных к де-
формациям построек.
С другой стороны, в случае слабых и сильносжимаемых грун-
тов часто вообще нет необходимости знать точные значения меха-
нических характеристик грунтов, и достаточно располагать лишь
минимумом данных, позволяющим установить непригодность
грунтов в качестве основания для данного сооружения. Тогда мож-
но принять решение о прорезке этих грунтов фундаментами
глубокого заложения или сваями, и либо более детальные иссле-
дования уже не потребуются, либо потребуются специальные ис-
пытания (вроде испытания свай пробной нагрузкой). Однако, ес-
ли грунтовые условия позволяют сравнивать в технико-экономи-
ческом отношении различные варианты фундаментов мелкого и
глубокого заложения, требуются детальные сведения о механичес-
ких свойствах грунтов основания.
Стадии проектирования и испытания грунтов. Как известно, в
настоящее время проектирование ведется в две стадии: разра-
ботка технического проекта и составление рабочих чертежей, при-
чем если строительство ведется по типовым или повторно применяе-
мым индивидуальным проектам, эти стадии объединяются в одну
(техно-рабочий проект). Стоимость сооружений определяется на
стадии технического проекта и, так как конструкция фундамен-
тов и работы по их устройству существенно влияют на эту стои-
мость, то уже на первой стадии проектирования необходимо рас-
полагать достаточно подробными инженерно-геологическими дан-
ными и результатами механических испытаний грунтов.
К сожалению, большинство современных методов инженерно-
геологической разведки требует для получения таких материалов
относительно больших сроков и нередко случается, что при про-
352
ектировании располагают либо далеко не полными инженерно-
геологическими данными, либо же продолжают вести изыскания
параллельно с проектированием, что создает значительные труд-
ности и приводит к необходимости вносить изменения в почти
готовые или даже совсем законченные проекты.
С целью преодоления этих трудностей сейчас наметились два
направления в подходе к объему и характеру испытаний грунтов..
Первое заключается в том, что либо исходя из необходимости всяче-
ского сокращения сроков и снижения стоимости инженерно-геоло-
гических изысканий, стремятся к созданию всевозможных инженер-
но-геологических карт и справочных таблиц механических характе-
ристик грунтов. Входами в такие таблицы должны служить сравни-
тельно простые и легко получаемые физические характеристики
грунтов, вроде гранулометрического состава, пористости, консистен-
ции и т. п. Типичным примером является таблица значений моду-
ля деформаций грунтов и показателей их сопротивления сдвигу
в строительных нормах 1962 г. (СНиП П-Б.1-62).
Эти характеристики даются для песчаных грунтов в зависи-
мости от их крупности и пористости, а для глинистых — от влаж-
ности на границе раскатывания и от естественной пористости.
Несмотря на оговорки в нормах, допускающие использование таб-
личных данных только для предварительных расчетов и не для
всех классов сооружений, практически ими пользуются гораздо ши-
ре, так как не всегда удается провести необходимые испытания грун-
тов, а иметь приближенные данные, очевидно, все же луч’ше, чем не
иметь никаких.
Второе направление исходит из того, что, во-первых, ни од-
на таблица не может охватить всего разнообразия естественных
грунтов и тех многочисленных факторов, от которых зависят их
строительные свойства и, что, во-вторых, пользование стандарт-
ными таблицами может приводить к грубым ошибкам. Сторонники
этого направления, признавая необходимость сокращения объема и
упрощения методики испытаний, считают, что необходимо совер-
шенствовать в соответственном направлении существующие ме-
тоды изысканий.
Надо полагать, что оба эти направления имеют право на су-
ществование и развитие, ибо оба они дают полезные результаты..
Не следует лишь забывать о границах применимости и условиях
целесообразного использования этих результатов.
Как известно, осадки сооружений и несущая способность ос-
нований определяются не только свойствами грунтов, но являют-
ся результатом совместной работы сооружения и основания и за-
висят от большого количества факторов, среди которых не менее
существенными, чем геологическое строение площадки и показа-
тели физико-механических свойств грунтов, являются конструк-
ция сооружения, его размеры, тип фундаментов, способы произ-
водства работ.
Именно поэтому Н. М. Герсеванов еще в 1937 г. [10] писал,
353-
что попытки составления всяких норм допускаемых давлений на
грунты являются пережитком прошлого, когда сооружения име-
ли относительно небольшие размеры, занимали небольшую пло-
щадь, имели однообразные системы фундаментов и возводились
единообразными способами. При современном же уровне строи-
тельной техники и масштабах сооружений подобный стандартный
подход к назначению допускаемых нагрузок на грунт не выдер-
живает, по его мнению, никакой критики, _равно как и приноров-
ленная к такому подходу классификация грунтов.
Вместе с тем нельзя отрицать полезности подобных классифи-
каций и норм, когда строго очерчены пределы их применимости
и указаны, во-первых, районы и геологические условия, в кото-
рых ими можно пользоваться, а во-вторых, дана примерная оцен-
ка тех погрешностей, к которым может приводить использование
табличных данных при тех или иных естественных колебаниях
свойств грунтов и инженерно-геологических условий. Надлежит
также иметь в виду, что по мере накопления опыта подобные
классификации должны систематически пересматриваться и уточ-
няться.
Значение методики испытаний. Необходимо помнить, что важ-
ные результаты испытаний можно во многих случаях получать и
на простом оборудовании, что эти результаты в весьма большой
степени зависят от правильности методики испытаний и что> даже
на превосходном оборудовании, но при дефектной методике бу-
дут получаться совершенно непригодные данные. Однако пра-
вильная методика испытаний должна прежде всего исходить из
верного представления о структурно-текстурных особенностях ис-
пытываемых грунтов и должна видоизменяться в соответствии с
этими особенностями.
Испытания материалов с целью определения их деформатив-
ных и прочностных свойств называют механическими. Эти испы-
тания необходимо вести таким образом, чтобы можно было пра-
вильно судить о внутреннем распределении в образце деформа-
ций и чтобы напряжения можно было легко рассчитать, исходя
из известной величины внешней нагрузки.
Такие условия осуществляются при однородных деформациях
типа простого растяжения или сжатия, при чистом изгибе и при
кручении тонкостенных цилиндрических образцов. Однако свойст-
ва грунтов позволяют проводить такого рода испытания лишь в
виде исключения, и в механике грунтов широко применяются ис-
пытания при сложных напряженно-деформированных состояни-
ях — на сжатие в обойме, на простой сдвиг и на трехосное сжатие,
на кручение сплошных цилиндров и толстостенных цилиндрических
образцов, на пенетрацию и т. п. Во второй части мы специально
остановимся на проистекающих из этого погрешностях.
Основные принципы исследования грунтов. Цель механики
грунтов состоит в том, чтобы по результатам испытаний грунтов
предсказать поведение оснований или земляных сооружений при
354
различных напряженных состояниях. В тех случаях когда теоре-
тический прогноз оказывается невозможным из-за сложности за-
дачи, прибегают к испытаниям в натуре или на моделях. Как пока-
зывает опыт, аппаратура и методика лабораторных и полевых ис-
следований и испытаний не могут быть однообразными и должны
соответствовать характерным особенностям не только состава, но»
и структуры данного грунта, отличающим его от всех остальных.
Так, для одних грунтов испытание на прочность должно выпол-
няться только по методу трехосного сжатия, для других— по мето-
ду кольцевого сдвига, для третьих — по методу кручения и т. д.
Это положение требует, в свою очередь, чтобы лаборатории
располагали достаточно разнообразным оборудованием для про-
ведения испытаний по различным методикам, в зависимости от
характерных особенностей всевозможных грунтов.
Такие современные методы инженерно-геологической разведки,
как шурфование и 'бурение, весьма трудоемки, требуют значитель-
ной затраты времени и средств и не всегда поэтому могут про-
водиться с надлежащей полнотой. При этом мы вынуждены судить
о грунтовой толще по данным, полученным в отдельных точках, в
которых проводилось бурение или зондирование, и прибегать к
широкой и не всегда оправданной интерполяции.
Поэтому в ряде случаев оказываются невыявленными сущест-
венные детали инженерно-геологической обстановки. Известны слу-
чаи, когда уже в процессе строительства обнаруживались такие
неожиданности в геологической картине основания, которые за-
ставляли полностью пересматривать проект.
Мы уже указывали, что даже высокое качество испытаний об-
разцов для определения основных физико-механических характе-
ристик, входящих в расчетные формулы, не дает еще уверенности
в правильности результатов расчета, так как поведение грунтов,
в образце может очень сильно отличаться от поведения того же
грунта в пласте в условиях естественного залегания. Поэтому, что-
бы правильнее оценить механические свойства грунтовой толщи на
основании подобных испытаний, необходимо обращаться к учету
особенностей процессов образования и преобразования грунтов,
носящих каждый раз региональный, специфический характер.
Весьма важно правильно оценить при разработке программы и
методики испытаний то существенное влияние, которое оказывают
методы производства работ при устройстве фундаментов или воз-
ведении земляных сооружений на последующее поведение грунтов
под нагрузкой, а также предвидеть возможные изменения свойств,
грунтов в период эксплуатации сооружения под влиянием различ-
ных естественных и искусственных воздействий.
Для строительных конструкций, рассчитываемых по правилам
строительной механики, достоверность исходных положений и ме-
тодов расчета может быть в большинстве случаев проверена пу-
тем сравнительно несложных экспериментов как над моделями, так
35S
и в натуре. Но проведение экспериментальных исследований та-
кого рода по отношению к основаниям и земляным сооружениям
отличается большой сложностью и дороговизной. Тем не менее
подобные исследования нередко позволяют получить гораздо бо-
лее экономичные решения, чем при проектировании сооружений, ис-
ходя только из данных инженерно-геологических изысканий.
Лабораторные испытания. Эти испытания подразделяются на:
а) испытание образцов для выяснения компонентных и агрегат-
ных свойств, б) испытание моделей (лотковые испытания).
Основная цель лабораторных испытаний образцов и моделей —
дать исходный материал для оценки поведения грунтов в натур-
ных условиях. Однако в некоторых случаях результаты этих испы-
таний, даже несмотря на тщательность работы персонала лаборато-
рии и должное качество аппаратуры, могут иметь мало общего
со свойствами грунтов в условиях естественного залегания. Глав-
нейшие причины возможных расхождений можно разбить на сле-
дующие семь групп.
1. Физическое состояние, в которое приводится грунт в процес-
се испытания, не соответствует действительному состоянию грун-
та при его работе в сооружении. Например, испытание на проч-
ность ведется таким образом, что влажность и плотность грунта в
процессе испытания не соответствуют влажности и плотности грун-
та в сооружении.
2. Напряженно-деформированное состояние образца в процес-
се испытания и граничные условия не соответствуют действитель-
ному характеру работы грунта в сооружении, причем теоретиче-
ский переход от одних условий к другим пока невозможен. Напри-
мер, испытание на прочность ведется путем сдвига, захватываю-
щего в образце зону всего в несколько миллиметров толщиной,
тогда как в натуре разрушение распространяется на гораздо более
мощную область.
3. Методика испытания в основе своей верна, но отдельные
детали не соответствуют действительным условиям работы грунта.
К такого рода ошибкам относится, например, загружение образца
при испытании с совершенно иной скоростью, чем это будет иметь
место в натурных условиях.
4. Методика испытания и ее детали правильны, однако испы-
таниям подвергаются не1представительные образцы. Например,
при определении прочности грунта с целью расчета на устойчи-
вость оползневого массива испытываются образцы не непосредст-
венно из зоны скольжения, а отобранные из других точек тела
оползня.
5. Методика испытания и ее детали правильны, и образцы ото-
браны там, где следовало, однако размеры образцов слишком ма-
лы, чтобы они могли характеризовать поведение натурного масси-
ва грунта. Например, массив глинистого грунта содержит много-
численные трещины, а испытанию на сдвиг подвергается малень-
356
кий образец, не имеющий трещин, либо, наоборот, сдвиг образца
происходит по трещине, тогда как в натуре поверхность скольже-
ния проходит частично по трещинам, частично по ненарушенному
материалу.
6. Не все факторы, определяющие поведение грунта в сооруже-
нии в данных условиях, известны и соответственно эти факторы
не могут быть воспроизведены или учтены при проведении испы-
таний.
7. Не произведена оценка степени однородности исследуемого
слоя грунта и соответственно не может быть определена доста-
точность количества испытанных образцов и надежность получен-
ных результатов.
Чтобы не допустить .подобных ошибок, необходимо выдержать
три условия.
1. Перед составлением программы испытания внимательно изу-
чить по материалам геологических изысканий структурно-текстур-
ные особенности и степень однородности исследуемого массива
грунта. Когда приходится испытывать для сравнения серию образ-
цов, размеры «и форма каждого из них должны быть строго одина-
ковыми.
2. При составлении программы предстоящих испытаний и раз-
работке их методики детально ознакомиться с характером и усло-
виями работы проектируемого сооружения и с предполагаемыми
схемами расчета деформации и устойчивости грунтов.
3. Не проходить мимо обнаруживаемых расхождений между
прогнозами, основанными на результатах испытаний, и действи-
тельным поведением сооружений, обстоятельно фиксировать их в
соответствующих отчетах, публиковать сообщения о них, настойчи-
во добиваться выяснения их причин. Следует помнить, что именно
такие расхождения и противоречия являются «точками роста»
науки.
Аллюзионные испытания. В ряде случаев детальные исследо-
вание того или иного свойства с определением соответствующих
числовых параметров требует затраты значительного времени или
представляет существенные технические трудности. Поэтому, преж-
де чем предпринимать такие исследования, необходимо простейшими
методами установить, обладает ли вообще грунт данным свойст-
вом и играет ли оно в его - поведении достаточно важную роль,
чтобы это оправдывало проведение специального исследования.
Так, например, прежде чем ставить опыты на компрессию грунта,
желательно знать, настолько ли велика его сжимаемость, чтобы
это могло сказаться на сооружении. Во многих случаях на такого
рода вопросы можно сразу ответить на основании чисто визуаль-
ных данных.
Однако иногда приходится обращаться к упрощенным и уско-
ренным испытаниям, носящим косвенный характер и позволяю-
щим оценить лишь порядок тех или иных показателей свойств
357
грунта для решения вопроса о проведении дальнейших испыта-
ний. Такого рода испытания называются аллюзионными (напри-
мер, пенетрация грунта для предварительной оценки несущей спо-
собности свай).
Иногда к полевым неправильно относят испытания образцов,
осуществляемые «в поле», т. е. непосредственно вблизи места от-
бора образцов из шурфов или скважин. В последнее время такие
испытания получили более правильное название коллекторских,
а соответствующие комплекты компактного переносного оборудо-
вания для этих испытаний называют коллекторскими лаборато-
риями.
Следует подчеркнуть, что во многих случаях отдаленность мест
изысканий заставляет создавать большие временные лаборатории
непосредственно в районе изысканий. Такие временные лаборато-
рии могут быть как стационарными, так и передвижными — в ва-
гонах или автофургонах.
В последние годы наряду с продолжающимся совершенствова-
нием техники отбора и методики испытания образцов особенно
усиленно разрабатываются методы исследований грунтов в их ес-
тественном залегании. Эти исследования, называемые полевыми,
подразделяются на: а) испытания для определения агрегатных
свойств грунтов в отдельных точках грунтового массива; б) ис-
пытания для определения механических свойств грунтового масси-
ва ’в целом (ситуационные испытания); в) крупномасштабные ис-
пытания моделей или сооружений в целом (эти последние испыта-
ния называют также натурными).
Однако при этом иногда забывают, что внедрение в грунт раз-
личных устройств может настолько нарушить его первоначальное
состояние, что результаты испытаний будут не только не лучше
лабораторных, но значительно уступать последним. Кроме того,
определяя при полевых испытаниях свойства грунта в отдельных
точках массива, упускают из виду необходимость обеспечить
оценку неоднородности и анизотропности механических свойств
массива и закономерности их изменений и колебаний в плане и по
глубине.
Между тем без этого невозможен правильный прогноз поведе-
ния фундаментов, опирающихся на различные участки неоднород-
ного основания. Кроме того, решающее значение нередко имеет
знание начального напряженного состояния грунтов и характера
испытывавшихся ими деформаций в прошлом.
Весьма большую (а в ряде случаев даже решающую) помощь
в оценке строительных свойств грунтовой толщи в целом могут
оказать геофизические методы исследования. Сущность этих мето-
дов заключается в изучении влияния свойств и особенностей за-
легания грунтов на те или иные естественные или искусственно
созданные физические поля. В практике инженерно-геологических
изысканий широкое применение получили пока электрометрические
358
и сейсмометрические методы, широко использумые как иллюзион-
ные испытания.
В отличие от лабораторных и «точечных» полевых испытаний,
геофизические исследования охватывают сразу целую площадку,
но для возможности интерпретации получаемых результатов их
необходимо сочетать с данными разведочного бурения и испыта-
ний проб грунта из выработок. Можно полагать, что решение про-
блемы исследования ситуационных свойств грунтов будет получе-
но именно в результате дальнейшего развития геофизических ме-
тодов, что следует считать первоочередной задачей исследовате-
лей, работающих *в области совершенствования методики и техни-
ки инженерно-геологической разведки.
Весьма целесообразный и эффективный способ преодоления
трудностей, возникающих при сложных инженерно-геологических
условиях,— это проведение в ходе самого строительства дополни-
тельных исследований свойств грунтов и поведения грунтовой тол-
щи по мере возведения сооружений и передачи от них нагрузки
на грунт. Подобный прием, получивший название «полевых геотех-
нических контрольных исследований», был впервые применен в
широком масштабе на Шведских 'государственных железных доро-
гах в 1912—1914 г., а в '1926 г. Терцаги применил этот метод при-
строительстве водохранилищной плотины Грэнвиль-Дэм, когда
вопрос о некоторых противофильтрационных мероприятиях можно
было решить лишь после заполнения водохранилища и проведе-
ния наблюдений за утечкой воды из него.
В СССР этот метод в широком масштабе был осуществлен при
строительстве гидротехнических сооружений на р. Свири в самом
начале тридцатых годов. На этой стройке Н. Н. Масловым была
организована первая в СССР современная лаборатория механики
грунтов, позволившая осуществить ряд исследований, а искусст-
венное регулирование осадок и наклонов сооружения на основе их
предвычисления, выполненное на этом строительстве, до сих пор
еще не превзойденное нигде в мире.
Наш собственный опыт создания контрольно-наблюдательных
станций и лабораторий механики грунтов на различных крупных
стройках убеждает в том, что для правильного решения большин-
ства сложных практических задач в области инженерной геологии
и геотехники важным подспорьем является производимое по мере
вскрытия котлованов уточнение первоначальных инженерно-геоло-
гических данных о свойствах грунтов и проведение необходимых ла-
бораторных и натурно-полевых исследований и испытаний. Одно-
временно изучается влияние, которое оказывают на грунт методы
производства работ, ведутся наблюдения за осадками сооружений,
с первых же моментов передачи нагрузки от сооружения измеря-
ются напряжения в грунтах, проводятся испытания опытных со-
оружений и т. п.
Все эти исследования позволяют в случае надобности своевре-
359
менно вносить в проект необходимые изменения, гарантирующие
прочность и устойчивость сооружений. Весьма важной положи-
тельной стороной организации таких исследований является нали-
чие на стройплощадке во время их проведения действующей стро-
ительной организации с опытным персоналом, механизмами, необ-
ходимыми материалами, что позволяет с большой легкостью осу-
ществлять такие опытные работы, о которых в условиях изыска-
тельской партии нельзя даже мечтать.
В связи с тем что организация строительно-полевых контроль-
ных станций и лабораторий механики грунтов на крупных строй-
ках становится правилом и благодаря высокому уровню развития
практики и теории моделирования, сейчас широко применяется в
случае надобности опытное строительство крупномасштабных мо-
делей фундаментов и земляных сооружений с целью их исследова-
ния в натурных условиях. Данные о поведении таких моделей
чрезвычайно ценны не только для решения вопросов проектирова-
ния конкретных сооружений, ради которых осуществлялось моде-
лирование, но и для развития механики грунтов в целом.
ЛИТЕРАТУРА
1. Алабужев П. М., Геронимус В. Б., Минкевич Л. М.,
Шеховцов Б. А. Теории подобия и размерностей. Моделирование. «Высшая
школа», 1968.
2. Артемьев А. В. Инженерно-геологическое изучение естественных пласти-
ческих и разрывных деформаций горных пород. «Наука», 1964.
3. Баландин П. П. К вопросу о гипотезах поочтшсти «Вестник инжене-
ра и техника», 1937, № 7.
4. Бартен ев 'Г. М., Зуев Ю. С. Прочность и разоушение высокоэластич-
ных материалов. «Химия», 1964.
5. Бленд Д. Теория линейной вязкоупругости. «Мир», 1965.
6. Болотин В. В. Статистические методы в строительной механике. Строй-
издат, 19'61.
7. Булан А. И., Рябченко В. Н., С<ухарев С. С. Основы физико-хи-
мии промывочных жидкостей и тампонажных растворов. «Недра», 1968.
8. Быковский В. Н. Сопротивление материалов во времени с учетом ста-
тистических факторов. Госстройиздат, 1958.
9. Вялов С. С. Реологические свойства и несущая способность мерзлых
грунтов. Изд. АН СССР, 1959.
10. Г е р се в а н о в Н. М. Основы динамики грунтовой массы, изд. 3. ОНТ'И,
1937.
11. Гольдштейн М. Н. Приложение термодинамики необратимых про-
цессов к электрокинетическим явлениям. Сб. «Вопросы геотехники», 1959, № 3.
12. Гольдштейн М. Н. Некоторые вопросы развития механики грунтов.
«Основания, фундаменты и механика-грунтов», 1960, № 1.
13. Гольдштейн М. Н., Б а б и цк а я С. С., Мизюмский В. А. Мето-
дика испытания грунто'в на ползучесть и длительную прочность. «Вопросы гео-
техники», сб. № 5, 1962.
14. Гольдштейн М. Н., Гольдштейн В. М. К теории вибропогруже-
ния свай-оболочек. «Вопросы геотехники», сб. №6, 1963.
'15 . Горькова И. М. Теоретические основы оценки осадочных пород в ин-
женерно-геологических целях, «Наука», 4966.
16. Гухман А. А. Об основаниях термодинамики. Изд. АН КазССР, 1947.
17. Д е в д а р и а н и А. С. Математический анализ в геоморфологии. «Нед-
ра», 1967.
18. Денисов Н. Я. О природе деформаций глинистых пород. Изд. Мини-
стерства речного флота СООР, 1951.
19. Зарецкий Ю. К. Теория консолидации грунтов. «Наука», 1967.
20. И в а н о в Н. Н., Ох о тин В. В. Дорожное почвоведение и механика
грунтов. Гострансиздат, 1934.
21. Иванов Н. Н. Взаимодействие колеса и дороги. Сб. ЛИИПС, № 100,
1929.
361
22. Кандауров И. И. Механика зернистых сред. Стройиздат, 1966.
23. К а ч а н о в Л. М. О времени разрушения в условиях ползучести. Изд.
АН СССР. ОТН, № 8, 1958.
24. Китайгородский А. И. Порядок и беспорядок в мире атомов, изд. 4.
«Наука», 1966.
25. К л а й н С. Дж. Подобие и приближенные методы. «Мир», 1968.
26. К о р ж е н к о Л. И. Особенности классификации элювиальных грунтов.
Труды Уральского политехнического института, сб. № 44. Госстройиздат, 19'53.
27. Коломенский Н. В. Инженерная геология, ч. I. Гос. изд. геологиче-
ской литературы, 1951, ч. II. Гос. изд. литературы по геологии и охране недр,
1956.
28. Коломенский Н. В., Комаров И. С. Инженерная геология. «Выс-
шая школа», 1964.
29. Кругл иц к ий Н. Н. Физико-математические основы регулирования
свойств дисперсий глинистых минералов. «Наукова думка», 1968.
30. Ксенофонтов А. И. Релаксационная теория консолидации и новый
метод расчета осадки во времени. Труды МИ1ИТ, выл. 197, 1965.
31. Леонова В. Ф. Термодинамика. «Высшая школа», 1968.
32. М а л ы ш е в М. В. О влиянии среднего главного напряжения на проч-
ность грунта и о поверхностях скольжения. «Основания, фундаменты и механи-
ка грунтов», 1963, № 1.
33. М а с л о в Н. Н. Инженерная геология. Гос. изд. литературы по строи-
тельству, 1941.
34. М а с л о в Н. Н. Требования, предъявляемые к лабораторному исследо-
ванию грунтов для гидротехнического строительства. Материалы по лаборатор-
ному исследованию грунтов. Госгеолиздат, 1952.
35. Маслов Н. Н. Условия устойчивости склонов и откосов в гидроэнерге-
тическом строительстве. Госэнергоиздат, 1955.
36. М а с л о в Н. Н. Инженерная геология. Госстройиздат, 1957.
37. Маслов Н. Н. Основы механики грунтов и инженерной геологии.
«Высшая школа», 1968.
38. М е с ч я н С. Р. Ползучесть глинистых грунтов. Изд. АН АрмСОР, 1967.
39. Сб. «Методы изучения осадочных пород», т. I, II. Госгеолтехиздат, 1957.
40. Мидлтон Г. В. Возникновение логнормального распределения частот
в осадках. Сб. «Вопросы математической геологии». «Наука», 1968.
41. Мизюмский В. А. Критерий для оценки степени устойчивости глини-
стых пород. «Транспортное строительство», 1962, № 4.
42. М и х а й л о в Н. В., Р е б и н д е р П. А. О структурно-механических
свойствах дисперсных и высокомолекулярных систем. «Коллоидный журнал»,
1955, т. XVII, № 2.
43. Миро любо в И. Н. К вопросу об обобщении теории прочности окта-
эдрических касательных напряжений на хрупкие материалы. Труды Ленинград-
ского технологического института, № 25, 1953.
44. Н а да и А. Пластичность и разрушение твердых тел, т. I. Изд. иностр,
лит., 1954.
45. Н овожилов В. В. О физическом смысле инвариантов напряжения,
используемых в теории пластичности. «Прикладная математика и механика»,
т. XVI, 1952, № 5.
362
46. Овчаренко Д. Д., Ничипоренко С. П., Круглицкий Н. Н.,
Третинник В. Ю. Исследования в области физико-химической механики дис-
персий глинистых минералов. «Наукова думка», 1965.
47. Пит л юк Д. А. Расчет строительных конструкций на основе моделиро-
вания. Стройиздат, 1965.
48. Покровский Г. И. Применение принципа Больцмана к расчету осад-
ки фундаментов. ВИОС. «Основания и фундаменты», сб. № 1, 1933.
49. Покровский Г. И., Некрасов А. А. Статистическая теория грун-
тов. «Вестник ВИА», 1934. -
50. Покровский Г. И. Исследования по физике грунтов. ОНТИ, 1937.
51. Покровский Г. И., Федоров И. С. Центробежное моделирование
в строительном деле. Стройиздат, 1968.
5'2. П о п о в И. В. Инженерная геология. Изд. МГУ, 1959.
53. Попо .в И. В. Инженерная геология СССР. Изд. МГУ, 1961.
54. При к л.о некий В. А. Сравнительная характеристика интенсивности
физико-механического диагенеза некоторых глинистых пород СССР. «Труды ла-
боратории гидрогеологических проблем АН СССР», т. 3, 1948.
55. Протодьяконов М. М., Чирков С. Е. Трещиноватость и прочность
горных пород в массиве. «Наука», 1964.
5'6 . Пэжина П. Основные вопросы вязкопластичности. «Мир», 1968.
57. Работнов Ю. Н. Ползучесть элементов конструкций. «Наука», 1966.
58. Р а д ч е н к о И. В. Молекулярная физика. «Наука», 1965.
59. Р а ц М. В. Неоднородность горных пород и их физических свойств. «На-
ука», 1968.
60. Ребиндер П. А. Физико-химические исследования процессов деформа-
ции твердых тел. Юбилейный сборник, посвященный тридцатилетию Октябрьской
революции. Изд. АН СССР, 1947.
61. Ребиндер П. А. Физико-химическая механика. «Знание», 1958, се-
рия IV, № 39, 40.
62. Рейнер М. Деформация и течение (введение в реологию). Гос. изд.
нефтяной и горнотопливной литературы, 1963.
63. Р е й н е р М. Реология. «Наука», 1965.
64. Р ж а н и ц ы н А. Р. Теория ползучести. Стройиздат, 1968.
65. Руппенейт К- В. Некоторые вопросы механики горных пород. Угле-
техиздат, 1954.
66. Руппенейт К. В., Либерман Ю. М. Введение в механику горных
пород. ГоСгортехиздат, 1960.
67. Руппенейт К. В., Долгих М. А., Матвиенко В. В. Вероятност-
ные методы оценки прочности и деформируемости горных пород. Стройиздат,
1964.
68. Рухин Л. Б. Основы литологии. Гостоптехиздат, 1953.
69. Седов Л. И. Методы подобия и размерности в механике, изд. 6. «Нау-
ка» 1967.
70. С е р г е е в Е. М. Общее грунтоведение. Изд. МГУ, 1959.
71. Сергеев Е. М., Максимов С. Н., Березкина Г. М. Методиче-
ское пособие по инженерно-геологическому изучению горных пород, т. I, И. Изд.
МГУ, 1968.
72. Слесарев В. Д. Механика горных пород. Углетехиздат, 1948.
363
73. С о к о л о в с к и й В. В. Теория пластичности, изд. II. Гостехтеориздатг
1950.
74. Справочное-руководство по петрографии осадочных пород, т. I, II. Гос-
топтехиздат, 1958.
75. Т а л о б р. Механика горных пород. Госгортехиздат, 1960.
76. Т е р н о в ск а я В. Т., Ар т юшков Е. В., Славяне в В. Н. Палео-
геоморфологический метод прогноза деформаций горных пород. «Наука», 1966.
77. Тер-Степанян Г. И. Графический метод сложения напряжений при
расчете оснований и земляных сооружений. «Основания, фундаменты и механи-
ка грунтов», 1960, № 6.
78. Т е р-С тепанян Г. И. Ближайшие задачи гео.механики. Сб. «Проблемы
геомеханики» № 1. АН Армянской ССР, 1967.
79. Терцаги К., Пек Р. Механика грунтов в инженерной практике. Гос.
изд. литературы по строительству, 1958.
80. Туровская А. Я., Тимофеева Т. А. Условия развития оползней в-
полускальных и скальных породах и особенности их изучения. «Вопросы геотех-
ники», 1965, № 9.
81. УилкинсонУ. Л. Неньютоновскиё жидкости. «Мир», 1964.
82. Фел там П. Деформация и прочность материалов. «Металлургия», 1968.
83. Филоненк о-Б о р о д и ч М. М. Механические теории прочности. Изд.
МГУ, 1961.
84. Френкель Я. И. Кинетическая теория жидкостей. Изд. АН СССР,
1945.
85. Френкель Я. И. Статистическая физика. Изд. АН СССР, 1948.
86. Ц ы т о в и ч Н. А. Механика грунтов, изд. 4. Стройиздат, 1963.
87. Я с и н с к и й Ф. С. Теория упругости. Спб., 1897.
88. Bishop A. W. Henkel D. J. The Measurment of Soil Properties in
the Triaxial Test., London, 1957.
89. Caquot A. Equilibre des massifs a frottement interne. Paris, 1934.
90. Dall aval e J. Micromeritics. The Technology of Fine Particles, N.-Y.,.
1943.
91. Goldstein M., Lapidus L., Misumsky V. Rheological Investi-
gation of Clays and Slope Stability. Proc. IV. Inter. Congr. Soil Meeh., vol. 111.
1960.
92. Gross B., Fuoss R. Ladder Structures for Representation of Viscoelas-
tic Systems. «Journ. Polim. Sci.», v. XIX, 1950.
93. H a e f e 1 i R. Erdbaumechanische Probleme im Lichte des Schneeforschung.
«Schweiz. Bauzeitung», Bd. 123, 1944.
94. Harr M. E. Foundations of Theoretical Soil Mechanics, N.-Y., 1966.
95. Yong R., Warkentin B. Introduction to Soil Behaviour, N.-Y.,
1966.
96. Korner H. Schnee und Eismechanik und einige ihrer Beziehungen zur
Geologie. «Felsmech. und Ing. Geologie», № 1, 1964.
97. L ossie r H. La crise de confience de la mechanique des sols. «Genie
Civil», v. 135, № 14, 1958.
98. Mur a у am a. On the Secondary Consolidation of Clay. «Proc. 11 Jap.
Congress Test. Mat.», 1958.
364
99. Peck R. Art and Science in Subsurface Engineering. «Geotechnique»,
№ 1, 1962.
100. Reynolds O. On the Dilatancy of Media Composed of Rigid Particles
in Contact. «Philosoph. Magaz.», 20(5), 1885.
101. Tan T. K. Investigations on the Rheological Properties of Clay. Delft,
1954.
102. Terzaghi K. Ends and Means in Soil Mechanics. «Eng. Journ.» (Cana-
da), v. 27, 1944.
103. Terzaghi K. Effect of Minor Geologic Details on the Safety of Dams.
«Amer. Inst. Min. and Metal. Eng.», TP 215, 1929.
104. Terzaghi K. Influence of Geological Factors on the Engineering Pro-
perties of Sediments. «Harvard Soil Meeh. Ser.», № 50, 1955.
105. Terzaghi K. Past and Future of Applied Soil Mechanics. «Journ. Bost.
Soc. Civ. Eng.», vol. 48, № 2, 1961.
106. Winterkorn H. The Bearing of Soil-Water Interaction on Water Con-
duction under Various Energy Potentials. «RILEM Symposium», Paris, 1964.
107. Wohlbier H., Feistcorn F., Herbst Ch. Die Geomechanik als
selbststandige Wissenschaft. «Proc. I Intern. Congr. Rock Meeh.», Lisboa, vol. 1,
1966.
ОГЛАВЛЕНИЕ
Стр,
Предисловие........................ . .........................
Глава I. Грунты, горные породы и сооружения........................ 6
1. Два основных класса грунтов........................................ 6-
2. Нескальные грунты как осадочные горные породы...................... 9
3. Особенности работы грунта в различных сооружениях и условиях . . 22
4. Основные виды нескальных грунтов ................................ 26
Глава 2. Грунты как объект исследования........................... 30
1. Науки, изучающие грунты ................... ....................... 30
2. Возникновение механики грунтов ,................................. 34
3. О физико-геологических основах механики грунтов.................... 42
4. Принципы построения расчетных и структурных моделей грунта ... 46
Г л а в а 3. О термодинамических системах......................... 54
1. Свойства и состояния систем............ ......................... 54
2. Изменение состояния системы............ ......................... 56
3. Энергия............................................................ 60
4. Энтропия...........................................................72
5. Характеристические функции к........... ......................... 76
6. Химический потенциал. Фазовые превращения...................... 83
7. Понятие о термодинамике необратимых процессов...................... 90
Глава 4. Грунты как объект механики сплошной среды................ 98
1. Механическое взаимодействие между частицами тела................... 98
2. Напряжения и деформации.................... . .................101
3. Однородные деформации............................................. 111
4. Тензор напряжений............................................... 117
5. Зависимость между напряжениями и деформациями..................... 140
6. Жидкое и аморфное состояния..................................... 150
7. Напряжения в фазовой модели грунта........................... . 152
8. Реологические свойства грунтов................................... 155
9. Сложные реологические тела....................................... 166
10. Спектральные реологические модели................................ 179
11. Потенциальная энергия деформации . ............................. 192
12. Рассеяние энергии при необратимых деформациях . ................. 195
13. Феноменологические реологические модели ................... ... 201
Глава 5. Грунты как объект статистической механики................204
1. Исходные понятия теории вероятностей....................... .... 204г
2. Сложение и произведение вероятностей....................... .... 207
3. Распределения вероятностей...................................... 209'
4. Нормальное распределение к . .................................... 214
5. Термодинамическая вероятность.................................... 218
6. Внутреннее трение и вязкость в гааах и жидкостях ..................225
7. Исходные положения математической статистики.......................230
8. Числовые характеристики статистического распределения..............238
9. Сыпучие тела..................................................... 248
10. Дисперсные системы................ ......................... 252
11. Приложение статистических методов к описанию некоторых свойств '
грунтов........................................................... 258
366
Стр.
Глава 6. Основы теории прочности...................................269
1. Понятие о прочности ................................................269
2. Энергетическая теория прочности....................................274
3. Теория прочности Кулона — Мора.....................................279
4. Обобщение теории прочности Мора. Условие прочности Филоненко-Бо-
родича . ............................................................ 283
5. Динамическая теория прочности......................................288
6. Длительная прочность...............................................293
7. Прочность структурированных систем ................296
Глава 7. Некоторые общие вопросы и исследования грунтов . . . 304
1. Ошибки измерений ...................................................304
2. Статистический анализ результатов испытаний....................... 314
3. Использование теории размерностей и подобия при исследованиях . . 327
4. О принципах классификации грунтов................................. 340
5. Показатели свойств грунтов........................................ 344
6. Основные принципы испытания механических свойств грунтов .... 352
Литература.......................................................: . 361
Гольдштеич, Михаил Наумович
МЕХАНИЧЕСКИЕ СВОЙСТВА ГРУНТОВ
* * *
Стройиздат
Москва, К-31, Кузнецкий мост, д. 9
* * *
Редактор издательства Н. М. Борщевская
Внешнее оформление художника А. С. Александрова
Технический редактор И. В. Высотина
Корректоры И* А. Зайцева, О. В. Стиенеева
Сдано в набор 29/VI—1970 г. Подписано к печати 2/11—1971 г.
Т-01656 Бумага 60X90V16— 11,5 бум. л.
23 печ. л.(уч.-изд. 24,35 л.)
Тираж 11 500 экз. Изд. № AVIII-41238. Зак. № 530. Цена 1 р. 66 к.
Подольская типография Главполиграфпрома
Комитета по печати при Совете Министров СССР
г. Подольск, ул. Кирова, д. 25
М. Н. ГОЛЬДШТЕЙН
ь ;
'Г; ! Нгн < :